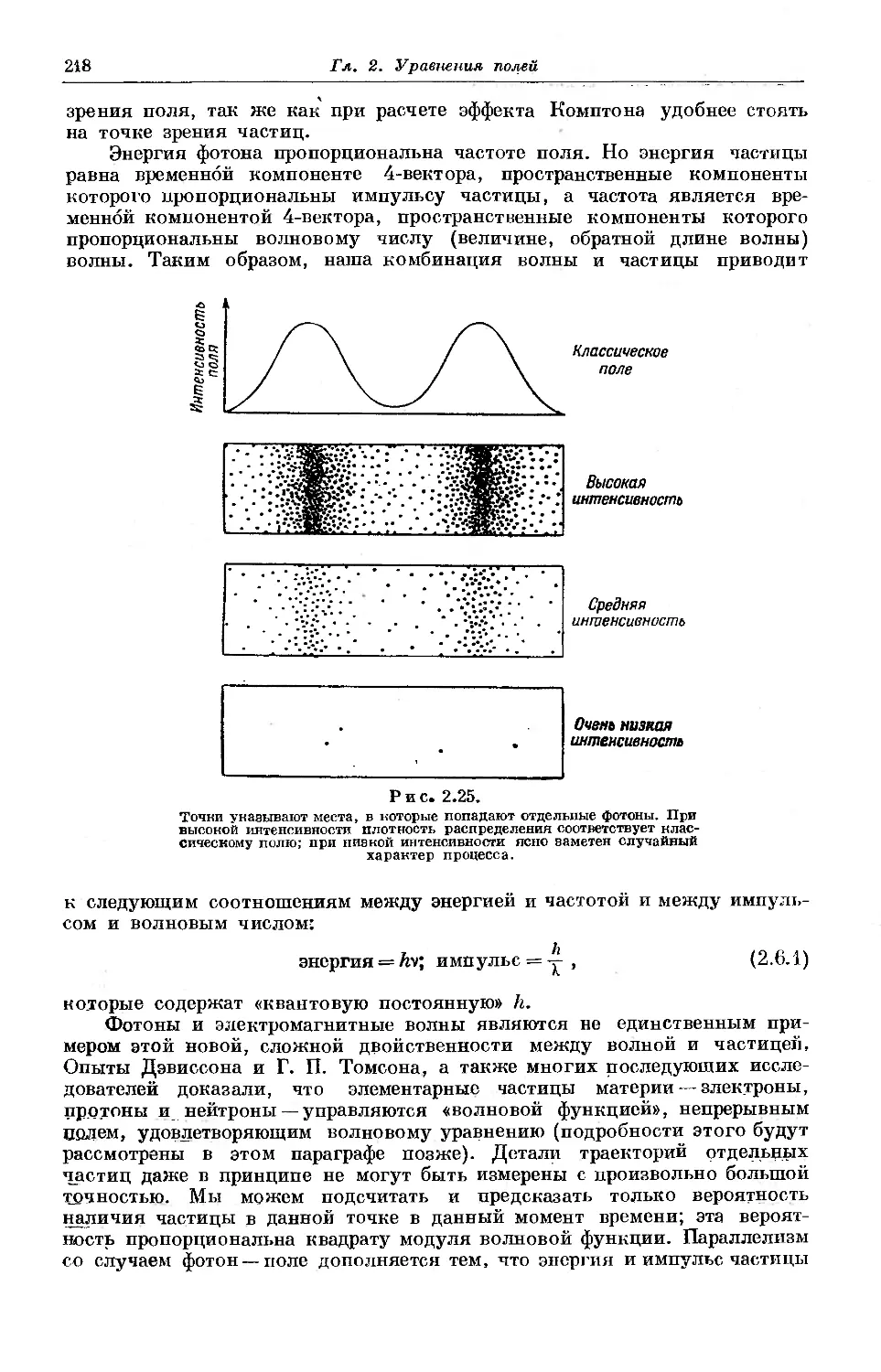
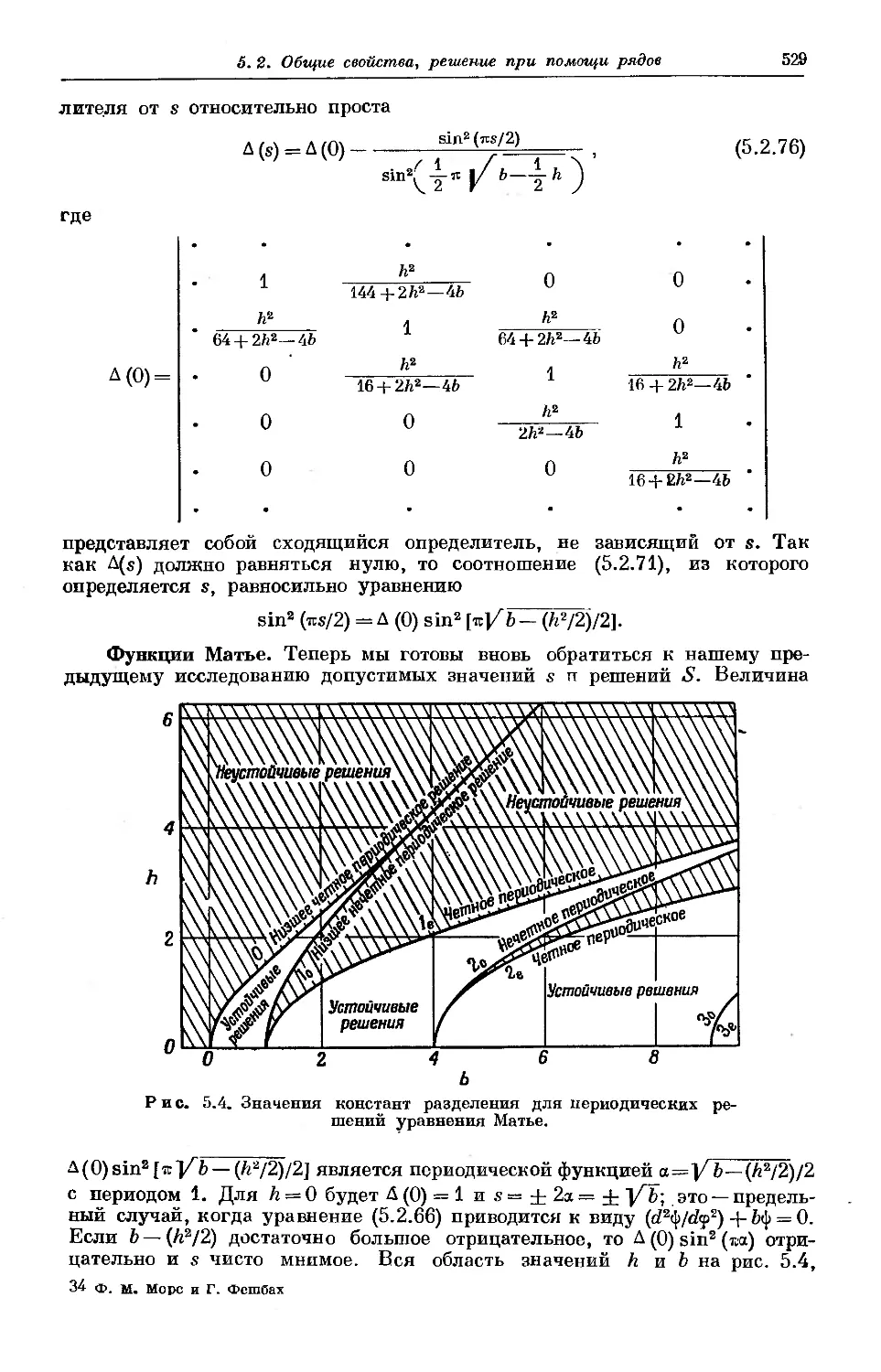
Текст
ФММорс, Г. Фешбах
МЕТОДЫ ТЕОРЕТИЧЕСКОЙ ФИЗИКИ, т.1
Двухтомный курс Ф. Морса и Г. фешбаха занимает особое место в литературе
по математической физике. Он написан физиками для физиков и инженеров и
показывает в действии математические методы, наиболее успешно применяемые
при изучении различных полей.
В книге излагается ряд важнейших разделов современной математики в плане
их применения к задачам физики и техники. Большим достоинством является то,
что авторы всюду стремятся выяснить основные идеи, существо и физический
смысл излагаемых методов. Поэтому книга представляет значительный интерес и
для математиков, которым она покажет новые стороны известных им методов.
Некоторые из излагаемых методов (например, метод теории возмущений во
втором томе) успешно применяются физиками, но еще недостаточно известны
математикам и ждут своего математического обоснования. И физики и
математики найдут в книге большое число подробно разобранных примеров
важных прикладных задач.
Курс Морса и Фешбаха лежит на стыке физики и математики. Он отличается
от обычных курсов математической физики своей значительно большей
физичностью, а от курсов теоретической физики тем, что в нем основное место
уделяется разработке математического аппарата.
Книга будет полезной студентам, аспирантам и научным работникам
математических, физических и инженерных специальностей Я вообще всем
лицам, сталкивающимся с применением современной математики.
Содержание
Предисловие к русскому изданию 5
Предисловие авторов 9
Глава 1. ТИПЫ ПОЛЕЙ 13
1.1. Скалярные поля 15
1.2. Векторные поля 19
1.3. Криволинейные координаты 31
1.4. Дифференциальный оператор Vnabla 40
1.5. Аппарат векторного и тензорного исчисления 52
1.6. Аффиноры и другие векторные операторы 60
1.7. Преобразование Лоренца, 4-векторы, спиноры 95
Задачи к главе 1 108
Таблица наиболее употребительных векторных и аффинорных 115
соотношений
Таблица свойств криволинейных координат 116
Литература 117
Глава 2. УРАВНЕНИЯ ПОЛЕЙ 119
2.1. Гибкая струна 119
2.2. Волны в упругой среде 146
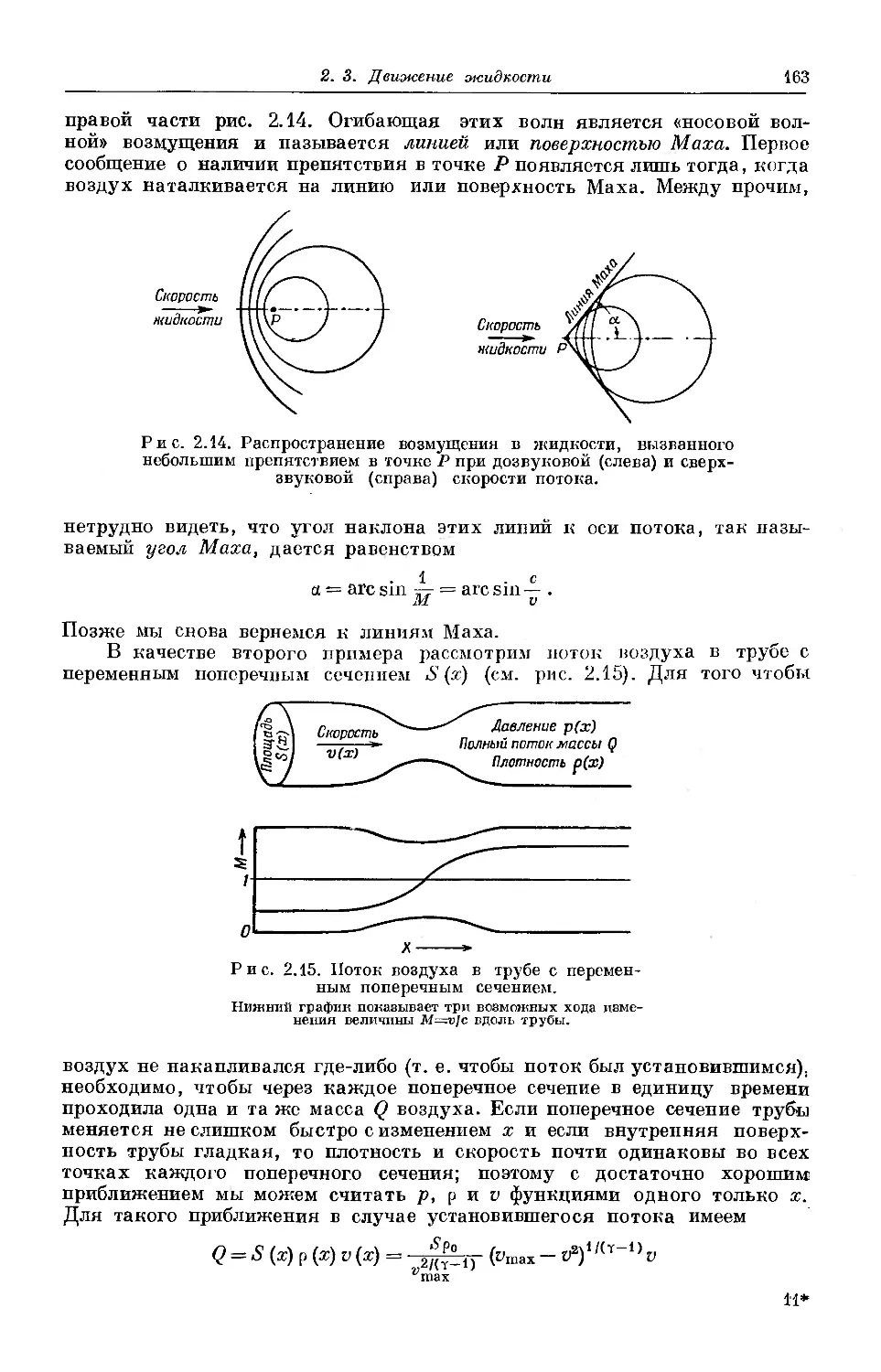
2.3. Движение жидкости 149
2.4. Диффузия и другие явления просачивания жидкости 168
2.5. Электромагнитное поле 195
2.6. Квантовая механика 215
Задачи к главе 2 256
Литература 262
Глава 3. ПОЛЯ И ВАРИАЦИОННЫЙ ПРИНЦИП 264
3.1. Вариационный нитеграл и уравнения Эйлера 265
3.2. Принцип Гамильтона и классическая динамика 268
3.3. Скалярные поля 288
3.4. Векторные поля 303
Задачи к главе 3 320
Сводка результатов главы 3 324
Литература 328
Глава 4. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО 330
4.1. Комплексные числа и комплексные переменные 331
4.2. Аналитические функции 337
4.3. Производные аналитических функций. Ряды Тейлора и Лораиа 354
4.4. Многозначные функции 376
4.5. Теория вычетов. Гамма-фуикция и эллиптические функции 386
4.6. Асимптотические ряды. Метод перевала 410
4.7. Конформное отображение 419
4.8. Преобразование Фурье 428
Задачи к главе 4 446
Основные свойства функций комплексного переменного 455
Часто встречающиеся специальные функции 461
Литература 466
Глава 6. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 468
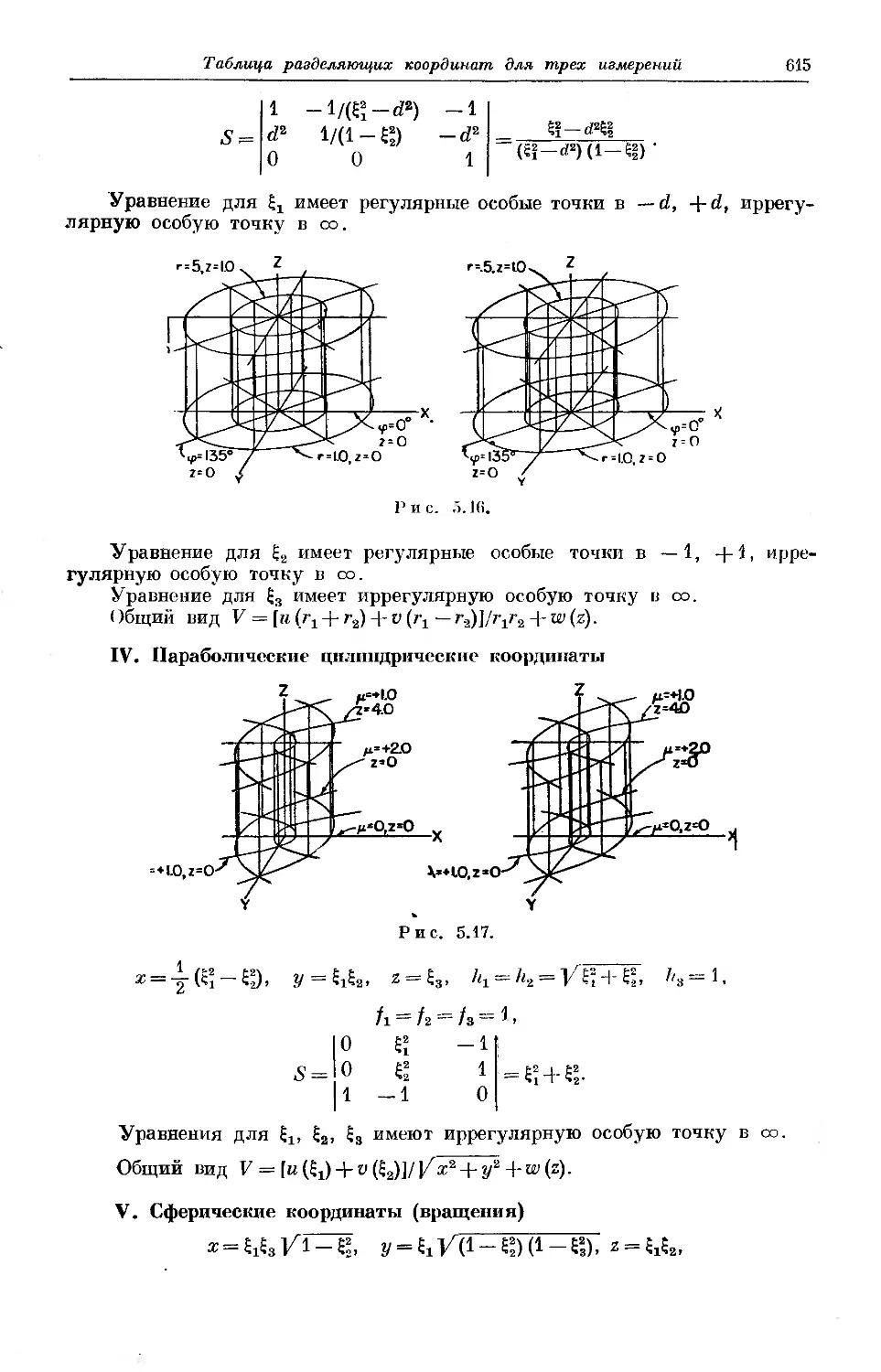
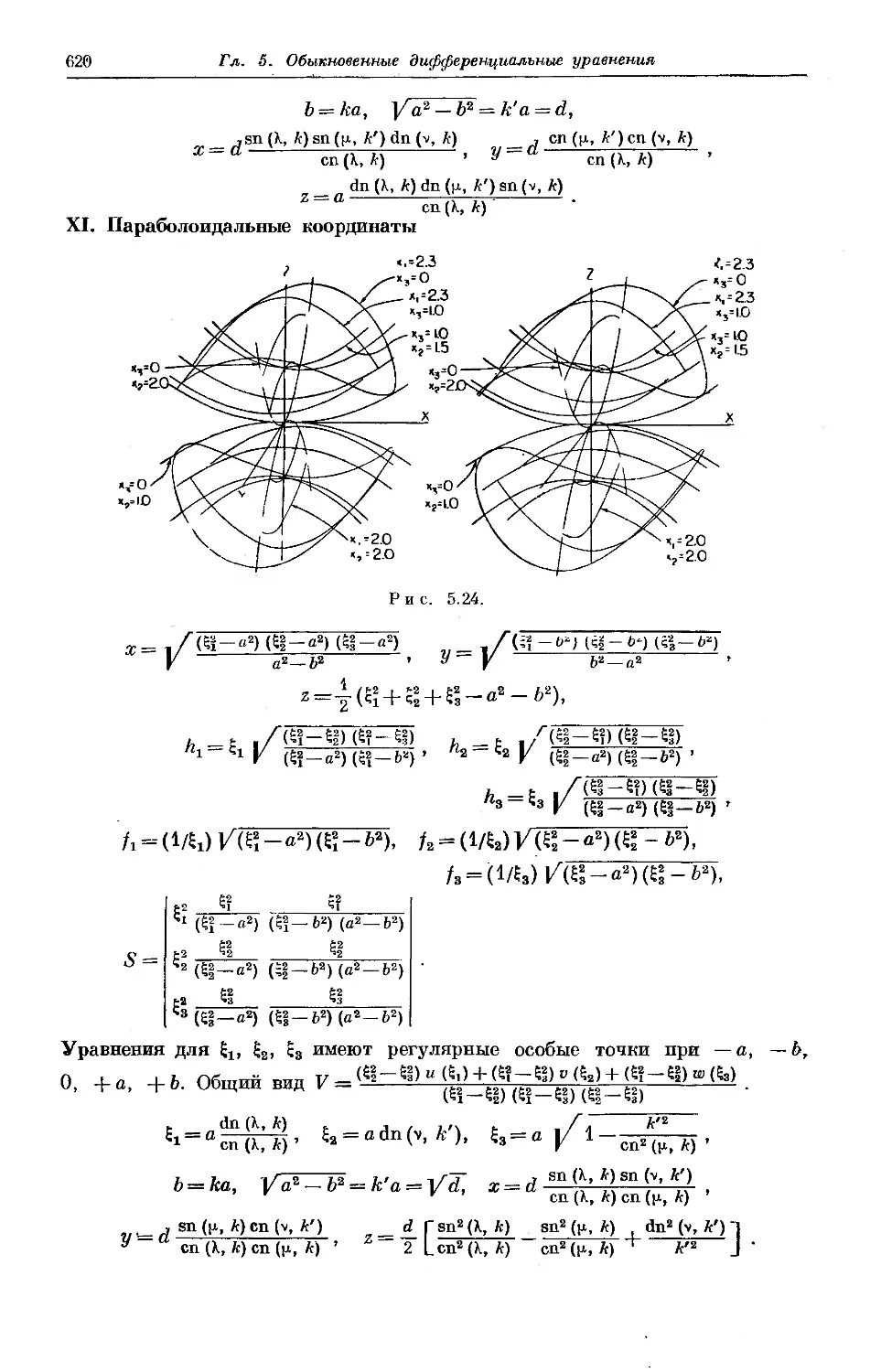
5.1. Координаты, в которых переменные разделяются 470
5.2. Общие свойства, решение при помощи рядов 495
5.3. Интегральные представления 542
Задачи к главе 5 604
Таблица разделяющих координат для трех измерений 612
Дифференциальные уравнения второго порядка и их решения 622
Литература 629
Глава 6. КРАЕВЫЕ УСЛОВИЯ И СОБСТВЕННЫЕ ФУНКЦИИ 631
6.1. Типы уравнений и краевых условий 631
6.2. Разностные уравнения и краевые условна 645
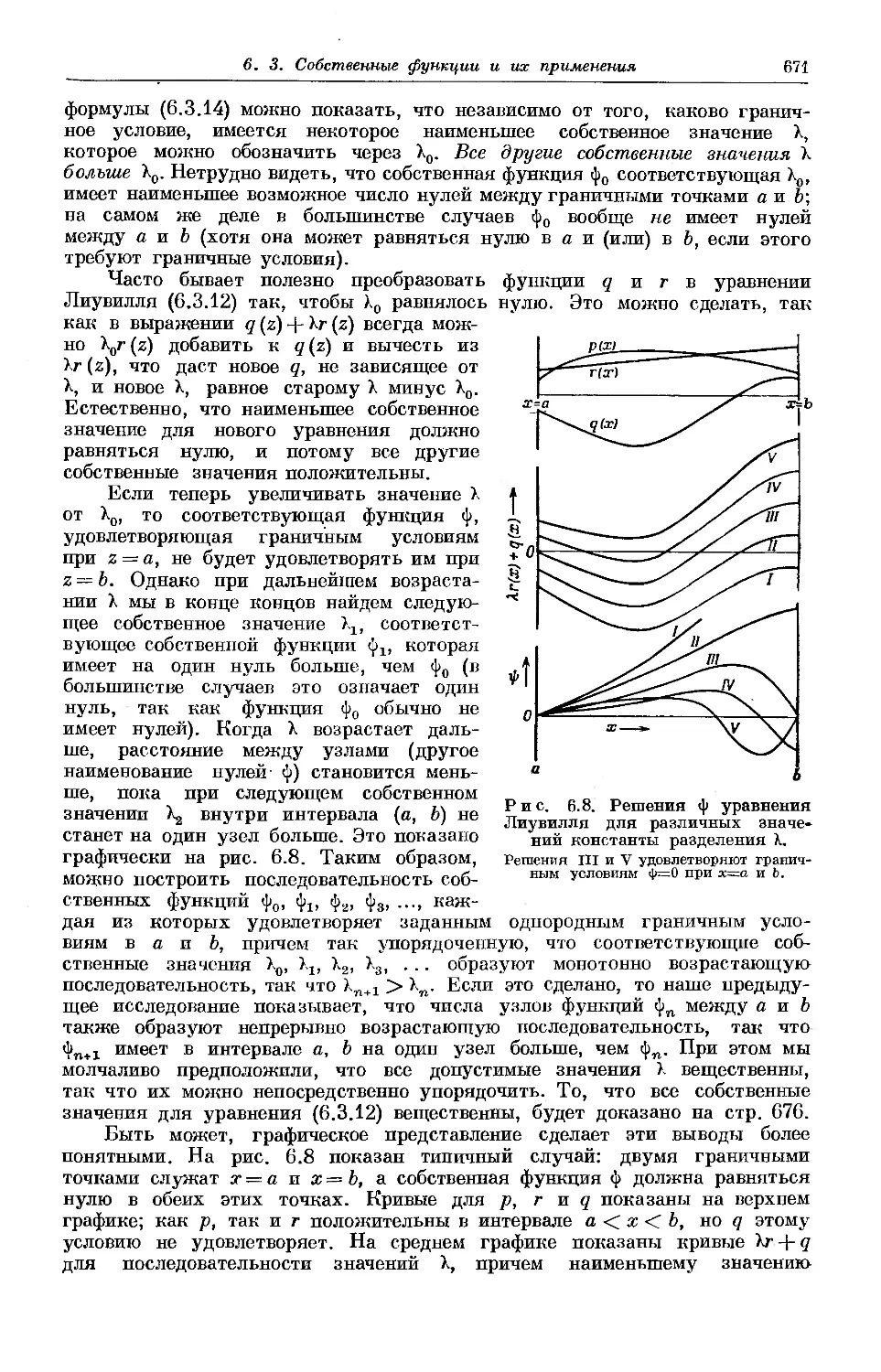
6.3. Собственные функции и их применения 658
Задачи к главе 6 722
Таблица полезных собственных функций и их свойств 725
Собственные функции, полученные при помощи метода факторизации 731
Литература 733
Глава 7. ФУНКЦИИ ГРИНА 735
7.1. Точки источников и граничные точки 737
7.2. Функции Грина для установившихся колебаний 745
7.3. Функция Грина для скалярного волнового уравнения 772
7.4. Функция Грина для уравнения диффузии 793
7.5. Функция Грина в абстрактной операторной форме 804
Задачи к главе 7 819
Таблица функций Грина 823
Литература 827
Глава 8. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 828
8.1. Интегральные уравнения физики; их классификация 828
8.2. Общие свойства интегральных уравнений 838
8.3. Решение уравнений Фредгольма первого рода 856
8.4. Решение интегральных уравнений второго рода 879
8.5. Преобразование Фурье и интегральные уравнения 883
Основные свойства интегральных уравнений и их решений 919
Литература 923
ПРЕДИСЛОВИЕ
К РУССКОМУ ИЗДАНИЮ
Предлагаемый вниманию читателей в русском переводе двухтомный
курс «Методов теоретической физики» весьма своеобразен и, пожалуй,
не имеет аналогов среди распространенных у нас книг. Написанный физи-
физиками (имя одного из которых — Филиппа Морса—хорошо известно нашим
читателям) для физиков и инженеров, этот курс содержит глубокое и
разностороннее изложение математической теории основных полей, рас-
рассматриваемых в физике. С содержанием книги читатель может познако-
познакомиться по подробному оглавлению, а установки авторов достаточно ясно
освещены в их предисловии. Сделаем только несколько общих замечаний.
Хотя математическая литература, предназначенная для нематемати-
нематематиков (физиков или инженеров), насчитывает большое число книг, однако
значительная се часть не полностью отвечает своему назначению. Стремле-
Стремление к современному уровню математической строгости, отбор материала
с традиционных математических позиций и другие проявления «узкове-
«узковедомственного» математического подхода приводят к тому, что многие из
этих книг являются лишь сокращенными вариантами университетских
курсов, предназначенных для математиков. Это влечет за собой, с одной
стороны, неоправданное усложнение и перегруженность изложения «нера-
«неработающим» материалом, а с другой стороны, приводит к тому, что многие
математические идеи и. методы, часто уже давно «принятые на вооруже-
вооружение» прикладниками, освещаются чрезвычайно слабо или даже совсем не
освещаются лишь из-за того, что их цока ещё не удается достаточно
строго изложить. В результате очень часто получается, что физик или
инженер, изучив математический курс и встретившись затем с применением
математики, вынужден овладевать рядом новых методов, понятий и тер-
терминов, перестраивая в какой-то степени свою «математическую психологию».
Поэтому наряду с традиционными курсами насущно необходимы и такие
книги, в которых математические понятия и методы излагались бы в том
плане (с той же. «мате'матите.ской психологией», с.теми же ассоциациями,
на том же уровне строгости и т. п.), в к,аком они впоследствии должны
применяться. Курс Морса и Фешбаха и является одной из таких книг,
причем он охватывает ряд важнейших отделов современной математики.
Думается, что. авторы со своей задачей в целом справились. Физики
и, иные специалисты, применяющие современную математику,- найдут
в книге очень много интересного материала, освещенного с естественной
для них точки , зрения, — как достаточно популярного, но оригинально
изложенного, так' и.' недостаточно распространенного, хотя и весьма по-
полезного. Мы надеемся, нто книга окажется очень интересной и для
математиков (если, конечно, они не будут предъявлять к ней требова-
требований, которым она и не должна удовлетворять); она не только,.! показывает
математику с точки зрения «потребителя» и содержит ряд важных недо-
¦6 Предисловие к русскому изданию
статочно популярных фактов, но и освещает, как это ни парадоксально
с первого взгляда, многие математические соотношения более глубоко,
чем это делается в «чисто математической» литературе (к примеру свой-
свойства функции Грина рассмотрены во многих книгах, однако при этом
очень редко объясняется, почему эта функция — функция влияния — появ-
появляется при решении краевых задач для однородных уравнений; можно
было бы привести и ряд других примеров). Особо хочется отметить живой
и образный язык книги, а также большое число подробно разработан-
разработанных важных примеров.
Книга не лишена недостатков. Изложение не всюду проводится наи-
наиболее простым и ясным образом. Порой авторы, нарушая свой собствен-
собственный стиль, пускаются в обсуждение излишних математических «тонко-
«тонкостей», что при принятом в книге уровне математической строгости не
является убедительным и может только запутать читателя. Иногда изло-
изложение становится, пожалуй, слишком небрежным, в результате чего
появляются ошибочные утверждения, а также ошибки в знаках, коэффи-
коэффициентах и т. п. Замеченные ошибки при переводе были выправлены,
однако, учитывая сложность работы над переводом этой книги, нельзя
поручиться за то, что все ошибки были замечены. В связи с этим сле-
следует предупредить читателя о необходимости известной бдительности,
если он захочет воспользоваться книгой не для ознакомления с поня-
понятиями, идеями и методами в освещаемых областях, а только в качестве
справочника формулировок и формул.
Из сказанного ясно, что книгу нельзя рекомендовать в качестве
учебника для первого ознакомления с трактуемыми в ней вопросами.
Однако, как нам кажется, читатели (и математики, и физики, и инже-
инженеры; и знающие предмет и изучающие его) найдут в ней много инте-
интересных идей, полезных методов и важных фактов, и книга займет свое
место в литературе по математической физике.
В процессе перевода книги над ней работала большая группа пере-
яодчиков и редакторов. Наибольшей опасностью для нас был соблазн
«улучшать» авторов, что нарушило бй характер и целевую установку
книги и в конечном счете привело бы к ее ухудшению. Поэтому мы ста-
старались без особой надобности не отступать от оригинала. В частности,
мы старались сохранить своеобразную терминологию авторов. В некоторых
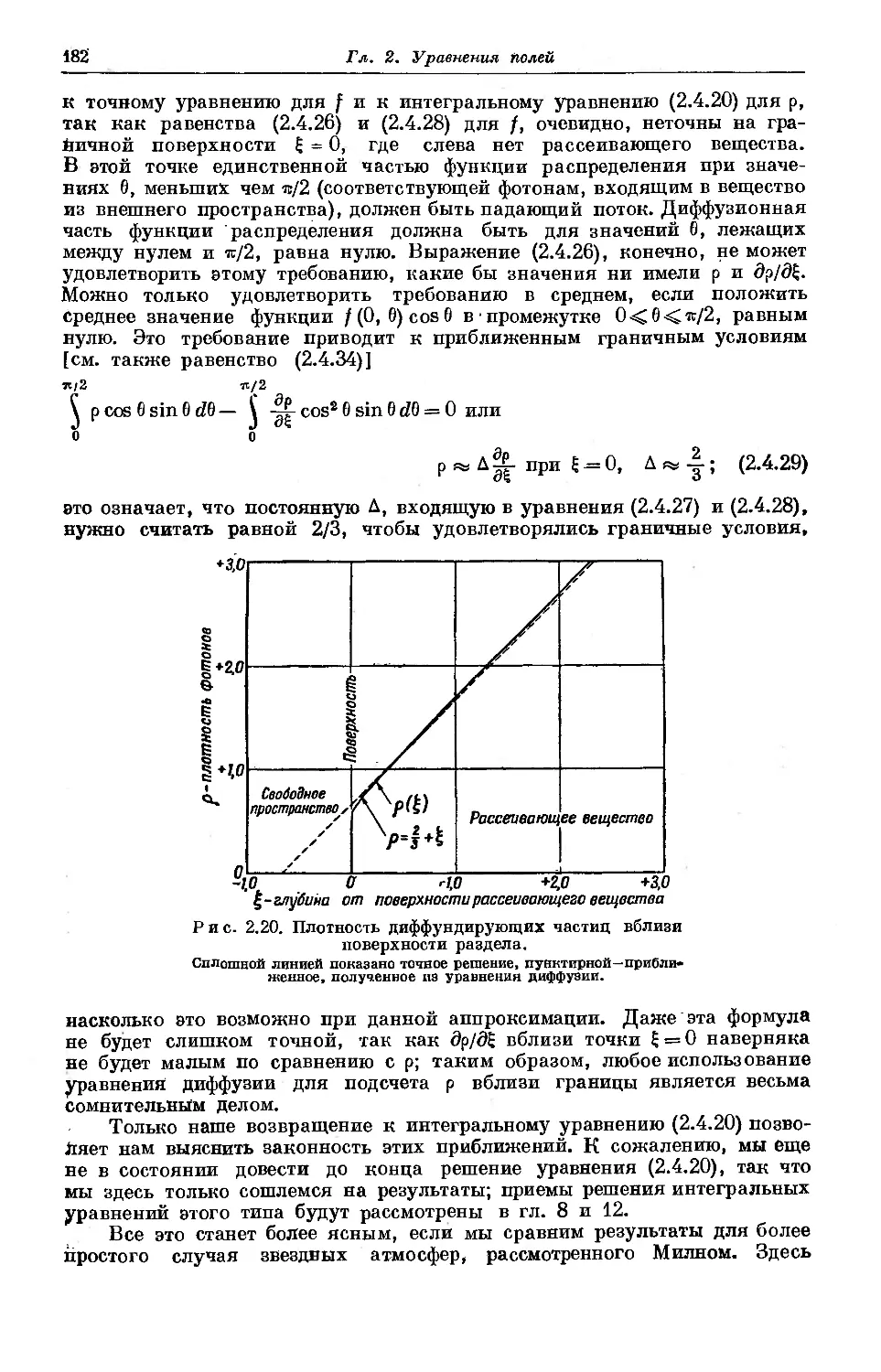
случаях добавлены небольшие пояснительные примечания; незначитель-
незначительные исправления внесены прямо в текст. Ряд довольно туманных мест
оставлен без изменения, так как и они всегда содержат какое-то «рацио-
«рациональное зерно», которое может оказаться полезным читателю. Несколько
пополнена библиография, главным образом указаниями на распростра-
распространенные у нас источники.
Книга издается в двух томах исключительно по техническим .при-
.причинам, ибо эти тома по существу представляют собой единое целое. Не-
Некоторые вопросы освещаются как в первом, так и во втором томе, разу-
разумеется, с различных точек зрения. Вследствие этого справочный аппарат
(предметный указатель и указатель используемых обозначений) сделан
общим и помещен во втором томе. Ряд указаний о пользовании книгой,
в частности о том, как рассматривать стереоскопические рисунки, чита-
читатель найдет в предисловии авторов.
Упомянем в заключение, что некоторые символы применяются
в разных местах книги в разных смыслах. Например, знак е^ асим-
асимптотического равенства означает иногда стремление к единице отношения
левой части к правой, иногда отличие левой части от правой на вели-
величину того или иного порядка малости. Впрочем, смысл употребляемых
символов всегда ясен из контекста.
Предисловие к русскому изданию
Работа но переводу книги распределилась следующим образом:
Д. А. Васильков ыеревел гл. 3, 4 и § 1, 2 гл. 8: Ю. И. Гросберг —гл. 11
и § 1, 2 гл. 12; В.-К. И. Карабегов —§ 7 гл. 1, § 3, 4 и о гл. 8, гл. 10;
В. И. Левин —§ 1 - E гл. 1; А. М. Молчанов —гл. 9; А. Д. Мышкис —
гл. 5, 6 и 7; А. Г. Свешников — гл. 13; В. С. Ялтуновскнй — гл. 2 и § 3
гл. 12. Редактировали: § 3 гл. 12 —С. П. Аллилуев; гл. 5, 6, 7, 8 и 13 —
]Н. С. Кошляков|; гл. 1, 2, 3, 4 и 9-А. Д. Мышкис; гл. 10, И и § 1. 2
гл. 12 —А. Г. Свешников. Весь текст книги пыл просмотрен
С П. Аллилуевым.
Редакторы.
ПРЕДИСЛОВИЕ АВТОРОВ
Этот трактат вырос из курса лекций, читанных тем или другим и»
авторов на протяжении последних шестнадцати лет. Сама книга находи-
находилась в процессе подготовки в течение более чем половины этого времени,
хотя, правда, было много перерывов, больших и малых. Проблемой не
последней важности являлось при этом достигнуть надлежащего понима-
понимания в вопросе о том, что должно составшъ основное содержание книги
и как это содержание должно быть представлено.
Современная теоретическая физика представляет собой весьма обшир-
обширную область; изложение всех относящихся сюда предметов не помести-
поместилось бы и на пятифутовой книжной полке, и оно находится далеко за
пределами возможностей и интересов авторов. Но не все участки этой
области в наше время интенсивно разрабатываются; части, в которых за
последние двадцать лет сделаны наиболее примечательные успехи, свя-
связаны главным образом не столько с частицами, сколько с полями, с вол-
волновыми функциями, силовыми нолями, электромагнитным и акустиче-
акустическим потенциалами, т. с. со всем, что является решениями дифферен-
дифференциальных уравнений в частных производных, определенными краевыми
условиями. Именно на этом общем подходе и концентрируется внимание
в настоящем трактате. Пятьдесят лет назад он мог бы быть назван «Диф-
«Дифференциальные уравнения в частных производных физики» или «Краевые
задачи». Сегодня, по причине распространенности концепции и методов
теории поля, не будет, быть может, неподходящим использование более
общего названия.
Но даже и эта ограниченная область не могла бы быть освещена
в двух томах курса. Описание физических понятий и экспериментальных
методов всех тех отраслей физики, которые пользуются полями, заняло
бы огромнейшую полку, причем в этом описании дублировалось бы основ-
основное содержание многих прекрасных книг, а единство предмета, имеющее
основное значение, в нем было бы погребено в массе деталей. II в самом
деле, единство теорий полей лежит в аналитическом.-'аппарате,- в тех
математических средствах, которые эти теории используют- для получе-
получения решений. Этот аппарат остается в своей сущности- одним и тем же,
изучаем ли мы поле, соответствующее нейтральному ме,зрну, или сигналу
радара, или звуковой волне, - или- облаку диффундирующих нейтронов.
Вследствие этого предлагаемый курс в первую очередь дает представле-
представление тех математических средств, которые оказались наиболее полезными
при изучении основных физических конструкций, связанных с полями,
а также дает ряд примеров, показывающих, как эти средства могут быть
использованы при решении различных физических задач. При этом сооб-
сообщаются только те физические сведения, которые необходимы, чтобы
сделать примеры понятными.
. Однако мы не утверждаем, что этот труд является математическим
сочинением. Физик, использующий математику как орудие, может также
10 Предисловие авторов
воспользоваться своими физическими знаниями для того, чтобы так
дополнить уравнения, как чистый математик не рискнет (и не должен
рисковать) это сделать. Например, он может пользоваться представлением
о точечном заряде; математик же должен добиваться выяснения аналити-
аналитических капризов дельта-функции Дирака. Физик обычно отправляется от
уже описанного и измеренного решения дифференциального уравнения
в частных производных; математик же часто вынужден детально разра-
разрабатывать сеть теорем и лемм, чтобы точно показать, когда данное урав-
уравнение имеет единственное решение. Рассуждения, приводимые в этой
книге, будут, мы надеемся, понятны и удовлетворительны для физиков
и инженеров, для которых написана эта работа; математик же зачастую
не сочтет их достаточно строгими.
Будучи ограничен в этих двух различных направлениях — в количе-
количестве физического материала и в математической строгости, — наш трактат,
надо надеяться, является сравнительно замкнутым и завершенным. Пред-
Предполагается, что читатель владеет физикой в объеме знаний, даваемых
физическими факультетами; математическая же подготовка предполагается
в объеме обычных курсов анализа и дифференциальных уравнений. Даль-
Дальнейший необходимый математический материал из векторного и тензор-
тензорного анализа и из теории линейных дифференциальных и интегральвых
уравнений, относящийся к нашему предмету, излагается в тексте.
Изложение ведется в довольно замкнутом стиле, так что лишь из-
изредка приходится прибегать к выражению «можно показать», столь рас-
расстраивающему читателя. Даже на ранней стадии обсуждения основного
математического аппарата сделана попытка сопоставить уравнения и методы
с физическими свойствами полей, являющихся главным объектом изуче-
изучения. Во многих случаях выводы даны дважды, сначала в полуинтуитивной
манере, чтобы выявить физическую сущность вопроса, а затем со всеми
символами и уравнениями, чтобы достигнуть необходимой степени стро-
строгости. Иногда часть рассуждения повторяется в позднейшей главе с дру-
другой точки зрения, чтобы избежать чрезмерного количества ссылок; это
было признано желательным, хотя и повлекло за собой некоторое увели-
увеличение объема книги.
Мы старались освободиться от тривиальных и слишком частных при-
примеров решений. В результате, конечно, включенные примеры, для того
¦чтобы выявить все то, что есть в них интересного, часто требуют длин-
длинных и сложных объяснений; однако эта книга и предназначена как раз
для того, чтобы объяснить, насколько трудные задачи могут быть решены,
а такое объяснение не может быть иллюстрировано простыми примерами.
Вариационные методы в применении к задачам дифракции, итерационные
методы, используемые при вычислении рассеяния волн на нерегулярных
границах, вычисление сходящихся рядов для собственных состояний, воз-
возмущенных сильными потенциалами взаимодействия, — все эти методы
обнаруживают свою подлинную силу только тогда, когда «ни применя-
применяются в задачах, неразрешимых иным способом.'
Другой общий принцип также работал в направлении удлинения
рассуждений. Авторы предпочитали, так часто, как только это было воз-
возможно, «атаковать» задачи «в лоб», стараясь не «зарыться в них». Они
предпочитали ' попытаться показать, как находить решение нового и
незнакомого уравнения, вместо того чтобы приводить список выражений,
относительно которых кто-то нашел, что они являются решениями инте-
интересных задач. Однако некоторого количества «раздражающих» примеров,
в которых решение появляется, так сказать, с неба, а затем доказывается,
¦что оно в самом деле является решением, нельзя было избежать. Обычно
такие примеры занимают меньше места и легче типографски воспроизво-
Предисловие авторов 11
дятся; однако в большом количестве они вызывают у изучающего состоя-
состояние подавленности или фатализма.
Мы надеемся, что эта работа окажется также сравнительно замкнутой
и в отношении численных таблиц ы списков употребительных формул.
Таблицы и перечни основных свойств, помещенные в конце каждой главы,
резюмируют основные результаты этой главы и позволяют легко обо-
;»реть основные свойства наиболее часто используемых функций. Вместо
того чтобы рассеивать литературные ссылки по всему тексту, мы собрали
их также в конце каждой главы; это позволяет легче находить их в слу-
случае надобности. Сюда были включены только названия тех книг и статей,
относительно которых авторы чувствовали, что они будут полезны чита-
читателю, дополняя материал данной главы; эти ссылки отнюдь не предназ-
предназначены для указания приоритета или кульминационных точек историче-
исторического развития. Историческое развитие теории, являющейся основным
предметом этой книги, было бурным и потребовало усилий многих зна-
знаменитых личностей. Методы переоткрывались и получали новое имя почти
всякий раз, как обнаруживалась новая ветвь физики. Полное библиогра-
библиографическое описание потребовало бы сотен страниц, многие из которых
были бы очень скучны. Мы давали ссылки, чтобы помочь читателю понять
предмет, а не для того, чтобы закрепить за каждым исследователем «его
долю». Искренне говоря, мы дали ссылки на те работы, которые мы
сами знаем и которые мы нашли полезными.
Была сделана попытка координировать выбор символов для обозна-
обозначения различных определяемых и используемых функций. В тех случаях,
когда символы, используемые в литературе, прочно установились, как,
например, для бесселевых функций, мы следовали принятым обозначениям.
Когда же имелось несколько различных символов, выбирался тот, кото-
который логически лучше подходил к остальному материалу и вызывал меньше
повторений, как это было сделано в случае функций Матье. В немногих
случаях функции были перенормированы, чтобы сделать их более удоб-
иыми для употребления; этим новым функциям даны новые обозначения,
как в случае полиномов Гегенбауера. Соотношение между используемыми
в этой книге обозначениями и другими обозначениями, которые доста-
достаточно часто появляются в физической литературе, указано в Приложении;
там же дан общий указатель символов.
Таблиц, помещенных в Приложении, будет достаточно для большин-
большинства вычислений, относящихся к основному предмету этой книги. Мы
предпочли включить большое количество таблиц с ограниченными диа-
диапазоном и точностью, нежели давать немного таблиц с большим числом
входов и значащих цифр. Табулировано большинство функций, исполь-
используемых в реально возникающих физических задачах, но некоторые вспо-
вспомогательные функции, такие, как гамма-функция или эллиптические
функции, не представлены, равно как и некоторые функции со слишком
многими независимыми параметрами, такие, как гипергеометрические
функции. Некоторые функции, такие, как параболические и сфероидаль-
сфероидальные волновые функции, мы хотели включить, но их полные основные
таблицы еще не опубликованы.
Некоторые из чертежей в этой книге, относящиеся к трем измере-
измерениям, выполнены для стереоскопического рассматривания. Их можно рас-
рассматривать либо при помощи какого-либо обычного стереоскопа, либо же
без какого бы то ни было дополнительного приспособления, расслабляя
фокусирующие мускулы глаз и заставляя каждый глаз смотреть на соот-
датствующий ему рисунок. При этом следует делать такое усилие, кото-
которое нужно было бы для того, чтобы рассмотреть нечто, находящееся за
плоскостью рисунка. Само собой разумеется, что эти рисунки можно рас-
12 Предисловие авторов
сматривать и как обычные перспективные, не обращая внимания на то,,
что они дублированы. Однако читатель, научившийся после недолгих
упражнений «стереоскопическому видению», будет рассматривать эти
рисуяки с удовольствием.
Авторам при выполнении их задачи помогали многие. Сотни аспи-
аспирантов, которые слушали соответствующий курс с 1935 года, вольно или
невольно помогли при выборе порядка изложения и при отборе относя-
относящихся сюда примеров. Они. исправили почти все опечатки литографиро-
литографированного издания записей лекций, на которых базируется эта книга;
однако, они еще не имели времени устранить те неизбежные ошибки,
которые имеются в этом издании. Любой из читателей может помочь
в этом, обратив внимание авторов на те ошибки, которые он заметит,
Была также и более специализированная помощь. Доказательство
теоремы Коши, данное на стр. 334, было предложено Р. Боасом. В чте-
чтении рукописи и корректур участвовали профессора Дж. А. Стрэттон и
Н. Г. Франк, доктора Гарольд Левин, К. У. Ингард, Вальтер Хойзер,
Роберт и Джейн Пис. С. Рубинов, а также Ф. М. Юнг, М. К. Ньюстейн,
Л. Сартори, Дж. Литтл, Э. Ломон и Ф. Дж. Корбато. Всех их следует
поблагодарить зэ многочисленные исправления и улучшения; на них не
должно взваливать вину за ошибки и неудобоваримые выражения, кото-
которые, без сомнения, еще остались. Мы выражаем также благодарность
профессору Юлиану Швингеру за беседы и советы, стимулировавшие
нашу работу.
Филипп М. Морс,
Герман Фешбах.
Май 1953.
Г Л А В А 1
Типы полей
Нашей задачей в предлагаемой книге является рассмотрение мате-
математического аппарата, используемого при расчете и анализе разных типов
полей, встречающихся в современной физике. Наше внимание будет
в первую очередь обращено на выявление взаимосвязи между уравнени-
уравнениями и физическими свойствами полей, причем временами мы будем жертво-
жертвовать математической строгостью, если она не содействует выяснению
физической сущности вопроса. Математическая строгость важна, и ею
нельзя пренебрегать, но физик-теоретик должен в первую очередь доби-
добиваться полного понимания физического смысла употребляемой символики,
без чего формальная строгость не может принести ему никакой пользы.
Существуют другие руководства, в которых математическая строгость
полностью выдержана; настоящая же книга достигнет своей цели, если
ее читатель получит ясное физическое представление о разнообразных
уравнениях полей, которые встречаются в современной теоретической
физике, а также полностью уяснит себе физическую сущность математи-
математического аппарата, применяемого для решения этих уравнений.
13 настоящей глаис мы рассмотрим общие свойства разных полей
и представления этих полей в различных системах координат. Вторая
глава будет посвящена рассмотрению различных типов дифференциаль-
дифференциальных уравнений с частными производными, которые описывают эти поля,
а третья. глава — связи между этими уравнениями и основными вариаци-
вариационными принципами, развитыми в классической динамике Гамильтоном
и другими учеными. Несколько дальнейших глав будет посвящено мате-
математическому аппарату, необходимому для решения этих уравнений,
а в остальной части книги мы рассмотрим решение отдельных уравнений.
Практически вся современная физика имеет дело с полями: потен-
потенциальными полями, полями вероятностей, электромагнитными, тензор-
тензорными и спинорными полями.
С математической точки зрения поле представляет собой систему
функций от координат точки в пространстве. С точки зрения, принятой
и этой книге, поле есть некоторая удобная математическая идеализация
физической ситуации, в которой протяженность является существенным
элементом, т. ё. которая не может быть исследована в терминах положения
конечного числа частиц. Поперечное отклонение струны, находящейся
под воздействием статических сил, от ее положения равновесия представ-
представляет собой . очень простой пример одномерного поля; отклонение у раз-
различно для разных частей струны, так что у можно рассматривать как
функцию расстояния х вдоль струны. Плотность, температуру п давле-
давление в жидкости, в которой распространяются звуковые волны, можно
рассматривать как функцию трех координат и времени. Поля такого типа,
очевидно, являются лишь приближенной идеализацией физической ситуа-
ситуации, так как они не учитывают атомных свойств материи. Мы можем
назвать их материальными полями.
14 Гл. 1. Типы полей
Другие поля являются конструкциями, позволяющими изучать про-
проблему действия на расстоянии, в которой относительное движенис-
и положение одного тела влияют на движение и положение другого тела.
Потенциальные и силовые поля, электромагнитные и гравитационные поля
служат примерами таких полей. Считают, что такие поля вызваны неко-
некоторым количеством материи, а значение поля в некоторой точке рас-
рассматривают как меру воздействия этого количества материи на некоторое
пробное тело, помещенное в рассматриваемой точке. В последнее время
стало очевидным, что многие из этих полей также являются лишь при-
приближенной идеализацией действительной физической ситуации, так как
они не учитывают различных квантовых законов, которым подчиняется
материя. В некоторых случаях теория этих полей может быть так
изменена, чтобы более или менее удовлетворительным образом учиты-
учитывались эти квантовые законы.
Наконец, поля могут, строиться для «объяснения» квантовых законов.
Примерами являются волновая функция Шредингера и спинорные поля,
ассоциируемые с электроном Дирака. Во многих случаях значение такого
поля в точке пространства тесно связано с вероятностью. Например,
квадрат модуля волновой функции Шредингера является мерой вероят-
вероятности присутствия элементарной частицы. Существующие квантовые тео-
теории поля встречаются со многими фундаментальными трудностями
и поэтому представляют собой одну из передовых линий фронта совре-
современной теоретической физики.
В_ большинстве случаев поля, рассматриваемые в настоящей книге,
оказываются решениями дифференциальных уравнений с частными про-
производными, чаще всего линейных уравнений второго порядка, однород-
однородных или неоднородных. Для того чтобы получить такие уравнения,
часто приходится упрощать действительную физическую ситуацию, при-
причем подобное упрощение может быть оправдано некоторыми прагмати-
прагматическими соображениями. Например, решением волнового уравнения
является лишь «сглаженная плотность» газа, что, однако, оказывается
достаточным для изучения звуковых волн, а значительно более сложные
вычисления фактических движений молекул газа немного добавили
бы к нашим знаниям о звуке.
Эта тенденция втиснуть физическую ситуацию в прокрустово ложе
дифференциальных уравнений с частными производными приводит к тому,
что получаемые поля оказываются одновременно и более и менее пра-
правильными, чем «фактические» состояния. Решение дифференциального
уравнения обладает в большей части пространства и времени' большей
степенью гладкости, чем соответствующая физическая ситуация, но мате-
математически оно обычно имеет конечное число разрывов, значительно более
«резких», чем те, которые «фактически» имеют место. Если упрощение
было не слишком далеко идущим, то большинство величин, которые
могут быть вычислены с помощью поля, достаточно хорошо соответствуе!
их измеренным значениям. В каждом случае, однако, обнаруживаются1
некоторые расхождения между вычисленными и измеренными значениями,
что объясняется либо «слишком гладким» поведением поля на большей
части его протяжения, либо наличием в математически построенном
поле разрывов и бесконечностей, отсутствующих в «действительности».
Иногда эти расхождения тривиальны в том смысле, что внесение в кон-
конструкцию поля дополнительных усложнений с целью получить лучшее
соответствие с экспериментом не приводит к принципиальному измене-
изменению самой теории явления; в некоторых же случаях эти расхождения'
далеко не тривиальны, и изменения в теории, необходимые для дости-
достижения лучшего соответствия с экспериментом, затрагивают коренным'
1. 1. Скалярные поля 15
образом основные понятия и определения. Для физика-теоретика важно
различать тривиальные и нетривиальные расхождения между теорией
и экспериментом.
Один из признаков того, что поле часто представляет собой упроще-
упрощение физической реальности, состоит в определении поля при помощи
предела некоторого отношения. Поле плотностей жидкости, в которой
распространяется звуковая волна, определяется посредством «плотности
в данной точке», которая является пределом отношения массы жидкости,
заключенной в некотором объеме, окружающем данную точку, к величи
не этого объема при стягивании этого объема к «нулю». Электрическая
напряженность «в данной точке» является пределом отношения силы,
действующей на пробный заряд в этой точке, к его величине при стрем
лении величины пробного заряда к «нулю». Величина квадрата модуля
волновой функции Шредингера есть предел отношения вероятности при-
присутствия элементарной частицы в некоторой области, окружающей дан-
данную точку, к объему этой области при сжимании этой области к «нулю»
и т. д. Аккуратное определение смещения «точки» колеблющейся
струны также должно использовать предел некоторого отношения.
Мы подчеркиваем здесь эти тривиальные с математической точки
зрения замечания потому, что техника предельных отношений должна
при определении и вычислении полей применяться с осторожностью.
Иными словами, для того чтобы получить результаты, соответствующие
«действительности», следует тщательно определить содержание понятия
«нуль» в предыдущих рассуждениях. Например, объем, встречающийся
в определении поля плотностей жидкости, должен быть на несколько
порядков меньше куба наименьшей длины волны распространяющегося
звука, если мы хотим, чтобы взятое отношение приводило к достаточно
точному решению волнового уравнения. С другой стороны, этот объем
нельзя уменьшать до величины, сравнимой с размерами атома, иначе
соответствующее отношение потеряет необходимые свойства гладкости
и не будет уже нам полезным. Если принять во внимание эти ограниче-
ограничения, то нетрудно понять, почему описание звуковых волн при помощи
поля, являющегося решением волнового уравнения, оказалось бы неадек-
неадекватным, если бы «длина волн» стала меньше межатомных расстояний.
Аналогичным образом мы определяем электрическое поле при помощи
пробного заряда, который должен быть достаточно мал, чтобы не влиять
на распределение зарядов, «порождающих» поле. Но если размеры проб-
пробного заряда уменьшить до порядка малости заряда электрона, то сле-
следует ожидать трудности, связанной с атомистичностью зарядов (кото
рая, однако, необязательно должна возникнуть).
В некоторых случаях предельное отношение может рассматриваться
при как угодно малых величинах его членов. Поля вероятностей волно-
волновой механики являются настолько «мелкозернистыми», насколько мы это
можем себе в настоящее время представить.
1.1. Скалярные поля
Когда рассматриваемое поле оказывается просто числом — значением
некоторой функции точки пространства и времени, - оно называется
скалярным. Отклонения струны или мембраны от их положения равнове-
равновесия представляют собой скалярные поля. Плотность, давление и темпера-
температура жидкости, определенные ранее через предельные отношения, также
являются скалярными полями. Как уже отмечалось, при вычислении
этих отношений объем не может быть уменьшен до атомных размеров,
16 Гл. 1. Типы полей
так как понятия плотности, давления и т. д. утрачивают смысл для
отдельных молекул. Отношения, определяющие эти поля, должны
приближаться к «макроскопическому пределу», когда объем мал по срав-
сравнению с объемом, занимаемым всей жидкостью, но все еще достаточно
велик по сравнению с размерами атома; иначе понятие скалярного поля
оказывается физически бессодержательным.
Все эти скалярные поля обладают свойством инвариантности отно-
относительно преобразований пространственных координат (инвариантность отно-
относительно преобразований временной и пространственных координат мы
рассмотрим далее в этой главе). Численное значение поля в точке
остается одним и тем же независимо от того, как выражены коорди-
координаты этой .точки. Форма математического выражения поля может меняться
в зависимости от выбора системы координат. Например, поле, выражен-
выраженное в прямоугольных координатах, может иметь вид Ь = у\ в сфериче-
сферических координатах оно будет иметь иной вид: 4 =/-sin 0 sin у, но в любой
системе координат в точке х = 10, у = 10, z = 0 (г = J/200 , <р = 45°, 6 = 90°)
оно имеет значение <1) = 10. Этому следует противопоставить поведение
^-компоненты скорости потока жидкости, где с изменением системы
координат может измениться и направление оси х. Поэтому численное
значение ж-компоненты скорости в данной точке будет изменяться
с изменением направления оси х.
Это свойство инвариантности скаляра будет играть важную роль
в дальнейших рассмотрениях, и его следует отличать от инвариантности
формы некоторых уравнений относительно некоторых преобразований
координат. Для таких упомянутых выше скалярных полей, как поля
плотности, температуры или электрического потенциала, свойство инва-
инвариантности совершенно очевидно из самого определения поля. Однако
это не всегда так для менее простых полей. В некоторых случаях свой-
свойство инвариантности должно быть использовано как пробный камень,
позволяющий найти правильное выражение для данного поля.
Поверхности уровня. Поверхности, определенные уравнением <Ь = const,
где <1> обозначает скалярное поле, называются поверхностями уровня.
Поверхности уровня являются очевидными обобщениями линий уровня
на топографической карте. В теории потенциала они называются экви-
эквипотенциальными поверхностями, в теории теплопроводности — изотерми-
изотермическими поверхностями и т. д. Они образуют семейство непересекаю-
непересекающихся поверхностей, которые часто оказываются полезными в качестве
одного из семейств координатных поверхностей, наиболее естественной
для данной проблемы системы координат. Например, если полем является
хорошо известный потенциал
то поверхностями уровня (в данном случае поверхностями постоянного
потенциала) являются концентрические сферы радиуса г = l/ж2 + у2 + z2 =
= const; поэтому естественными координатами для этой задачи явля-
являются сферические: г, 0, <р. Другая система поверхностей вместе с соот-
соответствующей системой координат показана на рис. 1.1. Поверхности
{1 = const могут рассматриваться как эквипотенциальные поверхности'
«округ круглого заряженного диска радиуса с, лежащего в плоскости
зу (ц=0).
Производные скаляра ty по прямоугольным координатам'х, у% z изме-
измеряют скорость, с которой изменяется поле при перемещении в простран-
пространстве. Например, изменение <Ь при перемещении из точки (х, у, z) в точку
1. 1. Скалярные поля
17
(x-\-dx, y-\-dy, z-\-dz) равно
«ty = |J- dx + -?J- dy +-f{- dz. =-
- V У ¦
A.1.1)
Если обе точки лежат на одной и той же поверхности уровня, тое?Ф = 0,
и дифференциальное уравнение этих поверхностей имеет вид
= 0. A.1.2)
ду
dz
Смещение {dx, dy, dz) перпендикулярно к поверхности уроння, если
составляющие смещения удовлетворяют соотношениям
dx
dy
A.J.3)
db/dx ду/ду
Эти соотношения являются дифференциальными уравнениями семейства
кривых, называемых нормальными линиями, которые в каждой точке
ею- г е^ зо°
9=90*
I' и с. 1.1. Примеры поверхностей уровня A = const, гдессЬ(л =
= -»-V'('> + cI! + zl!+ y^^—cJ + z2. 6 = const, где с cos 6 =
= -^- ~\f(r + сJ + z2 -^-1^('-—сJ-г z2 и ер = const, где t.g<p = —
иерпендикулярны поверхности уровня, проходящей через эту точку.
В сочетании с поверхностями уровня они могут быть использованы при
определении естественной для данного поля системы координат. Например,
для поля ф = (ж2-+ i/2+z2)-''2 поверхностями уровня являются (как было
отмечено выше) сферы, а нормальными линиями—радиальные лучи, что
наводит нас на мысль о сферических координатах г, б, <р (хотя эти эле-
элементы и не определяют полностью эту систему).
Нормальные линии имеют направление наиболее быстрого изменения ф.
Небольшие вычисления, основанные на уравнениях A.1.1) и A.1.3), пока-
показывают, что изменение ф ири смещении на расстояние ds вдоль нормаль-
нормальной линии равно
Квадратный корень в этом выражении называется величиной градиента 6.
Свойства градиента будут подробно рассмотрены несколько позже в насто-
настоящей главе.
Лапласиан. Чрезвычайно важное свойство скалярного поля выражается
посредством его вторых производных. В простейшем одномерном случае,
2 Ф. М. Морс и Г. Фешбах
18 Гл. 1. Типы полей
когда ф является поперечным отклонением струны от ее прямолинейного
положения равновесия, вторая производная сРф/da;2 непосредственно свя-
связана с разностью между значением ф в точке х и средним значением ф
в соседних точках. С точностью до малых второго порядка включительно
имеем
ф (х) - у [ф (х - dx) + ф (х + dx)\ =
= - |-{[ф (х + dx) - ф (х)] - [ф (х) - ф (х -dx)]} =
~" 2 da:
Следовательно, если вторая производная отрицательна, ф в точке х больше,
чем среднее значение ф в точках х +- dx и х — dx, так что график ф будет
обращдн в точке х своей выпуклостью кверху. Если вторая производная
равна нулю, то график ф не искривлен.
Нетрудно видеть, что уравнение, описывающее форму натянутой гибкой
струны, находящейся под воздействием поперечной силы F (х), отнесенной
к единице длины струны, должно содержать эту вторую производную.
Действительно, чем больше поперечная сила в некоторой точке, тем больше
должна быть кривизна струны в этой точке, для того чтобы натяжение Т
вдоль струны имело большую поперечную составляющую, которая уравно-
уравновешивает силу. Как показывает более подробное исследование, которое
мы проведем позже, уравнение, описывающее форму струны, имеет вид
Будем теперь искать трехмерный аналог этой меры кривизны ф. Раз-
Разность между значением ф в точке и средним значением ф в соседних
точках оказывается равной — -^(dxdydzJ V^, где
^ ^ ^ A14)
т дх1 ду2 dz2
является очевидным обобщением одномерного оператора второй производ-
производной. Математическая операция образования правой части уравнения A.1.4)
обозначается символом V2 (читается «набла квадрат») и называется опе-
оператором Лапласа. Результат этой операции, произведенной над функцией,
называется лапласианом ф. Если V^ отрицателен в некоторой точке,
то поле ф имеет тенденцию концентрироваться в этой точке. Прямым
следствием этого высказывания является тот факт, что скалярная функ-
функция ф (х, у, z) не может достигать своего максимального или минималь-
минимального значения в области, в которой Т2ф=0. Это—весьма важный факт.
Уравнение V2<J> = 0, называемое уравнением Лапласа, встречается
в физике столь часто, что полезно иметь ясное представление о его зна-
значении. Поэтому мы приведем без доказательств ряд фактов, касающихся
решений уравнения Лапласа, которые будут доказаны ниже в настоящей
главе.
Представим себе идеально упругую мембрану в состоянии равновесия,
находящуюся под воздействием равномерного натяжения, приложенного
к ее краю. Если край мембраны лежит в некоторой плоскости, то и мемб-
мембрана будет лежать в этой плоскости. Если плоская форма края будет
нарушена, то и мембрана перестанет быть плоской. Это искажение мембраны
может быть представлено функцией ф (х, у) — отклонением точки (х, у)
мембраны, перпендикулярным к этой плоскости. Оказывается, что это
отклонение удовлетворяет двумерному уравнению Лапласа Vs<{> = 0.
1. 2. Векторные поля
19
Последнее уравнение просто соответствует утверждению, что натяжение
иыравнивает все «выпучивания» мембраны, что отклонение в любой точке
равно среднему значению отклонений в соседних точках. Мы видим, что
уравнение Лапласа для мембраны соответствует требованию, что мембрана
принимает форму, требующую наименьшего растяжения.
Дополнительная нагрузка мембраны, перпендикулярная к плоскости
равновесия ф = 0, вызывает «выпучивание» мембраны. Как будет показано
далее, лапласиан ф в точке нагруженной мембраны пропорционален
нагрузке, отнесенной к единице площади в этой точке. Можно сказать,,
что двумерный оператор Лапласа измеряет «выпучивание» мембраны.
Обобщение этого рассмотрения на три измерения труднее представить,
но в принципе оно столь же просто. Мы можем представить себе, что скаляр-
скалярная функция ф соответствует концентрации некоторого вещества в растворе.
Трехмерный аналог «выпучивания» может быть назван «сгущенностью»;.
? г
Рис. 1.2. Форма круглой мембраны, равномерно нагружен-
нагруженной (Y24J = const) от г = 0 до /• = 1/2 и свободной от нагрузки
(у2ф = и) от г~г1^ до /•=!; край мембраны г=1 закреплен.
если есть тенденция вещества «сгущаться» в некоторой точке, то лапла-
лапласиан концентрации будет отрицателен в этой точке. Если V2$ = 0, то веще-
вещество вообще не имеет «сгущений», его плотность распределяется так, чтобы
различия в концентрации, порождаемые краевыми условиями, максимально
сглаживались. Как и в двумерном случае, уравнение Лапласа соответствует
требованию, чтобы ф в каждой точке было равно среднему значению ф
в соседних точках.
Наличие электрических зарядов плотности р вызывает (отрицательную)
концентрацию электрического потенциала ф, так что Т2ф = — р/г, где е —
постоянная. Наличие распределенных источников тепла Q в твердом теле
вызывает концентрацию температуры Т, так что ^2Т — —KQ, где К —
постоянная. Вообще во многих случаях на скалярное поле влияет функ-
функция источника q (х, у, z) (которая сама является скалярным полем, удовле-
удовлетворяющим некоторым другим уравнениям), причем это влияние описывает-
описывается уравнением
V^=-g. A.1.5)
Это уравнение называется уравнением Пуассона. Мы будем его подробнее
рассматривать в этой главе позже и уделим много места его решению
и дальнейших главах книги.
1.2. Векторные ноля
Мы рассмотрели в предварительном порядке ряд нолей, которые харак-
характеризуются в каждой точке одной единственной величиной. Такие поля:
были названы скалярными полями. Многие другие поля требуют для своего,
полного определения задания в каждой точке величины и направления.
Такие поля называются векторными полями. Они также часто могут быть
определены в терминах пределов отношений, хотя здесь определения, как;
2*.
'20 Гл. 1. Типы полей.
правило, более сложны, чем для скалярных полей. Сила, действующая
на некоторую массу жидкости в гравитационном или электрическом поле,
является вектором, имеющим величину и направление. Предел отношения
этой силы к объему, занимаемому той массой жидкости, на которую сила
воздействует, при уменьшении этого объема определяет в каждой точке
пространства некоторый вектор, задающий силовое поле. Как и для скаляр-
скалярных полей, в некоторых случаях оказывается важным не допускать умень-
уменьшения объема до атомных размеров.
Иногда векторное поле легче всего определяется черея скалярное
отношение, которое уже само учитывает направление. Например, в случае
проводника, через который течет ток, можно представить себе инструмент,
который измерял бы силу тока, проходящего через элемент площади dA
с центром в некоторой точке проводника. Тогда мы нашли бы, что измерен-
измеренная сила тока зависит не только от величины dA, но и от ориентации
элемента dA. Измерения соответствовали бы формуле J dA cos $, где Ь-
угол между нормалью кй4и некоторым направлением, характеристическим
для данного распределения тока. Величиной вектора поля в данной точке
будет, следовательно, J, а его направлением будет то, от которого отсчп-
тывается угол &.
Векторные поля в трех измерениях определяются заданием трех
количеств в каждой точке: величины и двух углов, определяющих направ-
направление, или трех составляющих (компонент) вектора по трем осям коор-
координат. Четырехмерные векторы будут рассмотрены позже.
Набранные жирным шрифтом заглавные латинские буквы (A, F, X)
обозначают в настоящей книге векторы; соответствующие буквы, набран-
набранные обычным шрифтом (A, F, X), обозначают величины соответствующих
векторов (обычный шрифт будет, как правило, применяться для обозначе-
обозначения скалярных величин). Составляющие А по трем осям координат будут
обозначаться через Ах, Ау, А,. Вектор единичной длины в направлении А
обозначается через а; единичные векторы в направлении осей х, у, z
обозначаются, как обычно, через i, j, k. Единичные векторы вдоль криво-
криволинейных осей координат будут обозначаться через а с индексом, указы-
указывающим соответствующую ось- (например, в полярных координатах единич-~
ный вектор в направлении г обозначается через аг, в направлении & —
через а& и т. д.). Если не оговорено противное, используются правые системы
координат: при вращении от х к у правый винт, расположенный вдоль
оси z, будет иметь поступательное движение в положительном направлении
оси z, или, что то же, наблюдатель, стоящий лицом к доске и видящий
на ней ось х, направленную вправо, и ось у, направленную вверх, смотрит
на плоскость ху со стороны положительных z.
В этих обозначениях векторы А и В удовлетворяют следующим общим
'Отношениям:
А + В = (Ах + Вх) i + (Av + By) j + D + Вг) k,
дающим определения составляющих и векторного сложения.
Векторы не инвариантны относительно замены координат в том же
смысле, как скаляры, так как составляющие изменяются с изменением
направления осей координат. Свойства преобразований векторов будут
рассмотрены ниже.
Умножение векторов. Два вектора могут быть перемножены двумя
различными путями: один тип умножения приводит к скаляру, другой —
к вектору. Скалярное произведение двух векторов А и В {произведение
1. 2. Векторные поля 21
с точкой) равно произведению величины одного из них на проекцию дру-
другого на направление первого:
А • В = ЛВ cos 0 = АХВХ + ЛуВи + AZB2, A.2.2)
где & — угол между А и В. Выражение /U5cos& не зависит от выбора
системы координат, примененной для вычисления составляющих Ах и т. д.,
так что значение скалярного произведения не зависит от системы коор-
координат. Скалярное произведение является поэтому истинным скаляром,
простейшим инвариантом, который может быть образован из двух векторов.
Скалярное произведение полезно для выражения многих физических
величин: работа, совершаемая при перемещении тела, равна скалярному
произведению силы на перемещение; плотность электрической энергии
в пространстве пропорциональна скалярному произведению электрической
напряженности и электрической индукции и т. д. Скалярное произведение
двух единичных векторов равно косинусу угла между ними. Максимальное
значение скалярного произведения двух векторов достигается, когда оба
вектора параллельны (и одинаково направлены); оно равно нулю, когда
они перпендикулярны. В некотором смысле скалярное произведение есть
мера равнонаправленности двух векторов.
Векторное произведение А X В двух векторов является вектором,
величина которого равна площади параллелограмма, определенного этими
двумя векторами, а направление перпендикулярно к этому параллело-
параллелограмму. Выбор того конца перпендикуляра, который должен быть снабжен
стрелкой, произвольно определяется тем условием, чтобы тройка А, В
и А х В была правой: если правый шшт расположить перпендикулярно
к А и к В, то вращение от А а В должно придавать шшту поступатель-
поступательное движение в направлении А - В. В праной прямоугольной системе
координат
А : В = (AyBz - ВЦАЛ * -г ИА - BZAX) J + (AJBy - ВхАу) k,
(l.Z.o)
Величина (А X В) = AB sin &.
Отметим, что векторное произведение некоммутативно, так как
А<В=-ВхА.
Аксиальные векторы. Хотя (как мы далее увидим) векторное произ-
произведение Двух векторов является вектором, обладающим при преобразова-
преобразованиях большинством свойств «истинного» вектора, здесь имеется все же
одно важное различие. Векторное произведение, определенное равенством
A.2.3), меняет знак при переходе от правой системы координат к левой.
Это один из аспектов того факта, что векторное прои-чведепие имеет скорее
свойства ориентации элемента площади, нежели стрелки. Направление,
связанное с, элементом площади, определено однозначно как направление,
нормальное к элементу, однако нет обязательного правилах) для выбора
положительной стороны элемента. Площадь определяет, так сказать, древко
стрелы, но не говорит о том, с какой стороны должен быть наконечник.
Этот вопрос должен быть решен каким-либо полностью произвольным
правилом, как, например, указанным выше правилом (правого винта),
которого мы и будем придерживаться.
Вообще векторы с данным «древком» (т. е. с заданной несущей прямой
и данной длины), но с заменяемыми стрелками называются аксиальными
1) Имеется в виду правило, не пвиоящее ог ориентации системы координат. —
Прим. перев.
22 Гл. 1. Типы полей
еекторами (они иногда называются также псевдовекторами). В дальнейшем
мы увидим, что три составляющие аксиального вектора фактически являют-
являются тремя компонентами трехмерного кососимметрического тензора второго
порядка. Кососимметрический тензор можно представить аксиальным
вектором в трехмерном пространстве.
Как указывалось выше, аксиальный вектор, связанный с элементом
площади dA, можно записать в виде
dA = n dA = dx x dy,
где n — единичный вектор нормали к элементу и где dx и dy — векторы,
соответствующие составляющим элементам dx и dy. Если применяются
первые два обозначения, необходимо дополнительно указать, какая сторона
элемента считается положительной; если используется последнее обозначе-
обозначение, наше правило правого винта автоматически решает и этот вопрос.
Другие аксиальные векторы также могут быть представлены в виде
векторного произведения: момент количества движения материальной
частицы относительно некоторой точки равен векторному произведению
вектора, представляющего импульс частицы, и радиус-вектора частицы;
момент силы равен векторному произведению вектора силы и вектора,
представляющего плечо, и т. д. Вращение определяет плоскость и ось,
нормальную к этой плоскости, т. е. характеристики аксиального вектора.
В соответствии с нашим правилом направление вектора, изображающего
вращение, совпадает с поступательным движением правого винта при рас-
рассматриваемом вращении.
Полезным примером произведения трех векторов является смешанное
тройное произведение
А-(В х С) = В(С х А) = С-(А х В) =
Ау 4
ву bz
су cz
A.2.4)
Это выражение равно объему (или объему, взятому со знаком минус)
параллелепипеда с ребрами А, В, С. Оно представляет собой скаляр,
являющийся скалярным произведением аксиального вектора и истинного
вектора, и меняет знак при переходе от правой к левой системе координат,
а также при перестановке двух векторов; поэтому такой скаляр называется
иногда псевдоскаляром. Заметим, что скалярное произведение двух аксиаль-
аксиальных векторов (или двух истинных векторов) является «истинным» скаля-
скаляром без неопределенности в знаке.
В частности, правилами умножения единичных векторов являются:
ixi=...=0, ixj = k, jxk = i. kxi = j. (""'
Линии тока. Как уже было указано, векторное поле определяется
заданием вектора в каждой точке пространства или, другими словами,
заданием вектора, являющегося функцией х, у, z: Г (ж, у, z). В большин-
большинстве интересующих нас случаев этот вектор является непрерывной функ-
функцией х, у, z, за исключением либо изолированных точек, или особенно-
особенностей, либо изолированных линий — особых линий. Там, где вектор непре-
непрерывен, мы можем определить линии тока поля, которые являются линиями,
касательными в каждой точке к векторх_в этой точке. Дифференциальные
уравнения этих линий выводятся из требования пропорциональности
1. 2. Векторные поля
23
составляющих dx, dy, dz смещения вдоль линии и составляющих F x, Fy,
Fz вектора поля в данной точке
Jcp. с уравнениями A.1.3)].
В некоторых простых случаях эти уравнения могут быть проинтегри-
проинтегрированы, что дает уравнения семейства линий тока.
Например, если Fx=—ay, F'y= ах, Fz — Ь(ж2 + у2), то линии тока
являются винтовыми линиями. Уравнение dx/Fх = dy/Fy. превращается
fl-2
<e =10, у
Рис. 1.3. Винтовые линии тока 6, ср = const с псевдопотенци-
псевдопотенциальными поверхностями ф = const (см. стр. 26).
в xdx — —у dy; интегрируя его, находим уравнение кругового цилиндра
хг _|_ у2 __ ^2^ Где ^ — произвольная постоянная, частично определяющая
выбор линии тока. Уравнение
dy dz
Fy Fz
п ревращается в
a dz
(если выразить х из уравнения, связывающего х и у). Интегрируя его,
находим
z = ^- arc sin -^ + 6 = — (ж2 + у2) a re tg ^ + б,
где б—другая постоянная интегрирования, которая необходима для пол-
полного определения линии тока. Уравнения
9 =
определяют дважды бесконечное семейство линий тока, причем каждая
отдельная линия тока задается парой значений <р и 6.
Другим примером является Fx = —g, Fy = \, Fz^=-^, где r2 = x2-{-
+ y*-\-z2. Уравнения для линий тока сводятся к системе
dx dy _ 'dz
х ~~ у ~~ z
Первое из уравнений этой системы дает In х = In у + const или х/у = const.
Аналогично мы находим, что либо ж/z, либо y/z = const или (ж2 + г/2)/г2 =
24
Г>. 1. Типы полей
= const. Наиболее удобной формой выражения постоянных интегрирова-
интегрирования является (по аналогии с предыдущим примером)
<р = arctg — , 6 = arctg -
У.
X
И в этом примере выбор значений для tp i 0 определяет индивидуальную
линию тока; она является в данном случае полупрямой, исходящей жл
начала координат.
С^ другой точки зрения <р и б могут рассматриваться как функции х,
у, z и называются функциями токд^. Значения <р и б в некоторой точке
вьщеляют_линито тока, проходящую через эту точку. Еще с одной точки
зрения два семейства поверхностей <р = const и б = const могут рассматри-
рассматриваться как семейства координатных поверхностей некоторой обобщенной
Ф--27СГ
-10
о--90?г=1.0.
ж
r=I.O
i
f
I/
%
L
j\
i 7
•w Si
г=Ю
Рис. 1.4. Радиальные линии тока и сферические эквипо-
эквипотенциальные поверхности для поля вокруг точечного источ-
источника.
системы координат. Пересечением двух таких поверхностей <р = <Ро и ^==^о
является линия тока, соответствующая паре значений (<р0, 60); это — коор-
координатная линия в новой системе координат.
Потенциальные поверхности. Линии тока могут также определять
другое семейство поверхностей, перпендикулярных к ним (если только
эти линии не «закручиваются» так, что такого семейства поверхностей
не существует). По аналогии с уравнением A.1.2) уравнение такой по-
поверхности имеет вид
F-Ax = Fxdx + Fydy + F2dz = U A.2.7)
в соответствии с тем фактом, что любой вектор смещения на поверхности
должен быть перпендикулярным к Г.
В некоторых случаях это уравнение интегрируемо. Если существует
такая функция (]>, что
то уравнением семейства поверхностей будет ф = const. Величина р. может
быть функцией х, у, z; она называется интегрирующим множителем.
Критерий того, существует ли уравнение поверхностей в интегральной
1. 2. Векторные поля 25
форме, может быть получен следующим образом. Рассмотрим выражение
х
ду dz)^ v\dz дх )^Гг\дх dy
Ото выражение равно нулю, если функция ф с указанными свойствами
существует. Обратно, если выражение
х\ ду dz ) • «V dz dar'y 2 V дх ду
оказывается ранным нулю, то интегрирование дифференциального уравне-
уравнения для поверхностей, перпендикулярных к линиям тока, возможно1).
Другими словами, если вектор с составляющими
ду ~dz )' \dz~ dx ) ' У дх ду
но осям х, у, z перпендикулярен к вектору F в каждой точке, то можно
получить уравнение нормальных поверхностей в интегральной форме
ф (х, у, z) = const. Подробнее этот вектор будет рассмотрен ниже. Функ-
Функция ф называется псеедопотеициалъной функцией.
В некоторых случаях [* постоянно и может быть положено равным —1,
так что
f = -д1 р = -°± р - _«!i
х дх' и ду ' -~ dz'
Позже будет объяснено, почему выбирается знак минус. В этих случаях
функция ф называется потенциальной функцией векторного ноля Г, а по-
поверхности ф =¦ const называются эквипотенциальными поверхностями*).
Для того чтобы это имело место, каждая из разностей
dFz dFv dFx__dF: dFy dFx
~~ду dz ' ~dz ~дх~ ' ~дх Ъу
должна быть раина нулю, как в этом можно убедиться, заменив выраже-
выражения для составляющих F производными функции ф.
В других случаях уравнение поверхностей не интегрируемо ни при
помощи интегрирующего множителя, ни без него; тогда невозможно
найти хорошо ведущее себя семейство поверхностей, всюду перпендику-
перпендикулярных линиям тока. Мы еще вернемся к этому рассмотрению на стр. 29.
В первом примере предыдущего пункта, где линиями тока являются
имптоиые линии, вектор с составляющими
dFz dFv_ dFx dF:_ dFu 0Fx_
oy oz u dz дх dx dy
перпендикулярен к вектору F. Поэтому дифференциальное уравнение
A.2.7) семейства поверхностей интегрируемо. После умножения уравнения
') Степанов 15. В., Курс дифференциальных уравнений, ГТТИ, М.—Л., 19Ы>.
гл. IX, § 2.—Прим. перев.
") В некоторых местах книги под потенциальной функцией понимается не <г.
а —-Ь. —Прим. ped.
26 Гл. 1. Типы полей
на интегрирующий множитель р. = (х2 -\- у2)'1 мы получаем в левой части
полный дифференциал. Полагая
находим, что
так что проинтегрированное уравнение, соответствующее уравнению
1.2.7), в этом случае имеет вид ф = const. Система поверхностей ф = const,
=const, <p = const образует систему обобщенных координатных поверхно-
поверхностей (которые в данном случае не являются взаимно перпендикулярными),
наиболее естественную для рассматриваемого векторного поля. Значения
<р и б в некоторой точке определяют линию тока, проходящую через эту
точку, а значение ф определяет положение точки на этой линии тока.
Во втором рассмотренном выше примере все разности
dFzdFjL 8FxdF\ dFy dFx
~ду dz~ dz дх ' ~дх ду~
равны нулю, так что уравнение A.2.7) интегрируется непосредственно
без применения интегрирующего множителя. Функция
поэтому является потенциальной функцией, а сферические поверхности
ф = const являются эквипотенциальными поверхностями. Компоненты. F
связаны с ф требуемыми соотношениями
вФ_ _х_ „ ?1=_ж__р dA-_±-_w
дх~ rs~~ ж' ду г3 У dz~~ r3" z'
Система координат, соответствующая линиям тока и эквипотенциальным
поверхностям, является сферической
г = ух2 -f- у2 ~р z2 .
В этом случае координатные поверхности взаимно-перпендикулярны.
Если для данного векторного поля F существует семейство эквипо-
эквипотенциальных поверхностей, то это поле может быть представлено через
скалярное потенциальное ноле ф, и тогда, как правило, гораздо легче
вычислить сначала это скалярное поле, а векторное поле получить диф-
дифференцированием .
Поверхностные интегралы. Векторные поля и их линии тока обла-
обладают рядом общих свойств, играющих важную роль для наших целей.
Одним из этих свойств является «расхождение» или «поток» линий тока,
отнесенное к данной области, причем это понятие учитывает как тот
случай, когда линии тока начинаются в этой области или пропадают
в ней, так и тот случай, когда они просто переходят через область
с одной ее стороны до другой. Другим интересным свойством является
мера «закрученности» линий, независимо от того, находятся ли в вектор-
векторном поле «завихрения» или нет.
Расхождение линий тока из области может быть измерено при по-
помощи поверхностного интеграла. Предположим, что мы рассматриваем
1. 2. Векторные поля 27
элемент площади поверхности, ограничивающей область, представленный
бесконечно малым аксиальным вектором dA, равным по величине пло-
площади элемента и направленным перпендикулярно к поверхности. Скаляр-
Скалярное произведение F-dA равно тогда произведению площади элемента по-
поверхности на составляющую вектора F, нормальную к поверхности. Если
вектор поля ?(х, у, z) представляет вектор скорости движения жидкости,
то F-dA равно объему жидкости, протекшему через элемент поверхности
(в единицу времени), а \ F-dA равен объему всей жидкости, протекшей
(в единицу времени) через ту поверхность, по которой распространяется
интегрирование. Знак интеграла зависит от выбора направлений аксиаль-
аксиальных векторов dA, т. е. от того, направлены ли эти векторы от одной
стороны поверхности или от другой. Абсолютная величина этого инте-
интеграла иногда называется числом линий тока поля, пересекающих поверхность
(являющуюся областью интегрирования), — термин, который определяет,
что следует понимать под «числом линий тока».
Если поверхность, по которой производится интегрирование, является
замкнутой и если векторы dA направлены от области, ограниченной
поверхностью, то интеграл будет записываться в виде
F dA
и называться потоком вектора F из области, ограниченной замкнутом
поверхностью интегрирования. Если F есть вектор скорости жидкости,
то этот интеграл равен «расходу жидкости» в рассматриваемой области.
Ограничивающая эту область поверхность не обязана состоять из одной
связной части, ограничивающей односвязную область; область может
быть ограничена несколькими поверхностями, например одной внутренней
и одной внешней (или даже несколькими внутренними поверхностями).
В этом случае внешняя ограничивающая поверхность может лежать
в бесконечности, так что область будет состоять из всего пространства,
внешнего относительно одной или нескольких замкнутых поверхностей.
Векторы dA в точках внутренних поверхностей должны быть направлены
внутрь от рассматриваемой внешней области.
Интеграл (A)F-dA является мерой числа линий тока, берущих свое
начало внутри области. Если таких линий нет, т. е. все линии тока
проходят с одной стороны границы области до другой, то этот интеграл
равен нулю.
Источник. Один простой пример векторного поля представляет для
нас особый интерес; он иллюстрирует важное свойство потока вектора.
Это тот случай, когда все линии тока берут свое начало в одной точке О,
причем вектор F в точке Р имеет величину Q/r2 и направлен вдоль г.
Величина г есть расстояние от О до Р, как показано на рис. 1.5,
а точка О называется простым источником линий тока; Q называется
мощностью источника. Элемент поверхностного интеграла в этом случае
равен
Но dA (cos О/г2) равно dQ — элементу телесного угла, под которым из
точки О виден элемент площади dA, когда нормаль к этому элементу
наклонена под углом G к радиусу. Поток вектора в этом случае сводится
к (}(T)dS, что равно нулю, если О лежит вне области, ограниченной
28
Гл. 1. Типы полей
поверхностью интегрирования, и равно 4тс(), если О лежит внутри этой
области. Более подробное рассмотрение, аналогичное приведенному выше,
доказывает, что это_справедливо для замкнутых поверхностей любой
формы и строения, ограничивающих область.
Изложенное выше дает нам довольно окольный путь для определе-
определения простого источника. Более непосредственным было бы „определение
простого источника мощности Q как точечной особенности векторного
поля, обладающей тем свойством, что поток вектора из любой области,
содержащей эту особенность (и не содержащей других), равен 4иф.
Полученный результат может быть сформулирован в виде равенств
О, если источник находится вне области,
, если источник находится внутри области.
Здесь аг обозначает единичный вектор, напра-
направленный от О вдоль г.
Иногда векторное поле является наложе-
наложением полей, порожденных несколькими про-
простыми источниками: одним в точке Ог мощ-
мощности Q13 другим в точке О2 мощности Q% и т. д.
Другими словами,
где гп — расстояние от точки Оп до Р, а агп —
единичный вектор, направленный вдоль гп.
В этом случае поток вектора будет равен
Рис. 1.5. Векторное поле вок-
вокруг точечного источника. Эле-
Элемент интеграла, выражающе-
выражающего поток вектора.
где штрих у суммы означает суммирование ш>
тем источникам, которые содержатся внутри
области, ограниченной поверхностью интегри-
интегрирования, а сумма без штриха распространяет-
распространяется на все источники.
Криволинейные интегралы. Вместо интегрирования нормальной со-
составляющей вектора по поверхности можно также интегрировать его со-
составляющую вдоль линии. Если ds — векторный элемент дуги вдоль неко-
некоторого пути, то интеграл \ F-ds, взятый вдоль этого пути, называется
криволинейным интегралом F (вдоль соответствующего пути). Если F —ве-
—вектор силы, то криволинейный интеграл является работой, совершенной
вдоль пути; если F — электрическая напряженность, то криволинейный
интеграл равен э. д. с. между концами пути и т. д.
Вообще говоря, значение криволинейного интеграла между двумя
точками зависит от выбора пути между ними. В некоторых случаях,
однако, оно зависит только от положения конечных точек. Это имеет
место в случае, рассмотренном на стр. 25, где составляющие F являлись
производными некоторой потенциальной функции <Ь. В таком случае кри-
криволинейный интеграл от точки О до другой точки Р вдоль некоторого
пути А равен по абсолютной величине и обратен по знаку криволиней-
криволинейному интегралу, взятому в обратном направлении от Р к О вдоль какого-
либо другого пути В. Поэтому интеграл вдоль замкнутого пути от О по
А к Р и затем обратно вдоль В к О для такого поля равен нулю. Вообще
же говоря, криволинейный интеграл векторного поля вдоль замкнутого
пути не равен нулю.
1. 2. Векторные поля
29
Криволинейный интеграл вдоль замкнутого пути обозначается
Fds
и называется циркуляцией ? вдоль этого пути. Этот интеграл является
мерой «закрученности» линий тока поля. Например, если линии тока
замкнуты (как, например, линии магнитной напряженности вокруг про-
проводника, по которому идет ток), то криволинейный интеграл F вдоль таких
линий будет, конечно, отличен от нуля. Этот интеграл называется цир-
циркуляцией потому, что если Г представляет вектор скорости в потоке
жидкости, то фр-ds является мерой циркуляции жидкости вдоль иы-
бранного замкнутого пути.
Мы видели, что в том случае, когда векторное ноле имеет потенци-
потенциальную функцию, циркуляция равна нулю. Поэтому мы называем все
Рис. 1.6. Пути для интеграла циркуляции-вокруг вих-
вихревых областей.
поля, имеющие потенциальные функции, полями без циркуляции или без-
безвихревыми полями. В полях, для которых существуют псевдопотенциалы,
циркуляция не обязательно должна быть равна нулю. Это будет иметь
место только в том случае, когда gradf* (см. стр. 25) в каждой точке
параллелен Г.
Существуют векторные поля, которые являются безвихревыми всюду
вне некоторой области пространства; точнее, в этих полях циркуляция
по замкнутому пути, охватывающему эту область, отлична от нуля,
а циркуляция по замкнутому полю, не охватывающему эту область, равна
нулю. По аналогии с задачей о потоке жидкости мы будем такую область,
«порождающую» циркуляцию, называть вихревой областью. Вихревые
области должны иметь форму трубки, которая не имеет ли начала, ни
конца. Она должна либо уходить в обе стороны в бесконечность, либо
иметь форму «баранки». Действительно, если бы вихревая область закан-
заканчивалась как V (см. рис. 1.6), то это означало бы, что циркуляция по
пути А отлична от нуля, тогда как интегралы по путям В, С и D равны
нулю. Однако нетрудно усмотреть, что если интеграл по А отличен от
нуля и, например, интегралы по Б и С равны нулю, то интеграл по D
не может быть равен нулю. Это следует из того, что интегралы по со-
соседним параллельным частям путей, проходимых в противоположных
направлениях, взаимно уничтожаются, так что сумма всех четырех инте-
интегралов по А, В, С и D должна быть равна нулю. Поэтому, если инте-
интегралы по В ж С равны нулю, то интеграл по D должен быть равен
30
Гл. 1. Типы полей
интегралу по А, взятому с обратным знаком, который по условию отли-
отличен от нуля. Следовательно, вихревая область не может заканчиваться
на V, а должна продолжаться каким-то образом, как, например, показано
пунктирной штриховкой на рис. 1.6. (При этом рассуждении мы молча-
молчаливо предполагаем, что поле непрерывно вне вихревой' области; в против-
противном случае положение может быть совершенно иным.)
Вихревая область может, конечно^ «разветвляться» на несколько тру-
трубок, из которых одни могут замыкаться, а другие — уходить в- беско-
бесконечность. Доказанное выше утверждение может быть обобщено и на этот
случай; в дифференциальной форме соответ-
соответствующая общая теорема будет приведена
на стр. 51.
Вихревая линия. Простейшим видом
вихревой области является простая вихре-
вихревая прямая линия, поле которой дается
уравнением
F = |-(Qxar)=^a9, A.2.11)
где Q, называемый иногда вектором зави-
завихренности, является вектором произвольной
длины, направленным вдоль вихревой пря-
прямой линии L. Пусть q —единичный вектор
в направлении Q. Вектор г перпендикуля-
Рис. 1,7. Векторное поле вокруг рен к Q и идет от L к точке Р, в которой
линии вихрей. Элемент цирку- рассматривается вектор поля F, аг — единич-
ляции. ный вектор в том же направлении и а,,, =
= qxar-единичный вектор, перпендику-
перпендикулярный к вг и к Q. Для пути в плоскости, перпендикулярной к L, цир-
циркуляция в этом поле равна
где а — угол между ds и а,,,.
Вторая часть рис. 1.7 показывает, что ds (cos a)/r = d<j>— элементу угла,-,
вращения г вокруг L. Поэтому циркуляция сводится к интегралу
2(?ф d<j>, который может быть непосредственно вычислен. Так, для пути
В, обходящего L, он равен AicQ, а для пути А, не обходящего L, он ра-
равен нулю. Это рассмотрение может быть обобщено на пути, не лежащие-
в плоскости, перпендикулярной к L, и окончательный результат для поля
простой вихревой линии имеет вид
г> /">п~\ - i 0, если путь не обходит L,
*f^K-ds= ' 3 ' A.2.12).
J ч г J * { -?- {lkQ, если путь один раз обходит L, v '
справедливый для всевозможных путей. Знак плюс следует брать, если
при интегрировании обход L совершается по часовой стрелке, если смот-
смотреть в направлении положительных Q; знак минус — если обход совер-
совершается в противоположном направлении.
Особенности полей. Интересно отметить параллелизм между свой-
свойствами интеграла, выражающего поток вектора вблизи простого источни-
источника, рассмотренными на стр. 28, и только что рассмотренными свойства-
свойствами интеграла циркуляции вблизи вихревой линии. Источник и вихревая
1. 3. Криволинейные координаты
31
линия являются простейшими примерами особенностей векторных полей.
В результате наших дальнейших рассмотрений мы убедимся в том, что
особенности, подобные этим, являются обычно наиболее важными момен-
моментами, характеризующими скалярные и векторные поля. Физическая
сущность задачи, как правило, тесно связана с типом особенностей поля.
Точно так же математические свойства решений дифференциальных урав-
уравнений определяются характером особенностей, которыми обладают урав-
уравнения и их решения. Нам придется много заниматься физическими и ма-
математическими свойствами особенностей в полях.
Поле, порождаемое простым источником, расходится из точки, а
поле, порождаемое вихревой линией, вращается вокруг этой линии.
Источники можно распределить вдоль линий, или поверхностей, или
даже по некоторому объему, а вихревые ли-
линии—по поверхностям или по объему, но
их нельзя стянуть в точку. Это связано с тем
фактом, что для вращения требуется ось,
т. е. линия, вокруг которой происходит
вращение.
Циркуляция и поток вектора в любых
полях обладают одним интересным общим
свойством, а именно, «аддитивностью». На-
Например, на рис. 1.8 циркуляция вдоль пу-
пути С равна сумме циркуляции по путям А
и В, так как интегрирование по внутренней
части D путей А и В совершается в проти-
противоположных направлениях и соответствую-
соответствующие интегралы взаимно уничтожаются, а
остатки в сумме дают интеграл по пути С.
Аналогично поток из любой области равен сумме потоков из всех частей
области, которые ее составляют. Это также объясняется тем, что интег-
интегралы по поверхностям, проходящим внутри исходной области, встречают-
встречаются парами и взаимно уничтожаются, так что сумма остающихся интег-
интегралов равна интегралу по поверхности, ограничивающей эту исходную
область.
Риг. 1.8. Аддитивность цирку-
циркуляции.
1.3. Криволинейные координаты
До сих пор мы молчаливо предполагали, что рассматриваемые поля
могут быть выражены через три прямоугольные декартовы координаты
х, г/, z (четвертая координата, время, будет рассмотрена позже). Век-
Векторные и скалярные поля всегда могут быть так выражены, но часто
оказывается гораздо более удобным выразить их в других системах коор-
координат. Мы уже видели, что иногда оказывается возможным построить
некоторую «естественную» для данного векторного поля систему коорди-
координат, используя для этого линии тока и потенциальные поверхности.
Во многих случаях природа поля определяется указанием его поведения
на некоторой граничной поверхности или указанием характера и распо-
расположения его особенностей (или тем и другим); при этом часто оказы-
оказывается, что «естественная» для поля система координат каким-то простым
образом связана с граничной поверхностью или с распределением особен-
особенностей (или и с тем и с другим). В этих «естественных» координатах вы-
выражение поля часто принимает простой и удобообозримый вид, тогда
как в координатах х, у, z это выражение становится очень сложным,
а необходимые вычисления — почти невыполнимыми.
32
Гл. 1. Типы полей
В силу этих и ряда других соображений, с которыми мы ознакомим-
ознакомимся при дальнейшем углублении в наш предмет, полезно сейчас заняться
выражениями полей, а также дифференциальных и интегральных опера-
операторов, которые действуют на них, в обобщенных трехмерных координа-
координатах. Мы ограничимся ортогональными координатами, для которых три
семейства координатных поверхностей взаимно перпендикулярны, так как
задачи, требующие неортогоналъных координат, почти никогда не ре-
решаются точно. Техника же приближенного решения таких задач обычно
использует решения в ортогональной системе координат.
Обобщенная система координат состоит из трех семейств поверхно-
поверхностей, уравнения которых в декартовой системе координат имеют вид
^(х, у, z) = const, 6а(ж, у, z) = const, ?3^» У' z) = const (мы предпола-
предполагаем, что читатель достаточно хорошо знаком со свойствами декартовых
Рис. 1.9. Элемент криволинейной системы координат с
единичными векторами а„ и направляющими косину-
косинусами -\пт-
координат х, у, z, так что нет необходимости заниматься ими здесь). Ути
равенства определяют ?х, ?2 и ?3 как функции от х, у ш z. Во многих слу-
случаях оказывается более удобным обратить уравнения и выразить х, у, г.
через ?1? ?2, ?8.
Линии пересечения этих поверхностей образуют три семейства кри-
кривых (вообще говоря) линий. От точки (ж, у, z) или (?lf !2> ?з) мы откла-
откладываем три единичных вектора а1? а2, а3, каждый из которых касателен
к проходящей через эту точку соответствующей координатной линии
криволинейной системы. Это новая тройка единичных векторов, чере:(
которые мы можем выразить векторное поле F. Повторяем, что векторы а
имеют единичную длину, скажем 1 см (или какая-либо другая примененная
единица длины), т. е. ту же длину, что и векторы i, j, k. Для ортогональ-
ортогональных систем координат векторы а в каждой точке взаимно перпендику-
перпендикулярны.
Направляющие косинусы. Обозначим направляющие косинусы еди-
единичного вектора ах относительно старых осей через a1 = a1-i, P1 = a1-j,
Y1 = a1-k; направляющие косинусы вектора а2 — через и2, ра, Чг и т.* д.
В общем случае эти направляющие косинусы изменяются от точки к точ-
точке, т. е. а, Р и у являются функциями ?lf E2, ?3. В силу свойств направ-
направляющих косинусов имеем равенства
<U + &+Y'«=l. ."=1.2, 3,
справедливые для всех значений координат.
Если новые единичные векторы а взаимно перпендикулярны в каж-
каждой точке, -то новая система координат ортогональна. В этом случае
1.3. Криволинейные координаты 33
я1, <х2, а3 являются направляющими косинусами i относительно векторов
а, и девять введенных направляющих косинусов симметричны относи-
относительно обеих систем координат. Чтобы подчеркнуть эту симметрию, мы
введем новые обозначения:
так что
и т. д.
Так как ii = l, i-j = O, а1а1=1, а1-а2 = О и т. д., указанные соот-
соотношения между направляющими косинусами и единичными векторами
приводят к ряду уравнений, связывающих значения утгг:
2 Y™ Y«e = 2 Ysm Y.n = W A-3.1)
s s
где omn— дельта-функция Еронекера, или символ Еронекера, равный нулю,
если т Ф п, и равный единице при т = п.
Обращаясь к равенству A.2.4), мы отмечаем, что если система коор-
координат ? правая (система х, у, z предполагается правой), то определитель
lYmnl Равен +1; если ? образуют левую систему, то этот определитель
равен — 1. Используя соотношения A.2.5) или решая уравнения A.3.1)
относительно одного из у, мы найдем, что
1тп=±Мтп, A.3.2)
где знак плюс имеет место в случае, когда ? образуют правую систему
координат, а знак минус —когда они образуют левую систему. Величина
Мтп является алгебраическим дополнением imn в определителе |утп|:
•™ 11 = Y22Y33 Y23
¦^12 = Y23Y31 - Y21Y33»
^31 = Y12Y23 - Y13Y22 и т. д.
Следует, конечно, иметь в виду, что соотношения A.3.1) и A.3.2)
Остаются в силе и в том случае, когда речь идет о двух произвольных
ортогональных системах, а не только о декартовой системе и одной про-
произвольной ортогональной системе. В равенстве A.3.2) знак плюс имеет
место, если обе системы правые или обе левые; знак минус —если одна
из них правая, а другая левая.
Так как мы предположили, что наша криволинейная система коор-
координат ортогональна, то любой вектор F в точке (?х, ?2> ?з) может быть
представлен разложением на составляющие по направлениям новых еди-
единичных векторов
F=2>mam, где /'m = F.am.
m
Используя направляющие косинусы утп, легко показать, что между этими
составляющими и декартовыми составляющими F имеют место соотно-
соотношения
m
3 Ф. М. Моро и Г. Фешбах
34 Гл. 1. Типы полей
Любая система трех величин, определенных относительно систем
координат так, что выбору х, у, z соответствует тройка функций от
х, у, z, а выбору ?а, $2> ?3 соответствует другая тройка функций от ^,
?г> ?з> может рассматриваться как система составляющих некоторого
вектора в том и только в том случае, когда эти две тройки функций
связаны между собой соотношениями вида A.3.3).
Коэффициенты Ламе. Проведенные выше рассмотрения не окажут
нам, однако, существенной помощи, если значения направляющих коси-
косинусов а, р, y B каждой точке остаются неизвестными. Как правило,,
нам задаются уравнения новых координатных поверхностей; исходя.из
них, мы должны вывести выражения для направляющих косинусов. На-
Например, обычное определение сферических координат z = ?1cos?2, x —
= ^sm^cosSg» У = %i sin?2sin?3 не дает непосредственно а, C, v, выра-
выраженных через ?lf ?2, ?з (Sx — сфррическая координата г, ?2 — сферическая
координата 6, ?3 —сферическая координата <р).
Необходимая нам связь обычно устанавливается при помощи эле-
элемента дуги. Длина ds бесконечно малого вектора дается в ортогональ-
ортогональной системе координат формулой
ds2 = dx* + dy2 + dz2 = 2 /& d&.
n
Простая подстановка показывает, что
fу]-
Величина hn называется коэффициентом Ламе (масштабным множи-
множителем) для координаты ?п. Изменению d^n этой координаты соответст-
соответствует смещение hnd?n см вдоль координатной линии. В общем случае hn
изменяется от точки к точке.
Отметим, что для вывода выражений коэффициентов h через коор-
координаты ? необходимо выразить старые координаты х, у, z через новые
?i> ?г> 53, как эт0 было сделано выше для сферических координат. Такой
способ записи соотношений между двумя координатными системами
является, как правило, наиболее целесообразным.
Так как hnd?n представляет собой величину смещения, соответст-
соответствующего d?n, то скорость смещения вдоль ^„-линии при перемещении
точки параллельно оси х равна hnd^Jdx. Эта величина равна, следова-
следовательно, направляющему косинусу an = Yni- Аналогично, если х выразить
через ?, то скорость смещения вдоль оси х относительно смещения
вдоль ?„-линии будет равна (l/hn) (дх/дЪп), что также равно Yni = <V
Таким образом, направляющие косинусы осей ?п относительно осей
х, у, z могут быть выражены через производные ? по х, у, z или через
производные х, у, z, по ?:
_ _ 1 дх _ , din _ о _ 1 ^У_ _ l. ?in
л a at A.O.0)
Y _Y -±*L = k -^
In3-4n~hndin пп dz .
в зависимости от того, выражены ли х, у, z через k или 5 — через
х, у, z.
Соотношения A.3.5) полезны, но применяются не так часто, как
этого можно было бы ожидать. Интересно отметить, что все дифферен-
дифференциальные выражения, которые мы далее получим и будем в дальнейшем
неоднократно применять, требуют для их вычисления в обобщенной си-
1.3. Криволинейные координаты
35
стеме координат только коэффициентов h, но не у- Очевидно, что мас-
масштаб новых координат и изменение масштаба от точки к точке выра-
выражают существенные свойства координат. Направления же координатных
Р и с. 1.10. Ортогональная система координат'с переменными коэффициентами Ламе Л.
В данном случае hi=/i» всюду, а в точке Р—точке концентрации системы—/ii=/i2=0.
линии в данной точке по отношению к осям х, у, z играют сравнитель-
сравнительно меньшую роль.
Кривизна координатных линий. Например, даже изменение направ-
направления единичных векторов а может быть выражено через коэффици-
коэффициенты h. Выражения для этих изменений подсказываются рис. 1.11.
Рис. 1.11. Изменение направления единичных векторов а„.
Из рис. 1.11, а мы видим, что изменение &х, соответствующее изменению
?2, равно а2 а, где
3*
36 Гл. 1. Типы полей
и, следовательно,
Аналогично из рис. 1.11, б находим, что изменение а.х, соответствующее
изменению ?г, имеет составляющую в направлении ?2, равную
и аналогичную составляющую в направлении <3. Таким образом, мы
приходим к следующим формулам:
да, а2 dhx а8 Shy д&х а2 dh2 aaj а8 dhs
да2 а8 а/га ai д/г2 За2 а8 dh3 Заа ai dh^ ,. « „.
9а3 at dhs а2 9Л3 9а3 ai dhy 9a3 a2 аА2
Мы можем доказать справедливость этих формул, выражая а через i, j,
к, производя соответствующие дифференцирования и используя опреде-
определения коэффициентов h из равенств A.3.4). Например,
с^а ~~аг2 L *155, +Л! а$! +лх аёг J ""
__ glnfet If д2х Гаг Эа; аа дх а3 дх 1
~ Й1 аё2 + к Хэъ зъ Lfti ^ + лаas2 + hsди3 J +
ЭгУ Г^-^-4-??^. • 5*^.1 I дЧ Г at аг а2 Эг а3 Эг 1 \
е!eea LAj в?! """AjaSj "•"Лв aes J "^a^a^ L^i а^ "^^а^"+" л8ве3 J J f
или ')
.^-—я a In/г, at dh\ a2
эе2 ~ ai ae2 + щ ага "'"гл^ вб! At a^
в соответствии с приведенным выше выражением.
Кривизна координатной поверхности ?х = const может быть дегко
вычислена при помощи формул A.3.6). Единичный вектор alf перпендику-
перпендикулярный к поверхности, при смещении ds в направлении ?2-линии изме-
1 аа, 1 гч и
няется на -j—-^r- ds. ото изменение имеет направление u-линии и является
п2 с*52
мерою кривизны поверхности ?, = const в направлении ?2-линии. Точнее,
1 aai ,-
величина а^-г--^- обратна радиусу кривизны нормального сечения рас-
^"»2
сматриваемой поверхности в направлении ?2-линии в точке (Slf ?2, ?3); если
эта величина положительна, то Е2-линия в положительном направлении
6Х выпукла, а если она отрицательна, то вогнута.
J) Сумма коэффициентов при а8 равна нулю, что можно показать хотя бы при
яомощи дифференцирования тождеств
дх дх ду ду dz dz n
dzm ае„ agm asn абт ае„ ^
до третьему 5.—Прим. рей.
1.3. Криволинейные координаты 37
Нетрудно показать, что полная кривизна поверхности ?х= const
в точке (?1? ?2, $3)_равна
где знак указывает направление вогнутости. Эта формула и соответ-
соответствующие формулы для поверхностей ?2 = const e E3= const будут в даль-
дальнейшем полезными при вычислении восстанавливающей силы искривленной
поверхности в напряженном состоянии.
В качестве простого примера рассмотрим сферические координаты
7"i 6) ?! здесь кривизна r-поверхности равна —2/г, так как сфера вогнута
внутрь и искривлена как в направлении 6, так и в направлени <р (чем
объясняется множитель 2). Кривизна конической поверхности 6= const
равна (— l/r)ctg6, а плоскость <p=const имеет кривизну нуль.
Во всяком случае, как только нам известны выражения х, у, z через
новые координаты, соотношения A.3.4)— A.3.6) позволяют вычислить
масштаб новой системы, составляющие вектора по осям этой системы,
их изменения и много других важных выражений, которые будут рас-
рассмотрены ниже.
Элемент объема и другие формулы. Другой величиной, играющей
важную роль в дальнейшем, является элемент объема в новой системе
координат. Так как элементам d?lt d?2, d?s соответствуют смещения h1d^1,
h2dt-2, /i3d?3 вдоль взаимно-перпендикулярных направлений, объем прямо-
прямоугольного параллелепипеда, определенного этими дифференциалами, равен
dv = hxh^d\xd^d^. A.3.7)
Это —элемент объема в новой системе координат. Он, конечно, всегда
положнтелеп.
Для примера рассмотрим упомянутую выше сферическую систему
координат х = ?j sin ?2 cos ?3, У = \\ sin 52 sin ?3, z — ?х cos ?2. Для коэффициен-
коэффициентов Ламе находим следующие выражения:
hx — \, к2 = ^г, ft3 = S1sin?2.
Направляющие косинусы единичных векторов в направлении сферических
осей поэтому равны
аг = sin ^2 cos?3> «2 — cos ?2 cos %з> аз= — sin?3,
Pi = sin E2 sin 631 P2 = cos^sin^3. P3 = cos?3,
Y1 = cos?a, v2=_sin?2, Ys = O-
Они удовлетворяют соотношениям ортогональности, приведенным
на стр. 33.
Элемент объема в новой системе координат dv=^sm^2-d^ld^2d^3,
а составляющие вектора по направлениям новых осей равны
Fx = Fx sin ?2 cos ?3 + Fy sin ?2 sin ?3 + Fz cos S2,
F2 = Fx cos ^2 cos ?3 + Fy cos $2 sin ^3 — Fz sin ?а,
x
Если функции Fx, Fy, Fz выражены через ?х, ^2, ^3, то новые составля-
составляющие выражаются только через новые координаты и преобразование будет
завершено.
Вращение осей. Другим примером преобразования координат является
тот случай, когда новая система координат, также прямоугольная,
38
Гл. 1. Типы полей
повернута относительно старой на углы Эйлера б, Ф, ф (см. рис. 1.12).
Уравнения преобразования имеют вид
х = (sin ф sin Ф -f cos ф cos Ф cos 6) ?x 4-
+ (cos ф sin Ф — sin ф cos Ф cos 6) ?2 -\- sin 6 cos Ф ?3,
у = (sin ф cos Ф — cos <]> sin Ф cos 6) ^ + A.3.8)
+ (cos ф cos Ф + sin <]> sin Ф cos 6) ?2 — sin 6 sin Ф ?3,
z = — cos ф sin 6 ?j + sin ф sin 6 ?2 + cos 6 ?3.
Коэффициенты Ламе в этом случае все равны единице, как и следова-
следовало ожидать, так как это преобразование не изменяет масштаба осей.
Рис 1.12, Вращение осей с указанием углов Эйлера.
Направляющие косинусы для этого преобразования являются коэффициен-
коэффициентами линейных уравнений A.3.8)
cos б
ax = sin(j) sini -f- совф cos® cos В и т. д.,
Px = sin ф cos Ф — cos ф sin Ф cos 6 и т. д.
При помощи этих направляющих косинусов можно получить формулы
преобразования вектора.
Законы преобразования векторов. Мы видели, что для того, чтобы
три функции точки могли служить тремя составляющими некоторого
вектора, они должны преобразовываться в соответствии с правилами,
содержащимися в соотношениях A.3.3) и A.3.5). Если мы преобразуем
составляющие из одной криволинейной системы координат ?х> ?2, ?3
с коэффициентами Ламе hx, h2, hs к другой системе ^, U, ?я с коэф-
коэффициентами Ламе h[, /г2', h'3, то составляющие в новой системе должны
выражаться через составляющие в старой системе формулами
^п = 2угшЛп. A-3.9)
где
hm дЧт __ hr^
Так как hmd?m и hnd?n являются расстояниями в сантиметрах, то новые
составляющие Fn измерены в тех же единицах, что и старые. Если мы,
развивая какую-либо новую теорию, найдем, что некоторые три величины
преобразуются согласно соотношениям A.3.9), то мы можем быть
вполне уверены, что найдены составляющие некоторого вектора.
Здесь уместно исследовать преобразование векторного произведения
А х В. Вспомним, что на стр. 21 было отмечено, что А X В не является
1.3. Криволинейные координаты 39
истинным вектором. Сейчас мы увидим, почему это так. Используя соот-
соотношения A.3.9), мы найдем, что составляющая А X В по ?[ равна
(А' X В')! = А'В; - А'& = ? (TsmTan -УзЛп) АА =
т., п
= 1 (ЪтЪп-ЪтЪп)(АтВп-А„Вт). A.3.10)
Используя соотношения A.3.2) (легко видеть, что эти соотношения оста-
остаются в силе и для рассматриваемых здесь общих преобразований, лишь бы
обе системы были ортогональны), мы находим, что
(A'xB'I=±2(AxB)nTln, A.3.11)
71
где знак плюс имеет место, если обе системы правые или обе левые,
а знак минус — если одна из них правая, а другая левая [кроме того,
равенства A.3.11) справедливы только для ортогональных систем].
Отсюда следует, что Ах В — аксиальный вектор.
Равенство A.3.9) также дает нам способ легко различать истинные
и аксиальные векторы, так как они ведут себя по-разному при преобра-
преобразовании правой системы в левую. Простым примером такого преобразо-
преобразования является изменение направления осей (инверсия) ?х = —х, |2= —у,
|3= —2. Если составляющие истинного вектора суть Ах, Ау, Аг, то
Ах= —Ах, А2= —Ау, А3= — Az, т. е. составляющие истинного вектора
при таком преобразовании меняют знак. С другой стороны, для аксиаль-
аксиального вектора Ах В при этом перемены знака не произойдет, так что
составляющие аксиального вектора при изменении направления всех осей
на обратные не меняют знака.
Аналогично истинный скаляр, или инвариант, примером которого
является А-В, не изменяется при изменении направления всех осей
на обратные. С другой стороны, псевдоскаляр, как например А-(ВхС),
при этом меняет свой знак на обратный.
Использование соотношений A.3.9) для установления того, являются ли
три величины составляющими некоторого вектора или нет, может оказаться
весьма громоздким. Другой способ заключается в использовании инва-
инвариантов, образованных при помощи этих величин. Например, если 2 AiBi
является инвариантом, a J54 суть составляющие истинного вектора, то
и Ai должны быть составляющими истинного вектора. Несколько приме-
примеров приложений этого метода встретятся нам дальше в этой же главе.
Контравариантные и ковариавтные векторы. Существуют еще два
способа записи составляющих вектора, которые иногда используются,
состоящие в применении разных «единичных векторов» для разложения F
на составляющие. Допустим, что «единичные векторы» определены как
векторы ап = йпап переменной длины, так что а„ соответствует единич-
единичному изменению ?п, а не имеет длину в 1 еж (как а„). Вектор F через
эти новые «единичные векторы» может быть записан в виде
В этом случае новые «составляющие» преобразуются по формулам
,m ( h
( '
40 Гл. 1. Типы полей
Величины f1 называются контравариантными составляющими векто-
вектора в системе координат Elf ?2, ?3. Они отличаются от «фактических»
составляющих множителем, обратным коэффициенту Ламе; они дают вектор
только в том случае, когда эти составляющие умножаются на «единичный
вектор» а„ = й„ап.
Если рассматривать «единичные векторы» aa = &Jhn вдоль координат-
координатных линий с масштабом, обратвым координатному, то соответствущие-
«составляющие» будут
и в этом случае /п преобразуется по формулам:
Величины fn называются ковариантными составляющими вектора в
системе координат ?lf ?2, ?3.
Эти формулы преобразований обладают несколько большей формаль-
формальной симметрией, нежели формулы A.3.9) для обычных составляющих, так
как коэффициенты h не входят под знаком суммы хотя бы в одно из вы-
выражений A.3.12) и A.3.13). Это сомнительное преимущество часто сводит-
сводится на нет тем фактом, что новые составляющие не обязательно сохраняют
свою размерность при переходе от одной координаты к другой, Например,
в сферических координатах, если F имеет размерность длины, составляю-
составляющие Fr, Fa, F9 после преобразования все еще имеют размерность длины»
тогда как /8 и р безразмерны, а /» и /ф имеют размерность площади.
Мы вернемся к этим обозначениям позже, когда будем говорить о тен-
тензорах. Там мы обнаружим, что составляющие / полезны в предваритель-
предварительных рассмотрениях задачи, когда формальная симметрия их формул пре-
преобразования может упростить выкладки. Но когда приходится проводить
подробные вычисления, то, как правило, оказывается проще использовать
«фактические» составляющие Fn, которые всегда имеют ту же размерность,
что и F, и единичные векторы а„, которые всегда имеют единичную длину.
1.4. Дифференциальный оператор v
После того как мы рассмотрели основные принципы преобразований
координат и указали, как можно распознавать скаляры и векторы по их
формулам преобразований, можно перейти к изучению общих дифферен-
дифференциальных свойств векторов. Выше мы изучали свойства в целом или макро-
макроскопические свойства векторных полей при помощи поверхностных и кри-
криволинейных интегралов. Теперь мы хотим подробно изучить их микро-
микроскопические свойства. По аналогии с дифференциальным оператором d/dx,.
который, действуя на скалярную функцию ф(ж), переводит ее в производ-
производную, выражающую наклон графика <р> мы имеем дифференциальный опе-
оператор, действующий по всем трем координатам, который, будучи приложен
к скалярным или векторным полям, переводит их в другие поля. Полу-
Получаемые таким образом поля являются мерою скорости изменения исходного
поля от точки к точке.
Градиент. Скорость изменения скаляра ф (х, у, z) изображается век-
вектором, направление которого совпадает с направлением наискорейшего-
возрастания ф, а величина равна этой максимальной скорости
1.4. Дифференциальный оператор V 41
возрастания. Мы уже указывали [см. формулу A.1.1)], что изменение ф
при переходе из точки с радиусом-вектором А = xi + yj -+ zk в соседнюю
точку A-fds, где элементарное смещение ds = \dx -\- jdy -f- kdz, равно
е?ф = ds-grad-ф, причем
grad^ = V^ = |ii + |i-j + |tk. A.4.1)
Если ds лежит на поверхности уровня ф = const, то с?ф должно быть рав-
равно нулю, так что вектор grad ф должен быть перпендикулярен к поверх-
поверхности уровня. Максимальное значение с?ф соответствует ds, перпендику-
перпендикулярному к этой поверхности, и в этом случае (как уже было отмечено выше)
Величина, обозначаемая символами grade]) или V<]> (читается табло.» ф),.
является, таким образом, мерой скорости изменения скалярного поля ф
в точке (х, у, z). Для того чтобы показать, что она является действительна
вектором, мы должны установить, что она преобразуется в соответствии
с формулами A.3.9). Это нетрудно сделать, так как очевидно, что выра-
выражение градиента в криволинейных координтах ?lf ?2, ?3 имеет вид
Если мы теперь преобразуем это выражение к другой системе координат
?i> ?г> ?з> пРеДполагая, что оно является вектором, мы придем к той же
форме в новых координатах, что и в старых. В самом деле, используя
соотношения A.3.9) и тождества
мы получим
2 hm azm - Ь а» Ь \ hm
т.
'как и должно быть, если gradф есть вектор, выражаемый в любой систе-
системе ортогональных координат формулой A.4.2).
Отметим, что gradф является истинным, а не аксиальным вектором.
Это доказывается тем фактом, что dф=gradф•ds является истинным ска-
скалярным инвариантом.
Так как ds—истинный вектор, gradф также должен быть истинным
вектором. Заметим также, что циркуляция градиента равна нулю
ф gradф•ds= ф с?ф = 0.
То обстоятельство, что циркуляция градиента всегда равна нулю, уже было-
отмечено на стр. 28.
Это краткое рассмотрение служит для того, чтобы подчеркнуть тот
факт, что если мы выражаем некоторую «физическую» величину через
коэффициенты Ламе h в системе координат 5, то в другой системе коор-
координат ?' она должна выразиться формулой того же вида через коэффи-
коэффициенты h'.
Производная по направлению. В наших уравнениях будет иногда
встречаться величина B•gradф. Если В —единичный вектор, эта величина
называется производной ф по направлению единичного вектора В; она пред-
42 Гл. 1. Типы полей
ставляет собой скорость изменения ф в направлении В. Независимо от
того, является ли В единичным вектором или нет,
Д* дх ^ПУ ду + * dz hj, в^ Л
Скалярный оператор (В • V) = (В ¦ grad) может быть также приложен
к вектору, что дает
(В-V) А = (B-grad) A = i (B-grad Аж) + j(B-grad А„) + k(B-grad A2).
В криволинейных координатах это выражение становится более сложным,
потому что единичные векторы а также являются переменными [см. фор-
формулы A.3.6)]. Используя формулы A.3.6), можно найти, что ^-состав-
^-составляющая рассматриваемого вектора равна
л ' h2 д%2 ' hs dia '
h2
A.4.3)
Остальные составляющие получаются из этой формулы круговой подста-
подстановкой индексов. Первые три слагаемых в правой части формулы A.4.3)
в сумме равны B-grad Аг; остальные слагаемые являются поправками,
возникающими вследствие того, что направления новых осей меняются
от точки к точке.
Элементарные повороты. Один из.типов преобразований координат,
который будет представлять для нас в дальнейшем особый интерес, полу-
получается в результате бесконечно малого вращения прямоугольной декар-
декартовой системы координат вокруг некоторой оси, проходящей через начало.
Предположим, что вектор du> по величине равен углу вращения (выра-
(выраженному в радианах), а по направлению совпадает с осью вращения
и указывает в сторону поступательного движения правого винта, вра-
вращаемого вместе с координатной системой. Точка с радиус-вектором
г = xi 4- yj -f zk при вращении с системой координат получит смещение,~
представляемое вектором du> х г= - rxdu>. Если, наоборот, точку считать
фиксированной в пространстве, то ее координаты в вращаемой системе
(которые мы будем снабжать штрихом) будут связаны с ее координатами
в исходной системе до вращения соотношением r' = r + rxdu>, или
х' = х + (г/ d<»z — z d<»y),
z' = z -J- (x du>y — у du>x).
Мы могли бы также записать: r = r' —r'xdu). [Эти соотношения справед-
справедливы только для очень малых поворотов; иначе мы должны применить
уравнения A.3.8), правые части которых отличаются от приведенных
выше на бесконечно малые высших порядков относительно 6 и Ф + ф.]
Допустим теперь, что некоторое скалярное поле ф медленно вращается
(поле может быть, например, плотностью медленно вращающегося твердо-
твердого тела). Благодаря этому вращению значение поля ф' в фиксированной
точке пространства связано с значением поля ф в этой точке до вращения
-соотношением
ф'(ж, у, г) = ф (ж, у, z)^-(гxdu))•gradф = ф(ж, у, z) —(гхУф)^ю, A.4.4)
1.4. Дифференциальный оператор V
43
так как (АхВ)-С= — (АхС)-В для любой тройки векторов. Поэтому
вектор rxV<}> является мерой воздействия на поле ф всякого рода элемен-
элементарных поворотов (инфинитезимальных вращений); чтобы получить измене-
изменение поля при элементарном повороте dw, нужно только образовать
¦скалярное произведение этого вектора на dw. Если ось вращения перпенди-
перпендикулярна к вектору rxV<}>, то малое вращение не отражается на ф; если
•ось вращения параллельна rxVф, то эффект вращения будет максималь-
максимальным. Так как любое поле вида / (г) инвариантно относительно вращений, то
гХ V [/ (г) g (ft, 9)] = / (г) [rx Vg (ft, ?)].
Дивергенция. Существуют две дифференциальные операции, приложе-
приложения которых к векторному полю играют важную роль. Одна приводит
к скаляру, который указывает скорость изменения числа линий тока,
другая — к вектору, характеризующему степень закрученности линий тока.
-Ч.У..О
К.У.А)
Л 1
1
Y У
Рис. 1.13. Поток вектора и дивергенция векторного поля.
Первая операция может быть получена предельным переходом из потока
вектора при стягивании замкнутой поверхности в точку, а вторая — ана-
аналогичным процессом, примененным к циркуляции.
Чтобы получить указанный скаляр, мы сначала вычислим поток
вектора F изнутри элемента объема dxdydz с центром в точке (х0, ц, z0).
Разлагая в ряд Тейлора ж-составляющую F в окрестности точки (х0, у0, z0),
найдем
Fx = Fx (x0, yo,zo)
(x - x0) + -? (y - y0) + -^- (z - z0)
{Здесь dFjdx и т. д. обозначают значения производных в точке (,т0, у0 z0).]
Поверхностный интеграл нормальной составляющей F по грани 1 (см.
рис. 1.13) равен
\ \ FJA = dy dz[Fx (x0, y0, z0) +--^.d
l
4- высшие степени дифференциалов.
Поверхностный интеграл по грани 2 равен
- $ \ FxdA= -dydz[Fx(x0, y0, zo)-±d-^
-\- высшие степени дифференциалов,
причем знак минус перед интегралом и перед скобками объясняется тем,
что интегрируется составляющая F по направлению внешней нормали,
44
Гл. 1. Типы полей
которая на грани 2 равна — Fx. Сумма поверхностных интегралов по
этим двум граням поэтому просто равна (dFx/ox)dxdydz, если не считать
величин высших порядков малости. Аналогичные выражения получатся
для двух других пар противоположных граней, так что с точностью до
величин высших порядков малости
Это выражение является векторным аналогом дифференциала du
скалярной функции и (х) одной переменной х. Аналогом производной
является поток, отнесенный к единице объема в точке (х, у, z). Эта
скалярная величина называется дивергенцией вектора F в точке (х, у, z)
и обозначается через
divF = li
dFv , 8FZ
= lim -L
объемно объем
dz
= v-F.
A.4.5)
Дивергенция равна скорости возрастания числа линий тока, отнесенной
к единице объема.
В соответствии с приведенным основным определением, дивергенция
поля F в точке Р является свойством поля F, характеризующим его
г
Рис. 1.14. Поток и дивергенция в криволинейных координа-
координатах.
поведение в окрестности Р; значение дивергенции не должно зависеть от
выбора системы координат. Можно, конечно, предполагать, что выражение
оператора дивергенции в обобщенных криволинейных координатах будет
иметь математическую форму, отличную от его выражения в декартовых
координатах; тем не менее численное значение divF в точке Р должно
быть одним и тем же в любых системах координат. Если преобразование
координат состоит только в повороте и не связано с растяжением ,или
сжатием (т. е. если все h равны единице), то не только значение дивер-
дивергенции, но и форма ее выражения должна оставаться неизменной. В ко-
конечном счете это и понимается под скалярным инвариантом.
Для того чтобы найти выражение дивергенции в обобщенных коорди-
координатах, рассмотренных на стр. 34, мы вернемся к основному определению
divF и вычислим поток изнутри элемента объема, определенного элемен-
элементарными смещениями hnd?n в новой системе. Поток через грань 1 (см.
рис. 1.14) равен
Мы должны были учесть коэффициенты hji3 под знаком производной во
втором слагаемом вследствие того, что поток через грань 1 отличается
от потока через сечение 3, проходящее через центр (^ ?2, ?3) элемента,
как благодаря тому, что Fx изменяется с изменением |lf так и благодаря
1. 4. Дифференциальный оператор V 45
тому, что в криволинейных координатах площадь грани 1 отличается
от площади грани 3;-именно, h2hs также зависит от ?i- Поэтому оба
коэффициента должны быть включены под знак производной.
Поток через грань 2 равен
а поток через обе грани, следовательно, равен
Таким образом, дивергенция F в обобщенных координатах равна
где dV = h^h^jd^d^g — объем элементарного параллелепипеда.
Это выражение, конечно, отлично по форме от выражения A.4.5)
в декартовых координатах. Для того чтобы показать, что оба эти выраже-
выражения принимают одно и то же значение в данной точке, мы прибегнем
к прямому преобразованию первого из них во второе, используя для
этого уравнения преобразования, приведенные на стр. 33 — 35. Выразим
Fx, F , F. через Flt F2, F3 по формулам A.3.3) и A.3.5). После вычисле-
вычисления некоторых производных и перегруппировки членов, мы найдем, что,
V 8Fz__ 1 Г дх dFt _dy_dF\ . dz 8Ft 1
i2 дх ""Г dq2 дУ "¦" di2 dz J "^ hs l ' " J "T"
дх dji/hj ду асуло ez a(i//,x)-i
h2 l'-;J"T l
h2
Выражения, заключенные в первые и четвертые скобки, могут быть при-
приведены к более простому виду, если учесть, что
дх д ду д dz д _ д
так что соответствующие слагаемые в сумме равны
1 dFt dji/hj д Г Ft\
Выражение, заключенное в седьмые скобки, может быть развернуто
•с учетом того, что
1=?к±+?кАл-?к± ит д
дх дх дс,^ дх S^" дх д^ М'
Используя соотношения
Эё, 1 дх
-дх-^цж и т- д->
следующие из формул A.3.5), и группируя слагаемые, мы найдем, что
соответствующее слагаемое равно
fdx_ д*х_ ду_д*у ,jfcjP
46 Гл. 1. Типы полей
Но из соотношений A.3.4), определяющих коэффициенты h, мы видим,
что выражение, заключенное в первые круглые скобки, равно тг-^г-,
так что все приведенное выше выражение равно
Таким образом, первое, четвертое и седьмое слагаемые в исходном выра-
8FX 8FV 8FZ
жении для Г^+~я +~я~^ B сумме дают
я
д ( Ft \
в?А *i J
д (h
т. е. первое слагаемое в выражении A.4.6). Аналогично получаются и
два других слагаемых в этом выражении. Тем самым преобразование
закончено, и мы действительно убеждаемся в том, что* div F в декарто-
декартовых координатах имеет в любой данной точке то же значение, что и
div F, выраженная в какой-либо другой ортогональной системе коорди-
координат. Поэтому мы можем назвать div F инвариантом относительно преоб-
преобразований координат.
Между прочим, этими несколько громоздкими выкладками мы пока-
показали, что поток изнутри инфинитезимальной поверхности зависит только
от объема, заключенного в этой поверхности, и не зависит от ее формы,
т. е. не зависит от того, имеем ли мы дело с элементом объема в де-
декартовых или криволинейных координатах. Мы могли бы также доказать
инвариантность div F, проверив зто последнее утверждение непосредст-
непосредственно, не прибегая к проведенным утомительным вычислениям.
Теорема Гаусса. Свойство аддитивности потока и определение div F
позволяют получить очень важный и полезный метод вычисления потока
изнутри любой области пространства. В силу свойства аддитивности поток
изнутри всей области должен быть равен сумме потоков изнутри всех
элементарных областей, заключенных внутри данной области. В силу
равенства A.4.5) интегралы по элементам объема dv могут быть записаны
в виде div F dv, так что должна иметь место важная теорема диверген-
дивергенции
^ ^^ divFdv, A.4.7)
где объемный интеграл распространяется на всю область, ограниченную
поверхностью, по которой распространяется интегрирование в поверх-
поверхностном интеграле в левой части. Равенство A.4.7) называется теоремой
Гаусса1).
Эта теорема подчеркивает тесную связь, которая должна существо-
существовать между поведением векторного поля на замкнутой поверхности и его
поведением всюду внутри этой поверхности. Она соответствует довольно
очевидному свойству линий тока: алгебраическое число линий тока,
выходящих из замкнутой поверхности, должно быть равно числу таких
линий, «начинающихся» внутри поверхности.
Решение уравнения Пуассона. Более того, сопоставление теоремы
Гаусса с упоминавшимися ранее фактами относительно векторных полей
*) В отечественной литературе обычно применяется более правильное название
«теорема Остроградского». —Прим. ред.
1. 4. Дифференциальный оператор V 47
и источников [см. равенства A.2.9)] позволяет получить полезное реше-
решение уравнения Пуассона V2<p =—q(x,y,z) [уравнение A.1.5)], где q —
ограниченная функция х, у, z, исчезающая на бесконечности, а реше-
решение <р подчинено единственному требованию, что оно также равно нулю
на бесконечности. Наводящим соображением здесь является образование
векторного поля F = grad<p и применение к этому полю теоремы Гаусса
(grad <р) • dA = \[ \ (V2?) dv
для любой области с, ограниченной замкнутой поверхностью S.
Другое наводящее соображение состоит в том, что векторное поло
(Q/r2) ar простого источника оказывается градиентом скалярного потен-
потенциала <р = — Qjr.
Объединяя эти факты, мы можем высказать предположение, что
решением уравнения Пуассона V2<p = — q (x, у, z) является интеграл
dx'dy'dz', A.4.8)
где R= ]/(ж — х'J+(у — у'J + (z — z'J есть расстояние от точки х, у, z
до точки х', у', z . Величина <р будет стремиться к нулю на бесконеч-
бесконечности, если потребовать еще, например, чтобы \ \ \ \ q\dxdydz < со.
Чтобы доказать, что у является решением, образуем векторное поле
?(х, у, z) = grad<p= — \ \ V ,1ш aRdx'dV'dz'>
где aR —единичный вектор направления от точки х', у', z' к точке х,
у, z. Далее образуем поток вектора F изнутри замкнутой поверхности S,
ограничивающей некоторую область с пространства. Используя соотноше-
соотношение A.4.7), найдем, что
(V2<?)dxdydz= -^dA ^C \ q {x'^ z>) aR dx' dy'dz',
S
где, конечно, V2 <p = div (grad 9). Последний интеграл распространяется
на все значения х', у', z' и на все значения х, у, z на поверхности S.
Порядок интегрирования может быть обращен, и мы рассмотрим сначала
интегрирование по S, в котором подинтегральной функцией является
q('>) aRdx'dy'dz'.
Применяя к интегралу потока для этой подинтегральной функции
равенства A.2.9), мы видим, что он равен q(x', у', z')dx' dy' dz', если
точка х', у', z' лежит внутри S, и равен нулю, если эта точка лежит
вне S. Поэтому интеграл по dx' dy' dz' равен интегралу от функции q'
по области с, и окончательный результат представится в виде
д(х', у', z')dx'dy'dz'.
Таким образом, мы показали, что интеграл от V2<p по любой области с
равен интегралу от —q по той же области, какой бы формы и каких
бы размеров эта область ни была.
Отсюда нетрудно заключить, что интеграл A.4.8) является решением
уравнения Пуассона 'V2<p= — q, где q — разумно ведущая себя функция,
стремящаяся к нулю ва бесконечности. Это решение —не единственное,
так как мы можем добавить к <р любое решение уравнения Лапласа
48
Гл. 1. Типы полей
V2<J) = 0 и все равно получим решение уравнения V2<p = — q с тем же
самым q.
Характер решения ф, которое мы добавляем, зависит от краевого
условия конкретной задачи. Если <р должно стремиться к нулю на беско-
бесконечности, то ф вообще не надо добавлять, так как <р» заданное интегра-
интегралом A.4.8), само уже стремится к нулю на бесконечности (при условии,
что q ведет себя, так же). Мы могли бы, конечно, попытаться найти
решение уравнения Лапласа, равное нулю на бесконечности и отличное
от нуля в некоторой области, но такая попытка не увенчалась бы успе-
успехом потому, что ни одно решение уравнения Лапласа не может иметь
ни максимума, ни минимума (см. стр. 18), а функция, равная нулю на
¦бесконечности и не имеющая ни максимума, ни минимума, должна быть
всюду равна нулю. Следовательно, функция <р, заданная интегралом A.4.8),
является единственным решением, если краевое условие требует исчезно-
исчезновения на бесконечности.
При других краевых условиях решением будет сумма <р и такого
решения <]> уравнения Т2ф = 0, что <p-t- ф удовлетворяет соответствующему
краевому условию. Весь этот вопрос будет гораздо подробнее рассмот-
рассмотрен в гл. 7.
Ротор (вихрь). Остается рассмотреть дифференциальный оператор,
который преобразует вектор в другой вектор. Этот оператор, являющийся
мерой «завихренности» векторного поля, так же
связан с интегралом циркуляции, рассмотренным
на стр. 29, как оператор дивергенции связан с
интегралом потока. Чтобы найти завихренность
векторного поля в точке Р, мы вычислим цирку-
циркуляцию вокруг элемента площади, содержащего Р,
и разделим ее на площадь элемента. Нетрудно
сразу же обнаружить, что в этом случае предель-
ный переход более сложен, чем при определении
дивергенции, так как результат зависит от ори-
ориентации элемента площади.
Например, если элемент площади перпендику-
перпендикулярен оси х, то интеграл циркуляции вдоль пути
на рис. 1.15 равен
Р7и"с. 1.15. Интеграл
циркуляции и ротор век-
векторного поля.
<6F-ds= &Fydy +
1 *
» zo) dV dT~2
7-i / \ 7
- Fv (x0, y0, z0) dy —
dz
. 4
(жо> ft» zo)
(x0, y0, z0
где мы использовали первые члены ряда Тейлора для Fy #и Fz. С другой
•стороны, циркуляция вокруг элемента, перпендикулярного оси у, равна
(-^ т^- )dxdz и т. д. Если элемент параллелен оси z, но образует
V oz ох /
угол 6 с осью х (как показано на рис. 1.16), то вычисление циркуляции
несколько сложнее. Например, смещение ds вдоль пути 1 соответствует
изменению — ds cos 6 абсциссы х и изменению ds sin 6 ординаты у. Аналогично
в средней точке пути 2 Fz имеет значение
„ , . ds с 8FZ , ds . о dFz
FA*** Уо> zo) = у cos 6- -ei + у sme'~ду- •
1.4. Дифференциальный оператор V
49
Принимая все это во внимание, найдем в данном случае для циркуляции
выражение
{Fy dssin 6-Fxdscos 6) — * (ds sin 6 ^ -ds cos 6^
- (Fv rfs sin 6 - Fx ds cos 6) - * (ds sin 6 ^ -ds cos 6 ^) -
ду 2
Циркуляция вокруг элемента произвольной ориентации в пространстве
представляется еще более сложной формулой.
Z Z
X X
Рис. 1.16. Циркуляция под углом к оси.
Однако все значительно упрощается, если мы будем рассматривать
ьеличины
\~ду дГ ) ' V~^z ~дх~) ' \.~dx~~J)y~ )
как, соответственно, х, у, z-компоненты некоторого вектора. В самом деле
тогда оказывается, что циркуляция вокруг элемента площади dA равна
просто составляющей этого вектора по направлению, перпендикулярному
к элементу, умноженной на dA. Так, например, направляющие косинусы
прямой, перпендикулярной к элементу, изображенному на рис. 1.16, равны
(sinG, cos6,0), и составляющая указанного вектора по направлению этой
прямой, умноженная на dsdz, как раз и дает полученный нами выше
результат.
Таким образом определенный вектор называется ротором {вихрем) F
Циркуляция вокруг элемента площади dA равна, следовательно, dA-rotF,
где dA — аксиальный вектор, соответствующий элементу площади. Вектор
rotF является мерой «завихренности» поля в точке (х, у, z). Если F
является скоростью в потоке жидкости, то направление rotF в точке Р
совпадает с направлением оси вращения жидкости, находящейся в окрест-
окрестности Р (согласованным по правилу правого винта с направлением самого
вращения), а длина rot F равна удвоенной угловой скорости вращения этой
части жидкости.
Ротор является оператором, аналогичным векторному произведению,
так же как дивергенция аналогична скалярному произведению. Отметим,
4 Ф. м. Морс и Г. Фешбах
50
Гл. 1. Типы полей
что rotF является аксиальным вектором, если F—истинный вектор, так
как интеграл циркуляции является скаляром, a dA — аксиальный вектор
и, следовательно, rotF также должен быть аксиальным вектором.
Чтобы завершить наше рассмотрение, мы должны еще показать, что
rotF ведет себя как вектор, т. о. преобразуется как таковой. В обобщен-
обобщенных координатах элемент площади, перпендикулярный к оси %1г показан
на рис. 1.17. Рассуждения, аналогичные тем, которые привели нас к вы-
выражению для циркуляции по пути, изображенному на рис. 1.15, показы-
показывают, что в данном случае
[hsF
Рис. 1.17. Циркуляция
и ротор в криволиней-
ных координатах.
Это выражение после упрощения и деления на
площадь hzhgd^d^ дает ^-составляющую ротора.
Дальнейшие вычисления показывают, что выражение
для ротора в обобщенных координатах имеет вид
rotF = -^
n2ns
д (haFa)
а2 Г
MaL
#.
d(hsFa)l
J *
A.4.10)
Чтобы показать, что этот иектор и вектор A.4.9) тождественны, рас-
рассмотрим ^-составляющую вектора A.4.9) rotF = С. По формулам A.3.3) она
равна
dy dz J '" dy\ dz dx J^ dz\ dx dy
Но по формуле A.4.10) при помощи соотношений A.3.2) и A.3.5) мы также
находим, что
1
Гдх 8FX dx dj\ dj}_dJ^_d^d?y ^dFz_dz_dF1
dz
8FZ
dF
dz
dy
dz
Hz
( dFx
V dz
ду
dx
dFz
dx
36i ( dFv dFx \ ^
~ dz\ dx dy J J '
откуда и вытекает, что формулы A.4.9) и A.4.10) определяют один и
тот же вектор. Чтобы показать, что rotF —аксиальный вектор, когда
F —истинный вектор, заметим, что выбор направления обхода в инте-
интеграле циркуляции вокруг элемента площади был произволен. Изменение
направления этого обхода на обратное привело бы к изменению знака
ротора на противоположный.
Вихревые линии. Вектор rotF определяет новое векторное поле
с новыми линиями тока. Эти линии называются вихревыми линиями
1.4. Дифференциальный оператор V 51
поля F. Например, для поля Fx = — ay, Fy = ax, Fz = 0 rot F имеет на-
направление орта к и по длине всюду равен 2а. Линиями тока поля F
являются окружности в плоскостях, перпендикулярных осп z. Для поля
Fx— —ay, Fy — ax, F:=b(x2 + y2), рассмотренного на стр. 23, rotF
имеет составляющие 2by, — 2Ьх, 2а. Мы видели, что винтовые линии
юка для этого поля определяются семействами поверхностей <р— 1^2 + 2/2,
!i=z (ж2 + г/2) arctg—. Методами, которые мы рассматривали па
стр. 25, можно установить, что вихревые линии определяются поверх-
поверхностями 9= V%~~Vy~, '^ = 2+ yarctg —.
В обоих примерах вихревые линии всюду перпендикулярны линиям
тока. Это, однако, не всегда так. Например, для поля Fx = az, F -=аху
F, = ay rot F = «i -j- oj + ак не перпендикулярен к F.
Вихревые линии любого поля обладают следующим очень интерес-
интересным свойством: они нигде не начинаются и нигде не кончаются. Это
соответствует рассмотренному на стр. 29 свойству вихревых трубок и
может быть доказано при помощи свойств ротора. Утверждение, что
линии тока нигде не начинаются и нигде не кончаются, равносильно
тому, что дивергенция соответствующего векторного поля всюду равна
нулю, так как тогда по формуле Гаусса A.4.7) поток изнутри любой
замкнутой поверхности равен нулю. Однако дивергенция любого ротора
равна нулю, так как по самому определению
I tF1-°2jF- d4v \&2Fx fflFz °*Fy d'Fx =0
(ГОЬ t) - дх ду -dxi)z^~dydz dydx~T~dzdx dzdy
Поэтому upocfeiiuinii способ получения векторного поля с равной нулю
дивергенцией состоит в образовании ротора какого-нибудь другого поля;
этим приемом часто пользуются в теории электромагнетизма.
Теорема Стокса. Существует теорема о роторе, аналогичная теореме
о дивергенции, выраженной формулой A.4.7); теорема о роторе может
быть выведена из его основного определения и свойства аддитивности
интеграла циркуляции, установленного на стр. 31. Рассмотрим любую
поверхность S, ограниченную замкнутой линией (или замкнутыми ли-
линиями) L, разобьем ? на элементы dA и сложим все циркуляции вокруг
этих элементов. По нашему определению ротора эта сумма может быть
записана ь виде \ rotF-dA, где dA — вектор, соответствующий dA, и
где интегрирование производится но всей поверхности S. В соответствии
с рассмотрениями на стр. 27 этот интеграл определяет число вихревых
линий, пересекающих поверхность S. В то же время вследствие свой-
свойства аддитивности интеграла циркуляции \ rotF-dA должен быть равен
циркуляции по контуру (или контурам) L,
rotFdA = (?)Fds.
= (?)Fds. A.4.11)
Это — теорема Стокса: она позволяет вычислить циркуляцию но любому
контуру. Она является еще одним соотношением, связывающим поведе-
поведение векторного поля на границе области с его поведением внутри обла-
области; в данном случае это соотношение устанавливает, что циркуляция
по контуру должна быть равна числу вихревых линий, охватываемых
контуром.
4*
52 Гл. 1. Типы полей
Векторный оператор V. Так же как оператор дивергенции является
аналогом скалярного произведения векторов, оператор ротора является
аналогом векторного произведения. Чтобы сделать эту аналогию более
совершенной, мы можем определить векторный оператор V, называемый
наблой, с составляющими, заданными формулой
дх
-^ + k'!-i. 1A.4.12)
ду ' '-dz., Л '
13 терминах этого оператора три дифференциальных оператора, рас-
рассмотренные в настоящем параграфе, могут быть символически записаны
в виде
Некоторые формулы, содержащие векторный оператор V, действую-
действующий на произведение двух величин, могут быть упрощены. Формулы
grad (фФ) = ф grad Ф + SJgrad ф,
div (aF) = a div F + fc" ¦ grad a,
div(AxB) = B-rotA-A.rotB, A.4.13)
rot (aB) = a rot В + (grad a) x BJ
rot(AxB)=AdivB — BdivA + (Bgrad) A — (A-grad)B
легко выводятся непосредственно из определений градиента, дивергенции и
ротора.
|1.5. Аппарат векторного и тензорного исчисления
Аналогия между V и вектором имеет, однако, лишь символический
характер, так как мы не можем указать направление и длину опера-
оператора V и сказать, что V перпендикулярен F, если divF = O, или что
rotF перпендикулярен V, как мы могли бы, если бы V был настоящим
вектором; даже перпендикулярность rotF и F не обязана иметь место.
Эта аналогия становится еще более слабой, если сделать попытку вы-
выразить V в обобщенных координатах, так как оказывается, что для
разных его применений V должен иметь разные представления:
V = адаЭ/dEt + аЛ д№2 + a^q1 д/д%3 для градиента,
V = (h^hs)-11агд (h^/d^ + a2d (hjij/db + а3д (hjij/d^] для дивергенций,
а для ротора вообще нельзя указать никакого представления. Для того
чтобы понять, как преобразуются эти операторы, и уметь легко соста-
составлять более сложные i выражения, мы должны углубиться в аппарат
тензорного исчисления.
Ковариантные и контравариантные векторы. Тензорное исчисление
было создано как аппарат для эффективного решения задач дифферен-
дифференциальной геометрии, но этот аппарат оказался существенно полезным
и при изучении общей теории относительности. Мы коснемся тензор-
тензорного исчисления кратко, лишь в той мере, какая необходима для уяс-
уяснения методов вычисления дифференциальных векторных операторов
в криволинейных координатах. Мы будем по-прежнему рассматривать
только ортогональные координаты в трехмерном пространстве, хотя тен-
тензорное исчисление достаточно мощно и для рассмотрения неортогональ-
неортогональных координат в пространстве любого числа измерений.
1.5. Аппарат векторного и тензорного исчисления 53
В связи с соотношениями A.3.12) и A.3.13) мы определили соста-
составляющие контравариантных и ковариантных векторов и их законы пре-
преобразования. Если Fn — составляющие обыкновенного вектора в трех-
трехмерной ортогональной системе координат с коэффициентами Ламе hn,
то величины /n = hnFn называются коеариантными составляющими век-
вектора в той же системе координат, а величины /n = Fn/hn — контраеа-
риантными составляющими. Таким образом, если /„ — составляющие
ковариантного вектора, то /n = fjh%. — соответствующие составляющие
контравариантного вектора в той же системе координат.
Как мы показали [формулы A.3.12) и A.3.13)], правила преобразо-
преобразования этих векторов при переходе от системы координат ?п к системе
In состоят в следующем:
</«.)'-2/» Л • (Л' = 2г||- A-5.1)
п п
Мы уже указывали на то, что эти формулы обладают математическим пре-
преимуществом формальной симметрии, но новые «векторы» имеют ряд недо-
недостатков с точки зрения физика. Один из них состоит в разной размерно-
размерности составляющих этих векторов; если обычный вектор имеет размерность
длины, то составляющие соответствующего контравариантного вектора имеют
размерность своей координаты, а размерность ковариантных составляющих,
вообще говоря, также отлична от обеих этих размерностей.
Для контравариантных векторов индексы, обозначающие различные со-
составляющие, ставятся наверху для того, чтобы отличить их от ковариант-
ковариантных составляющих. Существует, конечно, возможность смешения составля-
составляющих настоящих векторов и ковариантных векторов, так как и те и другие
пишутся с нижними индексами. В нашей книге это не окажется сущест-
существенным затруднением, ввиду того что мы редко рассматриваем ковариант-
ные векторы, а там, где они встречаются, их характер специально оговари-
оговаривается. Составляющая Fn без такой особой оговорки будет всегда относиться
к настоящему вектору.
Величины д§[д^х, дф/с??2, дф/д?3 являются составляющими ковариантного
вектора; они должны быть разделены соответственно на hx, h2, h3 для того,
чтобы стать составляющими настоящего вектора, именно grad<]>.
Величины btj, Ъг\ Ъ) называются составляющими соответственно кова-
ковариантного, контравариантного и смешанного тензора второго порядка
системе координат ?, если они преобразуются по формулам
hm
/, V ь h V h h V h ei . 9\
тп, n m, n rn, n
Попарные произведения составляющих двух ковариантных векторов
являются составляющими ковариантного тензора. Если векторы контра-
вариантны, то тензор также будет контравариантным. Если Аг и Bf —
составляющие двух обыкновенных векторов, то (hjhj) АгВ} = d являются
составляющими смешанного тензора.
Для смешанного тензора величина 2 ^т> называемая свернутым
¦т
тензором, не меняется при преобразовании координат, так как
2i'n X4 J-.m ^« ^fc XI J-.m d%h X1 J-.m
b* - Zj b* Wm Wn= 2j bk a^= 2j b™-
n [m, h, n ft, m m
Такую величину мы называли скаляром; она также часто называется
54 Гл. 1. Типы полей
инвариантом. Скалярное произведение двух векторов является сверну-
свернутым тензорсш 2 A-ifin = 2 7Г~ А»Д» и поэтому является инвариантом.
п п
Аксиальные векторы. При рассмотрении свойств векторного произ-
произведения мы должны учитывать ортогональность и ориентацию наших
обобщенных координат. Дальнейшая разработка полученных на стр. 33
формул, выведенных из соотношений а1ха2 = а3 и т. д. подобно
тому, как выводятся соотношения A.2.5), показывает, что при переходе
от одной ортогональной системы к другой
причем, если обе системы—правые, тройки (t, /, к) и (к, р, v) должны
быть циклическими перестановками тройки A, 2, 3). При помощи этой
формулы мы находим, что для любого тензора /i;- величины
сг= (fjk~fkj)' *> /> к=1, 2, 3 или 2, 3, 1 или 3, 1,2,
являются составляющими контравариантного вектора, так как по фор-
формулам преобразования тензоров
m, n " и
Точно так же hih2h3(f'k — fk') = ct являются составляющими ковариант-
ного вектора. Отметим, что эти векторы —аксиальные, как это следует
из произвольности правила выбора последовательности индексов A, 2, 3)
и т. д. Отметим также, что ат_и определения имеют место только для
трех измерений.
Таким образом, если Ат, Вп, Ck — составляющие обыкновенных век-
векторов и ат, Ъп, ck — составляющие соответствующих ковариантных век-
векторов, то i-я составляющая векторного произведения А и В
С —A By ~АкВ—-г^-(аЪг, — аъЪЛ = 1г,с1, A.5.3)
t } к k j Ьк^ \ } Ь h U г \ I
i, f, А=1, 2, 3 или 2, 3, 1 или 3, 1, 2.
Заметим опять, что это имеет место только для трех измерений.
Символы Кристоффеля. Для рассмотрения свойств дивергенции и
ротора мы должны ввести некоторые полезные обозначения, называе-
называемые символами Кристоффеля, и изучить их свойства. Эти символы опре-
определяются для ортогональных координат следующим образом:
f i \ __i_ dhj, f*l__fI"'l__Lf?*i / ¦ X = — hi dhi /л к /,\
I / i J hi dh ' I i / J 1 / i J h dtj ' \i i i i
| .l |=0, если г, /, к все отличны друг от друга.
Эти символы являются мерами кривизны координатных осей. По фор-
формулам A.3.6) изменения направлений единичных векторов at могут быть
выражены через символы Кристоффеля следующим простым образом:
1.5. Аппарат векторного и тензорного исчисления 55
Но единичный вектор at дает направление оси ?4 в точке Р ($х, ?2> ?з)>
a ht является масштабом этой координаты, т. е. hx равно фактическому
расстоянию между точками (^, ?2> У и (?i + ^?i> ?2» ?з)> разделенному
на приращение координаты d%v Поэтому вектор /г^ дает и направление
и масштаб координаты $4 в точке .Р. Скорость изменения этого вектора
относительно изменения координаты ^- является также вектором, ?-я со-
составляющая которого дает изменение масштаба, а две остальные состав-
составляющие, перпендикулярные к аи определяют изменение направления:
л-я составляющая этой скорости равна hn \ .". J- .
Мы замечаем, что символы Кристоффеля симметричны относительно
двух нижних индексов. Это означает, что вектор, представляющий ско-
скорость изменения /г4а4 относительно ?;-, равен по величине и направлению
вектору, представляющему скорость изменения fya, относительно ?4. Это
соответствует тому факту, что если масштаб координаты ?4 меняется
при изменении ?,-, то направление ^--линии меняется при изменении ?i;
и наоборот. В этом легко убедиться на рис. 1.11.
Символы Кристоффеля не являются тензорами. Можно показать, что
правило их преобразования задается формулой
^lJ \ m n J d^k d^sb d^h ^ч J-m^ \/i S J d^n
rn,n n
где штрих обозначает величины, выраженные в новых координатах ki-
Хотя символы Кристоффеля и не являются тензорами, они могут быть
очень полезными при образовании производных, имеющих уже тензорный
характер, от векторов. Обычная производная dfjd^j не является тензором,
в первую очередь потому, что координаты криволинейные, и изменение
направления координатных линий влияет на составляющие вектора,
вследствие чего производная учитывает не только изменения самого вектора,
но и привходящие изменения составляющих. Другими словами, в криво-
криволинейных координатах составляющие производной вектора не являются
производными его составляющих. Чтобы найти правильные выражения
для составляющих производной, мы должны сначала продифференцировать
сам вектор, а затем уже образовать составляющие производного вектора.
Ковариантная производная. Например, если f — составляющие кон-
контр авариантного вектора, то настоящий вектор F = 2 ar>^n/"- Производная
п
этого вектора по ?;- может быть приведена к виду
?=2 ¦-**!?
Поэтому составляющими контравариантного вектора, соответствующего
скорости изменения обыкновенного вектора F относительно ?,-, являются
величины
где /1 — составляющие контравариантного вектора, соответствующего F.
Эти составляющие производной уже содержат поправку на кривизну
координатных линий, и составляющие вектора hnfnj соответствуют факти-
фактическому изменению исходного вектора в зависимости от ^-. Запятая перед
нижним индексом обозначает производную.
56 Гл. 1. Типы полей
Величины ftj являются составляющими тензора, поскольку они
ковариантны по индексу i и контравариантны по индексу /. Это можно
показать, используя формулы A.5.1) и A.5.6):
m, ft
ft. 8 ' h, n, m,3
2 8/" mi dts ъ k as3 г d*%i , v ее; э^ с t v-i _
S n , a5/ Lsft
n, < h,e m,n
n
П,8 ft 71,8
Следовательно, /*,j являются составляющими смешанного тензора второго
порядка. Этот тензор называется ковариантной производной контравариант-
ного вектора с составляющими /г.
Аналогично если /4 — составляющие ковариантного вектора, то
F — 2 (ап/Лп) /п является обыкновенным вектором и
п m
также является обыкновенным вектором. Поэтому величины
являются составляющими ковариантного вектора, соответствующего
скорости изменения F относительно ^. Эти величины образуют кова-
риантный тензор второго порядка, называющийся ковариантной произ-
производной ковариантного вектора с составляющими fv
Определение ковариантного дифференцирования может быть распро-
распространено и на тензоры
и т. д. Эти величины являются составляющими тензора третьего порядкаТ
они преобразуются по формулам, являющимся очевидными обобщениями
формул A.5.2). Из формул A.5.9) можно усмотреть, что для ковариант-
ковариантного дифференцирования имеют место обычные правила дифференциро-
дифференцирования, например правило дифференцирования произведения (Я{ЬДь =
+ fy И Т. Д.
Тензорные обозначения для дивергенции и ротора. С ломощью
введенных определений мы можем теперь выразить дифференциальные
1.5. Аппарат векторного и тензорного исчисления
операции div и rot в симметричной форме. Свернутый тензор
2 т __ -у 9/"
т,п
в силу сказанного выше о таких тензорах является скалярным инва-
инвариантом. Если здесь положить /" = FJhn, где Fn — составляющие обык-
обыкновенного вектора, то свернутый тензор оказывается дивергенцией F
гО *Tx2rff^nV A.5.10)
Инвариантность дивергенции вытекает отсюда непосредственно как
следствие общих правил тензорного исчисления.
Выше мы также показали, что для ортогональных координат величины
С' = h^ths (/з"'k - fh- ^ tfk = 123> 231> 312>
являются составляющими контравариантного вектора. Если положить
fn = hnFn, где Fn — составляющие обыкновенного вектора, то величины hkch
также являются составляющими обыкновенного вектора. Выбирая опре-
определенную составляющую и используя определение символов Кристоффеля,
найдем, например,
V1=i {ж(Faha) -{Faha) i(ln ha) ~{FM ~k(ln hz) ~ i{F*K)+
+ РЫ'-щ (In A,) + (^з) -щ (In /г3)} ,
что, в соответствии с формулой A.4.10), дает ^-составляющую обыкно-
обыкновенного вектора rotF.
Другие дифференциальные операторы. Ознакомившись с техникой
тензорного исчисления и с определениями ковариантного дифференциро-
дифференцирования, мы можем теперь без тех утомительных осложнений, с которыми
мы встречались раньше, составлять правильные выражения для вектор-
векторных и скалярных комбинаций векторов, скаляров и операторов. Аппарат
тензорного исчисления сам заботится об устранении всех этих осложнений.
Мы можем, например, быть уверены в том, что комбинация 2
п
является 1-й составляющей некоторого ковариантного вектора, /ггкратной
соответствующей компоненте некоторого обыкновенного вектора. Полагая
bn = BJhn и аг = ]ггА-ъ, где А и В —обыкновенные векторы, мы получаем,
по делении на \\ составляющие обыкновенного вектора, ^-составляющая
которого равна
Сопоставление с формулой A.4.3) показывает, что этот вектор есть
(B-grad) А. Так аппарат тензорного исчисления опять позволяет находить
составляющие векторного оператора в любой ортогональной системе
координат.
58 Гл. 1. Типы полей
Стенографический метод записи в тензорном исчислении позволяет
записывать формулы в виде, пригодном для любой системы координат.
Как только записано тензорное равенство, в котором нижние и верхние
индексы в каждой части соответствуют друг другу, то можно быть
уверенным в том, что это равенство будет иметь место в любой системе
координат. Это отвечает общей цели теоретической физики, которая
стремится выразить законы в форме, не зависящей от системы координат.
Лапласиан, определенный равенством AД.4), также может быть
получен в общей форме при помощи тензорного исчисления
Как мы уже отмечали на стр. 19, лапласиан ф является мерой
«сгущенности» ф.
Лапласиан может быть приложен и к векторному полю F, что дает
также вектор, который может рассматриваться как мера сгущенности на-
направления или длины вектора F. Составляющие по осям х, у, z этого
вектора получаются приложением лапласиана к х-, у-, z-составляющим
вектора F. Чтобы получить его составляющие в произвольной системе
координат, используем соотношения
V2F = grad (div F) — rot (rot F),
Первое из этих соотношений легко проверяется в декартовых координатах;
оно справедливо, конечно, и в любой системе координат. Второе соотно-
соотношение показывает, что вектор V2F выражается через контра- и ковариант-
ные векторы, образованные двойным ковариантным дифференцированием
FJhi или h^i с последующим свертыванием получающегося тензора третьего
порядка. Запись окончательной формулы для V2F сложна, но для кон-
конкретных систем координат, которыми мы в основном пользуемся, эта
формула значительно упрощается.
Первое соотношение A.5.12) интересно само по себе, так как оно
показывает, что в выражение V2F входит rot F. Если F — скорость потока
несжимаемой жидкости, то divF = 0 и V2F = — rot(rotF). Поэтому для
того чтобы вектор, дивергенция которого равна нулю, имел лапласиан,
отличный от нуля, нужно, чтобы не только он сам был завихрен,
но и чтобы его вихревые линии также были завихрены.
Другие операторы второго порядка. Другие комбинации двух опера-
операторов V менее важны, чем лапласиан V2; однако и они иногда встретятся
в наших уравнениях, так что имеет смысл кратко рассмотреть их здесь.
Некоторые из этих операторов равны нулю. Равенство
rot (grad ф) =;V x (V«j>) = 0 <j A.5.13)
было уже использовано в § 1.2, где мы показали, что если вектор являет-
является градиентом потенциальной функции, то его ротор должен быть равен
нулю. Равенство
V-(VxF) = 0 A.5.14)
уже рассматривалось на стр. 51, где было показано, что вихревые линии
не могут ни начинаться, ни обрываться.
Равенство A.5.13) связано с одним свойством полей, которое рассмат-
рассматривалось на стр. 24 — 26, а именно, что если ротор поля всюду равен нулю,
1.5. Аппарат векторного и тензорного исчисления 59
то это поле может быть представлено в виде градиента некоторого ска-
скаляра, называемого потенциальной функцией1). Равенство A.5.14) связано
со сходным свойством, которое может быть легко установлено, а именно,
что если дивергенция поля равна нулю, то это поле может быть пред-
представлено в виде ротора некоторого вектора, называемого еектор-потен-
IIналом данного поля с нулевой дивергенцией.
Оператор grad (div) = V (V •) прилагается к вектору и дает вектор.
Он измеряет изменение дивергенции данного поля и отличается от лапласиана
этого поля F на величину rot (rot F), как это видно из формулы A.5.12).
Оператор rot(rot) = V X (V х ), последний из операторов второго порядка,
определен, таким образом, через два предыдущих оператора. Все эти
иыражения могут быть записаны в тензорной форме.
Вектор как сумма градиента и ротора. Мы теперь достигли такой
¦степени владения векторными формулами, что можем доказать следующее
предложение: любое векторное поле F, если оно, конечно, однозначно
и непрерывно и обращается в нуль на бесконечности, может быть пред-
представлено в виде суммы градиента некоторого скаляра <р и ротора некото-
некоторого вектора А, дивергенция которого равна нулю
divA = 0. A.5.15)
'Функция 9 называется скалярным потенциалом поля1) F, е А — его век-
векторным потенциалом; эта теорема называется теоремой Гелъмголъца.
Для доказательства этого утверждения мы должны показать, как, зная
F, можно вычислить 9 и А, а для этого мы должны воспользоваться
решением уравнения Пуассона V2o= —q, которое было дано формулой
/1.4.8):
Рассматривая по отдельности составляющие вектора, мы убеждаемся в том,
что решение векторного уравнения Пуассона V2F= — q может быть полу-
получено в таком же виде с заменой лишь <р на F и q на q. Кроме того, мы
покажем, что решение <р, А — единственное, если только интеграл от F
по всему пространству конечен. Если же это не так, если, например, одна
из составляющих вектора F = ах, то мы можем положить F= ах внутри
¦сферы очень большого радиуса и считать F = 0 вне этой сферы. После
выполнения всех вычислений можно устремить радиус сферы к бесконеч-
бесконечности. Если мы имеем дело с полем в ограниченной области, то мы
можем за F взять значение поля внутри этой области и положить F = О
вне ее. Во всех случаях, когда F само не обращается в бесконечность,
можно сделать \Fdv конечным.
Чтобы вычислить 9 п А, сначала вычислим векторную функцию
}dx'dy'dz', A.5.16)
которая является решением векторного уравнения Пуассона V2W= —F.
Отсюда видно, что если мы положим divW= —9й rotW = A, то [исполь-
[используя векторную формулу A.5.12)] придем к представлению A.5.15)
F= — V2W= — grad[(div|WL-rot (rot W) = grad <p +rot A.
') Потенциальная функция, введенная здесь, отличается знаком от той, которая
была введена ранее. — Прим. ред.
60 Гл. 1. Типы полей
Так как W однозначно определено интегралом A.5.16), то и <р и А опре-
определены однозначно, если только интеграл от F конечен (что может быть
всегда достигнуто указанным выше приемом, если только F не обращается
в бесконечность где-либо на конечном расстоянии от начала).
Мы можем выразить <р и А в несколько более простом виде, если мы
воспользуемся симметрией функции 1/7? относительно (х, у, z) и (ж', у', z")
и заметим, что градиент 1/7? по (х, у, z) (grad 1/7?) равен — grad'1/7?, где
grad' 1/7? означает градиент 1/7? по (х', у', z'). По теореме Гаусса A.4.7)
мы имеем
?= ~ \ W №V'F(X'* y'.*')/4*R]d*' dy' dz',
или
где ?F-dA'/4rc7? распространяется по Достаточно удаленной замкнутой
поверхности, на которой F всюду равно (или может быть сделано равным)
нулю.
Аналогично, используя соотношение, родственное теореме Гаусса,
именно
A.5.17)
мы можем преобразовать выражение для А к более простому виду
ИЛИ
Следовательно, <р и А могут быть получены непосредственно из дивер-
дивергенции и ротора F, если F удовлетворяет указанным выше условиям.
Это свойство любого векторного поля быть единственным образом
представимым в виде суммы двух полей: одного rot А, без дивергенции,
и другого grad<р, безвихревого, — составляет утверждение теоремы Гелъм-
еольца. Оно будет очень полезно нам в настоящей книге, особенно
в гл. 13, и будет еще рассмотрено с другой точки зрения в п. 2.31).
1.6. Аффиноры и другие векторные операторы
Мы уже рассматривали свойства векторных полей и их соответ-
соответствие различным физическим явлениям с целью приобрести «физическое
чутье» применительно к понятию векторного поля. Теперь мы должны
ознакомиться с физическими эквивалентами тензорных форм, определен-
определенных соотношениями A.5.2). Эти формы имеют в трех измерениях девять
составляющих, тогда как вектор имеет только три. В тензорном поле
эти девять составляющих могут изменяться от точки к точке; они Ч пре-
преобразуются при замене системы координат по формулам A.5.2).
Аффиноры. Так же как мы определяли «настоящие» векторы в от-
отличие от их контравариантных и ковариантных видов, мы должны здесь
г) Следует отметить, что указанная единственность представления имеет место
для всего пространства или при наличии необходимых краевых условий. Вообще же
говоря, каждое из полей-слагаемых определено с точностью до градиента гармони-
гармонической функции.— Прим. ред.
1.6. Аффиноры и другие векторные операторы 61
определить аффинор (dyadic) как совокупность девяти составляющих Ait
(функций трех координат), преобразующихся при переходе от одной
системы координат к другой по правилу
Уяч) - ZJ ЬЩ дЦ! дЦ Л™ - Ь hmhn дЦт din mn ~
т,п т,п
2 hi hn djj дс,п . _ V v V /I iM fi \\
m, n m, n
Аффинор как целое с составляющими, подчиненными соотношениям
A.6.1), будет обозначаться готической заглавной буквой?!. Соотношение
между составляющими аффинора и составляющими соответствующих
контравариантного, ковариантного и смешанного тензоров могут быть
выведены из соотношений A.5.2)
amn = AmJhmhn, amn = hmhnAmn, a™ = hnAmn/hn. A.6.2)
Можно сразу записать два общих свойства аффинора ЗД: его 'свертка
= 2«? A.6.3)
является скалярным инвариантом, значение которого в любой точке
не зависит от выэора системы координат; и в соответствии с формулами
A.5.3) величина
B1) = ах [A2i - А32] -и а2 [Ап - Л13\ + а3 [А12 - А21] A.6.4)
является аксиальным вектором, так -как она преобразуется как вектор
(а)П по-прежнему обозначают единичные векторы в трех направлениях
правой системы координат). Инвариант | ?! [ может быть назван следом
или коэффициентом расширения аффинора, а вектор (Щ называется
вектором вращения аффинора; вскоре обнаружатся основания для введе-
введения этих терминов.
Аффинор может сочетаться с вектором, образуя вектор
31-В = 2 атЛтгА, [В- И = 2 ВтАтпап. A.6.5)
тп тп
Применяя правила преобразования векторов и аффиноров, можно пока-
показать, что эти величины преобразуются как векторы («настоящие» векторы).
Этот результат наводит на мысль о следующей формальной записи
аффинора через его девять составляющих по осям
3]la1 _u nsAi2&2 + а34зза3. A.6.6)
Выражения aman не являются ни скалярными, ни векторными произве-
произведениями единичных векторов, а должны рассматриваться как такие опе-
операторы, что скалярное произведение (ата„)- В = Впат является вектором
вдоль оси %т, длины, равной составляющей В в направлении $п и т. д.
Отметим, что, вообще говоря, вектор B-St не совпадает с вектором ЗД-В.
Аффинор ЗД*, образованный из ЗД перестановкой индексов в каждой
составляющей (А*пп = АП1Г), называется сопряженным с ЗД. 'Нетрудно
видеть, что m-B = B-2I* и B-9l = 2t*-B.
Аффиноры как векторные операторы. Рассмотрения последнего
пункта подсказывают одно из самых полезных свойств аффиноров: они
62 Гл. 1. Типы полей
являются операторами, переводяшими один вектор в другой вектор. Новый
вектор получается из старого по определенной системе правил, пред-
представленной девятью составляющими А^. Значения этих составляющих
определяют, как новый вектор отличается от старого по длине и напра-
направлению. Это различие в длине и направлении зависит, конечно, и от на-
направления исходного вектора. Векторный оператор, представленный
аффинором, не является наиболее общим видом векторного оператора
(другие виды мы рассмотрим ниже), но он отвечает столь многим физи-
физическим явлениям, что заслуживает подробного изучения.
к
Рис. 1.18. Преобразование векторного поля аффинором
Черные векторы представляют исходное поле; светлые векторы—
преобразованное поле.
Примеры явлений, которые могут быть представлены при иомощи вен-
торных операторов, встречаются во многих разделах физики. Например,,
зависимость между угловым моментом М твердого тела и его угловой
скоростью «о имеет вид М = ^-ю, где g —аффинор моментов инерции.
Далее вектор скорости v жидкости, которая под давлением проса-
просачивается через анизотропную пористую среду, вообще говоря, не совпадает
но направлению с градиентом давления, а связан с ним аффинорным.
соотношением gradp = $i-x, где $i — аффинор сопротивления. Аналогич-
Аналогично зависимость между электрической напряженностью и электрической
поляризацией в неизотропном диэлектрике также имеет аффинерный
характер. Наиболее известный пример аффиноров получается при деформа-
деформации упругого тела, которая будет вскоре рассмотрена.
Понятие аффинора как векторного оператора, а также указанные-
выше соотношения приводят нас к следующим правилам алгебры аффи-
аффиноров:
tn, n
Первое соотношение показывает, что сложение аффиноров коммута-
коммутативно и что аффинор общего вида может быть построен как сумма аффи-
аффиноров более простых видов. Второе соотношение показывает, что аффи-
аффинор, умноженный на аффинор, есть вновь, аффинор и что умножение-
аффиноров некоммутативно. Третье соотношение определяет умножение-
на скаляр. Умножение на вектор было уже определено. Скалярное «дву-
«двуточечное» произведение 3(: S3 = 2 imBnm = I ^• S31 является, конечно,
m, n
полностью свернутой формой.
1.6. Аффиноры, и другие векторные операторы &6
Существуют, конечно, нулевой аффинор D и единичный аффинор §,
называемый также идемфактпором
где F —любой вектор.
Можно также определить ЭД, аффинор, обратный к %, как аффи-
аффинор, который, будучи умножен на 3(, дает идемфактор
Аффинор, обратный к нулевому аффинору, естественно, не определен.
Через девять составляющих аффинора 91 составляющие обратного аффп
нора выражаются следующим образом:
r/or-i\ __
/mn
—л
где А'тп—алгебраическое дополнение элемента Атп в определителе
1 2 3
1 2 3
Определение умножения аффиноров влечет за собой то, что аффинор,
сопряженный к произведению 91-58, выражается через сопряженные к 3(
и $8 формулой
так что переход ь произведении к сопряженному аффинору связан с пе-
перестановкой сомножителей. Аналогично выражается аффинор, обратный
произведению (Sl-58) = S8-St~1-
Так как аффинор определен в каждой точке пространства его девятью
составляющими по ортогональным осям [причем эти составляющие изме-
изменяются при вращении координат по формулам A.6.1)], то он может
быть построен в виде комбинации векторов, содержащих девять незави-
независимых параметров. Так как вектор определяется в каждой точке тремя
величинами, то аффинор может быть, например, образован при помощи
трех произвольно выбранных векторов Ат
91 = atA± + а2А2 + а3А3 = Afo + А*а2 + А*а3, A.6.7)
где а — единичные векторы ортогональной правой системы координат.
Сопряженным аффинором будет
$* = А^! -i- A2a2 f А3а3 = ахА* + а2А' + a3AJ.
Эти равенства определяют векторы Ап и А?. Их взаимосвязь дана ниже.
Вектор Ат может быть назван составляющим вектором но оси ?т. Для-
произвольного аффинора он может иметь любое направление и любую
длину. Вектор В, направленный вдоль ?т-линии, преобразуется опера-
операцией В-ЭД в вектор, имеющий направление Ат, а операцией ЭД-В —в век-
вектор, имеющий направление А^.
Нетрудно видеть, что составляющие векторы связаны с девятью-
составляющими Атп аффинора 91 по осям %г, ?2> ?3 1СМ- формулы A.6.6)]
формулами
64 Гл. 1. Типы полей
В декартовых координатах х, у, z аффинор может быть представлен в виде
Я = iAx + jAy + kA2 = A*i + A* j + AJk,
Ax = al Al
В более общем виде аффинор может быть представлен как сумма
комбинаций векторов1)
причем для такого представления произвольного аффинора в этой сумме
должно быть не менее трех членов.
Симметрические и кососимметрические аффиноры. Аффинор Аахаг
является особенно простым векторным оператором; он переводит любой
вектор F в вектор длины А(ах-?), имеющий направление ах. Он является
симметрическим аффинором, так как его составляющие в любой декар-
декартовой системе координат симметричны относительно индексов. Например,
в системе координат х, у, z его составляющие равны
где ax, pi? Yi — направляющие косинусы ах в системе х, у, z.
Наиболее общим видом симметрического аффинора является
'Us = a1A1a1 + a2A2a2 + a3Asas, A.6.8)
где а1} а2, а3 — любая тройка взаимно-ортогональных единичных векторов.
Так как симметрический аффинор содержит только шесть независимых
параметров (три пары его составляющих равны), то задание определен-
определенного симметрического аффинора однозначно определяет три постоянных
Аг, А.2, А3 и направления в пространстве трех взаимно-ортогональных
единичных векторов alf a2, а3 [которые задаются эйлеровыми углами ф,
Ф, 6, см. формулы A.3.8)]. Обращаясь к соотношениям A.6.7), мы видим,
что для того, чтобы аффинор был симметрическим, должна существо-
существовать такая тройка единичных векторов а, для которой составляющий
вектор Ах параллелен а± и т. д.
Обратно, любой симметрический аффинор может быть представлен
в виде A.6.8), и значения А и направления а могут быть найдены, так как
формула A.6.8) показывает, что симметрический оператор 9ls, воздействуя
на вектор в любом из трех взаимно-ортогональных направлений ах, а2
или а3, меняет только длину этого вектора, но не изменяет его напра-
направления, тогда как векторы в направлениях, отличных от ах, а2 и а3, пере-
переводятся в векторы с измененными направлениями. Эти специальные
направления, в которых оператор не изменяет направления вектора,
называются главными осями аффинора.
Направляющие косинусы главной оси ах аффинора
Я. = ^ii + Bzij + Byib + BJi 4-AJj + BJk + Byki
x) В нашей литературе вместо «комбинация векторов» говорят Неопределенное
или диадное произведение векторов (или просто «диада»).—Прим. перее.
1.6. Аффиноры и другие векторные операторы 65
могут быть найдены посредством решения уравнения
Я8-а:=М, A-6.9)
которое является математическим выражением данного выше определения
главной оси. Уравнение A.6.9) является первым встретившимся нам при-
примером задачи на собственные значения, но скоро мы познакомимся
и с другими такими задачами, например при рассмотрении «векторных
пространств» в квантовой механике, в теории волнового движения и во мно-
многих других вопросах теории поля. Единичные векторы at, дающие направле-
направления главных осей, называются собственными векторами, а постоянные А1г
А2, А3 —собственными значениями.
Для решения уравнения A.6.9) положим ах = axi + pxj + ухк. Подста-
Подставляя это выражение в обе части уравнения, мы найдем три линейных
однородных уравнения
Ута система уравнений имеет нетривиальное решение только в том слу-
случае, если определитель, составленный из коэффициентов при а1; Slt ух.
равен нулю
вч
Решая это уравнение третьей степени относительно Аг, мы найдем
чри корня, соответствующие трем числам Ах, А.2, А3. Этот определитель
известен под названием векового определителя. Он всегда возникает при
решении задач иа собственные значения при помощи линейной комбина-
комбинации векторов вида, принятого нами для ах.
Каждому из трех чисел Ai будет соответствовать система значений ait
д, Yi> которая дает направляющие косинусы i-й главной оси. Эти оси
взаимно перпендикулярны, что может быть показано следующим образом.
Так как 915-а1 = Л1а1 и 9fs-a2 = -l2a2, то, и силу симметрии 2L,
Но Ах и А2, как правило, не равны, так что последнее равенство может
иметь место только в случае а1-а2 = 0.
Можно показать, что след или коэффициент расширения является
инвариантом
как это, конечно, и должно быть, так как это выражение является ска-
скалярным инвариантом 19IS | аффинора. Мы теперь видим, почему этот ска-
скаляр называется коэффициентом. расширения: он равен утроенному произ-
производимому аффинором 2fs среднему относительному удлинению векторов,
направленных вдоль трех главных осей. Другой термин, «след» (по ана-
аналогии со следом крупной дичи), является картинным, но удобопонятным
описанием этой величины.
Отметим, что вектор (ЭД6), образованный для симметрического аффи-
аффинора, равен нулю и что для симметрического аффинора 2fs-F = F-9Is,
где F — произвольный вектор. Другими словами, всякий симметрический
аффинор совпадает с сопряженным себе.
5 Ф. м. Морс и г. Фешбах
66 Гл. 1. Типы полей
В кососимметрическом аффиноре диагональные составляющие Апп
равны нулю, а внедиагональные составляющие меняют знак при пере-
перестановке индексов: Атп = — Апт- Наиболее общий кососимметрический
аффинор Содержит только три независимых параметра. Он всегда может
быть представлен в виде
где $ = ii + jj + kk — идемфактор. Выбор кососимметрического аффинора
однозначно определяет вектор R, который равен минус половине вектора
вращения' (ЭДа)- этого аффинора. Отметим, что коэффициент расширения
кососимметрического аффинора равен нулю'. Отметим также, что для лю-
любого вектора F операция 91-F = RxF = -^ Cta)xF дает вектор, перпенди-
перпендикулярный к F, а также перпендикулярный к вектору вращения (9Ia).
Задача на собственные значения может быть также поставлена и для
кососимметрического аффинора
91а-а = Кха=).а;
формально решая это уравнение, мы получим «главные оси» S2fa. Состав
ление векового определителя показывает, что три значения X суть Аг — О,
А2 = Ш и А3 = — Ш, так что два корня чисто мнимы. Единичным векто-
вектором вдоль главной оси, соответствующей X = А1 = 0, является ай, парал-
параллельный R; два других единичных вектора невещественны. Сумма
А1-\-А2 + А3 = 0, как это и должно быть, так как коэффициент расшире-
расширения кососимметрического аффинора равен нулю.
Легко видеть, что любой аффинор может быть представлен в виде
суммы симметрического и кососимметрического аффинорон
Я = «, + «„,
1 1
( **s)mn == ~2 ' гпп ~Г -™пт), ( <Ха)тп = -? (Ann -™nm) •
Преобразованием к главным осям (которые всегда вещественны) мы можем
представить симметрическую часть 9IS в форме A.6.8), а надлежащим
выбором вектора R — кососимметрическую часть %а в форме A.6.10).
Мы можем, конечно, искать главные оси самого аффинора Ш., решая
уравнение
непосредственно (до разделения аффинора на симметрическую и кососим-
кососимметрическую части). Это приводит к вековому уравнению
Ах Azv
= 0.
Корни этого кубического уравнения можно обозначить через }. = Alt A2, А.6,
а соответствующие собственные векторы вдоль главных осей — через
Из алгебры известно, что взятый с обратным знаком коэффициент при
^2' А<х + А;« + 4к» Равен сУмме корней A1 + A2-\-As. Известно также, что
либо все три корня вещественны, либо один из них веществен, а два
1.6. Аффиноры и другие векторные операторы 67
других мнимы и комплексно сопряжены (при условии, что все девять
составляющих Атп аффинора % вещественны). Когда все три корня ве-
вещественны, то и все три собственных вектора ет вещественны, но когда
два из корней мнимы, то соответствующие два собственных вектора тоже
мнимы. Чтобы избежать этого осложнения, обычно сначала отделяют
кососимметрическую часть ЭДа и находят главные оси симметрической
части 2fs, так как ее собственные значения и собственные векторы обяза-
обязательно вещественны (если составляющие самого аффинора Ш вещественны).
Вращение осей и унитарные аффиноры. Специальный тин вектор-
векторного оператора соответствует такому преобразованию, которое можно
назвать жестким вращением. Рассматривая несколько векторов F как
своего рода координатный репер (каркас), мы будем под операцией
жесткого вращения понимать такое вращение всех векторов F, при
котором этот репер вращается как твердое тело, т. е. с сохранением
длин всех F и углов между ними. Если эти векторы F являются, напри-
например, радиус-векторами точек некоторого твердого тела, то рассматри-
рассматриваемой операции соответствует вращение этого твердого тела вокруг
начала координат.
Допустим, что мы представим такую векторную операцию специ-
специальным аффинором (У с составляющими ~[тп и т. д. Для того чтобы
преобразованный лектор 05-F имел ту же длину, что и F, для любого F
должно выполняться следующее условие:
(©.F)-(®)-F")= 2 [2 Y«nY,,J^«^ =*¦•«•-= S ^n- I, m,n = j-,y,z.
I. п in -и
или, другими словами,
2jTf™nYmI=a«l=| 0, 1ФП. A.6.11)
га
Аффиноры, составляющие которых удовлетворяют этому условию, назы-
называются (по причине, которая вскоре будет ясной) унитарными аффино-
аффинорами1). Между прочим, если у удовлетворяют этому условию, то, как
легко показывается, для любой пары векторов А и В их скалярное про-
произведение А-В остается неизменным при преобразовании, осуществля-
осуществляемом ©:
а следовательно (так как длины векторов остаются неизменными), опе-
оператор @ сохраняет неизменными и углы между векторами. Легко показать
также, что если аффиноры & и ^ представляют жесткое вращение, то и
аффинор C-$э имеет составляющие, удовлетворяющие соотношениям
A.6.11), т. е. также представляет жесткое вращение. Таким образом,
произведение унитарных аффиноров есть также унитарный аффинор.
Оказывается, что всевозможные вещественные значения составляю-
составляющих у, соответствующие всем вещественным вращениям вокруг центра,
могут быть выражены через эйлеровы углы вращения, [фигурирующие
х) Действительные матрицы, элементы которых удовлетворяют условиям A.0.II).
принято называть ортогональными. Унитарными матрицами называются матрицы
г комплексными элементами, удовлетворяющими условиям, которые, в случае сети
вес элементы действительны, превращаются в условия A.6.11). — Прим. ред.
68 Гл. 1. Типы, полей
в формулах A.3.8). Если составляющие аффинора © имеют вид
Узсзс = sin ф sin Ф-f-cos ф cos Ф cos 6,
Y3cy = cos(j' sinl- sinфcosФcos 6, yxz = sinflcos<!},
YUJC = sin<[> cos Ф — cos ф sin Ф cos 6,
YyH = cos ф cos Ф + siniji sin Ф cos 6, y(/. = — sin 6 sin Ф,
yzx= —cosф sin6, Yzu = sin 6sin 6, Yrz — 008®'
то, как видно на рис. 1.12, это преобразование соответстгует повороту
жесткого векторного репера на угол ф вокруг оси z с последующим
поворотом на угол 6 вокруг оси у и заключительным поворотом (уже
повернутого репера) еще раз вокруг оси z на угол —Ф.
Несложные выкладки показывают, что оператор ©, составляющие
которого имеют указанный выше вид, удовлетворяет условиям A.6.11)
и тем самым обладает всеми свойствами поворота осей. Действительно,
прежде всего аффинор, соответствующий произведению 9I-S3, где ЭД и 93 —
унитарны, также унитарен и представляет вращение, получающееся
в результате поворота осей на углы, определяемые аффинором 93 с по-
последующим поворотом на утлы, определяемые аффинором ЭД. Поэтому
утверждение, сделанное в предыдущем абзаце, означает, что © с указан-
указанными составляющими равно произведению 6-93•$, где три унитарных
множителя имеют вид
и представляют соответственно элементарные повороты на три эйлеровых
угла. Составляющие этого произведения вычисляются по формулам A.6.6').
Причина, по которой эти вращающие аффиноры называются унитар-
унитарными, состоит в том, что определитель, составленный из их элементов,
равен 1 [как легко усматривается с помощью соотношений A.6.11)]- Но
еще более полезное свойство может быть обнаружено сопоставлением
определений обратного и сопряженного аффинора с соотношениями A.6.11).
Оказывается, что если © — унитарный аффинор [удовлетворяющий усло-
условиям A.6.11)], то
©-! = ©*, или ©*-0 = & A.6.12)
Обратно, если для некоторого аффинора © выполняются соотношения
A.6.12), то его составляющие удовлетворяют условиям A.6.11)- Так как
©*¦© отдаленно напоминает квадрат длины вектора, то можно сказать,
что «величина» унитарного аффинора равна «единице».
Возвращаясь к формулам A.3.8) поворота системы координат, мы
видим, что если вектор F разложен на составляющие по осям х, у, z,
то составляющие ©-F являются составляющими F по осям ?17 ?2, ?3-
Таким образом, унитарный аффинор & представляет изменение состав-
составляющих вектора, происходящее вследствие поворота системы координат.
Поэтому вместо того, чтобы рассматривать систему координат как фик-
фиксированную, а вектор как изменяющийся, мы можем в данном случае
рассматривать вектор как неизменный по длине и направлению, а сие-
1.6. Аффиноры и другие векторные операторы 69
тему координат — как вращающуюся, причем новые составляющие векто-
вектора F определяются из (S-F1).
Если унитарный аффинор может представлять изменение составляющнх
нектора в результате поворота осей координат, то возникает вопрос,
нельзя ли изменения составляющих общего аффинора Ш в результате
того же поворота осей также выразить через тот же унитарный аффинор.
Ответ должен быть положительным, как это можно усмотреть из послед-
последнего равенства A.6.1) или из следующих рассуждений: если © — унитар-
унитарный аффинор, представляющий поворот осей, и если 3( — любой аффинор,
преобразующий вектор А в вектор В, 91-А = В, то 1#-А и ©-В дают соот-
соответственно новые составляющие Л и В; из соотношения же между А гт В
мы находим, что
©¦ В = ©¦?{¦ А = (@-«-©-1)- (©• А) = (©-И ¦&*)¦{&• А),
т. е. что аффино𠩦?(-©* переводит преобразованный вектор А в про-
прообразованный вектор В, а это, очевидно, и является определением пре-
преобразованного аффинора 'й. Другими словами, составляющие аффинора
(У-ЭД-®* являются составляющими ЭД в новой системе координат, полу-
полученной поворотом, производимым унитарным аффинором &.
В частности, если ©л представляет поворот осей х, у, z. перево-
переводящий их в главные оси симметричного аффинора SJ(S, то прообразованный
аффинор ©.д-91 -®3l имеет простую диагональную форму
/А о о\
i*4 = О А.2 О ] .
\о о aJ
Независимо от того, какой поворот представляется унитарным
аффинором © с вещественными составляющими, преобразованный аффинор
©•91-О = ($$-91-©* симметрический, если 91 симметрический, и кососим-
метрический, если 91 кососимметрический.
Аффинерные поля. До сих пор мы рассматривали свойства аффинора
в отдельной точке пространства. Аффинорное поле есть совокупность
девяти величин, преобразующихся по формулам A.6.1) и являющихся
функциями х, у, z или Б]., ?2> ?з- Б каждой точке пространства аффинор
представляет собой оператор, переводящий вектор в данной точке в дру-
другой вектор, причем само преобразование вектора в вектор меняется от
точки к точке. С другой точки зрения можно сказать, что коэффициент
расширения, главные оси и вектор вращения аффинора — псе являются
функциями точки.
Аффинорное поле 31 с составляющими Атп может быть получено
ковариантным дифференцированием векторного поля F [см. формулу A.5.8)]
Л"т = V 1пы ) '"•¦" = С ih^
A - д ( ЬтЛ+- 1 V Fn
o-.rn V "m У >lm ¦*~J "ii
Fn dhm
„,
J) Более точно: старые компоненты вектора F выражаются через новые, поле-
полеченные после преобразования осей аффинором ©, по тем же формулам, по которым
(старые) компоненты ©-F выражаются через (старые же) компоненты F. Чтобы вы-
выражать по тем же формулам новые компоненты через старые, надо оси координат
преобразовать аффинором 0*. —Прим. ред.
70 Гл. 1. Типы полей
Как уже было показано [формула A.5.10) и далее], коэффициент расши-
расширения | 911 этого аффинора равен div F, а вектор вращения EХ) = rot F.
Этот аффинор, следовательно, симметрический только тогда, когда F —
безвихревой вектор.
Аффинор, определенный формулами A.6.13), может быть символи-
символически записан в виде FVх) с составляющими по осям х, у, z, зада-
задаваемыми формулой
дх ду dz A.6.14)
A w
Сопряженным аффинором, очевидно, является
Приращение вектора F, соответствующее вектору dr = \dx-\-jdy-\-kdz,
получается воздействием оператора VF на dr
dr.(VF) = ^dx+^-dy + ^dz = dF. A.6.15)
Симметрический аффинор, соответствующий VF, равен, конечно,
-^-(VF + FV); он имеет равный пулю вектор вращения.
Изменение аффипорного поля от точки к точке может быть вычис-
вычислено при помощи дифференциального оператора V. Например,
V ¦ И = i • (d%/dx) + j • (Ш1&у) + k • (Ш/dz)
есть вектор, который получается в результате ковариантного дифферен-
дифференцирования соответствующего смешанного тензора с последующим свер-
свертыванием возникающего тензора третьего порядка
С помощью разложения на составляющие векторы, приведенного в фор-
формуле A.6.7), для этого вектора получаем выражение (дАх/дх)-\-(дАу/ду) +
+ (dAjdz), тогда как сопряженный вектор
9I-V =, V -91* = i (div Ax) + j(div Ay) + k(div A.). A.6.16)
Физический смысл этого вектора будет рассмотрен ниже.
Существует также аффинор, образованный при помощи оператора
ротора
_ ог . Ж , . Ж , , Ш
VxSt^.x-^ + jx^ + kx^^
/ад, дАул .
~ {"ду ЪГ) • 3
ЪГ) • 3у~дГ~ дх y + KV"9^ ду
= (rot AJ) i + (rot A*) j + (rot A*) k. A.6.17)
Наряду с этими дифференциальными свойствами аффиноров имеют
место также интегральные свойства, аналогичные теоремам Гаусса и
Стокса [формулы A.4.7) и A.4.11)]. Для интеграла, распространенного
х) При этом надо иметь в виду, что здесь, вопреки обычным правилам, диф-
дифференцирование в V действует на F, хотя V и стоит позади F. —Прим. ред.
1.6. Аффиноры и другие векторные операторы
71
no замкнутой поверхности, имеем
A.E.18)
где интеграл в правой части распространяется по объему «внутри» поверх-
поверхности и элемент поверхности dA направлен «изнутри» во внешнее про-
пространство, а S3 —произвольный аффинор. Каждый из интегралов является,
конечно, вектором. Для криволинейного интеграла по замкнутому кон-
контуру имеем
A.0.19)
где интеграл в правой части распространяется по поверхности,
опирающейся на этот контур, а S3—произвольный аффинор.
Деформация упругих тел. Важным приложением аффинорной алгебры
является представление деформации упругих тел. Твердое тело движется
и вращается как целое, но упругое тело способно еще, кроме того, изме-
изменять взаимное расположение своих внутренних частей. Для такого тела
смещение части, находившейся в исходном положении в точке (ж. у, z).
выражается суммой трех векторов
Т>(х, у, z)=T + F(x, у, z)-: s(a-, у, z),
где Т — постоянный вектор, представляющий средний|" перенос тела,
Р —часть смещения, учитывающая среднее вращение вокруг центра тяже-
тяжести, и s — дополнительное смещение, возникающее благодаря деформации
тела. По определению, s равен пулю в центре тяжести тела и
нулю всюду, если тело абсолютно твердое.
Рис. 1.19. Смещения в упругой среде, вызывающие
смещение s относительно центра массы и деформацию,
представляемую аффинором ® = Vs.
Вообще говоря, s гораздо меньше, чем могут быть Т и Р. Сейчас мы
лабудем про Т и Р и сосредоточим наше внимание исключительно на s,
так как мы не интересуемся движением тела в целом, а только его вну-
внутренними смещениями и деформациями.
Относительное смещение s не является, однако, хорошей мерой ло-
локальной деформации упругой среды, так как s является полным относи-
относительным смещением точки (х, у, z), которое даже при сравнительно рав-
равномерном распределении напряжений в среде может быть тем больше,
чем дальше точка (х, у, z) отстоит от центра тяжести. Нам нужна диф-
дифференциальная величина, измеряющая деформацию в точке (х, у, z). Она
получается вычислением изменения вектора dr = i dx -\- j dy -f- k dz, соеди-
соединяющего точки (х, у, z) и (x+dx, y + dy, z + dz) деформированного тела.
Точка (х, у, z) смещается на вектор s(x, у, z), а точка (x + dx, y + dy,
z-i-dz)~-na вектор s(x+-dx, y-\-dy, z-j-rfz). Изменение dr вследстпяе
72
Гл. 1. Типы полей
ож-r- + dy я- + dz д- = dr • Vs
Э •* ду dz
деформации с точностью до величин второго порядка малости равно
+ dy я- + d
ду
[в силу формулы A.6.15)]. Поэтому вектор dr переходит при деформации
в вектор dr', характеризующий новое относительное положение точек, где
dr' = dr-C + ®); ® = Vs. A.6.20)
Аффинор % является дифференциальным оператором, характеризую-
характеризующим деформацию в точке (x,y,z). Как было разъяснено на стр. 64, он
может быть разбит на симметрическую и кососимметрическую части:
5> = 9t + ®, 5R=--f (rots)x8,
A.6.21)
Аффинор Ш соответствует вращению элемента объема вокруг (х, у, z).
производимому деформацией среды. Ось вращения лежит в направлении
rots, а угол вращения, измеренный в радианах, равен длине -xvots. Отме-
Отметим, что этот член не происходит от вращения тела как целого (так как
эта часть движения была нами специально исключена из рассмотрений);
он фигурирует вследствие закручивания материала при деформации. Этот
тип вращения отсутствует, если rots = 0.
Симметрический аффинор <В называется аффинором чистой деформа-
деформации в точке (х, у, z). Если он равен нулю, то в рассматриваемой точке
напряженное состояние отсутствует.
Как уже указывалось, всегда можно найти три взаимно-ортогональ-
взаимно-ортогональных направления — главные оси с единичными векторами ах, а2, а3,
с помощью которых симметрический аффинор © представляется в виде
<3 = a^aj + a2e2a2 + а3е3а3. A.6.22)
Три величины ег, е2, е3 называются главными удлинениями в точке
(х, у, z). Прямоугольный параллелепипед со сторонами d%t, d%2, d%3, ребра
которого направлены вдоль главных осей, после деформации остается
L
/
/
/
\
/
//
\
/
7
Рис. 1.20. Изменение элемента упругой среды при
простом сжатии.
прямоугольным параллелепипедом (что уже не будет иметь места, если
его ребра наклонены к главным осям), но длины его сторон станут щв-
ными (I-\-ву) d?lt (I + e2)d?2, (^ + es)d^s. Поэтому относительное увеличе-
увеличение объема параллелепипеда равно
О = ег + е2 + е3 = еп + е22 + е33 = divs = | Ъ \. A.6.23)
Величина 6, коэффициент расширения аффинора ф (в любой системе
координат), называется коэффициентом объемного расширения среды
1.6. Аффиноры и другие векторные операторы
в точке (х, у, г). Этот коэффициент 6 также равен относительному умень-
уменьшению плотности среды в точке (х, у, z) (с точностью до малых второго
порядка относительно величин е).
Типы деформаций. Простейшим типом напряженного состояния ян-
ляется тот, которому соответствует постоянный аффинор, не зависящий
от положения точки; такая деформация называется однородной. Простей-
Простейшим типом однородной деформации является простое растяжение, соот-
соответствующее смещению s и аффинору чистой деформации S, заданным
формулами
s = e(xi + yj + zk), 2) = S = eg. A.6.24)
Этот тин деформации изотропен; любые оси являются главными осями:
отсутствует вращение вследствие деформации. Коэффициент объемного
расширения Ь = Зе.
Другой тин однородной деформации, называемый чистым сдвигом,
1 „
получается при е,= —е2=-^-е, e3 = v, так что
Коэффициент объемного расширения равен нулю, гак как растяжение
вдоль оси х компенсируется сжатием вдоль оси у. Если повернуть систему
К\
7К
/
\7
N
J
\
/
/
/
I/
\
/
Рис. 1.21. Изменение элемента упругой среды
при чистом сдвиге, задаваемом аффинором е (ii—jj).
координат на 45° вокруг оси z (\^2х = х' + у',
ние и аффинор чистой деформации примут вид
я1'—
, то смеще-
смещеЭтот тип деформации называется чистым сдвигом. Если его сочетап
с жестким вращением среды на угол, равный -^-е радиан, соответствую
щи» аффинору 9t = — -2 e(i'j'-j'i'), то результирующее смещение и сдви i
s = ey'i', ® = ej'i' A.6.25)
соответствуют так называемому простому сдвигу е направлении у'. Все
смещение происходит в направлении оси х', слои среды скользят дру!
над другом, как это можно проделать с колодой игральных карт.
Другой тип однородной деформации с коэффициентом объемного рас-
расширения, равным нулю, соответствует растяжению в направлении оси г
и соответствующему сжатию в направлениях осей у и z
). A-6-26>
Такого рода деформация возникает в материале типа резины, который
растягивается в направлении оси х. Эту деформацию можно назвать
растяжением с сохранением объема.
74
Гл. 1. Типы полей
Самая общая однородная деформация, отнесенная к ее главным
осям, может быть получена наложением простого растяжения, сдвига
и растяжения с сохранением объема по всем трем направлениям. После-
Последующий поворот осей дает наиболее общий вид для s и <3.
направление
сжатия
Направление
растяжения
Направление
растяжения
Р,ис. 1.22. Изменение элемента упругой среды при про-
простом сдвиге, задаваемом аффинором eji.
Простым типом неоднородной деформации является винтовое на-
накручивание в направлении оси х:
X = 9t -f © = е [iyk — izj
— kxj],
A.6.27)
-ij)]= - e [ii-{
= e [y (kf + ik) — z (ij + ji)].
• ho соответствует повороту элемента в точке (ж, у, z) вокруг оси х на
угол в ех радиан [член ezjk — e.zkj в ф, см. формулу A.6.10)] и сдвигу
в направлении оси х, пропорциональному длине вектора r = yj-\-zk,
соединяющему точку (х, у, z) с осью х [член eyik—ezij в ф, см. фор-
формулы A.6.25)].
Напряжения в упругой среде. Силы, действующие внутри упругой
«•реды, которые вызывают деформации, называются напряжениями. Они
Рис. 1.23. Изменение элемента упругой среды
при кручении, задаваемом формулами A.6.27).
также лучше всего представляются аффинорами. Сила, действующая на
элемент dydz, перпендикулярный оси х, равна ?xdydz, где F^ не обязан
быть параллелен оси х. Аналогично обозначим через F^ и F. силы, дей-
действующие на элементы, перпендикулярные к осям у и z, и отнесенные
к единице площади. Легко может быть показано, что сила, действующая
на элемент площади, представленный аксиальным вектором dA, равна
X ¦ dA, где
1.6. Аффиноры и другие векторные операторы
75
Более подробное рассмотрение соотношения между силами F и площа-
дями dA подтверждает, что 2 является аффинором и преобразуется как
нс.якнп аффинор.
4
т
/ ^f~
P.txl
/
Fy(V-dv)
A
:«(x*dx)
x
Рис. 1.24. Силы, действующие на грани элемента
упругой среды, соответствующие аффинору напряжений
При статическом равновесии эти силы не должны нриьодить ни кра-
крашение ни одну часть среды. Рассмотрение моментов, действующих на
элемент объема среды, показывает, что
'Следовательно, аффинор % — симметрический п равен своему сопряжен-
сопряженному 3/* = iFv -;- jF,, + kF2. При помощи главных осей и соответствующих
ортогональных единичных векторов ап мы можем записать % в виде
где постоянные Тп называются главными напряжениями но главным
-осям. Существуют различные простые типы напряжений, аналогичные
рассмотренным типам деформаций. Если, например, Т2= Т3 = 0, то мы
имеем растягивающее напряжение вдоль направления а^ если Т2= — 7\
и Т3 = 0, то мы имеем срезывающее напряжение, и т. д. Скаляр \%\ равен
утроенному давлению в точке, взятому с обратным знаком..
Статическая взаимосвязь между напряжением и деформацией в изо-
изотропном упругом теле. Если некоторая среда может находиться в равно-
несии при наличии срезывающих напряжений, то говорят, что она упру-
упругая. Если упругие свойства среды не зависят от направления, то она
называется изотропной. Когда оба эти требования выполняются, то ока-
окалывается, что главные оси деформации всюду совпадают с главными осями
напряжений и что деформации, порождаемые тремя главными напряже-
напряжениями, независимы друг от друга и аддитивны. Например, эффект глав-
главного напряжения Тх состоит в простом объемном расширении и удлине-
удлинении в направлении &г. Другими словами, уравнениями, связывающими
главные напряжения и главные удлинения, будут
Тп = X («! + е2 + е3) + 2аеп, п = 1, 2, 3,
где постоянные X и jj. определены упругими свойствами среды.
В декартовой системе координат х, у, z аффиноры напряжении и
деформаций принимают более общий симметрический вид
76 Гл. 1. Типы полей
Уравнения, связывающие % и S и их составляющие, могут быть полу-
получены преобразованием главных осей
x и т. д., A.6.28)
Тху = 2?еху и т. д.
Когда напряжения представляют собой изотропное давление, % = —/>^>
деформация является всесторонним сжатием и
Константа -^ C>. + 2jj.) = Р/Ь является поэтому модулем всестороннего ежа-
тия изотропной упругой среды. Если напряжение срезывающее
% = S (ii — jj), то деформация является чистым сдвигом © = Т (?/;л.) (ii — jj),
так что [л. есть модуль сдвига среды. Когда напряжение описывается аффи-
аффинором %=ТИ, т. е. является простым растяжением в направлении оси х,
аффинор деформации имеет вид
он представляет растяжение в направлении оси х и сжатие в направле-
направлениях осей у и z. Величина ;л. (ЗХ + 2[i)/(X 4- \>) называется модулем Юнга
материала. Отношение поперечного сжатия к продольному растяжению
2называется коэффициентом Пуассона.
Лффинорные операторы. Для того чтобы иметь возможность рассмо-
рассмотреть связь между аффинором напряжений и аффинором деформаций для
неизотропных сред, мы должны ввести операторы, которые преобразуют
аффиноры подобно тому, как аффиноры преобразуют векторы. Составляющие
должны иметь четыре индекса и должны преобразовываться по формулам»
аналогичным формулам A.6.1),
V-4jhU = 2j YimYynYkrY(s"rrmrs-
mnrs
Эти операторы могут .быть названы тетрадиками (tetradic) и обозначены
древнееврейскими буквами (чтобы отличить их от других операторов).
Например, символ,, представляющий 81 составляющую Gijhl, пусть будет 3
(гимель), а соотношение, определяющее характер преобразования аффн
нора, имеет вид
® = Д:Й, или #тп=2СтТ1Г8ЛГ8. A.6.2У)
rs
Тетрадик может быть представлен через неопределенное произведение
двух аффиноров аналогично тому, как аффинор может быть представлен
через неопределенное произведение двух векторов. Особенно простым
тетрадиком, например, является У (айн) =3S> который преобразует всякий
аффинор ь постоянную, умноженную на идемфактор:
У: 58 = | 58 |S, Ymnrs = omnbrt.
Существует, конечно, единичный тетрадик * (иод), который воспроиз-
воспроизводит любой аффинор, и сопряженный к нему **:
»:« = «, (»*):« = «*,
1.6. Аффиноры и другие векторные операторы 77
В этих обозначениях аффинор напряжений выражается для изотроп-
изотропных тел через аффинор чистой деформации следующим образом:
где тетрадик в квадратных скобках имеет столь простой вид благодаря
изотропности среды. Для неизотропных сред это соотношение более
•сложно, и составляющие тетрадика Т (далет)
re
is основном, не равны нулю. Так как и Ж и ©—симметрические аффиноры, то
должны иметь место равенства Dmnrs = Dnmrs и Dmnrs=Dmnsr, а также
Annrs = ^remn- Благодаря этим симметриям число независимых составляю-
составляющих Т сводится к 21. Эти составляющие называются упругими константами
неизотропного тела.
Можно было бы разнить анализ тетрадиков, определить их «главные
оси» и остальные свойства вполне аналогично тому, как мы это делали
для аффиноров. Однако недостаток места и меньшая значимость этого
«опроса для наших пелей не позволяют нам этого.
Комплексные числа и кватернионы как операторы. Прежде чем мы
перейдем к менее известным полям, полезно сделать обзор одного типа
векторных операторов, который настолько известен, что часто упускается
из виду. Использование комплексных чисел для представления векторов
п двух измерениях тривиально, но не всегда достаточно ясно понимают,
что комплексное число может также представлять линейный вектор-
векторный оператор л двух измерениях.
Комплексные числа и функции комплексного неременного будут под-
подробно рассмотрены в гл. 4, так как мы во всей книге будем пользоваться
комплексными числами при решении наших задач. Все, что нам нужно
здесь, состоит в следующем: вещественная единица 1 может рассматри-
рассматриваться как единичный вектор вдоль оси х, а мнимая единица ? = У — 1 —
как единичный вектор вдоль оси у; тогда двумерный вектор с составля-
составляющими х и у может быть представлен комплексным числом z — x + iy.
Такая величина удовлетворяет обычным правилам сложения векторов
{т. е. для этого нужно сложить составляющие) и умножения на скаляр
(т. е. az = ax-\-iay).
Вектор, являющийся зеркальным отображением z и оси х, называется
комплексно-сопряженным к z, z = x— iy. Угол между z и осью х равен
a rctg (у/ж), а квадрат длины z равен | z|2 = zz = a;2-f у2 = zz. Заметим, что
умножение комплексных чисел не соответствует правилам умножения
трехмерных векторов. Если z — x + iy и w = u-\-iv, то wz = zw = (их — vy) +
4- i(uy + vx) вновь является вектором в плоскости х, у. Произведение wz
не является ни скалярным произведением этих векторов (скалярное про-
произведение ux-\-vy является вещественной частью wz), ни их векторным
произведением (векторное произведение но величине равнялось бы мни-
мнимой части wz, но его направление должно было бы быть перпендикулярно
к w и к z, что требует третьего измерения). Фактически произведение wz
двух комплексных чисел в большей степени соответствует воздействию
аффинора w особого рода на вектор z.
Операция умножения на w изменяет и направление и длину z. Чтобы
записать это в обычной векторной и аффинорной форме, надо было бы
вектор z записать в виде xi 4- Vh a аффинор т — в виде ин —oij + oji + MJj.
т. е. в виде комбинации кососимметрического аффинора w(ji — ij) и сим-
78 Гл. 1. Типы полей
метрического аффинора M(ii + jj) с главными осями по осям хну Этот
аффинор, очевидно, не является самым общим двумерным линейным опе-
оператором (так как он содержит только два независимых параметра); это —
оператор особенно простого типа, который, как мы сейчас увидим, изме-
изменяет направление любого вектора на постоянный угол, а его длину
в постоянном отношении.
Комплексное число, символически представляемое в показательной
форме егВ (где 6 — вещественное число), но формуле Эйлера равно
е*в = cos б + i sin 6.
Рассматривая его как оператор, мы заключаемое, что оно поворачивает-
любой вектор z на угол 6 радиан (против часовой стрелки) и не изменяет
длины z. Следовательно, оператор w — Cei6 [С2 = w2 + w2, 0 = arctg(o/w)],
будучи умножен на любой вектор z = x-\-iy, поворачивает z на угол 6
и увеличивает его длину и С раз. Многие наши решения будут иметь вия
произведения некоторой комплексной величины ф на временной множи-
множитель е~*"!(. Этот множитель вращает вектор <|> с постоянной угловой ско-
скоростью »>, и если (как это часто бывает) физическое решение является
иещестьенной частью указанного произведения, то решение будет синусо-
синусоидально колебаться во времени с циклической частотой v = ш/2те.
Распространение этого типа представления величин на трехмерное-
пространство невозможно, вследствие чего мы и должны применять более
сложный аппарат векторов и аффиноров. Гамильтон показал, однако, что
векторы и операторы в четырехмерном пространстве могут быть пред-
представлены при помощи довольно очевидного обобщения комплексных чисел,
так называемых кватернионов.
Пусть число 1 представляет единичный вектор в четвертом измере-
измерении, и обозначим единичные векторы в трехмерном пространстве черел
/, /, к, правила перемножения которых аналогичны правилам для |/ — I
i2 = /2 = Аг2 = — 1, if = — fi = к, jk= —kj = i, Art = — iAr = /.
Тогда трехмерный вектор можно представить величиной ix-\- jy ~\- kzr
а общий кватернион q = a-\-ib-\-fc-\-kd представляет четырехмерный век-
вектор. Сопряженный четырехмерный вектор имеет вид q* = а— ib — /с— kd, так
что квадрат длины q равен | q |2 = q*q = а2 -\- Ь2 -\- с2 -\-d2, что является простым
распространением правила для обычных комплексных чисел на кватер-
кватернионы.
Как и для комплексных чисел, произведение кватернионов pq может
рассматриваться как результат операции, переводящей четырехмерный
вектор q в четырехмерный вектор pq. Если q = a-\-ib-\- jc-\- kd и р = а-
Р + йй, то
/>q = (aa — $b — ус — M) + i (ab + pa + -(d — Se) +
+ /(ac —pd + Yo + 8b)+Ar(oKZ + ?c—yb+ 8я) AА. За-
Заявляется новым кватернионом, представляющим новый четырехмерный
вектор. Отметим, что умножение кватернионов некоммутативно, т. е. что
pq ф qp. Мы не можем продолжать это рассмотрение дальше, хотя связь
между кватернионами и пространственно-временными векторами в теории
относительности будет еще упомянута ниже (заметим лишь, что //
не может представлять самый общий четырехмерный аффинор).
Полезно, однако, рассмотреть один специальный кватернион, кото-
который является интересным обобщением комплексного числа ег6. Примени»
правила умножения для i, /', к и разлагая показательную функцию в ряд,
1.IJ. Аффиноры и другие векторные операторы 7'.'
можно показать, что если а2-|-624-у2= 1, то
= cos 6 + sin б (ia
что является аналогом формулы Эйлера для eie. Показатель представляет
собой трехмерный вектор длины б и направления, определяемого направ-
направляющими косинусами а, [3, v. тогда как все выражение является кватер-
кватернионом единичной длины. Отметим, что любой кватернион может быть
представлен в виде
где Q — длина четырехмерного вектора, а угол й и направляющие коси-
косинусы определяют направление вектора в четырехмерном пространство
Можно ожидать, что, по аналогии с комплексным числом eie, этот оно
ратор (при (?=1) каким-то образом связан с оператором вращения, хотя
ясно, что эта связь не может быть столь простой, как в комплексной
плоскости.
Правильный путь здесь может подсказать следующее интересное
соотношение: если / — вектор в кватернионном обозначении / = ix -+- /у + kz.
то кватернион
f = x'i + y'j + z'k = e<e'2)(ia+^+'l'()/e^<e/2)<ia+^+ft1f>,
где a2 -|- L32 ---у2 = 1 представляет вектор, получающийся пл вектора / ново
ротом на угол 0 вокруг оси с направляющими косинусами а, $, Y- Заме-
Заметим, что угол поворота вокруг этой оси равен О, а пе 6/2. Это можно
показать в общем случае, однако выкладка становится нроще, если мы
козьмем частный случаи вращения вокруг оси .г. Тогда мы имеем
/' = e6i/2 (ix + jy
= ix + / (у cos 6 — z sin б) 4- k (у sin 6 -4- z cos 0),
4iо соответствует повороту у- и z-составляющих / на угол 6 в плоскости
yz, т. е. повороту всего вектора / на угол 6 вокруг оси х. Доказатель-
Доказательство в общем случае требует более громоздких выкладок.
Мы можем следующим образом обобщить этот результат: пусть дан
кватернион q, выраженный через его длину Q и «оператор направления»
e(+j0+fcY); МЫ можем формально образовать «квадратные корни» из кого
С = YQ e(e/2)(ie+its+fe-r) и ;* =
Тогда вектор / = ix-\- jy + kz преобразуется в вектор /', направление кото
рого получается из направления вектора / поворотом на угол G вокру!
оси с направляющими косинусами а, ,3> у ч длина которого равна длине
вектора /, т. е. ~\[х2Л~У2 ~ z2, умноженной на Q; это преобразование
осуществляется при помощи операции
= <,/„¦.
Последующая такая же операция еще одного вращения и изменения
длины, представляемая кватернионами -ц и тг]*, дает
Геометрический факт, что два последовательных вращения дают различ-
различные результаты в зависимости от порядка, в котором они выполняются,
находит свое выражение в том, что произведение кватернионов yj и Z
(так же, конечно, как и т,* и С*) некоммутативно. Число Q называется
тензором (tensor па латинском языке—«растягивающий»), а показатель-
показательный множитель — серзором (versor — «поворачивающий») оператора Z.
Гл. 1. Типы полей
Самый общий поворот четырехмерного вектора, представляемого ква-
кватернионом q = w-\-ix-\-]'y-\-kz, дается формулой
q' =
где а2 + р2 + у2 = 1 и X2-f fi2 + v2= 1. Когда и 6 и <р —мнимые углы, то это
преобразование соответствует преобразованию Лоренца, рассмотренному
к следующем параграфе.
В дальнейших частях этой тлавы и"в § 2.6 нам придется рассматри-
рассматривать обобщения верзора ?} = е1^, где 21 —общий аффинорный оператор.
Эта функция всегда связана с вращением вектора Г, на который дейст-
действует оператор 91, и во многих случаях преобразование вращения пред-
представляется формулой
как и в случае кватернионов.
Абстрактные векторные пространства. Трехмерные понятия векторов
и аффинорных операторов, рассмотренные нами выше, могут быть обоб-
обобщены на абстрактные пространства с любым числом измерений, часто
даже со счетным множеством измерений. Это обобщение стало одним из
наиболее мощных математических орудий, в особенности потому, что оно
позволяет синтезировать и яснее понимать очень многие результаты из
самых различных областей. Мы кратко рассмотрим здесь это обобщение,
иллюстрируя его физическими примерами.
Один из простейших примеров использования абстрактного вектор-
векторного пространства встречается при применении нормальных координат
для описания движения связанных осцилляторов. Число нормальных
х-соординат, т. е. число измерений соответствующего пространства, равно
числу степеней свободы осциллятора. Конфигурация, или состояние,
системы описывается вектором в этом пространстве. Главные оси про-
пространства соответствуют особым «элементарным» состояниям движения,
причем самое общее движение оказывается линейной суперпозицией этих
«элементарных» состояний.
Эти движения можно уяснить себе рассмотрением системы на
рис. 1.25. «Элементарных» движений — два: A) массы колеблются в одном
и том же направлении, т. е. двигаются вместе; B) массы колеблются
в противоположных направлениях, т. е. сначала движутся друг к другу,
натем друг от друга и т. д. Эти движения называются элементарными,
так как существует определенная простая частота для каждого из типов
движений. Самое общее движение системы является линейной суперпо-
суперпозицией этих «элементарных» движений и в результате не имеет опреде-
определенной частоты.
Построим теперь двумерное пространство, нужное нам для описания
этой системы. Мы можем, например, откладывать смещение хг одной из
масс по какой-либо оси, а смещение х2 другой массы по перпендику-
перпендикулярной оси. Пусть ег и е2 — единичные векторы в направлении этих
осей; тогда общий вектор в этом пространстве г= х1е1 + х2е2.
Уравнения движения имеют вид
или в векторной форме
d2t
1.6. Аффиноры и другие векторные операторы
81
где 21 —аффинор е1^41
-1 == "-1
2 + e2.A21e1-|-e2.A22e2, и
= — = -™21> -2 = Ч" -
«Элементарные» движения R имеют определенную угловую частоту со,
и поэтому они должны удовлетворять уравнению -^- = — u>2R;
Рис. 1.25. Связанные осцилляторы.
следовательно, уравнение движения для R примет вид
i-ii — гаш! А9,
— тш2
= 0.
Используя полученные выше результаты, мы найдем, что существуют
два элементарных решения Rx и U2> ортогональных друг к другу.
Их направления можно, очевидно, использовать для новых осей коорди-
координат, так что любой вектор в этом двумерном пространстве (т. е. любое
движение) может быть представлен в виде линейной суперпозиции двух
элементарных движений. Квадрат косинуса угла между вектором F и осью
Rj дает долю элементарного движения Rx в движении, представляемом
вектором F, и аналогичное значение имеет квадрат косинуса угла между
Г и R2; сумма этих долей равна, как и должно быть, единице (как
сумма квадратов направляющих косинусов). Другими словами, квадрат
косинуса дает долю общей энергии системы, приходящуюся на движение
типа R1#
Возвращаясь к уравнениям движения, мы теперь видим, что движе-
движение системы можно рассматривать как серию последовательных инфини-
тезимальных поворотов, производимых оператором 91, причем масштаб
времени определяется уравнением. Элементарные решения Rt обладают
тем важным свойством, что они не поворачиваются со временем, так как
оператор 51, действуя на Rt, восстанавливает его направление без измене-
изменений. Таким образом, R4 являются стационарными состояниями движе-
движения.
Эти рассуждения можно, конечно, распространить на случай N масс,
последовательно соединенных пружинами. Такая система может служить
одномерной моделью кристалла. Для этой системы потребуется про-
пространство N измерений. Мы будем иметь N элементарных состояний
движения, которые определяют систему фиксированных взаимно-орто-
взаимно-ортогональных направлений в абстрактном векторном пространстве.
Собственные векторы и собственные значения. Геометрический
характер этих абстрактных пространств полностью определяется опера-
оператором 91. Главные оси оператора идут по направлениям векторов еп
(мы будем через еп обозначать единичные векторы в абстрактном про-
пространстве в отличие от обозначения а„ единичного вектора в обычном
6 Ф. М. Морс и Г. Фешбах
82 Гл. 1. Типы полей
трехмерном пространстве), которые определяются уравнением
К-еп = Апеп, A.6.31)
где Ап— числа, называемые собственными значениями 91. Векторы епГ
называемые собственными векторами 91, взаимно-ортогональны и служат
для определения осей координат в пространстве. Любой вектор в этом
пространстве является тогда линейной комбинацией собственных векторов.
Это наводит на естественную мысль о целесообразности классификации
различных типов операторов, встречающихся в физике, и рассмотрения
соответствующих абстрактных векторных пространств. Мы более или
менее полно охватим все случаи, если ограничимся операторами, встре-
встречающимися в квантовой механике.
Операторы в квантовой механике. Абстрактная формулировка
квантовой механики, данная Дираком и фон Нейманом, опирается
в значительной степени на понятия, возникающие при рассмотрении свя-
связанных осцилляторов, проведенном выше. Состояние системы описывается
вектором абстрактного пространства, обычно бесконечномерного. Опреде-
Определение термина «состояние», употребляемого здесь, несколько затрудни-
затруднительно; он указывает на некоторую связь между типом системы, которую
мы рассматриваем (числом частиц, видами сил и т. п.), начальными
условиями для положения или скорости и т. д. и методами, применяе-
применяемыми для наблюдения системы; все это станет в дальнейшем ясным.
Один из основных постулатов квантовой теории состоит в том, что
наблюдение системы нарушает, т. е. изменяет, ее состояние. В абстракт-
абстрактном векторном пространстве это означает, что вектор, представляющий
состояние системы, испытывает в результате наблюдения, например
положения частицы или ее энергии, некоторый поворот. Так как поворот
может быть совершен при помощи аффинорного оператора в абстрактном
пространстве, мы приходим к заключению, что наблюдение должно быть
представлено оператором. Таким образом, механические величины, как,
например, энергия, положение, импульс и др., должны быть представлены
операторами. (Следовало бы говорить, что наблюдение этих величин
должно быть представлено операторами, но удобнее говорить более
кратко, как мы это сделали в предыдущей фразе.)
Как можно точно определить эти механические величины, имея
в виду, что измерение энергии и т. п. изменяет состояние системы?
Наши предыдущие рассуждения приводят к мысли, что это окажется
возможным только для некоторых специальных состояний, именно для
состояний, описываемых собственными векторами (главными осями в
случае обычного пространства) соответствующих операторов. Например,
собственные векторы оператора энергии E удовлетворяют уравнению
Это уравнение утверждает, что для собственных векторов еп (т. е. для
некоторых особых состояний, представляемых направлениями еп в век-
векторном пространстве) измерение энергий не изменяет состояния системы.
Только в этом случае можно быть уверенным в том, что наблюдение
дает точное значение энергии.
Каков же смысл постоянной Еп в этом уравнении? Обычно прини-
принимается, что можно нормировать оператор @ так, чтобы Еп были в точ-
точности равны энергиям состояний, представляемых векторами еп. Это,
конечно, автоматически имеет место в обычных трехмерных случаях,
рассмотренных выше. Например, собственные значения аффинора момента
2.6. Аффиноры и другие векторные операторы 83
инерции как раз равны трем главным моментам инерции, а собственные
значения аффинора напряжений суть главные напряжения.
Непосредственно очевидно, что такие две величины, как энергия
и импульс, будут одновременно измеримы (или наблюдаемы, как говорит
Дирак), если собственные векторы оператора энергии совпадают с собствен-
собственными векторами оператора импульса. Необходимое и достаточное условие
для одновременной измеримости двух величин состоит в том, чтобы
соответствующие им операторы коммутировали. Необходимость следует
из того факта, что если вектор еп является собственным вектором и для
© и для р, то (&-р-еп = p-(S-en. Так как по предположению любой вектор
является линейной комбинацией (суперпозицией) векторов еп, то msj
найдем, что E-р-е -= р.-б-е для любого вектора состояния е.
Доказательство достаточности в утверждении, приведенном курсивом,
несколько более трудно. Рассмотрим собственный вектор еп оператора (?,
Предположим коммутативность 6'(t)-eJ = ?n(p-en). Отсюда следует, что
р-еп является собственным вектором оператора 6 с собственным значе-
значением Еп. Если существует только один собственный вектор с собствен-
собственным значением Еп, то мы сразу заключаем, что р ¦ еп должно быть пропорцио-
пропорционально еп, что и доказывает требуемое утверждение. Если же существуют
несколько собственных векторов епт с собственным значением Еп (это
так называемый случай вырождения), то мы можем только заключить,
что р ¦ eni = 2 />mienm- В этом подпространстве, в котором все собственные
>mienm-
m
векторы имеют собственное значение Еп, мы можем теперь найти глав-
главные оси, т. е. собственные векторы оператора р и, таким образом, найти
состояния, в которых и р и 6 одновременно измеримы.
Очевидным, но важным следствием является то, что если два опе-
оператора не коммутируют, то соответствующие величины не могут быть
одновременно измердмыми.
Важным примером операторов, не все из которых коммутируют,
являются операторы, представляющие положение (х, ty, j) и соответствую-
соответствующие составляющие импульса (рх, ру, рг); для них
Щ = Щ и т. д., рж? - урх = h/i, 6
= *У* и т- Д-. ftA = !Jfcc и т. д.1)
где % — постоянная Планка h, деленная на 2х. Эти соотношения являются
основными уравнениями квантовой теории. (См. далее гл. 2.)
Направляющие косинусы и вероятности. Что можно сказать
о состоянии е, если этот вектор является не собственным вектором опе-
оператора энергии (S, а линейной комбинацией собственных векторов еп?
Используя аналогию с абстрактным пространством связанных осцилля-
осцилляторов, будем рассматривать квадрат косинуса угла между вектором состоя-
состояния е и собственным вектором еп как долю е, находящуюся в «состоянии
еп». Чтобы это выразить более физическим языком, можно сказать, что
если измеряется энергия ряда идентичных систем, находящихся в состоя-
состоянии е, то доля числа измерений, дающих энергию Еп, будет равна
квадрату косинуса угла между е и еп в абстрактном векторном простран-
пространстве системы. Для многих операторов в квантовой механике этот коси-
косинус является комплексным числом (что свидетельствует о возможности
интерференции между собственными векторами с произвольными фазами).
В таком случае употребляется квадрат модуля косинуса. Изменения, кото-
х) Здесь и далее при записи произведения операторов, а также оператора и век-
вектора иногда пропускается точка. — Прим. ред.
6*
84 Гл. 1. Типы полей
рые надо внести в математический аппарат абстрактного векторного прост-
пространства в связи с введением комплексных косинусов, будут рассмотрены
ниже.
Вероятности и неопределенности. Применительно к одному измере-
измерению мы можем истолковать квадрат модуля косинуса как вероятность
того, что состояние е будет иметь энергию Еп. Среднее значение энергии
для состояния е будет тогда равно 2^п(еп"еJ или -ЕСр = (е@е). Эта
п
формула правильна только для случая вещественных косинусов; соответ-
соответствующее обобщение на комплексные косинусы будет дано ниже.
Это позволяет нам рассмотреть результаты измерений двух величин,
которые не являются одновременно измеримыми. Допустим, например,
что е (х) — вектор состояния, для которого координата х известна точно.
Какова тогда вероятность того, что эта система будет иметь импульс рх,
если собственный вектор этого импульса равен f(px)? Наш формализм
дает на это следующий ответ: | е (ж) • f (рх) |2. Среднее значение импульса
равно ере. Можно также выразить среднеквадратическое уклонение изме-
измерения рх от его среднего
Только когда е является собственным вектором для рх, величина рх
для состояния е будет точно известна, и тогда мы будем иметь д/>ж = 0.
Величина &рх называется неопределенностью в измерении рх.
Комплексное векторное пространство. Мы должны теперь обобщить
понятия векторного пространства так, чтобы иметь возможность рассмат-
рассматривать комплексные косинусы. В этом случае длина вектора не может
уже определяться суммой квадратов его составляющих по осям координат,
так как эти квадраты могут оказаться неположительными, что противоречит
нашим обычным представлениям о длине. Ясно, что единственным путем
для получения положительных количеств в определении длины является
образование суммы квадратов модулей составляющих. Простой способ
достигнуть этого в рамках нашего формализма состоит в введении второго
пространства того же числа измерений, «комплексно-сопряженного» первому.
Пусть единичные векторы первого пространства суть ех, е2, ..., тогда
соответствующие единичные векторы в комплексно-сопряженном прост-
пространстве обозначим через е*, ё*, . Каждому вектору е=2М с состав-
i
ляющими Аг в первом пространстве сопоставляется в комплексно-сопря-
комплексно-сопряженном пространстве вектор е* = 2 е?А с составляющими Аг (Аг и Аг —
г
комплексно-сопряженные числа). Скалярное произведение (операцию,
существенную для определения длины) мы теперь определим следующим
образом:
е» е -8 -/ °' 1Ф}''
I i| l = ]•
Скалярное произведение еь и е,- не будет определено, да оно и не нужно.
Теперь ясно, что длина вектора е должна быть в данном случае связана с
величиной заведомо неотрицательной. «Длина» е, обозначаемая
определяется как ]/е* • е.
1.6. Аффиноры и другие векторные операторы 85
Из этих определений вытекает ряд важных следствий. Из них, напри-
например, следует, что еслие*-е = О, то| е|=0. Легко проверить, что если е и f—два
произвольных вектора, то
e*f = P^T
Векторы в обычном пространстве обладают тем свойством, что их
скалярное произведение не больше произведения их длин
АВ> А В.
Это так называемое неравенство Шварца1); в обобщенной форме оно
должно также иметь место в абстрактном векторном пространстве, так
как оно вытекает из того факта, что квадрат «длины» вектора не может
быть меньше нуля, т. е. положителен. Например, если е и f — два вектора
а а и Ъ — два комплексных числа, то
(ае*-М*)-(ае-М)>0.
Если положить а = j/(f*-f)(e*-f) и Ъ— j/(e*e) (f*e), то это неравенство
переходит в
V(e* • е) (f * • i) > Y(f* ¦ е) (е* • f) или |e|-|f| >|f*-e|, A.6.33)
что и представляет собой обобщенную форму неравенства Шварца. Это
неравенство будет ниже использовано при выводе соотношения неопре-
неопределенности Гейзенберга.
Другим неравенством, также имеющим свой аналог в обычном век-
векторном пространстве, является неравенство Бесселя, которое по существу
утверждает, что сумма длин двух сторон треугольника никогда не меньше
длины третьей стороны
A.6.34)
Обобщенные аффиноры. Перейдем теперь к рассмотрению операторов
в комплексных векторных пространствах. Рассмотрим сначала линейное
преобразование, поворачивающее оси пространства в другую систему
ортогональных осей
2
где е[ — единичный вектор в направлении i-й оси новой системы коор-
координат, а еп — единичные векторы в исходной системе. Соотношение
между ег- и (е4;)* должно быть таким же, как и между любыми двумя
сопряженными векторами, так что
Мы можем теперь составить аффинорный оператор, который, дейст-
действуя на вектор eit переводит его в новый вектор е[. Этот аффинор
имеет вид
& = J\en'(nie*i, A.6.35)
так что
(Мр • — ^ ^ v - — f* '¦
n
x) В нашей литературе оно обычно более правильно называется неравенством
Коши—Буняковского. —Прим- ред.
86 Гл. 1. Типы полей
Структура аффинора показывает, что мы должны векторы без звездочки
помещать всегда при умножении справа от оператора, а векторы с звез-
звездочкой — слева. Полезное свойство аффинорного оператора выражается
формулой
(e*®)f=e*(@f),
так что скобки вообще не нужны, и мы будем, как правило, писать
просто e*-@-f.
Наше обобщение таково, что произведение операторов, как и про-
произведение обычных аффиноров, есть вновь оператор
® • ? = (? enYTlieT) • B Л) ?
n,i i,h n,h j
так что (п, к)-п составляющая оператора ©•? равна
Возвращаясь теперь к оператору вращения ©, определенному форму-
формулой A.6.35), мы замечаем, что ef ¦& не дает (ej)*. Оператор, вращающий
е*, обозначим через ©* и определим его так, чтобы
Таким образом, оператор ©* связан с оператором © соотношением
Оператор &*, связанный с оператором & таким соотношением, назы-
называется эрмитово-сопряженным к О. Записывая это соотношение при
помощи составляющих, мы находим
так что
Y™ = (Y')in. A-6-36)
Это равенство означает, что (г, тг)-я составляющая эрмитово-сопряжен-
ного аффинора @* получается образованием комплексно-сопряженного
числа к (п, ^-составляющей @. Понятие эрмитовой сопряженности есть
обобщение понятия сопряженного аффинора, данного на стр. 61. Эрми-
Эрмитово-сопряженный оператор к произведению двух операторов @-? есть
(©-?)* = ?*•©*. Эрмитово-сопряженный оператор к произведению комплек-
комплексного числа на оператор есть произведение комплексно-сопряженного
числа на эрмитово-сопряженный оператор.
Эрмитовы операторы. Самосопряженный оператор (совпадающий
ео своим эрмитово-сопряженным), т. е. такой, что
@ = <Г, или Y«m = Ymn.
называется эрмитовым оператором. Все классические симметрические
аффинорные операторы являются эрмитовыми, так как их составляю-
составляющие вещественны. Операторы в квантовой механике, соответствующие
измеримым величинам, также должны быть эрмитовы, так как их
собственные значения должны быть вещественны (ведь в конечном
счете результаты фактических измерений суть вещественные числа). Чтобы
это доказать, заметим, что если собственные значения ап оператора 51 веще-
вещественны, тое*-ЭД-е вещественно для любого е, так как е можно разложить
по собственным векторам еп, что даст для е*-ЭД-е ряд с вещественными
1.6. Аффиноры it другие векторные операторы 87
членами. Пусть e = f+feg; тогда fe(g*-^-f) + fe (f*-9I-g) вещественно.
Но это возможно только в том случае, когда g*-5I-f комплексно сопря-
сопряжено с f*-2(-g, т. е. равно g*-$*-f. Следовательно, g*-($ — ?(*)-f = 0
для любых f и g, а поэтому Ж = S&*.
Оператор поворота &, определенный формулой A.6.35), принадлежит
к еще более узкому классу. Составляющие утп являются направляю-
направляющими косинусами, так что следует ожидать, что оператор имеет в ка-
каком-то смысле «единичную длину». Так как поворот осей координат
в векторном пространстве не изменяет величины скалярного произве-
произведения, то для произвольных векторов состояния е и f должно быть
Поэтому @*.© = g, где % — идемфактор 2 епе*. Это показывает, что
п
эрмитово-сопряженный оператор к © совпадает с его обратным оператором:
Такой оператор с «единичной длиной» называетря унитарным операто-
оператором. Оператор поворота, определенный формулой A.6.35), является
унитарным оператором [см. также формулы A.6.12)].
Большинство операторов в квантовой механике эрмитовы; их соб-
собственные значения вещественны, но эффект их приложения к векторам
состояний состоит и в повороте и в изменении длины. Кроме того,
встречаются и несколько полезных унитарных операторов; их собствен-
собственные значения не все вещественны, но эффект их приложения к векто-
векторам состояний состоит только во вращении без изменения длины.
Примеры унитарных операторов. Важные примеры унитарных опе-
операторов встречаются в теории распространения волн, квантовой меха-
механике и кинетической теории газов. Например, описание того, как
в месте сопряжения двух волноводов (скажем, разного поперечного сече-
сечения) отражаются волны, распространяющиеся вдоль них, может быть
дано с помощью аффинора отражения. Этот оператор переводит в соот-
соответствующем абстрактном пространстве собственный вектор падающей
волны в собственный вектор отраженной волны. Условие унитарности
является по существу требованием консервативности процесса. Равен-
Равенство &* = (З'1 сводится к теореме взаимности, т. е. взаимозаменяемости
источника и приемника. Мы подробнее остановимся на этом в даль-
дальнейших главах.
Унитарный оператор может быть построен из эрмитова оператора ?
следующим образом:
Оператор, эрмитово-сопряженный к ©, равен A —i?)/(l +i?), так что
<$-(У* = 3; и & унитарно. Если © — аффинор отражения, то формула
для (*5 дает соотношение, существующее между коэффициентами отраже-
отражения, составляющими ©, и коэффициентами импеданса, составляющими
аффинор импеданса 2.
Другим способом получения из эрмитова оператора $ унитарного
оператора & является следующий:
®=е**, A.6.37)
*) десь и в некоторых местах далее 1 означает идемфактор g.—Прим. ред.
88 Гл. 1. Типы полей
где е'? определено степенным рядом 1 -f Ш f 4(г'йJ + • • • • Для © =
= A+ Ш)/A — Ш) мы имеем, например, © = е1'®, где й —2arctg?.
В терминах приведенного выше физического примера это последнее
преобразование соответствует использованию для описания отраженной
волны сдвига фаз при отражении вместо самого коэффициента отра-
отражения.
Часто вектор является функцией параметра (в качестве типичного
параметра мы возьмем время t), причем вектор вращается при измене-
изменении параметра. Унитарный оператор, соответствующий этому враще-
вращению, оказывается полезным во многих задачах. Нетрудно вывести его
общий вид. Назовем его % (t). Тогда по нашему определению
® («О »(«о) = е («! + *„),
где tt и t0 — частные значения параметра t. Более того,
® (*s) Ф (*i) е (*0) = е (*х + t0 + *2) = ф («х +12) е (t0),
так что
Ф(««)Ф(«1) = Ф & + «,)¦
Чтобы это равенство имело место для всех t2 и tlt Ф должно быть
показательной функцией t. Так как этот оператор до.лжен быть унитарным,
то он должен иметь вид
ф = в**1,
где Jg —некоторый неизвестный эрмитов оператор.
Чтобы найти уравнение вращательного движения вектора е, мы
приложим ф к еB), изменяя t на инфинитезимальное dt. Тогда ф =
— l-{-ifQdt, так что
или %e(t) = -j?? . A.6.38)
Оператор ^ находится, конечно, из физических соображений. В кван-
квантовой механике, например, если t — время, то ^ пропорционален функ-
функции Гамильтона, в которой классические переменные — импульсы
и координаты положения заменены соответствующими операторами.
Преобразование операторов. В предыдущем рассмотрении мы имели
дело с вращением вектора при изменении параметра, от которого он
зависит. Этот эффект изменения параметра может быть получен также
вращением «пространства» при фиксированном векторе, т. е. приданием
параметрической зависимости всем встречающимся операторам. Другими
словами, мы изменяем значение операторов при изменении параметра,
оставляя векторы неподвижными. Посмотрим, как это должно быть
сделано, чтобы получить картину, эквивалентную той, которую мы
имели при вращающихся векторах и фиксированных операторах. Пусть
вращение векторов задается унитарным оператором
®е=е', ©f = f и т. д.
Соответствующее эквивалентное изменение ? на ?' можно найти, исходя
из требования, чтобы соотношение между ?-е' и Г (первая картина:
е и f изменяются, S не изменяется) было бы такое же, как между ?'-е
и f (вторая картина: е и f не изменяются, ? преобразовывается в ?')-
В алгебраической записи
f'*.?-e'=f'-S'.e. •
1.6. Аффиноры и другие векторные операторы
Подставляя сюда соотношение между F и f и вспоминая, что ©* = © *-,
мы найдем, что
f'*.?-e' = f*-(@-1?@)-e, или ?' = ©~1?@. A.6.39)
Исследуем теперь эффект этого унитарного (или, как его иногда
вазывают, канонического) преобразования с точки зрения свойств ?.
Сначала покажем, например, что собственные значения ? и ?' совпа-
совпадают. Пусть
?'e = L'e.
Отсюда
Умножая обе части на @, получим
= L'(@e).
Это означает, что если е — собственный вектор оператора ?' с собствен-
собственным значением L', то ©-е — собственный вектор оператора ? с тем же
собственным значением. Это сохранение собственного значения оказы-
оказывается иногда очень полезным свойством, так как если ? —сложный
оператор, то можно попытаться подобрать такое преобразование @,
которое дает более простой оператор ?' с собственными значениями,
совпадающими с собственными значениями оператора ?.
Вследствие соотношения между оператором и его эрмитово-сопря-
женным оператором мы можем записать
= ©*?* ((Г1)* =
Следовательно, эрмитов оператор остается эрмитовым и после унитар-
унитарного преобразования.
Унитарное преобразование не изменяет соотношений между опера-
операторами. Например, если
то
©-1?@©-1Ж© = ©-19<1©, или ?'SR' = 3t\
Два унитарных преобразования, примененные одно за другим,
соответствуют преобразованию, которое также является унитарным.
Если $ и © — унитарные операторы, то
что и доказывает наше утверждение.
Мы можем, наконец, рассмотреть, что произойдет с оператором 2
после преобразования унитарным оператором ®B) = el&'. Это позволит
нам вычислить изменение оператора, соответствующее изменению пара-
параметра t. Преобразованный оператор
Удобно, очевидно, ввести вместо ?' обозначение ?@, полагая ? = ?@),
так что
?(«) = е-'Ф-?@)-ег**.
Скорость изменения ? относительно t может быть получена из при-
приращения
?(*+*)-?(<) = «Г"*8 Л* Л
90 Гл. 1. Типы полей
так что
|-§ = ?•?-?•? [? = ?(*)]• A-6-40)
Оператор $ зависит, конечно, от конкретной физической задачи.
Например, во многих вопросах квантовой механики |) является опера-
оператором Гамильтона, a t — время; получающееся уравнение называется
уравнением движения Гейзенберга. Уравнение A.6.40) имеет широкие
приложения; для оператора ^, связанного с параметром вращения t век-
векторов состояния соотношением A.6.38), производная любого другого
оператора ?, связанного с той же системой, пропорциональна коммута-
коммутатору ?•?-?•?•
Операторы квантовой механики. Применим теперь некоторые из этих
результатов к операторам, встречающимся в квантовой механике. Вспом-
Вспомним, что среднее результатов измерений некоторой величины (энергии,
импульса и т. д.), представленной оператором р, в системе, находящейся
в состоянии, изображаемом вектором е, равно /?ср. = (е*-р-е). Отметим
также, что система, находящаяся в состоянии, представляемом векто-
вектором е (коротко, в состоянии е), с вероятностью, равной квадрату модуля
косинуса угла |(е*-е')|2, оказывается также в состоянии е'.
В силу последнего пункта это утверждение можно сформулировать
и в терминах унитарных операторов. Допустим, что мы найдем унитар-
унитарный оператор д, переводящий собственный вектор е(ап) оператора ЭД
с собственным значением ап в собственный вектор е' (Ьт) оператора 93
с собственным значением Ът
В (a, 6)e(an) = e'FJ.
Применяя теперь формулу A.6.35), мы видим, что вероятность того, что
измерение 93 даст значение Ът, если ЭД имеет значение ап, равна
I е* (а„) • е' (Ьт) |« = | е* (an) g (а, Ъ) е (ап) |» = | Yrm (а, Ъ) |«. A.6.41)
Здесь можно использовать неравенство Шварца A.6.33) для уста-
установления связи между квантовыми уравнениями A.6.32) и соотношением
неопределенности Гейзенберга. Мы уже показали, что если два оператора
не перестановочны, то они не могут быть одновременно измеримыми;
если один из них измерен точно, то другой не может быть точно изве-
известен. С физической точки зрения что-то, присущее измерению одного,
уничтожает наше одновременное точное знание другого. С математи-
математической точки зрения существует взаимность между их неопределенно-
неопределенностями. Как уже указывалось, неопределенность Д^4 в измерении опера-
оператора 31 определена формулой
1(для состояния е).
Чтобы применить эти общие формулы к квантовым соотношениям
A.6.32), определим операторы
= 3: — х,
так что "|/е*-(Д^J-е есть неопределенность в измерении х в состоянии е.
По формулам A.6.32) мы можем теперь показать, что
2.6. Аффиноры и другие векторные операторы 91
¦Взяв среднее значение этого выражения для состояния е, получим
Левая часть этого равенства равна удвоенной мнимой части
так что мы можем заключить, что
Но по неравенству Шварца A.6.33) произведение длин векторов никогда
не меньше модуля их скалярного произведения. Таким образом,
мы окончательно находим, что
(Арх)(Ах)>%/2.
Это неравенство и является знаменитым соотношением неопределенности
Гейзенберга. Оно показывает, что одновременное точное измерение какой-
либо координаты и соответствующей составляющей импульса невозможно
и что если предпринимаются одновременные измерения, то произведение
соответствующих неопределенностей не может быть меньше %/2.
Спиновые операторы. В предыдущем разделе были высказаны
утверждения, имеющие весьма общий характер, и теперь для уяснения
некоторых понятий необходимо обратиться к примеру. Для последующего
изложения полезен пример спина электрона. Эксперимент показывает,
что для составляющей магнитного момента электрона по каждому задан-
заданному направлению существуют только два допустимых значения. Поэтому
следует ожидать, что подобным же образом будет ограничено и число
допустимых значений для собственного момента количества движения
электрона. Момент количества движения частицы относительно начала
координат выражается через ее положение относительно начала коорди-
координат и ее импульс р следующим образом:
Прежде всего мы, используя квантовые уравнения A.6.32), вычислим
коммутатор для компонент 9JJ
шхшу - ак„зкх=(и - ьрг) ш>у - WJ = 1*тг, 6
Эти уравнения показывают, что точно знать все три компоненты спина
электрона мы не можем; в самом деле, если мы точно знаем значение
5Щ2, то мы не можем знать значений Шх и Шу.
Используя эти уравнения попарно, мы можем показать, что
Шг (s»x ± шу) - (шх ± mv) mz = ± л (а»х ± ®у)
или
+ Шу) == (SRX + №у) № + *)
A.6.43
- Шу) = (Шх -
Пусть известно, что значением Жг является т%; этому соответствует
вектор состояния ат (т. е. ат служит собственным вектором 9JJ, соот-
соответствующим собственному значению mh). Отправляясь от этого вектора
состояния ат, мы видим, что вектор (fflx-\-ii&iy) am является собствен-
собственным вектором для 9Лг, соответствующим собственному значению (т + 1)Л,
если только (Шх + ^у)^п отличен от пуля, и что (Шх— Шу)&т является
92 Гл. 1. Типы полей
собственным вектором для 5Ш2, соответствующим собственному значению
(т — 1)%, если только (fflx — i$Ry) am отличен от нуля, так как из урав-
уравнений A.6.43) имеем
5Щ2 (Шх + Шу) ат - №х + №у) 1№г + Л) ат] =
= (m+l)h[№x + imy)am] и т. д.
В частном случае спина электрона мы для обозначения момента
количества движения будем пользоваться буквой ©, вместо буквы Ш.
Для того чтобы т имело только два допустимых значения, отлича-
отличающихся друг от друга на единицу (как того требуют записанные выше
уравнения), и для того, чтобы эти значения были симметричными отно-
относительно направления оси z, допустимыми значениями ©2 должны
служить +%/2 (с собственным вектором а+) и — h/2 (с собственным век-
вектором а_) и должны удовлетворяться соотношения
(@3C + i©v)a, = 0 и (@х-1@и)а_ = 0.
Следовательно, спиновые операторы действуют на эти два собственные
вектора, а также умножаются друг на друга по следующим правилам:
@xa, = (ft/2)a_, @иа, = (Л/2)а_, <32а, = (Л/2) а+,
@ха_ = (Л/2) а,, ©уа_ = - (ift/2) а,, @2а_ = - (ft/2) a., .,„...
©х@у = (ад<з2= -©у@ж, @v@3-=(ft/2)@x= -©,©„, A-b-44)
@2©х = (ift/2) ©„ -= - @ж@г, (®J2 = (@/ = (@гJ = (V2J.
Здесь мы имеем довольно простое обобщение понятия оператора.
«Спиновое пространство» является двумерным пространством, одно
из направлений которого соответствует тому состоянию, при котором
z-составляющая спина наверняка равна %/2, а перпендикулярное направ-
направление соответствует тому состоянию, при котором @2 наверняка рав-
равняется — ft/2. (Теперь делается очевидным, что это пространство состоя-
состояний является удобной математической фикцией и не имеет ничего общего
с «реальным» пространством.) Единичный вектор состояния, имеющий
промежуточное направление, соответствует такому состоянию, при кото-
котором ©z иногда бывает положительной величиной и иногда отрицатель-
отрицательной, а относительная частота двух этих исходов зависит от квадрата
косинуса угла между этим единичным вектором и двумя осями коорди-
координат для ©2.
Оператор 22>х/% отражает каждый вектор состояния относительно
прямой, образующей с осями угол в 45°, т. е. меняет ролями положи-
положительные и отрицательные составляющие. Поэтому собственными векто-
векторами для <ВХ должны быть векторы (l/j-^2) (a+ + а,), соответствующие пово-
повороту осей координат в спиновом пространстве на 45° при повороте направ-
направления квантования в действительном пространстве на 90° (соответствующие,
например, изменению направления магнитного поля, при котором спин
электрона, ориентированный по оси z, станет ориентированным по оси х).
Поэтому, если мы знаем, что @2 равно ft/2, то значения ft/2 и — ft/2
для <ВХ являются равновозможными.
Далее, два собственных вектора для <&у суть —j=r (a+ + га_) и соот-
соответствуют мнимому повороту в спиновом пространстве (напомним, что
квадрат длины комплексного вектора такого вида равен скалярному
произведению комплексно-сопряженного вектора на данный).
Кватернионы. С абстрактной точки зрения операторы
1.6. Аффиноры и другие векторные операторы 93
совместно с .единичным оператором Qa = а и нулевым оператором оказы-
оказываются близкими по формальным свойствам к аффинорным операторам.
Они действуют на вектор (в данном случае на вектор в двумерном спино-
спиновом пространстве) и в результате получается новый вектор. Эти опера-
операторы можно складывать и перемножать, причем получаются операторы
того же класса. Таблица умножения для этих новых операторов имеет
вид
i« = f = P=_l; ij=f=_ji; jf = i=_fj; fl = j = - if. A.6.45)
Довольно любопытно, что операторы с точно такими же свойствами
изучил Гамильтон, пытаясь обобщить понятие комплексного числа,
задолго до того, как стала развиваться квантовая механика. Как гово-
говорилось на стр. 78, величину ? = "(/ —1 можно сопоставить операции пово-
поворота на 90° в комплексной плоскости. Для этого простого оператора
таблица умножения ограничивается равенством i2 = —1, где 1 есть еди-
единичный оператор. Каждой точке (х, у) на комплексной плоскости соот-
соответствует комплексное число z = x-\-iy, причем квадрат расстояния
до начала координат равен \z \2 = zz = (x-{-iy) (х — iy) = х2-{-у2. Для того
чтобы получить дальнейшее формальное обобщение, следует использовать
три. величины i, j и I, определенные в уравнении A.6.45), для образова-
образования кватерниона (см. стр. 78)
с\ + dt.
Квадрат длины здесь получается умножением р на его сопряженное
Поэтому единственным кватернионом с нулевой длиной является тот,
у которого а, Ъ, с и d одновременно равны нулю. Добавим, что кватер-
кватернион, обратный данному, легко находится
Кватернион можно соотнести повороту вокруг некоторой оси в трехмер-
трехмерном пространстве; направляющие косинусы этой оси должны быть про-
пропорциональны постоянным Ъ, с и d, а угол поворота определяется при
помощи отношения а2 к № + с2 + d2. Поскольку эти величины представ-
представляют теперь главным образом исторический интерес, то к сказанному
о них на стр. 78 и последующих нужно добавить очень немногое. Однако
спиновые операторы тесно связаны с этими величинами.
Операторы вращения. Унитарные операторы того типа, который
определяется уравнением A.6.37), весьма тесно связаны с общими опера-
операторами момента количества движения (а именно, пропорциональны им).
Изучение этих операторов даст нам возможность найти новые примене-
применения методов, развитых в разделе, посвященном абстрактным простран-
пространствам, и в тоже время поможет дальнейшему уяснению свойств момен-
моментов количества движения в квантовой механике.
Предположим, что вектор е из абстрактного пространства зависит
от ориентации вектора г в обычном пространстве, как от параметра.
Если мы теперь повернем г вокруг оси х на угол 6Ж> то е должен будет
совершить поворот в абстрактном пространстве. Оператор, который
нужно применить к е, для того чтобы получить этот новый вектор,
задается уравнением A.6.37). В данном случае мы пишем
94 Гл. 1. Типы полей
причем здесь 5ШХ является оператором. Аналогично можно определить
операторы %у и ©, через величины 6^ и 6Z. В большинстве случаев имеем
®зс®и ^ ®и®ж> так как вращение вектора г вокруг оси х не коммути-
коммутирует с вращением этого вектора вокруг оси у.
Тем не менее легко видеть, что для бесконечно малого вращения
на величины (db)x, (dB)y, (db)z эти повороты коммутируют и соответ-
соответствующий оператор в абстрактном пространстве имеет вид 1 + (i/%) x
x($flxdbx-{-'>fflydby-\-'3RzdBz). Так как действие этого инфинитезимального
оператора на вектор е не может зависеть от ориентации осей х, у, z,
то, следовательно, fflxdbx + Щуdby + SRZdbz должен быть инвариантным
относительно вращения. Так как (dbx, dBy, dbz) являются тремя соста-
составляющими пространственного вектора, то, следовательно, (Шх, Шу, 3J?Z}
также должны являться тремя составляющими некоторого вектора Ю1
и должны преобразовываться, например, так, как преобразуются x,.y,z
в уравнении A.3.8), ибо тогда этот оператор будет простым ска-
скалярным произведением, которое инвариантно относительно вращения.
Так как $Щ есть вектор, он должен преобразовываться как вектор.
В частности, если оси координат повернуты вокруг оси z на угол d6z,
то соотношения между старыми и новыми составляющими имеют вид
m'z=mz,' т?= dezmx+my, mx=mx-d%my. (i.6.46>
Однако 5Шг есть оператор, связанный с вращением в векторном про-
пространстве, и он зависит от параметра бг, аналогично тому, как опера-
оператор § в уравнении A.6.38) зависит от t. Более точно: этот оператор
связан со скоростью изменения вектора состояния е уравнением
Поэтому для любого другого оператора, связанного с этой системой,,
скорость изменения по отношению к 6Z должна задаваться уравнением
вида A.6.40).
Например, скорость изменения оператора Шх по отношению к па-
параметру 6Z задается уравнением
Но из уравнения A.6.46) d<$jljd6z= —gfty, и мы получаем соотношение-
гшу=mzmx—mxmz,
идентичное последнему из уравнений A.6.42) для операторов момента
количества движения.
Однако в этом выводе операторный вектор $ДО рассматривается
в связи с бесконечно малым поворотом осей в обычном пространстве.
В результате оказалось, что, поскольку речь идет об абстрактном про-
пространстве, этот оператор совпадает с оператором момента количества
движения, определенным равенством A.6.42). Причиной этого совпадения,
служит, конечно, тот факт, что измерение момента количества движе-
движения системы приводит обычно к повороту системы в пространстве (если
только состояние не соответствует собственному вектору оператора 5Щ),
точно так же, как измерение импульса р обычно приводит к изменению
положения системы.
В терминах аппарата абстрактного векторного пространства оператор*
Q==ei (ЗЛг/й) 62
1.7. Преобразование Лоренца, 4-еекторы, спиноры 95
осуществляет необходимое изменение ориентации векторов состояния,
соответствующее повороту обычного пространства на угол 6г вокруг оси z.
Так как в силу уравнений A.6.43) собственными значениями оператора Щг
являются mz%, где mz — либо целое число, либо полуцелое [в зависи-
зависимости от того, что подлежит изучению — обычный (орбитальный) момент
количества движения или спин], то, действуя на собственный доктор
оператора $ЭДг, оператор g не меняет ни величины, ни направления этого
вектора
ei (ЯЯх/Л) b--e(mz) = eim*°*e (m2).
Все эти вопросы квантовой механики и исчисления операторов будут
изучены более подробно в следующей главе.
1.7. Преобразование Лоренца, 4-векторы, спиноры
Вплоть до настоящего момента мы изучали векторы и другие вели-
величины в- трехмерном пространстве, и некоторые из формул и утвержде-
утверждений, полученных нами при рассмотрении аксиальных векторов, ротора
вектора и векторного умножения, остаются корректными только для трех
измерений. Поскольку в этой книге в большинстве случаев речь идет
только о трех пространственных измерениях, такое ограничение допу-
допустимо и эти результаты имеют значительную ценность. Однако во мно-
многих случаях возникает необходимость в четвертом измерении — времени.
В классической механике оно не вносит дополнительных осложнений,
так как предполагается, что ни одна из физически возможных опера-
операций не может так повернуть ось времени, чтобы совместить ее с одной
из пространственных осей или наоборот, и, следовательно, направле-
направление времени считается одним и тем же для всех наблюдений. Если бы
это предположение оказалось правильным, то единственными реализуе-
реализуемыми преобразованиями были бы преобразования трехмерного простран-
пространства, а время являлось бы неким дополнительным понятием и в физике
находил бы применение только изучавшийся до сих пор трехмерный
анализ.
Собственное время. Однако, как показывается в современной элек-
электродинамике и обосновывается в теории относительности, существуют
такие физически возможные преобразования, в которых участвует
время как измерение; и если относительная скорость двух наблюдателей
сравнима со скоростью света, то направления времени для них суще-
существенно не параллельны. Это не означает, что время просто является
еще одним пространственным измерением, так как в формулах оно
отличается от трех пространственных измерений мнимым множителем
i=Y — 1. Оказывается, что если некоторый объект в пространстве
передвигается на величины dx, dy, dz за время dt относительно наблю-
наблюдателя А, то время, измеряемое наблюдателем В, движущимся вместе
с объектом, будет равно dxp, где
^) ); A.7.1)
здесь с — скорость света, a diB называется собственным временем наблю-
наблюдателя Б' (dt =dxA есть, очевидно, собственное время наблюдателя А).
До тех пор, пока скорости dx/dt и прочие малы по сравнению со ско-
скоростью с, значения собственных времен dz^ и dxs мало отличаются
96 Гл. 1. Типы полей
друг от друга, но если относительная скорость приблизительно равна с,
различие этих промежутков времени может оказаться значительным.
Уравнение A.7.1) аналогично трехмерному уравнению для полного
дифференциала расстояния вдоль линии ds2 — dx2 + dy2 + dz2, и аналогия
делается более наглядной, если записать уравнение A.7.1) в виде
(icdxBJ = dx2 -f dy2 + dz2 + (icdtf.
Траектория, по которой движется объект в пространстве-времени,
называется его мировой линией, а расстояние вдоль нее измеряет соб-
собственное время объекта. Это уравнение показывает, что собственные
времена двух наблюдателей, движущихся один относительно другого,
связаны мнимым поворотом, а величина поворота зависит от охнр_с.и-
тельной скорости этих наблюдателей.
Преобразование Лоренца. Сначала, чтобы сделать изложение воз-
возможно более простым, предположим, что относительная скорость двух
наблюдателей параллельна оси х, в силу чего связанные с ними оси у
и z остаются параллельными. Мы предположим также, что их относи-
относительная скорость и постоянна, так что угол между их мировыми
линиями все время постоянен и преобразование от одной простран-
пространственно-временной системы к другой является простым (мнимым) пово-
поворотом. Рассмотрение относительных ускорений наблюдателей привело бы
нас к сложным вопросам общей теории относительности, включение
которых в данную книгу не является необходимым.
Преобразование, соответствующее повороту в плоскости (х, ict)
на мнимый угол га, имеет вид
х — х' cho + cf' sha,
г/ = г/\ z = z', A.7.2
ct = x' sha + сг' cha,
где (х, у, z, Z)— пространственно-временные координаты, связанные с на-
наблюдателем А, а (хг, у', z', t') — соответствующие координаты, связанные
с наблюдателем В, движущимся с относительной скоростью и, парал-
параллельной оси х. Для того чтобы ось времени для В двигалась относи-
относительно А со скоростью и (или наоборот), мы должны иметь
M = ctho, sha = и с . t cha =
—(U/CJ ' |Л_(„/сJ
Следовательно, мы можем записать преобразование в более привычной
форме
х' + ut'
X = -
(;L7.3)
Между прочим, это преобразование показывает, что если наблюдатель В
движется относительно наблюдателя А со скоростью м = с th о, а наблю-
наблюдатель С движется относительно В со скоростью w = cthp (имеющей
то же направление, что и и), то С имеет относительно А скорость,
равную
с th (a + р) = (и + v)/[l + (uv/c2)].
1.7. Преобразование Лоренца, 4-векторы, спиноры 97
Эта система уравнений, связывающая пространственно-временные
координаты двух наблюдателей, движущихся с постоянной относитель-
относительной скоростью, называется преобразованием Лоренца. Оно является сим-
симметричным преобразованием, в котором уравнения, выражающие х', t'
через х, t, можно получить из уравнений A.7.3) взаимной заменой штри-
штрихованных и нештрихованных величин и изменением знака и. В этом
можно убедиться, выражая х', V через х и t. Преобразование Лоренца
является весьма частным случаем замены координат, так как оно пред-
представляет собой простой (мнимый) поворот в пространственно-времен-
пространственно-временной плоскости, но его будет достаточно для большинства разбираемых
в этой книге вопросов, связанных с пространством-временем.
Уравнения для общего преобразования Лоренца, соответствующего
относительной скорости K = ctha, направление которой задается сфе-
сферическими углами в- и 9 относительно оси z, имеют вид
х= [1 -^- cos2 9 sin2 & (ch a — 1)] x' -j-cos <p simp sin2 & (cho— 1) y' -\-
-j- cos 9 cos & sin & (ch a — 1) z' -f- cos 9 sin & (sh a) ct',
y = cos9sin9sin2& (cho— 1) x' -\- [1 + sin2 9 sin2 & (cha— 1)] y' +
+ sin9 cos & sin & (cha— 1) z' + sin 9 sin & (sha)cZ',
z = cos 9 cos & sin & (ch a — 1) x' -f- sin 9 cos & sin & (ch a — 1) y' +
+ [1 + cos2 & (ch a — 1)] z' + cos & (sh a) ct',
ct' = cos 9 sin & (sh a) x' + sin 9 sin t> (sh a) y' +
+ cos & (sh0) z' + (cha)ct'.
Когда 9 = 0° и Э = 90°, эти уравнения сводятся к простому виду, задан-
заданному уравнениями A.7.2).
Для этого преобразования все коэффициенты Ламе h равны единице,
так как оно является вращением без растяжения. Очевидно, что здесь
коэффициенты Ламе включают четыре измерения
4
(КJ = 2 ("t^J' Ж1> х^ Х3' xi = x' У' z>ict-
Так как коэффициенты h все равны единице, то нет необходимости
различать ковариантные, контравариантные и «истинные» векторные
составляющие.
Четырехмерные инварианты. Точно так же, как и в случае трех изме-
измерений, весьма полезным для нас будет разыскание тех величин, кото-
которые не изменяются при преобразовании Лоренца. Иными словами, зна-
значение такой величины, измеренное любым наблюдателем, движущимся
с любой постоянной скоростью (меньшей скорости света), будет одним
и тем же. Эти величины аналогичны тем скалярным величинам, кото-
которые мы изучали выше, и во многих случаях соответствуют измеримым
величинам, так как, согласно теории относительности, многие физиче-
физические величины должны иметь одно и то же значение при измерении их
различными наблюдателями, движущимися с различными скоростями.
Такие величины называются лоренц-инвариантнылт.
Для движущейся без ускорения частипы пространственно-времен-
пространственно-временная длина данной части ее мировой линии является четырехмерным
инвариантом. Если перемещение этой частицы в системе координат,
связанной с наблюдателем В, равно х', а длительность этого переме-
перемещения во" времени, связанном с тем же наблюдателем, равна V, то квад-
7 ф. м. Морс и Г. Фегабах
Гл. 1. Типы полей
рат собственной длины мировой линии равен
s2=(ct'f-(x'f.
Для наблюдателя А, согласно уравнению A.7.3), квадрат собственной
длины равен
= (ctf -х* = —L^ [ (cl'f + lux'f
- (x'f - lux't' - (кГJ] = (ct'f - (x'f,
то есть имеет то же значение. Квадрат длины той же мировой линии
для наблюдателя, движущегося вместе с этой частицей, должен рав-
равняться квадрату его собственного времени, умноженному на с2; это
значение также совпадает с предыдущими.
Поэтому в теории относительности ни пространственная длина
линии, ни длительность времени не являются инвариантами. Простран-
Пространственная длина линии для наблюдателя А, движущегося вместе с ли-
линией, равна измеренному в один и тот же момент времени, связанного
с А, расстоянию хг — хх между точками на двух мировых линиях. Для
наблюдателя В, движущегося со скоростью и, пространственная длина
той же линии определяется расстоянием между точками на тех же
мировых линиях, измеренным в один и тот же момент времени, свя-
связанного с В, т. е. для t'2 = t[. Согласно уравнениям A.7.3), мы имеем
следовательно, расстояние, измеренное наблюдателем1 В, движущимся
относительно этой линии, равно
х'2 -х[ = (ж, - xj Yl
и оказывается короче расстояния, измеренного А, так как отличается
множителем J/1 — (и/сJ. Так как видимые размеры объектов изменяются
в зависимости от относительной скорости наблюдателя, то и видимая
плотность материи также не является инвариантной относительно пре-
преобразования Лоренца.
Многие другие величины, являвшиеся скалярами в трех измерениях
(т. е. для очень малых относительных скоростей), оказываются не ин-
инвариантными в пространстве-времени. Например, масса тела не является
четырехмерным инвариантом. Точным инвариантом является некоторая
комбинация массы и кинетической энергии тела, соответствующая
релятивистской зависимости между массой и энергией. Это будет дока-
доказано после того, как мы изучим четырехмерные векторы.
4-векторы. Сказанное до сих пор дает основание предполагать,
что, распространяя наши концепции на векторы в четырех измерениях,
мы также столкнемся с некоторыми неожиданностями. Как и 3-вектор,
4-вектор должен иметь инвариантную длину, но только теперь этой
длиной должна служить собственная длина в пространстве и времени.
Две точки (х'2, г/2, z2', t'2) и (х[, г/,', z[, Q при измерении наблюдателем В
определяют 4-вектор
Для наблюдателя А, движущегося относительно В со скоростью и
(в направлении х), компонентами этого вектора являются
„ _ Fi + (uF'Jc) р _„, „ _ F, v _(«?i
1.7. Преобразование Лоренца, 4-векторы, спиноры 99-
и, таким образом, для этого преобразования Лоренца направляющие,-
косинусы равны:
Ti2 = Y21 ~ Y13== Y31 = Y23= Y32 = Y24 == Y42 = Y3i == Y43 = ">
tha = K/c. A-7.4)
Это преобразование компонент типично для 4-векторов. Заметим, что
«сумма» квадратов четырех компонент F* = F\-\-F\-\-F% — F\ инвари-
инвариантна, как это и должно быть.
Очень важное значение имеет вектор, являющийся четырехмерным
обобщением импульса частицы, движущейся относительно наблюдателя Л
с постоянной скоростью и в направлении оси х. Для наблюдателя В,
движущегося вместе с частицей, масса частицы равна т0, а собствен-
собственное время — ъ. Относительно наблюдателя А частица проходит расстоя-
расстояние dx за время dt, где (okJ = (dtJ — (dx/cJ. Пространственная компо-
компонента вектора импульса не может равняться mo(dx/dt), так как было бы
трудно найти соответствующую временную компоненту, чтобы получаю-
получающийся в результате квадрат длины был инвариантом. С другой сто-
стороны, если выбрать пространственную компоненту равной величине
mo(dx/dz), которая преобразуется так же, как и dx, т. е.
dx mau dt mnc dx
p = m = p = mc = U = —r-
где ¦: является собственным временем рассматриваемой частицы (и, сле-
следовательно, наблюдателя В), то квадрат длины р будет равен р% — р\ =
= — (т0сJ, а эта величина инвариантна.
Для наблюдателя С, движущегося относительно Л со скоростью
v = сth8 в направлении х, вектор импульса преобразуется согласно
уравнению A.7.4)
р'х = Рх chр + Pt shp = moc sh (о + Р) = 1и0и'/1/1-(в'/сJ,
p't = рх sh р + pi ch р = moc ch (a + P) = moc/"|/l — (u'/cf,
где M = ctho есть скорость частицы относительно Л, а и' — cth(a + P) — ее
скорость относительно наблюдателя С. Таким образом, определение
импульса как 4-вектора согласуется с данным ранее правилом сложе-
сложения скоростей.
Поэтому 4-всктор, соответствующий импульсу, измеренному наблю-
наблюдателем А, дл» частицы, движущейся относительно А со скоростью и,
равен
_ mn (dx/dt) _ mo(dy/dt) _ mn(dz/dt)
х ~ /1 — (к/сJ ' Ру V'"l —(и/с)з ' г ~ J — (м/сJ '
mnc
2
VI —(и/сJ
где x, у, z, t являются координатами частицы для наблюдателя А.
Временная компонента этого импульса пропорциональна полной энер-
энергии частицы относительно наблюдателя Л,
г, ГПпС2 2 1 2
' У \—iujсJ ° 2 °
которая не инвариантна относительно преобразования Лоренца. Это урав-
уравнение показывает также, что полная энергия может быть разделена
7*
100 Гл. 1. Типы полей
на энергию покоя и на нерелятивистскую кинетическую энергию только
тогда, когда к мала по сравнению с ".
Другим 4-вектором является пространственно-временной градиент ? ф
некоторой скалярной функции ф от (х, у, z, t), где
(?*)> = ? -т. д., (ПФ). = 4#-
Так как коэффициенты Ламе все равны единице, а, следовательно, все
символы Кристоффеля равны нулю, эти компоненты являются также
компонентами четырехмерной ковариантной производной от <]>. Следова-
Следовательно, сокращенная производная второго порядка
является лоренц-инвариантной. Оператор Ц2 называется даламбертпаном.
С формальной точки зрения он аналогичен трехмерному оператору Лап-
Лапласа V2. Однако, как мы увидим в дальнейшем, ввиду наличия отрица-
отрицательного знака перед временным членом решения уравнения Лапласа
^2ф = 0 существенно отличаются от решений уравнения ?2ф = 0, которое
является волновым уравнением для волн, движущихся со скоростью света с.
Тензор напряжения-энергии. По аналогии с трехмерным случаем
можно построить аффиноры или тензоры для четырех измерений, преоб-
преобразующиеся при преобразованиях Лоренца по формулам, которые легко
¦определить, обобщая сказанное в предыдущем параграфе. Интересный и
полезный пример такого тензора получается при распространении на че-
четырехмерный случай аффинора напряжений для упругой среды, опреде-
определенного формулами A.6.28). Каждая из девяти компонент Tij напряжений
имеет размерность дина па квадратный сантиметр или грамм, деленный
на сантиметр и на квадрат секунды; они преобразуются согласно пра-
правилам, имеющим место в трехмерном случае. По аналогии с предыдущим
рассмотрением вектора импульса частицы мы должны ожидать, что вре-
временная компонента четырехмерного тензора может " оказаться пропор-
пропорциональной плотности энергии заданной среды. Другими словами, эта
четвертая компонента должна быть связана с членом рс2, выражающим
полную энергию (где р—плотность массы для данной среды), который
имеет размерность грамм, деленный на сантиметр и на квадрат секунды.
Поэтому мы полагаем, что тензор напряжения-энергии Ptj в точке
{х, у, z, ct) среды имеет для наблюдателя А, неподвижного относительно
помещающейся в (х, у, z, ct) части среды, следующие компоненты:
^11 = ^** и т. д., Р12 = Тху = Рп = Тух и т. д.,
Ри = ^24 = РМ = ^41 = ^42 = ^43 = 0, A-7.7)
-Р44 = С2РО.
где р0 —плотность среды в (х, у, z, ct), как ее измерил бы наблюдатель А.
Если эти величины являются компонентами истинного 4-тензора,
то компоненты Р, измеренные наблюдателем В, движущимся относительно
среды, находящейся в (х, у, z, ct), со скоростью и в направлениях х,
должны определяться общими правилами преобразования
ctha =
1.7. Преобрааоеание Лоренца, 4-еекторы, спиноры 101
В результате преобразования получим
Р'и = Т„ ch2 a -f Рос2 sh2 а, Р'ы = Р[х = Тху ch а,
P^P'31 = Txzcha, Р^ = Туу; PU = Ta,
P'2S = Р'л = Tyz, Р^ = Р'а = {Тхх 4 Рос2) ch а sh а, A.7.8)
Р^4 = Р'„ = Гж2 sh а,
Пространственные компоненты (РХ1, Р22 и т. д.) оказываются компонен-
компонентами напряжения, какими их измерил бы наблюдатель В в этой среде,
если принять во внимание конечную скорость света, а компонента />44
оказывается равной эффективной плотности, измеренной наблюдателем В,
умноженной на с2. Исследование компоненты Р'ъ1 показывает, что ее
можно рассматривать как величину, пропорциональную плотности парал-
параллельного оси х потока импульса среды, как ее измерил бы наблюда-
наблюдатель В. Соответственно компоненты P'%i и P'3i должны быть пропорцио-
пропорциональны потокам импульса в направлениях у и z, как их измерил бы
наблюдатель В.
Следовательно, мы приходим к важному и интересному результату,
который может быть проверен как дальнейшим анализом, так и экспе-
экспериментом: относительное движение преобразует напряжение в поток
импульса и наоборот. Более того, так как в системе, неподвижной
относительно данной среды (наблюдатель А), мы можем проверить, что
свернутые тензорные уравнения
VI Г дРтг,
или (в компонентах Т)
дТхх . 8TXV , &гхг г. д , . г.
—а^Н гГ^ + з ¦ = О и Т- Д-, -5г(сРп)=0
ox oy oz at x 'и/
являются справедливыми, то эти уравнения должны быть справедли-
справедливыми также для наблюдателей, движущихся относительно данной среди
(или, что то же, для среды, движущейся относительно наблюдателя).
Например, если определить вектор импульса М относительно наблю-
наблюдателя В как вектор с пространственными компонентами
Мх = A/с) (Рос2 + Тхх) ch a sh а = P'Jc,
а плотность относительно наблюдателя В как
р = Ро ch2 a + (Txx/c2) sh2 a = P'Jc2,
то одно из преобразованных уравнений должно иметь вид
-О, или
где штрихами снабжены те координаты, которые соответствуют наблю-
наблюдателю В. Очевидно, что это уравнение является уравнением неразрыв-
неразрывности для данной среды, связывающим плотность импульса (или поток
массы) с изменением плотности массы р. Остальные три преобразован-
преобразованных уравнения оказываются уравнениями движения этой среды.
102 Гл. 1. Типы полей
Спиновое пространство и пространство-время. Одним из самых
интересных выводов в современной теоретической физике является заклю-
заключение о том, что двумерное «пространство состояний», связанное со спи-
спином электрона, и четырехмерное пространство-время, описывающее дви-
движение электрона, находятся в тесной связи. В предыдущем параграфе
мы начали обсуждение вопроса о спиновом пространстве, соответствую-
соответствующем двум возможным спиновым состояниям электрона, и показали, что
изменение направления спина на 180° в обычном пространстве (опроки-
(опрокидывание спина) соответствует повороту вектора состояния в спиновом
пространстве на 90°. В зтом есть некоторая аналогия с соотношением
между векторами на комплексной плоскости, соответствующими (— 1) и
Y —1> и ПРИ желании пофантазировать можно рассматривать спиновое
пространство как своеобразный «квадратный корень» по отношению
к обычному пространству. В самом деле, можно показать, что двумер-
двумерное спиновое пространство является «пространством квадратного корня»,
причем не для трехмерного пространства, а для четырехмерного про-
пространства-времени. Более определенно мы найдем, что четыре компоненты
аффинора в спиновом пространстве могут быть отождествлены с ком-
компонентами 4-вектора в пространстве-времени.
Чтобы показать это, мы должны рассматривать компоненты векторов
в спиновом пространстве и даже сами единичные векторы как комплекс-
комплексные величины, имеющие комплексно-сопряженные (а и а для компонент,
являющихся числами, и е и е* для векторов состояния), так что аа и
е-е* являются вещественными положительными числами. Мы начнем
с двух взаимно-перпендикулярных векторов состояния ег и е2 (для них
комплексно-сопряженными являются е* и ef), представляющих состояния,
при одном из которых спин расположен в некотором определенном
направлении, а при другом — в противоположном. Для того чтобы два
комплексных вектора могли быть названы единичными ортогональными
векторами, должны выполняться соотношения
е1е* = е*-е1 = е2-е2 = е2-е2= 1
и
е1-е2 = е*-е2 = е2-е* = е?-е1 = 0.
Значения комплексных величин е1-е1, el-ea, е|-е* и т. д. роли не играют.
Любой лежащий в спиновом пространстве вектор может быть выра-
выражен при помощи этих двух векторов:
s = а1е1 + а2е2, s* — axet + а2е2,
и любой аффинор в спиновом пространстве может быть представлен
л виде
© = с^е? + c12ej.e§ -f c21e2ef + c22e2e|. A.7.9)
Аффинор в спиновом пространстве называется спинором второго
порядка. Он имеет обычные для аффиноров свойства, переводя вектор
состояния в спиновом пространстве в другой вектор состояния
<& -s = (сгхах + с12а2) ех + {с^аг + с22я2) е2,
s* • © = (ajCj.! + а2с21) е? + (ахс12 + а2с22) el.
Чтобы придать физический смысл этим определениям, мы должны найти
¦связь между изменением компонент спинора аг и компонент аффинора ci}
иод действием преобразования Лоренпа и их же изменением при пово-
1.7. Преобразование Лоренца, 4-векторы, спиноры 103
роте осей в спиновом пространстве. Например, величины, являющиеся
лоренц-пнвариантными, должны также оставаться инвариантными йри
повороте осей в спиновом пространстве. В силу наших предыдущих
замечаний мы должны потребовать, чтобы четыре компоненты ci;- спи-
спинора второго порядка п спиновом пространстве преобразовывались по-
подобно компонентам 4-вектора в обычном пространстве-времени. Аффинор
в спиновом пространстве есть вектор в пространстве-времени; тем самым
достигнута наша цель представить спиновое пространство как «про-
«пространство квадратного корня».
Спиноры и 4-векторы. До сих пор мы не разбирали тех специфи-
специфических правил преобразования для спинового пространства, благодаря
которым компоненты ci;- спинора второго порядка преобразуются подобно
компонентам 4-вектора. Наиболее общее преобразование задается следую-
следующим образом:
ei = anei + «i2e2, e*' = aue* + а12е*,
е2 = а21«1 + «22^2. <' = а21«1 + «22»*.
е1=аме1'— а12е^, е* = а22е*'-а12е*', A.7.10)
где нужно считать
alla22 ~~ al2a21 = 1» alla22 ~" al2a21 = If
для того чтобы масштаб в новых координатах совпадал с масштабом
в старых.
Под действием этого преобразования в спиновом пространстве компо-
компоненты произвольного спинора подвергаются следующей замене:
стп = 2 CiXma;-n. A.7.11)
п
Чтобы наиболее надежным путем двигаться дальше, нужно найти функ-
функцию от с, инвариантную относительно преобразований а в спиновом про-
пространстве, которую затем можно сделать инвариантной относительно
преобразования Лоренца. Используя правила, по которым перемножаются а,
мы легко можем показать, что одним из инвариантов является величина
сис22 — ci2c2i (это можно показать подстановкой и перемножением, с уче-
учетом того, что ana22 — a12a21 = 1 и т. д.). Эту величину можно сделать
также лоренц-инвариантной, если связать компоненты с с компонентами Fn
некоторого 4-вектора таким способом, чтобы
tllt22 t12t21 — L Г i Г 1 -"г ^3'
потому что такая комбинация из F, стоящая в правой части этого ра-
равенства, инвариантна. Это можно осуществить многими способами, но
наиболее прост следующий:
= (J/2)(c12-c21),
, A-7.12)
^i = A/2) (Сц-см).
Преобразование Лоренца для спиноров. Для наблюдателя В (штрихо-
(штрихованные координаты), движущегося со скоростью и в направлении х отно-
104 Гл. 1. Типы полей
сительно данного электрона, находящегося в покое относительно наблю-
наблюдателя А (нештрихованные координаты), компоненты F преобразуются
следующим образом:
Fa — F', F =F', M = c-tha.
Следовательно, преобразование компонент спинора имеет вид
— г'
A.7.13)
л л7 л— а ла -ш / '
С22— С22е > У С и
ла -ш /
У
а преобразование соответствующих направляющих косинусов при повороте
единичных векторов в спиновом пространстве имеет вид
ail = ea/2, a22 = e-a'2, a12 = a21 = 0. A.7.14)
Поэтому любой вектор состояния в спиновом пространстве, имеющий
относительно наблюдателя А вид s = а^ + с2е2, превращается в s' =
= a1ea/2e1' + a2e~a'2e2' относительно наблюдателя В, движущегося относи-
относительно А со скоростью M = c-tha.
Естественно, что формулы перехода для с и а в случае более общего
преобразования Лоренца будут сложнее приведенных здесь, но и они
могут быть разработаны теми же методами. Любая пара комплексных
величин, удовлетворяющих условиям преобразования для компонент век-
вектора состояния в спиновом пространстве, называется спинором первого-
порядка; четверка величин, удовлетворяющих условиям преобразования,
для компонент с, заданных уравнениями A.7.9) — A.7.11), называется
спинором второго порядка и т. д. Уравнения A.7.12) дают соотношения
между компонентами спинора и компонентами 4-вектора для рассмотрен-
рассмотренного нами простого преобразования Лоренца.
Пространственный поворот спиноров. В качестве следующего при-
примера соотношения «квадратного корня» между компонентами спинора
и компонентами вектора мы рассмотрим случай, когда временная коорди-
координата не меняется, а пространственные координатные оси поворачиваются
на соответствующие углы Эйлера, указанные на стр. 38. Под действием
этого преобразования временная компонента любого 4-вектора остается
неизменной, и потому, согласно уравнению A.7.12), сумма clx-\-c22 должна
остаться неизменной. Выражая си-\-с22 через компоненты а, мы видим,
что для чистого пространственного поворота, когда
мы должны иметь
О, пфт
Этот результат не является неожиданным, так как следствием из него
будет впв* = 1, а мы должны были ожидать, что «длина» вектора состоя-
состояния при пространственном повороте останется неизменной. Объединяя все
условия, содержащие а, мы увидим, что
aii = «22» ai2= — a2i и т. д. A.7.15)
Выпишем выражения для преобразований компонент F при простран-
пространственном повороте [модифицируя уравнения A.3.8) и заменяя Fz на Flf
1.7. Преобразование Лоренца, 4-векторы, спиноры MS
Fx на F2 и Fy на F3]
F2' = [cos Ф cos G cos d> — sin$smi5]F2 +
+ [sin Ф cos G cos >!> -f- cos Ф sin ty] F3 — sin 0 cos 0 Flt.
F's= — [cosФcosGsinty + sinФcosty] F2 —
— [sin Ф cos G sin Л — cos Ф cos <j>] Fs -f- sin G sin ф .F1;.
Fj = sinG cosФF2 + sin G sin Ф^3+ cos GFlt F't = F4
и подставим эти выражения в уравнение A.7.12) как для штрихованных,
так и для нештрихованных компонент, чтобы получить уравнения пре-
преобразования для с
с'ш = —sin (G/2) cos F/2) е1* (сп — с22) + cos2 F/2) е^+ф> с12 — sin2 @/2) е^'фк.21
и т. д. При помощи направляющих косинусов а связь этой компоненты
с нештрихованными выражается уравнением
а21С21 а21а22С2
21С21 а21а22С22-
Здесь мы обратили уравнения A.7.11) и использовали равенства A.7.15).
Сравнивая последние два уравнения, мы находим, что направляющие
косинусы а для поворота в спиновом пространстве, соответствующего
пространственному повороту с углами Эйлера Ф, 0, Ф [см. уравнения
A.3.8) и рис. 1.6], равны
a11 = cos(G/2)e-i^+<I))'2, а21 - - sin F/2) е^-®»2,
aM = sin @/2) е-'"«-ф)/2, аа„ = cos @/2) e*D«+<i»/2, (L''16)
где мы вновь прибегли к равенствам A.7.15), чтобы распутать эти урав-
уравнения. Поэтому при этом повороте пространственной системы координат
вектор состояниях в спиновом пространстве s = а^ -\- а2е2' превращается и
8=1^ cos @/2) е-*'«2 — a2 sin F/2) е*«2] е-1®'^ +
+ [ — % sin F/2) е-**/2 + а2 cos (G/2) е{ '2] е1ф1^„.
Это уравнение показывает, что углы поворота в спиновом простран-
пространстве равны половинам углов поворота в обычном пространстве. Поворот
на 180°(G = ti, Ф = Л = 0) переводит s = е^е,' 4- с2е2' в s=a2e1 — axe2, а это
есть поворот на 90° в спиновом пространстве.
Обычно представляют интерес преобразования A.7.14) я A.7.16). Все
другие случаи могут быть разобраны тем же способом при помощи урав-
уравнений A.7.12). Несмотря на то, что мы начали обсуждение этих вопро-
вопросов, стремясь удовлетворить довольно неопределенному условию, мы рам-
вили теорию величины, преобразующейся вполне определенным образом
при общем повороте координат (включая поворот Лоренца) и все же
не являющейся тензором, в соответствии с ранее проведенными рассуж-
рассуждениями. При первоначальном изучении спиноров этот факт казался
совершенно неожиданным.
Спиновые векторы и тензоры. В спиновом пространстве можно найти
четверку простых аффиноров, ведущих себя подобно единичным векторам
в пространстве-времени:
o4 = e1e* + eseg* = 3.
о, = е,е*4-еое*
A 7 17)
а2 = г(е2е]*-е]е*),
106 Гл. 1. Типы полей
Эти величины действуют на спиновые векторы е следующим, образом:
54-en = erl. 5i-e1 = e2, 52-е1 = ге2> s3-ei = ei и т- Д-
Сравнение с уравнениями A.6.44) показывает, что величины а1У <з2, <з3
равны спиновым операторам для электрона, умноженным на 2/Л. Они
называются спиновыми операторами Паули. Величина s4 есть, очевидно,
единичный аффинор. Мы видим также, что iax, ia2, — ia3 в точности
совпадают с кватернионными операторами Гамильтона.
Теперь мы можем переписать спинорный аффинор, заданный уравне-
уравнением A.7.9), в виде 4-вектора, используя уравнения A.7.12) и A.7.17):
+ F^, A.7.18)
где «единичные векторы» а являются операторами, действующими на век-
векторы состояния в спиновом пространстве, а' компоненты F представляют
собой обычные числа, преобразующиеся подобно компонентам обычного
4-вектора. Итак, мы видим, наконец, каким образом операторы в спино-
спиновом пространстве могут действовать подобно векторам пространства-
времени. Распространение зтого рассуждения на преобразование отражения
г'—> —г и его согласование со спиновым пространством требует, чтобы
мы рассматривали е* и е как независимые величины, так что преобразо-
преобразование одной в другую оказывается возможным. Однако мы не будем
углубляться дальше в эти вопросы, скажем только, что вектор а пре-
преобразуется подобно аксиальному вектору (см. задачу 1.34).
Можно перейти к образованию спинорных форм, преобразующихся
подобно аффинорам в пространстве-времени. Например, спинор четвертого
порядка
г (Flt + Fa -f iF23 - iF32) +
имеет компоненты ^v, которые ведут себя подобно компонентам аффи-
аффинора в пространстве-времени. Особо важной формой является свернутый
тензор, образованный умножением спинорного вектора на его сопряжен-
сопряженный
e1F1 + O2F2 + asF3) (a4cF4 - вЛ - g2F2 - a3Fa) =
-Fl-Fl-Fl) A.7.19)
и дающий квадрат длины 4-вектора. Это соотношение будет исполь-
использовано, когда мы перейдем к рассмотрению теории электрона Дирака.
Оператор вращения в спинорной форме. Обращаясь к исследова-
исследованиям Гамильтона о кватернионах (см. стр. 78), можно прийти к весьма
интересному и полезному спинорному оператору, для которого направ-
направляющие косинусы а спиновых векторов служат компонентами:
= ац^е* -4- agleje;f + a12e2e* + a22e2e* =
А . Л 1
¦Согласно уравнениям A.7.10), а являются направляющими косинусами,
связывающими в спиновом пространстве штрихованные и вгештрихован-
лые единичные векторы е. Если они имеют значения, задаваемые фор-
1.7. Преобразование Лоренца, 4-векторы, спиноры 107
мулами A.7.16), то они соответствуют повороту пространственных осей
координат на углы Эйлера 0, ф, Ф. Как мы показали выше, спинорный
оператор, имеющий вид Ш, преобразуется так же, как вектор, и это под-
подчеркивается тем, что мы записываем его при помощи его компонент R
«вдоль» единичных спиновых векторов а.
Однако вектор Ж (или спинорный оператор, в зависимости от того,
какая из точек зрения подчеркивается) имеет ту специфическую особен-
особенность, что его компоненты
R1 = i sin @/2) sin [(Ф — ф)/2], R2 = isin @/2) cos [(Ф - ф)/2],
R3 = i cos F/2) s in [(Ф -f- -i)/2], Rt = cos F/2) cos [(Ф + ф)/2]
сами связаны с частным видом преобразования, определенным углами
О, ф, Ф. (Это не означает, что вектор Ж не может быть выражен при
помощи любых координат, получающихся вращением на любые углы; это
означает только, что он особым образом связан с одним частным слу-
случаем поворота осей на углы 0, ф, Ф.)
Можно ожидать, что этот вектор обладает особой симметрией отно-
относительно этого поворота, так как если единичные векторы е' связаны
с векторами е теми же самыми углами [см. A.7.10) и A.7.16)], то тогда
оказывается, что выражение для Ж, содержащее штрихованные векторы,
не отличается от выражения с нештрихованными векторами
Ж = а^е* + а^е* + ... =
~ «12я21а22 + a22a2ia2l] ei'e*' ~
al2-*2lal2 ~Г a22a21ailJ ®l®2 ~Г • • • =
как это можно доказать, используя правила перемножения для а.
Однако ffi является также и оператором, действующим на спиновые
векторы. В действительности под действием этого оператора каждый
спиновый вектор поворачивается именно так, как он повернулся бы при
преобразовании е-^е'. Согласно уравнениям A.7.10), имеем:
9t-en = e;; 9Г-е* = е*', A.7.21)
где
91* = а^е^ел + а21е*е2 + a^e'ej. + а22е*е2.
Другой оператор 9Г1 осуществляет обратное преобразование е'—>е.
Из уравнений A.7.10) видно, что
ee* а12е2е* + a1]Le2e* =
следовательно,
а21е,'е*' — а12е2'е*' + а1Хе2'е*';
Но, так как а22 = а11, а12= — а21 и т. д., мы можем также показать, что
en.(9t-1)* = e; и е^-ЭГ^е*'
и что
e^.4R* = en и e*/-9i = e*, A.7.22)
откуда видна тесная взаимосвязь между оператором 9? и его обрат-
обратным Ж.'1.
108 Гл. 1. Типы полей
Особо важным свойством оператора Ш является то, что -он не только
порождает вращение векторов в спиновом пространстве, но и, кроме
того, может вызвать связанное с первым вращение 4-векторов в обычном
пространстве. Например, спинор
С21е2е1 ~
(где с имеют любые значения) преобразуется как 4-вектор [см. уравне-
уравнение A.7.18)] с компонентами Fn [см. уравнения A.7.12)]. Вектор, обра-
образованный воздействием оператора Ш «справа и слева» на <3
9* • © • ЭГ1 = с^'е*' + с12е;е*' + са^е*' + с22е2'е*' =
't + Fae', + Fte't, A.7.23)
имеет те же компоненты Fn, но теперь они являются компонентами
в разложении по штрихованным единичным векторам, повернутым отно-
относительно нештрихованных. Поэтому воздействие оператором 9} справа
и слева действительно повернуло вектор <3 на величину, задаваемую
углами О, ф и Ф. В соответствии с соотношением «квадратного корня»
между спиновым пространством и пространством-временем мы должны
были воздействовать на спиновый вектор оператором 9} один раз, чтобы
произвести поворот, но чтобы получить поворот 4-вектора на соответ-
соответствующую величину, на него надо подействовать дважды.
Заметим, что здесь мы имели дело с поворотами на конечные углы.
Если же поворот бесконечно мал, то углы Эйлера 6 и (Ф + ф) делаются
малыми и поворот может быть представлен при помощи бесконечно
малого вектора Дю, направление которого дает ось поворота, а длина —
угол поворота в радианах. Рассмотрение свойств векторного произведе-
произведения показывает, что операция перехода от обычного трехмерного век-
вектора А к другому вектору А' при помощи бесконечно малого поворота
задается уравнением
А' А ДА. A.7.24)
Изучение приведенных на стр. 105 уравнений для поворота, содержа-
содержащих углы Эйлера, показывает, что если 0 и (Ф4-ф) малы, то
(Аи)! ~ — (Ф + ф), (AwJ ~ —бвтф, (А(оK ~ — 6 cos ф.
Рассмотрение уравнений для компонент 9} приводит к соответствующей
системе уравнений
7?!= - (г/2) 6 sin ф,
когда 6 и (Ф + ф) малы.
Следовательно, для бесконечно малого поворота, представленного
вектором Дш, спинорный оператор вращения равен
91 -> <*4 + (i/2) [(Aw),ox + (AwJo2 + (Аю),о3]. A.7.25)
Эти уравнения иногда можно использовать, чтобы проверить, не под-
подчиняются ли компоненты какого-либо неизвестного оператора правилам
преобразования 4-векторов.
Задачи к главе 1
1.1. При постоянном ф поверхности, заданные уравнением
= а2, 0 < ф < и,
Задачи к главе 1 109
являются эквипотенциальными поверхностями. Выразить ф через х, у, z;
подсчитать направляющие косинусы нормали к поверхности ф в точке
х, у, z. Показать, что ф является решением уравнения Лапласа. Каков
вид поверхности ф = const? ф = 0? ф = ¦к?
1.2. Уравнение
[Ух2 + у2— ф]2 + z2 = ф2 — а2, а<ф<оо,
при фиксированном ф определяет одну из поверхностей, образующих
семейство. Каков вид зтой поверхности? Каков вид поверхности в пре-
предельных случаях ф — а, ф=оо? Выразить ф через х, у, z и подсчитать
направляющие косинусы нормали к поверхности ф в точке х, у, z.
Является ли ф решением уравнения Лапласа?
1.3. Компонентами векторного поля являются
Показать, что, интегрируя уравнения линий тока, можно получить
функции тока <р и р., где
х la \ х* + у2
Показать, что существует псевдопотенциал, равный ф, где
Показать, что поверхности, на которых соответственно о, р., ф постоянны,
являются взаимно-ортогональными.
1.4. Три компоненты векторного поля суть
Fx = 3xz, Fy = 3yz, Fz=2z*-x*-y*.
Проинтегрировав уравнения линий тока, получить функции тока
х (ж2 + г/2 +
и показать, что псевдопотенциал равен
Является ли ф решением уравнения Лапласа?
1.5. Вычислить для силовых полей задач 1.3 и 1.4 поток через сферу
радиуса г с центром в начале, а также через две полусферы: одну
соответствующую z < 0, вторую —z> 0 (замыкаемые диском в плоскости
z = 0). Вычислить поток через те же поверхности для векторного поля
F
Z
1.6. Вычислить циркуляцию вдоль лежащей в плоскости ху окруж-
лости радиуса г с центром в начале координат для поля
р _ (ж—о) ^__ р __ _л у
х ()* + * * + *' V 2 + 2 ( J 2'
110 Гл. 1. Типы полей
Для поля задачи 1.3 вычислить циркуляцию вдоль окружности, опреде-
определяемой уравнениями ср = 0, р- = const.
1.7. Параболические координаты определяются следующими урав-
уравнениями:
<Р = |
Описать координатные поверхности (или дать их набросок). Выразить
коэффициенты Ламе и направляющие косинусы для этой системы через
х, у, z. Выразить х, у, z через X, р, <р и отсюда получить коэффициенты
Ламе и направляющие косинусы как функции от X, р, <р. Выписать
выражения для rot F, V2$. Подсчитать составляющие по X, р, ср следующего
векторного поля
в виде функции от X, р., ^- Выразить дивергенцию F через X, р., <р.
1.8. Функции тока у, у. и псевдопотенциал ф, данные в задаче 1.3,
образуют тороидальную систему координат. Описать эти поверхности
(или дать их набросок). Найти коэффициенты Ламе как функции х, у, z,
а также как функции р., ф, ер. Выписать выражения для rotF, divF
и VZU. Найти выражения составляющих вектора F из этой же задачи
вдоль координатных линий тороидальной системы; вычислить направле-
направление его линий тока.
1.9. Семейство поверхностей, которое можно использовать в качестве
семейства координатных поверхностей, задается уравнением
при постоянных ?. Показать, что два семейства, образующих вместе
с данным трехмерную систему координат, имеют вид
т. е. показать, что зти семейства взаимно ортогональны. Эта система
координат может быть названа экспоненциальной. Почему? Подснитать
коэффициенты Ламе и направляющие косинусы для преобразования
компонент вектора.
1.10. Бисферическая система координат определяется уравнениями
_ a sin ft cos ср _ a sin 8 sin ср _ a sh jj.
~~ ch\i. — cos ft ' У" ch|j.—cos 8 ' ~ ch|j.—cos ft
Описать эти поверхности (или дать их наброски) и определить факти-
фактические промежутки изменения |л. Ь, <р. Подсчитать коэффициенты Ламе
и направляющие косинусы. Выписать выражения лапласиана и градиента.
Показать, что поверхвости р. имеют постоянную кривизну, т. е. показать,
что величина
J_ ^_ J_ ^e
hb " зь - h9 ' а?
не зависит от & и ср и что поэтому эти поверхности являются сферами.
Задачи к главе 1 111
1.11. Выписать выражения для компонент производных но направле-
направлению (a»-V)A и (acp-VJB в сферических координатах и в сфероидальных
координатах
х = a ch u cos & cos ср, у = a ch p. cos & sin 9,
z = a sh p.sin&.
1.12. Скалярная функция ф (?х, ?2, ?3) B ортогональной криволинейной
системе координат ?х, ?2> ?3 может быть превращена в вектор умножением
на единичный вектор а,, нормальный к координатным поверхностям :.у.
Другой вектор может быть получен как rot A = rol (ахф). Показать, что Л
касателен к поверхности ?х. Какому уравнению должна удовлетворять О
и какие условия должны быть наложены на коэффициенты Ламе, чтобы
вектор А удовлетворял уравнению
1.13. Пользуясь тензорной записью, найти выражение для V X (иУ7и)
в общих ортогональных криволинейных координатах.
1.14. Мы можем определить кривизну координатных поверхностей ?м
по направлению Ъ,т как составляющую но а^ скорости изменения а)г
по отношению к расстоянию в направлении ат. Выразить обе кривизны
поверхности ?„ при помощи символов Кристоффеля.
1.15. Вывести выражения для символ on Кристоффеля и для кова-
риантной производной компонент /;=/'^^ Для бисферических координат,
приведенных в задаче 1.10, и для параболических координат, определен-
определенных равенствами
a: = Xp.cos<p, у = Xp.sin о, z =-^ (X2 — |х2).
1.16. Дать явные выражения компонент симметрического аффинора
-„-(VA + AV) для сфероидальных координат, приведенных в задаче 1.11,
и для эллиптических цилиндрических координат, задаваемых равенствами
a;=achXcos«, г/ = ashXsin<p, z = z.
Дать также выражения для лапласиана вектора в обеих системах.
1.17. Найти главные оси аффинора деформаций
4?
+kk ~аху ^+&
в точке (х, у, z). Чему равны удлинения вдоль этих осей (главные
удлинения)?
1.18. Разбить аффинор
на симметричную и кососимметричную части. Найти вектор вращения
для кососимметричного аффинора и главные оси симметричного аффинора.
Какой вид будет иметь аффинор после приведения к этим главным осям0
1.19. Написать разложение аффинора
H2 Гл. 1. Типы полей
-на составляющие в цилиндрических координатах
г = Ух* + г/2, 9 = arctg JL , z.
После этого выделить его симметричную и кососимметричную части
и определить вектор вращения для кососимметричной части и главные
оси для симметричной.
1.20. Вектор смещения s можно представить в виде суммы градиента
скалярного потенциала 9 и вихря векторного потенциала А. Получить
в случае общих ортогональных координат $1? Ё2, ?3 выражение аффинора
напряжений
Г = —(Vs + sV), s = grad 9 + rot A,
через 9 H компоненты А вдоль ?х, ?2, ?3. Выписать явный вид этих выра-
выражений для цилиндрических координат ?', ф, z и для сферических коор-
.динат г, &, 9-
1.21. В некоторых случаях, вектор смещения s для упругой среды
может быть представлен выражением 8 = гоЦа2ф), где ф —некоторая
функция цилиндрических координат г, <р, z. Показать, что когда
ф = 7-2/(9, z) + g{r, z), то все три диагональных члена аффинора равны
нулю. Найти аффинор деформаций и определить главные оси и главные
удлинения для случая ф = zr2 cos 9-
1.22. Показать, что возможные смещения упругой среды, дающие
нулевые диагональные члены в тензоре деформаций ©, записанном для
сферических координат г, &, <р, могут быть представлены в виде суммы
двух векторов rot (a97* sin &g (9)) и rotasJ'/(&)). Найти аффинор деформаций,
главные оси и главные удлинения для двух случаев
s = rot (&9r sin & cos 9) и s = rot (a»7- sin B&)).
1.23. Три связанных осциллятора удовлетворяют системе уравнений
Выразить эти уравнения при помощи абстрактного векторного простран-
пространства и векторных операторов. Найти главные оси оператора и таким
образом собственные частоты этой системы.
1.24. Система из TV—1 связанных осцилляторов имеет следующее
уравнение движения в абстрактном векторном представлении:
JV
где R= 2 ^п(^)еп' с граничными условиями уо = уи = 0\ здесь оператор II
действует на единичные векторы еп (соответствующие амплитуде колеба-
колебаний уп для п-го осциллятора) согласно уравнению
Показать, что главные оси этого оператора U имеют направления
Задачи к главе 1 113
собственных векторов
(^)n, m = 1, 2, 3, ..., N- 1,
71=0
иными словами, что И• am = umam. Найти собственные значения ит и, таким
образом, допустимые частоты этой системы. Найти такие значения постоян-
постоянных Ст, чтобы новые векторы в.т были единичными векторами. Показать,
что векторы ат взаимно-ортогональны.
1.25. Доказать неравенство треугольника
1.26. Эрмитов оператор й, удовлетворяющий неравенству (е*-91-е)>0
для всех векторов е, называется положительно определенным. Показать,
что если ffi — положительно определенный оператор, то
1.27. а. Показать, что
где
[©, si = [©s:-a©] и is, [©,«]] = ©[©, Ж]-[©,г]©.
б. Из «а» получить разложение
, Щ +^[S, [©, Я]] +
в. Показать, что если р и q — два оператора, таких, что Ц), q] = i, то
1.28. Если еп и fn — два множества ортогональных векторов (т. е.
e*-f =0), то проекционный оператор ^J на множество еп определяется
равенствами феп = еп, 5}5fp = 0. Показать, что
а. $2 = $.
б. $* = $.
в. Если $Р2 = $Р, $* = $ и выбрано множество таких векторов еп,
что феп = еп, то $Р есть оператор проектирования на это множество.
г. Если ^ и $р2 являются операторами проектирования на два раз-
различных множества векторов, то необходимым и достаточным условием
для того, чтобы $^2 был проекционным оператором, будет ^^ — Ч$2$1 = 0.
1.29. Четырехмерной системой координат, аналогичных сферическим,
является система (х, а, и, ад), где
хА (= id) = ct ch a, x= ictshacosft,
г/ = icx sh a sin & cos 9, z = гсх sh a sin & sin 9,
а преобразованием Лоренца служит любое преобразование, оставляющее
масштаб t инвариантным. Вычислить коэффициенты Ламе и направля-
8 Ф. М. Морс и Г. Фешбах
114 Гл. 1. Типы полей
ющие косинусы и показать, что уравнение ?2ф=0 преобразуется к виду
Показать, что решением этого уравнения является ф=A/х3)сЬа. Найти
составляющие по х, у, z, t 4-вектора, являющегося четырехмерным
градиентом ф. Показать, что это есть истинный 4-вектор.
1.30. Частица с массой покоя т0, двигаясь со скоростью v в направ-
направлении х, сталкивается с другой частицей, находившейся в состоянии
покоя (относительно наблюдателя А) и имевшей ту же массу покоя.
Частицы отскакивают друг от друга без изменения суммарной энергии-
импульса, причем частица, наносившая удар, отклоняется от оси х
на угол 6 (относительно того же наблюдателя). Найти 4-векторы энер-
энергии-импульса для обеих частиц до и после столкновения относительно
наблюдателя А (неподвижного до момента удара относительно частицы,
получившей удар) и относительно наблюдателя В, неподвижного относи-
относительно центра инерции этой пары. Объяснить получающееся различие.
1.31. Для наблюдателя А, неподвижного относительно некоторой
жидкости, эта жидкость находится под однородным изотропным давле-
давлением р. Вычислить ее плотность, плотность импульса и давление в жидко-
жидкости для наблюдателя В, движущегося относительно жидкости со ско-
скоростью, равной 0,8 скорости света.
1.32. Найти направляющие косинусы преобразования спиновых векто-
векторов, соответствующего комбинации из преобразования Лоренца (вдоль
оси х) и пространственного поворота.
1.33. Пусть достоверно известно, что спин электрона ориентирован
в положительном направлении оси х для наблюдателя, находящегося
в покое относительно этого электрона. С какими вероятностями для
наблюдателя В, движущегося относительно этого электрона вдоль оси х
со скоростью и, спин может быть расположен в положительном или
отрицательном направлении оси х? Какова вероятность, что для наблюда-
наблюдателя А спин этого электрона будет расположен под углом 45° к поло-
положительному направлению оси х? А для наблюдателя В?
1.34. Пусть а является трехкомпонентным векторно-спиновым опера-
оператором с компонентами alt c2, с3.
а. Показать, что если А — вектор, то
(o-A)o==A + i(o X А),
О (О• А) = А — i (a x A),
О X a = 2ia,
а х (О X А) = i {а X А) — 2А.
б. Показать, что если а — единичный вектор, а X — постоянная, то
р- ехр.(г'Хо • а) = — ехр (?Хст • а)
и, следовательно,
ехр (ika -а) = cos X + i (о • а) sin X.
Таблица векторных и аффинорных соотношений 115
Таблица наиболее употребительных векторных
и аффинорных соотношений
А В = АХВХ + АуВу + AZCZ; A X В = i (AyBz - AzBy) +
+ 3 (AZBX - АхВг) + k (AxBy _ AyBx),
(Ах В) х С=(А-С)В-(В-С)А,
Ах (ВхС) = (А-С)В-(А-В)С,
А (В х С) = (А х В)-С = (С х А)-В = С-(А х В) = В(С х А) = (В х С)-А,
(А х В)-(С х D) = (A-C)(B-D)-(A-D)(B.C),
(А х В) х (С х D) = [А-(В х D)] С- [А-(В X С)] D =
= [А-(Сх D)]B-[B-(Cx D)]A,
VM = gradM, V-F = divF, VxF=rotF,
V (uv) = uVv + vVu, V -(kA) = (Vu) • A+ uV ¦ A,
V X (mA) = (Vb) X A + iiV X A,
V-(A x B) = B-(V X A)-A-(V X B),
V-(VxF) = 0, Vx(Vu) = 0, V-(Vu) = V4
V X (V X F) = V(V-F)-V2F,
где тройные интегралы берутся по всему объему, ограниченному замкну-
замкнутой поверхностью А, а двойные интегралы —по этой поверхности А
(вектор dA направлен наружу).
где двойной интеграл берется по площади, ограниченной замкнутой кри-
кривой С, а одномерный интеграл — по кривой С против часовой стрелки
для наблюдателя, смотрящего с конца вектора dA.
Векторное поле F (х, у, z) может быть представлено при помощи
скалярного потенциала ф и векторного потенциала А
F = grad ф + rot A, div А = 0.
Если поле F обращается в нуль на бесконечности, то выражения ф и А
через F имеют вид
где Я2 = (х-x'f л. {у-y'f + (z-z'f.
% = iAx + jAy -f kA2, 91* = iAS + jA* + kA2* = Aj + Ayj + Azk,
k-A,,
= i (Ax + AJ) Bx +1 (Ay + A*) By +1 (A, + A2*) Bz —I {Щ x B,
116 Гл. 1. Типы полей
x (V хВ) + Вх (V х А),
rot (А х В) = В • (V А) - А • (VB) + А (V • В) - В (V • А),
V • % = (дАх/дх) + (дАу/ду) + (dAjdz) = i div (A*) 4 j div (A*) + к div {At),
x V x F,
Таблица свойств криволинейных координат
Для ортогональных криволинейных координат ?х, ?2, ?3 с единичными
векторами в!, а2, а3, линейным элементом ds2 = ^ ft^ (d?nf и коэффициен-
тами Ламе hn, где
дифференциальные операторы принимают следующий вид:
I, m, n
I, т, п = 1, 2, 3 или 2, 3, 1 или 3, 1, 2,
VA = (VA), + (VA)a, (VA)a = I (rot A) x 3,
»n<n
а элемент объема равен h1h2hs d^ dl2 dl3 = dV.
Для цилиндрических координат
имеем /^ = 1, h2 = r, /г3 = 1, dV = rdrdydz.
t
т S [ Si ж "fef"+"й" жг "a?" J(атЭп+arAn)-
<
dAz
. д С 1 8АХ дА<р\ , С дАг дАг \ , Г 1 9 . I dAr \
rot А = а. ( = ^- -4- аф ( —^ ^— ) -+• ar I —^— гА,р ¦=— )
г \ Г Of OZ у г \ OZ ОГ у г \ Г ОГ Y Г Otf J
Литература Ц7
1 f dA<p , l дАг
[ +
2 [ dz
Для сферических координат ?1 = г, Е2 = &, Е3 = ю имеем й,=1,
rsin&, dV = г2 dr sin Sdbd
1 9 Г , 9d>
.-*[¦
r2 sin2 a+ r2 99 r2 sin2 » 9cf J
4r 2cos»
2 9ЛГ 2 cos» \ ,
9cf J +
os» ^» 1
in2a Я9 J'
l r l ал, sina 0 ^ av -\л
ЛИТЕРАТУРА
В предисловии уже упоминалось, что эта литература не претендует на полноту.
Включены только те книги и статьи, которые, по мнению авторов, содержат полезные
дополнения к данному тексту.
Общие справки по материалу этой главы:
Вебстер А. Г. и Сеге Г., Дифференциальные уравнения математической физики,
ч. 1—2, ГТТИ, М.—Л., 1933—1934.
Курант Р. и Гильберт Д., Методы математической физики, Гостехиздат,
М., 1951.
Соболев С. Л., Уравнения математической физики, Гостехиздат, М., 1954.
118 Гл. 1. Типы полей
Тихонов А. Н., Самарский А. А., Уравнения математической физики, Гос-
техиздат, М., 1950.
Франк Ф. и Мизес Р., Дифференциальные и интегральные уравнения математи-
математической физики, ГТТИ, Л.—М., 1937.
Jeffreys H. J., Jeffreys В. S., Methods of Mathematical Physics, Cambridge,
New York, 1946.
Joos G., Lehrbuch der theoretischen Physik, Lpz., 1956.
Margenp H., Murphy G. M., The Mathematics of Physics and Chemistry,
New York, 1943.
Murnaghan F. D., Introduction to Applied Mathematics, New York, 1948.
Slater J. C, Frank N. H., Introduction to Theoretical Physics, New York, 1933.
Дополнительный материал по векторному и тензорному анализу:
Кочин Н. Е., Векторное исчисление и начала тензорного исчисления, Изд. АН
СССР, М., 1951.
Фрезер Р., Дункан В. и Коллар А., Теория матриц и ее приложения к диф-
дифференциальным уравнениям и динамике, Изд. иностр. лит., М., 1950.
Шилов Г. Е., Лекции по векторному анализу, Гостехиздат, М., 1954.
С г aid H. V., Vector and Tensor Analysis, New York, 1943.
Gibbs J. W., Vector Analysis, ed. by E. B. Wilson, New York, 1901.
Phillips H. В., Vector Analysis, New York, 1933.
Rutherford D. E., Vector Methods Applied to Differential Geometry, etc., Edin-
Edinburgh, 1944.
Weatherburn С. Е., Elementary and Advanced Vector Analysis, 2 vols., London
1928.
Книги по теории упругости:
Ляв А., Математическая теория упругости, М.—Л., 1935.
Тимошенко С. П., Теория упругости, ОНТИ, М., 1937.
Brillouin L., Les tenseurs en mechanique et en elastique, Paris, 1938.
Sokolnikof f I. S., Mathematical Theory of Elasticity, New York, 1946.
Работы, содержащие полезные сведения по различным аспектам теории абс-
абстрактного векторного пространства:
Ахиезер Н. И. и Глазман И. М., Теория линейных операторов в гильберто-
гильбертовом пространстве, Гостехиздат, М., 1950.
В а н-д ер Варден Б., Метод теории групп в квантовой механике, ГТИ Украины,
Харьков, 1938.
Дирак П. Основы квантовой механики, Глав. ред. тех.-теор. лит-ры, Л.—М.,
1937.
К он дон Е. и Ш о р т л и Г Теория атомных спектров, Изд. иностр. лит., М.,
1949.
Шифф Л., Квантовая механика, Изд. иностр. лит. М., 1957.
Laporte О., Uhlenbeck G. E., Application of Spinor Analysis to Maxwell and
Dirac Equations, Phys. Rew., 37, 1380 A931).
Von Neumann J., Mathematische Grundlagen der Quantenmechanik, Berlin, 1932.
Rojansky V. В., Introductory Quantum Mechanics, New York, 1938.
Stone M. II., Linear Transformations in Hilbert Space, American Mathematical
Society, New York, 1932.
Книги, содержащие разделы, посвященные специальной теории относитель-
относительности:
Бергман П., Введение в теорию относительности, Изд. иностр. лит., М., 1947-
Голдстейн Г., Классическая механика, Гостехиздат, М., 1957.
Ландау Л., Лифшиц Е., Теория поля, ГТТИ, М., 1948.
Эддингтон А., Математическая теория относительности, Гос. научно-техн. изд.
Украины, Харьков—Киев, 1933.
Corben H. С, Stehle P., Classical Mechanics, Chaps. 17 and 18, New York, 1950.
Tolman Ft. C, Relativity, Thermodynamics and Cosmology, Oxford, New York, 1934.
Г Л А В А 2
Уравнения полей
Физические явления, которые могут быть описаны с помощью полей,
связаны с положением точек и со временем таким образом, что обычно
эту связь можно выразить посредством дифференциальных уравнений
с частными производными. Изменение поля в какой-либо точке влияет
на его значения в соседних точках, эти последние изменения отража-
отражаются на значениях в точках более отдаленных и так далее; имеет место
взаимозависимость, которая наиболее естественно выражается через
пространственные и временные частные производные. Таким образом,
поле, соответствующее определенной физической ситуации обычно
является решением некоторого дифференциального уравнения с частными
производными, а именно частным решением, удовлетворяющим определен-
определенной совокупности подходящих для данной ситуации «граничных условий».
Большая часть этой книги будет посвящена отысканию для специ-
специальных видов дифференциальных уравнений с частными производными
частных решений, удовлетворяющих данным граничным и начальным
условиям. Однако эта и следующая главы будут посвящены рассмотре-
рассмотрению способов нахождения дифференциальных уравнений, соответствующих
данной физической задаче. Этот процесс выделения наиболее важных
взаимозависимостей в изучаемом явлении с целью выражения и изучения
их в дифференциальной форме является одной из наиболее трудных
задач физика-теоретика.
Мы не будем пытаться рассмотреть все дифференциальные уравнения
с частными производными, которые оказались полезными в физике; зто
потребовало бы полного обзора всей физики. Даже относительно тех
уравнений, которые здесь выводятся, мы будем предполагать, что физи-
физическая сторона дела достаточно известна и что рассматриваемые вели-
величины не требуют подробных пояснений. Такие пояснения можно найти
в других источниках. Пас здесь интересует лишь процесс получения
дифференциального уравнения из условий физической задачи.
Мы обнаружим, что некоторые типы дифференциальных уравнений
вновь и вновь появляются в самых разнообразных ситуациях и что,
следовательно, детальное изучение решений этих сравнительно немного-
немногочисленных уравнений даст нам возможность решать проблемы в чрезвы-
чрезвычайно большом числе случаев, представляющих интерес с точки зрения
физики.
2.1. Гибкая струна
Прежде чем перейти к более сложным вопросам, полезно подвергнуть
детальному рассмотрению пример одномерной задачи, с тем чтобы выявить
некоторые приемы и понятия в их простейшей форме. Гибкая натянутая
120 Гл. 2. Уравнения полей
струна является хорошим примером этого рода, так как он достаточно
нагляден и хорошо знаком большинству читателей.
Физическим прототипом здесь является струна вижнего регистра форте-
фортепиано, представляющая собой более или менее равномерно нагруженную
проволоку, натянутую между двумя абсолютно жесткими зажимами.
Такая струна обладает жесткостью, но, как показывает опыт, сопро-
сопротивление перемещению струны из положения ее равновесия в значительно
большей степени вызвано ее натяжением, нежели жесткостью. Поэтому
при выводе уравнения струны обычно допускают упрощение, пренебрегая
жесткостью (в некоторых книгах по колебаниям и теории звука исследуется
и влияние жесткости и устанавливается, в каких случаях ею заведомо
можно пренебречь). Другие упрощающие предположения состоят в том,
что масса струны равномерно распределена вдоль ее длины, что натяже-
натяжение также равномерно и что отклонение точки струны от положения
равновесия мало по сравнению с расстоянием этой точки от ближайшего
закрепленного конца струны. Два последних предположения не незави-
независимы друг от друга.
Форма такой струны в любой момент может быть выражена через
ее отклонение от положения равновесия. Более точно: каждую точку
струны мы задаем ее расстоянием х от некоторой начальной точки,
измеренным в тот момент, когда струна находилась в положении равно-
равновесия (имела форму прямолинейного отрезка, соединяющего точки опоры).
Перемещение ф(ж) точки х, отсчитываемое от ее положения равновесия,
есть функция х (а иногда и времени). Если рассматривать движение
только в плоскости, то поле ф (ж)> соответствующее этому примеру,
будет скалярным одномерным полем.
Силы, действующие на элемент струны. Рассматривая рис. 2.1, мы
видим, что при малом наклоне dty/dx струны результирующая сила
FT(x)dx, действующая на участок струны между точками х и x-\-dxt
вызванная натяжением Т струны, равна
FT(x}dx = T-(d$/dx)x.dx-Щд$/дх)х или FT (x) = Т-(д2$/дх*) B.1.1)
и имеет направление, примерно совпадающее с направлением перпендику-
перпендикуляра к линии равновесия. Эта результирующая сила, вызванная натяже-
натяжением, действующим на элемент струны в точке х, которая стремится
вернуть струну в положение равновесия, пропорциональна скорости
изменения наклона струны в точке х. Она стремится выпрямить каждый
участок струны: если кривизна положительна, она направлена вверх,
если кривизна отрицательна, она направлена вниз. Таким образом, сила
зависит только от формы участка струны в непосредственной близости
от точки х и не зависит от формы струны в пелом. Однако если струну
предоставить действию этой силы, то струна только тогда придет в равно-
равновесие, когда каждый участок струны станет прямолинейным. Таким
образом, дифференциальное уравнение струны, хотя и имеет дело только
с формой каждого элементарного участка струны, в итоге налагает опреде-
определенные ограничения на форму всей струны в целом.
В действительности на струну фортепиано действуют и другие
силы —сила, вызванная жесткостью струны (которой, как мы уже гово-
говорили, во многих случаях можно пренебречь), и сила трения воздуха,
в котором струна движется, а также и некоторые другие силы.
Сила трения при движении в воздухе также относительно мала;
если нас интересует движение в течение короткого промежутка времени
или же форма струны, когда она неподвижна, этой силой также можно
пренебречь. Другие силы, которые могут играть роль —это сила тяжести,
2. 1. Гибкая струна
121
действующая на каждый участок струны (если струна натянута горизон-
горизонтально), и сила, исходящая от молоточка фортепиано, или пальца арфиста,
или смычка скрипача. Какие из этих сил нужно включить в уравнение,
определяющее форму струны, зависит от того, какой частный случай
рассматривается.
г
j j Лини» равновесии
x x*dx
Рис. 2.1. Силы натяжения Т, приложенные к
элементу струны, и их равнодействующая Fj.
Уравнение Пуассона. Струна может быть подвергнута, например,,
действию не зависящих от времени поперечных сил, распределенных по ее
длине, и нас может интересовать форма равновесия струны, возникшая
в результате одновременного действия этих внешних сил и сил, вызванных
натяжением. В этом случае зависимость от времени отсутствует и диффе-
дифференциальное уравнение, определяющее форму струны, имеет вид
Пх) = Ш-, B.1.2)
da:2
где поперечная сила, приложенная к элементу струны, лежащему между
х и x-\-dx, равна F(x)dx. Здесь эта приложенная поперечная сила уравно-
уравновешена в каждой точке результирующей поперечной силой, вызванной
натяжением Т. Уравнение B.1.2) представляет собой одномерный случай
уравнения Пуассона.
В качестве одного из случаев, описываемых этим уравнением, рас-
рассмотрим горизонтальную струну, на которую действует сила тяжести,
вызванная ее собственным весом. Если каждый сантиметр длины струны
весит р г, то сила F (х) равна — pg, где g — ускорение силы тяжести.
Общим решением полученного уравнения d2ty/dx? = pg/T является ф = а +
-\-bx + (pg/2T)x2, где с и Ъ определяются из «граничных условий». Если
оба конца струны закреплены жестко (т. е. если их смещениями можно-
пренебречь) и находятся друг от друга на расстоянии L, то эти гранич-
граничные условия имеют вид ф = 0 при х = О
и при x = L. Нетрудно видеть, что квад-
квадратичная функция от х со старшим чле-
членом (pg/2T)x2, обращающаяся в нуль
при х = 0 и при х = L, имеет вид ф =
= (pg/271) x(x — L). Это, следовательно, и
есть решение задачи. Форма струны —
* • /
Сила рд но единицу длины
Рис. 2.2. Форма натянутой струны,
парабола с приблизительно постоянной находящейся под действием по-
кривизной pg/T и наибольшим смеще- перечных сип тяжести,
нием в середине струны1).
Некоторые интересные общие свойства решений уравнения B.1.2)
вытекают из того факта, что ф входит в уравнение в первой степени.
Например, если ф есть решение уравнения B.1.2) для заданной функции
г) При малых по абсолютной величине значениях д\>/дх (что имеет место
в рассматриваемом случае) кривизна струны (82^>/дх2) ¦ [1 + (дЬ/дхJ]-3!?. приблизительно
равна 82]>/дх2. —Прим. ред
122 Гл. 2. Уравнения полей
f(x), то аф есть решение уравнения d2§/dx2= —af(x). Это новое решение
часто также удовлетворяет тем же граничным условиям, что и ф (это
имеет место, например, для струны с двумя закрепленными концами).
Аналогично если ф2 есть решение уравнения d^/dx2 = — f1 и ф2 — решение
уравнения d2ty/dx2 = — /2, то ф = фг + ф2 есть решение уравнения
Оба эти свойства будут многократно использованы в этой книге.
Сосредоточенная сила. Дельта-функция. Во многих случаях, имеющих
практический интерес, поперечная сила приложена лишь к малому
участку струны. Это внушает мысль о довольно оч евидной идеализации —
о силе, приложенной в «одной точке» струны. С математической точки
•зрения эта идеализация соответствует рассмотрению предельного случая
•силы
[о, *<«--§-,
(о, &+4
при стремлении к нулю длины Д участка струны, к которому приложена
¦сила.
Подобные идеализации сосредоточенных сил, электрических зарядов
и т. д. будут очень полезны в наших последующих рассуждениях. Они
все могут быть выражены с помощью одной «патологической функции»,
называемой дельта-функцией:
Го, *<-А
(О, А < х.
Мы. называем ее «патологической функцией» потому, что она не обладает
«физически нормальными» свойствами непрерывности и дифференцируе-
мрсти в точке ж = 01). Однако если от этой функции не требовать слишком
многого, она окажет значительную помощь в дальнейшем исследовании
многих задач. Вспоминая обычное определение интеграла, как предела
¦сумм, можно вывести следующее интегральное правило для дельта-функ-
дельта-функции:
со
" /E)8F-я) # = /_(*). B.1.5)
Тесно связанной с дельта-функцией и иллюстрирующей интегральные
свойства последней является единичная ступенчатая функция
0, х<0,
B.1.6)
1, х>0.
*) Дельта-функция даже не является функцией в обычном понимании этого
¦слова, представляя собой простейший пример обобщенных функций. См. об этом
Минусинский Я., СикорскийР., Элементарная теория обобщенных функций,
вып. 1, Изд. иностр. лит., М., 1958. —Прим. ред.
2. 1. Гибкая струпа 123
Эта функция является также не совсем обычной: дифференцирование
ее возможно только с известными предосторожностями1).
Обращаясь теперь к задаче о решении уравнения B.1.2), мы сначала
ищем решение уравнения в случае силы, сосредоточенной в точке х = ?
Решение этого уравнения ф удовлетворяет однородному уравнению
'х2 = 0 во всех точках, где х ф ?. Чтобы изучить поведение ф в точке
ж=?, интегрируем обе части урав-
уравнения по промежутку от х = ? — а до
# = ?-(-?, где г —исчезающе малая
величина. Воспользовавшись равен- - ,
ством B.1.6), мы видим, что в точ- ' F х~
ке i = J угловой коэффициент каса- Рис. 2.3. Форма струны, на которую
тельной к графику решения дол- действует одна сила в точке ж=5.
жен иметь единичный скачок. Если
опоры жестлше, то форма струны длины L для силы F = T, сосредото-
сосредоточенной в ж = ?, определяется равенствами
B.1.7)
Функция G(x\%) называется функцией Грина уравнения B.1.2) для точки
ж = ?. Отсюда мы видим, что решение для струны, находящейся под
действием силы F, сосредоточенной в точке ж=?, имеет вид (F/T) G (х | ?)
и что решение для двух сил —одной Fx, сосредоточенной в точке ?х,
и другой/^, сосредоточенной в Е2,—имеет вид (F1/T)G(x\%1)-\- (F2/T)G(x\?2).
Переходя от сумм к интегралам и пользуясь равенством B.1.5), мы
видим, что форма равновесия струны, на которую действует не завися-
зависящая от времени поперечная сила F (х) и которая находится под дейст-
действием натяжения Т между двумя жесткими опорами, удаленными друг
от друга на расстояние L, определяется равенством
L
*fi B.1.8)
Таким образом, функция Грина, которая является решением для случая
силы, сосредоточенной в точке ж=?, может быть использована и для
получения решения уравнения Пуассона в случае, когда сила имеет
произвольный вид и распределена вдоль струны.
Этот прием получения решения общего уравнения с помощью интег-
интеграла, содержащего функцию Грина, Ешторая является решением простого
частного случая уравнения, подробнее будет рассмотрен дальше.
Волновое уравнение. В связи с другими задачами нам представляется
¦более интересным изучение движения струны после того, как приложен-
приложенные силы исчезли, чем нахождение устойчивой формы струны под влия-
влиянием приложенных поперечных сил. Простейший случай, который
является также одним из наиболее интересных, —это случай, когда
можно пренебречь всеми силами, кроме сил, вызванных натяжением Т
струны. Если масса струны равномерно распределена и составляет р г
*) Из приведенного соотношения B.1.6) видно, что производной единичной сту-
ступенчатой функции является дельта-функция. —Прим. ред.
124
Гл.- 2. Уравнения полей
на единицу длины, уравнение поперечного движения получается при-
приравниванием произведения р (dx) (д2ф/Ш2) массы каждого элемента длины1
струны на его ускорение поперечной силе, вызванной натяжением'
и действующей на тот же элемент Tdx(d2ty/dxz), определенной равенством'
B.1.1). Полученное уравнение
а2ф 1 а2ф 2__2L (9 4 Qv
~дх2~~~с2"~д1г' с ~Т' у*л-уг
по причинам, которые вскоре станут ясными, называется волновым урав-
уравнением. Оно утверждает, что поперечное ускорение любого участка
струны пропорционально кривизне этого участка1).
Волна может быть грубо описана как некоторая конфигурация среды
(форма струны, распределение плотностей в жидкости и т. д.), переме-
перемещающаяся по среде с определенной скоростью. Скорость распространения
волны не связана необходимо со скоростью любого участка среды.
В самом деле, для волн, определяемых простым уравнением B.1.9),.
скорость волны совершенно не зависит от скорости участков среды;:
другими словами, если уравнение B.1.9) имеет место, то скорость любой
волны на струне будет одна и та же, какую бы форму ни имела эт„а
волна. Волна движется вдоль струны со скоростью с, в то время как
точка струны движется поперек струны вверх и вниз со скоростью dty/dtr
определяемой формой проходящей волны.
Представление для волны этого типа может быть найдено, если
принять, что отклонение струны от положения равновесия есть функция
от ж — ct для волны, распространяющейся в положительном направлении
оси х, и от x-\-ct для волны, распространяющейся в отрицательном
направлении оси х. Чтобы показать, что уравнение B.1.9) определяет
такое движение, можно сделать замену пе-
переменных, взяв за новые переменные вели-
величины % = х — ct и ti = x-\-ct.
f=i . is- ^j Тогда
д — д д^ х-— 0Y) д д
'=г "" ^"^ ^ ~дх ~~ ~Ш ~дх "*" ~дг\ дх ~ а? eh) '
8* _ а2 ^«> _??!__!_ _Ё!_
Их2
t'4
t~0
t=3
at2
as2
Следовательно, уравнение B.1.1) принимает
вид
Решением этого уравнения служит ф =
+ ^(т)), где / и F — любые функции, удо-
удовлетворяющие требованиям непрерывности
Рис. 2.4. Волновое движение и имеющие малые амплитуды, что было пред-
струны; доказаны волны, рас- положено при выводе уравнения B.1.9). Как
пространяющиеся в противо- мы увидим дальше, это и будет наиболее об-
полояшых направлениях. щИМ решением уравнения B.1.9), так что
наиболее общее движение струны всегда пред-
представляет собой наложение волны, движущейся направо, и другой волны,
движущейся налево, причем обе волны движутся с постоянной скоро-
скоростью, одной и той же для обеих волн, и имеют неизменную форму>
1) См. примечание на стр. 121. — Прим. ред.
2. 1. Гибкая струна 125
Заметим, что в случае, когда с есть скорость света, волновое урав-
уравнение будет инвариантным относительно преобразования Лоренца, так
как тогда выражение E2ф/дж2) — A/с2) (d2ty/dt2) является скаляром, полу-
полученным сверткой тензора второго порядка d2ty/dxndzm, и, следова-
следовательно, инвариантно относительно пространственно-временного враще-
вращения, имеющего вид, рассмотренный в первой главе. Линии \ = x — ct
и т]= х ct представляют собой мировые линии нулевой собственной
длины (c2dt% — dx2 = 0) и изображают лучи света.
Простое гармоническое движение, уравнение Гельмгольца. Иногда
волновое движение в его зависимости от времени будет синусоидальным,
так что можно выделить (как часто говорят, «отделить») множитель,
зависящий только от времени и имеющий вид е~ш. Так как мы усло-
условились применять только действительную часть комплексного решения,
этот множитель и дает синусоидальную зависимость от времени. Постоян-
Постоянная о) называется угловой скоростью колебания, а величина v = o)/2iu —
частотой колебания волны.
Подставив выражение ф = v [x) e~iat в волновое уравнение B.1.9),
¦получим для пространственной части ф уравнение
которое называется уравнением Гелъмголъца.
Мы увидим дальше в этой книге (но будет хорошим упражнением
.для читателя —показать самому это теперь), что функция Грина [см.
исследование уравнения B.1.7)] этого уравнения для бесконечной струны,
•соответствующая силе Te~iwt, сосредоточенной^ точке х = 0, имеет вид
4 КО,
•Общее выражение для любой приложенной силы, имеющей синусоидаль-
синусоидальную зависимость от времени с частотой <«/2ic, получается в виде инте-
.грала, аналогичного интегралу B.1.8).
Волновая энергия. Так как волны распространяются в обоих напра-
направлениях с постоянной скоростью и не изменяя своей формы, естественно
¦ожидать, что волновая энергия, однажды сообщенная струне, распро-
распространяется без потерь. Полная энергия струны составляется из суммы
кинетических энергий отдельных элементов струны
.(интегрирование производится по длине струны) и полной потенциаль-
потенциальной энергии струны. Если форма струны в момент t определяется функ-
функцией ф (х, t), то потенциальная энергия может быть найдена, если вообра-
вообразить, что эта форма струны получилась под действием поперечной рас-
распределенной силы такой величины, что, двигая медленно струву,
она перемещает ее из положения равновесия и придает ей окончатель-
окончательную форму ф (х, t). Можно принять, что промежуточные формы струны
определяются функцией Рф, где Р меняется от нуля до единицы по мере
того, как струна движется. Чтобы достигнуть промежуточной формы
струны Рф, нужно к элементу ее dx приложить силу — Т$ (d2ty/dx2) dx;
эота этой силы при перемещении этого элемента из положения рф
126
Гл. 2. Уравнения полей
в положение (Р + <ф)ф равна — Уф (о2ф/9х2)с?жрdp. Полная работа, соот-
соответствующая движению струны из положения равновесия ф = 0) к ее
окончательному положению ф(Р=1), равна, следовательно,
Полная энергия, которой обладает участок струны от точки х = а до х = Ь,
имеет поэтому вид
где окончательная симметричная форма получена интегрированием по ча-
частям члена, определяющего потенциальную энергию.
Если концы а и b струны жестко закреплены, то <]> равно нулю»
в точках а и Ъ и последний член в симметричном выражении обра-
обращается в нуль. Таким образом, энергия всей струны пропорциональна
интегралу по длине струны от квадрата скорости каждого элемента,
сложенного с произведением с2 на квадрат наклона каждого элемента.
Применение этого выражения для подсчета энергии только части
струны не дает единственно возможного результата, так как вопрос
об энергии «концов» выбранного участка не может быть решен одно-
однозначно. Вполне определенной величиной является энергия всей струны,,
включая опоры, так как только эта энергия сохраняется. Этот факт
может быть показан более наглядно, если подсчитать потенциальную-
энергию части струны другим спосббом и убедиться в том, что это
дает другой результат. Например, из-за отличия формы ф (х) от формы
равновесия струна растягивается. Соответствующая избыточная энергия,
вызванная растяжением, будет как раэ потенциальной энергией струны,
так как она равна работе, произведенной главной (горизонтальной)-
составляющей натяжения Т. Длина элемента dx струны благодаря рас-
растяжению становится равной J/1 + (dty/dxf dx. Потенциальная энергия,
получающаяся в результате действия постоянной силы Т, таким обра-
образом, имеет величину
Последнее выражение с точностью до членов второго порядка равно-
п q - 1 ri
так что энергии W..(«, Ь) имеет вид
Сравнивая это с нашим предыдущим выражением, мы видим, что оба
они различаются слагаемым — у ТЩд^/дх]\, которое зависит только»
2. 1. Гибкая струна 12?
от значений в концах а и Ь. Каждый из этих результатов одинаково
пригоден для всей струны, так как если а и b являются концами ее
(которые жестко или свободно закреплены1), так что энергия не пере-
передается опорам), то оба выражения совпадают друг с другом. Только
в этом случае результат будет единственным. Так как выражение B.1.11)
проще, мы будем употреблять его в дальнейших рассуждениях.
Поток энергии. Скорость изменения энергии части струны, лежащей
между а и Ъ, получается дифференцированием W{a,b) по времени
дх dt J J дх
а а
Таким образом,
W( Ь) Т \д±^УТ('д±дЛЛ _Т(д±д±Л
Эти два члена представляют собой поток энергии внутрь струны или
изнутри ее через два конца. Если —Т (db/dt) (д^/дх) представляет собой
поток энергии в положительном направлении оси х через точку х, то
первый член правой части представляет поток энергии внутрь участка
струны через его правый конец (Ь>а), а второй член—поток энергии
внутрь участка струны через левый конец.
Нетрудно проверить, что — Т (d<b/dt) (ду/дх) равно потоку энергии
вдоль струны в положительном направлении оси х, так как —Т (dty/dz)
равно поперечной силе, с которой часть струны, лежащая слева от х,
действует на часть струны, расположенную правее, вызывая ее движе-
движение, a dty/dt есть поперечная скорость точки ж струны. Сила, умноженная
на скорость, как известно, равна мощности или потоку энергии.
В этой связи член — Т (dty/дх) аналогичен напряжению в линии
электропередачи в некоторой точке, a dty/dt аналогично силе тока, про-
проходящего через ту же точку. Произведение этих двух величин равно
передаваемой мощности.
Мощность и волновой импеданс. Аналогия с линией передачи может
быть продолжена и далее. Для переменных токов комплексное отноше-
отношение напряжения к силе тока называется импедансом, или полным сопро-
сопротивлением линии. Часто этот импеданс2) является функцией частоты
переменного тока, но иногда, а именно когда импеданс есть чистое
омическое сопротивление, он не зависит от частоты.
1)На свободно закрепленном конце 9ф/9ж=0. —Прим. ред.
2) Так как для обозначения изменения во времени мы употребляем пока-
показательную функцию с отрицательным показателем e~vet, то знак членов реактанса
(реактивного сопротивления или мнимой пасти импеданса) будет противоположен
знаку соответствующих выражений, принятых в электротехнике. Их легко полу-
получить, поставив знак минус перед i. Например, если Z = R—iX, то X будет тем же
самым членом реактивного сопротивления, который встречается в электротехниче-
электротехнических инженерных обозначениях. Таким образом, формулы импеданса, употребляе-
употребляемые в этой книге, переходят в формулы в инженерных обозначениях при помощи,
замены —? всюду на -f /.
128 Гл. 2. Уравнения полей
Аналогичным электрическому импедансу является комплексное
¦отношение поперечной движущей силы к поперечной скорости, которое
можно назвать механическим импедансом. Для простой струны, доста-
достаточно длинной для того, чтобы волны не отражались от правого конца
(который предполагается находящимся в х—со), смещение точки х,
вызванное синусоидальной волной, идущей в направлении возрастания х,
может быть представлено выражением ф = Д.е* <№'с> (*-<*). Сила и скорость
в точке х равны
Следовательно, поток энергии через точку ж, т. е. среднее значение произведе-
произведения действительных частей этих двух выражений, есть
мощность = y Р с ш21A+ |2 = -
для синусоидальной волны, распространяющейся в положительном
направлении оси х. Величина U+ = —шА+ может быть названа ампли-
амплитудой скорости струны (но не волны) для синусоидальной волны.
Импеданс в точке х для этой простой волны равен
= рс. B.1.13)
Эта величина называется волновым импедансом струны. Для простой
струны в случае волн, распространяющихся в одном направлении, он
постоянен и не зависит ни от х, ни от частоты. На самом деле для
получения этого выражения для волнового импеданса не обязательно
рассматривать, как мы делали, распространяющуюся в одном направле-
направлении волну такого специального вида. Для любой волны /(ж — ct), рас-
распространяющейся в положительном направлении оси ж, поперечная сила
равна —Tf'(x — ct) (здесь штрих обозначает производную), соответствую-
соответствующая поперечная скорость равна —cf'(x — ct) и отношение силы к ско-
скорости, следовательно, равно Т/с = рс; оно не зависит ни от ж и t
ни от формы волны.
Конечно, если мы имеем дело с волнами обоих направлений, импе-
импеданс будет зависеть от частоты и положения точки. Если ф = [Д.е{иис'с +
-\-A_e~il<>xlc] e~Uot, тогда средний поток энергии, полученный как осред-
осреднение выражения B.1.12) по циклу, равен
МОЩНОСТЬ = -тг- рСОJ [ | Д_ |2—|А.|2]
я импеданс равен
Л Atoxic я .-моя/с
В этой главе встретится много случаев, в которых аналогия с на-
напряжением, силой тока, мощностью и импедансом может быть с поль-
пользой применена и обобщена. Например, в волновых движениях всех видов
можно обычно найти две величины, получаемые из волновой функции,
такие, что их произведение равно потоку энергии в волне, а их
отношение может быть принято за обобщенный импеданс. В боль-
большинстве этих случаев, когда волна перемещается только в одном напра-
направлении, импеданс является действительной постоянной, не зависящей
от положения и частоты; в этих случаях это постоянное значение может
быть названо волновым импедансом изучаемого волнового движения.
2.1. Гибкая струна 129
Более сложные выражения импеданса для более сложных форм волно-
волнового движения легче всего дать через этот волновой импеданс как мас-
масштабный множитель. Например, для струны постоянная pc = T/c=Y~p~T
является масштабным множителем в общем выражении импеданса.
Вынужденное движение струны. Как пример применения обобщен-
обобщенного понятия импеданса рассмотрим движение струны длины I, поддер-
поддерживаемой в точке х = I под натяжением Т зажимом (не являющимся
абсолютно жестким) и приводимой в движение поперечной силой в точке
х = 0. Отношение синусоидальной поперечной силы, действующей на зажим
в точке х — 1 и являющейся действительной частью выражения Fle~imt,
и поперечной скорости зажима ?/(e~ilc', вызванной силой, называется
поперечным механическим импедансом зажима Z( = Fl/Ul . Эта величина
зависит обычно от частоты w/2tc, но внутри известных границ не зави-
зависит от амплитуды F, и Ut.
Форма струны может быть представлена с помощью комбинации
синусоидальной волны д^еСйож/с)-™^ идущей из источника (х = 0) к за-
зажиму (х = 1), и другой волны у1_е~("с-т/с)~'1С', отраженной от зажима и дви-
движущейся назад к источнику:
6 = [A+xiti>xlc + А_е~г'"х!с] е~1ю( = A ch | l-^- -f- тах0 — in[
где
Следовательно, поперечная сила, с которой струна действует на за-
зажим, ра«на
F хе-™ =-Т (Щдх)^^
_ _ iwpc [Л+еМ«/с) 1 _ А_е~г ('"М '] e~iwt =
= — wpcAsb [i (o)Z/c) -f-до0 — iiup0] е~ш =
= ЗДе-** = Zt ( -di?ldt)x=l =
= —io>Zl [A^e1 <w/c>' + A_e~l (ю'сI] е~ш =
= — iwZtA ch [i (ib//c) + «x0 - in$0] е~ш.
Для получения четырех последних выражений мы воспользовались опре-
определением поперечного механического импеданса зажима.
Из этих уравнений мы можем выразить через импеданс ZL комплекс-
комплексное отношение амплитуд волн А_, А+, а также постоянные а0, р0 г)
гш1с а ф larthf-O-i^, B.1.14)
где X = c/v — 2т!С/ш — длина волн, распространяющихся по струне. Отноше-
Отношение А /А+ называется отношением стоячих волн или, иначе, коэффициен-
коэффициентом отражения. Если Z, чисто мнимое, т. е. является чистым реактив-
реактивным сопротивлением, то |^4_М+| = 1, так что амплитуды падающей и
отраженной волн равны, как это и должно быть, хотя, конечно,- фаза
отраженной волны будет отлична от фазы падающей волны. Связь между
коэффициентом отражения и Zt, устанавливаемая в B.1.14), является
примером соотношений между унитарным оператором отражения и опе-
J) См. примечание на стр. 127.
9 Ф. М. Морс и Г. Фешбах
130 Гл. 2. Уравнения полей
ратором импеданса, которые были рассмотрены в параграфе, посвящен-
посвященном абстрактным векторным пространствам. Из B.1.14) видим, что гра-
граничное условие в точке х = I определяет сдвиг фаз и отношение ампли-
амплитуд падающей и отраженной волн. Если эти величины известны, то отно-
отношение Zo приложенной силы к скорости в точке х = 0 приложения силы,
которое является для струны импедансом точки приложения силы,
может быть найдено сразу
Z° = PcTT(X/^T=pcth r*(ao-№ B-1.15).
Другими словами, если известна сила, может быть вычислена скорость,
струны в точке х = 0, равно как и выражения А+, А_, А, ф. Например,
если приложенная сила есть / (ш>) е~ш, то волна определяется выражением
= I - ' Г cth (тех. - iiuB0) cos — + i sin юЖ"|. B.1.16>
— iwpc L "с с J
iwpc
Переходная характеристика. Интеграл Фурье. Так же как и в слу-
случае уравнения Пуассона, рассмотренного на стр. 121, решение для не-
нескольких различных сил, действующих одновременно, равно сумме
решений для этих сил, действующих отдельно. Например, если действуют
силы всех частот и полную поперечную силу, действующую в конце
х = 0, струны можно выразить в форме интеграла
F(t)= ^ /(ш)е-»"Ао, B.1Л7)
— со
то форма струны как функция х и t определяется равенством
со
ф= \ фК х, t)dw, B 1.18)
где ф(о), х, t) дается выражением B.1.16).
В главе 4 мы покажем, что весьма многие функции от t могут быть
выражены с помощью интегралов типа, приведенного в равенстве B.1.17)
(интегралы этого вида называются интегралами Фурье), и мы увидим
там, как найти /(и>), если F (t) известно. Следовательно, интеграл B.1.18)
дает общее решение задачи о движении струны под действием прило-
приложенной в конце её поперечной силы, почти в любом физически реали-
реализуемом случае. Техника решения аналогична технике применения функ-
функции Грина, затронутой при выводе формулы B.1.8); она подскажет нам
также подобные методы решения других уравнений, которые дальше
встретятся в этой главе. Сначала находят решение для «силы» особенно
простого вида, зависящей от некоторого параметра (точки приложения
для уравнения Пуассона, частоты для волнового уравнения). Сила общего
вида может быть тогда получена в виде интеграла от простой силы,
взятого по параметру; полученное решение будет выражаться также
аналогичным интегралом от простого решения, взятым по тому же пара-
параметру. Это — общий принцип техники применения функции Грина; он
будет рассмотрен в гл. 7 и в некоторых других местах этой книги.
Операторные уравнения струны. Прежде чем закончить разбор задачи
о волновом движении простой струны, интересно наметить другой под-
подход к задаче, связанный с рассмотрением операторов в абстрактном
2.1. Гибкая струна 131
векторном пространстве, изложенный в гл. 1 и далее в этой главе.
Начнем с рассмотрения струны, состоящей из совокупности материаль-
материальных точек одинаковой массы, соединенных между собой невесомыми
участками струны, имеющими равные длины. Сначала предположим,
что имеется лишь конечное число N таких точек (очевидно, недостаточ-
недостаточное приближение к равномерной струне), а потом будем приближаться
к действительной струне, заставив N стремиться к бесконечности. Таким
образом мы обнаружим связь между связанными осцилляторами, разоб-
разобранными на стр. 80, и гибкой струной.
х-0
N+1
Рис. 2.5. Смещения материальных точек, лежащих на упру-
упругой струне.
Мы аппроксимируем струну постоянной плотности, находящуюся
под натяжением Т между двумя жесткими зажимами, удаленными друг
иг друга на расстояние I, посредством N равноудаленных материальных
точек, каждая из которых имеет массу pl/N и удалена от соседних
точек на расстояние l/(N 4-1). Беглый взгляд на рис. 2.5 показывает,
что если смещение п-й массы от положения равновесия есть уп, то дей-
действующая на эту массу поперечная сила, вызванная смещением сосед-
соседних масс, равна
(Последнее выражение в скобках является, конечно, разностным анало-
аналогом второй производной.) Следовательно, наша система совокупных
уравнений движения N частиц имеет вид
B.1.19)
где u>l=N(N+i)(T/pP).
Будем теперь считать смещения уп составляющими вектора у в аб-
абстрактном векторном пространстве Л' измерений; единичные векторы
этого пространства, расположенные вдоль осей координат, обозначим
через еи. Правые части уравнений можно рассматривать как результат дей-
действия аффинора u^jtt, который преобразует вектор еп в вектор с единичными
компонентами вдоль en_L и еп+1. Аффинор И назовем оператором единичного
сдвига, так как он сдвигает индекс п на единицу в ту и другую сто-
стороны. Оператор И может быть записан следующим образом через век-
Гл. 2. Уравнения полей
торы е:
U = e1e2 + e2(e1-f е3)+ ... + еп (еп_х + еп+1) + ... + е^е^. B.1.20)
Таким образом, уравнение, определяющее вектор у, изображающий сме-
смещение всех частиц,
N
у = 2 Упеп
71=1
может быть записано так:
Собственные векторы оператора единичного сдвига. Решение диф-
дифференциального уравнения для у производится легче, если использовать
собственные векторы ип оператора И:
где un —единичный вектор, направленный по главной оси оператора Ц.
Подставив в уравнение для у вместо у вектор un, получим уравнение,
определяющее зависимость ип от времени
так что зависимость un от времени выражается множителем е~ iu>oV 2-rm« .
Выражение вектора un через единичные векторы ет найдем, решив при-
приведенное выше уравнение для собственных значений.
Пусть un выражено через ет с помощью равенства
N
Un ~ 2j Ynm em>
l
где величины у являются направляющими косинусами преобразования.
Тогда у удовлетворяют уравнениям
Yn.m-1 - 7l«Y«.m+ Tn.mtl = °; B.1.21)
в первом и последнем уравнениях, т. е. при т = 1 и m — N, величины
Yno и Y«, iv+i. естественно, опущены. Однако и эти два уравнения можно
записать в том же виде, если мы предположим, что величины уп, о и
"(n,N*i всегда равны нулю.
Решение уравнений B.1.21) получается с помощью тригонометриче-
тригонометрической формулы
1 1
cos a sin та = — sin [(т — 1) а] + -«г sin \(m +1) а].
В самом деле, положив упт = .4 sin тап (зависимость от времени подра-
Вумевается) и т^ = 2 cos an, мы удовлетворим всем уравнениям. Одно из
дополнительных условий, именно ^п0 — 0, также выполняется; второе тре-
требование Yn, n+i = 0 может быть удовлетворено, если положим, что а„
равно mc/(N -4-1). Так как
( 0 п'=з«=п,
I
то значения постоянных А можно выбрать так, чтобы у были нормиро-
вйнными направляющими косинусами, а и — единичными векторами, если
2.1. Гибкая струна
е — единичные векторы. Окончательные результаты таковы:
N
2 XI • тгт Г „. . . пк ~\
лГ+1 Л ^sinFTIexp L -2ш°1 sm 2FTiy J •
l
m=l
VL •un = 2cos[rac/GV + l)]u,l. B.1.22)
Таким образом, мы нашли совокупность TV взаимно-ортогональных еди-
единичных векторов в абстрактном векторном пространстве; эти векторы
направлены вдоль главных осей оператора U (т. с. являются собствен-
собственными векторами оператора U).
В этой новой системе координат решение уравнения движения для
вектора у, представляющего движение N частиц, получается непосред-
непосредственно
Л" N
т= 1 п— 1
N
2 XI тт ¦ mrm Го- ¦ пт. ~\
ЛГ+Т Ь Unemsmw:ri ехр [ -2wot sin ^^ТГ) J •
и, m=i
Следовательно,
FTiL 2WTT)\ BЛ-23)
Г)=1
Допустимые частоты равны <в№/2те, где ши = 2да0 sin [ил/2 GV+1)]- Состав-
Составляющие движения un называются нормальными видами движения.
Если вначале частицы были смещены на расстояния у%, и все имели
начальные скорости, равные нулю, то значения Un могут быть найдены
с помощью первых уравнений стр. 132
2 ymsin^. B.1.24)
m=l
Таким образом, коэффициенты разложений ут могут быть выражены
через начальные значения у'т и направляющие косинусы преобразования.
Предельный случай непрерывной струны. Для того чтобы перейти
от набора N частиц к непрерывной струне, мы увеличиваем N до беско-
бесконечности, так что каждая «точка» струны отмечается своим значением п,
отличным от других значений. Если струна действительно непрерывна,
то N равно несчетной бесконечности, а это означало бы, что соответ-
соответствующее абстрактное векторное пространство имеет несчетное множе-
множество взаимно-перпендикулярных направлений. Такое векторное простран-
пространство представить себе довольно трудно, но мы можем утешить себя
тем, что здесь такие тонкости с различением типов бесконечности явля-
являются скорее академическими, так как на самом деле струна непре-
непрерывна лишь приближенно и наши теперешние решения недействительны
для частей, размеры которых равны размерам атома или меньше их.
Мы можем успокоить себя также тем, что только малое подпростран-
подпространство такого «сверхвекторного» пространства соответствует физической
стороне дела, так как из непрерывности следует, что значения уп и уп+1
должны сближаться друг с другом при стремлении к нулю расстояний
между последовательными точками.
134 Гл. 2. Уравнения полей
Во всяком случае, для непрерывной струны можно отказаться от
несчетного множества индексов тп, а характеризовать точки расстоянием х
ет одного из концов, т. е. положить x — ml/(N-\-1). Кроме того, так
как N столь велико, то разницей между N и 7V + 1 можно пренебречь.
Однако индекс п, которым отмечены различные допустимые виды дви-
движения, вовсе не имеет нужды становиться бесконечным или непрерыв-
непрерывным, так как мы обычно интересуемся небольшим (в пределах первой
сотни или около того) количеством допустимых частот. Таким образом,
п будет сохранять целые значения, и n/N будет мало. Более точно,
переход совершается следующим образом:
П, X
Последнее равенство дает обычный ряд Фурье для свободных коле-
колебаний однородной струны между жесткими зажимами. Функция
sin (птсх/Г) е~гшп', дающая форму и-ro нормального колебания, является
функцией преобразования, заменяющей счетное множество собственных
векторов un оператора И несчетным множеством единичных векторов е (ж),
каждый из которых соответствует отдельной точке непрерывной струны.
Суммирование по всем этим точкам обозначено символом суммирования 2»
х
хотя его можно было бы выразить также с помощью интеграла по х.
Предельный случай уравнения B.1.24), например, лучше выражается через
интеграл. Мы положим Yn равным предельному значению t/nl/2/(iV+l),
так что уравнения, выражающие Yn через начальные значения смеще-
смещений у'п (если начальные скорости равны нулю), имеют вид
N
v ,. Г 2 vi „ тппЛ xN
Yn=hm |-^ 2j VmSin-^-j, где m-^-j-.
rn=l
Число слагаемых этой суммы по т, лежащих между х и x-\-dx, будет,
следовательно, равно (N/l)dx. Таким образом, сумма для Yn в пределе
будет равна интегралу
i
уп = у )У {x)sin-rdx,
"о
который является обычным интегралом для коэффициентов ряда Фурье
и дает амплитуды различных нормальных колебаний.
Предположим теперь, что расстояние между зажимами безгранично
возрастает (мы помещаем начало координат в средней точке струны);
тогда другой способ предельного перехода, который подробно изложен
в гл. 4, приводит нас к общему решению в случае волнового движения
бесконечной струны, подвергнутой первоначально смещению у° (х) и осво-
освобожденной в момент t=*0:
со оо
У (ж' ') = Тп S еЫ (Х~а) da \ у° ® e~ial d*' B.1.25)
2.1. Гибкая струна 135
Действительная часть этого выражения дает истинное смещение точки х
в момент I.
Наконец, интересно посмотреть, какой вид принимает в пределе
оператор И для непрерывной струны. Чтобы подойти к уравнению для
вектора у, мы ищем предел выражения, полученного в результате при-
применения оператора со2, [И — 2] к вектору у = 2 Утет ~^ 2 У (х) е (х)- Д° пере-
m х
хода к пределу применение оператора давало для составляющих ут
вектора¦
Л'
о>02 [U - 2] -у - Л'(У)Г ^ 1(уп+1 - уп) - (уп - уп^)\ еп.
Так как расстояние между частицами становится все меньше и меньше,
разность уп+1 — уп приближенно можно заменить дифференциалом dy(x),
а расстояние между частицами l'(N +1) — дифференциалом dx. Следова-
Следовательно, (N11){уп+х — уп) при переходе к пределу дает dy/dx, и приведен-
приведенное выше выражение превращается в
X
так что уравнение движения для у в пределе принимает вид
X X
и, следовательно, уравнение для функции преобразования 2/(х) имеет вид
д*у _ ,^
а«а "с а»:2'
т. е. совпадает с волновым уравнением B.1.9).
Таким образом, проделав окольный путь через абстрактное вектор-
векторное пространство, мы снова пришли к дифференциальному уравнению
в частных производных для волнового движения простой струны. • Этот
экскурс мы предприняли потому, что подобные рассуждения будут про-
проводиться и в дальнейшем в этой главе там, где другие пути совершенно
не так прямы и просты, как в случае струны.
Влияние трения. До сих пор мы пренебрегали сопротивлением дви-
движению струны со стороны окружающей среды (воздуха или воды). Для
движений с малой амплитудой это сопротивление противоположно напра-
направлению движения каждого элемента длины и пропорционально его ско-
скорости. Сила, действующая на элемент, лежащий между х и x-\-dx, про-
пропорциональна скорости dty/dt этого элемента и направлена в сторону,
противоположную этой скорости. Коэффициент пропорциональности R
обычно зависит от частоты! колебаний струны, но в случае, когда вяз-
вязкость среды достаточно велика, он не зависит от частоты. Этот послед-
последний случай наиболее прост, и мы с него начнем.
Уравнение движения, если принять во внимание натяжение и тре-
трение среды, без учета жесткости и внутреннего трения струны имеет вид
Благодаря трению свободные колебания, конечно, становятся затухаю-
затухающими. Если струна натянута между двумя жесткими зажимами, нахо-
136 Гл. 2. Уравнения полей
дящимися друг от друга на расстоянии I, то форма нормальных коле-
колебаний не изменяется трением и по-прежнему будет иметь вид sin (жпх/1).
В то же время отдельные колебания затухают с течением времени, так
как решение этого уравнения имеет вид
Если к зависит от частоты, то для и-го нормального колебания оно
будет иметь значение-, соответствующее величине шп, так что ра'зличные
колебания будут затухать с различными скоростями.
С другой стороны, если струна имеет очень большую длину и при-
приводится в движение на одном конце действием синусоидальной силы .Fe—110',
то волны будут затухать при перемещении по струне в большей степени,
чем с течением времени. Решение в этом случае имеет вид
следовательно, а имеет положительную мнимую часть, которая и вызы-
вызывает затухание в направлении движения волны.
Уравнение диффузии. В одном из возможных предельных случаев
силы вязкости могут полностью преобладать над инерционными силами,
так что уравнение примет вид
R
2
** =
_
B.1.26)
Это уравнение много раз будет встречаться в этой книге. Так как оно»
также описывает поведение некоторого растворенного вещества, диффун-
диффундирующего в растворителе (где ф — плотность растворенного вещества),
то обычно его называют уравнением диффузии1).
Так же как и в случае волнового уравнения B.1.9), здесь имеет
место тенденция к выпрямлению искривленных участков, но здесь ско-
скорость любого участка струны пропорциональна и противоположна по
знаку кривизне этого участка, тогда как в волновом уравнении ускоре-
ускорение пропорционально кривизне и противоположно ей по знаку. Короче
говоря, мы и здесь по существу имеем дело с условием равновесия.
Для волнового уравнения скорость движения искривленного участка
непрерывно возрастает до тех пор, пока он не сделается прямолинейным,
и только тогда скорость начинает уменьшаться, что и вызывает колеба-
колебательное движение. В случае же уравнения диффузии скорость любого
участка становится равной нулю, как только этот участок окончательно1
выпрямляется, так что здесь колебательного движения нет. Таково пред-
предполагаемое поведение струны, не имеющей массы, движущейся в вязкой
жидкости, когда затухание больше критического.
В случае волнового уравнения общее решение может быть выражено
в виде результата наложения друг на друга двух волн, движущихся
в противоположных направлениях f (x + ct) + F (x — ct), что объясняется
симметричностью соотношений между х и t в уравнении. В уравнении
диффузии этой симметрии нет, и поэтому не существует простого выра-
выражения для общего решения. Кроме того, здесь имеется различие между
положительным и отрицательными направлениями времени, что вытекает
из того факта, что производная по времени, входящая в уравнение, есть
УравнениеB.1.26) называют также уравнением теплопроводности. — Прим.
2.1. Гибкая струна
137
1=0
производная первого порядка, тогда как в волновом уравнении она
является производной второго порядка.
Например, если струна имеет синусоидальную форму АеЫх'с, то для
волнового уравнения зависимость от времени имеет также синусоидаль-
синусоидальный характер е~ш. Но для уравнения диффузии множитель, дающий
зависимость от времени, имеет вид е-(ш/«J< и не является симметричным
относительно времени. Для положитель-
положительного времени синусоидальная форма зату-
затухает экспоненциально (по закону показа-
показательной функции), но рассматривая обрат-
обратное течение времени, мы видим, что амп-
амплитуда волны безгранично возрастает, ког-
когда t становится все больше и больше (по
абсолютной величине), оставаясь отрица-
отрицательным. Чем меньше длина волны флук-
флуктуации (т. е. чем больше ш), тем быстрее
функции затухают в положительном на-
направлении времени и тем быстрее они рас-
растут в отрицательном. Как мы покажем де-
детально дальше, для волнового уравнения
можно и предсказать дальнейшее движе-
движение., и восстановить предшествующее движе-
движение, если известно состояние в данный
момент. Для уравнения диффузии возможно
только предсказание, попытки восстановить
прошлое приводят только к расходящим-
расходящимся выражениям.
t=3
-2
Рис. 2.G. Последовательные гра-
графики решения уравнения диф-
диффузии; верхняя кривая относит-
относится к начальному моменту.
Уравнение Клейна — Гордона. Один из
видов уравнений, встречающихся в кванто-
квантовой механике (применяется для описания
скалярного мезонного поля), может быть также иллюстрирован с помощью
гибкой струны, на которую действуют дополнительные силы жесткости,
вызванные средой, окружающей струну. Если, например, струна заделана
в тонкий резиновый лист (или если она расположена вдоль оси резинового
цилиндра, внешняя поверхность которого остается неизменной), то допол-
дополнительно к восстанавливающей силе, вызванной натяжением струны,
появится восстанавливающая сила, вызванная влиянием резины на каж-
каждый участок струны. Если смещение элемента dx струны в точке х равно
ф (х), то эта восстанавливающая сила будет равна — Кф dx, где К — постоян-
постоянная, зависящая от упругих свойств и распределения резины.
Таким образом, уравнение движения струны имеет вид
1 дЧ 'дЧ „, „Г о К
с2 dt2 ~ дх* P V' c —p • f1 - т
где p — линейная плотность, а Т - натяжение струны. Это уравнение
в квантовой механике называется уравнением Клейна — Гордона. Заметим,
что в случае, когда с есть скорость света, это уравнение, как и волновое
уравнение, инвариантно по отношению ,к преобразованию Лоренца, так
что решения этого уравнения ведут себя соответствующим образом отно-
относительно пространственно-временных вращений специальной теории отно-
относительности.
Влияние па такую струну постоянной единичной поперечной силы,
приложенной в точке ж = Е, отличается от влияния такой силы на
струну, находящуюся под действием только натяжения. Форма упруго
B.1.27)-
138 Гл. 2. Уравнения полей
подкрепленной струны бесконечной длины, соответствующая форме B.1.7),
в этом случае дается уравнением
G(x\\) = l I B.1.28)
I
В случае обычной струны, находящейся под действием одного натя-
натяжения, мы должны были считать струну имеющей конечную длину, так
как конечные опоры были только «якорями», препятствовавшими силе
переместить струну на неопределенно большое расстояние. Напротив,
в данном случае упругая среда, в которой заключена струна, поглощает
почти полностью влияние силы; точное положение точек опоры важно
только для частей струны, находящихся на малых по сравнению с 1/ц
расстояниях от обоих концов. Следовательно, в этом случае можно взять
¦функцию Грина, не зависящую от конечных точек (т. е. для бесконечной
струны). Формула показывает, что часть среды, удаленная от точки при-
приложения силы на расстояние примерно 1/|л, поглощает большую часть
силы и смещение струны за пределами этого расстояния становится
весьма малым.
В случае, когда приложенные поперечные силы произвольного вида
распределены вдоль струны, соответствующая форма струны выражается
интегралом от функции Грина, определенной уравнением B.1.28); общая
форма такого интеграла дана в равенстве B.1.8).
Если упруго подкрепленная струна натянута между жесткими зажи-
зажимами, находящимися друг от друга на расстоянии L, она может коле-
колебаться; при этом последовательные нормальные виды движения аналогичны
по форме нормальным колебаниям для струны без упругой оболочки, но
отличаются от них частотой.
Ряд Фурье для свободных колебаний общего типа имеет вид
п=1
Допускаемые здесь частоты, благодаря наличию слагаемого (д.2, пропор-
пропорционального коэффициенту упругости К окружающей струну среды, все
будут больше соответствующих частот для обычной струны. Этот резуль-
результат не является неожиданным, так как добавленная жесткость среды
должна увеличить собственные частоты.
Вынужденное движение упруго подкрепленной струны. Струна, заде-
заделанная в резину и приводимая в движение на одном конце поперечной
переменной силой, также обнаруживает известные характерные особен-
особенности в поведении по сравнению с обычной струной.
Решение уравнения для волны, распространяющейся только вправо,
соответствующее случаю бесконечно длинной струны, имеет вид
| Аехр [ -xV^-(m/cf ~ Ш], а>2 < ?*<* = К/р, t
1 А ехр {i (oi/c)} [х |Л — (|лс/о)J — с/]}, ш*К/
Цри очень больших частотах приложенной силы волновое движение
очень похоже на движение обычной струны; только скорость волны *) всегда
1) Имеется в виду фазовая скорость. — Прим. ред.
2.1. Гибкая струна
139
несколько больше с и отличается от с множителем 1/У~1—(|лс/шJ. Здесь снова
добавочные упругие силы стремятся «ускорить» волны. Волновое число
2тг/Х = |/(ш/сJ — (л2 не является более линейной функцией от частоты. Таким
образом, дополнительно подкрепленная струна ведет себя подобно диспер-
диспергирующей среде. Общая волна составлена из волн, имеющих различные
значения ш; эти волны больше не удерживаются вместе, но расходятся
из их начального положения в последовательность волн, все более и более
Простая струна
Струна с трением
{
Струна с упругой опорой
t-0,
t=i
t=2
t=3
i/-u(t-x)J0(Vt2-x2)
Рис. 2.7. Последовательное изменение формы трех видов струн,
приведенных в движение у левого конца в момент г = 0.
рассеянных вдоль всей длины струны. Конечно, это поведение значительно
отличается от поведения волны, движущейся по обыкновенной, не под-
подкрепленной струне, так как там среда не была диспергирующей и форма
волны не изменялась по мере ее распространения.
При низких частотах влияние упругой среды преобладает над влия-
влиянием инерции массы струны, и для частот, меньших чем A/2 тс) ]ЛйГ/р,
уже вообще не будет подлинного волнового движения; точки струны
движутся взад и вперед, имея одну и ту же фазу, причем величина
отклонения от положения равновесия будет наибольшей вблизи точки
приложения силы и быстро убывает по мере удаления от приводимого
в движение конца.
Волновой импеданс для струны этого типа вычисляется аналогично
тому, как была получена формула B.1.13):
— ) , Ю < AС,
B.1.30)
При высоких частотах волновой импеданс имеет действительное значе-
значение и мало отличается от значения рс импеданса для простой струны.
Однако при уменьшении частоты волновой импеданс убывает,
а скорость волны возрастает до тех пор, пока при ш = («; = \/К/р волно-
волновой импеданс не станет раввым нулю, а скорость волны равной беско-
бесконечности. Это —частота резонанса для массы струны и упругости среды.
140 Гл. 2. Уравнения полей
При более низких частотах импеданс будет мнимым, и здесь нет под-
подлинного волнового движения.
Резюме. Различные причины побудили нас подробно рассмотреть
движения гибкой струны. Во-первых, наши рассуждения при изучении
струны являются простым примером тех рассмотрений, которые встре-
встретятся при изучении других уравнений полей. В каждом случае мы будем
рассматривать различные уравнения, получающиеся в предположении,
что та или другая сила становится преобладающей; таким образом, изу-
изучая различные предельные случаи, мы достигнем достаточно полного
понимания наиболее общего случая. Во-вторых, различные типы движе-
движения струны дают нам очень наглядное представление о формах решений
многих важных дифференциальных уравнений с частными производными,,
к которым приводит нас изучение многих физических явлений. Те же
уравнения появляются часто и тогда, когда они соответствуют физи-
физическим состояниям, которые представить себе наглядно гораздо труднее.
В-третьих, технические приемы решения, которые здесь были затронуты
в связи с физическими проблемами, имеют обычно применение во многих
других задачах, и ссылка на простое решение задачи в случае струны
поможет нам лучше понять и другие более сложные вопросы.
Мы теперь расширим область наших рассуждений и изучим несколь-
несколько типичных физических явлений, имеющих большое значение, чтобы
показать, какие типы полей могут быть использованы для описания
этих явлений и каким дифференциальным уравнениям с частными про-
производными должны удовлетворять эти поля.
2.2. Волны в упругой среде
Для нашего первого изучения трехмерной задачи о взаимной связи
физических явлений с дифференциальными уравнениями полей вернемся
к задаче о поведении упругой среды (которую мы начали рассматривать
в § Д.6), чтобы поставить вопрос о волновом движении в такой, среде.
Как и в случае струны, мы предполагаем, что смещения точек среды
малы и что нас не интересуют перенос или вращение среды в целом.
Пусть смещение s(xuy, z; l) элемента dxdydz среды в точке х, у, z
в момент времени t мало и его вращение, вызванное деформацией, также
мало. Инерциальное сопротивление элемента, вызванное ускорением изме-
изменения величины s, равно (d2s/dtz) р dxdydz, где р — плотность среды.
В § 1.6 мы определили аффинор напряжений % = FJL + Fj,j + FJk =
= 1РЖ + jF^ + kFz, сказав, что сила, действующая на элемент dA поверх-
поверхности среды, равна S?-dA. Например, сила, действующая на грань dydz.
элемента, перпендикулярную к оси х, равна ?xdydz. Таким образом,
результирующая сила, действующая на элемент dxdydz и обусловленная
разностью значений F,. на грани dydz элемента и на противоположной
его грани, равна dx(d?x/dx)dydz; поэтому результирующая сила, полу-
полученная от действия сил на все грани элемента, равна V-%dxdydz.
Но в уравнении A.6.28) мы показали, что аффинор напряжений ©
связан с аффинором деформаций соотношением % = X | C | Q -f- 2|л@, где ц
есть модуль сдвига среды и X + f-o-^J —ее модуль всестороннего сжатия
(отношение изотропного давления к относительному уменьшению объема).
Из формулы A.6.21) мы имеем соотношение между <& и смещением s,.
даваемое символически равенством E = V2 (Vs-f-sV). Сопоставляя все
эти уравнения, мы окончательно приходим к уравнению движения среды
2.2. Волны в упругой среде 141
под действием ее собственных восстанавливающих сил упругости
Р Qjf = v • [*$ div s + f^s + jisV] = (X + p.) grad divs -f ^ div grad s =
(Z.Z.i)
= (X-(- 2(i) grad div s — p rot rots.
Здесь мы использовали равенство A.5.12) для преобразования вектор-
векторных операторов.
Продольные волны. Форма уравнения движения наводит на мысль,
что по крайней мере часть вектора можно выразить через градиент ска-
скалярного потенциала ф, так как тогда уравнение значительно упрощает-
упрощается. Если s = grad<j), то уравнение для 6
divgrad<j, = V4» = Agf; c; = »±2? B.2.2)
является как раз волновым уравнением для скалярного волнового потен-
потенциала ф и представляет собой обобщение уравнения B.1.9) на случай
трехмерного пространства. Скорость распространения волн сс будет тем
•больше, чем больше модули X и ja (т. е. чем больше жесткость среды),
и тем меньше, чем больше р (т. е. чем больше плотность среды).
Когда решение уравнения B.2.1) является градиентом скаляра,
аффинорный оператор © = V (V6) симметричен, аффинор вращения Ш
равен нулю и © = @ является аффинором чистой деформации. В случае
такого решения отсутствует скручивание среды и имеются только растя-
¦жения и сжатия. Волны этого рода называются продольными или вол-
волнами безвихревого расширения. Они могут также распространяться
в жидкой и газообразной среде, где модуль сдвига jj. равен нулю.
Но градиент скалярного потенциала, как известно, не является
наиболее общим векторным полем, возможным для смещений s, как
было показано на стр. 59. Для определения наиболее общего векторного
поля необходимы три скалярные функции положения .по одной для
каждой компоненты, в то время как градиент скаляра определяется
единственной функцией — потенциалом. Следовательно, для задания само-
самого общего решения уравнения B.2.1) нужны еще две другие скалярные
•функции точки.
Конечно, можно найти уравнения для каждой декартовой компонен-
компоненты s, но тогда мы получили бы три уравнения, каждое из которых
¦содержит все три компоненты и которые нужно решать совместно, что
очень громоздко.
Поперечные волны. Для получения других решений гораздо лучше
воспользоваться некоторыми свойствами векторного оператора V, как
мы это делали для градиента потенциала; так как вихрь градиента
равен нулю, то один из членов уравнения выпал и мы получили волно-
волновое уравнение скалярного потенциала. Этот результат [совместно с ре-
результатом A.5.15)] наводит на мысль о том, чтобы испытать вихрь неко-
некоторого вектора, так как дивергенция вихря равна нулю и, следователь-
следовательно, член, содержащий дивергенцию, выпадет. В связи с этим в каче-
качестве другого решения для s возьмем rot А; полученное для А уравнение
имеет вид
-rotrotA=-?g?, €•=¦?•; B.2.3)
оно является, как дальше мы покажем, также волновым уравнением.
¦Скорость с6 этой волны меньше скорости продольной волны, будучи про-
142 Гл. 2. Уравнения полей
порциональной корню квадратному из модуля сдвига р. вместо корня
квадратного из комбинации X-f 2р. Это указывает на то, что эта часть
решения есть волна сдвига, который здесь и на самом деле имеет место.
Так как для этого вида смещений коэффициент объемного расширения
G = divs [см. формулу A.6.23)] равен нулю, то здесь не будет ни расши-
расширения, ни сжатия и, следовательно, деформация должна иметь вид
сдвига. Мы будем называть обычно этот тип волны поперечной волной
(волной равнообъемного искажения формы).
Такое разделение общего решения на продольную часть, которая
является градиентом скалярного потенциала ф, и поперечную часть,
являющуюся вихрем векторного потенциала А, по методу, изложенно-
изложенному на стр. 59, является очень удобным, так как получающиеся две
волв*ы движутся с различными скоростями; всякое другое разделение
решения привело бы к волнам, содержащим части обоих решений и,
следовательно, имеющим обе скорости, что, конечно, является более
громоздким.
Однако на первый взгляд два решения, которые мы получили, со-
содержат в себе много лишнего. Раньше мы отметили, что для того, что-
чтобы дать наиболее общее выражение для вектора s, нужны только три
независимые функции положения, здесь же мы имеем их четыре —одну
для скалярного потенциала и три —для компонент векторного потен-
потенциала. Но это излишество только кажущееся, так как мы не исполь-
используем всех степеней свободы векторного потенциала А. В процессе со-
составления вихря вектора А для получения s мы пренебрегаем частью
А, именно частью, которая может быть представлена как градиент ска-
скаляра, и используем только ту часть, для которой дивергенция равна
нулю. Таким образом, часть А, применяемая для составления общего
выражения для s, определяется только двумя независимыми функциями
положения, и они вместе со скалярным потенциалом и являются необ-
необходимыми тремя функциями.
Придавая нашим рассуждениям другой вид, мы скажем, что любое
векторное решение уравнения B.2.1) можно разбить на две части: про-
продольную часть, имеющую равный нулю вихрь, которая всегда (см. стр. 59)-
может быть представлена как градиент скалярного потенциала, и по-
поперечную часть, дивергенция которой равна нулю и которая всегда
может быть представлена (см. стр. 60) как вихрь векторного потенциа-
потенциала. Уравнение B.2.2) показывает, что если решение вначале было про-
продольным, оно продолжает оставаться продольным, и если оно вначале
было поперечным, оно будет оставаться поперечным все время, пока
величины X и (а имеют одни и те же значения. Если же X или р. или обе
величины резко изменяются на граничной поверхности или меняются
непрерывно в некоторой области пространства, то может произойти
отражение волны и при этом продольная и поперечная волны могут
перемешаться.
В настоящем случае продольная часть соответствует волновому
движению с определенной скоростью, а поперечная часть соответствует
волновому движению с другой, меньшей скоростью. В действительности,
здесь имеются две независимые поперечные части. Одна из них может
быть взята как вихрь некоторого решения А уравнения B.2.3) [между
прочим, вихрь решения уравнения B.2.3) является также решением
уравнения B.2.3), как можно легко проверить]. Эта часть называется
первым поперечным решением. Другая поперечная часть может быть по-
получена как вихрь первого решения [которое пропорционально, как легко
проверить, той части А, для которой дивергенция равна нулю]. Эту
часть будем называть вторым поперечным решением уравнения B.2.1).
2.2. Волны е упругой среде
143
Волновое движение в трехмерном пространстве. Волны на простой
струне могут быть только двух общих типов: волны, которые движутся
вправо и изображаются общей функцией F{x — ct), и волны, перемещаю-
перемещающиеся влево и изображаемые с помощью функции f(x-{-ct). В трехмер-
трехмерном пространстве возможно значительно большее количество типов вол-
волновых движений. Ограничиваясь пока случаем скалярного волнового
потенциала <Ь , мы получим, конечно, простое обобщение одномерной
волны
ф = /(а-г-сс0, B.2.4)
где r= xi-\-yj-\-zU., a a — единичный вектор некоторого произвольного
направления, определенного сферическими углами б и ф (см. рис. 2.8).
Движение волны происходит здесь всегда в одном направлении, и заме-
замечания, сделанные в § 2.1 относительно одномерных волн, могут быть
применены здесь без всяких изменений. По причинам, которые вскоре
станут ясными, такие волны называются плоскими волнами.
Неотъемлемой частью нашего представления о трехмерных волнах
является движение фронта волны. Гребни и Епадивы волны часто сохра-
сохраняются без изменения при их движении вперед, что может быть пред-
представлено с помощью поверхностей всюду перпендикулярных направле-
направлению движения волны и перемещающихся со скоростью распространения
волн с. Эти поверхности называются поверхностями постоянной фазы,
или просто фазовыми поверхностями. Для простой плоской волны вида
Рис. 2.8. Единичный вектор распростра-
распространения волны а и радиус-вектор г.
/(a-r — ct) такими поверхностями являются плоскости a-r= const, пер-
перпендикулярные к единичному вектору а, указывающему направление дви-
движения волны. Если волна является синусоидальной и представлена
в форме комплексной показательной функции ф = Aei^-lo'c^a'T~ct\ то для
всех точек какой-либо из этих поверхностей волновая функция имеет
одно и то же значение фазового угла комплексной показательной функ-
функции (что и является, причиной того, что эти поверхности называются
фазовыми поверхностями).
Мы можем спросить, существуют ли другие типы волн в трехмерном
пространстве, для которых гребни и впадины остаются неизменными
при продвижении волны? Небольшое исследование будет достаточ-
достаточным, чтобы убедиться в том, что только плоские волны вида, данного
равенством B.2.4), сохраняют при движении полностью их форму и раз-
размер. Однако могут существовать волны, отличные от плоских, которые
сохраняют свою форму, но не сохраняют размеров; такие волны имеют вид
ф = А (х, у, z) f [<р (х, у, z) — ct]. B.2.5)
Функция / обеспечивает движение волны, а поверхности tp= const являют-
являются поверхностями постоянной фазы; множитель А вызывает изменение
размера волны от точки к точке.
144 Гл. 2. Уравнения полей
Подставив это выражение в волновое уравнение V2(]> = A/с2) (d2ty/dt2),
получим
/VM + (f'/A) div [A2 grad <р] + Af" [grad2 <р - 1] = О,
где штрихи обозначают производные функции / по ее аргументу. Если /
есть произвольная функция ее аргумента <f — ct, то коэффициенты при
/, /' и /" должны быть равны нулю
VM=0, [grad у]2 = 1, div|>42grad<p] = 0. B.2.6)
Последнее уравнение эквивалентно утверждению, что вектор ^42grad<p
является вихрем некоторого вектора, второе равенство показывает, что
grad<p есть единичный вектор. Эти ограничения на А и <р достаточно
строги, и поэтому нельзя найти много решений. Другими словами, лишь
немногие типы волн сохраняют свою форму при движении в пространстве.
Одно из решений этих уравнений имеет сферические фронты волны
<р = г ¦= |/x2 + ^/2 + z2; амплитуда такого решения изменяется обратно
пропорционально расстоянию г от центра волны и имеет вид А = В/г
(В — постоянная). Решение
представляет собой сферическую волну, расходящуюся из центра г = 0.
Естественно, здесь может существовать также сходящаяся волна
D
Другой способ изучения той же общей задачи состоит в том, чтобы
найти, какие криволинейные координатные поверхности могут являться
фронтами волны. Если волновое уравнение в некоторой системе коорди-
координат имеет решения, являющиеся функциями только одной из трех коор-
координат, то решение, определяющее проходящую волну, может быть обра-
образовано из тех решений, которые будут иметь одну из систем коорди-
координатных поверхностей своими поверхностями постоянной фазы.
Предположим, что мы выбрали систему ортогональных криволиней-
криволинейных координат ?lf 52> S3 c коэффициентами Ламе hx, hs, h3 и единичны-
единичными векторами alf a2, а3. Согласно равенству A.5.11), волновое уравнение
в этих координатах имеет вид
' ' ? ? 1ф Л 1 в2-р .„ 0 7Ч
Для упрощения зависимость от времени дается в виде показательного
множителя е~1ш'. Если, кроме того, остальную пространственную часть
ф можно разложить на три множителя, каждый из которых зависит
только от одной координаты, уравнение называется разделяющимся;
в этом случае то или другое из трех семейств координатных поверхно-
поверхностей может быть семейством фазовых поверхностей. Другими словами,
если уравнение
_» д fh2hsdb\ Г«\\ = о
приводит к решениям, зависящим только от ^, то волновое уравнение
будет' разделяющимся по отношению к координате ?г
Если можно найти одно решение этого уравнения, то можно соста-
составить два независимых решения у (^) и F(y (это будет доказано в гл. 5),
и комбинация
2. 2. Волны в упругой среде 145
послужит нам выражением для простой гармонической волны, имеющей
координатные поверхности ?х = const в качестве поверхностей постоян-
постоянной фазы
ф = (у + iY) е~ш = А (^) е4<ш/с> Г* (^)-с]. B.2.8)
Эта форма волны представляет собой более частный случай, чем волна,
данная уравнением B.2.5), так как мы ограничились здесь синусоидаль-
синусоидальной зависимостью от времени. В обмен на это упрощение мы получаем,
что ограничительные требования, налагаемые на А и <р, не так строги,
как в B.2.6). Например, grade здесь не обязательно единичный вектор,
что соответствует утверждению, что поверхности постоянной фазы
не везде перемещаются со скоростью с. Функции А и <р могут зависеть
от и>, так что форма волны может быть различной для различных частот.
Тем не менее мы снова находим, что лишь немногие формы волнового
фронта допускают распространение волн в некоторой степени неиз-
неизменной формы. Как мы увидим в гл. 5, только небольшое количество
систем координат приводит к разделяющимся уравнениям. Таким образом
волновое уравнение довольно разборчиво относительно допускаемой
формы волнового фронта.
Дальнейшее обсуждение этих вопросов здесь бесполезно. Достаточно
заметить только, что имеется тесная связь между свойствами системы
координат, допускающей разделенные решения волнового уравнения
(т. е. решения, состоящие из множителей, каждый из которых является
функцией только одной координаты), и возможностью для соответству-
соответствующих координатных поверхностей быть поверхностями постоянной фазы
для некоторой волны. В гл. 5 мы рассмотрим проблему разделимости
более подробно.
Векторные волны. Теперь надо вернуться к волнам сдвига, которые
не могли быть представлены с помощью скалярной волновой функции,
но* могут быть изображены с помощью векторного потенциала, с исче-
исчезающей дивергенцией и удовлетворяющего уравнению
rot rot A+ ^-^- = 0.
Это уравнение также может иметь решения в виде плоских волн
A = (Bxa)/(a-r-d), B.2.9)
где В — некоторый постоянный вектор и, следовательно, (Вха) — постоян-
постоянный вектор, перпендикулярный к единичному вектору а, указывающему
направление распространения волны. Так как величина вектора А
не изменяется при перемещении вдоль линии, по которой направлен А
(т. е. так как градиент / перпендикулярен к Вха), дивергенция А равна
нулю, как это и требуется. Вихрь вектора А есть вектор, перпендику-
перпендикулярный к А и к а
rot A = (grad/) х (В х а) = [В - а (а-В)]/',
и^вихрь этого вектора снова параллелен вектору А
1
rotrotA= _(Вха)/"= --2-^
что, конечно, и должно быть, так как А удовлетворяет векторному
волновому уравнению B.2.3). Направления векторов А и rot А оба пер-
перпендикулярны к направлению вектора а, т. е. к направлению распро-
Ю Ф. М. Морс и Г. Фешбах
Гл. 2. Уравнения полей
странения волны, что является поводом для наименования этих волн
поперечными.
Здесь также имеется векторный потенциал, определяющий сфери-
сферическую векторную волну, аналогичную скалярной сферической волне
(B/r)f(r — ct), рассмотренной раньше. Если аг — единичный вектор, на-
направленный вдоль радиуса г, а9 — единичный вектор, перпендикулярный
к аг и к оси сферических координат и а» = а9 х аг — третий единичный
вектор, перпендикулярный к обоим прежним, то вектор А = (ae/r)/(r + ct)
является решением векторного волнового уравнения, пригодным всюду,
кроме точек сферической оси & = 0. Например, для расходящейся волны
rotA = ^/' (r-ct)
Вектор rot А, очевидно, также является решением векторного волнового
уравнения, так что наиболее общая расходящаяся сферическая вектор-
векторная волна имеет вид
Более сложный вопрос о разделимости векторного волнового уравнения
будет рассмотрен позже.
Интегральные представления. Более общие типы волн можно по-
построить, складывая плоские волны различных направлений. Как пока-
показано на рис. 2.8, вектор а (б, ф) есть единичный вектор распространения,
имеющий направление, определяемое сферическими углами б и ф, а г
есть радиус-вектор длины г, направление которого .определяется углами
& и у. Наиболее общий вид скалярной волны может быть представлен
с помощью интеграла
ф= \d<$> Csin6d6/^, б; г-а (б, ф)-с1], B.2.10)
где / есть проходящая волна, форма которой зависит от углов 6 и ф.
Интегрирование производится обычно в пределах от 0 до 2с для ф и от
0 до тс для б, но эти пределы могут быть и мнимыми или комплексны-
комплексными (так, например, от 0 до Ts/2 + ioo для б).
Наиболее общая векторная волновая функция может быть состав-
составлена подобным же образом
A= \ йф \ sinGdBFty, б; га(б, ф)-с^, B.2.11)
где Т(ф, б; z) есть векторная функция от ф, б и z; направление вектора
?(ф, б; z) перпендикулярно к направлению а (б, ф). Так как каждый эле-
элемент, стоящий под знаком интеграла, является поперечной волной, то
результат интегрирования имеет дивергенцию, равную нулю.
Тем же способом можно также выразить и более частные случаи
волн. Например, в очень важном случае простой гармонической волны
с временным множителем е~ш выражение для скалярной волны прини-
принимает вид
ф= С с1ф { У(ф, б) eH^/oec^-cOsiiiedo, B.2.12)
где г cos й = г [cos б cos&+sin6sin& cos (ф —<р)] = га (б, ф) и Y (ф, 6) — неко-
2. 2. Волны е упругой среде 147
торая функция сферических углов. Для векторного решения Y есть век-
вектор, перпендикулярный к а для каждого значения 6 н ф. В дальнейших
главах мы увидим, что чрезвычайно полезно выражать все решения вол-
волнового уравнения в такой интегральной форме.
Напряжение и деформация. Возвращаясь в область физики после
этого вторжения в область математики, подсчитаем напряжения в среде,
соответствующие различным видам волновых движений. Для волн рас-
расширения (продольных), проходящих направо вдоль оси х, скалярный
потенциал есть ф = / (х — cct) и смещение среды в точке х, у, z в момент
времени t равно
B.2.13)
Аффинор деформации имеет вид © = у [ Vs -f sV] = ii/" (x — cc«), а аффинор
напряжения равен
% = X3 div s + p (Vs + sV) = [(X + 2fi) ii + X (jj + kk)l /" (x - cc t),
Г F) = -^/F). B.2.14)
Другими словами, сила, действующая на единичную площадку, перпен-
перпендикулярную оси х, направлена вдоль оси х и имеет величину (Х + 2^)/",
тогда как сила, действующая на единичную площадку, параллельную
оси х, перпендикулярна к площадке и равна X/". Движение происходит
целиком в направлении оси х. Сдвига здесь нет.
Для волны сдвига (поперечной), проходящей направо вдоль оси х
со смещениями среды, параллельными оси z, векторный потенциал имеет
вид A=jF(x— cst), и смещение среды в точке х, у, z л момент t равно
s = rot A = \lF' (х — cst)t F' (E) — (d/dty F (?). B.2.15)
Аффинор деформации имеет выражение © = (ik-(-ki)i7" (x — cst), а аффинор
напряжений равен
% = (i(Vs + sV) = [a (ik + ki) F" (ж — cst), F" (Q = {d-/dt^) F (?), B.2.16)
так как div s равна нулю. В этом случае сила, действующая на единич-
единичную площадку, перпендикулярную оси х, направлена вдоль оси z и имеет
величину pF"; сила, действующая на площадку, перпендикулярную оси
z, направлена вдоль оси х и также равна pF". Усилий, приложенных
к площадке, перпендикулярной оси у, здесь нет. Эта деформация
является, конечно, чистым сдвигом в плоскости xz.
Волновая энергия и импеданс. Чтобы найти потенциальную энергию
некоторого объема среды, если ее аффинор деформации есть
© =-77 (Vs + sV), а аффинор напряжений равен 2 = X3|©| + 2(aS, мы
сперва найдем приращение потенциальной энергии, когда смещение s.
среды в точке х, у, z возрастает в а малую величии у us. Работа сил на-
напряжения среды в этом объеме может быть подсчитана с помощью ска-
скалярного произведения усилия (Z-dA), действующего на каждый элемент
dA поверхности рассматриваемого объема, и смещения 8s этого элемента
8ку =
где первый интеграл распространен на поверхность, ограничивающую»
10*
148 Гл. 2. Уравнения полей
рассматриваемый объем, а второй на сам этот объем. Чтобы вывести
¦второй интеграл из первого, мы воспользовались теоремой Гаусса A.4.7).
Однако манипуляции с компонентами показывают, что для вектора
А и аффинора S3 имеет место следующая формула:
где S3:® = J\ BmnDnm = |
ntn
Таким образом,
Так как (V-S)df есть результирующая сила, действующая на элемент
объема dv, которая равна нулю, когда среда находится в равновесии
(а это и имеет место, когда мы определяем потенциальную энергию), то
подинтегральная функция в интеграле потенциальной энергии прини-
принимает вид
где | S ¦ Vs | = | St-sV |, так как % симметрично. Полученное выражение
дает приращение потенциальной энергии, соответствующее приращению
смещения 8s. Поэтому ясно, что полная потенциальная энергия поля
смещения s дается интегралом по объему
Кинетическая энергия равна, конечно, интегралу от -^ р (ds/dtJ,
распространенному на тот же объем. Полная плотность энергии в среде
равна поэтому
A ^J B.2.18)
Для плоских волн расширения и сдвига, данных уравнениями
B.2.13) и B.2.15), плотности энергии принимают вид
о» = 4- гё [Л2+^ (х+ЗДI/"]2 = (х+2^) [/" & - сс<)]2>
t , B-2.19)
w == \pel [F"]2 + |(х [FT = fi [^" (х-cs0]2.
Поток энергии через любую данную замкнутую поверхность может
быть получен посредством определения скорости изменения полной
энергии внутри поверхности. Использовав в процессе вычислений
уравнение B.2.1), найдем, что
2. 3. Движение жидкости 149
Последним интеграл, являясь поверхностным интегралом, должен быть,
равен потоку энергии через поверхность, вызванному возрастанием W.
Он же со знаком минус впереди равен результирующему потоку энергии
через замкнутую поверхность наружу.
Таким образом, вектор, определяющий плотность потока энергии
и среде, в которой распространяются упругие волны, равен
).S. B.2.20)
Этот результат не является неожиданным; ds/dt есть скорость
частицы среды в точке х, у, z. Усилие, приложенное к элементу поверх-
поверхности dAu, перпендикулярной к ds/dt, равно St-dAu, а мощность равна
силе, умноженной на скорость. Так как размерность % есть сила
на единицу площади, размерность S есть мощность на единицу пло-
площади.
Для плоской продольной волны, данной уравнениями B.2.13)
и B.2.14), переносимая мощность равна
S = i (X + 2ц) сс [/" (х - cct)]\ B-2.21)
а для поперечной плоской волны, данной уравнениями B.2.15) и B.2.16),
она равна
S = ivcs[F"(x-cst)}\ B.2.22)
Плотность потока энергии для плоской упругой волны обычно назы-
называется интенсивностью волны. Мы видим, что в каждом случае вели-
величина интенсивности равна плотности энергии, умноженной на скорость
волны. В плоской волне энергия перемещается со скоростью, равной
скорости волны.
В приведенных случаях величины cj" и csF" — амплитуды скорости
среды —можно рассматривать как аналоги плотности электрического
тока, а величины (X + 2(а) /'' и jjJ*1" — амплитуды приложенных усилий —
как аналоги электрической напряженности. Произведение этих двух вели-
величин дает плотность мощности. Отношение их дает величину, которая
может быть названа импедансом среды для волн рассматриваемого типа.
Для волн сжатия импеданс равен (Х + 2(х)/сс = рсс, а для волн сдвига
2.3. Движение жидкости
Жидкость отличается от упругого тела тем, что она не оказывает
сопротивления при сдвиге. Мы не можем надеяться найти связь смеще-
смещения жидкости с тензором напряжений, так как напряжение сдвига,
может изменяться с течением времени, тогда как смещение остается
постоянным, и наоборот, при постоянном напряжении сдвига смещение
может изменяться. Требуется, чтобы постоянная скорость сдвига вызы-
вызывала бы постоянное усилие сдвига в жидкости.
Это указывает (если это еще было неясно!), что поведение жид-
жидкости удобнее выражать с помощью скоростей, чем с помощью пере-
перемещений. Употребляются два способа описания движения жидкости —
один, учитывающий скорость каждой частицы жидкости в каждый
момент времени, и другой, в котором рассматривается скорость движе-
движения жидкости в каждой точке пространства для каждого момента вре-
времени. В первом способе векторное поле следует за частицами жидкости
в их движении, во втором—поле отнесено к постоянной системе коор-j
150 Гл. 2. Уравнения полей
динат и вектор в данной точке определяет скорость той части жидкости,
которая в данный момент находится в этой точке.
Два способа описания движения жидкости отдаленно соответствуют
атомистическому представлению о жидкости и представлению о жид-
жидкости, как о непрерывной среде. Реальная жидкость является, конечно,
совокупностью молекул, каждая из которых движется под влиянием
сил. Некоторые из этих сил являются внутренними, вызванными воздей-
воздействием других соседних молекул; характер этих сил определяет сжимае-
сжимаемость жидкости. Другие силы являются внешними и вызываются телами,
находящимися на некотором расстоянии; таковы, например, силы тяже-
тяжести, электрические силы; эти силы действуют более или менее одинаково
на все молекулы, находящиеся в данной малой области.
Исследуя первый способ описания, мы должны начать с того, чтобы
охарактеризовать каждую молекулу ее положением в пространстве
при t = 0; чтобы иметь возможность детально определить последующие
движения молекул, мы должны также знать их начальные скорости.
Однако для многих проблем достаточно знать только среднее положе-
положение и скорость молекул в каждом элементе объема (например, dxdydz
в точке х0, у0, z0), имеющем большие размеры сравнительно с величиной
молекул, но малые по сравнению со всей, протяженностью рассматри-
рассматриваемой жидкости. Когда эти средние получены, внутренние силы взаимно
уничтожаются (за исключением задачи определения связи между давле-
давлением и плотностью) и остаются только внешние силы, действующие
на часть жидкости, находящуюся в рассматриваемом элементе. С по-
помощью этого приема осреднения мы получаем уравнения движения
жидкости в целом, в которых не учитывается разрывность ее строения
и которые соответствуют непрерывному, не имеющему зернистого строе-
строения приближению к реальной жидкости. Рассуждения в § 2.4 покажут,
как совершается этот переход от слишком детализированного молеку-
молекулярного изображения жидкости к сглаженному среднему ее изображению.
Второй способ описания обычно начинается сразу с рассмотрения сгла-
сглаженного приближения. Средние скорости частиц такой жидкости, близ-
близких в момент t к фиксированной точке х, у, z, считаются функциями t,
как будто жидкость действительно непрерывна.
Мы предпочитаем второй способ изображения, так как он более
соответствует типам полей, изученных в других частях этой главы.
Вектор v (х, у, z, t) есть скорость той части жидкости, которая нахо-
находится в момент t в точке х, у, z. Выражение divv есть поток жидкости
из «области вблизи х, y,z», так что dxdydzdiw есть поток жидкости
из элемента dxdydz наружу. Если divv везде равна нулю, то жидкость
несжимаема. Вектор w = yrotv представляет циркуляцию жидкости
«около точки х, у, z»; он называется вихревым век/пором жидкости (см.
стр. 49). Если w всюду равен нулю, поток жидкости называется без-
безвихревым (в этом случае вектор v является градиентом скалярного
потенциала скорости).
Все это напоминает нам основные понятия, связанные с векторным
полем, изучение которого проведено в § 1.2. В самом деле, мы исполь-
использовали там пример движения жидкости, чтобы облегчить описание век-
векторного поля; некоторые термины, такие как вихрь, линии тока и поток
были выбраны для того, чтобы аналогия была более полной. Мы можем
теперь вернуться к этой точке зрения, чтобы получить некоторые коли-
количественные характеристики движения жидкости.
Например, линии тока изображают средние траектории отдельных
частиц жидкости. Дифференциальные уравнения этих линий имеют вид
2. 3. Движение жидкости 151
dx/vx = dy/vy — dz/vz. Количество линий тока, пересекающих данную поверх-
поверхность, равное интегралу потока \ v-dA, распространенному на эту по-
поверхность, также равно среднему потоку жидкости через эту поверх-
поверхность и т. д. Если вихрь отсутствует (т. е. rotv = 0) и существует
иотенпиал скоростей, то линии тока везде ортогональны к экшшотен-
циальным поверхностям и дак>1 естественную систему координат для
нашей задачи.
Уравнение неразрывности. Прежде чем перейти к деталям, следует
указать два общих свойства поля скоростей жидкости. Одно из них
касается связи между суммарным потоком и изменением плотности
жидкости. Если v — скорость жидкости, а р —плотность жидкости в точке
х, у, z в момент t, то pv есть вектор, представляющий поток массы
через квадратный сантиметр и dx dy dz div (pv) дает тогда суммарное
истечение массы из элемента объема dxdydz. Так как масса не возни-
возникает и не исчезает в большинстве рассматриваемых случаев, это исте-
истечение массы равно потере массы pdxdydz жидкости в этом элементе.
Другими словами,
|-=-div(Pv). B.3.1)
Это уравнение называется уравнением неразрывности жидкости. Из этого
уравнения очевидно, что для жидкости постоянной плотности р (не-
(несжимаемая жидкость) суммарный поток divv должен быть равен нулю.
В отдельных задачах удобно предположить, что жидкость возни-
возникает (или исчезает) в некоторой точке или точках. Такие точки назы-
называются источниками (или стоками) жидкости. Естественно, что в этих
точках уравнение неразрывности не имеет места.
Второе общее свойство поля скоростей движущейся жидкости свя-
связано с тем, что система координат векторного поля не перемещается
вместе с жидкостью. Чтобы найти скорость изменения векторного свой-
свойства F (r, t) жидкости в выделенной частице жидкости (положение
частицы дается радиусом-вектором г в момент t) или вблизи нее, мы
не можем взять скорость изменения F в точке х, у, z, т. е. dF/dt, так
как выделенная частица не остается обычно в одной точке. Изменение F,
которое нас интересует, равно разности между значением F (г, /) в точке х,
у, z, где по предположению находилась частица жидкости в момент t,
и значением F(r + vdt, t-\-dt) в точке x-\-vxdt, у-\-vydt, z-\-vzdt, где
находится частица в момент t-\-dt. Эта разность в развернутой форме,
если ограничиться только членами первого порядка, имеет вид dF =
= [dF/dt-\-v-'VF]dt. Скорость изменения свойства F жидкости, обозна-
обозначаемая символом полной производной, дается поэтому уравнением
через скорость изменения функции F в точке х, у, z во времени (рав-
(равную частной производной F по t) и через скорость изменения функции F
при переходе от точки х, у, z к соседним точкам (определяемую чле-
членом VF).
Например, ускорение части жидкости, находившейся «в» точке х, у, z
в момент t, равно
dv __ dv _ dv 1 _
dt dt dt ,2 *¦ '
B.3. 3)
152
Гл. 2. Уравнения полей
Вторая форма этого выражения получается перестановкой компонент
1
вектора, а третья форма — заменой выражения -^-rotv вихревым векто-
вектором w. Согласно рассуждению, приведенному на стр. 49, величина век-
вектора w равна угловой скорости частиц жидкости, «близких» к точке х, у, z,
а направление вектора w совпадает с направлением поступательного
движения правого винта, вращающегося вместе с жидкостью.
Скорость изменения скалярных свойств жидкости подсчитывается
таким же образом. Скорость изменения плотности данного элемента
жидкости, оказавшегося в момент t «в» точке х, у, z, при его дальней-
дальнейшем движении, подсчитанная этим способом, оказывается равной
dp dp
Но уравнение неразрывности дает dp/dt= — div(pv), так что
-? = — div (pv) + v grad p = — p div v.
B.3.4)
B.3.5)
Решения для несжимаемых жидкостей. Если плотность р жидкости
везде постоянна, уравнение, определяющее v, принимает вид divv = O.
Ср= П
Рис. 2.9. Эквипотенциальные пинии ф и пинии тока Ф в двумер-
двумерном потоке несжимаемой жидкости.
Наличие циркуляции вызывает разрыв потенциала ф при 9=0.
Наиболее общее решение этого уравнения может быть выражено с по-
помощью скалярного и векторного потенциала (как показано на стр. 59)
v = rot A-+- grad ф;
> = div grad ф = 0.
B.3.6)
2. 3. Движение жидкости
153
А может быть любым достаточно правильным векторным полом, удовле-
удовлетворяющим граничным условиям. Уравнение для потенциала скоростей ф
называется уравнением Лапласа. Оно будет весьма подробно изучено
и этой книге позже. Линии тока, рассмотренные на стр. 23 для без-
безвихревого поля, будут, конечно, перпендикулярны к поверхностям,
на которых потенциал скоростей сохраняет постоянное значение.
Если вихри отсутствуют, то А = 0 и скорость полностью определяется
скалярным потенциалом. Если, кроме того, линии тока лежат в парал-
параллельных плоскостях, потенциал скоростей может быть сделан функцией
только двух координат и движение называется двумерным (или плоским)
потоком. Этот- частный случай имеет большое число важных примене-
применений в аэродинамике. Здесь линии тока и потенциальные линии обра-
образуют двумерную ортогональную систему криволинейных координат.
Уравнение линий тока (см. стр. 23) имеет вид
— = — или — i
Следовательно, если vy— — дФ/дх и ьх = дФ/ду, то
т— dx + g— dy — 0 или Ф (х, у) — const
вдоль линии тока. Функция Ф называется функцией тока: она связана
с потенциалом скоростей ф соотношениями
5Ф 5Ф дФ д'Ь
ду дх ' дх ду '
которые называются уравнениями Коши — Римана; значительно подроб-
подробнее они будут изучены в гл. 4 в связи с функциями комплексного пере-
переменного.
-Линии тока (-Линии тока
Рис. 2.10. Интеграл потока в двумерном случае.
Раньше мы упомянули, что «плотность линий тока» является мерой
полного потока и, следовательно, мерой скорости жидкости. Это легко
показать в случае двумерного потока, так как интеграл потока \ v-dA
между двумя линиями тока Ф (х, у) = Ф2 и Ф (х, у) = Ф1 может быть при-
приведен к криволинейному интегралу в плоскости ху. Речь идет об инте-
интеграле потока между двумя плоскостями, параллельными плоскости ху
и удаленными друг от друга на расстояние, равное единице; за эле-
элемент площади dA можно взять узкую полоску, длина которой раина
154
Гл. 2. Уравнения . полей
единице, а ширина равна ds, где ds —длина элемента дуги кривой,
идущей от Фх к Ф2 в плоскости ху.
Направление dA, конечно, перпендикулярно к направлению ds; именно,
dA = dsxk, где, само собой разумеется, ds всегда перпендикулярно к к.
Интеграл потока равен тогда
2 2 2 2 2
{ vdA= \ v-(dsxk) = ^ (vxds)-k= ^ (vxdy — vydx) = \ йФ = Ф2 —Фх.
iiii 1
Другими словами, полный поток жидкости вдоль области, заключенной
между плоскостями z = 0 и z=l и поверхностями, определенными
линиями тока 1 и 2, равен разности значений Ф2 и Фх функции тока.
Обычные граничные условия в потоке жидкости требуют, чтобы
направления скоростей в точках границы были касательными ко всем
ограничивающим поверхностям. Если вязкость значительна, мы должны
потребовать, чтобы жидкость в непосредственной близости к поверх-
поверхности двигалась вместе с поверхностью, иначе говоря, если поверх-
поверхность неподвижна, то и касательная компонента скорости на границе
должна быть равна нулю. Однако если вязкость невелика, можно с до-
достаточным основанием принять, что жидкость может скользить вдоль
поверхности без заметного торможения, так что допускается конечная
тангенциальная компонента скорости вблизи поверхности.
Примеры. Несколько простых примеров, может быть, разъяснят
некоторые из этих утверждений и определений. Скалярный потенциал
и соответствующее поле скоростей, данные уравнениями
Ф=—?: v = ^ar, B.3.7)
приводят, как было показано на стр. 27, в случае простирающейся
неограниченной жидкости к точечному источнику жидкости в начале
2 2
Рис. 2.11. Линии тока для точечного источника.
координат (г = 0). Как показано в уравнении A.2.9), полный поток
из источника равен 4в(?; эта величина называется мощностью источника.
Так как здесь векторный потенциал отсутствует, то вектор w = у rot v,
определяющий вихревое движение (см. стр. 150), равен нулю и поток
является безвихревым.
Другой случай представляет собой поток сдвига, который полу-
получается, когда жидкость находится между двумя плоскими параллель-
параллельными поверхностями (например, z = 0 и z = 1), одна из которых движется
относительно другой. Если поверхность z = 0 неподвижна, а поверх-
поверхность z = 1 движется в направлении оси х с единичной скоростью,
2. 3. Движение жидкости
155
жидкость между ними, как говорят, подвергается действию единичной
скорости сдвига. Поле скоростей остается неподвижным относительно
обеих поверхностей и равномерно распределено между ними; оно опре-
определяется векторным потенциалом
-///////////л
/СтрастъУ//
У/////////////
А= -y
B.3.8)
Здесь нет результирующего потока
{div v = 0), а вихревой вектор w = -^ j
постоянен во всей области.
Иным примером поля скоростей,
имеющего и векторный и скалярный по-
тенциалы, является следующий, выра-
выраженный в цилиндрических координатах г, <э, z:
Рис" 2Л2ПотокеРсдвигГИДКОСТИ
0,
0,
B.3.9)
г> а,
где ш —угловая скорость жидкости внутри цилиндра г=а. Вектор ско-
скорости тогда имеет вид
V =
ma2
- a,
r
¦?»
г <а,
г>а.
Вихревой вектор w = ^rotv равен cuaz (как этого и надо было ожидать
из его определения на стр. 49) для г < а и равен нулю при г > а. Заме-
Безвихревая
облвото
Безвихревая
область
Рис. 2.13. Скорости движения, линии тока и поверхность
нулевого давления (свободная поверхность) для простого
завихрения.
тим, что при г > а поле скоростей является полем, находящимся вне
простой вихревой линии, данной уравнением A.2.11). Здесь мы предпочли
сделать область вихревого движения конечной (г<а), вместо того
чтобы сконцентрировать ее в бесконечно узкой окрестности прямой
линии, как это было сделано в гл. 1.
Напряжения в жидкостях. Прежде чем идти в этом анализе дальше,
нужно изучить внутренние напряжения в жидкости. Конечно, здесь
имеется давление, которое может быть вызвано силами тяжести или
другими силами, действующими на жидкость, или может быть вызвано
сжатием жидкости либо и теми и другими причинами..
156 Гл. 2. Уравнения полей
Кроме того, имеются также напряжения трения, обусловленные
скоростью изменения деформации, пропорциональные вектору скорости v,
вместо вектора смещения s, как это было в случае упругого тела. Мы
видели на стр. 72, что деформация упругого тела может быть представ-
Л
лена с помощью симметрического аффинора 2>=-^ (Vs + sV). Скорость изме-
изменения этой деформации является также аффинором
Множитель расширения | И | = div v в силу уравнения неразрывности
пропорционален скорости изменения плотности жидкости (эта скорость
равна нулю, если жидкость несжимаема). «Остаток» U, который может
быть представлен с помощью аффинора
соответствует скорости чистого сдвига и изображает форму скорости
изменения аффинора деформации для несжимаемых жидкостей.
Перейдем теперь к рассмотрению формы аффинора напряжения
и зависимости ее от скорости деформации. Если жидкость неподвижна,
то единственным напряжением является статическое давление р, кото-
которое будет вполне симметричным
так что сила, действующая на элемент площади dA, |равна — рАА. (знак
минус обозначает давление, отрицательное натяжение). Если жидкость
расширяется без сдвига (Us = 0), то возможно возникновение трения
чистого расширения, а также изменение давления |из-за скорости рас-
расширения (это имеет место для всех жидкостей, кроме одноатомных газов).
В этом случае напряжение будет иметь вид
где X можно назвать коэффициентом трения расширения.
Если, кроме того, налицо и скорость сдвига жидкости, то суще-
существует и пропорциональное ей напряжение сдвига 2tjIIs, где т\ называется
коэффициентом вязкости. Полный аффинор напряжения поэтому связан
с давлением и со скоростью деформации следующим уравнением:
+ vV), B.3.10)
2
где у == "о" "Ч — ^ может быть назйано вторым коэффициентом вязкости.
Это уравнение аналогично уравнению A.6.28) для напряжений в упру-
упругом теле, но только там, где раньше стояло смещение s, теперь стоит
скорость v (и, конечно, добавлен член, содержащий давление). Однако
это различие не тривиально, так как сила, пропорциональная скорости,
является диссипативной силой, в то время как напряжения в A.6.28) —
консервативны.
Можно, конечно, было бы допустить, что постоянные \ и ц являются
аффинорами, а не скалярами, однако ожидать, что имеет место такое
усложнение, здесь менее обосновано, чем при изучении изотропных твер-
твердых тел. Мы полагаем, что жидкость изотропна и экспериментальные
данные подтверждают это.
Возвращаясь к нашим примерам, мы можем использовать выражение
аффинора -=- (Vv + vV) в сферических координатах, данное на стр. 117
2. 3. Движение зкидкости 157
для вычисления тензора напряжения
>?A. B.3.11)
соответствующего потоку в случае простого источника, данного уравне-
уравнением B.3.7). Другими словами, сила, действующая на элемент поверх-
поверхности, перпендикулярный к радиус-вектору, есть сила сжатия, величина
которой равна р + (A-qQ/r3), в то время как сила сжатия, действующая
на любую площадку, перпендикулярную предыдущей, равна р — Bг@/г3).
Поэтому при наличии вязкости (т) > 0) сила, действующая на элемент
жидкости, не будет изотропной и для достаточно мощного потока
(Q велико) или для достаточно малого г; сила, действующая «поперек»
радиальной линии тока, становится натяжением, в то время как сила,
действующая «вдоль» линии тока, всегда является сжатием. Силы такого
рода должны, конечно, изменять форму элемента жидкости при.его
перемещении от источника по радиусу; этот элемент должен расширяться
во всех направлевиях, перпендикулярных к радиусу, и соответственно
сжиматься в радиальном направлении. Если жидкость вязкая, такую
деформацию производит неизотропная сила. Постоянная у не фигури-
фигурирует здесь, так как мы предположили, что жидкость несжимаема
и div v = 0.
В случае единичной скорости сдвига, данного уравнением B.3.8),
тензор напряжения равен
л,— —р$ + 'q (ki + ik). B.3.12)
Здесь сила, действующая на единицу площади неподвижной поверх-
поверхности (z = 0), равна 2-к = — рк 1- Tji. Компонента — рк, нормальная
к поверхности, дает, конечно, давление (знак минус указывает на то,
что сила направлена к поверхности). Компонента тД параллельна
направлению движения верхней плоскости (z=l) и вызвана вязкостью
жидкости; именно здесь в точности осуществлены условия, соответству-
соответствующие основному определению коэффициента вязкости жидкости -q (tj есть
величина тангенциальной силы, действующей на единицу площади при
единичной скорости сдвига).
В последнем примере, данном уравнением B.3.9), имеем для напря-
напряжения
— Р$, г<а,
В той части жидкости, где г < а, имеется только напряжение, являю-
являющееся изотропным давлением, что, впрочем, неудивительно, так как эта
часть жидкости вращается, как твердое тело с угловой скоростью ш.
Вне этого вихревого стержня при г > а имеется сдвиг жидкости; сила,
действующая на единицу площади площадки, перпендикулярной к г,
имеет тангенциальную компоненту — (A-qwa2/r2)as, вызывающую тормозя-
тормозящее действие жидкости вне цилиндра радиуса г на жидкость, находя-
находящуюся внутри этого цилиндра (и наоборот).
Сила, действующая на элемент жидкости в точке х, у, z, равна, как
мы установили, (V-?-f F)dxdydz. Она должна быть равна ускорению
dv/dt элемента, умноженному на его массу pdxdydz. Вытекающее отсюда
158 Гл. 2. Уравнения полей
уравнение (которое получено с помощью формул стр. 116)
= F — grad [/>-(-|-7] + X^divv] +ijV2v= B,3.14)
= F — grad /)~(yTi"^^) ^v v ~~
где у=="з3~^> служит для вычисления давления, если известна скорость;
оно дает также возможность подсчитать поступательные или колебатель-
колебательные движения. Это уравнение вместе с уравнением неразрывности B.3.1)
и с уравнением состояния, связывающим давление и сжатие жидкости»
является основным во всех многообразных проблемах динамики жидко-
жидкостей. Различные частные случаи его получаются, если тот или другой
член исчезающе мал.
Уравнение Бернулли. Простейший случай соответствует установив-
установившемуся движению несжимаемой жидкости, для которого dv/dt и divv
равны нулю. Предположим дополнительно, что внешняя сила F может
быть получена из потенциальной энергии V, F— —gradF, и используем
векторное соотношение
gadw2 = v-Vv-f v,<rot v.
Окончательно получим
2т) rot w — 2pv x w = — grad U,
! •> l * B.3.15)
jpv2; w="rotv v '
Скалярную величину U можно рассматривать как плотность энергии
движущейся жидкости. Первый член в выражении для U равен плотности
потенциальной энергии положения, обусловленной внешними силами,
последний член равен плотности кинетической энергии. Если движение
жидкости безвихревое, вихревой вектор w равен нулю и U всюду
постоянно для потока данного вида. В этом случае скорость жидкости
определяем через потенциал скорости при помощи граничных условий
и потом находим давление из уравнения
p = U-V-^9v\ B.3.16)
где {/ — постоянная, определяемая из граничных условий. Это уравнение
называется уравнением Бернулли для несжимаемой жидкости (р = const).
Заметим, что, как может получиться, в некоторых областях для
решения требуется достаточно большая скорость, так что давление,
найденное по этой формуле, сделается отрицательным. В принципе это
произойти не может, так как иначе возникла бы кавитация и граничные
условия должны были бы быть изменены.
Очень многие задачи, представляющие практический интерес, могут
быть решены с достаточной степенью точности, если допустить, что
поток определяется потенциалом скоростей (т. е. что поток безвихревой),
который удовлетворяет уравнению Лапласа. Давление в любой точке
может быть найдено из уравнения Бернулли. Тем же способом могут
быть решены даже многие задачи аэродинамики, хотя воздух далеко не
является несжимаемым. Только в случае, когда скорость значительной
2. 3. Движение жидкости 159
части воздуха приближается к скорости звука, полученное приближение
оказывается непригодным. Более сложный случай сверхзвукового потока
будет затронут далее в этом параграфе.
Как пример безвихревого движения несжимаемой жидкости мы снова
рассмотрим поток жидкости из простого источника, данный уравне-
уравнением B.3.7). Если пренебречь гравитационным потенциалом, давление,
как функция г, будет иметь вид р^-— (р(?2/2г4), где р^ — давление на
бесконечном расстоянии от источника. Мы видим, что если действитель-
действительные размеры источника достаточно малы (г —достаточно мало), то давле-
давление может оказаться отрицательным и появится кавитация.
В заключение рассмотрим случай вертикального вихря радиуса а,
определенного уравнением B.3.9). Теперь мы примем во внимание грави-
гравитационный потенциал V = pgz. При г > а вихревой вектор w равен нулю,
так что U постоянно. Предположим, что жидкость, когда она неподвижна,
имеет свободную поверхность (р = 0) при z = 0. Постоянное значение U
в таком случае должно быть таким, что р—0 при z = 0 и при г=оо,
так что
2- = 0, r>a.
При г<а вихревой вектор w не равен нулю, но rotw = 0, так что
grad U = 2pv х w = 2po>2 rar.
Определив отсюда интегрированием U и выбрав постоянную интегриро-
интегрирования так, чтобы давление было непрерывным при г = а, получим
рог + р + Р? Bа2 - г2) = 0, г<а.
Уравнение свободной поверхности есть уравнение поверхности р = 0
z =
-о^лг, г>а.
г<а,
B-3.17)
В обоих рассмотренных случаях вязкость ке влияет на давление,
так как в уравнении, определяющем давление для установившегося дви-
движения несжимаемой жидкости, содержится единственный член, завися-
зависящий от вязкости, и этот член содержит также rotw; в наших же про-
простых примерах rotw = 0. Можно рассмотреть другие примеры, в которых
rotw не равен нулю и, следовательно, вязкость влияет на давление;
однако в примерах этого рода чаще всего \ и р зависят от времени.
Волновое уравнение. В качестве первого примера неустановившегося
движения рассмотрим колебания с малой амплитудой. В этом случае
в уравнении B.3.14) можно пренебречь членами, содержащими квадрат v,
и мы получаем более простое уравнение
р^= —grad (/> +F)+ ( |-•») +х") graddivv — Ti rot rot v, B.3.18)
где мы снова положили F= — gradT'; здесь мы более не предполагаем,
что жидкость несжимаема.
Чтобы пойти дальше, нужно рассмотреть связь между давлением
и сжатием жидкости. Поток материи, вытекающий из любого элемента
объема, уменьшает давление сжимаемой жидкости; именно для упругой
жидкости, если только сжатие невелико, скорость изменения р пропор-
пропорциональна дивергенции v, dp/dt = - /¦ div v. Постоянная х называется
160 Гл. 2. Уравнения полей
модулем сжатия рассматриваемой жидкости. Если смещения малы, это
равенство можно выразить через смещение s
На стр. 59 мы видели, что каждое векторное поле может быть един-
единственным образом разбито на две части, одна из которых является гра-
градиентом, а другая — вихрем. Это обстоятельство мы используем здесь дважды;
во-первых, положим, что неизвестная скорость v равна сумме градиента
потенциала скоростей ф и вихря векторного потенциала А. Подставив
это в B.3.18), мы приравняем отдельно градиенты и вихри в обеих частях.
Равенство вихрей дает
р ^ = — •») rot rot A. B.3.19)
Это уравнение не является векторным волновым уравнением, но пред-
представляет собой векторный аналог уравнения диффузии, упомянутого на
стр. 136, и будет рассмотрено в § 2.4. Так как здесь содержится произ-
производная по времени только первого порядка, а не второго, то решения
этого уравнения не будут истинными волнами, распространяющимися
с определенной скоростью и имеющими неизменную энергию; эти реше-
решения определяют возмущения, затухающие с течением времени и умень-
уменьшающиеся при распространении в пространстве. Эти решения будут рас-
рассмотрены более подробно в гл. 12. Отметим, что эти волны не влияют
на давление. Заметим также, что уравнение для вихря w = у rot v совпа-
совпадает с уравнением для А. Для нас не должно быть неожиданным, что
наличие вязкости вызывает распространение вихревого движения.
Собирая члены с градиентами в обеих частях уравнения, получен-
полученного из B.3.18), и дифференцируя обе части по времени, получим окон-
окончательно уравнение для продольных волн
Ж*) <2-3-20>
4
Если вязкость сжатия -^-tj + ^ мала, то в жидкости распространяются
о
обычные волны сжатия со скоростью с и все замечания, сделанные отно-
относительно волн сжатия в упругой среде, применимы и здесь. Если эта
вязкость не равна нулю, то нужно ввести еще член, характеризующий
затухание. Например, для простых гармонических волн в случае, когда
зависимость от времени выражена множителем e~iv>t, уравнение для вто-
второго множителя, выражающего зависимость <]» от положения точки в про-
пространстве, имеет вид
^= 0
Другими словами, функция ф содержит в качестве пространственного
множителя показательную функцию с комплексным показателем, опреде-
определяющую пространственное затухание волны.
С другой стороны, если построена стоячая волна, для которой часть,
зависящая от положения точки в пространстве, удовлетворяет уравнению
\72ф-)-Л2ф = 0, то уравнение для зависимости ф от времени имеет вид
2. 3. Движение жидкости 161
Это уравнение является уравнением колебаний, затухающих с течением
времени.
Безвихревой поток сжимаемой жидкости. Нашим следующим приме-
примером иного рода движения жидкости, представленного уравнением B.3.14),
будет установившееся безвихревое движение сжимаемой жидкости. Это —
важный в аэродинамике случай, когда скорость жидкости приближается
к рассмотренной в предыдущем пункте скорости распространения волны
сжатия с = 1Лс/р. Так как приводимые рассуждения почти всегда приме-
применяются к потоку воздуха, мы можем, кроме того, наше выражение для
сжимаемости х считать приспособленным для случая газа.
Мы не можем здесь углубляться в подробное рассмотрение термоди-
термодинамики идеального газа; для справок по этому вопросу имеется большое
число книг. Нам здесь нужно только записать два уравнения, связываю-
связывающих давление р, плотность р и температуру Т газа, подвергающегося
адиабатическому расширению (расширению без потери тепла, содержаще-
содержащегося в газе):
Ро'
где индексами 0 обозначены давление, плотность и температура в стан-
стандартных условиях (например, когда жидкость неподвижна). Эти уравне-
уравнения можно написать иначе, связав давление и плотность газа с его
энтропией S:
-Е- = AeaS.
Рг
Адиабатическое расширение газа является расширением при постоян-
постоянной энтропии S. Постоянная y равна отношению удельных теплоемкостей
при постоянном давлении и при постоянном объеме (ее значение для
воздуха равно 1,405).
Продифференцировав это уравнение при постоянном S, найдем
dp/p = Y^P/P> a воспользовавшись уравнением неразрывности B.3.5), по-
получим dp/p= —Y^divv. Сравнивая этот результат с определением мо-
модуля сжатия '/., мы видим, что x = y/) и чт0 скорость звука (волн сжатия)
в газе при давлении р и плотности р равна
c=J/ ±?-=у f- . B.3.22)
В потоке сжимаемого газа как давление, так и плотность (а следо-
следовательно, и скорость звука) меняются от точки к точке внутри газа.
Связь между этими величинами получается из уравнений B.3.15), при-
причем мы снова начинаем с рассмотрения безвихревого установившегося
потока (w = 0, dv/dt = 0; мы также пренебрегаем потенциалом V). Так
как теперь р не остается постоянным, то интегрирование уравнения
grad U - 0 несколько сложнее, чем раньше. И давление, и плотность
оказываются функциями скорости воздуха v в любой точке. Максимум
давления р0 и соответствующие значения плотности р0 и скорости
звука с0 достигаются в тех точках, где w = 0 (точки застоя). В любой
другой точке, согласно уравнениям B.3.15) и B.3.21), имеем
4 /^ РО
Р Ро > ^ ^ Т —1 Ро L V Ро
р
11 Ф. М. Морс и Г. Фешбах
162 Гл. 2. Уравнения полей
Это равенство указывает на то, что существует максимум скорости
потока
когда давление равно нулю. Такова будет, например, скорость истече-
истечения в пустоту. Для воздуха при температуре 15°С (То = 288) в точках
застоя эта предельная скорость составляет 75 700 см/сек. При этой пре-
предельной скорости скорость звука равна нулю (так как давление равно
нулю). В точках застоя воздух неподвижен и скорость звука V^YPo/P»
максимальна. Поэтому, когда v меняется от нуля до Umax» безразмерное
отношение M—v/c меняется от нуля до бесконечности. Это отношение
называется числом Маха в точке для потока воздуха. Если число Маха
меньше единицы, поток называется дозвуковым, если оно больше еди-
единицы, поток будет сверхзвуковым.
Формулы, выражающие давление, плотность, температуру, скорость
звука и число Маха в некоторой точке через скорость потока у в этой
точке и через давление р0 и плотность р0 в точке застоя, имеют вид:
) ;
i/Cr-l) f с Ч2/(тг-1)
U)
o I/ _L /v \\ /7,2 -,2\ - /О О ОО\
М = т =
с0 = ^max |/l^ = |/-^- = 34 100
Скорость vt, для которой число Маха М равно единице (скорость жид-
жидкости равна скорости звука), оказывается равной V(Y~^)/(Y + ^ ^max =
=^31100 см/сек для воздуха при температуре 15° С G'0 = 288) в точ-
точках застоя. Для этой скорости давление, плотность и т. д. равны:
ps = 0,528р0; Ps = 0,685 Ро; Т8 = 0,832Го = 240° К = -33°С; cs = v6.
Дозвуковой и сверхзвуковой потоки. Различные примеры показывают
важность области, где М=1, и обнаруживают, что явления в газовом
потоке, скорость которого превышает указанную (сверхзвуковой поток),
совершенно отличны от явлений в газовом потоке, скорость которого
меньше указанной (дозвуковой поток). В качестве очень простого при-
примера рассмотрим воздушный поток, набегающий на очень малый непо-
неподвижный предмет, находящийся в точке Р (рис. 2.14). Наличие этого
предмета постоянно тормозит движение воздуха перед ним, что непре-
непрерывно вызывает звуковую волну впереди него. Если скорость воздуха
меньше скорости звука, эти волны от препятствия в точке Р могут рас-
распространяться против течения и, так сказать, предупреждать среду
о предстоящей встрече с этим препятствием. Если же воздух движется
быстрее звука, то предостережение не может быть послано навстречу
и расширяющиеся фронты волн относятся по течению, как видно на
2. 3. Движение жидкости
163
правой части рис. 2.14. Огибающая этих волн является «носовой вол-
волной» возмущения и называется линией или поверхностью Маха. Первое
сообщение о наличии препятствия в точке Р появляется лишь тогда, когда
воздух наталкивается на линию или поверхность Маха. Между прочим,
Скорость
ншдкости
Скорость
жидкости
Рис. 2.14. Распространение возмущения в жидкости, вызванного
небольшим препятствием в точке Р при дозвуковой (слева) и сверх-
сверхзвуковой (справа) скорости потока.
нетрудно видеть, что угол наклона этих линий к оси потока, так назы-
называемый угол Маха, дается равенством
. 1 . с
а = arc sm ^ = arc sin — .
Позже мы снова вернемся к линиям Маха.
В качестве второго примера рассмотрим ноток «оздуха в трубе с
переменным поперечным сечением S (х) (см. рис. 2.15). Для того чтобы
Давление р(х)
Полный поток массы Q
Плотность р(х)
Рис. 2.15. Поток воздуха в трубе с перемен-
переменным поперечным сечением.
Нижний график показывает три возможных хода изме-
изменения величины M=vjc вдоль трубы.
воздух не накапливался где-либо (т. е. чтобы поток был установившимся);
необходимо, чтобы через каждое поперечное сечение в единицу времени
проходила одна и та же масса Q воздуха. Если поперечное сечение трубы
меняется не слишком быстро с изменением х и если внутренняя поверх-
поверхность трубы гладкая, то плотность и скорость почти одинаковы во всех
точках каждого поперечного сечения; поэтому с достаточно хорошим
приближением мы можем считать р, р и v функциями одного только х.
Для такого приближения в случае установившегося потока имеем
11*
164 Гл. 2. Уравнения полей
или
2 /¦ п -ч 1
In ? = г In umax + In ( — ) — In v г- In i
T—1 V Po У т —4
Дифференцируя по х последнее уравнение и пользуясь выражением
для с из B.3.23), получаем
L
da:
B.3.24)
Поэтому если поток всюду дозвуковой (М<1), то при уменьшении
размеров S скорость воздуха v возрастает, и наоборот; если же
поток всюду является сверхзвуковым (М>1), то при убывании
S скорость воздуха убывает, и наоборот. В обоих случаях при макси-
максимуме или минимуме S скорость v также достигает максимума или ми-
минимума. Эти случаи показаны на нижней части рис. 2.15.
Тем не менее, если давление /?0>хполный поток Q и т. д. подобраны
надлежащий! образом, число Маха М может оказаться равным 1 там,
где S достигает минимума. В этом случае при обращении dS/dx в нуль
dv/dx может не быть равным нулю и скорость при прохождении газа
через узкое сечение трубы, может возрасти от дозвуковой до сверхзву-
сверхзвуковой (конечно, скорость может быть и вначале сверхзвуковой, а в
конце —дозвуковой). Этот случай изображен средней кривой нижней
части рис. 2.15.
Потенциал скорости. Линейное приближение. Теперь мы должны
вывести уравнение, которое даст нам возможность рассчитать векторное
поле скоростей, удовлетворяющее любым заданным граничным условиям.
Как и в случае безвихревого потока несжимаемой жидкости, предполо-
предположим, что это поле может быть получено из скалярного поля потенциала
скоростей v = grad(J). Уравнение для ф получается из уравнения нераз-
неразрывности B.3.1) при dp/dt = O:
O = div(pv)=div [
ИЛИ
Следовательно, если v = grad(J>, то
4^|ЧЧ B-3-25)
т п т дхп
т, п=1
где хг = х, х2 = у, x3 = z и c2 = y(y —l)(wfnax —|grad(l>|2)
Для двумерного потока уравнение принимает вид
~"^\dxj J+SP4 ^Vdi) J -
Здесь существует также функция тока Ф, определяющая линии тока
и измеряющая поток массы воздуха между двумя линиями тока. Мы най-
найдем эту функцию из уравнения неразрывности для установившегося потока
div(pv)=0, так как можно положить
., _3* ро_ЗФ. =^.=:PoS*.
vx дх~—рду' v ду р дх '
2. 3. Движение акидкости 165
тогда div (pv) автоматически обращается в нуль. Подобно тому как мы
видели на стр. 154, полный поток массы между двумя линиями тока (на
единицу расстояния по оси z) равен произведению р0 на разность значе-
значений Ф для двух рассматриваемых линий тока. Уравнение для Ф анало-
аналогично уравнению для ф
= _2ГРЛа—--. B.3.27)
V рс J дх ду дх ду * '
Уравнение B.3.25) не является, конечно, линейным относительно ф;
его очень трудно решить точно. Если М мало (дозвуковой поток),
в первом приближении величиной / можно пренебречь и уравнение
сведется к линейному уравнению Лапласа, характеризующему несжи-
несжимаемые жидкости. Когда найдено решение ф0 уравнения Лапласа дли
интересующего нас частного случая, с помощью уравнения для / можно,
исходя из ф0, вычислить /0 для каждой точки. Тогда второе приближе-
приближение к истинному значению ф можно получить, решив уравнение Пуас-
Пуассона V2ty = /0 и т. д.
Однако, если М не мало, такие методы итераций не могут быть
использованы и нужно применять другие приближенные методы. Один
из приемов полезен в случае, когда поток незначительно отличается от
равномерного потока v = vu, где vu — постоянно. В этом случае напра-
направление невозмущенного потока можно считать совпадающим с напра-
направлением оси х, и мы можем положить
где vx мало сравнительно с vu, хотя vu не обязательно является малым
сравнительно с с. С точностью до величин первого порядка относительно
малого количества \^jc имеем
где Л/^ = [2/(у — l)][z^/(Dmax — vl)) = vl/cl есть квадрат числа Маха для
невозмущенного. потока.
Это уравнение, будучи линейным относительно ф1? может быть
решено, и тем самым установившийся поток может быть определен
вблизи неровностей граничных поверхностей, если только эти неровности
не вызывают вблизи себя значительных изменений скорости воздуха.
Линии Маха и ударные волны. Уравнение B.3.28) снова показывает
существенное различие между дозвуковым и сверхзвуковым потоками.
Это различие можно иллюстрировать в двумерном случае, когда уран-
нение принимает вид
^(l_Jil)+^i = 0. B.3.2!»)
Если Ми меньше единицы, это уравнение преобразуется в уравнение
Лапласа для ф2 путем изменения масштаба для у (полагаем у' = ^|/1 — М\,
х' = х). Поэтому линии тока и эквипотенциальные поверхности напоми-
напоминают линии тока и эквипотенциальные поверхности для потока несжимае-
несжимаемой жидкости, но только растянуты в направлении оси у в l/l/l — М? ран.
Если же Ми больше единицы, мы не можем преобразовать паше
уравнение в уравнение Лапласа, так как знак перед членом, содержа-
содержащим d2tyjdxz, становится отрицательным и уравнение больше напоминает
166
Гл. 2. Уравнения полей
волновое уравнение (см. стр. 124) с заменой t на х и с «волновой ско-
скоростью» cu= l/Y^Mli,— 1. Решения полученного уравнения имеют вид
Как было упомянуто на стр. 163, любая неправильность формы границы
(которая здесь, очевидно, является плоскостью, параллельной плоско-
плоскости xz) порождает «носовую волну», которая образует угол а = arc tgcu =
= arc sin j-r- с осью х, направлением невозмущенного движения. Этот
угол является углом Маха, упомянутым на стр. 163.
В двумерном случае мы можем также получить приближенное ура-
уравнение для функции тока Ф, рассмотренной на стр. 164. Предположим,
что Ф = (р/р0) vuy + Ф2; подставляя это в уравнение B.3.27) и пренебрегая
членами высшего порядка, получим уравнение
д (\ Мг\ I —0 19 Ч ЧГЛ
аналогичное приближенному уравнению для поправки к потенциалу ско-
скоростей ty.
Скорость в области В
Скорость в области С
Рис. 2.16. Двумерный сверхзвуковой поток;
линеаризированное решение.
Векторные диаграммы показывают способ определения
скоростей в областях В и С; скорость в областях А и D
равна vu-
В качестве примера рассмотрим поток воздуха, движущегося со сверх-
сверхзвуковой скоростью вдоль поверхности, совпадающей в основном с пло-
плоскостью xz; однако в некоторой точке на этой плоскости имеется складка,
образующая неправильность на границе, параллельную оси z, как пока-
показано на рис. 2.16. Если высота h этой складки невелика, то пригодны
приближения, даваемые уравнениями B.3.29) и B.3.30), и функция тока Фг
и потенциал скоростей фх являются в этом случае функциями от у — сих
или, что то же самое, от х - у \ГМ\ — 1. Функции от у + сих в этом
случае не нужна (почему?). Поэтому изменение скорости vt перпендику-
перпендикулярно к линии Маха, т. е. образует угол а с осью у.
Если граничная поверхность дана уравнением у=В{х), причем В(х)
равно нулю при х > х2 и при х < хх, то функция тока такова:
Линии тока Ф = const изображены в верхней части рис. 2.16. Заметим,
что линии тока не возмущаются в области А слева от линии Маха (х1г Р),
2. 3. Движение жидкости 167
а также и в области D справа от линии Маха {xz, Q); обе эти линии
наклонены к оси х под углом Маха а = arc sin тг .
Фактическая скорость v (для этого приближения) в областях В и С
рис. 2.16 может быть найдена графически, если воспользоваться следую-
следующими двумя очевидными фактами: во-первых, вектор v должен быть парал-
параллелен линиям тока, т. е. должен образовать угол б с осью х, и, во-вто-
во-вторых, вектор vx перпендикулярен к линии Маха, т. е. образует угол а
с осью у. Графическое построение показано на рис. 2.16. Так как v1? по
предположению, меньше чем vu, то для скорости воздуха, его плотности,
числа Маха я потока массы мы имеем следующие приближенные выра-
выражения для двух областей:
Область В v ss vu A — 6 tg a),
Область С v «te vu A + о tg a),
Интересно отметить, что для потока в области В, несмотря на
уменьшение скорости воздуха v, поток pv массы через единичную пло-
площадку возрастает. Изображение линий тока также подтверждает это,
так как на рис. 2.16 видно, что эти линии тока в области В распо-
расположены ближе друг к другу, чем в области А, а этому сопутствует
возрастание потока массы, как было выяснено на стр. 165. При пересе-
пересечении первой линии Маха скорость воздуха резко уменьшается и воздух
сжимается, при пересечении второй линии Маха движение ускоряется
и воздух расширяется, при пересечении третьей линии скорость умень-
уменьшается до первоначальной величины и воздух сжимается до первона-
первоначального состояния.
Если граница в самом деле искажена так сильно, как изображено
на рис. 2.16 (т. е. если углы 6 и 6 действительно так велики, как по-
показано), то v± не будет очень мало сравнительно с vu и первое прибли-
приближение не будет достаточным для того, чтобы рассчитать движение. Не-
Непосредственно возникающая трудность состоит в том, что угол Маха для
воздуха в области В заметно отличается от угла Маха для воздуха в об-
области А, если только скорости v заметно отличаются друг от друга
в этих областях. Возникает вопрос: каков должен быть угол между
осью х и линией Маха, отделяющей друг от друга области А и В?
Должен ли он совпадать с углом au = arcsin A/М„), соответствующим
области А, или с углом Маха, соответствующим движению воздуха
и области В (последний угол больше чем ам)? Подробное изучение точ-
точного решения показывает, что угол между осью х и действительным
«фронтом удара» является промежуточным между двумя указанными
выше углами и что воздух при пересечении этого фронта испытывает
практически мгновенное изменение состояния; его скорость, плотность
и давление становятся равными соответствующим величинам в области В.
168
Гл. 2. Уравнения полей
Линии Маха, соответствующие областям В и С, расходятся (как по-
показано пунктирными линиями Оа и Ob на рис. 2.17); в области, распо-
расположенной между ними, в точном решении происходит непрерывное изме-
изменение от состояния, соответствующего области Б, к состоянию, соответ-
соответствующему области С. Изменения давления вдоль линии тока Н также
показаны на рис. 2.17. Здесь видно, что при переходе от области более
быстрого движения к области, где скорость меньше, давление возрастает
скачкообразно, в то время как обратное изменение происходит более
плавно.
Точное решение
У/////////////////////,
Рис. 2.17. Двумерный сверхзвуковой поток; точ-
точное решение.
Показаны линии тока и распределение давления вдоль Н.
Еще очень многое можно было бы сказать здесь об аэродинамике сверх-
сверхзвуковых скоростей, но это слишком.далеко отвлекло бы нас от нашей
цели в этой главе. Мы здесь изучаем приемы получения уравнений полей,,
а не занимаемся исчерпывающим рассмотрением различных отделов физики.
2.4. Диффузия и другие явления просачивания жидкости
В предыдущем параграфе мы молча предполагали, что рассматри-
рассматриваемая жидкость одна заполняет пространство, что внутри жестких
границ, соответствующих изучаемой задаче, нет других жидкостей или
твердых тел, мешающих потоку жидкости. Однако многие интересные
задачи связаны с просачиванием жидкости через пористое твердое тело
(или через другую жидкость), которое в каждой точке взаимодействует
с диффундирующей жидкостью. Примерами могут служить проникновение
жидкости через пористую среду, или движение особых жидкостей,
например свободных электронов, через газ, или нейтронов через вещество.
Весьма важным является вопрос о расчете потока тепла через вещество.
Тепло является, конечно, внутренней энергией самого вещества, но оно
ведет себя во многих отношениях так, как будто бы оно было жидкостью
с «плотностью» и скоростью потока, которые могут быть измерены.
Во всех этих случаях мы все еще можем говорить об эффективной
плотности р рассматриваемой жидкости, равной средней массе на единицу
объема (или количеству тепла на единицу объема и т. д.) в каждой
точке, даже в том случае, когда каждый элемент объема содержит также
Другую жидкость или твердое тело. Во многих случаях мы не можем
говорить о средней скорости (что такое скорость тепла, например?),
но мы можем всегда говорить о потоке массы (или полном потоке тепла
и т. д.) через квадратный сантиметр в каждой точке. Это количество &
2. 4. Диффузия и другие явления просачивания 169
является вектором и равно pv, если здесь имеется такое понятие, как
скорость жидкости v.
Вообще говоря, рассматриваемая жидкость не исчезает (хотя в
случае, когда жидкость представляет собой нейтронный газ, некоторые
нейтроны исчезают благодаря поглощению их ядрами), так что уравнение
неразрывности обычно сохраняется
^¦=-divJ. B.4.1)
Однако, начиная с этого момента, наши рассуждения зависят от того,
какую именно жидкость мы изучаем.
Поток жидкости через пористое твердое тело. Например, для
жидкости, просачивающейся сквозь пористое твердое тело, обычно можно
пренебречь расширением и сжатием жидкости, т. е. положить dp/dt = O.
Можно пренебречь также вязкостью, так как влияние ее мало по срав-
сравнению с силами трения при просачивании; кроме того, можно пренебречь
вихревыми движениями. Таким образом, поток массы J можно рассмат-
рассматривать ка'к градиент скалярного потенциала, удовлетворяющего уравнению
Лапласа div [grad ф] = V2tJ> = 0, как и в случае безвихревого потока несжи-
несжимаемой жидкости. Отличие от других случаев, рассмотренных в предыду-
предыдущем параграфе, имеется в уравнении движения, определяющем давление
в каждой точке. В настоящем случае это различие состоит в наличии
силы, заставляющей жидкость течь через поры; в первом приближении
эта сила пропорциональна потоку.
Исходя из уравнепия B.3.14) мы видим, что уравнением для потока
массы в данном случае является уравнение
% + RJ = F-gv*dp, B.4.2)
где F — внешняя сила (тяжести и т. д.), действующая на единицу^ объема
жидкости, р - давление, а Л— удельное сопротивление потоку со стороны
пористого материала. Когда пористое вещество оказывает одинаковое
сопротивление во всех направлениях, Л можно считать скаляром; для
неизотропного вещества Л будет аффинором, действующим на J. Если
движение установившееся, причем J = grad ф и F является также градиен-
градиентом потенциальной функции V, это уравнение принимает вид
grad (V — р) — Л grad ф,
а в случае, когда Л — постоянно, оно дает просто p=V — /?ф, что и
служит для определения давления р в каждой точке.
Диффузия. Более интересные проблемы возникают в случае сжимаемой
жидкости, а также в случаях, когда вообще нельзя говорить о «силах»,
действующих на элемент жидкости. Таковы случаи потока тепла, диффузии
одной жидкости через другую и диффузии нейтронов через вещество.
В случае потока тепла понятие силы, действующей на жидкость, не
имеет смысла; в случае диффузии нейтронов существенными силами
являются внутренние силы, вызывающие столкновения между нейтронами
и частицами вещества.
Ни в одном из этих случаев уравнение движения B.4.2) не приме-
применимо. Поток вызывается не внешними силами и не градиентами давлений,
а просто градиентом концентрации. Жидкость по тем или иным причинам
стремится перемещаться из точек с более высокой плотностью к точкам
с меньшей плотностью, причем поток пропорционален градиенту плот-
170 Гл. 2. Уравнения полей
ности
J=-a2gradP; B.4.3)
достоянная а называется постоянной диффузии. Комбинируя это с урав-
уравнением неразрывности B.4.1), получаем уравнение диффузии
t = tt2V2P' B-4.4)
которое уже встречалось нам на стр. 136 и 160.
В случае потока тепла р есть «количество тепла» в единичном
объеме; оно пропорционально температуре р = СТ, где С — теплоемкость
вещества на единицу объема. Так как уравнение теплового потока имеет
вид J= — KgradT, где К — теплопроводность вещества, то, очевидно, Т
является решением уравнения диффузии при а? = К/С.
Доказательство того, что, например, поток нейтронного газа удов-
удовлетворяет приближенно уравнению B.4.3), и определение соответствующей
постоянной диффузии требуют подробного изучения механизма диффузии
нейтронов; это будет намечено позже в данном параграфе. В таком случае
диффузия является следствием беспорядочного движения частиц жидкости,
а постоянная диффузии является мерой сопротивления, оказываемого
этому движению другим присутствующим веществом.
Уравнение диффузии B.4.4) отличается от волнового уравнения B.2.2)
тем, что оно содержит производную первого порядка по времени вместо
производной второго порядка. Это соответствует тому факту, что диффузия
является необратимым процессом подобно движению при наличии трения,
при котором энергия теряется (или энтропия возрастает), в то время как
волновое движение является обратимым и консервативным. В одно-
одномерном случае уравнение
дР _„252Р
Tt~a дх*
является простейшей формой параболического уравнения с частными произ-
производными. Как отмечено на стр. 136, плотность жидкости здесь изменяется
так же, как изменяются смещения точек струны в случае полного зату-
затухания; плотность жидкости здесь стремится к тому, чтобы стать везде
постоянной, причем никогда не «перебарщивает» настолько, чтобы возникли
колебания, как это имело место для волновых и вибрационных движений.
Фазовое пространство и функция распределения. Прежде чем идти
дальше в изучении диффузии, нам надо будет рассмотреть подробно дви-
движения частиц диффундирующей жидкости; это значит, что мы должны
на время отказаться от представления о жидкости как о непрерывной,
гладкой среде и рассмотреть ее атомистическое, разрывное строение.
Такое исследование целесообразно выполнить именно в этой главе, если
только удастся показать, как можно описать поведение большого числа
атомов с помощью непрерывных полей, удовлетворяющих дифференциаль-
дифференциальным уравнениям с частными производными, а также показать, как
свойства отдельных атомов связаны с постоянными, содержащимися
в уравнениях поля.
Такая связь устанавливается, конечно, с помощью методов кинети-
кинетической теории. Пусть наша жидкость состоит из N атомов (или молекул),
каждый из которых имеет массу т. «Состояние» и-го атома в любой
момент задается его положением и скоростью (для молекул -существуют
еще другие внутренние движения, которые здесь нет надобности рассма-
рассматривать). Положение атома может быть задано с помощью радиус-вектора
2. 4. Диффузия и другие явления просачивания 171
проведенного к атому из некоторого начала координат;
скорость этого атома может быть задана с помощью вектора, изобража-
изображающего количество движения или импульс р = mv = ipx + jpy + kpz- Таким
¦образом, состояние атома (в той мере, как это нам здесь нужно) может
быть задано положением точки в шестимерном фазовом пространстве
с координатами х, у, z, px, ру, рг. Методы кинетической теории дают
способы, при помощи которых можно перейти от движения отдельных
атомов в фазовом пространстве, движений, вызванных влиянием внешних
и внутренних (межатомных) сил, к средним движениям множества
атомов.
Переход совершается с помощью функции распределения. Для опре-
определения этой функции рассмотрим жидкость частного вида, состоящую
из N атомов, удовлетворяющих данным начальным и граничным усло-
условиям обычного типа. В некоторый момент атомы этой жидкости изобра-
изображаются множеством N точек в фазовом пространстве. В одних областях
фазового пространства имеется концентрация точек, в других областях
они расположены очень редко. Если N — достаточно большое число, мы
обнаружим тенденцию к «гладкости» густоты этого множества точек. Мы
можем записать среднюю плотность точек в различных областях фазового
пространства, и эта плотность будет меняться более или менее гладким
образом от точки к точке. Предположим теперь, что для подобного
множества N атомов мы снова имеем те же начальные и граничные
условия, и рассмотрим распределение этих N точек в фазовом простран-
пространстве в соответствующий момент времени. Так как начальные и граничные
условия являются условиями макроскопическими и относятся только
к средним положениям атомов, то второе множество точек не будет в точ-
точности совпадать точка в точку с первым множеством. Однако средняя
плотность точек будет более или менее одинакова в обоих случаях.
Предположим, что мы проделали тот же самый опыт не дважды,
л много раз, отправляясь от N атомов, подчиненных условиям, тождест-
тождественным друг другу с макроскопической точки зрения. Тогда можно получить
плотность вероятности fix, у, z, px, py, pz, t) = /(г, р, t) для каждой точки
¦фазового пространства, так что величина f dxdydz dpxdpy dp, указывает,
для какой части из общего числа опытов какая-нибудь из рассматриваемых
точек находится в момент t внутри элемента dxdydz dpxdpydpz фазового
пространства в точке г, р. Функция / называется функцией распределения.
Если мы рационально поставим наш эксперимент, мы найдем, что / будет
достаточно непрерывной функцией г, р и t; можно ожидать, что она будет
удовлетворять некоторому дифференциальному уравнению, которое будет
служить звеном, связывающим микроскопические взаимодействия между
атомами жидкости и макроскопические движения жидкости в целом.
Мы можем получить макроскопические свойства жидкости, рассмот-
рассмотренные в предыдущем параграфе, с помощью интегралов, содержащих
функцию распределения. Обозначим элемент объема в фазовом пространстве
через dVxdVp, где dVx —dxdydz и dVp = dpxdpydpz; иногда применяются
сферические координаты г, &, <j> в обычном пространстве и р, б, ф в про-
пространстве импульсов; в этом случае соответствующие элементы объема
принимают вид dVx = <r2 dr sin Ь db dy> и dVp = p*dp sin QdQdfy.
Прежде всего, интеграл от функции /, распространенный на всю часть
пространства, лежащую внутри границ, будет как раз равен числу атомов
жидкости
Среднее число частиц на единицу объема обычного пространства будет
172 Гл. 2. Уравнения полей
равно интегралу от / по пространству импульсов; это число после умно-
умножения его на т — массу отдельной частицы — дает плотность
f (г, р, t) dVp, B.4.6)
упомянутую в этом параграфе раньше. Полный средний импульс, отнесен-
отнесенный к единице объема, т. е. к одному кубическому сантиметру,
J (я:, у, z, t) = ^ ^ p/ (r, p, t) dVp, B.4.7)
является вектором J потока массы, рассмотренным раньше. Полная кине-
кинетическая энергия жидкости равна
U = ^ \\ \ Р%1 (Г> Р) l) dVx dVp- B-4-8)
Если пренебречь силами, действующими между атомами, она равна
полной внутренней энергии газа и пропорциональна его температуре.
Эти интегралы показывают, что / должно стремиться к 0 для возрастаю-
возрастающих значений р настолько быстро, чтобы интеграл для U не был рас-
расходящимся.
Одно из дифференциальных свойств функции / имеет общую значи-
значимость и связано с уравнением неразрывности B.4.1). Все частицы
в данном элементе dVp пространства импульсов перемещаются с одной
и той же скоростью р/т. Внутри элемента dVx в точке г (ж, у, z) в мо-
момент t содержится / (г, р, l)dVxdVp таких частиц; в момент l-fdt они
будут находиться в точке r-{-(p/m)dl. Следовательно, плотность вероят-
вероятности / в точке г в момент t должна быть равна плотности в точке
r-{-(p/m)dt в момент t-^dt для частиц, имеющих импульс р:
= /(г, Р, t).
Разлагая левую часть в ряд и сохраняя только члены, содержащие
первые степени dt, получим уравнение неразрывности для функции рас-
распределения
7j-/(r, p, t) — —— -grader, р, t)], B.4.9)
где оператор градиента действует на /, как на функцию, зависящую
только от х, у, z. Сопоставив это уравнение с уравнениями B.4.6)
и B.4.7), непосредственно получаем обычную форму уравнения нераз-
неразрывности B.4.1). Оно может быть видоизменено благодаря влиянию
иных факторов, что будет рассмотрено дальше.
Давление и уравнение состояния. Очень простой пример покажет,
как можно использовать функцию распределения, чтобы связать сгла-
сглаженное давление, рассмотренное в предыдущем параграфе, с движениями
отдельных частиц. Рассмотрим сосуд, имеющий объем V и содержа-
содержащий N атомов газа, равномерно распределенных внутри него; термином
«равномерно распределенных» мы отмечаем, что / не зависит от г вну-
внутри F. Чтобы газ остался равномерно распределенным, / не должно
зависеть от t и J должен всюду равняться нулю. Для удовлетворения
всем этим требованиям проще всего предположить, что / = (N/AnV) ф (р),
где ф является функцией одной только величины р импульса частицы >
2. 4. Диффузия и другие явления просачивания 173
причем эта функция имеет следующие свойства:
е. B.4Л0)
Первый интеграл определяет произвольную постоянную, от которой
зависит величина ф (т. е. нормирует ф), так что typ2dp есть вероят-
вероятность того, что частица газа имеет величину импульса, заключенную
между р и p-\-dp. Величина s является тогда средней кинетической
энергией частицы.
Подставив это выражение / в интегралы, определяющие указанные
величины, связанные с полем, получим
р = -у-; J == 0; U = Ne.
Следует отметить, что предположение о том, что / равно (N/AkV) ф (р),
налагает известные ограничения на природу стенок сосуда, ограничи-
ограничивающих объем V. Во-первых, эти стенки должны отталкивать обратно
внутрь V каждую частицу, ударяющуюся о них, и не допускать утечки
этих частиц; иначе N и / будут изменяться с течением времени. Во-вто-
Во-вторых, при отражениях частиц от стенки должно сохраняться распреде-
распределение импульсов, даваемое функцией ф (р); так что образы частиц,
только что отраженных от стенки сосуда, не должны отличаться, по край-
крайней мере с точки зрения распределения скоростей, от образов неотра-
неотраженных частиц. Это вовсе не значит, что каждая частица должна отбра-
отбрасываться так же, как и в случае вполне упругих стенок; это значит
только, что для каждой частицы, отраженной с уменьшенной энергией,
существует частица, энергия которой после отра'жения возрастает. Иначе
распределение / изменялось бы при приближении к границе и, следова-
следовательно, / не могла бы быть независимой от г.
Предположим теперь, что эти несколько необычные требования
выполнены, и изучим среднее поведение таких частиц, близких к неко-
некоторому участку граничной стенки. Предположим, что этот участок будет
плоским, и расположим оси координат так, чтобы он лежал в плоско-
плоскости yz, причем сторона, соответствующая отрицательным значениям х,
обращена к газу, а сторона, соответствующая положительным значениям х,
лежит внутри стенки. Рассматривая тогда функцию / при х = 0, найдем,
что все частицы, для которых рх положительно, еще не ударялись
о стенку, а все те, для которых это значение отрицательно, уже отра-
отразились от нее.
Мы теперь в ¦ состоянии поставить вопрос о том, какое свойство
частиц газа вызывает постоянное давление на стенки сосуда. Очевидно,
это — взаимодействие при отражении между стенкой и частицами газа,
ударяющимися в эту стенку, то самое взаимодействие, которое отталки-
отталкивает частицы обратно внутрь сосуда после удара. Так как действие
равно противодействию, мы можем сказать, что сила, с которой газ
действует на квадратный сантиметр поверхности, будет та же самая,
что и сила, с которой квадратный сантиметр поверхности действует
на ударяющиеся частицы, отбрасывая их назад внутрь газа. Так как
сила равна скорости изменения импульса, эта реакция стенки равна
среднему изменению импульсов всех частиц, ударяющихся в стенку
в течение одной секунды. Число частиц, соответствующих элементу
импульса dVp для импульса р, которые ударяются о единичную пло-
площадку плоскости yz в течение секунды, равно vx(N/4nV) ф (p)dVp =
174 Гл. 2. Уравнения полей
= (N/AnWn) ф (р) psdp cos Ь sin ЬAЫф, где для этих ударяющихся частиц
О < б < тс/2. Полное среднее изменение импульса для каждой из этих
частиц равно 2рх = 2р cos б, так что сила, с которой квадратный санти-
сантиметр площадки действует на газ, (и, следовательно, величина давления),
нормальна к поверхности и имеет среднее значение
2и -ге/2
5
0 0
[в силу формулы B.4.10)]. Таким образом, получаем уравнение, связы-
связывающее давление Р, объем V и внутреннюю кинетическую энергию U,
PV = ^U, или /> = -|яР, B.4.11)
которое называется уравнением состояния газа. Величина E=U/Nm
есть кинетическая энергия единицы массы газа, a p = Nm/V— средняя
плотность газа.
Мы могли бы показать теперь, что при уменьшении объема такого
сосуда с отражающими стенками (это соответствует адиабатическому
сжатию, см. стр. 161) Е изменяется пропорционально (у —1)-й степени
плотности (здесь у — постоянная для рассматриваемого газа, равная
для воздуха 1,4) и что, таким образом, давление при адиабатическом
сжатии пропорционально у-й степени плотности р. Однако это нас
завело бы слишком далеко от нашей цели, и мы должны перейти к рас-
рассмотрению соотношения между внутренними силами, действующими
в жидкости, и диффузионными свойствами жидкости.
Средняя длина свободного пробега и эффективное сечение рассеяния.
Отдельные частицы (атомы, молекулы) газа удалены друг от друга
достаточно далеко, так что большую часть времени они двигаются как
свободные тела с постоянными импульсами. Только изредка сближаются
они друг с другом настолько, что на движение их начинают влиять
их взаимные силовые поля. Поэтому движение каждой частицы можно
разбить на две части: свободный полет, когда на частицах не сказывается
влияние других частиц, и кратковременная часть, в течение которой
импульсы меняются благодаря мгновенному сближению с другой части-
частицей, после чего частица снова возвращается к свободному полету; однако
скорость ее отлична от первоначальной. Эти мгновенные встречи с дру-
другими частицами, в течение которых импульс каждой частицы существенно
меняется, называются столкновениями. В случае прохождения нейтро-
нейтронов через твердое тело столкновение происходит между нейтроном и
ядром одного из атомов твердого тела, но и при этом наши рассуж-
рассуждения остаются в силе.
Если достигнуто термодинамическое равновесие, то при этих стол-
столкновениях будет в среднем сохраняться энергия и, следовательно,
столкновения можно считать упругими. Среднее количество изменений
направления движения зависит от закона действия сил между частицей
и «мишенью», которой может быть ядро атома в случае движения ней-
нейтронов или другой атом, подобный движущемуся, в случае газа. Простей-
Простейшее предположение состоит в том, что закон действия силы аналогичен
закону взаимодействия двух биллиардных шаров; сила равна нулю,
если расстояние между центрами больше чем R, для расстояний же
меньших чем R появляется значительная сила отталкивания; такое
предположение близко к действительности в достаточно большом коли-
количестве случаев. Биллиардные шары, если они вообще сталкиваются,
•2. 4. Диффузия и другие явления просачивания 175
отскакивают одинаково часто во всех направлениях, и аналогичное
явление отмечается во многих реальных случаях, особенно когда отно-
относительные скорости не очень велики. Если масса «мишени» имеет тот же
порядок величины, что и масса ударяющейся частицы, это равномерное
распределение углов рассеяния при столкновении имеет место относи-
относительно системы координат, движущейся вместе с центром тяжести
сталкивающейся пары, благодаря чему исследование становится несколько
сложным.
Чтобы избежать трудностей, мы сначала изучим случаи, в которых
мишень значительно более массивна, чем ударяющаяся частица, что,
например, имеет место, когда частицами являются нейтроны, а мише-
мишенями—тяжелые ядра или частицами служат фотоны, а мишенями —
частицы пыли в воздухе. В этих случаях мы будем считать, что мишени
были и остаются неподвижными и что щ из них случайным образом
распределены внутри каждого кубического сантиметра. Каждую мишень
можно представить себе как упругий шар радиуса R, а частицы —как
материальные точки. Здесь мы можем пренебречь столкновениями между
частицами и сосредоточить свое внимание на столкновениях между
частицами и мишенями.
Первый вопрос, на который следует ответить, касается относитель-
относительной частоты столкновений между частицами и расположенными случай-
случайным образом мишенями. Вероятность того, что столкновение происхо-
происходит после того, как частица прошла расстояние х, но раньше, чем она
прошла расстояние x-\-dx, пропорциональна числу, показывающему,
какая часть площади тонкого пространственного слоя толщины dx, пер-
перпендикулярного к пути частицы, заполнена мишенями. Площадь эффек-
эффективного поперечного сечения мишени равна Qe = тс/?2; число мишеней,
лежащих внутри слоя толщины dx, в основании которой лежит единич-
единичная площадка, равно ntdx. Часть единичной площадки, прегражденная
мишенями, выражается поэтому числом ¦KR2nidx = Qentdx, и вероятность
столкновения на участке пути подвижной частицы от х до x-\-dx равна
этой величине, умноженной на вероятность Р(х) того, что частица про-
прошла расстояние х без столкновений. Таким образом, получаем диффе-
дифференциальное уравнение для Р (ж)
¦^ Р (х) = — QentP (х), или Р (х) = е-Се",*; B.4.12)
здесь мы приняли (вполне обоснованно), что вероятность Р@) прохо-
прохождения по крайней мере нулевого расстояния от момента последнего
столкновения до ближайшего равна единице (это достоверный факт).
Таким образом, мы получили выражение вероятности того, что сво-
свободный пробег между двумя столкновениями имеет длину х, выразив
эту вероятность через плотность nt мишеней и площадь их эффектив-
эффективного сечения Qe для столкновений между частицами и атомами-мишенями.
Подробный подсчет силового поля между частицей и мишенью нужен,
таким образом, только для определения значения Qe, когда оно встре-
встречается при вычислении средних длин свободного пробега между стол-
столкновениями.
Средняя длина пути между столкновениями равна
где длина X называется средним свободным пробегом частицы среди мно-
множества мишеней.
176
Гл. 2. Уравнения полей
В случае обыкновенного газа средний свободный пробег частицы
является пробегом между столкновениями с другими подобными части-
частицами, так как здесь мишенями являются также молекулы газа. В слу-
случае более плотной среды, например такой, как жидкость, средний сво-
свободный пробег имеет приблизительно ту же величину, что и среднее рас-
расстояние R между частицами; поэтому здесь частица никогда не будет
долго свободна от влияния соседних частиц; но даже и здесь выраже-
выражение для вероятности Р (х) сохраняет силу. Можно сказать, что частицы
жидкости соприкасаются с атомами того вещества (атомами-мишенями),
через которое просачиваются, в среднем только после прохождения
расстояния, равного среднему свободному пробегу.
Возможность столкновений оставляет нам другой путь, при кото-
котором функция распределения изменяется от точки к точке и с течением
времени. Например, частицы из элемента импульсов dVv с импульсом р
в течение промежутка времени dt проходят расстояние dx = (р/Щ dt
и часть их, выражаемая числом (Qentp/m) dt, испытывает столкновения.
Те, которые испытывают столкновения, изменяют направления своих
импульсов и, следовательно, исчезают из элемента импульсов dV . Поэтому
имеется скорость убывания функции /, проистекающая из столкновений
и определяющаяся равенством
df (r, p, t) ¦¦
f(r,V,t)dt.
B.4.14)
Но здесь имеет место также и возрастание функции /, вызванное
столкновениями, так как существуют также частицы, первоначально
находившиеся в других элементах импульсов, которые после столкно-
столкновений отбрасываются внутрь dVp. Предположив (как мы это и делали
Рл
г /I г
Рис. 2.18. Импульсы и углы диффундирующей
частицы до и после столкновения с атомом-ми-
атомом-мишенью среды
до сих пор), что частицы рассеиваются во всех направлениях с одина-
одинаковыми вероятностями и что не происходит изменения скорости частиц
при рассеянии любой группы частиц, подвергшихся столкновению, мы
найдем, что часть всех частиц, выражаемая числом do)/4u, будет рас-
рассеиваться в направлениях движения, лежащих внутри телесного углами.
Рассматривая рис. 2.18, мы видим, что если в элементе импульсов
dV'v- d<j>'sin6'd6' (p'Jdp' находилось /(г, p',t)dVp частиц, то в элемент
импульсов dVp = йф sin G db p2 dp за время dt попадут (Qentp/4nm) x
X/(r, y>', t) dVvd§' sin6' db'dt частиц (р равно р', как мы предполагали
до сих пор). Полное возрастание /(г, р, t), вызванное рассеянием
частиц в последний элемент импульсов, равно интегралу от этого коли-
количества, распространенному на все начальные направления движения,
¦определенные углами б' и ф',
df (г, &, ф, р, б, ф, t) = %g- \]f(r, Ь, <р, р, в', ф') sin б' d6' d$' dt. B.4.15)
2.4. Диффузия и другие явления просачивания 177
Диффузия света, интегральное уравнение. Простой, но поучительный
пример применения этих уравнений относится к распространению света
через пластинку матового стекла (или слой тумана); освещенность предпо-
предполагается одинаковой во всех точках поверхности пластинки (например,
плоскости yz), так что / не зависит от у и z и является функцией
только х. Этот пример впервые изучал Милн в связи с потоком света
в атмосфере звезд; он называется проблемой Милна. «Частицами» являются
фотоны, имеющие одинаковые импульсы; в силу симметрии функция /
зависит от угла б между вектором р и осью хине зависит от ф. Поэтому /
можно записать, как f\x,b,t). Если достигнуто устойчивое состояние,
то скорости изменения /, как данные в B.4.9) и вызванные зависимостью /
от х, так и данные в B.4.14) и B.4.15) и обусловленные столкновениями,
взаимно уничтожаются и получающееся уравнение для / имеет вид
1С
cos 6 ±f (х, б) = - ntQJ (х, б) +1 ntQe \ f (x, 6') sin б' W
(мы сократили уравнение на общий множитель р/т). Решение этого
интегро-дифференциального уравнения позволит нам определить любые
требуемые свойства диффундирующего света. Мы здесь учли как возмож-
возможность поглощения фотонов рассеивающей средой (частицами тумана или
какой-либо другой средой), так и возможность рассеяния. Поэтому Qt
есть сумма эффективного сечения рассеяния Qe и эффективного
сечения поглощения Qa. Само собой разумеется, что Qa не входит в член,
содержащий интеграл, так как этот член соответствует фотонам, отбро-
отброшенным после столкновения в направлении, определяемом углом б,
а поглощенные фотоны столкновений не испытывают.
Если мы за единицу измерения расстояний примем средний свобод-
свободный пробег, то x = l/ntQt = l? и наше уравнение примет вид
B.4.16)
где х = QjQt — отношение эффективного сечения рассеяния к полному.
Член, стоящий в левой части уравнения, представляет зависимость
/ от движения частицы. Первый член правой части дает измене-
изменение /, вызванное поглощением и рассеянием; второй член правой части
выражает изменение /, вызванное отражениями в первоначальное напра-
направление.
Изменяя нормировку /, мы можем добиться того, чтобы
•к
с ^ cos б / (?, 6) sin б db = / (?), B.4.17)
где нравая часть есть средний поток световой энергии через единич-
единичную площадку за секунду в направлении положительной оси ж в точке ?.
Постоянная с есть скорость света. Тогда интеграл
" P(&) B.4.18)
равен средней плотности световой энергии в точке Е.
Предположим теперь, что пластинка рассеивающего материала огра-
ограничена плоскостями х = 0 и ж = жои что поток 1 F) падает на поверх-
12 Ф. м. Морс и Г. Фешбах
178
Гл. 2. Уравнения полей
ность х = 0, как показано на рис. 2.19. Функция / может меняться
произвольным образом с изменением б в пределах от 0 до тс/2, но она
должна быть равна нулю при (тс/2) < б <; ¦к, так как эти границы для 6
соответствуют потоку из пластинки и не могут соответствовать падаю-
падающему потоку. Это распределение потока, проникающего внутрь пластинки,
постепенно изменяется, по мере того как составляющие его фотоны
ударяются о мишени и поглощаются или рассеиваются. Часть потока,
-Mt/t W Yt/M\tM/M
ив)
Рис. 2.19. Диффузия света в пластинке из рассеиваю-
рассеивающего материала.
Задана интенсивность падающего света 1F)
образующая с осью х угол б, при проникновении на расстояние ж = Х?
внутрь пластинки проходит внутри ее вещества S sec б средних свободных
пробегов и в силу уравнения B.4.12) сохраняется только e~z se0 ° ее перво-
первоначальной величины. Поэтому одна часть /(?, б) имеет выражение
/F)e-=sec0.
Другая часть соответствует фотонам, отразившимся по крайней мере
один раз. Число фотонов, отраженных на расстоянии ?' свободных про-
пробегов от передней границы пластинки, будет пропорционально плотности
p(S'), определенной формулой B.4.18), а число таких фотонов, достигших
глубины ? под углом б, будет пропорционально величине р(?')е~1 ?~г'isec в,
где ?' меньше ?, если 6 меньше тс/2, и больше ? при б большем чем т:/2
(рассеяние назад). Следовательно, есть основание ожидать, что реше-
решение уравнения B.4.16), определяющее функцию распределения, имеет следую-
следующую общую форму:
-i * sec в
(г'-е)sec
*'. |.<б<тг.
B.4.19)
Это, конечно, еще не будет решением задачи, так как мы еще не вычис-
вычисляли плотности р. Однако р является более простой функцией, чем /, так
как оно зависит только от ? и не зависит от б.
Для того чтобы показать, что B.4.19) правильно определяет вид
функции /, преобразуем B.4.16) следующим образом:
—¦ f E, б) + sec б / E, б) = 1 «р (I) sec б.
Предполагая, что р известно, мы найдем, что решение этого линейного неод-
неоднородного уравнения, подчиненное условию / @, б) = / (Q), совпадает в точ-
точности с B.4.19) (мы, конечно, учитываем различие между значениями б,
меньшими -гс/2, и значениями б, большими -гс/2). Чтобы найти уравнение
для определения р, умножим уравнение B.4.19) на sin6d6 и проинтегри-
2. 4. Диффузия и другие явления просачивания 179
руем его по 6
• = Ро E) + 4- * ^i (| « - 6' |) Р (П #', B.4-20)
тс/2
Это интегральное уравнение стандартного типа, который будет подробно
исследован дальше. Если ?0 равно бесконечности, уравнение называется
уравнением типа Винера — Хопфа. Уравнение устанавливает, что значе-
значение р в точке ? зависит от значений р внутри интервала, равного сред-
среднему свободному пробегу, заключающего точку ?.
Диффузия света, дифференциальное уравнение. Мы переходим теперь
к выводу дифференциального уравнения для р и /, которое связано
с уравнением диффузии, так что дальнейшее рассмотрение интеграль-
интегрального уравнения откладывается. Хотя, как оказывается, интегральное
уравнение является точным, а дифференциальное — только приближенным,
дифференциальное уравнение решается настолько проще, что целесооб-
целесообразно пользоваться его решениями, если только они пригодны.
Дифференциальное уравнение типа уравнения диффузии дает хоро-
хорошее приближение всегда, когда относительное изменение р или / неве-
невелико на протяжении среднего свободного пробега. Это возможно, пока
эффективное сечение поглощения Q мало сравнительно, с эффективным
сечением упругого рассеяния Qe и пока не требуется слишком много
подробностей относительно поведения р и / на расстоянии одного сво-
свободного пробега от границы, так как- в~э'том случае функция распреде-
распределения / почти не зависит от угла , определяющего направление импульса,
и результирующий поток / значительно меньше; чем среднее квадратич-
квадратичное величины р.
Утверждение, что поток / мал, равносильно тому, что функция
распределения может быть приближенно выражена так:
/(&,6)~|-p(&) + -|cose^, B.4.21)
если только //с значительно меньше, чем р. Согласно уравнениям B.4.17)
и B.4.18), поток и плотность как раз равны величинам / и р в этом
выражении. Это простейшая функция от б, для которой значения р и j
могут быть независимыми.
Предположим, что мы составили уравнение, эквивалентное уравне-
уравнению B.4.16), содержащее, однако, производную по времени. За единицу
времени примем среднее время свободного пробега для фотонов Х/с,
В силу уравнений B.4.9), B.4.14) и B.4.15) имеем
-J-/(S. в. = -совв-^-/E, б, х)—i-op(E, х) +
б'. *)-/(&¦ в, x)]sine'de'f B.4.22)
о
где $ = (n,Qtx), v = (ntQtct), p/m — c, a = QjQt = l~in.. Подставляя сюда
вместо / его приближенное выражение через р и J B.4.21), получаем
12*
180 Гл. 2. Уравнения полей
довольно сложное интегро-дифференциальное уравнение. Однако последний
член, содержащий интеграл по б', может быть упрощен. В выражении
!/(?> О'> х) — /(?. О» хI члены, содержащие р, взаимно уничтожаются
и квадратная скобка превращается в -»- [cos б' — cos6]-(l/c) /(?, х); инте-
интегрируя это, получим — C/с)/(?, х) cose.
Полученное уравнение можно разделить на два уравнения, если умно-
умножить его на sin6d9 и проинтегрировать и, кроме того, умножить на
cos 6 sin 6 db и проинтегрировать. Эти интегрирования устраняют зависи-
зависимость от 6 и приводят к двум уравнениям, связывающим р и /. Первое
из них
-^-~--ж-аР B.4.23)
является как раз уравнением неразрывности B.4.1) для данного случая,
выраженным в безразмерных переменных х и ? и учитывающим потерю
фотонов, вызванную поглощением (член ар). Если, кроме того, за сред-
среднее время свободного пробега в кубе, ребро которого равно среднему
свободному пробегу, добавляются q фотонов, то величина q должна быть
добавлена к правой части уравнения.
Второе уравнение
связано с уравнением диффузии, содержащим градиент B.4.3). Оно имеет
дополнительный член dJ/di, дающий скорость изменения величины /
за среднее время свободного пробега. Так как при диффузии происходят
довольно медленные изменения, этот член незначителен по сравнению
с /, так что со степенью точности, принятой здесь, второе уравнение
имеет вид
/--|§. BА24)
Таким образом, при диффузии фотонов градиент Плотности фотонов
вызывает медленный поток в сторону более низкой плотности.
Комбинируя уравнения B.4.23) и B.4.24), получаем уравнение диф-
диффузии для плотности фотонов
Постоянная диффузии при наших единицах длины и времени равна
ЯбЧно j/l/З [см. уравнение B.4.4)]. Если где-либо функция источника q
велика, там р стремится быстро возрастать; если где-либо плотность
сильно сконцентрирована E2р/5?2 численно велико, но отрицательно),
там р стремится быстро убывать. Так как сюда входит только первая
производная по х, то решение не будет обратимым относительно вре-
времени, как это было бы для волнового уравнения.
Функция распределения с той же точностью выражается следующим
равенством:
/ E, 6) «, i- p (S) —!~Ц- cos 6 B.4.26)
через решение уравнения B.4.25). Это выражение пригодно, если только
д? мало по сравнению с р.
Для типичного решения уравнения B.4.25) мы можем вернуться
к решению, соответствующему установившемуся состоянию, в случае
2.4. Диффузия и другие явления просачивания 181
пластинки из рассеивающего материала. Предположим, что поток, падаю-
падающий на поверхность х = 0, имеет интенсивность / и полностью направ-
направлен в положительную сторону оси х, т. е. /F) =/о, где 8 = 8{l — cos б)
есть дельта-функция, рассмотренная на стр. 122. Мы также предпола-
предполагаем, что пластинка имеет бесконечную толщину (ж0=оо). Та часть
падающих фотонов, которая внутри пластинки еще не сталкивалась с рас-
рассеивающими мишенями, очевидно, не может бьггь представлена прибли-
приближенной формулой B.4.26); однако мы можем эту часть рассмотреть
отдельно [обозначим ее через /t = (//с) е~Щ и считать, что уравнение
B.4.25) применяется только к тем фотонам, которые испытали по край-
крайней мере одно столкновение. Для этой части решения падающие фотоны
появляются внутри пластинки в точке, где они испытывают свое пер-
первое столкновение, как если бы внутри вещества был распределен источ-
источник мощности q = A — a)/e~Vc (множитесь 1 — а = х появляется потому,
что только отраженные, но не поглощенные фотоны участвуют в диффу-
диффузии). Диффузионная часть плотности pd поэтому является решением
уравнения
которое получается из B.4.25) в результате подстановки вместо q его
величины и приравнивания производной по времени нулю (так как состоя-
состояние установившееся).
Решение этого уравнения имеет вид
]<2-4-27>
где постоянная Д выбирается так, чтобы удовлетворить граничному
условию при ? = 0.
Так как а—отношение поглощения к рассеянию при столкнове-
столкновениях — предполагается малым, то первая экспонента при возрастании ?
убывает медленнее второй; на значительном расстоянии внутри пластинки
плотность пропорциональна величине е~Уых. Иначе говоря, глубина
проникновения внутрь пластинки зависит только от относительной
частоты поглощения фотонов. Полная функция распределения имеет вид
/№, 6) *, ь + Ы--±=±. {[1
— (l + cos6)e-=}. B.4.28)
В интервале среднего свободного пробега от границы Е = 0 часть функции
распределения, соответствующая диффузии, с точностью до первых
степеней малых величин ?, Д и а становится равной
и соответствующая часть плотности становится равной C//с) X
Х[A — а)/A + j/З-)] (?-}-д)- Из этих разложений видно, что любое решение
уравнения B.4.25) непригодно вблизи границы ? = 0, если граничные
условия требуют, чтобы Д было мало, так как в случае, когда ?4-Д
невелико сравнительно с единицей, член, содержащий cosQ, не будет
больше мал сравнительно с членом, не содержащим 6, и то приближение,
на котором был основан вывод уравнения B.4.25), больше не имеет
места.
Граничные условия. Для того чтобы видеть, какое значение должно
иметь Д и какой вид примут / и р вблизи границы, мы должны вернуться
182
Гл. 2. Уравнения полей
к точному уравнению для f и к интегральному уравнению B.4.20) для р,
так как равенства B.4.26) и B.4.28) для /, очевидно, неточны на гра-
граничной поверхности ? = 0, где слева нет рассеивающего вещества.
В этой точке единственной частью функции распределения при значе-
значениях 6, меньших чем ъ/2 (соответствующей фотонам, входящим в вещество
из внешнего пространства), должен быть падающий поток. Диффузионная
часть функции распределения должна быть для значений 6, лежащих
между нулем и тс/2, равна нулю. Выражение B.4.26), конечно, не может
удовлетворить этому требованию, какие бы значения ни имели р и dp/dk-
Можно только удовлетворить требованию в среднем, если положить
среднее значение функции /@,6) cos 6 в промежутке 0<6<те/2, равным
нулю. Это требование приводит к приближенным граничным условиям
[см. также равенство B.4.34)]
pcos6sin6d6 — \ ||
= 0 или
при Е — О,
-|; B.4.29)
это означает, что постоянную Д, входящую в уравнения B.4.27) и B.4.28),
нужно считать равной 2/3, чтобы удовлетворялись граничные условия.
-1.0 О rio +2,0 +3,0
|-глубина от поверхности рассеивающего вещества
Рис. 2.20. Плотность диффундирующих частиц вблизи
поверхности раздела.
Сплошной линией показано точное решение, пунктирной-прибли-
пунктирной-приближенное, полученное из уравнения диффузии.
насколько это возможно при данной аппроксимации. Даже эта формула
не будет слишком точной, так как dp/dt вблизи точки ? = 0 наверняка
не будет малым по сравнению с р; таким образом, любое использование
уравнения диффузии для подсчета р вблизи границы является весьма
сомнительным делом.
Только наше возвращение к интегральному уравнению B.4.20) позво-
позволяет нам выяснить законность этих приближений. К сожалению, мы еще
не в состоянии довести до конца решение уравнения B.4.20), так что
мы здесь только сошлемся на результаты; приемы решения интегральных
уравнений этого типа будут рассмотрены в гл. 8 и 12.
Все это станет более ясным, если мы сравним результаты для более
простого случая звездных атмосфер, рассмотренного Милном. Здесь
2.4. Диффузия и другие явления просачивания
183
фотоны возникают значительно ниже поверхности слоя, диффундируют
вверх через внешние рассеивающие слои и излучаются через поверхность
во внешнее пространство. Толщина этих верхних слоев во много раз
превосходит средний свободный пробег, так что мы снова можем пред-
предположить, что х0 весьма велико. Однако при этом здесь нет потока,
падающего сверху на внешнюю сторону поверхности х = 0, так что
интегральное уравнение имеет вид
B.4.30)
зто уравнение называется уравнением Милна. Функция Ех определена
формулой B.4.20). Для простоты мы здесь предположили, что х—>1,
иными словами, что поглощения в веществе нет, а имеется только
рассеяние.
Решение приближенного уравнения диффузии B.4.25) в предполо-
предположении, что а и q равны нулю, удовлетворяющее граничным условиям,
B.4.29), имеет вид
Р~Л(? + Д), Л«-§* B.4.31)
Для функции распределения по углам потока, излучаемого поверхностью
во внешнее пространство, получаем приближенное выражение
cos6,
B.4.32)
Решение интегрального уравнения
B.4.30) приводит к следующему выраже-
выражению для функции плотности:
р «< А {? + 0,7104 [1 - 0,3429 Е2 (?) +
+ 0,3159 Я, F)]};
En (z)
"" е-"*
е-"* du, B.4.33)
Нормаль
к поверхности
+ f cos в
погрешность которого не превосходит
0,3% на всем промежутке изменения 5.
Так как и Е2, и Е3 быстро стремятся к
нулю при возрастании ?, мы видим, что
при ?, превышающем 1 (глубже, чем
«дин свободный пробег под поверх-
поверхностью), приближенное решение, данное „ о „. „
/о / o/i\ а Рис. 2.21. Полярная диаграмма
в B.4.31), вполне пригодно; только Д интенсивности частиц, испускае-
должно быть равно 0,7104 вместо 2/3. мых с поверхности рассеивающей
На расстоянии от поверхности, меньшем среды при различных углах испус-
чем средний свободный пробег, действи- кания 6.
тельная плотность падает ниже прибли- н^ГпуОввЛт^ео1-п^ГнеТнГ.е ???
женного решения на некоторую величи- ченное ив уравнения диффузии.
лу, как показывает рис. 2.20.
Точное решение для углового распределения потока, исходящего
от поверхности, имеет выражение слишком сложное для того, чтобы
«го стоило выписать здесь. Оно изображено на рис. 2.21 и сравнивается
здесь с распределением, полученным по приближенной формуле B.4.32).
Соответствие, как видим, не слишком плохое.
184 Гл. 2. Уравнения полей
Во всяком случае, мы видим, что решение уравнения диффузии дает
лучшее приближение к точному решению, чем мы были вправе ожидать,
если мы потребуем, чтобы оно удовлетворяло следующим граничным
условиям на каждой свободной границе:
плотность на поверхностнее0,7104 значения производной от
плотности по внутренней нормали к поверхности B.4.34)
Здесь при дифференцировании расстояние измеряется в средних свобод-
свободных пробегах. Только во внешней части рассеивающего вещества на расстоя-
расстоянии меньшем, чем величина свободного пробега от поверхности, действитель-
действительная плотность значительно отличается от вычисленной на основе этих согла-
соглашений. Внутри вещества решение уравнения диффузии, удовлетворяющее
этому граничному условию, дает вполне хорошие результаты, и даже
угловое распределение излучения, идущего от поверхности, достаточно
хорошо изображается с помощью приближенной формулы B.4.32).
Интересно отметить, что многие полезные расчеты, относящиеся
к диффузии нейтронов через твердые тела, могут быть также проведены
с помощью уравнения диффузии и граничных условий B.4.34).
Влияние иеизотропиого рассеяния. Рассмотрим теперь случай, когда
диффундирующие частицы рассеиваются не во всех направлениях равно-
равномерно; временно предположим, однако, что в процессе рассеяния энер-
энергия не теряется. Вероятность того что частица отскакивает внутрь
элемента телесного угла do, вместо того чтобы не зависеть от угла
и быть равной (QJ4k) dio, теперь будет иметь выражение c(a)diu, где а —
угол рассеяния внутрь элемента телесного угла du>. Как показано на
рис. 2.18, частица вначале имела импульс р', а после столкновения имеет
импульс р. Соотношение между о и эффективным сечением для упругого
рассеяния имеет вид
2п т.
Qe= С d3 \ о (a) sin a da; d<o = sinadad?. B.4.35)
о о
Существует также связанное с Qe эффективное сечение Qm, назы-
называемое эффективным сечением передачи импульса, которое выражается
через о с помощью интеграла
¦ <2m= ^d3 \ о (a) (I-cos а) sin я da. B.4.36)
о о
Если рассеяние одинаково во всех направлениях (т. е. если о постоян-
постоянная), то Qm = Qe- Если больше частиц отскакивают назад (л>90°), чем
вперед (а<90°), то Qm больше, чем Qe; в противоположном случае —
наоборот. Обе величины Qm и Qe, а также Qa— эффективное сечение
поглощения частиц зависят от импульса налетающей частицы.
Мы по-прежнему предполагаем, что величина импульса частицы не
изменяется при столкновении и что внешние силы не действуют на
частицы. Мы допустим, что в каждой точке пространства направление
потока J совпадает с направлением градиента функции распределения f.
Это предположение до некоторой степени предопределяет решение, но
это несущественно, так как можно доказать, что это предположение
на самом деле осуществляется. Однако сделать предположение, а потом
убедиться в его справедливости настолько облегчает дело, что мы, может
быть, можем извинить на этот раз подобную перестановку в рассужде-
рассуждениях. Вместе с требованием о том, чтобы часть /, зависящая от угла*
2.4. Диффузия и другие явления просачивания 185
была очень мала (что необходимо для того, чтобы уравнение диффузии
имело силу), все это соответствует предположению, что [см. B.4.21)]
где р и J определены уравнениями B.4.6) и B.4.7) и направление J
совпадает с направлением gradp, который на рис. 2.18 направлен вдоль
полярной оси (так что р-J = p/cos6). Отметим, что р и J все еще являются
функциями величины импульса р, поэтому они являются плотностью
и потоком частиц данной скорости. Чтобы получить средние величины,
рассмотренные на стр. 172, мы проводим осреднение по импульсам
со со
р (г, t) <= [ р2р (г, р, t) dp, 3 (г, t) = \j рЧ (г, р, t) dp;
о о
мы можем также определить и другие средние значения
СО оо
р- = \ Р3Р (г. Р> 0 dP> Ecv. =^- \ Р4Р (г> Р> t)dP- B.4.38)
6
о 6
Скорость изменения функции /, обусловленная свойствами нераз-
неразрывности, дается по-прежнему уравнением B.4.9). Скорость убывания f,
вызванная поглощением, равна (ntQap/m) /. Скорость изменения / вслед-
вследствие упругого рассеяния на основании уравнений B.4.14) и B.4.15)^
равна
2л тс
йф' J о (a) [cos б - cos 6'J sin 0' dO'.
о
Здесь мы выбрали за направление / направление полярной оси, пока-
показанной на рис. 2.18. Однако лучше полярную ось направить вдоль окон-
окончательного импульса; в этом случае cos 6' надо заменить на cos 6 cos a +
+ sin а cos (Р — ф), где 6 и ф постоянны, а а и [J — углы рассеяния, по
которым выполняется интегрирование. Учитывая уравнение B.4.36)
и соответствующее видоизменение уравнения B.4.22) (о зависит от угла
рассеяния а, но не от угла р ориентации относительно полярной оси),
мы окончательно получаем дифференциальное уравнение для р и J
до , Зт 83 1 , 3 л / ж\ nt /~>
¦? + -prV- if ~ —п P'grad p--^ p-grad (p- J)-—QaPP-
-jntQap.J-^ntQmP.3. B.4.39)
Приближение первого порядка. Уравнение диффузии. Как мы отме-
отметили при выводе уравнения B.4.24), членом, содержащим дЗ/dt, можно
пренебречь, когда мы имеем дело со сравнительно малыми скоростями
изменения J при диффузии. Некоторые из оставшихся членов меняют
знак при изменении направления р на противоположное, другие члены
при этом знака не меняют; все члены, содержащие p-J (gradp имеет
то же направление, что и J), меняют знак, но член, содержащий
p-grad (p-J), знака не меняет, так же как и члены, содержащие р.
Поэтому, в силу симметрии, мы можем разделить уравнение B.4.39) на
два уравнения, которые служат для выражения р и J через г (ж, у, z),
р и I.
Первое из этих двух уравнений может быть записано так:
J (г, р, t) ъ - -^^ grad p (r, p.t),Q = Qm + Qa, B.4.40)
186 Гл. 2. Уравнения полей
что, конечно, подтверждает наше предположение о том, что направле-
направления J и gradp одинаковы. Величина l/ntQ является средним свободным
пробегом частицы, когда учтены и поглощение и упругие столкновения.
Отметим, что в этом более тщательном анализе эффективное сечение
передачи импульса Qm [см. B.4.36)] играет большую роль, чем упругое
эффективное сечение Qe. Уравнение B.4.40) тесно связано с уравнением
{2.4.3) для средней диффузии. Величины Q, р и J в этом уравнении
являются функциями величины импульса р (т. е. скорости частиц), и для
приведения к B.4.3) надо произвести осреднение по р. Поэтому для
частиц, имеющих импульс р, постоянная диффузии пропорциональна
корню квадратному из произведения р на средний свободный пробег.
Уравнение, связывающее среднюю плотность и средний поток, имеет
вид
со
J (г> ') * "i PepAsp. grad [ р (г, t) ], Хор. = ~- ^ -JjL- р (г, р, t) dp,
что эквивалентно уравнению B.4.3). Поэтому, как мы увидим ниже,
величина j//>Cp.^cp./3/re равна постоянной диффузии для среднего рас-
распределения.
Рассмотрим теперь ту часть уравнения B.4.39), члены которой не
меняют знака при изменении направления р на противоположное. Все
эти члены, за исключением одного, не зависят от угла 6, определяю-
определяющего направление р, однако член, содержащий p-grad(p-J) является
функцией 6. Это, конечно, указывает на то, что предположение, содер-
содержащееся в уравнении B.4.37) относительно формы функции распреде-
распределения /, было только приближенным. Можно приближенно удовлетворить
¦соотношению, если произвести осреднение по всем направлениям р.
Такой процесс осреднения не вносит изменения в члены вида т (dp/dt) или
ntQaPP> но такие члены, как p-gradp, будут иметь среднее значение,
равное нулю. Единственный сложный член можно преобразовать, применяя
уравнение B.4.40) и проводя разложение по компонентам вектора р
[p-J] = pn*Qm P-grad [p-gradpj =
l f г jpp, a2P a2P
\Px lP* дх* +РУ дхду + P* dx dz
Если осреднить эти члены по всем направлениям вектора р, то слага-
слагаемые, содержащие смешанные множители типа рхру, pxpz и т. д., обра-
обратятся в нуль, в то время как р%, р%, р\ будут иметь средние значения,
равные -о-/?2, так что все выражение примет простой вид (p/3ntQm) V2p.
Второе уравнение, получающееся из B.4.39), принимает поэтому вид
i Р- '> -»Аа-? Р ('. P
и служит для определения плотности частиц, имеющих импульс вели-
величины р. Функция q есть функция источника, дающая количество частиц,
имеющих импульс р и «возникающих» в течение секунды в кубическом
¦сантиметре в точке г в момент времени t.
2.4. Диффузия и другие явления просачивания 187
Теперь нетрудно получить уравнение диффузии для средней плот-
плотности. С помощью средних значений, определенных в B.4.38), и поль-
пользуясь величинами
Ш ' V = 5! Р* р(, О
о ' о
получим окончательно
~ р (г, 0 ^ a2V2p (г, /) - хр (г, /) + q; B.4.42)
это — уравнение диффузии с двумя дополнительными членами, соответст-
соответствующими уничтожению и возникновению частиц. Как мы видели, это
уравнение пригодно только в тех случаях, где mJ/pcv- много меньше
чем р (или по крайней мере мы не можем быть уверены в его пригод-
пригодности, если mJ/pcp. не будет очень мало сравнительно с р). Граничные
условия на граничной поверхности, вне которой нет рассеивающих
мишеней, даются уравнением B.4.34).
Единичные решения. По аналогии с нашими рассуждениями отно-
относительно волнового уравнения и уравнения Пуассона мы ищем решение
уравнения B.4.42), представляющее возникновение единственной частицы
в момент времени ( = 0 в начале координат [q = %(t)b(x)b(y)b(z)]. Реше*-
ние должно быть сильно сконцентрировано около начала координат при
малых значениях t и с течением времени должно все больше и больше
распространяться. Можно попытаться выразить решение для случая
неограниченного пространства через функцию ошибок в пространстве
1р = В (t) e~T*DW, где г2 = х2-\- y2-\-z2], и в конце концов можно показать,
что требуемым решением уравнения B.4.42) является (предполагая, что
* — постоянная)
р = G (х, у, z; ,t) ^ { (^-^„(„л^о^ ' > о, B.4.43)
Показательная функция непригодна для отрицательных значений t\
если t положительно, но бесконечно мало, то р является дельта-функцией
вблизи начала (как это и должно быть), но когда t возрастает дальше
от значения t = 0, плотность выравнивается все больше и больше (на са-
самом деле в соответствии с нашими замечаниями на стр. 181 уравнение
диффузии, а следовательно, и его решение не пригодно до тех пор, пока
после появления частицы не пройдет промежуток времени несколько
больший, чем среднее время свободного пробега l/ntQcvvCVm). Если
имеется поглощение (х не равно нулю), решение в целом экспоненциально
убывает, так что интеграл от G, взятый по всему пространству (т. е.
вероятность того, что частица еще не поглощена), равен е~*'.
Если частицы возникают во всей области на протяжении некоторого
промежутка времени, так что они в количестве q(x0, у0, z0; t)dxodyodzodt
порождаются в элементарном объеме dxodyodzo, расположенном в точке
хо> Уо> zo. за промежуток времени между моментами t и t + dt, тогда
то же самое рассуждение, которое привело нас к формуле B.1.8), пока-
показывает, что получающаяся плотность частиц в неограниченном про-
пространстве в точке х, у, z в момент времени t равна
0= \ dz \ dx0 \ dyo\ dzoq (x0, y0, z0; z)G{x — x0, y — y0, z — zo;t — i).
B.4.44)
—CO —CO
188 Гл. 2. Уравнения полей
Это решение, а также и другие будут очень подробно рассмотрены в этой
книге дальше.
Когда достигается установившееся состояние и р больше не зависит
от времени, соответствующее поле является решением уравнения Гельм-
гольца (см. стр. 125), так как уравнение B.4.42) тогда принимает вид
— *р= —д.
В этом случае знак члена, содержащего р, противоположен знаку соот-
соответствующего члена в уравнении Гельмгольца, полученного из волнового'
уравнения и приведенного на стр. 125.
Потеря энергии при столкновении. До сих пор мы предполагали,
что атомы вещества (мишени), через которое диффундируют частицы
жидкости, жестко закреплены в пространстве, так что столкновения
вполне упругие и потери энергии в веществе не происходит. Это, конечно,
является идеализацией истинного состояния, которая лишь в немногих
случаях мало отличается от действительности (как в случае рассеяния
фотонов, рассмотренном раньше). Во много большем числе случаев, пред-
представляющих интерес, атомы-мишени также движутся и не являются
бесконечно более тяжелыми по сравнению с диффундирующими части-
частицами, так что эти частицы при столкновениях могут терять (а также
и приобретать) кинетическую энергию. Исследование наиболее общего-
случая возможно, но утомительно, оно отвлекло бы нас в сторону от
нашей цели дальше, чем это желательно. Мы в наших рассуждениях
продвинемся здесь лишь настолько, чтобы показать, какие новые эффекты
возникают при потере части энергии при столкновениях.
Предположим, что атомы-мишени имеют массу М, которая значи-
значительно больше массы т частиц жидкости, а также, что частицы жидкости
имеют в среднем намного большую кинетическую энергию, чем атомы-
мишени. В этом случае атомы-мишени можно считать неподвижными
в момент ударов частип, а также предположить, что только малая часть
кинетической энергии теряется при каждом ¦ отдельном столкновении.
Элементарный анализ баланса импульсов и кинетической энергии
показывает, что если начальный импульс частицы равен р' а ее оконча-
окончательный импульс после ее отклонения на угол а (см. рис 2.18) равен р,
то с точностью до членов первого порядка относительно малой вели-
величины т/М имеем:
] [] B.4.45)
В силу уравнений B.4.35) и B.4.36) мы можем сказать, что с точностью
до членов первого порядка относительно малой величины т/М для
частицы с первоначальным импульсом р'
средняя потеря кинетической энергии при упругом
столкновении равна произведению 2mQm/MQe на ее пер-
первоначальную кинетическую энергию;
средняя потеря величины импульса при упругом столк-
столкновении равна произведению mQm/MQe на ее первона- ^ B.4.46V
чалъный импульс р'\
среднее уменьшение передней компоненты импульса при
упругом столкновении равно произведению QmlQe наА ее
первоначальный передний импульс р', J
2.4. Диффузия и другие явления просачивания 189
Где среднее число упругих столкновений частиц, имеющих импульс р,
равно nfiep/m в секунду. Третье утверждение означает, что среднее
значение компоненты окончательного импульса по направлению перво-
первоначального движения (р-р7/О равно [1 — (Qm/Qe)]pr- Между прочим, эти
утверждения поясняют, почему Qm мы называем эффективным сечением
передачи импщгъса.
Вернемся теперь к рассмотрению уравнений B.4.14) и B.4.15),
дающих скорость изменения функции распределения / (г, р, t), вызван-
вызванного упругими столкновениями. Скорость убывания /, вызванного рас-
рассеянием частиц из элемента импульсов dVp = p2 dpd$ sin 6db (см. рис. 2.18),
равна, как и прежде,
2я я
{ d$\ alp, a)sinaefo/(r, р, в, у, t).
о о
Скорость возрастания /, обусловленного частицами, отброшенными
•внутрь элемента dVp из элемента импульсов dVp = (p'Jdp'd?' sind'dQ',
равна
2я я
^-sinddbdf^ d$ \ l(p')sa(p', а)/(г, р', 6', <р', t)dp'] sin.adx.
о о
Но согласно уравнению B.4.45) р' отличается от р на малую величину
(рт/М) A — cos-t). Выражение, стоящее в квадратных скобках, может
быть разложено в ряд Тейлора по степеням (рт/М), что даст в ка-
качестве первого приближения
.p»dp{a(p,a)f(T,p,V,9', 0+^A-cosа)
Мы допустили, что распределёлие частиц Почти изотропно и что
движение переноса мало по сравнению с случайным движением частиц
в соответствии с уравнением B.4.37), где mJ/p мало сравнительно с р.
Мы допустили также, что вектор J параллелен полярной оси 6 и <р-
При этих предположениях оба выражения могут быть объединены и
упрощены и мы получаем результирующую скорость изменения /, вызван-
вызванного приростом и потерей частиц при рассеянии
2я я
-™- dp sin б db dip { d?\ |— о (p, a) [cos 6' — cos 6] / (r, p, t) +
о о
A
+ A
Первый член этого выражения был выведен раньше [см. равенства
B.4.38) и следующие]; второй член - новый, он представляет изменение
функции /, вызванное потерей энергии при столкновении.
Другая часть скорости изменения, которая должна быть принята
во внимание, дается в уравнении B.4.9), соответствующем уравнению
неразрывности. Изменение имеет вид
если подставить приближенное выражение /, данное в уравнении B.4.37).
190 Гл. 2. Уравнения полей
Действие внешней силы. Учитывая влияние на функцию / потери
энергии при столкновениях, необходимо также принять во внимание-
возможность приобретения энергии частицами благодаря наличию внеш-
внешнего силового поля. Если, например, частицами являются электроны,
движущиеся через газ, то электрическое поле может вызвать движение-
переноса и изменить функцию распределения /. Мы предположим, что
действует постоянная сила F, параллельная потоку J. (Мы не будем
рассматривать случай, когда имеется внешняя сила и одновременно-
gradp отличен от нуля, поэтому в нашем исследовании в этом пара-
параграфе J направлено либо параллельно F, либо параллельно gradp,.
смотря по тому, какой из этих векторов отличен от нуля.)
Если приложить силу F, импульс каждой частицы изменится; ча-
частицы, имевшие импульс р в момент времени t, будут иметь импульс
p + Fdt в момент t-\-dt. Рассуждая подобно тому, как мы это делали
при выводе уравнения неразрывности B.4.9), мы должны принять, что»
плотность следует за ускоряемыми частицами, т. е. /(г, p-f Ydt, t + dt) =
= /(r, p, t); таким образом, скорость изменения величины fdVp, вызван-
вызванная внешним полем, равна
B.4.49>
Наконец, комбинируя выражения B.4.47) — B.4.49) и добавляя член.
— niQaP ?/m> соответствующий поглощению частиц, получаем выражение,
дающее скорость изменения р и /, вызванного столкновениями, ускоре-
ускорением переноса и поглощением
до , Зт г. 8J 1 т 3 , , ж.
¦fljT + y cos 6-g- о* —- p.grad p- -^p«grad (p- J) -
AfZA3mp cog2
- 3ntQmJ cos б + ^ -L (p*Qm9) - JL ntQaPP - ZntQJ cos 6. B.4.50>
Это уравнение может быть разделено на два, если воспользоваться сим-
симметрией относительно б (или относительно направления р); решение-
полученных уравнений позволит определить р (г, р, t) и J(r, p, t).
Далее будут рассмотрены два примера, оба в условиях установившегося
состояния, в случаях, когда члены, соответствующие потере энергии,
играют существенную роль при решении.
Равномерный перенос, вызванный силовым полем. В качестве пер-
первого примера рассмотрим равномерно распределенные частицы, движу-
движущиеся через среду под влиянием постоянной силы F. Таково, например,
движение электронов в газе под действием электрического поля. Здесь
grad p равен нулю и вектор переноса J должен быть параллелен F. Для.
установившегося состояния df/dt равно нулю; предположим, кроме того,
чт° Qa равно нулю. Остающиеся члены уравнения B.4.50) умножим
на sinGdG или на cos 6 sin 6 db и проинтегрируем по 6; получим два урав-
уравнения:
2.4. Диффузия и другие явления просачивания 191
Первое уравнение после интегрирования дает
Постоянная интегрирования К оказывается равной нулю, в чем можно
убедиться с помощью следующего рассуждения: интегрируя последнее
уравнение (при К = 0) еще раз относительно р, получим уравнение
баланса энергии [см. B.4.38)]
щОер
Левая часть как раз равна энергии, полученной от силового поля F
за одну секунду в одном кубическом сантиметре благодаря потоку плот-
плотности / переноса частиц. Выражение (р*/2т) BmQm/MQe), стоящее в пра-
правой части, как показывает уравнение B.4.46), дает среднюю кинетиче1
скую энергию, потерянную при столкновении и соответствующую импульсу
р; ntQep/m есть число столкновений частицы за секунду и р (р) р2 dp
есть число частиц в кубическом сантиметре, имеющих импульсы, лежа-
лежащие между р и p-\-dp; таким образом, интеграл как раз равен полной
энергии, теряемой благодаря столкновениям одним кубическим санти-
сантиметром за одну секунду. Если устойчивое состояние достигнуто, то коли-
количество энергии, потерянной при столкновениях, должно быть равна
количеству энергии, приобретенной от силового поля, и потому наше
уравнение удовлетворяется. Следовательно, К должно быть равным нулю.
Теперь можно вернуться ко второму из уравнений B.4.51) и найти
зависимость р от р. Так как /(р) = {ntQm/mMF)p3p (р), то, интегрируя,-
получим
Р(р) = Лехр [-%-{ Q^fjpdp] , B.4.52)
О
где А выбрано так, чтобы интеграл в B.4.38) был равен р, средн-ей плот-
плотности настиц. Если Qm не зависит от плотности, то
С помощью этой функпии распределения мы можем выразить среднюю-
кинетическую энергию scPi частиц и среднюю скорость переноса vcv.,
вызванные влиянием поля, через энергию ze = F/ntQm и скорость
ve = 1/r2F/mnlQm , которые приобрела бы частица при движении под дей-
действием поля из состояния покоя за величину среднего свободного про-
пробега. Эти величины равны
еср. = 0,4270 (^ Y2 ев, иср. = 0,6345 (-?У'" ve.
ср. — Ui^'u I — I =-e> ^ср.
Эти равенства верны только, если Qm не зависит от р. Отсюда видно,
что средняя энергия тем больше, чем тяжелее атомы по сравнению
с частицами, так как при увеличении М/т частицы могут терять при
столкновениях меньше энергии. С другой стороны, средняя скорость пере-
переноса убывает при возрастании М/т.
Этот пример мало связан с уравнением диффузии, но он показывает,
как уравнения, определяющие функцию распределения /, могут быть
приспособлены в различных случаях к очень обширному многообразию
условий и явлений. Он показывает, например, что распределение скоро-
192 Гл. 2. Уравнения полей
стей электронов, движущихся в газе под влиянием электрического поля,
не является распределением Максвелла, вызванным тепловым перемеши-
перемешиванием; здесь содержится четвертая степень скорости (вместо квадрата)
в показателе. Это, конечно, верно до тех пор, пока средняя кинетиче-
кинетическая энергия электронов много выше средней кинетической тепловой
энергии атомов газа, через который переносятся электроны. В против-
противном случае нельзя было бы считать, что атомы газа находятся в состоя-
состоянии относительного покоя и распределение электронов должно было изме-
изменяться на основе максвелловского закона распределения скоростей.
Уменьшение скорости частиц при столкновениях. Уравнение диф-
диффузии появляется в следующем (и последнем) примере, который интересен
при изучении замедления нейтронов в «замедлителе». Мы рассмотрим
здесь зависящие от х, у, z решения уравнения B.4.50), когда F равно
нулю и когда принимается во внимание замедляющее действие столкно-
столкновений.
Предположим, что частицы появляются в некоторой части првстран-
ства все с одним и тем же начальным импульсом р0; они сталкиваются
с атомами и постепенно замедляются и в то же время разбрасываются.
Так как здесь процесс установившийся, новые частицы непрерывно
появляются и заменяют те, скорость которых уменьшилась; функция
распределения не зависит от времени, но зависит от импульса р и от
пространственных координат. Как мы увидим, J в этом случае парал-
параллелен градиенту р.
Импульс может быть принят за меру среднего «возраста» отдельной
частицы, так как эта частица появляется, имея импульс р0. Когда этот
возраст увеличивается, распределение в пространстве изменяется; поэтому
можно надеяться найти уравнение, связывающее зависимость / от точки
пространства с зависимостью ее от возраста частиц тем же способом,
каким уравнение диффузии связывает зависимость /от точки простран-
пространства с ее зависимостью от времени для случая неустановившегося со-
¦стояния.
Среднее уменьшение импульса р при столкновении, как показывает
B.4.46), определяется равенством
dP ^, mQm
dx — MQ Г'
где х есть среднее число столкновений, которым подверглась частица;
следовательно, мы имеем соотношение между v и х
х_Хо== \MQdp_ 2453)
0 : rnQm p v '
V
Величина х — т0 называется возрастом частицы в распределении; она
заменяет время, когда мы рассматриваем случай установившегося состоя-
состояния при наличии замедления.
Возвращаясь снова к уравнению B.4.50), мы опускаем члены, содер-
содержащие силу и производную по времени, но включаем члены, характери-
характеризующие потерю энергии и поглощение. Член, зависящий от источника q,
аналогичный соответствующему члену в B.4.41), не включается, так как
он введен в «начальном условии» при ъ = т0. Если мы умножим на cos б
и проинтегрируем по всем направлениям б, мы получим, как и раньше
[см. B.4.40)],
2.4 Диффузия и другие явления просачивания 193
На этот раз уравнение получается точным, так как теперь мы имеем
дело с установившимся состоянием, так что производная по времени от J
равна нулю, в то время как раньше она была очень малой и мы ею пре-
пренебрегали»
Подставляя это обратно в B.4.50) и осредняя по всем направле-
направлениям, мы получим [по поводу члена, содержащего grad(p-J) см. стр. 186]
Полагая ф = (fy(?m/?4p/M) и подставляя вместо р его выражение через х
из B.4.53), получим окончательно уравнение для ф, имеющее вид урав-
уравнения диффузии
где вместо времени мы имеем (х — х0) — возраст частиц, имеющих импульс р.
Физический смысл величины ф вскоре станет ясным.
Решения этого уравнения полностью аналогичны решениям обычного
уравнения диффузии. Например, если частицы с импульсом р0 перво-
первоначально появляются в сконцентрированной области пространства,
то распределение более медленных частиц будет более равномерным; эта
равномерность будет тем больше, чем больше ъ (т. е. чем меньше р/р0).
Если только установившееся состояние достигнуто, мы можем сделать
перепись всех частиц, находящихся в данный момент времени в данном
кубическом сантиметре, чтобы определить количество тех из них,
импульсы которых попадают в данный промежуток (или, вернее, для
которых -. лежит в данном интервале dx). Из полученной плотности
относительно х можно найти функцию ty в точке как функцию х; нао-
наоборот, если ф известна, мы можем предсказать результаты переписи.
Чтобы определить «начальное значение» ф0, т.. е. значение функ-
функции ф при т = х0> мы должны установить связь между количеством частиц
на кубический сантиметр, появляющихся за секунду в данной точке,
и полной потерей импульсов за секунду в одном кубическом санти-
сантиметре, т. е. произведением числа частиц в одном кубическом сантиметре
на величину потери частицей импульса за секунду. Потеря импульса
при столкновении, согласно утверждению B.4.46), равна в среднем
mpQm/MQe. Число столкновений в секунду, приходящихся на одну
частицу, равно ntQep/m, так что полная величина потери импульса одной
частицей в секунду равна dp/dt = ntQmp2/M. Так как число частиц в одном
кубическом сантиметре, имеющих импульс в данном промежутке импуль-
импульсов dp, равно, согласно B.4.38), p2pdp, то полная потеря импульса в одном
кубическом сантиметре за промежуток времени dt равна р2р (dp/dt) dt =
= ntQmpipdt/M. Следовательно, величина ntQmpup/M = <!>(г) равна полному
числу частиц, имеющих в данное время импульсы, превышающие р,
но таких, что через секунду их импульсы становятся меньше чем р.
Это полная скорость уменьшения импульсов.
Например, если в каждом кубическом сантиметре ограниченной части
пространства каждую секунду появляется п0 частиц, то ф0 будет равно п0
всюду в этой ограниченной области (предполагается, что частицы появ-
появляются изотропно, т. е. все направления р0 равновероятны). Если гра-
границы области полностью отражают частицы, то ф при всех значениях х
не будет зависеть от пространственных координат и решение уравне-
13 Ф. м. Морс и Г. Фешбах
194 Гл. 2. Уравнения полей
ния B.4.54) будет иметь вид
«!> = noe~(Qa№K'r~'ro> при
S p ymQalMQm
или ( ? )
f p ^rnQalMQm Qm . \ B.4.55)
ty — no ( ) > если ~ не зависит от p i
v. Po У v J
и количество частиц, импульсы которых лежат между р и p-\~dpr
равно
9 J M4? 1 ПОМ С р \mQal'Mtm
при р < р0. Последняя форма решевия пригодна лишь в случае, когда
Qm/Q не зависит от р. Если отсутствует поглощение (Qa = 0), то <J> не зави-
зависит от -: и р будет обратно пропорциональным величине p4Qm- Это
и должно иметь место, так как при отсутствии поглощения быстрота •>
уменьшения импульсов должна быть одна и та же для всех скоростей.
Это решение, конечно', влечет за собой существование бесконечно боль-
большого числа частиц с бесконечно малыми скоростями. Если бы наше
исследование потери энергии при столкновениях сохраняло силу в пре-
пределе при обращении скорости в нуль, то такое бесконечное количество
должно было бы существовать, чтобы достичь установившегося состоя-
состояния. В действительности, конечно, атомы среды не остаются полностью
в покое, и поэтому для достаточно малых скоростей частиц приведенное
выше рассуждение, предполагающее, что частицы всегда теряют энергию,
становится неприменимым. Поэтому равенство B.4.55) непригодно для
частиц, имеющих кинетическую энергию той же величины или меньшую,
чем средняя энергия атомов.
В качестве второго примера рассмотрим случай, когда ц точке х0, уог
z0 неограниченного пространства появляется (изотропно) в секунду одна
частица с импульсом р0. Тогда •!> при z = -с0 будет равно дельта-функции
6 (х — х0) Ь (у — у0) 6 (z — z0); используя те самые методы, которые привели
нас к формуле B.4.43), получим <b = G(x — х0, у — у0, z — zc |т —10), где
G{x, у, z j -с — хо) =
О, 1 < V,
^ B.4.56)
MQ
Наконец, мы можем решить задачу, если на кубический сантиметр
в точке х0, у0, z0 неограниченного пространства в секунду появляется
изотропно д(х0, у0, z0 \po)dpo частиц, импульсы которых лежат между
р0 и po-\-dpo. Количество частиц, появляющихся в секунду между пре-
пределами «возраста» -0 и xo + d^o, будет тогда равно {pomQm/MQ)q(xo, yv,
zo\zo)dt(), где р0 связано с х0 так же, как р и i связаны в уравнении
B.4.56). Получающееся установившееся распределение в пространстве
частиц с различными импульсами р можно вывести из выражения для '!>
Т оо оо оо
•Ъ{:с, у, z|-)=^p \ podzo [ dx0 \ dy0 \ dzox
— ОО —ОС - г_п — ОС
>' Ч CV Уе> г„ ! -0) G{x- х0, у - ?/0, z - z0 \ -. - -й), B.4.57.)
2.5. Электромагнитное поле 195
где количество частиц, имеющих импульсы в промежутке между р и
p-\-dp, рассчитанное на один кубический сантиметр, равно p2pdp —
= (Mty/ntp2Qm) dp. При некоторых простых формах функции q интегриро-
интегрирование может быть выполнено и таким образом может быть получена
замкнутое аналитическое выражение для ф.
Резюме. Можно указать много других применений уравнения диффу-
диффузии. Для его появления требуется только, чтобы некоторая величина
(плотность, парциальное давление, количество теплоты и т. д.) удовле-
удовлетворяла двум условиям: во-первых, она должна подчиняться уравнению-
неразрывности, то есть скорость изменения этой величины с течением
времени должна быть равна дивергенции потока этой величины, взятой со
знаком минус, во-вторых, поток этой величины должен быть пропорционален
градиенту этой величины, взятому с обратным знаком. Другие случаи
будут рассмотрены в гл. 12.
Так как уравнение содержит производную по времени лишь первого
порядка, в то время как производные по координатам имеют второй
порядок, решения уравнения диффузии необратимы во времени. Почти
все другие уравнения, которые мы будем рассматривать, изображают
обратимые в термодинамическом смысле явления, в то время как урав-
уравнение диффузии изображает" возрастание энтропии (мы к этому вернемся
в следующей главе). Все это, грубо говоря, равносильно утверждению;
что явления, изображаемые уравнением диффузии, имеют статистический
характер.
2.5. Электромагнитное поле
Понятие поля играет большую роль еще в одной важной отрасли
физики, а именно в учении об электричестве. Некоторые элементарные
частицы вещества обладают электрическими зарядами и большая часть
их, если не все, имеют магнитные моменты. Электромагнитная теория
разработана для описания их взаимодействий в целом (взаимодействия
между отдельными частицами обычно включают квантовые явления,
которые мы опишем в этой главе позже).
Как и в случае полей, встречавшихся раньше в этой главе, электри-
электрический заряд часто удобнее рассматривать как непрерывную жидкость,
чем как мнЬжество заряженных частиц. Классическая электромагнитная
теория имеет дело с полями, порождаемыми различными расположениями
такой жидкости, а также и взаимодействиями этих полей с другими
частями жидкости. Конечно, можно было бы изучать силы, с которыми
одна часть- жидкости (или одна частица) действует на другую часть
(или частицу), вовсе не говоря о поле. Однако представляется значи-
значительно более простым и, быть может, также лучшим расчленить задачу
на две части: первую — о «создании» электромагнитного поля при нали-
наличии того или иного распределения зарядов и токов, и вторую—о влия-
влиянии этого поля на распределение зарядов и токов.
Электростатическое поле. Воздействие одной заряженной частицы
на другую вполне аналогично взаимодействию тяготения. Величина силы,
действующей на каждую частицу, обратно пропорциональна квадрату их
расстояния друг от друга и прямо пропорциональна произведению вели-
величин их зарядов; направление силы совпадает с направлением прямой
линии, соединяющей частицы (пока частицы остаются в покое одна отно-
относительно другой). В случае тяготения сила, всегда притягивающая,,
и величина гравитационного заряда пропорциональна массе частицы;:
13*
196 Гл. 2. Уравнения полей
между двумя электрическими зарядами действует сила отталкивания,
¦если заряды имеют один и тот же знак, и сила притяжения, когда
заряды противоположных знаков.
Сила, действующая на какую-либо частицу или часть заряда, будет,
следовательно, пропорциональна величине ее собственного заряда. Таким
образом, мы можем определить векторное поле, называемое электроста-
электростатическим (или гравитационным) полем Е, которое в какой-либо точке
является отношением силы, действующей на пробную частицу, помещен-
помещенную в эту точку, к величине заряда этой частицы. Вектор Е называется
электрической (или гравитационной) напряженностью поля в точке. Это
поле, определяемое суммой сил, величины которых обратно пронорцио-
нальны квадратам расстояний от различных имеющихся зарядов, является
полем, определенным некоторым числом точечных источников, рассмо-
рассмотренным на стр. 28. Мы показали в A.2.10), что для полей такого типа
поток через любую замкнутую поверхность изнутри наружу равен лроиз-
редению 4тс на сумму зарядов всех частиц, расположенных внутри неё.
До тех пор пока мы рассматриваем лишь макроскопические эффекты,
мы можем не обращать внимания на микроскопические неправильности
поля, возникающие благодаря тому, что заряды сосредоточены на отдель-
отдельных частицах, а не распределены непрерывно; нам надо рассматривать
тольк'о поля, осредненные по элементарным кускам поверхности, имеющим
площадь большую сравнительно с расстояниями между частицами,
но малую по сравнению со всей поверхностью. Если это возможно,- полу-
полученное среднее поле эквивалентно полю, возникающему при непрерывном
«сглаженном» распределении зарядов; в этом случае мы можем не бес-
беспокоиться по поводу точного положения каждой отдельной частицы.
Мы можем «вблизи» точки х, у, z выбрать элемент объема dxdydz, содер-
содержащий достаточно большое количество частиц. Величина полного заряда
внутри этого объема равна средней плотности заряда «в точке» х, у, z,
умноженной на dxdydz. Эта величина пропорциональна потоку через
поверхность рассматриваемого элемента, а этот поток, согласно равен-
равенству A.4.5), равен произведению dxdydz на дивергенцию поля Е.
Таким образом, рассматривая макроскопические явления, мы можем
заменить множество заряженных частиц гладким распределением заряда
с плотностью р (ж, у, z, t). Как показывает равенство A.4.5), в случае,
когда эта плотность не зависит от времени, получающееся статическое
поле Е связано с р уравнением
div Jb — — p.
Коэффициент пропорциональности з зависит от среды и называется диэлек-
диэлектрической постоянной среды. Если s меняется от точки к точке, то удобнее
рассматривать связанное с Е векторное поле D, называемое полем элек-
электрической индукции, причем
divD = 4Ti;p, D = eE. B.5.1)
Выразив D через р и зная г, найдем Е, а потом определим и силу рЕ,
действующую на кубический сантиметр электрической жидкости.
Как было показано на стр. 59, вектор Е всегда может быть выражен
через вихрь векторного и градиент скалярного потенциала. Но, так как
дивергенция вихря равна нулю, векторный потенциал для Е не опре-
определяется уравнением B.5.1) и поэтому не входит в выкладки в электро-
электростатике. Скалярный потенциал о Для Е должен удовлетворять следу-
следующему уравнению:
div[sgrad<p] = eV2?-f (grad j)- (grad?) = — 4тгр, Е=— grado. B.5.2)
2.5. Электромагнитное поле 197
Если s — постоянно, то это уравнение превращается в уравнение Пуассона
для ф [см. B.1.2)].
В случае тяготения величина г везде постоянна и в уравнении для
напряженности берется противоположный знак divE=—4гср/г, соответ-
соответствующий тому, что сила всегда является силой притяжения, а не отталки-
отталкивания. В этом случае также существует скалярный потенциал, являющийся
всюду решением уравнения Пуассона V2<p= —4-тф/г.
Магнитостатическое поле. Ферромагнитные материалы, атомы кото-
которых имеют не нейтрализированные магнитные моменты, ведут себя так,
как если бы они были заполнены магнитной жидкостьюг), подобной элек-
электрической жидкости, рассмотренной сейчас нами. Если поместить еди-
единичный положительный магнитный заряд, на него будет действовать сила,
определяемая векторным полем Н, аналогичным электрическому полю Е.
Диэлектрической постоянной е здесь соответствует магнитная прони-
проницаемость (л, а вектору электрической индукции D = sE соответствует
магнитная индукция В = цН.
Тем не менее важным различием между электричеством и магнетиз-
магнетизмом является отсутствие магнитных зарядов. Уравнение для поля магнит-
магнитной индукции В в отличие от уравнения B.5.1) имеет вид
divB = 0. B-5.3)
Конечно, можно было бы считать В градиентом скалярного потенциала,
обязательно удовлетворяющего уравнению Лапласа B.3.6), однако удобнее
воспользоваться тем фактом, что дивергенция вихря любого вектора
равна нулю, и выразить В с помощью векторного потенциала В = rot А.
В этих рассуждениях мы пока рассматривали магнитостатическое
поле, не учитывая того факта, что магнитное поле оказывается связан-
связанным с потоком электрических зарядов, т. е. с электрическим током.
Например, если вдоль прямолинейного провода, диаметром которого
можно пренебречь, течет ток I (направление вектора совпадает с на-
направлением тока вдоль провода), то магнитное поле вокруг провода
дается равенством
где г — есть вектор, перпендикулярный проводу и идущий от провода
к точке, в которой измеряется Н.
Но это как раз поле, порожденное простым вихрем, рассмотренное
на стр. 30. Принимая во внимание это, а также определение вихревого
вектора, данное на стр. 49, получаем общую связь между В и постоян-
постоянным током. Если заряженная жидкость движется, то произведение скоро-
скорости v -заряда на его плотность р называется плотностью тока J; этот
вектор определяет величину заряда, проходящего в секунду через один
квадратный сантиметр, и имеет в каждой точке направление скорости
заряда. Вектор J связан с вихревым вектором поля Н простым уравне-
уравнением
rotH = 4xJ. B.5.4)
(Между прочим, может оказаться, что имеется ток, но нет свободных
зарядов; так будет, если ток получается в результате движения
х) Так как не существует магнитных зарядов, а можно рассматривать только маг-
магнитные моменты, то было бы более логично выводить уравнения для магнитного поля,
рассматривая вращающий момент, действующий на магнитный диполь. Однако это не
книга по электромагнетизму и нас можно ийвинить (как мы надеемся) за то, что мы
экономим место, выводя наши уравневия по аналогии с электростатикой вместо
того, чтобы затратить еще несколько страниц на более логичный вывод, который
во всех подробностях дан в таких, например, книгах, как Дж. А. Стрэттон. Теория
электромагнетизма, ГТТИ, 1948, или Frank. Introduction to Electricity and Optics.
198 Гл. 2. Уравнения полей
в противоположных направлениях равных количеств положительных
и отрицательных зарядов.)
Наоборот, в магнитном поле возникает сила, действующая на ток.
Сила, действующая на один кубический сантиметр движущегося заряда
в точке х, у, z, равна
F=pvxB=JxB, В = цН. B.5.5)
Для решения вопросов, связанных с установившимся состоянием,
этих уравнений достаточно. Заряд вызывает появление электростати-
электростатического поля (Е, D), ток вызывает появление магнитного поля (Н, В).
В свою очередь электростатическое поле действует^ на заряд, а магнит-
магнитное поле —на ток. Электрическое поле возникает под действием стати-
статических зарядов и само вызывает силы, действующие на заряды; магнитное
поло возникает при наличии движущихся зарядов и само вызывает
силы, действующие на движущиеся заряды. Может быть установлена
довольно искусственная аналогия между скалярным потенциалом, опре-
определяющим электрическое ноле, и скалярным волновым потенциалом для
волн чистого расширения в упругой среде, а также между векторным
потенциалом, определяющим магнитное поле, и векторным волновым
потенциалом для волн сдвига. Однако здесь не может быть волнового
движения, так как мы рассматриваем только стационарное состояние.
Для неограниченного пространства, содержащего конечное устано-
установившееся распределение зарядов и токов и имеющего диэлектрическую
постоянную г, везде одну и ту же, и соответствии с равенством A.4.8)
решение уравнения B.5.2) имеет вид
о(х, у, z) = — \ ^ \ -^-р(х', у', z')dx' dy'dz, B.5.6)
— ОЭ
где
Я2 = (х - x'f + (у - у'J + (z - z'J
и Е= —grady, D= —sgrady.
Векторный потенциал А может быть выбран так, чтобы его дивер-
дивергенция была равна нулю (ибо нас интересует только та часть вектора
А, которая имеет ненулевой вихрь). Так как V2A = graddiv A — rot rot A,
то из уравнения B.5.4) имеем
V2A = - 4bhJ, B.5.7)
а из уравнения A.5.16) —
А (х, у, z) = |х \ \^ ^Цх', у', z") dx' dy' dz', B,5,8)
—со
где
В = rot A, H = — rot А.
Зависимость от времени. До сих пор мы рассматривали лишь
установившееся состояние, когда dp/dt и divJ равны нулю [divJ должна
быть равна нулю, если dp/dt равна нулю в силу уравнения неразрыв-
неразрывности B.3.1)]. Если же р и J меняются с течением времени, уравнения
B.5.1) и B.5.4) должны стать связанными друг с другом, так как
уравнение неразрывности связывает между собой плотность, заряда
2.5. Электромагнитное поле 199
и поток заряда. При этом надо связать единицы заряда, силы тока
и напряженности поля в этих двух уравнениях. Если мы пользуемся
системой единиц MKS (метр —килограмм —секунда), уравнения оста-
остаются прежними при е, равной для вакуума зо^-д--1СГ9, и при ц, равной
для вакуума ц0 ^ 1СГ7. Мы предпочитаем, однако, пользоваться смешан-
смешанной системой Гаусса, измеряя заряды в статических кулонах, ток-—
в статических амперах, магнитное поле — в электромагнитных единицах
<(ц для вакуума становится равной 1) и электростатическое поле —
в электростатических единицах (з для вакуума будет равна 1). Тогда
уравнение B.5.4) для установившегося состояния принимает вид
-crotH= -47TJ, B.5.9)
а уравнение B.5.5) принимает вид F = (l/c)JxB, где с = ]/l/noso о=;
~3-108 м/сек = 3-1010 см/сек.
Так как уравнение неразрывности dp/dt=—divJ остается в силе,
мы должны получить тождество, взяв дивергенцию от B.5.9) и произ-
производную по времени от B.5.1) и приравняв их друг к другу. Однако
левые части полученных уравнений оказываются неодинаковыми, так так
в одной из них содержится член div(dD/dt). Это не удивительно, так как
оба эти уравнения выведены для стационарных полей, благодаря чему
член, содержащий производную D по времени, должен был исчезнуть.
Уравнение для магнитного поля, зависящего от времени, очевидно,
должно иметь вид
crotH—^- = 4wJ, B,5.10)
что подтверждается и опытом. Это уравнение называется уравнением
магнитной индукции или контурным законом Ампера для Н. Магнитное
поле появляется не только при наличии электрического тока; измене-
вие электрического поля также вызывает появление магнитного поля.
Уравнения Максвелла. Мы уже почти пришли к симметричной форме
уравнений доля; мы имеем два уравнения, в которых содержатся дивер-
дивергенции векторов В и D [уравнения B.5.1) и B.5.3)], и одно уравнение,
содержащее вихрь вектора Н [уравнение B.5.10)]. Для получения сим-
симметричной формы уравнений нам недостает четвертого уравнения,
содержащего rotE. Однако четвертое уравнение не может быть полностью
•симметричным уравнению B.5.10), так как если не существует магнит-
магнитного заряда, то тем более не существует и магнитного тока. Наиболее
близко можно подойти к симметрии, составив уравнение, связывающее
rotE и дЪ/dt. Это уравнение также подтверждается опытом; оно назы-
называется законом электрической индукции Фарадея и связывает измене-
изменение магнитного поля с вихрем электрического поля. Экспериментальные
данные показывают, что в правую часть этого уравнения нужно ввести
множитель — 1/с. Таким образом, можно выписать четыре симметричных
уравнения, связывающих поля с токами:
1 sd , 1 . ? „ 1 ев
^-яГ + -^4е-*> rotE=-
div В = 0, divD==4rP, B.5.11)
В=цН, D = sE,
называемые уравнениями Максвелла. Сила, действующая на кубический
«антиметр движущегося заряда, равна
" B.5.12)
200 Гл. 2. Уравнения полей
Эти уравнения являются основными уравнениями, определяющими клас-
классическое электромагнитное поле, получающееся при «сглаживании» заря-
зарядов и плотности тока.
Уравнения для скалярного и векторного потенциала также изменятся,
если эти потенциалы зависят и от времени. Мы по-прежнему полагаем
В = rot А, так как тогда равенство div В = 0 автоматически выполняется.
Подставив это в уравнение для rotE, получим
rotE= rot( -д- ) или rot E-\ jr— =0.
с \ at / 1_ с at j
Вектор, вихрь которого равен нулю, может быть получен из скалярной
потенциальной функции, так что вектор [Е + A/с) (дА/dl)] будет градиен-
градиентом некоторого скаляра. В случае установившегося состояния, мы имели
Е= — grad<p, где <р — скалярный потенциал; в общем случае мы можем
функцию ф определить равенством
Подставив эти выражения для В и Е в уравнение для rot H (и приняв,
что е и [л — постоянные), получаем
1 ... s Г , дер , 1 д2А 1 , 1 , т
— rot rot A = grad -?- -\ тг^- + — 4icJ
\х с l dt с dt" ] с
или
V2A-
Это уравнение для А является обобщением уравнения B.5.7), если вели-
величина, заключенная в квадратные скобки, равна нулю. Так как до сих пор
определена только та часть вектора А, для которой вихрь отличен от
нуля, то всегда возможно подобрать дивергенцию А таким образом, чтобы
divA=-^^. B.5.14)
Подставляя Е и div А из уравнений B.5.13) и B.5.14) в последнее
уравнение Максвелла, определяющее divD (опять-таки предполагается,
что ц. и з —постоянны), мы получим уравнение для скалярного потен-
потенциала. Совместно, с окончательным уравнением для А имеем
5
что служит для определения скалярного и векторного потенциалов, если
известны р и J. Если р и J равны нулю, эти уравнения превращаются
в волновые уравнения с волновой скоростью," равной с ]/ 1/ejj. в гаус-
гауссовых единицах (или l/l/ец в системе MKS). Когда s и и. обе равны
единице (в вакууме), скорость волн равна скорости света 3-Ю10 см/сек;
в действительности она и является скоростью света. Из этих уравнений
мы видим, что соотношение B.5.14) между о и А является следствием
уравнения неразрывности для р и J. По аналогии с волнами в упругой
среде мы назовем, волны, связанные с <р,' продольными волнами, а волны,
связанные с А,—поперечными.
Запаздывание и релаксация. Рассуждая так же, как и при выводе
интеграла A.4.8) для решения уравнения Пуассона в неограниченном
пространстве, мы можем показать, что решения уравнений для <р(х, у, z, Z)>
2.5. Электромагнитное поле 201
и А (х, у, z, t) в неограниченном пространстве при конечном распределе-
распределении о {х, у, z, t) и J (х, у, z, t) имеют вид
9е(ж, у, z, t)= ^ -^ -^- p(V, г/', z', t — -^-jdx'dy dz ,
B.5.16)
где с'2 = с2/ец, и, как и раньше, R2 =(ж*— х'J + (у — у'J-г (z — z'J.
Эти интегральные решения показывают, что заряд и ток в точке
х', у', z' влияют на потенциалы в точке х, у, z с запозданием на проме-
промежуток времени R/c'. Действие потенциала запаздывает на промежуток
времени, в течение которого волна, движущаяся со скоростью с' = с/\/~гр,
проходит расстояние между точками х', у', z' и х, у, z. Так как волно-
волновое уравнение симметрично относительно изменения направления отсчета
времени, мы можем получить другие решения, заменив в подинтеграль-
ных выражениях t — (R/c') на t + (R/c'). Однако до настоящего времени
такие «опережающие» потенциалы почти не применяются на практике.
Задавая потенциалы, мы «переопределяем» соответствующие поля
или, что то же, одному полю может соответствовать более чем одно
семейство потенциалов. Решения, определяемые равенствами B.5.16),
могут быть видоизменены добавлением к каждому из них различных
функций, связанных только требованием выполнения равенства B.5.14).
Другими словами, мы можем взять любую функцию х, удовлетворяющую
подходящим граничным условиям, и образовать новые решения уравнений
B.5.15), полагая
A = A°-gradx, 9==9° + ±%-. B.5.17)
Тогда div A+(jj.s/c) (ду/dt) = — V2x + (t*s/c2) {.d2x/dt2), так что уравнения'
для новых А и у могут отличаться от уравнений B.5.15). Однако элек-
электрическое и магнитное поля (которые поддаются измерению) не зависят
от выбора х- При определении вихря вектора А (для получения В), член,
содержащий grad^, исчезает, а при подсчете Е по уравнению B.5.13)
члены, содержащие grad (dx/dt), уничтожаются. Эта инвариантность-
реальных полей при таких изменениях потенциалов, которые остав-
оставляют в силе уравнение B.5.14), называемая калибровочной, или гра-
градиентной инвариантностью, будет вновь рассмотрена позже1).
Решения уравнений Максвелла в областях, не содержащих свободных
зарядов, могут быть при помощи этих изменений упрощены. В этом
случае само у является решением волнового уравнения, так что мы
можем подобрать у^ таким образом, чтобы ср оказалось равным нулю;
тогда можно вовсе не рассматривать скалярного потенциала. Это обо-
обозначает в связи с уравнением B.5.14), что А будет иметь дивергенцию,
равную нулю; необходимые уравнения принимают вид
B = rotA, E=—~~, divA = 0,
яг* т B.5.18)
V2A= - rot rot А = -^г-^—Ч
Даже при наличии свободных зарядов мы можем выбрать А так, чтобы
divA = 0. Тогда на основании уравнений B.5.14) и B.5.15) скалярный
потенциал должен быть решением уравнения Пуассона V2ip= —4ир/з.
J) В обычном определении градиентной инвариантности выполнение условна
B.5.14) не требуется.—Прим. ред.
202 Гл. 2. Уравнения полей
Внутри металлических проводников нет свободных зарядов, а плот-
плотность тока пропорциональна Е, J = cE, где а — удельная проводимость
металла. В этом случае уравнение для векторного потенциала стано-
становится однородным
цз-^ +4*^-^ -c2V2A = 0. B.5.19)
Это уравнение очень похоже на уравнение B.3.20) затухающих волн
сжатия в жидкости. Член, содержащий dA/dt, вызывает появление в реше-
решении множителя затухания, зависящего либо от времени, либо от поло-
положения точки в пространстве, либо от того и другого вместе, как и в случае
волн сжатия.
Например, если волна янляется гармонической с частотой ш/2тс,
зависимость от положения точки и пространстве выражается уравнением
V2A ¦+--Jj- [fisu>2 + 4та>сш] А = 0,
если зависимость от времени дается множителем е~ш. Это, как и на
стр. 137, представляет собой затухание волны в пространстве. С другой
стороны, для стоячих волн, где V2A + A2A = 0, уравнение, определяющее.
зависимость от времени, принимает вид
- - — -яг- + -тг-А = 0
dt- ' e dt
и соответствует колебаниям, затухающим с течением времени. Такие
свободные колебания тока внутри проводника называются релаксацион-
релаксационными колебаниями.
Преобразование Лоренца. В пространстве, где р. и з обе равны еди-
единице, скорость распространения волн равна с, т. е. скорости света.
В этом случае следует ожидать, что уравнения B.5.11) и B.5.15),
связывающие поля и потенциалы с током и зарядами, имеют простую
¦связь с преобразованием Лоренца, рассмотренным в § 1.7. Оператор
<1)
называемый оператором Даламбера (даламбертианом), очевидно [см. A.7.6)]
обладает инвариантностью формы относительно преобразования Лоренца
(см. стр. 100). Говоря, что уравнения для А и <р являются инвариантами
преобразования Лоренца, мы подразумеваем, что они имеют ту же
форму для каждого наблюдателя независимо от его относительной ско-
скорости (до тех пор, пока она постоянна). Это будет иметь место, если
величина (Jx, Jy, J,, ipc) = I есть 4-вектор, преобразующийся по формулам
A.7.4). Наиболее простой способ проверить, что J является 4-вектором, состоит
в том, чтобы показать, что его «скалярное произведение» на какой-либо
4-вектор является инвариантом преобразования Лоренца. Известным четы-
четырехмерным векторным оператором является четырехмерный градиент с
компонентами
~Ыс ' ~ду ' SF' ~ic~dt) = '-'¦
«Скалярное произведение» этих двух величин
2.5. Электромагнитное поле 203
равно нулю в силу уравнения неразрывности [уравнение B.3.1) и стр. 199].
Нуль наверняка является инвариантом преобразования Лоренца, так что
мы доказали, что I, включающий в себя J и ipc, является 4-вектором.
Другими словами, выраженные в координатах
Х-± = X, Х2 = У> Я-3 = Z, X^ = ICt,
компоненты
I1 = JX, ra = Jv, /3 = JZ, /4 = icp
ш
V^AX, V2=Ay, V3 = AZ, F4 = *?
являются компонентами двух 4-векторов. Уравнения
инвариантные относительно преобразования Лоренца, являются как раз
уравнением неразрывности и уравнением B.5.14), связывающим А и <р.
Совокупность четырех уравнений для четырех компонент уравнения
представляет собой инвариантные относительно преобразования Лоренца
уравнения B.5.15), волновые уравнения потенциалов.
Электрическое и магнитное поля не являются 4-векторами. На осно-
основании уравнения B.5.13) (и вспоминая, что при s = fi=l имеем В = Н,
D = Е) получаем
я -_= дЛ~ дЛу = Г дУз dV* 1
х ду dz I дхг дх3 J '
Е
g^F 1 дАх = . Г dF4 дУ1 -1 ^
х дх с dt |_ дхх дх& J
Но выражения, стоящие в квадратных скобках, являются компонентами
кососимметричного тенз'ора (или, лучше сказать, четырехмерного аффи-
вора) % с компонентами
/ __ дУп 8Ут , _. _, _, _п
Iran— я-у- я-у- ' /11 — /22—/33 — /44 — и>
/12 = /21— "г> /13 = /31 ~ — "у> /23 = /З2'="х,
fit — /41 = ^ж> /24 = /42 = — iEy, /34 = /4З ^ l"^z-
Уравнения Максвелла можно теперь записать в форме, инвариантной
относительно преобразования Лоренца. Компоненты уравнения ? • 3 — D^/с) I
¦^Г = ~ та B.5.20)
71
соответствуют уравнениям
при т = 4 и rotН—-^--^-=-^-J при т=1, 2, 3.
Уравнения divH = 0 и rot E-f (l/c) (9H/9t) = 0, которые соответствуют
выражениям Н и Е через потенциалы А и <р [уравнения B.5.13) и
Н= A/р.) rot А], могут быть теперь записаны в форме уравнений
d/гз d/31 d/12 q ^/з4 . ^42 . й/гз _ п
. ^/l3 _
дх3 ¦ dxt ~
204 Гл. 2. Уравнения полей
которые, как можно доказать, являются также инвариантами преобразо-
преобразования Лоренца [поскольку для случая трехмерного пространства равенство
A.5.3) показывает, что величины с23— с32 = 61 и т. д. являются компо-
нентами трехмерного вектора, то для четырехмерного пространства вели-
величины с123 + с231 + с312 = Ь4 и т. д. являются компонентами псевдовектора].
В качестве примера применения к полям преобразования Лоренца мы
начнем с координат х[ и т. д., потенциалов А[ и т. д. и полей Е[ и т. д.
для наблюдателя В, неподвижного относительно штрихованных координат.
Для наблюдателя А, движущегося относительно В со скоростью M = ctha
вдоль оси х, координаты, ток, заряд и потенциалы принимают вид [см.
уравнения A-7.2) и A.7.4)]
х — х' cha + ct' sha, г/ = г/', z = z',
ct = х' sha + ci' cha,
p' sha, Jy = Jy, J, = JZ,
' B.5.21)
Ay = A'v, A, = A'Z,
p' cha,
tha = —> she. =— , cha =
c V c2 m2
V с2 — м2 Ус2 —м2
Мы должны были ожидать, что новая компонента тока по оси х содер-
содержит член с р', так как заряд теперь движется: но трудно было ожидать.
что новая плотность заряда содержит слагаемое, зависящее от компо-
компоненты тока по оси х.
' Поля, являясь компонентами тензора, подчиняются соответствующим
правилам преобразования
Ех — #14 = '2 "hnXiJmn — i ch2 a/14 -j- i sh2 а/41 = ?/{« = E'X и т. д.,
тэт
так что
у ha, Ег = Е'гсЪа-Щ sha,
НХ = Н^, IIу = Щ ch a - E'z sh a, Hz = H'z ch a + E'v sh a. B-5-22)
Мы видим, что электрическое и магнитное поля при движении переме-
перемешиваются; оно впрочем и не удивительно, так как мы видели раньше,
что неподвижный заряд порождает только электрическое поле, заряд те
движущийся порождает также и магнитное поле.
Калибровочное преобразование. Хотя в наших формальных рассужде-
рассуждениях и удобнее считать, что векторный и скалярный потенциалы являются
компонентами 4-вектора, однако они, вообще говоря, меняются при преоб-
преобразовании Лоренца не таким простым способом. Конечно, электрическое и
магнитное поля должны преобразовываться, как элементы четырехмерного
аффинора fnm, так как они являются физически измеримыми величи-
величинами и должны удовлетворять уравнениям Максвелла, согласующимся
с преобразованием Лоренца. Но при рассмотрении потенциалов, как
было указано на стр. 201, имеется известная свобода выбора. Если мы
свяжем потенциалы А и <р обычным уравнением div A + (l/c) (dy/dt) = Q,
то потенциал (A, i<p) окажется 4-вск тором. Но если мы произведем
калибровочное преобразование вида А' = А — gradx> 9 =Ч3 + A/с) (dy^/dt),
где / является решением волнового уравнения, то новые потенциалы
(А', ?<р') уже не обязательно образуют 4-вектор, хотя поля, полученные
с их помощью, совпадают с полями, полученными до преобразования.
2.5. Электромагнитное поле 205
Инвариантность полей при калибровочном преобразовании потенциа-
потенциалов дает нам возможность выбора либо такой формы для потенциалов,
которая при преобразовании Лоренца ведет себя, как 4-вектор, но
может оказаться не особенно простой для вычисления, либо такой
формы, которая легко вычисляется в частной системе Лоренца, но
поведение которой при преобразовании Лоренца труднее изучить.
Например, если для частной системы Лоренца мы выберем кали-
калибровку так, чтобы divA = 0, то мы сможем более полно, чем при любом
другом выборе калибровки, провести разделение между «продольными»
и «поперечными» полями (для этой системы Лоренца). Уравнения для
новых А и <р (которые мы будем обозначать через А° и ф°) можно полу-
получить, повторив вычисления, сделанные между выводами уравнений
B.5.13) и B.5.15); при новом предположении divA° = 0. Уравнение для
скалярного потенциала упрощается; оно принимает вид
VV= -~ • B.5.23)
то есть становится уравнением Пуассона, которое всегда играет основ-
основную роль в случаях установившегося состояния. Однако в данном слу-
случае мы не требуем, чтобы р было независимым от времени; скалярный
потенциал <р° должен изменяться без запаздывания в зависимости от
изменения р, так как здесь нет члена A/с2) (d2<p/dt2), вызывающего
запаздывание (это само по себе делает ясным, что <р° не может быть
временной компонентой четырехмерного вектора). Так как уравнение
Пуассона обычно решить легче, чем неоднородное волновое уравнение,
то уравнение B.5.23). решается проще, чем первое из уравнений B.5.15).
Получающийся потенциал <р° обусловлен свободным зарядом р.
Если уравнение B.5.23), выражающее <р° через свободный заряд,
решено, то может быть решено и уравнение для соответствующего А°
B.5.24)
¦если считать в нем <р° уже известным. Полученное решение обусловлено
только поперечным током, или током несвободных зарядов, так как J
может быть расщеплено на два слагаемых (см. стр. 59): одно J( с ди-
дивергенцией, равной нулю, может быть представлено как вихрь некото-
некоторого вектора, другое JL с вихрем, равным нулю, может быть записано
как градиент некоторого скаляра
J( = grad(), J( = rotC.
Но в силу уравнения неразрывности, связывающего Лир, имеем
<iiv J = div J( = —(dp/dt), уравнение, связывающее продольную часть J со
скоростью изменения свободного заряда. Сравнив это уравнение с про-
продифференцированным по времени уравнением B.5.23) (и вспомнив, что
V2 = divgrad), найдем, что
Поэтому уравнение B.5.24) можно переписать в форме, зависящей
только от поперечного тока J(, который не- связан со скоростью изме-
нени.я свободного заряда
Поэтому, если свободного заряда о нет и весь ток—поперечный,
•о° может быть сделано равным нулю и поля могут быть подсчитаны
206 Гл. 2. Уравнения полей
с помощью одного только векто'рного потенциала А°. Если же имеется!
свободный заряд, <р° вычисляется в зависимости от него, однако на А°
этот заряд не влияет. (Заметим, что эта калибровка не является лоренц-
инвариантной.)
Поле движущегося заряда. В к'ачестве примера приложения общих
преобразований, рассмотренных выше, найдем поле, порожденное точеч-
точечным зарядом, движущимся вдоль оси х со скоростью u = c\ha. Мы
можем найти это поле, подсчитав запаздывающие потенциалы из урав-
уравнений B;5.16); можно также найти статическое поле от неподвижного
заряда, а затем перейти к движущейся системе с помощью приведен-
приведенного только что преобразования Лоренца. Второй путь, как мы вскоре
увидим, проще.
Рассмотрим сначала неподвижный точечный заряд Q, находящийся
в начале координат штрихованной системы. Тогда потенциалы и поля
в точке (ж', у', z') будут
?' = ?, А' = 0, E' = ^5i-'> Н' = 0,
где г' — ix'-\- j«/' + kz'. Это 'поле, образованное простым источником,
рассмотрено на стр. 27.
Перейдем теперь к системе нештрихованных координат, двигаю-
двигающейся со скоростью M = ctha в направлении оси х. В момент времени t
заряд находится на расстоянии ut по оси х от начала координат. Связь
между штрихованными и нештрихованными координатами дается урав-
уравнениями B.5.21) или равенствами
х' —хсЬа — ctsha, y' = y, z'= z
ct' = — xsha+cfcha,
, 1 , к/с
ch a = , sh a =
Величина г' также должна быть выражена в нештрихованных:
координатах
2
1--.
г.де s2 = (ж — ut
Принимая во внимание уравнения B.5.21), мы видим, что потен-
потенциалы для движущегося заряда можно взять в форме [пользуясь калиб-
калибровкой B.5.14)]
где и = \и есть вектор, представляющий постоянную скорость заряда в не-
штрихованной системе координат. Воспользовавшись уравнениями
B.5.22) или продифференцировав соответствующим образом потенциалы,
мы получим электрическое и магнитное поля движущегося заряда
;,. B.5.26).
2.5. Электромагнитное поле 207
где г= (х — irf)i + «/j + zk — вектор, идущий от заряда к точке х, у, z,
в которой производятся измерения; положение заряда рассматривается
в момент измерения t.
Надо заметить, что в случае, когда величиной и2 можно пренебречь
по сравнению с с2, s становится равным г и получаются известные выра-
выражения для полей медленно движущегося заряда
Точные выражения, данные в B.5.26), приводят к некоторым искаже-
искажениям вследствие того, что они содержат релятивистскую поправку, зави-
зависящую от максимальной, не равной бесконечности относительной ско-
скорости с. Например, эквипотенциальные поверхности для <р не являются
сферами, а представляют собой сплющенные сфероиды, малые оси кото-
которых по направлению совпадают с направлением, движения заряда;
отношение малой и большой осей этих сфероидов равно j/l — (и2/с2).
В предельном случае, при высшей скорости частицы (и—»с), поле сжи-
сжимается в тонкий диск, перпендикулярный к и, в центре которого нахо-
находится заряд Q; практически мы имеем здесь дело с плоским волновым
импульсом.
Можно предположить, что эти потенциалы и поля должны быть
запаздывающими, то есть что они должны быть выражены через обычные
потенциалы, соответствующие некоторому более раннему положению,
заряда. Наивное рассмотрение уравнений B.5.16) подсказывает нам, что
<р должно быть ранно Q, деленному на гг, где гг — расстояние между
точкой х, у, z и положением заряда л момент времени на гг/с более.
ранний, чем / — момент намерения потенциала в точке х, у, z. Изуче-
Изучение рис. 2.22 показывает, что величина s, содержащаяся в выражениях
потенциалов, не равна гг — длине отрезка PQr, но равна длине отрезка,
PR, где QR нерендикулярно к PR. В самом деле, s равно
где аг — единичный вектор, направленный от точки Qr к точке Р. По-
Поэтому потенциалы могут быть выражены через расстояния и направле-
направления, соответствующие положению заряда в момент t—(rr/c), что и пони-
понимается под запаздывающим потенциалом. Если мы сможем выяснить,
как при вычислении <р из уравнения B.5.16) появляется неожиданный
множитель [1 — (l/c)aru], мы полностью согласуем друг с другом два
метода вычисления потенциалов (и, как это обычно бывает при таком
согласовании, немного больше познакомимся с математической физикой).
Причина трудности заключается в отмеченном на стр. 150 различии
двух способов описания движения жидкости. Уравнения B.5.16) для
запаздывающих потенциалов содержат под знаком интеграла множители,
определяющие заряд и плотность тока в системе координат, неподвиж-
неподвижной относительно наблюдателя* Однако в случае движущейся частицы
распределение плотности заряда остается постоянным, если оно выра-
выражено в системе координат, неподвижной относительно частицы (т. е.
движущейся относительно наблюдателя). Пренебрегая преобразованием
координат, которое должно быть сделано раньше интегрирования, мы
в результате теряем необходимый множитель [1 — A^с) аг ¦ и].
Это показако на второй части рис. 2.22, где мы увеличили рису-
рисунок настолько, чтобы показать размеры частицы и распределение заряда.
Отсюда видно, что как бы мала нп была частица, ее движение должно быть
208
Гл. 2. Уравнения полей
принято во внимание при выполнении интегрирования. Для той части
заряда, которая удалена от наблюдателя на расстояние гг, мы берем
положение частицы в момент t — (rr/c), для части же заряда, удаленной
на расстояние rr-\-drr, мы берем положение в момент t — (rr/c) — (drr/c),
учитывая смещение drr/c назад вдоль оси х. С помощью несложного
рассуждения можно убедиться в том, что при интегрировании величина
за«ряда dq, находящегося внутри элемента объема dA drr, равна не pdA drr,
Положение заряда
вовремя tr=l--f
Положение заряда
во время t\
Рис. 2.22. Расстояния и углы, встречающиеся при вычислении
запаздывающих потенциалов для заряда Q, двигающегося со ско-
скоростью и по отношению к наблюдателю, находящемуся в точке Р.
как было бы, если бы заряд не двигался, а [ 1 + (и/с) cos f3] pdAdrr. По-
Поэтому pdAdrr равно dq[l + (м/с) cosf^] и, если размеры частицы доста-
достаточно малы, интеграл4B.5.16) становится равным
что в точности совпадает со значением, полученным нами в уравнении
B.5.25) с помощью преобразования Лоренца статического потенциаль-
потенциального поля.
Таким образом, мы видим, что потенциал, вызванный в момент t
движущимся зарядом, отличается от потенциала, соответствующего этому
заряду в более раннем положении, множителем, связывающим скорость
частицы в этом более раннем положении со скоростью светового сигнала,
идущего от частицы к наблюдателю, т. е. множителем [1 — (u/c)-ar]. Это
более раннее положение частицы может быть определено, если мы пред-
представим себе, что частица посылает световые сигналы к наблюдателю;
положение, использованное в уравнениях B.5.25) и B.5.26), является
тем, из которого посланный световой сигнал достигает наблюдателя
точно в момент t.
Между прочим, уравнения B.5.25) для потенциалов сохраняют свою
силу даже в том случае, когда скорость частицы и изменяется с тече-
течением времени, если мы будем считать, что s равно гг [1 — (и/с) -аг] 1).
Выражения для Е и Н при наличии ускорения заряда будут, конечно,
отличаться от тех, которые даны в уравнениях B.5.26), так как и
г) Потенциалы произвольно движущегося.точечного заряда, записанные в форме
{2.5.25), с заменой s на ггA-
Прим. ред.
аг), называются потенциалами Льенара — Вихерта. —
2.5. Электромагнитное поле 209
теперь зависит от времени и это должно быть учтено при дифференци-
дифференцировании.
Сила и энергия. !Трехмерный вектор Г = рЕ +A/с)JxB определяет
силу, действующую на кубический сантиметр тока и заряда. Этот вектор
является пространственной частью 4-вектора, «временная компонента»
которого пропорциональна работе на кубический сантиметр, производи-
производимой полем в секунду при наличии тока, т. е. величине J-E. Рассмотре-
Рассмотрение уравнений B.5.20) показывает, что величина к с компонентами
4
Ат=42Л»,Л' т = 1, 2, 3, 4, B.5.27)
Т>=1
н является этим 4-вектором; пространственные компоненты к равны
трем компонентам вектора Г, а временная компонента А4 = i (Е • 3/с).
Интеграл от ckji по объему, лежащему внутри некоторой замкнутой
поверхности, равен полной величине работы поля за единицу времени,
затраченной внутри этого объема на перемещение заряда; эта величина
должна быть равна скорости уменьшения внутренней энергии U,
которой поле обладало в данном объеме, минус мощность, излучающаяся
через поверхность, ограничивающую объем. Воспользовавшись уравне-
уравнениями B.5.11) и предполагая, что ей цне зависят от времени, получим
div(E x
где
с/ === о— v*-i " ** ~т~ -И- " **) И о = т— *-* X -Н. I ^.О.^о)
Как и ожидалось, мы здесь имеем скорость изменения интеграла
по объему минус интеграл потока. Величина U, фигурирующая в ско-
скорости изменения интеграла по объему, должна быть плотностью энергии
поля, а вектор S, содержащийся в выражении интеграла потока, должен
быть плотностью потока энергии пбля. Вектор S называется вектором
Пойнтинга.
Возвращаясь к уравнению B.5.27) для 4-вектора к силы-мощности
(полагая снова s = [i=l) и подставляя в него вместо 1т пх выражения
через производные функций fmn, получаем
т 4тс Zl Imr QXg
Т, 8
Представляет некоторый интерес показать, что 4-вектор к может быть
получен свертыванием тензора «напряжения-энергии» X, где
г г, п
Свернутая форма имеет вид
B-5.29)
g/sr 1 -у dfmr . , i_ УГ\ f dfrn
r QXa 4„ Zj dxs '*r ~*~ 8тс Zj '"» dXm '
р ^_f у
dxs mi 4л Zj Imr QXa 4„ Zj dxs '*r ~*~ 8тс
r, a r, s r.
Ф. М. Морс и Г. ФешСах
210 Гл. 2. Уравнения полей
Первая сумма равна как раз кт, так как /sr= —frs. В третьей сумме мы
воспользуемся соотношениями ~т = _ 1т /m? j приведенными на
охт охп охг
стр. 203. Получаем, меняя обозначения индексов суммирования,
dfmr , dfnm-\ i_ -л dfmr , j_ -ст , dfmn __ 1 -ст а/„|Г ,
дг„ ' дхг J 8л Zj Sa;s '»+ 8л Zj '*" Sa.ft 4п Zl da:s '«'¦•
r, »i r, e ft, и г, s
что полностью уничтожает вторую сумму. Итак,
h - ^ly
где
7'n = ~ (El-??,-El + Hl-Щ-Щ а г. д.,
T12 = i (?x?y + Я^Я^) = ГЯ1 и т. д.,
Г14 = ^(ЕК Н)Х = 45Я=Г41 и т. д., B-
Ты =±(Е% + Е1 + Е*2 + Н% +.Щ + Щ) = С/.
Тензор ? называется тензором напряжения-энергии Максвелла. Он
аналогичен тензору напряжения-энергии, определенному в уравнении
A.7.8). Пространственные компоненты могут рассматриваться как своего
рода электромагнитные напряжения; пространственно-временнйе компо-
компоненты, пропорциональные потоку энергии, можно рассматривать как
величины, пропорциональные импульсу поля; член 74 определяет плот-
плотность энергии поля, аналогичную рассмотренной раньше плотности
массы среды.
Поверхности проводников и диэлектриков. Дватипа граничных условий
часто встречаются в вопросах электромагнетизма; граничные условия,
связывающие поля на поверхности, разделяющей два диэлектрика, где
диэлектрическая постоянная е (или магнитная проницаемость jx) резко
меняет свое значение и граничные условия на свободных поверхностях
металлического проводника. В случае границы между двумя диэлектри-
диэлектриками обычно можно пренебречь проводимостью среды и предположить,
что нет ни свободных зарядов, ни тока. Граничные условия, связываю-
связывающие нормальные и тангенциальные составляющие электрического поля
по обе стороны от границы, могут быть получены из уравнений Макс-
Максвелла B.5.11).
Выберем, как показано на рис. 2.23, элементарный контур и под-
подсчитаем циркуляцию Е по этому контуру. При малом 16 этот интеграл
(приближенно) равен /о | rot E |. Если о мало по сравнению с /, циркуля-
циркуляция вдоль указанного контура равна 1(Е° — Е\), где Е°, Е\ — тангенциаль-
тангенциальные компоненты полей по обе стороны границы. В случае стационар-
стационарного состояния rot E должен быть равен нулю, так что Е\ и Е\ должны
равняться между собой.
Поток поля D, взятый по показанной на рис. 2.23 поверхности,
равен А {Воп — Dln), если 8 исчезающе мало (здесь D°n и Z>^ — нормальные
компоненты поля D); согласно определению, этот интеграл пропорцио-
пропорционален divD. При отсутствии свободных зарядов div D равна нулю,
так что нормальные компоненты поля D меняются непрерывно при пере-
сечепии границы.
2.5. Электромагнитное поле
211
Подобно этому для границы, при пересечении которой меняется
проницаемость р, в случае установившегося состояния будут непрерывны
нормальные компоненты поля В и тангенциальные компоненты поля Н-
Нетрудно вывести соответствующие граничные условия и для потенциалов..
Металлический проводник имеет большую электропроводность а, иг
следовательно, малое время релаксации (см. стр. 202). Во многих слу-
случаях, включающих и случай полей с периодами колзоаний, боль-
большими, чем это время релаксации, можно предположить, что проводи-
проводимость металлического проводника равна бесконечности, а время релак-
релаксации его равно нулю. Свободный заряд может находиться только на
поверхности такого проводника, причем распределение этого заряда как
раз таково, чтобы уничтожить внешнее электрическое поле, так как вну-
внутри идеального проводника электрическое поле не может существовать.
Рис. 2.23. Элементарные контуры и площадки для нахождения
связи внутренних и внешних полей у граничных поверхностей.
Прежде всего на внешней стороне поверхности проводника танген-
тангенциальная составляющая электрического поля Е\ должна быть равна нулю;
векторы электрического поля всюду в точках поверхности нормальны
к ней. Воспользовавшись элементарной площадкой, показанной на
рис. 2.23, мы видим, что поток поля D будет равен AYf, так как D°
нормально к поверхности, a D1 равно нулю. Для того чтобы это имело»
место, нужно, чтобы на поверхности проводника имелся заряд с поверх-
постной плотностью р = D°/Atz [для того чтобы удовлетворялось уравнс-
иснпе B.5.1)]. Так как векторы электрического поля всюду в точках
поверхности проводника нормальны к этой поверхности, то эта поверх-
поверхность должна быть эквипотенциальной <р = const (по крайней мере в слу-
случае установившегося состояния).
Поведение магнитного поля вблизи проводника лучше рассмотреть
па примере.
Передача волн и импеданс. В качестве примера решения уравнений!
Максвелла рассмотрим и предварительном порядке поле внутри концен-
концентрической линии передачи, состоящей из двух длинных коаксиальных
цилиндров, являющихся проводниками; пространство между цилиндрами
заполнено однородной средой с постоянными диэлектрической постоян-
постоянной s, магнитной проницаемостью р. и проводимостью а (см. рис. 2.24).
Предположим, что внешний радиус внутреннего цилиндра равен а, вну-
внутренний радиус внешнего цилиндра равен Ь; обозначим через z расстоя-
расстояние по оси от одного из концов линии и через г — расстояние точки
от оси.
14*-
212
Гл. 2. Уравнения полей
Можно предположить, что в пространстве между проводниками нет
свободных зарядов, так что нужно пользоваться только векторным потен-
потенциалом и можно применять уравнения B.5.18) и B.5.19). Электрическое
поле должно быть нормальным к поверхностям обоих проводников, и,
следовательно, векторы поля направлены по радиусам при г = а и при
г = Ь. Для достижения зтого проще всего предположить, что поле Е
везде радиально; последнее проще всего получается, если предположить,
что векторы векторного потенциала А везде направлены по радиусам.
В то же время div А должна быть равна нулю; если А радиально
(А = Лаг), то div А = A/г) (д/дг) (гА), как указано на стр. 116. Чтобы
дивергенция А была равна нулю, нужно, чтобы модуль вектора А был
равен произведению 1/г на функцию от z, 9 и t (так как тогда гА не
V .Л
2bJ
2b -1
Рис. 2.24. Поля и токи в случае концентрической
линии передачи (бронированный провод).
зависит от г и производная этого произведения по г равна нулю). В про-
простейшем случае мы предположим, что А не зависит от <р
=-^ф(*. О-
B.5.31)
Ссылаясь опять на стр. 117, мы видим, что лапласиан от А
имеет вид
?гак что уравнение B.5.19) дает для части <]> амплитуды векторного
потенциала, зависящей от z и (, следующее простое уравнение:
B.5.32)
Уравнение этого вида встречалось в наших рассуждениях при изучении
движения струны на стр. 135. Решения этого уравнения определяют
волны, затухающие либо с течением времени, либо в зависимости
от расстояния.
Предположим теперь, что линия передачи подвергается в конце
z=0 воздействию с частотой ш/2тг. В этом случае зависимость от вре-
времени будет простой гармонической, т. е. >]> будет иметь множитель e~wl,
¦я, затухание будет происходить при перемещении в пространстве вдоль
оси z. Подставляя в B.5.32) ф = е-*ш'ф1(г), получаем
Решение в этом случае ьыражается через показательные функции
-:<«,/')("z-«*>, B.5.33)
2.5. Электромагнитное поле 21$
где
v^y \
Первый член представляет собой синусоидальную волну, распространя-
распространяющуюся в направлении положительных z со скоростью с/п, с затуха-
затуханием, пропорциональным х. Второй член определяет синусоидальную
волну, движущуюся в направлении отрицательных z с теми же скоро-
скоростью и затуханием. Это наиболее общее решение с колебаниями частоты
ш/215, зависящее от времени по синусоидальному закону. Если волна
порождается в конце z = 0, то остается только первое слагаемое и Тг3^-
Поля в этом случае имеют вид
Г^ A,
jXE, B.5.34)
Электрическое поле направлено по радиусам, как это и требовалось
первоначально. Разность потенциалов между внутренним и внешним
проводниками равна
Ь1
^ 1пе-«+*й/с)(пг-со;
если напряжение в конце z = 0 имеет вид Voe~iait, то будем иметь р=
= [F^c/iwln (t/a)] и напряжение между проводниками в точке z будет
равно
V (z>= Foe-^+^/cX'WTrt).
На поверхностях обоих проводников сосредоточивается заряд с поверх-
поверхностной плотностью Z)/4tc = з2?/4гс. Полный заряд, находящийся на поверх-,
ности внутреннего проводника, составляет на единицу длины
2) D или
2 In F/a) ' ~~ 2 In F/a) '
таков же, конечно, и заряд на. единицу длины внутренней поверхности
наружного проводника. Очевидно, емкость концентрической линии,
рассчитанная в той же системе единиц, составляет е/2 In (b/a) на единицу
длины.
Магнитными силовыми линиями являются концентрические окружности,
что указывает на то, что ток идет вдоль внутреннего проводника.
Его силу можно подсчитать с помощью правила циркуляции ^H>ds=
= 4тс/, получающегося из уравнений B.5.4) или A.2.12). Произведя вычис-
вычисления, получим
7 (z) = ^kr\ ( п +
4 ' 2 In (b/a) V
Сила тока затухает с возрастанием z, так как происходит утечка части
тока через частично проводящий материал, находящийся между идеально
проводящими цилиндрами. Если бы среда была полностью не проводя-
214 Гл. 2. Уравнения полей
хцей (о = 0), тогда волна не затухала бы (х было бы равно нулю)
т ток / имел бы ту же фазу, что и напряжение V.
Отношение напряжения в любой точке к силе тока
_21n(ft/«) B535)
п -\-1 (y.c/co) v '
называется характеристическим импедансом линии передачи. Если среда
полностью не проводит электричества (х = 0), этот импеданс будет
действительным (чистое «омическое» сопротивление).
Параллелизм между этим определением и рассуждениями стр. 128
•относительно волн на струне совершенно ясен. Можно, конечно, полу-
получить импеданс линии передачи и при наличии отраженной волны, как
это было сделано для струны; можно также составить интегралы Фурье
для переходной характеристики линии.
Между прочим, следует отметить, что так как V пропорционально
Е, а / пропорционально Н, то импеданс, подсчитанный выше, пропор-
пропорционален отношению между Е и Н. Во многих случаях злекро-
магнитного излучения, когда нельзя подсчитать V или /, все
¦же возможно найти отношение между ? и Я в каждой точке. Это
отношение часто называют импедансом среды или волны. Например,
для плоской электромагнитной волны, распространяющейся в положи-
положительном направлении оси х в открытом пространстве (о = ji= 1), вектор-
векторный потенциал имеет вид Аое*(и>'с>(ж~с'>, где Ао—вектор, перпендикуляр-
перпендикулярный к оси х. Поля имеют вид
Е = i -^ (Ао) е'Чш/оСх-со, Н = i -"- (i х Ао) е««''с><*-с<> = i x E. B.5.36)
В этом случае импеданс равен единице (в той же системе единиц)
Если s и (л не равны единице, импеданс равен |/fi/e.
Уравнения Прока. Все уравнения теории электромагнетизма экви-
эквивалентны лоренц-инвариантному требованию, состоящему в том, что-
чтобы оператор Даламбера от потенциалов, являющийся 4-вектором,
был пропорционален 4-вектору, представляющему заряд и плотность
тока. Это — обобщение на случай 4-векторов неоднородного волнового
уравнения для струны
fe2 с2 at2 ~'к ' >'
которое было рассмотрено в § 2.1. Проводя дальнюю аналогию, можно
сказать, что электромагнитные потенциалы имеют инерцию и своего рода
«восстанавливающую силу», так же как и простая струна, находящаяся
под действием натяжения; это свойство заставляет поле в какой-либо
точке стремиться к тому, чтобы сделаться средним по отношению к зна-
значениям поля в окружающих точках. Ток здесь аналогичен приложен-
приложенной силе /.
Мы видели в § 2.1, что, если струна заключена в упругую оболочку,
так что каждый участок струны стремится вернуться к положению равно-
равновесия, в волновом уравнении должен быть добавлен дополнительный член,
пропорциональный >]). Можно и для векторных потенциалов составить
подобное уравнение с дополнительным членом, пропорциональным потен-
потенциалам
1^-^, B.5.37)
Jz> icp),V = (Ax, A A,
2.6. Квантовая механика 215
которое аналогично уравнению, полученному из B.1.27) прибавлением
неоднородного члена, содержащего силовую функцию. Уравнение для ска-
скалярного поля без свободного члена называется уравнением Клейна-Гор-
Клейна-Гордона; оно пригодно для описания поведения скалярного мезонного поля.
Аналогичное уравнение для четырехмерного векторного потенциала назы-
называется уравнением Прока; его можно применить к описанию поведения
частицы, имеющей единичный спин (если такая частица существует!). Соот-
Соответствующие уравнения для полей в случае р = а == 1 (свободное пространст-
пространство), если ток равен нулю, имеют вид
rot Н = 5 а2А, rot E = ^- ,
с dt ' с dt '
div H = 0, div Е = — а2сф,
H = rotA, E=-grad<p-i--^ B-5.38)
л- a i да
dlvA=-T-^
|при другой калибровке см. стр. 205 и уравнение C.4.21)].
Наличие этого дополнительного члена заметно влияет на решение,
как это имело место и в случае струны. Поля быстро стремятся к нулю
везде, кроме ближайших окрестностей заряда или тока. Например,
потенциал вокруг точечного заряда равен Qe~^r/r и стремится к нулю
много быстрее, чем обычный потенциал Q/r. Подобная потенциальная
функция1) рассматривалась при изучении связи между нуклонами
(протонами или нейтронами) в атомном ядро. Поэтому уравнения Прока,
а также и уравнение Клейна — Гордона (для скалярного случая) могут
быть использованы в теории ядра.
2.6. Квантовая механика
На протяжении всей этой главы мы указывали случаи, когда
«сглаженное», непрерывное поле может заменить распределение масс и
зарядов, имеющее на самом деле дискретный характер. Пока мы инте-
интересовались макроскопическими явлениями, мы могли вместо беспоря-
беспорядочного распределения частиц рассматривать регулярную функцию по-
положения, значение которой пропорционально средней плотности частиц.
Однако, введя электромагнитное поле, мы приходим к существенно новой
связи между непрерывными полями и дискретными частицами, к связи,
которая является основой современной квантовой теории.
Существует два основных различия между прежними взаимосвязями
полей и частиц и новыми, квантовыми связями между ними. Прежде
всего, величина классического поля пропорциональна средней плотности
частиц или, что обычно то же самое, вероятности наличия частицы.
В квантовой же теории квадрат модуля поля пропорционален вероят-
вероятности наличия частицы. Это различие более существенно, чем могло бы
показаться с первого взгляда. Оно обозначает, например, что класси-
классические поля всегда выражаются действительными числами, так как они
должны равняться плотностям или вероятностям, являющимся действи-
действительными числами. Правда, во многих случаях и для классических
полей мы будем выполнять наши вычисления, пользуясь комплексными
числами, но всегда при этом будет ставиться условие, что только
1) Потенциал Юкава. — Прим. ред.
216 Гл. 2. Уравнения полей
действительная часть (или в некоторых случаях только мнимая часть)
этих чисел представляет поле. Напротив, в квантовой механике само
поле может быть комплексной величиной, так как только квадрат его
модуля (который всегда действителен) пропорционален вероятности
наличия частицы. Более того, во многих случаях важно, чтобы ком-
комплексная величина, сопряженная квантовому полю, была отлична от
•самого поля; таким образом, поле необходимо должно быть ком-
комплексным.
Во-вторых, связь между классическим полем и соответствующим
ему распределением частиц только допускается, но в принципе не тре-
требуется. В принципе можно всегда отказаться от понятия поля и рассчи-
рассчитывать индивидуальные движения самих частиц. Производить расчеты
с непрерывным полем, конечно, несравненно легче, чем вычислять дви-
движения отдельных частиц, но выбор того или другого является делом
соглашения и отнюдь не обязателен. С другой стороны, связь между
квантовыми полями и соответствующими им частицами необходима, а
не просто допускается. Основные принципы квантовой теории запре-
запрещают нам отказываться от понятия поля и рассчитывать подробно
движения отдельных частиц. Они утверждают, что полное описание
положений и движений соответствующих частиц невозможно получить
экспериментально и что поэтому такое описание не имеет физического
смысла. Только плотность вероятности, пропорциональная квадрату
модуля поля, может быть измерена и имеет физический смысл.
Смысл этих общих положений может быть лучше понят на специ-
специальных примерах.
Фотоны и электромагнитное поле. Отложим на время вопрос о связи
между движениями электронов и 4-вектором заряда-тока; предположим,
что каким-то способом мы нашли значения / и р, с помощью которых
можно рассчитать электромагнитное поле, подчиненное граничным
условиям, налагаемым потребностями эксперимента. Сосредоточим нашо
внимание на влияниях такого поля на другие заряженные частицы,
электроны и ионы.
Когда электромагнитная волна наталкивается на фотографическую
пластинку или поглощается металлической поверхностью, количество
энергии на квадратный сантиметр фронта волны, которое может быть
отдано галоидному кристаллу или затрачено на приведение фотоэлек-
фотоэлектрона в движение, равно интенсивности радиации, величине вектора
Пойнтинга (с/4тс) (Е х Н). Эта величина пропорциональна квадратам
амплитуд потенциалов, а в случае, когда эти потенциалы являются
комплексными величинами, она пропорциональна квадратам их модулей-
Поле будет действовать с данной энергией на галоидные крупинки или
на электроны, движущиеся по своим траекториям; полная потеря энергии
будет равна произведению общего количества частиц, испытавших воз-
воздействие, на среднюю величину энергии, отданной каждой частице.
Так как частицы, испытавшие воздействие, распределены не непрерывно,
нельзя надеяться на то, что ответ будет однородным вдоль всего фронта
волны. Однако можно ожидать, что чем сильнее радиация, тем большее
число частиц подвергнется значительному воздействию и в силу этого
окончательный результат будет более однородным. Это в действитель-
действительности и происходит; особенности квантовой теории сказываются только
при уменьшении интенсивности (при неизменной частоте) До очень
малых значений.
Само поле будет подобно непрерывному как при больших, так и
при малых значениях его интенсивности. Можно было бы ожидать, что-
2.6. Квантовая механика 217
реакция фотографической пластинки или фотоэлектронов в металле
постарается оставаться, насколько возможно, непрерывной при умень-
уменьшении интенсивности, причем уменьшение энергии будет происходить
более или менее в равной степени как из-за уменьшения числа частиц,
подвергшихся воздействию, так и из-за уменьшения количества энергии,
поглощенной каждой частицей. Однако, как ясно показывают много-
многочисленные опыты, этого не происходит. Энергия, поглощенная фото-
фотоэлектроном, не уменьшается; только количество порождаемых фото-
фотоэлектронов уменьшается при уменьшении' интенсивности. Это обсто-
обстоятельство проще всего объяснить, если предположить, что энергия
электромагнитного поля переносится дискретными частицами, каждая
из которых несет в себе определенное количество энергии^ Когда частица
света поглощается фотоэлектроном, она оставляет одно и то же коли-
количество энергии, какова бы ни была интенсивность радиации. Изменение
интенсивности отражается только на количестве имеющихся частиц света,
но не влияет на их индивидуальную энергию.
Как повторно показали многочисленные опыты, каждая из этих
«частиц» света, называемых фотонами, несет в себе энергию, пропорцио-
пропорциональную частоте v поля радиации E = h», где h — постоянная Планка.
Скорости этих частиц в свободном пространстве равны, конечно, ско-
скорости света с. Плотность их распределения определяется величиной
интенсивности соответствующего классического поля. Такое описание
электромагнитного поля с помощью фотонов не является конкурирующим
«объяснением» фактов электромагнитного взаимодействия с веществом;
оно дает дополнительное описание этих фактов не более и не менее
верное, чем описание с помощью классического поля. Фотоны не яв-
являются «реальными» в классическом смысле, так как мы не можем
ни рассчитать траекторию отдельного фотона, ни предсказать точно его
положение и направление движения в данный момент времени. Лучшее,
что можно сделать, — это подсчитать вероятность наличия фотона
в данной точке в данный момент; эта вероятность выражается через
квадрат значения классического поля в этой точке в этот момент вре-
времени. Частица не имеет смысла отдельно от интенсивности поля, и само
поле может быть сделано ощутимым только при помощи фотонов.
В качестве поясняющего примера рассмотрим поток света, падаю-
падающий на поверхность металла, снабженную приспособлением для реги-
регистрации выбрасываемых фотоэлектронов. Предположим, что интенсив-
интенсивность в разных точках поверхности, подсчитанная с помощью классичес-
классических полей, дается графически кривой, изображенной на верхней части
рис. 2.25. Если интенсивность очень мала и экспозиция короткая,
выделяется только небольшое число фотоэлектронов, благодаря чему
очень трудно восстановить кривую распределения интенсивности по изоб-
изображениям фотоэлектронов. Однако если интенсивность и экспозиция
возрастают, выделяется все больше и больше фотоэлектронов и относи-
относительные значения плотности точек могут быть измерены все с большей
и большей точностью. При очень большой интенсивности распределение
точек становится совсем «гладким» и с большой точностью следует изме-
изменениям классического поля.
Даже электростатические силы, действующие между двумя посто-
постоянными зарядами, могут быть «объяснены» с помощью фотонов. Наличие
зарядов вызывает обмен фотонов; некоторое количество их появляется
у одного заряда и исчезает у другого. Это количество связано с энер-
энергией поля, и комбинированное действие зтих фотонов «производит» силы.
могущие быть измеренными и действующие на каждый заряд. В этом
случае для подсчета этих сил удобнее, конечно, пользоваться точкой
218
Гл. 2. Уравнения полей
зрения поля, так же как при расчете эффекта Комптона удобнее стоять
на точке зрения частиц.
Энергия фотона пропорциональна частоте поля. Но энергия частицы
равна временной компоненте 4-вектора, пространственные компоненты
которого пропорциональны импульсу частицы, а частота является вре-
временной компонентой 4-вектора, пространственные компоненты которого
пропорциональны волновому числу (величине, обратной длине волны)
волны. Таким образом, наша комбинация волны и частицы приводит
I.
I
Классическое
поле
•••¦¦ЯК?.'-
ЯШ*:
Высокая
интенсивность
Средняя
интенсивность
Очень низкая
интенсивность
Рис. 2.25.
Точки указывают места, в которые попадают отдельные фотоны. При
высокой интенсивности плотность распределения соответствует клас-
классическому полю; при нивкой интенсивности ясно заметен случайный
характер процесса.
к следующим соотношениям между энергией и частотой и между импуль-
импульсом и волновым числом:
энергия = fo>; импульс = у
B.6.1)
которые содержат «квантовую постоянную» h.
Фотоны и электромагнитные волны являются не единственным при-
примером этой новой, сложной двойственности между волной и частицей.
Опыты Дэвиссона и Г. П. Томсона, а также многих последующих иссле-
исследователей доказали, что элементарные частицы материи —электроны,
протоны и нейтроны — управляются «волновой функцией», непрерывным
ищем, удовлетворяющим волновому уравнению (подробности этого будут
рассмотрены в этом параграфе позже). Детали траекторий отдельных
ч_астиц даже в принципе не могут быть измерены с произвольно большой
точностью. Мы можем подсчитать и предсказать только вероятность
наличия частицы в данной точке в данный момент времени; эта вероят-
вероятность пропорциональна квадрату модуля волновой функции. Параллелизм
со случаем фотон —поле дополняется тем, что энергия и импульс частицы
2.6. Квантовая механика
219
также связаны с частотой и волновым числом волновой функции урав-
уравнениями B.6.1).
Соотношение неопределенности. Теперь целесообразно рассмотреть
подробнее вторую особенность квантового поля — тот факт, что невозможно
«отказаться» от волновой функции для получения подробности движения
отдельной частицы. Предположим, что луч монохроматического света
>(или пучок электронов) падает на экран, имеющий две щели на некото-
некотором расстоянии друг от друга, как показано на рис. 2.26. Некоторая
часть света (или электронного пучка) пройдет через щели и может быть
обнаружена на пластинке Р. Согласно классической волновой теории,
интенсивность освещения пластинки изменяется благодаря интерференции;
именно точки, в которых интенсив-
интенсивность наибольшая, расположены под
таким углом 6, для которого sin 6 =
rik/a, а точки минимальной интен-
интенсивности— под углом 6, для которо-
котороГО Sin О =
-4 H
где п — це-
Монохромати-
чеашй пучок
I
Ри с. 2.26. Интерференция света в случае
двух щелей.
\
лое число.
Наша чувствительная пластинка
укажет отдельные частицы, фотоны
или электроны, и при значитель-
значительной интенсивности плотность таких
частиц вполне соответствует интер-
интерференционной картине, получающей-
получающейся с помощью волнового уравнения.
Чтобы понять, почему мы не можем
«отказаться» от плотности вероятности данной волновой функции, попы-
попытаемся сделать это и посмотрим, к чему это приведет нас. Попытаемся
проследить за фотоном (или электроном), когда он проходит через щель
и дадает на пластинку, где и обнаруживается. Не все частицы движутся
по одному и тому же пути, так как не все они попадают в одно и то же
место пластинки. Но проходит ли фотон, за путем которого мы пытаемся
следить, через одну щель, или через другую, или через обе щели? Если
он проходит только через одну щель, почему оказывается настолько
вероятнее, что он попадет в точки, соответствующие углам 6, где
sinG = nX/a, чем в точки, соответствующие промежуточным углам? Утвер-
Утверждение, что вероятность того, что фотон попадет в некоторую данную
точку пластинки, зависит от расстояния а между щелью, через которую
он прошел, и щелью^ через которую он не проходил, приводит к абсурду;
это и доказывает невозможность достаточно точного исследования путей
отдельных частиц. До тех пор пока местонахождение фотонов (или
электронов) определяется через квадрат величины волновой функции,
попытки описания пути отдельной частицы всегда будут приводить нас
к подобным логическим противоречиям.
Мы можем попытаться заставить фотоны пройти через щель А, закрыв
щель В. Но тогда мы не получим интерференционных полос на пластинке.
Этим мы не разрешаем парадокса, мы только разрушаем эксперимент.
Из сказанного следует, что мы не можем быть уверены в том,
каков поперечный импульс фотона на протяжении его пути- от щели до
пластинки, и что любая попытка точно измерить этот импульс разрушает
эксперимент так, что ничто другое не может быть точно измерено. Мы
могли бы, например, попытаться измерить поперечный импульс, измерив
220
Гл. 2. Уравнения полей
импульс, сообщенный экрану, когда частица проходит через щель и из-
изменяет направление своего движения. Но для того чтобы измерить
импульс отдачи, нужно, чтобы экран имел малую массу и был свободно
подвешен так, чтобы он мог заметно двигаться при отдаче; но если все
это имеет место, мы не можем быть уверены в точном положении экрана,
когда частица проходит через щель.
Факт состоит в том, что мы никогда не можем измерить одновре-
одновременно положение и импульс с произвольно большой степенью точности.
Рис. 2.27 показывает, как сделать это утверждение более определенным.
Здесь частицы должны пройти через одну щель ширины Дж« Согласно
теории диффракции Фраунгофера, волны, проходящие через щель шири-
ширины Ах, будут диффрагировать, разворачиваясь в расходящийся пучок.
X
Рис. 2.27. Диффракция света, проходящего через единственную
щель шириной Да;.
Кривая справа показывает классическое распределение интенсивности освеще-
освещения экрана Р.
окруженный диффракционными полосами, как показано в правой части рисун-
рисунка на кривой сглаженной интенсивности. Теория диффракции утверждает,
что угловая ширина Д6 основного пучка приближенно равна Х/Дж* Но
этот угол является мерой нашей неуверенности относительно попереч-
поперечного импульса фотона после того, как он прошел через щель; вероятнее
всего, что значения этого поперечного импульса лежат между границами
— Ар^-^-рАО и — у Ар^ — -у-рАй, где р~ импульс частицы в напраи
лении оси у, т. е. в направлении первоначального движения частицы.
Но, согласно уравнению B.6.1), имеем p = hfk, так что &р
(Х/Дж) или
ApAx<?h.
B.6.2)
Это соотношение называется соотношением неопределенности Гейзенберга:
оно является одним из основных соотношений квантовой физики.
Приспособление со щелью, показанное на рис. 2.27, дает метод изме-
измерения положения частицы только в направлении х. Пучок частиц,
движущихся в направлении у, падает на экран. Положение любой
из частиц в пучке до ее удара об экран неизвестно, но после того, как
она прошла через щель, мы можем сказать, что знаем ее координату х
(или по крайней мере знали ее координату х сразу после того, как она
прошла через щель) в пределах неопределенности Ах. Но так как пове-
поведение частицы подчиняется волновому уравнению с соответствующей
частотой и длиной волны, данными в уравнении B.6.1), самый факт ее
2.6. Квантовая механика 221
прохождения через щель влечет за собой неопределенность относительно
направления ее последующего движения; самый факт, что мы измерили
се координату х, влечет за собой неопределенность в компоненте по оси х
ее импульса. Соотношение волна — частица нуждается во взаимосвязи
между неопределенностью в нашем измерении х и неопределенностью
в соответствующем импульсе; эта связь дана в уравнении B.6.2), которое
содержит вездесущую постоянную h. Чем точнее мы измеряем х (то есть
чем уже щель), тем менее .точно.лы знаем импульс после, намерения.
Можно представить себе многие другие эксперименты для измерения
положения и импульса, но анализ показывает, что все они приводят
к тому же результату, пока мы имеем в виду квант, то есть взаимо-
взаимосвязь волна —частица. Например, мы можем пустить луч света на элек-
электрон и определить положение этого электрона, наблюдая под микроско-
микроскопом отраженный свет. Однако свет при отражении от электрона ведет
себя сам подобно частице, и это отражение сообщает электрону известный
импульс отдачи. Мы не можем быть уверены относительно направления
этой отдачи, так как линза микроскопа имеет конечные размеры, и мы
не знаем, через какую часть линзы прошел отраженный фотон, прежде
чем мы его увидели. Мы могли бы уменьшить неопределенность относи-
относительно направления импульса отдачи, уменьшив угловую апертуру мик-
микроскопа, но по законам диффракции это уменьшило бы разрешающую силу
микроскопа и поэтому увеличило бы неопределенность относительно поло-
положения, в котором находился электрон в момент столкновения. Если
провести все преобразования, то связь между неопределенностью в поло-
положении электрона в момент отражения фотона и неопределенностью в по-
последующем импульсе электрона снова дается соотношением B.6.2).
Затруднение (если это можно назвать затруднением) состоит в том,
что физические сущности нельзя дробить неограниченно. Мы не можем
осветить электрон бесконечно малым количеством света; наименьшее
возможное количество света все еще нарушает состояние электрона на
конечную величину. Самый факт, что материя (а также электромагнитное
излучение и т. д.) встречается только в конечных порциях, приводит
к неустранимым неточностям во всех наших экспериментах, что делает
неизбежным соотношение неопределенности. Рассматриваем ли мы взаимо-
взаимосвязь «волна —частица», содержащуюся в уравнениях B.6.1), как «объяс-
«объяснение» соотношения неопределенности, содержащегося в уравнении B.6.2),
или наоборот, оба они являются различными выражениями следствий
из существенно атомистического взаимодействия поля и материи; обе
эти точки зрения имеют общее клеймо — постоянную h.
Сопряженные переменные и скобки Пуассона. Положение х и им-
импульс рх являются на языке классической динамики каноническими
сопряженными переменными.Соотношение неопределенности сохраняет силу
для любой пары сопряженных переменных: угол и момент количества дви-
движения, энергия и время и т. д. Мы рассмотрим этот вопрос классической дина-
динамики несколько подробнее в ближайшей главе; здесь мы сошлемся только
на некоторые выводы теории преобразований прикосновения, чтобы осве-
осветить это понятие сопряженных переменных. Предположим, что мы можем
полностью выразить конфигурацию некоторой консервативной динами-
динамической системы в данный момент t с помощью некоторой подходящей
системы координат дг, д2, ..., qn. Мы можем тогда выразить кинети-
кинетический потенциал L— Т —V, разность между кинетической и потенциаль-
потенциальной эпергиями (иногда называемую функцией Лагранжа), через коорди-
координаты q и их производные по времени qm = dqm/dt.
222 Гл. 2. Уравнения полей
Импульс рт, сопряженный координате qm, определяется тогда для
рассматриваемой динамической системы формулой
Рт = -^-- B-6.3)
Кинетический потенциал, полная энергия или какое-либо другое свойство
системы может быть выражено через переменные q и р вместо перемен-
переменных q и q. По многим причинам употребление величин р и q предпо-
предпочтительнее перед применением величин q и q.
Существуют, конечно, и многие другие системы координат и сопря-
сопряженных импульсов, с помощью которых можно полностью выразить пове-
поведение динамической системы. Преобразование, позволяющее перейти
от величин <7i» <?2> ••¦> Яп', Pi, Р2> •••> Рп'. описывающих состояние-
системы, к другим переменным Qlt Q2, ..., Qn; Plt P2, ¦¦-, Pn, с по-
помощью которых также может быть описано состояние той же системы,
называется преобразованием прикосновения. Эти новые координаты
Qi, (?2> •••> Qn можно выбрать любым способом, но так, чтобы и с их
помощью можно было бы полностью описать рассматриваемую конфигу-
конфигурацию в любой момент. Кинетический потенциал L системы может быть
выражен через Q и Q, и тогда величины Р могут быть найдены из фор-
формулы B.6.3).
Другой способ нахождения соотношений, включающих величины Q
и Р, основан на применении скобок Пуассона. Предположим, что мы
лыразили две функции динамической системы кип через исходные
неременные q и р. Скобки Пуассона функций и и v определяются тогда
равенством
(и. у)= S Г#^^~#^хЧ ¦ B-6.4>
v > / ZJ [ дрт dqm dqm дрт J v- '
7П=1
Этп выражения подробнее будут рассмотрены в гл. 3.
Значение скобки (к, v) будет одним и тем же независимо от выбора
координат gt, q2, ¦ ¦ ¦, qn, если только эти координаты достаточны для
полного описания конфигурации системы и если сопряженные импульсы
определены равенствами B.6.3). Легко убедиться в том, что
. . ди , . ди
<В'Л»>=—а^ и (в> ^)=а^'
Интересное и полезное свойство таких выражений состоит в том, что
если и и и являются сопряженными переменными, то их скобка Пуассона
равна единице. Таким образом, полная совокупность координат Qm
и сопряженных импульсов Рт для рассматриваемой системы удовлетворяет
уравнениям
(Qi>Qi) = o> (Pi,Pi) = o, i, /=i, .... n,
(Л. <W = °> i, /=i, .... n, 1Ф], B.6.5)
(^m- <?J = 1- W=l, 2 П.
_\Гы находим также, что (и, v) = l, когда и и v выражены через любые
новые координаты Q и импульсы Р, если эта скобка была равна еди-
единице в старой системе q и р.
Наиболее общий вид соотношение неопределенности приобретает
поэтому для любых двух функций и и v динамических переменных р и q
данной системы. Если скобка Пуассона (и, v) равна постоянной К (если
2.6. Квантовая механика 223
она равна К в одной системе координат, то она будет равна if и во вся-
всякой другой), то произведение неопределенностей при одновременном изме-
измерении в и о равно Kh; вообще
ЛиЛу~|(и, v)h\cv., B.6.6)
где индекс «ср.» указывает на то, что должно быть взято среднее
в смысле квантовой механики (оно определено на стр. 224), если (и, v)
fie является постоянной.
Взаимосвязь волна —частица, а также соотношение неопределенности,
навязанные нам экспериментальными данными, подразумевают и требуют
такую формулировку основ динамики, которая говорила бы нам о том,
что мы должны знать относительно поведения системы, но которая не
говорила бы о том, чего мы не можем.знать.
В итоге рассуждений этого пункта мы можем сказать, что двой-
двойственность волна —частица, проявляемая как излучением, так и мате-
материей, требует существенного изменения описания физических явлений,
данного Ньютоном и Максвеллом, описания, в котором все координаты и
соответствующие им импульсы могли быть точно измерены, а потому
траектории частиц были полностью известны. Квантовая механика ут-
утверждает, что такие точные знания невозможны, что чем более настой-
настойчивы попытки получить их, тем более сильно исказится траектория. Эта
неотъемлемая неопределенность вытекает из того факта, что имеется
своего рода волна, связанная с частицей; эта волна может интерфериро-
интерферировать сама с собой. Интенсивность волны (т. е. квадрат ее модуля) связана
с вероятностью нахождения частицы в данной точке. Проблема единствен-
единственной частицы является центральной проблемой квантовой механики; эта
проблема будет некоторое время привлекать наш главный интерес. Если
ее решить, все еще остается проблема совокупности частиц, свободных
или взаимодействующих. Эта проблема включает в себя квантование
полей, в том числе, например, и поля вероятностей, рассмотренного
выше; в последнем случае часто говорят также о вторичном квантовании.'
Основные постулаты квантовой: теории. Количественная формули-
формулировка этих идей требует применения символического исчисления со-
состояний такого рода, как затронутое в гл. 1. Состояние системы имеет
смысл, хорошо определенный в классической физике. Например, траек-
траектория или орбита частицы описывает ее состояние; прежде чем описывать
состояние плоской электромагнитной волны, нужно знать направление
вектора поляризации и т. д. В квантовой физике может быть известно
не так много фактов относительно системы. Тем не менее, если бы мы поже-
пожелали остаться в полном неведении относительно одной из пары сопря-
сопряженных переменных, мы могли бы другую определить точно. Вообще
здесь имеется некоторое количество измерений, которые можно
выполнить одновременно. Совокупность результатов таких измерений
может быть принята за описание состояния системы. В самом деле,
в квантовой физике это является максимумом того, что можно сказать отно-
относительно системы.
Измерение, выполненное над системой, изменяет систему. Для на-
наглядного представления этого факта лучше всего построить абстрактное
векторное пространство, вектор которого представляет собой данное
состояние системы. Это, конечно, можно сделать в классической
физике так же, как и в квантовой; этот прием мы применяли, например,
при изучении связанных осцилляторов в параграфе, посвященном абстракт-
абстрактным пространствам, или при изучении колебаний струны в этой главе.
Как мы сказали, влияние измерения изменяет состояние, т. е. повора-
224 Гл. 2. Уравнения полей
чивает вектор, представляющий состояние в векторном пространстве.
Таким образом, измерение может быть представлено оператором в аб-
абстрактном пространстве; каждой динамической переменной соответствует
определенный оператор.
Вообще измерение значения данной динамической переменной нару-
нарушает состояние данной системы, так что последующие измерения той же
переменной дадут другие результаты; все, что можно получить с помощью
отих повторных измерений, — это среднее значение и средние отклонения
или неопределенность. Только для небольшого количества из всех воз-
возможных состояний неопределенность равна нулю и каждое измерение
данного количества приводит к одному и тому же значению. Если изме-
измерение этого единственного значения достаточно для задания состояния,
то вектор состояния должен быть собственным вектором оператора,
представляющего эту переменную (определенным на стр. 82). Если для
задания состояния требуются значения более чем одного переменного,
то вектор состояния, для которого неопределенность одного из этих
переменных равна нулю, не будет обязательно собственным вектором;
однако можно доказать, что совокупность собственных векторов всегда
может быть найдена.
Чтобы резюмировать некоторые наши рассуждения из гл. 1, обозна-
обозначим через 5J5 оператор, соответствующий импульсу системы; пусть
состояния, для которых неопределенность измерения р равна нулю,
изображаются векторами рп (собственные векторы оператора ф). Тогда,
согласно уравнению A.6.31), имеем
где рп — одно из измеренных значений импульса (мы выбираем длину
вектора рп так, чтобы рп было измеренным значением); оно называется
собственным значением оператора S$ для состояния, обозначенного че-
через рп. Так как рп должно быть действительным числом, оператор ф
должен быть эрмитовым оператором, согласно определению, данному на
стр. 86 (другими словами, оператор ф равен своему сопряженному опе-
оператору ф*).
Если система находится в произвольном состоянии, соответствующем
вектору состояния е, импульс, вообще говоря, не может быть точно
измерен. Можно определить только среднее значение результатов ряда
измерений. Как указано на стр. 83, вектор е может быть записан в виде
суммы произведений собственных векторов рт на соответствующие компо-
компоненты вектора е в направлениях рт, выражаемые скалярными произве-
произведениями Рт-е. В гл. 1 мы показали, что векторы рт взаимно-перпен-
взаимно-перпендикулярны и нормированы так, что скалярные произведения Pm-е экви-
эквивалентны направляющим косинусам, хотя вообще и являются ком-
комплексными числами. Это значит, что сумма квадратов модулей направ-
направляющих косинусов равна единице
2|Рт-е|в = 1, где е = ^рт(р^.е).
т т
Это уравнение подсказывает, что величину |рт-е|2 можно считать
вероятностью, а именно вероятностью того, что измерение величины р
в состоянии е приводит к значению рт (т. е. вероятностью того, что
состояние е находится в состоянии рт). Поэтому среднее значение р для
состояния е равно
Это среднее того самого типа, который содержится в уравнении B.6.6).
2.6. Квантовая механика 225
На стр. 83 мы показали, что если две динамические переменные не
измеримы одновременно, то соответствующие им операторы не переста-
нопочны, т. е. 91-S8 ф $8-91. В этом параграфе мы затратили некоторое
время на выяснение того, что данный импульс р и сопряженная ему
координата q не могут быть одновременно измерены, если принять во
внимание свойства физических взаимодействий, существенно обусловлен-
обусловленных атомистичностью и наличием комбинации волна —частица. Поэтому
коммутатор [^э - q -— q - ^>] (который в дальнейшем будем обозначать
через [р, q]) не равен нулю. Важно найти, чему он равен.
Прежде всего, [р, q] должен быть чисто мнимым, так как (e*-p-q-e)
является комплексным сопряженным с (e*-q-p-e) для любого вектора е
(так как q* = q и р* = )р) и разность между этими двумя величинами
(представляющая собой среднее значение [р, q] для состояния е) должна
быть поэтому чисто мнимой. Во-вторых, мы доказали на стр. 91, что
величина коммутатора [91, S3] пропорциональна произведению неопределен-
неопределенностей (ДаД2>). Комбинируя все это (а также и выводы из эксперимента),
мы приходим к уравнению [р, q] = h/i (где Ji = u/2u), уже полученному
раньше [уравнение A.6.32)].
Учитывая уравнение B.6.6), связывающее квантовые неопределен-
неопределенности с выражением классической скобки Пуассона, мы, наконец, при-
приходим к основному уравнению квантовой механики; это уравнение устанав-
устанавливает связь между двумя операторами, представляющими две динамиче-
динамические переменные некоторой системы, и скобкой Пуассона для соответ-
соответствующих классических переменных ¦
^| r*L^*L»H B.6.7)
здесь, если (я, b) не сводится к постоянной, мы должны считать эту
скобку функцией операторов рт и qm. Нужно, однако, сделать преду-
предупреждение о том, что порядок выписывания множителей (pqp вместо д/>а
и т. д.) для некоммутирующих операторов играет роль и что уравнение
B.6.7) выполняется только тогда, когда для написания скобки Пуассона
выбран правильный порядок множителей (см. стр. 226). Это очень инте-
интересное уравнение связывает операторы квантовой механики в абстрактном
векторном пространстве с чисто классическими динамическими функциями.
Оно представляет собой не единственное уравнение, которое можно при-
придумать, чтобы удовлетворить общим требованиям, намеченным на преды-
предыдущей странице, но является простейшим уравнением этого рода и его
оправдание заключается в правильности вытекающих из него результатов.
Подведем итог выводов этого параграфа, В квантовой механике
состояние задается значениями тех величин, которые могут быть одновре-
одновременно измерены для этого состояния. Соответствующие им операторы
оставляют состояние неизменным и попарно перестановочны друг с дру-
другом. Конечно, эти операторы не являются функциями друг друга. В этом
можно убедиться, составив оператор, перестановочный с одним, но не
перестановочный с другим. Если операторы не перестановочны, они удов-
удовлетворяют соотношению неопределенности, данному уравнением B.6.6).
Независимые квантовые переменные и функции от операторов. Суще-
Существует, конечно, много функций динамических переменных системы,
которые должны превратиться в операторы. Функция одного переменного
(например, рт или qn), которая может быть определена классическим
способом с помощью ряда по степеням этого переменного, может быть
очень просто преобразована таким образом, что любая такая функция,
15 Ф. м. Морс п Г. Фсшбах
226 Гл. 2. Уравнения полей
взятая, например, от рт, перестановочна с рт и ее значение может быть
точно найдено, если рт может быть точно измерено. Собственное значе-
значение функции может быть подсчитано, исходя из собственного значения рт.
Наконец, если оператор % перестановочен с оператором р и если каж-
каждый оператор, перестановочный с р, перестановочен также с %, то можно
сказать, что g- есть функция оператора р.
Однако во многих случаях, когда два оператора перестановочны, один
из них все же не является функцией другого. Так, многие системы тре-
требуют задания нескольких независимых операторов, чтобы полностью
определить состояние. Операторы рп и qm (n Ф т) независимы и перестано-
перестановочны, согласно равенству B.6.7). Однако ни один из них не является
функцией другого, так как можно найти много операторов, перестановоч-
перестановочных с рп, но не перестановочных с Q,m (например, любая функция опе-
оператора рт). Фактически если два оператора перестановочны, но можно
найти третий оператор, перестановочный с одним из них, но не переста-
перестановочный с другим, то, наверное, первые два оператора независимы друг
от друга.
Если мы имеем дело с функциями двух сопряженных переменных,
то с помощью уравнения B.6.7) и пользуясь инвариантностью скобок
Пуассона при преобразованиях прикосновения (т. е. при переходе от
одной совокупности сопряженных переменных к любой другой полной
совокупности) мы видим, что
[&fo«,/O.?U==yg. [&(<?„>/ОЛУ=-т^' B-6-8)
причем производные в правых частях переводятся в операторы после
того, как произведено дифференцирование. Прежде чем переводить в опе-
оператор любую функцию сопряженных переменных, нужно внимательно
расположить их в определенном порядке, так как эти переменные могут
быть не перестановочны. (Например, классическая функция pzq может
перейти в p-p-q, или в p-q-p, или в q-p-lp, а собственные векторы
каждого из этих операторов различны.) Часто правильный порядок может
быть найден только с помощью проб или под контролем опыта.
Предположим, например, что нужно найти квантово-механический
оператор, соответствующий импульсу, сопряженному со сферическим углом
<р = arctg (у/х). В классическом смысле — это компонента z момента коли-
количества движения, равная хру — урх; так как "^ в. ру перестановочны (так же,
как t) и рх), квантово-механический оператор может быть составлен
сразу в виде ?рц — tjpx. Легко проверить, воспользовавшись уравнениями
B.6.8), что
Рассмотрим более сложный пример. Требуется найти в квантовой
механике эквивалент «радиальному импульсу» рТ, сопряженному ради-
радиальной координате г=Ух2 + у2. Классический радиальный импульс равен
Это выражение не имеет единственного эквивалента в квантовой меха-
механике, так как, например, ? и рх не перестановочны. Форма, для которой
точно выполняется правило коммутатора, получается непосредственно
из написанного выше выражения, то есть
= 4-. B.6.10)
2.6. Квантовая механика 227
Так как мы требуем, чтобы оператор был эрмитовым, то должна быть
использована симметричная форма.
Собственные векторы для координат. До сих пор мы довольно под-
подробно рассматривали правила перестановочности, которые могут быть
выведены из уравнения B.6.7). Обратимся теперь к исследованию соб-
собственных значений этих операторов. Во-первых, мы покажем, что собствен-
собственные значения оператора q непрерывны. Чтобы убедится в этом, мы пока-
покажем, что если существует собственное значение q оператора q, то может
быть образован собственный вектор с собственным значением q-\-dq.
Предположим, что е (q) — собственный вектор оператора q, такой, что
q-e(g) = qe(q). На вектор e(q) будем действовать оператором
Ф = ехрГ — |-
Вектор %-e(q) является собственным вектором оператора q с собственным
значением qA-dq, так как
так что
Для получения этого мы воспользовались коммутационным правилом
Н>, q] = %/i.
Заметим, что при изучении колеблющейся струны на стр. 134 мы
нашли другой случай с непрерывным распределением собственных значе-
значений.
Отметим также, что
(О B-6Л1)
На стр. 133 мы отметили возможные осложнения при рассмотрении соб-
собственных векторов для несчетного множества собственных значений. Раз-
Различные собственные векторы е (q) для различных значений q перпенди-
перпендикулярны ко всем другим собственным векторам последовательности, так
что наверное е (q) не является непрерывной функцией от q. Поэтому
результат следующих действий
или
,.е(9) = арш1 [«<* + *«) —<«>] B.6.12)
не обозначает, что правая часть пропорциональна производной нектора
е (q) по переменному q, так как разность [е (q + &q) — е (q)] не стремится
к нулю непрерывным образом при стремлении &q к нулю. [Отметим, что
этот результат следует непосредственно из уравнения B.6.7) и может
быть написан для любой пары канонических сопряженных переменных
при непрерывном распределении собственных значений для одной из-
переменных.]
15*
228 Гл. 2. Уравнения млей
Тот факт, что q имеет континуум значений, вызывает также некото-
некоторые трудности при решении вопроса о том, какой функцией от q и q'
является скалярное произведение е* (q)e(qr). Можно предполагать, что
эта функция должна быть равна нулю для всех значений q и q', кроме
значений, для которых q — q', что приводит к разрывной функции.
Оказывается, что наиболее удобно определить ее с помощью интеграла.
Очевидную формулу У вт-еп=1, снраведливую для дискретных собствен-
п
со
ных лекторов, мы распространим на случай континуума \ е* (q) е (qr) dq' = 1.
—оо
Это равенство определяет величины векторов е (см. стр. 231).
Функции преобразования. Интегрируя по q, мы можем составить
интегралы, содержащие e(q) и равные пределам сумм подинтегральных
выражений для всех значений q между пределами интегрирования. Напри-
Например, произвольный вектор состояния f может быть выражен в виде суммы
всех различных собственных векторов для q
со
'= \ fD)e{q)dq, B.6.13)
где \f(q)\2dq есть вероятность того, что частица находится между д
и qA-dq, когда система имеет состояние f. Величина /(</), будучи
пропорциональна направляющему косинусу угла между i и е(<7), яплястся
комплексным числом и представляет собой обычную функцию непрерыв-
непрерывного переменного q. Аналогия между этим интегралом и интегралом
Фурье станет более ясной, если развить это рассуждение.
Этим способом, интегрируя собственные векторы онератора положения q,
мы можем поставить в соответствие каждому вектору состояния f
обыкновенную функцию f{q), которая называется функцией преобразова-
преобразования1'', так как она определяет связь между f и векторами e(q). Собствен-
Собственный вектор другого оператора может .быть, конечно, выражен через век-
векторы e(q). Например, если 51-е (а) = ае (а), то можно написать
СО
e(a)=\[^(a\q)e(q)dq, B.6.14)
— ОО
где \6(a\q)\2dq есть вероятность того, что координата системы имеет
значение, лежащее между q и q-\-dq, когда состояние системы таково,
что переменное, представляемое оператором ?t, наверное имеет значение а.
Такая функция преобразования была рассмотрена на стр. 134.
Если мы не хотим полагаться на наше умение производить вычис-
вычисления с векторами состояния, мы можем всегда перейти к вычислениям
над функцией f{q). Например, среднее значение динамической величины,
представляемой оператором 51, когда система находится в состоянии f,
имеет вид
оо со
f--«.f= $ dq J Hq)[e*(q)-%.e(q'))f(q')dq',
J) Функция / (q) называется обычно волновой функцией в ж-представлении. —-
Прим. ред.
2.6. Квантовая механика 229
так что, зная результат действия оператора на вектор e(q), мы можем
выразить результат действия оператора на любой другой вектор состояния
f через функцию преобразования f (q).
Например, мы можем вычислить результат действия оператора р,
являющегося канонически сопряженным координатному оператору q, на
произвольный вектор состояния f. Пользуясь уравнением B.6.12), имеем
. B.6.15)
Другими словами, результат действия оператора р на вектор состояния
f соответствует результату действия аналитической операции (Ь/i) (d/dq)
на функцию преобразования f{q). Так как / (q) — обыкновенная функция,
дифференциальный оператор имеет обычный смысл. Повторяя эти рас-
рассуждения, найдем, что оператору b (р)п соответствует оператор b (h/i)n (dnjdqn),
действующий на f(q). Таким образом, если функцию %(р) оператора р
можно разложить в степенной ряд, то соответствующий оператор, действу-
действующий на функцию f(q), получается подстановкой «место р дифферен-
дифференциального оператора (h/i) (d/dq).
Было бы нетрудно с помощью ypaimemiii B.6.5) и B.6.7) обобщить
этп замечания. Рассмотрим полную совокупность координат qm (m= 1,..., n),
с помощью которой можно задавать конфигурацию данной системы (в клас-
классическом смысле). Найдем имульсные переменные рт, сопряженные с г/
так, чтобы удовлетворялись уравнения B.6.5), содержащие скобки Пуас-
Пуассона. Каждое динамическое переменное B(p,q) системы может быть
выражено через р и q. Квантово-механический оператор S3, соответствующий
классической величине В, может быть получен, если подставить в В
операторы рт и qm вместо величин рт и qm. Этот оператор, действуя на
абстрактный вектор f, представляющий состояние системы, изменяет его
величину и (или) направление. Если вместо исследования действия опера-
оператора S3 (р, q) на f мы предпочтем изучить соответствующее влияние на
функцию преобразования /(<?!, <?2> •¦•><7П)> то мы можем воспользоваться
следующим обобщением уравнения B.6.15):
»(*>, q)' = \
Здесь дифференциальный оператор J? нод знаком интеграла, действующий
на функцию преобразования f (qlt ...,qn), обра.шван заменой каждого рт
в классической функции B{p,q) через (h/i) (д/ддт). И п S3, и в соответ-
соответствующем дифференциальном операторе, действующем на / (q), мы должны
быть внимательны к порядку множителей р и q в каждом члене В,
ибо сопряженные операторы рт и qm не перестановочны, что видно
из уравнений
0, тфп,
которые соответстлуют уравнениям B.6.5), содержащим скобки Пуассона.
Как было определено раньше, [Ч{, S3] обозначает коммутатор (?1-93 — 23-ЭД).
230 Гл. 2. У равнения полей
Операторные уравнения для функций преобразования. Например,
вместо применения векторного уравнения
для определения собственных векторов bm и собственных значений Ът
можно воспользоваться соответствующим дифференциальным уравнением
\д) B.6.17)
для нахождения функций преобразования ty(bm\g) и их собственных
значений Ьт для оператора S3. Собственные векторы Ьт (если в них есть
потребность) могут быть найдены с помощью формул
Ь,„ = I ¦ ¦ • I <НЬт | д) e (q) dqx... dqn, ^ g lg.
d
Вероятность того, что конфигурация системы определяется значениями
координат, лежащими между дх и q1 + dq1, ..., дп и qn + dqn, когда В
имеет значение Ьт, равна \ty(bm\q)\2dq1... dqn, а среднее значение дина-
динамической переменной А(р, q), когда В имеет значение Ьт, равно
l...dqn. B.6.19)
Так как совокупность собственных векторов Ъп может быть также
использована для разложения произвольного вектора состояния, мы
имеем аналогично
... dqn, B-6.20)
так как
0, афт, .
Таким образом, многие операции алгебры векторов состояний проходят
параллельно интегральным и дифференциальным операциям, совершае-
совершаемым над функциями преобразования. К настоящему моменту должно
быть ясно, что эти функции преобразования некоторым образом связаны
с волновыми функциями, рассмотренными довольно смутно в начале
этого параграфа. Квадраты их величин связывают между собой вероят-
вероятность того, что система имеет данную конфигурацию (например, что
частица находится в данной точке), и вероятность того, что система
находится в данном состоянии, характеризуемым собственным значением Ьт.
Эти функции характерны для нового анализа квантовых явлений; они
соответствуют тем типам фактов, которые можно надеяться найти для
динамической системы, взамен точных данных о траекториях, интере-
интересующих нас в классической динамике. Конечно, если содержащиеся здесь
энергии и импульсы настолько велики, что соответствующие период 1/v
и длина волны, определенные формулами B.6.1), намного меньше, чем
промежутки времени и расстояния, связанные с системой, то эти функ-
функции преобразования сжимаются к лучам, близко соответствующим траек-
траекториям классической динамики; допустимые состояния системы близко
соответствуют при этом различным, возможным в классической меха-
механике начальным условиям.
2.6. Квантовая механика 231
Преобразование к пространству импульсов. До сих пор мы выра-
выражали наши векторы состояния через основную систему векторов e(q)
для непрерывно изменяющихся координат qx, ..., qn системы. Тем не ме-
менее все можно выразить также и через сопряженные импульсы plt ...,pn,
так как между величинами р и q имеется симметрия в выражениях
классических скобок Пуассона и квантового коммутатора. Мы получаем
совокупность собственных векторов е (р) для всего несчетного множе-
множества допустимых значений импульсов рг, ..., рп, и всякий другой век-
вектор состояния можно выразить через интеграл
Ь,„ = [ ¦ ¦ ¦ U (Ьт | р) е (р) dPl... dpn, B.6.21
аналогичный интегралам B.6.18).
Воспользовавшись коммутационными соотношениями операторов р
и q, мы можем показать, что действие оператора q на вектор состоя-
состояния bm соответствует действию операции — (h/i) (д/др) на функцию пре-
преобразования ф (Ьт | р). Уравнения, соответствующие равенствам B.6.17)
и B.6.20), имеют вид
Величина | <1> (bm \ p) \2dpx . .. dpn является, само собой разумеется, вероят-
вероятностью того, что система попадает п элемент импульсов dpx ... dpn,
¦сели ее состояние дается величиной Ът.
Для того чтобы дополнить это описание, мы нуждаемся в знании
соотношений между собственными векторами е (q) для координат и соб-
собственными векторами е(р) для импульсов. Эти соотношения можно
•было бы также использовать для преобразования функции ф (fcm | q) в функ-
функцию §(Ьт\р) и обратно. Как и раньше, имеем:
B.6.22)
где мы для простоты рассматриваем только одну координату и один
¦сопряженный импульс. Функция преобразования ty (р | q) связывает состоя-
состояние, в котором мы точно знаем положение частицы (и не имеем сведе-
сведений об импульсе), с состоянием, в котором мы точно знаем импульс
частицы, но не имеем сведений об ее положении (это последнее соот-
соответствует нашим знаниям о частице, находящейся слева от экрана
на рис. 2.26 и 2.27). Чтобы найти ty(p\q), мы воспользуемся уравне-
уравнением ре (р) = ре (р) для собственного вектора оператора р и преобразуем
•его, опираясь на уравнения B.6.22) и B.6.15)
.для всех значений р и q. Таким образом, ty(p\q) равна сехр [(i/h)pq],
где с — нормирующая постоянная.
Функция «нормируется» так (см. стр. 228), чтобы выполнялось
равенство е*(р)-е (р') = о (р — р'O где о — дельта-функция Дирака, опре-
232 Гл. 2. Уравнения полей
деляемая уравнениями (см. также стр. 122)
0. s<--|U,
а (ж) = lim .
-z)dz = f(x), B.6.23)
О, у
Выразим сначала е* (р) и е(//) через векторы e(q)
Но [е* (q)-e(q')] = о (q — q')t так что интегрирование по qr дает
о (р -р') = с2
Этот последний интеграл не будет вполне сходящимся, но и дельта-
функций также не является функцией, ведущей себя хорошо. Лучше
было бы воспользоваться определением функции о (р — р') и проинте-
проинтегрировать обе части лрлиедешшго выше уравнения по р' в промежутке
от /; ——-А до/>-|-—Д (было бы, может быть, надежнее, если бы мы
интегрировали сначала по р', а потом по q', чем в обратном порядке,
но результат будет один и тот же)
dz
= 2c2k
Следовательно, с= 1/|^2гсЬ= l/^'/i и ф(р |tf) = [l/Y'Zieh] е№)и. Поэтому
функции преобразования / (д) и / (рI} для вектора состояния f связаны
следующими уравнениями:
|/2nft J
=:i. ^ dp ^ d5'/(9')eB"i/h)('-5')p- B.6.24)
—оо —со
Это последнее уравнение встречалось раньше (см. уравнение 2.1.25) и бу-
будет очень подробно рассмотрено в гл. 4. Правая часть его является одной
из форм интеграла Фурье.
*) Функция /(/>) называется обычно волновой функцией в ^-представлении
(ср. с примечанием на стр. 228). — Прим. ред.
2.6. Квантовая механика 233
Заслуживает упоминания физическое истолкование координатно-им-
пульсной функции преобразования. Так как | ф (р \ q) |2 является постоян-
постоянной, то вероятность | ф (/? | <?) |2rf<7 того, что частица, имеющая импульс р,
находится между точками q и q-\-dq, не зависит от q, а вероятность
I Ф (Р I ?) \2dp того, что частица, находящаяся в точке q, имеет импульс,
заключенный между р и p-\-dp, не зависит от р. Это является естествен-
естественным следствием из соотношения неопределенности Гейзенберга, которое
утверждает, что если р известно точно (А/?—>0), то частица с одинако-
одинаковой вероятностью может находиться где угодно (Дд—>оо), и наоборот.
Заметим, во-вторых, что е<4/й)рв, рассматриваемая как функция коор-
координаты q, могла быть множителем, зависящим от координаты, для про-
проходящей плоской волны ехр [Bш/И) р (q — ut)] длины h/p и частоты up/h,
распространяющейся с некоторой скоростью и. Мы еще не изучили зави-
зависимость векторов состояния и функций преобразования от времени, но
легко видеть, что соотношение \—(h/p) является таким, которое мы рас-
рассмотрели [см. уравнение B.6.1)], когда начали говорить о волнах и части-
частицах. Рассматривая это соотношение, мы должны ожидать, что величина
(hXчастота) = up будет соответствовать энергии частицы, хотя мы пока еще
не в состоянии определить скорость распространения волн и.
Появление функции преобразования, связывающей состояние, в ко-
котором частица имеет импульс р, с ее положением q, имеет существенную
связь с нашим предварительным рассмотрением волн и частиц. Для со-
состояния, в котором частица может иметь либо импульс р, либо импульс р',
собственный вектор имеет вид -^- \^2 [е (р) + е1*е (/?')], а функция преоб-
преобразования будет равна
(р, q) Д_ [e ( ]
уr'ih
и представляет собой пространственную часть двух линейно наложенных
друг на друга волн с различными длинами. Сюда включена произволь-
произвольная разность фаз <р, значение которой можно определить ара более точ-
точном задания состояния. Вероятность | ф j2 dq нахождения частицы между q
и g-fdg на этот раз не будет везде одной и той же, так как две части
«олны интерферируют, создавая узлы и пучности на протяжении волны.
Так как мы теперь не уверены относительно импульсов, то можем уточ-
уточнить положение частицы в пространстве.
Для состояния f, соответствующего широкому интервалу импульсов,
как показано в уравнетш B.6.24), интерференция отдельных поли
может быть такова, что f(q) велико только вблизи q0 (т. е. наиболее
вероятное положение частицы — положение вблизп q0) и состояние может
быть таким, в котором положение частицы достаточно точно известно.
Функция Гамильтона и уравнение Шредингера. Одной из наиболее
общих «постоянных движения» в классической динамике является пол-
полная энергия системы; действительно, она постоянна для всякой консер-
консервативной системы. Классическое исследование динамики таких систем,
проведенное Гамильтоном, основано на применении «функции Гамильтона»
H{p,q) (см. стр. 270), которая равна полной энергии системы, кинети-
кинетической плюс потенциальной, выраженной через координаты и сопряжен-
сопряженные импульсы (в то время как функция L Лагранжа обычно равна раз-
разности между кинетической и потенциальной энергиями, функция Гамиль-
Гамильтона Н равна их сумме). Уравнения, связывающие скорость изменения
во времени координат qm с импульсами, имеют вид
• dqm dll ,г)
234 Гл. 2. Уравнения полей
что соответствует уравнениям B.6.3). Уравнения движения, связывающие
ускорения с силами, имеют тогда вид
Эти уравнения подробнее будут рассмотрены в гл. 3.
В квантовой механике вектор состояния е(Е) данной системы, имею-
имеющей определенную энергию Е [е (Е), является собственным вектором,
соответствующим собственному значению Е энергии], может быть опре-
определен из уравнения
e(|Iq)-e(?) = ?e(?I B.6.27)
где оператор § получается из классической функции Гамильтона посред-
посредством замены величин рт и qm соответствующими операторами. Правиль-
Правильный порядок операторов в различных членах не определяется полностью
классической функцией Н (р, q), однако этот порядок обычно может быть
установлен с помощью проб, как указано на стр. 226.
Конечно, нельзя и думать решить уравнение, содержащее абстрактные
операторы и векторы состояния. Может оказаться легче решить соответ-
соответствующее дифференциальное уравнение для функции преобразования ф (Е | q),
квадрат модуля которой измеряет плотность вероятности различных кон-
конфигураций системы, если мы знаем, что энергия равна Е. Принимая во
внимание уравнение B.6.17), мы видим, что искомое уравнение имеет вид
B.6.28)
где каждое рт в выражении Н заменено на операцию (h/i) (d/dq), дей-
действующую на §(E\q). Это уравнение называется уравнением Шредингера
для системы.
Уравнение Шредингера часто оказывается имеющим общий вид урав-
уравнения Гельмгольца B.1.10), которое получается, когда из волнового
уравнения выделена зависимость от времени. Чтобы яснее показать это,
построим уравнение Шредингера для частицы, имеющей массу т и нахо-
находящейся под действием поля с потенциалом V (сила= — gradF). Соот-
Соответствующими координатами q являются декартовы координаты х, у, z.
^ . . .
Кинетическая энергия равна у тп (х2 4- у2 -f- z2) = Т, а кинетический потен-
потенциал L=T—V. Импульс рх в соответствии с уравнением [B.6.3) равен
¦dL/dx — mx и т. д. Выражая Т и V через р и qt мы в конце концов
получим классическую функцию Гамильтона
H{p,q)=~{p% + pl + Pi) + V(х, у, z).
Уравнение Шредингера получается подстановкой вместо суммы квад-
квадратов импульсов произведения — (ft2) на сумму производных второго
порядка (лапласиан):
или
2m,
2.6. Квантовая механика 235
В областях, где Е > V, ^ — осциллирующаяся функция; в областях,
где Е < V, решение изображается показательной функцией и будет либо
убывать, либо безгранично возрастать по своей величине. Это следует
сравнить с уравнением B.1.10).
Мы можем, конечно, составить аналогичное уравнение для функции
преобразования от ? к импульсу р. Для этого в И (р, q) вместо
каждого q нужно подставить дифференциальный оператор — (h/i) (д/др).
Иногда это сделать труднее, так как V часто является более сложной
функцией переменных q, чем Т — переменных р [как, например, истол-
истолковать оператор, образованный из 1/У xz + yz-\-zz, когда мы заменим х
через — (h/i) (д/дрх) и т. д.?]. Можно, конечно, сначала определить §(E\q),
а <Ь(Е\р) найти с помощью преобразования Фурье, данного в уравнении
B.6.24). Более прямой путь, который можно продемонстрировать на урав-
уравнении Гамильтона для одной частицы, заключается в следующем:
^ ; q = x,y,z.
Операция, соответствующая кинетической энергии, имеет выражение
со
Для потенциальной энергии мы можем применить второе преобразова-
преобразование к векторам е(р)
и на основании уравнения B.6.20)
со
S3• е (/>') = \ \ \ [е* (р) •»• е (р')] е (р) dpx dpy dpz,
—со
где
СО
[ е* (р) $8 • е (//)] = \] \ Ф (Р I 0) V (?) ф (р' | q) dx dy dz =
CO
Поэтому вместо дифференциального уравнения для ф (Е \ р) мы имеем
интегральное уравнение
A12т) (р% + Р\ + Р1) ф (Е|р) + ^ J Vw. ф (Е\Р') dp'xdp'y dp'z = ?ф (Е \р),
—со
которое, конечно, полностью эквивалентно уравнению
Какое из двух уравнений легче решить, зависит от вида функции Н.
Если V может быть разложено на простые многочлены относительно q,
236 Гл. 2. Уравнения полей
то, по-видимому, проще решать дифференциальное уравнение; в против-
противном случае предпочтительнее интегральное уравнение.
Гармонический осциллятор. Для иллюстрации приведенных общих
принципов будет полезно рассмотреть квантовую механику одномерного
гармонического осциллятора.
Сначала составим оператор, соответствующий функции Гамильтона //.
Для частицы с массой т на пружине с постоянной жесткостью К функ-
функция Гамильтона выражается равенством
так что уравнение для собственного лектора оператора энергии имеет вид
€¦ е = [ (р2/2т) +1 Кп?] е(Е) = Ее(Е). B.6.29)
Мы, конечно, могли бы составить соответствующее уравнение Шредип-
гера
и решить его относительно ф методом, который будет изложен в этой
книге позже. Однако и настоящее время будет более поучительным найти
сразу е(Е).
Отмстим, что классическая функция Гамильтона может быть раз-
разложена на множители
Н=—с.( - шп -J-
2 V т УЧ. »1
К
—
Квантово-механический оператор не может быть так легко разложен
на множители, но, следя за порядком р и q и пользуясь коммутацион-
коммутационным соотношением р • q — q • р = h/ i, получим
где
т& &. = ^ + ^- hw; '- т®, ¦&_ = !q-~ hw,
®+ = (р/т) + шщ if 03. = (р/т) - icoq = (S*.
Умножив еще раз на [(р/т) + icoq] и нреобра:шиан результаты, получим
; ?¦©_=©_¦[? —ftw]. B.6.30)
Эти уравнения показывают, что если имеется собственный вектор с(Е)
оператора § с собственным значением Е, то вектор (З^-е(Е) янляется
также собственным вектором оператора !о с собственным значением
(Е-\~ hw) [т. е. равен Ae(E+hm), где А — некоторая нормирующая постоян-
постоянная], а вектор (&-е(Е) будет также собственным вектором для § с соб-
собственным значением (Е — Ьш) [т. с. равен Be(E — ina)]. Это означает, что
при наличии одного собственного значения Е оператора !q существует
также бесконечная последовательность собственных значений (Е-\-п%ю),
где п — любое целое положительное или отрицательное число.
Этот результат является довольно неожиданным, так как в клас-
классической механике мы не могли ожидать возможности отрицательных
значений энергии. Более тщательное изучение уравнений B.6.30) и свя-
связанных с ними утверждений показывает, что мы можем избавиться от
неприятных отрицательных энергий, если значение Е выберем осторожно.
2.6. Квантовая механика 237
Дело в том, что мы должны были сказать, что лектор C_-е(Е) являет-
является собственным вектором с собственным значением B? —ftcu), если только
вектор © е(Е) не равен нулю. Поэтому, если мы не должны допускать
значения энергии меньшие, чем некоторое минимальное значение EmiU,
мы должны иметь
©_-е (?„,,„)= О
или
О = ©+ •«_ • е(Emin) = ($--!Лш)-е(Ет1п) = (я1111п-i-Ш)е(?min).
В действительности такой выбор является не просто более удобным;
только такой выбор имеет физический смысл. В самом деле, если бы
допустили отрицательное собственное значение для энергии, квадрат
соответствующего собственного вектора е*-е должен был бы быть отри-
отрицательным. Так как отрицательные вероятности не имеют смысла, то
допустимым является только указанный выше выбор.
Следовательно, наименьшее собственное значение энергии равно
1,
-g- Ъю и последовательность допустимых значении энергии дается равенством
jEn = fco>Qn + -|J, /г = 0, 1,2, ...;
различные собственные векторы могут все быть выражены через наиниз-
наинизший е0 = е (Emin), где ? ¦ с„ = т /коео.
Мы должны теперь нормировать собственные векторы так, чтобы
было е*-е=1. Предположим, что е*-ео=1. Ближайший вектор ех —
= е (EniiD-\- /ко) = Л1@+-е0. Для. определения Ах полагаем
I
Поэтому ег = i (т/2йсоJ ®+ -е0, где $¦ ех = у
Продолжая рассуждать так же и дальше, мы покажем, что
п. B.6.31)
Таким образом, мы решили задачу определения собственных значений
и собственных векторов этого оператора Гамильтона. Средние значения
других функций от операторов р и q могут быть определены с помощью
операторов &.
Уравнение для наиниэшей функции преобразования может быть по-
получено заменой уравнения @_-ео = О дифференциальным уравнением
для \(q)
h dtp0 . p.
im dq 'Q '
которое имеет решение
-P
J
— OO
238 Гл. 2. Уравнения полей
Дифференциальный оператор, соответствующий оператору ©+, имеет вид
G V
Воспользовавшись уравнением B.6.31) и переведя его в уравнение для
тг-й волновой функции, имеем
d "In
Таким образом, мы без особых трудностей получили выражения для раз-
различных волновых функций.
Этот пример, возможно, показал, что прямые действия с оператора-
операторами и собственными функциями в конце концов не трудны, а в некото-
некоторых случаях эти действия могут быть даже легче, чем вычисление сна-
сначала волновых функций.
Кстати, соотношение неопределенности может подсказать нам, что
наше состояние минимальной энергии не может иметь места при нуле-
нулевой энергии, так как при энергии, равной нулю, обе величины, р и q,
были бы равны нулю; но в силу соотношения неопределенности невоз-
невозможно одновременно знать точные значения р и q. Наименьшее коли-
количество энергии должно быть настолько большим нуля, чтобы произведе-
произведение возможного изменения q на амплитуду колебания р было не меньше
чем h. Подставив необходимые значения, мы увидим, что минимум
энергии не может быть меньше чем -«-Лю.
Зависимость от времени. Чтобы дополнить наше рассмотрение кван-
квантовой механики, теперь необходимо ввести переменную времени t, что
позволит развить кинематику, а в конце и динамику, так что мы смо-
сможем формулировать уравнения движения в квантовой механике.
В классической механике время появляется двумя существенно раз-
различными путями. В случае консервативных полей время является только
неявной переменной, т. е. употребляется как параметр, с помощью кото-
которого может быть описано движение. В самом деле, в случае двух или
трех измерений время может быть полностью исключено, и движение
может быть описано заданием траектории. Пространственные координаты
и временная координата играют не одинаковые роли. Тем не менее
в релятивистской механике время и пространство входят в теорию на
равных правах, так как при преобразовании Лоренца пространство и
время могут перемешиваться. Поэтому в настоящей релятивистской теории
переменная времени должна истолковываться совершенно иначе, чем в
нерелятивистской теории. Это различие сохраняется, когда мы переходим
¦к квантовой механике.
Время также появляется и как явная переменная, если силовое поле
неконсервативно, или если силовое поле меняется с течением времени
(например, поле, вызванное другой движущейся системой), или, нако-
наконец, при формулировке начальных условий. Во всех этих случаях вре-
временная переменная нужна для описания силового поля, действующего
на систему, так что временная координата и пространственные коорди-
координаты употребляются аналогичным образом.
Это раздвоение появляется также и в квантовой механике. Например,
в соответствии с Др^Дж^ft имеет место соотношение неопределенности
«* ft, B.6.32)
где ЬЕ измеряет неопределенность энергии, a kt — неопределенность во вре-
2.6. Квантовая механика 239
мени. Подобного соотношения можно было бы ожидать на основе реля-
релятивистских требований; в самом деле, здесь в точности повторяется рас-
рассуждение Де Бройля, употребленное им, когда он открыл соотношение
>. = h/p из 4 = E/h. По аналогии с нашим выводом уравнения коммутато-
Ра [Рж> ?]=ft/z" из соотношения неопределенности B.6.2) можно было бы
попытаться из уравнения B.6.32) получить коммутатор между операто-
оператором, соответствующим энергии, и оператором, соответствующим времени.
Но это рассуждение не было бы точным, так как соотношение неопре-
неопределенности B.6.32) применимо только тогда, когда время входит как
явная переменная.
Иначе говоря, когда время не входит явно в описание силового
поля, то время на самом деле является параметром. Измерение его на-
наблюдателем (например, с помощью наблюдения за часами) никак не
отражается на рассматриваемой системе. Это измерение не может по-
повлиять, например, на энергию такой системы. Но если время явно со-
содержится в описании силового поля, то неопределенность во времени
нлечет за собой неопределенность силы, а следовательно, и энергии.
В распространенном примере связи между Д.Е и At рассматривается
измерение времени движения между двумя точками 1 и 2 с помощью
волны, например световой волны. Использование волны, частота (а сле-
следовательно, и энергия) которой точно известна, потребовало бы беско-
бесконечной протяженности волны. Время движения было бы поэтому пол-
полностью неизвестным (Д?—>со, ЬЕ->0). Точность измерения времени
движения возрастает, если воспользоваться заслонкой, помещенной в
точке 1, которая в некоторый момент, скажем при t = 0, открывается,
и второй заслонкой (в действительности применяются зеркала), поме-
помещенной в точке' 2, которая должна открыться через некоторое время.
Легко видеть, что измеренная скорость есть скорость волнового пакета
ширины во времени, равной Д?, где Д? промежуток времени между дей-
действием двух заслонок. Однако такой волновой пакет должен состоять
из наложенных друг на друга волн с различными частотами, (интеграл
Фурье). Эти частоты размазаны в интервале, примерно равном 1/Д?, так
что AvAf *& 1 или АЕЫ *& h. Ясно, что функция Гамильтона, описываю-
описывающая этот опыт, зависит от времени; временная переменная требуется
для описания взаимодействия между материей (заслонки) и излучением.
Характерно, что зависимость от времени обусловлена тем фактом, что
все взаимодействующие системы (например, оператор заслонки) не вклю-
включены в рассмотрение.
Резюмируя, мы видим, что соотношение неопределенности B.6.32)
применяется только тогда, когда функция Гамильтона явно зависит от
времени. Если зависимость от времени неявная, это соотношение не
применимо, и само время может рассматриваться как параметр. Это
янусоподобное поведение отражается в том факте, что вывод уравнения
Шрёдингера, зависящего от времени, может различаться в зависимости
от обстоятельств. К счастью для релятивистских обобщений квантовой
механики можно найти единый вывод, пригодный в обоих случаях.
Время как параметр. В интересах простоты и ясности лучше рас-
рассмотреть нерелятивистский случай с консервативными полями, т. е. те
случаи, когда классическая нерелятивистская функция Гамильтона не
зависит от времени, так что временная переменная может быть принята
за параметр. В- гл. 1 (стр. 88) мы уже показали, что изменение с тече-
течением времени направления вектора состояния может быть получено
с помощью унитарного оператора. Мы показали там, что
240 Гл. 2. Уравнения полей
где оператор § пока не определен. В самом деле, при построении кине-
кинематики выбор $ будет одним из решающих шагов. Здесь мы написа-
написали — (ig/Jt) вместо Jg для того, чтобы согласовать это уравнение с урав-
нием B.6.11), связывающим р и q. В гл. 1 мы также показали, что
?-e = iftg, B.6.33)
где мы также ввели дополнительный множитель — (I/?1)- Это уравнение
аналогично уравнению B.6.12) для результата действия оператора Ь
на вектор e(q). Но имеется существенное различие, позволяющее нам
написать здесь de/dt, в то время как такой предельный переход в
B.6.12) был недопустим. В уравнении B.6.12), дающем результат дей-
действия оператора р, мы имеем дело с собственными векторами е(д) операто-
оператора q,Tai< что каждый е (q) перпендикулярен к другим, и это не давало воз-
возможности взять предел. В настоящем случае t — только параметр; е не
является его собственный! вектором, так как t не является оператором.
Все собственные некторы системы с оператором § являются непрерывными
функциями параметра t и вращаются в абстрактном пространстве при
возрастании t. Следовательно, мы здесь можем говорить о производной
вектора е по t. Оператор (!Q/ih) dt вызывает бесконечно малое вращение
вектора от его направления в момент t до его направления в момент
t + dt, и это различие направлений непрерывно уменьшается, когда dt
стремится к нулю.
Кинематика и классической механике занимается изменениями
с течением времени переменных, определяющих положение, таких, как,
например, q. Для того чтобы иметь возможность получить необходимые
аналогии в квантовой механике и таким образом определить Sq, нам
нужно рассмотреть изменение операторов с течением времени. В нашем
изложении квантовой механики в этой главе до сих нор предполагалось,
что оператор не зависит от времени, поскольку он действует на свои
собственные векторы, так что уравнение %-i — fi дает то же самое соб-
собственное значение / для всех значений времени (пока % явно не зави-
зависит от t).
Во многих случаях вектор состояния сам меняется с течением вре-
времени таким способом, как мы сейчас рассматривали. Однако мы можем
также предполагать, что вектор состояния не зависит от времени,
и возложить ответственность за все изменения с течением времени на опера-
оператор. Эта формальная замена, конечно, не должна влиять на измеряемые
величины, такие, например, как собственные значения / или коэффи-
циепты разложения, определенные в уравнении B.6.20). Другими слова-
словами, оператор 91 (t), содержащий время как параметр, может быть полу-
получен из постоянного оператора 91@) с помощью уравнения B.6.33) и тре-
требования, чтобы величина
f* (t) ¦ Ш @) ¦ f (t) = f* @) • 9t (t) - f @) = f* @) • e~W№ St @) e- №>*' • f @)
не зависела от t. Следовательно, равенство
% (t) = e<WM>' % @) е-(*№)*' B.6.34)
и дает зависимость 9t (t) от t, если мы должны рассматривать этот опе-
оператор как зависящий от времени.
Предположив, что t становится бесконечно малым dt, мы получим
уравнение, связывающее скорость изменения Оператора % (t) с течением
времени с неизвестным пока оператором $
Я@) [l-l^
2.6. Квантовая механика 241
или
Из того, как получе.но это уравнение, видно, что выражение
можно рассматривать как скорость изменения с течением времени опе-
оператора %, если мы оставляем векторы состояния постоянными и считаем
оператор 91 переменным во времени; это выражение можно также рас-
рассматривать как оператор, соответствующий классической скорости изме-
изменения динамической переменной А, если оставить операторы постоян-
постоянными, а векторы состояния изменять.
Например, оператор, соответствующий скорости изменения
qm координаты qm, может быть найден из B.6.35):
здесь для получения последнего выражения мы воспользовались уравне-
уравнением B.6.8). Но это последнее выражение является как раз тем, которое
нужно для определения природы оператора Jg. В пределе, при больших
энергиях и импульсах, это операторное уравнение сводится к классичес-
классическим уравнениям в обычных переменных. Это может быть верно, если
оператор § получается из функции Гамильтона для системы заменой
входящих в нее переменных р и q соответствующими операторами. Дру-
Другими словами, если ?j является оператором Гамильтона уравнения B.6.27),
то уравнение B.6.36) соответствует классическому уравнению B.6.25).
Этот результат можно перепроверить, так как если в уравнении
B.6.35) положить Ш = рт и воспользоваться равенством B.6.8), то мы опять
получим
что соответствует классическому уравнению B.6.26).
Таким образом, можно сделать вывод, что операторные ураввения
движения в квантовой механике имеют в точности ту же самую форму,
что и их классические аналоги, но с заменой классических переменных
р и q соответствующими операторами р и q. Например, уравнение дви-
движения Ньютона принимает вид т (d'q/dt2) = — (dSg/c'q). Взяв средние
значения для любого из этих уравнений, убеждаемся непосредственно,
что классическая ньютонова орбита является в точности средней для всех
возможных орбит квантовой механики1). Другими словами, влияние
соотношения неопределенности состоит во введении флуктуации от клас-
классической орбиты. При осреднении они устраняются. Конечно, среднее
значение квадратов отклонений не равно нулю и потому может быть
наблюдаемо, но в пределе при больших энергиях неопределенность ста-
становится ничтожной и квантовая механика незаметно переходит в клас-
классическую механику. Это утверждение известно как принцип соответствия.
Двойственным ему для уравнений является утверждение, что в пределе
коммутатор (i/h) [Ш, S3] переходит в классическую скобку Пуассона (А, В).
Из соответствия между коммутатором и скобкой Пуассона следует,
что каждая классическая постоянная движения является также квантово-
механической постоянной движения.
х) Это утверждение не совсем точное. При усреднении пр_авой_ части уравнения
получим — ЭЖ/dq, что, вообще говоря, не совпадает с —0d(q)/dq.—Прим. ред.
16 ф. м. Морс и Г. Фешбах
242 Гл. 2. Уравнения полей
Мы, конечно, можем пожелать иметь дело с функциями преобразо-
преобразования вместо собственных векторов. Эти функции также изменяются
с течением времени; в соответствии с уравнением B.6.33) мы имеем
зависящее от времени уравнение Шpeilumepa
^(tg), B.6.38)
rp,eH(p, q) — классическая функция Гамильтона, и вектор состояния,
зависящий от времени, выражается интегралом
Для стационарных состояний имеем, очевидно,
так что
е (Е, t) = е {Е, 0) е-« <Е'П>', B.6.39)
где Е — собственное значение энергии. Таким образом, зависимость от
времени для стационарного состояния является простой гармонической
зависимостью с частотой, равной значению энергии, деленному на h,
так что соотношение Планка E = h\, данное в B.6.1), удовлетворяется.
Таким образом, мы показали, что функция преобразования ф (Е, q)
является «волновой функцией», о которой мы говорили в начале этого
параграфа. Квадрат величины ее дает плотность вероятности различных
конфигураций системы, а интегралы вида \ t^J? — -~-, q j фйддают сред-
средние значения последовательности измерений динамической переменной
В{р, q), когда система находится в состоянии, соответствующем ф. Эта
плотность вероятности и эти средние значения исчерпывают все, что
может быть получено экспериментально для системы. Для больших
систем, имеющих значительную энергию, результаты будут очень мало
отличаться от точных предсказаний классической динамики, но для
атомных систем неопределенности пропорционально велики и результа-
результаты могут существенно отличаться от классических.
Мы показали также, что эти функции преобразования имеют волновые
свойства и им сопутствуют интерференционные эффекты, которые влияют
на плотность вероятности. Волновое число для волны в данном напран-
лении равно произведению 1//г на компоненту импульса в этом направ-
направлении, а частота волны равна произведению 1//г на энергию системы,
как указано в соотношении B.6.1). Только применяя аппарат теории
абстрактных векторов и операторов, а также пользуясь функциями пре-
преобразования, возможно построить теорию атомной динамики, которая
соответствовала бы экспериментально установленным фактам, например
таким, как необходимые неопределенности, возникающие при наблюде-
наблюдении атомных систем.
Функция Гамильтона, зависящая от времени. Обсудив случай, когда
время не входит явно в выражение энергии Н, причем тогда время
играет скорее роль параметра, чем оператора, рассмотрим теперь случай,
когда Н зависит явно от времени t. В этом случае время, применяемое
при описании изменения энергии, должно рассматриваться скорее как
оператор (так же, как и координаты), чем как параметр, удобный для
того, чтобы следить за развитием движения системы.
2.6. Квантовая механика 243
Различие становится яснее с точки зрения квантовой механики,
чем с классической точки зрения, так как в квантовой механике мы
можем отличать оператор, соответствующий времени, от непрерывного
распределения его собственных значений. В классической механике мы
пронодим различие, обозначая явно входящее время через qt, так что
полная энергия является функцией от qt, qlt q2---qn и импульсов рх,
Ръ-'-Рп' которую мы формально обозначаем через Н (qt, p, q).
Эта функция дает надлежащие классические уравнения движения
B.6.25) и B.6.26) для qlt q2-•-qn и Pi' /?2---/?n>H0 не дает соответствую-
соответствующей совокупности уравнений для qt. На самом деле мы еще не рассматри-
рассматривали сопряженного импульса pt. Таким образом в случаях когда Я явно
зависит от времени, мы должны изменить функцию Гамильтона так,
чтобы новая функция Гамильтона Н (pt, qt; p, q) удовлетворяла уравне-
уравнению
• _dqt_SB_
41 - dt dpi ¦
Но прежде чем решать вопрос о форме И, мы должны выяснить, какой
смысл имеет qt. Так как qt является явным временем, то надо ожидать,
что в классической динамике оно будет пропорционально временному
параметру t и что в действительности dqjdt = 1. Следовательно, новая
функция Гамильтона © должна быть связана с полной энергией
Н (Qi> Р> Я) и с новым импульсом pt уравнением
® (Pt> 4i'> P' 4)—H(qt; p, q)-\-Pi- B.6.40)
Тогда уравнения движения имеют вид
? = ^'?=-^' и = М. 2.....П. B,6.41)
Можно показать, что полная скорость изменения в с течением вре-
времени (обусловленная изменением всех р и всех q с течением времени)
равна нулю, так как, пользуясь уравнениями B.6.41), B.6.25) и B.6.26),
имеем:
d<d ее • . ее • , х-
Таким образом, новая функция Гамильтона остается постоянной, хотя
полная энергия Н явно изменяется с течением времени. Кроме того,
можно добавить подходящее слагаемое так, чтобы сделать эту по-
постоянную равной нулю: в = И -\- pt = 0. Это значит, что величина pt,
сопряженная переменная к явному времени qt, в точности равна значе-
значению полной энергии, взятому со знаком минус, pt = —Е (мы пишем Е,
так как И должно быть выписано как явная функция от q, и от других
р и q, в то время как Е является численным значением, изменяющимся
с течением времени). Таким образом, явное время является сопряжен-
сопряженным к значению энергии, взятому со знаком минус.
Выражения классических скобок Пуассона можно также обобщить,
включив в них новую пару переменных
/ , vi Г им ft) ди dv 1 .
(и, V) = > з— 5 ъ—ъ— i m — t, 1, ..., п.
v I АЛ [dpmdqm ддтдрт\
т
16*
244 Гл. 2. Уравнения полей
Скобка Пуассона, содержащая функцию Гамильтона, может быть вычис-
вычислена с помощью уравнений B.6.41)
_____
дрт dqm 3qm дрт
т
п
2 Г dv dqm dv dpm~\ Г dv 89 8v ~] _dv @ R A9>
ldqm dt+dp^-irj + leJi+dq-tdp-ti-dT' ^•°-^)
так как dv/dq, = dv/dt и dQ/dqt = 0.
Введение явного времени и его сопряженного импульса в квантовую
механику теперь осуществляется непосредственно. Мы вводим оператор
qf, имеющий несчетную, непрерывную последовательность собственных
значений t, которые могут быть использованы для задания частных
состояний, представляющих интерес. Сопряженный оператор pt имеет
собственные значения, равные допускаемым значениям энергии, взятым
со знаком минус. Эти операторы входят наравне с операторами для
различных координат и импульсов конфигураций. Коммутатор равен
№. ЧЛ=Т'
так что соответствующее соотношение неопределенности имеет вид
ДЕД^с^й.. Операторы pt и q, перестановочны со всеми другими р и q.
Уравнения B.6.8) и B.6.11) также остаются в силе для этой пары.
Оператор Гамильтона ig получается теперь заменой в функции пол-
полной энергии величин рт и qm соответствующими им операторами, при-
причем явное время заменяется оператором q(; значит,
B.6.43)
Унитарный оператор, преобразующий вектор состояния для момента
t в вектор состояния для момента V', имеет форму exp [(i/%) fe (t'— t)}
[см. уравнение B.6-11)]. Уравнение движения вектора состояния е при-
принимает: вид
[<' + %И] B.6.44)
аналогичный уравнению B.6.12), а уравнение движения для оператора
таково:
В частности.
где § —постоянный оператор, преобразующий каждый вектор в самого
себя (в гл. 1 мы называли его идемфактором):
Мы теперь можем перейти к свойствам функций преобразования
для систем в случае, когда функция Гамильтона явно зависит от вре-
времени. Функцию преобразования от q к Е (часто называемую волновой
функцией Шредингера) мы по-прежнему определяем равенством
^(O\q,t)dtdq1..Kdqne(q,t),
где t — собственное значение оператора q,, qm — собственное значение опера-
оператора qn и 0 — собственное значение для оператора §, данного в уравне-
уравнении B.6.43).
2.6. Квантовая механика 245
Раньше было показано, что оператор рт, действующий на вектор е,
соответствует дифференциальному оператору (h/i) (д/ддт), действующему
на функцию преобразования; точно так же здесь оператор pt соответствует
дифференциальному оператору (h/i) (d/dt), действующему на ф. Диффе-
Дифференциальное уравнение для ф, соответствующее векторному уравнению
ф-е = 0, имеет вид
Это уравнение называется зависящим от времени уравнением Шредин-
гера; его следует сравнить с B.6.38), где время рассматривалось просто
как параметр. Как мы видим, оно получается в результате закономер-
закономерного расширения описанного ранее метода замены классического уравне-
уравнения для зависящей от времени функции Гамильтона уравнением кванто-
квантовой механики для волновой функции ф. Величина | ф |2 есть плотность
вероятности данной конфигурации в данный момент времени. Среднее
значение плотности тока частицы в любой точке, как можно видеть,
пропорционально величине
за исключением того, что эта величина не будет обязательно действитель-
действительной. Тем не менее мы можем теперь подсчитать, каков ток.
Частица в электромагнитном поле. Например, для частицы с заря-
зарядом е (заряд электрона равен — е) и массой т, движущейся в электро-
электромагнитном поле с потенциалами А и о, сила, действующая на частицу
[на основании уравнения B.5.12)], равна е[Е + A/ст)рхН], и полная
энергия (нерелятивистская) частицы равна
как будет показано в ближайшей главе (стр. 283). Чтобы получить диф-
дифференциальное уравнение для ф, подставим (h/i) (d/dq) вместо каждого р
в выражении Н. Здесь нет неясности в порядке множителей в члене р-А;
если divA = 0, тогда правильный порядок есть А-р. Уравнение, полу-
полученное для ф, имеет вид
r?4l + -ф = О. B.6.46)
Как и в уравнении B.6.45), в этом уравнении явно содержится мнимая
величина i. Это означает, что уравнение для комплексной сопряженной
функции ф имеет вид
Если ефф является для электромагнитных уравнений плотностью
заряда р, то плотность тока J должна быть такой, чтобы удовлетво-
удовлетворялось уравнение неразрывности (dp/dt) + div J = 0. Применим уравне-
уравнения для фиф, чтобы определить J. Умножив уравнение для ф на ф,
а уравнение для ф —на ф и вычтя результаты, получим
*L (фУ2ф - фТ» ф) _ ig. A • grad (фф) + ih ±- (фф) = 0.
246 Гл. 2. Уравнения полей
Но на основе правил векторных операций мы можем показать, что
4>V2i — tyV2ty = div (ф grad ф — ф grad ф)
и если div A = 0, то A-grad (фф) = div (Афф). Поэтому
-|- ИЮ + div [ -^ (ф grad ф - ф grad ф) _ -fl Афф ] = 0
й если р = ефф, то плотность тока оказывается равной
i rad ф-<j> grad ф)--^-Афф. B.6.47)
Это выражение вещественно и, так 1*ак р и J удовлетворяют уравнению
неразрывности, можно предполагать, что они являются выражениями,
которые можно подставить в уравнения Максвелла вместо зарядов и тока.
Отметим, что эти выражения являются лишь вероятностными плотно-
плотностями, а не «истинными плотностями» в классическом смысле. Тем
не менее этот вывод находится в согласии с нашим новым пониманием
того, что является наблюдаемым; так как «истинные» положения и им-
импульсы отдельных электронов мы не можем знать точно, то из вол-
волновой функции должны вытекать пригодные выражения только для плот-
плотностей. Как сказано в начале этого параграфа, они содержат квадраты
модуля величины ф, характеризующие квантовые плотности и вероятности.
Относительность п спин. Соотношение между четырьмя импульсными
операторами для отдельной частицы и соответствующими дифференциаль-
дифференциальными операторами, действующими на функцию преобразования ф( |<7, ?)
(пустое место перед вертикальной чертой обозначает, что ф можно взять
для любого собственного вектора и собственного значения)
Ря"*Твад' Ят = х> У' z> 1> B.6.48)
является соотношением между четырехмерными векторами, которое может
удовлетворять требованиям специальной теории относительности. Тем
не менее зависящее от времени уравнение Шредингера B.6.46) не является
инвариантом преобразования Лоренца, даже в случае свободного движения,
когда А и <р равны нулю. Пространственные операторы содержатся в выра-
выражениях вторых производных, а оператор времени — в выражении первой
производной, и никакая комбинация р%, р%, р\ и /?,= —.? не может быль
инвариантом преобразования Лоренца.
Трудность лежит, конечно, в том, что выражение, которое мы при-
применяли для Н (р, д) в случае частицы, находящейся в электромагнитном
поле, не было релятивистски инвариантным, но являлось просто первым
приближением к правильной релятивистской функции Гамильтона. Эта
величина может быть получена, если, комбинируя четырехмерный вектор
Рх> Pv< Р?> — (г/с) Н (см. стр. 99) с четырехмерным вектором Лх, Ау, Az, гш
(см. стр. 203), составить инвариантное относительно преобразования Лоренца
уравнение
B.6.49)
Отсюда можно получить релятивистское выражение для функции
Гамильтона
c V m2c2 + р* - Bе/с) А-р + (е/с)М2. B.6.50)
2.6. Квантовая механика 247
Это и есть та функция, которая должна быть превращена в дифферен-
дифференциальный оператор, чтобы получить правильное зависящее от времени
уравнение Шредингера.
Однако этот результат ставит только более трудную задачу: как
интерпретировать оператор, содержащий квадратный корень из второй
производной? Понятно, мы могли бы разложить радикал в ряд по воз-
возрастающим степеням 1/т2с2 (функция Гамильтона на стр. 245 представляет
собой два первых члена такого ряда с отброшенным постоянным сла-
слагаемым тс2), но такой ряд содержал бы все производные высших порядкеш
функции ф и дал бы чрезвычайно «неаккуратное» уравнение, если даже
можно было бы надеяться на его сходимость. Возможное решение заклю-
заключается в том, чтобы воспользоваться уравнением B.6.49) в том виде, как
оно написано, помня, что величина — A/с) Н является четвертой компо-
компонентой вектора импульса и должна быть заменена через (h/ic) (d/dt). Если
поля равны нулю, это приводит к уравнению
которое является уравнением Клейна — Гордона [см. B.1.27)].
Это уравнение для функции преобразования является релятивпстски
инвариантным, но имеет тот недостаток, что если е | ф |2 есть плотность
заряда, то величина, данная в B.6.47), не является плотностью тока.
В самом деле, интеграл от |ф|2, распространенный на все пространство,
не будет больше всегда постоянным, как это имеет место для решения
уравнения B.6.46), так что не ясно, будет ли е|ф|2 плотностью заряда.
Мы отложим до следующей главы разыскание точных выражений для \>
и для /; необходимо только установить здесь, что уравнение Клейна —
Гордона не является точным уравнением для электронов или для любой
частицы со спином.
Зависящее от времени уравнение Шредингера B.6.46) является вполне
удовлетворительным для частиц, движущихся медленно по сравнению
со скоростью света, но оно не учитывает двух обстоятельств: относитель-
относительности и спина. Мы знаем, что электрон имеет спин, и рассмотрели
в § 1.6 и 1.7 свойства спиновых операторов. Эти спиновые операторы
соответствуют дополнительной степени свободы электрона, которой,
по-видимому, отвечают новые координата и импульс. Следовательно,
если бы мы пожелали, мы могли подсчитать функцию преобразования,
содержащую эту новую координату, и получить выражение для оператора
спина посредством дифференцирования по этой координате. Так как
правила действий со спиновым оператором очень просты, обычно легче
иметь дело с вектором состояния.
Поэтому функции, употребляемые здесь, являются смешанными,
состоящими из функций преобразования для пространственных компонент
и компоненты времени, а также вектора состояния а для части, соот-
соответствующей спину. Полный вектор состояния может быть, таким образом,
представлен следующим равенством:
со со
е (Е, s) = \ ... ^ <!f (E | glt q2, . .. qn) e (qx, .. . qn) a (s) dqt ... dqn,
- CO —CO
где s — то или другое из двух - собственных значений ?1/2 спинового
оператора © и а — один из спиновых векторов, определенных в уравне-
уравнениях A.6.44). Поэтому если мы имеем функцию Гамильтона (нереля-
(нерелятивистскую), которая содержит оператор спина B, так же как и р и q,
а также и время, то гибридный вектор волновой функции и спина имеет
248 Гл. 2. Уравнения полей
вид Ф = ф+ (| q, t) а (Л/2) -J- ф_ (| д, /) а (— Л/2) и уравнение принимает" вид
что соответствует уравнению B.6.45). Среднее значение величины
#?> 95 @) Для состояния, обозначенного через Ф, равно тогда
где часть оператора, связанная с S, действует на спиновые векторы а,
а дифференциальные операторы действуют на волновую функцию ф.
Но это решение все еще не дает нам волновой функции (для частицы),
которая содержала бы спин и была, бы релятивистской. Чтобы достигнуть
этого, мы обратимся к спинорным операторам, рассмотренным в § 1.7.
Единичные векторы <s1, ..., <j4, определенные в уравнении A.7.17), дают
операторы, которые ведут себя подобно компонентам четырехмерного
вектора. Они действуют на векторы состояния е, которые имеют только
два различных направления: одно соответствует z —компоненте спина,
равной Л/2, другое—компоненте, равной —(Л/2) (направление оси z про-
произвольно). Возникает мысль, что для получения волнового уравнения,
инвариантного относительно преобразования Лоренца и содержащего спин,
необходимо составить скалярное произведение четырехмерного вектора
Рху Ру> Pi* Pilc— —E/c на четырехмерный векторный спиновый оператор.
Так как скалярное произведение двух четырехмерных векторов является
инвариантом преобразования Лоренца, мы получим таким образом волновое
уравнение, которое содержит первую производную по времени [как
л уравнении B.6.45), но не в B.6.51)] и которое является также
релятивистским [как уравнение B.6.51), но не B.6.45)]. Мы можем
надеяться с помощью такого уравнения составить уравнение неразрыв-
неразрывности так, чтобы можно было определить плотность заряда и тока [как
мы это сделали в формуле B.6.47) для решений уравнений B.6.45)].
Простейшей формой такого уравнения является та, в которой резуль-
результат действия скалярного произведения четырехмерных векторов сир
на спинор е приравнен произведению постоянной' на е; для волновой
функции Ф, равной, как и раньше, сумме двух функций положения,
умноженных на два спиновых вектора, мы должны иметь
д . а т.,,
так как <J4 = 9 и Е для волновой функции заменяется через— (Л/г) (d/dt).
Трудность заключается только в том, что вектор <j=(<j1, <j2, <J3) является
аксиальным вектором (см. стр. 106), в то время как градиент есть истин-
истинный вектор, так что величина, стоящая в скобках в правой части
уравнения, будет псевдоскаляром (см. стр. 22), меняющим знак при
перемене ориентации координат. Чрезвычайно трудно видеть, какую
основную постоянную мы могли бы найти так, чтобы она была псевдо-
псевдоскаляром; в самом деле, это настолько трудно, что мы вынуждены искать
менее простую форму, которая позволила бы обойтись без псевдоскаляра.
Такая менее простая форма состоит из пары уравнений
(<;.p)e=[a + |-]f; (a-p) f = [b +^j e,
где е и f — различные векторы состояния. Исключая f и пользуясь
задачей 1.33, мы обнаруживаем, что Ь= —а; а тогда может быть настоя-
настоящим скаляром, а не псевдоскаляром, и е отлично от f. Любопытно
2.6. Квантовая механика 249
отметить, что эта пара уравнении аналогична уравнениям электромаг-
электромагнитного поля в свободном пространстве
rotH = ^-; rotE= 5-;
е ft ' с dt '
здесь опять-таки мы не могли бы описать электромагнитное поле с по-
помощью только одного вектора (скажем Е), пользуясь вихревым опера-
оператором в одной части равенства и производной по времени —в другой.
Действительно, если попробовать рассмотреть уравнение
rotE = a^-,
то вихревой оператор меняет знак при переходе от правой к левой системе
координат, в то время как d/dt знака не меняет. Поэтому а должно
было бы быть псевдоскаляром, что было бы истинным бедствием для
электромагнетизма, как и в случае волнового уравнения для е.
Величины е и f можно считать векторами одного и того же спино-
спинового пространства, связанного с приведенными выше уравнениями так же,
как мы считаем Е и Н векторами одного и того же трехмерного про-
пространства. Но так как е и f — независимые векторы (в том же смысле, что
и Е и Н) и так как спиновое пространство не является настолько
«физическим», как трехмерное пространство, то обычно рассматривают f
как вектор другого спинового пространства, перпендикулярного к про-
пространству, в котором находится е. Другими словами, мы составляем
четырехмерное спиновое пространство со взаимно-перпендикулярными
единичными векторами ех, е2, е3, е4 и обеспечиваем независимость векто-
векторов е и f друг от друга тем, что вектор е считаем комбинацией е1 и е2,
а вектор f — комбинацией е3 и е4.
При такой интерпретации переход от е к f является вращением
из одного подпространства в другое; это вращение может быть пред-
представлено оператором р таким, что p-e = f и р• f = e. Аналогичным образом
замена а на (— а) в приведенной выше паре уравнений может быть
выражена в операторной форме с помощью оператора р0 такого, чтор0е = е
и pof = —f. С помощью этих представлений два уравнения, написанные
выше, могут быть объединены теперь в одно уравнение
р. (в.р) е = [ - роа + (Е/с)]а, B.6.52)
где е стоит вместо е или f.
Мы теперь должны распространить наши операторные определения
спинового оператора а на четырехмерное пространство; эти определения
вместе с детализированными определениями р, р0 и а = р-а имеют вид
О2е3 = е3, а_е4=—е4,
рео = е,, ре4 = е2,
* S г * B.6.53)
еЗ> Г0с4 — C4>
= ie2, «„е4= — ie13
eze1 = es, e2e2= e4, аге3 = е1, a?e4= e2.
Заметим, что оператор p перестановочен с операторами ах, ау, az, ax, ау,
az, но что рРо + РоР —0- Оператор р0 поэтому перестановочен с операто-
°zei =
ре1 = .
Poei =
ei>
ei,
= »e4,
<j2e.
pe2
Те
2 = —
= e4,
s = e2,
e2,
i
(
ie3
250
Гл. 2. Уравнения полей
рами с, но не перестановочен с а. В матричной форме эти операторы
имеют вид
а =
z
4 0 О 0^
0 1 0 0
0 0-1 0
,0 0 0-1,
'0 0 0 -г'
0 0 г 0
о -г о о
J 0 0 0,
«/=
0 10 0
Л 0 0 Оу
¦О 0 1 0N
0 0 0-1
1 0 0 0
iO -i 0 Оу
при этом, начиная отсюда, символы а0 и р0 мы будем считать взаимо-
взаимозаменяемыми.
Операторное уравнение B.6.52), действующее на некоторый вектор е,
являющийся комбинацией единичных четырехмерных векторов elf е2, е3,
е4, мы можем составить с помощью этих операторов следующим образом:
или
1«хР* + ayPv + azPz + Роя] • е = (Е/с) е. B.6.54)
Мы должны теперь «возвести в квадрат» это уравнение, чтобы получить
форму его, аналогичную форме B.6.49).
Уравнение Дирака. Если электромагнитное поле равно нулю, уравне-
уравнение B.6.49) принимает вид
Взяв уравнение B.6.54) и возведя в квадрат операторы в обеих частях
^и помня о том. что ахау не равно ауах и т. д.), получаем
Чтобы это уравнение соответствовало уравнению B.6.49) в написанной
выше формуле, должно быть
= «J =
«I = «
«" = р; = 1; ахау + ауах = ... = azP
o +
= 0 B.6.55)
а = тс.
Изучение уравнений B.6.53) показывает, что операторы, определенные
там, удовлетворяют требованиям B.6.55), так что мы, наконец, получили
релятивистское уравнение для отдельной частицы массы т, которое
содержит член с первой степенью оператора, соответствующего Е (или
2.6. Квантовая механика 251
оператора pt). Для получения этого уравнения мы были вынуждены рас-
расширить наше «спиновое пространство» от двух до четырех измерений.
Два из этих состояний спина (elt е2) соответствуют члену + тс2 в вы-
выражении полной энергии, а другие два соответствуют члену (— тс2),
отрицательной энергии. Мы знаем теперь, что состояние с отрицательной
энергией связано с позитроном—частицей, имеющей заряд, противопо-
противоположный заряду электрона, но одинаковую с ним массу.
Волновое уравнение для отдельной частицы, имеющей заряд е,
и массу т, в электромагнитном поле является уравнением для комби-
комбинации волновой функции и спинового вектора
Ф = 41е1 + ф2е2 + <фяе» + №ь _ „
_ (Z.b.ob)
1+№:
где ф — функции от х, у, z и t, a e — ортогональные единичные векторы
в спиновом пространстве. Уравнение, называемое уравнением Дирака,
имеет вид
-А^ч/, B.6.57)
где оператор а представляет собой вектор с компонентами <хх, <ху, а,г
и где а0 = р0. Операторы подчиняются правилам, содержащимся в равен-
равенствах B.6.53) и B.6.55). Уравнение для Ф получается из B.6.57) при
перемене знаков у всех членов, содержащих i.
Мы должны теперь посмотреть, приводят ли все эти изыскания
к уравнению, допускающему разумные выражения для плотности заряда
и тока. Представляется целесообразным за плотность заряда принять
выражение
р = еФФ = е [| фх |» +1 ф, |» + | Ф» |» +1 Ф41; B-6.58)
рассуждая, как прежде, умножая уравнение для Ф на Ф, а уравнение
для Ф—на Ч* и вычитая результаты, мы получаем
— (d/dt) (ФФ) = с [Фа-grad Ф + Фа grad Ф] = с div (ФаФ).
Поэтому вектор с компонентами
се (Фажф) = се [ф1ф4 + ф2фз + ФзФг + ф4<Ы = Jx<
се (Фа^Ф) = — ice [фхф4 — ф2ф3 + ФзФг — Ф4Ф1] = Jy B.6.59)
се (Фа2Ф) = се [^фз — Ф2Ф4 ~ Ф3Ф1 — ФйФг!:= ^г
является вектором плотности тока J.
Интересно отметить, что, в то время как плотность импульса
частицы равна Фрф = (h/i) ф grad Ф, плотность скорости оказывается
равной сФаФ. Это может быть показано другим способом. Подставим
в уравнение Гамильтона дН/dp = q = и выражение B.6.50) (для простоты
мы не включаем поля и предполагаем, что ось х направлена вдоль р
или и). .Тогда
cd mu
U = г ИЛИ р == -
(м/сJ
252 Гл. 2. Уравнения полей
[см. уравнение A.7.5)] и
Н= , w°2 = ц-р + гас8УЧ-(и/сJ.
Сравнивая это классическое выражение полной энергии свободной
частицы (релятивистское) с уравнением B.6.54), мы видим, что при
переходе к уравнению Дирака вместо скорости частицы и ставится
векторный оператор са, а вместо |/l —(м/сJ —оператор а0.
Преобразования операторов а, спинового вектора е и волновой
функции при лоренцовом вращении пространства—времени или при вра-
вращении пространства могут быть выполнены на основе изложенного
в § 1.7. Например, если преобразование соответствует относительной
скорости K = cth6 вдоль оси х, величины р и А преобразуются по пра-
правилам, справедливым для четырехмерных векторов
Спиновые векторы е преобразуются согласно формуле е'=де, где
так как а|=1. Сопряженный оператор д*, такой, что е = д*-е', равен
в этом случае д. Поэтому новая волновая функция имеет вид
ЦТ = йц/ = ch F/2) [ф1в1 + ф2е2 + ф3е3 + ф4е4] +
+ sh (G/2) [ф4в1 + ф3е2 + 4>2е3 + Фа! • B.6.60)
Операторы а преобразуются по формуле g*-a-g = a'. Для симметрии мы
полагаем а, = ^/с [см. уравнение A.7.17)], где Q~- идемфактор. Имеем
тогда
а'х = ах ch б + ca, sh 6,
«у = еОа*/2 а^в^/2 = е6аж/2 е-8аж/2 ^ = а^
«z = «2; ао = ао>
так что (ах, а2, а3, а4) преобразуются подобно четырехмерному вектору
Поэтому скалярное произведение а на четырехмерный вектор импульса
является инвариантом преобразования Лоренца, так что
2 бХ8^= 2 «&?•
Поэтому уравнение в нештрихованных координатах можно преобразовать
следующим образом:
xyzt
= 6
при этом получается уравнение в штрихованных координатах
2.6. Квантовая механика 253
Для вращения в пространстве на угол 6 около оси х оператор враще-
вращения для величин е и а выражается достаточно хорошими равенствами
Q = e—Gava^2, g* = e6aW2 B.6.61)
и уравнения преобразования имеют вид
Pi = Pt, Px = Px, py = pvcosB+pzsmB,
Pz = — PySinQ-т p'zcosQ, e'=ge, a'=g*ag.
Более сложные вращения всегда могут быть разложены на несколько
вращений рассмотренных здесь типов; соответствующие операторы враще-
вращения g являются произведениями отдельных g для составляющих простых
вращений, взятых в надлежащем порядке.
Полные момент количества движения. В качестве упражнения
на применение операторов а и а мы покажем, что в случае отсутствия
электромагнитного поля полный момент количества движения частицы
не является только механическим моментом 9JJ [см. уравнение A.6.42)],
но представляет собой комбинацию момента $Щ и спинового вектора о.
Другими словами, мы должны включить спин частицы для того, чтобы
получить постоянную движения, которую мы называем полным моментом
количества движения. На основании уравнения B.6.35) мы видим, что
для постоянной движения, изображаемой оператором 51, мы должны иметь
где JQ — оператор Гамильтона.
В данном случае., при равенстве нулю потенциалов Аиу, мы имеем
для оператора Гамильтона, согласно уравнению B.6.57),
Q = ao/nc2 + с (ву>, + aj>y + <xzpz).
Оператор для компоненты вдоль оси z- механического момента количе-
количества движения имеет вид 9ftz=j:pv — typx. Составим коммутатор J§UJi2 —5Щ2^,
чтобы показать, что он не равен нулю. Здесь операторы а перестановочны
с операторами р и коордиватами, операторы р перестановочны друг с дру-
другом, так что в J§ только член с ахрх не перестановочен с первым членом
ffiz и только член с «upv не перестановочен со вторым членом 9Л7, так что
№ - ШЛ = - саурх (ад - \)\)у) + caxpu (ря? - ЕРя).
Но рхх — xpx = (h/i) и т. д., и наше выражение оказывается] равным
что, конечно,' не равно нулю, так что 5ЭД, не является постоянной дви-
движения.
Пользуясь правилами B.6.53) применения операторов, мы можем
показать, что [сравните с уравнениями A.6.44)]
(ахJ = (cj2 = (о2J = 1, axav = - avax = iaz,
\ х/ \ у/ \ z/ * х у ух ъг -су ^ АО\
<^2=-<*г<гж= -йу, ay<jz=-azay = i<jx.
Кроме того, так как оператор р перестановочен с операторами а и так
как a = pa, мы можем получить другие уравнения
»*«* = ахах = Р. «*°z = - az«x = iay, «yaz = - az«y = iax и т. д.
Следовательно, мы можем показать, что
254 Гл. 2. Уравнения полей
Сравнивая между собой коммутаторы для 5Щ2 и а,, мы видим, что комби-
комбинация [5ЭД2 + (ft/2) az] перестановочна с Q и, таким образом, является
постоянной движения. Это верно также для компонент по осям х та. у.
Таким образом, полный момент количества движения, являющийся
постоянной движения, равен сумме механического (орбитального) момента 9J}
и произведения Ь/2 на спиновой вектор о.
Волновая функция свободного поля. В качестве другого примера мы
получим волновую функцию, когда отсутствует внешнее поле. Для слу-
случая свободного поля уравнение Дирака B.6.57) принимает вид
Решением этого уравнения является
4f^{A1e1 + A^ + A3ea + Aiei]e^nv-r-Et)j B.6.63)
где А — численные коэффициенты, г = xi -\- г/j -(- zk — радиус-вектор, вектор
р = pxi + pyj -\-/>2k — классический вектор импульса с компонентами рх,
ру, pz, которые являются постоянными, а не операторами; число Е есть
величина энергии электрона для состояния, обозначенного через Ф.
Подставив это в уравнение Дирака, выполнив дифференцирования
и спинорные операции в соответствии с равенствами B.6.53), мы оконча-
окончательно получим (не уменьшая общности, мы положили pz = p, Рх = Ру=*®)
Отсюда следует, что четыре коэффициента при векторах равны нулю; это
приводит к четырем однородным уравнениям для четырех коэффициен-
коэффициентов А: двум, содержащим Аг и А3, и двум, содержащим А2 и At. Обе
пары могут быть решены, если выполняется равенство Е2 = т?с*-\-с2р2.
Таким образом, имеем четыре решения: два соответствуют значению
энергии
Е= -mc2Vl-}-{p/mcJ
и имеют вид
»1 = С [ -рех + A + у) е3] е , ^
2 = С [Ре2 + A+ 7) е4] <«/»> №+™*«)
другие два соответствуют значению энергии
Е = + /?гс2у р-0 [ /пс2 +1 (р*/т) ] ,
имеют вид
Ч*з = с [A + Y) ех +
Ч*4 = С [A + у) е2 -
где р = (р/тс) и Y = T/A1 + P2> а С — нормирующая постоянная. Функции Фг
и Ф3 соответствуют спину Л<тг/2, равному +%/2 (так как огФ1 = Ф1
и т. д.), а Ф2 и Ф4 соответствуют спину —й/2.
Резюме. В этой главе мы постарались наметить основные связи
между различными явлениями в классической и квантовой физике и раз-
различными видами полей, рассмотренными в гл. 1. Эту связь обычно можно
представить, с известной степенью приближения, с помощью дифферен-
дифференциальных уравнений, задающих поведение от точки к точке поля, кото-
2.6. Квантовая механика 255
рое должно описывать частное физическое явление. В классической
физике мы обнаружили, что надо было провести осреднение атомистиче-
атомистических дискретностей; в квантовой физике мы нашли, что принцип неопре-
неопределенности мешает нашему «изучению» непрерывной волновой функции,
являющейся корнем квадратным из вероятности; оказалось, что разрыв-
разрывные детали траекторий элементарных частиц невозможно измерять
и предсказывать. В обоих случаях мы пришли к непрерывному полю —
скалярному, векторному или аффинорному, подчиненному дифференциаль-
дифференциальному уравнению с частными производными и заданному однозначно
посредством некоторой совокупности граничных условий (или начальных
условий, или тех и других вместе).
Мы видели, что одни и те же поля и одни и те же дифференциаль-
дифференциальные уравнения оказываются в связи со многими и различными физи-
физическими явлениями. Мы нашли, например, что скалярное поле, удовле-
удовлетворяющее уравнению Лапласа, может представлять или электрическое
поле вблизи группы зарядов, или плотность диффундирующей жидкости
в стационарных условиях, или потенциал скорости установившегося
течения несжимаемой жидкости, или гравитационный потенциал вблизи
группы материальных тел и т. д. С точки зрения этой книги этот недо-
недостаток математической оригинальности со стороны природы дает большую
экономию сил и времени. Занимаясь изучением решений одного уравне-
уравнения, мы одновременно будем решать несколько дюжин задач из различ-
различных областей физики.
Мы не углублялись в подробности относительно физической стороны
различных примеров, рассмотренных в этой главе; эта книга в основном
занимается решением уравнений, если они уже получены. Например,
в области квантовой механики мы преодолели искушение выйти за рамки
беглого наброска новой точки зрения в динамике. Изложение достаточно
только для того, чтобы позже, при изучении решений уравнений Шрёдин-
гера и Дирака, можно было понять физический смысл решений. Превы-
Превышение этого сделало бы данный параграф учебником до квантовой меха-
механике, что было бы совершенно излишним.
Для подробного изучения затронутых физических явлений пригодны
другие книги, посвященные различным отделам физики. .
Нельзя отрицать того, что на рассмотрение уравнений квантовой
механики затрачено времени больше, чем на уравнения классических
полей. Эти более новые уравнения менее привычны, и, таким образом,
они дают возможность показать, какие способы рассуждений должны
быть использованы при выводе новых уравнений полей для описания
новых явлений. Классические уравнения полей выдержали проверку
нескольких поколений ученых, и логическая структура связи с «действи-
«действительностью» сделалась «второй природой» физиков. В квантовой механике
мы еше не закончили полностью процесс рационализации, преобразующий
«работающие» непривычные уравнения в логически обоснованную теорию,
«очевидную для каждого».
Новое уравнение для описания нового явления редко выводится
впервые с помощью строгих логических рассуждений из хорошо извест-
известных физических фактов; достаточно строгий вывод уравнения удается
обычно получить только тогда, когда теория становится «очевидной».
Первое получение уравнения обычно приходит менее дедуктивным путем,
с помощью аналогий, «работы назад», а также постоянного применения
современного аналога бритвы Оккама1). В уравнении Дирака, например,
*) «Бритвой Оккама» называют изречение этого философа: «Essentia non stmt
multiplicanda praeter necessitatem («Сущности не должны быть увеличиваемы в числе
без необходимости»). —Прим. ред.
256 Гл. 2. Уравнения полей
мы придерживались определенной общей формы уравнения, так как было
вероятно, что уравнение должно быть релятивистски инвариантным
и мы искали простейшее уравнение, которое привело бы нас к «разумным»
{т. е. не чрезмерно сложным) выражениям для заряда, тока и других
измеримых количеств. Результат мог показаться на первый взгляд
не очень простым, но читателю достаточно немного дней исследования
{или чтения старых номеров журналов, выпущенных в тот период
когда выводилось уравнение Дирака), чтобы убедиться в том, что много
легче составить более сложные уравнения, чем найти уравнение более
простое.
Среди общих принципов, которые можно использовать для того,
чтобы наметить направление поисков новых уравнений, одним из наибо-
наиболее важных является требование инвариантности, в частности инва-
инвариантности относительно преобразования Лоренца. Но существуют
и другие пути. Например, обычно сначала ищут линейные уравнения;
часто применяют оператор Лапласа.
Когда уравнение составлено, необходимо исследовать все входящие
в него величины, чтобы убедиться в том, достаточно ли они «соответ-
«соответствуют» различным физическим величинам. Обычно здесь встречается,
например, плотность энергии; тогда соответствующая выбранная величина
не должна обладать неприятным свойством становиться где-либо и когда-
либо отрицательной. В качестве путеводной нити при получении урав-
уравнения Дирака мы выбрали выражения для плотности тока и плотности
•чаряда, а также требование, чтобы эти выражения удовлетворяли урав-
уравнению неразрывности. Формальным аппаратом для получения этих вспо-
вспомогательных величин является вариационный метод, который мы рас-
рассмотрим в ближайшей главе. Когда эти величины обоснованы, можно
решить, являются ли они слишком сложными или нет.
Другой полезный способ испытать уже составленное уравнение
состоит в том, чтобы найти другое физическое явление, к которому можно
было бы применить то же самое уравнение. Свойство решений уравнения
Клейна — Гордона могут быть изучены с помощью струны в резиновой
оболочке (см. стр. 139), которая удовлетворяет тому же самому уравне-
уравнению и которую легче представить себе, чем волновую функцию, так как
движения струды достаточно хорошо известны. Аналогии этого вида
встречаются в теоретической физике повсюду и приводят к своего рода
перекрестному опылению, чрезвычайно полезному. Раннее изучение
переменного электрического тока было значительно облегчено благодаря
аналогии с более знакомым механическим осциллятором. Теперь, когда
«каждый слыхал» про переменные токи, мы склонны и при изучении
других видов колебательных и волновых движений (даже механического
осциллятора) говорить об импедансах, емкостях и т. д.
В ближайшей главе мы подробно рассмотрим аналогию между пове-
поведением поля и вариационными принципами классической динамики, раз-
развитыми Гамильтоном. Мы найдем, что эта аналогия является полезным
унифицирующим фактором при изучении всех уравнений, рассмотренных
в этой главе (а также и других).
Задачи к главе 2
2.1. Мембрана натянута на одной стороне герметического сосуда, так
что на нее действуют одновременно и ее натяжение Т и избыток давле-
давления воздуха внутри сосуда.
Задачи к главе 2 257
Показать, что
если \Р обозначает отклонение мембраны от положения равновесия; р, V
являются плотностью и объемом воздуха в сосуде в состоянии равновесия,
ас — скорость звука в воздухе.
Показать, что уравнение движения мембраны имеет поэтому вид
где - v- = Т/а, Г —натяжение, а с —масса единицы площади мембраны.
Какие допущения сделаны при выводе этого уравнения?
2.2. Пусть бесконечная упругая среда обладает пьезоэлектрическими
свойствами относительно сжатия в направлении оси х и электрического
поля в направлении оси у (при смещении s в направлении оси х электри-
электрическая напряженность Е и вектор электрической индукции D направлены
по оси у). Диэлектрическая поляризация Р, также в направлении у,
связана с D и Е обычным уравнением D = E-\ ~P, а с компонентой
.напряжения Х=ТХХ и Е — уравнением связи Р = ЬХ-1у^Е, где % — диэле-
диэлектрическая восприимчивость, а о — пьезоэлектрическая постоянная. С дру-
другой стороны, деформация Sxx = и связана с напряжением и электрической
напряженностью уравнением и = сХ-\-ЪЕ, где а —величина, обратная
модулю упругости. С помощью уравнений упругости и уравнений Максвелла
составить два совокупных уравнения для движения волн сжатия вдоль
оси х. Показать, что возможны две электроупругие волны; одна, движу-
движущаяся со скоростью несколько меньшей, чем волны безвихревого расши-
расширения (когда значение 8 равно нулю), и другая —со скоростью несколько
большей, чем скорость чистых электромагнитных волн.
2.3. Во время прохождения звуковой волны через вещество темпе-
температура областей сжатия выше средней температуры, в то время как
в областях расширения температура ниже средней. Эта разность темпе-
температур вызывает поток тепла от одной части вещества к другой.
а. Показать, что уравнения потока тепла и распространения звука
имеют вид
дТ/dt = {dTo/dPo)s (dp/dt) + (k/cvPo) V2Т,
d29/dt2 = фРо/дро)т V2P + (дРо/дТо)? V27\
где индекс нуль употребляется для обозначения значений при равновесии.
б. Предположим, что Тир распространяются как плоские волны
Т = A exp[i (kx — wt)]; p = ?exp[i (kx — Ы)].
Показать, что к и со связаны равенством
О = i (к/ср?оШ) 1{дРо/дРо)тк* - ш2] - {о,2 - /с2 1(дРо/д?о)т + (дТо/дРо)8 (дРо/дТо)9]}.
Определить скорость распространения волн при k/cpPow <C 1, при А/сррош>1.
Рассмотреть распространение волн при к/срРошса 1.
2.4. Проводящая жидкость (электропроводность о, проницаемость fi)
при движении вызывает магнитное поле, которое в свою очередь влияет
на движение жидкости. Показать, что уравнения, связывающие скорость v
17 ф. м. Морс и Г. Фешбах
258 Гл. 2. Уравнения полей
и магнитную индукцию В, имеют вид
дЪ _
"аГ=го1(
2.5. При .растворении в соответствующем растворителе многие соли
расщепляются на положительные и отрицательные ионы. Под влиянием
электрического поля они диффундируют. Показать, что уравнение, описы-
описывающее движение положительных ионов, в предположении, что они дви-
движутся в вязкой среде с их установившейся скоростью, имеет вид
ocjdt = А\\ЧХ -f- BXQ div (cx grad <p),
где с± — концентрация, A\ — постоянная диффузии, ^ — отношение устано-
установившейся скорости к приложенной силе, (? —ионный заряд и 9 — электро-
электростатический потенциал. Показать, что <j> удовлетворяет уравнению
где F — постоянная Фарадеяц
2.6. Частицы микроскопических размеров находятся в состоянии беспо<
рядочного движения, называемого броуновски л движением, вызываемого
молекулярными столкновениями. Пусть количество частиц, имеющих
в момент t0 положение между ж0 и xo-\-dxo и скорости между иош vo-\-dvo,
равно /(ж0, о0, to)dxodvo. Пусть число, указывающее, какая часть этих
частиц в момент т находилась в области между х и x + dx и имела ско-
скорости между о и o + do, равно w (&х, До, ъ\х0, v0, to)dxdv, где Ах = х — х0;
bv = v — v0, x = t — t0.
а. Показать, что
со
^ w (Дж, До, х | х0, o0J t0) f (х0, о0, t0) dx0 dv0.
—со —со
б. Показать, что для малых х, Да; и До
df(*,v,t0) _ д /^/Д^ д П~?>\ . 1
{ ) )^
f
dt0 ~~дх{ т ) dv\ т )^ г\дх*\ т
и2 /• f&zke \ д2 //Дг;2
где
со со
— ¦— г г
Дж = Дж (ж, о, t, г) = \ \ Джю (Дж, До, х |ж, о,
—со —со
с соответствующими определениями других средних величин.
в. Если частицы движутся в вязкой жидкости и если молекулярные
столкновения беспорядочны, тоДо= —аох и До2 = Лх, где а и А — постоян-
постоянные. Показать, что в пределе при малых t
г. Показать, что в условиях стационарного состояния
Задачи к главе 2 259
Показать, что среднее значение п-й степени скорости, определенное
равенством
vn= \ { tPf{x, v)dxdv,
удовлетворяет дифференциальному уравнению
-^- = — navn + -j An (n — 1) vn~z.
2.7. а. Пусть два оператора а и а* подчиняются следующему пра-
правилу перестановочности:
аа* — а*а = 1.
Показать, что собственными значениями оператора а*а являются 0,1, 2, 3,....
Если соответствующими состояниями будут еп, показать, что
б. Пусть два оператора а и а* подчиняются следующему правилу
перестановочности:
пусть также аа = 0, о*а* = 0. Показать, что собственными значениями
оператора а*й будут только 0 и 1. Если е0 и ех будут соответствующими
состояниями, показать, что
о*ео = е1? а*еа = 0, аео = 0, ое1=-е0.
2.8. Пусть электрон движется в кулоновом поле ядра, имеющего
заряд Z.
а. Полагая
доказать, что соответствующий сопряженный импульс рт равен
pr = (l/r)(r.p-ift).
б. Показать, что оператор Гамильтона для электрона может быть
записан следующим образом:
2m Pr + 2mr2
2
где S является оператором момента количества движения.
в. Определить значения энергии Еп электрона, имеющего данный момент
количества движения/, пользуясь следующим методом. Найти оператор % (г)
такой, что
Показать отсюда, что Еп1 не зависит от I, что для данного Еп1 сущест-
существует максимум величины I, который мы обозначим через и —1. Выра-
Выразить Еп1 через п.
2.9. Показать, что при преобразовании
е = ехр (— i%t/h) ?
17*
260 Гл. 2. Уравнения полей
уравнение Шредингера
принимает вид
где
& (t) = exp (i&f/h) & ехр (-
Показать, что
1 = Ш0,
где
a f0 не зависит от времени. Связать f0 с решениями уравнения
2.10. Разложить решение е волнового уравнения Дирака следующим
образом:
e = f + g; f = y(l + eo)e; g =-|-A - а0) е.
Показать, что
f*.g=^O
и что
(Е + eV + тс2) ( = с [а • (р + eA/c)]g,
(E + eV + mc2)g= -с [e-(p + eA/c)]f.
Показать для состояний с положительной энергией при малых еА и eV
сравнительно с тсг, что g*-g<Cf**f-
2.11. Определить совокупность четырех состояний ej, которые удовле-
удовлетворяют уравнению Дирака для Неподвижной частицы
(aomcf) ej = ?ое{.
Показать, что четыре решения уравнений Дирака для частицы с импуль-
импульсом р имеют вид
[с(а-р) + ао(/?гсг + |?|)]е{,
где
Стандартные формы некоторых уравнений с частными
производными теоретической физики
Номера уравнений
Уравнение Лапласа V2t[> = 0. A.1.4), B.3.6)
Векторная форма rot rot A = 0; div A = 0.
Уравнение Пуассона У2ф = —4яр. A.1.5), B.1.2) B.5.2)
Векторная форма rot rot A = 4irJ; divA = 0. B.5.7)
Стандартные формы некоторых уравнений 261
Уравнение Гельмгольца V24> -f- А2ф = 0. B.1.10)
Векторная форма rot rot A — А2 А =- 0; div А = 0.
Волновое уравнение П"Ф = V24>--i-^- = 0. B.1.9), B.2.2)
Векторная форма rot rot A + -^-дд" = ®>
divA = 0. B.2.3),B.5.15)
Уравнение диффузии V24>= —г" у-• B-4.4)
Векторная форма rot rot А -|—^—- = 0;
divA = 0. B.3.19)
Уравнение Клейна —Гордона ?24> = р.2ф. B.1.27)
Векторная форма rot rot A -}- -^ -™- + р-2А = 0;
divA = 0 (Уравнение Прока). B.5.37)
Уравнения Максвелла divB = 0; divD = 47tp; rotH= — -^-4- —4tcJ;
Cut С
rot E = - - ~ ; В = pH; D = sE. B.5.11)
С ut
Уравнения для электромагнитных потенциалов
= -4«P/s, Q2A= -4«p.J/c,
B = rotA, E=-grad?-»-~, divA=-^^- B.5.15)
(относительно видов этих уравнений при других калибровках см. стр. 201
и 315).
Уравнение упругих волн (изотропная среда)
s. B.2.1)
Уравнение вязкой жидкости
P^ = pv-(Vv) = V-[-(p + YdivvK + 1,(Vv) + 1J(vV)], B.3.14)
р -Q- = — grad р— f -о- т] + ^- ) div v + -^ pv2 — т, rot rot v + pv x rot v,
Уравнение Шредингера для одной частицы с массой тп при потенциале F
где Х = — к) —у.
^—V2 ф+ ^ф = г'й--^-, | ф|2 —плотность вероятности. B.6.38)
Уравнение Дирака для электрона в электромагнитном поле
V0; B.6.57)
4
= 2 епФп> Ч**-Ч* — плотность вероятности.
n=i
262 Гл. 2. Уравнения полей
ЛИТЕРАТУРА
Сочинения общего характера, затрагивающие материал этой главы:
Вебстер А. и Сеге Г., Дифференциальные уравнения в частных производных
математической физики, ч. 1—2, ГТТИ, М., 1933—1934.
Зоммерфельд А., Дифференциальные уравнения в частных производных физики,
Изд. иностр. лит., М., 1950.
Ландау Л., Лифшиц Е., Теория поля, ГТТИ, М., 1948.
Минусинский Я., Сикорский Р., Элементарная теория обобщенных
функций A вып.), Изд. иностр. лит., М., 1958.
Петровский И. Г., Лекции об уравнениях с частными производными, Гостех-
издат, М., 1950.
Рэлей Дне., Теория звука, Гостехиздат, М., 1955.
Соболев С. Л., Уравнения математической физики, Гостехиздат, М., 1954.
Тихонов А. Н., Самарский А. А., Уравнения математической физики, Гостех-
Гостехиздат, 1953.
Франк Ф. Мизес Р., Дифференциальные и интегральные уравнения математи-
математической физики, ч. 2, ОНТИ, М., 1937.
J о о s G., Lehrbuch der theoretischen Physik, Leipzig, 1956.
Lindsay R. В., MargenauH., Foundations of Physics, New York, 1936.
Margenau H., Murphy G. M., Mathematics of Physics and Chemistry, New York,
1943.
Slater I. C, Frank N. H.f Introduction to Theoretical Physics, New Vork, 1933.
Schaeffer C, Eiufiihrung in die theoretische Physik, 3 v. Berlin, 1937.
Дополнительная литература, представляющая интерес в связи с учением о коле-
колебаниях и звуке:
С о u I s о п С. А., Waves, a Mathematical Account of the Common Types of Wave
Motion, Edinburgh, 1941.
Lamb H., The Dynamical Theory of Sound, London, 1925.
Morse P. M., Vibration and Sound, New York, 1948.
Книги по теории упругости и упругим колебаниям:
Ляв А., Математическая теория упругости, ГТТИ, М., 1935.
Тимошенко С, Теория упругости, ГТТИ, М., 1934-
Brillouin L,. Les tenseurs en mechanique et en elastique, Paris, 1938.
Sokolnikoff I. S., Mathematical Theory of Elasticity, New York, 1946.
Дополнительная литература по гидродинамике и движению волн сжатия:
Зауэр Р., Введение в газовую динамику, ГТТИ, М., 1947.
Кочин Н. Е., КибельИ. А., Розе Н. В., Теоретическая гидромеханика, ч. 1,
Гостехиздат, М., 1955.
Ламб Г., Гидродинамика, ГТТИ, М., 1947.
Ландау Л. Д. и Лифшиц Е., Механика сплошных сред, Гостехиздат, М., 1954.
Chapman S., Cowling T. G., Mathematical Theory of Non-uniform Gases, Cam-
Cambridge, New York, 1939 x).
Hadamard G. S., Lemons sur la propagation des ondes et les equations de l'hydrody-
namique, Paris, 1903.
Milne-Thomson L. M., Theoretical Hydrodynamics, London, 1938.
Книги по диффузии, тепловому потоку и теории переноса:
Лоренц Г. А., Теория электронов и ее применение к явлениям света и теплового
излучения, ГТТИ, М., 1953.
Chandrasekhar S., Radiative Transfer, Oxford, New York, 1950.
Chapman S., Cowling T. G., Mathematical Theory of Non-uniform Gases, Camb-
Cambridge, New York, 1939 x).
Fowler R. H., Statistical Mechanics, Cambridge, New York, 1936.
H opf E., Mathematical Problems of Radiative Equilibrium, Cambridge, New York, 1934.
Книги по теории электромагнетизма, в особенности по основным понятиям
теории:
Стрэттон Дж. А., Теория электромагнетизма, ГТТИ, М., 1948.
Тамм И. Е., Основы теории электричества, Гостехиздат, М., 1954.
Abraham M., Becker R., Classical Theory of Electricity and Magnetism, Glas-
Glasgow, 1932.
*) Готовится к печати русское издание.— Прим. ред.
Литература 263
Van Vleck I. H., Theory of Electric and Magnetic Susceptibilities, Oxford, New
York, 1932.
Изложение основных принципов квантовой механики с различных точек зрения:
[а н-де р-Вар д е н Б., Метод теории групп в квантовой механике, Харьков, 1938.
,е Брольи Л., ^Магнитный электрон, Госуд. научно-техн. изд. Украины. Харь-
Харьков, 1936.
Дирак П., Основы квантовой механики, ГТТИ, М., 1932.
Зоммерфельд А., Волновая механика, Гостехиздат, Л. — М., 1933.
Зоммерфельд А., Строение атома и спектры, т. 2, ГИТЛЛ, М., 1956.
Кондон Е., Шорт л и Г., Теория атомных спектров, Изд. иностр. лит., М., 1949.
Ландау Л. Д. иЛифшицЕ. М., Квантовая механика, ч. 1, ГТТИ, М.—Л.,
1948.
Ш ифф Л., Квантовая механика, Изд. иностр., лит., М., 1957.
B4ohm D.. Quantum Theory, New York, 19511).
Jordan P., Anschauliche Quantentheorie, Berlin, 1936.
К e m h 1 e E. C., Fundamental Principles of Quantum Mechanics, New York, 1937.
Kramers H. A., Grundlagen der Quantentheorie, Leipzig, 1938.
J. von N e umann, Mathematische Grundlagen der Quantenmechanik, Berlin, 1932.
Готовится к печати русское издание.
ГЛАВА 3
Поля и вариационный принцип
Употребление превосходной степени прилагательных позволяет в сжа-
сжатой форме выразить общий принцип, охватывающий широкий круг явле-
явлений. Так, например, утверждения, что прямая есть кратчайшая линия,
соединяющая две точки, или что окружность есть кратчайшая линия,
охватывающая плоский участок заданной площади, с обманчивой просто-
простотой описывают определенные геометрические объекты. Говоря, что элект-
электрический ток в сети, состоящей из сопротивлений, распределяется так,
что наименьшая часть его энергии превращается в тепло, мы тем самым
даем описание постоянного тока, охватывающее множество индивидуаль-
индивидуальных случаев, не прибегая к сложному математическому аппарату (послед-
(последний, впрочем, неизбежно появляется при попытке применить этот общий
принцип к тому или иному индивидуальному случаю). Утверждение, что
некоторая физическая система эволюционирует так, что известная функ-
функция ее поведения принимает наименьшее (или наибольшее) значение,
часто оказывается как исходной точкой теоретических исследований, так
и конечным продуктом дистилляции соотношений, связывающих некоторые
явления в какой-либо обширной области физики.
Математическая формулировка принципа, содержащего «прилагатель-
«прилагательное в превосходной степени», обычно состоит в том, что интеграл от
некоторой функции, характерной для рассматриваемой системы, при
происходящей в действительности эволюции системы принимает значение
меньшее (или большее), чем при. любой другой мыслимой эволюции, под-
подчиняющейся известным, весьма общим условиям, характеризующим самое
систему. Подинтегральную функцию обозначим L; она зависит от неко-
некоторого числа переменных, характеризующих систему (координат, ампли-
амплитуд поля или других величин) и от производных этих переменных па
переменным интеграции (т. е. от скоростей или градиентов полей и т. п.).
Если переменные интеграции обозначены хг, ...,хт, переменные, харак-
характеризующие систему, фх, ... , фп, их производные 0фг/9ж8 = <prs, то интег^
рал, который требуется минимизировать, можно записать в виде
Ът
(g yl dxm.
Отыскивая минимум этого интеграла, мы можем получить диффе-
дифференциальные уравнения с частными производными, управляющие вели-
величинами ф как функциями от х, и еще целый ряд сведений. Такой метод
отыскания величин ф называется вариационным методом.
В этой главе мы сначала укажем общий прием, с помощью которого
вариационный метод приводит к уравнениям, определяющим искомые
функции ф, затем в качестве хорошо разработанного примера, показы-
показывающего пользу применения этого метода, мы более детально рассмотрим
3.1. Вариационный интеграл и уравнения Эйлера 265
вариационные принципы классической динамики; далее мы перейдем
к применению вариационного метода к исследованию различных1 полей,
с которыми мы встретимся в этой книге.
3.1. Бариационный интеграл и уравнения Эйлера
Функция L в интеграле, которому мы стремимся придать минималь-
минимальное (или максимальное) значение, называется плотностью функции
Лагранжа рассматриваемой системы. Она представляет собой функцию
от функций основных параметров системы. Так, в классической дина-
динамике основным параметром служит время, а в качестве функций выступают
координаты и скорости элементов системы в различные моменты времени,
по мере ее движения, обусловленного приложенными силами и началь-
начальными условиями. В случае поля основными параметрами являются
координаты, определяющие точки, в которых измеряется поле, а их функ-
функциями являются компоненты поля и их градиенты; эти функции опре-
определяются расположением «источников» (или зарядов) в пространстве
и граничными условиями.
Таким образом, требование, чтобы интеграл от L принимал наимень-
наименьшее (или наибольшее) значение, означает, что функции, через которые
выражена L (координаты и скорости или компоненты и градиенты),
должны быть выбраны так, чтобы интеграл C.1.1.) принимал наименьшее
(наибольшее) возможное значение. Функции <р должны быть таковы, чтобы
значение интеграла C.1.1), зависящего от этих <р и их производных д<р/дх,
было наименьшим из тех", которые он может принимать при заданных
условиях, определяемых существом задачи.
Для решения этой вариационной задачи мы сведем ее прежде всего
к системе уравнений, определяющей наилучший выбор функций <р.
Уравнения Эйлера. Но перед тем как сделать этот первый шаг, мы
должны уточнить, что именно мы понимаем под «минимизацией интег-
интеграла» и «наилучшим выбором функций». Для этого предположим, что мы
произвольным образом выбрали функции <pl7 ..., <рп параметров хг, ¦. ¦, хт.
Этот произвольный выбор определит, разумеется, функции <prs = 9<рг/9ж8
и тем самым однозначно определится значение X согласно формуле C.1.1),
Изменим теперь немного функции <р; пусть изменение функции <рг выра-
выражается в виде ег7]г, где ~г\г — произвольная функция параметров, а ег —
малая величина, не зависящая от параметров. Вместо sr7jr часто пишут
кратко 8'fr и рассматривают 6<р как произвольно малую «вариацию» функ-
функции <р. Изменения <р повлекут за собой изменения компонент <prs градиен-
градиентов. Те и другие связаны соотношениями д (егт1Г)/дхэ = згт]ге. В вариацион-
вариационных обозначениях эти соотношения имеют вид 8<prs = d(t'-pr)/dxs.
Разложив L в ряд Тейлора, мы обнаружим, что главная часть (члены
первого порядка малости) приращения интеграла X, вызванного малыми
вариациями функций <р, может быть представлена в виде
s=l
Допустим, что параметры выбраны так, что все пределы интегриро-
интегрирования постоянны и все tj обращаются в нуль при хг = аг и Ъг. Это имеет
место, в частности, тогда, когда значения аг и Ьг параметров соответст-
соответствуют каким-то физическим границам, где на <р наложены некоторые гра-
граничные условия. Обычно именно так и бывает, поэтому мы вводим здесь
266 Гл. 3. Поля и вариационный принцип
такое предположение; более общий случай, когда пределы интегрирования
переменны, будет затронут ниже.
Проинтегрировав по частям (dL/dyrs) (д1]г/дх8) по xs, мы получим
bs
b д 8L ,
as
В этом выражении первое слагаемое равно нулю, так как т]г = 0 при
xs = as жх—Ъ8. Таким образом, первая вариация ЬХ, т-. е. главная часть
приращения интеграла X, равна
™- \ ¦ ¦ • S 2 -г [Ц-2 ?(О ^ ¦ ¦ ¦ dxm. C.1.2)
°l arn r=l *=*
Если ЬХ отлично от нуля, то X не может достигать при ег = 0 ни
максимума, ни минимума. Если яке 8^ = 0 независимо от (малых) зна-
значений ег, то ьто означает, что при выбранных <р интеграл X как функ-
функция переменных гг имеет при ег = 0 либо минимум, либо максимум, либо
минимакс. Какая из этих возможностей действительно реализуется, обычно
удается выяснить из физических соображений; если же это неясно, то
можно вычислить следующий член ряда Тейлора для X (второго порядка
относительно ег) и посмотреть, положителен он, отрицателен или равен
нулю. Ради экономии места мы условимся впредь говорить «минимум»
вместо «минимум или максимум или минимакс» и «минимизировать»
вместо «отыскивать значение, соответствующее минимуму или максимуму
или минимаксу».
Мы видим, что для того, чтобы X имело экстремальное значение
(максимум или минимум), необходимо выбрать такие у, при которых
в C.1.2) коэффициенты при всех ег обращаются в нуль. Итак, для опре-
определения функций <р получается следующая система уравнений:
т
^а^=^' г-1' ••••"• (ЗЛ)
s=l
где <prs = d<frjdxs. Эти уравнения, служащие для отыскания оптималь-
оптимальных <р, называются уравнениями Эйлера. В этой главе мы будем широко
ими пользоваться.
В связи с полученными выводами следует сделать несколько общих
замечаний. Прежде всего, если описанный вариационный принцип пре-
претендует на универсальную применимость, то X должно быть инвариан-
инвариантом, а плотность функции Лагранжа L, или частное от деления L на
скалярный множитель, входящий в выражение элемента интегрирования,
должны быть инвариантны относительно преобразований координат
в пространстве параметров (переменных интегрирования). Этим обстоя-
обстоятельством мы воспользуемся в дальнейшем для отыскания других плот-
плотностей функций Лагранжа.
Другое замечание, еще более общего характера, состоит в том, что
вариационный принцип скорее способствует унификации теории, нежели
получению первых результатов в новом направлении. Обычно оказывается,
что дифференциальные уравнения, описывающие то или иное явление,
выводятся раньше, чем находится плотность функции Лагранжа L, по-
посредством которой эти уравнения можно получить только что описанным
методом. Это нисколько не умаляет роли плотности функции Лагранжа,
так как весьма полезно выяснить, какую именно физическую величину
3.1. Вариационный интеграл и уравнения Эйлера
267
следует минимизировать для того, чтобы получить дифференциальные
уравнения исследуемого явления, а сам вид вариационных уравнений
часто подсказывает плодотворные аналогии и обобщения.
Уравнения связи. Во многих случаях интеграл Лагранжа, подлежа-
подлежащий минимизации, подчиняется еще одному или нескольким условиям,
налагающим дальнейшие ограничения на независимые переменные
и параметры. В таких случаях для получения ответа мы прибегаем
к методу множителей Лагранжа.
Как работают эти множители, у
лучше всего показать на примере.
Пусть требуется найти мак-
максимум функции f(x, у). Если нет
никаких дополнительных усло-
условий, то мы решаем систему урав-
уравнений
дх
ду
C.1.4)
которая определит пару (или па-
пары) значений (ж0, у0) переменных
х и у, точку (или точки), где / Рис 3.1. Точка максимума (х0, у0) функции
имеет максимум, минимум или f(x, у), представленной линиями уровня
седловую точку (минимакс); соот- 0,1,2,.... Точка максимума (хх, уг) на
ветствующее значение функции линии у=уа(я).
есть /(х0, у0). Поскольку / пред-
представляет собой функцию двух независимых переменных, для отыскания
стационарных точек (х0, у0) нужны два уравнения C.1.4). Типичный
пример изображен на рис. 3.1, где функция / описана своими линиями
уровня.
Теперь предположим, что ищется максимум функции / (х, у) на
линии, заданной уравнением связи у = уа(%)- Эта линия, вообще говоря,
не проходит через точку (ж0, у0), поэтому искомая точка (или точки)
(Ж1» ^i) может не совпасть с (х0, у0) (см. рис. 3.1). Эти (хх, ух) можно
найти, подставив в / выражение у через х из уравнения связи. Получив
таким образом функцию / вдоль линии как функцию одного перемен-
переменного х, мы вычисляем ее производную и решаем уравнение
= 0.
C.1.5)
Искомая точка максимума будет определяться одним из корней хг урав-
уравнения C.1.5) и соответствующим значением yi = ya(xi)'
Однако эта же задача может быть решена другим методом, на пер-
первый взгляд более сложным и совершенно отличным от того, который
приводит к уравнению C.1.5). Пусть g (х, у) = 0 — уравнение связи. Введем
еще третье неизвестное X и попробуем минимизировать новую функцию
/ + Xg при соблюдении условия g = 0. При этом нам придется решать
систему уравнений
- = 0, g(x, y) = 0, C.1.6)
отыскивая одновременно значения" х, у и X.
Непосредственно не очевидно, что найденные из C.1.6) х и у совпа-
совпадают со значениями х, уа(х), найденными с помощью уравнения C.1.5).
Связь между ними станет яснее, если уравнение связи g(x, y) = 0 можно
представить в виде уа(х) — у = 0, как предполагалось выше. В этом
268
Гл. 3. Поля и вариационный принцип
случае первые два уравнения системы C.1.6) примут вид
дх ' dx ' ду
Выразив X из второго уравнения и подставив его в первое, мы получим
д/ , dyadf _0
дх ^ dx ду~ '
т. е. как раз уравнение C.1.5). Таким образом, в этом простом случае
метод множителей Лагранжа даёт тот же результат, что и первый, не-
непосредственный метод. Так будет и в других случаях. При этом если
в разобранном простом случае метод множителей более громоздок, чем
метод, основанный на применении уравнения C.1.5), то в более сложных
случаях он оказывается более простым.
В применении к задаче об отыскании минимума интеграла C.1.1)
метод множителей Лагранжа может быть сформулирован следующим
образом: пусть L (<pr, <prg, xs) (s=l, 2, . . ., т; r=l, 2, . . ., и)—плот-
и)—плотность функции Лагранжа, а уравнения связи имеют вид
bi Ът
( dyx1...dxm = Ct, C.1.7)
am
где С — постоянные (г = 1, 2, . . . , к;\ к<.т); берется вспомогательный
интеграл
bi bm
где
о,\
L' = L (9rl <prs, x.) + ^ \Gi (?,. ?r.. «.) C-1-8)
и требуемые <р и значения X отыскиваются из новых уравнений Эйлера
m
vJLf^ = ^L, C.1.9)
s=l
к которым добавляются к уравнений C.1.7). В этом случае метод мно-
множителей Лагранжа бесспорно является наиболее простым.
3.2. Принцип Гамильтона и классическая динамика
В классической динамике параметром является время t, а величи-
величинами у в функции Лагранжа служат координаты q, определяющие в каж-
каждый момент времени конфигурацию системы. Если система имеет п сте-
степеней свободы, то можно выбрать п независимых координат qlt ... , qn,
которые будут полностью определять конфигурацию системы; соответ-
соответствующие скорости будут qr = dqr/dt. Как бы ни были выбраны коор-
координаты q, кинетическая энергия инерц*иальной системы всегда предста-
представляет собой некоторую квадратичную форму относительно скоростей
3.2. Принцип Гамильтона и классическая динамика 269
коэффициенты а которой могут зависеть от координат q. Если система
консервативна (т. е. ее полная механическая энергия с течением времени
остается постоянной), то внешняя сила, действующая на систему, может
быть представлена как градиент некоторой скалярной потенциальной
функции, т. е. обобщенные силы, соответствующие координатам qr, вы-
выражаются в виде
Fr= -f-r. C.2.2)
Потенциальная энергия может явно зависеть от t, но она не является
функцией скоростей q.
В том случае, когда система консервативна, вариационный принцип,
определяющий уравнения движения, называется принципом Гамильтона
и в качестве функции Лагранжа берется кинетический потенциал (см.
стр. 221) Т — V. Получающееся уравнение
j{T-V)dt=:6 C.2.3)
to
гласит, что под действием консервативных сил при любых допустимых
начальных условиях система движется так, что разность кинетической
и потенциальной энергий имеет минимальное (или в редких слз'чаях
максимальное) среднее по времени.
Уравнения Лагранжа. Уравнения Эйлера для координат в рассма-
рассматриваемом случае:
d д(Т-У) _д(Т-У) , „ „„,
'dt—g-- dgr ' Г-1' *' •¦•' П' F-2Л>
называются уравнениями Лагранжа движения системы. Левые части этих
уравнений представляют ускорения системы, а правые части — соответ-
соответствующие силы, внешние (выведенные из потенциальной энергии V)
плюс «кинетические силы» (такие, как центробежные), обусловленные
самим движением системы. Когда эти силы не консервативны, то есть
не существует потенциальной энергии, вариационный принцип приводит
к уравнению
(О г==1
и уравнения Лагранжа принимают вид
dtdqr дЯт r V ;
Уравнения Лагранжа принадлежат к числу самых употребительных урав-
уравнений классической динамики.
Кинетическая и потенциальная энергии представляют собой скаляры,
инвариантные относительно преобразований координат; следовательно, они
могут быть выражены через любые обобщенные координаты, и в любой
системе таких координат уравнения Лагранжа будут иметь одинаковую
форму. В любом случае величина
А(Г_У) = ^=Р,
dqr dgr
270 Гл. 3. Поля и вариационный принцип
называется r-м импульсом. Таким образом, уравнения Лагранжа можно
представить в виде
— -д— в случае консервативной системы,
Fr в общем случае.
Если в качестве q мы возьмем прямоугольные координаты, то Т
будет зависеть лишь от q и не будет зависеть от q, и уравнения Лагранжа
сведутся к обычным уравнениям Ньютона
-г, (импульс) = сила.
Таким образом, принцип Гамильтона в простой инвариантной форме
охватывает все уравнения классической динамики.
Энергия и функция Гамильтона. В том случае, когда система кон-
консервативна, функцией координат и импульсов, сохраняющей постоянное
значение при движении системы, является полная энергия Е системы —
сумма кинетической и потенциальной энергий.
Эха последняя, выраженная через координаты q и импульсы р, назы-
называется функцией Гамильтона (гамильтонианом) системы и обозначается Н.
Так как функция Лагранжа L равна Т — V, а полная энергия Е — Т 4- V,
то E — 2T — L. Поэтому уравнение, к которому приводит вариационный
принцип, может быть записано в форме 8 \ B71 — E)dt = 0, а отсюда можно
получить уравнения, связывающие гамильтонову функцию со скоростями
и ускорениями. Хотя при этом получатся лишь новые формы «старых»
уравнений движения, но они оказываются особенно хорошо приспособлен-
приспособленными для перевода на язык квантовой механики.
Прежде всего нужно представить величину 2Т — Е, зависящую от q
и q, как функцию от q и р. Импульс рг, как было отмечено выше, полу-
получается дифференцированием кинетической энергии Т по qr. Выразив рг
через qr, мы легко исключим q из L и Т. В силу C.2.1)
п
Рг = S «rs?s
s=l
и, следовательно,
ji C.2.6).
Это уравнение дает ответ на вопрос, который до сих пор мы себе не
задавали: можно ли выразить И только через q и р, полностью исклю-
исключив д? В самом деле, взяв вытекающее из .C.2.6) равенство Н =^ pq — L
(в котором L, будучи функцией от q и q, в то же время не может быть
в общем случае выражена только через q и р) и придав величинам q, p>
и q малые приращения, мы получим
dq
Так как, по определению, p = dL/dq, то
3.2. Принцип Гамильтона и классическая динамика 271
Итак, полное приращение функции Н выражается через приращения q
и р, поэтому Н можно выразить только через q и р (впрочем, если L
зависит явно от t, то dH/dt= — dL/dt и Н оказывается функцией от q,
р и t).
Если энергия выражена через р и q (и через t, если это необходимо),
то ее называют функцией Гамильтона и обозначают Н. Вариация инте-
интеграла I Ldt принимает при этом вид
о J BT-H)dt= $
<о (о г=1
где од и Ьр означают вариации значений q и р, принимаемых вдоль
реальной траектории (эти вариации соответствуют ранее употреблявшимся
величинам etj). Интегрируя по частям слагаемые prbqr = pr(dbqr/dt), иы
расщепим вариацию подинтегральной функции на части, одна из которых
вызвана вариацией координат q, а другая — вариацией импульсов р
В силу предположения, что р можно варьировать независимо от q, каждое
из выражений в круглых скобках в отдельности должно обращаться в нуль,
и мы придем к другой форме уравнений движения
qr = dH/dpr, pr= ~(dH/dqr), C.2.7)
которые называются каноническими гамилыпоновыми уравнениями. Они
применялись несколько раз в предыдущей главе (см. стр. 222 и 233). Мы
вновь применим их в этой главе позже.
Легко видеть, что тогда, когда гамильтонова функция не зависит
от времени явно, она не изменяется с течением времени. Действительно,
в этом случае
dH_dHdq ЗН dp
dt ~ dq dt "" dp dt '
а это выражение #в силу уравнений C.2.7) тождественно равно нулю и,
следовательно, • при движении системы Н сохраняет постоянное значение
(т. е. полное изменение Н со временем для консервативных систем равно
нулю). Иногда Н явно зависит от времени, но и в этих случаях измене-
изменение q шр стечением времени не влияет на И и dH/dt — dH/dt, то есть пол-
полное изменение функции Н происходит лишь за счет того, что t является
одним из ее аргументов; заметим, между прочим, что, как мы уже
видели, dH/dt= —dL/dt.
Импеданс. В гл. 2 (стр. 128) мы ввели понятие механического импе-
импеданса как отношения гармонической движущей силы Foe-ta>t к соответ-
соответствующей скорости. Если система линейна, то это отношение не зависит
от амплитуды колебаний и является функцией от ш и констант системы.
Как мы увидим в следующей главе, введение импеданса дает воз-
возможность свести изучение реакции системы как функции времени к изу-
изучению импеданса кате функции частоты. Последняя задача часто оказы-
оказывается более простой.
Во всяком случае, канонические уравнения C.2.7) позволяют нам
подойти к понятию импеданса с новой точки зрения. Заметим сначала,
272 Гл. 3. Поля и вариационный принцип
что'если координате qr соответствует внешняя сила Fr, то канонические
уравнения примут вид
« P + F
Мы видим, что каждому из уравнений Лагранжа второго порядка соот-
соответствует пара канонических уравнений первого порядка как раз такого
вида, какой удобен для вычисления импеданса (если система такова,
что для нее импеданс имеет смысл). Действительно, если г-й координате
соответствуют внешняя сила FT и скорость qr, то отношение Fr к qT равно
как раз
7 pr + (8H/dqr)
С этой новой точки зрения мы можем представить себе, что мы изу-
изучаем основные свойства системы, «испытывая» ее воздействием сил, изме-
изменяющихся гармонически. Мы прилагаем такого рода силу поочередно
к каждой координате и измеряем отношение этой силы к соответствую-
соответствующей скорости. Если эти отношения не зависят от амплитуды, то с их
помощью можно восстановить систему. Обратно, если известна функция
Лагранжа системы, мы можем для любой координаты вычислить импе-
импеданс. Положим qr = Агеш (в гл. 2 и много раз в дальнейшем мы изобра-
изображаем с помощью множителя е~"°' простое гармоническое колебание; здесь
и в гл. 4 мы будем рассматривать Z при всех значениях ш, положитель-
положительных, отрицательных и мнимых, так что можно сначала вычислять Z
и при положительных показателях). Из равенства рт = dL/dqr мы можем
вычислить рг как функцию от qr и тем самым выразить рг через еш
и амплитуду Ат. Далее, мы можем выразить таким же образом дН/дрг,
dH/dqr и, следовательно, отношение Zr. Если это последнее не зависит
от А и от времени, то оно представляет собой импеданс.
Пусть потенциальная энергия системы достигает минимума, рав-
равного VmiTi, при некоторых определенных значениях координат q. Приняв
эту точку минимума за начало отсчета, мы получим, что при малых q,
т. е. при малых отклонениях от точки минимума, потенциальная энер-
энергия выражается в виде квадратичной функции от q:
C.2.8)
Г, S
т. е. мы получим выражение, сходное с C.2.1). Иногда этот минимум —
не абсолютный, а зависит от состояния «динамического равновесия».
Например, может оказаться, что один из импульсов, скажем рп, постоя-
постоянен; тогда dH/dqn = 0. В таком случае qn может быть исключено из урав-
уравнений и постоянную рп можно рассматривать как некоторую характери-
характеристику системы, определяемой меньшим числом координат. При этом
в выражении потенциальной энергии могут появиться дополнительные
члены, зависящие от рп, «вызванные» движением с постоянным импуль-
импульсом (их можно назвать динамическими потенциальными энергиями). Эта
новая система может иметь точки равновесия там, где «динамические»
силы уравновешиваются «истинными» силами, и тогда вблизи точек
равновесия потенциальная энергия опять будет выражаться в виде C.2.8),
где некоторые из Ь зависят от постоянной рп (которая уже не рассма-
рассматривается как импульс).
3.2. Принцип Гамильтона и классическая динамика 273
Итак, при достаточно малых отклонениях системы от (динамиче-
(динамического или иного) равновесия гамильтонова функция Н представляет
собой квадратичную функцию импульсов и координат. Приложенная
сила Fr имеет выражение
Рт + &z7 = 2 (arJlm + КтЯт) ¦
т
Это можно проще записать в абстрактной векторной форме. Координату qr
назовем г-ж компонентой вектора смещения q, a Fr — г-й компонентой
нектора силы F. Тогда соотношения, связывающие векторы силы, смещения
и ускорения, можно представить в виде
где % и S3 —аффиноры, имеющие соответственно компоненты атп и Ьтп.
Если теперь вектор F является простым гармоническим с частотой ш/2?с,
то F = F°ei€fi',rfle F° — постоянный вектор, и установившаяся скорость q имеет
вид Ueiu>t, где компоненты Ur вектора U — комплексные числа с модулями,
равными амплитудам скоростей qr.
В этом случае предыдущее соотношение может быть записано в виде
F° = 8-U, C.2.9)
где
называется аффинором импеданса системы вблизи рассматриваемой точки
равновесия. Итак, понятие импеданса всегда имеет смысл достаточно
близко от точек равновесия (если таковые имеются). Диагональный эле-
элемент Zmm называется входным импедансом, соответствующим т-й коор-
координате, а элемент Zmn (то Ф п) — переносным импедансом, соответствую-
соответствующим паре координат с номерами тип. Всегда можно (см. стр. 64)
преобразовать ,g к главным осям, т. е. перейти к нормальным коорди-
координатам ф, в которых все переносные импедансы равны нулю, а диаго-
диагональные элементы Z° (ш) представляют собой главные значения импеданса.
Такое преобразование может быть различным при различных «о. Через 3
и F° можйо выразить также смещения q = Aeiu>'
где | Ат | — амплитуда смещения по координате qm.
Переход к нормальным координатам представляет собой частный слу-
случай поворота осей в абстрактном векторном пространстве. Новые коор-
координаты q' связаны со старыми q формулами
тг
где 2 YrmYsm — \е- Другими словами, матрица (абстрактный векторный
тп=1
оператор) с элементами утп ~~ унитарная. Сами числа угт играют роль
направляющих косинусов (см. стр. 32). В случае преобразования пово-
поворота они не зависят от qr. Как было показано на стр. 66, сумма диа-
18 Ф. м. Поре ж Г. Фешбах
274 Гл. 3. Поля и вариационный принцип
тональных элементов Q остается инвариантной при поворотах, т. е.
п п
I -3 I =т 2j %тт = 2j %т,
m=l m=l
подобной же инвариантностью обладает и определитель
4z=|ZmJ=Z;(a>)Z»...ZS(<o).
Полезно еще вычислить аффинор 9), обратный по отношению к 3.
т. е. такой, для которого
где § ~ тождестпенный оператор (идемфактор). Согласно сказанному
на стр. 63, компоненты Ymn и Zmn связаны соотношениями
где Zmr—алгебраическое дополнение элемента Zmr в определителе Д2.
Далее очевидно, что 9) имеет те же главные оси, что $, и главные зна-
значения аффинора §) равны
?) = 8 называется аффинором полной проводимости (адмитанса) системы.
Если определитель Дг равен нулю, то 9), конечно, не может быть
вычислен. Это происходит тогда, когда значение угловой скорости ш
обращает в нуль одно из главных значений Zam импеданса. Вспомнив,
как именно Q зависит от ш, мы заметим, что определитель
( _ iw)n Д2 = | W2umr _ Kr | = ( _ iw)n Zo (w) Zo {w)_ Zon (w)
представляет собой многочлен n-й степени относительно <о2; последний
обращается в нуль при п определенных значениях ш2 (некоторые из них
могут совпадать). Так как порядок нумерации главных осей произволен,
то можно считать, что Z?(u>) обращается в нуль при ш = .^;и)г, где ш*,
(в*, ..., ш^ расположены в порядке возрастания. Отсюда будет следовать,
что главные значения импеданса могут быть представлены в виде
= ±Mr(w*-w*r) = j^, C,2.10)
где Мг и Кг — ш1Мг — постоянные, определяемые значениями атг и bmr.
Таким образом, мы видим, что главные значения импеданса консерватив-
консервативной системы чисто мнимые и представляют собой нечетные функции
от ш, то есть Z( — ш) = — Z(u>).
При ш = ±шг амплитуда колебаний, соответствующих г-й нормальной
координате, оказывается бесконечной (за исключением случая, когда
/7 = 0) и установившегося решения не существует. Частоты шг/2тс, соот-
соответствующие корням шг определителя Az> называются резонансными
частотами системы.
Заметим, между прочим, что постоянные Мг и Кг, так же как ш|,
положительны, так как в противном случае потенциальная энергия не до-
достигла бы абсолютного минимума при q — 0.
Канонические преобразования. Уравнения C.2.7) отличаются заман-
заманчивой простотой. Прежде всего, вместо уравнений Лагранжа C.2.4) вто-
второго порядка мы имеем пары уравнений первого порядка, которые для оты-
отыскания р и g должны решаться совместно. Это распадение переменных,
описывающих состояние системы, на две самостоятельных группы р и q
3.2. Принцип Гамильтона и классическая динамика 275
выражает отличительную особенность классической динамики: силе про-
пропорционально ускорение, то есть вторая производная; поэтому, как началь-
начальное положение, так и начальная скорость могут быть выбраны произ-
произвольно. Величины q являются обобщенными компонентами положения,
а величины р связаны с соответствующими скоростями таким образом,
что соотношения между q и р выступают в симметричной форме.
Канонические уравнения C.2.7) являются теми основными уравне-
уравнениями, которые связывают р и q для заданной системы и в то же время
определяют поведение самой системы. Выбор гамильтоновой функции Н
переменных р и q определяет семейство пар р и q, связанных уравне-
уравнениями C.2.7), при данной гамильтоновой функции Н величины р и q назы-
называются канонически сопряженными переменными для функции Н (или
просто сопряженными переменными).
Одна и та же, система, разумеется, может быть"] описана различ-
различными координатами (и сопряженными импульсами). Так же как теория
поля стала яснее после исследования того, как влияют на компоненты
поля преобразования координат, так и здесь рассмотрение эффекта пере-
перехода от одних сопряженных переменных р и q к другим помогает уяс-
уяснить дело. Для этого можно было бы, идя окольным путем, заменить q
новыми координатами Q, способными описать конфигурацию рассматри-
рассматриваемой системы, выразить функцию Лагранжа L через Q и Q, найдя
по уравнениям Pr = dL/dQr сопряженные импульсы Р и, наконец, соста-
составить новую функцию Гамильтона K = I,PQ—L, выраженную через новые
сопряженные переменные Р и Q. Но можно указать прием одновремен-
одновременного преобразования сопряженных пар р, q в новые пары Р, Q, оставляю-
оставляющего инвариантным форму уравнений C.2.7). Такие преобразования назы-
называются каноническими преобразованиями.
Канонические преобразования связаны с семейством преобразований,
которые математики называют преобразованиями прикосновения (контакт-
(контактными преобразованиями). Это — преобразования линейных элементов (т. е.
положенця и направления), а не точек. А так как мы.хотим нреобразовы-
вать как координаты qr определяющие положение системы, так и импульсы р,
связанные с направлением движения системы, то связь между теми и дру-
другими преобразованиями очевидна. В основу преобразования прикоснове-
прикосновения кладется некоторая функция S старых и новых координат.
В качестве примера рассмотрим двумерный случай (см. рис. 3.2),
когда S есть функция от х, у и х', у'. Каждой точке Р пространства
(х, у) (т. е. каждой паре фиксированных значений хну) ставится в соот-
соответствие кривая С в пространстве (ж', у'), изображаемая уравнением
S (ж, у; ж', у') = const1);
обратно, каждой точке плоскости (ж', у') таким же образом ставится
в соответствие некоторая кривая в плоскости (ж, у). Если точка в пло-
плоскости (х, у) описывает какую-нибудь кривую К, то соответствующее
семейство кривых в плоскости (ж', у') может иметь огибающую Е, кото-
которую мы сопоставляем с кривой К. Таким образом, точкам плоскости (ж, у)
поставлены в соответствие кривые в плоскости (х', у'), а кривым в пло-
плоскости (ж, у) — огибающие семейств кривых в плоскости (ж', у'). Поэтому
каждому линейному элементу (т. е. точке плюс направление) в плоско-
плоскости (ж, у) ставится в соответствие некоторый линейный элемент в пло-
плоскости (ж', у').
Эта константа в дальнейших рассуждениях фиксирована. — Прим. ред.
276 Гл. 3. Поля и вариационный принцип
Возьмем в плоскости (ж, у) две точки (ж, у) и (x-\-dx, y-\-dy), опре-
определяющие линейный элемент, и постараемся получить соответствующий
ему линейный элемент в плоскости (ж', у'). Кривые в плоскости (ж', у'),
отвечающие точкам (ж, у) и (x + dx, y + dy), имеют уравнения
S(x,y; x',y')=C,
S(x + dx, y±dy; x',y')=S(x,y; ж', y') + ^^
(последнее с точностью до бесконечно малых второго порядка). Если
\ ;
Плоскость (х\ у') Плоскость (х,у)
Рис. 3.2. Преобразование прикосновения в двумерном случае.
• • • ¦
положить dx — xds и dy = y ds, где у/х — угловой коэффициент заданного
линейного элемента, то мы придем к системе уравнений
S(x,y; x',y') = C, х^ + у^О,
решив которую, мы получим точку (х',у'), соответствующую точке (х, у).
Направление огибающей в точке (х', у') мы получим, взяв в первом
из уравнений дифференциалы по штрихованным аргументам
^rdx +^rdy =0
или
'ds r'-x-ds ,/-0
где dx' = x'ds, dy' — y' ds. Симметрия полученных уравнений относительно
производных свидетельствует о симметрии преобразования по отношению
к обеим плоскостям.
Поясним сказанное на простом примере. Пусть S = (ж — ж'J + (у — у')г —
функция, определяющая преобразование, и C = RZ. Точке х = а, у = Ь
отвечает в плоскости (ж', у') окружность радиуса R с центром в (а, Ь).
Если мы рассмотрим линейный элемент, определенный точками [(а, Ь)
я (a + dx, b), то при этом ж = 1, у—О, и мы получим систему уравнений
(x'-a)* + (y'-bJ = R*, 2(ж'-а) = 0.
Огибающей окружностей радиуса R с центрами на прямой у' ?=Ь служит
пара прямых у' = Ъ ± R. Поэтому преобразованный элемент будет опре-
определяться (бесконечно близкими) точками (а, Ъ ± R) и (a-\-dx, b±R)-
3.2. Принцип Гамильтона и классическая динамика 277
Заметим, что этот пример указывает на тесную связь между преоб-
преобразованиями прикосновения и принципом Гюйгенса.
В случае динамической системы с гамильтоновой функцией Н, не за-
зависящей явно от времени, как мы вскоре покажем, выражение ^]pdq —
2jPdQ как функция от р и q (или от Р и Q и т. д.) представляет со-
собой полный дифференциал, если переход от р, q к Р, Q осуществляется
с помощью канонического преобразования. При этом функция S может
быть получена интегрированием выражения
Как функция от Р и Q, S будет функцией, определяющей преобразование
прикосновения.
При таком преобразовании сохраняется вариационный принцип Га-
Гамильтона и, следовательно, не изменяется вид канонических уравнений
C.2.7); действительно, добавив в уравнении, определяющем dS, выраже-
выражение (K-H)dt (равное нулю, так как К есть новая гамильтонова фУнк"
ция) и проинтегрировав по времени, мы получим
to to , (О
Если концевые точки j!0 и tx фиксированы, то интеграл от dS не будет
меняться при деформации пути интегрирования, поэтому о \ B PQ—Kjdt
будет равно нулю, коль скоро о \ ( ^ pq — Ifjdt — O.
Итак, преобразование, определяемое полученной функцией S, пред-
представляет собой каноническое преобразование, и величины Р, Q и К свя-
связаны уравнениями
т. е. каноническими уравнениями C.2.7).
Даже тогда, когда Н (а следовательно, и К) явно зависит от времени,
функцию S можно получить, интегрируя уравнение
2 Prqr -H - 2 PTQr+ к =
или то же уравнение, записанное в дифференциалах,
2 Prdqr- 2 PrdQr + {K-H)dt = dS,
где e^S1 —полный дифференциал. Так как в любом случае
r=l
то, приравняв коэффициенты при дифференциалах, мы получим выраже-
выражения импульсов через координаты, участвующие в преобразовании
Скобки Пуассона. Изучение инвариантов канонических преобразова-
преобразований охватывает большую часть основных понятий классической динами-
динамики. Одним из таких инвариантов является энергия Н (если только Н не
зависит от t явно). Целый класс инвариантов наиболее удобно выразить
278 Гл. 3. Поля и вариационный принцип
посредством скобок Пуассона. Так называется для произвольных двух функ-
функций и и v от р и q выражение [см. формулу B.6.4)]
r=l
Скобки Пуассона обладают рядом интересных алгебраических свойств,
по форме напоминающих свойства производных. Так, если с — постоян-
постоянная, не зависящая от р и q, то
(в, с) = 0;
далее, выполняются соотношения
(и, v+w) = (к, v) + (и, w), (и + v,w) = (к, w) + (v, w),
(uv, w) ¦¦= и (v, w) + v (и, ш) и т. д.
Скобки Пуассона антисимметричны, т. е. (и, v) =—{v, и). Причина
пользы этих скобок заключается в том, что они инвариантны относительно
канонических преобразований. Если q, р и Q, Р связаны друг с другом
так, что выр 1Ж©ние 2! pdq — ^PdQ является полным дифференциалом,
то дяй любой пары функций и и v переменных р, q (или Р, Q)
п ' п
. . -л / ди dv ди dv Л ^, f ди dv ди dv
(U, V)= -2j \_~dq~rd~p~r~~dp~rdq~; )= ~ Ь \, ~Щ~Г ~дРг ~ Щ- Щ.
г=1 г=1
Таким образом, если уравнения динамики записаны посредством ско-
скобок Пуассона, то они инвариантны относительно канонических преобразо-
преобразований. Так, канонические уравнения движения C.2.7) можно записать в
виде
qr = (H,qr), pT=(H,pr).
В самом деле, из канонических уравнений и самого определения скобок
Пуассона вытекает, что для любой функции и переменных р и q
du irr ¦ \ ди . . ди , .
ш = (Н,и), ~^.{рг,и), — = (u,qr).
Скобками Пуассона можно также пользоваться для выяснения того,
является ли некоторое заданное преобразование преобразованием прикос-
прикосновения. Система п координат q и сопряженных импульсов связана с дру-
другой системой п координат Q и сопряженными импульсами некоторым пре-
преобразованием прикосновения тогда и только тогда, когда
(Qr, Q.) = 0, рг. Ps) = О, (Р„ Qs) = 6Г„
где &rs = 0 или 1 соответственно при г Ф s и при r — s.
Интеграл действия. Заметим, что функция S, определяющая преоб-
преобразование, имеет размерность действия и что если рассматривать S как
функцию от q при фиксированных Q, то вектор р, будучи градиентом
функции S, ортогонален поверхности S = const. Другими словами, выбор
значений переменных Q и функции К определяет семейство поверхностей
действия S = const и семейство траекторий системы, ортогональных этим
поверхностям. С некоторой точки зрения Q можно рассматривать как на-
начальные данные, а последующее поведение системы — как «развитие»'пре-
«развитие»'преобразования прикосновения с течением времени.
3.2. Принцип Гамильтона и классическая динамика 279
Дифференциальное уравнение, определяющее функцию действия S как
функцию начальных и конечных значений координат, можно получить,
записав условие, состоящее в том, что гамильтонова функция остается
достоянной Н (р, q) = Е, и введя в него dS/dqr вместо каждого рг согласно
уравнениям C.2.11). В результате мы получим дифференциальное урав-
уравнение
(j?)E, C.2.12)
называемое уравнением Гамильтона — Якоби. Его решение представляет
собой функцию п переменных q, величины Е и п постоянных интегриро-
интегрирования, которые мы можем обозначить Q2, , Qn, а (последними мы мо-
можем при этом так распорядиться, чтобы а было просто аддитивным пот
стоянным). Если мы положим E = QX, то остальные Q сможем рассмат-
рассматривать как новые координаты системы. Согласно C.2.11), сопряженными
импульсами будут Pr= —8S/dQr и преобразованные координаты и им-
импульсы будут удовлетворять каноническим уравнениям
так как при этом К — Н и Н не зависит от постоянных Qr, служащих
начальными данными. Таким образом, уравнения движения можно будет
записать в виде
8S . . dS in ч
где с —другая система постоянных (соответствующих, наряду с Q, на-
начальным данным). Следует отметить, что /\ связано с величиной qt (см.
стр. 243).
Интересна и важна связь уравнения Гамильтона — Якоби с уравнением
Шредингера B.6.28) е%? [(А/?) (д/dq), q] ф = Е§ для волновой функции <}> в
квантовой механике, но на этом мы не можем останавливаться. Нужно,
впрочем, заметить следующее: если положить ф = е^/А)8, то тогда, когда S
настолько больше Ь, что (i/%) (dzS/dqz) пренебрежимо мало по сравнению
с (i/h)z (dS/dq)z, уравнение Шредингера приводится к уравнению Гамиль-
Гамильтона — Якоби. В пределе, при больших значениях действия и энергии, по-
поверхности постоянной фазы волновой функции ф превращаются в поверхности
постоянного действия S Для соответствующей классической системы. Вол-
Волновая механика переходит в «геометрическую механику» так же, как вол-
волновая оптика переходит в геометрическую оптику при исчезающе малых
длинах волн.
Мы изложили здесь значительную часть классической динамики, не
разбавленную примерами. Прежде чем перейти собственно к предмету на-
настоящей главы, т. е. к приложению вариационного принципа к теории
полей, мы укрепим наши позиции, рассмотрев несколько примеров.
Двумерный осциллятор. Полезным примером может служить движе-
движение массы, помещенной на конце упругого стержня, который может из-
изгибаться в двух направлениях. При малых колебаниях движение массы
происходит в плоскости, и в качестве координат qx и q2 массы можно
язять прямоугольные координаты, выбрав в качестве направлений для
осей координат главные направления сил упругости, так что сила в на-
направлении qx будет пропорциональна только q1} и аналогично для q2- При
этом кинетическая энергия массы будет равна ^т(^1 + ^г)- Если упру-
упругость одинакова по обоим направлениям, то потенциальная энергия полу-
280 Гл. 3. Поля и вариационный принцип
чит выражение-|-muJ(?i + ?l). Уравнения Лагранжа C.2.4) совпадут с
уравнениями Ньютона
q1=-<o2q1, qz=-<o2q2,
и их решениями будут qx и qz, зависящие от t синусоидально с частотой
u)/2iu.
Сопряженные импульсы суть, разумеется, p1 = mq1, pz = mqz, так что
функцией Гамильтона явится
Я (р, q) = (l/2m) \р\ -г Pi + mW (gj + g»)]. C.2.13)
Хотя решения уже получены из уравнений Лагранжа, но для того, чтобы
проиллюстрировать основные понятия и величины, введенные выше, мы
попытаемся решить задачу при помощи преобразования прикосновения.
Было бы удобно, если бы новые импульсы оказались постоянны, а для
этого достаточно получить новую гамильтонову функцию К, не завися-
зависящую от (?! и Qz.
Проще всего положить К пропорциональной Рх + Pz, так как; при этом
Р = — dKjdQ = 0. В силу уравнений Q — ЭК/дР, Q будут пропорциональ-
пропорциональны времени t. Это приводит к следующему преобразованию:
q = A sin (wt), p — mwAcos(wt), Q ос wt и PccAzl),
то есть
<?х = arctg (moqjpj), Q2 = arctg (rmoqz/p2),
Pt = (i/2iwa)) 0* + mWql), P2 = A/2тш) (p\ + т2ш2^).
Величина p1dq1+p2dqz — PldQL — P2dQ2, если ее выразить через р
a q, имеет вид -^ {pidq1 + q1dpl-\-p2dq2-\-qzdpz) и является полным диф-
дифференциалом функции
5
2 4 C.2.14)
которая и определяет искомое преобразование. Значит, это — преобразова-
преобразование прикосновения. Выразив р, q через Р, Q, мы получим
qi = У2/яш VP~x sin Qly ch = /2/miD V^ sin <?2,
C.2. lo)
Pi—y 2m<o }/ /'j cos Qx, p2—y 2mm у Pz cos Qz.
Мы видим, что новой гамильтоновой функцией является
Так как мы осуществили преобразование прикосновения, то уравне-
уравнения Гамильтона C.2.7) по-прежнему выполняются, и в силу того, что
Q = дК/дР, мы получим
Так как P=—dK/dQ = 0, то Рг и Р2 постоянны.
Решение получено, так как мы можем, подставив эти простые выра-
выражения в C.2.15), получить формулы, выражающие координаты и импуль-
импульсы через время и энергию движения К.
г) ос—знак пропорциональности. —Прим. ред.
3.2. Принцип Гамильтона и классическая динамика 281
Заметим, что Р имеют размерность действия, a Q представляют со-
собой углы. Действительно, если проинтегрировать pdq по периоду колеба-
колебаний и выразить результат через Р и Q, то получится
— величина, пропорциональная Р. Эти канонически сопряженные пере-
переменные Q и Р так и называются соответственно угловой переменной и
переменной действия. Любая задача, связанная с колебательным процес-
процессом, имеющая синусоидальные решения, может быть упрощена и решена
посредством должным образом подобранного преобразования прикоснове-
прикосновения, вводящего эти переменные.
Возвращаясь к двумерному гармоническому осциллятору, мы можем
также вместо прямоугольных координат qx, q2 выразить движение в по-
полярных координатах г, <р. Соответствующее преобразование прикосновения
запишется в виде
г = Vfi + fi, ? = arctg (ft/ft), 2
Pr = Wr) (PlVl + Ptfi), Pt = (Ptfl - P1Q2),
а гамильтонова функция получит выражение
К = (l/2m) [pl + ifyr* + т-ш2г-\. C.2.17)
Так как дК/д<р = 0, то величина р9 — момент количества движения систе-
системы постоянна. Нетрудно видеть, что ото, верно, независимо от того, ка-
каково выражение потенциальной энергии; коль скоро последняя зависит
от г и не зависит от 9- Дальше, если нужно, можно воспользоваться ре-
решением в прямоугольных координатах.
Заряженная частица в электромагнитном поле. Бывают случаи, когда
не очевидно, каков должен быть вид функции Лагранжа L = T — V, фигу-
фигурирующей в вариационном интеграле C.2.3). Так бывает, в частности,
тогда, когда появляются силы, порожденные полем. Во многих таких
случаях для получения правильного ответа приходится сопоставлять
имеющиеся сведения о скалярных инвариантах системы с рассмотрением
простейших предельных случаев.
Например, когда рассматривается заряженная частица в электро-
электромагнитном поле, следует ли энергию взаимодействия между магнитным
полем и движением частицы считать частью кинетической энергии Т
(поскольку она зависит от скорости частицы) или отнести ее к потен-
потенциальной энергии V (раз она обусловлена воздействием поля)? Мы начнем
с того, что перечислим все скалярные инварианты (в трехмерном про-
пространстве) частицы и поля. Инвариантом должна быть сама функция
Лагранжа L=T — V, так как принцип Гамильтона действует при любом
выборе системы координат в пространстве. Кинетическая энергия Ymz}2
частицы, взятой сама по себе, будучи пропорциональна скалярному ква-
квадрату вектора v, также является инвариантом. Инвариантен и электри-
электрический потенциал 9 (в трехмерном пространстве). Инвариантны также
квадраты напряженностей Е2 и Н2 электрического и. магнитного полей
и квадрат А2 векторного потенциала. Оба поля получаются из потен-
потенциалов посредством дифференцирования, а силы, действующие на частицу,
получаются дифференцированием функции Лагранжа [см. формулы C.2.2)
и C.2.4)], поэтому естественно ожидать, что в функцию Лагранжа частицы
282 Гл. 3 Поля и вариационный принцип
войдут только потенциалы А и <р. Другим инвариантом, который может
появиться, является скалярное произведение v-A.
На частицу действуют силы еЕ = — е grad 9 — (е/с) (dA/dt) [в силу
{2.5.13)] и (е/с) v X В = (е/с) v X rot А [см. B.5.5)], и их выражение должно
получаться, согласно уравнениям Лагранжа C.2.4), дифференцированием
функции L. Так как при этом должна появиться производная от А по вре-
времени, то в выражение L войдет произведение v и А, предположительно
v-A. При рассмотрении уравнения для самой частицы (уравнения, опи-
описывающие поля, мы пока не рассматриваем) в него не войдут члены вто-
второй степени относительно А. Итак, L для частицы должна быть комби-
комбинацией членов, содержащих t>2, v-A и <р.
Первым из них, очевидно, является -^-mvz, кинетическая энергия ча-
частицы. Член, содержащий <р, представляет собой потенциальную энергию;
последняя, если частица несет заряд е, равна — еу. Третий член должен
дать — (е/с) (dA/dt), т. е. второе слагаемое в выражении еЕ и, кроме того,
(е/с) v X rot А. Так как grad (v- A) = v X rot A + v- (VA) (см. стр. 116)-, то тре-
третий член, видимо, должен иметь вид (е/с) v- А. Поэтому функция Лагранжа
для заряженной частицы в электромагнитном поле должна иметь выражение
L = ±-mv2+(e/c)v-A-e<{,. C.2.18)
Заметив, что аргументами А и у служат координаты х, у, z частицы
в момент /, мы сможем записать три уравнения C.2.4) (для трех коорди-
координат) в виде одного векторного уравнения. Так как
то таким векторным уравнением будет
-jr ( тп\ -\- — А ) = grad L = — е grad <р+-тх rot А+—v- (VA).
fit \^ Су С С
Слагаемое, входящее в выражение Е [см. B.5.13)], содержит частную
производную по времени dA/dt, характеризующую изменение А в фикси-
фиксированной точке пространства. В то же время левая часть последнего
уравнения есть полная производная А по времени, т. е. скорость измене-
изменения А для движущейся частицы. В силу B.3.2) для точки, движущейся
со скоростью v,
Поэтому векторное уравнение движения частицы сводится к виду
4"("»Ў)= -egrad<p--^ + -vX rot A = eE + -vX В, C.2.19)
который соответствует выражению B.5.12) для эффективной силы, дей-
действующей на заряженную частицу.
Теперь мы можем составить для рассматриваемой частицы функцию
Гамильтона. Импульсом частицы является вектор, компонента которого,
скажем, по оси х, есть dL/dvx
р = тх + (е/с) А.
В рассматриваемом случае скорость частицы должна непрерывно изме-
изменяться под действием поля, поэтому величина mv не может «сохра-
«сохраняться». Если мы все-таки хотим иметь закон сохранения импульса,
3.2. Принцип Гамильтона и классическая динамика 283
то мы не должны р приравнивать ту. Согласно C.2.6) функция Гамиль-
Гамильтона есть
// = р-v —L = f mv + — A J-v — -у mv2 — — v-
Это выражение встречалось на стр. 245 и 246.
Этот пример дает нам некоторое представление о том, каким образом
аппарат классической динамики охватывает поля и взаимодействие
с полями. Импульсы перестают быть просто пропорциональны скоростям,
менее ясным становится, что есть кинетическая-энергия, или Н, или L,
и для получения правильных выводов приходится в большей мере пола-
полагаться на формальные уравнения, такие, как C.2.4), C.2.6) и C.2.7),
чем на «интуицию».
В качестве частного примера рассмотрим частицу с массой т, несу-
несущую заряд е, в постоянном магнитном поле с напряженностью B — mcw/e,
направленной вдоль оси z. Скалярный потенциал 9 = 0, а векторный
потенциал
. теш . ...
А =-?-(—yi + sj).
Функцией Лагранжа служит
L = -^ /и (х2 + у2) + -j тш ( — ху + ух),
где x — dx/dt, y = dy/dt; импульсы выражаются в виде
1
Уравнения Лагранжа
dt* ~~ dt ' dt* ~ dt
имеют решения
х = JR sin (w? + a) + x0, y = R cos (wt + a) + y0,
изображающие вращательное движение по окружности радиуса R с цен-
центром в (ж0, у0). Функция Гамильтона равна, разумеется,
Заметим, что радиус орбиты равен о/ш, где ш равно произведению напря-
напряженности В магнитного поля на е/тс.
Упрощение функции Гамильтона достигается преобразованием при-
прикосновения
х = УТ/Ш^ [ ]/2Р[ sin Qi + P2] , рх - у VW [ /Щ cos & - Q2],
у = У 1/тсо[УЩcosQt + Q2] , ру = ~ \f^[-V2P~1sinQ1 + P2\ .
В том, что это—преобразование прикосновения, можно убедиться с по-
помощью равенств B.6.4), содержащих скобки Пуассона, взяв в этих
последних Р и Q в качестве независимых переменных. Эти преобразова-
284 Гл. 3. Поля и вариационный принцип
ния, после подстановки в Н, дают новую функцию Гамильтона
К = «>Р1.
В силу C.2.7) Рг, Р2 и Q2 оказываются постоянны, a Q1 зависит от вре-
времени линейно с коэффициентом пропорциональности, равным ю — угловой
скорости частицы при движении по окружностям.
Релятивистская частица. Другой пример применения уравнений клас-
классической динамики, который понадобится нам в дальнейшем в этой главе,
относится к описанию поведения частицы, движущейся со столь большой
скоростью, при которой нельзя пренебрегать отношением'у2 к с2. Выше
было отмечено, что L не является лоренц-инвариантом. Действительно,
вариационный интеграл \ Ldt, взятый вдоль мировой линии частицы,
должен быть таким инвариантом. Если частица движется со скоростью и
относительно наблюдателя, то дифференциал. dt времени наблюдателя
связан с дифференциалом собственного времени dz частицы соотношением
dx = l/l — (u/c)zdt. Из инвариантности ^ L dt = \ (L/j/l — (м/сJ) efr и dx
следует инвариантность подинтегральной функции Lj~\f\. — (м/сJ . Таким
образом, L выражается в виде некоторого лоренцова инварианта, умножен-
умноженного на УЧ — (м/сJ .
Например, для свободно движущейся частицы релятивистская функ-
функция Лагранжа есть1
L = — т0с2 ]/1 - (м/сJ ^ - т0с2 -+¦ ~ тои2> и < с- C.2.21)
Написанное выражение представляет собой кинетическую энергию
минус энергия покоя т0с2; из него следовало еще вычесть потенциаль-
потенциальную энергию, если бы она имелась. Дифференцируя L по компонентам м,
мы получим импульс
V
[см. A.7.5)].
Функцией Гамильтона будет служить
= тос2 У\ + (р/тос)* ^ т0с2 + (^)Р2 + . • ¦, Р € тос. C.2.22)
Этим выражением мы пользовались на стр. 246 и 252 в связи с уравне-
уравнением Дирака для электрона. Это выражение, разумеется, представляет
собой временную компоненту некоторого 4-вектора, пространственными
компонентами которого служат компоненты вектора ср. Слагаемое, соот-
соответствующее потенциальной энергии, если оно фигурирует, также должно
быть временной компонентой некоторого 4-вектора.
Диссипативные системы. Наконец, прежде чем обратиться к приме-
применениям принципа Гамильтона к теории полей, мы введем аппарат, позво-
позволяющий исследовать диссипативные системы (т. е. такие системы, в кото-
которых нельзя пренебрегать трением) так, как будто они были консервативны
(т. е. с пренебрежимо малым трением). Уловка будет состоять в том, что
одновременно с заданной системой, имеющей обычное трение, рассматри-
рассматривается ее «зеркальное отражение», обладающее отрицательным трением
3.2. Принцип Гамильтона и классическая динамика 285
и поглощающее ту энергию, которая теряется заданной системой. При
этом полная энергия остается постоянной, и мы можем получить инва-
инвариантную функцию Лагранжа ценой утраты «реального смысла» некоторых
побочных результатов.
Рассмотрим в качестве примера одномерный осциллятор с трением,
движение которого описывается уравнением
mx + Rx + Kx = 0. C.2.23)
Мы хотим получить это уравнение с помощью некоторой функции Лаг-
Лагранжа, применив обычный вариационный метод. Для этого мы чисто форг
мально составим выражение
L = т (И*) - ii? (х*'х-хх*) - Кхх* C.2.24)
и будем рассматривать его как функцию Лагранжа, в которую входят
две координаты х и х*. Координата х* изображает «зеркально отражен-
отраженный» осциллятор с отрицательным трением. Применив обычные выкладки,
мы получим импульсы
1 * 1
р = тх*—2~Rx*, р* = тх + у Rx,
имеющие, впрочем, мало общего с действительным количеством движения
осциллятора. Однако наш аппарат, продолжая действовать формально,
даст нам уравнения Лагранжа для той и другой системы
Уравнение, содержащее х, совпадает с исходным уравнением C.2.23).
Уравнение с х*, как уже говорилось выше, содержит —Rx*, что соответ-
соответствует отрицательному трению.
Функцией Гамильтона является
Н =рх-\- р*х*—L =mxx* -J- Кхх* =
= A/т)(р +4 Д**) (/>*-4Ла!) +Кхх*- .C-2.25)
Я остается постоянной в связи с тем, что амплитуда координаты х*
растет так же быстро, как убывает амплитуда х. В постоянстве Н легко
убедиться, умножив первое из уравнений Лагранжа на х, второе — на х*
и сложив их.
Этот прием позволяет нам оперировать с диссипативными системами
так, как если бы они были консервативными. Хотя он не может конкури-
конкурировать с другими способами решения тогда, когда таковые известны, но
совершенно необходим при изучении диссипативных полей, например, в слу-
случае уравнения диффузии. Заметим, что, хотя ранее мы считали L квадра-
квадратичной функцией от q, здесь L содержала член х*х; это указывает на то,
что подобные случаи далеко не. типичны.
Импеданс и полная проводимость для диссипативных систем. Сейчас
целесообразно вернуться к рассмотрению механического импеданса
(см. стр. 271 — 274) и выяснить, что получится при наличии сил сопро-
сопротивления. Как мы видели, если система обладает динамическим или ста-
статическим равновесием, то можно ввести такие координаты хх, х2, .... хп,
которые равны нулю в точке равновесия. При достаточно малых отклоне-
отклонениях от положения равновесия потенциальная энергия может быть пред-
286 Гл. 3. Поля и вариационный принцип
ставдена в виде
т, г
где S3 —аффинор с элементами bmr, a x — п-мерный вектор с компонен-
компонентами хТ. Кинетическая энергия, как всегда, задается формулой
* = ~2~ 2j amrxrnxr — ~2 х ' ™ 'х >
m, r
где vt —аффинор с элементами атг.
При наличии трения т-& координате соответствует сила сопротивле-
сопротивления, которую можно представить в виде
где fR — аффинор сопротивления, компонентами которого служат гтг.
Недиагональные элементы Ш, как и в случае кинетической и потенциаль-
потенциальной энергий, соответствуют связям различных" смещений хт.
Следуя образцу C.2.24), запишем функцию Лагранжа в виде
Г ¦*-* г "л' 1 /*¦ **ч I *
*~i— / | V-mr^ff-T •) rnr \ *^ г •*jm<br} ^тГ^тt-^rl —
m, r
= x*-Vt-x —x*-9t-x+— x*-9i-x x*-S3-x C 2 26)
где x* — вектор, сопряженный с х. Вектор импульса и сопряженный с ним
вектор имеют вид
1 -¦ 1
а функция Гамильтона
-x*-S3-x, C.2.27>
Гр +4
где 91 — аффинор, обратный по отношению к %, т. е. такой, что ФС-ЭД =
Изменения р* вызываются обобщенной силой, соответствующей смеще-
смещению хт, а не зеркально отраженному смещению. Каноническое уравнение
Гамильтона, соответствующее т-й координате, имеет вид
в абстрактном векторном пространстве эти [уравнения могут быть запи-
записаны так:
+ 93-х. C.2.28)
Если движущие силы имеют колебательный характер, F = F°ei(B', то
все отклонения (при установившемся движении) будут представлять собой
колебания с той же частотой х = Aeiu>' (компонентами вектора А будут
служить Ат — амплитуды колебаний по т-й координате); скорость выра-
3.2. Принцип Гамильтона и классическая динамика 287
зится в виде x=Ueiu>' (где U имеет компоненты Um). F° связано с А
и с U соотношениями
F = 8 -U = Ш8 • A, Zmr = йоатг + rmr + (i/ico) fcmr. C.2.29)
Аффинор импеданса теперь комплексный, а не чисто мнимый. Дейст-
Действительная часть каждого из его элементов называется активным сопро-
сопротивлением (резистансом), мнимая часть — реактивным сопротивлением
{реактансом). Обратный аффинор ^) = 3~* легко вычислить, зная опреде-
определитель Az=\Zmr\
. C.2.ЗО)
Здесь Z'rm — алгебраическое дополнение элемента Zrm в определителе Az-
SD называется аффинором полной проводимости (адмитанса); действитель-
действительная часть каждой из его компонент называется активной проводимостью
(кондуктансом), мнимая часть — реактивной проводимостью (сусептансом).
Так как $ — симметричный аффинор, для него можно найти главные
оси. Будучи приведен к главным осям (иначе говоря, записан в нормаль-
нормальных координатах) аффинор Q принимает диагональную форму; при этом
диагональные элементы Zr носят название главных значений импеданса.
Определитель Д2 оказывается равным произведению этих главных значе-
значений, так что
(- «о)пЛ2 = | (o2amr - iwrmr - Ьтт | = (- wZj (- ia)Z8) ... ( - wZn). C.2.31)
Так как все диагональные элементы St, 5R и fd положительны, то такой
определитель может быть разложен на п множителей вида Жш2 — Шш — К,
где коэффициенты М, R и К положительны. Расположим эти множители
в порядке возрастания действительных частей их корней i (R/2M) ±
± A/2М) J/4KM — R2. Множитель mZx имеет наименьшее значение
^jM^)-~(Rxl2M^J, остальные значения выражаются аналогично (кро-
(кроме тех множителей, которые, в силу неравенства i?2 > АКМ, имеют
чисто мнимые корни; такие множители мы расположим в порядке убыва-
убывания абсолютных величин корней). Таким образом, r-е главное значение
импеданса равно
— [Mrw2 - Шго> -Кг] = -^ К - 2»Лгю
ш
lkr
где kr = (Rr/2Mr), шг= \/(KrjMr) — k%, коль скоро A'r/Mr > ftp. Постоян-
Постоянные Mr, Rr, Kr, kr и a)r все определяются значениями amr, rmr и bmr.
Аффинор f) становится бесконечным при 2п различных комплексных
значениях ш, из которых п вида cor + iftr имеют положительные действи-
действительную и мнимую части и расположены так, что a)m_1^a)m, а осталь-
остальные п имеют вид — wr-{-ikr, то есть при соответственно тех же мнимых
частях имеют действительные части противоположного знака. Иначе говоря,
если нанести эти корни на комплексной плоскости, то все они окажутся
над действительной осью, причем те, у которых ш < 0, окажутся сим-
симметричны относительно мнимой оси корням с а) > 0 (если среди к% есть
большие Кг/Мг, то соответствующие корни окажутся на самой мнимой
оси над действительной осью). Найденные корни соответствуют свободным
колебаниям системы; зависимость r-го нормального колебания от времени
определяется множителем e~V+iuY', а компоненты смещения будут пропор-
пропорциональны компонентам единичного вектора вдоль r-й оси системы нор-
288 Гл. 3. Поля и вариационный принцип
мальных координат в абстрактном векторном пространстве. Вид множителя,
содержащего t, свидетельствует о том, что эти колебания — затухающие.
Сопряженным координатам, конечно, также соответствуют аффиноры
импеданса и адмитанса, с помощью которых можно выразить зависимость
между силами Fm = pm + dH/dxm и скоростями ж„. Компоненты этих
аффиноров отличаются от соответствующих компонент 3 й?) только тем,
что они имеют отрицательные сопротивления вместо положительных.
Иначе говоря, компоненты — iwQ* являются комплексно сопряженными
но отношению к компонентам — imQ, что отвечает указанному выше
зеркальному соответствию.
3.3 Скалярные поля
В классической динамике задача оказывается решенной, когда полу-
получены выражения координат системы как функций времени; вариационный
интеграл, служащий для отыскания решения, представляет собой интеграл
по времени от функции Лагранжа, выраженной через координаты и их
производные по времени. Материальные поля, рассмотренные в предыдущей
главе (упругая деформация, диффундирующая плотность, потенциал Скоро-
Скоростей жидкости), представляют собой «сглаженные» средние от величин, харак-
характеризующих поведение сложных систем, образованных множеством частиц.
Для решения задач такого рода мы можем взять уравнения движения
частиц и затем, усреднив эти уравнения, получить уравнения поля, как
это делалось, по крайней мере в принципе, в гл. 2. Или же, прежде чем
минимизировать интеграл, мы можем усреднить функцию Лагранжа для
всей системы и получить вариационный интеграл для поля; так мы
и будем поступать в этой главе.
Во многих случаях получается поле скалярной функции от времени
и координат, которые и служат параметрами интеграции. Само поле
варьируется для отыскания минимума интеграла от функции Лагранжа,
и уравнения Эйлера C.1.3) оказываются уравнениями в частных произ-
производных, выражающими зависимость поля от координат и времени.
Гибкая струна. Эти замечания мы проиллюстрируем на простом
примере натянутой гибкой струны; этот пример послужит нам ориенти-
ориентиром при рассмотрении более сложных задач. Мы начнем с того, что
составим функцию Лагранжа для каждого атома струны (следовало бы,
конечно, начать с уравнения Шредингера, но здесь мы рассматриваем
движения многих миллионов атомов, поэтому квантовыми эффектами
можно пренебречь и воспользоваться законами классической динамики).
Полная кинетическая энергия равна
JV
где iV —число наличных атомов. Движение каждого атома в элементе
струны между х и x-\-dx можно рассматривать как векторную сумму
среднего движения (dty/dt) j этого элемента [для простоты мы предпола-
предполагаем, что такое движение происходит в плоскости, ортогональной струне;
среднее смещение точки х струны от положения равновесия обозначено
О (ж)] и колебательных движений wg отдельных атомов около этого
среднего движения. Полная кинетическая энергия элемента струны равна
3.3. Скалярные поля 289
поэтому
da:
где члены j-ws имеют среднее по времени значение, равное нулю. Сумми-
Суммирование произведено по всем частицам, содержащимся в элементе струны
длины dx. Так как сейчас нас не интересуют колебания отдельных атомов,
то мы не станем составлять индивидуальные лагранжевы уравнения для
координат, соответствующих скоростям ws. Следовательно, мы выбросим
последние слагаемые в скобках не потому, что они пренебрежимо малы
(в действительности они соответствуют внутренней тепловой энергии
струны и не малы в совокупности), а потому, что мы не хотим сейчас
рассматривать эти движения молекул. Вторыми слагаемыми в скобках
мы пренебрегаем потому, что их производные по ф (входящие в уравне-
уравнение Лагранжа для ф) имеют средние по времени, равные нулю. Итак,
интересующая нас полная кинетическая энергия выражается в виде
C.3.1)
где pdx равно сумме масс та всех частиц, содержащихся в участке струны
между х и x-\-dx.
Потенциальная энергия струны представляет собой сложную функцию
координат всех атомов системы. В ней также можно выделить слагаемое,
выражающее среднее приращение потенциальной энергии струны, когда
последняя смещается на ф (х) от положения равновесия, и слагаемое,
соответствующее индивидуальным отклонениям частиц от их среднего
положения; последнее мы отбросим, как и при выводе формулы C.3.1).
Первое же слагаемое мы найдем, подсчитав работу, которая затрачи-
затрачивается на растяжение струны, когда ее выводят из положения равновесия.
Если натяжение струны равно То, то эта работа равна произведению То
на приращение длины струны при условии, что это последнее мало по
сравнению с длиной. Таким образом, интересующая здесь нас часть
потенциальной энергии выразится в виде
если только (dty/dxJ < 1 и струна натянута между точками х = 0 и х = 1-
Итак, для усредненного поперечного движения струны в заданной
плоскости функция Лагранжа равна
Она представляет собой взятый вдоль всей длины струны интеграл
от плотности функции Лагранжа
Как и раньше, мы стремимся к тому, чтобы минимизировать интеграл
19 Ф. м. Морс и Г. ФешСах
290 Гл. 3. Поля и вариационный принцип
функции X по времени. Эта задача приводит к уравнению Эйлера
) )
dt V d(dtydt) )~т~ дх\ d(dij[dx)
или
дх*
это—уравнение колебаний струны [см. B.1.9)].
Волновое уравнение. Итак, одномерное волновое уравнение — уравне-
уравнение колебаний струны —было выведено, исходя из требования, чтобы при
соответствующем усреднении и при соблюдении начальных и краевых
условий разность между полной кинетической энергией струны и ее потен-
потенциальной энергией принимала наименьшее возможное значение. Руковод-
Руководствуясь этим полезным замечанием, мы сумеем получить ряд других
результатов.
Если, например, к струне приложена сила, действующая перпендику-
перпендикулярно оси х и распределенная так, что в точке х сила, приходящаяся
на единицу длины струны, равна F (х), то к потенциальной энергии нужно
еще добавить — Fty; если струна погружена в упругую среду (см. стр. 137),
то нужно еще добавить слагаемое вида -к К§2. Окончательное выражение
плотности функции Лагранжа будет иметь вид
и мы получим такое уравнение движения
что согласуется с уравнением B.1.27).
Импульсу в динамике точки здесь будет соответствовать производная
X по ф; соответствующую плотность
р = dL/d$ = p (dtydt) C.3.4)
называют плотностью канонического импульса. В случае струны, как мы
видим, она равна импульсу единичного отрезка струны, движущегося
со скоростью dty(x)/dt.
Плотность функции Гамильтона, согласно C.2.6), есть
-F* C-3-5»
[ср. с B.1.11)]. Интеграл от Н, взятый вдоль струны, представляет
собой полную энергию, но, в отличие от классической динамики, Н зави-
зависит не только от р и ф, но еще и от dty/дх. Естественно поэтому ожидать,
что и уравнения, соответствующие гамильтоновым каноническим уравне-
уравнениям C.2.7), окажутся более сложными. С помощью принципа Гамиль-
3.3. Скалярные поля 291
тона, .интегрируя в двух слагаемых по частям, мы получим
О = 3 ^ dt^ dx [р\ -Н (р, ф, ф')] =
= \ dt\ dx [ф op + pty - (дН/др) ар - (дЯ/дф) 8ф - (дНЩ1) 8ф'] =
= ^ dt J dx{[ф - (дН/др)] Ър- [р + (dH/dCf) - (д/дх) (дНЩ')] Щ,
где
ф = дф/дг, p = dp/dt, ф' = 9ф/ах,
откуда следует, что
0ф _ аН dp __d_f дН\ дН ,ч о fiv
~а"~ ар ' а« ~" а* V, аф' J ~ зф ¦ ^.й.о)
Полученные уравнения отличаются от канонических присутствием члена
сШ/дф''. Комбинируя эти уравнения, мы придем к уравнению движения
струны
Положение оказывается более сложным по сравнению с динамикой
точки из-за того, что функция ф, соответствующая координате q в дина-
динамике, зависит не только от параметра t, но и от параметра х. Это озна-
означает, что соотношения между импульсами, полем и градиентом поля
сложнее соотношений, описываемых каноническими уравнениями C.2.7).
Большая сложность этих соотношений ясна также с точки зрения
теории относительности. Мы видели на стр. 99, что энергия частицы
есть временная компонента некоторого 4-вектора, пространственные компо-
компоненты которого пропорциональны импульсу. В то же время в рассматри-
рассматриваемом случае плотность энергии
гт 8L , г Эф вф т
оказывается 4,4-компонентой некоторого тензора ffis; последний имеет
компоненты
C.3.7)
Э1и компоненты удовлетворяют уравнениям дивергенции
ewu ewlt __ аф
«ф т а*ф „ „п _ п
имеющим интересное физическое истолкование. Взяв сначала второе из.
этих уравнений и проинтегрировав его по х от с до fc, мы получим
19*
292 Гл. 3. Поля и вариационный принцип
Но в силу B.1.2) WiX представляет собой поток энергии вдоль струны;
он, очевидно, связан с изменением энергии Н так, как описывается этим
уравнением. Таким образом, второе уравнение C.3.8) представляет собой
уравнение неразрывности потока энергии вдоль струны.
Первое уравнение C.3.8) связывает изменение во времени потока
энергии с распределением натяжения вдоль струны, так как WXi= — WA1/c2
имеет размерность плотности импульса, связанного с потоком энергии
еолнового движения. Интегрируя первое уравнение C.3.8), мы получим
ь
-ж
а
отсюда видно, что если WXi есть плотность волнового импульса, то
W1X — сила, которую можно назвать волновым напряжением. Это уравнение
утверждает, таким образом, что скорость изменения волнового импульса
на каком-либо участке струны равна разности значений волнового напря-
напряжения на концах участка.
Плотность волнового импульса Р = Wu теснее связана с самим волно-
бым движением, нежели плотность канонического импульса p=p(dty/dt),
так как р есть поперечный импульс в различных участках струны, а Р
связано с потоком энергии вдоль струны, обусловленным волновым движе-
движением.
Кстати, уравнения C.3.6) можно использовать для доказательства
того, что интеграл от плотности функции Гамильтона есть константа
движения, не зависящая от времени; в самом деле
i i
о
i
-" j L 9t ax эу+~щг ~te~dt J ~~ Lv ц' Jo'
о
так как й или дН/д^' обращаются в нуль на концах струны.
Уравнение Гелымгольца. Когда струна совершает простые гармони-
гармонические колебания, ее отклонения от оси х выражаются функцией ф (x,t) =
= Y (x)e~iwt, где функция Y удовлетворяет уравнению Гелъмголъца
(d2Y/dx2) + k2Y = 0, к = со/с,
в котором значение к определяется краевыми условиями. Это уравнение
можно получить также, исходя из вариационного принципа.
В качестве плотности функции Лагранжа можно взять член
— T(dY/dxJ, отвечающий потенциальной энергии. Получение ненулевого
решения можно гарантировать, добавив к вариационному уравнению
i
о
дополнительное требование, чтобы средняя квадратичная амплитуда У
отлична от нуля, например, чтобы
г
3.3. Скалярные поля 293
Согласно сказанному на стр. 267, такая вариационная задача может
быть решена методом множителей Лагранжа. Мы включаем дополнитель-
дополнительное требование (уравнение связи) тем, что будем минимизировать ин-
интеграл
где X — множитель, который заодно должен быть найден. Уравнение
Эйлера такой задачи совпадает с уравнением Гельмгольца
и искомые значения X окажутся равными требуемым значениям /с2.
Потенциал скоростей. Переходя к трехмерному случаю, рассмотрим
движение жидкости (см. § 2. 3). Если это движение безвихревое, то ско-
скорость жидкости может быть представлена как градиент потенциала ско-
скоростей ф. Плотность кинетической энергии выразится при этом в виде
г
Если жидкость несжимаема, то. потенциальная энергия постоянна п плот-
плотность функции Лагранжа L совпадает с Т. Уравнение Эйлера C.1.3)
в этом случае сводится к уравнению Лапласа
V2'A = 0.
Таким образом, уравнение Лапласа, описывающее установившееся
безвихревое движение несжимаемой жидкости, выражает требование, чтобы
при выполнении заданных начальных и краевых условий полная кинети-
кинетическая энергия жидкости имела наименьшее возможное значение.
Если жидкость сжимаема, но вязкость ее пренебрежимо мала, то
появится плотность потенциальной энергии, которая выражается через
потенциал скоростей ф. Эта энергия равна работе pdV, которая должна
быть затрачена на то, чтобы единицу объема жидкости перевести из
стандартных условий (относящихся к плотности и т. д.) в условия,
поставленные в задаче. Допустим, что такой переход сопровождается
относительно малыми изменениями соответствующих величин по сравне-
сравнению с их значениями в стандартных условиях; если в стандартных усло-
условиях плотность равна р, то мы считаем, что в условиях задачи она равна
p(l + s), где s — весьма мало по сравнению с единицей. Элемент жидкости,
имеющий объем 1 см3 в стандартных условиях, при плотпости, равной
p(l + s), будет занимать объем A — s) см3 (с точностью до величин пер-
первого порядка относительно малой величины s).
Для отыскания потенциальной энергии нужно знать, как при изме-
изменении состояния жидкости связаны между собой давление и плотность.
Так, например, в случае газа отношение давления к плотности вы-
выражается формулой B.3.21) (см. стр. 161). В рассматриваемом случае
давление в стандартных условиях мы обозначим р0, а давление в усло-
условиях задачи ро-\-р. Такие обозначения общеприняты в акустике (заметим,
что в этом пункте р означает давление, а не канонический импульс).
Уравнение B.3.21) в этих обозначениях примет вид
то есть
pipe's, C.3.10)
294 Гл. 3. Поля и вариационный принцип
где в случае газа с2 = у/?0/р. Для других жидкостей избыточное давление
также пропорционально относительному приращению плотности [так что
формула C.3.10) остается справедливой], но постоянная с2 определяется
различными свойствами рассматриваемой жидкости. Как мы вскоре увидим,
с в некоторых случаях равна скорости звука в жидкости.
Когда жидкость при переходе от стандартных условий к реальным
подвергается сжатию, элемент жидкости, занимавший объем dV, получит
новый объем dV (I — s) =dV [1 — (р/рс2)]. Работа, затраченная на такое
сжатие
^ pdVds = ^\pdp=(^)P4V,
о о
и есть потенциальная энергия сжатия элемента объема dV. Следовательно,
плотность потенциальной энергии равна р2/2рс2.
Но мы еще отсюда не можем составить вариационное уравнение, так
как нам надо связать р с потенциалом скоростей ф, хотя вполне можно
было бы составить вариационные уравнения для скаляра р, а не ф. Тре-
Требуемую связь проще всего найти из уравнения B.3.14). Если коэффи-
коэффициентами вязкости -г) и X можно пренебречь и внешняя сила F равна нулю,
то p(dv/d?)= — gradp. Если потенциал скоростей существует, то v = grad$
и, приравняв градиенты, мы получим уравнение
р=-РЩ№)+С0, C.3.11)
где постоянная интегрирования Со обычно приравнивается нулю. Таким
образом, давление представляет собой временную компоненту 4-вектора,
пространственные компоненты которого равны компонентам скорости
жидкости.
Волны сжатия. Теперь мы можем составить выражение плотности
функции Лагранжа для малых колебаний невязкой сжимаемой жидкости
C.3.12)
Это— инвариантная плотность, интеграл которой (по времени и прост-
пространству) должен быть минимизирован. Особенность ее в том, что скорость
выражена производными по координатам, а сила — производной по вре-
времени; объясняется это тем, что скорость представляет собой вектор (гра-
(градиент), а сила (давление) — скаляр.
Уравнением Эйлера C.1.3) для такой плотности функции Лагранжа
служит волновое уравнение в трехмерном пространстве
где с —скорость распространения волн.
Интересно отметить, что по сравнению с уравнением колебаний
струны, производные пространственные и производные по времени ме-
меняются ролями. Здесь производные <Ь по координатам соответствуют кине-
кинетической энергии, а производная по времени — энергии потенциальной.
Здесь так называемая «плотность канонического импульса» дЬ/д§ [см.
C.3.4)] пропорциональна давлению, а совсем не скорости жидкости. Поэ-
Поэтому простые методы, связанные с использованием канонически сопря-
сопряженных переменных q и р, применимые в динамике точки, должны быть
заменены более сложными. При этом оказывается полезен 4-аффинор 28 с
3.3. Скалярные поля 295
компонентами
Wu = L84j. - Р- -..^я ч, C.3.13)
Компонента W44 есть плотность энергии
]-1р^ + ^^ = Я, C.3.14)
интеграл от которой не зависит от времени (это можно показать так же,
как это было сделано на стр. 292 для случая струны).
Пространственно-временнйе компоненты аффинора 28 пропорциональны
некоторому 3-вектору S
Wu = Wtk = ±§-g- = 4-pvk=±Sk, Л= 1,2,3. C.3.15)
R4 4в с от ftcfe ic r " гс R '
S задает направление и величину потока энергии, обусловленного вол-
волновым движением. Вектор P = S/c2, имеющий размерность плотности
импульса, называется плотностью импульса поля. С другой стороны,
вектор pS/p = pv представляет собой плотность импульса движущейся
жидкости.
Заметим также, что 4-дивергенции векторов, образованных из 28, все
равны нулю. Это можно показать, взяв
Y dWjj = дЬ у Г й2ф dL 9\> д Г 8L ЛI
2л дх} dxi 2j [ dxidxj d'Jjj + dxi dxj V #y J J '
где tyj = d§ldXj. Если ? зависит от xt только через посредство функции ty
и ее производных, то,
и с помощью уравнений Эйлера C.1.3) мы приходим к равенствам
тп dWa _ dq, r dL v a ( дь \ i _n
4J 9ж/ ~ dxi I д<\> 2J дх}\ dtyj ) J — '
.доказывающим наше утверждение относительно дивергенций в том случае,
когда L не зависит от х явно. Отсюда мы можем получить уравнение
неразрывности для S и Н
divS+(dH/dt) = O,
которое показывает, что если Н — плотность энергии, то S — вектор плот-
плотности потока энергии (это было отмечено раньше). Хотя интеграл от Н
по всему пространству постоянен, значение Н в любой точке может из-
изменяться с течением времени, так как энергия может перераспределяться
в объеме, занятом жидкостью.
Волновой импеданс. Возвращаясь к уравнению Лагранжа-Эйлера
.для ф, мы видим, что если к ф приложена «плотность сил» /, то / будет
связано с приращением <1> уравнением
В классической динамике мы можем обычно приложить силу к одной
координат системы и найти соотношение между приложенной силой
296 Гл. 3. Поля и вариационный принцип
и перемещением или скоростью системы (см. стр. 272). Но в случае поля
сила, сконцентрированная в точке, как правило, вызывает бесконечное
смещение этой точки; для того же, чтобы вызвать физически реализуе-
реализуемый эффект, сила должна действовать на некоторый объем или на пло-
площадь. Обычно бывает так, что внешняя сила оказывается приложенной
к некоторому участку поверхности, ограничивающей поле. Так, например,
вибрирующая мембрана громкоговорителя служит источником звуковых
волн в жидкости, а эти волны в свою очередь воздействуют на мембрану.
Мерой этого воздействия (реакции) служит акустический импеданс жид-
жидкости перед мембраной, характеризующий тип возбуждаемых волн.
Если сила приложена к поверхности, служащей границей поля, то
для отыскания полной реакции следует интегрировать уравнение Лаг-
ранжа-Эйлера по всему объему, заключенному в этой поверхности. При
этом мы получим
где второе слагаемое преобразовано в поверхностный интеграл по фор-
формуле Гаусса [см. A.4.7)]. Любая сила, действующая на ф по граничной
поверхности, уравновешивается этим слагаемым, поэтому если F — «сила»,
действующая на ф, рассчитанная на единицу площади, то F = pgrac^. Если
F изменяется гармонически F= Foe~im', то соответствующая скорость изме-
изменения ф (соответствующая скорости) равна — гшф, так что отношение-
поверхностной плотности силы к скорости изменения ф равно
— F/адф = — (р/гшф) grad ф.
В силу того, что в рассматриваемом случае по сравнению с задачами
динамики градиент и производная по времени меняются ролями, то вели-
величина поф пропорциональна давлению, a grac^ пропорционален скорости
жидкости. В акустике обычно аналогом внешней силы мы считаем не F
(которое представляет собой «силу», вызывающую изменение ф), а дав-
давление, поэтому приведенное выше отношение соответствует скорее адми-
тансу, чем импедансу.
Обычно акустический адмитанс определяется равенством
^ C-ЗЛ6>
здесь р означает давление в какой-либо точке граничной поверхности,
где приложена внешняя сила, a v — скорость жидкости в этой же точке.
Чтобы вычислить Y, надо сначала решить волновое уравнение для отыска-
отыскания поля, порожденного вибрацией данного участка границы, после чега
можно будет вычислить A/шрф^гас1ф для различных таких участков;
если нужно, интегрируя, мы найдем акустический адмитанс всей поверх-
поверхности, воздействующей на поле.
Адмитанс Y представляет собой вектор, так как v —вектор, а р — ска-
скаляр. Обычно бывает достаточно вычислить нормальный акустический ад-
митанс—нормальную (к границе поля) составляющую Yn вектора Y,
равную
Обратная величина
называется нормальным акустическим импедансом. Она равна отношению
давления в граничной точке, где действует внешняя сила, к нормальной
3.3. Скалярные поля 297
составляющей скорости жидкости в той же точке. Так как эта скорость
равна скорости движения самой поверхности, то нормальный импеданс
является наиболее важной частью импеданса.
Плоская волна. В качестве примера тех разнообразных величин,
о которых мы так бойко здесь говорили, рассмотрим особенно простой
вид волнового движения, плоскую волну. Такая волна изображается
формулой
где С = | С j eicP — постоянная, определяющая амплитуду и фазу у потен-
потенциала скоростей, а к—постоянный вектор длины <о/с, указывающий
направление движения волны. Соответствующие волновые поверхности
представляют собой плоскости, перпендикулярные вектору к, движущиеся
по направлению к со скоростью с.
Выражения давления и скорости жидкости в случае плоской волны
можно получить, зная потенциал скоростей, с помощью ранее получен-
полученных соотношений. Они соответственно равны действительным частям
выражений
v = grad -Ь = гк Ceik -r-ш.
Иначе говоря, значение давления в точке х, у, z в момент t равно-
— сор \С\ sin[(u)/c) (аж + Ру + yz — ct) + y>], где а, р, у — направляющие коси-
косинусы вектора к и | к | = со/с. Жидкость движется по направлению век-
вектора к, т. е. перпендикулярно фронту волны, а скорость в случае плос-
плоской волны совпадает по фазе с давлением.
Для вычисления тензора напряжения-энергии надо взять действи-
действительные части обеих величин, так как его компоненты представляют
собой многочлены второй степени, содержащие ф. Обозначив
Q = (ш/с) (ах + Ру + yz — ct) + 9 = k • г — ш1 + <р,
будем иметь
, р= — cop|C|sinQ, v= — k|C|sinQ,
S = pv = pcok IС |2 sin2 Q = Pc2,
где a, p, у — направляющие косинусы вектора распространения (волно-
(волнового вектора) к. Следовательно, тензор напряжения-энергии для плоской
волны может быть представлен матрицей
298 Гл. 3. Поля и вариационный принцип
Нетрудно убедиться в справедливости для grg уравнений дивергенции
2л дхп
и в том, что пространственные компоненты 28 преобразуются, как
аффинор.
Одна из главных осей пространственной части 28 направлена вдоль к;
двумя другими служат любые два взаимно-перпендикулярных направле-
направления, ортогональных к. Если ?15 ?2, ?3~~К00РДинатЫ> соответствующие
.этим осям, то относительно них grg принимает вид
' —1 0 0 г>
0 0 00
0 0 00
- i 0 0 1,
Все компоненты оказываются пропорциональными квадрату частоты
и квадрату амплитуды волны.
Можно представить себе, что плоская волна вызвана колебаниями
ллоскости, перпендикулярной вектору к, совершающимися в направле-
направлении к, причем скорость колебаний равна gradф = ikCeik'r~iu)'. Акустический
•адмитанс, являющийся мерой реакции волны на колеблющуюся плоскость,
равен в этом случае
Рс k'
где afe, — единичный вектор, совпадающий по направлению с к. Следова-
Следовательно, акустический импеданс, нормальный к фронту плоской волны,
равен рс, т. е. имеет действительное значение. Другими словами, плос-
жая волна порождает резистивный импеданс1), действующий на колеблю-
колеблющуюся плоскость, не зависящий от частоты. Импедансы волн другой
»формы будут еще рассмотрены в этой книге.
Уравнение диффузии. Переходя к уравнениям, описывающим дисси-
лативные процессы, такие, как течение вязкой жидкости или диффузия,
мы воспользуемся формальным приемом, описанным на стр. 285. Напри-
Например, в случае уравнения диффузии плотность функции Лагранжа равна
L = — (grad ф).(grad ф*) — ^т0-2\ ф* -jr- — ф .7 ) , C.3.17)
1где ф — концентрация диффундирующего вещества, а2 — постоянная диф-
•фузии; ф* относится к зеркально отраженной системе, в которой про-
происходит процесс, обратный диффузии. Плотности канонических импуль-
«сов выразятся в виде
юни, впрочем, имеют мало общего с физическими импульсами.
Уравнения Эйлера для этой плотности функции Лагранжа имеют
вид
V2^ = а2 (дф/д*), V2<]>*= -а2 (db*/dt). C.3.18)
1 См. стр. 287.—Прим. ред.
3.3. Скалярные поля 299
Уравнение относительно ф — обычное уравнение диффузии; второе уравне-
уравнение относится к зеркально отраженной системе, поглощающей столько
же энергии, сколько теряет исходная система.
Плотность функции Гамильтона равна grac^-grad^*; интеграл ее
но объему не зависит от времени. Она представляет собой 4,4-компо-
ненту тензора дщ, определяемого равенствами
¦!¦*» ГЛ Sty d?j 5ф* dL #Q q Л Q\
тде фу = dty/dxj. Компоненты Wkt содержат компоненты вектора gradф,
определяющего направление и величину потока диффузии.
Метод введения «зеркально отраженного» поля ф* с целью образовать
функцию Лагранжа, из которой получается уравнение диффузии, может
быть, слишком уж искусственен для того, чтобы ожидать от него сущест-
существенных физических выводов. Он рассмотрен здесь затем, чтобы показать
возможность применения вариационного метода к диссипативным системам;
кроме того, введение подобных полей ф* оказывается необходимым в неко-
некоторых задачах квантовой физики, и задача о диффузии может служить
полезной подготовкой к этим более сложным задачам.
Аналогичный прием может быть использован для построения функ-
функции Лагранжа в том случае, когда при рассмотрении потока жидкости
учитывается вязкость.
Уравнение Шредингера. Нечто похожее может быть использовано
для вывода уравнения Шредингера B.6.38), хотя оно и не диссипативно.
Волновая функция ф принимает комплексные значения, поэтому ее дей-
действительную и мнимую части можно рассматривать как самостоятельные
(независимые) переменные или, что то же самое, можно рассматривать
отдельно (как независимые полевые переменные) скалярное поле ф и ска-
скалярное поле комплексно-сопряженной функции ф*. При этом произведе-
произведение фф* будет действительным в дри оптимальном выборе обеих пере-
переменных будет равно платности вероятности для наличия частицы,
т. е. для конфигурации системы, описываемой координатами х.
В качестве примера рассмотрим отдельную частицу с массой т,
находящуюся под действием потенциального поля V (х, у, z). Плотность
«функции Лагранжа оказывается равной
-ф*Гф; C.3.20)
искомые фиф* должны сообщать наименьшее значение интегралу
Уравнения Лагранжа — Эйлера получаются при этом
или
Легко видеть, что эти уравнения соответствуют уравнению B.6.38). Если
взять классическую функцию Гамильтона Н (р, д) = A/2то) (р% 4- р% + pi) + V
для частицы и заменить в ней рх, ... символами (%/i)(d/dx), ... , дей-
действующими на ф, то B.6.38) превратится в первое из уравнений C.3.21).
Уравнение, содержащее комплексно-сопряженную функцию ф*, получится
изменением знака при i в слагаемом, содержащем производную по времени.
300 Гл. 3. Поля и вариационный принцип
Два канонических импульса выражаются в виде
C.3.22)
Они бывают нужны при «вторичном квантовании», которое часто приме-
применяется в современной квантовой физике, но не рассматривается нами
в этой книге. Тензор напряжения-энергии 28 имеет компоненты, опреде-
определяемые равенствами
Wmn = <& -щ + Фт ~ - ЬтпЬ, C.3.23)
д\, _ , Г 0, тфп,
Хт~Х' У' Z< *• °mn[
где
Плотностью энергии служит 4,4-компонента 28
Следует отметить, что в рассматриваемом случае, как и в уравнении
диффузии, производные по времени (которые соответствуют величи-
величинам q) входят в L линейно, в отличие от классической динамики, где q
входят в L в виде квадратичной формы J] arsqrqs. А когда q входят в L
линейно, канонические импульсы dL/dq не зависят от q, а лишь от q,
поэтому р и q не являются независимыми переменными. В таком случае
гамильтонова функция Н^=2PQ — -^ зависит только от q и не зависит
от р и от q, а канонические уравнения не будут, конечно, иметь вид C.3.6).
Как в уравнении диффузии, так и в уравнении Шредингера, р представ-
представляет собой функцию от ф*> а р* —функцию от ф, поэтому нам не удастся
получить одно каноническое уравнение для р, другое для q, а придется
получить одно уравнение для ф и другое —для ф*. Как всегда,
*p*-H(ty, ф*, фп. <&
= С dt С dv [op ф + р Ц + ф*ор* + Ц*р* —
где ф2 = 9ф/бг/, ф| = бф*/9г и т. д. Но теперь ор = {йрД2ф*)8'!<*, и, интегри-
интегрируя по частям, мы получим \ dt /?8ф= — \ дЛрЩ= — \
и т. д. Как и раньше, мы будем также иметь
Подставив все эти выражения в интеграл, выражающий ЪЗв, мы найдем,
что ЬХ окажется равным интегралу от некоторого выражения, умножен-
умноженного на 8J), плюс некоторое другое выражение, умноженное на 8ф*. Так
как ЬХ должно обращаться в нуль при произвольных 8ф и 8ф*, то оба
множителя при Щ и 8ф* должны быть равны нулю, и мы придем к таким
3.3. Скалярные поля 301
двум уравнениям:
йр__ d^_ I ... ая у д г дн л
#* йф J - зф* Zj s*n V. эф* У ' C 3
*?_ dp_i _эн у д г ан
чЗто —новые канонические уравнения; если применить их к гамильтоно-
вой функции для уравнения диффузии или для уравнения Шредингера,
то мы снова получим уравнения движения C.3.18) или C.3.21). Не ясно,
впрочем, насколько полезными окажутся уравнения C.3.24), так как
не видно, чтобы они давали больше, чем уравнения Лагранжа —Эйлера.
Вектор плотности потока энергии в шредингеровском случае равен
• C-3.25)
S совместно с плотностью энергии Wit удовлетворяет уравнению не-
неразрывности div S + dH/dt = 0.
Плотность импульса поля представляется вектором
= -(ft/2i) ^grad^-^grad**]. C.3.26)
Обращаясь к стр. 246, мы замечаем, что (когда магнитное поле равно
нулю) плотность тока, соответствующая функции ф, равна J= — (e/m)P,
так что Р оказывается связанным с плотностью потока вероятности ча-
'Стицы, описываемой волновой функцией ty.
Уравнение Клейна—Гордона. Подобным же образом можно рассмо-
рассмотреть уравнение Клейна — Гордона B.6.51), могущее служить волновым
уравнением для релятивистской частицы (хотя для электрона или про-
протона оно неверно). Здесь мы снова используем два независимых поля
<i> и ф*. Величины (h/i) (dty/дх, д^/ду, dty/dz, dty/d {ict)) служат компонен-
компонентами некоторого 4-вектора, так же как соответствующие производные от ф*.
Скомбинировав их с 4-вектором (Д,., Ау, Аг, щ) электромагнитного по-
потенциала так, как это следует из уравнения B.6.49), мы получим плот-
плотность функции Лагранжа для «частицы» с зарядом е и массой т в электро-
электромагнитном поле
. C.3.27)
-i
Отсюда можно получить уравнение Лагранжа — Эйлера для ф
4
^ д / дЬ \ dL pi
где Сх = ж, С2 = 2/, C3 = z, ?4 = ^, Фп = 9ф*/9СП> приводящее к уравнению
Клейна — Гордона при наличии электромагнитного поля
Такой же вид имеет уравнение для ф*. При выводе мы несколько раз
должны воспользоваться соотношением div A + A/c) (df/dt) = 0. Когда
302 Гл. 3. Поля и вариационный принцип
А и <р равны нулю, уравнение C.3.28) упрощается и принимает вид
B.6.51).
Для простоты дальнейшие рассуждения проведем в предположении,
что А и <р равны нулю. При этом функция Лагранжа примет вид
C.3.29)
а канонические импульсы получат выражения
р = (дЬ/Ц) = (к*/2тс2)Щ*1д1), р* = (hz/2mcz) (Эф/Э*); C.3.30)
4,4-компонента тензора напряжения-энергии
Wmn- Гтщ + ^тщ-п-ЬтпЬ C.3.31)
является, конечно, плотностью энергии Н. Ее можно выразить через кано-
канонические импульсы р, р*, функции ф, ф* и их градиенты
= ^ (Р*Р) + ? (grad ф*) • (grad ф) + -1 тс^*ф = Я. C.3.32)
Отсюда с помощью канонических уравнений C.3.6) мы получим
йф _дН _ 2тс2 х
dt~~ dp ~~ № Р •
з
др* Ъ? д^Ь ^ д С дНЛ дН V- „ 1
dt 2mc2 6Р Zj dZn V ty*) d<h* 2m y 2 v
1
71=1
и еще два уравнения для d§*/dt и dp/dt. Эти уравнения снова дают урав-
ния Клейна — Гордона для ф и ф*.
Вектор плотности импульса поля равен
J|!gradф^-f gradф*] , C.3.33).
а вектор S плотности потока энергии есть — с2Р.
Выражения плотности тока и заряда для этого уравнения можно
вывести разными способами. Можно, например, — этот прием окажется
полезен в дальнейшем,—забегая вперед, обратиться к уравнению C.4.11)
и заметить, что то слагаемое в выражении функции Лагранжа, которое-
включает взаимодействие между электромагнитными потенциалами и
током, выражается в виде A/с) А ¦ J —<рр. Поэтому такой же вид должно
иметь то слагаемое в C.3.27), в которое входят ф и потенциалы, т. е.
Отсюда мы заключаем, что вектор плотности тока должен выражаться
в виде
J = (eh/2im) [ф*grad ф — фgradф*], C.3.34)¦
т. е. должен совпадать с выражением B.6.47) для уравнения Шредин-
гера при А и <р, равных нулю. Соответствующее выражение плотности
зарядов при ^1 = 0 и <р = 0 есть
3.4. Векторные поля 303
это выражение отлично от того, которое соответствует уравнению Шре-
дингера. Действительно, выражение C.3.35) не обязательно сохраняет
определенный знак (зависящий от знака е), а это не вполне удобно для
волновой функции (если только мы не имеем в виду рассматривать заряды
переменного знака!).
Между прочим, эти выражения для J и р могут быть получены и из
самих уравнений Клейна—Гордона так же, как на стр. 246 были выве-
выведены J и р для уравнения Шрёдингера.
3.4. Векторные пола
Если поле, потребное для описания какого-либо физического явле-
явления, имеет несколько компонент, исследование усложняется, но общие
принципы, изложенные выше, остаются в силе. Независимыми перемен-
переменными, которые должны быть подобраны так, чтобы интеграл от плотно-
плотности функции Лагранжа L принимал минимальное значение, служат ком-
компоненты <ЬХ, ... , <]>п, являющиеся функциями от параметров х, у, z, t
(или любых других четырехмерных координат). L есть инвариантная
функция от <1чиих производных tyiy = (%/#?,. (Ьх = х, %г = у, E3 = z> ?4 = 0>
и мы должны минимизировать интеграл
Уравнения Эйлера, то есть уравнения движения поля, имеют вид
д ( 9L\_dL . 2
Г~ 1
или 8~ C.4.1)
3
_??_v д ( dLЛ
~ % 2л ее, V, дь, J *
s-i
Заметим, что интеграл Лагранжа X и соответствующие уравнения Лаг-
Лагранжа — Эйлера обладают своего рода «калибровочной инвариантностью»
(см. стр. 205). Значение X не изменяется от прибавления к L 4-дивер-
4-дивергенции какой-либо 4-векторной функции от <]^ и их производных, обра-
обращающейся в нуль на границе поля. Действительно, такой четырехкрат-
четырехкратный интеграл от 4-дивергенции равен четырехмерному аналогу потока
этой векторной функции сквозь границу поля, а такой поток равен нулю,
так как сама функция равна нулю на границе. Так как X не изменяется
при замене L на L'=L + V ¦ F, то новая плотность функции Лагранжа
L' также удовлетворяет уравнениям Лагранжа — Эйлера C.4.1). Таким
образом, X и уравнения Лагранжа — Эйлера инвариантны относительно
замены L на L'
Общие свойства поля. Величина рг = дЬ/д^и называется плотностью
канонического импульса для i-й компоненты ф4, хотя, как мы уже ви-
видели, часто она имеет отдаленное отношение к тому, что обычно назы-
называют импульсом. Тем не менее величина dpjdt, участвующая в уравне-
уравнениях Эйлера, аналогична произведению массы на ускорение в более про-
простых системах. Следовательно, величина
F дЬ V д f dL
ri д^ A dtX&ks
s=l
304 Гл. 3. Поля и вариационный принцип
равная скорости изменения рг во времени, аналогична компоненте силы,
соответствующей компоненте ф| поля. Первое слагаемое dL/dfyi обычно
бывает обусловлено наличием внешних сил, действующих на поле. Вто-
Второй член часто представляет собой эффект воздействия самого поля на
•его г-ю компоненту в точке х, у, z, t.
Тензор SB с компонентами
W - У ^ ~ - о L C 4 2\
Wxi— Zl S5i di/rj JH^ C.4.Z)
представляет собой тензор напряжения-энергии. Его временная компо-
компонента Wi4. есть плотность энергии Н поля; интеграл от нее не зависит
¦от времени.
Так же, как и раньше, можно показать, что Н может быть выра-
выражено через фг, канонические импульсы рг и градиенты фг;-. Действуя
так же, как на стр. 290, мы можем получить канонические уравнения
Гамильтона посредством вариационного принципа. Эти уравнения имеют вид
~dF-™-Jp~;' dt-2jdxj\_'a^7jJ~'Wr' r-l'z n-
Из них также можно вывести уравнения движения C.4.1).
Тензор SS часто оказывается несимметричным, что может вызвать
серьезные затруднения, поскольку мы привыкли к тому, что аффиноры
напряжения симметричны. Если нам желательно пользоваться симметрич-
симметричными аффинорами, то этого можно добиться, воспользовавшись «калибро-
«калибровочной инвариантностью» функции 36 и уравнений Лагранжа. Мы приба-
прибавим к функции плотности L дивергенцию некоторой специальной вектор-
векторной функции от ф и от их производных и в то же время подберем мас-
масштаб по каждой из координат так, чтобы тензор 88 стал симметричен,
a W44 по-прежнему было плотностью энергии. То, что точный вид тен-
тензора напряжения-энергии оказывается неопределенным, аналогично неопре-
неопределенности выражения плотности энергии струны (см. стр. 126). Впро-
Впрочем, эта неопределенность лишь формальная, так как она не сказывается
на физически измеримых величинах.
Как было показано на стр. 295, 4-вектор, получаемый дифференци-
дифференцированием, имеющий компоненты
равен нулю.
Следует заметить, однако, что доказательство равенств C.4.3) осно-
основывается на предположении, что L и SB зависят от параметров ?;- только
через посредство функций фг. Если в! (а следовательно, и в SB) входят
еще и другие члены (такие, как потенциалы или плотности тока), зави-
зависящие явно от ?, то левые части C.4.3) будут равны некоторым выра-
выражениям, содержащим производные этих дополнительных членов по ?.
Явная зависимость L от координат имеет место только тогда, когда само
поле порождается некоторой совокупностью частиц или материальной
средой (такой, как электрический ток). Например, лоренцова сила, дей-
действующая на электрон, выражается через компоненты поля в определен-
определенной точке пространства, именно в той, где находится электрон. Взаимо-
„действие же различных частей поля выражается интегралами, распро-
3.4. Векторные поля 305
страненными по всему пространству, и поэтому зависимость от коорди-
координат проявляется только через посредство <]>.
Во всяком случае тогда, когда L и ЗВ зависят от ? только через ф,
тождества C.4.3) выполняются, и в этом случае 3-вектор
(= 2j— i-^+j-T^ + k-^4 C.4.4)
r=l
удовлетворяет уравнению неразрывности div S -\-(dH/dt) = 0. Следова-
Следовательно, он должен представлять плотность потока энергии поля. Этот
вектор можно назвать интенсивностью поля.
Дополнительный вектор
п
имеет размерность импульса, отнесенного к единице объема, и может
быть назван плотностью импульса поля. Если функция L видоизменена
так, что тензор SB оказывается симметричным, то Р = S; в любом случае
вектор Р тесно связан с вектором S.
Пространственная часть тензора SB есть 3-аффинор
где
2|fe[^ ^ ^] -Li C.4.6)
r=l
и т. д. Три других уравнения типа C.4.3), содержащих дивергенции,
задаются векторным уравнением
W ;
последнее указывает на то, что если Р — импульс, то производная от И
есть тензор силы, так что U связано с потенциальной энергией, порож-
порожденной полем.
Тензор напряжения-энергии имеет матрицу
р1
н
где \?г1 заданы равенствами C.4.2) и Wni = Pn, Win = Sn.
Вектор плотности момента количества движения можно (если это
необходимо) получить, взяв векторное произведение радиус-вектора г
точки (х, у, z) относительно некоторого начала на вектор Р в точке (ж, у, z)
В квантовой механике эта характеристика поля волновой функции ока-
оказывается связанной с вероятным моментом количества движения частиц,
ассоциированных с рассматриваемой волновой функцией. В случае,
20 Ф. м. Морс и Г. Фешбах
306 Гл. 3. Поля и вариационный принцип
например, невязкой сжимаемой жидкости плотность момента количества
движения, согласно C.3.10) и C.3.15), равна
М = (р/с*) (г х v) = ps (г х v).
Это —момент количества движения избытка плотности, вызванного дви-
движением жидкости.
Таким образом, изменение во времени плотности энергии Н требует
наличия вектора плотности потока энергии S, а изменение во времени плотно-
плотности импульса Р — аффинора «внутренних напряжений» УХ. По этой причине
тензор 38 и называется «тензором напряжения-энергии», хотя было бы
более точно называть его тензором напряжения-энергии-импульса.
Изотропные упругие среды. Теперь мы можем приложить эти общие
формулы к нескольким интересным случаям для того, чтобы посмотреть,
какой физический смысл приобретает этот аппарат. В качестве первого
примера рассмотрим движение упругого тела (ранее мы занимались этим
в §§ 1.6 и 2.2). Согласно § 2.2 [см. формулы B.2.17) и B.2.18)], плот-
плотностью функции Лагранжа для изотропной упругой среды является
dSy
dSx dSz у /- by 8sz
где вектор s представляет собой смещение точки (х, у, z) при деформации,
р — плотность среды, X и \х — постоянные упругости, © =-2" (Vs + sV) —
аффинор деформации, а 2 — аффинор напряжений
Переменными фп поля могут служить компоненты sx, sy, sz вектора
смещения; они должны быть такими, чтобы интеграл X = \ \ \ \ Ldxdydzdt
(полная функция Лагранжа) принимал минимальное значение. Уравнение
Лагранжа — Эйлера C.4.1) для sx имеет вид
то есть представляет собой первую компоненту векторного уравнения
р (d2s/dl2) = (X + v) grad (div s)
а это и есть уравнение движения B.2.1).
Временная часть тензора SB, определенного равенствами C.4.2), есть
плотность энергии
а вектор интенсивности поля, определенный равенством C.4.4), равен
S= -(ds/dt)-%,
3.4. Векторные поля 307
т. е. вектору плотности потока энергии [см. B.2.20)]. Он удовлетворяет
уравнению неразрывности энергии div S + (dH/dt) = 0 [см. уравнение C.4.3),
как было показано на стр. 295], так как в рассматриваемом случае L за-
зависит от координат только через посредство переменных поля s.
Тензор SB не симметричен. Его пространственная часть^ которая
соответствует аффинору сил, определенному равенствами C.4.6), есть
Плотность импульса поля, определенная равенством C.4.5), равна
Эти две величины удовлетворяют уравнению дивергенции U- V + (dP/dt) = 0.
Если Р — плотность импульса, то аффинор IX связан с плотностью напря-
напряжений, что вытекает из выражения U через тензор напряжений %.
Для того чтобы показать, насколько удобны и компактны вектор-
векторные и аффинорные обозначения, выпишем полностью первые две ком-
компоненты тензора напряжения-энергии S3:
Здесь уместно сделать еще несколько замечаний. Несомненно, вариа-
вариационный принцип позволил нам собрать и представить в сжатом виде
большую часть уравнений и формул, выведенных нами с таким трудом
в гл. 2. Независимо от того, можем мы или не можем выжать из этого
синтеза дальнейшее физическое содержание или использовать побочные
продукты, такие, как импульс поля или аффинор сил, мы во всяком слу-
случае владеем прямым и плодотворным методом вывода уравнений движения
с помощью плотности функции Лагранжа и получения таких важных
величин, как интенсивность и плотность энергии.
Решения типа плоской волны. Для того чтобы сделать более кон-
конкретными выведенные здесь формулы, применим их к плоской волне,
то есть к гармоническому решению уравнения движения B.2.1). Согласно
B.2.2), одним из решений является функция
s = grad'i,
где
Смещения можно определить, вычислив градиент функции <1>,
Г~ш = акАе*-г~ш, А = ikC = | А \ е1*,
') Конечно, в последней формуле к — единичный вектор координатной оси.—
Прим. ред.
20*
308 Гл. 3. Поля и вариационный принцип
где а, Р; y — направляющие косинусы волнового вектора к, определяющего
направление распространения волны. Таким образом, смещения в такой
волне сжатия, как уже было сказано, направлены вдоль к и амплитуда
их равна \А\. Тензор деформаций и тензор напряжений выражаются
в виде
© = ~ (Vs + sV) = - кк CeikT-i»« = ikah Ае*-Г~ш,
где кк — симметричный аффинор и его коэффициент расширения | kk | = (ш/ссJ.
Для того чтобы вычислить тензор напряжения-энергии, нужно взять
действительные части этих выражений. Так, например, плотность энергии
выразится в виде
^44 = P"
где Q = kr —a)i + l}> = (ш/сс) (аж + РУ +Yz~cc0 + (P- Вектор потока энергии
равен
а вектор импульса волны Р = S/cl. Пространственная часть аффинора ока-
оказывается равной
Все это, конечно, напоминает соответствующие выводы в- случае волн
сжатия в жидкости (см. стр. 298).
В случае поперечных волн или волн сдвига
где ар — единичный вектор, ортогональный вектору к. Аффиноры деформа-
деформации и напряжений задаются равенствами
Аффинор (aftap4-apafc) симметричен, но |aftap + араь| = 0, так что |Ж|и
равны нулю.
Различные части тензора напряжения-энергии равны
S = айРс5ш21В |2 sin2 Q, Р = S/
П = aftabP(D21В |2 sin2 Q,
где Q = (ш/с8) (ах + $у + yz — Cst) + «р,
то есть они имеют тот же вид, как и в случае плоских волн сжатия. Дру-
Другими словами, векторы потока энергии и импульса волны направлены вдоль
волнового вектора к, хотя смещения среды ортогональны к.
Импеданс. В случае неизотропной среды плотность функции Лагранжа
[см. A.6.29)] выражается в виде
где 3 («гимель») есть тетрадик1) с компонентами gmnrs, определяемыми
х) См. стр. 76.
3.4. Векторные поля 309
природой рассматриваемой среды. В силу симметрии аффиноров 8и2 всег-
всегда выполняются равенства gmnrs — grsmn = gmttsr- В случае изотропной среды
элементы 3 равны
gmnrs =
ИЛИ
В неизотропном случае уравнение движения записывается в виде
Это — сложное дифференциальное уравнение второго порядка с частными
производными относительно компонент s. В этом случае не всегда удается
отделить волны чистого сжатия от чисто поперечных волн; кроме того,
волны в различных направлениях распространяются с различными ско-
скоростями.
Элементами тензора напряжения-энергии являются
Wit = 4 Р (ds/dt)* + i- (Vs): У : (Vs),
S=-
Эти же обозначения могут быть использованы для изучения импеданса
волн в упругой среде. Как было сказано на стр. 296, внешние силы
обычно бывают приложены к поверхности, ограничивающей среду, и выра-
выражаются в виде объемного интеграла от инерционной реакции p(ds/dt). Но
эта реакция равна выражению V-J:(Vs), подобному дивергенции, поэтому
объемный интеграл равен интегралу по поверхности от
— аффинора поверхностной плотности сил. Это выражение представляет
собой аффинор (как и любое напряжение в упругой среде), так как сила,
действующая на поверхность, есть вектор, зависящий от направления нор-
нормали к поверхности. Плотность силы на элементе поверхности, внутрен-
внутренняя нормаль которой направлена вдоль единичного вектора ап, равна
an-J:(Vs), т. е. представляет собой вектор.
Когда движущая сила — гармоническая, вектор установившегося сме-
смещения также содержит множитель ei№' (или же е~ш, тогда импеданс, а
также адмитанс получат комплексно-сопряженные значения). Плотность
силы на участке граничной поверхности, колеблющемся со скоростью
v = Хеш ^= iws, равна
F = an.a:(Vs) = S-v=ico3-s,
где ап — единичный вектор, нормальный к поверхности, в точке, где изме-
измеряется F. Аффинор 3, который можно выразить через компоненты g и свой-
свойства решения s, есть аффинор импеданса, измеряющий реакцию среды на
действие приложенной силы.
Например, в изотропном случае, когда 3 = ^-У +^*+F1**, мы имеем
ап • 3 : (Vs) = (X div s) ah + ^an-(Vs + sV).
Если рассматривать плоскую волну сжатия, когда волновые поверх-
поверхности ортогональны вектору к, по направлению которого распространяется
310 Гл. 3. Поля и вариационный принцип
волна (т. е. когда 8^ = 8^), то Vs = iaftk.4eik'r~iu" = sV,
ak ¦ 3 : (Vs) = &ктрссАе1к-г-ш, рс? = Х+ 2р.
В этом случае движущая сила действует в направлении скорости
акш>Ае1к-Т~ш движения среды, поэтому аффинор импеданса будет равен
характеристическому импедансу сжатия рсс среды, умноженному на идем-
фактор.
В случае плоской волны сдвига скорость движения поверхности
1юарАе~ш перпендикулярна вектору к, и с помощью формул стр. 308 мы
получим
ah У : (Vs) = аршрс6Бе1к-г-{№;, рс| = р..
И в этом случае действующая сила параллельна скорости и аффинор им-
импеданса равен характеристическому импедансу сдвига pcs, умноженному
на идемфактор, хотя сила и скорости ортогональны направлению распрост-
распространения волны.
Электромагнитное поле. Рассмотрим теперь поле, выражающееся через
4-векторы, именно то, для которого предназначались преобразования Ло-
Лоренца,—поле электромагнитное. Согласно § 2.5, основными величинами
поля ф4 должны] быть компоненты 4-вектор-потенциала (см. стр. 203)
Vr=Ax, V^Ay, VS = AZ, V, = i9,
где А —векторный потенциал, а <р — скалярный потенциал. В этом случае
мы откажемся от координат ? в пользу лоренцовых координат хх = х, х2 — у,
a:3 = z, ж4=гс?, так же, как в § 2.5. Такой выбор координат обеспечит
лоренц-инвариантность, но потребует в некоторых местах добавления мно-
множителя ic для сохранения размерности. Производные потенциалов запи-
запишутся в виде
т/ дЛх т. . dtp
^12= -ej^-И Т. Д., ^1 = !^ИТ.Д,
v __ 1 дАх v 1 Эср
14 ~ ic at ' Vu~ с at ¦
В этих обозначениях векторы поля будут иметь вид
Ех = i (F41 - У14) = ifu, Ev = *(F42 - F24) = i/24,
^ = (^з2-^з) = /2з, ^y = (F13-F31) = /31, C.4.8)
если мы предположим, что [х и в равны единице.
По сравнению с упругой средой мы имеем здесь некоторое осложне-
осложнение, состоящее в том, что компоненты потенциала связаны между собой
дополнительным условием, накладываемым на дивергенцию
2 ^ C.4.9)
П=:1
что эквивалентно уравнению B.5.14), связывающему между собой А и ij>-
Эту равную нулю дивергенцию можно, таким образом, прибавлять к раз-
различным выражениям или вычитать из них с целью их упрощения.
Теперь мы" должны найти плотность функции Лагранжа, с помощью
которой можно было бы вывести уравнения движения [см. B.5.20)]
(V V \iVy V dW
f =y—(V -V \--i-Vy . V dWm - 4-" I C 4
Ьхп 'тп ZJ дхп
п п п
3.4. Векторные поля 311
эквивалентные уравнениям Максвелла или волновым уравнениям B.5.15),
и получить в качестве 4,4-компоненты тензора напряжения-энергии плот-
плотность энергии [см. B.5.28)]
если 4-вектор I равен нулю. Вектор I был определен на стр. 202 как че-
четырехмерный вектор плотности заряда-тока
Здесь было бы довольно трудно воспользоваться определением L как
разности между плотностью кинетической энергии и плотностью потен-
потенциальной энергии, так как не ясно, что отнести к кинетической, а что
к потенциальной энергии. Рассмотрение возможных инвариантов подска-
подскажет нам, что в L должно входить A/8тс) (Е2 — Н2); L должно предполо-
предположительно еще содержать скалярное произведение векторов I и V. Соста-
Составив для такого L уравнения Лагранжа — Эйлера и сравнив их с уравне-
уравнениями C.4.10), мы придем к заключению, что точное выражение плот-
плотности функции Лагранжа должно быть таково:
21)* + (F23 - V32f + (Vn -
hVx + I2V2 + I3VS + /4F4} =
. + TS^n^-i^-^ + ^J-A-py. C.4.11)
n, m
Таким образом, уравнения Максвелла в случае свободного пространства
(J = 0 и р = 0) соответствуют требованию, чтобы Е2 было настолько близко
к Н2, насколько это совместимо с краевыми условиями.
Уравнения Лагранжа — Эйлера C.4.1) как раз совпадают с уравне-
уравнениями Максвелла C.4.10). Вектор плотности канонического импульса р
с компонентами рп = A/ic) (8L/dVni) (re= 1,2,3), которые оказываются
равными A/4тас) (Vin — Vni), совпадает с вектором — A/4та) Е. «Вектор
силы», соответствующий скорости изменения этого импульса во времени,
будет равен (J/c) — (l/4ic)rotH. Временная компонента плотности кано-
канонического импульса dL/dVM равна нулю, а уравнение divE = 4n:p, «вре-
«временная компонента» уравнений Лагранжа — Эйлера C.4.10), представляет
собой своего рода уравнение неразрывности для вектора плотности кано-
ничесжого импульса р = — A/4тсс) Е.
Тензор напряжения-энергии. Временная компонента тензора энергии-
импульса SB должна быть плотностью функции Гамильтона
m=l
nt=l
m=i
312 Гл. 3. Поля и вариационный принцип
s, r n m
^ -ij.A + p9 + ^E.grad9. C.4.12)
Это выражение отличается от того, которое вытекает из B.5.28), при-
присутствием слагаемых рф+ A/4^) E-grad<p. Но E-grad<{> = div(<{>E) — (pdivE,
и, так как divE = 4rcp, мы видим, что эти дополнительные слагаемые
в сумме дают (l/4n:)div(<pE). Интеграл от дивергенции по всему прост-
пространству равен потоку поля на бесконечности, а этот последний равен
нулн), поэтому среднее значение W44 равно среднему значению плотности
функции Гамильтона
±
C.4.13)
где тензор % определен формулой B.5.30). Это — проявление свойств
калибровочной инвариантности поля, упомянутых на стр. 204, а также
отмеченного на стр. 126 обстоятельства, что плотность энергии и плот-
плотность потока энергии определяются неоднозначно, хотя и имеют одно-
однозначно определенные интегралы по всему пространству.
С другой стороны, для того чтобы правильно составить гамильто-
новы канонические уравнения (см. стр. 304), нужно воспользоваться
полным выражением Wiit введя в него канонический импульс р вместо
— A/4тс) Е. Тогда функция Гамильтона примет вид
с *->
П=1 ТП=1
Уравнение d§nfdt = icVnt = dH/dpn запишется в виде
*"c(Vn4-F4n)
откуда мы получим
в согласии с первоначальным определением рп. Уравнения
з
?Рп— V д ( дН Л дН
dt ~~ Zi dxr V.3Fnr ) 8Vr
r V.nr ) Vr
превращаются в уравнения Максвелла
Таким образом, для получения функции Гамильтона можно пользоваться
компонентой И^44, но, вычисляя принятое нами выражение для плот-
плотности энергии, нужно пользоваться величиной U.
Подобную же коррективу приходится вводить для получения известных
выражений вектора интенсивности и импульса поля из недиагональных
3.4. Векторные поля 313
элементов тензора напряжения-энергии. Мы имеем
4
yi- —V V С dL Л— LVy (V —V \ —
mn Zj ' rm V gy I ^n ^_j * rm Vr rn r nr/
r=l ГП r
= L V (Vrm — Vmr) (Vrn— Vnr) — 2 (^mr^ra-^mW- C.4.14)
r r
Вторую сумму в последнем выражении можно преобразовать, воспользо-
воспользовавшись вспомогательным условием C.4.9) и волновым уравнением для
потенциалов [см. B.5.15)] J] (dVnr/dxr) = — Dтс/п/с)
г
4п" J_J ' mr' rn ' mr' nr) == 4^" Zj 9ж~ I m ' rn ' nr)J 1
r r
+ Еи Г—Vf -V—f 1
4n L da;n ZJ rr Zj 9жг nr J "
r r
Первая сумма представляет собой 4-дивергенцию, и ее среднее значение
равно нулю. Вторая сумма равна нулю в силу C.4.9), третья же равна
Следовательно, среднее значение Wmn (при тфп) равно среднему от
4
Г=:1
В самом деле, среднее значение любой компоненты Wmn тензора 28 равно
среднему значению тензора, имеющего компоненты
где
Л У Л V
C.4.16)
Тензор % мы рассматривали ранее, на стр. 210.
В тех участках поля, где 4-вектор заряда-тока равен нулю, тензор %
совпадает с тензором напряжения-энергии. Компоненты его выражаются
через компоненты поля следующим образом:
тх1=±[е1-е1-е1+н1-н1-н1\ и т. д.,
Г44 = ± [El + El + El + Hi + H2V + Hl\ = U,
** C.4.17)
и т. д.,
ЕхН)ж = Г41 и т. д.
Импульс поля. То, что мы пренебрегли тензором 555 в пользу %, не должно
нас тревожить, так как 28 не удовлетворяет условиям дивергенции C.4.3),
кроме случая, когда Лир равны нулю, и слишком много пользы от Ш
314 Гл. 3. Поля и вариационный принцип
ожидать нельзя. Соотношение дивергенции для % не просты из-за выде-
выделения 4-дивергенционных членов. Мы имеем
г
Г Г, S Г
где кт — т-я компонента вектора плотности силы, определенного равен-
равенством B.5.27). Пространственная часть выражения
PE + (l/c)JxH
определяет величину и направление силы, действующей на распределение
зарядов и токов. Она должна равняться скорости изменения импульса
зарядов, которая в сумме со скоростью изменения импульса поля равна
силе, действующей на поле плюс заряды. Взяв интеграл, например, от кг
по некоторой области в пространстве и обозначив через 111 компоненту по
оси х импульса тока в этой области, мы получим
где F1 = T11i-b-Tl2j-\-Tl3k— сипа, действующая на ж-компоненты импуль-
импульсов поля и зарядов; последний интеграл берется по поверхности, ограни-
ограничивающей выбранную область. Если теперь
Р = ^ (Е х Н) = 4 [ТЫ1 + 72J + T3ik] C,4.19)
назвать импульсом поля (см. стр. 305), то предыдущее равенство озна-
означает, что напряжение Т, действующее на поверхность части пространства,
равно скорости изменения импульса П тока внутри поверхности плюс
скорость изменения импульса поля Р внутри этой же поверхности.
Временная компонента kt [см. C.4.18)] есть скорость изменения
во времени кинетической энергии Т тока. Соответствующее равенство
C.4.18) также имеет физический смысл, который станет более отчетлив,
если ввести вектор •
S = ic [741i + Ti2j + Г43к] = (с/4*) (Е X H), C.4.20)
характеризующий плотность потока энергии, так называемый вектор
Поинтшгеа. Компонента 74 представляет собой, конечно, плотность энер-
энергии U поля. При га = 4 уравнение C.4.18) принимает, таким образом, вид
W дТ
так что уравнение неразрывности для потока энергии означает, что поток
вектора S сквозь замкнутую поверхность равен сумме с обратным'знаком
скоростей изменения энергии тока Т и поля U внутри поверхности. Итак,
все компоненты тензора % имеют физический смысл.
Плотность момента количества движения поля при отсутствии зарядов
и токов равна
Полный момент количества движения поля относительно начала коорди-
координат получится интегрированием М по всему объему, занятому полем.
S.4. Векторные поля 315
Если электромагнитное поле, отделенное от токов, заключено в конеч-
конечном объеме (волновой пакет) и движется с течением времени, можно пока-
показать, что интеграл от
(РХ, Ру, Рг, U) = Wii/C, iT2i/C, iT3JC, Г44),
взятый по этому объему (точнее говоря, по соответствующей области
трехмерного подпространства, ортогонального оси времени, в любой задан-
заданный момент), ведет себя по отношению к преобразованиям Лоренца как
истинный 4-вектор. В самом деле, в этом случае 2 (дТтг/дхг) = 0, так
г
что если Ст — компоненты какого-либо постоянного 4-вектора, то 4-вектор В
с компонентами Вг — ^СтТтг имеет 4-дивергенцию ^(дВг/дхг), равную
т г
нулю; следовательно, интеграл по любой замкнутой поверхности в четы-
четырехмерном пространстве от нормальной составляющей вектора В равен
нулю. Возьмем в качестве такой поверхности поверхность «четырехмер-
«четырехмерной призмы» с образующими, расположенными вдоль оси времени парал-
параллельно движению волнового пакета, и с основаниями, перпендикулярными
этим образующим и настолько большими, чтобы призма содержала рас-
рассматриваемый волновой пакет. Интеграл по пространственной части
(по боковым граням призмы) будет равен нулю, так как поле равно
нулю вне пакета, поэтому интеграл временной компоненты 2 СгаГт4 век-
т
тора В по одному основанию четырехмерной призмы равен интегралу
по другому основанию, соответствующему более раннему моменту времени.
Таким образом, в данном случае интеграл от Jj CmTmi по объему, заня-
занятому пакетом, есть лоренц-инвариант, а соответствующие интегралы от Тт4
по пакету (по объемам, перпендикулярным оси времени) представляют
собой компоненты некоторого истинного 4-вектора, а это мы и хотели
доказать.
Из этого вывода следует, что если мы имеем волновой пакет элек-
электромагнитного поля, то вектор, компонентами которого служат интегралы
импульса поля-Р и энергии воля U, представляет собой истинный вектор
энергии-импульса, который ведет себя так, как если бы пакет был мате-
материальной частицей. Момент количества движения пакета мы получим,
взяв интеграл от М, как указано выше.
Вариационными методами можно получить много других интересных
свойств электромагнитного поля.
Изменение калибровки потенциалов. Многие трудности, которые нами
встретились при переходе от плотности функции Лагранжа к плотности
энергии, можно было обойти, изменив должным образом калибровку потен-
потенциалов поля. Если вместо того, чтобы исходить из уравнения div A +
-г A/с) (dfldt) = 0, задать новую калибровку потенциалов условием 9 = 0,
то уравнения Максвелла запишутся в виде
rot А = В = (хН, Е = - A/с) (дА/dt) = D/s,
div(aA/0O=-D*pc/s), C.4.21)
rot (rot A) + (з(х/с2) {d2A/dt2) = Dirp./c) J.
Другими словами, мы пользуемся как продольной, так и поперечной
частью вектора А, причем продольная часть определяется плотностью
зарядов, а поперечная часть —в значительной степени плотностью тока.
Такая калибровка особенно удобна тогда, когда отсутствуют свободные
заряды р, но она бывает полезна и в других случаях.
316 Гл. 3. Поля и вариационный принцип
Плотность функции Лагранжа при этой калибровке имеет вид
ЗА
dt
J-J-A = JL (E-D-H-B) + J_J.A. C.4.22)
Следовательно, плотность канонического импульса равна р = еА/4лс2 =
= — (D/4tcc). Уравнения Лагранжа—Эйлера приводят к последнему из урав-
уравнений C.4.21). Первые два связывают поля с потенциалом, третье — опре-
определяет калибровку.
При этом плотность функции Гамильтона имеет вид
Второе из видоизмененных канонических уравнений снова соответствует
последнему уравнению C.4.21).
Для отыскания остальных компонент тензора напряжения-энергии SB
при выбранной калибровке заметим, что аффинор второго ранга, (х, у)-ком-
понента которого равна dL/d (дАх/ду), есть (HxS/^TC)= ~ С5хН/4тс). Вос-
Воспользовавшись этим выражением, мы найдем, что вектор потока энергии
(при р. = е = 1) равен
S= -А-(^
то есть его выражение совпадает с C.4.20). Таким образом, наша специаль-
специальная калибровка приводит к стандартному виду плотность энергии и вектор
Пойнтинга и избавляет от возни с дивергенциями, которые неизбежны при
обычной калибровке, как мы это видели на предыдущих страницах. С дру-
другой стороны, вектор импульса поля имеет иной вид
Р= _^ |
Соответственно видоизменяются и пространственные составляющие тензора
напряжения- энергии
U=-ir(VA)xH-gL.
Эти величины нам не столь привычны, как плотность энергии и вектор
Пойнтинга, поэтому мы, вероятно, можем примириться с их видоизменен-
видоизмененными выражениями (можно, впрочем, придать им более знакомую форму,
опираясь на калибровочную инвариантность).
Аффинор импеданса. Для определения импеданса электромагнитного
поля наиболее удобно принять ту калибровку, которая была введена в
предыдущем пункте и привела к «правильному» виду плотности энергии
и плотности потока энергии. Вернемся к уравнениям Лагранжа—Эйлера
(или к каноническим уравнениям)
Выражение справа представляет собой «силу», вызывающую определенную
скорость изменения импульса р = еА/Акс2 = — D/4tcc. Той ее частью, ко-
которая прилагается к поверхности, ограничивающей поле, является, со-
согласно сказанному на стр. 296, аффинор ( — l/4s) ($xH), дивергенция
которого входит в приведенное здесь выражение плотности силы. Если
3.4. Векотрные поля 317
электромагнитная волна возникла на каком-либо участке граничной по-
поверхности, то «реакция» волны на элемент поверхности dA1) равна
то есть представляет собой вектор, ортогональный к Н и к dA (то есть
этот вектор лежит в касательной плоскости к поверхности). Сопоставив
этот вывод с правилом циркуляции ф Н ¦ ds = 4тс1 (см. стр. 214), мы
увидим, что если волна «вызвана» поверхностным током на граничной
поверхности поля, то вектор — (с/4тс) (d A x H) как раз равен, по величине
и направлению, току, несомому элементом dA. Интеграл от этого век-
вектора по всему участку поверхности, несущему ток, дает полный токо-
токовой лист2).
•
А= —сЕ есть вектор «скорости», поэтому величина, соответствую-
соответствующая импедансу для потенциала А, в направлении, определяемом единич-
единичным вектором а, есть аффинор, преобразующий вектор — сЕ в вектор
(a/4it)xH. Впрочем, роли «силы» и «скорости» определены нами так, что
обычное определение импеданса как отношения Z напряжения к силе тока
(Н пропорционально силе тока, а Е — напряжению) заменено на противо-
противоположное.
Итак, мы определим аффинор импеданса Q электромагнитного поля
как «отношение» электрического поля к магнитному, умноженному на
с/471, а аффинор адмитанса ^) — как обратный аффинор, то есть
Умножив единичный вектор а векторно на обе части второго из этих
равенств, мы найдем, что адмитанс поля в направлении вектора а ра-
равен ах§).
Между прочим, мы замечаем, что если Е и (c/4ic) а X Н соответственно
аналогичны напряжению и силе тока и, следовательно, импеданс есть
«отношение» одного к другому, то «произведение» (с/4тс) Е X Н есть коэф-
коэффициент расхода энергии, то есть плотность потока энергии [как и должно
быть в соответствии с C.4.20)]. Таким образом, аналогия оказывается
полной.
Плоская волна. Если отсутствуют токи и е = (л = 1, то простым ре-
решением уравнений C.4.21) будет
А = ap.4eik-r-iu)<, k = (ш/с) ай, А = | А | е*,
где ай и ар — взаимно-ортогональные единичные векторы; соответствую-
соответствующие поля —
к, Е и Н образуют правую тройку взаимно-ортогональных векторов.
Как обычно для плоских волн, соответствующее значение функции
Лагранжа равно нулю. Плотность энергии и вектор Пойнтинга выра-
х) Здесь случайное совпадение обозначений: А и dA. —Прим. ред.
2) «The total current sheet». —Прим. ред.
318 Гл. 3. Поля и вариационный принцип
жаются в виде
тт Е* <о2|Л|2 . 2О с <о2|,4|2 . 2О
и = -г-= . 2 sm2S, S = —j—Lafesm28
4л 4лс2 ' 4этс ft
где а, р, у — направляющие косинусы вектора к по отношению к осям
x,y,z. При этом аффинор VA = i (<D/c)afeapJeik-*-it0', так что плотность
импульса поля имеет выражение
4с Ь
и пространственная часть тензора напряжения-энергии представляет собой
симметричный аффинор
Сам тензор напряжения-энергии может быть записан в такой симмет-
симметричной матричной форме:
/а2 ар ау са
са ф су 1
Наконец, для случая плоской волны импеданс — отношение вектора Е
к вектору — (с/4тг) II — есть аффинор
а адмитанс
Импеданс волны в направлении распространения равен, таким образом,
Мы видим, что в гауссовых единицах, которыми мы здесь пользуемся,
«величина» импеданса плоской электромагнитной волны в вакууме равна
4тс/с.
Остаются еще лишь несколько полей, заслуживающих быть упомя-
упомянутыми в этой главе.
Уравнение Дирака. Нам следует, например, составить плотность
функции Лагранжа, относящуюся к уравнению Дирака для электрона
[см. уравнение B.6.57)]. Здесь мы имеем восемь независимых переменных
поля, компоненты фх, Ф2, <Ь3, ф4 [см. B.6.56)] волновой функции ф вдоль
четырех направлений спинового пространства и соответствующие компо-
компоненты ф*. С помощью небольших преобразований мы придем к такому
выражению плотности функции Лагранжа:
— еф*а • Аф + есф*<рф - тс2ф*а0ф, C.4.25)
где А и ф — электромагнитные потенциалы в точке, где находится элект*
рон, т и е —масса и заряд электрона,- ф и 4* представляют все четыре
3.4. Векторные поля 319
компоненты каждого из векторов, а операторы а = су + ayj + a2k и a0 оп-
определены в B.6.55).
Уравнения Лагранжа—Эйлера можно получить обычным способом, вы-
выразив предварительно фиф* через ф*, ф*, ф*, ф*, ф1; ф2, ф3) ф4 в уравне-
уравнении C.4.25) и выполнив необходимые действия, требуемые операторами а.
Так, например, уравнение
д Г 3L \ д Г 3L Ч д f dL Л д / 8L \ 8L _ »
перейдет в
то есть в одно из уравнений Дирака B.6.57). Однако тот же результат
можно получить проще, рассматривая только две переменных ф и о* и вы-
вычисляя формально частные производные так, как если бы это были обык-
обыкновенные функции, а не векторы в спиновом пространстве. Например, при
этом уравнение Лагранжа—Эйлера
ду V. еф* ) + dz v Щ ) + ~л \ еф* ) еф* ~ и
будет соответствовать всему уравнению B.6.57)
§)]=О, C.4.27)
одной из компонент которого является уравнение C.4.26). Соответствую-
Соответствующим уравнением для спинового вектора ф* явится
« + ( —|^--еФф*)] =0.
И в рассматриваемом случае энергия равна 4,4-ком-поненте тензора
= тс2 (ф*аоф) + еА • (ф*аф) - ее (ф*<рф) +
+ |f [ф*а- grad ф — grad ф* •*!»]. C.4.28)
Вектор «интенсивности поля» S и вектор «импульса поля» Р получают
соответственно выражения
| [^^] C.4.29)
Р = iwu + jW24 + bW3i = %r [(grad ф*) ф - ф* (grad ф)]. C.4.30)
Ни один из этих векторов не пропорционален вектору плотности тока
J = сеф*аф
[см. B.6.59)]. Так как L только линейно зависит от производных пере-
переменных поля по времени, то канонические импульсы пропорциональны
самим .переменным поля и весь аппарат гамильтоновых канонических
уравнений должен быть преобразован так, как описано на стр. 309. Впро-
Впрочем, более важно выражение интеграла, подлежащего минимизации, а
также выражения плотностей энергии и импульса.
320 Гл. 3. Поля и вариационный принцип
Задачи к главе 3
3.1. а. Показать, что может быть определена производящая функция
S' (?, Р, t) канонического преобразования следующим образом:
и
p = dS'/dq, Q = dS/dP, К = # + (dS'/dt).
б. Показать, что S' = qP определяет тождественное преобразование.
в. Показать, что если мы имеем бесконечно малое преобразование
р), е < 1,
то
Р-р=-в (дТ/dq), Q-q = * (дТ/дР).
г. Показать, что Д/= /(/>, Q) — f(p, q) выражается в виде
*/ = ¦(/. Т)
[где (/, Г) — скобки Пуассона] и отсюда вывести, что Т является константой
движения, если соответствующее преобразование оставляет инвариантной
функцию Гамильтона.
д. Показать, что для бесконечно малого поворота вокруг оси z
7 = (rXp)z = Mz.
3.2. Показать, что уравнения Лагранжа не изменятся, если к функ-
функции Лагранжа прибавить какую-либо полную производную по времени.
Показать отсюда, что для нерелятивистской частицы, движущейся в элек-
электромагнитном поле, функцию Лагранжа можно записать в виде
X = ~ mv2 - е<? - (е/с) [(дА/dt) + v-(VA)] ¦ г,
где VA — аффинор (градиент воздействует только на А). Показать, что
соответствующей функцией Гамильтона является
&в = {J?) \v + (e/c){VA)-r\* + {e/c)r.(dA/dt) + e? (Ричарде).
3.3. Показать, что в обобщенных ортогональных координатах ?х, ?2,
уравнение Лагранжа — Эйлера имеет вид
dL 1 д Г dL 1 0
J at I д (d],/dt) J - u>
Взяв в качестве плотности функции Лагранжа (VtJ)J, получить формулу
1 ^д 3 Г hih^hg d^i "I
3.4. Показать, что тензор третьего ранга
М^х = Тр.^хх — TVx^v
v = W,j.v. см. стр. 303) удовлетворяет уравнению неразрывности
только если тензор T^v симметричен. Показать, что Mijh есть плотность
момента количества движения и что, интегрируя уравнение неразрывности,
мы получим закон сохранения момента количества движения.
Задачи к главе S 321
3.5. а. Показать, что для бесконечно малого лоренцова преобразования
выполняются равенства @^= — ш011.
б. Опираясь на инвариантность плотности функции Лагранжа относи-
относительно лоренцовых преобразований, показать, что в случае электромаг-
электромагнитного поля, когда
(IV
мы имеем
где
Показать также, что
3.6. Если T^v не симметричен, то всегда можно найти тензор <S,j.v,
симметричный и обладающий всеми физическими свойствами 7^.
а. Показать, что S^w должен удовлетворять условиям
б. Показать, что ,Sp.v должен иметь вид
где
в. Воспользовавшись результатом задачи 3.5, б, показать, что
р р тт dL . 6L .
Вывести отсюда соотношения
г. Вычислить Sp.v для электромагнитного поля.
3.7. Показать, что однородное интегральное уравнение
ь
ф (ж) = X V К (х | х0) ф (х0) dx0
а
вытекает из вариационного уравнения
ь ь
о ^ ф(ж) Гф(ж) —х( K(x\xo)<i)(xo)dxAdx = O,
а а
21 Ф. м. Морс и Г. Фешбах
322 Гл. 3. Поля и вариационный принцип
если К(х|х0) = К(х01х). Показать, что при К(х\хо)Ф К(хо\х)
ь ь
о ^(х)[^{х)--К^ К(x\xo)^{xo)dxo~\dx = O,
а а
где &{х) удовлетворяет интегральному уравнению
ь
a
3.8. Уравнением движения мембраны, натянутой на отверстие в гер-
герметическом сосуде, служит
A/с2) (о2(])/от2) = V 2ф — (pc2/FjT)
(см. задачу 2.1). Найти соответствующие плотности функций Лагранжа
и Гамильтона.
3.9. Уравнение затухающих колебаний струны имеет вид
Показать, что соответствующей плотностью функции Лагранжа будет
L = UdZldt) (дШп -\-k\b Ш/dt) — &(dbldt)] - с2
и найти уравнение, которому должна удовлетворять ф. Найти канони-
канонические импульсы, соответствующие ty и ф, и пиотность функции Гамиль-
Гамильтона. Выяснить физический смысл полученных результатов.
3.10. Стационарному уравнению переноса при анизотропном рассеянии
на очень тяжелых рассеивающих частицах (см. § 2.4 и 12.2) можно при-
придать вид
со?6 {djld%) =-/(?, 6) + (*/4гс) ^ w(a-ao)/E, %)dQ0,
где ¦*. — постоянная, единичные векторы а и а0 имеют направления, опре-
определяемые соответственно сферическими углами 6, <р и 60, <р0, a dQ0 — элемент
телесного угла, охватывающий вд. Показать, что это уравнение может
быть получено из вариационного уравнения
So
b\d^ dQj(ti, 6) [ cose (df/dh) + f- (*/4*) ^ w(a-ao)f(S, %)dQ0] =0.
Показать, что / удовлетворяет уравнению
- cos 6 (df№) =-J(k,f)) + (*/4*) \w (a0 - a)/(?, 60) dQ0.
Истолковать эти результаты.ч
3.11. Диффузия заряженных частиц под действием внешнего поля Е
описывается уравнением
dc/dt = а?Х*с + Ъ (Vc»E)
(предположения, при которых это уравнение выводится, высказаны
в задаче 2.5). Показать, что соответствующая вариационная задача
Задачи к главе S 32%
ставится так:
о \\ dV dt <Г[(дс/&) — а?Х*с - b (Vc • E)] = 0.
Найти уравнение для с и истолковать его.
3.12. В теории дейтрона встречается пара интегральных уравнений,
которые можно записать в виде
со
% (г I r0) [f (т-0) и + g (r0) w] dr0,
в> (г) = X 5 С, (г | г0) [g (г0) и + h (г0) w] dr0,
о
где функции Go и G2 симметричны. Показать, что соответствующий
вариационный интеграл имеет вид
со
{ [к2/ + 2uwg + w2h] dr —
3.13. Взаимосвязь между механическим движением и распростране-
распространением тепла в звуковой волне описывается уравнениями
dT/dt = а (др/dt) + PV2Z', dzp/dt2 = yV 2p + sV 2Г,
где постоянные а, р, у и е заданы 9 айДаче„ 23. Покагать, что эти урав-
уравнения могут быть получены при помощи вариационного интеграла
Показать, что при должном подборе начальных условий Т и р удовлетво-
удовлетворяют аналогичным уравнениям с обращенным временем.
3.14. В задаче 2.2 описаны свойства бесконечной пьезоэлектрической
среды, связывающие электрическое поле Е, поляризацию Р, напряжение
и деформацию. Если оси х, у, z направлены по главным осям кристалла,
то соотношения между Е и Р, а также между аффинором напряжений ©
и аффинором деформаций % выражаются тремя системами из трех:
уравнений:
,„,и т. д.,
Txv = Тух = \xySxy + oxyPz и т. д.,
Ez = *zPz+oxySxy и т. д.,
где X — элементы тетрадика модуля упругости, приведенного к главным
осям, х —обратные величины диэлектрических восприимчивостей вдоль
координатных осей, о—элементы некоторого недиагонального «триадика»
(преобразующего вектор в аффинор и наоборот), который связывает дефор-
деформации и поляризацию. Комбинируя эти уравнения с уравнениями Макс-
2L*
024 Гл. 3. Поля и вариационный принцип
велла и с уравнениями упругих колебаний для частного случая попереч-
поперечной волны, движущейся вдоль оси z при смещениях, направленных вдоль
оси у, показать, что в результате получится пара связанных друг с дру-
другом волновых уравнений. Они будут соответствовать двум возможным
электрическим волнам сдвига, одна из которых распространяется со ско-
скоростью, несколько меньшей, чем скорость чистых волн сдвига (при равных
нулю с), а другая со скоростью, несколько большей скорости света
в рассматриваемой среде. Вычислить плотность импульса и аффинор
¦напряжения-энергии для плоских волн сдвига, движущихся вдоль оси z
(при Е, направленном вдоль оси у). В каком отношении находятся энергии,
несомые медленными волнами, соответственно электрического и упругого
лолей? Тот же вопрос, относящийся к быстрой волне.
Сводка результатов главы 3
Плотность функции Лагранжа L есть функция переменных поля
Ф4 (i = 1, 2, ..., п) и их производных 4>is = dtyjdbg (?х, ?2> Е3 — пространствен-
пространственные координаты, ?4 = ?). Иногда L зависит также от ? явно (например,
через посредство потенциалов или плотностей заряда и тока). Полный
лагранэФсев интеграл
$ [ b C.1.1)
СЦ О4
является инвариантом. Требование, состоящее в том, чтобы X принимал
максимальное или минимальное значение, то есть чтобы первая вариация
интеграла X обращалась в нуль, приводит к уравнениям Лагранжа —
Эйлера
2жШ-1й-0' <3-4Л>
s=l
служащих для отыскания 44. Если L — квадратичная функция от tyi4,
то плотность канонического импульса
_ 8L
Pi " д^ц
представляет собой линейную функцию от ^i4. Если L — линейная функ-
функция от <l»i4, то Pi и функция Гамильтона от 6i4 не зависят. Большинство
других важных физических свойств поля описывается тензором напряже-
напряжения-энергии 2В, компоненты которого равны
Л Г
Например, его 4,4-компонента
представляет собой плотность энергии. Если рг зависит от tyi4, то из Wti
можно исключить 'j>i4 и получить плотность функции Гамильтона
И — функцию от pit ''ii и их пространственных производных. В этом
Сводка результатов главы 3 325
случае уравнения движения могут быть также записаны в канонической
форме
з
tyi=nl>i4 = ——; рг = —~ =¦ у\ -gg- ( ¦ ¦ 1 . C.4.2)
8=1
Такие уравнения применимы только тогда, когда L содержит квадратич-
квадратичную функцию производных 4>i4. Если же L зависит от tyi4 линейно, то Н
не зависит от р (см. стр. 300). Вектор S интенсивности поля и вектор Р
импульса поля определяются формулами
8=1 1=1 8=1
3 п
8=1
Остальные компоненты 28 определяют так называемый аффинор напряжений
3
И= 2 ar^Vsas- Компоненты тензора 28 удовлетворяют уравнениям
Т, 8=1
4
dwms
C.4.3)
8 = 1
где dL/d?m — производная по параметру ?т, входящему в L явно (через
посредство потенциалов, токов и т. п.). Если L не зависит от $ явно,
то дЬ/д? — 0. В этом случае последние соотношения можно представить
в виде
Плотность момента количества движения поля относительно начала коор-
координат равна
Гибкая струна или мембрана
Переменная поля ф есть поперечное смещение.
Параметрами ?s служат х и t для струны, х, у и t — для мембраны.
Плотность функции Лагранжа L = yp [Г^) — c2grad2ф | , с2=—.
Уравнение Лагранжа — Эйлера с2Т2ф — (д2ф/д?2) = 0 (скалярное волно-
волновое уравнение).
Плотность канонического импульса р = р (dty/dt).
Плотность функции Гамильтона Н = (l/2p)/?2 + -2-7'0grada<J).
Интенсивность поля8= — T0(dty/dt)grad§.
Импульс поля Р = р (dtydt) grad 6 = — (l/c2)S.
Сжимаемая невязкая жидкость
Переменная поля ф есть потенциал скоростей; скорость поля = grad ф;
избыточное давление = — р {dty/dt).
Параметрами %s служат х, у, z и i.
326 Гл. 3. Поля и вариационный принцип
Плотность функции Лагранжа
" „2 _ Pot
Уравнение Лагранжа — Эйлера Т2ф — A/с2) (д2ф/дг2) = 0 (скалярное
волновое уравнение).
Плотность канонического импульса р = (р/с2) ф = — (избыточное дав-
давление) /с2.
Плотность функции Гамильтона Н = 1/2 A/рс2)/?2 + 1/2р (grad фJ.
Интенсивность поля S = — р (dtyldt) grad ф = (избыточное давление) х
X (скорость жидкости).
Импульс поля Р = (р/с2) (дЪ/dt) grad ф = — A/с2) S.
Уравнение диффузии
Переменными поля являются температурах) или концентрация ф и
«сопряженная» ей величина ф*.
Параметрами ?s служат х, у, z и ?. Плотность функции Лагранжа
Уравнение Лагранжа — Эйлера (для ф) Т^ф = a2 (d§/dt) (уравнение диффузии).
л л
Плотности канонических импульсов р= — — а2ф*: р* = — а2ф.
Плотность энергии U = W44 = (grad ф)-(grad ф*).
Интенсивность поля S= — ф*(gгadф) —(gгadф*)ф.
Импульс поля Р = у о2 [(gгadф*)ф = ф* (gгadф)].
Уравнение Шредингера.
Переменными поля являются волновая функция ф и ее сопряженная
ф* Произведение фф* есть плотность вероятности наличия частицы.
Параметрами ?,. служат х, у, z и t.
Плотность функции Лагранжа
V (х, у, z) — потенциальная энергия частицы.
Уравнение Лагранжа — Эйлера (для ф)
— (Ь2/2т) V2-^ + 7ф = ih {dty/dt) (уравнение Шредингера).
Плотности канонических импульсов р= — (Я/2г)ф*; р* — (
Плотность энергии {У==И/4i,==(^^2/2??г)(gradф*)•(gгadф) + ф*Fф.
Интенсивность поля S= -(%2/2m) [Eф*/9/) grad ф +gгadф*(9ф/90^•
Импульс поля Р= — (Я/2г)[ф*(grad*) —(gradф*)ф].
Плотность тока J = (eft/2im)[6*(grad6) — (gradd)*)»J»], где е — заряд
частицы, т — масса частицы.
Уравнение Клейна — Гордона
Переменными поля являются волновая функция ф и ее сопряженная ф*.
Плотность заряда частицы равна (Яе/2гтес2)[(9ф*/Ш)ф —ф*(9ф/Ш)], где
пг — масса частицы.
Параметрами ?s служат х, у, z и t.
1) В случае уравнения теплопроводности.— Прим. перев.
Сводка результатов главы 3 327
Плотность функции Лагранжа (в случае отсутствия поля)
Уравнение Лагранжа — Эйлера для <J>: ^24* —"^Г^О — СхТ^ (урав~
нение Клейна — Гордона).
Плотности канонических импульсов
Р ~ 2mc2 V dt ) ' Р ~ lmc% \dt
Плотность функции Гамильтона
Н = Bmc2/fc2) р*р + (ft2/2m) (grad 4»*) • (grad ф) + (тса/2L»*ф.
Интенсивность поля S= — 5— -тг- (grad ф) + (grad ф*) r^ I .
Импульс поля Р= — (l/c2)S.
Плотность тока 3 = (eh/2im) [ф* (grad ф) — (grad ф*) <]>], где е —заряд
частицы.
Уравнение упругих колебаний
Переменными поля фп служат компоненты вектора смещения s.
Параметрами ?s являются координаты х, у, z и t.
Плотность функции Лагранжа
где
у —аффинор деформации, & = X | © | §-f 2pS — аффинор напряжений для
изотропного твердого тела. Уравнение Лагранжа — Эйлера
р (d*s/dt2) = (X + {!.) grad (div s) + fi.Vas.
Плотность канонического импульса р = р (ds/dt).
Плотность функции Гамильтона H = Wit = A/2р)/?2-}-у |2-<3|.
Интенсивность поля S= — (ds/dt)-%.
Импульс поля P = p(Vs)-(ds/df).
Для неизотропного твердого тела аффинор напряжений выражается
в виде Ж = 3:>5, где 3 — тетрадик с элементами gmnrs; последние подчи-
подчинены общим условиям симметрии gmnrs~gnmra = gmnsr — Srsmn> a в осталь-
остальном произвольны.
Уравнение Лагранжа — Эйлера для этого случая
то есть
•• _ у „
mrs
Плотность функции Гамильтона
:J:(Vs), v = P(ds/dt).
Выражения S, P и т. д. в этом случае получаются подстановкой
нового % в формулы, определяющие S, Р и т. д., приведенные выше
^для изотропного случая).
328 Гл. 3. Поля и вариационнъш принцип
Уравнения электромагнитного поля.
Переменными поля служат компоненты векторного потенциала А и
скалярный потенциал <р. Для простоты выберем такую калибровку потен-
потенциалов, при которой <р = 0, так что rotA = B=fjJH, дА/dt— — сЕ = — cD/г
и Ai\(dA/dt) = — 4п:рс/г, где р — плотность свободных зарядов. Параметра-
Параметрами являются х, у, z и t.
Плотность функции Лагранжа L = -^-^ -jrr\ —=—^l rot A|2 + — J-A,
где J — плотность тока.
Уравнение Лагранжа — Эйлера rot (rot A) + (цг/с2) (dzA/dt2) =¦ (Аър/с) J.
Плотность канонического импульса р= —(D/4itc).
Плотность функции Гамильтона
Интенсивность поля S = (с/4и) (Е х Н).
Импульс поля Р = — (s/4iz)(VA)-(dA/dt).
Уравнение Дирака
Переменные поля — ф* и Фп (п=1> 2, 3, 4). Плотность вероятности
наличия электрона равна ^>*ilI + 'Ь|ф2 + фз^з ~Ь Ф^ф4 =^ 4**4*. Параметрами
являются х, у, z, t; Волновые функции — Ф = j>] е„фп и Ф* = 2 Ф* e?,
где еп — единичные векторы в спиновом пространстве. Операторы «х, ауу
а2, а0 воздействуют на векторы е„ согласно уравнениям B.6.53). Плот-
Плотность функции Лагранжа
" 'П1""" Ф-
- Ф* (j?- j ] - еф* (а • А) Ф + есф*<рф - тс2ф*аоф,
где А и <р — электромагнитные потенциалы, яг—масса частицы.
Уравнения Лагранжа — Эйлера
Плотность канонического импульса р = — (h/2i) Ф*, р* = (h/2i) Ф.
he
Ti
Плотность функции Гамильтона Н = ~ [ф*a•(gгad Ф) — (grad Ф*)-аФ} +
+ еФ*а • АФ - есф*<рф + тс2ф*а0Ф.
Интенсивность поля S = (bc/2i)[(d4!*/dt)a4i— 4>*a(d4!/dt)].
Импульс поля Р = (ft/2i) [(grad Ф*) Ф — Ф* (grad Ф)].
Плотность тока 1=сеф*аФ, где е—заряд частицы.
ЛИТЕРАТУРА
Лишь немногие книги сколько-нибудь подробно излагают основное содержание
этой главы, но по отдельным вопросам можно указать различные источники.
Общие вопросы вариационного исчисления изложены в следующих книгах:
Б лисе Д., Лекции по вариационному исчислению, Изд. иностр. лит., М., 1950.
Курант Р., Гильберт Д., Методы математической физики, т. 1, ГТТИ, М., 1951.
Рэлей, Теория звука, Гостехиздат, М., 1955.
Литература по теории преобразований, применяющихся в динамике, включая
принцип Гамильтона:
Литература 329
Голдстейн Г., Классическая механика, ГТТИ, М., 1957.
Уиттекер Е. Т., Аналитическая динамика, ОНТИ, М., 1937.
Burn M., Mechanics of the Atom, London, 1927.
Corben H. C, Stehle P., Classical Mechanics, Chaps. 10—15, New York, 1950.
Lanczos C, The Variational Principles of Dynamics, Toronto, 1949.
Webster A. G., Dynamics, Chaps. 4 and 9, New York, 1922.
Литература, посвященная приложениям принципа Гамильтона к физическим
полнм:
Венцель Г., Введение в квантовую теорию волновых полей, ГТТИ, М., 1947.
Гайтлер В., Квантован теория излучения, ГТТИ, М.—Л., 1940.
Ландау Л. Д. и Лифшиц Е. М., Теория поля, ГТТИ, М., 1948.
Ландау Л. Д. и Лифшиц Е. М., Квантовая механика, ч. 1, ГТТИ,
М.—Л., 1948.
Паули В., Релятивистская теория элементарных частиц, Изд. иностр. лит.,
М., 1947.
Шифф Л., Квантовая механика. Изд. иностр. лит., М., 1957.
Fermi E., Quantum Theory of Radiation, Rev. Modern. Phys., 4, 87 A932).
Weyl H., Theory of Groups and Quantum Mechanics, London, 1931, Chap. 2.
ГЛАВА 4
Функции комплексного
переменного
В двух предыдущих главах обсуждалась связь между некоторыми
физическими явлениями и дифференциальными уравнениями с частными
производными, изображающими эти явления. Несколько последующих
глав будет посвящено выяснению общих математических свойств диффе-
дифференциальных уравнений и их решений. Мы начали знакомиться с различ-
различными физическими интерпретациями величин, связанных с полями: тензо-
тензоров, дивергенции, криволинейных интегралов и т. п. Теперь нам предстоит
научиться распознавать различные типы уравнений и их решений. Мы
познакомимся с приемами, которые позволяют выяснить, как именно за-
заданная функция зависит от своего аргумента: где она стремится к нулю
или к бесконечности, где ее можно интегрировать и дифференцировать
и т. д. Мы должны научиться определять, какого рода функции служат
решениями данных дифференциальных уравнений, каким образом «особен-
«особенности» уравнения связаны с особенностями решений и т. п. В этой главе
мы рассмотрим общие свойства функций; связь между уравнениями и их
решениями является предметом следующей главы.
Точнее говоря, в этой главе мы рассмотрим функции комплексного
переменного z = x-\-iy, где i означает квадратный корень из —1. Мы уже
показали (см. стр. 77 и 78), что такая переменная может быть изобра-
изображена двумерным вектором, имеющим компоненты х и у по осям соответ-
соответственно абсцисс и ординат; было указано, что можно также рассматри-
рассматривать z как оператор, который поворачивает любой другой вектор, изобра-
изображающий комплексное число, на угол arctg (г//ж) и изменяет длину этого
вектора в ^гх2-\-у2 раз. В этой главе мы постоянно будем пользоваться
векторным представлением комплексных чисел и лишь время от времени
будем прибегать к представлению их в виде операторов.
Можно задать вопрос, почему необходимо изучать комплексные числа,
тогда как многие разделы физики нуждаются лишь в действительных
решениях уравнений. Казалось бы, изучения действительных функций
действительного переменного, изменяющегося от — со до + оо, достаточно
для того, чтобы во многих случаях исследовать интересные с точки зре-
зрения физики решения. На этот вопрос можно ответить, что переход к комп-
комплексным значениям переменных имеет своей целью законченность выводов
ш удобство формулировок.
Множества действительных чисел недостаточно даже для представле-
представления корней алгебраических уравнений. С другой стороны, все корни всех
алгебраических уравнений выражаются комплексными числами. Далее,
зная поведение функции / (z) при всех комплексных значениях z, мы
имеем картину основных свойств / (даже тех, которые относятся к дей-
действительным z), более полную, нежели та, которую мы получаем, когда
нам известно ее поведение лишь при действительных z. Так, расположе-
расположение на комплексной z-плоскости нулей и полюсов функции / (т. е. кор-
4.1. Комплексные числа и комплексные переменные 331
ней уравнений / = 0 и 1// = 0) определяет многое в поведении / при всех
значениях z. Часто вычисление интеграла функции / (z) по множеству
действительных значений z (вдоль действительной оси) можно значи-
значительно упростить, заменив искомый интеграл другим, взятым вдоль какого-
нибудь простого пути в комплексной плоскости. Обычно оказывается
полезным рассматривать решение некоторого уравнения в комплексной
форме, обращаясь с этим решением как с комплексным числом и выделяя
действительную или мнимую часть решения, соответствующую реальной
физической задаче, лишь тогда, когда нужно сравнить окончательный
ответ с данными измерений.
Однако наиболее важная причина, вызывающая необходимость изуче-
изучения комплексных функций, состоит в том, что такое изучение раскрывает
нам общие свойства функций. Так, например, различные типы особенно-
особенностей функции поддаются классификации. Как правило, эти особенности
•связаны с некоторыми физическими особенностями, такими, как источ-
источники, точечные электрические заряды и т. д. Оказывается возможным,
зная лишь особенности функции, полностью охарактеризовать всю
функцию. В электростатике этому соответствует тот факт, что электриче-
электрическое поле полностью определяется величиной и распределением зарядов.
Вследствие тесной связи, существующей между электростатикой и комп-
комплексными переменными, неудивительно, что нам удастся, кроме того,
получить метод решения уравнения Лапласа (иначе говоря, можно будет
указать расположение эквипотенциальных линий). В гл. 1 мы видели,
что эквипотенциальные линии и линии, им ортогональные, порождают
некоторую ортогональную систему криволинейных координат. Таким об-
образом, можно сказать, что мы получим метод построения новых коорди-
координатных систем, наилучшим образом соответствующих геометрии рассмат-
рассматриваемой задачи.
4.1. Комплексные числа и комплексные переменные
Впервые, может быть, изучающий физвку использует комплексные
числа тоща, когда он обозначает символом Аеш вектор длины А, вра-
щаюпгайся с постоянной угловой скоростью ю. Это представление полезно
также при изучении простых гармонических колебаний, так как' Л cos otf
является его действительной частью, a A sinwt —мнимой. Мы уже неодно-
неоднократно пользовались этим фактом в предыдущих главах.
Связь между векторами и комплексными числами устанавливают,
определяя должным образом символ i. Мы рассматриваем i как оператор,
который, воздействуя на произвольный вектор, поворачивает его на угол 90°
против часовой стрелки. Тогда оператор Р, действие которого состоит
в последовательном двукратном применении оператора i, будет поворачи-
поворачивать вектор на угол 180°. Такой поворот дает вектор, антипараллельный
исходному, а поэтому
г2=-1, D.1.1)
что согласуется с обычным определением символа i. Трехкратное приме-
применение оператора i сводится к повороту вектора на угол 270° или на
— 90°, так что i3— —i. Аналогично ?4=1.
Опишем теперь различие между действительными и чисто мнимыми
числами. Изобразим все действительные числа в виде векторов, парал-
параллельных оси х. Умножая действительное число на i, мы получаем вектор,
параллельный оси у. Векторы, параллельные оси у, называются чисто
мнимыми числами. Произвольный вектор1) / можно, конечно, выразить
г) Обычное обозначение полужирными буквами не [будет применяться к век-
векторам, изображающим комплексные числа.
332 Гл, '4. Функции комплексного переменного.
через его компоненты и и v вдоль осей х и у и записать в виде
/ = u + iw; D.1.2)
это равенство и выражает связь между комплексными числами и векто-
векторами. Длина или амплитуда вектора /, обозначаемая |./|, равна Y
т. е. абсолютной величине (модулю) комплексного числа u-\-iv, а угол <р,
образуемый вектором / с осью х и определяющий направление вектора,
равен фазе числа u-\-iv, т. е. aTCtg(v/u). Этот угол называется также
фазовым углом или аргументом числа и + iv. Число
f=u-iv,
сопряженное с и -\- iv, изображается вектором, получающимся из / посред-
посредством отражения относительно оси х.
Оператор вращения. Чтобы получить выражение оператора, осуще-
осуществляющего поворот на угол б, рассмотрим сначала оператор поворота
на бесконечно малый угол dti. Такой поворот прибавляет к исходному
вектору / вектор длины \fdO\, перпендикулярный /. Таким образом, / по-
получает приращение
df
а новый вектор имеет вид / + if dO = A + id6) f. Интегрируя это уравнение,
получаем вектор /, повернутый на 6 радиан. Пусть /0 — начальное значе-
значение / (при 8 = 0). Тогда при произвольном 8 вектор / будет равен
/в = **/„• D-1.3)
Следовательно, оператор, поворачивающий векторы на угол б радиан,
имеет вид eie (см. стр. 78).
Если этот оператор применить к единичному вектору, направленному
по оси х, то получится вектор, образующий с осью х угол 6. Выразив
этот новый вектор через составляющие и записав его в виде комплексного
числа, приходим к формуле Муавра eifl = cos O-fisinO, упомянутой на
стр. 78. Последняя согласуется с исходным определением i как опера-
оператора поворота на угол 90°, в чем нетрудно убедиться, положив 6 = тс/2.
Единичный вектор, вращающийся против часовой стрелки с угловой ско-
скоростью ш, запишется в виде eiu>', где, как обычно, опущена единица, на
которую воздействует этот оператор. Любой вектор / может быть выражен
через его модуль | /1 и оператор, нужный для поворота этого модуля от
оси х до направления /,
/ = |/|е*. 7 — |/| в—*»,
где (р — фазовый угол (аргумент) числа /.
Векторы и комплексные числа. Установив взаимно однозначное соот-
соответствие между комплексными числами и векторами, исследуем теперь
соотношения между различными возможными комбинациями комплексных
чисел и соответствующими комбинациями векторов. Два вектора склады-
складываются по правилу параллелограмма, т. е. так же, как два комплекс-
комплексных числа. Однако результат перемножения двух комплексных чисел,
если его выразить в векторных обозначениях, будет зависеть как от ска-
скалярного произведения, так и от векторного. Если / = u-\-iv и g — s + it, то
Jg = (us + vt) + i (ut — vs),
4.1. Комплексные числа и комплексные переменные 333
или в векторной. записи
7g = f-g + i(fxgK1). D.1.4)
Таким образом, если векторы / и g ортогональны, то вещественная часть
произведения /g равна нулю, если же они параллельны, то мнимая часть
этого произведения равна нулю. Следует заметить, что соотношение D.1.4)
подобно соотношению A.6.30), относящемуся к кватернионам. Это неуди-
неудивительно, так как Гамильтон первоначально строил алгебру кватернионов,
пытаясь распространить метод комплексных переменных на трехмерное
пространство и трехмерные векторы.
Дифференциальные свойства векторного поля выражаются через опе-
оператор V. Ограничиваясь здесь двумерным случаем, т. е. плоскостью пере-
переменных жиг/, можно записать V в виде
Применив оператор V к вектору g, в силу D.1.4) получаем
i(rotgK, D.1.6)
так что V сразу дает и дивергенцию и ротор вектора. Заметим, что воз-
воздействие оператора V на действительную функцию (т. е. на переменный
вектор g, направленный вдоль оси ж), в силу D.1.6) дает
ду'
т. е. именно нужное выражение. Мы видим, таким образом, что приме-
применение комплексных чисел для обозначения векторов имеет то достоинство,
•что оно позволяет «конденсировать» несколько векторных операций в одну.
Дальнейшей «конденсации» можно добиться, введя- вместо х и у новые
«переменные
(z + z), y=—~i{z--~z), D.1.7)
z — радиус-вектор точки (ж, у).
В этом месте у читателя обычно возникают сомнения относительно
возможности рассматривать гиг как независимые переменные (такие
¦сомнения не возникают при рассмотрении переменных ж—у, х-\-у), так
как часто говорится, что если известно z, то известно и z. Это, однако,
неверно. Если вектор z задан как отрезок, проведенный из начала в неко-
некоторую точку, то z еще не определено, так как должно быть еще задано'
направление оси х. Обратно, если даны векторы г и г, тс ось х может
быть получена как биссектриса угла, образуемого этими векторами, после
¦чего могут быть найдены ж и у2). С помощью D.1.5) нетрудно получить
выражения
21 = 2д*д эу a v = 2* D.1.8)
dz dz дх dz ду dz v '
l) Индекс З обозначает проекцию на третью ось координат (ось г), перпендику-
перпендикулярную осям х и у и составляющую с ними правую тройку.—Прим. ред.
г) Переменные z и z становятся независимыми только тогда, когда для х и у
допускаются комплексные значения. —Прим. ред.
334 Гл. 4. Функции комплексного переменного
Двумерное электростатическое поле. Предположим, что -мы имеем
электростатическое поле, порожденное линейными зарядами, перпендику-
перпендикулярными плоскости ху. Вектор напряженности поля Е будет, конечно,
лежать в плоскости ху, и мы будем иметь двумерное поле. Поэтому
вектор Е может быть представлен комплексным числом, скажем u—iv
(зачем берется знак минус, выяснится вскоре), где и и v представляют
собой функции от х и у, определяемые распределением линейных зарядов.
Рассмотрим сначала участки плоскости ху, свободные от зарядов. На
этих участках, согласно уравнениям Максвелла B.5.11),
divE = 0, rotE = 0. D.1.9)
В силу D.1.6) и D.1.8) оба эти условия могут быть записаны (только-
в двумерном случае) в чрезвычайно простой форме
?-«•
Это условие означает, что вектор Е зависит только от z = x-*iy и не зависит
от z — x-\-iy. Напротив, сопряженный вектор E = u-\-iv зависит только
от z и не зависит от z. Обычно мы будем иметь дело с функциями от z,
поэтому и здесь удобнее рассматривать вектор Е, зная который^ мы легко-
легконайдем, вектор поля Е. Итак, мы показали, что Е является функцией
переменного z, но не зависит от z. _
Выписав для Е уравнения, аналогичные D.1.9), или выразив 2(92?/dz) =
= V (и -\- iv) = 0 через производные по х и по у и отделив действительную
и мнимую части, получаем пару интересных соотношений между и и v:
дх дУ ' дУ дх* \*.
Это — так называемые условия Коши — Римана. Они получены для вектора
напряженности (двумерного) электростатического поля в области, свобод-
свободной от зарядов и токов, но сам вывод этих условий показывает, что им
удовлетворяет любая комплексная функция f = u-\-iv, зависящая только-
от z (и не зависящая от z). Всякая такая' функция, действительная и
мнимая части которой удовлетворяют уравнениям D.1.10)» называется
аналитической функцией комплексного переменного z = х + iy.
Всякая аналитическая функция переменного z может изображать дву-
двумерное электростатическое поле. Такую функцию можно получить, взяв,
любую достаточно хорошую функцию действительного переменного и введя
в нее комплексный аргумент z=x-\-iy [например, sin (х + iy), 1/[(ж + iyJ + a2],
In (ж -\-iy) представляют собой аналитические функции для всех значений zv
при которых они не обращаются в бесконечность].
В области, свободной от зарядов и токов, существует потенциал V поля Е,
т. е. такая функция V от х ж у, для которой Е = W = dV/дх -\- idV/dy. Обоб-
Обобщая, допустим, что V может принимать комплексные значения, причем
потенциалом в обычном смысле является только ее действительная или
мнимая часть. Тогда Е = 2dV/dz, и так как 8E/dz = 0, то
т. е. V удовлетворяет двумерному уравнению Лапласа. Разумеется,
действительная и мнимая части функции V в отдельности также являются
решениями уравнения Лапласа; с помощью уравнений D.1.10) легко полу-
получить, что действительная и мнимая части любой аналитической функций,
4.1. Комплексные числа и комплексные переменные
335
являются решениями двумерного уравнения Лапласа. Таким образом, или
аналитическая функция может непосредственно определять электростати-
электростатическое поле, или ее действительная и мнимая части могут служить потен-
потенциалами полей.
Контурные интегралы. Интегрирование комплексных функций пред-
представляет собой естественное обобщение интегрирования действительных
функций. Пусть требуется интегрировать аналитическую функцию /(z);
переменным интеграции служит, разумеется, z. Так как z может пере-
перемещаться по комплексной плоскости, а не только вдоль действительной
оси, то нужно еще задать определенную линию, вдоль которой должно
производиться интегрирование. Последняя называется контуром, и если
контур, замкнут, то сам интеграл на-
называется контурным интегралом и
обозначается ф / (z) dz или ф/е*? ds, где
ds — модуль вектора dz, а <р — его ар-
аргумент.
При таком обобщении понятия
интеграла мы не можем ограничиться
указанием нижнего и верхнего пре-
пределов интегрирования, а должны опи-
описать весь контур или начертить его,
как это сделано на рис. 4.1. Выра-
Выражение самого интеграла сходно с ин-
интегралами, выражающими циркуляцию
векторного поля вдоль контура или
поток сквозь контур в двумерном
случае (см. § 1.2). В действительности комплексный контурный интеграл
есть некоторая комбинация того и другого, в чем можно убедиться, взяв
интеграл от вектора электростатического поля и воспользовавшись фор-
формулой D.1.4):
Рис. 4.1. Контурное интегрирование в
комплексной плоскости.
Здесь j?, — компонента вектора Е вдоль ds, En — компонента, нормальная
к ds. Таким образом, действительная часть контурного интеграла от Е есть
циркуляция вектора Е вдоль контура интегрирования, а мнимая часть —
поток вектора Е сквозь цилиндр с высотой 1, образующие которого пере-
пересекают контур и перпендикулярны плоскости ху. (В рассматриваемом
случае, так как поле параллельно плоскости ху, поток вектора Е сквозь
цилиндр с образующими,! перпендикулярными плоскости ху, равен инте-
интегралу <T>Ends, умноженному на высоту цилиндра.)
В случае области, свободной от зарядов, и поток и циркуляция равны
нулю, поэтому для любого [контура, расположенного в такой области,
F2?dz = O. D.1.13)
Это равенство выражает теорему Коши, согласно которой, если /(z) —ана-
—аналитическая функния переменного z на некотором замкнутом контуре
и внутри его, интеграл ф / (z) dz вдоль этого контура равен нулю. На-
Наоборот, если интеграл вдоль любого замкнутого контура равен нулю, то
f (z)—аналитическая функция, а следовательно, вектор плоского элоктро-
336 Гл. 4. Функции комплексного переменного
статического поля может быть представлен посредством аналитической
функции во всех точках, где отсутствуют заряды и токи.
Применив формулу A.2.9) к цилиндрической поверхности, построен-
построенной на контуре, приходим к выводу, что если поле Е порождается сово-
совокупностью линейных зарядов, распределенных равномерно вдоль прямых,
перпендикулярных плоскости ху, причем линейная плотность зарядов
на г-й прямой равна qr, то в силу D.1.12)
im^'q,., D.1.14)
г
где суммирование распространяется на те линии, которые пересекают
плоскость ху внутри рассматриваемого контура.
Рассмотрим случай, когда лишь одна прямая, несущая заряды с ли-
линейной плотностью qx, пересекает плоскость ху в некоторой точке
zx = xx-\ iyx, лежащей внутри выбранного контура. Тогда поле Е может
быть представлено в виде суммы поля Es, порождаемого источником дх
внутри контура, и поля Ео, порождаемого внешними источниками. Эле-
Элементарное интегрирование уравнений электростатики дает выражение
Es = Bgj/r)ar, где r8 = (х — хг)*-\-(у — у1J = \z — zx\2 — квадрат расстояния
в плоскости ху от источника в точке гх и аг — единичный вектор, направ-
направленный от источника к точке (х, у). В комплексных обозначениях
Es = ^ (cos <p + i sin <p) = ^~- е**,
где ср —угол, образуемый вектором аг с осью х. Так как re^ — z— zx, то
Прибавив Ео к Es, получим
? = ^4г, D.1.16)
где / (z) = Ео (z — Zj) + 2qx — аналитическая-функция внутри контура и на нем.
Итак, для любой аналитической функции f(z) мы имеем формулу
DЛЛ7)
которая представляет собой более общую форму теоремы Коши.
Таким образом теорема Коши является перефразировкой, в терминах
аналитических функций, теоремы Гаусса из электростатики.
Подобным же образом магнитное поле, порожденное линейными токами,
перпендикулярными плоскости ху, можно изобразить посредством функ-
функции Я переменного z. Ток / вдоль прямой, пересекающей плоскость ху
я точке z0, внутри контура, порождает поле Я = 2(Ixar)/r, которое
изображается функцией Я = 2//г(г — z0). В случае нескольких токов 1Г
имеем в силу формулы A.2.11)
4TC ]>]'/,., D.1.18)
где суммирование распространяется на те токи, которые проходят внутри
контура интегрирования. Здесь контурный интеграл действительный, но
если мы подставим выражение функции И через z — z,,, то снова получим
теорему Коши.
4.2. Аналитические функции 337
Обратимся снова к рис. 4.1; мы видим, что интеграл вдоль (незамк-
(незамкнутого) пути, соединяющего точки А и В, может быть записан в виде
ВДВ
^Edz= ^Etds + i\ Ends=*W = V + iU. D.1.19)
А А А
Действительная часть V этого интеграла представляет собой разность
электростатических потенциалов в точках Аи В. Мнимая часть U измеряет
число силовых линий, пересекающих путь интегрирования от точки А
до точки В.
Заметим, что семейство кривых U = const ортогонально семейству
V = const, так что V и U могут служить ортогональными криволиней-
криволинейными координатами в плоскости. Если в поле помещен проводник, имею-
имеющий форму цилиндра с образующими, перпендикулярными плоскости ху,
то его поверхность должна пересекать эту плоскость по некоторой экви-
эквипотенциальной кривой V = const. Силовые линии будут при этом образо-
образовывать ортогональное семейство линий V = const, и поверхностный заряд
цилиндра на единицу его высоты на участке поверхности, ограниченном
точками А и В, будет равен U(B)— U{A). В гл. 2 (см. стр. 153) функ-
функция U была названа функцией тока.
В этом параграфе мы сопоставили комплексные переменные и электро-
электростатические величины и в качестве примера дали электростатическую
интерпретацию некоторым известным теоремам теории функций. В даль-
дальнейшем в этой главе мы разовьем более строгую теорию, но будем обра-
обращаться к электростатической интерпретации, чтобы сделать ощутимым
смысл излагаемых теорем, как это было сделано здесь в применении
к теореме Коши и интегралу Коши.
4.2. Аналитические функции
Электростатическая аналогия позволила нам вывести эвристическим,
путем некоторые основные теоремы теории функций. В частности, мы заме-
заметили, что аналитические функции образуют узкий класс, к которому
не принадлежат многие функции. В этом параграфе мы постараемся выяс-
выяснить сущность требований, определяющих аналитическую функцию, с точки
зрения геометра и аналитика. При этом получатся более строгие выводы
упомянутых теорем. (Строгость в этих вопросах действительно полезна!)
Аналитическая функция была нами определена грубо как функция,
зависящая только от z, а не от z и z вместе. Поэтому изучение анали-
аналитической функции комплексного переменного f{z) = u + iv, где и и v—дей-
v—действительные функции переменных жиг/, обладает меньшей степенью
общности, нежели изучение произвольных функций двух переменных, так
как в случае аналитической функции ими оказываются связанными
условиями Коши —Римана D.1.10). Более точное определение аналитиче-
аналитической функции можно получить, рассматривая поведение производной
функции / (z) no z в точке а. Само понятие производной достаточно ясно.
Функция f(z) изображается вектором. Спрашивается, как изменяется этот
вектор по величине и по направлению, когда z смещается из а в напра-
направлении, определяемом вектором dz. Если f(z) зависит только от z (как,
например, z2), то мы вправе ожидать, что производная Bz в нашем при-
примере) определяется только точкой, в которой она вычисляется. Однознач-
Однозначная функция является аналитической в точке а, если ее производная
в точке а определяется единственным образом, т. е. не зависит от направ-
направления dz, по которому она вычисляется. Независимо от того, куда мы
22 ф. м. Морс и Г. ФешСах
338 Гл. 4. Функции комплексного переменного
смещаемся из точки z, скорость изменения / с изменением z должна
быть одна и та же. Для произвольной комплексной функции u-\-iv,
в которой и и v зависят от х и у как угодно, это условие не выполняется.
Оно выполняется лишь тогда, когда и и v удовлетворяют уравнениям
D.1.10).
Преимущество такого определения аналитической функции перед
более простым определением, данным выше, состоит в его большей точ-
точности. Пользуясь им, легко проверить, является ли функция аналитиче-
аналитической в какой-либо заданной точке. Мы снова видим, как узок класс ана-
аналитических функций. Большинство функций не обладает «изотропной»
производной.
Нетрудно1 показать, что условия Коши —Римана необходимы для суще-
существования единственной производной. Для этого рассмотрим отношение при-
приращения Д/ функции / (z) при изменении z от а до a-f-Дгк приращению Дг:
Л/ _ /(g + Az)-/(g) = [(ди/дх) + i (dv/dx)] Ах + [(ди/ду) + i (dv/dy)] Ay _
Jb ~~ Az. Ax+iAy ~~
(ди/дх) + i (dv/дху f Ay С (dv/dy) — i (ди/ду) \ 1
1 + i (Ay/Ax) \ l + Ax V (ди/дх) + i (dv/dx) ) J "
Это равенство показывает, что, помимо некоторых исключительных слу-
случаев, производная df/dz = lim Д//Дг зависит от &у/&х, т. е. от направления
iz^ 0
вектора Дя. Для аналитической же функции такой зависимости быть
не должно. Достигается это только тогда, когда
D.2.1)
dv
ду
ди
дх """
. du
1~ду~
dv
ди
ди
ду ~ '
. dv
~1~дх~
dv
дх *
Последние равенства выражают условия Коши —Римана, необходимые для
того, чтобы функция была аналитической. Эти условия достаточны, если
дополнительно потребовать, чтобы входящие в D.2.1) производные были
непрерывны в точке а. Без этого требования производные ди/дх и другие
зависели бы от способа их вычисления, а это снова привело бы к неодно-
неоднозначной первой производной от /. Пусть, например,
_ Xs—у» ди __ a^ + 3arV + 2a^/3
U-~ х2 + у2 ' дх~~ (х2 + у2J
тогда lim lim (ди/дх) = 1 и в то же время lim lim (ди/дх) ^О1).
1-»0у->0 В-»О1-.О
Условия Коши—Римана показывают, что если действительная (или
мнимая) часть функции известна, то мнимая (соответственно действитель-
действительная) часть определяется однозначно с точностью до постоянного слагае-
слагаемого. Сейчас мы покажем на простом примере, как это осуществляется
(позже будут указаны специальные методы). Предположим, что известна
действительная часть и; попытаемся найти мнимую часть:
х) Это довольно тонкое различие между необходимостью и достаточностью
условий Коши—Римана для аналитичности функции установлено здесь недостаточно
корректно. По этому поводу заметим только, что во всех случаях, возникающих
при исследовании физических явлений, условия Коши—Римана необходимы и доста-
достаточны для аналитичности функции. —Прим. ред.
4.2. Аналитические функции 339
или
Значит, если и известна, то v определяется посредством интегрирования
по формуле D.2.2). Например, пусть и= Inr = A/2) In {х2-\-у2). Тогда
f —у dx , xdy у .
v= ^ —у,— +-pr = arc tg-|- +const,
так что 1п г -j- i arc tg (y/x) представляет собой аналитическую функцию;
последнюю можно записать проще в виде lnz.
Специальная природа аналитических функций сказывается также
в том, что если и и v удовлетворяют условиям Коши — Римана, то тем же
свойством обладает пара производных ди/дх и dv/дх, так же как ди/ду
си dv/ду. Это обстоятельство указывает на то, что если функция f (z) ана-
литична, то аналитичны и все ее производные. Эту полезную теорему
мы сможем доказать в следующем параграфе, так как пока еще не уста-
установлено существование самих высших производных; ее, однако, следует
запомнить, так как она позволяет обнаружить нарушение аналитичности
в тех точках, где не существует какой-либо из старших производных.
Точки, в которых рассматриваемые функции неаналитичны, назы-
называются особыми (особенностями). Мы уже встречали функцию с особен-
особенностью l/(z — а); она изображает электростатическое поле, которое порож-
порождено зарядом, находящимся в точке а. Точка « — особая, так как при
z = а эта функция не имеет производной. Сущесткуют функции, неанали-
тпческие во всех точках, как, например, |z|2. Эта функция равна zz я, оче-
очевидно, зависит не только от z. Функция zvlcj, где p/q — несократимая
дробь, неаналитична в точке z = 0. В применении, например, к функции z8/5
в этом можно убедиться, заметив, что при z = 0 ее вторая производная
бесконечна.
Конформное отображение. Любая аналитическая функция /(z) =
= H + jf (z = x+iy) может быть представлена геометрически как преобра-
преобразование переменных х, у в переменные и, v. Можно вообразить две ком-
комплексные плоскости: на одной пусть изображаются значения z, на дру-
другой—соответствующие значения /. Любой линии на плоскости z будет
при этом соответствовать некоторая линия на плоскости /. Разумеется,
такого рода отображения осуществляются произвольными парами функ-
функций и, v переменных х, у. Но в тех случаях, когда и и v служат дейст-
действительной и мнимой частями некоторой аналитической функции, соответст-
соответствующие отображения обладают некоторыми полезными и характерными
свойствами. Самое важное и очевидное из этих характерных свойств
состоит в том, что такие отображения «сохраняют углы», или являются
конформными.
Если в плоскости z взять две пересекающиеся кривые, то соот-
соответствующие им кривые в плоскости / также будут пересекаться. При
конформном отображении угол, под которым пересекаются эти кривые
в плоскости /, равен углу, образованному выбранными кривыми в пло-
плоскости z в их точке пересечения.
На рис. 4.2 кривые в плоскости z пересекаются в точке z = а, точкой
же пересечения соответствующих кривых в плоскости / является / (а)*
Элементарное перемещение вдоль кривой / можно записать в виде
dzx = \dzx\elIfj, элементарное перемещение вдоль кривой 2 есть dz2 =
= [ dza | егч>!!. Соответствующие элементарные перемещения в плоскости /
22*-
'340
Гл. 4. Функции комплексного переменного
^завны dzx(df/dz) и dz2 (df/dz). Если функция / аналитична в точке z = a,
то производная df/dz не зависит от направления dz; поэтому df/dz в точке а
равно \df/dz\eia, каков бы ни был угол f направления dzx или dz2. Следо-
Следовательно, элементарные перемещения вдоль кривых 1 и 2 в плоскости /
\равны соответственно \dzx (df/dz) \еНа+^ п \dz2(df/dz) |ei(a+ip2>. Эти кри
\те повернуты на угол а относительно соответствующих кривых в пло-
плоскости z, но угол между ними равен (а + <рх) — (ct-f ^2) = ^ — <р2, т. е. равен
углу между кривыми 1 и 2 в плоскости z. Таким образом, отображение,
осуществляемое аналитической функцией / (z) = и -f /и, конформно, т. е!
сохраняет углы. Повторяя в обратном порядке вес этапы этого рассуж-
рассуждения, мы убедимся в том, что если преобразование х,у в n,v конформно,
то оно осуществляется аналитической функцией f = u-\-iv переменного
z = x-i-iy и функции и и v удовлетворяют условиям Коши — Римана D.2.1).
г=а
f=f(a)\
Рис. 4.2. Сохранение углов при конформном отображе-
отображении.
Мы можем также нанести кривые на плоскость / и посмотреть, как
расположатся соответствующие кривые в плоскости z. Например, прямые
и = const, v = const служат координатными линиями прямоугольной системы
координат в плоскости /. Соответствующие кривые и (х,у) = const,
v (х,у) = const образуют ортогональную координатную сеть в плоскости z
{ортогональность обусловлена тем, что при отображении прямые углы
переходят в прямые). Воспользовавшись только что проведенным рассу-
рассуждением или определениями § 1.3 [см. A.3.4)], мы получим в силу урав-
уравнений D.2.1) (т. е. в силу аналитичности функции /) для обеих коорди-
координат u,v равные коэффициенты Ламе
ди
L
dz
Поэтому бесконечно малая фигура на плоскости / отображается в подоб-
подобную фигуру на плоскости z, отличающуюся, может быть, от исходной
положением и величиной, но заведомо сохраняющую углы и отношения
линейных размеров. Это свойство также может служить определением
.конформного отображения.
Простейшее конформное отображение задается равенством f = zel>-\-c,
где действительный угол б и комплексное слагаемое с постоянны. В этом
случае коэффициенты Ламе hu = hv= df/dz\—\, т. е. линейные размеры
сохраняются. Само преобразование состоит в смещении, определяемом
вектором с, и в повороте на угол 6. В других случаях происходит изме-
изменение линейных размеров, т. е. растяжение или сжатие, причем в раз-
различных участках это изменение неодинаково, так что в целом пло-
плоскость претерпевает искажения, несмотря на то, что преобразования ее
малых участков сводятся к преобразованиям подобия. Всякую аналити-
4.2. Аналитические функции
341
ческую функцию комплексного переменного, как мы видели, можно рас-
рассматривать как изображение некоторого электростатического поля, а поэтому
можно считать, что действие этого последнего состоит в искривлении
пространства и в замене первоначального поля простым электроста-
электростатическим полем Е = и + iv. Движение заряженной частицы можно при
этом объяснить либо непосредственным воздействием поля, либо ис-
искривленностью пространства под влиянием этого поля. Эта точка зре-
зрения напоминает подход Эйнштейна к гравитационным явлениям в общей
теории относительности.
На рис. 4.3 показано конформное отображение, осуществляемое функ-
функцией
/ = ;
1—х2
V =
—2у
z =
1 —/
Эта функция аналитична ьеюду, кроме точки z=—1, соответствующее
отображение конформно также всюду, кроме этой точки. Кривые и = const,
v — const в плоскости z образуют два взаимно ортогональных семейства
Плос
и=-2
и=-3-
:кость
(v=-Z
г
%
v=-4
У
и=0
J
X
1
Плоскость f
v=1
v=-1-
см
I
II
и и
а в
Рис. 4.3. Конформное отображение, осуществляемое функцией
/() A)/A )
касающихся друг друга окружностей. Другие случаи будут разобраны
и изображены ниже (см. § 4.7).
Заметим, что в точках, в которых коэффициент растяжения \df/dz\
обращается в нуль, отображение не конформно. Окрестность такой точки
в плоскости z претерпевает сильное сжатие при отображении на пло-
плоскость /. При обратном отображении соответствующая область на пло-
плоскости / подвергается сильному растяжению. Это наводит на мысль, что
для обратной функции z (/) точка, соответствующая той, в которой
/'(z) = 0, является особой. Мы увидим на примере, что это действительно
так. Простейшим примером может служить функция / (z) = z2, для которой
/' @) = 0. Как и следовало ожидать, / = 0 является особой точкой обрат-
обратной функции z — f42. Поэтому в этой точке отображение не может быть
конформным. Это можно доказать непосредственно, так как если отрезки
двух кривых пересекаются в точке z = 0 под углом <р2 —1Pi> T0 угол между
соответствующими кривыми в плоскости / равен 2(^2^-^). Ясно, что если
/'(а) = 0. то отображение в точке z = а не конформно, независимо оттого,
ведет ли себя / (z) вблизи z = а как (z — аJ, что имеет место в нашем
частном примере, или как (z — а)п с любым целым п > 2.
Однако там, где / аналитична и коэффициент растяжения \df/dz\ не
равен нулю, обратное отображение конформно. Математически это форму-
342 Гл. 4. Функции комплексного переменного
лируется так: если функция f (z) аналитична в точке z — a и f'(a) Ф 0, то
функция, обратная](z), аналитична в docmamo4HO малой области, окружаю-
окружающей ](а), и ее производная в точке ](а) равна 1//'(а).
Во-первых, что касается существования обратной функции, то мы
замечаем, что для отображения и = и(х,у), v — v(x,y) существует обрат-
обратное, если (du/dxJ + (du/dyJ Ф 0. При ]'{а)фО последнее условие выпол-
выполняется. Заметим также, что если ]'{а) равно нулю, то обратная функция
в точке ](а) не существует, а это означает, что /(а)— особая точка обрат-
обратной функции. Теперь нужно показать, что обратная функция аналитична,
т. е. что dx/du = dy/dv и dx/dv = —dy/du. Выразим дх/ди, .... через
производные ди/дх, .... Для этого из тождества
находим
откуда в силу D.2.
Точно так же
. дх ди
ди дх
1)
дх ди
ду дх
ду du
du ду
dx-
дх
+dv
dx
dv
, dJL
^ dv
dx
~du~
dv
dx '
du
dy '
du
dx '
dx
dv
„ dx du . dx dv
dudy"T~"dv"dy''
p. dx ди дх ди
du dy dv dx
~ dy ди ду ди
du dx dv dy
Решим полученную систему четырех уравнений с четырьмя неизвест-
неизвестными dx/ди, dx/dv, dy/du, dy/dv. Для производных от х получим выра-
выражения
дх
ди
du/dx
(ди/дхJ + (ди/дуJ'
дх —ди/ду
dv (ди/дх)*+ (ди/дуJ "
Найдя производные от у, мы увидим, что удовлетворяются условия
Коши —Римана дх/ди = dy/dv, dx/dv— —ду/ди. Вычислив производную
обратной функции
df ди~ ди ди dv (ди/дх) —i (ди/ду) df/dzr
мы докажем последнее утверждение теоремы. Значительная часть этой
главы будет посвящена дальнейшему изучению конформных отображений
ввиду важности этих вопросов для приложений.
Интегрирование в комплексной плоскости. Теория интегрирования
в комплексной плоскости в сущности есть теория криволинейных инте-
интегралов. Если С — какой-нибудь допустимый контур (см. ниже), то, согласно
сказанному на стр. 335 [см. абзацы, предшествующие формуле D.1.12)],
dz= *\ Etds + i \ Ends, ds = \dz\,
с с с
где Et — компонента вектора Е вдоль пути интегрирования, а Еп — нор-
нормальная компонента. Интегралы такого вида часто встречаются в физике.
Например, если Е—силовое поле, то \ Etds представляет собой работу,
с
которая совершается против сил поля при перемещении вдоль конту ра С.
Второй интеграл измеряет поток вектора Е через контур. Если Е — вектор
4.2. Аналитические функции
343
скорости движущейся жидкости, -то второй интеграл представляет собой
поток жидкости через рассматриваемый контур.
Для того чтобы оба эти "интеграла имели физический (а также мате-
математический) смысл, необходимо взять достаточно гладкий контур. Такой
гладкий контур (гладкая кривая) можно составить из непрерывно примы-
примыкающих друг к другу дут, каждая из которых имеет непрерывно изме-
изменяющуюся касательную. Последнее требование исключает возможность
появления таких патологических явлений, как дуги, имеющие бесконеч-
бесконечную длину. Для удобства предположим еще, что ни одна из дуг, состав-
составляющих контур, не имеет точек самопересечения, исключив тем самым
появление петель. Впрочем, контуры, имеющие петли, можно было бы
не исключать из рассмотрения, так как каждый контур с петлей может
быть разбит на замкнутый контур (петлю) ж некоторый гладкий контур,
и теорему, о которой идет речь, можно было бы применить отдельно
Во ос
Рис. 4.4. Примеры контуров в комплексной плоскости.
к обеим частям. Замкнутым контуром назовем замкнутую гладкую
кривую. Замкнутый контур описывается в положительном направлении
по отношению к области, ограниченной контуром, если по отношению
к наблюдателю, находящемуся в какой-либо внутренней точке этой области,
обход контура совершается против часовой стрелки. Отрицательным будем
считать обход по часовой стрелке. Интегрирование вдоль замкнутого
контура будет обозначаться знаком ф .
В дальнейшем мы будем часто пользоваться следующим достаточно
очевидным фактом: если /(г) —аналитическая функция внутри контура
и на самом контуре и если производная df/dz в этой области однозначна, то
В тех случаях, когда df/dz неоднозначна, это равенство может нарушаться.
Комбинируя контуры, составленные из гладких кривых, можно полу-
получать новые контуры. На рис. 4.4 приведены примеры. В примере б' окруж-
окружности не смыкаются и, следовательно, не образуют в совокупности еди-
единого замкнутого контура. Области, ограниченные контурами такого рода,
называются многосвязными; в остальных примерах на рис. 4.4 области
односеязные. Область односвязна, если любой замкнутый контур, лежащий
в ней, можно стянуть в точку, непрерывно деформируя его и не задевая
344 Гл. 4. Функции комплексного переменного
при этом границу области. В примере б' кривая Сх, лежащая в кольце
между двумя окружностями, не поддается такой деформации. Пример б
иллюстрирует тот факт, что любая многобвязная область может быть
превращена в односвязную, если дополнить ее границу разрезами так,
чтобы нельзя было провести нестягиваемых замкнутых контуров. Так, кон-
контур Сх в примере б', если его перенести в б, не лежал бы целиком внутри
заданной области. Необходимость принимать во внимание характер связ-
связности области и его физический смысл будет вскоре выяснена.
После этих геометрических замечаний мы можем сформулировать
центральную теорему теории функций комплексного переменного.
Теорема Коши. Если f(z)— аналитическая функция, непрерывная
внутри замкнутого гладкого контура С и на самом контуре, то
&f{z)dz = O. D.2.3)
Доказательство этой теоремы, принадлежащее Гурса, читатель может
найти в различных учебниках. Простое доказательство, приведенное выше,
предполагает не только существование производной /'(z) всюду внутри С,
но и ее непрерывность в этой области. Однако теорему Коши полезно
доказать при минимальных предположениях относительно /(г), так как
это расширит область ее применения. В настоящем параграфе мы удо-
удовольствуемся предположениями, что контур С ограничивает звездообразную
область и что /' (z) ограничена внутри и на С.
Геометрическое понятие «звездообразной» области нуждается в разъ-
разъяснении. Область называется звездообразной, если в ней существует такая
точка О, что любой луч, выходящий из О, имеет в точности одну точку
пересечения с границей области. Простым примером звездообразной области
служит круг. Кольцо, напротив, не является звездообразной областью.
То, что наше доказательство будет относиться лишь к звездообразным
областям, не нарушает общности теоремы, так как произвольная одно-
связная область с достаточно хорошей границей может быть разбита
на несколько звездообразных частей, к каждой из которых теорема Коши
применима. Например, на рис. 4.4,е область, представляющая собой полу-
полукольцо, может быть разбита на звездообразные части, подобные обла-
областям // и /// примера б. Применив теорему Коши отдельно к границам
этих частей, мы получим
II III
Но интегралы по общим участкам границ областей // и /// взаимно уни-
уничтожаются, и сумма интегралов в левой части равенства оказывается
равной интегралу от / по границе полукольца.
Переходим к доказательству теоремы Коши. Пусть точка О звездо-
звездообразной области является началом координат. Рассмотрим функцию
'Л. D.2.4)
Теорема Коши утверждает, что /"A) = 0. Для доказательства дифферен-
дифференцируем F (X):
F' (X) = & 1 (Xz) dz + X & zf (kz)dz.
4.2. Аналитические функции
345
Интегрируя во втором слагаемом по частям [что допустимо при условии
ограниченности /'(z)], получаем
где квадратные скобки указывают на то, что берется разность значении
заключенной в них функции в начальной и конечной точках контура. Так
как функция zf(Kz) однозначна, то [z/(Xz)/X] в случае замкнутого контура
обращается в нуль и /"(Х) = 0, т. е.
F(k) — const.
Для отыскания этой постоянной положим X = О в D.2.4) и получим
F@) = 0. Следовательно, /1A) = 0, и теорема доказана. Это доказательство,
кажущееся столь простым, на самом деле переносит трудность на другие
Рис. 4.5. Контуры в многосвязных областях.
вопросы, такие, например, как вопрос о возможности интегрирования по
частям. Последняя вытекает из предположения об аналитичности функции.
Теорема Коши в форме D.2.3) неприменима к многосвязной области,
так как ее граница не является замкнутым гладким контуром. Физичес-
Физические причины этого факта нетрудно обнаружить. На стр. 335 мы устапо-
пили, что в применении к электростатическому полю теорема Коши экви-
ьалентна утверждению, что внутри области, ограниченной контуром С.
ист электрических зарядов. Взяв многосвязную область, приведенную на
рис. 4.4,6', мы увидим, что существует контур (например, контур Сх).
целиком лежащий внутри рассматриваемой области, к которому теорема
Коши явно неприменима из-за того, что внутри маленького круга, т. е.
вне рассматриваемой области, могут находиться заряды. Теорему Коши
можно получить здесь при помощи вычитания
fdz=-O, D.2.5)
Ci С2
где С2 — малая окружность. Это равенство можно также установить непо-
непосредственно, соединив разрезом линии С1 и С2 и тем самым превратив
многосвязную область в односвязную. Если взять теперь (см. рис. 4.5)
контур, состоящий из контуров Сх (описываемого в положительном напра-
направлении), С2 (описываемого в отрицательном направлении) и границ разре-
:.ia С3 и С4, то к такому контуру теорема Коши применима. Интегралы
вдоль С3 и С4 взаимно уничтожаются, и мы получаем равенство D.2.5).
346
-Гл. 4. Функции комплексного переменного
Некоторые полезные следствия из теоремы Коши. Из теоремы Коши
следует, что если f(z) — аналитическая функция внутри области, ограни-
Z2
ченной некоторым замкнутым контуром С, то интеграл \ / (z) dz, взя-
взятый вдоль любого контура, лежащего внутри С, зависит только от zx
и z2. Таким образом, не только производная функции /(z), но и ее инте-
интеграл определяются однозначно. Это обстоятельство часто приводится в ка-
качестве довода в пользу важности теоремы Коши. Для доказательства
сравним интегралы \f(z)dz и \ f(z)dz, взятые вдоль двух различных
Ci Сг
С,
Область
аналитичности
Рис. 4.6. Независимость интеграла от пути внутри области анали-
аналитичности.
контуров Сг и С2, идущих от точки zx к точке z2 (см. рис. 4.6). Согласно
теореме Коти, \ f(z)dz—\ f(z)dz=&f(z)dz = O, что и требовалось до-
Сг Ci
казать. Из этого следствия вытекает весьма важный факт,, состоящий в
том, что, не изменяя значения интеграла, мы можем деформировать кон-
контур интегрирования, если только при такой деформации контур не пе-
пересечет ни одной особой точки под интегральной функции. Этой теоремой
мы постоянно будем пользоваться при вычислении контурных интегралов,
так как она позволяет выбирать наиболее удобный контур.
В силу однозначности интеграла \ fdz можно ввести неопределенный
интеграл функции / (z), положив
причем контур берется, разумеется, внутри области аналитичности функ-
функции /(г). Справедлива интересная теорема, состоящая в том, что если f(z)
-аналитична в некоторой области, то F (z) в этой области также является
аналитической функцией. Для доказательства достаточно установить од-
4. 2. Аналитические функции 2А1
нозначность производной функции F (z). С этой целью рассмотрим тожде-
тождество
z-C
В силу непрерывности и однозначности f(z), правая часть при прибли-
приближении z к С может быть сделана сколь угодно малой. Поэтому
Написанный предел является как раз производной F' (С), и теорема дока-
доказана.
Из уравнения D.1.19) и последующих рассуждений мы сделали вы-
вывод, что если /(z) —функция, сопряженная электростатическому полю, то
действительная часть функции F(z) является электростатическим потен-
потенциалом, а мнимая часть постоянна вдоль силовых линий поля, т. е. яв-
является функцией тока (см. стр. 337). Следовательно, двумерный электро-
электростатический потенциал и функция тока служат действительной и мнимой
частями некоторой аналитической функции комплексного переменного.
Возвращаясь к предыдущему абзацу, заметим, что, воспользовавшись
только непрерывностью и однозначностью /(z), а также одиозначностыо
интеграла, мы установили аналитичность функции F(z). Ниже мы пока-
покажем, что если функция /(г) аналитична в некоторой области, то анали-
тична и ее производная [см. формулу D.3.1)]. Забегая вперед и приме-
применяя эту теорему, приходим к заключению, что если F(z) аналитична, то
аналитична и /(г). Таким образом, мы получаем обращение теоремы Ко-
ши, именуемое теоремой Морера.
Если функция /(z) непрерывна и однозначна внутри некоторого зам-
замкнутого контура С и ф / (z) dz = 0 для любого замкнутого контура, ле-
лежащего внутри С, то f(z) аналитична внутри С.
Эта теорема позволяет проверять аналитичность функций и является,
таким образом, интегральным аналогом дифференциального признака, вы-
выражаемого условиями Коши — Римана. Последние, впрочем, требуют еще
непрерывности производной от /, и поэтому иногда бывает проще пользо-
пользоваться интегральным признаком.
Физический смысл теоремы Морера в применении к электростатичес-
электростатическому полю /(z) может шокировать физика своей очевидностью; она утвер-
утверждает,, что если полный заряд, заключенный внутри произвольного замк-
замкнутого контура, лежащего в данной области [вычисленный с помощью
/(z)], равен нулю, то и плотность зарядов в этой области всюду равна
нулю.
Интегральная формула Коши. Интегральная формула Коши, являю-
являющаяся прямым следствием теоремы Коши, играет основную роль в приме-
применениях теории аналитических функций в других областях математики и
в физике. Ее электростатическим аналогом является теорема Гаусса, ко-
которая утверждает, что интеграл от нормальной компоненты вектора эле-
электростатического поля вдоль замкнутого контура С равен сумме зарядов,
заключенных внутри С. В электростатике теорема Гаусса доказывается
таким образом, что поле, возбуждаемое внешними (по отношению к С) ис-
источниками, отделяется от поля, порожденного внутренними источниками.
Первое дает интеграл, равный нулю, а второе вычисляется путем сумми-
348 Гл. 4. Функции комплексного переменного
рования действий отдельных источников. Интегральная формула Коши
относится к случаю, когда внутри С имеется единственный точечный ис-
источник.
Рассмотрим интеграл (называемый интегралом Коши)
М?_, D.2.6)
взятый вдоль некоторого замкнутого контура С, причем предполагается,
что на контуре и внутри него /(z) аналитична. Согласно следствию из
теоремы Коши о деформировании контуров, С можно заменить малой ок-
окружностью радиуса р с центром в точке а. Положив z — a = pei<e, получим
i J [f {a + Ре*) - f (a)] d9. D.2.7)
В пределе при р—>0 второй интеграл в правой части обращается в нуль
в силу непрерывности /(z). Итак, интегральная формула Коши гласит,
что если функция /(z) аналитична внутри контура С и на нем самом и
а — какая-либо точка, лежащая внутри С, то
Если точка а выбрана вне С, то ф [/ {z)/(z — a)] dz = 0. Если точка а вы-
выбрана на самом контуре С, то главное значение Коши*) этого интеграла ран-
но rdf(a) (т. е. среднему арифметическому значений, получающихся в пре-
предыдущих случаях). Последний случай соответствует такому положению
точечного источника, когда одна его половина находится с внутренней
стороны контура С, а другая половина —с внешней. Итак,
\ 1, если а лежит внутри С,
D.2.9)
i 1, если а лежит внутри С,
<? Z(z) fa _ 2izif (a) x J ~2 (главное значение интеграла),
если а лежит на С,
0, если а лежит вне С.
Формула Коши дает интегральное представление функции /(z) и поз-
позволяет вычислить /(г) в любой точке, лежащей внутри контура С, коль
скоро известны значения /(z) на С. В физике часто встречаются такого
рода представления (в частности, в применениях функций Грина или фун-
функций источника) с разрывами такого же вида, как в D.2.9). Формула
D.2.8) в том случае, когда / определяет электростатическое поле, дает
возможность вычислить поле внутри контура С по его значениям вдоль С.
Аналогичные теоремы имеют место в теории распространения волн, где
они объединяются под названием принципа Гюйгенса.
*) Главное значение Коши несобственного интеграла определяется следую-
следующим образом: пусть q (х) —> с» при х —> а, тогда главное значение интеграла
с с
\ q (x) dz, обозначаемое 3й \ q (x) dx {Ъ < а < с), равно
Ь ь
а—д с
lim \ \ q(x)dx+ \ q(x) dx \ .
S->+0 I J J J
а+Ь
4. 2. Аналитические функции 349
Формула Коши представляет собой мощное орудие исследования
свойств аналитических функций. Она указывает на теснейшую связь, суще-
существующую между значениями аналитической функции во всей комплекс-
комплексной плоскости. Так, из формулы D.2.7) мы видим, что f(a) равно сред-
среднему арифметическому значений / на любой окружности с центром в точ-
точке а. Поэтому |/(а)| <.М, где М - наибольшее значение |/| на окружности.
Равенство \f(a)\ = M может иметь место лишь тогда, когда / постоянна
на окружности; в этом случае f постоянна и внутри круга. Эта теорема
легко может быть обобщена на области, ограниченные произвольными кон-
контурами.
В случае электростатического тюля последняя теорема означает, что
вектор поля в области, ограниченной некоторым замкнутым контуром С
и свободной от зарядов, принимает свое наибольшее (по модулю) значение
на границе области. Если /(z) не имеет нулей внутри контура С, то
¦функция l//(z) аналитична в этой области и |l//(z)| достигает своего наи-
наибольшего значения лишь на С. Следовательно, в этом случае |/(г)| при-
принимает свое наименьшее значение лишь на контуре С. Доказательство не
проходит и сама эта теорема несправедлива тогда, когда внутри С суще-
существуют нули функции f(z). Таким образом, модуль аналитической функ-
функции не может достигать внутри области аналитичности ни максимума, нп
{положительного) минимума. Если [/(г)| достигает наибольшего или наи-
наименьшего (положительного) значения внутри С, то / (г) — постоянная. Поэ-
Поэтому точки, в которых производная функции / (z) обращается в нуль и
f (г) ф 0, являются для | / (г) [ седловыми точками, а не точками максимума
или минимума.
В частности, вектор электростатического поля принимает своп наи-
наибольшее и наименьшее (по модулю) значения (когда последнее отлично
от нуля) на границе области.
Эти теоремы применимы не только к |/(z)|, но также к действитель-
действительной и мнимой частям аналитической функции / (z), а следовательно, и к
электростатическому потенциалу V. Чтобы это показать, запишем равен-
равенство D.2.7) в виде
2тс 2-л.
i/ (а) = 2т (u + iv) = i \ /(х - iy)dy = i \ (и-f- iv) d<p.
о о
Приравняв мнимые части второго и четвертого выражений, получим
D.2.10)
и мы видим, что значение и в центре окружности есть среднее арифмети-
арифметическое ее значений на самой окружности. Рассуждая точно так же, как
при рассмотрении |/(z)|, мы приходим к заключению, что и принимает
•свои наибольшее и наименьшее значения лишь на границе той области,
где / аналитична.
... Мы доказали, таким образом, теорему, которая гласит, что электро-
электростатический потенциал не может достигать ни максимума, ни минимума
внутри областей, свободных от зарядов. Этот факт был уже установлен в
гл. 1 (см. стр. 18) при обсуждении уравнения Лапласа, которому удовле-
удовлетворяет электростатический потенциал. Непосредственным следствием этой
теоремы является то, что электростатический потенциал V, если он посто-
постоянен на каком-либо контуре, внутри которого нет зарядов, оказывается
постоянным также внутри контура. Это свойство V находит свое истол-
350 Гл. 4. Функции комплексного переменного
кование в хорошо известном факте, что электростатическое поле внутри
проводника, образующего замкнутую поверхность, равно нулю.
Приведенные примеры показывают, насколько полезен интеграл Коши.
Кроме того, мы еще раз убедились в том, что аналитические функции
обладают весьма специальными свойствами. Более глубоким изучением
;>тих свойств мы займемся в этой главе позднее.
Действительная и мнимая части аналитической функции. Только что
приведенные рассмотрения указывают на то, что мы можем классифици-
классифицировать компоненты аналитических функций, т. е. их действительные
и мнимые части, и выяснять соотношения между ними так же, как в пре-
предыдущих пунктах это делалось с самими аналитическими функциями.
Опять-таки, в силу особой природы аналитических функций, поведение
этих компонент на одном участке комплексной плоскости оказывается
жестко связанным с поведением их на других участках. Кроме того, дей-
действительная и мнимая части тесно связаны между собой. В частности,
мы увидим, что, зная достаточно хорошо действительную или мнимую
часть аналитической функции, можно вычислить вторую компоненту.
Эта связь между действительной и мнимой частями аналитической
функции представляет значительный физический интерес. Например, в
электростатике ей соответствует связь между электростатическим потен-
потенциалом и полным зарядом, в теории колебаний — связь между действи-
действительной и мнимой частями импеданса, т. е. между активной и реактивной
составляющими. В последнем случае комплексное переменное представляет
комплексную частоту.
Некоторые простейшие съедения об аналитических функциях мы
смогли получить, воспользовавшись представлением аналитической функ-
функции посредством интеграла Коти. Такое представление возможно в лю-
любой области, лежащей внутри замкнутого контура, и, как мы видели,
оно связывает значения аналитической функции / внутри области с ее
значениями на границе. Простое выражение действительной части функ-
функции / (обозначаемой Re/) внутри области через значения Re/ на контуре
легко установить для случая круга. Ниже мы увидим, что с помощью
конформного преобразования внутренность любой области можно отобра-
отобразить на внутренность круга; поэтому и в случае произвольной области
можно, по крайней мере в принципе, установить связь между значениями
Re / внутри контура и ее значениями на самом контуре, хотя очень часто
это бывает нелегко осуществить практически. Однако в силу возможности
такого отображения установленные ниже теоремы с качественной стороны
справедливы для любой области. Всюду в последующем рассуждении бу-
будет предполагаться, что функция /(г) аналитична внутри рассматривае-
рассматриваемой области.
Многого удается достигнуть, рассматривая окружность бесконечного-
радиуса; для удобства мы предположим, что эта окружность совпа-
совпадает с осью х, а внутренняя к ней область —с верхней полуплоскостью.
Наша задача будет состоять в том, чтобы отыскать действительную и
мнимую части функции /=к + ш в верхней полуплоскости, считая и за-
заданной на оси х. Решение может быть подсказано соответствующей эле-
электростатической задачей, когда требуется по заданным значениям потен-
потенциала на оси у = 0 восстановить потенциал в верхней полуплоскости.
Такого рода задачи в электростатике решаются методом изображений
(см. гл. 7).
Интеграл Коши эквивалентен представлению решения с помощью
функции источника, причем множитель l/(z — ?) изображает «источник» в-
точке z = Z. — % + щ. Точку С мы поместим в верхней полуплоскости, так
4.2. Аналитические функции 351
что интеграл от f(z)/(z — С) вдоль охватывающего точку Z. замкнутого
контура, состоящего из оси х и полуокружности бесконечного радиуса,
будет равен 2та/(?). В то же время интеграл от f(z)/(z — ?) будет равен
нулю, так как точка ? лежит вне выбранного контура. Следовательно,
Коль скоро / аналитична во всей верхней полуплоскости, интеграл по
бесконечной верхней полуокружности обращается в нуль1), интеграл
D.2.11) сводится к интегралу, взятому вдоль действительной оси, и мы
получаем
= -
(х — «)
D.2.12)
где С = Е + г»). Знаменатель подинтегрального выражения, а также множи-
множитель перед интегралом действительны, поэтому формула D.2.12) справед-
справедлива отдельно для и и v. Например,
s-(;2+v*- <4-2-13>
Таким образом, если потенциал задан при у = 0, т. е. на оси ж, то
при условии, что / аналитична в верхней полуплоскости, формула D.2.13)
дает значения потенциала и во всех точках верхней полуплоскости.
Для того чтобы получить соотношения между и и v, следует повто-
повторить предыдущий вывод, сложив обе функции источника, вместо того
чтобы брать их разность. Мы получим
или
Отделив в последнем равенстве действительную и мнимую части, мы по-
получим искомые соотношения:
со
II- \ If (х—S) v (ж. 0)
— \ ~V >,, 2 dx D.2.1о)
т. J (ж—?J + тг]2 v '
оо
If (х ^) и
= -- \ —(х^
Зная поведение действительной (или мнимой) части функции / на оси х,
мы сможем посредством D.2.13) и формулы для v, аналогичной D.2.13),
а также формул D.2.15) и D.2.16) вычислить как и, так и и в верхней
полуплоскости. Эти формулы дают решение соответствующей задачи
электростатики, когда требуется найти поле в полуплоскости по задан-
заданному на границе распределению зарядов или потенциалу.
J) Это будет верно только при дополнительном условии, что | / (z)/z \ стремится
к нулю при z —> оо. — Прим. перев. '
352 Гл. 4. Функции комплексного переменного
Выражения D.2.13) и D.2.16) позволяют определить поведение и и v
на самой границе, если положить tj = O. Но при этом приходится про-
проявлять осторожность из-за получающихся несобственных (сингулярных)
-интегралов. Проще всего, пожалуй, снова вернуться к интегралу Копш,
который в том случае, когда точка С лежит на контуре, дает нам
[см. формулу D.2.9)]
Когда контуром служит ось х,
со
/(?, 0) = ^<И ^fdc, D.2.17)
—оо
откуда
±lz?? >S *?-?-«**. D.2.18)
Эти соотношения встречаются в теории преобразования Гильберта; функ-
функции и и v являются преобразованиями Гильберта одна для другой. Дальше
в настоящей главе мы подробнее рассмотрим эти трансформации. (Следует
еще раз подчеркнуть, что полученные формулы связывают между собой
действительную и мнимую части функции, аналитической в верхней полу-
полуплоскости.) Иногда удобно переписать формулы D.2.18) в таком виде,
чтобы особенность подинтегральной функции была «сглажена». Заметив,
со
что ?Р V dx/(x— S) = 0,
получим
D.2-19)
0F,0)=—L \ H*,0b-»(s,0)rfa;1)j
—оо
Импеданс. Среди аналитических функций, встречающихся в прило-
приложениях, одной из наиболее важных является полное сопротивление, или
импеданс Z (см. стр. 271 и 309). Электрический импеданс определяется
как отношение напряжения к силе тока в данной точке цепи в предпо-
предположении, что и напряжение и сила тока выражены в виде комплексных
показательных функций времени (V = Voeiuit и т. д.); механический импе-
импеданс есть комплексное отношение силы к скорости; волновой импеданс
колебаний струны был определен на стр. 128 и т. д.
Импеданс представляет собой функцию частоты v (или, иначе, угло-
угловой скорости «в = 27tv) и параметров системы. Когда <в действительна
и положительна (т. е. когда возмущающая сила или напряжение имеет
вид Foeiat), действительная часть функции Z называется активным сопро-
сопротивлением (резистансом) и обозначается R, а мнимая часть называется
х) Может оказаться, что на бесконечности эти интегралы надо понимать в смысле
N
главного значения, т. е. • как lim \ . Так будет, например, для приводимого
N— оо '
-N
ниже интеграла D.2.22), если %,фЫ. —Прим ред.
4. 2. Аналитические функции 353
реактивным сопротивлением (реактансом) и обозначается X. Однако мы
можем представить себе случаи, когда ш имеет комплексные значения
и возмущающая сила содержит вещественный множитель, являющийся показа-
показательной функцией времени, так что Z (а>) = JR (ш) -\- iX (ш) можно рассма-
рассматривать как аналитическую функцию комплексного переменного ш.
В большинстве физически реализуемых случаев Z оказывается анали-
аналитической в верхней полуплоскости ш (т. е. при положительной мнимой
части переменного ш). Природа импеданса такова, что при изменении
знака си (т. е. если возмущающая сила имеет вид Foe~iK>t) активная
составляющая не изменяется, а реактивная изменяет знак
Z(-u>) = Z(ui), Д(-со) = /?(«>), Jf(-ui)= -X(w). D.2.20)
Применяя к этим функциям формулы D.2.19), получаем равенства
со
2 С
=—\
It J
со
(x) — wX (w) , v, . 2ш Г R (х) — R (ю) , „ „ о.,
5-4 ?-LJdx, Х(ш)= \ —Ц w-^dx, D.2.21)
Я'1 О)-* ' V ' It J Ж2 ОJ ' V '
выражающие активную составляющую при действительных ш через реактив-
реактивную при действительных ш, и наоборот. Это показывает, что если Z ведет
себя достаточно хорошо (аналитична в верхней полуплоскости), то актив-
активная и реактивная составляющие импеданса связаны между собой опреде-
определенными соотношениями и их нельзя выбирать произвольно и независимо
друг от друга.
Помимо упомянутых здесь непосредственных приложений, формулы
D.2.19) могут служить для вычисления интегралов с бесконечными преде-
пределами. Это достигается применением формул D.2.19) к функциям, действи-
действительные и мнимые части которых известны. Пусть, например, / (z) = егг.
Тогда и (х, 0) = cos x, v (х, 0) = sin x и
со
,. А С sin а; — sin 6 , ,, о „„.
cos? = — \ .—i dx; D.2.22)
—оо
при 5 = 0 получаем
со
\ sin_^dx D.2.23)
Такого рода применения формул D.2.19) весьма многочисленны. В этой
главе, а также в задачах встречаются и другие примеры.
Формула Пуассона. Аналогичные соотношения могут быть получены в
том случае, когда рассматриваемой областью является круг. При этом точк*е С
мы ставим в соответствие ее изображение а2/?, где а — радиус круга
(при | С | < а точка а2/^ оказывается вне круга). Действуя так же, как при
выводе формул D.2.11) и следующих, напишем
f(z) /(z) 1 dz
где интеграл берется вдоль выбранной окружности. Переходя к полярным
координатам, имеем г — аегч, ? = rei6(r<a) и после некоторых простых
преобразований получаем формулу Пуассона
23 Ф. м. Морс н Г. Фешбах
354 Гл. 4. Функции комплексного переменного
Этот аналог формулы D.2.13) позволяет найти действительную (или мни-
мнимую) часть функции / внутри круга по заданным значениям ее на границе.
Формулы, подобные D.2.14), можно получить, преобразуя интеграл
Из формулы D.2.24) получаем
/(«») = f{P)-™X ."УЛ п, /(ае*)dy. D.2.25)
' v ' ' у ' я J а- + г2 — 2ar cos (ср — 0; ' v ' r v '
О
Приравнивая действительные и мнимые части, имеем
и (г, 6) = в @) + — ^ „"УЦ к о (а, 9) d9
v ' ' w к J a2 + r2 — 2аг cos (tf—о) \ ' т/ т
О
„(г, в) = 0@)—^- ( , 2Siro,
4 ' ' у ' л J а2 + г2—2a/-cos(tf — 6)
D.2.26)
sin(cp— 6) ,
где /=и + ш и значение и при r = 0 кратко обозначено и@).
- И в этом случае обнаруживается соотношение между функциями и и v
на окружности. Мы имеем равенство
JL-df ^ /(aei*)ctg^d?. D.2.27)
Воспользовавшись тем, что $Р \ cK,g~~—dy = O, и приравняв деиствитель-
U
ные и мнимые части обеих частей равенства D.2.27), получаем соотношения
2-ге
и (а, 6) = и @) + — \ [v (а, <р) — о {а, б)] ctg ^- dy,
D-2-28)
v{a, б) = у @)—п— \ [и (о, <р) — и (а,
о
являющиеся аналогами преобразований Гильберта для случая круга.
Различные выведенные здесь формулы еще раз демонстрируют тесную
связь между и и v, которую в дифференциальной форме мы уже видели
в условиях Коши —Римана D.2.1).
4.3. Производные аналитических функций.
Ряды Тейлора и Лорана
Одно из самых замечательных свойств аналитической функции состоит
в том, что все ее производные также аналитичны, причем в той же области,
где и исходная функция. Для доказательства этой теоремы мы восполь-
воспользуемся интегральным представлением аналитической функции, вычислив
производные путем соответствующего предельного перехода. Возможность
этого обеспечивается тем, что свойства интегрального представления опре-
определяются в основном свойствами функции l/(z — а), аналитичной при з Ф а.
4. 3. Производные аналитических функций. Ряды Тейлора и Лорана 355
Мы имеем
2mf> {а) =2ш lim/(fl + ^
- a — h z-aj J
f {Z
, \, dz.
(z —flJ
Предельный переход под знаком интеграла оправдывается соотношениями
| Д/Z,
>63 F-1 h I) »
где M — наибольшее значение |/(z)| на контуре, L —длина контура, b —
наименьшее значение | z — а | на контуре. При h —> 0 правая часть нера-
неравенства стремится к нулю, а следовательно, стремится к нулю и левая
часть.
Вычисляя таким же способом высшие производные, приходим к важ-
важной общей формуле, выражающей п-ю производную функции / в точке
z = a
В силу того, что -все производные существуют, все оыи оказываются ана-
аналитическими функциями внутри контура С. Заметим, что из этого доказа-
доказательства не следует существование высших производных на самом конту-
контуре С, так как интегральное представление D.2.9) функции /, которым мы
здесь пользуемся, разрывно на С.
Ряд Тейлора. С помощью формулы D.3.1) можно вывести ряд Тейлора
и найти его радиус сходимости. Ряд Тейлора представляет собой разло-
разложение f(a-\-h) в ряд по степеням h. Такой ряд 1) сходится внутри своего
круга сходимости и расходится вне его, 2) имеет аналитическую сумму
внутри круга сходимости и 3) имеет круг сходимости, простирающийся
до ближайшей к а особой точки функции f{z). Доказательство утвержде-
утверждений 1) и 2) читатель найдет в любом учебнике, в котором сколько-нибудь
подробно рассматриваются свойства степенных рядов. Предполагая, что
точка а лежит внутри контура С, а /(z) аналитична внутри и на С, из
формулы Коши получаем
В качестве С возьмем окружность с центром в а, поскольку область схо-
сходимости, получающаяся в результате, представляет собой круг.
В силу тождества
л. h ¦ h2 ¦ А"-* \z-a-h . ft"
"t"z-fl+ (z-flJ + ••• "^(z-o)"-1 ) z-a (z-o)"
мы имеем точное выражение
N
2 ^
23*
356 Гл. 4. Функции комплексного переменного
Подставляя его в интегральное представление f(a-\-h), получаем
§
или, в силу D.3.1),
/ (а + А) = ^ % /<">(«) + Я*. D.3.2)
п=0
Здесь i?w — остаточный член, т. е. разность между f(a-\-h) и суммой пер-
первых N -{-I членов ряда Тейлора. Чтобы найти радиус сходимости, заметим
прежде всего, что ряд наверное сходится в любом круге радиуса г с цент-
центром в а, где г меньше расстояния от а до ближайшей к а особой точки
функции /. Это следует из неравенства
где М — наибольшее значение | /1 на окружности радиуса г с центром в
точке о. Внутри такого круга |/г|<л-, а поэтому RN —» 0 при TV—»со.
Итак, внутри круга радиуса г
со
/(а + Л)=2 ^ГЧа): D.3.3)
полученный сходящийся ряд называется рядом Тейлора. Таким образом,
радиус сходимости не меньше расстояния от а до ближайшей особой точки.
Но он и не превосходит этого расстояния, так как мы не можем ожи-
ожидать от степенного ряда, чтобы он удовлетворительно представлял функ-
функцию в окрестности ее особой точки.
То обстоятельство, что радиус сходимости ряда Тейлора равен рас-
расстоянию до ближайшей особой точки, объясняет некоторые кажущиеся пара-
парадоксы в поведении функций и рядов, возникающие когда последние рас-
рассматриваются только при действительных значениях аргумента. Харак-
Характерным примером служит ряд Тейлора A — z)'1 = 1 -|-z + z2 + ... . Ясно,
что этот ряд «разлетается» при z = 1. Однако он расходится и при z= — 1.
а также при любом z = ebf, т. е. в любой точке единичной окружности
•с центром в начале. Доказанная выше теорема дает объяснение этому
явлению. В качестве другого примера рассмотрим функцию /(ж) = e-1'xS.
Все ее производные в точке х = 0 равны нулю, но если эти данные меха-
механически подставить в формулу Тейлора D.3.3), то получится очевидная
•бессмыслица. Дело здесь в том, что z = 0 — особая точка функции e~1/zS
комплексного переменного z.
Часто очень важно различать ряд, представляющий функцию, и «самое
функцию» (какой бы смысл не вкладывался в это выражение). Степенной
ряд, каковым является ряд Тейлора, как правило, представляет заданную
функцию / лишь в некоторой ограниченной области. За пределами этой
области функция / «существует», но это специальное представление в виде
ряда там непригодно. В примере, приведенном в предыдущем абзаце,
функция / = A—z) «существует» и аналитична всюду, за исключением
точки z= 1, но степенной ряд l-fz+z2+ ¦ • • «существует» (т. е. сходится)
и представляет / только внутри единичного круга с центром в точке z = 0.
11 1
Другой ряд—«- + "т (z~ 3) —-^-(z —3K-l- ... «существует» и представляет
4. 3. Проиэводные аналитических функций. Ряды Тейлора и Лорана 357
ту же функцию / только внутри круга радиуса 2 с центром в точке
z = 3 и т. д.
Степенные ряды (ряды Тейлора, Лорана и другие) подобны как бы
кускам клише, с помощью которого можно снять копию функции. Каж-
Каждый кусок клише воспроизводит / на всем своем протяжении, но не дает
непосредственной информации относительно поведения / за его пределами;
только если все куски клише сложены вместе и пригнаны один к дру-
другому, можно получить полное изображение функции. Такая пригонка от-
отдельных кусков клише с целью описать поведение / целиком называется
аналитическим продолжением; его мы рассмотрим ниже в этой главе.
Если / задана в конечном виде, например как A —z), то этот процесс
может быть интересен, но необходимости в нем нет, так как мы уже
знаем «самое функцию». Мы, так сказать, имеем рецепт, по которому
можем вычислить любое значение / конечным числом шагов (в нашем
примере следует вычесть z из 1 и взять обратную величину полученной
разности); бесконечный ряд, каким обычно является ряд Тейлора, дает
рецепт вычисления посредством бесконечного числа njaroB, и поэтому оно
выполнимо только тогда, когда ряд сходится (если каждый последующий
шаг вносит, так сказать, все меньшую поправку, то на самом деле для
получения удовлетворительной копии бесконечного числа шагов не тре-
требуется).
К сожалению, для большинства функций мы не имеем «конечных» алгеб-
алгебраических рецептов, позволяющих вычислять их значения. Даже пока-
показательная и тригонометрические функции, например, при подсчете тре-
требуют применения бесконечных рядов. При этом обычно дело обстоит так,
что мы не располагаем единым слепком «самой функции», а лишь отдель-
отдельными кусками клише, которые еще должны быть пригнаны друг к другу.
Так именно обстоит дело с большинством функций, изучаемых в этой
книге.
Для представления функций могут служить также интегралы (см.,
в частности, § 4.8 и 5.3); такие «клише» часто способны изобразить функ-
функцию в гораздо более обширных областях, нежели ряды. Например, :щко-
торые интегральные представления справедливы внутри полосы постояв-
ной ширины, пересекающей всю комплексную плоскость и простираю-
простирающейся до бесконечности, тогда как степенной ряд сходится внутри неко-
некоторого круга, т. е. в ограниченной области в случае конечного радиуса.
Однако и интегральные представления справедливы лишь в определенных
участках комплексной плоскости, и это следует иметь в виду во избежа-
избежание ошибок. Выяснение области сходимости интегральных представлений
часто является задачей гораздо более тонкой, чем в случае рядов. Ниже
мы встретимся с интегральным представлением постоянной; соответст-
соответствующий интеграл действительно равен этой постоянной в полуплоскости
Imz<l, а при Imz>l он «разлетается». Если бы нам было известно,
что «сама функция» всюду равна постоянной, то это интегральное пред-
представление показалось бы особенно нелепым представлением постоянной,
но трудность этого примера состоит в том, что задан только интеграл,
а нам приходится доказывать, что «сама функция» есть постоянная.
Ряд Лорана. Если мы хотим разложить функцию / в ряд в окрест-
окрестности ее особой точки а, то для этой цели ряд Тейлора, очевидно, непри-
непригоден. Однако некоторое разложение, справедливое сколь угодно близко к
особой точке а, можно получить. Для этого нужно воспользоваться конту-
контуром С, изображенным на рис. 4.7; этот контур, не охватывающий точку а,
может быть заменен, как показано, двумя окружностями Сх и С2, охваты-
охватывающими точку z = а и имеющими соответственно положительное и отри-
358 Гл. 4. Функции комплексного переменного
цательное направления обхода. Применив интеграл Коши и изменив на-
направление обхода Сg на положительное, мы получим
rfz §
2-ki •? z — a — h Zni у,
1 C2
то есть
D.3.4)
где в формуле для ап при и>0 взят контур Си а при п < 0 —контур С2, тот
и другой с положительным направлением обхода [хотя, так как подин-
тсгральная функция аналитична в области между Сх и С2, интеграл в
D.3.4) можно во всех случаях брать вдоль Сг].
Мы получили ряд Лорана. Рассуждая так же, как в случае ряда Тей-
Тейлора, можно показать, что полученный ряд сходится внутри некоторого
кольца с центром в точке а, внешняя граница которого проходит через
ближайшую к а особую точку функции /(z). Так как мы считаем, что внутри
С2, кроме z = a, нет особых точек, то радиус внутренней окружности С2
можно брать сколь угодно малым. Ряд положительных степеней h схо-
сходится всюду внутри внешней границы кольца, тогда как ряд, образован-
образованный отрицательными степенями h, сходится всюду вне внутренней гра-
границы кольца. Таким образом, пользуясь рядом Лорана, мы расщепляем
f (z) на две функции, одна из которых аналитична внутри внешней окруж-
окружности, а другая — вне внутренней окружности. При помощи интегралов
вдоль окружностей, ограничивающих' кольцо (или вдоль любых других
контуров, в которые в данной конкретной задаче эти контуры могут быть
преобразованы, например вдоль прямых, параллельных действительной
оси), мы разлагаем ряд для / на две части, суммы которых аналитичны
в разных областях комплексной плоскости.
Теперь обратимся к простой физической интерпретации такого разло-
разложения. Выше мы заметили, что функция l/h пропорциональна электро-
электростатическому полю линейного заряда, помещенного в точке h=0. Каков физи-
физический смысл функций 1/Л2, l/hs и т. д.? Так как 1/h2 можно получить
из l/h с помощью дифференцирования, то естественно ожидать, что 1/й2
изображает поле, порожденное линейным диполем (последний реализуется
наложением пары противоположно заряженных прямых). Важна ориента-
ориентация диполя; в настоящем примере он ориентирован вдоль оси х. Для до-
доказательства заметим, что поле, порожденное диполем, можно получить
при помощи наложения полей линейных зарядов, а именно, поместив в
точке h = 0 линейный положительный заряд q, а в точке h = г (г — дейст-
действительное положительное число) — линейный заряд — q и перейдя к пределу
при е—4s-0 так, чтобы произведение qs. оставалось постоянным и равным
моменту диполя р. Соответствующая выкладка
подтверждает нашу догадку. Аналогично l/hs изображает предельное (при
е—>0) поле, созданное положительным зарядом q в точке h = 0 и заря-
дами — -^ q в точках ±s, так что суммарный заряд равен нулю. Это — так
4. 3. Производные аналитических функций. Ряды Тейлора и Лорана
359
называемый квадруполь; его можно получить наложением двух ориенти-
ориентированных вдоль оси х диполей рассмотренного выше типа. Вообще функ-
функция h'n соответствует мулътиполю порядка 2й с суммарным зарядом,
равным нулю.
Рассматривая ту часть ряда Лорана, которая содержит отрицатель-
отрицательные степени h и сходится вне меньшей окружности, приходим к выводу,
что заряды, содержащиеся внутри меньшей окружности, порождают поле,
которое может быть представлено как линейное наложение полей, порож-
порожденных последовательностью мулыпиполей в точке а. Подобную же интер-
интерпретацию допускает ряд, содержащий положительные степени h: поле,
порожденное зарядами, лежащими вне большей окружности, может быть
представлено как линейное наложение полей, порожденных мультиполями,
находящимися в бесконечно удаленной точке. В § 10.3 это заключение
будет распространено на трехмерное пространство.
J* и с. 4.7. Контуры, употребляемые при выводе ряда Лорана
вблизи особенности z = a.
Неудивительно, что разложение в ряд Лорана невозможно тогда, когда
заряды имеются и внутри рассматриваемой области, так как их действие
нельзя свести к действию мультиполей, помещенных в точке h = 0 и на
бесконечности.
Изолированные особые точки. Выводы второй половины последнего
пункта приводят к классификации типов изолированных особых точек,
которые могут встретиться у аналитической функции. Если функция имеет
изолированную особую точку, то эта последняя является центром неко-
некоторого круга, в котором других особых точек нет; таким образом, сущест-
«ует круг с выброшенным центром, внутри которого функция, будучи
аналитической, допускает разложение в ряд Лорана. Из D.3.4) следует,
что если а — особая точка, то некоторые из коэффициентов ап с отрица-
отрицательными номерами п должны быть отличны от нуля. Если неравный нулю
коэффициент с наиболыиим (по абсолютной величине) отрицательным но-
номером есть а_д', то говорят, что в точке а функция имеет полюс поряд-
порядка N. Таким образом, полюсы тесно связаны с мультиполями: полюс
JV-ro порядка соответствует мультиполю порядка 2N~l.
Если ряд отрицательных степеней в лорановском разложении функ-
функции f бесконечен, то z= а называется сугцественно особой точкой этой
функции. Известным примером служит функция e"z, имеющая существенно
со
особую точку 2=0; соответствующий ряд Лорана имеет вид 2 1/ (n\zn).
Если z = а — существенно особая точка для /(z), то она одновременно
360 Гл. 4. Функции комплексного переменного
является существенно особой точкой функции l//(z). Действительно, если бы
точка z = a не была существенно особой для 1//, то она, самое большее,
оо
была бы ее полюсом, скажем, порядка N, и тогда мы имели бы 1//= ]?] bnh".
со
Но при этом f=hN/ 2 bm-nh™, и так как функция 1/ ^] bm-Nhm анали-
т=0
тична внутри Сг, то разложение / в ряд по степеням h начиналось бы
с hN, что противоречит предположению. Иначе ведет себя l//(z) вблизи
полюса функции f(z): легко видеть, что полюс iV-ro порядка функции /(z)
будет нулем того же порядка функции l//(z).
На примере функции el>z можно подметить еще одну важную черту
в поведении функции вблизи существенно особой точки. Рассмотрим зна-
значения этой функции, когда z по различным путям приближается к началу.
Например, если z стремится к нулю, принимая положительные действитель-
действительные значения, то е1/* стремится к бесконечности, но если z принимает
только отрицательные действительные значения, то e1<z при z—>0 стре-
стремится к нулю. Если же z приближается к нулю, оставаясь на мнимой
оси, то модуль рассматриваемой функции остается равным единице. Можно
доказать (теорема Пикара), что в любой окрестности существенно особой
точки функция принимает любое конечное значение, за исключением,
быть может, одного. Так, например, функция е1'* нигде не обращает-
обращается в нуль.
Мы видим, таким образом, что поведение функции вблизи существенно
особой точки в высшей степени сложно. Существенно особыми точками
обладают многие функции, встречающиеся в математических вопросах
теории поля. Поэтому в каждом конкретном случае поведение этих функ-
функций вблизи таких точек должно быть тщательно исследовано.
Разложение в ряд Лорана применимо только вблизи изолированных
особых точек однозначных аналитических функций. Но существуют осо-
особые точки, не являющиеся ни полюсами, ни существенно особыми. На-
Например, функции ]/z и In z не разлагаются в ряды Лорана вблизи точки
z = 0. Обе они неоднозначны в окрестности точки z = 0; если же мы попы-
попытаемся выделить однозначную аналитическую ветвь функции ]/z или lnz,
то она непременно окажется разрывной вдоль некоторой линии (хотя бы
вдоль отрицательной действительной полуоси), а поэтому z = 0 не
является для этих ветвей изолированной особой точкой. Такие особые
точки (называемые точками ветвления) будут рассмотрены ниже в § 4.4.
посвященном многозначным функциям.
Классификация функций; теорема Лиувилля. Функции с изолиро-
изолированными особыми точками мы можем теперь классифицировать по распо-
расположению и характеру их особых точек. Основную роль при этом будет
играть теорема Лиувилля, которая гласит, что функция, аналитическая
при всех конечных значениях z и ограниченная во всей плоскости, есть
постоянная. Доказательство следует сразу из оценки для производной,
получаемой в свою очередь из формулы
(z—aJ
В качестве контура возьмем окружность радиуса R с центром в точке
z — a, и пусть, согласно предположению, |/(z)|<M. Тогда
4. 3. Производные аналитических функций. Ряды Тейлора и Лорана 361
Положив теперь R—>оо, мы получим, что /'(а) = 0, т.е. что функция
/(а) постоянна. Из этой теоремы следует, что малейшее отклонение ана-
аналитической функции /(z) от постоянной на каком-либо участке комплекс-
комплексной плоскости неизбежно вызывает появление особой точки где-то в дру-
другом месте1). Таким образом, если функция гладко ведет себя недействи-
недействительной оси и не постоянна, то она имеет особую точку вне действитель-
действительной оси. Мы вновь замечаем тесную взаимосвязь между значениями ана-
аналитической функции на всей комплексной плоскости.
Подобным же приемом можно получить обобщение теоремы Лиувилля:
если функция f(z) аналитична при всех конечных значениях z и \f\ возра-
возрастает не быстрее \z\h, когда z—> оо (здесь к —целое число), то /(z) пред-
представляет собой многочлен степени <; /с. Б самом деле,
а значит, если |/(z)| c^A\z\h (z—>co), то
где А = постоянная. Когда R—>оо, правые части этих неравенств при
ге > к стремятся к нулю. Следовательно,
/(«) (а) = 0 при п> к,
и теорема доказана. (Если А Ф 0, то степень многочлена точно равна к.)
Многочлен степени к > 0 имеет особую точку на бесконечности 2).
Функции, аналитические в любой конечной области плоскости z, назы-
называются целыми. Например, многочлены являются целыми функциями.
К тому же классу принадлежат и другие фувкции, важные для прило-
приложений, как-то ez, cosz, бесселева функция Jn{z) порядка п и др. Ниже
мы увидим, что аналитичность этих функций в конечных областях ком-
комплексной плоскости и наличие у них существенно особой точки на бес-
бесконечности находят свое отражение в геометрических свойствах систем
координат, связанных с этими функциями (так, например, цилиндриче-
цилиндрическая система координат связана с бесселевыми функциями).
Мероморфные функции. Мы рассмотрели функции, всюду аналити-
аналитические (они постоянны), и функции, аналитические всюду, кроме беско-
бесконечно удаленной точки (многочлены относительно z, ez и др.). Следую-
Следующий по сложности класс образуют функции, все особые точки которых
(включая бесконечно удаленную, если она особая) являются полюсами.
Можно показать, что любая такая функция является рациональной, т. е.
представляет собой отношение двух многочленов.
Для доказательства заметим прежде всего, что каждая такая функ-
функция может иметь лишь конечное число полюсов. Действительно, если бы
полюсов было бесконечно много, то существовала бы неизолированная
особая точка (точка накопления полюсов), конечная или бесконечно уда-
удаленная, которая, следовательно, не была бы полюсом, что противоречит
предположению. Итак, допустим, что /(z) имеет TV полюсов, причем п-п
полюс находится в точке ап и порядок его равен in. Тогда функция
х) Быть может, на бесконечности.—Прим. ред.
2) Поведевие функции на бесконечности исследуетсн путем подстановки z=l/'C
с последующим рассмотрением результата при С ->¦ 0. При этом, например, zk пре-
преобразуется в функцию (l/?)ft, для которой ? = 0 служит полюсом порядка к.
362 Гл. 4. Функции комплексного переменного
аналитична всюду, кроме, быть может, бесконечно удаленной точки.
Независимо от того, является ли точка z=oo полюсом функции /(z) или
нет, |G(z)| при z—> оо растет не быстрее, чем |z|fe, где Л —некоторое
целое положительное число, и, согласно нашей предыдущей теореме, G(z)
есть многочлен. Следовательно, /(z) представляет собой отношение двух
многочленов G и JJ (z — an)ln, и теорема доказана.
п
К тому же выводу приводит рассмотрение электростатической ана-
аналогии: поле, порожденное каждым отдельным полюсом, может быть выра-
выражено в виде суммы конечного числа функций вида A(z — «n)~ft- (Полюс
в бесконечно удаленной точке создает поле, изображаемое многочленом
от z.) Сложив все такие выражения, мы получим рациональную функцию.
Теперь мы можем обобщить понятие рациональной функции. Допу-
Допустим, что все особые точки некоторой функции в заданной области ком-
комплексной плоскости являются полюсами. Такую функцию мы назовем
мероморфной в этой области. Функцию, мероморфную во всей плоскости,
за исключением бесконечно удаленной точки, можно разложить на эле-
элементарные дроби точно так же, как рациональную функцию. Различие
состоит в том, что, поскольку особых точек теперь может быть беско-
бесконечно много, мы получаем, вообще говоря, бесконечный ряд элементар-
элементарных дробей. Выведем это разложение для того случая, когда все по-
полюсы—первого порядка.
Пусть / (z) — заданная функция, ап — ее полюсы, занумерованные в по-
порядке возрастания их расстояний от начала, и предположим, что /(z) ана-
лытична при z = 0. Пусть / (z) ~ bnj{z — ап) при z —> ап. Рассмотрим
какую-либо окружность Ср радиуса Др, внутри которой находятся р полю-
полюсов (предполагаем, что на самой окружности полюсов нет). Тогда функция
аналитична внутри Ср. Взяв Ср в качестве контура интегрирования,
получим
Сумма в последнем выражении, как легко видеть, равна нулю и,
следовательно,
Возьмем теперь последовательность окружностей Ср с радиусами
Нр —> оо.. Ей будет соответствовать последовательность функций gp,
каждая из которых аналитична во все большей и большей области ком-
комплексной плоскости. Остается показать, что предел последовательности
функций gp представляет собой ограниченную 'функцию, и применить к ней
теорему Лиувилля 1). Легко видеть что
где М — наибольшее значение | /1 на Ср и R = | z |.
х) Ни существование предела последовательности gv, ни то, что этот предел
представляет собой аналитическую функцию, в приведенном здесь доказательстве
не установлено. — Прим. перее.
4.3. Производные аналитических функций. Ряды Тейлора и Лорана 3E3
Может случиться, что Мр остается ограниченным при возрастании р.
При этом lim | gp (z) | ограничен, и, согласно теореме Лиувилля, функция
g = limgp есть постоянная. Итак, в этом случае
оо
¦г- *•
/ (z) = постоянная +
¦*-> z~ ап
гг=1
Для того чтобы отыскать эту постоянную, положим z = 0; мы вправо
это сделать, поскольку в точке z = 0 функция / (г) аналитична. Тогда
D-3.6)
В том случае, когда / (z) не ограничена. на окружностях Ср при
р—>оо, иногда можно все же получить аналогичное выражение. Так,
например, часто удается подобрать такую степень z, скажем zn, что отно-
отношение f(z)/zn ограничено на рассматриваемых окружностях при р—> со;
при этом / (z) выражается в виде произведения ряда D.3.6) на zn.
Как уже указывалось, разложение D.3.6) имеет простой электростатиче-
электростатический смысл. Оно является также распространенной формой представления
адмитанса динамической системы (см. стр. 287). В качестве таковой оно
показывает, как система, имеющая много нормальных видов движения
(например, струна), реагирует на воздействие возмущающей силы. Знаме-
Знаменатели z— ап в D.3.6) соответствуют встречающимся резонансным зна-
знаменателям, постоянные Ъп — влиянию пространственного распределения
возмущающей силы на п-с нормальное колебание. В гл. 11 мы увидим при-
приложение этих фактов к исследованию движения полей.
Рассмотрим пример применения формулы D.3.6) к разложению функ-
функции в ряд частичных дробей. Возьмем функцию / (z) = tg z. Полюсами ее
служат точки ап = тсBп-{-1)/2. Из соотношений
(z -* ап)
зиы обнаруживаем, что Ьп= — 1. Выберем последовательность окружностей
с радиусами рк (/> —целое). На таких окружностях tgz ограничен для
«сох значений р и, согласно доказанной теореме,
СО
tgz= — 2j (^s —Bre+l)t/2 "+ B;г+1)х/2У =
— CO
3- у ( i .
Zj V z — Bn + l)n/2 "•
оо
у (
о
:2 [Bn+lW
«=0
364 Гл. 4. Функции комплексного переменного
Так как логарифмическая производная f (z)/f (z) целой функции f (z)
есть функция мероморфная, то с помощью формулы D.3.6) можно пред-
представить целую функцию /(z) в виде бесконечного произведения. В самом
деле, в конечной части плоскости особыми точками, а именно полюсами
функции /'(z)//(z) являются только нули ап функции /(z). Снова пред-
предположим для простоты, что все эти полюсы простые, т. е. что
/(z) ~ const • (z — an); при этом
откуда
71=1
/ (z) = / @) е«/'<о)//со) JJ Г 1 _ ±Л ei/«w. D.3.8)
71=1
Для того чтобы эта формула была применима, требуется, чтобы /(z) была
целой функцией, чтобы ее логарифмическая производная имела простые
полюсы, отличные от 0, чтобы эта производная была ограничена на
некоторой последовательности окружностей Ср и т. д.
Разложим в бесконечное произведение функцию sinz; этим разложе-
разложением мы часто будем пользоваться в дальнейшем. Так как sinz не удо-
удовлетворяет одному из требуемых условий, а именно обращается в нуль
в 'точке z = 0, то мы рассмотрим функцию sin z/z. Последняя имеет лога-
логарифмическую производную (z ctg z — l)/z, удовлетворяющую всем необходимым
требованиям. Итак, ап = тми, где тг Ф 0, и
sin z
= Ill A ) С"'"" =
«=1
«п О -?)ez/rra - п [ * - Ш] • D-3-9)
О 1
Подобные разложения можно получить и для других тригонометрических
функций, а также для бесселевых функций /n(z).
Поведение степенного ряда на границе круга сходимости. В мно-
многих задачах нерационально (или невозможно) получать в замкнутом виде
решение, являющееся аналитической функцией, и приходится доволь-
довольствоваться представлением этого решения в виде степенного ряда. Послед-
Последний имеет обычно конечный радиус сходимости, который можно найти,
если известно выражение коэффициента общего члена или по каким-либо
иным данным. Конечно, степенной ряд не полностью эквивалентен реше-
решению; внутри своего круга сходимости этот ряд совпадает с искомым реше-
решением, но вне этого круга понадобится новый ряд, сходящийся в некото-
некоторой другой области, и т. д. Как уже говорилось выше, дело обстоит так,
как будто искомое решение приходится изображать с помощью клише,
состоящего из разрозненных кусков, причем кусками являются как раз
ряды, изображающие решение на отдельных участках плоскости и ничего
не изображающие за пределами этих участков. А для того, чтобы отдель-
отдельные куски клише могли быть хорошо пригнаны один к другому, мы
4. 3. Производные аналитических функций. Ряды Тейлора и Лорана 365
должны выяснить соотношение между решением и изображающим его сте-
степенным рядом на границе круга сходимости последнего.
Заранее очевидно, что исследование поведения степенного ряда на
границе круга сходимости представляет собой чрезвычайно деликатную
задачу, требующую для своего решения привлечения весьма тонких
свойств аналитических функций. К счастью, формулировки соответствую-
соответствующих теорем достаточно понятны, и в этой книге нам нужны окончатель-
окончательные результаты, а не математические детали доказательств.
Поэтому мы опустим здесь большинство выводов и сосредоточим свое вни-
внимание на выяснении содержания указанных теорем. Доказательства чита-
читатель найдет в учебниках, перечисленных в конце главы.
Итак, предположим, что решение некоторой задачи представлено
степенным рядом вида
со
/=2 а?п- D.3.10)
71=0
Прежде всего нужно отыскать радиус сходимости R этого ряда. Если
коэффициент ап общего члена известен, то, как вытекает из признака
сходимости Даламбера,
D.3.11)
ап
(если только этот предел, конечный или бесконечный, существует). Пред-
Предположим, что радиус сходимости конечен. Тогда, произведя изменение
масштаба С = zR, мы получим новый ряд
/B)=IV (Ь« = «пЯп), D.3.12)-
имеющий радиус сходимости, равный единице. Такая нормировка рас-
рассматриваемого ряда оказывается полезной.
Делать заключения о поведении /(z) в заданной точке z единичной
окружности, основываясь на поведении коэффициентов Ъп при больших п,
можно* лишь с большой остррожностью. Так, если ряд D.3.12) сходится
или расходится в некоторой точке z = е1*, то отсюда не следует, что в этой
точке /(z) аналитична или неаналитична. Например, ряд ^.( — z)n, пред-
представляющий при |z|<l функцию 1/A +z), расходится в точке z = l,
хотя в этой точке 1/A -\-z) аналитична. С другой стороны, точка z=l —
особая для функции
(хотя эта функция конечна при z= 1), но соответствующий ряд 2 гп+1/7г(тг+1)
и точке z=l сходится. Существуют ряды, у которых Ьп —> 0, расходя-
расходящиеся во всех точках единичной окружности, и такие, которые сходятся
в точке z=l, а в остальных точках единичной окружности расходятся.
Предостерегши таким образом читателя от поспешных заключений, по-
посмотрим, что можно сказать об аналитических функциях и соответст-
соответствующих рядах на границе кругов сходимости этих последних.
Сначала мы рассмотрим признаки, по которым можно судить, является
ли заданная на границе круга сходимости точка особой или нет. Произ-
Произведем преобразование поворота так, чтобы рассматриваемая точка заляла
положение z = l. Для решения поставленного вопроса полезны следующие
дле теоремы. Первая утверждает, что если ряды f{z)=^bnzn и g(z) =
366 Гл. 4. Функции комплексного переменного
z" имеют радиусы сходимости, равные 1, и если Rein>0, то
z= 1 является особой точкой функции /(z). Другими словами, если аргумент
точки z на границе круга сходимости таков, что в этой точке все члены
ряда имеют неотрицательные действительные части, то такая точка особая
для /(z).
Так, применяя эту теорему к упомянутой выше функции /= 2 zn+1/n(n-t-1),
обнаруживаем, что z = l является особой точкой функции /, несмотря
на то, что ряд, изображающий эту функцию, сходится при z==l. В точке
z=l естественно ожидать осложнений, так как все коэффициенты
положительны и ряд, изображающий производную функции /, рас-
расходится.
Заметим, что если, согласно указанному признаку, z = 1 является
особой точкой, то точки z = е"Р, где <р мало, но отлично от нуля, могут
не быть особыми; действительно, положив z = Zelf, найдем, что /(z) = 2 BnZn,
где Вп = ine*w, и действительная часть коэффициента Вп получит мно-
множитель cos щ.
Более сильный признак дается следующей теоремой: Если Сп =
п
— п!
—т-.—:—тгЬт, то для того, чтобы точка z = l была особой для
т\ (п—ту. т '
функции ^E.bnzn, необходимо и достаточно, чтобы при /г-^со величина
\Cn\~iln не становилась меньше 1/21). Например, для ряда 2(~"z)n> ГДе
bn = ( — l)n, точка z = l не является особой. Для ряда 2z", c Другой
стороны, Сп = 2" и lim | 2n\~i/n = 1/2, так что s=l— особая точка. Более
драматичен пример/= 2! (п + 1) (я-|-2)( — z)n [этот ряд изображает функ-
функцию 2/A + zK], в котором Ъп = ( — l)"(n+ l)(nJ-2) и, следовательно, ряд
заведомо расходится при z=l, но Сп = 0 для номеров п > 2, так что /
аналитична в точке z=l.
Найдя радиус сходимости и выяснив расположение особых точек
на границе круга сходимости, полезно было бы получить общее представ-
представление о поведении /(z) на всей границе, в частности на ее части, запол-
заполненной особыми точками. Здесь полезна следующая теорема: Если /(z) =
= H*nznBg(z)=2C/, где Бе6„>0, ЯеСп>0, Im6n>0, 1тСп>0,
и если bnc^DCn при п—> оо (D — постоянная), то f(z)c^Dg(z) при
|z|-*l.
Следует заметить, что условие Бс Ъп > 0, Re С.п > 0 можно немного
ослабить, потребовав, чтобы Re bn и ReCn при достаточно больших п не
меняли знака; то же относится и к \mbn, 1тСп.
Попросту говоря, эта теорема утверждает, что если п-е члены степен-
степенных рядов, изображающих функции / и g, одинаково ведут себя при
больших п, то обе функции имеют одни и те же особые точки. С помощью
этой теоремы удается получить некоторые сведения об асимптотическом
поведении коэффициента Ъп. Например, мы можем утверждать, что если
bncaDnv'll{p— 1)! (п—>оо), то f(z)~D/(l-z)v при|г|—>1. Для доказа-
доказательства2) достаточно установить, что коэффициент Сп разложения.
2 Cnz" = (l — z)~p асимптотически совпадает с nv~~1l(p— 1)!. Но последнее
*) Точная формулировка этого условия такова: г = 1 является особой точкой
тогда, и только тогда, когда нижний предел последовательности { | Gn \ '"} равен
1/2.—Прим. перев.
2) Наше доказательство относится лишь к случаю целого р > 0. Его можно
обобщить и па нецелые р, заменив факториалы соответствующими значениями
гамма-функции (последняя рассматривается ниже в этой главе).
4. 3. Производные аналитических функций. Ряды Тейлора и Лорана 367
утверждение вытекает из равенства
A - z) -2а
В качестве второго примера рассмотрим гипергеометрическую функ-
функцию. Эта функция, которую мы подробно изучим в гл. 5, определяется
формулой
„, ,,,. . , аЪ , а (а 4-1) Ъ (Ь+ 1) г2
F(a,b\c\z)=l + — z + ;\ V"
Известно, что точка z = 1 является для нее особой. Общий член ряда
имеет коэффициент
п
Взяв целые а, Ь, с и предполагая, что а + Ь>с^>6>0, получим
, _ (с—1)? (а + гс— 1)!(Ь + га- 1)! _
° п— 1)! ~~
(с—1)! (ra+l).-.(fl+w-l) ^ (с—1I а+ь_с ,
__1)! (а—1I (Ь + п)...(с+ га—1)— (Ь—1)!(а —1)!
откуда можно заключить, что при с<а+Ь
(с — i)i (а + Ь — с — 1)!
F{a,b\c\z) (Ь1} (е1) (Т^
Выше мы привели пример ряда / = 2 zn+1M(n + 1), сходящегося в точке
z=l, которая является особой для /, хотя / при z=l конечна. Спраши-
Спрашивается, равна ли сумма ряда s = ^l/n(n + l) значению / в точке z = l?
Ответ на этот вопрос дает следующая теорема, принадлежащая Литтль-
вуду: Если f(z)—>s, когда z—>1 вдоль некоторой гладкой кривой, и числа
и|оп| ограничены, то 2 ап сходится к s. В нашем примере
в этом можно убедиться, непосредственно рассмотрев сам ряд.
Из приведенных здесь теорем ясно, что, зная разложение функции
в степенной ряд, можно получить довольно полное представление о цоис-
дении функции на границе круга сходимости представляющего ее ряда.
Можно ли использовать этот ряд для выяснения поведения функции вне
круга сходимости? Этому вопросу посвящен следующий пункт; ответ
при некоторых достаточно слабых ограничениях оказывается утверди-
утвердительным.
Аналитическое продолжение. Часто случается, что некоторая функ-
функция появляется в таком представлении, которое имеет смысл лишь
в ограниченных участках комплексной плоскости. Так, например, мы уже
не раз подчеркивали, что степенной ряд с конечным радиусом сходимости
непосредственно не дает сведений о поведении изображаемой им функции
вне круга сходимости. Часто встречается другой случай, когда функция
представляется интегралом, сходящимся не при всех значениях ее аргу-
368
Гл. 4. Функции комплексного переменного
мента. Например, интеграл
e~zt dt
представляет функцию 1/z лишь при Rez>0. Однако иногда удается,
сравнив ряд или интеграл с каким-либо другим представлением функции,
определить функцию за пределами той области, в которой действует
первоначально заданное представление. Так, например, исходя из ряда
/ (z) = 1 + z + z2 + ..., сходящегося при | z | < 1, можно найти значения
/(z) в круге |z|<l и отождествить / с 1/A —z), причем последнее выра-
выражение определено и при |z| > 1.
Такого рода действия (а также их результат) называются аналити-
аналитическим продолжением функции. Получающаяся в результате последова-
последовательного продолжения функция оказывается (в большинстве случаев)
определенной на всей комплексной плоскости независимо от того, где
она была первоначально определена.. Но бывает и так, что функцию
непозможно продолжить за пределы некоторой конечной области. При
этом граница такой области называется
естественной границей функции, а сама
область — естественной областью сущест-
существования функции.
Предположим, например, что функ-
функция / задана в окрестности точки z— О
степенным рядом, имеющим радиус сходи-
сходимости R, и пусть на границе круга схо-
сходимости имеется только одна особая точ-
точка функции /. Можно следующим образом
распространить эту функцию за пределы
круга радиуса R. Заметим, что в любой
точке z, лежащей внутри круга сходимо-
сходимости (| z | < R), можно вычислить не толь-
только /, но и значения всех ее производных,
так как производные имеют ту же об-
область аналитичности, что и /, и изобра-
изображающие их степенные ряды имеют тот
же радиус сходимости. Вычислив произ-
— z0, составим ряд Тейлора
f^ynpL{z_Zof. D.3.13)
\
\
Осооая точка
"^Г —Ълигкайшая
х особая точка
Рис. 4.8. Аналитическое продол-
продолжение посредством степенных рядов
(сначала ^ anzn; затем
2bn(z—zof и т. д.).
водные в некоторой точке z
Его радиус сходимости Ro равен расстоянию от z0 до ближайшей особой
точки z = zs (которая не обязательно лежит на окружности \z\ = R).
Соответствующий круг сходимости радиуса Ro изображен прерывистой
линией на рис. 4.8. Этот процесс можно продолжить, взяв в качестве
исходной новую точку, например z = zt, не обязательно лежащую в перво-
первоначальном круге, и построив новый ряд, подобный D.3.13). Продолжая
действовать таким образом, мы с помощью последовательности рядов
с перекрывающимися областями сходимости получим значения / во всей
комплексной плоскости, за исключением, разумеется, особых точек.
Это построение заведомо осуществимо, если на границе круга сходи-
сходимости имеется только одна особая точка zs. Если же особые точки
располагаются всюду плотно на окружности или на какой-либо другой
замкнутой кривой, то продолжить функцию за эту кривую невозможно.
Так обстоит дело с функциями, имеющими естественную границу.
4. 3. Производные аналитических функций. Ряды Тейлора и Лорана
369
У читателя естественно возникает вопрос о единственности продолже-
продолжения. В самом деле, если функция продолжена, как только что описано,
из одного участка плоскости в другой вдоль двух различных путей, то
будут ли ее значения и значения ее производных, полученные в конечном
участке, одинаковы в обоих случаях? Читатель спросит далее, получит-
получится ли один и тот же результат, если применять различные приемы ана-
аналитического продолжения? Сейчас мы попытаемся ответить на эти
вопросы.
Основные теоремы. Наиболее полезная теорема, служащая для раз-
разрешения этих вопросов, состоит в том, что если функция аналитична
е некоторой области и равна нулю вдоль какой-либо дуги непрерывной
кривой, лежащей в этой области, то эта
функция тождественно равна нулю в рас-
рассматриваемой области. В самом деле, если
условия этой теоремы выполнены, то в лю-
любой точке рассматриваемой кривой можно
вычислить все производные функции /, и
все они оказываются равными нулю. Все
члены соответствующего ряда Тейлора бу-
будут равны нулю, и в его круге сходимо-
сходимости / будет тождественно равна нулю. Возь-
Возьмем теперь какую-либо дугу внутри круга
сходимости, образуем новый ряд Тейлора и
продолжим это построение, оставаясь все
время внутри области аналитичности. Таким Рис. 4.9. Независимость ана-
образом, наше заключение о том, что / = О, литнческого продолжения от
г ' г ., ' пути. Если пересечение Ds oo-
оказывается верным н любой точке этой ластей Dx и D2 пересекается
области.
с D, то между этими тремя
Эта замечательная теорема еще раз по- областями нет особых точек и
казывает глубокую взаимосвязь между по- Л = /»=/»•
ведением аналитической функции в различ-
различных частях комплексной плоскости. Например, из нее вытекает, что если
две аналитические функции совпадают на какой-нибудь дуге кривой (сколь
угодно малой, но не сводящейся к единственной точке), то они совпа-
совпадают в их общей области аналитичности.
Теперь мы можем доказать основную теорему единственности аналити-
аналитического продолжения. Если функции fx и /2 соответственно в областях
Dx и D2 получены аналитическим продолжением функции /, заданной
первоначально в области D, и если область D3, общая часть областей Dy
и D2, перекрывается с D, то fj_ = f2 в области D3 (см. рис. 4.9). Эта
теорема дает утвердительный ответ на первый из поставленных выше
вопросов, по крайней мере (как это видно из формулировки теоремы) при
некоторых дополнительных ограничениях. Она немедленно вытекает из
предыдущей теоремы, так как функция f1 — /2, будучи аналитической
в области D3 и равной нулю в той ее части, которая заключена в D,
тождественно равна нулю в D3. Таким образом, в точках области, D3 мы
получим одни и те же значения /х и /2, каким бы путем мы ни продол-
продолжали функцию /.
Однако это доказательство существенно основывается на том, что
область D3 перекрывается с областью D. В противном случае теорема
единственности может нарушаться. Иначе говоря, если функция / про-
продолжена из точки z0 в точку zx вдоль двух различных путей и в резуль-
результате в точке zx получены два различных значения функции, то между
обоими путями содержится особая точка функции f(z).
24 Ф. м. Морс и Г. Фешбах
370 Гл. 4. Функции комплексного переменного
Последняя теорема очевидным образом следует из того факта, что
круг сходимости степенного ряда простирается до ближайшей особой
точки функции, изображаемой этим рядом. Если бы между двумя выбран-
выбранными путями не было особых точек функции /(z), то, осуществляя про-
продолжение посредством степенных рядов, мы заполнили бы всю эту область
их кругами сходимости и получили бы перекрытия, требуемые теоремой
единственности. Значения /(zj при том и другом продолжении были бы
равны, что противоречит нашему предположению. Следовательно, в усло-
условиях теоремы где-то между двумя путями, вдоль которых продолжается
функция^ есть особая точка.
Точки ветвления. Заметим, что последняя теорема не утверждает,
что при наличии особой точки между двумя путями продолжения непре-
непременно получатся различные значения функции. Такое расхождение обус-
обусловливается лишь особыми точками определенного типа! Рассмотрению
таких случаев мы посвятим несколько пунктов. Ясно, что, желая учесть
те случаи, когда различные пути продолжения приводят к различным
значениям /(z) в точке zly мы должны как-то обобщить понятие анали-
аналитической функции, чтобы охватить все такие значения. Мы условимся
теперь понимать под аналитической функцией не только функцию в том
виде, как она задана первоначально в некоторой области, но и все ее
аналитические продолжения, независимо от однозначности или неоднознач-
неоднозначности результатов. Если всевозможные аналитические продолжения при-
приводят в любой точке z к одному и тому же значению /(z), то полученная
функция / называется однозначной, в противном случае — многозначной.
В силу предыдущей теоремы многозначные функции имеют особые точки,
обладающие тем свойством, что аналитическое продолжение по различ-
различным путям, охватывающим эти особые точки, приводит к неоднозначным
результатам.
Такие особые точки называются точками ветвления, а различные
совокупности значений, полученных посредством аналитического продол-
продолжения, — ветвями аналитической функции. Более детальное определение
точки ветвления и примеры, поясняющие это понятие, будут даны в сле-
следующем- параграфе, целиком посвященном многозначным функциям. Здесь
достаточно будет сказать, что многозначные функции естественно возни-
возникают при рассмотрении аналитического продолжения и что всевозможные
значения функции в заданной точке могут быть получены посредством
аналитического продолжения вдоль путей, обвивающих точки ветвления
должное число раз.
Приемы аналитического продолжения. Обратимся теперь ко второму
вопросу, относящемуся к единственности: будут ли результаты анали-
аналитического продолжения функции зависеть от того, каким приемом это
продолжение осуществлено? Отрицательный ответ на этот вопрос выте-
вытекает непосредственно из основной теоремы, приведенной на стр. 369.
Любые два метода дадут, разумеется, тождественные значения в исходной
области задания функции. Одинаковые значения, в силу приведенной выше
теоремы, получатся поэтому в любой области, перекрывающейся с исход-
исходной. Повторяя это рассуждение на каждом этапе продолжения, мы докажем
наше утверждение.
Эти три теоремы единственности являются основными в теории ана-
аналитического продолжения. Однако с точки зрения приложений наиболее
важной была бы теорема, позволяющая решить, является ли функция /2
аналитическим продолжением функции /г Использовать мы будем обычно
не метод степенных рядов, но любой метод, естественный для той или иной
4. 3. Производные аналитических функций. Рж)ы Тейлора и Лорана
371
конкретной задачи. Любой прием опирается на следующую теорему:
Если fx и /2 — аналитические функции соответственно в областях Dx и D2
и если они совпадают на общей части этих областей, то функции Д и /2
представляют собой аналитические продолжения одна другой.
Справедливость этой теоремы обусловлена тем, что в силу анали-
аналитичности /j и /2 аналитическое продолжение с общей части областей
Dy и D2 на их неперекрывающиеся участки можно осуществить, начат*
с одного и того же степенного ряда. Фактически области D± и ZJ, ° кото-
которых идет речь в теореме, могут пересекаться лишь по некоторой линии,
служащей их общей границей. Покажем, что если /х аполитична в Dlr
Рис. 4.10. Продолжение контурного
интеграла, охватывающего точку
17.
V и с. 4.11. Аналитическое продолже-
продолжение посредством отражения относи-
относительно действительной оси.
а /2 аналитична о D2 и если /х и /2 совпадают и непрерывны на общей
границе С областей Dx и Z>2, то /2 является аналитическим продолже-
продолжением функции /х в область D2, а /х — аналитическим продолжением /.2
в область D±.
Для доказательства мы установим, «щ> функция- /, равная ft в Dt
$ /2 в 1>а,. аналитична во всей области Dt + D2 (см. рис. 4.10), а ив
этого уже будет следовать, что /2 служит продолжением функции Д.
Возьмем какую-либо точку z0 в ХJ. В силу свойств интеграла Коши
C+
Сложив эти равенства, получим
§
Ci+C2
dz,
так как интегралы вдоль L в силу совпадения fx и /2 на L взаимно
уничтожаются. Cx-\-C% представляет собой замкнутый контур. Восполь-
Воспользовавшись приемом, которым были получены формулы D.3.1), можно
вычислить производные функции / в точке z0. Так как эти производные
существуют, функция / аналитична в точке z0. В силу непрерывности
функции /, последняя формула остается справедливой также тогда, когда
z0 находится на L, и теорема доказана.
•Продолжим описание методов аналитического продолжения. Мы озна-
ознакомимся с методами двух типов: методы первого типа основаны на функ-
24*
372 Гл. 4. Функции комплексного переменного
циональных соотношениях, которым подчиняется продолжаемая функция;
методы второго типа —на непосредственных преобразованиях степенных
рядов. Рассмотрим два метода первого типа. Первый из них вытекает
из принципа отражения Шварца и основывается на функциональном соотно
шонии /(z) = /(z). Если функция /(z) аналитична в области D, которую
пересекает действительная ось, и f(z) на действительной оси принимает
действительные значения, то сопряженным значениям z соответствуют
сопряженные значения /(z). Иначе говоря, /(z) = /(z) (см. рис. 4.11). Для
доказательства разложим / (z) в ряд Тейлора в окрестности какой-либо
точки а действительной оси. В силу того, что значения / (z) действи-
действительны на действительной оси, все коэффициенты этого ряда Тейлора
также действительны. Итак, /(z) = 2 «« (z~a)n c действительными ап.
Отсюда / (z) = 2an (z~ a)n = /(z), и теорема доказана. Правда, она дока-
доказана лишь для точек, лежащих внутри круга сходимости выбранного
ряда, но при помощи аналитического продолжения ее можно распростра-
распространить на любые неособые точки, сопряженные каким-либо точкам обла-
области D. Таким образом, образование функции, сопряженной к /, непо-
непосредственно продолжает аналитическую функцию из области, примыка-
примыкающей к действительной оси сверху, в область, лежащую по другую
сторону действительной оси. Этот метод можно обобщить на тот слу-
случай, когда вместо действительной оси берется любая прямая линия.
Но формулировать это обобщение не стоит, так как всегда можно повер-
повернуть упомянутую прямую так, чтобы она совпала с действительной осью,
и после этого применить уже доказанную теорему.
Второй метод основывается на явных функциональных соотношениях,
таких, как теоремы сложения или рекуррентные соотношения. Простым
примером может служить формула сложения / (zx + z2) =/(zx)/(z2), кото-
которой, очевидно, подчиняется показательная функция. Если бы / была
задана лишь в некоторой ограниченной области, то, складывая коорди-
координаты всевозможных точек этой области и применяя указанную формулу
сложения, мы смогли бы определить / вне исходной области. Менее три-
тривиальный пример встречается в теории гамма-функции. Гамма-функция
часто определяется как интеграл
Г (,)=][
D.3.14)
б
который сходится только при Rez>0, так что Г (z) оказывается опре-
определенной лишь в правой полуплоскости. Из D.3.14), интегрируя по частям,
получаем соотношение, связывающее значения Г (z) и F(z-f-l),
zT(z) = T(z+l). D.3.15)
С помощью соотношения D.3.15) функцию Г(г) можно продолжить на полу-
полуплоскость Rez<0. Действительно, Г(г) задана в области х > 0
(см. рис. 4.12); зададим Г(г) посредством равенства D.3.15) в полосе
—1/2 < х < 1/2. Вновь полученная и заданная первоначально аналитиче-
аналитические функции оказываются определенными в перекрывающихся областях,
а следовательно,- первая служит аналитическим продолжением второй
в области, где х < 0.
Теперь рассмотрим методы непосредственного преобразования степен-
степенных рядов. Метод продолжения с помощью степенных рядов, при всей
его важности в теоретическом отношении, практически весьма громоздок,
поэтому прибегать к нему в конкретных задачах следует лишь в крайнем
случае. Если не удается воспользоваться какими-либо функциональными
4. 3. Производные аналитических функций. Ряды Тейлора и Лорана
373
соотношениями, можно обратиться к методу Эйлера. Этот метод состоит
в том, что ряд по степеням z (расходящийся при z = — 1) преобразуется
п ряд по степеням переменной
D.3.16)
При этом, если первоначальный ряд при z = 1 расходился или сходился
медленно, то новый ряд в соответствующей точке ? = 1/2 может оказаться
достаточно быстро сходящимся. Поскольку оба ряда имеют одинаковую
сумму в области их общей сходимости, ряд по степеням С является ана-
аналитическим продолжением ряда по степеням z.
Рис. 4.12. Аналитическое продолжение гамма-функции
с помощью рекуррентного соотношения D.3.15).
Рассмотрим это преобразование, приводящее к степенному ряду отно-
относительно С- Преобразование Эйлера удобнее всего применять к знако-
знакопеременным рядам вида
/(z)=2(-lf«r/\ D.3.17)
Ограничиваясь значениями z, лежащими внутри круга сходимости этого
ряда, умножим обе части равенства на 1 + z; перегруппировав члены
справа, получим
Здесь полезно воспользоваться обозначениями, которые мы будем
снова применять при изучении исчисления конечных разностей. Положим
Повторяя эту операцию, получим
8 (Зап) = 82о п = ап — 2an+1 + ап+2
и, вообще,
D.3.18)
р=0
где ( q j= , q'_ .,— биномиальные коэффициенты, так что (l-j-x)<3 =
374
Гл. 4. Функции комплексного переменного
= V ( q jxp. Воспользовавшись этими обозначениями, можно написать
v
со
/B) = r^; + :S («cn)(-l)»z». D.3.20)
п=0
Применяя к коэффициенту при X, в D.3.20) тот же прием, каким было
получено само это выражение, получаем
я=0
Продолжая это преобразование, приходим к формуле
гЬ D-3-21)
Продемонстрируем силу этого преобразования на каких-нибудь про-
простых примерах. Первым рассмотрим ряд
z2z3+ ) D-3.22)
Этот ряд имеет радиус сходимости, равный 1, и при z, близких к 1,
сходится чрезвычайно медленно. Вычислим коэффициенты d'n)a0:
71
,|
2
3
on
•]
2
1
3
1
4
8 on
1
2
1
6
1
12
1
20
1
3
1
12
1
30
азй„
1
4
1
20
...
Преобразованный ряд имеет вид
[ 44 ] D.3.23)
это равенство нетрудно проверить непосредственно. Ряд в D.3.23) схо-
сходится при |?| < 1, т. е. при (ж2 + г/2)/[A + з;J + г/2] < 1, последнее же
неравенство, коль скоро х > —1/2, выполняется при любом у. Таким
образом, мы получили аналитическое продолжение функции в полупло-
полуплоскость х >' —1/2.
Далее рассмотрим пример, обсуждавшийся выше на стр. 366, в котором
ап = п (п + 1). Из таблицы
п
0
1
2
3
an
0
2
6
12
8an
—2
—4
—6
—8
.on
2
2
2
2
аза„
0
0
0
0
...
4. 3. Производные аналитических функций. Ряды Тейлора и Лорана 375
мы заключаем, что все разности порядков > 2 равны нулю, а поэтому
преобразованный ряд обрывается и
Заметим, что исходный ряд расходился при z = 1. В этом примере пре-
преобразование Эйлера дает выражение /(z) в замкнутой форме, и, следова-
следовательно, /(z) оказывается продолженной на всю комплексную плоскость.
Преобразование Эйлера допускает различные обобщения. Быть может,
наиболее важное из них устанавливает соотношение между функциями
?Й=Ь/ и /(z)=f]CAzn- D-3.24)
п=0 п=0
Функция g считается заданной, и мы попытаемся связать между собой
/ Eg, основываясь на выражении коэффициентов Ъп через производные
функции g (z). Записав / в виде
мы исключим Ьо. Коэффициент Ь, можно исключить, заметив, что
п-\ Тогда
п
1
/ = Cog + (С, - Со) zg' + 2 bn l(Cn - Со) - п (С, - С„)] z".
2
Продолжая эти преобразования, окончательно получаем
V-... . D.3.25)
Полученное преобразование сводится к преобразованию Эйлера D.3.21)
в том случае, когда g = l/(l-+-z). Важное обобщение формулы D.3.21)
ролучается при g = l/(l + z)p. Формула D.3.25) принимает в атом случае
вид
D.3.26)
где
2! ' •••' ^~l+z-
Формулы D.3.25) и D.3.26) применимы во многих важных случаях.
Заметим, что формула D.3.25) представляет / (z) в замкнутой форме
всякий раз, когда ряд в правой части обрывается, а это имеет место,
¦если Сп являются многочленами относительно п. Значительного упроще-
упрощения можно достигнуть также тогда, когда g удовлетворяет какому-либо
дифференциальному уравнению, с помощью которого все ее производные
могут быть выражены через конечное число младших производных. В каче-
¦ ,'..— [т. е. положим о2 =
- (- 1)"/Bп)!, Ь2и+1 = 0] и Сп = п\ Тогда / = 2 (- 1)"§| ^ и' согласно
тг
формуле D.3.25),
/ = — z sin z — z^ cos z,
в чем нетрудно убедиться непосредственно.
376 -Гл. 4. Функции комплексного переменного
Рассмотрим более сложный пример, применив формулу D.3.26) к гипер-
гипергеометрической функции от — z
/ = l__z + _____ 2Г-... . D.3.2/)
Пусть р в формуле D.3.26) равно а. Тогда, положив Со = 1, C1 = fc/c,
С2 = b(b+ 1)/с(с + 1) и т. д., мы получим из D.3.26)
. а(с-Ь). а(а+\)(с-Ь)(с^
Выражение в квадратных скобках есть некоторая другая гипергеометри-
гипергеометрическая функция от z/(l-f-z). Кругом сходимости полученного ряда являет-
является |?|<1, и ему в плоскости z соответствует область х > —1/2. Таким
образом, формула D.3.28) в отличие от D.3.27) позволяет вычислять
значения заданной гипергеометрической функции вне круга \ z | < 1.
Существенное обобщение метода Эйлера принадлежит Барнесу; здесь
сумма заменяется интегралом в комплексной плоскости от функции, по-
полюсы которой подбираются так, чтобы интегральная формула Копш при-
приводила к требуемому ряду. В этом методе используются свойства гамма-
функции, и потому мы отложим его изложение до § 4.6.
4.4. Многозначные функции
Вопросы теории функций комплексного переменного, рассмотренные
до сих пор, почти полностью относились к однозначным функциям, кото-
которые, по определению, заданы при каждом данном z однозначно. Теперь,
переходя к изучению многозначных функций, мы должны заново рассмот-
рассмотреть многие теоремы (прежде всего теорему Коши и интеграл Коши).
Важно отметить, что большинство функций из тех, которые встретятся
нам в этой книге, либо сами многозначны, либо имеют многозначные
обратные функции.
Полезно сначала наметить основные понятия, рассмотрев типичный
пример
/(z) = z»fc. D.4.1>
Положим г=ге*ч и /(z) = _Re'*, тогда
Л_^/., 0 = у<р. D.4.2)
Эта функция многозначна. В самом деле, положение точки z на плос-
плоскости можно задать координатами г, <р и, в то же время, координатами
г, cp-f-2i., и соответственно этому мы получаем два значения функции /(z):
/j-z-r^e'*/2, /2 = /-1/-е'<!Р+2те).'2= — rV-e^,/2. D.4.3)
Причина полученной здесь многозначности лежит в том хорошо известном
факте, что квадратный корень из положительного числа может быть взят
со знаком + или—. Если вместо 1/2 взять показатель V4> то Для любого
2 Ф 0 мы получим четыре различных значения функции:
= е™ (zll*)lt
Если же z возводится в степень тс (или в какую-либо другую иррацио-
иррациональную степень), то получается бесконечное множество значений, отли-
4. 4. Многозначные функции
377
чающихся своими аргументами, причем эти аргументы можно выбрать
как угодно близко к любому наперед заданному числу. Поэтому, имея
дело со степенной функцией / = z", мы обладаем значительной свободой
is выборе arg/ в заданной точке, если он не задан.
Многозначность влечет за собой появление разрывов. Так, например,
в точке z = — г функция z1'2 принимает значения ir11* или — ir1!* в зави-
зависимости от того, представлено ли — г в виде re™ или в виде re~ni. Эти
разрывы могут соответствовать реальной физической картине, когда на
полуоси 9=+^ помещена преграда; математический аппарат в задачах
такого рода всегда использует многозначные функции.
Точки ветвления и линии ветвления. Разрывы, о которых сейчас
шла речь, могут быть легко обнаружены геометрически, если обратиться
к конформному отображению, реализуемому функцией/= z1^. На рис. 4.13
Плоскость г
Плоскость f
Фиг. 4.13. Конформное отображение f—~\fz (указана линия
ветвления этой многозначной функции аОЪ в плоскости z).
окружность, соединяющая точки а и Ъ, отображается в полуокруж-
полуокружность с концами А и В в плоскости переменного /=м + ш. Наличие
разрыва очевидно, так как точки А и В, являющиеся соответственно
образами точек а и 6, не совпадают. Так как радиус окружности в пло-
плоскости z может быть выбран произвольно, то мы видим, что всей плос-
плоскости z ставится в соответствие полуплоскость и > 0 плоскости /. Осталь-
Остальные точки плоскости / появятся лишь при вторичном обходе окружности
н плоскости z от точки а до точки Ь; иначе говоря, точки /, у которых
и < 0, будут соответствовать тем точкам z, аргументы которых заключёны
между тс и Зтс. Снова мы видим, что каждому z Ф 0 соответствуют два
различных значения /. Но теперь мы замечаем, что эти значения функции
/ могут быть разбиты на два самостоятельных множества, одно из кото-
которых появляется при первом обходе окружности от а до Ь, когда <р, аргу-
аргумент переменного z, изменяется от -х до и, а второе —при втором
обходе, когда <р изменяется от тг до Зт. Третий обход, соответствующий
значениям Зтс < <р < 5тг, приводит к тем же значениям /, какие получились
при — 1С < у < тт. Описанные здесь два независимых множества значений
z1/» называются ветвями этой функции. Линия <р = те, вдоль которой эти
ветви терпят разрыв, называется линией ветвления. На рисунках линии
ветиления мы будем изображать двойной жирной линией.
378
Гл. 4. Функции комплексного переменного
Необходимость такого выделения линий ветвления объясняется тем,
что, пересекая в плоскости z линию ветвления, хотя бы вдоль дуги cd
{см. рис. 4.13), мы переходим с одной ветви функции z1^ на другую.
Образами cd на плоскости / служат дуги CD, причем сплошной линией
изображена та дуга, для которой точка С принадлежит ветви z1^ c поло-
положительной действительной частью. Если взять С на другой ветви, то по-
получится дуга CD, изображенная пунктиром. В обоих случаях, когда z
пересекает линию ветвления, соответствующая точка / переходит с одной
«етви функции на другую.
К тому же выводу можно прийти, опираясь на теоремы об аналити-
аналитическом продолжении. Рассмотрим, например, окружность efg на рис. 4.13.
Если продолжить z1/^ вдоль efg, то мы придем к прежнему значению
этой функции, поскольку при этом особая точка функции лежит вне efg
Наглядно это проявляется в том, что образом окружности efg будет
замкнутый контур EFG. С другой стороны, если z1'* продолжить вдоль
Плоскость 2
Плоскость f
Фиг. 4,14. Преобразование /=|Лг (в точке г=0 нарушается
конформность).
окружности аЪ, то, как мы видели, мы придем к значению z1'" в точке Ь,
отличному от значения в ее исходной точке а. Из изложенной выше тео-
теории аналитического продолжения следует, что внутри этой окружности
должна находиться особая точка. Таковой является точка z = 0, так как
радиус окружности можно было взять произвольным; в этом можно убе-
убедиться и непосредственным изучением функции zl/2 вблизи z = 0. Такого
рода особая точка называется точкой ветвления (см. стр. 370).
Отметим еще некоторые свойства точек ветвления. Обычно значение
/ (z) в точке ветвления принадлежит одновременно всем ветвям функции
;(z). Чаще всего, хотя и не всегда, только точки ветвления являются
общими для всех ветвей функции. Далее, в точке ветвления отображение,
определяемое функцией /(z), не конформно. Это можно обнаружить на
рис. 4.14, где при отображении функцией z1^ углы между образами ради-
радиусов, выходящих из точки z = 0, вдвое меньше углов между самими ради-
радиусами. Для функции z1/o соответствующие углы уменьшаются в а раз.
Важно, наконец, заметить, что точки ветвления встречаются парами и что
линии ветвления соединяют точки ветвления. Так,, функция z1/2 имеет еще
точку ветвления z=co. В этом можно убедиться, сделав подстановку
z = 1/С; при этом zl'2 = ^-1/2) а функция С'2 имеет точку ветвления Г = 0,
которой соответствует точка z=co.
4. 4. Многозначные функции
379
Линия ветвления, которую мы рассматривали, соединяет точку вет-
иления z = 0 с точкой ветвления z == со вдоль отрицательной действитель-
действительной полуоси. Но линией ветвления могла бы служить с таким же успе-
успехом любая линия, соединяющая точки ветвления 0 и со. Например, в ка-
качестве промежутков изменения аргумента, определяющих первую и вторую
иетви функции z*'2, можно было бы взять соответственно 0 < <р < 2тс и
2тс < <р < 4ie. В плоскости / им соответствовали бы области v > 0 и v < О,
и линией ветвления оказалась бы положительная действительная полуось.
Ветви, выделенные таким образом, совершенно равноценны ранее опреде-
определенным ветвям. Вообще, мы можем выбирать в данной конкретной задаче
линии ветвления так, как нам удобно.
Римановы поверхности. Представление о том, что в случае функции
г1-2 областям —-к < <р <; тт и -ic < <р <1 3-гт плоскости z соответствуют различ-
различные области плоскости /, сопряжено с некоторыми геометрическими не-
неудобствами, так как каждая из областей — тс < <р<тс, тг < <р < Зтс пол-
полностью покрывает плоскость z (за исключением линии ветвления). Для
того чтобы восстановить однозначность и непрерывность и тем самым
Лист 1
Лчст \
A"
Д
1№-
—-/
—f" "/
— /
Линия
ветвления
Лист 2
Линия
ветвления
Лист 2
Лист 1
Лист 1
Линия
ветвления
Лист 2
Линия
ветвления
Фиг. 4.15. Склеивание листов римановых поверхностей
функций f = \Tz и / = yrz^—1 вдоль линий ветвления.
сделать применимыми теоремы, изложенные в предыдущих параграфах,
необходимо приписать самостоятельное геометрическое существование
обеим указанным областям плоскости z. ?Это может быть осуществлено
с помощью понятия римановой поверхности. Представим себе вместо плос-
плоскости z, существующей в одном экземпляре, целый набор плоскостей
(называемых листами), расположенных одна над другой. Каждая из них
ставится в соответствие определенной ветви функции. Таким образом, для
функции z1/2, имеющей две ветви, понадобятся два листа, причем точки
каждого из них будут взаимно однозначно соответствовать точкам опре-
определенной полуплоскости плоскости /. Пусть на листе 1 нанесена область
— тг < <р < л, а на листе 2 — область ir < <р < Зтс. Оба листа должны быть
как-то соединены друг с другом, потому что, как мы .помним, пересекая
линию ветвления, мы переходим с одной ветви функции на другую.
Обратимся к рис. 4.15. Оба листа, 1 и 2, разрезаются вдоль линии
ветвления (поэтому сами линии ветвления часто называются разрезами),
и оба края разреза на листе 1 склеиваются с соответственно противопо-
противоположными краями разреза на листе 2. Рассмотрим изображенный на рис. 4.1о
замкнутый контур AEBCDA. Дуга АЕВ этого контура принадлежит листу
1, но, пересекши разрез на листе 1, мы попадаем на лист 2 в точку С.
380
Гл. 4. Функции комплексного переменного
Дуга CD целиком принадлежит листу 2; двигаясь по этой дуге дальше,
мы пересекаем разрез на листе 2 и снова попадаем через точку А на
лист 1, в точку Е. Ясно, что следует разуметь под замкнутым контуром,
когда рассматривается такая поверхность, склеенная из нескольких лис-
листов: в нашем примере AEBCDA — замкнутый контур, а контур АЕВ — не-
незамкнутый. Теперь возможно применять теорему Копш и интеграл Коши.
Этим мы займемся в следующем параграфе, а сейчас продолжим изучение
поведения многозначных функций.
В качестве более сложного примера рассмотрим функцию
z = -/' /
Пиния ветвления
и=О
1'иг. 4.16. Линия ветвлении функции/ = \rW^
Точками ветвления для нее являются z= + I; z= со не будет точкой вет-
вления, так как, положив z=l/?, получаем / = |^A/С2) — 1 = j/"l— С2/С^
с* 1/? (? —>0), и, значит, беско-
бесконечно удаленная точка являет-
является простым полюсом функции /.
Плоскость г ^*\^^1 Точки z= —1 и z=l соеди-
соединим линией ветвления. Ее мож-
т но направить по отрезку оси
\ х, соединяющему эти точки,
1 V~Q как указано на рис. 4.15, но
х можно было бы в качестве ли-
линии ветвления взять отрезок
оси х, содержащий бесконечно
удаленную точку (состоящий из
точек этой оси от х = — 1 до
х— — со и от х=со до ж= 1);
есть, конечно, и множество других возможностей.
В точках действительной оси, где |ж|>1, значения |/z2 — 1 =
= Ух2 — 1 действительны, поэтому участок | ж | > 1 действительной оси
соответствует точкам Im/ = i/=O. При действительных х, для которых
|ж|< 1, arg/ может быть равен тс/2 или —тс/2. От этой неопределенности
можно избавиться, фиксировав линии ветвления множителей "j/z-j-l к
|/z —1. Тот или иной выбор их определит положение линии ветвления
произведения. Для того чтобы получить линию ветвления, изображенную
на рис. 4.15, мы возьмем для "|/z + l и |/z — 1 линии ветвления, идущие
вдоль оси х соответственно от — 1 до — со и от 1 до — со. Аргумент
произведения / = и -j- iv = (/z2 — 1 будет равен (xt + x_)/2, где -t = arg (z + 1),
a-_ = arg(z — 1) (см. рис. 4.16). Возьмем какую-либо точку, лежащую
между -1 и +1 непосредственно над действительной осью. В такой
точке -+ =0 и х_ =тс, а следовательно, / будет иметь аргумент тс/2. В соот-
соответствующей точке непосредственно под осью х имеем ~+=0, х_=— т.
и arg / = — тс/2. Таким образом, над линией у = 0 (в плоскости z) v > 0, а
под ней v < 0, что еще раз демонстрирует разрыв, имеющийся на линии
ветвления. Теперь обратимся к оси у. На ней, в тех точках, где у > 0,
имеем t+ -t-t_ =тг, ,arg/= тс/2 и, следовательно, к = 0. На отрицательной
полуоси у имеем равенство arg/= —тс/2.
Располагая этими сведениями, мы попытаемся наметить линии
и = const и v = const в плоскости z (см. рис. 4.17). Эти линии должны
быть взаимно-ортогональны всюду, за исключением точек ветвления,
в которых отображение плоскости z на плоскость / не конформно. (Так,
л точках z= + 1 пинии м=0 и v=0 служат продолжениями одна другой.
В точке z = 0 конформность также нарушается, так как в этой точке-
4. 4. Многозначные функции
381
=O.) Для больших z (т. е. при |z|»l) /<=*z, поэтому линии
н =const и v = const должны асимптотически совпадать соответственно
с линиями х = const и у = const. На рис. 4.17 показана линия н=0, со-
состоящая из оси у и отрезка оси х от х= —1 до ж= -|-1.
Между точками z — — 1 и z = О функция v изменяется от 0 до 1 над
осью х и от 0 до — 1 под осью х. Таким образом, линии v = C =/= 0 при
С\ < 1 подходят к оси х между точками х— — 1 и# = 1, образуя с ней
прямые углы. При | С | > 1 линии v = С пересекают ось у под прямым
углом. Сказанное позволяет наметить линии v= const. Линии м = const
можно построить, воспользовавшись свойством ортогональности. Выясним
теперь, где и положительно и где отрицательно. Для этого найдем arg /
и =-1,6 -1,2 -0J8 -Д4
0,8 1,2 1,6
-1.6
Рис. 4.17. Конформное отображение /=>^za—1 (в плоско-
плоскости г, нанесены линии Re / = u = const и Im/ = i>=const).
sia оси х при x <z — 1. В точках z, лежащих непосредственно над осью х,
левее точки ж= — 1, т+ = т_ =гс, и поэтому здесь arg/=is. Подобным же
образом мы обнаружим, что arg/= — ir непосредственно под осью х,
т. е. / имеет по существу тот же аргумент. Отсюда видно, что м<0
и полуплоскости х < 0; легко видеть, что в правой полуплоскости и по-
положительно.
На рис. 4.17 нанесены линии и= const и v = const, соответствующие
первому листу римановой поверхности функции \^z2 — 1 (ср. рис. 4.15).
Линии v = С при С > 0 продолжаются в нижней полуплоскости второго
листа, а при С<0 — в верхней полуплоскости. При переходе с одного
листа на другой области v < 0 и v > 0 меняются местами, а в остальном
рис. 4.17 годился бы и для второго листа. Действительно, на листе 2
~+ или i_ на 2тс отличаются от соответствующего угла на листе 1, и, рас-
рассуждая так же, как на стр. 380, мы обнаружим, что / в точках А ж В на
втором листе имеет аргумент, равный соответственно —тг/2 и тс/2. При
этом надо взять первый лист функции \^z -f-1 и второй лист функции
yz—i или наоборот; если взять в обоих случаях вторые листы, то мы
получим то же, что и в разобранном выше случае, когда для обоих мно-
множителей были взяты первые листы. Отсюда мы видим, что для двух ветвей
функции у z2 — 1 требуются только два листа. Листы 1 и 2 склеиваются
382
Гл. 4. Функции комплексного переменного
таким образом, что нижний край разреза от —1 до 1 на одном листе-
склеивается с верхним краем разреза на другом листе.
Наконец, поучительно указать физические поля, описываемые функ-
функцией |/z2 —1, для того чтобы показать, какой барьер в физической зада-
задаче соответствует разрезу в плоскости z. Так, например, и = const и
v = const могут изображать соответственно эквипотенциальные и силовые
линии однородного электростатического поля, направленного вдоль оси х,
н которое помещен проводник, имеющий форму бесконечной пластины,
сечение которого изображено на рис. 4.18, а. В гидродинамике и = const
могут изображать линии тока, возникающие при обтекании контур»
Рис. 4.18. Расположение граничных поверхностей в за-
задачах, в которых применимо отображение /=y^z2 — 1.
такой же формы потоком жидкости. В то же время и — const являются
силовыми линиями, a v = const — эквипотенциальными линиями поля, соз-
созданного пластинами, изображенными на рис. 4.18, б, если предположить,,
что они заряжены отрицательно относительно отдаленных участков оси.
(М1
Пример. В качестве последнего примера рассмотрим многозначную
функцию / переменного z, определяемую уравнением
-i
D.4.4)-
(см. рис. 4.19). Функция D.4.4) встречается при решении волнового урав-
уравнения (см. гл. 11). Она имеет простые полюсы в точках /= [Bи + 1)/2] та
(ft —целое число). Точками ветвления функции / служат нули производ-
производной от z. В каждой такой точке — обозначим ее а — отображение, опреде-
определенное уравнением D.4.4), не конформно. Объясняется это тем, что (см.
стр. 341) разность z — а имеет нуль порядка > 1 в точке / (а), так что-
/ — / (а) в окрестности точки z = а выражается дробной степенью разности.
z — а. Значения / в точках ветвления отыскиваются из уравнения sech2 /// —
— th///2 = 0, т. е. из уравнения
2/=sh2/. D.4.5>
Решение уравнения D.4.5) и соответствующие значения z = an (помимо-
«0 = 1) приведены в нижеследующей таблице.
Точки
ветвления
а2
«з
о4
/ = и + iv
и
1,3843
1,6761
1,8584
1,9916
V
3,7488
6,9500
10,1193
13,2773
s = reilf
г
0.23955
0,13760
0,09635
0,07407
а
63.00°
72,54°
76,85°
79,36°
и-действительная часть f(z)
Рис. 4.19. Конформное отображение (l//)^th f=z=rel<f.
В плоскости / нанесены линии r=coiist, v=con$t и_отмечеиы
первые три точки ветвления.
384
Гл. 4. Функции комплексного переменного
При больших v точки ветвления ап = u-\-iv (n > 1) асимптотически
выражаются в виде и ~ fin Dп +1) тг]/2, v ~ (n -|- 1/4)тс, в чем можно убе-
убедиться посредством подстановки в уравнение D.4.5). Мы имеем, таким
0.1
О
180
60° 120°
Фазовый угол z
Рис. 4.20. Конформное отображение первого листа римановой по-
поверхности функции f(w), где A//) th f = z = ew (/=7i3eie).
В плоскости w нанесены линии g=const, 6=const; а—одна из точек ветвления.
образом, бесконечное множество точек ветвления и соответственно беско-
бесконечное множество листов римановой поверхности. Следует отметить, впро-
впрочем, одно упрощающее обстоятельство: в любой точке ветвления а функ-
функция / ведет себя как (z aI^, так как z"(/(a))=?0. Поэтому все точки
ветвления имеют такой же характер, как точка z = 0 для функции z1/2,
уже нами исследованной. Поэтому мы сразу можем сказать, что в точке
z = а смыкаются лишь два листа римановой поверхности. Имея в виду эти
подробности, мы можем с помощью рис.. 4.20 и 4.21 наглядно представить
отображение D.4.4). Для удобства изображения плоскости z мы ввели еще
преобразование
Imw — y., Ret?> = lnr D.4.6)
= re*? = ew
4.4 Многозначные функции
385
и аналогично для /:
/ = u + Jt» = wPe?e=eF, lmF=d, Re.F=lnir|3.
8 качестве линии ветвления, выходящей из точки а, мы взяли линию
9 = 63°. Еще раз отметим очевидный разрыв F на этой линии. Разумеется,
линии 6 = const, пересекая линию ветвления <р = 63°, переходят на второй
' 0° 60° 120° ср 180'
Фазовый угол г
1. Конформное отображение второго листа римановой повер
ности функции /(ш), где A//) th/=z=eu) (/=7c?seie).
лист римановой поверхности, изображенный на рис. 4.21. На этом послед-
последнем рисунке, помимо <j> = 63°, изображена также линия ветвления 9 = 72,54°,
вдоль которой склеиваются второй и третий листы римановой поверхности.
Таким образом, любой лист склеивается со следующим, и в одной точке
могут склеиваться лишь два листа римановой поверхности. На рис. 4.19
изображен ряд линий <j» = const и г = const на плоскости /, причем отдельные
участки этой плоскости соответствуют различным ветвям функции. В за-
задачах к этой главе мы еще вернемся к дальнейшим подробностям, связанным
с этими рисунками.
25 ф. м. Морс и Г. Фешбах
386 Гл. 4. Функции комплексного переменного
4.5. Теория вычетов. Гамма-функция и эллиптические
функции
В предыдущих параграфах мы использовали интеграл Коши как сред-
средство обнаружения различных свойств аналитических функций. В этом
параграфе мы займемся более земными вещами. Так, например, формулу
Коши можно применить к вычислению интегралов. С примерами такого
рода мы встретились на стр.353 и 354, но в действительности область
применения интеграла Коши гораздо шире. Им можно пользоваться для
получения интегральных представлений функций, имеющих разрывы, или
таких, производные которых разрывны, а также для суммирования рядов.
Рассмотрим сначала задачу о вычислении интегралов. При этом мы
воспользуемся методами так называемой теории вычетов. Вычет опреде-
определяется следующим образом. Если а — изолированная особая точка функции
f(z), то в окрестности этой точки /(z) разлагается в ряд Лорана
^}an(z — а)п [см. D.3.4)]; коэффициент a_j есть вычет функции /(z) в точке
z — a. Сформулируем теперь основную теорему теории вычетов.
Если функция /(z) аналитична всюду в области, ограниченной кон-
контуром С, за исключением конечного числа особых точек, лежащих внутри
С, то значение интеграла <t/(z)dz, вычисленного вдоль С, равно умножен-
умноженной на 2да сумме вычетов подинтегралъной функции во всех ее особых точ-
точках, лежащих внутри С.
Для доказательства следует применить теорему Коши и проинтегри-
проинтегрировать почленно соответствующие ряды Лорана; мы предоставляем это
читателю. С помощью этой теоремы можно вычислять интегралы следую-
следующих трех типов:
2-п
1. \ /(cos6, sin6)d6, где / — рациональная функция cos 6 и sin6.
6
со
2- \ f(x)dx, где / (z) — функция, аналитическая всюду в верхней по-
—со
луплоскости, за исключением конечного числа особых точек, ни одна
из которых не лежит на действительной оси. Когда z стремится к оэ,
|/(z)| должен стремиться к нулю как |.4z|~m, где т > 1.
со
3. \ ху—1{(х)Aх, где /(z) — рациональная функция, аналитическая в
точке z = 0, имеющая только простые полюсы на положительной дейст-
действительной полуоси и такая, что z^f(z) стремится к нулю, когда z стре-
стремится к нулю или к бесконечности.
В задачах приводятся некоторые обобщения.
Для вычисления интегралов типа 1 следует sin 6 и cos 6 выразить че-
через z = eifl. Интеграл преобразуется при этом в интеграл вдоль единичной
окружности в плоскости z. После этого остается вычислить вычеты под-
интегральной функции относительно полюсов, лежащих внутри единичного
круга. В качестве простого примера рассмотрим интеграл
Пусть z=ei0; тогда
4. 5. Теория вычетов. Гамма-функция и эллиптические функции
387
где контуром интегрирования служит единичная окружность. Дальнейшие
вычисления зависят от величины р. Предположим, что | р | < 1. Тогда точка
z = p является полюсом подинтегральной функции в D.5.2). Соответствую-
Соответствующий вычет равен 1/A — р2)х), так что
/ = -гг=г. |р|<1. D.5.3)
Если | р | > 1, то полюсом является точка z = 1/р. Вблизи этой точки под-
интегральную функцию можно записать в виде — l/[ip(z — l/p)(z — p)],
поэтому соответствующий вычет равен —1/[Ц1 — р2)]. Итак,
В том случае, когда ^ — действительное число, оба результата можно
объединить, записав /= 2л/|/?2 —11.
Обращаясь к интегралам типа 2, проинтегрируем /(z) вдоль замкну-
замкнутого контура, состоящего из отрезка действительной оси от —R до Д
х
Рис. 4.22. Контур, служащий для вычисления
интегралов в пределах от —со до +оо с помощью
теории вычетов.
и полуокружности, лежащей в верхней полуплоскости (см. рис. 4.22).
В силу предположений, высказанных относительно /(z), интеграл вдоль
полуокружности при i?—>со будет стремиться к нулю, и мы получаем
формулу
/ (х) dx = 2та У С вычетов / (z) относительно особых точек,
^ ¦" члежащих в верхней полуплоскости).
f4 5 4)
В качестве простого примера вычислим этим методом интеграл
который, как известно, равен тт. Согласно формуле D.5.4), / = 2ти?х (вы-
(вычет в точке i), так как i — единственный полюс функции 1/A -f z2) =
= l/(z + 0 (z — г) в верхней полуплоскости. Искомый вычет равен l/2i,
а следовательно, / = та. Более сложные примеры приведены в задачах.
*) Если а—полюс первого порядка и / (z) = a_j/(z—а) + ао-\-а1 (z—а) + ... —соот-
—соответствующее разложение Лорана, то f(z)=g(z)/(z—а), где g (z)=a_i +aB (z~a) +
+ at(z—a)z+... . Отсюда следует, что e_lf вычет / (z) относительно z—a, равен
Mm [(*-«)/(«)].
Это—частный случай формулы D.5.6), выражающей вычет функции относительно
полюса п-го порядка.—-Прим. перее.
25*
388
Гл. 4. Функции комплексного переменного
Интегралы от функций, имеющих точки ветвления. Рассмотрим, на-
наконец, интеграл типа 3 от функции, не имеющей полюсов на положитель-
положительной действительной полуоси. Начнем с интеграла
замкнутый контур интегрирования которого не охватывает z = 0, точку
ветвления подинтегральной функции, и поэтому лежит целиком на одном
листе соответствующей римановой поверхности. Выберем контур, изобра-
изображенный на рис. 4.23 и состоящий из маленькой окружности, которая
охватывает z = 0 и радиус которой мы заставим стремиться к нулю, боль-
большой окружности, радиус которой будет в дальнейшем стремиться к бес-
бесконечности, и двух прямолинейных отрезков, направленных в противо-
противоположные стороны и лежащих на
противоположных краях разреза
вдоль оси х. Интегралы вдоль этих
прямолинейных отрезков не будут
взаимно уничтожаться, так как вдоль
разреза подинтегральная функция
разрывна. Аргумент множителя
( - zI1 выбираем так, чтобы (— zI1
х был действителен в точке Е. Тог-
Тогда в точке D, в которую переходит
Е при повороте на угол тс против
часовой стрелки, аргумент этого мно-
множителя равен те (р.— 1), и вдоль DC
подинтегральная функция имеет вид
еи1(и-1) xv—if(x). В точку А точка
Е переходит посредством поворота
Рис. 4.23. Контур, служащий для вычис- на угол тг по часовой стрелке,
ления интегралов функции с точкой вет- поэтому вдоль отрезка АВ под-
вления z=0. интегральная функция имеет вид
g-Ttidi-ij-pii-i дж)_ в силу предполо-
предположений относительно интегралов 3-го типа интегралы по обеим окружностям,
малой и большой, стремятся к нулю; следовательно, интеграл по выделен-
выделенному контуру в пределе, когда радиус внешней окружности бесконечно
велик, а радиус внутренней равен нулю, имеет вид
о
Первое слагаемое справа есть интеграл вдоль CD, второе — интеграл вдоль
АВ.
Объединив оба слагаемых, получим
со
& ( — zf~ f (z) dz = 2i sin щ \ ж11—1/ (х) dx.
Применяя основную теорему теории вычетов к коптурному интегралу
в левой части, получаем равенство
[вычетов функции(-г)^1/ (z)l D 5 5)
|_относительно всех полюсов /J. v '
4. б. Теория вычетов. Гамма-функция и эллиптические функции 389
«о
В качестве простого примера возьмем \ [xv-~l/ (I +x)]dx. Согласно форму-
о
ле D.5.5), значение этого интеграла при 0 < р. < 1 равно тс cosec тер..
Заметим, наконец, что подинтегральная функция может иметь полюсы
второго и более высокого порядка. Предположим, что точка z = a является
полюсом п-то порядка подинтегральной функции /(z), и представим по-
последнюю в виде / (z) = g (z)/(z — а)п, где g (z) — аналитическая функция в
окрестности z—a. Посредством несложного подсчета1) мы получим для
соответствующего вычета выражение
Тот же результат получается, если полюс п-го порядка рассматривается
как предельный случай п простых полюсов, слившихся в одну точку z = a.
Обращение рядов. Часто приходится иметь дело с задачей обращения
функции, заданной степенным рядом
71=1
Требуется найти такую функцию z = z (w), что / (z) — w es 0. Из уравнения
D.5.7) видно, что в силу теоремы, приведенной на стр. 342, эта обратная
функция может быть представлена степенным рядом
bn(w-w0)n. D.5.8)
71=1
Коэффициенты Ъп можно выразить через ап, подставив непосредственно
D.5.8) в D.5.7). Однако их можно вычислить и более изящным способом
при помощи интеграла Коши. Сначала мы возьмем контурный интеграл,
вычет которого равен как раз функции z(w). Таким интегралом является
(l/2iui)q)'[z df/(f — w)], где переменным интеграции служит /(z), а контур
охватывает точку f = w и не охватывает других нулей функции / — w.
Через z этот контурный интеграл выразится в виде
4 ' 2т j /(z)—ш v '
Дифференцируя его по w, а затем интегрируя по частям, получаем
D.5.10)
Последний интеграл можно вычислить. Записав
. со
1 1
71=1
и сравнив правую часть с рядом, полученным дифференцированием D.5.8)
по w, замечаем, что
[/(*)-мь1» '
См. примечание на стр. 387.—Прим. перее.
390 Гл. 4. Функции комплексного переменного
а этот интеграл равен
1 d"-1 / (z — z0)" -\
(n—1)! dz"-1 ^ [/(z) — шо1" Jz=z0'
Таким образом,
n n\
или
bn=^—\4^r( !+~х+ — **'+ ¦¦¦УП] ¦ D.5.11)
Производную, фигурирующую в D.5.11), можно вычислить явно с помощью
формулы
а-де
r+S + ^+ •••=/7.
Пользуясь этой формулой и взяв соответствующие производные, получаем
выражение Ъп в виде
fcn= D.5.12)
1 V/ A\*+t+u+... n(n+l)... (n—Y
где
w+ ... =n— 1.
Вычислим отсюда несколько первых &и:
•.-¦=¦•
3 За? L 21 V ai У 1!
=_1_Г 4-5-6/ aa у 4 °з *_^tl -
4 44 L 3! V % У + 1111 «! ах 1! ах \ ~
«4
Подставляя найденные коэффициенты в D.5.8), получаем искомое обраще-
обращение ряда.
Суммирование рядов. Следующее применение интеграла Коши, заслу-
заслуживающее быть рассмотренным, состоит в суммировании рядов вида
со
2 1(п)- Прежде всего такой ряд заменяется контурным интегралом.
«=—со
Для этого подбирается функция, которая имеет простые полюсы в точках
z=n и ограничена на бесконечности вне действительной оси. Такой функ-
функцией может служить rcctguz; действительно, она имеет полюсы в точках
2=71=0, ± 1, + 2, ... с вычетами 1 и ограничена на бесконечности
4. 5. Теория вычетов. Гамма-функции и эллиптические функции
391
в требуемом смысле. Другой функцией такого типа является тс cosec тк,
имеющая полюсы в точках г=и=0,+ 1,± 2,... с вычетами (— 1)п.
Интеграл (? тс/ (z) ctg tczdz вдоль контура Сг, изображенного на рис. 4.24,
равен умноженному на 2tci вычету функции тс/ (z) ctg tcz относительно точки
z = 0, который в свою очередь равен / @). Соответствующий интеграл
вдоль С2 равен
2ы {/ @) + / A) + / (- 1) + [Res тс/ (z) ctg ткЦ}
и т. д. [Сокращение Res (от французского residue) стоит вместо слова
вычет.] Беря последовательность расширяющихся контуров указанного
вида, получим в пределе
со
2тсг{ 2
Полюсы f(zu
-3
X
^•a2
Полюсы
я ctg (nz)
х
Р?ис. 4.24. Полюсы подинтегральной функции в интеграле,
выражающем ряд 2 / (")•
где вторая сумма берется по всем полюсам1) /(z). Предполагается, что
у /(z) нет точек ветвления.
Если, кроме того, |z/(z)|—>0 при |z|—>oo, то интеграл по бесконеч-
бесконечному контуру обращается в нуль и мы получаем
СО
2 / (п) = — 2 [Res тс/ (z) ctg tcz в полюсах / (z)]. D.5.14)
—ОО
Если вместо та ctg tuz взять Tccosecrcz, то тем же путем приходим к формуле
со
2 (— 1)" / (п) = — 2 [Resтс/ (z) cosec tcz в полюсах / (z)]. D.5.15)
—со
CO
Рассмотрим простой пример: в случае ряда 2 (~ 1)"/(G + пJ имеем функ-
—со
цию /(z) = 1/(а + zJ с полюсом второго порядка в точке z~ —а. Вычет
функции тс/ (z) cosec tcz относительно этой точки равен — тс2 cosec тга ctg тса
Здесь могут быть и изолированные существенно особые точки.—Прим. ред.
392 Гл. 4. Функции комплексного переменного
[см. формулу D.5.6)], и, следовательно,
2 (Smp=^cosec тса ctg т'
Этот метод суммирования рядов может служить иллюстрацией метода
интегрального представления рядов. Последний употребляется в тех слу-
случаях, когда решение дифференциального уравнения, полученное в виде
степенного ряда, нужно представить в виде интеграла (см. § 5.3).
Интегральное представление функций. Иногда бывает полезно пред-
представить функцию в виде некоторого интеграла. Объясняется это тем, что
зачастую очень сложные функции могут быть представлены интегралами
|т к
^ - Re*
Контур С
Рис. 4.25. Контур, по которому берется интеграл,
выражающий единичную ступенчатую функцию и (х).
от сравнительно простых функций. Кроме того, изменяя путь интегрирова-
интегрирования в соответствии с теоремой Коши, можно получить приближенные
выражения для таких интегралов. В главе, посвященной дифференциаль-
дифференциальным уравнениям, мы неоднократно будем прибегать к этому приему.
В качестве первого примера рассмотрим интеграл
e-ikx
-jTdk- D.5.16)
с
Контур интегрирования изображен на рис. 4.25. Эта функция и (х) встре-
встречается в операционном исчислении Хевисайда (см. § 11.1). Ее можно
вычислить с помощью интеграла Коши. При х > 0 мы замыкаем контур
полуокружностью бесконечно большого радиуса, лежащей в нижней полу-
полуплоскости. Интеграл вдоль такой полуокружности обращается в нуль.
Следовательно, и (х) = Res [e'lhx/k] в точке к = 0, т. е. и (х) = 1 при
х > 0. При х < 0 замыкающую полуокружность берем в верхней полу-
полуплоскости, и по такой полуокружности интеграл в пределе обращается
в нуль. Так как внутри такого контура полюсов функции е~гкх/к нет,
то и (х) = О при х < 0. Итак, мы нашли, что
¦«•Hi :<": <4-5-«>
Таким образом, интеграл D.5.16) представляет разрывную функцию. Часто
это представление оказывается более удобным, чем явное задание функции
и(х) в виде D.5.17).
В качестве второго примера рассмотрим интегральное представление
функции Грина для выведенного ранее уравнения колебаний бесконечной
струны [см. также вывод уравнений G.2.32) и A1.2.8)]. Возьмем интеграл
;*(*~* * dk. D.5.18)
4. 5. Теория вычетов. Гамма-функция и эллиптические функции 393
До тех пор, пока точно не определено положение контура С относительно
особых точек /с = ± К подинтегральной функции, этот интеграл остается
неопределенным. Выберем два контура, изображенные сплошной линией
и пунктиром на рис. 4.26, и сначала возьмем контур С1. При х — ж'> О
мы замыкаем этот контур полуокружностью большого радиуса, лежащей
в верхней полуплоскости. Когда радиус стремится к бесконечности, инте-
интеграл по этой полуокружности имеет предел, равный нулю. Значение рас-
рассматриваемого интеграла равно 2 кг х (вычет подинтегральной функции
в к~К). Следовательно, если выбран контур Си то
Ск(я-а/) = ^еис(х-х'), х-х'>0. D.5.19)
При х — х' < 0 замыкаем контур снизу. В этом случае интеграл равен
— 2ш X (вычет в к — — К), и, следовательно, если выбран контур Сг, то
-*'\ х-х'<0. D.5.20)
Im к
Контур С,
к--К
Reft
' Контур Cj
Рис. 4.26. Контуры для интегрального представле-
представления функции Грина задачи о колебаниях струны.
Комбинируя D.5.19) и D.5.20) для того случая, когда выбран контур С,
получаем
^ D.5.21)
С другой стороны, если взят контур С2, то мы получаем
GK{х-х') = -^е-« I*-*' I. D.5.22)
В полученном результате нет ничего неожиданного, если учесть, что кон-
контур С2 получается из Сх отражением относительно действительной оси.
Выбор контура Сх приводит к функции Грина при граничном условии,
соответствующем расходящимся волнам; иначе говоря, в этом случае
точка х' действует как источник. Выбор контура С2 приводит к» выраже-
выражению, соответствующему наличию стока в точке х'. В этом примере сами
представляемые функции непрерывны, но имеют разрывные производные.
И в том и в другом случае GK (x — х') можно в результате соответ-
соответствующих преобразований выразить через ступенчатую функцию и {х' — х).
Например, когда выбран контур С1г
-х) с .-i(h+K)(x'~x)
с „-i(h-К)(хГ-х) с .-i(h+K)(x'~x) ->
-*> е JK ' «№-«-"<--) $ ¦ k+к **} ¦
с с
Из этих интегралов первый имеет единственную особую точку k=Kt
поэтому нет надобности в том, чтобы контур, вдоль которого он берется,
обходил вокруг точки к = — К. Аналогично, вычисляя второй интеграл,
обходить нужно лишь вокруг точки к = — К. Сопоставив полученное выра-
394
Гл. 4. Функции комплексного переменного
жение с D.5.16) и принимая во внимание рис. 4.25, получим равенство
GK{x-x') = ^ {eiK(x-X') [ i _ ,ф' _ а)] + ,,-«<*-*'> и (ж' _ х)};
•согласующееся с D.5.21).
Интегралы, связанные с функцией ошибок. До сих пор мы имели
дело с интегралами, которые могли быть выражены через элементарные
трансцендентные функции. Теперь мы рассмотрим случай, когда это сделать
невозможно. Дифференциальное уравнение (d2tyjdz2) — 2z (dtyjdz) -\- 2htyi = О
имеет частное решение, выражающееся в виде интеграла
Д+1
dt;
D.5.23)
контур интегрирования изображен на рис. 4.27, а. Выберем линию ветвле-
яия подинтегральной функции вдоль положительной действительной полу-
полуоси. Вычислим теперь этот интег-
интеграл при некоторых частных зна-
Контур С чениях X для малых и для боль-
' Ret
In, \t
Гт
Рис. 4.27. Контуры для интеграла ошибок
и гамма-функции.
В
Ret
ших z. Если X равно целому чис-
числу п > 0, то 0 не является точкой
ветвления, и контур можно путем
деформации превратить в окруж-
окружность с центром в нуле. Тогда в
силу формулы D.3.1)
Чп ~~ п\ V Л"
Jt=o
или
(-1)"
dzn
D.5.24)
Полученные многочлены пропорциональны многочленам Эрмита (см. таблицу
в конце гл. 6).
При X < 0 рассматриваемый контурный интеграл можно свести к дей-
действительному интегралу следующим образом. Разбиваем контур на отрезок
действительной оси от -f- со до 0, малую окружность с центром в нуле
и отрезок от 0 до + со. При X < 0 интеграл вдоль указанной окружности
стремится к нулю вместе с радиусом окружности, поэтому остается рас-
рассмотреть лишь интегралы вдоль полуоси. Поскольку t = 0 — точка ветвле-
ветвления подинтегральной функции, нужно указать, какая именно ветвь этой
функции рассматривается. Лучше всего выбрать аргумент множителя
.?-(*+!) так, чтобы в точке А он равнялся нулю. Тогда интеграл по полу-
полупрямой от со до А будет равен
п „
a-r+2tz
1 Г e~l +ztz
-^- \ j^-j— dt (t действительное).
В точку D точка А переходит при повороте на угол 2тс в положительном
направлении. При таком повороте arg[?-(i+1>] принимает значение
— 2тс (X -J-1), и интеграл от D до со будет равен
e-r+2tz
Л + 1
-dt (t действительное).
4. б. Теория вычетов. Гамма-функция и эллиптические функции 395
Таким образом, для интеграла D.5.23) при X < 0 мы получаем выражение
-dt. D.5.25)
Так как интеграл в D.5.25) действителен, не обращается в нуль и не имеет
полюсов при целых отрицательных X, то при этих значениях X должна
обращаться в нуль <^к. В этом нет ничего неожиданного, так как при
таких X значения интеграла по верхнему и нижнему участкам контура
отличаются лишь знаком. Мы видим также, что, быть может, удобнее
было бы, чтобы ?-(*¦+!) была действительна в точке В контура, потому что
тогда в выражение D.5.25) не вошел бы показательный множитель.
Для того чтобы выяснить поведение ф^ при z—>0, разложим e2tz
в степенной ряд и запишем
п=0
Такие интегралы могут быть выражены через гамма-функцию. (Требуемая
для этого формула будет выведена в следующем пункте.) Поэтому мы
выносим вычисление D.5.26) в задачи, а здесь ограничимся лишь одним
интересным замечанием. Если X равно целому числу р > 0, то интеграл
в D.5.26) обращается в нуль при всех п> р. Следовательно, <Ьр представ-
представляет собой многочлен степени р. Это, конечно, подтверждается форму-
формулой D.5.24).
Наконец, рассмотрим значения фх ПРИ больших z. (Здесь особенно
отчетливо выступают преимущества интегрального представления фх- В нем
содержатся в наиболее доступной форме все сведения о функции; в частно-
частности, оно позволяет нам сопоставить поведение функции при z —»0 с ее
поведением при z —> оэ.) При z —» оэ и Re z ¦< 0 проще всего воспользоваться
подстановкой и = — 2tz ( \ Im z | < | Re z | ):
с v '
Разложив показательную функцию в степенной ряд, получим
). D.5.27)
Эти интегралы выражаются через гамма-функцию [см. формулу D.5.36)].
При очень больших | z | в этом ряде доминирует первый член, и ф\ ~ Azx.
При Rez<0, положив и = 2tz, получим
2
. \ZiZ) \ 6 ^ 1
¦ * == . \ г—^— аи.
с
Контур интегрирования при этой замене переходит в контур, изображенный
на рис. 4.27,6. Разложив в ряд e-(«/2zJ, получим
4>х = Bz)^ У! —' ~ 2п— -=-^ \ еи (мJп~А' du. D.5.28)
Последний интеграл также может быть выражен через гамма-функцию.
396
Гл. 4. Функции комплексного переменного
Гамма-функция. Выше [см. D.3.14)] гамма-функция была определен*
следующим образом:
T(z) =
D.5.29)-
Для того чтобы этот интеграл сходился, z должно иметь положительную
действительную часть. При z нецелом t = О служит точкой ветвления под-
интегральной функции. В качестве линии ветвления берется положительна»
действительная полуось. Элементарные преобразования приводят к следу-
следующим формулам:
Г(а) = 2
2 dt, Re z > 0;
Г(г) = 3 ^ [ In у ] Z~ldt, Re z > 0.
D.5.30>
Как уже говорилось в § 4.3, Г (z) может быть аналитически продолжен»
на полуплоскость Rez<0 посредством рекуррентного соотношения
гГ(г)=Г(г + 1). D.5.31)
Из этого же соотношения можно получить сведения об особых точках
функции Г(г).
Так как интеграл D.5.29) сходится при Re z > 0, то в верхней полу-
полуплоскости T(z) всюду конечна. Далее, так как производную Г'(г) при
Rez> 0 можно вычислить, дифференцируя в выражении D.5.29) под зна-
знаком интеграла, то Г (z) аналитична в полуплоскости Rez>0. Чтобы
выяснить поведение Г(г) при Rez < 0, выберем для заданного z настолько?
большое п, чтобы выполнялось неравенство Re(z + n-|- 1)^> 0. Пусть п —
наименьшее целое число, удовлетворяющее этому требованию. Тогда,,
очевидно,
r(z)= fg-in.w*+nLy(t+n-2) ...," ' D.5.32)
имеет определенную производную, если
только z не равно нулю или целому-
отрицательному числу.
Вблизи числа —п(п — целое по-
положительное число или нуль) мы мо-
можем положить z = — п + з, где | з | < 1„
и тогда в силу D.5.32)
тч « l=\_ ( 1)"Г A + е)
и мы видим что Г (z) конечна
и
-4
-3 -2
Рис. 4.28. Расположение полюсов
гамма-функции. а эта функция имеет при з = 0 про-
простой полюс. Итак, функция Г (z)
аналитична во всех конечных точках плоскости z, за исключением
точек z = 0, — 1, — 2, — 3, ..., которые являются ее простыми полюсами
(см. рис. 4.28). Так как ГA)=1, то вычет функции Г (z) относительно?
полюса z= - п равен ( —1)п/п!.
Правильным расположением своих полюсов, на одинаковом расстоя-
расстоянии один от другого, функция Г (z) напоминает такие функции, как
cosec -nz или ctgirz. Последние, впрочем, имеют полюсы и на положитель-
4. 5. Теория вычетов. Гамма-функция и эллиптические функции 397
иной действительной полуоси. На этой же полуоси расположены, очевидно,
аюлюсы функции Г( —z). Поэтому функция F(z) ГA — z) будет иметь полюсы
лари всех целых значениях z = n (положительных и отрицательных),
и других полюсов у нее не будет. Следовательно, произведение
sin mzF(z) ГA—z) будет аналитической функцией в любой конечной
точке плоскости. [Здесь нельзя было взять tgrcz вместо simrz, так как
tgirz имеет полюсы при всех z = Bр-\-1)п/2, где р — целое.] Мы сейчас
покажем, что на самом деле
r(z)r(l-z) = itcosecnz. D.5.33)
-Это тождество будет сначала установлено для действительных значений z,
заключенных между 0 и 1; на всю плоскость оно будет распространено
посредством аналитического продолжения (см. теорему на стр. 369).
Для доказательства формулы D.5.33), воспользовавшись первой
шз формул D.5.30), напишем двойной интеграл
Г(а)ГA — а) = 4 ^ { e-^+Wx^-ty-^-V dxdy.
о о
Переходя к полярным координатам х = г cosb^y = r sin 6, получаем
эт/2 со эт/2
Г(а) ГA — а) = 4 { (ctg бJ"-1 db \ re-* dr = 2 { (ctg бJ»-1 db.
О 0 0
Для того чтобы вычислить этот последний интеграл, прибегнем к под-
подстановке ctg 6 = s; при этом
и мы получили интеграл, к которому при 0 < о < 1 применима фор-
формула D.5.5). Таким образом,
¦если 0 < а < 1. Несложный подсчет дает Г(а) ГA — а) = та cosec тса. Далее,
как уже говорилось, применяется аналитическое продолжение.
Воспользуемся этой формулой для получения следующих двух
результатов. Во-первых, положив z = 1/2, получаем [ГA/2)]2 = тс, т. е.
ГA/2) = У~ъ. Во-вторых, мы покажем, что [F(z)] является целой функ-
функцией. Так как у F(z) нет других конечных особых точек, кроме полю-
полюсов, то достаточно убедиться в том, что F(z) не имеет нулей в конеч-
конечных точках. А это следует из D.5.33), так как если бы F(z) обращалась
в нуль в какой-либо точке, то в этой точке ГA—z) было бы бесконечно.
Но полюсы функции ГA—z) известны, и в них F(z) в нуль не обра-
обращается.
Контурные интегралы для гамма-функции. Получив известное общее
представление о поведении функции Г(г), мы займемся теперь выводом
таких выражений для F(z), которые . были бы справедливы в более
широких областях, нежели выражение D.5.29). Одно из таких
выражений получается непосредственно при решении разностного урав-
уравнения D.5.31). При этом нужно выбрать такое решение уравнения D.5.31),
которое при Rez>0 сводится к D.5.29). [Заметим, что любое реше-
решение уравнения D.5.31), умноженное на периодическую функцию с перио-
398 Гл. 4. Функции комплексного переменного
дом 1, снова дает решение того же уравнения.] Вид выражения D.5.29)
подсказывает нам, что решение следует искать в виде интеграла
Г(г) = \v{t)f-ldt,
где контур С и функция v (t) подлежат еще определению. Подставив
этот интеграл в D.5.31), получим
(г) ? dt = ^ v (t) ztz~l dt= J »@ т|- (?)dt-
е с
Интегрируя по частям во втором из этих трех интегралов, приходим
к равенству
где в правой части стоит разность в конечных точках контура. Выбе-
Выберем контур так, чтобы разность [v(t)tz] обратилась в нуль; тогда
в качестве v можно взять решение уравнения
то есть
v= const •e~l
Г (z) = A { (е-() (- ty~ldt, D.5.34)
с
где Л —некоторая постоянная. Выберем в качестве С контур, изобра-
изображенный на рис. 4.27,а. Теперь мы вычислим этот интеграл при
Rez>0 и выберем А так, чтобы D.5.34) совпало с D.5.29). Пусть
arg[(—tf'1] = 0 в точке В; тогда при Rez>0
О с»
T(z) = А И e-te-*il*-t)tz-i dt+\ c-tc*i(z-i)p-i dt\ =
со О
= 2iAsin[%(z — 1)]
Отсюда А= — l/Bjsimrz), и мы получаем
Г (а) = —4 С е-t (- tY-1 dt D.5.35)
— представление, справедливо для всех z. Комбинируя его с соотноше-
соотношением D.5.33), приходим к другому интегральному представлению
Поведение Г(г) при целых z можно найти из формулы D.5.35) или D.5.36)
непосредственно.
4. 5. Теория вычетов. Гамма-функция и эллиптические функции 39S>
Представление гамма-функции в виде бесконечного произведения.
Другое полезное представление функции Г(г) можно получить, восполь-
воспользовавшись формулой D.3.8), выражающей целую функцию в виде беско-
бесконечного произведения. Так как [F(z-f I)] 1 — целая функция, нулями
которой являются точки z= — 1,— 2,..., то, согласно D.3.8),
(v) D-5-37>
Постоянная у= — Г'A)/ГA), известная под названием постоянной
Эйлера-Маскерони, приближенно равна 0,5772157. Ее значение нетрудно
получить, положив z = 1 и прологарифмировав обе части равенства
D.5.37):
71=1
Из формул D.5.38) можно получить и другие выражения для у:
+ + +
Ы со
=1 0
)* D-5-40>
Производные гамма-функции. Для последующих приложений суще-
существенный интерес представляет логарифмическая производная гамма-
функции
Из D.5.37) следует, что
Когда z принимает целое значение N,
JV —1
Производная функции фх(г) имеет вид
«¦w-2ct- D-5-44>
«=о
Вообще
n=0
Таблицы этих функций для действительных z позволяют непосредственно-
вычислить суммы рядов, общие члены которых представляют собой
400 Гл. 4. Функции комплексного переменного
рациональные функции номера. Так, например, сумму
оо
5==2 (п+1
п=0
можно записать в виде
| ^ 1_
(a—IJ ZJ 1\ (п+1J "*" (п + аJ ^ о —lVn+1 n + aj) '
n=0
и поэтому
Функции фр («полигамма-функции») подчиняются простой рекуррент-
рекуррентной (по аргументу) формуле. В самом деле,
п=0
откуда следует, что
Mz+l) = <Mz)-K-l)p(/?-l)!]-^r. D.5.46)
Тем же приемом, каким была получена формула D.5.40) для у,
можно получить интегральные представления полигамма-функций ф .
Из формулы D.5.42) вытекает
Выражая у с помощью формулы D.5.40), получаем
D-5.47)
Последовательно дифференцируя по z, приходим к общей формуле для
полигамма-функций
Эта формула дает возможность выяснить поведение фр (z) при z —»со.
Последовательно интегрируя по z, получаем фх (z) = [din T(z)]/dz и затем
Г (z); таким образом можно выяснить поведение Г(г) при больших z.
Впрочем, из-за необходимости находить постоянные интегрирования мы
отложим рассмотрение этого вопроса до следующего параграфа. Здесь же
мы ограничимся тем, что приведем для справок асимптотическую формулу
Стерлинга для значений z, заключенных в первом квадранте,
(а-» со), D.5.49)
¦ч. — • — ч. ~ •
или
._i,. , 4 ^ B_>оо). D:5.50)
4.5. Теория вычетов. Гамма-функция и эллиптические функции 401
Формула удвоения. Применим теперь бесконечное произведение D.5.37)
к выводу формулы удвоения
. D.5.51)
Для доказательства рассмотрим отношение
p=i
В силу формулы D.5.37), выражающей гамма-функцию в виде бесконечного
произведения,
= r((zfff2) exp [z^ (--TtW)] • D.5.52)
p=i P
Для вычисления показательного множителя положим z = l в D.5.52)
и получим
Подставляя D.5.53) в D.5.52), приходим к формуле удвоения D.5.51).
Бета-функция. Рассмотрение гамма-функции мы заключим знакомством
с бета-функцйей; последняя определяется равенством
1
В (р, q)=\ t1 (I - tf~l dt D.5.54)
о
или, иначе,
о
Мы ограничимся тем, что установим формулу
'q)==2 \ sin^ecos^^ede. D.5.55)
о
Согласно первой формуле D.5.30),
оо
Г{р) V(g) =4[e х2х2р- 1 dx \ е-*у**-* dy; D.5.57)
о
26 ф. м. Морс и Г. «J't'iuOax
402 Гл. 4. Функции комплексного переменного
переходя к полярным координатам (х = г cos 6, у = г sin 6), получаем равен-
равенство
и/2
С ^1 bdb.
/
С si
о
Пользуясь снова формулой D.3.30), а также формулой D.5.55), приходим
к D.5.56).
Периодические функции. Много раз нам встретятся и будут нужны
функции, обладающие свойством периодичности, т. е. функции, значения
которых повторяются снова и снова. В математике функция /(z) назы-
называется периодической, если существует такое комплексное число а, что
для всех значений z из области, где / аналитична. Эта постоянная а назы-
называется периодом функции /. Когда z перемещается от zo + a до z0 + 2a,
функция / снова изменяется так же, как при переходе от z0 к zo-f а.
Разумеется, если а —период функции /, то 2а, а также любое целое
(положительное или отрицательное) кратное а является периодом /.
Иногда а/2, а/3 и т. д. также оказываются периодами. Однако такое
дробление периода не может продолжаться безгранично. Посредством
несложного рассуждения читатель может убедиться в том, что функция,
отличная от постоянной, не может иметь бесконечно малого периода.
(Необходимо воспользоваться непрерывностью функции / и свойством един-
единственности аналитических функций.) Расположив по порядку периоды
некоторой заданной периодической функции, мы обнаружим, что все они
являются целыми кратными некоторого основного периода т, характери-
характеристического для функции /. Функция / удовлетворяет тождеству
/2(z + x) = /;(z), D.5.58)
но если снабдить т множителем, меньшим 1 по модулю, то аналогичное
тождество не будет иметь места1).
Функции sing и tg(z/2) — периодические с основным периодом 2ir,
ег — периодическая функция с основным периодом 2iri и т. д. Функции
такого рода допускают представления в виде рядов или бесконечных про-
произведений, в которых проявляется наличие полюсов (или нулей), лежащих
на прямой (или на прямых) в плоскости z на расстоянии г один от дру-
другого. Таковы, например, рассмотренные выше представления
sm z z ¦*—i z"-
71=1 ' 71=1
Периодичность синуса можно было бы получить алгебраическими сред-
средствами непосредственно из этих выражений.
Периодические функции можно характеризовать также их дифферен-
дифференциальными уравнениями. Например, sinz является решением уравнения
х) Возможны также двоякопериодические функции, о которых будет сказано
ниже. —Прим. ред.
4.5. Теория вычетов. Гамма-функция и эллиптические функции 403
или уравнения второго порядка
5--У, D.5.61)
получающегося из предыдущего дифференцированием.
Для того чтобы обнаружить периодичность функции sin 2 при действи-
действительных z, воспользуемся уравнением D.5.60). Возьмем такое его реше-
решение у, которое обращается в нуль при z = 0; тогда уравнение показывает,,
что производная этого решения в той же точке принимает значение 1
(она может равняться ± 1, но мы возьмем -\-1). Когда z возрастает, воз-
возрастает шу, до тех пор пока у не обратится в 1; в этот момент dy/dz = O,
a d2y/dz2~ — 1 [см. уравнение D.5.61)]. Таким образом, 1 есть наибольшее
значение функции у на действительной оси. Когда z продолжает возра-
возрастать, у убывает, а производная dy/dz, оставаясь отрицательной, возра-
возрастает по абсолютной величине, и когда у снова обращается в нуль, dy/dz-
принимает значение — 1. При дальнейшем возрастании z функция у ста-
становится отрицательной, достигает —1, снова начинает возрастать и пра
некотором z принимает значение 0, а ее производная — значение 1, как
в начальный момент. При этом значении z функция у заканчивает свой
первый «цикл» и готова начать второй. Мы замечаем, что в силу сим-
симметрии самого уравнения этот полный период функции у разбивается,
на четыре равных участка, на первом из которых у растет от 0 до •!„
на втором убывает от 1 до 0 и т. д.
Возвращаясь к уравнению D.5.60), замечаем, что его решение, обра-
обращающееся в нуль при z = 0, определяется равенством
то есть z = arc sin §- Собственно говоря, здесь мы имеем выражение для
обратит функции (z как функция у), но оно позволяет легко отыскать
период функции у: Из рассуждений предыдущего абзаца вытекает, что
еслм х — период, то
VI — и2
Этот интеграл равен тс/2, а поэтому рассматриваемая функция у имеет
период 1 = 27t.
В учебниках анализа свойства тригонометрических функций, связан-
связанные с периодичностью, изучаются подробнее и гораздо более строго, чем
здесь, где мы не можем уделить этим вопросам много места; для нас эти
рассмотрения служат лишь подходом к изучению более общих периодиче-
периодических функций.
Существуют ли функции комплексного переменного z, имеющие деа
периода, скажем, ах и а2? Тождества у (z + аг) = у (z) и у (z + а2) = у (z)
не дают ничего нового в том случае, когда векторы ах и а2 имеют одина-
одинаковое направление в комплексной плоскости (т. е. когда отношение
aja2 действительно); в самом деле, одновременно с аг периодами являются
2alt 3% и 'т. д. Можно, конечно, еще спросить, не могут ли периоды ~г
и i2 иметь одинаковое направление, но несоизмеримые длины. Однако
этот случай исключается по тем же соображениям, в силу' которых
период функции (отличной от "постоянной) не может быть бесконечйЬ мал.
[В самом деле, если x2 = Xt1, где X —действительное, Но иррациональйое
число, то среди чисел (т-\-\пу.х нашлись бы периоды, сколь угодно. м!айо>
26*
404 Гл. 4. Функции комплексного переменного
отличающиеся друг от друга, а это невозможно.] Но если аг и а2 имеют
различные направления в комплексной плоскости (т. е. аг/а2 не является
действительным числом), то возникает совершенно иное положение, более
сложное, чем в случае однопериодической функции.
Прежде всего, вместо последовательности периодов, лежащих на одной
прямой, мы получаем на плоскости целую решетку параллелограммов,
в каждом из которых рассматриваемая функция ведет себя в точности
одинаково.
Наименьший параллелограмм, поведение функции в котором целиком
воспроизводится в других параллелограммах решетки, называется основным
параллелограммом для данной функции /; сторонами основного параллело-
параллелограмма служат основные периоды т2 и х2 этой функции. В окрестности
точки z-\- mi1-\-ni2 (т, и = 0, ±1, ±2, ...) функция / ведет себя так же,
как в окрестности точки z исходного параллелограмма. Точки z и z-\-
+ т~.г + т2 называются конгруэнтными (по отношению к /).
Можно задать вопрос, существуют ли функции комплексного перемен-
переменного, имеющие более двух независимых периодов? Доказательство того,
что таких функций нет, аналогично доказательству невозможности для
функции иметь два независимых периода с действительным отношением
и основывается по существу на том, что комплексная плоскость двумерна.
Итак, могут существовать однопериодические и двоякопериодические функ-
функции комплексного переменного, но периодичность тройная или более высо-
высокой кратности невозможна.
Основные свойства двоякопериодических функций. Прежде чем выво-
выводить какие бы то ни было формулы, касающиеся двоякопериодических
функций, мы установим некоторые свойства этих последних посредством
контурного интегрирования. Заметим, что интеграл вдоль границы основ-
основного параллелограмма, в силу периодичности подинтегральной функции,
равен нулю. Двоякопериодическая функция /(z), имеющая основные перио-
периоды xt и -2, может иметь нули и полюсы. Если это так, то в каждом
параллелограмме тех и других должно быть одинаковое количество (при
этом мы условимся выбирать основной параллелограмм так, чтобы на его
границе не было ни нулей, ни полюсов). Если функция имеет точки
ветвления, то эти последние в каждом параллелограмме появляются парами,
а поэтому линии ветвления можно провести так, чтобы они не пересекали
границ параллелограммов.
Займемся такими двоякопериодическими функциями, которые не имеют
точек ветвления, но могут иметь полюсы и нули целого порядка. [Это
означает, что вблизи таких точек z4 рассматриваемые функции имеют вид
{z—zi)riigi(z), где щ — целое число, положительное или отрицательное,
а функция gj(z) аналитична в zi и gi(zi)=^O; показатель nit когда он
положителен, представляет собой порядок нуля zt, а при щ < 0 порядок
полюса Zj равен \nt\.] Такие функции называются эллиптическими. Соглас-
Согласно сказанному на стр. 386, интеграл A/2та) j> / (z) dz no замкнутому кон-
контуру от такой функции / равен сумме ее вычетов в особых точках, лежа-
лежащих внутри контура. Но при интегрировании по границе основного парал-
параллелограмма интеграл равен нулю, и мы приходим к следующему выводу:
Сумма вычетов эллиптической функции во всех ее полюсах, | ., „_
лежащих в основном параллелограмме, равна нулю. J ' >
Если все полюсы некоторой эллиптической функции простые, то их
должно быть по меньшей мере два в каждом параллелограмме, чтобы соот-
соответствующие вычеты могли взаимно уничтожиться. Эллиптическая функция
может, конечно, иметь один полюс порядка :>2 в каждом параллелограмме,
4.5. Теория вычетов. Гамма-функция и эллиптические функции 405
если вычет в нем равен нулю. (Эллиптическая функция может, конечно,
и вовсе не иметь полюсов, но тогда она тождественно равна постоянной.
Почему?)
Если / — эллиптическая функция, то, очевидно, f-\-c, 1//, /', /" и f'/f
также являются эллиптическими функциями. Рассматривая интеграл
j>(l/f)dz по границе основного параллелограмма, убеждаемся в том, что
сумма вычетов l//(z) в ее полюсах, —а последние являются нулями функ-
функции /(z), —по основному параллелограмму равна нулю. Поэтому, если
все нули эллиптической функции / простые, то они встречаются парами
и в каждом параллелограмме их должно быть не меньше двух. Согласно
определению, эллиптическая функция не может иметь существенно особых
точек. У нее не может быть и бесконечного множества полюсов в основ-
основном параллелограмме, так как иначе в некоторой конечной точке появи-
появилась бы неизолированная особенность. Следовательно, в любом основном
параллелограмме эллиптическая функция может иметь лишь конечное число
полюсов и, соответственно, лишь конечное число нулей.
Возьмем теперь произвольную аналитическую функцию /(z), имеющую
внутри некоторого контура конечное число нулей и конечное число особых
точек, каждая из которых представляет собой полюс, и рассмотрим инте-
интеграл § [/' (z)/f(z)]dz (/' = df/dz), взятый вдоль этого контура. Функция /
вблизи полюса zt порядка щ имеет вид/ = (z —zi)~r'igi(z), где gj(z)— анали-
аналитическая функция и g% (zt) Ф 0. При этом /'// имеет в точке zt простой
полюс, а вычет ее относительно этого полюса равен —ni. Вблизи нуля
Zj f имеет вид f = (z — zi)mihj(z), где т}— порядок нуля, hj (z) аналити-
аналитическая функция, причем hj (zy) ф 0. Точка z- является также простым
полюсом функции /'//, и соответствующий вычет равен mjm Следовательно,
т. е. такой интеграл равен сумме порядков нулей минуе сумма поряд-
порядков полюсов функции /, лежащих внутри контура интегрирования- В том
случае, когда все эти нули и полюсы первого порядка, интеграл D.5.63)
равен разности между числом нулей и числом полюсов.
Применяя этот вывод к интегралу от эллиптической функции, взятому
вдоль границы основного параллелограмма, получаем теорему:
Для эллиптической функции сумма порядков всех полюсов,
лежащих внутри основного параллелограмма, равна сумме
порядков всех нулей, лежащих в этом параллелограмме.
Если все эти полюсы и нули простые, то число полюсов
равно числу нулей.
D.5.64)
Рассматривая интеграл j>[f'l(f — C)\dz, взятый вдоль границы основ-
основного параллелограмма, приходим к такому заключению:
Если I — эллиптическая функция, то число корней1)
уравнения f(z) = C, принадлежащих основному парал-
параллелограмму, при любом значении постоянной С равно
сумме порядков полюсов f в основном параллелограмме.
D.Э.65)
*) Корни zj уравнения /,(z)=C являются нулями функции f{z)—C порядка
»1). Числом корней уравнения /(г) = С называют сумму 2 ni- —Прим. перев.
406 Гл. 4. Функции комплексного переменного
Сумма порядков полюсов функции / в основном параллелограмме
{равная числу полюсов в основном параллелограмме в том случае, когда
все эти полюсы простые) называется порядком, эллиптической функции.
В силу теоремы D.5.62) не существует эллиптических функций первого
порядка. Эллиптическая функция нулевого порядка есть постоянная, так
что простейшими нетривиальными эллиптическими функциями являются
функции второго порядка.
Эллиптические функции второго порядка. Существует эллиптическая
функция, имеющая в основном параллелограмме один полюс второго
порядка и два простых нуля; это — эллиптическая функция Вейерштрасса.
Впрочем, более полезны эллиптические функции Якоби, имеющие по два
простых полюса и по два простых нуля в каждом основном параллело-
параллелограмме. В силу теоремы D.5.65) каждая из этих функций в любом основ-
основном параллелограмме принимает любое значение в точности два раза.
Такие функции, подобно тригонометрическим, могут быть построены
с помощью рядов или бесконечных произведений, либо путем обращения
некоторых интегралов. Для первой из функций Якоби мы выбираем на
действительной оси последовательность нулей, отстоящих на %J2 один
от другого, где (действительное) число ъх — первый основной период
функции. Считая, что второй основной период х2 чисто мнимый, поместим
над каждым нулем на расстоянии | х21/2 простой полюс. Над цепочкой
полюсов на том же расстоянии появится новая цепочка нулей и т. д.
По аналогии с рядом D.5.59) можно было бы составить ряд, «ведающий»
нулями, нашей функции. Потребуем, чтобы последняя вблизи своих нулей
вела себя как синус, т. е. имела производную, равную 1, а при т2—> оо,
становясь однопериодической, превращалась бы прямо в sinz. Об этих
свойствах напоминает обозначение snz конструируемой функции.
Полюсы функции 1/sn z (т. е. нули snz), лежащие на действительной
оси, можно получить, введя в ряд член B7t/x1)co§ecB7iz/x1). Последний
ведет себя требуемым образом вблизи каждого из действительных нулей
snz и сводится к 1/sinz, если x1—>2ir при t2—> оо. Следующая цепочка
полюсов функции 1/sn z образована точками z = ~2 + т%х/2, где t2 — чисто
мнимое число.
Выражение
cos
sin2 B?tis/ii;1) —sin2 B
имеет полюсы в точках z = ^ х2 -\-nzt/2, так же как l/sinBirz/-1) в точках
z = nxj/2. Комбинируя эти выражения, получаем
2 cos Bэтгг/гх) sin Bnz/-ci) _ 4 sin BюНЛ) cos
sin2 Bnz/v1) ¦—sin2 Bnz2t/z1) cosDn-2/T!)—cos Dmz/r2)
Учитывая всевозможные цепочки нулей snz, пересекающие мнимую ось
в точках iy = ± т2> составляем ряд
оо
1
snz
n=l
= JH Jcosecf-З^Л + 4 У. sfo(^) co8(W«,) | D566)
Tj \ V "i У -^-J COS Ditrecg/T:i) — COS Dэтг/т2) J ' v '
обеспечивающий требуемое распределение нулей функции snz во всей
комплексной плоскости. Нетрудно показать, что нули этого ряда (т. е.
полюсы функции snz) лежат посередине между любыми двумя соседними
полюсами [т. е. в точках z= тех1/2 + (и + 1/2)'с2]. Значительно труднее
было бы найти вычеты snz в этих точках.
4.5. Теория вычетов. Гамма-функция и эллиптические функции 407
К эллиптическим функциям можно подойти еше иначе. Ряд
со со
2 gn2cosBnu) D.5.67)
l
2
n=l
(где Im у > 0 и q = e7tiY) представляет собой периодическую функцию пере-
переменного и с периодом тт. Он сходится, когда мнимая часть у положи-
положительна, т. е. когда |д|<1. Интересно, что такой ряд псевдопериодичен
по и с периодом тсу, так как
F(u-\-Trv) = "У, e^iT(i2+2n)+2inu = e-7iiY-2iu V guiy (n+lJ+2i(n + l)u _
?г=—оо ?1=—оо
= g-le-2iuf (И).
Следующие четыре подобных ряда называются тэта-функциями:
н,9), D.5.68)
CO
(в, g) = 1 + 2 Д g«2 cos Bпв), &з (н + «,?) = &з (», Ч),
»4 (н, 9) = 1 + 2 V ( _ i)"gr,2 cos
51=1
»4(в + 1су, g)= — Л*»4(в, q),.
&2(в, д) = &1(^н + 2-tt, g"), &8(и, g) = &4(«+-g-it, g^ и т. д.
Здесь g = е7^ и N = д'ге~2ги. Эти функции не являются, конечно, соб-
собственно эллиптическими функциями из-за наличия множителя N.
Оперируя с тэта-рядами, можно показать, что выражения
Ц (и) + g&l (ц)
»! (и) ' »! М
представляют собой уже настоящие эллиптические функции. Подобрав
должным образом постоянные а и Ъ, можно добиться того, чтобы эти
отношения имели не более одного простого нуля в основном параллело-
параллелограмме со сторонами тс и у71- Тогда, в силу теоремы D.5.62) при таких
а и Ъ рассматриваемые отношения будут постоянны, и мы сможем выра-
выразить &| и &| через Ъ\ и Ь\. Для отыскания а и Ъ полагаем м = 0 и it/2.
Окончательно получаем
Ч («) Ч @) = Ч (В) »| @) - »? (н) &2 @),
и) ».2 @) = »г (в) е* @) - »5 (н)
? (в) ».2 @) = ft2 (в) &22 @) - Ь\ (и) &f @), D-5-69)
(в) &| @) = ft2 (в) »2 @) - Ц (в) »| @).
Второй аргумент q опущен для упрощения записи.
Исходя из тэта-функций, можно, как мы видели, построить настоя-
настоящие эллиптические функции. Для этого нужно взять их отношения,
408 Гл. 4. Функции комплексного переменного
чтобы освободиться от нежелательного множителя N. ¦ Так, например,
функция
имеет те же нули и так же ведет себя вблизи каждого из нулей, как
и функция, определенная равенством D.5.66), если только числа тс[&3@, д)]2
и тсу[&3@, д)]2 равны соответственно периодам ъг и т2. Далее в моногра-
монографиях по эллиптическим функциям из формул D.5.68) выводятся, не без
труда, дифференциальные уравнения для тэта-функций и для snz. Так,
например,
d
du
u если тг] = &j (к, g)/bi(u, g), то после некоторых преобразований получаем
Наконец, полагая у = [&3 @, ?)/&2 @, д)] к] и z = m[&3 @, <7)]2> получаем для
г/ уравнение
(S)8 = A-y')A-*V), D-5.71)
в котором V"fc = &2 @, g)/&3 @, ?) • Все свойства эллиптической функции
у = sn z могут быть получены из рассмотрения быстро сходящихся рядов
D.5.68). Однако для исследования некоторых свойств удобнее в основу
определения snz положить уравнение D.5.71).
Интегральные представления эллиптических функций. Уравнение
D.5.71) приводит нас к третьему способу определения эллиптических
функций второго порядка, самому полезному во всех случаях (исключая,
может быть, задачу табулирования функций). Формальным решением
дифференциального уравнения D.5.71) является
у
du D.5.72)
— функция, обратная эллиптической функции snz. Рассуждая так же,
как на стр. 403 в случае arc sin z, приходим к заключению, что y = snz —
периодическая функция с периодом i1 = 4i?, где
1 тс/2
J 1/A— и2) A — /с2м2) J
J 1A и) A /см) VI-ft2 sin2 cp
D.5.73)
it
2 ) y
) yv (i_^)(i_^2) г
[см. формулу E.3.16)]. Важно отметить, что sn(z + 2A')= —snz. Из D.5.71)
и D.5.72) следует, что snz при действительных z не превосходит 1 па
абсолютной величине.
Разложив интеграл D.5.72) в ряд по степеням у, мы обнаружим, чта
sn3 = z — A/6) A + ft2)z3 + ...; таким образом, snz —нечетная функция,,
а вычет функции 1/snz в ее простом полюсе z = 0 равен 1. Теперь посмот-
посмотрим, как ведет себя sn z вблизи точки z == К, в которой она принимает
значение 1. Смещаясь из точки z = К вдоль действительной оси, получаем
меньшие по модулю значения snz, а значит смещения параллельно мнимой
оси должны вызвать увеличение модуля snz (почему?). Смещаясь из точки
4.5. Теория вычетов. Гамма-функция и эллиптические функции 409'
= K вверх, получаем
v
du y s
Дифференциальное уравнение, связывающее v и у, показывает, что
у — периодическая функция от v с периодом 2К', причем
i/fc
К' = [ du ==«р(*- U\\k'A, D.5.74)
l
где /с'2 = 1 — к2. Следовательно, sn z — периодическая функция по z
с периодом %2 = 2iK', причем sniif = l, sn (К + iK') = \jk и т. д.
Наконец, чисто мнимым у соответствуют чисто мнимые значения z,
и у может стремиться к бесконечности при конечном z. Это означает, что
функция y = snz имеет полюс на мнимой оси, а именно, в точке га, причем
а=\ , dw = [ , du —=K\ u =
В результате этого исследования мы находим, что snz представляет
собой эллиптическую функцию с действительным периодом tj = iK и чисто
мнимым периодом x2 = 2iiif'. Эта функция имеет простые нули в точках
z = 0 шх = 2К и в соответствующих точках других параллелограммов.
Простые полюсы находятся в точках z = iK' и z == 2К +- iK' (и в конгру-
конгруэнтных с ними точках), причем вычет snz в z = iK' равен l/k, откуда
следует [см. D.5.62)], что вычет в z = 2J* + iK' равен— l/k. Параметр к
называется модулем функции snz; последнюю обозначают sn(z, к) в тех
случаях, когда нужно указать значение модуля. Выражение к через q ука-
указано в связи с уравнением D.5.71); впрочем, обычно к рассматривают как
исходный параметр, а К и К' определяют по формулам D.5.73) и D.5.74>
(К' выражается через к' = \Г1 — к2 так же, как К — через к), после чего
находят q = e~7l^K'fK). Проводя рассуждения в обратном порядке, убежда-
убеждаемся в том, что уравнение D.5.72) определяет ту же функцию snz, что
D.5.70) и D.5.66).
Аналогично определяются и остальные функции Якоби:
sn(z, /с) =
у
обратная функция z — F(k, у) — \ г 2ч
обратная функция1) z = ^ ,A__ 2+/,2B);
у
1
обратная функция1) z = \ .
х) Введенные здесь «обратные» функции могут быть, конечно, выражены обычным спо-
способом через эллиптические интегралы первого и второго рода, F(к, х) и Е(к, х). См.,
например, Смирнов В. И., Курс высшей математики, т. 3, ч. 2, изд. 6, Гостехиздат,.
М., 1956, стр. 584— 591.—Прим. ред.
Гл. 4. Функции комплексного переменного
здесь
а К и К' задаются формулами D.5.73) и D.5.74).
Используя формулы D.5.69) и наши предварительные сведения о
функции snz, можно показать, что
sn2(z, k) + cn*(z, Л) = 1, cn@,ft) = dn@, А)=1,
/с2 sn2 (z, А:) -f dn2 (z, /с) = 1, (d/dz) sn (z, A) = en (z, &) dn (z, /с). ( '
Теперь можно было бы установить множество других свойств этих функ-
функций. Некоторые из них приведены на стр. 462 — 466, с другими читатель
встретится в задачах. В этой книге мы еще не раз воспользуемся этими
•функциями.
4.6. Асимптотические ряды. Метод перевала
Для изучения поведения функции / (z) при больших значениях | z |
часто бывает целесообразно разложить ее в ряд по степеням 1/z и пред-
представить в виде
o + 71+lF + --
где <р (z) — некоторая функция, поведение которой при больших значениях
\z\ известно. Таково одно из выражений Г(г), указанное в предыдущем
параграфе [см. формулу D.5.50)]. В том случае, когда отношение f(z)/<p(z)
имеет в бесконечности существенно особую точку, ряд D.6.1) расходится.
Тем не менее этот ряд может быть полезен не только для качественного
исследования поведения функции, но и для вычисления ее значений при
больших | z |.
Для этого нужно, чтобы разность между / (z)/<p (z) и первыми п +1
членами ряда была порядка l/zn+1 и, следовательно, чтобы она могла быть
сделана весьма малой при больших |z|. Выражаясь точнее, говорят, что
такой ряд асимптотически представляет функцию /(z)/<p(z), и записывают
если при любом п
Последнее равенство утверждает, что при заданном п сумма первых п-\-1
членов ряда при достаточно больших | z | становится сколь угодно близка
к f(z)/<p(z). При заданном п отклонение будет порядка l/zn+1. Так как
ряд ^]Ajzp расходится, то заданному z соответствует такое п, при кото-
п
ром частичная сумма /jAp/zp точнее других представляет /(z)/^(z). Такое
оптимальное п одновременно определяет неустранимую ошибку. С возраста-
возрастанием z оптимальное п также возрастает, а неустранимая ошибка убывает.
4.6. Асимптотические ряды. Метод перевала
411
Пример. В качестве простого примера, разъясняющего эти общие
¦соображения, рассмотрим интегральную показательную функцию
Ei(-z)= -\eTdt.
X
Асимптотический ряд для нее можно получить последовательным интегри-
интегрированием по частям. Сначала получаем
а затем, продолжая,
Ряд, получающийся при п~^>са, расходится, так как
lim
= lim — =00.
n-»co L * J
В частности, мы замечаем, что при х =¦ п /г-й член ряда совпадает с
{и + 1)-м по абсолютной величине; это указывает на то, что при заданном
х оптимальным, грубо говоря, является значение п, ближайшее к х. Для
того чтобы доказать, что полученный ряд является асимптотическим,
достаточно обнаружить, что при х~>оо
a**i ех (п +1)! (- l)»i ^ ?sdt -* 0.
Это непосредственно вытекает из неравенства
со со
{ — At s- — С -(Ht — e'X
¦Ошибка приближения функции — Ei (— х) частичной суммой
по абсолютной величине меньше (и-(-1)! е'х/хп*2. Последнее выражение,
в точности равное по абсолютной величине следующему члену ряда,
с возрастанием п сначала убывает, а затем неограниченно возрастает.
В табл. 4.6.1 указаны приближения для значения —4e4Ei( — 4) = 0,82533.
Значениям 0,87500 и 0,78125 соответствует относительная погреш-
погрешность, меньшая 5%.
412
Гл. 4. Функции комплексного переменного
Таблица 4.6.1
п
0
1
2
3
4
5
6
7
8
9
п-й член ряда
1,00000
—0,25000
0,12500
— 0,09375
0,09375
— 0,11719
0,17579
—0,31013
0,62026
-1,39559
п-я частичная
сумма
1,00000
0,75000
0,87500
0,78125
0,87500
0,75781
0,93360
0,62347
1,24373
—0,15186
Верхняя граница
погрешности
0,25000
0,12500
0,09375
0,09375
0,11719
0,17579
0,31013
0,62026
1,39559
™
Усреднение последовательных членов ряда. Полученные в предыду-
предыдущем примере приближенные значения лежат по разные стороны от истин-
истинного значения; это наводит на мысль, что для лучшего приближения
нужно воспользоваться средними арифметическими двух последовательных
сумм. В нашем примере это среднее равно 0,82812 и дает относительную
погрешность, меньшую G2)%- Вообще, если
ТО, ПОЛОЖИВ
мы получаем
где
p
71+1
m=0
Sn + Sn+i
п+1
n+1 = ZJ
т==0
D.6.4)
Ряд из Un не является асимптотическим в узком смысле, т. е.
в смысле равенства D.6.3). Однако определение асимптотического ряда
можно обобщить (чтобы оно включало построенный ряд из Un), полагая
если при любом п
lim
|z|->oo
р=0
р=0
D.6.5)
Ясно, что замечания, сопровождавшие условие D.6.3) и относившиеся
к ряду вида D.6.1), применимы и к этому более общему случаю. Для U t
определенных равенствами D.6.4),
п п+1
2 ад =2 »»-T»n-i(*).
Р=-1 р=0
4.6. Асимптотические ряды. Метод перевала
413
и если 5] ир (z) — асимптотический ряд, т. е.
p=0
то 53 Up (z) также является асимптотическим рядом. Ряд из средних
арифметических, построенный согласно D.6.4), особенно удобен тогда,
когда исходный ряд — знакочередующийся. В табл. 4.6.2 приведены ре-
результаты такого преобразования (Un и Тп), относящиеся к примеру, изо-
изображенному в табл. 4.6.1.
Таблица 4.6.2
СУММИРОВАНИЕ АСИМПТОТИЧЕСКОГО РЯДА ПРИ ПОМОЩИ ОСРЕДНЕНИЯ
ЧЛЕНОВ [см. формулы D.6.4) и табл. 4.6.1]
п
— 1
0
1
2
3
Un
0,50000
0,37500
—0,06250
0,01562
0,00000
•
Тп
0,50000
0,87500
0,81250
0,82813
0,82813
п
4
5
6
7
8
—0,01720
0,02930
—0,06717
0,15508
—0,38767
Тп
0,81093
0,84023
0,77306
0,92813
0,54046 .
Прежде чем приобрести уверенность в обращении с асимптотическими
рядами, необходимо выяснить еще несколько вопросов. Заметим, прежде
всего, что асимптотический ряд не определяет однозначно представляемую
им функцию. Например, две функции
Щ и ф(8)==Ш
ср (z) ' W cp (Z)
имеют при Re z > 0 одинаковые асимптотические разложения. Далее, оче-
очевидно, что при, переходе от полуплоскости Rez>0 к полуплоскости
Re z < 0 асимптотическое разложение функции ф (z) заметно изменяется.
Таким образом, если z = |z|eie, то асимптотическое выражение ф (z) резко
изменяется при переходе через б = тг/2 и б = Зтс/2. Такого рода «разрывы» —
лишь кажущиеся и по существу обусловлены тем, что один и тот же
асимптотический ряд может представлять различные функции. Однако, когда
в дальнейшем мы будем обращаться к асимптотическим рядам, нам при-
придется внимательно следить за тем, чтобы не выйти за пределы тех значе-
значений аргумента z, для которых справедливо рассматриваемое разложение.
Кажущиеся разрывы асимптотических рядов часто дают о себе знать,
и в главе о дифференциальных уравнениях (см. § 5.3) мы с ними встре-
встретимся в связи с явлением Стпокса.
Надо отметить еще следующие общие свойства асимптотических рядов.
Асимптотические ряды можно почленно складывать; их можно и пере-
перемножать. Последнее означает, что если
р=0
р=0
то
414 Гл. 4. Функции комплексного переменного
п
где Сп = 2 А Вп_ . Асимптотический ряд можно почленно интегрировать-^
°° Av+i
p=i
С другой стороны, почленное дифференцирование асимптотического ряда
приводит к асимптотическому разложению производной только в том
случае, когда заранее известно, что эта производная допускает асимпто-
асимптотическое разложение.
Интегральные представления и асимптотические ряды. Нам часто-
придется выяснять асимптотическое поведение интегрального представле-
представления той или иной функции. Для этого применяется метод, называемый
методом скорейшего спуска или методом перевала (седловых точек).
Здесь мы рассмотрим этот метод и применим его к гамма-функции.
Прежде всего подчеркнем, что этот метод применим к функциям, до-
допускающим интегральное представление довольно частного вида
D.6.6>
причем контур С таков, что при приближении t к его концам подинтег-
подинтегральная функция стремится к нулю. Такое представление тесно связано с
преобразованием Лапласа (см. § 5.3). Можно ожидать, что многие интегра-
интегралы, интересующие нас в этой книге, должны иметь вид D.6.6); в самом
деле, решение . ф скалярного уравнения Гельмгольца (^2 4- к2) ф = 0 мож-
можно представить в виде наложения плоских волн eik"r, т. е. ф =
= \ eik-r/(k)rfQn, где dQn —дифференциал телесного угла в направлении
вектора к. Кроме того, часто удается искусственным путем придать таков
вид интегралу, первоначально выглядевшему иначе. Например, гамма-функ-
оо
ция Г(г+1) при Re z > — 1 представляется интегралом \ e-T>c2<fa, послед-
последний же подстановкой % = tz приводится к виду
Г (z + 1) = z2+1 [ e-tztzdt = zz*x ^ в*Пв|-')Л, D.6.7)
о о
и мы получаем, что функция Г (z +l)/zz+1 выражается интегралом вида
D.6.6).
Рассмотрим поведение интеграла / (z) при | z | —» оо и при заданном
значении <$> = argz. При больших | z | подинтегральная функция претерпевает
обычно быстрые колебания. Если z комплексно или если f(t) принимает
вдоль некоторых участков контура С комплексные значения, то мнимая
часть z/ (t), вообще говоря, возрастает вместе с | z |. Следовательно, множи-
множитель exp {ilm[zf(t)]} будет быстро колебаться, причем частота колебаний
будет при | z | —> оо возрастать. Наличие таких колебаний затрудняет пря-
прямое, без дальнейших преобразований, вычисление интеграла /(z). Действи-
Действительно, во многих случаях влияние больших положительных значений
подинтегральной функции на одних участках контура при интегрировании
почти полностью погашается большими по абсолютной величине отрица-
отрицательными значениями на других участках. В этих условиях для получе--
4.6. Асимптотические ряды. Метод перевала 415
ния удовлетворительного результата вычисление пришлось бы вести
с устрашающей точностью. Поэтому естественно попытаться так деформи-
деформировать контур, чтобы свести к минимуму вредное влияние колебаний под-
интегральной функции. В дальнейшем будет предполагаться, что такие-
деформации возможны и что можно каким-либо способом учесть влияние-
особых точек, если они встречаются.
Выбор контура. Контур интегрирования, вообще говоря, пересекает
как области, в которых Re[z/(?)]>0, так и области, где Re[z/(J)]<0.
Первые области важнее, так как в них модуль подинтегральной функции
больше, чем во вторых, а чем он больше, тем важнее уменьшить колеба-
колебания. Поэтому контур следует выбирать так, чтобы max Re [z/B)] был,
по возможности, меньше и чтобы на участке, где Re[z/(?)] принимает
наибольшие значения, вдоль контура мнимая часть zf{t) была постоянна.
Таким образом, на участке контура, вносящим основную долю в интеграл
/(z), мы будем иметь
/ (z) = { е2Н» dt = eiImr2>@] { еш !>«'>] dt. D.6.8)
с с
На тех участках, где значения Re[z/(?)] малы, контур можно выбрать
так, чтобы вдоль него \m[zf{t)] была переменной, если оказывается
необходимым соединить отдельные участки контура. Такой выбор-
контура в наибольшей степени обезвредит колебания подинтегральной
функции.
В точке t~t0, в которой Re[z/(?)] достигает наибольшего значения,
/'(д = 0. D.6.9),
Вблизи этой точки особенно важно избежать колебаний, а поэтому мы
выберем здесь контур так, чтобы вдоль него
Im[B/(Q] = Im[z/(«„)]. D.6.10),
Смысл этого условия легко пояснить геометрически. Представим себе-
поверхность w = Re/B) в трехмерном пространстве (Ret, lm t, и) (считая
для простоты z > 0 вещественным). В плоскости t нанесем линии уровня
функции Re/(?) (см. рис. 4.29). В точке t = t0 эта функция, будучи дей-
действительной частью аналитической функции, в силу сказанного на стр. 349
не может иметь ни минимума, ни максимума (т. е. соответствующая
поверхность не может иметь над точкой t0 ни вершины, ни впадины);
следовательно, это — точка минимакса, или седловая точка, или, упо-
употребляя топографический термин, перевал. На рис. 4.29 изображена окрест-
окрестность этой точки. *
В чем особенность выбранного пути lm[zf(t)] = const? Как мы пом-
помним, если u-\-iv — аналитическая функция, то семейства кривых и = const
и v = const взаимно ортогональны. Поэтому вдоль кривой Im[z/B)]=c
функция Re[zf(?)] изменяется быстрее всего. Но при c = Im[z/B0)] эта
кривая в окрестности точки t = t0 распадается на кривую CD, идущую
с одной «возвышенности» на другую, и на кривую АВ, идущую из одной
«впадины» в другую (см. рис. 4.30). Вдоль CD функция Re[z/(<)] быстрее
всего растет, вдоль АВ — быстрее всего убывает. В качестве пути должен
быть выбран, уча сток АВ, а не CD, в соответствии с исходным контуром
интегрирования. Таким образом, вдоль выбранного пути функция М)
-416
Гл. 4. Функции комплексного переменного
ходит к своим концевым значениям, изменяясь наиболее «быстро», причем
этот путь проходит через точку перевала t0. Основной вклад в значение
интеграла дает участок контура, близкий к t0, так как в этой точке
Рис. 4.29. Линии уровня Re/ = const вблизи седловой точки
модуль подинтегральной функции принимает максимальное значение на кон-
контуре интегрирования. Последнее обстоятельство тем более заметно, чем
z |, так как при больших | z | максимум оказывается особенно ост-
больше
рым, а
|, р | | у
ezib) | убывает к концевым значениям особенно быстро.
Первый член разложения. Воспользуемся тем, что было сказано
в предыдущем пункте, для вывода общей формулы, дающей первый член
асимптотического разложения J(z). В окрестности точки t = ta
(Может случиться, что f(to) = O; тогда приходится действовать иначе.]
Метод перевала указывает такой путь интегрирования, при котором под-
подинтегральная функция убывает как показательная функция. Поэтому
положим
•z=|z|ei<p t = ]/ei(«-t-<pty"it )(t t ). D.6.12)
Получаем
Мы видим, что при больших | z | подинтегральная функция имеет весьма
«острый» максимум, и потому становится важной только весьма малая
часть контура. Когда \z\ достаточно велик, подинтегральная функция
практически оказывается равной нулю вне области, где справедливо при-
приближение D.6.11). Вследствие этого можно заменить контурный интеграл
действительным интегралом, взятым в пределах от — оо до со. Направление
интегрирования будет определяться направлением обхода исходного контура
и преобразованием D.6.12). Допустим, что обход первоначального контура
4.6. Асимптотические ряды. Метод перевала
417
был таков, что новый интеграл берется по i от —ю до оо. Тогда при
jz|—> оо
/(z)~
;тс/«-*Г(«о)-
D.6.13)
Рис. 4.30. Выбор пути, проходящего через седловую точку.
В случае гамма-функции [см. D.6.7)] f(t) = In t — t. При этом /' (t) —
= 1/2—1, так что 20=1. Мы находим далее f(to)= — 1 и /"(*0)=—1.
Переменное t изменяется от 0 до -\- оо. Преобразование D.6.12) принимает
вид г = (t — 1) е1?'2. Формула D.6.13) применима и дает
Г (z-f- 1) <=**¦ \f2nzz+ll2e~г (z—> оо),
что согласуется с формулой D.5.50), если в последней удержать лишь пер-
первый член. См. также рассуждения, относящиеся к формулам E.3.77), где
рассмотрен другой пример.
Остаток ряда. К формуле D.6.13) мы пришли, рассматривая первый
член асимптотического ряда. Обобщим наш вывод с целью получить даль-
дальнейшие члены этого ряда. Для упрощения присоединим аргумент z к f{t)
и будем рассматривать z как действительный параметр.
Необходимо возвратиться к формуле D.6.11) и заменить ее на точную
подстановку
f(t) = f(to)-w2. D.6.14)
Заметим, что w — действительное переменное в силу выбора контура, вдоль
которого Im/B) = Imf(t0). Вводя D.6.14) в интеграл /(z), получаем
/(z) =
с
dt =
Предположим и теперь, что исходный интеграл таков, что интегрирование
по w следует производить от — оо до оо; таким образом,
С 2 dt
\ e~zw -г- <
D.6.15)
Остается вычислить dt/dw. Для этого нужно выразить dt/dw через w из
уравнения D.6.14) с помощью степенного ряда
D.6.16)
n=0
Подставляя D.6.16) в D.6.15) и замечая, что после интегрирования оста-
27 ф. м. Морс и Г. Фешбах
418 Гл. 4. Функции комплексного переменного
нутся лишь четные степени w, получаем асимптотический ряд
п=0
Коэффициенты ап можно найти, применив способ, описанный на стр. 389.
Там указывалось, что если
то
t — tn~\"+l
В рассматриваемом случае g (t) = Уf (t0) — f (t). Разложив в ряд функцию
/(*о)-/(*)._ у л (t-t0)p
v
приведем равенство D.6.18) к виду
1 Г «Г» Г лп А
другими словами, ап есть коэффициент при п-й степени х в разложении
B A xp)"n^2~il2 в степенной ряд.
Вот первые три коэффициента, выраженные через Ар:
1
^?_— 15. А2А'3 — — А А~2
. а0 - 8 Л1Л° 2 Л2Л" '
5-7-9-11 ,д,_я 5-7-9 ^_6
а0 ~~ 2'-3 Л»Ло 24
5-7 5
Снова, пользуясь гамма-функцией в качестве иллюстрации, получаем
—-In/ / / — 1
/(t0) —/W _(« —1)—lnt_l * — 1 (г — IJ:
(t—t0J ~~ (t—IJ ~~2 3" ' 4 ^~'"' '
а значит, Ап = ( — 1)п/(и + 2). Согласно D.6.19),
a0 "" 6 ' a0 ~ 216 •
В силу D.6.17) для r(z-}-l) получается асимптотическое разложение
Метод перевала будет не раз еще использован в дальнейшем, в част-
частности в § 5.3 с его помощью будет подробно исследовано асимптотическое
поведение бесселевых и некоторых других связанных с ними функций.
4. 1. Конформное отображение
419
Плоскость г
4.7. Конформное отображение
В большинстве интересных и важных геометрических приложений тео-
теории аналитических функций комплексного переменного к физике конформ-
конформное отображение играет важную роль. В качестве примера рассмотрим
электростатическое поле. Часто встречающейся задачей является отыскание
поля, созданного точечным зарядом q (линейным нарядом в трехмерном
пространстве) внутри замкнутой
поверхности С, представляющей
собой металлический проводник,
поддерживаемый при нулевом по-
потенциале (см. рис. 4.31). Силовые
линии (вдоль которых направлен
вектор поля Е) будут исходить из
источника и опускаться ортого-
ортогонально на поверхность С. На
рис. 4.31 нанесено несколько экви-
эквипотенциальных и силовых линий.
Конечно, семейства тех и других
образуют ортогональную сеть.
Можно поэтому ожидать, что су-
существует такая аналитическая
функция комплексного переменно-
переменного w (z) = и + iv, что кривые и (х, у) = const совпадают с силовыми линия-
линиями, а кривые v (х, 2/)= const — с эквипотенциальными. Эта функция,
если она вообще существует, должна иметь особенность в точке z = zq,
в которой помещен заряд. На самом деле эта функция в точке zq
имеет логарифмическую особенность; в гл. 10 мы увидим, что она должна
Рис. 4.31. Силовые и эквипотенциальные
линии в случае точечного источника, окру-
окруженного заземленным проводником.
и=0
Плоскость w
Рис. 4.32. Конформное отображение области, изо-
изображенной на рис. 4.31, на верхнюю полупло-
полуплоскость w = и + iv.
иметь вид: w= —2iq In (z — zq) плюс некоторая функция, аналитическая
в zq. Конформное отображение, осуществляемое функцией w = w(z), пере-
переводит линии и = const и v = const в прямые на плоскости w, параллельные
соответственно мнимой и действительной оси. Так как у=0 на С, то С
отображается на действительную ось в плоскости w. Образ области плос-
плоскости z, ограниченной контуром С, изображен на рис. 4.32. Заряд q в плос-
плоскости w оказывается в бесконечно удаленной точке (w=i со). Параллель-
Параллельные прямые и — const являются как раз силовыми линиями, которые по-
порождены зарядом, находящимся в бесконечности.
Общие свойства отображения. Искажение пространства, производи-
производимое преобразованием, о котором идет речь, может быть описано более
27*
420 Гл. 4. Функции комплексного переменного
наглядно; к описаниям такого рода часто прибегают, когда хотят
лучше «почувствовать» преобразование. В нашем случае преобразование
состоит в том, что контур С разрезается в какой-либо точке и растяги-
растягивается так, чтобы он заполнил всю действительную ось, а точка разреза
ушла в бесконечность. Далее, заряд передвигается бесконечно далеко вверх.
При этом эквипотенциальные линии и силовые линии превращаются в пря-
прямые, параллельные соответственно действительной и мнимой осям1).
Отметим следующее чрезвычайно важное обстоятельство: функция
w(z) отображает область, ограниченную контуром С, на верхнюю полу-
полуплоскость. Для того чтобы осуществить это преобразование, нужно только
найти функцию точечного источника, мнимая часть которой у ведет себя,
как — (<7/2iu)In|z — zQ\ вблизи заряда в точке zq, и удовлетворяет условию
Ь = 0 на кривой С. По самому физическому смыслу задачи такая функция
существует, а следовательно, существует конформное отображение об-
области, заключенной внутри С, на верхнюю полуплоскость. Очевидно также,
что'существует множество таких отображений, так как заряд можно по-
поместить где угодно внутри С.
Допустив существование функции / (z), осуществляющей требуемое
отображение, покажем, какую большую пользу можно извлечь из этой
функции для решения различных задач электростатики в области внутри С.
Существо дела состоит в том, что при помощи отображения возможно за-
задачу со сложной геометрией (рис. 4.31) свести к аналогичной задаче
с простой геометрией (рис. 4.32), решить которую значительно легче.
Пусть, например, вдоль С задан переменный потенциал, а зарядов внутри С
нет. В преобразованной задаче потенциал V будет задан вдоль действи-
действительной оси (у=0), а найти нужно V в верхней полуплоскости. Так как
известно, что V представляет собой мнимую часть функции, аналитиче-
аналитической в верхней полуплоскости, то можно применить формулу D.2.13),
и мы получаем
V(u,v) = -?-
Этот пример убеждает нас в том, что коль скоро известна отображаю-
отображающая функция, мы можем решить любую задачу электростатики, относя-
относящуюся к первоначально заданной области.
Преобразование Шварца — Кристоффеля. Обратимся теперь к практи-
практическому отысканию требуемого преобразования. Наиболее общим контуром
С, для которого эта задача может быть рассмотрена весьма детально,
является многоугольник. Другим важным частным случаем, для которого
решение известно, является эллипс и, в частности, окружность. Рассмот-
Рассмотрим сейчас случай многоугольника; соответствующее преобразование назы-
называется преобразованием Шварца — Кристоффеля. Многоугольник изображен
на рис. 4.33; вершины его обозначены а0, аг, ... , соответствующие внеш-
внешние углы — ц>0, <рг, ... , образы этих вершин в плоскости w~ b0, blt ....
Заметим, что
<Ро + ?! + ... = 2*. D.7.1)
т) В этом описании не учтена многозначность логарифма; скорее здесь ось и
плоскости ш наматывается на контур С плоскости г, как нитка на катушку. Строго
говоря, отображение w=w (z) не конформно, так как оно не однозначно. —Прим.
ред.
4.7. Конформное отображение
421
Читателю следует обратить особое внимание на то, каким образом отсчи-
тываются углы <р4, и на то, что при обходе многоугольника в направлении
отсчета углов внутренность многоугольника все время остается слева.
При тех вершинах, в которых контур при выбранном обходе поворачивает
влево, углы <$>| оказываются положительными; те <р$, которые соответствуют
вершинам входящих углов, будут отрицательными. Возможны и «случаи вы-
вырождения», когда <pt равно тс или —тс; какое из этих двух значений следует
выбрать, обычно определяется соотношением D.7.1).
Так как углы ^ при отображении не сохраняются, то аг должны
быть особыми точками функции w(z). Поэтому, обходя контур С, мы будем
X
Положительное
направление if,
Ьо
Рис. 4.33. Отображение Шварца—Кристоффеля.
внутренности многоугольника на верхнюю полу-
полуплоскость W.
«скруглять» вершины. Видоизменение соответствующего контура в пло-
плоскости w отмечено на рис. 4.33 маленькими полуокружностями, огибаю-
огибающими точки bt. Эти полуокружности исключают особые точки Ьг из верх-
верхней полуплоскости, где w (z) должна быть аналитической.
Рассмотрим поведение дифференциалов dz и dw при обходе многоуголь-
многоугольника в положительном направлении, указанном на рис. 4.33 стрелками.
Левее Ьо аргумент dw равен нулю (dw действительно), тогда как аргумент
dz определяется направлением отрезка а^а0. В точке а0 аргумент dz пре-
претерпевает скачок на величину <р0, а аргумент dw остается равным нулю.
Как же должна вести себя производная dz/dw вблизи 60? Согласно рис. 4.33,
dz/dw на оси и должна быть действительной при Ьо < и> < Ьг, а переход w
через Ьо, т. е. изменение arg(w — b0) на — тс, вызывает приращение arg (dz/dw)
на величину <р0. Отсюда однозначно вытекает представление dz/dw вблизи
Ьо в виде
^~A(w-bS (w->b0).
Требуемое изменение аргумента в точке Ьо будет обеспечено при а= — <$>0/тс,
так что
^9°/ЭТ (ю->6„). D.7.2)
Применяя это рассуждение последовательно ко всем Ъг, получаем
(w-
(w-
D,7.3)
422 Гл. 4. Функции комплексного переменного
Так как z не должно иметь ни нулей, ни особых точек, отличных от biy
то А в D.7.3) есть постоянная. Согласно принципу отражения Шварца
(см. стр. 372), функцию z можно продолжить на нижнюю полуплоскость,
и притом z не будет иметь там новых особых точек. Проинтегрировав
D.7.3), мы получим формулу, определяющую преобразование Шварца — Кри-
стоффеля
z = z0 + А ^ (w - Ьо) -*•'* (w - 6J"»1'* (w - Ь2Н2'* ...dw. D.7.4)
Итак, формула D.7.4) дает отображение внутренности некоторого мно-
многоугольника с внешними углами (р0, ^i. • - • на верхнюю полуплоскость
плоскости w. Выбирая постоянные z0, |.4| и arg.4, мы можем добиться
того, чтобы многоугольник в плоскости z имел нужное положение и раз-
размеры. Постоянные Ьо, Ьи ... должны соответствовать точкам а0, at,... .
Так как мы располагаем еще тремя произвольными постоянными, то из
чисел Ьо, Ъх, ... три можно задать как угодно. Остальные bt мы найдем,
проинтегрировав D.7.3), выбрав z0 ш А ш подставив значения г = а4. Вообще
говоря, bt являются точками ветвления функции z = z (w).
Одну из точек Ь4 обычно выбирают на бесконечности. Если это Ьо, то
формули D.7.4) принимает вид
z = z0 + А С (w - fci)-*1'71 (w - Ь2)-*21*... dw. D.7.5)
Функции D.7.4) и D.7.5) отображают на верхнюю полуплоскость об
ласть, лежащую внутри многоугольника. Однако часто приходится иметь
дело с областью, внешней по отношению к многоугольнику. При этом на
многоугольнике должно быть выбрано противоположное направление обхода
(т. е. по часовой стрелке), чтобы его внутренность при обходе остава-
оставалась справа. Углы (pt в D.7.4) должны быть взяты с обратными знаками.
Вызывает еще затруднение точка р в плоскости w, соответствующая бес-
бесконечно удаленной точке плоскости z. Точка w = p должна быть полюсом
функции z(w) (заметим, что р не может лежать на действительной оси
в плоскости w), и, следовательно, подинтегральные функции в D.7.4) или
D.7.5) должны еще содержать множитель вида 1/(ш — р). Но одного этого
множителя недостаточно, потому что его аргумент нарушит соответствие
между границей многоугольника в плоскости z и действительной осью
плоскости w. Чтобы избежать этого, введем такой множитель, который при
действительных w принимает действительные значения, т. е. не меняет
аргумента произведения. Таким множителем может служить 1/ [(w — p)(w — р)],
и вместо D.7.4) мы возьмем
(w—p) (w—
D.7.6)
Эта функция отображает область, внешнюю по отношению к многоуголь-
многоугольнику, на полуплоскость w. Напоминаем, что углы взяты, как указано на
рис. 4.33, но с противоположными знаками.
Рассмотрим теперь несколько примеров, чтобы показать, как дейст-
действует на практике изложенная теория. При этом мы ограничимся случаями,
когда интегралы выражаются в элементарных трансцендентных функциях.
Так бывает тогда, когда рассматриваются вырожденные треугольники
и прямоугольники. В случае треугольника функция D.7.5) принимает вид
w- ^H1'71 (w- b2)~nhldw.
Рассмотрим в качестве примера 1 область, изображенную на рис. 4.34.
Углы <рх и (р2 показаны на фигуре, угол <р0 при бесконечно удаленной вер-
4.7. Конформное отображение.
423
шине а0 можно вычислить, если считать заштрихованный многоугольник
пределом треугольника, вершина а0 которого удаляется в бесконечность
в направлении, отмеченном стрелкой.
В этом случае отображение задается функцией
Симметрия в расположении точек аг и а2 позволяет принять Ъх= —1,
Ь2=1; тогда
1 chw.
Для того чтобы вычислить z0 и А, положим z = 0; этой точке соответ-
соответствует w= 1, т. е.
откуда
0 = z0 + А Аг ch 1 = z0,
Случай '
Рис. 4.34. Отображение внутренности вырожден-
вырожденного треугольника на верхнюю полуплоскость ш
(заданные углы сро=л. tpi = cP2 = t/2)-
Далее, точке z = hi соответствует w= —1, т. е.
hi = А Аг ch (— 1) = Аш
и, следовательно,
А = h/v.
Итак, мы получили преобразование
z = — Аг ch йу, w = ch Г — z ).
D.7.7)
Проверить то, что эта функция отображает область, изображенную на
рис. 4.34, на верхнюю полуплоскость, можно, придав z какое-нибудь
конкретное значение. Пусть, например, z = p + ih/2. Тогда ch (tcz/Zz) =
= c\i(m/2 + 7cp/h)= i sh (ър/h), и мы видим, что полупрямая, параллельная
прямым у = 0 и у = h и проходящая посередине между ними, отобра-
отображается на мнимую полуось плоскости w. Отображение D.7.7) как бы рас-
расправляет границу полуполосы и накладывает ее на действительную ось
таким образом, что точки Ьх и Ь2 располагаются симметрично относительно
точки ш> = 0. Естественно, что при этом «средняя линия» полуполосы по-
попадает на мнимую полуось.
424
Гл. 4. Функции комплексного переменного
Если мы хотим отобразить на верхнюю полуплоскость область, внеш-
внешнюю по отношению к заштрихованной на рис. 4.34 полуполосе, то нужно
положить <р0 = — те, <pi = — те/2, <р2 = — тс/2. В этом случае р в формуле
D.7.6) можно положить равным i oo и мы получаем
— 1 dw,
то есть
\/w2 — 1 — Ar ch w).
Значению z = 0 соответствует w = 1, и поэтому z0 = 0; значению z = hi
1
соответствует о> = —1, и поэтому га= ^-Аъг, откуда А = —
Итак,
z = — (Ar ch и; — и; 1
D.7.8)
t f Г
a»
Плоскость г
х ¦
Случай 2
Рис. 4.35. В этом треугольнике углы таковы:
(ро = Зл/2, <f! = Tcf «fg =—тс/2.
В этой формуле нужно еще точно указать ветви функций Ar ch w и
j/ш2 — 1, определив их из условий задачи. Так, например, мы можем по-
потребовать, чтобы значению w=is соответствовали значения
= -^- +Arshs,
1= —Г
при этом
Значения Arshs всегда меньше, чем s j/l + s2, а поэтому z будет иметь-
отрицательную действительную часть. Таким образом, в плоскости w
точки верхней полуплоскости, лежащие на мнимой оси, перейдут в полу-
полупрямую, параллельную действительной оси в плоскости z и идущую от
точки ih/2 к точке — oo -\-ih/2. Мы можем быть уверены при этом, что-
незаштрихованная область рис. 4.34 отображается на верхнюю полу-
полуплоскость плоскости w.
Примеры. Для иллюстрации рассмотрим еще несколько примеров,
отображений настолько подробно, чтобы читатель мог следить за выво-
выводом формул. Область примера 2 изображена на рис. 4.35; это простой
пример поля, «огибающего угол». Если проводящий контур ауа^ай несет
один потенциал, скажем 0, а контур айах — другой, скажем Vo, то
в точке Р при х > d поле однородно, тогда как вблизи а0 силовые линии
имеют форму окружностей; особый характер этого поля обусловлен нали-
4.7. Конформное отображение 425
чием угла в точке а2. Естественно ожидать, что напряженность поля
в а2 бесконечна; интересен вопрос о том, каков порядок этой бесконечности.
В этом случае, если ^ = 0, Ь2=1, то
Чтобы полностью определить преобразование, нужно еще указать линии
ветвления как в плоскости z, так и в плоскости w. Естественно, что для
этого преобразования точки йу = О и а>=1, т. е. точки Ьг, а также оо,
будут особыми. В качестве линии ветвления удобнее всего взять участок
Reu><l оси 1ти> = 0. Из того, что прии>=1 должно бытьг = 0, следует,
что z0 = 0. Будем приближаться к точке w = 0 (z = ax) по двум различным
путям. Один путь, вдоль положительной действительной полуоси в пло-
плоскости w, соответствует пути а0 —> а2 —> а1 вдоль границы. Между а2 и ах
логарифм в последней формуле действителен и положителен, а поэтому
z = 2А (— too). Постоянная А должна быть чисто мнимой. Второй путь,
соответствующий участку границы а0—s-a.,, будет идти вдоль отрицатель-
отрицательной действительной полуоси. При этом логарифм имеет аргумент тс и
z = 2A[ — ico — A/2г) ш] = — Аъ -[- оо = — di -\- оо, откуда А = dijtt. Таким
образом,
z = -
Для проверки положим w=iv. Тогда z-^>(z'—1)оо при v—> оо и
z—> — A/2)di-{- сю при v-^0. Таким образом, мнимой оси в плоскости w
будет в плоскости z соответствовать линия, нанесенная на рис. 4.35
пунктиром.
В плоскости w исходной физической задаче соответствует следующая:
положительная действительная полуось имеет потенциал 0, отрицатель-
отрицательная— потенциал Vo. Решением является потенциал
где б —полярный угол в плоскости w.
Положим W = U-\-iV; тогда w = enWiv°. Наиболее непосредственный
физический интерес представляет электростатическое поле Е. Последнее очень
просто связано с функцией dW/dz = dU/dx -f- idV/dx. В силу условий
Коши —Римана [см. D.2.1)]
dW _ dV ,- <W _
откуда
F • F — • '^K
Полагая dW/dz =» (dW/dw) • (dw/dz), можно выразить Ех — iEy через j
Вблизи w = 0 выражение Ex — iEy оказывается чисто мнимым, ^ — по-
постоянным, а Ех = 0, как и подсказывают физические соображения. При
Re w > 1 это выражение принимает действительные значения, а Еу = 0>
426
Гл. 4. Функции комплексного переменного
как и должно быть вдоль пути az~^a0. При | w\ > 1 имеем
и
dyw
Вблизи а0 силовые линии имеют вид дуг окружностей, идущих от С к D.
Рассмотрим, наконец, поле вблизи а2, т. е. при w, близких к 1. Как
мы и предполагали, поле в этой точке бесконечно. Мы найдем поле в виде
функции от z в окрестност этой точки, выразив |/и>—1 через z при
w —> 1; имеем z ~ Brfi/3ir/) (w — IK'2, откуда Yw — 1 — zl/s и -^x — ^ — z-1/s.
Рассмотрим пример 3 (рис. 4.36), в котором электрическое поле соз-
создается двумя бесконечными пластинами, отстоящими друг от друга на
расстояние*/?, причем одна имеет потенциал 0, а другая Vo. Мы ограни-
ограничимся лишь построением самого отображения; что же касается самой физи-
Плоскость z
Случай 3 ,
Рис. 4.36. Отображение вырожденного четырех-
четырехугольника на верхнюю полуплоскость w.
«Внутренностью» четырехугольника служит вся плоскость г,
за исключением точек, охватываемых линиями aoaiaz и
агазао- В атом случае углы таковы: <jo=2jc, <?1=—я, ?2=2тс,
срз————5^.
ческой задачи, то она решается точно так же, как в примере 2. Сечения
пластин можно рассматривать как вырожденный четырехугольник с вер-
вершинами а0, ах, а2, fl3 (см. рис. 4.36).
Точки Ьг и 53 должны быть симметричны относительно Ь2, поэтому
мы положим feL= — 1, Ь3=1. Тогда
¦ ^ Ldw>
то есть
Значению и>= 1 соответствует z = c/2==zo + 2A, а значению w= — 1 соот-
соответствует z = — с/2 = z0 — 2Л. Отсюда следует, что z0 = 0 и А = с/4, так что
На рис. 4.37 изображено, как отображаются на плоскость w оси хш у
плоскости z. Отрезок оси х от точки — с/2 до точки с/2 превращается
в полуокружность единичного радиуса плоскости w. Ось у, «сжавшись»,
отображается в мнимую полуось от w = 0 до w = i со. Рассматриваемое
¦отображение как бы поворачивает линии а3 ~~> а2 и а2 —> aL от их исходного
положения в плоскости z на 180° через нижнюю полуплоскость и соеди-
соединяет их; на оси х появляется полукруглое вздутие, которое вбирает в себя
всю нижнюю полуплоскость плоскости z.
4.7. Конформное отображение
427
Метод инверсии. Формула Шварца — Кристоффеля может быть приме-
применена и к областям, ограниченным дугами окружностей, с помощью метода
инверсии. Преобразование инверсии естественно возникает при рассмотре-
рассмотрении изображения источника относительно круговой границы. С этим вопро-
вопросом мы уже встречались (см. формулу Пуассона на стр. 353); как уже
упоминалось, точка
а*
—
z
D.7.9)
называется изображением точки z относительно окружности радиуса а
с центром в начале. Преобразование, определяемое формулой D.7.9), назы-
называется инверсией (относительно указанной окружности). Оно отображает
область, лежащую внутри окружности, во внешнюю область, и наоборот.
Инверсия D.7.9) сохраняет величины углов, но изменяет направление
отсчета. Действительно, она представляет собой результат двух последо-
последовательных преобразований: отображения, осуществляемого функцией az/z,
и последующего зеркального отображения относительно действительной
%!=°f'/плоскость и//
Ь, Ь2] Ь3 и
Случай 3
Рис. 4.37. Верхняя полуплоскость ш в примере 3.
Показаны образ оси х и точки, соответствующие г=оэ.
оси. Первое отображение — конформное; второе сохраняет абсолютные вели-
величины углов, но изменяет их знаки.
В этом пункте нам понадобится применить преобразование D.7.9)
к окружности, проходящей через центр круга инверсии. Мы покажем, что
в результате получится прямая линия, проходящая, разумеется, через
точки пересечения обеих окружностей. В плоскости z окружность с цен-
центром в точке z0 (без ущерба для общности z0 предполагается действитель-
действительным и положительным), проходящая через начало координат, имеет
уравнение
ИЛИ
zz-(zzo4-zzo) = O. D.7.10)
Для того чтобы получить равнение соответствующего геометрического
места в плоскости w, нужно выразить z и z через шиш, пользуясь ра-
равенством D.7.9), и подставить в D.7.10). При этом мы получаем
о4 г о2 о2 -\ „
ww V w ' w J
Отсюда, обозначив и = Беи>, приходим к уравнению
и =-
что и доказывает наше утверждение.
Роль инверсии в обобщении формулы Шварца — Кристоффеля теперь
ясна. Пересекающиеся дуги окружностей, такие, как Р и Q на рис. 4.38,
428
Гл. 4. Функции комплексного переменного
подвергаются инверсии относительно окружности R радиуса а с центром
в точке пересечения Р и Q. Сама точка пересечения переходит при этом
в бесконечно удаленную точку, а дуги Р и Q — в части прямых Р' и Q'\
изображенные сплошными линиями. Теперь к этим прямым можно приме-
применить отображение Шварца — Кристоффеля.
Отображение Шварца — Кристоффеля применимо и к более сложным
контурам, состоящим из дуг окружностей. Однако рассмотрение их
Онрутнисть
Плоскость z
Р .
Плоскость иг
Р
Окружность В
Рис. 4.3S. Инверсия (относительно окруж- Рис. 4.39. Инверсия дуги окруж-
окружности В) дуг окружностей Р и Q, превра- ности Р относительно окружности
щающая их в части прямых Р1 и Q'. R, переводящая дугу Р плоскости z
в участок прямой Р плоскости ш.
завело бы нас слишком далеко. Поэтому мы ограничимся случаем, когда
имеется не более двух пересекающихся дуг окружностей, и отошлем любо-
любознательного читателя к другим руководствам, где рассмотрены более общие
контуры. На рис. 4.39 изображена одна дуга и преобразованный контру,
который был рассмотрен выше в примере 3.
4.8. Преобразование Фурье
В будущем нам часто придется применять преобразование Фурье, а также
связанные с ним преобразования Лапласа и Меллина. В настоящем пара-
параграфе мы изучим те свойства этих преобразований, которые окажутся
полезными нам в дальнейшем.
Преобразованием Фурье функции У (ж) называется функция F(k), опре-
определенная формулой
/-(*) =
/2л
e%hxf{x)dx.
D.8.1)
Здесь и в дальнейшем преобразование какой-либо функции будет обозна-
обозначаться той же буквой, что и исходная функция, но прописной. Того же пра-
правила мы будем придерживаться, применяя другие преобразования, так
как подчеркивать различие требуется не всегда. В тех случаях, когда
это нужно, мы будем приписывать индексы /, I и т, обозначающие соот-
соответственно преобразования Фурье, Лапласа и Меллина. Так, Ff будет
обозначать преобразование Фурье функции /. Впрочем в отдельных слу-
случаях будут употребляться буквы JF, X и eS, так что преобразование-
Фурье функции / будет также обозначаться JF(f).
4.8. Преобразование Фурье 429
Основную роль в этой теории играет интегральная теорема Фурье
•(или интеграл Фурье), согласно которой
со со
/ (х) = JL \ dk \ в«<5-*> / (С) «*С. D.8.2)
—СО —СО
Вводя в D.8,2) выражение для F(k), получаем
со
Цх)=-*= \ e~**F(k)dk.
—со
В талой форме D.8.2) часто называется формулой обращения Фурье.
Связь с рядами Фурье. Прежде чем сколько-нибудь подробно рас-
рассмотреть условия, при которых справедлива интегральная теорема Фурье,
полезно рассмотреть связь этой теоремы с рядами Фурье. Рассмотрим ряд
по синусам функции h (х) в промежутке 0<a;<Z
. ППХ
sin-p
Такого рода ряды мы рассматривали в гл. 2, где они играли важную
роль в задаче о колебаниях струны; мы вернемся к ним еще в гл. 6. Из
соотношений
г
ппх . тих , 1 „
sin -=- sin -j—dx = -^ h
I/O ?j
иолучаем выражения коэффициентов
t
А — 2 ^ h( \ ' тса;,7
О
Подставляя эти выражения в ряд для h (x), приходим к формуле
со I
п\х)— — Zi \ ) n^)sm — a^jsm-j-.
n=0 0
Посмотрим теперь, как будет вести себя этот ряд при I —» со. Для
этого введем функцию целочисленного аргумента к = кп = mz/l. Обозна-
Обозначив Д& = Ап+1 — кп = тс//, запишем
Довольно ясно, что при I—> со, когда ДА-^О, этот ряд имеет своим пре-
пределом интеграл
со со
-М dk{ h (С) sin AC sin kx d',. D.8.3)
о о
Эта формула справедлива лишь для нечетных функций. В случае
четной функции g(x) следует воспользоваться разложением в ряд по
430 Гл. 4. Функции комплексного переменного
косинусам, которое приводит нас к формуле
со со
g (х) = 1 ^ dk ^ g (С) cos Щ cos kx d?. D.8.4)
Ясно, что в формулах D.8.3) и D.8.4) можно, введя множитель 1/4, распростра-
распространить интегрирование на всю числовую ось, так что, например, первая и»
этих формул может быть записана в виде:
h (х) = g- \ dk \ h (?) sin Щ, sin kx dZ,.
-OO —CO
Для того чтобы получить формулу, пригодную для произвольной функции,
представим эту последнюю в виде суммы четной и нечетной функции, а
именно
В силу равенств
со со
\ h (x) cos kx dx = 0, \ g (x) sin kx dx = 0
мы
получаем
/(
—со
¦ ^ *
!
+ 4^
СО
\
— СО
со
—со
со
со
dk \
—СО
со
—со
со
-С)] сое ft? cos
—со —со
откуда
I 1X1 ^^ 7)—' \ tlfi \ / \^а) CUO /ь 1Ц XI иЦ* I *±.O.U J
—СО —СО
Для того чтобы получить формулу D.8.2), заметим, что
со со
i \ dk \ /(QsinA:(C-a;)dC = O, D.8.6)
— СО —СО
если только этот интеграл сходится, так как интеграл
представляет собой нечетную функцию переменного к. Предполагая, чта
интеграл D.8.6) существует, сложим почленно формулы D.8.5), D.8,6)
и. получим интеграл Фурье D.8.2).
Эти выкладки показывают, что интеграл Фурье представляет собой
аналог ряда Фурье для случая непериодической функции, заданной в про-
промежутке — сю < х < оо. В задаче о колебаниях струны интеграл Фурье
4.8. Преобразование Фурье 431
служит для описания движения бесконечной струны, простирающейся
от —со до +оо. В случае полубесконечной струны, простирающейся
от 0 до + со и закрепленной в точке х = 0, более удобна формула D.8.3).
Формулы D.8.3) и D.8.4) часто называются интегралами Фурье соответ-
соответственно по синусам и по косинусам. Функции
Fs(k)= У~ \ f(x)sinkxdx D.8.7)
о
Fc (k) = j/"^ \ f (x) cos kx dx D.8.8)
называются соответственно синус- и косинус-преобразованиями Фурье
функции f(x). Сами формулы D.8.3) и D.8.4) можно трактовать как фор-
формулы обращения
D.8.9)
б
CO
/(x)=j/-( Fc(k)coskxdk. D.8.10)
Некоторые интегральные теоремы. Только что приведенный вывод,
интеграла Фурье носит чисто эвристический характер и не дает никаких
указаний относительно границ применимости этой формулы. Теперь мы
должны подойти к этому вопросу с большей строгостью. Чтобы добиться
наибольшей общности результатов, необходимо прибегнуть к понятию
интеграла Лебега. Недостаток места не позволяет нам сколько-нибудь
подробно коснуться тонких вопросов, относящихся к теории меры и инте-
интеграла Лебега. С чисто практической точки зрения интеграл Лебега отли-
отличается от обычного интеграла Римана тем, что первый определен для любой
ограниченной функции, которая может реально встретиться в математи-
математическом анализе и в прикладных вопросах, каково бы ни было множество
ее точек разрыва, тогда как интеграл Римана от функции, имеющей
несчетное множество разрывов, вообще говоря, не существует *). С другой сторо-
стороны, для тех функций, для которых существует интеграл Римана, интеграл
Лебега также существует и совпадает с римановым интегралом. В то же
время, говоря образно, интеграл Лебега можно определить даже для таких
функций, которые в некоторой области колеблются «бесконечно часто».
В качестве примера, иллюстрирующего различие этих интегралов, можно
привести функцию f(x), определенную в промежутке @, 1) и принимающую
значения 1 и 0 соответственно при рациональных и иррациональных зна-
значениях х. Интеграл Римана такой функции не определен, лебеговский же
интеграл существует и равен нулю. Заметим, наконец, что интеграл Лебега
обладает всеми основными свойствами интеграла Римана.
*) По поводу интегрирования функций общего вида (т. е., вообще говоря,
неограниченных), играющих какую-либо роль в приложениях математики, заметим
следующее. Если функция такого рода не меняет знака, то ее интеграл Лебега либо
конечен (в этом случае функция называется интегрируемой по Лебегу), либо равен
бесконечности; интеграл же Римана от такой функции может вовсе не существовать-
Функция, меняющая знак, считается интегрируемой по Лебегу, если интегрируема ее
абсолютная величина. —Прим. ред.
432 Гл. 4. Функции комплексного переменного
О функции f(x) говорят, что она принадлежит лебеговскому классу
V (р > 0) на интервале (а, Ь), если | /(ж) |р интегрируема (в смысле Лебега)
на этом интервале.
Прежде чем доказывать интегральную теорему Фурье, мы выведем
формулу Парсееаля
оо оо
\ \F(k)\*dk = ^ \f{x)\4x. D.8.11)
—оо
Эта формула применима, если f(x) принадлежит классу L2 на интервале
(— со, со). Ниже мы увидим, что интеграл Фурье является почти непосред-
непосредственным следствием формулы Парсеваля. Для доказательства этой послед-
последней рассмотрим интеграл
оо
= С
Подставляя в / интеграл, выражающий F (А), получаем
со оо оо
) 7(
оо оо
= А- С f(x)dx \
Выполнив интегрирование по к, преобразуем / к виду
оо оо
1 = y=r \ ftxW* \ f?)e-<*-^*dt;. D.8.12)
—оо —оо
Теперь мы можем показать, что F(х) принадлежит классу L2 в интервале
(—со, со). Записывая / в виде
—со —со
и применяя к этому интегралу неравенство Шварцаг), получаем
СО ОО
4-т ( ^ [ \f(x)\ze-l*-tf№2dxdi, \ \
В пределе при о —» 0 отсюда имеем
\F(k)\4k<
*) Одна из форм неравенства Шварца была выведена в гл. 1. В том виде,
в каком оно используется здесь, это неравенство читается так: если функции и (х, С)
в v (х, ?) принадлежат L2, то
4.8. Преобразование Фурье 433
Мы видим, что F(k) принадлежит классу Lz в интервале ( — оо, оо), коль
скоро этим свойством обладает / (х).
В действительности, как мы сейчас докажем, последнее соотношение
сводится к равенству. Произведя в D.8.12) замену переменной интегриро-
интегрирования С = х + у, мы получим
о оо
J (x + y)f(x)dx. D.8.14)
Известно, что график функции е-ы2/28 jy\f2n8) становится все более и более
заостренным при о—>0, но интеграл ее по у при всех значениях 8 равен 1.
Поэтому если интеграл
«аи
= \
представляет собой достаточно гладкую функцию вблизи у = О, то есте-
естественно ожидать, что / стремится к h @) при 6=0. Справедливость этого
вытекает из интегрируемости квадрата модуля функции h (x), т. е. из того
факта, что h (у), как функция от у, принадлежит классу L? в интервале
( —оо, оо). Таким образом, для того чтобы получить предел функции /
при 8—>0, достаточно положить у=0 во внутреннем интеграле D.8.14);
при этом получаем формулу Парсеваля
k = ^ \f(x)\2dx. D.8.15)
—оо
Следует подчеркнуть, что это доказательство относится как к действитель-
действительным, так и к комплексным функциям /.
Интегральная теорема Фурье. Перейдем теперь к доказательству инте-
интегральной теоремы Фурье в том виде, как она была сформулирована
Планшерелем.
Предположим, что функция f (x) принадлежит классу L2 на интервале
(—оо, оо), и пусть
Тогда при а~> со функции F (к, а) сходятся в среднем к функции F(k)
на интервале (— оо, оо), и если
то f(x, а) сходятся в среднем к f(x).
Сходимость в среднем F (к, а) к F (к) на интервале (— со, с») означает,
по определению, что
оо
Ищ \ | F (к, a)-F (к) \Чк = 0. D.8.16)
а~>оо J
—оо
Иначе говоря, функция F (к, а) приближенно представляет функцию F (к)
со средней квадратичной погрешностью, стремящейся к нулю при а—э-оо.
28 Ф. м. Морс и Г. Фешбах
434 Гл. 4. Функции комплексного переменного
Для доказательства этой теоремы подставляем в D.8.15) F-\- С вместо
F и f-\-g вместо /. Мы получаем
\F + G\*dk=
В силу формулы Парсеваля отсюда следует, что
оо
Re(FG)dk = ^ Re{fg)dx.
Подобным же образом, подставив в D.8.15) F-j-iG вместо F и f + ig
вместо /, приходим к равенству
^ Im (FG)dk = \ Im (Jg)dx.
—сю —во
Следовательно^
оо оо
^ FGdk= ^ fgdx, D.8.17)
и из этой невинной маленькой формулы будут вытекать почти все нужные
нам теоремы, касающиеся преобразования Фурье.
Пусть функция g(x) равна 1 на интервале (О, С), а вне этого интер-
интервала равна нулю. Преобразованием Фурье этой функции служит
G (к) = —^ { eih*dx = -4=- elh-7* •
Отсюда, согласно предыдущему абзацу, вытекает равенство
оо С
-±=- \ F(k)^—ir—dk=\fdx.
г -со О
Пзяв производные по С от обеих частей, получим
т. е. обычную формулу обращения1).
Нам нужно еще показать, что функция F (к) существует, т. е. что
F(к, а) сходятся в среднем к F(к) при а—> оо. Так как
= ^=г^ f(x)eihxdx,
*) Это рассуждение, а также некоторые последующие рассуждения в этом пара-
параграфе проведены не вполне аккуратно. См., например, книгу Е. К. Титчмарша,
Введение в теорию интегралов Фурье, М.—Л., 1948.—Прим. ред.
4.8. Преобразование Фурье 435
то F (к, а) является преобразованием функции, равной / (х) при | х | < а
и тождественно равной нулю при j х | > а. Разность же Н (к, а) = F (к, а) —
— F(к) является преобразованием 'функции, равной нулю при |:г|<а
и совпадающей с / (х) при | х | > а. Применяя формулу Парсеваля, получим
\H(k,a)\*dk = $ \F(k,a)-F(k)\*dk = ^ \f{x) \2dx+ ^ \f{x)\*dx.
Мы видим, что \.\F(k,a) — F(k)\2dk—>0 при а—>со, т. е. соотноше-
соотношение D.8.16) справедливо.
Свойства преобразования Фурье. Доказав интегральную теорему
Фурье, обратимся теперь к выяснению свойств преобразования Фурье
в комплексной плоскости. Особенно ценной будет для нас следующая
теорема:
Пусть функция f(z) (z= x+iy) аналитична в полосе
У-<У<У+,
причем у+ > 0 и у_ < 0. Если в любой полосе, лежащей внутри исходной
полосы,
Ае*-Х при х —-> + оо,
где %_ < 0 и т:+ > 0, то функция F (к) (к = а + z't) аналитична в полосе
причем в любой полосе, лежащей внутри этой,
е~У*я при о—* + оо,
' I De-»-* при о-» —оо;
здесь А, В, С ж D — действительные постоянные.
Для доказательства достаточно заметить, что аналитичность функции
со оо
=~=- \ f(z)e-<*e*»<dx
сю
обусловлена характером сходимости определяющего интеграла. Если
ч;_<х<'с+, то модуль подинтегральной функции убывает как е<т— г>х или
как е(-с*~^х соответственно при х—> + оо или при х—> — оо. Тем самым
обеспечивается равномерная (относительно к = о -\- гт) сходимость рассма*
триваемого интеграла и, следовательно, аналитичность функции F(k).
Рассмотрим теперь поведение F (к) в полосе х_ < х < х+. Так как /(z) —
аналитическая функция, то интеграл, определяющий F (к), можно взять
вдоль прямой, параллельной оси х и лежащей в полосе у_ < у < у^. Тогда
=-
—оо — -х
Отсюда мы заключаем, что при | о | —> оо
| F (к) | < Ее—У.
Для значений у, близких к г/+, сходимость рассматривается лишь при
а > 0, а для у, близких к у_, — при о < 0. Тем самым теорема доказана.
28*
436 Гл. 4. Функции комплексного переменного
В том случае, когда функция / (ж) не принадлежит классу L2 на интер-
интервале (— со, со), например из-за ее поведения при ж—>-}-оо, может случить-
случиться, что некоторая функция вида
все-таки принадлежит классу ZA Применяя к g(x) формулу обращения,
получаем
g(a) = /(aOe-V= * С G(k)e-ihxdk,
откуда
—оо
\ §
Г
-oo+iT0
Функция G(C —гЧ0) весьма просто связана' с F(k). В самом деле,
и
G (С - к0) = -^
откуда получается следующая формула обращения:
F(k)e-ik*dk. D.8.18)
-оо+гт0
Однако часто случается, что одного множителя вида е~тож недостаточно
для всего интервала — со < ж < оо. Тогда мы вводим функции
О, ж < О,
О, ж>0,
/ (х) е~^х, х < 0 (х1 < 0).
При этом постоянная х0 выбирается по возможности меньшей, а ~х— боль-
большей, но так, чтобы /+ (х) и /_ (х) принадлежали L2 при ж—> ± со. Соот-
Соответствующими преобразованиями являются
о
где А = о -|- гЧ.
" Согласно интегральной формуле Фурье,
4.8. Преобразование Фурье 437
оо+гт0
=ik 5
откуда следует, что
*AJ \ lit/ ^* V/1
О (х<0)
-оо+1Т0
Аналогично
co-f iTt
U (z>U) | i r F_(k)eihxdk.
f(x)(x<O)j V2*_J+iH
Складывая почленно, получаем формулу обращения
со+гт0 oo+i^
/(a;) = -Lr \ F+(k)e'ihxdk+ [ F_(k)e'ihxdk. D.8.19)
—oo+iTn —оо+гт,
0 1 ¦
Аналитичность функций Ft и F_ вытекает из предыдущей теоремы. В силу
определения функции Ft интеграл, ее представляющий, сходится при х > х0,
а поэтому Ft аналитична в полуплоскости k = a-{-ix, расположенной над
прямой х — х0. Аналогично функция F_ аналитична в полуплоскости х < хх.
Рассмотрим, например, функцию / (х) — еш. В этом случае можно поло-
положить хо=1-(-з и хх= —1 — г, где е — сколь угодно малое положительное
число. Функции F + и F_ будут, следовательно, аналитическими соответ-
соответственно при х > 1 и при х < — 1. Чтобы убедиться в этом, вычислим эти
функции:
со
= -4= \
F =
Для функций F_ и jP+ точки /с = г и к= — i соответственно являются
особыми; эти точки определяют области аналитичности F+ и F_. Функция
Ft, например, аналитична выше прямой ImA=l.
Асимптотические значения преобразования. Здесь уместно рассмотреть
асимптотическое поведение функций F\ и /+, а также функций F_ и /_.
Предположим что F+(k) можно разложить в ряд по степеням \/к
г п=1
Вводя это разложение в формулу обращения D.8.19)
" -co+iT0
получаем
оо+й„
p-ikx
438 Гл. 4. Функции комплексного переменного
Воспользуемся теперь равенством
то+гт0
2п , J ik 10 г <Г О
которое получается из формулы обращения, поскольку непосредственным
интегрированием легко убедиться в том, что ( — 1/|А2ге) (i/ik) представляет
собой преобразование функции, равной 1 при х > 0 и 0 при х < 0. После-
Последовательно интегрируя по х обе части этого равенства, приходим к формуле
co+vr
х° .-ita Г
= \ (п-1)!
Отсюда получаем
то есть
. «. = /"-» (О).
1аким образом,
F №==_j_y?
Мы замечаем, что поведение Ft(k) при больших значениях \к\ в верхней
полуплоскости связано с поведением / вблизи нуля.
Общая формулировка. Рассмотрим теперь вопрос об обращении фор-
формулы D.8.19). Предположим, что нам дано выражение
=
G(k)e-ikxdk+
-оо+гт0
При каких условиях G и Н можно отождествить соответственно с F+ и F_ ?
Согласно предыдущему, одна из этих функций должна быть аналитической
выше некоторой прямой, параллельной действительной оси, а другая — ниже
некоторой другой прямой, также параллельной действительной оси. Далее
если области аналитичности этих функций перекрываются, то должно быть
Ft = — F_ и, следовательно, G= —H. Это следует из определения функций
Ft mF_, так как, разлагая / в ряд по степеням а; и интегрируя почленно (если
это возможно), мы получим для F+ и —F_ одно и то же разложение по степе-
пям\ХЦК. Таким образом, F+ и — F_ совпадают в общей части их области
аналитичности и, следовательно, F+ служит аналитическим продолжением
функции — F_ в верхней полуплоскости, a F_ — аналитическим продолже-
продолжением] — jF+ в нижней полуплоскости. Отсюда мы можем заключить, что
если G не равна — Н, то G и Н могут быть отождествлены с F+ и F_
лишь в том случае, когда не существует области, в которой обе эти
функции были бы аналитичны.
Функции G и Н не могут быть отождествлены с F+ и F_ и тогда,
когда G и Н являются аналитическими не в полуплоскостях, а в непере-
неперекрывающихся полосах. Однако в этом случае важный вывод можно сделать
тогда,1* когда / = 0, т. е. при условии
oo+iTQ oo+i^j
^ G(k)e'ikzdk+ ^ H(k)e-ihzdk = 0. D.8.20)
4.8. Преобразование Фурье
439
Точнее говоря, предположим, что выполняется D.8.20) и, кроме того:
1) G аналитична в полосе -с^ < t < т^', содержащей прямую ъ = ъ0;
2) Н аналитична в полосе T^<t<x^, содержащей прямую х = х1;
3) <<<;
4) G и Н принадлежат классу L1 в интервале ( —оэ, сю);
5) G и Я стремятся к нулю, когда |о|-^оо в соответствующей полосе
(А = о -f- iz).
При выполнении всех этих условий можно показать следующее:
1) функции G и Н обе аналитичны в полосе z[ < ¦z < i?,
2) в этой полосе G -\- Н = 0.
Области, о которых идет речь в условиях и в утверждении теоремы,
изображены на рис. 4.40 соответственно слева и справа.
Для доказательства умножим D.8.20) на eKz и проинтегрируем по z.
В силу абсолютной сходимости интегралов в D.8.20) порядок интегрирова-
интегрирования можно обратить. При этом мы получаем
D.8.21)
-оо+й,
. ^ /Q аполитична //
////////////^
у///////////////////////////,;.
г;
плоскость k=a*ix
Плоскость i
Рис. 4.40. Области аналитичности функций Рис. 4.41. Контуры при аналити-
G и. Н. ческом продолжении функций G и Л.
Выберем С так, чтобы ImC была заключена между т0 и \. Применяя инте-
интеграл Коши к контуру, изображенному на рис. 4.41, получаем
oo+iin
-OO + IT.
Отсюда
tT"
-oo+it"
D.8.22)
где tj > i± > Tj. Значение Im ? в левой части может быть любым между
t'o и tj, а следовательно, формула D.8.22) дает аналитическое продолжение
функции G(C) за пределы ее исходной области аналитичности.
Точно так же
D-8.23)
где 1[ < Im Z < V
440 Гл. 4. Функции комплексного переменного
Мы видим, что при tj < Im С < t0 справедливы обе формулы D.8.23)
и D.8.22). Фиксировав ? в этой области, вычитаем D.8.22) из D.8.23):
oo+ii'jj
Так как ? лежит вне контуров интегрирования, то оба последних интеграла
равны нулю. Тем самым теорема доказана.
Полученных сведений из общей теории для нас достаточно. Мы позна-
познакомились с интегралом Фурье, выяснили аналитические свойства преобразо-
преобразования Фурье и получили выражения преобразований и формулы обращения
для тех случаев, когда из-за поведения функции при ж—> + со или ж—> — оо
не удовлетворяются условия теоремы Фурье. Теперь мы перейдем к при-
приложениям.
Свертка. Интеграл
со
= \f(y)h(x-y)dy D.8.24)
называется сверткой функций / и h. Название связано с тем, что аргумент
ж—у функции h свернут по у. Мы покажем, что если и / и h принадлежат
классу L2 в интервале (— оо, оо), то преобразованием Фурье этого инте-
интеграла служит F(k)H(k), т. е. произведение преобразований функций /
и h. Эта теорема оказывается чрезвычайно полезной при решении некоторых
интегральных уравнений (см. § 8.4). Вытекает она непосредственно из фор-
формулы Парсеваля D.8.17). В самом деле, если g{y) = h(x — y), то
G"= L ^ e-ihvh(x —
V2n J
— OO
Положим ж— у;=?, так что
оо
—со
Отсюда в силу D.8.17)
77=- \ 1 (У) h (х - у) dy = -1=, ^ F (к) Н (к) е'^ dk, D.8.25)
—оо —оо
что и требовалось» доказать. Таким образом, интеграл D.8.24) является как
раз обратным преобразованием Фурье функции FH. В силу взаимности,
существующей между функциями и их преобразованиями Фурье, формуле-
D.8.25) можно придать иной вид
4.8. Пресбрааование Фурье 441'
так что преобразованием произведения fh служит свертка преобразований
функций / и h (т. е. свертка функций F и Н).
Эту теорему можно обобщить. Рассматривая правую часть формулы
D.8.25) как функцию от х, умножим обе части этой формулы на p(z— х)
и возьмем интеграл по х. Получим функцию от z, равную
со
p{z-x)h(x-y)f(y)dydx= \ P(k)H(k)F(k)e-ikzdk.
В качестве примера применения формулы D.8.25) рассмотрим простое
интегральное уравнение
в котором функции g и h даны, а искомой является функция /. Подвергая
обе его части преобразованию Фурье, приходим к уравнению
откуда
/27C Я (ft)
и
Н (к)
—оо
Это, конечно, только частное решение рассматриваемого интегрального
уравнения; кроме того, оно годится лишь в том случае, когда функция
G/H принадлежит классу L2 в интервале ( — оо, оо). Уравнения такого
вида будут рассмотрены более полно в § 8.4.
Формула суммирования Пуассона. Интеграл Фурье иногда помогает
также при вычислении сумм рядов. Так, например, сумма ряда весьма
оо
общего вида S= ^] f{an) может быть вычислена следующим образом.
п=— оо
Допустим, что / принадлежит классу L2 в интервале ( — оо, оо). Если
взять функции
то
eo+ii0
\ FWe-ihxdk D.8.26)
где в силу предположения относительно / постоянную х0 можно считать
отрицательной. Преобразование Ft (к) представляет собой аналитическую
функцию при t > 1д, где х0 > %'о (см. рис. 4.41). Мы имеем также
/_0г) = -7^ С F_(k)e'ikxdk, D.8.27)
¦442 Гл. 4. Функции комплексного переменного
где tx можно выбрать положительным, и F_ (к) аналитична в области
¦с < tj , где %г < %{.
Имея это в виду, расщепим S на две суммы
п=0 п=—оо
Сначала рассмотрим S+. Вводя D.8.26) в выражение «S+f получаем
—co+i-:0
В силу абсолютной сходимости интеграла, представляющего /+, сумми-
суммирование можно внести под знак интеграла
со+гто оо oo+ixo
~~ \f~2H V 1—e-i
dk.
ifca
—co+ito
Функция /*+ аналитична в верхней полуплоскости, и, если она достаточно
¦быстро убывает при | к \ —> со, мы можем в правой части прибавить интег-
интеграл по полуокружности бесконечно большого радиуса, лежащей в полу-
полуплоскости над прямой -с = т0 и соединяющей точки — со ¦+ j"x0 и со 4- «0.
Постоянная t0 отрицательна, поэтому мы можем применить теорему Коши
и найти вычеты подинтегральной функции в нулях знаменателя, т. е.
в точках к=2тп/л, где т принимает целые значения, положительные
и отрицательные. Таким образом, мы получаем, что
Аналогично
rtt=—оо
¦Следовательно,
то есть
D-8-28)
где /"—преобразование Фурье функции /. Это и есть формула суммиро-
суммирования Пуассона.
Возьмем в качестве простого примера функцию / (п) = 1/A -j- n2).
Преобразование Фурье
F(k)= \f\e-\*\
этой функции легко найти с помощью теории вычетов. Применяя фор-
4.8. Преобразование Фурье 443
мулу D.8.28), получаем
21 _" f V
1 + aW ~ a \2j
0 т=—со
1 _в-2«/а J'
т=:0
или
со
У, * . =JLcth-. D.8.29)
В последующих главах мы часто будем пользоваться формулой Пуассона
Jcm., в частности, формулу G.2.30)].
Преобразование Лапласа. Преобразование Лапласа функции.
определяется формулой
СЮ
F^p) = [ f (x) e~px dx. D.8.30)
Изучение свойств преобразования Лапласа может быть сведено к изуче-
изучению свойств преобразования Фурье, потому что, как мы увидим, первое
приводится ко второму. В самом деле, рассмотрим функцию
J f{x), x>0,
МаИо, х<0.
Взяв ее преобразование Фурье
и сопоставив это выражение с D.8.30), мы замечаем, что
^ D-8.31)
Вооруженные этим соотношением, мы сможем, исходя из известных
теорем для преобразования Фурье F+, получить соответствующие теоремы
для преобразования Лапласа Ft. Например, из формулы обращения D.8.19)
[ Ft{k)e~ihxdk
—oo+ito
посредством подстановки к = ip получаем формулу обращения преобразо-
преобразования Лапласа
то+it»
^(Ж) = ^Г \ Fi(P)eVXdP (Rez>0). D.8.32)
То—ioo
Рассмотрим в качестве примера функцию / (х) = егдх. Для нее
Подставляя это преобразование в формулу D.8.32), получаем интеграл
To+ioo
1 С ег>х
•СО—i
444 Гл. i. Функции комплексного переменного
который легко вычисляется с помощью теории вычетов. При х > О мы
замыкаем контур интегрирования полуокружностью, лежащей в левой
полуплоскости, и получаем выражение /+ = eiqx. При х < О вспомогатель-
вспомогательную полуокружность следует взять в правой полуплоскости, а так как
в этой области подинтегральная функция аналитична, то /+ = 0, когда
х < 0, как и следовало ожидать.
Теорема о свертке играет важнейшую роль в приложениях преобра-
преобразования' Лапласа. Так как /+ (у) <= 0 при у < 0 и h+ (х — у) = О при х < у, то-
{x — y)dy=^ f(y)h(x — y)dy.
Подставляя это выражение в формулу D.8.25), получаем теорему о свертке
для преобразования Лапласа
О -oo+iT0
ИЛИ
то+ioo
±. \ F^H^e^dp. D.8.33)
0 To—ioo
Иначе говоря, преобразование Лапласа функции \ / (г/) h (x — у) dy равно
произведению преобразований Лапласа функций / и h.
В качестве примера применения этой теоремы возьмем интегральное
уравнение типа Вольтерра, встречающееся в теории начальных задач:
=Д k{t-z)g{z)dx;
здесь / — заданная функция, a g — искомая. Это уравнение будет рассмот-
рассмотрено в гл. 8. Здесь же мы, без доказательства, ограничимся лишь ука-
указанием на то, как можно его решить. Следует подвергнуть обе части урав-
уравнения преобразованию Лапласа, в результате чего получим
Отсюда
F{p)
To+ioo
То—too
Дальнейшее рассмотрение преобразования Лапласа и его применений
читатель найдет в гл. 5, 8, 11 и 12.
Преобразование Меллина. Другое важное преобразование, тоже тесно
связанное с преобразованием Фурье, определяется формулой
оо
Fm(s)=\f{x)x-1dx. D.8.34)
4.8. Преобразование Фурье 445
Так, например, преобразованием Меллина функции е х служит Г (s). Для
того чтобы установить связь преобразования D.8.34) с преобразованием
Фурье, положим х = ez. Тогда
S(z) = /(е2)- Сравнивая это выражение с преобразованием Фурье
функции g(z), замечаем, что
Fm{s) = V2^G(-i8). D.8.35)
Теперь можно перефразировать теоремы, относящиеся к преобразованию
•Фурье, применительно к преобразованию Меллина. Начнем с рассмотрения
условий существования преобразования. Существование интеграла (в смысле
¦Лебега)
\gWdz
эквивалентно существованию интеграла
f(x)\*^. D.8.36)
о
Теперь выведем формулу обращения. Так как
оо loo
TO
Если условие D.8.36) не выполнено, то интеграл D.8.34) может существо-
существовать лишь в некоторой полуплоскости вида Res>o0, а вне этой полу-
полуплоскости функция Fm (s) может быть определена путем аналитического
продолжения. Пример такого рода мы имели в § 4.5 при рассмотрении
гамма-функции. При этих условиях формула обращения D.8.37) перестает
быть справедливой. Однако в этом случае наши выводы могут быть приме-
применены к функции a?of(x), где а'о > с0. Преобразованием ее является функ-
функция Fm(s-\-a'o). Формула D.8.37) при этом дает
откуда, положив s + Cj = 5, мы получаем
446 Гл. 4. Функции комплексного переменного
В тех случаях, когда нет такого значения Res, при котором интег-
интеграл D.8.34) сходится при всех х, приходится разрезать область опреде-
определения /(ж) и брать две различные функции, обладающие каждая своим
множителем, которым обеспечивается сходимость, так же, как это дела-
делалось с преобразованием Фурье [см. формулу D.8.18) и следующие за ней
абзацы]. Это построение, вполне аналогичное приведенному выше, вынесено-
в задачи.
Обратимся, наконец, к теореме о свертке, относящейся к преобразо-
преобразованию Меллина. Взяв формулу D.8.25) и осуществив подстановки
«"-¦ч. /(у) = о(ч).
ех = ?, Л (ж - у) = го («*"*) = го
приходим к формуле
со °0+io°
О °0~io°
которой можно придать еще такой вид
со <rO + io0
JoWro^e-MS-JL \ Vm(j>)Wm{s-P)dp. D.8.40)
В качестве примера применения формулы D.8.40) вычислим интеграл
o0'-io
Заметив, что f(x) — e~xxa, если Fm (s) = Г (а + s), воспользуемся форму-
формулой D.8.40):
С»
3'1 dx = Г(°ц+8) .
Положим s = а в / и вычислим интеграл вдоль мнимой оси. Мы получим
следующее интересное соотношение между значениями F(z) при действи-
действительных z = а и комплексных z = a-{-it:
Изучив поведение функций комплексного переменного, мы перейдем
в следующей главе к исследованию их связи с дифференциальными урав-
уравнениями.
Задачи к главе 4
4.1. Доказать, что
2тс
Г sin2 6 db
j a + b cos В
о
Задачи к главе 4 44?
4.2. Доказать, что
q cos о (Cos — sin 1 cos
t (?sin6) p (?sm6 + 6)d6 = 2rc
4.3. Доказать, что
со
cos ж da;
С
У
Каково значение этого интеграла при а = b, Re а > О?
4.4. Доказать, что
^ eccsl cos (пб - sin G) dti = -2J-.
о
4.5. Доказать, что
со
\ -у——г- da; ¦= -к- и cosec тга @ < а < 1).
4.6. Вычислить интеграл
со
Г x2dx
J A + ж2) A —2
— оо
4.7. Доказать, что
4.8. Доказать, что
J 1 + z2 ^Z = "8~ "
4.9. Рассмотреть действительный интеграл
ь
^(b-xy(x-a)n^-1F{x)dx,
а
где а и Ь — действительные числа, Ъ > а, р. > — 1, и —целое число, боль-
большее р., и znF(z)~^0 при |z|—» оо. Функция F(z) предполагается аналити-
аналитической во всей плоскости z, за исключением конечного числа полюсов ск,
ни один из которых не лежит на действительной оси левее точки z = b..
Показать, что заданный интеграл равен
где контур С идет от точки 6 + е к — оо непосредственно под действитель-
действительной осью, затем вдоль окружности бесконечно большого радиуса против
часовой стрелки и от — оо возвращается к точке Ъ -\- е, идя непосредст-
непосредственно над действительной осью. Вывести отсюда, что этот интеграл равен
те cosec f№ 2(Res (z — fcf (z — a)'11 ^ (z) в ch).
448 Гл. 4. Функции комплексного переменного
Показать, что при 0 < р < 1, /с > 1
4.10. Доказать, что
со
х~а dx тс sin aft
J 1 + 2х cos 6 + х2 smna sin
о
4.11. Воспользовавшись формулами D.2.19), показать, что
sinkxsmk'x , __«_ | sin kl cos /c'S (/c</c'),
Л s/c?sin/c'? (k>kr).
4.12. Пользуясь формулами D.2.19), показать, что
cos рж —cos да;
4.13. Пользуясь формулами D.2.19), показать, что
— (а;2—ab) sin x + (a + b) x cos ж , __ л
4.14. Показать, что
оо—г^
1
i L4
4.15. Рассмотреть интеграл
при действительном z, где путь интегрирования идет вдоль действительной
оси, но обходит точку z по малой полуокружности против часовой стрел-
стрелки. Показать, что
где аР — главное значение этого несобственного интеграла.
4.16. Пусть /(z) — аналитическая функция в полосе |Imz[<a. Пока-
Показать, что
/(*) = /_(*)-/¦(*),
где
3 i
—co+i3 — оо—iji
причем Р < a. Показать, что функции /_ и /+ аналитичны соответственно
при Im z < р и Im z > — р.
Задачи к главе 4 449
4.17. Функция ф (х) определена равенством
оо+го oo+ix
rV ' Ьп \ J (z2
(z2—z§)(z+w) J (z2 —z2)(z—ш)
—oo+io —oo+iT
где t < 1 и о > — 1. Показать, что
Ф(ж)=-ТтЛв«1*Ч Z° + * гп.ц Г »¦ I т. I - я rr.f.g ±) .
lU a2 + 2g ^zo/a2 + zg V01 ' *4J
4.18. Показать, что z = 1 является особой точкой функции, представ-
представляемой (внутри круга сходимости) рядом
n=o
4.19. Обобщенная гипергеометрическая функция Fia^a^... ,ae|c1,c2,...,ce| z)
определяется посредством степенного ряда
-as , «о (
c1.. .cs ' ci (ci + 1) cs (cs + 1) 2! ~r ' ¦ ' '
Показать, что z = 1 является особой точкой функции F, и если а4 < ct,
то
Z -^ 1 ,
(l-z)P \j Т(ат)
тп=О
где р = ао+ 2
n=l
4.20. Доказать, что
оо г
2 1 _ 51 sh (тса У 2) + sin (па У2)
4 i 4 — ~Г~~ Т~
71=;— ОО
4.21. Доказать, что
2
(и2 + а2) (п2 + Ь2) Ъ2—а2[
П=:—оэ
cthicbN
4.22. Показать, что четная целая функция может быть представлена
в виде
п=1
где / (ап) = 0 и в произведение из каждой пары нулей ап, — ап входит
только один. Пусть /(z) подчиняется условиям, сформулированным при
выводе формулы D.3.8). Показать тогда, что если /@) = 1, то
СО ОО
Jl=l 71=1
29 ф. м. Морс и Г. Фешбах
450 Гл. 4. Функции комплексного переменного
Воспользовавшись представлением D.3.9) функции sinz/z, показать, что
оо со
n=l n=l
4.23. Доказать, что
со
рО,? рЪъ __ In /A 2g(a + b)z/2 T Г
п=1
4.24. Доказать, что
со со
/i ;—г~,—2i/ ii—«г =-г cth ait ¦ cth ото.
4-i (m2 + a2) (n2 + a2) ab
m=—со n=—oo
4.25. Пользуясь обобщенным преобразованием Эйлера, показать, что
F (a0, аи...\ Ьи Ья> ... 12) ==
К + !).¦•
2!
4.26. Вычисляя интеграл функции e'^z" вдоль границы сектора,
заключенного между действительной осью, прямой q> = a (z = rei<p), дугой
окружности малого радиуса r = s и дугой окружности большого радиуса
г —Я, доказать, что
sm
где 6<^тг/2, а и р — действительны и положительны.
4.27. Вычисляя интеграл функции za~1ez вдоль пути, идущего от точ-
точки, примыкающей к началу справа (z = &), к точке —со непосредственно
под действительной осью, далее соединяющего последовательно точки
— со—гсо, Ъ — гсо, b^-ico, —co + ico, —со и затем идущего к точке
z = s непосредственно над действительной осью, показать, что при 0 < а < 1
и 6>0
оэ
[ elv (b + iy)a~i dy = 2е~ь sin air Г (a)
—oo
и, следовательно,
7t/2
{ cos [tg 6 - A — a) 6] seca+1 6 db = -i sin a% Г (a).
4.28. Показать, что интеграл
Задачи к главе 4 451
взятый по октанту объема, ограниченного поверхностью (х/а)р + (yfb)Q-
4- (z/c)r = 1, равен
glbmcn Г (I/р) Г (то/g) Г (я/г)
4.29. Доказать, что
4.30. Выразить интеграл
входящий в формулу D.5.26), через гамма-функцию.
4.31. Показать, что
| _C0S_O7t _
4.32. Показать, что
4.33. Показать, что
| Г (z+ 1) |»
_L_
где z = a; + i2/, r2 = a;2 + j/2, <j> = arctg (y/x).
Показать, что argF(z) асимптотически выражается в виде
4.34. Рассмотреть интеграл
причем линией ветвления служит отрицательная действительная полуось,
а контур С идет из — оо под линией ветвления, обходит точку ветвления
(начало координат) в положительном направлении и идет к — со над
линией ветвления. Разбив этот интеграл на три интеграла, из которых
два берутся от — со до — з0) где е0 мало, а третий вдоль окружности
радиуса е0 с центром в нуле, показать, что при s0—->0 последний интег-
интеграл имеет предел 1/х, а сумма остальных может быть выражена в виде
2
п=0
Показать, что
\i\TT
е-"' si ( Уп) У \
' sin (X
\
п) ~ = Уъ \
"о
29*"
452 Гл. 4. Функции комплексного переменного
л, следовательно, что
°° A/V7
4^? S
4.35. Рассмотреть интеграл
g(z)=
где функция GB) аналитична в полуплоскости Re?>0, a G(t)zl/T ()
стремится к нулю с возрастанием Re t. Интегрирование производится
вдоль мнимой оси, но с обходом нуля вдоль малой полуокружности по
часовой стрелке. Замкнув этот контур большой полуокружностью в полу-
полуплоскости Re t > 0, показать, что
Вывести отсюда выражение
со
с 1„ ы л I „ч _ г (С1_ К
(o)r 2j Г(с + п)
п=0
Г (с)
2тпГ (о) Г (Ь)
— гсхэ
для Re (а+ 6 — с)<0 (а, 6 ^fc 0, — 1, — 2,.., ). Показать, что исходный кон-
контур может также быть замкнут полуокружностью в левой полуплоскости.
Вывести отсюда, что
[см. формулу E.2.49)].
4.36. Доказать, что
V
где a > 1. Для этого вычислить интеграл
где С идет от -М к — i вдоль мнимой оси и возвращается к -|- i вдоль
правой половины единичной окружности.
4.37. С помощью метода перевала показать, что для функции Н$\
определенной равенством
7С/2—ico
-ivto/ с
=\
/2
Задачи к главе 4 453
справедливо асимптотическое равенство
_
4.38. Показать, что в интеграле
оо
/= С
—оо
вычисленном вдоль действительной оси, можно взять новый путь интегри-
интегрирования, составив его из полупрямой 9 = 5^/6 (* = ге*?), идущей от —оо
к 0, и полупрямой 9= тс/6, идущей от 0 до оо. Отсюда будет следовать,
что
¦)'
ml
Почему g должно быть при этом действительным?
4.39. Метод перевала может быть несколько модифицирован при малом
|/"(*о)|- в интеграле D.6.6)
/= С ezfV)dt
с
разложим fit) по степеням t —10, причем f'(to) = O. Показать, что при
малом |/"| целесообразно преобразование
где
/'"(to) ' P
Показать, что
/ - ехр
где
6i
4.40. Показать, что при р —> оо
«/2—tco
5
5
— 7С/2 + 1СО
4.41. Показать, что при конформном отображении
z = х + г'г/ = w + |/ш2 — 1 (ш = м + it»)
действительная ось плоскости ш переходит в участок | х | > 1 действитель-
действительной оси плоскости z и в единичную окружность z = eil?. Нанести на
плоскости z линии, соответствующие прямым и = 0, ± 1 и о = 0,±1-
454 Гл. 4. Функции комплексного переменного
4.42. Показать, что при отображении
w + iae19 tg ф
(a, 9, ф — постоянные) окружность радиуса a sec ф с центром в начале на
плоскости w переходит в дугу окружности, которая стягивается хордой
длины 4а, образующей угол 9 с осью х. На плоскости z нанести кривые,
соответствующие линиям и = 0, [v| >a sec<|> и и = О, | и | > asecф при
а=1, ф = 30°, <|>=15°. Какова угловая мера дуги в плоскости z, соответ-
соответствующей окружности w = a sec tye*'?
4.43. Показать, что формула Шварца — Кристоффеля дает для функ-
функции, отображающей внутренность четырехугольника со сторонами х = 0,
у>0; у — О, ж>0; у=— а, ж > —Ь; х= —Ъ, у> —а на верхнюю полу-
полуплоскость плоскости w выражение
z = — Аг th I/ -г— arc tg I/ г*
К С О! 1 + Ш 51 Б V Ъ2
Найти на плоскости w образы точек z = 0, z= —b — ai, z= —b, z= — ai.
4.44. Показать, что функция
w = tg f — arc cos z2 J
отображает «крест» у = 0, —1<ж-<1; ж = 0, —1-<у<;1 на действитель-
действительную ось плоскости w. Найти на плоскости w образы точек z=l, z=i,
z= — 1, z= —г. Какие физические задачи могут быть решены с по-
помощью этого конформного отображения?
4.45. Тонкий металлический киль, поддерживаемый при температуре
То, расположен перпендикулярно к металлической пластинке, поддержи-
поддерживаемой при нулевой температуре, так что кромка киля параллельна этой
пластинке и находится на расстоянии а от нее. Посредством преобразо-
преобразования Шварца — Кристоффеля показать, что стационарное распределение
температуры в окружающей (теплопроводящей) среде может быть опреде-
определено функцией (преобразованием)
г п <U+iT) \
—~ ;•
причем линии Т = const представляют собой изотермы. Показать, что
полоса киля длины L и высоты Ь (последняя отсчитывается от кромки)
испускает
Аг сп ( —¦— J калории в секунду,
где х — коэффициент теплопроводности среды.
4.46. Посредством преобразования Шварца — Кристоффеля показать,
что участок плоскости z, лежащий над прямой у = — а вне двух частей
ж>0 и ж< —Ь вещественной оси (это соответствует двум параллельным
плоскостям, расположенным на расстоянии а друг от друга, в верхней
из которых имеется щель ширины Ь), отображается на верхнюю полупло-
полуплоскость плоскости w функцией
а Г(е$—1)(
5= — — ^ '-
п L w — e
Основные свойства функций комплексного переменного 455
где 6 = Bа/тг) ф + shp). Для случая Ь = а (при этом р = 0,7493) вычислить
{с двумя значащими цифрами) образы в плоскости w точек z= —а,
— а/2, —a/2 — ia, — a/2 + ia.
4.47. Показать, что если
оэ
/И= S Л**""*" {-КХ<1),
п=—оо
ТО
г
А« = ё \ f (х)е~ы™11 dx-
-i
Внося эти выражения Ап в ряд, представляющий функцию f(x), и пере-
переходя должным образом к пределу при I—> оо, вывести интеграл Фурье.
4.48. Обобщенные преобразования Меллина определяются равенствами
F_ (s) = ^ / (ж) ж8 йж, F+ (s) = ^ / (ж) Xs'1 dx.
о Г
Показать, что F_ аналитична в некоторой полуплоскости вида Res>a0,
a F+—b некоторой полуплоскости вида Res<o1. Показать, что если су-
существует преобразование Меллина в обычном смысле, то о0 < ог. Показать,
что ДЛЯ а > а0 и 1 < ах
4.49. Найти преобразования Фурье F+ и F_ функции cosaa; при ком-
комплексном а и определить их области аналитичности.
4.50. Найти преобразования Фурье F+ и F_ функции хп е"х и опре-
определить их области аналитичности.
4.51. Посредством формулы суммирования Пуассона показать, что
со
»3(и, е~а2/2)= ^ ^ e-B
'(функция &з определена на стр. 407).
Основные свойства функций комплексного переменного
Функция f = u-\-iv комплексного переменного z = x + iy называется
аналитической в области R плоскости z, если она удовлетворяет одному из
следующих трех эквивалентных условий:
а. Производная dfldz в любой точке z == а области R существует и не
зависит от направления dz; эта производная непрерывна в области R.
б. du/dx = dvjdy, ди/ду= —dv/dx, причем все эти производные непре-
непрерывны в Л.
456 Гл. 4. Функции комплексного переменного
в. ф / (z) dz = О для любого замкнутого контура С, который можно
с
стянуть в точку внутри области R.
Если хоть одно из этих условий выполнено (следовательно, выполне-
выполнены и остальные), то производные всех порядков функции f no z существуют
и аналитичны в области R.
Далее, для любого замкнутого контура, заключенного внутри одно-
связной области R, в которой / аналитична,
когда а лежит внутри контура; если точка а находится вне контура, та
эти интегралы обращаются в нуль (см. § 4.3).
Точки, в которых / (z) не аналитична, называются особыми точками злой
функции (см. стр. 339, 359). Особая точка z == а есть простой полюс, когда
где g (z) — аналитическая функция при z = a и g(a)=f=O. Вообще, если
где п — целое положительное число, g (z) — аналитическая функция лри
z = a и ё{о)фО, то z = а является полюсом порядка п. Если при z—> а
функция /(z) не имеет определенного предела, ни конечного, ни бесконеч-
бесконечного, то z = а — существенно особая точка функции /(z).
С другой стороны, если особая точка z = a функции /(z) такова, что
/(a + se1*) при возрастании 9 на 2тг, изменяясь непрерывно, приобретает
значение, отличное от исходного, то z — a называется точкой ветвления
функции /(з выбирается так, что a-fee1* для всех 9 находится в области
аналитичности функций /). Так, например, точка а является точкой вет-
ветвления функций f=(z — ayg(z) и / = In (z — a) g(z), где v —нецелое число
(положительное или отрицательное), а g (z) — аналитическая функция в точ-
точке а. Полюсы и существенно особые точки представляют собой изолирован-
изолированные особые точки; точки же ветвления (никогда не существующие в оди-
одиночку) являются неизолированными особыми точками, так как любая ветвь /
оказывается неаналитической вдоль некоторой линии, оканчивающейся
в точке ветвления.
Если точка w = 0 является особой для f(l/w), то говорят, что /(z)-
имеет особенность в бесконечно удаленной точке.
По характеру и расположению своих особых точек функции могут быть
классифицированы следующим образом:
1. Если /(z) вовсе не имеет особых точек, to/(z) — постоянная.
2. Если / (z) имеет единственную особую точку — полюс п-то порядка
в бесконечности, то / (z) — многочлен n-й степени относительно z.
3. Если / (z) имеет единственную особую точку в бесконечности, то / (z)
называется целой функцией (целыми функциями являются, в частности,
многочлены).
4. Если /(z) не имеет других особых точек, кроме полюсов (тогда их
может быть лишь конечное число), то /(z) представляет собой отношение
двух многочленов от z. Функция, не имеющая в заданной области особых
точек, отличных от полюсов, называется мероморфной в этой области. Та-
Таким образом, рациональная функция мероморфна во всей плоскости z.
5. Если в конечных точках плоскости / (z) не имеет других особенно-
особенностей, кроме полюсов (тогда как бесконечно удаленная точка может быть
Основные свойства функций комплексного переменного 457
существенно особой), то /(z) называется мероморфной функцией перемен-
переменного z (в частности, рациональные функции являются мероморфными).
6. Функции, имеющие точки ветвления, являются многозначными (все
ранее перечисленные функции однозначны).
Мероморфная функция может быть разложена в ряд элементарных
дробей, каждый член которого соответствует некоторому полюсу функции
в конечной точке плоскости. В частности, если все ее полюсы z = an в ко-
конечной части плоскости простые, причем точка z = 0 не является полю-
полюсом, то [см. D.3.6); дополнительные условия см. на стр. 363]
м=/«>>+2 0^г+?
где Ьп — вычет функции относительно полюса ап.
Целая функция может быть представлена в виде произведения множи-
множителей, соответствующих всевозможным нулям функции (в конечных точ-
точках). Так, если все нули z = %, а2, ... функции / простые (т. е. 1//
имеет лишь простые полюсы) и ни одно ап не равно нулю, то
/(a) = /(O)e»'<
[см. D.3.8); дополнительные условия см. на стр. 364].
Алгорифм Эйлера для вычисления сумм рядов. Пусть задан ряд
со
п=0
и пусть другой ряд
со
п=0
получается из первого введением множителей Сп в коэффициенты. Тогда
/ (z) = Cog (а) - (ЬС0) zg' (a) + (S2C0) J f (z) ~ • • •'
где
О Cq = Со <*
В частности, если g(z)= 1/A + z)= У, ( — 1JV, то
где ?=z/(l + z). В том случае, когда Сп или ап представляют собой мно-
многочлены относительно п степени JV', все разности ofe порядка к > iV
обращаются в нуль и /(z) выражается через известную функцию сравне-
сравнения g{z) в конечном виде.
Представление интегралов посредством асимптотических рядов. Часто
удается представить функцию ф (z) в виде интеграла
'/О) dt,
458 Гл. 4. Функции комплексного переменного
где С — некоторый контур (замкнутый или уходящий в бесконечность) в
плоскости t. Для вычисления ф (z) при Re z > 1 мы деформируем С (в до-
допустимых пределах) так, чтобы Re/ всюду принимала возможно меньшие
значения. Тогда наибольшее значение Re/ на контуре будет достигаться
в седловой точке t = t0 для Re /, где df/dt = 0. В окрестности t = t0 будем
иметь
и в этой окрестности контур следует направить по линии, вдоль которой
Im/ постоянна и равна Im/(Z0). Из двух возможных линий выбираем ту,
вдоль которой Re/(Z) имеет максимум (а не минимум) при t = t0. При ин-
интегрировании по такому пути часть интеграла, соответствующая участку
контура, близкому к точке t = t0, будет доминировать, и для больших зна-
значений Re z получаем асимптотический ряд
где
L> Л ГУ 1
О » -*-'l — A'j iff
[по поводу дальнейших деталей см. формулы D.6.14) — D.6.19)].
Преобразование Фурье. Если функция / (z) такова, что интеграл
со
\ \f(z)\2dz имеет конечное значение, то функция
— со
оо
Ч) гт
со
называется преобразованием Фурье функции /(z); при этом
со
k= [ \f(z)\*dz.
Далее, если в окрестности точки z = 0 функция /+ (z) задается равенствами
О, z<0,
то поведение F при больших к описывается функцией
Если F(k) и G(к) — преобразования Фурье функций /(z) и g(z), то
преобразованием Фурье функции
Основные свойства функций комплексного переменного
459
является произведение F(k)G(k) (теорема о свертке). В то же время пре-
преобразованием Фурье произведения f(z)g(z) служит функция
Имеет место равенство
оо оо
^ F(k)G(k)dk= ^ f(z)'g(z)dz.
—со —со
Если F(k) — преобразование Фурье функции f(z), то
оо оо
п=—со rn=—оо
(формула суммирования Пуассона).
со
В случае когда интеграл \ |/(z)|2dz бесконечен, но при некотором т0
— оо
со
конечен интеграл \ |/(z)|2e-2-oz dz и преобразованием Фурье функции
— GO
f(z)e~~oz является G(k), преобразованием Фурье функции /(z) служит функ-
функция F(k) — G(k — ix0), причем
-оо+гто
[другие условия сходимости см. в связи с формулой D.8.19)].
Функция /(z)
f(az)
izf(z)
1
(z — iZq)'1 (Re z0
[(z — iz0) (z-j- iz1)]~1(Rez0 ]
sech (/coz)
th(/coz)
z-a-ieijz
е-гЩ2
>0)
>0,Rez1>0)
)
Ее преобразование Фурье F (fc)
(l/a)F (к/а)
-ikF(k)
e-ihzop (fy
*-j/2TO-ife2° (Re/c>0)
/2^" } e~z°fe (Re Л > °)>
zo + % I e^fe (Reft<0)
(i//c0) У те/2 cosech (irft/2ft0)
460
Гл. 4. Функции комплексного переменного
Преобразование Лапласа. Если функция /(ж) равна нулю при х < 0
со
нтеграл \ | / (х) |2 e~2rx dx конечен при т _> г0, то функция
e-P* dx
называется преобразованием Лапласа функции f(x); при этом
t+ioo
"C+ioo
Теорема о свертке гласит, что
Дальнейшие сведения о преобразовании Лапласа см. в конце гл. 11.
Преобразование Меллина. Если функция f(x) задана в интервале
GO
0 < х < оо и интеграл \ \f(x)\2x2a~i dx конечен при а > а0, то
называется преобразованием Меллина функции f(x)\ при этом
а 4-too
Теорема о свертке может быть выражена так:
ИЛИ
o+ioo
o-ioo
a+ico
Функция / (x)
Щх)
flflx)
x*f(x)
d
f(x) In x
Ее преобразование Меллина Fm(s)
Wm(s)
a-*Fm(s)
Fm (s -f- a)
(s \\p (s ^\
Часто встречающиеся специальные функции
461
Функция / (х)
Ее преобразование Меллина Fm(s)
F(a,b\c\ х)
T(s)
Г (с) Г(я)Г(а—s)V(b—s)
Г (а) Г (Ъ) Г (c-s)
T(s)T(a-s)/T(a)
Artha;
F(a\c\-x)
xj\(x)
[Г E)/Г A - s)} [T (m - s)/T (m)f
T(s)T(a-s)T{c)/T(a)T(c-s)
sin ж
cos ж
Г (s) sin (us/2)
Г (s) cos (ад/2)
-2:чт>
Функции Jv, /v, F, Pm и 7VV, встречающиеся в этой таблице, опре-
определены в конце гл. 5, 10 и 11.
Часто-встречающиеся специальные функции
См. также в конце гл. 5, 6, 10, 11 и 12.
Гамма-функция (см. стр. 396).
-tf-1dt (Rez>0), ГB+1) = 2ГB).
= ze"z П A + ^
n=l
(Y = 0,577215 ...).
462 Гл. 4. Функции комплексного переменного
Г (z) ~ l/^nz* 2 e~z (z > 1).
7С/2
= 2 С sin2*-19cos2l/-1<pd9 (Rez>0,
Эллиптические функции (см. стр. 404).
х
/1ч f dx
x = sn(v, k), если w= \ .
i /(!-*•) A-fcV)
1
f da
ж = en (и, /с), если v — \ ,
K ' J >'(! — a;2)(l
x = dn (u, &), если d = \ —
J у
da:
ж = tn (о, /с), если и = \ dx
Ж2)A + /с'2
1
J V^(l — ж2)A — /c2a^") ' J Y(i— x2) A —/c'
(/с = sin a, &' = cos a).
X
x — sn(v, к), если t> = -^
1
•. r~ /7ч If dx
у x — cn(v,k), если u = —\
1
Vra;=dn(u) /с), если v = -^ \ ,
^~~ /7\ * i dx
I 9*1 /^ 1 О/1 II тт у| ^ *
cn2 (м, A) = 1 - sn2 (m, A), dn2 (M> A) = 1 - k2 sn2 (в, k),
. i 7 s sn (u, k)
tn (m, k) = —; ' ,: .
v.' ' cn (к, k)
sn@, A) = 0, cn@, A) = 1, dn(Ot"A)=l,
sn(— u, k)= — sn(M, k), cn( — u,k) = cn(u,k), dn( — м, k) = dn(u, k).
Часто встречающиеся специальные функции
463
СВОЙСТВА ПЕРИОДИЧНОСТИ ЭЛЛИПТИЧЕСКИХ ФУНКЦИИ
iu
u + K
u + 2K
u + iK'
u + K+iK'
u + 2iK'
u + 2K + 2iK'
sn (ti, fe)
itn («,*')
en (и, к)
dn (в, к)
—sn (и, к)
1
к sn (и, к)
dn (и, к)
Л сп (и, к)
sn(u, к)
— sn {и, к)
СП G), fe)
1
8П(И, *)
dn (и, к)
— сп (и, к)
i dn (и, к)
к sn(u, к)
ik'
к сп(и, к)
— сп (и, к)
сп(и, к)
dn(ti, fe)
dn {и, к')
сп (в, к')
к'
dn {и, к)
dn (к, к)
i
tn (к, к)
ik' tn (и, к)
— dn(u, к)
— dn(u, к)
tn (t>, fe)
i sn (и, к)
1
к tn (в, к)
tn(u, к)
i
dn (в, к)
к'
— tn(u, Л)
— tn(B, к)
[Например, cn(u + 2K, k)=—en (u, k), dn (u + K + iK') = ikr tn (к, к) и т. д.]
СООТНОШЕНИЯ МЕШДУ ПАРАМЕТРАМИ ЭЛЛИПТИЧЕСКИХ ФУНКЦИИ
[При достаточно малых к (< ОД) хорошим приближением служит к = 4е~эт?'/2А =
= i\rq; при К/К' > 1,0 вместо К, к и а берутся соответственно К', к' и 90° — а.]
К
К'
к
к'
а
0,0
1,571
со
0
1,000
0
0
0,1
1,571
15,71
—
1,000
—
—
0,2
1,571
7,855
0,00156
1,000
5°4'
—
1
5
0
1
1°
D,3
,571
,237
0213
,000
11,7'
—
1
3
0,
0
4
0,
3,4
,573
,933
0784
,998
°30'
0004
К/К'
с
1
3
0
0
9
0,
,5
583
166
171
985
°50'
0019
0,6
1,604
2,673
0,265
0,965
15°22'
0,0053
0
1,
2,
0,
0,
,7
643
347
407
913
24 °0'
0,
3114
с
1
2
0
0
31
0,
,8
699
124
520
853
°23'
0197
0
1,
1,
0,
0,
38
,9
768
966
622
784
D30'
0,0307
1,0
1,854
1,854
0,707
0,707
45°
0,0432
Далее мы кое-где опускаем второй аргумент эллиптических функций,
т. е. к. Он предполагается во всех членах одинаковым:
sn к en v dn v + сп и sn v dn и
sn(u + v) = - - -
4 ' 1 — &2sn2Ksn2p
/ . ч en и en v—• sn к sn v dn к dn v
сп (и -f- и) =
dn (м + и) =
. , , ч tn м dn v + tn у dn к
' 1 — tn и tn г; dn к dn v
1 — /с2 sn2 и sn2 у '
dn и dn v— к2 sn и sn v en к en v
464
Гл. 4. Функции комплексного переменного
Функции snw, спи, diiM имеют простые полюсы в точках 2тК-\-
+ Bn-\-l)K'i, где т и п — целые числа, положительные или отрицатель-
отрицательные. Значения вычетов этих функций (Resu /) относительно полюсов при-
приведены в следующей таблице:
>\
sn и
en и
dn и
iK'
l/k
—i/k
— i
—iK'
l/k
i/k
i
2K+iK'
— l/k
i/k
2K-iK'
-l/k
-i/k
i
Нулями функции sn(u,k) служат точки и = 2тК-\-2пКЧ (т,п =
= 0, ±1, ±2, ...); далее, en[Bm + 1)К + 2nK'i, к] = 0, dn[{2m+l)K +
+ Bn + l)K'i, к] = 0, sn(u, k) = u + O(u?) (м-»0). Поведение сп(и, к) и
•dn (и, к) вблизи их нулей можно выяснить, воспользовавшись свойствами
периодичности.
1
sn(«, к) 2К
= ^cosec-
sin (тси/2-й:) ch jnnK'/K)
cbBnnK'/K) — cos(r.u/K) '
dn ( к, к) _
sn (и, к)
Если а — е~г
cn(u,k) _ тс тем тс. ^
sn (м, к) ~~ 2К g 2К + 2К Zj ch
и=0
!L_ V
2К ZJ ch[Dn
sin {пи/К)
— cos
sin (izu/K)
тем , 2тс -у ,
n=l
К'/К] — cos (г.и/К) '
„ sin (nu/2K) ch (ппК'/К)
' ch BnnK'/K)—cos (пк/Ji:) -
, то
СО
(л 2п—1 -v 2
_ . 1 —
1 — 2qzn cos (пи/К) +д"
An—2 '
in
1_гд2"-1 cos (tcu/A") + 54n~2 '
В, Л)- 11
71=1
fe /л 2К *а(™
(B,A)_ — tg^
d
„2и-1
4n-2
4n-2 '
„2и
¦^-sn(M, /с) = сп(м, A)dn(M, A),
-г—
сп(м, /c)= —
n(M, A),
-j— dn(M, A)= —A2 sn(M, А)сп(м, А),
sn (ж, A) = sin (am ж), en (x, k) = cos (am x),
4n
Часто встречающиеся специальные функции 465
\ dn (х, k) dx = arc sin [sn (x, к)] = am x,
Г 1
\ en (ж, k)dx = — arc cos fdn(a;, k)],
С dx — ln sn (x, fc)
j sn(a;, fc) en (ж, fc) + dn (ж, fc) '
С dx _ 1 - fc' sn (x, k) + dn (x, k)
) cn{x,k) ~Tr en (x, k) '
С dx 1_ k'snjx, fc) — en (ж, fc)
J dn (x, fc) ~~ fc' аГС tg fc'sn (ж, fc) + en (x, fc) '
Тэта-функции. Определяются эти функции так:
со ' 1 \2
»! (в, ш) = 2 2 (- Ife1" [П+~г> sin Bn + 1) ъи = - »2 ^в + у,
00 / 1 \2
(в,io) = 22 е"ИГ l"+TJ cos Bn
»3{м, ш) = 1 + 2 2 е-™ cos 2тш = &0 Г м + -|-, ю\
со
»0 (к, го) = 1 + 2 2 ( - !)" е
и + Т if, if J = ie ? »0 (м, iu),
(« v —
Ьг {и, iv +1) = e*»/*»! (в, iw), »! (в, fr) = ^=- e-"-1'^ (JL , 1) ,
»2 (в, fo+ 1) = e^4»2 (и, ш),
—nv—inu
-j- V.V—VKU
e
%0 (в, fc + 1) = », (и, fc), К (и, iv) = ^ е-™2'»&, (-2L , -1
30 ф. м. Морс и Г. Фешбах
466 Гл. 4. Функции комплексного переменного
Нули тэта-функций
n + miv
»¦
n + ^ + miv
».
1 / 1 Л
(m, n —целые числа).
ЛИТЕРАТУРА
Имеется, конечно, очень много учебников, в которых рассматриваются различ-
различные вопросы теории функций комплексного переменного. Рекомендуется изучение
некоторых из следующих книг:
Гурвиц А., Теория аналитических и эллиптических функций, Гостехиздат,
М.—Л., 1933.
Курант Р., Геометрическая теория функций комплексной переменной, Гостех-
Гостехиздат, М.—Л., 1934.
Л а II ре и т ьев М. А. и Шабат Б. В., Методы теории функций комплексного
переменного, изд. 2, Физматгиз, М., 1958.
Map куше вич А. И., Краткий курс теории аналитических функций Гостех-
Гостехиздат, М., 1957.
Полна Г. и Сеге Г., Задачи и теоремы из анализа, изд. 2, Гостехиздат, М.,
1956.
Привалов И. И., Введение в теорию функций комплексного переменного, изд. 7,
Гостехиздат, М.—Л., 1945.
Смирнов В. И., Курс высшей математики, т. 3, ч. 2, изд. 6, Гостехиздат, М.,
1956.
Тит ч марш Е., Теория функций, Гостехиздат, М.—Л., 1951.
Уигтекер Е. Т. и ВатсонГ. Н., Курс современного анализа, ч. 1 и 2, Гос-
Гостехиздат, М.—Л., 1934.
Франк Ф. и М и з е с Р., Дифференциальные и интегральные уравнения матема-
математической физики, Гостехиздат, М.—Л., 1937, гл. 3.
Фукс Б. А. и Левин В. И., Функции комплексного переменного. Специаль-
Специальная часть, Гостехиздат, М.—Л., 1949.
Фукс Б. А. и Шабат Б. В., Функции комплексного переменного и некоторые
их приложения, Гостехиздат, М.—Л., 1949.
Cops on К. Т., Theory of Functions of a Complex Variable, Oxford, New York, 1935.
McLachlan N. W., Complex Variables and Operational Calculus, Cambridge, New
York, 1939.
Книги, в которых рассматриваются ряды, и асимптотические разложения:
Ват со н Г. Н., Теория бесселевых функций, т. 1, Изд. иностр. лит., М., 1949.
Евграфов М. А., Асимптотические оцонки и целые функции. Гостехиздат, М., 1957.
Hadamard J., Mandelbrojt S., La serie de Taylor et son prolongeuient ana-
lylique, Paris, 1926.
Landau E., Darstellung und Begrundung einiger neuerer Ergebnisse der Funktio-
nentheorie, Berlin, 1929.
Книги, представляющие интерес в связи с многозначными и специальными
функциями:
Ахиезер Н. И., Элементы теории эллиптических функций, Гостехиздат, М.—Л.,
1948.
Лебедев Н. Н., Специальные функции и их применения, Гостехиздат, М., 1953.
Forsyt-he A. R., Theory of Functions of a Complex Variable, Cambridge, 1893.
Neville E. H-, Jacobian Elliptic Functions. Oxford, New York, 1944.
Nielsen N., Theorie der Gammafunktion, Leipzig, 1906.
Книги, в которых рассматривается конформное отображение и его приложения:
Каратеодори К., Конформное отображение, Гостехиздат, М.—Л., 1934.
Кочин Н. Е., Кибель И. А. и Розе Н. В., Теоретическая гидромеханика,
ч. 1, изд. 5, Гостехизлат. М.„ 1955.
Лаврентьев М. А., Конформные отображения, Гостехиздат, М.—Л., 1946.
Литература 467
Milne-Thomson L. M., Theoretical Hydrodynamics, London, 1938.
Ramsey A. S., Treatise on Hydromechanics, Part 2, Ch. 6, London, 1920.
Rothe R., Ollendorff F., Pohlhausen K., Theory of Functions, Cambridge,
1933.
Книги по теории преобразований Лапласа и Фурье, а также по другим преоб-
преобразованиям:
Гарднер М. С. и Берне Дж. Л., Переходные процессы в линейных системах
с сосредоточенными постоянными, Гостехиздат, М. — Л., 1949.
Диткин В. А. и Кузнецов П. И., Справочник по операционному исчислению,
Гостехиздат, М.-Л., 1951.
Контор о вич М. И., Операционное исчисление и нестационарные явления в электри-
электрических цепях, изд. 2, Гостехиздат, 1953.
Лурье А. Н., Операпионное исчисление, Гостехиэдат, М., 1950.
Снеддон И., Преобразования Фурье, Изд. иностр. лит., М., 1955.
Титчмарш Е. К., Введение в теорию интегралов Фурье, Гостехиздат, М.—Л.,
194о.
Трантер К. Дж., Интегральные преобразования в математической физике, Изд.
иностр. лит., М., 1956.
Campbell G. A., Foster R. M., Fourier Integrals for Practical Applications,
Bell System Techn. Publ. B-584, 1942 (таблица преобразований Фурье).
Carslaw H. S., Theory of Fourier Series and Integrals, New York, 1930.
Churchill R. V., Fourier Series and Boundary Value Prohlems, New York, 1941.
Doetsch G., Theorie und Anwendung der Laplace-Transformation, Berlin, 1937.
Pale у R. E. A. C, Wiener N., Fourier Transforms in the Complex Domain, New
York, 1934.
30*
ГЛАВА 5
Обыкновенные дифференциальные
уравнения
После обзора видов полей, встречающихся в физике, и описывающих
их уравнений с частными производными, после исследования аналитиче-
аналитического характера различного рода решений этих уравнений мы должны
¦теперь перейти к центральной части нашей работы, именно, к нахождению
решения конкретных уравнений поля. Для этого обычно требуется два
основных шага: первый, исследуемый в настоящей главе, состоит в на-
нахождении всех (или почти всех) возможных решений уравнения, а второй,
изучаемый в дальнейших главах,—в выборе из них того частного реше-
решения, которое удовлетворяет краевым условиям рассматриваемой задачи.
Уравнения, которые мы предполагаем изучать в данной книге, приве-
приведены в таблице на стр. 260, 261. Мы уже указали, что они являются далеко
не единственными встречающимися в физике уравнениями поля, но мы
отметили и то, что они составляют неожиданно большую часть важных
в современной физике уравнений поля. Зная, как найти решение приве-
приведенных уравнений, мы будем в состоянии изучать многочисленные теоре-
теоретические проблемы во всех важных в настоящее время областях физики.
Все приведенные в таблице уравнения имеют несколько существенных
общих свойств, которые дадут нам возможность сузить круг вопросов, изу-
изучаемых здесь и далее. Эти уравнения можно единообразно записать в виде
р%?ф = р.
где поле ф представляет собой скалярную либо векторную функцию коор-
координат и времени (рассматриваемые векторы могут принадлежать как
обычному пространству, так и абстрактному векторному пространству
или обоим). Оператор &€ представляет собой комбинацию функций коор-
координат и времени, частных производных по пространственным координатам
и времени, а также иногда векторных операторных функций в обычном
или абстрактном векторном пространстве. Величина F представляет собой
скалярную или векторную функцию пространства и времени. ?№ и F
известны; поле ф неизвестно.
Первым общим свойством, на которое надо указать, является то, что
такие уравнения линейны относительно неизвестной ф; ни один из членов
не содержит ф2, или произведений двух компонент ф, или высших степе-
степеней. Обычно линейные уравнения решаются значительно проще, чем не-
нелинейные, и мы в наших рассмотрениях будем много раз пользоваться
этим свойством линейности.
Если F равно нулю, уравнение называется однородным, так как
каждый из его членов содержит ф. Однородные линейные уравнения об-
обладают следующим чрезвычайно полезным свойством: если фг, ф2, ...
являются решениями уравнения, то любая линейная комбинация 2 апФп
этих решений также представляет собой решение. Читатель легко прове-
проведет доказательство этого утверждения.
Введение 469
Если F не равно нулю, уравнение называется неоднородным, так как
некоторые из его членов не содержат ф. Неоднородные линейные уравнения
также обладают полезными свойствами: если tyt является решением неод-
неоднородного уравнения &€^i = F, а % — каким-либо решением соответствую-
соответствующего однородного уравнения <^ф^ = 0, то сумма ф4 + ф;, представляет собой
решение неоднородного уравнения; если tyt является решением уравнения
e^i — ^ii Фг~решением уравнения <^?фа = /'2 и т. д., то сумма ф= 2 апФ51
представляет собой решение неоднородного уравнения eW ф = 2 anFn- Оба
эти результата, которые нетрудно доказать, окажутся в дальнейших иссле-
исследованиях весьма полезными.
Другим свойством уравнений, приведенных в таблице на стр. 260, 261,
является то, что ни одно из них не имеет порядка выше второго, то есть
ни одно из них не содержит производных выше второго порядка. Число
уравнений поля порядка выше второго, используемых в физике, невелико
(например, уравнение поперечных колебаний упругой пластинки); наиболее
важные уравнения, которые рассматриваются в нашей книге, имеют по-
порядок либо первый, либо второй. Это также позволит нам сберечь время
и место за счет проведения общих рассмотрений только для этих случаев".
Уравнения с частными производными, содержащие более одного неза-
независимого переменного, решить значительно сложнее, чем обыкновенные
дифференциальные уравнения, содержащие только одно независимое пере-
переменное. За исключением небольшого числа случаев, когда решение удается
угадать, а затем проверить, известно только два общих эффективных ме-
метода решения, именно интегральное представление решения и решение
при помощи разделения переменных1). Пример интегрального представления
решения приведен на стр. 47 для уравнения Пуассона V2(J>= — q(x, у, z).
Решение можно записать, как было показано выше, в виде
«К*, У, *)= $5 5 [<?(*', У',
где R — расстояние между точками (х, у, z) и (ж', у', z'). Это —типичная
запись решения в виде интеграла. Неоднородная часть уравнения q нахо-
находится под знаком интеграла, а остальная часть подинтегральной функции
1/iizR, называемая функцией Грина, одна и та же для любой функции q.
Решения аналогичного типа можно получить также для однородных урав-
уравнений, причем тогда функция q определяется по краевым условиям,
а функция Грина — по виду решаемого уравнения.
Преимуществом метода интегрального представления решения является
общность этого метода, так как обычно интеграл остается инвариантным
при преобразовании координат, и, построив функцию Грина один раз, как
показано в гл. 7, в принципе можно найти любое требуемое решение
однородного или неоднородного уравнения. Однако выражение «в принципе»
указывает, что интегральное представление решения не всегда является
достаточно удовлетворительным, так как во многих случаях интеграл не
берется и тогда численные значения решения получить чрезвычайно
трудно.
Другим методом решения линейных уравнений с частными производ-
производными является метод разложения на множители или разделения перемен-
переменных, в котором исходное уравнение, содержащее несколько независимых
переменных, разбивается {разделяется) на ряд обыкновенных дифферен-
дифференциальных уравнений, каждое из которых содержит только одно незави-
х) Имеется в виду получение точного решения. Существует также ряд эффек-
эффективных приближенных методов, часть которых освещена и в этой книге.—Прим.
перев.
470 Гл. б. Обыкновенные дифференциальные уравнения
симое переменное. Этот прием не обладает такой универсальностью, как
предыдущий (основанный на интегральном представлении решения), так
как разделение переменных проходит различным образом для различных
систем координат и возможно лишь для немногих таких систем. Однако
если этот метод применим, то он обычно является значительно более удов-
удовлетворительным, так как решения обыкновенных дифференциальных ура-
уравнений найти гораздо легче, чем решения уравнений с частными произ-
производными.
В этой главе мы будем изучать метод разделения переменных. Мы
укажем, в каких системах координат уравнение допускает разделение пе-
переменных, после чего перейдем к изучению получающихся обыкновенных
дифференциальных уравнений и покажем, как их можно решить и как
можно связать аналитические свойства решений с характеристиками урав-
уравнений и, в конечном счете, с геометрией выбранной системы координат.
5.1. Координаты, в которых переменные разделаются
Чтобы не ограничиваться замечаниями столь общими, что их затруд-
затруднительно понять и применить, мы проведем исследование для одного из
уравнейий общего вида $?ф = F; оно послужит нам примером, с которым
можно сравнивать остальные уравнения. Дифференциальный оператор
^?= (V2 + /c2), соответствующий линейному однородному уравнению второго,
порядка вида
V24> + /c2<? = 0 E.1.1)
для скалярного поля ф, где V2 —оператор Лапласа (см. стр. 18), является
достаточно типичным; поэтому его рассмотрение представляет общий инте-
интерес. Если к = 0, уравнение превращается в уравнение Лапласа для стати-
статических потенциальных полей; если к— положительная постоянная, имеем
волновое уравнение для синусоидальной зависимости от времени (уравление
Гельмгольца) или уравнение диффузии для показательной зависимости от
времени; а если А2 представляет собой функцию координат, то получается
уравнение Шредингера для частицы с постоянной энергией Е (тогда А2
пропорционально разности между Е и потенциальной энергией частицы).
Уравнение вида E.1.1) обладает бесконечным множеством различных
решений, что затрудняет выбор одного из них. Бесконечности и нули
решений могут быть расположены где угодно; можно найти решение,
имеющее любое заданное, достаточно (а иногда и недостаточно) непре-
непрерывное распределение его значений на произвольным образом выбранной
поверхности. Поэтому вопрос состоит не в нахождении всех решений,
а в нахождении частного решения или решений, соответствующих той
частной задаче, которую мы хотим решить.
k Эти различные частные задачи обычно отличаются одна от другой по
характеру налагаемых краевых условий; меняется либо вид границы, либо
заданное поведение поля на границе. (Начальные условия являются, ко-
конечно, краевыми условиями, заданными на поверхности г = 0.) Это наводит
на мысль классифицировать решзняя различных уравнений с частными
производными в соответствии с видом граничных поверхностей, «поро-
«порождающих» решение, а также в соответствии с характером краевых условий
на этих поверхностях. Такая классификация утомительна и сложна; мы
обсудим ее здесь только в объеме, необходимом для наших текущих целей.
В дальнейшем изложении этому вопросу будет посвящено еще несколько
параграфов.
5. 1. Координаты, .в которых переменные разделяются 471
Граничные поверхности и системы координат. Прежде всего надо раз-
различать два общих класса граничных поверхностей: открытые и замкнутые
поверхности. Замкнутая граничная поверхность — это такая поверхность,
которая окружает поле со всех сторон, заключая его в конечный про-
пространственный объем. В этом случае граничная поверхность расположена
вне поля и вся уходящая из поля энергия поглощается на границе. От-
Открытая же поверхность не вполне ограничивает поле, а оставляет его
простирающимся в бесконечность по крайней мере в одном напраплении,
так что поле занимает бесконечный объем и энергия может уходить
«в бесконечность» равно как и поглощаться границей. Это определение
открытой поверхности несколько отличается от обычного смысла этого
термина; например, сфера является замкнутой поверхностью по отпошевию
к содержащемуся внутри нее полю, но открытой для поля, находящегося
вне ее.
Рассмотрим сначала открытые границы. Краевые условия, обычно
накладываемые на поле, состоят в задании значения поля в каждой точке
граничной поверхности, или в задании нормальной составляющей градиента
на этой поверхности, или же и того и другого. В краевой задаче Ди-
Дирихле задаются значения ф на поверхности; в краевой задаче Неймана на
ней задаются значения Зф/Зп; в задаче Когии на ней задаются как значе-
значения поля, так и значения нормальной составляющей его градиента. Каж-
Каждое из этих условий свойственно различным типам уравнений и различным
граничным поверхностям. Например, условия Дирихле на замкнутой по-
поверхности однозначно определяют решение уравнения Лапласа внутри
этой поверхности, в то время как условия Коши для этого поля были
бы «переопределяющими». Эти вопросы будут детально обсуждаться
в гл. 6.
Можно было бы ожидать, что для открытой поверхности требуется
задание на ней значений решения и его градиента (то есть условий Коши),
чтобы однозначно определить решение дифференциального уравнения вто-
второго порядка вне этой поверхности. Это верно, однако имеются другие
¦способы однозначного определения решения. Чтобы упростить исследова-
исследование, целесообразно, если только это возможно, на границе «соорудить»
координатную систему, приспособленную к этой границе. Под этим мы
понимаем такой выбор системы координат El7 E2> ?з> чтобы граничная по-
поверхность стала одной из координатных поверхностей, скажем, ?, = Х,
где X — постоянная. (Имеются варианты, в которых методика несколько
усложняется, хотя принципиально и не изменяется: например, можно
одну часть поверхности записать в виде ?1 = Х, другую—в виде ?2 = Y
и т. д.) Если граничная поверхность не слишком «патологического» вида,
можно найти по крайней мере одну подходящую ортогональную систему
координат (см. стр. 17). Во многих случаях можно найти более одной
такой системы; это не должно нас беспокоить, надо выбрать одну из них
и придерживаться ее.
Уравнение с частными производными [например, уравнение E.1.1),
•которое мы выбрали как пример] можно записать в новых координатах,
причем решения будут функциями этих переменных ?. Конечно, в виде
функций от ? можно выразить всевозможные решения уравнения, однако
мы теперь в состоянии классифицировать решения в соответствии с крае-
краевыми условиями, которые должны удовлетворяться на поверхности ?t = X.
Например, имеются решения, обращающиеся в нуль на поверхности
%1=Х; они должны содержать (?t — X) в качестве множителя. Имеются
также .решения с нулевой нормальной составляющей градиента на поверх-
поверхности; , в-третьих, имеются решевия с постоянными значениями самого
решения и нормальной составляющей его градиента на всей поверхности.
472 Гл. 6. Обыкновенные дифференциальные уравнения
Как мы указали выше и докажем позже, для решений третьего вида
осуществляется взаимно однозначное соответствие между решениями
и краевыми условиями: каждой паре значений ф, дф/ди на поверхности
соответствует одно и только одно решение. Некоторые из них являются
кратными других и не должны рассматриваться как новые решения. На-
Например, решение, соответствующее условиям ф = аа, 5ф/ди = аЬ на поверх-
поверхности ?1=Х, получается умножением на а решения при условиях ф = а,
д&/дп = Ь. Эти решения нельзя рассматривать как независимые, так же
как вектор А нельзя рассматривать как независимый с единичным век-
вектором а, направленным вдоль А. Однако мы получим различные решения,
если будем менять отношение ф к д^/дп.
Допустим, что мы упорядочим эти решения в соответствии со значе-
значением отношения [§х/(д$/дп)х] = Р. Решение для /> = 0 (имеется бесконеч-
бесконечное число решений для Р = 0, но все они различаются только постоянным
множителем, так что могут рассматриваться как одно решение) соответ-
соответствует граничному условию ф = 0 при ?i = X. Если взять теперь решения,
когда Р убывает, принимая отрицательные значения, то мы обнаружим,
что поверхность ф=0 удаляется от поверхности ^ = Х. Вообще говоря,,
семейство порожденных таким образом поверхностей не совпадает с семей-
семейством поверхностей ?х = const, но в некоторых случаях такое совпадение
имеет место. В этих специальных случаях решение ф должно обладать
множителем ^i(Si), функциональный вид которого зависит от Р. Если
Fx (?х) равно нулю, соответствующая поверхность ф = О совпадает с одной
из координатных поверхностей ?х = const.
Поверхность ф = 0 называется узловой поверхностью (или узлом) для ф.
Семейство поверхностей, порожденное при изменении Р, может не вклю-
включать все узловые поверхности. Вообще говоря, эти дополнительные по-
поверхности не будут ортогональными к поверхности ?i = const, так что-
они не совпадают и с другими координатными поверхностями.
До сих пор мы говорили о решениях специального вида, имеющих
на поверхности ?г = Х постоянные значения или постоянную нормальную-
составляющую градиента. Для большинства решений значения и градиент
вдоль граничной поверхности меняются, то есть являются функциями
координат ?2 и ?3* Их узловые поверхности, вообще говоря, не связаны
простыми соотношениями с координатными поверхностями $х. Однако
в некоторых случаях и для некоторых простых граничных поверхностей
из всей совокупности различных решений можно выделить множество-
таких, для которых все узлы либо совпадают с координатными поверхно-
поверхностями ?1? либо же ортогональны к ним. Такими будут решения, пред-
представляющие собой произведение двух сомножителей
Ф = /'1F1)ФFа, У,
один из которых F1 является функцией одного ?1? нули которой поро-
порождают узлы, совпадающие с поверхностями ?lf а другой Ф является
функцией ?2 и 53> н0 не 5i> и порождает узлы, ортогональные к поверх-
поверхностям Si-
Для еще более ограниченного множества систем координат можно
найти совокупность решений ф, у которых все узловые поверхности сов-
совпадают с координатными поверхностями всех трех семейств и которые
можно выразить в виде произведения трех сомножителей
Такие решения являются разделенными на множители, каждый из кото-
которых зависит только от одной координаты. Для большого числа систем
координат можно найти лишь небольшое число решений, у которых не-
5.1. Координаты, в которых переменные разделяются 473-
которые узловые поверхности совпадают с координатными, и только
в немногих координатах можно найти достаточно полное семейство реше-
решений, все узлы которых имеют такой вид.
Конечно, даже в этих специальных координатах семейство разделен-
разделенных (на множители, зависящие от одной координаты) решений образует
небольшую часть множества всех решений уравнения E.1.1). Однако
интересным и важным свойством этого подмножества является то, что
все решения уравнения с частными производными могут быть получены
из линейных комбинаций членов семейства разделенных решений. Вычислив
разделенные решения, мы можем найти и остальные.
Системы координат, обладающие семействами разделенных решений
данного уравнения, при помощи которых можно построить все решения
уравнения, называются разделяющими системами координат для рассмат-
рассматриваемого уравнения. Только в таких системах возможно получить реше-
решения в более удобной для применения форме, чем в виде громоздких рядов
или интегралов со многими переменными.
Для представления картины в целом рассуждения, приведенные на
последних страницах, проводились догматически. Для анализа и доказа-
доказательства всего нами сказанного потребуется несколько глав. В дальней-
дальнейшей части этого параграфа мы покажем, как находить разделяющие
системы координат и как можно получить разделенные решения.
Двумерные разделяющие координаты. Начнем со случая двух изме-
измерений, когда выбранное для рассмотрения уравнение E.1.1) имеет вид
3+Э+^=°- <5Л-2>
Если к постоянно, это уравнение допускает разделение переменных
в прямоугольных координатах х, у, так как, подставляя ф =X(x)Y(y)
в уравнение E.1.2), после простых преобразований получаем
X dx* + Y 1у
Первый член этого уравнения является функцией только х, второй —
только у, а третий постоянен. Чтобы это уравнение удовлетворялось при
всех х и у, необходимо, чтобы каждый член был постоянным, а сумма
всех трех постоянных равнялась нулю. Отсюда
A/Х) (d2X/dx2) = - а2, A/У) (d*Y/dy2) = - Р2, а2 + р2 = Л2
или
(d2X/dx2) + a2X=0, (d*Y/dyz) + (ft2 - а2) Y = 0. E.1.3)
Таким образом, мы расщепили уравнение с частными производными по двум
переменным на два обыкновенных дифференциальных уравнения, каждое
из которых содержит лишь одно независимое переменное. Постоянная а2
называется константой разделения. Семейство разделенных решений урав-
уравнения E.1.2) состоит из произведений решений уравнений E.1.3) для всех
значений параметра а. Общее решение уравнения E.1.2) можно предста-
представить в виде линейной комбинации разделенных решений для различных
значений параметра а. Другими словами, так как произведение решений
уравнений E.1.3) имеет вид eiax+v V-b»i то общее решение можно пред-
представить в виде интеграла
СО
= \
474 Гл. б. Обыкновенные дифференциальные уравнения
имеющего вид интеграла Фурье (см. стр. 428). Этот интеграл иногда
берется как контурный по комплексным значениям а.
Если к2 является функцией координат [когда уравнение E.1.2) пред-
представляет собой уравнение Шредингера], то для возможности разделения
переменных надо, чтобы она имела общий вид к2 = &2 + f{%) + g(y), где/
и g —произвольные функции одного переменного. Тогда разделенные ура-
уравнения приобретают вид
(d*Xldx*) + [а2 + / (ж)] X = 0, (d*Y/dy*) + [в» - а2 + g (у)] 7=0,
где а2 опять константа разделения.
Чтобы исследовать другие координаты, можно для упрощения приме-
применить аппарат теории аналитических функций комплексного переменного
z=x-\-iy, так как уравнение E.1.2) можно выразить через производные
по z и по его комплексно сопряженному z = х — iy (являющимися незави-
независимыми переменными). В соответствии с уравнением D.1.11) можно преобра-
преобразовать уравнение E.1.2) в
4 {дЦ/dz dz) + Щ = 0.
Произведем теперь конформное преобразование координат, перейдя
¦от х, у к ?i, ?2* Поскольку преобразование конформное, функция w = Ех -f- /?2
должна быть аналитической функцией z = х + iy (а сопряженная функция
w =¦ ?j — i?2 — аналитической функцией z = x — iy). Новые координатные
линии задаются уравнениями ?, (ж, у) = const, 52 (ж, у) = const. Так как
д/dz = (dw/dz) (d/dw) и д/dz = (dw/dz) (д/dw) (dw/dz и dw/dz равны нулю),
то преобразованное уравнение примет вид
dw dw ~ 8% +Щ~ | dw/dz |» - tto dw Ф' ^ }
где мы выражаем теперь z как функцию w (a z как функцию до).
Разделяющие координаты для двумерного уравнения Лапласа. Заме"
тим прежде всего, что для уравнения Лапласа, когда А = 0, все коорди-
координаты, полученные конформным преобразованием из прямоугольных коорди-
координат х, у, являются разделяющими координатами для уравнения Лап-
Лапласа в случае двух измерений. Разделенные решения имеют общий вид
ф 5i ± оЕ2 или
где константа разделения а может иметь любое вещественное или ком-
комплексное значение. При помощи интегралов или сумм этих элементарных
решений для различных значений а, C или у можно представить любое
решение двумерного уравнения Лапласа. Этот вопрос будет детально
исследован в § 10.2.
Надо заметить, что имеется тесная связь между геометрическими
-спойстнами координат и поведением решений. Геометрические свойства
координат ?,, ?3 наиболее ясно выражаются при помощи коэффициентов
Ламе hl=\/(dx/d?lJ-[-(dy/dtl)'i и h2 (см. стр. 34). Так как преобразова-
преобразование конформное, то коэффициенты Ламе hx и h2 должны быть одинаковы,
а используя условия Коши — Римана, легко показать, что эти коэффици-
коэффициенты равны \dz/dw\. В точках, где w(z) имеет полюс, коэффициент Ламе
| dzldw | обращается в нуль и система координат 5 имеет точку концен-
концентрации. Обратно, там, где система координат имеет точку концентрации,
•функция w(z) имеет полюс, а решение ф = e±aw — существенную особен-
особенность.
5.1. Координаты, в которых переменные разделяются 475
Разделение переменных, в вблновом уравнении. Для двумерного
уравнения Гельмгольца (волнового уравнения с синусоидальным премен-
нйм множителем) к постоянно и равно ш/с. В этом случае уравнение
E.1.5) не допускает разделения переменных, если только произведение
(dz/dw) (dz/dw), представляющее собой функцию ?г и ?2, не является сум-
суммой функций, одна из которых зависит только от ?и а другая — только
от ?2. Другими словами,
или, в дифференциальной форме,
и чтобы найти., чему может равняться \dz/dw\2 для разделяющих коорди-
координат, надо решить это уравнение.
Так как величина
{здесь мы применили условия D.2.1) Коши —Римана] представляет собой
коэффициент Ламе И.г = h2 для обеих координат ?lf 5г (для конформного
преобразования коэффициенты Ламе обязательно равны, см. стр. 440),
то нами тем самым получено уравнение для коэффициента Ламе разде-
разделяющей системы координат, для уравнения E.1.5). Неудигительно, что
мы пришли к такой задаче; мы уже говорили на стр. 34, что если мы
знаем коэффициенты Ламе, то мы знаем также все важнейшие свойства
соответствующей системы координат.
Уравнение для hlt Нг нуждается в дальнейшем преобразовании. Так
как величина dz/dw является функцией w, a dz/dw — функцией w, то диф-
дифференциальный оператор надо преобразовать к переменным w, w. Имеем:
и так как dz/dw не зависит от w, a dz/dw от w, то уравнение E.1.6)
приобретает вид
Kdw J dwi \dwj~\dw
ИЛИ
dz ~\ _
d~z
dz/dw dw* \dw J dz/dw dw2
Левая часть последнего уравнения зависит только от w. Чтобы она рав-
равнялась правой части (зависящей только от w) для всех значений шиш,
надо, чтобы обе части равнялись одной и той же постоянной, которую
мы обозначим X. Таким образом, мы получаем
d? С dz\ .(¦ dz\ d2 fd~z\x(dz^ (г.,7
^) \) )\) E 7)
Только если dz/dw удовлетворяет первому уравнению (a dz/dw — сопря-
сопряженному уравнению), то \ dz/dw \ является коэффициентом Ламе для раз-
разделяющей системы координат. Чтобы определить, какие координаты
476
Гл. 6. Обыкновенные дифференциальные уравнения
являются разделяющими для уравнения E.1.1), надо решить полученные
уравнения E.1.7).
Прямоугольные и параболические координаты. Простейшим, конечно,
является случай Х = 0. Тогда решением уравнения для dz/dw служит
и если у принять равным нулю, получим (a=a + ib, $ = c + id)
E.1.8)
Это соответствует простому вращению, изменению масштаба и переносу,,
причем координаты остаются прямоугольными. Новый коэффициент Ламе
равен \dz/dw\ = \$\ = \rc2 -\-d2, а новое уравнение имеет тот же вид, что
и E.1.2), но к2 заменяется на &2|р|2.
Рис. 5.1. Параболические координаты.
Если у не равно нулю, достаточно рассмотреть лишь член с у, так
как члены сайр добавляют просто вращение и перенос. Так как изме-
изменение масштаба также несущественно, то для простоты положим у=1
(и опустим постоянные интегрирования). Таким образом, имеем
г __ J_ ц|2 ж _ Г?. /t2 j
=w2,
E.1.9)
Получились параболические координаты, координатные линии для которых
образуют два ортогональных семейства софокусных парабол, осью которых
служит ось х. Эти линии определяются уравнениями ?х = []/ж2 + у2 + ж]1'2 =
— ж]1'2 = const, как показано на рис. 5.1. Такие
й
= const и ?2= ± [1/ ] , р
координаты удобны, например, для границы, состоящей из отрицательной
полуоси (которой соответствует уравнение ?i = 0).
Уравнение E.1.5) теперь приобретает вид
E.1.10)
5.1. Координаты, в которых переменные разделяются
который допускает разделение переменных, как это и должно быть. При-
Применяя обычный прием, видим, что разложенное на множители решение
имеет вид ф = F (?х) G (?2), где сомножители удовлетворяют обыкновенным
дифференциальным уравнениям
(d»/yd®+ (*• + *¦?¦) *" = (), {dW/d?2) + (-v.* + k%)G = 0 E.1.11)
Решения этих уравнений мы исследуем в настоящей главе позже.
Надо сделать несколько замечаний. Прежде всего, хотя функция
z = -тр w2 аналитична всюду, за исключением бесконечности, точка w = О
является точкой ветвления конформного преобразования, так как в ней
коэффициент Ламе h обращается в нуль. Мы избежали двузначности,
приняв, что ?х принимает только положительные значения, в то время как ?2
может изменяться от —со до + оо. Таким образом, линия ?х = О,
представляющая собой отрицательную полуось х, производит разрез, выше
которого ?2 принимает положительные значения, а ниже — отрицательные.
Мы будем, если только это возможно, исключать этот разрез из рассма-
рассматриваемой области, полагая, что граница поля совпадает с одной из линий
?г = const, а само поле расположено во внешней части этой параболы,
что можно сделать в значительном числе случаев, когда граница откры-
открытая; однако для замкнутых границ, состоящих из линий ?х = const,
?2 = const, когда поле расположено внутри границы, часть разреза попа-
попадает в интересующую нас область. В этом случае мы избегнем разрыва
решения вдоль разреза, положив, что G является четной или нечетной
•функцией ?2, и выбирая затем соответствующую функцию F (^) так, чтобы
•если G четная, то dF/d%1 = 0 при ^ = 0, и если G нечетная, то F{0) — 0
(этот вопрос детально исследуется в § 11.2).
В соответствии с единственной особенностью функции w2, расположен-
расположенной на бесконечности, мы покажем позже, что решения F и G также
имеют особенности только при бесконечных значениях ?t и ?2.
Для уравнения Шредингера в параболических координатах функция к2
.должна иметь вид еа + [/ (Si) + ^ (?гI/(^1 + 51) - В этом случае разделенными
уравнениями будут
® + [а2 + *Ч1 + f (Wl F = 0, (daG/dfe22) + [ - а2 + в»** + g F,)] G = 0,
где / и g —любые функции одного переменного. Функции F и G будут
иметь особенности при Z = со и в каждой особой точке соответственно / и g.
Полярные и эллиптические координаты. Возвращаясь к уравнению
E.1.7), исследуем теперь случай, когда X не равно нулю. Примем сначала,
что X положительно, и положим Х=1, так как изменение численного
значения X меняет только масштаб и не дает новых систем координат
(а поскольку X больше нуля, оно может быть и единицей). Имеем
dz/dw = e±v> или z = aew + be~w.
Возьмем сначала крайнее значение 6 = 0 (и положим а = 1, так как
изменение а меняет только масштаб). Тогда преобразование в координатах
задается соотношениями
; E.1.12)
| dz/dw | = \ = hz = e?i = r.
Получились полярные координаты, причем семейство ^ = const (или г = const)
-состоит из концентрических окружностей, а множество ?2 = <р = const —
478
Гл. 5. Обыкновенные дифференциальные уравнения
из радиальных лучей, как показано на рис 5.2 (заметим, что коэффициент-
Ламе кг равен г для координаты ?lt а не для координаты г, для кото-
которой скалярный множитель hT = 1). Эти координаты применимы для круго«
вых границ и для границ, состоящих из двух лучей, образующих угол.
Уравнение E.1.5) принимает вид
(дЦ№1) + (дЦ/д%) + е2'ъЩ = 0 E.1.13>
и разделяется на уравнения
O, E.1.14),
где постоянная а2 опять является константой разделения.
Для общего случая, когда z = aew + be~w, можно получить результаты
в более удобной форме, положив
так что если d, а и fS вещественны, то
E.1.15>
| dz/dw ! = *! =
cos fa), у = dsh(^ -p) singa>
?? |/ch2 Ft - p) - cos2
tp=Zir
Рис. 5.2. Полярные координаты. Рис. 5.3. Эллиптические координаты..
Это — эллиптические координаты, состоящие из софокусных эллипсов
и гипербол с фокусами в точках x=±d, у = 0, как показано на рис. 5.3.
Постоянная р обычно для удобства полагается равной нулю. (Однако надо
заметить, что если положить а = C -f- In 2 и затем устремить ?$ к отрица-
отрицательной бесконечности, то фокусы эллипса сольются с началом координат
и вся система координат перейдет в пределе в полярную.) Уравнение-
с частными производными в рассматриваемых координатах и обыкновен-
обыкновенные дифференциальные уравнения, полученные в результате разделения,
переменных, имеют вид
+
E.1.16)
cos2 E2 - a2] G = 0,
где a2 вновь является константой разделения.
Коэффициенты Ламе и геометрия систем координат. Мы увидим
в этой главе позже, что вид уравнений, полученных при помощи разде-
5.1. Координаты, в которых переменные разделяются 47&
ления переменных в полярных или- эллиптических координатах и имеющих
в качестве коэффициентов при F и G показательные (или гиперболические)
функции, не является наиболее удобным для исследования. Трудность
проистекает прежде всего из геометрии систем координат и из того, что
они получены при помощи конформного преобразования. Обе эти системы
имеют точки концентрации, где коэффициент Ламе \dz/dw\ обращается
в нуль. Вблизи таких точек в соответствии с малостью коэффициента Ламе
координатные линии расположены очень густо, а так как преобразование
конформное, то в этих точках обращаются в нуль коэффициенты Ламе
для обеих координат.
Однако, поскольку мы определили геометрию разделяющих систем
координат, мы можем видоизменить коэффициенты Ламе для каждой коор-
координаты в отдельности так, чтобы сохранить геометрию координат и в то же
время привести разделенные уравнения к более удобному для исследова-
исследования виду. Например, так как в разделенных уравнениях в качестве коэф-
коэффициентов при F и G более желательны алгебраические функции, чем
показательные, мы можем принять в полярных координатах е-1 за новую
координату г, а в эллиптических координатах ch (?х — Р) — за р. Преобра-
Преобразование тогда не будет конформным, но вид координатных линий остается
неизменным и координаты все равно будут разделяющими.
Возвращаясь вновь к уравнению E.1.6), мы видим, что как для вол-
волнового уравнения, так и для уравнения Шредингера в случае разделения
переменных должно быть kz\dz/dw\2= k2h2 = / (Б^ + g (?a)- В этом случае
разделенные уравнения имеют вид
E.1.17)
В соответствии со сказанным выше выберем некоторую функцию р-(?,}
от переменной ?х, для которой функция / (S^, выраженная как /(р-), является
простой алгебраической функцией р.. Так как f + g пропорционально ко-
коэффициенту Ламе \dz/dw\2, то в точках концентрации системы коорди-
координат /и g могут одновременно обратиться в нуль. Можно выбрать новую
координату р. так, чтобы точка концентрации получилась при некотором
стандартном значении р., например 0 или 1 (или, может быть, бесконеч-
бесконечности). Коэффициент Ламе для р. связан с коэффициентом h для ?х и ?2 сле-
следующим соотношением:
К = V(dx/dtf + (ду/dtf = кФ», Ф^^/dfs E.1.18)
так как дх/др — (дх/д^) (d^/dp). Если h^. не обращается в нуль в точке
концентрации системы координат (где h равно нулю), то в этой точке
Фр. = h^/h обращается в бесконечность.
Чтобы перейти в первом уравнении E.1.17) к независимой перемен-
переменной р., применим формулы
dy. dp dti ' d6, "" Ф^ d;x ' d\\ ~ Ф2 d\>? Ф? dp ' * d\J* '
Мы можем, если нужно, сделать то же для ?2, перейдя к новой функции
т]E2) и получив новый коэффициент Ламе йч=/гФТ|, и т. д. Тогда новое
преобразование и получающиеся разделенные уравнения приобретают вид
й,=Ф,А,
E.1.19)
80 Гл. 5. Обыкновенные дифференциальные уравнения
Последние два обыкновенных дифференциальных уравнения выглядят более
сложными, чем уравнения E.1.17), однако если Ф^/Фр. и Ф?Д — а2 + /(р.)]
станут алгебраическими функциями р., вместо трансцендентных, то ура-
уравнения E.1.19) легче исследовать и решить.
Как мы указали выше, при значениях р, соответствующих точкам
концентрации системы координат, функция Ф^., или функция Ф^/Ф,,., или
обе вместе могут обратиться в бесконечность, так что особенности коэф-
коэффициентов при dF/dp и F в уравнении для F тесно связаны с геометрией,
соответствующей системы координат. На эту связь мы будем ссылаться
в данной главе позже.
Для конкретизации рассуждений применим их к полярным коорди-
координатам E.1.12). Мы хотим так изменить шкалу радиальной координаты,
чтобы функция e2=i стала алгебраической. Очевидно, можно выбрать
fi = r = eei или ^ = 111A., где р. (или г) —обычное расстояние. Начало коор-
координат — единственная точка концентрации для этой системы координат —
получится тогда при г = 0. Коэффициентом Ламе и результирующим ура-
уравнением для F тогда будут
^ = \пг, Фг = 4> Ф;=-^, K = l, %+-j^r+^f(r)F = O, E.1.20)
где для случая волнового уравнения f(r) = r2k2 — a2. Следовательно, мы
видим, что оба коэффициента при dF/dr и при F имеют особенности
в полярном центре, при г = 0.
Шкала координаты ?2 не нуждается в изменении, так как последнее
из уравнений E.1.14) не имеет трансцендентных коэффициентов. Тем
не менее ?2 представляет собой угол, так что решение G является пери-
периодической функцией, a w — многозначной функцией z. Для устранения
этой многозначности иногда бывает полезно совершить преобразование
7] = cos52, причем •») меняется от — 1 до +1. Соответствующими уравне-
уравнениями будут
>где для волнового уравнения g(f\) равно а2, константе разделения. Коэф-
Коэффициенты здесь имеют особенности при т]=±1, т. е. на концах интер-
интервала изменения ч\.
Теперь очевидно, что для случая эллиптических координат простейшее
преобразование имеет вид ch (^ — Р) = р-, cos ?2 = т], причем р. меняется от 1
до со, а т) — от — 1 до +1. Преобразование и видоизмененные уравне-
уравнения таковы (для р = 0):
S1=Archp., fe2 = arc cost],
_o d2G у dG g(ti) r
где для волнового уравнения / (fi) = d2fc2p.2 — a2, g (tj) = — d2kzif + a2. Здесь
опять коэффициенты этих уравнений имеют особенности только в точках
концентрации координат (р= 1, ¦»] = ± 1).
Следует также заметить, что p- + "»] = (l/d) 1/(ж + dJ + г/2 = rx/d, p- — ¦»] =
= A/d) |/"(ж - dJ + у2 = r2/d, то есть
E.1.23)
5.1. Координаты, в которых переменные разделяются 4Й1
где rlt r2 — расстояния от точки (ж, у) до обоих координатных фокусов
(ж= Я- d, у = 0). Отсюда линия р. = const представляет собой геометрическое
место точек, сумма расстояний которых до обоих фокусов постоянна,
то есть является эллипсом. Подобным образом уравнение линии •») = const
содержит разность расстояний и представляет гиперболу.
Константы разделения и граничные условия. Если в координатах,
приспособленных к граничной поверхности данной задачи, переменные
разделяются, то в принципе возможно удовлетворить разумно поставлен-
поставленным граничным условиям посредством правильной комбинации решений
разделенных уравнений (какие граничные условия являются «разумными»
и как находить «правильные комбинации», будет сказано в гл. 6 и 7).
Например, границей может служить линия ?i = const в одной из рассмо-
рассмотренных разделяющих двумерных систем координат. Эта граница может
иметь конечную длину (такой будет замкнутая граница); в этом случае
множитель G(?2) должен быть непрерывным, когда мы, меняя ?2, обходим
линию ?i = const, начиная движение в некоторой точке и заканчивая его
в ней же.
Например, для полярных координат г, <р линия г = const представляет
собой окружность конечного радиуса, которая полностью пробегается
при изменении угла ср от 0 до 2и\ Разделенное уравнение для множителя,
зависящего от <р, имеет вид
где а —константа разделения, и имеет решениями cos(aop), sin (aop) и их
линейные комбинации. Чтобы Ф была непрерывной вдоль границы г = const,
это решение должно при ср = 2гс иметь то же значение, что причр = 0;
другими словами, решение Ф должно быть периодическим по ср с перио-
периодом 2ic. Это требование периодичности накладывает ограничение на допу-
допустимые значения константы разделения а. В нашем примере, чтобы функ-
функция cos (дер) или sin (дер) была периодичной по <р с периодом 2тс, константа
разделения а должна равняться целому то = О, 1, 2, 3,... Ив других
случаях, когда ?2 является периодической координатой, накладываются
аналогичные ограничения на значения константы разделения для решений,
остающихся непрерывными при обходе границы ?i = const.
Мы всегда можем упорядочить эти допустимые значения, обозначив
наименьшее через ах и т. д., так что an+1 > an, а соответствующие мно-
множители в решениях — через Х\ (?2), XI (?2), ... Множитель с ?, также зависит
от а, так что полное решение, соответствующее допустимому значению ап
константы разделения, имеет вид Х"(^)Х^(^2).
В гл. 6 будет показано, что каждую функцию периодической коор-
координаты ?2, удовлетворяющую разумным ограничениям, можно разложить
в ряд по указанным допустимым функциям
п=1
Правило для подсчета коэффициентов Ап будет также дано позже. Отсюда,
если интересующее нас решение ф (?lf ?2) должно удовлетворять граничному
условию ф(с, 62) = /(?3) вдоль границы %х = с, то это решение можно
выразить через разделенные решения, взятые для допустимых значений
константы разделения
= 2 К
31 Ф. м. Морс и Г. Фешбах
482 Гл. 5. Обыкновенные дифференциальные уравнения
Другим, более сложными граничным условиям можно удовлетворить по-
подобным же образом.
Заметим, что окончательное решение ф (?х, ?2) не является разделенным,
но может быть выражено в виде ряда из разделенных решений. В каждом
случае условия периодичности выделяют последовательность допустимых
значений константы разделения, и общее решение получается в виде ряда
по этим допустимым значениям. Даже для открытых границ обобщенные
условия периодичности также дают возможность выразить решение, удовле-
удовлетворяющее определенным граничным условиям, в виде ряда (или интеграла)
из разделенных решений, взятых для допустимых значений константы
разделения.
Однако эти рассмотрения увели нас в сторону от того, что здесь
необходимо; сейчас мы должны исследовать вопрос о разделении перемен-
переменных для уравнений с частными производными в трехмерном случае.
Разделение для трех измерений. Разделение переменных для двух
измерений особенно просто по следующим причинам. Прежде всего имеется
только одна константа разделения, так что разложенные на множители
решения образуют однопараметрическое семейство, в результате чего при-
применение граничных условий приводит к относительно простым рядам.
Во-вторых, условия разделения просты; так, для уравнения
дЦ>
dz
член к21 dz/dw |2 должен просто представлять собой сумму функций, зави-
зависящих только от к и только от v, в противном случае переменные не раз-
разделятся. И, в-третьих, семейства узловых поверхностей, совпадающих
с координатными, получаются только в случае, когда решения представлены
в виде X1{k1)X2{k2).
Во всех этих трех отношениях трехмерная проблема разделения пере-
переменных оказывается сложнее. Так как имеется три разделенных уравне-
уравнения, то констант разделения вместо одной будет две. Каждое из трех
уравнений может содержать обе константы, и в этом случае каждый
из трех множителей в разделенном решении сложным образом зависит
от обеих констант разделения, в результате чего удовлетворить граничным
условиям даже в виде ряда из разделенных решений — утомительное
и трудное дело. Однако для некоторых систем координат получается, что
одно (или два) из разделенных уравнений содержит только одну константу
разделения; в этих случаях ряд, представляющий общее решение, при-
принимает более простой и удобный для применения вид.
Что касается третьего пункта, то оказывается, что для трехмерного
уравнения Лапласа V2i]> = 0 имеются такие координатные системы, в кото-
которых решение принимает более сложный вид Я (?lf Ё2) ^з)-^1(^1)-^2(^2)-^з(^з)>
где дополнительный множитель И (который можно назвать модуляционным
множителем) не зависит от констант разделения. Для этих систем раз-
разделение происходит с точностью до общего множителя, и граничным
условиям все равно можно удовлетворить, так как после вынесения этого
общего множителя R за знак суммы, взятой по всем допустимым значениям
констант разделения, эта сумма принимает тот же общий нид, как и
в случае, когда модуляционный множитель отсутствует.
Возвращаясь ко второму из перечисленных пунктов, отметим, что для
трехмерного уравнения с частными производными член, соответствующий
слагаемому к2 \ dz/dw |2 для двумерного случая, не обязан быть простой
суммой функций, каждая из которых зависит только от одной координаты;
разделения можно достичь и в более сложных случаях, чем этот.
5.1. Координаты, в которых переменные разделяются 483.
Определитель Штеккеля. Общий метод 'разделения для нашего стан-
стандартного трехмерного уравнения с частными производными
связан со свойствами определителей третьего порядка. Такой определи-
определитель S строится по своим элементам Фтп при помощи следующего-
соотношения:
11 $12 $13 I
$21 $22 $23 =$11$22$33 + $12$2зФ31 + $13$21$32-
$31 $32 $33
$21.
$31
будут
Мг = 3S,
М% = OS
M3 = dS,
/дФ11 = Ф22Ф33-ФчзФ32,
/аФ21=Ф13Ф32-Ф12Ф33,
/5ф31 = ф12ф23-ф13ф22.
- $13Ф22Ф31 - $11$23$32 - $12$21$33- E.1.25>
Алгебраическим дополнением элемента Фтп называется множитель при
элементе Фтп, если Фтп вынести за скобки из членов, где он встречается.
Например, алгебраическими дополнениями элементов первого столбца Ф11г
Ф $ б
E.1.26)
Так как нам потребуются здесь только алгебраические дополнения элемен-
элементов первого столбца, то мы не будем писать у М двойных индексов.
Важным свойством определителей, которое мы будем применять при
разделении переменных для уравнений с тремя аргументами, является
свойство ортогональности, связывающее элементы и алгебраические допол-
дополнения. Так. для E.1.26) имеем
2^„Фщ = ^ %МпФпт = 0, т = 2,3, E.1.27)
Т1=1 71=:!
как если бы Фп2 или Фп3 были компонентами векторов, перпендикулярных
вектору с компонентами Мп.
Значит, если бы разделенными уравнениями для трехмерного случая
были
то мы могли бы скомбинировать эти три уравнения таким образом, чтобы
исключить константы разделения А| и Щ. Действительно, умножая уравне-
уравнение для Хх на (M1/S)X2X3 и т. д. и складывая, получаем
Это уравнение соответствует нашему стандартному уравнению
если выражение для оператора Лапласа в координатах 5
совпадает с первым слагаемым в уравнении E.1.29).
Чтобы это было так, надо наложить некоторые ограничения на коэф-
коэффициенты Ламе h и на элементы Фпт определителя 5. Во-первых, так как.
уравнения E.1.28) предполагались разделенными, все функции /п, Фп1,.
Фп2 и Фп3 должны зависеть только от $п. Определитель, элементы Ф17П,
верхней строки которого, являются функциями только ?1( элементы Ф2т
31*
484 Гл. 5. Обыкновенные дифференциальные уравнения
второй строки — функциями только ?2 и элементы Ф3т нижней строки —
только ?3> называется определителем Штеккеля. Он является основным
понятием при изучении разделения переменных в трехмерном случае.
Заметим также, что если Ф1т является функцией ?х и т. д., то первый
минор Мх зависит от ?2 и %й, но не зависит от \х и т. д.
Далее, величина h^hg/hn должна равняться произведению функции /п
только от ?п на некоторую функцию gn от остальных ?. Тогда, например,
член с ^ в операторе Лапласа приобретает вид
_i е г h^i^ аф ] _ g, F,, У а г . , , j_i ?__?_["* ^
hjh^hs дЦг L fef as, J fe,V*s d?, L'1^1' S5, J ~~ /if/, 35, L'1 «5,
й имеет ту же общую форму, что и член (M1/Sf1)[d(f1d^/d^1)/d^1] в урав-
уравнении E.1.29). Чтобы эти члены совпадали, должно быть
l/hl = Mn/S, E.1.31)
а это вместе с исходным ограничением на hji^h^h^. приводитх) к условию
Рвбертсона
S = U &) /2 F.) /3 F,), E.1.32)
которое дает выражение для определителя Штеккеля и одновременно огра-
ограничивает виды систем координат, допускающих разделение переменных.
Если оно имеет место, то величина ^hjijh^ равна произведению /х, функ-
функции сх, на функцию Mi/з/з от ?2 и ?3, но не ^ и, таким образом, удовле-
удовлетворяет сформулированному выше требованию.
Эти требования, наложенные на коэффициенты Ламе, резко ограничи-
ограничивают число независимых систем координат, отвечающих условиям задачи.
Детальный анализ того, какие системы удовлетворяют этим требованиям,
является значительно более громоздким, чем соответствующее исследование,
проведенное на стр. 475 для двумерного случая. Там мы показали, что
разделяющие координатные системы (для волнового уравнения) состоят
из софокусных конических сечений (эллипсов и гипербол) или их вырожден-
вырожденных форм (окружностей и радиусов, софокусных парабол или параллель-
параллельных прямых). Детальный анализ трехмерного случая приводит к анало-
аналогичному утверждению: в эвклидовом пространстве координатные поверх-
поверхности системы разделяющих координат для волнового уравнения состоят
из софокусных поверхностей второго порядка или их вырожденных
форм.
Софокусныо поверхности второго порядка. Уравнение
Ь E.1.33)
при различных значениях параметра ? представляет три семейства софо-
софокусных поверхностей второго порядка. Для 5 > о- получается полное
семейство софокусных эллипсоидов, пересечение которых с плоскостью
yz дает эллипсы с фокусами в точках у = 0, z = ± Yb2 — с2, с плоскостью
жг —эллипсы с фокусами в точках ж = 0, z=±l/ra2 — с2 и с плоскостью
ху - эллипсы с фокусами в точках х = 0, у = ± Y0? — ^2- Предельная
поверхность этого семейства получается при Иов представляет собой
Ч Из этих условий вытекает, что gi/(M1/2/8)=g2/(M2/1/8) = g8/(Af3/1/2), откуда
следует, что эти отношения постоянны и получается соотношение E.1.32) с точ-
точностью до несущественного постоянного множителя.—Прим. перев.
5.1. Координаты, в которых переменные разделяются 485
часть плоскости yz, расположенную внутри эллипса с большой осью
2 "\/ ег — с2 вдоль оси z и малой осью 2 \/ а2 — Ь2 вдоль оси у.
Для а > ? > Ь получается полное семейство софокусных однополостных
гиперболоидов, перзсечение которых с плоскостью yz дает эллипсь}
с фокусами в точках у = 0, z = ±\/ Ъ2 — с2, с плоскостью . xz — гиперболы
с фокусами в точках ж = 0, z = ± Т^о2 — с2 и с плоскостью ^ — гипер-
гиперболы с фокусами в точках ж = 0, y=±Va2 — Ь2. Одна из предельных
поверхностей получается при ? —¦» а и представляет собой часть плоскости
2/z, расположенную вне эллипса с большой осью 2|/а2 — с2 вдоль оси z
и малой осью 2 |/а2 — Ь2 вдоль оси у; другая предельная поверхность
получается при ?-^Ь и представляет собой часть плоскости xz, рас-
расположенную вне -гиперболы с вещественной осью 2"|/Ь2 —с2 вдоль оси z
и мнимой осью 2 j/a2—Ь2 вдоль оси ж.
Наконец для Ь > ? > с имеем полное семейство софокусных двупо-
двуполостных гиперболоидов, пересечение которых с плоскостью yz дает
гиперболы с фокусами в точках у = 0, z = ± |/Ь2 — с2, с плоскостью xz —
гиперболы с фокусами в точках ж = 0, z= ±"|/а2 —с2, а с плоскостью жу
эти гиперболоиды не пересекаются. Одна из предельных поверхностей
получается при 5—>Ъ и представляет собой часть плоскости, xz, распо-
расположенную внутри гиперболы с вещественной осью 2 |/Ь2 с2 вдоль оси z
и мнимой осью 2 1/а2— Ь2 вдоль оси ж; другая поверхность получается
при 5—>с и совпадает с плоскостью ху. Между прочим, без ограниче-
ограничения общности мы можем положить с = 0.
Так как построенные три семейства поверхностей попарно ортого-
ортогональны, можно положить, что указанным трем интервалам изменения
параметра ? соответствуют три семейства координатных поверхностей:
параметру ?х (?х > а) соответствуют эллипсоиды, ?2 (а > ?2 > Ь) — однопо-
лостные гиперболоиды и ?3 (Ь > ?3 > с) - двуполостные гиперболоиды. Легко
убедиться, что соотношения между координатами х, у, z и эллипсоидаль-
эллипсоидальными, координатами ?х, ?2, |3 (для с = 0) с их коэффициентами Ламе
таковы:
52
ь =
1
Следуя проведенным выше рассуждениям, найдем, что h^hg/hl равно
произведению
на функцию V - (V, ~ %)*/(% - а<) (? - Ь2) FJ - а2) (% - Ь2), не содержащую ^.
Следовательно, функция
/п«п) = "/1(й-«8)(й-Ья)| E.1.35)
является одной из функций, участвующих в уравнении E.1.32). Это в свою
очередь дает значение определителя Штеккеля
486 Гл. 5. Обыкновенные дифференциальные уравнения
откуда, учитывая соотношения E.1.31),
что дает возможность найти элементы определителя Штеккеля. Они равны
Поэтому уравнение Гельмгольца и получающиеся разделенные обык-
обыкновенные дифференциальные уравнения в этих координатах имеют вид
Gnfn д_ Г f д]> ,,. _ п
E1-Si) (q-g) (Sf-51) в5п |_'я esn J + "i* ~ u>
1 = ^ 1 JC_ = 0. E.1.37)
Eb2) (aa62) J n v '
Этот вид обыкновенных дифференциальных уравнений встретится нам в
дальнейшем.
Заметим, что в случае трехмерного уравнения Шредингера для частицы
член к2 (который мы обозначили через kl) не является постоянным, а
представляет собой разность между постоянной к\ (полной энергией час-
частицы) и зависящей от 5 потенциальной энергией частицы. Для возмож-
возможности разделения переменных потенциальная энергия частицы должна
быть такой, чтобы в уравнении E.1.37) из коэффициента при Хп вычита-
вычиталась некоторая функция pn(kn), зависящая только от ?п. Это означает,
что допустимым видом потенциальной энергии будет
з
^ф1 E.1.38)
Заметим также, что для эллипсоидальных координат каждое из трех
разделенных обыкновенных дифференциальных уравнений содержит кх и
обе жшстанты разделения к2 и к3. Напоминая наши квантово-механические
рассуждения гл. 2, мы можем рассматривать процесс разделения как про-
процесс вращения, переводящий множество векторов в абстрактном векторном
пространстве, определенных координатами ж, у, z (или ?х, 5а. ?3). в мно-
множество векторов, определенных параметрами кг, к2, к3. Разлагающиеся на
множители решения представляют собой функции преобразования (напра-
(направляющие косинусы) от собственных значений для координат к собствен-
собственным значениям для к. То, что мы нашли, означает, что это преобразование
в случае эллипсоидальных координат приводит к функциям преобразова-
преобразования, разделяющимся (на множители) относительно координат, но не раз-
разделяющимся относительно параметров к. Для некоторых вырожденных
форм эллипсодиальных координат разложенные на множители решения
разделяются также относительно параметров, что значительно упрощает
манипуляции с решениями.
Эти вырожденные формы эллипсоидальных координат, полученные,
когда а, Ъ, с полагаются равными друг другу, нулю или бесконечности,
более полезны и интересны, чем общая форма. Имеется 10 таких форм,
признающихся «различными» системами координат и обладающих специаль-
специальными наименованиями. Эти 11 систем (общая эллипсоидальная система
5.1. Координаты, в которых переменные разделяются 487
и 10 вырожденных форм) являются единственными системами, допускаю-
допускающими разделение переменных ш для волнового уравнения или уравнения
Шредингера в трехмерном случае [причем уравнение Шредингера разде-
разделяется, только если потенциальная энергия имеет определенный функцио-
функциональный вид, см. E.1.38)]. Эти формы вместе с отвечающим им видом
коэффициентов Ламе h, определителя S и т. д. приведены в таблице в
конце этой главы.
Вырожденные формы эллипсоидальных координат. Отправляясь от
о реобразования
(х\~gg) (aj—a2) (ajj — а2)
для общих эллипсоидальных -координат, мы можем получить все десять
вырожденных форм, приведенных в конце главы, при помощи растяжения,
сжатия и переноса. Например, бесконечное растяжение всех фокальных
расстояний дает у центра эллипсоидов:
I. Прямоугольные координаты. Положим х\ в приведенных выше со-
соотношениях равным а2 + k\, х\ = р2 + ?|, а х3 = ?3; положим Р = а sin <p, где
<р может быть произвольным, и после этого устремим а к бесконечности.
Это даст координаты, приведенные под номером 1 в конце главы. С другой
стороны, стремление р к нулю симметризует эллипсоиды, выравнивая их
в поверхности вращения.
IX. Сплющенные сфероидальные координаты. Полагая а = а, х\ —
= a2 + Si, xl = a2 — a2%l, х3 = р?3 и УстРемляя Р к нУлю, мы перейдем от
эллипсоидов к сплющенным (выровненным) сфероидам, от однополостных
гиперболоидов к гиперболоидам вращения (также однополостным) и от
двуполостных гиперболоидов к парам плоскостей, проходящих через ось
«ращения. Чтобы получить форму, данную в таблице в конце главы, надо
положить еще х' = ?, у' = у, z' = x, что сделает ось z осью вращения. Если
превратить эллипсоид в поверхность вращения около большой оси, мы
получим
VIII. Вытянутые сфероидальные координаты. Они получаются при
Р—»<х, согласно формулам а = а, Р2 = а2 —г, х1 = ?1, а^ = я2 — г?|, ж| = а2?|,
s —» 0. Бесконечное вытягивание при этом большой оси даст
II. Круговые цилиндрические координаты. Если обозначить а —а,
Р2 = а2 — з, ж^ = а2-}-?*, х\=а2 — з|2, х3 — \ъ и положить г—>0, а затем
а—*со, то получатся простейшие координаты вращения. Бесконечное, вы-
вытягивание большой оси до симметризации дает
III. Эллиптические цилиндрические координаты. К такой системе мы
¦приходим, обозначая Р2 = а2 + а2, х\ = а?-{-1\, х\ = а2-{-а2^\, ж3=?3 и пола-
полагая а —> со, но оставляя при этом а конечным. С другой стороны, если
мы вместо удлинения укоротим большую ось вытянутых сфероидальных
координат, то мы получим полностью симметричные
V. Сферические координаты. Обозначив ос = а, р2 = а2 —е, Xy^ — ^i,
х\ = а2 — cfc2,, ж3 = аЕз1 мы положим сначала е—>0, а затем а—>0, что даст
488 Гл. 5. Обыкновенные дифференциальные уравнения
полную симметрию. Полагая, наконец, р пропорциональным а и устремляя
их одновременно к нулю, получим
VI. Конические координаты. Они имеют своими координатными по-
поверхностями сферы и эллиптические конусы, а получаются, если обозна-
обозначить а = ка, р=Л'а, к2 + к'2=1, x\ = FJ{k2-k'% xl = a2[2k2k'2 + (k*-
— k'2)klh х% = а2[2к2к'2 -(к2 — k'2)?s] и затем положить а~>0.
Параболические системы получаются, если переместить положение
начала координат на «край» эллипсоида до удлинения последнего. Самым
общим случаем являются
XI. Параболойдальные координаты. Здесь мы полагаем a2 = d2-\-a2d,
Р2 = с?2 -f- ЪЫ и помещаем новое начало координат в точку z' = d, так что-
х = ж', у = у' и z = z' — d. Обозначим х\ — d2-\-iftd, х\ = d?-\- -rfed, х\ = d2 |?
и примем, наконец, что d—> сю. Новыми координатами будут
- У
У
они соответствуют поверхностям
ж2
tf—а2 ' if—б2 '
Для т] = % > а получается семейство эллиптических параболоидов, пере-
пересекающихся с плоскостями xz и yz по параболам, а .с плоскостью
ху — по эллипсам. Для т\ = % (где а > т]2 > Ь) поверхности представляют
собой гиперболические параболоиды, пересекающиеся с плоскостями xz
и yz по параболам, а с плоскостью ху — по гиперболам. Наконец, для
tj = Tj3 < b (мы должны допускать для tj| и отрицательные значения, чтобы,
исчерпать все это семейство) вновь получаются эллиптические парабо-
параболоиды, направленные относительно оси z в противоположную сторону.
Предельная поверхность при tj1 —> а представляет собой часть плос-
плоскости yz, расположенную внутри параболы с вершиной при z = -^a% и е
фокусом при z = -K-b2; при tj2 —> а — остальную часть плоскости yz; при
7]2 —> Ъ — часть плоскости xz, расположенную вне параболы с вершиной
1 1
при z = y62 и с фокусом при z = -=-«, наконец, при т]3-^ о предельная
поверхность представляет собой остальную часть плоскости xz. Коэффи-
Коэффициенты Ламе и связанные с ними функции этих координат приведены
на стр. 620.
Как и выше, другие координатные системы можно получить при по-
помощи изменения междуфокусных расстояний. Например, полагая а = Ь,
получаем координаты вращения, именно
VII. Параболические координаты. Обозначив Ъ2 — а2 — е, t)i = Ei + g2i
т)! = а2 — sS|, Tjg = Ъ2 — ?а и положив затем г—=> 0, получим эту более простую
систему. С другой стороны, если мы будем растягивать большую ось
эллипсов, то в конце концов получим
IV. Параболические цилиндрические координаты. Здесь мы обозна-
обозначаем -»Ji = a2 + ^, 7J = Ь2 + ^, -п1=Ъ2 — ?|, x = z'~~b2,y=y',z = x'/a и за-
затем полагаем а—> со.
5.1. Координаты, в которых переменные разделяются 48&
Этим исчерпываются все различные вырожденные системы, которые
можно получить из эллипсоидальных координат. Было бы интересно ис-
следовать определители Штеккеля и окончательно разделенные уравнения
для этих случаев, чтобы узнать, имеются ли у них характерные общие
черты.
Слияние особенностей. Мы выбрали шкалу всех рассмотренных здесь
координат так, чтобы функции /п и Фпт представляли собой алгебраи-
алгебраические функции kn, а если разделенные уравнения записать в виде
(*«). E-1.39).
то функции р и q имеют особенности в точках концентрации соответ-
соответствующих систем координат. Например, для эллипсоидальных координат
р и q имеют полюсы при ?= ±а, +Ь и на бесконечности (то есть если
сделать замену переменной и = 1/?, то соответствующие функции р и q бу-
будут иметь полюс при и= 0 или, что то же, ? = оо). Вырожденные формы
систем координат получаются при сближении до совпадения двух или
более из этих особенностей. Точки, в которых р или q имеет особенность,
называются особыми точками соответствующего уравнения, а указанный
процесс сближения особых точек называется слиянием особых точек.
В случае вытянутых сфероидальных координат, например, имеет
место слияние особых точек а и Ъ, а также — а и — Ъ; это вместе с за-
заменой шкалы приводит к тому, что -уравнение для ^ имеет особые точки
±а и на бесконечности, а уравнение для ?2 и ?3 —особые точки ±1 исо.
В сферических координатах а становится равным нулю, так что уравне-
уравнение для ?i имеет особые точки в 0 и в оо и т. д.
Где бы ни была особая точка дифференциального уравнения, там
общее решение этого уравнения имеет особенность (полюс, точку ветвле-
ветвления или существенную особенность). Следовательно, можно сказать, что
разложенное на множители решение ф = ХгХ2Х3 обычно имеет особенность
во всех точках концентрации соответствующей системы координат. Можно
также сказать, что все обыкновенные дифференциальные уравнения, на
которые разделяется уравнение V2ф + /с2ф = 0 (включающее большую часть
уравнений, которые мы будем изучать), получаются из общего уравнения
с пятью особыми точками при помощи слияния их до четырех, трех или
двух. Так же как указание нулей и особенностей определяет функцию
комплексного переменного, указание положения и строения особых точек
дифференциального уравнения, как мы увидим позже в этой главе, опре-
определяет само уравнение и его решения. Это является, конечно, совсем дру-
другим путем выражения того обстоятельства, что геометрия системы коор-
координат определяет структуру решений разделенных уравнений, что не уди-
удивительно.
Константы разделения. Рассмотрение определителей Штеккеля для
11 систем координат, приведенных в конце главы, показывает, что среди
элементов этих определителей имеется целый ряд равных нулю. Например,
для всех координат вращения Ф31 = Ф32 = О- Это значит, что множители Х3 (?3)
для координат вращения включают только константу разделения &3.Так как
для координат вращения ?3 соответствует углу вокруг оси вращения, то
не удивительно, что этот множитель особенно прост. Мы видим также, что-
-490 Гл. б. Обыкновенные дифференциальные уравнения
для всех цилиндрических координат два из трех элементов Фп1(Еп)
равны нулю; это означает, что только один из множителей Хп зависит
от кх.
¦ Таким образом, для некоторых вырожденных форм эллипсоидальных
координат решения, разложенные на множители, осуществляют определен-
определенное разделение параметров к.
Другим путем это можно установить посредством самого процесса
(в~его обычном виде) разделения переменных в уравнении. Возьмем урав-
уравнение
и пусть ф = Х1Х2Х3. Если координаты разделяются, так что выполняются
соотношения E.1.29) и E.1.31), то имеем •
В некоторых случаях представляется возможным умножить это уравнение
ла некоторую функцию от ? так, что по крайней мере один из четырех
членов полученного уравнения зависит только от одной координаты, в то
время как остальные члены от нее не зависят. Мы можем тогда этот член
положить равным постоянной а (так, как функция от одного Еп может
совпадать с функцией от остальных ?, только если эта функция предста-
представляет собой не зависящую от Ё постоянную), и тогда соответствующий
множитель X будет зависеть только от одной постоянной а (которая яв-
является тогда константой разделения, либо к\, либо к\).
Возможность разделения уравнения таким способом зависит от строе-
строения коэффициентов Ламе hn, на что ясно указывает уравнение E.1.40)
(все остальные множители в и-м члене зависят только от ?„, так что если
hn постоянно или является функцией одного ?п, то этот член уже готов
для разделения без каких-либо преобразований). Здесь можно различить
три случая:
А. Решение, вполне разделяющее константы разделения. В этом слу-
случае можно найти такой множитель p{klt ?а, ?3), что каждый из двух членов
зависит от одной координаты (допустим, что так будет для ?2 и ?3)- Тогда
член с ?2, то есть (p/h\f2X2) [d(/2dX2/d$2)/d$2] можно положить равным
постоянной к\, а соответствующий член с Х3~Равным постоянной к\. Сле-
Следовательно, для Хг получается уравнение
а решение, разложенное на множители, принимает вид
(А) ф = ХгFi; klt *„*,)*,&; к2)Х3(Ц3; *,), E.1.41)
где два из множителей зависят только от одного параметра к, так же
точно, как и от одной координаты 5. Сравнение с методом разделения при
помощи определителя Штеккеля показывает, что решение может иметь
вид E.1.41), только если каждая из двух строк определителя Штеккеля
имеет два нуля, и просмотр таблицы в конце главы показывает, что этим
простым поведением обладают только решения для прямоугольных и кру-
круговых цилиндрических координат. [Сферические координаты имеют ре-
решение вида Хг(?х; klt k2) X2(?z; k2, к3)Х3(?3; к3), который для уравнения
5.1. Координаты, е которых переменные разделяются 491
Лапласа, когда кх = 0, так же прост, как и E.1.41)]. Этот тип разделения
требует высокую степень симметрия системы координат.
Б. Решение, частично разделяющее константы разделения. В этом
•случае только один член (например, с ?3) можно отделить непосредственно;
оставшееся уравнение
у- d С, &Х%~\ ,. ]r*-ni\
Л/а ~Ж~) + ^ + 3 ~ )
должно быть умножено на другой множитель v(S1, ?2), чтобы можно было
отделить другой член. Поэтому решения, разложенные на множители,
имеют один из следующих видов:
\"l) Ф =-^1 (Sl> ^2> )^2(^2; "С2>"'з)-^з(^31 ^> ^з)> /К А ЛО\
/ft v v it- j 1 l \ v tt- 1 ? j \ v- /f. ? \ tD.l-.ЧЛ)
Л 2/ т -^-1 \^1» 1) 2) 3/ 2 \Ч2» *^1> "'З» *^3/ 3 \^3» 3/'
Просмотр таблицы показывает, что виду (Бг) соответствуют параболиче-
параболические цилиндрические координаты, а виду (Б2) — эллиптические цилиндри-
цилиндрические, параболические, сплющенные сфероидальные и вытянутые сферо-
сфероидальные (то есть все оставшиеся цилиндрические координаты и коорди-
координаты вращения). Здесь только последняя строка определителя Штеккеля
имеет два нуля.
В. Решение, не разделяющее констант разделения. В этом случае
ни один из элементов второго и третьего столбцов не равен нулю и для
осуществления разделения надо применить всю технику, связанную
с определителем Штеккеля. Возможные виды таковы:
(Вх) ф=Х1(?1; къ к2, к3)Х2(^2> к2, к3)Х3(?3; к2, к3), ._ . ,„
<Ва) ф-Х^; К К, *.)ХаFа; klt k2, kz)X3{k?; кг, к2, к3). ^ ЛО)
Форму (БЛ) имеют только конические координаты. Эллипсоидальные
и параболоидальные координаты имеют вид (В2), где ни один из элемен-
элементов определителя Штеккеля не равен нулю.
Должно быть очевидным, что вид (А) сравнительно прост для при-
применения к рассматриваемой задаче, виды (Б) более сложны, а виды (В)
несравненно сложнее для применения.
Уравнение Лапласа для трех измерений, модуляционный множи-
множитель. Очевидно, что уравнение Лапласа V2cJ> = 0, к которому приводится
наше стандартное уравнение при кг = 0, допускает разделение переменных
в каждой из 11 систем координат, перечисленных в таблице. Но так как
двумерное уравнение Лапласа допускает разделение переменных для боль-
большего числа систем, чем двумерное волновое уравнение, то нам следует
проверить, не будет ли это верно и для трех измерений. Исследования
показывают, ' что систем координат, в которых решения уравнения Лап-
Лапласа принимают вид ^1(^)^2(^2)^3(^3) типа (А), (Б) и (В), больше нет.
Однако обнаруживается, что можно найти другие системы, в которых
можно построить множество решений уравнения Лапласа, имеющих более
общий вид.
ф = Х1 (^)Х2(У Х3(?,)/Д&, 6„ 5,), E-1.44)
где R не зависит от констант разделения к2 и А;3 (см. стр. 482). То же
исследование показывает, что волновое уравнение не допускает этого
Член \ik\ может отсутствовать; это приводит к случаю (Б]).—Прим. перее.
492 Гл. 5. Обыкновенные дифференциальные уравнения
рбобщения, так что дополнительные системы координат являются разде-
разделяющими только для уравнения Лапласа.
Множитель -ft можно назвать модуляционным множителем', он изме-
изменяет все семейство разложенных решений одним и тем же образом.
Его присутствие несколько видоизменяет технику применения определит
теля Штеккеля. Например, теперь мы полагаем [вместо E.1.32)]
hxh2h3lS = U (У U F.) /з E,) ЯЧ E-1.45)
где к —функция \х, ?2, ?3. Мы также] требуем, чтобы [вместо E.1.31)]
E.1.46)
причем в этих двух уравнениях определитель Штеккеля S и его алгебраиче-
алгебраические дополнения Мп удовлетворяют тем же условиям, что и выше (элементу
Фпт этого определителя являются функциями только ?„, и потому Мп
не зависят от %п). Подставляя все это в уравнение Лапласа, мы сначала
получим уравнение
1
У 1 df , dXn I _ у 1 Ifj JH
^ h2f |7 J L7
h2nfnxn
I _
Получившееся разделение членов с X и членов с И и является причиной
включения Л в оба соотношени'я E.1.44) и E.1.45). Если теперь мы смо-
сможем найти функцию R, удовлетворяющую уравнению
то, применяя E.1.46), мы получим в результате уравнение
которое, подобно волновому уравнению, разделяется на обыкновенные
дифференциальные уравнения
из коих можно определить множители Хп.
Софокусные циклиды. Циклиды — это класс поверхностей четвертого
порядка, очень близких по своим свойствам к поверхностям второго
порядка (эллипсоидам, гиперболоидам, параболоидам). Одним из интерес-
интересных свойств поверхностей этого класса является то, что их инверсия
в сфере снова представляет собой циклиду. Уравнение этих поверхостей
просто выражается в однородных координатах X, ?i, v, p
z = Vp, У = ф, z = v/p E.1.50)
или в «пентасферических координатах»
р») = if (х» + y2 + z2+l),
= p2(.T2 + y2 + z2-l), E.1,51)
xa = 2pX= 2р2ж, a;4 = 2pp. = 2p2y; xa = 2pv = 2p2z.
Поверхность, определенная уравнением
2'Т^ = 0' "n+1>«n, E-1.52)
5.1. Координаты, в которых переменные разделяются 493
где ? и а постоянны, и называется циклидой. Поверхности, полученные
при выборе различных значений ? для фиксированных а, образуют семей-
семейство поверхностей, которое можно назвать семейством софокусных
циклид.
Одно полное семейство получается, если брать все значения $ между а2
и а3, другое —если брать все значения между а3 и а4 и третье —между
а4 и аъ. Оказывается, что эти семейства попарно ортогональны, так что
они могут быть приняты за семейства координатных поверхностей.
Мы обозначим \ = \х между а2 и а3, ?2 между а3 и а4 и ?3 между а4 и а5
Так как ж = ж3/2р2, у = ж4/2р2, z = #5/2р2, р = — (ж2 + г'.т1)/2р, то уравнение
Лапласа V2<J> = 0 равносильно уравнению
Одновременно, так как хх и х2 входят в комбинации х2 + ixl7 мы видим,
что
Этот результат можно обобщить следующим образом: если а^,..., х5 —
лентасферические координаты, связанные с четырьмя однородными
•координатами X, ц, v, p при помощи уравнений второго порядка
так, что
Б
2 з»=0, E.1.53)
71=1
то решение уравнения Лапласа удовлетворяет также уравнению
Для окончания рассуждения надо перейти от пентасферических
координат к софокусным пдклидным координатам ?• Для этого рассмот-
рассмотрим сначала координаты хп, как обычные ортогональные координаты
•в пятимерном пространстве, не требуя, чтобы удовлетворялось уравнение
E.1.53). Совершим тогда переход к другим пяти координатам, опреде-
определенным пятью уравнениями:
Т2_? (ei-ai)(^2-ai) E3—М F4—Qi) ,t л сеч
или равносильными уравнениями
5
"V
Z
5 2 5
5
Заметим, что при этом ?5 = ^ %п и конечном счете обратится в нуль.
71=1
Уравнение, соответствующее уравнению E.1.54), получается после
ряда алгебраических преобразований и имеет вид
494
Гл. б. Обыкновенные дифференциальные уравнения
где
/ (х) = (х
х - а2) (х — а3) (х — а4) (х — а6).
Оно равносильно пятимерному уравнению Лапласа в новых координатах.
Но мы не занимаемся пятимерным уравнением, а хотим в конце
концов получить трехмерное уравнение в координатах ?lf ?2, ?»• Однако
эти координаты тесно связаны, так как, решив уравнения
5 2 5
мы получим соотношения
тг=1
а3) (о,—
оБ)
и т. д., E.1.57)
которые определяют хп через трехмерные координаты ?1( ^2» 5з и в ко"
нечном счете определяют ж, у, z через циклидные координаты.
Заметим, что преобразование E.1.57) связано с E.1.55). В последнем
случае лишь три координаты присутствуют явно, то есть можно сказать,,
что преобразование E.1.57) представляет трехмерное подпространство'
преобразования, данного в уравнении E.1.55). Оно и ясно, так как
мы знали, что ?s = 2 х\ должно быть равно нулю, а ?4 также должно-
быть положено равным некоторой постоянной, чтобы мы могли полу-
получить в результате трехмерное уравнение. Сравнение уравнений E.1.57).
и E.1.55) показывает, что если мы одновременно устремим ?6 к нулю,
а ?4 к бесконечности так, что ^^5—> — 2 апхп, то мы придем к циклид-
ным координатам.
Возможно, что ф будет функцией 54 и ?5. Если она является функ-
функцией произведения ?ЖЕ5, то усложнения в виде дополнительных нулей-
или бесконечностей не будет. В частности, если <]> содержит множи-
множитель (?4?6)а> то в пределе этот множитель обратится в [^,апх^]а. Если
мы хотим, чтобы на больших расстояниях потенциал обращался в нуль,
как 1/г, то показатель а может равняться —1/4 и мы можем положить.
E-1.58)
Подставляя эту форму для решения в E.1.56) и устремляя \± к беско-
бесконечности, получаем в результате уравнение с частными производными
для <р. Умножим его на ??'4 и произведем разложение по степеням 1/?4.
Члены с первой степенью ?4 исчезнут автоматически. Члены же с нуле-
нулевой степенью Е4 дадут уравнение ^цля <р
E.1.59).
71=1
5.2. Общие свойства, решение при помощи рядов 495-
где / (ж) = (ж — uj) (х—а2)(х — а3) {х — а4)(х— а5). В этом уравнении можно
разделить переменные при помощи определителя Штеккеля, так же как
и для уравнения в эллипсоидальных координатах. Однако в этом случае
полное решение ф будет произведением неразделенной части [2 апх%\ 4 =
на разделенную часть <р, как мы уже установили.
Можно получить различные вырожденные формы циклид, полагая
одну или более из постоянных ап равными друг другу или бесконеч-
бесконечности. При этом эллипсоидальные координаты и все их вырожденные
формы включаются в качестве частного случая. Включаются также торо-
тороидальные координаты, определенные следующими уравнениями:
п (x* + yZ + z*-aY , 4я«»« „„
=и> Тг '"Р—г- —и. ^o.i.ouj
Это — вырожденные формы уравнения E.1.52) причем мы применили обо-
обозначения & и а2 вместе ?п и ап; им соответствуют (для ?х = const)
тороиды, полученные вращением вокруг оси z окружности радиуса а/\/?\ - 1
с центром z = 0, х — a^jY^\ — 1, и (для ?2 = const) сферы радиуса a/\fl — %\
с центром х=у — 0, z = tt?8/V^l —?1 (все эти сферы проходят через окруж-
окружность z = 0, x2-{-y2 = a2, соответствующую предельному тороиду ^=00).
Выражения х, у, z через ?, а также вид скалярных множителей h,
модуляционного множителя R и определителя Штеккеля для этого полез-
полезного частного случая приведены на стр. 621 и 622 этой главы. На этих
страницах приведен также другой полезный частный случай бисфериче-
ских координат.
Представляется, что общие циклидные координаты (и их вырожден-
вырожденные формы) содержат все системы координат, в которых уравнение
Лапласа разделяется с модуляционным множителем или без него, так же
как эллипсоидальные координаты содержат все системы, в которых раз-
разделяется волновое уравнение. Теперь мы должны перейти к исследова-
исследованию обыкновенных дифференциальных уравнений, полученных в резуль-
результате разделения переменных.
5.2. Общие свойства, решение при помощи рядов
Мы должны теперь перейти к изучению обыкновенных дифференци-
дифференциальных уравнений, полученных при разделении переменных в уравнении
с частными производными V24 + A:2<p=0 в различных разделяющих коор-
координата^. Как мы показали на стр. 483, все разделенные уравнения
имеют общий вид
где
a fn и ФП7П — функции ? (обозначенной здесь через z). Мы выбрали шкалу
координат так, чтобы функции р и q представляли собой простые алге-
алгебраические функции z с конечным числом полюсов, соответствующих
точкам концентрации системы координат.
Уравнение E.2.1) является линейным однородным уравнением второго
порядка. Как указано на стр. 469, такие уравнения могут иметь раз-
496 Гл. 6. Обыкновенные дифференциальные уравнения
личные решения. При этом, если фи Фг. •••» 4>п~~решения уравнения
<5?(ф) = 0, то и 2 Ап$т (гДе ^т —произвольные постоянные коэффициенты)
также есть решение. Иногда встречается соответствующее неоднородное
уравнение X (ф) =r (z). Мы уже указали раньше, что если ЧР"П—решение
уравнения X (ф) = гп, то \Fm + X ^тФт — также решение уравнения X (ф) = гп,
т
a 2 lpn + 2 Д„Фт — решение уравнения X (ф) = 2 /"„•
Таким образом, имеется бесконечное число различных решений урав-
уравнения E.2.1), соответствующих различным выборам постоянных Ап.
Однако в действительности многие из этих решений различаются только
постоянным множителем. Картина станет, пожалуй, более ясной, если
рассмотреть ее с точки зрения абстрактных векторных пространств. Каж-
Каждой функции y{z) можно поставить в соответствие вектор ? несчетно-
мерного пространства, причем для каждого z величина y{z) принимается
за компоненту Y вдоль направления, соответствующего этому значению z
(см., например, стр. 134). Дифференциальной операции X соответствует
векторная операция, которая, вообще говоря, преобразует каждый век-
вектор A (z) в некоторый другой вектор. Однако если у представляет собой
решение уравнения X(у) = 0, то соответствующий вектор Y при помощи
этой векторной операции переводится в нуль. Каждому решению и (г),
отличающемуся от y(z) постоянным множителем, соответствует вектор U,
имеющий то же направление, что и Y, хотя и другую длину. Возникает
вопрос: сколько различных направлений могут иметь векторы, соответству-
соответствующие решениям уравнения E.2.1)?
Определитель Вронского. Если двум решениям ух и у2 соответствуют
векторы одного направления, то у2 — аух и у, = ау[ (в этой главе мы будем
применять краткие обозначения у' = dy/dz и у" = d2y/dz2) и выражение
д&1- Уя) = У1У'2-Уш!/1 E.2.2)
¦обращается в нуль для всех значений z. С другой стороны, если Y2
имеет отличное от Yx направление, то &{ylt y2) нигде не равно нулю.
Выражение Д {у1г у2) .определенное формулой E.2.2) (где ух и у2 оба являются
решениями уравнения X (у) = 0), называется определителем Вронского для
решений уг и у2 данного однородного уравнения. Если определитель Врон-
Вронского равен нулю, то одно решение отличается от другого постоянным
множителем. Если определитель Вронского отличен от нуля для любого
интервала изменения z, то Y2 имеет отличное от Yx направлени'е и два
решения у1 и у.2 называются независимыми.
При помощи свойств определителя Вронского можно непосредственно
показать, что имеется по крайней мере одно решение, независимое
с ух ф 0. Предположим, что решение уг известно, и попробуем построить
другое решение у2, связанное с yt в некоторой начальной точке z=z0
соотношениями у2 = ауи у'2 — №[{& ф Р). Тогда определитель Вронского
A (z/i У2) = Ф~а) У\У\ в точке z = z0 отличен от нуля (мы допускаем, что
ни уи ни у[ не равно нулю при z = z0). Посмотрим, какие значения при-
принимает Д для других значений z, если у2 является решением уравнения
¦^(у)==0- Взяв производную от Д по z и применив уравнение E.2.1),
получим
^Г = У1У1 ~ УъУ'х = - У1 (РУ2 + ЧУъ) + У2 (Py'i + ЧУ1) =
6.2. Ofivive свойства, решенье при помощи рядов 497
Это уравнение для Д можно проинтегрировать, что дает
^ E.2.3)
Отсюда, за исключением того несчастного случая, когда / при выбранном z0
равно нулю, если Д отлично от нуля при z — z0, то оно отлично от нуля
и при других значениях z, пока / (z) Ф 0; таким образом возможно вайтп
второе решение, независимое от уг.
Так как &(z) = yly'2 — y2y'1 = y21(z)d[y2(z)/y1(z)]/dz, то немедленно
получаем, что
го
z
=А (zo) / (z0) Vi (z) \ f.dut u . E.2.4)
го
Нетрудно убедиться в том, что выражение E.2.4) представляет собой
решение уравнения E.2.1), так как если подставить y = uv, то уравне-
уравнение E.2.1) принимает вид
+ 2u'v' = 0, y = uv, X (у) = 0. E.2.5)
Полагая и = уг, X (и) = 0, а и= \{&/yl)dz, мы легко убедимся в том, что
уравнение E.2.5) удовлетворяется. Таким образом, у2, определенное фор-
формулой E.2.4), представляет собой решение уравнения X (у) = 0, незави-
независимое с уу\ соответствующий вектор Y2 в абстрактном векторном простран-
пространстве имеет направление, отличное от \v Если имеем диа независимых
решения, то, так как уравнение E.2.1) линейное, любая -комбинация
Аух + Ву» также является решением. Отсюда каждому вектору е плоскости,
определенной векторами Yx и Y2, отвечает решение соответствующего
уравнения.
Независимые решения. Мы только что показали, что если одно реше-
решение yl (z) уравнения ? {у) = 0 известно, то второе решение можно получить
посредством интегрирования
^-!**-^ E.2.6)
Это решение независимо с y±{z), так как определитель Вронского
г*
равен Бе~^ р *. Далее возникает следующий вопрос: нельзя ли все воз-
возможные решения уравнения E.2.1) выразить в виде линейной комбивации
Ау1 + Ву2 или же можно найти решение, у которого соответствующий
вектор не лежит в плоскости, определенной векторами Yt и Ya. Возьмем
какое-нибудь решение у3 и посмотрим, можно ли его выразить через ух
и yv Выбрав точку z = z0, мы всегда можем найти значения А и В, для
которых
Уz (zo) = Ayi («о) + Ву2 (z0), у'г (z0) = Ау[ (z0) + Ву'2 (z0). E.2.7)
Это можно сделать, поскольку определитель Вронского Д(У1»-Уа) отличен
от нуля или, другими словами, поскольку уг и у2 — независимые решения.
32 ф. м. Морс и Г. Фешбах
Гл. б. Обыкновенные дифференциальные уравнения
Итак, всегда можно найти такую комбинацию уг и у2, что определи-
определитель Вронского у3 и этой комбинации равен нулю при z = z0. Но чтобы
убедиться, что функция у3 действительно равна Ау1 + By , надо проверить,
что их высшие производные при z = z0 также равны. Однако, применяя
уравнения E.2.1) и E-.2.7), мы видим, что
У'г (zo) = - РУз -ЯУз=-р№А + ВУ'Л -q[Ayx + Byt[*= Ay", (z0) + Byl (z0 j.
Продолжая дифференцирование и применяя уравнение E.2.1), находим,
что если имеют место соотношения E.2.7), то и п-я производная от уъ
в точке z0 равна такой же комбинации п-х производных от ?/г и у2. Сле-
Следовательно, ряд Тейлора около точки z = z0 дает
так что решение у3 представимо в виде комбинации Ау1-\-Ву2 во всей
области изменения z, где сходится ряд Тейлора.
Таким образом, в этом смысле каждое решение у3 уравнения X (у) = О
представимо в виде линейной комбинации двух независимых решений ух и у2.
С точки зрения абстрактного векторного пространства получается, что
векторы, представляющие решения уравнения X (у) = 0, все лежат в одной
плоскости. Нетрудно показать, что при рассмотрении уравнения третьего
порядка потребуется уже три независимых решения для построения базис-
базисной системы, через которую можно выразить все остальные решения;
другими словами, в этом случае векторы, соответствующие решениям, все
лежат в трехмерном подпространстве абстрактного векторного пространства;
для дифференциальных уравнений высшего порядка размерность этого под-
подпространства равна порядку линейного дифференциального уравнения,
порождающего решения.
Интегрирующие множители и сопряженные уравнения. Выражение
решения незнакомого дифференциального уравнения через известные алге-
алгебраические или трансцендентные функции является обычно более сложной
задачей, чем интегрирование незнакомой функции; действительно, опре-
определению первообразной функции и = \ vdz соответствует решение очень
простого дифференциального уравнения первого порядка du/dz — v (z) = О.
Для интегрирования в замкнутом виде обычно, по существу, просто
испытывают несколько возможных решений и, чтобы проверить, не будет
ли производная и' какого-нибудь из них равна v. Результаты этого иссле-
исследования собраны в таблицах интегралов. Если требуемый интеграл
не содержится в таблицах, обычно необходимо прибегнуть к разложению
в ряд (при этом область применимости ряда ограничивается областью его
сходимости) или к численному подсчету (с аналогичными или более жест-
жесткими ограничениями).
Основной задачей этой главы будет классификация уравнений (то есть
составление таблицы, аналогичной таблице интегралов), по которой можно
было бы узнавать виды уравнений, имеющие известные и табулированные
решения, а также исследование различных о^щих методов решения таких
уравнений, что позволит нам найти общий характер поведения решений
других незнакомых уравнений. Во многих случаях мы будем считать
решение найденным, если его можно выразить через один или более инте-
интегралов, даже если интегрирование возможно осуществить только при
помощи разложения в ряды (или численного подсчета). Это называется
5.2. Общие свойства, решение при помощи рядов 499
«приведением к квадратурам»—выражение, посредством которого математик
как бы уклоняется от остальной части задачи нахождения решения.
Например, простейшее линейное дифференциальное уравнение
E.2.8)
можно привести к квадратурам посредством перегруппировки членов
y = Ae-$pdz E.2.9)
или при помощи интегрирующего множителя. Для этого заметим, что
если умножить уравнение E.2.8) на множитель е*р г, то результат будет
представлять собой полный дифференциал, который можно немедленно
проинтегрировать
Имеется обширная литература, в которой излагаются полезные приемы
нахождения интегрирующего множителя для более сложных уравнений
первого порядка.
Уравнения второго порядка вида E.2.1) также ивогда можно привести
к квадратурам при помощи интегрирующего множителя. Из тождеств
y"v - v"y = {d/dz) {y'v — v'y), {d/dz) (pyv) = vpy' + у {pv)'
получаем следующее тождество для любых разумных функций у и v пере-
переменной z:
v [у" + ру' + gy] — y [V - {pv)' + qv] = {d/dz) [vy' - v'y + vpy],
которое можно символически записать в виде
vX{y)-y?{v) = {d/dz)P{v, у), E.2.10)
где оператор X тот же, что и в исходном дифференциальном уравнении
•# (у) = У" + РУ' + qy = ®- Дифференциальный оператор X, преобразующий о
по формуле
? W = S - -Ж №) + ЧР = ^ - Pv' + (Я ~ Р') v E.2.11)
называется сопряженным оператору X (у), преобразующему функцию у,
а дифференцируемое по z выражение
[?? '] E.2.12)
называется присоединенной билинейной формой, зависящей от функций
v и у и независимой переменной z.
Если мы можем решить сопряженное уравнение X (и) = 0, то решение
исходного уравнения X (у) = 0 сводится к решению уравнения первого
порядка
Р =vy [{y'ly) — {v'/v) + p] = const.
Так как годится любое решение последнего уравнения, то мы выберем
простейшее, положив постоянную равной нулю, так что если v — решение
уравнения X {v) = 0, то
~ = — -pdz, yx = ve I E.2.13)
500 Гл. б. Обыкновенные дифференциальные уравнения
(мы не обращаем внимания на произвольные постоянные, так как можем
ввести их позже). Второе, независимое от ух решение можно найти
по формуле E.2.6)
\^\^%, E.2.14)
причем надо выполнить еще одно интегрирование. Тогда общим решением
будет $ = Ау1 + Ву2.
К общему типу дифференциальных уравнений второго порядка, кото-
которые можно решить таким путем, принадлежит случай, когда g = dp/dz,
так как тогда сопряженное уравнение [см. E.2.11)] принимает простой вид
и двумя независимыми решениями для у будут
— \pdzC fpdz, v
у1 = е i \ei y dz = -y ,
E.2.15)
(lei dzy
при подходящем выборе постоянных интегрирования.
В некоторых из наших разделенных уравнений множитель /п имеет
вид (? — а)л, так что соответствующее выражение р в уравнении равно
d In ]ld% = u/(? — а). Если при этом элементы определителя Штеккеля
таковы, что <7== — а/(? — аJ, то уравнение X (у) = 0 приобретает вид
у" + (a/z) у' - (а/з2) у = 0, z = 5 - а;
тогда условие д-р' удовлетворяется и можно применить формулы E.2.15).
В этом случае \ pdz — alnz, v' =za, v = za+1/(a + l), так что общим реше-
решением уравнения X (у) = О будет
ф = 4'ух + ?'у2 = 4z + (B/z«), E.2.16)
которое имеет точки ветвления (если а не целое) порядка а при z = 0
(то есть при \ = а, в точке концентрации координат) и при z = co, полюс
порядка а при z = 0 и простой полюс при z = со (то есть после подста-
подстановки z = 1/w функция ф имеет простой полюс при w = 0), если а целое
положительное, и полюс порядка \а\ при z = оо, если а< — 2 целое.
Решение E.2.16) имеет место, кроме случая а= — 1, когда член Bz~a
не является независимым с первым решением Az. В этом случае р = — 1/z
в второе решение можно получить прямо из E.2.6)
- \" pdz
_ С ej> , _ Г zdz ,
t/o ~~* *4л \ " a uZ —"¦ 2 \ ¦*' и ¦—— 2 1П 2j
так что общее решение будет тогда равно
ф = z (Л + В In z) E.2.17)
и опять будет иметь точки ветвления при z = 0 и z = оо.
Решение неоднородного уравнения. Зная два независимых решения ух
и. у2 однородного уравнения ? {у) = 0, мы можем найти общее решение
неоднородного уравнения ? (ф) = t (z) при помощи дополнительного инте-
5.2. Общие свойства, решение при помощи рядов 501
грирования. Аналогично уравнению E.2.5) подставляем .(]> = ни в уравне-
уравнение X (ф) = г и получаем
vX (и) + uv" + {up + 2м') v' = г.
Если теперь положить и равным одному из решений уг однородного урав-
уравнения X (у)=0, получится
f + lp + 2 (y,7yi)I и' = r/yi. E.2.18)
Однако так как второе решение и определитель Вронского связаны соот-
соотношением (у2/У\)' = '-Vz/i, то из указанного на стр. 497 свойства опреде-
определителя Вронского вытекает, что
У\ Z У\ Р У\ Ух И '
откуда (yJy^)"-\ [p + ^iy'Jy,)] (y2/yi)' = 0. Умножая это уравнение на и',
а уравнение E.2.18) на {у21у^)' и вычитая, получаем
При помощи этого преобразования мы привели исходное неоднород-
неоднородное уравнение второго порядка X (ф) = г к простому неоднородному урав-
уравнению первого порядка
dz L (У-г/yi) J 4
где уи у2 и Д = 2^2 — 2/2^1 получены из однородного уравнения X (у) = 0
и предполагаются известными функциями z. Интегрируя это уравнение
первого порядка без больших усилий, получаем
или
Так как v=ty/y1, то мы отсюда получаем формальное решение неодно-
неоднородного уравнения X (<]>) = г
где интегралы неопределенные, а постоянные с выбираются в соответ-
соответствии с краевыми условиями. В соответствии с обсуждением на стр. 4;N
это решение состоит из суммы частного решения
\r{w) Г у.(»)и(')-у«Му.(») 1 dw
и произвольного решения однородного уравнения X (у) = 0.
Решение при помощи рядов около обыкновенных точек. Как мы
указали несколько выше и докажем вскоре, общее решение уравнения
X (у) = 0 имеет особенности в точках полюсов функций р a q. Все другие
значения z, в которых р и q являются аналитическими функциями, назы-
называются обыкновенными точками уравнения. Точки, в которых р или q (или
обе) имеют особенности, называются особыми точками уравнения.
Чтобы показать, что общее решение в обыкновенной точке анали-
тично, и также проиллюстрировать один из приемов решения дифферен-
дифференциальных уравнений, подсчитаем разложение в ряд решения уравне-
вия E.2.1) в обыкновенной точке z=a. Так как z= а — обыкновенная
точка, то как р, так и q аналитичны и могут быть около z = a разложены
502 Гл. 5. Обыкновенные дифференциальные уравнения
в ряды Тейлора
p(z) = p(a) + (z-a)p'(a) + ±{z- af рГ
Решение у (если оно аналитично) также можно выразить в виде ряда
y=ao + a1(z — a) + a2(z — aJ+ ... .
Подставляя его в уравнение E.2.1), получаем
0 = [2a2 + alP (a) + aoq (a)] +
+ [6а3 + 2а2р (а) + ахр' (а) + аод' (а) + агд (a)] (z - а) + ... .
Приравнивая коэффициенты при каждой степени z — а нулю, получаем
последовательность уравнений для определения коэффициентов ап ряда,
представляющего решзние. Первое уравнение выражает а2 через а0 и at
[и известные величины р(а) и q(a)]. Из второго можно выразить а3
через а2, ах и а0 и потому через а0 и а1 и т. д. Эти уравнения можно
решить, что и даст ряд для у.
Таким образом, разложение у в ряд можно записать в виде
где г/х и у2 — независимые решения. Они образуют особенно удобную для
применений пару решений, так как одно имеет единичное значение
и нулевую производную при z = a, а другое — нулевое значение и единич-
единичную производную; эта пара называется основной системой решений для
обыкновенной точки z = а. Любому начальному условию у (а) — А, у' (а) = В
легко удовлетворить, положив у = Аух + Ву.2. Решение, представленное
в виде ряда, пригодно внутри круга сходимости радиуса, равного расстоя-
расстоянию от а до ближайшей особой точки дифференциального уравнения.
Например, основной системой решений дифференциального уравнения
у" _)- у = 0 в обыкновенной точке z = 0 служит ух = cos z, y2 = sin z. Так
как ближайшая особая точка находится на бесконечности, то ряды, в кото-
которые разлагаются косинус и синус, пригодны на всей конечной части пло-
плоскости z.
Интересно отметить, что если р имеет при z = а полюс, в то время
как q аналитична в а, то одно решение уравнения аналитично, а второе
имеет особенность. Подставляя р= F (z)/(z —a)", где /' — аналитическая
функция, отличная от нуля при z = a, а затем проводя такое же разло-
разложение в ряд, как и выше, мы найдем в общзм случае, что ах = а2 = ...
...=ап = 0, в то время как an+1, an4.2 и т. д. можао выразить через а0.
Например, если в выражении для р будет п = 2, то ряд, соответствующий
уравнению X (у) = 0, имеет вид
0= ?~Ta1F(a)+l^
так что одно из решений уравнения будет (полагая а0 = 1)
5.2. Общие свойства, решение при помощи рядов 503
Второе решение можно подсчитать, применяя формулу E.2.6). Так как
\ pdz = — ^М + F' (a) In (z - а).-Ь4-^4°) (z — а) + ..., то ивтеграл
\ dze* v Чу\ имеет существенвую особенность общего вида (z — aJ~F'(a)X
хер(а)/(г-а)ф Поэтому общее решение Аух + Ву2 имеет при z = a существен-
существенную особенность.
Особые точки, определяющие уравнение. Мы только что увидели,
что вблизи такой особой точки, где q аналитичва, а р имеет полюс, одно
решение, аналитпчно, в то время как второе имеет точку ветвления (или
полюс), если р имеет простой полюс, или существенную оссбенвссть,
«ели р имеет полюс высшего порядка (эта особенность может одновре-
одновременно являться точкой ветвления). Это исследование имеет значение
¦с общей точки зренпя: можно определить регулярную особую точку как
такую, в которой общее решение имеет полюс или точку ветвления (или
их комбинацию), а иррегулярную особую точку как такую, в которой
-общее решение имеет существенную особенность.
Чтобы найти, какой тип особых точек получается при различном
поведении р и q, выделим особенность у у, положив y = uv, где и пред-
предполагается аналитической и и (а) Ф 0. Применяя формулу E.2.5), получаем
и" + Яв' + /в = 0, H = p + 2{v'/v), J = q + (v"/v)+ p(v'/v). E.2.21)
Теперь предположим, что уравнение X (у) = 0 имеет при z = а особую
точку, то есть р = F (z)/(z — a)m, q = G (z)/(z — a)n, где F и G аналитичны
при z = a. Чтобы функция и была аналитической, потребуем, чтобы коэф-
коэффициент / был аналитическим: и может тогда быть аналитическим реше-
решением уравнения и"-\- Ни' -\-Ju = 0, у которого коэффициент / аналити-
аналитический, а 77 имеет полюс.
Прежде всего посмотрим, какие ограничения надо наложить на р и q
(то есть на т и п), чтобы г = абыла регулярной особой точкой. В этом
•случае, по определению, v=(z— a)% v'/v — s/{z — a), if'/v = s(s — l)/(z — aJ.
Чтобы функция / была аналитической, полюс q должен быть не выше
второго порядка (п= 2), а полюс р — не выше первого (/п = 1). Таким
образом, если р имеет вид F {z)/(z — a), a q — cud G(z)/{z — aJ, где функ-
функции F и G аналитичны при z = а, то точка z = а является регулярной
особой точкой для уравнения X (у) = 0 и общее решение имеет, в ней точку
ветвления (u/iu полюс). Уравнение для 5 получается иэ E.2.21)
s2-!- [F (a) - 1] s + G (а) = 0, E.2.22)
и оно называется определякщим уравнением для решения. Два корня sx
и i*2(sj.>s2) соответствуют двум решениям yx={z — a)s'ul, г/2 = (z — a)s*u2,
где их и ы2 — функции, аналитические в точке а.
Если sx = s2 и, во многих случаях, если sx — ss — целое, н2 оказы-
оказывается равным (z — a)*1"8*^, так что определяющее уравнение и ряд для и
дают одно решение, но не дают второго. В этом случае для получения г/2
применяется формула E.2.6). Так как е~* Р z равно произведению (z — a) ~*'(°)
на аналитическую функцию и так как 1 — / (a) = Sj. + s2, то подинтеграль-
ная функция в формуле E.2.6) имеет вид
(г — a)Sl^S2 (аналитическая функция) (аналитическая функция)
(г — а)-Ь1и? (а—я)81-*2+1
Если s1 — s2 целое, то подинтегральная функция имеет при z=a полюс,
а не точку ветвления и, разложив аналитическую функцию в ряд
5.04 Гл. 5 . Обыкновенные дифференциальные уравнения
bo + b1(z — а)..., получим ряд для второго решения в виде
он имеет характерный член их (z — aNi In (z — a).
Этот логарифмический член обязательно появляется во втором реше-
решении, если s, = s2 (см. стр. 500), и почти обязательно, если sx— s2 целое.
Поэтому можно сказать, что общее решение уравнения E.2.1) имеет
в регулярней особой точке уравнения точку ветвления, так как если
st и s2 оба целые и можно было бы ожидать отсутствие точки ветвления,
то как раз в этом случае во втором решении появляется логарифмический
член, приносящий вместе с собой свою точку ветвления. Это правило
имеет исключения, одно из них дается формулой E.2.16).
Если q имеет полюс выше второго порядка, или если р имеет полюс
выше первого порядка, или если имеет место и одно и другое, то одно
решение или оба должны иметь существенную особенность и особая точка
является иррегулярной. Если при этом порядок полюса q не превосходит
более чем на единицу порядок полюса р, то только одно из решений
имеет существенную особенность.
Это можно просто показать, подставив ряд
со
у = (z — a)s ^ с4 (z — a)\ то есть v = (z — a)s, и = 2 с, (z — аI
i=0
в уравнение E.2.1). Тогда, если р и q можно представить рядами Лорана,.
р = а_т (z - а)~т + a_m+1 (z - a)'m*1 +...,
Q = b-n (z — аУп + Ь-n+i (z — a)""*1 + • • •» m,n — целые,
то следующий ряд
+ coa_ms {z - а Г"* + [coa_ntls + Cla_m (s +1)] (z - a)s"m + ... +
+ cob_n (z - ay-n+ [cob_ntl + Cl6.n] (z - a)*-™
должен равняться нулю для тех z, для которых ряд для и сходится.
Следовательно, коэффициент при каждой степени z — а должен обращаться
в нуль. Если полученная бесконечная последовательность уравнений
неразрешима, то наше исходное предположение о форме у-нереализуемо
и у должен иметь существенную особенность при z=a.
Оказывается, что если коэффициент при младшей степени z — а можно-
сделать равным нулю, то всем дальнейшим уравнениям можно удовлетво-
удовлетворить при помощи подходящего выбора коэффициентов ct. Это основное
уравнение для низшей степени z — а как раз совпадает с определяющим
уравнением E.2.22), если т и п таковы, что удовлетворяют условиям,
при которых это определяющее уравневие было введено. Мы видели, что-
если /п<;1 и п<,2, то это уравнение относительно s имеет вторую степень;
например, для т = 1 и п = 2 имеем
что позволяет найти для s два значения, следовательно, оба независимые-
решения у1 и у2 имеют указанный вид (точку ветвления при z=a),
то есть точка z==a, по определению, является регулярной особой точкой.
(Если корни равны, то мы уже видели, что второе решение имеет лога-
логарифмический член.)
5.2. Общие свойства, решение при помощи рядов 505
Если 1<т>и— 1, то уравнение для низшей степени z — a линейво
по s, так что только одно решение у может иметь указанный гид, а если
2 < п > /гс + 1, то определяющее уравнение отсутствует и ни одно решение
не имеет указанного вида. Такая точка является иррегулярной особой
точкой, так как одно или оба решения должны иметь при z — a сущест-
существенную особенность. Имеется определенная иерархия иррегулярных особых
точек, основанная на виде существенной особенности, которой обладает
решение. Например, если решение в некоторой иррегулярной особой точке
имеет вид
то характер существенной особенности у при z = а определяется значе-
значением к. Можно распределить особые точки по различным видам в соот-
соответствии с требуемым значением к. Если р или q имеет точку ветвления-
или существенную особенность, то у имеет еще более «патологическую»
особенность. К счастью, нам не потребуется забираться в эти дебри
осложнений, чтобы решать уравнения, с которыми мы работаем.
Классификация уравнений, стандартные формы. Теперь очевидно,
что первое, с чего надо начинать, приступая к решению линейного диф-
дифференциального уравнения неизвестного вида, состоит в выяснении поло-
положения всех особенностей функций р и q. Если все эти особенности
являются полюсами, то можно перейти к следующему шагу; если веко-
торые из них являются точками ветвления или существенными особенно-
особенностями, то надо попытаться так заменить независимое переменное z, чтобы
все они стали полюсами (если этого нельзя сделать, что иногда бывает,
то приходится применять численное интегрирование). Затем мы разделяем
регулярные особые точки и иррегулярные и, решая определяющие урав-
уравнения для всех регулярных точек, находим значения индексов s, опреде-
определяющих структуру точек ветвления решений вблизи этих значений z.
Если это иррегулярные особые точки, мы также определяем характер
существенной особенности при помощи упомянутых выше методов.
Характер бесконечно удаленной точки определяется при помощи
подстановки z = 1/w, в результате чего получается уравнение
E.2.23)
По структуре полюсов Р и Q при w = 0 мы узнаем характер особой точки
на бесконечности. Например, если решением определяющего уравнения
для w = 0 будет sx, то решение у имеет вид ws'F(w) = (l/z)si/'(l/z), где
функция F(w) аналитична при w — 0.
Особые точки всех уравнений, получающихся при разделении пере-
переменных в уравнении V2<]j + &24> = 0, приведены в таблице в конце этой
главы.
Обычно лучше всего оказывается преобразовать уравнение к стан-
стандартному виду, со стандартным положением особых точек и по возмож-
возможности с более простыми индексами s решений. Например, если имеется
только две особых точки, то обычно лучше расположить их в нуле и в
бесконечности; если их три, то их обычно размещают в нуле, единице
и бесконечности. Это делается при помощи замены независимой nepjMeH-
ной. Если особыми точками первоначально были а, Ъ и с, то преобразо-
вание
z = (w — a)Yl(w — с), w = (-(a — cz)/("( — z),y = (b — c)/(b — a) E.2.24)
506 Гл. 5. Обыкновенные дифференциальные уравнения
меняет положение особых точек, не изменяя их структуры, то есть
определяющего уравнения в каждой точке. Уравнения для нового и старого
независимого переменного связаны следующим образом:
E.2.25)
Здесь и до конца этой главы мы будем обозначать через ф общее реше-
решение, а черен у — частные решения специального вида.
Найти преобразование, перемещающее четыре произвольные точки
в четыре стандартные позиции и не меняющее индексов, невозможно, так
что не существует простой стандартной формы уравнений, имеющих более
трех особых точек. Л1ы обычно располагаем иррегулярную особую точку
.(если она сдинстьедная) на бесконечности, так как тогда рассмотренный
выше множитель v имеет сравнительно простой вид
exp (ahzb + Oft^z* + ... + ak_szk-s).
Если особая точка в нуле регулярна, то обычно целесообразно заме-
заменить искомую функцию, положив ф = ни, чтобы, используя равенства
E.2.21), получить сравнительно просто решаемое уравнение для и. Обычно
при этом полагают, что v имеет точку ветвления, соответствующую мень-
меньшому корню определяющего уравнения для нулевой особой точки, так что
одно из решений уравнения для и апалитично при z = 0. Однако детальные
соображения, которыми надо руководствоваться при выборе преобразо-
преобразования независимой и зависимой переменных, лучше всего могут быть
показаны па примерах.
По этой и другим причинам полезно более или менее систематически
исследовать некоторые из менее сложных уравнений, чтобы познакомиться
•с их видом и кое-что узнать о поведении их решений. Мы приступим
к рассмотрению различных случаев в порядке возрастания числа и слож-
сложности особых точек. Для этих случаев мы сначала исследуем общий
вид, а затем преобразование к стандартному виду, для которого мы опре-
определим стандартные решения. Простейшим является, конечно, случай одной
регулярной особой точки. Если этой точкой будет w = а, уравнение имеет
вид
-a)]<J>' = 0, E.2.26)
где коэффициент при члене <b'/(w — а) должен равняться 2, чтобы не было
-особой точки на бесконечности [см. E.2.23)]. Общим решением служит
ф = А + B/(w — а). Стандартная форма для этого уравнения могла бы быть
с особой точкой на бесконечности; уравнением и решениями будут тогда
ф" = 0, ф = Л + ?2. E.2.27)
Две регулярные особые точки. Здесь общей формой уравнения будет
1)-д(Х + ц + 1) djf , 1у.{а-с)* ,, _ п
к — a) (w — с) Аи +(ш—аJ(ш —с)8* ' К0-*""*)
причем коэффициент P(w) выбран в таком специальном виде (в частности,
член 2w в числителе), чтобы на бесконечности была обыкновенная точка.
5.2. Общие свойства, решение при помощи рядов 507
Определяющее уравнение E.2.22) для w = a имеет вид s2 — (X-|-^) s + ^ = 0
и корни X и ц, так что решениями служат y1 = (w— а)хи1, у2 = {w — а)*и%.
Определяющее уравнение для w — c имеет вид а2 + (X-|-р) а + Хц = 0 и корпи
— X и — ц, так что решениями будут 2/1 = (ш—с)-хи\, y2 = (w - c)~v-u%.
Прямая подстановка (или решение с помощью ряда) показывает, что
u« = (w — с)~х, Щ = (ги — а)х, и% = (w — с)-*, u% = (w — a)v-, так что общее
решение имеет вид
Однако задача о нахождении решения была бы проще, если бы мы
совершили преобразование z = (w — a)/(w — c), переводящее одну особую
точку в нуль, а другую на бесконечность. Преобразованное уравнение
тогда имело бы вид
Из этой стандартной формы нетрудно вывести, что решением будет
ф = Azx +Вг^. Таким образом, если имеются только две особые точки
и они регулярны, то решение должно иметь особенно простой вид,
¦& индексы в одной из особых точек лишь знаком отличаются от индексов
в другой.
Исключительный случай здесь будет, если X=fi. В этом случае
решение, полученное по формуле E.2.6), имеет вид
У ] E.2.31)
Одна иррегулярная особая точка. Вот уравнение с единственной
иррегулярной особой точкой &у = а:
"Л^~+ w— a dw (ш-о)* ^~~и- \р.*.М)
Мпожитель (w — а) указывает на иррегулярность особой точки, а из-за
коэффициента 2/(w — а) не возникает особой точки при w = oo. Решение
.этого уравнения таково:
ф = Aeh^w~a) + Be' -'«/(«'-"), E.2.33)
что можно найти прямой подстановкой или при помощи преобразования
к z = l/(w — а), так как стандартная форма уравнений этого типа полу-
получается при перемещении иррегулярной особой точки на бесконечность
(d2(])/dz2) - кЦ = 0. E.2.34)
Следует заметить, что уравнение E.2.34) не является единственным
уравнением, имеющим одну иррегулярную особую точку на со, так как
могут быть различные виды иррегулярных особых точек. Например,
уравнение, получающееся из волнового уравнения в параболических
цилиндрических координатах
имеет одну иррегулярную особую точку на со, но его решения не явля-
являются простыми показательными функциями.
Интересная взаимосвязь между регулярными и иррегулярными осо-
особыми точками обнаруживается, если посмотреть, что будет в случае
двух регулярных особых точек, если эти особые точки сближать до
-совпадения, сохраняя при этом коэффициенты дифференциального уравне-
508 Гл. 5. Обыкновенные дифференциальные уравнения
ния конечными. В уравнении E.2.28) положим а = с —з, Х = — jt = ft/e в
затем устремим е к нулю: получится уравнение E.2.32). Решение
соответствует одному из известных определений показательной функции
Такое сближение двух особых точек с соответствующим изменением;
индексов называется слиянием (конфлюенцисй) особых точек.
Три регулярные особые точки. Уравнения, более сложные, чем при-
приведенные выше, имеют решения, которые нельзя выразить через элемен-
элементарные функции. Однако таблица в конце этой главы показывает, что-
большинство приведенных там уравнений, получающихся при разделении»
переменных, имеет либо три регулярные особые точки, либо же одну
регулярную и одну иррегулярную особые точки, так что нам следует
детально рассмотреть эти случаи.
Для дальнейшего ознакомления с методами исследования особых,
точек уравнений построим уравнение (с независимой переменной w)r
имеющее три регулярные особые точки при w = а, Ъ, с. Это означает,
что функция p(w) должна иметь простые полюсы при w = a, Ь, с и больше-
нигде. Отсюда p(w) должна иметь одну из двух равносильных форм
" v I (w—а) (га— Ь) (ш—с) w—a w — Ь "¦ w—с ~"~
Мы будем применять вторую форму, так как с ней легче работать^
Обращаясь к уравнению E.2.23) мы видим, что для юго, чтобы бесконеч-
бесконечность была обыкновенной точкой, функция (w= 1/и)
2_ J_ / 1 \ _ 2_ а/и р/ц -у/» 8_
и и2 '' \ и ) и 1 — аи 1 — Ъи 1 — си и2
должна быть аналитической при и = 0. Отсюда вытекает, что S = O
и a p Y
Аналогично так как q может иметь в точках а, Ъ, с полюсы не выше
второго порядка и так как функция §A/и)/и4 должна быть аналитической
при и = 0, то q должна иметь вид
"\ ' (w—a) (w—b) (w—с) |_ w—a w—b w — с J
Чтобы найти связь между индексами решения при w — а и постоян-
постоянными a, p, y> ^» е> /> обратимся к уравнению E.2.22). Вблизи точкд
1
(w—ay ' v ' {a — b)(a — c
Если два индекса при w = a должны быть равными s = X и s = X'
(то есть если два решения вблизи w = a имеют вид yl = (w — а)хщ (ш)
и y.2—(w — a)*' u2(w), где их и и2 аналитичны и отличны в точке а от
нуля), то в уравнении s2 + [F(a)— 1] s + G{a) — 0 член 1—^@) должен
равняться сумме корней \ + \', а член G(о) — произведению корней XX'.
Отсюда а=1—X —X', a d = Х>/ (а— Ъ) (а — с). Если индексы в точке Ъ
равны [х и [/, а в точке с —v и v', то остальные постоянные также выра-
выражаются через эти индексы. Однако, как мы показали, чтобы бесконечна
5.2. Общие свойства, решение при помощи рядов
509
удаленная точка была обыкновенной, должно быть а + Р + у=2, то есть
X+X' + n + n' + v + v' = l. E.2.35)
Предполагая выполненным это условие, мы можем теперь написать самое
общее уравнение с тремя регулярными особенностями
I *¦ + *.'-! ц + ц'-l . v + v'-l I d^
L w—a w—b w—с J dw
XX' (a — b) (а —с) цц' (b—a) (b — c) ,c о oRn
«feu*
— af(w — b) (w — c)
~а) (ш—
— c)
(ш
w'(t-a)(c-t) "] д, —Q
—о)(ш— Ь)(ш — сJ J Y
Оно называется уравнением Папперица. Как мы видели, это урав-
уравнение (и потому его решения) вполне определяется указанием положений
трех его особых точек и значением обоих индексов в каждой из трех
точек (или, скорее, пяти из шести индексов, поскольку шестой полу-
получается из соотношения E.2.35)). Другими словами, символическая
табличная запись
а Ъ с
X ц v z | E.2.37)
йолпостью равносильна (если сумма элементов второй и третьей строки
равна единице) утверждению, что ф является решением уравнения E.2.36).
Этот симвил, введенный Риманом, будет иногда применяться для сокра-
сокращения записи.
Решение уравнения E.2.36) при помощи ряда было бы очень гро-
громоздким, и поэтому мы поместим особые точки в их стандартные поло-
положения. Полагая а = 0, 6 = 1, с—» со и вводя z вместо w, получаем
dz2
или
L_ Г
2 I
р'-1 1 <Ц>
— 1 J dz
-["Г CT
^ E.2.38)
0
GO
A (J. V
X' ц' 1-Х — X'—[i-[j.'— v
Рекурсивные формулы. Теперь мы знаем, что решение ф можно выразить
при помощи следующих разложений вблизи особых точек:
п=0
= {z - If 2 «n (z - l)n +(z- If % bln(z-lf=
E.2.39)
n=0
П=0
=:0
илп через фундаментальную систему решений вблизи любой обыкновенной
точки (см. стр. 502). Сейчас мы должны определить соотношение между
510 Гл. 5 Обыкновенные дифференциальные уравнения
коэффициентами рядов ап и Ъп при различных п, так чтобы можно было
выразить ап через а0 и Ьп через Ьо и тем самым получить ряд для реше-
решения. Подстановка любого из шести возможных рядов в уравнение и при-
приравнивание коэффициентов при степенях z, z — 1 или 1/z нулю дают после-
последовательность уравнений общего вида
Д„ К) = Гп1а„_ь+1 + rn2an.ft+2 + ... + l\kan = 0, E.2.40)
которые надо решить, чтобы выразить ап через а0 (или Ьп через Ьо). Такие
уравнения называются к-членными рекурсивными формулами. Коэффи-
Коэффициенты Гпу являются функциями постоянных, входящих в уравнение,
различны для различных оеббых точек и выбранных индексов и зависят
также от своих значков п и /(/ = 1,2, ...,&). Так как ряды E.2.39)
являются решениями, то Гп^ = 0 (и> 1, п — & + /< 0); это означает, что
нет надобности вас отрицательными значками.
Например, для уравнения E.2.38), точки z = 0 и индекса X рекурсив-
рекурсивная формула имеет вид
-l)]an-
- [(и + 1) Bя + 2Х - 2Х' - |i -р' + 3) - №' - (v + X) (X' + (х + ц' + v - 1)]ап+1 +
= 0. E.2.4i>
Однако с помощью такой трехчленной рекурсивной формулы получить-
явное выражение для ап/а0 чрезвычайно сложно.
Во всяком случае, мы привели задачу о нахождении решения диф-
дифференциального уравнения к задаче о решении бесконечной последователь-
последовательности алгебраических уравнений, определяющих последовательные коэф-
коэффициенты ряда для решения. Другими словами, мы совершили еще одно-
преобразование от непрерывной переменной z к последовательности целых
значений индексов п коэффициентов ап и Ъп степенных рядов; соответ-
соответственно совершается переход от дифференциального уравнения Xz ($) = О*
к разностному уравнению Ьп (an) = 0. Коэффициенты разностного уравне-
уравнения соответствуют коэффициентам р и q дифференциального уравнения-
и определяются ими. Взаимосвязь между дифференциальным уравнением-
и рекурсивной формулой становится более ясной, если выразить Dn через
разностные операторы
е2(«„) = 8E(«„)) = а„-2ап+1 + аТ1,2 и т. д.
Например, рекурсивная формула E.2.41) для ряда, определяющего решение-
уравнения E.2.38), может быть переписана так:
п К) = (» + >¦ - у + 2) S2 («О - (^ + И' + 3) S (пап) +
+ (X + v) (X + v') S (ап) - №'S (ап) + (№' + 2га) ап = 0 •
Если ограничиваться построением решений в виде степенных рядов,
то желательно преобразовать независимое и зависимое переменные в диф-
дифференциальном уравнении к виду, порождающему по возможности более-
простую рекурсивную формулу. Например, трехчленная рекурсивная фор-
формула E.2.41) соответствует разностному уравнению второго порядка; воз-
возможно, что преобразование зависимой переменной заменит ее на двучлен—
5.2. • Общие свойства, решение при помощи рядов 511
ную рекурсивную формулу, которой соответствовало бы ргзиостное уравне-
уравнение первого порядка; последнее же решить гораздо проще.
Гипергеометрическое уравнение. Преобразовав независимое перемен-
переменное так, чтобы особые точки попали в их стандартные положения, мы
теперь преобразуем зависимую переменную, чтобы сделать по возможности
более простыми индексы в особых точках, расположенных в конечной
части плоскости. Такая замена переменной <]> межет изменить только сумму
индексов в особой точке, но не может изменить их • разности. Однако
мы можем произвести деление на z*-(z — If", так что в обеих особых точ-
точках одно решение станет аналитичным, в то время как второе будет иметь
индексы X' — X или ц' — р. Другими словами, наше решение приобретает
вид <}> = zx(z — i-Y'y, где символом Римана для у будет
f 0 1 оо
у=р\ 0 0
I X* — X ц' - ц 1 _ X' - ц' — v
Соответствующее уравнение для у (полученное подстановкой
<j) = zx(z—II* у в уравнение E.2.38) или изменением этого уравнения в соот-
соответствии с новым символом Р) имеет вид
У"
ix' + l 1 , (у + Х + цН1-А'-ц'-у) _fi
2—1 J У "•" Z(Z—1) J
Однако здесь слишком много постоянных фиксируемых величин. Для
фиксирования индексов нужны только три постоянные: имеется четыре
индекса, не положенных равными нулю (по одному при 0 и при 1 и два
при оо), однако их сумма должна равняться единице, так что достаточно
трех постоянных. Более удобно положить два индекса на сю равными
а и Ъ, один при 0 равным 1 — с, так что один при 1 равен с — а — Ъ^
Символ Римана Р тогда приобретает вид
F-
а соответствующее дифференциальное уравнение
z{z-l)F"+[{a+b+l)z-c]F' + abF = O, E.2.42)
называемое гипергеометрическим уравнением, является стандартным урав-
уравнением для случая трех регулярных особых точек.
Аналитическое вблизи г^О решение этого уравнения называется гипер-
гипергеометрической функцией. Чтобы получить разложение ее в ряд, полагаем
F=^ anzn и подставляем в E.2.42). Коэффициент при z" порождает рекур-
рекурсивную формулу для ряда
п-(п + Щп+ с) ап+1 =
an) + [n(a + b-l)-(n+l)c + ab]an = 0. E.2.43)
Это — двучленная рекурсивная формула, то есть разностное уравнение пер-
первого порядка, с простым решением
, а(а+1) ... (а + п-1)Ъ(Ъ+1) ... (Ъ+п-1)
"о *> «п- 1-2 ... п.с(с + 1) ... (с + и—1)
512 Гл. б. Обыкновенные дифференциальные уравнения
•Соответствующий ряд
называется гипергеометрическим рядом (см. стр. 367). Он является анали-
аналитическим вблизи z = О решением уравнения E.2.42). Он сходится при
|г|< 1, так как ближайшей особой точкой служит z=l. Через этот ряд
можно выразить все решения уравнения E.2.42) вблизи любой их особен-
особенности.
Например, если в уравнение E.2.42) подставить функцию zx~°F% (где
F2 должна быть аналитической, так как второй индекс при z = 0 равен
1-е), получим уравнение
которое является другим гипергеометрическим уравнением с аналитиче-
аналитическим решением в виде гипергеометрического ряда F2 = F(b — c +1,
а — с+1|2 —c|z). Поэтому общее решение уравнения E.2.42) имеет вид
AF(a, b\c\z) + Bzl-cF(b-c+l, a-c + l\2-c\z). E.2.45)
Возвращаясь к предыдущим уравнениям, получаем общее решение
уравнения E.2.38) вблизи z = О
а общее решение уравнения Папперица E.2.36) вблизи w = а равно
' ' w—с b—a J '
/f + Mv, iv,|x + |^
E.2.46)
Решения уравнения Папперица вблизи w = b или w = с можно получить
заменой X, У на ц, ц' и т. д., так как уравнение симметрично относи-
относительно перестановки особых точек и соответствующих индексов (если
иметь в виду, что V = 1 — X — X' — р - ц' — v).
Формула E.2.45) дает общее решение, за исключением случая, когда с
целое, так как в этом случае ряд для одного из решений будет иметь
во всех членах, начиная с некоторого, нулевой множитель в знаменателе
(а при с = 1 эти ряды совпадают). Например, для с = 3 ряд для второго
решения будет иметь два первых члена конечными, а все высшие члены
бесконечными из-за сомножителя 2 —с+1 в знаменателе. Это —пример
того специального случая, указанного на стр. 500, когда индексы в дан-
данной особой точке различаются на целое число. Как указано на стр. 503,
в этом случае надо находить второе решение при помощи формулы
E.2.6).
Здесь y1 = F(a, b\c\z) и p = (c/z) + [(a + b+1 — c)/(z — 1)], так что
е- Jp dz = z-= A _ z)c-°-b-i_ Вторым решением будет
yt = F{a,b\c\z)^[F(a,b\c\ z)] z"c A - zf^-^ dz.
Если |z|<l, можно разложить A — z)c"a"b~1f/r(a, b\ c|z)]~2 в ряд по сте-
степеням z, который можио записать в виде #0~b#iz~b*-* • ^*ЯД Для ПОД"
5. 2. Общие свойства, решение при помощи рядов 513
интегральной функции тогда имеет вид
+ + +
причем мы предположили с целым положительным, так что gc множится
на нулевую степень z, g^ делится на первую степень z и т. д., а дроб-
дробные степени не участвуют. В этом случае gc_Jz даст при интегрировании
логарифмический член и вторым решением будет
у2 = F (а, Ъ | с | z) [g^ Inz + (l/z0-1) (fc0 + V + ... + hc_^^ + hcic +...)),
¦где коэффициенты hn являются функциями a, b, с и к.
Функции, предетавимые гипергеометрическими рядами. При помощи
рядов E.2.44) можно выразить большое число функций. Например, про-
простейшими случаями являются
Разделенное уравнение для ?2 в круговых цилиндрических координатах
и для ?з в сферических, параболических, вытянутых и сплющенных сферо-
сфероидальных координатах имеет вид
1 d Г т/"| ^2 ^-^ I *5 X = О
или
-^ "я ^^ г»
Оно имеет общий вид уравнения E.2.36), причем о= +1, 6= — 1, с = оо,
Х' —1= -1/2 = (х+(х' —1, U' = №'=0, vv'=— /с2 (и, конечно, обыч-
обычное условие E.2.35): Х + Х' f- p. -j - p.' -J— v -J- v' = 1). Поэтому символ Римана
для его решения будет
Х = Р
1 -1 СО
i/2 i/2 k3 a
О 0 -к3
а общее решение вблизи 5= +1 (из формулы E.2.46))
Эти решения называются функциями Чебышева. Оказывается [см. фор-
формулы E.2.54)], что они Пропорциональны соответственно sin (&<р) и cos(/c<p),
дде ? = cos<p, что можно показать и преобразованием приведенного выше
гифференциального уравнения. Эти функции будут исследованы в § 5.3.
Разделенное уравнение для ?3 в сферических координатах, а также
в сфероидальных координатах в случае кг = 0 имеет вид
dX Г -к\ Щ/2
di
и называется уравнением Лежандра. Ему отвечает уравнение E.2.36)
са=+1, Ь= — 1, с=со, Х= —X'=/га/2 = {1= —ji', v= —п, У = п+1,
где мы положили к3 = т и ft2 = n(n + l), чтобы результаты было легче
33 Ф. м. Морс и Т. ФешСах
514 Гл. 6. Обыкновенные дифференциальные уравнения
выписать. Поэтому решение соответствует символу Римана
1 —1 оо
т/2 т/2 — п
— т/2 —т/2 п + 1
и общее решение вблизи ? = 1 равно [см. также формулу E.2.52)]
E.2.47)
Первое решение называется функцией Лежандра первого рода, а вто-
второе — функцией Лежандра второго рода. Если т целоэ положительное,
то так записанное второе решение теряет смысл и тогда второе решение
надо строить при помощи формулы E.2.6) (см. стр. 503). Эти функции
Лежандра и связанные с ними функции Гегенбауера будут вновь рас-
рассмотрены через несколько страниц и очень детально в § 5.3 и 10.3, так
как они имеют очень большое значение для наших дальнейших исследо-
исследований.
Аналитическое продолжение гипергеометрического ряда. В качестве
упражнения в действиях с этими решениями мы выведем выражение,
описывающее поведение гипергеометрического ряда, когда z стремится
к единице. Обращаясь к символу Римана, указанному перед уравнением
E.2.42), мы видим, что индексы в особой точке z—1 равны 0 и с - а — Ъ.
Применяя уравнение E.2.46) с а — 1, 6 = 0, с=оо, Х = 0, У = с — а — Ь,
|х = 0, |х' = 1 —с, v = a, v' = b (другими словами, меняя ролями особые
точки 0 и 1), видим, что общим решением гипергеометрического уравне-
уравнения E.2.42) вблизи z =1 является
AF{a, b\a + b-c + l\l — z) + B{l—z)c^bF{c-b, c-a\c-a~b+l | 1 -z).
Однако гипергеометрический ряд F (a, b\c\z) является решением
уравнения E.2.42), и потому после аналитического продолжения он должен
равняться некоторой комбинации двух решений вблизи z = 1. Другими
словами, должно быть
F(a, b\e\z) = aF{a, b\a+ fc-
z)c~a-bF(c-b, e~a\c-a-b + l\l — z). E.2.48)
Если бы мы смогли как-то определить значения коэффициентов аир,
то мы имели бы средство подсчета точвого поведения F(a, b\c\z) при
Z = 1 и даже за этим значением, почти вплоть до z = 2.
На стр. 367 мы показали, что при b <c < а + Ь
где мы подставили гамма-функцию вместо факториалов, чтобы a, b и с
могли иметь нецелые значения. Это соотношение показывает только,
что если с<а-\-Ь, то главный член вблизи z=l имеет вид A — z)c'a'b,
что позволяет определить коэффициент при нем. Ковечво, имеются другие
члены вида A z)c~a~b*1, A — z)c~a~b+2 и т. д., часть которых может также
стремиться к бесконечности при z—> 1, но в достаточной близости от
z=^l' они <<поглощаются» членом A—zH"". Остальные члены можно
получить при помощи формулы E.2.48).
б. 2. Общие свойства, решение при помощи рядов 515
Так как F(с — Ь, с — а\с — а — fc -f-111 — z) —> 1, то при z —> 1 глав-
главный член правой части равенства E.2.48) равен $(l — z)c~a~b, если только
с<Са + Ь. Сравнивая это с предыдущим результатом, мы видим, что
откуда определяются коэффициенты во всех членах с отрицательными
степенями 1 — z:
Однако в случае с > 1 можно пойти дальше. Можно применить приве-
приведенную выше предельную формулу в обратном порядке, чтобы посмотреть,
что будет с равенством E.2.48) при z—>0. Левая часть, конечно, при
этом стремится к единице. Применяя же предельную формулу, приве-
приведенную на стр. 367 к пранэй части, получаем
Г(а + Ь—с + 1)Г(с-1) Г(с-д-
Г (а) Г F) +Р Г (с — а) Г (с— 6)
Отсюда если с > 1, то оба члена в правой части должны взаимно унич-
уничтожиться. Это дает соотношение между а и Р, на основании которого-
можно решить задачу. Подставляя уже полученное значение р и приме-
применяя свойство гамма-функции Г (и-\- 1) = мГ (и), получаем
Чтобы это имело место при с > 1, выражение, стоящее в квадратных
скобках, должно обратиться в нуль, откуда и получаем а. Следовательно,
по крайней мере при 1 < с < а +¦ Ъ получаем полезную формулу
+ Г (Сг wai46)~C) <* ~ '>"'' * (с - Д, с - »| с - « - » +111 - «), E-2.49)
которая позволяет продолжить решение через особую точку z=l. В сле~
дующем параграфе мы покажем, что это соотношение справедливо: для
значительно более обширной области значений с, чем мы сейчас полагали
(например, для с, больших чем а + Ь). В действительности эта формула
имеет место всегда, за исключением тех случаев, когда гамма-функция
в числителях обращается в бесконечность.
Другие полезные формулы для гипергеометрических рядов можно
получить при помощи «уравнения связи» и некоторого преобразования
гипергеометрического уравнения E.2.42). В этом уравнении мы полагаем
а = 2л, 6 = 23, с = а + Р + "р- и переходим от z к новой независимой пере-
переменной и = 4z (I — z); это дает уравнение
которое вновь является гипергеометрическим уравнением с новыми пара-
параметрами а, Р и а + р + у, вместо а, Ъ и с. Значит, функция
является решением уравнения E.2.42) при а = 2а, Ь = 23, с = о+-Р+ -~
и должна выражаться через два решения вблизи z = 0 [см-: E.2.45)-}
33*
Гл. о. Обыкновенные дифференциальные уравнения
|-о ~
Однако F ( а, р | a + р -|- —- 4z— 4z2 J является аналитической функцией z
вблизи z = 0; отсюда второе решение, имеющее точку ветвления, не может
присутствовать и В равно нулю. Кроме того, так как F—\ при z = 0,
то А должно равняться единице. Отсюда имеем
4|) E.2.50)
Эту формулу, связывающую значение Z1 для 2а, 2,3 и z с значением /'
для а, р и z2, можно назвать формулой удвоения для гинергеометрической
функции.
Функции Гегенбауера. Мы указали раньше, что иногда желательно
иметь такую каноническую форму для трех регулярных особых точек,
в которой две из них равнялись бы 4-1 и — 1, а не 0 и 1. Так будет,
в частности, если индексы при +1 те же, что и при — 1. Это порождает
символ Римана
-1
0
1
0
-3
-а
¦Соответствующее уравнение
(z2 - 1) Ф" + 2 (Р + 1) г'У
a (a + 2,3 + 1) ф = 0
E.2.51)
называется уравнением Гегенбауера (ср. с уравнением Лежандра на стр. 513).
Оно является хорошей формой уравнения для Е2 в круговых цилиндриче-
цилиндрических и сферических координатах. Решения, конечно, можно выразить
через гипергеометрические функции
или
Решение, которое будет для нас очень полезным, можно дать в различных
формах:
E.2.52)
2-«Г(-+1)г№ + 1) situ™?)
причем мы применили равенства E.2.49) и sinG:M)r (к) Г A — и) = ir, чтобы
лояучить вторую форму. Функция Tl(z) называется функцией Геген-
5. 2. Общие свойства, решение при помощи рядов 517
бауера. Если а не целое, Т имеет точку ветвления в z= — 1 (если только
Р не целое). Если а равно нулю или целое положительное, Т является
конечным полиномом относительно z и, конечно, аналитично при z = +_ 1.
Иногда применяется второе решение вблизи z = l, причем это реше-
решение, умноженное на A —z2)
2<)Г(а +
часто называют обобщенной функцией Лежандра от z.
Если а равно целому и = 0, 1, 2, ... , то при помощи разложения
многочлена и почленного сравнения можно показать, что
и, следовательно,
«(z) = ; A — z ) , _ 1 х—z ) (O.z.
Этот многочлен можно назвать многочленом Гегенбауера (он отличается
численным множителем от многочлена Сп z , часто также называемого
многочленом Гегенбауера).
Если р равно целому m — 0, 1, 2, ... , а а не таково, то, как будет по-
показано в следующем параграфе, 71™ имеет логарифмические точки ветвле-
ветвления при z=±l, в то время как A — z2)~m/2.P™ (z) аналитична во всей
области — 1 < z < 1. Наконец, если оба аир целые положительные (или
равны нулю), то Т™ (z) = A — z2)~~m'2P™(z) и обе функции аналитичны в
этой области изменения z. Так как
¦Й^Г"^ ' -V-1) („ + 2m)l dzr, + 2m (z -1)
+ 2m)l
TO
эти полиномы иногда называются тессеральными (клеточными) полинома-
полиномами. Особенно важен случай т = 0; он настолько важен, что многочленам
присваивается специальное обозначение и наименование. Функция
518 Гл. 5. Обыкновенные дифференциальные уравнения
называется многочленом Лежандра [см. формулу E.2.47)]. Б нашей книге
эти многочлены будут в дальнейшем часто встречаться. Мы видим, что
п ' dz™
В следующем параграфе нам придется много говорить об этих функциях.
В специальном случае Р=± -^ , а = п = 1, 2, 3, ... можно показать
(при помощи' прямого разложения), что многочлены Т имеют следующий
вид:
Тп1/2 (z) = A1/A ch (п Аг ch z),
chz]; E.2.54)
такие многочлены называются многочленами Чебышева.
Отметим, между прочим, что общее решение уравнения для ?2 ПРИ
разделении в круговых цилиндрических координатах и для ?3 в парабо-
параболических и вытянутых и сплющенных сфероидальных координатах
(z2 — 1) ф"+ zil/ — а.Ц = О
имеет вид
^тУи (г),
как это показывает сравнение с уравнением для Т.
Одна регулярная и одна иррегулярна* особые точки. Для таких
уравнений обычно располагают регулярную особую точку при z = 0, а
иррегулярную при z=co. Уравнения этого вида появляются при разде-
разделении переменных в следующих системах координат:
1. Для волнового уравнения в круговых цилиндрических (z = /c151,
t< = X1), сферических (z =¦ k^lt ф = ]/гХ1) и конических (z=/c1^1, ty = |/гХх)
фоординатах получается уравнение Бесселя
dz*
2. Для волнового уравнения в параболических цилиндрических коор-
координатах (z = S;/2, 6|/2; ф = Х1? Ая)
3. Для волнового уравнения в параболических координатах (z = \-\
ХХ
dz
это уравнение включает параболические цилиндрические функции как
частный случай.
4. Для уравнения Шредингера в случае одной частицы в кулоновском
поле 1/г в сферических координатах для радиального множителя (г = ^,
5. 2. Общие свойства, решение при помощи рядов 519
Это приводит к исследованию общего уравнения
^ ^ = О, р-!=^. E.2.55)
_
¦Это не самое общее уравнение с регулярной особой точкой при z = 0 и
иррегулярной на бесконечности. К выражениям, указанным в E.2.55),
можно было бы прибавить постоянную (к функции р), члены az и bz
(к обеим р и д) и т. д. Однако эти дополнительные члены сделали бы су-
существенную особенность решения при z = co еще более «особой», и так
как ни одно из уравнений, полученных при разделении волнового урав-
уравнения, не имеет этих дополнительных членов, то мы и не включаем их
здесь. Все же некоторые более сложные случаи будут включены в
упражнения!
Возвращаясь к уравнению E.2.55), мы видим, что н силу опреде-
определяющего уравнения разложения около регулярной особой точки z = О
имеют вид zxux(z) и zx'u2(z), где их и м2 аналитичны при z=-0. Как и
раньше, мы переходим к случаю, когда одно решение аналитично, поло-
положив <!> = z*/(z), так что f(z) = Ащ (z) + Bzx'~ku2 (z). Уравнение для / имеет
тогда вид
/" + [A + X - V)/z\f' + I Ba/z) - **]/ = 0. .56
Для исследования особой точки на бесконечности мы полагаем
я = 1/w. Уравнение относительно аргумента w приобретает вид
Г 1 + У-*1 df r^__Jf] ,_
L w J dw^ lw3 xifl J '
dw*
который в соответствии с членами 2а/ш3 и к2/гл)* указывает на иррегу-
иррегулярность особой точки w — 0. Однако, полагая f=e~h'wF, мы можем пе-
перейти к уравнению .
„„ Г 2fc 1-X+V-] „, г кA + \-\')^-2л-\ „
F + lw+—w—J F ~ L *—•—J F=
которое имеет определяющее уравнение с одним корнем
2/cs - f/с A + X - X') - 2о] = 0.
Следовательно, имеется решение F = w$v1(w), где vx — аналитическая при
w = 0 функция, а Р = [A + Х —Х')/2] —(u/А). Другим решением для / будет
ekiwwyV щ где р' = [A j X \')/2] + (а/к) а v аналитична при w = 0
( )] (/) Дру р /
i щ^ где р' = [A _j- X — \')/2] + (а/к), а v2 аналитична при w =
Таким образом, существенная особенность при йу = О (z—> оо) имеет вид
±fc/ й
Мы можем теперь возвратиться к уравнению E.2.56) с аргументом
z и, положив f=e~hzF(z) (или ty = z*e~ta/'), можем быть уверенными, что
одно из решений для F аналитично при z = 0 и имеет точку ветвления
только при z—> оо. Уравнение для F с аргументом z имеет вид
и приводится к простейшей форме, если положить z = x/2k, c = l + 7- — X,
[(l XX'J(A)
S (с - х) ^ -aF=°; E-2-57)
последнее уравнение называется вырожденным или конфлюентным (полу-
(полученным в результате слияния) гипергеометрическим уравнением. Это наи-
520 Гл. б. Обыкновенные дифференциальные уравнения
менование связано с тем, что уравнение E.2.57) получается из гипергео-
гипергеометрического уравнения E.2.42) при помощи соответствующего слияния
особых точек z = 1 и z = со.
Легче увидеть слияние, если отправляться от уравнения Папперица
E.2.36) в случае а = 0, с=со
-Ц'Ь
Г -Ц'
Положим теперь Х = 0, 1 — Х' = с (здесь с — новая постоянная, а не аффикс
третьей особой точки, расположенной на бесконечности), (*'=—b и
(х = а —v (здесь а тоже новая постоянная, а не аффикс первой особой
точки). Мы придем теперь к вырожденному гипергеометрическому урав-
уравнению E.2.57), если заставим вторую особую точку стремиться к совпа-
совпадению с третьей на бесконечности, то есть если положим Ь—->со. При
этом в процессе совпадения особых точек один из индексов в каждой из'
них (то есть ft' и ¦/) также стремится к бесконечности.
Одно из решений уравнения E.2.57), аналитичное при х = 0, можно
найти подстановкой ряда общего вида F = ~^апхп в уравнение. Коэффи-
Коэффициент при хп порождает рекурсивную формулу
n = 0, E.2.58)
которая вновь является двучленной и имеет простое решение. Следоьа-
тельно, аналитическое при z = 0 решение дается рядом
E.2.59)
который называется вырожденным гипергеометрическим рядом. Этот
ряд сходится при — со < re < со. Применяя методы, приведенные на
стр. 367, можно получить сведения об асимптотическом поведении этого
ряда. Для больших значений z превалируют члены с высшими степе-
степенями z. Но в качестве первого приближения относительно z/n, если а и с
целые, член ряда с zn(n большое) приобретает вид
(«?-!)! (а + я) I rn_ (е-1I па-с »_ (с-1I
n!(a — l)!(c + n)! ~" (a— 1) ! n! — (a—1I (га—a + c)! "
Следовательно, для достаточно больших z ряд аппроксимируется рядом
(«-1I V *" ^ (с-1)' za-c V ^L = fc-1)' za-c^
(а—1)! ^J (n —а + с)! — (с—1)! ZJ то! (а—1) !
и m
Подставляя гамма-функцию вместо факториалов, получаем в результате,
что
F(a\c\z)/*-V —If Щ ¦ E-2-60>
В следующем параграфе мы покажем, что эта асимптотическая формула
справедлива для более широкой области значений а, с и z, чем это допус-
допускалось при нашем выводе.
Вспоминая связь между функциями F и if, мы видим, что общее
решение уравнения E.2.55) вблизи z = 0 имеет вид
—%-| 1 -X + X' | 2te) , E.2.61)
5. 2. Общие свойства, решение при помощи рядов 521
если только X —X' не целое; в последнем случае второе решение содержит
логарифмический член и должно быть получено при помощи формулы
E.2.6).
Из этого общего решения можно также видеть, что вторым реше-
решением вырожденного гипергеометрического уравнения является
xl-cF{a — с-Ь 11 2 — с\х).
Однако можно видеть также и то, что если в уравнении E.2.57) положить
х= — &, F = e^Fz, то уравнение для F2 снова определяет вырожденную
гипергеометрическую функцию. Другими словами, еще одним решением
уравнения E.2.57) будет exF(c — а \с | — х). Однако это не третье независи-
независимое решение, так как разложение в ряды и умножение рядов показывают,
что
exF(c-a\c\~x)=F{a\c\x). E.2.62).
Между прочим, сравнение с формулой E.2.60) показывает, что асимпто-
асимптотическая формула, которая может быть удовлетворительной для z боль-
больших положительных, может в то же время быть совершенно неудовлетво-
неудовлетворительной для z больших отрицательных. Действительно, поскольку соот-
соотношение E.2.62) справедливо, а E.2.60) имеет место при Rez—=>оо, то
Однако мы отложим дальнейшее обсуждение этого вопроса до следующего
параграфа, когда мы будем подготовлены к этому значительно лучше.
Сравнение уравнений на стр. 518 с равенством E.2.61) показывает,
что общим решением уравнения Бесселя является
Ф = е-*' [ AznFA + п 11 + 2п \ 2iz") + Bz-nF {^~- п | 1 - 2п \ 2iz
или, применяя соотношение E.2.62),
1 + 2п| 2 iz*\ + BJH^F fj - п\ 1 — 2» | — 2i
Общее решение уравнения, получающегося при разделении переменных в
волновом уравнении в параболических координатах, включающее решение
уравнения, получающегося при разделении в параболических цилиндри-
цилиндрических координатах, имеет вид
С-
2т \ 2ikz Л
| - т —^ 11 - 2/и | - 2ikz
а общее решение уравнения Шредингера для частицы в кулоновом потен-
потенциальном поле при Е— —/с2 таково:
-n _-^. | _ 2и | -
Много других функций (таких, как функция ошибок и неполная гамма-
функция) можно выразить через вырожденную гипергеометрическую функ-
функцию.
Асимптотические ряды. Хотя мы отложили полное рассмотрение по-
поведения вырожденной гипергеометрической функции вблизи z= со, мы ис-
522 Гл. 5. Обыкновенные дифференциальные уравнения
следуем разложение решений в надлежащим образом выбранные ряды
вблизи особой точки z=co. Совершая в уравнении E.2.57) преобразо-
преобразование ау=1/ж, мы видим, что вблизи бесконечности вырожденное гипергео-
гипергеометрическое уравнение имеет вид
dw
E.2.64)
Хотя бесконечность — иррегулярная особая точка, все же имеется одно ре-
решение s=a определяющего уравнения. Подставляя F=^anwa*n в урав-
уравнение E.2.64), мы вновь найдем двучленную рекурсивную формулу для ап
Отсюда разложение F в ряд вблизи оу = О (z=oo) имеет вид
1 , q(q + l)(q-
E.2.65)
где мы опять вместо w подставили 1/z. [Этот ряд следует сравнить с фор-
формулой E.2.63).J Сравнение с формулой E.2.60) приводит к мысли, что вто-
второе решение должно иметь вид zif~aeilw^_bnwn. При подстановке для Ьп
получается двучленная рекурсивная формула, подобная приведенной выше.
Отсюда вторым решением, построенным в виде ряда, вблизи z=oo является
1 4- A-0) (с-а) 1 , (l-fl)B-q)(c-q)(c-q + l) 1
^ -г- y\ Г+ 2! "i*""*" — J-
Главное несчастье с этими двумя рядами для решений состоит в том,
что они нигде не сходятся, кроме точки z= со. Однако эта расходимость
особого типа, так как если z большое, но конечное, то ряд сначала схо-
сходится, а затем, если брать все больше и больше членов, в конце концов
расходится. Точнее говоря, оказывается, что разность Д„(г) между Fv и
суммой первых п членов ряда E.2.65) при возрастании п сначала умень-
уменьшается, а затем беспредельно возрастает. Для малых значений z наимень-
наименьшее значение Ап получается при относительно малом значении п, и это
наименьшее значение относительно велико. Если z возрастает, то минимум
Ап достигается при все больших и больших значениях п и значение этого
минимума становится все меньше и меньше. Поэтому для любого конечного
значения z возможно получить довольно точное значение F, взяв конечное
число членов, в то время как повышение числа членов даст менее точный
результат. Пока z конечное, имеется некоторая непреодолимая ошибка в
результате подсчета, даже если взято оптимальное число членов, однако
эта ошибка быстро уменьшается с возрастанием z. Во многих интересных
случаях эта непреодолимая ошибка во всяком случае меньше 0,1, когда z
больше 10. Во многих таких случаях один первый член разложения дает
удовлетворительное приближение при z > 20.
Такие ряды, которые расходятся, но могут быть применены для
подсчета значений, не точно равных «истинным» значениям, но быстро
приближающихся к «истинным» значениям при возрастании z, называются
асимптотическими рядами. Они были детально исследованы в § 4:6.
В некоторых отношениях они оказываются полезней сходящихся рядов,
¦если с ними обращаться с тактом и пониманием. Кое-что необходимое
для понимания будет приведено в следующем параграфе; такт же должен
проявить тот, кто их применяет.
5. 2. Общие свойства, решение при помощи рядов 523
Две регулярные, одна иррегулярная особые точки. Уравнение для
?! и ?, в эллиптических цилиндрических координатах имеет вид (ф =Xlt Х2;
(z2 -1) ф" + гф' + (&2z2 - b) ф = О,
а уравнения для ?г и ?2 в вытянутых и сплющенных сфероидальных коор-
координатах — вид (X = (z2 — 1)а/2ф)
(z2 - 1)ф" + 2 (а + 1) гф' + (?2z2 — Ь) ф = 0. E.2.66)
Первое уравнение является частным случаем второго (а= —^ Л. Чтобы
выяснить, каковы особые точки, перепишем второе уравнение так:
Оно имеет регулярные особые точки z= i 1 с индексами 0 и — а в обеих
и иррегулярную особую точку при z=co. Это уравнение не является
самым общим из тех, которые имеют две регулярные и одну иррегуляр-
иррегулярную особые точки, но оно встретилось в нашей работе. Особые точки
находятся в стандартных положениях (мы могли бы поместить регулярные
точки в 0 и 1, но f 1 удобнее), и одно решение в каждой регулярной
точке аналитично, как мы раньше требовали для канонического вида;
таким образом, мы будем рассматривать уравнение E.2.66) в качестве кано-
канонического вида уравнений этого типа.
Если подставить в уравнение E.2.66) ряд по степеням z, получится
трехчленная рекурсивная формула
(п + 1) (п + 2) а„+2 + [Ь-п(п+ 2а + 1)] ап -Ь?а^г = 0,
из которой можно получить два фундаментальных решения около регу-
регулярной точки z = 0. Разложения в ряды около особых точек по степеням
1 — z или 1 -f z порождают четырехчленные рекурсивные формулы, которые
еще труднее для подсчета и анализа.
В таких случаях мы пытаемся произвести разложение в ряд по
соответственно выбранным функциям, а не в ряд по степеням 1 ± z. На-
Например, преобразовав независимое переменное в случае эллиптических
цилиндрических координат (а= —1/2), мы можем получить
z = cos 9, ji + {b - h2 cos29) ф = 0, E.2.67)
Первое из этих уравнений называется уравнением Матье. Второе очень
интересно тем, что оно по форме алгебраическое, и переход от z к х так
изменил особые точки, что теперь имеется две иррегулярные особые точ-
точки, одна при 0, другая при оо.
С помощью первой формы уравнения можно получить интересное
свойство решений. Так как функция cos29 периодична по <р с периодом тс,
то если ф(ф) является решением уравнения, то и ф(9 + тс) также. Напри-
Например, если ф\ и ф2 —два независимых решения, то будем иметь
4»i (? + "О = аиФ1 (?) + а12<Ь (?)
и
ф2 (? + я) = а21ф,. (
524 Гл. 5. Обыкновенные дифференциальные уравнения
где а — постоянные, определяемые параметрами Ъ и h и частным выбором
решений (J>j и ф2.
Отсюда можно показать, что возможно найти решение уравнения
E.2.67), равное произведению els? на функцию, периодическую по 9- Это
решение (назовем его W), конечно, должно быть некоторой комбинацией
фх и ф2, W = Лфх (9) + ^Ф2 (?)= eist*F(<p), где функция F периодична по <р
с периодом it, то есть F (9 + it) = F (9)- Применяя свойства функций ф,
имеем, что
*) = A$i (9+ 1г) + Вфя(?+ та) -
2) ф2 (9) =
= е"» в*8* Z1 (9) = е"
Приравнивая коэффициенты при фхОр) и ф2(9), мы получаем систему
двух уравнений для А, В и e™s
А (ои - в»*) + ?а21 == 0, Аа12 + В (а22 - е™8) = 0.
Чтобы она имела ненулевое решение, определитель из коэффициентов
должен равняться нулю
Получилось квадратное уравнение относительно e™s с двумя корнями,
соответствующими двум независимым решениям уравнения E.2.66).
Теорема о существовании таких решений уравнения E.2.67) называется
теоремой Флоке.
Для второй формы уравнения E.2.67) теорема Флоке устанавливает,
что можно выбрать два независимых решения, равных произведению
Xs (х = eitp) на ряд Лорана по х2, так как ряд Лорана по х2 содержит все
положительные и отрицательные степени х2 и потому одновременно является
рядом Фурье по 29. Такой ряд периодичен по <р с периодом it, как
и должно быть, согласно предыдущему, и может представлять функцию
вблизи обеих иррегулярных особых точек х = 0 и х = со. Поэтому мы
берем в качестве решения
ф= 2 апх*+2п = е**? 2 «пе21"ф- E.2.68)
«= —со п——со
Подставляя этот ряд во второе уравнение E.2.67), мы приходим к основ-
основной рекурсивной формуле
4* Y
Это — трехчленная рекурсивная формула с неизвестными ап и s. Выло
бы желательней совершить другое преобразование зависимой -и независи-
независимой переменных, чтобы получить двучленную рекурсивную формулу.
К несчастью, как будет показано позже в этом параграфе, такой приятный
результат невозможен для столь сложных уравнений, и потому мы
принуждены взяться за анализ трехчленных рекурсивных формул.
Если мы начнем с произвольно выбранных значений а0, аи и s, то
мы можем подсчитать все другие а для положительных и отрицательных
п. Но в этом случае коэффициенты а не будут обязательно уменьшаться
5. 2. Общие свойства, решение при помощи рядов 525
с возрастанием п, так что ряд, вообще говоря, не будет сходиться. Только
для некоторых значений s и ajao ряд будет сходиться, и нам надо найти
путь подсчета этих значений.
Непрерывные дроби. Прежде всего, конечно, мы должны убедиться
в том, что ряд может сходиться для некоторых значений ajao и s. Для
этого мы подсчитаем значение anlan-i Для больших положительных п
и ajan+x для больших отрицательных п. Если эти значения с достаточной
скоростью стремятся к нулю при п—»±оо, то можно быть уверенным
в сходимости ряда при 0 < х < со. Однако
^
16 [п+ (s/2)]2+ 2h* — 4b + 1гЧп+1/ап '
ап+1 16 [n +
Первое из этих равенств показывает, что для больших положительных п
отношение ап/ап^1 стремится к нулю, как 1/п2, если только отношение
ап+1/ап ограничено, так как тогда для достаточно больших п член
16 [п + (s/2)]2 превалирует над всеми остальными членами знаменателя
и п2ап/ап_1~^- — /га/16. Применение метода, приведенного на стр. 367,
показывает, что для больших значений х (т. е. для <р> больших по модулю
и расположенных на отрицательной мнимой полуоси) функция ф приблизитель-
приблизительно пропорциональна Xs cos (kx/A).
Подобным образом второе равенство E.2.70) показывает, что если
ап_Л1ап ограничено для. больших отрицательных п, то nzan/an+l—> — h-/16.
Отсюда для очень малых х (для 9 больших по модулю и расположенных
на положительной мнимой полуоси) ф приблизительно пропорциональна
Xs cos (h/Ax). Однако нам надо еще узнать, как подсчитывать отношение
aJan-\ Ддя малых значений п, а также, как определять нужные значения s.
Тем не менее равенства E.2.70) дают способ стать на правильный
путь. Если мы не можем начать с а0, at и идти вперед, то, может быть,
можно начать с очень больших значений п и идти назад. Предположим.,
что мы начинаем с настолько большого значения п, что а^:1.1/ап очень
близко от — &2/16[n + (s/2)]2. Подстановка в первое равенство дает почти
точное выражение для ajan^; подстановка его в аналогичную формулу
для а-п-\1ап-2, Дает еще более точное выражение для dn^xlan-2, и т- Д-> так
что мы приходим к значению
%— ft 2
16 1+-^-я +2fc2 — 4Ь-
J-2/г2 — ЛЬ -
h*
1
Подобным образом применение второго равенства для отрицательпых п
•дает нам
2 ^s )J-2A;2 —4Ь —
б( 3-
526 Гл. 5. Обыкновенные дифференциальные уравнения
Эти выражения называются непрерывными дробями. На вопросы об их
сходимости можно ответить, применяя соответствующие правила для рядов.
Применение уравнения E.2.69) для п = 0 дает формулу, связывающую
и а_х/а0,
Эта формула вместе с двумя предыдущими приводит к уравнению, из
которого можно определить s через Ь и h. Подсчитаем непрерывные
дроби для предполагаемого значения s и затем проверим результат при
помощи равенства E.2.71). Если оно не удовлетворится точно, возьмем
квадратный корень из правой части равенства за новое значение s и под-
подставим его в непрерывные дроби и т. д. Если только первоначальный
выбор не слитком плох, то этот процесс последовательных подстановок
быстро сходится и значение, верное с точностью до пяти или шести
значащих цифр, можно обычно получить меньше чем за дюжину шагов.
Конечно, для малого h этот итеративный процесс можно осуществить
аналитически. С точностью до первого порядка относительно Л2 имеем
s= [/fc —(&2/4|/l>). Подставляя это в обе непрерывные дроби (и опуская
в них члены с №), получаем
или
h* h* 2 — 3,
если только Ъ не близко к 1; в противном случае нужно включить высшие
степени h2.
Заметим, что из симметрии соотношения E.2.71) и непрерывных
дробей [или из формулы E.2.68)] следует, что если s является решением,
то и — s также; также и fsi 2т, где т любое целое число, является
решением.
Если s подсчитано, то аг и a_t можно выразить через а0 (которое
можно положить равным ,1), а остальное а можно подсчитать при помощи
вспомогательных непрерывных дробей
-А2
4ip
Ш у s — п— 1 J
и тем самым вычислить весь ряд. Соответствующая функция
со
&'(b,h,ei*) = eis* ^ апе21п<е> E-2.72)
Т1=—СО
включающая эти значения s и а, является одним из решений уравнения
E.2.66). Другое решение получается при противоположном знаке s
и перемене мест ап и а_п
со
if (b, h, e*) = е'1** ^ ane-2iT"f;
6. В. Общие свойства, решение при помощи рядов
527
оно комплексно сопряжено с первым. Соответствующие вещественные
функции получаются при слежении или вычитании
Se (b, h; z) =
i
So(b,h;z)= ^i ansm[(s+2n)<p].
E.2.73)
Эти функции четны или нечетны относительно <р — 0> но не периодичны
по <р с периодсм -а или 2it, если только s не целое.
Для некоторых областей значений Ъ (например, для отрицательных
Ъ или для Ъ, близких к 1, 4, 9 и т. д.) s оказывается комплексным
числом. В этом случае вещественные решения Se и So имеют несколько
более сложный вид. При увеличении h увеличивается также область
значений Ь, где s комплексно. Эти области называются областями
неустойчивости решений, так как вещественный показательный множитель,
присутствующий тогда в решениях, становится как угодно большим для
больших z, положительных или отрицательных.
Определитель Хилла. Прежде чем продолжить наше исследование
решения уравнения Матье, мы рассмотрим совершенно иной метод под-
подсчета s и коэффициентов an, успех которого проистекает из особенной
симметрии рекурсивных формул E.2.69). Эти формулы образуют, конечно,
систему однородных уравнений первой степени относительно ап (в беско-
бесконечном числе, поскольку число коэффициентов ап бесконечно). Чтобы ее
можно было решить и выразить, например, ап через а0, определитель из
коэффициентов при неизвестных ап должен равняться нулю. Он является
бесконечным определителем, так что вадо проследить за его сходимостью.
Однако для улучшения сходимости можно до образования определителя
разделить п-ю рекурсивную формулу на 2/г2 —4fc +16п2. Получающийся
определитель
(, + 2)-a2
Z2 — a2
I2 —a2
0
0
•
•
P2
22 — a2
I2 — a2
P2
— a2
0
•
0
»2 p2
I2 —a2
c2 —a2
P2
I2—a2
•
• •
0
0
к
Г т
(j-lJ-a2
I2 —a2
• •
, E.2.74)
1 11
где a = —s, a2 = — b—^ h2 и р = /г/4, называется определителем Хилла.
Нам остается лишь разрешить уравнение Д (s) = 0 относительно si
Замечательным является то, что из-за периодического характера
зависимости от о, устанавливающего связь Д с тригонометрическими
функциями, такое решение возможно. Прежде всего, упростив наш опре-
528 Гл. 5. Обыкновенные дифференциальные уравнения
делитель при помощи умножения n-й строки (считая от строки п = 0) на
{п2~а2)/[(а + пJ — а2], получим новый определитель D (о), где
ДМ - Г) (а\ ТТ
и2 —a2 ~ — a2 11 [1 —(a//iJ]2
n=—со n= 1
Определитель _5 (о) имеет вдоль главной диагонали последовательность
единиц, на обеих соседних диагоналях — последовательность вида
B2/[(a + rcJ —a2], а все остальные элементы равны нулю. На основании
формулы D.3.9) мы видим, что
л / \ r*i / \ sin п (з -4- a) sin 7г (_— а) г\ / \ sin2 (пес) — sin2 G13) /г- о г7Р-\
A^)=-jD(°) LIin2(,a) =D(°) sin2(TCa) ' E-2-75)
это соотношение уже говорит кое-что о периодической зависимостд
от а и о.
Однако определитель D (о) также имеет определенную периодичность
по о и простые полюсы при а = ±п ±^а, порожденные элементами
Р2/К° -\~пJ — а2]. При этом полюсы _5(о) расположены только в этих точ-
точках, и к этой функции, очевидно, применимы рассмотрения стр. 360—364.
Мы сперва вычтем функцию, имеющую такие же полюсы,
где С равно вычету в каждом полюсе D. Однако подобно тому как мы
пришли к соотношению D.3.7) (см. задачу 4.21, стр. 449), мы получим
так что функцию К (о) можно переписать. Эта функция
К (о) = D (о) -j- ~ [ctg % (а + а) — ctg it (о — а)]
не имеет полюсов ни для одного значения s и ограничена при s~» оо. По
теореме Лиувилля (стр. 360) она должна быть постоянной, и, полагая
°—»со, мы видим, что постоянная _Г равна единице. Отсюда получаем
довольно удивительный результат
D (о) = 1 ~ S
Возвращаясь к равенству E.2.75), мы видим, что
а , ч . sin2 (т) пС . ,
A (s) = 1 ^-j-)—( ctg (тга),
х Sin2(n2) а б ^ ''
где единственной еще не определенной постоянной является постоянная С,
вычет в полюсах D (о). Его можно1 подсчитать, положив с = 0; получится
(ъС/s) ctg (т;а) = 1— Д @). Следовательно, возвращаясь к исходным обо-
обозначениям, получаем, что функциональная зависимость исходного опреде-
б. 2. Общие свойства, решение при помощи рядов
529
лителя от s относительно проста
Д(8) = Д(О)
sin2 (ms/2)
E.2.76)
где
Д@) =
1
ft2
34 + 2&2— 46
0
0
0
*
ft2
144+2ft2—46
1
ft2
16 + 2ft2—46
0
0
*
0
ft2
64 +2ft2—46
1
ft2
2ft2—46
0
0
0
h2
16 + 2ft2—46
1
ft2
16 +2ft2—46 '
представляет собой сходящийся определитель, не зависящий от s. Так
как A(s) должно равняться нулю, то соотношение E.2.71), из которого
определяется s, равносильно уравнению
sina (us/2) = Д @) sin2 [%Vb^J
Функции Матье. Теперь мы готовы вновь обратиться к нашему пре-
предыдущему исследованию допустимых значений s п решений S. Величина
\ \ \ \ \ \ \ \
www
8
Рис. 5.4. Значения констант разделения для периодических ре-
решений уравнения Матье.
A@)sin2[7i:"j/~& — (k*/2)/2] является периодической функцией а=|^Ь—(Л2/2)/2
с периодом 1. Для h = 0 будет Д @) = 1 и s = ± 2а = ± УЪ; это — предель-
предельный случай, когда уравнение E.2.66) приводится к виду (dzty/d<p2) -f bty = 0.
Если b—(Л2/2) достаточно большое отрицательное, то Д @) sin2 (от) отри-
отрицательно и s чисто мнимое. Вся область значений h и Ъ на рис. 5.4,
34 ф. м. морс и Г. Фешбах
530 Гл. 5. Обыкновенные дифференциальные уравнения
лежащая слева от линии 0 и заштрихованная, соответствует неустой-
неустойчивым решениям с вещественным показательным множителем.
Для некоторого значения Ъ, зависящего от h и изображаемого на
рис. 5.4 кривой 0, произведение Д @) sin2 (тах) равно нулю, так что и s
равно нулю. В этом случае решение if (fc, h; e**) вещественно, симметрично
по ф и периодично по <р с периодом тг [так как ап — а_п и if является
рядом Фурье по cos {2щ)\. Эта функция называется функцией Матье
нулевого порядка и обозначается специальным символом
со
Se0 (й, г) = 2J #2n cos Bn<p), z = cos 9,
71=0
где В пропорциональны а, но подобраны так, что Seo(h,l) = l. Если
s = 0, то два решения if (fc, /г; е1*) и ^F, /г; e"i(P) равны и второе решение,
независимое от Se0, надо находить при помощи формулы E.2.6). Оно
содержит логарифмический член и потому не периодично по <р-
В области изменения Ъ, h, которой на рис. 5.4 соответствует неза-
штрихованная область между линиями 0 и 10, выражение Д @) sin2 (на)
меньше единицы, и потому уравнение для s имеет решение, которое веще-
вещественно и меньше единицы. Функции Se и So, данные формулами
E.2.73), являются независимыми решениями, а наилучший способ подсчета
s и коэффициентов ап основан на применении непрерывных дробей
в соотношении E.2.71).
Для множества значений Ъ, h, изображаемого кривой 10) произведение
Д @) sin2 (тис), а потому и s равно единице. Оказывается, что ап= —o_n_lt
так что оба решения if (b, h, е*?) и if (fc, h, e1?) пропорциональны функции
со
So, (Л, z) = 2 В*п+г sin B" + *) 9-
n=0
которая называется нечетной функцией Матъе первого порядка. За ним,
в следующей заштрихованной области, Д @) sin2 (тссс) больше единицы, s
комплексно и имеет значение 1 + si и, следовательно, решение неустойчиво.
На правом краю этой области неустойчивости s опять равно единице, но
в то же время ап = а_п_1г так что оба решения if пропорциональны
со
Sex (h, z) = 2 #2n+i cos Bn + 1) 9
n=0
четной функции Матъе первого порядка. Второе решение вновь имеет
логарифмический член.
Такое поведение продолжается и для возрастающих значений Ь:
чередующиеся области устойчивости и неустойчивости, разделяемые
граничными линиями, соответствующими тому специальному случаю,
когда s целое и когда одно решение периодично и является либо четной
функцией (разлагающейся в ряд Фурье по косинусам), либо нечетной
функцией (разлагающейся по синусам), а другое решение непериодично
и содержит логарифм. Для остальной части области изменения Ъ, h, вне
граничных линий, решение непериодично, колеблется и имеет вид E.2.73)
или же непериодично, неустойчиво и является произведением комплекс-
комплексного показательного множителя на ряд Фурье.
Во многих случаях, имеющих физический интерес, координата,
соответствующая 9» является периодической и повторяется при возраста-
возрастании 9 на 2тс. В этом случае единственно пригодными являются перио-
периодические решения, названные нами функциями Матъе, для целых
5. 2. Общие свойства, решение при помощи рядов 531
значений s (одна нечетная функция Som и одна четная функция Sem
для каждого целого значения s = т). Если h обращается в нуль, то Sem
становится равной cos mo, a Som — равной sin mcp.
Чтобы подсчитать допустимые значения константы разделения Ьу
соответствующей этим периодическим функциям, можно вместо опреде-
определителя Хилла применять формулу E.2.71), включающую непрерывные,
дроби, причем, в отличие от предыдущего, находя Ъ при данном s.
Полагая s равным целому т, находим при помощи последовательных,
приближений решение уравнения
где отношения aja^, a_x/a0 приведены на стр. 526 в виде непрерывных
дробей. Для каждого значения т, за исключением т=0, имеется два
различных решения, из которых одно порождает ряд по синусам, а
другое —по косинусам (т. е. «п=±«2т-„).
Если s = 0, то а1/о0= «^^Ор, и мы решаем уравнение
А4
16 + 2Л2—4fc—
16-4+2fc2—ib— ...;
отсюда
со со
Se0 {h,z)= ^ #2n cos 2n9, B2n = ап / ^ ап,
где коэффициенты В нормированы так, что Seo--=l при 9 = 0. Соответ-
Соответствующее значение Ъ в этом случае можно обозначить be0 (k).
Однако если мы интересуемся только функциями Матье, т. е. перио-
периодическими решениями, то мы можем значительно упростить выкладки,
используя тот факт, что решения являются суммами рядов Фурье. Пре-
Преобразуем первое из уравнений E.2.67) в
Как мы показали, имеется четыре различных типа периодических реше-
решений этого уравнения:
I. Четные решения периода к, s = целому четному = 2т, соответ-
соответствующее значение Ъ = Ье2т
со
SeZm(h, cos9)= 2 В2п cos Bn9).
п=0
II. Четные решения периода 2тс, s = целому нечетному = 2т -г 1,
для Ь = Ье2т+1
Se2m+1{h, cos 9)= 2?2«+iC
III. Нечетные решения периода я, s = целому четному = 2т, для Ъ =. boirr
со
So2m (h, cos 9) = 2 В2п sin B"ф)-
34*
532 Гл. 5. Обыкновенные дифференциальные уравнения
IV. Нечетные решения периода 2тс, s = нечетному целому = 2т-\-1,
для b=bo2mtl
оо
&>«m*i (Л> cos ?) = 2 ^2«*i sin Bn + 1) ср,
п=0
где коэффициенты В зависят от h, m (то есть от значения s или от свя-
связанного с ним значения Ь) и, конечно, от п.
Подставляя ряд Фурье типа I в дифференциальное уравнение и при-
1 1
меняя тождество cos a cos Ъ—-^ cos (а -f fc)-f-^-cos (а — b), имеем
Б2 = k0B0, Д, = &2Б2 — 2В0, къпВ2п — В2г1<.2
где
/сто = /г2 D6 - 2/г2 — 4т2).
Из этих уравнений, преобразованных в непрерывные дроби, мы можем
подсчитать отношение коэффициентов, а также соответствующее значе-
значение Ь, то есть Ье%т. Полагая отношение представленным в виде
имеем две возможные совокупности уравнений для G:
2 ^ 1
ге > 1 E.2.77)
или G2 = Ао, G4 = А2
re>2, E.2.78)
причем можно пользоваться той или иной в зависимости от относитель-
относительной простоты выкладок и от скорости сходимости.
Приравнивание двух выражений для G2 дает уравнение с непрерыв-
непрерывной дробью для определения соответствующего значения Ь. Полагая
1 1
a = fc—«-й2, 6=-т-/г2, имеем уравнение
262 В2
"=g_4 J! В*
16
*" а — ЗС — ...
которое равносильно уравнению стр. 531. Можно найти бесконечную
последовательность решений а в виде функций 6, откуда можно опреде-
определить значения Ье%т. Некоторые из этих значений имеются в таблицах.
Эти значения показаны также графически на рис. 5.4.
Для решений типа II при помощи тех же методов можно прийти
к следующим уравнениям для отношений коэффициентов G и для кон-
константы разделения beimtl = а + ^-й2:
5.2. Общие свойства, решение при помощи рядов 533
к^=.... п > О,
• = l + » + ^r
а—25—
a—49— . . .
В обоих этих случаях удобно нормировать функцию так, что Sem — 1
при 9 = 0. Это означает, что ЕВП = 1.
Для решений типа III имеем Во = 0, и уравнениями для G и bo
будут
1 1
_=0, G4 = U2I С2„ = А2„_2-7-_4_
«2
а—10—
а — 36 — ...
Наконец, для решений типа IV имеем:
п>0,
fj2
a = 1 - 6 ¦ U
t — 9—
а_25 — ...
Для обоих рядов по синусам удобно провести нормировку так, чтобы
скорость изменения функции dSom/d<p равнялась единице при <р = 0. Это
означает, что ?i?n = l.
При вычислении значений а (и тем самым Ь) мы можем преобразо-
преобразовать непрерывные дроби, чтобы облегчить работу. Например, для реше-
решений типа I при значении а, близком к 16, можно в уравнении E.2.77)
дважды перейти к обратным величинам, что даст
A2 Q2
+ 62
а—64— . . .
Оказывается, что (если только h не слишком велико) значения Вп наи-
наибольшие при пй^т. Поэтому Gn = Bn/Bn_% мало для п>т и велико для
ге < т. Опыт показывает, что конечные непрерывные дроби,' подобные
E.2.78), лучше применять при подсчете Gn для п < т, а бесконечные
дроби, подобные E.2.77), лучше для значений п, больших т.
Функции Матье второго рода. Как мы указали на стр. 526, если s
целое, то обе функции <У(Ъ, h, е1?) и ef (b, h, е~^) пропорциональны Sem
или Som, то есть функции Матье первого рода, отвечающей значению
b = bem или Ьот, соответственно. Для этих частных значений b второе
решение имеет логарифмическую особенность относительно z == е"? (дру-
(другими словами, оно не периодично по <р), и мы должны ввести специальцые
534 Гл. 5. Обыкновенные дифференциальные уравнения
решения в этих специальных случаях. Мы укажем здесь метод для полу-
получения вторых решений, соответствующих четным функциям Se%m (h, cos<p).
Так как <р = 0 представляет собой обыкновенную точку для уравне-
уравнения Матье
ь - i h2 ~ i h2 cos 2? ) Ф=0)
то можно построить фундаментальную систему решений, из которых одно
имеет единичное значение и нулевую производную, а другое нулевое зна-
значение и единичную производную при <р = 0. Для Ъ = fce2m первым реше-
решением будет функция Se.2m(h, cos 9), имеющая единичное значение и нуле-
нулевую производную. Второе решение должно быть общего вида
со
Fe2m (h, cos 9) = Ьт [ TSe2m (h, cos 9) + % #•„ sin Bn<p) ] , E.2.79)
n=l
имеющего логарифмическую особенность относительно z при <р = arccos z = 0.
Оно также не периодично по <р. Подставляя это выражение в уравнение
Матье и вспоминая, что 6"е2т = 2 -^2n cos ^n9 представляет собой решение
того же уравнения для того же значения Ъ, в конце концов получаем
п=1
+ ( Ье2п -1 й» ) D2n + \ h* /Jп+2 ] sin Bп9) = 0'
причем член D2n_% для п=1 отсутствует. Отсюда вытекает система сово-
совокупных уравнений
i-й»-16]/L + i-*»/), = 8В4 и т. д.,
ид которых можно выразить Z) через В (это не просто, но тем не менее
можно найти решение, для которого ряд сходится). Мы выберем значение
постоянной Y2rn> положив, что производная Fe при <р = 0, равная
у2то [l + S2nZJn], должна обратиться в единицу, то есть
Отсюда имеем фундаментальную систему решений относительно
Определитель Вронского АF"е, Fe) относительно у постоянен и потому
Se2m (h,r cos 9) щ Fe2m (fe, cos cp) - Fe2m (^,^cos 9) -^ Se2m (h, cos 9) = 1
для всех значений <р. [См. также соотношение E.3.91 и далее.]
Вторые решения для других функций Матье получаются подобным
образом. Например, для Ъ = Ьо2т+1 второе решение имеет вид
n=0
5.2 Общие свойства, решение при помощи рядов 535
где уравнения для D подобны написанным выше. В этом случае норми-
нормировка такова, что Fo2m+1 = 1 при <р = О (и имеет там нулевую производ-
производную), что приводит к уравнению для
•а определитель Вронского для этой пары решений равен — 1.
Итак, мы во всяком случае указали вид вторых решений для тех
-значений Ь, для которых функции of (b, h, e~i!f) и ef {b, h, e*?) не незави-
независимы. Для всех остальных значений Ъ обе функции of независимы и обра-
образуют требуемую пару.
Еще о рекурсивных формулах. Теперь мы в состоянии несколько
больше разобраться в решениях дифференциальных уравнений при помощи
рядов и в связанных с ними рекурсивных формулах. Пусть нам дано диф-
дифференциальное уравнение X (ф) == ф" + рф' + <?ф = 0, для которого мы хотим
получить решение, разложенное в ряд около одной из его особых точек.
Для простоты подсчета мы поместим рассматриваемую особую точку в на-
начало координат, что можно сделать без изменения прочих особых точек-.
Тогда р, или q, или обе эти функции имеют полюс при z = 0. Если р
имеет только простой полюс, a q — полюс не выше второго порядка при
z = 0, то данная особая точка регулярная и мы можем при желании пред-
представить решение прямо в виде суммы двух рядов по степеням г. Каждый
из рядов имеет вид zs ^ «nz", где s является одним из двух корней опре-
определяющего уравневия
причем P=limzp(z), a Q= limz2q(z). Приравнивание нулю коэффициента
при zn+s в ряде, полученном после применения «5? (ф) к ряду Xanz"+S'
дает рекурсивную формулу Dn (ап) = 0 для степенного ряда вблизи осо-
'бенности z = 0. Эта формула вместе с формулами для других значений п
образует бесконечную последовательность линейных уравнений относи-
относительно неизвестных коэффициентов ап. Если р, или q, или обе эти функ-
функции z требуют для своего представления бесконечный ряд, то каждая
рекурсивная формула /)п = 0 включает все а от а0 до ап (возможно, даже
дальше).
В принципе, эти совокупные уравнения всегда можно решить, полу-
получив тем самым отношения ап к а0. Однако если каждая из рекурсивных
формул содержит более двух членов (то есть включает более чем пару
смежных а), то задача о подсчете ряда и об испытании его на сходимость,
-асимптотическое поведение и т. д. становится гораздо более сложной.
Посмотрим, что мы можем сказать о возможности получения двучлен-
двучленных формул.
Короткие рекурсивные формулы можно получить только если р и q
представляют собой рациональные функции z, то есть отношения много-
-членов относительно z (см. стр. 361). Если они не являются рациональ-
рациональными функциями, то можно пытаться так преобразовать независимое пере-
переменное, чтобы новые р и q стали рациональными функциями; если это
можно сделать, то можно продолжать далее, в противном случае мы при-
принуждены иметь дело с бесконечными рекурсивными формулами.
Знаменатели р и q, если эти функции рациональны, определяются
лоложением особых точек уравнения. По крайней мере один из этих зна-
знаменателей имеет z множителем, так как хотя бы одна из двух функций
536 Гл. 5. Обыкновенные дифференциальные уравнения
имеет при z = О полюс. Если имеются другие особые точки для конечных
значений z (скажем, для z = zi\ i = 1, 2, ... , N), то знаменатели р, или q,
или обеих этих функций должны содержать множители вида z — z{. В»
всяком случае если мы избавимся в уравнении X (ф) = 0 от дробей, то
оно приобретает вид
JV JV
П(г-«4)гчФ" + ^B)Ф' + С(г)ф = 0, М= 2*4, zo = 0,
i=0 1=0
где F и G — многочлены относительно z. Отметим, между прочим, что
если на бесконечности нет особой точки, то многочлен G (z) должен иметь
степень М — 4 или меньше, a F должен быть многочленом степени М — 1
и иметь старший член 2zM-1 (почему?).
Нетрудно видеть, что, вообще говоря, такое уравнение будет иметь
Л/-членную рекурсивную формулу. Если бесконечность является регуляр-
регулярной точкой, то количество членов в этой формуле можно понизить на
один или два посредством преобразования w = z/(z — z;-) независимого пере-
переменного, переводящего /-ю особую точку на бесконечность. Когда это сде-
сделав о (если только это возможно) и особые точки имеются и в нуле, и
в бесконечности, то уравнение все еще будет иметь указанный выше вид,
но степени многочленов, на которые множатся ф", ф' и ф, будут наимень-
наименьшими возможными степенями для рассматриваемого частного уравнения.
Теперь можно усмотреть, что обычно получить двучленную рекурсив-
рекурсивную формулу возможно только тогда, когда имеется лишь одна особая
точка, помимо расположенных в нуле и в бесконечности, так как коэф-
коэффициент при ф" должен иметь вид zn»(z— гг), многочлен F должен иметь-
вид azno -\- bzno-1, a G — вид az**»-! -\-$zn<>-2, для того чтобы степени z в раз-
разложении X (ф) в ряд располагались так, чтобы был возможен вывод дву-
двучленных рекурсивных формул. Другой, несколько худший случай — это
если имеются две другие особые точки, расположенные симметрично
(то есть z2 = —zx), так что коэффициент при ф" имеет вид zn°(z* — z*^
Если тогда F = azn»+i -\-Ъгп°~х, а G = azn° + Pzn°-, то получается двучлен-
двучленная формула, связывающая ап и ant2 (а не ап и antl).
Даже если другая особая точка только одна, то функции F и G
могут не иметь требуемого простого вида. В этом случае, иногда может
помочь преобразование зависимой переменной по формуле ф = к(г)/(г),
где и представляет собой произведение некоторых степеней z и z — zt.
Обычно в качестве показателей степеней подходят какие-либо из индек-
индексов s в каждой из особых точек, так что уравнение для новой зависи-
зависимой переменной / имеет как при z = 0, так и при z = zt одно из решений,
аналитическим. Это часто понижает степень многочлева G и дает дву-
двучленную рекурсивную формулу. Этот прием был нами успешно применен
при преобразовании уравнения Папперица в гипергеометрическое урав-
уравнение.
Если имеется более одной иррегулярной особой точки, то F или G
не имеют вида, приводящего к двучленной рекурсивной формуле. Как мы
видели, лучшее, что можно сделать в случае двух иррегулярных точек,,
равно как и в случае двух регулярных и одной иррегулярной точки, —
это получить трехчленную формулу. Большее число особых точек или,
высший вид иррегулярности порождают еще более сложные формулы..
К счастью, оказывается, что такие случаи не приобрели до сих пор боль-
большого практического значения, так что мы их опустим без дальнейших
церемоний, заметив только, что если эти случаи приобретут значение,
то потребуются дальнейшие исследования для создания техники работьв
с этими более сложными рекурсивными формулами.
5.2. Общие свойства, решение при помощи рядов 537
Функциональные ряды. Нам, однако, не обязательно ограничиваться
рядами по степеням z; можно также применять ряды по некоторой системе
функций /„
Чтобы увидеть, как можно осуществить это обобщение, возвратимся
к методу степенных рядов и спросим, почему множество функций
было таким полезным. Очевидный ответ гласит, что в этом случае функ-
функции /п удовлетворяют чрезвычайно простым рекуррентным соотношениям
Применяя эти соотношения, возможно привести дифференциальный опе-
оператор X к виду, содержащему только различные степени zn. Чтобы при-
применить другое множество функций /„ для представления решений, это
новое множество также должно удовлетворять рекуррентным соотношениям.
Другое важное и полезное свойство степенных рядов—это свойство
полноты. Под полнотой мы понимаем то, что при выполнении опреде-
определенных условий линейную комбинацию степеней z можно применить для
представления любой функции. Это утверждение является следствием
теоремы Лорана [см. D.3.4)] и имеет место при выполнении условий
этой теоремы. Прежде чем применять другие множества функций, мы
должны выяснить, какие функции могут быть представлены с их помощью,
а какие нет. Позже, в главе о собственных функциях, мы уделим значи-
значительное внимание, исследованию этого вопроса. Однако стоит рассмотреть,
что можно сделать в этом отношении при помощи уже развитой нами
техники. Мы приведем несколько примеров, после чего возвратимся к ис-
исходному вопросу о решении уравнений при помощи функциональных
рядов.
Обычно применяемый метод состоит в установлении связи между
используемым функциональным рядом и степенным рядом. Тогда на
основании известных свойств степенного ряда возможно получить сведе-
сведения и о множестве /я. В качестве первого примера установим полноту
рядов Фурье по еш прямо из рядов Лорана. Из формулы D.3.4) имеем
Рассмотрим теперь значения $(z) на единичной окружности, z=e%i. Тогда
Из свойства полноты степенных рядов мы можем теперь заключить, что
с помощью множества функций ein> можно представить любую достаточно
хорошую периодическую функцию 6 периода 2%. Необходимость "перио-
"периодичности проистекает из того, что ряд Фурье представляет значения ф на
окружности, при обходе которой эти значения повторяются. При рассмо-
рассмотрении четных или нечетных функций 6 мы немедленно приходим к рядам
Фурье по косинусам или синусам.
В качестве второго примера исследуем первое решение уравнения
Лежандра E.2.47) для и = Ои целых значений п
538 Гл. 6. Обыкновенные дифференциальные уравнения
Для целых значений п X является многочленом относительно z; поли-
полиномы Лежандра Рп будут более детально исследованы позже, на стр. 558.
Подсчитаем несколько первых из этих функций:
Р2 = Cz2 - 1)/2, Р5 = F3z5 - 70z3 + 15z)/8 и т. д.
На основании этой последовательности можно доказать, что любую сте-
степень z" можно выразить в виде линейной комбинации многочленов Рп.
Для 1 и z это очевидно. Выпишем результат для нескольких следующих
степеней:
z* = 4
и т. д.
Из того что степенные ряды по положительным степеням z полны для
функций, не имеющих особенностей, можно заключить, что эти функции
можно равным образом выразить через полиномы Лежандра. Чтобы охва-
охватить функции с особенностями, было бы необходимо вовлечь в наше ис-
исследование второе решение уравнения Лежандра (соответствующее отри-
отрицательным степеням z).
В данный момент нет необходимости определять явно коэффициенты
указанных выше разложений. Достаточно показать возможность такого
представления. Например, при решении уравнения Бесселя для целого п
(см. стр. 521) мы получаем одну совокупность решений
. формулу E.2.63) и далее]. Можно полагать, что посредством подхо-
подходящей комбинации этих функций было бы возможно представить z". Ана-
Аналогично для z"n были бы пригодны вторые решения, функции Неймана
(см. стр. 585). Это утверждение проверить несколько труднее, чем подоб-
подобное утверждение для функций Лежандра, так как функции Бесселя пред-
представляют собой не многочлены, а суммы бесконечных рядов. Однако отно-
относительно просто доказать, что принципиально представление через функ-
функции Бесселя возможно.
Теперь мы в состоянии обратиться к некоторым примерам примене-
применения функциональных рядов, откуда мы сможем вывести способ рассужде-
рассуждений, который должен обычно применяться. Как первый пример, рас-
рассмотрим исследованное ранее (стр. 523) уравнение Матье
Это уравнение до некоторой степени походит на уравнение, которому
удовлетворяют показательные функции:
5.2. Общие свойства, решение при помощи рядов 539
со
(член cos2<p отсутствует). Подставим ^ Anfn в уравнение Матье
со
2 ^„
Группируя члены с общим множителем е21(я+вI? получаем
2 {-т
^ + ^[ь4(Л+«I]}e2i(n+s)J =
На основании полноты системы функций е1 (ri+s) ° коэффициент при каждом
члене должен равняться нулю. (Здесь мы используем тот результат, что
если сумма степенного ряда тождественно равна нулю, то коэффициент
при каждой степени должен равняться нулю.) Таким образом, мы полу-
получаем трехчленную рекурсивную формулу
1^2 г~ Jj2 "| k2
Она тождественна с E.2.69) (естественно).
В качестве второго примера рассмотрим специальный вид уравнения,
лолученного в результате разделения в сфероидальных координатах
(z2 - 1N" + 2гф' -\- (h2z2 — b) ф = 0.
Сравним его с уравнением, которому удовлетворяют полиномы Лежандра
(Z2 - 1) Рп + 2z/>; - П {П + 1) Рп = 0.
Если потребовать, чтобы ф не, имела особенностей в ± lf то есть в осо-
особых точках дифференциального уравнения, то естественно ожидать, что
выбор /„ = Рп окажется полезным; итак, положим
Здесь применимо следующее рекуррентное соотношение, которое будет
выведено позже:
-гп _
(" + !)* 1 р
г+1)Bп + 3) J "
(п +2)
р
4na— 1 ^B/г+1)Bп + 3) J " Г Bп +
Подстановка в дифференциальное уравнение дает
{,1 ,2 (я+ 2) (в+'l)
" \лп-2Н Bи4 з) B7г + 5
Полученная трехчленная рекурсивная формула теперь должна быть раз-
разрешена относительно Ап при условии, что A t = Л_2 = 0.
То, что здесь сделано, сводится к указанию полного множества функ-
функций fn (z), по которым мы хотим разложить наше решение. На практике
540 Гл. б. Обыкновенные дифференциальные уравнения
мы выбираем функции / так, что их дифференциальное уравнение
сМп (/„) = 0 не очень отличается от уравнения X (ф) = 0, которое мы хотим
решить. После этого мы применяем соотношения между последователь-
последовательными /„, чтобы выразить разность между X (/„) и еЖп (/„) в виде ряда по /„
lX-cSm]fm = Y-(mnfn- E-2-80)
п
Например, для рядов по полиномам Лежандра, о которых мы говорили
выше, [X — еЖп](Рп) = [hH* — b + n(n+l)]Рп, что можно подставить в ряд
вида E.2.80), включающий только три члена (с Рп^, Рп и Рп+^).
В случае удачного выбора ряды по /„ будут конечными с небольшим
числом членов. Мы назовем эти формулы, выражающие результат примене-
применения простых операторов к /„ в виде простых рядов по fm, рекуррентными
формулами, чтобы отличать их от рекурсивных формул E.2.40). Подстав-
йяя наш ряд в оператор X, имеем
X (I am U = 2 {X - aSm) ajm + 2 ameSm (/J =
m иг
= 2flmS Ymn/n = 2 B «m YmJ /» = 0,
m ix n m
где о^то(/то) = 0 по определению. Если множество /„ полное, то можно каж-
каждый коэффициент при fn последнего ряда приравнять в отдельности нулю
2 ат(тп = 0,
«I
что дает рекурсивные формулы для коэффициентов ат. Если эти формулы
можно разрешить, мы получаем решение уравнения X (ф) = 0.
Общая применимость разложения рассматриваемого вида зависит, ко-
конечно, от скорости сходимости, которая в свою очередь зависит от пове-
поведения ап при п —> со. Чтобы его получить, рассмотрим указанное выше
уравнение в пределе при п—> со
Это —как раз рекурсивное соотношение E.2.69), выведенное для функций
Матье, если совершить подстановку
s = 0, Л+2 = уС«+2, "=2Р-
Напомним, что рекурсивные соотношения для уравнения Матье влекут за
собой сходимость для ап при п ~^ со, если Ъ при данном s принимает толь-
только некоторые частные значения. Эти значения следует определять из ре-
рекурсивных формул для ап при помощи методов, описанных в разделе о
непрерывных дробях.
Далее в этой книге будет указано много иных случаев разложения
функции в ряд по другим функциям. Особенно полезными будут ряды по
функциям Лежандра (гипергеометрическим функциям, см. стр. 557) и по
функциям Бесселя (вырожденным гипергеометрическим функциям, см.
стр. 579).
Вообще то, что мы можем пытаться сделать при помощи таких ря-
рядов, — это применить решения уравнения с данным множеством особых
точек для выражения решений уравнений, имеющих на одну особую точ-
точку больше (или имеющих более сложные особые точки). Например, согла-
согласно уравнению E.2.30), степень z является решением дифференциального
уравнения с двумя регулярными особыми точками в 0 и со. Отсюда ре-
5.2. Общие свойства, решение при помощи рядов 541
шения уравнения с тремя регулярными точками (гипергеометрические
функции) или с одной регулярной и одной иррегулярной точкой (вырож-
(вырожденные гипергеометрические функции) можно выразить сравнительно про-
просто в виде рядов по степеням z. С другой стороны, решения уравнения
с двумя регулярными точками и одной иррегулярной точкой (сфероидаль-
(сфероидальные функции) можно наиболее просто выразить в виде ряда по гипергео-
гипергеометрическим функциям (функциям Гегенбауера) или по вырожденным ги-
гипергеометрическим функциям (функциям Бесселя). Мы рассмотрим ряды по
функциям Бесселя и ряды по любым другим более сложным функциям
в этой книге позже [см. формулы E.3.82) и A1.3.87)].
В заключение заметим, что можно обобщить ряд San/n(z)> перейдя
к интегралу, так же как, обобщая ряд Фурье, мы приходим к интегралу
Фурье. Например, вместо й (z) = 2 an /n (z) мы могли написать
Ясно, что здесь целочисленная переменная п заменилась на непрерывную
переменную t, функции /„ (z) перешли в K(z, t), а коэффициенты ап пре-
превратились в v(t). Сравнивая это с аналогичным процессом для рядов, мы
можем наметить способ получения интегрального представления ф (как
называется приведенный выше интеграл).
Прежде всего применяем оператор X, причем теперь для указания
того, что X действует только по переменной z, мы будем писать Хг вме-
вместо X. Имеем
t)]v(t)dt = O.
В нашем исследовании X, [/„ (z)] мы применяли рекуррентные соотноше-
соотношения для fn, чтобы заменить дифференциальный оператор на систему раз-
разностных операторов при помощи рекуррентных соотношений
¦с численными коэффициентами inp. Это привело к замене операции по пе-
переменному z на операцию по индексу п. В случае интегрального предста-
представления это означает, что мы можем выразить XZ[K (z, t)] = <Mt [К (z, t)],
где cSt представляет собой дифференциальный оператор по t, так что
0= \ <Л, [К (z, t)]v(t)dt.
Следующим шагом в представлении в виде ряда /п была перегруппи-
перегруппировка членов ряда, в результате чего /„ становился общим множителем;
приравнивание нулю коэффициента при /п, включающего несколько ап,
приводило к рекурсивным соотношениям для ап. Таким образом, операция
над fn была преобразована в операцию над ап. Подобным образом здесь
операция &#, должна быть преобразована теперь в операцию над V. Это
можно осуществить при помощи интегрирования по частям или, что рав-
равносильно, при помощи определенного ранее (стр. 000) оператора сопряжен-
сопряженного с a/Ht. Напомним, что
VaMt [и] — UoMf [V] = -3- Р (К, V).
Отсюда
0 = [ К (z, t) e?? {v) dt + [Р (и, v)].
542 Гл. 5. Обыкновенные дифференциальные уравнения
где второй член зависит от пределов интегрирования. Выберем теперь пре-
пределы или контур интегрирования так, чтобы член с Р(и, v) обратился в
нуль; тогда исходное дифференциальное уравнение удовлетворится, если
«амплитуда» v (t) в интегральном представлении удовлетворяет уравнению
оМ\ (v) = 0.
Это уравнение аналогично рекурсивным формулам для ап. Если мы смо-
сможем решить дифференциальное уравнение для v (t), то мы получим реше-
решение исходного дифференциального уравнения для ф (z), имеющее некото-
некоторые преимущества перед решением, представленным в виде ряда. Однако
это достаточно обширная тема, и мы лучше посвятим ей отдельный пара-
параграф.
5.3. Интегральные представления
Теперь у нас достаточно данных, чтобы увидеть, к чему приводит
способ нахождения решений в форме рядов. Разложение около обыкновен-
обыкновенной точки осуществляется непосредственно. Необычные случаи осущест-
осуществляются вблизи особых точек дифференциального уравнения, где общее
решение имеет особенность. Мы указали, как можно получить вблизи
каждой особой точки два независимых решения в виде рядов, сходя-
сходящихся вплоть до ближайшей особой точки (или в виде асимптотических
рядов, из которых можно подсчитать достаточно точные значения реше-
решений в более ограниченной области). Другими словами, мы выработали
средство для анализа поведения любого решения линейного дифференци-
дифференциального уравневия второго порядка в непосредственной близости любой
точки комплексной плоскости. В частности, мы можем применить разло-
разложения в ряд для нахождения частного решения, удовлетворяющего любо-
любому допустимому краевому условию (в гл. 6 будет исследовано, что озна-
означает «допустимость» для краевых условий).
Очень часто эти краевые условия ставятся в особых точках дифферен-
дифференциального уравнения. Мы видели, что такие особые точки соответствуют
геометрическим «точкам концентрации» соответствующей системы коорди-
координат. Часто вид физической границы можно идеализировать так, чтобы ей,
в силу ее простоты, соответствовала особая точка в одном из измерений
(например, значению г = 0 в сферических координатах соответствует начало
координат, значению ц. = 0 в сплющенных сфероидальных координатах —
диск, значению е> = 0, тс в эллиптических цилиндрических координатах —
плоская щель и т. д.). Часто только одно решение лишь с одним из ин-
индексов (если особая точка регулярная) может быть приспособлено к кра-
краевым условиям, так что будет пригодным одно из решений, исследованных
в предыдущем параграфе.
Если нам требуются значения рассматриваемого решения вблизи
особой точки, то разложение в ряды пригодно и, более того, является
единственным путем подсчета этих промежуточных значений. Но очень
часто нам бывает нужно вычислить значения решения и его производной
вблизи следующей особой точки, где ряд, пригодный для первой особой
точки, либо сходится чрезвычайно медленно, либо даже расходится. На-
Например, мы часто должны удовлетворять краевым условиям в обоих кон-
концах области изменения переменной, соответствующих двум последователь-
последовательным особым точкам. При этом требуются коэффициенты перехода, связы-
связывающие ряд около одной из особых точек с двумя решениями около дру-
другой точки, так как тогда нет нужды добиваться сходимости ряда. Пусть
Kj, vx — два независимых разложения в ряды около особой точки z = alv
5.3. Интегральные представления 543
а и2, v2 — ряды около z = a2- Если мы можем найти соотношения вида
ui — Yu Н2 + У12и2 и т- Д-> т0 мы можем тогда при подстановке краевых
условий в ах пользоваться решениями их, vt, а при подстановке условий
в а2 — решениями и2, v2. He будет никаких проблем сходимости, если мы
сможем выразить каждое решение у одного конца через решения у другого.
Для простейших видов дифференциальных уравнений эта связь между
поведением у одной особой точки и поведением у другой проста. По-
Поскольку решения представляют собой либо рациональные функции E.2.29),
либо элементарные трансцендентные функции E.2.33), то мы знаем поведе-
поведение решений в обоих концах; «связь» уже нам дана. Для дальнейших более
сложных уравнений эта связь не так проста. Примером такой связи слу-
служит формула E.2.49), однако наш вывод этой формулы на основе разложе-
разложения решений в ряды не был вполне строгим и не годился для всей обла-
области изменения параметров. Решение при помощи рядов, как выразился
Стоке, «имеет преимущество в широкой приложимости, но совершенно
лишено элегантности». Мы предпочли бы выразить решения через рацио-
рациональные или элементарные трансцендентные функции каким-либо кон-
конченым способом, сходящимся как в одной особой точке, так и в другой.
Для некоторых уравнений это можно сделать, если перейти от рядов;
к интегралам.
Выражение
^(z,t)v{t)dt E.3.1)
является достаточно общим для хорошего представления любого решения.
Если функции К и v оказываются рациональными или элементарными
трансцендентвыми, то мы имеем «замкнутый» вид, который можно приме-
применить для подсчета решения где угодно в комплексной плоскости. Нам
остается только установить, как надо находить правильный вид К и v для
данного уравнения.
Некоторые простые примеры. Наше знакомство с техникой контурного
интегрирования дает возможность составить несколько простых примеров,
для иллюстрации взаимосвязи между интегральным представлением и ре-
решением при помощи рядов. Например, так как
со со
тс ctg -xt = V. —¦— или it cth irf = V. ——^~
7l=—CO 71— — CO
(см. стр. 528), то можно применить вычеты этой функции для 'получения
ряда Фурье. Так, интеграл
cth vt -F (t) е-1 dt
с
можно разложить в ряд, если F представляет собой рациональную функ-
функцию t (см. стр. 390), имеющую все полюсы справа от мнимой оси и при-
притом такую, что tF(t) при г—>оэ стремится к нулю. Контур С включает
прямую, проходящую справа от мнимой оси, в ее непосредственной близо-
близости от s — ico до е+г'оэ, а затем возвращается к —гоэ, проходя вдоль
полуокружности бесконечного радиуса, расположенной в полуплоскости
Ret < 0. Так как t*-F(t) не обращается в бесконечность при \t\—-> оэ, то
интеграл по бесконечной полуокружности равен нулю (поскольку cth irt —-» — 1
при 11! —> оо для Re t < 0), если z > 0.
Поэтому полюсы внутри контура совпадают с полюсами cthirt, то есть^
имеют вид + in. Внутри контура мы предположили F всюду аналитиче-.
544 Гл. 5. Обыкновенные дифференциальные уравнения
ской. Вдоль мнимой оси (в случае вещественных коэффициентов) F имеет
симметричную и антисимметричную части
Контурный интеграл равен произведению 2ш на сумму вычетов по
всем полюсам cth %z
iao+e oo
^ cth (nt) F(t)e* ;=2iRe Fo +Ы %[ReFn cos (nz) - Im Fn sin (nz)], E.3.2)
—ioo+e 71=0
где Fn = F(in).
Более непосредственное применение интегрального представления мож-
можно получить из свойств гамма-функции Г( — t). Функция
Г@^^A)П " 012
имеет простые полюсы при t = 0, 1, 2, ... Если после включения в под-
интегральную функцию множителя zl интеграл будет сходиться, то сумма
вычетов превратится в ряд по целым степеням z. Как было указано ша
стр. 462, асимптотическое выражение для Г(? + 1) имеет вид
t-*CO
Значит, если функция G(t) такова, что G (t) z'/Г (t -J-1) sin izt —> 0 при t—> oo
для Re t > 0, и если все особенности G расположены слева от мнимой
оси, то
ioo oo
{ G(t)T(-t)(-zydt = 2та 2 G(»)z"/n!. E-3-3)
—ioo n=0
где контур проходит слева от полюса при < = 0и дополняется полуокруж-
полуокружностью бесконечного радиуса, проходящей в полуплоскости Re (t) > 0 от
-|-гоо обратно к —ioo. Тем самым мы получаем способ непосредственного
перехода от ряда к интегралу. Если G(n) является «замкнутой функцией» п
(то есть если последовательные коэффициенты связаны простой формулой,
вроде двучленной рекурсивной формулы), то подинтегральная функция
имеет замкнутый вид.
Применения такой формулы и предосторожности, необходимые для
обеспечения сходимости, хорошо иллюстрируются на приложении ее
к гипергеометрическому ряду E.2.44)
F(a b\c\z)~ Г(с)
г (a, o|c|z;-r(
2j T(c + n)n\
0
a v n T(c)/2niT(a + t)T(b + t)
Ясно, что функция G должна равняться „. '. v г. . -, еслипослед-
няя имеет полюсы слева от мнимой оси и если частное Gz'/Г (t +1) sin тЛ
ведет себя требуемым образом при t —> oo. Применяя асимптотическую
формулу для гамма-функции, находим, что если t —Rei6 — RcosB + iRsin 6,
б.З. Интегральные представления
545
то для достаточно больших R
Г (а +1) Г (b +1) ^ +r._n_bjjn+b-r.-i et(a+b-c-l) О
Г (c + t)T (t + 1)
Кроме того, если z = rei<f и — z = re1?-™ = elD r+i (ч1-"), то
(— z)( = exp {/? [(In r) cos 6 + (it — 9) sin 6] -f iLR [(9 — it) cos 6 + (In r) sin б)},
- 2i exp [№/? cos 6 — iri? sin 6], 0 < 6 < x,
i exp — [iicR cos 6 + it/? sin 6], 0 > 6 > — it.
sin (тег)
Отсюда, отбрасывая мнимую часть в показателе, оцениваем модуль под-
интегральной функции
Г (с-и) Г (г+1) sin (те
Я In г cos О
О < 6 < (тс/2),
eBB7c-9)sin0j 0>6>— (тс/2).
Отсюда если модуль z меньше единицы (то есть In г < 0), а аргумент z
больше нуля и меньше 2тс @ < ^ < 2it), то подинтегральная функция обра-
Плоскость t
-4-Ъ -3-Ь -2-6
-4-е -
Контур С
Рис. 5.5. Контур для интегрального пред-
представления гипергеометрическои функции при
помощи преобразования Меллина.
щается в нуль на полуокружности, входящей в контур (R—»оо, — тс/2 <
< 6 < тс/2). Поскольку эти условия выполнены, интегральное представление
гипергеометрического ряда имеет вид
F(n
У (а,
Г(С)
(a + t)T(b + t)
—ioo
если только мы сможем провести контур от — i 00 до 4-?°° так, чтобы
все полюсы Г ( — t) остались справа, а полюсы Г (a-\-t)T (b-^-t) — слева.
Рис. 5.5 показывает, что это можно сделать, даже если Re a и Re Ъ отрица-
отрицательны, если только ни а, ни Ъ не являются целыми отрицательными.
Если а либо Ъ целое отрицательное, то формула E.2.44) показывает, что F
будет конечным многочленом, а не бесконечным рядом (она показывает
также, что с не должно быть целым <0).
Это интегральное представление не кажется полезным или элегантным;
на первый взгляд оно представляется менее элегантным, чем представление
в виде ряда. Однако нетрудно показать, что возможность деформации
35 ф. м. Морс и Г. Фешбах
546 Гл. б. Обыкновенные дифференциальные уравнения
контура без изменения значения интеграла делает полученный результат
настолько гибким, что при его помощи удается связать разложение у одной
особенности с разложениями у другой особенности.
Например, дальнейшее рассмотрение асимптотического поведения под-
интегральной функции в E.3.4) показывает, что она стремится к нулю
при Н—>со для tj/2 < 6 < Зтс/2 (f = Reie), то есть на бесконечной полу-
полуокружности, проходящей в левой части плоскости t. Отсюда контур, содер-
содержащий внутри себя все полюсы V( — t) (и приводящий, как указано выше,
к гипергеометрическому ряду), можно заменить на контур, содержащий все
полюсы Г (а +1) Г {Ь -|-1). Применяя соотношения Г {а +1) = тс/Г A - а — t) х
X sin тс (a f 0 и т. д. и вычисляя вычеты в парах полюсов, получаем
¦у r(a + n)V(l — c + a+n) Sinn (с— а — и) , ,^_„
Zi ГA + и) ГA+а — Ь + n) cos (ил; sin я (Ь — а—и) ^ Z' "*~
п=0
2У
Г
У(Ь+п) ГA — c + b + n) simi(c — Ь — п) . \-ь-п_
")ГA — а+ Ь +и) cos (ил) sin л (а — 6— и)
E.3.5)
Если |а—fcj целое или нуль, то один из этпх рядов теряют силу, так как
второе решение должно содержать логарифмический член.
Ряд в левой части сходится при \z\ < 1, в то'время как ряды в правой
части сходятся при |z|>l. Строго говоря, эти два ряда нельзя при-
приравнивать; лучше было бы сказать, что интегральное выражение, приве-
приведенное в формуле E.3.4), обладает разложением в ряд, определяющий
F(a, b\c\z), справедливым при |z|<l; оно также обладает другим раз-
разложением в ряд, указанный в правой части формулы E.3.5), справедливым
при | z | > 1. Интегральное представление справедливо для всех (или почти
всех) значений z и может рассматриваться как «истинное решение» урав-
уравнения E.2.42). Разложения в ряды можно считать, частными представле-
представлениями этого «истинного решения», пригодными в ограниченной области
изменения z. При помощи интегрального представления мы можем осуще-
осуществить аналитическое продолжение решения из одной области сходимости,
содержащей одну особенность, в другую область сходимости, содержащую
другую особенность.
Таким образом, можно назвать интеграл, стоящий в правой части
формулы E.3.4), гипергеометрической, функцией F (а, Ъ \ с \ z), одним из реше-
решений уравнения E.2.42). Если |z|< 1, то эту функцию можно подсчитать
при помощи представления ее рядом E.2.44), гипергеометрическим ^рядом
по z. Для других областей изменения z гипергеометрическую функцию
можно подсчитать, применяя гипергеометрические ряды по 1/z, данные
в формуле E.3.5), или по 1 — z, которые будут даны позже, и т. д. Сама
функция, показывающая свои различные стороны при различных подходах,
дается* интегральным представлением.
Общие уравнения для подинтегральной функции. Свойства, раскрыва-
раскрывающиеся при представлении гипергеометрической функции, являются типич-
типичными для интегральных представлений вообще. Они превращают аналити-
аналитическое продолжение решения почти в тавтологию .хли такое представле-
5.3. Интегральные представления 547
ние мозкно найти, то обычно бывает не трудно применить краевые условия
в обоих концах области изменения z. Если представления нельзя найти,
то такое применение проходит сложно и «неизящно».
Методы, примененные в предыдущем пункте для получения интеграль-
интегральных представлений, были далеко не прямыми; нам нужна техника перс-
хода от дифференциального уравнения прямо к виду подинтегральной
функции. Мы будем пользоваться сначала видом E.3.1) с ядром К (z, t)
и модуляционным множителем. v {t). Для этого мы выбираем вид К, кото-
который нам представляется подходящим, а затем выясняем, какому дифферен-
дифференциальному уравнению удовлетворяет v. Если это уравнение достаточно
простое (существенно проще, чем уравнение для ф), то можно получить
замкнутый вид v и тем самым построить интегральное представление.
Дифференциальное уравнение, которое надо решить, имеет второй
порядок и независимое переменное, преобразованное таким образом, что
коэффициенты являются алгебраическими. До использования выражения
E.3.1) лучше освободиться от дробей, перейдя к уравнению
где /, g и h — многочлены относительно z. Дифференциальный оператор X,
примененный к интегралу вида E.3.1), можно внести под знак интеграла,
действуя на ядро К по z
t))v(t)dt,
если интеграл достаточно хорошо сходится. Операция J6,, произведенная
над К (z, t), порождает новую функцию z и t. Если вид ядра К нами
выбран удовлетворительно, то эта новая функция z ш t равна результату
применения к К (z, t) некоторого оператора по t
(в некоторых случаях достаточно, чтобы %z (К) равнялось результату при-
применения оператора &#, к какому-либо другому ядру К' (z, f)).
Эта эквивалентность между операторами по z и по t, примененными
к ядру К, дает возможность определить v(t) и одновременно резко огра-
ограничивает выбор видов К (z, t). Немногие функции z и t обладают простыми
взаимосвязями, подобными тем, которые обнаруживают показательное ядро
[примененное в формуле E.3.2)]
(d/dz) ezt = tezt, ze2' = (d/dt)ezt,
для которого дифференциальный оператор, содержащий производные по z
и степени s, преобразуется в оператор, содержащий соответствующие сте-
степени t и производные по t. Тем не менее найдено много других ядер,
применимых в" различных случаях: z' (примененное в формуле E.3.3),
(z — if, различные функции произведения zt и т. д. Во многих случаях
можно воспользоваться несколькими различными ядрами, что приводит
к нескольким различным интегральным представлениям одного и того же
решения. Выбор ядра, порождающего наиболее приспособленное к при-
применениям представление, зависит от связи между особенностями ядра
и особыми точками дифференциального уравнения. Например, для гипер-
гипергеометрического уравнения с тремя регулярными особыми точками можно-
ожидать, что ядро вида (z — t)^ окажется лучше, чем ядро ezt, имеющее
существенную особенность на бесконечности. С другой стороны, вырожден-
вырожденное гипергеометрическое уравнение, имеющее иррегулярную особую точку:
на бесконечности, представляется подходящим для ядра etl.
35*
а48 Гл. б. Обыкновенные дифференциальные уравнения
Однако возвратимся к нашей непосредственной теме, состоящей в по-
построении уравнения для v(t). Мы достигли того, что подинтегральная
функция представляет собой произведение функции v переменной t на диф-
дифференциальный оператор oMt, действующий по t над ядром К (z, t). На основе
формулы E.2.10) мы видим, что подинтегральную функцию можно теперь
преобразовать к виду суммы произведения К на результат применения
сопряженного (см. стр. 499) дифференциального оператора сМ к v и про-
производной присоединенной билинейной формы Р. Символически это осуще-
осуществляется следующим образом:
^(z, t)v(t)dt,
(У) = [ %z (К) v dt = ^ °*« (^) Vdt=
где при а€(К) = аA)(A2К/A^) + ^(t)(dK/dt)-^r^(t) К сопряженный оператор
имеет вид
а соответствующая присоединенная билинейная форма
P(v, K) = av^-K-K-±-{
Если теперь пределы интегрирования и контур, вдоль которого взят
интеграл, таковы, что Р возвращается к своему начальному значению в конце
контура, то интеграл от dP/dt равен нулю и
Отсюда если v(t) является решением дифференциального уравнения
е^( (v) = 0, то интеграл у = \ Kv dt представляет собой решение дифферен-
дифференциального уравнения 36z(y) — 0, которое мы и хотели решить. Если мы
удачно выбрали ядро К, то уравнение cMt (v) = 0 будет проще, чем J6Z (у) — 0,
и v будет простой функцией t. Обычно имеется несколько различных воз-
возможных путей и пределов интегрирования, для каждого из которых
\ (dP/dt) dt = 0. Эти различные интегралы соответствуют различным неза-
независимым решениям уравнения Xz (у) = 0.
Подходя с другой точки зрения, можно сказать, что нами сейчас были
исследованы интегральные преобразования типа преобразования Фурье
/ (v) = ^F 0») e*v dflj Ffa) = -± J / (v)
рассмотренного в § 4.8. Мы преобразуем функцию ф (z) в функцию v (t)
посредством ядра К (z, t)
и пытаемся найти тип преобразования, при котором функция v, служащая
образом ф, будет проще, чем ф.
5.3. Интегральные представления 549
Например, если ядро равно е'2, то этот переход называется преобразова-
преобразованием Лапласа. Его легко получить из приведенного только что преобра-
преобразования Фурье; полагая ft = — it, v = z, F (— it) = — iv (t), f (v) = ф (z), получим
ico oo
(z) e~z dz. E.3.8)
А если ядро равно z1, переход называется преобразованием Меллина. Его
также можно получить из преобразования Фурье, положив fi= —it, v=lns,
/Aпг) = фB), F( — it)= —iv(t), что дает
too со
4(z)= ^ v(t)z'dt, v(t) = ^-^{z)z-t-1dz. E.3.9)
Однако можно найти и другие преобразования, причем не все они будут
так тесно связаны с преобразованием Фурье, как эти два. Таким будет,
например, преобразование Kv(t)(z — t)[l'dt, называемое преобразованием
Эйлера (см. также § 4.8).
Дальнейшая часть этого параграфа будет посвящена изучению ряда
примеров интегральных представлений, чтобы проиллюстрировать технику
получения решений и методы применения результатов, а также чтобы ближе
познакомиться с некоторыми функциями, которые будут широко применяться
позже в этой книге. Особенно детально будут изучаться два типа ядер:
(z — 1)^ — преобразование Эйлера,
ezt—преобразование Лапласа.
Другие типы преобразований, менее широко применимые, будут рассмотрены
менее детально.
Преобразование Эйлера. Как указано ранее, надо ожидать, что ядро
(z — tY' должно дать удовлетворительное представление решений уравнений,
имеющих только регулярные особые точки, как, например, уравнение Пап-
перица E.2.36) или его канонический вид, гипергеометрическое уравнение
E.2.42). Ограничение, которое приходится накладывать на форму уравне-
уравнения, чтобы к нему было применимо преобразование Эйлера, обнаруживается
несколько необычным образом при применении дифференциального опера-
оператора 36 к ядру (z — t)^.
Вид 36 дается формулой E.3.6), причем гипергеометрическос уравне-
уравнение E.2.42) как раз имеет такой вид. Если применить оператор X к ядру
(z — 1)*, то получится сложная алгебраическая функция z и t
Ее нужно теперь представить в виде результата применения некоторого
дифференциального оператора oMt к некоторой степени z — t. Можно найти
вид сМ громоздким путем, если произвести деление на (z —1)^~ , предста-
представить частное в виде билинейной формы z и t, а затем попытаться составить
вид оМ, который давал бы такой результат. Более красиво получится тре-
требуемый результат, если разложить функции /, g, h в ряды Тейлора около
z = t (это всегда можно сделать, так как /, g и h — многочлены по z).
а50 Гл. б. Обыкновенные дифференциальные уравнения
Например, f(z)=f(t) r(z-t)f (t) + -i(Z-*J/"@+ ... и т. д. Получится
причем коэффициент четвертого члена ряда представляет собой линейную
комбинацию третьей производной от /, второй производной от g и первой
производной от /г и т. д.
Чтобы полученное выражение представляло собой результат применения
оператора второго порядка над (z — t)^, четвертый и все высшие члены ряда
должны равняться нулю. Имеется много способов выбора функций /, g, h,
чтобы это было так, но простейший путь (и достаточный для наших целей
здесь) — это потребовать, чтобы все производные / выше второго порядка,
g выше первого и h выше нулевого порядка равнялись нулю. Другими
словами, если /(z) представляет собой многочлен второй степени по z,
g(z)— многочлен первой степени и h(z) — постоянную, то приведенное
выше выражение будет иметь только три выписанных члена, все высшие
члены пропадут.
Мы видим, что это автоматически ограничивает нас уравнениями
с тремя регулярными особыми точками, так как /, будучи квадратичной
функцией, имеет два нуля, и если уравнение записать в виде E.2.1)
<1Ц , g (») <Ц> h(z) n
rfr" "+" /(*) dz "•" f(z) *
то мы легко убедимся в том, что, вообще говоря, оно имеет три регуляр-
регулярные особые точки — две в корнях уравнения / (z) = 0 и одну на бесконеч-
бесконечности. Гипергсометрическое уравнение имеет как раз такой вид (как,
конечно, и должно быть). Обращаясь к уравнению E.2.42), мы видим, что
/ = z(z-l), g = (a + b + l)z-c, h = ab.
Однако достигнув столь многого, мы можем пойти еще дальше вперед
в упрощении уравнения, так как мы свободны в выборе значения р.. Коэф-
Коэффициент при (z — t)^ теперь не зависит от z и t, так как /", g' и h постоянны.
Следовательно, положив
1A([А-1)/" + ^' + /г = 0, E.3.10)
мы получим в качестве решений два значения р., каждое из которых можно
применить и интегральном представлении.
Значит, дифференциальный оператор cMt имеет вид
где
-1) f + Р#'Ч-Л E.3.11)
а сопряженное уравнение и присоединенная билинейная форма таковы:
= 0, E.3.12)
р (v, K) = fv-^(z~- ty — (z — ty ^{fv) — Pt)(z — ty =
= — ф (z — ty-* — (fi/'u + /ц! + gt)) (z — «)^.
5.3. Интегральные представления 551
Если ft выбрано так, что E.3.10) имеет место, то у = 0 и уравнение
для v можно быстро решить
ПЛИ
-l)f + |] Л}
/>(», /0= ~tf(t)v(t) (z-ty-i, ф = $ (z-tyv{t)dt, E.3.13)
где интеграл для ф таков, что Р имеет одно и то же значение в начале
и в конце пути интегрирования.
Заметим, что можно построить дифференциальное уравнение, которое
можно пытаться решить при помощи преобразования Эйлера, имеющее
четыре регулярные особые точки (из них одна на бесконечности), если
принять за / многочлен третьей степени, за g — многочлен второй степени
и за h — первой степени, а затем положить, что коэффициент при (z— ty+1
и ряде для %z((z — ty) равен нулю
Так как /'", g" и h' постоянны, то это уравнение может служить для
определения ft, взамен E.3.10), после чего нам надо решать уравнение
E.3.12) для v, в котором у не равно нулю. Однако ложкой дегтя в бочке
меду в этом случае является то, что уравнение v€(v) = 0 столь же сложно,
как уравнение X (ф) = 0, так как имеет столько же особых точек. Следо-
Следовательно, преобразование Эйлера совсем не облегчает нам работы, как
в случае уравнения с тремя особыми точками, когда у можно положить
равным нулю. Решение v не имеет простого вида, подобного E.3.13), оно
по-прежнему должно быть разложено в бесконечный ряд.
Отсюда видно, что преобразование Эйлера специально приспособлено
к уравнениям типа Папперица E.2.36) и, в частности, к гипергеометри-
гипергеометрической функции и к ее специальным случаям, функциям Лежандра
E.2.47) и функциям Гегенбауера E.2.52).
Преобразование Эйлера для гипергеометрической функции. Гипергео-
.метрическое уравнение.
Xz (ф) = (z2 - z) ф" + [{а + Ъ + 1) z - с] ¦>' + айф = О
допускает решение при помощи преобразования Эйлера. Выражения для
коэффициентов в операторе cMt таковы:
*(*-!), Р = (а + Ы-2Р—1)« —(с + р—1),
я корнями уравнения у = 0 являются fi= —a, (i= —Ь. Мы выберем fi= — a;
подстановка в E.3.13) [при g = (a-\-b + l)z — с] дает
Отсюда решением гипергеометрического уравнения будет интеграл
Ф = A \(t~ z)~a ta~c (t — IH-6-1 dt,
552 Гл. б. Обыкновенные дифференциальные уравнения
взятый в таких пределах и вдоль такого контура, что соответствующий
интеграл от dP/dt обратится в нуль. F3 этом случае подинтегральная
функция имеет точки ветвления (если только a, b и с не все целые)
при (=0,1, г я оо. Если Р обращается в нуль в двух из них, то мы
можем принять их за пределы интегрирования; в противном случае мы
можем взять интеграл по замкнутому контуру, чтобы Р возвратился
к своему исходному значению в конце обхода. Например, если с > Ъ > 0,
то Р обращается в нуль при t = 1 и t = со.
Чтобы получить разложение интеграла в степенной ряд для сравне-
сравнения с гипергеометрическим рядом, разложим (t — z)~a под знаком интег-
интеграла
и применим формулу [см. D.5.54)]
1 '
Сравнение с определением гипергеометрического ряда, данным формулой
E.2.44), показывает, что
F(a,b\c\z)= Т{Ъ^_Ъ) $ (* -*)~°*-« (t- I)-6-1 dt, E.3.14)
причем это справедливо при Re с > Re Ь > 0, если z не является веще-
вещественным числом, большим единицы. Для случая Refc< 0 в этой формуле
можно переставить а и Ъ и получить другое равносильное представление,
так как F(а, Ь\ с \z) =F (b, a\c\z).
Таким образом, интеграл E.3.14) можно рассматривать как «истинную»
гипергеометрическую функцию, для которой можно получить разложение
в ряд около любой точки. Интересно заметить, что это интегральное
представление имеет совершенно иной внешний вид, чем равносильное
представление E.3.4). Однако на самом деле это различие является поверх-
поверхностным, так как гамма-функция тесно связана с преобразованием Эйлера,
что выяснится при решении некоторых задач.
В качестве интересного применения этой формулы получим выраже-
выражение для одного из решений уравнения Папперица E.2.36), данных фор-
формулой E.2.46). Полагая t — (и — а)(Ь — с)/(и~ с)(Ь — а) (где а, Ъ и с теперь
представляют собой положения особых точек, а не индексы, как выше),
имеем:
fz—аЪ — с~\*. f z — b а — сЛи- „ Г . , . м. ,, . .,z—ab — c\
т ) 1 ) г[ X-4-u.-4-v.A-4-u.4-v А— К -4-1 j ) =
\z—cb—aj \z — са — bj \ ' г ' ' ' г ' ' ' lz*-cb — aj
- Г frff + V )V+h'+ v) ('-«)*(«- Ы (« - с? (а - сГ {с - ЪГ (Ъ - a) v
с
X ^ (и — z)~b-v-v(u — a)-^-v-'-v (и — b)-^-v-*'(u — c)~x'-^'^du, E.3.15)
где X-f X' -\- u. + u.' -\- v-}- v' «= 1. Эта формула примечательно симметрична
относительно особых точек и их индексов. Из нее, полагая а, Ъ, с рав-
равными 0, 1, оо в различном порядке, можно получить целый ряд полезных
5.3. Интегральные представления
553
интегральных представлений для различных решений гипергеометрического
уравнения около каждой из особых точек.
Интеграл E.3.14) допускает различные видоизменения, из которых
получается большое число полезных и интересных соотношений. Например,
формулу E.2.49), связывающую решение вблизи z = 0 с решениями вблизи z = 1,
можно вывести значительно более удовлетворительным способом, чем это
Плоскость t
Контур
Рис. 5.6. Контур интегрирования для получения
соотношений, связывающих гинергеометрическую
функцию.
Подинтегральная функция вещественна в точке .4, если
только z вещественно.
было сделано на стр. 515, где пришлось сделать различные ограниченияг
суживающие пределы" справедливости результата. Мы отправляемся от
интеграла
взятого по контуру, показанному на рис. 5.6, тщательно обходящему все
особенности подинтегральной функции. Будем считать подинтегральнук>
функцию вещественной в точке А, показанной на рисунке, то есть для I,
лежащего на вещественной оси и несколько меньшего z, но большего нуля
(мы предполагаем здесь, что z вещественно; это не необходимо, но делает
преобразования несколько менее сложными; действительно необходимым
является, чтобы z не лежало на вещественной оси менаду +1 и + со).
Если теперь Re fc<Rec< l-f-Rea<2, то можно применить методы,
описанные на стр. 388, чтобы показать, что приведенное выше равенство
равносильно
sin (iza) \ (t
— tf-b-1 dt
— sin
in r. (a-\-b — c) { (t — z)-a
-sirnr(a-c)
554 Гл. 5. Обыкновенные дифференциальные уравнения
Теперь мы при помощи фурмулы Г(г)ГA—z) = тс/siri vz заменим
sin тс (с —а) Г(с —а —&)Г(а + Ь —с+1) sin (тса)
suite (с — а — Ь) Г (с — a)F(a—с+1) sinTi(a4-b — с)
на —— с jC а '. В первом интеграле положим t =
а в третьем t = 1 — и; это после преобразований даст
\ (t ?\ -« /о—с d 1\с—Ь — 1 /If —
¦откуда, после применения соотношения E»3.14) в обратном порядке, сразу
следует формула E.2.49). В данном случае нами было поставлено ограни-
ограничение Re &«. Rec<! 1-j- Rea<.2. Так как результат получен при помощи
изменения контуров интегрирования и подстановки гамма-функции и дру-
других конечных действий, то он, возможно, производит более надежное впе-
впечатление, чем когда он был ранее выведен при помощи жонглирования
с бесконечными рядами.
В результате обоих выводов и при помощи аналитического продол-
продолжения можно продолжить эту формулу перехода на более обширную область
изменения а, Ъ и с. Так, в предыдущем выводе предполагалось, что
Refc^Rec— Re a, a в данном —что Refc<.Rec; таким образом, в резуль-
результате обоих выводов получаем, что формула имеет, место для всех тех Ь,
для которых функции аналитичны. Поскольку z не равно единице, функ-
функция F (а, Ъ | с | z) аналитична по а, Ь и с, за исключением значений а и Ъ = оо
и с, равных нулю или отрицательным целым. Правая часть равенства
¦E.2.49) аналитична по а, Ь и с, за исключением значений для с отрица-
отрицательных целых или нулевого и для a + b — с любых целых. Для любого
из этих параметров можно найти область, в которой выполняется одно или
другое ограничение, сделанное нами при выводе формулы E.2.49), и кото-
которая в то же время покрывается белее широкой областью, где F анали-
аналитична. Значит, при помощи аналитического продолжения справедливость
равенства распространяется на всю область значений а, Ь и с, где его
.левая и правая части аналитичны. Другую формулу связи E.3.5) можно
продолжить подобным же образом. Вместе обе они дают возможность
выразить любое решение гипергеометрического уравнения вблизи одной из
трех особых точек через решения, построенные вблизи любой из двух дру-
других особых точек. Таким образом, для случая уравнений с тремя регу-
регулярными особыми точками мы полностью решили проблему коэффициентов
перехода, упомянутую на стр. 542.
Аналитическое продолжение гипергеометрического ряда. Другую
совокупность формул, полезных для дальнейших выкладок, можно полу-
получить посредством дальнейших видоизменений интегрального выражения
¦E.3.14). Положив t = l/u и м = 1— w, получим
F(a, b\c\z) =
5.3 Интегральные представления 555
E.3.16)
Наконец, применяя ото соотношение к правой части равенства E.2.50),
мы можем получить еще одно соотношение
^|±!±i|-i> E.3.17)
Можно применить также интегральное представление F для вывода
различных рекуррентных соотношений между смежными функциями. Напри*
мер, так как
(z — t)~a ta~c (t - ly-b-t = z (z _ *)-«-» ta~c (t — 1)с-ь-1 _
— (z —^-«-Ч"-^1^ —IH-6,
TO
-/'(a, fc|c|z) = (fcz/c)^(a+l, 6 + 11 c+ 1 \z) ~F{a+ 1, 6|c|z).
А из (d/dz) (t — z)~° fa-c («— 1)с-ь-1 = a (t — z)-°-J ta~c (t — 1)с-ь-1 получаем
Y F (a, b\c\z) = — F (a + 1, fc + 11 с + 11 z); обе эти формулы, конечно, можно
легко вывести при помощи преобразования гипергеометрического ряда.
Прежде чем окончить наше рассмотрение гипергсометрической функ-
функции, следует еще убедиться в справедливости утверждения, сделанного
на стр. 548, что различные независимые решения дифференциального урав-
уравнения можно получить при помощи изменения пределов интегрирования
и интегральном представлении, не меняя вида подинтегральной функции.
Если в случае гипергеометрического уравнения взять за первое решение
F(a, b\c\z), вторым решением около z = 0, согласно формуле E.2.45),
будет
y2 = zl~cF(b — с+1, a —c-J-l|2 —c|z).
Применение формулы E.3.14) для интегрального представления новой
F дает выражение
оо
AT B-е) ,
J
где подинтегральная функция имеет отличный вид от того, который был
у первого решения E.3.14). Однако, полагая u=-zjt и
_Г(с)Г(а-с + 1)ГA —а)
Г(Ь)Г(с —Ь)ГB —с) '
•(Ь)Г(с-Ь)ГB-с)
мы получаем в результате интегральное представление второго решения
E.3.18)
556
Гл. 5. Обыкновенные дифференциальные уравнения
справедливое при Rec<Rea+l<2. Эта формула для второго решения
отличается от формулы E.3.14) для первого решения лишь пределами
интегрирования, что и доказывает наше предыдущее утверждение, во вся-
всяком случае, для гипергеометрического-
уравнения.
Заменяя 2— с на с, Ь — e-j-1 на а и
й-с+1 на Ъ, мы найдем, что
X
Рис. 5.7. Контур С для интеграль-
интегрального представления гипергеометри-
гипергеометрической функции при помощи пре-
преобразования Эйлера.
X \ (z—t
E.3.19)
Подинтегральная функция вещественна в
точке А, если z вещественно.
и. таким образом, получим еще одно пред-
ставление первого решения при Re с >
>Refc>0, как и выше. Этот интеграл
можно заменить на интеграл по замкну-
замкнутому контуру вокруг 0 и z, если мы смо-
сможем выбрать контур так, чтобы подин-
подинтегральная функция после обхода возвратилась к своему исходному значе-
значению. Для этого требуется двойной обход, показанный на рис. 5.7, при
котором каждая точка обходится по одному разу в обоих направлениях.
Обозначая интеграл в E.3.19) через /, имеем
(t —
— t)~adt = eixb [еы <С-2Ь> - ei7tc-f e-i7t <c~2b> — e~inc] J =
2-Й br
= 4е*-ь sin {щ sin n {c _ b) j = Г(Ь)ГA_Ь)Г(С_Ь)ГA + Ь_С
Отсюда контурный интеграл для F имеет вид
F(a, b\c\z) =
Т (с)Г {1 + b-c)T {1- Ъ)х
X
&{t — zy-b-i I*-1 A - 0~° dt. E.3.20)
Эту формулу можно теперь распространить при помощи аналитического
продолжения на всю область значений а, Ъ и с, кроме тех, при которых
гамма-функция обращается в бесконечность.
Наконец, при помощи подстановки t = (и — z)/(l — и) в E.3.19) можно
получить формулу
F{a,b\c\z) =
Г(с)г1-СA-
Г(Ь)Г(с-Ь)
E.3.21)
которую опять можно было бы преобразовать в контурный интеграл,
подобно E.3.20).
Итак, мы нашли интегральные представления обоих решений гипер-
гипергеометрического уравнения, справедливые в широких областях значений
параметров а, Ъ, с. При помощи соотношений между значениями F можно
было бы получить другие представления, справедливые в других областях.
Однако в этом обычно нет необходимости, так как интегральные предстаь-
ления применяются главным образом для получения других формул,
таких, как рекурсивные соотношения, разложения в ряды и т. п. Получив
такие формулы при помощи интегральных представлений, можно посред-
5.3. Интегральные представления 557
ством аналитического продолжения распространить их на другие области
параметров за пределами области применимости представления, если в этом
есть необходимость и если сами формулы допускают это.
До перехода к дальнейшему детальному исследованию свойств общей
гипергеометрической функции будет полезно рассмотреть некоторые частные
случаи, представляющие особый интерес для последующего изложения.
Функции Лежандра. Функции Гегенбауера, определенные на стр. 516,
представляют собой частный случай гипергеометрических функций, поскольку
они зависят от двух параметров а и Р, вместо трех а, Ь и с. Однако эти
функции охватывают значительное большинство функций гипергеометри-
гипергеометрического типа, встречающихся в настоящее время в математической физике,
так что их специальные свойства важно рассмотреть в некоторых деталях.
Уравнение имеет вид
B*_1)ф» + 2(Р + 1)*ф'-а(о + 2? + 1)ф = 0 E.3.22)
и обладает тремя регулярными особыми точками — 1, +1 и оо с индек-
индексами @, —Р), @, + Р) и (—a, a-j-23 + 1) соответственно.
Интересно и полезно заметить, что непосредственное дифференцирова-
дифференцирование уравнения дает
откуда видно, что если Т\ (z) есть решение уравнения E.3.22), то Т^1[ (z) —
решение последнего уравнения. Это показывает, что решения для целых
значений [3 > О можно получить из функций Т„ (z) посредством дифферен-
дифференцирования. Легко видеть также, что если Т$ (z) есть решение уравнения
E.3.22), то Ti!-H-20-i (z) ~ также решение того же уравнения.
Уравнение для T°a(z)
(г2-1)ф" + 2гф'-а(а+1)ф=0 E.3.23)
называется уравнением Лежандра. Если а целое положительное, то его
можно получить при помощи (а -{- 1)-кратного дифференцирования из
уравнения
(z2 - 1) dV/dz — 2azV = О,
где F = (z2— 1)а, если в полученном уравнении принять d"V/dza за ф. Сле-
Следовательно, если а целое положительное, то одно решение уравнения
Лежандра пропорционально d°(z2 — l)a/dza.
Отметив эти простые свойства, применим технику настоящего параг-
параграфа для определения решений уравнения E.3.22) при всех значениях а
и р и для разложений этих функций вокруг трех особых точек.
Возвращаясь к стр. 550, • где был указан общий метод построения
интегральных представлений для уравнений с тремя регулярными особы-
особыми точками, положим в этом уравнении f(t)=ti — I, g{t) = 2 ([3 + 1J,
h = —а (а+ 234-1). Уравнение E.3.10) для определения (i приобретает вид
так что р = а или — а —2,3—1. Поэтому из формул E.3.13^ мы получаем
два различных интегральных представления решения и две присоединенные
•билинейные формы
, . Г (z— tf ,t n (z— Г)а~1
Ф = А \ — Ц—г dt, Р = — а — '—— , \х = а.
1*= -а-2Р-1;
558 Гл. 5. Обыкновенные дифференциальные уравнения
как обычно в таких представлениях один интеграл можно преобразовать
в другой при помощи подходящей замены переменной интегрирования и
пределов интегрирования. Для начала мы можем считать вещественные
части аир положительными, так как противоположный случай можно
потом получить посредством аналитического продолжения. Если Re а и
Rep>0, то подходящими пределами интеграла в первом представлении
будут t=z и г = оэ; кроме того, интеграл можно взять по замкнутому
контуру вокруг точек — 1, +1 и z в таком порядке, чтобы после обхода
Р возвратилась к своему исходному значению.
Отправляясь от случая Р = 0, найдем сначала решение, пропорциональ-
пропорциональное производной порядка а от (z2 — 1)а, если а > О целое. Из формулы
D.3.1) мы видим, что проще всего взять второй упомянутый интеграл
по замкнутому контуру, окружающему точку t = z, и, например, точку
t = 1. Соответственно положим
• = л Ф 1* Т-м * = ^^(z2 - 1)",
с '
где я ==п = 0, 1, 2, ..., а контур обходит против часовой стрелки обе
точки t — \ и t — z, как это показано на рис. 5.8. Подинтегральная
Плоскость t
Контур D
Рис. 5.8. Контур D для интегрального предста-
представления функции Лежандра первого рода.
функция предполагается вещественной в точке А, если z расположено на ве-
вещественной оси между -+-1 и — 1. Заметим, что если z находится на ве-
вещественной оси слева от — 1, то (если а не целое) интеграл принимает
различные значения в зависимости от того, проходит ли контур сверху
или снизу точки t = — 1. Поэтому мы сделаем разрез вдоль отрицатель-
отрицательной вещественной полуоси от — 1 до — со, чтобы сохранить функцию
Т°а (z) однозначной.
Для — 1 < Re a < 0 интеграл по замкнутому контуру можно заменить
на простой интеграл от t = z до t — 1. Отсюда, полагая t=l — 2u и при-
применяя формулу E.3.19), получим разложение Ра в ряд
1
Tea(z)= -2iAsin(T.a) ^ {t-zf^1 (I - t)"A + t)a dt =
(i -z)/2
2niA2a С f I — z N-o-i
Г(а+1)Г(-а) I
О
= 2шА2а Z1 [ - а, я + 111 | A - з)/2],
причем окончательный результат можно распространить при помощи ана-
аналитического продолжения на всю область значений а, для которых
5.3. Интегральные представления
55»
гипергеометрический ряд аналитичен. Так как удобно считать У?A)=1,
то полошим А = 1/2а+1 тл, так что
(г2—1)"
C.3.24)
эту формулу можно принять за основное определение функции Лежанора
Pa(z). Заметим, что Р_н_ , (z) = Pa{z) в силу симметрии /\
Плоскость t
Рис. 5.9. Контур Е дли интегрального представлении
функции Лежандра первого рода.
Эта формула позволяет также подсчитать поведение JJa(z) для очеш>
больших значений z. На основе соотношения E.3.17)
Применяя формулу E.2.49) и равенства Г (ж)Г A — х) = -n/smitx и
|/"те Г Bх) — 22Ж~1 Г(ж)Г( ж-f у), в конце концов получаем, что
Г(°+1) tg(TCa) ,
2a+3
так что при положительном а для очень больших z Pa имеет порядок za.
Другое полезное интегральное представление можно получить из фор-
формулы E.3.24), если положить и = -^-{t2 — l)/(t — г)илп? = ({-}-у'и2 — 2uz-\-1,
где t веществевно для вещественных -; им, |z|< 1 и к> 1. Преобразо-
Преобразованный интеграл имеет вид
иа du
где контур Е показан на рис. 5.9; часть А, соответствующая обход}'
около t = l, переходит и обход вокруг к —0, а часть Б, бывшая обходом
вокруг t — z, переходит в обход на очень большом расстоянии вокруг точ-
точки и = 0 вне й=1 п u = z. Функция \fl—2uz + u2 имеет, нули при
560 Гл. 5. Обыкновенные дифференциальные уравнения
и = z ±У z2— 1 (на рис. 5.9 точки Р и Р'), так что наш контур приво-
приводится к контуру, обозначенному через Е, обходящему эти две точки.
Так как Ра (z) = /*_a-i (z), то имеем также
Pa (Z) = П (Z) = ^ ^ , ГГ1^ " E-3-26^
в- '—2kz+1
Если а целое положительное, то интеграл по большой окружности В
обращается в нуль и Е приводится к окружности А с центром в к=0,
так что по формуле D.3.1)
*> W - п\ I dun у#_2ия+1 }и=0
а при помощи ряда Тейлора D.3.3) имеем
оо
1 XI inn /„\ 1^4 97\
¦г/ | *2Jiz -4- Л2 ^"^
где | ЛI должно быть меньше расстояния от начала координат до точек Р
или Р рис. 5.9, а |z|<!l. Аналогично при помощи ряда Лорана и ин-
интеграла с иа получаем
где |Л| должно быть больше чем \z ±"V^z2— 1| либо z<l. Отсюда полу-
получаем полезную общую формулу
У rf — 2rYrz cos 6 + r| ^0
n (cos 6), г2 < гг. E.3.28)
Функции Лежандра второго рода. Второе решение уравнения Ле-
Лежандра должно получиться при помощи контура, отличного от того, кото-
который был в интегральном выражении E.3.24). Мы не можем просто при-
применить вид второго решения гипергеометрического уравнения, данный
в формуле E.3.18), так как для с = 1 г/2/1- В данном случае, так как
присоединенная билинейная форма для E.3.24) обращается в нуль при
/ = ±: 1, для образования второго решения можно применить интеграл
1
Л
Поэтому мы определяем функцию
E'3-29)
как функцию Лежандра второго рода. Для этой формы Rea>—1, а г не
должно быть вещественным числом между — 1 и +1-
Для отрицательных значений Re a (Re a < — 1) нам надо взять контур-
контурный интеграл вокруг +1 и —1. Чтобы присоединенная билинейная фор-
форма вернулась к своему исходному значению, сделаем контур имеющим
вид восьмерки, обходящей вокруг t —- — 1 в положительном направлении.
5.3. Интегральные представления
561
а вокруг t = 4 1 в отрицательном направлении. Отсюда, после преобразо-
преобразований,
если только а не целое. Об оставшемся случае, когда а целое отрицатель-
отрицательное, можно позаботиться, положив Q_n(z) — Qn-i(z), что допустимо в силу
нашего замечания на стр. 559. Обе интегральные формулы показывают,
что для однозначности Q надо произвести разрез
от г=+1 до z = — 1.
Если а целое положительное или нуль, ин-
интеграл E.3.29) берется, что даст
-;
Плоскость t
*}
i-zlnKz + l)/(z-l)]-l и т. д.
Даже если а не целое, Qa (z) имеет логариф-
логарифмические особенности при z = ± 1. Для больших
значений z можно произвести разложение в ряд
по степеням 1/z следующим образом:
BZ)
H+'
-I
I V Г(а+т+1)/- t
4 ^J Г(« + 1)т! V. z
m = 2w.
Интегралы для нечетных т равны нулю, так что
можно положить и = t2 и получить
1
B2)'
«+i
Г(а42тг41)
Г(а4-1)ГBга+1)
О
X
п~5,
го<=2п
Рис. 5.10. Преобразова-
Преобразование контура для установ-
установления связи Ра(—z) с
Ра (*) и <?о («).
Применяя формулу D.5.54) для [подсчета интегралов и равенство
У^гГ Bж) = 22Ж~1 Г (ж) Г Г ж 4-- J несколько раз, мы в конце концов придем
к выражению для Qa, полезному для больших значений z
'тГ Г(а + 1)
Q» (') =
B»Г
1) , E.3.30)
если только а не является целым отрицательным (в последнем особом
случае Q_n = Qn^t). Отсюда мы видим, что Qa(z)~> 0, если только
Z—5-OO
Rea>—1; сравните это с соответствующим выражением E.3.25) для
Имеется несколько интересных взаимосвязей между функциями Ле-
жандра первого и второго рода. Одну из них можно получить посредством
показанного на рис. 5.10 преобразования контура для Ра (— z). Положим
сначала t — — и в контурном интеграле для Pa{ — z), а затем заменим
36 ф. м. Морс и Г. Фешбах
562 Гл. 6. Обыкновенные дифференциальные уравнения
контуры, как показано
Но контур С как раз такой, как при представлении функции Qa, а кон-
контур В — функции Ра. Кроме того, z — и во втором интеграле надо заме-
заменить на u — z, чтобы получилось так же, как в E.3.24). Если lmz>0,
как показано на чертеже, то z—u = ein(u — z); если lmz<0, то z — u =
= е~*Л(и— z). Отсюда получаем
Ра (- z) = - [B/™ sin (-a)] Qa (z) + е*™ Pa (z), E.3.31)
где знак — в показателе надо взять, если Im z > 0, 'а знак +, если Im z < 0.
Это равенство показывает природу особенности Pa{z). Если только а не
целое, то Ра (z) (равное единице при z = 1) имеет логарифмическую осо-
особенность при z= — 1; если же п целое, то Рп( — 1) = ( — 1)пРпA) = ( — 1)п.
Эта формула дает также возможность получить выражение @_a_i
через Qa и Ра для любых значений а. Так как для всех а имеем
Pa(z) = P-a-i (z), то выведенное равенство можно прообразовать в
(?_a_! (Z) = Qa (Z) - Ъ Ctg (та) />a (Z), E.3.32)
что законно для всех не целых а. Для а = п = 0, 1, 2, ... имеем простую
формулу @_n_i (z) = @n (z).
Так как Р ш Q - независимые решения, то их определитель Вронского
Ра Q'a — Pa Qa не должен равняться нулю. В силу формулы E.2.3), по-
поскольку p=2z/(z2 — 1) = d In (z2 — i)/dz, получаем
где постоянную С можно найти, подсчитав ее значение для некоторого
частного значения z. Выберем точку на, бесконечности, где мы сможем
применить формулы E.3.25) и E.3.30). Так как для очень больших z
Ра (z) с- 2" Г (a +1) z«/]/^Г (a + 1),
то подсчет дает
Р* (z) ^i (z) - ^; (z) ^a (z) ^ (- a - 1 - o)/[Bo +1) z2], z -* со,
так что С = — 1 и потому для всех значений z имеем
Д (^«. W = ^« (z) ^; (z) - Qa (z) />; (z) = 1/A - z2). E.3.33)
Следовательно, из E.2.4) получаем
Наконец, мы можем применить интегральные представления E.3.24)
или E.3.29) для Р или Q, чтобы получить рекуррентные формулы для
функций Лежандра. Пусть pa(z) равно Pa(z) или Qa(z) или любой ли-
6.3. Интегральные представления 563
нейной комбинации этих двух функций (с коэффициентами, не зависящи-
зависящими от а). Тогда
P«(z) = ;
где интеграл взят по любому из числа допустимых контуров, в зависимо"
сти от выбранной линейной комбинации. В любом случае контур таков,
что интеграл \ d[(t2 — l)a+i/(t — z)a+l] равен нулю. Отсюда
¦ _ К С d \(t*-Da+i]dt_
2°+» J I («-*)"*1 (t-Z)a+2 J
Дифференцируя по z и разделив на a-\-i, имеем
p'a+i (z) - zp'a (z) = (a + 1) pa (z),
где штрих, как обычно, означает производную по z.
Для другого соотношения произведем разложение интеграла
d [t (<2 - 1)"Д« - z)a] = 0, что даст
(о + 1) pe+ j (z) - Bа + 1) zpa (z) + a/?a_, (z) = 0.
Комбинируя и дифференцируя эти равенства, получим
zpa (z) = [l/Ba + 1)] f(а +1) pa+t (z) + op«_t (z)],
p'a+l (z) - K-i (z) = Ba + 1) pa (z), E.3.34)
/>4 (z) = [a/(z2 -1)] [zjDa (z) - pa_i (z)],
где ра равно Ра, или ^a, или линейной комбинации этих функций.
Наконец, применяя равенство E.3.33), получаем еще одно соотношение
между Р и Q
а [Ра (z) Qa^ (z) -Pa_t (z) Qa (z)] = 1.
Полиномы Гегенбауера. Теперь довольно легко распространить наши
выкладки на более общие функции, определенные формулами E.2.52)
и следующими. В качестве основного решения мы можем взять либо
_i
функцию Ti, конечную при целом а, либо же функцию A — z2) 2m/>3+p^
упрощающуюся при целом р (если и а и р целые, то обе функции равны).
Мы предпочтем первый выбор, так как случай, когда а целое, а р не целое
более интересен, чем противоположный. Соответственно определим
[см. E.3.21)]
-a|l + p|i— 4-0 =
(t2_1)g+P
С
где контур С тот же, что на рис. 5.7, обходящий вокруг точек t — 1 и f = z
как в положительном, так и в отрицательном направлениях. Если а целое,
интеграл можно преобразовать к виду производной, данному в E.2.53).
36*
о64 Гл. 5. Обыкновенные дифференциальные уравнения
С другой стороны, если бы мы предпочли другое решение, мы могли
определить
sin
которое при целом положительном р = m равно Т™ (z), совпадающей в дан-
данном случае с т-п производной функцией Лежандра /)m+o(z). Если как а,
так и р целые, то
(n + 2m)l I rf" 2 .
z2—1)'" dz" v '
E.3.37)
как указано в E.2.53). Эти полиномы называются присоединенными поли-
полиномами Лежандра.
Из симметрии гипергеометрических функций имеем
и для р = т (целому), применяя формулу F(a, b|с| w) = A — к))с~"~ь х
X F (с — fc, с — а\ с\ w), видим, что
-a>a~m !
(- ir/vm w=
Можно найти совокупность формул, аналогичных E.3.26) и E.3.27),
и показать, что производящая функция для полиномов Гегенбауера имеет
вид
г У 2 Anr« (z)- Iл К *• E.3.39)
t 2
+ * п=0
2—2hz)
Применяя формулу E.3.5) и равенство
6.3. Интегральные представления 565
тесно связанное с E.3.17), получаем выражение этих решений для боль-
больших значений z:
COS [тг (а + р)] Г ( а + р + -|
+
,2ч~|ЭрЗ ,Л Г (а + 23+ 1) Sin frc (а + 23)] я—**-*
— z) -^о+р vzj — —z г~; т ч~\
+ 23 + 2|
|
которое показывает, что обе эти функции стремятся к бесконечности при
z —> со , кроме случая 0 > a > — 2,3 — 1.
Если выбрать первым решением уравнения E.2.51) функцию Та (z),
то богатый набор вторых решений может нас даже затруднить. Функция
Г?_а_2[*-1 (z), конечно, пропорциональна Tl(z) и потому не независима.,
но функции, которые можно обозначить одним из следующих способов
)-"г (; ;^i:X% TzL
т»v () (* irg r
независимы от Т\ (z) (если только р не целое), так же как Та( — z)
и A — z2) ^ />^+?( —z) Кроме того, имеются функции с противополож-
противоположным знаком аргумента. С помощью формулы E.2.49) можно показать, что
^
sin (-Ф) Tl (z) = sin «(a + p) 7S (- z) - sin sa A - z2) 2 Pa+p (- z);
отсюда также получаются соотношения специального вида, если р или a
целое.
Однако все эти функции стремятся к бесконечности при z—»со
(за исключением случая, когда 0 > a > — 2?S— 1). Часто будет предпочти-
предпочтительней иметь второе решение, стремящееся к нулю при z—> со для a > О,
как это было для функций Q, определенных формулой E.3.29). Кроме
того, желательно иметь решение, остающееся независимым от Та (z), даже
если р целое.
Такую функцию можно получить, если в формуле E.3.36) взять дру-
другой контур интегрирования. Положим
dt =
2«+*+2?Г(а+р+1)Вш[«(а
566 Гл. 6. Обыкновенные дифференциальные уравнения
±1
—1)
Tl(-z)} =
!-l)~2p$+p(z). E.3.41)
Контур у интеграла имеет вид восьмерки, обходящей +1 и —1, как это
было для Qa (z). Вторая строчка показывает, что V стремится к нулю при
z—>со, если Re (a + 2,3 + 1) > 0, что мы и желали. Третья строчка указы-
указывает взаимосвязь между V и двумя независимыми решениями Т. Четвертая
строчка, подобно E.3.31), связывает решения для -\-г и для —z; верхний
знак надо брать при Im z > 0, а нижний — при Im z < 0. Последняя строчка
показывает, что это второе решение выбрано так, что перемена знака
у верхнего индекса не порождает независимой функции, в противополож-
противоположность Т„, для которого соотношение E.3.38) имеет место только для
целого р. С другой стороны, V-a-z$-i не пропорционально Va, но
V'i (z) = Fia_2^_i (z) + [ве«*е cos ™(o +P)/sin(«*)]71« (z).
Если р = тп целому, то третье выражение в E.3.41) стремится
к конечному пределу; однако в этом случае имеют место следующие, более
простые формулы:
F« (z) = ^<?«+m(z). У—21В-1 == Г (я + 1} (Z2-I)m ^-«-l- ^.<J.4Z)
Случай Р= i-g- особо интересен как из-за получающихся полиномов,
так и в силу раскрывающихся специальных свойств гипергеометрических
функций
./~
-У Ц
2~chfaArchz] _ 1 Yz*—
Ц ~T
p- -2l
^ ("j") exp [ - a Ar ch z] = - -^ y'z^l Ff _, (z); E.3.43)
для целого а они пропорциональны полиномам Чебышева.
Вырожденная (конфлюентная) гипергеометрическая функция. Гипер-
Гипергеометрическое уравнение для F {а, Ъ + с | с | z/b) имеет вид
Это уравнение имеет регулярные особые точки в 0, Ъ и со с индексами
@, 1-е), @, —а — Ь) и (а, b + с) соответственно. Если Ъ стремится к беско-
5.3. Интегральные представления 567
нечности, то при этом две особые точки (Ь и со) совпадают друг с другом,
а один из индексов в каждой из совпадающих точек стремится к беско-
бесконечности (индекс —а — Ъ в точке Ъ и индекс Ъ-\-с в точке оо). Этот двой-
двойной процесс предельного перехода называется слиянием особых точек;
он был указан ранее на стр. 508. Получающееся уравнение
Zjr + (c_z)F'-aF = 0 E.3.44)
называется вырожденным (конфлюентным) гипергеометрическим уравне-
уравнением [см. E.2.57)]. Решение, аналитическое при z = 0, получается в пре-
пределе из F[a, b-\-c\c\z/b), когда b стремится к бесконечности
оно называется вырожденным гипергеометрическим рядом.
Чтобы увидеть, как действует это слияние на интегральное представле-
представление, мы отправимся от представления, полученного из E.3.14) заменой t
на 1/г
1-—E-
b
Г (а) Г (с-а) _
Предельный переход Ъ—» со меняет природу ядра A — zt/byb~°, делая его
показательной функцией, вместо алгебраической, так как
1-|] ^е
при
Особенность взамен точки ветвления при х = Ъ становится сушественной
особенностью при ж=со, и в результате интегральное представление для
вырожденной гипергеометрической функции имеет вид
если только Rec>Rea>0. Для других областей значений a и с можно
построить представление при помощи соответствующих контурных инте-
интегралов, которое будет пригодно, если только с не будет целым отрица-
отрицательным или нулем, когда даже разложение в ряд «разлетается». В этих
случаях, которые будут рассмотрены позже, решение имеет логарифмиче-
логарифмическую точку ветвления при z = 0.
Второе решение уравнения E.3.44) можно найти, производя слияние
во втором решении z1 ~CF (a — c-\-l, fc +112 — с\z/b) гипергеометрическо-
гипергеометрического уравнения или в результате подстановки в уравнение E.3.44) вместо
решения функции z1'cf(z), в результате чего для / вновь получится урав-
уравнение вида E.3.44). В любом случае найденное второе решение имеет вид
и пригодно, если с не равно 2, 3, 4, ... Если с = 1, этот ряд сходится,
но совпадает с первым решением -^ (a j 11 z), так что данное выражение
не представляет собой второго решения ни для какого целого положи-
положительного с. Второе решение в этих частных случаях будет получено
позже. Нет необходимости исследовать отдельно случай с < 1, так как
при с = 2-с'<1 можно умножить наши решения, на zc~l = zl~c' и на-
568 Гл. 5. Обыкновенные дифференциальные уравнения
звать исходное второе решение первым, и наоборот, в результате чего с',
то есть новое с станет больше 1.
Из интегрального представления можно вывести интересное соотно-
соотношение, впервые указанное в E.2.62); именно, из
следует, что F (a\c\z) = ezF(с — а|с | — z). Подобным образом другой фор-
формой второго решения является z1'cezF(l — а\ 2 — с\ — z).
Преобразование Лапласа. Однако до перехода к дальнейшему иссле-
исследованию решения нам надо более тщательно рассмотреть новый вид ин-
интегрального представления, так как мы теперь перешли от преобразования
Эйлера к преобразованию Лапласа, указанному на стр. 549. Согласно
стр. 547, где мы исследовали интегральные представленич вообще, мы
видим, что показательное ядро имеет некоторые преимущества. Напри-
Например, так как dezi/dz = tezt и zezt — dezt/dt, то если наше исходное уравнение
имеет вид
т, п
т т m
то соответствующее преобразованное выражение таково:
т, п
и сопряженное к нему даст уравнение
t», п
Если это уравнение проще решить, чем <5fz(^) = 0, то преобразование Лап-
Лапласа будет пригодно для интегрального представления.
Например, если в исходном уравнении X (¦?) =/Ф" + g*y + Л'1» = 0, мно-
многочлены /, g и h не выше первой степени относительно z, то в дифферен-
дифференциальном операторе <М t не будет производных по t выше первого порядка
и v (I) можно легко найти. Наиболее общим видом уравнения такого рода
является
причем о можно исключить при помощи подходящего изменения начала
отсчета z. Это уравнение для у можно получить из следующего уравнения
для ф, где ty = zay
оно, в свою очередь, имеет общий вид E.2.55). Это уравнение имеет регу-
регулярную особую точку при z = 0 с индексами а и а + 5+1 и иррегулярную
точку z = oo. Подстановка у = F ехр [(— = -f j/e — -ц) z] приводит к вырож-
вырожденному гипергеометрическому уравнению для F. Итак, именно вырожден-
вырожденное гипергеометрическое уравнение особенно хорошо поддается решению
при номощи преобразования Лапласа.
5.3. Интегральные представления 569
Другие уравнения, имеющие в качестве /, g или h многочлены выше
первой степени, также можно решать при помощи преобразования Лапласа,
однако получающееся уравнение для v будет иметь второй порядок (или
выше) и должно быть особенно простым, чтобы его решение имело замкну-
замкнутый вид.
Во всяком случае, мы начнем наше изучение интегрального предста-
представления Лапласа с применения его к вырожденному гипергеометрическому
уравнению. Согласно этому уравнению, если положить F= \ er'v(t)dt, то
выражение М, (е*'), соответствующее E.3.44), имеет вид
(«2 -t) (d/dt) ezt + (ct - a) e2',
и сопряженным уравнением будет
(Ж (v) == (d/dt) (t2 — t) v + (ct — a) v = 0
с решением и присоединенной билинейной формой
v = At"'1 A — tf0-1, P = — Af (I - t)c~aezt.
Отсюда возможными путями интегрирования являются или путь от 0 до 1
при Re с > Re а > 0, как это было дано в формуле E.3.46), или путь от
— со до 0 при Re а > 0 и Rez > 0, или же двойной контур вокруг 0 и 1,
возвращающий Р к его исходному значению. Различные интегралы будут,
конечно, представлять различные решения. Интеграл, представляющий
вырожденный гипергеометрический ряд, дается формулой E.3.46) или
имеет вид контурного интеграла
—та о
F(a\c\z) = ~r Г (с) Г A - а) Г (а — с + 1) ф е2'^^ — IH"" dt, E.3.47)
с
где подинтегральная функция вещественна для вещественного z, если t
находится на вещественной оси справа от t — 1, а контур проходит против
часовой стрелки вокруг t=\ и t = 0, а затем по часовой стрелке вокруг
этих точек, как на рис. 5.7. Это представление имеет место, за исключе-
исключением точек, где гамма-функция не аналитична (то есть если 1 — а, с или
а — с+1 являются целыми отрицательными).
Асимптотическое разложение. Исследуем теперь поведение F (а | с | z)
для очень больших значений z, применяя представление E.3.46). На
стр. 520 мы уже обсуждали осложнения, свойственные асимптотическим
разложениям около иррегулярных особых точек, и указали, что если ве-
вещественная часть z велика и положительна, то
F(a\c\z) ca ^za-ce?.
Мы указали также, что это выражение несправедливо для Rez больших
по абсолютной величине отрицательных; в этом случае будет, вероятно,
F(a\c\z) ~
Мы должны теперь обосновать эти предварительные результаты и попы-
попытаться понять, какие свойства асимптотического разложения порождают
это любопытное, неопределенное поведение функции, придающее ей один
вид для z больших положительных и другой — для z больших отрица-
отрицательных.
570 Гл. 6. Обыкновенные дифференциальные уравнения
Из формулы E.3.46) мы видим, что если z вещественно, положи-
положительно и велико, то важнейшая часть подинтегральной функции сосредо-
сосредоточена вблизи t = 1 и интеграл не может существенно измениться, если
продолжить интегрирование по t от 0 до — оо. Более точно, мы можем
написать
1 0
что имеет место для положительного Rez. Полагая t = l — n/z в первом
интеграле ш t— — w/z во втором, имеем
+ (- z)-° ^ e-V-1 A + -j- У"" &г>} • E.3.48)
Оба интеграла теперь имеют один и тот же вид и оказываются прибли-
приближенно равными Г (с —а) и Г (а) соответственно. Отсюда первый член, со-
содержащий множитель ег, для большого положительного Rez несравненно
больше второго, и потому второй член может быть опущен (хотя нам надо
помиить о том, что мы его опустили, так как в этом и заключается
основная причина указанного выше неопределенного поведения F).
видоизменение рассуждения, примененного на стр. 356 для разложе-
разложения в ряд Тейлора, показывает, что
я—1
иу-1_ ^ Г (а) ( Ц>
z J — 2а Г(т+1)Г(о — т)\. г }
m=0
n+1
если га > Re а — 1. Подставляя это
в интеграл, имеем
Г(с —
| (CC)(CO + 1)A — с) B-е)
Л 2!
где
A-е) ... (п—с)Г(с + п—а+ 1)
n! г"*1 "" ' "
Мы видим, что для конечных значений z ряд расходится, но сумма первых
п членов ряда приближается к «истинному» значению, если п остается по-
постоянным, a z беспредельно возрастает. Например, для z = 10, \с — а|<2,
11 — а | < 1 первые четыре члена ряда дают значение интеграла с точностью
примерно до одной десятой процента, тогда как первые сто членов для
тех же значений z и параметров дают значение, далекое от истинного.
5.3. Интегральные представления
571
Плоскость t
Это свойство типично для асимптотических рядов, как об этом говорилось
на стр. 410.
Из первых нескольких членов мы получаем почти точное значение, но
свести ошибку к нулю можно только, делая z бесконечным.
Обычно нас интересуют значения асимптотического ряда для z, значи-
значительно больших единицы (например, для z > 1000). В этом случае для нас
достаточен первый член ряда. Следовательно, в нашем случае мы можем
написать, что F (a\ c\z)<=^ [Г (с)/Г (a)\za~cez для вещественных положитель-
положительных больших z. Это соответствует формуле E.2.60). Мы не включили
член [Г (с)/Г (с — a)\z~a, появляющийся
из второго интеграла, так как этот член,
вообще говоря, меньше, чем ошибка, при-
присущая первому асимптотическому ряду,
так что включать его было бы бессмыс-
бессмысленно.
Положение совершенно отличное,
если z вещественное, отрицательное и
большое по абсолютной величине. В этом
случае нодицтегральная функция в E.3.46)
наиболее велика при t, близком к нулю,
и второй интеграл в E.3.48) значительно
больше первого. В этом случае, отправ-
отправляясь от формулы E.3.46) и сохраняя
только главный член, имеем (причем
полагаем z = — | z |, t = и/\ z |
У О
Рис. 5.11. Видоизмепение контура
для подсчета асимптотического пове-
поведения вырожденной гипоргеометри-
ческой функции.
w
Независимой переменной является2=|г|е ,
причем | z | ^> 1.
F(a\c\z)~
Г (с) Г (с — а)
— а) }
c'a~idu-' Г(с) Isl-
для вещественного отрицательного большого z. Это соответствует формуле
E.2 63). Здесь мы опустили член с е2 = е~'г1, появляющийся из первого
интеграла в E.3.48), так как этот член, вообще говоря, меньше чем ошибка,
присущая асимптотическому разложению второго интеграла.
Явление Стокса. Уже из простого рассмотрения формулы E.2.60)
можно было бы видеть, что асимптотический вид F не может иметь такое
выражение для всех положений z на бесконечной окружности. Если под-
подставить г = |г|е^, где Jz| очень велико; в выражение [Г (с)/Г (a)]zacez, то
мы видим, что это выражение не возвращается к своему исходному зна-
значению, когда <р возрастает от 0 до 2тг. Однако, так как функция F(a\c\z)
аналитичнЯ во всей конечной части плоскости z, то из формулы, справед-
справедливой для больших z, должно следовать, что F возвращается к своему
исходному значению, когда <р меняется от 0 до 2%, описывая окружность
большого радиуса около начала координат. Выражение, включающее z",
как в E.2.60), не может правильно изображать F при больших \z\ для
всех фазовых углов у точки z. И мы только что показали, что это так:
для z вещественных и отрицательных правильным является выражение
[Г(с)/Г(с — a)] ( — z)'a (это второе выражение в свою очередь не может
быть пригодным для всех <р, так как оно содержит член z'a, который по-
породил бы многозначность).
Чтобы увидеть более детально, как это получается, возьмем случай
г = |г|е^, где |s| очень велико. Сначала возьмем <р между нулем и и (т.
е. z в верхней полуплоскости). При этом путь интегрирования
в E.3.46) деформирован в путь, показанный на рис. 5.11 сплошной
572 Гл. S. Обыкновенные дифференциальные уравнения
линией, идущий из t — О в t= — сое** и возвращающийся оттуда
a t — i. Таким образом, интеграл вновь распадается на два. В первом
положим t= —we~if!\z\ = wei(n-f'>/\z\, а во втором t — I — ue-lf/\z\, где
как и, так и w вещественны. Интегральное представление тогда при-
приобретает вид
Fta\r.\*\ = r(f)
E.3.50)
при 0 < «р < тс. Записывая только главные члены в разложениях
[1 ± (^ или u/z)] (то есть предполагая, что эти величины практически
равны 1 в области значений w илп и, для которых подинтегральная
функция не является пренебрежимо малой), мы получаем асимптотическую
формулу для z = |z|е*?, \z\ большое, 0 < ср < тс
F (а | с | z) сы.„ , . | z [а~с е* (°-c> *elz Ie'9 + ¦ ^с' | z |~а eia («-?).
Каждый из этих членов имеет неустранимую ошибку, присущую
асимптотическим рядам, малую при большом г, но равную нулю только
для бесконечного z. Если ср равно нулю (z вещественно и положительно),
то второй член, в этом выражении меньше неустранимой ошибки в пер-
первом (и потому не должен включаться), а если ср равно тс (z вещественно
и отрицательно), то первый член меньше неустранимой ошибки во вто-
втором (и потому не должен включаться). Если ср = тс/2 (z мнимое положи-
положительное), то оба члена имеют сравнимую величину и для нахождения
правильного значения надо пользоваться обоими.
Чтобы найти выражение для 0 > ср > — тс, мы используем путь интег-
интегрирования, показанный на рис. 5.11 пунктиром, причем на соответствую-
соответствующих прямых t = — те~^1\ z \ = we~l ("Р+те)/| z | и t=\—ие-^/\г\. Здесь
в выражении для w мы полагаем 1/ — z = e~l (<p+7t)/| z | вместо применен-
примененного выше выражения е**7*—*ty|zj, так как мы хотим, чтобы w было
вещественно и положительно, когда t находится на пунктирной линии,
и так как мы провели для подинтегральной функции разрез от t — 0
до t= — со. При этом найдем, что
F (а I с I z) ~ ~г\ I z |a"c е1 (°-с) f e121et<p + „, ^ . I z |~a e~ia («+'?),
если z=\z\elf и 0 > <p > —ir. Заметим, что если <р меняется от 0 до — тг/2,
то второй член выходит из своего «затмения» при ц> = 0* отличаясь
от соответствующего члена при ср = тс/2 на множитель e~2rtia. Это внезап-
внезапное изменение второго члена при ср = 0 не влечет за собой разрыва F,
когда <р проходит через нуль, ибо как раз при <р = 0 второй член меньше
ошибки, присущей первому члену, и любое изменение второго члена
не играет роли.
С другой стороны, это изменение как раз то, которое требуется,
чтобы сделать второй член вещественным как при ср = ъ, так и при
9 = — тс. Если бы дополнительный множитель е~27"а не был включен
в выражение для второго члена при 0 > у > — тс, то асимптотическая
формула при tp= — v давала бы результат, отличающийся от результата
при <р = + тс множителем e27tia, чего не должно быть, так как функция F
аналитична около z = 0. Чтобы соблюсти эту аналитичность, два члена
в асимптотическом разложении «играют в прятки» друг с другом; когда
6.3. Интегральные представления 573
один из них испытывает «затмение», становясь меньше чем ошибка в другом,
то он скачком меняет фазу, выходя из тьмы как раз с таким допол-
дополнительным фазовым множителем, чтобы обеспечить непрерывность в той
области ср, где этот член велик.
Это подобное игре в прятки поведение членов асимптотического раз-
разложения называется явлением Стокса, который первым обратил на него
внимание. Оно должно проявляться в первом члене при ср = тс, где пер-
первый член меньше чем ошибка во втором. Например, чтобы F при ер = 2тс
равнялась F при ср = О, в области тс < ср < 2тс должно быть
F{a\c\z)~ Щ-1 z\а~се
j
с дополнительным множителем е2те{(с~а> в первом члене. Этот результат,
конечно, получается из асимптотического вычисления интегралов; так,
при тс < ср < 2тс мы должны в первом интеграле положить t=l — uel Bте-"Р)/| z |,
чтобы нейтрализовать разрез от Z=0 до г= — оо.
Собирая все наши формулы, мы можем написать для z = | z j е1?,
где |z| большое,
|T(a)|z|-«, ,,= -*,
Г (с — а) |z |a-ce* (a-c> f ez + Ца)\z\~ae-ia<7t+<P>, — тс
Г (с — a)|z|«-cez, 9 = 0,!
f\ 0 < cp < it, E.3.51)
Г (с — a) | z |°-c el (a-c> (?-2n) ег + Г (a) | z |~a eia («-?), тс < cp < 2-я,
T{c — a)\z\a-cez, 9 = 2тс и т. д.;
отсюда ясно видно явление Стокса, так как когда ср становится целым
кратным тс, каждый член по очереди исчезает, появляясь с другой сто-
стороны как раз с такой переменой фазы, чтобы сохранить однозначность
функции при совершении обхода.
Решения третьего рода. Для удовлетворения граничных условий
при больших значениях z более удобно применять решения, стремящиеся
к z~a или к za~cez, но не к обеим функциям сразу. Формула E.3.50)
показывает, как это можно сделать. Для z=|z|eItp определяем
О < <р < 2тс, ъ
со
О
— тс <^ ср <^ iu.
Если Re (а — с) > 1, интеграл для U1 не пригоден и надо применить
контур вокруг точки ветвления при и = 0. Пригодный для этого контур
574 Гл. б. Обыкновенные дифференциальные уравнения
показан на рис. 5.12, причем подинтегральная функция вещественна
в точке А, если z находится на отрицательной вещественной полуоси.
Соответствующие контурные интегралы для U имеют вид
E.3.53)
F
и пригодны, если только с —а (или соответственно а) не является целым
положительным. Так как точка u—^z должна находиться вне контура,
то мы видим, что надо провести разрез для иг вдоль положительной
0
Контур F
ПлССКостл и
• Z
А
Рис. 5.12. Контур для интегрального представле-
представления вырожденной гипергеометрической функции
третьего рода.
Подинтегральная функция вещественна в точке А, если
z вещественно и положительно.
вещественной полуоси, а для U2 вдоль отрицательной вещественной полу-
полуоси. Это делает явление Стокса для U несколько отличным от того,
которое было для F; оно будет рассмотрено на стр. 576.
Эти решения можно называть вырожденными гипергеометрическими
функциями третьего рода. Они являются такими же хорошими решениями
уравнения E.3.44), как F(a\c\z) и zl'cF(a — с + 11 2 — c\z), и через них
можно выразить любое решение. Значение определителя Вронского для
двух независимых решений уравнения E.3.44) таково [см. E.2.3)]:
Значение А получается из применения асимптотического вида реше-
решений Ux и U2
иг U'% - U2 Щ ~ Г - а - - (а - с) - - 11 z~c ег+^,
и так как это асимптотическая формула, то можно пренебречь членами
с 1/z по сравнению с — 1. Следовательно,
Д (C/j, U2) = — z-c ez+ialT- E.3.54)
для всех значений z. Обычную вырожденную гипергеометрическую функцию,
конечно, можно выразить через эти новые функции
F{a\c\z)=^U1(a\c\z) + f^iUa{a\c\z) E.3.55)
для 0 < 9 < п.
Между прочим, следует отметить, что для выражения независимых
решений обычного гипергеометрического уравнения вблизи других
5.3. Интегральные представления 575
особых точек нам не требуется придумывать новые формы решений. Все
три особые точки были регулярными, и потому каждую пару решений
можно было выразить через ряды F (а, 0 \ с \ z) с различными значениями а, Ь,
с и z. В случае вырожденного гипергеометрического уравнения одна осо-
особая точка регулярная, а другая иррегулярная, и не удивительно, что
пара решений Ult Uz, соответствующая иррегулярной точке, имеет вид,
отличный от пары решений F(a\c\z) и zl~c F (а— с+1|2 — c\z), соот-
соответствующей регулярной точке.
Для окончания нашего рассмотрения нам надо выразить zi~cF (а — с -\-
-h 112 — c\z) через решения Ux и U2. Применяя формулу E.3.46) и про-
проводя такое разбиение, как для формулы E.3.50), получаем
Г B с\ (-git (a-c+1)
Г(в-с+1)ГA
оо
(-git (a-c+1) n
I ? V P-w zofi
-в) \ z« У ^
a-cez f e-uu
0
eu-a
0
Но это выражение должно быть комбинацией иг и U2. Сравнивая асимп-
асимптотическое поведение, мы видим, что первый член пропорционален U%,
а второй — Ux. Таким путем мы получаем новую совокунность интеграль-
интегральных представлений функций U
§
а также- получаем выражение z1~c/i'(a — с + 112 — с | z) через U1 и
при 0 < <р < it
alclz), E.3.57)
справедливое для области изменения 0 < <р < те фазового угла z. Явление
Стокса для этой функции можно выявить, применяя интегральные пред-
представления E.3.56) для асимптотических интегралов. Получится
1 (А с)
Г(а — с+1)е-ы^-с)\г\~а, tp=—it,
Г A - а) | z |°-с ё («-<=) ? ег + Г (а - с +1) | z [-« е{я («-!)-*» <«+»> - те < ср < 0,
ГA-а)|г|°-сег, ср = О,
Г(а —
Г A —a)|z|«-c е-2та+{(о-с)<рег + г (а — с +1) |z|-aeiTCA-c)+ia<TC-tp),
те < ср < 2it,
576 Гл. 5. Обыкновенные дифференциальные уравнения
и т. д. В силу того, что второе решение равно произведению zi~c на аналити-
аналитическую функцию, получаем, что асимптотическое значение, вещественное при
9 = 0, должно равняться произведению e~"i7tA"c) на вещественное число при
9= —тс, произведению е27"A~с) на вещественное число при ср =2тс и т. д.; это
делают фазовые углы, порождаемые явлением Стокса.
Для полноты нам надо выразить решения третьего рода через реше-
решения первого рода. Эти соотношения можно получить, решая совместно
уравнения E.3.55) и E.3.57). Преобразования являются несколько громозд-
громоздкими и включают применение формулы Бт(тс:г)Г (я)ГA — х)= it. Например,
имеем
г(с) *1в|Ч*Л- гB_с) z г (а-
В конце концов, получаем
1,\
Г Г7а)] еЫа zl"c ^ (а — с + ! I 2 — с Iz). - тс < 9
Явление Стокса для функций U (и для функций, связанных с U и F)
можно получить из этих соотношений, применяя таблицу изменений
фазы F и zi~cF. Если Ux, U2 представляют собой решения, асимптоти-
асимптотически пропорциональные соответственно za~cez и z~a для всех значений
фазового угла <р, и если формулы E.3.58) считаются определяющими Ux
и C/g при 0 < <р < it, то можно вывести правило, регулирующее фазовые
углы в соотношениях E.3.55), E.3.57) и E.3.58), а также для U. Напри-
Например, при—2тс<4<0
^ в г Ц-а) е" (°"е) ^ (а I с I g) - TT^^f ei" (OC) zl"c/1 (fl - c + 11 2 - c 1z) -
^^/ g2wi (a— с) 2°—с ег.
(Так как для U1 имеется разрез вдоль положительной вещественной полуоси,
то для перехода от положительных к отрицательным значениям ср надо
перейти от 0 + е к 2ъ — е.) Подобный же скачок появляется для U2 при
<р = чс или — тс.
Решение второго рода. До сих пор мы оставляли в стороне вопрос
о том, что делать с решением, независимым от F(aic\z), если с целое
отрицательное. Если с = п + г, где п целое, большее 1, а s обращается
в нуль, то оказывается, что первые п— 1 членов ряда для zl~cF(a—с +
+112 — с | z) остаются конечными, а остальные члены имеют мно-
множитель 1/( —s), и потому обращаются в бесконечность. Очевидный
прием, заключающийся в умножении на з до перехода к пределу, не по-
помогает, потому что, как мы увидим, предел (п — c)zl~cF(a — c-t-l|2— c\z)
при с—>п оказывается пропорциональным первому решению y'(a[c|z),
5.3. Интегральные представления 577
и потому не является независимым решением. Эта трудность про-
проявляется также в формуле E.3.57), содержащей множитель Г B —с)
стремящийся к бесконечности при с-^2, 3, 4, ... Решения иг и С/2 при
этом не становятся бесконечными, поэтому надо построить второе реше-
решение при помощи функций U. Это можно довольно просто сделать, если
изменить знак у одного из членов Формулы E.3.55V выражающей F {а \ с \ z)
через функции U.
Поэтому мы определяем вырожденную гипергеометрическую функцию
второго рода формулой
G(a\c\z) = ^UAa\c\z)-1^L_U2(a\c\Z) E.3.59)
при 0 < ср < к. Как показывает асимптотическое выражение, эта функция
независима от F. Она удобна тем, что порождает простые формулы,
выражающие U через F и G; например, U1= [Г (а)/Г (с)] (F + G),
а С/2 = [Г (с — а)/Т (c)](F — G). Она также остается конечной при целом с,
как будет вскоре показано, хотя оказывается, что она в этих случаях
имеет логарифмическую особенность при z = 0. Но это как раз то, чего
надо ожидать, так как для целого с индексы вырожденного, гипергеоме-
гипергеометрического уравнения при z = 0 различаются на целое число, а в этом
случае, как мы видели на стр. 504 и 513, следует ожидать у второго
решения логарифмическую особенность.
Чтобы получить разложение G около z = 0, выразим U в формуле E.3.59)
через F и zl~cF при помощи E.3.58). В результате преобразования гамма-
функций получаем
b(a\c\z)-e Г(а) j ГA_а) Iе + sin (па) Jr\a\c\z)
} E.3.60)
Эта формула не выглядит слишком многообещающей, так как теперь оба
члена в фигурных скобках стремятся к бесконечности, когда с —> п, целому.
Однако, как было указано выше, при с = п оба решения равны друг
другу, а коэффициенты в этом выражении так подобраны, что бесконеч-
бесконечные части как раз взаимно уничтожаются, и остается конечное выраже-
выражение, пропорциональное производной от F(a\c\z) no с. Эта производная
от F по параметру является решением, которое мы искали.
Теперь нам следует доказать высказанные утверждения и на самом
деле подсчитать разложение этого решения второго рода около z = 0.
Прежде всего надо доказать, что г1-с/'(а — с+ 11 2 — с\ z) пропорцио-
пропорционально F(a\c\z), когда с—>п, целому. Это просто при с-^1, так как
тогда zl-°F(a — с+ 112 — clz)—>F(a\ 11 z). Отсюда (так какГ(с — 1)~!
~1/(с-1) и ГA-с)~1/A-е)),
Каждый член в квадратных скобках имеет вид /(с) — /A), так что предел
этой величины, разделенной на с — 1, равен производной от /(с) по с
37 ф. м. Морс и г. Фешбах
578 Гл. 5. Обыкновенные дифференциальные уравнения
при с=1. Значит,
eiTCa f I d Г .•_. , sin it (a — с) ,-, . . . .
"I" I x I z)— Y(a) I 1A — a) dc \_ ' sin ma J v ' ' '
— 2-j- Г*1
Г- 4/^(a—c + 112—c|z)]l
Lr(c — a) v ' ' • ' J J c-1
Ho dzc/dc = zclnz и dT(a + c)/dc = 4)(a + c)r(a + c), где ф(ж) — логарифми-
логарифмическая производная от Г (ж)
r=0
v= -фA) = 0,5772 . . . ,
' ти ' a; ' a;+1
ф A — c) = <
Отсюда
—a) I dc L + sin(na) J
Г _А Г/ I
Г(а)ГA —a) I dc L + sin(na) J Zj т!Г(а)Г(с +
т0
т=;0
9Г М _ ^ -1 Г 1 V Г(а-с + 1 + т)ГB-с)^1-с "I 1
Zi ^ "^ dc Lr(c-a) Zj т!Г(а — с + 1)ГB — с + т) J J с=1
0
т=0
л "
2 Hic
т=0
т_
^ го1Г(а)Г(т-
_ e ""Г -[ [2 In z + те ctg (теа) — iw + 2ф (а)] f (а 111 z) -f-
oo
g ТУ.(а + ^2 [ф (а + m) - ф (а) + 2ф A) - 2ф (т + 1)] zm\ . E.3.61)
Это решение независимо от /"(a|l|z) (это показывает логарифмический
член, даже если по остальной части это не так очевидно). Его вид инте-
интересен тем, что представляет собой сумму логарифма величины, пропор-
пропорциональной z, умноженного на первое решение, и бесконечного ряда,
сходящегося для всех конечных значений z и также независимого от F (а 111 z).
Для с = 2, 3, ... процесс вполне подобен приведенному выше, хотя
выкладки несколько сложнее. Разложение в ряд показывает, что для исче-
зающе малого с — п (п — 2, 3, 4, . . . ) функция
эт-2
_, „\ -у Г(с —а)Г(с —т —
-^J то!Г(с —а —т)Г(с —1)
т=0
. „ч Г (а) Г B-е) ^
Г (и) Г (а —с+ 1) ^ Г(г+1+п—с)Г(а)Г(п + г)
г=0
5.3. Интегральные представления 579
v Г (а) Г (re—а) sin Ыа) „ . . . .
превращается в функцию ' у, '_ *—-F{a\n\z), так как (с — /г) X
ХГB — c)czL ~ и потому первый член в E.3.60) приближается
С-*П * (С Ч
kq второму, но оба становятся бесконечно большими. Добавляя и вычитая
член 2[Г(п — 1)/(Г(п — a)]Fn(a\n\z)/(c — n) внутри фигурных скобок, имеем
v ' ' ; г(а)с-+п IГ (с) те (с—и) L втте(а —n) J VII/
!1 ?
с+п (с) те (с—
а) sin (пя)
Г (re—а) (с — re) n
Отсюда
2тега л «
G ( а |п | z) = 2д. |[2Inz + rcctg(«a)- iw]F(a\n\z)~
-2 2
m=l
и-i
Г (a) ^J T (n—r) T (r—a+l) ¦ V"-*'-"^
Это выражение отличается от общего вида G (a 111 z) присутствием конеч-
конечной суммы отрицательных степеней z. Она, а также логарифмический
член показывают, что G в отличие от F не аналитична при z = 0. Нет
надобности исследовать G, когда с равно целому отрицательному или нулю,
так как если уравнение удовлетворяется функцией z1 +n F (а + п -\-112 -f- n | z),
то мы принимаем ее за первое решение и следуем далее, как описано
выше. Так как индексы вырожденного гипергеометрического уравнения
при z = 0 равны 0 и 1-е, то если при первой попытке мы найдем, что с
меньше 1, то уравнение для zi"cy имеет новое с больше 1, и мы будем
работать с ним.
Этой формулой завершается наше общее рассмотрение вырожденной
гипергеометрической функции, так как мы теперь записали выраже-
выражения обоих решений для больших и для малых значений z и для всех
значений параметров [разложение функций U в ряды можно получить
при помощи рядов для F и G и соотношений E.3.55) и E.3.59)], включая
те значения, для которых второе решение имеет логарифмическую особен-
особенность. Остается пока только рассмотреть некоторые из более важных
частных случаев этих функций.
Функции Бесселя. Самой важной специальной функцией, представи-
мой через вырожденную гипергеометрическую функцию, является функция
Бесселя. Она представляет собой решение уравнения, упоминавшегося на
стр. 518,
z dz \
37*
580 Гл. 5. Обыкновенные дифференциальные уравнения
называемого уравнением Бесселя. Это уравнение имеет регулярную особую
точку z = 0 с индексами \ и — \. Подстановка ф = zv e~iz F приводит урав-
уравнение к вырожденному гипергеометрическому виду
zF" + [Bv+ 1) - 2iz] F'-iB4 + l)F = 0
с решением /Y-v-|-y|2v+l| 2iz J. Решение уравнения Бесселя, остающееся
конечным при z = 0, называется функцией Бесселя первого рода
1 2iz") =
f'V
V2y
Интегральные представления можно получить из представления У
( при помощи формулы Г B\ + 1) = B2v/j/^) Г (¦» + у") Г (v + 1), если поло-
1 1 1 \
жить t — —{\ — iu) или у—5"cos б J или непосредственно из преобразо-
преобразования Лапласа. Ряды можно получить из интегралов или посредством
перемножения рядов для показательной функции и для F (интересно заме-
заметить, что произведение вырожденного гипергеометрического ряда с мнимым
аргументом и показательной функции с мнимым показателем может ока-
оказаться вещественной функцией). Если Rev — -^-< 0, то линейный (обычный)
интеграл можно заменить на интеграл по замкнутому контуру, обходя-
обходящему точку в = 1 в положительном направлении и — г в отрицательном
направлении.
Посредством манипуляций с интегральным представлением или с рядами
можно получить следующие рекуррентные формулы для функций Бесселя:
_, (z) + /v+1 (z) = Bv/z) /v (z), з
vZt (Z) - /v+1 (Z) = 2 (d/dz) /j)
Так как эти формулы можно получить из интегрального представления,
то они будут иметь место и для других решений уравнения Бесселя,
полученных при помощи изменения пределов интегрирования; именно они
будут иметь место для решений второго и третьего рода.
Из последней формулы E.3.63) в результате ряда преобразований
можно получить другой вид интегрального представления, который будет
нам полезен позже во многих приложениях; его можно выразить в различ-
5.3. Интегральные представления 581
ных формах (для целого п)
Д eizcos?cos/icp dcp = E.3.65)
lo
~ ^ Scos ^пб ~z sin e*de>
—7Ъ
где контур в первом равенстве представляет собой окружность с центром
в начале координат, проходимую в положительном направлении. То, что
это представление на самом деле дает функцию Бесселя, можно показать
при помощи разложения в ряд и сравнения результата с рядом E.3.63)
или проверив, что интеграл удовлетворяет уравнению Бесселя и имеет
необходимое значение при z = 0.
Это представление с помощью формулы D.3.4), определяющей ряд
Лорана около существенной особенности в а, можно применить для полу-
получения очень полезного разложения в ряд. Функция ег('2-1>'2' имеет
существенную особенность при t = 0. Поэтому около t = 0 она разлагается
в ряд Лорана с коэффициентами
Поэтому ряд имеет вид
со
^(i2-.)/2i= 2 t"Jn{z);
71=; —со
его можно применить для определения свойств функций Бесселя целого
порядка. Например, рекуррентные формулы E.3.64) можно получить
при помощи дифференцирования по z или t и т. д. Мы исследуем это
далее в гл. 11.
Это разложение можно применить для получения других. Например,
имеет место простое разложение
= ^ ein*Jn(z).
71=— СИ
Более сложное, но более полезное соотношение можно получить при помощи
следующего разложения (здесь Z = У~х2 + у2 — 2ху cos <p, Zsin а = х — у cos у,
Zcosa = г/siiKp):
2
1 Г
о
27t
i (x — у cos <p) sin
x) \eivsin (tp"e)+jneм=
n=—со О
= 2 JnV)Jn{y)^= Ц /n(a:)/n(!r)co8(ii«p). E.3.66)
582 Гл. б. Обыкновенные дифференциальные уравнения
Применяя другие контуры интегрирования по б, получаем общую формулу
| Ym(x)Jm(y) cos (гщ),
m=—со
где символ Y может означать любой из видов функций Бесселя — /, N, Нау
или ЯB), которые будут вскоре определены. Много других подобных
разложений будет выведено и применено в этой книге позже. Данное
разложение выведено здесь, так как оно будет использовано в этой главе
ниже.
ДРУГУЮ формулу, которая будет полезна впоследствии, связывающую
функции Бесселя и полиномы Гегенбауера, можно получить при помощи
формулы E.2.53) и интегрирования по частям модифицированного интеграль-
интегрального представления E.3.63)
(z) =
1
eizt.
I
nl z
E.3.67)
Если v полуцелое, то есть равно п + -^ , то получающиеся функции
Бесселя имеют особенно простой вид. При помощи сравнения разложений
в ряды можно видеть, что
/4 (z) = |^2/irz sin z и / 4 (z) = \^2/tczcos z.
2 ~~2
Мы увидим позже, что для волнового уравнения в сферических координа-
координатах удобно пользоваться сферическими функциями Бесселя, определенными
формулами
/n (Z) = j/^Г Jn+l (Z)^i- COS [ Z - I W (П +
*« (z) = /n (z) + г'ип (z) ^ (Vz) exp [ iz - Y in (n
Некоторые рекуррентные формулы для этих функций имеют вид
[Bm + l)/z] fm (z) = fm^ (z) + /mtl (z),
Bm + 1) (d/dz) /m (z) = m/m^ (z) - (m +1) /m+1 {z),
{d/dz) [z-mfm (z)] = - z~mfm+1 (z),
где fm(z) есть jm(z), nm(z) или hm{z). При помощи формулы E.3.67)
6.3. Интегральные представления 583
можно показать, что интегральным представлением для jn(z) будет
/n (Z) = [г
Дифференциальное уравнение, которому удовлетворяют эти функции, таково:
dz2 z dz
Уравнение Бесселя имеет иррегулярную особую точку при z = со.
Как и надо ожидать для таких уравнений, разложение около этой точки
является разложением асимптотического типа, расходящимся для конеч-
конечных значений z, если взять слишком много членов, но приближающимся
к истинному значению при неограниченно возрастающем z, если восполь-
воспользоваться только конечным числом членов. Предельную форму (первый
член асимптотического ряда) можно получить из формул E.3.51), дающих
асимптотический вид F(a\c\z), или же прямо из интегрального пред-
представления при помощи деформации пути интегрирования (например,
в первом представлении E.3.63) в путь, идущий из — г в — со и из
— со в —?). Таблица асимптотических выражений, показывающая явле-
явления Стокса для функции Бесселя первого рода, имеет вид (при z= \z\e**)
__iir<?<^7Cj E3.68)
-) r г 1 / 1 \ i 1 4
1J y2/iczcos у z + y те( v + -^- J I , -j те < <j- < утг и т. д.
Независимое решение вблизи z = 0 можно взять таким
«ели только v не равно нулю или целому положительному. Оно стремится
к бесконечности, как z~~v, если z стремится к нулю.
Функции Ганкеля. Функции, соответствующие 17г и U2 E.3.52), при-
приспособленные для удовлетворения граничным условиям при больших зна-
значениях z, получаются подобным же образом при помощи продолжения
пути интегрирования в E.3.63) до — со и разбиения его на дне части.
Верхняя половина дает функцию с положительным показателем степени
(мы множим интеграл дополнительно на 2 по причинам, которые станут
ясными позже).
^ \ el'
1 С izcos ?+iv (<P—2«)
. 1.1 1
м~2** lV+2
е
_±7и<?<4те; E.3.69)
584
Гл. б. Обыкновенные дифференциальные уравнения
она называется функцией Ганкеля первого рода (или первой функцией
Бесселя третьего рода). Путь интегрирования во втором интеграле [выве-
[выведенном из.E.3.65)], показанный на рис. 5.13, проходит из +гоо вплотную
слева от мнимой оси в — гоо вплотную справа от мнимой оси (причина
такого выбора состоит в том, что в заштрихованных участках плоскости <р
Рис. 5.13. Контуры для интегрального пред-
представления функций Бесселя.
подинтегральная функция беспредельно возрастает при удалении от
вещественной оси, а в незаштрихованных участках подинтегральная функ-
функция стремится к нулю, так что нам надо закончить наш интеграл в неза-
незаштрихованных областях). Этот же интеграл представляет также другие
функции, так как
J -у (Z) — -
г cosjp+iv (ф—2
а контур С представляет другое решение для больших значений z
—00 }
J (У2Г
(z) =
dt =
nv+l.V.—iz
2
= — \ e
—i2Cos<p+iv [<p—gtj
2/itze 2 v 2У
E.3.70)
Эта функция называется функцией Ганкеля второго рода. Во многих
случаях, если мы будем иметь дело только с первой из этих функций,
мы будем опускать верхний индекс; Н„ будет всегда означать Н™ и назы-
называться функцией Ганкеля {просто), если это не может вызвать недоразу-
недоразумения.
Эти два решения независимы, как показывает их асимптотический
вид. Определитель Вронского для независимых решений уравнения Бесселя
равен A/z [см. формулу E.3.2)]. Постоянную для этих двух решений
можно определить при помощи их асимптотического вида, и в итоге мы
5. 3. Интегральные представления 585
получаем
н™) = я?» ~ н? - нт -^ я;и = -4^. E.3.71)
Так как обе функции Н'? и Н™ удовлетворяют рекуррентным форму-
формулам E.3.64) (и другим формулам, получающимся при помощи комбини-
комбинирования этих), то соотношение E.3.71) можно выразить различными спо-
способами, как например
Н™ (z) H?U (z) - Я;1' (z) Hfti (z) = k/mz и т. д.
Имеется тесная связь между функциями Ганкеля и показательными
функциями с мнимым показателем, с одной стороны, и функцией Бес-
Бесселя / и косинусом, с другой. Совсем так же, как
cos ж = -jj (ete + е-**),
здесь имеем
/v (z) = 1 [HfXz) + НТ (z)], E.3.72)
что можно установить из приведенных определений или из простого рас-
рассмотрения рис. 5.10.
Аналогично из формул E.3.58) и определений / и Н через F и U
получаем
Я?1^ = -ВД" [<Wv(z)-/-v(z)], E-3-73>
откуда мы можем вывести разложение функций Ганкеля вблизи z = 0.
Но прежде чем провести выкладки до конца, мы лучше исследуем пове-
поведение второго решения в случае целого v.
Функция Неймана. Рассмотрение разложения Jv (z) в ряд E.3.63) пока-
показывает, что если v отрицательно, то /v (z) становится бесконечным при z = 0,
если только v не целое отрицательное. Чтобы исследовать этот особый
случай, положим v = — п — г
- /J \ ч Т{т)Т{т — n — e)
m=l
- Zj ^ x^ Г (m) Г(т — n—s) + ^ > Zi У х> Г (г — в)
«1=1 Г=1
что переходит в пределе (е = 0) в простое равенство
/_n(z) = (-l)Vn(z), 11 = 0,1,2,... E.3.74),
Отсюда, если п целое или нуль, решение /_„ (z) не является более неза-
независимым от Jn(z), и нам надо позаботиться о втором решении.
Эта ситуация должна быть нам теперь знакома: если п целое, индексы
уравнения Бесселя при z = 0 различаются на целое число и второе реше-
решение должно иметь логарифмическую особенность. Ни /„, ни J_n не имеют
такой особенности, так что надо подыскать что-нибудь другое. Конечно,
две функции Ганкеля не становятся пропорциональными одна другой
при v = n, а потому одна из них или обе должны иметь там логарифми-
логарифмическую особенность (на самом деле обе они имеют). Но мы хотим иметь
•586
Гл. 5. Обыкновенные дифференциальные уравнения
решение, более тесно связанное с /v. Аналогия между /v и косинусом
наводит нас на мысль определить функцию Бесселя второго рода, то есть
функцию Неймана, аналогичную синусу
N, (z) = A/20 ttfv1' (z) - НТ {z)\ =
= ctg (т) /v (z) — cosec (irv) /_v (z) =
w. E.3.75)
Эта функция пригодна для всех значений v (нам надо, конечно, рас-
рассматривать только значения, для которых Rev>0, так как в противном
случае мы можем взять за первое решение /_v). Если v не целое, члены
по отдельности конечны, и так как функция содержит кое-что от 7_v
(при v = n + -7r она целиком равна /_v), то она должна быть независима
от /v. Если v целое, члены по отдельности бесконечны, но взаимно
уничтожаются, порождая решение с логарифмической особенностью
при z = 0. Для получения этого решения можно применить формулу E.3.61)
или же вновь вычислить ряд. Так как настоящий случай проще, то мы
произведем вычисление заново, чтобы вновь продемонстрировать метод.
-Полагая v=n-f-s и устремляя е к нулю, получаем
-Vn B) = 1Ш [ ~ /п+е B) - -Ь^- /_„_. (
= -?- lim Г
- (- 1)"
'где мы добавили и вычли /п( = (
равна
Производная от /v при v = п
Г d Z
m=l
Г (m) Г (m +
)
)T{m + n)
¦ ' гЦп+rV. 2j ~7 '
г+п
г=1
s=l -i n
где
= л (V) +1 + —L- + .. . -] L__ и у = 0,5772 ....
нелогично производная от (—l)n/_v равна
^
ds ZJ Г(
=0
т + 1)Г(т
2)-"-^"' ,Ду( r-i^ W2)"~s~2+2r 1 e
—и+1 —s ¦ deZl V ; Г (r—s) Г (г + n) J s = 0
n-l
5.3. Интегральные представления 587
-l)! у 1У-1Г]ПЯ
m! (z/2)"-2m Zi \ *> L 2 V *•Г) J Г (г) Г (n + г)
O r=l
ri—1 oo
m=0 m=l s=l
Складывая полученные два выражения, получаем в итоге разложение
функции Неймана около z = О
п-1
п^-J^ ' ml (n+ m)\ -Zj [_ s ' s + n J
71 = 0, E.3.76)
[ *(n-i)! ^z J ' n>U-
Если n = 0, конечная сумма (от 0 до п — 1) отсутствует. Это разложение
имеет тот же общий вид, что разложение E.3.61) для вырожденной
гипергеометрической функции второго рода; оно содержит член, включаю-
включающий произведение Jn на In z, конечную сумму отрицательных степеней z
(за исключением случая п = 0, когда она отсутствует) и добавочный бес-
бесконечный ряд, начинающийся с члена z"+2.
Приближенные формулы для высокого порядка v. Асимптотические
формулы E.3.68), E.3.69), E.3.70) и E.3.75) предполагают, что аргумент z
значительно больше порядка v функций Бесселя. Полезные формулы для
/v(z),' когда и z, и v велики, можно получить, применяя метод кратчай-
кратчайшего спуска (см. § 4.6). Если как z, так и v велики, интеграл
из которого мы получили предыдущие асимптотические разложения, уже
не имеет наибольшего значения подинтегральной функции вблизи t = i,
как это было ранее. Следовательно, первый член асимптотического разло-
разложения не дает хорошего приближения, и мы должны позаботиться
о другой формуле. Оказывается, что интегральное представление
(е~2*1У/те) С ei (z cos w+vu>) dWt
приведенное на стр. 584, контуры которого показаны на рис. 5.13, наибо-
наиболее подходит для нашей цели. Так, если взять контур А, то интеграл
равен 2/v (z); если взять В, то интеграл равен //"' (ZY> если же контур
состоит и из Б, и из С (причем В проходится в обратном поряде, сверху
вниз), то интеграл равен 2iVv(z).
Каждый из этих контуров проходит из области, где подинтегралыгая
функция исчезающе мала (на рис. 5.13 незаштрихованные участки вдалеке
от вещественной оси), через область, где эта функция велика, в другую
область, где подинтегральная функция исчезающе мала. Если мы проведем
588 Гл. б. Обыкновенные дифференциальные уравнения
контур произвольного вида между этими пределами, то подинтегральная
функция будет меняться сложным образом, часто меняя знак и часто
приобретая большую мнимую часть, но при интегрировании все эти
дополнительные осложнения взаимно уничтожаются и результат будет
один и тот же, как бы мы ни провели промежуточную часть контура (так
как подинтегральная функция имеет особенность только при w = co).
Если нам надо подсчитать приближенное значение интеграла, то мы долж-
должны сначала выбрать путь, вдоль которого подинтегральная функция
ведет себя по возможности наиболее просто. Например, так как подинте-
подинтегральная функция является показательной, то вещественная часть пока-
показателя определяет модуль этой функции, а мнимая часть — фазу. Чтобы
исключить излишние колебания подинтегральной функции, надо условиться
производить интегрирование вдоль контура, на котором фаза постоянна.
Мы должны сейчас попытаться найти маршрут, для которого подинтеграль-
подинтегральная функция велика только на его коротком участке, так что подсчет на
этом ограниченном участке будет достаточным, чтобы дать ответ с хорошим
приближением.
Любой из контуров, показанных на рис. 5.13, представляет собой
путь через горную цепь. Мы хотим оставаться в долине по возможности
долго, чтобы пройти через самый низкий перевал и по возможности
быстро достичь долины с другой стороны. Оказывается, что путь для
этого является также путем, вдоль которого фаза подинтегральной функции
остается постоянной, как это было показано в § 4.6.
Так как в показателе нашей подинтегральной функции стоит функция
комплексного переменного w = u -f- iv, то вещественная часть этой послед-
последней определяет модуль, а мнимая — фазу подинтегральной функции
F {w) = i (z cos w + \w) = f{u, v) + ig (u, v),
/ = zsinusht> — w, g = zcosucht> +w.
В белых участках рис. 5.13 / становится большой отрицательной, а в
заштрихованных — большой положительной. Мы хотим пройти по самому
низкому проходу в поверхности f(u,v).
Так как / представляет собой вещественную часть функции комплексного
переменного, то она является решением уравнения Лапласа по и и о (см.
стр. 334) и не может иметь максимумов или минимумов в конечной части
плоскости. Это означает, что вершина самого низкого прохода должна
быть седловой точкой, где поверхность искривляется книзу в одном направ-
направлении и кверху в направлении, перпендикулярном первому. Другими
словами, вершина перехода является точкой, где dF/dw = 0, и вблизи этой
точки
F = Fs + b{w-'wsJ+ ... =
= /8 + а t(^2 — У2) cos 26 — 2ху sin 26 + ... ] +
+ igs + ia [(ж2 — у2) sin 26 + 2ху cos 26 + ... J;
здесь b—ae2il = {d2F/dwz)s и х = и — us, y = v — vs. Вдоль линий у= — xtgb
и y = xctgB (под углом —6 и ~2^ — 6 к вещественной оси) мнимая часть
F постоянная (g = gs), а вещественная имеет наибольшую кривизну. Вдоль
линии у= — a;tg6 вещественная часть F равна
ReJF = / = /s + yaz2sec26+ . .a = /e + i-ad2+ ...,
где d = \fx2-\-yz представляет собой расстояние вдоль линии у— — xtgd.
Отсюда вдоль линии, составляющей угол —6 с вещественной осью,
5.3. Интегральные представления
589
(и потому подинтегральная функция) возрастает, когда мы отходим от
седловой точки w = ws. Отсюда эта линия идет вдоль оси горного хребта,
и мы не должны по ней следовать, так как она приведет нас к еще
большим высотам.
Однако вдоль линии у — х ctg 6 вещественная часть F равна
где s = |/ жа + у2 представляет собой расстояние вдоль этой линии от
седловой точки. Поэтому вдоль этого пути в любом направлении от вер-
вершины прохода мы держим курс вниз к долине. Если наш контур не
v=-Z-
v=-2
Случай z= I.543 v Случай z=d86Bv
Рис. 5.14. Пути интегрирования для получения асимптотических
представлений функций Бесселя, если и z, и v велики.
должен пересекать других горных цепей, то приближенным выражением
для интеграла тогда будет
"ds=i/^
еР («О dw
Если контур (в направлении интегрирования) вблизи w = ws образует угол
-jic-o с вещественной осью, то элемент dw равен е- ds, где as ве-
вещественно. ( Если интеграл взять в противоположном направлении, то
надо в окончательном результате добавить множитель — 1 или заменить
в показателе -Q-^t на—-г7"- ) *^то выРажение тем лучше приближает
истинное значение интеграла, чем выше и уже проход, через который мы
должны итти (то есть чем больше /s и а).
Для преобразования интеграла, представляющего функцию Бесселя,
положим F (w) = iz cos w + hw. В седловых точках, где dF/dw равно нулю,
будет sin ws = v/z. Если z вещественно, возможны два случая: если z > v,
то ws находится на вещественной оси в точках Arc sin (v/z); если же z < v,
то ws комплексно и находится в точках ( 2n+-^J тс + i Arch (v/z).
Оба случая показаны на рис. 5.14, где оба рисунка начерчены на
плоскости w = u — iv, причем для правого z = 0,866v, а для левого z= l,543v.
590 Гл 5. Обыкновенные дифференциальные уравнения
Тонкие линии — линии равного значения / = Re F. Жирные линии — контуры,-
проходящие через одну или обе седловые точки S, S' и вдоль которых
g" = Im ^ постоянно. Контур А, проходящий из i оо —-тс через S (или
о
через S и S' на правом рисунке) в ? со Ч-у1*, дает 2/v(z). Контур С, про-
1 1
ходящий из гсо—^ъ через S' (слева) или S (справа) в — г со-f-^-1*, дает
Hly}(z)y а контур D дает H™(z). Если применить С и D вместе, начиная
из ? со — -^-т: и ioo4--ric и кончая оба контура в — гсо + —-к, получаем
2Nv(z). На контурах В и В' значение g постоянно, но в этих случаях
/ убывает, когда мы отходим от седловой точки. Если как . v, так и %¦
велики, то значение / в седловой точке много больше, чем, например, ее
значения в любом другом месте вдоль Л, так что вне непосредственной
близости S можно полностью пренебречь подинтегральной функцией.
Взяв сначала случай z<v (и полагая для удобства z = vsecha), мы
найдем, что dF/dw = 0 при w = wg = у те i- ia. Верхняя точка S пересекает-
пересекается контуром А, построенным для 2/v(vsecha). Значение / в ws равно
/s = v(tha — a), а значение g там равно gs = ~2-™. Вторая производная
d2F/dw2 при w=ws равна —vtha, так что вблизи точки S значение F
приближенно равно
F с* v (th a — a) + 4" *"w ~ 4 v th a'(w ~ wsJ = ^'s + 4"аеШ (w ~ ^sJ.
a = vtha, 6 = —-тс.
Согласно нашим предыдущим рассуждениям, контур, спускающийся
с прохода, составляет угол -^- тс — 6 = 0 с вещественной осью, и приближен-
приближенное значение интеграла равно
—„-7siv
2/v (у sech a) ~ \ eF I w~>dw = l/ —re— eV ^th a~a' ¦
A
Контуры для функций Ганкеля проходят через <S", где
/s = v(a — tha), gg=-|-icv, (d27^/d^2)s = vtha, 6 = 0,
a = v th a.
Для первой функции Ганкеля контур проходит через <S" в отрицательном,
а для второй —в положительном направлениях, так что
и потому соответствующим выражением для функции Неймана будет
-./Vv(vsecha)~|/ -———ev(a-tha>.
v ' Г nv th a
Если z > v, полагаем z = v sec P; тогда седловыми точками будут
=-2-ie±p. Вторая производная {d2F/dw2)s = ±htg$, так
и 6 = ± тг/4; далее, /8 = 0 и gs = -^ tcv T v(tgP — P). Контур С для первой
5.3. Интегральные представления
591
функции Ганкеля пересекает s( ws==-^-'n~ PJ в отрицательном направле--
нии, так что
I'J' (v sec P) c^ -
vtgp
с другой стороны, вторая функция приобретает вид
2 iv (tg p—Р)-т- mi
«vtg?1
2 -iv (tg g—р)+-т-яг
e 4
С помощью этих двух функций мы можем подсчитать /v и iVv.
Если z очень близко к v, обе седловые точки приближаются друт-
к другу и в конце концов становятся неразличимыми. При z = v в точке-
w=-^tz как dF/dz, так и d2F/dzz равны нулю, так что нуль будет высшего,
порядка, и надо ожидать тройной симметрии осей. Контуры, на которых
g = const, приближаются к точке w = -^ it вдоль мнимой оси или вдоль
направлений ± те/6, или тс ^ тс/6. По направлениям тс/6, тс —тс/6, Зтс/2
функция /убывает при возрастании расстояния от «седловой точки» (седло,
для трехногого всадника). Для /v(v) мы применяем первые два направлен
ния, причем первое в обратную сторону. Интеграл оказывается равным
'A L L
Если z —v очень мало сравнительно с v, то все равно можно пользоваться
этим путем интегрирования, причем можно подсчитать малый поправоч-
поправочный член.
Таким образом, мы можем написать следующие приближенные фор-
формулы для больших значений v и z для различных областей z по отношению,
к v (при вещественном v):
(¦ ev (th a-a)
j/^Ttvtha
= l/l — (z/vJ,
sin (я/3) Г (\ Л sin B«/3) Г Г -f ^
37= {Z./
Зя {z/Qf
f _
th a
2 sin (л/3) Г( ^r- I 2 sin Bл/3)
VjW + .
3jt (z/6)
3n (z/6)
. E.3.77),
(z —v), z~
v-
592 Гл. 5. Обыкновенные дифференциальные уравнения
Кулоновская волновая функция. Радиальная часть уравнения Шредингера
для электрона с массой т, зарядом — ей полной энергией Е в центрально-
симметричном потенциальном поле V (г) имеет вид
1 df'2dR\ 1A+1) Km
г* dr V dr ) г2 П+^1
где множитель Z(Z+1) представляет собой константу разделения, появля-
появляющуюся ив углового множителя; если потенциал зависит только от г, то /
целое. Если потенциал V представляет собой кулоновское поле, порождае-
порождаемое частицей заряда Ze (достаточно тяжелой, так что частица находится
в центре тяжести), то V равно — e2Z/r. Полагая Е — —{^^2J
x = 2*z = B*me2Z/fc2) г и R = e 2 xlF (x), получим уравнение для F
которое является вырожденным гипергеометрическим уравнением с а = / +
+ 1 — 1/ч и с = 21 + 2. Поэтому решение данного уравнения, конечное при
z = 0, имеет вид
с, (.,
221*
Если х вещественное (то есть энергия Е отрицательная), это решение,
хотя и конечное при z—>0, становится бесконечным при z—>co, еслм
только Г(/+1 — 1/у) не бесконечное. Если 1/к равно положительному
целому п, большему /, то Г (/ -f-1 — 1/х) представляет собой значение гамма-
функции от нуля или от отрицательного целого, равное бесконечности.
Только в этих случаях имеется решение, конечное от г = 0 до г= оо.
Таким образом, допустимые отрицательные значения энергии таковы:
Еп = — (me4Za/2ft2n2), n = Z+l. *+2, Z + 3, ... ;
эти значения были впервые подсчитаны Бором.
Если ч мнимое (ч = ik в случае положительной энергии), то С, конечно
во всей области изменения z для любого вещественного значения А (любого
положительного значения энергии). В этом случае первое (конечное) реше-
решение принимает различные формы:
С, (»*,*) = -
BikzI
?21 +
1 !__i ? /b2z2— 1 =
E.3.79)
5.3. Интегральные представления 593
где
Второе решение, имеющее особенность при z = О, можно записать
в виде
(nI/2)~(n/2ft)
Разложение в ряд около z = 0, показывающее структуру особенности в этой
точке, можно получить из формулы E.3.62).
Другие решения, пригодные для других интересующих нас уравнений,
будут исследованы после постановки задач. Так, например, волновые функ-
функции для параболических и параболических цилиндрических координат
можно выразить через функции F и G. Они будут рассмотрены в гл. 11.
Функции Матье. Мы указали на стр. 550, что интегральное представ-
представление наиболее полезно в случае уравнений с тремя регулярными особыми
точками или с одной регулярной и одной иррегулярной точками. Поэтому
мы не разочаруемся, найдя, что оно не так хорошо применимо к более
сложным уравнениям. Чтобы проиллюстрировать возникающие трудности
и показать, что представление все же приносит некоторую пользу, при-
применим преобразование Лапласа к уравнению Матье (в одной из его алге-
алгебраических форм)
(z2 -1) ф" + *ф' + (Л«*« - Ь) ф = 0. E.3.80)
Легко проверить, что применение преобразования Лапласа даст уравнение
для v (/) того же общего вида:
(г2 + h2) v" + 3tv' - {t2 + b - 1) v = 0.
Таким образом, чтобы решить уравнение для v, требуется столько же
работы, как и для 4; v тоже пропорциональна функции Матье, и наше
интегральное преобразование приводит к интегральному уравнению.
Однако интегральное уравнение может иметь некоторую ценность, так
что стоит его рассмотреть подробнее. Целесообразно изменить шкалу t,
чтобы уравнение для v стало по возможности близким к уравнению для ф.
Положив 'b(z)= I elhlzv(t)dt, получим уравнение для v и присоединенную
билинейную форму следующего вида:
(;2 _ !) v» + з^' + {hH* - Ъ +1) v = 0,
Р {v, eihlz) = - iheihlz {(t* -l)v' + [t- ihz («» - 1)] v].
Если v положить равным / (t)l\fl — t*, то уравнение для / оказывается
тем же самым, что уравнение E.3.80) для ф. Следовательно, можно ска-
сказать, что если / представляет собой решение уравнения Матье E.3.80),
то другим решением того же уравнения будет
$p=i. E-3.81)
38 ф. м. Морс и Г. Фешбах
594 Гл. 5. Обыкновенные дифференциальные уравнения
Если постоянная А и пределы интегрирования выбраны соответственным
образом, то ф может равняться / и мы получаем интегральное уравнение
ДЛЯ ф.
Однако даже в таком виде этот интеграл может нам помочь при ана-
аналитическом продолжении решения, из-за чего нам и нужно интегральное
представление.
Например, решением уравнения E.3.80) (см. стр. 531) для частного
значения b(.= beZm) будет
со
Se2m(h, z) = У. BincosBn<p), z = cos<p.
n=0
Из формулы E.3.81) мы видим, что другим решением уравнения E.3.80)
будет
27Е СО СО
ф (z) = A J е^ ™ * 2 В*п cos BnT) d9 = 2vA 2 (- 1)" BinJin (hz),
0 n=0 n=0
причем мы применили формулу E.3.65) для получения функций Бесселя.
Это особенно интересное и важное соотношение; то, что решение уравне-
уравнения Матье можно выразить в виде ряда по функциям Бесселя, интересно
и само по себе, но то, что числовые коэффициенты ряда равны (с чере-
чередующимися знаками) коэффициентам разложения решения в ряд Фурье,
представляет собой один из тех факторов, которые укрепляют нашу веру
в значительное единство и простоту математики.
Мы могли, конечно, предоставить себе этот приятный сюрприз в пре-
предыдущем параграфе, когда мы говорили о разложении функций Матье
в ряды. Мы могли бы попытаться применить ряды по функциям Бесселя
для решения уравнения E.3.80) (см. стр. 540) и нашли бы, что рекурсив-
рекурсивная формула для коэффициентов е точности та же, что и формула E.2.69)
для коэффициентов ряда Фурье (с чередующимися знаками перед а).
Затем мы сказали бы, что рекуррентные формулы E.3.64) для функций
Бесселя, приводящие к рекурсивной формуле для коэффициентов, тесно
связаны с рекуррентными формулами для тригонометрических функций,
так что для столь симметричного уравнения, каким является уравнение
Матье, рекурсивные формулы оказываются эквивалентными. Так как мы
прождали с демонстрацией этого свойства до настоящего момента (чтобы
лучше познакомиться с функциями Бесселя), то теперь мы предпочли бы
сказать, что тесная интегральная взаимосвязь между тригонометрическими
и бесселевыми функциями, осуществляемая преобразованием Лапласа,
является свойством, порождающим это совпадение. Конечно, эти два
утверждения являются только двумя выражениями одного и того же
общего свойства.
До сих пор мы показали только, что ряд по функциям Бесселя
является решением уравнения E.3.80); мы не показали, как он связан
с функцией Sem (h, z), которая также есть ряд (аналитический при z= ± 1).
Для этого мы перейдем в Se от z = cos <j> к z = ch 6 F = i<p) и затем при-
применим формулы E.2.54), связывающие гиперболические функции с функ-
функциями Гегенбауера
z) = 2 В*п Л Bn6) = |/у 2 B*nT*nh (z).
п=0 п=0
При помощи разложения этого выражения по степеням z и разложения
функции Бесселя также по степеням z можно показать, что оба ряда
5.3. Интегральные представления 595
пропорциональны и потому образуют одно и то же решение. Таким обра-
образом, мы получили аналитическое продолжение решения Se, определенного
при — 1 < z < 1, на интервал 1 < z < со.
Для области 1 < z < со мы предпочтем применять функцию, имеющую
простые асимптотические свойства. Пользуясь асимптотическим поведением,
функций Бесселя E.3.68), определяем
, z) = |/ -I ^ (-1Г BtnJtn{hz)~-^=
n=0
E.3.82)
поскольку 2 ^2n= 1 • ^то асимптотическое выражение имеет место для
1 , 1 гг
аргумента z между —о~7:И ~^"л' к как этоРешение пропорционально
Se%m, то можно найти коэффициент пропорциональности посредством срав-
сравнения значений при любом подходящем значении z. Наиболее подходит
значение z 0 так как
ея р
значение z = 0, так как
% и Seim(A,O) = 2
п=0
Отсюда
2т (Л, г) = (- 1Г Во |/у^^2т (h, z). E.3.83)
Теперь мы в состоянии получить второе решение уравнения E.3.80)
при помощи замены функций Бесселя на функции Неймана
E.3.84У
Это решение имеет особенности при г= ± 1 и является, конечно, неза-
независимым от Se2m и Jeim. Ряд E.3.84) нельзя применять при |z|<l
(на самом деле он не сходится хорошо и для малых значений z, несколько
больших 1), и надо пользоваться различными разложениями. Так как
второе решение в области | z | < 1 редко требуется в физических задачах
(в силу его непериодичности по <р), то мы не будем заниматься этим
вопросом дальше.
Преобразование Лапласа и разделенное волновое уравнение. До про-
продолжения нашего исследования функций Матье и сфероидальных функций
будет полезно для ясности изложения ввести особо важный метод решения
волнового уравнения, который будет широко применяться в последующих
главах. Здесь мы применим его только для выражения новой точки зрения
на преобразование Лапласа, которая даст нам возможность строить новые
интегральные преобразования фактически по нашему желанию. Для этого
мы возвратимся к исследованию разделения переменных для двумерного
волнового уравнения, рассмотренного на стр. 473 — 478.
Если координаты ^ и ?2 являются разделяющими и осуществляют
конформное преобразование плоскости х, у, то уравнению Гельмгольца
можно придать вид
|f ^ 0. E.3.85)
38*
596 Гл. 5. Обыкновенные дифференциальные уравнения
Любое решение уравнения Гельмгольца, разделяющееся по ?1; Е2 на мно-
множители или нет, должно быть решением последнего уравнения. Например,
elkx или J0(kr), если х или г выразить через ?lf ?2, удовлетворяет уравне-
уравнению E.3.85). Если решение окажется разделяющимся в этих координатах
^ = X1{^1)Xi (?2), то Хг и Х2 будут решениями разделенных уравнений
i) ~ «2J Xi = 0, (d2X,/<^) + /c2 [g2 F,) + a2] X2 = 0,
где a2 - константа разделения.
Новым здесь является то, что, как мы можем сейчас показать, каждое
решение уравнения Гелъмголъца является подходящим ядром для инте-
интегрального представления одного из разделенных решений Х1 через другое Х2.
Допустим, что K(z, t) представляет собой решение уравнения Гельмгольца
\2К -\-к2К~ 0, выраженное в координатах (z = ?г, t = ?.2 для избежания
индексов), в которых решения Хи Х2 разделяются. Например, К может
равняться егкх, а разделяющими координатами могут быть полярные коор-
координаты (z = lnr, Z = <p); тогда K = eikrcost. В этом случае К удовлетворяет
уравнению E.3.85)
Если теперь получающаяся при разделении функция Хг(г) удовлетво-
удовлетворяет уравнению
Xz (ZJ = (d^Xjdz2) + k* (gl - a2) Хг = 0,
то можно применить интегральное представление Хг(г) = \ К (z, t) v(t)dt.
Действительно,
Xz (К) = М, (К) = - d*K/dt* - k? [g2 @ + a2] K
и в силу отсутствия члена с первой производной и того, что вторая про-
производная не имеет множителя, зависящего от t, сопряженный оператор
o/Ht = vM,. Поэтому уравнение для v
d*v/dt* + k2 [g2 (t) + a2] v = 0
есть как раз уравнение, которому удовлетворяет другой, получающийся
при разделении множитель Х2, образующий вместе с Хг решение уравне-
уравнения Гельмгольца.
Таким образом, мы сейчас показали, что если К (z, t) есть любое
решение уравнсзния (V2 + k2) К =0, выраженное в разделяющих координа-
координатах z и t, а X2(t)—решение уравнения, дающего после разделения зави-
зависимость от координаты t, то решзние уравнения, дающего зависимость
от координаты z представим в виде
Хг {z) = ^K (z, t)Xz {t)dt, E.3.86)
a X,(z)X2(<) является разделенным решением уравнения (V2 -\-ki)XlX2 = 0
в координатах z, t. Если функция Х2 проще чем Хг, то мы получаем
интегральное представление более сложной функции через более простую
{если К достаточно простое).
Как первый пример этого возьмем полярные координаты S1 =
р2 = <р, где уравнение E.3.85) приобретает вид [см. E.1.13)]
Решением уравнения (V2 + к2) К = 0 является К — егкх = exp (i/ce-1 cos <p) =
_ eifer cos 9> а решением уравнения для ср-множителя будет cos a<j> (где
5.3. Интегральные представления 597
а — константа разделения). Отсюда решением уравнения для г-множителя
будет
Хг (г) = { eihr cos * cos a? df,
и из формулы E.3.65) мы видим, что если интегрирование производится
от 0 до 2ти. то получается интегральное представление функции Бес-
Бесселя Ja (кг). Вполне разделенное решение для константы разделения а
имеет вид /а (кг) cos ау.
Мы могли, конечно, применить любое из других решений в качестве Х2,
как sin а? или е1а* и т. д., чтобы получить другие представления функций
Бесселя или Неймана. Или же мы могли применить другие волновые реше-
решения в качестве ядра. Или, наконец, мы могли переставить порядок мно-
множителей и выразить тригонометрические функции как интеграл от функ-
функций Бесселя вида
С eift cos 9-e«/a (kez) dz={ eihr c°s *Ja (кг) у,
который, если интегрирование производится от нуля до бесконечности,,
оказывается пропорциональным eia*. Однако выражение простой показа-
показательной функции в виде интеграла Бесселя было бы излишним усердство-
усердствованием.
Переходя к функциям Матье, мы можем воспользоваться координа-
координатами ?6 = ^ — р, Ф = ?2! Данными в формулах E.1.15), где х — d cos 0 cos 9,
у = id s in 6 s in ф. Мы вновь пользуемся ядром eihx = eih cos e cos * (h = kd)
и получаем интегральное представление
Х1 F) = С eih cos оcos *Ха (?) d<p,
где как Xv так и Х2 удовлетворяют уравнению [см. E.2.67)]
(d2X/df) + [b-h2 cos2 <p] X = О,
в котором <р есть либо ф либо 6, а X —либо Хи либо Х2. Здесь мы имеем
полную симметрию, так что если пределы интегрирования и постоянные
множители выбраны соответственно, то Хг = Х2 и вместо интегрального
представления получается интегральное уравнение для X. Из соотноше-
соотношений E.3.81) —E.3.83) мы видим, что решение Se2m (h, cos 6) удовлетворяет
интегральному уравнению
2те
Se2m (A, cos 6) = X2m ^ е* cos"cos *Sein (h, cos 9) d9, E.3.87)
Мы могли бы так же успешно взять е№у = eih sln °sln 9 в качестве ядра. Посред-
Посредством этого возможно показать (см. аналогичный вывод на стр. 595), что
1егт (A, ch (х) = s^lb) ( - 1Г 2 B.2J2n (A sh (x), E.3.88)
где (л = ^ —p = i6.
Значительно более важное и полезное разложение для Je получается
при помощи интегрального представления, ядром которого является функ-
функция Бесселя. Решением уравнения Гельмгольца в полярных координатах
598 Гл. 5. Обыкновенные дифференциальные уравнения
служит функция
Jo (kr) = J0[k ух* + у*) = /0 (ft Vcos2
= Jo у1 у у cos 2e + ? cos 2'f) •
Отсюда другим решением уравнения Матье E.2.67) будет интеграл
o[h у 4"cos 2е+тcos 2? ^ <s'e2m (Л> cos
Он конечен для всех вещественных значений 6, периодичен по 6 и четен
по 6 (то есть его значение не меняется при перемене знака 6). Поэтому
он должен быть пропорционален Se%m(h, cos 6). Таким образом, мы полу-
получили другое интегральное уравнение
2те
?е2т (h, cos G) = v2m ^ Jo (h j/i cos 26 + i- cos 2?j ?e2m (A, cos ?) dT. E.3.89)
Для определения v2m и, что более важно, для построения нового раз-
разложения Je2m мы применим формулу E.3.66) для разложения ядра. Поло-
Л А
жив в E.3.66) <р = 2<р, x = -7rheiB, y= —-^-he-w, получим
0(h |/1
J0(h |/1 cos 26 + | cos 2<p)=
п=—оэ
2т
найдем
комбинируя это с рядом Фурье для Se2m (см. стр. 594), мы в конце концов
Se2m (h, cos 6) =
71=0
Подстановка 6 = 0 дает нам выражение для постоянной
п=0
так как Se.2m(h, 1) = 1.
2те
Можно показать, что \ /2n (h cos 6) d6 = 2~Д Г у J • Из формул E.3.82)
о
и E.3.83), где z = cos6, при помощи интегрирования по 0 получаем
, cos 6) d% = 2тсБ0 =
5
= i [ S
n=0 " n=0
5.3. Интегральные представления 599
откуда мы можем в итоге получить выражение v2rv только через В2п
ею
2 A)пв
n=0
Еще о функциях Матье. Собирая все наши результаты о четных
периодических функциях четного порядка, мы получаем, что угловая
функция имеет вид
Se2m (A, cos <p) — 2 В2п сор Bщ),
п=0
где коэффициенты!?подсчитываютсяметодами, рассмотренными на стр. 531 —
533', и нормируются так, что У] Д> =1. «Радиальными» функциями первого
рода являются
оо
Jp2m ih< c}l f) = -g Ih л 2 ( ~~ If^/sn (h c}l V) =
2Ш ' n=0
Se2m(h,l)Se2m{h,0) 2j
n-0
n=0
-^2(-ir^^d^O^^6"')- E-3-90)
n=0
Подобным образом для второго радиального решения имеем
Ne2m (h, ch,0 = ^^у 2 (- ^"
,^^^). E.3.91)
Второй ряд сходится, только если sh|i>l; третий ряд сходится вполне
удовлетворительно при (л>0. Для нормировки функции Se%m, примененной
здесь нами, Se2m (А, 1) = Y в2п = 1, а ?е2т (А, 0) = ^. ( - 1)пВ2п, но формулы
записаны так, что они справедливы при любой нормировке.
Чтобы удовлетворить граничным условиям, часто бывает важно знать
значения обепх функций Уе и /Ve, а также их производных при р- = 0
(что соответствует предельному эллиптическому цилиндру, то есть полосе
ширины d = h/k). Для первого решения можно легко найти, что прир. = 0
Je2n (h, ch ^ = (- l)m j/\ Z(_^nBgn , ^ Je2m (A, chp) = 0.
Для получения производной от Ne, мы применяем значение определителя
600 Гл. 5. Обыкновенные дифференциальные уравнения
Вронского
Д (Je, Ne) = /e2m ^ Ne2m - Neim -jL Je2m = 1,
в чем легко убедиться при помощи асимптотического вида Je и Ne. Так
как при р. = 0 второй член равен нулю,* то значение производной от Ne
при }i = 0 должно равняться обратному значению Je.
Найти значение Ne при р. = 0 труднее, так как надо пользоваться
разложением функции Неймана около начала координат. Наиболее прямой
метод состоит в применении значений / и N в довольно хорошо сходя-
сходящемся разложении
оо
п=0
Другой метод основан на том, что, согласно стр. 534, Ne2m представляет
собой линейную комбинацию Seim и второго решения Fe2m> определенного
формулой E.2.79). Сравнивая значения функций и их производных при
^ = 0, получаем соотношение
Ne2m (h, ch ,1) ,= [ (-1™) ?^L 2 ( - l)nB2n ] Fe2m (h, ch v) +
n
+ [Ne2m (h, 1)] Seim (h, ch ц), E.3.92)
которое показывает поведение решения вблизи р = 0.
До сих пор мы рассматривали только четные функции Матье,
Sen функции, связанные с ними. Имеются также нечетные решения для
различных значений константы разделения (b=bo,n). Анализ этих решений
проходит аналогичным путем с небольшими изменениями из-за перемены
характера симметрии. Например, мы не можем пользоваться тем же
интегральным уравнением E.3.89), так как интеграл по синусоидальному
ряду был бы равен нулю. Возвращаясь к формуле E.3.81), заметим, что
если F (t) есть решение уравнения Матье, то
ih2tF {t) dt
также является решением. Заменяя z = ch[i., ? = cos<p и интегрируя один
раз по частям, имеем (например, для нечетных значений т):
ОЭ 27С
Jo2mtl (h, ch р) = A sh [i ^ B-2n*i \ sin ?eih sh "¦cosф sin Bn + 1)9 d'f —
n=0 0
= ( тИ1'111 2 ^2n+il2"+1 B« + 1)/2mi (h ch p)-
rv=O
Дальнейшие преобразования проводятся до конца с аналогичными заме-
заменами и дают
n=0
5.3. Интегральные представления 604
o) ^
n=0
где So' представляет собой производную от So (h cos <р) по <р.
Второе решение No строится аналогичным образом. Так как первое
решение Jo имеет нулевое значение для р. = 0, то при этом величина No-
связана с производной от Jo при помощи определителя Вронского. Про-
Производную от No при р. = 0 можно вычислить посредством ряда из произ-
произведений бесселевых функций
No2m+1(h, _
п=0
как было указано для значения функций Ne.
Возможно ввести также функции Матье третьего рода, подобно
функциям Ганкеля, комбинируя функции первого и второго рода. Например,
Не2п (h,z) = Je2n {h, z) + iNe2n (h, z) = j/-J ^ (- if-mB2nH2n (hz)
n=0
и т. д. Однако дальнейшее исследование специальных свойств функций
Матье лучше отложить до последующей главы, когда наша техника будет
более развита, а в этих функциях будет более непосредственная надобность.
Сфероидальные волновые функции. Более общее уравнение
(г2 - 1) <!>" -}- 2 (а + 1) гф' + (u2z2 - Ь) ф = 0
получается в случае сфероидальцых координат. Если, например, взять
вытянутые сфероидальные координаты р., г>, <р, то после разделения полу-
получатся уравнения:
2Ф
Решая первое уравнение, мы получаем, что если решение должно быть
периодическое по координате <р, то т должно быть целым. Если во вто-
втором уравнении подставить cos& = z, «S = sin7" & - ф (z) или в третьем
chp. = z, i? = shm[j.-(J)(z), то уравнение для ф будет иметь вид E.2.66),
повторенный выше, причем а равно целому т.
На стр. 538 и 541 мы рассмотрели вопрос о возможности решения
этого уравнения при помощи ряда по функциям Гегенбауера. Мы указали,
что решение можно записать в виде
Sml (A, z) = A - г2)'"'2 2 d.2nT?n (z), E.3.95)
no
602 Гл. б. Обыкновенные дифференциальные уравнения
если I четное целое. Если / нечетное, то суммируются d2n+1T2n+i (z).
Соответствующие значения константы разделения, при которых S конечна
на отрезке —l<z< 1, обозначаются через Ът1. Нормировка коэффициен-
коэффициентов d такова, что Sml имеет то же значение или ту же производную при
z=»l, что Tf_m{z). Например, если т = 0, то мы требуем, чтобы Sol(h, 1) =
= У?A) = />,A) = 1, так что для m = 0jXn = l или 2d2n+1=l.
тг п
«Радиальные» решения, аналогичные функциям Je, Jo для эллипти-
эллиптического цилиндрического случая, получаются при помощи применения
интеграла E.3.67) вместе с интегральным уравнением для этих функций
(которое можно получить посредством преобразования Лапласа или при
помощи метода стр. 595 — 599)
ф (ft, z) = A (z2 - l)m/2 ^ &™ A - i2)m/2 / (t) dt.
Если f(t) есть решение уравнения E.2.66) для а — т, то ф также является
решением того же уравнения. Далее, для а = т формулу E.3.67) можно
переписать
Bn)l (hz)'n
где ]\(х)=ут./2х7 . i (x) — сферическая функция Бесселя, упомянутая на
2
стр. 582. Комбинируя эти две формулы и подставляя вместо / (t) ряд
для Smi (h, t), можно показать, что решением «радиального» уравнения
при b=--bml будет
jeml (h, с/г р) =
тг=О
[4] E-3-96)
Второе решение neml (/г, cli ;л) можно получить посредством подстановки
ит+2п(^сЬ^)> вместо /m+2n(^ch(a), где и — сферическая функция Бесселя,
определенная на стр. 582.
Для этих функций можно получить также интегральные уравнения
с функциями Бесселя, но будет легче исследовать эти функции позже
в книге (гл. 11). Мы закончим этот параграф рассмотрением дрзтих типов
интегральных представлений, которые иногда оказываются полезными.
Ядра, являющиеся функциями от zt. Мы уже рассмотрели свойства
ядра ezt, связанного с преобразованием Лапласа. Однако любое ядро вида
К (zt) обладает тем свойством, что zdK/dz = tdK/dt. Это само по себе
не особенно полезно, но если К (w) удовлетворяет дифференциальному
уравнению
где Л [w (d/dw)] — сравнительно простой дифференциальный оператор, то
мы можем использовать К как ядро для некоторых интегральных пред-
5.3. Интегральные представления 603
ставлений. Покажем эту технику на нескольких примерах.
Функция Бесселя /v (w) удовлетворяет уравнению
Следовательно, любое уравнение вида
можно решить при помощи подстановки <1>= \ Jy(zt)v (t)dt, так как опера-
оператор Xz, действуя на Jy(zt), дает
Выражение в квадратных скобках как раз равно —/v(o>), так что
^z ( \ JJ> dt\= V о#( (/v) w cfr, где е.#( (/v) = at (d/dt) /v + (аи — /2) ./v.
Сопряженный оператор порождает уравнение
ВМ1 (о) = — (d/d«) (а«о) + [сф. — f2] о = 0,
имеющее решение v (t) = А^'1е'1212а, и присоединенную билинейную форму
Поэтому решением уравнения E.3.97) будет
со
ф(г) =А ^ t'-4-l^-aJ^{tz)dt, E.3.98)
если только Rep. + Rev>0. Это решение представляет некоторый интерес,
так как волновое уравнение в параболических координатах, которое можно
записать в виде
обладает решением
со
F = Ае-&* [ tW^e-W^Jv (tz) dt. E.3.99)
о
Наконец, уравнение
имеющее три регулярные особые точки при z = 0 и ±1 и одну иррегу
лярную точку на бесконечности, также обладает решением вида
(]>(z)=^ J^{zt)v{t)dt.
В этом случае оператор сМ (J) имеет вид
а сопряженное уравнение
604 Гл. 5. Обыкновенные дифференциальные уравнения
вновь связано с уравнением Бесселя, обладая решением A/1I^A). При-
Присоединенная билинейная форма равна
Р (/v> V) = J-i (%t) /p. (t) + -7- [tJv (zt) /p. (t)] — 2/v (Zt) -г- [i/,j. (Z)],
и если только Rep.+ Rev>— 1, можем получить
со
т I \ г , \ dt
О
Как известно, эта величина имеет разрыв при z = 1.
Имеется много других интегральных представлений, играющих неко-
некоторую роль в совсем специальных случаях, но мало пригодных к любому
другому уравнению. Такие решения обычно находятся в результате проб
и ошибок или «нюхом». Во всяком случае, было бы мало смысла тратить
время на их каталогизацию или на указание рецептов, когда их надо
применять. Мы рассмотрели здесь наиболее полезные преобразования,
а прочие можно отыскать в специальной литературе.
Задачи к главе 5
5.1. Построить уравнение Гельмгольца в конических координатах
и разделить переменные. Какой вид имеют координатные поверхности?
В каких физических задачах это уравнение было бы полезным?
5.2. Построить уравнение Лапласа в бисферических координатах
и разделить переменные. Показать, что постоянная к\ для уравне-
уравнения E.1.47) равна -г и что R = (x2 + y2) '4.
5.3. Построить уравнение Шредингера для электрона в двухатомной
молекуле в вытянутых сфероидальных координатах
5 = К + r2)/a, tj = (гг — r2)/a, w =
где гх представляет собой расстояние от одного ядра, а г2 — от другого,
причем ядра предполагаются расположенными в точках z=±ya> х = у = 0.
Выразить х, у, z через ?, т\, <р, получить коэффициенты Ламе; построить
уравнение Шредингера и определитель Штеккеля. Показать, что для
потенциальной функции —cJr-^ — cJr^ уравнение Шредингера разделяется.
Получить разделенные уравнения.
5.4. Показательные координаты задачи 1.9 имеют вид
t = ln(x2 + y2) — z, тг] = у(ж2 + у2) + г, <p = arctg{y/x).
Набросать гповерхности, найти коэффициенты Ламе, построить волно-
волновое уравнение и показать что оно не разделяется.
5.5. Гиперболоидальные координатьГЪпределяются уравнениями
Набросать некоторые из координатных поверхностей, подсчитать коэффи-
коэффициенты Ламе, построить волновое уравнение и показать, что оно не
разделяется.
Задачи к главе 6 605
5.6. Координаты вращения характеризуются наличием оси симметрии
вращения (например, оси х); они имеют вид Х(г, х), ;л(г, а;)
и <р = arctg(z/?/) (г2 = ?/2 + z2). ф-Множитель, если Ф отделяется, равен sin ?щ
или cos /?г<р, и если положить решение ф трехмерного уравнения Лапласа
равным eiirr"PJ& (г, х)/г, то уравнение для Ф имеет вид
1-Я!»
Эж2 ^ Sr2
Исследовать разделимость этого уравнения в координатах X и р. следующим
образом. Положить z = x-\-ir и т = ^-\-щ, так что z будет функцией до,
и наоборот. Воспользоваться техникой, примененной в уравнении E.1.6)
и далее, чтобы показать, что требование равенства \z'\2/r2~ — 4z'z'/(z — zJ
выражению /(X) + g([i) приводит к уравнению
2zG -\-~z2H = F+ 2zG + z2#,
где
F = (l/z') (z'"z2+6z'8-6z"z'z),
G = 3z" — (z'"z/z'), Я = z'Vz',
a z' = dz/dw и т. д. Показать, что наиболее общее решение этого уравне-
уравнения получается при
что в конце концов приводит к решению
(dz/dwJ — а0 -f- axz -f- a2z2 -f- aszs -f a4z4.
Решить это уравнение для различных видов систем координат iz(w),
допускающих разделение X, ^.-части уравнения Лапласа
Показать, что в случае z — w получается обычная цилиндрическая система
координат: z'2 = z, z ¦-=-у-до2 — параболическая система; z' = z, z = ew — сфе-
сферическая система; г'2 = z2 ± 1—две сфероидальные системы; z' = l±z2 —
бисферическая и тороидальная системы координат. Набросать системы
координат, соответствующие z'2 = z3 и z'~z2.
5.7. Для координат вращения, рассмотренных в задаче 5.6, исследовать
случай z'2 = аA — z2) A — k2z2), что дает z== a sn(w, к) [см. формулу D.5.74)].
Набросать на плоскости z = x-\-ir для к = 0,6 достаточное число коорди-
координатных линий Х= const, fi = const, чтобы указать строение системы.
Построить X, ц-часть уравнения Лапласа и разделить в ней переменные.
Для каких физических задач была бы эта система координат полезной?
5.8. Провести анализ системы координат вращения (см. задачу 5.6),
соответствующей соотношению z = acn(w,k) (z = x-\-ir, до = Х+1'р.).
Набросать вид координатных линий X, р. = const на плоскости z. Разделить
уравнение Лапласа в этих координатах. В какой физической ситуации
была бы эта система полезной? [См. формулу D.5.77) для определения сп].
5.9. Провести анализ системы координат вращения (см. задачу 5.6),
соответствующей соотношению z = a dn (w, к) (z = x+ ir, до = X + ip) [см. фор-
формулу D.5.77)J. Набросать систему координат, разделить уравнение Лап-
606 Гл. 5. Обыкновенные дифференциальные уравнения
ласа и указать физическую ситуацию, в которой эта система была бы
подходящей.
5.10. Построить уравнение Лапласа в полярных координатах г, <р
и разделить их. Найти основную фундаментальную систему решений полу-
полученных двух уравнений около точек г = а, <р = 0.
5.11. Уравнение Шредингера для электрона в одномерном потенциаль-
потенциальном поле V = (h2/2M)x2 имеет вид ф" + (А-ж2)ф = 0, где /c = 2MW/ft2.
Одно решение этого уравнения при /с=1 равно фх = ехрГ —^-х2 J. Найти
фундаментальную систему решений около ж = 0.
5.12. Найти общее решение уравнения
(d2tydx2) — F/а?2) ф = ж In х.
5.13. Одним из решений уравнения Лежандра
служит ф = х. Найти фундаментальную систему около х = 0. Каков опре-
определитель Вронского для этой системы? Какое решение имеет значение 2
при х— 1? Какие решения имеют значение 2 при ж = 0? Почему ответ
однозначен в одном случае, но не в другом?
5.14. Уравнение Ламе имеет вид
определить местонахождение особых точек этого уравнения и указать
индексы решений в каждой точке. Какова фундаментальная система реше-
решений вблизи z = 0? Чему равен определитель Вронского для этой системы?
5.15. Показать, что единственная особая точка уравнения
ф' — 2агф' + [E + 2bcz — (а2 — в2) z2] ф = 0
— это иррегулярная точка при z—>со. Показать, что если положить
ф = exp(az-f ftzz)F(z) и согласовать значения аир, то для F получится
уравнение, на основании которого можно разложить F в ряд около
z—> со. Выписать три члена этого ряда. Записать уравнение, имеющее
только иррегулярную особую точку на бесконечности, для которого реше-
решением будет ф = exp (az + |3z2 + yz3) ^ (z)> гДе G (z) ~ РОД виДа ao zS + «iZs+1 + • • •
Сравнить это уравнение с предыдущим и с уравнением ф" + /с2ф = 0, также
имеющим особую точку при z —> со. Что можно высказать относительно
классификации иррегулярных особых точек?
5.16. В уравнении E.2.26) с одной лишь регулярной особой точкой
сумма показателей двух решений около этой точки равна — 1. Для урав-
уравнения с двумя регулярными особыми точками E.2.28) сумма показателей
решений около одной точки плюс их сумма для решений около другой
точки Х + р,—X —(х равна нулю. Каково соответствующее утверждение отно-
относительно уравнения E.2.36) с тремя регулярными особыми точками? Какой
вид имеет уравнение с четырьмя регулярными особыми точками без ирре-
иррегулярных точек и каково соответствующее утверждение? По индукции,
чему равна сумма показателей около всех особых точек для уравнения
с iV регулярными точками, но без иррегулярных точек?
Задачи к главе 5 607
5.17. Показать, что решением уравнения
является функция
ф = A—ехJ е 2 ^(a,6|c|e*).
Для каких значений а, Ъ и с гипергеометрический ряд является конечным
многочленом и ф конечно в области 0<ж<со?
5.18. Построить одномерное уравнение Шредингера для частицы массы М
в потенциальном поле—(%2А2/2М) sech2 {x/d). Заменив независимое пере-
1 1
менное на z = y + у th(x/d), показать, что получающееся уравнение отно-
относительно z имеет три регулярные особые точки. Выразить решения этого
уравнения через гипергеометрические функции z. Какое решение остается
конечным при х~>— со? Найти значения энергии, для которых это реше-
решение представляет собой конечный многочлен относительно z. Рудет ли
это решение конечным при z —> со ?
— с -— z —
5.19. Показать, что уравнение для <]>(ж) = (г2 е 2 /}fz')F(a\c\ z),
где z — функция ж, имеет вид
причем z' = dz/dx и т. д. Показать, что уравнение для
ф (х) = z~*c A -?)"а" (о+ь-с+1) (Z')-T /¦ (в, 61 с | я)
таково:
Каков вид этих уравнений при z = ж"? При z = е~х?
5.20. Разделить переменные в уравнении Гельмгольца для сфериче-
сферических координат и показать, что радиальное уравнение, где x = kr
1 d (^dit-\ rt n(n+1I _Q
имеет решения jn (x) = ]/ iz/2z J i (x), nn (x) = |Лг/2ж iV i_(x). Показать,
n+— n+—
что решением этого уравнения является функция
Показать, что она имеет асимптотический вид eix/in+1x и потому hn = fn -f- mn.
5.21. Построить уравнение Шредингера в сферических координатах
г, Ь, ср для электрона в потенциальном поле V = — e2Z/r. Разделить пере-
переменные и показать, что решение радиального уравнения можно выразить
608 Гл. S. Обыкновенные дифференциальные уравнения
через вырожденную гипергеометрическую функцию. Найти два асимпто-
асимптотических ряда для решения, независимого от Ь и <р. Найти, при каких
значениях энергии асимптотические ряды обрываются и превращаются
в конечные многочлены (в этом случае ряд не является асимптотическим,
а дает точное решение). Для каких энергий это решение конечно для
всех значений г@<г<оо)?
5.22. Каков асимптотический ряд около z = со для сфероидального
уравнения
Каков асимптотический ряд около z = 0 для уравнения
ф" + B/z) ф' + [(o/z«) - F/z6)] ф = 0?
5.23. Очень близким выражением для потенциала электронов прово-
проводимости в металлической решетке является
у" )
Показать, что все разделенные уравнения имеют вид уравнения Матье
E.2.67), в котором /г2 = l'2U0/n2, а Ь пропорционально энергии электрона.
Применяя формулу E.2.71), подсчитать значения фазового множителя s
для /г=1 и 6=0,3, 0,469, 1,0, 1,242 и 1,5. Какие из этих значений b
приводят к допустимому решению (конечному при —оо<;;к<.оо)?
5.24. Применяя формулу E.2.77) и дальнейшие формулы, подсчитать Ье0
и коэффициенты Фурье функции Se0 (/г, cos 9) для h = 2.
5.25. Построить уравнение Гельмгольца в вытянутых сфероидальных
координатах (VIII) и показать, что если решение независимо от Е3, то
уравнения для ?,- и ?2~М1ЮЖИтелей имеют вид
(ж2 -1) ф" + 2х<Ъ' + {h2x2 - b) ф = 0.
Исследовать особые точки этого уравнения и построить трехчленную
рекурсивную формулу для коэффициентов разложения в ряд около а: = 0.
Указать равенство, связывающее с помощью непрерывных дробей b и а,
которое должно выполняться, чтобы ряд сходился при х — ±: 1 (отрица-
(отрицательные степени х отсутствуют, а ряд должен сходиться) для решения,
имеющего нулевую производную при ж = 0 для Л=1.
5.26. Разложить решение уравнения задачи 5.25 по сферическим
гармоникам Рп (х) (см. стр. 539) и получить трехчленную рекурсивную
формулу для коэффициентов. Получить из нее соотношение, связывающее
с помощью непрерывных дробей h2 и а. Решить его относительно b для
7г=1 и провести сравнение с результатами задачи 5.25.
5.27. Применив преобразование Лапласа, показать, что решение
уравнения
где Dfy = dydx, D^ = d2'b/dx2, и т. д., а / и F представляют собой конеч-
конечные многочлены по степеням D, имеет вид
ь
ф= \ exp {zt+ J [F(t)/f(t)]dt} [dtlf(t)\.
Задачи к главе 609
где а и b выбраны так, что
для всех значений х. Применить эту формулу для подсчета интегрального
представления вырожденной гипергеометрической функции.
5.28. Показать, что решение уравнения
z (z — 1) (z — a) ф" - (а — 1) z Bz — а) ф' + <* (а - 1) (z + 1) ф = 0
имеет вид
ф = А ^ (z -*)"(*-1)»—»-1 (г - а)Р-а?+а-
где р = (а — 1)/(а — 1)» Каковы должны быть пределы интегрирования, чтобы
ф было решением? Какой выбор пределов и А дает решение, равное
единице при z = 0? Каково поведение этого решения вблизи трех осталь-
остальных особых точек?
5.29. Показать, что решением уравнения
(<Г-1фА2гп-1)-гф = а
будет
п— 1 со
ф = 2 AseZnis'n { exp [zte2nUin — (t"/n)] dt,
s=0 0
где
s=0
5.30. Показать, что решением уравнения
будет
ОО j
С — —-1
ф= \ sin (z/к) е 2
о
о
5.31. Взяв определение гамма-функции и заменяя переменные инте-
интегрирования, показать, что
1
Г (р) T(q)=T(p + q)\ и*'* A -нГ1 du =
I
- _
Л
С
;
S111 71J3 S1I1 71$ Л
С
где контур С подобен показанному на рис. 5.7, но обходит точки 0 и 1
(где подинтегральная функция вещественна?). Разложить F(a, b\c\z) около
z = 0, воспользоваться последней формулой для замены Г (Ь + п)/Г (с + п)
в ряде (полагая р = b-\-n, q = с — 6) и получить, таким образом, ряд по
(mz)" внутри контурного интеграла. Показать, что этот ряд можно просум-
просуммировать и в конце концов получить
F (а, Ъ I с | z) = г(с>ГA-Ь) ic р мь-1 A _ ц)с-ь-1 ^ _ MZx-a dM
4 I ' ' 4тс sin тс (с — Ь) Л
с
39 Ф. М. Морс и Г. Фешбах
610 Гл. 5. Обыкновенные дифференциальные уравнения
Показать, что эта формула равносильна первой части соотношений E.3.16).
5.32. Применяя преобразование Эйлера, показать, что решением
уравнения
A — z2) ф" - 2гф'+ [п (п + 1) - /и2/A - z2)] ф = О
является присоединенная функция Лежандра (п, т не обязательно целые)
где контур проходит как вокруг +1, так и вокруг z в положительном
направлении. При помощи изменения переменной интегрирования пока-
показать, что
1[z+(z2 - ^ *г cos м
о
Показать, что эта функция равна функции, определенной формулой E.3.36).
Показать, что эти функции входят во все потенциальные и волновые
задачи в сферических координатах.
5.33. При помощи формулы E.3.33) и дальнейших формул показать,
что для п целого
<?п (*) = -§•*» (*) 1П [A + Z)/A - Z)] - W^! (Z),
где Wn_1(z) — многочлен относительно z степени п — 1. Отсюда вывести
что если х вещественное между — 1 и -\-1, то
lim [Qn (x + ie)-Qn(x-i в)] = шРп (х).
5.34. При помощи теоремы Коши показать, что
гл i ч 1 Г ? Qn (oO dw С Qn {w) dw и
Л/ (z) ^= т;—: I CD (D I ,
xn\ / 2t^i [_ J ш—z J ш—z J
C* C,
где контур Сх содержит точки w = ± 1 внутри, а точку а> = z вне себя,
а контур С2 представляет собой окружность радиуса R > \z\ и 1. Показать,
что интеграл по С2 равен нулю, если п = 0 или целому положительному.
Привести контур Сх к обходу вплотную к отрезку между +1 и при
помощи второго результата задачи 5.33 показать, что
пч ' Z — W
1
5.35. Показать, что полиномы Wn_1(z) задачи 5.33 равны
^ (> Р (Z> + ^(z) + ^ W
-з
5.36. Можно определить второе решение гипергеометрического уравне
ния около z = 0, как
Задачи к главе 6 611
Показать, что оно равно
sin л (с—a) sin л (с—b) + sin -на sin тсЬ „ , , ¦ i \ .
sinTc(c—a)sinTc(c—b)—sin iza sin ъЪ * ' II'1
2nz1~<: sin тсс Г (с) Г (с — 1) F(a — с + 1, Ь — с + 11 2 — с | z)
"¦ sin тс (с — a) sin тс (с — Ь) — sin тса sin тсб Г (а) Г {Ь) Г (с — а) Г (с — Ь)
Показать, что предельным видом этой функции при с —> 1 является ряд,,
приведенный на стр. 624.
5.37. Доказать, что
Лп (z) = 9"^ \ е" cos " cos mudu-
\ р iz cos и
— 2тс;п ) е
5.38. Найти асимптотический ряд для функции Уиттекера U2(a\c\z).
Из него при помощи формулы E.3.3) получить соотношение
.
Каков точный вид контура? Повторяя процесс, примененный к выводу
формулы E.3.5), получить формулу E.3.58) (исследовать пределы схо-
сходимости при каждом шаге).
5.39. Показать, что радиальный множитель для решений уравнения
Гельмгольца в полярных, сферических и конических координатах удовле-
удовлетворяет уравнению Бесселя
dz J
Определить местонахождение особых точек и описать их; составить три
первых члена разложения в ряд решения /v. регулярного при 2 = 0 около
каждой особой точки. При помощи преобразования Лапласа вывести
интегральное представление E.3.53). Показать, что вторым решением этого
уравнения является
7V\ (z) = ctg xk• Jx (z) — cosec ^-J_\ (z).
Подсчитать первые три члена разложения Nx в ряд (для X не целого);
около z = 0 и первые три члена асимптотического разложения этой
функции. Показать, что для Х = 0
ТП=1 8=1
5.40. Показать, что решение уравнения Шредингера в параболических
Л Я
координатах ж = У^Хр. cos <p, у = l/Xp. sin <p, z = у (X — р.), г = -у (X + fi) для час-
частицы массы М при потенциале V = if/г равно
39*
612 Гл. 5. Обыкновенные дифференциальные уравнения
где о + г= —iMyf/h2k и к2 = 2ME/h2 = (Mv/hJ. Показать, что при
т = 0, о=—g- и N — Г A — i rf/hv) e7"<2/2m> решение имеет асимптотиче-
'СКИЙ ВИД
ф ~ exp [ikz — i (vf/Kv) In k (r — z)] +
, ri2expfi(Yi2/?H!) lnfl — z/r) — 2(8]
где Г A — iri2/hv) = | Г | ei6. Исследовать физическое значение этого резуль-
результата и получить закон рассеяния Резерфорда.
5.41. При помощи способа, аналогичного указанному в тексте для
/e2m (h, ch p.), вывести разложения в ряды для «радиальной» функции
Матье
Je2m+1 (Л, ch tx) = |/i* 2 (- 1)"
где Z?2ri+1—коэффициенты ряда Фурье для «угловой» функции ¦S'e2m+1 (h, cos 6),
определенной на стр. 531.
5.42. При помощи преобразования Лапласа показать, что если
со со х
u(s)=[e-stK(t)dt и v (s) = С е-*'<р (г) dt, то /(ж) = ^ К (х- t) y(t) dt,
со
где и (s) v(s)= V е-»'/ (г) df. Отсюда доказать, что
Таблица, разделяющих координат для трех измерений
Система координат определяется соотношениями между прямоуголь-
прямоугольными координатами х, у, z я криволинейными координатами ?lt ?.,, ?3
или при помощи коэффициентов Ламе hn = V (д%/д?п)*+(ду/с)?пJ+(()г/д?пУг
ш т. д., обладающих свойством (см. стр. 34)
dsB = dx2 + dy* + dz2 = 2 /A #„*•
n
Выражения для оператора Лапласа, градиеЕ1та, вихря и т. д. через эти h
приведены в табл. на стр. 116. Стандартное уравнение с частными про-
производными Т2ф + Л:^ф = 0 приобретает вид
2 1 д Г h,hji3 Ц_ Л , 2, _ ft
Таблица разделяющих координат для трех измерений
615
где /Ci = O для уравнения Лапласа, k\ = const для волнового уравнения
и /с? = ег — V (?) для уравнения Шредингера для одной частицы в потен-
потенциальном поле V.
Для разделения величина h-jiji^lh^ должна разлагаться на множители
следующим образом:
hjiji3lh\ = gx F2, &3) /i (&i) и т. д.
Определитель Штеккеля равен
31
32
33
Алгебраическое дополнение iS элемента Фт1 (?т) связано с коэффициентами
Ламе соотношением
где
Отсюда
6Х, 6а) = ФиФая - ф12ф33,
Фтп (€т) 1 У! ф м _>
а также
д.
Поэтому стандартное уравнение с частными производными приобретает вид
а тремя разделенными уравнениями для волнового уравнения (kl = const)
служат [ф = Х1F1)ХвFв)Х3F,)]1
—U-4-1/ (a
= О,
где /c'j и /c| — константы разделения. Уравнение с частными производными
получается при помощи умножения ураваения при т = 1 на (M1/S)X2Xa,
и т. д. для т — 2 и т = 3 с последующим суммированием по т.
Для разделимости уравнения Шредингера потенциал V должен иметь
вид
где fm' зависит только от с,т. Разделенными уравнениями в этом случае
являются
где s2 и е3 — константы разделения.
614
Гл. 5. Обыкновенные дифференциальные уравнения
В следующей таблице приведен список коэффициентов Ламе hm, свя-
связанных с ними функций fm и определителей Штеккеля для 11 различных
разделяющих трехмерных координат для волнового уравнения. Особые
точки трех разделенных уравнений в их каноническом виде также даются.
В отдельных случаях, когда применяются различные шкалы координат,
приводятся различные выражения. Указан также общий вид потенциаль-
потенциальной функции V, для которой уравнение Шредингера разделяется.
I. Прямоугольные координаты
S =
1
0
0
-1
1
0
_ I
0
1
= 1.
Иррегулярная особая точка на бесконечности во всех трех уравнениях.
Общий вид V = u(x)-{~v(y)-{-w(z).
II. Круговые цилиндрическпе координаты (вращения)
Рис. 5.15.
1 -A/© -
О 1/A-© О
О 0 1
Уравнение для ?х: регулярная особая точка в 0, иррегулярная особая
точка на со.
Уравнение для ?2: регулярные особые точки в —1, +1, со.
Уравнение для ?3: иррегулярная особая точка на со.
Общий вид V = и (г) + A/г2) v ((р) + w (z).
III. Эллиптические цилиндрические координаты
d ch tx = -i fo +
ЗЦ, /3 = l,
z, a2 = cos T = (l/2d) (rx - r2) (см. стр. 523)
Таблица разделяющих координат для трех измерений
615
-dz) —1
d2 1/A-SJ -d2
0 0 1
Уравнение для ^ имеет регулярные особые точки в — d, -\-d, иррегу-
иррегулярную особую точку в со.
=5,z=i.o z
г=.5.г=Ю>
РИС. .1.10.
Уравнение для ij2 имеет регулярные особые точки в — 1, +1, ирре-
иррегулярную особую точку в со.
Уравнение для ?3 имеет иррегулярную особую точку и со.
Общий вид V = [u(r1 + r2) + v(r1—r2)]/r1r2+w(z).
IV. Параболические цилиндрические координаты
2*0
=*l.0,z=
Рис. 5.17.
s =
1 -1
Уравнения для ?1; Е2, ?3 имеют иррегулярную особую точку в сю.
Общий вид V = [и I
V. Сферические координаты (вращения)
х = 5 % l/"l и, ?/ = I
616
Гл. S. Обыкновенные дифференциальные уравнения
<P'
r=I.O
и с. 5.18.
0
|-1) 1/E!-1)«
0 l/($23-l)
Уравнение для ^ имеет регулярную особую точку в 0, иррегулярную
особую точку в со.
Уравнения для ?2, ?3 имеют регулярные особые точки в — 1, +1, со.
Общий вид V = u(r) + {l/r2)v(b) + (l/r*sin2b)w(<p).
VI. Конические координаты
г
, a), ?3 = p en (p., P),
Таблица разделяющих координат для трех измерений
617
сп —одна из эллиптических функций, так что
4 a)sn(n,
0 gil
о JX
k, a)dn(p.,
= r en (X, a) сп(ц,
" (a2-
Уравнение для ?х имеет регулярную особую точку в 0, иррегулярную-
особую точку в со.
Уравнение для ?2 имеет регулярные особые точки в fa, ± ф, со.
Уравнение для ?3 имеет регулярные особые точки в ± ia-, НЬ Р, оо.
Общий вид V = и (г) + [v (а2) + w (?3)]/F1 + Щ.
VII. Параболические координаты (вращения)
,1-IJD
V=2.0
Рис. 5.20.
Если r2 =
', то 5j =
с __
—z.
i/а2
О О
Уравнения для ?х, 52 имеют регулярную особую точку в 0, иррегу-
иррегулярную особую точку в со.
Уравнение для ?3 имеет регулярные особые точки в — 1, +1, со.
Общий вид V = ^
VIII. Вытянутые сфероидальные координаты (вращения)
618
Гл. 5. Обыкновенные дифференциальные уравнения
4 62 J2 4 Л 62 4 ЛГ\ fc2
( + r) a cose
r2), S3 =
С __.
1
1
1-1
О
¦ F1
A —61) (i — 65) '
Рис. 5.21.
Уравнение для ?,г имеет регулярные особые точки в —d, -\-d, ирре-
иррегулярную особую точку в со.
Уравнение для ?2 имеет регулярные особые точки в —1 и -f 1, ирре-
иррегулярную особую точку в со.
Уравнение для ?3 имеет регулярные особые точки в —1, +1, оо.
Общий вид V = —
IX. Сплющенные сфероидальные координаты (вращения)
Рис. 5.22.
1-
Таблица разделяющих координат для трех измерений
619
s=
1
О
О
Уравнение для ^ имеет регулярные особые точки в — id, -f й/, ирре-
иррегулярную особую точку в со.
Уравнение для ?2 имеет регулярные особые точки в —1, +1, ирре-
иррегулярную особую точку в со.
Уравнение для ?3 имеет регулярные особые точки в — 1, -Ь 1, со.
X. Эллипсоидальные координаты
«г=2.С
Рис. 5.23. «п=Ьжп> а=2Ь.
Ж =
а2 (а2 — Ь2)
6j6j6,
. _ I/(?iZI6|H6|II6i) , _ ./F1-6!) F1-61)
1- У F?-о2) F? -Ь2)' 2~ I7 (?1-а2)(?1-62) '
I, _,/F|-6j)FI-
3"" V №-а*)(Щ~
-g)
= /(?!-в1)й-
.-a')V4-
1 W-
\ '.
1 .-=-
1
F1-Ь«) (а2-Ь2)
Уравнения для ?х, ?2, ?3 имеют регулярные особые точки в
со общий вид г -(д-з^жазмыге*»
, со. иощии вид v
—а, —6,
Fi-6»F!-ej)Fi-6I)
b k'), Z3 =
620
Гл. 6. Обыкновенные дифференциальные уравнения
Ъ = ка, ya2 — bz = k'a = d,
_ jsn (К, к) sn (ц, к') dn (v, к) , сп (ц, к') en (v, к)
сп(Х, к) ' у сп (X, А)
z = a-
n(n, /c')sn(v, к)
XI. Параболоидальные координаты
сп (К, к) '
х, = 2.0
Рис. 5.24.
1 5l
1 — a2) E1 —
Уравнения для ?1( ?2> ^з имеют регулярные особые точки при
О, +а, + Ь. Общий вид V = и ' >2!'^ »" |]+ iz ~ ^
dn (X, А) р , . .,. .
— a, — i
сп (А., А) сп ([х, А)
, snpx, A) en (v, A') _ d |~sn2(X, к) sn2 (ix, A) dn2 (v, .
У ~ сп (X, fc) en (ix, А) ' Z "~ 2 L сп2 (X, А) "" сп2 (|х, А) "* А72"
Таблица разделяющих координат для трех измерений
621
Двумерное уравнение Лапласа разделяется в любой системе коорди-
координат, получающейся конформным преобразованием из прямоугольной си-
системы х, у.
Трехмерное уравнение Лапласа разделяется во всех приведенных
выше 11 системах координат, в которых волновое уравнение разделяется.
Кроме того, решение уравнения Лапласа можно разделить по следующей
формуле:
тогда разделенные уравнения для X можно получить, несколько видоизме-
видоизменяя предыдущие уравнения. Полагаем
Тогда уравнение Лапласа приобретает вид
2_1_1_й_Л dXn \ _ XI 1 1 d / , дН\
hUn /n din Vn dkn J- Zj h\R fn dSnV" dkn ) '
Если правая часть этого уравнения равна —Щ/и,(Ь1г 52.
стоянно. и если
)> гДе
п0"
где iS— определитель Штеккеля, то уравнение приводится к такому, для
которого применима описанная выше техника.
Двумя системами координат, в которых уравнение Лапласа разделяется
в этом смысле, являются бисферическая и тороидальная системы.
Бисферические координаты
х = а?3
z — а
= а V (^
^ - У,
. _^g 2,
622
Гл. 5. Обыкновенные дифференциальные уравнения
S =
1
1
о
о о
1-11
1
й-1) A-ф A—eg) •
Тороидальные координаты
г
Рис. 5.26.
X = t
z —
?х = ch ji, ?a = cos 6, ?3 = cos <p,
1 —1 —l
О
О
О
?f — 1) A —SI) A — Ц) •
Дифференциальные уравнения второго порядка
и их решения
Одна регулярная особая точка (см. стр. 506).
Канонический вид, точка в со:
0 = 0; решения y1(z) = l; y2(z)=z.
Общий вид, точка в а:
~г А — = 0; решения w, = 1; у.? = .
dw*^w—adw i/i ' 1/2 w—я»
Дифференциальные уравнения второго порядка и их решения 623.
Одна иррегулярная особая точка (см. стр. 507).
Канонический вид, точка в с»:
^ — k2y = O; решения ух = &г; y2 = e-hl.
Общий вид, точка в а:
р> + _g_j» *\4 = 0; решения у 1 = <*/<»-«>;
Мы не рассматриваем уравнения с иррегулярной особой точкой выс
шего вида.
Две регулярные особые точки (см. стр. 506).
Канонический вид, точки в 0, с», индексы 0 и — а(а>0):
если а = 0, ?/2 = In z.
Общий вид, точки в а и с, индексы X и \i (\ ф (i):
d^2" (ю-а) (ю-с) do;" (w—aJ(w —
¦^1ГС) ; V^yj^J ' если A==Х. y8
Три регулярные особые точки (см. стр. 508 и 509).
Канонический вид: точки 0, 1, с»; индексы 0, 1 —с (в 0); 0, с — а — Ь
(в 1); a, b (в со) (мы всегда можем считать, что Reol, как для выро-
вырожденной гипергеометрической функции)
z (z — 1) -т-f + [(а 4- b 4-1) z — с] -^ 4- а^У — 0 (гипергеометрическое уравнение)..
Решения yt(a, b\c\z) и yz(a, b\c\z) вблизи особых точек.
Разложение уг в ряд при | z | < 1, справедливое при Re с > 0
о с/ м i \ Г (с) vi Y{a + n)V(b + n)zn , „ ,
у\ = F (а, Ъ | с | z) = г-фУр) 2j Г(с + и)п1 (гипергеометрическии ряд);
эт=0
a\c\z) = (\-z)c-l'hF{c~a, c-b\c\z) =
/•(с, 6|с|1) = Г(с)Г(с-с-6)/[Г(с-с)Г(с-6)],
zf (a, b|c|z) = [(c-l)/(c-b)]/'[(o-l, b\c-l\z)-F(a, b- 1 |c-
/"(o, b[c|z) = [l/(a—b)] ^(a+l, fe|c|z)-W(a, b+l|c|z)],
(d/dz)F(a, b\c\z) = (ab/c)F(a + l, fc+1 |c + 1 jz).
•624 Гл. 5. Обыкновенные дифференциальные уравнения
Вторым решением около z = 0 является zl~cF (а — с + 1, b — с + 11 2 — с | z);
.однако оно не независимо от у\, если с = 1, 2, 3, ... Независимым ре-
дпением для всех значений Re о 1 будет
о ,-, , 7114 sin it (с—a) sin it (с — b) + sin тса sin'rcb p . ,, . . .
w° = G(a, b\c z) = - ) '—. ) ' . : , F(a, b\c\ z)-\-
¦Уг v * II/ smit(c — a)sinit(c—b)— siiiMSinrf ч ' ' '
2tcz1-c sin тссГ (с) Г (с — 1) F (a—c + 1, b— c + l|2 — c\z)
"¦"sinit(c — a) sin л (с — Ь) — sin яо sin-пб Г (а) Г (Ь) Г (с — а) Г (с — Ъ)
Из определения F можно построить ряд для G, за исключением
*=1, 2, 3
Если с целое, при помощи предельного процесса можно показать, что
/~i I 11 л 1 \ 2 sin эта sin тсЬ
Д( bll|)
1 1
— irctgiua + yiuctgTifeJ /"(а,
b + n) v /11 2\»l
""" ?1 Г (в) Г F) [n'J* Zj Уа + г^ b + r r+lj )'
n=0 r=0
Для то = 2, 3, 4, ...
G(a, b\m\z) — : ;—-=т X
v ' ' ' ' —it sin it (a + 6)
f Г i \ 1 1
X -I In z + Y +Ф (a) +Ф (") — ty (m) + "у w ctg ta + -=- it ctg ico
n—1
Г(а)Г(Ь)Г(п+т) л! ^J Vva + '- Ь + r r + 1
r=0
m-l
у Г (а—я) Г (Ь—п) Г (n) Г (w)
Zi Г (а) Г(Ь)Г(т —и)
п=1
Интегральное представление для первого решения около z = <
ioo
Г (я) Г (Ъ) У 2nir (с
где контур проходит слева от точек t = 0, 1, 2, ... и справа от точек
— а, — а — 1, —а —2, ... и — Ь, — Ь—1, — й —2, ... (а, й не могут
¦быть целыми отрицательными).
cIz) = r^nib) \ С - z)^a" (г - 1)С"Ь'1 dt
ИЛИ
если Re с > Re b > 0 и если (для второго представления) fe + 1 не является
вещественным числом, большим единицы. Перестановка букв а и Ь в этих
Дифференциальные уравнения второго порядка и их решения 625
интегралах даст представление ух для Re с > Re а > 0.
Z
y°(a,b\c\z) = rJh^*l°[(z-t)c-b-4b-1(l-t)-adt =
о
= -^J- Г (с) Г A - 6) Г A + 6 - с) z1 § (< - гH-"*"-1 A - f)~° A =
с
ВТТГ1} Г(с)ГA - 6)ГA + 6 - с)**- A - 2)с—" $ («- z)b-V-«-i (I - tf"dt,
где контур С заворачивает как восьмерка, проходя вокруг t = z ъ поло-
положительном направлении (против часовой стрелки), вокруг ( = 0 в положи-
положительном направлении, а затем вокруг t = z ш t = 0 в отрицательном на-
направлении. Представление при помощи контурного интеграла имеет место
для любых значений параметров, если только —с+1, -\-Ь ш с—6 не
целые положительные.
Решения вблизи z = 1 и z = со:
у\ (a, b | с | z) = F (a, b \ а -\- Ъ — с + 1 |1 — z); ряд пригоден для 11 — z | < 1;
yl(a, b\c\z)=(l-z)c-a-hF(c-a, с- Ь\ с- а-Ь+ 111 -z),
однако при а + b — с -\-1 = 1, 2, 3,... надо применять G (а, Ь\а-\- Ь — с+ 111 — z);
у^(а, b | с | z) = z~aF (а, 1 — с-\-а\\ — Ь-\-а\ 1/z); ряд пригоден для | z \ > 1;
yf (a, b\c\z)= z'bF(b, 1— c + fe|l— a-\-b\ 1/z),
1 — b + a
l — a + b
однако для а — b = 1, 2, ... применяется 2~°С (а, 1 — с + а
0 1 2 bb
р (
а при а — й = 0, —1, —2, ... применяется z~bG(b, l—c+b
1/z).
Основные формулы, связывающие решения в виде рядов вокруг одной
и другой особенности, таковы:
zl-cF(a — c+l, fe —c + 1 12 — с | z) =
Следовательно, уравнения перехода, связывающие решения для z
с решениями для z = 1 и оо, имеют вид
о/ Mix Г(с)Г(а + Ь —с) w , , . . , Г (с) Г (с— а — Ь) х , ,
У?(«» Ь|с|г)= Ч(а)Г(Ь) yl(a,b\c\z) + Y(c_a)T(c_byi(a,b\c\z),
п/ .1 I \ T(c)Y(a + b — с) Л, ,|,ч Г (с) Г (с —а —Ь) ,, , , , ч
У«(аb\c\z)= ^\ ;y;(flb|c|g);yi(ablclz)
(а' b I С I Z> = rSrialc} e"irta^ К fe I CI Z> + rSri'-ci *-**& (°. fe I C
ф. М. Морс и Г. Фешбах
626 Гл. 5. Обыкновенные дифференциальные уравнения
[sin тс (с — a) sin % (с — Ь) — sin it a sin %Ъ] у\(а, b \ с \ z) =
= {sin , (с - «) sin . (с - ft) [ 1 + е'« Г Vw+r?-Ц^
+ sinnа sin тсйr|^r((°H^} е~™у? (а, fc | с | z)+
sin»(с- «)sin.(c-ft) [1+ ^Г(^)+гУЛ"С
+ sin ,ш sinTCfc Ig^g~«>| e-inbyf {a,b\c\z).
Одна регулярная и одна иррегулярная особые точки (см. стр. 518
и 567).
Канонический вид: особые точки в 0 (регулярная), в со (иррегуляр-
(иррегулярная), индексы в 0 равны 0 и 1 —с (с>1)
z-p-,-\-(c — ?)-У- — ау = 0, вырожденное гипергеометрическое уравнение.
Если условие Re с >¦ 1 не выполнено, полагаем у = z1~cF; тогда урав-
уравнение для F будет иметь тот же вид, причем вещественная часть нового,
с будет больше единицы.
Решения г/° (а | с | z) и г/" (а | с | z) около z = 0 таковы:
Разложение г/х в ряд около 0, справедливое для конечных \z\:
вырожденный гипергеометрический ряд
zF(a\c\z)=(c-l)[F(a\c-l\z)-F(a-l\c-l\z)],
{d/dz) F(a\c\z) = (а/с) F(a + l\c+l\z).
Разложение уг в ряд около О (G — функция Гордона):
(c) jrjl-cj Г
(a) \.ГA — a) L
sin* (a-c)
sm(na)
Ряд можно построить из приведенного выше определения F, за исключе-
исключением значений с= 1, 2, 3, ...
При помощи предельного процесса (см. стр. 577) «можно показать,
что формула для G при целом с приобретает вид
G(a|l|z)«= —
Если с = п = 2, 3, 4, ...
G(a\n\ z) = ^-sin(ua) |[21nz + u ctgica — m]F (a\ n\z)
Дифференциальные уравнения второго порядка и их решения 627
¦22H
»n=l
Интегральное представление для у\
ico
V
Г (а) ZJ (п —г — 1I Г (г— а + 1) '
г=1
где контур проходит слева от ? = 0, 1, 2, ... , справа от —а, —а—1, ...
Справедливо для а Ф 0, — 1, — 2, ...
= -^-Г(с) ГA - а)Г(а — с + 1)^>ё'ta'1(t-l)caidt, Rec > Rea >0r
с
где контур заворачивает как восьмерка, проходя в положительном па-
правлении вокруг 1 и 0, а затем в отрицательном направлении вокруг
этих точек. Подинтегральная функция вещественна для z вещественного
и t вещественного > 1. Формула справедлива для всех значений а и с,
для которых участвующая гамма-функция аналитична. Асимптотические
выражения для z = | z | е1* > 1, а или с при 0 < <р < -к
t/^a|c|z)_r(e)z г Г(с_а) I z; •
Для других областей изменения ф см. стр. 573 и 575.
Интегральные представления для решения вблизи z = оо (функциш
Уиттекера):
?= U2(a\c\Z) =
Г(в-с + 1) _
о
Первый интеграл имеет место при Re с > Re а, второй— при Re а < 1 и т. д.
Для других значений см. контурные интегралы формул E.3.53) и E.3.56).
Уравнения перехода, связывающие решения около 0 и около оо:
40*-
628 Гл. 5. Обыкновенные дифференциальные уравнения
Я(а\с\г) = Щу?(а\с\г)- F*Wa) yf[a\c\z).
Две иррегулярные особые точки (см. стр. 523 и 597).
Канонический вид, точки в Ои со:
Полагая z = е»*, получаем уравнение Матье
(См. также уравнение для двух регулярных и одной иррегулярной точек.)
Для общих значений а (или Ь) двумя решениями являются
со со
df (b, h, е1?) = eis? 2 ane2in'('' <У(Ь> h> е-^) = е-^ 2 ane~2nif,
П— — CO П=;—СО
причем коэффициенты ап подсчитываются при помощи формул, содержа-
содержащих непрерывные дроби (см. стр. 526).
Если Ъ принимает частные значения, делающие s целым, эти два
решения периодичны и не независимы. В этих периодических случаях
мы пользуемся функциями (называемыми функциями Матье), определен-
определенными следующим образом:
Четные угловые функции около <р = 0; b = be2m или fee2m+1:
оо
Se2m (h, cos <p) = 2 В2п cos 2щ, %В2п*=1,
•Se2m+1 (h, cos 9) = 2 В2„+1 сой Bп + 1) ?, 2 Б2ЭТ+1
эт=0 эт
Нечетные угловые функции около <р = 0; b=bo2m или feo2m+1:
со
6"о2т (/г, cos <р) = 2 ?2п sin 2
+1 (Л, cos <?) = 2 52n+isi
гг=1
sin
где коэффициенты В являются функциями h и различны для различных
Se или So.
Вторыми решениями для тех же значений константы разделения
являются [см. формулу E.2.79)]:
со
Л, /),„, sin
Литература 629
[ 9$е2т*1 (Л> COS 9) + 2 D*n*l S"
гг=0
Y2m + 1 =
Foim (fi, cos 9) = T|m [ 9 ,So2m (A, cos 9) + 2 Anc°s 2"? ] -
0
CO
cos9)+ 2 An+i cos Bn+ 1)9] ,
0
По поводу дальнейших деталей подсчета коэффициентов В ш D см.
стр. 532 и далее. По поводу поведения решений для комплексных значе-
значений 9 см- стр. 594 и далее, а также таблицы в конце гл. 11.
ЛИТЕРАТУРА
Статьи и книги, связанные с проблемой разделения переменных:
В о с he г М., Uber die Reihenentwickelungen der Potentiallheorie, Leipzig, 1894
(диссертация).
E is en hart L. P., Separable Systems of Staeckel, Ann. Math., 35, 284 A934).
Eisenhart L. P., Separable Systems in Euclidean 3-space, Phys. Rev., 45 427
A934).
Eisenhart L. P., Potentials for Which Schroedinger Equations Are Separable,
Phys. Rev., 74, 87 A948).
Michel, Exhaustion of Neumann's Mode of Solution for the Motion of Solids of
Revolution etc., Messenger of Mathematics, 19, 83 A890).
Redheffer R. M., Separation of Laplace's Equation, Massachusetts Institute of
Technology, Cambridge, 1948 (диссертация).
Robertson H. P., Bemerkung uber separierbare Systeme in der Wellenmechanik,
Math. Ann., 98, 749 A927).
Дополнительный материал по решению обыкновенных дифференциальных урав-
уравнений:
Айне Э. Л., Обыкновенные дифференциальные уравнения, ГНТНУ, Харьков, 1939.
Голубев В. В., Лекции по аналитической теории дифференциальных уравнений,
Гостехиздат, М., 1950.
Уиттекер Е. Т. Ватсон F. Н., Курс современного анализа, ГТТИ, Л. — М.,
1933—1934.
Франк Ф., Мизес Р., Дифференциальные и интегральные уравнения математиче-
математической физики, ГТТИ, М. — Л., 1937.
BatemanH., Partial Differential Equations of Mathematical Physics, Cambridge,
New York, 1932.
Forsyth A. R., Theory of Differential Equations, vol. 4, Cambridge, New York, 1880.
Работы, содержащие дальнейшие подробности о специальных функциях, иссле-
исследованных в § 5.2 и 5.3:
Ватсон Г. Н., Теория бесселевых функций, Изд. иностр. лит., М., 1949.
Г об сон Е. В., Теория сферических и эллипсоидальных функций, Изд. иностр.
лит., М., 1952.
Грей Э., Мэтьюз Г. В., Функции Бесселя и их приложения к физике и меха-
механике, Изд. иностр. лит., М., 1949.
Мак-Лахлан Н. В., Теория и приложения функций Матье, Изд. иностр. лит.,
М., 1953.
¦630 Гл. 5. Обыкновенные дифференциальные уравнения
€третт М. Д. О., функции Ламе, Матье и родственные им в физике и технике,
ГНТИУ, Харьков —Киев, 1935.
Klein F., Vorlesungen fiber die hypergeometrische Funktion, Berlin, 1933.
M а с R о Ь е г t Т. М., Spherical Harmonics, London, 1927.
McLachlan N. W., Bessel Functions for Engineers, Oxford, New York, 1934.
Stratton J. A., Morse P. M., Chu L. J., HutnerR. A., Elliptic Cylinder and
Spheroidal Wave Functions, New York, 1941.
Книги, содержащие таблицы формул, связывающих интересующие нас функции,
в дополнение к таблицам о конце глав настоящей работы:
Янке Е., Эмде Ф., Таблицы функций с формулами и кривыми, ГТТИ, М.—Л., 1948.
Madclung E., Mathematische Hilfsmittel des Physikers, Berlin, 1936.
Magnus W., Oberhcttinger F., Formeln und Satze fur die speziellen Funktio-
non der mathcmatischen Physik, 2 Aufl., Berlin, 1948.
ГЛАВА 6
Краевые условия
и собственные функции
Мы уже исследовали методы решения обыкновенных дифференциаль-
дифференциальных уравнений, которые будут встречаться при изучении многих задач
о поведении сплошных сред. Как мы видели, заданием только дифферен-
дифференциального уравнения, которому должно удовлетворять решение, задача
определяется не однозначно, так как каждое уравнение рассмотренного
нами типа имеет бесконечное число решений. Чтобы сделать задачу опре-
определенной, имеющей однозначный ответ, надо из всего множества возмож-
возможных решений выбрать такое, которое обладает некоторыми определенными
свойствами на определенных граничных поверхностях. Любая физическая
задача должна давать не только дифференциальное уравнение, которое
надо решить, но также и краевые условия, которым должно удовлетворять
решение. Удовлетворить краевым условиям часто "так же трудно, как и
решить дифференциальное уравнение.
Первый факт, который надо заметить, состоит в том, что мы не можем
пытаться подчинить решения данного уравнения краевым условиям про-
произвольного вида, мы не должны, так сказать, пытаться «запихнуть правую
ногу в левый башмак». Для каждого типа уравнений, исследованных
в гл. 2, имеется определенная совокупность краевых условий, определяю-
определяющих ответ однозначно, в то время как при условиях другого вида ответ
неоднозначен или невозможен. При этом, конечно, в реальной физической
задаче краевые условия всегда должны быть правильного вида и опреде-
определять ответ однозначно (по крайней мере, так мы все надеемся!), и при
постановке задачи в соответствии с реальной действительностью мы будем
иметь всегда правильные краевые условия для уравнений. Однако не
всегда легко сказать, какие именно краевые условия соответствуют «ре-
«реальной действительности»; поэтому желательно знать, какие условия
подходят для того или иного уравнения; это может дать указание, каким
образом формулировать наши математические задачи, чтобы они возможно
точнее соответствовали физическим.
6.1. Типы уравнений и краевых условий
Рассмотрим сначала двумерный случай, чтобы осветить понятия, не
путаясь в дополнительных усложнениях. Все двумерные уравнения с част-
частными производными для скалярных полей, исследованные в гл. 2 и 3,
а также многие уравнения для компонент векторных полей имеют общий вид
g , у) »*; + €&, y)% = F(X,y; Ф,^!> F.1.1)
причем если уравнение линейно по ф, то F имеет вид
D {х, у) ^ + Е(х, у) g +G (х, у) ф + Н (х, у).
632
Гл. 6. Краевые условия и собственные функции
Это, конечно, наиболее общее линейное уравнение с частными производ-
производными по двум переменным х и у. Эти две координаты могут быть либо
обе пространственными, либо одна пространственной, а другая временной.
Имеется несчетное множество решений этого уравнения; дополнитель-
дополнительные условия, налагаемые в задаче и используемые для выбора одного
подходящего частного решения, называются краевыми условиями. Обычно
они заключаются в указании поведения решения на некоторой граничной
линии (или поверхности в трехмерном случае) или вблизи нее. (С этой
точки зрения начальные условия представляют собой краевые условия во
времени.) Конечно, интересно знать, какой вид могут иметь эти граничные
линии и какое условие должно быть наложено на поле вдоль линии, чтобы
получился однозначный ответ.
Для двумерной задачи решение ф (х, у) можно изобразить при помощи
поверхности z = ty(x, у). Границей является определенная кривая в плос-
плоскости (х, у), а не край поверхности 2 = ф(ж, у), который расположен над
Граница
Граница
Рис. 6.1. Краевые условия для двух измерений.
Поверхность х=ф (ж, у), граничная кривая ж=с (s), y=r, (s); а, и ап—еди-
ап—единичные векторы в плоскости ж, у; а—вектор, касательный к поверхно-
поверхности у границы.
граничной кривой. Граничные условия при этом изображаются высотой ф-
поверхности над граничной кривой и (или) наклоном ф-поверхности в направ-
направлении нормали к граничной кривой (см. рис. 6.1). Край ф-поверхности,
расположенный над граничной кривой (который, вообще говоря, не яв-
является плоской кривой), иногда называется несущей кривой для границы.
Если расстояние вдоль границы от некоторой начальной точки равно .s,
а параметрические уравнения граничной кривой имеют вид х = ? (s), у — rt (s),
то уравнение несущей кривой записывается в виде z = ф (?, kj) = ф (&¦)¦
Единичный вектор а(, касательный к границе в ее точке s, равен
idt/ds + jdri/ds, а единичный вектор ап, нормальный к кривой, равен
a(xk= — jdt/ds + idri/ds. Выражения для этих векторов особенно про-
просты потому, что по нашему условию s представляет собой расстояние вдоль
граничной кривой, откуда ~[f(d'?/dsJ-\-(drjdsJ = 1 (почему?). Аксиальный
вектор а„ мы направим (в этом параграфе, но не в гл. 7) внутрь области,- где
ищется решение. Составляющая градиента ф, нормальная к границе в точно
s, выражается через этот вектор и производные от ф так:
где д^/ду и дф/дж берутся в точке x = t(s), y=ri(s). При помощи этих
определений мы можем теперь обозреть различные типы краевых условий.
Типы краевых условий. В каждом случае, конечно, мы должны
указать вид границы. Для двумерного уравнения Лапласа она может пред-
представлять собой замкнутую кривую, для струны (волновое уравнение, вклю-
включающее время и одно пространственное измерение) с закрепленными кон-
6. 1. Типы уравнений и краевых условий 633
цами и с данным начальным состоянием в данный момент времени она
будет открытой U-образной, состоящей из отрезка, параллельного про-
пространственной оси, и двух полупрямых, параллельных оси времени,
и т. д. Как указано на стр. 643, граница называется замкнутой, если она
полностью окружает область, в которой имеется решение (даже если часть
границы расположена на бесконечности), и открытой, если она уходит
в бесконечность и если на части, расположенной на бесконечности, не
ставится граничных условий.
В одномерном случае решение уравнения второго порядка определяется
однозначно, если задать начальные значения решения и его производной.
По аналогии можно было бы ожидать, что если граница параллельна одной
из координатных осей, например оси х, то указание значения на границе
(то есть указание ф (s)) и нормальной составляющей градиента (то есть
указание N (s), в данном случае д^/ду) однозначно определяет решение.
Это, вообще говоря, верно, как будет показано позже, но этот случай
слишком частный, чтобы нас удовлетворить. Часто требуется, чтобы гра-
граница не только не была координатной линией, но могла иметь достаточно
произвольный вид. Не так легко ответить на вопрос, какой должна быть
граница для того, чтобы указание на ней значений решения и его нормаль-
нормальной производной определяло это решение однозначно (тем не менее обычно
это верно, хотя и не очевидно!).
Краевые условия типа, указанного в предыдущем абзаце, состоящие
в" задании решения и его нормальной производной, называются краевыми
условиями Коши, и задача об определении решения, которое им удовлетво-
удовлетворяет, называется задачей Коши. Нас будет интересовать, для какого вида
границы и для каких уравнений задача Коши приводит к однозначному
и приемлемому решению. Указание начального вида и начальной скорости
бесконечной гибкой струны соответствует условиям Коши вдоль линии
t = const. Как мы знаем, это указание определяет решение однозначно.
С другой стороны, если решение строится внутри замкнутой границы,
то можно* ожидать, что условия Коши предъявляют слишком много тре-
требований и могут исключить все решения. Быть может, требуется указать
только значение ф (s) или только нормальную производную N (s) вдоль
границы, чтобы получить однозначный ответ.
Краевые условия, состоящие в задании только значений решения вдоль
границы, называются условиями Дирихле, а условия, при которых указы-
указываются значения только нормальной производной, называются условиями
Неймана. Задача из теории потенциала, скажем, об определении электри-
электрического потенциала внутри системы проводников, потенциалы которых
заданы, соответствует условиям Дирихле. С другой стороны, определение
потенциала скорости жидкости вокруг твердых тел, когда она должна
течь тангенциально к поверхности тел и нормальная составляющая градиента
потенциала равна нулю, приводит к условиям Неймана. Кроме этого,
иногда требуется задание значения некоторой линейной комбинации реше-
решения и его нормальной производной; это одно граничное условие, и оно-
является промежуточным между условиями Дирихле и Неймана.
Для нашей несущей линии, изображенной на рис. 6.1, условиям Коши
соответствует указание не только линии ф (s) — z, но также наклона в нор-
нормальном направлении у края поверхности ф (ж, y) = z. Получается, как
будто вместо несущей линии для ф-поверхности имеется тонкая лента,
изгибы которой задают как высоту ф-поверхности по оси z, так и наклон
ф-поверхности (но не высшие производные). Для условий Дирихле несущая
линия действительно является линией, а не лентой. В случае условий
Неймана лента свободно движется вверх и вниз, задан только «наклон»
этой ленты. Эти условия могут быть однородными, если аф (s) p/V() O
634 Гл. 6. Краевые условия и собственные функции
где а и В заданы и не зависят от s, или неоднородными, если аф (s) -{- QN (s) =
= F(s). Это различие будет проводиться в § 6.3.
Однако сейчас нам надо вернуться к нашему общему уравнению
F.1.1) и рассмотреть, в каком случае условия Коши вдоль кривой x = ?(s),
y = ri(s) приводят к однозначному решению.
Задача Коши и характеристические линии. Чтобы подсчитать ф на
некотором расстоянии от границы, мы можем прибегнуть к помощи дву-
двумерного ряда Тейлора:
где ф и все ее производные в правой части равенства вычислены в гра-
граничной точке (?, т]). Если все эти частные производные от ф вычислены
на границе, то ф однозначно определяется внутри круга сходимости ряда,
то есть в полосе, примыкающей к граничной линии, причем ширина этой
полосы зависит от природы уравнения и может оказаться бесконечной.
Если мы можем составить правило для подсчета частных производных,
то задача Коши окажется разрешимой. Это делается не так непосред-
непосредственно, как может показаться сначала, потому что нам даны только
уравнение для ф, параметрические уравнения границы и значения ф (s)
и N (s) на границе, и на основании этих данных надо подсчитать всю
бесконечность в квадрате значений частных производных для каждой
точки (?, т;) на границе.
Выразить первые производные через известные величины не очень
трудно. Этих производных всего две, и для них имеется два уравнения,
одно из которых дает заданная нормальная производная N (s), а другое —
скорость изменения известной величины ф (s) вдоль границы:
при ж = е' у = ъ
Так как определитель из коэффициентов (d^/dsJ-Jr(dri/ds)z— ^, то эти
уравнения всегда имеют решение
Однако следующий шаг с целью получения вторых производных не
так прост. Он является также решающим шагом, так как если можно
найти три вторые производные, то, как мы увидим, нахождение высших
производных осуществляется повторением того же вычисления. Теперь,
когда мы решили уравнения для первых производных, мы знаем р и q,
данные формулами F.1.3), как функции параметра s. Два из требуемых
трех уравнений для вторых производных получаются, если выписать
выражение для известной скорости изменения р и q относительно s через
эти вторые производные; третьим уравнением является само дифферен-
6. 1. Типы уравнений и краевых условий 635
циальное уравнение F.1 1), которому ф должна удовлетворять:
92ф _ dp
dl дх*
d? д2ф drj 924) _ dg
Us дх ду ~* ~ds Ijy2 ~~ds '
где A (s) и т. д. представляют собой известные значения коэффициентов
в точке ?(s), rt (s) на границе.
Эти три уравнения можно решить и тем самым найти три частные
производные, за исключением того случая, когда определитель из коэф-
коэффициентов
ds ds °
о dA d3
ds ds
A 2B С
равен нулю. Если определитель Д отличен от нуля, то все высшие част-
частные производные можно найти при помощи последовательных дифферен-
дифференцирований известных величин по расстоянию s вдоль границы и полу-
получающийся ряд Тейлора будет однозначно определять решение внутри не-
некоторой области сходимости. Таким образом, мы показали, что условия
Коши на границе определяют частное решение, если только граница не
такова, что вдоль лее определитель А равен нулю.
Уравнение Д = 0 представляет собой уравнение кривой
С {х, у) dx2 — 2В (х, у) dxdy + A (ж\ у) dy* = 0 F.1.5)
(где мы заменили дифференциалы d?, drk на более обычные dx, dy) или,
лучше сказать, двух семейств кривых, так как левую часть этого уравнения
можно разложить на множители, что даст
B*-AC)dz, Ady= (В-УВ2- AC) dx. F.1.6)
Эти кривые характеризуют уравнение с частными производными F.1.1)
и называются характеристиками этого уравнения. Как будет ниже показано,
если граничная линия окажется совпадающей с одной из них, то задание
условий Коши не будет однозначно определять решение; если граница
пересекает каждую кривую каждого семейства один раз, то условия Коши
вдоль нее будут однозначно определять решение.
Гиперболические уравнения. Чтобы это утверждение было содержа-
содержательным, характеристики обоих семейств должны быть вещественными
кривыми. Это значит, что наше утверждение (в приведенной формулировке)
применимо только к тем уравнениям с частными производными, для ко-
которых В2 (х, у)> А (х, у) С (х, у) всюду. Такие уравнения называются
гиперболическими уравнениями. Волновое уравнение
дх* с2 dt2
является гиперболическим уравнением, если t рассматривать как вторую
координату у. Уравпение B.3.29) для сверхзвукового потока также являет-
является гиперболическим уравнением.
636 Гл. 6. Краевые условия и собственные функции
Для гиперболических уравнений естественная система координат
образуется из двух семейств характеристик, которые вещественны. Инте-
Интегрирование первого из уравнений F.1.6) дает решение Х(ж, у) = const,
интегрирование второго дает |х (х, у) = const, и естественными координа-
координатами являются X и р.. Так как при движении вдоль одной из характери-
характеристик X = const мы имеем (dtydx) dx + (д~к/ду) dy = O (градиент функции X
ортогонален вектору i dx 4- j dy при движении вдоль характеристики
Х = const), то подстановка этого соотношения обратно в уравнение F.1.5)
показывает, что
(рУ + 2В+с(^У = О; F.1.7)
\дх J ' дх ду ' V дУ /
рассматривая другое семейство, получаем аналогичное уравнение для
производных от ц.
Вернемся теперь к исходному уравнению F.1.1) и запишем его в
новых координатах. Например,
9ж2~ d\2\dxj + дкдр дхдх + ду*\
плюс члены с д§/дх и д§[ду. В итоге мы получаем
^ д\ д\>. I дх дх ^ \дх ду ~Т~ ду дх )^ ду ду
Однако первое и третье выражения в квадратных скобках равны нулю, так
как X и р. являются характеристическими функциями уравнения. Если
уравнение однородное, то функцию G можно записать в виде ад§/д~к +
+ &<Эф/дц-|-сф, и выражение во вторых квадратных скобках (отличное
от нуля), а также а, Ъшс можно считать функциями от Х'и (х.
Таким образом мы приходим к нормальной форме гиперболического
уравнения
где Р, Q и R являются функциями от X и (х. Если эти величины Р, Q и
R равны нулю, как это часто бывает (например, для волнового уравнения
в одном пространственном измерении и для уравнения сверхзвукового-
потока), то решение уравнения F.1.8) имеет вид
*?=fW + g(v-), F-1.9)
где / может быть любой функцией от X, a g —любой функцией от [i.
Например, для волнового уравнения \=x — ct и ц=ж+й, так что ф =
= f(x — ct)-\-g(x-\- ct), что соответствует волнам произвольного вида,
распространяющимся в положительном и отрицательном направлении оси
х со скоростью с. Случай, когда Р и Q не равны нулю, мы рассмотрим
на стр. 641.
Итак, мы показали, что решения по крайней мере некоторых гипер-
гиперболических уравнений подобны проходящим волнам, а семейства характе-
характеристик соответствуют фронтам волн. Если нормальный вид уравнения имеет
особенно простую форму
"''=0, F.1.10)
21,
д\х
6. 1. Типы уравнений и краевых условий
637
то могут быть волны произвольного вида с фронтом вдоль X = const и вдоль
(X = Const.
Если граница пересекает оба семейства характеристик (как на первой
части рис. 6.2), то условия Коши однозначно* определяют как /(X), так
и g(n). Каждой точке границы, характеризуемой расстоянием s от начала
отсчета, соответствуют определенные значения X и (х. Указание ф(я) и N (s)
в этой точке дает два уравнения, которые служат для определения как
/, так и g для этой пары значений X и ц. Если граница пересекает кйж-
дую^из обоих семейств характеристик,. то / и g будут указаны для всех
Граница
Граница
Рис. 6.2. Пересечение граничной линией семейств характери-
характеристик для гиперболического уравнения.
значений X и ц и поле будет однозначно определено всюду. Если харак-
характеристики всюду вещественны, а ф (s) и N (s) ограничены и непрерывны,
то будут также ограничены и непрерывны / и g, а потому и ф(ж, у).
Условия Коши и гиперболические уравнения. Мы теперь можем видеть,
почему условия Коши не задают решения, когда граница совпадает с ха-
характеристикой. Если, скажем, граница идет вдоль кривой ц=|*0, то усло-
условия Коши содержат данные о g((x) и о производной от g([i) только при
ц = [i0 и совсем ничего не говорят о поведении g для любого другого (х. В этом
случае /(X) определена, поскольку линия |х = |х0 пересекает все семейство
Х-характеристик, так что значение ф(в) (которое в этом случае можно
записать как ф(Х)) равно /(X). Нормальная производная N (s) определяет
dg/d\>. при (J.= ^o, но никаких высших производных определить нельзя, и
потому g(n) для любых других р. полностью неопределенна. В общем же
случае значения / и g определены только для тех значений X и р., кото-
которые пересекаются граничной линией.
Другим способом это можно выразить так: граница, совпадающая
с характеристикой, проходит вдоль фронта волны. Так как он никогда не
¦соприкасается с любой другой частью волны, проходящей в его направ-
направлении, то он может воздействовать только на волну, проходящую
в противоположном направлении (то есть он может определить только /,
но не g). Теперь должна быть очевидной тесная связь между этими утвер-
утверждениями и рассмотрением на стр. 165 ударных волн, появляющихся при
течении жидкости мимо границы со скоростью, большей скорости звука.
Теперь мы можем также видеть, что случится, если граница завора-
заворачивает так, что она пересекает семейство характеристик дважды, как на
второй части рис. 6.2. В точке P(^t, (X() граница касается характеристики
638 Гл. 6. Краевые условия и собственные функции
(х=(х(; для всех значений |х > ц( граница пересекает [х-характеристику
дважды, а характеристики [х < [х( совсем не пересекаются. Предположим,
что условия Коши заданы на части РА границы. Это определяет /(А) для
А < А, и g(n) для (х>ц(. То, что g(|x) не определена для |х<[х(, несуще-
несущественно, так как эти значения [х лежат вне границы; однако нам надо
знать значения /(А) для А>А(. Они должны быть определены из гранич-
граничных условий вдоль части РВ границы.
Если условия Коши (как ф (s), так и N (s)) заданы вдоль дуги РВ,
то решение будет «переопределенным», так как вдоль этой дуги функция
g((x), определенная из условий Коши на РА, уже фиксирована и при по-
помощи условий на РВ требуется определить только /(X) для А > Х(. Это
можно сделать, если указать либо ф (s), либо N (s) вдоль РВ (или линей-
линейную комбинацию ф и N), но не обе. Следовательно, для РВ достаточны
условия Дирихле или Неймана (или промежуточная комбинация). Конечно,
мы могли бы получить также однозначный ответ, задав условия Коши на
РВ и условия Дирихле или Неймана на РА.
Вообще, можно сказать, что если граница искривлена так, что она
пересекает семейство характеристик дважды, то условия Коши нужны па
части границы с одной стороны от точки, где граница касается характе-
характеристики, а с другой стороны достаточны условия Дирихле или Неймана.
Нетрудно перенести это заключение на случай, когда имеется более одной
точки касания. Например, для U-образной границы условия Коши нужны
вдоль основания U, а вдоль боков достаточны условия Дирихле или Ней-
Неймана; для Z-образной границы подходят условия Коши вдоль верхней инижней
частей Z, а вдоль диагональной части — условия Дирихле или Неймана.
Нетрудно также видеть, что если граница замкнутая, так что каждая
внутренняя характеристика пересекает ее дважды, то условия Коши на
произвольно выбранной конечной части границы, вообще говоря, могут
переопределять решение. Однако не очень легко усмотреть, будут ли до-
достаточны условия Дирихле (или Неймана) вдоль всей границы, и потому
нам придется отложить исследование этого вопроса; мы вернемся к нему
позднее в этой главе.
Быть может, полезно рассмотреть простой случай задачи описанного
типа, чтобы увидеть, как она решается практически. Простейшее гипербо-
гиперболическое уравнение мы имеем в случае гибкой струны, где зависимость
смещения ф струны от х и t определяется уравнением (см. стр. 124)
дх* с2 dt2 ~~
Характеристическими функциями являются А = ж — ct и (х— x-\-ct, в нор-
нормальной форме уравнение имеет вид
= 0,
и решением служит ф = / (X) 4 g (|х).
Задание начального смещения и начальной скорости бесконечной стру-
струны соответствует условиям Коши на простой открытой границе, пересекаю-
пересекающей характеристики только один раз. Если начальная форма струны при
t == 0 есть ф0 (х) ( = ф (s)), а начальная скорость равна Vo (x)(=N (s)), то фун-
функции / и g надо подобрать так, чтобы
и -
6. 1. Типы уравнений и краевых условий 63У
где штрих указывает на дифференцирование по аргументу. Нетрудно видеть,
что
70(w) dw. F.1.11)
Отсюда следует, что решение равно ф(ж, t) = f(x — ct)-\-g (ж-f ct) и состоит
из суммы двух волн, проходящих в противоположных направлениях со
скоростями си —с. Это показано на первой части рис. 6.3.
Если теперь струна закреплена при х — 0, то граница L-образна
и пересекает ^.-характеристики в двух точках. Значения / (X) и g (ц) для
X и ц, больших нуля, получаются при помощи условий Коши, в которых
начальные смещение и скорость заданы на части границы, где t = 0, ж>0;
значение / (X) для X < 0 определяется из условия Дирихле ф = 0 для части
границы х — 0, t > 0. Значения g для (х < 0 не определяются из граничных
условий, но эти значения и не требуются.
f(x-ct).
д(х *ct)
Рис. 6.3. Начальная форма (сплошная линия) и на-
начальная скорость (стрелки) струны.
Последующее движение дается суммой пунктирных линий fug,
движущихся в противоположных направлениях.
Процедура удовлетворения этим граничным условиям состоит в выборе
значения /( — X) в виде «отражения» g(i>), чтобы для любого значения t
обе волны как раз уничтожались при ж = 0. Легко проверить, что началь-
начальному смещению ф0 (х) и начальной скорости Уо (х) отвечает решение ф =
-\-ct), где
1 1 С
8 (v) = у Фо \V) 4" зг \ ^о (w) dw при р. > 0;
о
л
oMd™ при Х<0.
Это показано на второй части рис. 6.3. Мы видим, что значения /(X) для
отрицательных X порождают отраженную волну, получающуюся из [х-волны
отражением от закрепленного конца.
Закреплению обоих концов струны соответствует U-образная граница,
приводящая к периодичности отражений, так как начальные условия
(Коши) на конечном участке струны отражаются сначала от одного конца,
а затем от другого. Для замкнутости границы в этом случае надо было бы
€40 1'л. 6. Краевые условия и собственные функции
задавать «конечные условия» в момент Ц_, как и начальные условия при
.1 = 0. Если мы задаем условия Коши (и смещение, и скорость) при 2 = 0,
то смещение и скорость при t = 1г определяются, и в нашем конечном
условии нельзя задавать произвольные значения фг и F1; чтобы не полу-
получить противоречия. Можно было бы ожидать, что задание ф0 только при
t = 0 и <!>! только при 1~1г (условия Дирихле) определяет решение одно-
однозначно, однако периодическое движение конечной струны опровергает это.
Как известно, такая струна допускает свободные колебания периода 21/пс,
где Z — расстояние между закрепленными концами, а п — любое целое поло-
положительное число. Если tx равно любому кратному какого-нибудь из этих
периодов (то есть произведению любого рационального числа на 21/с), то
струна может испытывать периодическое колебание (любой амплитуды)
такой частоты, чтобы проходить через нуль при ( = 0 и также при t — t^,
такое колебание не проявилось бы в значениях ф ни в начале, ни в конце.
Отсюда мы видим, что условия Дирихле (или Неймана) на замкнутой
границе не определяют однозначно решения этого простого гиперболи-
гиперболического уравнения. В сущности, трудно усмотреть, какой вид граничных
условий на замкнутой границе не переопределяет и не не доопределяет
решение. Однако мы видим также, что замкнутая граница не очень
«естественна» для гиперболического уравнения, так что это затруднение
не должно отвлекать нас.
Волны для нескольких пространственных измерений. Распространение
рассмотренных выше общих понятий на случай нескольких пространствен-
пространственных измерений не очень трудно. В уравнении гиперболического типа
имеется одна координата, которой соответствует член со второй произ-
производной со знаком, противоположным остальным. Это приводит к уравне-
уравнениям для вещественных характеристических поверхностей, которым часто
отвечают волновые поверхности.
В двумерном случае (одно пространственное измерение) возмущение,
возникшее в момент t в точке х, распространяется в обоих направлениях
с конечной скоростью и без изменения своей формы при прохождении
волны. Волна, представленная функцией f(x — ct), движется направо, не
меняя своего вида при перемещении, й аналогично для волны g(x+ct),
идущей налево. Поставим вопрос, будут ли волны, возникающие из возму-
возмущения в точке, распространяться без изменения своего вида при любом
числе измерений.
Как будет показано в гл. 7, возмущение в точке (хг, х2, . .., хп)
«-мерного пространства в момент t распространяется одинаково во всех
направлениях из этой точки. Поэтому нас будут интересовать здесь реше-
решения волнового уравнения, зависящие только от времени и от расстояния г
¦от одной точки до другой в n-мерном пространстве. Гиперсферические
координаты для п измерений определяются следующим образом:
F.1.13)
хп-\ = r sin eisin 62 • • • sin 6n_2 cos 6П_Х,
хп = г sin Ьг sin 62 ... sin6n_2sin6n_1.
¦Отбрасывая производные по каждому из углов, мы находим, что волно-
волновое уравнение для «сферически симметричной» волны в n-мерном про-
пространстве имеет вид
или
или
^0 или -- _
6. 1. Типы уравнений и краевых условий 641
Последнее уравнение, очевидно, является гиперболическим уравнением
вида F.1.1), и будет интересно рассмотреть его как таковое. Характе-
Характеристиками, как и выше, будут X = r — ct и p = r-\-ct. Нормальная форма
уравнения такова:
Только при п = 1 решением будет ф = / (X) -j- g (p.); это уже рассмотренный
случай. Поскольку во всех случаях, кроме одномерного, невозможны
решения в виде волн, распространяющихся наружу и внутрь без измене-
изменения формы, попытаемся посмотреть, нельзя ли найти решение, изменение
которого сводится лишь к уменьшению его амплитуды при удалении
волны от точки возмущения. Другими словами, мы попытаемся найти
решение в форме ф = /"(Х, ц) (X + ц)" = F (X, ц)Bг)а, надеясь, что функция F
окажется имеющей вид / (X) -j- g (ц).
Подстановка в уравнение F.1.15) показывает, что, за исключением
случая а = A — п)/2, уравнение для F еще хуже, чем уравнение для ф.
Если а=A—п)/2, то есть если ф = F/Br)<-n~i'>/2, то уравнение для F имеет
вид
Только при п = 1 или п = 3 функция F будет просто суммой функции
от X и функции от (х. Случай п=\ уже исследован, и теперь видно, что
для трех пространственных измерений можно получить решение
lf(rct) + g(r + ct)], где ^ = a* + y* + z*, F.1.16)
представляющее уходящие и приходящие волны, при распространении
которых изменение их формы состоит только в уменьшении амплитуды
с возрастанием г. Очевидно, что для двух пространственных измерений
форма волн, излучаемых из точки, меняется более существенно.
Дальнейшие шаги в этом направлении означали бы чрезмерное втор-
вторжение в гл. 7. Достаточно здесь сказать, что взрывные (одноимпульсные)
волны для нечетного числа пространственных измерений (п=1, 3, 5, ...)
распространяются радиально как резкие толчки, уменьшающиеся по ам-
амплитуде, но все время имеющие резко очерченные передний и задний
фронты; эти волны не дают предупреждения о своем приходе и не остав-
оставляют за собой следов после прохождения. Напротив, в пространстве
четного числа измерений (п = 2,4,6, ) волны, порождаемые резким
толчком, распространяются, радиально и все время обладают резко очер-
очерченным передним фронтом; они не дают предупреждения о себе до момента
t = г/с, но оставляют за собой след, так как возмущение продолжается
долго после прохождения гребня. Мы коснемся причин этого интересного
различия также в гл. 11.
Эллиптические уравнения и комплексные переменные. Теперь надо
вернуться к уравнению F.1.6) характеристик, чтобы посмотреть, что
следует делать, если характеристики не являются вещественными кривы-
кривыми. Если А(х, у)С(х, у)>В2(х, у) для всех значений % и у, то уравне-
уравнение F.1.1) называется эллиптическим. Уравнения для характеристик
комплексно сопряжены одно другому, и если характеристической функ-
функцией служит X(z, y) = u(x, y) + iv(x, у), то другой характеристической
функцией является ее комплексно сопряженная (х(ж, у) = и(х, y) — iv(x, у)
41 Ф. м. Морс и Г. Фешбах
642 Гл. 6. Краевые условия и собственные функции
(где и и v — вещественные функции от х, у). Замена уравнения F.1.1 У-
на F.1.8)
Р о
здесь уже не так полезна, потому что X и р.-^- комплексные переменные.
Более полезно и естественно применить в качестве координат и и v ве-
вещественную и мнимую части X и р..
Следовательно, нормальной формой эллиптического уравнения является
°±+*L = S3L+T$- + U). F.1.17)
да2 dv^ ди dv ~ v '
Уравнение Лапласа является эллиптическим уравнением, так же как
уравнение для дозвукового (с числом Маха < 1) потока сжимаемой
жидкости (см. стр. 165) и уравнение Гельмгольца. Уравнение Пуассона
представляет собой неоднородное эллиптическое уравнение с дополнитель-
дополнительным членом р (х, у) в правой части.
Если Р, Q и R (или S, Т и U) равны нулю, то решения можно
вновь выразить в виде
ty = fW + g(v-) = f(u+iv) + g(u~iv). F.1.18)
Другими словами, ф равна сумме любой функции комплексного перемен-
переменного u-\-iv ш любой функции его сопряженного. Приложения теории функ-
функций к решениям двумерного уравнения Лапласа были затронуты в гл. 4
и будут рассмотрены более детально в гл. 10.
Связь между аналитическими функциями и решениями двумерного
эллиптического уравнения проливает некоторый свет на соотношения между
этими решениями и краевыми условиями. Для иллюстрации возьмем дву-
двумерное уравнение Лапласа V2(]> = 0 и попытаемся применить условия Коши
вдоль оси х для определения ф в верхней полуплоскости. Характеристи-
Характеристическими функциями для уравнения Лапласа являются >. = x + iy, p = x — iy,
а общее решение записывается в виде ф = f (x-\-iy)-\-g {х — iy). Краевые-
условия, которым надо удовлетворить, таковы: ф = % (х) и д^/ду = —No (x),
если у = 0. Решение имеет вид
ВДЮ^ F-1.19)
Ф = Re ф0 (х + iy) - Tm Хо (х + iy);
Следовательно, ф равна вещественной части функции фоB)-МхоB)
переменного z — х -f iy- Для физически разумных краевых условий ф0 и Ха
являются любыми приемлемыми функциями на вещественной оси (то есть
вдоль границы). Однако имеется много функций от z, конечных на ве-
вещественной оси и все же имеющих полюсы и (или) существенные осо-
особенности где-либо вне этой оси. (В самом деле, мы в гл. 4 доказали, что
единственной функцией от z, остающейся всюду конечной, является по-
постоянная.) Значит, за исключением случая, когда наши краевые условия
имеют вид ф0 = const, No = 0, функция ф (х, у) наверняка обращается в бес-
6. 1. Типы уравнений и краевых условий 643
конечность где-либо на комплексной плоскости. Конечно, все особенности
могут оказаться лежащими в нижней полуплоскости вне границы, а потому
безвредными, но малейшее неудачное колебание ф0 или 7V0 в какой-либо
части границы может породить бесконечность где-либо в верхней полу-
полуплоскости. Другими словами, функция от x-\-iy просто слишком чувстви-
чувствительна к малым колебаниям ее значений или значений ее производной
вдоль вещественной оси, чтобы подчиняться контролю краевых условий
этого вида.
Становится также очевидным контраст со случаем гиперболического
уравнения. Формула F.1.11) выражает значения ф (х, у) для гиперболического
уравнения через ф0 и 7V0 для вещественных значений аргумента, и если ф0
и интеграл от 7V0 ограничены и непрерывны вдоль границы, то ф также
будет ограниченной и непрерывной во всем пространстве. Формула же
F.1.19) показывает, что ф(ж, у) для эллиптического уравнения выражается
через ф0 и No для комплексных значений аргумента, и как раз поэтому,
если ф0 и интеграл от 7V0 ограничены и непрерывны вдоль вещественной
оси, нет гарантии, что они будут ограничены и всюду в верхней полу-
полуплоскости Z.
Другое фундаментальное отличие между гиперболическими и эллипти-
эллиптическими уравнениями состоит в общем поведении их решений. Например,
решения уравнения Лапласа (которое является эллиптическим уравнением)
не могут иметь максимумов и минимумов (см. стр. 18); отсюда следует,
что если граничные условия порождают решение, возрастающее в опреде-
определенном направлении, то решению ничего не остается, кроме как продол-
продолжать возрастать, пока оно не обратится в бесконечность в некоторой точке
(там будет не максимум, а особенность!), если только пе встретится со
временем другой край границы. С другой стороны, решения волнового
уравнения (которое является гиперболическим уравнением) могут иметь
максимумы и минимумы; значит, если в силу краевых условий решение
возрастает в определенном направлении, то может получиться так, что
после перехода гребня волны в этом направлении градиент решения обер-
обернется. Позже мы возвратимся к этой чрезмерной чувствительности решений
эллиптических уравнений к условиям Коши на открытой границе.
Но если условия Коши на открытой границе для решений эллипти-
эллиптических уравнений слишком разборчивы, чтобы встречаться в физических
задачах, то условия Дирихле или Неймана на открытой границе недоста-
недостаточны для того, чтобы определять ответ однозначно. Поэтому дело пред-
представляется таким образом, что для элипптических уравнений предпочти-
предпочтительней замкнутые границы с условиями Дирихле или Неймана (так как
условия Коши для замкнутых границ переопределяют их решение). Труд-
Трудность, к которой мы пришли, решая гиперболическое уравнение при замк-
замкнутой границе (проистекающая из возможности наличия волн, не ощутимых
на границах), не может появиться для эллиптического уравнения, так
как в этом случае волновое движение невозможно. Позже мы покажем
более детально, что условия Дирихле или Неймана на замкнутой границе
для эллиптических уравнений обычно дают единственное решение.
Надо, конечно, отметить, что «замкнутая граница» в этих случаях
может частично располагаться на бесконечности. Дело в том, что ф0
(или No) надо задавать даже для расположенной на бесконечности части
границы, чтобы получить единственное решение. С другой стороны, для
рассмотренного вьппе случая гиперболического уравнения краевые условия
на бесконечности не являются необходимыми; более того, они излишни,,
если заданы условия Коши на конечной части границы.
Подобным образом решения вида F.1.16) не особенно полезны для
эллиптических уравнений, отчасти из-за упомянутых выше трудностей-
41*
644 Гл. 6. Краевые условия и собственные функции
с комплексными характеристиками, но также из-за того, что ни одна
из координат не отличается от другой по знаку перед второй производной,
как это было для временной координаты у волнового уравнения. Соот-
Соответственно для эллиптического уравнения (скажем, для уравнения Ла-
Лапласа) целесообразно рассматривать все координаты как равноправные.
Для точечного источника в тг-мерном пространстве уравнение для «сфери-
«сферически симметричного» решения имеет вид
Решение 4 равно а-\-Ъ/гп~2, где а и Ь — постоянные (исключая случай п = 2,
когда решение равно а + Ыпг). Для эллиптического уравнения это вполне
удовлетворительное решение, так как оно конечно зсюду, кроме источника
г = 0. Подобное решение можно построить для волнового уравнения
с г2 — э^ + х1+ ... -\-Zn-t — сНг, но из-за последнего члена решение обра-
обращается в бесконечность всегда при сЧ2 = z\ -\- х\ + ... -f Жп-ь оно не столь
полезно, как только что приведенное решение эллиптического уравнения.
Параболические уравнения. Следует рассмотреть предельный случай
уравнения F.1.1), когда B2(z, y) = A{z, y)C(z, у) всюду. В этом случае
имеется только одно семейство характеристик, определяемых интегралом
уравнения Ady — Bdz [см. F.1.6)], который мы обозначим через ^(z, у).
Выражая уравнение F.1.1) в новых координатах X и z, получаем в конце
концов в качество нормальной формы параболического уравнения
^ ^ ^ F.1.20)
поскольку оба члена
дх J ' дх ду ' V. ду J дх ' ду
равны нулю. В этом случае имеется лишь один член со второй произ-
производной; по характеристической функции участвует только первая про-
производная.
Такой.вид имеет уравнение диффузии, в котором t занимает место X:
±_ 1
дх* ~а at '
Это уравнение «кривобокое» относительно времени: если изменить знак.г,
то получаем решение другого вида, тогда как волновое уравнение симме-
симметрично относительно времени. Это различие в основном обусловлено тем,
что уравнение диффузии выражает «не консервативный» процесс. Энтропия
непрерывно возрастает с течением времени (и обычно свободная энергия
убывает), в то время как для волнового уравнения энергия остается по-
постоянной (если не включается трение). Как можно было бы ожидать
(см. стр. 136), с возрастанием времени все неправильности решения урав-
уравнения диффузии «сглаживаются», так как вблизи максимума ф кривизна
d2ty/dz2 отрицательна и ф там со временем убывает. Только если кривизна
(и потому неправильность) ф всюду равна нулю, ф может быть незави-
независимой от времени.
Следует ожидать, что для этого уравнения подходят условия Дирихле,
а границу надо брать открытую в направлении возрастания t. При дви-
движении во времени в обратном направлении неправильности в решении
стремятся возрасти; чем короче область иррегулярности, тем быстрее
возрастание; значит, хотя мы можем предсказать, каким станет данное <J>
6. 2. Разностные уравнения и краевые условия 645
через время t, но мы не можем с уверенностью сказать, каким было то же <|>
на время t раньше (другими словами, решение при отрицательных t пере-
переопределено граничными значениями при t = 0). Это различие между пред-
предсказанием и предисторией типично для параболического уравнения и не
имеет места, например, для волнового уравнения: в случае последнего
так же легко заглянуть в прошлое, как и в будущее.
У n-мерного параболического уравнения по одной из координат
(назовем ее хп+1) присутствует только член с первой производной, в то
время как по остальным координатам присутствуют вторые производные.
Уравнение для «сферически симметричного» решения в пространстве п
измерений [ср. с уравнением F.1.14)] имеет вид
и само является параболическим уравнением. Решение в виде отрица-
отрицательной степени г возможно, но практически бесполезно, если есть зави-
зависимость от t. В § 7.4 мы покажем, что самым полезным «примитивным»
решением является решение, полностью сконцентрированное при 1 = 0
и диффундирующее во все стороны с возрастанием t. Выбирая форму
ф = F (t) e~r2lai, обладающую этими свойствами, мы легко находим, что F
обратно пропорциональна tn/2. Итак, мы находим в результате, что реше-
решением уравнения F.1.21) будет
*>0, F.1.22)
где г2 = ж* + а^-f ... 4- %п- Оно нормировано так, что интеграл от него
по всему n-мерному пространству равен единице. Эта функция очень
сконцентрирована для малых значений t, совсем «размазана» для больших
значений t и недействительна для отрицательного t. Ее свойства будут
более основательно исследованы в § 7.4.
6.2. Разностные уравнения и краевые условия
Мы несколько раз (стр. 131 и 227) говорили о предельном переходе
от величин, определенных только для целых значений некоторого пара-
параметра, к непрерывным переменным, от рядов к интегралам, от частиц
к сплошной среде. Имеется соответствующая связь и между дифферен-
дифференциальными уравнениями и разностными уравнениями, которой мы касались
при рассмотрении рекурсивных формул (см. стр. 510) и которая очевидна
из определения производной как предела. Величине уп, определенной для
каждого целого значения п и представляющей счетный набор значений у,
отвечает непрерывная функция у (ж) от непрерывного переменного х. Первой,
второй и т. д. разностям
и т. д. F.2.1)
соответствуют различные производные от у (х). (Взаимосвязь была бы
несколько теснее, если бы мы рассматривали b(yn)/h и т. д., где h -при-
-приращение х, отвечающее единичному изменению индекса п и стремящееся
к нулю при измельчении разбиения; однако в предварительном анализе
можно обойтись без h.)
Дифференциальным уравнениям, рассмотренным в предыдущей главе,
соответствуют разностные уравнения, которые в принципе легче анали-
анализировать, но на практике часто труднее решать. Однако в некоторых
отношениях полезно противопоставить и сопоставить поведение решений
разностного уравнения и решений соответствующего дифференциального
646 Гл. 6. Краевые условия и собственные функции
уравнения. Это особенно относится к взаимосвязи между решениями
и краевыми условиями, так что здесь целесообразно заняться исследова-
исследованием общих свойств разностных уравнений.
Линейные разностные уравнения первого порядка.- В предыдущей
главе мы нашли несколько рекурсивных формул (см., например, стр. 511),
которые содержат только два последовательных коэффициента разложения
в ряд,
Апап 4- Dnantl = О,
и из которых можно определить коэффициенты ап, например, через а0.
Это равносильно разностному уравнению первого порядка
Д(У„) = С-яУп; Сп=-1-%-. F.2.2)
Очевидно, что для уп можно получить определенное решение, если зафик-
зафиксировать значение одного из уп. Обычно это граничное условие (равно-
(равносильное условиям Дирихле) выражается посредством задания значения у0.
Тогда у для больших значений п равно произведению
Уп = Уо Й (С,.+ 1) = г/оехр ? In(l+Cr). F.2.3)
Соответствующее дифференциальное уравнение имеет вид dyjdx = / (х) у,
и решение его есть
X
y(z)-yoexv \ f{x)dx.
о
Связь между этими решениями очевидна. Для неоднородного уравнения
Ь(Уп)-СпУп = Вп F.2.4)
можно пытаться искать решение в виде yn = ^nJJ (Cr-fl). Подставляя
это выражение в F.2.4), получаем
п п—1 п — 1
ЛЛ1 (Сг+1)-ЛгП (С, + 1)-С,АгЦ (СГ + 1) = ВП,
г=0 г=0 г<=0
п п
д(Лг)П (СГ + 1) = ВП, или Д(Л„) = ВП/П (Сп + 1).
г=0 г=0
Отсюда следует, что полное решение уравнения F.2.4) имеет вид
2/»= [П (*+cr)] {y.+"s e Bs } ; (в-2.5)
оно тесно связано с решением
\FdxY
6. 2. Разностные уравнения и краевые условия 647
дифференциального уравнения
Например, если Сп = с~ш Вп = Ь не зависят от п, то решение равно
п
, vi Ь
8=1
Мы могли бы перейти к разностным уравнениям второго порядка,
следуя рассмотрениям гл. 5 почти во всех деталях. Однако мы сейчас
посмотрим, как применить разностные уравнения, чтобы лучше разобраться
в поведении уравнений с частными производными.
Разностные уравнения для нескольких измерений. Очень полезный
метод приближенного вычисления решений обыкновенных дифференциаль-
дифференциальных уравнений и уравнений с частными производными состоит в замене
непрерывных независимых переменных разрывными переменными, значе-
значениями которых могут быть только целые кратные некоторого шага h.
Например, для дифференциального уравнения
"¦*" ду2
дх2 ' ду
мы строим прямоугольную решетку (сетку) шага h в обоих направлениях
и подсчитываем ty только в точках сетки, где ее линии пересекаются.
Величину ф для x=mh, y = nh обозначим через ф(т, п). Если h доста-
достаточно мало, то хорошим приближением дифференциального уравнения
будет разностное уравнение
1
или
-т-[ф(то—1, м)-)-ф (яг-j- 1, тг)-1-ф(т, и — 1)-(-6(т, и + 1)] ='1»(то, п). F.2.6)
Возможно развить методы численного решения таких уравнений, чтобы
применять их, когда соответствующие дифференциальные уравнения
нельзя решить точно; однако здесь мы ограничимся рассмотрением парал-
параллелизма между дифференциальными и разностными уравнениями в отно-
отношении их реакции на краевые условия.
В этом параграфе мы рассмотрим среду, или поле, которое сначала
не будет непрерывным, а будет иметь вид решетки с шагом h, где
h конечно, хотя и мало. Поле ф будет иметь смысл только в узловых
точках, а конечные разности между значениями ф в соседних точках
регулируются разностными уравнениями. Мы получим результаты о реше-
решениях краевых задач для разностных уравнений, соответствующих рассмот-
рассмотренным в предыдущем параграфе трем типам уравнений с частными про-
производными. Отправляясь от этих результатов, полученных для решетки
конечного шага, мы можем затем сделать шаг бесконечно мелким и быть
уверенными, что выводы обычно справедливы и для соответствующих
дифференциальных уравнений. Процесс перехода к пределу не всегда
648 Гл. 6. Краевые условия и собственные функции
так прост, как это может показаться; однако можно проверить, что для рас-
рассматриваемых нами теорем не возникает непредвиденных осложнений.
При доказательстве зтих теорем нам следует ограничиться только
двумя измерениями; большее число измерений вносит непринципиальные
усложнения. Мы будем также пользоваться лишь простейшими видами
для трех типов уравнения. Например, простейшим эллиптическим уравне-
уравнением является уравнение Лапласа; ему соответствует разностное уравне-
уравнение F.2.6). В качестве неоднородного эллиптического уравнения можно-
взять уравнение Пуассона
Соответствующее ему разностное уравнение имеет вид
-ф(т, n)^—^-F(m, n). F.2.7>
Простейшим гиперболическим уравнением для двух измерений является
волновое уравнение
W д^ -О v~ct
соответствующее разностное уравнение имеет вид
-1, га) = ф(т, и + 1)+Ф(т, га-1). F.2.8>
Подобным образом простейшим параболическим уравнением является
уравнение диффузии
34» _
_ „
2
at
для которого соответствующее разностное уравнение можно записать-
в виде
, л),
или
ф(|и, и—1)= —С[ф(т + 1, и) + 4>(т—1, и)-2ф(|и, и)] + ф(т, п) F.2.9,
в зависимости от того, хотим мы двигаться вперед или назад по п (вре-
(временной переменной). При этом мы положили С = l/ha2. >
Эллиптическое уравнение и условия Дирихле. Как пример такого-
анализа, рассмотрим сеточный аналог эллиптического уравнения
с условиями Дирихле вдоль замкнутой границы. Мы указали на стр. 643,
что эти граничные условия для такого уравнения определяют единствен-
единственное решение; посмотрим, может ли метод сеток помочь нам доказать,
это утверждение. Основная решетка показана на рис. 6.4. Пусть гранич-
граничные точки (светлые кружки) заполняют ряды т = 0, п = 0, т = М и п = N;
мы задаем значения ф во всех этих точках. При заданных таким обра-
образом граничных значениях мы хотим определить (единственные) значе-
значения ф во всех внутренних точках (черные точки) при помощи разност-
разностного уравнения F.2.6). Если будет развит сходящийся процесс для под-
подсчета каждого ф через граничные значения ф, дающий однозначный ответ
для всех внутренних точек, то мы. можем считать задачу решенной,,
а тот факт, что условия Дирихле дают однозначный ответ, доказанным.
6. 2. Разностные уравнения и краевые условия
649
4 о
Зо
2 о
I о
О
Физическим примером этой сеточной задачи служит сетка из рези-
резиновых связок, натянутая между равноотстоящими стержнями, каждый
из которых поднимается над плоскостью на свою высоту. Высота каждой
жз узловых точек над * плоскостью
соответствует значению ф (то, п). Раз- n о о о ° ее
ностное уравнение (и также модель _««,«.»_-» • о
из резиновых связок) утверждает, что
значение ф в узловой точке (то, п) n-2<
равно среднему из значений ф в четырех ¦
соседних узлах. Мы уже говорили п
(стр. 18), что в этом состоит физи-
физический смысл уравнения Лапласа.
Это можно применить для под-
подсчета значений ф во внутренних узлах.
Например, значение ф во внутренней
точке B,1) можно подсчитать через
значения в ее соседних точках:
ф B,1) = 1[ф C,1) + ф A,1) + ф B,2)] +
+ ?Ф B»0), Рис. 6.4. Основная решетка для
решения разностного уравнения, ана-
где ф B,0) равно значению ф в гра- логичного дифференциальному урав-
ничной точке B,0) и тем самым зада- нению Пуассона,
но. Остальные три значения ф в пра-
правой части взяты во внутренних точках и еще не известны. Однако их
можно выразить как средние из значений для их соседей, что даст
16
то есть фB,1) выражается через граничные условия и значения ф в точ-
точках, еще дальше отстоящих от границы.
Вновь выражая ф для внутренних точек как среднее значение
из соседних значений, получаем третье последовательное уравнение
О I 2 '3 4
о
Т 5
+ 3-М1,3)+4фB,2)] + |
и таким же образом далее получаем одно уравнение за другим. После
каждой подстановки значение ф B,1) будет выражено через значения ф
в других узлах с некоторыми коэффициентами и через. граничные значе-
значения (которые заданы) с другими коэффициентами. При продолжении под-
подстановок мы заметим два важных факта: коэффициенты при внутренних
потенциалах быстро стремятся к нулю (так быстро, что даже сумма
всех коэффициентов при всех внутренних потенциалах в уравнении
стремится к нулю), тогда как коэффициенты при граничных потенциалах
стремятся к конечным значениям. Например, значение коэффициента
1 1
при ф C,1) равно -г Для первого уравнения, 0 для второго, ^7 Для третьего
и т. д., тогда как коэффициент при граничном значении фB,0) равен
14 5
Т' 13' 16 и Т- Д-
650 Гл, 6. Краевые условия и собственные функции ¦
Это означает, что если продолжать подстановки достаточно долго,
то в уравнении для ф B,1) члены, содержащие значения ф в других внут-
внутренних точках, можно сделать произвольно малыми по сравнению
с соответствующими членами для граничных значений. Значит, в пре-
пределе ф B,1) можно выразить через только одни граничные потенциалы,
и если все они заданы, то значение ф B,1) будет однозначно определено.
С помощью тех же аргументов можно показать, что потенциал в каждом
узле однозначно определяется, если только граничный потенциал задан
вдоль всей замкнутой границы, окружающей сеть. Если часть границы
находится на бесконечности, то вывод сохраняет силу; на самом деле
все, что обычно требуется знать о граничных значениях ф на бесконеч-
бесконечности для получения однозначного значения ф (т, п), это то, что все они
не бесконечны.
Разработан способ, называемый методом релаксации, посредством
которого эта последовательность вычислений проводится четко и с быст-
быстрой сходимостью. Однако нам здесь надо только знать, что это можно
сделать; это как раз и было сейчас доказано. Отсюда, полагая h стре-
стремящимся к нулю, можно доказать, что условия Дирихле на замкнутой
границе однозначно определяют решения уравнения Лапласа. Простое
обобщение того же вывода оказывается достаточным, чтобы распростра-
распространить это утверждение на общее эллиптическое уравнение F.1.17) и число
измерений, большее двух.
Не намного труднее провести тот же вывод для условий Неймана.
Здесь для сети задаются все разности между граничным значением и значе-
значением -j в ближайшей внутренней точке сети. Можно показать, что если
эти разности удовлетворяют простому общему ограничению, то описанный
выше метод и здесь сходится и позволяет получить единственные значения
для внутренних 41 с точностью до произвольного постоянного слагаемого.
Природу этого общего ограничения в случае условий Неймана можно
выяснить на следующем примере. Допустим, что все граничные разности
заданы так, что они делают решение возрастающим внутрь; как же найти
решение, не имеющее максимума внутри (ведь уравнение F.2.6) не допус-
допускает такого максимума)? Очевидно, все граничные градиенты не могут
иметь одинаковый знак. Ограничение можно указать более точно, если
вспомнить, что потенциал скорости несжимаемой жидкости подчиняется
уравнению Лапласа и что в этом случае условиям Неймана на поверх-
поверхности соответствует задание потока жидкости через поверхность. Если бы
такой поток через замкнутую поверхность был направлен всюду внутрь,
то это означало бы, что количество жидкости внутри поверхности возра-
возрастает с положительной скоростью, что для несжимаемой жидкости невоз-
невозможно. Следовательно, в нашем случае надо требовать, чтобы интеграл
от заданной нормальной составляющей градиента по всей граничной
поверхности равнялся нулю; в рамках этого простого ограничения на гра-
границе могут быть заданы любые значения нормальной производной.
Значит, можно ожидать, что для уравнения Лапласа корректными
граничными условиями могут служить условия Неймана на замкнутой гра-
границе, если только заданные граничные условия удовлетворяют некоторому
интегральному соотношению на граничной поверхности. Кроме того,
поскольку в граничных условиях задаются градиенты, а не значения,
для получения однозначного ответа надо задать значение <Ь в одной какой-
либо точке.
Собственные функции. Рассмотрим особенно простой случай, чтобы
показать, что еще можно сделать при помощи сеточных вычислений. Возь-
Возьмем изображенную на рис. 6.5 (стр. 652) решетку с четырьмя внутренними
6. 2. Разностные уравнения и краевые условия 651
и восемью граничными точками. Мы приступим к построению нашего
решения для любых граничных условий при помощи решений для простых
граничных условий. Это можно сделать, так как наше разностное уравне-
уравнение линейно; если ф(т, п) есть решение, когда граничные значения
равны %@, п), %(т, 0) и т. д., то А$(т, п) представляет собой реше-
решение для граничных значений А%, а если ф' (т, п) есть решение для
граничных значений <Ь'й, то решение при граничных значениях &О + Фо
равно ф(т, п) + <Ь'(т, п).
Например, можно решить разностное уравнение для простого случая,
когда ф1A,0) = ф1B,0) = 1, а все остальные граничные значения 6 равны
нулю. Тогда, по симметрии, Л A,1) = ф B,1) и фA,2) = фB,2). Записывая
разностные уравнения для Двух внутренних точек, имеем
К21>+К12) или l-
), или |
Эти уравнения можно решить и получить
0AД) = фB,1) = §, фA,2) = фB,2) = |. F.2.10)
Полученную матрицу значений обозначим через ^(т.тг).
Можно также найти решение для случая, когда ф2A,0) = — ф2B,0) = 1,
а остальные граничные значения ф равны нулю. Это даст
фA,1)=-фB,1) = ^, фA,2)=-фB,2)=4; F.2.11)
полученную матрицу значений обозначим через W2 (т, п).
Теперь нетрудно видеть, что если фA,0)=а, 6B,0) = Ь, а псе
остальные граничные значения ф равны нулю, то получится решение
W(m, п) = Ц^Ч>\(т, n) + ^W2(m, n).
Решения для других трех частей границы можно получить, повернув это
решение на 90, 180 или 270°. При помощи соответствующего сложения
можно получить решение для любого задания значений граничных
потенциалов.
Этот метод можно распространить на области с прямоугольной гра-
границей любого размера. Мы сначала допускаем, что граничные значения
ндоль одной стороны имеют особенно простой вид, а вес остальные гра-
граничные значения равны нулю. Например, мы полагаем й(т, 0) = <р(т)
{где ф надо определить), ф@, п) = <Ь(т, N) = ф(М, п) = 0. Затем мы раз-
разделяем переменные в разностном уравнении, полагая ф(»г, п) — f{ri)<p(m)\
разностными уравнениями для / и <р будут
Т (т) = ^ [? {т +1) + <р (ш - 1)] + Of (in)
F.2.12)
где С —константа разделения. Разностное уравнение F.2.6) получается
при помощи умножения первого из этих уравнений на / (п), второго на <р (т),
сложения результатов и деления на 2. Аналогия между этим и процессом
разделения переменных в уравнении с частными производными очевидна.
652 Гл. 6. Краевые условия и собственные функции
Мы видим, что для простоты данного метода функции ^(т), опреде-
определяющие простые граничные условия вдоль одной стороны и нулевые-
условия на остальных сторонах, должны удовлетворять разностному
уравнению
)(™l) +
a <f>v @) и <j»v (M) должны равняться нулю. Согласно сказанному на стр. 132,
возможными решениями являются
<Pv (т) = sin (m/M), Cv = 2 sin2 (irv/2M), v = 1, 2 M. F.2.13)
Эти М различных функций от т обладают тем свойством, что их соот-
соответственно подобранная линейная комбинация может равняться вдоль
части границы, где гс = 0, произвольно заданной системе значений гранич-
граничных потенциалов, оставаясь равной нулю на остальной части границы.
Далее надо найти соответствующие функции /v(^) как решения
уравнений
/v(и) = i/v(п- 1) + у/v(n+ 1)- 2sin*(«v/2M)/v(n), F.2.14)
равные нулю при п = N и единице при п = 0. Общее решение для про-
произвольных граничных значений вдоль части границы, где и = 0, равно
линейной комбинации произведений <p\>(m)fw(n), где v = l, 2, ...,М.
Функции вида F.2.13) называются собственными функциями; они
будут исследованы позже в этой главе в связи, с дифференциальными
уравнениями. С их помощью можно получить решения, удовлетворяющие
любым граничным условиям на граничных поверхностях особенно про-
простого вида.
Функции Грина. Однако мы можем также перегруппировать исследо-
исследоф чтобы подойти к решениям с другой стороны.
Решения F.2.10) и F.2.11) для простой решет-
решетки, изображенной на рис. 6.5, можно скомбини-
скомбинировать, чтобы получить специальное решение
Gi(m, n)= i-\F1(m,n) + y\F2(m.n),
ванные выше
7
@,2)
8
«ДО
Рис.
стых
6
о
аз;
A,2)
а,1)
i
0.0)
функции,
5
B%
.2,2)
B,1)
2
B.0)
6.5. Решетка для
примеров задания
4
о
C.2)
i
о
C.1)
про-
гра-
-!
1- =Gl(l,2),
F.2.15)
ничных значении.
разностного уравнения F.2.6), удовлетворяю-
удовлетворяющее простым граничным условиям: <1> в гранич-
граничной точке 1 A,0) равна единице, а во всех
остальных — нулю. Решение, равное единице в
граничной точке 2 B,0) и нулю во всех осталь-
ных точках, имеет вид G2 (m, n) = -^ Wt (m, п) —
- цг2 (т, п) и равно функции Gx, отраженной от вертикальной оси сим-
2 17 1
метрии решетки (то есть G2 A,1) = ^2 = G2B,2); G2B,l) = 24-, G(l,2) = ;^),
а функции для других граничных точек можно получить, последовательно
отражая первое решение от различных осей симметрии решетки.
6. 2. Разностные уравнения и краевые условия 653
Эти величины, которые можно рассматривать как функции граничной
точки и внутренней точки, называются функциями Грина для границы.
Так как Gs(m, n) соответствует граничному условию <5>s = l, Л = 0 в осталь-
остальных граничных точках, то можно быстро построить решение для гранич-
граничных условий 4 = ф8 B S~H граничной точке с помощью суммы
Ф (»», п) = 2 Фзсз (т> п)- F.2.16)
S
Мы умножаем функцию Грина для s-й граничной точки на граничное зна-
значение в этой точке и производим суммирование по всем граничным точ-
точкам. В гл. 7 мы рассмотрим обобщение этого приема на решения диффе-
дифференциального уравнения.
Решение разностного уравнения Пуассона F.2.7) можно найти при
помощи весьма сходного приема. Мы решаем это уравнение, когда все
граничные потенциалы равны нулю, /^A,1) = 4//г2, а все остальные F
равны 0:
G A,111,1 ! i |
, G(l,l|l,2) = G(l,l|2,l) = -i
¦Отсюда решение, когда все граничные значения равны нулю, а функция
F (т, п) принимает любую фиксированную совокупность значений, равно
<Ит, n) = ^.^]F(r, s)G{r, s\m, n), F.2.17)
4 Г,!
•сумме значений F в различных внутренних узлах, каждое из которых
умножено на решение ф Для этого узла. Если некоторые из граничных
потенциалов отличны от нуля, то для удовлетворения этим граничным
условиям достаточно сложить функции F.2.17) и F.2.16).
Решение G(r, s\ rn, п) называется функцией Грина для внутренних
точек (г, s) и (т, п). Оказывается, что она симметрична относительно
перестановки точек, то есть потенциал в точке (т, п), порожденный единич-
единичным «зарядом» F в точке (г, s), равен потенциалу в (г, s), порожденному
единичным зарядом в (т, п). Это — выражение принципа взаимности, который
«будет рассмотрен несколько позже.
Между прочим, решение G для решетки с границей любого вида
непосредственно связано со следующей чисто воображаемой задачей. Допу-
Допустим, что решетка изображает улицы симметрично разбитого города.
На углу г-ш стрит и s-й авеню находится салун. Как-то рано утром
из салуна был изгнан посетитель, который отправился наобум или
по r-й стрит или по s-й авеню. На улицах довольно скользко, и каждый
раз, когда человек пересекает стрит или авеню (то есть в каждой встре-
встречающейся ему узловой точке), он скользит и падает. При этом он на-
настолько пьян, что когда вновь становится на ноги, то полностью забывает
направление, по которому шел, так что его прогулка вдоль следующего
квартала одинаково вероятна во всех четырех направлениях от последнего
места падения. Так он продолжает ставить себе новые и новые синяки,
пересекая различные стриты и авеню (некоторые из них по нескольку
раз), пока в конце концов не достигает граничной точки. На всех гранич-
граничных перекрестках стоят полисмены, один из которых живо доставляет
пьяного бродягу в ближайший участок.
Конечно, имеется много возможных путей, по которым этот человек
может пройти от салуна до ареста, и мы, естественно, не можем точно
предсказать, какой путь он изберет. Однако можно предсказать матема-
математическое ожидание того, что он упадет на углу т-ш стрит и и-й авеню.
,Для этого нужно сложить математическое ожидание (шанс) того, что он
654 Гл. 6. Краевые условия и собственные функции
упадет там только один раз, математическое ожидание того, что он упадет
там два раза, и т. д., или же, если эти прогулки достаточно часты, то
это математическое ожидание равно осредненному по всем прогулкам числу
падений в точке (т, и). Эта возможность как раз равна функции Грина
G(r,s\m,ri), которую мы подсчитали. Рассмотренный здесь пример
является частным случаем задачи о случайных блужданиях, изучавшейся
несколькими выдающимися математиками и интересной для исследования
брауновского движения, а также движения звезд в галактике.
Эллиптическое уравнение и условия Коши. Для пополнения нашего
исследования эллиптических уравнений следует выяснить, что будет, если
вдоль границы п = 0 задать условия Коши. Это означает, что для всех
значений т задаются ф(т, 0) и ф(т, 1). Тогда из уравнения F.2.6) можно
найти все $(т, 2):
ф(то, 2) = 4ф(го, 1)-ф(го, 0)-ф(го+1,1)
и так далее последовательно для всех п. Если имеются боковые границы
(скажем, при т = 0 и т = М), то вдоль них нельзя задавать условий
Коши, так как тогда некоторые ф (для т=1 и т — М — 1) были бы
переопределенными; допускаются только условий Дирихле или Неймана.
Так как значения <1> уже заданы условиями Коши при тг = О, то мы
не можем на верхней границе, скажем при n — N, задавать произвольно
граничное условие любого вида. Для эллиптического уравнения внутри
замкнутой границы условия Коши на любой части границы дают слишком
много условий.
С другой стороны, если нет верхней границы, то ф (т, п) будет,
вообще говоря, беспредельно возрастать при возрастании п. Раз ф не может
иметь максимумов или минимумов, то если ф начинает возрастать или
убывать с ростом и, оно должно продолжать возрастать или убывать
неограниченно при возрастании п. Любое бесконечно малое изменение
условий Коши при и = 0 послужит причиной неограниченно большого
изменения ф для очень больших значений п. Такая чувствительность
к граничным условиям не имеет физического смысла.
Все приведенные выше выводы справедливы независимо от величины
шага, так что они будут также верны и при стремлении h к нулю.
Поэтому можно ожидать, что никакое решение уравнения Лапласа не мо-
может иметь внутри своей области существования максимумов или мини-
минимумов; условия Дирихле или Неймана на замкнутой границе дают кор-
корректную задачу; условия Коши даже на части замкнутой границы дают
слишком много, а на открытой границе вызывают слишком высокую-
чувствительность к малым изменениям условий, чтобы быть физически
удовлетворительными. Эти заключения о граничных условиях применимы
также к уравнению Пуассона (на самом деле даже к любому эллиптиче-
эллиптическому уравнению), хотя решения уравнения Пуассона могут иметь макси-
максимумы и минимумы.
Гиперболическое разностное уравнение. Для гиперболического урав-
уравнения можно начертить сетку, в направлениях х, у, как для уравне-
уравнения F.2.8), или же провести решетку вдоль характеристик и сделать раз-
разностное уравнение аналогичным уравнению в нормальной форме F.1.8),
которая для волнового уравнения принимает вид д2ф/дХф = 0:
*+1), F.2.18)
где характеристиками являются линии решетки у = const или v = const
(см. рис. 6.6). Здесь связаны потенциалы,* углах ромбообразной фигуры;
6. 2. Разностные уравнения и краевые условия 65S
уравнение F.2.18) утверждает, что среднее значение потенциалов на концах
горизонтальной диагонали равно среднему из значений на концах верти-
вертикальной диагонали. Условиям Коши соответствует задание значений
в светлых точках на рис. 6.6, в двух нижних рядах. При этих заданных
значениях можно применить уравнение F.2.18) для подсчета потенциалов
в первом ряде черных точек, затем в следующем и т. д. Если функция
начинает возрастать в некоторой точке, например если f в а больше,
чем среднее в Ъ и d, то ф в с станет вновь меньше (так как среднее в а
и с должно равняться среднему в Ъ и d). Следовательно, функция удержи-
удерживается в определенных границах и не может беспредельно возрастать
• • • д •••-
• • » г* •••••••
• с* • • ч • • •с# • • •
je d • • • ••6»»d»»«
о о О О О ^ОООООООО
о о о о О ОООООООО
Я7 -—'>
Рис. 6.6. Различные решетки для гиперболического урав-
уравнения.
Ряды *=^к (?H-f rc)=const и v=^ (m—n)=const :i влгаотся характеристиками.
на любом ограниченном участке изменения временной переменной, как это
делает решение уравнения Лапласа. Значит, незначительные изменения
граничных условий порождают лишь незначительные изменения функции,
которые делаются незаметными при удалении от границы; другими словами,
решение устойчиво относительно условий Коши на открытой границе.
На этом примере можно также пояснить трудности, встречающиеся,
когда граница совпадает с характеристикой. Допустим, что значения
заданы вдоль линий v = 0 и v=l. Применяя уравнение F.2.18), мы видим,
что уравнения при v = 0 требуют внутренней совместимости граничных
значений. Система уравнений вида
не может дать однозначного решения, так как каждое уравнение содержит
два неизвестных, и если граница простирается в бесконечность в обе
стороны, то решение системы бесконечного числа уравнений не сходится
(определитель из коэффициентов не сходится). Если граница в некоторой
точке заворачивает, так что значение одного из ф (*, 2) дано, то можно
получить остальные ф(х, 2). Но это может случиться, если граница не всюду
идет по характеристике; если же она совпадает с характеристикой, един-
единственного решения найти нельзя.
Возвратимся к (х, г/)-виду F.2.8) разностного уравнения, соответству-
соответствующему второй решетке рис. 6.6. Здесь опять узлы, связанные уравнением,
образуют ромбообразную фигуру, причем среднее от значений в концах
горизонтальной диагонали равно среднему значений в концах вертикаль-
вертикальной диагонали. Это постоянство формы связи не должно нас удивлять,
так как волновое уравнение должно представлять некоторую взаимосвязь,
656 Гл. 6. Краевые условия и собственные функции
не зависящую от координат, в которых оно выражено. Для горизонталь-
горизонтальной сети это значит, что в уравнениях не участвует значение функции
в центре ромба (так было и для (х, v)-представления, но там не было так
заметно, потому что при проведении сети центральные точки пропускались).
Пропуск центральной точки является одним из выражений коренного
различия между уравнением Лапласа и волновым уравнением. Это — основ-
основная причина того, что условия Дирихле на замкнутой границе не при-
приводят к однозначному ответу для волнового уравнения, но дают такой
ответ для уравнения Лапласа.
Чтобы сделать это еще яснее, можно упростить сеточную задачу
Дирихле для замкнутой границы до наиболее простого случая, показан-
о ного на рис. 6.7, с четырьмя граничными точ-
точками и одной внутренней точкой решетки. Если
рассматривается уравнение Лапласа, то значе-
значение <1) в центральной точке равно среднему из
значений в четырех граничных точках, и если
о • ° все эти четыре значения заданы, получается
единственное решение. Однако если рассматри-
рассматривается волновое уравнение, то это уравнение
связывает значения в граничных точках и ни-
ничего не говорит о значении в центральной точке,
о Значит, если значения в четырех граничных
точках даны, то они могут быть совместными с
Рис. 6.7. Решетка для самим волновым уравнением или не совместны-
'^^краТойТадачи™41100 ми- н0 в обоих слУчаях ° значении во внутрен-
ней точке решетки ничего не известно.
Возвращаясь к решетке для т, п в правой части рис. 6.6, мы можем
удовлетворить краевым условиям, разделяя F.2.8) на разностные уравне-
уравнения по т и по п:
7 (ш + 1) + f (т - 1) + (А:2 - 2) 7 (иг) =-Д»7+ А*Р = °« F.2.19)
/ («+1) + / (п- 1) + (Р-2) / (п) = Дг/ +Р/= 0.
Мы решаем уравнение для <р(т) в функциях особенно простого типа [через
которые можно легко выразить краевые условия, например, применяя
функции F.2.13)], а затем решаем уравнение для соответствующего мно-
множителя /; окончательное решение будет суммой таких произведений,
удовлетворяющей краевым условиям при я = 0 и 1. Или же-можно решить
задачу, когда краевые условия имеют вид единичной функции или про-
производной для т = М, при остальных краевых значениях, равных нулю,
что нам даст функции Грина для границы. Окончательное решение будет
опять равняться сумме этих функций Грина, умноженных на граничные
значения в граничных точках.
Параболическое разностное уравнение. Взяв, наконец, уравнение
F.2.9), как простейшее параболическое уравнение, мы видим, что если
вдоль горизонтальной части границы и = 0 поставлены условия Дирихле,
то первое уравнение допускает единственное решение для точек решетки,
где п=1, затем где и = 2 и т. д. Будет ли решение устойчивым или нет,
зависит от значения С. Если ф(т, п) при т = т0 больше, чемф(то+1, п)
и Ф(т0 — 1, и), то ф(т, и + 1) имеет меньшее значение, чем ф(т, и), так
как
6. 2. Разностные уравнения и краевые условия
657
Если С не настолько велико, чтобы ty(m, и + 1) сделалось отрицательным
и начались неустойчивые колебания, то неправильности решения стремятся
выровняться, и при больших значениях п все ф стремятся принять одина-
одинаковое значение (см. задачу 6.3).
Если, с другой стороны, пользоваться вторым видом уравнения для
движения назад в направлении п (времени), то мы найдем, что непра-
неправильности в значениях ф стремятся увеличиться и легкая неправильность
в краевых значениях порождает в конце концов очень большую непра-
неправильность у функции для достаточно больших отрицательных п. Поэтому
решение неустойчиво для любых краевых условий (оно неустойчиво для
условий Дирихле и Неймана; условия Коши переопределяют решение).
После перехода к пределу можно утверждать, что решения параболических
уравнений дают устойчивый и единственный результат для условий
Дирихле на открытой границе при движении в положительном направле-
направлении от характеристики, но неустойчивы в отрицательном направлении.
С физической точки зрения это происходит из-за того, что парабо-
параболические уравнения (примером является уравнение диффузии) предстань
ляют ситуации, в которых энтропия возрастает с возрастанием нремени.
Поэтому неправильности поля ф стремятся сгладиться при возрастании
времени; чем резче неправильность, тем быстрее она исчезнет. Если мы
хотим вести исследование в обратном направлении по времени, чтобы
узнать, каким было поле, диффундирующее в конце концов в заданное
распределение, минуту (или час) назад, то мы не сможем сказать, сколько
тогда было резких неправильностей, которые потом практически исчезли
и не проявляются заметно в заданном распределении.
Результаты исследования этого параграфа можно резюмировать в сле-
следующей таблице:
Условия
Дирихле или
Неймана (за-
(задается функ-
функция или нор-
нормальная про-
производная)
Коши (задают-
(задаются функция
и нормальная
производ-
производная)
Граница
Откры-
Открытая
Замкну-
Замкнутая
Откры-
Открытая
Замкну-
Замкнутая
Гиперболиче-
Гиперболическое уравнение
Недостаточно
Решение не
единственно
Единственное
устойчивое
решение
Решение пере-
переопределено
Эллиптическое
уравнение
Недостаточно
Единственное устой-
устойчивое решение (от-
(относительно условий
Неймана см. стр.
650)
Решение неустой-
неустойчиво
Решение переопре-
переопределено
Параболическое
уравнение
Единственное устойчи-
устойчивое решение в поло-
положительном направле-
направлении, неустойчивое
в отрицателвном на-
направлении
Решение переопреде-
переопределено
Решение переопре-
переопределено
Решение переопреде-
переопределено
42 ф. м. Морс и Г. Фешбах
658 Гл. 6. Краевые условия и собственные функции
Приемлемые комбинации уравнений и краевых условий указаны жир-
жирным шрифтом. Заметим еще раз, что условия Дирихле — Неймана могут
быть однородными ?<х ф (s) -f- р N (s) = 0] или неоднородными [а ф (s) + р N (s) =
= F(s)]. Однородные условия Дирихле означают, что функция ф должна
равняться нулю на границе; неоднородные условия Дирихле означают, что
ф должна иметь заданные ненулевые значения на границе и т. д.
6.3. Собственные функции и их применения
Теперь мы достигли пункта, когда от обобщений надо начать пере-
переходить к частным случаям. Мы потратили первые два параграфа этой
главы, чтобы показать вообще, для каких уравнений с частными произ-
производными пригодны те или иные виды краевых условий и при каких усло-
условиях можно ожидать, что, нашему заданию будет отвечать единствен-
единственное решение. Сейчас* мы детально изучим технику получения этого един-
единственного решения в отдельных случаях.
Процесс подчинения достаточно общего решения краевым условиям
до некоторой степени аналогичен процессу решения обыкновенного диф-
дифференциального уравнения. Ни в том, ни в другом случае метод не яв-
является прямым; мы должны выбрать общую форму решения, которая
представляется подходящей для удовлетворения нашим требованиям, а
затем провести подгонку деталей (конечно, если это окажется возмож-
возможным!). Даже, например, для сравнительно простого процесса интегриро-
интегрирования функции f (х) по х надо, в сущности, угадать вид интеграла
и затем проверить правильность этой догадки посредством дифференциро-
дифференцирования. Многие из форм, в которых мы угадываем решение дифференци-
дифференциальных уравнений, имеют очень общий вид, как, например, степенные
ряды или интегральные представления; частное решение находится при
помощи подстановки выбранной формы в дифференциальное уравнение
и попытки его удовлетворить.
Общие формы, применяемые для удовлетворения краевым условиям,
также выражаются либо через ряды функций, либо через интеграл от
некоторой функции по границе. Как и для решений обыкновенных диф-
дифференциальных уравнений, мы сначала рассмотрим применение рядов;
следующая глава будет посвящена использованию интегралов для удовле-
удовлетворения краевым условиям. На практике приложение рядов обычно тре-
требует разделения уравнения с частными производными в приспособленных
к границе координатах; прежде чем погрузиться в технические детали,
мы проработаем простой пример, чтобы увидеть, как это получается.
Ряды Фурье. Пусть мы хотим решить краевую задачу для двумерного
уравнения Лапласа
в прямоугольнике, заключенном между прямыми ж = 0, х = а, у = 0, у = Ъ.
Очевидно, что для этой границы подходят прямоугольные координаты
х, у, так что мы можем разделить переменные и прийти к двум обык-
обыкновенным уравнениям:
где к2 — константа разделения. Это — эллиптическое уравнение, так что
подходят условия Дирихле или Неймана на замкнутой границе; см. 'ис-
'исследование для случая решетки на стр. 650.
6. 3. Собственные функции и их применения 659
Допустим для начала, что наши граничные условия являются осо-
особенно простыми условиями Дирихле, а именно ф должна равняться нулю
(однородные условия) при ж = 0, х = а и у = Ь и принимать произвольные
значения <1>8(ж) (неоднородные условия) при у = 0. Решением ж-уравнения,
равным нулю при ж = 0 и при х = а, является sin(¦кпх/а), где п целое
(мы положили к = ъп/а), а решением «/-уравнения, равным нулю при ?/ = fc,
является sh k (b — у). Другими словами, единственными значениями к, при
которых решение может удовлетворять нулевым граничным условиям на
трех сторонах, являются значения к = тсп/а (и= 1, 2, 3, ...), а при этих
значениях единственными решениями, пригодными для данных условий,
являются функции, указанные в предыдущем предложении.
Следовательно, наиболее общее решение уравнения V2<!> = 0 в дву-
двумерном случае, удовлетворяющее однородным условиям ф = 0 при ж = 0,
х = а, у=Ъ, можно представить при помощи ряда
ф- 2^nsh[^(fe_2/)]sin^. F.3.1)
Чтобы сделать такое категорическое утверждение, как это, надо быть
уверенным в том, что в виде этого ряда можно представить все возмож-
возможные решения, удовлетворяющие нулевым условиям вдоль трех, сторон,
независимо от того, какие (неоднородные) граничные условия выполня-
выполняются вдоль четвертой стороны у = 0. Для этого нам надо будет доказать,
что ряд F.3.1) может удовлетворить любым возможным граничным усло-
условиям при у = 0. Так как условия Дирихле на замкнутой границе опре-
определяют единственное решение, то тогда мы сможем ручаться, что такой
ряд представляет решение, соответствующее заданным граничным усло-
условиям при г/ = 0. Если мы найдем также другую форму функции (замкну-
(замкнутую форму или интегральную форму), удовлетворяющую этим условиям,
то можно будет утверждать, что эта новая форма совпадает с рядом и,
обратно, что ряд может представлять эту новую форму.
Следовательно, решающий шаг в обосновании приведенного выше
утверждения состоит в доказательстве того, что ряд F.3.1) может удовле-
удовлетворить всем возможным условиям Дирихле вдоль г/ = 0. Конечно, выра-
выражение «всем возможным» является довольно оптимистическим по своей
общности, и нам следует несколько ограничить его при помощи более
точных определений.
Однако в простом случае, который мы теперь рассматриваем, ряд
F.3.1) для у —0 является рядом Фурье. Мы увидим позже в этой главе,
что такой ряд можно подобрать для любой функции, непрорывной вместе
с производной при 0 < х < а всюду, за исключением конечного числа
точек разрыва самой функции или се производной (и, конечно, стремя-
стремящейся к нулю при ж—»-0 и х—>а). Такие функции называются кусочно-
гладкими. Ряд Фурье пригоден для любой непрерывной части такой про-
произвольной функции (и, конечно, непригоден, вообще говоря, в точках
разрыва, если функция обладает пиками нулевой ширины, которые, к сча-
счастью, имеют малое физическое значение).
Уточняя, можно придать утверждению о том, что ряд
<р (ж) = 2 #« sin
может отвечать кусочно-гладкой функции f(x) в области 0<ж<а, сле-
следующий смысл: возможно выбрать значения Вп, при которых
42*
660 Гл. 6. Kpaeetie условия и собственные функции
Это требование, конечно, не затрагивает различия в бесконечных пиках
нулевой ширины, так как площадь под такими пиками равна нулю.
С физической точки зрения это удовлетворительно. Можно сказать, что
наше требование о выборе ряда является требованием сходимости в сред-
среднем или требованием наименьших квадратов. Обоснованием нашего утвер-
утверждения о подборе в смысле сходимости в среднем как ряда Фурье, так и
рядов из других функций мы займемся в этом параграфе позже.
Если нам известно, что ряд может удовлетворить требуемым гранич-
граничным условиям, то нетрудно подсчитать необходимые значения коэффи-
коэффициентов Ап. Напишем равенство, соответствующее граничному условию
вдоль у = 0,
оо
, (ж) = 2j Кsh —'sm —'
71=1
умножим обе части на sin (тстж/а) и проинтегрируем по ж от 0 до а. Все
интегралы в правой части, кроме одного, как легко проверить, равны нулю.
Один оставшийся, при п = т, равен -^ aAmsh(bmb / а). Значит, коэффи-
коэффициенты Ат в формуле F.3.1) можно легко подсчитать, и решением урав-
уравнения V2<j> = 0, удовлетворяющим граничному условию ф = 0 при ж = 0,
х = а, у=Ь и условию ф = ф8(ж) при у = 0, оказывается ряд
со ft
ф(ж, w) = > I — \ фЛ^эш—dk sin ( — )—1V. ; ':. . ". F.3.2)
yv i it) ZJ L о I a J V a J sb(%nb/a) • \ /
n=l 0
Этот ряд удовлетворяет граничным условиям и является решением урав-
уравнения Лапласа по жиг/. Следовательно, он должен быть тем самым
единственным решением, которое мы искали.
В предельном случае,*когда Ъ —> со, область внутри границы становится
бесконечной, но согласно сказанному на стр. 643, условия Дирихле надо
все-таки налагать на всей границе, чтобы получить единственный резуль-
результат. Отношение гиперболических синусов приводится к простой экспо-
экспоненте ехр( — югу/а), а в остальном ряд остается тем же. Если теперь
продолжить границы в направлении х, то в конце концов мы перейдем
от ряда Фурье к интегралу Фурье. Следуя § 4.8, мы найдем, что реше-
решение двумерного уравнения Лапласа в верхней полуплоскости, удовлетво-
удовлетворяющее граничным условиям ф = ф8 (ж) при г/ = Оиф = О на бесконечно-
бесконечности, равно
У) = i { \ eihx+hv dk
со
v dk ^ ф,
^ e \ ф,.($)сов[*(а:-е)]#, F.3.3)
0 —"со
где интегрирование по к разбивается на две части так, что зависимость
от у обязательно исчезает при у—> со (то есть мы применяем e+hv для
отрицательного к и е~й" для положительного к). Если г/ = 0, мы полу-
получаем обычный интеграл Фурье D.8.2).
6. 3. Собственные функции и их применения 661)
Функция Грина. Заметим, что как.для конечных границ (когда при-
применяется ряд F.3.2)), так и для бесконечных границ (когда применяется
интеграл F.3.3)), мы можем преобразовать решение в интеграл по гра^
нице у = 0:
\ F.3.4)
где для конечной границы интегрирование производится между концами
границы 0 и а, а функция G представляет собой ряд
со
г, , ... 2 v) sh Uiznja) (b — у)] . лет . пп?
G (ж, у ?) = — У. — J, ), > sin • sin ,
71=1
тогда как для бесконечной границы интегрирование по границе S про-
производится от — оо до оо, а функция G равна
Функция G называется функцией Грина для граничной поверхности S
(в нашем случае для у = 0).
Таким образом, мы видим, что наше решение задачи Дирихле можно
выразить через интеграл по границе от функции Грина (соответствующей
уравнению и виду границы), умноженной на заданную граничную функ^
цию. Однако развитие этой идеи будет осуществлено в следующей главе;
здесь нам надо сконцентрировать внимание на процессе определения функ-
функций, образующих ряд, и на том, как этот ряд составляется.
До сих пор мы рассматривали случай, когда только на части у = 0
границы граничные значения tys были отличны от нуля. Чтобы удовле-
удовлетворить условиям, когда ф отлично от нуля вдоль других частей прямот
угольной границы, мы пользуемся очевидным видоизменением функций,
примененных в ряде F.3.2) или интеграле F.3.3). Например, для удовле-
удовлетворения условиям вдоль а; = 0 мы пользуемся рядом
sin
и аналогично для х = а и у=Ь; для получения окончательного решения
мы складываем отдельные ряды. После этого мы можем построить и
функцию Грина для ее применения в подинтегральной функции при
любых граничных значениях в любой точке вдоль прямоугольной границы.
См. стр. 651—653 по поводу аналогичного случая для решетки.
Собственные функции. Функции sin (nnz/a) для целых значений п— это
простейший пример последовательности собственных функций, которые
составляют основу метода рядов для удовлетворения граничным условиям.
Мы видим, что этот метод включает в себя разделение переменных в урав-
уравнении с частными производными в таких координатах ?п, что границе
соответствует одна или более из координатных поверхностей ?s = const.
Множитель в решении, зависящий от точки граничной поверхности (в на-
нашем примере—множитель sin (чспх/а) для границы у = 0), включает кон-
константу разделения и должен удовлетворять некоторым простым граничным
условиям (в примере в двух концах: х'=0 и х = а), и мы находим, что
лишь для некоторых значений константы разделения (в примере для
662 Гл. 6. Краевые условия и собственные функции
целого п) эти условия будут удовлетворяться. Другой множитель
(sh[(im/a) (b — у)] в примере) выбирается затем так, чтобы удовлетворить
условиям на другом конце области (у=Ь в примере), и тогда полное
решение представляет собой сумму этих произведений по всем допусти-
допустимым значениям константы разделения.
Центральной частью метода, как нетрудно видеть, является определе-
определение вида множителя, выражающего зависимость решения от точки гра-
границы (множителя sin (ъпх/а) в примере), и соответствующих допустимых
значений константы разделения, которые удовлетворяют условиям на кон-
концах 0, а границы. Решения обыкновенного дифференциального уравнения,
содержащие константу разделения, которые удовлетворяют простым гра-
граничным условиям в двух концах области изменения независимого пере-
переменного, называются собственными функциями, а значения константы раз-
разделения, допустимые при заданных условиях, называются собственными
значениями (иногда применяются термины характеристические функции и
характеристические значения). В приведенном выше примере функции
sin (-кпх/а) являются собственными функциями, а значения (тгп/аJ (п целое) —
собственными значениями. Следует ожидать, что ряд из этих собствен-
собственных функций, для всех собственных значений константы разделения,
может представлять любые граничные значения. Нам надо показать вообще,
что такой ряд может представлять любую выбранную функцию в необхо-
необходимой области изменения независимого переменного, а также показать,
как подсчитывать коэффициенты ряда. (Нужно отметить, что можно рас-
рассматривать собственные функции для более чем одного измерения и соб-
собственные функции, являющиеся решениями интегральных, а не дифферен-
дифференциальных уравнений.)
Например, в общем двумерном случае мы выбираем такие координаты
?!, E2i чтобы граница соответствовала значениям ^1 = а1, %1=а2, ^2 = Ьг,
Е2 = Ь2. Затем мы строим решение, для которого функция ф равна О
вдоль трех частей границы (например, при Ei = «i, ?1 = а2, ^2=^г)> а
вдоль четвертой части ?2 = ^i — некоторой произвольно выбранной функ-
функции /(^). Это можно сделать, если мы сможем разделить уравнение
в координатах ?. Решения ^-уравнения, обращающиеся в нуль при
il = a1 и 51 = а2) являются тогда собственными функциями задачи.
Типы краевых условий. До сих пор мы рассматривали случай условий
Дирихле на замкнутой границе, но ту же технику можно применить для
других типов краевых условий. Например, для условий Неймана на гра-
границе, имеющей вид прямоугольника со сторонами размеров а и Ь, при-
примыкающего в первом квадранте к координатным осям, мы сначала удо-
удовлетворяем условиям вдоль стороны у = 0, считая условия вдоль осталь-
остальных трех сторон однородными, так что там нормальная производная равна
нулю. Тогда подходящими собственными функциями являются cos (-кпх/а),
где п— целое, а ряд, имеющий нормальную производную Ns(x) вдоль
оси а; от 0 до а и нулевую нормальную производную вдоль у=Ь, х = 0
и х = а, записывается в виде
cos — • ch [Gw/a) (b~y)]
a ch {nnbla)
n=i о
В этом случае, как мы указали на стр. 650, надо требовать, чтобы
6. 3. Собственные функции и их применения 663
Если граница не замкнутая, а уравнение гиперболическое, то, воз-
возможно, надо задать условия Коши на части границы. Например, для
гибкой струны длины а, закрепленной при х = 0 и х = а, граничные усло-
условия являются однородными условиями Дирихле (ф = 0) при х = 0 и х = а
для всех значений t, но начальные условия (краевые условия вдоль ? = 0)
должны задавать как начальное смещение ty = 40(#), так и начальную
скорость d&/dt = U0(x) (см. стр. 639). Соответствующий ряд, дающий ре-
решение волнового уравнения с2д2Л/д#2 = d2ty/dt2, имеет вид
со
¦Knot . -г, . 7mct"\
+BSm )
= 2j sin— • ( An
l
Tl=l
Собственными функциями будут sin (-кпх/а), а собственными значениями —
числа тт/а. Значения коэффициентов Ап, Вп определяются по ф0, Uo спо-
способом, подобным тому, который был применен на стр. 660.
Иногда граничные условия, определяющие собственные функции,
состоят не в задании нулевого значения или нулевой производной на
двух концах интервала. Может быть поставлено общее однородное усло-
условие, состоящее в том, что отношение значения к производной равно по-
постоянной, не зависящей от значения константы разделения; например,
адф/д# = Рф при ж=0 и ж=а.
Если а = 0, оно приводится к однородному условию Дирихле, а если
Р = 0—к однородному условию Неймана. Заметим, что граничные условия
для собственных функций всегда однородны (см. стр. 633), если гранич-
граничная точка является обыкновенной.
Пример граничного условия другого типа мы имеем в случае реше-
решения уравнения Лапласа внутри круга радиуса а при условиях Дирихле
на окружности. Соответствующими координатами являются, конечно,
полярные координаты г, <р, а уравнение Лапласа и уравнения, получаю-
получающиеся после разделения переменных, имеют вид
p dr
Решением ^-уравнения будет a cos ту + b sin ту с произвольными
значениями a, b и т. Если мы ищем имеющее физический смысл реше-
решение внутри окружности г = а, то оно должно быть в этой области непре-
непрерывным и конечным. Угол <р пробегает непрерывно значения от 0 до 2-к,
возвращаясь к 0, когда радиус-вектор делает полный оборот. Значит,
ФBтс) должно равняться Ф@), и вообще Ф (у) = Ф (у + 2-к). Чтобы это было
возможно, константа разделения т должна быть целой, и потому соб-
собственными функциями по у являются sinm<p и cosm<p с целым т. В этом
случае нет задания значений функции на концах <р = 0 и ^ = 2тг области
изменения <р. Условие было просто условием непрерывности, и ему соот-
соответствует требование, чтобы Ф была периодична по <р с периодом 2-к.
В последующих главах нам будет часто встречаться требование перио-
периодичности как граничное условие.
Интересующая нас область изменения г формально ограничена двумя
точками, г = 0 и т=а, хотя физическая граница имеется только при
г = а. Мы могли бы начать беспокоиться о том, какое граничное условие
применить при г = 0, где нет физической границы, а имеется лишь точка
.концентрации системы координат, но следует вспомнить, что точке кон-
концентрации соответствует особая точка для дифференциального уравне-
664 Гл. 6. Краевые условия и собственные функции
ния, и простого требования, чтобы ф была там конечной, или непрерыв-
непрерывной, или аналитической, достаточно для ограничения нашего выбора
функции. Общее решение уравнения для R равно
а^г
-\- b0 In г при т = 0,
при m > 0;
чтобы R было конечным и непрерывным внутри границы, второй член
надо опустить. (Заметим мимоходом, что если бы окружность г = а была
внутренней границей, а от функции требовалось бы, чтобы она была
ограниченной на бесконечности, то надо было бы опустить первый член
при и>0 z член с In г при m = 0.)
Решение уравнения Лапласа внутри окружности г = а, равное ф = ф (<p)
вдоль границы, выражается, таким образом, рядом
^ncosn9-t-/3nsin
где
2я
2я
1 Г
(a) cos иа с?а, -Вп = —\ ф8 (a) sin na da.
о
В других случаях граница может простираться от одной точки концентра-
концентрации до другой; тогда двумя граничными точками будут две смежные особые
точки дифференциального уравнения для собственных функций, а гранич-
граничные условия могут просто заключаться в том, что решение должно оста-
оставаться конечным в обеих особых точках. Трехмерное уравнение Лапласа
в сферических координатах
подстановкой ф =7?(г)вF)Ф(ф) разделяется на уравнения
Если краевая задача решается в шаре г < а, то последние два уравнения
служат для нахождения собственных функций, причем граничные условия
непрерывности и конечности служат для определения допустимых значе-
значений п и тп. Так как азимутальный угол <р непрерывно меняется от 0 до
2тс, то, как и выше в случае круговой границы, мы заключаем, что m должно
быть целым, а собственными функциями будут sinm<p, cos тщ. Решениями
уравнения для в являются функции Лежандра (см. стр. 514). В гл. 5 мы
видели, что решения, остающиеся конечными в обеих особых точках z = 1
и z = — 1, могут иметься лишь при целом п. Требование конечности мно-
множителя R в особой точке г = 0 также определяет его вид. Поэтому реше-
6. 3. Собственные функции и их применения 665-
ние должно выражаться в виде ряда
Ф= 2 2 (Am
7П=0 т1=тп
где Т представляют собой полиномы Гегенбауэра, определенные формула-
формулами E.2.53) и E.3.36). Функции sinme-71^_rn(cose) иногда называются
присоединенными функциями Лежандра.
Граничные условия могут быть условиями Дирихле на сфере, г = а.
Тогда они выражаются равенством ф == фй(б, <р) при г = а, где (J>s представ-
представляет собой кусочно-гладкую функцию от 6 и у. Позже мы покажем, что-
интеграл
тс
[ Sin2m+1 6 • УЯ-m (с OS 6) 7T-m (COS 6) db
О
при к, отличном от п, равен нулю, и подсчитаем значение интеграла при
& = п. Сейчас нам достаточно знать, что если умножить обе части ряда
для <|> на
cos /<р • sin1*16 ¦ Tlh_i (cos 6) dy db
и проинтегрировать по-поверхности сферы г=а, то все члены ряда исчез-
исчезнут, кроме одного, для которого m — l и п = к, а этот член можно запи-
записать в виде AlhAlh, где Alh — известная постоянная. Этим путем можно-
показать, что коэффициенты ряда равны
2тс тс
Amn=-^-\ cosm<pdT С фБ(в, 9)sin*1 Ъ-П-п(cos6)dS,
о о
2п тс
Втп = /Г" \ Sin m<Pd<P ^ ^S F' *¦> Sinm+1 6- Г--п (COS 6) ?Й,
чем коэффициенты ряда окончательно определяются через граничные зна-
значения <]>sF, <p).
В этих примерах мы указали общие свойства некоторых собственных
функций и их отдельные применения. Эти функции могут быть решения-
решениями обыкновенных дифференциальных уравнений, появляющихся в резуль-
результате разделения одного из полученных выше уравнений с частными про-
производными, соответствующими частным значениям константы разделения?
(собственным значениям). Эти собственные значения определяются тогда
из условия, чтобы собственные функции удовлетворяли некоторому виду
граничных условий в двух концах данной области значений независимого
переменного. Если эти концевые точки являются особыми для дифферен-
дифференциального уравнения, то граничные условия могут состоять просто в тре-
требовании, чтобы решение оставалось там конечным. Если концевые точки
являются обыкновенными, то условия могут быть однородными и заклю-
заключаться в требовании, чтобы отношение между функцией и ее произ-
производной равнялось некоторой постоянной, не зависящей от константы раз-
разделения, или чтобы решение было периодическим с некоторым постоян-
постоянным периодом и т. д.
Нужно выяснить, как определять собственные значения и собствен-
собственные функции из граничных условий, но надо также, и это еще более
важно, показать, что из последовательности так определенных собствен-
собственных функций можно образовать ряд, который может изображать любую-
666 Гл. 6. Краевые условия и собственные функции
кусочно-гладкую функцию между граничными точками. Оставшаяся часть
этого параграфа будет посвящена исследованию этого общего вопроса
с частыми паузами для иллюстрации понятий на примерах. Свойства
собственных функций как решений интегральных уравнений будут изу-
изучены в гл. 8.
Абстрактное векторное пространство. Собственные функции, с кото-
которыми мы пока познакомились на отдельных примерах, скажем члены
sin (тс/гж/а) ряда Фурье, имеют некоторые свойства, аналогичные свойствам
компонент векторов, рассмотренных в § 1.6 и 2.6. Компоненты вектора
?h в п-мерном пространстве можно записать в виде Fhm (то есть если ат
представляет собой единичный вектор в направлении оси хт, причем
«i, ..., а„ попарно ортогональны, то /Tbm = Fft«am). При этом скалярное
произведение вектора Fft на другой вектор F; имеет вид
п
17 Т? ^1 /л /7
k I ^—I ktYl It?1
m=l
и равно нулю, если Fb и F( взаимно ортогональны (перпендикулярны
•один другому). В частности, длина вектора Fft равна квадратному корню
из скалярного произведения этого вектора на себя:
Функция sin (птх/а) зависит от целого т и непрерывного переменного
х. Ее можно рассматривать как координатное представление некоторого
вектора Sm в абстрактном векторном пространстве бесконечного числа
измерений. Скалярное произведение двух таких векторов Sm и Sn можно
определить при помощи интеграла
Tzrnx . tztix
sin
m-Sn= ^sin —-sin —da:, F.3.5)
о
который является типичным предельным видом обычной суммы произве-
произведений компонент. Получается так, как будто каждому значению х из
интервала @ < х < а) соответствуют свое направление и свой единичный
вектор е (х) в функциональном пространстве, причем вектор е для любо-
любого х ортогонален вектору е для любого другого х, а величина sin (кпх/а)
для данного х является как бы компонентой вектора Sn в направлении,
определяемом е (х).
Отсюда длина Sn равна квадратному корню из скалярного произведе-
произведения Sn на себя:
а 1/2
. F.3.6)
Собственная функция sin (¦кпх/а) определяет, таким образом, собствен-
.ный вектор Sn. В силу ортогональности собственных функций каждый
собственный вектор ортогонален любому другому, так как скалярное
произведение (Sm-Sn), определенное формулой F.3.5), равно нулю при тф п.
Если разделить каждый вектор Sn на ]/а/2, мы получаем совокупность
попарно ортогональных единичных векторов
6. 3. Собственные функции и их применения 667
которые определяют систему нормальных координат в функциональном
пространстве, столь же полезных, как и исходные координаты и единич-
единичные векторы е (ж).
В частности, единичный вектор е (х) можно представить посредством
новых единичных векторов в виде
ssi
а нормированные собственные функции у 2/а sin (-кпх/а) аналогичны
направляющим косинусам, определяющим одну систему осей через другую
[см. A.3.1)].
Довольно трудно поверить в то, что пространство, характеризуемое
несчетным множеством единичных векторов е(х), можно полностью пред-
представить при помощи счетного множества собственных векторов е„. И
в действительности это, конечно, не так, потому что произвольно выбран-
выбранный вектор в пространстве е (х) изображается «функцией» от х, имеющей
бесконечное число разрывов. Мы же выбрали из несчетномерного про-
пространства подпространство, состоящее из всех функций, непрерывных
вместе с производной всюду, кроме конечного числа точек (то есть
кусочно-гладких функций). Эти функции, имеющие существенно специ-
специальный вид по сравнению со всеми возможными бесконечно-разрывными
функциями, можно представить посредством счетного множества собствен-
собственных векторов еп. Это ограничение надо иметь в виду в наших дальнейших
исследованиях.
При указанном ограничении мы уже можем выразить произвольный
вектор F в абстрактном векторном пространстве через его компоненты
вдоль нормальных осей:
Тот же вектор можно выразить и через исходные единичные векторы
е(х) с компонентами F(x), связанными с Fn соотношениями
F.3.8)
Получились как раз формулы, определяющие разложение функции F (х)
в ряд Фурье.
Направления, даваемые собственными векторами Sn (или еп), как-то
•определяются дифференциальным уравнением
для синуса и однородными граничными условиями tl» = 0 при ж = 0 и х = а.
Мы можем сопоставить этому дифференциальному уравнению и этим
граничным условиям операторное уравнение (см. § 2.6)j
•с соответствующими граничными условиями, служащее для выделения
нормальных осей для оператора Л и собственных значений для постоян-
постоянной к.
668 Гл. 6. Краевые условия и собственные функции
Другое дифференциальное уравнение и (или) другие граничные условия
определяют другие нормальные оси, соответствующие новым собственным
векторам Еп, определенным новыми собственными функциями фп(#)
(которые могут быть комплексными). Эти векторы также ортогональны,
так что (ср. стр. 65)
с — ( 0 при пфт,
Е?-Ет = \ фп(х) фт (х) dx = { El при п= т F.3.9>
где Еп представляет собой длину вектора Е„. Любой вектор F вновь
можно выразить через эти собственные векторы, и соотношение между
компонентами F по новым нормальным осям и его компонентами F(x}
по направлениям е (х) имеет вид
^ ^\ F.3.10)
что дает формулы, посредством которых любую функцию F (х) можно
разложить по собственным функциям фп (х).
Наконец, можно подсчитать скалярное произведение собственного
вектора, соответствующего <!>п (х), и собственного вектора, соответствую-
соответствующего siri (-кпх/а) [это можно сделать, если функциональные пространства
для обоих векторов тождественны, то есть если оба множества собственных
функций определены на одном и том же отрезке @, а)]. Это скалярное
произведение равно
Еще одно свойство этих собственных векторов будет полезно позже.
Так как е (х) ортогонален е (х') для х' Ф х, то при помощи формулы,
аналогичной F.3.7), получаем
е (х)-е(х ) = _2j-^г ф„(ж)фп(ж )— (х—х). F.3.11)
Эта величина равна нулю при х Ф х, а при х = х' имеет такое значе-
значение, что
b(z~x')dx=l.
Другими словами, это дельта-функция Дирака, определенная на стр. 122.
Естественно, что остаются вопросы, которыми мы займемся потом, свя-
связанные со сходимостью этих разложений в ряды.
Однако мы все еще не приступили к овладению деталями. Векторная
аналогия является плодотворной идеей, полезной в общих понятиях, но она
очень абстрактна. Чтобы вполне понять все ее значение, надо возвратиться
к нашим дифференциальным уравнениям и граничным условиям.
Задача Штурма—Лиувилля. Обыкновенное дифференциальное уравне-
уравнение, получающееся при разделении из уравнения с частными производными
) = 0, можно [см. уравнение E.1.28)] записать в виде
= 0. F.3.12)
6. 3. Собственные функции и их применения 669
Это уравнение называется уравнением Лиувилля. Параметр X представ-
представляет собой константу разделения (в некоторых случаях появляется более
одной константы разделения; мы на время отложим рассмотрение этих
¦случаев). Каждая из функций р, q, r характеризует координаты, приме-
примененные при разделении, и для исследованных в § 5.1 разделяющих коорди-
координат р и г являются простыми алгебраическими функциями от z, имеющими
конечное число нулей и полюсов. Функция q, особенно для уравнения
Шредингера, более сложна, но и тогда q не имеет особенностей внутри
области изменения z (хотя может иметь особенность на одном или обоих концах).
Точки, в которых p(z) равна нулю, являются особыми точками уравнения,
и обычно область изменения z простирается от одной из таких точек до
другой; во всяком случае, особые точки могут находиться в начале или
в конце этой области, но никак не в середине. Другими словами, функ-
функция p(z) нигде в области изменения z не меняет знака, и потому ее
можно всегда считать положительной. Оказывается также, что и г не
¦меняет знака (в интересных случаях), так что и г можно считать всегда
положительной.
Задача Штурма — Лиувилля состоит, в основном, в выяснении зависи-
зависимости общего поведения ф от параметра X и зависимости собственных
значений X от однородных граничных условий, наложенных на ф.
В некоторых наших рассмотрениях мы будем сравнивать решения при
различных значениях константы разделения X; для этого решение при
X = Хп обозначим через фп. Для такого сравнения очень полезно умножить
уравнение для фг на ф2, уравнение для ф2 на tyi и вычесть одно из другого:
«тли
d
~dz
•Столь простое соотношение для сравнения можно получить потому, что
уравнение Лиувилля самосопряженное. В случае уравнения для фх более
•общего типа
иадо было бы для ф2 пользоваться сопряженным уравнением
•чтобы выразить разность в виде суммы полной производной и произведе-
произведения Хх — Х2 на функцию (см. стр. 499). Уравнением, сопряженным к урав-
уравнению Лиувилля, является оно само (проверьте!).
Теперь проинтегрируем соотношение F.3.13) по z от левой гранич-
граничной точки (которую мы обозначим через а) до некоторой произвольной
точки z, лежащей левее правой граничной точки. Получим
где величина в круглых скобках была бы определителем Вронского
для фх и ф2, если бы \ было равно Х2 (но нам нужно именно Х2 Ф Х2).
Если а является особой точкой дифференциального уравнения, то р
равно нулю и величина в квадратных скобках обращается в нуль при
условии, что фх и ф2 конечны в особой точке. Если точка регулярная,
670 Гл. 6. Краевые условия и собственные функции
а граничное условие однородно и имеет вид adty/dz — Рф = 0 при z = a
(где а и Р не зависят от X, см. стр. 663), то
при z = a и опять-таки величина в квадратных скобках равна нулю.
Отсюда почти для любых обычных граничных условий при z = a имеем
Для некоторой области значений X решение ф, удовлетворяющее гранич-
граничному условию при z = a, колеблется, то есть возрастает до максимума,
при z, большем а, затем уменьшается по величине, проходя через нуль
и достигая отрицательного максимума и т. д. Допустим, что мы выбрали
Хх в области значений X, для которых ф колеблется, а ?— наименьшее
значение z (значение, ближайшее к z — a), для которого ф^О. Тогда
формула F.3.14) приобретает вид
с
с= (Ха ~ Xl) \ г^ dz; Ф*(С) = °- F.3.15>
Так как С представляет собой наименьший нуль функции фх, то фг
не меняет знака между z = a и z = ?, а потому фх можно считать положи-
положительной при а < z < С- Мы уже сказали на стр. 669, что для уравнений,
которыми мы занимаемся, как р, так и г положительны во всем интер-
интервале а < z < Ъ, где Ъ — правая граничная точка. Можно также утверждать,,
что производная dtyjdz при z = ? отрицательна, так как в этой точке фх.
переходит через нуль от положительных значений к отрицательным.
Выберем Х2 большим Хъ чтобы величина ^2~~^i стала положительной..
Что теперь говорит формула F.3.15) о поведении ф2 (в предположении,
что ф2 удовлетворяет тем же краевым условиям при z = а и соответ-
соответствует Х2)? Обращается ф2 в нуль при а < z < ? или нет?
Допустим, что ф2 не обращается в нуль при а < z < С- В этом случае ф2
можно считать также. положительной во всем этом интервале и даже
при z = ?. Тогда величина в левой части равенства F.3.15) будет отрица-
отрицательной (р положительна, dtyjdx отрицательна, ф2 положительна при z = Q,
тогда как величина в правой части — положительной (Х2 — Х2 положительна,
фх, ф2 и г положительны). Это противоречие показывает, что ф2 должна
пройти через нуль где-нибудь в интервале а •< z •< ?. Повторение тех же
рассуждений на участке z от первого нуля фх до второго и т. д. показы-
показывает, что расстояние между последовательными нулями функции ф2 меньше-
расстояния между последовательными нулями функции ф2, если Х2 > Хх.
Другими словами, чем больше значение X, тем ближе друг к другу
лежат нули функций ф (в предположении, что р и г всюду положительны
на интервале о < z < J). Или, обратно, если значение X уменьшается, то-
расстояние между последовательными нулями функций ф возрастает.
Для достаточно низкого значения X (т. е. малого в алгебраическом смысле;
оно может быть отрицательным) внутри интервала а < z < Ъ не будет нуле-
нулевых значений ф. Для некоторого значения Х=Х0 функция ф будет иметь
нуль в другой граничной точке z = Ъ и ни одного нуля между а и Ь; для
X < Хо при а< z <fe нулей не будет. Если граничное условие при z = b-
имеет вид ф = 0, то Хо представляет собой собственное значение X, причем
нет собственных значений, меньших Хо. Подобным образом при помощи..
6. 3. Собственные функции и их применения
671
формулы F.3.14) можно показать, что независимо от того, каково гранич-
граничное условие, имеется некоторое наименьшее собственное значение X,
которое можно обозначить через Хо. Все другие собственные значения X
больше Хо. Нетрудно видеть, что собственная функция ф0 соответствующая Хо,
имеет наименьшее возможное число нулей между граничными точками а и Ь;
на самом же деле в большинстве случаев ф0 вообще не имеет нулей
между а и Ъ (хотя она может равняться нулю в а и (или) в Ъ, если этого
требуют граничные условия).
Часто бывает полезно преобразовать функции q и г в уравнении
Лиувилля F.3.12) так, чтобы Хо равнялось нулю. Это можно сделать, так
как в выражении q (z) + Xr (z) всегда мож-
можно Xor (z) добавить к q (z) и вычесть из
Xr (z), что даст новое q, не зависящее от
X, и новое X, равное старому X минус Хо.
Естественно, что наименьшее собственное
значение для нового уравнения должно
равняться нулю, и потому все другие
собственные значения положительны.
Если теперь увеличивать значение X
от Хо, то соответствующая функция ф,
удовлетворяющая граничным условиям
при z = a, не будет удовлетворять им при
z == Ъ. Однако при дальнейшем возраста-
возрастании X мы в конце концов найдем следую-
следующее собственное значение \, соответст-
соответствующее собственной функции ф1; которая
имеет на один нуль больше, чем ф0 (в
большинстве случаев это означает один
нуль, так как функция ф0 обычно не
имеет нулей). Когда X возрастает даль-
дальше, расстояние между узлами (другое
наименование нулей- ф) становится мень-
меньше, пока при следующем собственном
значении Х2 внутри интервала (а, Ь) не
станет на один узел больше. Это показано
графически на рис. 6.8. Таким образом,
можно построить последовательность соб-
собственных функций фо> фц ф2, Фз! ••¦> каж-
каждая из которых удовлетворяет заданным однородным граничным усло-
условиям в а и Ь, причем так упорядоченную, что соответствующие соб-
собРис. 6.8. Решения ф уравнения
Лиувилля для различных значе-
значений константы разделения X.
Решения III и V удовлетворяют гранич-
граничным условиям ф=0 при х=а и Ь.
ственные значения X,
о,
Х1; Х2
Х3
образуют монотонно возрастающую
о 1
последовательность, так что Хп+1 > Хп. Если это сделано, то наше предыду-
предыдущее исследование показывает, что числа узлов функций фп между а и Ь
также образуют непрерывно возрастающую последовательность, так что
фп+1 имеет в интервале а, Ъ на один узел больше, чем фп. При этом мы
молчаливо предположили, что все допустимые значения X вещественны,
так что их можно непосредственно упорядочить. То, что все собственные
значения для уравнения F.3.12) вещественны, будет доказано на стр. 676.
Быть может, графическое представление сделает эти выводы более
понятными. На рис. 6.8 показан типичный случай: двумя граничными
точками служат х — а и х=Ь, а собственная функция ф должна равняться
нулю в обеих этих точках. Кривые для р, г и q показаны на верхнем
графике; как р, так и г положительны в интервале а < х < Ъ, но q этому
условию не удовлетворяет. На среднем графике показаны кривые ~kr-\-q
для последовательности значений X, причем наименьшему значению
€72 Гл. 6. Краевые условия и собственные функции
соответствует нижняя кривая и т. д. На нижнем графике изображены
решения уравнения Лиувилля, равные нулю при х — а, для тех же значе-
значений X, что и средняя система кривых.
Отметим несколько интересных моментов, относящихся к связи
между ф и соответствующими линиями Xr + g. Если Xr + g отрицательно,
то ф поворачивает от прямой ф = 0. Это свойство возрастания производ-
производной с возрастанием х, если ф положительно, и убывания, если ф отрица-
отрицательно, характеризует любую комбинацию экспонент еах, е~ах и будет
называться экспоненциальным поведением. Во-вторых, если 1-r-\-q положи-
положительно, то ф искривляется к оси, то есть если ф положительно, то про-
производная убывает с ростом х, и наоборот. Это свойство характеризует
тригонометрические функции и будет называться синусоидальным поведе-
поведением.
Этот характер поведения функции ф можно обнаружить, интегрируя
уравнение Лиувилля один раз:
Если У-r + q отрицательно при ж1 < х < х2, а ф положительно в этом
интервале, то значение pdty/dx в точке х2 больше, чем в точке х1; и т. д.
В случае, приведенном на у>ис. 6.8 под номером I, значение X таково,
что Хт- + <7 всюду отрицательно; соответствующая функция ф, обладая
экспоненциальным поведением, не имеет возможности вновь «повернуть
обратно» и прийти к нулю при х—Ъ. В случае II V + g положительно
на коротком участке изменения х, достаточном, чтобы несколько отог-
отогнуть ф назад, но еще недостаточном, чтобы довести ее до нуля. В слу-
случае III мы достигли как раз такого значения X (собственного значения Хо),
для которого участок положительности ~kr-\- q достаточен, чтобы завернуть
ф обратно к нулю как раз при х = Ъ. В случае IV значение X еще больше
и колебание ф более заметно. Появился один узел, но он еще не настолько
приблизился к х = а, чтобы до Ъ вместился другой полуцикл колебания.
Наконец, в случае V X достигает значения, для которого ф проходит через
нуль и вновь направляется обратно так, чтобы обратиться в нуль как раз
при х = Ь.
Продолжение этого рассуждения очевидно; ясно также, что те же
рассуждения можно провести при других граничных условиях. Далее,
нетрудно показать, что разность Хп+1 — Хп не может быть бесконечо
малой, если расстояние Ъ — а конечно, даже в пределе для больших п.
Для этого, применяя формулу F.3.14) вновь, мы полагаем пределы инте-
интегрирования равными а и Ъ. Положим, далее, \ равным Хп — собственному
значению, а фх —равным соответствующей собственной функции фп (при
граничных условиях, например, ф = 0). Допустим, что Х2 взято меж-
между Хп и Хи+1, так что ф2 = 0 при х = а, но йф2/йж = 0 при х — Ъ. Рассмо-
Рассмотрение ф-кривых, приведенных на рис. 6.8, показывает, что если между
а и b имеется четное число узлов фп, то d§Jdx при х = Ь отрицательна
и функция ф2 (определенная в предыдущем предложении) также отрица-
отрицательна при х = Ъ; если же число узлов фп нечетно, то как d^^Jdx,
так и ф2 положительны при х = Ъ. Отсюда следует, что в равенстве
ъ
{К - К) [ Ф« (*) Ф-2 (ж) г (х) dx = ф2 (Ь) ф; (Ь) р (Ь)
величина в правой части обязательно положительна и не бесконечно мала,
как бы велико ни было п.
6. 3. Собственные функции и их применения 673
Так как Х2, по определению, больше Xft (но меньше Хп+1), то инте-
интеграл обязательно положителен. Если Ъ — а не бесконечно, то интеграл
не может быть бесконечным, так как обе функции ф (и г) всюду конечны.
Следовательно, разность Х2 — Хп может быть бесконечно малой, только
если Ъ — а бесконечно. Так как Xn+i>X2, т0 мы получаем полезный
результат, заключающийся в том, что разность Хп+1 — Хп не может быть
бесконечно малой, как бы велико ни было п, если только Ъ — а не бес-
бесконечно. Значит, последовательность значений Хо, Хх, ..., Хп, Хп+1, .. -
не может иметь ни предельной точки, ни верхней границы, а должна
продолжаться до +со. Этот результат будет полезен в нашем последу-
последующем анализе. Таким образом, непрерывное распределение собственных
значений может получиться, только если Ъ — а бесконечно.
Выводы о том, что имеется наименьшее собственное значение \ и что
упорядочение собственных функций по возрастанию собственных значений
одновременно упорядочивает их по возрастанию числа узлов в интервале
(а, Ь), являются полезными результатами в изучении задачи Штурма —
Лиувилля. Они основаны на нашем предположении положительности г
всюду в интервале а < z < Ъ, а также положительности р всюду в этом
интервале (последнее равносильно утверждению, что внутри интервала
(а, Ъ) нет особых точек дифференциального уравнения). Эти предположе-
предположения выполняются для всех уравнений, к которым мы пришли при раз-
разделении переменных в § 5.1. Результаты получены при помощи теоремы,
утверждающей, что чем больше значение константы разделения X, тем
меньше расстояния между узлами соответствующего решения ф (z) (эта
теорема называется первой теоремой Штурма о сравнении).
Хотя имеется наименьшее собственное значение Хо, но, как мы уже
видели, наибольшего собственного значения нет, и для каждого собствен-
собственного значения Хп с собственной функцией фп всегда имеется ближайшее
большее собственное значение Хп^х > Хп с собственной функцией фП4Л,
имеющей в интервале (а, Ь) на один узел больше, чем фп. Таким образом,
последовательность собственных значений бесконечна и простирается
от наименьшего собственного значения Хо до бесконечности.
Как пример этого поведения можно рассмотреть случай уравнения
d2ty/dz2 + Хф = 0 с граничным условием Неймана dty/dz = 0 при z — Ош более
сложным- однородным условием dty/dz = ф/а при z = а. Здесь ни одна из конце-
концевых точек не является особой точкой уравнения.
Если X отрицательно, то решение, имеющее при z = 0 нулевую про-
производную, равно ф = сЬ/сг, где Х= —к2. Значение к, для которого ф удо-
удовлетворяет условию при z = a, получается из решения трансцендентного
уравнения
— cth w = 1, w = ка.
Аналогичная функция была исследована в § 4.4 (см. рис. 4.19). Можно
легко показать, что для w имеется лишь один вещественный корень; все
другие корни мнимые, если а вещественно и положительно. Единственное
вещественное решение к0 приближенно равно fco~ 1,200/а. Отсюда един-
единственное отрицательное значение X (которое должно быть наименьшим
собственным значением) приближенно равно
Х = Х„= -А^~ -1,440/а2
(с четырьмя значащими цифрами), а соответствующая собственная функ-
функция равна
фо(г)~сЬ A,200 z/a)
и в интервале 0, а не имеет узлов.
43 Ф. м. Морс и Г. Фешбах
674 Гл. 6. Краевые условия и собственные функции
Все другие собственные значения должны быть положительны, поэтому
можно взять ф = cos kz; X = А;2. Эти косинусы удовлетворяют условию Ней-
Неймана при z = 0; чтобы удовлетворить условиям при z = a, надо выбрать к
так, что
f d<b\ i ¦ i Ф cos ka . .
( ~- ) =—ksmka=-j=—-—, или ctgay=—w, w — ka.
Это уравнение имеет бесконечвую последовательность решений
*! ~ 2,798/а = (тс- 0,344 )/а,
Л, с* 6,121/в = Bтс - 0,162)/в.
или, несколько менее точно,
кп ~ пп/а — 1/птса, п = 1, 2, 3, . . . ,
откуда
Нетрудно доказать, что фп имеет как раз п узлов в интервале 0 < z < a.
За исключением отрицательного наименьшего собственного значения Хо,
все собственные значения положительны и не имеют верхней грани.
Конечно, можно преобразовать наше уравнение, записав его в виде
g+(-^o+x°H = o, p = i. q=-K, r=i,
причем новые собственные значения равны \°п = Хп + к\. Посредством этого
преобразования мы сделали наименьшее собственное значение Х° равным
нулю и обеспечили отсутствие отрицательных собственных значений.
Вырождение. Некоторые граничные условия могут быть недостаточ-
недостаточными для определения единственного решения при каждом допустимом
значении X. Например, для уравнения е?2ф/й<р2 + Хф = 0 в некоторых слу-
случаях (см. стр. 481 и 663) единственным граничным условием является
требование периодичности функции ф по <р с периодом 2тс. В этом случае
допустимые значения X оказываются равными m2(m = 0, 1,2,...), но
для каждого значения т условию периодичности удовлетворяет любая
линейная комбинация sinmip и cos m<p, так что имеются два независимых
решения. Такие случаи, когда одному собственному значению принадле-
принадлежит более одной собственной функции, называются вырожденными слу-
случаями.
В случаях двойного вырождения можно применить любую пару неза-
независимых решений хп и ^п> соответствующих данному собственному значе-
значению Хп, чтобы выразить наиболее общую собственную функцию для этого
собственного значения. Однако обычно лучше выбрать два решения орто-
ортогональными друг другу (см. стр. 668), то есть так, чтобы
Это обычно можно сделать, добавляя к граничным условиям некоторые
требования симметрии, выделяющие ту или иную совокупность независи-
независимых решений.
6. 3. Собственные функции и их применения 675
Например, для уравнения d2ty/d<p2 + m2ty = 0 и для периодических условий
функции sin тткр являются нечетными функциями <р, а функции cos my —чет-
—четными функциями <р, и они взаимно ортогональны, так как
2тс
\ sin mrp- cos щ d-f = 0.
о
Польза этого требования ортогональности вскоре станет очевидной.
Во всяком случае мы могли бы обозначить функции cosny через <j>en(z)
(индекс е —для четных функций), а функции sin п<р—через фоп (индекс
о—для нечетных) и получить последовательность фе0 для \ = 0, фе1 и фо1
для \ = 1, фе2 и фо2 для \, = *к и т. д., по две собственные функции- для
каждого собственного значения, кроме наименьшего.
Ряды по собственным функциям. Как мы видели раньше в этом
параграфе, собственные функции дают возможность удовлетворить краевым
условиям при помощи рядов. Получив нашу последовательность соб-
собственных функций <]>n(z), мы в состоянии выразить любую кусочно-глад-
кусочно-гладкую функцию F (z) в виде ряда
F(z)= fUn<L(Z)
71=0
между граничными точками а, Ъ [см. формулы F.3.8)]. Чтобы доказать
возможность этого, надо показать, что последовательность собственных
функций полна. Это до некоторой степени аналогично требованию, чтобы
система собственных векторов в функциональном пространстве, соответ-
соответствующих системе собственных функций, покрывала все «измерения»
в функциональном пространстве, определяемые произвольным вектором,
соответствующим F(z) [см. рассуждение, следующее после формулы F.3.7)].
Если F (z) аналитична в некоторой области вокруг z — 0, то необходимо
показать только, что степенным рядам соответствуют ряды по собственным
функциям.
Например, если каждую степень z можно выразить в виде равномерно
сходящегося ряда по собственным функциям, то можно перейти прямо
от степенного ряда к ряду по собственным функциям и быть уверенными,
что второй ряд будет сходиться в области, где F(z) аналитична.
Но часто можно пойти дальше этого. Например, мы покажем позже,
что если функция и ее производная имеют в интервале (а, V) конечное
число разрывов, то эту функцию можно представить при помощи ряда
по собственным функциям, дающего совпадение с ней в смысле сходи-
сходимости в среднем (стр. 660). Такие ряды нельзя дифференцировать, и обычно
они не являются равномерно сходящимися. Но их обычно можно инте-
интегрировать, и получающийся после интегрирования ряд будет сходиться
равномерно. Следовательно, ряды по собственным функциям могут идти
дальше, чем степенные, и представлять некоторый класс неаналитических
функций, хотя с получающимися рядами надо обращаться с осторож-
осторожностью.
Чтобы представление функции в виде ряда по собственным функциям
в смысле сходимости в среднем было легко получить, члены последова-
последовательности должны быть взаимно ортогональными, то есть соответству-
соответствующие собственные векторы в функциональном пространстве должны быть
взаимно ортогональными [см. формулу F.3.5)]. Это значит, что
м, ( 0, если тфп;
(z) dz = если т = п F.3.16)
I
43*
67G Гл. 6. Краевые условия и собственные функции
Равенство F.3.14) дает возможность доказать это важное свойство, если
положить верхний предел интегрирования равным верхней граничной
точке Ъ; тогда, если фп удовлетворяет подходящим граничным условиям
в точке Ъ (конечность, если Ъ — особая точка; определенное не зависящее
от X однородное линейное соотношение между функцией и производной,
если Ъ—обыкновенная точка), то левая часть равенства равна нулю и
а это показывает, что если собственные функции фп и фт принадлежат
различным собственным значениям (Хп Ф Хт), то они ортогональны. Заме-
Заметим здесь, что, как будет показано в § 11.1, если граничные условия меняются
с изменением X, то система собственных функций не является ортогональной.
Даже для общего периодического граничного условия получающиеся
собственные функции, если они принадлежат различным собственным
значениям, ортогональны. Действительно, если проинтегрировать равенство
F.3.13) от а до Ъ, мы получим
и выражение в квадратных скобках в силу периодичности принимает
одинаковые значения в а и Ъ, так что они взаимно уничтожаются.
Этим не доказывается, что в вырожденных случаях несколько собствен-
собственных функций, принадлежащих одному и тому же собственному значению,
ортогональны друг другу, но на стр. 674 мы указали, что эти функции
всегда можно выбрать так, чтобы они были взаимно ортогональными.
Значит, будет ли случай вырожденным или нет, собственные функции фи,
образующие нашу последовательность, можно сделать взаимно ортого-
ортогональными, и любую произвольную кусочно-гладкую функцию F{z) можно
представить при помощи ряда
^ щ\ F.3.17)
n=0
в интервале а < z < fe (если система фп полна).
Между прочим, эта ортогональность обеспечивает то, что собственные
значения уравнения Лиувилля F.3.12) вещественны, если только функции р,
q, r вещественны в рассматриваемом интервале z. Если бы существовало
комплексное допустимое значение X, то по симметрии его комплексно
сопряженное тоже было бы собственным значением. Две соответствующие
собственные функции также были бы комплексно сопряжены одна другой;
скажем, фп равна и -f- iv, а фт равняется и — iv. Однако если все-таки
верно, что две собственные функции, соответствующие различным соб-
собственным значениям, ортогональны, то
что невозможно при наших предположениях о г, и и у. Значит, уравне-
уравнение Лиувилля не может иметь комплексных собственных значений, и наши
опасения, выраженные на стр. 671, были напрасными.
6. 3. Собственные функции и их применения 677
В соответствии с нашими рассуждениями на стр. 666 можно при-
принять, что плотность единичных векторов e(z) между z и z + dz пропор-
пропорциональна г (z) dz, а не dz (по этой причине г (z) иногда называется
функцией плотности). Таким образом, скалярное произведение двух век-
векторов F и G будет равняться
ь
(F*-G)= ^ F(z)G(z)r(z)dz,
а
где F(z) и G(z) представляют собой компоненты Г* и G вдоль различных
направлений, определяемых векторами e(z). Собственные функции ф„
являются компонентами взаимно ортогональных собственных векторов Еп;
длина такого вектора
l/2
называется нормирующим множителем для фп.
Значит, компоненты единичных собственных векторов еп имеют вид
§п(х)/Еп; они равны направляющим косинусам е(ж) относительно нор-
нормальных осей, определенных собственными векторами еп. Следовательно,
обобщая формулу F.3.11), получаем
^mr dz = hm> Ц =^Г Фп И Фп (*) = 8 (Ж - Z),
где 8 (ж— z) представляет собой дельта-функцию Дирака (см. стр. 122)-
Ряд во втором равенстве не является абсолютно сходящимся, так что
его можно применять только в случаях, когда последующее интегрирова-
интегрирование обеспечит сходимость. Например, из равенства
ь
F(х) 8 [х-z)dx = F{z),
определяющего о (ж — z), при помощи симметричного ряда по собственным
функциям мы немедленно получаем формулу F.3.17).
Собственные функции, разделенные на амплитуду Еп, так что они
являются направляющими косинусами, компонентами единичных векто-
векторов, называются нормированными. Система собственных векторов, попарно
ортогональных и одновременно нормированных, называется ортонормиро-
ванной системой. Свойство ортогональности очень важно и полезно,
в то время как свойство нормированности имеет лишь формальную выгоду.
Мы будем почти всегда применять ортогональные системы собственных
функций, но редко будем заниматься нормировкой их, предпочитая включать
нормирующие множители 1/Еп в наши уравнения явно.
Разложение уравнения Штурма—Лиувилля (факторизация). Впервые
мы встретились с задачей о собственных значениях в гл. 1 в связи с опре-
определением главных осей линейного векторного оператора. Исследования,
проведенные там, в особенности в части, относящейся к операторам
в абстрактном векторном пространстве, тесно связаны с рассмотрениями
настоящей главы, как мы только что видели. Эту связь можно выявить
¦еще яснее при помощи дальнейшего изучения операторной техники,
описанной на стр. 91—92 и 236. Там было показано, что чисто операторные
678 Гл. 6. Краевые условия и собственные функции
вычисления, применяющие «разложенные» операторы, повышающие или
понижающие собственное значение, также дают решения соответствующего
уравнения Шредингера, являющегося уравнением Штурма — Лиувилля.
Теперь мы покажем, что при выполнении некоторых условий оператор
Штурма—-Лиувилля можно «разложить» на линейные дифференциальные
операторы, которые можно применить для получения собственных зна-
значений и собственных функций по методам, аналогичным методам гл. 1.
Процесс получения этих линейных дифференциальных операторов
из дифференциального уравнения называется разложением на множители
(факторизацией). Возвращаясь к выводу задачи о гармоническом осцил-
осцилляторе на стр. 236 и далее, мы видим, что уравнение
равносильно паре дифференциально-рекуррентных уравнений первого порядка
связывающих собственную функцию фп с ее «ближайшими соседями» фп-1
и фп+1- Обратно, из этих двух уравнений первого порядка можно полу-
получить собственное значение 2п -j- 1 для исходного уравнения второго порядка
и явные дифференциальные выражения для соответственно нормированных
собственных функций.
Для обобщения этого результата мы заменим уравнение Штурма —
Лиувилля
уравнением, которое будем называть видоизмененным уравнением Штурма
Лиувилля:
где
Оно имеет общий вид одномерного уравнения Шредингера с потенциалом V.
Мы рассмотрим здесь случай, когда две границы интервала х (а и Ь)
являются смежными особыми точками уравнения. В этом случае ни р,
ни г не обращаются в нуль в интервале а < х < Ъ, и единственное требо-
требование, наложенное на функцию Ф, заключается в том, что она должна
ь
/•
быть конечной в а и Ъ, или же в том, что интеграл V Ф2 dx должен
а
быть конечным (другими словами, чтобы Ф была интегрируемой в квадра-
квадрате).
Теперь мы исследуем, можно ли оператор, стоящий в левой части
уравнения для Ф (без X), разложить на пару дифференциальных операторов
®~=Ы1(х)-4-, ©+ = ы(ж) + |-
v ' dx ' v ' ' dx
6. 3. Собственные функции и их применения 679
так, чтобы
®*®-фп = (Хп + в)Фп, (Г®*Фп=(Хп-а)Фп.
Складывая и вычитая два предполагаемых уравнения, мы видим, что
Следовательно, если а не должно зависеть от х, то и должно линейно
зависеть от х, и потому и2, равное V, должно быть пропорциональным ж2,
что приводит нас к уравнению для гармонического осциллятора. Диф-
Дифференциальные операторы C~ и ®+ соответствуют абстрактным векторным
операторам, определенным в формуле B.6.30), и с ними надо действовать
так, как описано в гл. 2, для получения собственных значений и соб-
собственных функций.
Этот процесс можно обобщить, чтобы он соответствовал другим фор-
формам V, если V является (или может быть формально сделано) зависящим
от некоторого параметра т, который для удобства нашего анализа можно
предположить принимающим значения, различающиеся на единицу. Мы будем
считать и и а также функциями этого параметра и построим два уравнения:
\х) = [ит+1 (х)- d/dx]Фп (т | х) = /Xn ~am+iфп (т +
®+тФп (т\х) = [пт (х) + d/dx]Фп(jn\x) = УК-атФп(т-Цх),
или эквивалентную пару
®^+1®т+1Фп(т\х) = (Хп- ат+1)Фп(т\х),
®-т®шФп(т\х) = (К-ат) Фп {т\х), (°' ' °J
подобрав эти уравнения так, чтобы они были эквивалентны видоизменен-
видоизмененному уравнению Штурма — Лиувилля
[Vm (х) -d*/dx*]Фп(т\х) = \Фп(т\х).
Чтобы найти соотношение между ит (х), ат и потенциалом Vm (x),
мы вычтем друг из друга и сложим уравнения второй пары (заменяя
в первом т на т—1), а затем сравним результаты с соответствующими
разностью и суммой для уравнения с Vm,
^ 4 4 (х) + Vm (x)],
если X считать не зависящим от т. Так как ат предполагается не зави-
зависящим от х, то можно продифференцировать второе уравнение, в резуль-
результат подставить первое и в конце концов получить
(П +V)/(Vi -Vm),
F.3.19)
где V = dV/dx. Таким образом, видоизмененное уравнение Штурма —Лиу-
—Лиувилля равносильно уравнениям F.3.18), в которых величины ит и ат свя-
связаны с потенциалом Vm формулами F.3.19).
Очевидно, что не все виды V будут давать'удовлетворительное раз-
разложение. Прежде всего, мы предположили, что допустимые значения X
не зависят от т, а это требует, как мы увидим, чтобы ат не зависело
от х. Следовательно, Vm (x) должно быть такой функцией х и т, чтобы
выражение для ат, приведенное в F.3.19), не зависело от х. Это приводит
680 Гл. 6. Краевые условия и собственные функции
к ограниченному числу возможностей, причем некоторые из них дают
полезные последовательности собственных функций. Ряд этих возможно-
возможностей приведен в таблице в конце этой главы; здесь же мы рассмотрим
только один пример, приводящий к полиномам Гегенбауэра (или сфери-
сферическим гармоникам), определенным формулами E.2.52) или E.3.35), а также
в конце этой главы.
Уравнение для этих полиномов имеет вид
где для Т = ТТ (z) собственное значение Х° оказывается равным I (l+2m + 1),
причем l = n—m. Заметим здесь, что параметр m не обязательно ограни-
ограничен целыми значениями. Наша факторизация связывает собственные функ-
функции для данного значения m с собственными функциями для другого тп,
отличающегося на единицу, но часто можно начать от любого значения тп
и передвигаться вперед или назад на единичные шаги. Значения m могут
ограничиваться другими условиями, но в данном случае этого не будет.
Если перейти к видоизмененной форме, положив
z = cos х, Ф = sin ^х-Т,
то уравнение примет вид
«РФ т2"Т
dx2 sinz x
В этом случае потенциальная функция равна
и, следовательно, ит (х) = ( т — -гг J ctga;; om = f m-y J , так что в этом
случае ат не зависит от х, как и требуется.
Раз мы разложили рассматриваемое уравнение Штурма—Лиувилля
частного вида и ат не зависит от х, можно приступить к решению
посредством методов, аналогичных примененным в § 2.6. Например, можно
показать, что дифференциальный оператор ©+ сопряжен к оператору 6Р,
так что
если только / и Ф интегрируемы в квадрате на интервале х между
точками а и Ъ (которые, по предположению, являются особыми точками
уравнения).
Уравнения F.3.18) показывают, далее, что если уп (т | х) представляет
собой собственную функцию видоизмененного уравнения Штурма—Лиувилля
(тем самым функцию, интегрируемую в квадрате при а<ж<6) для соб-
собственного значения Хд, то ®тУп {щ \ #) является собственной функцией
(следовательно, также интегрируемой в квадрате) для того же собствен-
собственного значения Хп, но для значения т, уменьшенного на единицу; эту
функцию можно обозначить через уп(т— 1\х). (Функции у не обязательно
нормированы; мы сохраним символ Ф для собственных функций, норми-
нормированных в интервале а<ж<6.) Другими словами, ®туп {т \ х) =
= Уп{™ — 11 ж); так же &m+iyn{"i\x) = yn(m + l\x), до тех пор, пока
6. 3. Собственные функции и их применения 68
левая часть того или другого выражения не обратится тождественно
в нуль.
Далее мы применяем технику § 2.6 для получения допустимых зна-
значений Хп. Если ат является возрастающей функцией от т, то есть если
am+i > ат> то мы полагаем
ь ь
(т + * I ж)№ = ^ &™+iyn (т | х) ®т+\Уп (т \x)dx =
а
Ь Ь
п(тI х) ®m+i©m+i2/n(т\x)dx = (Хп — ат+1) ^ [уп(т\ x)f dx,
а а
так что если уп (т\ х) интегрируема в квадрате, то и уп(т-\-11 х) такова же,
если только лп — ат+1 не отрицательно; но отрицательным оно не может быть
из-за вещественности у. Следовательно, для т, большего чем некоторое
максимальное значение п, собственных функций быть не может; чтобы убе-
убедиться в этом, достаточно положить Хп = ап+1, чем собственное значение Хп
определяется, поскольку ап+1 известно.
Для определения собственных функций заметим, что
®n+iyn(n\x)= [un+1 (ж) -ж ] уп(п\х) = О,
так как Хп = ап+1, и потому уп (п -{-11 х) тождественно равно нулю.
Следовательно,
Уп (п\х) = ехр [ ^ ип+1 (х)dx J
уп(т\ х) = ®m+i®m+2 ... &п ехр [ ^ un+i (ж) da; j .
Далее, из у можно получить нормированные собственные функции Ф.
Имеем
Фп (п\х) = Сп ехр [ ^ untldxJ , Сп = [ ^ ехр ^2
а
Ь
и если \ [Фп(т\х)]Ых= 1, то можно видеть, что
Таким образом, мы показали, что уравнения F.3.18) равносильны паре
уравнений, непосредственно предшествующих формулам F.3.18), если
функции Ф нормированы, и что второе из уравнений этой пары дает
средство для определения нормированной собственной функции Фп (т \ х)
по известной функции Фп (п \ х):
Фп(т | z) =
... (an+1 — am+
= п, п — 1, п —2, ....
С другой стороны, если аш является убывающей функцией от /те
(ат+1 < ат), то мы обращаем вывод и показываем, что должен существо-
682 Гл. 6. Краевые условия и собственные функции
вать некоторый нижний предел п параметра т, для которого @„ уп {п \ х)
равно тождественно нулю. Тогда Хп = ап и
Сп
У (an—antl) ... (ап—ат)
т = п, и+1, п + 2
причем здесь
Сп = [ j ехр ( - 2 ^ М*) d
а
Таким образом, оба уравнения, предшествующих F.3.18), порождают
нормированные собственные функции, независимо от того, что собой пред-
представляет функция ат от т, но мы пользуемся первым уравнением для
получения Фп (т \ х), если ат+1 < ат, и вторым, если ат+1 > ат.
Возвращаясь к нашему примеру присоединенных функций Лежандра
(или полиномов Гегенбауера), мы видим, что пределы для х равны 0 и тс
A Л2
m-f-yj > am. Отсюда собственные значения равны
где Z = n — т. Так как т = п, п — 1, ..., то I никогда не может быть
отрицательным. Начальная функция равна
„ (п | х) = Сп ехр [ ^п + ~^ ^ ctg (ж) da; J = Сп sinn+1 /2ж,
ж другими собственными функциями являются
n+i/2
1 (»-»)! dn-n
и /л 72^п
2«n! (I —z2J 4
где z = cosx. Сравнение этого результата с таблицей, приведенной в конце
настоящей главы, показывает, что если т и п — целые и 1 = п — т, то
полиномы Гегенбауера и присоединенные функции Лежандра связаны
с Ф соотношениями
=(- iy л[—д±^1^ A _z»)-!-^ (m|arccos
6. 3. Собственные функции и их применения 683
В таблице в конце этой главы мы перечислим другие виды Vm (ж)
и соответствующие ит (х), для которых ат не зависит от ж и которые,
следовательно, допускают факторизацию по описанному выше способу.
Ясно, конечно, что этот метод вычисления собственных функций тесно связан
€ абстрактным векторным представлением. Операторы & можно также
применить для доказательства ортогональности собственных функций.
Описанная выше техника непосредственно дает различные рекуррентные
формулы, связывающие различные собственные функции; эти формулы
полезны для дальнейших вычислений.
Многие уравнения можно разложить несколько иным путем. Например,
уравнение
1 dr. dp\ , г . ... т2 -\ п А
-г-! Sin X —г- )+ и(и+1) ^-=- /> = 0
sin х dx \ dx J ¦ L sin x J
для P™ (cos x) = sin™ x • T™_m (cos x) является уже разложенным по пара-
параметру т, если положить Х= га(га+1) и Фп(т|ж) = С~^Лзтж Р™ (cos ж).
Однако можно также рассмотреть — т? как собственное значение X и про-
вести разложение по п; полагая 1 = \пЩ-^-х, получаем уравнение
которое можно разложить, приняв un(t) = ntht, an= —и2. В этом слу-
случае ап является убывающей функцией от п, так что применима вторая
форма <])т (п 11), значения п не могут быть меньше определенного зна-
значения т, где Хт = — /и2, и первая нормированная собственная функция
равна
Другие собственные функции, для п = т, иг +1, иг + 2, ..., имеют вид
...X
Рекуррентные соотношения для ф удобно выразить через переменную
= 2arctge':
— и cos ж + sin ж-^-j 6m(w|0 = Vr(w — m)(n+m)^m(n — l\t).
Так как
1 = 5 №» (»10Г* = C2 J f^ (cos ж)]2 ^ = C2
—CO 0
то мы видим, что
<!) (П I t) - 1/ m(" —m>! p"
= (- 1Гт 1/7 pv Ф« ("»I arccosth«).
( ~2 )sirxx
684 Гл. 6. Краевые условия и собственные функции
где Ф представляет собой собственную функцию, полученную при первой
факторизации.
Таким образом, мы получили четыре дифференциально-рекуррентных
соотношения для собственных функций Ф или для связанных с ними
функций <]> (мы предпочитаем иметь дело с функциями Ф, так как они
нормированы по углу х, который является переменной во многих физи-
физических задачах). Из этих соотношений можно получить другие полезные
рекуррентные равенства. Например, при помощи сложения формул
/
(n + m + j) (и—m + l) Bи+Т)
выведенных из уравнений для <]>, мы получаем обычное рекуррентное
соотношение для нормированных функций Лежандра
а подставляя это выражение в одно из равенств, выведенных ранее для Ф,
Фп(т\х) =
)(n — m) si
или
у(п + т -}-1) (п — т) sin х ¦ Фп (т \ х) = (п + т +1) cos х¦ Фп (т +11 х) —
мы получаем
Этим же путем можно вывести многие другие полезные соотношения.
Некоторые из них будут получены другими методами позже в этом пара-
параграфе (см. стр. 696). Однако теперь нам надо вернуться к нашей основ-
основной теме —к исследованию полноты системы собственных функций.
Собственные функции и вариационный принцип. Полная система
собственных функций —это такая система, которая может осуществить
представление в смысле сходимости в среднем (см. стр. 660) любой
кусочно-гладкой функции. Чтобы показать, что рассмотренные нами
системы собственных функций полны, мы обратимся к вариационной тех-
технике, развитой в гл. 3. Согласно сказанному в конце, решение уравне-
уравнения Штурма—Лиувилля представляет собой функцию, минимизирующую-
6. 3. Собственные функции и их применения 685
интеграл
и подчиненную дополнительному условию
ь
\ 0>2r (z) dz = const.
а
Другими словами, уравнением Эйлера для этой вариационной задачи
является как раз уравнение Лиувилля F.3.12).
Рассмотрим это утверждение несколько более детально. Допустим, что
мы выбрали в качестве пробной функции функцию <Ь (z), удовлетворяющую
граничным условиям в точках а и b и нормированную с функцией
плотности г:
(это одно из немногих мест, где несомненно выгодно нормировать функции).
Подсчитаем интеграл
|>(!J] F-3-20)
и будем менять пробную функцию произвольным образом (но так, чтобы
она оставалась нормированной и удовлетворяющей граничным условиям),
пока не найдем ф, дающую наименьшее возможное значение Q. В силу
того, что уравнение Лиувилля соответствует вариационному уравнению,
функция ф, для которой Q принимает наименьшее возможное значение,
равна низшей собственной функции <]>0, а соответствующее значение Q равно
то есть наименьшему собственному значению. Здесь мы проинтегрировали
член p(d§/dzJ по частям, применили уравнение F.3.12) для получения
последнего интеграла и использовали граничные условия в точках а и b
для доказательства равенства нулю выражения в квадратных скобках.
Для последующих рассуждений мы предположим q и X преобразованными
так, что Хо = 0.
Для нахождения следующей собственной функции и соответствующего
собственного значения мы минимизируем Q, отыскивая нормированную
функцию ф, которая удовлетворяет граничным условиям в точках а и b
и, кроме того, ортогональна найденной выше функции ф0. Это минималь-
минимальное значение Q равно Х1; а соответствующая пробная функция есть ^.
Таким же образом мы действуем и дальше: для нахождения фп и Хп мы
подсчитываем Q для пробных функций, удовлетворяющих граничным
условиям при z = a и Ь, нормированных и ортогональных подсчитанным
перед этим функциям <]>0, ф1? ..., фп_!. Функция, придающая Q минималь-
минимальное значение, равна <]>п, а значение Q (фп) есть Хп.
686 Глл 6. Краевые условия и собственные функции
Для вырожденных случаев мы найдем целую совокупность функций,
дающих одно и то же минимальное значение Q. Однако из соображений
симметрии или из других дополнительных требований всегда можно выбрать
систему взаимно ортогональных решений, которые можно рассматривать
как стандартные решения для этого вырожденного значения Хп.
Полнота системы собственных функций. Результаты предыдущего
пункта можно выразить еще следующим образом. Пусть F' — любая 'функ-
'функция, удовлетворяющая граничным условиям и нормированная в интервале
(а, Ъ)\ тогда интеграл Q(F), определенный формулой F.3.20), не меньше \.
Поскольку мы преобразовали q и X так, что Хо = 0, Q (F) не может быть
отрицательным. Аналогично, если для функции Fn
= 0, 1, 2,..., и-1, п,
то интеграл Q (Fn) не меньше Хп+1.
Для полноты системы собственных функций нужно, чтобы ряд
со Ь
2 Ст$т (z). Ст = 4" \ 1 (Z) ^m (z) r (z) dz, F.3.21)
m=0 a
сходился (в среднем) к функции /(z) в интервале (а, Ь). Чтобы это было-
так, разность между функцией / и первыми n+l членами ряда
п
/П V / J \ / JL-1 Г71ТГ71 V /
¦m=0
должна стремиться к нулю (в среднем), когда п стремится к бесконечности.
Другими словами, чтобы ряд давал хорошее приближение в среднем,
в соответствии со сказанным на стр. 660, величина
ь ь п
<?= ^ fn(z)r(z)dz= ^ frdz - 2 Е*тС2т
а а тп=0
должна стремиться к нулю, когда п стремится к бесконечности.
Теперь можно применить наши вариационные соображения для оценки
величины ап, так как функция
*"» = /„(*)/*„
обладает указанными выше свойствами:
\ F%r dz = 1 по определению ап,
Г р
(Е2т/ап)(Ст-Ст) = 0, если т<п,
(Е%п/ап) Ст, вообще говоря, ф 0, если т > п,_
6. 3. Собственные функции и их применения 687
в силу ортогональности ф и определения Ст. Следовательно, в соответ-
соответствии со сказанным в первом абзаце этого пункта
S
а т=0
Ь п
а s=0
Первый из полученных членов равен 2 (/)/е& и потому, как мы видели
выше, неотрицателен. Первый член во втором интеграле можно проинте-
проинтегрировать по частям, и, используя то, что фт удовлетворяет уравнению
Лиувилля и что как /, так и ф удовлетворяют граничным условиям,
получаем для второго интеграла
i if i с. [?(*?>«.] *-$ [ i с^
a m=0 m=0
—
= -4- 2
n m=:0
Аналогично находим, что третий интеграл равен — ^ С^ктЕ^п, так что
п)=-V Г Q (У) -
т=0
Так как величина 2 ^mOm должна быть положительной (ни одно из
не отрицательно), то отсюда
1, или a^
Однако 2 (/) положительно и не зависит от п, а мы доказали, что
Хп+1 стремится к бесконечности, когда п стремится к бесконечности. Сле-
Следовательно, ап стремится к нулю, когда п стремится к бесконечности,
и тем самым мы доказали, что ряд F.3.21) сходится е среднем к функции
/в интервале а < z < b. Таким образом, если фп — последовательность
собственных функций—решений уравнения F.3.12) (которое можно преоб-
преобразовать так, что Хо = 0), удовлетворяющих граничным условиям, в силу
которых [/?ф (d$/dz)]a равно нулю, то система фп полна. Это доказатель-
доказательство существенно пополняет наше исследование основных свойств собственных
функций. Теперь мы можем обратиться к частным случаям и к исследованию
общей техники, которая будет использована позже.
Асимптотические формулы. Иногда бывает полезно получить прибли-
приближенные выражения для собственных функций и собственных значений
высокого порядка (и велико). Мы вернемся к уравнению Лиувилля
и сделаем подстановку
688 Гл. 6. Краевые условия и собственные функции
для получения уравнения
сРу/с?в + [Ля-а;F)]у:=О, F.3.22)
где
ap, q и г надо выразить через ?. Новое независимое переменное изменяется
в пределах 0<С?<Стс.
Если X велико, то /с2 велико сравнительно с w, и можно ожидать, что
зависимость у от ? приближенно синусоидальная. Для уточнения этого
можно переставить члены уравнения
и решать его так, как будто шг/— неоднородная часть. На основании фор-
формулы E.2.19) мы видим, что выражением для у будет
! sin[k(Z—t)]w(t)y(t)dt, F.3.23)
где ?0 — подходящий нижний предел интегрирования. Это, конечно, не реше-
решение, а интегральное уравнение для у. В гл. 8 мы будем детально изу-
изучать его решение. Однако здесь мы занимаемся только решениями, для
которых X очень велико, настолько, что интегралом по сравнению с пер-
первыми двумя членами можно пренебречь (если X велико, то к велико и под-
интегральная функция, умноженная на 1//с, исчезает). Значения А, В и к
должны быть выбраны так, чтобы удовлетворялись граничные условия.
Если ни а, ни Ъ не являются особыми точками, то задача о приспособ-
приспособлении нашей асимптотической формы к граничным условиям довольно
проста. Если требование состоит в равенстве ф нулю в точках а и Ь, то
первое приближение, полученное путем отбрасывания интеграла в уравне-
уравнении F.3.23), есть просто
к=п, <l>n^[l/G7>I/4]sinK), Xn = (n//J, F.3.24)
что имеет место, если п2 больше w всюду в интервале 0 < ? < и. Более
точное приближение можно получить, если теперь подставить результат
обратно в интеграл в формуле F.3.23) и подсчитать поправочный член,
но пока мы опустим такие подробности.
Если граничные условия состоят в требовании аф -J- Р dty/dz = 0 при
z = а и в аналогичном соотношении, возможно, с другими постоянными а
и р, при z — b, то этот процесс несколько усложняется. Мы полагаем
в качестве первого приближения
где фазовый угол 6 надо определить из граничных условий. Так как к2
должно быть больше w (?) всюду в интервале 0 < ? < тс, то
так как для большого к производная от множителя (рг)-1!* мала сравни-
сравнительно с производной от cos(/c$ + 6). Решение для 6 получается из урав-
уравнения
-«-И!/
6. 3. Собственные функции и их применения 689
Если к достаточно велико, то отсюда
Подобное удовлетворение граничному условию при z = b определяет допу-
допустимые значения к и тем самым Х = (Л//J:
1 1, F.3.25)
фп
где и—целое.
Таким образом, если а и Ъ — обыкновенные точки, то высшие собствен-
собственные значения уравнения Лиувилля приближенно равны квадрату произве-
произведения тс на большое целое п, разделенному на квадрат интеграла от \^г/р
по интервалу от а до Ъ. Соответствующая собственная функция прибли-
приближенно равна косинусу произведения чсп на отношение интеграла от У г/р
по интервалу от а до z к интегралу от ~[/~г/р по интервалу от а до b
(с дополнительным «амплитудным множителем» (jw)~1/4, изменяющим
амплитуду).
Если а, или Ь, или и а и b являются особыми точками, в которых р
обращается в нуль, то интегралы, определяющие J и ? (приведенные
непосредственно перед уравнением F.3.22)), могут расходиться, и тогда
наши определения надо несколько видоизменить. Кроме того, в таких
точках может обратиться в бесконечность функция q; во всяком случае,
там обратится в бесконечность функция w. Конечно, мы можем решить
уравнение Лиувилля вблизи особой точки при помощи степенных рядов
и найти там природу особенности обоих решений. Если наше уравнение
имеет физический смысл, то одно из решений будет там конечным.
Чтобы увидеть, как это получается, возьмем частный пример уравне-
уравнения Бесселя, к которому мы приходим при разделении волнового уравне-
уравнения в полярных координатах (см. стр. 518 и 579),
dz1
F.3.26)
где z = r=?1, m — целое (получается из граничных условий периодичности
для ?2-множителя), а X—константа разделения. В этом случае имеем
p=z, r=z, q= —m2/z. Допустим, что в качестве предела а берется особая
точка z = 0.
Совершая подстановку для перехода к уравнению F.3.22), имеем
<Ь=-
d2y/d^ + [kz - (m2—l/4)/?2] у— 0; и интегральное уравнение для у будет
иметь вид
где пределы интеграла выбраны так, чтобы обеспечить сходимость. Для
больших значений к и z первый член дает достаточную точность, и об
интеграле не нужно беспокоиться, если только Z не близко к нулю. Если
44 ф. м. Морс в Г. «Гешбах
690 Гл. 6. Краевые условия и собственные функции
бы мы могли найти значение фазового угла 6, соответствующее требова-
требованию конечности ф для z = 0, то нам вообще не требовалось бы пользо-
пользоваться асимптотической формой для малого ? (где она неточна).
Мы найдем значение 6, используя явление Стокса (см. стр. 571),
потребовав для этого, чтобы изменение асимптотической формулы для
ф, когда ? берется на окружности с центром ? = 0, соответствовало изме-
изменению ряда, дающего решение около С = 0. Рассмотрение определяющего
уравнения (см. стр. 503) для уравнения F.3.26) показывает, что решение,
конечное при z = 0, имеет вид произведения zm на ряд Тейлора по z. Сле-
Следовательно, если ф вещественно для больших z вдоль положительной
вещественной полуоси (фазовый угол ф = 0), то оно равно произведению
eim-n на вещественную функцию для ф = тс (z отрицательно и велико) и его
главный член должен равняться произведению eim<e на вещественную функ-
функцию, если ф не является целым кратным тс (z комплексно и велико по
модулю).
Положим ф ~ A/2 У^г) [e№!:+ie4- e-ikZ~i6]; это выражение вещественно
при <р = 0, и мы исследуем сначала его поведение для <р = тс/2 (? = i | ? |).
Здесь первый член в квадратных скобках незначителен при больших t,
и асимптотическая формула дает
ф == eirrm/2.вещественная функция *==< (l/2 ~[/r\ z () е % * , z = \z\eVK ,
1 f IN
так что 6= —-jT-тс (m+~<r )• Для проверки этого результата положим
также ф= —тс/2 (?= — i|?|). Здесь второй член незначителен и
ф = e-imTt/^-вещественная функция<^A/Z у \z\)e , z = \z\e ,
так что опять 6= —jT^v m ~^~~2j ¦ Значит, асимптотической формой для
собственных функций в этом случае будет
что совпадает с асимптотическим поведением, которое дается формулой
E.3.68). Если граничное условие при z = b имеет вид ф = 0, то асимпто-
асимптотическое выражение для собственных значений таково:
2; и велико.
Ту же технику можно с успехом применить для других случаев,
когда один или оба предела являются особыми точками. Более полное
исследование асимптотических формул будет проведено в гл. 9. Из при-
приведенного здесь рассуждения можно заключить, что для любого из
обычных видов граничных условий (все равно, в особых или обыкновен-
обыкновенных точках) можно указать асимптотическую формулу, дающую подхо-
подходящее приближение, если подобрать фазовый угол 6 в выражении
F.3.27)
6. 3. Собственные функции и их применения 691
Подобным образом асимптотическая формула для высших собственных
значений оказывается такой:
где значение а зависит от частного вида граничных условии как в а, так
и в Ъ.
Сравнение с рядом Фурье. Из этого исследования мы видим, что
в высших членах любой ряд по собственным функциям ведет себя подобно
ряду Фурье. Можно доказать, что разность между первыми п членами
ряда по собственным функциям и первыми п членами ряда Фурье, взятых
для одного и того же интервала и для одной и той же функции, является
равномерно сходящейся к нулю при неограниченном возрастании п.
Чтобы это показать, перейдем к новой независимой переменной ?
и новой зависимой переменной у, как указано в F.3.22). Обозначим через
/(?) представляемую функцию F(z), умноженную на (ргI'* и выраженную
через Z,. При этих операциях в / не появится новых особенностей или
разрывов. Разложение / в переменной Z, имеет вид [см. формулы F.3.17)
и F.3.18)]
Ь со
/ (С) = №) г (z)]1/* \f (t) 2 ^г фт (z) <L @ r (t) dt =
о nt=0
a m=0
тс со
(*) 2 ^УтЮуМЛъ, F.3.28)
О m=O m
где
= Ут ШРГI'*, F(t) =
Ь Л 2
Е2т=\ фтг cfa, 7V^- \ y2n(Q dQ = ^
Однако функцию / можно выразить^ в интервале 0]< Z, < it рядом
Фурье. Например, можно применить ряд по косинусам
•к
/(С) =5
0
8-f cos mZ-cos mzdz, F.3.29)
n>=0
где so=l, en = 2(n>0) называются множителями Неймана.
Если граничные условия, налагаемые на функцию ф, таковы, что
асимптотический вид ф„ дается формулой F.3.25), то вид членов с у в ряде
с возрастанием п будет приближаться к виду косинусоидальных членов.
Оба ряда будут приближаться почленно один к другому, и в конце кон-
концов отдельные члены станут совсем близкими друг к другу, совпадающими
в гораздо больших деталях, чем можно было бы ожидать. Многие ряды
44*
-Гл. б. Краевые условия и собственные функции
по собственным функциям сходятся лишь условно (то есть сходятся только
из-за того, что члены имеют чередующиеся знаки и частично взаимно
уничтожаются). Многие из трудностей, сопровождающих исследование
представления отдельных функций при помощи собственных функций, про-
проистекают из этой слабой сходимости. Эти трудные случаи детально изуче-
изучены для рядов Фурье, и потому если мы сможем показать, что то, что
имеет место для ряда Фурье, справедливо и для других рядов по собствен-
собственным функциям, то мы избавимся от значительной части работы. Если
окажется, что разность между рядами F.3.28) и F.3.29) абсолютно сходится
(то есть ряд из абсолютных величин разностей сходится), то тем самым
будет установлено требуемое детальное соответствие рядов.
Например, согласно формуле F.3.11), ряд
оо
1
2 тг
„ "ffl
тп=0
в определенном смысле представляет дельта-функцию Ь (? — х). Такой ряд
далек от абсолютной сходимости, но можно показать, что если из гранич-
граничных условий следует формула F.3.25), то функция
т=0
при стремлении п к бесконечности ограничена. Мы докажем это интерес-
интересное соотношение, применяя еще раз асимптотическую форму для ут, по-
полученную из формулы F.3.25):
= -jt-1/ — при z = a, В—то же выражение при z=b,
sin mX, ->
и нормирующие постоянные имеют вид Щп с^ ъ + члены порядка 1/т2
и выше. Разность между членами в квадратных скобках в выражении Фп
велика для малых значений т, но для все больших и больших значений
т (если л достаточно велико) эта разность приближается к малой величине
— — { [ — {В— А) + А 1 sin mZ cos mz —
— I ~ (B — ^4)+^4 I sin тех cos m?J j + члены порядка 1/m2 и выше.
Члены порядка 1/т2 сходятся абсолютно, и потому их сумма ограничена;
¦vn sin mt
ряд 2j m ¦ сходится, и потому сумма членов, умноженных на 1/т, также
¦ограничена, чем и доказывается ограниченность функции Ф„ при п -^ оо.
Мы можем утверждать, что она всегда меньше некоторой конечной вели-
величины D, независимо от значений п, ? или г (если 0 < ? < те, 0 < х < те).
6. 3. Собственные функции и их применения
693
При помощи тех же рассуждений можно показать, что разность
между первыми ft членами разложения непрерывной функции /(?) по соб-
собственным функциям уп и первыми п членами разложения / (?) в ряд по
косинусам равномерно стремится к нулю при п —> оо. Здесь мы сравниваем
наш ряд по собственным функциям с рядом по косинусам. При других
граничных условиях надо сравнивать с рядом по синусам и т. д.; оказы-
оказывается, что для каждого разложения по [собственным функциям можно
построить ряд Фурье, имеющий с этим
разложением такую же тесную связь,
как показано выше.
Сформулируем наши выводы на фор-
формальном языке: разложение любой непре-
непрерывной функции по собственным функ-
функциям сходится или расходится в любой
точке так же, как соответствующий
ряд Фурье. В любом интервале оно схо-
сходится абсолютно тогда и только тогда,
когда соответствующий ряд Фурье схо-
сходится абсолютно в этом интервале.
а х0 х-
¦х-
JLD-
Р и с. 6.9. Явление Гиббса.
Разрывная функция F (х), приближенная
и-й частной суммой Sn (эс) ряда.
Явление Гиббса. Мы показали, что
соответственно выбранный ряд по соб-
собственным функциям может дать совпаде-
совпадение в смысле сходимости в среднем,
даже если функция имеет конечное число
разрывов. Однако надо отметить некоторые трудности, появляющиеся при
применении такого ряда для подсчета значений функции вблизи разрыва.
На рис. 6.9 показана функция F(x) с разрывом при х = х0. Первые
п -\-1 членов соответствующего ряда по собственным функциям
Ь п
р (м) 2 ~ ф™ (х) ф™ wr (M)du
не могут дать разрыва, так как конечное число непрерывных функций не
может дать бесконечного наклона, требуемого при разрыве. Как показы-
показывает тонкая линия на рисунке, частная сумма Sn(x) пытается достичь
бесконечного наклона при х = х0, и при этом она перебегает за разрыв на
некоторое расстояние. Получающаяся кривая для Sn походит на кривую
интенсивности света при диффракции у края экрана, причем длина свето-
световой волны обратно пропорциональна п. Даже при сколь угодно больших п
это «перебегание» сохраняется и полный ряд имеет «закраины» на концах
разрыва, отмеченные буквами D* и D~ на второй части рис. 6.9. Эти
дополнительные пики нулевой ширины не мешают ряду сходиться к функ-
функции в среднем, но указывают на ограничения, связанные с представлением
функций при помощи рядов по собственным функциям.
Можно исследовать явление Гиббса более точно, если взять в качестве
примера ряд Фурье. Рассмотрим представление функции
*М-1 +1 ДЛЯ °<ж<*'
694 Гл. ¦ 6. Краевые условия и собственные функции.
при помощи ряда, периодического по ж с периодом 2ттг, которое имеет вид
•к 2-я оо
S (х) =— ( \ dt — \ dt }\ у+ 2 (cosm&'cosmt + sin mx ¦ sin mt) =
О -К 7П=1
оо
=42 г^81
8=0
Здесь перед нами вырожденный случай, однако применение суммы произ-
произведений для всех собственных функций под знаком интеграла' все еще
возможно.
Подсчитаем сумму всех членов от sin x до sin пх (это не будет суммой
первых п членов, так как в данном случае все члены с четными п отсут-
отсутствуют), производя суммирование под знаком интеграла до интегрирования.
Подинтегральная функция равна
¦^¦ + 7 2 cos[m(a-l)] =-^ У, etm <*-<> = JL e-i« <*-*>
JL
s=0
3 30)
так что сумма до sin пх включительно равна
0
It—X
—X
X
sin [(и+1/2)
si
db-
sin
!
inl<!-*
~ \ Ctv
J
X
(n+1/2)
3inF/2)
¦)/2] J
sin[(n + l/2)(t—ж)]
sin[(t—a;)/2J
1 sin (n +1/2) 6
J sin F/2)
,6 7*
j
sin(ra + l/2N ,fll
sin F/2) Й j
Если 0 < ж < it, а и велико, то первый из двух интегралов в послед-
последних двух формах значительно больше второго. Последняя форма показы-
показывает, что если п—> со, а ж не стремится одновременно к нулю или тс
(то есть х на некоторую конечную величину больше нуля и меньше тг),
то второй интеграл стремится к нулю, а первый — к
1С
те j
Значит, в интервале е < х < тг — е, где е мало, но, конечно, сумма Sn схо-
сходится к 1 при п—>со; подобным образом для ъ-\-е. <х<2ъ~е (а также
для — тг + е < ж< — е)?п—> — 1 при п—> оо.
3. Собственные функции и их применения 695
Однако будем теперь подсчитывать значение Sn для х = тс/B/г +1)» когда я
стремится к бесконечности (то есть одновременно с я—> со устремлять
х—>0 по выбранному закону). Вновь отбрасывая второй интеграл, который
опять стремится к нулю, имеем
и/2
-я/2
Следовательно, ряд, пытаясь следовать разрыву при ж = 0, перебегает
отметку почти на 18% в области исчезающе малой ширины, прежде чем
он возвратится к правильному единичному значению.
Мы уже показали, что ряды по другим собственным функциям по
отношению к сходимости ведут себя подобно ряду Фурье. Поэтому надо
ожидать подобного перебегания у точек разрыва и для других рядов.
Так как область перебегания имеет исчезающе малую ширину, то интеграл
от ряда дает правильное значение, даже если интегрирование распростра-
распространяется на разрыв. Однако требуется соблюдать осторожность при диф-
дифференцировании таких рядов. Если данный ряд равномерно сходится, то
ряд, получающийся из него почленным интегрированием, сходится навер-
наверняка, однако ряд, получающийся при почленном дифференцировании, — не
обязательно.
Производящие функции, полиномы 'Лежандра. Для большинства
систем собственных функций имеются простые соотношения между после-
последовательными собственными функциями (рекуррентные формулы), а выра-
выражения для нормирующих постоянных часто довольно просты. Многие из
зтих полезных равенств наиболее легко найти, детально изучая разложение
по собственным функциям некоторой более или менее простой функции.
Мы ищем функцию двух переменных Ф (<, z), имеющую разложение вида
(.HS V*w(). ()
п=0
где <]>„ — изучаемая система собственных функций, а коэффициент ап не
зависит от z ж t. Другими словами, функция Ф должна быть так связана
с системой 4»п, чтобы каждый член ее разложения равнялся произведению
степени t на соответствующую собственную функцию от z и на коэффи-
коэффициент, не зависящий от z и t. Такая функция Ф называется производящей
функцией для системы собственных функций фп. Сравнение формулы F.3.32)
с формулами D.3.3) и D.3.1) показывает, что производящая функция
связана с тем или иным интегральным представлением собственных
функций.
Производящие функции часто тесно связаны с построением решений
при помощи функции Грина, которое было указано на стр. 653 и 661
и будет изучаться в следующей главе. В качестве примера того, какую
помощь могут оказать производящие функции, выведем свойства полиномов
Лежандра (см. стр. 560). Эти полиномы появляются при решении уравне-
уравнения Лапласа в сферических координатах и связаны с функцией Грина 1/R,
где R2 = г\ -\- /•§ — 2т>17>2 cos 6, соотношением [см. формулу E.3.28)]
696 Гл. 6. Краевые условия и собственные функции
Упростим его для получения производящей функции для Рп (z):
Отсюда при помощи дифференцирования по t получаем
4? = Z~l .„, ИЛИ (l + f«-2fz) 4g- + (f-z) Ф = fl-
flat (l + t2 — 2tz)a/* ' dt ^v ;
Подставляя ряд в это уравнение, получаем
2 rntm-iPm(Z) + % sts+iPs(z)- 2 2nztnPn(z) +
Л s=0 n=:0
s=0 n=0
Приравнивая коэффициенты при tn, находим рекуррентные соотношения
2и +1) zPn (a) = (#» + !) />mI (z) + nP^! (z) дли п = 0, 1, 2, 3, ... . F.3.33)
Дифференцирование Ф по z дает другое соотношение:
dz ~
откуда
CO OO OO
8=0 7П=0 П=0
Приравнивая коэффициенты при степенях tn+1, получаем
/>q = 0, Р[=Р0, Pn+i + Pn-i = 2zPn + Pn, n>0. F.3.34)
Можно вывести также
что приводит к реккурентным формулам
/>5=о, />j = p0) Bn+i)jpn=jp;+1-jp;_lf n>jo. F.3.35)
При помощи комбинирования этих трех равенств или же посредством
дальнейшего манипулирования с производящей функцией можно получить
дальнейшие формулы:
F.3.36)
и, наконец,
A - z2) Р'п - 2zPn + п (п + 1) Рп = 0.
Последнее, конечно, является дифференциальным уравнением [см. E.3.23)]
для функций Лежандра Pn(z).
При помощи прямого разложения ФB, z) находим, что P0(z) = l,
P1(z) = z; остальные Р можно получить из формулы F.3.33). Громоздкие,
но не вызывающие затруднений выкладки дают общую формулу
Р (z\ ¦ BПI fz" "("-Ц =" -2 . я(в-1)(я-2)(в-3) 4 \ ^6
r-nW- 2«(n!Jl 2Bn—1)Z + 2-4Bn-l)Bn-3) •¦•/' У0-
6. 3. Собственные функции и их применения 697
откуда можно найти, что
О, если п нечетно,
F-3.38)
2 4 6
еСЛИ П четно-
Отсюда или при помощи подстановки г=±1 в выражение для Ф и срав-
сравнения коэффициентов при tn получаем
РпA) = 1, Рп(-1) = (-!)". F.3.39)
Мы видим, что каждая из этих собственных функций представляет
собой полином относительно z степени п, имеющий при четном п только
четные степени z, а при нечетном п — только нечетные степени. Обратно,
каждую степень z можно выразить через конечное число Рп, причем нечет-
нечетную степень — через Рп с нечетными значениями п, не превосходящими
показателя степени z, а четную степень — через Рп со всеми четными п,
не превосходящими показателя. Эти разложения можно получить также
при помощи непосредственных выкладок:
„n_ Bв + 1)в(в-2) ... 2
n —1)... {n
B1.-3I.A.-2)... 4
n = 4, 6, 8,
1) Bтг — 1) ... (n + 2) n
Bв-3)(И-1)(Д-3)...4
п = 5, 7, 9, ... F.3.40)
Значит, любая функция, аналитическая в круге | z \ < 1 и потому
допускающая в нем разложение в сходящийся ряд по степеням z, может
быть разложена в сходящийся ряд по функциям Pn(z). Производящая
функция Ф для Рп тесно связана с ядром интегрального представления
E.3.26) для jPbi как это, конечно, и должно быть.
Следует, кстати, заметить, что функции Лежандра можно получить
следующим образом. Если мы хотим представить любую аналитическую
в круге | z | < 1 функцию z, то это можно сделать посредством степенного
ряда, но степени z не ортогональны при интегрировании от — 1 до +1
(хотя они ортогональны при интегрировании по окружности с центром
в начале координат); поэтому мы начинаем с 1 и z (которые ортогональны),
(выбираем комбинацию z2 и 1, ортогональную 1 (и z), и т. д., выбирая
каждую функцию tyn (z) в виде линейной комбинации zn, zn~2, ..., ортого-
ортогональной tj)m (m < п) при интегрировании от — 1 до +1. Получающиеся Оп
будут пропорциональны сферическим гармоникам Pn(z) (см. таблицу в
конце этой главы).
Формулу, приведенную на стр. 517 и выражающую Pn(z) черев
n-ю производную от (z2 — 1)п, можно также получить из производящей
л
функции. Решение квадратного уравнения y = z + -^t(y^ — l), стремящееся
к z при t —> 0, равно
откуда -|=
•698 Гл. 6. Краевые условия и собственные функции
Однако это решение квадратного уравнения можно получить и при помощи
разложения Лагранжа [см. D.5.8)]:
откуда
X-l 2nn\ dzn
n=l
Приравнивая коэффициенты при одинаковых степенях t, имеем
^^Г(Я«_1)- F.3.41)
Последняя формула дает возможность подсчитать нормирующий
интеграл для функций Лежандра. Допустим сначала, что п > т. Тогда
1 1
/ = К Р (z) P (z)dz — —
-1 -1
Интегрируя т раз по частям, получаем
(_l)m*n-l
-1
(-1)"
-1
( — l)"-mBm)!
•С другой стороны, если п = т, то последний интеграл равен
F-3.42)
Таким образом, мы показали, что эти функции взаимно ортогональны
¦(как это, конечно, и должно быть, поскольку они являются собственными
функциями), и подсчитали нормирующие постоянные Еп [см. формулу F.3.16)].
Для доказательства того, что система полна и что ряд
[ 2 ^ Рп (*) рп (Q ] К F.3.43)
0
п=0
.дает хорошее совпадение в смысле сходимости в среднем для произволь-
произвольной кусочно-гладкой функции f(x), можно применить наши общие вариа-
вариационные соображения. Можно ожидать, конечно, что вблизи каждого раз-
разрыва будет наблюдаться явление Гиббса, но что ряд можно интегрировать,
•будучи уверенным, что такие интегралы всегда равны соответствующим
интегралам от функции /. (Однако можно встретиться с затруднениями
при дифференцировании ряда.) Например, если / — непрерывная функция,
то ряд в квадратных скобках в формуле F.3.43) можно считать эквива-
эквивалентным дельта-функции 6 (х — Q в области — 1 < (ж, Q < 1.
б, 3. Собственные функции и их применения 699
Кроме дельта-функции, при помощи ряда по полиномам Лежандра
можно представить, другую чрезвычайно полезную функцию:
п=0
Если z не находится на вещественной оси между — 1 и +1, то интеграл
в квадратных скобках сходится и может быть подсчитан при помощи
интегрирования по частям:
где Qn(z) [см. формулу E.3.29)] —функция Лежандра второго рода.
Мы получаем полезный ряд
со
^ z)Pn(Q. F.3.44)
Он сходится только при |z|>l и | ? | < 1, но интегралы от этого ряда,
умноженного на аналитические функции, можно рассматривать для еще
более широких областей переменных, чем в случае ряда для дельта-функ-
дельта-функции. Однако важно помнить, что область определения функции Qn(z)
из-за ветвления имеет разрез вдоль вещественной оси z между — 1 и -|" !•
Последнее равенство имеет некоторые интересные и полезные след-
следствия. Во-первых, разложение функции / (z), аналитической внутри эллипса С,
имеющего фокусы^в точках ± 1, и на. нем, записывается в виде
где коэффициент ап определяется любой из следующих формул:
1
-1
~f(x)dx. F.3.45)
Первая форма интеграла полезна для функций, аналитических при боль-
больших значениях | z |, так как на контуре С можно применить асимптоти-
асимптотическую формулу E.3.30) для Qn вдоль большого эллипса. Во-вторых,
применяя производящую функцию для Рп, мы находим, что
F.3.46)
чем определяется производящая функция для Qn (хотя Qn не является
собственной функцией).
Из подходящих производящих функций можно вывести много других
полезных систем одномерных собственных функций. Некоторые из них
будут приведены в таблице в конце этой главы, некоторые другие войдут
в задачи.
700 Гл. 6. Краевые условия и собственные функции
Собственные функции для нескольких измерений. До сих пор мы
исследовали собственные функции для одного измерения, именно, реше-
решения уравнения Лиувилля с одним независимым переменным, удовлетво-
удовлетворяющие граничным условиям довольно общего типа в двух концах интер-
интервала. Уравнения с частными производными по трем или более переменным
порождают собственные функции, зависящие от более чем одного перемен-
переменного. Это — решения уравнения с частными производными, полученного при
отделении одной из координат, оставившей взамен себя константу разделения.
Решение этого уравнения должно удовлетворять некоторому простому гра-
граничному условию вдоль некоторой граничной линии или поверхности
(обычно однородным условиям Дирихле или Неймана или же их однород-
однородной комбинации). Это обычно возможно только для некоторых дискретных
значений (собственных значений) константы разделения.
Многие из выводов теории Штурма-Лиувилля можно перенести на
многомерный случай. Для большинства видов уравнения имеется наимень-
наименьшее собственное значение, и собственная функция, соответствующая этому
наименьшему (низшему) значению, обычно не имеет узловых линий (или по-
поверхностей) внутри границы. Однако собственные функции нельзя расположить
в каком-либо простом, линейном порядке, как это было в случае одного
измерения. Трудность состоит в том, что имеется более одного решения с одним
узлом (даже если нет вырождения). Однако можно расположить решения
в своего рода двумерном порядке, так как обычно оказывается, что узлы
в двумерном случае распадаются на два семейства (см. стр. 472) и возра-
возрастание числа узлов одного рода всегда влечет возрастание соответствую-
соответствующего собственного значения.
В тех случаях, когда имеется наименьшее собственное значение,
когда собственные значения не имеют верхней грани и существует вариа-
вариационное уравнение, эквивалентное дифференциальному уравнению для
собственных функций, можно применить рассуждения, изложенные на пре-
предыдущих страницах, для доказательства того, что эти более общие соб-
собственные функции образуют полную ортогональную систему (а в вырож-
вырожденных случаях они могут быть сделаны ортогональными), при помощи
которой можно представить в виде ряда любую кусочно-гладкую функ-
функцию внутри границы.
Если уравнение с частными производными для собственных функций
само разделяется, эти факты легко доказать. Каждая собственная функ-
функция равна тогда просто произведению собственных функций от разделен-
разделенных координат (за исключением вырожденных случаев, когда решения
могут быть конечными комбинациями произведений для каждого из
вырожденных состояний). Ортогональность и полноту можно вывести
из ортогональности и полноты одномерных множителей.
В качестве примера можно рассмотреть случай однородной гибкой мем-
мембраны плотности р (на единицу площади), натянутой на жесткую опору
с равномерной силой натяжения Т на единицу длины. Уравнением движе-
движения будет волновое уравнение
•' 2 j_a^ = 0 2 т_
где W — смещение мембраны от ее положения равновесия. Предполагая
простую гармоническую зависимость от времени, можно отделить времен-
временной множитель, так как W = ф (х, у )е~ш, где
3 ^ 0, ft-i; F.3.47)
получается уравнение Гельмгольца в двух переменных х и у (или, после
преобразования, в переменных г и <р и т. д.) с константой разделения &2.
6. 3. Собственные функции и их применения 701
Если опора имеет вид прямоугольника со сторонами, лежащими на
прямых х = 0 и а, у = 0 и Ъ, то собственные функции и собственные
значения равны
Ф«т (х> У) = sin (ътх/а) sin (кпу/Ь),
ftjm = ir2 [{mlaf + (n/b)% m, n = 1, 2, 3, 4, ... . F.3.48)
Так как отдельные множители взаимно ортогональны, то и произведения
обладают этим свойством, и при помощи тех же рассуждений, что
и выше, получаем, что <]>mn образуют полную систему. Узловые линии
{линии внутри прямоугольника, где ф = 0) либо перпендикулярны оси х,
либо же перпендикулярны оси у. Число первых и вторых равно соответ-
соответственно т—1 и п — 1. Значит, хотя расположение kmn в порядке возрас-
возрастания не порождает простой последовательности чисел тп и п, тем не
менее возрастание тп на 1 увеличивает на 1 число узлов, перпендику-
перпендикулярных оси х, и увеличивает соответствующее к2, а возрастание п на 1
увеличивает число узлов, перпендикулярных оси у, и также увеличивает к2.
Если а—Ъ, имеем вырожденный случай, так как тогда ктп = кпт
и для одного и того же собственного значения к имеется по крайней
мере две собственные функции. В этом случае в качестве собственной
•функции можно было бы взять любую линейную комбинацию функций
Фтп и Фпт- Поскольку уже фтп взаимно ортогональны, целесообразно
пользоваться ими самими.
Значит, любую кусочно-гладкую функцию / (х, у) можно разложить
в ряд
а Ь
/ (*, У) = 2 [ ~ь
тп,п
Если /(ж, у) является аналитической функцией при 0<ж<а и 0<у<Ь,
то ряд будет равномерно сходиться в этих интервалах; если / имеет
разрывы, то для ряда может обнаруживаться явление Гиббса у разрывов,
однако почленно проинтегрированный ряд будет сходиться.
Если в соответствующих границе координатах уравнение не разделяет-
разделяется, то его анализ несколько более сложен. К сожалению, подробно иссле-
исследовано только два неразделяющихся случая, в одном из которых граница
представляет собой прямоугольный равнобедренный треугольник. Возможно,
что это слишком простой случай, чтобы выявить все сложности; тем не
менее он заслуживает некоторого внимания (см. § 11.2).
Чтобы сделать наше изложение конкретным, вновь рассмотрим мембрану,
но сейчас будем считать, что граница состоит из трех прямолинейных
отрезков, соединяющих начало координат и точки @, а) и (я, 0). Уравне-
Уравнения будут те же, что и выше, и для простой гармонической зависимости
от времени получится уравнение Гельмгольца F.3.47). Решение, равное
произведению sin (ртж/а) ¦ sin (vicy/a), обращается в нуль на частях осей
.жиг/, принадлежащих границе, но не равно нулю вдоль третьей, диаго-
диагональной части. Однако комбинация
sin (fiir:a;/a) sin (чъу/а) Т- sin (ръу/а) sin (vicx/a)
равна нулю и вдоль этой части (знак — или -\- ставится в зависимости
• от того, будет ли число | fi — v| четным или нечетным). Значит, для этого
702
Гл. 6. Краевые условия и собственные функции
случая собственными функциями являются
Фтп (х> У) — sin I — (/» + «) ж I sin Г — nw I —
L J L ^ J
— (- 1)т sin [^ (то + п) уЛ sin Г -^ пх 1 , F.3.50)
где то и и —целые положительные числа. Чтобы показать, как удовлетворить
граничным условиям вдоль диагональной части границы, повернем наши
оси на те/4, положив
а=|/2а,
где координатные оси ? и -ц показаны^на
рис. 6.10. Совершая несколько тригоно-
тригонометрических преобразований, получаем
— sin — (то + 2n) tj I sin Г — тоМ
при то = 2, 4, —,
= cos f -^- (то + 2п) ¦»] 1 cos | — тоМ —
— cos -^ (то + 2/г) ? 1 cos f ^- то-»]
при то = 1, 3, —»
откуда видно, что ф обращается в нуль
? 2
ф
Рис. 6.10. Собственные функции при ? = <х/2, чему соответствует диаго-
для треугольной мембраны. нальная часть границы.
Линии внутри границы обозначают поло- ГпЯртпрннир чпядання а чтпм
шение узловых линий, на которых ф=о, ^ооственные значения и атом
для малых значений квантовых чисел т равны
(Jm2 + 2mn + 2n2]; F.3.51)
они имеют наименьшее значение (то = п = 1) и не имеют верхней грани.
Собственные функции взаимно ортогональны и являются решениями
вариационного уравнения
*SS
Следовательно, эти функции образуют полную систему. Однако взаимо-
взаимосвязь между значениями А2, с одной стороны, и числом и расположением
узловых линий, с другой, не очевидна.
Узловые линии для некоторых из собственных функций показаны на
рис. 6.10. Заметим, что эти линии не распадаются на два взаимно ортогональ-
ортогональных семейства, как это будет для прямоугольной границы (и в действитель-
действительности для всех случаев разделения). Можно сказать только, что если то
или п возрастает, то число узлов увеличивается и /с2 возрастает (это является
существенным результатом теории Штурма —Лиувилля).
6. 3. Собственные функции и их применения 70S
Разложение функции f(x, у) до этим собственным функциям имеет тот
же вид, что и F.3.49), однако интегралы в квадратных скобках берутся
по внутренности треугольника вместо внутренности прямоугольника,
а множитель А/а2 перед интегралами заменяется на 8/а2. Относительно
сходимости можно сделать такие же замечания, какие были сделаны несколь-
несколько выше.
Разделимость констант разделения. Осложнения, появляющиеся, если
для данной границы нет подходящих разделяющих координат, обычно столь
существенны, что систему собственных функций нельзя подсчитать, а краевую
задачу нельзя решить. Но даже если разделение можно осуществить, могут
возникнуть некоторые до сих пор не отмеченные осложнения, которые делают
решение краевой задачи практически весьма затруднительным. Эти труд-
трудности появляются в случаях, рассмотренных на стр. 489 — 491, когда нет
полного разделения констант разделения.
Если константы разделения разделяются [случай А, формула E.1.41)], то
уравнения для ?2~ и ?3"множителеи содержат только одну константу разделения
каждое и тем самым отвечают простому виду уравнения Лиувилля, которое
мы уже подробно исследовали. Граничные условия для множителя А
определяют собственные значения к2, а условия для Xs — собственные
значения к3, и эти значения можно подставить как известные постоянные
в уравнение для Х1г чтобы определить собственные значения kv Ряд по
собственным функциям, получающийся при удовлетворении граничного
условия на поверхности ^ = const, представляет собой тогда простой двойной
ряд по всем собственным значениям к2 и всем собственным значениям й3.
В случае В2, указанном в формуле E.1.42), все еще возможно полу-
получить собственные значения для одного множителя, а именно Х3, не зная
значений других констант разделения.
Однако в других случаях константы разделения не разделяются
и построение рядов по собственным функциям для удовлетворения граничных
условий требует для каждого члена ряда одновременного решения системы
уравнений для двух собственных значений. В качестве примера возникаю-
возникающих осложнений и в то же время для указания метода решения рассмотрим
случай колебаний эллиптической мембраны. Разделяя уравнение Гельмгольца
22» = 0 в эллиптических координатах:
у = dsin <
получаем
+(hCVp-b)M=0, ^
где h = kd, а к связано с частотой колебания ¦v = w/2k (поскольку примене-
применение уравнения Гельмгольца соответствует допущению, что движение
является простым гармоническим, с временным множителем e~iwi) соотноше-
соотношением к — ш/с = 2т/с. Постоянная Ъ представляет собой константу разделения,
однако, конечно, h = 2nvd/c также является константой разделения, так
что оба уравнения содержат обе константы. Согласно сказанному в § 5.2,
второе из этих уравнений совпадает с уравнением E.2.67).
Граничное условие для Ф состоит в периодичности по <р, а граничное
условие для М— в том, что М должно быть конечным и непрерывным при
|л = 0 и обращаться в нуль на эллипсе [i = jj.o, соответствующем границе.
Надо выбрать Ъ и h одновременно так, чтобы оказались выполненными обе
системы условий.
Для этого мы решим уравнение относителььо Ф, считая И известным.
Как показано на стр. 530, периодические решения уравнения Матье выра-
704 Гл. 6. Краевые условия и собственные функции
жаются в виде рядов Фурье. Их два сорта: одна система решений Sem(h, cos <р),
четных по <р, и другая система решений Som (h, cos <р), нечетных по <р;
первой системе собственных функций соответствуют собственные значения
bem (h), а второй системе — собственные значения bom (h). Эти собственные
значения перемежаются, так что для данного h
be0 <bo1<be1< ... < bom < bem < bom+1 < ...
Значит, если h было бы произвольным образом фиксировано, то последова-
последовательность Se, So образовывала бы полную ортогональную систему собственных
функций.
Однако h не фиксировано, и поэтому мы получили только взаимосвязь
между h и последовательностью значений Ь, при которой удовлетворяются
граничные условия для Ф.
Решения уравнения для М даются формулами E.3.90) и E.3.91),
и потому нам надо сначала выяснить, будут ли функции Je и Ne удовле-
удовлетворять условию непрерывности при р. = 0. Рассмотрение данных координат
показывает, что ("¦ = (), <р = а) и (р- = 0, <р= — а) определяют одну и ту же
точку (x = dcosa, у = 0), и после нескольких минут размышления мы уви-
увидим, что для непрерывности ф и ее производной при переходе через линию
fi = 0 множитель М должен иметь на ней нулевую производную, если
множитель Ф четен по у, и М должен обращаться в нуль при f* = 0, если
множитель Ф нечетен по <р. В силу сказанного на стр. 595, мы видим, что
для Sem (h, cos <р) подходит решение Jem (h, ch \i) с теми же значениями h
п т (то есть с тем же значением Ь), а для Som подходит решение Jom
с соответствующими /гит. Значит, в этой задаче функции Ne, No не
применяются.
Наконец, потребуем, чтобы выполнялось условие М = 0 при f*- = fv Для
любого данного значения b можно выбрать h так, чтобы это имело место, но,
конечно, Ъ также зависит от h, так что hub надо определять одновремен-
одновременно. На практике следует подсчитать ряд кривых, дающих последователь-
последовательность значений \i, при которых Jem(h, chp-), например, обращается в нуль
для каждого из различных значений h. Эти значения можно обозначить
через fimn (h), причем индекс т соответствует индексу для Jem, а индекс п
указывает, какую точку мы имеем в виду из последовательности нулевых
точек (р.т1 может быть наименьшим значением, рт2 — следующим и т. д.).
Таким образом, мы имеем двойную последовательность значений р.
в соответствии с различными значениями т и различными значениями п.
Каждое из этих значений является функцией от h. Теперь мы обращаем
задачу, находя значение h, которое делает один из корней pmn(h) равным
координате р.о границы. Корень уравнения \ьетп (h) = р0 обозначим через
hemn, а уравнения td (h) = p.o — через homn. С помощью этих значений
можно затем подсчитать допустимые значения частоты v свободных коле-
колебаний эллиптической мембраны. Частному значению частоты ш„Г1/2ти =
= (с/2тий) hemn будет соответствовать • двумерная собственная функция
Sem{hemn, cos^)-Jem(hemn, ch [i), а частоте i«w/2tc = (c/2toZ) homn — другая
собственная функция Som(homn, cos<p) Jom(homn, chp.). Отсюда полное реше-
решение будет записываться в виде
2 [A,nnSemJem cos (w^nt + amB) + BmTlSomJom cos {w°mnt + Pmn)],
m,n
где числа А, В, a и р определяются начальными значениями смещения и
скорости мембраны.
Очевидно, конечно, что множители iSe, So взаимно ортогональны, если
see они соответствуют одному и тому же значению h. Однако члены пос-
6. 3. Собственные функции и их применения 705
леднего ряда берутся для различных значений h каждый, так что ни множи-
множители Sem, ни множители Som не являются все взаимно ортогональными
(хотя все Se все еще ортогональны всем So). Однако общие рассуждения,
ароведенные на стр. 676, показывают, что рассматриваемые двумерные соб-
собственные функции взаимно ортогональны, так что функции Jem(hemn, ch^),
а также функции Jom (homn, ch p.) должны быть взаимно ортогональными
в интервале 0<A<р.0 для различных значений п, тогда как функции
Sem (hemn, cos <р) должны быть взаимно ортогональными для различных значе-
значений т. Значит, все члены ряда ортогональны друг другу, и коэффициен-
коэффициенты^!, В и фазовые углы а, ,В можно определить обычным образом.
На этом примере мы показали, что технику удовлетворения гранич-
граничным условиям при помощи собственных функций можно применить всегда,
если в соответствующих границе координатах уравнение разделяется, даже
если константы разделения не разделяются в получающихся обыкновенных
уравнениях. Такие случаи требуют значительно больших подсчетов для
получения решения, чем случаи, когда одно из разделенных уравнений содер-
содержит только одну константу разделения; однако эти выкладки являются
прямыми, не требующими привлечения новых принципов.
Плотность собственных значений. Довольно случайное распределение
собственных значений, обнаруживающееся уже для простых двумерных слу-
случаев, вызывает вопрос, который мы до сих пор не ставили: можно ли что-
либо сказать о числе собственных значений между X и X-j-e? Это число
является разрывной функцией от X и е (так как собственные значения обра-
образуют дискретное множество), однако можно попытаться подсчитать среднее
число собственных значений между X и Х + е. Возможно, что эта величина
будет «сглаженным» приближением истинного числа и будет непрерывной
функцией от X и е.
Такую асимптотическую функцию плотности собственных значений
можно получить для одномерного случая при помощи асимптотической
формулы, следующей за формулой F.3.27). При этом мы будем подсчи-
подсчитывать плотность чисел кп, где &? = ХП. Это, вообще говоря, более полезно.
Например, если мы имеем дело с волновым уравнением, то к пропорциональ-
пропорционально допустимой частоте свободных колебаний системы. Условно будем
называть кп также собственным значением. Асимптотическая формула для
кп имеет вид
кп = У\ ~ (пти + а)/ \ |/-^ dz
Эта формула указывает на то, что большие значения к распределены
вдоль вещественной оси к равномерно. Асимптотически расстояние между
аоследовательными значениями равно тг/S V^r/pdz, откуда число соб-
собственных значений, меньших к,
и потому среднее число собственных значений между к и к-^-dk
ь
dn са Г i- ^ у — dz I dk, F.3.52)
где величину в квадратных скобках можно назвать средней плотностью
собственных значений к для больших значений к.
45 ф. м. Моро и Г. Фешбах
706
Гл. 6. Краевые условия и собственные функции
Заметим, что эта плотность пропорциональна интегралу от функции
У^г/р, взятому по интервалу (а, Ь). Если г и р имеют одинаковую размер
ность (в этом случае 1/к имеет размерность длины), то интеграл от уг/р
имеет размерность длины. Для одномерного волнового уравнения ги/i
равны единице и средняя плотность собственных значений равна как раз
произведению 1/ти на расстояние от а до Ь. Подинтегральная функция
\/ г/р связана с коэффициентами Ламе криволинейных координат, так
что отклонение |/ r/р от единицы некоторым образом связано с кри-
кривизной рассматриваемой координаты. Интеграл \ Уr/p dz можно назвать
эффективной длиной интервала для изучае-
III мОи координаты и границы.
f " " ' ' ~ Обращаясь теперь к двумерному случаю,
мы находим здесь, что плотность собствен
ных значений к уже не является даже при
ближенно не зависящей от к. Например,
рассматривая значения, данные в формуле
F.3.48), для прямоугольной мембраны, мы
найдем, что плотность собственных значений
возрастает с возрастанием к. Это легко
показать вследствие особенно простой взаи-
\У мосвязи между к и целыми т и п в случае
у/Л / прямоугольной мембраны. Формула F.3.48)
¦*— ^—— аналогична соотношению, определяющему
расстояние от начала координат до точки,
заданной декартовыми координатами кт/а и
тсп/Ь. Эти точки, для целых значений тип,
на рис. 6.11 являются точками пересечения
линий прямоугольной сетки. Допустимые
значения к отвечают расстоянию любой из
этих точек решетки от начала координат.
Можно поэтому говорить о «плотности
допустимых точек в пространстве к». Так
как интервалы решетки в двух направлениях
равны тг/а и ж/b, то средняя плотность точек
равна ab/ти2, где ab = A, то есть площади,
заключенной внутри границы. Следовательно, для этого простого случая
среднее число собственных значений к, меньших некоторого к,
f
n ш
Рис. .6.11. Распределение соб-
собственных гначений для прямо-
прямоугольной и треугольной мембран.
Длина вектора к равна значению УТ.
тс2 V 4 J An
где величина в круглых скобках представляет собой площадь, заключен
ную между линиями г = к, у = 0 и х = 0. Дифференциал
Г—1
dk
F.3.53)
дает плотность собственных значений к для этого простого случая (вели-
(величина в квадратных скобках). Мы видим, что она пропорциональна к (это
мы и хотели доказать), а также пропорциональна площади А, заключен
ной внутри прямоугольной границы.
Однако можно пойти дальше, так как мы замечаем, что на рис. 6.11
точки покрывают не весь первый квадрант. Так как точки с т = 0 или
с /г = 0 отсутствуют (для граничного условия ф = 0), то надо удалить
половину полос решетки, примыкающих к обеим осям, и более точная
6. 3. Собственные функции и их применения 707
формула будет иметь вид
п (к) ~ (afc/ти2) [~ тиЛ2/4 - (кп/2а) - (кп/2Ь) 1 = (А/4ти)/с2 - (L/4ic) Л,
или
2«) - (L/4w)] dk, F.3.54)
где L = 2a + 2b представляет собой периметр границы.
Этот второй член в выражении для плотности собственных значений
зависит от граничных условий. Например, если граничные условия
на прямоугольнике состоят в равенстве нулю нормальной производной
от ф, а не самой ф, то выражение для собственных значений к будет
то же, но точки с т = 0 и ?г = 0 теперь допускаются. Следовательно,
в этом случае функция плотности имела бы вид (ЛЛ/2т:)-|- (Z,/4m).
Получается, что первый член в средней плотности не зависит от точ-
точного вида поставленных граничных условий, по крайней мере для неко-
некоторых типов граничных условий, а зависит только от площади, заключен-
заключенной внутри границы. Второй член зависит от частного вида наложенного
граничного условия.
Можно разобрать другие случаи, когда известны точные решения
двумерного уравнения Гельмгольца (например, случай круглой мембраны).
Оказывается, что если вид границы меняется, но площадь А остается
постоянной, то точки, изображающие допустимые значения к, перемеща-
перемещаются на «^-плоскости», однако средняя плотность точек не меняется.
Кроме того, можно показать, что если граничные условия не меняются при
варьировании вида границы, то поправочный член (член с периметром Ь
границы) не меняет своей формы. Можно проверить оба эти утверждения,
рассмотрев случай треугольной мембраны. Здесь удаление половины пло-
площади исключает половину точек в первом квадранте. Детальный подсчет
показывает, что для граничного условия ф = 0 формула F.3.54) имеет
место, причем А = а2/2 и L=2a + Y2a2.
По-видимому, формула F.3.54) справедлива для границы любого вида
при условиях ф = 0 на границе. Доказано, что форма первого члена (кото-
(который является главным членом для больших к) сохраняется в общем случае.
На второй член доказательство не было распространено, хотя во всех
подробно разработанных случаях не было найдено ни одного противореча-
противоречащего примера. Во всяком случае, если мы имеем дело с большими значе-
значениями к, то можно пренебречь вторым членом в плотности и пользоваться
только первым членом, о котором известно, что он пригоден для любых
границ и любых разумных граничных условий.
Таким образом, для собственных функций с большими номерами плот-
плотность собственных значений не зависит от Л в одномерных случаях, про-
пропорциональна к в двумерных случаях и, аналогично, пропорциональна Лг
в трехмерных случаях. В каждом случае плотность также пропорциональна
«размеру» части пространства, заключенного внутри границы: длине для
одного измерения, площади для двух и т. д. Если уравнение есть уравне-
уравнение Гельмгольца, а интервал не искривлен, то эти «размеры» являются
настоящими длинами, площадями и т. д.; но если координаты криволиней-
криволинейные и линии или поверхности, составляющие границу, искривлены, то «раз-
«размеры» являются эффективными длинами, площадями и т. д., равными инте-
интегралам от некоторых комбинаций KO3<j$H4HeHTOBj Ламе, подобным инте-
интегралу \ j/Y/pdz для одномерного случая.
45*
708 Гл. 6. Краевые условия и собственные функции
Непрерывное распределение собственных значений. Из предыдущего
рассуждения мы видим, что при возрастании размера области промежутки
между собственными значениями уменьшаются. Например, в одномерном
случае средняя разность между последовательными собственными значе-
значениями, согласно формуле F.3.52), равна отношению it к эффективной длине
\ Уг/pdz интервала. Если эта длина стремится к бесконечности, то про-
промежутки между собственными значениями стремятся к нулю, и в конце
концов все значения X (или к), большие наименьшего значения, становятся
собственными значениями. В этом предельном случае получается непре-
непрерывное распределение собственных значений, и наши представления рядами
превращаются в интегральные представления.
Этот переход можно показать, развивая наш первый пример, при-
приведенный на стр. 659. Допустим, что расстояние а между концами интер-
интервала изменения х неограниченно возрастает. Тогда длина волны собствен-
собственной функции sin (ъпх/а) при данном п, а также нормирующая постоянная
Еп = У а/2 этой функции будут расти. Ряд Фурье
7Ш?
сохранит свой общий вид, но каждый отдельный член будет уменьшаться
по величине и (для данного конечного значения х) будет изменяться все
менее и менее быстро при переходе от и к следующему п; при росте п
каждый член становится исчезающе малым, а скорость изменения коэф-
коэффициентов в квадратных скобках — исчезающе медленной. При переходе
к пределу целесообразно применять не п в качестве переменной суммиро-
суммирования, а квадратный корень к = тт/а из константы разделения X. Про-
Промежутки между допустимыми значениями этой переменной становятся все
меньше и меньше, пока в конце концов к не станет непрерывной пере-
переменной и суммирование по п не превратится в интеграл по к от нуля
до бесконечности.
Когда а растет, среднее число (а/тс) dk собственных значений к между
к и k-\-dk, выражаемое формулой F.3.52), становится все ближе и ближе
к истинному числу, так как на любом конечном сегменте dk находится
все больше и больше допустимых значений к. В то же время последова-
последовательные члены суммы, взятые для собственных функций при этих собст-
собственных значениях внутри dk, отличаются друг от друга все меньше
и меньше (во всяком случае, для конечных значений х), так что в конеч-
конечном счете можно представить сумму всех членов между п = ак/ти и
+ (a dk/n) в виде
а
— sinкх- — \ /(С) sin kZi
и, когда а стремится к пределу, сумма в конце концов переходит в инте-
интеграл
оо со
/ (х) = -?- ^ sin kx ^ f (Q sin ft? 0% dk, F.3.55)
о о
который можно применять для представления любой кусочно-гладкой
функции в интервале 0 < х < оо, обращающейся в нуль на концах интер-
интервала. Это — один из видов интеграла Фурье (см. стр. 429). К более общему
виду
6. 3. Собственные функции и их применения 709
/ (х) = ±- ^ eihx dk ^ f (С) е~ы dC F.3.56)
— СО
можно прийти, рассматривая более общие граничные условия, чем усло-
условие периодичности с периодом а функций от х.
Однако вовсе не обязательно получать свойства собственных функций
для непрерывных собственных значений при помощи неуклюжего предель-
предельного процеса. С точки зрения функционального пространства вектор F,
представляющий любую функцию F, можно выразить через его компоненты
F (х) вдоль единичных векторов е (х) (соответствующих каждому значе-
значению х из рассматриваемого интервала) или через его компоненты /(&)
вдоль другой системы единичных векторов е (&) (соответствующих каждому
допустимому значению к). Вместо одного непрерывного множества и одного
дискретного множества мы имеем теперь два непрерывных множества, что
дает более симметричную картину.
Собственные функции по-прежнему являются проекциями векторов
е (к) на векторы е (х), но так как здесь получаются две системы единич-
единичных векторов, то эти собственные функции представляют собой теперь
направляющие косинусы, и весь формализм приобретает значительную сим-
симметрию. Собственные функции ф (к, х) являются в одно и то же время
как компонентами векторов е(к) по векторам е(х), так и компонентами
векторов е (х) по векторам е(&). Распространяя формулы F.3.17) на рас-
рассматриваемый случай, получаем, что компонента F (х) произвольного век-
вектора F по направлению е (х) связана с компонентой / (к) вектора F
по направлению, задаваемому вектором е (к), при помощи соотношений
F(z)=^f(kL>(k,lz)r(k)dk, f(k)=^F(z)b(k,z)r(z)dz, F.3.57)
где функция г (к) связана с плотностью собственных значений к вдоль
оси к так же, как г(х) связана с плотностью собственных значений вдоль х.
Интегрирование здесь производится по областям допустимых значе-
значений Лих, иногда от 0 до со, но чаще от — со до со. Возможность
устремления к к — со не означает, что собственные значения X не имеют
нижней границы, так как X = к2, и если только к вещественно, то X > 0.
Кроме того, когда мы включаем отрицательные значения к, можно счи-
считать ф комплексной величиной (как elbx в примере), если пользоваться
комплексно сопряженной величиной ф во втором интеграле.
Свойства нормированности и ортогональности этих собственных функ-
функций выражаются при помощи формул, обобщающих формулы стр. 677:
г (к) { ф'(/с, z)"u> (*,. z) r (z) dz = о (к - %),
._ " F.3.58)
г (z) ^ ф (к, z) ф, 0 г (к) d* = 8 (z - С),
причем оба интеграла соответствуют дельта-функции. Функции ф пред-
представляют собой направляющие косинусы, поскольку и е(х), и с (А)
являются единичными векторами, так что множители Ет равны единице
и не присутствуют в формулах явно. Как всегда, для выражений, соот-
соответствующих дельта-функциям, они должны применяться в интегралах,
а не в дифференциалах или сами по себе. Наиболее полезный вид норми-
нормирующего интеграла, соответствующего обычному определению дсльта-функ •
710 Гл. 6. Краевые условия и собственные функции
ции, таков:
_гд i 1 при |z| < Д.
Другими словами, в пределе при Д —> 0 получаем
fto+д
¦ • при |Л-«„|>«, F359)
при |/с-Л0|<Д
и аналогичное соотношение с переставленными z и к, соответствующее
6(z — Q. Обычно пределы второго интеграла сначала полагаются конеч-
конечными, но большими @ и R или —R и R, где R велико), а затем рас-
распространяются до бесконечности для удобства вычислений.
В качестве примера рассмотрим уравнение Бесселя, получающееся
при разделении уравнения Гельмгольца в полярных координатах:
где т представляет собой константу разделения, которая порождается
«^-множителем и является целой, если <р изменяется от 0 до 2ти (другими
словами, если Ф периодична по у).
Если граничные условия для R состоят в том, что R конечна в осо-
особой точке г = 0 н R = 0 при г = а, то собственными функциями являются
функции Бесссля [см. формулу E.3.63)]:
ФП1ГIат/ГПГ/й\1т0(а1)=20' <6-3-М>
Эти функции ортогональны (с функцией плотности г):
I Ф п,
так что мы имеем полную систему собственных функций (га = 0, 1, 2, ...)
для каждого значения т.
Если а взять бесконечным, то собственные значения к будут образе
вывать непрерывное множество от & = 0 до бесконечности. Поэтому функ-
функция Jm (кг) пропорциональна собственной функции для непрерывного к.
Для нормировки положим <!) (к, z) = AJm (kz) и определим А, применяя
формулу F.3.59). Как указано выше, для упрощения вычислений следует
положить верхний предел второго интеграла равным R, а затем устре-
устремить R к со. Применяя асимптотическое выражение для / и производя
нычисления при т > 0, имеем
R
йо-Д 0
fco+Д
*°+Л - - 'л2 при \к-ко\<\
при \к — к01 > Л.
"г , Г 2/тс . . Dii f А
О-Д l U
6. 3. Собственные функции и их применения 711
Окончательный результат справедлив также при т = 0. Поэтому нормиру-
нормирующая постоянная А равна единице, нормированная собственная функция
равна как раз Jm (kz), а выражение, соответствующее интегральной фор-
формуле Фурье F.3.55), имеет вид
оо со
Jn{kz)kdk \ /(С)/т(ВДс? F.3.62)
и называется интегралом Фурье — Бесселя.
Собственные значения для уравнения Шредингера. При решении
уравнения Шредингера встречаются случаи, когда собственные значения
дискретны для одного интервала значений и непрерывны для другого. Рас-
Рассмотрение взаимосвязи между уравнением Шредингера [см. формулу B.6.28)]
и задачей Штурма — Лиувилля покажет, как это получается, и, быть
может, прольет новый свет па результаты теории Штурма — Лиувилля
[см. также исследование уравнений A2.3.25) и A2.3.27)].
Уравнение Шредингера для одного измерения имеет вид
™JL+*!LlE-V(z)]C> = O, F.3.63)
где т — масса рассматриваемой частицы, Е — ее полная энергия в рассма-
рассматриваемом состоянии, V — потенциальная энергия и % = /г/2ти — видоизменен-
видоизмененная постоянная Планка. Вероятность того, что частица находится между х
и x-^-dx, пропорциональна |О|2йх, а средняя «плотность тока» частицы
пропорциональна мнимой части <b-d<b/dx (то есть если ^> является вещест-
вещественной функцией для вещественного х, то результирующий средний ток
равен нулю).
Согласно классической механике, частица может находиться только
там, где энергия частицы Е больше потенциальной энергии V; в таких
областях чем больше значение Е — V ( = кинетической энергии), тем больше
плотность тока и тем меньше плотность вероятности нахождения частицы.
Плотность вероятности нахождения частицы пропорциональна величине
A/скорость) ~ \\\f E — V, а вероятная плотность тока пропорциональна
[/Е—V . Энергия Е, всюду меньшая V, невозможна; возможны все энер-
энергии Е, для которых Е где-либо больше V. Если частица находится в мини-
минимуме потенциала, отделенного от другого минимума пиком высоты, боль-
большей Е, то эта частица не может перейти из одного минимума в другой.
В противоположность этому уравнение Шредингера больше ограничи-
ограничивает допустимые значения энергии, но меньше ограничивает расположение
частицы, как показывает вывод уравнения (стр. 234 и 299). Рассмотрим
случай, когда V (х) имеет минимум (который можно для удобства рас-
расположить в х = 0), а асимптотическое значение V больше этого минимума,
и исследуем уравнение с точки зрения задачи Штурма — Лиувилля
{см. стр. 671).
Если Е всюду меньше V, то решение уравнения F.3.63) —не коле-
колеблющееся; оно ведет себя скорее как вещественные экспоненты еж и е~х,
и никакая комбинация двух независимых решений не даст решения, конеч-
конечного как при х= — со, так и при х= +оо. Как указано на рис. 6.8, если
решение стремится к нулю при х—>—со, то оно будет стремиться к бес-
бесконечности при ж-^+оо. Значит, энергия, меньшая V (х) всюду вдоль
вещественной оси х, не допускается.
Если Е меньше, чемУ(—со) и F(+co), но больше, чем F@), мини-
минимальное значение V, то 4 все еще ведет себя подобно вещественным экспо-
712 Гл. в. Краевые условия и собственные функции
нентам в тех областях, где Е < V, заворачивая от оси х\ но там, где
Е > V, она заворачивает к оси, подобно тригонометрической функции.
Функция ф, начиная от нуля при х = — со, будет экспоненциально возра-
возрастать, пока х не достигнет значения, где V (х) = Е, после чего ф будет
в течение некоторого времени искривляться обратно к оси. После второй
точки, где V = Е, она будет вновь иметь экспоненциальное поведение. Для
некоторого значения Е, большего V @), это обратное искривление будет
как раз" достаточным для того, чтобы ф плавно перешла в функцию, подоб-
подобную е~ах справа от начала, так что ф искривляется вверх как раз настолько,
чтобы обратиться в нуль при х= +со.
Это значение Е является наименьшим собственным значением энергии.
Соответствующая собственная функция имеет максимальное значение
где-то вблизи ж = 0, в области, где E>V- Это —область, внутри которой
должна содержаться частица, согласно классической физике. Однако вели-
величина |фJ не становится внезапно равной нулю при V > Е; она убывает
со экспоненциальному закону к нулю в обе стороны, если Е — собствен-
собственное значение, так что, согласно волновой механике, имеется малая, но
конечная вероятность нахождения частицы в области, где потенциальная
энергия больше полной (то есть где кинетическая энергия отрицательна).
Если Е возрастает дальше, то соответствующая функция ф вновь
становится бесконечной при х= + со или х= —- со, пока при следующем
собственном значении функция ф не сможет опять обратиться в нуль
в обоих концах интервала. Эта собственная функция имеет узел где-то
в области, в которой Е > V.
И так этот процесс продолжается и дает только дискретное мно-
множество энергий, значения которых определяются требованием конечности ф,
пока мы не достигнем энергии, равной наименьшему асимптотическому
значению V (мы принимаем для упрощения формулировок, что
V(—со) < V (+оэ)). Выше этой энергии Е больше F от — со до неко-
некоторого конечного положительного значения х, и ф колеблется во всей
этой области х. Значит, ни одно решение рассматриваемого дифферен-
дифференциального уравнения не стремится к бесконечности при х~-> — ос, и мы
можем выбрать для любого значения Е подходящую линейную комбинацию,
которая будет стремиться к нулю по экспоненциальному закону при
ж—> + оо. Таким образом, любое значение энергии, большее V ( — со).
является допустимым.
Так как экспоненциально исчезающие решения являются веществен-
вещественными функциями для вещественного х, то собственные функции для
дискретных энергий [меньших либо V( — со), либо F(oo)] всюду вещест-
вещественны (более точно, фазовый угол этих собственных функций не зависит
от ж и вполне может быть взят равным нулю). Так как они вещественны
и их производные вещественны, то средняя плотность тока (пропорцио-
(пропорциональная мнимой части ф-йф/dz) равна нулю. Классическое объяснение
этого состоит в том, что в точках, где V возрастает выше Е, частица
обращает направление своего движения, так что в каждой точке частицу
можно с равной вероятностью найти идущей в любом из двух направле-
направлений и результирующий ток равен нулю.
Это верно и для непрерывной области собственных значений Е между
V ( — со) и F( + co), так как частица здесь выходит из —со, отражается
от потенциального «барьера» и возвращается в — со.
Если Е больше и V(— со), и V(-\-co), то оба решения уравнения
всюду конечны, так что можно выбирать любые их линейные комбинации.
Некоторые из этих комбинаций дадут ненулевые значения для средней
плотности тока в соответствии с классическим утверждением, что если Е
больше V( — со) и F( + co), то частица может пройти от — со до + о:
6. 3. Собственные функции и их применения 713
без отражения. Весь этот вопрос будет рассмотрен позднее, в другой
главе.
Дискретные и непрерывные собственные значения. В качестве при-
примера этого рода поведения возьмем симметричный случай потенциальной
функции V= — Vo eh'2 (z/d) [см. формулу A2.3.22)]. Этот потенциал
имеет минимум —Vo при ж = 0 и возрастает асимптотически до нуля
при х —> ± оо. После подходящего выбора маштаба и констант уравнение
Шредингера ( 6.3.63) приобретает вид
(d2ty/dw2) + (l + (?с1Г2ш)ф = 0, w = x/d. F.3.64)
Дальнейшие преобразования, а именно подстановки X =¦•—К2,
z= (l + tbw)/2 = ew/(ew + e~w) и ф = cb~Kw-F (z), приводят к уравнению
которое является как раз уравнением E.2.42) для гипергеометрической
функции
где Р = 1/ Q-\--r- Имеется и второе решение, но оно становится беско-
бесконечным при z = 0. Значит, решение остающееся конечным при х = —оо,
имеет вид
k{ ± \ ?) F.3.65)-
Рассмотрение формулы E.2.49) показывает, что эта функция стано-
становится бесконечной при z = l (w—э-со), кроме случаев, когда величина
K + -z—Р является целой отрицательной, то есть когда К=у Q + t —
—^—п, где п может быть нулем или любым целым положительным
Г 1
Q+-r—о" ¦ Поэтому дискретные собственные значе-
значения X, пропорциональные энергии, таковы:
F.3.66>
Для таких значений X собственная функция ф представляет собой много-
многочлен относительно z. Заметим, что если Q положительно (то есть если
имеется потенциальная «яма»), то будет существовать по крайней мере
одно дискретное состояние (п = 0),. хотя других может не быть, если Q
мало.
Для положительных значений энергии К мнимое и можно положить
K = ik, где \ = к2. В этом случае двумя независимыми решениями вблизи
z = 0 (ш—» = оо) являются
714 Гл. в. Краевые условия и собственные функции
.которое можно обозначить через ф (к), и
-ikwр(р , J_ jo 1 1 | 1 ik\ eW Л
которое можно обозначить через ф( — к). Таким образом, для каждого
значения X имеются две собственные функции. Для очень большого отри-
отрицательного w эти два решения приводятся к eihw = eihxld и e'lhw = е~Шх'д,
причем обе эти функции конечны при w<= —со. Одна представляет волну,
идущую в положительном направлении (и соответственно имеющую поло-
положительную плотность тока), а другая —в отрицательном направлении
(с отрицательной плотностью тока). Подобным образом оба решения
конечны и вблизи w = -f- со для всех значений к, так что допускается
любое положительное значение параметра энергии X.
В этом случае имеются как дискретные, так и непрерывные собствен-
собственные значения. Наше разложение по собственным функциям должно включать
ряд по немногим дискретным ^значениям ( сумму по п для п, меньших
I/ (? + х—о") и интеграл по к от —со до + °° (включающий, таким
образом, обе собственные фувкции для каждого положительного собствен-
собственного значения X). Чтобы получить явный вид суммы и интеграла с соот-
соответствующими значениями нормирующих множителей, требовался бы более
подробный анализ задачи, чем это стоит делать здесь. Он будет проведен
вновь в § 12.3,
Дифференцирование и интегрирование как операторы. Это исследование
уравнения Шредингера (а также трактовка факторизации на стр. 678)
может напомнить нам, что иногда полезно рассматривать дифференциро-
дифференцирование и умножение на постоянную (и также интегрирование) как операто-
операторы. Рассмотрим вектор f с компонентами / (х), вектор at с компонентами
af(x), вектор aPt с компонентами df(x)/dx и вектор &t с компонентами
х
\ / (w) dw.
Эти операторы можно складывать (то есть" они удовлетворяют законам
дистрибутивности и коммутативности для сложения); например, вектор
{ЗР + 3%) = B. -|- еТ5) f имеет компоненты
х
-y-f(x)+ \ f(w) dw= \f(w)dw + -j-f (x).
0 0
Как еР, так и й коммутируют со скалярным оператором а, но &*
не коммутирует с й, так как
и потому
<^J = 1, тогда как йЗ> ф 1, F,3.67)
где 1 — единичный оператор. Однако если следить за порядком перемноже-
перемножения, то интегральный оператор 3. можно рассматривать как обратный
к дифференциальному оператору &" и записывать в виде аР'1.
в. 3. Собственные функции и их применения 715
Как аР, так и SP"'1 можно итерировать. Компонентами еРТ являются
(dn/dxn) f (x), а компонентами di~n{—
и1 ип-1
duj(un).
Положительные степени ef, действующие на постоянный вектор А, дают
нуль, в то время как отрицательные степени дают ненулевой результат.
Например, компонентами ^'"А служат Ахп1п\ При помощи интегрирования
по частям можно видеть, что компонентами ?Р~Ч служат
\ du \ / (w) dw — \ {x — w)f (w) dw.
0 0 0
Повторное применение этого соображения показывает, что компонентами ef nf
являются
х
] AГ- F-3-68)
С рядами из операторов (при обычных условиях сходимости) можно
обращаться в точности так же, как с обыкновенными рядами. Например,
компонентами вектора
если ряд из интегралов сходится. Посредством этого можно определить
смысл выражений, содержащих обратные операторы, таких, как [^^/(l —
— aaP'^i. Подходя к этому выражению формально, мы подсчитаем его при
помощи разложения в ряд по степеням сР'1. Компоненты получающегося
при этом вектора (Ф'1 + аоР~2-\-а2оР~3 + . ..)f равны
=^- + a2 {х~^)г f ...jf(w)dw = eaxi\je-awf(w)dw; F.3.69)
результат неожиданно компактный.
Чтобы увидеть, как можно применить эту технику, и, кстати, чтобы
до некоторой степени сделать законным это несколько беззаботное обра-
обращение с символами, подсчитаем решение дифференциального уравнения
первого порядка
^L-ay = f(x). F.3.70)
Обычными средствами можно найти, что решение этого уравнения имеет
«ид
х
у(х) = у @) еах + еах { e~aw f (w) dw.
о
Для решения уравнения F.3.70) символическим методом заметим, что оно
эквивалентно операторному уравнению (ef — а) у = f, которое после интегри-
интегрирования по х приобретает вид
716 Гл. 6. Краевые условия и собственные функции
Применяя формулу F.3.67) и деля обе части на 1 — аЗ*~г, мы найдем,
что у(х) как раз равно компонентам вектора
[$>~Ч4 у @)]/A — а^) = у @) + iP'1 [f + ау @)]/A — atf*'1),
то есть в силу F.3.69) равно
х
у @) + еах { e"aw [f (w) + ay @)] dw,
о
что совпадает с решением, полученным обычным путем.
Надо заметить, что обе части уравнения F.3.70), записанного в опе-
операторном виде, нельзя было непосредственно делить на ?Р — а. В противном
случае у равнялось бы компонентам вектора (е?> — а)~Ч, и результат не
включал бы необходимую постоянную у@).
Эта техника, намеченная здесь, будет исследована более подробно позже.
Сейчас мы хотим указать только, что дифференциальные уравнения
можно рассматривать как изображения операционных уравнений с операто-
операторами ef и ё"'1, соответствующими дифференцированию и интегрированию,
и что такие операционные уравнения поддаются некоторому количеству
алгебраических преобразований, если учитывать ограничения в отношении
коммутирования.
Задача о собственных значениях в абстрактном векторном про-
пространстве. Вопрос о дискретных собственных значениях и о допустимых
решениях имеет значительно более широкую область приложений, чем
только дифференциальные уравнения, как показывает внимательный
просмотр § 2.6 и подсказывает аналогия в абстрактном векторном про-
пространстве. Во многих случаях в теоретической физике имеет место
ситуация, которую можно описать при помощи некоторого рода оператора,
действующего на вектор. Так, в случае упругости это оператор растяже-
растяжения (или сжатия), действующий на обычный трехмерный вектор и даю-
дающий результирующее смещение; в случае обыкновенного дифференциального
уравнения это комбинация только что определенных операторов $", дейст-
действующая на «вектор», соответствующий функции Л (х) (которую можно рас
сматривать как компоненту вектора вдоль направления единичного векто-
вектора е (х)); в случае уравнения Дирака оператор представляет собой комби
нацию операторов, переставляющих четыре компоненты <bi(a;)> ¦¦•> %(х)*
и дифференциальных операторов, действующих на х. В каждом из этих
случаев можно говорить о векторе F и об операторе 21, который,
вообще говоря, переводит F в другой вектор Е, как об этом говорилось
в § 1.6.
Вектор F можно описать при помощи его компонент вдоль подходя-
подходящих осей координат (х, у, z-компоненты вдоль декартовых осей для упругого
смещения, значения F (х) при каждом х как компоненты вдоль осей, соответст-
соответствующих векторам е (х), для дифференциальных уравнений, различные спи-
спиновые состояния для уравнения Дирака и т. д.); Оператор должен быть
задан соответственно при помощи матрицы компонент
[см. формулу A.6.35)],
«l-F
где матрица (Лтп) изображает $[. Если рассматриваемые оси повернуть, то
6. 3. Собственные функции и их применения Til
компоненты F и 31 изменятся в соответствии с обычными правилами пре-
преобразования, данными в гл. 1.
Представлением о системе осей, соответствующих единичным векто-
векторам с,,, можно пользоваться и в случае, когда «индексы» являются непре-
непрерывными переменными (как для е(х)), и скалярное произведение надо
изображать в виде интеграла по х вместо суммы по индексу п. Таким же
образом необходимо перейти от сумм к интегралам и в других местах,
где это требуется. В связи с этим надо напомнить рассуждения, следо-
следовавшие за формулой F.3.7).
Например, пусть операторному уравнению 8-F = E соответствует диф-
дифференциальное уравнение &XF (х) ~Е(х), где &х представляет собой обык-
обыкновенный дифференциальный оператор вида
который мы исследовали в этой главе. Тогда скалярному произведению
(G*•91 • F) будет соответствовать интеграл
ь
G(xj&xF (x) dx
{G является комплексно сопряженным к G) и т. д.
Почти во всех интересных случаях оператор % является эрлштовым;
это означает, что его эрмитово сопряженный оператор ЭД*, получающийся,
если заменить в матрице строки на столбцы и затем перейти к комплексно
сопряженной матрице, равен самому St. Мы вывели некоторые следствия
этого требования на стр. 86—90. Посмотрим, что это значит для диффе-
дифференциального оператора, компоненты которого соответствуют континууму
значений х.
Эрмитово сопряженным к оператору ЭД является такой оператор %*,
что если 9l-F = E, то E* = F*-'2l*, другими словами,
G*s(9l.F) = Cl*.G)*-F. F.3.71)
Если оператор вещественный, то понятие эрмитовой сопряженности соот-
соответствует понятию сопряженности для дифференциальных операторов,
данному на стр. 499. Например, в интегральном виде левую часть фор-
формулы F.3.71) можно записать как
a a
Но согласно формуле E.2.10), последний интеграл равен
ь
где &х представляет собой сопряженный дифференциальный оператор,
определенный равенством
и исследованный на стр. 548. Если как F(x), так и G(x) удовлетворяют
соответствующим граничным условиям при х = а и Ъ, то присоединенная
718 Гл. 6. Краевые условия и собственные функции
билинейная форма Р (G, F) равна нулю в а и Ъ, и мы получаем
ь ь
G&JFdx= ^ [?XG] Fdx,
а
что соответствует соотношению F.3.71), определяющему оператор, сопря
жеыный к &х. Это значит, что наше применение слова сопряженный
в связи с обобщенными .операторами ЭД соответствует нашему применению
того же слова для обыкновенного дифференциального оператора &х, если
оператор &х вещественный. Если оператор &х не вещественный, то его
эрмитово сопряженный будет комплексно сопряженным к его сопряженному
оператору, .#* = .#. Следовательно, обыкновенный дифференциальный опе-
оператор, самосопряженный в смысле, указанном на стр. 669, соответствует
вещественному эрмитову оператору, самосопряженному в операторном
смысле. (Мы уже видели, что уравнение Лиувилля является самосопря
женным.) Этот вопрос мы исследуем более полно в § 7.5.
Если §t эрмитов, то, будет ли он дифференциальным оператором или
оператором более общего вида, имеет место равенство
(G*-a-F) = (F*9l*-G*). F.3.72)
Это означает, что если ЭД эрмитов, то величина (F*-?l-F) вещественная, неза
висимо от того, каков вектор F. Б квантовой механике эта величина обыч
но называется средними значением 21 в состоянии, характеризуемом векто
ром F. Если 21 соответствует физической величине (положению, импульсу
и т. д.), то его среднее значение, конечно, должно быть вещественным.
Б большом числе случаев это среднее значение (F*-3l-F) не только
вещественно, но всегда положительно для всех (ненулевых) векторов F.
Б таких случаях оператор называется положительно определенным эрми
товым оператором.
Каждому оператору % отвечает совокупность собственных векторов Еп
для которых
Я-Еп = апЕ„,
где ап представляет собой собственное значение ЭД, соответствующее Еп
Из сказанного выше легко вывести, что если оператор ЭД является эрми
товым или положительно определенным, то все его собственные Значения
будут соответственно вещественными или положительными. Как мы видели
выше, собственные значения могут образовывать ряд дискретных значе
ний, или непрерывную область, или же комбинацию и того и другого.
Мы уже исследовали собственные векторы несколько раз; наша цель
здесь — увязать наши предыдущие результаты с результатами настоящего
параграфа о собственных функциях. Например, в связи с формулой A.6.9)
мы показали, что собственные векторы заданного оператора взаимно орто-
ортогональны, чему соответствует тот результат, что собственные функции
для данного дифференциального уравнения и данных граничных условий
являются взаимно ортогональными. Можно, конечно, нормировать наши
собственные векторы, чтобы получить ортогональную систему единичных
векторов еп. Их имеется столько же, сколько «измерений» в абстракт
ном векторном пространстве, соответствующем оператору %. Следовательно,
любой вектор в том же абстрактном пространстве можно выразить черен
его компоненты вдоль главных осей оператора %:
Y=y F e F
6. 3. Собственные функции и их применения 71*.)
Это кажущееся очевидным утверждение соответствует основной теореме
о разложении для собственных функций. Чтобы показать общность этой
теоремы, доказанной ранее для дифференциальных операторов, наметим
здесь рассуждение для общего оператора Я. Для того чтобы собственные
векторы данного оператора 81 образовывали полную систему, достаточно,
чтобы выполнялись следующие условия:
1. Я самосопряженный (или эрмитов), то есть для любого вектора F
скалярное произведение (F*-8t-F) вещественно.
2. Я положительно определенный, то есть для любого вектора F
произведение (F*-8t-F) больше нуля.
3. Уравнение для собственных векторов
Я-Еп = атЕп; F.3.73)
соответствует некоторому вариационному принципу. Такой принцип может
быть совершенно общим. Например, можно подсчитывать скалярную (веще-
(вещественную и положительную) величину
Z)(F) = (F*-$-F)/(F*-F) F.3.74)
для произвольного вектора F. Вариационное требование, чтобы F был
вектором, для которого D имеет минимальное значение, дает собственный
вектор Ео уравнения F.3.73), а значение D при F = E0 как раз равно
собственному значению а0.
Для доказательства этого рассмотрим вариацию D, когда F и F*
меняются на произвольные малые величины 6F и 8F*, и потребуем, чтобы
qD=0. Умножая F.3.74) на (F*-F) и варьируя, мы получаем с учетом,
того, что 6D =0,
D [(qF* • F) -+- (F* -8F)] = [(qF* • Я • F) + (Г* • Я -3F)],
или
[8F* • (Я ¦ F - DF)] + [(F* ¦ Я - ?F*) • 6F] = 0.
Так как 8F* и 8F являются произвольными независимыми вариациями,
то вариационное требование, таким образом, эквивалентно равенству F.3.73)
и его сопряженному, причем D равно а.
Как было указано выше, вектор, дающий минимальное значение D,
равен Ео, а соответствующее значение D равно наименьшему (низшему)
собственному значению а0 (которое больше нуля, поскольку 21 — положитель-
положительно определенный оператор).
Вектор, дающий минимальное значение D при дополнительном требо-
требовании ортогональности к Ео, равен Ех, а соответствующее значение D
равно следующему собственному значению аг. Для доказательства этого
утверждения надо считать, что с оператором ЭД можно обращаться, как
если бы он был аналитической функцией, то есть что операторы Я, |/^Я
и т. д. имеют тот же смысл, что и их алгебраические двойники. Мы ука-
указывали, что это возможно для дифференциальных и интегральных опера-
операторов.
Если это так, то можно показать, что собственные векторы любой
функции ^(Sl), которую можно выразить в виде ряда по степеням Я,
равны соответствующим собственным векторам 81, а собственные зна-
значения равны эквивалентной функции Н (ап) от соответствующих собствен-
собственных значений ап. Отсюда следует, что решения вариационной задачи
оВ = 0, где
720 Гл. 6. Краевые условия и собственные функции
равны как раз собственным векторам Еп, решениям уравнения F.3.73),
если соответствующая алгебраическая функция Н (а) всегда вещественна
и положительна для вещественного положительного а. Получающиеся
стационарные значения В равны значениям Н (ап). (Доказательство этого
утверждения можно предоставить читателю; конечно, оно верно, только
если оператор ЭД положительно определенный.)
Произведение К = [F* • B1 — а0) ¦ F], где а0 — наименьшее собственное
значение %, не может быть отрицательным, независимо от выбора век-
вектора F, как показывает рассмотрение вариационного уравнения. Также
не может быть отрицательным произведение / = [F*-Bt — ао)B1 — ах) ¦ F],
где аг—следующее собственное значение, так как минимальные значения
выражения
l-4-(flo + «i)l2-F .
достигаются для F, равного либо Ео, либо Ег Для этих двух векторов J
равно нулю, тогда как К равно нулю только для F = E0. Следовательно,
величина J/K нигде не отрицательна и равна нулю лишь при F=EX.
Из этого последнего предложения можно вывести, что утверждение,
которое мы сделали выше и хотели доказать, уже доказано. Для этого
мы построим вектор G = уг<& — а0 ¦ F, который автоматически ортогоналев
низшему собственному вектору Ео (G*-E0 = 0), а в остальном совершенно
произволен. Составим затем вариационное отношение
Предложение, выделенное курсивом, показывает, что минимальное значе-
значение D достигается для d = yrar—ao-^i и равно а1, что и надо было
доказать.
Показав, что минимальное значение D для вектора, ортогонального
к Ео, равно аг, а соответствующий вектор равен Ej, можно продолжить
рассуждения и прийти к тому, что
#(G)>as+1, если G*-Em = 0, т = 0, 1, . . . , s; F.3.75)
это равносильно утверждению, приведенному перед формулой F.3.21).
Для общего случая произвольного оператора может не быть беско-
бесконечной последовательности собственных значений. Если векторное про-
пространство имеет только п измерений (то есть если все векторы в пространстве
можно выразить в виде линейной комбинации лишь п взаимно ортогональных
векторов), то имеется ровно п собственных векторов и п собственных
значений (в вырожденных случаях некоторые из собственных значений
могут равняться друг другу, но все равно будет п взаимно ортогональ-
ортогональных собственных векторов), так как пока можно составить вектор, орто-
ортогональный первым s собственным векторам, по-прежнему можно найти
новый собственный вектор и соответствующее собственное значе-
значение. Только при s = n будет невозможно найти вектор, ортогональ-
ортогональный предыдущим, и тогда последовательность оборвется. Следовательно,
для векторного пространства конечного числа измерений число взаимно
ортогональных собственных векторов равно числу измерений, и эта система
собственных векторов будет полной, так как, по определению, любой
вектор в этом пространстве можно выразить в виде линейной комбинации
такого числа попарно ортогональных векторов.
в. 3. Собственные функции и их применения 721
Для векторных пространств бесконечного числа измерений доказа-
доказательство полноты -не так просто [см. рассуждения, следующие за фор-
формулой F.3.7)]. Сначала надо доказать, что последовательность собствен-
собственных значений стремится к бесконечности, когда п стремится к бесконеч-
бесконечности. Однако доказательство этой теоремы для положительно определен-
определенного эрмитова оператора наиболее общего вида завело бы нас слишком
далеко в сложные вопросы современной алгебры. На стр. 673 мы показали,
что это верно для дифференциальных операторов типа Лиувилля. Это верно
также для квантовомеханических операторов, имеющих бесконечное число
допустимых состояний. Если мы допустим, что это верно в общем случае,
то наше доказательство полноты получится по той же схеме, что и дока-
доказательство, приведенное на стр. 685—687. Так как рассуждения в терми-
терминах абстрактных операторов «чище», чем рассуждения для дифференциальных
уравнений, то мы вновь бегло проведем доказательство.
Желая выразить произвольный вектор G через единичные собственные
векторы ет, мы построим конечную сумму
i)Cmem, Cm = e^G, F.3.76)
m=0
где
Вектор
ортогонален первым п-\-1 собственным векторам %, так как
прп т<7г. Отсюда по формуле F.3.75) получаем, что
ИЛИ
^ [(G*- 2 ?.*
0
) (
m=0 m=0
m=0
Однако второй член в квадратных скобках положителен, так как он равен
сумме произведений квадратов величин на собственные значения (которые
все положительны). Значит,
Поскольку ни одна из величин в скобках (так же как и an+1) не может
быть отрицательной и (G*-3t-G) не зависит от п, а ап+1—*¦ со при п—>оо,
мы имеем (J*-Jn)-^>0 прп п-^-со, и потому 3п, равпый разности между
произвольным вектором G ц первыми п -\-1 членами его разложения в ряд
по собственным векторам ет, стремится к нулю, когда п неограниченно
возрастает. Значит, полный ряд (п—>оо) равен вектору G, и "мы вновь
доказали, что еп образуют полную систему собственных векторов.
Подобным образом любой оператор (в том же абстрактном простран-
пространстве) можно выразить через его компоненты вдоль главных осей для ЧЛ.
40 Ф. м. Морс и Г. Фешбах
722 Гл. 6. Краевые условия и собственные функции
В частности, сам оператор 91 имеет особенно простой вид
^ = 2епапе*, т. с. Amn = aJmn,
п
где ап есть собственное значение оператора 91, соответствующее собствен-
собственному вектору еп. Другими словами, матрица оператора, отнесенная к соб-
собственным главным осям, является диагональной матрицей.
Другие общие свойства, применимые равным образом к абстрактным
векторным операторам и к обыкновенным дифференциальным операторам,
были уже рассмотрены в §§ 1.6 и 2.6; еще некоторые будут выведены
позже. Теперь должно быть очевидно, что абстрактное векторное изобра-
изображение имеет значительное преимущество в простоте из-за наличия про-
простой геометрической аналогии, делающей неоценимой эту новую точку
зрения почти во всех наших задачах.
Задачи к главе (»
6.1. Сеточный потенциал ц>(т,п) удовлетворяет разностному уравне-
уравнению F.2.6) и должен удовлетворять граничным условиям на граничных
линиях п = 0, п = Ъ, т = 0, т= 5. Показать, что решение, удовлетворяю-
удовлетворяющее требованию, что <р принимает значение <pv в v-й граничной точке,
имеет вид
где G(m,ra|v) представляет собой решение уравнения F.2.6), равное нулю
во всех граничных точках, кроме v-й, где оно имеет единичное значение.
Показать, что все G можно получить из этих функций, построенных для
точек @,1) и @,2). Подсчитать эти две G с точностью до трех десятичных
знаков для каждого внутреннего узла.
6.2. Показать, что решение разностного уравнения Пуассона
ф (т+1, иL-ф (т — 1; и) + ф (т, п+ 1) + ф (т, п— 1) — 4ф (т, n) = F (т, п),
где F(т, п) — заданная функция и ф=0 во всех граничных точках, равно
ф (т, п) = У G (т, п \ jj., v) F (p, v),
где G (m, n | fj-, v) представляет собой решение разностного уравнения Пуас-
Пуассона, если / (р, v) = 1, все прочие /1 = 0mG = 0bo всех граничных точках.
Каковы значения G для 4х4-сетки задачи 6.1? Как можно скомбиниро-
скомбинировать эти результаты с результатами задачи 6.1, чтобы получить общее
решение уравнения Пуассона, удовлетворяющее общим граничным усло-
условиям?
6.3. Дифференциальное уравнение является простым параболическим
уравнением
д*\> _ Эф
дх2~ dt '
а граница состоит из линий ж = 0, ж=ти и t = 0. Показать, что при гра-
граничном условии ф = 0 для х = 0 и х = ти решение при t > 0 имеет вид
со
ф (ж, t) = 2 -^v sin чх ¦ exp ( — чН),
v=l
Задачи к главе 6 723
где А выбираются в соответствии с начальным значением ф при г = 0.
Рассмотреть сеточное приближение этого уравнения, полученное деле-
делением интервала 0<;ж<7и на N равных частей длины A = Tc/iV, а оси t
на интервалы длины к=ъ/М. Показать, что решение соответствующего,
уравнения
-р- [ф (те+1, п) + ф (те -1, »)- 2ф (те, п)] = ~ [ф (т, п + 1)- ф {т, п)]%
ф @, п) = ф GV, и) = 0, и>0,
равно
N-1
ф(/и, и)= 2 ^vSinvmA-oxp и In Г 1— ^sin'2^-Av I .
Что произойдет с этим решением, если к выбрать большим А2? Какое огра-
ограничение надо наложить на величину к, чтобы решение было устойчивым?
Пусть начальные условия таковы, что коэффициенты А, в точном реше-
решении для v > vmax можно не учитывать. Что можно сказать о выборе h и к„
который приведет к достаточно точному (скажем, до 1%) сеточному реше-
решению в области 0<г<ти и в то же время не будет настолько «мелкозер-
«мелкозернистым» (N и М слишком велики), чтобы сделать численные подсчеты
чересчур трудоемкими?
6.4. Пусть начальные значения ф (х, t) задачи 6.3 таковы:
при 0 <:?<: —
| -j- тс (тс — X) при -^~ тс < X <
11 11
Подсчитать значения ф (х, t) при ж = -т-тс, —тс; t^-j-к, -утг для точного
решения. Затем подсчитать значения ф при помощи разностного уравнения
ф (т,- п-\-1)= 1 —р- I ф (Щ, п)-\--щ [ф (те -|- 1, п) + <Ь {т — 1, п)],
начиная от п = 0 и вычисляя вперед (для возрастающего п) при тех же
начальных условиях. Принять А = -т-ти (TV = 4) и произвести подсчеты с
к = тс/4 и к = тс/16. Сравнить с четырьмя ужо подсчитанными точными
значениями.
6.5. Будет ли уравнение с частными производными
дх^ " ду2 " ду
эллиптическим или гиперболическим? Каковы уравнения характеристик?
Набросать несколько из них. Показать, что если условия Коши ставятся
на границе у = у0 > 0, то решение для у > у0 име*ет вид
Уо
где фо(ж) есть значение ф при г/=г/0, a <po(z)= \ vo(z)dz, причем v0 (ж)
есть начальное значение <9ф/<9г/ при у — у0- Почему это решение непри-
непригодно для у0 = 0?
46*
724 Гл. 6. Краевые условия и собственные функции
6.6. Построить последовательность взаимно ортогональных полиномов
от х для интервала — 1 <х<1. Начать с г/0= 1, уг = х, ..., а полином уп
степени п выбирать так, что
1
-1
Получить первые четыре таких полинома. Показать, что эти полиномы
для четных п но имеют нечетных степеней х, а для нечетных п не
имеют четных степеней. Показать, что полученные полиномы пропорцио-
пропорциональны полиномам Лежандра Рп(х). Будет ли этот процесс построения
системы ортогональных полиномов однозначным? Если нет, то какие огра-
ограничения надо добавить, чтобы сделать процесс однозначным? Будет ли по-
получающаяся система функций полной? Как в этом можно убедиться?
6.7. Повторить процесс, указанный в задаче 6.6, для интервала
О -< х <! 1 и требования ортогональности
1
Начать вновь с уи = 1 п получить первые четыре полинома. Сравнить это
с системой функций <рп (х) =/0 (каопх), где аоп есть п-й корень уравнения
dJ0(i;a)/d3. = 0. Показать, что эти функции также взаимно ортогональны
для того же интервала а- и функции плотности х. Для каких задач полезны
эти системы функций?-
6.8. Полиномы Чебышева Тп (х) определяются производящей функцией
со
1 — t2 __ у гр . . „
1—2te + i2 ^J n\ /
п=0
Получить первые четыре полинома и при помощи действий с производя-
производящей функцией показать, что
Тг (х) - 2хТ0 (х) = 0; 2Т0 (х) - 2хТ, (х) + Т2 (х) = 0;
Гп+1 (х) - 2хТп (х) + Тп_г (х) = 0, п > 1,
и, следовательно, что Тп (х) = sncos (иагесовж). Показать, что
1
6.9. Полиномы Якоби определяются как
/„ (а, с | х) — F (а 4- п, — п \ с | х).
Выписать первые четыре полинома и показать, что система полна (для
какого интервала?). При помощи контурного интеграла, полученного из
формулы E.3.21), и последующего применения формулы D.3.1) показать,
что
gl-c A _Ж)С-« Г (С) d" „я-! A Г,„-С1
¦/«(Й'С1Ж)- Г(с + п) ^«l V ^ '•
Таблица полезных собственных функций 725
Показать, что
diJn(a, с|ж)= —
и что
1
-1/л \а-с т i р \ т 1 I \ 7 п![Г(с)]2Г(п + а —с+1) s
1A-хУ cJn(a, c\x)Jm(a,c\x)dx = (J+l\\4l + n)T(c + ri>) ь1ПГ1.
Выразить Рп(х) и Т^{х) через /.
6.10. Радиальная функция для уравнения Гельмгольца в сферических
координатах равна /п(йг) = У"тс/2йг.7п+1/2(йг). Показать, что собственные
функции для стоячих акустических волн внутри жесткой сферической обо-
оболочки имеют вид jn (к$птг/а), где Р„т— т-й. корень уравнения [djn (i$)/d|3] = 0.
Показать, что они образуют полную ортогональную систему на интервале
а. Полагая а—>оо, показать, что
f{v)jn{uv)v*dv.
о о
6.11. Показать, что
--4?L* (t) dt = [Г (в + п
о
6.12. Доказать, что
Нп (х) Нп (у) ^j = у=
П=:0
Таблица полезных собственных функций и их свойств
Выберем интервал переменной z и функцию плотности /¦ (z) так, чтобы
интеграл по этому интервалу от произведения г (z) на любую положитель-
положительную степень z был конечным. Выберем затем собственную функцию %(z)= 1.
Следующая собственная функция 4>1(z) выбирается в виде комбинации 1 иг,
ортогональной <Ь0 в выбранном интервале при выбранной плотности г. Затем г1/2 (z)
возьмем как комбинацию z2, z и 1, ортогональную 'Ьо и <blt и т. д. Таким
образом, при помощи чисто механического метода, называемого методом
Шмидта, можно построить систему собственных функций, которая будет
служить базисом для разложения любой кусочно-гладкой функции z в вы-
выбранном интервале. Обычно оказывается, что полученные таким образом
собственные функции получаются также из решения некоторого уравнения
Лиувилля с граничными условиями или из некоторой производящей функ-
функции. Здесь будут рассмотрены три полезных случая для трех областей
изменения z и различных функций плотности г (z). См. также таблицу поли-
полиномов Якоби в конце гл. 12.
726 Гл. 6. Краевые условия и собственные функции
I. Интервал — 1 <# < 1; функция плотности A — г2)^; полиномы Гегсн-
бауера Т™(г).
Производящая функция:
2?L_ v tTHz)
ч4>
Частные случаи: Т°п (z) = Рп (z) — полиномы Лежандра [см. E.3.24)];
A — z2)m'27T_m (z) = P% (z) — присоединенные функции Лежандра [см. E.3.38)];
пТ~1'2 (z) = |/ — ch (n arch z) —полиномы Чебышева [см. E.3.43) ];
У z*—lTn-i(z)= A/ —sh (n arch z) — полиномы Чебышева [см. E.3.43)];
для р = 0, 1, 2, ...;
2 для р = 0, 1,2, ....
Рекуррентные формулы, связывающие эти полиномы и полученные из
производящей функции:
-j- Уп(г)=У„_1 B),
А [B«- 1KГ^ (z)] = (,г + 1) (п+ 2Р) (z9— 1)р-!Г?;+1 (z);
B3 + 2;г + 1) z?t (z) = (п + 1) T^+i (z) + Bр+ п) r?_i (z);
B? + 2п + 1) Г^, (z) = А [Га+i (г) - Tl-i (z)] = П+1 (z)- Г^| (z);
<2? + 1) Ti (z) + 2z А П (г) = 7t+1 (z) + Г^* (z);
(„ + 2,8 + 1) it (z) = T^+f (z) - zTit\ (z);
n^ (z) = zli+_\ (z) - Г^| (z);
B? + 2и + 1) (z3 - 1) Tit\ (z) = ;г (n + 1) Г* + , (z) - (n + 23) (n + 2? + 1) TLi (z);
/-a
Таблица полезных собственных функций 727
последнее уравнение связано с гипергеометрическим уравнением, так как
имеет три регулярные особенности. Случай, когда р равно целому п,
приводит к присоединенным полиномам Лежандра:
рт
грт п+т d'n .р
п ~~ (l"i/2 ~ "dim" )
ТО А гр\ л rp2 'J гръ Л ЕГ
„— 1, Io— I, Jo — О, 10=1Э,...
Tro _ Bn+2m)! Г n _ n(n—1) „
1 n — 2"™n!(n+m)! L 2Bn+2m —1)
, в(в-1)(в-2)(я-3) n-
"• 2-4Bn + 2m —l)Bn + 2m—3)
см. также формулы F.3.37) и F.3.40).
Нормирующий интеграл:
* (z\T*(z\dz-b 2Г(я + 2р+1)
-1
Частные значения:
=0 для и!=
, для п = 0,2, 4,
Сеязь с гипергеометрической функцией:
Формула сложения:
(cos 6 cos 60 4- sin 6 sin 60 cos 9) =
X Tit™ (cos 6) T^t™ (cos 60) Tt1/2 (cos 9)
728 Гл. 6. Краевые условия и собственные функции
II. Интервал 0<# < оо; функция плотности »ае~"; полиномы Лагерра
?" (*).
Производящая функция:
- 2jr(n + e + i)^»W-
Частные случаи: L°n (z) = ег -^уг (zne~2),
LjJ(z) = r(o+l),
Рекуррентные формулы:
(z)= — L^i
e-zL° (z)] = („ + 1) 2a-le-«L^l B),
-r^Ln(z)= — L^i'i (z), за исключением случая и = 0;
~ U (z) = B - o) Lan (Z) - (n +1)
последнее уравнение является вырожденным гипергеометрическим уравне-
уравнением с регулярной особой точкой при z = 0 и иррегулярной точкой на с».
Если а равно целому т, получаются присоединенные полиномы Лагерра:
L°0=l, LJ=1, L; = 2, L; = 6,..., Lom = m!;
LJ=l-z, 1^ = 4 —2z, L; = 18-6z, LJ = 96-24z, ...
L3° = 2 - 4z + z2, LJ = 18 - 18z + 3z2, L"^ = 144 - 96z + 12z2,
a p, „, ,,, ,
где F представляет собой вырожденный гипергеометрнческпй ряд с п -\-1
членами.
Нормирующие интегралы:
] zve-.
dz - о
az — omn
o!(m — o)! (n — о)! (з + ;л — m)!
Таблица полезных собственных функций 72&*
где т, п, [t, -v —целые, а а принимает все целые значения, большие либо
т — р., либо п — v и меньшие либо т, либо п (если этим требованиям
нельзя удовлетворить, то интеграл равен нулю).
Связь с вырожденным гипергеометрическим рядом для общих значений я:.
Формула сложения и другие соотношения:
га , , \ „VI ( — l)m I
^п {Л -г у) — е ^ , г.
т=0
"«-'= 2 ттй
ZJ (те—п)
п=0
B у5) =
С е-«/2 M
О
где т и и — целые, в то время как а и v не осязательно целые.
III. Интервал — оо < s < сю; функция плотности e~z2; полиномы
Эрмита Нп(%).
Производящая функция: e~t2+2tz = 2j—r^n(z)-
Рекуррентные формулы:
(z+a)-e
730
Гл. 6, Краевые условия и собственные функции
последняя является уравнением для вырожденных гипергеометрических
функций
Н3 = 8z3 - 12z, Я4 = 16z4 - 48z2 + 12,
тт , лчи/2 и!
G»I
.|("-О
n!
1 1 N
„=1|3> 5
= 2 гп.,^-2.). g-
s=0
Нормирующий интеграл и другие формулы:
1 '2
ехр -! — — [(и2 + у2) cos 9 + 2uv sin <j>] V =
Можно ввести лидоизменсиные полиномы, аналогично тому, как
в случаях I и II были введены полиномы с верхними индексами $ и а,
•если выбрать функцию плотности e-z2+2az, вместо е~г2. Однако это сведется
к перемещению центра полиномов с z = 0 в z = а. Новая производящая
•функция имеет вид
m=0
где
m=0
-a
m=0
Собственные функции
ИЛИ
Hn(z-a) =
m=0
+ 2 ".w
m=n-fr- i
Все рекуррентные формулы будут те же, но с новым началом. Нормирую-
Нормирующий интеграл равен
оо со
= ea2 \ e~^-^- [Hn(z-a)]2dz = 2nnl у Те.
—оо
На этих трех системах собственных функций мы видим различные
возможности для особенностей функции- плотности в концевых точках:
полиномы Гегенбауера соответствуют плотности, имеющей точки ветвления
в обоих концах интервала, полиномы Лагерра — функции плотности, имею-
имеющей точку ветвления в одном конце и существенно особую точку в дру-
другом, и полиномы Эрмита — функции плотности с существенно особыми
точками в обоих концах. При этом значения независимой переменной
в обоих концевых точках можно сделать равными данным выше стандарт-
стандартным значениям при помощи очевидных преобразований. Например, для
интервала от z = - а до z=oo при функции плотности, имеющей точки
ветвления в обоих концах, мы применяем систему собственных функций
Tn[z/(z-\-2a)] с функцией плотности r= 22^+1a3+1 (z + a)$/(z-\- 2aJs+2 и т. д.
Собственные функции, полученные при помощи метода
факторизации
Основным уравнением является уравнение типа Шредингера
сРФ/dx* + [X - Vn (х)] Ф = О,
где X — собственное значение, а от соответствующей сообствошгой функ-
функции Ф требуется интегрируемость в квадрате в интервале а <#<:&,
причем а и Ъ — соседние особые точки уравнения. Параметр т может
меняться непрерывно или принимать только дискретные значения (в послед-
последнем случае масштаб выбирается таким, чтобы эти значения были целыми).
Это уравнение иногда равносильно следующим операторным уравнениям:
©m+i@m+i®n (т\х) = (Х„ - от+1) Фп (т\х),
®т®т&п (т\х) = (Хп- ат) Фп (т| х),
где
— взаимно сопряженные операторы. Если Vm(x) такова, что факторизацию
можно осуществить, причем ат зависит от т, но не зависит от х,
то собственные значения не зависят от т, и если ат+1 > ат, то Хп = оп+1,
732 Гл. 6. Краевые условия и собственные функции
п=т, т-\-1, т + 2, ...,
-1/2 \un*i(.x)dx
b
Фп (m | x) Фп< (т | x) dx — Inn',
а если am+1 < am, то \ = ап, n = m, m — 1, m — 2, ...,
r ь
Ф(У) I Tl I \ ftyn / V \ 1] ftT 1 ft IT I pa
L J V J .' J
a
Ф„ (m\x)= — [вт (ж) - d/tfo] Фп (m - 11 ж),
J an am
где Фт — снова ортонормированная система.
Различные виды функций V, допускающих факторизацию, можно
получить, определяя такие функции ит, которые удовлетворяют соотно-
соотношениям
а а , d , d
причем ат не зависит от х. Тогда соответствующая функция V для исход-
исходного уравнения равна
Vm (х) = и2т (х) ~^ит (х) + ат = и2т+1 (х) +~ ит+1 (х) + ат+1.
Тривиально простым случаем является тот, когда ит не зависит от х;
тогда ат = — u^, Vm = 0, а собственными функциями являются тригоно-
тригонометрические функции. Другие возможности дают
um = v(x)+mw(x),
где для того, чтобы ат не зависело от х, должно быть w2 -\-w' = const,
v' -f-m) = const;
um = A/m) г/ (ж) + иг о» (ж),
где должно быть г/= const и ю2 -j-ю' = const. Любой другой выбор зависи-
зависимости от т и х не допускает независимости ат от ж.
Решая эти уравнения для v, w и у при различных значениях постоян-
постоянных (включая нулевые значения), мы получаем следующие частные виды
ит(х), ат и Vm (x), содержащие все возможные случаи описанного выше
метода факторизации:
], am=b2(m+cJ,
-\-2bd ( т + с+~2 j cos [b (x i-p)] | cosec2 [b (x -\- p)],
откуда при помощи преобразования переменных и выбора значений постоян-
постоянных Ь, с, d и р можно получить сферические гармонические функции
Литература 733
и другие собственные функции, связанные с гипергеометрической функцией.
(Б) um=debx~m~c, am = fc2 (m + сJ,
Fm= -d*e*bx
откуда при помощи преобразования можно получить функции Лагерра
и другие собственные функции, связанные с вырожденной гипергеометри-
гипергеометрической функцией.
+ bx a 2b + b
Vm=-(m + c)(m + c+l)±—±bx+b(m-c),
что также дает вырожденные гипергеометрические функции.
(Г) um=bx + d, am=—2bm,
что дает обобщение полиномов Эрмита.
'(Д) um = mactglb{x + p)] + ^-, am=b2m2-^,
Vm = — т (т + 1) b2 cosec2 [b (x + p)] — 2bq ctg [b (x + p)];
это связано с гипергеометрической функцией [см. формулу A2.3.22)].
та о2
. I ' п -^ *
х т ' т тг
что приводит к полиномам Лагерра [см. формулу A2.3.38)].
ЛИТЕРАТУРА
Рассмотрение различных типов уравнений с частными производными, типов
краевых условий, а также разностных уравнений:
Вебстер А., Сеге Г., Дифференциальные уравнения в частных производных мате-
математической физики, ч. 1 и 2, ГТТИ, М.—Л., 1934.
Зоммерфельд А., Дифференциальные уравнения в частных производных физики,
ИЛ, М., 1950.
Курант Р., Гильберт Д., Методы математической физики, т. И, Гостехиздат,
" М. —Л., 1951.
Курант Р., Фридрихе К., Леви Г., О разностных уравнениях математической
физики, Успехи матем. наук, VIII, 125 A941).
Смирнов В. И., Курс высшей математики, т. II, изд. 14, Гостехиздат, М., 195C;
т. IV, изд. 3, Гостехиздат, М., 1957.
Соболев С. Л., Уравнения математической физики, изд. 3, Гостехиздат, М., 1954.
Тихонов А. Н. и Самарский А. А., Уравнения математической физики, изд. 2,
Гостехиздат, М., 1953.
Трикоми Ф., Лекции по уравнениям в частных производных, ИЛ, М., 1957.
Bateman H., Partial Differential Equations of Mathematical Physics, Cambridge,
New York, 1932.
Hadamard J., Lectures on Cauchy's Problem in Linear Partial Differential Equations,
New Haven, 1923.
Phillips H., Wiener N., Nets and the Dirichlet Problem, J. Math. Phys., 2, 10o
(March, 1923).
Poeckels F., Uber die Partielledifferentialgleichung V2m + /c2m = 0, Leipzig, 1891.
734 Гл. 6. Краевые условия и собственные функции
Книги, содержащие довольно полное исследование свойств и применений собствен-
собственных функций:
Айне Э., Обыкновенные дифференциальные уравнения, НТЛУ, Харьков, 1939,
гл. 10 и 11.
Зоымерфе льд А., Строение атома и спектры, т. II, Гостехиздат, М., 1956.
Курант Р., Гильберт Д., Методы математической физики, т. 1, Гостехиздат,
М.—Л., 1951.
Левитан В. М., Разложение по собственным функциям дифференциальных уравне-
уравнений второго порядка, Гостехиздат, М. — Л., 1950.
Наймарк М. А., Линейные дифференциальные операторы, Гостехиздат, М., 1954.
Франк Ф., Мизес Р., Дифференциальные и интегральные уравнения математиче-
математической физики, ч. 2, ГТТИ, М. — Л., 1937.
Bateman H., Partial Differential Equations of Mathematical Physics, Cambridge,
New York, 1932.
Bibliography of Orthogonal Polynomials, National Research Council, Washington, 1940.
Infeld L., Hull Т., Factorization Method, Rev. Modern Phys., 23, 21 A951).
Kemble E., Fundamental Principles of Quantum Mechanics, ch. 3, 4, New York, 1937.
Magnus W., Oberhettinger F., Special Functions of Mathematical Physics.
Herlin, 1943.
Szego G., Orthogonal Polynomials, American Math. Soc, New York, 1939.
ГЛАВА 7
Функции Грина
В предыдущей главе мы начали изучение центральной задачи теории
поля, состоящей в построении решения данного дифференциального урав-
уравнения при заданных граничных условиях. В ней мы исследовали тех-
технику разложения по собственным функциям — метод, приводящий к цели
прямым путем, если только можно найти подходящую для рассматриваемых
границ систему координат, допускающую разделение переменных в рассма-
рассматриваемом уравнении с частными производными. Однако результат обычно
получается в виде бесконечного ряда, который часто сходится довольно
медленно, что затрудняет общий анализ поведения решения в целом, его
особенностей у краев и т. д. Для некоторых видов задач более желательно
иметь решение в замкнутой форме, хотя бы в форме интеграла, включаю-
включающего замкнутые функции. Использование функций Грина представляет
собой как раз такой подход^
Этот метод достаточно очевиден физически. Для получения поля,
порожденного некоторым распределением источников (зарядов, или источ-
источников тепла, или чем бы то ни было, что порождает поле), мы подсчи-
подсчитываем эффект от каждой элементарной части источника и складываем
все эти эффекты. Если G(r|r0) представляет собой ноле в точке наблюде-
наблюдения г, порожденное единичным точечным источником в точке источника г0,
то поле в г, порожденное совокупностью источников, распределенных
с плотностью р(г0), равно интегралу от G-p по всей области изменения
г0, занятой источником. Функция G называется функцией Грина.
Этим методом можно также строить решение, удовлетворяющее задан-
заданным граничным условиям. Именно, мы подсчитываем поле в г, когда гра-
граничные значения решения (или его нормальной производной, в зависимости
от того, рассматриваются ли условия Дирихле или Неймана) равны нулю
в каждой точке поверхности, за исключением точки гЦ (которая находится
на поверхности). В г^ граничное значение имеет характер дельта-функциц,
так что интеграл от него по малому участку поверхности вблизи г* равен
единице. Это поле в г (не на границе) можно обозначить через G(r|rjj);
тогда общее решение для произвольного выбора граничных значений ф0 (rg)
(или нормальной производной No) равно интегралу от бф0 (или GN0)
по граничной поверхности. Эти функции G также называются функциями
Грина.
Тот факт, что решение неоднородного уравнения для поля, порожден-
порожденного распределением источников, можно найти в виде интеграла по про-
пространству от произведения плотности источников на функцию Грина,
не особенно удивителен, так же как и то, что решение однородного уравнения,
имеющее заданные значения на границе, можно получить в виде инте-
интеграла по граничной поверхности от произведения этих значений на другую
функцию Грина. Однако полезно и (возможно) неожиданно то, что эти две
функции Грина не являются различными; по существу это одна и та же
функция. Для каждого из линейных уравнений с частными производными
736 Гл. 7. Функции Грина.
гл. 1—3 можно получить функцию, которая, будучи проинтегрирована
aio объему, изображает поле распределенных источников. Если же ее (или ее нор-
нормальную производную) проинтегрировать по поверхности, то она будет изо-
изображать поле, порожденное граничными условиями, заданными на поверхности.
Физически это означает, что задание граничных условий на поверх-
поверхности эквивалентно заданию распределения источников на этой поверхно-
поверхности. Для электростатического случая это, возможно, не новое положение.
Граничное условие на заземленном проводнике состоит в равенстве потен-
потенциала на поверхности нулю. Помещая поверхностное распределение диполей
непосредственно около границы проводника (двигаясь из проводника внутрь
.области, занятой полем, мы пересечем сначала поверхность проводника,
затем бесконечно близкую поверхность, на которой распределен заряд плот-
зности +°,и затем бесконечно близкую поверхность с зарядом плотности — а),
мы получим, что значения потенциала непосредственно около дипольного слоя
.отличаются от нуля на величину, пропорциональную плотности момента
дипольного слоя (произведению с на расстояние между -\-с и —о). Это
не так ново и в случае потока несжимаемой жидкости. Граничное условие
на твердой поверхности состоит в равенстве нулю нормальной производной
от потенциала скорости на поверхности. Помещение бесконечно близко
,от этой твердой границы простого слоя источников даст на ней значения
нормальной производной потенциала скорости, пропорциональные поверх-
поверхностной плотности слоя источников. Как мы увидим, такая возможность
удовлетворять граничным условиям при помощи поверхностных интегралов
от функций источника делает применение функций источника (функций
Грина) особенно полезным.
Желательно подчеркнуть связь между источниками и граничными
условиями посредством выбора терминологии. Уравнение поля в присут-
присутствии источников является неоднородным уравнением с частными произ-
производными (например, уравнением Пуассона V24= — 4тср). Неоднородный
член, не содержащий Ф, содержит плотность источников р. Обратно, урав-
уравнение поля, в котором отсутствуют источники, является однородным
уравнением (например, уравнением Лапласа V2<!> = 0).
Аналогично можно сказать (и мы уже говорили), что граничные
условия, требующие равенства поля нулю на поверхности, являются одно-
однородными граничными условиями (нулевые значения дают однородные
условия Дирихле; нулевая нормальная производная — однородные условия
Неймана; требование равенства аф + Ьд^/дп нулю на поверхности дает одно-
однородные смешанные условия).
Обратно, требование, чтобы •!> принимало заданные значения 60 (не всюду
равные нулю) на поверхности, называется неоднородным условием Дирихле;
в этом случае граничные значения можно считать «порожденными» поверх-
поверхностным дипольным слоем источников, соответствующих неоднородному
уравнению. Подобным образом требование, чтобы д^/дп = No (No — не всюду
нуль) на поверхности, называется неоднородным условием Неймана, а требо-
требование а'Ъ -\- bdty/dn = Fo на поверхности можно назвать неоднородным
смешанным условием. Если либо уравнение, либо граничные условия неод-
неоднородны, то можно считать, что источники присутствуют; если и уравне-
уравнение, и граничные условия однородны, то источники отсутствуют.
Конечно, имеется другая, более очевидная причина того, что в обоих
случаях применяется одно и то же определяющее прилагательное. Решения
однородных уравнений, умноженные на произвольный постоянный множи-
множитель, все равно остаются решениями, и то же можно сказать о функциях,
удовлетворяющих однородным граничным условиям; решения неоднородных
уравнений или функции, удовлетворяющие неоднородным граничным усло-
условиям, нельзя так преобразовывать.
7. 1. Точки источников и граничные точки 737
Поэтому функция Грина является решением для случая, когда однород-
однородность имеет место всюду, кроме одной точки. Если точка на границе, то функ-
функцию Грина можно применять, чтобы удовлетворить неоднородным граничным
условиям; если точка находится в пространстве вне границы, то функцию
Грина можно применять, чтобы удовлетворить неоднородному уравнению.
Таким образом, при помощи нашей терминологии мы в состоянии выска-
высказывать утверждения, справедливые одновременно для граничных условий
и для распределений источников.
7.1. Точки источников и граничные точки
В предыдущей главе мы применяли понятия абстрактного векторного
пространства для «геометризации» наших функциональных идей. Функ-
Функция F (х, у, z) рассматривалась как удобное обозначение для записи компо-
компонент вектора F вдоль каждого направления из несчетного множества
направлений, соответствующих всем точкам (х, у, z) области внутри границы.
Дельта-функция 8 (г — г0) изображала единичный (относительно интегриро-
интегрирования в первой степени) вектор е (г0) в направлении, соответствующем точке
(х0, у0, z0) (где г = xi + уз + zk; следует заметить, что г представляет собой
вектор в трехмерном пространстве, тогда как е и F являются векторами в аб-
абстрактном векторном пространстве).
Формулировка в абстрактном векторном пространстве. В гл. 6 и § 1.6
мы исследовали преобразование координат при переходе от осей, направ-
направленных вдоль единичных векторов е (г), к осям, направленным вдоль еди-
единичных векторов е„, которые соответствовали собственным функциям —
решениям фп определенных дифференциальных уравнений
•*(Ф») = *»*„•
Векторы еп являются собственными векторами абстрактного векторного
оператора ?, соответствующего дифференциальному оператору X:
fi(en) = Xnen. G.1.1)
Мы показали, что единичные векторы е„ взаимно ортогональны и что
вектор, соответствующий искомому решению, удовлетворяющему заданным
граничным условиям, можно построить однозначно в виде суммы отдель-
отдельных собственных векторов:
F=2Aien, или F(x, у, z) = *2jAn$n(x, у, z).
Так как дифференциальные операторы X и соответствующие векторные
операторы ? линейны, то решения можно складывать; на основе этого
строится решение в виде ряда. Был развит метод непосредственного вычи-
вычисления компонент Ап, в результате чего наша абстрактная схема дала
сильную, практичную технику решения краевых задач.
Очевидно, что возможны и другие полезные разложения F. Одна
из таких возможностей проявляется при изучении неоднородного уравнения
X{F)=-^P(x,y,z). G.1.2)
Для решения этого уравнения при помощи собственных функций мы раз-
разлагаем как р, так и F по собственным функциям. Если вектор, соответ-
соответствующий р, равен Р = V. Вп еп и если принять, что F = 2 ^п &п, то неиз-
неизвестные коэффициенты Ап можно определить при помощи подстановки
в уравнение
47 Ф. м. Морс и Г. Фешбах
738 Гл. 7. Функции Грина
Однако неоднородный вектор Р можно было бы разложить по еди-
единичным векторам е(х0, у0, z0) вместо е„:
Р= ^ p(z0, Уф ?0)е(а;0, у0, z0),
Х0' V Z0
что соответствует формуле (представляющей собой одно из определений
дельта-функции)
р(х, у, z) = ^ ^ р (г0) а (г - r0) dx0 dy0 dz0.
Затем мы решаем более простое неоднородное уравнение
C(G)= -4ъе(хо>Уо, z0) G.1.3)
(если это возможно). Компоненты решения G в (х, у, г)-системс являются
решениями более простого неоднородного дифференциального уравнения
,S?(G)=_4*8(r-r0). G.1.4)
Компоненты G, полученные из решения уравнения G.1.4), являются
функциями как координата;, у, z (независимыхпеременных дифференциального
оператора ¦?), так и х0, у0, z0 (положения «источника» дельта-функции),
соответствующих единичному вектору е(х0, у0, z0), выбранному в уравнении
G.1.3). В конце §7.5 мы покажем, что функции G (х, у, z\x0, y0, z0) = G(r|r0)
для различных значений х0, у0, z0 являются компонентами вдоль направле-
направления е(г) скорее оператора, чем вектора. Этот оператор переводит вектор Р,
неоднородную часть, в вектор F —решение. Ввиду линейности мы ожидаем,,
что решением уравнения
?(F)=-4* ? P(r0)e(r0) будет F= ? p(ro)G (г|г0), G.1.5)
т. е. сумма всех отдельных решений для единичных векторов в правой
части, каждое из которых умножено на соответствующую амплитуду р (г0).
Следовательно, надо ожидать, что решенлем неоднородного дифференциаль-
дифференциального уравнения G.1.2) будет
F {х, у, z)=^^G(x,y,z\ х0, у0, z0) р (х0, у0, z0) dx0 dy0 dz0, G.1.6)
где G является решением уравнения G.1.4) и называется функцией Грина.
Таким образом, с абстрактной векторной точки зрения получается, что
решение посредством функций Грина есть представление через единичные
векторы е (х, у, z), тогда как решение посредством собственных функций
есть предста"вление через единичные векторы е„. Значительно более полное
исследование этого представления будет дано в конце этой главы.
В этой главе мы наметим, как находить единичные решения G и опре-
определять, когда представления сходятся, а также рассмотрим другие уточ-
уточняющие детали, аналогичные тем, которые мы изучили в предыдущей
главе, прежде чем смогли уверенно применять технику собственных
функций.
Граничные условия и поверхностные заряды. Мы еще не показали,
чем может помочь возможность решать неоднородное уравнение (с одно-
однородными граничными условиями) при решении однородного уравнения
с неоднородными граничными условиями. Прежде чем вдаваться в детали,
разберем простой пример, который, быть может, пояснит принцип. Позже
будет показано, что решение уравнения Пуассона
7'. 1. Точки источников и граничные точки
739
с однородными условиями Дирихле (G = 0 на поверхности S на рис. 7.1)
представляет собой функцию, стремящуюся к бесконечности как 1/|г—го|
при г—>г0. Здесь мы хотим лишь указать, что упомянутое решение G
Рис. 7.1. Точка источника, точка наблю-
наблюдения и граничная поверхность для функ-
функции Грина.
можно применить как для построения решения при произвольном распре-
распределении заряда внутри поверхности S, так и для построения решения при
произвольных граничных условиях Дирихле на S (т. е. для ф = ф8
на поверхности).
Действительно, заменим неоднородные граничные условия на- однород-
однородные, но при этом добавим поверхностное распределение зарядов, располо-
расположенных внутри области, где ищется решение, бесконечно близко к гранич-
граничной поверхности. Увеличим картину вблизи граничной поверхности, как
Слой
заряда сг
{раничная
поверхность S
Рис. 7.2. Потенциал слоя источника з на малом
расстоянии s вне заземленной поверхности.
показано на рис. 7.2. Плотность поверхностного заряда, заменяющего
неоднородные граничные условия, возьмем равной с/г, где е—малое рас-
расстояние от поверхности S. Возьмем s значительно меньшим радиуса
кривизны поверхности, а также меньшим расстояний, на которых а
заметно меняется. Итак, мы заменяем неоднородные условия на одно-
однородные плюс этот слой заряда, так что мы теперь требуем, чтобы
потенциал на граничной поверхности равнялся нулю. Для расстояний
порядка s поверхность можно считать плоскостью (которую можно принять
за плоскость у, z), а плотность заряда с/г можно считать равномерной.
47*
740 Гл. 7. Функции Грина
Таким образом, мы приходим к задаче о плоском поверхностном заряде
с постоянной поверхностной плотностью с/е, расположенном на расстоянии е
параллельно заземленному плоскому проводнику при х = 0. Из элементар-
элементарной электростатики вспоминаем, что при переходе через поверхностный
заряд с плотностью с/з нормальная составляющая градиента потенциала
меняется скачком на величину 4тсс/з. Так как г очень мало, то градиент
между зарядом и границей должен быть несравненно больше, чем градиент
по другую сторону поверхностного заряда вблизи от него, и вторым
по сравнению с первым можно пренебречь.
Следовательно, градиент между х = — е и х = 0 должен приближенно
равняться — 4ио/е, а потенциал в этой области должен быть равным
ф = - Dгсо/е) X, -s<a;<0,
и потому потенциал по другую сторону поверхностного заряда .при х = — ?
вблизи него должен быть равен ф = 4тса. Отсюда, если сделать поверх-
поверхностную плотность с/г слоя поверхностного заряда, бесконечно близкого
к заземленной поверхности, равной ф8/Dтсз), то потенциал при прибли-
приближении к поверхностному заряду со стороны х < — s будет как раз рав-
равняться ф8-, т. е. граничному значению, которому мы хотели удовлетворить.
Таким образом, мы сделали правдоподобной идею о том, что решение
однородного уравнения, удовлетворяющее неоднородным граничным условиям,
эквивалентно решению неоднородного уравнения, удовлетворяющему одно-
однородным граничным условиям, с неоднородной частью, представляющей
поверхностный слой заряда с плотностью, пропорциональной неоднородным
граничным значениям, бесконечно близкий к граничной поверхности.
Конечно, мы не доказали этой эквивалентности; мы сделали только ее правдопо-
правдоподобной. Мы также не увидели, где эквивалентность теряется (можно ожи-
ожидать, например, что эквивалентность нарушается между слоем заряда
и поверхностью). Однако, указав цель, мы сможем легче найти путь к ее
достижению.
Между прочим, было бы нетрудно сделать правдоподобным удовлет-
удовлетворение неоднородных условий Неймана при помощи подобной замены
на однородные условия (нулевая dty/dn на S) плюс поверхностный слой
у границы с поверхностной плотностью, пропорциональной заданной
на границе нормальной производной. Таким образом, мы начинаем видеть,
как решения неоднородных уравнений связаны с решениями для неодно-
неоднородных условий и как поверхностный слой может заменить граничные
условия.
Простой пример. Прежде чем разбирать задачу во всей ее общности,
мы рассмотрим некоторые подробности на простом примере. Возьмем дву-
двумерное уравнение Пуассона
^=-3-+^=-4-р(*. у) с7-1-7)
внутри прямоугольной границы х = 0, х = а, г/ = 0, у = Ь. Прежде
всего мы напомним полученное методом собственных функций решение
в случае р = 0 (однородное уравнение) при однородных граничных усло-
условиях (ф = 0) на трех сторонах х = 0, х = а, у = 0, но неоднородных усло-
условиях (ф = фь (х)) вдоль стороны у = Ь. Согласно формуле F.3.2), это решение
имеет вид
7. 1. Точки источников и граничные точки 741
где
Г" /¦->• о. I ЕЛ * X1 °"r"»'") oJ^^ri cir. % П А Я\
U IX, и I С I — ' / 1 —\—; т"»—Г" ЫП о 111 . I I . J. .О 1
17 а ^—1 shGtreo/a) а а ч '
П=:0
Величина Gb в квадратных скобках является функцией координат жиг/,
а также положения ? на линии у = Ъ. Ее можно назвать функцией Грина для
граничных условий на этой линии у= Ъ. Для получения решения мы умножа-
умножаем эту функцию на заданное граничное значение ф и интегрируем по границе.
Чтобы показать, как связана эта функция с решением уравнения
Пуассона для точечного источника (точечный источник для двух измере-
измерений— это то же, что линейный источник для трех измерений), мы далее
исследуем две формы решения неоднородного уравнения (которое, согласно
формуле G.1.4), является уравнением для функции Грина с точечным
источником в х0, у0)
с л0) о (у — у0) (i.i.у)
при однородных граничных условиях ф = 0 на всех четырех граничных
линиях.
В непосредственной близости от источника [R2—(x—жоJ+(у—-у0J < а2, Ь2]
решение должно вести себя так, как если бы границы вообще не было.
Решение уравнения G.1.9) для границы на бесконечности есть ф = — 2 In R =
= — In [(ж — хоJ+ (у — г/0J], так что можно было бы ожидать, что решение
уравнения G.1.9) для конечной границы стремится к бесконечности как
— 2lnR, когда расстояние R становится значительно меньшим расстояния
между точкой источника (х0, у0) и ближайшей границей.
Имеются два пути решения уравнения G.1.9) (и потому также урав-
уравнения G.1.7)). Один, более простой аналитически и более тяжелый с вычис-
вычислительной точки зрения, состоит в разложении в двойной ряд Фурье
Ф^Л . . НИМ . ¦КПЦ
— у. Лт„ sin sin —-~ .
"fcj ТИП q A
т, п
Этот ряд не является решением уравнения Лапласа Т2ф = 0, но мы вскоре
покажем, что он может быть решением уравнения Пуассона G.1.7); при
этом, чтобы быть решением уравнения G.1.9), он должен удовлетворять
уравнению Лапласа всюду, кроме одной точки (х0, у0). Для решения
уравнения G.1.7) разложим р(х, у) в ряд Фурье:
Р (*,»)= 2 Pr,mSi
гп, п
и подставим оба ряда в G.1.7). Тогда можно будет определить коэффи-
коэффициенты Атп , и в результате мы получим решение
•Ь(х, у) = — > , , ., " ,,.„ sin sin —?- =
j), G.1.10)
742 Гл. 7. Функции Грина .
где
„ , |? , _ 16 ^i sin (гопж/а) sin (mzy/b) sin (miz%/a) sin (геятд'6)
<* № У I 6, TJ) =- ^ 2j (^p + (re/6J —
m, n
есть функция Грина для неоднородного уравнения. Нетрудно видеть, что G
является решением уравнения G.1.9) для однородных граничных условий.
Она равна потенциалу в точке (х, у) от единичного точечного заряда
в (?, 7j). Плохая сходимость ряда проистекает из того, что он должен
стремиться к бесконечности как логарифм, когда (х, у) стремится к (?, ¦»))
(как мы указали несколько выше и докажем в следующем параграфе).
Для более хорошего распределения р ряд G.1.10) сходится быстрее.
Еще одно свойство G, которым вообще обладают все эти функции
Грина: она симметрична относительно перестановки (х, у) и (Е, tj). Дру-
Другими словами, потенциал в (ж, у), порожденный зарядом в (?, tj), равен
потенциалу в (Е, tj), порожденному тем же зарядом в (х, у), если гранич-
граничные условия не меняются. Этот вывод, что перестановка источника и наблю-
наблюдателя не меняет G, иногда называется принципом взаимности.
Связь между объемной и поверхностной функциями Грина. Однако
ряд G.1.10) все еще далек от выражения, стоящего в квадратных скобках
в G.1.8). Прежде всего это выражение является простым рядом, тогда как
ряд G.1.10) — двойной. Попытаемся решить уравнение G.1.7) при помощи
простого ряда. Для этого положим
2l^ 2^ G.1.11)
т т
где Fm требуется подсчитать, а
о
Подстановка в уравнение G.1.7) дает для Fm(y) обыкновенное неодно-
неоднородное уравнение
d2 „ f пт Л2 г,
Чтобы применить формулу E.2.19) для решения такого уравнения, заме-
заметим, что двумя независимыми решениями однородной части будут
у1 = sh (жту/а), у2 = sh [(жт/а) (Ь — у)].
Эти решения независимы, так как их определитель Вронского
, тсго /7 . , . тс/га/ , тсго ,,
hF2/Hchsh (fc2
= — (пт/а) sh (izmbia)
отличен от нуля (и постоянен, как это и должно быть). Подставляя все
это в E.2.19) и выбирая пределы интегрирования такими, чтобы Fm рав-
равнялось нулю при у = 0 и у = Ъ, имеем
F {y)= Ja
т\У> msh(nmb/a)
У
v
7. 1. Точки источников и граничные точки 743
где
4а \ sh(vmy/a)-sh[(Tzm/a)(b— tj)] для tj > у,
Х
msh(nmb/a) ' \ sn (ът-ц/а) -sh [(кт/а) (b- y)\ для y\<y.
Функция gm{y\t\) обращается в нуль, когда у или tj равно нулю .или Ъ,
и ее производная имеет разрыв (см. стр. 123) величины — 4тг при j/ = tj.
Наконец, подставляя все эти решения вновь в формулу G.1.11), мы
получаем простую форму для решения:
а Ь
•1>(ж, у) = \ d? \G(x,y\f-, tj) p (?, tj)rfirj, G.1.12)
о о
где
ЯШ
G (х I ? - V 8sm a Sm a ., (sh (ъту/а) ¦ sh [(nm/a) (b — tj)] для tj > у,
КХ>У\ ,Ю— 2j msh(nmb/a) л|sh(жт-ц/а)¦ sh[(vm/a) (b — y)] для tj < y.
Так как этот интеграл для ф имеет тот же вид, что и интеграл в фор-
формуле G.1.10), то и функция G, данная здесь, должна равняться G, дан-
данной там. Простой (но утомительный) процесс разложения gm в ряд Фурье
по у показывает, что обе функции G в самом деле тождественны.
Однако при помощи этого последнего выражения для G можно лучше
ныяснить связь между решением неоднородного уравнения при однородных
граничных условиях и данным в G.1.8) решением однородного уравнения
при неоднородных граничных условиях; действительно, если единственным
зарядом внутри границ является поверхностный заряд с плотностью
(l/4ic?) фь (?), расположенный на исчезающе малом расстоянии s от поверх-
поверхности у = Ь, то при tj = b — з, т. е. в единственном месте, где р отлично
от нуля, имеем
G(x, у E, b~ s) ~ У sin sin ,-7—rV-r , У <b — z.
m
Так как область Ъ — s < у < Ъ должна стать исчезающе малой, то она
не будет участвовать в нашем рассмотрении, хотя надо помнить, что в этой
бесконечно узкой области производная от G претерпевает разрыв, обра-
обращаясь в нуль при у=Ь. Подставляя последнее значение для G в формулу
G.1.12), можно видеть, что потенциал, порождаемый тонким слоем заряда
поверхностной плотности A/4тсг)фь(ж) на бесконечно малом расстоянии е
от заземленной пластинки у = Ъ, представляется точно тем же интегралом,
что и потенциал G.1.8), получающийся, когда на поверхности у=Ь
задается неоднородное граничное условие фь(ж).
Общее решение. Можно прийти к тому же равенству двух решений
несколько иным путем, возможным при более общих условиях. Заметим, что
*-G(x, y\k, tj) 1 -*-4«Gb(*l y\%), G.1.13)
гдр Gb определено формулой G.1.8), так что равенство G.1.8) можно
переписать следующим образом:
<f{x, y)= -± $%(So)[^G(z, y\S0)]dS0, G.1.14)
So
где величина в квадратных скобках есть производная функции G(x, у\х0, у0)
от х0, у0 по нормали к граничной поверхности So (в данном случае So
ость у0 = Ъ, так что производная берется по у0 или -ц), причем координаты
744 Гл. 7. Функции Грина
хо' Уо берутся на этой поверхности. Интеграл от этой производной, умно-
умноженной на заданное граничное значение ф0, берется по поверхности (в дан-
данном случае интегрирование производится по х0 или ?).
Эта стенографическая запись раскрывает соотношение между функ-
функцией Грина для неоднородного уравнения и функцией Грина для неодно-
неоднородных граничных условий, но о некоторых вещах ничего не говорит.
Например, в ней не указана структура разрыва функции G, получающе-
получающегося, когда точка (х0, у0) стремится к поверхности So (производная от G
имеет разрыв при у = уо = 'Ц, который попадает прямо на поверхность,
когда точка (ж0, у0) достигает поверхности). Получающееся решение <1>
не имеет разрыва внутри области, окруженной граничной поверхностью,
но должен иметься разрыв как раз на самой границе (на самом деле этот
разрыв должен быть таким, чтобы ф равнялась нулю непосредственно
за поверхностью и равнялась ф0 (So) непосредственно внутри поверхности
в области, окруженной границей).
При дальнейшем применении формулы G.1.14) надо заботиться о том,
чтобы при получении функции Грина для граничных условий из G (г | г0)
сначала устремить «точку источника» (х0, у0) к поверхности So и только
после этого позволить точке (ж, у) приблизиться к соответствующей гра-
граничной поверхности S пространства «точек наблюдения». Переходя к пре-
пределу в этом порядке, мы видим из формул G.1.13) и G.1.8), что, когда
сначала -ц стремится к Ъ, а затем у стремится к Ъ, предел равен
^G(x, y\t, ¦,)_> __2]sin —.sin —= ~4irS (*-?)•
n
Значит, функция Грина для поверхности (вычисленная на поверхности)
является дельта-функцией, соответствующей граничным условиям, равным
нулю всюду, кроме точки ж=?. Это, конечно, соответствует нашему инту-
интуитивному представлению о природе функции Грина.
Подведем итоги: для решения краеиых задач, помимо техники собствен-
собственных функций, имеется другой метод, в котором решается неоднородное
уравнение при однородных граничных условиях для «точечного источника»
в некоторой точке г0 внутри границы. Получающаяся функция G(rjr0),
функция Грина для внутреннего объема, симметрична относительно пере-
перестановки г и г0, разрывна или имеет разрывную производную при г = г0.
и удовлетворяет по г однородным граничным условиям на граничной поверх-
поверхности S, а по г0 — на аналогичной поверхности So. Решение общего неодно-
неоднородного уравнения имеет вид G.1.12), т. е. Л (г) получается при интегри-
интегрировании Gp по г0-области внутри So.
Если однородные граничные условия, которым удовлетворяет G, состоят
в том, что G = 0 на б1 и So, то решение для неоднородных граничных
условий [ф = фF') на S] имеет вид G.1.14), где производная от G берется
в координатах г0 по нормали к So для г0, исчезающе близкого к So. Далее,
точка г0 устремляется «на» So и интегрирование после умножения на ф (So)-
производится по граничной поверхности.
Если однородными граничными условиями на G служат условия Ней-
Неймана (нулевая нормальная производная от G на S), то решение для неод-
неоднородных условий (dty/dn = N (S) на S) имеет вид
ф (х, у) = 4ir ^N (So) G(x,y\ So) dS0. G.1.15>
So
Это будет доказано позже. Рассмотрения зтого параграфа не заканчивают
нашего «доказательства» формулы G.1.14); они только начинают наше-
исследование.
7. 2. Функции Грина для установившихся колебаний 745
Функция Грина и производящие функции. Формулы G.1.8) —G.1.12)
показывают, что функции Грина и собственные функции тесно связаны.
Позже в этой главе мы получим общую формулу для разложения функции
Грина по собственным функциям. Нетрудно показать, что такие формулы
разложения служат обильным источником производящих функций для соб-
собственных функций [см. формулу F.3.32)]. В случае, исследуемом в этом
параграфе, мы получаем производящую функцию, интегрируя функцию
Gb(x, у\%), определенную формулой G.1.8), по ? от нуля до а. Только
члены с нечетным п дают ненулевые интегралы, так что, разлагая гипер-
гиперболический синус на составляющие его экспоненты, имеем
sin
Gb (ж, j,, ч, „ч - n ^j gh + _^
71=0
Это соотношение не особенно полезно, так как функция Gb не дана в замк-
замкнутом виде. Однако легко видеть, что если возможно получить замкнутый
вид для G, то тем самым можно построить производящие функции для соот-
соответствующих собственных функций.
7.2. Функции Грина для установившихся колебаний
Прежде чем приступить к более сложным случаям, целесообразно
упростить обозначения, возвратившись к векторной символике. Точке х, у, z
в трехмерном пространстве соответствует радиус-вектор г = xi + г/j -f- zk.
Функция Грина G(r|r0) зависит от положения двух точек: точки наблю-
наблюдения, в которой поле измеряется, имеющей радиус-вектор г и координаты х,
у, z наблюдателя, и точки источника, в которой помещается единичный
источник, имеющий радиус-вектор г0 и координаты источника х0, у0, z0. Гра-
Граничная поверхность в координатах х, у, z обозначается буквой б1, а в коорди-
координатах х0, у0, z0 — буквой So. Функция Грина с точкой наблюдения в г и с
источником на границе обозначается через G(r|r?). Элемент объема в про-
пространстве переменных х, у, z обозначается через do (— dxdydz), аксиальный
вектор, изображающий элемент граничной поверхности S, обозначается че-
через dA, и элемент граничной поверхности So—через dA0. Оба эти векто-
вектора направлены наружу, из объема, заключенного внутри границы.
Элемент нормальной составляющей градиента G на поверхности в коор-
координатах источника можно тогда записать в виде grad0 G (r | rg) ¦ dA0, где
индекс нуль у градиента указывает, что производную надо брать по х0,
у0, z0. Дельта-функцию для трех измерений можно записать в виде 8 (г— г0);
она имеет интегральное свойство
Наконец, V? с индексом нуль есть оператор Лапласа в координатах
источника, тогда как в координатах наблюдателя он обозначается просто V'-.
Теорема Грина. Чтобы получить вполне строгий вывод свойств функ-
функции Грина, будет выгодно воспользоваться вариантом теоремы Гаусса.
Для любой замкнутой поверхности S теорема Гаусса, записанная форму-
формулой A.4.7), утверждает, что поток любого «достаточно гладкого» вектор-
векторного поля через поверхность S (наружу) равен интегралу от дивергенции.
746 Гл. 7. Функции Грина
этого поля по всему объему, заключенному внутри S. Под «достаточной
гладкостью» мы понимаем то, что вектор не должен иметь разрывов в ве-
величине или в производной на б1 и что дивергенция интегрируема.
Рассмотрим теперь две «достаточно гладкие» скалярные функции U (г)
и V (г) от г. По ним построим вектор U grad V. Теорема Гаусса утверждает,
что поток этого вектора через S равен интегралу от дивергенции U grad V
по объему, заключенному внутри S. Так как
div (С/grad V) = (grad U) ¦ (grad V) + UV2V,
то в указанных выше обозначениях имеем (где dA направлено наружу
из области, заключенной внутри границы)
С/grad V -dA = ^ ^ (grad f/grad V) dv+^^U VW dv.
Однако можно получить также подобное соотношение для другого вектора
I7 grad С/. Вычитая одно из другого, получаем
(?[?7gradF-Fgrad?/]-dA= \\\ [C/V2F -VV*U]dv, G.2.2)
где поверхностный интеграл берется от наружной нормальной компоненты
вектора, заключенного и квадратные скобки, по замкнутой поверхности S,
а объемный интеграл берется от скалярной величины в квадратных скоб-
скобках по всему объему внутри S- Граничная поверхность может быть конеч-
конечной (по протяженности) или бесконечной. Например, она может быть
конечной сферой, причем объемное интегрирование распространяется по вну-
внутренности сферы, a dA направлено от центра сферы. Или же она может
состоять из этой конечной сферы и бесконечной сферы, причем «внутрен-
«внутренностью» в этом случае будет бесконечный объем между этими сферами,
и dA на конечной сфере направлено к центру (от «внутренности»), а на бес-
бесконечной сфере — наружу. Аналогично можно построить и другие частные
примеры.
Это соотношение между поверхностным и объемным интегралами назы-
называется теоремой Грина. Как мы видели, она является частным случаем
теоремы Гаусса. Вскоре мы увидим, как она применяется к выводу свойств
функции Грина.
Функция Грина для уравнения Гельмгольца. Начнем с изучения функ-
функции Грина для уравнения Гельмгольца
Щ = V2<j) + /c24> = 0 G.2.3)
при некоторых граничных условиях на замкнутой поверхности S. В соот-
соответствии с нашим кратким введением в § 1, нам надо сейчас доказать
следующие свойства функции Грина.
1. Функция Грина является симметричной функцией координат двух
точек, именно, координат точки наблюдения и точки источника:
Gh(r\r0) = Gh(r0\r) G.2.4)
(соотношение взаимности). Эта функция удовлетворяет некоторым однород-
однородным граничным условиям как на S, так и на So и имеет разрыв (вида,
который надо определить) при г=г0.
2. Используя эту функцию, можно получить решение неоднородного
уравнения с данными однородными граничными условиями или же реше-
решение однородного уравнения с неоднородными граничными условиями. В силу
линейности уравнения мы можем также решить неоднородное уравнение
с неоднородными граничными условиями при помощи наложения обоих
частных решений.
7. 2. Функции Грина для установившихся колебаний 747
3. Решения для неоднородных граничных условий имеют разрыв на гра-
границе. Например, если ф задано на поверхности (условия Дирихле), то реше-
решение будет иметь заданное значение ф непосредственно внутри границы
it будет равно нулю непосредственно за ней. В случае условий Неймана,
когда задается нормальная производная, будет разрыв у этой производной.
Требуемая функция Грина является решением неоднородного уравне-
уравнения Гельмгольца
V*Gk (г | г0) + кЮк (г | г0) = - 4* 8 (г - г0) G.2.5)
для единичного точечного источника в г0, удовлетворяющим однородным
граничным условиям (либо нулевое значение, либо нулевая нормальная
производная от G) на граничной поверхности S (и также, в координатах
источника, на So). Дельта-функция определена формулой G.2.1) и симмет-
симметрична относительно вращения около г0. Более сложные источники — диполи
it т. д. — можно рассматривать как состоящие из этих простых источни-
источников. Отметим, что V2 в G.2.5) действует в координатах наблюдателя.
Мы хотим теперь показать, что решение неоднородного уравнения
V2<]> А- Щ = - 4тгр (г) G.2.6)
при произвольных условиях Дирихле (или Неймана) на замкнутой гранич-
граничной поверхности S можно выразить через функцию G. Для этого мы умно-
умножим G.2.5) на ф, а G.2.6) на G и вычтем один результат из другого,
и то же время меняя местами г и г0:
G* (Го I г) Vft (г0) - ф (r0) VlGh (г0 | г) = 4* [ф (г0) 8 (г - г0) - Gh (г01 г) р (г0)].
Интегрируя это равенство по всем координатам источника х0, у0, z0 внутри St>,
мы получаем в силу свойства дельта-функции н формулы G.2.4)
G"(r'Го) v°*(Го) - *(Го) V°G*(r'ГоI' dv<>+
<Ь (г) для г внутри S,
Ш
Интересно указать, какое значение имеет правая часть, если точка
наблюдения находится на S. До некоторой степени это дело соглашения;
но если такое соглашение принято, то надо проводить его последовательно.
В дальнейшем мы будем всегда считать, если не оговаривается против-
противное, что эта разрывная функция равна ф (г) внутри и на S и равна
нулю вне S.
Теперь мы применяем теорему Грина G.2.2) для упрощения левой
части. В соответствии с нашим соглашением, мы измеряем градиент
по направлению изнутри наружу (или, что то же, элемент поверхности dA
указывает изнутри объема, где надо вычислить поле), так что интеграл
по поверхности равен обычному потоку. Применение формулы G.2.2) дает
' Gh (г I г*) grad0 •!> (rs0) — ф (/•{;) grad0 Gh (r
Ф (г) для г внутри и на S,
п с G-2-7)
q для г вне g^ \ r
откуда можно найти наше решение как для неоднородного уравнения, так
и для неоднородных граничных условий.
Решение неоднородного уравнения. Например, для неоднородного
уравнения (рфО) с однородными граничными условиями Дирихле (ф = О
на S) мы выбираем G также равной нулю как на S, так и на So. Тогда
748 Гл. 7. Функции Грина
поверхностный интеграл по So равен нулю и
для г внутри или на S. Эта функция автоматически удовлетворяет одно-
однородным граничным условиям (d» = 0 на 5) и является решением уравне-
уравнения G.2.6). Если граничным условием служит однородное условие Неймана
(нормальная производная ф равна нулю на S), то мы выбираем Gh удовле-
удовлетворяющей тем же условиям в обеих системах координат, как наблю-
наблюдателя, так и источника. Тогда опять поверхностный интеграл равен
нулю и имеет место формула G.2.8). Значит, формула G.2.8) дает реше-
решение неоднородного уравнения G.2.6) для однородных граничных условий,
если Gk удовлетворяет тем же условиям, что и ф.
На самом деле зта формула имеет место также, когда граничные усло-
условия состоят в том, что функция ф на S равна произведению функции /(г^)
на нормальную производную от ф на S, если только Gh удовлетворяет
тем же условиям. Наиболее общие однородные граничные условия имеют вид
^ г0) = /(,-) A Gk> Gh^
Если / = 0, получаются однородные условия Дирихле; если 1// = 0 — одно-
однородные условия Неймана. Вне зависимости от значений / поверхностный
интеграл в формуле G.2.7) исчезнет, что приведет к формуле G.2.8) для
решения. Конечно, не все условия допустимы в физических задачах. На-
Например, если суммарный заряд внутри S отличен от нуля, то нельзя ожи-
ожидать, что нормальная производная ф равна нулю на всей границе, так что
нельзя ожидать, чтобы для решения уравнения Лапласа производная dG/dn
была равна нулю на границе. Что именно возможно, обычно указывают
физические соображения.
Для неоднородных граничных условий, если они являются условиями
Дирихле [ф = ф0 (гЦ) на So], мы полагаем Gh равной нулю на 5 и также
на So. Тогда получаем уже исследованное на стр. 743 решение
i§Ao G.2.9)
для г внутри и на S при неоднородных условиях Дирихле для ф, если Gh
равно нулю на S и So- Заметим вновь, что вектор dA0 направлен наружу
из области, где ищется поле, так что интегрируемая компонента гра-
градиента—это наружная нормальная компонента. Здесь мы получаем наше
решение в виде интеграла только по граничной поверхности; неоднородные
граничные условия удовлетворяются посредством расположения слоя заряда
на поверхности. Для условий Дирихле получается двойной слой, что
явствует из рассмотрения gradG.
Если ф должно удовлетворять неоднородным граничным гусловиям
Неймана, т. е. производная от ф по внешней нормали к S равна N (rs), то
мы полагаем нормальную производную Gk на S равной нулю и получаем
решение
i$ G.2.10)
для г внутри или на S, причем N представляет собой заданную нормаль-
нормальную составляющую градиента функции ф и нормальная производная G на
S и So равна нулю. В этом случае поверхностный заряд, порождающий
нормальную производную N, равен как раз iV/4ir и представляет собой
простой, а не двойной, слой заряда.
7. 2. Функции Грина для установившихся колебаний 749
Наконец, если граничные условия имеют общий неоднородный вид
то мы требуем, чтобы G удовлетворяла соответствующему однородному
условию
где обе нормальные производные внешние; тогда решение однородного
уравнения при условии G.2.11) имеет вид
I
1
Можно пользоваться любым из двух видов поверхностного интеграла. Пер-
Первый более полезен, если / мало или равно нулю (условия Неймана); вто-
второй— если 1// мало или равно нулю (условия Дирихле), но F/f огра-
ограничено.
Решения, данные формулами G.2.9), G.2.10) и G.2.12), построены для
однородного уравнения (р = 0 внутри границы). Если мы хотим решить
неоднородное уравнение G.2.6) с неоднородными граничными условиями,
то надо сложить объемный интеграл типа G.2.8) с соответствующим по-
поверхностным интегралом, взяв G в объемном интеграле удовлетворяющей
тем же однородным граничным условиям, что и G в поверхностном инте-
интеграле.
Общие свойства функции Грина. Теперь мы совсем точно доказали
большую часть утверждений, сделанных в § 7.1 и на стр. 744. Граничные
условия удовлетворяются посредством расположения на поверхности рас-
распределения диполей (для условий Дирихле) или простого заряда (для
условий Неймана) с плотностью, пропорциональной требуемому значению
функции ф или ее нормальной производной, которое надо умножить на
значение нормальной производной от соответствующей функции Грина G
или значение самой G. Мы также обратили внимание на разрыв решения,
так как интеграл равен ф на и внутри S, но равен нулю вне S.
Но мы еще не доказали, что G является симметричной функцией г
и г0, как это утверждает формула G.2.4). Как функция от г, G удовле-
удовлетворяет уравнению G.2.5), а для источника в г, — уравнению
V2Gfe (г | Г1) + /c2Gh (г | п) = - 4^ 8 (г - гх).
Умножая G.2.5) на G^lr^ и это новое уравнение на G(r|r0), вычитая
-один результат из другого и применяя теорему Грина G.2.2), имеем
§[G(r|r1)gradG(r|r0)-G(r|r0)gradG(r|r1)].rfA =
Так как обе функции G удовлетворяют одним и тем же однородным гра-
граничным условиям, то поверхностный интеграл исчезает, и мы получаем
условие взаимности GOblrJ = G(r1|r0), если только как г0, так и тг нахо-
находятся внутри или на поверхности.
Остается изучить еще более важный вопрос о поведении G(r|r0),
когда точка наблюдения находится вблизи точки источника, т. е. когда
длина вектора R = г — г0 мала в сравнении с расстоянием любой из этих
750 Гл. 7. Функции Грина
точек до ближайшей точки на граничной поверхности. Из структуры уран-
нения G.2.5) мы видим, что если
R = V(*-*J*r(y-yo)' + (z - zof
мало по сравнению с расстоянием от S или So, то функция G зависит
только от R. Другими словами, ввиду полной симметрии источника функ-
функция G не может зависеть от направления R, она может зависеть только
от его длины. Как мы заметили раньше, надо ожидать, что функция G
должна иметь особенность при R = 0.
Говоря на более математическом языке, надо ожидать, что G(r|r())
можно разделить на две части: во-первых, часть, которая всюду регулярна
и непрерывна внутри S и зависит от граничных условий, наложенных на
G у S, и, во-вторых, часть, которая регулярна и непрерывна всюду внутри S,
кроме г = г0, является функцией только от R и имеет особенность при
R=0. Эту последнюю часть можно обозначить через gk(R). Значит, можно
сказать, что если точка наблюдения и (или) точка источника не находятся
бесконечно близко к S, то
Gft(r|r0) ~gh(/?), R = r-r0. G.2.13)
Чтобы выяснить поведение gh при малых R, мы проинтегрируем
(в координатах наблюдателя х, у, z) обе части урапнения G.2.5) по малому
шару радиуса s с центром в г0. Это даст
Интеграл в правой части равен —4it в силу свойств дельта-функции, так
как шар, по которому производится интегрирование, содержит точку г=г0.
Сделаем теперь е достаточно малым, чтобы соотношение G.2.13) имело
место, и подставим gh вместо Gh в остающиеся интегралы. Кроме того,
предположим, что оператор Лапласа от особенности является более «особен-
«особенным», чем сама особенность, так что в пределе первый интеграл преобла-
преобладает. Тогда получим
72gh(R)dv—> — 4тс при е—> О,
где координатами при интегрировании по шаровому объему будут R, 6, <р,
а элемент объема равен dv = RzdR-sin bdbdy.
Применяя теорему Гаусса A.4.7), мы получаем, что суммарный поток
gradg наружу через поверхность сферы с центром в г0 радиуса е равен — 4ir:
ф grad gh ¦ dA —> — 4it.
Так как gh зависит только от радиальной координаты R маленькой сферы,
то gradgfe имеет всюду радиальное направление, параллельное dA, и- его.
величина всюду на поверхности .одинакова. Значит, поверхностный интеграл
в пределе равен произведению dgh/dR при R = з на площадь 4ite2 сферы,
и мы приходим к формуле
(dgk/dR)R=e 4ite2 —» — 4тс при е —> 0,
или, что то же,
Таким образом, мы в результате получаем gk (/?) ^ -щ-, или
когда i? = |r^ro|->0, G.2.14)
7. 2. Функции Грина для установившихся колебаний 751
если ни г, ни г0 не находятся слишком близко к S или So. Теперь не-
нетрудно видеть, что выше мы законно пренебрегли объемным интегралом от G.
Итак, можно сказать, что, как функция координат (х, у, z) точки
наблюдения, функция Грина ¦ представляет собой регулярное непрерывное
решение однородного уравнения V2G-fA2G = 0 внутри S, за исключением
точки г = г0, где она имеет особенность, указанную формулой G.2.14). Эта
особенность проистекает из наличия единичного точечного источника, при-
причем уравнение G.2.5) неоднородно только в этой точке. Заметим, что пре-
предельная форма 1/jR не зависит от к, так что этот результат имеет место
также для уравнения Лапласа.
Формула G.2.14) справедлива для трех измерений. Можно провести
подобное рассмотрение для двумерного случая, причем можно показать,
что для. двух измерений
G(r|ro)^-21ni?, Д-*0. G.2.15)
В одномерном случае уравнение G.2.5) принимает вид
Как указано на стр. 743, здесь будет разрыв производной, так что если
проинтегрировать по х от х0— е до жо + а, то интеграл от k2G будет стре-
стремиться к нулю, тогда как интеграл от второй производной
\ -rTdx=\ -г- —> —4it, е —-0. G.2.16)
J dx2 l_dxjxo-s ' К '
Значит, для одного измерения функция Грина G имеет разрыв производной,
равный — 4ти, при х = х0.
Возвращаясь к сказанному на стр. 123—125, мы видим, что функции
Грина для уравнения Гельмгольца, указанные выше, удовлетворяют требо-
требованиям, приведенным в формулах G.2.14), G.2.15) или G.2.16), в зависимо-
зависимости от числа измерений. Например, после формулы B.1.10) мы указали, что
функция Грина для струны равна B'Ki/k)-eik'<x~x»\; она удовлетворяет со-
соотношению G.2.16). Подобным образом, мы знаем, что функция Грина для
точечного источника в трех измерениях равна elkR/R.
Эффект граничных условий. Рассмотрим, как влияют граничные усло-
условия на функцию Грина, чтобы можно было видеть, как построить требуе-
требуемую функцию в каждом интересном случае. По-видимому, простейшим
является случай, когда граница расположена на бесконечности, так как
тогда се эффект должен быть наименьшим. Для трех измерений нам тре-
требуется решение уравнения (V24- k2)G = 0, определенное всюду, за исключе-
исключением г=г„, которое стремится к нулю [и (или) производная которого
стремится к нулю] при R—> со и которое имеет особенность порядка 1/R
при R—^0. Имеются два линейно независимых решения с такими свой-
свойствами (и пригодна любая линейная комбинация этих решений):
eihR/R, e~im!R, cos(kR)/R и т. д.; i? = |r-ro|.
Очевидно, что даже если граница находится на бесконечности, то выбор
все-таки должен производиться на основании граничных, условий.
Чтобы сделать выбор, мы обратимся к исходному зависящему от вре-
времени решению волнового уравнения V2lF= (l/c2)d2yV/dt&. Мы получили
уравнение Гельмгольца, приняв простую гармоническую зависимость реше-
решения волнового уравнения от времени. На стр. 125 и 700 мы положили это
решение равным tbe~iw( = Ы~^а, откуда ф есть решение уравнения Гельм-
Гельмгольца. Следовательно, если G надо применять к простому гармоническому
752 Гл. 7. Функции Грина
решению волнового уравнения, то полным решением будет Ge~ihcl. Отсюда,
если мы хотим иметь волны, идущие от точки источника, то надо при-
применять
?»t (r I ro) = Eh (Щ — eihR/R, граница на бесконечности, G.2.17)
так как тогда полное решение A//?) eih(R~c|) представляет расходящуюся
волну. В тех редких случаях, когда нам нужны сходящиеся волны, надо
выбрать функцию e-ihR/R. Для границы, расположенной всюду на конечном
расстоянии от г0, может не быть полного поглощения энергии поверхно-
поверхностью. Часть может отражаться обратно к источнику, и тогда надо поль-
пользоваться комбинацией расходящихся и сходящихся волн. Однако в боль-
большинстве случаев мы пользуемся решением в виде расходящейся волны,
данным формулой G.2.17).
Решения уравнения Гельмгольца иногда используются при решении
уравнения диффузии V2lF = A/а2) dW/dt. Здесь для описания процесса рас-
распространения диффундирующего вещества, концентрация которого изме-
измеряется величиной W, мы полагаем W = фе-^2'; ф вновь будет решением
уравнения V2<j)-|-/с2Ф = 0. Обычно требуют, чтобы ф была всюду веществен-
вещественной; отсюда
Gk(r\r0) = сов (kR)/R,
так что возможная функция Грина для уравнения диффузии равна
что соответствует «выходящей» диффузии, когда граница находится на бес-
бесконечности, а «источник» диффузии обладает экспоненциально затухающей
зависимостью от времени. Как будет показано позже, для функции Грина
уравнения диффузии на самом деле обычно применяется совсем другое ре-
решение уравнения диффузии, соответствующее «источнику» значительно
более «правильного» вида.
В случае двух измерений решения уравнения Гельмгольца, симметрич-
симметричные относительно R = О, являются решениями уравнения
которое представляет собой уравнение для функций Бесселя нулевого по-
порядка [см. формулу E.3.63)]. Нам требуются решения, имеющие при /? = 0
особенность, причем такую, как указано в G.2.15). Возможными реше-
решениями являются функции Ганкеля [см. формулу E.3.69)], в частности,
функция
"' ' " "' " " '" ~" при R —> О,
.„) G.2.18)
при R —> со
представляет собой точную функцию Грина в двумерном случае для гра-
границы на бесконечности и расходящихся волн. Если требуются сходящиеся
волны, то применяется вторая функция Ганкеля, а если нужна веществен-
вещественная функция (как в частном случае уравнения диффузии), то можно поль-
пользоваться произведением тс на функцию Неймана N0(kR) [см. формулу
<5.3.75)].
Наконец, в одномерном случае функция Грина для расходящихся волн,
простирающихся до бесконечности в обоих направлениях, уже дана фор-
формулой G.2.16). Она равна
?^-^. G.2.19)
7.2. Функции Грина для установившихся колебаний
753
Метод изображений. Теперь мы обратимся к задаче получения функ-
функций Грина для ограниченных областей. Сначала рассмотрим один метод—
метод изображений, в котором непосредственно применяется полученная
выше функция gh(R). Каков физический эффект введения границы? Без
границы соответствующая функция Грина равнялась gk (/?). Если введена
граница, то, скажем, в электростатике возникает потенциал, порождаемый
индуцированным зарядом на граничной поверхности, который в свою
очередь порождается приложенным электрическим полем gk (R). В аку-
акустике эффект границы состоит в возникновении отражений, которые надо
добавить к волне, выходящей из источника, чтобы получить полное дав-
давление. Значит, можно ожидать, что
(г I г0) = gk (Я) + Fk (r | г0),
G.2.20)
где Ffe(r|r0) представляет граничный эффект. Fh(v\v^ не может иметь осо-
особенности внутри области, так что Gk (г | г0) —> gk (R) при г—>г0. Метод изо-
изображений, описывающий отраженные волны в акустике или индуцирован-
индуцированный заряд в электростатике, можно применить для определения /*h(r|r0).
— Граница
<Г\
Начало координат
Рис. 7.3. Изображение точки источника
(*о» Уо) в плоскости х--0.
Рассмотрим простой случай, показанный на рис. 7.3. Единичный ли-
вейный заряд расположен при (ж0, у0) перед бесконечной проводящей ме-
металлической пластинкой. Потенциал на поверхности пластинки при х = 0
должен равняться нулю, так что функция Грина должна удовлетворять
граничным условиям Дирихле. В методе изображений вводится линейный
заряд противоположного знака в зеркально-симметричной точке (— х0, у0),
как показано. Полный потенциал для ж>0 равен тогда
Go(rK)=-21n(i?/i?o), ж>0. G.2.21)
На эквипотенциальной плоскости R = R0 и Go = 0, так что граничные усло-
условия удовлетворяются. Так как g0 (R)= — 2 lni?, то мы видим, что Fo = 21ni?0.
Единственная особенность, имеющаяся в области, представляющей физиче-
физический интерес (х > 0), находится в месте расположения заряда, R — 6. Дру-
Другая особенность получается при i?0 = 0 (ж < 0), т. е. в области, где выра-
выражение G.2.21) уже не применимо.
Легко обобщить формулу G.2.21) для нахождения Gk. Введя отраже-
отражение, как выше, найдем
Gk (г | г0) = ш [tf(i> (Щ-ЩЧ (kR0)]. G.2.22)
Отражение падающей волны зеркалом, требующее в этом случае равенства
G нулю, дается выражением Яу)(/с/?0). {Начиная отсюда, мы в этом пара-
48 ф. м. Морс и Г. Фешбах
754 Гл. 7. Функции Грина
графе не будем писать верхний индекс A), так как мы всегда будем поль-
пользоваться функцией Ганкеля первого рода.)
Если, с другой стороны, поверхность жесткая или если, в случае урав-
уравнения Лапласа, требуется решать задачи с известными распределениями
заряда, а не потенциалами, то соответствующими граничными условиями
будут условия Неймана д'Ь/дп = О. Метод изображений можно применить
и здесь; заряд или источник в зеркально-симметричной точке надо взять
того же знака (или той же фазы), так что
Go (г | г0) = - 2 In (RR0), Gk (г | rj = т [Но (kR) + Но (kR0)].
Граничные условия удовлетворяются, в чем можно убедиться, подсчитав
производную по х при ж = 0.
В качестве иллюстрации подсчитаем эффект от потенциала /(г/) (уже
не нулевого) на плоскости. Из формулы G.2.9) имеем
f{y0)(dG0/dx0)Xo=0dy0.
Вводя функцию Грина G.2.21) и подсчитывая производную, находим
Мы встречались с этой формулой раньше. Она была выведена при помощи
теории функций комплексного переменного в гл. 4 [формула D.2.13)] при един-
единственном требовании, чтобы ty удовлетворяла уравнению Лапласа. Интересно
проверить непосредственно, что решение удовлетворяет граничным условиям.
Как указано на стр. 744, это должно дать представление 6-функции.
Для этой цели рассмотрим функцию
1 х
со
Заметим, что \ А (ж, 7j)d7j = l. Для исследования ее свойств при х—>0,
—ОО
т) —» 0 перепишем А (ж, tj) в виде
Если положить tj = O, то при ж—» 0 функция А (ж, 0) (= 1/гас) строго воз-
возрастает. С другой стороны, для т] ф 0 при х~->0 функция А (ж, г,) (c^l x/wf)
стремится к нулю. Мы видим, что НшД(ж, т\) представляет собой функцию,
зс-»0
интеграл от которой всегда равен единице и значения которой при к) = 0
возрастают к бесконечности для х~»0, а при -ц Ф 0 стремятся к нулю.
Значит,
ШпД(ж, 7]) =
0
Отсюда в G.2.23)
lim ф (г) = \ 6 (у - у') f (у') dy' = / (у),
как и требуется. Функция А (х, у) особенно полезна для задач, связанных
с уравнением Лапласа, так как, будучи вещественной частью аналитической
функции 1/tcz = l/%(x + iy), она является решением уравнения Лапласа.
Метод изображений можно применить и к границам другой формы.
Например,, его можно применить, если граница представляет собой окруж-
7. 2. Функции Грина для установившихся колебаний
755
ность. Применение теории функции Грина приводит к интегральной формуле
Пуассона D.2.24). По поводу дальнейших подробностей мы отошлем чита-
читателя к задачам и к гл. 10, так как метод изображений для окружности
будет действовать только для уравнения Лапласа.
Применение метода изображений допускают и некоторые другие границы
симметричного вида. Однако, вообще говоря, при этом получаются бесконеч-
бесконечные ряды с обычными ограничениями их пригодности. В качестве примера
x=-h
-с
см
I
X
I
J
ч
1
x=h
1
x=2h
i
•с
см
x*3h
•f
-с
О)
Рис. 7.4. Поле между па-
параллельными плоскостями
от источника в точке
(*о> Уо)-
Рис. 7.5. Последовательность образов источника
рис. 7.4.
рассмотрим расположение, показанное на рис. 7.4, где источник находится
между двумя бесконечными плоскостями х = 0, x = h, на которых на функ-
функцию Грина накладываются граничные условия Неймана дф/ди = О.
Ряд изображений. Мы применяем метод изображений посредством
последовательных шагов, не учитывая каждую из границ ж = 0 и x = h
по очереди. Учитывая только границу х = 0, мы вводим изображение источ-
источника при х= —х0, а учитывая только х = h — изображение приж = 2& — х0'.
Они обозначены цифрами 1 и 2 на рис. 7.5. Однако, хотя 1 и 0 ¦ вместе
порождают потенциал, удовлетворяющий условиям Неймана при х = 0, надо
добавить эффект источника 2, который, конечно, не удовлетворяет условию
дф/5п = 0 при ж = 0. Чтобы устранить эффект точки 2, мы вводим теперь
изображение 3 в (х0 — 2h, у0) точки 2 относительно х = 0. Подобным
образом для устранения эффекта точки 1 в плоскости x = h вводится источ-
источник 4 при x~2h + x0. Однако теперь становится необходимым устранить
эффект точки 3 при x = h; необходимо ввести изображение 6 в C& — х0, у0).
Процесс продолжается неограниченно, приводя к бесконечному числу изо-
изображений основного источника. Это не должно удивлять, так как любой
луч, выходящий из источника, испытывает бесконечное число отражений.
Каждое изображение соответствует одному из этих отражений.
Выпишем теперь получающуюся функцию Грина. Источники располо-
расположены в (xo-\-2nh, у0) и в Bmh — x0, у0), где т и и —целые. Значит,
48*
756 Гл. 7. Функции Грина
(где мы имеем в виду функции Ганкеля первого рода, не выписывая верх-
верхнего индекса). Записывая более сжато, имеем
Gh = i« 2 Г#„(*|г-г;|)+Я0(*|г-г;|)], G.2.24)
П=—СО
где
г; = аж [2nh + х0 ] + ауу0, г"п = аж [2nh - х0] + &уу0.
Ряд G.2.24) применим, если играют роль только сам источник и, быть
может, его несколько первых отражений. Так будет, если точка наблюде-
наблюдения г очень близка к точке источника, т. е. г—» г0 из-за особенности функ-
функции H0(k\r — ro'|). Остающиеся отражения дают поправку к непосредствен-
непосредственному эффекту источника. К сожалению, ряд G.2.24) сходится не очень
быстро, так что подсчет поправки является довольно утомительным делом.
Для подсчета ее порядка выясним поведение отдельных членов при | п | —¦> со.
Тогда
|r-r;| ~ 2\n\h±(x-z0), |r-r;| ~ 2\n\h±(x + x0). G.2.25)
| n |-»oo I n |->-oo
Заметим, что эти приближения справедливы, только если
2\n\h>V(x-x')* + (y~y')\
Ясно, что эта асимптотическая форма достигается тем более быстро, т. е. для
тем меньших значений п, чем ближе находится точка наблюдения к источ-
источнику. Для больших значений 2nhk функцию Ганкеля можно заменить ее
асимптотическим выражением, так что (полагаем для определенности п>0)
Поэтому высшие члены ряда для Gh аппроксимируются рядом
G-2-26)
со
где N выбирается достаточно большим, чтобы обеспечить справедливость
приведенных выше приближений. Бесконечную сумму оцениваем, заменяя
ее на соответствующий интеграл:
™ ihh ?
?, ^" *
= . G.2.27)
2ikhYN
Этот интеграл можно также вычислить непосредственно через интегралы
Френеля. Если
и и
С (и) = ^ cos -|-12 dt, S (и) = ^ sin ^-1* dt, G.2.28)
то
Если применить простое выражение G.2.27), то ? приобретает вид
2 са 2 е" * ™е2Ш Vu-ih* Cos /сж0. G.2.29)
7. 2. Функции Грина для установившихся колебаний 757
Таким образом, мы видим, что если kh значительно больше единицы,
то весь ряд G.2.24) можно выразить простой формулой G.2.29) с ЛГ;ч=1.
Для волнового уравнения к = 2тс/Х, где X — длина волны, так что для всей
суммы можно применить простое выражение, если X значительно меньше
расстояния h между пластинками. Единственным членом, не включенным
в Е, будет тогда член с п = О, выражающий непосредственное влияние
источника на наблюдателя. Повторяем: если h > X и | х — х0 | < Л, то значе-
значение <j> в точке наблюдения (х, у) равно сумме основного слагаемого
жШ0 (к | г — г01) и малой поправки, пропорциональной 2.
Другие разложения. В случае если одно или оба из этих условий
.не выполняются, требуется более тщательное исследование. Если г находится
на некотором расстоянии от источника, a kh ни велико, ни мало, то раз-
разложение по изображениям источника можно преобразовать, чтобы получить
более быстро сходящийся ряд. Это можно осуществить с помощью формулы
суммирования Пуассона D.8.28)
где
ОО
C(*)e-^efr. G.2.30)
Для применения формулы суммирования Пуассона к данной задаче требуется
преобразование Фурье функции Н0(к\г—го|). Позже в этой главе (см. стр. 762)
мы покажем, что
] dKx \ \2_KZ dKy. G.2.31)
—CO —OO
Интеграл не вполне определен, если не указать, каким способом обходится
полюс К = к. Это будет сделано в процессе вычислений.
Теперь нам надо подсчитать значение
/=
Если ввести G.2.31) в подинтегральную функцию, / примет вид
7=i
— СО —ОО —СО
(*+*„-^)+К„ <„_„„)]
758
Гл. 7. Функции Грина
Интеграл по t можно непосредственно выразить через дельта-функцию (при
этом мы применяем интегральную теорему Фурье):
eiKy (V-V
е Х C0S
оэ
— OO —CO
Интеграл по Кх легко подсчитать, применяя основное свойство о-функции,
оо *
состоящее в том, что \ b(z)f(z — a)dz = f (a). Имеем
«,«/* сое
iKy (i/-tf0)
Окончательно интегрирование можно выполнить только после указания пути
интегрирования в плоскости Ку. Специальный путь С, показанный на рис. 7.6,
Плоскость Ку
Контур С
-j^z
. 7.6. Контур С для интегрирования в формуле G.2.31).
выбран так, чтобы / удовлетворяло тому граничному условию, что точка
х — х0, у = Уо является только источником, а не стоком или и источником,
и стоком.
Подсчет этого интеграла при помощи интегральной формулы Копии
D.2.8) был рассмотрен в гл. 4, стр. 392, Мы находим, что
У-Уп
cos
/ = e cos ^.
Окончательное разложение для функции Грина приобретает вид
i I V-Vo
8 /
i I У-
e
ev cos -j- cos —r1
h h
G.2.32)
Этот результат особенно полезен при | у — у0 \ > 1, так как если irv/Л > к,
то члены ряда экспоненциально убывают. Таким образом, число членов,
требуемое для получения хорошей аппроксимации, имеет порядок hk/ъ = 2/г/Х.
(Заметим, что если v становится большим, то соответствующие члены в G.2.32)
становятся независимыми от к.) Мы видим, что последнее разложение допол-
дополняет разложение для ?. Разложение G.2.24) по изображениям источника
осуществимо, если hk > 1, а разложение G.2.32) применимо, когда М< 1.
7. 2. Функции Грина для установившихся колебаний 759
Разложение по изображениям источника пригодно для коротких длин волн
и вблизи источника, так как тогда эффект границы менее важен; разложе-
разложение G.2.32) пригодно для больших длин волн и на значительном расстоя-
расстоянии от источника. Ряд G.2.32) представляет собой разложение Фурье, вполне
аналогичное формуле G.1.12); его можно получить более непосредственно,
чем в примененном здесь окольном методе, основанном на отражениях
и на формуле суммирования Пуассона. Значение данного нами вывода
состоит в раскрытии связи между двумя типами разложений.
Выражение G.2.32) в отличие от G.2.29) точно равняется ряду G.2.24)
и всегда сходится. За исключением случая, когда hk/ж = 2/г/Х. имеет порядок
единицы, ряд сходится не очень быстро, так что надо поискать средства
улучшения его сходимости. Для этого мы обратимся к замечанию, приведен-
приведенному в скобках в последнем абзаце, что члены разложения G.3.32) для
большого v не зависят от к. Это приводит к мысли использовать функцию
Грина Go (r | г0) для уравнения Лапласа, которую часто можно выразить
в замкнутом виде. Если написать
то разложение для Gh — G0 будет сходиться быстрее, чем для одной Gh.
Если выбрать условия Дирихле при х = О и х = к, то соответствующая
статическая функция Go получится в замкнутом виде; Go (r | г0) тогда
равна статическому потенциалу для единичного заряда в (х0, у0) между
двумя заземленными пластинками. С целью рассмотреть более трудную
задачу мы выберем условия Неймана, при которых Go соответствует уста-
установившемуся потоку жидкости, порожденному единичным источником
в (жо> Уо)- Однако установившийся поток нуждается в стоке (в данном
случае на бесконечности), как и в источнике, а это не включено в условия.
Таким образом, требуется небольшое видоизменение, которое мы сейчас
сделаем, чтобы принять в расчет и сток.
Мы начнем с ряда
2 ^p'-|'ol, G.2.33)
v=l
« которому приводится G.2.32) при /с = 0 (если опустить член с v = 0).
Применяя повторно соотношение
со
2 Ie-*= -ln(l-e-b),
мы получаем
ro = R(x + xo\y-y^ + R(x-xo\y-yo), G.2.34)
где
R (а | Ь) = — In [1 - 2е~* I b Vh cos (гса/Л) + е-2* I b Uh].
Нетрудно показать (например, подсчитывая Т2Г0), что Го представляет собой
решение уравнения Пуассона
V2r0= -tefb(r-T0)-(l/h)b(y-y0)], G.2.35)
которое соответствует единичному положительному заряду в (х0, у0) и еди-
единичному отрицательному заряду, равномерно распределенному вдоль линии
У — Уо> перпендикулярной обеим граничным линиям х = 0 и x = h. Так как
полное распределение заряда между двумя граничными линиями в среднем
равно нулю, то можно удовлетворить условиям Неймана без того, чтобы
760 Гл. 7. Функции Грина
статическое решение принимало бесконечные значения на бесконечности.
Можно также непосредственно убедиться, дифференцируя G.2.35), в том, что
дГ/дх равно нулю при х = 0 и x = h.
Поэтому окончательным выражением для Gh будет
-V
_.и-(»у/ьIУ-у,П . G.2.36)
Этот ряд сходится достаточно быстро. Другие случаи, когда статическая
функция Грина оказывается замкнутым выражением, можно разобрать
на основании результатов гл. 10.
Возможность применения метода изображений ограничивается случаями,
в которых граница составлена из прямых линий для двух измерений или
плоскостей для трех измерений. Из этого правила имеется одно исключение.
Именно, в случае уравнения Лапласа (с условиями Дирихле) метод изображе-
изображений можно применить для окружности в двух измерениях и для сферы
в трех измерениях. Указанное ограничение для метода изображений есте-
естественно ожидать на основании элементарных соображений геометрической
оптики, так как хорошо известно, что единственным зеркалом, для которого
образ точечного источника снова представляет собой точку, является пло-
плоское зеркало. Конечно, это не значит, что метод изображений нельзя при-
применить к границам другого вида, но тогда он применяется только прибли-
приближенно. Поэтому мы обратимся к более общему представлению функций
Грина посредством собственных функций.
Разложение функции Грина по собственным функциям. Метод соб-
собственных функций, исследованный в гл. 6, лимитируется только простотой
определения требуемых собственных функций. Так как точные решения
достижимы только в разделяющих системах координат, то разложение
функций Грина по собственным функциям практически осуществимо только
в этих случаях.
Пусть собственные функции равны <]»„, а соответствующие собственные
значения равны кп, т. е.
ЎЧ # 0 G-2-37)
Здесь п представляет все требуемые индексы, определяющие все рассматри-
рассматриваемые частные функции фп. Кроме того, как показано в предыдущей главе,
функции фп образуют ортонормированную систему:
mdV = Znm, G.2.38)
где область интегрирования R ограничена поверхностью, на которой tyn
удовлетворяет однородным граничным условиям. Функция Грина Gh (г | г0)
удовлетворяет тем же условиям. Дополнительно предполагается, что функ-
функции фп образуют полную систему, так что Gh (r | г0) можно разложить в ряд
Введя это разложение в уравнение с частными производными, которому
удовлетворяет Gh,
мы находим, что
Y (г) = - 4* о (г - г0).
7. 2. Функции Грина для установившихся колебаний 761
Пользуясь формулой G.2.38), мы умножаем обе части последнего уравне-
уравнения на фп (г) и интегрируем по объему R. Получаем
. 4пфп (го)
п
так что
Г /» I - \ /л- V Фп (Гр) Фп (г) /7 о 4Q1
У-Жи \Т I Tqj = г№ ?. ^ ( ' .^.Ot7|f
п
— требуемое разложение. Пример такого разложения мы имеем в формуле
G.1.10).
Неожиданной особенностью формулы G.2.39) является ее несимметрич-
несимметричная зависимость от г и г0 для комплексного фп вопреки приведенному выше
доказательству того, что Gh должно зависеть от этих переменных симме-
симметрично. Конечно, это только кажущееся противоречие. Дело в том, что так
как скалярное уравнение Гельмгольца не включает явно никаких комплекс-
комплексных чисел, то фп также является решением уравнения G.2.37) и потому
также включено в ортонормированную систему фп. Таким образом, здесь
будет простой случай вырождения, так как одному собственному значению
принадлежат две собственные функции — как <ЬП, так и фп. Поэтому в сумму
G.2.39) будет включен как член
Фп (Гр) Фп (Г)
1.2 /^2 '
так и член
"фп (г) фп (Го)
fcn-*2 •
так что в действительности выражение G.2.39) симметрично и вещественно.
Другим интересным моментом является поведение Gh при к —*• кп. Мы
видим, что Gh как функция от к аналитична всюду, за исключением прод-
продетых полюсов при к= ± кп с вычетами Я- 214^ (г0) фп (г)/кп. Значит, если
функция Грина известна в замкнутом виде, то собственные функции ф„
и собственные значения кп можно найти, исследуя Gk в ее полюсах.
Эти особенности имеют простое физическое истолкование, так как они
являются как раз бесконечностями, появляющимися, когда недиссипативная
колебательная система возбуждается одной из ее резонансных частот.
Чтобы сделать это соответствие более ясным, мы напомним, что уравнение
с частными производными, которому удовлетворяет потенциал скорости,
созданный точечным источником в г0 с угловой частотой ш, имеет вид
Однако ф = e~iwtGk, к = шс. Отсюда если к=кп, то система возбуждается
одной из ее резонансных частот, что при отсутствии трения приводит
к бесконечной амплитуде. Имеется одна ситуация, в которой это возбужде-
возбуждение не будет бесконечным. Так будет, если функция, выражающая про-
пространственную зависимость источника, ортогональна <Ьп. Действительно,
если ф удовлетворяет уравнению
ТО
GhdV0 = 4* У. ^т^°)р(,Гао)^0 фт (г). G.2.4U)
762 Гл. 7. Функции Грина
Если \ фп (г) р (г) dV = 0, то п-й член исчезает. Тогда в ряде G.2.39)
я-й член отсутствует и к может равняться кп, не обращая Gk в бесконеч-
бесконечность. Функция Грина для таких задач (мы будем употреблять здесь
термин «видоизмененная функция Грина» и обозначение Thn) удовлетворяет
уравнению
Значит,
у. Ф"»(;о)Фт(» ? G241)
где под записью т Ф п мы понимаем, что опускаются все члены, для которых
кт = ± /сп. Мы уже исследовали один такой случай для функции Грина
уравнения Лапласа, когда граничными условиями служили однородные усло-
условия Неймана. В этом случае одним из собственных значений было & = 0,
и ему соответствовала постоянная как собственная функция. Значение к
для уравнения Лапласа также равно нулю, и мы нашли целесообразным
применить видоизмененную функцию Грина Го.
Теперь мы дадим некоторые примеры применения формулы G.2.39). Они
совсем просты, если рассматриваются полностью ограниченные области, так
как если в этом случае собственные функции и соответствующие собственные
значения известны, то функции й> надо только нормировать, чтобы их можно
было подставить в формулу. Пример разложения такого вида дает формула
<7.1.10).
Разложения для бесконечной области. Поэтому мы обратимся к другим
типам областей, из которых простейшей является неограниченная бесконеч-
бесконечная область. Мы показали ранее в этом параграфе [формула G.2.18)], что
в этом случае для источника (а не для стока) двумерная функция Грина
равна ?dH0{k\v — v0\). Полную ортонормированную систему, по которой ее
можно разложить, дают, в частности, плоские волны
_L/>iK-r
2% е '
где K-v = Kxx + Kyy, а Кхи Ку могут принимать любое численное значе-
значение. Чтобы получить полную систему, необходимо в соответствии с инте-
интегральной теоремой Фурье иметь совокупность значений К, простирающуюся
от — со до -Ь со вдоль пути в комплексной плоскости Кх и Ку, соединя-
соединяющего эти две точки. Так как Кх и Ку являются непрерывными перемен-
переменными (см. стр. 708 по поводу перехода от дискретного к непрерывному),
то в формуле G.2.39) сумму надо заменить интегралом:
со
= ± ^ dK
Это представление было применено в формуле G.2.31) (isT2= K\)
Опять важно заметить, что интеграл не определен, если не задан путь
интегрирования около полюсов подинтегральной функции. Путь интегриро-
интегрирования в плоскости Ку дан на рис. 7.7. Он выбран так, чтобы привести
к волне, выходящей из точки источника R = 0. Тогда можно осуществить
интегрирование по Ку, что даст для Y > 0
dKx.
7. 2. Функции Грина для установившихся колебаний
763
Пусть Кх = k cos F -f <р)> гДе ? = arctg(y/X); тогда
-ioo
too
При этом контур интегрирования по § должен, конечно, быть таким, чтобы
дать сходящийся интеграл. Принимая во внимание исходные пределы, мы
Плоскость Л„
Контур С
г
7
Рис. 7.7. Контур С для интегрирования в формуле G.2.42).
видим, что этот контур должен идти от + гоо до — гсо . Сходимость полу-
получится, если контур провести несколько слева от мнимой оси в верхней
полуплоскости и справа от нее в нижней полуплоскости, как показано
Плоскость в
Рис. 7.8. Контур В для интегрального
представления функции Но (kR).
на рис. 7.8. Нашим окончательным результатом будет хорошо известное
интегральное представление для функции Ганкеля [см. формулу E.3.69)]:
¦п/2—ioo
G.2.43)
-эт/2+ico
Полярные координаты. Формула G.2.42) дает представление функции
Грина gh (r) в бесконечной двумерной области, пригодное для задач, в кото-
которых наиболее удобны прямоугольные координаты. Рассмотрим теперь общую
формулу G.2.39), применяя собственные функции, отвечающие полярным
координатам. Этими функциями будут
764 Гл. 7. Функции Грина
Их также нужно нормировать. Нормирующий множитель для функции,
выражающей зависимость от <р. равен 1/~|/2tc. Нормирующий множитель Nm
для радиальной функции получается из соотношения, отвечающего непре-
непрерывным собственным значениям (в данном случае к):
k+Ak R
lim lim [ N2n J dk' ^ Jm (kr) Jm (k'r) г dr ] = 1.
Значение неопределенного интеграла jno г равно (см. формулы в конце гл. 11)
Q т п \ т /1' \ j ¦k'rJmtkr)Jrn_1(k'r)—krJm(k'r)Jm+x(kr)
^ Jm (kr) Jm (k r)rdr= 1 р — к1* *
Так как R велико, можно воспользоваться асимптотическим поведением
1
Jm (х) ~l/2/техcos ?ж —
данным в формуле E.3.68). Мы находим, что Nm не зависит от m и равно
\Hi. Поэтому нормированными собственными функциями будут
Ук/2ъе™ч>1т(кг). G.2.44)
Подстановка G.2.44) в G.2.39) дает
где контур интегрирования еще надо уточнить. Фактический подсчет дока-
доказывает, что для расходящихся волн требуется как раз такой контур, какой
показан на рис. 7.7, с полюсами при ± к. Последнее разложение можно
переписать так, чтобы оно включало только положительные т следующим
образом:
2 emcosm(9<p0) ^ ^lfrkiKdK. G.2.45)
tn=O
Возможно подсчитать интеграл по К методами теории функций. Однако
это осуществляется довольно сложными выкладками. Предпочтительнее
вывести разложение G.2.45) другим приемом, который можно распростра-
распространить на другие системы координат и граничные поверхности.
Общая техника. Это как раз метод, который был применен в § 7.1
для установления связи между поверхностной функцией Грина G.1.8) и объем-
объемной функцией Грина G.1.10). Мы разлагаем объемную функцию Грина
по полной системе функций, содержащих все координаты, кроме одной
(в настоящем случае имеются только две координаты, г и 9)» с коэффи-
коэффициентами, являющимися неопределенными функциями не включенной коор-
координаты. Таким образом, мы положим
2 i eim(9~9°41 (r I r0). G.2.46)
—ОО
Сравнивая с G.2.45), мы замечаем, что
Рт(г\ro)=] Jm(К?!Гк1КГо)КdK.
7. 2. Функции Грина для установившихся колебании 765
Мы подставим G.2.46) в уравнение для gh(r \ г0):
В полярных координатах оно имеет вид
^ G.2.
(Правая часть этого уравнения содержит выражение о-функции в полярных
координатах. Это выражение должно удовлетворить требованиям, чтобы
о (г — г0) исчезало всюду, кроме г = г0 и <р = <Ро> а интеграл по всему про-
пространству давал единицу: \ \ о (г — ro)rdr dy= 1. Легко проверить, что эти
требования удовлетворяются.)
Если подставить разложение G.2.46) в G.2.47), то получится
Умножим обе части этого равенства на e-int и проинтегрируем по <р от О
до 2те. При интегрировании левой части мы используем ортогональные
свойства системы функций eim<?. Получаем
^^- G-2-48)
Мы видим, что рт (г | г0) является одномерной функцией Грина для опера-
оператора Штурма—Лиувилля
(см. уравнение F.3.12)]. Решение линейного неоднородного дифференциаль-
дифференциального уравнения второго порядка «S? (<}>) = о дается формулой E.2.19) в виде
где z — независимая переменная, у,и уа-два независимых решения одно-
однородного уравнения
— определитель Вронского
У* 2
Функция v представляет собой неоднородный член, в данном случае
4Ъ(
Пределы интегрирования в выражении для ф зависят от специального
выбора независимых функций уг и у2 и от граничных условий на рт. Мы
возьмем пределы (это допустимо, так как мы не выбрали уг и у2) меньшим
z( = r) в первом интеграле и большим z во втором. Тогда
г Ь
и — ro)yz(u)du
766 Гл. 7. Функции Грина
Для г < г0 первый интеграл равен нулю, тогда как для г > г0 равен нулю
второй интеграл. Отсюда
УгИУгЫ Для г>г0,
причем определитель Вронского подечитывается в г0. Граничные условия опре-
определяют, какие из решений однородного уравнения надо применять. В рассма-
рассматриваемом случае решениями являются функции Бесселя Jm(kr), Nm(kr)
и любая их линейная комбинация. Граничные условия состоят в следующем:
A) Рт должна быть конечной при г = 0, так как gh имеет единственную
особенность при г = г0, и B) точка /• = /•„ должна быть источником, потому
что gh (R) взята в виде расходящейся волны. Отсюда уг = Jm (kr)
У2 т()
Наконец, надо подсчитать Д(ух, у2) приг = г0. Здесь полезно применить
формулу E.2.3), выражающую зависимость определителя Вронского] от
аргумента:
если дифференциальное уравнение для ух (или у2) имеет вид
В рассматриваемом случае f — r, так что Д (yv у.г) = const/r. Чтобы опре-
определить постоянную, можно воспользоваться первыми членами степенного
ряда около нуля (г = 0) или асимптотического ряда около г = со, так как
соотношение А (ух, у2) = const/r должно удовлетворяться каждым членом
степенного или асимптотического ряда для А^, у2)- Например, применяем
соотношения
)
fir-» со
Определитель Вронского равен асимптотически
2Г-7 Г/ 1 С , 1М i[ftr-|'t(m+l)] ,
+ A;sin ykr — yw{ т + т
e
Но это выражение равно 2i/«r, так 4toJ &(ylt y2) = 2i/nr. Объединяя все
наши результаты, получаем окончательно
Jm (kr) Нт (кгЛ
I Jm(krO)Hm(kr) ДЛЯ Г>Г0.
Заметим, что рт равно значению интеграла, получающегося в формуле
G.2.46). Вводя G.2.50) в разложение для gh (R) = ЫН0 (kR), получаем раз-
разложение для Но (kR):
для r<r0,
(kr) для г > r0;
7. 2. Функции Грина для установившихся колебаний 767
Мы привели подробный вывод формулы G.2.51), так как он будет
служить образцом для подсчета разложений других функций Грина. Эти
разложения очень полезны, как показывает следующее вычисление. Мы
выведем разложение функции elkx (плоской волны, проходящей слева
направо) в полярных координатах, а затем из него получим интегральное
представление функции Бесселя Jm [указанное в формуле E.3.65)]. Заме-
Заметим, что Но (kR) изображает волну, выходящую из источника в г0. Чтобы
получить плоскую волну, проходящую слева направо, необходимо поместить
источник в — со, т. е. считать, что г0—> со и <р0—> те. Тогда
= Vг*- 2rr0cos(?-9о) + г» f* r0 ( 1 + -f-
90 =я
Отсюда
" 'го -»со Г пкгп
со Г 1 I 1М
тп=0
ИЛИ
со
eifex= ^ emimcosm?-ym(A;r) G.2.52)
— требуемое разложение. Этот ряд был приведен в гл. 5 в ином виде
[см. формулу E.3.65)].
Наконец, пользуясь свойствами ортогональности системы cos/n<p,
можно вывести интегральное представление для Jm (кг). Умножаем обе
части равенства G.2.52) на cos-v^ и интегрируем от 0 до те. Получаем
/v (kr) = ^-\ eiftr cos f cos vy dy. G.2.53)
Это соотношение было выведено другим способом в гл. 5 [см. формулу
E.3.65)].
Общая формула. Обратимся теперь к задаче вывода разложения функ-
функции Грина для любой из обобщенных систем координат, в которых скаляр-
скалярное уравнение Гельмгольца разделяется. Напомним некоторые результаты
исследования техники разделения переменных (см.. стр. 612 и далее). Если
?lf Е2 и Ез — ТРИ ортогональные обобщенные координаты с коэффициентами
Ламе к1г h2 и h3, то оператор Лапласа равен
п=1
Величина /п зависит только от ?п (т.е. /х является функцией только от ?х);
S есть определитель Штеккеля E.1.25), элементы которого Фпт являются
функциями только от ?п (т. е. Ф1т зависит только от ?х); Мп представляет
собой алгебраическое дополнение определителя <S\ на который в разложении
S E.1.26) умножается Фп1. Мх зависит от Е2 и ?3, но не зависит от
Ех. В скалярном уравнении Гельмгольца, записанном в координатах ?lt ?8,
768 Гл. 7. Функции Грина
?3, переменные разделяются, так что
4» = Х1(?1)Х2(УХ3(?3),
где
kkO^> 21 = О, G.2.55)
f 21 *п»
ТП=:1
причем к\ == к2, а к\ и к% — две константы разделения. Множители /п
и элементы определителя iS приведены в таблице в конце гл. 5. Нам потре-
потребуется также условие Робертсона h-Ji2h3 — Sfxf?,f3 E.1.32).
Чтобы увидеть, как разложить функцию Грина в этих общих коорди-
координатах, целесообразно вернуться к выводу разложения G.2.51) функции
Грина в полярных координатах. Там ^-множители оказываются собствен-
собственными функциями, не зависящими от постоянной к, входящей в уравнение
Гельмгольца. С другой стороны, r-множители зависят и от к и от соб-
собственных значений т для <р~множителей; по этой и по другим причинам
/•-множители не могут быть приняты за собственные функции.
Таким образом, функция G была разложена в ряд по собственным
функциям для <р-множителей. Поэтому г-множители для каждого члена
ряда удовлетворяли неоднородному уравнению, решение которого можно
было выразить через два независимых решения соответствующего однород-
однородного уравнения, придя таким способом к разложению.
Мы испробуем тот же метод для трех общих координат ^Л^Лз- Из
трех констант разделения кг = к, к2, к3 значение первой, к, определяется
уравнением Гельмгольца, которое мы решаем. Другие две, &2 и к3, при-
пригодны, чтобы стать собственными значениями для системы двумерных соб-
собственных функций, по которым мы разлагаем функцию Грина G. Обычно
выбор того, какие два из координатных множителей должны быть собст-
собственными функциями, очевиден. Например, в сферических координатах две
из трех переменных, <р и 6, являются углами и имеют конечную область
значений, причем граничные условия, которые можно наложить для полу-
получения собственных функций, достаточно просты (периодичность и конечность).
В других случаях (таких, как круговые цилиндрические координаты г, <р. z)
только одна из координат (для цилиндрических координат это <р) имеет
конечную область значений, а любой из Остальных двух (например, z)
должна отвечать система собственных функций для бесконечного интервала,
в результате чего для одной из констант разделения &2 или к3 получается
непрерывная совокупность собственных значений.
Пусть мы нашли, что ?2-и 13-множители можно превратить в собствен-
собственные функции с соответствующими парами собственных значений для к2
и к3. Упорядочим некоторым способом допустимые значения к2 и к3; напри-
например, наименьшее собственное значение й2 можно обозначить через &20, сле-
следующее—через к21 и т. д., т-е через к^т, тогда как допустимые значения
к3 — через к30, к31,..., кзп,• • •', собственная функция, соответствующая
значениям &2m, k3n, равна Xът (Е2) -^зп (Ез)> хотя Х% может. также зависеть
от п, а!8- от т. Для упрощения записи мы будем обозначать пары целых
чисел (т, п) одной буквой р или д, а произведение собственных функций —
одной буквой W. Тогда р-я собственная функция в координатах \2, ?3 рав-
равна Wp(k2, E3) для собственных значений kZp, k3p. В дальнейшем мы будем
считать, что как ?2» так и ?з изменяются на конечных интервалах, так
что значения как к2р, так и к3р дискретны и разложение по собственным
функциям представляет собой ряд по р (т. и п). Переход к случаям, когда
одна или обе из совокупностей собственных значений представляют собой
континуум, так что разложение превращается в интеграл (подобно тому
как интеграл Фурье заменяет ряд Фурье), обычно нетруден.
7. 2. Функции Грина для установившихся колебаний 769
Следовательно, мы допускаем существование полной системы собствен-
собственных функций Wq ft,, Е3) (мы выбрали ?2 и ?3 для определенности, так как
пригодна любая пара, для которой выполняются необходимые условия),
удовлетворяющих условиям ортогональности и нормированности
j q ft, У Wp ft, 6Я) р (?2)у d?2 dg3 = 83p, G.2.56)
где р — весовая функция. (Относительно весовой функции в одномерном
случае см. стр. 725.) Мы будем предполагать, что эта система собственных
функций существует при произвольном к для значений ?2 и ?3 в интересу-
интересующей нас области. Конечно, функция Wq может зависеть от к. Тогда
по аналогии с G.2.46) мы напишем
Gh (г | г') = 2 Xlq ft | ад BJft, 6i) Wg ft, l=3), G.2.57)
где функции Xg и J3g надо определить.
В обобщенных координатах уравнение, определяющее Gh, имеет вид
п=1
G258)
Заметим, что представление функции о (г — г'), стоящее в правой части
с коэффициентом — 4тг, обладает обычными свойствами дельта-функции: оно
равно нулю при всех ?х, ?2, ?3, за исключением ?х = ?j, k2 = Sj» ?3 — К>
а интеграл от него по всему пространству равен единице. Приступим теперь
к подстановке ряда G.2.57) в уравнение G.2.58). Нам потребуется резуль-
результат применения оператора V2 + k\ к И/в(?2, ?3)- Только два из членов суммы
в G.2.58) содержат производные от Wq. Так как Wq равно произведению
решений Х2(?2) и Х3(?3) уравнений G.2.55), то отсюда вытекает, что
^J nm K n) mQ J «'
^ Sfn dnJ nj
n=2 - n=2
где мы придали константам разделения дополнительный индекс q, указы-
указывающий на их соответствие функции Wq. ¦
Сумму по п можно упростить, пользуясь свойством определителя S
[см. формулу E.1.27)]:
Значит,
n=2,3
Отсюда, если подставить ряд G.2.57) в G.2.58), получится
2 Bq (б;, ад wQ ft, у ^ [ ± -^ ( л
^ ^ )
m=i
^^ __ iTt ¦ гz—j .
п1п2п3
Воспользовавшись условием ортонормальности G.2.56) и условием Роберт-
сона E.1.32), мы находим, что
В« (Е«' ^s) = л/,(«.«)/,(Ч)^,(«) ( >59)
ж") + ( S А^Ф-) Х^= -^»«i-«D. G-2.60)
m=J
49 ф. м. Морс я Г. Фешбах
770 Гл. 7. Функции Грина
Таким образом, как в разобранном вьипе примере полярных координат, Х1ф
является одномерной функцией Грина. Следуя методу, примененному при
решении уравнения G.2.48), можно выразить Xlq через два независимых
решения {у1 и у2) однородного уравнения
Мы
получаем
где Д — определитель Вронского, вычисленный в ?j. Как в исследовании
на стр. 765, выбор применяемых решений уг и у2 зависит от граничных
условий задачи1). Определитель Вронского в данном случае имеет вид
tjk что множитель &(у1г 2/2)/i постоянен.
Значит, разложение Gfe(r|r') таково:
С„(г|_г')= _4ir-^-p(^, k'a) 2wj({,', ?3
х 1 х f 2/i9 (Ei) 2/2, Fi) для Si < 6J,
где коэффициенты Ламе h и определитель Вронского Д являются функциями
координат со штрихом, а р — весовая функция, определенная в формуле
G.2.56). Из этого разложения методом, примененным в рассмотренном выше
случае полярных координат, возможно, вообще говоря, получить разложе-
разложение плоской волны и интегральные представления участвующих в них
функций. Наконец, так как теперь можно выразить плоские волны и функ-
функцию Грина в различных системах координат, то становится возможным
выразить решения уравнения Гельмгольца в одной системе координат
через решения, соответствующие другой системе.
Функции Грина и собственные функции. Функцию Грина для задачи
Штурма—Лиувилля (см. стр. 668)
можно выразить в виде бесконечного ряда G.2.39) по собственным функ-
функциям однородного дифференциального уравнения, соответствующего G.2.64):
- = 0 „G.2.65)
с однородными" граничными условиями при х = а и х = Ъ. Эти собственные
функции можно взять так, чтобы они образовывали полный ортонормаль-
ный ряд, так что
ь
*я (*) Фт И г"шйх = Ьпт. G.2.66>
*) Решение j/ioEi) 'должно удовлетворять однородному граничному условию,
наложенному на G^ при, ?i = a, а решение ?/2qEi)—-соответствующему условию при
&! = &, где а<Ъ — границы интервала изменения переменной S,.—Прим. ред.
7. 2. Функции Грина для установившихся колебаний 771
Бесконечный ряд для бЛ (х \ х0) имеет вид
Gx (х| х0) = 4и 2 ^(У . G.2.67)
С другой стороны, функцию G можно выразить через два независимых
решения yt и у2 уравнения G.2.64) при помощи метода, которым была
выведена формула G.2.49). Получается
| х0) = , ** х / У1 {Х) У* {Хо) ДЛЯ Х< Жо' G.2.68)
Сравнивая это выражение, имеющее различный вид для различных
областей значений х, с формулой G.2.67), можно получить информацию
о функциях фп и соответствующих собственных значениях Хп. Это дает очень
сильный метод исследования свойств собственных функций, который дейст^
вительно время от времени применялся как основа всей описанной в гл. 6
теории. Здесь мы удовлетворимся исследованием тех результатов, которые
представляют практическое значение.
Основная идея состоит в том, что Gi (x \ х0) как функция У. имеет
простые полюсы при Х = ХП с вычетами— 4тг4»п(х)фп(х0). Эти же самые осо-
особенности должно иметь и представление G.2.68), имеющее замкнутый вид
{а не вид бесконечного ряда, как G.2.67)]. Отсюда, рассматривая G.2.68),
возможно (в принципе) получить собственные значения Хэт, а также соответ»
ствующие собственные функции tyn, уже нормированные.
Поясним предложенный метод на простом примере. Пусть уравнение
G.2.65) имеет вид
а граничные условия состоят в том, что ф = 0 при х — а, x=b(a<_b). Тогда
соответствующее у1 равно sin|/^X(x—a), a y.z = sin |/X(x—b). Значение
A(Vi, У2) Равно
sinl/X(a; — a)»cos]/X(a: — b) —
— j/X cos j/"X(ж — a)-sin ~|/X (ж — 6) = y^Xsin"|/X (fc — a).
Сдедовательно,
sinl/X(x —a)-sin]/X(x0—6) для ж<х0,
sin")/X(x0— a)-sin j/X(x— 6) для х>х0.
Собственные значения являются нулями функции sin]/rXF — а), так что
получается хорошо знакомый результат }/Хп = лтг/F — а). Вычеты здесь
равны
— [8тг/F — а)] (— 1)" sin [пте (х — а)/(Ь — a)] -sin [me (z0 — ?>)/(& — а)],
и*я
— [8тг/F — a)] sin [птг F — x)/(fc — а)] ¦ sin [mcF — xo)/(b — а)].
Отсюда фп (ж) *„ (х0) равно
[2/(Ь — a)] Bin [mu (b — x)/(b — a)] -sin [тип (b — xo)/(b — a)],
так что нормированные собственные функции имеют вид
I . гт (Ъ — х)
1772 Гл. 7. Функции Грина
Эти собственные функции удовлетворяют условиям ортогональности и норми-
нормированное™ G.2.66) при г=1и образуют полную систему. Таким образом,
мы видим, что если можно найти два независимых решения и составить
из них комбинаций, из которых одна' удовлетворяет граничному условию
в одной граничной точке, а другая —в другой, и если можно подсчитать
определитель Вронского, то можно найти нормированные ортогональные
¦собственные функции и собственные значения.
Сравнивая этот метод с более обычным методом, рассмотренным
в гл. 6, мы видим, что в итоге получается то же самое. Однако описанный
сейчас метод дает также нормировку, что в других методах часто требует
вычисления сложных интегралов.
Мы будем иметь случай воспользоваться этим методом для более
сложных функций в задачах к этой главе, а также при определении
и нормировке собственных функций, возникающих в задачах для двух
о более измерений. С тем же процессом в несколько ином виде мы встре-
встретимся в § 11.1.
7.3. Функция Грина для скалярного волнового уравнения
Функция Грина для скалярного уравнения Гельмгольца, только что
исследованная в § 7.2, особенно полезна при решении неоднородных задач,
т. е. задач, возникающих при наличии источников внутри объема или на
граничной поверхности. Функция Грина для скалярного волнового уравне-
уравнения должна нести аналогичные обязанности, т. е. также должна давать
возможность решать скалярное волновое уравнение при наличии источников.
Для получения некоторого представления об уравнении, которому должна
удовлетворять эта функция, рассмотрим типичную неоднородную задачу.
Пусть <1> удовлетворяет уравнению
v24—4"S-=-4w«<'•*>• G-3.1)
Функция д (г, t) описывает плотность источников и дает не только распре-
распределение источников в пространстве, но также зависимость источников от
времени в каждой точке пространства. Кроме уравнения G.3.1), необхо-
необходимо сформулировать граничные и начальные условия, чтобы получить
единственное решение этого уравнения. Условие на граничной поверхности
может быть условием Дирихле, или Неймана, или линейной комбинацией
обоих. Условия по временной координате должны быть условиями Коши
(см. стр. 638, гл. 6). Следовательно, необходимо задать значения ф и dty/dt
при t = t0 для каждой точки рассматриваемой области. Пусть эти значения
равны <J>0 (г) и v0 (г) соответственно.
Вид уравнения G.3.1) подсказывает, что уравнение, определяющее
функцию Грина G(r, t1 г0, t0), имеет форму
^ri^= -4«&(r-ro)8(«-g. G-3.2)
Мы видим, что источник имеет характер импульса при I = t0 в точке
г=г0. Поэтому G описывает эффект от этого импульсного источника с тече-
течением времени, распространяющийся от г — г0. При этом, как и в случае
скалярного уравнения Гельмгольца, G должна удовлетворять однородным
граничным условиям, наложенным на функцию <J> на границе. Для началь-
начальных условий представляется разумным допустить, что G и dG/dt должны
равняться нулю при t < t0; это значит, что импульсный источник, действо-
действовавший в момент t0, не должен проявлять себя в предшествующее время.
7. 3. Функция Грина для скалярного волнового ураенгния 773
Не следует думать, что примененное здесь соотношение между, причи-
причиной и следствием очевидно. Направленность течения времени несомненна
для макроскопических событий, но возможность экстраполяции этого опыта
на микроскопические явления не ясна. Действительно, как уравнения
движения в механике, так и уравнения Максвелла, которые могут привести
к волновому уравнению, не имеют никакой асимметрии по времени. Поэ-
Поэтому для микроскопических событий могут оказаться возможными «эффекты»
распространения во времени назад; в последние годы начали оформляться
теории, применяющие такие решения волнового уравнения. Однако исследо-
исследование вопроса о том, как такие решения могут все-таки привести к связи
между причиной и следствием во времени для макроскопических событий,
увело бы нас слишком далеко.
Пока мы будем в основном пользоваться нулевыми начальными усло-
условиями для G (r, 11 г0, t0) и dG/dt при t < t0, хотя не следует забывать
существования иных возможностей.
Соотношение взаимности. Вытекающая из условий Коши, как ука-
указано выше, направленность времени означает, что, обобщая соотношение
взаимности Gfe (г j г0) = Gk (г01 г) посредством включения времени, мы не при-
приходим к равенству G (г, t | г0, t0) = G (г0, 101 г, t). Действительно, если t > t0,
то второе выражение равно нулю. Чтобы получить соотношение взаимности,
необходимо обратить направление течения времени, так что соотношение
взаимности приобретает вид
G(r,t\ r0, t0) = G (r0, -10 | г, - 0. G-3.3)
Для истолкования этого равенства удобно положить to = O. Тогда получим,
что G(r, t\r0, 0) = G(r0, 01 г, —t). Мы видим, что эффект в точке г в момент
t от импульсного источника, действовавшего в г0 в момент 0, равен эффекту
в г0 в момент 0 импульсного источника, действовавшего в г в момент — t,
т. е. на время t раньше.
Для доказательства соотношения G.3.3) напишем уравнения, которым
удовлетворяют обе функции Грина:
, -t\rlt -*1)-jr
Умножая первое на G(r, — t\rx, —tj, а второе на G(r, Z j г0, *0), вычитая
один результат из другого и производя интегрирование по исследуемой
области и по времени t от — с» до t', где t' > t0 и t' > tx, получаем
G (г, 11 r0, t0) VaG (r, -t | Г1) -tx)-G (г, -t | rlt ~tx) V*G (r, t \ r0, to) +
-LG(r,t\ r0, to)^G (r, -11 rlt - h) -
J J [
—CO
+ -LG(r,t\ r0, to)^G (r, -11 rlt
= 4* [G (r0, -101 rlf - h) - G (r1? ^ | r0, t^]. G.3.4)
Левую часть последнего равенства можно преобразовать при помощи
теоремы Грина и тождества
I
If [G(r,f|ro,g^-G(r, -t|rlf ~h)-G(r, -t\rlt -*x)-|-G(
= G(r,tjro,to)-^-G(r, -t\rlt -tJ-Glr, -t\rlt -h)^-
774 Гл. 7. Функции Грина
Тогда левая часть примет вид
r, -t\rlt -tj-
- G (г, - i | rlf - ij grad G (r, 11 r0> *„)] +
Первый из этих интегралов равен нулю, так как обе функции Грина
удовлетворяют одинаковым однородным граничным условиям на S. Второй
также равен нулю, как мы сейчас увидим. На нижнем пределе как
G (г, — с» | r0, t0), так и ее производная по времени равны нулю в силу
условия причинности. В момент t — t' функция G (г, —t'\rlt —h) и ее
производная по времени обращаются в нуль, так как момент — t' пред-
предшествует моменту — tv Значит, левая часть равенства G.3.4) обращается
в нуль, что приводит к теореме взаимности G.3.3).
Теперь покажем, как с помощью функции Грина можно выразить реше-
решение неоднородной задачи (включающей начальные условия) для скалярного
волнового уравнения. Нам потребуется уравнение G.3.1)
vo V А> fo) - -г ~щ- = - 4тг g (г„, t0),
а также
Это последнее равенство можно получить из G.3.2) при помощи соотноше-
соотношения взаимности. Как обычно, умножаем первое уравнение на G, второе
на <J> и вычитаем один результат из другого. Интегрируем по интересую-
интересующему нас объему и по t0 от 0 до t*. Под символом t* мы будем понимать
^ + е> где е произвольно мало. Этот предел вводится, чтобы избежать окон-
окончания интегрирования точно в пике дельта-функции. Пользуясь оконча-
окончательными формулами, важно иметь в виду, что предел равен t*, а не
точно t. Получаем
(г, 0- $ dt0 ^ dV0-q(r0.to)G].
Вновь применяя теорему Грина и т. д., находим
о §dS0-
^- $ dV0 [ -g- ф - G
Подинтегральная функция в первом интеграле задана граничными усло-
условиями. Во втором интеграле при подстановке t = t* подинтегральная функ-
функция обращается в нуль в силу начальных условий для G. Оставшийся
7. 3. Функция Грина для скалярного волнового уравнения 775
предел включает только начальные условия. Отсюда
«*
(г, t) = 4ти { dt0 \ dV0G (г, 11 r0> t0) q (r0, t0) +
о J
о § dSo • (G grad0 ф - ф grad0 G) - G.3.5)
где фо(го) и г>0 (r0) — начальные значения ф и d§/dt.
Формула G.3.5) дает полное решение неоднородной задачи, включая
удовлетворение начальным условиям. Поверхностные интегралы, как и в слу-
случае уравнения Гельмгольца, надо аккуратно определить. Как и в том слу-
случае, мы примем, что значение на поверхности равно пределу значений
функции при приближении к поверхности изнутри.
Первые два интеграла в правой части последней формулы G.3.5) имеют
почти такой же вид, как интегралы, получающиеся в аналогичной формуле
для случая уравнения Гельмгольца. Первый представляет эффект объемных
источников; второй — эффект граничных условий на (пространственной) гра-
границе области. Последний член содержит начальные условия. Его можно
истолковать, если спросить, какой требуется вид источника q, чтобы функ-
функция ф началась при t = 0 требуемым образом. Можно ожидать, что это
потребует силу импульсного типа в момент t = 0+. На основании G.3.5)
можно показать, что член с источником, требуемый для воспроизведения
начальных условий, равен
где под о' (t0) мы понимаем производную от 2-функции, Она обладает
•следующим свойством:
г , . , ( — /'@), если ж = 0 находится внутри интервала (а, Ь);
\ f (х)Ь (х)ах— (
^ I и, если ж = и находится вне интервала (а, о).
Можно понять физический смысл написанных членов. Член типа
voo (t0) требуется, чтобы представить импульсную силу, придающую каждой
точке среды начальную скорость vo(ro). Чтобы получить начальное смеще-
смещение, импульс, действующий в момент t0 = 0, должен длиться короткое
время, пока не будет достигнуто требуемое смещение. В этот момент при-
прилагается второй импульс, чтобы уменьшить скорость до нуля, но оставить
¦смещение неизменным. Можно заметить, что первый член ф (г0, t0) 8' (t0)
имеет!такой вид, если записать его в форме
Вид функции Грина. Чтобы сделать формулу G.3.5) применимой,
нужно знать функцию G. Как и в случае скалярного уравнения Гельм-
Гельмгольца, мы найдем ее сначала для бесконечной области. Обозначим эту
•функцию через g. Метод, примененный в случае скалярного уравнения
Гельмгольца, включает оценку относительного порядка особенностей функ-
функций V2g и dug/dt2 в уравнении
776 Гл. 7. Функции Грина
Можно обосновать, что функция V2g имеет более сильную особенность,
так как она содержит вторую производную от трехмерной Й-функции
8(г — г') = 8(ж— х')Ъ(у — y'N(z — z'). Такое обоснование не очень удовлетво-
удовлетворительно. Однако в данный момент допустим, что это верно. Позже мы
возвратимся к последнему уравнению и выведем более строго результат,
который сейчас получим.
Интегрируя обе части уравнения по малому шаровому объему с центром
в точке г = г0, т. е. R = 0, и пренебрегая членом с производной по времени,
получаем, как в предыдущем параграфе,
G.3.6)
Как и ранее, мы приступим теперь к отысканию такого решения однород-
однородного уравнения, которое удовлетворяет этому условию, так как ясно, что
g удовлетворяет уравнению
r_J|- = 0, когда R и t —10 не равны нулю.
При R = 0 надо воспользоваться условием G.3.6). Так как мы имеем
дело с точечными источниками в бесконечной среде, то g является функ-
функцией от R, а не от г и г0 в отдельности. Отсюда
ag \ I d*g n a*(gR)
Решениями этого уравнения служат функции
h[R/c—(t—tD)] + k[R/c + (t— tD)]
g R
где h и к — любые функции. Сравнивая с условием G.3.6), мы видим, что
представляются две возможности (или любая их линейная комбинация):
g=b[R/c-(t-to)]/R и g = b[R/c+(t-to)]/R.
Но вторую из еРих надо исключить, так как она не удовлетворяет наложен-
наложенному ранее условию, которое требует, чтобы эффект от импульса, действо-
действовавшего в момент 10, ощущался на удалении R только при t>t0. Следо-
Следовательно,
gssblBfc-(t-b)] (/u_,o>O), G.3.8)
что представляет сферическую волну, распространяющуюся от источника
с радиальной скоростью с.
Теперь можно сделать апостериорную проверку нашего начального
допущения о том, что особенность у V2g более высокого порядка, чем
у d2g/dt2. На это указывает наличие множителя 1/R, но для доказательства
требуется довольно тонкий учет бесконечностей. Поэтому мы задержимся,
чтобы придать формуле G.3.8) более прочное обоснование, и только после
этого вернемся к обсуждению выводов, вытекающих из этой формулы.
Применяя сферические координаты для 8 (R) = 8 (г — г0) и обозначив
х = *-*„,
можно, делая те же шаги, которые привели к G.3.7), получить более
общее уравнение, справедливое также для R и х, равных нулю:
84Rg) 1 аг(Д§) _ 28 (Д)
ЗД2 С2 д** R ( h
Численный множитель 2 появляется из-за того, что переменная R пробе-
оо
Г 1
гает только неотрицательные значения. Отсюда \ о (R) dR = -^ .
7. 3. Функция Грина для скалярного волнового уравнения 777
Чтобы перейти к дальнейшему, желательно воспользоваться соотноше-
соотношением
^L=-b'{R). G.3.9)
Для его доказательства умножим o(R)/R на дифференцируемую функ-
функцию f(R) и проинтегрируем по R. Пусть
Тогда
RZ(R)dR+....
Первый из полученных членов представляет собой интеграл от нечетной
функции, так что его главное значение по Коши равно нулю; второй член
дает /' @); третий и все высшие члены дают нули. Следовательно,
Это равенство можно также вывести более непосредственно из определения
производной следующим образом:
v (Д) =
Возвращаясь к уравнению, мы можем теперь написать
Ясно, что следует ввести координаты
k = R—cz, -q = R + ci. G.3.10>
Надо определить также смысл произведения о'(Л) о (т) в новых переменных.
Для этого заметим, что
—оо —оо
Это выражение можно переписать как— (d//d?-f df/dri)iiTl==o. Следовательно,
после преобразования G.3.10)
8' (R) о (т) = 2с [o'L(S) 6 (tj) +8' (•»]) 8 F)]. G.3.11)
Появившийся множитель 2с как раз компенсирует изменение элемента пло-
площади при переходе от переменных R, т к переменным ?, tj.
Таким образом, уравнение, которому удовлетворяет Rg, в новых пере-
переменных S и tj приобретает вид
У^ = с [8' (S) S (tj) + S' (tj) о
или
со со
—СО —СО
778 Гл. 7. Функции Грина
Пределы интегрирования выбраны так, чтобы привести к решению, удов-
удовлетворяющему требуемым начальным условиям. После интегрирования по-
получаем
Rg = с о ($) и (tj) - с о (tj) [1-й F)], G.3.12)
О для tj < 0, Г 1 для g < О,
где в hi = , . откуда i-eu =, „ „ _
м v'; ^ 1 для •»] > О, JM w I 0 для ? > 0.
Второй член в G.3.12) можно отбросить; можно показать, что всюду один
или оба из его сомножителей равны нулю. Функция о (tj) отлична от нуля,
только если tj = O (т. е. если сх= —R), но в этой точке ? = 2/?, так что
1 — и (?) = 0. С другой стороны, в первом члене о (?) отлично от нуля, если
ci = R, т. е. когда tj = 2/? и u(tj) = 1. Заменяя в G.3.12) ? на R — c(t —10),
a u(tj) на 1 (для R, t — to>O) и разрешая относительно g, мы приходим
к G.3.8), что и требуется.
Чтобы получить некоторое представление о значении формулы G.3.8),
рассмотрим случай бесконечной области с начальными условиями ф = dty/dt = 0
при t = 0. Тогда
, о- ^^'^v^gfa, w, «¦=«+.,
_ /\ С g(r0' Д/с) Jr/ /7 Q 4 Q\
г, г) = \ -д а\ 0 . (/.o.id)
о
ж окончательно
Мы видим, что эффект в г в момент t определяется значением функции
источника q в г0 в момент t |г — г„|. Это утверждение как раз означает,
что скорость распространения возмущения равна с. Если скорость распро-
распространения становится бесконечной, то решение приводится к известному
решению уравнения Пуассона, имеющему вид потенциала, как это и должно
¦быть, поскольку неоднородное скалярное волновое уравнение в этом пределе
превращается в уравнение Пуассона. Вследствие этого решение G.3.13)
часто называют запаздывающим потенциалом.
Поле подвижного источника. В качестве простого примера рассмотрим
точечный источник, движущийся в бесконечной среде со скоростью v.
Тогда g=go6(r— xt), где q0 определяется интенсивностью источника. Из
.G.3.5) имеем
г
о
Положим
Тогда
\ .
о
7. 3. Функция Грина для скалярного волнового уравнения 779
так что
dpb(p-t)
г/с
Особенность 8-функции здесь находится в р = t. Этим должен опреде-
определяться такой момент t0, что сигнал, вышедший из источника в момент t0,
достигнет г в момент t (см. рис. 7.9). Время t —10 должно быть равно
пройденному расстоянию | г — \t0 |, деленному на с; t —10 = | г— vt0 |/с, что
г"
Рис, 7.9. Запаздывающий потенциал
подвижного источника.
как раз равносильно p = t. Таким образом, величина | г — vt01 = р равна рас-
расстоянию источника от точки наблюдения г в момент t — p/c. Время t0,
называемое запаздывающим временем, представляет собой решение уравне-
уравнения р = t и дает момент времени и потому положение источника vt0 в за-
запаздывающий момент. Интегрируя по р, получаем
Вводя р = г— vt0, имеем
где р представляет собой вектор, проведенный в момент to = t — р/с из поло-
положения источника в точку наблюдения. Это решение другим методом мы
получили в гл. 2, где было показано, что множитель 1 — v-p/cp надо ввести,
чтобы принять в расчет движение источника в течение интегрирования,
так как этот множитель требуется для нормировки источника (см. стр. 208).
Двумерное решение. Если распределение источника q не зависит от z,
получается задача, в которой <J> зависит только от двух пространственных
координат — от х и у. «Двумерный точечный источник» для такой задачи
представляет собой однородный линейный источник, простирающийся от
z0 = — со до z0 = + со вдоль прямой, параллельной оси z и проходящей
через (х0, у0). Поэтому функцию Грина для двумерных задач можно найти,
интегрируя трехмерный точечный источник от zo= —со до zo= -{-co:
где р = х\ + уj — радиус-вектор в плоскости х, у. Можно ожидать, что g
является функцией от |р — ро\ = Р и t — to = t. В самом деле, последнее
780 Гл. 7. Функции Грина
равенство можно переписать в виде
где С = z0 — z и
Отсюда
g (*>,*) =
или окончательно
2с D ^
== ДЛЯ Р <СХ,
р2 G.3.15)
О для Р > ст.
На соотношении G.3.15) видно поразительное различие между двумер-
двумерным и трехмерным случаями. Для трех измерений эффект от импульсного
источника по истечении времени х оказывается сосредоточенным на сфере
радиуса R = сх с центром в точке источника. Так будет из-за функции
6(R/c — x), участвующей в формуле G.3.8). Для двух измерений эффект
импульсного источника в момент х распространяется на всю область Р < ст.
Конечно, при Р = сх имеется особенность, но по сравнению с особенностью
о-функции в трехмерном случае она очень слабая. Объяснение этого разли-
различия можно легко получить, рассматривая линейный источник для трех
измерений. По истечении времени х эффект каждого точечного источника,
которые составляют линейный источник, обнаружится в своей области пло-
плоскости ху. Таким образом, мы заключаем, что импульсный линейный источ-
источник испускает цилиндрическую волну с возмущением, имеющимся не только
на волновой поверхности Р = сх. За этой волновой поверхностью остается
«след». Этот след характерен для двумерных задач и не появляется ни
в трехмерных, ни, как мы увидим, в одномерных задачах. Это было уже
упомянуто на стр. 641.
Одномерные решения. Трехмерное распределение источника, соответ-
соответствующее функции Грина, зависящей только от х— х0 (не зависящей от
у —у0 и z — z0), представляет собой плоский источник, по которому точеч-
точечные источники (или, что то же, линейные источники) распределены равно-
равномерно. Такие функции Грина полезны для задач, в которых нет простран-
пространственной зависимости от у и г. Эту функцию можно получить из G.3.15),
интегрируя g(P, х) по у0 при фиксированных х и х0. Положим ? = ж— х0,
у 2—t2—if
= 0 для | ?_| > сх.
Интегрирование по ij легко осуществляется и дает 2сти, так что
\ G.3.16)
!) В формуле G.3.16) и[х)—\ ПрИ Х ' как и на стр. 778.—Прим. ред.
\ 0 нри х < 0,
7. 3. Функция Грина для скалярного волнового уравнения
781
Вновь заметим, что эффект импульсного источника, действующего
в момент t0 в точке х0 в одномерном случае (или эффект плоского источ-
источника, помещенного на плоскости х = х0 в случае трех измерений), не скон-
сконцентрирован в точках \x — xo\ = c(t — to), а проявляется во всей области
протяженностью 2c(t — t0), середина которой находится в х = х0.
Начальные условия. Чтобы лучше понять различные выражения G.3.8),
{7.3.15) и G.3.16), рассмотрим начальную задачу. Допустим, что начальная
скорость v0 и начальное смещение <]>„ известны в каждой точке простран-
пространства; каковы скорость и смещение в момент I, если считать, что источники
отсутствуют, т. е. д = 0? Решение этой задачи можно получить из G.3.5):
*<'•*> = 15Т И* -0&° (r°> ~ Ш<о=о *° <'«)} dV° ¦ <7-ЗЛ7>
Интегрирование распространяется по всему пространству [мы приняли также,
что поверхностный интеграл в G.3.5) исчезает на бесконечности].
Рассмотрим сначала одномерный случай, где можно просто подсчитать
G.3.17) и непосредственно истолковать результат. Для одного измерения
выражение G.3.17) принимает вид
-(U )
<о=о
где g дается формулой G.3.16). Функции gtD=o и (dg/dto)to=o имеют значе-
значения 2стс[1 —и(| ? \/c — t)] и —2ciuo(J %\/c — t) соответственно, где|Е| = \х—хо\.
Нетрудно выполнить интегрирование и получить
x+ct
Ф (я, 9 = Т { Т S ие fro) dx0 + % (х + ct) + ф0 (х - ct)} . G.3.18)
x-ct
Это общеизвестное решение Даламбера одномерной начальной задачи
[см. формулу A1.1.58)]. Его можно также получить непосредственно из
дифференциального уравнения (см. стр. 639).
Рис. 7.10. Слева показано движение струны, которую
оттянули и отпустили (т. е. в начальный момент дано лишь
емещение). Справа показано движение струны после удара
(т. е. в начальный момент ей лишь сообщили скорость).
Сплошные ливии изображают струну в последовательные моменты, а
пунктирные — вид двух «частичных волн» (идущих в противоположных
направлениях), сумма которых дает форму струны.
Из формулы G.3.18) мы видим, что если для среды, скажем для струны,
дано начальное смещение без скорости, то начальное отклонение разбивается
782 Гл. 7. Функции Грина
на две одинаковые волны, из которых одна идет в положительном направле-
направлении оси х, а другая —в отрицательном. Сумма обеих волн при t = 0 дает
начальное смещение %. В течение некоторого времени, когда они частично
перекрываются, вид составного отклонения будет довольно сложным, пока
они в конце концов не разделятся. Это показано на рис. 7.10 слева.
Заметим, что позади каждой волны не остается следа. В двумерных зада-
задачах, как мы увидим, такой след возникает.
Начальная задача для двух измерений решается формулой G.3.17).
Здесь удобно поместить начало координат в точку наблюдения. Тогда
где g выражается формулой G.3.15). Отсюда, вводя полярные координаты
и замечая, что dg/dto= —dg/dt, получаем
ct 2и ct
Эта формула показывает, что значение <1> в точке зависит от исходных
значений d§/dt и Ф внутри круга радиуса ct с центром в точке наблюдения.
Как и при исследовании одномерного случая, рассмотрим начальное
условие vo = O. Кроме того, пусть ф0 (р0) = о (р0 — р), т. е. начальное движе-
движение имеет вид импульса в точке р. Тогда
T &M^] если 9<[а'
2лСагЧ ?
i У**~Я J I 0, если P>ct.
Этот результат можно записать в виде
t\ ¦ 1 д Гц(с*~~р)~1- 1 Г ctu(ct-p) Ib(ct-p) Л
. Ч - 2ис dt L УсЧ*-р*-1 ~ 2^ I (с^_ р2K/2 "Г /c2j2_p2 J '
Таким образом, до момента, когда с? = р, в начале координат нет никакого
эффекта. В этот момент в начало координат приходит возмущение в виде
импульса (второй член последнего выражения). Однако за этим возмуще-
возмущением остается след, описываемый первым членом, который при ct > p убывает
со временем как 1/с222. Сопоставим это с результатами, полученными для
аналогичного импульсного возмущения в х0 в одномерном случае. Там
сигнал достигал точки х в момент | х — х0 \/с. Он был точной копией исход-
исходного сигнала, за исключением уменьшения амплитуды в два раза; следа
не было. Это различие между одномерным и двумерным случаями показано
на рис. 7.11.
Наличие следа характерно для распространения в однородной среде
в двумерном случае. Для трех измерений, как и для одного, форма возму-
возмущения, вызванного импульсом, остается неизменной при распространении
от его исходного положения. Это непосредственно видно из формулы G.3.8)
для функции Грина в случае трех измерений. Наличие 8-функции предот-
предотвращает создание следа. Этим не обязательно гарантируется неизменность
вида возмущения. В одномерных задачах сохраняется вид возмущения,
которое создается начальным смещением (с нулевой скоростью). Для трех
измерений верно обратное. Сохраняется вид возмущения, для которого на-
начальное смещение равно нулю, но задана начальная скорость.
Это можно показать при помощи вывода формулы, аналогичной G.3.19)
ж G.3.18). Вводя трехмерную функцию Грина в G.3.17) и беря начало
7. 3. Функция Грина для скалярного волнового уравнения
783
координат в качестве точки наблюдения, имеем
0
ob(^-t)vo (r0) - ro8'.( ? - «) % (r0)
где dQ0 — элемент телесного угла на сфере в «нуликовых» координатах (т. е.
sin6u d0od<po). Непосредственно ясно, что эффект, получающийся в точке
жаблюдения в момент t, определяется условиями, имевшими вначале место
Р л с. 7 II1 Поведение струны и поведение мембраны.
Верхние рисунки показывают начальные очертания, а нижние—
картину в последующие моменты. Четвертая часть мембраны
вырезана, чтобы показать ее форму, со «следом» позади перед-
переднего крутого фронта волны.
на поверхности сферы радиуса ct с центром в точке? наблюдения. Теперь
можно выполнить интегрирование по г0. Нам нужно явно записать зависи-
зависимость ф0 и v0 от координат 60, <р0 на поверхности сферы, например, ф0 (г0) =
= Фо (ro> fy>> ?o)- Первый интеграл вычисляем, пользуясь свойствами о-функ-
ции. Получаем c4vo(ct, %, <р0).
Чтобы подсчитать второй член, можно проинтегрировать по частям или
воспользоваться свойством производной о' (см. стр. 775)
/ {х') V (х' - х) dx' = - /' (х).
Моэтому второй член равен — c2{d[tty0(ct, 60, <po)]/dt}. Объединяя эти ре-
784 Гл. 7. Функции Грина
зультаты, получаем окончательно
! } G-3-20)
Непосредственная зависимость Ф от в0 и появление производной, дей-
действующей на ф0, находятся в соответствии с нашими предварительными
замечаниями. Формула G.3.20) известна как решение Пуассона.
Принцип Гюйгенса. Функцию Грина для бесконечной области можно
также применить для получения математического выражения принципа
Гюйгенса. С элементарной точки зрения принцип Гюйгенса постулирует,
что каждая точка фронта волны ведет себя как точечный источник,
испускающий сферическую волну, которая распространяется со скоростью
¦с. Поэтому поле в данной точке через некоторое время равно сумме полей
от каждого из этих точечных источников; огибающая этих волн для всех
точек представляет собой фронт волны в это время.
Для вывода этого принципа обратимся к общему уравнению G.3.5)
и рассмотрим случай, когда источников нет (т. е. q = 0 внутри поверхно-
поверхности S) и, кроме того, начальные значения ф и dty/dt равны нулю. Мы ви-
видим, что объемный интеграл в формуле G.3.5), включающий начальное
условие, равен нулю, так что в левой части остается только
о
где мы подставили G.3.8) в левую часть G.3.5). Проинтегрировать по t0
первый член не слишком трудно:
t*
S жь ('» -1+т) erado Ф <г°'г»)л» = ж erad» * Сго-1 - т
о
Второй член проинтегрировать не намного труднее, если следить за наши-
нашими 6 и 8'. Имеем
д Г8(«о — t + R/c)
L
о
о
Следовательно, функция ф в точке г в момент t внутри S, где нет
источников, имеющая внутри S нулевые начальные значения, целиком оп-
определяется интегралом от поверхностных значений на S:
dS° • [ i rad * (r l) +
Если теперь часть поверхности So расположена вдоль фронта волны,
а остальная часть — на бесконечности или там, где ф равно нулю, то мож-
7. 3. Функция Грина для скалярного волнового уравнения 785
но сказать, что значения поля ф в (г, t) определяются полем ф в точках
фронта волны в более ранний момент t — R/c. С другой точки зрения, дей-
действие фронта волны в точках перед ним в более позднее время эквивалент-
эквивалентно действию распределенных по поверхности волнового фронта лсточников:
во-первых, действию простого поверхностного слоя источников, пропорци-
пропорционального составляющей градиента ф по нормали к фронту волны; во-вто-
во-вторых, действию двойного слоя, пропорционального самой ф, и, наконец, дей-
действию любопытного простого слоя, пропорционального скорости изменения
ф во времени на поверхности. Это последнее действие наиболее сильно про-
проявляется прямо впереди поверхности, но ослабевает пропорционально косинусу
угла между нормалью к поверхности и направлением распространения (т. с.
направлением R).
В большинстве случаев (за исключением простых и тривиальных) точные
значения ф, grac^ и dty/dt вдоль всего фронта волны точно не известны.
Но во многих интересных случаях эти величины приближенно известны,
так что формулу G.3.21) можно применять для приближенного подсчета
значений ф в более позднее время. Этот вопрос будет подробно рас-
рассмотрен в § 11.4.
Границы в конечной части пространства. Теперь обратимся к эффекту,
получающемуся при введении границы, на которой функция Грина должна
удовлетворять заданным граничным условиям. Техника, которая может
здесь служить, вполне подобна той, которая была рассмотрена в предшест-
предшествующем § 7.2 для стационарного случая.
Как и в том случае, имеются два метода:
метод изображений и метод собственных
функций. Исследуем сначала метод изобра-
изображений, причем воспользуемся знанием функ-
функции Грина для бесконечной области. Един-
Единственная особенность, естественно, имеется
в точке источника в момент его действия,
так что вообще
" \т> Ч ГО> lo) — r г r \т> l\ ro> lo)i g Начало
"•координат
где /' — решение однородного волнового урав- р-ис 7 12. образ / импульсного
нения, свободное от особенностей в рассма- * источника волны в Q.
триваемой области.
Здесь полезен простой пример. На рис. 7.12 источник находится в Q;
он действует в момент t0. Бесконечная жесткая плоскость расположена при
х — 0. Чтобы удовлетворить граничным условиям на плоскости, мы добав-
добавляем отраженное импульсное возмущение, возникающее в изображении /
точки Q в тот же момент t0. Чтобы получить требуемое обращение в нуль
нормальной производной при х = 0, эффекты этих импульсных возмущений
надо сложить, так что
! +
Легко проверить, что (dG/dx)x—o равно нулю для всех t. Эффект второго члена
состоит в том, что он дает отражение от плоскости х = 0 в соответствую-
соответствующее время. Это — единственное отражение, и потому требуется только один
дополнительный член к функции Грина для бесконечной области. Заметим,
что в случае волнового уравнения необходимо задавать не только поло-
положение изображения источника, но также и момент V', в который возникает
отраженный импульс. К счастью, в большинстве задач это решается про-
просто, а именно, все отраженные импульсы возникают в тот же момент f,
50 Ф. м. Морс и Г. Фешбах
786 Гл. 7. Функции Грина
что и исходный импульс. Для достаточно регулярных геометрий возможно
пользоваться методом изображений почти так же, как и для случая урав-
уравнения Гельмгольца.
Разложение по собственным функциям. Мы применяем функцию Грина
для уравнения Гельмгольца. Выражение Gfe(r|ro)e~iu)' представляет собой
решение волнового уравнения с простым гармоническим точечным источни-
komj расположенным в г0. При ш = кс имеем
V2 [Gk е~™ <'-<<»] _ 1|L [Gk е-** С-'о)] = _ 4ти 8 (г - r0) e~™ «-<<».
При помощи соответствующего наложения этих простых гармонических ре-
решений можно получить функцию Грина для импульсного источника в точке
пространства, соответствующего уравнению G.3.2). Для этой цели мы вос-
воспользуемся интегральным представлением о-функции:
— ОО
На основании линейности надо ожидать, что функция Грина для импульс-
импульсного источника связана с решением уравнения Гельмгольца соотношением
оо
G(r,t\ r0, t0) = -L ^ G (г | г01 к) е-- «"'о) dm, G,3.22)
—со
где ю = кс и G(r[ro|/с) = Gfe(r| г0). Это соотношение будет более тщательно
выведено в §11.1. Простота формулы G.3.22) обманчива. Следует вспом-
вспомнить, что для конечных областей функция Gh имеет особенности всякий раз,
когда к = кп, где кп — собственное значение скалярного уравнения Гельмгольца
для решения A>„, удовлетворяющего тем же граничным условиям, что и Gh.
Более определенно, если функции фп нормированы, то в силу G.2.39)
Поэтому интегрирование в G.3.22) нельзя производить вдоль вещественной
оси ш (или к), а надо эти особенности некоторым способом обойти. Выбор
контура диктует рассмотренный выше принцип причинности. Чтобы это
увидеть, внесем разложение для Gk в интеграл G.3.22):
СО
G (г, 11 r0, t0) = Ъ? ^ Фп Ы Фп « \ ^Г-ш^ «Ч ">« = скп.
п —оо
Контур надо выбрать так, чтобы G(r,t\r0, to) = O для t < t0. Соответствую-
Соответствующий контур показан на рис. 7.13. Он параллелен вещественной оси и про-
проходит непосредственно над ней. Если t > t0, то контур можно замкнуть в
нижней полуплоскости полуокружностью большого (—> со) радиуса без из-
изменения значения интеграла. Теперь можно воспользоваться интегральной
формулой Кошй D.2.9), что даст Bти/шп) sin шп (t —10). Если t < t0, контур мож-
можно замкнуть полуокружностью в верхней полуплоскости. Так .как в верхней
полуплоскости нет особых точек, то значение интеграла для t < f0 равно
нулю. Отсюда
G (г, 11 г0) *0) = 4ъс* ^ 81П[Ш;^~гоI» (* -10) *„ (г0) Фп (г), G.3.23)
7. 3. Функция Грина для скалярного волнового уравнения 787
где и (t —10) — единичная функция, равная нулю при t < t0 и единице при
t>t0.
Воспользовавшись формулой G.3.23), можно теперь явно подсчитать
решение задачи с начальными и граничными значениями, данное в форму-
Плоскость си
Контур С.
Рис. 7.13. Контур для интеграла
G.3.22).
ле G.3.5). Рассмотрим каждый член формулы G.3.5) в отдельности. Пер-
Первый член <{I дает эффект источников, распределенных по всему объему:
^ = ^ dt0 ^ G (г, 11 r0, t0) q (r0, t0) dV0 =
о
t*
= i7ZC* 2 i; \ Ло \ sin [% (* -10)] $n (r0) <?„ (r) q (r0) t0)
n 0
Пусть
Тогда
r
{ ^ !^iI ^ ^ ('о. ^o) ?n («-о. ^o) dV0 } . G.3.24)
Мы видим, что амплитуда возбуждения n-й гармоникой пропорциональна
кратному интегралу в G.3.24). Возбуждаемая амплитуда велика, если про-
пространственная зависимость q очень близка к фп, а временная зависимость — к
е-4'*"', как и следовало ожидать. В случае точного резонанса q ~ е-"""* заме-
замечаем, что <bt линейно возрастает со временем и более не колеблется.
Второй член формулы G.3.5) дает эффект источников, распределенных
на границе. Результаты до некоторой степени подобны тем, которые полу-
получены из первого члена. Третий член включает удовлетворение начальным
условиям. В дальнейшем нам понадобятся Gto=o и {dG/dto)io=0:
G(v,t\v0, 0) = ^c^s^f-u{t)^Ji)^n(r0), G.3.25)
n
[~G{r,t\ r0, t0)] jo=o = -4kc* ^ cos К/) и(t) фп(г) фп(г0), G.3.26)
где мы подставили [sin (и>пг)/шп] S (t) = 0. Третий член в G.3.5) приобретает
вид
+ cosmnt фп (г) \ ф„ (г) \ (r0) dV0 \ . G.3.27)
50*
788 Гл. 7. Функции Грина
Можно непосредственно проверить, что ф^ (/ = 0) как раз равно ф0, а
(dfy3/dt)t—о = ^0> как и требуется. Это также показывает, что мы могли бы
получить формулу G.3.27) прямо, не используя функцию Грина. С другой
стороны, этим подтверждается законность основной формулы G.3.5) для
случая конечных областей.
Нестационарные малые колебания круглой мембраны. В этом месте
будет полезен пример, показывающий характер результатов, полученных для
задач, содержащих зависимость от времени. Пусть для круглой мембраны
радиуса а с натяжением Т и массой о на единицу площади дано начальное
смещение малого участка вокруг ее центра. Края мембраны закреплены,
так что граничные условия имеют вид ф (г) = 0 при г = а. Мы представим
начальные условия при помощи S-функции:
, о0(г) = 0. G.3.28)
Здесь А — постоянная. Вводя G.3.28) в G.3.27), получим решение началь-
начальной задачи
ф(г, t) = A2 cos%*-фп(г)фп(О). G.3.29)
п
Для перехода к дальнейшему необходимо получить собственные функ-
функции фп(г). Это будет очень подробно рассмотрено в §11.2. Сейчас заметим,
что уравнение Гельмгольца в полярных координатах (г, <р) разделяется и что
общее решение, конечное и однозначное для г < а, является суммой членов
e±im* Jm(kr), где Jm — функция Бесселя первого рода порядка то (то — целое
число).
Теперь необходимо ввести граничные условия при г = а. Это приводит
к уравнению, определяющему к:
Jm{ka) = 0. G.3.30)
Обозначим значения к, удовлетворяющие этому уравнению, через ктр, где
индекс т указывает порядок функции Бесселя, а буква р — номер корня
уравнения G.3.30). Для целей этого примера достаточно воспользоваться
асимптотическим видом Jm(kd) E.3.68):
Jm(ka) ~
Таким образом, Jm {ka) равно нулю, когда аргумент косинуса равен нечет-
нечетному числу, умноженному на тс/2:
1 1
/стра~-^Bто + 1)^ + -2B/? + 1)тс, р-целое.
Теперь можно вернуться к выражению G.3.29), дающему решение при
начальном смещении импульсного вида при г = 0, t = 0. Таким образом,
функции фп равны
где каждому п мы поставили в соответствие определенную пару целых чи-
чисел (т, р) и определенный знак в показателе. Множитель Nmp выбран так,
что
где областью интегрирования служит мембрана. Для G.3.29) требуется
/т@). Так как /m(z) = O(zm), to мы видим, что /m@) = 6Om fCM- формулу
г-* 0
,E.3.63)]. Поэтому сумма G.3.29) приводится к сумме по функциям Бесселя
7. 3. Функция Грина для скалярного волнового уравнения 789
нулевого порядка. Отсутствие угловой зависимости неудивительно, если при-
принять во внимание круговую симметрию начального смещения G.3.28). Ре-
Результирующее отклонение в последующий момент t в положении г дается
формулой
ф (г, t) = А ^ cos (kOp ct) NIP /0 (kOpr). G.3.31)
p
Формула G.3.31) точная. Заметим, что система функций iVOpcos (kOpct) X
X Jo (&oP r) описывает свободные радиальные колебания мембраны. В общем
случае результат воздействия начального смещения можно выразить в виде
наложения свободных колебаний, причем каждое из них происходит со своей
собственной частотой. Другим будет результат постоянного действия на
мембрану силы данной частоты. В последнем случае вынужденное коле-
колебание мембраны будет иметь ту же частоту, что и действующая сила, а прост-
пространственная зависимость будет представлять суперпозицию функций ф„(/1),
каждая из которых выражает колебание с частотой действующей силы.
Рассмотрим результат воздействия в самой начальной точке г = 0.
Формула G.3.31) принимает вид
v
Введем приближенное значение нулей:
.>@^)~^2cos(^±3.^OVV G.3.32)
р
Когда смещение вновь сосредоточится в /- = 0? На первый взгляд мо-
может показаться, что это произойдет при t = laic, т. с. после того как пе-
передний фронт смещения дойдет до края мембраны и вернется обратно в
центр. Однако это не так. Как можно видеть из асимптотического поведе-
поведения функции
/0 (z) ~ y^/iuz cos f z — -r ти J ,
при прохождении от области г са 0 до г ~ а появляется изменение фазы на
ти/4. Это характерно для распространения в двух измерениях. Ни для од-
одного, ни для трех измерений не получается такого изменения фазы.
Из-за этого изменения фазы передний фронт возмущения должен сде-
сделать два перехода от центра до края, чтобы получилось окончательное из-
изменение фазы на ти и смещение вновь сосредоточилось н точке г = 0. Поэ-
Поэтому можно ожидать, что толчок воссоздастся при г—0, когда ct—ia. В
этом легко убедиться при помощи подстановки в G.3.32), так как
v
[Начальный толчок ф@, 0) равен А^Ы\Р.] Нам хотелось бы подчеркнуть,
что это явление имеет место только в двумерном случае; в случае одного
или трех измерений его не будет. Толчок в центре сферы радиуса а вос-
воссоздается в центре в момент t = 2а/с.
Имеется еще один, последний момент, также показывающий удивительную
разницу в распространении волн для двух измерений в сравнении с* одним
или тремя. В последнем случае начальное смещение в соответствующее время
точно воссоздается. Для двух измерений это не так, потому что при про-
продвижении волны остается след. Это можно видеть в настоящем примере
следующим образом. Выражение G.3.32) приближенное, так как применя-
применялись приближенные значения корней функции Бесселя /0. Если восполь-
790 Гл. 7. Функции Грина
зоваться точными значениями корней, то оказывается, что не существует
значений ct, для которых фаза kOpct точно одна и та же для всех р. Дру-
Другими словами, не было бы значений ct, для которых повторились бы перво-
первоначальные соотношения фаз между всеми свободными колебаниями, возбуж-
возбужденными начальным смещением. Таким образом, свободные колебания
никогда не будут интерферировать настолько, чтобы точно воссоздать на-
начальную ситуацию.
В качестве другого примера построения функции Грина для скаляр-
скалярного волнового уравнения выведем выражение G.3..8) функции Грина для
бесконечного пространства при помощи непосредственного применения метода
наложения. В этом случае
Gk(r\r0) = e*R/R, Л = со/с,
так что
Следует заметить, что мы сознательно выбрали знак между величинами kR
и сох таким, чтобы е1 (feR-u)'r)/i? изображало волну, расходящуюся из источ-
источника с течением времени, т. е. с возрастанием ъ. Этим способом мы удовле-
удовлетворяем принципу причинности. Теперь воспользуемся интегральным пред-
представлением S-функции [см. формулу, предшествующую G.3.32)] и получим
Уравнение Клейна—Гордона. Функция Грина для зависящего от вре-
времени уравнения Клейна — Гордона удовлетворяет уравнению
™-У-^-Ж=-^ЪA-10)Цт- г0). G.3.33)
Легко убедиться, что функцией Грина для уравнения Клейна — Гордона
можно пользоваться почти так же, как функцией Грина для скалярного
волнового уравнения. Например, условие взаимности G.3.3) и общее реше-
решение G*3.5) имеют место также и здесь. Однако имеются важные физические
различия между обеими функциями. Это легче всего показать, рассматри-
рассматривая клейн-гордонову функцию Грина для бесконечной области, т. е. полу-
получив аналог функции G.3.8). Функцию g(r,t\ro,to) можно получить путем
наложения решений с простой гармонической зависимостью от времени
g-tu)(j-jo)i вместо того чтобы решать уравнение с правой частью, имеющей
импульсную зависимость 6(t —t0) от времени. Необходимое наложение
дается формулой G.3.22). Частные решения имеют вид g(.R|l/uJ—сгх2)
и удовлетворяют уравнению
[V2 + (<»/с)г - *2] g [R | j/a>2-(ocJ] = - 4tuS (г - r0).
Решение этого уравнения есть
yj^t д = |г_Го|. G.3.34)
В пределе при ш/с > v. формула G.3.34) принимает вид g = e* И«) R/R, как
и должно быть. Для противоположного случая ш/с <С *
что дает характерную «затухающую» пространственную зависимость. Это,
конечно, не связано с какой-либо диссипацией. Из одномерной механичес-
7. 3. Функция Грина Зля скалярного волнового уравнения
791
кой аналогии (гл. 2, стр. 137 и далее) со струной, погруженной в упругую
среду, мы видим, что это получается как следствие жесткости среды.
Воспользовавшись G.3.22), можно теперь написать в качестве решения
^7.3.33), пригодного для бесконечной среды,
g{t,t\ г0, /0) = JL. ^ exp i [V(m/cf-Y.* Я - сох] dm,
G.3.35)
где x = t — tQ. Функция g является функцией только от R и х, как и ожи-
ожидалось. Теперь надо 'задать путь интегрирования. До этого удобно для
изучения вопросов сходимости ввести такую функцию h (R, х), что
dh{R, t)/3i? = i?g(r, 11 r0, t0). G.3.36)
'9 %) = — V — -dw. G.3.37)
•Отсюда
Подинтегральная функция имеет точки ветвления ш= ±^с%. Расположение
пути - интегрирования относительно этих точек ветвления определяется
условием причинности. Выберем путь и линию ветвления, как показано
Контур^
со=-Сх
Плоскость си
У w=+Cx
^Линия ветвления
Рис. 7.14. Контур для интеграла G.3.37) при R > ст.
«а рис. 7.14. Заметим сначала, что /г = 0, если R > сх, как требует для
этого случая принцип причинности. В пределе для большого ш показатель
экспоненты в G.3.37) приближается к iw[(R/c) — x] =z'u>| (R/c) — x\. Поэтому
путь интегрирования можно замкнуть в верхней полуплоскости ш без
изменения значения интеграла. Так как подинтегральная функция не имеет
особенностей в верхней полуплоскости, то интеграл равен нулю.
Рассмотрим теперь h для /?<сх. Тогда контур деформируется так,
как показано на рис. 7.15. Его можно теперь привести к более известному
виду. Введем новую переменную 6 так, что
м положим со = с* ch х. Тогда
,x) = ?-. \ ехр [ - Ыс
оо+— тег
1 ch(х- 6)] dx.
792
Гл. 7. Функции Грина
Наконец, положим х — 6 = г?; тогда
1
Это — как раз интегральное представление функции Бесселя нулевого
порядка [см. формулу E.3.65)], так что
h {R, х) = - с/0 [xc>V - (R/cJ], R<cz.
Комбинируя это с выражением для ее < R, окончательно получаем:
h (R, z) = - cJ0 [xcVx»-(R/c)»} и [х- (R/c)].
Поэтому функция Грина равна
-J»
или
6 [%-{R/c)\
х [хс /г2 -
u[% — {R/c)]. G.3.38)
Плоскость су
Мы замечаем, что g {R, т) в пределе при х—>0 приводится к функции
Грина для скалярного волнового урав-
уравнения G.3.8), как это и должно быть.
Если мы будем наблюдать возму-
возмущение на расстоянии R от импульсного
источника через время t после его
действия, то найдем, что при R > с-
возмущение отсутствует, т. е. волнаt
порожденная импульсным источником Т
не имела достаточно времени, чтобы
достичь точки наблюдения R. При
R = cx приходит импульс от началь-
начального возмущения, уменьшенный по
амплитуде, как это и должно быть, в.
1/R раз. За ним остается след, который
выражается вторым членом формулы
G.3.38). Этот след для больших зна-
^ Линия
ветвления
Рис. 7.15. Контур для интеграла
G.3.37) при R < ст.
чений времени убывает по амплитуде из-за множителя |Ч2 — (Д/сJ]~3/4.
Нетрудно объяснить это явление, если заметить, что фазовая скорость
плоской волны, удовлетворяющей уравнению Клейна—Гордона, является
функцией от (о:
или — =
С
Так как возмущение от импульсного источника составлено из гармони-
гармонических возмущений различных частот, то не удивительно, что соответствую-
соответствующие этим гармоническим возмущениям плоские волны достигают точки
наблюдения, имея относительные фазы, отличные от тех, которые они
имели в начале. Равносильное описание можно получить, рассматривая
пример из механики для уравнения Клейна — Гордона, данный в § 2.1.
7. 4. Функция Грина для уравнения диффузии 793-
ЧА. Функция Грина для уравнения диффузии
Уравнение диффузии во многих аспектах качественно отличается от
скалярного волнового уравнения, и, конечно, на функциях Грина эти
различия будут проявляться. Наиболее важной характерной особенностью
является асимметрия уравнения диффузии относительно временной перемен-
переменной. Если, например, $ (г, t) — решение скалярного волнового уравнения,
то и $ (г, — t) будет решением. Однако если <J» (r, t) — решение уравнения
диффузии
G.4.1)
то функция ф (г> — 0 Уже не будет его решением; она будет решением
совсем другого уравнения
Таким образом, уравнение приносит вместе с собой направленность во
времени, т. е. оно различает прошедшее и будущее. Скалярное волновое
уравнение и вообще все уравнения, приложимые к микроскопическим
(например, атомным) явлениям, симметричны во времени. Направленность
во времени уравнения диффузии является следствием того, что поле,
в котором происходит диффузия, изображает поведение некоторого среднего
свойства совокупности многих частиц. Как можно вывести из теорем
термодинамики, неправильности таких средних, которые первоначально
могли существовать, с течением времени сглаживаются. Обращаясь в буду-
будущее, мы видим, что энтропия возрастает; обращаясь в прошлое, видим,
что энтропия была меньше.
Причинность и взаимность. Как и в случае скалярного волнового
уравнения, можно решать различные неоднородные задачи и начальную
задачу для уравнения диффузии при помощи функции Грина, которая
удовлетворяет однородным граничным условиям и условию причинности:
G(r, *|r0, го)=О, если t<t0. G.4.2)
Уравнение, которому удовлетворяет G, содержит импульсный точечный
источник:
V*G-a*dG/dt= -4rcS(r-ro)o (t -t0). G.4.3)
Чтобы истолковать G.4.3), будем считать G температурой среды. Тогда
импульсный точечный источник означает введение единичного количества
тепла в г0 в момент t0. При этом функция G дает температуру в дальней-
дальнейшие моменты для любой другой точки среды и потому описывает распро-
распространение тепла от его исходного распределения.
Функция G удовлетворяет условию взаимности, в котором, как и для
скалярного волнового уравнения, время надо обратить, так как причинность
требует выполнения соотношения G.4.2). Мы покажем, что
G(rft|r0,/0) = G(r0,-*0|r,-0. G.4.4)
Функция G (г0, —10 | г, — t) дает эффект в г0 в момент —10 от источника
тепла, помещенного в среду в точке г в момент — t. Так как t0 < t, то
последовательность моментов расположена в требуемом порядке. Другое
истолкование можно получить, рассматривая сопряженную функцию-
794 Гл. 7. Функции Грина
G (г, 11 r0, t0), определенную соотношением
G (г, -11 г0, - У = G>, 11 r0, «„). G.4.5)
Функция G удовлетворяет уравнению с обращенным временем
V2G + a2 9G/5f = - 4m о (г - r0) S (г - f0).
Условие G.4.2) заменяется на G (r, t | r0, ?0) = 0 при 2 > ?„. Другими сло-
словами, G дает развитие обратно во времени источника, помещенного в г0
в момент t0. Условие взаимности теперь записывается так:
G(r,«|ro,g = S(ro,to|r,l). G,4.6)
Функция G описывает развитие при возрастании времени, приводящее от
исходного источника к конечному распределению. Функция G описывает
тот же процесс в обратном порядке, начиная от конечного распределения
и идя обратно во времени к исходному источнику. Вопрос о сопряженных
функциях будет рассмотрен позже в этой главе.
Доказательство формул G.4.4) или G.4.6) проходит по тому же
образцу, что и в предыдущем параграфе. Надо рассмотреть два уравнения;
V*G (г, 11 г0, *0) - с2^G (г, 11 г0, «„) = - 4гс 6 (г- г0) 6 (/ - *0),
"Умножаем первое из них на G(r, — t\r1, — t1), второе на G(r, t\ r0, t0),
вычитаем одно из другого и интегрируем по интересующей нас области
л^по t от —оо до t^. Применяя затем теорему Грина, получаем
«о*
^ dt ^ {G (г, -11 rlt - /х) grad [G (г, 11 r0, t0)] -
-CO-
- G (r, 11 r0, t0) grad [G (r, -11 rlf - tj]} • dS -
= 4m [G (rlf t21 r0, /0) - G (r0, - t01 rlf - «J].
Первый из интегралов обращается в нуль в силу однородных граничных
условий, которым удовлетворяет функция G. Во втором можно произвести
.интегрирование по времени, что даст
[G (г, - 11 rlf - 1г) G(r,t\ r0, «oJI^co.
На нижнем пределе второй из двух множителей обращается в нуль в силу
условия G.4.2). На верхнем пределе первый множитель равен нулю опять
в силу G.4.2), причем мы молчаливо предполагали, что tt находится внутри
интервала интегрирования.
Теперь условие взаимности получается непосредственно. Можно также
шолучить уравнения, которым удовлетворяют G и G как функции t0. Например,
7. 4. Функция Грина для уравнения диффузии 795
из G.4.6) имеем
дС
VIG + с2 ?- = - 4гс о (г- г0) 6 (t -10),
G.4.7)
Неоднородные граничные условия. Теперь мы с помощью функции С
получим решение неоднородного уравнения диффузии с неоднородными
граничными условиями и заданными начальными условиями. Надо решить
уравнение
V204 - a2 dtydt0 = - 4тг р (r0, t0), G.4.8)
где р, функция источника, является известной функцией пространственных
и временной координат. Умножим это уравнение на G, а первое из уравне-
уравнений G.4.7) —на ф; вычтем одно равенство из другого, проинтегрируем по
пространству и по времени от 0 до t*:
\ dt0 \ [bVlG-GVli?]dV0 + a* [ dV0 i
с
= 4it { dt0 { pGdV0-4n$(r, l).
К первому из этих интегралов можно применить теорему Грина. Во втором
можно произвести интегрирование по времени. Заметим, что G(r, t\ro,t*) = 0.
Окончательно
t*
ф (г, 0 = J *о J Р (го.М G (r, 11 г01 to)dVo +
о
I*
+ 57 J *« 5 dS°"[G grad° ф ~ * grad° G] +1 \ dV° №Ъ*=ь. G.4.9)
о
Функция G выбирается так, чтобы удовлетворить однородным граничным
условиям, соответствующим тем граничным условиям, которым удовлетворяет
функция ty. Например, если ф удовлетворяет однородным или неоднородным
условиям Дирихле, то G берется удовлетворяющей однородным условиям
Дирихле. Первые два члена в G.4.9) представляют знакомые эффекты
•объемных источников и граничных условий, тогда как третий член вклю-
включает эффект начальных значений % функции ф. Если были бы даны началь-
начальные значения d§/dt, то лучше вместо уравнения для ф рассмотреть уравне-
уравнение, которому удовлетворяет dty/dt. Пусть v = d§/dt. Тогда из G.4.8)
получаем
т. е. уравнение того же вида, что и G.4.8), так что его можно анализиро-
анализировать тем же способом. Следовательно, при помощи G.4.9) можно рассмотреть
любой тип начального условия. Как мы видели в гл. 6, для уравнения
диффузии нельзя задавать как начальное значение, так и начальную
производную.
Функция Грина для бесконечной области. Теперь мы приступим.
к построению частных примеров функций Грина для этого случая. Как1
796 Гл. 7. Функции Грина
обычно, сначала надо исследовать функцию Грина g(R, х), R = |r — г01^
х = t — t0, для бесконечной среды. Можно вывести выражения для одного,
двух или трех измерений одновременно. Пусть g —одно-, дву- или трех-
трехмерный интеграл Фурье:
где п равно 1, 2 или 3 в зависимости от числа измерений и такова же
размерность переменной интегрирования dV'p. Так как
^ e4>-R Г — n2v— я2
то мы получаем для у уравнение
a2 dy/dx + /?2у = 4тг S (х),
которое имеет решение у = Dт/а2)е~(р /а )тм (т); при этом мы выбрали реше-
решение, согласованное с требованием причинности. Отсюда
или
Преобразуя экспоненты в интеграле, можно точно подсчитать каждый
член произведения. В первом члене
Р
— 4r - a^ 4r •
Поэтому интеграл можно записать в виде
2r '
—«o
и при помощи подходящей замены переменной можно показать, что он равен
= а
Подставляя этот результат в выражение для g, получаем
g(R, х) = §-(^=г )V(aaK*/4,)M(x). G.4.10)
Функция g обладает важным интегральным свойством, имеющим место для
всех значений п:
G.4.11)
Эта формула выражает сохранение тепловой энергии. В момент t0 в г0
введен источник тепла. Теплота диффундирует в среду, но таким образом,
что полная тепловая энергия не изменяется.
7. 4. Функция Грина для- уравнения диффузии
797
Функция g(R,%) в одномерном случае, п = 1, изображена на рис. 7.16
для нескольких значений т. Заметим, что кривая имеет строгий максимум
при R = 0 и что ширина кривой возрастает с ростом t. При т = 0 ширина
нулевая, так как тепло только что введено и все сконцентрировано при
R = 0. Так как соотношение G.4.11) тем не менее имеет место, то мы
видим, что
¦Z-+0 °
¦чем часто пользуются в качестве примера о-функции. Когда т становится
отличным от нуля, температура немедленно поднимается повсюду, причем
наиболее резко выраженное повышение происходит, конечно, вблизи
i? = 0, т. е. при R < "j/t/a2. Позже мы рассмотрим случаи, в которых
из-за соответствующей инерции скорость распространения конечна.
¦2
ах -—
Рис. 7.16. Функция Грина уравнения диффузии в
одном измерении для единичного источника, введен-
введенного при ж = 0, f = 0, как функция х для различных
моментов t.
Введем теперь G.4.10) в формулу G.4.9), что даст выражение ф(г, t)
¦через функцию Грина, начальное значение, распределение объемных
источников и граничные условия. Рассмотрим начальную задачу. Пусть
р равно нулю, а интересующий нас объем представляет собой бесконеч-
бесконечную область, так что во втором члене G и ее производные равны нулю.
Тогда
G.4.12)
G.4.12а)
В случае одного измерения эта формула приводится к
=
Формулу G.4.12) нетрудно истолковать с помощью плотности мгновенных
источников. При t0 = 0 в каждом элементе пространства было задано
некоторое количество тепла, равное для одномерного случая ф0 (х0) dx0.
798 Гл. 7. Функции Грина
Эффект этого источника при t > t0 получается при помощи умножения на
функцию (a/2y~Td)e-a2^x-x^2lit, описывающую, как это тепло диффундирует
от х0. Результирующее ф в х получается линейным наложением эффектов
в х каждого из источников при различных х0.
Конечные границы. Функцию G для ограниченных областей можно
получить методом отражений или методом собственных функций. Метод
отражений полностью аналогичен ¦ уже описанному для скалярного уравне-
уравнения Гельмгольца. В качестве простого примера рассмотрим полупро-
полупространство ж>0. Допустим, что температура ф является функцией только
от х и t, а температура на границе х = 0 меняется во времени по простому
гармоническому закону
ф@, t) = T0coswt.
Чтобы воспользоваться формулой G.4.8), нужно иметь функцию Грина,
значения которой при ж=0 равны 0. Она получается при помощи метода
изображений:
САт 1 I T t \ = — - Гр-а2(ж-хсJ/4(«-<о) p-°2(*+*o)8/4(l-lo)l П L 1 ЧЛ
К ' ° °' a22fa{t-t0) I \ f
Подставим функцию Грина G.4.13) в G.4.9). Чтобы получить установив-
установившееся решение, перенесем «начало времени» на t = — со, когда начальные
значения равны нулю. При отсутствии источников
г
ИЛИ
cos
Более удобной переменной интегрирования является 5, где
Тогда
со
= |Z±Re К efc
оо
Можно показать, что интеграл справа равен постоянной, не зависящей
от х. Положим
/(*) =
6
7. 4. Функция Грина для уравнения диффузии 799>
Интеграл / можно записать в другом виде, если подставить т] = а2Д:
Отсюда
0= ^
Дифференцируя первое выражение для /, находим
о о
Следовательно, / не зависит от а и равно своему значению при a = 0r
т. е. -г-У~ъ. Отсюда
~ |Ло/2аж]. G.4.14)-
Это выражение, очевидно, удовлетворяет граничному условию при х = 0.
Функция ф (х, t) изображает температурную волну, которая движется со
скоростью }/2а)/с, но ослабевает с ростом х. Скорость волны, как мы
видим, зависит от частоты колебания температуры, причем эта скорость
тем больше, чем выше частота, и стремится к бесконечности, когда и>
неограниченно возрастает; этот кажущийся парадокс мы вскоре рассмотрим.
Из решения для гармонически колеблющегося граничного значения «1»
при помощи интеграла Фурье можно получить решение для граничного
значения с любым видом зависимости от времени.
Пусть
со
ф@, t) = T(t) = ±Re { \ 7»е-**do} .
— OD
Тогда
ОО
ф (ж, t) = ^ Re | ^2" (со) «*¦*-Vtoax da)} . G.4.15)
—со
Для полубесконечного одномерного случая можно воспользоваться этим
выражением вместо G.4.9). Техника нахождения преобразований Фурье
будет рассмотрена в § 11.1, а ее приложения к задачам диффузии —в § 12.1.
Решения при помощи собственных функций. Функцию Грина можно
также разложить по собственным функциям. Пусть ип — решение скаляр-
скалярного уравнения Гельмгольца в области, ограниченной поверхностью S, на
которой ип удовлетворяет однородным граничным условиям. Тогда
Так как функции ип образуют полную систему, то G можно разложить
по ним; конечно, коэффициенты разложения будут зависеть от времени.
Пусть
G (г, 11 rOf t0) = 2 Сп С. 1о) и„ (г) пп (г0).
-800 Гл. 7. Функции Грина
Подставляя это разложение в уравнение G.4.3), которому должно удовле-
удовлетворять G, и замечая, что
получаем для Сп простое дифференциальное уравнение первого порядка
¦откуда
С -— -,-(*>2)('-<о) и(t - t0).
п ~~ а?
Следовательно,
G(r,t\ г0, О = g- и (t -10) ^ e-<ft>2><'-'°> ип (г)пп (г0). G.4.16)
Это выражение можно теперь применить в формуле G.4.9) для реше-
решения задач, включающих объемные источники, неоднородные граничные
условия и начальные значения. Предположим, например, что объемных
источников нет, а граничные условия однородны. Выберем собственные
функции ип, удовлетворяющие тем же однородным граничным условиям.
Тогда из G.4.9) имеем
п(ГоLо(Го)^о для *>0. G.4.17)
При 2 = 0 формула G.4.17) сводится к разложению <Ь0 по ип. Обратно,
легко вывести выражение G.4.17), если от обычного разложения по соб-
собственным функциям потребовать выполнения начальных условий. Пусть
Полагая 2 = 0, получаем
откуда следует разложение G.4.17).
Максимальная скорость передачи тепла. Как мы указали в § 2.4,
уравнение диффузии, управляющее передачей тепла в газе, является только
приближением к довольно сложному закону движения молекул газа. Один
из непосредственно очевидных недостатков этого приближения заключается
в том, что, согласно этому уравнению, если сообщить тепло некоторой
точке тела, то температура этого тела начнет мгновенно повсюду подни-
подниматься (хотя и не одинаково). Например, функция точечного источника
G (R, т) G.4.10) становится отличной от нуля для всех значений R сразу же,
как только z станет положительным. Так как такое мгновенное распростра-
распространение тепла невозможно, то нужно принять, что уравнение диффузии спра-
справедливо только по истечении достаточно большого промежутка времени. Это
время, естественно, зависит от скорости распространения тепла, которая
в свою очередь зависит от средней длины свободного пробега X молекул
газа. Скорость распространения возмущения в газе является, конечно,
скоростью звука с. Если время, требуемое, чтобы изменение температуры
достигло рассматриваемой точки, превышено, то можно предполагать, что
7. 4. Функция Грина для уравнения диффузии 801
уравнение диффузии приложимо. Уравнение с частными производными,
учитывающее этот эффект, имеет вид
К этому уравнению можно также прийти с другой точки зрения, рас-
рассматривая изменение уравнения звуковой волны из-за диссипации. Мы встре-
встретимся с этим уравнением, рассматривая эффект потерь на сопротивление
при колебании струны, а также распространение электромагнитных волн
в проводящей среде.
Соответствующая функция Грина для G.4.18) удовлетворяет уравнению
§ g -r0)8(*-i0). G.4.19)
Мы вновь примем принцип причинности. Условие взаимности имеет вид
G (r, 11 r0, t0) = G (r0, —10 | г, -1).
Аналогом формулы G.4.9) служит формула
I*
Ф (г, t) =\dto\j dV0 (PG) +? ^ dV0 [фС],0=0 +
t*
i S dt° § dS° ¦[G grad« * - * grad«G]+
0
Теперь займемся функцией Грина g (R, т), отвечающей G.4.20), для
бесконечной, неограниченной области. Пусть
G.4.21)
Подставляя это выражение в G.4.19), получаем дифференциальное уравне-
уравнение, определяющее у(Р, ъ):
где пространственная размерность п равна 1, 2 или 3. Заметим, что у является
функцией только от р2 и т, так что интегрирования по углам, определяю-
определяющим направление р, которые требуются в G.4.21), можно немедленно вы-
выполнить. Пути интегрирования в каждом случае выбираются так, чтобы
удовлетворялись требуемые граничные условия:
при » = 3,
оо
= tz \ H0(pR)f(p,x)pdp при /г = 2,
—СО
оо
= \ eiPR^(p,i)dp при /г=1. G.4.23)
—со
51 Ф. м. Морс и Г. Фешбах
'802 Гл. 7. Функции Грина
Заметим, что трехмерная функция Грина связана с одномерной. Пусть
g3(R, х) — трехмерная функция Грина, a gt — одномерная. Тогда
)
где мы привяли во внимание различие функций у, которое дает правая
часть уравнения G.4.22).
Для определения у сначала надо рассмотреть решения однородного
уравнения, соответствующего G.4.22). Они равны
е-«оч и ^
где ш* и а)" —решения уравнения оJ + гша2с2— /?2с2 = 0:
ш*= |-[ — ш2с2 + У 4jd2c2 — а4с4], аГ = у [ — ю2с2 — У4/?2с2 - а4с4].
Подходящая линейная комбинация решений, удовлетворяющая условию
у (-с) = 0 при х < 0, равна
Интеграл, определяющий glt приобретает вид
где в качестве контура берется линия в верхней полуплоскости р, парал-
параллельная вещественной оси р. Линия ветвления проводится от р = а2с/2
до р = — а2с/2 вдоль вещественной оси. Рассмотрим теперь интеграл, содер-
содержащий е""**":
л 2 —
27е
Если R > сх, то контур можно замкнуть полуокружностью в верхней
полуплоскости. Тогда интеграл равен нулю, так как внутри контура нет
особенностей. Если R < сх, то контур деформируется так, чтобы он про-
простирался вдоль отрицательной мнимой полуоси. После этого надо подсчи-
подсчитать интеграл, весьма близкий к тому, с которым мы имели дело при вы-
вычислении функции Грина для уравнения Клейна—Гордона. Мы получаем
(см. таблицу преобразований Лапласа в конце гл. 11)
TCI _
-е
Jo\ -^azcyH*—сгъг \u(c-—R).
Рассмотрим теперь слагаемое, интеграл в котором содержит e~ixa~'z:
jl_ _1а2с2т Г exp [ipR+i Yp*—.a*cilli сх\ ,
2се ^ ар.
С |/2А2
Этот интеграл равен нулю при R-\-cz>0 (напомним, что в одномерном
случае R может быть отрицательным), но отличен от нуля при R-\-cz < О.
Отсюда получаем
6
С
7. 5. Функция Грина для уравнения диффузии '803
Комбинирование этих двух выражений приводит к формуле
gx {R, х) = 2ъс e-ia2c2lz Jo [^ VR'-c*x> ] и (сх- | R |). G.4.25)
Читатель может убедиться в том, что это выражение стремится к точным
предельным формам G.4.10) и G.3.16), когда с—> оо или а—>0 соот-
соответственно.
Теперь можно получить трехмерную функцию g из дифференциального
уравнения G.4.24):
.G.4.26)
Функцию Грина для двумерных задач проще получить, интегрируя g3 С^> х)
по компоненте z вектора R, чем при помощи прямого рассмотрения фор-
формулы G.4.23). Пусть Я2 = ?2 + р2. Тогда
ИЛИ
G.4.27)
Здесь мы воспользовались формулой
х B2 sin 6) d6 =
где /1(ж)= —iJ^iioc) (см. таблицы в конце гл. 10 и 11).
Рассмотрение трехмерного случая показывает физические явления, ко-
которые учитываются включением скорости распространения в уравнение диф-
диффузии или диссипативного члена в волновое уравнение. Оба члена в G.4.26)
при R > cz равны нулю, как и надо ожидать во всех случаях, когда
эффекты распространяются с конечной скоростью. Первый член воспроиз-
воспроизводит начальное возмущение импульсного типа, уменьшенное, однако, двумя
множителями. Первый, 1/R, — это геометрический множитель, появлявшийся
в решении простого волнового уравнения. Второй—множитель е z — гово-
говорит нам, что эта часть волны, порожденной точечным источником, убывает
со временем при движении через среду. Второй член в G.4.26) образует
след. Для достаточно больших промежутков времени cz > R этот член при-
приводит к обычному приближению диффузии.
Эти различия можно выявить другим способом. Решим одномерную
начальную задачу. Из G.4.20) находим
51*
804 Гл. 7. Функции Грина
Значит,
¦i = ~ е~2агс2' [ф0 (х + ct) + %(х- а)] +
х+Ы
1 *±
~-ct
— fi f* 1/ p t -^— I v — *тм I > A\ i v \ dv 1
2 u. t, у l, i \j,0 j;) I Г то \."*"о/ tt-*'o i
x+ct
^-e 2 \ /0 a2cl/c2f2— (ж0 - жJ уо(жо)сгжо, G.4.28)
3C-C<
где фо(жо) и v0 (x0) — начальные значения ф и 5ф/5^ соответственно. Заме-
Заметим, что эта формула при а—>0 переходит в решение Даламбера G.3.18).
Первый член тот же, что и в формуле Даламбера, за исключением убываю-
j
щего во времени множителя е % . Второй член новый и представляет
эффект диффузии. Третий член при а —> 0 приводится к соответствующему
члену в формуле Даламбера.
7. 5. Функция Грина в абстрактной операторной форме
До сих пор наше рассмотрение ограничивалось специальными видами урав-
уравнений с частными производными. Пространственный оператор имел вид V2,
а временной оператор отсутствовал, был равен d/dt или равнялся dz/dt2
для уравнений Гельмгольца, диффузии и волнового соответственно. В на-
настоящем параграфе мы обобщим эти рассмотрения так, что они станут
применимыми к любому оператору, это позволит применять теорию к лю-
любому уравнению физики, если только оно линейное. Наш план— выделить
существенные элементы предыдущего исследования и затем посмотреть,
как их лучше всего обобщить.
Естественно, что рассмотрения будут несколько абстрактными. Напри-
Например, вместо выписывания частного вида рассматриваемого однородного
уравнения мы запишем его в операторном виде
,#ф = 0, G.5.1)
где А действует на координаты, от которых зависит ф. Например, в урав-
уравнении диффузии &=V2— a2d/dt и действует на г ж t. Другие примеры
линейных операторов дают интегральные уравнения, с которыми мы встре-
встретились в гл. 2 (см. стр. 177) и которые будут исследованы более полно
в гл. 8. Для них оператор & имеет вид
ь
& = 1 — \ К (х, х0) ... dx0
а
и уравнение ,#ф = 0 читается так:
ь
ф (ж) - ^ К (х, х0) ф (ж0) dx0 = 0.
a
Переменные могут включать не только пространственную и временную
зависимость. Так, в задачах переноса (§ 2.4) функция распределения /
зависит не только от г и (, но также от импульса р и энергии Е.
7. б. Функция Грина в абстрактной операторной форме 805
В тех же обозначениях уравнение для функции Грина G имеет вид
|xo) = -4*8(x-xo), G.5.2)
где х—обобщенный вектор, представляющий все участвующие независи-
независимые переменные; ,# действует на х. Так, для волнового уравнения х = ахх-\-
-\-ayy-\-azz-\-att, где а,,, и т. д.— единичные взаимно ортогональные век-
векторы. При этом 6(х —х0) становится произведением 6-функций по отдель-
отдельным координатам; например, для волнового уравнения
l(x-xo) = b{x-xo)o(y-yo)o(z~zo)b(t-to).
Обобщение теоремы Грина, сопряженные операторы. Наиболее важ-
важным математическим инструментом, применявшимся в исследованиях пред-
предшествующего параграфа, была теорема Грина; первая наша задача—обоб-
задача—обобщить ее. В дифференциальном виде теорема Грина утверждает, что
Непосредственно напрашивается обобщение этого равенства для оператора .#:
—vfiu=V - Р(м, v), G.5.3)
где Р—обобщенный вектор, выражающийся через те же единичные векторы,
что и х, тогда как V — соответствующий градиентный оператор. Отсюда
V Р = dPJdx + дРу/ду + dPjdz + dPt/dt + ....
Например, в случае волнового уравнения, когда & = V2 — A/с2
из G.5.3) мы находим, что
д
dul 1 S Г dv du
\[V
Здесь P = uVv — vVu, где V — общий градиентный оператор.
Соотношение G.5.3) удовлетворяется не всеми операторами й-. На-
Например, в случае одномерного уравнения диффузии, й- = д2/дх2 — аг d/dt,
мы находим, что
- м д Г dv dul Л а» ди!
дх \_ дх dx J L dt dt J
Первая пара членов в правой части имеет подходящий вид. Однако вто-
вторую пару нельзя записать в виде производной по времени от функции от
и и v. Поэтому надо обобщить теорему Грина по сравнению с G.5.3):
u&v— v&u = V .Р(м, v), G.5.4)
где i?- — оператор, называемый сопряженным к ,#. Если ,# = ¦#, т. е. если
имеет место равенство вида G.5.3), оператор ,# называется самосопряжен-
самосопряженным. В случае уравнения диффузии & = д2/дх2 + a^d/dt. Определение G.5.4)
является непосредственным обобщением определения сопряженного опера-
оператора, которое было дано в гл. 5 (см. стр. 499). Согласно формуле E.2.10)
оператор & был определен соотношением
v (z) Л- [у (z)] - у (г) M[v(z)] = ~P {v, у),
где Р (р, у) — присоединенная билинейная форма. Это не что иное, как соот-
соотношение G.5.4) для одномерных задач.
806 Гл. 7. Функции Грина
Вспоминая о том, каким способом применялась теорема Грина, мы
видим, что нам придется заниматься решениями уравнения
.#0 = 0 ' G.5.5)
и соответствующей функцией Грина для сопряженного оператора
.#G(x|xo) = — 4тио(х-хо). G.5.6)
Уравнение G.5.5) называется сопряженным к уравнению G.5.1), содержа-
содержащему ,#, а функция ф называется сопряженной к ф. В случае одномерного
уравнения диффузии уравнение ,# ф = 0 имеет вид
Мы видим, что ф удовлетворяет уравнению диффузии с обращенной времен-
временной переменной. Отсюда, если ф (t) есть решение уравнения G.5.1), то
>b(t) = ф (— t) -- решение уравнения G.5.5).
Раз мы обладаем обобщением теоремы Грина, становится возможным
решить неоднородную задачу
Щ= -4тер(х) G.5.7)
с неоднородными краевыми условиями. Так как в теорему Грина G.5.4)
входит сопряженный оператор «#¦, то ясно, что надо сравнить G.5.7)
и G.5.6). Умножаем последнее равенство на ф(х), а первое на G(x|x0)
и вычитаем одно из другого:
Пользуясь G.5.4), интегрируем по объему в пространстве х (который
включает всю нужную с точки зрения физической задачи область измене-
изменения каждой компоненты х). Например, в случае волнового уравнения мы
интегрируем по времени от 0 до to и по координатам х, у и z внутри
поверхности, на которой должны удовлетворяться граничные условия.
Получаем
ф (х0) = ^ р (х) G (х | х0) dv + A/4«) ^ V -Р [G (х | х0), ф (х)] efot
или
¦Нхо)= J P(x)G(x|x0)tft; + (l/4*)§n-P[G(xs|x0), b(x*)]dS, G.5.8)
где п — направленный наружу единичный вектор, ортогональный к поверх-
поверхности S, ограничивающей объем в пространстве х. Для скалярного волно-
волнового уравнения последний член имеет вид
Эффект краевых условий. Для дальнейшего необходимо рассмотреть
краевые условия, которым должно удовлетворять ф. Рассмотрим случай,
когда ф удовлетворяет однородным краевым условиям на S; другими сло-
словами, на поверхности S нет источников поля ф. Согласно принципу нало-
наложения, решение можно получить в виде интеграла от распределения объем-
объемных источников р (х), умноженного на решение, выражающее эффект от
точечного источника в х. Для этого надо рассмотреть два вопроса. Прежде
всего надо связать G с G. Как мы увидим, это приведет к обобщенному
7. S. Функция Грина в абстрактной операторной форме 807
условию взаимности. Мы отложим доказательство этой теоремы на корот-
короткое время. Во-вторых, чтобы получить решение в подходящем виде, необхо-
необходимо, чтобы член в G.5.8), содержащий поверхностный интеграл, исчез..
Однородные краевые условия, которым удовлетворяют функция Грина G
н функция ф, должны быть так согласованы, чтобы
n.P [G(xs| х0), ф (х8)] ^ = 0. G.5.9)
В простейшем рассмотренном нами случае скалярного уравнения Гельм-
гольца член с интегралом по поверхности исчезает, если функция Грина
и функция ф удовлетворяют одним и тем же однородным граничным усло-
условиям. Кроме того, в случае скалярного волнового уравнения, где мы
пользовались начальными значениями для dty/dt и ф, т. е. условиями Коши,
для функции Грина мы применяли также условие причинности (см. стр. 772).
С другой стороны, можно определить подходящие краевые условия,
которым должна удовлетворять ф (как мы указали это ранее, в § 7.2).
Например, для уравнения Гельмгольца поверхностный член содержит зна-
значения ф и д^/дп на поверхности. Положить оба эти значения равными
нулю явно не годится, так как в этом случае поверхностный интеграл
обращается в нуль автоматически, краевое условие на G остается произ-
произвольным и решение неоднородного уравнения становится не единственным.
Так как решение на самом деле единственно, то такое допущение о значе-
значениях ф и dSf/дп на поверхности неправильно, и мы приходим к ослабле-
ослаблению граничных условий до однородных условий Дирихле, или Неймана,
или некоторой их линейной комбинации. Определив граничные условия
для ф, добиваемся, чтобы поверхностный член исчез. В случае уравнения
Гельмгольца G должна для этого удовлетворять тому же граничному
условию, что и ф. Подобным же способом испытание формулы G.5.9) при-
приводит к определению подходящих краевых условий для ф и соответствую-
соответствующих условий для G.
Определив таким образом краевые условия на ф и G (x | x0), мы можем
теперь вернуться к условию взаимности. Сравним уравнения, которым
удовлетворяют G и G:
|хо)= — 4itu(x-x0), %G(x\x1) = -4тсо(х — х,).
Умножаем первое из них на G, второе па G, вычитаем одно из другого
и интегрируем по соответствующему объему в пространстве х. Пользуясь
обобщенной теоремой Грина G.5.4), получаем
Чтобы решение неоднородной задачи об источниках с Годнородными крае-
иыми условиями можно было выразить через G, не используя G, необ-
необходимо, чтобы между ними имелось простое алгебраическое соотношение,
которое требует в свою очередь, чтобы член с поверхностным интегралом
в последнем равенстве исчез. Сравнивая этот член, содержащий поверх-
поверхностный интеграл, с G.5.9), мы видим, что G(x|x0) удовлетворяет тем
же условиям на S, что и ф; этого можно было бы ожидать на основании
наших интуитивных представлений о G и о ее связи с ф.
Окончательно получаем
G(x|xo) = G(xo|x). G.5.10)
808 Гл. 7. Функции Грина
Выражаясь словесно, левая часть этого равенства описывает эффект
в точке х от точечного источника в х0, причем распространение возмуще-
возмущения описывается оператором .59" и краевыми условиями. Выражение в правой
части соответствует случаю, когда источник помещен в х, эффект
измеряется в х0, а распространение возмущения, происходящее от х до х0,
описывается оператором Л и соответствующим краевым условием для 6'.
Если G отлична от G, то в пространстве х должна существовать направ-
направленность при распространении возмущения, так как обращение направле-
направления распространения изменяет результат наблюдения. Эта необратимость
должна проявляться в операторе & или в краевых условиях. Например,
оператор fl для уравнения диффузии V2 — a2d/dt не инвариантен относи-
относительно изменения направления времени, т. е. относительно подстановки — t
вместо -\-t. Оператор для волнового уравнения &¦¦= V2 — A/с2) (d2/dt2)
самосопряженный (<#=.#-), так что из него нельзя получить направлен-
направленность, например, временной координаты. Однако эту направленность можно
сразу вывести из наложенных краевых условий. Так, применение условия
причинности накладывает определенную асимметрию по отношению к про-
прошедшему и будущему. Как следствие этого, принцип взаимности для функ-
функции Грина волнового уравнения при этих начальных условиях читается
так:
G{t, t\t0, to) = G(to,-to\r, —t),
так что
G(T,t\T0,t0) = G(r,-t\T0,-t0). G.5.11)
Мы видим, что G описывает распространение от точки источника г0 до
точки г, которое, однако, обращено во времени, так что событие в момент t
происходит на некоторое время раньше, чем импульс, порождающий это
событие в момент t0 (заметим, что t < t0). [Например, в случае функции
Грина для бесконечной области
При данном R эффект ощущается в момент t = to — R/c, т. е. на время Я/с
раньше, чем начало движения в t0. По этой причине G часто называется
опережающим потенциалом, тогда как G = {1/R) о [R/c — (t —10)] — запазды-
запаздывающим потенциалом. Оба они являются решениями задачи об источнике
при различных начальных условиях.
Из-за эффекта краевых условий полезно обобщить идею сопряженности.
Мы введем два термина: сопряженные краевые условия и сопряженная
задача. Сопряженная задача удовлетворяется функцией <|», являющейся
решением уравнения
,#ф = 0
и удовлетворяющей сопряженным краевым условиям. Мы определим послед-
последние требованием
п-Р[ф, ф] = 0 на граничной поверхности. G.5.12)
Отсюда если ф удовлетворяет некоторому краевому условию, то ty будет
удовлетворять соответствующему краевому условию, которое мы назовем
сопряженным краевым условием. Задача считается самосопряженной,
если & — & и краевые условия для фиф одинаковы. Для самосопряженных
задач G (х | х0) = G (х | х0).
7. б. Функция Грина в абстрактной операторной форме 809'
Еще о сопряженных дифференциальных операторах. Перейдем теперь
к более определенному рассмотрению некоторых операторов и им сопряжен-
сопряженных. В качестве первого примера рассмотрим одномерную ситуацию. Здесь
мы вообще будем интересоваться операторами второго порядка, так что
можно написать
Сопряженный оператор ра'вен (см. формулу E.2.10) и далее)
¦#M = ?^M)-iteM) + ™- G.5.14>
Присоединенная билинейная форма записывается в виде
G.5.15)
При каких условиях ,# будет самосопряженным? Приравнивая «#¦ и ,#, мы
находим, что dp/dz должно равняться д. Отсюда
d Г dv
Уравнение &v = 0 является как раз уравнением Штурма — Лиувилля, иссле-
исследованным в § 6.3. Мы видим, что среди дифференциальных операторов
второго порядка только оно соответствует линейному самосопряженному
оператору.
Если dp/dz = q, то присоединенная билинейная форма Р равна
„ / dv du \
P=pl U-, V—7- ).
r \ dz dz J
Требование п-Р(М) = 0 "состоит в том. чти 0 = р( ty-X— й-г^ ) =
= p ( d)-J- — ф -p- ) , где а и Ъ — точки, в которых удовлетворяются гра-
\^ uz dz yz^b
ничные условия. Если р конечно (и отлично от нуля) в концевых точках,
то возможными условиями являются условия Дирихле (ф = 0 в точках а и Ь)Т
Неймана (dty/dz = 0 в точках а и Ъ) или смешанные (dty/dz = рф в точках
а и Ь). Все эти граничные условия самосопряженные, так как ф Должно
удовлетворять тем же граничным условиям, что и Ф. Периодические гра-
граничные условия ф (а) = <J< (b) и (dty/dz)z=a = (d'])/dz)z=b также самосопряженные.
Другой тип граничного условия получится, если р имеет нуль в а или Ъ.
В этом случае Р равно нулю в точке, если функции фиф только ограни-
ограничены. Это граничное условие опять самосопряженное. Конечно, эти же
самые условия мы рассматривали в гл. 6. Для всех них функция Грина
должна быть симметричной.
Можно обобщить выражения G.5.13) —G.5.15) на операторы, содержа-
содержащие производные высшего порядка и более чем одно измерение. Рассмотрим
Сначала оператор
*»° = P-S- G-5Л6>
Любой одномерный оператор является, конечно, линейной комбинацией
операторов типа &п. Сопряженный оператор равен
() G.5.17)
¦S10 Гл. 7. Функции Грина
Присоединенная билинейная форма равна
Р(и T,\-ni,dn~~4
G.5.18)
Для нескольких измерений наиболее общий дифференциальный оператор
.имеет вид
f n, G.5.19)
& = р(хг, х2, ...) f
ох1 ох2.. ¦ oxs
r;ic* х1г xt, . .., xs— координаты. Сопряженный оператор ,# равен
^Г ,Ъ, ...)••¦]• G-5.20)
Присоединенная билинейная форма Р (и, v) записывается в виде
1 l J 2 L fe« a^-1... a** a^aar,
где ay — единичный вектор, соответствующий координате
В качестве простого примера рассмотрим оператор
^^P^+^lyT + ^^^ + t- + m
Тогда
Id
Р(Ы> ») =
«и - й2 (* ,?М, р8г(гЦ) a (tit)
Г Sx> S(om) од(ги) , ~[
+ а,, аи -з if— 0—2 \ v + muv .
vL4dy ду дх J
Ввиду симметричной зависимости члена с г от а; и у, можно получить дру-
другое выражение для Р(м, v) [его можно получить из общей формулы G.5.21),
•если написать другое выражение для Р, положив х^ — у и х2 = х, и осред-
нить его с последним выражением, в котором xt = х и х2 = у]'.
dv д (qu) . dv д (ги)
В v+rukJ
v+muvj-
u-8x-—k
Условия, при которых онератор & будет самосопряженным, имеют вид
др , дг n dq дг п
дх ду ' ду ' 9ж
7. 5. Функция Грина в абстрактной операторной форме 811
Для совместности этих двух равенств надо также потребовать, чтобы
дх V дх J ду V ду J'
Тогда Р (u,v) значительно упрощается и принимает вид
ди \ , / dv
Сопряженные интегральные операторы. Определение сопряженного
оператора, данное в G.5.4), не очень подходит для интегрального опера-
оператора G.5.1), и попытка воспользоваться этим определением без изменений
не была бы плодотворной. Мы воспользуемся интегральным определением,
которое во многих отношениях слабее, чем G.5.4), но тем не менее остав-
оставляет большую часть наших результатов без изменения. Специальный выбор,
который мы намерены сделать, устранит все члены с поверхностными
интегралами, содержащие Р, из результата G.5.8); условие взаимности
{7.5.10) будет тем не менее иметь место. Для интегральных операторов мы
определяем сопряженный оператор ,# равенством
u&vdx- \ v&udx = 0. G.5.22)
Это определение получается из равенства G.5.4), взятого для одномер-
одномерного случая, при помощи однократного интегрирования G.5.4) от а до Ъ:
ъ
&V - V &U] dx = [Р (и, О)]?=а.
[ [U
Мы видим, что G.5.22) получается, если [Р (к, v)]?2a равно нулю. Напомним,
что для дифференциальных операторов так будет, если граничные условия,
которым удовлетворяют и и v, однородны и сопряжены одно другому
и смысле формулы G.5.12). Рассмотрим теперь следствие определения G.5.22).
Для примера исследуем оператор
ь
•#?>= \К(х, xo)v(xo)dzo.
а
Тогда, если А определен формулой
ь
Ъи = ^ К (х, х0) и (х0) dx0,
то определяющее равенство G.5.22) приобретает вид
ь
dx ^ [v (х) К (х, х0) и (ж0) - и (х) К (х, х0) v (x0)] dx0 = 0.
a a
Если переставить переменные интегрирования в первом интеграле, то это
равенство перепишется так:
ь ь
{v (ж0) и (х) [К (ж0, х) - К (х, ж0)]} dx0 = О»
812 Гл. 7. Функции Грина
Так как оно должно иметь место для произвольных к и v, то мы опре-
определяем К следующим образом:
К(х0, х) = К(х, х0), G.5.23)
что напоминает формулу G.5.10), где делае.тся подобное утверждение для
функции Грина. Как мы увидим в следующей главе, К очень часто
является функцией Грина или тесно связана с ней, так что получающаяся
здесь аналогия не слишком удивительна. В силу G.5.23) теперь можно написать
ь
&v= ^ К(х0, x)v(xo)dxo.
а
Условие, при котором & = Й, т. е. оператор является самосопряженным,
имеет вид
К(х0, х) = К(х, х0), G.5.24)
т. е. функция К должна быть симметричной относительно переменных х0 и х.
Другой тип интегрального оператора получается, если взять неопреде-
неопределенный интеграл
= ^ K(x, xo)v(xo)dxo.
а
Этот оператор можно привести к виду с постояиныме гределами, если
ввести единичную функцию, так что
ь
&v = ^ и (х — х0) К (х, х0) v (х0) dx0.
Положим
М(х, хо) = и(х — хо)К(х, х0).
Тогда сопряженный оператор & включает функцию
М(х, х0) = М (х0, х) = к (х0 — х) К (х0, х).
Отсюда
ь ь
.Яш = ^ к (х0 — х) К (х0, х) w (х0) dx0 = ^ К (х0, х) w (x0) dxu.
а х
Для самосопряженности оператора & должно быть М (х, х0) = М (ж0, х),
или
и (х — х0) К (х, х0) = и (х0 — х) К (х0, х).'
Это соотношение никогда не может удовлетворяться, так как к (ж — х0)
равно нулю всюду, где к (х0 — х) равно единице, и обратно. Поэтому Л для
неопределенных интегралов не является самосопряженным.
Обобщение этих определений на случай более одного измерения
не требует привлечения каких-либо новых принципов, и потому мы пере-
перенесем исследование этого случая в задачи в конце главы.
Обобщение на абстрактное векторное пространство. Как и при раз-
развитии теории собственных функций, полезно и поучительно распространить
теперь наше исследование на представление результатов этой главы
в абстрактной символике векторного пространства и векторных операторов.
Эта символика была впервые рассмотрена в § 1.6 и широко применялась
7. 5. Функция Грина в абстрактной операторной форме 813
в §§ 2.6 и 6.3. Там мы показали, что любой вектор F абстрактного про-
пространства можно выразить либо через его компоненты по ортогональной
системе собственных векторов еп,
F= У. F e F — F*-e
п
множество которых счетно, либо через его компоненты по системе единич-
единичных векторов е(х), соответствующих 8-функциям,
F = [ F (х) e (х) dx, F (x) = F*e{x),
множество которых несчетно (отметим, что х здесь изображает совокупность
координат, как, например, х, у, t, а интегрирование производится по области
изменения этих переменных внутри границы). Векторы в абстрактном про-
пространстве задаются одномерной системой компонент, Fn или F(x).
Кроме того, мы имели дело с операторами 91, обобщениями в абстракт-
абстрактном векторном пространстве дифференциальных операторов, рассмотренных
в первой части этого параграфа. Они задаются при помощи двумерной
матрицы с компонентами Атп или А(х\х0):
® = 2 «WWS = [ dx \ е (х) А {х \ х0) е* (х0) dx0, G.5.25)
mn
где можно было бы писать г, г0 вместо х, х0 и dV вместо dx, чтобы
подчеркнуть, что сюда может быть включено более одного измерения. Если
матрица Атп диагональная (Атп = ат6тп), то единичные векторы еп явля-
являются для 91 собственными векторами, удовлетворяющими уравнению
2I-en = arien; если Атп — не диагональная матрица, то система еп является
системой собственных векторов для некоторого другого оператора, а не 91.
Оператору §1, действующему на вектор F, соответствует дифференциаль-
дифференциальный оператор .#г, действующий на функцию F (г):
И-F = J [&rF (г)] е (г) dV = ^ dV ^А (г | г0) F (г0) е (г) dV0,
где &г — дифференциальный (или интегральный) оператор, рассмотренный
в первой части этого параграфа. Вторая форма иллюстрирует тот факт, что
любой оператор можно выразить в интегральном виде. Для дифференциаль-
дифференциальных операторов зто легче всего показать при помощи дельта-функции и ее
производных. Например, если &x = g(x) (d/dx) + r(x), то матрица для 91,
выраженная через х-ы, имеет вид
А(х\хо)= -g(x)b' (хо-х)+г(х)Ъ(хо-х),
так как тогда (см. стр. 775)
I{х|х0)F(х0)dx0 = g(x)^-F(x) + r (x) F(х). G.5.26)
Высшие производные можно выразить через высшие «производные» дельта-
функции; нетрудно видеть, что все операторы, с которыми мы до сих пор
имели дело в этом параграфе, можно выразить через эквивалентную функ-
функцию А (х | х0), включающую дельта-функцию и ее производные, функции
от х и х0 и, быть может, единичную функцию и(х0 — х) (см. стр. 778).
Для обобщения метода функций Грина нам надо сначала найти опера-
операторное обобщение теоремы Грина, затем найти обобщение дельта-функции,
соответствующей единичному источнику в правой- части неоднородного урав-
уравнения, и, наконец, найти искомое решение обобщенного операторного
уравнения.
814 Гл. 7. Функции Грина
Мы уже обобщили теорему Грина формулой G.5.22). Она в то же
время определяет, что понимается под сопряженным оператором и что
требуется от сопряженных краевых условий, а также служит основой для
соотношения взаимности. Все эти вопросы надо теперь перевести на векторно-
операторный язык.
Сопряженные, комплексно сопряженные и эрмитовы операторы.
Формула G.5.22) равносильна теореме Грина. Запишем эту формулу
в несколько ином виде:
[к (х) &xv (ж) - v (х)&хп (х)] dx = 0. G.5.27)
Она до некоторой степени подобна формуле, определяющей оператор, эрми-
эрмитово сопряженный к данному [см. стр. 86, а также формулу F.3.72)],
которая в компонентах вдоль векторов е(х), соответствующих 8-функциям,
имеет вид
\ {к (x) &xv (x) — v(x) [&*u (x)]
или
dx {и (х) А {х | х0) v (х0) — v (х) А* (х | х0) и (х0)} dx0 = 0,
где и(х) и v(x) — соответствующие компоненты векторов U, V. Так как
компоненты А* (х \ х0) эрмитово сопряженного к ЭД оператора комплексно сопря
жены компонентам оператора, транспонированного к % (который получается
заменой строк на столбцы), то последний интеграл автоматически равен
нулю.
Однако формула G.5.27) не точно такая же, так что мы отметили
различие, употребив тильду (&) вместо звездочки (&*). Чтобы выяснить
характер этого различия, надо вернуться к определению сопряженного
дифференциального оператора. Тогда становится очевидным, что если
А (х | х0) — компоненты оператора 91 вдоль осей е (х), то компонентами ?(
служат А(хо\х), тогда как компонентами 91* являются А(хо\х). В одпом
случае мы заменяем строки на столбцы (х на х0), а в другом мы, кроме
того, переходим к комплексно сопряженным величинам.
Чтобы показать, что переход к обычному сопряженному оператору
соответствует перестановке х и х0 в компонентах по е (х), можно рассмотреть
формулу G.5.27) для случая дифференциального оператора gd/dx + r. Здесь
компоненты оказываются равными
А (х | х0) = — g (ж) о' (х0 — х) + г (х) о (х0 — х).
Простая перестановка х и х0 дает
А(х | х0) = А (х01 х) = — g (х0) о (х — х0) + г (х0) о (х- х0),
чему соответствует дифференциальный оператор
V (*) = \ Чх | х0) F (х0) dx0 = - A (gF) + r(x)F {x);
то, что мы действительно получили сопряженный оператор, видно из фор-
формулы G.5.14).
Теперь можно резюмировать наши соглашения относительно эрмитовой
сопряженности, сопряженности и комплексной сопряженности. Компоненты
7. 5. Функция Грина в абстрактной операторной форме 81&
вектора F*, комплексно сопряженного к F, комплексно сопряжены компо-
компонентам F:
f=2 Ла. = \F (*)е (*) *c F*=2 е«7п = ^ °* (^^dx G-5-28>
(можно также просто называть вектор F* сопряженным к F). Компоненты
оператора 91, сопряженного к 91, получаются в результате перестановки
строк и столбцов (транспонирования); компоненты оператора 91, комплексно
сопряженного к 91, равны комплексно сопряженным к компонентам 91, и,
наконец, эрмитово сопряженный- оператор 91* получается в результате пере-
перестановки строк и столбцов и перехода к комплексно сопряженным величинам:
« = 2 eAraeL 31* = f = 2 en JmBe-, G-5-29)-
nm nm
91 =!•, 1 = 9>.
Если 91 эрмитов, то 91* = 91, однако 91 =? 91, за исключением случая, когда
все элементы 91 вещественны. Если 91 вещественный, то 91 = 91, однако
91 Ф 91, за исключением случая, когда 91 эрмитов, и т. д.
Заметим, что свойство оператора быть эрмитовым инвариантно относи-
относительно поворота осей в векторном пространстве, тогда как свойство быть
вещественным (или быть самосопряженным) не инвариантно. Например,
матрица из компонент 91 вдоль ах и а2
эрмитова, но не вещественна и не самосоцряженна. Эта матрица имеет
собственный вектор ех = 1/ -ц [ах— а2/A — i)] с собственным значением О,
а также собственный вектор е2= I/ -5-[a2-l-a1/(l^-i)] с собственным значе-
значением 2. Относительно этих новых осей матрица 91, конечно, диагональна,
*~\0 2
т. е. все еще эрмитова, но, кроме того, вещественна и самосопряженна.
Функция Грина и оператор Грина. Таким образом, аналогом неодни-
родного уравнения &rty (г) = — 4тс р (г) является операторное уравнение
91-F= — 4тсР, где F и Р—абстрактные векторы, а 91—один из описанных
нами операторов. Что является аналогом уравнения &rG(r | г0) = — 4тс S (г — г0)
для функции Грина? Мы видели раньше, что компоненты вдоль осей е(г)
оператора тождественного преобразования (идемфактора)
3 = \ е (г) е* (г) dV, %¦? = F для любого F G.5.30)
как раз равны дельта-функции о (г—г0), так что аналогом правой части
уравнения для функции Грина могло бы быть — 4к^.
Это сделало бы также функцию Грина скорее аналогичной абстракт-
абстрактному векторному оператору, а не абстрактному вектору, так как если
правая часть уравнения является оператором, то такой же должна быть
816 Гл. 7. Функции Грина
и левая часть. Этот результат не удивителен, так как если аналогом плот-
яости источника — функции р — является абстрактный вектор Р, то аналогом
функции G должен быть оператор, преобразующий Р в решение F. Отсюда
аналогом неоднородного уравнения
^rG(r|r0)= -4icd(r-r0)
является
a.@=-4icg, G.5.31)
или в компонентах вдоль е(г)
А (г | г') G (г' | r0) dV = - 4* 8 (г- г0),
что эквивалентно дифференциальному уравнению для С Таким образом,
¦обобщением функции Грина является оператор Грина ®.
Глядя на уравнение G.5.31), мы сразу видим, что подходящей формой
для оператора Грина служит
@=-41сИ-1. G.5.32)
Другими словами, функция Грина получается представлением в компонентах
е (ж) произведения —4тг на оператор, обратный оператору Щ,, соответствую-
соответствующему однородному уравнению. Поэтому решение общего неоднородного
уравнения ЭД • F = — 4даР равно
F=@-P= -4яЯ.Р,Э G.5.33)
что является в этих общих понятиях очень простым и очевидным ответом.
Умножение на функцию Грина и интегрирование равносильны умножению
на обратный оператор; функция \ G (х \ х0) р (х0) dx0 дает компоненты вдоль
осей е (х) вектора — Aiz'u'1 -P.
Соотношение взаимности. Мы видели, что обобщение теоремы Грина
приводит к условию
где и и v удовлетворяют «самосопряженным» краевым условиям на гранич-
граничной поверхности. Оператор ЧЦ сопряжен к 91 (если ЭД эрмитов, то ЭД также
комплексно сопряжен к Ш). Его функцией Грина служит §, где §•$( =
= — 4icQ. Однако если транспонировать равенство G.5.31), то получается
(*> ¦ ЭД = — 4тсЗ; следовательно, Sq = (&. Другими словами, оператор Грина
для сопряженного оператора ЭД сопряжен к оператору Грина &:
S(r|>0) = G(r0|r), G.5.34)
что является обобщением теоремы взаимности G.5.10). В понятиях вектор-
векторного пространства этот результат является до некоторой степени тавтоло-
тавтологией. Если мы убеждены в том, что обобщением функции Грина является
оператор, то G.5.34) служит как раз определением сопряженности; с другой
-стороны, формула G.5.34) может служить подтверждением того, что опет
ратор ® на самом деле обладает достаточно хорошими свойствами.
Теперь мы видим, почему исследование в начале этого параграфа было
неполным и не могло быть полным в тот момент. Мы должны были рас-
рассматривать понятие «сопряженности» для дифференциальных (или интеграль-
интегральных) операторов, для функций Грина и для граничных условий до того,
как мы смогли увидеть, что G.5.27) на самом деле может содержать все
7. б. Функция Грина в абстрактной операторной форме 817
существенное из граничных условий и из свойств дифференциальных опе-
операторов, чтобы дать возможность определить операторы Грина. И мы
должны были исследовать поведение функций Грина до того, как мы могли
понять их связь с операторами.
Разложение оператора Грина в эрмитовом случае. Иногда бывает
полезно разлагать операторы и векторы по некоторым другим системам
собственных векторов, кроме бесконечной несчетной системы е(г). Так, если
оператор 'й равняется ? — X, где X — мультипликативная постоянная,
то можно было бы соблазниться разлагать участвующие величины по соб-
собственным векторам еп уравнения
где операторное уравнение включает в себя как граничные условия, так
и дифференциальный оператор. Например, оператор тождественного пре-
преобразования Qi равен ^_ епе*, и можно было бы выразить оператор Грина
через компоненты его матрицы до его же осям:
®= 2 emGm^. G.5.35)
m. n
Если ?— эрмитов оператор (и если краевые условия эрмитовы), то все
собственные значения \ вещественны и сопряженный оператор будет ком-
комплексно сопряженным к ?. Функции <j) (функции преобразования), входящие
в соотношение между еп и е (г),
e(r)=2i(r)em, G.5.36)
комплексно сопряжены к функциям <j) для сопряженного оператора ?. Если
оператор ? самосопряженный, то либо 0> — вещественные функции г (х, у, z, t),
либо же, если они комплексны, их комплексно сопряженные также входят
в систему собственных функций, так что при желании (и если это позволяют
краевые условия) можно было бы сделать все ty вещественными (например,
для угла <р можно пользоваться функциями eim? с положительным или
отрицательным т или же функциями cos m<p и sin m<p).
Чтобы решить неоднородное уравнение (й — X) • F = — 4тсР, надо сначала
решить операторное уравнение
(?_Х).@=-4*3- G.5.37)
Действуя затем обеими частями этого уравнения на вектор Р, соответству-
соответствующий функции плотности, мы видим, что решением уравнения (й —X)-F =
= — 4тсР будет F = t#-P.
Мы знаем, что (У равно —4тс(й — X), но это формальное решение
не очень полезно. Более плодотворным было бы получить разложение &
по собственным векторам еп. Подставляя G.5.35) в уравнение G.5.37),
мы видим, что матричные компоненты Ф по собственным векторам еп равны
^. G.5-38)
Функция Грина равна матричной компоненте & по векторам е(г):
Сопряженной к G будет функция G (r01 г), которая комплексно сопряжена
к G (г | г0). Это, конечно, является следствием того, что если оператор ?
52 ф. м. Морс и Г. Фешбах
818 Гл. 7. Функции Грина
эрмитов, то функция G также [см. формулу G.5.29)]. Если оператор ?
к тому же самосопряженный, так что все его элементы в этом разложении
вещественны, то функция G также самосопряженная и G(r | ro) = G(ro|r).
В этом случае или все 0> вещественны, или, если имеются комплексные ty,
их сопряженьые также являются собственными функциями, так что сумма
G.5.39) симметрична относительно г и г0.
Следовательно, вообще для эрмитового оператора функция Грина
с точкой наблюдения в г и источником в г0 комплексно сопряжена функции
Грина с точкой наблюдения в г0 и источником в г, тогда как для само-
самосопряженного оператора (с самосопряженными краевыми условиями) источник
и точку наблюдения можно переставить без изменения G. Это окончатель-
окончательное обобщение соотношения взаимности.
Неэрмитовы операторы; биортогональные функции. Иногда мы бываем
вынуждены рассматривать дифференциальные уравнения или краевые усло-
условия, которые не соответствуют эрмитовым операторным уравнениям. В этом
случае оператор ?* отличается от оператора ? и собственные векторы также
должны отличаться. Мы определим обе системы обычными уравнениями
где, конечно, em и fn имеют сопряженными векторами е*г и f?.
Собственные значения Хп для ? можно в принципе получить, если
известен эффект ? для некоторой стандартной системы взаимно ортогональ-
ортогональных единичных векторов ап (которыми, конечно, могут быть е (х)):
т, n m, n
согласно формуле A.6.36). Как показано в § 1.6, уравнениям G.5.40)
отвечают системы уравнений
2j Lmn (an• ev) = \ (am • ev), 2. Lnm (an • fv) = (j.v (am • fv)>
n n
которые для получения собственных значений Xv u ^ надо решить, находя
корни уравнений, полученных приравниванием нулю определителя из коэф-
коэффициентов при a?-ev и a*fv'-
|Z-mn-XvomJ = O, |?пт-^8тП| = 0- G.5.42)
Система корней Av тесно связана с системой корней ^, что станет очевид-
очевидным, если взять сопряженное к первому из уравнений G.5.40),
(? • ev)* = е* ¦ ?* = ^е*,
что даст
с вековым определителем
I Lnm — }-Фпт | = 0,
который совпадает со вторым определителем G.5.42). Следовательно,
система корней (iv совпадает с системой корней Xv, и можно упорядочить
индексы так, что fiv = Xv. Однако это не означает, что em = fm или ej = fn.
Если ? не эрмитов, то система собственных векторов е^ не является
ортогональной, но векторы in имеют ортогональную взаимосвязь с векто-
векторами ет; действительно,
Задачи к главе 7 819
так что
Следовательно, скалярное произведение f*-em равно нулю, за исключе-
исключением случая, когда m = п. Поэтому разложение любого вектора F имеет вид
F = 2*>». гДе *"„ = Я-Г. G-5.43)
Двойная система собственных векторов ет и in называется биортогоналъ-
ной системой собственных векторов. Об их представлениях через векторы
е(х)
говорят, что они образуют биортогональную систему собственных функций.
Отсюда оператор тождественного преобразования 3 равен 2 еп^*>
а разложение оператора Грина имеет вид
т, п
и соответствующая функция Грина равна
G-5-44)
Эта функция симметрична, только если <р„ = фи (как будет в некоторых
случаях).
В § 11.1 [формулы A1.1.21) и далее] мы рассмотрим случай колеблю-
колеблющейся струны с однородными граничными условиями, зависящими от часто-
частоты (наклон графика О на границе зависит как от значения ф, так и от ее
скорости). Эти граничные условия не самосопряженные, и соответствующий
оператор не эрмитов, так что надо применять биортогональные собст-
собственные функции. Мы решаем задачу для данных условий, а также для
сопряженных граничных условий, комплексно сопряженных к A1.1.22).
Оказывается, что в этом случае <р„= фя, так что ряд A1.2.25) соответствует
формуле G.5.44).
Задачи к главе 7
7.1. Круговой проводящий диск радиуса а с постоянным потенциалом V
помещен целиком в бесконечный плоский проводник (совпадающий с пло-
плоскостью z = 0), на котором поддерживается нулевой потенциал. Показать,
что функция Грина, соответствующая этой задаче, равна
Показать, что потенциал в точке (ж, у, z), порожденный этой комбинацией
проводников, равен
2те а
ф (г, Щ = ^ \ df jj у dy (г2 + уг - 2ry sin 9 cos ?)~3/2 ,
о о
где г2 = х2 4- у2 + z2 и tg 8- = A/z) V х2 + у2 . Найти плотность заряда на диске
и на бесконечном проводнике в виде определенных интегралов. Найти ф
для г, больших по сравнению с а, и для г, малых по сравнению с а.
52*
820 Гл. 7. Функции Грина
7.2. Пусть граничное условие на плоскости z = 0 состоит в том, что
= V на диске радиуса а и = 0 в остальной части плоскости. Пока-
Показать, что функция Грина равна
К* ~ ЧГ + (У - УоГ + (z - 20JГ1/2 + 1(х - xof + (у - yof + (z + zo)*r112 .
Подсчитать потенциал ф на поверхности диска и его градиент при г ^ а.
7.3. Пусть диск, о котором говорится в задачах 7.1 и 7.2, колеблется
нормально к своей плоскости со скоростью Ve~iwt, излучая звук в области
г > 0. Показать, что соответствующая функция Грина равна (eihR/JR)-\-
+ (eikR'/R'), где /с = ш/с и
Я2 = (х - х0
(Л'J = (х- *0
Показать, что если г2 = х2 4- у2 + z2 J> а2, то асимптотическое выражение
для 41 имеет вид
4» ~ (Va2/r) ёш~™Чх (ка sin 6)/ка sin б.
Применить этот результат для исследования диффракции Фраунгофера волн,
исходящих из круглого отверстия.
7.4. На внутренней поверхности сферы радиуса а поддерживается потен-
потенциал фа(&, <р), где & и <р —угловые координаты сферической системы, кон-
концентрической с данной сферой. Показать, что функция Грина, соответству-
соответствующая этой задаче, равна
2rr0'cos 6Г{ '2 - [{rrjaf + а* - 2rr0 cos 6]-1/2 7
где 6 —угол между радиусом-вектором г точки наблюдения и радиусом-
вектором г0 точки источника [cos 6 = cos & cos &0 + sin & sin &0 cos (9 — <p0)J.
Показать, что внутренний потенциал равен
r а т\ - а Г1 С r Y I
Найти разложение ф в ряд по степеням г/а, применимый для точек, нахо-
находящихся вблизи начала координат.
7.5. Показать, что в сферических координатах функция Грина для
уравнения Лапласа равна
n m I (/У ) Для
а для уравнения Гельмгольца
n, m
^m, n ч ( fn(kr) hn(kr0) ДЛЯ Г<Г0,
X/>™(cos&0)-{ . „ ч . „ ч
l /и (^ro) "-n К^П Для г > г0,
где /п и hn — сферические функции Бесселя (см. задачу 5.20 и таблицы
в конце гл. 11).
7.6. Решение уравнения Гельмгольца первоначально имеет вид
Фо (г) = 2 Amn COS (т? + ат) Р™ (COS &) l'n (кг)
Задачи к главе 7 821
и определено во всем пространстве. Вводится сфера радиуса а с центром
в начале координат, на которой ty должна удовлетворять граничному
условию
Показать, что новое решение ty уравнения V2ty 4- k2ty — О вне сферы, удо-
удовлетворяющее указанному граничному условию при г = а и тому условию, что
4» при г—> со должна равняться сумме % и расходящейся волны, является
решением следующего интегрального уравнения:
где G —второй ряд задачи 7.5, а интегрирование производится по поверх-
поверхности сферы.
7.7. Проволока радиуса b погружена в масляную ванну бесконечного
объема. Коэффициент тепло-диффузии как масла, так и проволоки равен а2.
Как масло, так и проволока сначала имели нулевую температуру. Через
проволоку послан электрический импульс, мгновенно нагревающий ее до
температуры То. Показать, что температура на расстоянии г от оси про-
провода через время t равна
При помощи разложения в ряд и асимптотического выражения для /0 под-
подсчитать Т для двух предельных случаев, когда 2a2t/r значительно меньше
или значительно больше Ъ.
7.8. Определить одномерную функцию Грина Gh (г | г0) для дифферев-
циального оператора Бесселя
где Gh (а \ г0) = 0. Показать, что Gk имеет особенности при к = кп, где
/0 (kva) = 0. Из поведения Gh в такой особенности определить нормиру-
нормирующий интеграл
а
\rJl{knr)dr.
о
7.9. Показать, что в цилиндрических координатах
\g- = 2 B - 50m) cos [m (? - %)] \ Jm (Xp) Jm (XPo) - ^-^ X dk.
[( rnZ 0
7.10. Пусть k = ?x и v— —Ey, где Е —двумерное электрическое поле.
Показать, что уравнения, которым удовлетворяют кии, можно объединить
следующим образом:
/д/дх ~(
\д/ду д/дх)\о
822 Гл. 7. Функции Грина
Определить аффинор Грина
in п
'11 2
\G9/I G99 I
Удовлетворяющий уравнению
/д/дх ~д/ду\ , _ .., J1 О
\д/ду д/дх/
Показать, что
д/дх д/ду
где G — функция Грина для двумерного уравнения Лапласа. Исследовать
смысл @ и получить при помощи ($ решение неоднородного вида уравне-
уравнений для и и v.
7.11. Пусть <{> удовлетворяет следующему уравнению:
и граничному условию Ф @) = О и Ф (I) = /'!*' @> гДе / — комплексная постоян-
постоянная. Показать, что собственными функциями служат s'm(knx), где tg kn = fkn.
Показать, что сопряженное решение удовлетворяет тому же уравнению,
что и 0>, но с граничными условиями Ф@) = 0, Ф(/) = /Ф'(/). Показать, что
<Ьп — <Ьп. Показать, что
i _ г
\ W» ^ = ^ Ф^фт da; = 0, и # т.
о о
Рассмотреть нормировку функций Ли и проверить результат при помощи
исследования функции Грина, которую можно получить в замкнутом виде
для этой задачи.
7.12. Пусть самосопряженный оператор J6 можно разбить на две само-
самосопряженных части Хт и J6D, где J6r действует только на переменную /¦,
а «??р — только на р:
jo = at- j, -f- jo о.
Пусть ортогональными п нормированными собственными функциями опера-
оператора <3?р служат <р„(р):
Показать, что функция Грина Gx(r, p |г0, р0), удовлетворяющая уравнению
[^(r,P)-X]G,= -o(r-/-0)o(p-p0),
выражается формулой
Gx = 2 ?*->.„ (/• I ''о) Т« (р) Ч>„ (Ро).
где
[ifr-(X-
7.13. Пусть
Таблица функций Грина 823
Показать, что
Gx (г | г0) = Go (г | г0) - ^ G^r | гх) б^х К)
7.14. Пусть G — функция Грина скалярного уравнения Гельмгольца для
нолубесконечной области х > О, удовлетворяющая смешанным граничным
условиям
д&/дх = Fty при х = 0;
показать, что
8х tU~ ^дх^* ) \ R R'
где /? = | г — ro|, a R' =|г-|-го|. При помощи интегрирования показать, что
G = (eikR/R) + Т.
Определить Т.
Таблица функций Грина
Общие свойства. Функция Грина Gx (r | г0) удовлетворяет уравнению
— XG= -4тго(г-го)
и некоторым однородным граничным условиям на граничной поверхности S.
Сопряженная к пей функция [см. формулу G.5.4)] Gx(r|r0) удовлетворяет
уравнению
S{G)-yG= _4тго(г-г0)
и сопряженным граничным условиям [см. формулу G.5.9)] на граничной
поверхности S- Принцип взаимности состоит в том, что
Если оператор X эрмитов (если его сопряженный и комплексно сопря-
сопряженный операторы совпадают), то функция СЛ также эрмитова. Б этом слу-
случае собственные значения \х оператора X,
¦вещественны, собственные функции Фи взаимно ортогональны и
где Nn= \ |<!>tl|2dF. Если X не эрмитов, то собственные функции Фп эрми-
эрмитово сопряженного уравнения
могут отличаться от собственных функций <Ьп, и как в той, так и в дру-
другой системе функции могут не быть взаимно ортогональными. Однако
824 Гл. 7. Функции Грина
в этом случае двойная система ф, Ф биортогональна и
а сопряженная функция G не обязательно равна комплексно сопряжен-
сопряженной G Г см. формулу G.5.44); Nn= { Q>n<bndv ] .
Функция Грина для уравнения Гельмгольца. Функция G является
решением уравнения
V2Gft (г | г0) + /с2 Gh (г | г0) = - 4* 8 (г- г„),
удовлетворяющим однородным граничным условиям на некоторой поверх-
поверхности S. Тогда соотношение взаимности имеет вид Gh (г|г0) = Gh (r| г0), так
как уравнение самосопряженное. Если <1> представляет собой решение урав-
уравнения (V2 -f- /с2) ib = — 4тср, имеющее на поверхности S значение ф0 (Is)
и производную по направлению внешней нормали iV0 (r8) = (dty/dn)s, то вну-
внутри в на 5
* « = J Р К) Gh (г | г0) dv0 + ± § [ Gh (г | rg) N'a (vl) - % (i-) A Gft (r | r«) ] dA0,
где первый интеграл берется по объему, ограниченному поверхностью S,
а второй представляет собой поток через всю S наружу. Нормальная
производная берется по внешней (указывающей наружу) нормали.
Если поверхность S находится на бесконечности и задаются расходя-
расходящиеся волны [условие причинности, формула G.2.17)], то G принимает про-
простой вид gfc(r|r0) для бесконечной области:
, 3 измерения; Л2 = (х-хо
(кР), 2 измерения; i>2 = (х - ж0J + (у - yof;
_2^ieiftl3c_:c0|> i измерение.
Функция Грина для уравнения Пуассона V2ty= — 4тср равна G0(r|r0),
т. е. X = 0. Соответствующий вид для бесконечной области:
ёо (г I го) = !/#, 3 измерения;
= — 2 In R, 2 измерения.
Если S целиком или частично совпадает с одной из координатных поверх-
поверхностей разделяющей системы координат, исследованных в § 5.1, то G
можно разложить в ряд по разделенным решениям. Допустим, что гранич-
граничные условия (конечность, периодичность или однородные условия на гра-
границе) таковы, что два из множителей могут быть собственными функциями,
скажем ?2- и ?3~множители- ^-множитель должен также удовлетворять
однородным условиям на поверхности, которую мы считаем соответству-
соответствующей поверхностям ?х = а, ^ = Ь, Ъ > а. Пусть координаты имеют коэф-
коэффициенты Ламе hlt /г2, /г3, определитель Штеккеля S с элементами Фтп (?т)
и алгебраические дополнения Мт = д?/дФт1 [см. формулы E.1.25) и далее].
Тогда в уравнении Гельмгольца
Таблица функций Грина 825
переменные разделяются, если положить ф = Ха (?х) Х2 (?2) Х3 (?3), где
эт=1
и в качестве Х2 и Х3 берутся решения, имеющие вид собственных функций
для соответствующих граничных условий:
\Y (t j ? \ _ gv ^ \ х (? ) v, ц. = 0, 1, 2
Они ортогональны относительно функции плотности р (часто р = h2h3),
так что
О для р ф д,
Nq для р = д,
причем функции W образуют полную систему для координат ?2, ?3 внутри
поверхности S.
В качестве ^-множителя выбираются два независимых решения ylq (?х)
и y2q(ki), каждое из которых соответствует константам разделения в Wq,
причем эти решения выбраны так, что у1 удовлетворяет требуемому гра-
граничному условию при ?j = а, а г/2 — при ?х = b (b > а). Тогда
где коэффициенты Ламе являются функциями координат со штрихами,
а Д — определитель Вронского для двух ^'-решений:
Д = Д (ylq, y%q) = y^ny'iq — у'\чУ±п== const/flf функции от %[.
Разложение функции Грина для бесконечной области в обобщенном сейчас
виде приведено для двумерных полярных координат в формулах G.2.51) и
A1.2.23), для прямоугольных координат в формуле A1.2.11), для парабо-
параболических координат в формуле A1.2.70) и для эллиптических координат
в формуле A1.2.93). Разложения для трехмерных систем прямоугольных
координат имеются в формуле A1.3.10), для сферических координат в фор-
формуле A1.3.44) и для сфероидальных координат в формуле A1.3.91). Подоб-
Подобные разложения для векторных решений даны в формулах A3.3.15) и
A3.3.79).
Функция Грина для волнового уравнения. Функция G является реше-
решением уравнения
V*G (г, 11 то,%) - -1-J G (г, 11 r0> 10) = - 4* S (г - г0) & (t -10),
удовлетворяющим однородным граничным условиям на поверхности S и под-
подчиняющимся требованию «причинности», состоящему в том, что G=0 и
dG/dt = 0 всюду при t <.t0. В этом случае соотношение взаимности имеет
вид
G(r,t\ro,to) = G(ro, -to\r, -t).
Если ф (г, t) — решение уравнения V4 — A/с2) (д2ф/дг2) = — 4тгр (г, г), имеющее
на поверхности S значение Ф8 (г4) и производную по внешней нормали Ns (rs),
а внутри S при t = 0 начальное значение % (г) и начальную производную
826 Гл. 7. Функции Грина
по времени v0 (г) = Зф/3^=0, то для I > О внутри и на S
•!» (г, 0 = \ Ло \ dF0 -G (г, *| г„, t0) p (г0> *„)
о J
1+е
Замкнутый вид функции Грина для бесконечной области таков:
g(r,t\ г0, t0) = A/Д) о [(R/c) -(t-10)] для 3 измерений,
В2 = (х - х0J + (у - уоу + (z- zoy;
= [2c/l/c2 («—10J — P2] и [(t —10) — (Р/с)] для 2-измерений,
Р* = (х-хо)* + (у-у0Г;
= 2съи[A —10) — (| x — x0 \/c)] для 1 измерения,
где
u(x) = 0, x<0, u(x) = l, x>0, o(x) = u'(x),
6' (x)/(x + a) dx= -/' (a).
—oo
Функция Грина для волнового уравнения связана с функцией Грина
для уравнения Гельмгольца интегральным соотношением Фурье
•G (г, 11 г0, 4) = -^ ^ Gk (г | г0) e-ifec('-">) dk =
—oo
¦ _. 1 -
= 4тс C2M(f — t0) 2j — Фп (ro) <i>n (r) sin [wn (< — *o)I.
n
где фп является собственной функцией — решением уравнения V2tl» + ^n^n = О
внутри iS, причем % = ft^c. Контур интегрирования по к расположен не-
непосредственно выше вещественной оси.
Функция Грина для уравнения диффузии. Функция G является ре-
решением уравнения
V2Ga (г, 11 г0, г0) -a2-lfGa (г, 11 г„, t0) = - 4тго (г - г0) 8 (t -10),
удовлетворяющим однородным граничным условиям на поверхности S и под-
подчиняющимся требованию причинности, состоящему в том, что G при t < t0
равна нулю. Сопряженная функция Ga (г, t\ r0, t0) = Ga (г, — ? | г0, — ^0) удовлет-
удовлетворяет сопряженному уравнению V2G + a* dG/dt — — 4ъ6 (г— ro)o(f —10).
•Соотношение взаимности имеет вид
a \l> I *0> 1о/ — о \ О» 'о I ж> lJ — а \*0> l0 I *> 1)~
Если ф(г)— решение уравнения V2tl> — a?d&ldt = — 4тгр (г), имеющее
на поверхности 5 значение 4*8 (rS) и производную по внешней нормали
iVg (rs) = д<Ь/дп, а внутри S при t = 0 — начальное значение фо(г), то для
Литература 827
t > 0 внутри и на S
Л (г, t) = [ dt0 \ р (r0, t) G(v,t\ r0, «0)
(г, «| rg, g iVs (,*) - ф8 (,«) -^-G (г, г I r*.
Вид функции Грина для бесконечной области в случае п измерений:
где t = f—10 и /?=|г — го|. Функция Грина для уравнения диффузии свя-
связана с собственными функциями фи соответствующего уравнения Гельм-
гольца (V24- kn) ф„ = 0 для области, заключенной внутри 5, соотношением
= _ в («_ «„) 2 i _ ф„ (г0) ф„ (г),
ЛИТЕРАТУРА
Сведения по функциям Грина и их приложениям разбросаны по разным работам.
Удовлетворительное изложение различных аспектов этой теории можно найти в сле-
следующих книгах:
Вебстер А., Сеге Г., Дифференциальные уравнения в частных производных ма-
математической физики, Гостехиздат, М.—Л., 1934.
Зоммерфельд А., Дифференциальные уравнения в частных производных
физики, ИЛ, М., 1950.
Карслоу X. С, Теория теплопроводности, Гостехиздат, М.—Л., 1947.
Курант Р., Гильберт Д., Методы математической физики, т. I, Гостехиздат,
М.—Л., 1951.
Смирнов В. И., Курс высшей математики, т. IV, изд. 3, Гостехиздат, М., 1957.
Соболев С. Л., Уравнения математической физики, изд. 3, Гостехиздат, М.—Л., 1954.
Тихонов А. Н. и Самарский А. А., Уравнения математической физики, изд. 2,
Гостехиздат, М.—Л., 1953.
Франк Ф., Мизес Р., Дифференциальные и интегральные уравнения математиче-
математической физики, ч. 2, ГТТИ, М.—Л., 1937.
Bateman H., Partial Differential Equations of Mathematical Physics, ch. 2, Cam-
Cambridge, New York, 1932.
Kellogg O., Foundations of Potential Theory, Berlin, 1939, перепечатка, New
York, 1944.
Murnaghan F., Introduction to Applied Mathematics, New York, 1948.
ГЛАВА g
Интегральные уравнения
В предыдущих главах при описании распространения некоего поля 4*
мы полагались главным образом на дифференциальные уравнения. Дополни-
Дополнительно задавались краевые условия, так как само дифференциальное урав-
уравнение описывает Ф лишь локально, связывая значения ф в точках г и г 4-dr.
Дифференциальное уравнение позволяет, начав с какой-либо заданной
точки г, шаг за шагом строить различные возможные решения. Краевые
условия призваны для того, чтобы можно было выбрать решение, соот-
соответствующее интересующим нас физическим условиям.
Поскольку граничные значения ty играют столь важную роль, естест-
естественно попытаться так задать уравнение, определяющее $, чтобы оно сразу
включало в себя краевые условия. Такое уравнение должно связать ty (г)
не только со значениями $ в точках, близких к г, но и со значениями
во всех точках области, включая граничные точки. Интегральные уравнения
обладают именно таким свойством. Включая в себя краевые условия, такое
уравнение в весьма компактной форме представляет всю физику задачи и
оказывается, как мы увидим на многих примерах, удобнее, чем диффе-
дифференциальное уравнение.
Это не единственная причина для изучения интегральных уравнений.
Мы уже видели при рассмотрении диффузии и явлений переноса, что
во многих случаях дифференциальные уравнения не могут служить средством
описания таких явлений. Это имеет место в тех задачах, где поведение ф
в точке г зависит не только от значений <1> вблизи г, но и от значений <3>
в точках, удаленных от г.
В первом параграфе этой главы мы рассмотрим некоторые из интег-
интегральных уравнений, встречающихся в физике, и опишем отдельные типы
таких уравнений, обладающие различными свойствами и требующие раз-
различных способов решения. После обсуждения общих математических свойств
этих уравнений, будут изложены способы их решения.
8. 1. Интегральные уравнения физики;
их классификация
Рассмотрим сначала гпример из теории переноса. Пусть некоторая
частица, движущаяся в заданном направлении и обладающая определенной
энергией, в результате соударения с другой частицей приобретает значение
импульса р, отличное по величине и направлению от первоначального зна-
значения р0. Обозначим через Р (р | р0) dp dt вероятность того, что частица,
обладающая импульсом р0, за время dt, в результате соударений, приоб-
приобретет значение импульса, заключенное между р и р + ^р. Если в окрест-
окрестности точки г доля частиц, имеющих импульсы, заключенные между р0 и
po + dpo, равна /(г, р0, t)dp0, то вычисляя /(г, р, t + dt), мы должны учесть
8.1. Интегральные уравнения фиаики
829
приращение /, получающееся за счет соударений, т. е. величину
[^(Р|Ро)/(г. Ро. t)dpo]dt.
Мы сразу же замечаем, что значение /(г, р, t) при фиксированном р опре-
определяется значениями /(г, р0, t) при всех р0, совместимых с законами сохра-
сохранения импульса и энергии. Для того чтобы получить полную картину,
составим уравнение для /, учтя полное приращение / за время dt. Выра-
Выражение, приведенное выше, дает число частиц, рассеянных в элемент фазо-
фазового пространства, определяемый величинами г и р. Некоторое число частиц
покинет этот элемент из-за соударений и за счет поглощения. Пусть
Рт (р) — вероятность того, что частица покинет окрестность значения р
за единицу времени. Если поглощения нет, то Рт (р) = \ Р (р01 р) dp0. Число
частиц, покидающих эту окрестность за время dt, равно
Наконец, даже если нет соударений, / изменяется просто потому, что
частицы движутся. Частица, находящаяся в точке г, за dt секунд до этого
занимала положение г— (p/m)dt. Итак,
/|(г, Р, t + dt) = f[r-(p/m)dt, p, t]-PT(p)f(r, p, 0*4-
4- [ § -Р (Р | Ро) / (г, Ро. 0^Ро]Л-
Согласно этому уравнению, число частиц, находящихся в окрестности
точки г в момент t + dt, равно числу частиц, достигших окрестности этой
точки в результате движения, минус число частиц, поглощенных или рас-
рассеянных из интервала (р, p + dp), плюс число частиц, рассеянных в этот
интервал в результате соударений.
Разложив первый член правой части по степеням dt, получаем
{см. § 2.4_и 12.2) интегро-дифференциальное уравнение
Ж= -(^-V)f-PTf+ \P(P\Vo)f(r> Ро, ОФо- С8-1-1)
В стационарных условиях / не зависит от t, и мы приходим к уравнению
(-2—V )/= ~Prf+ \ Р(р |Ро)/(г, ро)фо. (8.1.2)
Подчеркнем еще раз, что / при любом р связано со всей совокуп-
совокупностью значений /, а не только со зна-
значениями, отвечающими близким р. В § 2.4
•была установлена связь вероятностей Рт
и Р с эффективными сечениями и соот-
соответствующее уравнение посредством ин-
интегрирования из интегро-дифференциаль-
¦ного было превращено в интегральное.
Уравнения переноса будут еще рассмо-
рассмотрены в гл. 12.
Твердая
пластина
\
-—Мембрана
х—-
Пример из акустики. Не следует ду-
думать, что уравнения такого типа встре-
встречаются только в задачах переноса, где
-соударения являются естественной при-
причиной скачкообразного изменения импуль-
импульса р. Можно взять пример хотя бы из Рис. 8.1. Излучение мембраны, за-
акустики.Интегро-дифференциальные урав- крепленной в твердой пластине.
нения появляются, как мы увидим, тог-
тогда, когда имеются две взаимодействующие друг с другом системы с
распределенными массами или с какими-либо другими характеристическими
830 Гл. 8. Интегральные уравнения
параметрами. Рассмотрим в качестве примера колебания мембраны, натянутой
на отверстии в твердой пластине (см. рис. 8.1). Колебания мембраны вызы-
вызывают звуковые волны, которые в свою очередь оказывают на мембрану
обратное воздействие, вызывая ее колебания, и т. д. Пусть смещения точек
мембраны описываются функцией <b(y,z); соответствующая скорость в
направлении оси х равна dty/dt = — шф, если предположить простую гармо-
гармоническую зависимость от времени. Согласно уравнению G.2.10), в среде,
примыкающей к мембране справа, существует потенциал скоростей
k(x,y,z\0, у0, z0) vn (y0, z0) dS0,
где Gh — функция Грина, удовлетворяющая условию
4^ = 0 при х = 0.
Здесь к=ш/с, с—скорость распространения звука, a vn — нормальная
составляющая скорости, т. е. составляющая по оси х в отрицательном
направлении. Таким образом, vn = гсм|>. Функция Gh может быть получена
методом изображений (см. стр. 753):
eikR eikR>
Gk (z, У, z\%o> Уо> zo) — —^ 1—~gi— i
где
Я2 = (х - хХ + (У - У of + (z ~ z0J,
Звук, порожденный в области х > 0, вызывает появление давления, которое
в свою очередь играет роль возмущающей силы в уравнении колебаний мем-
мембраны. Давление связано с потенциалом скоростей соотношением
дз
PP
где р0 — средняя плотность среды, в которой распространяется звук. Урав-
Уравнение движения мембраны запишется в виде
V2(]) 4- **'!> = —
Р
где x = o)/V, V =1/ГТ/A, Т — натяжение, jj. — поверхностная плотность мемб-
мембраны. Подставив выражение для р, получим
(8.1.3)
Мы видим, что и в этом уравнении значение Л в какой-либо точке мембраны
связано посредством интеграла в правой части не только со значениями tU
в соседних точках, но и с ее значениями во всех точках мембраны Это-
уравнение — интегро-дифференциальное, но, если воспользоваться функцией
Грина для мембраны, его можно свести к интегральному уравнению.
Приведенный пример ясно показывает, что интегральное уравнение
появляется всякий раз, когда возбуждение в какой-либо точке среды может
быть передано другим точкам через посредство некоторой среды, взаимо-
взаимодействующей с первой. При этом уравнение, описывающее колебания
первой среды, будет содержать член, учитывающий распространение возбуж-
возбуждения во второй среде. Он будет зависеть от значений Ф во всех точках
соприкосновения обеих сред; в приведенном примере таковым является член
с интегралом в уравнении (8.1.3). Проблемы излучения волн, в которых
нельзя пренебречь реакцией излучения на источник, естественным образом
8.1. Интегральные уравнения физики 831
приводят к интегральным уравнениям. Решение такого интегрального урав-
уравнения позволяет точно определить сопротивление излучения или, что
является более общей задачей, импеданс излучения. Такого рода проблемы
будут рассмотрены в гл. 11 и 13.
Пример из волновой механики. Последний пример мы заимствуем
из квантовой механики. Уравнение Шредингера должно записываться
в виде интегрального уравнения тогда, когда потенциальная энергия зави-
зависит от скоростей. Пусть
V(t, ftV/i)
— потенциальная энергия, причем вместо оператора импульса уже под-
подставлено (h/i)V. В дифференциальной форме уравнение Шредингера
имеет вид
Это уравнение имеет конечный порядок только в том случае, когда V явля-
является многочленом от V. Для того чтобы получить эквивалентное интеграль-
интегральное уравнение, введем преобразование Фурье функции Л:
V (г)= ,„ ».з/,
Подставляя это выражение в уравнение Шредингера, умножая
па Bmft)~3'2e~<i'fiL-r и интегрируя по г, мы получаем
(8.1.4)
V(p-q, Р) = 7г^ \ e*<P-Q>-v»V(r, V)
Это интегральное уравнение, определяющее <р (q), было приведено ранее
в § 2.6. Смысл фигурирующего здесь интеграла легче всего понять, рас-
рассматривая задачу о рассеянии, вызываемом потенциалом V. Если плоская
волна с амплитудой <р (р) приходит в область, где существует потенциал,
то она рассеивается. Иначе говоря, часть начальной волны изменяет
направление, возможно, с потерей импульса. Интеграл в приведенном
выше уравнении показывает, как меняется импульс q под влиянием сово-
совокупности плоских волн с разными импульсами, появляющейся при рас-
рассеянии на потенциале V. Здесь имеется аналогия с явлением переноса,
ранее рассмотренным в этой главе, которая может быть использована для
получения наглядного представления о некоторых квантовомеханических
явлепиях.
Мы рассмотрели некоторые задачи, требующие применения интеграль-
интегральных уравнений. Ранее мы указывали также, что даже те задачи, которые
описываются дифференциальными уравнениями, могут быть сформулиро-
сформулированы в виде интегральных уравнений. Приведем теперь несколько приме-
примеров этого рода.
Краевые условия и интегральные уравнения. Особенно хорошо под-
поддаются формулировке в виде интегральных уравнений краевые задачи
для дифференциальных уравнений с частными производными. В примере,
приведенном ниже, дифференциальное уравнение с частными производ-
производными второго порядка в двумерной области переформулировано в виде
одномерного интегрального уравнения. Такое сведение двумерной задачи
832
Гл. 8. Интегральные уравнения
к одномерной очень важно, конечно, для нахождения как точного, так
и приближенного решения.
Рассмотрим задачу1), связанную с уравнением Гельмгольца. На отрица-
отрицательной полуоси х поместим преграду (см. рис. 8.2). Плоская волна eik-r,
движущаяся по направлению вектора к, набегает на эту преграду. Пол-
Полное поле ф должно удовлетворять уравнению Гельмгольца V^-f/с2ф =0.
Нас интересует воздействие преграды на волну в случае, когда решение ф
9
Преграда ¦
х
Контур С
Т
Рис. 8.2. Дифракция на полуплоскости у = 0, х < 0.
Указан контур интегрирования для интегрального представления.
удовлетворяет краевому условию д^/ду = 0 на преграде. На больших рас-
расстояниях от начала координат это решение должно удовлетворять еще
-следующим условиям. В нижней полуплоскости у < 0
ф = 2 cos (kyy) е*хх + ф~, (8.1.5)
где ф~ представляет уходящую волну при г—> оэ, у < 0. В верхней по-
полуплоскости у > 0 полагаем
Ф = Ф*. (8.1.6)
где ф* представляет уходящую волну при i—> со, у > 0.
Именно из-за асимметрии условий на больших расстояниях, мы берем
для ф различные выражения при г/> 0 (8.1.6) и при г/< 0 (8.1.5). Необ-
Необходимо, значит, проверить непрерывность ф и д^/ду на общей границе
этих областей, т. е. в точках у = 0, х > 0. Согласно теории функций Грина,
изложенной в гл. 7, ф (г) при г/<0 должна иметь вид
ф(г)=2соз
dS0.
Путь интегрирования указан на рис. 8.2. Так как Gk должна удовлетво-
удовлетворять условиям излучения, то интеграл вдоль большой полуокружности
обращается в нуль. Поскольку, кроме того, dGk (г | х0, уо)/дуо = 0 при у0 = 0,
интеграл вдоль оси х упрощается, и мы получаем
, у < 0,
(8.1.7)
Gk (г | го) = m [Яо (kR)+H0 (fcR')l
*) В нижеследующем примере в переводе исправлены неточности оригинала.—
Прим. ред.
8.1. Интегральные уравнения физики 833
В области у > 0 при той же Gh получаем
со
-о da;°' у > °- (8Х8>
При таком выборе выражений для ф условие д§/ду = 0 при у = 0, х < О,
очевидно, выполняется.
Теперь нужно ввести условия непрерывности. Значения производ-
Н0Й (~ёОу=о- И (^)и)-1 вычисленные из формул (8.1.7) и (8.1.8),
совпадут, если взять -?— ) = ( -^— = ( -^— ) . Кроме того,
должны совпадать при у = 0, х > 0 и значения (ф)„_0+ и (ф)у==0-. Это
условие дает
или
(8-1.9)
Мы получили для производной (д$/ду0)уо—о интегральное уравнение.
Коль скоро (д$/ду0)уо~о найдена, мы подставляем ее в (8.1.7) и в (8.1.8)
и находим ф при у < 0 и у > 0.
Заметим, что можно было бы для этой задачи составить и другое
интегральное уравнение, если за неизвестную функцию взять скачок
(ф)у=0+ — (ф)и=_0_ при х < 0. При этом выражения для Л при у < 0 и у > 0
надо было бы выбрать так, чтобы они удовлетворяли условиям непрерыв-
непрерывности при х > 0 и затем подчинить их условию ( ~^~ ) = 0 при х < 0.
ч "У у у=о
Полученное тем или иным способом одномерное интегральное уравне-
уравнение включает в себя краевые условия. Задавая другие краевые условия,
мы придем к другому интегральному уравнению.
Уравнения, определяющие собственные функции. Интегральное
уравнение другого типа получается из уравнения Шредингера
которое мы запишем в виде
(^24-/е2-[/)ф = 0, (8,1.10)
где
/,2_ J^L w и- — V
Переписав (8.1.10) в форме (V2 + /c2)ty= С/ф, видим, что решением этого
уравнения является
^ (8.1.11)
53 ф. м. Морс и Г. Фешбах
834 Гл. 8. Интегральные уравнения
где выбор функции Грина Gk определяется краевыми условиями, которым
должна удовлетворять ф. Уравнение (8.1.11) представляет собой интеграль-
интегральное уравнение относительно функции ф.
От уравнения (8.1.9) оно отличается тем, что в (8.1.11) ф входит как
под знаком интеграла, так и вне интеграла.
Для того чтобы более отчетливо представить себе смысл уравне-
уравнения (8.1.11), рассмотрим одномерный пример. Обратимся к задаче Штурма —
Лиувилля, о которой шла речь в § 6.3. Неизвестная функция ф удовлетво-
удовлетворяет уравнению
^[^] )^ = °- (81Л2>
Для того чтобы свести (8.1.12) к уравнению (8.1.11), введем функцию
Грина, удовлетворяющую уравнению
-S(z-zo). (8.1.13)
Теперь мы должны задать какие-нибудь краевые условия для G И4ф.
Для определенности будем считать заданными ф @) и ф(/), т. е. подчи-
подчиним ф условиям Дирихле. Соответственно для G имеем G @1 z0) = G (I | z0) = 0.
Перенося в (8.1.12) Хт-ф в правую часть, получаем
=г- (8.1.14)
Это — интегральное уравнение относительно ф. Если ф должна удовлетво-
удовлетворять однородным условиям Дирихле: ф @) = 0, ф (I) = 0, то это интеграль-
интегральное уравнение принимает вид
i
ф (z) = X^ G B1 2о) г Bо) ф Bо) dv (8Л.Щ
Краевые условия фигурируют в уравнении (8.1.14), так сказать,
в «явном» виде, и мы опять видим, что интегральное уравнение включает
в себя все данные, относящиеся к задаче. Никаким дополнительным
условиям подчинять Ф не нужно.
Интегральные, уравнения некоторых собственных функций. Для
иллюстрации уравнения (8.1.15) приведем интегральные уравнения, кото-
которым удовлетворяют классические ортогональные функции»
(а) -g
0
z(l~zo)' z<zo'>
zo(l — z
Решения: sin (nizz/l), X = (nir//J, n — целое.
т I л 1 / z(l~zo)'
Gzzo=T a \
1 I [ zo(l — z), z
8.1. Интегральные уравнения фиаикц 835
-^Ть ] +4 = 0, ф конечна при z = ± 1.
1 1
= x\ G(z\z0) ty(zo)dzo —
Решения: полиномы Лежандра Pn(z), X = n(n+1), n —целое.
конечна
(¦?¦)"¦ «>v
Решения: бессёлееы функции Jn (]/х z).
(г) ^•+(Р2-Ля)Ф = 0>
или
g ; Х = ^ + а2; ф(оо), ф(- со) конечны.
—ео
2
e.ti/2 С e-«5«d6e.A2 ^ e-^Ve, z < zOl
/a i —со
V -сю
$, z > z0.
Решения: функции Эрмита e~az*l2Hn("|/az), X = 2(n-f-l)a, n —целое.
*(oo) конетаы-
Параметр X можно отождествить либо с 2а, либо с а2 — р2.
В первом случае
со
ф (z) = X ^ G (z | z0) z^xl» (z0) dz0, I = 2a,
о
Решения: e-$zL\ B^z), LnB^z) — полиномы Лагерра, a/p—l = n, «г —целое.
53*
836 Гл. 8. Интегральные уравнения
Во втором случае эквивалентное уравнение имеет вид
Г *Г
I \
z>z0.
Типы интегральных уравнений; уравнения Фредгольма. Перейдем теперь
к классификации рассмотренных интегральных уравнений и к некоторым
обобщениям. Возвращаясь к (8.1.14), видим, что это уравнение имеет вид
(8.1.16)
где в рассмотренном конкретном случае К (z| z0) = /-(zo)G(z| z0), a <j>(z) —
некоторая заданная функция; а и b — фиксированные точки, в которых ф
удовлетворяет краевым условиям. Интегральное уравнение относительно ф
вида (8.1.16) называется неоднородным уравнением Фредгольма второго
рода. Функция A'(z|z0) называется ядром этого интегрального уравнения.
Ядро симметрично, если A (z | z0) = A (zo| z). В (8.1.14) ядро несимметрично
при r(z0) ф 1.
Отбрасывая <j> (z), превращаем (8.1.16) в однородное уравнение Фред-
Фредгольма второго рода:
ь
(8.1.17)
Однородными уравнениями Фредгольма второго рода являются Уравнение
(8.1.15) и уравнения в примерах (а) —(д). В примерах (а), (б) и (г) ядра
симметричны. В примерах (д) и (е), а также в уравнении (8.1.14) фигури-
фигурируют так называемые полярные ядра, т. е. ядра вида
A(z|zo) = G(z|zo)r(zo), где G(z\zo)=G(zo\z). (8.1.18)
Во всех этих примерах ядра являются определенными в заданной области,
т. е. при 0<z</ в примере (а), при 0<z<oo в примере (в), и т. д.
Положительно определенное ядро A (z | z0) характеризуется неравенством
которое должно выполняться для любой функции ф. В случае отрицательно
определенного ядра этот интеграл всегда меньше нуля. В том и в другом
случае ядро называется определенным. Если знак такого интеграла зави-
зависит от выбора ф, то ядро называется неопределенным.
8.1. Интегральные уравнения физики 837
Уравнение (8.1.9) представляет собой пример уравнения Фредгольма
первого рода, которое имеет общий вид
ь
dzo, (8.1.19)
где ф— искомая функция, а функция <р известна.
Уравнения Вольтерра. В уравнения Фредгольма (8.1.16), (8.1.17)
и (8.1.19) входят определенные интегралы. Если сделать пределы этих
интегралов переменными, то мы получим уравнения Вольтерра. Уравнению
(8.1.16) соответствует неоднородное уравнение Вольтерра второго рода,
имеющее вид
Z
ф (г) = ^ К (z | z0) ф (z0) dz0 + 9(z). (8.1.20)
a
В соответствующем однородном уравнении <р = 0. У равнение Волътерра
первого рода, соответствующее уравнению (8.1.19), имеет вид
)dz0. (8.1.21)
Уравнение Вольтерра можно, если угодно, рассматривать как частный
случай уравнения Фредгольма, ядром которого служит
К (z\z0), z0 < z,
oU°' z°>2 (8.1.22)
Некоторые функции Грина, встретившиеся нам в предыдущей главе, обла-
обладали свойством (8.1.22). Стоит напомнить, что в задачах, в которых одним
из параметров служило время, мы имели при t < t0 равенство G(r, t\ r0, t0) = 0;
последнее является следствием принципа причинности, согласно которому
никакое событие, происходящее в момент t0, не может как бы то ни было
влиять на события, происшедшие ранее t0. Можно ожидать, что интеграль-
интегральное уравнение, для которого такая функция Грина G служит ядром, будет
уравнением типа Вольтерра.
Чтобы показать, как появляется уравнение Вольтерра, рассмотрим
движение простого гармонического осциллятора, описываемое уравнением
Возьмем импульсную функцию o(t —10) и зададим функцию Грина
G(t 110), положив d2G (t | to)/dtl = —6(t — t0) при t > t0 и G (t 110) = 0 при t < t0.
Умножая уравнение движения на G, а равенство d4i/dtl = — о (t —10) —
на ф, вычитая из первого получившегося равенства второе и интегрируя
по t0 от го = 0 до to = t* (обозначение t* указывает на то, что при инте-
интегрировании следует устремить t0 к t с той стороны, где t0 > t), получаем
или
Г^1КП Л (8-1.23)
где ф0 и v0 — начальные значения смещения ф и скорости dty/dt. Уравнение
(8.1.23) представляет собой неоднородное уравнение Вольтерра второго рода.
В нем учтены начальные условия, которым должна удовлетворять Ф.
838 Гл. 8. Интегральные уравнения
Из этого примера видно, что уравнения Вольтерра должны появляться
в тех задачах, в которых существует предпочтительное направление изме-
изменения независимого переменного; в только что рассмотренном примере это —
направление возрастания времени. То же имеет место в явлениях переноса,
когда рассматриваются соударения частиц с рассеивающими центрами,
обладающими большой массой. При этом энергия рассеиваемых частиц
"не возрастает в результате столкновений. Следствием этого является изве-
известная деградация энергии, которая и определяет предпочтительное напра-
направление изменения энергетической переменной.
В качестве примера такого рода рассмотрим пучок рентгеновских лучей,
проходящий через вещество в положительном направлении оси х. Будем
считать, что пучок при рассеянии сохраняет это направление. Рассмотрим
совокупность лучей с заданной длиной волны. Проходя через слой веще-
вещества толщины dx часть этих лучей поглощается, а часть изменяет длину
волны из-за рассеяния. Одновременно эта совокупность обогащается за счет
тех лучей, которые, обладая первоначально большей энергией (иначе говоря,
имея меньшую длину волны X, так как энергия обратно пропорциональна X),
теряют часть своей энергии из-за рассеяния. Итак, если /(X, ж)с?Х— доля
лучей, длины волн которых заключены в промежутке от X до X + dX, то
= - fl/ (X, х) + \ Р (X | Хо) / (X,,, х) d\,
где (л — коэффициент поглощения, а Р (X | X,,) d~k — вероятность того, что луч
с длиной волны X,,, проходя слой единичной толщины, приобретает длину
волны, заключенную между X и X-j-dX. Мы получили интегро-дифферен-
интегро-дифференциальное уравнение. Его можно свести к интегральному уравнению, если
положить
/(X, x)= \ е-*>*ф(Х, p)dp;
о
при этом fy (X, p) будет удовлетворять однородному уравнению Вольтерра
второго рода
&»-/>)* (*.*>) = ^(XlXoHfXo, jD)dX0.
о
8.2. Общие свойства интегральных уравнений
При рассмотрении общих свойств интегральных уравнений полезно
воспользоваться некоторыми результатами теории операторных уравнений
в абстрактном векторном пространстве. Мы сейчас покажем, что ранее при-
приведенное уравнение Фредгольма есть не что иное, как координатная запись
операторного уравнения. Рассмотрим в векторном пространстве неоднородное
уравнение
Так как функция Грина, постоянно фигурирующая в интегральных урав-
уравнениях, тесно связана с обратным оператором (см. стр. 816), то целесооб-
целесообразно записать (8.2.1) в виде
g = 9T1-f. (8.2.2)
8.2. Общие свойства интегральных уравнений 839
Желая придать этому уравнению классическую форму, разложим все век-
векторы по координатным ортам e(z0), соответствующим z0. Пусть
с=
) = J e (Zl) A' (Zl | z0) dzx,
= ^ e(zo) dzo $ A' (z01 zx) ф (zx) dZl.
Вводя эти выражения в (8.2.2), мы получаем неоднородное уравнение
•Фредгольма второго рода
ф (z0) = X \ К (z01 zx) <1 (Zl) dzx + ? (z0). (8.2.4)
Пределы интегрирования включены в определение функции К.
Таким образом, интегральное уравнение часто эквивалентно «обращен-
«обращенному» дифференциальному уравнению. Вместо дифференциального опера-
оператора 81 рассматривается интегральный оператор 81. Уравнение Фредгольма
первого рода
I — ? (zo) = \к (zo I Zi) ф (Zi) dzx
¦соответствует операторному уравнению
-g=ST1-e, (8.2.5)
которое должно быть решено относительно е (или, в координатной трак-
трактовке, относительно ф). Однородное уравнение Фредгольма второго рода
ф(го)=Х$ A'(zo|z1)«l>(z1)dz1
•соответствует уравнению
тогда как неоднородное уравнение (8.2.4) соответствует (8.2.2).
Ядро К (х01 хх), входящее в уравнение Фредгольма любого из трех
видов, тесно связано с оператором. ЭД. Поэтому нам надлежит изучить
свойства К и извлечь из них свойства оператора 31. Однако не всякий
оператор имеет обратный; если оператор 81 соответствует интегрированию
с ядром К, то оператор 91, изображающий какую-то дифференциальную
¦операцию, может и не существовать (например, когда 9l-1-f = 0 при неко-
некотором t Ф 0, оператор SI не может быть однозначно обращен). Полезно
выяснить, какие типы ядер соответствуют операторам, имеющим обратные,
является ли дифференциальный оператор ЭД самосопряженным и т. д.
Однородное уравнение Фредгольма второго рода (уравнение (8.2.4)
при ip = 0) в том случае, когда для ЭД" существует обратный, эквивалентно
уравнению ЭДе = Хе, определяющему собственные значения оператора 81,
или дифференциальной форме этого уравнения; поэтому мы вправе ожидать,
что существует последовательность допустимых значений Хо, Хх, Х2, ...
{Хп < Хп+1) параметра X, которым соответствуют решения — собственные
функции фп. Что касается неоднородного уравнения, то естественно ожидать,
что оно эквивалентно уравнению 9l-e = Xe-|-f, решения которого предста-
вшмы с помощью функции Грина (см. гл. 7). Хотя мы и не собираемся,
решая интегральные уравнения, предварительно обращать их в уравнения
дифференциальные, тем не менее, изучая свойства ядер различных инте-
тральных уравнений, следует помнить о связи между теми и другими,
символически выражаемой записью %~г и 91.
S40 Гл. 8. Интегральные уравнения
Ядра интегральных уравнений. Возможность решить интегральное
уравнение в значительной мере зависит от двух свойств его ядра: симмет-
симметрии и свойства, состоящего в том, что существует оператор 91, обратный
по отношению к 91 ~*. Симметричное ядро соответствует самосопряженному
оператору. Если 91 существует, то
91 = % (8.2.6)
коль скоро К(хо\х1) = К(х1\хо).
Ядро называется определенным, если интеграл
/ (г \ dr \ К (г I г W (г
либо для всех функций / положителен, либо для всех / отрицателен (в том
и в другом случае значение этого интеграла всегда действительно). Ана-
Аналогичные операторные свойства соответственно для положительно опреде-
определенного и отрицательно определенного операторов выражаются неравен-
неравенствами
(e*-9t-1-e)>0,
(e*-9t-e)<0. (8-2'7)
В обоих случаях существование оператора 91, обратного по отношению
к W1, обеспечено. (Заметим, что если 91 ^ — определенный оператор, то
таков же и оператор 91.) К сожалению не все ядра являются определен-
определенными; часто оказывается возможным найти функцию, соответствующую
такому вектору е, для которого (e*-9t~1-e) = O, а при этом оператор 91
оказывается не единственным. В некоторых случаях имеют место неравен-
неравенства (е*-9(~1-е)>0 или (е*-91~1-е)<0, причем нулевое значение дости-
достигается. Такие ядра и соответствующие операторы называются полуопре-
полуопределенными (это название может ввести в заблуждение, так как полуопре-
полуопределенное ядро немногим лучше любого другого неопределенного ядра).
Бывает, что интегральное уравнение первоначально задается в таком
виде, что его ядро оказывается несимметричным и (или) неопределенным;
поэтому полезно знать, можно ли преобразовать это уравнение так, чтобы
новое уравнение имело симметричное определенное ядро.
Полярное ядро (см. 8.1.18) имеет вид
K(x\xo) = r{xo)G(x\xo),
где G симметрично по а; и х0. Такое ядро преобразуется в симметричное
путем замены неизвестной функции ф (z) = ip(z)/l/A/'(z)- Например, подста-
подставляя ф = q>/\/~r в однородное уравнение второго рода
ф (z) = X ^ G (z | z0) /• (z0) ф (z0) dz0,
приходим к уравнению
\ УТЩ G (г | z0) У7(Г0) ср (z0) dz0,
? (z) = X \
в котором новое ядро |/ г (z) G (z \ z0) j/V (z0) симметрично. Полезно указать
операторный аналог уравнения с полярным ядром. Зто — операторное урав-
уравнение
9X-e = XS3-e, (8.2.8)
в котором 91 — симметричный оператор. Проведем преобразование, анало-
аналогичное переходу от ф к ip. Пусть
8.2. Общие свойства интегральных уравнений 841
тогда
f = X(/»-St-*-l/»)-f. (8.2.9>
В действительности полярное уравнение является весьма частным случаем
уравнения (8.2.8). В самом деле, уравнению е = ХЭД-158-е соответствует
интегральное уравнение
где
М (z | z0) = J К (z | Zl) L (zx | z0) dzx
Полярное уравнение получается тогда, когда
L(zl\z0) = b(zl~z0)r(z0),
где Б —функция Дирака. Вычисляя интеграл, выражающий М, получаем*
Переход к определенным ядрам. Мы желаем, если это окажется воз-
возможным, преобразовать наше уравнение так, чтобы новое уравнение имело
симметричное определенное ядро. Выбором знака ядра К можно добиться
того, чтобы оно было положительно определенным. Считая К определен-
определенным ядром, мы неизбежно ограничиваем себя рассмотрением задач, в кото-
которых ядра действительны, а соответствующие операторы в абстрактном про-
пространстве — эрмитовы. Кроме того, не должно существовать собственных векто-
векторов е, для которых ЭД-е = 0. Прежде всего полезно перечислить те операторы,
которые тем или иным путем могут быть преобразованы в операторы ука-
указанного типа. Вообще говоря, преобразованные операторы будут лишь-
полу определенными, так как если не исключено равенство ЭД • е = 0 при неко-
некотором" е Ф 0, то этот вектор е после действия преобразованного оператора
даст также нуль.
Любой действительный эрмитов оператор превращается в определенный
оператор посредством итерации. Пусть
2Ье = Хе.
Подействовав на это уравнение оператором 91, т. е. итерируя, получаем
Я2-е = Х2е.
Оператор ЭД2 по меньшей мере полубпределенный, так как
Оператору 9t~2 соответствует ядро
K2 (x \xo)=\ К (x | xt) К (Xl | x0) dxx , (8.2.10>
и, значит,
коль скоро
-842 Гл. 8. Интегральные уравнения
В качестве первого следствия этой теоремы мы замечаем, что антиэр-
антиэрмитов оператор 31, определяемый тем свойством, что 31* = — 31, также
может быть преобразован в определенный оператор. Антиэрмитов оператор
соответствует антисимметричному ядру, для которого
K{x\xo)=-K{zo\z), (8.2.11)
¦если К действительно (если же К — комплексное ядро, то при перестановке
аргументов действительная часть К изменяет знак, а мнимая часть
не изменяется). Для доказательства заметим, что антиэрмитов оператор 51
можно записать* в виде
31 = Й8,
где $8 — эрмитов оператор. Тогда из 31 ¦ е = Хе следует равенство
Sg.e= —iXe.
Подействовав на это уравнение оператором $8, получаем
$82.е=_Х2е, (8.2.12)
так что 932— по крайней мере полуопределенный оператор.
Вторым следствием является то, что полярное интегральное уравнение
может быть сведено к интегральному уравнению с действительным, сим-
симметричным и определенным ядром. Соответственно этому покажем, что если
где ЭД и 58 — либо оба эрмитовы, либо оба антиэрмитовы и один из этих
операторов определенный, то е удовлетворяет некоторому операторному
уравнению, в которое входят только определенные операторы. Докажем это
для того случая, когда 31 и $8—эрмитовы операторы, $8 — положительно
определенный, 3( — неопределенный. Для положительно определенного
оператора 58 существует обратный оператор S3". Поэтому
то есть
Оператор ЗШ^ЭД'в левой части —»по меньшей мере полу определенный.
Для изложенных здесь преобразований характерно, что получающееся
в результате ядро и соответствующий оператор не зависят от X. Любой
оператор может быть сведен к эрмитову, но этот последний в большинстве
случаев будет зависеть от X. Действительно, если
C1-Х)-е = 0,
то, подействовав на обе части этого равенства оператором 31* — X, получаем
или
Ясно, что X3I* 4- ХЭД — 31*31 — эрмитов и, по самому его построению, опре-
определенный оператор. Однако, по сравнению с более простым уравнением
31е = Хе, употребление последнего уравнения затруднительно, так как в нем
сам оператор содержит X и X. Поэтому в дальнейшем мы не будем поль-
пользоваться этим приемом. Ниже в этом параграфе будет изложен другой,
практически более ценный метод.
8.2. Общие свойства интегральных уравнений 843
Итак, если ЭД-е = Хе, то в отдельных случаях для е можно построить
аналогичное уравнение с оператором, по меньшей мере полуопределенным
и не зависящим от собственного значения X. Это возможно тогда, когда
91 —эрмитов или антиэрмитов оператор. Подобное же преобразование тогда
применимо к уравнению вида ЭД ¦ е = XS3 ¦ е, когда операторы ЭД и S3 — эрми-
эрмитовы или антиэрмитовы и один из них определенный.
Свойства симметричного определенного ядра. Займемся изучением
действительного положительно определенного симметричного ядра. Соот-
Соответствующий оператор — эрмитов. Из § 6.3 мы можем извлечь следующие
результаты. Однородное уравнение 9i ¦ е = Хе имеет ненулевые решения лишь
при некоторых специальных значениях Хот параметра X, называемых соб-
собственными значениями. Соответствующие собственные векторы ет образуют
ортогональную систему векторов, быть может конечную, которую мы можем
считать нормированной:
e*-em = onm. (8.2.13)
Будем предполагать, что вырожденных собственных значений нет. Все
собственные значения действительны и могут быть расположены в возра-
возрастающую последовательность. Среди них есть наименьшее собственное
значение Хо (положительное, если 91 — положительно определенный оператор),
следующее по величине \ и т. д. Эти результаты могут быть обоснованы
с помощью экстремального свойства собственных значений:
(8.2.14)
Второе экстремальное свойство, если исходить из уравнения е =
может быть сформулировано так:
Неоднородная задача, соответствующая неоднородному уравнению
Фредгольма второго рода, имеет решение при любом значении ~кф~кт. Решение
может быть получено применением оператора, обратного по отношению
к ЭД — X. Если
то
e = C(-X)-1-f = @x.f, (8.2.16)
где &\— эрмитов оператор, называемый оператором Грина [см.G.5.35)].
Установим некоторые свойства оператора &^. Сначала выясним его
связь с SI. Из (8.2.16) непосредственно следует, что
является оператором, соответствующим ядру К. Далее,
©* = («- X)-1 = 9Г1 A - ХЗД-*)~\
или
®х=2 ЗД-(П+|)Х» (8.2.17)
п
для тех X, для которых этот ряд сходится. Из (8.2.17} вытекает следую-
следующая общая формула:
Г 1
844 Гл. 8. Интегральные уравнения
Оператор C\ может быть также представлен с помощью собственных
векторов оператора ЭД:
Щ; . (8.2.18)
т
Отсюда при X = 0 получаем разложение
И-1 = @„= У.0^^ . (8.2.19)
т
Для Ut~p имеем
эд-р=2^^- (8.2.20)
т т
Возвращаясь к формуле (8.2.18), видим, что собственные значения Х = Хт
оператора ЭД являются особыми точками @ как функции от X. Это — общее
свойство, не зависящее от того, является ли 9( эрмитовым либо опреде-
определенным или нет; в самом деле, если 8l-em = Xmem, то
и мы видим, что @х-ет—> со при X—>Хт.
Характер соответствующих особенностей проще всего выяснить с помощью
следа | 0&к | (Spur) оператора &к (в главах 1 и 3 это выражение называлось
также коэффициентом расширения; см. F.1.3)). Согласно разложению (8.2.18),
Мы видим, что | ®х | представляет собой мероморфную функцию перемен-
переменного X, имеющую простые полюсы в точках X = Хш, причем соответствующие
вычеты равны —1. Скалярная функция |@х|» согласно (8.2.17), выра-
выражается через | %~р | по формуле
l@x! = 2^n|^~(n+1)l, (8.2.21')
где в силу (8.2.20)
Sir- <8-2-22>
Перефразируем теперь эти результаты применительно к теории инте-
интегральных уравнений. Однородное уравнение второго рода
с действительным, симметричным, положительно определенным ядром К
имеет решения лишь при некоторых специальных значениях Хт параметра X.
Этим Хт соответствуют решения — собственные функции фт. Последние
образуют ортонормированную систему функций, быть может конечную, т. е.
п(*)Фт(*)<Ь = «пт- (8-2.23)
Числа Хт образуют возрастающую последовательность; наименьшее из них Хд
положительно, если К — положительно определенное ядро. Экстремальное
свойство чисел Хт в соответствии с (8.2.15) записывается так:
( ^ d7(z) ф (z) dz )
X = min — iYK ;VV ; . (8.2.24)
{^(z)K(zlz)^(z)dzdz\
8.2. Общие свойства интегральных уравнений 845
Ядра и функции Грина для неоднородных уравнений. Обратимся
теперь к неоднородному уравнению
ф (z) = X J К (z | z0) ф (z0) dz0 + x (z), (8.2.25)
которое мы собираемся решать с помощью функции Грина. Последнюю мы
выбираем так, чтобы она соответствовала оператору №>х из (8.2.16). В аб-
абстрактном векторном пространстве аналогом (8.2.25) служит уравнение
Решение для е может быть получено следующим образом:
(l-X8l-i).e = q,
или
B(-X).e=2l-q.
Отсюда
е=(ед.ч,
где
@x = (Sl-X)-1.
Неудобство этого решения состоит в том, что оно выражается через произ-
произведение двух операторов. Это неудобство легко обойти, записав
тогда
e = q + X@x-q. (8.2.26)
Тем самым решение уравнения (8.2.25) выражено через @^; в координат-
координатной записи имеем
Ф И = X W + * 5 Gx (z | z0) x (zo) dz0. (8.2.27)
Входящую сюда функцию Грина в теории интегральных уравнений принято
называть резольвентой.
Для того чтобы формулу (8.2.27) получить прямо, не обращаясь
к операторным уравнениям, нужно получить интегральное уравнение
для &1. Из уравнения (8.2.16), определяющего @Л, следует, что
а отсюда
ЭГ1 {% - \) ©х = 2Г1 = ©х - Х9Г1 ©х
и
©х = «-1 + ХЧ1 ©х. (8.2.28)
Уравнению (8.2.28) соответствует интегральное уравнение для G^
Gx (z | z0) = Я (z | z0) + X ^K (z | Zl) Gx (zx | z0) dZl. (8.2.29)
Из этого интегрального уравнения следует, что
Комбинируя уравнения (8.2.25) и (8.2.29), можно, воспользовавшись сим-
симметрией G\ и К, получить выражение ф в виде (8.2.27). Следует подчерк-
подчеркнуть, что именно эти свойства симметрии позволяют изменять порядок
интегрирования.
846 Гл. 8. Интегральные уравнения
Для дальнейшего нам полезно получить содержащее Gi интегральное
уравнение, которому должно удовлетворять ядро К. Снова прибегая;
к операторам в векторном пространстве, замечаем, что
откуда
Соответствующее уравнение имеет вид
К (z | z0) = Gx (z | z0) - X ^ Gx (z | zt) К (Zl | z0) dzx. (8.2.30).
Отличие этого уравнения от (8.2.29) только кажущееся. Поменяем местами z.
и z0 в уравнении (8.2.30); при этом
Теперь, пользуясь свойствами симметрии К и Gx, мы можем от (8.2.30)
перейти к (8.2.29). Эти соотношения между К и Gx дали основание Воль-
терра назвать К и —G\ взаимными функциями.
Формулы разложения (8.2.18) и (8.2.19) для ©х и ЭД могут быть
перенесены на Gi и К в такой форме (см. сказанное на стр. 839):
- V
— Zj
m
m
^Ы?)±тЫ. (8.2.32)
Для того чтобы вывести формулы, аналогичные формулам (8.2.17), (8.2.20)
и (8.2.22), нужно выяснить, что соответствует операторам ЧЩ-р. Выражению.
ЭД^р-е соответствует
где функция Kp(z\z0) подлежит определению. Будем исходить из выра-
выражения U(~1-e, которому соответствует интеграл
Заметив, что результат воздействия ЭД~2 на е есть ЗГ^^Щ^-е) и, следова-
следовательно,
2 (z | z0) ф (z0) dz0 = ^ if (z | zx) /i: (Zl | z0) ф (z0) dz0 dzlt
получаем, что
K2{z\z0)^^K{z\z1)K{z1\z0)dz1.
Далее, так как 2Г3е = 2t~1-(?l~2-e), то подобным же образом получаем
К3 (z | z0) = $ Я (z | Zl) K2 (Zl | z0) dz,.
Ясно, что из общего соотношения ЭД-(р+з> = Щ-Щ-ч вытекают равенства
| z0) = ^ /iCp (z | zx) ^TQ (Zl | z0) dZl = J Kq (z | Zl) /JCp (Zl | z0) dzx. (8.2.33)
8.2. Общие свойства интегральных уравнений 847
Теперь мы можем написать формулы, аналогичные (8.2.17), (8.2.20),
(8.2.21) и (8.2.22). Аналогом первой будет служить разложение
со
Gk (z | z0) = 2 *n+i (* I z0) X", (8.2.34>
аналогом второй —
К (., I 7 \ — V ^m B) Фт (Zp) /о ? осч
AP\z\z0>— 2j (Ог.ЛО),
P\z\0> 2j \r>• (),
m m
Утверждения, относящиеся к @х и 8l~~p, в которых говорится о следах
операторов, можно будет перенести на G^ и Кр, если определить скаляр,
соответствующий |@х|. Для этого положим z = z0 в ядре, что соответствует
взятию диагонального элемента матрицы, изображающей @х. и> вместо того
чтобы суммировать диагональные элементы, возьмем интеграл по z. Сле-
Следующие формулы будут тогда соответствовать (8.2.21) и (8.2.22):
\p{z\z)dz^^±=Cp, (8.2.37)
а отсюда получаем
^ x (z | z) dz = ^ Cn+1 X". (8.2.38),
Полуопределенные и неопределенные ядра. Во многих случаях ядра
являются неопределенными и соответствующие операторы — неэрмитовыми,
а поэтому предыдущие рассуждения к ним не применимы. Иногда даже
в результате итерации получается не определенный, а лишь полуопреде-
полуопределенный оператор, так что и в этих случаях приведенные выше теоремы
непригодны.
Что можно сказать о неопределенных ядрах? Прежде всего, их соб-
собственные значения не обязательно действительны. В некоторых случаях
может быть лишь конечное число собственных значений. Например, п слу-
случае уравнения Вольтерра собственных значений нет вовсе, так что одно-
однородное уравнение не имеет решений (см. стр. 851). В качестве примера
рассмотрим следующее уравнение Фредгольма с весьма простым ядром;
1
ф (z) = X ^ (z — 2z0) ф (z0) dz0.
о
Ясно, что ф (z) должна быть линейной функцией
Постоянные а и р можно найти, подставив az + P в интегральное уравнение;
1
a.z + р = X ^ (z - 2z0) (az0 + р) dz0,
о
848 ' Гл. 8. Интегральные уравнения
и приравняв коэффициенты при одинаковых степенях z. Мы получаем
— систему однородных линейных уравнений относительно аир. Ненуле-
Ненулевое решение можно получить только при равном нулю определителе системы,
т. е. когда
1-1х _х
2 =0-
|Х 1 +
Двум корням последнего уравнения
соответствуют решения
Итак, в этом примере имеется всего два комплексно сопряженных собствен-
собственных значения и столько же решений заданного уравнения.
Число собственных значений и собственных функций может быть
конечно, и в этом случае нельзя разложить произвольную функцию в ряд
по собственным функциям; свойство полноты может быть сохранено лишь
по отношению к какому-то специальному классу функций. Так, в только
что рассмотренном примере по собственным функциям может быть разло-
разложена любая линейная функция от z. Важнее, однако, то, что собственных
функций оказывается достаточно много для того, чтобы по ним можно
было разложить ядро K(z\z0) и функцию Грина (?x(z|z0). Таким образом
сохраняется возможность решить методом собственных функций соответ-
соответствующее неоднородное уравнение.
Необходимый для подобных случаев аппарат был рассмотрен в гл. 7.
Задача о собственных значениях в абстрактном векторном пространстве
ставится в форме уравнения
Я-е = Хе. (8.2.39)
Поставим теперь эрмитовски сопряженную задачу о собственных значениях
[см. G.5.40)]:
m*-f = Xf. (8.2.40)
Решения уравнения (8.2.39) и решения уравнения (8.2.40) взаимно орто-
ортогональны, и поэтому мы можем положить, что
i^-en = onm. (8.2.41)
С помощью этих соотношений можно вычислить коэффициенты разложения
по еп тех [векторов, которые допускают такое разложение [см. G.5.43)]:
g=)j?nei.. gn = (f«-g)- (8.2.42)
п
Справедливо следующее разложение оператора Грина ©^ — ffi — ^)~1;
/-м XI &тт'т (Q О /,Ч\
\S\ = У, г г- . \O.Z,.tO)
8.2. Общие свойства интегральных уравнений 849
След оператора % выражается через ет и fj, следующим образом:
Следы ISt], |ЭД~Р|, |©х| и разложение \&\\ по следам |ЭД~Р| выражаются
формулами (8.2.22), (8.2.21) и (8.2.21'). Если существует лишь конеч-
конечное число собственных значений, то следы различных степеней опера-
оператора ЗД^1 связаны некоторыми соотношениями. Если, скажем, имеется
ровно q различных собственных значений, то эти последние выражаются
через следы первых q степеней оператора ЭД. Отсюда следует, что след
| ЭД-(«+1)| может быть выражен через l^!, |ЭД~2|, •••, |91~9|.
Экстремальное свойство решений уравнений (8.2.39) и (8.2.40) состоит
в том, что
X = экстремальное значение '—^ . (8.2.45)
Варьируя f* в этом уравнении, мы находим [см. F.3.74)], что условие
оХ = 0 приводит к уравнению (8.2.39), а варьируя е находим, что условие
оХ = 0 приводит к (8.2.40). Равенство (8.2.45) аналогично (8.2.14). Анало-
Аналогом (8.2.15) является равенство
X = экстремальное значение ^ ' . (8.2.46)
Особого внимания заслуживает случай антиэрмитова оператора (соот-
(соответствующего антисимметричному действительному ядру), когда ЭД* = — ЭД.
В этом случае из уравнения
следует, что
= -Х2е.
— определенный оператор, т. е. (е* • ЭД*21 • е) > 0, а поэтому — Х2>0,
т. е. значения X чисто мнимые. Далее, интересно отметить одну особен-
особенность сопряженной задачи о собственных значениях: в случае антиэрми-
антиэрмитова оператора еп = fn. В самом деле, если
ад. о — X е
ТО
Обращаясь к соотношению ортогональности (8.2.41), мы видим, что век-
векторы еп для антиэрмитова оператора ортогональны, так же как собствен-
собственные векторы эрмитова оператора. Таким образом, при этом сохраняется
формула разложения оператора Грина и, следовательно, остаются в силе
формулы, выведенные для случая положительно определенного оператора.
Ядра, отличные от действительных определенных. Теперь посмотрим,
как применяются формулы (8.2.39) — (8.2.46) к интегральным уравнениям.
Ввиду большой сложности уравнений рассматриваемого типа некоторые
выводы будут лишь продемонстрированы на примере интегрального урав-
уравнения с уже упоминавшимся ядром z — 2z0.
Уравнение
й> (z) = X J К (z | z0) ф (z0) dz0 (8.2.47)
54 ф. м. Морс и Г. Фешбах
850 Гл. 8. Интегральные уравнения
с действительным ядром K(z\z0), не являющимся положительно опреде-
определенным, имеет ненулевые решения лишь при некоторых специальных зна-
значениях X, которые мы обозначим Хт. Этим Хт соответствуют собственные
функции фот — решения уравнения (8.2.47). Числа Хш не обязательно обра-
образуют бесконечную последовательность, и они не обязательно действительны.
Система собственных функций может быть не полной, эти функции могут
быть даже не ортогональны. Поэтому мы рассмотрим эрмитовски сопря-
сопряженное уравнение [соответствующее уравнению (8.2.40)]
Ф(г) =Л [K*{z\ z0)ф(z0) dz0. (8.2.48)
Как уже отмечалось выше, собственные значения сопряженной задачи ком-
комплексно сопряжены с собственными значениями задачи (8.2.47). Далее,
<p%dz = opQ, (8.2.49)
где Фр и фд — собственные функции.
Собственные значения и собственные функции для ядра z — 2z0 были
указаны выше. Сопряженное уравнение имеет вид
1
? (z) = V- \ (zo — 2z) ?'{zo) dzo-
о
(Ядро К* этого уравнения комплексно сопряжено ядру К, в котором пере-
переставлены z и z0.)
И здесь мы видим, что ф зависит от z линейно, т. е. <p = az-j- b.
Отсюда получаем уравнения
и уравнение
определяющее ^. Последнее совпадает с уравнением, служившим для на-
нахождения X. Положим
тогда
11 11
2 2Х.! Г 2 2Х2
Сопоставляя фх и <р2 с фх и ф2, найденными выше, мы замечаем, что фх и §х
не являются комплексно сопряженными. Очень легко показать, что в со-
согласии с (8.2.49)
8. 2. Общие свойства интегральных уравнений 851
Функции <pj и ф4 еще не нормированы так, как это предписывают соотно-
соотношения (8.2.49). Для нормировки нужно вычислить интеграл
и аналогичный интеграл для пары функций <р2, <|>2.
Возвратимся к общим соображениям, касающимся функции Грина
и однородного уравнения Фредгольма второго рода. И теперь решение
неоднородного уравнения может быть получено с помощью функции Грина,
Подобно (8.2.27),
Снова функция Грина Gx удовлетворяет интегральным уравнениям (8.2.28)
и (8.2.30). Из (8.2.43) можно получить разложение Gx(z\z0):
ск (Z ю=2 Фт11}!-Ты - (8-2-50)
m
где фт и <рт нормированы, разумеется, согласно (8.2.49). В рассмотренном
нами примере
* 1 V1 Ф1(«)?1(«о) , ( 1 1 у^
где нормирующие множители выписаны явно. Так как $i = 4*2. ?i = ?2
и Х1 = Х2, то Gx при действительном X принимает действительные значения.
Однако мы замечаем, что Gx (z | z0) Ф GK (z01 z), т. е. нарушен принцип
взаимности. Читатель без труда докажет, подставив в (8.2.27) ядро z — 2z0
и найденную выше функцию Грина, что при любом выборе функции "/
получается решение соответствующего неоднородного уравнения.
Интегральное уравнение Вольтерра. Интегральное уравнение Вольтерра
[см. формулу (8.1.21) и следующие] представляет собой пример уравнения,
ядро которого не имеет собственных значений. Это верно для любого урав-
уравнения Вольтерра с ограниченным ядром. Представим уравнение Вольтерра
в виде уравнения Фредгольма
с ядром [см. (8.1.22)]
Предположим, что ядро К ограничено. Отсутствие собственных значений
будет доказано, если мы установим, что ряд
где Мп есть п-я итерация М, сходится при всех значениях X. Действи-
Действительно, если бы существовало хоть одно собственное значение, то соответ-
соответствующая конечная точка плоскости X была бы особой для G\ (z | z0) [см.
54*
852 Гл. 8. Интегральные уравнения
формулы (8.2.34) и (8.2.31)]. Необходимо оценить итерированные ядра.
Сначала рассмотрим
i
М2 (z \zo)=\ M (z | zx) M {zx | z0) dzx.
При z > z0 разобьем промежуток интегрирования на отрезки от 0 до z0,
от 20 до г и от г до I. Интеграл вдоль первого отрезка обращается в нуль,
потому что здесь гг < z0 и, следовательно, М (zx | z0) = 0. Интеграл от z
до / также равен нулю, так как при % > z обращается в нуль М (z | %).
Итак,
M2 (z | z0) =}K{z\z1)K (zx | z0)dz^ z > z0.
20
Рассуждая аналогично, убеждаемся в том, что M2(z\zo) = 0 при z < z0 и,
далее,
\[ G I ~ \ _ \ Д/ /у | -у \ Д/ /л, | 7 \ А7
\J G \ 7 \ ТС G I -7 ^ /^ 7 ^> 7
0, z < z0.
Воспользуемся теперь тем, что М ограничено. Пусть | К \ <: т; тогда
\М\<т,
| М31 < ^- т31 z — z0 |2,
Следовательно,
и мы видим, что Gx (z | z0) как функция переменного X не имеет особен-
особенностей в конечных точках; тем самым доказано, что уравнение Вольтерра
с ограниченным ядром не имеет собственных значений.
Сингулярные ядра. Характер особенностей ядра оказывает сильнейшее
влияние на распределение собственных значений уравнения Фредгольма
второго рода. Ядро называется сингулярным, если оно или A) имеет раз-
разрывы, или B) имеет особые точки внутри области интегрирования, или C)
область интегрирования не ограничена. Случай C) сводится к случаю A)
посредством замены переменного. Например, если интегрировать нужно от
нуля до бесконечности, то подстановка С = 1/A + z) приводит к интегралу
в конечных пределах, но ценой появления полюса в конечной точке пло-
плоскости ?.
Интегральные уравнения, содержащие функцию Грина уравнения Гельм-
гольца или Лапласа, часто оказываются сингулярными, причем встреча-
8. 2. Общие свойства интегральных уравнений 853
ются особенности всех трех типов. Например, интегральное уравнение
(8.1.9), к которому была сведена задача дифракции на полуплоскости, имеет
ядро Н™(к\х — xo\) с логарифмической особенностью при х = х0. Кроме
того, бесконечен один из пределов интегрирования. Ядра, перечисленные
после уравнения (8.1.15), имеют разрывные производные.
Ядра с интегрируемым квадратом приводятся к ограниченным ядрам
с помощью итерации. Так, если ядро К (z \ z0) имеет конечное число раз-
разрывов, то уже К2 (z [ z0) непрерывно. Проиллюстрируем это, положив
к (z | z0) при z < z0,
h (z | z0) при z > z0,
где функции k(z\z0) и h(z\z0) непрерывны, но могут иметь различные
значения при z = z0. Итерированное ядро задается формулой
ь
A-(zlzo)={
К* {z\zo)=^K(z\ Zj) К (Zj | z0) dzv
a
Для того чтобы вычислить К2, подставим в этот интеграл выражение А.
При z^z0
Къ (z | Zo) = ^ h (z | Zj) k (zx | z0) dz1 + ^ h (z | z2) h (Zl | z0) c/zj +
a ' г0
а при z <! z0
z го
A'g(z|z0)= ^ /г(z| Zl) k(zx| z0)dzx + ^ Л(z| zx)Л(zx| z0)dzx
20
Функция A^2(z|z0) непрерывна, так как при z = z0 приведенные выражения
совпадают.
Сингулярное ядро вида1)
A-(z|zo) = tf(z|zo)/|z-zo|°, \H(z\zo)\<M, (8.2.51)
может быть сведено к несингулярному посредством нескольких итераций,
если a < 1. Оценим итерированные ядра. Так как
— zo
> dZl,
то, очевидно, уже Кг при а<Ч/2 ограничено; если а = 1/2, то К2 растет
как InA/1 z—z01) при z-^-z0, а потому следующая итерация К3 будет
ограничена; если, наконец, 1/2<^а<^1, то
ь
dz1
М*
\z~z0 >2а~
__^ ^_ _< М2 2ai с д
*) В нижеследующем рассуждении в переводе исправлены неточности ориги-
оригинала.— Прим. ред.
854 Гл. 8. Интегральные уравнения
где Р = (b— zo)/(z— z0), y= (a~zo)/(z—z0). Последний интеграл легко выра-
выразить через бета-функцию, и мы получаем
где Co—значение интеграла, выписанного выше.
Как мы видели, К2 ограничено при 2<х— 1 <^0, т. е. при а<1/2. Если это
неравенство не выполняется, то следует продолжить процесс итерации.
Покажем, что при а < 1 мы рано или поздно дойдем до ограниченного
итерированного ядра. Доказательство основывается на неравенстве
| Кр [z | z0) |< ^ | К (г | Zl) 11 Кр_х(zx | z0) | dzx.
a
Отсюда получаем, что К3 при a <^ 2/3 ограничено, при a = 2/3 имеет лога-
логарифмическую особенность, а при 2/3<а<1
-2o|3a-2 J ц-cricl2»-1 '
так что
где Сг— некоторая другая постоянная. Вообще при (n—l)/n<^a<^l
\Kn(z\z0)\<CMn/\z-z0 |"--(«-«), (8.2.52)
а при па— (га— 1) < 0, т. е. при
a<(re-l)/n, (8.2.53)
n-с итерированное ядро оказывается ограниченным. Значит, для заданного
а < 1 существует такой номер п, что ядро Кп ограничено.
Особенности, весьма близкие к только что рассмотренным, встречаются
у ядер, связанных с функцией Грина уравнения Лапласа. Трехмерная функ-
функция Грина пропорциональна
[(х- хоJ + (У-УоГ + (*- *оJГ'. (8-2-54)
двумерная — пропорциональна логарифму соответствующего расстояния на
плоскости. Во втором случае мы только усилим особенность, если возьмем
ядро
Этот прием позволяет нам трактовать трех- и двумерный случаи аналогично.
Остановимся на случае трех измерений. Пусть
|#(г|.
Тогда
8. 2. Общие свойства интегральных уравнений 855
Пользуясь неравенством
(х -xxf + {у- У1Г + (z- zx)* > 3 [(х- х,Г (У -УгГ (z - zj*\* ,
получаем оценку, подобную найденной ранее,
уу Г С ^ I
Таким образом, К% ограничено. В двумерном случае, рассуждая анало-
аналогично, находим, что ограничено ядро К3.
Функция Грина уравнения Гельмгольца имеет в отличие от (8.2.54)
существенную особенность при |г—г0 |—> со [см. интегральное уравнение
(8.1.9)]. Такие ядра называются существенно сингулярными. Для них
процесс итерации не приводит к ограниченным ядрам.
Основное различие, важное для нас, между существенно сингулярными
и ограниченными ядрами проявляется в строении спектра собственных
значений соответствующего однородного уравнения Фредгольма второго рода.
Можно показать, что в случае ограниченного ядра множество собственных
значений конечно или счетно. Существенно сингулярное ядро может иметь
непрерывный спектр собственных значений, т. е. при любом X из неко-
некоторого промежутка может существовать ненулевое решение ф^.
Это различие можно истолковать следующим образом. Если некоторое
ядро Кп интегрируемо в квадрате, то оно может быть разложено в ряд по
собственным функциям, образующим счетную ортогональную систему, и такой
ряд будет сходиться в среднем (см. стр. 687). Такое ядро, в частности, может
быть представлено двойным рядом Фурье. Иначе обстоит дело в случае ядра
с неинтегрируемым квадратом. Для представления функции с неинтегрируемым
квадратом, вообще говоря, требуется интеграл Фурье со специальным кон-
контуром интегрирования (который должен обходить особые точки). Мы уже
видели при рассмотрении функций Грина, что в разложениях функций
Грина (уравнений Лапласа и Гельмгольца) по собственным функциям в не-
неограниченной области фигурируют интегралы типа интеграла Фурье; это
согласуется с тем, что такие функции Грина не интегрируемы в квадрате.
В заключение этого параграфа приведем пример интегрального урав-
уравнения с существенно сингулярным ядром, имеющим непрерывный спектр
собственных значений:
<!> (z) = X \ е-' г-г<>' <}• (z0) dz0. (8.2.55)
[-00
Ядро имеет особую точку в бесконечности. Это уравнение сводится к диф-
дифференциальному уравнению
откуда следует, что
Однако интеграл в (8.2.55)) существует только при Re [|/ 1 — 2к] < 1. Все
X, удовлетворяющие этому ограничению, являются собственными значениями
{8.2.55), а соответствующие фх — собственными функциями. Мы имеем
непрерывный спектр собственных значений. Такого же типа случай (б)
в примерах, следующих за уравнением (8.1.15).
856 Гл. 8. Интегральные уравнения
8. 3. Решение уравнений Фредгольма первого рода
Мы ограничимся изучением только тех случаев, когда может быть
получено точное решение. Приближенные методы будут рассмотрены в гл. 9.
Следует подчеркнуть, что приближенные методы решения физических проп-
лем наиболее удобно основывать на интегральных уравнениях. И так как
мы не в состоянии точно решить подавляющее большинство интегральных
уравнений, то приближенным методам будет отведено особое место и они
будут подробно изложены в гл. 9.
Общий метод, который будет здесь изложен, аналогичен методам реше-
решения дифференциальных уравнений, изученным в гл. 5. Главное в этом
методе — разложение искомой функции по полной системе функций. Это
разложение имеет вид суммы или интеграла по этой системе с неизвестными
коэффициентами. Подставляя это разложение в дифференциальное уравне-
уравнение, получаем соотношения между искомыми коэффициентами. Иными словами,
дифференциальное уравнение оказывается преобразованным в уравнение или
систему уравнений, определяющее коэффициенты. Полное семейство функ-
функций, если это возможно, выбирается так, чтобы эти новые уравнения легко
решались. Например, если разложением является степенной ряд ф = ^ anzn*s,
то преобразованное уравнение оказывается разностным уравнением относи-
относительно коэффициентов ап. Для некоторых, изученных в гл. 5 типов, это разност-
разностное уравнение содержит только два различных значения п и легко решается.
Решения уравнений Фредгольма в форме рядов. Мы применим теперь
этот метод к интегральным уравнениям Фредгольма первого рода, для
которых он особенно хорошо приспособлен. Это интегральное уравнение
[см. (8.1.19)] имеет вид
ь
)dz0. (8.3.1)
В соответствии со сказанным положим
vBi== /аи \z\w\zL (o.o.^i
п
где функции gn образуют полную систему на интервале {a, b); w(z) является
весовой функцией, которую можно выбрать близкой к <'j (z) и тем самым
улучшить сходимость ряда (8.3.2). Тогда
ь
9 (z) = 2 аг> \ К (z I z«) &n (^o) a» (*o) cZzo = 2 апЛ»(*), (8-3.3)
тг а п
Ь
К (z) = ^ ^ (z I zo) &n (zo) a» («o) rfzc •
а
где функции hn известны.
Таким образом, решение интегрального уравнения сводится к нахожде-
нахождению коэффициентов ап по известным <р и hn. Это особенно просто делается
в двух случаях. Если функции hn пропорциональны степеням z, то (8.3.3)
оказывается степенным рядом, так что неизвестные коэффициенты можно
получить путем сравнения этого ряда с разложением <р по степеням z. Во
втором случае, если функции hn образуют ортогональное семейство:
ь
8. 3. Решение уравнений Фредголъма первого рода 857
то коэффициенты ап можно определить при помощи квадратур
ь
Как мы увидим ниже, существует важный класс уравнений, для кото-
которого осуществляется один из этих двух специальных случаев. К сожалению,
чаще функции hn не являются ни степенями z, ни элементами ортогональ-
ортогональной системы, и в этом случае необходимо преобразовать разложение <р но
функциям полной системы в ряд по hn. Точнее, пусть у разложена в ряд
по функциям y_q, образующим полную систему
z). (8.3.4)
Тогда возникает необходимость выразить функции yq при помощи функции
(8.3.3).
К-
Подставляя эти выражения в уравнение (8.3.4), получаем
<? = 2 /«««Л. =2B /«««„) К-
q,n n q
Сравнивая с (8.3.3), имеем
«„=2/Ли- (8-3.6>
Q
Таким образом, для решения данного интегрального уравнения достаточно.
найти коэффициенты аеп из системы (8.3.5).
Определение коэффициентов. Мы изучим три метода определения
коэффициентов. Первый из них предполагает, что yq образуют произвольное
множество функций, не связанных каким-либо частным способом с функ-
функциями hn. Во втором методе функции yq строятся из hn при помощи про-
процесса ортогонализации, т. е. находятся линейные комбинации из функций
hn, образующие полное семейство и попарно ортогональные. Наконец, функ-
функция <р может быть непосредственно разложена в ряд по yq, коэффициенты
которого вычисляются при помощи квадратур.
В первом методе мы разлагаем функцию hn из уравнения (8.3.5) в ряд
по функциям y_q:
Уравнение (8.3.5) при этом дает
Хд == 2^ ag»i"npXp >
n,v
а следовательно,
2«eAp=V (8-3-7>
71
Теперь система уравнений (8.3.7) должна быть решена относительно aqn~
858
Гл. 8. Интегральные уравнения
Обозначим через Н определитель, составленный из элементов hnp:
Ко
Ко
0
Кг
Къ • ¦ •
&12 • • •
h22 ...
(8.3.8)
Пусть Mnp—алгебраическое дополнение, соответствующее элементу h
Так как
ny.
то
М.
пд
н
(8.3.9)
Из полученного результата явствует, что этот метод может быть эффектив-
эффективным только в том случае, если, каждая функция hn является комбинацией,
составленной из небольшого числа функций ур, так как тогда нетрудно
вычислить определитель Н и его миноры.
Ортогонализация. Процесс Шмидта упоминался в таблице, помещен-
помещенной в конце гл. 6. Теперь мы его изучим подробнее. Ставится следующая
задача. Дано полное семейство неортогональных функций hn; построить
новое семейство функций yq, являющихся линейными комбинациями hn
и образующих полное ортогональное семейство. Процесс Шмидта состоит
в последовательном построении функций у^. В качестве функции ^о берется h0.
Функция Хг представляет собой линейную комбинацию h0 и hx, подобран-
подобранную так, чтобы она была ортогональна у0; функция Хг представляет собой
линейную комбинацию h0, hx, h%, ортогональную уЛ и ^о-
Можно выписать рекуррентное соотношение, выражающее yq через hq
11 Хр» Р < 9- Из способа построения видно, что hq должна быть линейной
комбинацией функций хр при р^д. Используя. условие ортогональности
получаем функцию hq в виде суммы
dz
р=о
р
где р — весовая функция. Разрешая относительно yq, находим
ь
p=0
Теперь мы можем так нормировать функции
ь
^, чтобы было
(8.3.10)
8. 3. Решение уравнений Фредволъма первого рода 859
Тогда выражение для у^ приводится к виду
ь
в-1 I XphqP dz
У =h _V Л у (8.3.11)
р=0
и
ь
7Vg = ^ | hQ
hQ |
a
Более подробно:
a
Ъ
Xo = К No = \ I Ло |2Р dx,
Ъ
Xi = K- ( ^
a
b
/.2 = К — ( ^ ХЛР ^z/A^ ^ xi - (^ Хо^-зР ^z/^o ) Zo и т. д.
a
b Ь
ь
W1 =
В качестве примера произведем ортогонализацию семейства степеней zn
на промежутке (—1, 1), р=1. Этот процесс должен привести к полиномам
Лежандра. Мы покажем, что это действительно так, вычислив функции уЛ
и Х2> которые должны быть пропорциональны соответственно z и 3z2— 1.
Интегралы, входящие в выражение для ул, имеют значения
ь 1
No = 2, V Xo^iP dz = \ z dz = 0.
a —1
Отсюда следует, что
Xi = z> Ni = -3 •
Интегралы, необходимые для определения уя, имеют значения
1 Ь 1
\Xi^2p^z— \
a -I a -I
Следовательно,
2 2 1 2 1
/а 3 ""~ 3 '
а это выражение действительно пропорционально Р2. Нормирующий интег-
интеграл равен
N-1-9-8
860
Гл. 8. Интегральные уравнения
Продолжая этот процесс, получаем другие полиномы Лежандра и их норми-
нормирующие интегралы. В таблице, помещенной в конце гл. 6, приведены дру-
другие ортогональные полиномы, получающиеся при использовании других
промежутков интегрирования и других весовых функций. Например,
полиномы Эрмита соответствуют промежутку интегрирования (—со, сю)
и весовой функции e~z2, в то время как полиномы Лагерра L^ соответствуют
промежутку интегрирования @, со) и весу х?е~х.
Однако коэффициенты aqn уравнения (8.3.5) не получаются непосред-
непосредственно из процесса Щмидта и потому мы в нашем рассмотрении не можем
ограничиться этим процессом. Теперь мы должны получить явные выраже-
выражения для aQm. Из формулы (8.3.5) и из процесса получения функций у имеем
q
Х« = S
Так как функции у ортогональны, то
ь
y,:/,s> dz = О,
% А-
если Р =? Я-
Условия ортогональности будут выполнены для всех р и q при р < q, если
потребовать, чтобы
ь
==0' Р<9-
(8.3.13)
Теперь можно использовать условие (8.3.13) для определения aQn, так как
после подстановки выражения для хд в (8.3.13) получаем
71=0
где
и
z-
При р = q эта сумма обращается в 7Vg. Коэффициенты aqn можно выразить
при помощи миноров элементов dnp в определителе, составленном из этих
элементов.
Рассмотрим определители D'.
, = <?
001
^
00
"o
«02
^
20
(8.3.14)
И Т. Д.
Коэффициент aqn пропорционален алгебраическому дополнению Мт эле-
элемента dm в Dq. Это следует из условия, которому удовлетворяют Mnq:
Поскольку мы хотим, чтобы коэффициент при hq в выражении для /Q
равнялся единице, следует положить aqn = Mm/Mqq и теперь разложение y(j
S. 3. Решение уравнений Фредголъма первого рода
861
запишется так:
(8.3.15)
п=0
Этот ряд как раз и является другим представлением формулы Шмидта
(8.3.11) и притом таким, которое дает явное выражение коэффициентов
в разложении уд.
В качестве примера рассмотрим снова полиномы Лежандра, т. е.
положим уА = Рп, un=z", р=1, а в качестве промежутка интегрирования
возьмем (—1, 1). Для определения Р2 нам необходимо рассмотреть опре-
определитель
О | О
А о 2
Теперь из (8.3.15) следует, что
]\1п ]№ 1
Л*22 •'2 &
а это выражение действительно пропорционально Р2.
Нормирующие интегралы также можно выразить при помощи опреде-
определителей Dq. Интеграл
в силу уравнения (8.3.13) оказывается равным
z =
то есть
р=0
Эта последняя сумма в точности равна значению определителя Dn, в то
время как Mqq равняется Dq_x. Следовательно,
Nq = Dq/DQ_1. (8.3.16)
В примере, разобранном выше,
л_32^ п _.? -Y — А
2 "" 135 ' г ~~ 3 ' 2 ~ 45 -
Биортогональные ряды. Вернемся к нашей исходной формуле (8.3.3),
где функция (р разложена в ряд по известным, но не ортогональным функ-
функциям hn:
Коэффициенты ап могут быть вычислены, если найдено семейство функ-
функций wn, удовлетворяющих условиям
(8.3.17)
862 Гл. 8. Интегральные уравнения
Тогда ап определяются при помощи квадратур
n9{Z)dZ. (8.3.18)
В этой формуле мы не уточняем пределов интегрирования или, в более
общем случае, пути интегрирования в плоскости комплексного перемен-
переменного z. Необходимо только, чтобы область, в которой интегралы (8.3.18)
имеют смысл, включала область определения интегрального уравнения.
Непосредственные попытки прямого определения функций wn(z) обычно
не бывают удачными. Вместо этого мы рассмотрим метод, применение
которого целесообразно тогда, когда разложения последовательных hn
начинаются со все более высоких степеней z (как, например, для функций
Бес селя):
Коэффициент Апп всегда можно положить равным единице, хотя исторически
так делали не всегда. Следовательно, функция кп регулярна в начале
координат. Теперь мы покажем, что в этом случае функции wn получаются
из разложения
(8.3.20)
Для доказательства вычислим интеграл
взятый по некоторому замкнутому контуру, охватывающему точку z и начало
координат и лежащему в области аналитичности hn(z). Тогда, согласно
интегральной формуле Коши, левая часть этого уравнения в точности равна
2mhg(z). Сравнивая с правой частью, убеждаемся, что равенство возможно
только в том случае, когда
wn @ \ Wydt = 2™П9 (8.3.21)
Соотношение (8.3.21) не зависит от предположения о поведении hn,
выраженного равенством (8.3.19); оно является общим и применимо всегда,
когда hn аналитична в области, ограниченной контуром интегрирования.
Это требование является ограничением только в том случае, когда hn имеет
существенную особенность в точке z. В таких случаях разложение <р в ряд
по hn должно исследоваться особо тщательно.
Определение функций wn зависит от возможности осуществления разло-
разложения (8.3.20). Однако в том случае, когда выполняются условия (8.3.19),.
для определения wn можно дать общий алгорифм. Возьмем q-ю производ-
производную по z от (8.3.20), а затем положим z = 0. Получим
n
Используя условия (8.3.19), находим, что
=° 1 0 д < п.
8. 3. Решение уравнений Фредгольма первого рода 863
Следовательно,
Эти равенства образуют систему рекуррентных соотношений, последова-
последовательно разрешая которые, получим функции wn(t). Это особенно удобно
сделать, переписав уравнение (8.3.22) в следующем виде:
q-i
71=0
Прежде всего положим q = 0. Тогда
wo(t)=l/t.
Пусть q=i. Тогда
Ниже приведены первые четыре функции wn, полученные таким способом:
= -1 = 1 Ло
-, . [р.б.гд)
1 — A3l — Aso + A
... _ 1 As2
W3 — Ji — tS -Г t2 t
Отсюда можно вывести общую формулу.
Ясно, что функции wn являются полиномами относительно l/t, и наи-
наибольшая степень l/t, фигурирующая в wn, равна п-\-1.
Вернемся теперь к исходному вопросу о получении разложения произ-
произвольной функции <р в ряд по hn. Теперь этот вопрос сводится к вычисле-
вычислению интеграла (8.3.18). Контур интегрирования выбран так, что он охва-
охватывает начало координат. Если мы запишем
р=0
то равенство (8.3.18) преобразуется к виду
Si §«М*М«)* = 25 2 *-
р=0
Из интегральной формулы Коши вытекает, что
где q>(p) @)—значение /j-й производной от <р по ее аргументу в начале
координат. Следовательно,
р=0
Это и есть выражение, определяющее ап. Ясно, что в случае, когда hn
удовлетворяют условию (8.3.19) (ряды начинаются с n-ii степени z), вычи-
вычисление ап можно довести до конца, ни разу не прибегнув к бесконечным
864 Гл. 8. Интегральные уравнения
процессам. Однако, если условие (8.3.19) не выполнено, процесс разыска-
разыскания функций wn (t) уже не будет столь простым. В этом случае более
эффективным оказывается метод ортогонализации, описанный выше. Факти-
Фактически здесь можно провести некоторую аналогию с процессом Шмидта.
Мы закончим это рассмотрение примером. Предположим, что hn явля-
являются функциями Бесселя Jn(z). Тогда искомыми будут коэффициенты ряда
Ряды такого твпа называются рядами Неймана. Соответствующие биорто-
гональные функции называются полиномами Неймана On(t). Соотношения
.между /„ и Оп имеют вид
Функции Оп не совладают и точности с функциями wn, так как первый
член в разложении Jn ранен zn/2nn\, а не / и разложение (8.3.20) не со-
содержит ен. Однако это различие не принципиальное, а касается, скорее,
деталей. Уравнения (8.3.22) можно легко решить и в том случае, когда
Aqq ф 1. Полипомы Неймана определяются соотношениями
2пп\
ггРп @ = -JJTTT
— 2) + 2-4-Bп—2)B/г — 4) +¦¦
Первые несколько полиномов таковы:
(8.3.27)
о гл- 5 , 120 , 1920
Козффициенты а„ могут быть определены согласно формуле (8.3.25):
" in s{n + s)/2\
{ )Wh nv (8.3.28)
Штрих над знаком суммирования означает здесь, что следует брать сумму
только по четным или только по нечетным s, если п соответственно
четное или нечетное; ( * J — биномиальные коэффициенты.
Интегральные уравнения первого рода и производящие функции.
Теперь мы на нескольких примерах проиллюстрируем развитую выше общую
теорию. Рассмотрим прежде всего случай &n=zn; это имеет место тогда,
когда ядро интегрального уравнения служит одновременно производящей
функцией для семейства ортогональных полиномов.
Согласно сказанному на стр. 729, производящую функцию для поли-
полипомов Эрмита Hn(z0) можно записать в виде
п\
8.3. Решение уравнений Фредгольма первого рода 865
Это разложение можно применить для решения интегрального уравнения
)dZo. (8.3.29)
Проблема такого типа может возникнуть в задачах о распространении
тепла, когда искомым является первоначальное распределение источников,
порождающее некоторое заданное распределение температуры. Положим
в равенстве (8.3.29)
Используя разложение ядра и нормировку функций Эрмита (см. стр. 730)
сводим уравнение (8.3.29) к виду
9(s) =
Следовательно,
и решение ty имеет вид
Если решено некоторое интегральное уравнение первого рода с задан-
заданным ядром, то можно найти другие примеры разрешимых уравнений, при-
применяя операторы по z, скажем, к обеим частям уравнения (8.3.29); (8.3.30)
остается при этом решением. Ясно, что в рассматриваемом примере можно
получить при помощи дифференцирования производящей функции новые
ядра, разложимые в ряды по функциям Эрмита и "в степенные ряды.
Используя соотношения
мы получаем
s=0
Следовательно, уравнение
со
9 (z) = J в-(«-'в)« Нр (г -z0) ф (z0) dz0 (8.3.31)
—СО
имеет решение
Ф (Z) = 2 «Л (Z) + S=g ? ^f Яр+6 (*). (8.3.32)
q=0 " s=0
Здесь коэффициенты aQ при q < p — 1 произвольны, так как их нельзя
определить из интегрального уравнения (8.3.31),. поскольку Hq ортого-
ортогонально ядру е-(*~гоJ i/p(z — z0).
55 ф. м. Морс и Г. Фешбах
866 Гл. 8. Интегральные уравнения
Наконец, можно взять линейную комбинацию нескольких ядер такого
вида и получить новое ядро
#(Z|Zo) = e-<^o)*2<zptfp(z-2o). (8.3.33)
р
Ясно, что каждое ядро, являющееся функцией от (z — z0), можно разложить
в такой ряд. Значит, имея решения соответствующих интегральных урав-
уравнений первого рода, можно найти решение интегрального уравнения, ядром
которого является произвольная функция от (z — z0). Дальше, в этой же
главе, мы увидим, что к таким ядрам можно также применить метод,
использующий интегралы Фурье.
Теперь мы перепишем (8.3.33) в виде ряда по степеням z:
р=0 s=0 р=0
Подставляя это разложение в интегральное уравнение, получаем
Пусть
~ CqHg(z)
5=0
тогда
со
TW@)= S(-1LCp- (8-3.34)
р=0
для любого s. Уравнения (8.3.34) образуют систему, определяющую коэф-
коэффициенты Ср. Выпишем несколько таких уравнений:
9 @) = Со — ахСх + а2С2 — agCg + а4С4 — ...,
*A) @) = Сг - ахС% + а2С3 -а3СЛ+...,
где а0 считаем равным единице.
Решение этой системы можно получить методом итераций. Здесь мы
приведем только результаты. Решение является линейной комбинацией <р*6* @):
Ср = 2 ?<"+¦> @)Гв> (8.3.35)
s=0
причем коэффициенты 1\ имеют вид
Г. - 2j (- *) (п (вЛ (й) (fl)
где при суммировании должны быть учтены все такие комбинации rt, что
r1 + 2ra + 3r, + 4r4+...=*. (8.3.3в)
Выпишем несколько первых Ts:
То = 1, Т1 = а1, Та = а[ — а2, Т3 = а\ — 2аха^-\-аъ,
7ь = а\- 3afa2 -j- a\ + 2asax -a4, (8.3.37)
'ia\a3 + 'Sala^ — 2а3а2 — 2a4ax + а6.
8.3. Решение уравнений Фредгольма первого рода 867
Аналогичным образом можно решать интегральные уравнения, ядрами
которых служат производящие функции других ортогональных полиномов.
Подробное решение мы приведем для полиномов Лагерра. Производящая
функция имеет вид
? [Г(п+1 + а)]« '
причем нормировка такова:
Тогда решение уравнения
jMffl , 0<z<c», (8.3.38)
(«о)""
имеет вид
?г=О
Упомянем также о другом разложении, из которого можно получить раз-
разрешимое интегральное уравнение. Это разложение основано на более общей
производящей функции для /4,а) (см. стр. 728):
i 2 r
Если эта функция используется в качестве ядра, то решение соответству-
соответствующего интегрального уравнения первого рода имеет вид
¦ = V S [rti+a + i)]. ^d) e>B). (8.3.40)
п=0
Применение полиномов Гегенбауера. Производящая функция для
полиномов Лежандра или, в более общем случае, для полиномов Геген-
Гегенбауера также порождает интегральные уравнения первого рода, которые
можно решить. Рассмотрим, например, следующее ядро:
Тогда интегральное уравнение записывается так:
Используя разложение К и полагая ф = 2 a^n> получаем
п=0
55*
868 Гл. 8. Интегральные уравнения
где мы воспользовались равенством
•Следовательно,
П=:0
Аналогичные результаты можно получить для системы полиномов
Гегенбауера T^(z) с любым v, для которых производящая функция имеет
вид (см. таблицу в конце гл. 6)
- 2zz0
при нормировке
Используя производящую функцию в качестве ядра и ограничиваясь про-
промежутком изменения z от — 1 до 1, получаем решение интегрального
уравнения первого рода (8.3.41), в котором ядро l/j/~l— 2zzo-\-z2 заменено
ядром (8.3.42), в виде
—Л A— z2)v
SaH2 ^Ййзг (8-3.44)
Придавая v соответствующие значения, можно получить важные част-
частные случаи: при v = 0 — полиномы Лежандра, при v целом — присоединенные
функции Лежандра. При v = 1/2
1 —2zzo + Z2 = у Y 2 Тп
Т 2
п=0
Здесь Гп2 —полиномы Чебышева. Условие нормировки имеет вид
1
Решение интегрального уравнения
дается формулой
. . со
Ф - V i (* - z2I/2 2 ^ 71"'2 (*)• (8-3.45)
Во всех рассмотренных выше случаях можно получить новые разре-
разрешимые интегральные уравнения дифференцированием или интегрированием
обеих частей по z.
До сих пор мы рассматривали производящие функции, которым "соот-
.ветствовали ортогональные системы функций. Такое благоприятное положе-
8.3. Решение уравнений Фредгольма первого рода 869-
ние не всегда имеет место. Представляется интересным найти подход
к решению задачи и в более общем случае. Рассмотрим, например, инте-
интегральное уравнение, ядром которого служит производящая функция для
функций Бесселя:
eizco&ub{u)du, 0<z<oo. (8.3.46)
Интегральное уравнение такого вида возникает в задаче о распространении
двумерных волн, амплитуда которых подчинена определенному условию
на некоторой полуплоскости. Первый шаг при решении уравнения (8.3.46)
состоит в разложении как ядра, так и функции ty (и) в ряды Фурье
по cos (пи):
2 = 2 ет/п (Z) COS ПК-
ет/п
Тогда
?(*) = « 2 «УпСО- (8-3-47)
п
Коэффициенты ап можно непосредственно выразить через значения функ-
функции <р и ее производных при z = О, как это было сделано при получении
формул (8.3.28).
Интегральные уравнения первого рода и функции Грина. Если оказы-
оказывается, что ядром интегрального уравнения служит функция Грина,
то решение получается легко. Это следует из того факта, что каждую
функцию Грина можно разложить в ряд по собственным функциям [см. фор-
формулу G.2.39)]. Для симметричной функции Gk
С^К) = 4*2^|^> , (8.3.48)
где функции %п ортогональны и нормированы на отрезке
Решение уравнения
ь
<р (х) = ^ G {х | х0) ф (х0) dx0
а
теперь может быть легко получено. Рассмотрим разложение для функции ф:
Тогда
причем коэффициенты ап вычисляются при помощи квадратур:
ъ
а« = ^ (*"" - F") \ Zn № 9 W **• (8-3-49)
а
Аналогичный процесс можно осуществить для дву- и трехмерных функ-
функций Грина, если только выражение
г0) = 4*2^^М, (8.3.50)
870 Гл. 8. Интегральные уравнения
•определяющее Gk, допускает разделение переменных. Функции, стоящие
лод знаком этой суммы, зависят от двух или от трех переменных. Тем
не менее, предполагая, что переменные разделяются, мы можем записать
каждую функцию у^п в виде произведения функций от одной переменной. Более
того, семейство всех этих функций от какой-либо переменной ортогонально (для
каждой из переменных):
Если при этом фиксировать значение двух переменных, например жа и х3,
пак для г, так и для г0, то выражение (8.3.50) для Gk приводится к виду
К (х \х0) = 2«, Хк1 (х0) Хк1 (х). (8.3.51)
k .
Интегральное уравнение первого рода, ядром которого служит К (х\хо)р
легко решается. Решение имеет вид
ф {х) = р (Ж) 2 [ ^Ь1(Жо)^о)р(Жо)^0] хм (я). (8.3.52)
Придавая переменным х2 и х3 различные значения и составляя линейные
комбинации получаемых таким образом ядер, можно получить много ядер
типа (8.3.51).
Поясним теперь эти замечания примером. Функция Грина двумерного
уравнения Лапласа пропорциональна inR, где
R = ]/>2 — 2rr0 cos (<р — 9о) +¦ т* = |г — г01.
Используя общую теорию разложения функций Грина, развитую в преды-
предыдущей главе (см. также гл. 10), находим, что в. полярных координатах
^(т) г>г°-
n=i
Пусть теперь г=го = 1. Тогда это разложение приводится к виду
= -2 4 cos[n (?-
или
In J 2 sin Г1^") I = - 2 4"tcos (n?) cos (n<p°) + sin (n<p) sin (™Р°Н- (8-3-54)
Интегральное уравнение первого рода с ядром
где 0<9<2i:, теперь легко решается.
Мы можем построить другое ядро с простым билинейным разложе-
разложением типа (8.3.51) в виде суммы
In | 2 sin (^Jfo) | + In | 2 sin (^4p ) | = In [2 (cos cp - cos %)].
Тогда
CO
In [2 I cos у — cos <p01 ] = — 2 ~ cos (nip) cos (n'f0). (8.3.55)
7l=i
8 3. Решение уравнений Фредгчяьмп первого рода 871
Следовательно, интегральное уравнение
я
W (?) = ^ In [2 | cos 9- cos9o IJ ф (%) efy0 (8.3.56)
6
имеет решение
= flo- ^ 2 п [ 5 ^ feo) cos (/г%)d% ] cos (n<p)> (8-3.57)
71 0
где а0 произвольно.
Дифференцируя только что приведенные ядра, можно получить другие
полезные ядра. Дифференцирование In | 2 sin (<р — <ро)/2 | и In [21 cos 9 — cos <р01 ]
соответственно дает
_ ctg (^~^° J = 2 tsin (ncp) cos G190) — cos (гор) sin (n<p0)],
71
= - У 2 .v ^' cos (n<pQ).
— COS<p
Интегральное уравнение
I COSCf0 — COScp
о
ядром которого служит функция l/(cos<p0— cos 9), можно преобразовать
в другое уравнение, представляющее интерес для гидродинамики Пусть
Тогда
J
Операции, при помощи которых из функции Грина lni? мы получили
много различных ядер, очевидно, могут быть использованы и для других
функций Грина. Пример, который мы выбрали, особенно прост. В самом
деле, перечисленные выше разложения можно было получить прямым путем
быстрее, чем используя предварительное знание разложения функции Грина,
и в принципе такое непосредственное разложение всегда возможно. Однако
в последующих главах (гл. 10 и следующие) будут указаны разложения
для многих функций Грина в системах координат, допускающих разделение
переменных, и таким образом будут автоматически выделены многие инте-
интегральные уравнения первого рода, разрешимые при помощи разложения
по собственным функциям.
Интегральные преобразования и интегральные уравнения первого
рода. В равенстве
функция W (z) часто называется (интегральным) преобразованием функции <]> (z).
Решение интегрального уравнения, выражающее й через W, называется
обращением этого преобразования. Преобразования, в которых соотно-
соотношение между ? и | особенно просто, изучены весьма подробно. Здесь мы
рассмотрим несколько примеров.
872 Гл. S. Интегральные уравнения
Наиболее изученным и наиболее важным является преобразование
Фурье (см. § 4.7)
W(k) = —\=- [ eihz$(z)dz. (8.3.59)
— .JO
Его обращение имеет вид
со
<!>(*) = -/= \ e~ih*W(k)dk, (8.3.60)
и, таким образом, интегральное уравнение (8.3.59) с известной функцией х?
и ядром К (к | z) = ebhz имеет своим решением (8.3.60). Мы отсылаем чита-
читателя к § 4.7, где излагаются условия, при которых такое обращение воз-
возможно.
Преобразование Фурье можно обобщить на широкий класс функций.
Как было показано в гл. 6, преобразование Фурье вытекает из условия
полноты для семейства собственных функций с непрерывным спектром соб-
собственных значений. Напомним прежде всего, как выражается условие
ортогональности и нормировки для случая непрерывного спектра. Если
к — собственное значение, то
? (ft I x)<p (fto'| x) dx = 8 (ft- ft0), (8.3.61)
где область интегрирования простирается до бесконечности хотя бы в од-
одном направлении, а о.— дельта-функция Дирака. Произвольную функцию ф
можно разложить по функциям ф только при условии, что существует
интеграл
ф (х) = ^ W (ft) 9 (ft | х) dk. (8.3.62)
Для получения функции W (к0) умножаем обе части этого равенства
на <р (к0 | х) и интегрируем по х:
dz= ^ W(k)y(ko\x)9(k\x)dkdz.
Меняя порядок интегрирования (эту операцию следует обосновать в каж-
каждом частном случае) и используя уравнение (8.3.61), получаем
jj 9 (ft0! х) ф (х) dx = jj W (ft) 8 (ft - k0) dk.
Следовательно,
цг (/С) = J ^ (ft | ж) <t (x) dx. (8.3.63)
Мы видим, что если W (ft) является преобразованием функции ф (х) при помощи
функции <р, то ф является преобразованием функции W при помощи
функции <р. В случае преобразования Фурье, рассмотренного выше,
а интегральные соотношения Фурье (8.3.59) и (8.3.60) как раз являются
частными случаями уравнений (8.3.63) и (8.3.62) соответственно.
Таким образом, ясно, что каждая функция двух переменных, которую
можно нормировать в соответствии с уравнением (8.3.61), может быть
использована для построения преобразования и его обращения. Иными
8.3. Решение уравнений Фредеолъма первого рода 873
словами, для тех интегральных уравнений первого рода, ядрами которых
служат указанные функции, решение дается формулой обращения.
Например, преобразование Ганкеля можно получить, используя свой-
свойства ортогональности функций Бесселя Jm (kr) с произвольным т. В гл. 7
[см. также уравнение F.3.62)] мы показали, что
со
ущ 5 jjm jjm rdr=8 (к - ю-
о
Следовательно, в предыдущих рассуждениях можно положить
Следуя традиции, мы опускаем множитель У к в преобразовании Ганкеля.
Таким образом,
(8.3.64)
о
Его обращение определяется так:
со
^(r)=[jm(kr)W(k)kdk. (8.3.65)
о
Из уравнений (8.3.64) и (8.3.65) получаем
[оо оо
•> (г) = J ft dft J p [Jm (kr) Jn (ftp) ф (рI dp.
О и
Итак, решение интегрального уравнения (8.3.64) дается формулой (8.3.65).
При изучении некоторых интегральных уравнений важную роль играют
различные преобразования, тесно связанные с преобразованием Фурье
(см. также § 4.7). Преобразование Лапласа, которое мы применим в даль-
дальнейшем к интегральному уравнению Вольтерра, имеет вид
W (р) = { е~ш ф (z) dz. (8.3.66)
о
Его обращение имеет вид
c+ioo
^ (8.3.67)
Преобразование Меллина определяется формулой
оо
W (S) = ^ z8 ф (z) dz. (8.3.68)
о
Его обращением является
c+ioo
z-sW(s)ds. (8.3.69)
Как выражение (8.3.67), так и выражение (8.3.69) можно рассматривать
как решения интегральных уравнений первого рода (8.3.66) и (8.3.68)
соответственно.
874 Гл. 8. Интегральные уравнения
Наконец, упомянем еще о двух преобразованиях, получаемых в теории
аналитических функций, которые, по существу, выводятся из интеграль-
интегральной формулы Коши. Их называют преобразованиями Гильберта. Из фор-
формулы D.2.18) следует, что если
оо
± \ ^zo, (8.3.70)
то
оо
V (8.3.71)
Знак аР перед интегралом показывает, что интеграл берется в смысле
главного значения. Если (8.3.70) рассматривать как интегральное уравне-
уравнение с искомой функцией ф(г), то решение дается формулой (8.3.71).
Из D.2.28) получаем аналогичную пару:
2я
L
<8-3-72)
Мы уже говорили об этом частном виде ядра в предыдущем пункте, посвя-
посвященном функциям Грина [см. (8.3.57)], где решение было найдено с по-
помощью рядов Фурье. Эта связь не вызывает особого удивления, так как
формула D.2.28) основана на соотношении D.2.25), в которое входит функ-
функция Грина.
В этом пункте была подчеркнута связь между интегральными пре-
преобразованиями и интегральными уравнениями первого рода. Ниже в этой
главе мы используем преобразования для приведения интегральных ура-
уравнений к видам, более удобным для решения.
Дифференциальные уравнения и интегральные уравнения первого
рода. В предыдущих пунктах мы видели, как можно решать уравнения
первого рода довольно разнообразных типов. Еще большее количество
разрешимых уравнений можно построить, действуя на обе части уравне-
уравнения каким-нибудь оператором, дифференциальным или интегральным (или
и тем и другим). Например, предположим, что мы знаем решение ф {ура-
{уравнения
<2>(z)=^ К (z | z0) ф (z0) dzQ,
где К и <р—известные функции. Тогда мы можем найти решение уравнения
X (z) = ^ %№ B1 2о)] 4> Ы dz0 (8.3.73)
в том случае, когда известно решение уравнения
.*?*[? (*)] = х(*). (8-3-74)
и выразить ф через х- Обратно, если мы знаем решение уравнения с не-
неизвестной х> т0 мы можем решить уравнение с неизвестной <р. Таким обра-
образом, мы можем перейти от решения простого интегрального уравнения
к решению более сложных интегральных уравнений в том случае, когда
8.3. Решение уравнений Фредгольма первого рода 875
мы можем решить уравнение, выражающее <р через х- Если оператор,
переводящий К в X {К), является дифференциальным оператором, то ура-
уравнение, которое следует решить, чтобы получить <р, является дифферен-
дифференциальным уравнением. Таким образом, если мы в состоянии решить диф-
дифференциальное уравнение, то мы можем решить и интегральное уравнение,
и, наоборот, если мы в состоянии решить интегральное уравнение, то мы
дюжем решить дифференциальное уравнение.
Пусть, например, К (z | z0) = e~zz°, так что
Это как раз преобразование Лапласа; решение ф дается формулой обраще-
обращения {8.3.67). Значительно более общий класс ядер можно получить из ядер
или
S« (z | z0) = 2 (- l)ng« B) ^ (е-и°) = ^z [K (z | z0)],
n
где
X = У ( - l)ngn (z) — (8.3.75)
n
В данном случае (8.3.74) является дифференциальным уравнением относи-
относительно <р, изученным довольно подробно в гл. 5:
Решение этого дифференциального уравнения может оказаться нелегким.
Для того чтобы воспользоваться более доступными методами, необходимо,
чтобы сумма была, конечной. Действительно, даже если дифференциальное
уравнение имеет первый или второй порядок, разрешимость его маловероятна.
Другой пример получим с помощью полиномов Эрмита. Пусть К (z | z0) —
= е-<2-2«J. Если
ТО
Z[K(z\ z0)] = S ane-lt-xJ*Hn{z- z0):
h
Это последнее соотношение весьма расширяет область выбора ядер для новых
интегральных уравнений. Если ап постоянны, то ядро X {К) является функ-
функцией общего вида от'(z — z0), определенной на интервале (— со, оо). Если
же ап зависят от z, то ядро оказывается даже ещ~ более общим. Соответ-
Соответствующее дифференциальное уравнение
решается особенно просто, если коэффициенты ап постоянны; следовательно,
здесь мы имеем способ решения любого интегрального уравнения первого
876 Гл. 8. Интегральные уравнения
рода, ядром которого служит функция от (z — z0), определенная на интер-
интервале (— оо, со).
С интегральным уравнением может быть связано также другое диф-
дифференциальное уравнение. Его можно получить из равенства (8.3.73) совер-
совершенно аналогично тому, как были получены интегральные представления
для дифференциальных уравнений (см. § 5.3). Предположим, что
XzK(z\z0)=e?zK(z\z0),
где индекс указывает, на какую из переменных действует оператор. Напри-
Например, если X задается равенством (8.3.75), то
(Другие примеры см. в § 5.3.) Введем теперь сопряженный оператор
определяемый соотношением
иЛ [v] -
Применяя эти соотношения к уравнению (8.3.73), получаем
ь
х(г) + Р[К (z|а), ф(а)]-P[K(z\ Ъ), ф (Ъ)] = \ К(z\ z0)ЛЩ (z0)] dz
Согласно нашему предположению, это интегральное уравнение можно решить
относительно &#[ф], так что
c?[ty(z)]^r(z). (8.3.76)
Может оказаться, что это дифференциальное уравнение решается проще,
чем (8.3.74). Методы и примеры нахождения cS по оМ, а также примеры
операторов X приведены в § 5.3.
Оператор X не обязательно должен быть дифференциальным. Например,
он может оказаться операцией взятия преобразования и тогда проблема
(8.3.73) сводится к проблеме обращения этого преобразования. Однако этот
сильный метод заслуживает сам по себе целого параграфа и мы вернемся
к нему в § 8.5.
Проблема моментов. Момент /г-го порядка Мп функции (или, как это
обычно бывает в физике, распределения) ф определяется следующим образом:
ь
\)dz0, (8.3.77)
где р (х) — весовая функция. Во многих случаях, в частности при рассмотре-
рассмотрении явлений переноса (см. § 2.4 и 12.2), возможно вычислить последова-
последовательность моментов Мп, и искомой является функция ф.
Прежде чем изучать методы, применяемые здесь, заметим, что линей-
линейной заменой переменной можно изменить пределы интегрирования. В резуль-
результате мы изменим область определения ф и новые моменты будут линейно
выражаться через конечное число исходных. Например, пусть
Тогда
S.3. Решение уравнений Фредголъма первого рода 877
Положим
Тогда
ь
Pn = {j^l)n+t \ (zo - а)"Ф Bо) Р («о) dzo
а
и, следовательно,
^=(^T+1 2 (Г )(—)п-^.. (8-3.78)
8=0
Отсюда ясно, что в силу линейности преобразования пределы интегрирова-
интегрирования а и Ь в (8.3.77) можно изменить, не прибегая к каким-либо бесконеч-
бесконечным процессам. Обычно рассматриваются пределы ( — со, об), @, со)
и (-1, 1).
Метод, пригодный для решения проблемы моментов, заключается в том,
что устанавливается соотношение между моментами и коэффициентами
разложения функции ф по полиномам, ортогональным с весом р в про-
промежутке (а, Ъ).
Например, предположим, что интервалом интегрирования является
( —оо, со), а весовой множитель равен e~z°. [Можно, конечно, выделить
множитель е~2о из функции ф (z0) и определить новую неизвестную функ-
функцию 9 соотношением ф B„) = e~z»p (z0).] Соответствующими ортогональными
полиномами будут Hn(z0). Разложим теперь ф (z0) следующим образом:
Ф (*о) = 2 апНп (г0), ап = -^А— \ ф (z0) Нп Bо) е-В dz0.
—оо
Так как Нп — полиномы, то интеграл, входящий в выражение для ап, можно
непосредственно выразить через Мп. Например, H0(z0) = 1, так что
В общем случае
( — l)hn\
п—2Л)!
где при четном п последним членом разложения является постоянная, а при
нечетном — член с первой степенью х. Тогда
При помощи (8.3.79) легко найти функцию ф.
Существует и другой подход к проблеме моментов, в принципе более
общий, но не всегда более эффективный практически. Можно показать, что
эта проблема эквивалентна интегральному уравнению первого рода. Вернемся,
878 Гл. 8. Интегральные уравнения
например, к разобранному выше случаю. Умножая обе части уравнения
(8.3.77) на e-z2Bz)n/n\, получаем
Суммируя теперь в обеих частях по п, имеем
^ { 2 (JTMn } = J ^B~гА Ы *о- (8.3.80)
п=0 —со
Предполагая, что ряд в левой части сходится, мы видим, что проблема
моментов свелась к интегральному уравнению первого рода. Конечно, это
уравнение можно решить, разложив ф по полиномам Эрмита. Однако суще-
существуют приближенные методы решения интегральных уравнений (см. гл. 9),
которые часто могут оказаться более практичными, чем использование соот-
соотношения (8.3.79).
Подобным же образом можно поступать и в случаях других промежут-
промежутков интегрирования. Интервалу @, оо) соответствуют весовая функция е~~г°-
и полиномы Лагерра. Промежутку (—1, 1) и р=1 соответствуют полиномы
Лежандра. Если р = |/г1— z\, то соответствующими полиномами являются,
полиномы Чебышева. Весьма важно заметить, что разложение ф по орто-
ортогональным полиномам зависит от весовой функции р. Действительно, харак-
характер сходимости для различных весовых функций может быть совершенно
различен. Однако, как указывалось выше, выделяя множитель из ф (z0)
и рассматривая оставшийся множитель как неизвестную функцию, можнги
произвольным образом менять вес. Обозначим вес через ш (z), так что
ь
zo9 (zo) <° (zo)9(zo) dzo' гДе Ф = ">?•
Наиболее подходящей (т. е. обеспечивающей наиболее быструю сходимость)
будет такая весовая функция о», которая возможно более близка к неиз-
неизвестной функции ty. Очевидно, если она в точности равна ф, то в разложе-
разложении ср по полиномам будет только один член, а именно <р = 1. Весьма
выгодно использовать любую доступную информацию, чтобы построить
наилучшее возможное приближение к 6, и затем взять это приближенно
в качестве ш.
Резюме. Мы исследовали те решения интегральных уравнений Фред-
гольма первого рода, которые получаются при помощи разложения неиз-
неизвестной функции в ряд по функциям какой-либо полной системы. Наиболее
общие ядра, для которых могут быть получены точные решения, характери-
характеризуются разложением вида
где как фп, так и <рп образуют полные и ортогональные семейства. Орто-
Ортогональность, вообще говоря, не существенна, но на практике весьма удобна.
Однако же обсуждались и методы, применяемые в случае, когда одно из этих
семейств не является ортогональным.
Следует подчеркнуть, что уравнения Вольтерра первого рода могут
быть решены некоторыми из описанных в этом разделе методов, хотя,
вообще говоря, операции оказываются более трудными и требуют привлече-
8.4. Решение интегральных уравнений второго рода 879
ния всего аппарата метода Шмидта или биортогональных рядов. К счастью,
"многие ядра уравнений Вольтерра имеют специальную форму v(z — z0),
что позволяет развить для них более эффективные методы; этот случай
довольно подробно будет рассмотрен в § 8.5.
8.4. Решение интегральных уравнений второго рода
Методы, применяемые для решения интегральных уравнений Фредгольма
второго рода, также можно классифицировать в соответствии с типом раз-
разложения ядра. Эта классификация, конечно, весьма похожа на ту, которая
была дана в § 8.3, но оперировать с уравнениями второго рода приходится
совсем иначе. Вследствие этого целесообразно подойти к классификации
иным путем, отличным от того, которому мы следовали в § 8.3, хотя, как
мы увидим, будут изучаться те же типы ядер, что и раньше. Как и в пре-
предыдущем параграфе, мы будем заниматься здесь методами точного решения;
приближенным методам будет полностью посвящена гл. 9. Один из методов
решения при помощи рядов, называемый методом Фредгольма, весьма важен
для изучения теории возмущений и поэтому мы откладываем его изложение
также до следующей главы.
Уравнение, подлежащее изучению, имеет вид
fe. (8.4.1)
Эта задача имеет решения только для некоторых специальных значений л
Мы будем их обозначать через Хп, а соответствующие им решения — через фп.
Если ядро К симметрично и несингулярно, то собственные значения веще-
вещественны, а спектр собственных значений дискретен. Если ядро симметрично,
но сингулярно, то часть спектра может быть непрерывной, если же ядро
не симметрично, то собственные значения не обязательно вещественны.
Мы можем разложить К (z | z0) в ряд по функциям hn(z), образующим
полное семейство; тогда коэффициентами будут функции gn(z0) от z0:
(8.4.2)
Это наводит нас на мысль, что решение можно искать в виде
(Следует подчеркнуть, что в дальнейших рассуждениях будет предполагаться,
что это разложение сходится.) Значит,
ь
) dz° для всех п'
Ап = * 2 АР 5 ?п (*о) К (z
880
Гл. 8. Интегральные уравнения
Обозначив
получаем
или
(8.4.5)
Это — система линейных однородных уравнений с неизвестными А .
Ненулевые решения Ар существуют только тогда, когда равен нулю опреде-
определитель, составленный из коэффициентов,
Xa00 —:
4)i
Xa02
^«03
Xa10
Xau-1
Xa,,
Ха21
Xa;
Xa.
Xa,
30
31
'32
Xa33 -
= 0
или в сокращенной записи
l4»-Vl = 0. (8.4.6)
Все возможные решения Хп этого уравнения, записанного с помощью опре-
определителя, можно найти, а затем из уравнения (8.4.5) находим соответ-
соответствующие значения Ар и с помощью формулы (8.4.3) определяем ф. Для
того чтобы установить связь с задачей интегрирования дифференциального
уравнения, заметим, что (8.4.5) представляет собой последовательность
рекуррентных соотношений для определения Ар, очень похожих на соот-
соотношения, получающиеся при подстановке степенного ряда (или иного ряда
по функциям полной системы) в* дифференциальное уравнение.
Для разыскания «наилучшего» типа разложения ядра К не существует
«столбовой дороги», не существует всегда пригодного правила, указывающего,
какое из разложений в наибольшей степени упрощает решение. В самом
деле, обычно для каждого типа ядер возможно несколько разложений и часто
приходится испытывать каждое из них для того, чтобы найти наиболее
удобное в данном, конкретном случае. В соответствии со сказанным наша
классификация методов решения будет связана скорее с типами разложений,
чем с ядрами, связана с природой коэффициентов арп, получающихся для
данного К после выбора множеств gn и hp. Часто для данного К можно
применить разложения различных классов, хотя, обычно, одно из разложе-
разложений представляется наиболее подходящим. Сейчас мы дадим обзор наиболее
употребительных классов разложений К, приводя примеры тех типов ядер,
для которых эти разложения оказываются подходящими, а также остано-
остановимся на некоторых деталях решения уравнений.
Разложения первого класса. Наша классификация будет зависеть
от свойств матрицы арп, т. е. от того, как связаны функции gn и hp.
Например, первым назовем тот класс, для которого арп— диагональная
матрица, т. е. apn = an6pn. Это означает, что каждая функция gn орто-
S. 4. Решение интегральных уравнений второго рода 88
тональна всем функциям hp, за исключением hn. В этом случае
Х« = ^Г' (8А7)
причем
Проверить это решение можно непосредственной подстановкой в интеграль-
интегральное уравнение (8.4.1).
Ядра, являющиеся функциями Грина, дают примеры разложений диа-
диагонального типа. В предыдущем параграфе мы получили из разложения
для In Я выражение (8.3.54)
СО
= — 2 -^ fcos (Щ) °os (щ0) + sin (щ) sin (щ0)].
71=1
При 0<<р<2тс собственными функциями соответствующих интегральных
уравнений являются cos (щ>) и sin(n<p); обе они соответствуют собственному
значению Хп = — п/ъ.
Второй пример получаем, объединяя In 12sin (<р — <ро)/21 и In 12sin (<р4-<ро)/21
так, чтобы иметь (8.3.55)
со
к (ф 19о) = Ь [2 [ cos <р — cos <р0 |] = — 2 — cos (щ) cos (щ>0).
71=1
При 0 <; <р <; л соответствующее интегральное уравнение имеет собственные
функции cos (щ) и собственные значения ^п= —п/и.
Дифференцируя только что выписанное ЛС (ер ] ц>0) [см. (8.3.55)], мы
получаем пример, иллюстрирующий существенную разницу между уравне-
уравнениями первого и второго рода:
cos <р — cos ср0 ^—1
71=1
Заметим, что хотя функции sin (ntp) и cos (nw) образуют полные семейства,
они не являются попарно ортогональными в промежутке 0<!<p<;ir. При ре-
решении уравнения первого рода (см. § 8.3) это обстоятельство не порождало
трудностей, так как свободный член не был связан никаким явным соот-
соотношением с функцией Ь\ напротив, для уравнения второго рода дело обстоит
совершенно иначе.
Разложения второго класса. Разложениями второго класса мы будем
считать такие, для которых
"рп
ИЛИ
а =0, если р<п (типа),
арп = 0, если р > п (тип Ь). (8.4.8)
Такие разложения мы будем называть полу диагональными. Функцию gn
можно следующим образом разложить в ряд по функциям hp, которые
56 ф. м. Морс и Г. Фешбах
882
Гл. 8. Интегральные уравнения
полагаем ортогональными и нормированными:
(8.4.9>
Р=0
Рекуррентное соотношение, связывающее коэффициенты Ар в случае а,
имеет вид
. = * 2
р=п
Это соотношение включает как частный случай (если для заданного п
отличны от нуля только два арп) двучленные рекуррентные соотношения,
имеющие столь важное значение в случае дифференциальных уравнений.
Уравнение, определяющее Хп, выглядит в случае а весьма просто:
,-1
\а
о
о
о
10
_ \
о
о
Ха21
а22 —1
6
.-1
= 0.
Разложение этого определителя имеет вид (Ха00¦— 1) (ХаХ1 — 1) ..., так что
собственными значениями служат Хп = 1/апп. Соответствующие собственные
функции представляют собой линейные комбинации функций hp, р<и.
Таким образом, как это следует из рекуррентных соотношений для Ар 9
К и т. д.
Поучительно рассмотреть частный случай типа а, когда арп
от нуля только при р=п и р + 1 Т
приобретает вид
отличны
у рп
Тогда рекуррентное соотношение
.» = о.
Это — двучленная рекуррентная формулами она легко решается:
Мы видим, что выбор [X = Хп = 1/я„п влечет за собой равенства Ар = 0
при р > п; другими словами, ряд для ф„ по функциям hp обрывается
при р— п. Почему же не каждое X может быть использовано при под-
подсчете А и, следовательно, не существует непрерывного спектра X? Един-
Единственным ограничивающим условием является сходимость ряда для Л. Воз-
Возможны только те значения X, для которых ряд для <]> сходится. Положе-
Положение здесь вполне аналогично тому, которое имеет место в теории диффе-
дифференциальных уравнений. Например, решая дифференциальное уравнение
Эрмита при помощи степенных рядов, мы получаем двучленную рекуррент-
рекуррентную формулу. Сходящиеся степенные ряды нельзя получить без отбора
8. 4. Решение интегральных уравнений второго рода
883
специальных значений, соответствующих специальным значениям X в ис-
исследуемом случае (ср. стр. 713). В случае интегральных уравнений важно
понять, что, помимо решений, соответствующих ХГ1 = 1/аГ1Г1, могут также
существовать решения, для которых спектр X непрерывен.
Рассмотрим теперь тип Ъ. Рекуррентное соотношение и уравнение,
определяющее Хп, имеют вид
п
Ко -'
Ха
01
р=О
о
о
<х .
Чз
Ха
Ха.
О
О
О
Ха33 —'¦
= 0.
Как и для типа а, собственные значения равны \п=1/апп. Соответству-
Соответствующие собственные функции не являются конечными линейными комбина-
комбинациями функций hp, как это было в случае а. Например, уравнения, опре-
определяющие коэффициенты разложения для ф0, имеют вид
Следовательно,
п—1
2
р=0
1 = 1 \а ' ' 2
или
-Vii + 02J
и -т. д. Все сказанное для тица а относительно осторожности, необходи-
необходимой при рассмотрении спектра X, применимо также и здесь.
Примеры ядер полудиагонального типа дают производящие функции.
Рассмотрим
Независимая переменная меняется от —1 до +1. После подстановки
в интегральное уравнение ф = 2 -^р^р (z) получаем
zn0Pp(z0)dz0.
(8.4.10)
-1
Если р > п, то интеграл обращается в нуль. Следовательно, К является
полудиагональным ядром типа Ъ. Для собственных значений имеем
zn0Pn(Zo)dzo..
Для того чтобы вычислить этот интеграл, заметим, что z" можно выразить
в виде линейной комбинации Рр, р <п, и что при интегрировании этой
линейной комбинации «выжить» может только тот член, который содержит Рп.
56*
884 Гл. 8. Интегральные уравнения
Следовательно, в представлении z" при помощи Рр следует рассматривать
только член, содержащий Рп. Так как
Р = у '; гzn — ...1,
то
После интегрирования получаем
__ Bге + 1)! .
П ОП+1 /„|\2
С4-) '
» _ * х -гз х -15
Ло — 2 ' * — 2 ' 2 — 4 ' "" * '
Коэффициенты Д, для каждого частного значения X можно получить непо-
непосредственно из рекуррентных соотношений (8.4.10). Меняя в вышеприве-
вышеприведенных рассуждениях ролями z и Рп, можно получить полубесконечное
ядро типа а. Это ядро имеет вид
Тогда для
-1
получаем
п -1
Если положить
то
р -1
Так как \ PnzP dz = 0 при р <.п, то мы можем написать
-1
-1
V 2
"Собственные значения определяются равенствами Хп = 1/а„п и совпадают с
(Собственными значениями предыдущей задачи. Однако в этом случае соб-
8. 4. Решение интегральных уравнений^ второго рода 885
ственные функции определяются легче:
--2 |
1-(аоо/а2а) И Т- Д-
где значения арп приведены выше.
Разложения третьего класса. Обратимся теперь к третьему классу
разложений, которые мы назовем конечными. Эти разложения определяются
условием
арп —0, когда р или п больше, чем г. (8.4.11)
В этом случае в уравнении (8.4.6), определяющем Хп, определитель имеет
конечный порядок г (г строк и г столбцов). Раскрывая этот определитель,
получаем полином степени г. Таким образом, наше уравнение имеет г кор-
корней, которые могут быть определены обычными методами. Очевидно, как
диагональные, так и полудиагональные ядра могут быть конечными.
В простейшем примере из этого класса K(z\z0) представляется в виде
произведения
K(z\zo) = h
Интегральное уравнение имеет вид
Так как этот интеграл равен постоянной, то сразу видно, что Ф (z) = h (z).
Следовательно,
Этот результат можно получить также непосредственно из уравнения (8,4.6),
так как в этом случае только элемент а00 не равен нулю. Согласно ура-
уравнению (8.4.6), имеем
Х«оо-1 = 0, Х=^
в соответствии с результатом, полученным из интегрального уравнения.
Решения можно получить в явном виде также и в случае, когда в раз-
разложении К фигурируют только два члена. Мы приводим эти результаты
для справок. Уравнение, определяющее X,
(Чо-1)
имеет два решения
1а01
' ±
2(aooau— o10a01) * \ • • /
где Х+ соответствует знак плюс перед квадратным корнем. Соответству-
Соответствующие собственные функции таковы:
886 Гл. 8. Интегральные уравнения
Другие случаи. Наконец, может случиться, что выбор hn был сделан
столь неудачно, что привел к разложению ядра К, не относящемуся
ни к одному из рассмотренных выше классов, т. е. разложение полу-
получилось не диагональное, не полудиагональное и не конечное. Тогда, вообще
говоря, невозможно получить точное выражение для собственного значения Хп
и следует прибегнуть к приближенным или численным методам. Эти методы
будут изучены в гл. 9. Однако существует один случай, заслуживающий
рассмотрения, когда уравнение для Хп достаточно просто. Именно, предпо-
предположим, что
арп = 0, когда рФп — 1, п, п + 1. (8.4.14)
Другими словами, разложение gn по функциям hn состоит только из трех
членов. Предполагая, что функции hn ортогональны и нормированы, полу-
получаем это разложение в виде
Xa00 - 1
Xa01
0
Xa10
XaL1 —
Xa12
8n — an-i, пЛп_1 -\-ап<n
Уравнение, определяющее Хп, имеет вид
0
Xa21
Ха22 — 1
О 0 Ха23 Ха33—1 Ха43 0 . . =0.
Рекуррентное соотношение, связывающее неизвестные коэффициенты Ар
в разложении функции Ф, согласно (8.4.5), имеет вид
Xan_i,n An_1 + (Un,n-l)An + htn+i,n Л„+1 = 0. (8.4.15)
0
0
Xa32
33
•
•
1
#
0
X«43
•
•
. • •
• • •
• • •
0 . .
• • •
• Ф •
• • •
Это — трехчленная рекуррентная формула. Мы изучали решение таких
разностных уравнений в гл. 5 на стр. 532, где подобная проблема воз-
возникла при решении дифференциального уравнения Матье.
Сначала введем новые неизвестные
Тогда
Ха„_1>п + (Хап>п — 1) Gn ¦+- Xan+i>n Gn+l Gn = 0.
Для упрощения обозначений положим
an,nA*n-i,n = — Pni «n+i.n/an-i.n = — <7„>
1/Х = [1, l/an_1>n = — г„.
Теперь (8.4.15) можно переписать в виде
- 1 + (Рп - ?rn) Gn + qnGnGntl = 0. (8.4.16)
Выражая из этого уравнения Gn через Gn+1, получаем
G 1
Подставляя в это выражение аналогичное выражение для Gn+lt находим
Г
Рп V-rn
8. 4. Решение интегральных уравнений второео роба
887
Продолжая этот процесс, получаем Gn в виде непрерывной дроби:
9n+i
Для Gx имеем
(8.4.17)
Ра —
Рз —
Мы можем также разрешить (8.4.16) относительно Gn+1:
г _ Рп—У-Гп . 1
n+1 ~ 9п 9пС„ •
Отсюда получаем конечную непрерывную дробь:
+¦
— (Рп-1 —
Яп-i
+ ¦
9п-2 '" 9о
(8.4.18)
При п = 0 (8.4.18) дает
Приравнивая зто выражение выражению (8«4.17), получаем уравнение для
определения р = 1/Х: [
¦ *—„ (8-4.19)
Ро—
Л—
Pt —
Численные методы, которые следует применять для решения этого уравне-
уравнения, описаны в гл. 5 на стр. 532, и нет необходимости вновь говорить
о них. Во всех случаях, когда разложение ядра имеет вид (8.4.14), все
сводится к решению уравнения (8.4.19). Как только jj. определено, соответ-
соответствующие Gn+1 можно найти из (8.4.18) и, следовательно, при помощи со-
соотношений Gn = AjAn_1 можно вычислить АЛ.
Неоднородное [интегральное уравнение Фредгольма второго рода.
Решение неоднородного уравнения второго рода рассматривалось в § 8.2.
Будет поучительно вновь вывести прямым путем результат, полученный
там. Это уравнение имеет вид
(8.4.20)
Пусть
888 Гл. 8. Интегральные уравнения
где
Кроме того, можно разложить К в ряд по биортогональным собственным
функциям:
71
где
ь
ФпТп. dz = Sum-
а
Тогда, подставляя полученное выражение в (8.4.20), получаем
п п, р
ИЛИ
Следовательно,
T"dz- (8A21>
Конечно, записывая решение в форме (8.4.21), мы предполагаем, что
нам известно достаточно много <1>п. В случае когда этих решений мы не
знаем, иногда оказывается удобным переписать интегральное уравнение
(8.4.20) в виде интегрального уравнения первого рода. Затем можно при-
применить методы § 8.3. Уравнение (8.4.20) можно записать так:
где о (z — z0) — дельта-функция Дирака. Это — уравнение первого рода
с ядром o(z — z0) — Xif (z|z0). Из формулы (8.4.21) явствует, что те значе-
значения X, при которых ф, рассматриваемая как функция от X, имеет полюсы,
являются собственными значениями Х„.
8. 5. Преобразование Фурье и интегральные уравнения
В § 5.3 был рассмотрен метод преобразования одного дифференциаль-
дифференциального уравнения в другое, которое иногда оказывается более простым.
Вместо того чтобы пытаться тепосредственно решать заданное дифферен-
дифференциальное уравнение, мы изучали уравнение для соответствующего преоб-
преобразования Фурье или Лапласа, Меллина или'Эйлера. В случае когда одно
8. 5. Преобразование Фуры и интегральные уравнения 889
из^ этих уравнений для преобразования оказывалось проще первоначаль-
первоначального, мы получали интегральное представление решения исходного урав-
уравнения, и этот способ, как мы видели, был весьма эффективным.
Иногда такой же метод может облегчить работу по решению инте-
интегральных уравнений. Мы находим интегральное уравнение, которому удов-
удовлетворяет преобразование исходной искомой функции; если оно оказывается
более простым, чем первоначальное уравнение, то мы можем получить
интегральное представление для исходной неизвестной функции.
Конечно, этот процесс является частным случаем развитых в § 8.3-
методов разложения неизвестных функций по полной системе собственных
функций. Если спектр собственных значений непрерывен в некоторой об-
области, то такое разложение является интегралом, распространенным по
этой области собственных значений, т. е. является интегральным пред-
представлением, а не разложением в ряд. Например, коэффициент в разложении
Ф(ж) по собственным функциям "|/1/2тс elhx, причем областью непрерывности
служит — оо < к < оо, как раз и является преобразованием Фурье функции <!>.
Этот метод особенно хорош, когда интегральное уравнение после инте-
интегрального преобразования сводится прямо к алгебраическому уравнению,
что имеет место, когда преобразованное ядро оказывается диагональным.
Несколько примеров лучше проиллюстрируют вопрос, чем дальнейшее общее
рассмотрение. Заметим сразу же, что мы не будем слишком заботиться о
тонкостях (таких, как вопрос о существовании данного преобразования!). Мы
вернемся к ним, после того как поясним на примерах общие черты метода.
Преобразование Фурье и ядра вида v(x — яс0). Прежде всего отметим,
что область изменения независимой переменной в преобразовании Фурье
есть весь промежуток от — оо до -f- оо, а поэтому наше внимание сначала
будет сосредоточено на уравнениях вида
(8.5.1)
{уравнение Фредгольма второго рода на промежутке (—оо<а;<^оо)].
Возьмем теперь преобразования Фурье от обеих частей уравнения. Предпо-
Предполагая, что эти преобразования существуют (в дальнейшем мы будем более
осторожны; настоящее рассмотрение упрощено, с тем чтобы не затемнять
центральную идею деталями), мы находим
со
?(Л) = Ф(/с) + Х<р[ ^ w(x\xo)C?(xo)dxo].
—СО
Чтобы найти преобразование Фурье
со оо с»
dx0]=-l= ^ eikxdx ^ w(x\xo)t?(xo)dxOT
—СО — СО
мы выразим Ф (х0) через W (к0) при помощи формулы обращения
Затем запишем
со со
JF [ 5 w(x\xo)*(xo)dxo] = ^ W(qko)W(ko)dko,
890 Гл. 8. Интегральные уравнения
где
СО СО
= ± ^ dx0 ^ e-a°*°w(x\x0)eihxdx. (8.5.2)
—со
Преобразованное интегральное уравнение имеет вид
W(k\ko)W(ko)dko. (8.5.3)
Применение преобразования имеет смысл, если новое ядро проще старого.
Часто случается, что довольно сложная функция может быть представлена
в виде интеграла Фурье от функции сравнительно простого вида.
Из уравнения (8.5.3) явствует, что если W(k\k0) имеет вид
W^k\k0) = V^HV(k)o(k-k0), (8.5.4)
где о — дельта-функция Дирака, то преобразованное интегральное уравне-
уравнение решается немедленно. В этом случае уравнение (8.5.3) переходит
в уравнение
W (к) = Ф (к) +Уък W (к) У (к).
Это уже простое алгебраическое уравнение относительно Чг(/с):
(8.5.5)
Применяя теперь формулу обращения Фурье, можно получить ty(x).
Требование, чтобы преобразованное ядро было диагональным (т. е.
было пропорциональным дельта-функции от к — к0), накладывает опреде-
определенные ограничения на вид исходного ядра w(x\x0). Если мы научимся
распознавать ядра, подчиняющиеся этим ограничениям, то мы будем в со-
состоянии распознавать те интегральные уравнения, которые стоит подвер-
подвергать преобразованию Фурье. Выражение (8.5.2) для преобразованного ядра
является двойным преобразованием Фурье по обеим координатам х и х0;
его обращением служит
— СО —СО
w(x\xo) = -^ \
— СО
Подставляя частное выражение (8.5.4) в это уравнение, получаем
оо со
= ^ V(k)e-ihxdk J eih°*ob (к - к0) dk0 =
—со
dk^vix-Xo), (8.5.6)
где
СО
Vlk)e-ihxdk
— преобразование Фурье функции V. Следовательно, уравнение Фредголъма
второго рода (где переменная меняется от — оо до оо) может быть упро-
упрощено при помощи преобразования Фурье, если его ядро является функцией
от разности (х~х0).
8. 5. Преобразование Фурье и интегральное уравнения 891
Преобразование Ганкеля. Если переменные меняются в промежутке
от 0 до оо, то мы можем испробовать преобразование Ганкеля [см. фор-
формулу F.3.62)]:
со
&в (/) - ^ (к) = 5J / (х) /0 (кх) х dx. (8.5.7)
о
Формула обращения для него имеет вид
fix) = ^F (к) /0 (кх) kdk^m (F). (8.5.8)
Если применить преобразование Ганкеля к уравнению
то
V (к) =
или
со
У(к) = Ф(к) + \\ш(к\,
где
со со
О О
Обращением этого двойного преобразования Ганкеля будет
w (х | х0) = \ к dk $ fto/0 (fee) W (к | ft0) /0
о о
Как и раньше, для того чтобы это преобразование было полезным для
нас, преобразованное ядро W должно быть диагональным:
W(k\k0) = (l/k)V(k)o(k-k0).
Отсюда следует соотношение, которому должно подчиняться первоначаль-
первоначальное ядро w:
] Л (кх) V (к) /0 (кх0) kdk. (8.5.10)
о
Это ограничение не может быть выражено в такой же простой форме!
как его аналог для преобразования Фурье, и, таким образом, труднее
охарактеризовать те ядра, которые подчиняются этому ограничению.
Приведем два примера таких ядер:
(а) V(к) = е-Р*\ w(x\x0)^^(g)
где /0 —функция Бесселя от мнимого аргумента;
<б) V (к) = е~°\ w[(x\\х0) = (ЩУ^о) Q-щ [(ж2 + а»+ а*)/2хх0],
де Qn— Бтсрсе решение уравнения Лежандра [см. формулу E.3.29)].
892 Гл. 8. Интегральные уравнения
Возвращаясь к общему случаю, заметим, что ядро w(x x0), удовлетво-
удовлетворяющее уравнению (8.5.10), симметрично, т. е.
Чтобы получить более определенную информацию, разложим J0(kx) в фор-
формуле (8.5.10) в степенной ряд:
со
(J™ [ *W (к) Jo (kx0) dk.
0
Пусть V (/с) — преобразование Ганкеля от v(x), т. е.
о(*о)=5 kV{k)J0(kx0)dk.
и
Мы можем выразить интеграл более общего вида через v (x), заметив, что
Следов тельно,
W »*)- a WCt.)"[
и
m=0
Итак, убедиться в том, что преобразование Ганкеля заданного ядра
является диагональным, можно, проверив, что w симметрично по х и х0
и что коэффициенты в разложении и; по степеням х имеют форму (8.5.11).
Ядро v(x—ас0) в бесконечной области. Преобразование Фурье (8.5.5)
решения уравнения Фредгольма второго рода (8.5.1) с ядром w(x\x0) —
= v(x— x0) можно также получить более прямым путем при помощи тео-
теоремы о свертке [см. D.8.25)]:
со
& [ \ v (х- х0) Ь[(х0) dx0 ] = У2к V (к) W (к).
—со
Преобразование Фурье уравненияА(8.5.1) в силу этой теоремы имеет вид
W (к) = Ф (к) + VbXV (к) W (к). (8.5.12)
Разрешая (8.5.12) относительно W (к), получаем выражение (8.5.5). Такой
подход возможен только в том случае, если существует область плоскости
комплексного переменного к, в которой равенство (8.5.12) выполняется.
В § 4.8 мы видели, что интегралы, являющиеся преобразованиями
Фурье, во многих случаях не сходятся во всей плоскости комплексного пе-
переменного к. В большинстве случаев интеграл дает представление преобра-
преобразования только в полосе плоскости к, ограниченной сверху или снизу или и
сверху и снизу прямыми, параллельными действительной оси. Внутри этой по-
полосы преобразование всюду аналитично; наличие особенностей определяет верх-
верхнюю и нижнюю границы полосы. Следовательно, когда мы имеем дело с урав-
8. 5. Преобразование Фурье и интегральные уравнения 893
нением, в которое входят преобразования Фурье нескольких функций, мы дол-
должны заботиться о том, чтобы их полосы аналитичности имели общую часть.
В § 4.8 мы видели также, что преобразование Фурье функции <р(ж)
можно обобщить, введя две функции, аналитичные в двух различных поло-
со
сах плоскости к. Например, если интеграл \ <р (х) е~~х dx сходится только
о
о
при х>Хд, а интеграл \ ев (х) е~"-хйх— только при х<х,', то мы видели,
—со
что <р можно выразить следующим образом [см. уравнение D.8.19)]:
9(а;) = -Дг-| \ ФЛк)е-а*Aк+ ^ Ф_ (к) e-ih*dk}, (8.5.13)
—co+ito —oo+iti
где Ф+ аналитична всюду в полосе Im к > ь'о, а Ф_ аналитична всюду в по-
полосе ImA;<iEj. В этом случае желательно, чтобы полоса, в которой ана-
литично преобразование V, имела бы общую часть (перекрывалась) с поло-
полосой, в которой аналитична функция Ф+, а также с полосой, в которой ана-
аналитична функция Ф_.
Подобным же образом преобразование Фурье неизвестной функции <]>
может появиться в обобщенном виде, т. е. в виде двух функций, одна из
которых ЧР*+ аналитична всюду в полосе 1тА;>т:о, а другая ЧР*_ — анали-
аналитична при 1тк<Съ1. Пусть преобразование V(к), как и в предыдущем
параграфе, аналитично всюду в полосе
xi"<Im&<x6", (8.5.14)
причем
tj'' < "Ч и tl, io" > х0' и т|).
При этих условиях формулу обращения (8.5.13) можно применить ко всему
интегральному уравнению, и мы получаем
оо+гт0
со+iTj
^ Ф+(Л)е-«*»сгл+ 5
—оо-Нт0
oo+iti
-ikxdk+ { W_ к)f]/2^XF(к)]s~ihxdk,
—oo+tTo —oo+tTi
ИЛИ
¦oo+i-c,,
^ {A- V2^W)W.-<&Je-ih*dk +
oo+iTi
+ ^ [A _ Y2^\V) »F_ -Ф_] e-ift*dk = 0. (8.5.15)
—oo+it,
Здесь х0 больше чем max (dJ, xq), но меньше чем хб", a xx меньше чем
min(t/, tJ), но больше чем xi". Тогда условие теоремы, сформулированной
на стр. 439, выполнено и мы можем заключить, что
[A - \/^Щ W, -Ф+] + [A - V2^W) W_ -Ф_] = 0.
894 Гл. 8. Интегральные уравнения
В силу этой же теоремы не только сумма двух подинтегральных функ-
функций должна быть равна кулю, нб, кроме того, каждое слагаемое в отдель-
отдельности должно быть аналитично во всей полосе ¦to<Imfc<t1. Таким обра-
образом, додинтегральная функция
должна быть равна некоторой функции S+ (к), аналитичной в полосе
х0< Imк<Xj и настолько быстро стремящейся к нулю, когда | ReAj| —> со,
что интегралы в (8.5.15) сходятся. Тогда, для того чтобы сумма двух под-
подинтегральных функций равнялась нулю, необходимо
[A - У2а IV) ?_ - Ф_'] = S_ (к) = - S+ (к).
Следовательно, уравнению (8.5.15) эквивалентна пара уравнений
jM/o+5^ у к <d_w+j_w (8516
где S+= —S_ — функция, аналитичная всюду в полосе т0 << Im к < хг. Эти
уравнения сводятся к уравнению (8.5.5), если i'o и %[ можно положить
равными нулю, так что Ф+ = Ф_ (в этом случае S+ должна равняться S_ и
поэтому обе должны обращаться в нуль). Подставляя в формулу обращения
(8.5.13) выражения (8.5.16) для W+ (/с) и W_ (к), получаем решение в виде
e~ikx
/ ч 1 f f Ф+е~'"ж ., , V Ф_е-шх , „ ,
(ж) = —=- J \ —=г ак 4- \ = [ак +
|/2mJ I J. I—V2jcX.F J. 1— y2nlV
s+e~*X dk\ . (8.5.17)
1—1^2я^У J
Первые два интеграла соответствуют установившемуся решению (частное
решение) неоднородного дифференциального уравнения, а последний интег-
интеграл, взятый по замкнутому контуру, лежащему внутри полосы аналитич-
аналитичности функций V ш S+, соответствует «переходному» решению, которое су-
существует и в случае, когда <р = 0.
Однородное уравнение. Изучим прежде всего «переходное» решение
однородного уравнения
со
[ v(x-xo)b(xo)dxo. (8.5.18)
Согласно (8.5.17), решением этого уравнения служит
ф (ж) = (? s*^U~lhx м $.5.19)
где V (к) — преобразование Фурье функции v(z), а замкнутый путь интег-
интегрирования лежит внутри полосы аналитичности V(k), z[" < lm/c < ч'о",
причем S> аналитична всюду внутри этой полосы. Таким образом, интег-
интеграл (8.5.19) равен нулю, если только функция [1— }/2izXV (к)) не имеет
нулей или точек разветвления внутри указанной полосы.
Такое поведение не является неожиданным, так как из § 8.2 известно,
что ненулевые решения однородного уравнения появляются только при не-
некоторых определенных значениях X, называемых собственными значениями.
В настоящем случае дело обстоит таким образом, что собственные значе-
значения X заполняют некоторые непрерывные полосы; это происходит потому,
что промежуток интегрирования бесконечен и, следовательно, уравнение
8. б. Преобразование Фурье и интегральные уравнения 895
является сингулярным [см. уравнение (8.2.55)]. Допустимыми будут все
значения X, при которых функция A — |/2iuXF) имеет внутри полосы ана-
аналитичности один или более нулей. Для большинства значений X, при ко-
которых существуют ненулевые решения, нули функции A —j/2rcXF) являются
простыми, функция стремится к нулю линейно вместе с к — кТ, так что осо-
особенности подинтегральной функции в выражении (8.5.19) обычно оказы-
оказываются простыми полюсами. Предположим, что внутри данной полосы
лежат полюсы к0, кг,..., кг,..., кп (каждый из них является
функцией от X), и пусть вычет множителя 5+/A — |/2n:XF) в точке кг равен
Ar/2m; тогда
Фс (х) = 2 Л e~ihrX- (8.5.20)
г=0
(Может оказаться, что некоторые отдельные значения [X [являются нулями
1 — \^2izW высшего порядка, и в этом случае в выражении для <]> появятся
члены вида В^с'-1 e~iksX.) При этом постоянные Аг произвольны, так как
до сих пор S+ является произвольной аналитической функцией от к. Зна-
Значения Ат могут быть определены, если заданы начальные или граничные
условия, совершенно так же, как в случае дифференциального уравнения.
В некоторых случаях приходится выбирать известное число отношений
коэффициентов таким образом, чтобы выражение (8.5.20) было решением
первоначального интегрального уравнения; это легко сделать, подставляя
(8.5.20) в (8.5.18).
Может оказаться поучительным проверить, что Ar e~ihrX является реше-
решением однородного уравнения (8.5.18). Непосредственной подстановкой по-
получаем, учитывая, что V (к) является преобразованием Фурье функции v (z),
Ar e~ih>-x = 1А
= Х.ЛГ
Поэтому Are~ihrX будет решением (8.5.18), если
(8.5.21)
Последнее уравнение, очевидно, удовлетворяется, так как кг с самого начала
было определено как корень этого уравнения.
Пример. Рассмотрим интегральное уравнение
1> (x0) dx0. (8.5.22)
Начнем с решения соответствующего однородного уравнения
zo (8.5.23)
[это решение дается равенствомД8.5.20)]. Наукнеобходимолвайти нули разности
1—X|/2itF, где V—преобразование Фурье функции е~'*!. Имеем
со
V (к) = -^ \ e-W e** dx, или V {к) = \^ .
•896
Гл. 8. Интегральные уравнения
Таким образом, V.(к) аналитична в полосе |1т/с|<^1. Следовательно,
1 -1/2UXF = [/с2- BХ- 1)]/A + к2).
Эта функция имеет простые нули при к = ± к0, где /со =
чйт, решениями однородного уравнения являются функпии
x = e±ikext (8.5.24)
•если только точки ± к0 лежат внутри) полосы регулярности V, |1т/со|<1,
.а это соответствует условию (Im XJ < 2Re X. Эти решения можно проверить
непосредственно подстановкой в первоначальное интегральное уравнение
для х или сведением этого уравнения к дифференциальному уравнению
посредством двукратного дифференцирования обеих частей, что дает
Теперь мы рассмотрим решение неоднородного уравнения, представ-
представленное в формуле (8.5.17) двумя первыми членами. С этой целью потре-
потребуем, чтобы выполнялись равенства
Ф+ = —^
о
о
ф
' = V_ \ e-ax eik
V^2n J
dx =
2n.(i^—a)
, Im к > а,
, Im к < — а.
Решение (8.5.17) имеет смысл только при a < 1. Тогда
Т T
-?{- Т
причем к этому выражению мы можем добавить любое решение однород-
однородного уравнения, т. е. любую линейную комбинацию двух решений, зада-
задаваемых формулой (8.5.24). Пределы интегрирования удовлетворяют усло-
условиям Хд < 1, т^> — 1, как это показано на рис. 8.3. Рассмотрим два слу-
случая: ж>0иж<0. В первом случае мы можем добавить к контуру каж-
каждого из интегралов по полуокружности, расположенной в нижней полу-
полуплоскости, и получить таким образом замкнутый контур. Затем эти инте-
интегралы вычисляются при помощи интегральной формулы Коши. Второй
интеграл обращается в нуль, так как все особенности подинтегральной
функции находятся вне контура. Первый член вычисляется легко, и мы
получаем
2ко(ко-1а)
2fcB(fco+ia)
При х < 0 полуокружность лежит в верхней полуплоскости, так что
отличен от нуля только второй интеграл:
8.5. Преобразование Фурье и интегральные уравнения
897
Комбинируя эти два выражения, мы получаем
• <8-5-26'
Ясно, что функция ф непрерывна и равна А при х — 0; однако ее
первая производная разрывна. Этот скачок при ж = 0 нельзя изменить,
добавляя решение однородного уравнения, так как такое решение может
!
Im к
К
Контур первого
интеграла
Контур второго
интеграла
/ -fro
Плоскссть к
•*1<п
Re A —
Рис. 8.3. Контуры интегрирования для формулы (8.5.25).
изменить только значение ф при х = 0. Заметим, что к интегралам, входя-
входящим в выражение (8.5.25) и образующим частное решение, всегда можно
добавить «переходную» функцию х так> чтобы значение ф @) сделалось
равным А.
Проведенный выше анализ применим, если только V (к) аналитична
в полосе, содержащей вещественную ось плоскости к. Единственной труд-
трудностью, которая может здесь встретиться, является вычисление интегралов,
входящих в обращение преобразований Ф+, Ф_, V.
Точки ветвления. Не представляет больших трудностей распространить
эти результаты на случай, когда V (к) имеет точки ветвления внутри по-
полосы, содержащей вещественную ось плоскости к. Однако здесь сущест-
существенно наличие полосы, в которой аналитичны V (к) и Ф+, и аналогичной
полосы для V (к) и Ф_. Если эти условия выполнены, то необходимо только
ввести разрезы и убедиться, что в процессе вычисления мы не интегрируем
по контурам, пересекающим линии разреза. Это может породить извест-
известные трудности при выражении ф(ж) через W+ и W_, так как вычислять
интегралы в формуле обращения при помощи интегральной формулы Коши
теперь уже невозможно. Появляются интегралы вдоль линии разреза, ко-
которые в одних случаях легко выражаются через элементарные функции,
а в других — нет.
В связи с этим важно вспомнить, что преобразование Фурье содержит
информацию об асимптотическом поведении функции ф (х). На основании
результатов, изложенных на странице 437, мы знаем, что
ИЛИ
В рассмотренном выше примере
?+ (к) ~ - (A/ik V~2k) , а - > оо.
57 Ф. М. Морс и Г. Фешбах
898 Гл. 8. Интегральные уравнения
Следовательно, ty@) = A, что согласуется с результатом, полученным из
формулы (8.5.26) для полного решения.
Ядро v(oc-\-oc0) в неограниченной области. Здесь также можно при-
применить теорему о свертке. Мы вновь можем представить 6 (ж) и <р (х) при
помощи формулы обращения (8.5.13). Представление интеграла
получается заменой переменной интегрирования х0 на — So, а затем приме-
применением теоремы о свертке. Мы находим, что
:*F(*)]e-i
Ч\ (- к) [УЪк V (к)] е-*** dk.
-co+iT,
Здесь предполагается, что функция W_( — k), так же как Ф+ (/с) и W+ (к),
аналитична при Imft>x0. Соответственно, функции W+ ( —/с), Ф_(/с) и ?„(/с)
предполагаются аналитическими при Im/c<'c1. Заметим, что если Ф+ (ft)
аналитична при Imk>z'o, то Ф+( — к) аналитична при Imft< — i'o. Таким
образом, уравнение, соответствующее уравнению, следующему за (8.5.15),
имеет вид
+ (ft) - /2^XF (к) «Г_ (- к) - Ф+ (к)} +
+ {W_(к)- V2^W (к) W+ ( — к)— Ф_(/с)} = 0.
Члены, заключенные в скобки, аналитичны в некоторой полосе, парал-
параллельной вещественной оси, как и в (8.5.15). Опуская члены S+ и S_, фи-
фигурирующие в уравнениях (8.5.16) и порождающие, как мы убедимся ниже,
решения однородного уравнения, получаем частные решения неоднородного
уравнения. Следовательно,
ЧТ„ (к)- У2ЙЩ*) Ч-'_( ~ к) = Ф+(/с),
Ч/_ (к) - Y2mkV{k) W+{- к) = Ф_(/с).
Заменим во втором из этих равенств А на — к. Это можно сделать только
при условии, что функции Ф_ (— к) и V ( — к) аналитичны в области, где
аналитичны как Ф+(/с), так и V (к). Теперь второе уравнение записывается
так:
W (-к)- ]/2^XF (- к) Ч\ (к) = Ф_ (- к).
Разрешая полученную пару уравнений относительно М\ (к), находим
Аналогично
8.6. Преобразование Фурье и интегральные уравнения 899
Формула (8.5.17), полученная для ядра v(x — х0), заменяется теперь
формулой
-co+vr0
+ _^_°°Г1 Г Ф-W + /^F(ft) Фл-fc
+ /& J L l-2^«F(ft)F(-fc)
—OO+iT,
В первом интеграле подинтегральная функция аналитична при Im/c>-:0T
во втором—при Im/c<x1.
Решение однородного уравнения получаем из (8.5.29), заменяя Ф+ на
5+, Ф_ на ,S_ и учитывая, что 5_ = —S+. Таким образом,
1—2rA*F(ft)F(—ft)
где контур интегрирования расположен внутри области, в которой V (/<;)•
и V (— к) аналитичны. Выполнив во втором члене замену переменной,
интегрирования, мы можем записать <!>• в виде
ф
Так как обе функции S+ и 1 + "|/2icXF (— к) аналитичны в области, огра-
ограниченной этим контуром, то решение однородного уравнения может быть
представлено в виде ряда
ф = 2^4г,жв-1е- *<•«, (8.5.31)
I", S
где предполагается, что
=
1—2jtX*F(fc)F( —fc) (fe—
Коэффициенты Ars должны быть определены из начальных или граничных
условий, но вместе с тем должны выполняться некоторые соотношения
между ними, так как выражение (8.5.31) должно удовлетворять исходному
интегральному уравнению.
Пример. В качестве примера рассмотрим интегральное уравнение
оо
4»(ж) = Ае*\ х I + X ^ е-1х + Vljl -Ь(х„)dx0.
Из результатов, полученных при изучении интегрального уравнения (8.5.22),
имеем
, ]m/c>o,
к (ik -a), Im к < - а.
Рассмотрим прежде всего решение однородного уравнения. Для этого
исследуем корни уравнения 1 — 2тсХ2Т/(/с) V ( — к) =0, которые даются
формулами
/с=±/с0, /?„
57*
'i-ЮО Гл. 8. Интегральные уравнения
На основании (8.5.31) мы можем записать решение однородного уравнения
в виде
ф = ахе -**•* + a2eift°x + bxe~^x -f b2e-^x.
Для того чтобы получить соотношения между коэффициентами этого выра-
выражения, его необходимо подставить в данное интегральное уравнение.
Получаем
4» (х) = \УШ KF(/c0) еш°х + a2V( - к0) e~ih
Приравнивая коэффициенты при одинаковых экспонентах, получаем две
независимые системы уравнений:
*o)aa = 0, Ц/~2ъУ (ко) % -а2 = 0
(ikx) fc2 = О, \V2^V (— iAJ ^ - &2 = 0.
Условие существования ненулевых решений — обращение в нуль определителя
системы — приводит к уравнению, уже использованному выше для опреде-
определения /с0 и /сх, и поэтому удовлетворяется автоматически.
Теперь можно найти отношение коэффициентов. Для решений, соответ-
стлующих к0, оно равно
Следовательно, d> = cos kox является решением однородного уравнения.
Аналогично, сЬкгх является вторым независимым решением.
Обращаясь теперь к неоднородному уравнению (8.5.29), мы видим, что
процесс вычисления интегралов, вполне аналогичный использованному
в примере (8.5.22), с применением интегральной формулы Коши не встречает
существенных затруднений.
Применения преобразования Лапласа. Из предыдущего изложения
можно заключить, что преобразование Лапласа наиболее выгодно применять
к интегральным уравнениям, к ядрам которых приложима теорема, о свертке
для преобразования Лапласа:
(х~ х0 (х0) <fe0] = V (р) F (р),
где V (р) и F (р) - преобразования Лапласа функций v (x) и / (х) соответствен-
соответственно. Это наводит на мысль о том, что нам следует рассмотреть интеграль-
интегральное уравнение Вольтерра
X
^ x>0. (8.5.32)
Примеры уравнений Вольтерра, возникающих при решении задач о колеба-
колебаниях и о поглощении энергии рентгеновских лучей в веществе, мы обсу-
обсудили на страницах 837, 838.
Здесь мы рассмотрим общий случай. Возьмем преобразование Лапласа
от обеих частей уравнения (8.5.32). Допустим, что преобразование функции
ср аналитично в полуплоскости Rep > -с0 и что область аналитичности пре-
преобразования v содержит полосу, параллельную мнимой оси плоскости р
8.6. Преобразование Фурье и интегральные уравнения 901
и принадлежащую полуплоскости Rep > т0. В этой полосе
F(P) = *{
Решая относительно F(p), имеем
Следовательно, частное решение уравнения (8.5.32) получается обраще-
обращением цреобраз.ования Лапласа [формула D.8.32)]
(8.5.34)
Однородное уравнение Вольтерра не имеет ненулевых решений, и, таким
образом, формула (8.5.34) дает единственное решение уравнения (8.5.32).
В качестве примера рассмотрим интегральное уравнение Вольтерра,
получающееся из дифференциального уравнения
с начальными условиями: <|> = %, db/dt = v0 при t — О. Эквивалентное инте-
интегральное уравнение дается формулой (8.1.23):
Функция Грина G определяется из условий
-др = — 0(t — t0) При f> , t\ t0) = 0 При t < t0.
Отсюда
G (t\t0) = (to~ t) u(t — t0),
где и (г) — единичная функция (см. стр. 778). Подставляя это выражение
для G в интегральное уравнение, получаем
i|> (t) = -!i0 + vot -\-к2^ (tti — Щ (t0) d t0, t>0.
о
Это уравнение имеет теперь вид, как раз пригодный для применения
вышеуказанного приема:
? @ = Фо + V• ф (Р) = (Фо/Р) + ЫР2),
v(t~ t0) = /с2 (t0 — t), V(p)=— k2/p*, Re p > 0.
Подставляя в решение (8.5.34), получаем
-гоо+т,
Этот интеграл мы можем вычислить, добавляя бесконечную полуокруж-
полуокружность, как это указано на рис. 8.4, и затем применяя интегральную
формулу Коши. Конечно, мы получим уже знакомый результат
•Ь = ф0 cos kt + (vjk) sin kt.
902
Гл. 8. Интегральные уравнения
Интегральное уравнение Вольтерра с пределами (х, оо). Преобразова-
Преобразование Лапласа можно применить также к интегральным уравнениям следую-
следующего вида:
со
(8.5.35)
<Ь (х) = <р (х) + ^ v(х- х0) ф (х0) dx0,
возникающим в связи с задачами переноса, причем х может обозначать
энергию после столкновения, а х0 — энергию до столкновения (см. § 2.4
и 112.2). Для столкновений с неподвижными системами, не имеющими
внутренних степеней свободы, жо>ж; это означает, что столкновения всегда
приводят к уменьшению энергии падаю-
\
-Imp
ik
\
\
-ik
щей частицы.
Для того чтобы решить уравнение
Плоскость р (8.5.35), применяя преобразование Лапла-
Лапласа, необходимо вывести теорему о свертке
для выражений вида
v (х — х0) <Ь (х0) dx0.
Re p -
-Контур
Мы начнем с теоремы о свертке для пре-
преобразования Фурье:
хо) ? Ы dx0} =
/^ (к) Ф, (к).
Рис. 8.4. Контур интегрирования
для обращения преобразования Пусть g (х) = v_ (х), т. е. g(x) равна v(x)
Лапласа. при х < 0 и равна нулю при х > 0; по-
подобным же образом пусть 9 0е) —Ф+ (х)>
т. с. у(х) равна О (ж) при 1>0и равна нулю при х < 0. Тогда приве-
приведенное выше уравнение переписывается так:
со
\v {х - f 0) ф (х0) dx0)
Для того чтобы перейти от преобразования Фурье к преобразованию
Лапласа, вспомним, что FL (p) = Y2tz[F+ (ip)h. Следовательно,
X { \v (х - я;0) ф (я;0) dx0) = j/2^ [F_ (ip)], [У+ (р)],.
Мы можем выразить [У^тсV_ (ip)h через преобразование Лапласа:
0
[У2%У_ (ip)]f — \v(x) е-** dx, [V2nV
—CO
Поэтому, положив и( — x)—w(x), мы получаем
со
= ^ v
0
8.5. Преобразование Фурье и интегральные уравнения 903
Окончательно
со
[ S}Wl(-p)%(P)- (8-5.36)
Теперь мы можем вернуться к интегральному уравнению (8.5.35). Взяв
преобразование Лапласа от обеих частей (начиная с этого момента мы не
пишем индекс I, так как мы будем иметь дело только с преобразованием
Лапласа), получим
8537)
= Ф ()/[ 1W ()]
Наконец, выражение
является частным решением интегрального уравнения (8.5.35). Следует
подчеркнуть, что для того, чтобы решение (8.5.37) или (8.5.38) имело смысл,
необходимо, чтобы области аналитичности W (—р) и Ф{р) перекрывались.
Как упоминалось выше, если это установлено только для некоторой опре-
определенной области изменения параметров, от которых зависят Ф или W, то
иногда оказывается возможным расширить эту область при помощи анали-
аналитического продолжения.
В качестве примера, иллюстрирующего этот случай, пусть <р(х) = С,
v(x)=Aeax, А ж а вещественны и положительны, так что (8.5.35) сводится
к уравнению
Ь (х) = С + А ^ е»**-*") ф (х0) dx0.
Применим теперь преобразование Лапласа (хотя мы должны отметить,
прежде чем погрузимся в этот анализ, что для этого частного вида
функции v (х) интегральное ура'внение можно свести к дифференциальному
уравнению первого порядка, которое легко решается). Фигурирующие
в формуле (8.5.38) функции Ф(р) и W(— р) имеют вид
Re»>0,
-a)xdx = A/(a — p), Re p < а.
Заметим, что W(—р) и Ф (») имеют общую полосу аналитичности только
в случае а > 0. Равенство (8.5.38) дает
(> ei» dp,
6 (х) = V ,Г
1 v ' 2tii J р[р — (а — А)]
—ioo+^o
где 0 < х0 < а. Мы вновь замыкаем этот контур, добавляя полуокружность,
лежащую в левой полуплоскости плоскости р, как показано на рис. 8.4.
Тогда интеграл, определяющий ф, можно вычислить по интегральной
формуле Коши, причем простые полюсы имеются при р = 0 и р=а — А
(последний появляется при х0 > а—А). Этот произвол, связанный с вычетом
в точке а— А, которую по желанию можно включать или нет, соответствует
произволу при выборе переходной функции, т. е. решения однородного
904 Гл. 8. Интегральные уравнения
уравнения, которое в случае включения пропорционально разности двух
частных решений линейного неоднородного уравнения. Мы получаем
Первый член является частным решением, которое представляет «устано-
«установившийся процесс», порожденный «источником», соответствующим члену С,
если а<С.А. Второй член, пропорциональный е^а~А^х, описывает «переход-
«переходный процесс» и является решением однородного уравнения.
Преобразование Меллина. Мы начнем этот пункт с того, что напомним
определение и формулу обращения, приведенные в гл. 4 и задаче 4.48.
Преобразование Меллина функции f(x) определяется так:
со
F(s) = ^ f(x)xs'ldx.
Если интеграл не существует, то часто оказывается возможным ввести
обобщенные («полуплоскостные») преобразования, аналогичные обобщенным
преобразованиям, введенным в теории преобразования Фурье:
F_ (s) = ^ /(х) Xs'1 dxk F+ (s) = ^ /(х) Xs-1 dx. (8.5.39)
о 1
Функция F _ существует при Re s > а0, в то время как F+ существует нри
Re s < Cj. В том случае, когда F (s) не существует, а0 > аг; если же F (s)
существует, то имеет место противоположное неравенство.
В соответствии с этим формула обращения может быть записана так:
ico+ao' ico+aj'
i'
гДе Go > co и Gi ^ °i" Теорема о сьертке имеет вид
оо
{s E)?}¦ (8-5'41)
Эта формула наводит на мысль о том, что преобразование Меллина осо-
особенно выгодно применять при решении интегральных уравнений следующего
типа:
со
ф (х) = ф) + J о (-J У Ы ^ • (8-5-42)
Анализ, при помощи которого находится решение этого уравнения, до
такой степени подобен тому, который был дан для случая преобразования
Фурье [см. решение (8.5.17)], что здесь мы можем дать только его результаты:
ico+oo ico+oi
Ф d С Ф+ ds
i+oo +oi
If Г Ф_ ds . С Ф+
где контурный интеграл берется по пути, лежащему внутри области а'о <
< Rep < Oj, внутри которой функция S должна быть аналитической. Решение
X соответствующего однородного уравнения выражается именно этим кон-
8.5. Преобразование Фурье и интегральные уравнения 905
турным интегралом. Если нули 1 — V лежат в точках sr и если эти нули
имеют кратность t, то
X^2Brt(lnx?-lx-sr, (8.5.44)
где Вг1 — произвольные постоянные.
В примере на применение преобразования Меллина положим
интегральное уравнение (8.5.42) принимает вид
ф (х) = Ае~ах + С\ е-*'*°б (х0) ^ .
о
Преобразования Меллина соответствующих функций равны
/а8], Res>0,
), Res>0.
Нет нужды разбивать Ф на Ф+ и Ф_, так как области регулярности Фи Г
совпадают.
Рассмотрим сначала решения однородного уравнения. Согласно пра-
правилу, выражаемому формулой (8.5.44), мы находим, что
X=2,Brx-r, (8.5.45)
г
где sr — корни уравнения
Нули выражения Г (s) — 1/С простые; существует бесконечное множество
решений.
Неоднородное уравнение имеет частным решением
T(s) ds > п
-гоо+о'0
Этот интеграл можно вычислить при помощи интегральной формулы Коши.
При ах > 1 контур интегрирования замыкается полуокружностью, лежащей
в правой полуплоскости. В этом случае единственная особенность подин-
тегральной функции лежит в точке s0, в которой 1 — CT(so) = O. Тогда
ф, ах>1, (8.5.46)
где <]I(s0)—логарифмическая производная гамма-функции в точке s0. При
ах < 1 особенностью оказывается каждый отрицательный корень выраже-
выражения 1 —CT(s), так что
со
r=l ^а2;) ^х ^г)
[Заметим, что эти выражения для ф не являются решениями однородного
уравнения. ] Ряд для ф в области ах < 1 сходится весьма быстро, так как
корни sr образуют последовательность отрицательных чисел, абсолютные
величины которых возрастают вместе с г.
906 Гл. 8. Интегральные уравнения
Метод Винера—Хопфа. Можно расширить класс интегральных урав-
уравнений, которые решаются при помощи преобразования Фурье, так, чтобы
включить в него следующий тип:
ф (ж) = \^v(x- х0) ф (ж0) dx0, (8.5.48)
о
так же как и соответствующие неоднородные уравнения первого и второго
рода. Важно отметить, что записанное выше уравнение, по предположению,
имеет силу для всех вещественных значений х, как положительных, так
и отрицательных. Для того чтобы этот факт был яснее виден из записи
этого уравнения, введем функции ф+ и ф_, определенные обычным образом:
ф+ (х) = ф (ж) при х>0, ф+(ж) = 0 при ж<0,
ф_ (х) = ф (ж) при х < 0, ф_ (ж) = 0 при ж > 0.
Тогда уравнение (8.5.48) перепишется так:
'К (ж) + ф_ (х) = X ^&(ж — ж0) ф+ (ж0) Лс0 = X ^ & (ж — ж0) ф„ (ж0) ?*ж0. (8.5.49)
0 —оо
Другими словами, как ф_, так и ф+ можно выразить через ф+:
жо, ж<0,
(8.5.50)
6+ (ж) = X ^ и (ж — ж0) <Ь+ (ж0) йж0, ж > 0.
о
Такие интегральные уравнения, называемые уравнениями типа Винера —
Хопфа, возникают всякий раз, когда мы имеем дело с граничными зада-
задачами, где границы являются полубесконечными, а не бесконечными; послед-
последним соответствуют интегральные уравнения, рассмотренные ранее в этом
параграфе. Один пример нам дает задача о дифракции волн, на полупло-
полуплоскости, другие примеры будут рассмотрены в гл. 11 и 12.
• При изложении метода Винера — Хопфа мы сосредоточим внимание
сначала на применяемых здесь формальных операциях и условиях, при
которых эти операции законны, а в заключение проиллюстрируем этот
метод примерами. Мы сделаем это без подробных, строгих доказательств;
многие элементы этих доказательств были изложены в гл. 4. Те дополне-
дополнения, которые потребуются, будут по мере надобности доказываться в ходе
решения проблемы.
Как и при обсуждении ранее изученных в этом параграфе задач, мы
предполагаем, что функция V (к), являющаяся преобразованием Фурье
функции v (ж), регулярна в области
— и < Imk<z0,
что аналогично условию (8.5.14). Это требование соответствует асимптоти-
асимптотическому поведению v (ж):
v (ж) с^ е~~~1х, ж —> оо, v (ж) са ето*, ж —> — оо.
Мы рассматриваем решения уравнения (8.5.48), которые ведут себя подобно
е-1Х при #—>со (где р. < — ix). Условие в скобках необходимо для сходи-
сходимости интеграла, входящего в интегральное уравнение. Мы можем опреде-
8.5. Преобразование Фурье и интегральные уравнения
907
лить асимптотическую зависимость для Ф_ непосредственно из уравнения
(8.5.50):
оо со
ф_ ~ }Л е~~в(ж~хо)ф+ [х0) dx0 = >-етож ^ е~~-ох° й+ (х0) dx0> х->. — оо .
о о
Следовательно, необходимо, чтобы [i < х0 и чтобы ф_ вела себя при
х —> — со как ё'ох. Полосой регулярности для ЧГ+ будет полуплоскость
1тк>^, а для 'F_ такой полосой будет 1т&<т0. Эти полосы показаны
на рис. 8.5, на котором можно видеть, что существует полоса р < Im к < т:0,
где все интересующие нас преобразования," V, W+, W_, регулярны. Этот
результат, как мы увидим, является основным в методе Винера—Хопфа.
Рис. 8.5. Области регулярности функций ЧГ+ и Ч"_ в
плоскости к.
Теперь можно, применяя теорему о сиортке, составить преобразование
выражения (8.5.49)
или
- Ч-_ = 0. (8.5.51)
Для того чтобы определить из этого уравнения как W+, так и W_, нужны
дополнительные сведения об этом уравнении. Эти сведения можно получить,
разлагая на множители функцию 1—j/2icXF. Это выражение регулярно
в полосе —Xj < Im к < i0. Попытаемся разложить это выражение на мно-
множители Г+ и 1/Г так, чтобы иметь
W = Г+ (Л)/Г_ (к). (8.5.52)
Эти множители должны быть регулярными и отличными от нуля соответст-
соответственно в полуплоскостях Im&>[i и 1т&<-0. Обычно дополнительно тре-
требуют, чтобы Г+ и Г_ имели алгебраический рост, а не экспоненциальный.
Возможность такого разложения на множители была показана Винером и
Хопфом в их оригинальной работе.
В каждой данной задаче это разложение на множители должно быть
явно осуществлено. Допуская, что равенство (8.5.52) имеет место, мы можем
переписать уравнение (8.5.51) для W+ и W_ следующим образом:
4rX=-4P'_rj. (8.5.53)
908 Гл. 8. Интегральные уравнения
Левая часть этого уравнения регулярна в области lm к > р., в то время
как правая часть регулярна при 1т&<т0. Так как они имеют общую
область регулярности х0 > \т.к > р, в которой они равны, то мы можем
утверждать, что—Ч^Г, является аналитическим продолжением W+Y+ в
нижнюю полуплоскость. Следовательно, функция Ч?'Д+ регулярна во всей
комплексной плоскости и потому является целой функцией, которую мы и
обозначим через Р(к).
Приведенного рассуждения совместно с уравнением (8.5.52), очевидно,
еще недостаточно для того, чтобы найти вид Чг+Г+; необходимо еще учесть
поведение этой функции при больших к. Заметим, что функция Г+ уже
выбрана так, что имеет алгебраический рост, т. е. при больших к она
ведет себя как полином. Поведение ЧР"+ при больших к определяется пове-
поведением ф+ (х) при х ~-> 0+. Условие интегрируемости ф+ (х) в начале коорди-
координат, необходимое для существования XV+, приводит к асимптотической зави-
зависимости
<|)+(/с)~0, |&|-^оо.
Итак, мы видим, что Р (к) представляет 'собой полином степени, меньшей
чем порядок роста Г+ (так как /*/Тт стремится к нулю при больших |&|).
Этим определяется вид Р (к); неопределенные постоянные можно найти под-
подстановкой в исходное уравнение (8.5.48).
Теперь уравнение (8.5.53) можно решить относительно Ч*+ и W :
\р _ Р(к) (О г; гь
4+ 1\{к) ' -~ r_(fc) • (й.э.щ
Формула обращения имеет вид
со+1т
-К (х) = -^ ¦ ^ -?Ц e~ikxdk, р < т < v (8.5.55)
Если известна функция ф+, то ф_ можно определить подстановкой в (8.5.50)
или более прямым путем:
co+i-
ф (х)= т=- \ „ ./ e~lkxdk, v. < х <х„. (8.5.56)
" -co+iT
Этим завершается решение интегрального уравнения Винера — Хопфа (8.5.48).
Проиллюстрируем теперь эти рассуждения несколькими примерами.
Примеры применения метода. Весьма простой пример доставляет
интегральное уравнение
со
I ~ ^> I
0
Преобразование функции е~И — функция V (к) — равно
V (к) = . А_ 2 , хо = х1=1.
Выражение, которое должно- быть представлено в виде произведения Xt и
1/Г , согласно равенству (8.5.52), имеет вид
l — V2ikV = -
Разложение на множители можно осуществить, заметив, что
k+i k—i
8.5. Преобразование Фурье и интегральные уравнения 909
Следовательно,
Первая из этих функций Г+, очевидно, регулярна и не имеет нулей при
Im к > [>., где ц. меньше чем хо= 1, в то время как Г_ регулярна и не об-
обращается в нуль при 1т&<т0, если только ReX>0 и (ImXJ<2ReX.
Следовательно,
" V4 = —1 , . = — (Л — I) Ч: _ (К).
Функция Р (к) определяется из того условия, что она должна быть
регулярной во всей конечной плоскости комплексного переменного к, в то
время как ?+(&)—^0 при \к\~><х>. Из этого условия следует, что в дан-
данном примере Р (к) должна равняться постоянной С. Она не может расти
так быстро, как к, ибо из этого предположения вытекало бы, что Чг+ (к) —> 1.
Она не может убывать быстрее чем постоянная, так как отсюда вытекало
бы существование особенности (полюса или точки разветвления) в конечной
части комплексной плоскости. Теперь мы можем найти W+ и W_:
ИГ = °(fc+t) ИГ =: ^_
+ к2—BК— 1)' - к— i
В
С* 7 i *
V*=C ) /V-2_BA-1) e dX-
-co+i-г
Так как в этом выражении х > 0, то мы можем замкнуть контур интегри-
интегрирования полуокружностью, лежащей в нижней полуплоскости. Применяя
интегральную формулу Коши, получаем
(8.5.57)
где D — новая постоянная. Таким же способом находим
ф_ == Dex, x<0. (8.5.58)
Конечно, для решения этого уравнения не было необходимости при-
применять метод Винера —Хопфа. Исходя непосредственно из интегрального
уравнения, легко убедиться, что при х > 0 функция ty = ty+ удовлетворяет
дифференциальному уравнению
При ж < 0 функция ']» = ф_ задается так:
со со
ф = X \ e-l*-*o I (i)+ (а;0) drr0, или 0_ = Хеж \ е-*» б+ (Жо) da;0.
о 6
Это выражение, очевидно, той же формы, что и (8.5.58). Решение, которое
дается равенствами (8.5.57) и (8.5.58), является непрерывным и имеет
непрерывную производную при х = 0.
Наше разложение на множители не является столь непостижимым,
как это может показаться. Прежде всего оно не обязательно единственно,
так как условия, налагаемые ва Р = ЧГ+Г^= — \F_T_ и на асимптотический
910
Гл. 8. Интегральные уравнения
вид W, не являются вполне жесткими. Тем не менее оказывается, что
соотношения между Р, Г+, Г_, W+ и W_ таковы, что окончательное решение
определяется однозначно, независимо от выбора, сделанного вначале.
Во многих случаях разложение на множители оказывается единственным.
Это имеет место в только что приведенном примере. Например, мы могли
бы попытаться разложить так:
r.- , г_ = (*-о<*Р)-
Если Г+ не должна обращаться в нуль в области 1т&>ц(а< 1), то сле-
следует положить Imp< [i([i< 1); но в этом случае Г_=0 в точкеч& = [3, где,
по предположению, не должно быть нулей функции Г_. Либо мы могли бы
испробовать
(k-%) ' - А —? •'
но тогда появился бы полюс в той области плоскости к, где его не должно
быть. Следовательно, единственная комбинация, для которой нули и полюсы
функции Г+ остаются ниже прямой Im к = 1, а пули и полюсы Г_ выше
Imк = 1, —это та, которую мы выбрали, если только мы хотим ограни-
ограничиться функциями, стремящимися к бесконечности при \к\—> со как
конечная степень к.
В качестве второго примера мы обратимся к задаче, рассмотрениол
Хейнсом:
•Ъ (х) = >.
ф (х0) dx0
ch[(*-*0)/2]
Преобразование Фурье от sech[(:r — xo)/2] можно легко получить при
помощи контурного интегрирования.
Функция, подлежащая разложению на множители, такова:
Пусть cosira = Xir, где |а|<1/2. Тогда
, , о . я (а 4- ik) n (a—ik)
ch тс к — с-оя тса = 2 s m ——^ — s in —5— .
Эти множители можно в свою очередь выразить непосредственно через
их нули, представляя их в виде бесконечных произведений [формула D.3.8)],
или эквивалентным образом при помощи гамма-функции, используя соотно-
соотношение [формула D.5.33)]
sin nz
Следовательно,
a + ik
I-гГ1.+1^г>.-1.-1Т
и подобным же образом
sin. -к ( 01
8.5. Преобразование Фурье и интегральные уравнения 911
Значит,
ch izk = —
Отсюда вытекает, что
1 - 1/2гё W = -
Исходя из этого, мы можем с некоторой степенью произвола написать
пГ A—ik*) (a+_ik) e* (fe>
Функция х(^) определяется из условия, чтобы Г+, Г_ имели алгебраи-
алгебраический рост при больших значениях к. Для исследования их поведения
при больших к применим формулу Стирлинга:
In Г (z) ~ z —2~ lnz — z"b^n 27г' z~> ос"
Тогда
In Г+ ~ z— гЛ In 2 + In (ik) +..., \к\~>оэ.
Для того чтобы функция Г+ вела себя при больших | к \ п одобно полиному
мы должны выбрать у =ikln2, и в этом случае будем иметь
Г+ ~ ik, | к\~> со.
Конечно, это соотношение имеет место только там, где Г+ регулярна.
Теперь мы можем определить Р(к). Так как Ч'+~0, \к\—> со, то из
регулярности Р(к)= —4P"_i"_ = \Р+Г+ следует, что Р (к) является постоян-
постоянной, которую мы обозначим через С. Таким образом, определяется функ-
функция Ф+:
IF __C__ С chnfc
"* 1"+ У— сЪкк—cos па
В данной задаче оказывается более полезным именно это представле-
представление. Функция ф+ (х) равна
oo+it
С С ^ах сЪпк dk
chnfe — cos па ТС_
-oo+iT
При х > 0 мы можем замкнуть контур в нижней полуплоскости, где Г_
регулярна. Тогда полюсы подинтегральной функции лежат только в точках,
где разность ch тг& — cos дах обращается в нуль, т. е. при —ik= —2n±a,
я=0. 1, 2, .... Поэтому
51=0
912 Гл. 8. Интегральные уравнения
где С" — новая постоянная. Подставляя выражение для Г , получаем
, _r,ctg™~ Г(т+я + 2")B^)-<^-)
'^+ it Zj I r(l + o + n) n!
п=0
n! J -
ГA —a + n)
Это выражение можно свести к линейной комбинации гипергеометри-
гипергеометрических функций от е2ж; для этого надо использовать формулу удвоения
гамма-функции
Отсюда
тс Zj | ГA + а+п) п\
•п=0
All Л/31
г (^ т~та+п)г ^т^та+п; Р-B"-*>»I
ГA — а + n) n! J '
где С" — еще одна новая постоянная. Сравнивая полученные ряды с гипер-
гипергеометрическим рядом, получаем
гA—о) е
Это выражение можно в свою очередь преобразовать при помощи вторых
решений дифференциального уравнения Лежандра Q i , Q i - Мы имеем
2 2 2
Применяя формулу удвоения для гамма-функции, получаем
•К = С-Щ^- к [Qa_t (ех) - Q_ai (еж)] . (8.5.59)
Наконец, из соотношения между функциями Лежандра первого и второго
рода
имеем
1
\ = - С'"е2 ХР j (ех), х > 0. (8.5.60)
а~2
Таким образом, мы можем выразить решение этого интегрального уравне-
уравнения для х > 0 через гипергеометрические функции или функции Лежандра,
8.5. Преобразование Фурье и интегральные-уравнения 913
а этого, учитывая формулы аналитического продолжения (см. таблицы
б конце гл. 5), достаточно для представления ф при всех значениях х.
Задача Милна. Предыдущие примеры показывают, что разложение
на множители выражения 1 — )Л2тиХУ является единственным шагом в про-
процессе Винера —Хопфа, при проведении которого можно натолкнуться
на существенные трудности. В приведенных выше примерах это разложе-
разложение было получено путем догадки и последующей проверки. Мы займемся
сейчас задачей, в которой преобразование Фурье ядра имеет точку вет-
ветвления, делающую разложение на множители по догадке почти невозмож-
невозможным. Теперь мы увидим, как можно преодолеть эту трудность вполне общим,
но зато достаточно громоздким приемом. Эта задача — задача Милна — воз-
возникает в связи с прохождением, излучения (или любого другого множества
частиц с независимыми скоростями, таких, например, как медленные ней-
нейтроны) через неабсорбирующую однородную среду, в которой излучение
изотропно рассеивается (см. § 2.4). Эта среда берется полубесконечной
по протяжению и мы рассмотрим случай, когда функция распределения /
[см. уравнение (8.1.2)] не зависит от х, у, так же как в от величины
импульса |р|.
В этих предположениях уравнение (8.1.2) принимает вид
где 6 — угол между направлением движения частицы и осью z. Мы можем
осуществить интегрирование по азимутальному углу ф0. Кроме того, удобно
ввести переменные
?, = (z/vPT), ц = cos 6.
Заметим, что PT = Na, где iV—число атомов в единице объема, а о—полное
эффективное сечение рассеяния. Тогда это уравнение приводится к виду
[см. уравнение B.4.16)]
1
$ /(С, po)tffv (8-5.61)
-1
Для того чтобы превратить это уравнение в интегральное, рассмотрим
его как уравнение первого порядка по С и соответствующим образом про-
проинтегрируем. Получим
С 1
^ \ /(Co, PoMfV
-1
Постоянная интегрирования во втором члене и постоянный коэффициент А
определяются из граничных условий. Рассмотрим две области изменения
углов: 0 < ц •< 1 и —1<[1<0 (первая — для частиц, движущихся вправо,
вторая —для частиц, у которых проекции скорости на ось z отрицательны).
Обозначим соответствующие / через /о и /ь, т. е. положим
/ь = 0. /а = / при 0<(х<1,
/ь = /, /а = 0 При -1<ц<0.
Тогда граничные условия примут вид:
/а — Л) (?) ПРИ С = 0, 1
/ =0 при ?=аэ / /«' /ь>° для всех конечных ?. (8.5.62)
Здесь /0 — функция распределения для падающего пучка частиц.
V4 58 Ф. м. Морс и Г. Фешбач
914 Гл. 8. Интегральные уравнения
Эти граничные условия удовлетворяются следующими выражениями
{см. B.4.19)]:
с 1
L = he-" + ^ \ е-*-Ы» dl0
6 -1
со 1
\ с(Сад/1141 ^ 5 /(S ) * (8.5.63)
Для того чтобы свести их к одному интегральному уравнению, полезно
заменить зависимую переменную /:
1 1
р (Q = \ f (С, р) ф = \ (/„ + /ь) ф. (8.5.64)
-1 -1
Подставляя fa и /ь из (8.5.63) в (8.5.64), получаем
1 1 со
6 0 0
порядок интегрирования, находим [см. B.4.20)]
1
р 0 = [ Io (fi) е-'iv- dfi + ^ о (С - Со) Р Go) ^o, (8.5.65)
о
1
о
Мы узнаем в (8.5.65) неоднородное уравнение типа Винера — Хопфа.
Опуская в этом уравнении член, связанный с источником, мы получаем
однородное уравнение, которое называется уравнением Милна:
Сравнительно простое изменение в процессе Винера — Хопфа, которое нужно
произвести для случая неоднородных уравнений, мы обсудим ниже. Реше-
Решения уравнения (8.5.66) дают асимптотический (при большом С) вид реше-
решений неоднородного уравнения.
После определения р полное распределение можно найти, интегрируя
выражение (8.5.63). Особенно интересным является распределение выходя-
выходящего излучения у нижней поверхности при С = 0. Здесь
или
где R+ (к) — преобразование Фурье функции р+(С). Этот результат особенно
интересен, так как он показывает, что для нахождения распределения
выходящего излучения на поверхности вещества нет необходимости обращать
преобразование Фурье решения уравнения (8.5.66).
Теперь мы возвратимся к уравнению (8.5.66) и рассмотрим его решение
методом Винера—Хопфа. Преобразование от v равно
8.5. Преобразование Фурье и интегральные уравнения 913
Следовательно, функция Г, которую надо представить в виде Г+/Г_, имеет вид
Г = 1 - yi^kV = к~&™ь%к . (8.5.67)
V аналитична в полосе [ Im к \ < 1; однако при к = ± i она имеет точки
ветвления, из-за которых уже невозможно применить простой метод двух
предшествующих примеров.
Общий метод разложения на множители. Метод, который мы изучим,
основан на теореме о том, что каждая функция f(k), аналитическая
в полосе | Im к \ < а, является суммой двух функций, одна из которых
аналитична при ImA:>— a, a вторая — при 1тк<^а. Легко убедиться,
что это —частный случай теоремы о разложении в ряд Лорана [равенство
D.3.4) и рассуждения, следующие за ним]. Процесс, используемый здесь,
заключается в применении интегральной формулы Коши, причем контуром
интегрирования служит граница области аналитичности f(k); как и при
выводе ряда Лорана, этой границей является граница полосы, которая
представляет собой частный случай кругового кольца, когда центр кольца
расположен на бесконечности. Интеграл Коши разбивается на два инте-
интеграла: один, по внешней окружности, берется в положительном направле-
направлении, другой, по внутренней, — в отрицательном Направлении (для полосы
эти окружности обращаются в прямые, ограничивающие полосу). Функция.
представленная интегралом вдоль внешней окружности, аналитична внутри
внешней окружности, т. е. внутри кольца, а также во внутреннем
круге, а функция, представленная интегралом по внутренней окружности,
аналитична вне внутренней окружности. Переходя к случаю полосы
и помещая центр кольца в точку к= —ico, мы получаем
где
(8.5.68)
—со— Si
Слагаемое q_ аналитично при ImA:<j3, a q+ аналитично при p
где р < а; а определяется границей полосы аналитичности преобразования V
ядра уравнения.
Теперь мы можем использовать равенства (8.5.68) для того, чтобы
выполнить разложение на множители Г = Г+/Г_ сбгласно равенству (8.5.52).
Эта задача эквивалентна задаче о представлении In Г в виде 1пГ+ —1пГ_,
которая может быть решена при помощи равенства (8.5.68), если только
In Г не имеет особенностей в данной полосе. Так как функция Г анали-
аналитична в этой полосе, то трудности могут возникнуть только в точках,
где Г обращается в нуль; мы обозначим эти точки кг. Кроме того, для
обеспечения сходимости интегралов, фигурирующих в (8.5.68), мы должны
потребовать, чтобы <?(tj)—»0, когда |тг)]-^>оэ и tj остается внутри данной
полосы. Если q (к) должно равняться логарифму Г, то для выполнения
последнего требования Г должно стремиться к единице при |А;|—> ос.
Функция q не может в точности равняться логарифму Г, так как мы
должны ввести под знак логарифма сомножители, которые «компенсируют»
нули Г, лежащие внутри области аналитичности V, т. е. при |ImA|-<a;
затем мы должны заставить все выражение, стоящее под знаком логарифма,
58»
916 Гл. 8. Интегральные уравнения
стремиться к единице при j Л; j ¦—> оо. Как уже было сказано, нулями Г,
лежащими внутри области аналитичности, являются точки кг (г = 1, 2,..., N).
Поэтому отношение Г/П (к — кг) не имеет нулей внутри данной полосы
[некоторые из нулей могут иметь кратность, большую единицы, и в этом
случае множитель (к — кт) должен фигурировать в произведении И в соот-
соответствующей степени]. Однако это отношение не стремится к единице при
| к |—> оо, и поэтому мы должны умножить его на некоторый полином
от к (не имеющий нулей в этой полосе). Если, например, [Г/П (к — kr)] ~
сы.к~м1С, когда \к\—>оо, то мы можем умножить это выражение на
С(/с2 + а2)м'2 и положить
q = In [CI,(k) (Аа + а2)м'2/П (к- Аг)]. (8.5.69)
г
Соображения, по которым мы выбрали множитель (к2-{-а2)' , довольно
очевидны. Этот множитель не должен иметь нулей внутри области анали-
аналитичности Г (| Im к | < а), и поэтому мы выбираем его так, чтобы нули были
расположены на границе полосы. Кроме того, нам удобно, чтобы нули
располагались парами, один на верхней, другой на нижней границе полосы,
с тем чтобы q+ имела все нули на одной из границ, а #_ — на другой,
Постоянная С выбирается как раз так, чтобы величина в скобках стреми-
стремилась к единице при | /с j —> оэ.
Записав q= —<?+ + ?_ и выполнив вычисления по формулам (8.5.68),
получим
Г = [][ (А - кгIС (А* + a2)M/2] е<«-«->.
Теперь разложение Г очевидно:
Г+ = [[] (к - кг) е-**/С (к + io)M/zJ, Г_ = (к - ia)M/2e-e-. (8.5.70)
Таким образом, искомое разложение на множители формально получено,
и этот общий процесс всегда применим при решении методом Винера —
Хопфа (если мы можем найти q+ и q_\).
Задача Милна; продолжение. В задаче Милна Г задается равен-
равенством (8.5.67) в виде 1 — arc tg к/к. Эта функция имеет в точке к = 0 един-
единственный нуль второго порядка. Следовательно,
arc
откуда
в выражение для q_ входят те же подинтегральные функции, но преде-
пределами интегрирования служат oo-|-3i, —co-f-3i. В качестве заключитель-
заключительного шага мы должны определить Р(/с) = 1Г+Г+ = — \F Г_, где, согласно,
(8.5.70),
, r_ = (A-i)e-«-. (8.5.72)
Из сходимости интегралов, выражающих q+ и q_, следует, что обе эти
функции ограничены при больших к, каждая в своей области регулярности.
Следовательно, е~ч* стремится к постоянной и, значит, Г+ си к. Далее, так
как ЧГ+ (к) он 0, а Р — целая функция, то Р должна равняться постоянной;
эту постоянную обозначим, например, через А. Итак, преобразование
8.5. Преобразование Фурье и интегральные уравнения 917
Фурье функции р+ имеет вид
Д, = ^-= ^(*+0 <*»<»>, (8.5.73)
где д+ задается равенством (8.5.71).
Для получения углового распределения теперь необходимо [согласно
(8.5.67)] найти /?+(г'/|р|)- Здесь основной трудностью является вычисление
интеграла для д+. Мы можем свести его к виду, удобному для численного
интегрирования. С этой целью положим р = 0 и будем интегрировать
вдоль действительной оси tj (при к Ф 0). Тогда при кфО получаем
q (A) = 4.^br^fl-H?M^1_J*!L_. (8.5.74)
Для нахождения асимптотического вида р (Q необходимо иметь разло-
разложение R+ в степенной ряд по к. Вычислим q+ @) и затем высшие члены
из выражения (8.5.74). Интеграл (8.5.71) при & = 0 можно вычислить,
рассматривая контур, состоящий из действительной оси, часть которой
заменена малой полуокружностью с центром в точке "ч = 0, лежащей ниже
¦этой точки. Сумма интегралов по частям вещественной оси равна нулю
в силу нечетности подинтегральной функции. Интегрирование по окруж-
окружности дает
1 , 1
т. е. — In -5-, так что
Z* О
Чтобы найти следующий член, мы используем выражение (8.5.74), которое,
прибавляя равный нулю интеграл, записываем в виде
3G]*+1)
к
о
Здесь подннтегральная функция регулярна при к = 0, tj = 0. Следовательно,
Ч (8.5.75)
Возвращаясь к 7?+, получаем
откуда
Р+ (С) ~ const • [1 + iq'+ @) + С], ,? ->0.
Постоянная l-\-iq'+@) может быть вычислена интегрированием [в равен-
равенстве (8.5.75) по частям. Мы получим 1 -\-iq'+ @) =& 0,7104... . Это уравне-
уравнение и его решение будут изучены более подробно в § 12.2.
Неоднородное уравнение Винера —Хопфа. Уравнение
со
Ф(ж) = ?(ж) + Х^(ж-яоЖ*о)<Ч (8.5.76)
59 Ф. М. Морс н Г. Фсшбах
918 Гл. 8. Интегральные уравнения
можно решить тем же методом, который применялся в случае однородного
уравнения. Так же находим преобразование Фурье
(8.5.77)
Разлагая на множители 1 — УтсХУ = Г+/Г_, мы можем переписать это
равенство так:
\рд+ + Г_ (?_ -Ф_) - Г_Ф+ = 0. (8.5.78)
Первые два члена имеют требуемый вид, причем они аналитичны в общей
части двух полуплоскостей. Третий член не имеет нужного вида и поэтому
должен быть представлен в виде суммы двух слагаемых, одно из которых
аналитично в верхней полуплоскости, другое — в нижней. Для этого необхо-
необходимо, очевидно, чтобы существовала полоса, в которой регулярны и Г_
и Ф+. Если это так, то мы можем применить разложение, даваемое равен-
равенством (8.5". 68), где теперь д=Г_Ф+. Поэтому мы пишем
Г_Ф+ = ?_-д+.
Переписывая (8.5.78), получаем
ЧМГ„ + q. = q_ + Y_ (Ф.- W_) == Р. (8.5.79)
Левая часть уравнения аналитична в верхней полуплоскости, а пра-
правая—в нижней. Существует полоса регулярности, общая для них, так
что, как и в случае однородного уравнения, правая часть является анали-
аналитическим продолжением левой части в нижнюю полуплоскость. Определен-
Определенная таким образом функция Р регулярна в любой конечной части плоскости
и потому является целой функцией. Как и в случае однородного уравне-
уравнения, характер функции Р определяется асимптотическим поведением одного
из определяющих ее выражений. После того, как Р определена, имеем
ip; = *=*if (8.5.80)
и это выражение можно внести в формулу обращения для получения ф+ (х).
Если интегральное уравнение является уравнением первого, а не вто-
второго рода, т. е. если
то решение можно выразить в виде (8.5.79) и (8.5.80), полагая
На этом мы закончим общее изучение интегральных уравнений. Мно-
Многие из методов, которых мы здесь коснулись, будут применены в последу-
последующих главах. Читая эту главу, можно было заметить, что теория инте-
интегральных уравнений развита далеко не с той полнотой, как теория обыкно-
обыкновенных дифференциальных уравнений. Не существует правил, столь же
простых, как правила для нахождения особых точек, которые давали бы
нам возможность классифицировать ядра интегральных уравнений и легко
распознавать, какое из представлений для неизвестной функции в виде
интегралов или рядов быстро приводит к решению. Это положение отчасти
обусловлено тем, что интегральные уравнения, вообще говоря, представляют
более сложные физические и математические явления. Только в редких
случах интегральное уравнение оказывается эквивалентным дифференциаль-
дифференциальному уравнению второго порядка. Чаще они соответствуют дифференциаль-
дифференциальным уравнениям бесконечного порядка.
Основные свойства интегральных уравнений 919
Тем не менее существуют случаи, для которых мы можем получить
решение прямым путем. Например, для ядер вида v(x — х0) применимо
преобразование Фурье. Однако для многих случаев еще не найден подхо-
подходящий алгорифм для получения общего решения. Несмотря на это, сведе-
сведение задач к интегральным уравнениям оказывается полезным, потому что,
как мы увидим в следующей главе, интегральные уравнения служат осно-
основой для развития многих приближенных методов решения уравнений
физики.
Основные свойства интегральных уравнений и их решений
Типы уравнений. В уравнениях Фредгольма фигурируют интегралы
с фиксированными пределами; в уравнениях Вольтерра — интегралы,
у которых один из пределов переменный; в уравнения первого рода неиз-
неизвестная функция ф входит только под знаком интеграла; в уравнениях
второго рода ф имеется также и вне интеграла.
Уравнение Фредгольма первого рода:
ь
9 (z) = \ К (z | z0) ф (z0) dz0, 9 и К известны.
а
Уравнение Фредгольма второго рода:
ф (z) = 9 (z) + X \ К (z | z0) ф (z0) dz0, 9 и К известны.
а
При 9 = 0 это уравнение становится однородным.
Уравнение Вольтерра первого рода:
Z
9 (z) = \ К (z\z0)ty(z0)dz0, cp и К известны.
о
Уравнение Вольтерра второго рода:
Z
Ф (z) = 9 (z) + \ К (z | z0) ф (z0) dz0, 9 и К известны.
а
Соответствующее однородное уравнение, возникающее при 9 = 0, не имеет
ненулевых решений. Функция К (z \ z0) называется ядром уравнения.
Типы ядер. Симметрическое ядро удовлетворяет равенству К (z | z0) =
= К(zo\z). Полярное ядро имеет вид r(zo)G(z\zo), где функция G сим-
симметрична. Уравнение Фредгольма с симметрическим ядром самосопряженное,
уравнение Вольтерра с симметрическим ядром не является самосопряжен-
самосопряженным. Ядро является определенным, если
\ / (z) dz \ К (z | z0) f (z0) dz0 > 0 (положительно определенное)
или
\ / (z) dz \ К (z | z0) f (z0) dz0 < 0 (отрицательно определенное)
для любой функции /, конечной в промежутке интегрирования, соответ-
соответствующем уравнению с ядром К.
59*
920 Гл. 8. Интегральные уравнения
Ядро называется эрмитовым, если для него К(zo\z) —К(z\z0), и анти-
антиэрмитовым, если K(zo\z)= —K(z\z0). Ядра обоих этих типов можно пре-
преобразовать в определенные или полуопределенные (полуопределенными назы-
называются ядра, для которых в предыдущих определениях знаки > или <
заменены на > или <; соответственно) при помощи итераций [см. фор-
формулу (8.2.10) и следующие]. Уравнение с полярным ядром можно преобра-
преобразовать в уравнение с симметрическим ядром [см. формулу (8.2.8)].
Вещественное, положительно определенное, симметрическое ядро в урав-
уравнении Фредгольма обладает следующими свойствами. Однородное уравне-
уравнение второго рода имеет ненулевые решения для некоторой последователь-
последовательности значений параметра X; называемых собственными значениями
{0 < Хо < \ < Х2 ...); соответствующие решения фп (z) являются собствен-
собственными функциями и образуют семейство, ортогональное на отрезке a<C%*Cb
|см. стр. 844). Эти собственные функции удовлетворяют вариационному
принципу
;И
(см. F.3.20) по поводу аналогичного соотношения для дифференциальных
уравнений]. Стационарными значениями выражения, стоящего в скобках,
являются собственные значения Хп [см. (8.2.24)].
Сингулярное ядро имеет разрывы или особенности внутри промежутка
интегрирования или же бесконечные пределы интегрирования. Некоторые
из этих ядер можно свести к несингулярным при помощи итераций; те
ядра, которые не могут быть сведены к несингулярным, называются суще-
существенно сингулярными (см. стр. 855). Однородные уравнения Фредгольма
с существенно сингулярными ядрами могут иметь несчетное множество
собственных значений; могут оказаться допустимыми все значения X из неко-
некоторой области.
Функция Грина для неоднородного уравнения. Неоднородное уравне-
уравнение Фредгольма второго рода можно решить при помощи функции Грина
Gx (z [ z0), являющейся решением уравнения
Решение исходного уравнения имеет вид
<Ь (z) = ? (z) + X ^ Gx (z | z0) <р (z0) dz0.
Функция Грина Gx может быть разложена в различные ряды, содержащие
собственные функции <!>„, собственные значения Хп или итерированные
ядра Кп:
G\ (z i z0) = ^j '"* X .. , &m нормированы.
m
CO
n=0
= \ Kn (z| z±) К (Zl 1 z0) dzx =
Основные свойства интегральных уравнений 921
Следом функции Грина является
Решение уравнений Фредгольма первого рода. Обычно это уравнение
решается при помощи разложения у, К и искомой функции ф в какие-
либо ряды и приравнивания коэффициентов. Тип применяемых рядов зависит
от типа ядра К.
а. К является производящей функцией для некоторого множества соб-'
ственных функций хп> соответствующих данным пределам интегрирования:
Полагая ф = 2апХп> мы получаем ф (z) = 2 атАгг"' л неизвестные коэф-
коэффициенты ап могут быть определены при помощи сравнения с разложением
в ряд функции f.
б. К является функцией Грина, которую всегда можно выразить при
помощи соответствующих собственных функций уп:
Полагая ф = 2 а«Х«. мы получаем ап = A/fcJ t 9 (г) ун (z) dz, т. е. полу-
получаем формулу, выражающую коэффициенты ап.
Если нельзя воспользоваться ни одной из этих возможностей, то коэф-
коэффициенты ап можно найти по методу Шмидта [см. равенства (8.3.10) и сле-
следующие] или при помощи биортогональных функций [см. равенства (8.3.19)
и следующие], или же численными методами (см. гл. 9).
Для бесконечного промежутка интегрирования, когда ядра являются
сингулярными, иногда можно воспользоваться тем, что уравнение Фредгольма
первого рода представляет собой соотношение типа интегрального пре-
преобразования между известной функцией <р и неизвестной О при помощи
ядра К:
в. К (z | z0) = etZ7or интегрирование от — оо до со, —преобразование
Фурье. Решение [см. (8.3.59)]
г. К = е zz°, интегрирование от 0 до со, — преобразование Лапласа.
Решение [см. (8.3.66)]
ioo+e
—ioo+e
д. К = Jm(zz0)z0, интегрирование от 0 до оо, —преобразование Ган-
келя. Решение [см. (8.3.64)]
е. К = (zgJ'1, интегрирование от 0 до со, —преобразование Меллина.
Решение [см. (8.3.68)]
z sip (s) ds.
—ioo+e
922 Гл. 8. Интегральные уравнения
Решение уравнений Вольтерра первого рода. Здесь отсутствуют типы
а и б; обычно приходится прибегать к методу ортогонализации Шмидта
или к биортогональным рядам. Для ядер вида К = v(z — z0) можно исполь-
использовать преобразование Лапласа [равенство D.8.30) и следующие]:
а. K = v(z — z0), интегрирование от 0 до z. Решение [см. (8.5.34)]
ioo+e
... 1 f Ф(р) rvr , т-, Л
Ф (z) = ^—г \ , \ е dp, Re z > и,
2iti j v \p)
—ioo+e
где
V (p) = ^ v (x) e~vx dx, Ф (p) = \ <p (а:) е"рж ckc.
о о
б. A^ = a(z —z0), интегрирование от z до оо. Решение
где
(- х) ерх dx.
о
Решение уравнений Фредгольма второго рода. Ядро можно предста-
представить при помощи соответствующего ортонормированного семейства собствен-
собственных функций Хп. К (z| z0) = ^. gn (z0) Xn (z). Тогда, полагая ф=2апХт..
мы сводим однородное уравнение к системе уравнений
2 а" famn — A/Х) Ьтп] = °. amn = } Xrri (zo) ?n (zo) dzo-
n
Определитель этой системы | amn — A/X) 8mn | должен равняться нулю (веко-
(вековое уравнение). Корни этого уравнения являются собственными значе-
значениями Хп, а соответствующие ряды для ф — собственными функциями. Неко-
Некоторые случаи упрощения:
а. К является функцией Грина; тогда функции gn пропорциональны х„,
%1 = аАт- Определитель, входящий в вековое уравнение (вековой опре-
определитель), диагоналей, собственными значениями служат l/an, а собствен-
собственными функциями —Хп-
б. К является производящей функцией или каким-либо другим выраже-
выражением, для которого вековой определитель полудиагонален [см. (8.4.3)].
в. К таково, что вековой определитель конечен [см. (8.4.11)].
Соответствующее неоднородное уравнение можно решить при помощи
ряда по собственным функциям фи однородного уравнения и по биорто-
биортогональным решениям <рп сопряженного уравнения (если К симметрично,
то <р„ = ф„)
и частное решение имеет вид
где 9 (z) — неоднородный член в интегральном уравнении.
Литература 923
При бесконечном промежутке интегрирования появляется континуум
•собственных значений X, вековой определитель превращается в интеграл,
и следует применять метод интегральных преобразований.
г. K = v(z — z0), интегрирование от —со до со, —преобразование
Фурье. Если оба преобразования Ф(к) и V (к) регулярны при lm/c<i:,
— со < Re /c< со, то решением является
co+iT
, , . 1 f Ф(к)е~^Aк
1 — \/2
-со+гг
Если приходится вводить различные преобразования при z < 0 и при z > О
{обобщенное преобразование Фурье), то применима формула (8.5.17).
д. К = о (z — z0), интегрирование от 0 до со, — уравнение типа Винера —
Хопфа. Для решения см. формулы (8.5.55), (8.5.56), а также (8.5.76)
и следующие.
е. К = v(z + z0), интегрирование от —со до со, —преобразование
Фурье. Для решения см. формулу (8.5.29).
ж. К= (l/z0)v(z/z0), интегрирование от 0 до со, —преобразование
Меллина. Для решения см. формулу (8.5.43).
Решение уравнений Вольтерра второго рода. Однородное (несингуляр-
(несингулярное) уравнение не имеет ненулевых решений. В случаях когда К = о (z — z0)
и интегрирование производится от 0 до z или от z до со, можно восполь-
воспользоваться преобразованием Лапласа, так же как для уравнений Вольтерра
первого рода. Для решения неоднородного уравнения второго рода см. фор-
формулы (8.5.34) и (8.5 38).
ЛИТЕРАТУРА
Книги, в которых излагаются вопросы общей теории интегральных уравнений:
Курант Р. и Гильберт Д., Методы математической физики, т. 1, изд. 3, Гос-
Гостехиздат, М.—Л., 1951, гл. 3.
Ловитт У. В., Линейные интегральные уравнения, изд. 2, Гостехиздат, М., 1957.
Михлин С. Г., Сингулярные интегральные уравнения, Успехи матем. наук, 3, вып. 3
B5) A948). ^
Петровский И. Г., Лекции по теории интегральных уравнений, Гостехиздат,
М., 1951.
Привалов И. И., Интегральные уравнения, изд. 2, ОНТИ, М.—Л., 1937.
Смирнов В. И., Курс высшей математики, т. 4, изд. 3, Гостехиздат, М., 1957, гл. 1.
Уиттекер Е. Т. и Ватсон Г. Ш, Курс современного анализа, ч. 1, Гостехиздат,
М.—Л., 1934, гл. 11.
Ham el G-, Integralgleichungen, Berlin, 1937.
Kneser A., Integralgleichungen und ihre Anwendung in der Mathematischen Physik,
Brunswick, 1911.
Kowalewski G. W. H., Integralgleichungen, Berlin, 1930.
S ho hat J. A. and Та mark in J. D., The Problem of Moments, New York, 1943.
Vivanti G., Elemente der Theorie der linearen Integralgleichungen, Hanover, 1929.
Книги, в которых рассматривается применение преобразований Фурье и Лапласа
для решения интегральных уравнений:
Ван дер Подь Б. и Бреммер X., Операционное исчисление на основе двусторон-
двустороннего преобразования Лапласа, Изд. иностр. лит., М., 1952.
Титчмарш Е. К., Введение в теорию интегралов Фурье, Гостехиздат, М. — Л., 1948.
Doetsch G., Theorie und Anwendung der Laplace-Transformation, Berlin, 1937.
Hopf E., Mathematical Problems of Radiative Equilibrium, Cambiidge, New York, 1934.
Paley R. E. A. C. and Wiener N., Fourier Transforms in the Complex Domain, New
York, 1934.
Smithies P., Singular Integral Equations, Proc London Math. Soc, 46 A939), 409.
ОГЛАВЛЕНИЕ
Предисловие к русскому изданию. . 5
Предисловие авторов ... 9-
Глава 1. ТИПЫ ПОЛЕЙ 13
1.1. Скалярные поля 15
Поверхности уровня. Лапласиан.
1.2. Векторные поля 19-
Умножение векторов. Аксиальные векторы. Линии тока. Потенциаль-
Потенциальные поверхности. Поверхностные интегралы. Источник. Криволиней-
Криволинейные интегралы. Вихревая линия. Особенности полей.
1.3. Криволинейные координаты 31'
Направляющие косинусы. Коэффициенты Ламе. Кривизна коорди-
координатных линий. Элемент объема и другие формулы. Вращение осей.
Законы преобразования векторов. Контравариантные и ковариантные
векторы.
1.4. Дифференциальный оператор у 40
Градиент. Производная по направлению. Элементарные повороты.
Дивергенция. Теорема Гаусса. Решение уравнения Пуассона. Ротор
(вихрь). Вихревые линии. Теорема Стокса. Векторный оператор у.
1.5. Аппарат векторного и тензорного исчисления 52
Ковариантные и коятравариантные векторы. Аксиальные векторы.
Символы Кристоффеля. Ковариантная производная. Тензорные обозна-
обозначения для дивергенции и ротора. Другце дифференциальные операто-
операторы. Другие операторы второго порядка. Вектор как сумма градиента
и ротора.
1.6. Аффиноры и другие векторные операторы 60
Аффиноры. Аффиноры как векторные операторы. Симметрические
и кососимметрические аффиноры. Вращение осей и унитарные аффино-
аффиноры. Аффинерные поля. Деформация упругих тел. Типы деформаций.
Напряжения в упругой среде. Статическая взаимосвязь между на-
напряжением и деформацией в изотропном упругом теле. Аффинорные
операторы. Комплексные числа и кватернионы как операторы. Абст-
Абстрактные векторные пространства. Собственные векторы и собственные
значения. Операторы в квантовой механике. Направляющие косинусы
и вероятности. Вероятности и неопределенности. Комплексное векторное
пространство. Обобщенные аффиноры. Эрмитовы операторы. Примеры
унитарных операторов. Преобразование операторов. Операторы кванто-
квантовой механики. Спиновые операторы. Кватернионы. Операторы вращения.
Оглавление 925
1.7. Преобразование Лоренца. 4-векторы, спиноры 95
Собственное время. Преобразование Лоренца. Четырехмерные инва-
инварианты. 4-векторы. Тензор наиряжения-энергии. Спиновое простран-
пространство и пространство-время. Спиноры и 4-векторы. Преобразование Ло-
Лоренца для спиноров. Пространственный поворот спиноров. Спиновые
векторы и тензоры. Оператор вращения в спинорной форме.
Задачи к главе 1 108
Таблица наиболее употребительных векторных и аффинерных соотношении 115
Таблица свойств криволинейных координат . . . 116
Литература . .......... 117'
Глава 2. УРАВНЕНИЯ ПОЛЕЙ 119
2.1. Гибкая струна 119
Силы, действующие на элемент струны. Уравнение Пуассона. Сосредото-
Сосредоточенная сила; дельта-функция. Волновое уравнение. Простое гармониче-
гармоническое движение, уравнение Гельмгольца. Волновая энергия. Поток энер-
энергии. Мощность и волновой импеданс. Вынужденное движение струны.
Переходная характеристика; интеграл Фурье. Операторные уравнения
струны. Собственные векторы оператора единичного сдвига. Предельный
случай непрерывной струны. Влияние трения. Уравнение диффузии.
Уравнение Клейна—Гордона. Вынужденное движение упруго подкреплен-
подкрепленной струны. Резюме.
2.2. Волны в упругой среде 146
Продольные волны. Поперечные волны. Волновое движение в трехмер
ном пространстве. Векторные волны. Интегральные представления.
Напряжение и деформация. Волновая энергия и импеданс.
2.3. Движение жидкости . 149
Уравнение неразрывности. Решения для несжимаемых жидкостей.
Примеры. Напряжения в жидкостях. Уравнение Бернулли. Волновое
уравнение. Безвихревой поток сжимаемой жидкости. Дозвуковой и
сверхзвуковой потоки. Потенциал скоростей; линейное приближение.
Линии Маха и ударные волны.
2.4. Диффузия и другие явления просачивания жидкости 168
Поток жидкости через пористое твердое тело. Диффузия. Фазовое
пространство и функция распределения. Давление и уравнение состоя-
состояния. Средняя длина свободного пробега и эффективное сечение рас-
рассеяния. Диффузия света, интегральное уравнение. Диффузия света,
дифференциальное уравнение. Граничные условия. Влияние анизотроп-
анизотропного рассеяния. Приближение первого порядка; уравнение диф-
диффузии. Единичные решения. Потеря энергии при столкновении. Дей-
Действие внешней силы. Равномерный перенос, вызванный силовым полем.
Уменьшение скорости частиц при столкновениях. Резюме.
2.5. Электромагнитное поле 195
Электростатическое поле. Магнитостатическое поле. Зависимость от
времени. Уравнения Максвелла. Запаздывание и релаксация. Преобра-
Преобразование Лоренца. Калибровочное преобразование. Поле движущегося
заряда. Сила и энергия. Поверхности проводников и диэлектриков.
Передача волн и импеданс. Уравнения Прока.
2.6. Квантовая механика - 215
Фотоны и электромагнитное поле. Соотношение неопределенности.
Сопряженные переменные и скобки Пуассона. Основные постулаты
квантовой теории. Независимые квантовые переменные и функции от
операторов. Собственные векторы для координат. Функции преобра-
преобразования. Операторные уравнения для функций преобразования. Преоб-
926 Оглавление
разование к'пространству импульсов. Функция Гамильтона и уравне-
уравнение Шредингера. Гармонический осциллятор. Зависимость от времени.
Время как параметр. Функция Гамильтона, зависящая от времени.
Частица в электромагнитном поле. Относительность и спин. Уравне-
Уравнение Дирака. Полный момент количества движения. Волновая функ-
функция свободного поля. Резюме.
Задачи к главе 2 256
Стандартные формы некоторых уравнений с частными производными тео-
теоретической физики 260
Литература ...... 262
Глава 3. ПОЛЯ И ВАРИАЦИОННЫЙ ПРИНЦИП 264
3.1. Вариационный интеграл и уравнения Эйлера . 265
Уравнения Эйлера. Уравнения связи.
3.2. Принцип Гамильтона и классическая динамика 268
Уравнения Лагранжа. Энергия и функция Гамильтона. Импеданс. Кано-
Канонические преобразования. Скобки Пуассона. Интеграл действия.- Дву-
Двумерный осциллятор. Заряженная частица в электромагнитном поле. Реля-
Релятивистская частица. Диссипативные системы. Импеданс и полная про-
проводимость для диссипативных систем.
3.3. Скалярные поля .... 288
Гибкая струна. Волновое уравнение. Уравнение Гельмгольца. Потев-
циал скоростей. Волны сжатия. Волновой импеданс. Плоская волна.
Уравнение диффузии. Уравнение Шредингера. Уравнение Клейна —
Гордона.
3.4. Векторные поля 303
Общие свойства поля. Изотропные упругие среды. Решения типа пло-
плоской волны. Импеданс. Электромагнитное поле. Тензор напряжения-
энергии. Импульс поля. Изменение калибровки потенциалов. Аффинор
импеданса. Плоская волна. Уравнение Дирака.
Задачи к главе 3 ' . . 320
Сводка результатов главы 3 324
Гибкая струна или мембрана. Сжимаемая невязкая жидкость. Уравне-
Уравнение диффузии. Уравнение Шредингера. Уравнение Клейна — Гордона.
Уравнение упругих колебаний. Уравнения электромагнитного поля.
Уравнение Дирака.
Литература... ..... , . . 328
Глава 4. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО . 330
4.1. Комплексные числа и комплексные переменные 331
Оператор вращения. Векторы и комплексные числа. Двумерное электро-
электростатическое поле. Контурные интегралы.
4.2. Аналитические функции 337
Конформное отображение. Интегрирование в комплексной плоскости.
Теорема Коши. Некоторые полезные следствия из теоремы Коши.
Интегральная формула Коши. Действительная и мнимая части анали-
аналитической функции. Импеданс. Формула Пуассона.
4.3. Производные аналитических функций. Ряды Тейлора и Лорана . . 354
Ряд Тейлора. Ряд Лорана. Изолированные особые точки. Классифи-
Классификация функций; теорема Лиувилля. Мероморфные функции. Поведе-
Поведение степенного ряда на' границе круга сходимости. Анали-
Аналитическое продолжение. Основные теоремы. Точки ветвления. Приемы
аналитического продолжения.
Оглавление 927
4.4. Многозначные функции 376
Точки ветвления и линии ветвления. Римановы поверхности. Пример.
4.5. Теория вычетов. Гамма-функция и эллиптические функции .... 386
Интегралы от функций, имеющих точки ветвления. Обращение рядов.
Суммирование рядов. Интегральное представление функций. Интегралы,
связанные с функцией ошибок. Гамма-функция. Контурные интегралы
для гамма-функции. Представление гамма-функции в виде бесконеч-
бесконечного произведения. Производные гамма-функции. Формула удвоения.
Бета-функция. Периодические функции. Основные свойства двоякопери-
одических функций. Эллиптические функции второго порядка. Инте-
Интегральные представления эллиптических функций.
4.6. Асимптотические ряды. Метод перевала 410
Пример. Усреднение последовательных членов ряда. Интегральные
представления и асимптотические ряды. Выбор контура. Первый член
разложении. Остаток ряда.
4.7. Конформное отображение 419
Общие свойства отображения. Преобразование Шварца—Кристоффеля.
Примеры. Метод инверсии.
4.8.1 Преобразование Фурье 428
' Связь с рядами Фурье. Некоторые интегральные теоремы. Интеграль-
Интегральная теорема Фурье. Свойства преобразования Фурье. Асимптотические
значения преобразования. Общая формулировка. Свертка. Формула сум-
суммирования Пуассона. Преобразование Лапласа. Преобразование Мелпина.
Задачи к' главе 4 446
Основные свойства функций комплексного переменного 455
Алгорифм Эйлера для вычисления сумм рядов. Представление интег-
интегралов посредством асимптотических рядов. Преобразование Фурье. Пре-
Преобразование Лапласа. Преобразование Меллина.
Часто встречающиеся специальные функции 461
Гамма-функция. Эллиптические функции. Тэта-функции.
Литература 466
Глава 5. ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ .... 468
5.1. Координаты, в которых переменные разделяются 470
Граничные поверхности и системы координат. Двумерные разделяю-
разделяющие координаты. Разделяющие координаты для двумерного уравнения
Лапласа. Разделение переменных в волновом уравнении. Прямоуголь-
Прямоугольные и параболические координаты. Полярные и эллиптические коор-
координаты. Коэффициенты Ламе и геометрия систем координат. Константы
разделения и граничные условия. Разделение для трех измерений.
Определитель Штеккеля. Софокусные поверхцости второго порядка.
Вырожденные формы эллипсоидальных координат. Слияние особенно-
особенностей. Константы разделения. Уравнение Лапласа для трех измере-
' ний, модуляционный множитель. Софокусные циклиды.
«5.2. Общие свойства, решение при помощи рядов 495
Определитель Вронского. Независимые решения. Интегрирующие мно-
множители и сопряженные уравнения. Решение неоднородного уравнения.
Решение при помощи рядов вблизи обыкновенных точек. Особые точки,
¦ определяющие уравнение. Классификация уравнений, стандартные
формы. Две регулярные особые точки. Одна иррегулярная особая точка.
Три регулярные особые точки. Рекурсивные формулы. Гипергеометри-
Гипергеометрическое уравнение. Функции, представимые гипергеометрическими рядами.
Аналитическое продолжение гипергеометрического ряда. Функции Геген-
бауера. Одна регулярная и одна иррегулярная особые точки. Асимн-
928 Оглавление
тотические ряды. Две регулярные, одна иррегулярная особые точки.
Непрерывные дроби. Определитель Хилла. Функции Матье. Функции
Матье второго рода. Еще о рекурсивных формулах. Функциональные
ряды.
5.3. Интегральные представления 542
Некоторые простые примеры. Общие уравнения для подинтегральной
функции. Преобразование Эйлера. Преобразование Эйлера для гипер-
гипергеометрического ряда. Аналитическое продолжение гипергеометриче-
гипергеометрического ряда. Функции Лежавдра. Функции Лежандра второго рода.
Полиномы Гёгенбауера. Вырожденная (конфлюентная) гипергео-
гипергеометрическая функция. Преобразование Лапласа. Асимптотическое
разложение. Решения третьего рода. Решение второго рода. Функции
Бесселя. Функции Ганкеля. Функции Неймана. Приближенные фор-
формулы для больших v. Кулоновская волновая функция. Функ-
Функции Матье. Преобразование Лапласа и разделенное волновое уравне-
уравнение. Еще о функциях Матье. Ядра, являющиеся функциями от zt.
Задачи к главе 5 604
Таблица разделяющих координат для трех измерений 612
Прямоугольные координаты. Круговые цилиндрические координаты
(вращения). Эллиптические цилиндрические координаты. Параболи-
Параболические цилиндрические координаты. Сферические координаты (вра-
(вращения). Конические координаты. Параболические координаты (вра-
(вращения). Вытянутые сфероидальные координаты (вращения). Сплю-
Сплющенные сфероидальные координаты (вращения). Эллипсоидальные коор-
координаты. Параболоидальные координаты. Бисферические координаты.
Тороидальные координаты.
Дифференциальные уравнения второго порядка и их решения 622
Одна регулярная особая точка. Одна иррегулярная особая точка. Две
регулярные особые точки. Три регулярные особые точки. Одна регу-
регулярная и одна иррегулярная особые точки. Две иррегулярные особые
точки.
Литература 629
Глава 6. КРАЕВЫЕ УСЛОВИЯ И СОБСТВЕННЫЕ ФУНКЦИИ 631
6.1. Типы уравнений и краевых условий 631
Типы краевых условий. Задача Копти и характеристические линии.
Гиперболические уравнения. Условия Коши и гиперболические уравне-
уравнения. Волны для нескольких пространственных измерений. Эллиптиче-
Эллиптические уравнения и комплексные переменные. Параболические уравнения.
6.2. Разностные уравнения и краевые условия 645
Линейные разностные уравнения первого порядка. Разностные урав-
уравнения для нескольких измерений. Эллиптическое уравнение и условия
Дирихле. Собственные функции. Функции Грина. Эллиптическое урав-
уравнение и условия Коши. Гиперболическое разностное уравнение. Пара-
Параболическое разностное уравнение.
0.3. ¦ Собственные функции и их применения 658
Ряды Фурье. Функция Грина. Собственные функции. Типы краевых
условий. Абстрактное векторное пространство. Задача Штурма—Лиу-
вилля. Вырождение. Ряды по собственным функциям. Разложение
уравнения Штурма—Лиувилля (факторизация). Собственные функции
и вариационный принцип. Полнота системы собственных функций.
Асимптотические формулы. Сравнение с рядом Фурье. Явление Гиббса.
Производящие функции, поливомы Лежандра. Собственные функции для
Оглавление 929
нескольких измерений. Разделимость констант разделения. Плотность
собственных значений. Непрерывное распределение собственных значе-
значений. Собственные значения для уравнения Шредингера. Дискретные
и непрерывные собственные значения. Дифференцирование и интегри-
интегрирование как операторы. Задача о собственных значениях в абстракт-
абстрактном векторном пространстве.
Задачи к главе 6 722
Таблица полезных собственных функций и их свойств 725
Интервал —1^2^ 1; функция плотности A — z2)^; полиномы Геген-
бауера Тп (z). Интервал 0 ^ z < оэ; функция плотности z e ; поли-
номы Лагерра L п (=). Интервал — оо < z < оо; функция плотности е ;
полиномы Эрмита Нп (z).
Собственные функции, полученные при помощи метода факторизации . . 731
Литература 733
Глава 7. ФУНКЦИИ ГРИНА 735
7.1. Точки источников и граничные точки 737
Формулировка в абстрактном векторном пространстве. Граничные усло-
условия и поверхностные заряды. Простой пример. Связь между объемной
и поверхностной функциями Грина. Общее решение. Функция Грина
и производящие функции.
7.2. Функции Грина для установившихся колебаний 745
Теорема Грина. Функция Грина для уравнения Гельмгольца. Решение
неоднородного уравнения. Общие свойства функции Грина. Эффект гра-
граничных условий. Метод изображений. Ряд изображений. Другие раз-
разложения. Разложение функции Грина по собственным функциям. Раз-
Разложения для бесконечной области. Полярные координаты. Общая тех-
техника. Общая формула. Функции Грина и собственные функции.
7.3. Функция Грина для скалярного волнового уравнения 772
Соотношение взаимности. Вид функции Грина. Поле подвижного источ-
источника. Двумерное решение. Одномерные решения. Начальные условия.
Принцип Гюйгенса. Границы в конечной части пространства. Разложе-
Разложение по собственным функциям. Нестационарные малые колебания
круглой мембраны. Уравнение Клейна—Гордона.
7.4. Функция Грина для уравнения диффузии 793
Причинность и взаимность. Неоднородные граничные условия. Функция
Грина для бесконечной области. Конечные границы. Решения при
помощи собственных функций. Максимальная скорость передачи тепла.
7.5. Функция Грина в абстрактной операторной форме 804
Обобщение теоремы Грина, сопряженные операторы. Эффект краевых .
условий. Еще о сопряженных дифференциальных операторах. Сопря-
Сопряженные интегральные операторы. Обобщение на абстрактное векторное
пространство. Сопряженные, комплексно сопряженные и эрмитовы опе-
операторы. Функция Грина и оператор Грина. Соотношение взаимности.
Разложение оператора Грина в эрмитовом случае. Неэрмитовы опера-
операторы; биортогональные функции.
Задачи к главе 7 8J9
Таблица функций Грина • - ¦ 823
Общие свойства. Функция Грина для уравнения Гельмгольца. Функ-
Функция Грина для волнового уравнения. Функция Грина для уравнения
диффузии.
Литература 827
930 Оглавление
Глава 8. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ 828
8.1. Интегральные уравнения физики; их классификация 828
Пример из акустики. Пример из волновой механики. Краевые условия
и интегральные уравнения. Уравнения, определяющие собственные
функции. Интегральные уравнения некоторых собственных функций.
Типы интегральных уравнений; уравнения Фредгольма. Уравнения
Вольтерра.
8.2. Общие свойства интегральных уравнений ... 838
Ядра интегральных уравнений. Переход к определенным ядрам. Свой-
Свойства симметричного определенного ядра. Ядра и функции Грина для
неоднородных уравнений. Полуопределенные и неопределенные ядра.
Ядра, отличные от действительных определенных. Интегральное урав-
уравнение Вольтерра. Сингулярные ядра.
8.3. Решение уравнений Фредгольма первого рода . . . .• 856
Решения уравнений Фредгольма в форме рядов. Определение коэффи-
коэффициентов. Ортогонализация. Биортогональные ряды. Интегральные урав-
уравнения первого рода и производящие функции. Применение полиномов
Гегенбауера. Интегральные уравнения первого рода и функции Грина.
Интегральные преобразования и интегральные уравнения первого рода.
Дифференциальные уравнения и интегральные уравнения первого рода.
Проблема моментов. Резюме.
ЯЛ. Решение интегральных уравнений второго рода 879
Разложения первого класса. Разложения второго класса. Разложения
третьего класса. Другие случаи. Неоднородное интегральное уравнение
Фредгольма второго рода.
8.5. Преобразование Фурье и интегральные уравнения 88}
Преобразование Фурье и ядра вида v(x—х0). Преобразование Ганкеля.
Ядро v(x—x0) в бесконечной области. Однородное уравнение. Пример.
Точки ветвления. Ядро v(x-{-x0) в неограниченной области. Пример.
Применения преобразования Лапласа. Интегральное уравнение Вольтерра
с пределами (х, оо). Преобразование Меллина. Метод Винера—Хопфа.
Примеры применения метода. Задача Милна. Общий метод разложения
на множители. Задача Милна; продолжение. Неоднородное уравнение
Винера—Хопфа.
Основные свойства интегральных уравнений и их решений 919
Типы уравнений. Типы ядер. Функция Грина для неоднородного урав.-
нения. Решение уравнений Фредгольма первого рода. Решение урав-
уравнений Вольтерра первого рода. Решение уравнений Фредгольма второ-
второго рода. Решение уравнений Вольтерра второго рода.
Литература ' 923
ЗАМЕЧЕННЫЕ ОПЕЧАТКИ
Стр.
401
450
452
474
529
541
576
586
602
647
652
653
684
713
7
726
726
Строка
5 св.
5 сн.
1 сн.
22 св.
2 св.
5 сн.
12 св.
1 сн.
17 сн.
5 св.
3 сн.
18 св.
2 сн.
2 сн.
4 св.
5 св.
Напечатано
Ы)
е~
е-гчп/
dw{dz и ~dw~ldz
стр. 000
eii7C
ds 2л Г(т+1)Г(т—п+1-е*
=0
со
г=
A+с
G(l,2)
г.
в конце,
W—>=ОЭ
A+ta—2tzf+i/2
линсмы
1.3.5).....2Р-1)
Следует читать
(•+*)•""¦
е-Ь
е—iV7c/2
dwldz и dwldz
стр. 499
ei7C
ds 2j Г(т+1)Г(т-п+1-Е) +
m==0
Bn)!
A + c)-1
G2(l,2)
У
r,s
в конце § 3.1,
W—> —OD
(l+fi_2f*)P+1/2
полиномы
1.3-5... ..BP-1)
По
вине
ТИП.
»
»
»
»
ред.
ТИП.
ред.
ТИП.
ред.
ТИП.
»
*
*
»
в
Зак. 249