Автор: Коли Г.
Теги: общая генетика общая цитогенетика иммуногенетика эволюционное учение видообразование филогенез биология зоология позвоночные
Год: 1979
г. КОЛИ
АНАЛИЗ ПОПУЛЯЦИЙ
ANALYSIS
OF VERTEBRATE POPULATIONS
GRAEME CAUGHLEY
Senior Lecturer in Biology
School of Biological Sciences
The University of Sydney
A Wiley—Interscience Publication
John Wiley and Sons
London New York Sydney Toronto
1977
г. КОЛИ
АНАЛИЗ ПОПУЛЯЦИЙ
ПОЗВОНОЧНЫХ
Перевод с английского
Е. П. КРЮКОВОЙ
под редакцией
канд. физ.-мат. наук А. Д. БАВЫКИНА
Издательство «Мир»
Москва 1979
УДК 575.3/.7
В настоящее время становится все более очевидной
необходимость рационального отношения к окружающей
среде, в частности к популяциям диких позвоноч-
ных животных. В книге бывшего профессионального
охотника, а ныне известного австралийского эколога
описаны количественные методы, используемые для
оценки численности популяций, их возрастного соста-
ва, предсказания их динамики и т. п. Рассмотрены пред-
ставления о динамике естественных популяций, о ме-
тодах получения данных, необходимых для решения
практических задач по регуляции их численности. Кни-
га не предполагает наличия у читателя специальной
математической подготовки.
Предназначена для зоологов, экологов, охотоведов
и специалистов по охране природы и эксплуатации при-
родных ресурсов.
Редакция литературы по биологии
© 1977, John Wiley and Sons Ltd. All Rights Reserved.
Authorised translation from the English language edi-
tion published by John Wiley and Sons Ltd.
© Перевод на русский язык, «Мир», 1979
21002-136
041(01)—79
136—79
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В наше время необходимость рационального обраще-
ния с окружающей средой становится все более акту-
альной и пропагандируется достаточно широко. В по-
следнее время воздействие человека на природные сис-
темы резко возросло, и поэтому совершенно ясно, что мы
должны предвидеть возможные последствия наших дей-
ствий и разумно их планировать.
Однако, несмотря на явную актуальность исследо-
ваний в этом направлении и на быстро растущее число
публикаций, в отечественной и мировой литературе на-
метился и продолжает расширяться определенный раз-
рыв между работами чисто теоретического характера с
результатами, не часто доводимыми до практических ре-
комендаций по управлению природными популяциями, и
работами в основном описательными, в которых резуль-
таты математического моделирования популяций и при-
родных сообществ либо вовсе не используются, либо
используются лишь в самой незначительной степени.
Положение усугубляется еще и тем, что публикации на
эти темы чрезвычайно разбросаны, и методы, развивае-
мые, например, в ихтиологии, зачастую остаются неиз-
вестными специалистам по охотничьему хозяйству, хотя
сами количественные методы анализа могут быть совер-
шенно безразличны к таксономической принадлежности
исследуемых животных.
Все же в самое последнее время исследователи посте-
пенно начинают осознавать, что такие имеющие на пер-
вый взгляд мало общего проблемы, как рациональная
организация промысла самых различных животных, борь-
ба с вредителями сельского и лесного хозяйства или пред-
сказание последствий воздействия загрязнения окружаю-
щей среды на природные популяции, в принципе являются
проблемами родственными, требующими для своей пра-
вильной постановки и решения разработки одного круга
6
Предисловие редактора перевода
идей, методов сбора исходных данных и методов мате-
матического анализа и моделирования.
Все это вместе взятое вызвало в последние годы
зарождение и формирование нового направления —
учения об управлении природными популяциями
и сообществами, в рамках которого синтезируются
идеи, накопленные в описательной, эксперимен-
тальной и теоретической экологии, в науках, зани-
мающихся управлением и разработкой математических ос-
нов и вычислительных методов математического модели-
рования природных систем.
Уместно заметить, что поскольку в капиталистичес-
ких странах в результате бесконтрольного ведения хо-
зяйства пагубные последствия многих воздействий на
окружающие системы стали очевидными широкой общест-
венности раньше, чем у нас в стране, то и разработка
методов управления природными системами также была
там начата ранее. Однако следует помнить, что несомнен-
ные преимущества планового ведения хозяйства не реа-
лизуются автоматически, а могут быть осуществлены лишь
на основе разработки теоретических и методических основ
управления природными системами. С этой точки зрения
актуальным и оправданным является внимательное от-
ношение к уже накопленному за рубежом опыту, как по-
ложительному, так и отрицательному.
Конкретному и важному разделу возникающего но-
вого направления в науке — анализу динамики числен-
ности природных популяций позвоночных животных и
использованию результатов анализа для управления попу-
ляциями — посвящена предлагаемая советскому читате-
лю книга бывшего профессионального охотника, а ныне
известного эколога, преподавателя Сиднейского универ-
ситета Грэма Коли, в значительной степени заполняющая
пробел между сугубо описательными и чисто теоретичес-
кими исследованиями.
Книга рассчитана в первую очередь на экологов и на
быстро расширяющийся круг специалистов в области ра-
циональной эксплуатации природных ресурсов и не пред-
полагает у читателя знания математики, выходящего
за рамки элементарной алгебры и статистики. Уже за-
головок книги свидетельствует о том, что автор будет го-
Предисловие редактора перевода 7
ворить о позвоночных животных, и, действительно, исполь-
зуемые автором в тексте конкретные примеры, основы-
вающиеся в значительной степени на его собственных
исследованиях, относятся к млекопитающим и птицам;
однако круг применения описанных и систематизирован-
ных автором методов может быть значительно расширен,
а книга в целом заслуживает внимания всех,, кто инте-
ресуется проблемами взаимоотношений человека с окру-
жающей средой.
А. Базыкин
ПРЕДИСЛОВИЕ
Описания методов анализа, необходимых для понима-
ния того, что собой представляют и как живут популяции
позвоночных, разбросаны по нескольким тысячам книг
и научных журналов. Крайняя распыленность этой ли-
тературы часто тормозила и мои собственные исследова-
ния, особенно когда ближайшая библиотека находилась
в соседнем городе или в соседней стране. Те же неудоб-
ства испытывают и другие экологи. Мои студенты, спе-
циализирующиеся в прикладной популяционной эколо-
гии и в области эксплуатации природных популяций,
также тратят массу времени из-за отсутствия единого ру-
ководства, которое охватывало бы эти дисциплины.
Предлагаемая вниманию читателей книга представляет
собой введение в данную область и является попыткой
исправить существующее положение. Я отобрал в лите-
ратуре такие методы анализа и такие подходы к пробле-
ме, которые кажутся мне пригодными для непосредствен-
ного использования. Оставшиеся при этом пробелы в це-
лостном изложении я попытался временно заполнить
собственными модификациями этих методов. Некоторые
из существующих подходов, будучи математически без-
укоризненными, требуют данных, которые очень трудно
или даже невозможно собрать в полевых условиях.
Другие основаны на предпосылках, или вовсе не свя-
занных с реальной жизнью животных, или связанных с
ней лишь косвенно. Ни те ни другие не включены в эту
книгу. Все методы анализа подверглись тщательному от-
бору. Будучи экологом, а не математиком, я выбирал наи-
более понятные и простые для использования методы.
Большинство из них я применял в своей собственной ра-
боте и поэтому имею некоторое представление об их дос-
тоинствах и недостатках.
Любая книга по методам популяционного анализа
представляет собой компромисс между строгостью и дос-
Предисловие
9
тупностью. Когда приходится жертвовать одним из этих
качеств, я жертвую строгостью. Поскольку многие чита-
тели не знакомы с дифференциальным исчислением и мат-
ричной алгеброй, эта мощная математическая техника
здесь не используется, и от читателя требуется лишь зна-
ние элементарной алгебры и статистики.
Книга преследует четыре конкретные цели:
1. Дать читателю, изучающему экологию и управление
природными популяциями, понятие о динамике числен-
ности популяций, позволяющее ему, в первую очередь,
представить себе сами популяционные процессы, а не
просто последствия, к которым эти процессы приводят.
2. Дать представление о том, какая информация тре-
буется для решения задач популяционной динамики, по-
рождаемых проблемами экологии и управления природ-
ными популяциями.
3. Показать, как обращаться с этой информацией,
чтобы получить ответы на интересующие его вопросы.
4. Показать, как популяционный анализ может ис-
пользоваться для решения разного рода практических
задач — снижения численности популяций, стимулиро-
вания их роста или поддержания постоянного уровня
промысла.
На протяжении всей книги для иллюстрации методов
анализа я пользовался примерами, относящимися к са-
мым различным видам животных и условиям их обита-
ния. Непосредственной целью каждого примера является
знакомство читателей с методами расчетов, но кроме того,
существуют еще два критерия отбора. Во-первых, при-
мер сам по себе должен быть биологически интересным и,
во-вторых, он должен концентрировать внимание чита-
теля не только на арифметических вычислениях, но и на
том, как от алгебраического результата перейти к био-
логическим выводам. Этот переход представляет собой
наиболее трудный шаг и наиболее важный этап в попу-
ляционном анализе.
Я бесконечно благодарен Л. Бёрчу и другим сидней-
ским экологам за многочасовые дискуссии, способство-
вавшие созданию этой книги. Многим главам книги пошли
на пользу критические замечания А. Ходсона, Дж. Мон-
ро, Т. Ринея и Дж.Гулланда. Мне хотелось бы выразить
10
Предисловие
признательность моей жене, которая по причинам осо-
бого характера выступает то как Джудит Коли, когда
работает с млекопитающими, то как Джудит Бэдхем,
когда работает с рептилиями. Будучи чистым практиком
и не занимаясь разработкой теоретических вопросов,
она подсказала мне многие идеи, лежащие в основе этой
книги.
Грэм Коли
Глава 1
Введение
Популяционный анализ оперирует количественными
характеристиками популяций — численностью, соотно-
шением полов, скоростью роста и т.п., а также свойства-
ми животных и окружающей среды, определяющими зна-
чения этих характеристик. Различные исследователи по-
разному определяют термин «популяция». Наиболее под-
ходящее для наших целей рабочее определение популя-
ции дал Коул (Cole, 1957). «Популяцией называется био-
логическая совокупность, выделяемая на уровне эколо-
гической интеграции, для которой при описании ее
.свойств имеет смысл говорить о рождаемости, смертности,
соотношении полов и возрастной структуре».
Существуют разные подходы к описанию динамики
популяции. При простейшем подходе все особи считаются
тождественными, численность популяции выражается как
среднее за несколько лет значение и исследуются при-
чины, по которым численность принимает именно такое
значение. Следующим шагом является изучение колеба-
ний численности в связи с изменением условий окружаю-
щей среды. Далее исследователь может поставить перед
собой цель — изучить скоростх, изменения численности в
зависимости от изменений рождаемости и смертности, в
свою очередь зависящих от влияния факторов среды. При
более детальном подходе приходится отказываться от
упрощающего, но не реалистического предположения о
тождественности всех особей в популяции. Такой под-
ход предполагает, что факторы окружающей среды влия-
ют на численность косвенно, воздействуя на плодови-
тость и выживаемость различных возрастных категорий.
Факторы окружающей среды непосредственно связаны
именно с этими характеристиками, а не с самой числен-
14
Глава 1
человека и популяций насекомых, вторая — анализ попу-
ляций рыб и китов, причем динамику популяций послед-
них стали изучать явно с опозданием, третья — боль-
шинство исследований по млекопитающим и птицам.
Каждая категория располагает своей собственной систе-
мой обозначений и своими собственными методами анали-
за.* Демаркационные линии поразительно четки и нару-
шаются лишь считанными безрассудными исследова-
телями, игнорирующими эти границы. Такие работы пред-
ставляют собой явные исключения; это свидетельствует
о том, что исследователи, изучающие какую-то одну группу
животных, редко читают работы, относящиеся к другим
группам, и принадлежность животного к определенному
таксону, как правило, считается более существенной чер-
той по сравнению с исследуемым биологическим процес-
сом. Это, конечно, абсурд. Рождаемость есть рождаемость
независимо от того, идет ли речь о медведях или о жуках,
и вычисления в обоих случаях проводятся одни и те же.
Но существуют и различия. Жуков можно изучать в бан-
ках, а медведи — неподходящий объект для исследова-
ния в лабораторных условиях, поэтому данные по этим
группам животных должны собираться разными спо-
собами. При исследовании популяций медведей порой не-
возможно получить данные, позволяющие непосредст-
венно оценивать определенные параметры, здесь требу-
ются специальные косвенные методы, связанные с про-
блемой величины выборки. Некоторые из этих методов
будут описаны, но скорее применительно к конкретным
проблемам, чем к конкретным таксонам. Большинство
примеров в этой книге относится к млекопитающим и
птицам, однако я приведу также несколько примеров,
связанных с использованием некоторых методов на дру-
гих группах, и, разумеется, большинство описанных ме-
тодов с небольшими изменениями можно применять при
решении проблем, касающихся рыб, пресмыкающихся,
беспозвоночных, растений.
Отдельные методы, изложенные в этой книге, могут
показаться не очень удобными для ихтиологов. Широко
используемые здесь параметры повозрастной плодо-
витости и смертности у рыб обычно оцениваются с большим
трудом или вовсе не могут быть оценены и соответствен-
Введение
15
но редко используются при анализе их популяций.
Исследователи, работающие в этой области, обходным
путем решают острые проблемы выборки, используя кос-
венные математические подходы (см., в частности, Bever-
ton and Holt, 1957; Ricker, 1958), впечатляющие своей
бесконечной сложностью и всеобъемлющей широтой.
Я не способен что-либо добавить к ним и не хочу рисковать,
настраивая ихтиологов против них, однако может ока-
заться, что некоторые методы, представленные здесь,
могут послужить полезным дополнением к традиционно
используемым в исследованиях популяций рыб. Приме-
нение параметров, исходно введенных исследователями
в области демографии, для изучения популяций сардин
(Murphy, 1967), показывает, что через пропасть, лежа-
щую между этими двумя подходами, можно перекинуть
мосты.
В последующих главах описываются проблемы попу-
ляционной динамики, данные, которые необходимо прив-
лекать для их исследования, и методы, посредством ко-
торых следует анализировать данные, чтобы решать эти
проблемы. Методы полевых исследований рассмотрены
лишь вкратце. Эти методы описаны в широ ко доступных
руководствах, касающихся отдельных групп животных:
насекомых (Southwood, 1966), рыб (Allen, 1951; Rounse-
fell and Everhart, 1953; Gerking, 1967), птиц (Wolfson,
1955; Giles, 1969), рептилий (Goin and Goin, 1962) и мле-
копитающих (Davis, 1956; Southern, 1964; Giles, 1969.
Глава 2
Популяция
Для описания популяции часто привлекают самые
разнообразные аналогии; одна из них, предложенная
Фарнером (Farner, 1955), представляется наиболее удач-
ной. Фарнер подметил близкое сходство между динами-
кой популяции и динамикой озера. Вода поступает в озе-
ро (рождение особей) и уходит из него (их гибель), причем
взаимодействие этих процессов в значительной степени
определяет уровень воды в озере (численность животных).
Продолжая указанную аналогию, можно заметить, что
на уровень воды в озере непосредственно влияют выпа-
дающие осадки (иммиграция) и испарение (эмиграция).
Популяции представляют собой системы более сложные,
чем озера, и сходство между ними на этом кончается, но
основные свойства обеих систем имеют много общего. И
те и другие относятся к открытым системам, и их можно
описывать одинаковыми уравнениями.
2.1. Границы популяции
Привычное нам представление о популяции как о
группе скрещивающихся между собой особей, почти или
полностью не контактирующей с другими такими же
группами, далеко от того, что мы в действительности на-
блюдаем в природе. На рис.2.1 показана гораздо более
распространенная структура пространственного рассе-
ления. На нем изображено мозаичное распределение, в
котором можно выделить отдельные группы животных,
но ни одну из групп нельзя рассматривать как полностью
изолированную. Прямоугольниками на диаграмме огра-
ничены четыре «популяции». Границы прямоугольника
А не имеют никакого отношения к границам других
Популяция
17
трех групп животных. Здесь «популяция» объединяет
животных, обитающих на территории произвольного
размера и формы. Таковы «популяции» мышей какого-
либо поля или оленей штата Нью-Йорк.
Прямоугольник Б проведен с учетом границ группы
животных, но то же самое можно сказать и о прямоуголь-
Рис. 2.1. Наложенные друг на друга прямоугольники означают ис-
следуемые территории на ареале популяции.
пиках В и Г. Каждый из них ограничивает некую «попу-
ляцию»; в данном случае термин «популяция» понимается
в том смысле, как он определен в гл. 1; какую из популя-
ций выбрать в качестве объекта исследования — дело
вкуса.
Важно не то, что границы популяции трудно выявить
в пространстве и во времени, а то, что исследователь дол-
жен иметь четкое представление о соотношении между
границами исследуемой им территории и частичной или
полной изолированностью обитающих па ней групп жи-
вотных. В противном случае оценки размера популяции,
скорости роста и тому подобное могут иметь отношение не
18
Глава 2
только к «популяции», обитающей на исследуемой терри-
тории, но также и к животным, живущим за ее предела-
ми. Так, например, оценка числа животных, обитающих
в прямоугольнике А (рис.2.1), посредством мечения и
повторных отловов, будет завышенной за счет переме-
щения животных в границах прямоугольника Б. Ошиб-
ка будет тем меньше, чем большую территорию — в пре-
делах наших возможностей — мы исследуем. С увели-
чением территории уменьшается отношение периметр
/площадь, а вместе с ним уменьшается и доля животных,
пересекающих границу очерченной территории.
2.2. Системы размножения
Демографические свойства популяции определяются
характером жизенного цикла ее членов. Коул (Cole,
1954) исследовал различия в демографической динамике
популяций с различными жизненными циклами особей и
показал, что при достаточно большой величине популя-
ции и при достаточно длительном времени исследования
эти различия в целом невелики. Таким образом, хотя демо-
графическое поведение, присущее каждому типу жизнен-
ного цикла, строго говоря, описывается специальными
уравнениями, однако общие для разных жизненных цик-
лов демографические уравнения обычно оказываются не
менее точными.
Некоторые типы жизненных циклов являются ‘част-
ными случаями более общих типов. Например, существу-
ют популяции с перекрывающимися и неперекрывагощими-
ся поколениями. Популяции многих насекомых относятся
ко второму типу. Такие насекомые достигают полово-
зрелости в возрасте одного года и погибают сразу же после
размножения. Для описания этих двух случаев исполь-
зуются различные уравнения, однако дискретные поко-
ления представляют собой с математической точки зре-
ния частный случай перекрывающихся, и математичес-
кий метод, адекватно описывающий второй случай, пол-
ностью применим и в первом.
Преимущества описания всех популяций с помощью
одной-двух моделей, а не с помощью десятка или более
моделей совершенно очевидны. Единственным критерием,
Популяция
19
по которому мы будем здесь для удобства статистических
выкладок разделять популяции, '.будет служить харак-
тер размножения, а именно: производят ли животные по-
томство с более или менее постоянной скоростью на про-
тяжении всего года или приносят потомство лишь в опре-
деленное ограниченное время года. Хотя оба эти случая
могут быть описаны одной и той же системой уравнений,
более удобно исследовать их, используя две модели.
Первая — модель’ «непрерывной» (birth-flow) рождае-
мости — описывает популяции, у которых скорость раз-
множения постоянна на протяжении всего года. Вторая —
модель сезонной («импульсной», birth-pulse) рождае-
мости — описывает демографическое поведение попу-
ляции, в которой все потомство из года в год появляется
в какой-то один определенный день. Никакая популяция
в точности не соответствует ни одной из этих моделей, но
большинство определенно тяготеет к тому или иному типу.
Если скорость размножения популяции имеет тенденцию
сохраняться в течение года постоянной, что характерно,
папример, для популяций человека, рыжего кенгуру
Megaleia rufa (Frith and Sharman, 1964) и андской зоно-
трихии Zonotrichia capensis (Miller, 1962), то они могут
быть с достаточной точностью описаны параметрами
непрерывной модели. Те же популяции, у которых стан-
дартное отклонение даты размножения составляет мень-
ше 30 дней, как это имеет место в большинстве популя-
ций животных, могут быть описаны «импульсной» мо-
делью. В немногих промежуточных случаях можно ис-
пользовать оба способа, а параметры определить как
средние по двум моделям.
Поскольку «импульсные» популяции наиболее распро-
странены в природе, им и отводится в книге основное
место, анализ же популяций с непрерывным размноже-
нием приводится там, где это необходимо.
2.3. Выбор параметров
Для того чтобы понять динамику какой-либо попу-
ляции, мы должны знать, какова численность популя-
ции, сколь быстро она растет или уменьшается, знать
число новорожденных, появляющихся на свет в единицу
20
Глава 2
времени, и скорость сокращения популяции за счет
смертности. Такие характеристики называются парамет-
рами; значения этих параметров оцениваются статисти-
чески. Популяцию можно описывать бесчисленным мно-
жеством параметров, однако в большинстве случаев доста-
точно лишь нескольких. Трудность состоит в том, чтобы
решить, какие именно параметры использовать.
Если бы мы имели дело не с популяциями, а с прямо-
угольниками, то мы вернее всего сравнивали бы их по
ширине и длине. Такие параметры хорошо описывают раз-
мер прямоугольника, а их отношение дает представление
о его форме. Мы можем сравнивать эти объекты еще по
каким-либо иным параметрам, например по длине диа-
гонали, но никакой другой параметр ничего не приба-
вит к описанию, задаваемому длиной и шириной.
Как и в случае с прямоугольниками, выбор параметров
для характеристики популяций зависит от: 1) простоты
(легкости) оценки; 2) степени, в которой они в совокуп-
ности описывают существенные свойства популяции;
3) возможности экстраполировать их за рамки данных,
для которых они были вычислены; 4) непосредственности
их отношения к процессам, протекающим в популяции;
5) их общности, т.е. степени, в которой они приложимы
ко всем, а не только к нескольким специфическим типам
популяций.
При выборе параметров мы должны отыскивать ком-
промиссное решение, руководствуясь при этом указан-
ными выше требованиями. В'данной книге в качестве ос-
новных используются следующие параметры:
1) выживаемость в зависимости от возраста;
2) плодовитость в зависимости от возраста;
3) возрастное распределение;
4) отношение численности полов;
5) численность или плотность.
Этот набор статистически связанных между собой
величин может быть использован для оценки следующих
параметров: а) рождаемости, б) скорости вымирания,
в) скорости роста.
Если один или несколько из перечисленных выше пара-
метров невозможно оценить, могут быть использованы
другие параметры. Ихтиологи оценивают параметр, пазы-
Популяция
21
ваемый «пополнение», числом рыб, добавляющихся еже-
годно к стаду, служащему объектом лова. Этот параметр
не соответствует ни одному из перечисленных выше кри-
териев, кроме одного. Он зависит и от плодовитости, и
от смертности мальков и связан не столько с возрастом,
сколько с размером особей; его оценка в зависимости от
методов лова различна. Но этот параметр очень важен в
одном отношении: по чисто практическим причинам он
часто служит единственным критерием, с помощью кото-
рого ихтиолог может оценить плодовитость. Наш выбор
параметров столь же часто определяется самыми неожи-
данными на первый взгляд факторами — дождями, на-
личием гор, лесов и морей, как и требованиями алгебры
и логики.
Глава 3
Возраст
Наиболее существенные параметры, характеризующие
животных, зависят от возраста. Плодовитость, например,
можно определить как число потомков, производимых в
популяции за год, деленное на общее число самок. Но
поскольку эта величина изменяется с изменением в попу-
ляции доли молодых неразмножающихся особей, опа
говорит нам не столько (и если угодно — не только) о
процессе размножения, сколько о возрастной структуре
популяции. Для более точного определения плодовитос-
ти надо учитывать приплод для каждой возрастной груп-
пы в отдельности.
Возраст человека можно выражать в месяцах, годах
или десятилетиях. Выбор единицы измерения не игра-
ет большой роли, поскольку физиология человека прак-
тически не связана жестко с какими-либо временными ин-
тервалами, кроме 24-часового и 28-дневного. Для челове-
ка время течет равномерно. Для большинства других
млекопитающих время, по сути дела, периодично. Все
аспекты жизни животного — питание, гормональный ба-
ланс, поведение, линька, рост, размножение, выживае-
мость — тесно связаны с чередованием времен года.
Лишь очень немногие виды, в основном из числа тропи-
ческих и пустынных форм, не подчиняются смене времен
года. Год, единица времени, произвольная для челове-
ка, является реальной величиной для других позвоноч-
ных.
При изучении влияния возраста на плодовитость и
смертность мы должны объединять в группы одновозраст-
ных животных, рожденных в одно время года (хотя и не
обязательно в один и тот же год), а в качестве единицы
измерения возраста должны выбрать один год. В против-
ном случае различия между, возрастными группами бу-
дут в большей степени связаны со временем года, нежели
с возрастом как таковым. В последующих главах год
Возраст
23
используется не как произвольная единица времени, а
как естественная единица измерения возраста.
Изучение динамики популяций сильно зависит от
возможности определять возраст отдельных особей. Воз-
раст рыб определяется подсчетом годовых колец на че-
шуе, отолитах и плавниковых лучах, а также подсчетом
числа позвонков и просто путем разбиения на возрастные
классы в соответствии с размерами тела. Возраст рептилий
обычно определяется по их размерам, причем кривые роста
строятся либо по- показателям скорости роста, измеряе-
мым в полевых условиях для особей неизвестного возраста,
либо по данным о росте особей, отловленных сразу после
вылупления из яиц. Используется также подсчет остео-
логических зон роста. Возраст птиц старше 1—2 лет
трудно определить с помощью морфологических крите-
риев, поэтому орнитологи делят птиц па ювенильных и
половозрелых или относят их к младшему, среднему и
старшему возрастным классам. Обычно ограничиваются
точным определением возраста только тех особей, которые
были окольцованы до того, как оперились. Для опреде-
ления возраста млекопитающих существует множество
разнообразных методов, так что среди них обычно всегда
можно найти метод, применимый к конкретному изучае-
мому виду. Ключевыми признаками для определения
возраста служат прорезывание новых и снашивание ста-
рых зубов, размеры тела, распределение по характерным
размерам, степень слияния эпифизов, вес хрусталика
число годовых колец на клыках, рогах, а также в зубах
и костях, подсчет числа плацентарных пятен или желтых
тел у самок. Методы определения возраста рыб описаны
в работе Раунсфелла и Эверхарта (Rounsefell and Ever-
hart, 1953), а млекопитающих и птиц — в работе Табера
(Taber, 1969). Некоторые методики, не вошедшие в
эти обзоры, описываются в публикациях Пибоди (Pea-
body, 1961) по остеологическим зонам роста, Лоу и Ко-
вана (Low and Cowan, 1963) и Митчелла (Mitchell, 1967)
о годовых слоях в зубах, Фабенса (Fabens, 1965) по ис-
пользованию кривых роста животных неизвестного воз-
: раста, а также Касси (Cassie, 1954, 1962) и Тейлора
(Taylor, 1965), где обсуждается разбиение частотного
Глава 3
распределения размеров тела животных в популяции на
составляющие возрастные классы.
Таким образом, здесь нет необходимости специально
рассматривать различные методики определения возрас-
та; отметим лишь некоторые, приводящие к ошибочным
результатам.
Показатели возраста можно классифицировать сле-
дующим образом:
А. Индивидуальное мечение (например, кольцевание
или прикрепление каких-либо меток к молодым жи-
вотным с указанием даты).
Б. Морфологические показатели:
а) признаки, которые с возрастом меняются непре-
рывно (например, вес хрусталика или стачивание
зубов);
б) признаки, которые меняются скачкообразно:
1) ежегодно (например, кольца роста на рогах,
чешуе и в зубах);
2) неежегодно (например, смена оперения или
появление новых зубов).
Никакие критерии определения возраста, кроме ос-
нованных на индивидуальном мечении, не застрахованы
от ошибок, хотя одни из методов более, а другие менее
надежны. Методы, основанные на признаках, претерпе-
вающих ежегодные целочисленные изменения, дают наи-
более точные оценки, в особенности для половозрелых
животных, но и они не безупречны. Морфологические
признаки, непрерывно изменяющиеся с возрастом, и
целочисленные признаки, не связанные с временем года,
обладают изменчивостью, которая автоматически приво-
дит к некоторым ошибкам в определении возраста. Хо-
рошим примером является прорезывание зубов, посколь-
ку этот признак часто используется для определения воз-
раста млекопитающих. В табл.3.1 приводятся данные по
изменчивости возраста, в котором прорезываются постоян-
ные резцы, у гималайского тара Hemitragus jemlahicus
(горного козла) и у крупного рогатого скота. Крупный
рогатый скот содержался в домашних условиях, а гор-
ные козлы жили на воле. Коэффициент вариации для
возраста появления новых зубов составляет около 8%
у коров и 12% у тара.
Возраст
25
Таблица 3.1
Средний возраст и изменчивость сроков появления
постоянных резцов у крупного рогатого скота
и гималайского тара (Wiener. Donald, 1955; Caughley, 1965)
Резцы Крупный рогатый "скот Гималайский тар
средний возраст, мес возрастной интер- вал, в котором прорезывается 95% резцов, мес. средний возраст, мес возрастной интер- вал, в котором прорезывается 95% резцов, мес
1-й 25,1 21,3—28,9 17 12—22
2-й 31,8 27,6—36,0 26 23—29
3-й 37,8 31,6—44,0 42 31—53
4-й (С) 45,0 38,0—52,0 64 45-85
Возрастные интервалы, в которых прорезывается
95% новых зубов, перекрываются у тара только для
третьего и четвертого резцов. Тем не менее возраст жи-
вотного с любым набором зубов может быть определен
ошибочно. Допустим, пойман тар, у которого второй
постоянный резец уже прорезался, а третий зуб еще мо-
лочный. Наиболее подходящим возрастом, промежуточ-
ным между средними возрастами прорезывания этих двух
зубов, будет возраст 34 мес. Если измерять время в годах,
то данный экземпляр может быть либо двух-, либо трех-
годовалым. Но на самом деле животному может быть
от 23 мес (нижняя граница возрастного интервала, в
котором прорезывается 95% вторых резцов) до 53 мес
(верхняя граница соответствующего интервала для треть-
его резца), т. е. оно может быть двух-> трех- или четырех-
годовалым.
При измерении признаков, меняющихся непрерывно,
возникают сходные проблемы. М. Дж. У. Дуглас и я
изучали связь снашивания зубов у тара с возрастом.
Было обнаружено, что начиная с 3-летнего возраста ре-
грессия возраста на высоту коронки первого коренного
зуба является линейной функцией. Казалось бы, этот
признак чрезвычайно многообещающий в качестве пока-
зателя возраста. Однако в дальнейшем обнаружилось, что
стандартное отклонение возраста от линии регрессии со-
26
Глава 3
ставляет 1,7 года. Таким образом, возраст лишь 22%
экземпляров был оценен правильно, тогда как возраст
40% особей был оценен с ошибкой в 1 год, еще 22% —
с ошибкой в 2 года, 10% — с ошибкой в Згода и6% —
с ошибкой в 4 года. На этом этапе мы решили отка-
заться от данного метода. В нашем исследовании сте-
пень стачивания зубов мы обычно измеряли, а не оценива-
ли эту величину визуально. Риль, Фей и ван Эттен (Ry-
el, Fay and van Etten, 1961) показали, что визуальные
оценки износа зубов различными исследователями сильно
различаются и, таким образом, к разбросу за счет ес-
тественной изменчивости прибавляется разброс за счет
ошибок оценки.
Большинство экологов сходятся на том, что ошибки
при определении возраста неизбежны. Вопрос лишь в
том, как велики такие ошибки. Робинетт и др. (Robi-
nette et al., 1957) придерживаются оптимистической точ-
ки зрения: «Авторы признают, что при определении воз-
раста отдельных оленей возможны ошибки. Однако если
исходить из того, что эталонные значения возраста были
получены при изучении возрастной структуры оленей,
добытых охотниками, то использование адекватных по
размеру выборок должно компенсировать ошибки». Коли
(Caughley, 1967а), напротив, показал, что ошибки в опре-
делении возраста в действительности не компенсируются.
Роль ошибок в определении возраста можно проиллюс-
трировать на модельной популяции, состоящей из двух
возрастных классов, содержащих 100 и 10 особей соот-
ветственно. Если при определении возраста 10% осо-
бей каждого класса ошибочно помещено в другой класс,
то оценка численности классов составит соответственно
91 и 19. Различия между отношениями 100/10 и 91/19
достаточны, чтобы исказить значение демографических
параметров, оцениваемых по возрастному распределению.
Ошибка не уменьшается при разбиении возрастного рас-
пределения на более узкие возрастные группы.
Правильное определение возраста — дело крайне
важное. Когда у исследователя нет точного критерия
возраста, как это обычно и бывает на практике, он вы-
нужден прибегать к менее надежным методикам. Но
тогда необходимо отдавать себе отчет в том, как часто
Возраст 27
приблизительные оценки приводят к ошибкам,’и исхо-
дя из этого судить о правомерности делаемых выводов.
Определение регрессии возраста на такие морфологи-
ческие признаки, как размер, снашивание зубов, число
плацентарных пятен — рискованное занятие, если при
этом не оценивать стандартное отклонение возраста от
линии регрессии.
Глава 4
Обилие
Обилие можно определять тремя способами: как
число животных в популяции, как число животных, при-
ходящихся на единицу площади, занимаемой популя-
цией (абсолютная плотность), и как плотность одной по-
пуляции по отношению к другой (относительная плот-
ность), Кажется, что оценка численности популяции
обладает несомненными преимуществами перед оценка-
ми ее абсолютной и относительной плотности, однако на
самом деле это часто бывает не так. Число рыб в пруду
еще кое о чем говорит нам, тогда как, например, число
лосей в популяции провинции Саскачеван лишено боль-
шого биологического смысла. Первая оценка имеет ка-
кое-то отношение к реальной популяции, члены которой
составляют некое биологическое единство. Вторая попу-
ляция представляет собой единицу лишь в чисто админис-
тративном смысле. Численность популяции имеет био-
логический смысл только тогда, когда границы популя-
ции очерчены; в тех же случаях, когда границы популя-
ции либо неизвестны, либо вовсе не существуют, либо
существуют, но лишь в нашем воображении, именно плот-
ность популяции, а не абсолютная численность является
с биологической точки зрения более реальной мерой
обилия.
Оценки обилия сами по себе не имеют самостоятель-
ного значения, и их никогда не следует рассматривать
как самоцель. Решение многих биологических проблем
(например, некоторых вопросов генетики, зоогеографии,
поведения и управления численностью популяции) не
требует оценок обилия. При решении же других про-
блем, в частности проблем, связанных с использова-
нием местообитаний, скоростью роста, расселением или
Обилие
29
реакцией популяции на ее эксплуатацию, часто поль-
зуются оценками относительной плотности. Лишь не-
многие проблемы (например, поддержание постоянного
уровня промысла, некоторые топкие вопросы генетики и
исследования, связанные с плотностью популяции, с од-
ной стороны, и с поведением, размножением, выжива-
нием, эмиграцией и иммиграцией — с другой) требуют
для своего решения оценок численности популяции или
ее абсолютной плотности.
К большинству экологических проблем можно под-
ступиться, используя лишь индексы плотности, абсолют-
ные же оценки плотности являются в этих случаях из-
лишней роскошью. Индексом плотности в таком смысле
может быть любая измеримая величина, коррелирующая
с плотностью. В идеале она должна быть линейно свя-
зана с абсолютной плотностью, но иногда достаточно бы-
вает и нелинейных индексов. Примерами таких индек-
сов, связанных с плотностью популяции, могут являться:
улов на единицу промыслового усилия; количество фе-
калий, приходящихся на 1 м2; плотность рыбьей икры;
плотность самцов птиц, обладающих индивидуальным
участком; число павших оленей, обнаруживаемых на
единице площади за единицу времени. Индексы плотности
имеют смысл лишь в сопоставлениях. Когда одна попу-
ляция сравнивается с другой или плотности одной и
той же популяции сравниваются в различные годы, ин-
дексы плотности часто служат достаточной мерой обилия.
Во многих работах исследователи пользуются оценками
абсолютной плотности, хотя столь же полную информа-
цию можно было бы извлечь из индексов плотности.
Проблема, очерченная в терминах абсолютной плотности,
часто может быть заново сформулирована таким образом,
что ее удастся решить с использованием оценок относи-
тельной плотности. Такая возможность сберегает иссле-
дователю время, деньги и нервы, а точность результа-
тов часто оказывается выше, чем в тех случаях, когда мы
исходим из оценок абсолютной плотности.
Биолог должен быть знаком со многими методами
оценки обилия, однако ему совершенно не обязатель-
но держать в голове все подробности. Важнее, чтобы он
умел оценить область применения каждого метода и
Рис. 4.1. Последовательность решений, в процессе принятия кото-
рых выбирается метод проведения учета численности (не считая ме-
тода мечения с повторным отловом).
Обилие
31
R. примерно представлял себе, какой метод применим в
< каждой конкретной ситуации. В настоящей главе, а так-
К- же в гл.10, в которой разбираются методики мечения с
* повторным отловом, автор преследует две цели. Во-пер-
Ж' вых, он пытается дать некоторое представление о раз-
Т личных методах оценки обилия и о ситуациях, в которых
V' приемлем тот или иной метод, и, во-вторых, предоставить
в распоряжение исследователя справочный материал,
(содержащий детали конкретного метода, описание дан-
ных, необходимых для его использования, и предполо-
жения, на которых он основывается. Поскольку методы,
связанные с мечепием обитающих на воле животных,
используются не только при оценке численности попу-
ляции животных, но и при оценках рождаемости, смерт-
ности и скорости роста популяции, целесообразно отло-
у жить обсуждение этих методов до тех пор, пока читатель
не усвоит материал, изложенный в гл.7, 8 и 9.
Рис. 4.1 помогает нам выбрать метод оценки обилия
(за исключением методов, связанных с мечением). На
9:. нем изображена схема последовательных решений, при-
ft: водящих к выбору подходящего метода.
S 4.1. Оценки относительной плотности
'•t (индексы)
_ На рис.4.2 показано несколько возможных^ зависи-
. йостей между абсолютной плотностью и индексом плот-
j ' ности.
- " Прямая Аа соответствует простейшей зависимости —
Линейной регрессии, проходящей через начало коорди-
нат. Можно предполагать, что таким образом связана
плотность китов с числом фонтанов, наблюдающихся за
-Д 1ч хода судна. Прямая Аб также соответствует линей-
жЖвой регрессии, которая, однако, не проходит через на-
‘ - чало координат. Так часто бывает связана плотность
-.“^птиц с числом обладающих собственной территорией сам-
^,/Цов, приходящихся на единицу плотности популяции.
График Б на фиг. 4.2 соответствует отрицательной ре-
грессии плотности на индекс. Примером такой связи мо-
й<ет служить иногда наблюдаемая связь между плот-
32
Глава 4
ностыо травоядных и средней высотой предпочитаемого >’
кормового растения.
График В соответствует нелинейной положительной ре-
грессии. Так связана плотность популяции мышей с
процентом ловушек, в которые за ночь попались мыши.
Рис. 4.2. Различные типы регрессии абсолютной плотности на ин-
декс плотности.
А. Возрастающая пинейпая зависимость. Б. Убывающая линейная зависи-
мость. В. Нелинейная регрессия. Г. Нелинейная неоднозначная регрессия.
График Г соответствует «двойственной» зависимости
между плотностью и индексом, при которой для каждого
значения индекса имеется два возможных значения плот-
ности. В некоторых случаях так связана плотность мле-
копитающих со средним размером тела.
Эти различные типы зависимостей плотности от ин-
декса следует интерпретировать по-разному. Пример Аа,
при котором график зависимости проходит через начало
координат, допускает простейшее толкование. В данном
случае индекс удваивается при удвоении плотности, или,
в общей форме, увеличение или уменьшение индекса в х
раз соответствует увеличению или уменьшению в такое же
число раз плотности популяции. Если же регрессия
плотности на индекс имеет вид А б, Б и В, то сравнение
Обилие
33
индексов для популяции позволяет лишь расположить
популяции в порядке убывания или возрастания их
плотности, за исключением тех редких случаев, когда
известна точка пересечения линии регрессии с осью ор-
динат. В случае Г сравнение индексов не позволяет даже
сказать, плотность какой из сравниваемых популяций
больше. Совершенно ясно, что зависимость плотности от
индекса, изображаемая прямой Аа (линейная и прохо-
дящая через начало координат), наиболее полезна. За-
висимость типа В (криволинейная и проходящая через
: начало координат) также полезна, поскольку часто может
быть преобразована в линейную зависимость плотности
от индекса.
В большинстве случаев тот или иной индекс плотности
выбирается потому, что его зависимость от плотности
примерно линейна, и потому, что существуют веские
теоретические соображения, свидетельствующие о про-
> хождепии линии регрессии через начало координат.
Угол наклона линии регрессии известен редко, и потому
t абсолютная плотность популяции не может быть оценена
непосредственно по индексу, но это и не важно, если ис-
ходная проблема формулируется в терминах относитель-
ной плотности. На вопрос: к какому относительному
уменьшению плотности популяции оленя приведет удвое-
ние интенсивности охоты, — можно ответить, лишь зная
индекс, зависящий от плотности по типу Аа. Для ответов
на менее конкретные вопросы, вроде: «Зависит ли чис-
ленность популяции от доступности корма (воды, убе-
жищ)?»— обычно достаточно индексов типа Лб, В и В.
'4.1.1. Линейная зависимость плотности
от индекса
Когда регрессия плотности на индекс линейна, соот-
ношение между ними может быть записано в таком виде:
v" Плотность = а + b X Индекс,
"/'где а — плотность популяции, соответствующая нулево-
му индексу, а b — увеличение плотности популяции,
, связанное с возрастанием индекса на единицу. Исполь-
--..;3уя индекс, мы должны знать, положительна или отрица-
.^/2—334
34
Глава 4
тельна величина Ь, для чего обычно достаточно сообра-
жений, основанных просто на здравом смысле, и в зави-
симости от решаемой нами проблемы нам иногда нужно
знать, равна ли нулю а. Последнее обычно становится
ясным из ответов на следующие вопросы: измерим ли
индекс, если животные вовсе отсутствуют (если да, то а
отрицательна), а если животных мало, то может ли ин-
декс быть равным 0? Вопрос о равенстве индекса нулю не
тождествен вопросу о возможности его измерения при
низкой плотности популяции.. Второй вопрос относится к
изменчивости выборки, а не к функциональной зависи-
мости между плотностью и индексом. Большинство ин-
дексов непосредственно отражает активность животных;
низкой плотности соответствует низкий индекс, пулевой
плотности соответствует пулевой .индекс и, следовательно,
а = 0.
Учет животных
Наиболее широко используемые индексы плотности
основаны на учетах числа животных, например: 1) числа
пролетных птиц, пересекающих диск луны за час; 2) чис-
ла антилоп, замеченных на миле пути; 3) числа оленей,
встреченных за час пешего маршрута; 4) числа слонов,
отмеченных на водопое за ночь; 5) числа греющихся на
солнце крокодилов на милю берега реки; 6) числа оле-
ней-карибу, замеченных за минуту с самолета, летящего
па высоте 150 м над землей.
Эти примеры объединяются тремя общими свойства-
ми: мы имеем основание полагать, что регрессия абсо-
лютной численности на индекс приблизительно линей-
на, что она проходит через начало координат и что на-
клон ее положителен. Однако эти предположения, хотя
они и обоснованны, могут быть ошибочными. Часто не-
линейной бывает регрессия плотности оленей на число
встреченных за час (Thane Riney, личное сообщение);
иногда нелинейно связан с плотностью каждый из пере-
численных выше индексов. Если требуется строго ли-
нейный индекс, то, прежде чем тот или иной индекс будет
признан подходящим, соотношение между индексом и:
плотностью необходимо тщательно исследовать.
Обилие
35
Данные учета числа животных часто используются в
качестве индексов плотности, однако они обладают не-
которыми недостатками, причем наиболее неприятные
из них связаны с тем, что точность методов учета зави-
сит от строгой страндартизации условий, при которых
производятся учеты. Недопустимо, например, сравнивать
относительные плотности двух популяций газелей по
данным маршрутных учетов, если один из них был про-
веден в первой половипе дня, а другой — в сумерки.
. Также недопустимо использовать данные учетой для срав-
нения плотности двух популяций ящериц, если одна из
них обитает на территории, покрытой высокой травой,
| а другая — низкой. Результаты учета числа животных
| также сильно зависят от способностей того, кто произ-
| водит учет. Квалифицированный исследователь не толь-
ко замечает больше животных в поле зрения, но и меньше
j искажает дапные учетов фактом своего присутствия. От
' неопытного наблюдателя значительно большее число жи-
| вотных ускользает незамеченным. Сам факт наблюдения
! оказывает влияние на число учитываемых животных —
принцип неопределенности Гейзенберга не является ис-
ключительной принадлежностью физики.
Ж. Учет следов животных
>7 Часто учеты следов животных дают более точный ин-
Д. деке плотности, чем учеты числа самих животных. Все
животные оставляют такие улйки, как следы, помет,
сброшенные рога, помятую или выеденную раститель-
Д; мость, останки жертв (если речь идет о хищниках), сво-
бодно плавающие икринки, брошенные гнезда и т. п.
.Д' Данные, основанные на таких следах пребывания живот-
пых, имеют некоторые преимущества перед данными пря-
мого учета числа животных: их точность менее зависит
от квалификации наблюдателя; измерения, выполненные
различными наблюдателями, легче стандартизировать;
они менее подвержены влиянию условий наблюдения, и
сам факт наблюдения не влияет на количество учитывае-
мых следов. К недостаткам такого метода учета по срав-
пению с методами, основанными на учетах числа живот-
ных, следует отнести менее’прямую зависимость между
2*
36
Глава 4
количеством следов и реальной плотностью популяции и
разрыв во времени между моментом, когда животное ос-
тавляет след своего пребывания, и моментом, когда этот
след учитывается. Учет следов дает скорее индекс сред-
ней плотности популяции за некоторый промежуток вре-
мени, а не индекс плотности в данный момент.
Плотность следов животных оценивается по данным
ограниченных выборок точно так же, как плотность са-
мих животных — по данным прямых учетов. Соответ-
ствующие методы расчетов обсуждаются в разд. 4.2.3.
Улов на единицу промыслового усилия
Добыча на единицу промыслового усилия служит
хорошим индексом плотности в том случае, когда вылов
не слишком сильно снижает численность популяции.
В тех же случаях, когда добыча велика по сравнению с
численностью популяции, более подходящим индексом
будет абсолютная добыча за единицу времени.
Добыча на единицу промыслового усилия может ис-
пользоваться в качестве индекса плотности только для
эксплуатируемых популяций. Получение этого ин-
декса связано с большой затратой труда, оказывает боль-
шое влияние на исследуемую популяцию, а сам индекс,
вообще говоря, менее точен, чем большинство других.
Но если мы исследуем популяцию, так или иначе являю-
щуюся объектом охоты или промысла, или если иссле-
дователь должен добыть экземпляры животных для це-
лей, не зависящих от задачи учета численности, то этот
индекс может быть вычислен с небольшой дополнитель-
ной затратой сил. Этот индекс особенно полезен для неза-
висимой проверки других оценок относительной числен-
ности. При использовании улова на единицу промысло-
вого усилия в качестве индекса предполагается, что:
1) условия лова стандартизированы; бессмысленно срав-
нивать уловы рыбы, приходящиеся на одно судпо в двух
различных районах, если в одном случае лов проводил-
ся в шторм, а в другом — в хорошую погоду;
2) стандартизована эффективность добычи; нельзя
сравнивать популяции оленя по числу добытых оленей,
приходящихся на охотника за день в двух различных
Обилие
37
областях по данным отстрелов, если в первом случае от-
стрел проводился профессионалами, а во втором — лю-
бителями;
3) стандартизованы орудия лова; совершенно оче-
видно, что сравнивать количество рыбы, пойманной за
день сетью и на удочку, бессмысленно, однако следует
принимать во внимание и гораздо более тонкие особен-
ности орудий лова. Количество отлавливаемых мелких
млекопитающих в расчете на сотню ловушко-суток за-
висит не только от плотности животных, но и от типа ло-
вушек и вида приманки. Число отстреленных крупных
млекопитающих в расчете на 1 человеко-день, по-видимому,
слабо зависит от того, какого калибра ружье использова-
лось и нарезное ли оно или гладкоствольное, но может
очень сильно зависеть от того, были ли ружья снабжены
телескопическими прицелами;
4) поимка одного животного не должна сказываться
на вероятности поимки другого. Ихтиологи говорят о «на-
сыщении орудий лова», о переполнении сети или трала,
но это лишь один из аспектов проблемы. Животное, по-
павшее в ловушку, может отпугивать других (Kennedy,
1951) или, наоборот, привлекать их (Ricker, 1958). Отно-
шение числа крупных млекопитающих, добытых одним
охотником за сезон, к числу тех, которых, он видел, за-
висит от среднего числа животных в группе. Когда груп-
па состоит из двух или трех животных, охотпик обычно
убивает всех животных в группе, но по мере того как раз-
мер группы возрастает, доля животных, убиваемых в
группе, падает. Это, правда, скорее временной эффект,
а не эффект, связанный с насыщением орудий промысла,
поскольку охотник может убивать животных, лишь пока
они находятся в пределах досягаемости. «Одноместные»
капканы представляют собой частный случай орудий лова,
характеризующихся эффектом насыщения. Среднее чис-
ло животных, пойманных за ночь в расчете на одну ло-
вушку, никогда не может быть больше единицы, и регрес-
сия плотности на эту величину поэтому нелинейна. Одна-
ко при индексе ниже 0,2 регрессия почти линейна и «кон-
куренция» за ловушку не оказывает сильного влияния на
число отлавливаемых животных. При индексе, большем
0,2, число животных, в среднем попадающих за ночь в
38
Глава 4
одну ловушку, все менее точно отражает относительную
плотность, и индекс необходимо спрямить по методу,
описанному ниже в разделе «Измерение частот»;
5) животные не должны научаться избегать ловушек
или проявлять к ним повышенный интерес. И то и другое —
две оборотные стороны непреднамеренного обучения. Ме-
Годы
Рис. 4.3. Использование числа успешных охот в качестве индекса
плотности популяции олепя (по Dasmann and Dasmann, 1963).
I. Число проданных лицензий. II. Число убитых оленей. III. Доля успеш-
ных охот.
тоды отлова, связанные с такого рода эффектами, не дол-
жны применяться в тех случаях, когда скорость отлова
используется в качестве индекса плотности. Однако если
другие методы отлова неприменимы, то время, на которое
расставляются ловушки, должно быть настолько малым,
чтобы животное не успело научиться избегать ловушку
или заинтересоваться ею. В тех случаях, когда индексом
плотности служит добыча на единицу промыслового уси-
лия, должны применяться методы отлова, к которым жи-
вотные в принципе не могут приспособиться.
Обилие
39
В случаях когда соблюдаются все 5 перечисленных
выше условий, регрессия абсолютной плотности на добы-
чу, приходящуюся на единицу промыслового усилия,
имеет вид линейной зависимости, проходящей через на-
чало координат (Ricker, 1940).
Примеры квалифицированного использования этого
индекса можно найти в работах Лесли и Дэвиса (Leslie,
Davis, 1939) по мелким млекопитающим, Гуланда (Gul-
land, 1955) по рыбам, Рини (Riney, 1956) и Батчелера
и Логана (Batchelor, Logan, 1963) по альпийским копыт-
ным, а также Чайлда, Смита и Ричтера (Child, Smith,
Richter, 1970) по африканской дичи. Дасман и Дасман
(Dasmann and Dasmann, 1963), используя показатель та-
кого типа, отметили, что плотность оленей в Калифорнии
между 1936 и 1943 гг. претерпела резкий подъем. Эти
авторы графически изобразили отношение числа добы-
тых оленей к числу ежегодно продаваемых охотничьих
лицензий в 1927 по 1960 г. На рис. 4.3 представлены два
набора исходных данных: число проданных лицензий и
зафиксированное число добытых оленей, и рассчитанный
по ним индекс плотности (частота успешных охот).
Для правильной оценки плотности эту частоту следова-
ло бы преобразовать в соответствии с методом, описанным
ниже в разделе «Измерение частот», но поскольку она,
как правило, не превышает величину 0,2, то ипепреобра-
зованное значение частоты, вероятно, представляет со-
бой достаточно точный индекс обилия.
4.1.2. Нелинейная зависимость плотности
от индекса
Когда регрессия абсолютной плотности на индекс кри-
волинейна, удвоение индекса уже не соответствует удвое-
нию плотности. Индексы могут быть использованы лишь
для того, чтобы оценить, плотность какой из популяций
больше, а какой — меньше. Этого основного недостатка
можно избежать, либо вычисляя криволинейную регрес-
сию, с тем чтобы получить уравнение, дающее зависи-
мость плотности от индекса, либо спрямляя зависимость.
Первый способ требует много дополнительной информа-
ции. Второй способ обычно гораздо проще и не требует
никаких новых данных.
40
Глава 4
Измерение частот
Пусть плотность популяции определяется подсчетом
на случайно распределенных пробных площадках слу-
чайно распределенных животных. Среднее число живот-
ных, приходящихся на одну пробную площадку, делен-
ное на площадь площадки, представляет собой несмещен-
ную оценку абсолютной плотности. Предположим теперь,
что животные очень осторожны и что появление наблюдате-
ля на площадке вспугивает многих животных. В этом случае
наблюдатель легко может судить о том, были ли вообще
животные на площадке, но ему будет трудно определить их
число. Данные учета будут, следовательно, представлены
в виде констатации присутствия или отсутствия животных
на площадке и могут быть сведены к доле участков, на
которых было обнаружено одно или более животных.
Таким образом, измеряемая величина представляет со-
бой «частоту», а не «плотность», причем связана частота
с абсолютной плотностью нелинейно.
Если животные распределены случайно, то среднюю
частоту / без труда можно преобразовать в среднюю плот-
ность х. Доли участков, содержащих 0,1,2 ... животных,
задаются распределением Пуассона, в котором первый
член равене~х. Доля участков, не содержащих ни одного
животного, составляет
!-/ = «"*,
а доля участков, содержащих одно или более животных,
составляет
/=1-е .
Следовательно, х может быть непосредственно определен
по / как 1—/ с помощью таблиц значения экспоненциаль-
ной функции (Приложение 1) или же прямо по графику
на рис.4.4, если обеспечиваемая им точность достаточна.
Описанная выше ситуация, вероятно, нечасто встре-
чается в полевых условиях, но она может служить ил-
люстрацией перехода от частот к плотности, который
можно использовать применительно к широкому кругу-
Обилие
41
экологических данных. Так, например, в качестве ин-
декса плотности мелких млекопитающих часто исполь-
зуется число зверьков, попадающих в «одноместные»
капканы. Каждый раз, когда животное попадает в кап-
кан, он срабатывает, и, таким образом, число заряжен-
ных капканов в течение ночи постепенно уменьшается.
Рис. 4.4. Зависимость между частотой и плотностью (см. текст).
Лесли и Дэвис (Leslie, Davis, 1939) обратили внимание
на то, что эта ситуация описывается простой зависи-
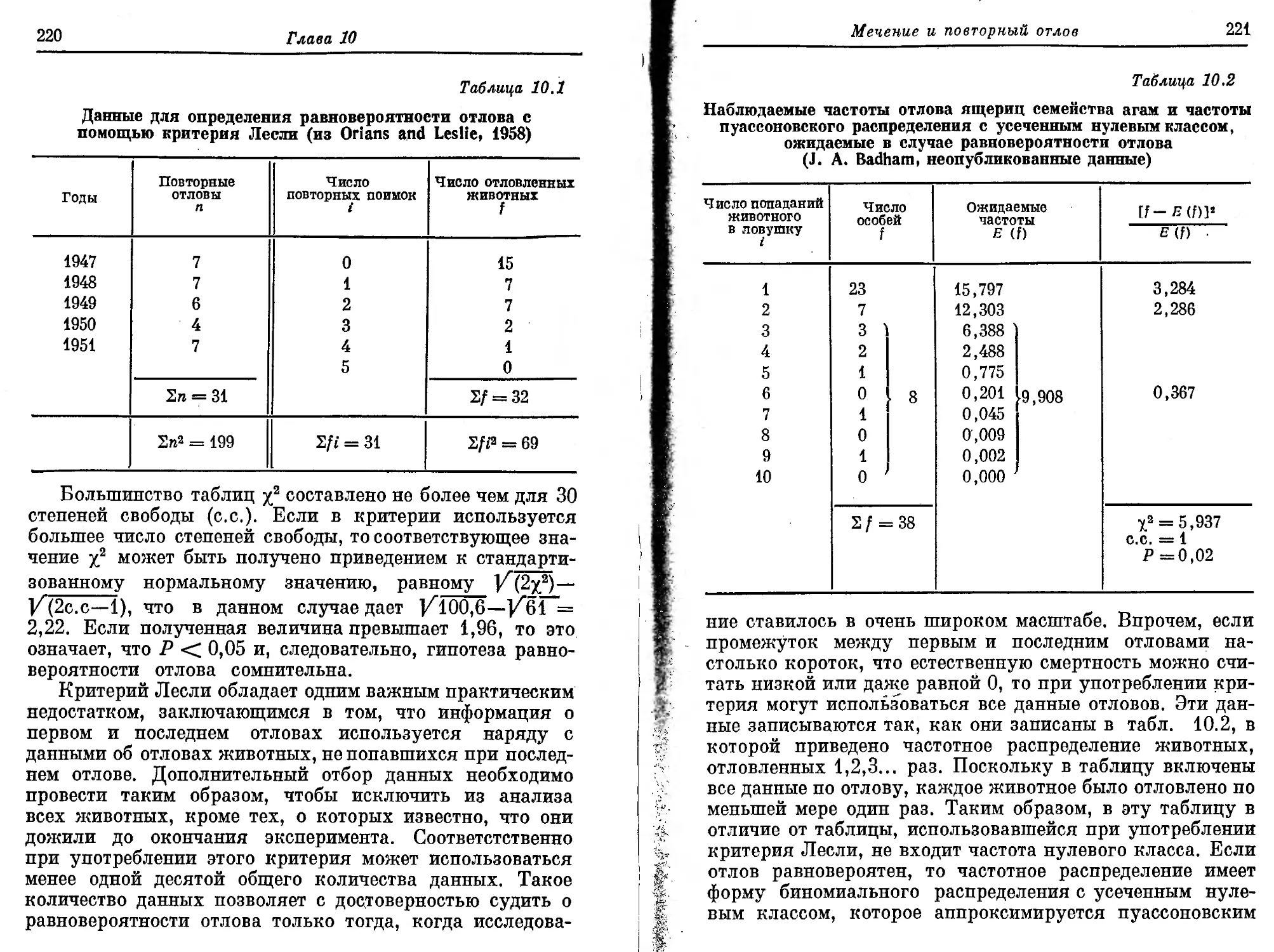
мостью между частотой и плотностью. Доля капканов, в
которые за ночь попались животные, представляет со-
бой частоту по отношению к тому числу животных, ко-
торые были бы пойманы в расчете на один капкан, если
бы капканы были способны срабатывать многократно.
Последняя величина представляет собой «плотность пои-
мок» (захватов)*и легко может быть вычислена из «часто-
ты поимок».
Предположим, что относительные плотности крыс в
районах Л и В измерялись при помощи ста одноместных
капканов, настороженных на одну ночь в каждом из
районов, и что в одном месте попалось сорок, а в другом —
42
Глава 4
восемьдесят крыс.Тогда частоты поимок могут быть пре-
образованы в плотности поимок:
а в
Доля сработавших капканов (/) 0,4 0,8
Доля несработавших капканов (1—/) 0,6 0,2
Плотность поимок х, рассчитанная по формуле (1—/)== 0,5 1,6
= е~х
Сравнение преобразованных индексов показывает, что
плотность крыс в районе В больше плотности в районе
А не вдвое, как можно было бы заключить, исходя из
сравнения непреобразованных частот поимок, а более
чем в три раза.
Наличие или отсутствие животных на пробной пло-
щадке и частота попадания животных в капканы — это
лишь наиболее яркие примеры перехода от частоты к
плотности. Некоторые другие индексы обилия имеют
менее явное отношение к категории «частот», но и они
также могут быть преобразованы указанным способом
для того, чтобы спрямить их зависимость от плотности.
Доля съеденных за ночь приманок, доля разорванных ни-
ток, натянутых поперек звериных троп, доля объеденных
растепий, доля сломанных или примятых животными по-
бегов, доля обитаемых нор, число успешных охот, во вре-
мя которых нельзя убивать больше одного зверя, — все
это примеры частот, которые должны быть преобразованы
в линейные индексы плотности.
Преобразование частот в плотности хорошо проил-
люстрировано в двух исследованиях сумчатого Trichosu-
rus vulpecula. Батчелер, Дарвин и Прейси (Batcheler,
Darwin, Pracy, 1967) использовали это преобразование
для получения оценок плотности по данным частоты по-
падания животных в ловушки, а Бемфорд (Bamford,
1970) прообразовал частоту съеденных за ночь при-
манок в индекс, линейно связанный с абсолютной плот-
ностью.
Частоты ниже 0,2 связаны с плотностью почти линей-
но, и нет необходимости прибегать к их преобразованию.
Так, если животные встречаются на пробных площадках
с частотой 0,05, то этому соответствует плотность 0,051
Обилие
43
животного на 1 площадку. Для частоты 0,2 соответствую-
щие плотности составляют 0,22 животного на 1 площадку.
При частотах, больших 0,2, значения частоты и плотности
расходятся, причем чем больше частота, тем больше рас-
хождение; в этом случае пепреобразованная частота уже
не может служить хорошим индексом плотности.
Метод преобразования частоты в плотность основан на
предположении о том, что вероятности оказаться на проб-
ной площадке в момент учета одинаковы для всех особей
или, если отлов производится капканами, что вероятность
попасться в капкан одинакова для всех особей. Эти пред-
положения часто не соблюдаются на практике, первое —
из-за того, что животные склонны скучиваться, второе —
из-за того, что разные животные по-разному избегают
капканов. Оба указанных обстоятельства ведут к зани-
женной оценке плотности, причем ошибка тем больше,
чем выше плотность. Соответственно сравнение индек-
сов плотности популяций, обитающих в двух различных
районах, как правило, приводит к заниженной оценке
различия в плотностях. В тех случаях, когда оценка
смещена, смещение обычно носит именно такой харак-
тер. Заниженные оценки плотности реже, чем завышен-
ные, ведут к ошибкам в решениях, касающихся интен-
сивности эксплуатации популяции.
Геррард и Чанг (Gerrard, Chiang, 1970) разработа-
ли видоизмененный метод преобразования частоты в
плотность, который позволяет работать с неслучайными
распределениями. Вместо того чтобы принимать за час-
тоту число участков, на которых встречено одно или не-
сколько животных, они подсчитали число участков, на
которых встречалось j или более животных, где j может
быть любым целым числом. Они показали, что для лю-
бого отклонения от нормального распределения сущест-
вует оптимальное /, которое можно определить из пред-
варительного исследования. Использование этого мето-
да для оценки преобразования требует большой предва-
рительной работы, но, после того как эта работа уже про-
делана, плотность рассчитывается быстро и точно, фак-
тически часто даже более точно, чем при полном учете
числа животных на пробных площадках.
44
Глава 4
Расстояние до ближайшего соседа
Набор расстояний от случайно выбранной точки (или
случайно выбранной особи) до ближайшей соседней мо-
жет служить нелинейным индексом плотности. Если осо-
би распределены случайно, то по этому набору расстоя-
ний 'можно оценить абсолютную плотность. Если w —
квадрат расстояния до ближайшего соседа, a w — сред-
ний квадрат расстояний по выборке из п расстояний, то
среднее число животных па единицу площади определя-
ется по формуле
nwn '
Если средний квадрат измеряемых в метрах расстояний
по выборке из 50 соседей составляет 220, то плотность
равна
N =----------------= 0,0014 животного на 1 м2, или
3,1416 X 220 X 50
.1400 животных на 1 км2.
Это уравнение дает несмещенную оценку плотности
лишь тогда, когда животные распределены случайно,
и поэтому, приведенная нами формула представляет, ка-
залось бы, лишь академический интерес. Однако па са-
мом деле ее можно использовать и на практике. Она
преобразовывает набор расстояний до ближайших со-
седей в линейный индекс плотности. Если порядок эф-
фекта, связанного с неслучайностью распределения осо-
бей, не зависит от плотности популяции, то регрессия
абсолютной плотности на преобразованный индекс не
сильно отклоняется от прямой линии.
Набор расстояний до ближайших соседей как тако-
вой еще не позволяет судить, случайно ли распределены
животные (Pielou, 1969:114). Некоторым типам конта-
гиозных распределений соответствует распределение рас-
стояний до ближайших соседей, неотличимое от такового
при случайном распределении особей. Батчелер и Белл
(Batcheler, Bell, 1970) разработали видоизмененное
Обилие
45
преобразование, которое позволяет оценивать абсолют-
ную плотность даже тогда, когда распределение сущест-
венно контагиозно. Поскольку они рассматривают случай-
ное и регулярное распределения как частные случаи
контагиозных, при использовании этого преобразования
не требуется предварительной оценки характера распре-
деления.
Классы плотности
Часто бывает, что нам нужен лишь грубый индекс.
Лицо, ответственное за установление правил охоты на
куропаток в масштабах штата, не может не интересо-
ваться вопросом, достаточно ли разработать правила охо-
ты, общие для всего штата, или продолжительность
охотничьего сезона в разных частях штата должна быть
различной. Для этого в числе прочего необходимо знать,
постоянна ли примерно плотность популяции куропа-
ток в различных частях штата. С этой точки зрения су-
ществование незначительных различий в плотности экви-
валентно отсутствию различий. Достаточно знать, что в
каждом определенном округе куропатки отсутствуют, ред-
ки, обычны или многочисленны.
Такие категории называются классами плотности, и
оценки обилия по этой шкале часто позволяют дать впол-
не удовлетворительные ответы на удивительно широкий
круг вопросов. Недостатки указанной шкалы совершенно
очевидны:
1. Популяцию, которую один наблюдатель оценива-
ет как «обычную», другой может оценить как
«многочисленную».
2. Абсолютная плотность обычно нелинейно связана
со шкалой классов плотности.
3. Поскольку разбиение на классы субъективно, его
точность зависит от квалификации наблюдателя.
Основная проблема, связанная с определением клас-
са плотности, в действительности проблемой не является.
_ Дело в том, что многие склонны рассматривать классы
плотности как оценку, более точную, чем она является
на самом деле, и использовать эти классы для решения
46
Глава 4
проблем, которые требуют более совершенной оценки
плотности. Если же мы отдаем себе отчет в неизбежной
неточности, сязанной с оценкой плотности по классам,
и пользуемся классами плотности только в исследова-
ниях, требующих лишь грубой оценки плотности, то они
могут быть весьма полезны.
Точность разбиения по классам плотности возрастает
в том случае, когда критериям «редкий», «обычный» и
«многочисленный» дается определение. Если критерий
«обычный» определяется как «от 20 до 50 животных, за-
меченных в течение дня», то эта оценка воспроизводима
в других условиях. Конечно, в разных районах и в раз-
ное время мерки «обычного» различны. Когда путешест-
венник XIX в. писал, что кенгуру «обычны», он имел в виду,
что каждый день встречал одного или двух. В наше вре-
мя, когда фермер говорит, что кенгуру «обычны», это зна-
чит, что, проведя день в седле, он встретил от 50 до 100
штук.
По. некоторым причинам человек склонен оценивать
плотность не в арифметическом, а скорее в логарифми-
ческом масштабе. Если наблюдатель за обычную плот-
ность принимает примерно, утроенную редкую плотность,
то многочисленной он будет считать популяцию, в сред-
нем втрое более плотную, чем обычная, и соответствен-
но в 9 раз более плотную, чем редкая. Если классам
плотности присвоить номера 1, 2, 3 и т.д., то регрессия
абсолютной плотности на этот индекс будет спрямляться,
если мы'. возьмем антилогарифмы этих величин.
В качестве индекса плотности часто пользуются кри-
терием «присутствия или отсутствия». Может показаться,
что это объективно дихотомический критерий, во в дей-
ствительности он приводит нас к тем же трудностям, что
и более развитые классификации. Оценки по этому крите-
рию всегда занижены, поскольку если «присутствие»—
понятие обычно недвусмысленное, то «отсутствие» озна-
чает, что животные, может быть, есть, а может быть, их
нет. Важно помнить, что «отсутствие»означает не то, что
животных нет, а то, что они не были замечены. Оценку
«отсутствуют», основанную на наблюдении с автомобиля,
нельзя приравнивать к такой же оценке, выведенной в ’
результате пешего похода по этой же территории. Точ-
Обилие
47
ность критерия «присутствия—отсутствия» также тесно
связана с продолжительностью наблюдений.
Иногда все это*не имеет существенного значения. При
решении некоторых проблем низкая плотность приводит
к тем же последствиям, что и отсутствие животных. Био-
лог, наносящий на карту распределение вида-вредителя
с целью контролировать его численность в тех местах,
где он приносит вред, интересуется местами с низкой
плотностью не более, чем местами, где вид полностью
отсутствует. Низкая плотность и отсутствие животных —
для него одно и то же. Если же он ставит целью сохранение
вида, находящегося на грани вымирания, то «редкий» и
«отсутствует»—ситуации, резко различающиеся, и эти два
класса должны быть четко отделены один от другого. В пер -
вом случае уже поверхностное обследование может дать
информацию, достаточную для принятия решений, ка-
сающихся управления численностью популяции, во вто-
ром случае требуется более тщательное исследование.
Число животных в группе
Средняя величина групп у стадных животных имеет
тенденцию возрастать с увеличением плотности популя-
ции. Причина этого не вполне понятна, по само утвержде-
ние может быть, правда с некоторой осторожностью,
принято в качестве эмпирического обобщения.
Если группы обладают рыхлой социальной структу-
рой, склонны раскалываться, снова сливаться и обмени-
ваться отдельными особями, то регрессия размера груп-
пы на плотность будет определяться корреляцией между
абсолютной плотностью и частотой, с которой встреча-
ются группы. Коли (Caughley, 1964) предположил, что
такой механизм обусловливает регрессию плотности на
размер группы у кенгуру. Однако неслучайный состав
групп у копытных и других общественных животных ука-
зывает па то, что у этих видов размер группы определя-
ется иным механизмом и что такое объяснение слишком
упрощенно даже для кенгуру. Так или иначе, безотноси-
тельно к лежащему в основе явления механизму, размер
группы обычно может служить эффективным индексом
плотности. Кристи и Эндрьюс (Christie, Andrews, 1964)
48
Глава 4
показали, что этот индекс можно использовать для опре-
деления классов плотности у тара, а кроме того, он рав-
ным образом бывает полезен при исследовании многих
других видов общественных животных.
Средний размер группы обычно может быть опреде-
лен с большой точностью и с высокой воспроизводимос-
тью. Уже по одной этой причине его всегда следует рас-
сматривать как ценный индекс плотности. Обладает он
и некоторыми недостатками: связь индекса с плотностью
меняется в зависимости от времени Тода и различна для
разных местообитаний. Индекс полезен лишь при срав-
нении плотностей популяций в одно и то же время года
и в районах со сходной топографией и растительностью.
Регрессия плотности на размер группы редко бывает
линейной, и линия регрессии обычно пересекает верти-
кальную ось ниже начала координат. Таким образом,
индекс позволяет расположить популяции в порядке
возрастания плотности, но не позволяет количественно
сравнивать плотности популяций между собой.
4.2. Оценки абсолютной плотности
4.2.1. Абсолютные учеты
Иногда, когда исследуемая территория невелика, а
животные хорошо заметны, можно произвести полный
учет общего числа животных, обитающих на исследован-
ной территории. Попытки произвести переписи такого ро-
да предпринимались для альпийских копытных (Douglas,
1967), млекопитающих долины Серенгети (Talbot, Stewart,
1964), для пернатой дичи на озерах (во многих исследо-
ваниях) и т. п. Полный учет можно произвести, только
если животные относительно малоподвижны или когда
время, за которое наблюдатель способен учесть всех
животных на участке, настолько мало, что существенны-
ми перемещениями животных можно пренебречь. В про-
тивном случае некоторые животные будут учитываться
дважды, тогда как другие — ускользать от учета.
Обилие
49
4.2.2. Прикидочные оценки
Когда исследователь хорошо знаком с определенной
областью и ее фауной, он может реалистически оценить
примерное число населяющих эту область животных.
В тех случаях, когда не требуется особой точности, та-
кие прикидки могут служить в качестве оценок плот-
ности. Явные и многочисленные недостатки таких прики-
док не должны заслонять от нас их достоинств. Иногда
основанные на хорошем знании предмета прикидки быва-
ют ближе к истине, чем объективные оценки, полученные
мечением с повторным отловом, методами, вызывающими
изменение демографической структуры популяции, или
с помощью каких-либо иных косвенных методов. При-
кидки плотности или численности, дают ли они цифры
более или менее точные по сравнению с объективными
методами или нет, могут служить полезным орудием неза-
висимой проверки результатов объективных оценок. Если
косвенные методы дают результаты, сильно завышенные
или заниженные по сравнению с основанными на хорошем
знании материала прикидками, то вполне уместен здо-
ровый скептицизм в отношении точности таких объектив-
ных оценок, и предпосылки, на которых основываются
эти оценки, должны быть более тщательно проанализи-
рованы.
В то же время следует полностью отдавать себе от-
чет в том, чем по сути дела являются прикидки. Прикид-
ки — это не то же самое, что «визуальные оценки» или
предварительные учеты, и точность прикидок не увели-
чится от того, что мы будем называть их этими затейливы-
ми терминами. Прикидки — это и есть прикидки. Мы
не должны поддаваться соблазну и думать, что хорошее
знание конкретной территории и населяющих ее видов
гарантирует хорошее соответствие наших прикидок дей-
ствительным численностям. Прикидки даже высококва-
лифицированных наблюдателей обычно бывают занижен-
ными.
О масштабе ошибок, которыми могут страдать даже
основанные на хорошем знании объекта прикидки, гово-
рится в работе Андерсена (Andersen, 1953). По данным
охотоведов, ответственных за состояние некоего леса пло-
50
Глава 4
щадью 3,4 км2 в Дании, численность косуль в этом лесу
оценивалась примерно в 70 голов. Поскольку охотоведы
проводили в этом лесу много времени, имелись веские
основания считать эту оценку достаточно точной. Одна-
ко, когда всю эту популяцию полностью истребили для
того, чтобы заселить лес оленями другого вида, число
убитых животных превысило 213. Прикидки охотоведов
оказались заниженными втрое.
Точность прикидок должна оцениваться на основе
некоторой дополнительной информации; в частности,
как много времени провел наблюдатель на исследуемой
территории, основана ли его оценка на учете следов, кри-
ков животных, каких-либо других примет их существо-
вания или же на комбинации этих критериев; следует
также учитывать опытность исследователя. Простым спо-
собом оценки точности прикидок может служить сравне-
ние различных прикидок, сделанных независимо не-
сколькими наблюдателями. Численность популяции оле-
ня на плато Кайбаб в 1924 г. оценивалась в 100 тыс.,
70 тыс., 50тыс. и ЗОтыс. голов (Rasmussen, 1941; Coughley,
1970а). Разброс в оценках указывает на то,, что пи одна
из них не заслуживает большого доверия.
4.2.3. Выборочные учеты
Хотя интуитивно абсолютный учет кажется наиболее
точным методом оценки плотности, в действительности
выборочные учеты обладают по сравнению с ним рядом
преимуществ:
1) выборочные учеты требуют меньшей затраты сил;
2) они значительно снижают вероятность многократ-
ного учета одних особей и вероятность того, что
другие не будут учтены совсем;
3) такие учеты в отличие от абсолютных не обязатель-
но полностью проводить в течение короткого про-
межутка времени;
4) они оказывают мепыпее возмущающее воздей-
ствие на саму популяцию.
В большинстве статистических моделей выборочных
учетов предполагается, что случайно распределенные
по территории животные подсчитываются на случайно
Обилие
51
распределенных пробных площадках. В действитель-
ности же щивотные распределены не случайно, а, как
правило, склонны в той или иной степени скучиваться.
Точно так же разместить пробные площадки случайным
образом удается лишь при исключительно благоприятных
обстоятельствах. Такая организация выборки чаще пред-
ставляет собой идеализированную схему, нежели ре-
ально достижимую цель. В соответствии с основным прак-
тическим принципом органпзации выборочных учетов
распределение пробных площадок вне зависимости от
того, является ли оно вполне случайным, ни при каких
обстоятельствах не должно быть смещенным.
В процессе выборочных учетов плотность оценивается
посредством разбиения исследуемой территории на проб-
ные площадки и подсчета животных на некоторых за-
ранее отобранных площадках. Средняя плотность на ото-
бранных площадках принимается за оценку средней плот-
ности на использованных и неиспользованных для учета
площадках, вместе взятых. Достоверность оценки вычис-
ляют по разбросу в оценках плотности по отдельным
площадкам. На точность оценок оказывают влияние два
основных фактора. Во-первых, если мы разбиваем тер-
риторию, на которой обитают, допустим, 100 животных,
на 10 участков, а учет проводим только на двух из них,
может оказаться, что случайно ни на одном из них не бу-
дет ни одного животного. Такой сильно заниженной (ну-
левой) оценки плотности можно избежать, если взять
для учета четыре площадки. Во-вторых, допустим, что
100 наших животных — это косяк рыбы в озере. Оче-
видно, что в каждый момент времени косяк будет нахо-
диться лишь на одной из пробных площадок. Если
пробных площадок всего две, то оценка плотности по
ним будет равна либо 0, либо 50, и соответственно общее
число рыбы в озере по этим оценкам будет равно либо 0,
либо 500. Эти примеры иллюстрируют два основных прин-
ципа организации выборочных учетов: чем больше число
пробных площадок, тем выше точность оценки и чем более
скучены животные, тем большее число пробных площа-
док требуется для достижения разумной точности оценки
плотности.
52
Глава 4
Стратификация
До сих пор мы предполагали, что животные распре-
делены по исследуемой области равномерно, даже если
при внимательном рассмотрении характера распределения
оказывалось, что они держатся группами. В действитель-
ности же гораздо чаще на исследуемой территории пред-
ставлено несколько типов растительных ассоциаций, в
одних из которых плотность животных высока, тогда
как другие служат прибежищем лишь отдельных осо-
бей. В таких условиях наиболее точные оценки средней
плотности получаются, если всю область разбить на зо-
ны, внутри которых плотность одинакова, и вычислять
общую плотность, исходя из значений плотности, изме-
ренных отдельно для каждой зоны. Этот процесс назы-
вается стратификацией, а зоны — стратами.
Стратификация обладает следующими преимущест-
вами:
1. Поскольку плотности оцениваются отдельно по
каждой страте, их можно сравнивать. Так как каждая
страта обычно соответствует отличному от других место-
обитанию, такая информация биологически важна.
2. Суммарные усилия, затрачиваемые на определение
средней плотности, распределяются наиболее эффек-
тивно, когда участки изучаются тем детальнее, чем бо-
лее плотно они заселены: вряд ли имеет смысл тщатель-
но исследовать страту, населенную считанным числом
особей. Даже если мы вдвое завысим плотность живот-
ных в такой зоне, эта ошибка слабо скажется на оценке
средней плотности по территории в целом.
3. Точность оценки плотности тем меньше, чем боль-
ше изменчивость плотности по территории в целом.
Стратификация подразделяет неоднородно населенную
территорию на некоторое число страт, в каждой из ко-
торых плотность относительно постоянна. В резуль-
тате точность оценки возрастает, поскольку теперь она
становится функцией изменчивости выборок в стратах,
а не изменчивости по территории в целом. Сайниф и
Скуг (Siniff, Skoog, 1934) показали, что точность оценки
плотности карибу, полученная ими методом стратифи-
кации, была вдвое выше точности оценки плотности,
Обилие
53
полученной при простом, случайном распределении вы-
борок.
Стратификация предполагает, что нам известен ха-
рактер распределения животных по террритории. В иде-
альном случае вся территория делится на страты еще до
того, как начнется ее детальное изучение, и густота, с
которой распределяются единичные пробные площадки,
зависит от плотности животных в стратах Формально
математически наиболее точную оценку общей плотности
(т.е. наименьшую стандартную ошибку) можно полу-
чить тогда, когда густота выборок пропорциональна
рассчитанному по страте стандартному отклонению числа
животных, приходящихся на единичную пробную площадку
(Tschuprov, 1923; Neyman, 1934). Часто имеет смысл
поэтому для получения грубых оценок этих стандартных
отклонений провести предварительные исследования.
Разумеется, если последовательно проводится несколько
обследований, то при распределении размещения выборок
в последующем обследовании следует руководствоваться
результатами, полученными в предыдущем. Если же пред-
варительное обследование невозможно и территория ра-
нее не исследовалась, относительную плотность в каж-
дой страте следует оценить по десятибалльной шкале.
Выборки тогда размещаются с густотой, пропорциональ-
ной полученному индексу, поскольку для большинства
видов стандартное отклонение числа животных на проб-
ной площадке обычно линейно связано со средней плот-
ностью на этой площадке.
Точность в проведении границ между стратами не
существенна. Значительные ошибки при проведении гра-
ниц будут увеличивать стандартную ошибку, но но будут
смещать оценку плотности. При явно неоднородном за-
селении территории даже грубая стратификация лучше,
чем ее отсутствие.
В последующем разделе описываются методы анали-
за, применяемые при стратификации. Хотя рассмотренные
вопросы касаются только обследований с самолета, мето-
ды анализа носят общий характер и полностью применимы
к любым способам разбиения территории на страты при
оценке плотности посредством прямых подсчетов жи-
вотных.
54
Глава 4
Обследования с воздуха
Важным методом в лесном и охотничьем хозяйстве
является перепись животных с воздуха. Проблемы, свя-
занные с применением этой методики, подробно описаны
в ряде статей (Petrides, 1953; Fuller, 1953; Banfield
et al., 1955; Gilbert and Grieb, 1957; Stewart, Geis and
Evans, 1958; Erickson and Siniff, 1963; Bergerud, 1963;
Siniff and Skoog, 1964; Goddard, 1967; Watson et al.r
1969; Caughley, 1974 и LeRescho and Rausch, 1974).
В 34-м томе Восточноафриканского журнала сельского
и лесного хозяйства за 1969 г. опубликованы труды пре-
восходного симпозиума по проблемам и методам про-
ведения учетов животных с воздуха. В приведенной в
этом сборнике работе Джолли (Jolly, 1969) описаны по-
становка эксперимента и методы анализа данных таких
учетов; в этой главе мы будем придерживаться его под-
хода.
На рис.4.5 представлены четыре способа разбиения
изучаемой территории на участки которые могут быть
отнесены к двум стратам по плотности учитываемых жи-
вотных. На первой (4) представлено стратифицирован-
ное случайное разбиение с пробными площадками оди-
накового размера. На схеме Б территория разделена на
участки неравной площади, и вероятность того, что будет
выбран тот или иной участок, пропорциональна его
размеру. На схеме В площадки представляют собой поло-
сы заданной ширины, расположенные в строго опреде-
ленном направлении, но на произвольном расстоянии
одна от другой. Схема Г отличается от схемы В лишь
тем, что полосы расположены на одинаковом расстоянии
друг от друга. Мы рассмотрим методы анализа, наиболее
удобные для каждого из четырех случаев, и возникаю-
щие при этом проблемы.
Площадки равных размеров. На карту территории
накладывают прямоугольную сетку с пронумерованными
строками и столбцами. Из таблицы случайных чисел
выбирают пару, причем первое число соответствует номе-
ру строки, а второе — столбца. Квадрат на карте, зада-
ваемый этими двумя числами, отмечается в качестве объ-
екта учета. Этот процесс повторяется до тех пор, пока
Обилие
55
число отмеченных участков не достигнет заранее выбран-
ного числа для каждой страты. Так, например, на
рис. 4.5, А для обследования отобрано 50% территории
с высокой плотностью населения и 25% редко населенной
•страты. Отобранные площадки шрихуются, и число
обнаруженных на каждой из них животных записывается.
Используемые обозначения взяты главным образом
из статьи Кочрена (Cochran, 1963), в которой намечены
Рис. 4.5. Четыре способа организации сбора данных на территории,
подразделенной на страты с высокой (левый верхний квадрат па
каждой карте) и низкой плотностью популяции.
А. Случайно распределенные пробные площадки одинаковых размеров.
Б. Случайно распределенные площадки разных размеров; вероятность вы-
бора площадки пропорциональна ее площади. В. Одинаково ориентиро-
ванные случайно распределенные трансекты. Г. Упорядоченно располо-
женные трансекты. Во всех Случаях интенсивность сбора данных на стра-
не с высокой плотностью вдвое выше, чем на страте с низкой плотностью,
56
Глава 4
основы теории и методов стратификации. Индекс h озна-
чает номер страты, a i — номер пробной площадки в дан-
ной страте. Все перечисленные ниже обозначения от-
носятся к страте h.
Nh — общее число пробных площадок;
nh — номер пробной площадки;
yhi — число животных на г-й площадке;
yh — среднее число животных на площадке;
«2(/й — дисперсия числа животных по обследованным
площадкам;
Yн — Nhyh ~ оценка'общего числа животных в страте.
Приведем вычисления, пользуясь данными Сайнифа
и Скуга (Siniff, Skoog, 1964) по учету оленей. Авторы
выделили 6 страт и на каждой из них выбрали для про-
ведения учетов некоторое количество участков площадью
4 квадратных мили каждый. Их данные приведены в
табл. 4.1.
Таблица 4.1
Расчет численности популяции карибу с использованием
стратифицированных случайных выборок
(данные из работы Siniff, Skoog, 1964)
(1) Страты (2) Nn (3) "ft (4) Nh^h~nh'> (5) s2 yh (в) «h (7) YK=Nh yh.
nh
А 400 98 1233 5575 24,1 9640
В 30 10 60 4064 25,6 768
С 61 37 40 347 556 267,6 16 324
D 18 6 36 22 798 179,0 3222
Е 70 39 56 123 578 293,7 20 559
F 120 21 566 9795 33,2 3984
Сумма 699 211 7=54497
Сумма значений столбцов 4 и 5 равна 34 305 121.
SEy=K 34 305 121 =5857.
Полное число животных в каждой страте оценива-
ется как
Обилие
57
Yh — Nhyh = 9640 в страте A,
768 в страте В,
3984 в страте F.
Тогда число животных на всей территории будет равно
их сумме по всем стратам:
У = S Уй = 54497,
что почти не отличается от оценки Сайнифа и Скуга
(Siniff, Scoog, 1964), которые использовали другой метод
расчета.
Стандартная ошибка У вычисляется из данных, при-
веденных в столбцах (4) и (5):
SEr=l/2^^*4..
V h. nh
где s2yh определяется для каждой страты как
= 1 w2 _ \ ,
у1г лг гад /
Отсюда SEr = }^34 305 121 = 5857, и 95%-ный дове-
рительный интервал равен +2SEy = +11 714.
Пробные площадки неравных размеров. Предыдущий
метод используется только в тех случаях, когда все проб-
ные площадки имеют одинаковый размер. Чаще, однако,
приходится проводить учеты на трансектах постоянной
ширины (обычно по 100 метров по каждую сторону от
самолета), но не равной длины. Максимально точная
оценка получается при этом, когда трансекты располо-
жены на случайном расстоянии друг от друга, как это
изображено на рис, 4.5, В, однако не следует пренебре-
гать и более удобным в практическом отношении распо-
ложением трансект в правильном порядке (Г).
Обозначив площади пробных площадок через zh
а общую площадь обследуемой территории — через Z,
58
Глава 4
запишем выражение для оценки суммарной численности
животных по всем стратам:
у
S Nhzhi
h
Чтобы рассчитать стандартную ошибку определения сум-
марной численности, определим прежде всего среднюю
плотность:
R = Y/Z
и
что дает
Г------------------------------------
SEr= ]/ Z nh} (^й -2Rsh2y + ДV.) ,
где s%ft — дисперсия численности животных, прихо-
дящихся на одну пробную площадку в Л-й страте, а «2гй —
дисперсия площади пробных площадок в той же страте.
Такой способ вычисления стандартной ошибки представ-
ляет собой усовершенствование метода, использованного
в примере с пробными площадками равных размеров.
Его можно применять аналогичным образом, табулируя
данные, подобно тому, как это сделано в табл.4.1, лишь
добавив столбцы л2гй и shzy.
Пробные площадки равных или неравных размеров,
выбираемые с вероятностью, пропорциональной площади
территории.^ горных районах проводить учет по прямым
трансектам, а также использовать пробные площадки
равной площади невозможно. Территорию следует под-
разделять на участки, которые можно легко осмотреть с
самолета.
Пробные площадки с прямолинейными границами на-
носятся на карту. Они могут быть любой формы, но
использование трех-и четырехугольников упрощает рас-
Обилие
59
чет площадей. Пробные площадки по-прежнему выбира-
ются из каждой страты с помощью пары случайных чи-
сел, но числа эти в данном случае обозначают не номер
участка, а координаты определенной точки на карте.
Выбор площадок продолжают до тех пор, пока число их
для каждой страты не достигнет заданной величины.
Площадки, на которые попала одна или более точек,
предназначаются для проведения учетов. В дальней-
шем при вычислениях данные по каждой площадке
используются столько раз, сколько случайных точек па
них попало, хотя учет на каждой площадке проводится
лишь однократно. На рис.4.5, Б приводится пример такого
выбора пробных площадок. Числа в кружочках обозна-
чают число точек, попавших на соответствующую площад-
ку. При применении такого способа вероятность выбора
'определенной площадки пропорциональна ее размеру, а
это свойство дает некоторые преимущества при примене-
нии статистики и ведет к упрощению вычислений.
По исходным Данным прежде всего рассчитываются плот-
ности для каждой пробной площадки Dt = y-Jz^ Затем
число животных в каждой страте оценивается по формуле
~ ZhDlV
где zh — общая площадь страты, a Dh — средняя плот-
ность по пробным площадкам, принадлежащим к этой
страте. Общее число животных на всей территории оце-
нивается суммированием животных по всем стратам:
У = 2УЛ.
Стандартная ошибка рассчитывается по формуле
SEK
2
SDh ’
где
2 1
S°h ~ nh-i
VDhjp
Систематические и случайные выборки. Методы, опи-
санные в предыдущем разделе, основаны на предположе-
нии, что пробные площадки расположены случайно.
60
Глава 4
Хотя получаемая таким образом оценка численности
наиболее точна, при этом возникают такие трудности
практического характера, которые часто приводят к
снижению точности, сводящему на нет скромный вы-
игрыш, который дает использование идеальной схемы на-
блюдений.
Трудности эти состоят в следующем.
1. Случайное размещение пробных площадок очень
неудобно для летчика. В местах, где ориентиры редки,
трудно прослеживать границы пробных площадок, и
возможны многочисленные ошибки. Лучше всего рабо-
тать, когда биолог хорошо знает местность, но и тогда
ему приходится делить свое время между подсчетом жи-
вотных и инструктированием летчика. Если же он ведет
самолет сам, то ему не удается полностью сосредоточить-
ся на подсчете животных и соответственно точность учета
падает.
2. Самолет сильно шумит, а дикие животные пугливы
и убегают от пролетающего над ними самолета. Соответ-
ственно пробные площадки следует размещать таким
образом, чтобы избежать перемещения животных с одних
площадок на другие, пока учет не закончен. Если же пло-
щадки расположены случайно, то некоторые из них могут
оказаться в непосредственной близости друг от друга, что
приведет к повторным учетам животных, перебежавших
на соседние площадки.
3. Случайное размещение пробных площадок приво-
дит к наименее полному обследованию территории из
расчета на час летного времени.
Хотя упорядоченное размещение пробных площадок
встречает возражения с теоретической точки зрения, за-
то оно лишено перечисленных выше недостаткрв. Регу-
лярно расположенные маршруты сильно облегчают по-
леты. Если исходные точки маршрутов точно фиксируют-
ся (а маршруты лучше всего начинать, от извилистой
дороги или реки, задающих таким образом основной
навигационный ориентир), то летчик может выдерживать
направление по компасу, используя заметные ориен-
тиры на местности для корректировки сноса. Маршруты
обычно располагаются на расстоянии 2—3 км друг от дру-
га. Потревоженные самолетом животные при этом редко
Обилие
61
добегают до следующей учетной линии до возвращения
самолета. Упорядоченное размещение площадок сводит
к минимуму «пустое время» между последовательными
учетами. Правда, это не всегда является преимуществом,
поскольку наблюдатели должны делать паузу для отды-
ха примерно каждые 15 мин, однако это обстоятельство
важно в тех случаях, когда необходимо наилучшим обра-
зом оценить плотность животных, уложившись в ограни-
ченное время или определенную сумму денег.
Во многих книгах, посвященных организации выборок,
подчеркивается, что оценка доверительных интервалов
при выборочных учетах правомочна, лишь когда выборка
случайна, и это так и есть в действительности, если огра-
ничиться определением правомочности, принятым в статис-
тике. Статистическое утверждение правомочно, только
когда данные, на которых оно основано, удовлетворяют
аксиомам соответствующей статистической модели. В ос-
нове большинства статистических методов лежат такие
аксиомы, как нормальное рапределение переменных, не-
зависимость наблюдений и случайность выборки, но в
большинстве случаев, в которых используются эти мето-
ды, соответствующие аксиомы не выполняются; иногда
данные не удовлетворяют аксиомам лишь незначительно,
а иногда очень сильно. Математическая правомочность
или неправомочность статистического метода — это еще
не самое важное. Нам нужны не столько математически
корректные, сколько' грубые методы, способные давать
близкие к истине результаты, даже когда исходные .дан-
ные не вполне удовлетворяют аксиомам статистики.
Рассматривая тот или иной статистический метод, мы
прежде всего интересуемся не корректностью его приме-
нения, а тем, достаточно ли он груб для того, чтобы можно
было пренебречь содержащимися, как мы знаем, в наших
данных отклонениями от лежащих в основе статистики
аксиом. Иногда мы вынуждены признать, что наши дан-
ные слишком плохо удовлетворяют условиям, лежащим
в основе модели, и мы не вправе пользоваться соответ-
ствующим методом. Иногда удается преобразовать данные
таким образом, что использование соответствующего ме-
тода становится возможным. В других случаях применяют
-статистический метод к исходным несовершенным данным,
62
Глава 4
но при этом, чтобы застраховать себя от ошибок, Снижают
приемлемый уровень значимости с 5 до 1 %. Математи-
ческая статистика — точная наука, но наиболее неточная
область использования статистических методов — это об-
работка биологических данных.
Доверительный интервал, рассчитанный по неслу-
чайным выборкам, может быть не вполне корректным, но
он, как правило, не сильно отличается от доверитэльно-
го интервала, рассчитанного по случайным выборкам.
До тех пор пока регулярное расположение трансект не
повторяет рельефов местности, аксиомы статистической
модели не сильно нарушаются. Разумеется, если топо-
графия изучаемой территории имеет регулярную струк-
ТУРУ> а маршруты полетов лежат вдоль хребтов или до-
лин, оценка числа животных может оказаться очень не-
точной. Это же относится и к случаю, когда проводится
учет уток на озерах, но исследуются лишь озера, на кото-
рых заведомо обитают только крупные популяции. Та-
кие методы обследования непригодны с точки зрения
здравого смысла, и именно здравым смыслом следует
руководствоваться, решая, использовать или не исполь-
зовать ту или иную конкретную схему выборок.
Методы наблюдений с самолета. По указанным выше
причинам популяции обычно учитываются с воздуха при
полетах по маршрутам, расположенным через регуляр-
ные промежутки. Животные подсчитываются в 100-
метровой полосе по обе стороны от центральной линии
полета, причем высота полета должна составлять при-
мерно 75 м. Границы этой полосы для наблюдателя от-
мечаются двумя линиями, нанесенными на видимую из
окна распорку крыла. Когда самолет находится на за-
данной высоте, в промежутке между этими двумя от-
метками наблюдателю видна 100-метровая полоса земли.
Хотя необходимые отметки можно нанести, пользуясь
геометрическими построениями, все же более надежно
определять место их нанесения опытным путем.Одна
постоянная отметка наносится на распорку около фюзе-
ляжа (внутренняя отметка), а выше нее — через равные
интервалы вверх по распорке — наносятся временные от-
метки. Самолет на заданной высоте пролетает над отме-
ченной на земле полосой 100-метровой ширины, наблю-
Обилие
63
датель помогает пилоту направить самолет таким обра-
зом, чтобы внутренняя постоянная метка на распорке сов-
падала с внутренней границей полосы на земле. Затем
наблюдатель находит точку на распорке, зрительно сов-
мещающуюся с внешней границей 100-метровой полосы, и
. Рис. 4.6. Подсчет животных с воздуха (X) и фиксация границ тран-
секты с помощью меток на распорке крыла самолета (.Б).
отмечает ее положение по временным меткам. Нанесен-
ные таким образом внутренняя и внешняя отметки явля-
ются зрительными границами полосы наблюдения
(рис.4.6).
Когда учет проводится в горных районах, получение
систематических выборок невозможно. В этом случае
• наиболее приемлемой схемой учета являются случайные
выборки, организованные так, чтобы вероятность выбора
той или иной пробной площадки была пропорциональна
ее площади.
Наблюдения проходят наиболее спокойно, если один че-
ловек ведет самолет, а другой проводит подсчет живот-
ных. Хотя многие пилоты с готовностью предлагают свою
помощь при подсчетах, такой практики следует избе-
гать. В горных районах ведение самолета требует неослаб-
64
Глава 4
ного внимания, и любая оплошность может привести к
катастрофе.
Поскольку наблюдатель должен не отрываясь следить
за полосой наблюдения на протяжении всего полета, мно-
гие записывают результаты своих подсчетов на магнито-
фон. После того как мне несколько раз довелось уже после
учета обнаружить, что магнитофон был неисправен, я
предпочитаю полевой дневник. Для этого трансекта де-
лится на отрезки, соответствующие двум минутам полета
и отделенные друг от друга обязательной паузой в семь
секунд. Пространство, над которым самолет пролетает
за эти эти семь секунд, исключается из области наблюде-
ния, а тем временем вы успеваете записать число живот-
ных, замеченных на предыдущем участке маршрута.,
Такая система имеет дополнительные преимущества.
Она позволяет периодически переводить взгляд с удалэн-
ных на близлежащие предметы, размять мышцы шеи, а
также сверить с напарником порядковый номер участка,
на котором ведется учет. Кроме того, этот способ — про-
тивоядие против своего рода гипноза, которому подвер-
жены наблюдатели с самолета; его симптомы легко
распознать по утрате способности сосредоточиваться, сон-
ливости и спорадической потере памяти, когда наблюда-
тель забывает, записал ли он данные последних наблю-
дений.
Если животные держатся скученно, очень удобно поль-
зоваться фотокамерой. Точно подсчитать животных в
большой группе за то короткое время, что они находятся
в поле зрения, практически невозможно. Опытным на-
блюдателям часто удается довольно верно оценить число
животных, очень быстро считая пятерками или десятками,
но точный подсчет позволяет произвести только фотогра-
фия. Камера должна быть закреплена в направлении
взгляда наблюдателя, и ограничивающие поле зрения
отметки на распорке должны попадать в кадр, чтобы из-
бежать учета животных за границами 100-метровой по-
лосы. В статье Уотсона (Watson, 1969) обсуждается со-
четание объективов, пленки, освещения и высоты съем-
ки, дающее наилучшие результаты.
Поправка на неполный учет. Лишь очень немногие на-
блюдатели, в том числе и я сам, осознают, что, летя на
Обилие
65
высоте 75 м при хорошем освещении, они: все же могут
пропустить находящихся в учетной полосе животных.
Действительно, каждый раз, когда проводится: соот?-
ветствующая проверка, оказывается, что часть животных
не учитывается, но как это происходит — почти невоз-
можно ощутить. Однажды я проверял точность учетов с
воздуха, сидя позади штатного наблюдателя и проводя
'учет по ту же сторону от самолета. Мы считали млекопи-
тающих в африканской саванне и в конце каждой линии
сравнивали результаты. В общем наши данные оказались
близкими, хотя у меня они были несколько занижены,
чего, впрочем, и следовало ожидать, так как я хуже знал
африканских животных. При последнем полете и он, и
я вслух указывали на каждое замеченное нами животное.
Разница была ощутимой. Он замечал животных, кото-
рых пропускал я, и наоборот. То он, то я иногда пропус-
кали даже, казалось бы, бросающихся в глаза жирафов.
Это поучительное упражнение рекомендуется проде-
лать каждому наблюдателю, полагающему, что он заме-
чает 95% животных на трансекте.
В табл.4.2 приводятся некоторые оценки эффективности
учетов с воздуха, показывающие, что численность живот-
пых неизбежно оказывается заниженной. Ошибка обыч-
но достаточно велика для того, чтобы усомниться в Приме-
нимости подсчетов с самолета в качестве метода пол-
ного учета. Эти подсчеты остаются хотя и полезным, но не
безупречным показателем многочисленности животных,
а также могут служить оценками минимальной числен-
ности. Для того чтобы их можно было использовать в
качестве оценок абсолютной плотности, должна быть вне-
сена, соответствующая поправка. Коли и Годард (Caughley,
Goddard, 1972), используя методы моделирования с
помощью ЭВМ и данные полного учета численности
черных африканских носорогов, показали, что правиль-
ная оценка полной численности может быть получена по
средним значениям и дисперсиям многократных пол-
ных учетов, распадающихся на две серии с сильна раз-
личающимися условиями наблюдений. Этот метод можно
Продемонстрировать, используя данные по учета^ чис-
ленности чернохвостого оленя (табл.4.3) (Gilbert, brieb,
1957), Численность оленя определялась с роздуха р шта-
3—334 '
ф
03
mJ
И
и
3
«
я
S
X
S
®
о
н
§
о
СП
л
Ьи
л
СП
§
тз
л
'тз
-о
о
0
ф ч
’Я 'О
'ъл
ьс й
Й °
то
га
s
о
И
3
в
ь
о
и
я
%
«
о
h
ф
л
н
«
Я
м
я
£
ф
Контроль* Хороший Слабый » Хороший 1 » J ьтрогии Слабый » Удовлетвори- тельный
Условия наблюдений Равнина и редкий кустар- ник Джунгли и заросли пеннп- сетума Равнина с редкими деревь- ями Равнина (с самолета) Равнина (с вертолета) Снег и редкий лес Луг с редкими деревьями Редколесье
Процент учтенных животных CH CD СО LO Ю Ю Г— СО 03 Ю 00 О Г- Г- Г- CD V V V
о
о
к
о
я
S
я
* Точность учета с воздуха определяется по тому, сколь мало общее число учтенных животных отличается от оцененного
при помощи другого, как мы надеемся, более точного метода. Точность этого контрольного значения также может быть раз-
личной, и оценки, проставленные в этом столбце, выражают моо собственную субъективную оценку достоверности контроля,
основанную на описании этих методов цитированными авторами. Оценка «слабый контроль» указывает на то. что контроль-
ная оценка, вероятно, занижена, и поэтому соответственно значение процента животных, учтенных с воздуха, завышено.
Обилие
67
Таблица 4.3
Учеты с воздуха и наземные учеты численности
чернохвостого оленя (Gilbert, Grieb, 1957)
Ж
Время и условия наблюдений Последовательные учеты с воздуха Наземные учеты
1-я серия учетов (отдель- 246
ные пятна снега) 229 220 238 255 7= 237,6 695
2-я серия учетов (сплошной снежный покров) а2 = 189,3 339 312 345 353 342 7 = 338,2 s2 = 241,7 690
те Колорадо-на площади примерно 20 км2. Во время пер-
вой серии из пяти учетов условия наблюдения были не
очень хорошими из-за скудности снежного покрова. Во
время второй серии учетов, проводившихся через месяц,
вся территория была покрыта снегом и условия наблю-
дения были превосходными. Полученные результаты об-
разуют, следовательно, два набора данных, относящих-
ся к учетам, проведенным при
условиях. Эта модель приводит
х = s2 — 4- х2
к
сильно различающихся
к уравнению
1
N ’
где N — истинная численность популяции, х — средняя
численность животных по данным каждой серии, s2 —
дисперсия этих учетов, к — постоянная, характеризую-
3*
68
Глава 4
щая степень изменчивости условий наблюдений при раз-
личных учетах в обеих сериях1.
Таким образом, мы -имеем два неизвестных, опреде-
лить которые можно, если есть по две оценки для сред-
него значения и дисперсии. Например,
237,6 = 189,3 -j- 4- (237,6)2-^ ,
338,2 = 241,7 -±- + (338,2)2-^- .
Умножая первое уравнение на 241,7, второе — на 189,3,
получаем
57428 = 45754 — + 13 644 874 — ,
к [ N
64021 = 45754 — + 21 651 990— ,
к ' N
откуда, вычитая первое уравнение из второго, имеем
6593 = 8007116 —,
N
и наконец,
N = 1214 оленей на территории.
Исходя из этого результата, мы можем заключить, что
во время учетов с воздуха регистрировалось не более
24% оленей; наземные учеты позволяют единовременно
учесть тоже всего лишь 58%. В этом примере состояние
снежного покрова удачным образом создало условия, при
которых различались эффективности учета в двух сериях
наблюдений. Чаще же мы должны создавать такие раз-
личия сами, либо летая один раз на высоте 100, а второй
раз — 200 м, либо увеличивая число наблюдателей во
второй серии учетов.
1 Предполагается, что эта константа одинакова в обеих сериях
наблюдений, что, вообще говоря, неочевидно. — Прим. ред.
Обилие
6Й
Поскольку этот метод основан на суммарных подсче-
тах, он бесполезен при оценке истинной плотности на
территории, на которой могут быть проведены лишь вы-
борочные учеты. В этих случаях используется другой ме-
тод (Caughley, 1974), при котором истинная плотность
оценивается как точка пересечения линии регрессии на-
блюдаемой плотности на скорость полета (5), высоту
полета (Н) и ширину трансекты (71) с осью ординат. Так,
например, при учете рыжих кенгуру па открытой мест-
ности уравнение, предсказывающее процент учтенных
животных, имеет вид (Caughley et al., 1976)
Процент учтенных животных = 100 — 0,17185 —
- 0,0123// - 0,007Я2 — 0,0982т1.
Из этого уравнения можно рассчитать поправочный
множитель для любого сочетания переменных, характе-
ризующих постановку учета. При ширине трансекты
100 м наблюдатель, летящий на высоте 75 м со скоростью
160 км/ч, регистрирует лишь 58% попадающихся ему кен-
гуру. Таким образом, прежде чем анализировать данные
учета по каждой пробной площадке, их необходимо умно-
жить на поправочный множитель, равный 1/0,58 = 1,72.
Наземные учеты
Данные учетов с воздуха можно заменить наземными
учетами. Схема организации учета и методы анализа в
этих двух случаях аналогичны, с той лишь незначитель-
ной разницей, что ширина трансекты при наземных уче-
тах, как правило, уже, поскольку меньше становится
зона видимости. Каждой схеме учета с воздуха соответ-
ствует аналогичная схема организации наземного учета.
Так, например, подсчет животных с воздуха при полете по
прямым в точности соответствует подсчету с автомобиля,
снабженного специальной рамкой-видоискателем, при-
Ь чем методы обработки данных остаются теми же самыми.
5 Более существенное отличие наземных учетов от учетов с
Р воздуха заключается в том, что первые сильнее распуги-
вают животных. Учеты с воздуха также вспугивают жи-
70
Глава 4
вотных, но на самолет животные реагируют уже после
того, как он пролетел, а не до его появления.
Совсем иначе обстоит дело при наземных учетах. Если
обозреватель передвигается зигзагами между учетными
площадками, подсчитывая пугливых и подвижных жи-
вотных, то к тому времени, как он объедет половину тер-
ритории, на второй половине останутся лишь единичные
животные. Таким образом, наземные обследования дол-
жны быть организованы с учетом особенностей поведе-
ния животных. Если животные очень подвижны, площад-
ки должны иметь форму узких и длинных полос. Иногда
проведение корректного наземного учета в принципе не-
возможно. Если животные обитают в условиях, когда
средняя видимость составляет 10 м, а убегают они при
появлении наблюдателя в радиусе 20 м, то никакая орга-
низация учета не позволит получить оценку плотности.
В таких случаях следует использовать косвенные методы.
Эберхарт (Eberhardt, 1968) предлагает следующую
классификацию условий, влияющих на проведение на-
земных учетов:
внимательности
наблюдателя
Обнаружение за-
висит в первую
очередь от
ярко выраженной
реакции живот-
ного на прибли-
жение наблюда-
теля
хорошо заметные жи-
вотные
. условия ограниченной
видимости или живот-
ные с покровительст-
венной окраской
животное подпускает
наблюдателя на опре-
деленное расстояние
вероятность вспугива-
ния животного зависит
от расстояния до на-
блюдателя
В зависимости от того, какая из перечисленных ситуаций
реализуется, следует использовать различные схемы орга-
низации учета. Больше всего проблем, связанных с на-
земными учетами, сопряжено с выбором между двумя
альтернативами: проводить ли учет на трансекте фикси-
рованной ширины, определяемой исходя из поведения жи-
вотного и его заметности, или учитывать всех животных,
обнаруживаемых на маршруте.
Обилие
71
Трансекты фиксированной ширины. Первая стратегия
приводит к более простым методам анализа и особенно
удобна при высоких плотностях животных. Расстояние от
линии маршрута до границ трансекты, лежащих парал-
лельно по обе стороны маршрута, должно быть таким, что-
бы обнаруживались все животные, находящиеся в этой
полосе. Это может быть 1 м, если учитываются лягушки,
10 м, если учитываются крупные млекопитающие в густом
лесу, или 500 м, если животные того же размера под-
считываются в степи, прерии или саванне. Каждый раз
очень важно бывает определить, внутри или за грани-
цами полосы находится животное. Если ширина трансек-
ты больше 100 м, необходимо использовать специальный
видоискатель. Если учитываемых животных не смуща-
ет присутствие человека, не следует отмечать животное
до того, как была достигнута ближайшая по отношению к
нему точка маршрута. С этой точки легче всего оценить
расстояние от линии маршрута и решить, находится ли
животное внутри полосы учета. Что же касается скрытных
животных или тех, которые обнаруживают свое присут-
ствие, только когда срываются с места, вопрос о том, на-
ходятся они внутри или вне полосы учета, следует каждый
раз решать немедленно. За исключением очевидных ситуа-
; ций, для этого следует вычислять расстояние от животного
до наблюдателя и определять по компасу угол, под кото-
рым оно находилось в момент обнаружения, к линии мар-
шрута.
Схема организации учетов и методы анализа для уче-
тов на трансектах фиксированной ширины те же самые,
что были описаны выше в разделе «Учеты с воздуха» для
площадок неравного размера. Вся территория стратифи-
цируется на карте, во-первых, по плотности животных и,
во-вторых, по условиям их видимости. Ширина трансект
для различных страт зависит от условий видимости,
а необходимое число трансект определяется размерами
страт, шириной трансект и плотностью животных. Плот-
ности животных можно грубо оценить при беглом предва-
рительном исследовании.
Трансекты неопределенной ширины. Эберхарт (ЕЬег-
vhardt, 1988) отмечает, что, поскольку точность оценки
плотности животных пропорциональна квадратному кор-
72 Глава 4
ню из числа животных, обнаруженных при учете, нужно,
насколько это возможно, принимать во внимание всех
животных, замеченных во время учета. Такого рода данные
должны обрабатываться иначе, чем данные, получен-
ные при учетах на трансектах фиксированной ширины.
Рис. 4.7. Вероятность обнаружения животных на различном рас-
стоянии от линии маршрута.
В этом случае требуется следующая дополнительная ин-
формация:
1) кратчайшее расстояние от каждого животного до
линии маршрута (в случае учета на трансектах
фиксированной ширины требуется лишь знать,
внутри или за пределами зоны учета находится жи-
вотное);
2) форма кривой, связывающей вероятность обнару-
жения животного с его расстоянием от линии мар-
шрута ;
3) крутизна этой кривой.
Поскольку каждая из этих величин определяется с
некоторой ошибкой, решение вопроса о том, использовать
ли метод трансект фиксированной или неопределенной
I
I
>
I
1
4
।
'i
Обилие
73
ширины, упирается в выбор между простотой метода и
меньшими экспериментальными ошибками в первом слу-
чае и повышением точности за счет увеличения числа
учитываемых животных во втором. В общем случае второй
способ более приемлем при низкой плотности живот-
ных.
Схема организации учета и методы обработки данных
можно проиллюстрировать на следующем воображаемом
примере. Допустим, нам нужно оценить плотность степ-
ных птиц. Для этого мы определяем кратчайшие рас-
стояния до всех птиц, обнаруживаемых по обе стороны
от 10-километровой линии маршрута, а затем представ-
ляем эти данные в виде гистограммы (рис.4.7), на которой
высота столбцов обозначает число птиц, обнаруженных на
расстоянии 0—10, 10—20 ит.д. метров от линии маршрута,
деленную на их число в интервале 0—10 м. Если считать,
что в ближайшей к линии маршрута зоне учитываются все
птицы (вероятность обнаружения равна 1), то тогда наши
гистограммы представляют собой распределение вероят-
ности обнаружить птицу в зависимости от расстояния
между ней и линией маршрута, и вероятность эта убыва-
ет с расстоянием.
Эберхарт (Eberhardt, 1968) предложил следующую гиб-
кую зависимость для описания такого рода данных:
Рх = 1-(—
х \w)
где Рх — вероятность обнаружить животное, находящееся
на расстоянии х м от линии маршрута; W — максимальное
расстояние, на котором может быть обнаружено животное.
Постоянная к описывает форму кривой. При к = 1 ре-
грессия линейна, к > 1 соответствует выпуклой, а £<1 —
вогнутой кривой.
В табл. 4.4 представлены последовательные этапы
определения параметров кривой вероятностей, изобра-
женной на рис. 4.7. Константы к и W оцениваются по ре-
грессии log (1 — Рх) на log я: для всех интервалов, кроме
первого. Константы регрессии а и Ь являются оценками
соответственно —к log W и к. Табл. 4.4 и рис. 4.7 пока-
зывают, что значения к п W, оцененные таким образом,
дают кривую, хорошо описывающую наблюдаемое умень-
74
Глава 4
Таблица 4.4
Расчет параметров кривой вероятности обнаружения птиц
па различном расстоянии от линии маршрута
Интервалы, в ко- торых произво- дится учет е до антер- Число замечен- ных птиц Вероят- ность обнару- жения рх log X log (i-PJ Приведенная ве- роятность Р*
И 3 и Л С •1
0—10 Е 50 1,00 1,00
10—20 15 49 0,98 1,1761 —1,6990 0,98
20—30 25 43 0,86 1,3979 —0,8539 0,88
30—40 • 35 31 0,62 1,5441 —0,4202 0,61
40—50 45 5_ п= 178 0,10 1,6532 —0,0458 0,07
Регрессия: log (1 — Рх) = к log х — к log W = 3,444 log х — 5,723,
к = 3,444; W = 45,92 м.
( х )3’444
Следовательно, Рх = 1 — | 1
_ (5x50) + (15X49) + ... +(45X5)
Среднее расстояние х = —--------------—----------1-----==18,93м.
178
Число обнаруженных птиц п = 178.
Длина маршрута L = 10 000 м.
шепие вероятности обнаружения животных с расстоя-
нием.
Построив эту кривую и установив, что она хорошо соот-
ветствует нашим данным, мы теперь можем оценить плот-
ность популяции. В соответствии с моделью Эберхарта
(1968) выражение для плотности на единицу территории
имеет вид
Z) =
п(к+ 1)а
4Lxk(k + 2)
где п — число наблюдавшихся животных, равное 178;
т — среднее расстояние животных от линии маршрута,
равное 18,93 м; L — длина маршрута, равная 10 000 м.
Обилие
Для
нашего примера
178 X 4,4442
4 X 10000 X 18,93 X 3,444 X 5,444
= 0,000248 птиц на 1 м2 = 248 птиц па 1 км2.
Полезно сравнить эту оценку с оценкой, получаемой
.Ж из учетов на трансекте фиксированной ширины. Если за
Т основу для определения ширины полосы принята ширина
# первого интервала (поскольку по предположению в этом
интервале учитываются все птицы), то оценка плотности
составит
Число птиц, обнаруженных на трансекте
Длина X Ширина
Ж. = 50/(10 000 х 20) = 0,000 250 птиц на 1 м2 =
= 250 птиц на 1 км2.
& 7 Заметим, что ширина трансекты составляет не 10 м, как
1^ ширина первого интервала, а 20 м, поскольку птицы под-
/ считываются в двух десятиметровых коридорах по обе
стороны от линии маршрута. Эта оценка очень близка к
оценке, полученной в предыдущем случае, но поскольку
: она основана на подсчете лишь 50, а не 178 птиц, зарегис-
7 трированных на трансекте неопределенной ширины, ее
Г точность вдвое меньше (1/50/1/178 = 0,53).
В модели, предложенной Хоглундом, Нильсоном и
%. Столфельтом (Hoglund, Nilsson, SUlfelt, 1967) и обсуж-
/ давшейся Эберхартом (Eberhardt, 1968), предполагается,
И), что вероятность обнаружить животное уменьшается с
расстоянием экспоненциально. В этом случае нет необхо-
димости вводить предельное расстояние, на котором мо-
жет быть обнаружено животное, и оценка плотности в.ы-
Жг глядит проще:
D =
2L х
Эберхарт приводит теоретические соображения в поль-
зу того, что эта модель хорошо соответствует действитель-
ности, когда обнаружение животного определяется в
76
Глава 4
первую очередь условиями наблюдения, а не поведением
животных. Можно показать, что эта оценка является наи-
лучшей при учетах павших животных (трупов), а также при
наземных учетах дичи в Африке. Применимость метода
можно проверить построением графика зависимости ло-
гарифма числа животных, замеченных в некоторой поло-
се, параллельной линии маршрута, от расстояния сере-
дины полосы до линии маршрута. Если регрессия при-
мерно линейна, то экспоненциальная модель дает
удовлетворительную оценку плотности.
4.2.4. Селективное добавление и изъятие
(метод Келкера)
Если популяция подразделяется на два или большее
число классов, например, по окраске животных, полу или
возрасту, то численность ее можно оценить посредством
добавления в популяцию или изъятия из нее известного
числа животных, принадлежащих к одному из классов.
Этот метод состоит в проведении предварительного об-
следования популяции для определения отношения чис-
ленностей различных классов, затем изъятии или добав-
лении в нее определенного числа животных, принадлежа-
щих к одному из классов, и, наконец, повторном обследо-
вании популяции с целью определения нового отношения
численностей. Метод впервые предложил Келкер (Ке1-
ker, 1940; 1944) для оценки численности популяции оле-
ней, в которой охота разрешалась только на самцов.
В дальнейшем ряд исследователей (Petrides, 1949; Chap-
man, 1954, 1955; Lander, 1962; Chapman, Murphy, 1965,
и Rupp, 1966) усовершенствовали и обобщили его.
Введем следующую систему обозначений:
индексы х и у — первый и второй классы соответ-
ственно;
Л\ — численность популяции во время первого обсле-
дования;
А 2 — численность популяции во время второго об-
следования;
Pi — доля особей, принадлежащих к классу х, в
популяции А/,
Обилие
77
р 2 —доля особей, принадлежащих к классу х, в
популяции JV2;
Сх — число особей класса х, добавляемых или изы-
маемых из популяции между обследования-
ми (положительное значение С х соответствует
добавлению, отрицательное — изъятию);
Су — число особей, принадлежащих к классу у, до-
бавляемых или изымаемых из популяции меж-
ду обследованиями (положительное значение
Су соответствует добавлению, отрицательное —
изъятию); С = Сх—Су.
Численность популяции во время первого обследования
равна
ДГ _ С-Г Pip
Рг Pi
Допустим, мы изучаем популяцию ящериц, иссле-
дуя биологию размножения самок. В качестве побочного
результата этого исследования мы можем получить оцен-
ку численности популяции. Прежде всего мы оцениваем
долю самок в популяции; предположим, она составляет
рг = 0,64. Затем производится отлов 50 самок (С х =
= —50) и 10 самцов (Су = —10). При втором обследова-
нии, проводимом непосредственно после изъятия особей
из популяции, доля самок в популяции оказывается рав-
ной р2 — 0,51. Следовательно, численность популяции
составляет
дг = (-50)-0,51 (-60) = -19,4 =
' 1 ~ 0,51—0,64 —0,13 ~
= 149 ящериц обоих полов.
Этот метод допускает самые разные постановки экспери-
мента: величины Сх и Су могут быть обе положительны
или отрицательны, одна положительна, а другая отри-
цательна, и, наконец, одна из них может быть положи-
тельна или отрицательна, а другая равна 0. Метод Кел-
..кера часто используется сотрудниками Охотничьих хо-
зяйств при оценке численности популяций дичи, когда
Охота ведется главным образом на сашщв. Отношение
' численностей полов в популяции оценивается до и после
78 Глава 4
охотничьего сезона, а число убитых за сезон особей уста-
навливается по данным контрольных станций. Метод хо-
рошо работает и в случае, когда в популяцию выпуска-
ют новых особей (Rupp, 1966); он может также исполь-
зоваться для решения таких проблем, как оценка числен-
ности популяции фазанов, в которую выпускаются сам-
цы, выращенные на специальных фермах.
Чепмен (Chapman, 1955), Рикер (Ricker, 1958) и
Рапп (Rupp, 1966) предложили новую модификацию ме-
тода, пригодную Для случая, когда х и у — два разных
вида, а не два класса особей в рамках одного вида. Пред-
положим, мы хотим оценить численность особей
вида, являющегося объектом охоты и обитающего сов-
местно с видом, охота на которого запрещена. Тогда
Сх — численность особей промыслового вида, изымае-
мых из популяции, а Су = 0 — численность особей вида,
находящегося под защитой, изымаемых из его популяции.
Когда один из видов используется таким образом в ка-
честве контрольного, позволяющего следить за уменьше-
нием численности другого, мы, как правило, интересуемся
не суммарной численностью обеих популяций, а размером
лишь одной из них, а именно Nх. По аналогичной формуле
iy _ Pl (С х РгС)
Pi —Pl
«Метод двух видов» особенно удобен, когда изучается
определенный вид лягушек или ящериц, обитающих сов-
местно с еще одним или несколькими видами, экологи-
чески и таксономически близкородственными изучаемому.
При этом численность популяции изучаемого вида может
быть оценена без непосредственного воздействия на попу-
ляцию и ее членов. Метод Келкера основан на следующих
пр едпо ло жениях:
1. Оба класса равнодоступны для наблюдений при
обоих обследованиях.
2. Между обследованиями не происходит естествен-
ной гибели особей.
3. Между обследованиями не происходит притока осо-
бей из соседних популяций.
4. Число изымаемых из популяции или добавляемых
в нее особей известно.
Обилие
79
Чепмен и Мэрфи (Chapman, Marphy, 1965) обобщили
метод Келкера на случай существования естественной
смертности. Они вывели уравнения, позволяющие оце-
нить интенсивность эксплуатации популяции для случаев,
когда животные изымаются из популяции в течение корот-
кого промежутка времени и когда эксплуатация популя-
ции ведется круглогодично.
4.2.5. Нееелективное добавление и изъятие
Метод Лесли
Если в популяции отсутствуют естественная смертность
- и приток особей извне, то, откладывая по оси ординат
улов (добычу) в расчете на единицу промыслового усилия,
а по оси абсцисс — суммарную добычу, мы получаем
прямую, пересекающую ось абсцисс в точке, соответствую-
щей численности популяции до начала отлова (Leslie,
Davis, 1939). Если при каждом из последовательных от-
ловов применяется одно и то же промысловое усилие, что
может быть лишь в случае специально поставленного
эксперимента (но не в условиях рыбного промысла), то
по оси ординат можно откладывать просто добычу (на-
пример, тонны рыбы, число животных), а не добычу
на единицу промыслового усилия.
На рис. 4.8 изображен типичный график зависимости
добычи на единицу промыслового усилия от суммарной
предыдущей добычи. Наклон этой линии регрессии (знак
отрицателен) характеризует эффективность лова, т. е.
представляет собой долю популяции, отлавливаемую при
применении единичного промыслового усилия. В данном
примере наклон b = —0,186 указывает на то, что в сред-
нем пара охотников-промысловиков каждую неделю от-
стреливает 18,6% численности популяции оленей, оби-
тавших на их охотничьем участке к началу недели. Точ-
ка пересечения графика с осью абсцисс дает оценку чис-
ленности популяции перед началом охоты:
Ni = — а/Ъ = — 18,85/(— 0,186) = 101 олень.
Циппин (Zippin, 1956) отметил, что применение ме-
тода наименьших квадратов при проведении линии ре-
80
Глава 4
грессии слегка смещает оценку, и предложил ввести весо-
вой фактор, с тем чтобы [компенсировать этот эффект.
Однако Рикер (Ricker, 1958) считает, что поскольку раз-
брос точек определяется главным образом изменениями
ото дня ко дню эффективности промысла, а не чисто ста-
Рис. 4.8. Использование линейной регрессии еженедельной добычи
па суммарную добычу при оценке численности популяции по методу
Лесли.
тистическими причинами, то повышение точности, дости-
гаемое введением весового фактора, редко оправдывает
затрачиваемые усилия.
Метод Лесли основан на трех предположениях. В фор-
мулировке Морена (Могап, 1951) они выглядят следую-
щим образом:
1. Вероятность попасться все время постоянна для
всех животных.
2. Плотность популяции не настолько велика, чтобы
отлов одного животного оказывал влияние на веро-
ятность отлова какого-либо другого.
3. За время проведения эксперимента не происходит
Обилие
81
& рождений, гибели, иммиграции или эмиграции
животных.
Ж Мало кто из биологов сможет признать хоть одно из
этих допущений близким к реальности. Однако экспери-
Ж* мент можно поставить таким образом, чтобы минимизи-
W ровать различия между предположениями, заложенными
в модель, и реальной ситуацией. Справедливость первого
Яу допущения проверяется линейностью линии регрессии.
Ж Если экспериментальные точки явно не ложатся на пря-
& мую, метод отвергается. Второе условие может быть вы-
полнено при тщательной постановке эксперимента. Если,
фЛ например, используются одноместные капканы, то число
Ж; их должно быть настолько велико, чтобы от проверки до
«^•проверки срабатывало не более чем 20% из них.
Й Третье предположение может хорошо соответствовать
реальности, если эксперимент проводится в течение ко-
.'1-роткого промежутка времени. Число последовательных
»! отловов должно быть сделано возможно меньшим* а до-
ЖЬ-быча за каждый из них, напротив, возможно большей.
^МДиппип (Zippin, 1956) и Зебер и Ле Крен (Seber, Le Cren,
1967) проанализировали такую постановку эксперимента.
Они показали, что если производится только два отлова
С! и С 2 с одним и тем же промысловым усилием, числен-
»j;; ность популяции до первого отлова оценивается выра-
4k : жением
^ = С?/(С1-Сг),
а эффективность лова определяется по формуле
S" Р = (С1-С2)/С1.
Ж'... Если предположить, что оценка эффективности лова,
определенная по этой формуле, справедлива и для неко-
торой второй популяции, то ее численность можно оце-
нить по данным одного отлова (Seber, Le Cren, 1967) по
формуле
. N^C./p.
ж'тТакая операция выглядит довольно сомнительно, по-
скольку успешность одного отдельно взятого отлова во
, многом определяется, например, погодой. Однако, если
I' 4—334
Ж
82
Глава 4
условия отловов в точности одинаковы, удается получить
приемлемую оценку.
Метод Лесли вполне применим в тех случаях, когда мы
не просто изымаем животных из популяции, а метим от-
ловленных животных и выпускаем их снова. Тогда при
повторных отловах меченые животные игнорируются и
добычей считаются только немеченые животные. Однако
этот метод, в сущности представляющий собой вариант
метода мечения с повторным отловом, довольно неэффек-
тивен. Метод Петерсена (разд. 10.3) позволяет более точ-
но оценить численность популяции при тех же самых уси-
лиях. Дисперсия оценок, полученных по методу Лесли,
больше, чем для оценок, получаемых из других моделей.
Этим методом следует пользоваться лишь в тех случаях,
когда все другие неприемлемы или когда оценка числен-
ности популяции получается как побочный результат
мероприятий по учету или регуляции численности попу-
ляции.
Метод Делури
Делури (DeLury, 1947) показал, что между суммарным
промысловым усилием, затраченным за время до конкрет-
ного лова, и логарифмом добычи на единицу промыслового
усилия для данного лова существует линейная зависи-
мость. Угол наклона линии регрессии b связан с эффек-
тивностью лова р соотношением
1 — р — antilog105,
а начальная численность популяции определяется при
этом по формуле
1 — (1 — р)п '
где С — суммарный улов, а n — суммарное промысло-
вое усилие в выбранных единицах.
Тесная связь между этим методом и методом Лесли
очевидна, и действительно, оба они могут быть выведены
из одного уравнения (Ricker, 1958). Соответственно на при-
менение этого метода накладываются те же самые огра-
Обилие
83
ничения, которые были перечислены в предыдущем раз-
В- деле.
Метод Делури можно продемонстрировать на данных,
<+ собранных Хартом (Harte, 1932) и обработанных Рике-
Е ром (Ricker, 1949; 1958). В течение 7 последовательных
F' недель проводился лов сига в озере Шекспир-айленд,
к. штат Онтарио. Размер сетей, их расположение и время, па
II, которое они каждый раз ставились, были стандартизо-
f ваны, и, таким образом, недельный улов можно было при-
пять за улов на единицу промыслового усилия. В табл,
к.. 4.5 приводятся данные лова и результаты их обработки.
j Таблица 4.5
(. Оценка численности популяции методом Делури
’ Недели Суммарное время лова в неделях Недельный улов logic (недельного улова)
t 1 0 25 1,40
L • 2 1 26 1,42
Г з 2 15 1,18
1 . 4 3 13 1,11
5 4 12 1,08
: 6 5 13 1,11
К? 7 6 5 0,70
Ь = —0,1007; 1 — р = antilog 10 6 =0,793; р =0,207;
С= 25 + 26 + ... + 5 = 109;
У1= С/[1 — (1 —/>)"] = 109/(1—0,793’) = 136 рыб.
, ' Двукратное использование индекса
Численность популяции можно оценить по линейному
индексу плотности, измеренному дважды — до и после
того, как некоторое известное число животных добавлено
ДЕ-7- в популяцию или изъято из нее. В обоих случаях исполь-
gj-.; зуется один и тот же метод обработки данных с учетом
ж.того- обстоятельства, что число животных, добавляемых
1? 4*
84
Глава 4
в популяцию, считается положительным, а изымаемых
из популяции — отрицательным.
Рини (Riney, 1957) изучал популяцию благородного
оленя Cervus elaphus, обитающего в Новой Зеландии,
на территории леса площадью 30 кма. Он определял ин-
декс плотности, подсчитывая число кучек помета на 2160
пробных площадках площадью 4 м2 каждая. Среднее
число кучек помета составило 0,17 на площадку. После
этого два охотника-промысловика в течение двух с поло-
виной месяцев проводили отстрел на этой территории
и убили 66 оленей. Через месяц определение индекса
плотности было повторено, и его значение упало до
0,07 кучек помета на пробную площадку.
Следовательно, мы имеем:
Индекс плотности до охоты 1Х =0.17
Индекс плотности после охоты 72 =0,07
Число животных, изъятых из популяции за С =—66
охоту
Численность популяции до охоты оценивается сле-
дующим образом:
лг ДС 0,17 х (— 66)
Л( —-----1:----------------— = 112 оленей,
Д — Д 0,07 — 0,17
а численность популяции после охоты равна
1ЪС
h-h
0,07 X (— 66) ,п
—------*----- = 46 оленей.
0,07 — 0,17
Точность оценки зависит от справедливости пред-
положения о том, что популяция в течение всего экспери-
мента является замкнутой. На самом деле, как правило,
некоторое количество животных за время, прошедшее
между оценками N х и JV2, погибает естественной смертью,
и, следовательно, обе оценки получаются заниженными.
Для того чтобы минимизировать это смещение, все три
этапа эксперимента — первое определение индекса, до-
бавление или изъятие животных, второе измерение ин-
декса — следует как можно теснее совмещать во времени.
Этот метод особенно хорош, когда в популяцию, слу-
жащую объектом спортивной охоты или рыболовства,
выпускаются особи, выращенные на специальных фер-
Обилие
85
мах, инкубаторных станциях или рыборазводных хозяй-
ствах. Поскольку эти особи добавляются, а не изымаются,
значение С положительно. Однако здесь есть одно тон-
кое место. Выпущенные животные не должны оказывать
на уровень индекса плотности при втором его измерении
большее влияние, чем следует ожидать, исходя из их
численности. Так, например, в случае когда в популя-
цию форели выпускаются особи, выращенные в рыбораз-
водном хозяйстве, улов на промысловое усилие нельзя
использовать в качестве индекса обилия, поскольку вы-
ращенные в рыборазводных хозяйствах рыбы ловятся лег-
че, чем рыбы, выросшие в природных условиях. Такой
индекс дал бы завышенную оценку плотности.
4.2.6, Коррекция индекса
Индекс и эталонный вид
В некоторых случаях на территории, где обитает ин-
тересующий нас вид, живет еще один вид, плотность кото-
рого нам известна. Тогда плотность изучаемого вида можно
оценить по известной плотности вида у, если мы знаем
индексы обилия обоих видов хну.
Этот метод можно проиллюстрировать на примере уче-
та кенгуру в Квинсленде, Австралия. Кенгуру и овцы
подсчитывались на упорядоченно расположенных тран-
сектах на пастбище площадью 15 км2, где, как было за-
ранее известно, содержалось 1430 овец. В результате учета
на трансектах было зарегистировано 24 кенгуру и 160
овец. Обозначая неизвестное число кенгуру через Nх,
известное число овец через Ny, а число кенгуру и овец, уч-
тенных на трансектах, через пх и пу соответственно, полу-
чаем следующую оценку для общего числа кенгуру на паст-
бищах:
Nynx 1430 x 24
Nx =-------==-----------= 214 кенгуру.
пу 160
Известную плотность одного вида можно, таким обра-
? зом, использовать для оценки плотности другого вида
только в том случае,если индексы обилия обоих видов экви-
86
Глава 4
валентны. В нашем примере мы считаем, что и овцы и кен-
гуру одинаково реагируют на присутствие наблюдателя,
что они одинаково заметны, а характер их распределения
на обследуемой территории примерно одинаков. По из-
вестной плотности чернопятой антилопы можно, напри-
мер, оценить плотность коровьей антилопы, однако ее
нельзя использовать для оценки плотности львов, по-
скольку последних трудно наблюдать днем, тогда как и
чернопятая и коровья антилопы одинаково хорошо за-
метны на любом расстоянии.
Калибровка индёкса
В тех случаях, когда для широкого интервала плот-
ности известна зависимость между индексом плотности и
абсолютной плотностью, из любого единичного значения
индекса можно получить оценку истинной плотности.
Количество данных, необходимых для определения ре-
грессии плотности на индекс, зависит от характера этой
зависимости. Если известно, что линия регрессии — пря-
мая, проходящая через начало координат, то угол ее
наклона может быть определен по одному измерению плот-
ности при известном значении индекса. Если регрессия
линейна, однако не проходит через начало координат,
необходимы по меньшей мере две точки, а если регрессия
криволинейна, то наименьшее число точек для опреде-
ления линии регрессии равно трем.
Соотношение между плотностью, определяемой во
время учетов с воздуха, и абсолютной плотностью пред-
ставляет простой пример вычисления регрессии. В боль-
шинстве случаев линия регрессии — это прямая, прохо-
дящая через начало координат. Если число тщательно
подсчитанных животных на 1 км2 равно D, а число жи-
вотных зарегистрированных с самолета на той же терри-
тории, равно /, то любые данные самолетных учетов по
местообитаниям этого типа пересчитываются в истинную
плотность умножением на коэффициент D/I. На самом
деле, чтобы получить точное значение коэффициента
пересчета, следует определить этот множитель незави-
симо несколько раз. Когда линия регрессии плотности
на индекс линейна, но не проходит через начало коорди-
Обилие
87
нат, соответствующая зависимость имеет вид
D = а + Ы,
Постоянные а и Ъ оцениваются стандартным приемом ре-
грессионного анализа по двум или более парам точек
плотность — индекс.
Если зависимость между индексом и плотностью не-
прямолинейна, ее характер можно определить тремя
способами.
1. Если общий вид зависимости может быть выве-
ден теоретически, индекс обычно удается преобразовать
таким образом, чтобы регрессия плотности на него стала
линейной. Далее переход от индекса к абсолютной плот-
ности проводится так, как описано выше.
2. Зависимость между плотностью и индексом можно
преобразовать в линейную эмпирически. Для этого не-
обходимы по меньшей мере три пары точек, а если нужно
точно знать поправочный множитель, то несколько боль-
ше. Чаще всего применяют логарифмирование и извле-
чение квадратного корня из одной или обеих переменных,
а затем оценивают отклонение преобразованной регрес-
сии от линейной. После того как достигнута приемлемая
степень линейности, по постоянным линии регрессии
вычисляют поправочный множитель. Преимущество этого
метода состоит в легкости, с которой можно последова-
тельно вычислять поправочные множители для различ-
ных местообитаний. Если логарифм плотности линейно
зависит от квадратного корня из индекса в местообита-
нии А, то есть веские основания полагать, что та же за-
висимость сохранится и в местообитании В, хотя наклоны
прямых и точки пересечения с осью ординат могут быть
различны. Таким образом, поправочный множитель для
второго местообитания можно вычислить на основе зна-
чительно меньшего количества исходных данных, чем
это необходимо для установления формы зависимости
плотности от индекса в первом местообитании.
3. Вместо линеаризации нелинейной зависимости мож-
но непосредственно по исходным данным строить кривую,
описываемую уравнением регрессии, преобразующим лю-
бое значение индекса в соответствующее значение плот-
ности. Вероятно, наиболее полезны в этом случае полило-
88
Глава 4
миальные уравнения регрессии, позволяющие строить са-
мые разнообразные кривые, на одну из которых обычно
удовлетворительно ложатся экспериментальные точки.
Уравнение регрессии в общем виде выглядит так:
D =a + bj + v2 +V3'....
Новые члены можно последовательно добавлять до
тех пор, пока не получится удовлетворительное совпаде-
ние с экспериментальными данными (этот метод описан
в большинстве учебников по статистике).
Когда по значению одной переменной предсказыва-
ется значение второй переменной, эта вторая переменная
называется зависимой и значение ее традиционно откла-
дывается по оси ординат. В рассматриваемом случае за-
висимой переменной является плотность, и поправочный
множитель, позволяющий преобразовывать значение ин-
декса в значение плотности, должен определяться из ре-
грессии плотности на индекс, а не индекса на плотность.
Разумеется, с биологической точки зрения индекс за-
висит от плотности, а не наоборот, но термин «зависи-
мость» в статистическом смысле не обозначает зависи-
мости причинно-следственной.
Регрессия, определенная методом наименьших квад-
ратов, будет несмещенной, лишь если значения незави-
симой переменной фиксированы. Примером регрессии
случайной переменной на фиксированную является, на-
пример, регрессия численности популяции на время.
Время — величина неслучайная и формально может опре-
деляться без ошибки. Когда же абсолютная плотность
оценивается по регрессии на индекс, то обе величины —
случайные, и оценка наклона регрессии будет несколько
занижена. Соответственно, когда уравнение регрессии
используется для вычисления значений плотности по
значениям индекса, значение плотности, как правило,
занижается, а не завышается.
Глава 5
Скорость роста численности
популяций
В этой главе вопрос о скорости роста рассмотрен лишь
вкратце с той целью, чтобы читатель мог освоить следую-
щие три главы. В дальнейшем, в частности в гл. 9, это
понятие будет рассмотрено более глубоко.
5.1. Конечная и экспоненциальная скорость
роста
Простейшей мерой скорости роста численности по-
пуляций является отношение численностей за два по-
следовательных года. Это так называемая «конечная
скорость роста», иногда именуемая также «множителем
роста» (Rogers, 1968), которую мы временно обозначим
символом к. Таким образом,
X=^±L,
Nt
где N — численность, a t — время. При л > 1 числен-
ность популяции от момента времени t до t-\- 1 возраста-
ет, при X < 1 убывает.
Численность популяции, растущей с постоянной ско-
ростью, будет увеличиваться следующим образом:
Годы 0 1 2 3 и т. д.
Численность No N0Xk NoxXxk 2УохХхХхХ
или, в более сжатой форме,,
2V0 ;У0л2 7УОХЗ И т. д.
Другими словами, численность увеличивается в соот-
ветствии с формулой
Nt = N0X‘.
00
Глава 5
В большинстве статей, посвященных позвоночным,
скорость роста численности выражают в процентах, за-
давая ее следующим выражением: (X—1) X 100. Таким об-
разом, X = 1,2 соответствует скорости роста, равной 20%. j
При высоких скоростях роста такая практика приводит
к путанице. Трудно понять, например, что имеется в
виду, когда говорят, что скорость роста популяции со-
ставляет 170%. Напротив, если сказать, что численность
популяции ежегодно увеличивается в 2,7 раза, то ника-
кой путаницы не возникает.
В дальнейшем вместо символа X мы будем использо-
вать обозначение ег. Постоянная е — это основание нату-
рального логарифма; она равна 2,71828. Величина г
представляет собой степень, в которую надо возвести е,
чтобы ег равнялось X; г называется экспоненциальной
скоростью роста. На первый взгляд замена простого обо-
значения X на более сложное ег кажется варварством,
однако на самом деле это приводит к упрощению выкла-
док и способствует более четкому пониманию смысла по-
нятия «скорость роста».
Конечная скорость роста ег связывает численности
популяций в два последовательных момента времени со-
отношением !
Nt = N<>ert,
которое можно записать также в виде j
2V0 = Nte~rt, ;
или
или
ln7Vf = ln2V0 4- rt.
Последняя форма записи особенно удобна. Поскольку
In е = 1, уравнение принимает вид у = а + Ьх, т. е. ста-
новится уравнением прямой.
Мерой скорости роста может быть либо конечная
скорость ег, либо экспонециальная скорость г. Последняя
более удобна по следующим причинам:
Скорость роста численности популяций
91
1. Постоянной численности популяции соответству-
ет г = 0, в то время как при этом ет = 1. Соответ-
ственно одно и то же абсолютное значение г означает ско-
рость роста численности популяции при г > 0 и скорость
убывания численности, популяции при г < 0, тогда как
конечные скорости роста имеют значения, которые трудно
интерпретировать. Так, если известно, что конечная ско-
рость роста численности одной популяции составляет
ег = 1,649, а второй — ег = 0,607, то из непосредствен-
ного сопоставления этих чисел не следует, что скорость
роста численности первой популяции равна скорости
убывания численности второй. Значения же соответствую-
щих экспоненциальных скоростей в этом случае состав-
ляют г = 0,5 и г = —0,5, т. е. это равенство скоростей
совершенно очевидно.
2. В отличие от конечной скорости е^для экспонен-
циальной скорости г переход к новым единицам времени
не составляет труда. Если х — экспоненциальная ско-
рость роста численности за год, то скорость роста за день
составляет гг/365. Удобной мерой скорости роста числен-
ности популяции является время удвоения численности.
Оно легко вычисляется из г и равно 0,6931/г. Так, напри-
мер, при годовой скорости г = 0,23 время удвоения чис-
ленности равно 3 годам. Если же г = —0,23, то числен-
ность популяции за три года вдвое убывает.
По этим причинам удобнее пользоваться экспонен-
циальной скоростью роста г, а не конечной скоростью ег.
Впрочем, от одной к другой легко перейти с помощью
формулы
Дп ег = г.
Значения натуральных логарифмов можно найти в боль-
шинстве сборников математических таблиц, а можно и
рассчитать из десятичных логарифмов по формуле
In х = 2,3026 Igx»
Таблица переходов от ет кг дается в Приложении 1.
Из рис.5.1 видно, что график зависимости численности
популяции от времени при постоянной скорости роста
представляет собой экспоненту. Тангенс угла наклона
касательной к кривой непрерывно изменяется и в каждой
92
Глава 5
точке равен rN. Использование натуральных логарифмов
позволяет получить простое соотношение между накло-
ном, экспоненциальной скоростью роста и численностью
популяции. По этой причине в популяционном анализе
чаще используются натуральные, а не десятичные лога-
Рис. 5.1.
А. Зависимость численности популяции от времени для популяции, ра-
стущей с постоянной скоростью. В любой точке тангенс угла наклона
кривой равен b=rN. Б. Рост той же самой популяции, когда по оси орди-
нат откладывается натуральный логарифм численности; угол паклона
линии регрессии равен г.
рифмы. Когда скорость роста численности популяции
постоянная, график зависимости натурального логарифма
численности популяции от времени представляет собой
прямую с тангенсом угла наклона, равным г.
5.2. Меры скорости роста
Идеальная скорость роста
Идеальной скоростью роста, обозначаемой гт, назы-
вается экспоненциальная скорость роста популяции с
устойчивым возрастным распределением (разд. 9.5), если
внешние ресурсы (т. е. пища, вода, пространство и убе-
жища) неограниченны. Она определяется генетической
Скорость роста численности популяций
93
структурой популяции и ее взаимодействием с окружаю-
щей средой (Andrewartha, Birch, 1954); под условиями
окружающей среды понимается погода, наличие пищи,
удобство мест гнездования и т. п. Идеальная скорость
роста может быть с равными основаниями названа «иде-
альной скоростью убывания численности», поскольку для
большинства видов тт в большинстве местообитаний мень-
ше 0. Так, в Антарктике rm для императорского пингвина
положительна, однако популяция такого же вида, вы-
пущенная на свободу в тропиках, будет характеризо-
ваться отрицательной rm. Следует отметить, что пищи и
других ресурсов в этих условиях вполне достаточно>
однако пингвины не смогут выжить при высокой темпера-
туре и влажности.
Скорость роста при фиксированной зависимости
выживаемости и плодовитости от возраста
Эта скорость, обозначаемая символом rs, представля-
ет собой экспоненциальную скорость роста численности
популяции в условиях, когда устойчивое возрастное рас-
пределение соответствует зависимости выживаемости и
плодовитости от возраста в момент исследования. Эти
термины будут строго определены в гл. 7 и 8, но основ-
ная идея довольно проста. Скорость роста численности
популяции зависит от средней плодовитости каждой воз-
растной категории,и от средней выживаемости животных
в каждом возрасте. Если эти величины остаются постоян-
ными в течение Достаточно длительного промежутка
времени, то возрастное распределение популяции стаби-
лизируется и скорость ее роста становится постоянной.
При этом имеется в виду, что заданная таким образом
скорость роста популяции определяется возрастным рас-
пределением выживаемости и плодовитости в момент из-
мерения. Она обычно отличается от действительной, ско-
рости роста, поскольку возрастное распределение редко
остается постоянным. Однако возрастное распределение
отражает в основном условия недавнего прошлого, а не
характер распределения выживаемости и приспособлен-
ности по возрастным категориям в данный момент. Опре-
деленная таким образом скорость роста, не учитывающая
94
Глава 5
влияния особенностей возрастного распределения попу-
ляции, отражает потенциальную способность популяции
в данный момент увеличивать свою численность. Она так-
же соответствует той действительной скорости роста
численности, которая установится, если выживаемость и
плодовитость не будут меняться с возрастом.
Скорость rs отличается от скорости гт тем, что в ее
определение не входит требование неограниченности внеш-
них ресурсов. Таким образом, гт представляет собой
частный случай rs.
Наблюдаемая скорость роста
Наиболее общей мерой скорости роста является на-
блюдаемая скорость роста г. Это экспоненциальная
скорость, с которой популяция увеличивает свою числен-
ность на протяжении некоторого промежутка времени.
При этом не делается никаких предположений относи-
тельно постоянства скорости роста, возрастного распре-
деления в течение этого промежутка времени или относи-
тельно неограниченности ресурсов.
Рассмотренные выше три скорости роста — rm, rs
и г — взаимосвязаны и иногда конгруэнтны. Разрежен-
ная популяция, растущая со скоростью гт, характери-
зуется также скоростью rs = гт и г = гт. Скорости rs
и гт часто путают, поскольку они рассчитываются одина-
ковым образом по возрастным распределениям плодови-
тости и выживаемости (гл. 9), и единственное различие
состоит лишь в условиях их измерения, В то время как
гт — это максимальная скорость, с которой популяция
может увеличивать свою численность в некотором кон-
кретном местообитании, rs — это скорость, с которой опа
может увеличивать свою численность при данном уровне
обеспеченности ресурсами на особь.
5.3. Демографический потенциал
Скорость роста численности популяции, определен-
ная так, как это сделано выше, говорит о популяции мно-
го больше, чем просто прирост поголовья за единицу вре-
Скорость роста численности популяций
95
мени. Она характеризует уровень благосостояния популя-
ции в целом, описывая усредненную реакцию всех чле-
нов популяции на совокупное действие всех окружаю-
щих факторов внешней среды. Ни одна другая величина
не характеризует в столь сжатой форме демографический
потенциал популяции.
Мерой демографического потенциала являются и rm
и rs, ио они характеризуют его с разных сторон. Бирч
(Birch, 1960) предложил рассматривать rm как экологи-
ческий показатель генетической приспособленности попу-
ляции. В данном контексте rm является мерой врожден-
ной способности популяции к росту в определенных усло-
виях. За исключением ситуаций, когда плотность низка,
rm не является мерой действительной скорости роста по-
пуляции. Таким образом, rm — это потенциальная ско-
рость роста, а действительная скорость обычно оказы-
вается ниже этого уровня из-за ограниченности пищи,
пространства и убежищ. Скорость rm удобна для сравнения
приспособлеиностей двух видов к одним и тем же усло-
виям или для сравнения того, какое пз двух занимае-
мых видом местообитаний больше ему подходит.
Напротив, rs — величина более общая; при ее оценке
учитывается и суммируется демографический потенциал
обоих полов и всех возрастных классов популяции при
условиях, отражающих недостаток ресурсов, с которым
действительно сталкивается популяция. Любое изменение
условий приводит к быстрому изменению rs, будь то при-
лив извне новых животных в популяцию, устойчиво хо-
рошая погода, изменение условий местообитания или за-
суха. Благоприятное или неблагоприятное изменение
окружающих условий сразу отражается в направлении
и величине изменения rs. С этой точки зрения rs может
также служить мерой приспособленности популяции, но
не в смысле долгосрочной приспособленности, а в смысле
немедленной реакции на небольшие изменения окружаю-
щей среды. В данном контексте rs можно именовать «де-
мографическим потенциалом», отличая таким способом ее
от г — просто характеристики постоянной скорости роста
популяции. Демографический потенциал популяции опре-
деляется, таким образом, как уровень ее благосостояния,
отражаемый в плодовитости и выживаемости и оценивае-
96
Глава 5
мый величиной rs. Эта величина не говорит пам ни о том,
как будет популяция реагировать на существенное изме-
нение окружающих условий, ни о том, уцелеет ли она
через 10 лет, но показывает, как популяция справляется
со своими насущными проблемами. Хотя демографичес-
кий потенциал — величина, не имеющая большого смыс-
ла с генетической или эволюционной точки зрения, оце-
ненная таким образом приспособленность может быть
использована при эксплуатации популяции.
Для оценки благосостояния популяции существует
ряд показателей — жировые отложения, размеры тела,
отношение численностей полов и различных возрастных
категорий, вес, — которые измерить гораздо легче, не-
жели г,. Эти показатели могут служить индексами
«состояния популяции», однако обычно само понятие
«состояние популяции» либо вообще не определяется, либо
описывается в весьма расплывчатых терминах. Данные
показатели полезны лишь в отношении конкретных приз-
наков, которые они описывают. Если одна популяция по
какому-то конкретному показателю находится в лучшем
состоянии, чем другая, то что это означает в экологичес-
ком смысле — неясно. Эта семантическая сложность сни-
мается, если мы определяем «состояние популяции» с
помощью демографического потенциала. Таким образом,
все перечисленные выше показатели полезны в той мере,
в какой они способны предсказывать значение rs. Пока-
затель, не корррелирующий со значением rg, несомнен-
но, может служить мерой чего-то, но не дает представ-
ления о шансах популяции на выживание и размножение,
а, следовательно, связан с элементарными процессами
взаимодействия популяций с окружающей средой лишь
в небольшой степени.
Потенциальная скорость роста
Идея, нашедшая свое выражение в понятии «демогра-
фический потенциал», может быть видоизменена для
эксплуатируемых популяций. При квалифицированной
эксплуатации популяции значение rs будет равно 0,
но на самом деле представляет интерес значение потен-
циала rs, достигаемое при резком прекращении эксплуа-
Скорость роста численности популяций
97
тации. Этот потенциал тождествен скорости неселектив-
ного изъятия особей из популяции, поддерживающего
ее в состоянии гг = 0.
При описании эксплуатируемых популяций требуется
ввести еще одну скорость роста — гр. Это так называе-
мая потенциальная скорость роста, определяемая как
экспоненциальная скорость, с которой растет численность
популяции в первый момент после того, как снимается
один из факторов смертности.
Для эксплуатируемой популяции гр можно либо
измерить непосредственно, прекратив эксплуатацию, ли-
бо рассчитать косвенным образом по демографическим
таблицам, в которых отдельно указаны естественная и
промысловая смертность (разд. 8.3). Более удобна оцен-
ка с помощью косвенных показателей. Вероятность того,
что в эксплуатируемой популяции какая-то особь окажет-
ся добычей промысла, не находится в тесной связи с ее
способностью к размножению или способностью противо-
стоять естественным факторам смертности. Соответствен-
но такие показатели, как запас жиров, плодовитость и
скорость естественной смертности, коррелируют
скорее с гр, чем с rs, искусственно поддерживаемой в экс-
плуатируемой популяции. Если известна зависимость
какого-либо показателя от значения rs для неэксплуа-
тируемой популяции, то этот показатель можно исполь-
зовать в качестве индекса гр для эксплуатируемой попу-
ляции. Несколько зависимостей такого типа было по-
строено для популяции благородного оленя в 'работе
Коли (Caughley, 1971b).
Глава 6
Расселение
Расселение можно .определить как перемещение жи-
вотных от места их появления на свет до места, где они
размножаются или где они могли бы размно-
житься, если бы уцелели и нашли себе бран-
ного партнера (Howard, 1960). Расселение не следует пу-
тать с локальными перемещениями (т.е. передвижениями
внутри собственного индивидуального участка) и с мигра-
циями (переселениями с зимних местообитаний на лет-
ние и наоборот). Расселение может проявляться в причуд-
ливых формах — примерами тому служат происходящие
время от времепи массовые перемещения антилопы-пры-
гуна Antidorcas marsupialis (Child, Le Rich, 1969). Однако
гораздо чаще расселение представляет собой непрерыв-
ный скрытый процесс, выявляющийся лишь при тща-
тельном изучении.
Способность к расселению определяет шансы вида па
выживание не в меньшей степени, чем способность к раз-
множению и продолжительность жизни особи. Пригод-
ные для обитания места редко остаются неизменными в
течение длительного промежутка времени, и вследствие
этого эфемерными являются сами населяющие их попу-
ляции, возникающие, размножающиеся и снова вымираю-
щие по мере того, как возникают и исчезают удобные
местообитания. Особенно четко это выявляется в том слу-
чае, когда условия, пригодные для существования
данного вида, реализуются лишь на какой-то одной ста-
дии лесной сукцессии. Участки, на которых могут обитать
локальные популяции, представляют собой тогда рассеян-
ные острова в море леса, непригодного для жизни вида.
Они непрерывно возникают при пожарах, бурях и опол-
знях и непрерывно разрушаются в процессе сукцессии.
В результате некоторые популяции по мере изменения
условий местообитания вымирают, тогда как в местах,
Расселение
99
вступающих в благоприятную стадию сукцессии, возни-
кают новые популяции. Для того чтобы вид выжил, по
крайней мере некоторые особи должны обладать способ-
ностью расселяться из одних местообитаний в другие.
Жизненный цикл большинства локальных популя-
ций имеет такой характер: популяции возникают, растут
и существуют до тех пор, пока изменение окружающих
условий не приведет их к гибели. Если популяция жестко
связана с определенной стадией сукцессии, этот процесс
проявляется особенно ярко, однако он в такой же степе-
ни характерен и для видов с менее специфической эко-
логией; разпица лишь в том, что сам процесс более дли-
телен. Местообитание вида редко бывает сплошным. Обыч-
но оно представляет собой множество пятен, рассыпанных
наподобие элементов мозаики. В результате колебаний
климата, изменения погодных условий от года к году,
сукцессий растительных сообществ и деятельности чело-
века и других животных эта мозаика изменяется, как
картинка в калейдоскопе, и вместе с нею изменяется
распределение популяций животных. Одни пятна место-
обитаний растут, другие сужаются, третьи возникают,
четвертые исчезают. Популяция может уцелеть за счет
следующих факторов:
1. Она может измениться генетически или фенотипи-
чески, оставаясь на прежнем местообитании.
2. Она может обладать высокой экологической плас-
тичностью, т.е. быть способной существовать в ши-
роком спектре местообитаний.
3. Некоторые члены популяции способны к рассе-
лению.
Каждое из этих достоинств превращается в недоста-
ток, если условия существования относительно стабиль-
ны. Первый способ требует поддержания генетической
изменчивости популяции, т.е. предполагает у большин-
ства членов популяции наличие субоптимальных ком-
бинаций генов при постоянных условиях. Второй способ
обрекает членов популяции на роль особей, потенциально
способных существовать в широком спектре условий, а
это значит, что лишь в очень редких случаях они могут
быть максимально для своих возможностей приспособлены
к определенному набору условий обитания. Способность к
100
Глава в
расселению сама по себе не является недостатком, однако
расселение — процесс расточительный. Расселение сни-
жает скорость роста популяции, препятствуя быстрому
восстановлению популяции после того, как плотность ее
была снижена из-за неблагоприятных условий. Очень
хорошо продемонстрировал этот эффект Гентри (Gentry,
1968). Он оградил участок, заселенный сосновыми полев-
ками (Microtus pinetorum), не позволяя им таким обра-
зом покинуть пределы участка и расселиться на новые
территории. В результате популяция, обнесенная изго-
родью, достигла много большей плотности по сравнению
с контрольной, где расселение не было ограничено.
Говард (Howard, 1960) выделяет два типа расселения.
«Естественным расселением» он называет спонтанные
перемещения, причины которых — не внешние условия,
а генетические особенности расселяющихся особей. «Вы-
нужденное расселение» — это, напротив, поведенческая
реакция животных на неблагоприятные внешние условия,
например недостаток пищи или жизненного пространства.
Эти два типа расселения приводят к различным резуль-
татам. Для естественного расселения, вообще говоря, не су-
ществует предпочтительного направления; животные, оби-
тающие на краю ареала, с одинаковой вероятностью могут
как расселяться к центру ареала, так и осваивать новые тер-
ритории. Вынужденное расселение менее случайно. Рас-
селяющиеся особи склонны уходить от неблагоприятных
условий, обычно перемещаясь в направлении от высоких
к низким плотностям популяции. При естественном рас-
селении особи часто совершают путешествия, во много раз
превышающие средний радиус индивидуального участка,
тогда как при вынужденном расселении эти путешествия,
как правило, коротки и заканчиваются сразу после того,
как особь достигнет мест с благоприятными условиями
существования.
6.1. Процесс расселения
Для тщательного исследования расселения требуется
знать следующее:
1. Пол и возраст расселяющихся особей и особей,
остающихся на прежнем месте.
Расселение
101
2. Случайно ли направление расселения особей или
зависит от градиента плотности, направления пре-
обладающих ветров и ориентации на страны света.
3. Изгоняются ли расселяющиеся особи со своих
родных мест или покидают их по доброй воле.
4. Вероятность того, что данная особь отправится в
путешествие, а также сведения о том, постоянна ли
эта вероятность или она является функцией плот-
ности, скорости роста, обеспеченности пищей или
еще каких-либо факторов.
5. Среднее значение и дисперсию расстояния, преодо-
леваемого при расселении, а также то, постоянны
эти величины для вида или изменяются в зависи-
мости от внешних условий; сколько максимумов
имеет частотное распределение расстояний, на кото-
рые расселяются особи,— один или несколько.
6. Вероятность того, что расселившаяся особь доживет
до размножения, в сопоставлении с той же вероят-
ностью для нерасселяющихся особей.
7. Генетические различия между расселяющимися и
оседлыми особями.
Пока мы не располагаем такой информацией, собран-
ной для нескольких видов, никакие обобщения, каса-
ющиеся процесса расселения, невозможны. К сожалению,
в настоящее время таких данных нет ни для одной попу-
ляции [правда, работа Майерса и Кребса (Myers, Krebs,
1971) по полевкам приближается к этому идеалу] — факт
удручающий, хотя вряд ли удвительный. Расселение —
самый трудный для изучения популяционный процесс,
и в большинстве экологических исследований о нем пред-
почитают просто не говорить. Однако изучение популя-
ционной экологии без учета расселения аналогично таксо-
номической работе, пренебрегающей изучением процесса
эволюций. И в том и в другом случае процессы описы-
ваются так, как если бы они были статическими. Иссле-
дования расселения очень трудоемки и технически слож-
ны, однако они позволяют так глубоко понять экологию
животных, что это с лихвой окупает затраченный труд.
Всеобъемлющих исследований по расселению не су-
ществует, но есть ряд хороших работ по одному или не-
скольким аспектам этого процесса.
102
Глава 6
Направление расселения
Работы Фриса (Frith, 1959,1963) по нескольким видам
уток показали, что расселение их идет во всех направле-
ниях. Однако по результатам кольцевания автор не смог
доказать отсутствия предпочтительного направления рас-
селения, поскольку кольца возвращались охотниками,
а их число в разных направлениях было неодинаковым.
Тэнтон (Tanton, 1965) обнаружил, что на исследован-
ной им территории расселение лесной мыши Apodemus
sylvaticus идет одинаково во всех направлениях. Он из-
мерял угол между определяемыми по двум последо-
вательным отловам направлениями расселения различ-
ных особей, а для проверки случайности этого угла ис-
пользовал критерий Релея (Durand, Greenwood, 1958).
Критерий этот прост. Если А г А 2, А 3 ...Ап —углы, и
W — sin At -Р sin А2 4- sin А3 + • • • 4- sin Ап,
V = cos Ai + cos A2 4- cos A3 -|- • • • 4- cos An,
вероятность того, что направление случайно, меньше
5%, если (И-’2 + V2)/ п > 3. При п < 6 этот критерий
непригоден и следует пользоваться точным вероятностным
методом (Durand, Greenwood, 1958).
Коли (Caughley, 1970b) показал, что в Новой Зелан-
дии популяция тара расширяет ареал в северном на-
правлении вдвое быстрее, чем в южном; это же справедли-
во и для популяции серн Rupicapra rupicapra (Chris-
tie, Andrews, 1965; Christie, 1967), обитающих в той же
местности. Таким образом, может показаться, что ско-
рость расселения отдельных особей должна быть различ-
на в разных направлениях. Однако эти наблюдения рав-
ным образом могут отражать различия в скорости роста
популяций, населяющих склоны северной и южной экс-
позиции, а также различия в вероятностях успешного
расселения через долину в одном случае и через горный
хребет, разделяющий долины,— во втором. Как будет
показано ниже (разд.6.3.2), информации относительна
характера расселения популяции в целом недостаточна
для понимания поведения расселяющихся особей.
Расселение
103
Пол и возраст расселяющихся особей
Говард и Чайлдз (Howard, Childs, 1959), отлавливая
расселяющихся гоферов Thomomys bottae в специаль-
ные конусы, расположенные вдоль передвигавшейся лов-
чей линии, обнаружили, что все 197 пойманных ими го-
феров были молодыми неполовозрелыми особями. Среди
608 других грызунов, относящихся к 8 видам,-большин-
ство также оказались неполовозрелыми (Howard, 1960).
Коли (Caughley, 1960) исследовал останки 28 тюленей-
крабоедов (Lobodon carcinophaga, совершивших 25-кило-
метровое путешествие по скалам и осыпям в свободную
ото льда долину в Антарктике. Все они также были не-
половозрелыми. Еще несколько аналогичных примеров
явно врожденной склонности к расселению у молодых
птиц и млекопитающих привели Говарда (Howard, 1960)
к выводу о том, что «расселение идет в основном за счет
молодых животных в момент их приближения к полово-
зрелости».
Говард, вероятно, прав — ив том, что касается самого
вывода, и в том, какова причина этого явления. Однако
4 специальных исследования показали, что все-таки
нельзя a priori считать, что расселение данной популя-
ции всегда происходит просто за счет расселения молодых.
Стодарт (Stoddard, 1950) обнаружил, что большинство рас-
селяющихся водяных крыс Arvicola terrestris — это по-
ловозрелые самки, а Тает (Tast, 1966) пришел к тому же
заключению относительно полевки-экономки Microtus
oeconomus. Коли (Caughley, 1970b), определив возрастное
распределение популяции тара на границе области раз-
множения, выявил его аномальный характер, но среди
расселяющихся особей было и несколько половозрелых
самок. Майерс и Кребс (Myers, Krebs, 1971) обнаружили,
что склонность к расселению сильно связана с наступле-
нием половозрелости, однако расселение взрослых осо-
бей также распространено весьма широко.
Генетика расселяющихся особей
Специалисты по гепетике насекомых располагают кое-
какими данными о взаимосвязи между генетикой и рас-
селением (Ford, 1964; Baker, Stebbins, 1965); что же ка-
104
Глаеа 6
сается позвоночных, то исследования по выяснению взаи-
мосвязи между генетическими факторами и склонностью
к расселению практически отсутствуют. Можно надеять-
ся, что статья Майерса и Кребса (Myers, Krebs, 1971)
является лишь первой ласточкой.
Таблица 6.1
Характерные признаки расселяющихся полевок
Microtus pennsylvanicas на четырех стадиях вспышки
численности (Myers, Krebs, 1971)
Рост численности
1. Число расселяющихся особей велико
2. Большая часть убыли животных в контрольной популяции
происходит за счет расселения
3. Расселяются самки фенотипа Tf—С/Е
Приближение к максимуму численности
1. Среди расселяющихся особей молодые самцы составляют лишь
малую часть
2. Значительная часть расселяющихся молодых самцов готовы
к размножению
3. Среди расселяющихся большинство составляют молодые самки
4. Расселяющиеся самцы характеризуются агрессивным поведением
и менее склопны уклоняться от опасности
5. Расселяются самки фенотипа Tf—С/Е
6. Увеличивается отношение численности полов среди расселяю-
щихся животных (самцов больше)
Начало спада численности
1. Расселяются самцы фенотипов Tf—Е и LAP—8
2. Расселяющиеся самцы ведут себя менее агрессивно
3. Расселяющиеся самки весят меньше оседлых
4. Для всей популяции характерно ознакомительное поведение
Спад численности
1. Число расселяющихся особей низко
2. Расселение пе ответственно за смертность популяции
3. Вес тела контрольных и расселяющихся самцов низок
4. Среди расселяющихся особей значительную часть составляют
молодые самки
5. Большинство расселяющихся молодых самок готовы к размно-
жению
6. В популяции в целом у малой доли почти взрослых самцов-,
(subadultus) развиты половые органы
7. Расселяются самцы фенотипа Tf—Е
Расселение
105
Эти авторы исследовали несколько признаков у рас-
селяющихся особей, принадлежащих к двум видам поле-
вок, и сравнили их с признаками у оседлых особей на
четырех стадиях вспышки и спада численности.
В табл. 6.1 суммированы результаты их исследований.
Частоты генотипов в отношении двух полиморфных бел-
ков плазмы — лейцинаминопептидазы (ЛАП) и транс-
феррина (ТФ) — для выборок расселяющихся и оседлых
особей оказались различными. Один из трансферринов
был обнаружен только у расселяющихся самцов. Эти
различия варьировали в зависимости от стадии вспышки
численности. Полученные результаты показывают, что
причины-расселения отдельных полевок непросты, они
кроются в сложном взаимодействии между генетическими
и внешними факторами.
6.2. Определение расселения
Перемещения животных можно подразделить на четы-
ре типа: 1) расселение, 2) локальные перемещения по ин-
дивидуальному участку, 3) кочевничество, 4) миграции.
Установить сам факт перемещения, как правило, доволь-
но просто; гораздо труднее определить, к какому из
типов оно относится. Миграцию можно отличить от рас-
селения посредством мечения новорожденных. Если они,
повзрослев, покидают свою родину, но возвращаются для
размножения, это миграция; если же они и размножа-
ются в другом месте, то это расселение.
Кочевничество представляет собой форму расселения,
однако его трудно отличить от локальных перемещений.
По определению, кочевничество предполагает отсутствие
индивидуального участка, и, следовательно, эти два типа
перемещений можно различить по тому признаку, где
происходит перемещение — в замкнутой или в неограни-
ченной области. Измерение среднего расстояния, на кото-
рое происходит перемещение, само по себе еще не дает
ответа на вопрос, с чем мы имеем дело — с кочевни-
чеством или локальным перемещением. Пространства,
которые покрывают кочующие животные, не всегда больше
территорий, по которым перемещаются оседлые животные.
Поэтому кочевничество должно определяться исходя из
106
Глава в
соотношения между радиусом перемещения и временем.
Кочевые перемещения подобны случайным блужданиям
(разд. 6.3.1), отличительным признаком которых являет-
ся свойство животного оказываться со временем в среднем
все дальше и дальше от места, где оно было впервые обна-
Месяцы между мечением и отловом
Рис. 6.1. Расстояния между точками мечения и повторного отлова
рыжих кенгуру (Frith, 1964).
ружено. Если же перемещение животного ограничено
областью его оседлости, то расстояние от места, где оно
было встречено впервые, до места, где оно встречается
впоследствии, сперва растет со скоростью, пропорцио-
нальной размеру области его обитания, а достигнув этой
величины, стабилизируется и в дальнейшем остается по-
стоянным.
На рис. 6.1 приведены результаты измерения расстоя-
ния между точками, где были помечены и впоследствии
встречались рыжие кенгуру Megaleia rufa, в зависимости
от времени, прошедшего с момента мечения до повторной
встречи. Наклон линии регрессии составляет 0,11 км/мес
и не отличается достоверно от 0 (Р = 0,6—0,7). Таким
Расселение
107
образом, характер наблюдавшихся перемещений свиде-
тельствует о том, что меченые животные не были кочевни-
ками, а перемещались в пределах большой, но все же огра-
ниченной территории.
6.3. Модели расселения
До сих пор мы рассматривали понятие расселения
лишь применительно к отдельным животным. Посмотрим
теперь, как эти перемещения, совершаемые многими жи-
вотными независимо, влияют на пространственное рас-
пределение популяции, и в частности остановимся на ис-
следовании суммарного эффекта естественного и вынужден-
ного расселения, с тем чтобы определить, как эти два типа
расселения влияют на пространственное распределение
популяции.
В случае естественного расселения доля расселяющих-
ся животных не зависит от численности популяции и ее
плотности. Если же расселение вынужденное, то доля рас-
селяющихся особей с ростом плотности будет иметь тен-
денцию повышаться, хотя и не обязательно монотонно.
Воспользовавшись аналогиями из области физики, это
различие можно кратко сформулировать так: естествен-
ное расселение аналогично диффузии, вынужденное —
процессам, происходящим под действием давления. «Рас-
селение под действием давления» не обязательно предпо-
лагает вытеснение расселяющихся особей с их родных
мест; они вполне могут покидать их «по собственному же-
ланию». Однако результат будет таким же, как если бы
они расселялись вынужденно.
6.3.1. Случайные блуждания
Представьте себе тушканчика, свалившегося в узкий
ров и в панике мечущегося взад и вперед. Если он каж-
дую секунду совершает один прыжок длиной в один
метр, а направление прыжков случайно, то мы можем
рассчитать вероятность того, что тушканчик в данный
момент окажется в данном месте. Будем считать точку, в
которой он свалился в ров, точкой отсчета и измерять
108
Глава 6
расстояние от нее в метрах. Таким образом, один метр левее
точки отсчета соответствует минус единице, а один метр
Таблица 6.2
Вероятность того, что тушканчик, совершающий каждую
секунду прыжки длиной 1 м в произвольном направлении,
в данный момент окажется на определенном расстоянии
от точки отсчета
правее — плюс единице. В табл. 6.2 представлено это
распределение вероятностей. Числители дробей образуют
треугольник Паскаля — каждый из них равен сумме
числителей дробей, стоящих в расположенном выше ряду
справа и слева от данной дроби. Вероятности симметрич-
ны относительно точки отсчета, и распределение монотон-
но расширяется, причем дисперсия прямо пропорцио-
нальна времени. Если бы в ров попала сотня тушканчи-
Расселение
109
ков и если бы каждый из них перемещался независимо
от других, мы получили бы то же самое распределение.
Через 5 с примерно 31 = 100 X 10/32 тушканчик ока-
зался бы в одном метре справа от точки отсчета, 15 — в
трех метрах справа и 3 — в пяти метрах справа. Слева от
точки отсчета картина была бы аналогичной.
Эта воображаемая ситуация иллюстрирует характерные
свойства одномерной диффузии:
1. В любой момент времени наиболее вероятным
местонахождением является точка отсчета.
2. Распределение вероятностей симметрично относи-
тельно точки отсчета.
3. Дисперсия распределения растет со временем.
4. Скорость распространения постоянна.
Эти характерные особенности являются наиболее су-
щественными свойствами одно-, двух- и трехмерных
случайных блужданий. Если через точку отсчета провести
любую прямую, то безотносительно к размерности про-
странства, в котором происходит расселение, распре-
деление вероятностей вдоль этой прямой будет иметь
сформулированные выше свойства.
6.3.2. Сложные модели
Рассмотренная нами модель является простейшим при-
мером расселения путем диффузии, и ее следует тщатель-
но проанализировать, прежде чем приступать к модели-
рованию расселения реальных животных. Если в центре
однородного ареала выпущено на свободу несколько жи-
вотных и тем положено начало популяции, то процесс
расселения будет отличаться от рассмотренного выше в
следующих отношениях:
1. Расселяется лишь небольшое число животных.
2. Расстояние, на которое происходит расселение,
разное для разных особей.
3. Поскольку животные размножаются, численность
популяции, а следовательно, и число расселяющих-
ся особей возрастает со временем.
4. Расселение животных по меньшей мере двумерно.
С математической точки зрения такой более сложный
процесс был исследован Фишером (Fischer, 1937), Кендэ-
по
Глава 6
лом (Kendall, 1948), Скелэмом (Skellam, 1951, 1955) и
Пилу (Pielou, 1969 : 129), которые пришли к выводу, что
усложнение мало сказывается на течении процесса: ра-
диус расселения растет со временем линейно.
На рис. 6.2 графически представлены результаты ма-
шинного эксперимента по одномерному расселению попу-
Рис. 6.2. Стохастическое моделирование расселения в процессе
простой диффузии.
ляции. В начальный момент популяция состоит из 10
животных, которые размножаются со скоростью г =
0,1 за Ггод. Каждый год в среднем одно из 10 животных
расселяется в среднем на расстояние 1 км со стандартным
отклонением, равным 0,4 км. Направление расселения
случайно; расселяющиеся особи и направление, в кото-
ром они перемещаются, определяются случайным обра-
зом. На вставке рис. 6.2 изображены зависимости средне-
го радиуса расселения от времени для двух реализаций
машинной модели, результаты обсчета одной из которых
изображены на основной части диаграммы. Регрессия
приблизительно линейна, радиус расселения возрастает
каждые 10 лет примерно в одно и то же число раз. Если
бы рост популяции был не экспоненциальным, а логисти-
ческим, то основной результат остался бы тем же самым:
Расселение
111
радиус расселения увеличивался бы со временем линейно.
Альтернативой диффузионному расселению является
расселение под действием давления. При этом предпола-
гается, что животные расселяются не в случайных на-
правлениях с постоянной скоростью, а начинают рассе-
Рис. 6.3. Расселение вследствие превышения пороговой плотнос-
ти; стохастическая модель расселения популяции (два обсчета) для
случая, когда особи расселяются лишь после того, как локальная
плотность превысит некоторое пороговое значение.
ляться, лишь когда плотность популяции достигнет не-
которого порогового значения, и прекращают расселение
сразу по достижении ближайшего места, где плотность
популяции ниже пороговой.
На рис. 6.3 изображен результатат стохастического
машинного моделирования такого процесса с учетом
пороговой плотности. Исходными являются две одинако-
вые популяции по 10 животных в каждой, размножаю-
щиеся со скоростью г = 0,1 в год. Характер увеличения
ареала популяции, описываемый зависимостью среднего
радиуса ареала от времени, резко отличается от того,
который имеет место при диффузионном расселении
(рис.6.2). Размер ареала сначала почти не увеличивается,
пока плотность популяции в области, где были выпущены
112
Глава 6
на волю перйые животные, не достигнет порогового зна-
чения, а затем радиус популяции увеличивается с постоян-
но возрастающей год от года скоростью, так что зависи-
мость его от времени становится экспоненциальной (Caug-
hley, 1970b.) Эти два примера — простое диффузионное
расселение и расселение после достижения пороговой
плотности — представляют собой два крайних случая
в спектре процессов, посредством которых популяции
увеличивают область своего обитания. Ни один их этих
крайних случаев не является, по-видимому, нормой в
естественных условиях. Простая диффузионная модель
может вполне удовлетворительно описывать движение
молекул газа, однако для анализа перемещения социаль-
ных животных такой механистический подход вряд ли
пригоден. С другой стороны, строго направленное рассе-
ление, принимаемое в модели с пороговой плотностью,
также представляет собой лишь приближение к реальной
ситуации. Трудно себе представить, чтобы животные без-
ошибочно выбирали направление движения к ближайшему
месту с плотностью ниже пороговой, хотя на их переме-
щения вполне могут накладывать отпечаток локальные
градиенты плотности. Общим для обеих моделей является
то, что каждая их них описывает эффекты, обусловленные
лишь одним из типов расселения: естественного рас-
селения в диффузионной модели и вынужденного — в мо-
дели с пороговой плотностью популяции, и не рассматри-
вает никаких процессов, возникающих в результате со-
четания этих двух типов расселения.
Гораздо лучше описывает процесс естественного рас-
селения модель, занимающая промежуточное положение
между этими двумя крайними, случаями. Предположим,
что доля животных, расселяющихся ежегодно, не зависит
от плотности (как в диффузионной модели), однако рас-
селяющиеся особи перемещаются в направлении от места
максимальной плотности (как в модели расселения под
действием давления). Рис. 6.4 иллюстрирует результат
такого процесса, представленный в виде зависимости ра-
диуса ареала от времени при расселении двух модельных
популяций, причем для каждой проведено два машинных
эксперимента. Скорость роста численности каждой из по-
пуляций составляла г = 0,1 в год, а средняя доля еже-
Расселение
ИЗ
годно расселяющихся особей была равна 10%. В первой
популяции среднее расстояние ежегодной миграции при-
нималось равным 2 км, а во второй — 1 км. Несмотря на
заложенную в модели направленность расселения, сред-
ний радиус ареала популяции зависит от времени прибли-
зительно линейно, также как в диффузионной модели.
Рис. 6.4. Стохастическая модель расширения ареала двух популя-
ций (для каждой из них поставлено два машинных эксперимента).
В первом случае расселяющиеся особи преодолевают ежегодно расстояние
2 км, во втором — 1 км. Механизм расселения определяется частично
простой диффузией, а частично популяционным давлением.
По зависимости радиуса ареала от времени дифференциро-
вать данную и диффузионную модели невозможно.
Используя машинное моделирование, легко показать,
что справедливо более общее утверждение, а именно: вне
зависимости от того, расселяется ли ежегодно некая по-
стоянная доля животных или эта доля растет с ростом
плотности популяции, случайно ли направление расселе-
ния или животные расселяются в направлении от локаль-
но го максимума плотности, подчиняется ли рост числен-
ности популяции логистическому или экспоненциальному
закону, радиус ареала растет примерно с постоянной
скоростью, и, таким образом, процесс невозможно отли-
5—334
114
Глава 6
чить от процесса, описываемого диффузионной моделью.
Рассмотренные здесь модели служат яркой иллюстра-
цией трудностей, с которыми сталкиваешься, пытаясь по
данным о динамике ареала популяции определить меха-
низм и характер расселения отдельных особей.
6.4. Типы роста ареала
На рис. 6.5 представлены зависимости, описывающие
расселение двух популяций, которые ведут свое начало
от выпущенных на свободу особей. Первый график отно-
Годы с момента выпуска на свободу
Рис. 6.5. Динамика расширения ареала выпущенных на свободу
ондатр в Европе и гималайских таров в Новой Зеландии (Skellam,
1955; Caughley, 1970b).
сится к распространению ондатры Ondatra zibethica,
завезенной в Центральную Европу в 1905 г. Распростра-
нение ондатры картировалось по данным пяти обследова-
ний па протяжении последующих 25 лет. Второй график
суммирует данные по расселению гималайского тара, за-
везенного в Новую Зеландию в 1904 г., по Южным Аль-
пам. Распространение тара картировалось в 1936, 1946,
Расселение
115
1956 и 1966 гг. В обоих случаях площадь ареала живот-
ных выражалась через радиальные эквиваленты, т.е.
через радиус круга, площадь которого была равна соот-
ветствующей площади расселения по данным картиро-
вания.
Распространение ондатр происходило примерно с по-
стоянной скоростью, из чего был сделан вывод о простом
диффузионном расселении (Skellam, 1951, 1955; Caug-
hley, 1970b). Однако приведенные в разд. 6.3.2 результа-
ты моделирования показывают, что такое лежащее на
поверхности заключение необоснованно. Характер рас-
пространения ондатры явно несовместим и с гипотезой
о расселении при превышении пороговой плотности попу-
ляции, однако зависимость радиуса ареала от времени не
позволяет сделать выбор между простой диффузией и на-
правленным расселением, между процессом, при кото-
ром всегда расселяется постоянная -часть популяции, и
процессом, при котором эта доля растет с ростом плот-
ности, или между различными комбинациями этих про-
цессов, так как в любом из этих случаев радиальный экви-
валент площади ареала растет со временем приблизи-
тельно линейно.
Расселение популяции тара подчиняется, по-видимому,
еще более сложной закономерности. Эта популяция рас-
ширяла свой ареал примерно с постоянной скоростью на
протяжении тех 30 лет, когда велось картирование, одна-
ко экстраполяция этих данных на предшествовавший про-
межуток времени показывает, что до этого скорость рас-
пространения была ниже. Такой характер расселения мог
бы служить свидетельством порогового механизма рас-
селения, если бы не постоянство скорости увеличения ра-
диального эквивалента за каждые 10 лет между 1936 и
1966 гг. Хотя такую динамику можно «объяснить» мно-
жеством различных способов, в отсутствие информации о
поведении отдельных животных все объяснения являются
равноценными (или одинаково бесполезными).
Характер роста радиального эквивалента со временем
мало что дает для понимания механизмов процессов
распространения популяции. Он в состоянии отвергнуть
крайние гипотезы, но не позволяет сделать выбор между
множеством сильно различающихся возможностей.
116
Глава 6
6.4.1. Скорость расширения ареала
Скорость, с которой популяция расширяет область
своего обитания, может быть выражена множеством раз-
личных способов. Здесь используются только два из них.
Если имеются карты границ ареала животных для двух
последовательных моментов времени, скорость распро-
странения в любом направлении может быть определе-
на по кратчайшему расстоянию между новой грани-
цей и заданной точкой на старой. Максимальное из всех
таких расстояний соответствует направлению максималь-
ного распространения популяции, а это расстояние, де-
ленное на время между картированиями, дает максималь-
ную скорость распространения популяции за этот период.
В соответствии со вторым способом средняя скорость рас-
пространения рассчитывается как скорость роста ради-
ального эквивалента ареала (|/площадь ареала /те) за
время между картированиями.
Оба метода имеют свои недостатки. Первый дает оцен-
ку, которая может не иметь ничего общего с процессом
распространения в целом за период между обследова-
ниями, а второй имеет биологический смысл, лишь когда
перемещения животных происходят неограниченно во
всех направлениях. Если ареал популяции ограничен
морем или высокими горами, то популяция, разумеется,
не может распространяться в соответствующем направ-
лении. Средняя скорость распространения в этом случае
представляет собой абстрактную заниженную оценку
скорости распространения в других направлениях. Так
как распространение большинства популяций на некото-
рых участках границы ареала сталкивается с препятст-
виями, первый метод обычно дает более точный критерий
сравнения различных видов. В табл. 6.3 сравниваются рас-
пространения некоторых видов на основе критерия макси-
мальной скорости расширения ареала.
Приведенные данные представляют собой лишь грубые
оценки, их следует понимать не как константы, характе-
ризующие перечисленные виды, но лишь как скорости
распространения за определенный промежуток времени
на определенной территории; скорости распространения
сильно зависят от внешних условий. Тем не менее, вообще
Расселение
117
Скорости расширения ареала
Таблица 6.3
Вид Км в год Источник данных
Европейский кролик 64 Myers, 1970
Лошадь 48 Darwin, 1845
Землеройка 19 Buckner, 1966
Ондатра 15 Skellam, 1955
Хлопковая крыса 12 Cockrum, 1948
Зяблик 11 Kalela, 1949
Первобытный человек 11 Данный раздел
Девятипоясный броненосец 10 Humphrey, 1974
Черный дрозд 9,2 Kalela, 1949
Серна 8,7 Caughley, 1963
Европейский хорек 5,1 Kalela, 1949
Серый кенгуру 4,8 Caughley, не опубл.
Гималайский тар 3,2 Caughley, 1970 b
Благородный олень 1,6 Caughley, 1963
Японский олень 1,6 To же
Белохвостый олень 1,0 »
Лань 0,8 »
Замбар 0,8 »
Замбар 0,6 »
Вапити 0,6 »
говоря, эти оценки позволяют сравнивать различные ви-
ды. Они показывают, что виды отличаются друг от дру-
га по способности к расширению ареала и что эта способ-
ность лишь слабо коррелирует со средней подвижностью
в пределах индивидуального участка. Мало кто мог бы
предсказать, например, что ондатры способны распростра-
няться в несколько раз быстрее, чем белохвостые олени.
Скорость распространения первобытного человека мож-
но определить лишь предположительно, однако, восполь-
зовавшись данными о заселении Северной и Южной Аме-
рики, удается получить кое-какие приближенные оценки.
В археологической литературе приводятся некоторые
оценки времени проникновения человека на Аляску.
118
Глава 6
Они группируются вокруг даты 10 000 лет до нашей эры,
хотя отдельные данные по радиоуглеродному анализу
(достоверность которых, правда, горячо дискутируется)
свидетельствуют о том, что это произошло гораздо рань-
ше. Данные по датировке наиболее древних стоянок перво-
бытного человека на юге Южной Америки относят время
его первого появления там примерно к 8500 году до нашей
эры. Если эти две даты заслуживают доверия, они дают
среднюю скорость распространения, равную И км в год.
Даже если истинная скорость вдвое больше или вдвое
меньше полученного значения, то и тогда это означает,
что скорость распространения первобытного человека
лежит в ряду скоростей, характеризующих и других
млекопитающих. Человек, может быть, и уникальное
существо, но не в отношении скорости своего расселения.
Одичавшие лошади распространяются гораздо быстрее.
Группа лошадей, выпущенных на свободу в районе Буэ-
нос-Айреса в 1537 г., положила начало популяции, гра-
ницы ареала которой достигли Магелланова пролива к
1580 г. (Darwin, 1845: 222); средняя скорость распростра-
нения составила 48 км в год. Что бы мы ни думали о по-
учительности этого прецедента расселения популяции,
трудно удержаться от размышлений о том, сколь быстро
мог бы расселяться вид, объединяющий в себе интеллект
человека и выносливость лошади. С какой скоростью в
действительности стал расселяться человек после того,
как он оседлал лошадь, и как быстро стали расселяться
лошади после того, как они были оседланы? Грубую
оценку можно получить, исходя из скорости распростра-
нения монгольского нашествия, сперва при Чингис-Хане
и потом при его сыне Угедее. Поход на Запад был начат
в 1219 г. и продолжался до 1242 г., когда Батый и Субе-
тай, два блистательных полководца, возглавлявших на-
шествие, отменили поход на Западную Европу, получив
известия о смерти Угедея (Lister, 1969). К этому времени
передовые отряды монгольской кавалерии были на под-
ступах к Вене, в 7000 км от своей родины, лежащей к югу
от озера Байкал. Скорость нашествия была поистине
фантастической—она составляла 300 км в год. Грубо гово-
ря, всадники, расселяются в 6 раз быстрее неосед-
ланных лошадей и в 30 раз быстрее пеших людей.
Глава 7
Плодовитость
Плодовитость самки измеряется числом новорожден-
ных, появившихся у нее за определенный промежуток
времени, обычно за один год. С точки зрения популяцион-
ной биологии плодовитость одной конкретной самки —
величину тривиальная; интерес представляет лишь сред-
няя плодовитость самок каждого возрастного класса.
В популяционном анализе она выражается средним числом
новорожденных самок, приходящихся на одну самку дан-
ного возрастного класса. Полный набор этих значений,
относящихся ко всем возрастам, начиная с новорожден-
ных и кончая самым старшим возрастом, наблюдаю-
щимся в популяции, называется таблицей плодовитости.
Чтобы составить такую таблицу, для каждого возраст-
ного класса матерей необходимо знать среднее число
новорожденных в помете,_среднее число пометов в год и
отношение численности полов у новорожденных.
В зависимости от того, какой из моделей — с круголо-
годичным или сезонным размножением описывается дина-
мика популяции, способы использования таблиц пло-
довитости могут быть различными, поэтому первым шагом
при исследовании плодовитости является определение
средней календарной даты размножения и ее стандартно-
го отклонения.
7.1. Сезон размножения
Смена времен года определяет годовой цикл размноже-
ния в большинстве популяций. Хотя этот цикл не имеет
естественного начала или конца, какое-то произвольное
начало все же необходимо задать, чтобы иметь возмож-
ность делить популяцию на возрастные классы. Наибо-
120
Глава 7
лее удобным «началом» годового цикла является средняя
календарная дата появления новорожденных. В се-
зонно размножающейся популяции возраст всех особей в
популяции без большой потери точности можно считать
равным целому числу лет, отсчитываемому от этой даты.
Большинство опубликованных данных о времени размно-
жения неточно. В этих работах обычно приводится про-
должительность временного интервала, когда появились
новорожденные, и «период пика» рождений. Мой опыт
показывает, что субъективные оценки «периода пика»
дают завышенную оценку средней даты рождений, а
оценки продолжительности времени появления ново-
рожденных мало что говорят о длительности периода раз-
множения. Если нам необходима точная оценка сезона
размножения, то мы должны отказаться от таких рас-
плывчатых понятий, как «пик размножения» или про-
должительность времени появления новорожденных.
Дата рождения должна вычисляться как среднее или
медианное значение по одному или более сезонам,
а длительность периода размножения — как стандарт-
ное отклонение дат размножения от среднего зна-
чения.
Прямой метод
Строгий метод вычисления этих параметров состоит
в том, что сезон размножения делят на равные интервалы
и подсчитывайт число рождений в каждом из них. Этот
метод используется только в том случае, когда популяция
или выборка из нее находится под непрерывным наблю-
дением. В табл.7.1 представлен набор данных, поддаю-
щихся прямому анализу. Они взяты из работы Брэнда
(Brand, 1963), в которой приводятся данные по времени
рождения 103 гималайских таров в зоопарке Претории с
1908 по 1959 г. Эти данные представлены в виде гисто-
граммы числа рождений за каждые полмесяца. Двое
новорожденных — один, родившийся в конце марта,
и другой — в конце апреля — из таблицы исклю-
чены.
Плодовитость
121
Таблица 7,1
Частота рождений тарой в зоопарке Претории за каждые
полмесяца (Brand, 1963)
Половины месяцев Номер временно- го интер- вала X Число ро- дившихся f fx fx*
Октябрь, а 0 0 0 0
Октябрь, б 1 5 5 5
Ноябрь, а 2 22 44 88
Ноябрь, б 3 39 117 351
Декабрь, а 4 17 68 271
Декабрь, б 5 17 . 85 425
Январь, а . 6 2 12 72
Январь, б 7 1 7 49
Февраль, а 8 0 0 0
Sf=103 Sfa=338 2fx*= 1261
Сначала средняя дата рождения и стандартное откло-
нение рассчитываются в масштабе выбранного промежутка
времени:
Средняя дата = —|у~ = = 3,28.
дисперсия = = 1261 —— 3382/103_t 49
(S /) - 1 .102
Поскольку дисперсия рассчитана из данных, сгруп-
пированных по интервалам однаковой продолжитель-
ности, она является слегка завышенной; ее можно скор-
ректировать, вычитая 1/12 квадрата интервала (поправ-
ка Шеппарда для сгруппированных данных), что дает
Дисперсия = 1,49 — — = 1,41,
поскольку интервал в использованном масштабе времени
равен 1. Стандартное отклонение вычисляется как
квадратный корень из дисперсии: $ = 1^1,41 = 1,19.
Теперь можно перейти от исходных полумесячных ин-
тервалов к реальным данным:
122
Глава 7
Средняя дата = 3,28 интервала (один интервал = 15,2 дня) =
= 50 дней после середины нулевого интервала =
= 7 октября 4- 50 дней = 26 ноября.
Стандартное отклонение = 1,19 интервалах 15,2 = 18,1 дня.
Стандартная ошибка = 18,1/1^103=1,8 дня.
Как правило, максимум распределения числа рожде-
ний на протяжении сезона размножения смещен влево,
т.е. частота рождений сначала резко возрастает до мак-
симальной, а затем плавно спадает. В этом случае луч-
шей оценкой середины сезона размножения в популя-
ции является медианное, а не среднее значение даты рож-
дения. На протяжении первого года жизни смертность
более сильно сказывается на позднорожденных, сдви-
гая среднюю дату рождения выживших назад от среднего
значения к медианному. Медианное значение даты рожде-
ния, согласно Симпсону и др. (Simpson et al., 1960), есть
1
l~ —
M = L +-------— ,
/
где L — нижняя граница интервала, на который прихо-
дится медианное значение; i — номер соответствующего
наблюдения в классе и f — абсолютное значение числа
рождений в медианном классе.
Для примера из табл.7.1 имеем
М = 2,5 + (23 — 0,5)/39 = 3,08 интервала = 23 ноября.
Косвенный метод А
Прямой метод применим лишь в том случае, если жи-
вотные содержатся в неволе или если за размножающими-
ся популяциями ведется тщательное наблюдение. Воз-
можности его применения ограничиваются практичес-
кими трудностями оценки доли новорожденных, появ-
ляющихся на свет в последовательные промежутки вре-
мени. Много легче получить оценку числа рожденных к
какой-то конкретной дате, отнесенного к общему числу
новорожденных за весь сезон размножения. По этим дан-
ным можно косвенно оценить статистические параметры,
Плодовитость
123
рассчитанные в предыдущем параграфе. Из рис.7.1 видна
связь между числом рождений за данный интервал, т.е.
величиной, по которой интересующие нас параметры рас-
считаны выше прямым методом, и числом рождений к опре-
Рис. 7.1. Сезонная динамика размножения гималайского тара;
гладкая кривая изображает процент новорожденных, появившихся
к определенной дате, гистограмма — процент новорожденных, по-
явившихся на свет за конкретные промежутки времени (Caughley,
1971а).
деленному сроку, которым можно воспользоваться в
качестве исходных данных для косвенного анализа.
Такого рода данные приводятся в табл. 7.2. Объектом
исследования снова является гималайский тар, но на
этот раз мы имеем данные по популяции животных, сво-
бодно живущих в горах Новой Зеландии. В таблице для
124
Глава 7
пяти дат, приходящихся на сезон размножения, приво-
дится число беременных и кормящих самок, отстрелян-
ных за пятидневные интервалы, серединой которых яви-
лись указанные даты. Кормящие самки дали потомство
до момента отстрела; беременные самки не успели ро-
дить. Таким образом, доля рождений, происшедших к
конкретной дате выборки, равна доле кормящих самок в
выборке за эту же дату.
Таблица 7.2
Число самок гималайского тара, находящихся на различных
стадиях репродуктивного цикла, в различные моменты
сезона размножения (Caughley, 1971а)
Дата День X Log Дня X Число бере- менных Р Число кор- мящих L Сумма В Число рож- денных к да- те 100 L/В в % Пробит, в % У
17 ноября 1 0,00 23 3 26 12 3,83
22 ноября 6 0,78 18 6 24 25 4,33
12 декабря 26 1,41 12 26 38 68 5,47
6 января 51 1,71 2 15 17 88 6,18
31 января 76 1,88 3 49 51 94 6,56
5 февраля 81 1,91 0 34 34 100 —
Все дни выборок пронумерованы, причем за первый
день, естественно, принимается первый день первого от-
стрела. Число рождений к определенной дате в процен-
тах пересчитывается в пробиты по таблицам, приведенным
в работах Финнея (Finney, 1947) и Фишера и Ета (Fis-
her, Yates, 1948). 5 февраля учет был завершен, посколь-
ку к этому времени кончился сезон размножения.
Если число рождений на протяжении соответствующего
сезона подчиняется нормальному распределению, пере-
ход к пробитам переводит сигмоидную кривую числа
рождений к определенной дате в процентах в прямую.
Таким образом, первый шаг анализа — это проверка ли-
нейности зависимости пробита от дня наблюдения X.
Если получившаяся зависимость отклоняется от прямой
вверх, максимум соответствующего распределения числа
Плодовитость
125
рождений сдвинут влево. Такое распределение обычно
можно нормализовать последующим переходом от номе-
ра для выборки X к 1g X, обозначенному здесь через х.
Затем вычисляется регрессия пробита (р) на х:
п = 5
х = 1,156
2 х = 5,780
2 я2 = 9,055
(2ж)2/п = 6,682
SSX = 2 г2 - (2 *)> = 2,373
у = 5,274
2?/= 26,370
2зд = 33,991
(2Ж) (2 УУп = 30,484
SSy = 2 Ху — (2 X) (2 у)/п = 3,507
Из SSX и SSху можно рассчитать наклон линии регрессии
b и точку ее пересечения с осью ординат а:
b = SSxy/SSx = 1,48,
а = у — Ъх = 3,56.
Медианное значение даты рождения рассчитывается по
формуле
,,М“ = (5 —а)/5 =0,97,
но это — значение для номера дня на логарифмической
шкале. Истинное значение медианы равно его антило-
гарифму, т. е. 9, что соответствует 26 ноября.
Стандартное отклонение для распределения числа
рождений задается величиной, обратной наклону линии
регрессии
,,5“ = 1/5 = 0,68 X log (дни).
Оценку истинного значения стандартного отклонения
можно найти по формуле
126
Глава 7
antilog (, ,М' • — ,,§“) — antilog (, ,Ml ‘ + , ,S“) __
s _ _
_ antilog (0,97 — 0,68) — antilog (0,97 + 0,68) _2j
Изложенный здесь метод регрессии представляет со-
бой упрощение более сложного метода, известного под
названием пробит-анализа. В большинстве случаев точ-
ность, которую дает применение простой регрессии,
вполне достаточна, однако если размеры выборок зна-
чительно различаются или нужна максимальная точность,
следует использовать пробит-анализ. Сущность этого ме-
тода изложена в работе Финнея (Finney, 1947). Данные,
приведенные в табл.7.2, представляют собой часть боль-
шей по объему сводки данных (Caughley, 1971а),
отобранную для иллюстрации этого метода. Пробит-ана-
лиз полной совокупности данных дает медианное значе-
ние даты рождения 30 ноября и стандартное отклоне-
ние, равное 18,5 дня.
Для прямого метода анализа необходимо знать час-
тоту рождений за равные промежутки времени. Напро-
тив, изложенный выше косвенный метод требует лишь
суммарной информации об общем числе рождений к опре-
деленной дате. В идеале выборки, представленные в
табл. 7.2, должны были бы составляться по данным от-
стрелов за каждый последующий день. Если же, как в
нашем случае, такой интенсивный отстрел нецелесо-
образен, промежутки между отстрелами должны тем не
менее быть как можно более короткими.
Этот метод допускает большое разнообразие в выборе
постановки эксперимента. По сравнению с прямым ме-
тодом он обладает следующими преимуществами:
1. Промежутки времени, в течение которых произво-
дятся выборки, не обязательно должны непре-
рывно следовать один за другим.
2. Интервалы между выборками могут быть различ-
ными.
3. Число животных в выборке, а следовательно, и
затрачиваемые при этом усилия не обязательно
должны быть одинаковыми.
4. Расчеты числа рождений к определенной дате
Плодовитость
127
(в %) статистически независимы друг от друга.
Недостаток данных за какой-то один период не
смещает медианного значения и стандартного от-
клонения.
5. Не обязательно иметь данные для начала и конца
сезона размножения, что представляет собой явное
преимущество в тех случаях, когда соответствую-
щие даты трудно определить.
В работе Коли и Коли (Caughley, Caughley, 1974)
приводится модификация этого метода, позволяющая
обойтись без отлова или отстрела животных.
Косвенный метод Б
Орнитологи обычно определяют продолжительность
сезона размножения,, подсчитывая несколько раз за се-
зон гнезда с яйцами; на каждый подсчет затрачивается
при этом одинаковые время и силы. Максимум соответ-
ствующего распределения числа кладок по сезону обычно
смещен влево (Davis, 1955). Такое распределение сум-
марного числа гнезд с кладками, последовательно обна-
руживаемых на протяжении йезо на, не совпадает с распре-
делением дат появления новых кладок или дат вылуп-
ления птенцов, хотя часто считается, что это одно и то
же. Средняя дата для распределения суммарного числа
кладок приходится на более поздний срок, чем средняя дата
появления новых кладок, соответствующее распределение
менее асимметрично, чем распределения для дат появ-
ления новых кладок и вылупления птенцов, и характе-
ризуется большей дисперсией, чем они оба.
Распределение суммарного числа кладок можно пре-
образовать в распределение дат появления новых кладок,
если пренебречь вкладом, вносимым в дисперсию про-
должительностью времени насиживания птенцов. Если
подсчеты проводятся через одинаковые промежутки вре-
мени, то результат каждого подсчета можно рассматри-
вать как ординату соответствующего частотного распре-
деления, временной интервал которого соответствует вре-
мени между последовательными подсчетами. Индексы
при среднем значении хп и дисперсии этого распределе-
ния sn2 указывают на то, что эти параметры относятся к
128
Глава 7
распределению общего числа кладок, а не к распределе-
нию дней появления новых кладок. Единицей измерения
времени при этом является промежуток между последо-
вательными подсчетами.
После этого определяется вклад в дисперсию, вноси-
мый временем насиживания птенцов. Пусть время наси-
живания составляет 20 дней, а подсчеты проводятся че-
рез каждые 5 дней. Тогда продолжительность периода
насиживания в наших единицах составит z = 4, а соот-
ветствующий вклад в дисперсию будет равен дисперсии
набора чисел 1, 2, 3, 4, т.е. зг2 = 1,667.
Оценка стандартного отклонения для распределения
дат появления новых кладок в наших единицах времени
задается формулой
Средняя дата появления новых кладок оценивается из
среднего для распределения суммарного числа кладок
и среднего времени насиживания птенцов по формуле
Средняя дата появления птенцов может быть рассчитана
как среднее время появления новых кладок плюс средняя
продолжительность времени насиживания.
Расчет стандартного отклонения для распределения
дат появления новых кладок дает разумную, хотя и слег-
ка заниженную, оценку стандартного отклонения для
времени появления птенцов. Несмещенная оценка пред-
ставляет собой квадратный корень из суммы дисперсии
даты появления новых кладок и дисперсии продолжи-
тельности насиживания. В данном случае дисперсия
2
продолжительности насиживания — это не зг, рас-
считанное выше, а дисперсия по нескольким сезонам раз-
множения. Этот метод можно применять не только для
анализа популяции птиц или рептилий. Он равным об-
разом применим и для млекопитающих. В последнем
случае соответствующими величинами являются доли
беременных половозрелых самок в выборках, произ-
водимых регулярно на протяжении всего сезона беремен-
Плодовитость
129
ности. При этом затрачиваемые на подсчеты усилия не
обязательно должны быть каждый раз одинаковыми.
Данный метод особенно удобен для анализа популяций
мелких млекопитающих, которые приносят несколько
пометов за сезон размножения и к которым не применим
поэтому косвенный метод А.
7.2. Частота рождений
Среднее число пометов, приносимых самкой в течение
года, оценивается в два этапа. На первом требуется оце-
нить среднюю встречаемость беременности на протяжении
той части года, когда можно обнаружить беременных са-
мок. Встречаемость беременности, т.е. доля беременных
самок в данный момент, определяется несколько раз за
этот период времени. Для получения средней встречае-
мости Р эти оценки усредняются. Предположим, напри-
мер, что беременные самки встречаются 5 месяцев в году
и что подсчет производится в каждый из этих месяцев.
Отношения числа беременных самок к их общему числу
составляют 3/30, 24/48, 12/30, 12/40, 7/70. Средняя
встречаемость беременности за этот период равна, сле-
довательно,
Р = (0,1 + 0,5 + 0,4 -J- 0,3 + 0,1)/5 = 0,28.
Р представляет собой невзвешенное среднее; оно не равно
частному от деления суммы числителей месячных отно-
шений на сумму их знаменателей, как это делается при
вычислении взвешенного среднего.
Дэвис и Голли (Davis, Golley, 1963 : 214) показали,
что средняя повторяемость беременности I, т. е.
число раз, которое самка в среднем становится бере-
менной на протяжении года, может быть оценено по Р.
Введем величину D — среднюю продолжительность
видимой беременности — как среднюю продолжитель-
ность периода истинной беременности, в течение которо-
го она может быть обнаружена. Эта величина всегда
меньше продолжительности истинной беременности, по-
скольку обнаружить беременность на ее ранних стадиях
довольно трудно. Рассматривая наш пример дальше,
130
Глава 7
предположим, что мы может выявить беременность лишь
на последнем месяце. Так как беременные самки встре-
чаются на протяжении пяти месяцев в году, D = 1/5 =
= 0,2. Тогда повторяемость беременности можно рассчи-
тать как
7 = PlD =0,28/0,20 = 1,4,
т.е. в среднем самка бывает беременной 1,4 раза в году.
Завышение оценки продолжительности сезона бе-
ременности не влияет на точность определения повторяе-
мости беременности. Предположим, что, оценивая встре-
чаемость беременности, мы провели два лишних обсле-
дования: одно до начала периода течки, а другое — уже
после появления на свет молодняка. Оба обследования да-
дут нулевое значение для встречаемости беременности, а
среднее значение встречаемости беременности, оценен-
ное по периоду продолжительностью 7 месяцев, составит
Р = (0 -J- 0,1 + 0,5 + 0,4 + 0,3 + 0,1 + 0)/7 = 0,2.
При этом средняя длительность видимой бременности
равна
D = 1/7 = 0,143,
откуда
7 = 0,2/0,143 = 1,4,
т.е. мы получаем тот же результат, что и выше.
Строго говоря, I —это не среднее число пометов, при-
носимых в среднем одной самкой за один год, а число по-
метов, которые донашиваются до середины видимого пе-
риода беременности. Если же некоторые эмбрионы абор-
тируются или рассасываются, то I будет завышенной
оценкой среднего числа производимых на свет пометов.
Обычно мы определяем I для того, чтобы составить затем
таблицы плодовитости, в которых указывается числен-
ность потомства, производимого каждым возрастным клас-
сом матерей, а следовательно, и I нужно определять для
каждого возрастного класса. D смело можно считать не-
зависимым от возраста, тогда как Р в различных возраст-
Плодовитость
131
ных классах может быть существенно разным. Соответ-
ственно и выборки для определения встречаемости бере-
менности должны производиться таким образом, чтобы Р
оценивалось для каждого возрастного класса отдельно,
с тем чтобы затем можно было рассчитать значения I для
каждого возраста.
7.3. Соотношение численностей полов
У большинства позвоночных отношение численнос-
тей полов при рождении столь близко к 1:1, что незначи-
тельным избытком самцов можно пренебречь. Если же
предполагается, что численности полов заметно различа-
ются, наблюдаемое значение их отношения должно быть
исследовано с помощью критерия у2.
В табл. 7.3 приведены данные по соотношению полов у
еще не покинувшего материнские сумки молодняка серых
и рыжих кенгуру. Соотношение численностей полов в
Таблица 7.3
Критерий выявления различий в соотношении полов
у детенышей двух видов кенгуру (Caughley, Kean, 1964)
Вид Пол Наблюдае- мое число О Ожидаемое число Е (Р-Н)2 Е р
Рыжий Самцы 202 410/2 3 0,004
кенгуру Самки 208 410/2 3 0,004
410 Х2=0,008 0,95 (с.с.=1)
Серый кен- Самцы 242 420/2 32 4,876
гуру1 Самки 178 420/2 32 4,876
420 7.2=9,752 0,005(с.с.=1)
1 Эта выборка получена в юго-западном Квинсленде. Отношение полов
в выборке из 555 Детенышей кенгуру из Нового Южного Уэльса (Poole, 1973)
существенно не отличается от представленного здесь, тогда как другой ис-
следователь, Киркпатрик, в выборке из 260 детенышей с юга центрального
Квинсленда получил совершенно другое соотношение полов.
132
Глава 7
выборке рыжих кенгуру незначительно отличается от
ожидаемого соотношения 1:1; значение /2 для выборки
серого кенгуру достаточно низко для того, чтобы пред-
положить, что наблюдаемая асимметрия в сторону сам-
цов вполне реальна, а не обусловлена просто ошибкой
выборки.
При использовании соотношения численностей полов
в популяционном анализе эту величину определяют как
долю самок в популяции Pf. Следовательно, для молодня-
ка рыжего кенгуру Pf составляет 0,50, а для серого —
0,42. Стандартная ошибка Pf при этом равна
SE = VPf(i-Pf)/n,
где п — число самцов и самок в выборке. Для серых кен-
гуру
SE = V (0,42 х 0,58/420) = 0,024
и 95%-ный доверительный интервал составляет Pf +
+ 2SE = Pf ± 0,048. Это означает, что если мы имеем
100 выборок по 420 особей, то в 95 из них наблюдаемая
доля самок будет находиться между 0,372 и 0,468.
Иногда соотношение численностей полов представляют
в виде числа самцов на сотню самок. Согласно этому кри-
терию соотношение численностей полов у молодняка се-
рого кенгуру равно (242 X 100)/178 = 136 с 95%-ным
доверительным интервалом, равным ± 200]/Мп/F3 =
= ± 200]/(242 X 420)/1783 = ± 27 (Riney, 1956).
7.4. Таблица плодовитости
Плодовитость животного — это число потомков, про-
изводимых за определенный промежуток времени. Пло-
довитость млекопитающих определяется числом новорож-
денных, а плодовитость рыб, рептилий и птиц — чис-
лом отложенных яиц или икринок или реже числом вы-
лупившихся птенцов или мальков. Поскольку плодо-
витость зависит от возраста животного, полное описание
процесса воспроизведения требует отдельных расчетов
для каждого периода жизненного цикла. Для популяции
с однократным ежегодным размножением в качестве еди-
Плодовитость
133
яичного возрастного интервала выбирается один год, а для
животных, дающих в год более одного помета, единичный
возрастной интервал обычно меньше.
Структура плодовитости популяции изображается в
виде таблиц плодовитости или перечня значений (вектора)
плодовитости, в которых указываются средние плодови-
тости для животных каждого возрастного класса. Ино-
гда составляют две таблицы — по одной для каждого пола.
Для популяционного анализа достаточно одной из них, а
поскольку плодовитость самок легче измерять, то всегда
выбирается таблица плодовитости самок. Как следующее
упрощение из новорожденных учитывают лишь самок. В та-
блицах плодовитости, используемых в популяционном ана-
лизе, перечисляются средние значения числа новорож-
денных самок, приходящихся на одну самку, для каждого
возрастного интервала. Эта величина для сезонно размно-
жающихся популяций обозначается символом тпх, гДе
индекс х обозначает возраст. Так, например, т3 — это
среднее число новорожденных самок, производимых за
сезон размножения трехлетними самками. Аналогичная
величина для круглогодично размножающейся популя-
ции обозначается символом тх,х+1 и представляет со-
бой среднее число новорожденных самок, производимых
одной самкой в возрасте от а: до х + 1. Если за едини-
цу возраста принять один год, то величина ш2|3 будет
означать плодовитость самок в возрасте от 2 до 3 лет.
В табл. 7.4 приведен перечень плодовитости для двух
популяций благородного оленя Cervus elaphus, одна из
которых обитает на острове Рам у побережья Шотлан-
дии, а другая — на крайнем юге Новой Зеландии. Когда
плодовитость выписана таким образом, характер пло-
довитости популяции виден с первого взгляда. Чтобы по-
казать, что общая плодовитость популяции Новой Зе-
лапдии много больше плодовитости оленей, живущих на
Раме, не требуется детального анализа.
При составлении таблиц плодовитости сезопно и круг-
логодично размножающихся популяций используются не-
сколько разные методы. Ниже приводится по одному при-
меру применения каждого из них.
Таблица 7.4
Таблицы плодовитости для двух популяций благородного оленя
(Lowe, 1969; Caughley, 1971b)
Возраст в годах X Число новорожденных самок, приходящихся на одну самку
остров Рам тх Новая Зеландия
0 0,000 0,000
1 0,000 0,000
2 0,000 0,063
3 0,311 0,415
4 0,278 0,400
5 0,302 0,455
6 0,400 0,414
7 0,476 0,486
8 0,358 0,476
9 0,447 0,455
10 0,289 0,500
>10 0,283 0,375
Таблица 7.5
Перечень плодовитостей, рассчитанных для серн
(Caughley, 1970с)
Возраст в го- дах X Численность выборки fx Число беремен- ных или кормя- щих самок Вх Число новорожден- ных самок на одну самку (Bx/2fx) тх
0 — — 0,000
1 60 2 0,017
2 36 14 0,194
3 70 52 0,371
4 48 45 0,469
5 26 19 0,365
6 19 16 0,421
7 6 5 0,417
>7 10 7 0,350
Плодовитость
135
Плодовитость при сезонном размножении
В табл. 7.5 приводятся данные, необходимые для со-
ставления перечня плодовитостей серны Rupicapra ru-
picapra. За сезон деторождения было отстрелено 275
самок в возрасте одного года и старше. Каждое животное
было отнесено к размножающимся или яловым в этом се-
зоне в зависимости от того, было оно беременным или
кормящим или нет. Отношение полов среди новорожден-
ных принималось равным 1:1 и размер помета равным 1.
Плодовитость при круглогодичном размножении
Табл. 7.6 демонстрирует расчет перечня плодовитос-
тей для содержащихся в лабораторных условиях оркней-
Таблица 7.6
Перечень плодовитостей, рассчитанных для оркнейских полевок (Leslie et al., 1955)
Возраст (единич- ный интервал равен 6 неделям1) х,х-}-1 Среднее число самок Число живых детенышей вх,х+1 Число новорожден- ных самок на одну самку (®х,х+1 /2^х,х+1)
0, 1 38,5 30 0,390
1, 2 43,0 114 1,326
2, 3 45,0 135 1,500
3, 4 44,5 137 1,539
4, 5 43,5 142 1,632
5, 6 43,0 142 1,651
6, 7 42,0 145 1,726
7, 8 40,0 139 1,737
8, 9 40,0 94 1,175
9, 10 40,5 86 1,062
10, И 39,0 72 0,923
11, 12 38,0 42 0,553
12, 13 36,5 29 0,397
13, 14 31,0 22 0,355
14, 15 20,0 13 0,325
15, 16 12,5 6 0,240
16, 17 12,5 6 0,240
1 Нулевой возраст равен 9 неделям после рождения.
136
Глава 7
ских полевок Microtus orcadensis. В этих условиях по-
левки размножались на протяжении всего года. Лесли и
др. (Leslie et al., 1955) подробно описали процесс раз-
множения 51 самки. Поскольку некоторые самки иногда
содержались отдельно от самцов, среднее число прини-
мавших участие в размножении самок за каждый дан-
ный промежуток времени могло быть дробным.
7.5. Упрощение таблицы плодовитости
У большинства млекопитающих и птиц по достижении
половозрелости плодовитость сначала резко возрастает,
а затем выходит на плато. «Плато» всегда немного выпукло
Рис. 7.2. Зависимость плодовитости от возраста у домашних овец
(Hickey, 1960).
и его кривизна в разных группах может быть разной.
У мелких млекопитающих и птиц по достижении средне-
го возраста плодовитость уменьшается, тогда как у крупных
млекопитающих отклонения от постоянного значения пло-
довитости у половозрелых особей столь незначительны
(рис.7.2), что для того, чтобы их обнаружить, требу-
ются большие выборки. Для целей популяционного ана-
лиза плодовитость на «плато» можно считать постоянной
и равной ее среднему значению, если только кривизна
плато не слишком велика. Однако, если хотят найти точ-
Плодовитость
137
ную зависимость плодовитости от возраста (например,
при изучении биологии размножения), необходимо иметь
полную таблицу плодовитости.
Среднее значение плодовитости для возрастов, при
которых плодовитость примерно постоянна, может вы-
числяться либо как взвешенное, либо как невзвешенное
среднее. Взвешенное среднее для возрастов, больших
или равных трем годам, вычисляется по формуле
— п3 п4 4- + • • •
w Ns + Ni + N5+---
где п — число новорожденных самок в потомстве N са-
мок данного возраста. Если в выборке нет самок, возраст
которых меньше, чем нижняя граница определяемого
возрастного интервала, определять возраст самок нет
необходимости.
Невзвешенное среднее определяется по формуле
Пз I nt . ге5 .
- _ Ns N< Ns
mu —
c
где с — число возрастных классов, для которых произ-
водятся расчеты. Прежде чем вычислять невзвешенное
среднее, необходимо определить возраст всех самок,
В тех случаях, когда в популяционном анализе ис-
пользуют среднее значение плодовитости, лучше брать
взвешенное среднее. Невзвешенное среднее больше под-
ходит для исследований по биологии размножения и в
тех случаях популяционного анализа, когда возрастное
распределение самок в выборке сильно отличается от воз-
растного распределения в популяции. Иногда та и дру-
гая величины равноценны. Численные различия между
взвешенным и невзвешенным средним зависят от постоян-
ства, с которым сохраняется плодовитость в исследуемых
возрастах. Взвешенное и невзвешенное средние значения
плодовитости, рассчитанные для самок благородного оле-
ня трехлетнего возраста и старше по приведенным выше
данным для популяции юга Новой Зеландии (табл.7.4),
составляют соответственно 0,437 и 0,442; различие столь
мало, что его можно не принимать во внимание.
Глава 8
Смертность
8.1. Демографическая таблица
Зависимость смертности от возраста описывается не-
которой абстрактной, но удобной схемой: смертность опре-
деляется для больших совокупностейодновременно родив-
шихся животных постепенно уменьшающейся числен-
ности. Такая группа одновременно родившихся животных
называется когортой. Хотя реальные когорты
исследуются редко, значения смертности косвенно вычис-
ляются именно для таких воображаемых когорт.
Характер смертности когорт формально представля-
ется в виде таблицы зависимости демографических пара-
Таблица 8.1
Демографическая таблица для самок тара (Caugley, 1966)
Возраст в го- дах X Число до- живших до данного воз- раста fx Выживае- мость 1х Смерт- ность dx Удельная смерт- ность Qx Удельная выживае- мость ?х
0 205 1,000 0,533 0,533 0,467
1 96 0,467 0,006 0,013 0,987
2 94 0,461 0,028 0,061 0,939
3 89 0,433 0,046 0,106 0,894
4 79 0,387 0,056 0,145 0,855
5 68 0,331 0,062 0,187 0,813
6 55 0,269 0,060 0,223 0,777
7 43 0,209 0,054 0,258 0,742
8 32 0,155 0,046 0,297 0,703
9 22 0,109 0,036 0,330 0,670
10 15 0,073 0,026 0,356 0,644
11 10 0,047 0,018 0,382 0,618
12 6 0,029
>12 И
Смертность
139
метров от возраста. Табл. 8.1 является примером такой
схемы для популяции гималайского тара. Сами животные
вполне реальны, тогда как когорты представляют собой
воображаемые образования, поскольку животные не рож-
дались одновременно. Тем не менее таблицы строятся
таким образом, как если бы 205 самок родились в один
день, а затем в каждую последующую годовщину со дня
их рождения регистрировалось число выживших самок.
Таблица состоит из 6 столбцов.
Столбец 1: возраст (х), выраженный в годах.
Столбец 2: число доживших до 1, 2, 3 и т.д. лет из
числа исходных 205 новорожденных.
Столбец 3: переписанный в другом масштабе стол-
бец 2, элементы которого получены делением соответ-
ствующих элементов второго столбца на исходную чис-
ленность когорты (т.е. на 205) и представляют собой,
таким образом, долю животных, доживающих до данного
возраста. Каждое из этих значений обозначается симво-
лом 1Х—вероятность новорожденного дожить по крайней
мере до возраста х — и называется выживаемостью.
Столбец 4: вероятность умереть в возрастном интер-
вале от х до х + 1. Эта величина, обозначаемая как
ах, представляет собой частоту гибели особей и вычисля-
ется как разность между двумя последовательными зна-
чениями 1Х. Хотя величины dx как относящиеся к гибелям
в промежутке между возрастом х и х + 1 логично было
бы писать в таблице на уровне, промежуточном между
этими двумя возрастами, по традиции их выписывают в
строке, соответствующей началу возрастного интервала.
Поскольку первый элемент в третьем столбце всегда равен
1, сумма всех dx равна по определению 1.
Столбец 5: удельная смертность qx означает долю жи-
вотных в возрасте х, погибающих до достижения возрас-
та х + 1. Эти величины равны dХ/1Х.
Столбец 6: удельная выживаемость рх — это доля
животных в возрасте х, доживающих до возраста х -j-1;
Рх = 1—qx-
Демографические таблицы не всегда составляются
именно таким образом. Иногда величины 1Х и dx пред-
ставляют не в виде вероятностей (табл. 8.1), а как число
животных, доживающих до соответствующего возраста,
140
Глава 8
из каждой тысячи, десяти тысяч или ста тысяч животных,
принадлежащих к когорте, если исходно когорта была
достаточно многочисленна. Хотя судьбы тысячи живот-
ных легче зримо представить, чем оперировать с набором
зависящих от возраста вероятностей, при анализе ис-
пользуются именно вероятности. По-видимому, нет смыс-
ла выписывать демографическую таблицу в виде истории
100 животных, если в ходе анализа все равно каждый
элемент в таблице придется переводить в вероятность;
и уж совсем не имеет смысла составлять такие таблицы,
если не использовать их затем для популяционного ана-
лиза.
Демографические таблицы исходно были разработаны
для популяций человека (по-видимому, первая попытка
такого рода была предпринята Дж. Граунтом в 1667 г).
Точные демографические таблицы для человека первона-
чально использовались для расчетов величины страхово-
го полиса при страховании жизни. Следовательно, они
имели еще один столбец, не содержащийся в табл. 8.1,—
ожидаемую продолжительность жизни для каждого воз-
раста. Эти величины дают весьма ценную информацию для
страхования, но мало что добавляют к пониманию попу-
ляционных процессов. Поскольку методы, принятые в
страховом деле, были переняты биологами и иногда не-
критически использовались применительно к другим по-
пуляциям, демографические таблицы для животных часто
содержат столбец ожидаемой продолжительности жизни.
Вычисление ожидаемой продолжительности жизни для
каждого возраста, за естественным исключением е0,
ожидаемой продолжительности жизни новорожденного,
представляет собой пустую трату сил.
Не следует думать, что каждый из 4 параметров таб-
лицы — lx, dx, qx и рх — содержит независимую инфор-
мацию. На самом деле это лишь 4 способа записи одной
и той же информации, позволяющие представить харак-
тер смертности с четырех различных точек зрения. Пере-
счет элементов одного столбца в элементы другого — не
более, чем арифметическое упражнение. В табл. 8.2 при-
водятся алгебраические соотношения между величинами
dx, qx и рх, а на рис.8.1 эти соотношения изображены
графически.
Смертность
141
Таблица 8.2
Соотношения между демографическими параметрами
lx дх рх
1х —G+i 1 (Gr+l/M Ix+tllx
со S dy у—х d-x 8н У l-(dxl 2 dy) y=x
X — 1 П (l-9v) г/=о <7г ’П (1—<7У) г/=о Рх i-Px
х—1 П Ру д=о х—1 (1-Рх) П Ру г/=о 1— Рх Px
2 — сумма, П — произведение.
Выживаемость 1Х
Смертность dx
Удельная смертность qx
Удельная еыживаемостьРх
Рис. 8.1. Графическое изображение зависимости четырех параметров
демографической таблицы от возраста для самок гималайского тара
(Caughley, 1966).
Параметры таблицы используются в разных целях:
1Х применяется почти во всех уравнениях популяцион-
ной динамики; dx особенно удобен при изучении гене-
тических и эволюционных последствий смертности того
или иного характера; дх наименьшим образом подвержен
142
Глава 8
влиянию ошибок выборки, дает непосредственное пред-
ставление о характере смертности и наиболее удобен при
сравнении различных видов и популяций одного вида;
рх используется при расчетах степени эксплуатации по-
пуляций и при моделировании популяционных процес-
сов с помощью ЭВМ.
В. 1.1. Роль возрастной структуры
Факторы, определяющие возрастную структуру по-
пуляции, подробно обсуждаются в следующей главе;
здесь же мы сделаем несколько замечаний вводного ха-
рактера, поскольку возрастные распределения часто ис-
пользуются для расчета демографических таблиц.
Не следует путать два типа возрастного распределения:
«текущее» возрастное распределение для когорты, дающее
долю доживающих до каждого определенного возраста
животных, и «мгновенное» возрастное распределение для
популяции, указывающее численность животных, принад-
лежающих к каждому возрастному классу в опреде-
ленный момент времени, относительно численности ново-
рожденных. Эти два возрастных распределения совпа-
дают лишь в одном случае: если экспоненциальный пока-
затель роста численности популяции равен 0 и к тому же
если он был равен 0 в течение некоторого времени перед
этим, а кроме того, в течение некоторого времени оста-
вались постоянными векторы выживаемости и плодови-
тости; только тогда мгновенное распределение совпадает с
текущим и оба они в равной степени характеризуют струк-
туру популяции. Во всех других случаях эти два распре-
деления различны.
На рис. 8.2 это положение иллюстрируется на некотором
воображаемом примере. Здесь представлена популяция,
ежегодно удваивающая свою численность, причем удель-
ная смертность не зависит от возраста. Соответственно в ло-
гарифмическом масштабе численность когорты со временем
будет убывать линейно. Мгновенное возрастное распре-
деление в каждый момент времени складывается из живот-
ных, рожденных в последний сезон размножения, из одно-
летних животных, принадлежащих к предшествующей
возрастной когорте, двулеток, принадлежащих к когор-
Смертность
143
те, рожденной два года назад, и так далее. Следователь-
но, мгновенное распределение должно отличаться от рас-
пределения для любой когорты, за исключением случая,
когда число новорожденных из года в год остается по-
Возраст , годы
Рис. 8.2. Сплошные прямые — текущие возрастные распределения
последовательных когорт для воображаемой популяции, ежегодно
удваивающей свою численность; пунктирная прямая — мгновенное-
возрастное распределение в момент появления на свет когорты VI.
На рис. 8.2 мгновенное возрастное распределение
представлено в терминах абсолютных численностей воз-
растных категорий, но обычно возрастная структура пред-
ставляется в виде численностей животных различных воз-
растных категорий относительно числа новорожденных.
Это возрастное распределение 5х определяется как
Sx = F X/F о,
где Fх — число животных возраста х в популяции, а
Fo — число новорожденных. Sx обычно оценивается по
выборке как
Sx = f xlffr
где fx и /0 — соответствующие частоты в выборке.
144
Глава 8
Если скорость роста популяции в течение некоторого
времени остается постоянной, то Sx связано с выживае-
мостью соотношением
lx = Sxerx,
или
Sx = lxe'rx.
В табл. 8.3 представлена зависимость возрастной струк-
туры от скорости роста популяции. В ней приведены мгно-
венные возрастные распределения для пяти воображае-
мых популяций с одинаковым вектором выживаемости
1Х и различными скоростями роста.
Таблица 8.3
Зависимость возрастной структуры от скорости
роста популяции
Возраст X Выжива- емость 1х Устойчивое возрастное распределение Sr
г=-0,4 /=—0,2 /=0,0 г=0,2 /•=0,4
0 1,000 1,000 1,000 1,000 1,000 1,000
1 0,700 1,044 0,855 0,700 0,573 0,469
2 0,600 1,335 0,895 0,600 0,402 0,270
3 0,400 1,328 0,729 0,400 0,220 0,120
4 0,100 0,495 0,226 0,100 0,045 0,020
Табл. 8.3 составлена по результатам расчета устойчи-
вого возрастного распределения из соотношения между
вектором выживаемости 1Х и скоростью роста популяции
г. Возможна и обратная операция. Демографическую таб-
лицу можно построить из данных по устойчивому возраст-
ному распределению, если известна скорость роста по-
пуляции г. Соотношение между Sx, 1Х и г справедливо
лишь тогда, когда векторы выживаемости и скорость
роста популяции остаются постоянными достаточно долгое
время для того, чтобы при данных их значениях возраст-
ное распределение приняло устойчивую форму. Воз-
растное распределение всегда стремится к устойчивому
состоянию и остается таковым до тех пор, пока 1Х и г по-
стоянны, безотносительно к тому, положительна, от-
рицательна или равна 0 скорость роста. Распростра-
Смертность'
145
ненная ошибка состоит в том, что скорость роста по-
пуляции считается в течение некоторого времени
равной нулю, если за это время в возрастном распределе-
нии исследуемой популяции не выявляется никаких из-
менений.
Прямым следствием устойчивости возрастного распре-
деления является установление устойчивого распреде-
ления возрастов гибели. Пусть все случаи гибели особей
в популяции за год представлены в виде распределения в
зависимости от возраста, а соответствующее значение для
каждого возрастного класса поделено на общее число жи-
вотных этого возраста, с тем чтобы получить удельную в
отношении возраста величину. Вектор таких величин дает
распределение возрастов гибели, обозначаемое в тех слу-
чаях, когда оно устойчиво, символом Sx. Это распре-
деление совпадает с распределением возрастов гибели в
отдельных когортах (dx) только в том случае, если г =
=0, — обстоятельство, которое нужно иметь в виду, со-
ставляя демографическую таблицу по выборке собран-
ных черепов. Если возрастное распределение устойчиво,
то и распределение возрастов гибели также устойчиво.
Оно связано с распределением смертности в когорте со-
отношением
dx = Sxerx,
откуда
Si = dxe~rx,
что означает, что dx — Sx , только когда г = 0.
Возрастные распределения могут быть разбиты на три
категории: неустойчивые, устойчивые и стационарные;
последняя относится к возрастным распределениям в
популяциях, скорость роста которых равна 0. Устой-
чивое и стационарное возрастные распределения по сути
дела не различаются. Оба опи описываются соотношением
Sx = lxe-rx,
которое при г = 0 сводится к
Sx = 1Х.
6—334
146
Глава 8
Стационарное возрастное распределение — это просто
частный случай устойчивого возрастного распределения;
все стационарные возрастные -распределения устойчивы,
по лишь некоторые из устойчивых стационарны.
8.1.2. Составление демографических таблиц
Сбор данных для демографических таблиц позвоноч-
ных — дело дорогостоящее и трудоемкое. Поэтому ме-
тоды сбора данных и их анализа должны тщательно от-
бираться, чтобы использоваться с максимальной эффек-
тивностью. Прежде чем приступить к сбору данных, био-
лог должен решить, действительно ли демографическая
таблица необходима для решения данной проблемы, и
если это на самом деле так, то как следует организовать
сбор данных, чтобы достичь требуемой точности с наимень-
шими затратами сил. Перечисленные ниже методы в це-
лом охватывают весь спектр используемых методов, хотя
и не исчерпывают всех существующих возможностей.
Метод 1. В группе особей, рожденных за один сезон
размножения, регистрируется число животных, поги-
бающих в последовательные промежутки времени. Зна-
чения смертностей dx получают делением каждого из этих
Таблица 8.4
Расчет демографических параметров по частотам
гибели животных в зависимости от возраста
fx в когорте
Параметры Обозначения Расчет
Возраст Число погибших в каждом возраст- ном интервале от х до х-|-1 Вероятность гибели в интервале от X ДО х+1 Вероятность для новорожденного дожить до возраста х Удельная смертность Удельная выживаемость X f'x dx lx Рх Рх Собранные данные f'x / ^Х Л -1 1— S dx 0 dXHx l-<7x
Смертность
147
чисел на исходную численность когорты. В табл.8.4
приводятся последовательные этапы расчета параметров
демографической таблицы. Этот метод применим лишь к
интенсивна обследуемым природным популяциям или к
животным, содержащимся в неволе.
Метод 2. Численности принадлежащих к опреде-
ленной когорте животных регистрируются через равные
промежутки времени. Разделив эти числа на исходную чис-
ленность когорты, получают выживаемости для соответ-
ствующих возрастов. Дальнейший анализ данных поня-
тен из табл. 8.5.
Таблица 8.5
Расчет демографических параметров по числу животных
в когорте, доживших до различных возрастов
Параметры Обозначения расчет
Возраст X —
Число доживших до определен- ного возраста х fx Собранные данные
Вероятность для новорожденно- го дожить до возраста х lx fxlfo
Вероятность погибнуть в возраст- ном интервале от г до х 1 dx lx — lx+1
Удельная смертность Рх d-х/lx
Удельная выживаемость Рх 1 — Рх
Метод 3. Животные, рожденные в разные годы, ме-
тятся при рождении, затем регистрируется возраст, в
котором они погибают, и вся совокупность данных рас-
сматривается так, как если бы животные принадлежали
к одной когорте. Дальнейший расчет проводится в со-
ответствии с методом 1.
Метод 4. Число животных, принадлежащих к возраст-
ному классу х, сравнивается с числом животных, не до-
живших до возраста х + 1. Число погибших, деленное на
численность возрастного класса в начале интервала, дает
оценку удельной смертности qx. Таким образом, как пра-
вило, составляются демографические таблицы для попу-
6*
148
Глава 8
ляции человека, и этот же метод был использован для до-
машних овец (Hickey, 1960, 1963). Он применим и к
природным популяциям. Предположим, что в два после-
довательных сезона размножения при одинаковых затра-
тах производятся две выборки. Тогда число животных
различных возрастных классов в выборках будет про-
порционально частоте соответствующих возрастных клас-
сов в популяции в момент взятия выборки. Сравнение
численности любого возрастного класса первой выборки
с численностью следующего возрастного класса во второй
выборке дает оценку числа погибших за год, прошедший
между выборками.
Оценка qx для каждого возрастного интервала опре-
деляется из соотношения
___ /г (в момент 0) — /х+1 (в момент 1)
х__jx (в момент 0) ’
которое в свою очередь определяется по формуле
kdxe-rx
х klxe~rx
где постоянные к й е~тх можно сократить. Этот метод ред-
ко использовался при исследовании природных популя-
ций, поскольку очень трудно в двух последовательных
выборках изымать из популяции одну и ту же ее часть, а
небольшое отклонение в численности выборки сильно
сказывается на точности значений вычисляемых парамет-
ров1. Более того, обе выборки должны составлять лишь
очень малую часть популяции, или животные, отловлен-
ные в первой выборке, после изучения должны снова вы-
пускаться на волю в ту же популяцию. Тем не менее
этот метод был успешно использован для популяции бело-
хвостого оленя (Eberhardt, 1969а), а его применение
к популяции благородного оленя будет обсуждаться в
разд. 9.6.
Метод 5. В популяции с устойчивым возрастным рас-
пределением и известной скоростью роста регистриру-
1 Неявно предполагается равная улавливаемость животных
разных возрастов. — Прим. ред.
Смертность 149
ются возрасты гибели всех животных. Эти данные пред-
ставляются в виде распределения частот гибели живот-
ных в зависимости от возраста через равные промежутки
времени, а затем все частоты умножаются на егх. Полу-
ченные данные пересчитываются в значения смертности
dx в соответствии с тем, как это сделано в табл. 8.4. Метод
5 обычно используется в случае, когда скорость роста по-
пуляции считается равной 0, т.е. когда erX = 1 и распре-
деления частот гибели в зависимости от возраста можно
непосредственно пересчитывать в значения смертности
dx. Этот метод впервые использовал Диви (Deevey, 1947)
при расчете демографических таблиц для барана Далля
Ovis dalli. Мури (Murie, 1944) исследовал скелеты бара-
нов в национальном парке горы Мак-Кинли и определял
возраст, в котором погибли отдельные особи, подсчи-
тывая годовые кольца на рогах. Диви, предположив, что
скорость роста равна 0, а возрастное распределение по-
пуляции устойчиво, пересчитал это распределение частот
гибели в значения смертности в зависимости от возраста.
МетгТд 6. Возрастное распределение популяции с
устойчивой возрастной структурой и известной скоростью
роста рассчитывается в момент размножения. Числен-
ность «нулевого» возрастного класса вычисляется исходя
из таблиц плодовитости. Затем численность каждого
возрастного класса умножается на етх и делится на чис-
ленность «нулевого» возрастного класса. В результате
получается таблица значений выживаемости 1Х.
Обычно данные, обрабатываемые таким методом, полу-
чаются на основе выборки самок, взятой в сезон размно-
жения. Хотя раньше этот метод использовался только для
популяций, скорость роста которых предполагалась ну-
левой, здесь его можно проиллюстрировать (табл. 8.6) на
примере данных по растущей популяции, с тем чтобы под-
черкнуть, что г не обязательно должно быть равно 0.
Для использования методов 1, 2 и 3 необходимо мечение
отдельных особей. Идя на постановку такого сложного и
дорогого эксперимента, нужно организовать его таким
образом, чтобы из полученных данных можно было из-
влечь максимум информации. Как наиболее полно исполь-
зовать метод мечения с повторным отловом, обсуждается
в гл. 10.
150
Глава 8
Таблица 8.6
Построение демографической таблицы по устойчивому
возрастному распределению самок тара со скоростью
роста г = 0,12х
Возраст х Число животных в выборке Поправочный множитель егх (г = 0,12) Частоты после коррекции °гх Сглаженные частоты Fx Демогафическая таблица
1х dx чх
0 432 1,00 43,0 43 1,00 0,37 0,37
1 25 1,13 28,3 27 0,63 0,02 0,03
2 18 1,27 22,9 26 0,61 0,03 0,04
3 18 1,43 25,7 25 0,58 0,03 0,05
4 19 1,62 30,8 23 0,55 0,05 0,09
5 11 1,82 20,0 22 0,50 0,05 0,10
6 12 2,05 24,6 19 0,45 0,06 0,13
7 8 2,32 18,6 17 0,39 0,06 0,15
8 2 2,61 5,2 14 0,33 0,06 0,18
9 3 2,94 8,8 11 0,27 0,06 0,21
10 4 3,32 13,3 9 0,21 0,05 0,23
1 Упрощение анализа, проведенного Коли (Caughley, 1970а).
г Нулевая численность оценивается по удельным плодовитостям.
1
I
Методы 1—4 являются более общими, поскольку при
их применении нет необходимости делать какие-либо
предположения относительно скорости роста популя-
ции или устойчивости возрастного распределения. Мето-
ды 5 и 6, напротив, могут использоваться лишь тогда,
когда нам известна скорость роста популяции, а возраст-
ное распределение устойчиво. Практически всегда ско-
рость роста выбранной для исследования популяции в
течение некоторого времени остается близкой к 0. Если
предполагается, что г = 0, то при использовании метода
5 dx = fxI'Zfx, а ПРИ использовании метода 6 1Х =
= fx/f0, где/х и fx — соответственно число гибелей в
интервале между х и х + 1 и число животных в возрасте
х в наших выборках. Хотя методы 5 и 6 могут исполь-
Смертность
151
зоваться только в строго ограниченном числе случаев,
часто они оказываются практически единственным спо-
собом получения данных для демографических таблиц и
поэтому нередко используются при обработке данных, не
удовлетворяющих необходимым требованиям. Ниже пере-
числяются ситуации, когда эти два метода нельзя при-
менять, даже если скорость роста популяции равна 0.
Случаи неприменимости метода 5
1. Когда для получения выборки используется отстрел,
то выборка характеризует возрастное распределение во
всей популяции. То, что собранные животные при этом бы-
ли убиты, никак не сказывается на распределении естест-
венной смертности в популяции; пользоваться в этом слу-
чае следует методом 6, а не 5.
2. Когда число гибелей в зависимости от возраста ре-
гистрируется лишь в местах летнего или зимнего обитания
популяции, полученные данные отражают характер смерт-
ности только в эти периоды и не годятся для составления
демографических таблиц.
3. Когда выборка получена в результате гибели жи-
вотных от таких редких событий, как лавина, наводне-
ние или лесной пожар, опа характеризует возрастное
распределение в природной популяции, и соответствующее
распределение но может быть пересчитано в вектор смерт-
ности dx. Если случайно катастрофа произошла в сезон
размножения или непосредственно до или после него, то
для обработки этих данных может быть использован ме-
тод 6, в случае когда выполняются остальные условия его
. применимости.
4. Если скорость естественного разложения скеле-
тов или легкость их обнаружения зависит от возраста
погибшего животного, то получающееся распределение
возрастов гибели будет смещено и без точного определения
и учета этого смещения нельзя будет получить вектор
смертности dx. Смертность на первом году жизни, оце-
ненная по выборке обнаруженных черепов, обычно бывает
занижена.
5. Если одни животные, имеющиеся в выборке, по-
гибли естественной смертью, а другие — при отстреле,
152
Глава 8
во время лесного пожара или по другим причинам, то
эти данные отражают совместное действие факторов, свя-
занных с характером смертности dx и выживаемости 1Х,
и потому не могут быть использованы для получения ни
вектора смертности dx, ни вектора выживаемости 1Х.
Существует, однако, ситуация, когда сочетание естест-
венной смертности и смертности за счет отстрела позво-
ляет получить данные, вполне пригодные для дальнейшего
анализа. В том случае, когда отстрел занимает значитель-
ное место среди различного рода опасностей, с которыми
постоянно сталкивается популяция, может понадобиться
демографическая таблица,учитывающая все факторы смерт-
ности, в том числе и отстрел. Тогда естественная гибель
и гибель от отстрела могут включаться в одну выборку,
впрочем, только если соотношение числа случаев гибели
от этих двух причин в выборке пропорционально соот-
ветствующему соотношению для естественной популяции.
Получить такую пропорциональную выборку, как прави-
ло, очень трудно, а часто даже невозможно. Когда воз-
раст гибели устанавливается в охотничьих хозяйствах,
то регистрируется большинство отстреленных во время
охоты животных, и немногочисленные данные по естест-
венной смертности тонут среди учетов охотничьих тро-
феев.
При использовании колец, которыми метится боровая
и водоплавающая дичь, задача становится еще более
сложной. Возвращаемые с большой территории на стан-
цию кольца бывают обычно сняты с подстреленных птиц
и лишь очень редко с птиц, погибших естественной смер-
тью.
Даже в тех случаях, когда скелет убитого животного
остается на месте, а охотник довольствуется лишь шку-
рой, рогами или фотографией, организация выборки слу-
чаев естественной гибели и гибели в результате отстрела
в правильной пропорции остается трудным делом. Под-
стреливают животных, как правило, на открытом месте, а
естественной смертью они умирают в потаенных убежи-
щах. Относительное число случаев гибели в результате
отстрела обычно оказывается сильно завышенным при
всех обследованиях, за исключением наиболее тщатель-
но выполненных, и демографические таблицы, построен-
Смертность
153
ные на основе этих данных, могут привести к неверным вы-
водам. Один из таких примеров изображен па рис. 8.3.
На нем приведены две кривые зависимости удельной
смертности от возраста: первая получена по выборке из
черепов 142 таров, из которых одни умерли естественной
смертью, а другие были убиты охотниками. Вторая, более
Рис. 8.3. Зависимость удельной смертности от возраста, рассчитан-
ная для самок гималайского тара двумя разлитыми способами.
Пунктирная кривая рассчитана по выборке собранных черепов, сплош-
ная — по возрастному распределению.
точная кривая была построена на основе возрастного
распределения популяции в сезон размножения и сильно
расходится с первой. Различия в кривых отражают за-
вышение оценки числа погибших от отстрела и относи-
тельно более быстрое естественное разложение черепов
молодняка.
Случаи неприменимости метода 6
1. Популяции с круглогодичным размножением и ну-
левой скоростью роста характеризуются устойчивым воз-
растным распределением, которое может быть эквива-
лентно описано вектором выживаемости 1Х начиная с воз-
раста в полгода. При этом полную демографическую табли-
цу можно составить по возрастному распределению толь-
ко в том случае, если удельная смертность па протяжении
154
Глава 8,
первых шести месяцев жизни оценивается независимо.
2. Ту же самую информацию дают выборки, произво-
димые в сезонно размножающейся популяции в середине
интервала между последовательными сезонами размно-
жения. Возрастное распределение характеризует выжи-
ваемость только начиная с возраста шесть месяцев. Точно
так же невозможно составить полную демографическую
таблицу по выборке, полученной из популяции вследствие
какого-нибудь катастрофического события, если только
катастрофа произошла не в сезон размножения или не-
посредственно до или после него.
3. Выборка, полученная по данным спортивной охо-
ты, в особенности если целью охотников является добы-
ча мяса или трофеев, по-видимому, дает сильно смещен-
ное возрастное распределение, не пригодное для состав-
ления демографических таблиц. Однако эти данные мо-
гут быть использованы для получения таблиц плодови-
тости, на точность составления которых смещение возраст-
ного распределения влияния не оказывает (гл. 7).
В тех случаях, когда возрастные распределения со-
ставляются по результатам отстрела, отстрел должен
производиться опытными охотниками, способными про-
тивостоять естественной склонности стрелять в самых
крупных животных группы, Методы определения такого
рода смещений описаны в работе Коли (Caughley, 1966)
Скрытые опасности на пути применения
обоих методов
•“i7 Если предположения, на которых основываются те
или иные методы, не выполняются хотя бы приблизи-
тельно, пользоваться этими методами не следует. Ско-
рость размножения должна быть известна с разумной
точностью и оставаться примерно постоянной на протя-
жении двух или трех поколений. Колебания скорости
роста г, происходившие незадолго до выборки, исключа-
ют возможность применения метода 6, однако если перио-
дичность этих колебаний много меньше времени, в течение
которого производился сбор черепов, то метод 5 все же
позволяет составлять достаточно точные демографические
таблицы.
Смертность
155
Некоторые из опубликованных демографических таб-
лиц основаны на очень малых выборках. Никакого аб-
солютного критерия для определения минимального раз-
мера выборки существовать не может, поскольку он
зависит от требуемой точности, которая в свою очередь
зависит от того, где и для чего будут затем использоваться
демографические таблицы. В любом случае при исполь-
зовании методов, основанных на возрастном распреде-
лении, таблица, построенная по данным менее чем 150
определений возраста, вряд ли может быть достаточно
точной, для чего бы она ни применялась.
Точность построения возрастного распределения зави-
сит от размера выборки, числа возрастных классов, сме-
щенности выборки и точности определения возраста.
Последнее часто бывает наиболее существенным. Некото-
рые показатели возраста очень изменчивы, и, хотя они
могут быть полезны для разбиения выборки на грубые ка-
тегории, их нельзя использовать для составления демогра-
фических таблиц. Все методы определения возраста, за
исключением мечепия и кольцевания, дают в той или иной
степени смещенную оценку, и в результате возрастные
распределения, построенные с их помощью, являются в
какой-то степени искаженными. Решение вопроса о том,
достаточно ли точен метод определения возраста для того,
чтобы имело смысл составлять демографическую таблицу,
всегда остается на усмотрении конкретного исследова-
теля.
8.2. Сглаживание возрастных распределений}
Демографические таблицы можно строить непосред-
ственно по стационарному возрастному распределению
только в том случае, когда численность каждого возраст-
ного класса х больше или равна численности класса
х + 1. Если это не так, то одно или несколько значений
смертности dx получится отрицательным, что лишено био-
логического смысла. Если изменчивость выборки или ее
смещенность приводит к нарушению этого требования,
то, прежде чем строить демографическую таблицу, сле-
дует сгладить возрастное распределение. Сглаживающая
формула должна обладать двумя свойствами: она дол-
156
Глава 8
жна быть достаточно «гибкой» для того, чтобы можно было
строить кривые, пригодные для описания широкого спек-
тра различных возрастных распределений, и при этом
заранее не должно делаться никаких предположений о
характере зависимости между удельной смертностью и
возрастом. Этим требованиям удовлетворяют две фор-
мулы: логарифмически-полиномиальная и пробит-регрес-
сия, каждая из которых дает кривые, хорошо описываю-
щие большинство возрастных распределений, начиная
с одного года.
Логарифмически-полиномиальная формула имеет вид
log fx = а 4- Ьх ex'2 -f- dx3 + • • ,
где fx — частота встречаемости возраста х в выборке,
a tz, b, с и d — постоянные. Распределение описывают
поэтапно, последовательно добавляя члены все более и
более высокого порядка и оценивая на каждом шагу улуч-
шение точности. Простое объяснение этого метода дано в
работе Снедекора и Кохрана (Snedecor, Cochran, 1967),
и большинство ЭВМ имеют стандартные программы для
этой операции. На первом этапе вычисляется функция
log fx = а + Ьх, удовлетворительно описывающая рас-
пределения, если удельная смертность не зависит от воз-
раста. Если совпадение расчетной и экспериментальной
кривых неудовлетворительно, то гипотеза независи-
мости удельной смертности от возраста отвергается и рас-
считывается регрессия
log/д. = а + Ьх 4- сх3.
Этот процесс повторяется до тех пор, пока добавление
последующих членов пе перестанет заметно уменьшать
сумму квадратов. Мне не встречались возрастные распре-
деления начиная с возраста одного года, для аппроксима-
ции которых логарифмически-полиномиальной зависи-
мостью понадобились бы члены, порядок которых был бы
выше двух.
Квадратичный многочлен представляет собой уравнение
параболы с вертикальной осью. Возрастное распределение
начиная с возраста в один год описывает только правая
нисходящая ветвь, и ось параболы обычно проходит
Смертность
157
близко к этому возрасту. Если почему-либо ось прохо-
дит правее него, кривая уже не годится для описания рас-
пределения, поскольку соответствующие частоты будут
сперва расти с возрастом, а уже затем убывать.
Вторая возможная кривая описывается формулой
. Пробит = а + Ьх1,
где я, b и i — постоянные, рассчитываемые по часто-
там начиная со второго возрастного класса. Расчет ко-
эффициентов в этом случае более трудоемкий, чем при
использовании логарифмически-полиномиальной зави-
симости, поскольку постоянную i приходится определять
методом последовательных приближений. Расчет про-
водят следующим образом:
1. Находят величины fxlfi начиная со второго воз-
раста.
2. Эти величины преобразуют в пробиты (Finney,
1947).
3. Рассчитывают компоненты вектора х1 для I = 0,1.
4. Рассчитывают линейную регрессию пробита
(/x//i) на х1.
5. Найденные значения пробитов начиная с возраста
1 переводят в значения частот соответствующих
возрастных классов, вычисляют средний квадрат
отклонения рассчитанного значения от наблюдае-
мого для каждого возрастного класса и их сумму.
6. Шаги 3, 4 и 5 повторяют для i = 0,2; 0,3; 0,4 и
т.д.,с тем чтобы найти значение г, соответствующее
наименьшей сумме квадратов отклонений между рас-
считанными и наблюдаемыми частотами.
Сглаженные значения частот F х в табл 8.6 рассчитаны
именно таким образом. Этот расчет довольно утомителен,
но результат оправдывает затраченные усилия. Пробит-
кривые позволяют осмыслить распределение частот ги-
бели взрослых особей (т.е. начиная с возраста 1) как ве-
роятностное распределение. Это позволяет глубже по-
нять характер смертности, что не удается при рассмотре-
нии демографической таблицы. Характеристики распре-
деления частот гибели взрослых особей в зависимости от
возраста могут быть получены непосредственно из пара-
метров пробит-кривой; медианное значение возраста равно
158
Глава 8
aV/i
а стандартное отклонение для распределения частот ги-
бели составляет
_1
2
ГМ — a y/t
1Д ъ )
/ 6 — а \1/<
Г b J
Показатель асимметрии распределения задается выраже-
нием —Ini. При Ini = 0 распределение нормально.
Если значение логарифма отрицательно, максимум кри-
вой смещен вправо, а если положительно — влево.
8.3. Разложение удельной смертности
на составляющие
При эксплуатации популяции возникает необходи-
мость в определении удельного веса различных факторов
смертности. Обычно пытаются отделить эффект гибели за
счет охоты от всех других причин смертности, объеди-
няемых под названием «факторы естественной смертности».
Если их и wx — это отношения числа особей возраста
х, погибших в течение года в результате охоты и от естест-
венных причин соответственно, к суммарной численности
данного возрастного класса, a qx — соответствующая сум-
марная удельная смертность, то
qx = ux+wx.
Величины их и wx не являются независимыми. Если
охота запрещена, то значение wx увеличивается, посколь-
ку в отсутствие охоты многие животные из числа тех, ко-
торые были бы отстреляны, теперь рискуют погибнуть по
другим причинам. Таким образом, разложение суммарной
удельной смертности, на их и и>х — не слишком хороший
способ представления ее в виде суммы составляющих, за-
висящих от двух различных причин. Для решения этой
проблемы вводят удельные смертности: hx — отношение
числа животных, которые погибли бы в результате охоты,
если бы от естественных причин животные не погибали вов-
се, к общей численности возрастного класса х и пх — от-
ношение числа животных, которые погибли бы от естест-
Смертность
159
венных причин в отсутствие охоты, к общей численности
возрастного класса х. Эти величины означают соответ-
ственно «изолированную» удельную смертность вслед-
ствие охоты и «изолированную» естественную удельную
смертность. Они связаны с суммарной удельной смерт-
ностью соотношением
Qx = hx “Ь ПХ ^ХПХ1
которое можно также записать в виде
Рх = (1 - Ю (1 - пх).
Рикер (Ricker, 1958) отмечает, что при использовании
этого выражения нет необходимости предполагать, что
соотношения между изолированными удельными смерт-
ностями остаются неизменными в течение всего года.
Удельные смертности hx = 0,5 и пх = 0,5 дают суммар-
ную удельную смертность qx = 0,75 вне зависимости от
того, как действуют оба фактора смертности — одновре-
менно или последовательно. Для реальных удельных
смертностей их и wx этого утверждать нельзя.
Предположим, что мы хотим далее разложить смерт-
ность в результате охоты на компоненты, определяемые
спортивной и профессиональной охотой. Обозначим изо-
лированную удельную смертность за счет спортивной охо-
ты символом gx, а за счет профессиональной охоты — сим-
волом hx. Тогда
рх = (1-?х)(1-/»х) (1-««)••
Перейдя к qx = 1— рх, получим
Qx = Sx + hx + ПХ - Sxhx — gxnx — hxnx + SxhxKx •
Аналогичные уравнения могут быть выписаны для любо-
го числа факторов смертности.
8.4. Зависимость смертности от времени года
При решении большинства задач пользуются демогра-
фическими таблицами с возрастным интервалом, равным
одному году. Однако в отдельных случаях необходимо
исследовать смертность более детально, в частности опре-
160
Глава 8
делить ее в различные времена года. Ход сезонной измен-
чивости смертности лучше всего определять путем еже-
месячного учета всех случаев гибели животных па обсле-
дуемой территории. Затем от этих данных можно перей-
ти к удельной месячной смертности с помощью метода, в
равной мере применимого к популяциям с круглогодич-
ным и ежегодным сезонным размножением. В приводи-
мом в табл. 8.7 примере используются подсчеты числа
погибших взрослых куропаток, полученные при обследо-
вании некоторой территории в Шотландии (Jenkins,
Watson, 1962). В таблице сведены вместе данные этих
авторов за 1957—1958 и 1958—1959 гг., а для того чтобы
проиллюстрировать метод анализа, я произвольно пред-
положил, что годовая удельная смертность взрослых осо-
бей составляет 40%.
Таблица 8,7
Анализ сезонной изменчивости удельной смертности
шотландских куропаток (данные из работы Jenkins,
Watson, 1962)
Месяц т Число погиб- ших fm Оцененная числен- ность г т Удельная смертность fm/Fm Удельная выживаемость ‘-Ол)
Июль 14 1160 0,012 0,988
Август 9 1146 0,008 0,992
Сентябрь 17 1137 0,015 0,985
Октябрь 17 1120 0,015 0,985
Ноябрь 42 . 1103 0,038 0,962
Декабрь 92 1061 0,087 0,913
Январь 37 969 0,038 0,962
Февраль 64 932 0,069' 0,931
Март 57 868 0,067 0,933
Апрель 46 811 0,057 0,943
Май 50 765 0,065 0,935
Июнь 19 715 0,027 0,973
S = 464
П = 0,600
Смертность
161
Анализ проводится следующим образом:
1. Записывают число взрослых погибших особей, об-
наруженных в течение месяца, начиная с месяца, следую-
щего за сезоном размножения.
2. Делят общее число обнаруженных погибших птиц
(464 в данном случае) на годовую удельную смертность
взрослых особей (0,4). В результате получают теорети-
ческую численность популяции взрослых особей в пред-
шествующий сезон размножения. Выписывают это зна-
чение (1160) в первой строке таблицы.
3. Последовательно вычитают из теоретической чис-
ленности популяции число ежемесячно погибавших осо-
бей и выписывают результаты в соответствующих строках
таблицы.
4. Делят числа особей, погибавших каждый месяц,,
на теоретическую численность популяции в этот месяц;
при этом получают значения удельных месячных смерт-
ностей.
5. Вычитают каждое из значений удельной месячной?
смертности из единицы и получают таким образом зна-
чения удельных месячных выживаемостей.
6. Проверяют расчет, перемножив все значения удель-
ных месячных выживаемостей. Полученный результат в
сумме с годовой удельной смертностью, использованной
на этапе 2, должен дать единицу.
8.5. Характерные зависимости смертности
от возраста
Млекопитающие
В 1966 г. Коли (Caughley, 1966) суммировал всю имею-
щуюся информацию по зависимости смертности от воз-
раста у млекопитающих и пришел к выводу, что, как пра-
вило, эта зависимость имеет U-образную форму. Демо-
графические таблицы для некоторых млекопитающих,
опубликованные после 1966 г., подтвердили это заклю-
чение. Удельная смертность до достижения половозре-
лости в разных популяциях одного и того же вида может
сильно варьировать. Человек в этом отношении не явля-
ется исключением. По моим оценкам, проделанным в
162
Глава 8
1968 г., в горах Непала смертность до достижения полово-
зрелости составляла примерно 70%, в то время как в
Канаде она составляет примерно 3% (ВОЗ, 1972). Удель-
ная смертность взрослых особей у млекопитающих варь-
ирует в гораздо меньшей степени. По сравнению с коле-
баниями смертности до достижения половозрелости из-
менения от года к году удельной смертности взрослых
•особей являются лишь небольшой добавкой к колеба-
ниям скорости роста численности популяции.
Птицы
Превосходный обзор зависимостей смертности от воз-
раста у птиц опубликован Фарнером (Farner, 1955). Каж-
дый исследователь, интересующийся этим вопросом, дол-
жен полностью прочесть его. Демографические таблицы
для птиц с трудом поддаются истолкованию по двумя при-
чинам.
1. В первых работах в этой области (Nice, 1937; Kraak
et al., 1940; Lack, 1943 a, b, с ) выявилась тенденция к
независимости удельной смертности от возраста. Хотя
эти данные были немногочисленными и точность их не
контролировалась, они послужили основой для появле-
ния гипотезы о постоянстве удельной смертности вне за-
висимости от возраста. Так уж повелось в истории орни-
тологии, что гипотезы не рассматриваются как утвержде-
ния, подлежащие дополнительному изучению и проверке.
Они просто принимаются, сначала как вывод, затем —
как принцип и наконец — как аксиома. В настоящее
время многие исследования смертности у птиц исходят
из аксиомы о том, что удельная смертность после первого
года жизни остается постоянной. Постановка опытов и их
последующий анализ основываются в той или иной сте-
пени на аксиоме, что гипотеза постоянства удельной смерт-
ности взрослых особей не требует дополнительных обос-
нований.
2. Почти все исследования смертности основаны на
кольцевании, а кольца легко теряются. Меры, прини-
маемые против утери колец, в разных исследованиях раз-
личны. В некоторых случаях сношенные кольца заме-
няются новыми при повторном отлове птиц, но в больший-
Смертность
163
стве случаев на это просто не обращают внимания
и удельная смертность рассчитывается так, как если бы
никаких потерь колец не происходило. Я не знаю ни одной
работы, в которой бы аккуратно учитывались потери ко-
лец и демографические таблицы составлялись с по-
правкой на это обстоятельство.
Такая поправка приводится в гл.10, но в данный мо-
мент нас интересует вопрос, искажаются ли демографи-
ческие таблицы вследствие потери колец. Этот вопрос мож-
но исследовать с помощью простой модели, в которой
частота потери колец исходно невелика, но непрерывно
растет со временем, истекшим с момента кольцевания.
Если скорость потери колец на первом году после кольце-
вания равна А и увеличивается год от года в е1 раз, то
скорость потери на if-м году после кольцевания составля-
ет Aeli. От общего числа окольцованных птиц через
t лет кольца сохранит лишь часть, равная
р4 = П(1-^/у)-
!/=0
На рис. 8.4 эта модель изображена графически. «Кажу-
щаяся» удельная смертность рассчитывается по числу
а
§ 0,5
ъ_!_____- 1 .-J_______I______L
0 3 _ 6 9 12
Возраст, годы
Рис. 8.4. Возможное влияние потери колец на расчет зависимости
смертности от возраста (см. текст).
Светлые кружки — действительная смертность, темные — кажущаяся.
164
Глава 8
-обнаруженных погибших птиц и составляет 0,45 в год.
«Действительная» удельная смертность вычисляется на
основе предположения, согласно которому на первом
году жизни в когорте теряется один процент колец, а
затем число потерянных колец каждый год увеличивает-
ся в е°’3раз. Характер зависимости «кажущейся» и «дей-
ствительной» удельной смертности от возраста совер-
шенно различен. Этот результат не может служить дока-
зательством ни того, что внешне постоянная удельная смер-
тность в действительности характеризуется U-образной
зависимостью от возраста, ни того, что параметры моде-
ли соответствуют действительности, ни даже того, что мо-
дель правильна сама по себе. Но не в этом дело. Модель
строится для того, чтобы показать, что утеря колец может
исказить показатели смертности и что демографические
таблицы, построенные на основе данных по возвращенным
кольцам без учета потерь колец, должны восприниматься
с разумным скептицизмом.
Несмотря на все эти трудности, можно сделать не-
сколько обобщений. По-видимому, действительно у птиц
удельная смертность зависит от возраста меньше, чем у
млекопитающих. Это ясно показывают составленные Рич-
дейлом (Richdale, 1954) демографические таблицы для
желтоглазого пингвина, не основывающиеся на данных
о возвращении колец. Различие между удельной смерт-
ностью до достижения половозрелости и сразу после ее
достижения у птиц, вероятно, также меньше, чем у мле-
копитающих.
Рыбы
Наблюдающееся у большинства промысловых популя-
ций рыб убывание с возрастом численности возрастных
классов соответствует постоянству удельной смертности
после достижения половозрелости. Однако данные по по-
пуляциям, не являющимся объектом промысла, или лишь
слабо облавливаемым популяциям (Ricker, 1949; Ken-
nedy, 1953, 1954; Wohlschlag, 1954; Tester, цитирую по
Ricker, 1958) показывают, что в этих популяциях рыбы
-старших возрастов характеризуются более высокой удель-
ной смертностью, чем рыбы среднего возраста.
Смертность
165
г Земноводные и пресмыкающиеся
I Полные демографические таблицы не опубликованы
ни для одного вида лягушек. Наилучший материал для
построения таких таблиц дают возрастные распределения
по претерпевшим метаморфоз бесхвостым земноводным.
Однако наиболее полные из них, а именно данные по
Bombina bombina (Банников, 1950), Pseudacris brachi-
phona (Green, 1957) и Rana pretiosa (Turner, 1960a, 1962),
выявляют весьма необычную^картину. Если по этим дан-
ным построить кривые выживаемости, то окажется, что
у половозрелых особей Bombina удельная смертность
убывает с возрастом, у Pseudacris она не зависит от воз-
раста, а для Rana результаты, полученные по данным за
несколько последовательных лет, сильно разнятся от года
к году. Эти явные различия не обязательно свидетель-
ствуют о существовании значительных различий в ха-
рактере зависимости удельной смертности от возраста
между разными родами бесхвостых амфибий. Скорее все-
го дело здесь в неточности определения возраста и в из-
менчивости скорости роста популяции. В каждом из пере-
численных случаев возрастное распределение строилось
непосредственно по распределению размеров особей, а
этот метод приводит к искажению кривых выживае-
мости, пропорциональному изменчивости размеров в дан-
ном возрасте.
Орган (Organ, 1961) рассчитал кривые выживаемости
по возрастным распределениям пяти видов саламандр
рода Desmognathus. Эти кривые значительно отличаются
друг от друга даже в рамках отдельных видов, но данные,
сведенные воедино, свидетельствуют о том, что удельная
смертность растет с возрастом.
До недавнего времени полных демографических таб-
лиц для пресмыкающихся не существовало. Однако за
последние несколько лет, по-видимому в результате сти-
W мулирующего воздействия пионерских работ Типкла
£ (Tinkle, 1967, 1973), герпетологи интенсивно разрабаты-
вают такие таблицы. Оказывается, что характер зависи-
2^ мости Удельной смертности от возраста у пресмыкающихся
Ж: примерно такой же, как у млекопитающих: высокая
«£ удельная смертность на первом году жизни, меньшая на
166
Глава 8
втором году и затем последовательно растущая с каждым:
годом. В качестве характерного примера можно привести
данные по удельной смертности в популяции Sceloporus-
graciosus за первые четыре года жизни: удельная смерт-
ность составляет 0,77; 0,38; 0,47 и 0,55 соответственно
(Tinkle, 1973), большинство ящериц погибают молодыми.
Тинкл (Tinkle, 1967) показал, что треть ящериц Uta
stansburiana, умирающих на первом году жизни, поги-
бают в первую же неделю.
8.6, Неправильное понимание демографических
параметров
Потенциальная продолжительность жизни
В большинстве работ по популяционной экологии про-
слеживается некоторая явным образом не высказанная
точка зрения на смертность. Считается, что смертность —
это событие, которое должно в свой черед произойти по
достижении некоторого заранее предопределенного сро-
ка; смерть до достижения этого возраста — это роковое
(в средневековом смысле слова) стечение обстоятельств.
Из такого взгляда на смерть проистекает «концеп-
ция потенциальной продолжительности жизни» как воз-
раста, которого могли бы достичь все члены популяции,
если бы не внешние причины (в особенности см. Boden-
heimer, 1958). Характер смертности в популяции рас-
сматривается при этом как результат сочетания двух фак-
торов: присущей животным неспособности оставаться »
живых по достижении определенного возраста и проти-
водействия (враждебности) среды, обрывающей многие*
жизни до достижения отмеренного срока.
Яспо, что продолжительность жизни отдельного жи-
вотного — это промежуток времени между его рождением
и его смертью. Таким же точным является определение
средней продолжительности жизни особи в популяции1
1 Средняя продолжительность жизни — это предполагаемая
средняя продолжительность жизни новорожденных при условии,
что повозрастная смертность (т. е. число умерших на 1000 особей
определенного возраста) на всем протяжении жизни данного поко-
ления будет такой же, как в год рождения. — Прим. ред.
Смертность
167
или предполагаемой средней продолжительности жизни
новорожденных, но эти понятия ничего не говорят нам о
том, сколько может прожить, скажем, слон. Спрашиваю-
щий хочет получить ответ на вопрос о потенциальной про-
должительности жизни, но правильно на него можно от-
ветить лишь следующим образом: такого возраста не су-
ществует. Тогда часто следует какая-нибудь вариация
контрвопроса: «Неужели вы думаете, что животное может
прожить тысячу лет?» Этот вопрос не имеет отношения к
делу, поскольку он уводит в сторону от понятия потен-
циальной продолжительности жизни — возраста, до ко-
торого животное данного вида может дожить в исключи-
тельных условиях, но сверх которого оно жить не может.
Животное заведомо не может прожить тысячу лет или
жить бесконечно, однако у нас нет никаких оснований
устанавливать предельный возраст ниже этого значения.
Если бы такой возраст существовал, мы бы очень прос-
то это обнаружили. Он выявлялся бы в виде перегиба на
диаграмме зависимости удельной смертности от возраста,
в особенности для содержащихся в певоле популяций, жи-
вущих в условиях, близких к оптимальным. Однако даже
наиболее точные демографические таблицы, составленные
для человека и домашних животных, не обнаруживают ни
малейшего намека на существование фиксированной по-
тенциальной продолжительности жизни или средней по-
тенциальной продолжительности, сопровождающейся не-
которым разбросом.
«Потенциальная продолжительность жизни» — это в
корне неправильная концепция. Опа должна быть заме-
нена вероятностным утверждением: животные не живут
бесконечно долго не потому, что они физически не могут
преодолеть некоторый пороговый возраст, но потому,
что вероятность его преодоления даже при постоянном
риске гибели становится исчезающе малой. Данное ут-
верждение не следует рассматривать как дань математи-
ческой софистике. По-видимому, это более точная аппрок-
симация для биологической реальности, чем модель,
включающая понятие порогового возраста. Пороговые
эффекты в биологических системах встречаются очень
редко, и никаких данных, говорящих о необходимости их
введения в модель смертности, не существует.
168
Глава 8
Предполагаемая продолжительность жизни
Предполагаемая продолжительность жизни — это
средний возраст гибели членов одной когорты; хотя это
определение вполне однозначно, его, как правило, пони-
мают неверно.
Предполагаемая продолжительность жизни в Мабута
равна 30 годам. Это не означает ни того, что жители
Мабута умирают между 25 и 35 годами, ни того, что в
Мабута мало стариков, ни того, что 50-летние жители
Мабута физиологически старше своих ровесников в Ка-
лифорнии; это свидетельствует только о том, что в Мабута
высока детская смертность. Когда в результате развития
общественного здравоохранения снизится детская смерт-
ность, предполагаемая продолжительность жизни возрас-
тет. Такой рост есть просто арифметическое следствие
снижения детской смертности; он не зависит от того, сни-
жается ли также смертность взрослых.
Заблуждения, связанные с понятиями «потенциальной»
и «предполагаемой» продолжительности жизни, могут
кое-чему научить. Затруднения, с которыми мы сталки-
ваемся, встречаясь с первым понятием, показывают, что
термины, используемые при описании смертности, дол-
жны быть строго определены. В противном случае мы
скатываемся к метафизике. Второй случай показывает,
что описание смертности одним параметром может при-
вести к неправильному пониманию того, что в действи-
тельности происходит в популяции.
8.7. Представление демографических таблиц
в сжатом виде
Для решения той или иной проблемы зачастую не
требуется полной демографической таблицы, а еще чаще
такая таблица является заветной целью, достичь которой
не удается в связи с трудностями практического характе-
ра. Иногда при составлении детальной демографической
таблицы с самого начала оказывается, что в дальнейшем
можно ограничиться несколькими возрастными классами.
В каждом из этих случаев составляют сжатую демогра-
фическую таблицу, а насколько она сжата, зависит от
Смертность
169
того, для чего будет далее использоваться таблица. В де-
мографических таблицах для человека данные обычно
суммируются по пятилетним интервалам; таким же объ-
единением данных можно воспользоваться и для других
видов с низкой удельной смертностью взрослых особей.
Однако чаще данные суммируются по возрастным ин-
тервалам различной продолжительности, каждый из ко-
торых объединяет в себе возрасты, в некотором смысле
одинаковые. Как правило, это деление на «молодых»,
«годовиков» и «взрослых» или даже просто «молодых» и
«взрослых». Смертность для каждого интервала задает-
ся как средняя годовая смертность в данном возрасте.
Удельную смертность для молодых и годовиков можно
взять прямо из демографической таблицы, это q0 и q х
соответственно. Для взрослых же особей ее рассчитыва-
ют подформуле
х=2
где 92,оо — средняя взвешенная годовая удельная смерт-
ность по всем возрастам, начиная с двух лет. Если взрос-
лые далее подразделяются на «зрелых» (скажем, в воз-
расте от 2 до 10 лет) и «старых» (в возрасте старше 10 лет),
соответствующие удельные смертности могут быть рас-
считаны по формулам
^2 ~Ь ^3 ^4 ~Ь ‘ • 4-^9
___ «2 ~Г ц3 ~т~ ц4 т • Т“|
2’ 10 ^2 + h + Ц + ’ • ’ + ^9
— ^10
910,0=“ ll° 2 lx\
x=10
Средняя взвешенная удельная смертность для популя-
ции в целом дает долю животных, погибших между дву-
мя последовательными сезонами размножения, от всех
животных, доживших до первого из этих сезонов:
? = 2^/2^-",
170
Глава 8
что сводится к соотношению
Q =
когда популяция стационарна. Последнее уравнение ма-
тематически эквивалентно более сложной формуле, ис-
пользуемой в орнитологии, где q, обычно обозначаемое
символом Mw, рассчитывается из числа смертей D в
когорте в первом, втором, третьем и т. д. возрастных ин-
тервалах:
jjf = ^1 + ^2 + Д3 +
Z>i + 2D2 -|- 3D3 + 4D4 + • • •
q является более точной мерой удельной смертности по-
пуляции, чем «время обновления». Этим термином обознача-
ется время, необходимое для естественной замены всех
особей в популяции. «Время обновления» и его модифика-
ции, «время 95%-го обновления» и «время 90%-го обновле-
ния», используются в исследованиях, посвященных управ-
лению природными ресурсами. Однако эта величина обла-
дает лишь некоторыми достоинствами удельной смерт-
ности q и рядом собственных недостатков.
Методы, использующие относительные величины
Существуют многочисленные формулы (Kelker, 1949,
1950, 1952; Robinette, 1949; Petrides, 1954; Selleck, Hart,
1957; Hanson, 1963; Kelker, Hanson, 1964) для оценки об-
щей смертности и смертности за счет охоты для различ-
ных частей популяции. В них входят доли молодняка,
годовиков и взрослых особей в выборке. Многие из этих
методов дают удельную смертность в одной части популя-
ции по отношению к удельной смертности в другой части
популяции, а не в виде абсолютного значения. Зачастую
полученные результаты имеют весьма отдаленное отно-
шение к большинству практических или теоретических
задач. Подавляющая часть этих методов основана на не-
явном предположении, что популяция обладает устой-
чивым возрастным распределением, соответствующим ну-
левой скорости роста. Таким образом, с их помощью нель-
зя проследить изменение удельной смертности от года^к
Смертность
171
году. Среди различных методов, основанных на относитель-
ной численности различных возрастных классов, для оцен-
ки удельной смертности могут быть рекомендованы только
два, и то лишь при определенных условиях. Один из них
(метод Келкера) обсуждался в разд. 4.2.4, поскольку глав-
ным в этом методе является оцепка плотности, а оценка
смертности носит вспомогательный характер. Второй ме-
тод дает грубую оценку q для популяций, близких к ста-
ционарному состоянию. Если j — число новорожденных
во взятой в сезон размножения случайной выборке об-
щей численностью п, то
Предполагаемая продолжительность жизни для новорож-
денных
Когда эти формулы применяются к данным, полученным
на популяциях с непрерывным круглогодичным размно-
жением, q является оценкой удельной смертности на про-
тяжении первых шести месяцев жизни, а е0 — оценкой
предполагаемой продолжительности жизни для этих жи-
вотных. Вывод формул и примеры их применения приве-
дены в работе Коли (Caughley, 1967b).
8.8. Применеиие демографических таблиц
Для эколога основное значение демографических таб-
лиц заключается в том, что они отражают стратегию,
используемую популяцией для выживания. Эколога
интересуют демографические механизмы, посредством ко-
торых скорости вымирания особей и рождения новых по
прошествии достаточно большого периода времени урав-
новешиваются и средняя скорость роста численности
популяции поддерживается равной 0. Попытки решения
этой проблемы можно найти во многих работах (Cole,
1954; Lewontin, 1965; Murdoch, 1966; Holgate, 1967;
Frank, 1968; Murphy, 1968; Reddingius, den Boer, 1970;
Meats, 1971).
172
Глава 8
Эколог также должен знать, как изменяется структу-
ра смертности популяции за сравнительно небольшие
времена в ответ на флуктуации внешних условий. Па-
радоксально, что и в том случае, когда цель состоит в
понижении численности популяции, и когда требуется
стимулировать рост численности, эколог должен обна-
ружить наиболее слабое звено в жизненном цикле. Имен-
но на эту фазу жизненного цикла следует оказывать воз-
действие и в том случае, если требуется подавить попу-
ляцию, и в том, когда целью является охрана популяции.
Ахиллесовой пятой популяции обычно является возраст-
ной класс, обнаруживающий максимальную изменчи-
вость удельной смертности, или плодовитости, или соче-
тания этих параметров от года к году. Такой класс уда-
ется идентифицировать только при последовательном срав-
нении за несколько лет векторов смертности и плодови-
тости. Возможности этого метода были убедительно про-
демонстрированы в исследованиях канадских ученых по
еловой листовертке-почкоеду (Morris, 1957, 1963).
Менее эмпирический вариант такого подхода состоит
в предсказании реакции популяции на заданную совокуп-
ность обстоятельств посредством моделирования дина-
мики популяции. Изменение численности популяции во
времени рассчитывается обычно с помощью ЭВМ для
различных начальных возрастных распределений (см.,
например, Niven, 1970) или для различных вариантов
векторов плодовитости и выживаемости, постоянных или
меняющихся со временем (например, Lefkovitch, 1967;
MacArthur, 1968). Такие имитационные модели особен-
но полезны при оценке влияния избирательного в отно-
шении возраста промысла. Моделирование применяется
очень широко, и не на последнем месте стоит использо-
вание его для быстрого выявления ошибочных гипотез.
Для того чтобы отвергнуть такие заведомо неверные гипо-
тезы, бывает достаточно рассмотреть очень простые мо-
дели. Тогда остаются лишь такие гипотезы, которые можно
проверить, поставив всего один тщательный эксперимент.
Оценка идеальной скорости роста численности попу-
ляции, т.е. скорости, с которой растет не ограниченная
ресурсами популяция, часто бывает необходима для ре-
шения проблем» экологии (Birch, 1948; Nagel, Pimentel,
Смертность
175
1964), генетики (Fisher, 1930; Hairston, Tinkle, Wilbur,
1970), эволюции (Birch et al., 1963), непрерывного сбора
урожая и организации промысла (Beverton, Holt, 1957;
Ricker, 1958; разд. 11.2). Наиболее точные оценки вы-
числяются по демографическим таблицам и таблицам пло-
довитости (разд.9.2).
Глава 9
Связь между параметрами
9.1. Основное уравнение
Векторы выживаемости и плодовитости связаны со
скоростью роста численности популяции (Lotka, 1907а, Ь)
уравнением
2 = 1.
Это основное уравнение популяционной динамики; из
него можно получить большинство параметров, исполь-
зуемых в популяционном анализе. Оно описывает дина-
мику части популяции, состоящей из самок, с фиксиро-
ванными векторами выживаемости и плодовитости; дру-
гими словами, удельная выживаемость и плодовитость
могут быть различными в разном возрасте, но вектор как
характеристика популяции со временем не меняется.
Это, разумеется, идеализация, поскольку в природе
векторы выживаемости и плодовитости, как правило, не
остаются постоянными. Однако свойства естественных по-
пуляций во всей их сложности нельзя понять до тех пор,
пока эти популяции не исследованы в рамках понятий,
входящих в основное уравнение, и не рассмотрены от-
клонения их от простых систем, описываемых этим урав-
нением.
Смысл уравнения выявляется при рассмотрении сле-
дующей воображаемой ситуации. Пусть в сезон размно-
жения, соответствующий нулевому моменту времени, рож-
дается одна самка. Скорость роста популяции равна г, а
векторы плодовитости и выживаемости постоянны. Сле-
довательно, число самок, родившихся в предыдущий
сезон размножения, было равно е~т. Из них Z1e-r выжили в
течение минувшего года и представляют популяцию в
момент времени t = 0. Число же самок, рожденных ими
в этот нулевой сезон размножения, равно Z1e_,'m1. Ана-
Связь между параметрами
175
логичный расчет можно проделать для каждого возраста.
Так, например, при t = —3 родилосье~гХ е~гХ е~т — е~гЯ
самок, I Зе~гз из них дожили до трехлетнего возраста и в
момент t = 0 в соответствующий цикл размножения про-
извели на свет Z3 e~r3m3 самок. (Если читателю трудно
представить себе дробное число самок, он может считать,
что в начальный момент t = 0 родилась не одна, а 1000
самок.)
Таблица 9.1
Вклад различных возрастных классов в число самок,
родившихся в пулевой сезон размножения
Время Число родившихся самок Возраст этих самок в момент t «0 Число доживших до момента /=0 Численность ново- рожденных самок, рожденных в мо- мент t = 0
0 1 0 1 0
—1 е~г 1 Z1e-r?n1
—2 е-п 2 12е~т^ lae~ram2
-3 е-гй 3 13е'гз l3e~™m3
—4 e~ri 4 ^е~'*т4
—5 е-гъ 5 1ье~г* 1{,е~гъть
Общее число родившихся = Ихе~тхтх = 1
В табл. 9.1 представлены все эти параметры для попу-
ляции, состоящей из 5 возрастных классов. В последнем
столбце приведены численности новорожденных самок,
произведенных на свет в момент t — 0 самками различных
возрастных классов; сумма этих значений дает общее
число новорожденных самок в момент t = 0. Но это число
исходно было положено равным 1, и, следовательно,
сумма содержащихся в последнем столбце табл. 9.1 вели-
чин равна 1 по определению, т.е.
%lxe~r*mx = 1.
Входящие в это уравнение переменные определены для
части популяции, содержащей только самок. С равными
основаниями они могли бы означать выживаемость сам-
цов и количество сыновей, родившихся от одного отца.
176
Глава 9
Если векторы выживаемости и плодовитости фиксирова-
ны и для самцов, и для самок, то значение г для части по-
пуляции, содержащей лишь самцов, будет тем же самым,
что и для «женской» части популяции. Это остается спра-
ведливым впе зависимости от того, одинаковы ли векторы
выживаемости и плодовитости в «мужской» и «женской»
частях популяции.
Основное уравнение не обязательно должно быть выра-
жено через выживаемость, считая от момента рождения, и
число новорожденных, приходящихся на одну самку.
Момент рождения является произвольной точкой отсче-
та в жизненном цикле, и в качестве граничной точки,
«отделяющей» плодовитость от выживаемости, с тем же
успехом может быть взята любая другая произвольная точ-
ка. До нее существование особи в популяционном ана-
лизе игнорируется, в момент достижения возраста, соот-
ветствующего этой точке, особь учитывается в качестве
•составляющей плодовитости, а затем как компонента вы-
живаемости. Если плодовитость определяется по числу
приходящихся на одну самку оплодотворенных яйцекле-
ток, из которых потенциально могут развиться самки, вы-
живаемость следует определять как вероятность для такой
оплодотворенной яйцеклетки дожить до соответствующего
возраста. Плодовитость может быть также определена как
количество приходящихся на одну самку дочерей, достиг-
ших возраста одного года, и выживаемостью тогда будет
вероятность для однолетних животных достичь возраста
двух, трех и т. д. лет. Нельзя делать только одного: если
плодовитость и выживаемость определены для различ-
ных моментов жизненного цикла, например плодовитость
(определяется как частота зачатий, а выживаемость как
вероятность новорожденных дожить до определенного воз-
раста, то основное уравнение не может быть использовано
для описания связей между выживаемостью, плодовитостью
и скоростью роста.
9.2. Вычисление г
В гл. 5 приведено несколько различных определений
скорости роста. Они различаются скорее по смыслу, не-
жели способом их оценки.
Связь между параметрами
177
ж \ г — наблюдаемая скорость роста;
* rs — скорость роста по плодовитости-выживаемости,
ж т.е. скорость роста, определяемая существующими
• векторами выживаемости и плодовитости;
rm — идеальная скорость роста, т.е. скорость, дости-
гаемая в отсутствие перенаселенности и ограни-
7 ченности ресурсов;
р — идеальная скорость роста при оптимальных вне-
j шних условиях (Cole, 1957);
? гр — потенциальная скорость роста — скорость рос-
та, которая достигается при устранении некото-
£ рого данного фактора смертности.
Скорости эти обозначаются символом г, а индексы при-
меняются только тогда, когда хотят подчеркнуть, что
именно понимается под скоростью роста. Допустим, я
VL занимаюсь организацией содержания в естественных ус-
ж ловпях популяции оленей, с тем чтобы поддерживать по-
W стоянпый уровень их добычи. Я должен знать, как меня-
Ж ется численность популяции от года к году, для чего надо
№ в течение нескольких лет подряд измерять скорость г.
ЯГ. Мне могут также понадобиться данные о том, в какой сте-
ж. пени изменения г определяются изменениями выживае-
Е мости и плодовитости, а в какой они зависят от изменения
ж возрастного распределения. Оценки значения rs дают
SL скорости роста, определяемые существующими векторами
Ж" выживаемости и плодовитости за вычетом эффектов, свя-
Е ванных с неравповесностью возрастного распределения.
Ж Правильную интенсивность промысла можно определить
Ж; исходя из оценок гр, т.е. скорости роста популяции при
ж полном прекращении охоты. Интенсивность промысла
Ж' должна быть такой, чтобы среднее значение скорости
'Ц; роста численности популяции поддерживалось равным 0.
Если я хочу максимизировать добычу, мне следует оце-
нить максимальную скорость, с которой популяция может
Расти ПРИ Данных внешних условиях, если полностью
:.Й устранить эффекты, связанные с перенаселенностью и
; ограниченностью ресурсов. Эта скорость обозначается сим-
волом rm. Ее нужно знать для вычисления максимального
уровня устойчивого промысла или урожая (гл. 11).
178
Глава 9
Расчет г по оценкам численности популяции
Наблюдаемую экспоненциальную скорость роста г
можно рассчитать методом регрессионного анализа по
двум или нескольким оценкам численности популяции.
Если размножение популяции носит сезонный характер,
то оценки численности следует производить ежегодно
примерно в одно и то же время. Оценки численности или
индексы этих величин прежде всего преобразуются в на-
туральные логарифмы, обозначаемые символом N. Изме-
ренные в годах временные интервалы обозначаются сим-
волом t. Желательно, чтобы первый интервал был равен
одному году. Тогда средняя за период наблюдений экспо-
ненциальная скорость роста будет равна
r= (SO/”
где h — число оценок численности.
Вычисление г по выживаемости
и плодовитости
Регрессионный анализ позволяет рассчитать сроднее
значение г за некоторый промежуток времени. Оценки гт и
rs — значения этих величин в данный момент времени и
должны рассчитываться по векторам приспособленности
и плодовитости с помощью основного уравнения
'£llxe~rxmx = 1.
Однако непосредственно относительно г это уравнение
удается решить лишь с помощью сложных методов, изло-
жение которых выходит за рамки данной книги. Вместо
этого можно просто подобрать такое значение г, при под-
становке которого в левую часть уравнения мы полу-
чили бы 1.
Осуществление такого процесса последовательных при-
ближений должно быть поручено ЭВМ. В Приложении 2
приводится программа на ФОРТРАНе, которая позво-
ляет за несколько секунд рассчитать значение г.
Существует несколько приемов, позволяющих уско-
рить вычисления, если их приходится проводить на руч-
Связь между параметрами
179
ном калькуляторе. В этом случае проделывают такие
последовательные операции:
1. Выписывают составляющие вектора lxmx.
2. По формуле
d 2
рассчитывают приближенные значения г,
3. Для каждого возраста выписывают значения гах, .
а затем с помощью таблицы, приведенной в Приложении 1,
находят е-г« х •
4. Выписывают составляющие вектора lxmxe~raх и
определяют их сумму. Как правило, она оказывается
больше 1, указывая на то, что приближенное значение
•. га меньше истинного.
5. Выбирают второе пробное значение г умножением
’ га примерно на 1,3. Это значение обозначается гь. Затем
повторяют операции 3 и 4. Если получившаяся сумма
меньше 1, значит, гь больше истинного значения г, ко-
' торое заключено, следовательно, между га и гь. Если же
" сумма больше 1, ть следует увеличивать до тех пор, пока
; сумма не станет меньше 1.
6. Строят графики зависимости га и ть от соответству-
ющих значений суммы '2Лхе~гхтх и проводят прямую
Значение г на этом графике, соответствующее 2^е_'’Лтпж=1,
£ является достаточно хорошим приближением к истин-
ному значению г для решения практических задач. На
самом деле такое приближение слегка завышено, по-
скольку регрессия пробных значений г на решение
'Ыхе~гхтпх не прямолинейна, а слегка изогнута.
7. В тех случаях, когда требуется большая точность,
полученную в результате интерполяции оценку г под-
? ставляют в основное уравнение и производят суммирова-
ние; второе суммирование производят с чуть меньшим
пробным значением г. Затем графически определяют более
точное интерполяционное значение г.
Расчет г с помощью методов матричной
алгебры
С помощью прямого альтернативного метода, исполь-
зующего матрицы удельной приспособленности и плодо-
7*
180
Глава 9
витости Лесли—Леви, г определяется как натуральный
логарифм. В ряде недавно вышедших экологических ра-
бот сказано очень много слов об изяществе этого метода,
но совершенно упускаются из виду трудности практичес-
кого характера, связанные с его применением. Выжи-
ваемость (Рх) и плодовитость (Fx), используемые в матри-
цах Лесли—Леви, отличаются от рх и тх, с которыми мы
имеем дело в нашей книге. Особенно трудно рассчитать
по данным полевых наблюдений Fx. Плодовитость Fx
определяется (Leslie, 1948) как «приходящееся на одну
самку из числа достигших в момент t возраста от х до
х + 1 число дочерей, рожденных между временем t и
t + 1, доживших до момента t + 1 и составивших воз-
растную группу от 0 до Ь (курсив мой). Что касается то-
го, как оценить эти сложные биологические параметры
по данным полевых исследований,— это уж дело иссле-
дователя. Формально Fx = ermx (Pielou, 1974), но, как
правило, это соотношение не дает возможности непосред-
ственно оценить значение Fx, поскольку г — это вовсе
не независимо вычисляемый параметр, а неизвестная вели-
чина, которую мы определяем по независимо оценивае-
мым удельным плодовитостям и выживаемостям.
Так как операции, производимые в матричной алгебре,
легко реализуются на ЭВМ, матрицы удобны для моде-
лирования роста популяции. Менее пригодны они на так-
тическом уровне, при анализе динамики природных по-
пуляций, поскольку их трудно строить по данным поле-
вых исследований.
Расчет г по выживаемости и возрастному
распределению
Когда возрастное распределение устойчиво, величина
Sx, получаемая .делением числа самок в возрасте х на
число новорожденных самок, связана с выживаемостью
соотношением
Sx = lxe~rx.
Следовательно, если известны 1хи8х хотя бы для од-
ного возраста для популяции с сезонным размножением,
Связь между параметрами
181
г можно вычислить по формуле
r _ In lx — In Sx
X
Более точной оценкой является невзвешенное среднее
ряда значений г, рассчитанных по этой формуле для не-
; скольких возрастных классов.
9.3, Максимальная скорость увеличения
численности популяции
Максимальная скорость, с которой может увеличи-
ваться численность популяции при данных внешних
условиях, равна гт. В наилучших из всех возможных усло-
виях гт достигает своего максимального значения р.
В обоих случаях выполняется соотношение
s S lxe~rxmx = 1,
где г может быть равно г g, гт или р в зависимости от усло-
вий, в которых определяются векторы 1Х и тх. Скорости
роста численности популяции являются результатом
/ взаимодействия двух факторов — плодовитости и смер-
• тности.
Но существует еще и другая скорость — «максималь-
ная скорость роста», которой очень часто пользуются,
но редко дают точное определение. Именно эта величина
неявным образом присутствует в таких утверждениях, как
«если бы рост численности кроликов ничем не ограничи-
вался, они покрыли бы поверхность Земли за 8,3 года» или
«потомство одной пары бурундуков через пять лет в иде-
альных условиях составило бы 363 271 486 штук». Хотя
обычно отмечают, что эти оценки нереальны, поскольку
идеальные условия недостижимы, на их полную бес-
мысленность, как правило, не указывают. Такие оценки
получаются в предположении, что максимальная скорость
роста задается максимальной плодовитостью в отсут-
ствие смертности. По весьма понятным чисто психологи-
ческим причинам никогда не рассматривается «макси-
мальная скорость убыли» численности популяции, за-
даваемая смертностью в отсутствие рождаемости, тогда
как эта величина с точки зрения логики не более аб-
сурдна, чем «максимальная скорость роста».
182
Глава 9
Концепция «максимальной скорости роста» не только
в высшей степени умозрительна, но и далеко не безобидна.
Она может использоваться для оправдания весьма сом-
нительных мер по управлению численностью популяций
и экологических исследований, в которых акцент делается
на изучение размножения, в то время как смертность
игнорируется. Такое упущение создает мнимое удобство,
поскольку плодовитость измерить много легче, чем смерт-
ность; это различие четко отражено в разнице объемов
7-й и 8-й глав. Часто считается, что основной популя-
ционный процесс — это размножение, а смертность —
процесс подчиненный, но гибель особей — биологический
процесс не более и не менее реальный, чем размножение.
Понимание динамики популяций основывается на пони-
мании и определении и того и другого. Отдельно взятая
плодовитость ничего не говорит о максимальной или дей-
ствительной скорости роста популяции; то же самое от-
носится и к смертности. Максимальная скорость роста
при данных внешних условиях измеряется одновременно
и по плодовитости, и по смертности. Ее значение редко
Таблица 9.2
Оценка идеальной скорости роста гт для популяций
_________________некоторых видов_________________
Виды гт/год Популяция (условия существования) Источник данных
Короткохвостая полевка 4,56 Лабораторная Leslie, Ranson, 1940
Серая крыса 3,91 » Leslie et al., 1952
Оркнейская по- левка 3,74 » Leslie et al., 1955
Белохвостый олень 0,55 Дикая Kelker, 1947
Тихоокеанская сардина 0,39 » Murphy, 1967
Олень-вапити 0,27 » Murphy, 1963
Косуля 0,23 » Andersen, 1962
Человек 0,04 По нескольким ис- точникам
Связь между параметрами
183
превышает 0,4 в год для крупных млекопитающих и 4,0
для мелких млекопитающих и птиц. Оценки rm для неко-
торых видов приведены в табл. 9.2.
9.4. Устойчивость связей между параметрами
Если векторы выживаемости и плодовитости фикси-
рованы, то возрастные распределения для самцов и самок
стремятся к устойчивым и скорость роста популяции
становится постоянной (Lotka, 1907а, b; Sharpe, Lotka,
1911). Это утверждение справедливо вне зависимости от
того, меняется удельная смертность с возрастом или нет,
одинаковы или различны векторы приспособленности и
плодовитости для самцов и самок, и от того, больше, мень-
ше или равна 0 идеальная скорость роста популяции,
обусловленная этими векторами. Из этого принципа сле-
дуют два вывода:
1. После того как скорость роста популяции становит-
ся устойчивой, любая часть популяции (т.е. самцы, сам-
ки, возрастные классы, размножающиеся инеразмножа-
ющиеся части популяции, молодь и взрослые, а также лю-
бая комбинация или любое подразделение этих частей)
растет с одной и той же скоростью г.
2. Если скорость роста любой части популяции, за
исключением пострепродуктивных возрастов, принимает
новое значение и остается равной ему, то скорость роста
всех других частей популяции будет стремиться к тому же
значению.
На рис. 9.1 представлена диаграмма, изображающая
связь между четырьмя частями популяции. Светлые стрелки
указывают на то, что скорость роста одних частей попу-
ляции жестко определяется скоростью роста других. Тем-
ные стрелки означают, что связи более слабые, для уравни-
вания скоростей роста требуется больше времени.
Эти взаимосвязи важны при управлении дикими по-
пуляциями, поскольку они выявляют огромную гибкость
в способах управления численностью и скоростью роста
популяции. Если, например, цель воздействия состоит
в том, чтобы стабилизировать численность растущей по-
пуляции, ее можно достичь, воздействуя лишь на какую-
либо одну часть этой популяции. Численность всех ос-
184
Глава 9
тальиых частей популяции будет при этом стабилизиро-
ваться автоматически, т.к. скорости их роста будут стре-
миться к скорости роста управляемой части популяции,
в данном случае — к нулю. Возможность управлять по-
пуляцией в целом, воздействуя лишь на одну-две ее части,
г для
молодых
самок
г для
молодых
самцов
г для
взрослых
самок
г для
взрослых
самцов
Рис. 9.1. Зависимость скорости роста т одной из частей популяции
от скорости роста других частей.
очень важна в тех случаях, когда представители некоторых
частей популяции имеют покровительственную окраску,
ведут скрытный образ жизни или опасны. Направления
светлых стрелок на рис. 9.1 указывают на то, что быстрой
стабилизации численности популяции можно достичь,
поддерживая равной нулю скорость роста численности
неполовозрелых или размножающихся самок. При стаби-
лизации численности неполовозрелых или размножаю-
щихся самцов стабилизация общей численности достигает-
ся за гораздо большее время.
Связь между параметрами
185
9.5. Постоянство структуры популяции
Если векторы выживаемости и плодовитости фикси-
рованы и популяция достигла постоянной скорости раз-
множения, то относительные численности различных
частей популяции также фиксированы. Такое положение
сохраняется до тех пор, пока векторы выживаемости и
плодовитости остаются неизменными. Следующий отсюда
вывод — устойчивость возрастного распределения — уже
упоминался. К этому можно добавить устойчивость от-
ношения численностей полов, устойчивость отношения
размножающейся и неразмножающейся частей популя-
ции, устойчивость доли новорожденных, вливающихся
в популяцию ежегодно.
Устойчивое возрастное распределение
После того как скорость роста достигнет постоянного
значения, определяемого фиксированными векторами вы-
живаемости и плодовитости, относительные частоты всех
возрастных классов оказываются жестко связанными с
выживаемостью. Для сезонно размножающейся популя-
ции
/я//0 = 1хе~гх,
где fx — число животных в возрасте х в момент размноже-
ния, а /0 — число новорожденных в популяции в тот же
самый момент. Это отношение представляет собой устой-
чивую частоту встречаемости возрастного класса S х,
и вектор S х, составленный по всем возрастам, представ-
ляет собой устойчивое возрастное распределение. Устой-
чивые возрастные распределения для самцов и самок,
вообще говоря, различны, за исключением случая, когда
одинаковы векторы выживаемости.
Устойчивое возрастное распределение непрерывно раз-
множающейся популяции связано с выживаемостью и
скоростью роста соотношением
fx, x+i _ Lxe~rx
/о,1
186
Глава 9
где Lx — средняя выживаемость в возрасте между х и
х + 1, приблизительно равная
т __ kr 4~ Аг+1
х 2
В популяции с непрерывным размножением возрастной
класс объединяет особей, возраст которых находится в
интервале между двумя фиксированными значениями.
Так, /ж,х+1 — это число животных, возраст которых в дан-
ный момент времени лежит между х и х + 1- Устойчивое
возрастное распределение в популяции с непрерывным
размножением остается неизменным на протяжении все-
го года. В популяциях с сезонным размножением ус-
тойчивое возрастное распределение различно в различ-
ные времена года, но остается одним и тем же для данного
времени года в течение ряда последовательных лет.
Хотя устойчивое возрастное распределение формально
определяется лишь через величины г и lx, тх также ока-
зывает на него влияние, поскольку от плодовитости
зависит скорость роста г. Изменение удельной выживае-
мости или плодовитости какого-либо одного возраста будет
смещать установившееся устойчивое возрастное распреде-
ление. Постепенно оно примет новую устойчивую форму,
соответствующую новому набору выживаемостей и плодо-
витостей. Если эти векторы непрерывно пзменяются, то
возрастное распределение также изменяется, отставая
на несколько тактов и стремясь к устойчивой форме, соот-
ветствующей уже изменившемуся набору выживаемости
и плодовитости.
Лесли (Leslie, 1948) показал, что поголовное изменение
удельной смертности, затрагивающее равным образом все
возрастные классы, не меняет возрастного распределе-
ния. Меняются и вектор выживаемости, и скорость роста,
но эти два изменения в точности компенсируют друг дру-
га, оставляя возрастное распределение неизменным.
В табл. 9.3 представлен пример сохранения постоян-
ного возрастного распределения, построенный на основе
демографической таблицы для овец (Hickey, 1960, 1963),
видоизмененной Коли (Caughley, 1967а). Скорость роста,
определяемая заданным вектором 1хтх, составляет г, =
0,2; устойчивое возрастное распределение соответствует
Связь между параметрами
187
Таблица 9.3
Неизменность возрастного распределения при введении
дополнительной, не зависящей от возраста смертности
Возраст X Исходные данные Переработанные данные
выживаемость 1х возрастное распределение Sx выживаемость 1Х возрастное распределение 4
0 1,ООО' 1,000 1,000 1,000
1 0,845 0,692 0,761 0,692
2 0,824 0,552 0,667 0,552
3 0,795 0,436 0,579 0,436
4 0,755 0,339 0,495 0,339 •
5 0,699 0,257 0,413 0,257
6 0,626 0,189 о.ззз 0,189
7 0,532 0,131 0,255 0,131
8 0,418 0,084 0,180 0,084
9 0,289 0,048 0,112 0,048
10 0,162 0,022 0,057 0,022
11 0,060 0,007 0,019 0,007
Г = 0,2000 г' =0,0945
этой скорости. Вторая пара столбцов представляет
собой значения 1Х и 5х, отражающие последствия введения
во всех возрастных классах дополнительного фактора
смертности, в изолированном виде действующего с ин-
тенсивностью 0,1 за год. Таким образом, новое значение
удельной смертности для всех возрастных классов со-
ставляет qx = qx + 0,1 — О,!*/^ (разд.8.3). Отсюда мож-
но рассчитать новые значения выживаемости 1Х. Зна-
чения плодовитости остаются неизменными. Скорость
роста, соответствующая новому вектору /жтх, составляет
г' = 0,0945. Однако
lxe~rx = l 'xe~r x,
188
Глава 9
и, следовательно, возрастное распределение остается тем
.же самым. Этот эффект имеет практическое значение при
определении устойчивого уровня промысла или урожая.
Устойчивое отношение численностей полов
В популяции с фиксированными векторами выживае-
мости и плодовитости отношение числа самок к числу сам-
цов задается выражением
сТс? _ о S lxe~rx
9? 9 5/^-"*
Даже если векторы выживаемости для самцов, и самок
различны, число самцов и самок в популяции будет уве-
личиваться с одной и той же скоростью г, и, следователь-
но, отношение численностей полов будет оставаться по-
стоянным. Более того, устойчивость отношения числен-
ностей полов не зависит от знака г, от рождаемости и от
отношения численностей полов у новорожденных.
Хэнсон (Hanson, 1963: 58) полагает, что «если постоян-
но сохраняющееся различие в выживаемостях приводит
к тому, что отношение числа взрослых самцов к числу
взрослых самок превышает величину, примерно равную
150/100, то популяция птиц или млекопитающих неиз-
бежно обречена на вымирание, даже если компенсирую-
щая рождаемость очень велика». Хэнсон, очевидно, спу-
тал устойчивость численности с устойчивостью отношения
численностей полов. Это положение можно проиллюстри-
ровать примером. Рассмотрим модель популяции с нуле-
вой скоростью роста и с одинаковым для самцов и самок
вектором выживаемости. Другими словами,
9 Е 1хтх — 1
и
=
99 9^х
Предположим теперь, что местообитание изменилось та-
ким образом, что выживаемость самцов сильно увеличи-
лась, тогда как выживаемость самок и их плодовитость
остались неизменными. Отношение численностей полов
Связь между параметрами.
189
при этом примет новое равновесное значение, соответ-
ствующее новой выживаемости самцов 1Х\
сГсГ _с? S 1Х > ।
99 "
и стабилизируется на этом уровне. Заметим, что соотно-
шение
9 S lxmx = 1
остается в силе и, следовательно, число новорожденных,
вливающихся ежегодно в популяцию, не меняется. После
того как отношение численностей полов стабилизируется
на новом уровне, скорость роста численности популяции
в целом снова становится равной 0, как и раньше; един-
ственное отличие заключается в том, что популяция те-
перь более многочисленна, а отношение численностей
полов не равно 1. Отношение численностей полов может
достигать 10 или даже 100, не создавая никакой неус-
тойчивости и не требуя компенсирующего изменения пло-
довитости самок.
Устойчивое отношение численностей
размножающейся и неразмножающейся частей
популяции
Лэк (Lack, 1966: 293) рассмотрел модель популяции
птиц, размножение которых ограничивается числом мест
на острове, годных для гнездования. Он считает, что хотя
численность размножающейся части популяции ограни-
чена, тем не менее «численность неразмножающихся осо-
бей будет устойчиво и непрерывно расти до тех пор, пока
они не столкнутся с истощением источников пищи в ок-
рестностях острова, после чего начнет сказываться за-
висящая от плотности смертность вследствие голода».
Другими словами, Лэк считает, что даже при г = 0 для
размножающейся части популяции г для неразмножаю-
щейся части может оставаться больше 0 неограниченно
долго или до тех пор, пока выживаемость не изменится
за счет смертности от внешних причин.
На первый взгляд модель Лэка приводит к нарушению
двух демографических законов сохранения: закона ра-
190
Глава 9
венства скоростей роста всех частей популяции и зако-
на постоянства отношения численностей различных час-
тей популяции. Таким образом, эта модель может рас-
сматриваться как вызов закону, на котором испыты-
вается его мощь и справедливость. С этой точки зрения
роль зависящих от плотности факторов не имеет ни ма-
лейшего отношения к делу; интересно лишь, вытекают ли
логически сделанные Лэком выводы из начальных усло-
вий и предпосылок о механизме популяционных процес-
сов.
Для простоты предположим, что удельная смерт-
ность не меняется с возрастом. Это предположение не
является существенным, и окончательные выводы от него
не зависят. Пусть
N — фиксированное число размножающихся птиц;
т — число потомков, приходящихся ежегодно на од-
ну принимающую участие в размножении пти-
цу;
п — число неразмножающихся птиц;
q — удельная смертность неразмножающихся птиц.
Убыль неразмножающейся части популяции за счет
того, что некоторые птицы занимают гнездовые места
особей, выбывших из размножающейся части популяции,
представляет собой компоненту суммарной «смертности».
В сезон размножения численность неразмножающейся
части популяции составляет
п = Nm + Nm (1 — q) + Nm (1 — g)2 + • • -\-Nm (1 — g)°° =
= ^[l+(l-g) + (l-g)2 + ..- +(!-<?)“] =
=у41-<1--П=—•
ч J 1
Таким образом, число птиц в неразмножающейся части
популяции в каждый сезон размножения определяется
исключительно значениями N, т и q, каждое из которых
постоянно. Следовательно, постоянна и численность не-
размножающейся части популяции, а соответственпо ско-
рость роста этой части популяции равна нулю. Если
N = 100, т = 3 и q = 0,6, то устойчивая численность
неразмножающейся части популяции равна 500. Непо-
Связь между параметрами
191
средствепно перед следующим сезоном размножения она
снижается до величины
iVw(l-g) _ 200
9
и снова поднимается до 500 за счет новорожденных. Мо-
дель Лэка полностью согласуется с законами сохранения.
Неверны не законы, а его выводы. Экологи должны на-
Время после стабилизации численно-
сти размножающихся птиц,
годы
Рис. 9.2. Зависимость от времени численности неразмножающихся
птиц вследствие стабилизации численности размножающихся (см.
текст).
учиться распознавать явные нарушения этих законов и
относиться к ним с таким же скептицизмом, с каким фи-
зики принимают новые проекты вечного двигателя.
Рис. 9.2 показывает, с какой скоростью в предыдущем
примере устанавливается постоянство отношения чис-
ленностей неразмножающейся и размножающейся частей
популяции. Численность неразмножающейся части попу-
ляции достигает уровня, соответствующего 97% равновес-
ного значения, лишь спустя 4 года после того, как стаби-
лизируется численность размножающейся части попу-
ляции. Полное равновесие достигается еще через 5 лет.
192
Глава 9
9.6. Интерпретация возрастного
распределения
Тавтология, связанная с возрастным
распределением
Тавтологией называется несомненно истинное утвер-
ждение, не содержащее никакой информации. «Если у
меня была возлюбленная, которую звали Мэри, то ее
имя начиналось на букву М» — это пример тавтологии.
Таким утверждением не сказано ничего ни о моей личной
жизни, ни об имени моей возлюбленной, ни даже о том,
была ли она у меня.
Тавтологические утверждения встречаются и в мате-
матике. На первый взгляд уравнение
имеет смысл. Из него, казалось бы, можно определить
численное значение х. Однако, решая его, мы получаем
всего лишь х = х.
Тавтологические утверждения широко распростране-
ны в популяционном анализе. Наиболее типичные из них
— оценка г или проверка равенства г нулю по возраст-
ному распределению. Иногда расчеты проводятся на осно-
вании одного лишь мгновенного возрастного распре-
деления, но чаще возрастное распределение используется
в сочетании с распределением возрастов гибели и век-
тором повозрастной плодовитости. Эти математические
упражнения представляют собой порочный круг,, постро-
енный на использовании основного уравнения
S lxe~rxmx = 1.
Его нельзя разрешить относительно г, если 1Х рассчитан по
возрастному распределению Sx в предположении, что
S х = 1Х. Точно так же решение для г не имеет смысла и
в том случае, когда вектор выживаемости строится по
распределению возрастов смерти Sx в предположении,
что Sx = dx. Оба эти предположения подразумевают
равенство г нулю. Решение для г попросту возвращает
нас к этой оценке. В тех случаях, когда для оценки г
Связь между параметрами
193
используется не вектор выживаемости, а возрастное рас-
пределение, следует использовать не выписанное выше
уравнение, а уравнение
S Sxe~rxmx = 1.
Логическая ошибка становится очевидной при подста-
новке вместо Sx выражения 1хе~гх, что дает
Появление в уравнении второго г должно обязательно
привести к решению г = 0 безотносительно к истинному
значению г. Вычисленное же значение г обычно отличается
от ожидаемого нулевого значения, но получившееся от-
клонение не имеет ничего общего со скоростью роста по-
пуляции. Оно отражает лишь изменчивость и смещен-
ность выборки.
Тавтологии не обязательно бывают столь изощренными,
как в приведенном примере. Рассмотрим соотношения
S 1хе~гхтпх — S Sxmx = S dx = l0 = So = 1.
Все они верны по определению. Значения г из этих ра-
венств определить нельзя. Констатация того, что S =
= 10, например, ничего не говорит о скорости роста по-
пуляции, хотя иногда это равенство приводится в ка-
честве «доказательства» того, что г = 0.
Различных вариантов тавтологии, связанных с воз-
растным распределением, очень много, однако распоз-
нать их при беглом чтении бывает довольно трудно. Тав-
тологию, связанную с возрастным распределением, не-
возможно выявить до тех пор, пока автор точно не ука-
жет, каким образом он собирал свои данные и как их об-
рабатывал. Решение уравнения относительно г имеет
смысл в том случае, когда 1Х оценивается с помощью мето-
да мечения и повторных .отловов, и бессмысленно, когда
1Х строится на основе возрастного распределения по вы-
борке, полученной отстрелом, или на основе распреде-
ления возрастов смерти, полученного, например, по вы-
борке черепов. В работе Коли и Бирча (Caughley, Birch,
1971) приводится несколько примеров тавтологического
анализа такого рода.
194
Глава 9
Таблица 9.4
Возрастные распределения самок благородного оленя
на острове Рам в Шотландии (Lowe, 1969)
Возраст в годах
Годы 0 1 2 3 4 5 6 7 8 9 10 И 12 13
154 129
131 129
113 ИЗ
129 110
129
96
81 78 59 65 55 25 9 8 7 2
107 69 75 51 59 43 12 5 6 3
1957
1958
1959
1960
1961
1962
1963
1964
1965
75
52
37
23
19
В табл. 9.4 представлен пример того, как два или более
набора очень похожих данных могут полностью разли-
чаться по способности служить основой для оценки г.
Приведенные данные представляют собой часть совокуп-
ности (Lowe, 1969) возрастных распределений благород-
ного оленя на острове Рам в Шотландии, построенных по
результатам определения возраста обнаруженных мерт-
вых животных. Из этих данных оценивалась дата рожде-
ния каждого животного и продолжительность его жизни.
Поскольку обнаружены были трупы почти всех погибших
животных, данные могли быть использованы для опре-
деления численности животных всех возрастных классов
за каждый из нескольких последовательных лет.
Исходя из табл.9.4, можно было построить 4 демогра-
фические таблицы.
1. По мгновенному возрастному распределению
1957 г. в предположении, что г = 0.
2. По мгновенному возрастному распределению 1958 г.
в предположении, что г = 0.
3. По ежегодному убыванию между 1957 и 1965 гг.
численности когорты, рожденной в 1957 г. (числа,
расположенные по диагонали).
Связь между параметрами
195
4. По различию между численностью данного возраст-
ного класса в 1957 г. и численностью следующего
возрастного класса годом позже.
Однако не все 4 таблицы в сочетании с таблицей пло-
довитости могут служить основой для оценки г s. Для этого
подходят лишь таблицы 3 и 4, поскольку две первые по-
строены в предположении, что г = 0. В сочетании с при-
веденным в работе Лоу (Lowe, 1969) вектором плодови-
тости демографическая таблица 3 дает оценку rs =0,136,
а таблица 4 — оценку rs = 0,082. Эти оценки скорости
роста определяются векторами выживаемости и плодо-
витости. Поскольку возрастное распределение при этом
было неустойчиво, они не дают действительного значения
скорости, с которой увеличивалась численность популя-
ции во время проведения измерений.
Ихтиологи часто считают, что линейное убывание ло-
гарифма численности возрастных классов является сви-
детельством того, что г = 0. Оставляя в стороне вопрос
о том, всегда ли стационарное возрастное распределение
имеет такую форму, заметим, что из такого характера
возрастного распределения нельзя сделать вывод о ра-
венстве г пулю. Если qx постоянно для всех возрастных
классов популяции, служащей объектом промысла, то
логарифм численности возрастных классов действитель-
но будет линейно зависеть от возраста при скорости
роста популяции, равной 0. Однако эта регрессия будет
оставаться линейной и в тех случаях, когда популяция
увеличивает или уменьшает свою численность с любой
скоростью.
Возрастное распределение как показатель г
В предыдущем разделе мы рассмотрели причины, по
которым г нельзя рассчитать по стационарному устойчи-
вому распределению и вектору плодовитости. Можно или
нельзя по виду возрастного стационарного распределения
хотя бы приблизительно оценить знак г — совсем другой
вопрос, и в большинстве случаев это действительно уда-
ется. В крайних ситуациях (например, в случае, когда за-
суха приводит к почти полной гибели годовалых и двух-
летних кенгуру в популяции) резкое изменение в возраст-
196
Глава 9
ном распределении наверняка указывает на изменение
скорости роста, однако такой вывод можно сделать и по
многим другим данным. Гораздо чаще нас интересует
знак г в том случае, когда эта величина отклоняется от О
в том или другом направлении не слишком сильно, но
именно при этом возрастное распределение, как правило,
не указывает на знак изменения г вне зависимости от
того, подразделена популяция на два или на десять воз-
растных классов.
Этот вывод кажется обескураживающим в особенности
потому, что он в точности противоположен утверждению,
принимаемому в качестве аксиомы при исследовании и
управлении природными популяциями. Однако эта при-
вычная точка зрения в значительной степени основыва-
ется на неправильной интерпретации данных по возраст-
ным распределениям городского населения, приведенных
в графической форме в работе Боденгеймера (Boden-
heimer, 1938). Он показал, что у людей возрастные рас-
пределения бывают различны в зависимости от того,
возрастает, убывает или остается постоянной числен-
ность популяции, и предложил провести подобные иссле-
дования для других видов. Многие авторы использовали
эти диаграммы (рис.9.3) для диагностики скорости роста
популяций различных видов, от мышей до человека.
Однако специфическая особенность городских популя-
ций человека состоит в том, что там очень низка детская
смертность. Таким образом, возрастное распределение у
человека отличается от возрастного распределения у дру-
гих видов. Диаграмма А может соответствовать росту по-
пуляции, ее убыванию или поддержанию численности на
постоянном уровне для большинства видов млекопитаю-
щих и птиц. Возрастные распределения типов Б и В в
природе встречаются очень редко. Они соответствуют очень
быстрому убыванию численности.
Изменение устойчивого возрастного распределения мо-
жет быть обусловлено одной из трех причин.
1. Изменением выживаемости по крайней мере одного
возрастного класса.
2. Изменением плодовитости в одном или нескольких
возрастных классах.
3. Изменением и плодовитости, и выживаемости.
Связь между параметрами 197
Однако, если возрастное распределение не является
устойчивым, его изменение не обязательно предполагает
изменение 1Х или тх. Оно может представлять собой пере-
ходный процесс к устойчивому возрастному распреде-
лению, соответствующему значениям 1Х и тх, установив-
шимся за некоторое время до того.
АЛО
А Б В
Рис. 9.3. Возрастные распределения городского населения (Boden-
heirner, 1938).
А — растущая популяция; Б — стабильная популяция; В — убывающая
популяция.
Даже когда возрастное распределение меняется от
одной устойчивой формы к другой, тем самым выявляя
изменения, происшедшие в выживаемости или плодови-
тости, далеко не просто интерпретировать такие изменения
возрастного распределения как увеличение или уменьше-
ние скорости роста популяции. На рис. 9.4 графически
изображено устойчивое возрастное распределение неко-
торой модельной популяции млекопитающих со следую-
щими векторами выживаемости и плодовитости:
Возраст 0 1 2 3 4 5
1х 1,000 0,400 0,320 0,192 0,077 0,015
тх 0 . 0,6 1,2 1,4 1,3 0,5
Несложный расчет показывает, что эти векторы описы-
вают стационарную популяцию с г = 0. Пунктирные кри-
вые изображают устойчивые возрастные распределения,
к которым постепенно перейдет эта популяция, если ско-
рость ее роста резко возрастет до 0,33 в результате удвое-
198
Глава 9
ния выживаемости на первом году жизни (/) или удвое-
ния плодовитости во всех возрастных классах (II).
Хотя модельные популяции I и II характеризуются
одинаковой скоростью роста и имеют общее происхож-
дение, они обладают различными возрастными распре-
делениями. Это различие отражает различие в способах,
которыми было достигнуто увеличение г.
Рис. 9.4. Влияние изменения скорости роста популяции на устой-
чивое возрастное распределение.
Возрастное распределение при нулевой скорости роста (сплошная кри-
вая) при увеличении скорости роста до г=0,33 принимает вид I, если это
произошло за счет удвоения выживаемости на первом году жизни, и
вид II, если причиной является удвоение плодовитости всех возрастов.
Различие возрастных распределений, изображенных
на рис. 9.4, хорошо отражает трудности, возникающие
при определении г по возрастному распределению. Тако-
го способа или критерия, с помощью которого этим трем
распределениям можно было бы однозначно поставить в
соответствие растущую, убывающую или стационарную
популяцию, не существует. Задача нисколько не облег-
чается, если возрастное распределение представлено в
форме отношения численностей различных возрастных
классов, например неполовозрелых ко всем остальным
или годовалых к половозрелым. Пока в нашем распоряже-
нии имеется только возрастное распределение и нет ни-
Связь между параметрами
199
каких других дополнительных данных, лишь очень ред-
ко по изменению возрастного распределения мы можем
выяснить, увеличивается, уменьшается или остается по-
стоянной скорость роста популяции.
Хотя эти замечания вполне справедливы, не следует
слишком падать духом. Боденгеймер (Bodenheimer, 1938)
показал, что возрастные распределения у человека под-
даются интерпретации; то же самое не в меньшей сте-
пени должно относиться и к другим видам. Но диагнос-
тические особенности возрастных распределений, которые
свидетельствовали бы об убывании, возрастании или
поддержании постоянной численности популяции, дол-
жны определяться отдельно для каждого вида или груп-
пы видов. Имея представление о процессах, в результате
которых увеличивается или уменьшается численность по-
пуляции данного вида, можно соответствующим образом
истолковывать возрастное распределение.
Процессы, ответственные за изменение скорости роста
популяции, хорошо изучены, например, для тара (Caug-
hley, 1970а). Положительная скорость роста популяции
обусловлена ростом выживаемости на первом году жиз-
ни и плодовитости на втором. Убывание численности по-
пуляции бывает вызвано падением выживаемости на пер-
вом году жизни и плодовитости в целом. Такой характер
зависимости, по-видимому, является правилом для тара
и, я думаю, для многих других видов копытных. Подоб-
ная информация позволяет с той или иной степенью дос-
товерности интерпретировать вид возрастного распреде-
ления тара, поскольку число способов, которыми может
меняться возрастное распределение, ограничено. Одна-
ко без априорных знаний такого рода попытки интерпре-
тации возрастного распределения представляют собой
бесплодные упражнения в ясновидении.
9.7. Продолжительность поколения
Продолжительность поколения — это понятие, мало
пригодное при изучении популяций одного вида. Его при-
менение ограничивается рамками сравнительного ана-
лиза различных видов, в особенности когда исследуются
скорости изменения частот генов. Сравнение скоростей
200
Глава 9
эволюции мышей и слонов, по-видимому, имеет весьма
ограниченный демографический и генетический смысл
(хотя может быть вполне осмысленным в эволюционном
плане), если скорости определяются в абсолютных еди-
ницах, а не в расчете на одно поколение. Таким образом,
продолжительность поколения используется в качестве
фактора, компенсирующего различия в скоростях, с кото-
рыми через популяции этих двух видов течет поток энер-
гии.
Наиболее общее определение средней продолжитель-
ности поколения задается уравнением
Ro = егТ,
где Ro — суммарная скорость размножения, или «конеч-
ная скорость роста за поколение», определяемая как
Ro =
Приравнивая правые части уравнений, получаем со-
отношение
Т = -£-1п %1хтх,
которое выглядит вполне разумно до тех пор, пока мы
не решаем это уравнение для г = 0 и не получаем Т
Это значение Т, казалось бы, можно считать единичным
возрастным интервалом. Если единичный интервал при-
нят равным году, то и Г равно одному году. Но если те
же самые данные записаны для двухгодичного интервала,,
значение Т таинственным образом также увеличивается
до двух лет, хотя смертность и плодовитость остаются
неизменными. Таким образом, Т — явно неудобная мера
продолжительности поколения. Некоторые авторы (на-
пример, Andrewartha, Birch, 1954; Cole, 1960; Laughlin,
1965) считают, что за продолжительность поколения мож-
но принять среднее время между рождением матери и
рождением ее потомства. Лолин (Laughlin, 1965) пред-
ложил для этой величины термин «продолжительности
поколения когорты 7’с», которым я и буду пользоваться.
Связь между параметрами
201
В алгебраических обозначениях
гр _ 1хПЪхХ
с S lxmx
Введенная таким образом величина дает логичную меру
продолжительности поколения для фиксированной когор-
ты и с этой точки зрения полезна, однако применимость
ее резко падает, когда мы переходим к популяциям, со-,
стоящим из нескольких пересекающихся поколений. В
таком случае следует использовать формулу, взвешенную
пропорционально долям животных в каждом, возрастном
классе, и правильным термином будет «средний возраст
матерей всех новорожденных самок по устойчивому воз-
растному распределению». Для сезонно размножающейся
популяции эта величина определяется по формуле
где, как и ранее, S х — устойчивое отношение числен-
ности самок возраста х к численности новорожденных
самок, f тождественно Тс, за исключением случая, когда
текущее возрастное распределение в когорте (/ж) заме-
няется устойчивым возрастным распределением (1хе~гх\
Концепция средней продолжительности поколения Т
была предложена независимо Лесли (Leslie, 1966) и Гуд-
меном (Goodman, 1967). Поскольку эта концепция вполне
общая, Т во всех случаях следует использовать в ка-
честве меры средней продолжительности поколения. Ана-
логичная величина для популяций с круглогодичным
размножением определяется по формуле
т = ^хе mx> x+l (х + уJ .
Приняв Т за меру продолжительности поколения, мы
можем теперь строго определить конечную скорость роста
за поколение (7?) как
гТ
И = е = ехр (г S Sxmxx).
202
Глава. 9
9.8, Рождаемость и скорость вымирания
Демографическую таблицу и таблицу плодовитости
можно свести к паре скалярных параметров — рождае-
мости и скорости вымирания. Конечная рождаемость еь
определяется (Caughley, 1967а) как скорость, с которой
растет популяция в отсутствие смертности. Для популя-
ции с сезонным размножением прик устойчивом возрастном
распределении
. S lxe~rx S Sx
(SSJ-1 *
Может показаться странным, что в уравнение для опреде-
ления рождаемости не входит плодовитость, однако на
самом деле плодовитость неявно входит в это уравнение
как составляющая г. Впрочем, для определения рождае-
мости не обязательно знать даже г, поскольку еь можно
рассчитать непосредственно по устойчивому возрастному
распределению.
Для вычисления конечной скорости вымирания e~d,
которая по аналогии с рождаемостью определяется как
конечная скорость, с которой убывает численность попу-
ляции в отсутствие рождаемости, аналогичного прямого
способа не существует. В популяции с сезонным размно-
жением при устойчивом возрастном распределении
e-d = 1 _
Хотя можпо рассчитать'по устойчивому возрастно-
му распределению, ^dxe~rx нельзя найти из одного рас-
пределения возрастов смерти, не зная г. Равным образом
его нельзя оценить и из устойчивого возрастного распре-
деления, так как
dxe~rx =^lxe~rx — W^1’,
за исключением частного случая г = 0. Конечные рож-
даемость и скорость вымирания связаны с конечной ско-
ростью роста популяции соотношением eb-e~d = еТ, от-
куда для соответствующих экспоненциальных скоростей
имеем b — d = г.
Связь между параметрами
203
Интерпретация bud
Увеличение рождаемости проявляется лишь в том, что
в расчете на одну особь появляется на свет больше ново-
рожденных; при этом совсем не обязательно возрастают
одно или несколько значений тх или скорость роста по-
пуляции г. Так, уменьшение г вследствие увеличения смерт-
ности неполовозрелых особей в какой-то год повлечет за
собой пропорциональное увеличение доли животных в
интенсивно размножающихся возрастных классах. В
результате число новорожденных, приходящихся на одну
особь в популяции, возрастет, несмотря на то что абсо-
лютное число новорожденных может даже понизиться.
При этом не требуется никакой причинно-следственной
обратной связи, ответственной за увеличение рождае-
мости, следующее за увеличением смертности. Возрос-
шая рождаемость есть попросту арифметическое следствие
определения понятия «рождаемость», проистекающее из
взаимодействия между повозрастной плодовитостью и
возрастным распределением. Соответственно рождаемость
равным образом чувствительна как к изменениям плодо-
витости, так и к изменению смертности.
Точно так же скорость вымирания не является мерой
лишь смертности. Увеличение плодовитости приводит к
возрастанию доли неполовозрелых особей в популяции,
которые характеризуются более высокой удельной смерт-
ностью, чем взрослые, и в результате скорость вымирания
растет, несмотря на то что вектор 1Х остается постоянным.
По этим причинам, исследуя смертность и плодови-
тость, следует оперировать величинами 1Х (или <?х) и
тх. Рождаемость и скорость вымирания полезны в по-
пуляционном анализе, но они приводят к неоднозначным
выводам относительно популяционных процессов. Они
описывают эффекты, но не выявляют их причин.
9.9. ~Рост численности популяций
Этот раздел преследует две цели: показать, как раз-
личные отношения между популяционными параметра-
ми определяют характер роста популяций, и дать макси-
204
Глава 9
малым краткое введение в методы моделирования динами-
ки популяций.
Модели можно подразделить на два класса: общие (или
стратегические) и частные (или тактические). В страте-
гических моделях пренебрегают деталями взаимоотноше-
ний внутри популяций и между популяциями, а также
между популяциями и окружающей средой и концентриру-
ют внимание на наиболее существенных свойствах систем.
Функция этих моделей состоит в выявлении наиболее об-
щих свойств процесса. Делающиеся при этом выводы носят
качественный характер и могут быть, например, такого
рода: результатом данного процесса является вымирание
(или устойчивое равновесие, или колебания). Они обычно
остаются справедливыми для большинства популяций,
характеризующихся заложенными в модель свойствами
системы.
Тактические же модели направлены на определение
вероятности того или иного альтернативного исхода для
конкретного набора начальных условий, параметров и
отношений между параметрами. Стратегическая модель,
например, может указывать на то, что имеется широкий
класс систем, куда относится и интересующая нас популя-
ция, для которых почти наверняка существует устойчи-
вое равновесие. Это полезная информация, но нам инте-
ресно знать, достигнет ли когда-нибудь наша конкретная
популяция этого равновесия и какова вероятность того,
что она не вымрет за это время. Решение этих вопросов
находится в компетенции тактических моделей, которые в
отличие от стратегических принимают во внимание вре-
менные задержки, стохастические эффекты, колебания
внешних условий, пространственную неоднородность ме-
стообитаний, расселение, возрастные распределения и
сезонную изменчивость. Они имитируют динамику кон-
кретной популяции, растущей в заданных условиях. Хотя
такие модели и полезны для предсказания того, что в
действительности произойдет в популяции, они редко
позволяют проникнуть в суть экологических процессов.
Для решения двух основных задач, которые мы поста-
вили перед собой в данном разделе, лучше всего прибегнуть
к стратегическим моделям. Попробуем выяснить, к
какому детерминистическому результату приведет про-
Связь между параметрами
205
цесс роста при постоянных внешних условиях, если пре-
небречь возмущающим влиянием меняющихся возраст-
ных распределений и считать, что результат следует за
причиной без запаздывания, а скорость размножения и
смертность не зависят ни от возраста, ни от времени года.
9.9.1. Первый трофический уровень
Скорость роста растений обычно определяется наличием
воды и света, т.е. ресурсами, скорость возобновления ко-
торых не зависит от плотности растений. Пусть ресурс
поступает на каждый квадратный метр поверхности
земли со скоростью g, а единица растительной биомассы,
для того чтобы поддержать свое существование и воспро-
извести себя в следующем поколении, должна потреблять
этот ресурс со скоростью Ъ. Если на один квадратный метр
поверхности приходится растительная биомасса, равная
V, то доля ресурса, потребляемая ею, составляет b/Vg,
тогда как избыток, равный 1 — bV/g, может быть исполь-
зован на рост популяции. Когда растения достаточно уда-
лены друг от друга, почти вся доступная энергия может
идти па увеличение их числа. По мере роста плотности
популяции растет также доля ресурсов, которая идет на
поддержание биомассы и ее возобновление до тех пор,,
пока в конце концов на это не израсходуются все ресур-
сы и рост популяции не прекратится. Модель такой си-
стемы можно описать следующим уравнением:
Экспоненциальная скорость роста популяции т\ при
низкой плотности растительности близка к идеальной
скорости роста rml, но по мере роста биомассы V она по-
степенно убывает, стремясь к rt= 0. V при этом дости-
гает постоянного значения К = g/b. Подставляя К в
уравнение, получаем
r = (1-y)’
т.е. уравнение логистического роста. Заметим, что по-
стоянные скорости возобновления ресурса и скорости по-
206
Глава 9
требления его единицей биомассы уже не фигурируют в
уравнении, они неявным образом входят в константу К.
Такая замена возможна только в том случае, когда ско-
рость возобновления ресурсов совершенно не зависит от
плотности популяции — свойство, которое, за немногими
V
-------1-------!-------;— ---г--------
/
I
I
20000 - I
I
I
I
I
10000 - /
/
/
/
0 10 20 30 40 50
Годы
Рис. 9.5. Модель динамики численности певыедаемой популяции
растений.
исключениями, реализуется лишь на первом трофичес-
ком уровне. Рост популяции, изменяющей уровень ре-
сурса, которым будет обеспечено следующее поколение,
как это имеет место у травоядных, формально не может
описываться логистическим уравнением. Однако если,
например, животные, питающиеся мякотью плодов, не
трогают семян или косточек, они не оказывают влияния на
уровень этого ресурса в следующем году, и, следова-
тельно, логистическое уравнение применимо. Кроме того,
рост популяций, которые за счет небольшой величины гт
влияют на уровень ресурсов в следующем поколении
Связь между параметрами
207
лишь незначительно, также можно с приемлемой прагма-
тически точностью описывать логистическим уравнением.
Соответствующая кривая отличается от логистической,
но для практических целей этим расхождением, как пра-
вило, можно пренебречь.
На рис.9.5 изображена кривая логистического роста
популяции для rml = 0,8 и К =30 000. Примерно так
будет расти со временем биомасса травы на вашем газоне,
если семена высеяны в чистую почву и газон не подстри-
гается. Разумеется, кривая не будет в точности совпадать
с логистической, поскольку скорость возобновления ре-
сурсов и температура непостоянны, и, кроме того,
со временем меняется возрастное распределение, однако
совпадение будет достаточно хорошим. Кривая на рис.9.5
описывает динамику вида, растущего медленнее, напри-
мер кустарника, требующего для достижения равновес-
ной плотности примерно 20 лет.
9.9.2. Второй трофический уровень
1 ост популяций второго трофического уровня опре-
деляется факторами, существенно отличающимися от тех,
которые действуют на первом трофическом уровне. Ско-
рость роста популяции второго трофического уровня за-
висит от запасов лимитирующего его ресурса, а в том слу-
чае, когда этим ресурсом является пища, на уровень его
запаса в свою очередь оказывает влияние сама популя-
ция. Таким образом, система циклична: запас пищи в
значительной степени определяется животными, а уро-
вень численности животных — доступностью пищи. Со-
ответственно мы должны составить два уравнения: од-
но — для скорости роста растительности, а второе — для
скорости роста популяции травоядных.
В качестве первого уравнения возьмем приведенное
ранее уравнение для скорости роста растительности, до-
полнив его членом, описывающим уменьшение этой ско-
рости за счет выедания растений травоядными:
П = Гт1 (1 - y) “ С1Я(1 “ e~d^/V‘
208
Глава 9
Постоянная q обозначает скорость потребления расти-
тельности одним травоядным в условиях, когда пища
неограниченна (т.е. когда V велико и, следовательно,
1,— e~d'v ~1). При более низких значениях V животное
не может полностью удовлетворять свой аппетит, и коли-
чество потребляемой им в единицу времени пищи ста-
новится равным произведению с х на 1 — e~^v, которое
стремится к нулю при V, стремящемся к 0. Постоянная
d х характеризует скорость уменьшения этой величины от
1 до 0. Таким образом, величина с 1(l—e—d>v) описывает
«функциональную реакцию» травоядного, т.е. изменение
скорости потребления пищи в зависимости от её коли-
чества. Запишем теперь уравнение для скорости роста
популяции травоядного:
г2 = - а2 4- с2 (1 — e^iV},
Здесь а 2 — скорость убывания численности популяции в
расчете на одно животное в отсутствие пищи, а с2 —ско-
рость, с которой это убывание компенсируется ростом
популяции при избытке пищи. Следовательно, идеаль-
ная скорость роста популяции равна
гт2 — с2 ~ а2‘
При убывании количества доступной пищи с2 умножа-
ется на (1 — e-d»v), меняющуюся от 0 до 1 в зависимости
от значения V. Таким образом, величина с 2(1—e-d»v)
описывает «численную реакцию» популяции травояд-
ных на количество пищи, т.е. зависимость выживае-
мости и размножения от плотности пищи. Итак, система,
описывающая динамику популяций растительности и
травоядных, состоит из двух связанных уравнений:
Г1 = rmi (1 — — Cl (1 — е dlV)/V,
г2 = — а2 + с2(1 - е"су/).
На рис.9.6 изображена динамика процессов, описыва-
емых этими уравнениями. Исходная плотность расти-
тельности полагается равной равновесной плотности,
представленной на рис. 9.5, а затем в эти райские кущи
Связь между параметрами
209
мы запускаем 20 травоядных, характеризующихся сле-
дующими значениями параметров: сх = 2,5; = 0,0001;
а 2 = 1,2; с 2 = 1,7; d2 = 0,00008. Рост популяции рас-
считывался на ручном калькуляторе путем определения
Рис. 9.6. Модель динамики численности популяции травоядных
и биомассы популяции растений, служащих им пищей,
скорости роста двадцать раз в течение года и введением
каждый раз соответствующей поправки к численности по-
пуляции. Для этого указанные выше годовые скорости
роста (rml, сх, а 2 и сг) делились на число проводившихся
за год итераций. Большинство специалистов, имеющих
дело с природными популяциями, воспримут изображен-
ные на рис.9.6 кривые как график динамики вспышки
численности травоядных, и поэтому с достаточным осно-
ванием мы можем считать, что модель отражает свойства
системы растительность— травоядные. Она воспроизво-
дит основные черты динамики роста, которые мы наблю-
даем в полевых условиях.
Для того чтобы йолучить качественный результат, не
обязательно численно просчитывать рост популяции.
8—334
210
Глава 9
Его можно оцепить аналитически. Р. Мэй и Е.Робин-
сон проанализировали устойчивость этой модели и лю-
безно разрешили мне воспользоваться их результатом.
В двух словах этот результат можно сформулировать так:
еелй между растительностью и травоядными возможно
сосуществование, то биомассы этих двух составляющих
системы будут стремиться к равновесным значениям, рав-
ным
У* = J_ 1п,
^2 \с2 — а2 /
(1-У*/£)
- •
Эти два уравнения дают возможность понять общие зако-
номерности работы системы растительность—травоядные,
которые не являются ни тривиальными, ни a priori оче-
видными.
1. Равновесное значение биомассы растительности V*
при ее выедании травоядными никак не связапо ни с иде-
альной скоростью роста этой растительности гт1, ни с
ее равновесным значением в отсутствие выедания К.
Если бы в результате мутации, распространившейся по
всей популяции растений, идеальная скорость роста
удвоилась бы, то новыми равновесными значениями био-
масс стали бы V* и 2Н*. Точно так же равновесное зна-
чение биомассы растительности 7* остается неизменным
при увеличении значения К в результате дополнитель-
ного орошения. Избыточный ресурс при этом опять же
используется на увеличение популяции травоядных.
2. Если одних травоядных заменить другими, погло-
щающими вдвое больше пищи, а во всех остальных отно-
шениях тождественными своим предшественникам, то
равновесная биомасса растительности ие изменится, а
равновесная биомасса травоядных уменьшится вдвое.
3. Изменение идеальной скорости роста популяции
травоядных (rm2 = с2—а2) влияет и на V*, и на Н*,
причем повышение скорости роста приводит к уменьше-
нию V* и к увеличению Н*.
На равновесную биомассу растений, вообще го-
воря, не влияет ни один из параметров, характеризую-
Связь между параметрами
211
щих рост растений, а также интенсивность выедания.
Напротив, изменение любого параметра, характеризую-
щего рост популяции травоядных, сказывается и на V*,
и на Я*.
Читателю, желающему подробнее ознакомиться с мо-
делями систем, состоящих из двух видов, следует обра-
титься к книге Мэя (Мау, 1973).
9.9.3. Третий трофический уровень
Итак, теперь стратегия моделирования роста популя-
ций ясна. Мы должны написать уравнение для роста са-
мой популяции и по крайней мере по одному уравнению
для каждого из лежащих ниже трофических уровней.
Модель одной из очень простых систем может быть описана
следующим образом:
Растительность
Травоядные
Хищники
\ Л /
г2 = — д2 + с2 (1 — e~d*v) —
— fP II.
r3=-a34-c3(l — e~dlH'),
где Р во втором уравнении — это уровень численности
хищников, а выражение, в которое он входит, представля-
ет собой функциональную реакцию хищников, логичес-
ки эквивалентную функциональной реакции травоядных в
первом уравнении. Система, описываемая этими уравне-
ниями, может в зависимости от значения постоянных
либо находиться в устойчивом равновесии, либо совершать
колебания. Это в точности совпадает с тем, что мы видим
в полевых условиях. Некоторые из систем раститель-
ность—травоядное—хищник относительно устойчивы, тог-
да как параметры других систем (особенно в высоких
широтах) колеблются. На рис.9.7 показано, что проис-
ходит, когда в систему, динамика численности которой
была представлена на рис. 9.6, выпускают 20 хищников.
Соответствующие значения констант составляют : / =2,0;
d3 = 0,005; а3 = 1,0; с3 = 1,4; = 0,005. Биомасса
8*
212
Глава 9
растительности возрастает, а биомасса травоядных па-
дает в ответ на рост популяции хищников, и система при-
ходит к новому состоянию равновесия. Графики, изо-
браженные на рис. 9.6 и 9.7, в общих чертах соответствуют
истории событий, происходивших, как я читал, на остро-
ве Айл-Роял (Meeh, 1966; Allen, 1974), где сначала обос-
Рис. 9.7. Модель динамики численности популяций хищников, тра-
воядных, которыми они питаются, и растений, служащих пищей
травоядным.
повались и размножились лоси, а затем на них стали
охотиться проникшие туда волки. Численность лосей
сначала достигла равновесия, определяемого доступной
для них пищей, а затем после появления волков, перешла
к новому, более низкому равновесному значению.
Прежде чем мы расстанемся с хищниками, остановим-
ся на одном из наиболее безжалостных из них — совре-
менном человеке. Допустим, что он охотится на популя-
цию травоядных и интенсивность охоты регулируется
постоянным числом лицензий, выдаваемых ежегодно,
Связь между параметрами
213
причем на владельца лицензии уже не накладывается ни-
каких дополнительных ограничений. Для большей про-
стоты предположим, что каждый владелец лицензии —
это квалифицированный охотник-профессионал, сопро-
вождаемый подручным, который занимается его добычей.
При этих условиях динамику системы будут описывать
следующие уравнения:
Растительность
Травоядные
Хищники
П = rmi — — e dlV)/V.
r2 = — а2 4- с2 (1 — e-d,v) — fP.
r3 = 0.
Функциональная реакция хищника в пересчете на одного
травоядного, в предыдущем случае составлявшая /Р(1 —
—e~d*H)/H, теперь будет равна просто jP. Таким об-
разом, теперь количество травоядных, добываемых хищ-
ником, становится функцией только его квалификации и
численности травоядных. Хищник будет добывать одну
и ту же часть популяции при ее высокой и низкой плот-
ности, поскольку эффекта насыщения, обеспечивающего
максимальное значение добычи хищника, не существу-
ет. Равновесием этой системы будет
V* = — In (----1,
d2 \с2 — а2 — fPJ
тт* V»rml(i-V*/V
Р* = Р.
Мы вернемся к обсуждению практического значения та-
кого вида равновесия в гл. 11 при рассмотрении вопроса
о постоянном уровне добычи.
Глава 10
Мечение и повторный отлов
Развитие методов мечения и повторного отлова име-
ет длинную историю; они насчитывают множество моди-
фикаций, касающихся постановки и анализа, и им посвя-
щено ошеломляющее количество статей. К счастью, су-
ществует очень полный обзор этой литературы (Seber,
1973), который в сочетании с другим обзором (Cormack,
1968) дает введение в широкий спектр различных техни-
ческих приемов и методов анализа; потребность в тех
или иных приведенных в обзорах методах может возни-
кать при решении самых необычных проблем. Ме-
нее полный, но очень полезный обзор опубликован Хэнсо-
ном (Hanson, 1967).
В этой главе рассматриваются лишь те методы, кото-
рые представляют непосредственный интерес для эколо-
га, изучающего позвоночных животных.
Все эксперименты по мечению и повторному отлову
проводятся в основном в одном и том же порядке. Отлавли-
вается некоторое количество животных, составляющих
выборку, животные метятся и затем снова выпускаются
на волю, с тем чтобы характеристики этой опознаваемой
выборки могли быть в дальнейшем использованы для
оценки свойств популяции в целом. Целью этого меро-
приятия может быть исследование одного или нескольких
из перечисленных свойств:
1) подвижности;
2) скорости роста;
3) удельной повозрастной плодовитости;
4) удельной повозрастной смертности;
5) численности популяции;
6) увеличения численности за счет рождений и
иммиграции;
Мечение и повторный отлов
215
7) уменьшения численности за счет гибели и эмигра-
ции;
8) интенсивности добычи или сбора урожая;
9) скорости роста популяции.
Использование меченой выборки зависит от цели экс-
перимента. Экспериментальные приемы, пригодные для
достижения одной цели, могут быть совершенно непри-
годны для другой. Выбор техники эксперимента очень ва-
жен. Слишком часто биологи метят и повторно отлавли-
вают животных, прежде чем решить, какую, собственно
говоря, информацию они хотят получить; большинство
специалистов по математической обработке данных био-
логических экспериментов и наблюдений могут расска-
зать чудовищные истории на эту тему. Прежде чем при-
ступать к эксперименту, биолог должен решить, какие
параметры ему нужно оценить, какая экспериментальная
техника необходима для достижения этой цели и каков
требуемый уровень точности. Если нужную информацию
можно получить другими, более простыми способами,
не прибегая к методу мечения и повторного отлова, то
именно этот другой метод и следует использовать. Метод
мечения и повторного отлова трудоемок и дорогостоящ,
а получаемые результаты часто бывают неточны, посколь-
ку модели, положенные в основу метода, как правило,
не более чем грубое приближение к реальности.
10.1. Вероятность отлова
Эксперименты по мечению и повторному отлову можно
разделить па 2 класса. К первому, классу относятся
эксперименты, позволяющие решать вопросы 1—4, пере-
численные в приведенном выше списке, а ко второму —
вопросы 5—9. При постановке экспериментов первого
класса требуется лишь, чтобы меченые животные могли
быть опознаны. Для этого изучается только выборка ме-
ченых животных. Поведение и численность немеченных
животных не имеют отношения к оценке интересующих
нас параметров. Нам не важно, с равной ли вероятностью
отлавливаются меченые и немеченые особи, однако мы
должны предположить, что все меченые особи отлавли-
ваются с равной вероятностью. Ко второму классу экс-
216
Глава 10
периментов относятся те, в которых одинаковая вероят-
ность попадания в ловушки всех особей, меченых и неме-
ченых, имеет решающее значение для точности экспери-
мента. Не следует начинать какие бы то ни было экспе-
рименты по мечению и повторному отлову, относящиеся ко
2-му классу, до тех пор пока справедливость этого пред-
положения не проверена в предварительных экспери-
ментах или если такая проверка не входит в саму поста-
новку эксперимента.
Многие авторы, описывая результаты своих экспери-
ментов по мечению и повторному отлову, допускают, что
предположения, лежащие в основе проведенного анализа,
возможно, в некоторой (не поддающейся оценке) сте-
пени нарушаются, но при этом считают, что они сделали
все от них зависящее; затем, свято выполнив ритуал ста-
тистической обработки, интерпретируют полученные ре-
зультаты так, как если бы никакой вероятности ошибки не
существовало. Двоемыслие такого рода весьма опасно.
Мечение с повторным отловом — это не очень грубый ме-
тод, . и небольшие отклонения от заложенных в его
основу предпосылок могут приводить к большим ошиб-
кам в результатах. Основным источником ошибок следует
считать неодинаковую вероятность отлова животных.
Эберхарт (Eberhardt, 1969b), дополняя схему, предло-
женную Кормаком (Cormack, 1966), дал следующую клас-
сификацию причин этого явления:
1. Наследственные свойства особей (проявляющиеся
в поведении животных в непосредственной бли-
зости от. ловушки).
2. Результат обучения (животные могут проявлять
любопытство или, наоборот, начинают бояться ло-
вушек).
3. Свойства, зависящие от относительной вероятности
попадания в ловушку (животное не попадет в ло-
вушку, если в пределах его индивидуального участ-
ка нет ни одной ловушки).
Первую причину трудно выявить по данным повтор-
ных отловов, поскольку в предельном случае некоторые
особи будут характеризоваться вероятностью отлова,
равной нулю. Присутствие таких животных никоим обра-
зом не может быть выявлено по результатам экспе-
Мечение и повторный отлов
217
|римента. Вторую причину легко обнаружить, если одни
и те же меченые животные более одного раза выпуска-
ются на волю и снова отлавливаются (разд. 10.1.1).
Для компенсации этого эффекта следует изменить метод
отлова на такой, при котором шансы животного быть пой-
манным менее зависят от его поведения, использовать мо-
дели анализа, которые могут учитывать любопытство жи-
вотных или, наоборот, их страх перед ловушками,
появившийся в результате обучения (разд.10.6), и, на-
конец, снизить число повторных отловов, с тем чтобы жи-
вотные не успели обучиться положительному или отри-
цательному отношению к ловушкам. Третья причина
неодинаковой улавливаемости — неравенство для раз-
личных животных априорной возможности встретить
на своем пути ловушку; эта причина, вероятно, наиболее
важна, но она явно привлекает наименьшее внимание ис-
следователей. Надежность методов анализа, основанных
на оценке отношения числа меченых и немеченых живот-
ных, зависит не столько от случайного перемешивания
этих Животных, практически никогда не осуществляю-
щегося, сколько от того, случайным ли образом размеще-
ны на территории, занятой популяцией, пункты, на ко-
торых производится мечение животных, и ловушки, ко-
торыми они повторно отлавливаются. Эксперименты по
мечению и повторному отлову мелких млекопитающих
часто страдают тем недостатком, что животные повторно
отлавливаются в тех же местах, где они метились. За ис-
. ключением тех случаев, когда сеть ловушек очень густа —
настолько, что на каждый индивидуальный участок при-
j; ходится по крайней мере по одной ловушке, пренебреже-
ние взаимной случайностью расположения мест, где жи-
вотные метятся и повторно отлавливаются, неизбежно
приводит к очень большой частоте повторных отловов
-X меченых животных, и соответственно к заниженной оцен-
ке численности популяции. Этой погрешности можно из-
бежать, размещая ловушки для первичного отлова жи-
вотных с последующим мечепием случайным образом при-
мерно лишь в 25% узлов сети. Перед повторным отловом
& ловушки переставляются в другие узлы сети, положение
которых определяется по таблице случайных чисел. Слу-
чайным образом, разумеется, некоторые из ловушек мо-
218
Глава 10
гут оказаться оба раза в одних и тех же узлах сети. Если
постановка эксперимента требует более чем однократного
повторного отлова, то ловушки должны аналогичным обра-
зом переставляться перед каждым отловом.
Такая процедура делает для животного возможность
попасть в ловушки вполне случайной только тогда, когда
все животные имеют одинаковый радиус перемещения.
Если же, например, самцы более подвижны, чем самки, то
для них вероятность натолкнуться на ловушки будет боль-
ше, чем для самок. Такое различие в поведении требует,
чтобы число самцов и число самок оценивалось незави-
симо.
Неравная для разных особей вероятность попасться
в ловушку независимо от причин, которыми она опреде-
ляется, представляет собой не исключение, а скорее
правило. Это явление установлено для популяции мле-
копитающих (Getz, 1961; Kotte, 1965; Tanton, 1965,
1969; Marten, 1970), птиц (Orians, Leslie, 1958; Taylor,
1966) и лягушек (Turner, 1960a). Часто полагают, что
рыбы, как правило, не могут обучиться избегать крюч-
ка, однако Бьюкема (Beukema, 1970) показал, что карпы,
один раз попавшиеся на крючок, спустя год попадаются
в три раза реже, чем никогда не попадавшиеся карпы.
10.1.1. Критерии равновероятности отлова
Рофф (Roff, 1973) проанализировал обычно исполь-
зуемые критерии равновероятности отлова и показал, что
эти критерии не дают возможности отличить популяцию,
в которой вероятность отлова действительно случайна,
от популяции, которая состоит из двух или нескольких
классов, различающихся по средней вероятности быть
отловленными. На основе этих критериев нельзя отли-
чить простое пуассоновское распределение от суперпо-
зиции нескольких пуассоновских распределений, и во
втором случае, когда в действительности вероятность от-
лова разных животных различна, эти критерии тем не
менее будут давать положительный ответ на вопрос о
равновероятности отлова. Если какой-либо из этих кри-
териев указывает на неравновероятность отлова, то с
уверенностью можно сказать, что различия в вероятности
Мечение и повторный отлов
219
быть пойманными для разных животных существуют^на
самом деле; если же критерий указывает па равную i ве-
роятность, то этот результат может быть интерпретиро-
ван двояко. Таким образом, упомянутые нами критерии
применимы для выявления лишь некоторых типов нерав-
новероятности отлова, а в результате метод мечения с
повторным отловом применяется в отношении популяций,
для которых неравная вероятность отлова не обнаружи-
вается, хотя, возможно, и существует в действительности.
Предположим, что помеченные одновременно животные
выпускаются в популяцию, подвергающуюся затем шести
последовательным отловам. Очевидно, что все меченые жи-
вотные, попавшиеся при последнем отлове, были живы и
могли попасться при любом из предыдущих пяти отловов.
Число животных, попадавшихся в ловушки один, два и
т.д. до пяти раз, дает нам данные, необходимые для того,
чтобы судить о случайности отлова, т.е. о равновероят-
ности попадания в ловушку различных животных.
В табл. 10.1 представлены данные такого рода. Это —
распределение повторных отловов для 32 буревестни-
ков, помеченных в 1946 г., о которых известно, что они
еще были живы в 1952 г. (Orians. Leslie, 1958). За это
время отлов производился пять раз, и, следовательно, каж-
дая птица также могла быть отловлена максимум пять
раз. Лесли подчеркивает, что если отлов для различных
особей равновероятен, то частоты повторных отловов
должны образовывать биномиальное распределение. Сле-
довательно, гипотезу можно проверить, сравнивая на-
блюдаемую дисперсию с ожидаемой дисперсией биноми-
ального распределения. Для этого можно воспользовать-
ся критерием х2 с (S/)—1 степенями свободы:
2Л-2-^
2 2 /
X ------------~
Zfl _
2/ (2/)2
„„ 312
69------
32
31 199 ’
32 “ 322
что дает х2 = 50,32 с числом степеней свободы, равным 31,
для Р < 0,02. Таким образом, гипотеза о том, что распреде-
ление повторных отловов биномиально, т.е. вероятность
отлова одинакова, явно не подтверждается этим резуль-
татом.
220
Глава 10
Таблица 10.1
Данные для определения равновероятности отлова с
помощью критерия Леели (из Orians and Leslie, 1958)
Годы Повторные отловы п Число повторных поимок i Число отловленных животных f
1947 7 0 15
1948 7 1 7
1949 6 2 7
1950 4 3 2
1951 7 4 1
5 0
2п = 31 2/= 32
2п2 = 199 Zfi = 31 2/i2 в 69
Большинство таблиц /2 составлено не более чем для 30
степеней свободы (с.с.). Если в критерии используется
большее число степеней свободы, то соответствующее зна-
чение х2 может быть получено приведением к стандарти-
зованному нормальному значению, равному К(2/2)—
У(2с.с—1), что в данном случае дает j/100,6—]/бГ~=
2,22. Если полученная величина превышает 1,96, то это
означает, что Р < 0,05 и, следовательно, гипотеза равно-
вероятности отлова сомнительна.
Критерий Лесли обладает одним важным практическим
недостатком, заключающимся в том, что информация о
первом и последнем отловах используется наряду с
данными об отловах животных, не попавшихся при послед-
нем отлове. Дополнительный отбор данных необходимо
провести таким образом, чтобы исключить из анализа
всех животных, кроме тех, о которых известно, что они
дожили до окончания эксперимента. Соответстственно
при употреблении этого критерия может использоваться
менее одной десятой общего количества данных. Такое
количество данных позволяет с достоверностью судить о
равновероятности отлова только тогда, когда исследова-
Мечение и повторный отлов
221
Таблица 10.2
Наблюдаемые частоты отлова ящериц семейства агам и частоты
пуассоновского распределения с усеченным нулевым классом,
ожидаемые в случае равновероятности отлова
(J. A. Badham, неопубликованные данные)
Число попаданий
животного
в ловушку
i
Число
особей
f
Ожидаемые
частоты
Е (f)
Е (f)
1
2
3
4
5
6
7
8
9
10
23
7
3
2
1
0
1
0
1
0
15,797
12,303
6,388
2,488
0,775
0,201
0,045
0,009
0,002
0,000
9,908
3,284
2,286
0,367
8
2/ = 38
Х2 = 5,937
с.с. = 1
Р=0,02
ние ставилось в очень широком масштабе. Впрочем, если
промежуток между первым и последним отловами на-
столько короток, что естественную смертность можно счи-
тать низкой или даже равной 0, то при употреблении кри-
терия могут использоваться все данные отловов. Эти дан-
ные записываются так, как они записаны в табл. 10.2, в
которой приведено частотное распределение животных,
отловленных 1,2,3... раз. Поскольку в таблицу включены
все данные по отлову, каждое животное было отловлено по
меньшей мере один раз. Таким образом, в эту таблицу в
отличие от таблицы, использовавшейся при употреблении
критерия Лесли, не входит частота нулевого класса. Если
отлов равновероятен, то частотное распределение имеет
форму биномиального распределения с усеченным нуле-
вым классом, которое аппроксимируется пуассоновским
222
Глава 10
распределением с усеченным нулевым классом, в тех слу-
чаях, когда число отловов относительно велико по срав-
нению со средним числом повторных отловов животных.
Дарроч (Darroch, 1958) указывает, что ожидаемое рас-
пределение никогда не совпадает в точности с усечен-
ным пуассоновским, но для наших целей усеченное пуас-
соновское распределение служит хорошей аппроксима-
цией. Усеченное пуассоновское распределение может хо-
рошо соответствовать наблюдаемым частотам, и степень
соответствия проверяется с помощью критериях2- Мате-
матические_ожидания частоты, вычисленные по среднему
значению X полного пуассоновского распределения, свя-
заны со средними значениями усеченного пуассоновско-
го распределения соотношением
X
X —-------- •
1-е-^
Среднее значение наблюдаемого частотного распределения
отловов приравнивается х, а по нему оценивается X.
Набор соответствующих значений х и X приводится в
табл. 10.3. Если требуется большая точность, то X может
быть рассчитан по приведенному выше уравнению мето-
дом проб и ошибок с использованием в качестве исходного
ближайшего значения X в табл. 10.3 и таблицы значений'
экспонент, приведенной в приложении 1. Если х > 2,
то прямое решение (Irwin, 1959) задается полиномами Лаг-
ранжа:
X = z- Z-Z2- 1,5Z® - 2,6Z4 - 5,21Z\
где Z = хе~х .
В табл. 10.2 приведено распределение частот отловов
38 ящериц семейства агам (Amphibolurus barbatus),
отлавливавшихся 21 раз в течение 37 дней. Среднее зна-
чение распределения х — 'Zfi/'Zf = 1,974. Из табл. 10.3
следует, что значение X составляет немногим больше
чем 1,5; в действительности оно равно 1,558. Теперь мож-
но рассчитать математическое ожидание значений час-
тот E(f) для всех ' i:
Мечение и повторный отлов
223
Таблица 10.3
Зависимость между средним значением X (основная
часть таблицы) в пуассоновском распределении и эквивалентным
средним значением х в пуассоновском распределении с
усеченным нулевым классом
X 0 1 2 3 4 5 6 7 8 9
1 — 0,194 0,376 0,550 0,715 0,874 1,027 1,175 1,318 1,458
2 1,594 1,726 1,856 1,983 2,109 2,232 2,353 2,472 2,590 2,706
3 2,821 2,935 3,048 3,160 3,271 3,381 3,490 3,599 3,707 3,814
4 3,921 4,027 4,133 4,238 4,343 4,447 4,551 4,655 4,759 4,862
5 4,965 5,068 5,170 5,273 5,375 5,477 5,579 5,680 5,782 5,883
Д(/1) .2L,
17 1 — е-х i!
причем первый член постоянен для всех значений I. Сле-
довательно, для i = 1 математическое ожидание часто-
ты равно
Я(Л) = 38 x 0,2107 х 1,558 = 15,8,
vv 0,7893
а каждая последующая ожидаемая частота равна преды-
дущей, умноженной на X/i. Так,
Е(/2) = 15,8 Х-^- = 12,3,
2
Е(/3) = 12,3 х=6,4
И т.д.
Сравним теперь рассчитанные математические ожида-
ния частот (табл. 10.2) с наблюдаемыми частотами отлова.
Объединим вместе последние 8 частот, с тем чтобы все мате-
матические ожидания значений частот были больше 5,
сведя таким образом число классов в распределении на-
блюдаемых и ожидаемых частот к трем. Значение у2 =
= 5,937 (табл. 10.2) соответствует одной степени свободы,
224
Глава 10
т.е. числу, на 2 меньшему, чем число классов в критерии,
а это, в свою очередь соответствует вероятности Р =
= 0,02, иными словами, указывает на то, что наблюдаемые
частоты почти заведомо не описываются пуассоновским
распределением. Мы, следовательно, можем заключить,
что либо вероятность отлова различных животных неоди-
накова, либо значительное число животных погибло за
время эксперимента. Поскольку эксперимент был спе-
циально поставлен таким образом, чтобы исключить вто-
рую альтернативу, истинным следует считать первое пред-
положение.
Дополнительные критерии равной вероятности отлова
приводятся в работах Лесли (Leslie, 1952) и Кормака
(Cormack, 1966).
10.1.2. Поправка на потерю меток
Метод мечения и повторного отлова дает достаточно
точные данные лишь при условии, что животные не утра-
чивают метки. К сожалению, надежными являются лишь
очень немногие метки. Наихудшей в этом отношении сле-
дует, вероятно, считать систему кольцевания птиц, по-
скольку кольца часто изнашиваются и сваливаются
(Blake, 1951; Hickey, 1952; Orians, Leslie, 1958; Rowley,
1966; Fordham, 1967), срываются самими птицами (Lo-
vell, 1948), а нередко, будучи слишком крупными для
птенцов, сваливаются с них сразу после кольцевания.
Фарнер (Farner, 1949) предложил использовать в ка-
честве индекса частоты потери колец долю птиц, потеряв-
ших одно кольцо, от числа птиц, меченных двумя коль-
цами. Этот индекс может быть преобразован в прямую оцен-
ку скорости потери колец. Группе птенцов на обе ноги
надеваются хорошо заметные кольца, принципиально
не отличающиеся от колец, используемых для обычного
кольцевания. В выборке птиц, наблюдаемых через время
t после кольцевания, будут представлены птицы, отно-
сящиеся к четырем категориям:
а) В2 птиц с кольцами на обеих ногах,
б) В f птиц, у которых сохранилось лишь одно из двух
колец,
в) Во птиц, потерявших оба кольца,
Мечение и повторный отлов
225
г) птицы, не принадлежащие к группе меченных дву-
мя кольцами.
Идентифицирована может быть лишь принадлежность к
категориям а и б.
Обозначим вероятность потери кольца птицей, околь-
цованной одним кольцом, за время t через р, тогда ве-
роятность того, что кольцо сохранится, будет равна 1— р..
Если потери колец с правой и левой ног происходят неза-
висимо, то вероятность потери обоих колец птицей, околь-
цованной двумя кольцами, за время t будет равна р2,
вероятность потери одного из колец равна 2р(1—р) и
вероятность сохранения обоих колец — (1—р)2. Следо-
вательно,
р2: 2р (1 - Р): (1 — Р)2 = Во: В{: 52.
Предположим, что в наблюдаемой выборке имеется Вх =
= 32 птицы с одним кольцом, В 2 = 64 птицы с двумя коль-
цами, а у остальных птиц колец нет, и, следовательно,
мы не можем сказать, были ли они исходно мечены двумя
кольцами. Число
быть оценено по
5о =
птиц, потерявших оба кольца, может
формуле
322 ,
---— = ------= 4 птицы.
Вероятность потери кольца птицей, исходно окольцо-
ванной одним кольцом, за тот же промежуток времени
равна
2В2 + BL 128 + 32
Оценка р может использоваться для коррекции дан-
ных по вторичному отлову птиц, окольцованных одним
кольцом. Если такая выборка содержит тп окольцован-
ных птиц, то истинное число в этой выборке птиц, которые
были окольцованы, составляет
, m
ТП — ----- .
1-р
В случаях, когда посредством мечения и повторного от-
лова оценивается удельная смертность, требуется опре-
226
Глава 10
делить значения р для нескольких значений t — времени
между мечением и повторным отловом, с тем чтобы выя-
вить характер зависимости р от времени.
Такая коррекция представляет собой приближенное
и, конечно, не точное решение. Эта неточность происте-
кает главным образом от положенного в основу нашего рас-
суждения предположения о том, что потеря кольца с пра-
вой и левой ног происходит независимо. Такое предпо-
ложение вряд ли всегда можно считать справедливым.
10.2. Интерпретация оценки численности
популяции, полученной методом мечения
и повторного отлова
В случаях, когда популяция имеет четкие и известные
нам географические границы, единственной проблемой,
которая стоит перед нами, является вопрос о том, как
следует поставить эксперимент по оценке численности
этой популяции. Однако часто у популяции нет четких
границ, и мы знаем лишь, что некоторая часть популя-
ции обитает на исследуемой территории произвольной
величины. При использовании метода мечения и повторного
отлова для оценки численности популяции в этой ситуа-
ции наш первый вопрос — как я должен оценивать чис-
ленность популяции? — превращается во второй: что
представляет собой популяция, численность которой я
определяю? Предположим, что популяция облавлива-
ется посредством одной ловчей линии из близко располо-
женных друг от друга ловушек в центре изучаемой тер-
ритории и что ловушки остаются на тех же местах при
первом и втором отловах. Получающаяся при этом оценка
не является оценкой общего числа животных, обитающих
на исследуемой территории, а относится лишь к числу
животных, индивидуальные участки которых включают
в себя ловчую линию. Если длина ловчей линии составля-
ет L метров, а средний диаметр индивидуального участка
равен D метрам, то мечение с повторным отловом даст
•оценку численности популяции, обитающей в полосе с
общей площадью, примерно равной D(D + L) м2. Если
же, однако, расстояние между соседними ловушками замет-
но больше среднего диаметра индивидуального участка,
Мечение и повторный отлов
227-
ТО мы оцениваем численность популяции, обитающей на*,
цепочке изолированных участков общей площадью при-
мерно пк (-i-D)2 м2, где п — число ловушек. Предполо-
жим теперь, что метятся животные, попавшиеся в ловушки,,
размещенные по всей изучаемой территории случайным-,
образом, и что перед повторным отловом ловушки заново
случайным образом размещаются, по территории.. Пусть-
популяция замкнута в том смысле, что иммиграция равна
эмиграции. Тогда оценка численности популяции по Пе-
терсену (одно мечение — один повторный отлов) дает чис-
ленность популяции, населяющей изучаемую территорию,
плюс полосу, окружающую территорию по периферии,,
ширина которой примерно равна половине среднего диа-
метра индивидуального участка. Более того, такая оцен-
ка будет завышенной даже и для этой территории, по-
скольку, в то время как эмиграция не сказывается на.
оценке, иммиграция повышает ее.
Эти проблемы интерпретации оценок встают всякий
раз, когда метод мечения с повторным отловом применя-
ется в отношении популяций, не имеющих естественных,
границ. Постановка эксперимента по мечению с повтор-
ным отловом для оценки численности уток Северной Аме-
рики не создает принципиальных проблем, тогда как по-
становка эксперимента по точной оценке? численности
уток США практически невозможна.
10.3. Оценка Петерсена
Простейший метод оценки численности мечением с
повторным отловом предполагает однократное прове-
дение мечения при первом отлове и затем определение-
доли меченых животных в выборке, полученной при пов-
торном отлове. Такая оценка базируется па основной акси-
оме теории выборок: доля особей, обладающих определен-
ным признаком в популяции, может быть оценена по их
доле в выборке, взятой из популяции. С точностью
до ошибок выборки
М т
228
Глава 10
где М — это число меченых животных в популяции об-
щей численностью N (IV неизвестно), а т — число ме-
ченых животных в повторно отловленной выборке общей
численностью п. Нетрудно преобразовать это уравнение
таким образом, чтобы оно давало оценку численности
популяции:
ЛГ I ГО »г Мп
N = М — , или N =----------,
/ п т
т.е. численность популяции в момент лечения оценивается
как общее число меченых животных, деленное на долю
меченых животных в повторно отловленной выборке.
Такая оценка называется оценкой численности популя-
ции по Петерсену.
Смертность не смещает этой оценки при условии, ко-
нечно, что смертность меченых и немеченых животных
одинакова. Если за время между мечением и повторным
отловом погибает 70% животных, то уравнение может быть
переписано в форме
N = М
m (1—0,7)
п (1—0,7) ’
где (1—0,7) — удельная выживаемость — сокращается.
Уравнение Петерсена лежит в основе большинства
оценок численности посредством метода мечения с пов-
торным отловом. Это уравнение привыкли настолько тесно
связывать с указанным методом, что любопытно вспомнить,
что впервые оно было использовано для оценки числен-
ности популяции, члены которой не метились и не
отлавливались. Лаплас (Laplace, 1786, цит. по Cor-
mack, 1968) оценил численность населения Франции
посредством деления зарегистрированного числа новорож-
денных по всей стране за год, М, на долю, которую
новорожденные в том же самом году составляли от из-
вестного общего числа прихожан нескольких церковных
приходов. Таким образом, новорожденные в данном слу-
чае рассматривались как «меченые особи», а доля ново-
рожденных, представляющая собой «повторно отлавли-
ваемых» в выборке известного размера, использовалась
для оценки общей численности населения. Лаплас при
Мечение и повторный отлов
229
этом не нуждался в предположении, что все новорожден-
ные тщательно регистрируются (это и не соответствова-
ло действительности), ему достаточно было предположить,
что доля новорожденных, регистрируемых в приходах,
являвшихся объектом выборки, не отличалась от таковой
по стране в целом.
Идею использовать мечение особей для оценки чис-
ленности популяции впервые предложил Петерсен еще
в 1896 г. (Petersen, 1896), однако ее практическая реали-
зация осуществилась только в 1919 г. Далом (Dahl,
1919), который использовал этот метод для оценки чис-
ленности популяции рыб. По праву первенства оценка
получила имя Петерсена. Линкольн (Lincoln, 1930) ис-
пользовал метод Петерсена для оценки численности уток,
и с тех пор орнитологи, маммологи и охотоведы часто
называют его оценку индексом Линкольна. Такое назва-
ние неудачно, во-первых, потому, что метод дает не ин-
декс, а оценку численности, во-вторых, потому, что Лин-
кольн был не первым, предложившим его. Хотя бы из
соображений единообразия, не говоря уже о других при-
чинах, этот метод следует называть оценкой Петерсена.
Оценка Петерсена дает правильный результат лишь
при выполнении следующих условий:
1) вероятность попадания в ловушку одинакова для
всех особей в популяции;
2) за промежуток времени между мечением и повтор-
ным отловом на изучаемой территории не рождают-
ся новые животные и не происходит иммиграции;
3) смертность и выживаемость животных на изучае-
мой территории одинаковы для меченых и неме-
ченых животных;
4) животные не теряют метки.
Интуитивно, казалось бы, вполне обоснованная фор-
мула
m
в действительности дает смещенную оценку, причем при
больших промежутках времени результат получается за-
вышенным (Chapman, 1951; Bailey, 1951, 1952). Бейли
считает, что в тех случаях, когда до повторного отлова не
230
Глава 10
оговаривается число меченых животных, которое должно
быть отловлено (прямая выборка), более точной является
оценка
N M(n + i)
т 4- 1
причем стандартная ошибка (SE) составляет
SE
, /" (Af2 (п + 1) (п — т) ]
|/ I (т + I)2 (т + 2) J
Если же число меченых животных, которое должно быть
отловлено, оговаривается до начала отлова и отлов про-
должается до тех пор, пока это число не будет достигну-
то (обратная выборка), то несмещенная численность попу -
ляции определяется по формуле
дг. . n (М + 1)
т — 1
со стандартной ошибкой, равной
SE =
У I m(m + 2)
Недостатком обратной выборки является необходи-
мость заранее решать, какое число меченых животных
должно быть отловлено. Биолог может поставить себе
целью отловить т животных, а в действительности эта
цель может оказаться практически недостижимой, на-
пример из-за того, что заранее не имеется ни малейшего
представления о численности популяции. Однако пре-
имущества обратной выборки столь велики, что сл'едует
пренебречь трудностями, связанными с получением не-
обходимой для ее использования информации.
Еще до того, как мы приступим к повторному отлову,
следует решить, какая точность оценки численности нам
требуется. Тогда число меченых животных, которое дол-
жно быть отловлено, можно определить, исходя из извест-
ного общего числа меченых животных и предполагаемой
численности популяции. Предположим, что исследова-
тель считает, что популяция насчитывает 200 особей, и из-
Мечение и повторный отлов
231
вестно, что помечено 40 из них. Требуется получить оцен-
ку численности, стандартная ошибка которой составляет
примерно 10% численности популяции, т.е. примерно 20
особей. Число меченых животных, которое должно быть
отловлено для достижения такой точности оценки, может
быть определено по формуле
ш —
/• ( (N+i) (N-M)
|/ I SE2
4 (У+1) (N—M) (М+1)
SE2
2
(У + 1)(У-М) '
“ "" -4—
SE2_________
2
, / <201 + 160 Л2 <4X201X160X41^ <201x500
|/ V 400 + J + \ 400 ) [ 400 + J
= 29,45, т. е. 30 меченых особей.
Таким образом, заранее заданная требуемая точность
оценки показывает, что повторный отлов должен про-
должаться до тех пор, пока не будет поймано 30 меченых
животных.
Предположим теперь, что в процессе повторного отло-
ва вместе с 30 мечеными животными в ловушки попалось
155 немеченых особей. Тогда
М = 40,
m = 30,
’ д=30 + 155 = 185.
Оценка численности популяции в соответствии с уравнени-
ем Бейли составляет
/V = п (^ + О _ 185x41/29 = 262 животных.
тп — 1
232
Глава 10
Стандартная ошибка этой оценки равна
SE =
, / ( (М —m + l)(N + l) (N —7И)'
|/ I т (т 4- 2)
(40—30+1) X (262 + 1)х222
30 X 32
и тогда N ± SE = 262 + 26, или 262 ±10%.
Общее число меченых животных (М)
Рис. 10.1. Число меченых животных, которое должно быть отловле-
но для того, чтобы стандартная ошибка оценки Петерсена составля-
ла 10%.
Это число является функцией численности популяции (V) и общего числа
меченых животных (М).
На рис.10.1 изображены несколько вариантов зависи-
мости числа меченых животных, которое должно быть
отловлено для того, чтобы стандартная ошибка составля-
ла примерно 10% численности популяции, от общего числа
Мечение и повторный отлов
233
меченых животных при различных численностях популя-
ции. На кривых видно, что даже если исходно метится
более трети популяции (ситуация маловероятная), то
заранее предполагаемая численность популяции не ока-
зывает существенного влияния на точность окончательной
-оценки. Даже в тех случаях, когда заранее предполагае-
мая численность популяции вдвое больше или меньше
истинной, это исказит стандартную ошибку оконча-
тельной оценки лишь на несколько процентов. Если желае -
мая точность оценки численности составляет 10%, а чис-
ленность самой популяции лежит в пределах между 100
и 1000 особей, то хорошим общим правилом для выбора
числа меченых и повторно отлавливаемых животных может
’ служить следующая табличка
’ М 100 200 250
тп 55 80 90
Появление в популяции в промежутке между мече-
! нием и повторным отловом новорожденных и иммигрантов
завышает оценку Петерсена. По этой причине мечение и
повторный отлов лучше всего производить в промежутке
между двумя последовательными сезонами размножения.
Смещение оценки, происходящее за счет иммиграции,
может быть сведено к минимуму сокращением промежутка
> времени между мечением и повторным отловом. Если в
промежутке между мечением и повторным отловом все
же появляются новорожденные, то для получения не-
смещенной оценки требуется проведение по меньшей мере
Jf трех последовательных отловов. Описание постановки
эксперимента и проведения анализа для этого случая
содержится в разд.10.5 и 10.6.
10.4. Метод Шумахера
Оценка Петерсена предполагает одновременное ме-
чение всех предназначенных для этого животных. Очень
часто такая задача невыполнима, поскольку мы пе можем
одновременно отловить и пометить число животных, до-
статочное для получения требуемой точности оценки чис-
ленности популяции. При альтернативной постановке
234
Глава 10
эксперимента, когда мечение производится в процессе
нескольких последовательных отловов, численность по-
пуляции оценивается по скорости, с которой растет в
популяции доля меченых животных по мере того, как их
метится все больше и больше.
Метод получения максимально точной оценки числен-
ности при такого рода постановке эксперимента разра-
ботал Шнабель (Schnabel, 1938), но поскольку предло-
женное им уравнение допускает решение лишь методом
последовательных приближений, мы воспользуемся мо-
дифицированным вариантом этого метода (Schumacher,
Eschmeyer, 1943), дающим решение в явном виде. Этот
вариант не менее эффективен, чем дающий максимальное
приближение (Turner, 1960b, Phillips, Campbell, 1970),
а часто, быть может, даже более точен, поскольку он ме-
нее зависит от степени случайности в перемешивании ме-
ченых и немеченых особей (DeLury, 1958).
Если N — постоянная численность популяции, Mt —
число особей, меченых до i-го отлова, а пг — число осо-
бей, пойманных при г-м отлове, из которых тпг оказались
меченными ранее, то численность популяции можно
оценить по формуле
N =------1— •
Стандартную ошибку в оценке численности N рассчиты-
вают косвенным методом (DeLury, 1958; Ricker,
1958 : 101). В первом приближении стандартная ошибка
величины i/N составляет s/|/"SAf;2rai, где
S (и?/пг)-(^Л/гтг)2/(^М?пг)
S — ' «
/-1
причем / — общее число отловов. Доверительные интер-
валы вычисляются для i/N умножением стандартной ошиб-
ки на величину t, соответствующую у — 1 степеням сво-
боды. Доверительные интервалы для N представляют
собой величину, обратную доверительным интервалам
для i/N. Допустим, оценка для N составляет 100 и соот-
ветственно i/N = 0,01. Стандартная ошибка для i/N, рас-
считанная для пяти повторных отловов, составляет
Мечение и повторный отлов
235
± 0,001. Тогда 95%-ный доверительный интервал для
1/7V заключен между
i/N + (0,001 х 2,776) = 0,0128
и
i/N — (0,001 X 2,776) = 0,0072,
где 2,776 — это значение t для уровня вероятности 0,05
при числе степеней свободы, равном 4. Вычисляя обрат-
ные величины, получаем, что 95%-ный доверительный
интервал для N лежит между 78 и 139.
Основное достоинство этого метода состоит в том, что
он позволяет проверить справедливость предположения
о постоянстве вероятности отлова для всех особей. Если
это предположение справедливо, то регрессия тп^/щ на
представляет собой проходящую через начало коор-
динат прямую с наклоном i/N.
Применение метода Шумахера требует выполнения
более строгих ограничений, чем использование оценки
Петерсена. В частности, предполагается, что численность
популяции остается постоянной на протяжении всего
времени эксперимента, животные не погибают и не по-
кидают исследуемую территорию. Так же как и при ис-
пользовании оценки Петерсена, предполагается, что за
время эксперимента на исследуемой территории новые жи-
вотные не рождаются и не иммигрируют, а кроме того,
что вероятность отлова меченых и немеченых животных
одинакова.
10.3. Метод троекратных отловов Бейли
Ни метод Петерсена, ни метод Шумахера не дают пра-
вильной оценки общей численности популяции в тех слу-
чаях, когда в промежутке между мечением и повторными
отловами на исследуемой территории появляются новые
животные — новорожденные или иммигранты. Один из
нескольких методов оценки численности популяции в такой
ситуации содержится в работах Бейли (Bailey, 1951,
1952). Кроме определения численности популяции, его
метод позволяет оценить также рождаемость и смерт-
ность.
236
Глава 10
Использование метода троекратного отлова требует
данных по двум последовательным мечениям и двум
последовательным повторным отловам. Данные по пер-
вому из повторных отловов и второму мечению получаются
по одной и той же выборке, так что всего требуется про-
извести три отлова. В табл.10.4 приведены данные, необ-
ходимые для оценки численности популяции методом
троекратного отлова.
Таблица 10.4
Данные, используемые для анализа методом
троекратных отловов Бейли
Время, Число меченых животных Число животных, отловленных для повторного мечения Отловленные из числа м0 Отловленные из числа Mi
0 Ма = 600
1 = 518 = 700 т01 = 182
2 п2 = 700 т02 = 146 т12 = 158
В момент времени «нуль» было отловлено, помечено
и выпущено на волю 600 животных. В момент t = 1 было
отловлено 700 животных; 182 из них, оказавшихся ме-
чеными, были сразу выпущены на волю, а остальные
518 были сначала помечены новыми метками, отличными
от использовавшихся при предыдущем мечении, и лишь
затем выпущены на волю. В момент t = 2 было снова от-
ловлено 700 животных, при этом оказалось, что 146 из
них были помечены в момент t = 0, а 158 — в момент
t = 1. Обратите внимание, что ни на одном из животных
не могло быть двух меток. Бейли [151 ] считает, что не
следует в момент t = 1 повторно метить особей, уже по-
меченных в момент t = 0. Если все же поступать таким
образом, то некоторые из животных будут одновременно
принадлежать к двум выборкам — тп02 и иг12. Это об-
стоятельство хотя и выгодно с точки зрения статистики,
однако оно приводит к увеличению любого смещения
оценки, возникающего за счет изменения реакции жи-
вотных на ловушки после первого попадания в них.
Мечение и повторный отлов
237
Вычисления довольно просты:
Мх (тгх + 1) та02 518 X 701 X 146 _
(m01 + 1) (тп12 + 1) 183 X 159
где N-l — численность популяции в момент t = 1. При-
ближенная стандартная ошибка определяется по формуле
.2 (гах + 1) (пх + 2) (m02 — 1) ге02
1 (mnl -f- 1) (zn01 + 2) (m12 -|- 1) (w12+2)
518^ * 701 x 7Q2 * 145 x 146
183 X 184 X 159 X 160
= 238 (t. e. 13% от N^).
В промежутке между моментами t = 1 и t = 2 ско-
рость увеличения численности популяции за счет появ-
ления новорожденных и иммиграции определяется по
формуле
jg __ moi (и2 1) __ 182 X 701 ___ 240
12 «1 (®02 +1) 700 X 147 - ’
Скорость убыли популяции в промежутке между момен-
тами £ = 0и£ = 1за счет гибели особей и эмиграции
определяется по формуле
^1^02
DOi = 1------= 0,207.
(™12 + О
Так как продолжительности промежутков между момен-
тами £=0и£ = 1, с одной стороны, и< =1и< = 2-
с другой, часто бывают различны, прежде чем сравнивать
эти скорости, следует привести их к эквивалентной про-
должительности времени:
В12 = виг, откуда i12 = 0,215.
и
Doi = (1 — e"d)01, откуда doi = O.,233.
Если продолжительность промежутка (0,1) составляет
4 нед, а промежутка (1,2) — шесть недель, то соответ-
ствующие «недельные» скорости будут равны: Ь12 =
238
Глава 10
= 0,215/6 = 0,0358 и . doi = 0,233/4 = 0,0583. Считая,
что эти скорости остаются постоянными на протяжении
всех 10 недель эксперимента; можно получить скорость
роста численности популяции в промежутке между мо-
.ментами t = 0 и t = 2:
г = Ь - d = 0,0358 - 0,0583 = — 0,0225.
Зная скорость изменения численности популяции и оцен-
ку численности в момент t = 1, мы можем рассчитать
значения численности в моменты t = 0 и t = 2:
No = Nf'1 = 1822Г(0’0225 х4) 1994
и
Дг2 = Ni6rt = 1822е(-0’0225х6> = 1592.
Метод троекратного отлова разработан для случаев,
когда в промежутках между последовательными отлова-
ми в популяции рождаются новые особи. Однако даже в
тех случаях, когда численность популяции измеряется в
промежутке между двумя последовательными сезонами
размножения, предпочтительно пользоваться не оценка-
ми Петерсена, а методом троекратных отловов, посколь-
ку последний позволяет учесть эффект иммиграции
и ввести на него поправку.
Существует несколько вариантов метода троекратного
отлова, изложенных в работах Лесли (Leslie, 1952),
Лесли и Читти (Leslie and Chitty, 1951), Лесли, Читти и
Читти (Leslie, Chitty and Chitty, 1953), Мак-Леода (McLeod,
1958), Кулсона (Coulson, 1962) и Санлейтнера и Бейт-
мена (Sonleitner and Bateman, 1963). В последней ста-
тье дается также метод оценки величины выборки, не-
обходимой для получения определенной величины стан-
дартной ошибки.
10.6. Метод Джолли — Зебера '
Джолли (Jolly, 1965) и Зебер (Seber, 1965) независи-
мо друг от друга разработали изящный метод стохасти-
ческого анализа, позволяющий оценивать демографи-
ческие параметры популяции в случаях, когда прово-
дятся два или более повторных отлова меченых животных.
Мечение и повторный отлов
23»
Метод этот существенно отличается от методов Петерсена
и Бейли. В этих уже рассмотренных методах 10%-ная
смертность, например, означает, что в популяции из каж-
дой сотни животных погибает ровно десять. Это детерми-
нистические модели. В модели же Джолли — Зебера
10%-ная вероятность гибели означает, что в точности 10%
особей погибает в популяции лишь при рассмотрении
очень больших промежутков времени. Если взят малый
промежуток времени, из каждой сотни особей за принятое-
за единицу время может погибнуть 6, 10, 13, 14 или ка-
кое-либо другое число особей, причем каждой из этих
ситуаций в свою очередь может быть приписана опреде-
ленная вероятность. Такие модели называются стохасти-
ческими.
Использование этого метода требует, чтобы в нашем
распоряжении были подробные сведения относительно ме-
чения и отловов каждого конкретного животного. Каж-
дое животное при каждом повторном отлове метится мет-
кой с указанием времени мечения, так что в конце экспе-
римента у каких-то животных может оказаться либо
несколько различных меток, либо одно индивидуальное-
нумерованное кольцо или индивидуальная нумерованная
метка. В последнем случае каждый раз фиксируется дата
очередного отлова каждого конкретного животного.
Обычно для данных, полученных при i-м отлове, ис-
пользуются следующие обозначения:
Nt — оценка численности популяции;
и, — размер выборки;
Mi — общее число животных, помеченных в популя-
ции до г-ro отлова;
mt — число меченых животных в выборке;
Rt — число меченых и отпущенных на волю живот-
ных;
гг — число животных из числа 7?г, выпущенных на
волю после г-ro отлова и затем снова попав-
шихся при последующих отловах;
Z; — число животных, помеченных до i-ro отлова г
не попавшихся при i-м отлове, но попавшихся
при одном из последующих;
аг — доля меченых животных среди попавшихся при
г-м отлове.
240
Глава 10
Использование метода Джолли—Зебера покажем на
примере определения численности популяции бабочки
голубянки-икар (Polyommatus Icarus) (Рагг, Gaskell and
-George, 1968). Для большей наглядности добавим к зна-
чениям частот по нескольку «воображаемых», в действи-
тельности не наблюдавшихся экземпляров. Табл. 10.5
составлена таким образом, чтобы суммировать всю ин-
формацию по мечению и повторным отловам. Так, числа
в четвертой строке означают, что при четвертом отлове
было поймано 8 бабочек (ге;), из которых 0 + 2 + 1 =3
были помечены ранее. Две из них уже попадались при
втором отлове и одна — при третьем. Пять немеченых
бабочек из выборки иг были затем помечены, но при этом
одна, nf — Rt = 1, была нечаянно убита. Однако три,
уже имевшие метки ранее, и четыре, только что помечен-
ные (Rt =7), были выпущены на волю. Кроме того, в
каждом столбце приведено число rt бабочек, уже имевших
метки, из числа 7?г, выпущенных на волю после г-го
отлова. Например, в выборке, полученной при втором
отлове, rt = 12.
Таблица 10.5
Значения щ, R; и Г; для анализа методом Джолли — Зебера
Число пойманных бабочек ni Число выпущенных на волю Число раз. которое бабочки попадались прежде (числа, выделенные курсивом)
9 9 1
13 12 5 2
14 14 2 7 3
8 7 0 2 1 4
18 16 1 2 3 1 5
14 14 0 1 2 1 2 6
G = 8 12 6 2 2
Г1 г*
Табл. 10.6 получена из табл.10.5 (не считая колонок
,пг и Rt) суммированием общего числа меченых бабочек,
Мечение и повторный отлов
241
пойманных при предшествовавших отловах. В скобках
приведено суммарное число меченых бабочек. Так, на-
пример, числа в шестой строке получены следующим
образом: 0, 0 + 1, 0 + 1 + 2, 04*1 + 2 + 1и(0 + 1 +
+ 2 + 1+2). Эти величины, стоящие вверху каждого
столбца, представляют собой значения тп^ причем соот-
ветствующее г каждый раз выделено курсивом и стоит
справа. Сумма этих значений по каждому столбцу дает
значение Z. Так, для третьего отлова т; =9, a Z( = 6.
Таблица 10.6
Значения иц и Zt, полученные из табл. 10.5 для анализа
методом Джолли—Зебера
1
(5) 2
2 (9) 3
0 2 (3) 4
1 3 6 (?) 5
0 1 3 4 (6) 6
Zi+i= 3 6 9 4 . 4—.
zs Zi zt
В табл.10.5 и 10.6 содержится вся информация, необ-
ходимая для оценки демографических параметров попу-
ляции. Численность популяции при взятии последова-
тельных выборок, за исключением первой и последней,
оценивается по формуле
"ЧП
откуда
Nn = 13 + 13x3x12 = 20,8,
5 X 12
дг 14 + 14x6x14 = 35 8
Лг4 = 92,0 и Лг5 — 100,3. Для каждого значения числен-
ности может быть вычислена стандартная ошибка по фор-
муле
9—334
242
Глава, 10
SEi =
Mj — mj+ Rj /1_______1 \ j 1—аг
Afj Vi Ri) mi
rj\e at = mi/rii (например, a4 = 0,375) и ЛГг = me -f-
+ (например, Л/4 = 34,5).
Так, стандартная ошибка для JV4 составляет
se4=
34,5 — 3+7 / 1.. 1 \
34,5 (.2 7 /
= 55,50.
. 1 — 0,376
ф 3
Вероятность того, что некоторая конкретная особь,
присутствующая в популяции при i-й выборке, сохранит-
ся, т.е. не погибнет и не эмигрирует с изучаемой терри-
тории к моменту проведения следующей выборки, со-
ставляет
Mi — mi + Ri
и для четвертой выборки равна р4 = 39/(34,5 — 3 + 7) =
= 1,013, что невозможно, так как значение вероятности
не должно превышать единицы. Поэтому соответствующее
значение должно быть принято равным единице.
Численность пополнения популяции за счет новорож-
денных и иммигрантов в промежутке между i-й и i +- 1-й
выборками, если, разумеется, считать лишь особей, до-
живших до i + 1-й выборки, оценивается по формуле
= 7Vi+1 - Pi (Nt — nt + R^,
откуда
Л4 = 100,3 - 1,013(92 - 8 + 7) = 8,12.
В работе Джолли (Jolly, 1965) приведены также вычис-
ления, позволяющие определить стандартную ошибку
для pi и At.
Этот метод не позволяет точно оценить численность
популяции в моменты взятия первой и последней выборок,
однако эти величины могут быть приблизительно оцене-
ны с помощью метода, не менее точного, чем тот, который
Мечение и повторный отлов
243
используется при троекратных отловах по Бейли
(разд. 10.5). Скорость роста популяции в промежутке меж-
ду вторым и третьим отловами ([1пА3 — 1пА2 ]//) при-
нимается равной скорости роста между первым и вторым
отловами. Численность Ni оценивается по численности
JV2 и найденной скорости роста популяции посредством
экстраполяции в прошлое. Точно таким же образом чис-
ленность популяции в момент последнего отлова может
быть оценена экстраполяцией, исходя из значения чис-
ленности при предпоследнем отлове и скорости роста
популяции, рассчитанной по значениям численности при
предпоследнем и предшествовавшем ему отловах. В
тех случаях, когда постановка эксперимента предусма-
тривает лишь троекратное проведение отловов, метод
Джолли—Зебера может быть использован наряду
с методом Бейли.
В работе Уайта (White, 1971) приводятся написанные
на ФОРТРАНе программы для расчета на ЭВМ по мето-
ду Джолли—Зебера численности популяции и других
параметров.
10.7. Оценка удельной смертности
Предположим, что М животных помечены и затем вы-
пущены на свободу. При последующих отловах коли-
чество меченых (и вновь выпускаемых на свободу) жи-
вотных составляет соответственно т0, mlt т2 и т3. Эти
данные позволяют оценить значение удельной смертности
даже в тех случаях, когда промежутки времени между
последовательными отловами были неодинаковы.
Примем за точку отсчета времени момент проведения
отлова, при котором в выборке оказалось т0 меченых
животных. Тогда угол наклона b линии регрессии нату-
рального логарифма In т на время b дает оценку мгно-
венного значения удельной смертности —d в используе-
мых единицах времени. По этой величине может быть опре-
делена доля особей в популяции, погибающих за единич-
ный отрезок времени: q = 1—e~d. В табл. 10.7 приведен
пример такого расчета.
9»
244
Глае a 10
Таблица 10.7
Вычисление удельной смертности из частот повторных отловов
М=200 меченых особей
Время, кед X Повторные отловы т 1п повторных отловов (у)
0 88 4,477
5 53 3,970
17 10 2,303
21 8 2,079
Ег = 43 Еу = 12,829
Ег2 = 755 Егу = 102,660
, Ежу — (S х )(Еу)/я 102,66—(43х12,829)/4 - я
х)2/п ~ 755 — (43х43}/4 ’ "
Мгновенная удельная смертность = d = 0,120
Конечная удельная смертность =g = 1 — e~d =0,113 в неделю
Конечная удельная смертность = q = 1 — e-62d = 0,998 в год
Конечная удельная смертность =7 = 1 — e~dji = 0,017 в день
Если промежутки времени между последовательными
отловами одинаковы, то процедура оценки упрощается:
~ 1 + w2 + т3
т0 4- 7П1 + т2
причем единицей времени в этой оценке является Про-
межуток между последовательными отловами. Мгновен-
ное значение удельной смертности d следует рассчитывать
лишь в тех случаях, когда нам надо определить значение
q для различных единичных отрезков времени. Если доля
особей q, погибающих в течение недели, составляет 0,113,
то
d = In —= 0,12
1 — 7
и, следовательно,
q = 1 — е-0,12^7 = 0,017 в сутки.
Мечение и повторный отлов
245
Этот метод часто применяется неправильно, когда в
в соответствующие значения частот включаются
не только меченые животные, попавшиеся при данном
отлове, но и отловленные впоследствии; при этом исхо-
дят из того, что хотя эти животные и не попались при
данном отлове, они тем не менее были живы и присутство-
вали в популяции в момент его проведения. Такая про-
цедура дает завышенное значение q. Другой широко
распространенной ошибкой является включение в фор-
мулу для оценки удельной смертности числа исходно
меченных животных М:
р ' . ~ j_m0 ~4~ + m3
' - М -|- ZTIq -j- 777 j -|- 7712
При вычислении по такой неправильной формуле значения
q получаются заниженными.
Значения удельной смертности не могут быть оце-
нены по дапным, на основе которых (исходя из частот
попадания в ловушки) оценивается численность поцуля-
ции. Точность оценок численности зависит от того, на-
сколько хорошо выполняется допущение об отсутствии
гибели особей в популяции в течение эксперимента. Та-
ким образом, постановка эксперимента, в котором оце-
нивается численность популяции, и эксперимента, в
котором оценивается смертность, должна быть различ-
ной. В первом случае эксперимент проводится за возмож-
но более короткое время, тогда как во втором случае
эксперимент должен быть достаточно продолжителен для
того, чтобы успела погибнуть заметная доля меченых осо-
бей. ....
10.8. Модели частот попадания в ловушки
Большинство моделей мечения с повторным отловом
основано на умозрительных конструкциях типа «что
будет, если...?», где после «если» следует перечень не-
вероятных предположений, наименее реалистическое из
которых требует, чтобы вероятность попадания в ловушку
была одинакова для всех животных. В последнее время
появилось много новых идей, связанных с построением
246
Глава 10
моделей мечения и повторного отлова; эти идеи делают
модели более реалистичными и соответственно основанные
на них оценки более правдоподобными. Большая часть
попыток была предпринята с целью разработать модели
частот попадания в ловушки, в которых не обязательным
было бы выполнение требования равновероятности попа-
дания различных животных. В настоящее время в этом на-
правлении наблюдается лишь незначительный прогресс, но
хотя опубликованные анализы такого рода еще явно не-
совершенны, они знаменуют начало пути, который
в ближайшие годы, несомненно, приведет нас к созданию
более совершенных моделей.
При анализе частот отлова мы имеем дело с численнос-
тями животных, 1, 2, 3 и т.д. раз попадавшихся в ловушки
при последовательных отловах. Эти данные образуют
распределение с усеченным нулевым классом, в который
входит неизвестное нам число животных, ни разу не по-
падавшихся в ловушки. Цель анализа заключается в по-
пытке оценить частоту встречаемости нулевого класса,
исходя из формы усеченного распределения. Числен-
ность популяции при этом рассчитывается как общее
число животных, по меньшей мере один раз попадавших в
ловушки, плюс оценка числа животных, не попадавшихся
ни разу.
Все эти методы анализа обладают одним общим по-
ложительным свойством. Применимость каждого из них к
конкретному набору данных может быть оценена по сте-
пени совпадения ожидаемых частот с наблюдаемыми. По-
этому нет необходимости пользоваться этими методами
вслепую, бездумно принимая на веру лежащие в их основе
гипотезы. Равным образом нет необходимости ограничи-
ваться при анализе какой-то одной моделью; правильная
стратегия заключается в том, чтобы из нескольких распре-
делений выбрать то, которое дает наилучшее совпадение
с экспериментальными данными. Три изложенных здесь
метода анализа основываются на различных предполо-
жениях относительно вероятности попадания в ловушки.
Вместе взятые, эти методы описывают, хотя и не исчер-
пывающим образом, довольно широкий круг возможных
распределений вероятностей попадания в ловушку. Метод
Пуассона основан на предположении о постоянстве ве-
Связь между параметрами
247
роятности попадания, тогда как геометрическая модель
и модель отрицательного биномиального распределения
предполагают существование возникающей различными
способами неравнрвероятности попадания в ловушку.
Продемонстрируем использование этих моделей на
данных по частотам отлова самцов агам Amphibolurus
barbatus (J. A. Badham, неопубликованные данные). Экс-
перимент продолжался 37 дней между последовательными
периодами размножения, из них на протяжении 21 дня
проводились повторные отловы. Таким образом, пополне-
ние популяции было равно 0, а удельная смертность от-
носительно низка. В табл. 10.8 приведены численности
ящериц, попадавшихся в ловушки 1, 2, 3 и т.д. раз, при-
чем максимальное число попаданий составило 9 на
21 отлов.
Таблица 10.8
Усеченное пуассоновское, отрицательное биномиальное
и геометрическое распределения, соответствующие частотам
поимки самцов ящериц семейства агам
Число пос- ледователь- ных попада- ний в ловуш- ки i Число особей fi Распределения
пуассоновское E(ft) отрицательное биномиальное геометрическое
1 13 8,180 5,191 11,017
2 6 8,150 2,244 6,349
3 2 5,413 1,186 3,659
4 21 2,6971 0,6841 2,1081
5 1 1,075 0,414 1,215
6 0 0,357 0,259 0,700
7 1 0,102 0,165 0,403
8. 0} 5 0,025 4,263 0,107 1,842 0,233 4,976
9 1 0,006 0,071 0,134
10 0 0,001 0,047 0,077
>10 0 0,000 0,095 0,106
X2 5,687 24,007 1,128
с.с. 2 1 " 2
р 0,06 <0,001 0,5
Оценки N 30 117 45
248
Глава 10
Оценки по пуассоновскому распределению
Пуассоновское распределение с усеченным нулевым
классом может хорошо соответствовать наблюдаемым ча-
стотам в том случае, если вероятность попадания в ло-
вушку постоянна. Мы уже имели дело с этим распреде-
лением в разд. 10.1.1, где оно использовалось для провер-
ки гипотезы о равновероятности попадания в ловушки.
В настоящем разделе оно используется для оценки чис-
ленности популяции. Этот метод был предложен Крейгом
(Craig, 1953), а впоследствии использовался. Киккавой
(Kikkawa, 1964) и Эберхартом (Eberhardt, 1969b).
Процесс определения параметров распределения опи-
сан в разд. 10.1.1. Среднее число попаданий в ловушку
среди особей, попадавшихся по крайней мере один раз, х,
рассчитывается как среднее по наблюдаемому распре-
делению частот попадания в ловушку, и на основе этого
значения оценивается среднее значение числа попаданий
в' ловушку X на одну особь по популяции в целом. В нашем
примере (табл. 10.8) х — = 2,3077, исходя из
чего X = 1,9927. Предполагая, что вероятность по-
падания в ловушку постоянна, а смертность за время
эксперимента пренебрежимо мала, мы оцениваем числен-
ность популяции, составляющую
N = = 30.
X 1,9927
Оценка по отрицательному биномиальному
распределению
Отрицательное биномиальное распределение обычно
используется для описания частотных распределений,
характерных для процессов, при которых вероятность
свершения тех или иных событий не постоянна. Отрица-
тельное биномиальное распределение лучше, чем пуассо-
новское, описывает, например, распределение числа не-
счастных случаев, еженедельно происходящих на фабри-
ке. Это обстоятельство, вероятно, отражает неравную
предрасположенность различных рабочих к несчастным
Мечение и повторный отлов
случаям. Так как предрасположенность к несчастным слу-
чаям и предрасположенность к попаданию в ловушки —
явления сходного порядка, можно ожидать, что отрица-
тельное биномиальное распределение также хорошо будет
соответствовать распределению частот попадания вдо-
вушки. Этот метод оценки численности популяции был
предложен Тентоном (Tanton, 1965) и Холгейтом (Hol-
gate, 1966).
Как и при использовании пуассоновского метода,
численность популяции рассчитывается по средней часто-
те X, с которой в ловушки попадаются особи по популяции
в целом. В свою очередь X оценивается по среднему числу
попаданий в ловушки х для особей, попавшихся по мень-
шей мере одип раз. Для того чтобы произвести такую
оценку, нам необходимо знать еще один параметр, з2,
дисперсию среднего числа попаданий в ловушку среди
особей, попадавшихся по меньшей мере один раз. В нашем
примере
Е/.г = 13 4-6 + 24---=26,
Zfti = (13X1) +(6 х 2) + (2 X 3)... = 60
и
S/ii2 = (13- 12)+(6х22) + (2х32)... =242.
Для этого набора данных среднее значение и дисперсия
распределения числа попаданий в ловушки с усеченным
нулевым классом оценивается по формулам
я = -^- =— = 2,3077
26
и
S2
”1
“ 25
Брасс (Brass, 1958) показал, что среднее значение пол-
Vi
242 -
26
4,1415.
ного распределения может быть оценено по формуле
1
Х = х-—^---,
* (s/i —Л)
где /1 — наблюдаемая частота однократных попаданий
в ловушку. При условии что наблюдаемое распределений
250
Глава. 10
действительно представляет собой отрицательное биноми-
альное распределение с усеченным нулевым классом, этот
метод дает приближенную, но эффективную оценку X.
В нашем примере
X = 2,3077-----44415x13— = 0,513.
2,3077 (26 — 13)
Неизвестное число особей, пи разу не попадавшихся в
ловушки, может быть теперь оценено по формуле
= S/ft-XS/,- _ 60-(0,513 X 26) _g.
'° X 0,513 ~ *
Общая численность облавливаемой популяции составляет
^fii 60
N == ц7.
X 0,513
В качестве проверки можно оценить общее число попадав-
шихся в ловушки особей: N — /0 = 2/г- = 26.
О приемлемости моделей, основанных па отрицатель-
ном биномиальном распределении, и, следовательно, о
возможной точности оценки численности популяций мож-
но судить, сравнивая наблюдаемые частоты с ожидаемыми.
Для того чтобы рассчитать ожидаемые частоты, мы прежде
всего должны определить значения еще двух параметров.
Определение максимально приближенных оценок этих
параметров (Sampford, 1955) требует многочасовых вы-
числений. Но существуют приближенные оценки (Brass,
1958), пригодные для большинства целей:
w = — (1-------= 0,2786,
к __ = о 1981.
1—и>
Если наблюдаемое распределение является отрицательным
биномиальным с усеченным нулевым классом, то матема-
тическое ожидание частот определяется по формуле (Fis-
cher, 1941)
E(fi) = ZfiX х r(fe + 0' X (1 - w)1,
V i-w Г(Л)»! . V '
Мечение и повторный отлов
251
где Г ( ) — гамма-функция, Е ( ) «математическое ожида-
ние», I —факториал, a i может принимать значения 1,
2, 3... . Значения гамма-функции могут быть рассчитаны
по формуле Стирлинга (Cramer, 1945)
In Г (х) = (х----—In х — х + 0,91767 -}— -----------— ,
' ’ \ 2 ) 12г 360г»
последний член в которой может быть опущен при х > 3.
Рассчитанные таким • образом частоты приведены в
табл.10.8.
Оценки по геометрическому распределению
Эберхарт (Eberhardt, 1969b) проанализировал воз-
можность использования геометрического распределения,
являющегося предельным случаем отрицательного бино-
миального распределения. Оп мог бы привести неко-
торые теоретические соображения, свидетельствующие
о том, что геометрическое распределение хорошо опи-
сывает распределение частот попадания в ловушки, одна-
ко он предпочел просто ввести этот метод как эмпири-
ческий результат, показав, что может быть достигнуто
хорошее совпадение теоретического и эксперименталь-
ного распределений.
Геометрическое распределение характеризуется од-
ним параметрам q, имеющим смысл вероятности того, что
данная особь попадается в ловушку по меньшей мере один
раз. Предложенное Эдвардсом и Эберхартом (Edwards
and Eberhardt, 1967) уравнение, видоизмененное с уче-
том поправки Чепмена и Робсона (Chapman and Robson,
1960) на смещение для малых выборок, дает следующую
оценку для q:
q = = 6Q~26 = 0,5763.
S ft i — 1 59
Оценка численности популяции при этом составляет N —
= S/Jq = 26/0,5763 = 45, а ожидаемые частоты рас-
считываются, начиная с i — 1, по формуле
Е (f i) = (£ f (i — q) у‘~г.
252
Глава 10
Соответствующие значения для рассматриваемого примера
приводятся в табл.10.8,
Интерпретация совпадения
В табл. 10.8 приводятся математические ожидания
частот, если наблюдаемое распределение частот попадания
в ловушки описывается соответственно пуассоновским,
отрицательным биномиальным и геометрическим распре-
делениями с усеченным нулевым классом. Степень сов-
падения в каждом случае может быть охарактеризована
значением величины х2, рассчитываемым по формуле
[л-я(/да(/о
для каждого i от i = 1 до i = 3, где некоторые из на-
блюдаемых частот объединены в один класс, так что общее
число классов равно четырем. Для пуассоновского и
геометрического распределений значения х2 обладают
п — 2 = 2 степенями свободы, тогда как для отрицатель-
ного биномиального распределения число степеней сво-
боды равно п — 3 = 1.
Значения вероятностей, определяемые по значениям
X2, не должны рассматриваться сами по себе, изолиро-
ванно. В данном случае мы должны определить по этим
значениям, какая из трех моделей наилучшим образом опи-
сывает характер наблюдаемого распределения числа по-
паданий в ловушки. Для нашего примера ясно, что лучше
всего экспериментальным данным соответствует геометри-
ческое распределение, хуже всего — отрицательное бино-
миальное. То, что отрицательное биномиальное распре-
деление плохо описывает экспериментальные данные,
в значительной степени определяется приближенностью
расчетов, — эта приближенность может быть оправдана
лишь в том случае, когда наблюдаемое распределение хо-
рошо соответствует отрицательному биномиальному рас-
пределению. Однако наиболее существенным следует счи-
тать тот факт, что модель отрицательного биномиального
распределения не пригодна для описания данных анали-
зируемого эксперимента.
Модели распределений с усеченным нулевым классом
не должны использоваться порознь, независимо друг от
Глава 10
253
друга. Они должны использоваться вместе, «триплетом»,
и тогда по меньшей мере один из методов позволит дос-
тигнуть цели. Приведенные здесь данные лучше всего
описываются геометрическим распределением, а осталь-
ные два должны быть отвергнуты. При других полевых
условиях более приемлемым может оказаться пуассонов-
ское или отрицательное биномиальное распределение.
В приложении 3 приводится написанная на ФОРТРАНе
программа для расчета численности популяции и соот-
ветствующих частот по каждой из этих трех моделей.
Эти методы не могут служить для оценки численности
популяции, если животные погибают за время проведения
эксперимента. Равным образом наличие или отсутствие
совпадения между теоретическим и наблюдаемым распре-
делениями ничего не говорит о равновероятности попада-
ния животных в ловушки, если популяция является
открытой, не замкнутой. Тантон (Tanton, 1969) построил
отрицательное биномиальное распределение с усеченным
нулевым классом для описания частот попадания в ловуш-
ки представителей двух видов мелких млекопитающих с
небольшой продолжительностью жизни, отлавливавших-
ся на протяжении двух с половиной лет. Его оценку чис-
ленности популяций нельзя считать ни средним мгно-
венным значением численности популяции за этот период,
ни суммарным числом особей, обитавших на исследуе-
мой территории в течение этого периода. Ничего не дают
нам и данные, приведенные в работах Бастарда (Bustard,
1969, 1970), показавшего, что распределение частот попа-
даний в ловушку представителей двух видов ящериц,
которых он ловил в течение двух лет, пе описывается пуас-
соновским распределением. Возможно, он прав, утверж-
дая, что вероятность попадания в ловушку пе одинакова
для различных ящериц, но плохое совпадение пуассо-
новского распределения с наблюдавшимся пе может слу-
жить тому доказательством.
10.9. Анализ возврата меток охотниками
Обсуждавшиеся выше методы эффективны лишь в тех
случаях, когда биолог полностью контролирует ход
всего эксперимента. Однако гораздо чаще биолог постав-
254
Глава 10
лен в определенные условия, которые он изменить не в
силах и, следовательно, должен приспосабливаться к ним
при постановке экспериментов. Это особенно справедливо
в отношении популяций, являющихся объектом охоты.
Меченые животные в этом случае не отлавливаются и за-
тем выпускаются на волю, а отстреливаются охотниками,
которые могут вернуть, а могут не вернуть метку или коль-
цо в соответствующее бюро кольцевания. По каждой воз-
вращенной метке биолог может определить лишь где и
когда было помечено животное и в лучшем случае где и
когда оно было убито. Он редко может определить, какая
часть общей добычи была помечена. В общей форме полу-
чаемые от охотников данные всегда характеризуются этими
свойствами, однако приемлемые методы анализа могут
быть различными; это зависит от продолжительности
охотничьего сезона, от того, метятся ли животные на
протяжении короткого или длительного периода, и от
того, представляют ли собой меченые животные несме-
щенную выборку из популяции или преимущественно ме-
тятся животные определенного возраста.
Численность популяции определяется с помощью ме-
чения и повторного отлова по отношению численностей
меченых и немеченых животных в случайной выборке.
Этот параметр может быть легко определен в экспери-
менте, полностью идущем под контролем эксперимента-
тора, с большими трудносятми, — когда возвращение ме-
ток связано с китобойным или рыболовным промыслом и
с самыми большими трудностями — когда возврат меток
зависит от охотников-спортсменов. Теоретически отноше-
ние численностей меченых и немеченых животных можно
оценить по выборке из охотничьих трофеев, однако
практически такая информация очень ненадежна. Воз-
вращенные охотниками метки редко могут использовать-
ся для оценки численности популяции, являющейся объ-
ектом охоты. По данным большинства экспериментов,
использующих возвращаемые охотниками метки, оцени-
вается лишь значение удельной смертности.
Описываемые ниже методы анализа основываются на
предположении, согласно которому для принадлежащего
к данному возрастному классу животного вероятность
быть подстреленным пропорциональна частоте этого воз-
Мечение и повторный отлов
255
растного класса в популяции. Данное предположение
представляется и логичным и реалистичным одновремен-
но, однако большинство опубликованных результатов
анализа смертности у пернатой дичи основывается на почти
противоположном предположении. В большинстве таких
анализов используются методы Беллроуза и Чейза (Bellrose
and Chase, 1950). Эти методы основываются на неявном
предположении (противоречащем утверждению, выска-
зываемому авторами) о том, что для птицы вероятность
быть подстреленной в течение охотничьего сезона пропор-
циональна вероятности погибнуть от естественных причин
в следующем году, если она уцелела к окончанию охот-
ничьего сезона. Таким образом, считается, что все факторы,
обусловливающие смертность, оказывают влияние на
результаты отстрела, что в высшей степени сомнительно.
Приводимые ниже модели не ограничиваются также
обычным требованием постоянства удельной смертности
по прошествии первого года жизни. Эта гипотеза не была
доказана ни для одной из групп позвоночных животных.
Она не является также необходимым условием математи-
ческого анализа.
Независимо от условий эксперимента мы обычно можем
оценить для популяции в целой или по крайней мере для
какого-либо одного пола или возрастного класса долю
особей, погибающих за год от всех возможных причин.
Если охотники-спортсмены возвращают все метки, обна-
руженные на добытых животных, то эта доля может быть
разделена на животных, добытых в течение охотничьего
сезона, и на животных, погибших за год от других при-
чин. Включим также во вторую категорию тех особей,
которые были отстрелены, но не учтены, и тех особей,
которые были учтены, но метки с которых пе были воз-
вращены. Охотники-спортсмены возвращают не все мет-
ки. Доля возвращаемых меток в США оценивается при-
мерно в 30% (Crissey, 1967), 40% (Tomlinson, 1968),
45% (Bellrose, 1955) и 50% (Geis and Atwood, 1961) и
сильно различается для разных штатов. Оценки такого
рода дают значение коэффициентов коррекции, которые
следует использовать при оценке удельной смертности
животных за счет охоты.
Значения удельной смертности за счет охоты и естест-
256
Глава 10
венной удельной смертности могут быть рассчитаны по
отдельности лишь в тех случаях, когда охотничий сезон
короток, а животные метились незадолго до открытия
сезона.
Описываемые ниже методы охватывают широкий круг
ситуаций, с которыми сталкиваются специалисты в об-
ласти лесного и охотничьего хозяйства. Описание других
подходов можно найти в работах Зебера (Seber, 1970,1972)
и Джонсона (Johnson, 1974).
Общие допущения и обозначения
В основе всех методов анализа, рассмотренных в этом
разделе, лежат перечисленные ниже допущения. До-
полнительные допущения, характерные для той или иной
конкретной модели, приводятся при описании соответству-
ющих моделей.
1. Меченые животные не теряют меток или же, если
они их теряют, то эффект потери может быть скор-
ректирован.
2. Интенсивность охоты не возрастает и не убывает
со временем, хотя от года к году она может претер-
певать колебания.
3. При анализе во внимание принимаются лишь мет-
ки, возвращенные охотниками.
4. Животные всех возрастных классов в равной мере
подвержены истреблению на охоте.
Для всех моделей общеприняты следующие обозначения:
М — число животных, помеченных и выпущенных на
свободу;
т — число меток, возвращаемых в течение охотни-
чьего сезона;
х — возраст в годах, определяемый в разных моделях
по-разному; в первой модели, например, воз-
раст х = 0 эквивалентен возрасту 6 мес и соот-
ветственно возраст х= 1 эквивалентен 1,5 годам;
и — доля особей в возрасте старше фиксиро-
ванного базового (т.е. х = 0), добываемая
охотниками в течение одного года;
w — доля особей в возрасте старше фиксированного
Мечение и повторный отлов
257
базового, погибших в течение года от других
причин;
h — изолированная удельная годовая смертность за
счет охоты;
п — изолированная удельная годовая смертность за
счет других причин;
q — общая удельная годовая смертность, т.е. доля
особей, погибших от всех причин в течение
года.
Когда значения этих смертностей зависят от возраста,
нижний индекс означает нижний граничный возраст соот-
ветствующего возрастного класса. Так, qx — это общая
удельная годовая смертность в возрасте от х до х + 1.
Черточка над символом означает среднегодовую удель-
ную смертность по всем возрастам выше базового, взве-
шенную в соответствии с представленностью каждого воз-
растного класса в популяции. Различные удельные ха-
рактеристики смертности связаны между собой соотно-
шениями
q = и 4-w и q = h п — hn.
10.9.1. Методы анализа, пригодные в случаях,
когда метятся только молодые особи
Модель 1. Животные метятся лишь в одном году, мет-
ки возвращаются на протяжении нескольких последую-
щих лет, охотничий сезон короток, животные метятся
незадолго до открытия сезона, интенсивность охоты оста-
ется из года в год постоянной.
В табл. 10.9 приводятся данные Болхема и Майерса
(Balham, Miers, 1959) по результатам возвращения ко-
лец после кольцевания 1069 птенцов черных австралий-
ских уток Anas superciliosa, произведенного в 1950 г.
Базовым возрастом (х = 0) является средний возраст
утят к достижению ими первого охотничьего сезона, что
в данном примере составляет около полугода.
Прежде всего рассчитывается общая удельная смерт-
ность для каждого возрастного класса по формуле
qх = 1 —f"'ir+1 = 1 -— = 0,333 для возраста х = 2*
258
Глава 10
Таблица 10.9
Возврат колец и удельная смертность самцов черных
австралийских уток, окольцованных птенцами в один и тот же
год (данные из работы Balham and Miers, 1959)
Возраст Число возвратов Исходное число X тх М 0 314 1069 1 69 2 18 3 12 4 2 5 1
Парциальные (и ? 0,294 0,294 0,294 0,294
удельные j ™Х 0,486 0,445 0,039 0,539
смертности 1 пх 0,688 0,630 0,055 0,763
Общая удельная
смертность 1х 0,780 0,739 0,333 0,833
Для возраста х = 4 удельная смертность не рассчиты-
вается, поскольку частота возвращенных колец слишком
мала для того, чтобы служить основой для достоверной
оценки; эти данные не позволяют также определить смерт-
ность qx для возраста х = 5. Взвешенная среднегодовая
удельпая смертность вычисляется по формуле
=_з1£ = 0 755
4 £т, 416
Доля убитых на охоте в течение года может быть оценена
только для возрастного интервала между 0 и 1. Мы пред-
положим, что она остается постоянной для всех возраст-
ных интервалов и составляет
й = = 0,294.
М 1069
Тогда доля особей, погибающих в возрастном классе в
течение года от других причин, составляет
wx = qx — u =0,333 — 0,294 = 0,039 для возраста х = 2.
Если мы считаем возможным предположить, что смерт-
ность в промежутке между кольцеванием и началом пер-
вого охотничьего сезона настолько мала, что ею можно
пренебречь, то изолированная удельная смертность и
естественная смертность могут быть рассчитаны соответ-
Мечение и повторный отлов
259
ственно по формулам hx = и и
Q Y ~~~ h у 0,039 Л ЛГГ Г»
n _ jdx----= -------= о Q55 дЛя возраста х = 2 .
х 1 — hx 0,706
В табл. 10.9 приведены оценки смертности для различных
возрастных классов, рассчитанные таким способом.
Модель 2. Молодые особи метятся незадолго до на-
чала ограниченных охотничьих сезонов последовательно
несколько лет подряд, и на протяжении нескольких по-
следующих лет кольца возвращаются охотниками.
Если для оценки удельных смертностей некоторые ко-
горты могут быть объединены в группы, то постоянство
интенсивности охоты, требовавшееся в первой модели,
теперь больше не является обязательным. Расчеты ана-
логичны тем, которые проводились в первой модели, за
исключением того, что значение М теперь зависит от воз-
раста.
В табл. 10.10 приведены такого рода данные. Значения
частот, равные 0, соответствуют реальной ситуации. Про-
черки соответствуют классам, существование которых не-
возможно. Например, не существует годовалых птиц и
птиц старших возрастов, окольцованных в году 7, по-
скольку эксперимент был завершен до начала охотни-
чьего сезона в этом году. Точно так же не может быть
колец на птицах старше одного года,, которые были бы
окольцованы птенцами в году 6, или птиц старше 2 лет,
окольцованных в году 5, и т.д. Этот эффект «последова-
тельного усечения» должен быть скорректирован в тех слу-
чаях, когда несколько когорт объединяется в группы для
оценки значений удельной смертности в зависимости от
возраста. Поскольку М уже не является постоянной, за-
висящие от возраста значения рассчитываются как
численности исходно окольцованных птиц, которые мог-
ли бы внести свой вклад в совокупность возвращенных ко-
лец шх. Мх определяется путем вычитания из общего
числа окольцованных птиц числа птиц, окольцованных
в годы, для которых в таблице возвращений колец стоят
прочерки (табл. 10. 10). Исходная численность «когорты»,
в которой было возвращено 54 кольца с двухлетних птиц,
составляет М 2 = 2489 — 27 — 124 = 2338.
260
Глава 10
Таблица 10.10
Возврат колец и удельные смертности самцов черной
австралийской утки, окольцованных птенцами, за несколько
последовательных лет (данные из работы Balham and Miers, 1959)
Год кольцева- ния Число окольцо- ванных Число возвратов колец (т) в зависи- мости от возраста (х) Годовая удельная СМЕРТ- НОСТЬ за счет охо- ты
0 1 2 3 4 5 6
1 2 3 4 5 6 7 175 1069 452 330 312 124 27 64 15 4 1 0 0 1 314 69 18 12 2 1 — 112 28 12 4 0 — — 92 11 10 4 — — — 80 17 10 — — — — 17 9 — — — — — 8 — — — — — _ 0,366 0,294 0,248 0,279 0,256 0,137 0,296
Итого 2489 687 149 54 21 2 1 1 из из из из из из из 2489 2462 2338 2026 1696 1244 175
Число возвратов тх Исходное число мх
Парциальные ? ,u = hx удельные J и>х смертности ( пх Общая удель • ная смертность дх 0,276 0,276 0,276 0,276 0,505 0,342 0,275 0,610 0,698 0,472 0,380 0,843 0,781 0,618 0,551 0,886 ” = 0,731
Значения удельных смертностей оцениваются с по-
мощью уравнений, аналогичных использовавшимся в мо-
дели 1 :
qx = 1 — = 1 — 2338 \21 =0,551 для возраста 2;
Мх+1тх 2026 X 54
-------- ------------= 0,731;
M0S (тх/Мх) 2489 X 0,3777
Мечение и повторный отлов 261
1V1 Q &4cSJiJ
hx = и = 0,276;
wx — Чх ~~и = 0,551 — 0,276 = 0,275 для возраста 2
и
qx — hr 0,551 —0,276 n 9On o
nx = —-------— =--------------= 0,380 для возраста 2.
L1 — hx 0,724
Эти оценки для каждого возраста можно проверить с
помощью соотношения
qx = и 4- wx = hx 4- пх — hxnx.
Доля погибающих каждый год на охоте и может быть рас-
считана лишь для первого после кольцевания охотничь-
его сезона. При проведении этих расчетов предполага-
ется, что охотники возвращают все попадающиеся им
кольца. Поскольку это предположение является в той или
иной мере несправедливым, оценка и оказывается зани-
женной, а, следовательно, оценка wx — завышенной,
тогда как оценка qx остается несмещенной. Такие смеще-
ния оценок неизбежны, если только в значение тп0 не
вводится поправка на обнаруженные, но не возвращенные
кольца. Смещение в оценке и не оказывает большого влия-
ния на ее эффективность в качестве меры интенсивности
охоты, и и можно с уверенностью использовать как
критерий колебания интенсивности охоты от года к году,
В последнем столбце табл. 10.10 приводятся оценки годо-
вых значений и. В году 4, например, удельная смертность
за счет охоты составила 92/330 = 0,279. Эти оценки от
года к году заметно меняются, что оправдывает объеди-
нение последовательных когорт в группы, с тем чтобы сгла-
дить эти ежегодные различия. Однако до тех пор, пока ди-
намика этих оценок не обнаруживает тенденции к не-
уклонному росту или уменьшению, общее допущение 2
остается в силе.
Модель 3. Молодые животные метятся на протяжении
нескольких последовательных лет незадолго до начала
продолжительных охотничьих сезонов, и на протяжении
262
Глава 10
нескольких последовательных охотничьих сезонов ре-
гистрируются возвращаемые кольца.
В этой модели мы отказываемся от требования малой
продолжительности охотничьих сезонов, но при этом жер-
твуем возможностью получить оценки для hx и пх.
С этой точки зрения такая модель хуже модели 2, и ее сле-
дует использовать лишь в тех случаях, когда предполо-
жения, лежащие в основе модели 2, явно нереалистичны.
Специально неоговоренное условие применимости моде-
ли 2, заключающееся в том, что на протяжении охотничь-
его сезона смертность от естественных причин, не свя-
занных с самой охотой, настолько мала, что ею можно
пренебречь, не может считаться выполненным, если охот-
ничий сезон продолжается больше месяца. Однако если
наибольшее число охот приходится на начало сезона, то
эффект может быть таким же, как если бы сезон был ко-
ротким; в этом случае данные могут анализироваться
с помощью модели 2. В примерах, использовавшихся для
иллюстрации первых двух моделей, продолжительность
сезона охоты на черных австралийских уток составляла
от 2 до 4 нед, однако Болхем и Майерс (Balham, Miers,
1959) показали, что в каждом сезоне на первые 2 дня при-
ходилось 64% добычи.
Различие между моделями 1 и 2 наиболее просто оце-
нить, интерпретируя данные, приведенные в табл. 10.10,
так, как если бы они собирались во время охотничьих
сезонов продолжительностью 6 мес. Когорты группируют-
ся точно так же, каки в модели 2, и соответствующие зна-
чения частот тпх и Мх получаются такими же. Различие в
обработке данных сводится к новой интерпретации воз-
раста х ив отказе от расчета величин hx и пх. Изолиро-
ванная удельная смертность за счет охоты hx не может
быть рассчитана, поскольку количество колец, возвращае-
мых в течение охотничьего сезона, является теперь функ-
цией как интенсивности охоты, так и удельной смертности
от других причин на протяжении охотничьего сезона. Эти
факторы не могут быть разделены. По тем же самым при-
чинам не может быть рассчитано и значение пх. В преды-
дущих моделях возраст определялся таким образом, что
х = 0 соответствовало возрасту, примерно равному
6 мес. В этой же модели возраст х — 0 — это средний воз-
Мечение и повторный отлов
263
раст птенцов к середине охотничьего сезона. Если охот-
ничий сезон продолжается 6 мес и начинается в тот же
день, что и короткие сезоны, рассмотренные выше, то
х = 0 эквивалентно возрасту, равному примерно 3/4 го-
да, а х = 1 — возрасту 13/4 года. Таким образом,
средняя удельная смертность q представляет собой долю
всех птиц в возрасте старше 9 мес, погибших от различ-
ных причин в течение года.
Модель 4. Мечение и возврат колец происходят на
протяжении нескольких лет. В промежутке между мече-
нием и первым охотничьим сезоном наблюдается значи-
тельная смертность особей.
Анализ проводится так же, как и при использовании
модели 3, независимо от продолжительности охотничьих
сезонов. Так как численность окольцованной когорты
снижается за счет естественной смертности еще до начала
первого охотничьего сезона, величины hx и пх не могут
быть рассчитаны ни для одного возраста. Базовый воз-
раст х = 0 означает средний возраст птенцов к середине
первого в их жизни охотничьего сезона.
10.9.2. Методы анализа, используемые в случаях,
когда метятся особи всех возрастов
В большинстве случаев, когда проводятся массовые
операции по мечению, метятся все отлавливаемые особи.
Таким образом, выборка меченых животных в момент,
когда они выпускаются на свободу, представляет собой до-
вольно случайную выборку из популяции в отношении воз-
растного распределения и соотношения численности полов.
Кольца, возвращаемые на следующий год, уже нельзя счи-
тать случайной выборкой, поскольку все меченые особи
стали теперь на год старше. Кольца, возвращаемые через
2 года после мечения, могут быть сняты с животных лишь в
возрасте старше 2 лет. Следовательно, возрасты животных,
отстреливаемых через 0, 1, 2, Зи т. д. лет после мечения,
характеризуют набор возрастных распределений, по-
следовательно усекаемых снизу.
Модель 5. Незадолго до начала короткого охотничь-
его сезона метится случайная по возрасту выборка жи-
вотных. В табл. 10.11 приводятся данные по возвращению
264
Глава 10
колец, которыми исходно были окольцованы самцы чер-
ных австралийских уток всех возрастов (Balham, Miers,
1959). Поскольку предполагается, что окольцованные
птицы представляют собой случайную в отношении воз-
растного распределения выборку из популяции в момент
мечения, данные, приведенные в таблице, теперь уже
связаны не с возрастом х, а со временем, прошедшим после
кольцевания, i.
Значения удельных смертностей, рассчитаные по этим
данным, уже не зависят от возраста, но представляют со-
бой средние значения по всем возрастным классам, причем
вклад каждого класса в среднее значение пропорциона-
лен доле численности животных этого возрастного клас-
са в популяции в целом. Для анализа требуются лишь зна-
чения четырех частот Мо, М lf т0 им,. Остальные частоты
излишни.
Сравнение табл. 10.10 (анализ черных австралийских
уток, окольцованных птенцами) и табл. 10.11 (анализ
черных австралийских уток, окольцованных безотноси-
тельно к возрасту) дает информацию, которую нельзя по-
лучить, если рассматривать эти две таблицы порознь.
Такое сопоставление часто бывает возможным, поскольку
многие операции по кольцеванию представляют данные и
того и другого типа.
Сравним прежде всего значения удельных смертностей
за счет охоты. Для птенцов оно составляет и = 0,276,
тогда как для выборки, в которой представлены все воз-
расты, и = 0,267. Близость этих значений позволяет пред-
положить, что птенцы и взрослые особи имеют одинаковые
шансы погибнуть в течение охотничьего сезона и что риск
стать жертвой охоты не зависит от возраста. Затем срав-
ним векторы wx для птиц, окольцованных птенцами, с
w для выборки, в которой представлены все возрасты, с
тем чтобы определить, зависит ли от возраста изолирован-
ная удельная смертность, обусловленная естественными
причинами, не связанными с охотой. Оказывается, что эта
удельная годовая смертность для всей популяции в целом
(ш = 0,510) отражает главным образом удельную смерт-
ность на первом году жизни (и:0 = 0,505); в последующие
годы удельная смертность сначала понижается, а затем
Мечение и повторный отлов
265
Таблица 10.11
Возврат колец и удельные смертности самцов черной
австралийской утки, кольцевавшихся независимо от возраста
в течение нескольких лет (данные из работы Balham and Miers,
1959)
Год кольце- вания Число окольцо- ванных Число возвратов колец (т) в зависимо- сти от года кольцевания (t) И | о III О Ч ft и: ® а? pgs сть за счет ОХОТЫ
0 1 2 3 4 5 6
1 2 3 4 5 6 7 212 1419 590 411 358 138 27 71 17 4 1 1 0 1 395 90 30 19 5 2 — 146 35 18 5 1— — 112 14 14 4 — — — 89 21 10 — — — — 20 9 — — — — — 8 — — — — — — 0,335 0,278 0,247 0,273 0,249 0,154 0,296
Итого 3155 Число возвратов mi Исходное ЧИСЛО Mj 841 186 76297 2 1 из из из из из из из 3155 3128 2990 2632 2221 1631 212
Парциальные удельные смертности ] _ 7— т0 841 „ „ и = й = "Щ = 3155 = 0,267 17= q — u = 0,777— 0,267 =0,510 п = 4=^- = 0,696 1 —h
Общая — Mam1 3155x186
удельная 1 - 1 — мгтй ~ 3128x841 “0,777
смертность
снова возрастает. Значение удельной смертности, обус-
ловленной естественными причинами, явно зависит от
возраста. И наконец, мы сравним q = 0,731 для птиц,
окольцованных птенцами, с q = 0,777 для птиц, околь-
цованных независимо от возраста. Это по существу две
оценки одного и того же параметра: доля популяции, по-
266
Глава 10
гибающая ежегодно. Различия в значениях, вероятно,
отражают случайность выборки. Если бы это различие
было большим, то мы могли бы предположить, что либо
птицы, окольцованные независимо от возраста, не пред-
ставляют собой случайную выборку из популяции в от-
ношении возрастного распределения, либо скорость роста
популяции сильно отличается от 0. Это сравнение может
служить контролем для интерпретации различий между
другими характеристиками смертности. К различиям в
величинах следует относиться серьезно лишь в том слу-
чае, если они больше различия между двумя оценками q.
Более тонкие различия можно обнаружить при срав-
нении птиц, окольцованных птенцами, с птицами, околь-
цованными взрослыми, а не с выборкой, в которой пред-
ставлены все возрасты. Болхем и Майерс (Balhem, Miers,
1959) приводят необходимые данные, но их анализ ничего
не добавляет к выводам, сделанным выше.
Метод анализа, представленный в табл.10.11, исполь-
зуется редко. Гораздо чаще рассчитывается общая смерт-
ность за каждый год после кольцевания, а затем усредне-
нием получается «среднегодовая удельная смертность».
Рассмотрим эту процедуру. Суммарная удельная смерт-
ность на первом году после кольцевания представляет
собой долю птиц всех возрастов, погибающих в течение
года от самых различных причин. Смертность на втором
году после кольцевания дает оценку для птиц всех возрас-
тов, за исключением однолетних. Та же самая оценка на
третий год после кольцевания относится ко всем птицам,
за исключением одно- и двухлетних. «Среднегодовая
удельная смертность», рассчитанная посредством усредне-
ния этих последовательных оценок, является сильно взве-
шенной, причем вес возрастного класса тем больше, чем
он старше. Взвешивание следует считать правильной опе-
рацией, если вклад каждого возрастного класса в сред-
нее значение оценивается в соответствии с долей птиц
этого возрастного класа в популяции в целом (таким обра-
зом оценивается величина q в табл.10.И), однако процесс
усреднения значений удельной смертности, полученных в
последовательные годы после кольцевания, дает в точ-
ности противоположный эффект; веса возрастных классов
Мечение и повторный отлов
267
являются обратно пропорциональными их представлен-
ности в популяции. Так, удельная смертность трехлетних
птиц дает вес втрое больший, чем смертность молодых
особей, хотя молодых особей в большинстве популяций
пернатой дичи примерно в 10 раз больше, чем трехлетних.
Оценка доли ежегодно погибающих птиц, полученная с
помощью такой процедуры, неточна всегда, за исключением
случаев, когда удельная смертность не зависит от возраста.
Модель 6. Животные всех возрастов метились в течение
нескольких лет, предшествовавших продолжительному
охотничьему сезону.
Удельные смертности рассчитываются так же, как и в
модели 5, но поскольку h уже нельзя оценить исходя из
и, то ни значение h, ни значение и не могут быть получе-
ны при использовании данных по кольцеванию. Суммар-
ная удельная смертность (/определяется как доля особей в
популяции в целом, погибающих от всех возможных причин
в промежутке между серединой одного охотничьего сезона
и серединой следующего. Эта оценка представляет собой
взвешенное среднее по всем возрастным классам, за ис-
ключением класса животных, возраст которых меньше, чем
промежуток между серединой периода вылупления из яиц
и серединой охотничьего сезона.
Модель 7. Мечение и охота происходят непрерывно на
протяжении всего года.
Поскольку в этом случае животные метятся на протя-
жении того же промежутка, во время которого на них
охотятся, данные, собираемые таким способом, существен-
но отличаются от данных, обсуждавшихся выше. Такого
рода данные можно обрабатывать двумя способами. Если
для каждого животного, с которого было снято кольцо,
известны даты мечения и гибели, то эти. данные могут быть
сгруппированы по промежуткам времени, прошедшим
между мечением и гибелью, безотносительно ко времени
года, когда произошло каждое из этих событий, и анализи-
роваться с помощью модели 6. Этот метод игнорирует се-
зонную изменчивость смертности, поэтому результаты
должны интерпретироваться с осторожностью. Напротив,
если нас интересует динамика смертности в процессе сме-
ны времен года, то данные следует сгруппировать по году
268 Глава 10
смерти, причем год может быть определен произвольным
образом как промежуток времени, например, с января по
декабрь или с июля по июнь. Таким образом, мы можем
выбрать дату начала года так, чтобы в одну группу попа-
дали особи, погибшие в сезон, когда смертность высока.
Например, в случае когда большинство животных по-
гибает с декабря по февраль, следует считать, что год на-
чинается, скажем, в июле.
Второй подход приводит нас к новой проблеме. Число-
колец, возвращенных в год, когда они были надеты, не
может интерпретироваться так, как это делалось в пре-
дыдущих моделях. Вероятность того, что кольцо, надетое
в начале года, будет возвращено в течение того же года,
намного больше, чем та же вероятность для кольца, на-
детого в последний месяц года. Соответственно частота воз-
врата колец в год кольцевания несравнима с частотами
возвратов в последующие годы. Мы оказываемся перед вы-
бором: либо оценивать смертность на протяжении года
кольцевания, исходя из предположения относительно
динамики скорости мечения и удельной смертности на про-
тяжении года, либо исключить данные по животным, от-
стреленным в том же году, когда они были помечены, и
оценивать удельную смертность, исходя из оставшихся
данных. Рикер (Ricker, 1948 : 62; 1958 : 118) привел урав-
нения для оценки значений q и и по данным о возвратах
меток в год мечения и в последующие годы. Надежность
этих оценок зависит от того, насколько постоянными на
протяжении года остаются скорость мечения и интенсив-
ность охоты. Бивертон и Холт (Beverton, Holt, 1957:199)
показали, что решение теоретически возможно даже
в тех случаях, когда эти скорости подвержены сезонной из-
менчивости, но такой анализ требует дополнительной ин-
формации, которая редко бывает доступна.
Фрис (Frith, 1963), анализируя данные по возвратам
колец, которыми были окольцованы серые чирки Anas
gibberifrons в Австралии (табл. 10.12), исключил из
анализа кольца, возвращенные в год кольцевания,
поскольку в его распоряжении не было информации, необ-
ходимой для правильного использования этих данных.
Фрис произвольно принял за начало года 1 июля, с тем
чтобы последовательные месяцы лета южного полуша-
Мечение и повторный отлов
269
рия (декабрь, январь, февраль), на которые, по его пред-
положению, должна была приходиться максимальная
смертность, не попадали в разные годы.
Числа в последнем столбце табл.10.12 снова получены
в результате деления числа колец, возвращенных в течение
года мечения, на число птиц, окольцованных за этот же
год. Их теперь уже нельзя интерпретировать как долю
популяции, добытую на охоте в течение года, но они слу-
жат для проверки общего допущения, согласно которому
интенсивность охоты не убывала за время проведения экс-
перимента. Цифры эти не отличаются постоянством, но не
обнаруживают явной тенденции к монотонному изменению.
Таблица 10.12
Число возвратов колец и удельные смертности чирков,
кольцевавшихся и отстреливавшихся круглогодично
(данные из работы Frith, 1963)
е S я я п »околь- ных Число возвратов колец в зависимости от времени, прошедшего от начала кольцевания U3 га - 3 4) О S Н £ о ^g g §
ЕТ Л ' И е? О о Рч Я ga 2 я 0 1 2 3 4 S Рн й Ф ? S о S О S Я о
1954-55 21 1 1 0 0 0 0 0,048
1955—56 291 26 15 4 0 2 1 0,089
1956-57 1724 201 71 26 И 3 2 0,117
1957—58 11 295 618 168 131 77 34 9 0,055
1958—59 1802 174 63 48 12 6 — 0,097
1959—60 254 14 5 7 0 —— — 0,055
1960—61 536 27 10 5 — — — 0,050
Итого Число 15 923 1061 333 221 100 45 4
возвратов пц Исходное число Mt из 15 923 из 15 923 из 15 923 из 15 387 из 15133 из 13 331
— , M.m 2 9 “ 1 М2тх “ 15 923x221 = 0,336
1 — 15 923X333
По этим данным может быть оценена лить величина
q. Она интерпретируется как доля популяции старше
270 Глава 10
определенного возраста, погибавшая от всех возможных
причин в промежутке с 1 июля по 30 июня. Значение «опре-
деленного возраста» зависит от того, характеризуется ли
популяция сезонным или круглогодичным размножением,
и если размножение носит сезонный характер, то пред-
ставляет собой интервал между сезоном размножения и
произвольной датой, принятой за начало года. Если коль-
ца, возвращаемые за несколько последовательных лет, объ-
единяются в группы, то популяция серого чирка в Австра-
лии может рассматриваться как популяция с круглогодич-
ным размножением (Frith, 1959). Таким образом, базовый
возраст для q в табл.10.12 равен среднему возрасту птен-
цов при кольцевании (1/2 года плюс) 1 год. Ника-
кой другой информации из этих данных извлечь нельзя.
Глава 11
Использование популяционного анализа
при эксплуатации и охране популяций
Цели, преследуемые при эксплуатации природных по-
пуляций, понимаемой в самом широком смысле, немного-
численны и конкретны. Мы сталкиваемся здесь фактичес-
ки всего лишь с тремя проблемами:
1. Повышение плотности малых и убывающих попу-
ляций.
2. Получение постоянного уровня промысла или уро-
жая с эксплуатируемой популяции.
3. Снижение плотности слишком многочисленных по-
пуляций или стабилизация численности слишком
быстро растущих популяций.
Эти три проблемы можно назвать соответственно про-
блемами охраны популяций, поддержания оптимального
уровня промысла и регуляции численности. В ряде от-
раслей охотничьего, рыбного или заповедного хозяйства
нам приходится сталкиваться лишь с одной или двумя
из этих проблем. Так, например, когда мы имеем дело с
рыбными популяциями, основной целью почти всегда
является обеспечение стабильного уровня промысла;
остальные две проблемы возникают очень редко. Что же
касается популяций насекомых, то здесь основная зада-
ча — подавление их численности. При организации запо-
ведного и охотничьего хозяйств, которые будут рассмот-
рены здесь наиболее подробно, приходится иметь дело
со всеми тремя вопросами. В любом из рассмотренных слу-
чаев проблемы решаются путем воздействия на динамику
популяции, и в этом смысле популяционный анализ яв-
ляется основным орудием их решения, однако сами спо-
собы воздействия на динамику популяций могут быть в
разных ситуациях весьма различны.' В одних случаях
желаемые изменения скорости роста популяций дости-
272
Глава 11
гаются воздействиями на убежища животных, на источни-
ки воды или пищи, в других используются более пря-
мые методы воздействия.
Хотя при управлении природными популяциями, поми-
мо трех перечисленных, возникают и другие проблемы,
решение вопроса о том, что, где и когда следует предпри-
нять, определяется не ими. Ни одна из них сама по себе
не является проблемой. Популяция, ее взаимоотношения
с окружающей средой или положение вещей в целом ста-
новятся предметом беспокойства лишь в том случае,
когда вступают в противоречие с какими-то нашими
целями.
Все аргументы обычно концентрируются вокруг вопроса
о том, чего мы, собственно, хотим для той или иной тер-
ритории, для людей и прочих обитателей, ее населяющих;
без четкого ответа на этот вопрос невозможно принятие
каких бы то ни было мер воздействия на конкретные по-
пуляции. Только после того как сформулирована основ-
ная цель, мы можем судить о том, верна ли система орга-
низации промысла, иными словами — действительно
ли та или иная популяция настолько широко распростра-
нена и многочисленна, что это противоречит государствен-
ным интересам.
Если мы хотим превратить некоторую территорию
в национальный парк, то популяция крупных тра-
воядных, обитающая на этой территории, будет являться
для нас предметом радости и гордости. Если же мы пред-
полагаем разбить здесь огороды, наша точка зрения на
этих животных будет совершенно иной. Значительная
доля усилий, предпринимаемых в области взаимоотношения
с природными популяциями, направлена на решение во-
проса о том, существует ли в действительности задача,
которую нужно решить, и если да, то как подойти к ее ре-
шению: охранять популяцию, подавлять ее или поддержи-
вать промысел на оптимальном уровне. Здесь популяцион-
ный анализ бессилен. Это метод, который может быть
крайне полезен для решения конкретных проблем, но он
совершенно непригоден в том случае, если не определено,
в чем состоит проблема.
Популяционный анализ и эксплуатация популяций
273
11.1. Охрана популяций
Многие проблемы, связанные с охраной природы, при
ближайшем рассмотрении оказываются не техническими,
а экономическими и социальными. Как правило, не тре
буется большой проницательности для того, чтобы рас-
познать причины убывания численности популяции, и
даже если меры, препятствующие этому, не всегда уда-
ется непосредственно реализовать, их по меньшей мере
можно теоретически сформулировать. Основная трудность
состоит в том, чтобы убедить компетентных лиц предпри-
нять соответствующие действия. Ярким примером труд-
ностей, возникающих в такой ситуации, может служить
промысел горбатого кита Megaptera novaeangliae. Читл-
боро (Chittieborough, 1965) свел воедино и резюмировал
данные по истории популяции, проводящей лето в южной
части Индийского океана южнее Западной Австралии (по-
пуляция, относящаяся по принятой классификации к
группе IV). В 1912—1934 гг. в антарктических водах и во
время миграций к западному побережью Австралии еже-
годно добывалось лишь по нескольку штук китов. На
протяжении последующих пяти лет промысел интен-
сифицировался, и суммарная добыча китов составила, по
мепыпей мере 12 700 штук. К концу этого периода рез-
кое падение добычи на единицу промыслового усилия сви-
детельствовало о превышении оптимального уровня про-
мысла и об «истощении» популяции. Затем началась война.
За последующие 10 лет было добыто лишь несколько ки-
тов, и популяция, оказавшаяся как бы под охраной, уве-
личивала свою численность. Затем, когда в 1949 г. кито-
бойный промысел возродился, он был в антарктических во-
дах поставлен под контроль Международной комиссии по
китобойному промыслу, которая сначала ввела систему
квот, а затем — ограниченный (обычно четырьмя днями)
ежегодный период разрешенного промысла. Для австра-
лийских береговых китобойных станций квоты были уста-
новлены австралийским правительством. В 1960 г. Между-
народная комиссия по китобойному промыслу, обеспо-
коенная падением численности горбатых китов, предло-
жила приостановить на три года промысел популяции
группы IV. Правительства Японии, Норвегии, СССР и
10—334
274
Глава 11
Великобритании отклонили эту рекомендацию, и про-
мысел продолжался. Квоты, устанавливаемые австралий-
ским правительством для береговых китобойных станций,
начиная с 1959 г. постепенно снижались. Однако измене-
ние год от года квот и уловов, ни в коей мере не являю-
щихся оценками устойчивого уровня промысла (табл. 1 у
Chittieborough, 1965), почти ничего не дает для понимания
динамики численности популяции, если только не пред-
положить, что эти квоты могут служить оценкой макси-
мальной численности китов, остающихся в живых при ра-
боте береговых китобойных станций на полную мощность.
Такая жестокая интерпретация, может быть, и ошибочна,
но я в этом сомневаюсь. В условиях непрерывного под-
держания такого безжалостного промысла с береговых
китобойных станций и в открытых водах к 1962 г. популя-
ция была практически полностью истреблена. Падение
численности популяции было очень резким: в течение од-
ного года она упала до уровня, .который уже не мог обес-
печивать коммерческий промысел одних лишь горбатых
китов ни с береговых станций, ни в открытом море.
По оценке Читлборо, при полном запрещении промы-
сла па восстановление популяции потребуется около
50 лет.
С одной стороны, это наглядный пример того, что пробле-
ма сохранения популяции в действительности является
экономической. Мудрость часто отступает перед непреду-
смотрительностью, но в данном случае люди, которые при-
нимали решение, знали, что решение это экологически
вредно, и руководствовались экономическими соображе-
ниями. Никаких технических трудностей не было, дина-
мика популяции была в общих чертах понятна. Колос-
сальное количество данных, относящихся к этой популя-
ции, можно было истолковать лишь одним способом:
численность популяции падает и это падение является
прямым следствием неумеренного промысла.
С другой стороны, история падения численности попу-
ляции группы IV горбатого кита не типична для большин-
ства проблем охраны популяций. В настоящее время за
счет охоты снижается численность лишь очень немногих
популяций; основную опасность для популяций позво-
ночных представляет собой разрушение и видоизменение
Популяционный анализ и эксплуатация популяций
275
их источников пищи и местообитаний. С моей точки зре-
ния, примерно 95% проблем, связанных с охраной попу-
ляций, относится к этой категории. Даже в тех случаях,
когда на первый взгляд главной причиной убывания чис-
ленности популяции представляется охота, более тщатель-
ное исследование обычно показывает, что, помимо этого,
изменяются убежища, источники воды и пищи. Техни-
ческая часть проблемы охраны популяций — выявление
причин убывания численности и решение вопроса о том,
что можно с этим сделать — бывает и очень простой, и
очень сложной. Вряд ли имеет смысл затевать пятилетнее
исследование, если есть вероятность, что ответ можно полу -
чить за одну неделю, и поэтому исследование лучше раз-
бить на два этапа. Если задачу не удается решить на пер-
вом этапе, предпринимают более тщательные исследования.
Первая стадия
Исследование причин падения численности данной
популяции существенно упрощается, если мы имеем дос-
туп к популяции того же вида, обитающей в благоприятных
условиях. Тогда местообитание, источники воды и пищи,
жировые запасы особей и распространенность болезней в
исследуемой популяции можно сравнить с аналогичными
характеристиками контрольной популяции. Выявляемые
различия в дальнейшем можно исследовать более тща-
тельно. Если, например, изучаемая популяция обитает на
территории, служащей пастбищем для овец, а на терри-
тории обитания контрольной популяции овцы отсутствуют
и в этом заключается единственное различие, которое уда-
ется обнаружить, исследуя условия обитания обеих попу-
ляций, можно предположить, что овцы каким-то образом
являются причиной убывания численности исследуемой
популяции. Это заключение можно проверить, удалив
овец и проследив, замедляется ли падение численности
популяции, а затем вернув овец снова. Многие проблемы
охраны популяций решаются именно таким образом. Дан-
ный метод хорош тем, что предпринимаемые меры позво-
ляют одновременно предотвратить падение численности
популяции и проверить справедливость нашей гипотезы.
10*
27 6
Глава 11
Некоторые из вопросов охраны популяций нельзя ре-
шить на первой стадии исследования, и требуется более
глубокое их изучение.
Вторая стадия исследования
Итак, основываясь на отрицательных результатах
предварительного исследования, мы выяснили, что при-
чины падения численности не являются ни простыми,
ни очевидными. Следовательно, нам нужно изменить так-
тику, не пытаясь взять проблему приступом и перейдя к
планомерной осаде.
Прежде всего мы измеряем удельные плодовитости, с
с тем чтобы определить, не является ли причиной убы-
вания численности популяции нарушение ее размножения.
Если это так, мы должны исследовать вопрос более под-
робно и выявить конкретную причину этого явления.
Нарушение размножения — довольно редкая причина убы-
ли численности популяции, если не считать популяции не-
которых хищных птиц. Это явление может быть обус-
ловлено либо болезнями, либо, присутствием в окружаю-
щей среде метаболических ядов.
Убывание численности популяции может быть обуслов-
лено или падением плодовитости, или увеличением смерт-
ности, и поэтому если обнаружено, что удельная плодо-
витость остается на нормальном уровне, можно сделать
вывод, что причиной убыли численности является уве-
личение смертности популяции. Если необычно велика
смертность взрослых особей, а ювенильная смертность
сохраняется на нормальном уровне, первое предположе-
ние, которое можно сделать, состоит в том, что все дело в
неумеренной охоте. Большинство других факторов смерт-
ности воздействует в первую очередь на молодых особей.
Если убывание численности популяции связано с истоще-
нием источников пищи или ухудшением условий место-
обитания, характерными диагностическими чертами такого
явления будут увеличение ювенильной смертности обыч-
но в сочетании с уменьшением плодовитости молодых
особей.
Процесс выявления наиболее уязвимой части попу-
ляции можно ускорить, если для данной популяции име-
Популяционный анализ и эксплуатация популяций
277
ется демографическая таблица. Сравнение этой таблицы с
таблицей для нормальной популяции сразу же показы-
вает, какой именно возрастной класс затронут неблаго-
приятным воздействием. Составление демографической
таблицы для вымирающей популяции требует изобрета-
тельности — ясно, что нельзя добывать данные от-
стрелом. Иногда мы можем рассчитать распределение
возраста гибели особей S'x по выборке собранных чере-
пов, а затем по формуле dx = S'хегх определить вектор
dx‘, г — в данном случае скорость убывания численности
популяции и, следовательно, отрицательна (разд.8.1.2,
метод 5).
После того как выделен наиболее уязвимый возраст-
ной класс популяции, вне зависимости от того, характе-
ризуется он пониженной плодовитостью или повышенной
смертностью, причины убывания его численности находят
с помощью простого стандартного исследования.
Если предположительно уменьшение численности обу-
словлено ухудшением качества местообитания, проще
всего выяснить у местных жителей, не заметили ли они
за последние 10 лет каких-либо изменений в плотности
растительности, глубине болот и т.п. Более точным мето-
дом является сравнение данных аэрофотосъемок. Лишь
очень немногие районы земного шара еще не сфотографи-
рованы с воздуха. В ряде районов аэрофотосъемка про-
изводилась по меньшей мере дважды, и таким образом
можно выявить изменения, происшедшие в местообита-
нии за время между двумя последовательными съемками
и между последней съемкой и той, которую мы специаль-
но провели в нашем исследовании. Мне приходилось
видеть аэрофотоснимки десятилетней давности, которые
требовалось тщательно изучить, чтобы убедиться, что на
них отснята та же самая территория, что и сегодня, —
так сильно изменились местообитания в результате пожа-
ров, выпаса домашнего скота и расширения сельскохо-
зяйственных угодий.
11.2. Принципы организации промысла
Когда говорят о промысле, большинство людей пред-
ставляют себе китобойный, тюлений и рыбный промыслы,
278
Глава 11
т.е. отрасль, в которой многие люди заняты профессио-
нально. Однако если говорить о человеко-часах, затрачи-
ваемых на добычу диких животных, то основная часть при-
ходится на охотников-спортсменов, а профессиональный
промысел поставляет лишь незначительную часть общего
числа добываемых животных.
Вне зависимости от того, является ли популяция объ-
ектом промышленного промысла, спортивной охоты или
рыболовства, справедливы одни и те же принципы. Цель
организации промышленного или спортивного промысла
заключается в поддержании постоянного уровня добычи
(ПУД), т.е. такого, который оставался бы неизменным
из года в год и это не приводило бы к уменьшению чис-
ленности популяции. Для каждой конкретной популя-
ции существует не единственное значение, а целый набор
постоянных уровней добычи. Каждый уровень соответ-
ствует определенной организации промысла. Таким об-
разом, целью организации промысла является разработ-
ка такой схемы, которая обеспечивала бы максимальный
постоянный уровень добычи (МПУД) или чаще макси-
мальный доход или максимальное удовлетворение рекре-
ационных потребностей (оптимальный постоянный уро-
вень добычи — ОПУД).
Интенсивность промысла, при которой скорость роста
популяции поддерживается равной 0,— это интенсив-
ность, соответствующая скорости роста популяции в от-
сутствие промысла. Так, популяция с конечной скоростью
роста ет = 0,20 и, следовательно, с экспоненциальной
скоростью г = 0,182 может облавливаться с интенсив-
ностью, обеспечивающей добычу Н = 0,182. Данная ве-
личина называется мгновенной интенсивностью промыс-
ла и требует некоторого пояснения: Н — это интенсив-
ность, с которой популяция может облавливаться на про-
тяжении года. Обозначая среднюю численность популя-
ции в течение года символом N, мы получаем значение
постоянного уровня добычи за год, равное HN животных.
Однако в тех случаях, когда популяция облавливается
лишь в течение части года, значение ПУД рассчитывает-
ся не из мгновенной интенсивности промысла, а из изолиро-
ванной интенсивности промысла h, где h = 1 — е~н.
Популяционный анализ и эксплуатация популяций 219
Поясним это на конкретном числовом примере. Предпо-
ложим, что популяция с сезонным размножением, расту-
щая со скоростью г = 0,182, насчитывает непосредствен-
но после сезона размножения 1000 особей и что естест-
венная смертность постоянна на протяжении всего года
и составляет п — 0,25 в год (что эквивалентно 0,0236 в
месяц). Численность необлавливаемой популяции в ме-
сяцы, следующие за сезоном размножения, представлена
Таблица 11.1
Влияние охоты, проводящейся один раз в год, на годовую
динамику численности популяции с сезонным размножением
(см. текст)
Месяцы Численность популяции, в которой запре- щена охота Охота на первом месяце Охота ""на пятом месяце
1 1000 /1=0,167 1000 >833 1000
2 976 813 976
3 953 794 953
4 930 775 930
5 908 757 /1=0,16 7 908 757
6 887 739 739
7 866 722 722
8 846 705 705
9 826 688 688
10 806 672 672
И 787 656 656
12 768' 640 640
1 750+750 m 625+625 m 625 + 625 пг
= 1200 = 1000 =1000
пг = 0,6 m =0,6 m = 0,6
г = 0,182 г = 0,0 /• = 0,0
ПУД = 0 ПУД = 167 ПУД = 151
в табл. 11.1. К концу года численность популяции по-
нижается за счет естественной смертности до 750 особей,
что в случае, когДа плодовитость составляет m = 0,6 на
280
Глава 11
одну особь, дает по прошествии второго сезона размноже-
ния численность, равную 750 + 750 т = 1200.
Предположим теперь, что на нашу гипотетическую
популяцию разрешена охота, интенсивность которой тако-
ва, что скорость роста становится равной 0, и пусть охота
происходит в течение короткого охотничьего сезона.
Для расчета интенсивности промысла и соответственно
числа животных, которое может быть добыто охотниками,
мгновенную интенсивность промысла Н = 0,182 следует
пересчитать в изолированную удельную смертность за
счет охоты (или, что то же самое, в изолированную ин-
тенсивность промысла h) по формуле
h= 1 — е“я = 0,167.
В любое время года 0,167 животных от их общего числа в
этот момент могут быть добыты на протяжении короткого
промежутка времени, и это обеспечит поддержание ско-
рости роста популяции на нулевом уровне. Ясно, что пра-
вильное значение ПУД будет зависеть от времени охоты,
поскольку естественная смертность постоянно уменьшает
численность популяции в промежутке между последо-
вательными сезонами размножения и тем самым уменьша-
ется число животных, рискующих погибнуть на охоте.
Это явление иллюстрируют данные, приведенные в
табл. 11.1: непосредственно после сезона размножения
отстреляно 167 (1000 X 0,167) животных, тогда как в
течение пятого месяца после сезона размножения это число
равно лишь 151 (908 X 0,167). При любом режиме охоты
численность популяции по прошествии следующего сезона
размножения должна составлять 1000 особей, и тогда
скорость роста численности популяции будет поддержи-
ваться на нулевом уровне.
Если мы хотим охотиться дважды на протяжении года,
то правильную интенсивность промысла для каждого
охотничьего сезона можно рассчитать как значение изо-
лированной удельной смертности за счет охоты, соответ-
ствующее вдвое меньшей мгновенной интенсивности про-
мысла :
2й = 1-е"н/2 = 0,087.
Популяционный анализ и эксплуатация популяций
281
В табл.11.2 приведены данные, характеризующие та-
кой режим охоты для двух случаев: в первом случае охота
проводится на девятом и одиннадцатом месяцах после
сезона размножения, во втором— на шестом и седьмом.
Окончательный результат остается тем же самым: чис-
ленность популяции после последующего сезона размно-
жения остается той же, что была после предыдущего,
т.е. скорость роста популяции г = 0.
Таблица 11.2.
Влияние охоты, проводящейся два раза в год, на годовую
динамику численности популяции с сезонным размножением
(см. текст)
Месяцы Численность попу- ляции, в которой запрещена охота Охота на девятом и одиннадцатом месяцах Охота на шестом и седьмом месяцах
1 1000 1000 1000
2 976 976 976
3 953 953 953
4 930 930 930
5 908 908 908
, h = 0,087
6 887 887 887 > 810
2 Л = 0,087
7 866 866 772 > 791
8 846 846 705
, h = 0,087
9 826 826 >754 688
10 806 736 672
, h = 0,087
11 787 656< 719 656
12 768 640 640
1 750+750 m = 1200 625 + 625/77 = 1000 625 + 625 //г = 1000
m = 0,6 777 = 0,6 777 = 0,6
г = 0,182 Г = 0,0 Г = 0,0
ПУД = 0 ПУД = 134 ПУД = 146
Аналогичным обр азом мы можем рассчитать правиль-
ную интенсивность промысла для любого числа охот в
282
Глава 11
течение года. Например, если охота в течение года про-
изводится 12 раз через одинаковые промежутки времени,
то правильная интенсивность каждой охоты определя-
ется по формуле
12/i =1 -е~"/12 = 0,015.
Это соответствует значению ПУД, равному 146 животным
в год. Но при такой интенсивности охоты она может вес-
тись на протяжении всего года, эффект будет тем же са-
мым. При непрерывной охоте на протяжении всего года
и правильно выбранной интенсивности промысла средняя
численность популяции в течение года составляет N =
= 800, а годовая добыча, следовательно, равна
ПУД =HN =0,182 х 800 =146 животных.
Эти числовые, примеры иллюстрируют следующие об-
щие правила организации промысла:
1. Значение ПУД рассчитывается по мгновенной ин-
тенсивности охоты Н, которая равна скорости роста попу-
ляции гр в отсутствие промысла.
2. Если охота производится один раз в год на протя-
жении короткого промежутка времени, то правильная
интенсивность охоты определяется по формуле h = 1—е~н
и означает долю животных, которые могут быть отстре-
лены, от общей численности животных в этот момент.
3. Если охота проводится несколько раз в год в течение •
коротких промежутков времени, правильная интенсив-
ность промысла для каждого из них определяется по фор-
муле h = 1 — e~Hlv, где у — число охот в течение года.
4. Для поддержания постоянного уровня добычи про-
мысел организуется таким образом, чтобы при охоте в
течение нескольких коротких интервалов интенсивности
охот, выраженные в форме мгновенных величин, в сумме
составляли мгновенную интенсивность Н, где Н = гр —
скорость роста популяции в отсуствие промысла.
5. Сформулированные выше 4 правила с достаточ-
ной степенью точности остаются справедливыми вне зави-
симости от характера естественной смертности (постоянна
она на протяжении года или зависит от времени года) и
характера размножения популяции — сезонное оно, круг-
Популяционный анализ и эксплуатация популяций 283
логодичное или промежуточного типа; важно только, чтобы
определяющие динамику численности популяции величи-
ны оставались постоянными из года в год.
В рассмотренном числовом примере мы имели дело с
гипотетической популяцией, характеризующейся в от-
суствие промысла положительным значением г. Мы мате-
матически рассчитали интенсивность промысла, при ко-
тором скорость роста популяции поддерживается равной
нулю, а численность остается на постоянном уровне, на
котором она находилась до начала промысла. Такая си-
туация очень редко реализуется на практике, поскольку,
хотя численности большинства популяций и претерпе-
вают флуктуации год от года, средняя по нескольким
годам скорость роста численности, как правило, близка к
нулю (см., например, график динамики численности по-
пуляции оленей, изображенный на рис.4.3). Если бы ин-
тенсивность промысла определялась только скоростью
роста популяции, как это было принято в предыдущем
примере, то популяции с нулевой средней скоростью роста
всегда соответствовала бы нулевая интенсивность охоты
(II = 0) и, следовательно, ПУД также был бы равен нуля.
Популяция постоянной численности может служить
объектом охоты только после того, как скорость роста
ее численности каким-то образом сделана большей нуля.
При организации промысла используется тот факт, что,
вообще говоря, скорость роста популяции тем больше, чем
больше пищи и других ресурсов приходится на одну особь.
Таким образом, для увеличения г необходимо понизить
плотность популяции и увеличить, следовательно, до-
лю ресурсов, приходящихся на одну особь. Если такую
популяцию предоставить затем самой себе, она неизбежно
восстановит свою исходную плотность, при которой сред-
няя скорость роста численности равна нулю. Но если сна-
чала снизить численность популяции, а затем начать про-
мысел с интенсивностью, соответствующей скорости, с
которой популяция в отсутствие промысла возвращалась
бы к прежней плотности, то численность популяции стаби-
лизируется на новом уровне.
Можно ожидать, что в известных пределах чем сильнее
снижается плотность необлавливаемой популяции, тем
больше индуцированная скорость роста популяции и соот-
284
Глава 11
ветственно тем выше интенсивность промысла, необхо-
димая для того, чтобы поддерживать плотность популя-
ции на новом уровне. Таким образом, для каждой плот-
ности существует потенциальная скорость роста числен-
ности популяции гр, проявляющаяся в отсутствие промыс-
ла (разд.5.3). Другими словами, каждой плотности попу-
ляции соответствует интенсивность промысла Н — гр,
поддерживающая постоянную численность популяции.
Переходя от интенсивности промысла к уровню добычи
для любой заданной плотности популяции, мы можем
оценить число животных, которых нужно ежегодно до-
бывать, чтобы стабилизировать численность популяции.
В то время как интенсивность охоты монотонно увеличи-
вается с понижением плотности, зависимость ПУД от
плотности носит другой характер. Когда плотность пони-
жена слабо, Н мало, а ПУД составляет небольшую часть
сравнительно большой популяции. Когда плотность попу-
ляции понижена значительно, сравнительно небольшая
популяция обладает высокой потенциальной скоростью
роста тр и соответственно высоким значением Я; ПУД те-
перь составляет значительную часть малочисленной попу-
ляции. Максимальный постоянный уровень добычи для
популяции, облавливаемой одинаково для обоих полов и
всех возрастных классов, соответствует такой численности
популяции Я, при которой значение HN максимально.
Таким образом, задача оценки МПУД довольно сложна и
состоит из двух этапов. Мы должны оценить, во-первых,
плотность, при которой может быть достигнут МПУД, и,
во-вторых, интенсивность промысла, стабилизирующего
плотность на этом уровне. Наиболее трудоемкий метод,
используемый при анализе эксплуатации природных по-
пуляций, — метод последовательных приближений — для
этой задачи непригоден. Вероятность того, что нам удастся
с приемлемой точностью найти значения HN независи-
мой подгонкой II и N, столь мала, что эту задачу можно
сравнить с пресловутыми поисками иголки в стоге сена.
Рис. 11.1 иллюстрирует это положение. На нем
представлена идеализированная зависимость численнос-
ти (или плотности) популяции в данном году от числен-
ности в предыдущем. Идущая по диагонали прямая дает
совокупность всех возможных значений NM = Nt, т.е.
Популяционный анализ и эксплуатация популяций
285
набор ситуаций, когда численность популяции не меня-
ется год от года. Точки, лежащие слева от диагонали,
соответствуют возрастанию численности за время от t до
t + 1, а справа — убыванию численности. Кривая на этом
Рис. 11.1. Возможная зависимость численности животных в данном
году от численности в предыдущем (кривая линия).
Длина пунктирных прямых пропорциональна значению постоянного уров-
ня добычи при соответствующих значениях Nt (Ricker, 1958).
рисунке соответствует взаимосвязи, которая будет иметь
место между численностями популяции за два последова-
тельных года, если источник питания популяции будет
пополняться с постоянной скоростью. Форма этой кривой у
разных видов и разных популяций одного и того же вида
может быть различной. Значение численности Nf, при ко-
тором кривая пересекает диагональ, соответствует стацио-
нарному состоянию, т.е. средней численности необлавли-
ваемой популяции.
286
Глава 11
Ни одна популяция не характеризуется в точности та-
кой зависимостью. Колебания от года к году внешних
условий обусловливают флуктуации выживаемости, пло-
довитости, возрастного распределения и скорости роста
популяции, и зависимость численности популяции в дан-
ном году от численности в предыдущем оказывается до-
вольно слабой. Кривая может хорошо описывать ситу-
ацию, когда численность простой популяции колеблется
под влиянием изменений внешних условий. Можпо наде-
яться, что влияние среды и факторов, связанных с огра-
ниченностью выборки, могут лишь слегка исказить эту
зависимость, но не изменить полностью ее характер.
На рис. 11.1 изображены три стратегии, позволяющие
поддерживать в этой идеализированной популяции по-
стоянный уровень добычи. В первом случае плотность
популяции понижена от стационарного уровня до зна-
чения, при котором ее численность Nt = А. Пунктир-
ный отрезок а, связывающий по вертикали диагональ с
популяционной кривой, изображает увеличение числен-
ности популяции за год. Длина отрезка пропорциональ-
на ежегодному уровню добычи, при котором численность
популяции будет поддерживаться на уровне Nt = А.
При этом ПУД составляет малую часть большой популя-
ции. Напротив, когда численность популяции снижается
до Nt = В и ПУД пропорционален длине отрезка Ъ,
добыча составляет значительную часть малой популяции.
МПУД достигается при такой численности популяции,
когда расстояние между диагональю и популяционной
кривой максимально, т.е. при Nt — М.
Рис. 11.1 при всей его абстрактности может служить
иллюстрацией нескольких утверждений, справедливых
для промысла в реальных популяциях.
1. Если исходная численность популяции устойчи-
ва, то, прежде чем начинать промысел, необходи-
мо понизить стационарную численность.
2. Для каждого значения плотности популяции, ле-
жащего ниже равновесного, существует соответ-
ствующий ПУД.
3. Каждому уровню ПУД соответствуют два уровня
плотности популяции, при которых этот ПУД мо-
жет достигаться.
Популяционный анализ и эксплуатация популяций
287
4. МПУД может достигаться лишь при одном’значении
плотности популяции.
5. Ежегодный ПУД должен быть меньше числа осо-
бей, изъятых из популяции при первоначальном
понижении ее численности.
6. Если в популяции ежегодно добывается постоян-
ное число особей, то численность популяции будет
сначала снижаться, а затем стабилизируется на
большем из двух значений численности, которым
соответствует данный уровень добычи. Если чис-
ленность особей, ежегодно добываемых в популя-
ции, превысит МПУД, то популяция обречена на
вымирание.
7. ПУД должен рассчитываться не для исходной ста-
ционарной численности популяции, а для числен-
ности, к которой сведена популяция после исход-
ного изъятия из нее некоторого количества особей.
Последнее утверждение существенно. Вопрос о том,
какой процент от общей численности популяции можно
добывать ежегодно, неправильно поставлен. Его нужно
перефразировать следующим образом: если исходно чис-
ленность популяции снижена на 20% (или на 30%, или
на 40%), то какую часть популяции с новой числен-
ностью мы должны добывать ежегодно, чтобы числен-
ность популяции устойчиво поддерживалась на этом уров-
не? Еще лучше, если оба неизвестных сведены в одном
вопросе: до какого уровня необходимо снизить числен-
ность популяции и какая часть популяции должна после
этого добываться ежегодно, чтобы постоянный уровень
добычи был максимальным?
11.2.1. Оценка уровня добычи с помощью
логистической модели
Если характер зависимости Nt+l от Nt точно опреде-
ляется из полевых наблюдений, то нахождение МПУД и
соответствующей численности популяции сводится к прос-
той чисто технической задаче. К сожалению, набор
экспериментальных точек, описывающих такую зависи-
мость, обладает значительным разбросом, не позволяю-
щим однозначно выяснить характер зависимости, и мы ока-
288
Глава 11
зываемся перед выбором: либо продолжать эксперимент
до тех пор, пока не накопится столько данных, что удаст-
ся ясно проследить характер зависимости на фоне шума,
либо выбрать правдоподобную кривую и подобрать зна-
чения параметров в соответствии с экспериментальными
данными. Эти возможности не являются взаимноисклю-
чающими. Первоначально МПУД можно оценить методом
последовательных приближений, пока не будет накоплено
достаточное количество данных для расчета более точной
оценки. Хотя всегда лучше определять характер зависи-
мости непосредственно из экспериментальных данных,
скудность и неопределенность исходной информации
обычно вынуждает нас сначала сделать некоторые общие
предположения о характере зависимости, а затем, исходя
из экспериментальных данных, подбирать соответствующие
значения параметров. Поскольку такая процедура сама
потенциально заключает в себе источник ошибок, необ-
ходимо проверить, действительно ли оцененные значения
ПУД обеспечивают поддержание численности на расчет-
ном уровне.
Число моделей роста численности популяций доста-
точно велико. Бивертон и Холт (Beverton, Holt, 1957:
327) составили обзор таких моделей, связанных с вопро-
сом поддержания постоянного уровня добычи, по состоя-
нию дел на 1953 г. и предложили несколько собственных
моделей. Позднее в ряде работ (Andrewartha, Birch,
1954; Ricker, 1954а, b, 1958; Leslie, 1959; Gulland, 1962,
1968; Lefkovitch, 1966, 1967) были рассмотрены новые
модели или новые модификации ранее разработанных мо-
делей.
Из всех этих моделей в первую очередь и наиболее
подробно мы рассмотрим логистическую модель. Она не
относится к числу лучших, поскольку является чрезмерно
упрощенной, но такая простота позволяет выработать
общую стратегию оценки постоянного уровня добычи.
Зная закономерности динамики некоторой конкретной
популяции, исследователь сможет модифицировать мо-
дель таким образом, чтобы она подходила для конкретной
популяции, являющейся объектом промысла, и условий
ее существования.
В ряде вопросов, связанных с определением постоян-
Популяционный анализ и эксплуатация популяций
289
ного уровня добычи, логистическая модель может исполь-
зоваться непосредственно. Биологи, занимающиеся ки-
тами, обнаружили, что модель дает довольно точные пред-
сказания, а эксперименты с лабораторными популяциями
показали (Silliman, Gutsell, 1958), что она также приме-
нима при описании динамики по крайней мере некоторых
видов рыб.
Основное допущение логистической модели состоит
в том, что гр, а следовательно, и Н считаются обратно
пропорциональными плотности популяции. Другими сло-
вами, поступление каждого нового пополнения в популя-
цию снижает либо выживаемость, либо плодовитость,
либо и то и другое у всех членов популяции. Вряд ли
такая ситуация в точности реализуется на практике,
однако, по-видимому, что-то близкое к этому все-таки
имеет место. Разумнее было бы считать, что истощение
ресурсов, вызываемое пополнением популяции, в первую
очередь сказывается на сравнительно молодых особях.
Отражающую такой эффект модель построил Рикер
(Ricker, 1954а, 1958), а в работе Марфи (Murphy, 1966)
суммированы лежащие в основе этой модели предполо-
жения. Основное предположение, заложенное в модели
Рикера, почти диаметрально противоположно главной
аксиоме логистической модели (Frank, 1960): плодови-
тость и выживаемость взрослых особей не зависят от по-
ступающего в популяцию пополнения, а выживаемость
пополнения, напротив, определяется численностью взрос-
лых. особей в популяции. Можно было бы ожидать, что
предсказания, даваемые моделью Рикера о динамике
численности популяций, будут заметно отличаться от
предсказаний логистической модели, однако Марфи (Mur-
phy, 1967) показал, что в случаях, когда rm меньше 0,34
в год, различия невелики, а при rm = 0,2 пренебрежимо
малы.
Эти данные позволяют по-новому взглянуть на ло-
гистическую модель. Динамика численности популяций
позвоночных, по-видимому, подчиняется закономернос-
тям, в каком-то смысле промежуточным между теми,
которые лежат в основе логистической модели и модели
Рикера, а характер динамики популяции, предсказы-
ваемый обеими моделями для не слишком больших ско-
290
Глава 11
ростей роста популяции гт, почти одинаков. Поэтому мож-
но ожидать, что логистическое уравнение будет хорошо
описывать динамику численности даже такой популяции,
которая подчиняется закономерностям, отличным от по-
ложенных в основу логистической модели. Именно по
этой причине мы и рассматриваем логистическую модель.
Для того чтобы использовать ее при оценке постоянного
уровня добычи, не обязательно считать, что реальные по-
пуляционные процессы согласуются с предположениями,
заложенными в логистическую модель.
Как было показано в разд.9.9.1, логистическая мо-
дель описывается уравнением
г = гго(1-У/К),
где N — численность популяции, г — экспоненциальная
скорость роста, гт — идеальная скорость роста, К —
стационарная численность популяции. Первым, кто ис-
пользовал логистическую модель для оценки постоянного
уровня добычи, был Грэхэм (Graham, 1935), хотя модели,
близкие к логистической, применялись в этих целях и до
него (Баранов, 1926; Hjort et al., 1933). Грэхэм показал,
что, поскольку rN — это мгновенный прирост численности
популяции, приводящий ее к стационарному состоянию,
эта же величина определяет и постоянный уровень до-
бычи. Определив Н как мгновенную интенсивность охоты,
необходимую для поддержания численности популяции
на уровне N, мы можем переписать уравнение в виде
HN = rmN(l—N/K),
или
HN = rmN-^- №.
К
Последнее уравнение может быть записано в общем виде как
у = Ъх — сх2,
а это — уравнение параболы, проходящей через начало
координат. Поскольку для любых значений N. справедли-
во равенство ПУД = HN, соотношение между числен-
ностью популяции и ПУД дает очень простой рецепт
вычисления максимального постоянного уровня добычи:
Популяционный анализ и эксплуатация популяций
291
МПУД достигается при численности популяции N = К/2
и мгновенной интенсивности охоты, равной Н = тт/2,
и составляет HN = гт К! к животных в год. Другими сло-
вами, численность популяции должна составлять половину
стационарной в отсутствие промысла, а интенсивность
охоты — половину идеальной скорости роста популя-
Рис. 11.2. Логистический рост численности популяции и параболи-
ческая зависимость постоянного уровня добычи от численности по-
пуляции (Ricker, 1958).
ции. Рис.И.2 иллюстрирует’связь между логистическим
ростом и постоянным уровнем добычи.
Если предположить, что логистическая модель пра-
вильно описывает характер динамики численности попу-
ляции, то для оценки МПУД достаточно знать К и гт.
Метод оценки МПУД зависит от того, идет ли в популяции
в момент оценки промысел или она находится в естест-
венном стационарном состоянии.
292
Глава 11
Численность популяции растет;
К и гт неизвестны
Если численность популяции растет, стремясь к не-
известному нам стационарному уровню, то по данным о
зависимости численности популяции от времени мы можем
построить логистическую кривую и оценить значения гт и
К. Морисита (Morisita, 1965) показал, что при логисти-
ческом росте величина (NM — линейно связана
с NM, так что
(NM-Nt)/Nt = a-bNM,
где а = егт — 1 и b = а/К. Соответственно если мы зна-
ем значения численности популяции 2V за три или более
последовательных года,то гтл К можно оценить методом
наименьших квадратов. Затем, определив мгновенную ин-
тенсивность охоты Н — гт!2 и уровень, на котором сле-
дует поддерживать численность популяции К/2, мы можем
оценить МПУД.
Численность популяции растет;
К известно, а гт неизвестно
Если нам известен стационарный уровень численности
К, а исходно численность популяции была снижена, то по
скорости, с которой численность популяции стремится i
принять прежцее значение К, мы можем оценить значение
гт, и, следовательно, МПУД. При логистическом росте
1П(^~ )=а~г^
где гт — наклон линии регрессии In (K—N)/N на время
t. Табл.11.3 иллюстрирует такой расчет на примере гипо-
тетической популяции, численность которой исходно была
понижена от К = 1000 до 800 особей. На следующий год
численность популяции возросла до 850 особей, а еще
через год достигла значения 890 особей. Значение МПУД,
рассчитанное в предположении, что охота ведется на про-
тяжении всего года с постоянной интенсивностью, опре-
деляемой по значению мгновенной интенсивности охоты
Н, составляет 86 животных в год. Если же охота ежегод-
Популяционный анализ и эксплуатация популяций 293 Таблица 11.3 Расчет максимального постоянного уровня добычи для популяции с известной стационарной численностью К — 1000 животных
Годы t Численность K-N N / К—N N j У
0 1 2 800 850 890 0,250 0,176 0,123 —1,39 —1,74 —2,10
ЪГу-Vt )(Sy)/n ~Гт~ К = 1000 п = 3 St = 3 2у = —5,23 3/2 = 5 Sty=—5,94 S/3— (3/ )Чп = 2 3/!/ - (St )(3у )/п = -0,710 -rm =-0,710/2 = —0,355; rm = 0,355 Я = г_/2=О,177 при У = К/2 = 500 МПУД = 0,177 X 500 = 86
но разрешена на протяжении короткого промежутка вре-
мени, то значение МПУД следует рассчитывать, исходя из
значения конечной интенсивности охоты h.
Известны К и одно из значений ПУД
Предположим, что популяция в течение нескольких
лет являлась объектом промысла, причем нам известны
значения численности популяции и ПУД. Допустим
также, что нам известна исходная стационарная числен-
ность популяции до начала промысла. Таким образом,
нам известпы значения К, ПУД в год и численности, соот-
ветствующей этому уровню добычи. По этим данным мы
можем рассчитать идеальную скорость роста популяции
по формуле
KHt
Г' »Т *
л — Nj
294
Глава 11
где Н t — мгновенная интенсивность охоты, соответствую-
щая известному значению ПУД и известной численности
популяции NI. Теперь, зная правильную мгновенную ин-
тенсивность охоты Н — гт/2 и соответствующую числен-
ность популяции К/2, мы можем определить значение
МПУД.
Известны значения ПУД для двух
интенсивностей охоты
Предположим, что нам известны значения ПУД для
двух интенсивностей промысла, но значение К мы не зна-
ем.
Так может быть, например, в том случае, когда в по-
пуляции в течение многих лет производится охота с по-
стоянной интенсивностью и устанавливается соответствую-
щая численность популяции, а затем интенсивность охоты
увеличивается и численность популяции переходит к
новому равновесному значению. Такая ситуация может
быть либо при наличии хорошо поставленного охотничь-
его хозяйства, либо просто при удачном стечении обстоя-
тельств.
Для того чтобы оценить МПУД и соответствующий
уровень численности, на котором нужно поддерживать
популяцию, мы должны определить гт и К. Рассмотрен-
ный ниже пример является гипотетическим, однако зна-
чения параметров примерно соответствуют популяции бе-
лохвостого оленя. Пусть в течение 10 лет численность
популяции к началу охотничьего сезона составляла в
среднем 4800 оленей, а добывалось ежегодно в среднем
384 оленя, Затем управление охотничьего хозяйства ре-
шило, что число лицензий на отстрел оленей может быть
удвоено. В новых условиях средний уровень добычи со
временем стабилизировался на значении 546 оленей в год, а
средняя численность популяции перед началом охотничь-
его сезона составляла 3900 особей. Так' как охотничий се-
зон короток, а большая часть оленей добывается в первые,
же дни после открытия сезона, то интенсивность охоты
можно оценить как ежегодную добычу, деленную на чис-
ленность популяции, что равно изолированной удельной
смертности популяции за счет охоты h. По этим данным с
Популяционный анализ и эксплуатация популяций
295
помощью формулы Н = —In (1—h) мы можем опреде-
лить мгновенные интенсивности охоты.
Первый уровень интенсивности Второй уровень инте нс ивност и
у = 4800 3900
ПУД = 384 546
Л= ПУД/У 0,080 0,140
Н = — 1п(1—h) 0,083 0,151
Идеальная скорость роста численности популяции при
каждом уровне интенсивности охоты связана с числен-
ностью популяции и уровнем добычи соотношением
КНХ КН2
Гт - к —N,. “ K — N2
Из этих соотношений можно получить формулу для оцен-
ки значения К:
к _ HtN2 — H2Ni _ (0,083 X 3900) — (0,151X 4800) =
Hr — Н2 ~ 0,083 — 0,151
= 5900 оленей.
По значению К для любого из уровней интенсивности
охоты мы можем определить идеальную скорость роста
популяции гт:
КН
I'm
Первый уровень
5900 X 0,083 _0 45
5900 — 4800 ~ ’
Из этих оценок для гт~а К мы получаем, что соответствую-
щая МПУД численность популяции составляет К/2 =
= 2950 оленей, а мгновенная интенсивность промысла
гт/2 = 0,22. Этому значению соответствует интенсивность
охоты в течение короткого охотничьего сезона, равная
h = 1 — е"°-22= 0,20, что дает для МПУД значение 0,20 X
K — N
Второй уровень
5900 X 0,151 _ q
296
Глава 11
X 2950 = 590. Это значительно превышает уровень
добычи в предыдущие годы при обеих интенсивностях
охоты.
Популяция не является объектом промысла1,
не известны ни К, ни гт
Очень часто численность популяции, которая в силу
экономических или других причин должна быть неза-
медлительно сделана объектом промысла, совершенно не
известна. Такое положение не столь безысходно, как это
может показаться. Если начатая в популяции охота носит
планомерный и управляемый характер и при этом на про-
тяжении нескольких первых лет регистрируется числен-
ность популяции, то и МПУД, и соответствующий ему
уровень численности популяции можно определить не-
посредственно из данных, получаемых в процессе про-
мысла. Сама охота при этом является орудием, позволяю-
щим получить параметры динамики роста популяции,
по которым затем определяется максимальный постоянный
уровень добычи.
Поскольку до начала промысла популяция пребывала
в естественном состоянии, ее численность в это время мо-
жет служить оценкой К. Это значение определяется с
помощью любой из описанных в разд. 4.2 методик
учета, хотя наиболее удобным, по-видимому, является
метод двукратного использования индекса (третья часть
разд. 4.2.5), так как популяция в любом случае подвер-
гается внешнему воздействию в результате охоты, а при-
меняя данный метод, мы можем этим воспользоваться.
Численность популяции рассчитывается по разности ин-
дексов до и после первого сезона охоты. Пусть индекс
численности популяции до охоты равен 11 = 145,3, а
после первой охоты, во время которой было отстреляно
С — —75 животных, индекс оказался равным /2 = 134,4.
Тогда численность популяции до охоты определяется по
формуле
„ 1ГС 145,3 Х(-75) .лол
Л =-----1---=-------------— = 1000 животных.
У2 —А 134,4-145,3
Популяционный анализ и эксплуатация популяций 297
Заметим, что значение С отрицательно, поскольку жи-
вотные изымаются из популяции, а не добавляются к ней.
Если мы будем продолжать добывать ежегодно по 75
животных, численность популяции будет сначала убы-
вать, а затем стабилизируется на уровне, отвечающем боль-
шему из двух значений плотности популяции, соответ-
ствующих ПУД = 75. При этом по скорости убывания
численности после начала промысла можно оценить идеаль-
ную скорость роста популяции. Для такого расчета необ-
ходимы значения численности популяции по крайней мере
за три последовательных года непосредственно после нача-
ла промысла. Последовательные значения численности свя-
заны друг с другом приблизительно таким соотношением:
Nt+i Nt (1 - К) e^~bNt\
где Ъ — это постоянная, равная уменьшению rm при уве-
личении плотности популяции на единицу, а другие обоз-
начения были определены ранее. Подставляя h — C/Nt
и логарифмируя, получаем
In ( N,+1 } = rm-bNt.
\ Nt — C ) 1
Это уравнение позволяет найти rm из эксперименталь-
ных данных; оно определяется точкой пересечения линии
регрессии с осью ординат. В табл.11.4 даны соответству-
ющие расчеты для модельной популяции, параметры
которой близки к параметрам популяции пернатой дичи.
Точность оценки rm, полученной таким способом, тем
больше, чем меньше продолжительность охотничьего се-
зона. С формальной точки зрения в процессе эксперимента
годовая добыча может быть различной, однако из практи-
ческих соображений удобнее всего, чтобы она поддержи-
валась из года в год постоянной.
Теперь нам известны значения К и rm, из которых мож-
но оценить МПУД так же, как мы это делали раньше.
Если, например, К = 1000, a rm = 0,66, то для поддер-
жания МПУД численность популяции должна быть рав-
ной 500 особям, а интенсивность промысла Н = 0,33.
Тогда МПУД, достигаемый за короткий сезон охоты, со-
ставляет 500 h, где h = 1 — е~н\ таким образом, ежегод-
ная добыча составляет 140 птиц.
298
Глава 11
Таблица 11.4
Оценка гт по убыванию численности популяции в результате
ежегодного отстрела С = 75 птиц
Nt X NM Nt — C У
925 893 1,050 0,0488
893 877 1,072 0,0695
877 869 1,084 0,0808
869 865 1,089 0,0854
865 863 1,092 0,0880
х = 885,8 • Ъх = 4429 7 = 0,0745 2^ = 0,3725
2г2 = 3 925 589 2^ = 328,398
2ж2 = (2ж)2/п= 2380,8 2гг/ — (2ж )(2у )/п = —1,5628
Ь = —1,5628/2380,8 = —0,000656
гт = 7~~ б7= 0,0745 + (0,000656X885,8) =0,66
11.2.2. Оценка уровня добычи в моделях
взаимодействующих популяций
В разд. 9.9.2 мы рассмотрели модель динамики
численности популяции травоядных, рост которой опре-
деляется не только собственными параметрами, но и ди-
намикой растительности, служащей пищей этим траво-
ядным. Такая модель ближе к реальности, чем логисти-
ческая.
В разд. 9.9.3 мы дополнительно усложнили модель,
введя в рассмотрение популяцию хищника, и из соот-
ветствующей системы уравнений нашли равновесные зна-
чения численности популяций растений и животных для
частного случая, когда в роли хищника выступает хо-
рошо вооруженный охотник. Эта модель содержит во-
семь постоянных, характеризующих особенности роста
популяций растений и животных. Если бы эти постоянные
Популяционный анализ и эксплуатация популяций
299
удалось определить, то с хорошей точностью можно было
бы рассчитать максимальный постоянный уровень добы-
чи травоядных в такой системе и соответствующую чис-
ленность их популяции. Однако в настоящее время на это
не приходится надеяться. Как бы то ни было, специалистам,
занятым организацией промысла наземных животных, сле-
довало бы беспокоиться о реалистичности используемых
ими моделей не меньше, чем это принято у занимающихся
прикладными вопросами ихтиологов, и что-то предпри-
нимать в этом направлении.
Существуют приближенные методы оценки МПУД в
системах взаимодействующих популяций, позволяющие
обойтись без определения всех характеризующих систему
параметров. Будучи приближенными, эти методы тем не
менее позволяют получать более точные оценки,' чем с по-
мощью логистического уравнения. Соответствующие рас-
четы приведены, например, в работе Коли (Caughley,
1976), здесь же мы лишь отметим, что они дают обычно
более низкие значения МПУД, чем логистическое уравне-
ние. Кроме того, эти методы приводят к более высокому
значению (0,7 К) численности, обеспечивающей МПУД.
Расхождение между соответствующими Оценками служит
еще одним аргументом против некритического подхода
к выбору моделей для оценки МПУД.
11.2.3. Оценка МПУД по соотношению между
промысловым усилием и добычей
В тех случаях, когда удельные плодовитость и смерт-
ность мгновенно изменяются при изменении обеспечен-
ности пищей или другими ресурсами, т.е. эти факторы
сразу же проявляются в изменении скорости роста
популяции, МПУД можно оценить по зависимости добы-
чи от промыслового усилия.
Рис.11.3 служит иллюстрацией этого метода на приме-
ре популяции желтоперого тунца. На графике пред-
ставлены данные Шафера (Schaefer, 1957) по уловам между
1934 и 1955 гг. в зависимости от промыслового усилия.
Аналогично тому как в случае логистического роста по-
пуляции для регрессии ПУД на плотность мы получаем
параболическую зависимость, регрессия ПУД на про-
300
Глава 11
мысловое усилие, затраченное на достижение такой до-
бычи, также имеет вид параболы. Построенная по данным
Шафера и изображенная на рис. 11.3 парабола имеет
максимум в точке, соответствующей 18,6 млн. фунтов
(8,5-10е кг), что и является оценкой МПУД. Сам Шафер
использовал несколько другой метод анализа, но в прин-
ципе пришел к тому же самому заключению.
Промысловое усилие в тысячах дней
промысла
Рио 11.3. Аппроксимация параболой зависимости улова желтоперо-
го тунца от затраченного промыслового усилия как метод оценки
максимального постоянного уровня добычи (Schaefer, 1957).
Поскольку этот метод основан на отсутствии задержки
во времени между причиной (снижение плотности попу-
ляции вследствие промысла) и следствием (достижение
значения гр, соответствующего новому уровню плотности),
он может использоваться лишь для быстро перестраива-
ющихся популяций. В популяциях крупных млекопитаю-
щих, состоящих из представителей нескольких перекры-
вающихся поколений, изменение плотности скажется на
скорости роста популяции не сразу. Изложенный метод
для таких популяций не годится, но он вполне применим
к популяциям пернатой дичи и мелких млекопитаю-
щих.
Популяционный анализ и эксплуатация популяций 301
Для применения метода требуется детальная инфор-
мация о величинах промысловых усилий и добычи, и для
более успешного его применения лучше, если исследова-
тель может в той или иной степени контролировать ин-
тенсивность промысла. Его можно при этом поэтапно
увеличивать, причем этапы должны разделяться перио-
дами, когда интенсивность остается постоянной. На гра-
фике следует откладывать лишь добычу в годы, предшест-
вующие каждому очередному изменению интенсивности
промысла. Этот уровень добычи, достигаемый в конце пери-
ода, в течение которого интенсивность промысла поддер-
живалась постоянной, наиболее точно соответствует равно-
весному уровню добычи при данном годовом промысловом
усилии.
Экспериментальные точки на графике зависимости
добычи от промыслового усилия следует получать до тех
пор, пока линия регрессии не начнет загибаться вниз.
Затем методом наименьших квадратов (Snedecor, Cochran,
1967: 453) через эти точки проводят параболу, описывае-
мую уравнением у = а + Ьх + сх2, и определяют ее мак-
симум, дающий оценку МПУД в случае, если а близко
к 0.
11.2.4. Промысел социальных видов
В тех случаях, когда популяция подразделена на со-
циальные группировки, возможны две схемы постановки
промысла: либо полностью истребляют некоторые груп-
пы, оставляя другие в неприкосновенности, либо в каждой
группе добывают некоторую часть особей. Выбор тактики
определяется социальной организацией групп и харак-
тером дробления вида на группы.
Стратегия организации промысла направлена на уве-
личение скорости роста численности популяции за счет
увеличения количества ресурсов, приходящихся на одну
особь, и тактика промысла должна быть построена с уче-
том этой цели. Вообще говоря, в тех случаях, когда тер-
ритории, принадлежащие отдельным группам, перекры-
ваются, а также для кочующих видов промысел должен
быть направлен против целых групп, а не против отдель-
ных особей. При этом уменьшается неблагоприятное воз-
302
Глава 11
действие одних групп на другие, а кроме того, в резуль-
тате изъятия одних групп некоторое дополнительное коли-
чество пищи и других ресурсов становится доступным для
других групп. Если же принадлежащие отдельным груп-
пам территории не перекрываются, а расселение в незаня-
тые, но благоприятные для обитания области идет мед-
ленно, то промысел следует вести, добывая некоторую часть
каждой группы. Увеличение количества ресурсов, при-
ходящихся на одну особь, ничего не дает, если эти допол-
нительные ресурсы никак не используются.
11.2.5. Избирательный промысел
До сих пор мы рассматривали неизбирательный про-
мысел, при котором вероятность для особи стать добычей
не зависела ни от ее возраста, ни от пола. Этот метод
хотя и неэффективен, но часто является единственным
практически осуществимым. Мелкие пушные млекопитаю-
щие и пернатая дичь при отсутствии полового диморфиз-
ма добываются только таким способом. То же самое от-
носится и к рыбам, если не считать слабой избиратель-
ности, обусловленной размерами ячеи или запретом на лов
особей размеров меньших, чем минимально допустимые.
При организации коммерческого промысла' или спор-
тивной охоты на крупных наземных млекопитающих
имеется больший выбор между различными способами
избирательного отстрела. Если в полевых условиях на
глаз можно распознать несколько категорий особей,
различающихся между собой по возрасту и полу, не-
избирательный отстрел не является ни необходимым, ни
желательным. Решение вопроса о наиболее эффективной
организации промысла зависит от того, хотим ли мы сде-
лать промысел избирательным в отношении пола или в
отношении возраста. В действительности выбор типа
«либо-либо» отсутствует — в конечном итоге интенсивность
промысла должна быть оптимальной в отношении каждого
класса особей определенного пола и возраста, однако для
ясности изложения мы сначала рассмотрим эти две взаи-i
мосвязанные проблемы так, как если бы они были изоли-
рованными.
Популяционный анализ и эксплуатация популяций
303
Избирательный по возрасту промысел
Принципы, лежащие в основе организации избира-
тельного промысла, лучше всего можно понять, еще раз
рассмотрев влияние неизбирательного промысла на воз-
растное распределение самок в сезонно размножающейся
популяции. Как мы уже видели (разд. 9.5), такой промы-
сел не меняет возрастного распределения в популяции,
оставляя его таким же,каким оно было до начала промысла.
Устойчивое возрастное распределение Sx в популяции,
не являющейся объектом промысла, связано с ее выживае-
мостью и скоростью роста соотношением Sx = lxe~rx.
При неизбирательном промысле и при поддержании
постоянного уровня добычи выживаемости понижаются
до значения l'x = 1хе~гх. Таким образом, поддержание ПУД
при неизбирательном промысле изменяет 1Х и снижает
г до 0, так что при этом составляющие нового вектора вы-
живаемости 1Х становятся равными значениям частот соот-
ветствующих возрастных классов в необлавливаемой попу-
ляции. Вопрос заключается в том, является, ли такая
организация промысла наилучшей или же 1Х можно из-
менить другим образом, не отказываясь от требования ра-
венстващулю скорости роста популяции при наличии про-
мысла. Фактически единственным ограничением, накла-
дываемым на популяцию при поддержании постоянного
уровня добычи, является Т>1хтх = 1. Это равенство дос-
тигается, при очень широком наборе тактик промысла,
дающих соответственно различные векторы 1Х.
В разд. 8.3 было показано, как удельную смертность
qx для данного возрастного интервала (ж, х + 1) можно
разложить на две составляющие — изолированную
удельную смертность за счет охоты hx и удельную естест-
венную смертность пх, удовлетворяющие равенству
Qx = hx + пх — hxnx или при переходе к удельной вы-
живаемости рх = (1 — hx) (1 — пх). Соответственно
^х'тх — 1, уравнение, смысл которого состоит в том, что
при поддержании ПУД скорость роста ? = 0, также может
быть’записано в виде
ОО X— 1
2тх П Ру = 1
1 »=0
304
Глава 11
(см. табл. 8.2 перехода от 1Х к рх) и, следовательно,
П(1-/гу)(1-пу) = 1.
1 у=о
Записанное в такой форме уравнение позволяет опреде-
лить, правильно ли составлен набор интенсивностей охоты
в зависимости от возраста, и проверить, дает ли выбран-
ная стратегия избирательного промысла г — 0. Зная век-
торы пх и тх и желаемый набор hx интенсивностей охо-
ты в зависимости от возраста, мы можем подставить все
эти значения в уравнение. Если получающаяся сумма не
равна 1, то выбранная стратегия промысла не обеспе-
чивает равенства 0 скорости роста популяции. Но это еще
не все. В действительности мы интересуемся в первую оче-
редь не тем, поддерживает ли данная стратегия промысла
постоянной численность популяции; мы хотели бы знать,
какая из многих возможных стратегий обеспечивает под-
держание максимально возможного постоянного уровня
добычи. Это сложная проблема. Возрастное распределение
добычи задается распределением интенсивностей охоты в
зависимости от возраста и в свою очередь задает возрастное
распределение, которое установится в популяции на сле-
дующий год. Оптимальная стратегия промысла представ-
ляет собой компромисс между добычей максимально воз-
можного числа самок из возрастных классов, дающих
наименьший потенциальный вклад в значение скорости
роста популяции, и необходимостью обеспечить такое
возрастное распределение остающихся в живых особей,
при котором на следующий год те же самые возрастные
классы самок будут достаточно многочисленны для того,
чтобы быть объектом эффективной охоты.
Противоречивость этих двух устремлений не дает
возможности достичь ни одной из целей. За исключением
довольно специальных случаев, промысел различных
возрастных классов с различной интенсивностью обычно
дает очень немного или вовсе ничего не дает. В результа-
те оптимальной стратегией снова оказывается неизбира-
тельный промысел. Если при данной плотности потен-
циальная скорость роста состоящей из самок части попу-
ляций равна, скажем, гр — 0,2, то никакая зависимость
Популяционный анализ и эксплуатация популяций 305
интенсивностей от возраста охоты не позволит при под-
держании плотности популяции постоянной сделать
значение гр устойчиво большим 0,2. Исключения из этого
правила тривиальны. Во-первых, если плодовитость са-
мок резко падает по достижении некоторого возраста, то
промысел старых самок с более высокой интенсивностью
увеличит значение МПУД по сравнению с тем, которое
достижимо при неизбирательном промысле. Я не знаю,
однако, ни одного вида позвоночных, у которых плодо-
витость падала бы по достижении некоторого возраста
достаточно круто для того, чтобы с экономической точки
зрения имело смысл организовывать промысел старых
самок с более высокой интенсивностью. Во-вторых, если
изъятие из популяции молодых особей сильно увеличива-
ет жизнеспособность следующего приплода, может ока-
заться оправданной более высокая интенсивность промыс-
ла самого молодого возрастного класса. Однако изменение
эффективности промысла на единицу промыслового уси-
лия вряд ли будет при этом значительным. В-третьих,
если связанное с присутствием в популяции данной самки
уменьшение гр не зависит от веса самки, а сам вес животных
быстро растет с возрастом и в пределе достигает высокого
значения, избирательный промысел самок старших воз-
растов увеличивает значение МПУД, выраженное в еди-
ницах убойного веса добычи. И опять-таки я не знаю такого
вида млекопитающих, у которого эти свойства были бы
развиты столь значительно, чтобы организация избира-
тельного промысла была экономически выгодной. Таким
образом, с практической точки зрения неизбирательный
промысел не менее эффективен, чем промысел, избира-
тельный по возрасту, а поскольку он дешевле, то и пред-
ставляет собой более правильную стратегию.
Эти утверждения высказаны здесь таким решительным
образом, чтобы не проглядеть их за математическими вы-
кладками. Избирательный по возрасту промысел не
является полезной стратегией, поскольку имеет место почти
полная взаимозависимость между скоростями роста раз-
личных возрастных классов. Допустим, состоящая из са-
мок часть популяции подвергается промыслу с целью дос-
тижения МПУД. В полевых условиях мы можем разли-
чать возрастные классы 0,1,2 и > 2 и охотиться на них с
11-334
306
Глава 11
различной интенсивностью. При любой организации
промысла устойчивое возрастное распределение в сезон-
но размножающейся популяции может быть записано в
таком виде:
Для возраста 0
Для возраста 1
Для возраста 2
Для возраста >2
1.
(1 — Ло) (1 - п0).
(1 — Ло) (1 — n0) (1 — (1 — Tij).
(1—ho) (1—n0) (1—fct) (1—nt) (1—h2) (1—ra2)
ha+na~ha na
причем
1 У—0
Это равенство означает, что выбранные интенсивности
промысла стабилизируют численность популяции. Когда
устойчивое возрастное распределение 'записано в такой
развернутой форме, обнаруживается, что формула, опре-
деляющая устойчивую частоту для каждого возрастного
класса, содержит члены, зависящие от интенсивностей
промысла всех младших возрастных классов. В силу со-
отношения, обозначающего равенство нулю скорости
роста популяции, устойчивая частота нулевого возрастного
класса является функцией интенсивности охоты на каж-
дый из возрастных классов. Такая замкнутая система
подчиняется общеизвестному в физике правилу, согласно
которому поведение изолированной системы никак не ме-
няется при перестройке внутренних взаимосвязей. Оце-
нивая поведение являющейся объектом промысла популя-
ции по МПУД, мы можем заключить, что добыча при пере-
ходе от неизбирательного к избирательному промыслу
существенно не увеличивается. Непосредственное след-
ствие из этого вывода очевидно: при эффективной орга-
низации промысла введение ограничения на минималь-
ный размер отстреливаемых животных влияет на МПУД
лишь незначительно или вовсе не оказывает никакого
влияния.
Хотя эти выводы были сформулированы только для
части популяции, состоящей из самок, они применимы (по
Популяционный анализ и эксплуатация популяций
307
крайней мере в общем виде) и к самцам/ В высшей сте-
пени маловероятно, чтобы избирательный по возрасту про-
мысел мог увеличить добычу самцов по сравнению с
МПУД, достигаемым при неизбирательном промысле.
В тех случаях, когда МПУД измеряется не в числе до-
бытых животных, а в ценах, убедительные аргументы,
высказанные против избирательного по возрасту промыс-
ла, перестают быть справедливыми. Любую комбинацию
промысловых усилий и добычи можно выразить также
через затраты и прибыли. В тех случаях, когда животные
определенного возраста обладают более высокой рыноч-
ной стоимостью, чем животные других возрастов, макси-
мальный постоянный уровень добычи — это уже не мак-
симальное число животных, которое может устойчиво
добываться в данной популяции, а постоянная комбина-
ция представителей разных возрастов, обеспечивающая
максимальную суммарную прибыль. Правильные зависи-
мые от возраста значения интенсивностей промысла опре-
деляются максимизацией выражения
оо - X—1
Wvh0 (1 - пу + 2 Wx+Vhx (1 - пху П (1 - (1 - ”у)
х=1 У=0
при условии
2 П (2 * 4 * * * В - hy) с1 - пу) = v
1 у=о
где v —это часть года между сезоном размножения и се-
зоном охоты, Wx — весовой фактор, выражающий отно-
сительную прибыль от добычи животного возраста х, а
индекс означает возраст в годах. Максимизация этого
выражения «вручную» абсолютно невозможна, однако
сравнительно легко составить программу для ЭВМ и
провести такой анализ.
В табл.11.5 приведены векторы пх и тх, оцененные
для состоящей из самок части популяции тара, растущей
примерно со скоростью г — 0,12. Для простоты предпо-
лагается , что плотность популяции составляет половину
стационарной, а к началу сезона размножения популяция
насчитывает 1000 особей. Три набора весовых коэффициен-
11*
308
Глава 11
тов относятся соответственно к ситуациям, когда макси-
мизируются: а) численность добытых особей;' б) убой-
ный вес и в) прибыль. Коэффициенты в столбце «б» — это
просто средний вес особей данного возрастного класса
в килограммах. Коэффициенты в столбце «в» выбраны в
данном примере произвольно, а в реальных условиях
они должны представлять собой чистую прибыль, полу-
чаемую от добычи одной самки соответствующего возраста.
Эта величина может убывать с возрастом в тех случаях,
когда промысел ведется ради шкур (например, кара-
кулевые овцы или котики), а может возрастать, если за-
готовляется мясо. Может быть и по-другому. Если слу-
жащая объектом промысла популяция обитает в мало-
доступной местности, то добыча молодого животного может
дать большую чистую прибыль, чем более старого и тя-
желого. Маленькую тушу охотник может доставить к
дороге на вьючной лошади, тогда как для транспорти-
ровки более крупного животного обычно приходится вы-
зывать вертолет. Чистая прибыль в этом случае оказы-
вается выше для более мелких животных, поскольку сни-
жаются накладные расходы.
В нижней половине табл. 11.5 приводятся резуль-
таты определения с помощью ЭВМ максимальной интен-
сивности охоты и суммарной добычи для случаев, когда
в промысловой популяции максимизируется численность
добычи, ее убойный вес и получаемая прибыль соответ-
ственно. Анализ показывает, что, когда мы хотим оптими-
зировать численность добычи, объектом промысла дол-
жен быть только первый возрастной класс, Однако уровень
добычи при этом остается почти тем же самым, что и при
неизбирательном промысле. Этот результат не является
неожиданным, он лишь свидетельствует о том, что на мак-
симизирующей добычу поверхности имеется несколько
максимумов. Рекомендовать такую организацию промысла
на практике не имеет смысла, поскольку избирательный
по возрасту промысел не повышает уровня добычи по
сравнению с неизбирательным, но обходится дороже.
Рекомендации по максимизации добычи в отноше-
нии убойного веса также неприемлемы, посколь-
ку незначительные преимущества, которые- дает из-
бирательный промысел, не оправдывают дополнительных
Популяционный анализ и эксплуатация популяций 309
Таблица 11.5
Максимизация добычи самок тара. Популяция после сезона
размножения насчитывает 1000 самок и служит объектом охоты
на протяжении в мес после сезона размножения
Естествен- ная удельная смерт- ность пх Удельная Весовые коэффициенты
Возраст х ' ПЛОДОВИ- ТОСТЬ тх а x+v b а
0 0,37 0,00 1 9 2
1 0,03 0,00 1 25 10
2 0,04 0,33 1 32 5
>2 = а 0,16 0,45 1 40 1
Максимальная Интенсивность промысла Добыча
л, ЧИС-
добыча, выражен-
пая в: Йо h1 лен- ность лары
а) численности 0,460 0,000 0,000 0,000 100 900 200
б) весе 0,000 0,000 0,000 0,203 52 2095 52
в) цене 0,000 0,460 0,000 0,000 72 1800 720
неизбиратель-
ный промысел 0,113 0,113 0,113 0,113 100 2062 398
затрат, связанных с его организацией. Избирательный по
возрасту промысел дает четкий экономический эффект
только в тех случаях, когда добыча выражается через
прибыль. Правда, произвольные значения коэффициен-
тов, выбранные в рассмотренном примере, различаются
для разных возрастных классов сильнее, чем это обычно
бывает в действительности. В большинстве реальных
ситуаций чистый доход от избирательного промысла не-
намного превышает доход при поддержании МПУД неиз-
бирательного промысла. По крайней мере на первых эта-
пах реализации программы промысла избирательная по
возрасту охота вряд ли оправданна.
Промысел, избирательный по полу
В тех случаях, когда промысел является избиратель-
ным в отношении возраста, изменение интенсивности охо-
ты на какой-либо один возрастной класс сказывается на
310
Глава 11
допустимых интенсивностях охоты для всех остальных
классов. В динамике двух полов такие взаимосвязи выра-
жены значительно слабее (рис. 9.1). Связи между частя-
ми популяции, состоящей из самцов и состоящей из самок,
гораздо более гибкие, и это позволяет нам использовать
их в своих целях. При численности популяции, поддер-
живаемой на постоянном уровне, увеличение или умень-
шение интенсивности охоты на самцов не обязательно
отражается на допустимой интенсивности охоты на са-
мок. В большинстве популяций самцов больше, чем это
необходимо для оплодотворения всех самок, способных
к размножению. Постепенное уменьшение доли самцов в
популяции мало сказывается на плодовитости самок до
тех пор, пока не будет достигнут некоторый критический
пороговый уровень. Он может быть очень низок, осо-
бенно в популяциях с промискуитетом или в случаях,
когда несколько доминирующих самцов монополизи-
руют всех способных к размножению самок1. В таких
условиях МПУД можно значительно увеличить, отка-
завшись от невыборочного промысла и уменьшив долю
самцов в популяции. Так как в потомстве отношение
численностей полов остается неизменным, то тенденции к
восстановлению устойчивого отношения численностей по-
лов (разд. 9.5) должна постоянно противостоять более'
высокая интенсивность промысла самцов.
Уровень, до которого можно снизить численность сам-
цов, еще не влияя на плодовитость самок, определяют два
независимых фактора. Первый — это плотность. Кломп,
ван Монтфорт и Таме (Klomp, van Montfort, TammeSj
1964) показали, что число контактов между самцами и
самками пропорционально квадратному корню из плот-
ности популяции и что ниже определенного порога по
мере снижения плотности популяции доля оплодотворен-
ных самок падает со все возрастающей скоростью. Этот
эффект не очень сказывается на организации промысла,
1 Данные по котикам, по-видимому, свидетельствуют о том, что
избыточный промысел якобы лишних самцов («холостяков») снижает
репродуктивную способность секачей — обладателей гаремов. Это
говорит о том, что к оценке числа лишних в популяции самцов
следует подходить с большой осторожностью — в учет должны
приниматься поведенческие, этологические факторы,— Прим. ред.
Популяционный анализ и эксплуатация популяций 311
поскольку плотности, соответствующие МПУД, всегда
много выше пороговых. Вторым фактором, влияющим на
плодовитость, является отношение численности самцов
к численности самок. Данное число самцов способно опло-
дотворить лишь определенное число самок. Если R =
NmlNf ~~ отношение численности самцов к численности
самок; а к — это среднее максимальное число раз, кото-
рое самец способен спариваться в течение сезона размно-
жения,' то среднее число спариваний для самки будет равно
kR. Это число определяет долю способных к размножению
самок, которые будут оплодотворены. Пара упрощенных
моделей поможет понять суть дела. В первой модели
(модель I) самки спариваются лишь однократно в те-
чение периода размножения и после этого не подпускают
к себе самцов. Доля оплодотворенных самок составит
Р = kR — g, где g — индекс нереализованной плодови-
тости самцов, то есть величина, на которую kR превы-
шает 1. В модели II самки спариваются с самцами вне
зависимости от того, спаривались ли они до этого. Доля
самок, спаривавшихся 0, 1, 2 и т.д. раз, будет описы-
ваться пуассоновским распределением, из чего следует,
что суммарная доля оплодотворенных самок в популяции
составит Р = 1 — e~kR-.
На рис. 11.4 графически изображена связь между
плодовитостью и отношением численностей полов для
этих двух моделей. В действительности доля оплодотво-
ренных самок зависит также от таких факторов, как про-
должительность сезона скрещивания, подвижность обоих
полови организация иерархического доминирования. Одна-
ко эти факторы могут изменить лишь наклон кривых на
рис. 11.4, но не их характер. Приведенные зависимости
показывают, что в популяциях, описывающихся и мо-
делью I, и моделью II, существует пороговое значение, и
при снижении отношения численностей полов ниже поро-
гового этот фактор неизбежно начинает оказывать влия-
ние на плодовитость и, следовательно, на постоянный
уровень добычи. В рассматриваемом примере это поро-
говое значение составляет R = 0,05 для модели I и 7?~0,2
для модели II. На практике порог должен определяться
экспериментально, с помощью воздействий на отношение
численностей полов.
312
Глава 11
Рассмотрим теперь преимущество, которое дает орга-
низация избирательного по полу промысла по сравнению
с неизбирательным, считая, что доля самок в популяции
Pf остается в пределах, когда значение плодовитости
еще не зависит от отношения численностей полов.
Рис. 11.4. Зависимость плодовитости от отношения численности
полов для случаев, когда самки спариваются лишь однократно за
сезон размножения [/J и остаются способными к спариванию вне
зависимости от того, спаривались ли они до этого (//).
В этом примере самцы в среднем способны участвовать в 20 спариваниях
за сезон (й=20).
Предположим, что популяция с равной численнос-
тью полов во всех возрастах (т.е. Pf = 0,5) поддержи-
вается при плотности, соответствующей МПУД. Пусть
удельная плодовитость составляет т = 0,5 доче-
рей на одну самку в год, а средняя удельная выживае-
мость в отсутствие промысла р — 0,8. В этом случае р =
= 1 — h, где Л — средняя удельная изолированная смерт-
ность. Популяция ежегодно облавливается непосредствен-
но после сезона размножения, так что в живых остается
1000 особей. Таким образом, вследствие естественной смерт-
ности к началу следующего сезона размножения ее чис-
Популяционный анализ и эксплуатация популяций
313
ленность понижается до Np = 800 животных, затем в
течение сезона размножения рождается Npm = 400 ново-
рожденных и численность популяции достигает значения
1200 особей. Следовательно, ПУД, возвращающий попу-
ляцию к исходной численности, равной 1000, составляет
200 особей. Итак,
ПУД = Np + Npm — N = 800 + 400 - 1000 =
= 200 животных,
а интенсивность промысла
= . =0)1667.
Np -j- Npm
Это уравнение можно упростить введением величины
егр, конечной скорости роста популяции в отсутствие
промысла, равной р + pm, что дает
h = 1 - е“Ч
соотношение, уже полученное ранее в разд. 11.2 другим
способом.
Для того чтобы эти формулы можно было использо-
вать при организации выборочного по полу промысла, их
следует выписать отдельно для каждого пола. ПУД для
самок составляет
ПУД$ = NPfp + NPfpm - NPf =
== NPf[(p + pm — 1) = 500 (0,8 + 0,4 — 1) = 100 самок.
При этом интенсивность охоты равна
h = ,р + р»-1 = 0)2/1^2 _ 0>1667>
Р + pm
Соответственно для самцов
ПУД^ = N (1 - Pf)~р + NPfpm - N (1 - Pf) =
=N (Pf~pm — P~p+ Pf + p-i) =
= 1000 (0,,2 - 0,4+0,5+0,8 - 1) = 100 самцов,
314
Глава 11
причем интенсивность промысла составляет
N(l-Pf)p+NPfpm-N(i-Pf)
%’ =
N (1 — Pf) р + Njpm
= 1 -
= 1 -
i-Pf
Pt\ — Pf + Pfm)
1—0,5
0,8(1—0,5 + 0,25)
= 0,1667.
Предположим теперь, что численность популяции по-
прежнему поддерживается на постоянном уровне, состав-
ляющем 1000 особей по окончании охотничьего сезона,
однако охота при этом производится избирательно, так
что численность самок составляет 600 особей, а самцов —
400, т.е. Pf — 0,6, а не 0,5, как раньше. ПУД для самок
равен теперь
ПУД9=^/(р + рш-1) =
= (1000 х 0,6) (0,8-(-0,4 — 1) = 120 самок,
а для самцов
ПУДс? = Лг(75/рт-Р/р + Р/ + р-1) =
= 1000 (0,24 — 0,48 + 0,6 + 0,8 — 1) = 160 самцов.
Рассчитанные по тем же формулам, что и ранее, интен-
сивности охоты составляют соответственно /и? = 0,1667 и
/V = 0,285. Заметим, что изменилась только интенсив-
ность промысла самцов. Таким образом, при новой, из-
бирательной по полу организации промысла постоянный
уровень добычи поддерживается при сохранении прежней
интенсивности промысла (но не уровня добычи) для самок,
тогда как интенсивность промысла самцов возрастает.
Для популяции фиксированных размеров ПУД рас-
тет линейно с ростом Pf:
ПУД = (2Урш) Pf - N (1 - р),
тде — Лт(1 — р) — точка пересечения прямой с осью
ординат, 2Npm — наклон этой прямой. Точка Пересе-
Популяционный анализ и эксплуатация популяций
315
чения графика с осью абсцисс (1 — pj/Zpm дает зна-
чение Pf, ниже которого никакой уровень избиратель-
ности промысла не может поддерживать постоянным
Pf и численность популяции.
Рис. 11.5 иллюстрирует выигрыш, которого можно ожи-
дать от организации избирательного промысла, т.е. от
Рис. 11.5. Зависимость постоянного уровня добычи от отношения
численностей полов для популяции, "в которой промысел ведется
избирательно в отношении пола.
поддержания значения Pf на уровне выше 0,5 для попу-
ляций пернатой дичи (р = 0,3; тп — 0,4), копытных
(р = 0,8; тп — 0,5) и крупных млекопитающих, например
слонов (р = 0,9; тп — 0,145). Во всех случаях увеличение
добычи значительно. Эта простая модель в действитель-
ности является лишь весьма далеким приближением к
реальной ситуации. Самое большое упрощение состоит
в том, что мы считаем р не зависящим от возрастного рас-
пределения. Это не существенно в отношении самок, воз-
растное распределение которых не меняется при пзбира-
316
Глава 11
тельном в отношении пола промысле, однако для самцов,
средний возраст которых в стационарной популяции
снижается при изменении отношения численностей полов
в пользу самок, этой зависимостью пренебрегать нельзя.
Такое смещение возрастного распределения, вероятно, по-
влечет за собой повышение средней удельной естествен-
ной смертности. Следовательно, р будет убывать по мере
роста Pf, и линии регрессии, изображенные на рис. 11.5
прямыми, в действительности, вероятно, будут искрив-
ляться. Однако в рамках практически реализуемой в по-
левых условиях избирательности промысла приведенные
здесь формулы обычно дают достаточно хорошую оценку
уровня добычи при избирательном по полу промысле.
Избирательный промысел в системе
нескольких видов
В тех случаях, когда промысловый вид использует
те же ресурсы, что и некоторые другие совместно с ним
обитающие виды, взаимосвязь между численностями попу-
ляции в последовательные годы вряд ли будет столь прос-
той, как это изображено на рис. 11.1. Обусловленное
охотой снижение плотности популяции промыслового
вида может повлечь за собой увеличение плотности одного
или нескольких не являющихся объектом промысла видов,
обитающих на той же территории, если рационы или тре-
бования, предъявляемые этими видами к местообитаниям,
перекрываются. В такой ситуации постоянное снижение
численности промысловой популяции не обязательно
повлечет за собой соответствующее увеличение уровня ре-
сурсов, приходящихся па каждого члена данной популя-
ции, а так как именно это повышение обеспеченности ре-
сурсами и было основой ранее описанных моделей, то в
новой ситуации эти модели могут оказаться совершенно
непригодными для оценки МПУД.
Когда плотности популяций связаны таким образом,
пе следует, если это возможно, ограничивать промысел
одним видом. В группе видов со сходными экологичес-
кими требованиями промысел необходимо организовы-
вать так, как если бы эти группы представляли собой еди-
ную популяцию, и МПУД оценивать в единицах суммар-
ного убойного веса или общей прибыли. Такая постановка
Популяционный анализ и эксплуатация популяций
317
промысла формально аналогична организации изби-
рательного в отношении пола промысла одного вида.
В обоих случаях мы стремимся максимизировать суммар-
ную добычу, оптимизируя интенсивности промысла в
каждой из частей облавливаемой популяции. Однако в
отличие от избирательного по полу промысла, результа-
ты которого в значительной степени можно предсказать на
основе минимальной информации о социальной органи-
зации вида, при постановке избирательного промысла в
группе видов нас могут подстерегать неожиданности.
Если не считать общих слов и умозрительных рассужде-
ний, в настоящее время мы не в состоянии предсказать
влияние убывания плотности одного вида на плотность
другого. Межвидовые связи обычно не являются прямыми
и носят весьма деликатный характер. Можно, конечно,
строить простые модели взаимодействия между видами
п использовать их затем в качестве первого приближения
для оценки МПУД в такой системе видов [отправным
пунктом в этом вопросе может служить работа Рифен-
бурга (Riffenburg, 1969) по максимизации суммарной до-
бычи сельди, анчоуса и хека], но такие модели не за-
меняют прямых экспериментов по исследованию эффек-
тов взаимодействия между видами.
11.2.6. Промысел в переменных
внешних условиях
Методы, описанные выше для оценки МПУД, пригод-
ны, лишь когда колебания условий существования попу-
ляций год от года весьма умеренны. Такие модели приме-
нимы для большинства популяций. Однако для ряда
популяций характерна динамика «бумов и кризисов»,
когда численность популяции резко увеличивается при
благоприятных условиях и резко падает, когда условия
меняются к худшему. К этой категории можно отнести
большинство видов, обитающих в пустынях и полупусты-
нях, многие виды океанических рыб и некоторых позво-
ночных северной тундры. Упрощающее предположение о
существовании стационарной плотпости, даже в лучшем
случае представляющее собой очень смелую идеализа-
цию, практически теряет связь с реальностью, когда мы
318
Глава 11
имеем дело с популяцией, численность которой резко ме-
няется. Аналогичным образом для популяций, числен-
ность которых изменяется в широких пределах, нельзя
использовать плотность в качестве показателя количества
ресурсов, приходящихся на одну особь, и соответственно
в качестве индекса гр. При таких условиях плотность
популяции и количество доступных ресурсов, как прави-
ло, не сбалансированы и ни одну из них нельзя предска-
зать по значению другой.
К проблеме организации промысла в меняющихся
условиях можно подойти с двух сторон. Во-первых, мы
можем просто игнорировать изменчивость внешних
условий и оценивать МПУД так, как если бы популя-
ция обладала стационарной численностью, принимая за
таковую среднюю за несколько лет численность популя-
ции. Это так называемая «усредненная» стратегия. Во-
вторых, можно использовать «следящую» стратегию, ког-
да интенсивность промысла увеличивают при увеличении
скорости роста популяции и, наоборот, промысел ос-
лабляют или временно прекращают, когда г принимает
отрицательное значение. Таким образом, стратегию про-
мысла меняют вместе с изменениями, происходящими в
популяции, прослеживая динамику популяции.
Усредненная стратегия обладает многими преимущест-
вами, в особенности когда амплитуда колебаний числен-
ности и среднее время между колебаниями не слишком
велики. Экономически она также является более выгодной,
чем следящая, поскольку позволяет минимизировать коле-
бания рыночных цен. По этой причине ей отдают предпоч-
тение занимающиеся проблемами промысла ихтиологи,
показавшие, что усредненная стратегия приемлема в ра-
зумных пределах даже в тех случаях, когда численность
пополнения претерпевает год от года значительные и
несистематические колебания. Недостаток такой стра-
тегии заключается в том, что есть опасность подвергнуть
слишком интенсивному промыслу популяцию при низкой
плотности и таким образом серьезно подорвать ее спо-
собность к восстановлению при благоприятных внешних
условиях. Принятие усредненной стратегии требует зна-
чительной информации. Крайне неразумно делать выбор
между усредненной и следящей стратегиями в ситуации,
Популяционный анализ и эксплуатация популяций
319
когда о размахе колебаний внешних условий или о дина-
мике популяции мало что известно. Да и вообще усреднен-
ная стратегия требует от организатора известной стой-
кости. Когда численность популяции низка, всегда су-
ществует сильный соблазн перейти от усредненной стра-
тегии к следящей1.
Следящая стратегия безопаснее, в особенности когда о
самой популяции и об условиях ее существования мало
что известно, но опа приводит к колебаниям рыночных
цен, спроса па рабочую силу и обычно соответствует мень-
шей средней добыче. Однако это единственная приемле-
мая стратегия в тех случаях, когда колебания внешних
условий значительны или когда их средняя продолжи-
тельность превышает 5 лет.
На начальных стадиях реализации программы промысла
не следует пользоваться усредненной стратегией, если
только она не основывается на значительной информации.
Правильнее в этом случае применить следящую стратегию
и пользоваться ею до тех пор, пока не накопится доста-
точно данных, чтобы можно было сделать обоснованный
выбор между двумя подходами
11.2.7. Обсуждение проблем промысла
В простейшем случае максимизацию добычи проводят
следующим образом:
1. Оценивают стационарную численность популяции К.
2. Иа протяжении нескольких последовательных лет
добывают ежегодно постоянное число животных
и по скорости, с которой убывает численность попу-
ляции, оценивают значение rm.
3. Оценивают (по К) численность популяции, соот-
ветствующую МПУД, и (по rm) мгновенную ин-
тенсивность промысла Н для популяции такой
числепности.
4. Промыслом доводят численность популяции до
уровня, соответствующего МПУД, и затем продол-
1 К сожалению, автор не касается случая, когда колебания чис-
ленности популяций определяются не флуктуациями внешних ус-
ловий, а внутри- и межвидовыми взаимодействиями, носят довольно
закономерный характер и могут быть предсказаны. Прим. ред.
320
Глава 11
жают промысел с интенсивностью И, если он ве-
дется круглогодично, или с интенсивностью h,
если охотничий сезон ограничен.
5. Если в полевых условиях самцов можно отличить,от
самок, то определяют отношение численностей
полов, еще не оказывающее влияния на плодови-
тость самок.
6. Организуют промысел самцов с более высокой ин-
тенсивностью, чтобы отношение численностей по-
лов поддерживалось на оптимальном уровне.
При таком описании оценка МПУД выглядит просто
как немудреное упражнение в области полевой экологии
и прикладной арифметики, не требующее ничего, кроме
соответствующего полевого оборудования и минимального
знания математики. Это впечатление ложно. Аналити-
ческие методы, использующиеся для вычисления МПУД,
дают не точные, а приближенные решения. На каждом
этапе осуществления описанной программы необходимо
следить за реакцией популяции, с тем чтобы эмпири-
чески определять, действительно ли расчетные значения
МПУД стабилизируют плотность популяции на соот-
ветствующем, предсказываемом моделью уровне. Боль-
шинство методов оценки МПУД основано на упрощенных
моделях реакции популяции на снижение плотности.
И хотя мы можем быть совершенно уверены в том, что
популяция не ведет себя в точности так, как это предска-
зывает модель, однако мы не знаем заранее, достаточна
ли точность модели для практических целей или модель
совершенно не годится.
Описанная в предыдущих разделах логистическая
модель применима не во всех случаях. При ее использо-
вании предполагается, что скорость производства пищи и
других потребляемых животными ресурсов не зависит от
числа потребляющих их животных; считается также, что
животные потребляют некоторую часть прироста расти-
тельной массы и не трогают «основного капитала».
В действительности большинство популяций травоядных
зависят от того, сколько видов растений произрастает на
территории их обитания, что это за виды и какова плот-
ность каждого из них, и в свою очередь оказывают влияние
на все виды растительности. Искусственное снижение
Популяционный анализ и эксплуатация популяций
321
плотности животных и поддержание ее на таком уровне в
течение достаточно длительного времени приводят к из-
менениям в растительном сообществе. При поддержании
режима МПУД плотность являющейся объектом промыс-
ла популяции начнет по прошествии нескольких лет
медленно увеличиваться в результате того, что увели-
чится суммарная биомасса источника питания. Этот
эффект был четко продемонстрирован при изучении тен-
денции изменения числа крупных млекопитающих, от-
стреливавшихся в Ботсване в качестве меры борьбы с му-
хой цеце (Child, Smith, von Richter, 1970). Простейший
способ, которым можно реагировать на этот эффект, со-
стоит в том, чтобы оставить интенсивность промысла
равной Н = rm/2, отбирая тем самым тот же процент жи-
вотных, но от более высокой численности, в силу чего сум-
марная годовая добыча, естественно, возрастает. Плот-
ность при этом неизбежно стабилизируется на более вы-
соком уровне, составляющем примерно половину истинной
стационарной плотности Д, обычно несколько превышаю-
щей первоначальную оценку.
Основной причиной неточности при оценке МПУД
является разрушение социальной организации популя-
ции в результате промысла. Группы животных — это,
как правило, не случайное сборище особей, и они часто
неожиданным образом реагируют на потерю некоторых
своих членов. Не следует организовывать промысел
социальных видов до тех пор, пока не будет вполне понята
их социальная организация. Мы должны уметь предска-
зывать, во-первых, разрушает ли промысел социальную
организацию групп и, во-вторых, какое влияние это ока-
зывает на гр.
В предыдущих разделах МПУД вне зависимости от
того, измеряли ли мы его в числе животных, убойном ве-
се или рыночной стоимости, рассматривался так, как
если бы единственной целью организации промысла было
достижение максимального уровня добычи. Иногда это
действительно так, но часто бывает и иначе. Оптимальная
плотность являющейся объектом охоты популяции может
быть выше рассчитываемой по критерию МПУД в тех слу-
чаях, когда мы хотим удовлетворить интересы не только
людей, любящих охоту, но и людей, желающих видеть
322
Глава 11
самих животных. Напротив, оптимальная плотность по-
пуляции может быть ниже плотности, обеспечивающей
МПУД, если целью организации промысла является
добыча крупных животных, служащих охотничьими тро-
феями, или когда высокая численность животных пре-
пятствует мероприятиям по защите территории от эрозии
и наводнений.
Иногда наилучшим способом действия является без-
действие. Мероприятия, направленные на повышение
продуктивности популяций, могут вступать в противо-
речие с ценностями, не имеющими денежного выражения.
В окружении, в котором я вырос, считалось, что благород-
ный олень с размахом рогов в 2 м стоит дороже тонны
мяса, а олень с рогами в 2 м 15 см вообще пред-
ставлял собой бесценный трофей. Воспитанный в тех же
традициях — а они еще существуют — достаточно ква-
лифицированный охотовед может в естественных условиях
вырастить стадо, в котором такие гигантские самцы будут
встречаться довольно часто. Его пе следует благодарить.
Такие олени должны быть детьми природы, а не объекта-
ми фабричного производства. Они заслуживают того,
чтобы умирать естественной смертью. Используя свое
искусство для того, чтобы удовлетворить по собственно-
му разумению запросы определенного узкого круга лю-
дей, подставляя константы в написанную на ФОРТРАНе
программу, рассчитывающую параметры оптимального
равновесия, в действительности являющегося оптимальным
лишь в его воображении, такой охотовед тем самым отри-
цает любую систему ценностей, противоречащую его соб-
ственной. Нужно быть очень осторожным, имея дело с
ценностями, не подчиняющимися простым арифмети-
ческим правилам. Такие ценности могут иметь немате-
риальный характер.
Даже когда достижение МПУД представляется до-
стойной целью, существуют ситуации, в которых оно ока-
зывается экономически невыгодным. Затраты на промы-
сел резко возрастают с падением плотности популяции, и
максимальной чистой прибыли зачастую удается достичь
лишь при плотности более высокой,чем отвечающая МПУД.
В частности, организация избирательного в отношении
пола промысла требует привлечения более квалифици-
*
Популяционный анализ и эксплуатация популяций
323
ровапных исполнителей и больших средств, чем неизбира-
телышй промысел. Выигрыш, получаемый при той или
иной организации промысла, должен быть тщательно
сопоставлен с уменьшением чистой прибыли, приходящей-
ся на одно добытое животное.
Цель этих призывающих к осторожности замечаний —
подчеркнуть, что достижение МПУД чревато различными
неожиданными трудностями. Вычисление МПУД можно
рассматривать лишь как первое приближение, и для опре-
деления режима, максимально близкого к оптимальному,
необходимо тщательно проследить различные эффекты
промысла. В цитируемом ниже отрывке из книги Бивер-
тона и Холта (Beverton, Holt, 1957: 436) речь идет о ры-
бах, но эти замечения равным образом относятся и к
промыслу птиц и млекопитающих. «Изменения, возни-
кающие в характере рыбного промысла в результате ре-
гулирующих мероприятий как таковых, вне зависимости
от того, были ли эти мероприятия самыми первыми или,
наоборот, последними в ряду, направленном па достиже-
ние оптимального режима, при специальном исследова-
нии могут дать как раз ту информацию, которой не хва-
тало раньше. Таким образом, прогресс достигается одно-
временно в двух взаимно дополняющих направлениях.
Мы больше узнаем о том, что собой представляет опти-
мальный режим, и в то же время постепенно приближаемся
к нему; выгоды, которые получает от этого рыболовство,
вряд ли можно переоценить».
11.3. Регуляция численности
Большинство популяций, истребленных человеком,
было уничтожено не умышленно, а зачастую вопреки
энергичным мероприятиям, предпринимавшимся для того,
чтобы предотвратить вымирание. Напротив, многочис-
ленные попытки умышленно искоренить популяцию ока-
зывались безуспешными. Это явление становится менее
парадоксальным, если вспомнить, что незапланированные
истребления популяций обычно были вызваны изменения-
ми местообитаний животных, тогда как при умышленном
уничтожении воздействию, как правило, подвергались
сами животные. Мораль ясна. Популяции более чувстви-
324
Глава 11
тельпы к воздействиям, направленным на их местообита-
ния, чем к прямым воздействиям на их численность. Изме-
нение условий существования обычно качественно меняет
одну или несколько составляющих окружающей среды, и
при таких вредных изменениях популяция оказывается
не в состоянии приспособиться к ним понижением плот-
ности, как это происходит, когда изменения касаются лишь
количества доступных ресурсов. Популяции, атакован-
ной « в лоб», т.е. путем отстрела или применением ядохими-
катов, не приходится вступать в борьбу с ухудшившимися
условиями местообитания. Совсем наоборот, вызванное
применением мер борьбы снижение плотности популяции
никак не мепяет качество необходимых ресурсов, тогда
как количество ресурсов, приходящихся на одно уцелев-
шее животное, увеличивается. Таким образом, мероприя-
тия по истреблению автоматически приводят к увеличе-
нию значения гр, что, в сущности, в точности составляет
цель программ оптимизации промысла. Большинство опе-
раций по борьбе с вредителями в действительности пред-
ставляет собой неумышленную реализацию программ по
поддержанию постоянного уровня добычи.
Одна из наиболее разработанных программ по ис-
треблению млекопитающих преследовала цель уничтоже-
ния крупных млекопитающих в некоторых районах рас-
пространения мухи цеце в Африке. Чайлд, Смит и фон
Рихтер (Child, Smith, von Richter, 1970), подводя итоги
результатам программы в районе Мауна Фронт в северной
Ботсване, писали: «За двадцать три года охоты не был ис-
треблен ни один вид животных; исключенпе составляет,
пожалуй, лишь лошадиная антилопа, которая была очень
распространена в этих местах в начале операции и чис-
ленность которой упала во многих районах ее обитания
в Северной Ботсване. В последние годы снизилось лишь
число отстреливаемых зебу, гну и куду, однако имеются
данные, что снижение ежегодной добычи последних двух
видов связано с факторами, не имеющими отношения к
охоте. Добыча всех остальных видов увеличивается, что
в сочетании с данными другого характера никак не может
свидетельствовать об уменьшении численности популяций
на территории, где производилась охота».
На рис. 11.6 и 11.7 изображены результаты опреде-
Рис. 11.6. Динамика численности популяции в случае, когда из
нее ежегодно изымается постоянная доля особей; максимальный
постоянный уровень добычи достигается при скорости, равной 0,3.
Годы
Рис. 11.7. Динамика численности популяции в случае, когда из по-
пуляции ежегодно изымается постоянное число особей; максималь-
ный постоянный уровень добычи составляет 150 особей в год.
326
Глава 11
ления с помощью ЭВМ мер по поддержанию постоянного
уровня добычи в популяции, растущей логистически с
параметрами К = 1000 и гт = 0,6. Из первой гипотети-
ческой популяции (рис. 11.6) изымалась ежегодно по-
стоянная доля, особей, а из второй (рис. 11.7) — постоян-
ное число. Таким образом, интенсивность истребления в
первой модели поддерживалась постоянной, тогда как
во второй модели для поддержания постоянства числа
ежегодно изымаемых особей интенсивность истребления
должна была постоянно расти по мере падения численности
популяции.
Из рис. 11.6 видно, что если скорость истребления
меньше чем Н = 0,6 в год, то численность популяции со
временем стабилизируется, причем уровень численности
при этом обратно пропорционален интенсивности ис-
требления. В том же случае, когда в популяции ежегодно
истребляется постоянное число особей (рис. 11.7), она
может вести себя по-разному. Если ежегодная добыча
была менее 150 особей, численность стабилизировалась
на равновесном уровне. Если же число ежегодно добы-
ваемых особей составляло более 150 особей, популяция
быстро вымирала. Эти наблюдения отражают некоторые
общие принципы, в значительной степени не зависящие
от характера роста популяции и значений соответствующих
параметров.
1. Когда из популяции, первоначально находившейся
в стационарном состоянии, изымается постоянное
число особей, численность популяции стабилизиру-
ется, если только число ежегодно изымаемых осо-
бей не превышает МПУД.
2. Уровень, на котором стабилизируется плотность
популяции при ежегодном изъятии постоянного
числа особей, больше или равен плотности, соот-
ветствующей МПУД.
3. Когда из популяции ежегодно изымается постоян-
ная доля особей, плотность популяции стабили-
зируется на постоянном уровне, если только доля
изымаемых особей не превышает идеальной ско-
рости роста популяции гт.
4. При ежегодном изъятии из популяции постоян-
ной доли особей плотность популяции в зависи-
Популяционный анализ и эксплуатация популяций
327
мости от скорости изъятия может стабилизироваться
*на любом уровне, начиная от исходного и кончая
нулевым (вымирание).
Для популяций, характер роста которых близок к ло-
гистическому, эти общие правила можно сделать более
конкретными.
1. Когда из популяции ежегодно изымается постоянное
число особей С, меньшее, чем МПУД (равный rm/C/4),
численность популяции стабилизируется на уровне
v rm + /( r2m-iCrm/K)
2rm/K
2. Когда из популяции ежегодно изымается постоян-
ная доля, меньшая rm, численность популяции стабили-
зируется на уровне
N=K-™-,
Гщ
где Н — мгновенная скорость изъятия’ особей из попу-
ляции.
3. Если ежегодно из популяции извлекается постоянная
доля особей, большая, чем rm, или число особей, боль-
шее, чем ттК./к, то популяция обречена на вымирание.
В данном контексте термин «стабилизация» означает
не больше, чем временное поддержание равновесия. Если
в течение длительного времени общий запас ресурсов на-
ходился в равновесии с плотностью животных, то пони-
жение этой плотности вызовет увеличение абсолютного
уровня запасов этих ресурсов. При этом, если усилия,
затрачиваемые на изъятие особей из популяции, постоян-
ны, численность популяции будет увеличиваться. В уже
цитированном в этом разделе отчете Чайлда, Смита и фон
Рихтера приводился факт общего увеличения добычи на
промысловое усилие в популяции крупных млекопитаю-
щих, много лет подвергавшейся истреблению с целью
полного уничтожения. Несомненно, увеличение добычи
связано с ростом плотности популяции. Конечно, мы не
можем с уверенностью говорить, что такая тенденция
отражает реакцию на увеличение запасов ресурсов, но
эта гипотеза представляется очень вероятной.
328
Глава 11
Как отмечалось выше, большинство попыток истре-
бить популяции сводились к непредвиденным и не соот-
ветствующим намерениям исполнителей упражнениям
по поддержанию постоянного уровня добычи. В конеч-
ном счете это не так уж и плохо: стало ясно, что боль-
шинство попыток такого рода экологически неоправдан-
но и экономически невыгодно.
Здесь я должен сознаться в том, что у меня есть свое,
предвзятое мнение на этот счет. Хотя я не имею ничего
против мер по поддержанию плотности популяции на
уровне, лежащем ниже /С, когда к тому есть достаточно
веские основания, я болезненно реагирую на утверждения,
что та или иная популяция должна быть истреблена. Я не
считаю, что не бывает исключений; например, я под-
держивал истребление одичавших коз на некоторых мел-
ких океанических островах. Но, вообще говоря, я не
обладаю ни необходимыми знаниями, ни даром предви-
дения, а стало быть, и правом принимать или содейство-
вать принятию решений такой важности. Когда,' как в
случае истребления популяций, потери от принятия не-
правильного решения несравненно перевешивают вы-
игрыш, который дает правильное решение, все действия,
ведущие к необратимым последствиям, необходимо тща-
тельно анализировать. Здесь я в основном остановлюсь
на экономических аргументах в пользу этого положения,
хотя сам я пришел к этой точке зрения совсем другим пу-
тем и придерживаюсь ее по причинам, не имеющим ничего
общего с экономикой. Я знаю, что не все биологи разделя-
ют мою личную точку зрения, но я надеюсь, что те, кто со
мной не согласен, готовы рассмотреть экономические ас-
пекты попыток истребления. Эти задачи сложны и доро-
гостоящи. Приниматься за такую операцию, не оценив
сначала выигрыш и затраты, — это не только админи-
стративная и профессиональная безответственность, это
еще и экономическая тупость. Минимальными данными
для оценки прибыли могут служить оценки тт и /С,
затраты на проведение операции и достигаемое при этом
пропорционально затратам снижение плотности популяции.
В качестве примера рассмотрим гипотетическую попу-
ляцию, динамика которой при разных воздействиях
изображена на рис. 11.6. В данном случае «единичное
Популяционный анализ и эксплуатация популяций
329
усилие» может быть определено как деятельность, необ-
ходимая для изъятия из популяции животных с мгновен-
ной годовой скоростью, равной Н — 0,1. Чтобы предста-
вить себе конкретную ситуацию, будем считать, что мы
хотим истребить небольшую популяцию копытных сред-
него размера; для достижения такой интенсивности ис-
требления требуется работа одного охотника в течение
года. Таким образом, за единичное усилие можно принять
один человеко-год охоты. Ясно, что интенсивность ис-
требления должна превышать величину rm = 0,6 в год, в
противном случае наша операция сведется просто к под-
держанию постоянного уровня добычи. Если Н = 0,65,
для того чтобы удовлетворить требуемым условиям, ис-
треблением популяции должны быть заняты в течение года
в среднем 6,5 человека. Эти люди должны работать 72
года, и, таким образом, суммарное усилие на истребле-
ние популяции составит 468 человеко-лет. При Н = 0,7
популяция достигнет порога вымирания через 42 года, и
суммарные усилия при этом составят 294 человеко-
года. Затраты на операцию уменьшаются по мере роста
интенсивности истребления: при Н — 0,8 требуется всего
лишь 184 человеко-года. Такие интенсивности истребле-
ния лежат много выше обычно рассматриваемых. Из всех
проанализированных мною попыток истребления попу-
ляции интенсивность истребления лишь в редких случаях
превышала Н =0,1 в год— интенсивность, позволяющую,
как правило, лишь поддерживать постоянный уровень
добычи, да ито неэффективно.
Оценка усилий, требуемых для истребления малень-
кой популяции, вычисленная с помощью ЭВМ, сама по
себе производит достаточно сильное впечатление, однако
в действительности такая оценка очень сильно занижена,
поскольку модель не учитывает двух важных свойств
реальной популяции. Во-первых, за исключением тех
случаев, когда популяция истребляется очень быстро,
увеличение уровня запасов ресурсов, вызванное убы-
ванием плотности популяции, приводит к увеличению по-
тенциальной скорости роста популяции гр и соответ-
ственно к увеличению усилий, необходимых для дальней-
шего снижения численности популяции. Во-вторых, в моде-
ли предполагается, что единичное промысловое усилие по-
so
Глава 11
зволяет истреблять постоянную часть популяции вне за-
висимости от ее плотности. В нашем примере это озна-
чает истребление 100 животных, когда N = 1000; 50, когда
N = 500, и 10, когда N = 100. На практике это пред-
положение разумно, по-видимому, до тех пор, пока чис-
ленность популяции больше /С/2. Но когда численность
популяции падает ниже этого уровня, предположение бы-
стро становится совершенно необоснованным. Животные ис-
требляются не с равной вероятностью; при проведении
операции в первую очередь истребляются наименее ос-
торожные. Среди сохранившихся при низкой плотности
большую часть составляют либо животные, крайне осто-
рожные, либо те, индивидуальные участки которых на-
ходятся в труднодоступных местах. Таким образом, еди-
ница промыслового усилия при низкой плотности попу-
ляции будет приводить к истреблению меньшей доли, чем
когда плотность популяции высока.
Регуляция численности популяции — операция, ко-
торую осуществить гораздо легче, чем полное истребление,
к тому же она допускает рациональное планирование.
Здесь снова важен подсчет затрат: выигрыш, получае-
мый за счет поддержания популяции при данной плот-
ности, следует сравнить с затратами. Требуемую интен-
сивность истребления можно рассчитать по оценкам гт
и /(, а суммарные затраты рассчитываются по оценке уси-
лия, необходимого для поддержания такой интенсивности
истребления. Я не знаю ни одной программы управления
численностью, которой предшествовало бы такое иссле-
дование. В настоящее время (1975 г.) ряд стран разра-
батывает программу регуляции численности, которая на
взгляд стороннего наблюдателя требует больших затрат,
чем, как можно полагать, принесет дохода. В этом я мо-
гу ошибаться, но так как анализ затрат и получаемой
прибыли недоступен ни мне, ни заинтересованным пра-
вительствам, мое любопытство остается недоувлетво-
ренным. Поскольку регуляция численности популяций с
помощью охоты, отлова или ядохимикатов в сущности
то же самое, что и поддержание постоянного уровня до-
бычи, безотносительно к тому, используется добыча или
нет, то рассмотренные выше методы оптимизации промысла
в точности совпадают с методами, необходимыми для ре-
Популяционный анализ и эксплуатация популяций
331
гуляции численности популяций. Прямая регуляция чис-
ленности популяций и организация промысла — это опе-
рационно тождественные задачи. Эффективность регуля-
ции численности определяется тем, насколько хорошо
разработаны методы анализа и техника оптимальной ор-
ганизации промысла.
Довольно соблазнительной представляется регуля-
ция численности животных с помощью возбудителей
инфекционных болезней, и успехи, рекламируемые энто-
мологами, привлекают к этому методу еще большее вни-
мание. К сожалению, существует только один пример
успешного использования болезнетворных микроорга-
низмов для управления численностью популяции позво-
ночных — это использование возбудителей миксоматоза
против кроликов. История этого успеха (по крайней мере
в Австралии) подробно описана Феннером и Рэтклифом
(Fenner, Ratcliffe, 1965). Вирус был впервые описан в
1896 г. как возбудитель заболевания с летальным исхо-
дом у лабораторных кроликов (Oryctolagus) в Южной
Америке. Он существует в естественных условиях как
возбудитель нелегального заболевания американских кро-
ликов Sylvilagus. Европейские кролики Oryctolagus эво-
люционировали в условиях, где вирусы группы мик-
соматоза никогда не встречались, поэтому они оказа-
лись высокочувствительными при первом контакте с этим
вирусом. Как подчеркивает Барнет (Burnet, 1962), равно-
весие между свободно распространяющимся вирусом
и хозяином, для которого он является высоколетальпым,
не может долго существовать, так как снижение числен-
ности хозяина будет препятствовать эффективному рас-
пространению болезни и таким образом приведет к эли-
минации вируса. Как и следовало ожидать, через два или
три года после интродукции этого вируса в Австралию
вирулентность его сильно снизилась, а через 8 лет у кро-
ликов выявилась генетическая устойчивость к нему.
Данный пример хорошо обнажает трудности исполь-
зования болезнетворных организмов для регуляции чис-
ленности позвоночных. Во-первых, мы должны найти мик-
роорганизм, который никогда не контактировал с интере-
сующим нас видом, но хозяином которого является близко-
родственный вид. Во-вторых, необходимо быть уверенным
332
Глава 11
в том, что объектом воздействия патогенного микроорга-
низма будет лишь вид-мишень и возбудитель не затронет
никаких других обитателей этой территории. В-третьих,
мы должны отдавать себе отчет в том, что применение воз-
будителей инфекций дает лишь временную передышку,
поскольку и возбудитель,и вид-мишень будут под действием
интенсивного естественного отбора быстро взаимоприспо-
сабливаться. Эти трудности служат веским аргументом
против использования патогенных микроорганизмов в
качестве орудия регуляции численности позвоночных.
Шансы найти подходящую болезнь очень невелики, и
даже когда она найдена, это не решает проблемы в корне.
Всегда по возможности следует пытаться понижать
численность популяции животных, действуя на их место-
обитания. Этот метод обладает очень немногими недо-
статками по сравнению с прямым управлением или уп-
равлением с помощью патогенных микроорганизмов.
Большинство популяций восприимчивы к изменению
ключевых компонент их местообитаний, и поэтому сни-
зить плотность популяции можно лишь с небольшой за-
тратой усилий. Примером опять может служить европей-
ский кролик. В Новой Зеландии в отличие от Австралии
кроликов не заражали вирусом миксоматоза, поскольку
там недостаточно многочисленными были комары, яв-
ляющиеся переносчиками этого вируса (Filmer, 1953).
Плотные скопления кроликов обычно опрыскивали ядом
1080 с самолета. Говард (Howard, 1959) показал, что,
когда плотность кроликов была снижена и в результате
восстановился непрерывный травяной покров, кролики
оказались неспособными к новой вспышке численности.
В дальнейшем их плотность уже можно было регулировать
более эффективно с помощью ограничения выедания тра-
вы овцами и применения удобрений для поддержания в
хорошем состоянии дерна и травяного покрова. Кроли-
ки — это в основном пустынные животные, и они не могут
поддерживать высокую плотность популяции нигде, кро-
ме пустынь или мест, где близкие условия созданы ис-
кусственно.
Наиболее действенный и тонкий метод управления чис-
ленностью популяций — это воздействие на ключевые
компоненты их местообитаний.
Приложения
Приложение 1А. Значения функции ех
X 0 1 2 3 4 5 6 7 8 9
0,0 1,0000 1,0101 1,0202 1,0305 1,0408 1,0513 1,0618 1,0725 1,0833 1,0942
0,1 1,1052 1,1163 1,1275 1,1388 1,1503 1,1618 1,1735 1,1853 1,1972 1,2092
0,2 1,2214 1,2337 1,2461 1,2586 1,2712 1,2840 1,2969 1,3100 1,3231 1,3364
0,з 1,3499 1,3634 1,3771 1,3910 1,4049 1,4191 1,4333 1,4477 1,4623 1,4770
0,4 1,4918 1,5068 1,5220 1,5373 1,5527 1,5683 1,5841 1,6000 1,6161 1,6323
0,5 1,6487 1,6653 1,6820 1,6989 1,7160 1,7333 1,7507 1,7683 1,7860 1,8040
0,6 1,8221 1,8404 1,8589 1,8776 1,8965 1,9155 1,9348 1,9542 1,9739 1,9937
0,7 2,0138 2,0340 2,0544 2,0751 2,0959 2,1170 2,1383 2,1598 2,1815 2,2034
0,8 2,2255 2,2479 2,2705 2,2933 2,3164 2,3396 2,3632 2,3869 2,4109 2,4351
0,9 2,4596 2,4843 2,5093 2,5345 2,5600 2,5857 2,6117 2,6379 2,6645 2,6912
1,0 2,7183 2,7456 2,7732 2,8011 2,8292 2,8577 2,8864 2,9154 2,9447 2,9743
1,1 3,0042 3,0344 3,0649 3,0957 3,1268 3,1582 3,1899 3,2220 3,2544 3,2871
1,2 3,3201 3,3535 3,3872 3,4212 3,4556 3,4903 3,5254 3,5609 3,5966 3,6328
1,3 3,6693 3,7062 3,7434 3,7810 3,8190 3,8574 3,8962 3,9354 3,9749 0,0149
1,4 <♦,0552 4,0960 4,1371 4,1787 4,2207 4,2631 4,3060 4,3492 4,3929 4,4371
1,5 4,4817 4,5267 4,5722 4,6182 4,6646 4,7115 4,7588 4,8066 4,8550 4,9037
I,6 4,9530 5,0028 5,0531 5,1039 5,1552 5,2070 5,2593 5,3122 5,3656 5,4195
1,7 5,4739 5,5290 5,5845 5,6407 5,6973 5,7546 5,8124 5,8709 5,9299 5,9895
1,8 6,0496 6,1104 6,1719 6,2339 6,2965 6,3598 6,4237 6,4883 6,5535 6,6194
1,9 6,6959 6,7531 6,8210 6,8895 6,9588 7,0287 7,0973 7,1707 ’,2427 «.3155
-_;W
2,0 7,3891 7,4633 7,5383 7,6141 7,6906 7,7679 7,8460 7,9248 8,0045 8,0849
2,1 8,1662 8,2482 8,3311 8,4149 8,4994 8,5849 8,6711 8,7583 8,8463 8,9352
2,2 9,0250 9,1157 9,2073 9,2999 9,3933 9,4877 9,5831 9,6794 9,7767 9,8749
2,3 9,9742 10,0744 10,1757 10,2779 10,3812 10,4856 10,5910 10,6974 10,8049 10,9135
2,4 11,0232 11,1340 11,2459 11,3589 11,4730 11,5883 11,7048 11,8224 11,9413 12,0613
2,5 12,1825 12,3049 12,4286 12,5535 12,6797 12,8071 12,9358 , 13,0658 13,1971 13,3298
2,6 13,4637 13,5991 13,7357 13,8738 14,0132 14,1540 14,2963 14,4400 14,5851 14,7317
2,7 14,8797 15,0293 15,1803 15,3329 15,4870 15,6426 15,7998 15,9586 16,1190 16,2810
2,8 16,4446 16,6099 16,7769 16,9455 17,1158 17,2878 17,4615 17,6370 17,8143 17,9933
2,9 18,1741 18,3568 18,5413 18,7276 18,91-58 19,1060 19,2980 19,4919 19,6878 19,8857
3,0 20,0855 20,2874 20,4913 20,6972 20,9052 21,1153 21,3276 21,5419 21,7584 21,9771
3,1 22,1980 22,4210 22,6464 22,8740 23,1039 23,3361 23,5706 23,8075 24,0468 24,2884
3,2 24,5325 24,7791 25,0281 25,2797 25,5337 25,7903 26,0495 26,3113 26,5758 26,8429
3,3 27,1126 27,3851 27,6604 27,9383 28,2191 28,5027 28,7892 29,0785 29,3708 29,6660
3,4 29,9641 30,2652 30,5694 30,8766 31,1870 31,5004 31,8170 32,1367 32,4597 32,7859
3,5 33,1155 33,4483 33,7844 34,1240 34,4669 34,8133 35,1632 35,5166 35,8735 36,2341
3,6 36,5982 36,9661 37,3376 37,7128 38,0918 38,4747 38,8613 39,2519 39,6464 40,0448
3,7 40,4473 40,8538 41,2644 41,6791 42,0980 42,5211 42,9484 43,3801 43,9160 44,2564
3,8 44,7012 45,1504 45,6042 46,0625 46,5255. 46,9931 47,4654 47,9424 48,4242 48,9109
3,9 49,4024 49,8990 50,4004 50,9070 51,4186 51,9354 52,4573 52,9845 53,5170 54,0549
Приложение 1 А (продолжение)
336
X 0 1 2 3 4 5 6 7 8 9
4,0 54,5982 55,1469 55,7011 56,2609 56,8263 57,3975 57,9743, 58,5570 59,1455 59,7399
4,1 60,3403 60,9467 61,5592 62,1779 62,8028 63,4340 64,0715 64,7155 65,3659 66,0228
4,2 . 66,6063 67,3565i 68,0335 68,7172 69,4079 70,1054 70,8100 71,5216 72,2404 72,9665
4,3 73,6998 74,4405 75,1886 . 75,9443 76,7075 77,4785 78,2571 79,0436 79,8380 80,6404
4,4 81,4509 82,2695 83,0963 83,9314 84,7749 85,6269 86,4875 87,3567 88,2347 89,1214
4,5 90,0171 90,9218 91,8356 92,7586 93,6908 94,6324 95,5835 96,5441 97,5144 98,4944
4,6 99,4843 100,4841 101,4940 102,5141 103,5443 104,5850 105,6361 106,6977) 107,7701 108,8532
4,7 109,9472 111,0522 112,1683 113,2956 114,4342 115,5843 116,7459 117,9192 119,1044 120,3014
4,8 121,5104 122,7316 123,9651 125,2110 126,4694 127,7404 129,0242 130,3209 131,6307 132,9536
4,» 134,2898 135,6394 137,0026 138,3795 139,7702 141,1750 142,5938 144,0269 145,4744 146,9364
5,0 148,4132 149,9047 151,4113 152,9330 154,4700 156,0225 157,5905 159,1743 160,7741 162,3899
5,1 164,0219 165,6704 167,3354 169,0171 170,7158 172,4315 174,1645 175,9148 177,6828 179,4686
5,2 181,2722 183,0941 184,9342 186,7928 188,6701 190,5663 192,4815 194,4160 196,3699 198,3434
5,3 200,3368 202,3502 204,3839 206,4380 208,5127 210,6083 212,7249 214,8629 217,0223 219,2034
5,4 221,4064 223,6316 225,8791 228,1492 230,4422 232,7582 235,0974 237,4602 239,8467 242,2572
5,5 244,6919 247,1511 249,6350 252,1439 254,6780 257,2376 259,8228 262,4341 265,0716 267,7356
5,6 270,4264 273,1442 275,8894 278,6621 281,4627 284,2915 287,1486 290,0345 292,9494 295,8936
5,7 298,8674 301,8711 304,9049 307,9693 311,0644 314,1907 317,3483 320,5377 323,7592 327,0130
5,8 330,2996 333,6191 336,9721 340,3587 343,7793 347,2344 350,7241 354,2490 357,8092 361,4053
5,9 365,0375 368,7062 372,4117 376,1545 379,9349 383,7533 387,6101 391,5057 395,4404 399,4146
12—334
Приложение 1 В. Значения функции е~х
X 0 1 2 3 4 5 6 7 8 9
0,0 1,0000 0,9900 0,9802 0,9704 0,9608 0,9512 0,9418 0,9324 0,9231 0,9139
0U 0,9048 0,8958 0,8869 0,8781 0,8694 0,8607 0,8521 0,8437 0,8353 0,8270
о,а 0,8187 0,8106 0,8025 0,7945 0, 7866 0,7788 0,7711 0,7634 0,7558 0,7483
0,3 0,7408 0,7334 0,7261 0,7189 0,7118 0,7047 0,6977 0,6907 0,6839 0,6771
0,4 0,6703 0,6637 0,6570 0,6505 , 0,6440 0,6376 0,6313 0,6250 0,6108 0,6126
o,s 0,6065 0,6005 0,5945 0,5886 0,5827 0,5769 0,5712 0,5655 0,5599 0,5543
0,6 0,5488 0,5434 0,5379 0,5326 0,5273 0,5220 0,5169 0,5117 0,5066 0,5016
0,7 0,4966 0,4916 0,4868 0,4819 0,4771 0,4724 0,4677 0,4630 0,4584 0,4538
0,8 0,4493 0,4449 0,4404 0,4360 0,4317 0,4274 0,4232 0,4190 0,4148 0,4Ю7
0,9 0,4066 0,4025 0,3985 0,3946 0,3906 0,3867 0,3829 0,3791 0,3753 0,3716
1,0 0,3679 0,3642 0,3606 0,3570 0,3535 0,3499 0,3465 0,3430 0,3396 0,3362
1,1 0,3329 0,3296 0,3263 0,3230 0,3198 0,3166 0,3135 0,3104 0,3073 0,3042
1,2 0,3012 0,2982 0,2952 0,2923 0,2894 0,2865 0,2837 0,2808 0,2780 0,2753
1,3 0,2725 0,2698 0,2671 0,2645 0,2618 0,2592 0,2567 0,2541 0,2516 0,2491
1,4 0,2466 0,2441 0,2417 0,2393 0,2369 0,2346 0,2322 0,2299 0,2276 0,2254
1,5 0,2231 0,2209 0,2187 0,2165 0,2144 0,2122 0,2101 0,2080 0,2060 0,2039
1,6 0,2019 0,1999 0,1979 0,1959 0,1940 0,1920 0,1901 0,1882 0,1864 0,1845
1,7 0,1827 0,1809 0,1791 0,1773 0,1755 0,1738 0,1720 0,1703 0,1686 0,1670
1,в 0,1653 0,1637 0,1620 0,1604 0,1588 0,1572 0,1557 0,1541 0,1526 СР 0,1511 ' СР
1,9 0,1496 0,1401 0,1466 0,1451 0,1437 0,1423 0,1409 0,1395 0,1381 0,1367
Приложение I Б (продолжение)
ьо
X 0 1 2 3 4 5 6 7 8 9
2,0 0,1353 0,1340 0,1327 0,1313 0,1300 0,1287 0,1275 0,1262 0,1249 0,1237
2,1 0,1225 0,1212 0,1200 0,1188 0.1177 0,1165 0,1153 0,1142 0,1130 0,1119
2,2 0,1108 0,1097 0,1086 0,1075 0,Ю65 0,1054 0,1044 0,1033 0,1023 0,1013
2,3 0,1003 01,0993 0,0983 0,0973 0,0963 0,0954 0,0944 0,0935 0,0926 0,0916
2,4 0,0907 0,0898 0,0889 0,0880 0,0872 0,0863 0,0854 0,0846 0,0837 0,0829
2,5 0,0821 0,0813 0,0805 0,0797 ' 0,0789 0,0781 0,0773 0,0765 0,0758 0,0750
2,6 0,0743 0,0735 0,0728 0,0721 0,0714 0,0707 0,0699 0,0693\ 0,0686 0,0679
2,7 0,0672 0,0665 0,0659 0,0652 0,0646 0,0639 0,0633 0,0627 0,0620 0,0614
2,9 0,0608 0,0602 0,0596 0,0590 0,0584 0,0578 0,0573 0,0567 0,0561 0*0556
2,9 0,0550 0,0545 0,0539 0,0534 0,0529 0,0523 0,0518 0,0513 0,0508 0,0503
Э*,0 0,0498 0,0493 0,0488 0,0483 0,0478 0,0474 0,0469 0,в464 0,0460 0,0455
3,1 0,0450 0,0446 0,0442 0,0437 0,0433 0,0429 0,0«4 0,0420 0,0416 0,0412
3,2 0,0408 0,0404 0,0400 0,0396 0,0392 0,0388 0,0384 0,0380 0,0376 0,0373
3,3 0,0369 0,0365 0,0362 0,0358 0,0354 0,0351 0,0347 0,0344 о,оэ40 0,0337
3,4 0,0334 0,0330 0,0327 0,0324 0,0321 0,0317 0,0314 0,8311 0,0308 ' С, 0305
3,5 0,0302 0,0299 0,0296 0,0293 0,0290 0,0287 0.0284 0,0282 0,0279 0,0276
3,6 0,0273 0,0271 0,0268 0,0265 0,0263 0,0266 0,0257 0,0255 0,0252 0,0250
3,7 0,0247 0,0245 0,0242 0,0240 0,0238 0,0235 0,0233 0,0231 0,0228 0,0226
3,8 0,0224 0,0221 0,0219 0,0217 0,0215 0,0213 0,0211 0,0209 0,0207 0,0204
Э,9 0,0202 0,0200 0,0198 0.0194 «.от 0.0193 0,0191 0,0189 0,0187 0,0105
як Г.
- у. --
4,0 0,0183 0,0181 0,6180 о.опа 6,6176 0,0174 0,0172 0,0171 0,0169 0,0167
4,1 o,oi66 0,0164 0,0162 0,0161 0,0159 0,0158 0,0156 0,0155 0,0153 0,0151
4,2 . 0,0150 0,0148 0,0147 0,0146 0,0144 0,0143 0,0141 0,0140 0,0138 0,0137
4,3 0,0136 0'0134 0,0133 0,0132 0,0130 0,0129 8,0128 0,0127 0,0125 0,0124
4,4 0,0123 0,0122 0,0120 0,0119 0,0118 0,0117 0,0116 0,0114 о,оиз 0,0112
4,5 0,0111 0,0110 0,0109 0,0108 0,0107 0,0106 8,0105 „0,0104 0,0103 0,0102
4,6 0,0101 0,0100 0,0099 0,0098 0,0097 0,0096 0,0095 0,0094 0,0093 \ 0,0092
4,7 0,0091 0,0090 0,0089 0,0088 0,0087 0,0087 0,0086 0,0085 0,0084 0,0083
4,в 0,0082 0,0081 0,0081 0,0080 0,0079 0,0078 0,0078 0,0077 0,0076 0,0^79
4,9 0,0074 0,0074 0,0073 0,0072 0,0072 0,0071 0,0070 0,0069 0,8069 0,8068
5,0 0,0067 0,0067 0,0066 0,0065 0,0065 0,0064 0,0063 0,0063 0,0062 0,006?
5,1 0,0061 0,0060 0,0060 0,0р59 4,0059 0,0058 0,0057 0,0057 0,0056 0,0056
5,2 0,0055 0,0055 0,0054 0,0054 0,0053 0,0052 8,0052 0,0051 0,0051 0,0050
5,3 0,0030 0^0049 0,0049 0,0048 0,0048 0,0047 0,0047 0,0047 0,0046 0,0046
5,4 0,0045 0,0045 0,0044 0,0044 Q,0043 8,0043 0,0043 0,0042 0,0042 0,0041
5,5 0,0041 0,0040 0,0040 0,0040 0,0039 0,0039 0,0038 0,0038 0,0038 0,0037
5,6 0,0037 0,0037 0,0036 0,0036 0,0036 0.0035 0,0035 0,0034 0,0034 0,0034
5,7 0,0033 0,0033. 0,0033 0,0032 0,0032 0,0032 0,0032 0,0031 0,0031 0,0031
5,8 0,0030 0,0030 0,0030 0,0029 0,0029 0,0029 0,0029 8,0028 0,0028 0,0028
5,9 0,9027 0,0027 0,0027 0.0427 0,0026 0,0026 0,0026 0,0026 0,0025 0'0025
со
8S
339
340
Приложение 2. Программа на ФОРТРАНе для расчета
значения г по выживаемости и плодовитости
с
С ESTIMATING EXPONENTIAL RATE OF INCREASE FROM THE LIFE TABLE ANO
C THE FECUNDITY TABLE. DATA ARF ARRAY V OF SURVIVAL X FECUNDITY
C PRODUCTS FOR EACH AGE BEGINNING AT ZERO AGE. LAST DATA CARO HAS
C 99. BEGINNING FROM COLUMN 1.
C
DIMENSION V(16)
I READ (5. 2» V
2 FORMAT (1655.3)
IF (V(l) .EQ. 99.) GO TO 8
SUM! = 0.
SUM2 = 0.
DO 3 I = If 16
SUM! = SUM! + V(I)
3 SUM2 = SUM2 + V(D • <!-!»
R = ALOG(SUMl) * SUM! / 5UM2
4 R = R + .00001
SUM 0.
DO 5 ! = If 16
S SUM « SUM + V(f) / EXP(R) •• (1-1)
IF (SUM - 1.) 6t 6. 4
6 WRITE (6. 7) R. SUM
7 FORMAT </// 20X. 4HR = f Г6.4/ 20X. 12HSUMMATION = • F6.V/>
GO TO 1
В CONTINUE
STOP
END
Примечание. В большинстве случаев вместо величин.’! 0,00001 в пунк-
те 4 можно взять 0,001. Точность при этом практически не уменьшается,
а машинное время сокращается в 100 раз.
341
Приложение 3. Программа на ФОРТРАНе для расчета
численности популяций по данным о частоте попаданий в
ловушки
с
С ESTIMATING POPULATION SIZE FROM CAPTURE FREQUFNCIES. THREE
C DIFFERENT MODELS ARE USED - NEGATIVE BINOMIAL* GEOMETRIC ANO
C POISSON DISTRIBUTIONS» EACH IN TRUNCATED FORM. DATA ARE ARRAT
C FREO OF CAPTURE FREQUENCIES» I.E, NUMBER OF ANIMALS CAPTURED
C ONCE* TWICE» THREE TIMES AND SO ON. LAST DATA CARD HAS 99.
C BEGINNING FROM COLUMN 1.
C
DIMENSION FREQ(20)
GAM(Z) = EXP(IZ-.5)«ALOG(21-Z+.918+(I./(12.)-(1•/(360.*7«*3))>
I READ (5» 2) FREQ
2 FORMAT (20F4.0)
IF (FREQ(l) .EQ. 99.) GO TO 15
^•••••CALCULATE NEGATIVE BINOMIAL ESTIMATES
SF = 0.
SFI = 0.
SFI2 » 0.
DO 3 i,= 1« 20
SF « SF + FREQ(I)
SFI s SFI + FREQ(I) * I
3 SFI2 « SFI2 + FREQ(l) * I •• 2
AVI = SF1/SF
VAR » (5FI2 - (SFI»«2)/SF)/(SF - 1.)
AV2 = AVI - ((VAR*FREQ11))/IAVI *(SF - FREQ(I))))
TOT s SFI/AV2
W s (AV1/VAR)*(1.- (FREQ(1)/SF))
Rs <(W * AV 1)-(FREO(1)/SF))f(I.- W)
WRITE (6» 4) TOT» AV2« W» R
4 FORMAT (1HI. 27Х» 27HNEGATIVE BINOMIAL ESTIMATES/30H0ESTIMATED
1P0PULAT10N SIZE = » F9.4/ 33H0MEAN OF COMPLETE DISTRIBUTION « •
2 F7.4/ 5H0W = » F9.6Z 5H0K a .F11.6ZZZ)
WRITE (6. 91
IF (R .LT. 0.) GO TO 7
F « 1.
DO 5 I = 1» 20
F = F * I
DIST = SF * W**R*GAM(R+I)*(1.-W)*»I / ((I.-W)«GAM(R)#F!
5 WRITE (6» 6) I» FREQ(I)» DIST
6 FORMAT (1H0. 151» F7.0» F12.3)
C«**«**CALCULATE GEOMETRIC ESTIMATES
7 TOT = SF » (SFI - l.)/(SFI - SF)
Q = (SFI - SF)/(SFI - 1.)
WRITE (6» 8) TOT» Q
8 FORMAT (1H1. 27Х» 32HGEOMETRIC DISTRIBUTION ESTIMATES/28H0ESTIMAT
1ED POPULATION SIZE = , F9.4Z 4H0Q = • F6i4)
WRITE 16* 9)
9 FORMAT tlHO* SOX. 19HT DATA FITTED///!
DO 10 1 = 1. 20
O1ST = TOT * <1. -0) ♦ Q**I
10 WRITE (6. 6) I. FREQ(I)» DIST
^«•••♦CALCULATE POISSON ESTIMATES
TMEAN = AV!
11 TMEAN = TMEAN - 0.001
EST = TMEAN / (1. • EXP(-TMEAN!)
IF (AVI - EST) 11» 12» 12
12 TOf = SFI / TMEAN
WRITE (6» 13) TOT» TMEAN
13 FORMAT (1НЬ 27Х» 17HPOISSON ESTIMATES/29H0ESTIMATED POPULATION
1SIZE a , F9.4/ 33H0MEAN OF COMPLETE DISTRIBUTION - • F7.4///I
WRITE (6« 9)
DIST 2 TOT * EXP(-TMEAN)
DO 14 I = 1» 20
DIST = DIST ♦ TMEAN / I
14 WRITE (6» 6) 1» FREQ(I)» DIST
GO TO 1
IS CONTINUE
STOP
ENO
СПИСОК ЛИТЕРАТУРЫ
Allen. D. L. (1974). Of fire, moose and wolves, Audubon, 76, 38—49.
Allen D. L. (1951). The Horokiwi Stream: a study of a trout popula-
tion, New Zeal. Marine Dept. Fish. Bull., No. 10, 1—231.
Andersen J. (1953). Analysis of a Danish roe-deer population (Capre-
olus capreolus (L)) based upon the extermination of total stock,
Danish Rev. Game Biol., 2, 127—155.
Andersen J. (1962). Roe-deer census and population analysis by means
of modified marking release technique, pp. 72—80. In: Le Cren
E. D. Holdgate M. W. (eds.), The Exploitation of Natural Animal
Populations, Blackwell, Oxford.
Andrewartha H. G., Birch L. C. (1954). The Distribution and Abundan-
ce of Animals, University of Chicago Press, Chicago.
Bailey N. T. J. (1951). On estimating the size of mobile populations
from recapture data, Biometrika, 38, 293—306.
Bailey N. T. J. (1952). Improvements in the interpretation of recaptu-
re data, J; Anim. Ecol., 21, 120—127.
Baker H. G., Stebbins G. L. (1965). The Genetics of Colonizing Species,
Academic Press, New York.
Balham R. W., Miers К. H. (1959). Mortality and survival of grey and
mallard ducks banded in New Zealand, New Zeal. Dept. Int.
Affairs Wild!. Pubs, No. 5, 1—56.
Bamford J. (1970). Evaluating opossum poisoning by interference with
non-toxic, baits, Proc. New Zeal. Ecol. Soc., 17, 118—125.
Banjield A. W. F., Flook D. R., Ketsall J. P., Loughrey A. G. (1955).
An aerial survey technique for northern big game, North Amer.
Wildl. Conf., 20, 519-532.
Банников А. Г. (1950). Возрастное распределение и динамика попу-
ляции Bombina bombina, Труды Академии Наук СССР, 70,
101-103.
Баранов Ф. И. (1926). К вопросу о динамике рыбного промысла,
Бюллетень рыбного хозяйства за 1925 год, 8, 7—11.
Batcheler С. L., Bell D. J. (1970). Experiments in estimating density
from joint point and nearest-neighbour distance samples, Proc.
New Zeal. Ecol. Soc., 17, 111—117.
Batcheler C. L., Darwin J. H., Pracy L. T. (1967). Estimation of
opossum (Trichosurus vulpecula') populations and results of poison
trials from trapping data, New Zeal. J. Sci., 10, 97—114.
Batcheler C. L., Logan P. C. (1963). Assessment of an animal-control
Список литературы
343
campaign in the Harper-Avoca Catchment, New Zeal, For. Res.
Notes, 27, 1—27.
Bellrose F. C. (1955). A comparison of recoveries from reward and stan-
dard bands, J. Wildl. Mgmt., 19, 71—75.
Bellrose F. C., Chase E.B. (1950). Population losses in the mallard,
black duck and blue-winged teal, Ill. Nat. Hist. Survey Biol.
Notes, No. 22, 1—27.
Bergerud A. T. (1963). Aerial winter census of caribou, J. Wildl.
Mgmt., 27, 438-449.
Beiikema J. J. (1970). Angling experiments with carp (Cyprinus carpio
L.). II. Decreasing catchability through one trial learning, Ne-
therlands J. Zool., 20, 81—92.
В ever ton B. J. H., Holt S. J. (1957). On the dynamics of exploited
fish populations, Min. Agr. Fish and Food, Fisheries Investiga-
tions, Ser. 2, 19,1—533. (Имеется перевод: БивертопР., ХолтС.,
Динамика численности промысловых рыб, М., Пищепромиздат,
1969).
Birch L. С. (1948). The intrinsic rate of natural increase of an insect
population, J. Anim. Ecol., 17, 15—26.
Birch L. C. (1960). The genetical factor in population ecology,
Amer. Nat., 94, 5—24.
Birch L. C., Th. Dobzhansky P. 0., Elliott, Lewontin В. C. (1963).
Relative fitness of geographic races of Drosophila serrata, Evolu-
tion, 17, 72—83.
Bird J. B. (1970). Paleo-Indian discoidal stones from southern South
America, Amer. Antiquity, 35, 205—290.
Blake С. H. (1951). Wear of towhee bands, Bird-banding, 22,179—180.
Bodenheimer F. S. (1938). Problems of Animal Ecology, Oxford Uni-
versity Press, London.
Bodenheimer F. S. (1958). Animal Ecology Today, Monogr. Biol., 6.
Brand D. J. (1963). Records of mammals bred in the National Zoolo-
gical Gardens of South Africa during the period 1908 to 1960,
Proc. Zool. Soc. Lend., 140, 617—659.
Brass W. (1958). Simplified methods of fitting the truncated negative
binomial distribution, Biometrika, 45, 59—68.
Buechner H. K., Buss I. O., Bryan H. F. (1951). Censusing elk by
airplane in the Blue Mountains of Washington, J. Wildl. Mgml.,
15, 81-87.
Buckner С, H. (1966). The role of vertebrate predators in the biologi-
cal control of forest insects, Ann. Rev. Ent., 11, 449—470.
Burnet F. M. (1962). Evolution made visible: current changes in the
pattern of virus disease, pp. 23—32. In: Leeper G. W. (ed.), The
Evolution of Living Organisms, Melbourne University Press,
Melbourne.
Bustard H. B. (1969). The population ecology of the gekkonid lizard
(Gehyra vartegata (Dumeril and Bibron)) in exploited forests
in northern New South Wales, J. Anim. Ecol., 38, 35—51.
Bustard H. B. (1970). A population study of the scincid lizard Egernia
striolata in northern New South Wales, Proc. Koninkl. Nederl.
Akad. Wetenschappen, C73, 186—213.
Cassie В. M. (1954). Some uses of probability paper in the analysis
344
Список литературы
of size freguency distributions, Austral. J. Mar. Freshw. Res.,
5, 513-522.
Cassie R. M. (1962). Frequency distribution models in the ecology of
plankton and other organisms, J. Anim. Ecol., 31, 65—92.
Caughley G. (1960). Dead seals inland, Antarctica, 2, 270—271.
Caughley G. (1963). Dispersal rates of several ungulates introduced
into New Zealand, Nature, 200, 280—281.
Caughley G. (1964). Social organisation and daily activity of red kanga-
roos and grey kangaroos, J. Mammal., 45, 429—436.
Caughley G. (1965). Horn rings and tooth eruption as criteria of age
in the Himalayan thar, Hemitragus jemlahicus, New zeal. J. Sci.,
8, 333-351.
Caughley G. (1966). Mortality patterns in mammals, Ecology, 47,
906-918.
Caughley G. (1967a). Parameters for seasonally breeding populations,
Ecology, 48, 834-839.
Caughley G. (1967b). Calculation of population mortality rate and
life expectancy for thar and kangaroos from the ratio of juveniles
to adults, New Zeal. J. Sci., 10, 578—584.
Caughley G. (1970a). Eruption of ungulate populations, with emphasis
on Himalayan thar in New Zealand, Ecology, 51, 54—72.
Caughley G. (1970b). Liberation, dispersal and distribution of
Himalayan thar (Hemitragus jemlahicus) in New Zealand, New
Zeal. J. Sci., 13, 220—239.
Caughley G. (1970c). Population statistics of chamois, Mammalia,
34, 194-199. ‘
Caughley G. (1971a). Season of births for northern-hemisphere ungu-
lates in New Zealand, Mammalia, 35, 204—219.
Caughley G. (1971b). Demography, fat reserves and body size of a po-
pulation of red deer Cervus elaphus in New Zealand, Mammalia,
35, 369-383.
Caughley G. (1974). Bias in aerial survey, J. Wildl. Mgmt., 38, 921—
933.
Caughley G. (1976). Wildlife management and the dynamics of ungula-
te populations, Advances Appl. Biol., 1 (in press).
Caughley G., Birch L. C. (1971). Rate of increase, J. Wildl. Mgnft.,
35, 658—663.
Caughley G., Caughley J. (1974). Estimating median date of birth,
J. Wildl. Mgmt., 38, 552-556.
Caughley G., Goddard J. (1972). Improving the estimates from in-
accurate censuses, J. Wildl. Mgmt., 36, 135—140.
Caughley G., Sinclair R., Scott-Kemmis (1976). Experiments in aerial
survey, J. Wildl. Mgmt., 40, 290—300.
Caughley G., KeanR. I. (1964). Sex ratios in marsupial pouch young,
Nature, 204, 491.
Chapman D. G. (1951). Some properties of the hypergeometric distri-
bution with applications to zoological sample censuses-, Univ.
Calif. Pubs. Stat., 1, 131—160.
Chapman D. G. (1954). The estimation of biological populations, Ann.
Math. Stats., 25, 1—15.
Chapman D. G. (1955). Population estimation based on change of com-
Список литературы
345
position caused by a selective removal, Biometrika, 42, 279—290.
Chapman D. G., Murphy G. I. (1965). Estimates of mortality and popu-
lation from survey-removal records, Biometrics, 21, 921—935.
Chapman D. G., Robson D. S. (1960). The analysis of a catch curve,
Biometrics, 16, 354—368.
Child G., Le Riche J. D. (1969). Recent springbok treks (mass move-
ments) in south-western Botswana, Mammalia, 33, 499—504.
Child G., Smith M. В. E., von Richter W. (1970). Tsetse control
hunting as a measure of large mammal population trends in the
Okavango Delta, Botswana, Mammalia, 34, 34—75.
Chittieborough R. G. (1965). Dynamics of two populations of the hum-
pback whale, Megaptera novaeangliae (Borowski), Austral. J.
Mar. Freshw. Res., 16, 33—128.
Christie A. H. C. (1967). The sensitivity of chamois and red deer to
temperature fluctuations, Proc. New Zeal. Ecol. Soc., 14, 34—39.
Christie A. H. C., Andrews J. R. H. (1964). Introduced ungulates in
New Zealand, (a) Himalayan thar, Tuatara, 12, 69—77.
Christie 4. H. C., Andrews J. R. H. (1965). Introduced ungulates in
New Zealand, (c) Chamois, Tuatara, 13, 105—111.
Cochran W. Gi. (1963). Sampling Techniques, John Wiley and Sons,
New York, 2nd edition.
Cockrum E. L. (1948). The distribution of the cotton rat in Kansas,
Trans. Kansas Acad. Sci., 51, 306—312.
Cole L. C. (1954). The population consequences of life history phenome-
na, Quart. Rev'. Biol., 29, 103—137.
Cole L. C. (1957). Sketches of general and comparative demography,
Cold Springs Harb. Symp., Quant. Biol., 22, 1—15.
Cole L. C. (1960). A note on population parameters in cases of complex
reproduction., Ecology, 41, 372—375.
Cormack R. M. (1966). A test for equal catchability, Biometrics, 22,
330—342.
Cormack R. M. (1968). The statistics of capture-recapture methods,
Oceanogr. Mar. Biol. Ann. Rev., 6, 455—506.
Coulson J. C. (1962). The biology of Tipula subnodicornis Zetterstedt,
with comparative observations on Tipula paludosa Meigen, J.
Anim. Ecol., 31, 1—21.
Craig С. C. (1953). On the utilization of marked specimens in estima-
ting populations of flying insects, Biometrika, 40, 170—176.
Cramer H. (1945). Mathematical Methods of Statistics, Princeton Uni-
versity .Press, Princeton.
Crissey W. F. (1967). Aims and methods of waterfowl research in North
America, Trans. 8th Int. Congress Game Biologists, 37—46.
Dahl K. (1919). Studies of trout and trout-waters in Norway, Salmon
and Trout Mag., 18, 16—33.
Darroch J. N. (1958). The multiple recapture census. I. Estimation
of a closed population, Biometrika, 45, 343-359.
Darwin C. (1845). The Voyage of the Beagle, Everyman’s Library Edi-
tion, 1906, Dent and Sons, London.
Dasmann W. P., Dasmann R. F. (1963). Abundance and scarcity of
California deer, Calif. Fish, and Game, 49, 4—15.
Davis D. E. (1955). Breeding biology of birds, pp. 264—308. In: Wolf-
346
Список литературы
son A. (ed.), Recent Studies in Avian Biology, University
Illinois Press, Urbana.
Davis D. E. (1956). Manual for Analysis of Rodent Populations, Ed-
wards Bros., Ann Arbor.
Davis D. E., Galley F. B. (1963). Principles in Mammalogy, Reinhold
Publishing Corp., New York.
Deevey E. S. Jr. (1947). Life tables for natural populations of animals,
Quart. Rev. Biol., 22, 283—314.
DeLure D. B. (1947). On the estimation of biological populations, Bio-
metrics, 3, 145—167.
DeLury D. B. (1958). The estimation of population size by a marking
and recapture procedure, J. Fish. Res. Bd Canada, 15, 19—25.
Douglas M. H. (1967). Control of thar (Hemitragus jemlahicus): eva-
luation of a poisoning technique, New Zeal. J. Sci., 10, 511—526.
Durand D., Greenwood J. A. (1958). Modifications of the Rayleigh
test for uniformity in analysis of two-dimensional orientation
data, J. Geol., 66, 229—238.
Eberhardt L. L. (1968). A preliminary apprasial of line transects,
J. Wildl. Mgmt., 32, 82—88.
Eberhardt L. L. (1969a). Population analysis, pp. 457—495. In:
Giles R. H. Jr. (ed.), Wildlife Management Techniques, 3rd
edition revised, Wildlife Society, Washington, D. C.
Eberhardt L. L. (1969b). Population estimates from recapture frequen-
ces, J. Wildl. Mgmt., 33, 28-39.
Edwards B. Y. (1954). Comparison of aerial and ground census of
moose, J. Wildl. Mgmt., 18, 403—404.
Edwards W. R., Eberhardt L. L. (1967). Estimating cottontail abun-
dance from live-trapping data, J. Wildl. Mgmt., 31, 87—96.
Erickson А. И7., Sinifj D. B. (1963). A statistical evaluation of factors
influencing aerial survey results, North Amer. Wildl. Conf.,
28, 391-408.
Fabens A. J. (1965). Properties and fitting of the von Bertalanffy
growth curve, Growth, 29, 265—289.
Earner D. S. (1949). Age groups and longevity in the American robin:
comments, further discussion, and certain revisions, Wilson Bull.,
61, 68-81.
Earner D. S. (1955). Birdbanding in the study of population dynamics,
p. 397—449. In: Wolfson A. (ed.), Recent Studies in Avian Bio-
logy, University Illinois Press, Urbana.
Fenner F., RatcltfjeF.N. (1965). Myxomatosis^ Cambridge University
Press, Cambridge.
Filmer J. E. (1953). Disappointing tests of myxomatosis as rabbit cont-
rol, New Zeal. J. Agric., 87, 402—407.
Finney D. J. (1947). Probit Analysis: a Statistical Treatment of the
Sigmoidal Response Curve, Cambridge University Press, Cambrid-
ge.
Fisher R. A. (1930). The Genetical Theory of Natural Selection, Claren-
don Press, Oxford.
Fisher R. A. (1937). The wave of advance of advantageous genes,
Ann. Eugen., 7, 355—369.
Список литературы
347
Fisher R. А. (1941). Note on the efficient fitting of the negative bino-
mial, Biometrics, 9, 197.
Fisher R. A., Yates F. (1948). Statistical Tables for Biological and
Medical Research, 3rd edition, Oliver and Boyd, Edinburgh.
Ford E. B. (19641. Ecological Genetics, Methuen, London.
Fordhan R. A. (1967). Durability of bands on dominican gulls, Notor-
nis, 14, 28—30.
Frank P. W. (1960). Prediction of population growth form in Daphnia
pulex cultures, Amer. Nat., 94, 357—372.
Frank P. W. (1968). Life histories and community stability, Ecology,
49, 355-357.
Frith H. J. (1959). The ecology of wild ducks in inland New South
Wales. IV. Breeding, CSIRO Wildl. Res., 4, 156-181.
Frith H. J. (1963). Movements and morality rates of black duck and
grey teal in south-eastern Australia, CSIRO Wildl. Res., 8, 119—
131.
Frith H. J. (1964). Mobility of the red kangaroo Megaleia rufa, CSIRO
Wildl. Res., 9, 1-19.
Frith H. J., Sharman G. B. (1964). Breeding in wild populations of
the red kangaroo, Megaleia rufa, CSIRO Wildl. Res., 9, 86—114.
Fuller W. A. (1953). Aerial surveys for beaver in the Mackenzie Di-
strict, Northwest Territories, North Amer. Wildl; Conf., 18, 329—
336.
Geis A. D., Atwood E. L., (1961). Proportion of recovered waterfowl
bands reported; J. Wildl. Mgmt., 25, 154—159.
Gentry J. B. (1968). Dynamics of an enclosed population of pine mice,
Microtus pinetorum, Res. Popul. Ecol., 10, 21—30.
Gerking S. D. (1967). The Biological Basis of Freshwater Fish Produc-
tion, Blackwell, London.
Gerrard D. J., Chiang H. C. (1970). Density estimation of corn root-
worm egg populations based upon frequency of occurence, Ecolo-
gy, 51, 237—245.
Getz L. L. (1961). Response of small mammals to live-traps and weather
conditions, Amer. Midi. Nat., 66, 160—170.
Gilbert P. F., Grieb J. R. (1957). Comparison of air and ground deer
counts in Colorado, J. Wildl. Mgmt., 21, 33—37.
Giles R. H. Jr. (1969). Wildlife Management Techniques, 3rd edition
revised, The Wildlife Society, Washington, D. C.
Goddard J. (1967). The validity of censusing black rhinoceros popula-
tions from the air, East African Wildl. J., 5, 18—23.
Goin C. J., Goin О. B. (1962). Introduction to Herpetology, Freeman,
San Francisco.
Goodman L. A. (1967). On the reconciliation of mathematical theories
of population growth, J. Roy. Stat. Soc., A130, 541—553.
Goodman L. A. (1968). An elementary approach to the population pro-
jection-matrix and to the mathematical theory of population
growth, Demography, 5, 382—409.
Graham M. (1935). Modern theory of exploiting a fishery, and appli-
cation to North Sea trawling, J. Conseil Expl. Mer., 10, 264—
274.
348
Список литературы
Green N. В. (1957). A study of the life history of Pseudacris brachyphona
(Cope) in West Virginia with special reference to behaviour and
growth of marked individuals, Dissertation Abstr., 17, 23692.
Gulland J. A. (1955). Estimation of growth and mortality in commercial
fish populations, U.K. Min. Agric. Fish.; Fish Invest. Series
2, 8, 1-46.
Gulland J. A. (1962). The application of mathematical models to fish
populations, pp. 204—217. In: E. D. Le Cren and M. W. Holdgate
(eds.), The Exploitation of Natural Animal Populations, Black-
well, Oxford.
Gulland J. A. (1968). Manual of methods for fish assessment, Pt. I
Fish population analysis, FAO Fish. Tech. Paper., No. 40, Re-
vision 2.
Hairston N. G., Tinkle D. W., Wilbur H. M. (1970). Natural selection
and the parameters of population growth, J. Wildl. Mgmt.,
34, 681-690.
Hanson W. R. (1963). Calculation of productivity, survival and abun-
dance of selected vertebrates from sex and age ratios, Wildl.
Monog., No. 9.
Hanson W. R. (1967). Estimating the density of an animal population,
J. Res. Lepidoptera, 6, 203—247.
Harte J. L. (1932). Statistics of the whitefish (Coregonus clupeaformis)
population of Shakespeare Island Lake, Ontario, Univ. Toronto
Studies, Biol. Ser., No. 36, 1—28.
Hickey F. (1960). Death and reproductive rate in relation to flock
culling and selection, New Zealand J. Agric. Res., 3, 332—344.
Hickey F. (1963). Sheep mortality in New Zealand, New Zealand Agri-
culturalist, 15, 1—3.
Hickey J. J. (1952). Survival studies of banded birds, U. S. Fish.
Wildl. Serv., Spec. Sci. Rept., Wildl., 15, 1—177.
Hjort J., Jahn G., Ottestad P. (1933). The optimum catch, Hvalradets
Skrifter, 7, 92-127.
Hoglund N., Nilsson G., Sthljelt F. (1967). Analysis of a technique
for estimating willow grouse (Lagopus lagopus) density, Trans.
8th Int. Cong. Game Biologists, 156—159.
Holgate P. (1966). Contributions to the mathematics of animal trapping,
Biometrics, 22, 925—936.
Holgate P. (1967). Population survival and life history phenomena,
J. Theoret. Biol., 14, 1—10.
Howard W. E. (1959). The rabbit problem in New Zealand, New Zeal.
Dept. Sci. Indust. Res., Info. Ser., No. 16, 1—47.
Howard W. E. (1960). Innate and environmental dispersal of
individual vertebrates, Amer. Midland Nat., 63, 152—161.
Howard W. E., Childs H. E., Jr. (1959). Ecology of pocket gophers with
emphasis on Thomomys bottae mewa, Hilgardia, 29, 277—358.
Humphrey S. R. (1974). Zoogeography of the nine-banded armadillo
(Dasypus novemcinctus) in the United States, Bioscience, 24, 457—
462.
Irwin J. O. (1959). On the estimation of the mean of a Poisson distri-
bution from a sample with the zero class missing, Biometrics,
15, 324-326.
Список литературы
349
Jenkins D., Watson A. (1962). Fluctuations in a red grouse (Lagopus
scoticus (Latham)) population, 1956—9, pp. 96—130. In: E. D.
Le Cren and M. W. Holdgate (eds.), The Exploitation of Natural
Animal Populations, Blackwell, Oxford.
JohnsonD. H. (1974). Estimating survival rates from banding of adult
and juvenile birds, J. Wildl. Mgmt., 38, 290—297.
Jolly G. M. (1965). Explicit estimates from capture — recapture data
with both death and immigration — stochastic model, Biometri-
ka, 52, 225-247.
Jolly G. M. (1969). Sampling methods for aerial censuses of wildlife
populations, East African Agr. Fot. J., 34, 46—49.
Kalela 0. (1949). Changes in geographic ranges in the avifauna of
northern and central Europe in relation to recent changes in cli-
mate, Bird-banding, 20, 77—103.
Keiber G, H. (1940). Estimating deer populations by a differential
hunting loss in the sexes, Proc. Utah Acad. Sci. Arts and Letters,
17, 65-69.
Kelker G. H. (1944). Sex ratio equations and formulas for determing
wildlife populations, Proc. Utah. Acad. Sci. Arts and Letters,
20, 189—198.
Kelker G. H. (1947). Computing the rate of increase for deer, J. Wildl..
Mgmt., 11, 177—183.
Kelker G. H., (1949—50). Sex and age class ratios among vertebrate
populations, Proc. Utah. Acad. Sci. Arts and Letters, 27, 12—21.
Kelker G. H. (1952). Yield tables for big game herds, J. Forestry, 50,
206-207.
Kelker G. H., Hanson W. R. (1964). Simplifying the calculation of
differential survival of age-classes, J. Wildl. Mgmt., 28, 411.
Kendall D. G. (1948). A form of wave propagation associated with the
equation of heat conduction, Proc. Camb. Phil. Soc., 44, 591—594.
Kennedy W. A. (1951). The relationship of fishing effort by gill nets
to interval between lifts, J. Fish. Res. Bd. Canada, 8, 264—274.
Kennedy W. A. (1953). Growth, maturity, fecundity and mortality in
relatively unexploited whitefish, Coregonus clupeaformis, of
Great Slave Lake, J. Fish. Res. Bd. Canada, 10, 413—441.
Kennedy W. A. (1954). Growth, maturity and mortality in the relati-
vely unexploited lake trout, Cristivomer namaycush, of Great Slave
Lake, J. Fish. Res. Bd. Canada, 11, 827—852.
Kikkaina J. (1964). Movement, activity and distribution of the small
rodents Clethrionomys glareolus and Apodemus sylvaticus in wood-
land, J. Anim. Ecol., 33, 259—299.
Kirkpatrick T. H. (1965). Studies of the Macropodidae in Queensland.
3. Reproduction in the grey kangaroo, Qd. J. Agric. Anim. Sci.,
22, 319-328,
Klomp H., van Montfort M. A. J., Tammes P. M. J. (1964). Sexual
reproduction and underpopulation, Arch. Neerlandaises Zool.,
16, 105—110.
Klott E. (1965). Factors Affecting Estimates of Meadow Mouse Popu-
lations, Ph. D. Thesis, University of Toronto.
Kraak W. G., Rtnkel G. L., Hoogerheide E. (1940). Oecologische hewer-
350
Список литературы
king van de Europese ringgegevens van de kievit (Vanellus vanell
us (L.)), Ardea, 29, 151—175.
Lack D. (1943a). The Life of the Robin, H. F. and G. Witherby, Lon-
don.
Lack D. (1943b). The age of the blackbird, Brit. Birds, 36, 166—175.
Lack D. (1943c). The age of some more British birds, Brit. Birds,.
193-197, 214-221.
Lack D. (1966). Population Studies of Birds, Clarendon Press, Oxford.
Lamprey H. F. (1964). Estimation of large mammal densities, biomass
and energy exchange in the Tarangire Game Peserve and the Masai
Steppe in Tanganyika, East African Wildl., J., 2, 1—46.
Lander R. H. (1962). A method of estimating mortality rates from a
change of composition, J. Fish. Res. Bd. Canada, 19, 159—168.
Laughlin R. (1965). Capacity for increase: a useful population statis-
tic, J. Anim. Ecol., 34, 77—91.
Lefkovitch L. P. (1966). A population growth model incorporating
delayed responses, Bull. Math. Biophys., 28, 219—233.
Lefkovitch L. P. (1967). A theoretical evaluation of popualation growth
after removing individuals from some age classes, Bull. Ent.
Res., 57, 437-445.
LeResche R. E., Rausch R. A. (1974). Accuracy and precision of aerial
moose counting, J. Wildl. Mgmt., 38, 175—182.
Leslie P. H. (1948). Some further notes on the use of matrices in popu-
lations analysis, Biometrika, 35, 213—245.
Leslie P. H. (1952). The estimation of population parameters from data
obtained by means of the capture—recapture method. II. The
estimation of total numbers, Biometrika, 39, 363—388.
.Leslie P. H. (1959). The properties of a certain lag type of population
growth and the influence of an external lag factor on a number
of such populations, Physiol. Zool., 37, 151—159.
Leslie P. H. (1966). The intrinsic rate of increase and overlap of
successive generations in a population of guillemots (Uria aalge
Pont.), J. Anim. Ecol., 35, 291—301.
Leslie P. H., Chitty D. (1951). The estimation of population parameters
from data obtained by means of the capture—recapture method.
I. The maximum likelihood equations for estimating the death-
rate, Biometrika, 38, 269—292.
Leslie P. H., Chitty D., Chitty H. (1953). The estimation of popula-
tion parameters from data obtained by means of the capture—
recapture method. III. An example of the practical applications
of the method, Biometrika, 40, 137—169.
Leslie P. H., Davis D. H. S. (1939). An attempt to determine the abso-
lute number of rats on a given area, J. Anim. Ecol., 8, 94—113.
Leslie P. H., Ranson R. M. (1940). The mortality, fertility and rate
of natural increase of the vole (Microtus agrestts) as observed in
the laboratory, J. Anim. Ecol., 9, 27—52.
Leslie P. H., Tener T. S., Vizoso M., Chitty H. (1955). The longevity
and fertility of the Orkney vole, Microtus orcadensis, as observed
in the laboratory, Proc. Zool. Soc. Lond., 125, 115—125.
Leslie P. H., Venables U. M., Venables L. S. V. (1952). The fertility
and population structure of the brown rat (Rattus norvegicus) in
Список литературы
351
corn-ricks and some other habitats, Proc. Zool. Soc. Lond., 122,
187-238.
Lewis E. G. (1942). On the generation and growth of a population,
Sankhya, 6, 93—96.
Lewontin R. C. (1965). Selection for colonizing ability, pp. 77—91.
In: Baker H. G., Stebbins G. L. (eds.), The Genetics of Colonizing
Species, Academic Press, New York.
Lincoln F. C. (1930). Calculating waterfowl abundance on the basis of
banding returns, Cir. U. S. Dept. Agric., No. 118.
Lister R. R. (1969). The Secret History of Genghis Khan, Peter Davies,
London.
Lotka A. J. (1907a). Relationship between birth rates and death rates,
Science, 26, 21—22.
Lotka A. J. (1907b). Studies on the mode of growth of material aggre-
gates, Amer. J. Sci., 4th Series, 24, 199—216.
Lovell H. B. (1948). The removal of bands by cardinals, Bird-banding,
19, 70-71.
Low W. A ., Cowan I. McT. (1963). Age determination of deer by annu-
lar structure of dental cementum, J. Wildl. Mgmt., 27, 466—471.
Lowe V. P. W. (1969). Population dynamics of the red deer (Cervus
elaphus L.) on Rhum, J. Anim. Ecol., 38, 425—457.
MacArthur R. (1968). Selection for life tables in periodic environments,
Amer. Nat., 102, 381—383.
MacLeod J. (1958). The estimation of numbers of mobile insects from
low-incidence'recapture data, Trans. Roy. Ent. Soc. Lond., 110,
363-392.
Marten G. G. (1970). A regression method for mark-recapture estima-
tion of population size with unequal catchability, Ecology, 51,
291-295.
Martin P. S. (1973). The discovery of America, Science, 179, 969—
974.
May R. M. (1973). Stability and Complexity in Model Ecosystems,
Princeton University Press, Princeton.
Meats A. (1971). The relative importance to population increase of
fluctuations in mortality, fecundity and the time variables of the
reproductive schedule, Oecologia, 6, 223—237.
Meeh L. D. (1966). The wolves of Isle Royale, Fauna Nat. Parks U. S. A.,
' Fauna Series, 7, 1—201.
Miller A. H. (1962). Bimodal occurrence of breeding in an equatorial
sparrow, Proc. Nat. Acad. Sci., U. S., 48, 396—400.
Moran P. A. P. (1951). A mathematical theory of animal trapping,
Biometrika, 38, 307—311.
Morisita M. (1965). The fitting of the logistic equation to the rate of
increase of population density, Res. Popul. Ecol., 7, 52—55.
Morris R. F. (1957). The interpretation of mortality data in studies
on population dynamics, Canad. Ent., 89, 49—69.
Morris R. F. (1963). The dynamics of epidemic spruce budworm popu-
lations, Mem. Ent. Soc. Canada, 31, 1—,332.
Murdoch W. W. (1966). Population stability and life history pheno-
mena, Amer. Nat., 100, 5—11.
352
Список литературы
Murie А. (1944). The wolves of Mount McKinley, Fauna Nat. Parks
U. S., Fauna Series, 5.
Murphy D. A. (1963). A captive elk herd in Missouri, J. Wildl. Mgmt.,.
27, 411—414.
Murphy G. I. (1966). Population dynamics and population estimation.
In: Calhoun A. (ed.), Inland Fisheries Management, Calif. Dept,
of Fish and Game, San Francisco.
Murphy G. I. (1967). Vital statistics of the Pacific sardine (Sardinops
caerulea) and the population consequences, Ecology, 48, 731 —
736.
Murphy G. I. (1968). Pattern in life history and the environment,
Amer. Nat., 102, 391—403.
Myers J. II., Krebs C. J. (1971). Genetic, behavioral and reproductive-
attributes of dispersing field voles Microtus pennsylvanicus and
Microtus ochrogaster, Ecol. Monog., 41, 53—78.
Myers К. (1970). The rabbit in Australia, pp. 478—506. In den Boer
P. J., Gradwell G. R., eds., Dynamics of Populations. Adv.
Study Inst. Dynamics Numbers Popul. (Oosterbeck).
Nagel W. P., Pimentel D. (1964). The intrinsic rate of natural
increase of the pteromalid parasite Nasonia vitripennis (Walk.}
on its muscoid host Musca domestica L., Ecology, 45, 658—660.
Neyman J. (1934). On the two different aspects of the representative
method: the method of statified sampling and the method of purpo-
sive selection, J. Roy. Stat. Soc., 97, 558—606.
Nice M. M. (1937). Studies on the life history of the song sparrow.
I. A population study of the song sparrow, Trans. Linn. Soc. N. Y.,
4, 1—247.
Niven B. S. (1970). Mathematics of populations of the quokka, Setonix
brachyurus (Marsupialia). I. A simple deterministic model for
quokka populations, Austral. J. Zool., 18, 209—214.
Organ J. A. (1961). Studies of the local distribution, life history,
and population dynamics of the salamander genus Des nognathus
in Virginia, Ecol. Monog., 31, 189—220.
Orians G. II., Leslie P. H. (1958). A capture-recapture analysis of a
shearwater population, J. Anim. Ecol., 27, 71—86.
Parr M. J., Gaskell T. J., George В. J. (1968). Capture-recapture methods
of estimating animal numbers, J. Biol. Educ., 2, 95—117.
Peabody F. E. (1961). Annual growth zones in living and fossil verte-
brates, J. Morph., 108, 11—62.
Petersen C. G. J. (1896). The yearly immigration of young plaice into
Limfjord from the German sea etc., Rept. Danish Biol. Stn., 6,
1-48.
Petrides G. A. (1949). Viewpoints on the analysis of open season sex
and age rations, Trans. N. Am. Wildl. Conf., 14, 391—410.
Petrides G. A. (1953). Aerial deer counts, J. Wildl. Mgmt., 17, 97—
98.
Petrides G. A. (1954). Estimating the percentage kill in ring-necked
pheasants and other game species, J. Wildl. Mgmt., 18, 294—297.
Phillips B. F., Campbell N. A. (1970). Comparison of methods of esti-
mating population size using data on the whelk Dicathats aegrota
(Reeve), J. Anim. Ecol., 39, 753—759.
Список литературы
355
Pielou Е. С. (1969). An Introduction to Mathematical Ecology, Wiley-
Interscience, New York.
Pielou E. C. (1974). Population and Community Ecology, Gordon
and Breach, New York.
Poole W. E. (1973). A study of breeding in the grey kangaroo Macropus:
giganteus Shaw and M. fuliginosus (Desmarest), in central New
South Wales, Aust. J. Zool., 21, 183—212.
Rasmussen D. I. (1941). Biotic communities of Kaibab Plateau, Ari-
zona, Ecol. Monogr., 3, 229—275.
Reddingius J., den Boer P. J. (1970). Simulation experiments illust-
rating stabilization of animal numbers by spreading the risk,.
Oecologia, 5, 240—284.
Richdale L. E. (1954). A Population Study of Penguins, Oxford Uni-
versity Press, London.
Ricker W. E. (1940). Relation of “catch per unit effort” to abundance'
and rate of exploitation, J. Fish. Res. Bd. Canada, 5, 43—70.
Ricker W. E. (1949). Mortality rates in some little-exploited popula-
tions of freshwater fish, Trans. Am. Fish. Soc., for 1947, 77,114—
128.
Ricker W. E. (1954a). Stock and recruitment, J. Fish Res. Bd. Canada,
11, 559-623.
Ricker W. E. (1954b). Effects of compensatory mortality upon popu-
lation abundance, J. Wildl. Mgmt., 18, 45—51.
Ricker W. E. (1958). Handbook of computations for biological statis-
tics of fish populations, Fish. Res. Bd. Canada Bull., No. 119r
1-300.
Riffenburgh R. H. (1969). A stochastic model of interpopulation dy-
namics in marine ecology, J. Fish Res. Bd. Canada, 26, 2843—
2880.
Riney T. (1956a). Differences in proportion of fawns to hinds in-
red deer (Cervus elaphus) from several New Zealand environments.
Nature, 177, 488—489.
Riney T. (1956b). Comparison of occurence of introduced animals with
critical conservation areas to determine priorities for control,
New Zeal. J. Sci. Tech., B38, 1—18.
Riney T. (1957). The use of faeces counts in studies of several free-
ranging mammals in New Zealand, New Zeal. J. Sci. Tech., B38,
507—522.
Robinette W. L. (1949). Winter mortality among mule deer in Fishla-
ke National Forest, Utah. U. S. Fish, and Wildl. Serv., Spec. Sci.
Report, 65, 1—15.
Robinette W. L., Jones D. A., Rogers G., Gashwtler J. S. (1957).
Notes on tooth development and wear for Rocky Mountain mule
deer, J. Wildl. Mgmt., 21, 134-153.
Roff D. A. (1973). An examination of some statistical tests used in
the analysis of mark-recapture data, Oecologia, 12, 35—54.
Rogers A. (1968). Matrix Analysis of Interregional Population Growth
and Distribution, University of California Press, Berkeley.
Rounsefell G. A., Everhart W. H. (1953). Fisheries Science: Its Methods,
and Applications, John Wiley and Sons, New York.
354
Список литературы
Rowley I. (1966). Rapid band wear on Australian ravens, Austral.
Bird Bander, 4, 47—49.
Rupp R. S. (1966). Generalized equation for the ratio method of esti-
mating population abundance, J. Wildl. Mgmt., 30, 523—526.
Ryel L. A., Fay L. D., van Etten R. C. (1961). Validity of age determi-
nation in Michigan deer, Pap. Mich. Acad. Sci., 46, 289—316.
Rampford M. R. (1955). The truncated negative binomial distribution,
Biometrika, 42, 58—69.
Schaefer M. R. (1957). A study of the dynamics of the fishery for yellow-
fin tuna in the eastern tropical Pacific Ocean, Inter-American
Trop. Tuna Comm. Bull., 2, 247—267.
Schnabel Z. E. (1938). The estimation of total fish in a lake, Am.
Math. Mon., 45, 348—352.
Schumacher F. X., Eschmeyer R. W. (1943). The estimation of fish
populations in lakes and ponds, J. Tenn. Acad. Sci., 18, 228—
249.
Seber G. A. F. (1965). A note on the multiple-recapture census, Bio-
metrika, 52, 249—259.
Seber G. A. F. (1970). Estimating time-specific survival and reporting
rates for adult birds from band returns, Biometrika, 57, SIS-
SIS.
Seber G. A. F. (1972). Estimating survival rates from bird-band re-
turns, J. Wildl. Mgmt., 36, 405—413.
Seber G. A. F. (1973). The Estimation of Animal Abundance and
Related Parameters, Griffin, London.
Seber G. A. F., Le Степ E. D. (1967). Estimating population para-
meters from catches large relative to the population, J. Anim.
Ecol., 36, 631-643.
Selleck D. M., Hart С. M. (1957). Calculating the percentage of kill
from sex and age ratios, Calif. Fish and Game, 43, 309—316.
Sharpe F. R., LotkaA. J. (1911). A problem in age-distribution, Phil.
Mag., 21, 435-438.
Silliman R. P., Gutsell J. S. (1958). Experimental exploitation of fish
populations, Fish. Bull., Fish Wildl. Serv., 58, 215—252.
Simpson G. G., Roe A., Lewontin R. C. (i960). Quantitative Zoology,
Revised edition, Harcourt, Brace and Company, New York.
Siniff D. B., Skoog R. 0. (1964). Aerial censusing of caribou by stra-
tified random sampling, J. Wildl. Mgmt., 28, 391—401.
Skellam J. Gr. (1951). Random dispersal in theoretical populations,
Biometrika, 38, 196—218.
Skellam J. G. (1955). The mathematical approach to population dyna-
mics, pp. 31—45. In: Cragg J. B., Pirie N. W. (eds.), The Num-
bers of Man and Other Animals, Oliver and Boyd, Edinburgh.
Snedecor G. W., Cochran W. G. (1967). Statistical Methods, 6th edition,
Iowa State University Press, Ames.
Sonleitner F. J., Bateman M. A. (1963). Mark-recapture analysis of a
population of Queensland fruit-fly, Dacus tryoni (Frogg.), J. Anim.
Ecol., 32, 259-269.
Southern H. N. (1964). The Handbook of British Mammals, Blackwell,
Oxford.
Southwood T. R. E. (1966). Ecological Methods with Particular Refe-
Список литературы
355
гепсе to the Study of Insect Populations, Methuen, London.
Stewart R. E., Geis A. D., Evans C. D. (1958). Distribution of popula-
tions and hunting kill of the convasback, J. Wildl. Mgmt., 22,
333-370.
Stoddart D. M. (1950). Individual range, dispersion and disper-
sal of water voles (Avicola terrestris (L.)). J. Anim. Ecol., 39,
403-425.
Taber R. D. (1969). Criteria of sex and age, pp. 325—401. In Giles-
R. H. (ed.), Wildlife management Techniques, The Wildlife-
Society, Washington, D. C. 3rd edn, revised.
Talbot L. M., Stewart D. R. M. (1964). First wildlife census of the-
entire Serengeti-Mara region, East Efrica, J. Wildl. Mgmt., 28,.
815-827.
Tanton M. T. (1965). Problems of live trapping and population esti-
mation of the wood moMse Apodemus sylvaticus (L.), J. Anim. Ecol.,
34, 1-22.
Tanton M. T. (1969). The estimation and biology of the bank vole
(Clethrionomys glareolus (Schr.)) and wood mouse (Apodemus syl-
vaticus (L.)), J. Anim. Ecol., 38, 511—529.
Tost J. (1966). The root vole Microtus oeconomus (Pallas), an inhabi-
tant of seasonally flooded land, Ann. Zool. Fenn., 3, 127—171.
Taylor B. J. R. (1965). The analysis of polymodal frequency distri-
butions, J. Anim. Ecol., 34, 445—452.
Taylor S. M. (1966). Recent quantative work on British bird popula-
tions. A review, The Statistician, 16, 119—170.
Tinkle D. W. (1967). The life and demography of the side-blotched
lizard, Uta stansburiana, Misc. Publ. Mus. Zool. Univ. Mich.,
132, 1-182.
Tinkle D. W. (1973). A population analysis of the sagebrush lizard,.
Sceloporus graciosus, in Southern Utah, Copeia, 1973, 284—296.
Tomlinson R. E. (1968). Reward banding to determine reporting rates-
of recovered mourning dove bands, J. Wildl. Mgmt., 32, 6—11.
TschuprowA. 4.(1923). On the mathematical expectation of the mo-
ment frequency distributions in the case of correlated observati-
ons, Metron, 2, 461—493, 646—683.
Turner F. B. (1960a). Tests of randomness in recapture of Rana p.
pretiosa, Ecology, 41, 237—239.
Turner F. B. (1960b). Size and dispersion of a Louisiana population
of the cricket frog, Acris gryllus, Ecology, 41, 258—268.
Turner F. B. (1962). The demography of frogs and toads, Quart.
Rev. Biol., 37, 303-314.
Watson R. M. (1969). Aerial photographic methods in censuses of ani-
mals, East African Agric., For. J., 34, 32—37.
Watson R. M., Freeman G. H., Jolly G. M. (1969). Some indoor expe-
riments to simulate problems in aerial censusing, East African
Agric. For. J., 34, 56—59. .
Watson R. M., Jolly G. M,, Graham A. D. (1969). Two experimental
censuses, East African Agric. For. J., 34, 60—62.
Watson R. M., Parker I. S. C., Allan T. (1969). A census of elephants
and other large mammals in the Mkomazi region of northern Tan-
zania and Southern Kenya, E. Afr. Wildl. J., 7, 11—26.
356 Список литературы
White Е. G. (1971). A computer program for capture-recapture studies
of animal populations: a Fortran listing for the stochastic model
of J oily G. M., New Zeal. Tussock Grasslands and Mountain Lands
Inst. Spec. Pub., 8, 1—33.
W. H. 0. (1972). World Health Statistics Annual for 1969, I. W. H. 0.,
Geneva.
Wiener G., Donald H. P. (1955). A study of variation in twin cattle.
IV. Emergence of permanent incisor teeth, J. Dairy Res., 22,
127-137.
Wohlschlag D. E. (1954). Mortality rates of whitefish in an Arctic
lake, Ecology, 35, 388—396.
Wolfson A. (1955). Recent Studies in Avian Biology. University of
Illinois Press, Urbana.
Zippin C. (1956). An evaluation of the removal method of estimating
animal populations, Biometrics, 12, 163—189.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Бейли, метод троекратных отло-
вов 235—238, 243
Беременность
— встречаемость 129
— повторяемость 129
Биномиальное распределение
Ближайший сосед 44,
Возрастное распределение ,142
— — в демографических таб-
лицах 150, 157J 194
:----устойчивое 144, 180, 185
Возрастные.^ классы 198
— — отношение численностей
171
Вспышка численности 209
Вторая скорость роста популя-
ций 207
Второй трофический уровень
— промысел 299
Выборка
— систематическая 59, 63
— случайная 50, 51, 59
Выедание растительности траво-
ядными 210
Гамма-функция 251
Геометрическое распределение
247, 251
Делури метод 82
Демографические таблицы
— — для млекопитающих 161
Демографические таблицы для
птиц 162
— — интерпретация 194
— — методы составления 146—
151
— — применение 171, 277
Демографический потенциал 94,
177
Джолли-Зебера метод 238—243
Иммиграция
— оценка 237
— смещение оценок, полученных
методом мечения с повторным
отловом 233
Индивидуальный участок 105,
226
Интенсивность охоты 256, 257
Келкера метр, 76, 171
Когорта 138, 161, 162
Кольцевание
— возврат колец 255
— утеря колец 162, 224, 256
Кочевничество 105, 301
Лесли метод 79
Линкольна индекс см. Петерсена
оценка
Ловушки
— избегание 38, 216, 236
— интерес к ним 38, 216, 236
Логистическая модель
— — в регуляции численности
326
— — оценка уровня добычи
287
— — роста популяции 206
358
Предметный указатель
Мечение и повторный отлов 214
— — возврат меток охотника-
ми 253—270
— — модели частот попадания
в ловушки 245
— — неравная вероятность от-
лова 216—224, 246, 253
— — оценка смертности 237,
243, 253—270
— птиц 253—270
Миграция 105
Определение возраста 23
— — ошибки 25
Отрицательное биномиальное
распределение 247
Охрана популяций 271, 273—
275
Петерсена оценка 227—233
Плодовитость
— определение 119
— охраняемых популяций 276
— при низкой плотности 310
— среднее значение 137
— таблица 132
Плотность, индексы 31
— классы 45
— метод двукратного использо-
вания индекса 83
— оценки 31
— прикидочные оценки 49
Полевки 100—104, 135, 136, 182
Полиномиальная регрессия 156
Популяция, границы 16
— определение 11
— численность 28
Постоянный уровень добычи 271,
278-323
Потенциальная продолжитель-
ность жизни 166
Предполагаемая продолжитель-
ность жизни 168, 171
Пресмыкающиеся 77, 165, 222,
247, 253
Пробит-анализ 124, 125, 157
Продолжительность поколения
199
Промысел в переменных внешних
условиях 317
Промысел избирательный, в
системе нескольких видов 316
----- по возрасту 303
-----— полу 309, 322
— принципы организации 277
— социальных видов 301, 321
Противодействие (враждебность^
среды 166
Пуассона распределение 40, 218,
221, 247, 311
Расселение, возраст расселяю-
щихся особей 103
— генетика расселяющихся осо-
бей 103
— диффузионная модель 109
— «естественное» 100
— модели 107
— монгольское нашествие 118
— определение 105—107
— первобытного человека 117,
118
— пороговое значение плотнос-
ти 111
Регуляция численности 271, 328
— — воздействием на место оби-
тания 332
— — затраты на 330
— — охотой 324
— — с помощью инфекций 331
Релея критерий 102
Рождаемость 202
Сезон размножения 119
— — оценка средней даты рож-
дений 120
Скорость вымирания 202
Скорость роста., вычисление 178
— — идеальная 92, 177, 210,
290, 326
— — конечная 189
— — максимальная 181
— — наблюдаемая 94, 177
— — потенциальная 96, 177,
282, 321, 329
-----при фиксированной зави-
симости выживаемости и пло-
довитости от возраста 93, 177
Случайные блуждания 107—109
Предметный указатель
359
Смертность, зависимость от вре- мени года 159 — разложение на «изолирован- ные» составляющие 158, 258, 266 — средняя удельная 169, 257 Состояние популяции 96 Стирлинга формула — — расчета гамма-функции 251 Стратификация 52—54 Учеты с воздуха, методы наблю- дений 62 — поправки 64 — разбиение территории 54 Функциональные реакции 208 Характер размножения 19 Хищники 211
Травоядные, динамика популя- ции 207, 208 Трансекты 55, 71, 72 Частоты, измерение 40 — преобразование в плотности 39, 40 Численная реакция 208 Численности полов, соотношение 131, 188, 310
Улов на единицу промыслового усилия 29, 36, 79, 300 Управление природными попу- ляциями 171—172 Успешные охоты, доля 38 Шеппарда поправка 121 Шнабеля метод 234 Шумахера метод 233—235
ОГЛАВЛЕНИЕ
Предисловие редактора перевода........................... 5»
Предисловие ............................................. 8
Глава 1. Введение.............................. 11
Глава. 2. Популяция .................................... 16
• 2.1. Границы популяции ............................. 16
2.2. Системы размножения ........................... 18
2.3. Выбор параметров ............................... 19
Глава 3. Возраст ........................................ 22
Глава 4. Обилие.......................................... 28
4.1. Оценки относительной плотности (индексы) .... 31
4.1.1. Линейная зависимость плотности от индекса . 33
4.1.2. Нелинейная зависимость плотности от индекс а 39
4.2. Оценки абсолютной плотности.......... 48
4.2.1. Абсолютные учеты .................... 48
4.2.2. Прикид очные оценки ................. 49s
4.2.3. Выборочные учеты ......................... 50
4.2.4. Селективное добавление и изъятие (метод
Келкера) ........................................ 76
4.2.5. Неселективное добавление и изъятие . . 79
4.2.6. Коррекция ипдекса ........................ 85
Глава 5. Скорость роста численности популяций ... 89
5.1. Конечная и экспоненциальная скорость роста . 89
5.2. Меры скорости роста ............................ 92
5.3. Демографический потенциал....................... 94
Глава 6. Расселение ..................................... 98
6.1. Процесс расселения ......................... 100
6.2. Определение расселения ...................... 105
6.3. Модели расселения ........................... 107
6.3.1. Случайные блуждания..................... 107
6.3.2. Сложные модели ......................... 109
6.4. Типы роста ареала............................ 114
6.4.1. Скорость расширения ареала .... 116
Оглавление
361
Глава 7. Плодовитость ................................. 119
7.1. Сезон размножения ........................ . 119
7.2. Частота рождений . . . . . . . . . . 129
7.3. Соотношение численностей полов .....' 131
7.4. Таблица плодовитости ......................... 132
7.5. Упрощение таблицы плодовитости . . . • . 136
Глава 8. Смертность ................................... 138
8.1. Демографическая таблица .............. 138
8.1.1. Роль возрастной структуры .... 142
8.1.2. Составление демографических таблиц . . 146
8.2. Сглаживание возрастных распределений . . . 155
8.3. Разложение удельной смертности на составляющие 158
8.4. Зависимость смертности от времени года . . . 159
8.5. Характерные зависимости смертности от возраста 161
8.6. Неправильное понимание демографических пара-
метров ............................. 166
8.7. Представление демографических таблиц в сжатом
виде .............................................. 168
8.8. Применение демографических таблиц .... 171
Глава 9. Связь между параметрами . . ................. 174
9.1; Основное уравнение :...........................174
9.2. Вычисление г.................................. 176
9.3. Максимальная скорость увеличения численности по-
пуляции ........................................... 181
9.4. Устойчивость связей между параметрами . . 183
9.5. Постоянство структуры популяции .... 185
9.6. Интерпретация возрастного распределения . . 192
9.7. Продолжительность поколения .................. 199
9.8. Рождаемость и скорость вымирания .... 202
9.9. Рост численности популяций............. 203
9.9.1. Первый трофический уровень .... 205
9.9.2. Второй трофический уровень....... 207
9.9.3. Третий трофический уровень .... 211
Глава. 10. Мечение и повторный отлов................... 214
10.1. Вероятность отлова ........................... 215
10.1.1. Критерии равновероятности отлова . . 218
10.1.2. Поправка на потерю меток .............. 224
10.2. Интерпретация оценки численности популяции, полу-
ченной методом мечения и повторного отлова. . 226
40.3. Оценка Петерсена ............................ 227
10.4. Метод Шумахера . . . ........................ 233
10.5. Метод троекратных отловов Бейли .... 235
10.6. Метод Джолли — Зебера ....................... 238
10.7. Оценка удельной смертности................... 243
10.8. Модели частот попадания в ловушки . . . 245
362
Оглавление
10.9. Анализ возврата меток охотниками .... 253
10.9.1. Методы анализа, пригодные в случаях, когда
метятся только молодые особи .... 257
10.9.2. Методы анализа, используемые в случаях,
когда метятся особи всех возрастов . . 263
Глава 11. Использование популяционного анализа при экс-
плуатации и охране популяций..................... 271
11.1. Охрана популяций ........................... 273
11.2. Принципы организации промысла .... 277
11.2.1. Оценка уровня добычи с помощью логисти-
ческой модели ................................. 287
11.2.2. Оценка уровня добычи в моделях взаимодейст-
вующих популяций ............................... 298
11.2,3. Оценка МПУД по соотношению между про-
мысловым усилием и добычей . . . 299
11.2.4. Промысел в социальных видах .... 301
11.2.5. Избирательный промысел ............... 302
11.2.6. Промысел в переменных внешних условиях 317
11.2.7. Обсуждение проблем промысла . . . 319
11.3. Регуляция численности ...................... 323
Приложения ........................................... 333
Список литературы .................................... 342
Предметный указатель ............................... 357
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформле-
нии, качестве перевода и другие просим присылать по
адресу:
129820, Москва, И-110, ГСП,
1-й Рижский пер., д. 2,
издательство «Мир»
Г. Коли
АНАЛИЗ ПОПУЛЯЦИЙ ПОЗВОНОЧНЫХ
Редакторы М. Б. Николаева, Н. Н. Шафрановская
Художественный редактор Б. Н, Юдкин
Технический редактор Н. И, Манохина
Корректор Н. В. Спичкина
ИБ № 1547
Сдано в набор 19. 04. 78. Подписано к печати
30 . 08 . 78. Формат 84Х1081/зг- Бумага кн.журн. №2.
Гарнитура обыкновенная. Печать высокая. Объем,
5,75 бум. л., 19,32 усл. печ. л., 18,19 уч.-изд. л.
Изд. №4/9816 Тираж 4200 экз. Зак. 334. Цена 2 р. 40 к.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2.
Ярославский полиграфкомбинат Союзполиграфпрома
при Государственном комитете Совета Министров.
СССР по делам издательств, полиграфии и книж-
ной торговли. 150014, Ярославль, ул. Свободы, 97,
ИЗДАТЕЛЬСТВО «МИР»
Выйдет в свет в 1979 году
ГУДВИН Б. Аналитическая физиология клеток и
развивающихся организмов. Пер. с англ., 18 л.
В книге рассмотрены внутриклеточные биохими-
ческие процессы в ходе развития и дифференцировки.
Изложены общие представления о регуляции обмена
веществ, активности ферментов, митотических циклах
в клетках прокариотов и эукариотов. Используя со-
временные данные о динамике внутриклеточных про-
цессов, автор пытается раскрыть механизмы, лежащие
в основе временной и пространственной дифференци-
ровки клеток.
Предназначена для биофизиков, биохимиков, эм-
бриологов, молекулярных биологов, а также для мате-
матиков и других специалистов, интересующихся воп-
росами развития организмов. Доступна студентам стар-
ших курсов и аспирантам.