Текст
Министерство высшего и среднего специального образования РСФСР
ЛЕНИНГРАДСКИЙ ОРДЕНА ЛЕНИНА
ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
имени М. И. КАЛИНИНА
Г. А. ЖУКОВА-МАЛИЦКАЯ, Ю, Н. КУЗЬМИН
МАТЕМАТИЧЕСКАЯ ФИЗИКА
УЧЕБНОЕ ПОСОБИЕ
S
Ленинград
19 7 4
Министерство высшего в среднего специального образования РСФСР
ЛЕНИНГРАДСКИЙ ОРДЕНА ЛЕНИНА
ПОЛИТЕХНИЧЕСКИЙ ИНСТИТУТ
имени М. И. КАЛИНИНА
Г. А. ЖУКОВА-МАЛИЦКАЯ. Ю. Н. КУЗЬМИН
МАТЕМАТИЧЕСКАЯ ФИЗИКА
УЧЕБНОЕ ПОСОБИЕ
Ленинград
19 7 4
Г Г°с-
би®0;“Гс^я
| ЭКЗЕМПЛЯР
L^AJTbr.yc зд/,д
ftf- 33 633
Учебное пособие является практическим руко*
водством для изучения математической физики
во втузе. Оно содержит задачи и методические
указания по применению метода Фурье и метода
собственных функций, метода интегральных пре-
образований Фурье и Ханкеля, операционного и
вариационного исчисления, интегральных урав-
нений.
Пособие предназначается для студентов фи-
зико-механического факультета, факультета ра-
диоэлектроники, гидротехнического и электроме-
ханического факультетов.
Рецензент — доктор физ.-матем. наук, про-
фессор Я. С. Уфлянд.
©
Ленинградский политехнический институт
имени М. И. Калинина, 1974 г.
ПРЕДИСЛОВИЕ
Настоящее пособие предназначается для практических
занятий студентов, изучающих курс математической физики
на физико-механическом факультете и факультете радио-
электроники Ленинградского ордена Ленина политехниче-
ского института имени М. И. Калинина.
В основу пособия положен сборник задач по математи-
ческой физике [9], однако оно не может рассматриваться как
задачник стандартного типа ввиду большого числа включен-
ных в текст указаний теоретического и методического харак-
тера. Необходимость в таком пособии вызвана специфиче-
скими трудностями изучения курса математической физики
в техническом вузе, существенно отличающегося по своей
программе и целям от соответствующих университетских
курсов. Последнее обстоятельство не позволяет использовать
в качестве основных пособий существующие учебники по ма-
тематической физике.
При подборе задач авторы руководствовались програм-
мой читаемого курса и многолетним опытом преподавания
на кафедре математической физики института.
В пособие введено -некоторое количество задач по вариа-
ционному исчислению и интегральным уравнениям в объеме
читаемых курсов, а также задачи на теорию собственных
функций задачи Штурма — Лиувилля и преобразование
Лапласа.
Кроме практических занятий иа физнко-механическом
факультете и факультете радиоэлектроники, настоящее по-
1* 3
собие может быть использовано студентами и другими ли-
цами, изучающими математическую физику, для самостоя-
тельной работы.
Данное пособие следует .рассматривать как введение
в практикум по математической физике. Для более глубо-
кого изучения предмета можно обратиться, например, к [1],
И, [9], [И].
Авторы.
Глава I
ЗАДАЧА ШТУРМА — ЛИУВИЛЛЯ
Задачей Штурма — Лиувнлля пр-инято называть задачу
о нахождении нетривиальных (ненулевых) решений однород-
ного дифференциального уравнения вида
[₽ w +iXr w - ? W] у=0
при однородных граничных условиях. Функции р(х), г(х) и
q(x) известны, к— параметр.
Те значения параметра X, при которых существуют нетри-
виальные решения задачи Штурма — Лиувилля, называются
собственными значениями или собственными числами, а сами
нетривиальные решения — собственными функциями задачи.
Совокупность собственных значений называется спектром.
1. Найти собственные значения н собственные функции
для уравнения
если х меняется в промежутке 0<^х</ прн следующих гра-
ничных условиях:
а) У = 0. У|х=1 = 0;
б) у|л.„ = о, -g-|x=i = 0;
в>4 .^ = 0. VU = 0;
г) =0, #1 =0;
' Ах л-=ю Ах | х=1
д) у I -ь hy I x-i = °;
е> -4r + ^UO = O, y|.v..,=0;
о тг L_o = °> +
5
3)-^- + AyU = °- 4L-. = °:
и)-4 + ^|.-о = °. 4 + *У ^ = °;
к)-у|,_о=.уи> -М=о=4Ь^
Ответ:
а) \, = ^, y„ = C„sin^-(«=l, 2, 3,...);
б) s-'2w 4,'1"8 , y„^C,,sin (2" + Ч" (я = 0, 1, 2,..,);
в) X„ = l?^i>y„ = C„cos^±^(« = 0, I, 2....);
>г) Хо = 0, Уо = Со — const,
, л2^2 rntx , 1 п о \
= y„ = C„cos ——(га = 1, 2, 3,...);
д) оде уп — положительные корни уравнения
tgV = —Уп=Сп$т^^;
е) %п совпадают с собственными числами пункта «д»,
y„=C„SinlL(!zLi);
У 2
ж) , где уп — положительные корни уравнения
, м г, 1>,х
tgv=—, у* = с»,cos I ;
з) Хп совпадают с собственными числами пункта «ж»,
и) в этом случае спектр состоит из двух независимых
наборов собственных чисел , где уп — положи-
, 2т г- - 7n(f—2*)
тельные корни уравнения tgy =------yn=Cnsin---------j----
и Ль==^~-у, где yk — положительные корни уравнения
, hl г-, ta(Z — 2х)
tgV = -27‘> >4 = Oacos----;---,
<к) ло = О, Уо= Со = const,
4п2л2 2лпх . г. , 2пкх , » п \
^ = —р-. y„ = C„cos —+ D„sin—— (п= I, 2,...).
Здесь Сп и Dn — независимые произвольные постоянные;
таким образом, одному собственному числу соответствуют
две линейно .независимые собствешше функции.
2. Найти собственные значения и собственные функции
для уравнения
dx2 1 J ’
если к меняется в промежутке —при следующих
граничных условиях:
а) у4=-<=о;
б) -У- =о, #1 =0;
' dx |л=/ ’ dx [x—z ’
в) ^+М.=<=0.
Ответ:
ч (2л 4- 1)2п2 (2п + И ях , п 1 \
а) К = -—5Г~ > y« = C«cosi-gjJ—(л = 0, 1, 2,...),
Ь2ге2 __ Ъ-у-
= Ул = -О*81п —7—(А = I, 2, 3,...);
б) %о‘—0, yQ — Cq= const,
>™=7Г> y» = C„cos-^(«=l, 2, 3,...),
— 4^2 ’ Vfe — Г/уШ 2/ — U, i, 2, • . )•,
в) = где yn — положительные корни уравнения
tgv =------Уп= C„sinJy,
v «,2
Лк = -~-, где Yh—положительные корпи уравнения
Ук = Dtcos Jy;
г) Лю = 0, Уо= Со — const,
' n2rt2 Z-. ппх г-. . пкх . f А о \
'•» = —> У» = cos—2~ — D„ sin~^—(га= 1, 2, 3,.. .)
3. Найти собственные значения для уравнения
[р’тг] + V<*)у = 0 (a<x<bt
при граничных условиях:
a ) = УНг-* = °>
б ) =0,^1 =0,
7 dx Iх-а dx Ix=b
для следующих частных случаев:
1)Р(Л) = Л-, г(х) = Ц~;
2) р(х) = х\ г(х)^х'-;
3) р(х) — X, Г (х) =Х
Ответ:
1) Для уравнения (х~3т) + 1У = 0;
а) К
пп 1п-^~
y„ = C„sin---------^(«=1, 2,...);
In----
б) Ло = 0, г/о = Со = const,
пЫ
КГ
ПК In —
y„ = C„cos-Л(я=)> 2>
In —
2) Для уравнения +Хх2у = 0:
Ч ' Я2к3 Си . пк [Ь — х) . I О о \
а) К«= > У-^-Г81'1 (f —Д> (Я=1’ 2’
б) Ло = О, у0= Со = const,
^п=_Где уп — положительные корни уравнения
tg-(= \,at, y,.=e.4HabCos'«y-^+
+ |d-a)2
+ {b-a) sin '(„fEr] •
3) Для уравнения + >.xy = 0:
а) \. = "Г' У^ = сч^п(уп, x),
где
Л(т, ^)=л(ч-у-) ^o(l) — А(т) (т-г)>
\'п — положительные корни уравнения /?(у, я)=0;
б) Ло = о, уо~ Со= const,
= ’ У»=
8
где
Z(7, *) = ./, (7-^) Г, (7)(7) Г„ (7-^).
</Z I п
Yn — положительные корни уравнения — О-
4. Найти собственные числа и собственные функции для
уравнения
yIV - ;.у = О,
если х меняется в промежутке 0<х< I при следующих гра-
ничных условиях:
a) J' U = °’ У” |,=<>=<О U=i = 0, у" =
б) У" | = 0, у’" | л.о = 0, у" | = 0, у’" |= 0;
в) У | ,_о = О, У' | _,.-о 0, у | x_t = 0, у' | х_, = 0;
г) у 1^0 = 0. У' Uo=o. У'"|х-< = 0;
л) У | ,=.0 = О, У' | .,=0 = О, У | - о, у" ] = 0;
е) У"|.-о=0- У"'|._о = О> У Ь=; = 0, У" |._< = 0.
Ответ:
a) = — > Уп = С„8\п — (п= 1, 2, 3,..,);
б) /.о~О, уо = С(1х 4- Do,
Хл = , где у„ — положительные корни уравнения
ch у cosy = 1,
у„ = с„ [(ch cos-,-„l[sh-!y + sin-3^-) -
- (sh т„ - sin 7„) (ch + cos ;
B) = > гДе — положительные корни уравнения
ch у cos у = 1,
Уп = С„ [(ch 7„ - cos 7„) (sh - sin ~
- (sh т„ - sin 7„) (ch - cos )] ;
9
г) Хп= , где Yn — положительные корни уравнения
ch у cos у = — 1;
У» = с„ [(ch + cos т„) (sh - sin -
- (shy„ + sin7„) (ch jy — cos^y)] ;
д) кп=-~- , где уп—положительные корпи уравнения
tg у = th у,
Уп = С„ [(ch cos 7„) (sh — sin -
- (shT„ + sin-(„)(ch^ -cos^c)] ;
е) Ло = 0, £о = Со(1 — х/1); кп = ^~, где уп — положи-
тельные корни уравнения tg у = th у,
Уп = С„ [(ch-(„-I-cosT„)(sh-^ + sin -
- (sh T„ + sin T„) (chl£- + cos^)].
5. Найти собственные числа и собственные функции для
(V с Л
уравнения у —/л/=0, если % меняется в промежутке
— 1<х<1> при следующих 'Граничных условиях:
а) у |i=i=0, у" |.v=/ = 0, у |Л__, = 0, у" ^__, = 0;
б) У |.г_< = °- У’ Ь-( = 0, У Ь—1 = °. У' К—/ = 0;
в) у";,_, = 0, у"'|.г_, = о, у"|^_, = о. у"'|х__/ = о.
Ответ:
a) У» = С„со8^ЦУ^(л = 0, 1, 2,...),
Ч = yb = DkSln-^-(k=\, 2, 3,...);
б) \г=, где уп — положительные корни уравнения
tg 7 = - th у, ул == Сп (cos ь ch уп ~ - ch cos ,
10
Xfe==-^-, где ул — положительные корни уравнения
tg т = th -у, ук = Dk (sin 1s sb ь - sh yk sin ;
в) %o — 0, Уй~ Сох + Do,
1 tn4
— где y« — положительные корни уравнения
thy = — tgy,
Уп = Cn [cosf„ch7„^ + ch^cos ,
\.= -jr , где уь — положительные корпи уравнения
th-f = tgY,
Уь = £>к [sinbsh tk -I- sh ~k sin f4 .
6. Решить следующие сингулярные задачи Штурма —
Лиувилля для уравнения
(х2 ) -|- Хх2у =0. 0 < х < а
dx \ dx / 1 7
при условиях:
а) _У Л-=Д —0, у|х_0 —ограничено;
б) '^'|х-»=0, у|ж_о~огРаничен°;
в) + hy | г„а = 0, у л. .о— ограничено.
Ответ:
а) Хп=-^~, л=^-81п —(л= 1. 2, 3,.
б) Ло = 0, у0 — Со = const,
Y 2
Хя = —^2—, где уп — положительные корни уравиеиия
igv = v, Уп= 4^sin^r;
в) \п — t где Yn — положительные корни уравиеиия
‘8Т = Г^>
}’„= -V'sin-!F-
И
7. Решить следующие сингулярные задачи Штурма —
Лиубилля для уравнения
= °<х<а
при условиях:
а) У I х-а = У । х-о ~ ограничено;
б) 1 t_e = 0, у | V=CI — ограничено;
в) -Jj- + ty | х-о =°> У | х_о~ограничено.
Ответ:
2
а-) Хп — £ , где уп— положительные корни уравнения
W = 0, у„ = Сп/0(^);
б) Хо = О, у0 = Со = const, Хп^=~- , где уп— положи-
тельные корни уравнения Л (у) —0, yn^CTlJ0
в) %п —где уп— положительные корни уравнения
yJtM=haJ0(iy, уя = С,л(^).
8. Решить следующие сингулярные задачи Штурма —
Лнувилля для уравнения
И*) ? wo=о
при условиях:
а) - 1 < х < 1, р (х) = 1 - л-2, г (х) = 1, ?(л)=0,
ограничено;
б) — 1 < х < 1, р (х) = ]/1 л3, г (х)— 5(х)=О_.
у 1 ~ хз
У | х--! 1 — ограничено;
в) 0 < X <со, р (х) — х, г(х) = 1, 9(x) = -~f у(_^о —
ограничено, у|л._то = 0;
г)_сс<х<со, р(х)==1, г(х)=1, з(х),= — х\
yi^±w=0.
12
Ответ:
а) Хп = «(я+1)» Уп = СпРп(х) (п = 0, 1, 2,...),
I d'1
Р„(х) = (л2 — 1)” — п-й полином Лежандра;
б) Кп = п2, уп = СпТп(х) +DnUn(x) (п = 0, 1, 2,...),
7„ = (- 1 -^(\ -х2) ® = cos(narccosx),
= sin (narccos x) — полиномы Чебышева;
В) \, = « + 4-, У« = С,е 2 L„(x} (n = 0, 1, 2,...),
L„ (a) = (е~ххг‘У п-й полином Лагерра;
г) z.n —2/f+l, j/„ = C„e 2 H„ (x) (n = 0, 1, 2,...),
dn — rs
7/n(x) =(—1)лел’-^ e ’ —n-й полином Эрмита.
9. Найти собственные функции для уравнения
^ + ХУ = 0
при следующих условиях:
а) У |х=о = 0, — ограничено;
б) ^’L-o=0, огРаничен°'’
в) — + hy | v=0 = 0, у [^-ограничено.
Отв ет:
а) л — v3, 0< v<оэ, у^ = C(v) sin vx;
б) X = v2, 0 О <оо, у, — С (v) cos vx;
в) ^ = v2t 0<v<co, yv = С (v) (v cos vjc + Л sin *х).
10. Найти собственные функции для уравнения
^г + хУ = °
при условии — ограничено
13
Л = v2, О v < °0, = С (v) sin vx cos ^х>-
C(v), D(v) —произвольные функции от v.
11. Найти собственные функции уравнения
d f dy \ I ч 1 п
-J- (х-/-) 4-л—у = 0
dx \ dx I 1 х J
при следующих условиях:
а)у|х_й = 0, у|х=0— ограничено;
б) -^“-|v_a = 0, у |А.=0—ограничено.
Ответ;
а) х — v2, 0<v<oo, уч — С (v) sin In ;
6) A, = v2, 0 v < oo, у, — C (v) cos (v In.
12. Найти собственные функции уравнения
4Н^)+иу=0
при условиях:
у | д._а — ограничено, у | х_, х — ограничено-.
Ответ:
Л = >2, о < V < оо, yv -- С W Jo (vjc).
Из 'Приведенных задач видно, что спектр собственных значе-
ний может иметь различный характер. Так, совокупность,
собственных значений в задачах 1 — 8 образует дискретное
множество. В этих случаях -говорят, что задача Штурма —
Лиувилля имеет дискретный спектр. В задачах 9—12 спектр
собственных значений непрерывный.
Собственные функции задач 1—8, имеющих дискретный
спектр собственных значений, обладают очень, важным свой-
ством — так называемой ортогональностью.
Пусть а^х^Ь, Две функции ср(х) и ф('х). называются
ортогональными на промежутке (n, ft] с весом г(х), если вы-
полняется равенство
ь
J <р (х) ф (х) г (х) dx — 0.
Покажем, что собственные функции задачи Штурма —•
Лиувнлля, соответствующие различным собственным значе-
ниям, ортогональны с весом г(х).
14
Так как собственные функции являются частными реше»
ниямн уравнения Штурма'—'Лиувилля при соответствующем
собственном значении параметра к, то для каждого кп н
уп(х) выражение
^[?W^] + IMW-?W]y.=o
является тождеством. Для другой пары, например Х™ и уто(х),
получим аналогично
+ [vwо.
Если первое из написанных тождеств умножим на ут, а вто-
рое — на уп и вычтем одно из другого, то получим
(Х„ - М г (х) уя (х)ут (х) = у„ (р - ут -±- (р .
Как нетрудно видеть, правая часть последнего равенства
представляет собой полную производную. Поэтому
/. \ ч|____& Г„ (dy?n ,, &Уп\ ]
( ‘п т)ГУпУт dx \Р \Уп dx Ут dx •
Если а х Ь, то после интегрирования по х от а до b по-
лучим
(>'„ - KJ J’ ry„ymdx = р (у„ % - ym 4f) | •
а а
Если собственные функции при х = а и х=Ь удовлетворяют
одному из условий: Уь=®— условие I рода; = 0—L
условие II рода; +йу& = 0 — условие III рода, то пра-
вая часть последнего равенства есть нуль. Тогда при Кт=/=^п
(разные собственные числа) выполняется соотношение
ь
Jr(x)y„(x)ym(x)dx = 0.
а
Если, как в задачах 6—8, на одном или обоих концах
промежутка заданы условия ограниченности, то ортогональ-
ность сохраняется для уравнений, в которых функция р(х)
на этих концах обращается в нуль. Для указанных задач 6—8
последнее условие выполняется. Например, в задаче 6
р(х) =х2 обращается в нуль при х = 0, а в задаче 8 р(х) =
= 1 —х2 обращается в нуль на обоих концах х~ + 1.
Для так называемых условий периодичности (см. зада-
чи 1,к и 2,г) ортогональность сохранится, если р(а)=р(Ь)._
16
Для указанных задач (1 и 2) это условие, очевидно, выпол-
нено, так как р(х)==1.
Таким образом, во всех указанных случаях собственные
функции образуют системы ортогональных функций с весом,
равным г(х). Пусть теперь задана некоторая функция f(x)
в промежутке [а, 6]. Разложим ее в ряд по собственным
функциям задачи Штурма — Лиувилля
/W ~ Хс4у6(*)-
(Ч>
Ряды такого вида получили название рядов Фурье. Фор-
мально коэффициенты ряда Фурье можно найти следующим
несложным приемом. Умножим левую и правую части ряда
на произведение уп(х)г(х) и проинтегрируем по х от а до Ь.
После почленного интегрирования ряда в правой части
остается только n-н член, так как все остальные члены ряда
ь
будут содержать множители J* УпУк^йх, равные нулю в силу
ортогональности собственных функций:
if W г (х) у„ (х) dx = C„iy„2(x)r(x)dx
а а
ИЛИ
17 (х) г (х) у„ |х) dx
jj'n= (x)r(x)dx
а
Следует подчеркнуть, что указанные операции были про-
деланы формально. Они будут справедливы не для всякой
функции f(x). Этому вопросу посвящена обширная литера-
тура (см., например, [10]). Укажем здесь лишь наиболее важ-
ные результаты.
1. Если функция f(x) непрерывна и ее ряд Фурье равно-
мерно сходится, то сумма ряда совпадает с функцией !(х).
2. Если функция f(x) удовлетворяет условиям Дирихле,
т. е. является кусочно-непрерывной и кусочно-монотонной
(последнее означает, что она имеет конечное число максиму-
мов и минимумов), то сумма ряда Фурье внутри промежутка
разложения равна
’ _ /i-у 4~Q) + ft* — 0)
а па краях
16
В этом случае сумма ряда Фурье во всех точках непре-
рывности функции f(x), кроме, может быть, концов, совпа-
дает со значением этой функции, Сам ряд Фурье может ока-
заться неравномерно сходящимся.
Собственные функции задач Штурма — Лиувилля с непре-
рывным спектром собственных значений дают возможность
представлять заданные функции в виде интегральных разло-
жений.
Наиболее часто в математической физике встречаются
следующие интегральные разложения.
Интеграл Фурье
(““<х< + ^),
гдеЛ(у)*= J f(x)ebxdx.
Для справедливости указанной формулы достаточно, если:
а) /(х) удовлетворяет условиям Дирихле в любом конеч-
ном промежутке;
б) интеграл f |/(х) \dx сходится.
В вещественной форме интеграл Фурье записывается так:
/(л) =-1- J (v) co’svx ф- С(») sin vx] dv.
о
где S(v) = f f(x) cos vxdx- C(v) = f f(x) sin vxdx.
Для функций, заданных в промежутке (0, +<»), могут
быть получеиы разложения;
1) S(v)cosyxdv — косинус-интеграл Фурье,
о
B(v)**=J fix) cosvxdx;
о
2) /(х) = —J C(v) sin yxdv — синус-интеграл Фурье,
о
C(v)**= J* f (х) sin vxdx;
* Л ('>) называется интегральным преобразованием Фурье функ-
ции Дх). -------------——
** В (v) и С(\) называются косинус-преобразованием Фурьер ^Ьб.пична-я
нус-преобразованием Фурье функции /(х) соответственно. научно-технкчзская
2 библиодека CCGP
ЭКЗЕМПЛЯР
ЧИТАЛЬНОГО ЗАЛ/
з) /w=4j£,<’)
о
У COS NX -|- л sin NX
/ V2 + Л2
n , . f ,, . n cosnx + h sin nx , . . n
D(v) = I f(x)--------. -----ах, л > 0.
4 ’ У 7/ № + Й*
Интеграл Ханкеля
f(x) = f'iM(->')J(vx)dy (0<x<+co).
u
/И (v)« = f xf(x) (ух) dx (y. > - 4*)
0
Для справедливости указанной формулы достаточно, если
a) f (х) удовлетворяет условиям Дирихле в любом конеч-
ном промежутке;
6) J У-х \f (х) | dx сходится,
о
13. Разложить в ряды Фурье по собственным функциям
задачи Штурма — Лиувилля
y"-f-ty = O, У |Х=,1 = УУ'|л_г = У'|х—I
следующие функции:
(0 — /
а)/(х) = х2; б)/(х)= »
Ответ:
X 9 I2
а) *2 = —
б) /(х) =
ппх .
cos—Т- +
* М (n) называется интегральным преобразованием Ханкеля функ-
ции /(х).
18
14. Разложить в ряд Фурье по собственным функциям за-
дачи Штурма — Лиувилля
у"^Ху = О, y|v_o = O, у|х=( = 0
функцию
/(%)=№.
Ответ:
~ Пт.Х
[<->)” (4- -0-4^У4-
(1=1
15. Разложить в ряд Фурье по собственным функциям за-
дачи Штурма — Лиувилля
у"+>.у = О, - у' + hy | = 0, у|х_„ = 0
линейную функцию
/(х) ~ 1 -г сх.
Ответ;
V 1+с«-(1------. х
4- сх = 4 / ।---о-------------sin г- ( 1--),
1 sin 2-рг ,л\ а /’
л—1
где уп — положительные корни уравнения tgy = —.
16. Разложить в ряды Фурье по собственным функциям
задачи Штурма — Лиувилля
4 (*4) + 4-^=« у 1-=°> у и ~0
следующие функции: a) f(x) = l; б) f(x)=x.
17. Разложить в ряд Фурье по собственным функциям
задачи Штурма — Лиувилля
^г(х3^-)+,х2>' = 0’ ~<М_а = 0’ У|,=о-ограничено
функцию f(x) = X2.
Ответ:
ЗД2 ,
5 '
4дЗ sin ь
х 7«s sin in ’
П=1
где уп—'положительные корни уравнения tgy = y-
18. Разложить в ряд Фурье по собственным функциям
задачи Штурма — Лиувилля
+>'Х2У = О, ^г + Ау|,..„^0, ограничено
функцию f(x) = С2 — X2.
Ответ:
,2 _ ,2 _ ™ VI 1А l^-^-2a]+6^ • их
п=1
где уп— положительные корни уравнения tgy—
19. Разложить в ряды по собственным функциям задачи
Штурма — Лиувилля*
л-)+иУ = 0’ = У Ц=о-ограничено
следующие функции:
а)/(х) = 1; б) f(x) =0? — в) f(x)=J0(ax).
Ответ:
а’ 1=22j4h^
П = 1
б) а2 — х2 = 8а2
* Ряды по этим функциям носят название рядов Фурье—Бесселя.
20
в) Jq (ал) = 2J0 (аа)
Здесь у—положительные корни уравнения J0(y) =0.
20. Разложить в ряд по собственным функциям задачи
Штурма — Лиувилля*
-гг(л^-) У ограничено
фукнцию f (х) = X2.
Ответ:
а +4 7,4(7») ’
где уп — положительные корни уравнения /| (у) = 0.
21. Разложить в ряд по собственным функциям задачи
Штурма — Лиувилля*
~^(х~7ьг) + )'хУ = 0’ + АУ |х_« = °, у |,_0-ограничено
функцию f(x) = 1.
Ответ:
;,У Л(7,)л(ъ-^)
•Xrf 7» №! 1Ы +Л’(7»)1 ’
Л = 1
где уп — положительные корпи уравнения Ла/0(у) == Wi('[)•
22. Получить интегральные разложения функции /(х) =
= е~ах (0<х<оо, а>0) по собственным функциям за-
дач 9.
Ответ:
б) е-«=2±Г_^£_Л;
7 Л J ч2 -L- а2 1
О П
2 (о + Л) f » cos чх + h sin :х ,
’ ~ " J (»г + Л2) I'-2 + а2)
Ряды в задачах 20 и 21 носят общее название рядов Дини.
21
23. Получить интегральные разложения функции
fl, 0 < х < а,
'Но, а<х<оо,
по собственным функциям задач 9.
Отв ет:
Г
а) /(х)=_ I _____-__sinvXfA;
nJ v
о
,, •. 2 f sin ча ,
б) Дх) = — J —-—COS vxd'i\
о
Of ча ча\
л I I ч cos -к-+ п sin -я- I sin ча
в) f(x) = — J --,Р + А—б) 7---('cos« + hsinw)di.
О
24. Получить интегральное разложение по собственным
функциям задачи Штурма — Лиувнлля
^(?£?x)+''xy = 0’ У |*_о~огРаничено’ У | „.-ограничено
следующих функций:
fl 0 < х < а,
a) f(x) = „ .
(0 х> а;
( х2 0<х< а,
б)/« = |о х>а-
в) =
О тв ет:
а) /(^) = л|Л (ш) y0(vx)rfv;
б) / (х) = a J л
и
. Г1 С 4(4X1 ,
в)—
о
22
Глава II
ПОСТАНОВКА ЗАДАЧ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
25. Написать начальные -и граничные условия в задаче
о колебаниях струны с закрепленными концами
которая в начальный момент времени / = 0 оттянута в точке
х = с на заданную величину h и отпущена без начальной
скорости.
Ответ:
«|(=0 =/(•*) =
ди I
dt I г=о
— 0; •
26. В точке х = с струны (0 х I) укреплен сосредо-
точенный грузик массой Написать уравнения, опреде-
ляющие процесс колебаний при произвольных начальных
условиях, предполагая, что концы струны закреплены.
Ответ:
_ | ult 0< х<с,
U I «2, с < х < Z, д*а
1 d2ut „ /. , лх
7г — 0 (^ — 1, 2).
Граничные условия:
__ /п0 д?и I
— ~Т~ ~д&\х=с''
начальные условия:
“|(=0=/W> "5г|м = г(4
27. Получить дифференциальное уравнение продольных
колебаний тонкого стержня постоянного сечения 5.
Сформулировать начальные и граничные условия задачи
о продольных колебаниях стержня для следующих частных
случаев:
а) стержень длиной I закреплен на конце №0 и растянут
силой F, приложенной к другому концу; в момент I — 0 дей-
ствие силы внезапно прекращается;
б) к концу х = 1 стержня, находящегося в состоянии рав-
новесия, прикладывается в момент £ = 0 растягивающая
сила F(t);
23
в) стержень, закрепленный в точке х = 0, с грузом мас-
сой Мо на свободном 'конце х = 1 совершает продольные ко-
лебания при произвольных начальных условиях.
Ответ:
д2и____1 д‘2и _р __ -| Г Е .
дх2 v2 dt2 ’ гр’
= >L = 0' “I--0- ^=/ = 0;
б)«|;=0=о, 4fLo=o, «|^=о, ;
В) ^-0=/W. »|.r=o = °- 4rUi =
__ Л10 д2и |
” “ ~ES It2'1 •
28. Получить дифференциальное уравнение поперечных
колебаний тонкого стержня постоянного сечения S.
Сформулировать граничные условия, если колец стержня:
а) заделан, б) подперт, в) свободен.
Ответ:
<>Ц I I „ п Л2 _
дх± “г b2 dt2 и’ и р5'’ ।
где р — плотность; /—момент инерции сечения; Е — модуль
Юнга материала стержня.
На границе:
а) и = 0, -4^- = 0;
' 'ох ’
29. Бесконечный цилиндрический проводник радиуса а,
начальная температура которого совпадает с температурой
окружающей среды, принимаемой за нуль, нагревается с мо-
мента / = 0 постоянным током, выделяющим в единице объе-
ма проводника тепло Q. Дать математическую формулиров-
ку задачи теплопроводности, предполагая, что отдача тепла
с поверхности проводника происходит: а) -по закону Ньюто-
на; б) через тепловую емкость.
24
Ответ:
Температура Т (г, t) удовлетворяет уравнению
i а / ^L\ — Л.____( .kt \
г дг \ дг ) ~ дх k V ср ) ’
начальному условию 7J,t=0=O и граничным условиям
а) 4г-ЛГ1,-«^°-
_ дТ , 1 дТ I л Со
б) ЯТ>Г + Т 'дТ - °’ Я = 1^Г’
где Со — тепловая емкость на единицу длины.
30. Однородный шар радиуса а в течение длительного
времени нагревался источниками тепла, распределенными по
его объему с постоянной плотностью. Написать уравнения,
определяющие процесс остывания шара после выключения
источников, считая, что теплоотдача с поверхности шара
в окружающее пространство как во время нагрева, так и
при охлаждении происходила по закону Ньютона.
Ответ:
_!__ /iT'i —о
г2 dr \ dr / dx ’ dr Ir=a ’
ri —- М2 _ r2i j______2fL
1 I т=о 6A M
31. Две пластинки толщиной at и a2, изготовленные из.
различных материалов и нагретые до температур Т° и Т2°,.
в момент t = Q вводятся в соприкосновение одна с другой.
Написать уравнения, определяющие процесс выравнивания
температур, считая, что свободные грани теплоизолированы
от окружающего пространства.
Ответ:
гл
дх? ft, dt {
д?Т2 _ с2р2 дТ2 ,
дх? Л2 dt 1
а,);
Граничные условия:
тг-1 =°> Лк
дх I х~к * 11 х
- k «i I
. дТ\ :
«1 “3— :
1 дх ;
начальные условия:
6Т, I
дх |
= 0;
Ч -02
Т.\
25
32. Пластинка толщиной а нагрета до температуры То.
К грани х — а присоединена тепловая емкость Со, а грань
х — 0 излучает тепло в окружающую среду по закону Ньюто-
на. Написать уравнение задачи, начальные и граничные
условия.
Ответ:
&Т _ с? дТ
дх* k dt '
Граничные условия:
дТ , , ,г| Л , дТ | „ дТ [
““Э7 + Л/Ъ-о-°’ ’ C»“STl.r-0’
начальное условие
Г|(_о=7’о.
где Со — тепловая емкость на единицу площади.
33. Сформулировать начальные и граничные условия
в задаче распространения колебаний в линии, обладающей
самоиндукцией L, емкостью С, сопротивлением R и утечкой
G на единицу длины, для следующих частных случаев:
а) в момент ^ = 0 на одном конце линии через сосредо-
точенное сопротивление Ro включается постоянное напряже-
ние Е, а другой конец замкнут на катушку с самоиндук-
цией Lq',
б) в момент t = 0 на одном конце линии через емкость Со
включается постоянное напряжение Е, а другой конец ра-
зомкнут;
в) один конец линии заземлен, а на другом конце, через
катушку с самоиндукцией Lo, включается постоянное напря-
жение Е.
Ответ:
а) иj х=-)= ~ | .t==o’ и | x=t= [ x=i ’
б) «|,=0 = £-^-р|^Л, 0;
' о
в) —£0-зг| wj.v„j = O, «|(=о=0, /|f^0=O.
26
Глава Hl
МЕТОД СОБСТВЕННЫХ ФУНКЦИЙ
В настоящей главе рассматриваются задачи математиче-
ской физики, описываемые уравнениями вида
-?««}+-Ч« = у) (‘)
(а<х. <6, c<.y<Zd),
Л(^), В(у), С(у), F(x, у) — заданные функции своих аргу-
ментов.
Граничные н начальные условия, накладываемые на иско-
мую функцию и(х, у), могут быть различными. Если уравне-
ние (1) не имеет особых точек в промежутке {а, Ь], включая
его концы, то искомая функция и{х, у) по переменной х
обычно удовлетворяет граничным условиям вида
aa^\x_a + ^\x.a-L(y).
а4-^[л_4+МЬ_6 = Л(>').
(2)
где Оа? Ра, аь и рь — постоянные, часть которых может рав-
няться нулю, нли
ди 1
дх | л=а
ди I
дх |х=ь'
(3)
Характер условий по второй переменной у определяется на
всем промежутке функцией А (у).
В случае, если А>0, эти условия имеют вид граничных
условий, т. е.
(4)
При Л<0 и Л = 0 переменная у играет роль времени и
условия принимают вид
^-\y.=sM (5)
ИЛИ
«|^с-/(%). (6)
27
В случае, когда уравнение (1) имеет особенности на
одном или обоих концах (сингулярные концы) промежутка
(а, Ь) или промежуток (а, Ь) бесконечен, то граничное усло-
вие, относящееся к такому сингулярному концу или к концу
х = Ь->оо, обычно заключается в требовании ограниченно-
сти решения на этом конце. На другом конце промежутка,
если он не сингулярный, ставится обычное граничное условие.
Для поставленной задачи математической физики соб-
ственные функции Х(х) по переменной х будут решениями
следующей задачи Штурма — Лиувилля:
(7)
при условиях
°-<Х' I + РЛ = °- “Л' I х=„ = о,
если искомая функция и удовлетворяет (2), и при условиях
если и удовлетворяет (3).
Одним из важнейших методов решения рассматриваемых
задач математической физики, имеющих дискретный спектр
собственных значений, является метод собственных функций.
Основная идея этого метода заключается в том, что реше-
ние представляется в виде ряда по собственным функциям
данной задачи
и(х, у) = s Г„(у)Х„(л)®. (8}
<х«>
Если уравнение (1) и условия по переменной х однород-
ны, то коэффициенты разложения Уп(#) в (8) можно найти,
методом разделения переменных (метод Фурье). Согласно
методу Фурье частные решения уравнения (1) разыскива-
ются в виде произведения двух функций, каждая из которых
•зависит от одной переменной
« (х, у) — X (х) Y (х).
Чтобы и(х, у) удовлетворяло однородным условиям по-
переменной х, функции Х(х) должны 'быть собственными,
функциями данной задачи.
* В случае условия (3) функция Хп (х) может иметь вид
и - С„Х<Ч (JT) + о„4г) W.
где 4”" х„2> — линейно-независимые функции.
28
Для функции Уп(#), (соответствующей собственной функ-
ции Хп(х), после разделения переменных получаем урав-
нение
Л^(Гл)-л„Г„=0,
где л,( — n-е собственное число.
Общий интеграл последнего уравнения может быть запи-
сан в виде
+ (у),
тде и У„2> (у) —линейно-независимые решения урав-
нения.
Таким образом, мы получим совокупность частных реше-
ний вида
у) = Г,(у)А'лМ)-
Чтобы удовлетворить условиям по переменной у, состав-
ляем суперпозицию в виде ряда
= 2 [W (У> + (8')
Коэффициенты этого ряда определяем, подставляя (8')
в условия по переменной у, что приводит к разложению за-
данных функций в ряды по собственным функциям.
Задачи математической физики с неоднородными диффе-
ренциальными уравнениями и неоднородными граничными
условиями могут быть решены методом Фурье, если с по-
мощью того или иного приема они приводятся к однородным.
К таким приемам относится, например, нахождение частного
решения и* уравнения (1), удовлетворяющего условиям (2).
Поэтому, если и{х, у) представить в виде и(х, у) =
= w* + wi, то «1(х, у) есть решение соответствующего одно-
родного уравнения при однородных граничных условиях, т. е.
может быть найдено методом Фурье.
В общем случае коэффициенты ряда (8) для неоднород-
ных задач могут быть найдены методом Гринберга (метод
конечных интегральных преобразований). Так как собствен-
ные функции Хп(х) ортогональны, Yn(y) может быть пред-
ставлена в виде
_ ь ь
где «„(y)=J«(x,y)X„(x)r(jc)a'x; N„ = Г Хп2 (x)r (jc) dx.
а а
Если в операторе Му Л (у) =0, то решение и (х, у) имеет вид
«у) = 2 Y’1 w %п W-
29
Для определения мп(//) построим дифференциальное-
уравнение, умножив все члены уравнения (1) на г(х)Хп(х)
н проинтегрировав по х в пределах от а до Ь. Это уравнение
имеет вид
/Иу(и„)-Х.А=/„(у),
где функции fn(y) оказываются известными благодаря тому,
что Xn(x) есть собственные функции данной задачи.
В случае непрерывного спектра собственных значений
искомое решение строится в форме разложения в интеграл
по собственным функциям. Неизвестные функции от у в ука-
занном разложении могут быть найдены методом разделе-
ния переменных в случае однородных задач, что приводит
к разложению заданных функций в интегралы Фурье, Хан-
келя, Вебера и т. д.
В случае неоднородных задач применяются методы ин-
тегральных .преобразований (Фурье, Ханкеля, Вебера и т. д.).
34. Найтн собственные частоты:
а) продольных колебаний стержня длиной 1\
б) поперечных колебаний струны с закрепленными кон-
цами (О % О-
Ответ:
а) —ст, я = 0, 1, 2,...;
6)wn = -^v, п= 1,2,3........
35. Определить собственные частоты радиальных колеба-
ний круглой мембраны радиуса а.
Ответ:
= К= 1, 2, 3,...,
где уп — положительные корни уравнения /о(у)=О-
36. Струна длиной I закреплена в точках х = 0 и х=1.
Найти форму вынужденных колебаний, вызванных силой
A sin (со/ 4-ф), если она:
а) сосредоточена в точке х — с струны (0<с<Ч);
б) равномерно распределена
Ответ:
И(Л-, С = .sl1' +
' ' о>/ . <о/
sin-----
V
по длине струны,
шХ . ш {[ — С) '
sin — sin—-------
wt? . w (I — X) , , }
sin----sin —i, c <T X t;
MX 0) (/ — X)
6) «CM) = -|^- —— S‘n,„f W -sin(«rf H)-
COS
30
37. Найти форму вынужденных продольных колебаний
стержня, конец х = 0 которого закреплен, а конец х=1 на-
ходится под действием силы Л sin (о>/ + ф).
Ответ:
. S1D-------------------------
, Av о . . , . ,
11 (*’ ------------- sln
cos---
38. Круглая мембрана радиуса а закреплена по контуру.
Найти, форму вынужденных колебаний, вызванных нагрузкой
плотностью q sin (o>f-}-<p), если она равномерно распределена:
а) по всей поверхности мембраны;
б) по кругу радиуса
Ответ:
б) и t) =
а) и (г, 1)=—^
' ' ’ ‘ ПфЛ
Ttbqv sin (<о/
2^7
sin (ш£ 4* ?)•
Гг0(——
L 0 \ V J 1 \ V ) J\ V / 1\O /J ПшЬг
4v“j
39. Найти собственные частоты поперечных колебаний
стержня длиной I с закрепленными концами.
Ответ: ___
“» = 4ь2; «=1,2,3,...; =
у — положительные корни уравнения chyoosy=l.
40. Найти форму вынужденных колебаний стержня,
опертого в точках х = 0 и х—1 н находящегося под дей-
ствием равномерно распределенной натрузки плотностью
<7 sin cot
Ответ:
31
41. Струна, концы которой закреплены в точках х = 0 и
х = 1, оття.нута в начальный момент времени в точке х=с
и отпущена без начальной скорости.
Определить смещение и{х, t) любой точки струны, если
и(с, 0) = h.
Ответ:
И (х, f) =
2hP
т;2с (/ — с)
П~ 1
пкс . ЛПХ nnvt
-у- sin —т— COS —7— .
42. Найтн закон колебаний струны, начальная форма
смещения которой изображена на рис. 1, а начальная ско-
рость всех ее точек равна нулю.
43. Дать решение предыдущей задачи при условии, что
в начальный «момент времени точки струны отклонены по
параболе, симметричной относительно центра струны, при-
чем максимальное начальное смещение равно А.
Ответ:
2n + 1 2« т 1
cos—кх cos ^-wt.
44. В начальный момент времени центру струны, закреп-
ленной на концах х = — I и х = 1, сообщается ударный им-
пульс величиной Р. Определить дальнейшие колебания точек
струны.
Ответ:
и (х, t)=
2л+ 1
cos 21 ~х . 2и-|-1 ,
32
Указание. Рассмотреть ’Колебания струны при следую-
щих начальных условиях:
I л I I ^0=^7 при |л|<г,
«;(=о=о, -*-!„„=
[ 0 при < I,
и в дальнейшем осуществить предельный переход при е-»-0.
М — масса струны.
45. Изучить колебания струны, закрепленной в точках
Л' —О И х—1, вызванные внезапно приложенной нагрузкой,
распределенной с постоянной |Плотностью q по длине струны
и остающейся в дальнейшем неизменной. В начальный мо-
ьмент времени струна находилась в покое.
Отв ет:
и (х,
Sin--t-Лх
I 2n-4-I ,
—гтгСОЗ—~KVt
46. Струна длиной I с закрепленными концами колеб-
лется под действием равномерно распределенной пульсирую-
щей нагрузки 7 sin at Найти форму колебаний струны, счи-
тая, что в момент времени f = 0 опа находилась в состоянии
покоя.
Ответ;
и (х, t) =
~^Т
sin м/ -
л=0
. 2п 4-1 , . 2л -|- I
Sin --------T.l't Sin-----J---7ГХ
(2«+O! [1
(2n+ 1)J
47. Решить предыдущую задачу в предположении, что
пульсирующая нагрузка действует только на участке струны
а<^х<^Ь.
Ответ:
3
48. Исследовать колебания струны, вызванные сосредото-
ченной пульсирующей силой A sin wt, приложенной в момент
t — Q в произвольной точке х=с струны.
Ответ:
49. Стержень длиной I, закрепленный в точке х = 0, рас-
тянут силой F, приложенной на его другом конце. Исследо-
вать продольные колебания стержня при условии, что в мо-
мент времени f = 0 действие силы внезапно прекращается.
Ответ:
, хч 8F/ VI (—’У2 . 2л+1 2л -j-1 .
2d С^+ ‘Fя"™cosT'vt-
50. Рассмотреть вертикальные продольные колебания
стержня длиной I, подвешенного за конец х=0, совершаю-
щиеся под действием собственного веса. Начальные условия
считать нулевыми. \
Ответ:
“(*> — Л'(1 21 )
51. Исследовать продольные колебания стержня, конец
х = 0 которого закреплен, а конец х = 1 начиная с момента
времени t = Q движется по закону и(1, £)=Л5шсйЛ
Ответ:
ИХ
sin---- 9
п (х, t) = А-----sin <•>£-!—Д
' ’ ' ш/ 1 ГС2и
sin----
V
/?=1
52. Найти смещение точек закрепленного на конце % —О
стержня, совершающего продольные колебания под дейст-
вием пульсирующей силы A sin cot, прикладываемой к его
34
свободному концу х — l. До начала действия силы стержень
находится в состоянии покоя.
Ответ:
sin---
V . j_
------7- S ПС)Г —
ш/
cos---
V
53. Грани пластины толщиной 2а (рис. 2), нагретой до
температуры То, начиная с момента времени t — 0 поддержи-
ваются при температуре, равной пулю. Найти распределение
температуры в пластине.
Ответ:
т, s 4Г0 W-l)" ' 2fl ’ 2И-1-1
cos-^b«-
п-0
54. Найти закон выравнивания заданного начального
распределения f(x) температуры в пластине, грани которой
х=0 и х = а не пропускают тепла.
Ответ:
1 а м _ п2л27 а
= “3 созЛуу(Е)со<.'у.Й.
О /2=1 О
55. Пластина толщиной 2а (—а х а) с заданным
начальным распределением температуры Т(х, 0)=/(х) на-
чиная с момента времени г1—0 излучает тепло-в окружаю-
щую среду, температура которой принимается равной нулю.
Считая, что излучение подчиняется закону Ньютона, найти
распределение температуры в пластине в произвольный мо-
мент времени.
Ответ:
7(E)cos^-<&4-
7(E) sin-^dE,
35
где yn — положительные кор-нн уравнения tgy—яй/у; ул —
положительные .корни уравнения tgy = — (y/ah).
56. В пластине толщиной 2а (—а х а) начиная с мо-
мента £ = 0 происходит тепловыделение с постоянной плот-
ностью Q. Найти распределение температуры в пластине при
условии, что ее грани поддерживаются при температуре нуль,
начальная температура также равна нулю.
Ответ:
V ( -1)”
а2 / rJk 12л -j- ll3
л-0
(2л ' 1 )^1J
4«s
: 2/1^1
COS -75--XX.
2a
57. Исследовать процесс нагрева пластинки, через грань
х== 0 которой начиная с момента t = 0 подается тепловой
Рис, 2
Рис. 3
поток постоянной плотности q3 а грань х = 0 поддерживается
при температуре То. Найти распределение температуры
в-любой момент времени, считая, что в начальный момент
она равна нулю,
Ответ:
Пх,х)=Го + ^(1-^)-
(2«+ 1р
58. Через проводник, сечение которого изображено на
рис. 3, пропускается, начиная с момента t = Q, постоянный
ток, выделяющий джоуле во тепло плотностью Q. Найти рас-
пределение температуры в проводнике, считая, что отдача
36
тепла в окружающую среду происходит по закону Ньютона
и начальная температура равна нулю.
Ответ:
59. В пластине толщиной а на грань х~а подается теп-
ловой поток постоянной плотности q, а грань х = 0 излучает
тепло по закону Ньютона. Найти Т(х, /), если начальная
температура пластины равна нулю. ।
Ответ:
где уп — положительные корни уравнения ctgy=—
60. Линия без потерь длиной I с параметрами С заря-
жена до постоянного напряжения Е и разомкнута на обоих
концах. Определить величину тока в каждой точке линии,
предполагая, что конец х = 1 замыкается в момент f = 0 на
катушку самоиндукции Lo.
Ответ:
/ (x, t) =
где у„ — положительные корни уравиеиия tgy = —; а==
— -и=-т=; Z^Lu.
Lo / kC
61. Линия с параметрами L, С, R коротко замкнута на
конце х = 1, а другим концом х — 0 присоединяется к источ-
нику постоянной э. д. с. Е. Найти распределение напряжения
вдоль линии, считая начальные условия нулевыми.
37
Ответ:
ll(x, ^ = £(1-^-)-
Zn = Lvn.
1 /". /?2С/2
где vn = , 1 / 1----------
/ТС у 4nWL
62. Линия длиной I с параметрами L, С, R. присоединена
да конце х=0 к источнику постоянной э. д. с. Е, а на другом
конце замкнута на сопротивление /?о. Найти значение напря-
жения в линии -после внезапного отключения нагрузки RQ.
Ответ:
fit »
“ (х, t) = E - (1 + 0) е [cos ~
л=0
. . „ . 2л + 1
W . 2« + 1 J ЬЧ-
Ktv„(2n + l) Sln '21 ’"’“Ч (2 л + 1?
1 1/1 ЮСР
’Vn~ /ЛС V (2и-£ 1)=Д™= ’
А
IR
63. Решить задачу об остывании однородного стержня
с теплоизолированной боковой поверхностью, если его на-
чальная температура Т(х, 0) = 2Тй~, конец х=0 теплоизо-
лирован, а другой конец х = 1 поддерживается при постоян-
ной температуре Tq.
Ответ:
T(x,^=.TQ-
n(2nd-1)
64. Решить задачу теплопроводности для пластины тол-
щиной а при условии, что грань х = 0 поддерживается при
температуре 7 = f(x), а грань х = а имеет температуру, рав-
38
ную нулю. Рассмотреть частные случаи: a) f(r)=7'0;
б) /(т)=Лт. Начальная температура пластины равна нулю.
Ответ:
Т('х’ л sin (“j" S>ds-
n=l 0
В частных случаях:
а) Т(х,т) = Т0 I
а
б) Т(х, г) = А I - v)T
_2Л/2-^-'| +
6 у а ! \ а J
Л = 1
65. Найти распределение температуры в пластине, грань
х=0 которой излучает тепло в окружающую среду по зако-
ну Ньютона, а другая грань х = а поддерживается при тем-
пературе То, равной начальной температуре пластины.
Ответ:
(?-V^sin7,Ll£^)'|
Т(х, г) = Та
Г I + Ллг
[ 1 + ha
4 V1 cos tn
2-(„ — sin 2у„
Л = 1
где уц — положительные корни уравнения tgy =
66. Найти напряжение в кабеле (£=G = 0) длиной /,
конец х = 0 которого подключен к источнику постоянной
э. д. с. Е, а конец х — 1 замкнут на омическую нагрузку /?0-
Ответ:
Здесь у?1— положительные корни уравнения tqу =----;
39
67. Кабель сопротивлением /? и емкостью С на единицу
длины заземлен в точке х = 1. При 2 = 0в точке х = 0 к ка-
белю через сопротивление Ro приложена постоянная э. д. с. Е.
Определить потенциал в точке х.
где \п— положительные -корни уравнения tgy = —
68. Свободная от искажений (RC = LG) линия длиной I
заземлена в точке х—1. Начальные ток и заряд равны нулю.
В момент времени t — Q в точке х = 0 приложена постоян-
ная э. д. с. Е. Найти потенциал в точке х.
Ответ:
sh VRGt‘ (I -4-')
« (л, f) = Е----------_
' sh/ftGZ-’
_ /? »
_ L 1 n ( nizvt , R1 . nnvt\ , nr.x
2, +*a‘2' ‘+sin ’
/1—1
69. Найтн распределение потенциала электростатического
поля и(х, у) внутри вытянутой коробки прямоугольного се-
чения (рнс. 4), две противоположные грани которой нахо-
дятся при потенциале V, а две другие заземлены.
Ответ:
(-!)«
ц=0
. 2п Н- 1 2л + I
сп—— -х COS-—;—itv
b b J
^n+1 2n + 1“
ch-7-™ - •
40
70. Найти распределение электростатического потенциала
внутри полубесконечнон прямоугольной -коробки (рис. 5),
вертикальная стенка которой поддерживается -при потенциа-
ле V, а горизонтальные стенки — при потенциале, равном
нулю.
Ответ:
K(x,y) = ^arctgr^.
8,1 “Г
Указание. Для представления решения в замкнутой
форме воспользоваться разложением
e~(2n+i).r I sin у ,
2j —2V+ 1— sin (2л I)у = -5- arctg (х > 0).
71. Найти распределннс потенциала электростатического
•поля между двумя бесконечными параллельными пластина-
ми, одна из которых (у = 0) находится при потенциале, рав-
ном нулю, а на другой поддерживается заданное периодиче-
ское распределение потенциала u\y=sh = f(x), где f — перио-
дическая функция с заданным периодом 2а.-
Ответ:
2а 2а
sin J/ (Е) Sin + J/(Е) di.
О о
72. Рассчитать плоское электростатическое поле для кон-
струкции электродов, изображенных на рис. 6.
О т в ет:
а) и(х,у) =
п—I
4-sh-~[a-'r/2(y-.r)]}
п пк
И
73. Найти распределение потенциала электростатического
поля в электронно-оптическом устройстве, представленном на
рис. 7. Получить выражение для распределения потенциала
в плоскости симметрии.
Ответ:
Рис. 6 Рис. 7
74. Найти стационарное распределение температуры
Т(х, у) в бесконечно длинном брусе прямоугольного сечения
(рис. 8), три грани которого находятся при температуре,
равной нулю, а па четвертой поддерживается заданное рас-
пределение температуры Т(х, b)=f(x). Применить получен-
ные общие формулы к частному случаю f (х) = То-
Ответ:
а
Vsh ПГ'У С*
/(=)Sin^Ld£.
z I sh-----
a v
n=i о
В частном случае:
. 2л+ 1
sin !—
2л-г'1 ‘
42
75. Прямоугольный брус состоит из двух кусков с различ-
ными коэффициентами теплопроводности (рис. 9). Найти
распределение температуры в брусе, предполагая, что две
противоположные грани (*/ = + ^) находятся при темпера-
туре То, а две другие — при температуре нуль.
Ответ:
Л <Х) =
sinsin , 0<x< a,;
а-! ’ *’
• 'in а-, — х\ .
sin м -- sin 7Л, О; < х < 4" «2-
Рис. 8 Рис. 9
Здесь уп — последовательные положительные корни урав-
нения
где ki и k2—коэффициенты теплопроводности материалов.
76. Найти распределение температуры в брусе прямоуголь-
ного оечеиия, две противоположные грани y=Q и у — b ко-
торого находятся соответственно при температурах пуль и
То, а две другие излучают тепло по закону Ньюто-
на в окружающую среду с температурой, равной нулю.
Ответ:
sh7„-^
ч п.,, Ж swr. 1 а
Т (Х, у ) = 2 1 о у -----:-:--------------j— COS -
v / I + sm 7/1 cos & *”
sn 'М а
л=1
, ah
где ул — положительные корни уравнения tgy ——
43
77. Найти форму равновесия прямоугольной мембраны со-
сторонами 2а и 2Ь, находящейся под действием равномерно
распределенной нагрузки q.
Ответ:
и (х, у) = X
78. Две грани прямоугольного бруса покрыты тепловой
изоляцией, две другие поддерживаются при температуре,
равной нулю (рнс. 10). Найти стационарное распределение
температуры при условии, что в брусе выделяется тепло
плотностью Q.
Ответ:
Н-мЬ^х
79. Найти стационарное распределение температуры
в брусе прямоугольного сечеиия (0 х а,
если грани х — а и у — Ь поддерживаются при температурах
Г1 и Тз соответственно, а остальные грани — при температу-
ре, равной нулю.
Ответ;
-= 1
( —l)"]}sh пк 4+(~shnn —-
b
nshnn-^-
Sln
44
80. Найти стационарное распределение температуры
в проводнике прямоугольного сечения, нагреваемом постоян-
ным током, выделяющим тепло Q в единице объема, считая,
что теплоотдача с поверхности проводника происходит по за-
кону Ньютона.
Ответ: Т(х, У)=~^Х
где уп — положительные корни
уравнения tgy = a/2./y.
81. Поток тепла Q втекает
через две противоположные гра-
ни бруса прямоугольного сече-
ния и вытекает через две другие
(рис. II). Найти стационарное
распределение температуры в
брусе, предполагая, что втекаю-
Рис. 13
щий и вытекающий потоки распределены по граням с равно-
мерной плотностью.
Ответ:
т = “2^г 1у (* -.у) - * ~ x)i +const
82. В брусе (рис. 12) происходит выделение тепла плот-
ностью Q. Найти стационарное распределение температуры
в предположении, что тепло отводится потоком постоянной
плотности через участок |х|<^ с верхней грани, а остальная
часть поверхности покрыта тепловой изоляцией.
Ответ:
-г/ ч Q Р2
Па У) = --А~ у"
----7 cos-- 1 — const.
пкЬ а
sh— I
83. В брусе прямоугольного сечения (О^х^а, О^у^Ь)
происходит объемное тепловыделение с постоянной плот-
ностью Q. Найти стационарное распределение температуры
при следующих граничных условиях (рис. 13):
дТ дТ\ J ~/Г ’
rUo=?-«. rU=o, О, С<х<а.
45
О т в е т:
х \1 sh~X-[z'° + ^5'1-msT°l] ch^~У1 х
I 2y„ - sin 2T„) ch
X sin ,
где yn — положительные корни уравнения1 tg-y^----X-..
84. Дать общее решение задачи об охлаждении ш&ра
.радиуса а при условии, что начальное распределение тем-
пературы шара задано Т(г, 0) =f(r), а температура поверх-
ности равна нулю. Рассмотреть частный случай, f(r) = Tq.
Ответ:
Т(-г- sinZXp(p)psin2,Frfp-
л=1 0
В частном случае
” п**!
X 2a.Tr, V (—I)"-1 at . n-r
n = 1
85. Найти распределение температуры в шаре радиуса
а, поверхность .которого начиная с момента / = 0 излучает
тепло по закону Ньютона, а начальная температура равна То.
Ответ:
Г (г - -ЛГ^а3__ V C0Sb : г --тН
* ’ ' r[l — ha] 2Tw -sin2bm 1Л а е
где \г> — положительные корни уравнения tgy = } _^Ла»
86. Тело, имеющее форму шара радиуса а, длительное
время подвергалось нагреву путем объемного тепловыделе-
ния плотностью Q. Исследовать процесс -выстывания после
прекращения нагрева, принимая, что охлаждение происходит'
46
путем излучения с (Поверхности, и считая температуру воз-
духа в камере, где производился нагрев, равной То-
Ответ:
Т(г, х) = Т(> х У si„ > ,
где ул — положительные корпи уравнения tgy = ^—1~.
87. Найти распределение температуры в шаре радиуса а,
внутри которого начиная с момента / = 0 происходит выде-
ление тепла плотностью Q. Начальная температура шара
равна нулю, а на границе:
а) поддерживается постоянная температура То;
б) происходит теплоотдача потоком постоянной плотно-
сти q\
в) происходит излучение в окружающую среду по закону
Ньютона.
Ответ:
а) = н
+ d+ *p’sln-;
"r / । n L kn2n2 J a
n =1
b ’ ] — ha '
88. Решить задачу об обтекании шара радиуса а пло-
скопараллельным потоком идеальной жидкости. Начало сфе-
рической системы координат (г, 0, ср) выбрать в центре шара
и ось z направить в сторону, противоположную направлению
потока.
47
Ответ;
и (г, 0) = г,Дг+-^-)cos6 4-const,
где Voo — значение скорости потока вдали от шара.
89. Найти электростатическое поле точечного заряда 7,
помещенного на расстоянии b от центра проводящего шара
радиуса а (а<Ь), находящегося ори потенциале и = 0.
Отв ет:
и(г, 0) = -^- + J-,
где R = ]f Ь2 ~г г'2 — 2br cos 0 , R - уЛЬ‘г 4- г2 — 2br cos 6,
/Го- й
ЬЬ = а-, <? = -<?—
90. Решить предыдущую задачу, предполагая, что шар
изготовлен из диэлектрика проницаемостью е.
Ответ:
внутри шара
=4 S (£+"?Л1 Стр» <cos
вне шара
“ 9М- - “ ') S (Г+Л4ПЛ ( р» («s 0)-
91. Найтн потенциал точечного заряда q, помещенного
между проводящими заземленными 1концентрическими сфе-
рами радиусов а и Ъ.
Ответ:
Заряд помещен в точке с координатами г — го и 0 = 0.
48
92. Найти стационарное распределение температуры
в шаре .радиуса а, часть шовepixnости которого Si имеет по-
стоянную температуру То, а остальная часть S2 — темпера-
туру, равную нулю (рис. 14).
Ответ:
Т(г, 0) =
= - cos “ - [/’„„(cos (cos o:)](y)\(cos 9)|.
93. Дать решение предыдущей задачи, предполагая, что
в шаре происходит объемное тепловыделение плотностью Q,
а тепло отводится через поверхность Si нормальным потоком
постоянной плотности. Поверхность S2 не пропускает тепла.
Ответ:
Т(г, 6) = Г — +
к ’ ik [ 2а2 т
. 1 \?Л,+1 !cosa) -P„-i(cos«) ( г у ]
Т 1-cOSa 2J-----------П--------- Ы Р" (C°S ’] + C°nSt
П=1
94. Шар рядиуса а нагревается плоскопараллельным
потоком тепла плотностью q, падающим на его поверхность,
и отдает тепло в окружающую среду в соответствии с зако-
ном Ньютона. Найти стационарное распределение темпера-
туры в шаре.
Ответ:
т (Г, 0)=^-Х
Г 1 , Г cos 0
12ah 1 а 1 4- ah
(4“)2"jP2»(COS °)] •
yi (4к ; 1)^(0)
1 ah) (2п— ])(2я 1 2)
n=i
Указание. Граничное условие
даче имеет вид
в рассматриваемой за-
дТ
or
cosQ,
й
0,
2
95. Два металлических полушария радиуса а, разделен-
ных тонкой изолирующей прокладкой, поддерживаются при
потенциалах V (верхнее) и нуль (нижнее). Найтн распреде-
4 49
пение электростатического потенциала в пространстве между
полушариями.
Ответ:
« (СЮ = 4 [' + S Ш (0) «+1 и(cos 0>]
96. Бесконечный цилиндр радиуса а помещен в плоско-
параллельный поток идеальной жидкости. Найти потенциал
скоростей, считая, что начало координат выбрано в центре
цилиндра, направление оси х противоположно направлению
потока (рис. 15).
Ответ:
и (г, ср) — v* (г + -у-) cos ср 4- const,
где их — значение скорости потока вдали от цилиндра.
97, Найти электростатический потенциал внутри беско-
нечного цилиндра радиуса а, если на поверхности цилиндра
потенциал распределен по закону
U 1г=а = ^COS-’cp.
Ответ:
'?) = -2~(1 +^COs2<f)-
98. Найти функцию и(г, <р), гармоническую в круге радиу-
сом а (рис. 16), при следующих граничных условиях:
a) u|,=<. = f(q>);
б)
в) +Ла|r__„=/(<?).
50
Ответ:
а) 2zJ a- — 2ar cos (т - 8) - г2 7
'о
_ч .• \ , a C^/a\i а2 — 2ar cos (ф — 8) + № .ц
б) И (г, ?) = const — -g— ^ / (») In------'----dB;
О
в) » (г, ?) —
= 4-1 fWd» f Г 4— 2г , r9<-aCO,S(<f-,8i Ml
2л J J v ' J ah a- — 2art cos (<p — 8) r2/2 J
о о
99. Определить стационарное распределение температу-
ры в' брусе, сеченне которого представляет собой криволи-
Рис. 16 Рис. 17 Рис. 18
нейный прямоугольник, две стороны которого образованы
дугами концентрических окружностей, а две другие — отрез-
ками радиусов (рис. 17). Одна из изогнутых граней г=Ь
имеет температуру То, остальные поддерживаются при тем-
пературе, равной нулю.
Ответ:
Т(г,'4) =
2п 1
sin—
2п - 1
100. Решить предыдущую задачу в предположении, что
прн температуре То поддерживается одна из плоских граней
<р = а, остальные грани имеют температуру нуль.
4* 51
Ответ:
T(r, <?) = —
101. Найти распределение температуры в брусе, сечение
которого есть криволинейный прямоугольник
при следующем распределении температуры по
контуру сечения:
Г|_ = о, Г1^ = Г„, а=0 = о, 7-|^ = Т.
Ответ:
102. Решить плоскую электростатическую задачу для
внутренней области прямоугольного сектора (рис. 18), счи-
тая потенциалы дуги и радиусов заданными.
Отв ет;
Другая форма решения:
9 ( P^sh^shU.
и (г, <р) = — I ----- sin и In ) d'i.
J vsh-^- Х
52
103. Внутри заземленной металлической коробки, сечение
которой представляет собой 'криволинейный прямоугольник
(a^r^b, О^ф^а), помещена заряженная иить с заря-
дам q на единицу длины. Определить распределение потен-
циала внутри .коробки.
Рассмотреть частные 'случаи задачи:
а) а = 0, 6 = оо (заряженная нить внутри двугранного
угла);
б) а = 0, 6 = оо, сс = 2л (нить вблизи края проводящей
полуплоскости);
в) 6 = со, а = л, <ро = л/2 (нить под плоскостью с высту-
пом в форме полуцилиндра).
О т в ет:
«(Г, <?) =
Здесь г0, Фо — координаты нити.
В частных случаях:
а)
и [г, с) = q In
б)
,_2(£).СО5М^ + (£р
Я 2тс 5
1 о/ г \~ п (?<}-¥) . ( г \~
I — 2( —- ) COS --- — I — )
\ Го / а \ Го /
в) и (г, ф) = q In
г / г V а2 / л2 \21
1 + Ы 1 - 2 .
1 - 2~sinT + (-^-) 1 ! 2 sin т -
Го т \ Го / Г0Г \ Г0Г/ J
53
104. 'Решить задачу о равновесии полукруглой мембра-
ны радиуса а (рис. 19) под равномерной нагрузкой q.
Ответ:
И (Г, т)=4т{4-[('Г--г)81п'?~
-4((^+^cos2?^2)arctg2^+
г I / г'2 а2 \ . Л . а? + г2 — 2аг cos » "| г2 sin2 <f
+ Т - тг) Sln 2'? 1П ^ + Г^2агсо5?]-
105. Поток тепла Q втекает через плоскую часть поверх-
ности бруса полукруглого «сечения и вытекает 'через осталь-
ную часть его поверхности (рис. 20). Найти стационарное
Рис, 19
Рис. 20
распределение температуры по сечению бруса, считая, что
втекающий и вытекающий потоки распределены с постоян-
ными плотностями.
Ответ:
Т (г, I3) — const —
106. Цилиндр радиуса а нагрет до температуры То и
охлаждается с поверхности таким образом, что ее темпера-
тура начиная с ‘момента t = Q поддерживается равной нулю.
Найти закон охлаждения цилиндра, считая, что распределе-
ние температуры во всех поперечных сечениях одинаково.
Ответ:
54
где y-п — (последовательные положительные корни уравнения
/0(у) = 0.
107. Найти стационарное .распределение температуры
в цилиндре (O^r^a, верхний торец которого
имеет температуру То, а остальная поверхность — темпера-
туру, равную нулю.
Ответ:
V4?) sh<
T(r, z) = 2T„ У } ’--------.
Z_l sh^-
n=l
где уп — последовательные положительные корни уравнения
/о(т) =0.
108. Торец полубесконечного цилиндра
0^z<^oo) поддерживается при постоянной температуре То,
а боковая поверхность находится при температуре, равной
нулю. Получить стационарное распределение температуры
в цилиндре.
Ответ:
где у« — положительные корни уравнения 7о(у) ~ 0.
Другая форма решения
7-=7'„h _Г(
L я J * J
о
109. Исследовать осесимметричные колебания круглой
мембраны радиуса а, вызванные ударным импульсом Р,
приложенным в момент времени Z — 0 и распределенным по
площади круга радиусом е.
Ответ:
. > 71 \'in~) , ( г \ . ynvt
J° v“ « /sm “ ’
/1=1
где Yn — последовательные положительные корни уравнения
7о(у)=О; Т — натяжение на единицу контура; р —поверх-
ностная плотность мембраны.
55
ПО. Найти закон выравнивания заданного осесиммет-
ричного начального распределения температуры Т(г, 0) ==/(г)
в бесконечном цилиндре .радиуса а, баковая -поверхность
которого не пропускает тепла.
Ответ:
Т (г, т) =
а
0
_2
Д2'
О
Г
Рис. 21
где уп — последовательные положитель-
ные 'корни уравнения Л(*у)=О.
111. Постоянный ток силы / посту-
пает через один торец цилиндрического
проводника, изготовленного из материа-
ла с проводимостью а, и отводится с про-
тивоположного торца. Определить рас-
пределение тока внутри проводника,
считая, что подводящие контакты есть
диски радиуса Ь<^а (а — радиус ци-
линдра) -и ток по иим распределен с по-
стоянной плотностью (рис. 21).
Ответ: распределение токового по-
тенциала
и (г, Z)
, 2/ л(^)л(Л-), t
~.аъ+ т.Ьа / ’(„/г 7»Ц)2(Ъ> + Cons ,
ch------
где уп—шоследовательные положительные корни уравнения
Л(у)=0.
112. Бесконечный цилиндр радиуса а, нагретый до на-
чальной температуры Го, охлаждается, излучая тепло в окру-
жающую среду по закону Ньютона. Найти закон остывания
цилиндра.
Ответ:
Г (г, т) = 2Т0
Л2Ы + Л2 Ъ
где уп — 'последовательные положительные корни уравнения
haJ0(y) ==уУ1(у).
56
113. Найти стационарное распределение температуры
в цилиндре радиуса а и длиной I, торцы которого поддер-
живаются при нулевой температуре, а температура баковой
поверхности равна Го-
Ответ:
2п ^1
sin ——7tZ
2л + 1
114. Дать решение предыдущей задачи, считая, что торцы
цилиндра не пропускают тепла, а на боковой поверхно-
сти поддерживается заданное распределение температуры
T\r=a = f(z).
Ответ:
115. Стенки цилиндрического канала, просверленного
в неограниченной пластине толщиной h (рис. 22), поддержи-
ваются при заданной температуре Го. Найти стационарное
распределение температуры в пластине, если ее страны имеют
нулевую температуру.
Ответ;
116. Решить задачу 113 при условии, что торцы цилиндра
охлаждаются путем теплоотдачи по закону Ньютона
Ответ:
где у« — положительные корни уравнения tgY = /t//2y.
57
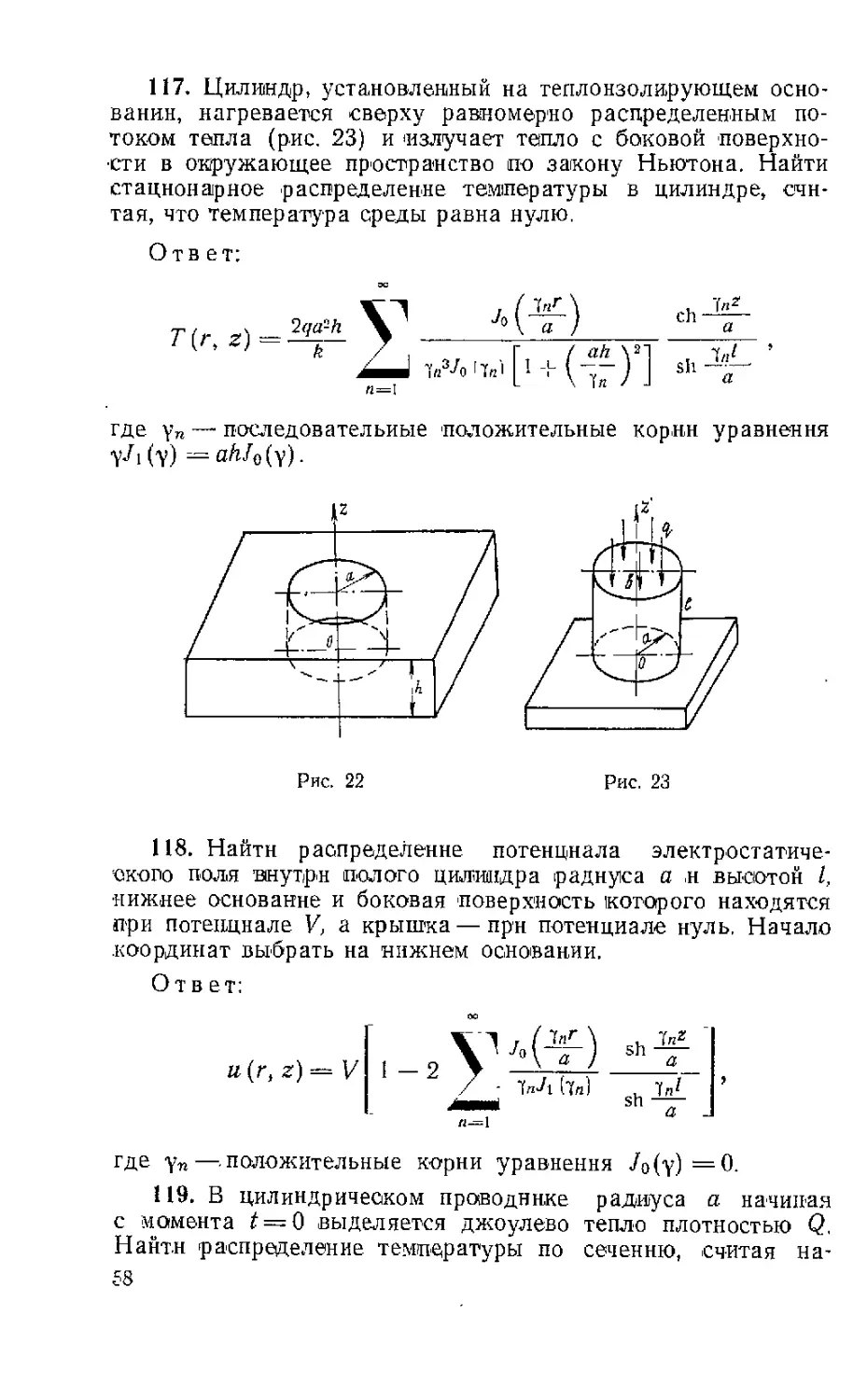
117. Цилиндр, установленный на теплоизолирующем осно-
вании, нагревается сверху равномерно распределенным по-
током тепла (рис. 23) и излучает тепло с боковой поверхно-
сти в окружающее пространство по закону Ньютона. Найти
стационарное распределение температуры в цилиндре, счи-
тая, что температура среды равна нулю.
Ответ:
7 (г, 2) =
t. w
ch——
shbL
где \'п —~ последовательные положительные корни уравнения
yJi (у) — ahlo(y).
Рис. 22
Рис. 23
118. Найти распределение потенциала электростатиче-
ского поля внутри полого цилиндра радиуса а и высотой I,
нижнее основание и боковая поверхность которого находятся
при потенциале V, а крышка — при потенциале нуль, Начало
.координат выбрать на нижнем основании.
Ответ:
u(rtz) = V
где уп — положительные корни уравнения /0(у) =0.
119. В цилиндрическом проводнике радиуса а начиная
с момента £ = 0 выделяется джоулево тепло плотностью Q.
Найти распределение температуры по сечению, считая на-
58
чальную температуру и температуру -поверхности проводника
равными -нулю.
Ответ:
Т(г, т) =
Qcfi
4k
n=l
где у» — последовательные положительные корни уравнения
Zo(Y)=O.
120. В цилиндре высотой / и радиуса а происходит теп-
ловыделение с постоянной плотностью Q. Найти стационар-
ное распределение температуры, если отвод тепла совер-
шается через часть поверхности верхнего торца, ограничен-
ную .юругом г = Ь<а, а остальная поверхность цилиндра
не пропускает тепла. Принимается, что поток тепла, выте-
кающий из цилиндра, равномерно распределен по сечению.
Ответ:
Т< 1 Qal г! 21 ,
k 2a= ' b 2^ b2-VIW shb? 1
n=l
где уп — положительные корни уравнения Л(у)—0.
121. Цилиндрический проводник радиуса а длительное
время нагревался током, выделявшим тепло плотностью Q.
Исследовать процесс охлаждения проводника после выклю-
чения тока при условии, что охлаждение проводника с по-
верхности в течение всего процесса совершалось по закону
Ньютона, причем температура среды принята равной нулю.
Ответ:
где уп — последовательные положительные корни уравнения
haJG(y) = yA(y)-
122. Круглая мембрана радиуса а находится в состоя-
нии покоя при постоянном натяжении Т. В момент времени
59
/ — О к поверхности мембраны приложена равномерно рас-
пределенная нагрузка <?q. Найти колебания мембраны.
Ответ:
«('•> О = - 1
га=1
где уп—последовательные положительные корни уравнения'
/о(у)=О-
123. Определить осесимметричные колебания круглой
мембрады радиуса а, вызванные пульсирующей нагрузкой
q sin (at, равномерно распределенной по всей площади
мембраны и начинающей действовать с момента Z = 0.
Ответ:
и (г, t) = —X
' ’ ' рш2
где уп — последовательные положительные корни уравнения
Л(у)=0.
124. Найти электростатическое поле внутри цилиндра-
(O^r^a, O^z^Z), торцы и боковая поверхность которого
имеют соответственно потенциалы Vo, Vi и V.
Ответ:
и(4‘, г) = Ц, (1 - +
4- 2 V I1 -i-H"! И,- ;°( 4 ) =|п mz
1 ” I„ (^) 1
я—I ' y
Другая форма решения:
«(г, v+2(Vl-V)X
60
где у» — последовательные положительные корни уравнения
/0(у) =0.
125. Найти стационарное распределение температуры
в цилиндре радиуса а и высотой h, если температура его
нижнего основания 0, верхнего То, а боковая поверхность
имеет температуру, равную
Ответ:
Г(г|2)=Г0^-
•(2м - 1)-<
h
'(2n+ 1) т.а
А
(2п -L 1) KZ
Sln /I
12п + 1]3
Другая форма решения:
А — 2? ( j^_\
?\ — д_ ~ И 47> X1 сМя <2а J(>\{n а'
’ z) А2 2№ & 7 1 t h -tf-K Ы ’
Ch^-2S-
где уп — последовательные положительные корни уравнения
Л>(у) =о.
126. Найти распределение температуры Г(г, т) в ци-
линдре радиуса а, температура поверхности которого изме-
няется по закону Т|г=о = /(т). Начальная температура ци-
линдра принимается равной нулю. Рассмотреть частные слу-
чаи: а) /(т) =Лт; б) f (т) = A sin сот; в) f (т) = Аге~“'.
Ответ:
б) Т(г, т) — A |sin 4-
+2ша3 S [е
л=1
— cos <ВТ - sin от] J„ ;
в)
а«
61
где yn — последовательные положительные корни уравнения
/о (у) =0.
127. Получить распределение потенциала в электронно-
оптическом устройстве, изображенном на рис. 24.
Ответ:
где уп — положительные корни уравнения /о(у)=0.
Рис. 24
128. Найги распределение температуры в цилиндре ра-
диуса а, нагревающемся вследствие объемного тепловыде-
ления, считая, что поток тепла с поверхности имеет задан-
ную плотность и начальная температура цилиндра равна
нулю.
Ответ:
A S -;„Ч (ь) G" а ,
Л=1
где уп — последовательные положительные корни уравнения
Л(у) = о.
129. Поток тепла Q втекает через торцы цилиндра
(Ог^гг^а, 0^2^/) и вытекает через его боковую поверх-
ность. Найти распределение температуры, считая, что вте-
кающий и вытекающий потоки имеют постоянную плотность.
62
Ответ:
Т(-Г’ *> = 2^(4---T--2?)+COnSt-
130. Через цилиндрический образец (рис. 25) пропущена
тонкая проволока, нагреваемая -постоянным током, выделяю-
щим тепло Q на единицу длины. Найти распределение тем-
пературы в образце, считая, что температура боковой поверх-
ности цилиндра равняется нулю, а торцы
в окружающую среду по закону Ньютона.
Ответ:
Т (Г’ г~> = S Ш Х
излучают тепло
«Л ch у,, ~
I ' Г~
in sh 'tn -v “!i ch т„ —
где у„ — положительные корни уравнения
Ш = о.
131. Найти распределение температуры
в цилиндре внутри
'которого происходит тепловыделение, а
поверхность излучает тепло в окружающую
кону Ньютона.
Ответ:
'Г/ \ 2Q/2
i х
Рис. 25
среду по за-
cos
где уп — положительные корни уравнения tgy = A//y.
Другая форма решения
ч 2(?Лдз
т (''> = ~*Г~ х
ah z
ch —
_________|Л_________и
I ah
sh — cli у,
где уп — положительные Корин уравнения у/j (у) = ahJ0(y).
63
132. В цилиндрическом проводнике вследствие прохожде-
ния постоянного тока начиная с момента t = 0 выделяется
джоулево тепло плотностью Q. Найти распределение тем-
пературы по сечению проводника в предположении, что теп-
лоотдача с его поверхности происходит по закону Ньютона,
а начальная температура равна нулю.
Ответ:
Т(г, .) = ^Х
где уп— положительные корни уравнения уЛ (у) == haJQ (7).
133. Исследовать колебания круглой мембраны радиуса
а, вызванные нагрузкой, приложенной в момент времени
t = 0 и равномерно распределенной с 'Плотностью q(t) по пло-
щади кольца 6<г<с. Рассмотреть случай sincotf.
Ответ:
и. (г, t) = X
где уп —1 последовательные положительные корни уравнения
/о (у) = 0.
В частном случае
u(r, О =
134. Решить задачу о колебаниях круглой мембраны, воз-
никающих под действием силы A sin приложенной в мо-
мент времени t = 0 и -равномерно распределенной по окруж-
ности радиуса (а — радиус мембраны). •
64
Ответ:
П = 1
sln^--^sin“z
tnJi2 nJ
где yn — положительные 'корни уравнения 7о(уп)=0.
135. Найти распределение температуры в трубе (а^г^Ь),
через внутреннюю поверхность которой втекает поток тепла
плотностью q, а внешняя находится при температуре нуль.
Начальная температура трубы равна нулю.
Ответ:
ьг
(г) = Го (т) Л (14г) ~ Л (т) (П)'
где уп— последовательные корни уравнения /?’ (д) = 0.
136. Полубесконечная трубка со стенками, образован-
ными 'коаксиальными цилиндрами радиусов а и Ь, нагре-
вается с торца и охлаждается с боковой поверхности. Найти
стационарное распределение температуры в трубке, считая,
что температура торца равна Го, а температура боковых сте-
нок поддерживается равной пулю.
Ответ:
Г(г, z) = r.TQ
(a^r^b, 2>0);
2°(‘‘ а ) — ('* а) СО (т >
где уп—корни уравнения 0, расположенные
в порядке возрастания.
5 65
137. Дать решение задачи о .распределении температуры
в 'бесконечном стержне для следующих частных случаев за-
дания начального распределения температуры Г|<=0 = /'(х):
б) f(x} = Тае л'.
Ответ:
а) ПХ,О = ^[Ф(^) + Ф(^
б)
Т(х, т) =
У 1 + 412Т
138. Полубесконечное тело, ограниченное плоскостью
х = 0, имеет заданное начальное распределение температуры
Г|г=0 = /(х) (0<Д<со), Найти последующее распределе-
ние температуры, считая, что с момента £ = 0 его граница
поддерживается при нулевой температуре. Применить полу-
ченные формулы к частному случаю f(x) = Го.
Ответ:
— J е sSf (— х -{- 2 У ts) ds
в частном случае
Ж.)=7-0Фу=).
139. Найтн стационарное распределение температуры
Т (к, у) в полубесконечном теле, ограниченном плоскостью
у = 0, часть которого (|х|<Х<1) находится при заданной тем-
пературе То, остальная часть (|х|>а) — при температуре,
равной нулю (рис. 26).
Ответ:
где ф— угол, под которым отрезок —у —О
видеи из точки М (х, у).
66
140. Найти стационарное распределение температуры
Т(х, У) У края 'пластины (Ог^я<оо, Q^y^b), две грани
которой находятся при температуре нуль, а грань у=Ь —
прн температуре То. ,
Ответ:
Т(.х, у) = arctg (th .
141. Тепловой поток Q поступает через участок |х,|<а
плоской границы полубесконеч.ного тела (рис. 27). Найти
Рис. 26
Рис. 27
стационарное распределение температуры в теле, считая по-
ток равномерно распределенным н предполагая, что поверх-
ность тела излучает тепло в окружаю-
щую среду по закону Ньютона.
Ответ:
Т (х,у) = ? ^n^L_g~Ху cos Ixdk.
* ’-х/ 7tak J К (X + h]
о
142. Решить плоскую стационар-
ную задачу теории теплопроводности
для квадранта (рнс. 28), одиа грань
(г/= 0) которого находится прн тем-
пературе нуль, а другая покрыта теп-
ловой изоляцией, за исключением участка 0 у ь, через
который втекает поток тепла заданной постоянной плотно-
сти q. Получить распределение теплового потока через
грань у = 0.
Рис. 28
Ответ:
_, . 2о р 1 - cos \b - .
т (X, у) = }--------J5-----е sin lydl.
О
Я (х, 0) = -?- In ( 1 + .
5*
67
143. Дать решение плоской электростатической задачи
для полупространства (—• оо < х<^ 4-оо, t/^О) при усло-
вии, что плоскость у — О находится при заданном распреде-
лении потенциала m|j,=0 = /(x).
Ответ:
Г f
Ч(х, у) = ^-
/(x + ytg9)d8-
2"
144. Найти распределение электростатического потенциа-
ла в плоских электронных линзах, изображенных на рис. 29.
Рис. 29
Отв ет:
\ / \ И2 + К . К? — V. f ch Ху sin Хх
a) + Л;
. т, . .. I7. —- lzo Р sin Ха cliXy .
б) «(X, у) -14 + 2 J —— cos мгЛ..
О
145. Найти распределение потенциала в цилиндрической
электронной лннзе, изображенной на рис. 30.
Рис. 30
Ответ:
4- V2 х И3 - И, Г /0 (Хг) sin Хг ,
2 ‘ z J70(Xa) X ДЛ*
68
146. Найти стационарное распределение температуры
в квадранте (х^О, г/^0), грань t/ = 0 которого поддержи-
вается при температуре TQ, а грань х = 0 отдает тепло
в окружающую среду по закону Ньютона.
Ответ:
'г/ ч 'г Г 1 2Л f е sin Ху ,.1
Т(х, У)=/,[!--] Л(Х + Й/ dxj.
О
147. Найти потенциал бесконечной нити с линейной плот-
ностью заряда q, помещенной на расстоянии b от проводя-
щей зазе>мленной плоскости у—0 параллельно этой пло-
скости.
Рис. 31 Рис. 32
Ответ:
и (х, у) = — 2q In /?! 4- 2д In /?2,
/?, = Ухг + (у - 6)!, /л2(у + *)“
148. Найти распределение потенциала внутри заземлен-
ного квадранта (рис. 31), если источником поля является
заряженная бесконечная нить с плоскостью заряда q на еди-
ницу длины, проходящая через точку с .координатами (а, 6).
Ответ:
Н(л,у) = -291п-^-,
/?, = V (л-а)Ч (У ~ *)! > «а = /У + а)2 + (У - - by2,
Яз = УУ + а)2-+(у +Ь)!, R4 = /(x-a)2 + (y + ЬУ.
149. Тонкая заряженная нить с зарядом q на единицу
длины помещена между двумя проводящими плоскостями
(рис. 32). Найти распределение электростатического потен-
циала, а также плотность заряда на плоскостях.
69
Ответ:
и (*» У) = 4^ ~YsK77T^' sh cos У<^~а-
о
Соответствующая формула для у^>а получается из преды-
дущего выражения перестановкой букв у. и а. Плотность за-
ряда на пластинах
, > а . ~а
tzx -а
c"——ms~iT
A — +COS-J-
(У=0);
Су = h).
150. Между плоскими
изготовленных из железа
массивных тел,
границами двух
с магнитной проницаемостью ц,
помещен линейный ток / (рис. 33).
Найти магнитное поле в воздуш-
ном зазоре.
2J
Рис. 33
.-л---------err cos х“к |
ch kb + u-sh kb J
2J
ch kb 4- |x sh kb
151. Найти потенциал точечного заряда 7, помещенного
на оси бесконечного проводящего цилиндра радиуса а.
Ответ:
и (г, z) = - —— f /0 (>-г) cos л zdl.
о
Указание.
Ко (Хй) = f
J/a’ + zs
о
152. Найти стационарное распределение температуры
в полупространстве (г>0), на границе которого поддержи-
70
4
J
вается заданное распределение температуры Т|2==о = f(r).
Рассмотреть частный случай
[То, г < а;
о, г>;
Ответ:
Т(г, z) = f е “ J„().r)XdXJf (f)(Хр) р dp.
О о
В частном случае
Т (г, z) — Т9а [ е~ ‘'г Ja (Xr) (Ха) dX.
о
153. Решить предыдущую задачу в предположении, что
полупространство нагревается тепловым потоком постоянной
плотности q, падающим на площадь круга а, а отвод тепла
осуществляется путем теплоотдачи с границы тела в окру-
жающую среду по закону Ньютона.
Ответ:
T(r, z) = S±^l~TTJ1(Ka)JII(l.r)d)..
О
154. В неограниченную среду, начальная температура
.которой принимается равной нулю, вставляется цилиндри-
ческий стержень радиуса а, нагретый до температуры /(г).
Найти распределение температуры Т(г, т), предполагая теп-
ловые постоянные материалов стержня и среды одинаковыми.
Рассмотреть частные случаи:
а) /(г) = 7’о; б) Г(г)=ЛЛ
Ответ:
а) Т (г, т) — Т„а f е~ '*’Jl (Ха) Л, (Xr) t/X;
б
б) Т(г, Т) =Ла^[л (Ха) + 2 ]е~l^J0Q~r) dl.
б
155. Найти распределение потенциала электростатиче-
ского поля в пространстве между двумя заземленными пло-
скими электродами z = + a, созданного зарядом q, помещен-
ным в точке г = 0, z = 0.
71
Ответ:
" (Г'г)“ТЙ=7?^'7У!
О
156. Найти электростатическое поле точечного заряда q,
помещенного вблизи плоской границы раздела двух сред
с различными диэлектрическими постоянными ((рис. 34).
157. Найти электростатическое поле двух точечных заря-
дов + q и —q, между которыми помещена .пластинка из
диэлектрика с постоянной 8 (рис. 35). Вычислить распреде-
ление поля иа линии, соединяющей заряды.
Ответ:
в> ch Xz
sh lb 4- s ch \b
И<&;
Л,
-----?----- X a f sh Xfr — £ ch Л& J)
r 7 J sh AZ? -echXb^ '*!>*•
о
72
Глава IV
ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Преобразованием Лапласа от функции f(t), заданной
в промежутке (0, оо), называется интеграл
= (1)
О
где р— некоторый комплексный параметр, обеспечивающий
существование данного интеграла. Можно показать, что при
определенных ограничениях, наложенных на функцию f(t)t
существует такое число С, что в области Rep^>C преобра-
зование Лапласа (1) является аналитической функцией ком-
плексного переменного р и справедлива теорема обращения
Римана — Меллина
где L —прямая, параллельная мнимой оси и лежащая в об-
ласти Rep>C. Имеют место следующие важные теоремы.
Теорема смещения:
если F(p) =№ + «), то F(t)=/(f)e'".
Теорема запаздывания:
еслиЛ(р)=/е , то Г (i) = |/(f f>*
Теорема подобия:
если А(р) =7(°Р), то =
Теорема Бореля (о свертке):
если F—f}f2,
то F (t) = JA (г)/2 (* -г) dr = (/, (t - т)/2 (г) dr,
, о 6
причем равные интегралы, входящие в последнюю формулу,
называются сверткой Лапласа двух функций, В частном
случае
О
73
Теорема о производных:
JW = p.f-/-/(О) - ... (0),
в частности,
Г=р7-/(0), Г=р7-р/(0)-Г(0).
158. Найти функции по нх преобразованиям Лапласа без
помощи теоремы обращения Римана — Меллииа:
Э) / = ’ б) f~ ai!)2 • В) f= р4 _р4»
r)/=^r; =
“) /К
Jit)
О Т 'll Jf к 5t
Рис. 36
1/И/Ж
О % 2ч: Зт 4т 5т t
Ответ:
а) /(*) = « 2 Усо8]Л&-4-^+ г—-^51пУГ/,--ТЧ''
\ V ь /
б) f(t) = -^-sincrf; в) f (t) =—l-(sin£ chi — cos ish t);
r) f it) = е'Ф (у? I + ; д) f it) = -L Jo (4-).
159. Найти преобразо!вание Лапласа от следующих функ-
ций, заданных графически (рис. 36).
В следующих примерах требуется найти решения диффе-
ренциальных уравнений >и систем уравнений, удовлетворяю-
щих определенным начальным условиям.
160. г/"+3^+2//^4, г/(0)=2, /(0) = 0. •
Отв ет: у= 2.
74
161. y"+n1y = asm (mt+'a), m=y=n, y(0) = y'(0) = 0-
Ответ:
y = д^Лд!)' I"! cos a sin nt -|- n sin a cos nt — nsin (nit -J- a)].
162. y"+n2y = asin (nt+a), y(0) =/(0) =0,
Ответ:
у ~ [sin nt cos a — nt cos (nt -|- a)].
163. y"-4y = eK, y(O) = yo, У'(О) = У1.
Ответ:
у =y0 ch it -f- y1 - sh 2f + "T
164. у"'+у = 1, у (0) = у' (0) = у" (0) = 0.
Ответ:
. 1 -t 2 Т i /Т
• у = 1 —y-e ~ ~3e cos —Ь— •
165.
x' = y
y' = z x(0)=.x0, y(0) —y0, z(0) = z0.
z' — x
Ответ;
-X (t) = I (x0 + y0 + z0) e‘ - 1 [<~ 2*» + У» + ’ ’ >cos -
-(Уо — го) /3 sin-Цр^].
f x" — 8л: +/6У = О,
166. r Z , о n Л(0)=1’ ^Ч0)-у(0)=У(0)-0.
( —-|/6x'+y-4-2y = 0,
О т в ет:
jc = ~ (3 ch — cos 2/), у = (sh 2t — sin 2t).
167.
x" — 4л — y' — 2y + z' — 2г = sin
2x! — y" + 3y -J- z" — 4z = 0,
x' —2x—у+г"—4г=0, начальные условия— нулевые.
75
Ответ:
jc=--^sinM+4shf+i^sh-3t
I x' = — cxn + ex ,, n = 1, 2,,..
168. , n n~v
I x0' = — cxQ,
x0 = 1, x} = x2 — ... xn = 0 при t = 0.
Ответ:
X„ = 4 (с0"е“ "
169. Найти ток в электрической цепи, изображенной на
рис. 37, если /|<=о==О и /=о=О, для следующих случаев:
Рис. 37
Рис. 38
а) !/(/)—произвольная функция времени, ключ замы-
кается в момент времени t=Q. Рассмотреть конкретные
частные случаи:
V(f) = Е = const и V'(Z) c=Esine)^;
б) V(/) =£; в момент времени / = 0 замыкается ключ
а в момент t~T — ключ Кз.
170. Найти движение частицы массой т и зарядом е,
находящейся в электрическом поле Е, параллельном ОХ, и
магнитном поле Н, параллельном OZ. Частица в момент-
t = Q обладает скоростью (и, v, w} и находится в начале
координат.
Ответ:
Hv — сЕ ,, ,ч , и ,
X —-----7j (I — cos at) Н---sin at;
па ' ' 1 a ’
у = vt------— (at — sinaO--------— (1 — cosetf);.
z = <wt.
Здесь c — скорость света, a,-=eHlmc.
76
171. Частица массой т и зарядом в вылетает из начала
-координат со скоростью (и, 0, 0). На нее действует магнит-
ное поле И, параллельное оси OZ, и сопротивление среды
kmV, где V — скорость частицы. Показать, что ее координаты
в момент времени t равны:
ku ku — kt
а2 ~ д2 *2 6
, , хи -kt . ,
cos аг 4- е sin-ctf,
। а2_|_Д2 ’
Я/Z । И — kt / I I г • j\
У = - + дцДЗ е (acos^-i-Asinai),
еН
тс
172. Найти закон движения материальной точки под дей-
ствием силы f(t), заданной графиком (рис. 38).
Ответ:
*w=4
‘2 х •
2 6(Х3 — Т,|’ < 2’
173. Конец л' = 0 полубесконечной линии, обладающей
самоиндукцией L и емкостью С на единицу длины, присоеди-
няется в момент времени 1 = 0 к источнику э. д. с. Е = f (t).
Найти напряжение и(х, t) в каждой точке линии.
Ответ:
и(х, t) —
0,
Л'-v)-
174. К концу х=0 п-олубеоконечиой лии-ии без -искаже-
ний (kC=^LG) подключается источник э. д. с. E =
Найти напряжение и(х, t) в линии.
Ответ:
175. Конденсатор емкостью Со, заряженный до потенциа-
ла V, разряжается в момент / = 0 на полубесконечную ли-
нию без потерь (R=G~Q). Найти распределение, тока.
1(х, I) в линии.
Ответ:
о,
t < —;
V
/(X, 0 =
t> —
V
где —волновое сопротивление линии, *
176. Вход линии без потерь (/?=6=0) подключается
к источнику постоянной э. д. с. Е, а конец х = I замыкается
на землю через нагрузку. Найти напряжение на нагрузке,
если она представляет собой;
a) Ro — сосредоточенное сопротивление;
б) Со—сосредоточенную емкость;
в) Lq — сосредоточенную индуктивность.
Ответ:
а) и ] x=i — Е X
Л=1
1С
Со ’
78
в) « L-j = E Г т *_ о — 4 V г—-|in 9 cos -У ,
> l*=* L I + p Xj — Sin27,; 1л T J ’
n=I
‘g- = -T- ? = -!-
177. Найти форму колебаний струны (—l^x^l) с сосре»
доточенным грузиком массой т0, укрепленным в ее средней
точке. При решении задачи считать, что начальная форма
струны соответствует смещению грузика на заданную малую
величину h, а начальная скорость точек струны равна нулю.
Ответ:
и (х, t) = 2Ла
cos 7„ sin ьг
b2(7/i--sin7„cos-r„) C0S I
где уп— положительные корни уравнения tgy=a/Y> а =
= tn/mQt m — 2pl— масса струны.
178. Исследовать продольные колебания стержня, конец
х = 0 которого закреплен, а на конде х = 1 находится сосре:
доточенный груз массой Мо, получающий в момент времени
t = Q заданное смещение 6 без сообщения начальной ско-
рости.
Ответ:
cos Tnsin7/t-^- ,
и (х, t) = 28а z J —г;-:—:? cos ,
к ’ .ЯШЛ -(п3 Ил I sin COS ул) I
где уп — положительные корни уравнения tgy —а/у, а =
— М/Мо, M — plS— масса стержня.
179. Линия, свободная от искажений, длиной I заряжена
до потенциала 1. Конец х = 1 изолирован, и в момент вре-
мени, ( = 0 конец х — 0 заземляется. Определить потенциал
в точке х.
О т в е т:
, 4
«(-V, о = — е
sin 21
2я + 1 C0S 21
180. Кабель сопротивлением R и емкостью С па единицу
длины заземлен в точке х = 1. При t = Q в точке х = 0 к ка-
79
белю через емкость Со приложена постоянная э. д. с. Eq.
Найти потенциал и(х, t).
Ответ:
и (х, /) = 2Е
где уп— положительные корни уравнения yigy=Cl/C0.
181. Получить решение задачи 64 в форме, удобной для
малых времен т и больших толщин а.
Ответ:
а) Г(х, .) = 7-.^ [ф(2а--ф
л—О
б) 7-и = +
- (х |- 2па) у — е ' — 17 Н-§- х
Г /О . Г) , •> г- (2я-х-г2лс)г
х[1-ф(”7=—+ }•
182. Грань х = 0 пластинки поддерживается при темпера-
туре Го, а к грани х = а присоединена тепловая емкость.
Получить выражения для плотностей теплового потока на
гранях пластины.
В начальный момент времени температура равна нулю.
Ответ:
, _ 2feT(> у 1-^т2л
V I х=о - а Д|1_а_ а2ь2е ’
л—1
I = Т<> V ___________7л ________ “ V ~а^
Ч\х=а а Д| 1.1-На i а2Тн2) sin
Л=1
где уп — последовательные положительные-корни уравнения
ctgy = ay; a = C0/Cpa; Со — тепловая емкость на единицу
•площади.
80
183. В цилиндрическом проводнике радиуса а начиная
с момента времени t = 0 выделяется тепло плотностью Q.
Найти температуру на оси проводника, считая, что отвод
тепла с его поверхности совершается через тепловую емкость
и начальная температура проводника равна нулю.
Ответ;
7’1 = — (___-___a3g^ ~ -I- 9а2а _____е_^_^______|
' |r=0 k 12а<1 4(2а —I)2 ^Ь2Л(7„)(а2тя2^2а-Ы)1’
Л=1
где \п — положительные корни уравнения Л (у) Н-ссу^о (т)= 0;
а = С0/2ла2Ср; Со —тепловая емкость на единицу длины.
184. На холодный цилиндр радиуса а в момент времени
t = Q надевается нагретая тонкая цилиндрическая оболочка,
покрытая снаружи теплоизолирующим слоем (рнс. 39).
Найти распределение температуры в цилиндре, считая на-
чальную температуру цилиндра и оболочки равной соответ-
ственно нулю и Тй и пренебрегая температурным перепадом
по толщине оболочки.
Ответ:
Здесь уп — положительные корни уравнения Му) +
+ ау/о(у)=0; а = С0/2ла2Ср; С€ —тепловая емкость обо-
лочки на единицу длины.
185. Плоская граница полубесконечиого тела начиная
с момента t = 0 поддерживается при температуре, изменяю-
щейся по заданному закону 7’|хг=0 = /:(т). Найти значение
температуры в каждой точке тела, принимая его начальную
температуру равной нулю. Рассмотреть частные случаи:
( Т Q х
a) f№=T„; б) в) fb) = [ q’
Ответ:
7'(Х-Т)=^Г J <х>0)'
2 VT
&
81
В частных случаях:
в) Т (х, -^ = Т0
‘-’ЬМ
0<т <ТО,
ф—
\ 2 у 1! — Т0
> V
186. Решить предыдущую задачу, считая, что на границе
вместо температуры задан тепловой поток постоянной плот-
ности д0.
Ответ:
Т(х, =
k I у-
187. Полубеюконечное тело, нагретое до начальной тем-
пературы То» излучает тепло с плоской границы х = 0. Найти
распределение температуры в теле, считая, что излучение
происходит по закону Ньютона.
Ответ:
’)=w<'+"[' -ф(лг?+^)])-
188. Через плоскую границу полубесконечного тела на-
чиная с момента времени /=0 осуществляется импульсная
подача теплового потока по закону 9 = /(т), где
Г дп, 0 < '=<“о.
/(т)=1 о,
Найти распределение температуры в теле после большого
числа циклов, считая, что начальная температура тела равна
нулю, и пренебрегая теплоотдачей с поверхности тела в окру-
жающую среду.
Ответ: для ограниченных хит
Т' —~ ,
82
189. Два полубесконечных тела из различных материа-
лов, одно из которых нагрето до температуры То, а другое
имеет температуру, равную нулю, приводятся в контакт
своими плоскими границами начиная с момента t~ О
(рис. 40). Найти закон вы<ра>вн1И1ва1Ния температур.
Ответ;
nv) = ^[i + >(^|)], х>о;
т^ = Т^ *<0’
190. Тело, ограниченное изнутри сферической поверх-
ностью радиуса а, снаружи неограничено. Начальная темпе-
ратура равна нулю, а иа его поверхности температура рав-
на То. Найти температуру в момент времени t.
Ответ:
191. К концу * = 0 полубесконечного кабеля (1 = 0)
подключается в момент времени t — 0 постоянная э. д. с. Е.
Найти напряжение в каждой точке линии.
Ответ:
+ ^[1-ф(4- /4+/4)]).
6*
83
192. Найти распределение температуры внутри тела,
Имеющего форму двугранного угла (х>0, У > 0), поверх-
ность которого с момента времени t = 0 поддерживается при
температуре TQ (начальная температура принимается рав-
ной нулю).
Ответ:
Т(х,у, .) = Го[1 ~ Ф(^=)ф(у^)].
Указание. Решение искать в форме Т= Го(1 -н
+ w(x, Z)].
193. Найти распределение температуры внутри октанта
(х>0, ^>0), грани которого начиная с момента t = 0
поддерживаются при постоянной температуре То, а началь-
ная температура равна нулю.
Ответ:
Т(х, у, г, Т, [1 - Ф(^-) Ф (^) Ф (^)].
194. Диффузионное вещество распределено в полупро-
странстве с заданной начальной концентрацией
Найти плотность потока вещества через границу х = 0, на
которой начиная с момента t = 0 поддерживается концентра-
ция, равная нулю.
Ответ:
195. Линия бесконечной длины (х>0) обладает сопро-
тивлением R и емкостью С па единицу длины. Начальные
ток и потенциал равны нулю. При / = 0 в точке X — 0 при-
ложена единичная э. д. с. через импеданц. Найти потенциал
в произвольной точке х линии, если импеданц представляет
собой:
а) /?о” сосредоточенное сопротивление;
б) Со — сосредоточенную емкость.
84
Ответ:
а) «(х, Z) = 1 —
196. Граница полупростра<н-ства(ОС*<°о, —00<С^<С + 00)
начиная с момента времени t = 0 поддерживается прн тем-
пературе, являющейся заданной функцией координаты
У*Т\х==0 = [(у). Дать решение задачи теплопроводности,
считая начальную температуру рав-
ной нулю.
197. Диффундирующее вещество поступает в полупро-
странство г>0 через отверстие в непроницаемой стенке
z —0 нз тонкой цилиндрической трубки длиной I, закрытой
с другого конца (рис. 41). Определить количество вещества,
заключенного в трубке, как функцию времени, считая, что
поток вещества в сечении трубки имеет постоянную плот-
ность, а начальное значение концентрации вещества в трубке
и полупространстве равно соответственно Со (на единицу
длины) и нулю.
Ответ:
Dtx2
где а — радиус трубки; — начальное количество вещества,
заключенного в ней (М0 = С0/).
85
198. Решить задачу 176 волновым методом.
Ответ* *:
О,
О < t < Т,
а) и|
(2^—l)7'<^<(2^^- Г)Т,
N — 1, 2, 3,...;
О, 0<t<r,
б) “|л_г=2/?
3T<t <5Т,
2 J i„(2s)e ‘ds
(2W-1)7’<£<(2W+1)Т, w= 1,2,3,...; ' 0, О < t < т.
е , Г<7<ЗГ,
в) и | л=/ = 2Е е [1-2? (ф-з)] е \ ЗТ< £<5Г,
£(-1)"б [4-(2n+ 1)]} (2.V-1) r<i<(2W+ 1) Т.
199. Исследовать процесс распространения волн вдоль
неоднородной линии, состоящей из конечного участка дли-
ной I с волновым сопротивлением Zi и бесконечной линии
с волновым сопротивлением Z2. Получить отраженную и пре-
ех dn
* В задачах 198, 200, 201 и 204 Ln (х) = (0_jrxn) — поли-
номы Лагерра. Преобразования Лапласа от полиномов Лагерра приве-
дены в таблице (приложение II).
86
ломленную волны, возникающие в месте стыка, считая, что
в момент времени t — Q к началу линии подключается э. д. с.
£ = /(/) (рис. 42).
Рис. 42
Ответ:
О,
w)>
Л] (x, t) =
U2(x, t) =
2NT-^-<t<2NT-\-^-,
г-/[1 - 2NT — + а» [/(г - 2пТ — -
_Я^-2«Г + ^], 2NT + ±<t<2(N+l)T~^
О, 0<t<T+^_
t'2 ’
а)
л = 0
(2N - 1) Т + ^-1 < t < (2N + 1) Т + .
N=}, 2, 3,...; ^ = 4“^; Т = 7Г’
^1 ~~ 2 ^1
200. Получить выражения для 'Преломленных волн в линии
из предыдущей задачи, если f(t) — £' = cosntJ а в месте стыка
(х = 1) включается:
а) /?о—сосредоточенное сопротивление;
б) Со —сосредоточенная емкость;
в) Lq —- сосредоточенная индуктивность.
87
Ответ:
а) м2 (х, t) =
о, 0<1<7Ч^,
ЕА Г, / Z, - Z3 - Д,
X. + Z2 [ \ Z) -г Z, -г Л>„ j ]
(2/V— i) Г4-^1<г<(2лч-1)7Ч-^,
N= I, 2, 3,...;
r+
б) и2 (х, t) = Е (1 — а)
-PU-WX
/V — 1 - а? Г/ - (2/1-1 1) Т — --------
2 а-е 1
п = О
Х^(?(1+«)[/--(2« + 1)Г-^-2р
(2N- I) Г+ < t<+ 1) Т + ,
N= 1,2,3,...,
ct —
Z1 + Z2
Р (Zi-ZeKV
88
0 Q<t<T^r—
i V2
1 Vt I '
1 — e ’
7’ + ^T<*<37’+^,
I - a — e [a + 7 (I -L а) X
4
37- X AzlI < t < 5T 4- ^L,
1 t'2 Vi
,V-1 тр-СЙ-ЩТ-^]
S(-l)” J " La [(!+«) s] e~sdS
n=O 0
(2N - 1) 7-+ t < (4N + 1) 74 ,
N= 1, 2, 3,...;
0__ ~~ Z2 __ Zi ~F Z2
~ Z^z2 > £0
201. Решить предыдущую задачу, если место стыка
(х = 1) замыкается на землю через; а) /?0, б) Со, в) Lo.
Ответ:
0,
0<t<T + ±—
V2
а) иг (х, t} =
р Г, / гл - z,za гл ^1
[ (. гл + гл-г гл ) ]
(2jV_ 1) Т+^- < t<(2N + 1) Т 4-
N=l, 2, 3,...;
89
0<t<T + ±--L,
^2
V2
6) U2(xt t)=E(l —a)
3r+^2<f<5r+^,
,. т[^-(2я-г1) T--—П
Л — 1 t ®! J
J Лл[(1 — a)s]£-Tds
(2AMpx £ J<f<(йгЧ)Г lJ,
;V=1, 2, 3,...,
_ 7--Z zl + z3 .
+ z, ' > c»z,z3 ’
0, 0<t<
T + ^L<t<3T + ^,
ap p- 7'-£Z_T|
3r+i^<<<sr+x=i,
90
-»4'-<2“+1)г-М
2 л х
л=0
I L ‘г JJ
(2N-l)r+^'<^<(2N+l) + ^;
N = 1, 2, 3,...,
Z, Z2
?! + ?2
Z-o (^i — 2Tn)
p = -----
202. Исследовать процесс распространения упругих про-
дольных колебаний в 'полубесконечном стержне, вызванных
силой F(/), приложенной в момент / = 0 « концу стержня
х= 0.
Ответ:
0, o<f<—,
’ V
н(х, t) =
203. Исследовать продольные колебания в стержне дли-
ной /, конец х = 0 .которого закреплен, а на конце х=1 на-
fft)
О Т 2Т Зт 4т
F(i)=Fft4)
Рис. 43
чиная с момента t = 0 приложена сжимающая сила, изме-
няющаяся по пилообразному закону (рис. 43). Найти реак-
цию в заделке, считая, что период т равен времени пробега
волны вдоль стержня.
91
Ответ:
2Л
О, 0 <t < Т (2л 4- 1) Т< t< (2л 4-3) Г,
л=1, 3, 5,...,.
4- ~~k, kT<t <(&+ 1) Т, k= 1,2; 5, 6; 9, 10;...
204. Консольный стержень, заделанный на конце х = 0,
начинает колебаться под влиянием удара по сосредоточенной
массе MG, укрепленной на конце x = L Найти динамическую
реакцию заделанного конца, считая, что в момент удара
массе ЛГ0 сообщается скорость и0.
Ответ:
«Lh=v£^(z);
/(0 =
о,
_|_е-.<1-ЗГ) J] _2j(Z_37.)]>
0 < t < Т;
Т <t<3T-r
3T<t<_bT;
*2' е~- <2',+1> rl L„ {2а [t - (2л 4- 1) Г] |
п = 0
(2N- 1) T<t < (2N+ 1) Т, N= I, 2, 3,...;
7’== — • а =
v ' Мгр *
Глава V
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
В следующих задачах предлагается решить интегральные
уравнения Вольтерра.
205. ф (х) = — 1 - f (х — у) 'f (у) dy.
о
Ответ:
ср (х) = — COSX.
206. <р (х) = — 2 cos х + х 4- 2 + J (у — х) f (у) dy.
Ответ:
’?(•'£) = ( 1 + •*) sinx.
92
207. <f(x) = e x4-f sin(x — y)cp(y)iZy.
“ I
Ответ:
с? (x) = x — 1 2e~x.
208. <p (x) = 5 sin x + ^ex~y <p (y) dy.
о
Ответ:
<p (x) = e2x — cos x 4- 3 sin x.
209. <p (у) dy = x.
о
Ответ:
ср (x) = 1 — X.
210. f Jo(x — y) ?(y)dy = sinx.
b
Ответ:
ср (х) = ^(х).
<p W = i + J (x - у) Ф O')
0
211.
ф(х)=х -И(*- y'lvly'tdy-
0
Ответ:
tp (x) = 4 (e-v + cos x - sin x),
di (%) = 4(e-t — cosx+ sin x).
212. = 1.
J Vx-y
0
Ответ:
7 \ 1
? W = —7=
X
213. p(x)=|«':--'y-t^Tp"W*-
0
Ответ:
о (x) = 8х.
93
В следующих задачах найти собственные числа и- соб-
ственные функции уравнений Фредгольма с вырожденными,
ядрами.
1
214. со (л) = х|(х + у) (y)dy.
Ответ:
X, =-4Г'3-6, <Pl(x) = C1(x + -i^-),
Х2 = -4/3-6, <р8(х) = С2(х-
1
215. <р(х) = Х Jxy <?(y)dy.
и
Ответ:
X = З3 <р (х) = Сх.
216. о (х) = X j [Зху + 1 - ~ (х + у)] <? (y)dy.
О
Ответ:
Х = 4, <f, = Ct, ®2 = С2 (х — X) •
т
217. <р (л*) =Х f (sin х -г sin у) ср (y)dy.
о
Ответ:
Х’ = 2^Г~ ’ ¥ 1 W = С> (8‘П Х +
Z-j/2-iTt \ z/
= ?2(х) = C2(slnx-X2-j..
218. ®(х) = Х j [sinlx + у)]-f (y)dy.
0
Ответ:
Xl, 2 = 2"ГГ > 2 Ci, 2 <Sln X ± C0S *>•
94
219. ч>(х) = М'г+5>(У)«'.
о
Ответ;
о
л = ~-f, ? (х) = Сех.
220. у (х) = Х pgyy(y)dy.
(J
Ответ;
л == -ПГ2" ’ ® = С-
221. При ’каких Л система имеет нетривиальные решения?
1
?(х)=л J (х — у) ф (у) dy,
О
1
ф (x) = /J(y-x)y(y)dy.
О
Ответ:
1-12 /3.
Решить уравнения:
222. °(x) = 4Jxyy(y)dy +4л-.
О
Ответ:
у (х) =Г X.
1
223. f (х) = Зх — 2 + 3 I ху а (у) dy.
()
Ответ:
о (х) --- Сх — 2;
1
224. ср (х) — х2 4- 2J (1 + Эху)? (у) dy.
о
Ответ;
f , , 1 5
?(х)=х2--1-х-тг.
95-
225. ? (х) — sin x J cosx sin у ф (_y) dy.
о
Ответ:
<р (х) — sin х -4- — (тг — 2) cos х.
226. т (х) = х 4- J sin (х + у) ? (у) dy.
О
Ответ:
ср (х) = х — 8 •.]' sin х — 2 4 ~s2‘~ ~t cos х.
Т \ / J-2 — 4 я2 — 4
227. ® (х) = + — ( г-? У d~.
к ’ 1 х* ' г. J 1 -г (% - у!
Ответ;
, ч Г sin х'> л ,, 1
?0) = J-7Zrr=^-cth«--2r-
О
228. ®(х) = е '’| + 4_ ( К (х ~ у)(у) dy,
«W = { о
Ответ:
229.
? (*)=
®(х) =
ФО) =
л-»О,
4-е2 , х<0,
Й2-|-1Х — у)2’
ft Г V (у) Лу
Т.
(0<b<k)
л - л
& + th - бр
96
Ответ:
tp(x) =
~.b
sin ~k~
XX r.b
ch—J- cos —
В следующих задачах требуется свести задачу Штурма —
Лиувилля >к интегральному уравнению.
230. ё-+^=°
при условиях:
а) У | х_о = °’ Пг-/ = °;
б) у о = О, 4^! =°;
1 ' । -r=o ’ dx | ’
bOU = °- 4riy|.t__, = 0;
r) --^ + Mx=o = O, -^^-^1^ = 0.
Ответ:
/
У = X I G(x, £)y
о
где функция G(x, g) определяется формулами:
97
г)
О(л',Е) =
[1 + h{l - л)) il + th'}
Л (2 hl]
ll-h[l-in]l | xh]
h(2 + hl]
231. -Мл+ —•>’ = °. У|, a = °. У|, ь
dx \ dx / ' x z и ’ z |-t=t>
Ответ:
ь
у = h § G(x,;) 4-y (i)d£,
232. P®) + 'Y’y = °’ y lx-0 “ ограничено, у
О т в e т:
y(x) = /jG(%, 9?y(E)^,
о
G(x, ?) =
233- S7 {х + ^ху = °’ У -о ~ ограничено, _у|
Ответ:
У = к]'б(л, Е) ;у (E)dE,
О
О(х, =
98
234- + = У|,-о=О. Ч-.=о.
fl= 1,2, 3,...
Ответ:
y = XJ G(x, S)fy(s)dt,
О
ЖЯ-Й"]
235. Найти собственные числа и собственные функции
1
интегральных уравнений вида у(х)=Л/*(х, t)y(t)dt, если:
о
б) k(x, t') =
(2 — л) (t + 1), t < х,
(2-0(х + 1), t>x-
( — x(l + t),
OWH-m+x),
t> x;
r) *(*./) = {
e * sh t,
e~‘ shoe,
Ответ:
а) Л„ = п2л2, yn (x) = Cn sin nnx («=1,2, 3,...);
б) кп = 4yn2, где yn — положительные корни уравнения
tgV = —2y> ^n==C„sinyn(l — 2x);
Ак = 4уь2, где ул — положительные корни уравнения
4вт=1/2у, p(, = Dftcosyfl(l — 2х);
в) Zo= 1, p»=aI;
Л„ = п2л2, = С„(sin«лх + шгcos«кх) (п=1, 2,...);
г) Лп = Тп2+1, где у» — положительные корни уравне-
ния tgy = — у, y„ = C„siny„x.
236. Найти собственные числа и собственные функции
интегральных уравнений вида y(x)=Xjfe(x, t)y(t)dt, если:
7* 99
в) /г(-М)-
Ответ:
а) = 1 ' - (л + -i-)2, у„ = С„ cos (я + 4") х
(га = 0, 1,2,...),
б) + * y» = c»sln (га + 4") *
(11 = 0, 1, 2,...);
в) —*• где V» — положительные корни урав-
a 2т s- , ‘tn (n -
нения tg у = — —, уп — Сп sin * _--- ;
дЛ ——g---1, где yk — положительные корни урав-
ления tg у = -^, У'-- = Dk cos
Глава VI
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
Среди линий, соединяющих точки А и В, найти ту, кото-
рая дает экстремум функционалам:
В(1, 0)
237. J [у (х)] = j (у'2 2уу' — 1 бу2) (Ух.
д (о, о>
Ответ; */=0.
'’СМ
238. J[^(x)== J (4y2-y'24-8y)rfx.
Д(0, -I)
Ответ: y = sin2x—1.
100
Я (1.2) ______
239. J[y(x)] = J rfx.
Л (0,1)
Ответ: (х — 2)2 + у2 = 5.
В(1,!)
240. 7[у(*)] = f ^dx.
А (0, 0)
Ответ: у = sh[xln (1 +|2)].
ь
241. Для функционала /(«/(*)] = J F (х, y)dx, заданного
а
на у^С[а, 6], FsC2[g, b]*, установить достаточные условия
экстремумов.
Указание. Рассмотреть полное приращение функцио-
нала.
1
242. Показать, что функционал •/[#(*)]= J y'2dxt задан-
о
ный на ysCjfa, 6], у(0) = 0, у'(0) = 1 (условия Коши),
не имеет экстремума.
Решить следующие вариационные задачи и исследовать
характер экстремумов по полному приращению функционала.
243. ^[y(x)]=Jy'(l гх3у')с/х, у (1) = 3, у (2) = 5.
1
Ответ: у=—i- + 7(min).
244. J [у (х) ] = J (ху'3 — у) dx, у (I) = 0, у (2) = 1.
Ответ: у = -'^1 (т1п).
* Пространство С [а, &] состоит из всех непрерывных на [а, 6] функ-
ций. Близость между двумя функциями у(х) и z(x) определяется рас-
стоянием р (у, z) = тахн/(х)—г(х) |. Пространство Сп [а, состоит из
а<х<о
всех функций на [а, 6], имеющих непрерывные производные до порядка п
включительно, где п=1, 2, 3,.... Расстояние между функциями у(х)
и z(x) определено формулой
Р 'У. г) = 2 max | »(|!) (х) - гт Iх) |.
А—9акхкЬ
101
245. S[y(x)] = ((ISxy+yy' + y'^dx, y(O) = l, y(l)=4.
0
Ответ: у = x3 -|- 2x 1 (min).
246. d(y(x)] = J(xy'4-2yy'3)dx, у (I) = 0, y(2) = l.
Ответ: у = x — 1 (mln).
247. /[y (x)J = j (x2y'2 + 12y2)dx, y(-l) = -l, y(l)=l.
-1
Ответ: у = x3 (mln).
248. J [y (x)] = f (xy' + y'2) dx, у (0) = I, у (2) = 0.
0
Ответ: _y=l-----(min).
249. J [y (x)] = f x3 y'2dx, y(— 1) = — 1, y(l) = l.
Ответ: y=y/x (mtn).
250. J [y (x)] = J (y'2 + y2 + 2ye2jc) dx, у (0) = •
0
у(1)=Ц-е2.
Ответ: y = —e2x (mln).
251. Sly(x)]=J(y2H-y'2H-6ysin2x)dx, y(0)=0, у(^)=1-
0
Ответ: у = -8sh-------1-sin2x (min).
5sh-^-
252. /[y(x)]=j-^, y(0) = 0, y(l)=l.
0
Ответ: y — x (min).
102
253. 7[y(x)] = J'[№.ry2+yy'] dx, y(0) = 0, y(l) = O.
0
Ответ: у —0 (min).
254. J [у (л)] = J у' Vdx, y(0) = 0, _y(l)=l.
0
i-7T
Ответ: у —--------1— (min).
l-«? 2
2
255. J [y (x)]= fy(!) = 0, у (2) — 1.
Ответ: у = 1/j-f ~1 ) (mtn).
F x yf 2 — 1 /
1
256. J[y (x)] = f y"t'~xdx. _y(0)=l, y(l) = 2.
о
Ответ: y = —(mln).
257. /[yWhjff + fl*. y(0) = 0, y(l) = l.
Ответ: y = -^f- (min).
3
258. 7[y(x)] = J’(12A:y + y'2)rfA:, у(1)=0, у(3) = 26.
Ответ: у = jc8 — 1 (min).
259. J[y(x)]= f [ys-f-y'2 — 2xy] dx, v(0) = 0, y(2) = 3.
b
Ответ: y= ^2 4~*
Найти функцию, для которой может достигаться экстре-
мум функционала.
260. [у(х)|= С (у2 — y’2+y)dx, у(0) = 0, у -
не задано.
103
Ответ;
у = --(sinл cos х — I).
261. I [у (л)] — J —У 2tfx, y(0)=0, у (2) —не задано,
о
Ответ:
V = ±/4 - (л - 2)2.
i
262. /[у (х)] = J (ху' -j- у'2) dx, у (0) — не задано, у (1)=1.
о
Ответ:
5-л’
У =—•
263. / [у (х)] = У (у- -j- у'2 - - 2у sin х) dx, у (0) — не задано.
У (-) = 0.
Ответ:
1
264. / [у (х)] = J(y2 + v'342yex)dx, у(0), у(1) —незаданы.
Ответ:
V- 1 I С11(1
У - 2 [_х<? ’С Sh 1 J •
265. /[y«]=j[y2+y'3+-^^x, y{0), y(l)-
0
не заданы.
Ответ:
у = х sh х -j- ch x [in ---vi~] •
J 1 L chx sh 1 J
1
266. 7[y(x)| = j* [‘-7“У/2 +уул если значения у на
6
концах интервала не заданы.
104
Ответ:
у = -1-(х2-Зх+ 3).
Найти экстремали функционалов:
267. I [у] = ? (1бу2 - у"2 + х2) dx.
-v0
Ответ;
У = ch 2х 4- С2 sh 2х 4- С3 sin 2х -j- С4 cos 2х.
268. /[у] = )'(2ху x"'-')dx.
ХВ
Ответ:
У = ~7г+ СХ° + С,х‘ + С.х3 + С,х2 -I- С,х 4- С„.
269. / [у] = J (у"2 - 2у'2 + у2 2у sin х) dx.
-то
Ответ;
у = (Ct С2х) sin х 4- (С3 4- С4х) cos х — s^n * .
270. I [у] = J (у'"2 + у2 - 2ух3) dx.
Ответ:
у = С,ех + С2е~х + (с„ cos d~~ х + С, sinх)е2 +
+ ^С3 cos-Ц^-* + C„sin ~~х^е 2 4-х3.
Найти функции, на которых могут достигаться экстре-
мумы функционалов:
271. I [у] ==У(у")*£?л при условиях:
а)у(О)=О, у(1) = 0, у'(0) = «, /GW;
б) у (0) = 0, у(1) = 0, У(0), У (1) — не заданы.
Ответ:
а) у = х(л- 1) [(а 4- ?) х-а];
б) у = 0.
105
272. /[у] =Л(у")2 + 4У2] dx, y(0), /(0) - не заданы,
y(l) = y'(l)=0.
Ответ:
У = 0.
273. /[у] = ПОТ--У'2-W*. У(0)=0, у(1) = 1,
о
у' (0), у' (1) — не заданы.
Ответ:
л । 1 r _ Il sinx + sin(l -х)
У — 2 Z ' 2 1 sin 1
274. I [у] = J [(у'Т - 2ху] dx, у (0) == у'(0) = О, у(1)=^,
О
у' (1) — не задано.
Ответ:
’ м. ! Х2-Л3
У ~ 120 + 24
Найти экстремали функционалов:
275- / [у (х), г (х)] = J (у'г + г'2 — 4хг' — 4г) dx.
Ответ:
у = С}х -р С21 % == ~р С%,
276. / [у (х), г (х)] = / (2уг - 2у2 + у'2 - г'2) dx.
Ответ:
у = Сг cos х -р С2 si их -J- С3 (cos х — ~ sin xj +
-Р С4 (sin х + cos х) ,
г = Сх cos х -р С2 sin х х (С4 cos х -р С3 sin х).
Найти функции, дающие экстремум функционалам:
277. / [у, z] = J (У2 + г'2) dx, у (0) = г (0) = 0,
у(1) = г(1)=1.
Ответ:
у =г = х.
106
‘278. Z[y, г] — J [у'2 — ху' — z'2] dx, у (0) — нс задано,
г(0)-0, y(I)=z(I) = l.
Ответ: ,
Найти геодезические линии:
279. Сферы радиуса /?.
Ответ: дуги больших кругов.
280. Круглого цилиндра г = /?.
Ответ: винтовые линии 2 = Лср + В, лежащие на цилинд-
ре r~R.
281. Параболоида вращения r2 = 2z.
Ответ:
z-i < и ~f- I I /" 2г -j- 1
<P = C1-arctgC« + Cln-;77T, и=У 2г_С2
282. Кругового конуса r = z.
Ответ:
j Найти экстремали следующих изостериметрических задач:
283. / [у (jc)] = J у dx, у (а) = у (— а) = 0,
— а
У VI + J1'2 dx — (const), / > 2а.
—а
Ответ: дуга окружности (^ + УХ2 — а2)2 + лг2 = X2,
>.sin^ = a, Х>-2-.
284. / [у (л)]= У(у'2 + л2)йл, у(0)=у(1) = 0, У y*dx = 2.
0 о
Ответ:
у = + 2 sin п~х (п = 1, 2, 3...).
107
285. /[у (х)] = \y'2dx, y(O) = y(w) = O при условиях:
о
a) f y2dx — 1; б) J ydx — I.
о о
Ответ:
а) у = sin&x (£—1,2,3...); б) у = -^г(я — х).
286. 1 [у (х)] — ? (у")2 dx, у (0) — у (я) = О при условиях:
и
a) ]y2dx — I; б) \y'2dx — 1.
о о
Ответ:
а) у = + sin nx; б) у = ± “ sin пх.
287. Один конец тяжелой цепи длиной I закреплен, а вто-
рой скользит по вертикальному стержню, отстоящему от
вертикали, проходящей через закрепленный конец цепи, на
расстоянии а < I. Найти форму цепи.
Указание. В состоянии равновесия центр тяжести цепи
занимает иаинизшее положение.
Ответ:
y=-^{ch7'»(1 -v) -ch4
где 7]о — положительный корень уравнения sh ц = ~ тр
Написать уравнение Эйлера для задачи об экстремуме.-
функционала:
288. /[2(x,v)]=JJ2[(4y + ^y]d.vdy.
Отв ет:
^+(4У+«У=о.
289. / [„ (х, у, г)] = JJJ + + dx dy dz:
Ответ:
Au = 0.
108
290. Написать уравнение Эйлера для задачи на экстремум
функционала
J [г (X, у)] = JJ + (~гг)2 +2г/<-х- J')]dx аУ
при условии z|s = <p(x, у). Получить естественное граничное
условие и показать, что функция, удовлетворяющая уравне-
нию Эйлера н одному из написанных условий, дает J[z] ми-
нимум.
Указание. Рассмотреть полное приращение Д/.
Ответ: уравнение Эйлера &z = f(x, у)-, естественное
граничное условие = где ~ означает дифференци-
рование по 'Направлению внешней нормали к S.
291. Написать уравнение Эйлера .и естественное гранич-
ное условие для функционала
J [«(х„ х2, Л8)] = JJJ f У ал + 2иД dx,dx2dx3*
D \i,k = \ /
3
Ответ: уравнение Эйлера = f',
t,k = \ k 1
естественное граничное условие
3 Z\
У «Л-^7 cos I-V = °-
292. Показать, что функция, удовлетворяющая уравнению
Эйлера задачи 291, условию и|8=ф(х(, х2, х3) или естествен-
ному граничному условию, сообщает /[и] минимум, если сим-
метричная матрица а^(хь х2, х3) такова, что при любых
X,, х2, х3е£) и любых t2, Ь будет 2а^бл>0 (ailt = a6i).
Указание. Рассмотреть полное приращение функцио-
нала.
293. Написать уравнение минимальной поверхности. Ми-
нимальной поверхностью называется поверхность z=z(x, у),
натянутая на заданный (в пространстве) контур L, и имею-
щая наименьшую площадь. Предполагается, что для кон-
тура L г|г = ф(х, у), где /•—проекция L иа плоскость хОу.
D—-плоская или трехмерная область с гладкой границей S.
109
Ответ:
fi j_ —i— Fi a. ( dz VI d‘2z о dz dz — л*
L ! X dy ) J <№ L 1 \ dx ) J dys dxdy dx dy “ u'
294. Доказать, что функция, удовлетворяющая уравнению
задачи 293, дает поверхность с наименьшей площадью.
Указание. Рассмотреть полное приращение функцио-
нала
у[г1=ЛК'+Ш+«Г^
D
и воспользоваться неравенством
1 •}- 2xr 4- г2 — 1 — гх > О при | х j < 1, г О'.
295. Получить уравнение, которому удовлетворяет г(х,У)
(аадача 293), если контур, на который натянута поверхность,
мало отличается от плоского.
Указание. Ввести малый параметр е следующим
образом:
z|; = Ах 4- By С 4- (х, у)>
2 = Ах 4- By 4- С 4- еф (х, у), А, В, C-const,
н линеаризировать уравнение Эйлера.
Ответ:
(1+«2)^ + (1+^-^-2ДВ^ = 0,
296. Найтн уравнение минимальных поверхностей, для
которых
г(х, у) = Л(х) +В(у).
Ответ:
где К — const.
При Л = 0 *< = ax + by-\-d есть уравнение плоскости.
Получить методом Ритца приближенное решение следую-
щих задач:
297. у" + у4-я = О5 у(0) = у(1) = 0.
Ответ:
y = -х>-
по
298. (х/)' + у = х, у(0) = 0, у(1) = 1.
Ответ:
У = Х+х(1 — х) (-jg-
299. Л/г =- 2, и|х_±а = О, tt|y_±b = O.
Ответ:
Найти собственные частоты .колебаний:
300. Однородной струны длиной 2а с закрепленными
в точках а и — а концами.
Отв ет:
1,57 — .
а
301. Однородной мембраны, имеющей форму:
а) полукруга (рис. 44) х2+#2 = я2, */> 0.
Ответ:
л 1 V
4,1 —
а
у
б) параболического сегмента (рис. 45) -у = I, у>0.
Ответ:
»=^/Ж + 4). приа=йщ«4,2^;
в) косинусоиды z/ = bcos (рис. 46), £/>0.
Ответ:
v 1/99 / а3 . 5г.2\ , _. q v
Ш = м). приа = й »~4,3-.
111
302. Получить методом Ритца приближенные значения
первых двух собственных чисел задач Штурмана — Лиувилля
и сравнить с точными значениями:
а) ^-4->-У = 0, J’|.v=0 = O, у|х_, = 0;
б>4М-)+^=°- ^U=o’ у|-1=°-
У
6
Рис. 46
ЛИТЕРАТУРА
1. Будак Б. М., С а м а р с к и й А. А., Тихонов Л. Н. Задачи
по уравнениям математической физики. ГИТТЛ, 1956.
2. Гринберг Г. Л. Избранные вопросы математической теории
электрических и магнитных явлений. АН СССР, 1948.
3. Гюнтер Н. М, Куз ьмин Р. О. Сборник задач по высшей
математике. Ч. 3, ГИТТЛ. 1951.
4. Кузьмин Р. О. Бесселевы функции. Гостехиздат, 1935.
5. Курант Р. Уравнения с частными производными. «Мир», 1964.
6. Курант Р., Гильберт Д. Методы математической физики-
Т. 1—2, Гостехиздат, 1951.
7. Лаврентьев М. А., Шабат Б. В. Методы теории функций
комплексного переменного. Физматгиз, 1958.
8. Лебедев Н. Н. Специальные функции и их приложения. Физ-
матгиз, 1963.
9. Лебедев Н. Н., Скальская И. П., Уфлянд Я. С. Сборник
задач по математической физике. ГИТТЛ, 1955.
10. Смирнов В. И. Курс высшей математики. Т. 2 и 4, ГИТТЛ, 1954.
11. Смирнов М. М. Задачи по уравнениям математической физики.
ГИТТЛ, 1954.
12. Тихонов А. Н.. Самарский А. А. Уравнения математической
физики. «Наука», 1966.
ПРИЛОЖЕНИЕ I
Таблица некоторых рядов Фурье
О < х
а.
8
2а
т('"4
О -С х К а.
{2п -г 1) кх
sin-----2л----
_ IV________________
(2«^1)2
8а
О < х < а.
113
О < х < а.
Ж^Ч 2л - 1 ~л-
12 ____= 0<л.<а.
‘> |2/г+1|3 32 ( а? ’ и л
«=0
13. = 0<х<п.
4 1 п1 — a2 2 sine*
п — 1
VI/ <у< Rin (2л г
/J |>4 1р
~ Sin ах
4а COS —2~
ix|< 2 .
15.
_________sin {‘2п -I- О х
[2п -- 1) [(2л + Г;а — а2]
ах а
- sin -у sin ~2 — х}
2а cos —2—
Sxn 1
~ COS Я<5 ----< In (1 — 2x COS O — x'~), ! X < 1.
n— I
l7- S 2л 4 1 sin + 1)T = 4arctg
л ~ 0
18- cos(2«-i-1)'fi=4arctg-T^L- и<!-
n = 0
!9. У ^LLcos(2«+ |)?=±|п^±^£^4^, И<1-
2n -• 1 v 1 ' 1 4 1 — 2x cos -г x2 1 1
114
ПРИЛОЖЕНИЕ И
Таблица преобразований Лапласа
/(<) f (/>) = у (') «“"'Л fW f w= J/U) e-"‘M 0
1 1 sh at a
р p" — a2
г rL+n. v> i Ch at P
pv+I , - 1 P- - »‘J I
С p-а Ju (a/) )/"/?3 — a-
sin at a /„ w 1
/₽=-«»
P 1 (, _ 1 у
cos at p^ + ^p- Ln P v p )
СОДЕРЖАНИЕ
Предисловие ..............................................
Глава 1. Задача Штурма—Лиувилля ..........................
Глава II. Постановка задач математической физики..........
Глава 111. Метод собственных функций..............
Глава IV. Преобразование Лапласа..........................
Глава V. Интегральные уравнения...........................
Глава VI. Вариационное исчисление ........................
Литература -..............................................
Приложение I. Таблица некоторых рядов Фурье...............
Приложение II. Таблица преобразований Лапласа...............
Галина Александровна Жукова-Малицкая,
Юрий Николаевич Кузьмин
Математическая физика
Учебное пособие
Издание второе, дополненное
Редактор А. П. Алексеева
Корректоры С. Д. Рутковская и Н. Н. Тарасова
М-07794, Подписано к печати 20/VII-74 г. Формат бумаги бОХ^О1/^,
Обьем 7,25 нем, л. Заказ 354. Тираж 5000. Цена 26 коп.
Лаборатория полиграфических машин Ленинградского ордена Ленина
политехнического института им. М. И. Калинина
195251, Ленинград, Политехническая ул., 29.'
Замеченные опечатки
Стр. Строка Напечатано Должно быть
50 4-я снизу сом а ... са а ...
69 10-я снизу ... с плоскостью за- ... с плотностью за-
ряда ... ряда...
112 2-я сверху .,. задач Штурмана — —- Лиувилля ... задач Штурма — — Лиувилля
Заказ 364. Тираж 5000,
26 коп.
ь77 1 У