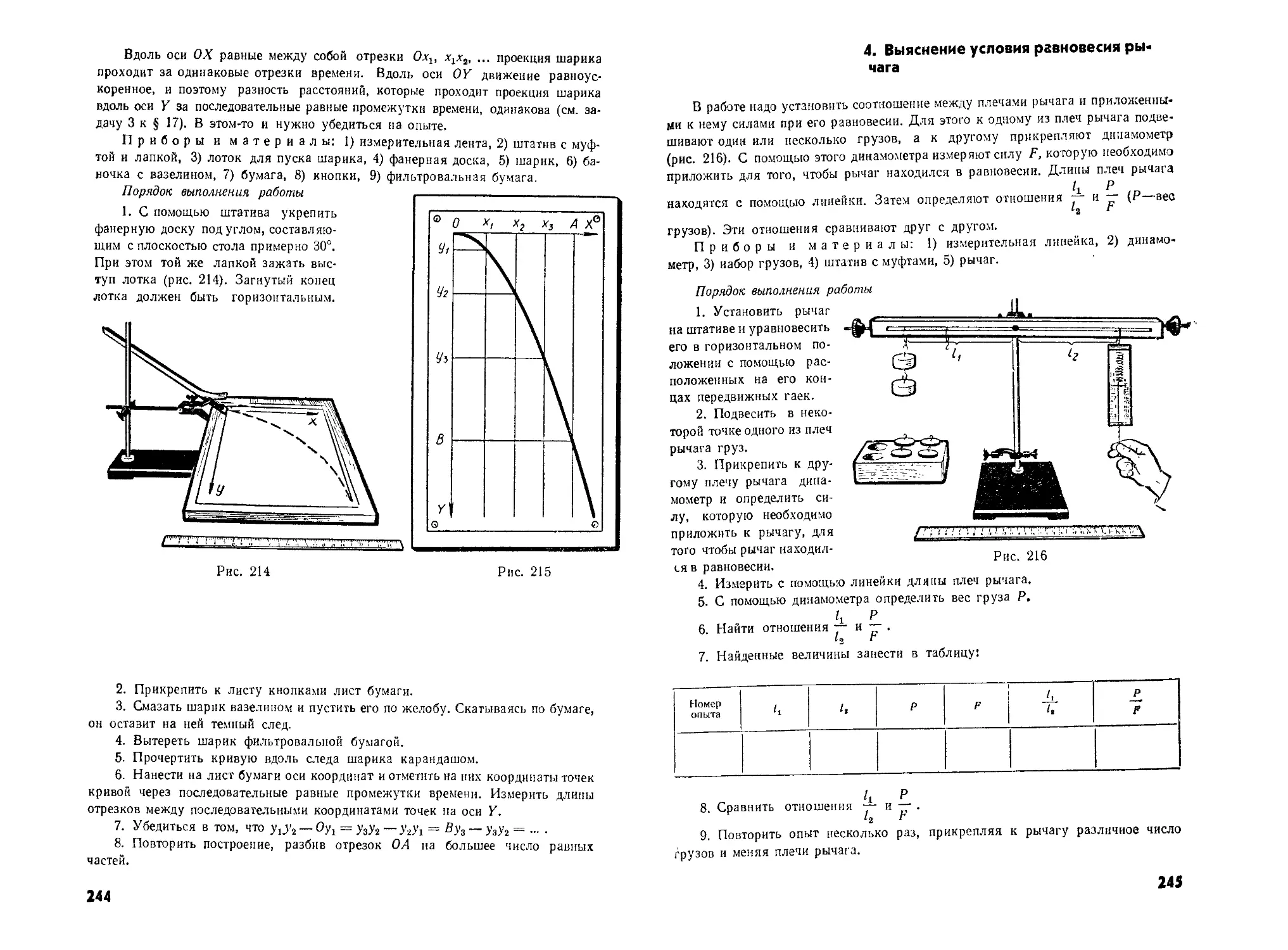
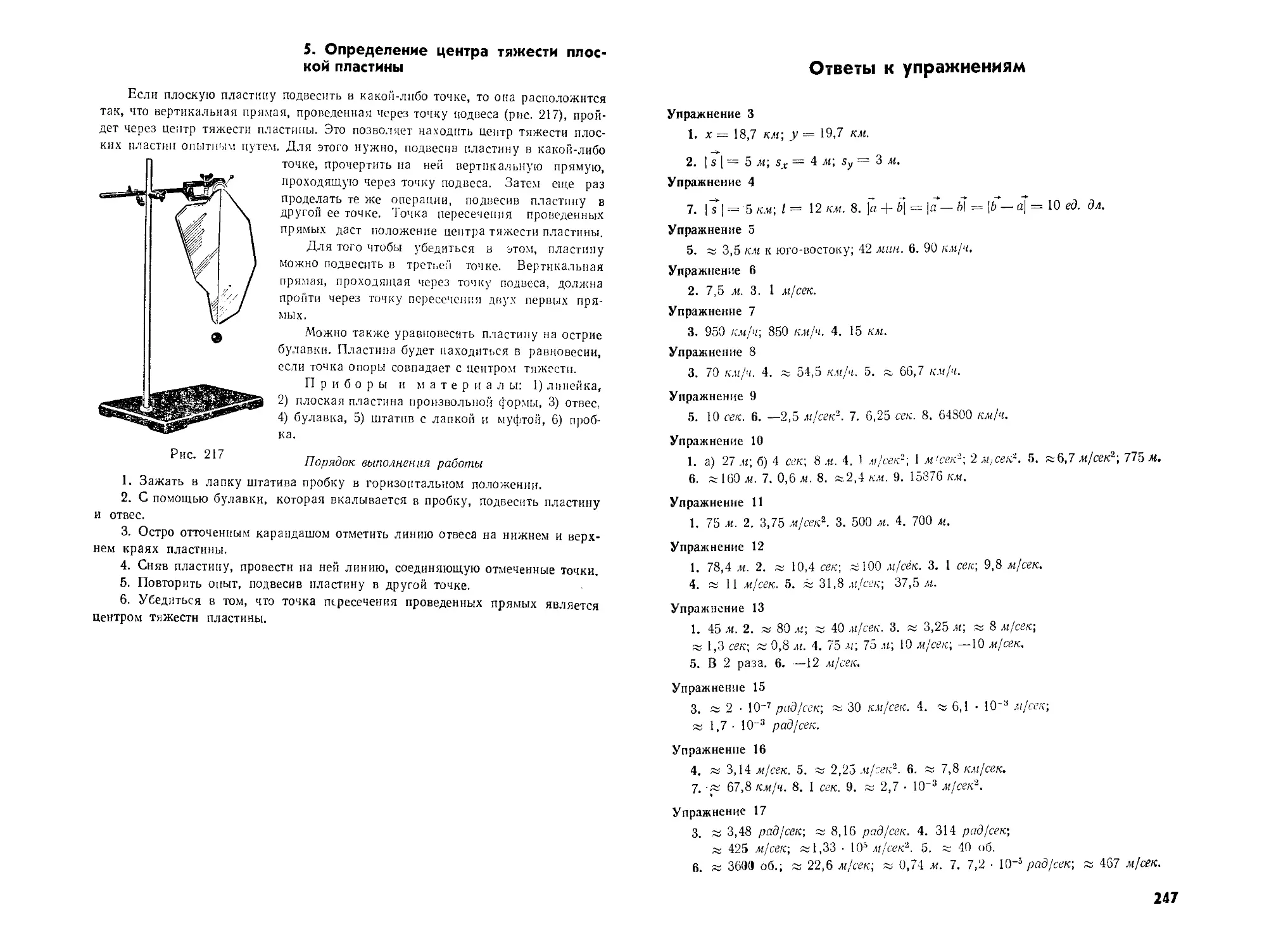
Автор: Кикоин И.К. Кикоин А.К.
Теги: физика математическая физика учебник учебник по физике издательство просвещение
Год: 1973
Текст
ФИЗИКА 8
Основные механические единицы
Международной системы (СИ)
метр
м
килограмм
кг
секунда
сек
I м приближенно равен части
40 000 000
длины земного меридиана, проходящего
через Париж
Эталон метра
I м равен I 650 763,73 длин волн
оранжевой спектральной линии
излучения атома нриптона с
атомной массой 86
I нг приближенно равен массе
1 л чистой воды при температуре 15 С
Эталон килограмма
I сен приближенно равна части
31 556 925, 9747
времени обращения Земли вонруг Солнца
в 1900 году
1 сен равна 9 192 631 770 периодов из-
лучения, соответствующего переходу
между двумя определенными уровнями
атома цезия с атомной массой 133
И. К. КИКОИН, А. К. КИКОИН
УЧЕБНОЕ ПОСОБИЕ
ДЛЯ 8 КЛАССА
СРЕДНЕЙ ШКОЛЫ
Утверждено Министерством
просвещения СССР
ИЗДАНИЕ ЧЕТВЕРТОЕ, ПЕРЕРАБОТАННОЕ
Москва
«Просвещение»
1973
53 (075)
К 38
0661 — 276
М 103 (03) — 73
Кинематика
Глава 1
Общие сведения о движении
ВВЕДЕНИЕ
Все, что реально существует в мире, на Земле и вне Земли,
все, что мы можем видеть, осязать или вообще ощущать с помощью
наших органов чувств, называют в науке материей. К ней относят-
ся всевозможные тела, окружающие нас: воздух, камни, растения,
вода, небесные светила и т. д., и вещества, из которых эти тела со-
стоят. Материей является и то, что телами обычно не называют, на-
пример свет, позволяющий нам видеть мир, или радиоволны, кото-
рые делают возможным радиосвязь и телевидение.
Выражение «реально существует» означает, что тот или иной
предмет существует независимо от того, ощущаем мы его непосред-
ственно или нет. Например, автомобиль, который мы видим проез-
жающим мимо нас, конечно, реально существует. Но он не переста-
ет существовать и тогда, когда он повернул за угол улицы и видеть
его нам уже нельзя.
Одно из самых важйых свойств материи — ее изменчивость.
Еще 2500 лет назад греческий философ Гераклит высказал заме-
чательную мысль: «Все течет, все изменяется». В этой как будто бы
простой фразе выражена мысль вовсе не простая и не очевидная.
Ведь каждый из нас видит вокруг себя не только изменяющиеся,
но и, казалось бы, «неизменные» вещи. Здание школы, куда вы приш-
ли сегодня, кажется совершенно таким же, каким оно было вчера;
улицы, по которым вы прошли, как будто такие же, какими они
были и раньше; мебель в квартире, деревья в парке, звезды на не-
бе и многое другое как будто бы остается неизменным. Но на самом
деле эта неизменность только кажущаяся. В действительности все
окружающее нас, может быть, незаметно на первый взгляд, но из-
меняется. Новое здание в результате накопившихся в нем изменений
3
постепенно приходит в ветхость. Любое дерево рано или поздно
погибает, уступая место молодому растению, и т. д.
То или иное изменение материи мы называем явлением природы.
Науки о природе изучают эти явления, чтобы узнать законы, по
которым происходят всевозможные изменения материи. А знать
это нужно для того, чтобы дать в руки людей методы, с помощью
которых можно заранее узнать, как будет протекать то или иное
изменение в природе (явление), т. е. предсказать будущее и объяс- •
нить прошлое. Только при этом условии явления природы можно
использовать на благо людям. Если бы, например, химики не изу-
чили, что происходит при взаимодействии различных веществ, не
могло бы быть современной химической промышленности, которая
обеспечивает людей огромным количеством нужных им веществ.
Если бы не было изучено, как ведут себя растения, как они пита-
ются и произрастают, трудно было бы развивать сельское хозяй-
ство, нельзя было бы предвидеть, что получится в результате
посева тех или иных семян, той или иной обработки почвы. Вся
современная техника основана на предвидении будущего. Когда ин-
женер конструирует какую-нибудь машину, он заранее представля-
ет себе, как она будет работать, потому что пользуется данными
науки.
О любом явлении всегда можно сказать, что оно происходит
где-то и когда-то. Все события происходят в пространстве
(г д е?) и во времени (к о г д а?). Поэтому материя и ее изменения
неразрывно связаны с пространством и временем.
Нельзя говорить о материи вне времени и пространства так
же, как нельзя говорить ни о совершенно пустом пространстве,
ни о времени, которое течет само по себе.
Из всех изменений, происходящих в окружающем нас мире,
из всех явлений природы наиболее знакомо всем механиче-
ское движение. Что это за явление?
Каждое тело в любой момент времени занимает вполне опре-
деленное фиксированное положение в пространстве по отношению
к другим телам. Если с течением времени положение тела изменяет-
и ж е т с я.
Механическим движением тела на-
зывают изменение его положения в
пространстве относительно других
тел с течением времени»
Изучением явления движения за-
нимается часть физики, которую на-
зывают механикой. Основная
задача механики заключается в том,
чтобы определять положение движу-
щегося тела в любой момент време-
ни. Так, астрономы, пользуясь зако-
нами механики, могут точно вычис-
лять положение небесных тел в любой
ся, то говорят, что тело д в
Рис. 1
4
момент времени и поэтому предсказывать различные небесные явле-
ния, например такие, как солнечные и лунные затмения.
Больше того, законы механики позволяют определить поло-
жение тела не только в будущем, но и в прошлом. Если бы, напри-
мер, историки не знали точную дату начала похода князя Игоря
против половцев, то ее легко могли бы вычислить астрономы,
потому что в знаменитом «Слове о полку Игореве», в котором вос-
пет этот поход, указано, что перед вступлением Игоря в землю по-
ловецкую произошло полное солнечное затмение. Этого достаточно,
чтобы установить, что на границе половецкой земли Игорь со своей
дружиной был 1 мая 1185 г.1.
§ 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ.
МАТЕРИАЛЬНАЯ ТОЧКА
Чтобы изучать движение тела, т. е. изменение его положения в
пространстве, нужно прежде всего уметь определять само это
положение. Но здесь возникает некоторое затруднение. Каждое
тело имеет определенные размеры; следовательно, разные его ча-
сти, разные точки тела находятся в разных местах пространства.
Как же определить положение всего тела? В общем случае это тру-
дно сделать. Но оказывается, во многих случаях нет необходи-
мости указывать положение каждой точки движущегося тела.
Этого не нужно делать в тех случаях, когда все точки тела
движутся одинаково. Зачем, например, описывать движение каж-
дой точки санок, которые мальчик тянет в гору, если их движения
ничем существенным не различаются между собой?
Одинаково движутся все точки баржи, плывущей по реке, че-
модана, который мы поднимаем с пола (рис. 1), и т. д.
Движение тела, при котором все его точки движутся одинаково,
называют поступательным.
В дальнейшем мы будем рассматривать главным образом по-
ступательное движение.
Не нужно описывать движение каждой точки тела и тогда,
когда размеры тела малы по сравнению с расстоянием, которое оно
проходит, или по сравнению с расстояниями от него до других тел.
В этих случаях размерами тела можно пренебречь. Так поступают,
например, в астрономии при изучении движений небесных тел.
Планеты, звезды, Солнце, конечно, не малые тела. Но радиус Зем-
ли, например, в 24 000 раз меньше, чем расстояние от Земли до
Солнца. Поэтому можно считать Землю точкой, которая движется
вокруг другой точки — центра Солнца.
Во всех таких случаях тела можно считать точками. И говоря
о движении тела, мы в действительности будем иметь в видудвиже-
1 Ошибиться здесь нельзя, потому что известно, что в одном и том же месте
полное солнечное затмение бывает примерно один раз в 200 лет. В XII в. в райо-
не донских степей могло быть всего одно затмение.
5
Рис. 2
нельзя.
ние какой-нибудь точки это-
го тела. Не надо забывать
при этом, что эта точка мате-
риальна, т. е. она обладает
всеми свойствами обычного те-
ла, кроме свойства иметь раз-
меры.
Тело, размерами которо-
го в данных условиях дви-
жения можно пренебречь,
называют материальной точ-
кой.
Слова «в данных условиях»
означают, что одно и то же те-
ло при одних его движениях
можно считать материальной
точкой, а при других нет.
Когда, например, мальчик,
возвращаясь из школы, про-
ходит до дома расстояние в
1 км (рис.. 2, а), то маль-
чика в этом движении можно
рассматривать как материаль-
ную точку, потому что его раз-
меры малы по сравнению с
расстоянием, которое он про-
ходит. Но когда тот же мальчик выполняет упражнения утренней
зарядки (рис. 2, б), то материальной точкой считать его никак
Упражнение!
В каких из следующих случаев тела можно считать материальными точками:
1. На станке изготовляется спортивный диск. Тот же диск после броска
спортсмена пролетает расстояние в 55 м.
2. Пассажирский самолет совершает рейс из Москвы в Хабаровск. Самолет
выполняет фигуру высшего пилотажа.
3. Конькобежец проходит дистанцию соревнований. Конькобежец-фигурист
выполняет упражнения произвольной программы.
4. За движением космического корабля следят из центра управления на
Земле. За тем же кораблем наблюдает космонавт, осуществляющий с ним
стыковку в космосе.
§ 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА)
В ПРОСТРАНСТВЕ
Как определить положение тела? В одном древнем документе,
относящемся к началу нашей эры, приведено такое описание место-
нахождения клада, содержащего слитки золота и серебра: «Стань
у восточного угла крайнего дома села лицом на север и, пройдя
6
120 шагов, повернись лицом на восток и пройди 200 шагов. В этом
месте вырой яму глубиной в 10 локтей и найдешь 100 талантов
золота». Если бы указанные в документе село и дом сохранились
до наших дней, то этот клад было бы нетрудно найти. Но, по по-
нятным причинам, от села и дома не осталось и следа, и найти
клад поэтому невозможно. Этот пример показывает, что положение
тела или точки можно задать только относительно како-
го-нибудь другого тела, которое называют телом отсчета.
Тело отсчета можно выбрать совершенно произвольно. Им мо-
жет служить, например, дом, в котором мы живем, вагон поезда,
в котором мы едем, и вообще любое другое тело. Телами отсчета
могут служить Земля, Солнце, звезды. Нам, живущим на Земле,
удобно указывать положение тела относительно Земли. Впрочем,
астрономы предпочитают вести отсчет относительно звезд.
Если тело отсчета выбрано, то положение тела задается рас-
стоянием или расстояниями, отсчитываемыми от этого тела до тела
отсчета.
Допустим, что тело может двигаться только вдоль некоторой
линии. Так движется поезд по железной дороге, автомобиль по
шоссе и т. д. Так как тело может находиться либо с одной, либо с
другой стороны от тела отсчета, то расстояния, отсчитываемые в
одну сторону от него, например вправо, считают положительными,
в другую (Влево) — отрицательными.
Как определить, например, положение автомобилей на дороге
(рис. 3)?
В качестве тела отсчета выберем придорожное селение А. Мыс-
ленно проведем вдоль дороги прямую со стрелкой, указывающей
направление отсчета, которое мы примем за положительное. Ее на-
Рис. 3
7
зывают координатной осью.
Отметим на координатной оси точку О,
соответствующую селению А (начало
отсчета). Тогда положение автомоби-
ля / определится длиной отрезка ОВ. Чис-
ло, выражающее эту длину в определенном
масштабе, называют координатой
автомобиля/. На рисунке 3 масштаб
выбран так, что координата получилась
равной 1200 м.
Для автомобиля // координата выра-
жается числом 400 м, но так как ее при-
ходится отсчитывать влево от начала от-
счета, то ей нужно приписать знак «—».
Таким образом, положение тела на
линии определяется одной координатой —
расстоянием вдоль линии от этого тела до
тела отсчета.
Если тело может двигаться в преде-
лах некоторой плоскости (например, лод-
ка на озере), то через выбранную на теле
отсчета точку проводят две взаимно пер-
пендикулярные прямые — оси коор-
динат.
Их принято обозначать, как это сде-
лано на рисунке 4, ОХ и 0Y, а назы-
вают просто осями X и Y. Они образуют
так называемую прямоугольную
систему координат X0Y.
Из курса алгебры VII класса известно, что положение точки на
плоскости определяют двумя координатами, отсчитываемыми от
начала координат О вдоль осей X и Y. Эти два числа, выражающие
расстояния от начала координат, обозначают малыми буквами х и у.
Например, у точки А (см. рис. 4): х= 3, у = 4; у точки В: х = 2,
у = —1,5.
Наконец, чтобы задать положение тела в пространстве (на-
пример, положение самолета в воздухе), нужно мысленно провести
через тело отсчета три взаимно перпендикулярные прямые (три
оси координат). Их принято обозначать OX, 0Y и 0Z (рис. 5).
Соответственно этому положение тела (точки) в пространстве опре-
деляется тремя координатами: х, у и г.
Именно такая система координат использована в документе
о кладе, о котором рассказано в начале параграфа. Чтобы найти
клад, нужно только знать, где находится начало координат, от ко-
торого следует отсчитывать расстояние по осям X, Y и Z.
Итак, положение точки на линии, плоскости и в пространстве
определяют соответственно одним, двумя и тремя числами — ко-
ординатами. Пространство, в котором мы живем, является, как
8
говорят, пространством трех измерений, или трехмерным
пространством.
В дальнейшем мы будем иметь дело главным образом с движе-
ниями вдоль линий или на плоскостях. Поэтому нам придется поль-
зоваться либо одной, либо двумя координатами.
Мы уже говорили, что механика — это наука о том, как опре-
делять положение тела в любой момент времени. Поскольку поло-
жение тела определяется его координатами, то задача механики
сводится к тому, чтобы уметь вычислять координаты тела в лю-
бой момент времени.
При движении тела его координаты изменяются. Если, на-
пример, координата, отсчитанная по оси X, в какой-то начальный
момент времени была х0, а спустя промежуток времени t она стала
равной х, то это значит, что координата изменилась на величину
X — ха.
Чтобы решить задачу механики, надо знать, как изменяются
координаты тела со временем. Но как это узнать? Какими данными
нужно для этого располагать? Что’должно быть известно заранее?
Ответы на эти вопросы дает раздел механики, который называ-
ют кинематикой. В нем мы ознакомимся с различными ви-
дами движения и с тем, как в разных случаях можно определять
положение тела в любой момент времени.
§ 3. ПЕРЕМЕЩЕНИЕ
Если тело движется равномерно вдоль некоторой заданной ли-
нии, то его положение на этой линии в любой момент времени на-
ходится просто. Из курса физики VI класса известно, что, умножив
скорость тела v на время I, протекшее до интересующего нас мо-
мента, мы получим длину пройденного пути I.
И если известна точка, в которой находилось тело в начальный
момент времени, то, отложив от нее вдоль линии, по которой дви-
жется тело, пройденный путь I, мы найдем точку, где тело окажется
в момент времени t.
Но задача решается так просто только тогда, когда известна
линия, вдоль которой движется тело, или, как говорят, известна
траектория движения тела. Так, траекторией для поезда
будет железная дорога, для автомобиля — шоссе и т. д.
В тех случаях, когда траектория движения не задана, Опреде-
лить положение тела, т. е. его координаты, в конце пути нельзя,
даже если положение тела и длина пройденного им пути известны.
Так, например, если мы знаем начальное положение корабля и
длину пройденного им пути, мы не сможем вычислить координаты
корабля в конце этого пути: корабль может пройти его в любом на-
правлении и по любой траектории.
Для того чтобы и в этом случае найти положение тела, надо знать
не длину пройденного пути, а совсем другую величину — пере-
мещение тела. Что это за величина?
9
Рис. 6
Допустим, что в какой-то начальный
момент времени движущееся тело (точка)
занимало положение Л1х(рис. 6), а через
некоторый промежуток времени оно оказа-
лось в другом положении на расстоянии $
от начального. Как найти это новое поло-
жение тела? Очевидно, что для этого недос-
таточно знать расстояние s, потому что
есть бесчисленное множество точек, уда-
ленных от точки М на это расстояние
(рис. 6).
Чтобы найти конечное положение тела,
надо еще знать направление отрезка s,
соединяющего начальное положение тела
с его конечным положением. Этот направ-
ленный отрезок прямой и представляет со-
бой перемещение тела. Конец отрезка, изоб-
ражающего перемещение, для нагляд-
ности отмечают стрелкой (рис. 7, а).
Приставив отрезок к точке Mlt мы у кон-
ца стрелки найдем новое положение тела
М2 (рис. 7, б).
Перемещением тела называют направ-
ленный отрезок прямой, соединяющий
начальное положение тела с его конеч-
ным положением»
Итак, чтобы найти положение тела в
любой момент времени, нужно знать его
начальное положение и перемещение, совер-
шенное к этому моменту времени.
Перемещение тела надо отличать от
траектории его движения. Из того, что
тело переместилось из точки в точку
М2 (рис. 8) и длина его перемещения равна
отрезку М1М2, не следует, что тело дви-
галось по прямой М1М3. Траектория дви-
жения тела, т. е. линия, по которой оно
действительно двигалось, может не совпа-
дать с этой прямой. Следующий пример
поясняет это.
На рисунке 9 изображена географическая карта района Черно-
го моря. Расстояние между Одессой и Севастополем по прямой со-
ставляет 270 км, и, для того чтобы попасть из Одессы в Севасто-
поль, нужно совершить перемещение, направленное примерно на
юго-восток и численно равное 270 км. Если мы отправимся в
путешествие на теплоходе, то его действительное движение может
происходить по прямой, совпадающей с перемещением. Но из
Одессы в Севастополь можно ехать и на поезде. Линия железной
10
дороги проходит через Ни- ;
колаев, Херсон, Джанкой
и Севастополь. Ее протя-
женность 660 км. При пу-
тешествии по железной до-
роге траектория движения
уже не будет совпадать с
перемещением.
Ясно, что если нас ин-
тересует конечное положе-
ние поезда относительно
Одессы, то оно определя-
ется перемещением Одес-
са — Севастополь. Если мы
знаем, что перемещение
направлено на юго-восток
и составляет 270 км, то
этих сведений достаточно .
для того, чтобы узнать, где
расположен поезд. Но если
нам сказано, что поезд прошел путь в 660 км, то это не поможет
нам узнать, где, он находится: из Одессы поезд мог отправиться
в Москву, Киев, Харьков или в любой другой город.
Упражнение 2
1. Наблюдения над движениями футболистов показали, что нападающий за
время матча пробегает примерно 12 км. Как следует называть приведен-
ную величину: перемещением или длиной пути?
2. Штурман, определяя утром положение корабля, обнаружил, что корабль
находится в точке, расположенной на 100 км к северу от пункта, в кото-
ром находился корабль накануне вечером. Что выражает приведенное
здесь число: перемещение или пройденный путь?
3. Дежурный по гаражу, принимая автомашину у закончившего работу
шофера, записал увеличение показания счетчика на 300 км. Что будет
означать эта-запись: пройденный путь или перемещение?
§ 4. ПОНЯТИЕ О ВЕКТОРАХ.
ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ГЕЛА
Перемещение — это особая величина. Особая потому, что она
задается не только определенным числом, но и направлением. Та-
ких величин в физике известно много; их называют векторны-
ми величинами или просто векторами.
Векторные величины изображают отрезками прямых со стрел-
ками, как это сделано на рисунке 7, а и б. Длина отрезка в опре-
деленном масштабе показывает абсолютное значение (модуль)
векторной величины, а стрелка указывает ее направление. Вектор-
ные величины обозначаются буквами со стрелочкой над ними.
Например,® — вектор перемещения. Модуль (или длина) вектора
перемещения — число, показывающее, скольким единицам длины
Рис. 10
(метрам, километрам и т. д.) равно перемещение. Модуль вектора
мы будем обозначать той же буквой со стрелкой, что и сам вектор,
но перед буквой и за ней будем ставить вертикальные линии. На-
пример, |s|—модуль вектора перемещения s. Вектор определя-
ется его модулем и направлением.
Два вектора считают равными, если равны их модули и они оди-
наково направлены.
Величины, не имеющие направления в пространстве, т. е.
просто числа, хотя и именованные, называют скалярными
величинами или просто скалярами. Скалярными ве-
личинами являются, например, время, объем, температура и т. д.
Зная вектор перемещения и координаты начального положе-
ния тела, можно найти значения координат его конечного положе-
ния. Как это сделать, поясним на примере движения тела на плос-
кости .
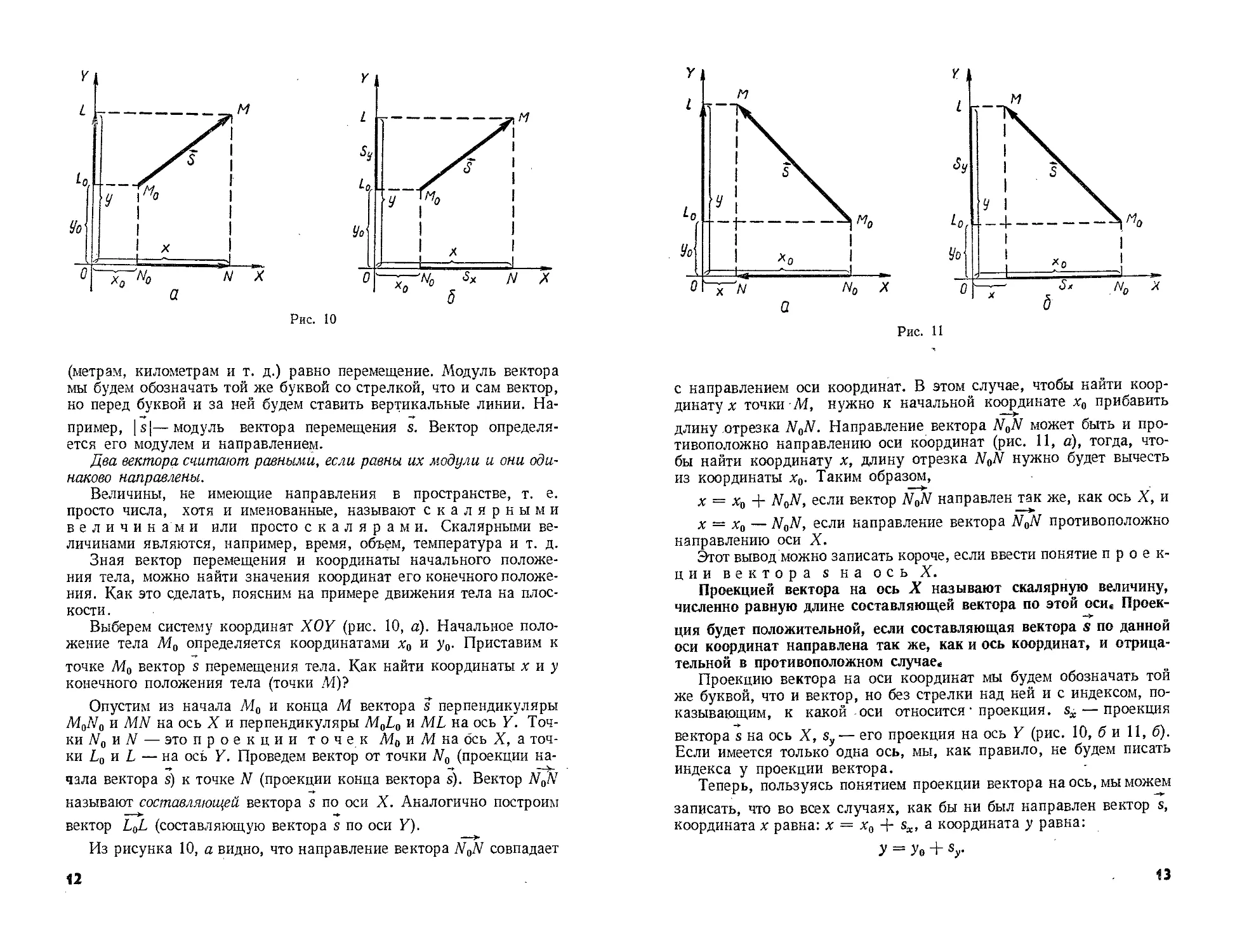
Выберем систему координат X0Y (рис. 10, а). Начальное поло-
жение тела Л1о определяется координатами х0 и у0. Приставим к
точке Л1о вектор s перемещения тела. Как найти координаты х и у
конечного положения тела (точки Л1)?
Опустим из начала Л10 и конца М вектора s перпендикуляры
M0N0 и MN на ось X и перпендикуляры M0L0 и ML на ось Y. Точ-
ки No и N — это проекции точек Л10иЛ1на ось X, а точ-
ки Lo и L — на ось Y. Проведем вектор от точки Ао (проекции на-
чала вектора s) к точке N (проекции конца вектора s). Вектор N0N
называют составляющей вектора s по оси X. Аналогично построим
вектор LjL (составляющую вектора s по оси Y).
Из рисунка 10, а видно, что направление вектора N0N совпадает
12
У
Рис. 11
с направлением оси координат. В этом случае, чтобы найти коор-
динату х точки-М, нужно к начальной координате х0 прибавить
длину отрезка N0N. Направление вектора N0N может быть и про-
тивоположно направлению оси координат (рис. 11, а), тогда, что-
бы найти координату х, длину отрезка N0N нужно будет вычесть
из координаты х0. Таким образом,
х — х0 + N0N, если вектор N0N направлен так же, как ось X, и
х = х0 — N0N, если направление вектора iVoJV противоположно
направлению оси X.
Этот вывод можно записать короче, если ввести понятие проек-
ции вектора s на ось X.
Проекцией вектора на ось X называют скалярную величину,
численно равную длине составляющей вектора по этой оси. Проек-
ция будет положительной, если составляющая вектора s по данной
оси координат направлена так же, как и ось координат, и отрица-
тельной в противоположном случае.
Проекцию вектора на оси координат мы будем обозначать той
же буквой, что и вектор, но без стрелки над ней и с индексом, по-
казывающим, к какой оси относится • проекция. sx— проекция
вектора s на ось X, sy— его проекция на ось У (рис. 10, би 11, б).
Если имеется только одна ось, мы, как правило, не будем писать
индекса у проекции вектора.
Теперь, пользуясь понятием проекции вектора на ось, мы можем
записать, что во всех случаях, как бы ни был направлен вектор s,
координата х равна: х ~ х0 -У sx, а координата у равна:
У = У о + sr
13
Следовательно, зная перемещение, а значит, и его проекции на
оси координат, можно найти координаты тела, т. е. решить основ-
ную задачу механики.
Если вектор N0N направлен так же, как ось X, то проекция sx
положительна (sx = N0Ny, если направление вектора N0N проти-
воположно направлению оси координат, то проекция sx отрица-
тельна (sx = —N0N). Подобные рассуждения можно провести и
для вектора L0L и проекции s„.
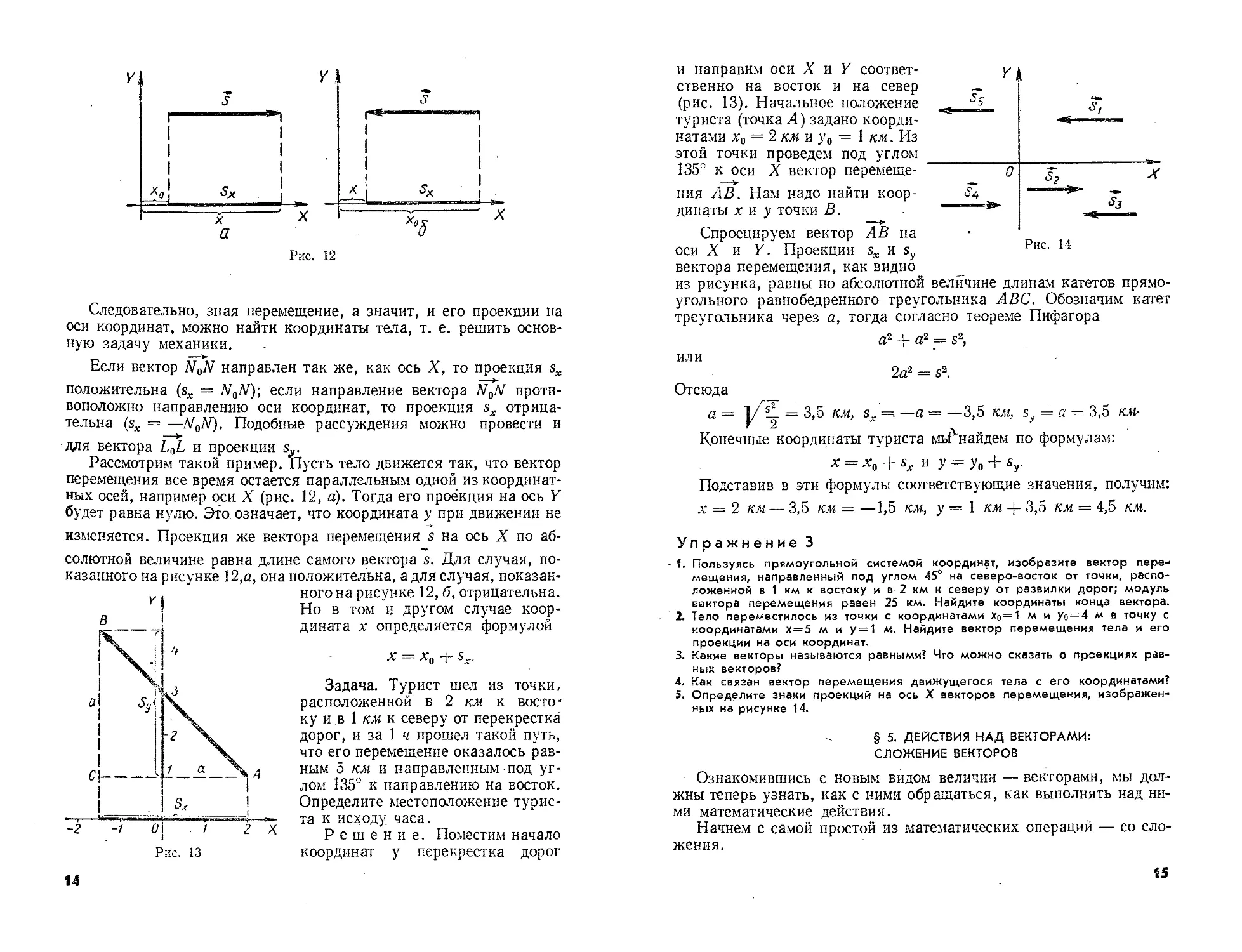
Рассмотрим такой пример. Пусть тело движется так, что вектор
перемещения все время остается параллельным одной из координат-
ных осей, например оси X (рис. 12, а). Тогда его проекция на ось Y
будет равна нулю. Это, означает, что координата у при движении не
изменяется. Проекция же вектора перемещения s на ось X по аб-
солютной величине равна длине самого вектора s. Для случая, по-
казанного на рисунке 12,а, она положительна, а для случая, показан-
ного на рисунке 12, б, отрицательна.
Но в том и другом случае коор-
дината х определяется формулой
х = х0 + s „
Задача. Турист шел из точки,
расположенной в 2 км к восто-
ку и в 1 км к северу от перекрестка
дорог, и за 1 ч прошел такой путь,
что его перемещение оказалось рав-
ным 5 км и направленным под уг-
лом 135° к направлению на восток.
Определите местоположение турис-
та к исходу часа.
Решение. Поместим начало
координат у перекрестка дорог
14
и направим оси X и Y соответ-
ственно на восток и на север
(рис. 13). Начальное положение
туриста (точка Л) задано коорди-
натами х0 = 2 км и у о — 1 км. Из
этой точки проведем под углом
135° к оси X вектор перемеще-
ния АВ. Нам надо найти коор-
динаты X и у точки В.
Спроецируем вектор АВ на
оси X и Y. Проекции sx и sy
Рис. 14
вектора перемещения, как видно
из рисунка, равны по абсолютной величине длинам катетов прямо-
угольного равнобедренного треугольника АВС. Обозначим катет
треугольника через а, тогда согласно теореме Пифагора
a2 J- а2 = s2,
или
2а2 = s2.
Отсюда
а = = 3,5 км, sx =. —а = —3,5 км, sy = а = 3,5 км-
Конечные координаты туриста мьРнайдем по формулам:
х = ха + sx и у = у0 + sy.
Подставив в эти формулы соответствующие значения, получим:
х = 2 км — 3,5 км = —1,5 км, у = 1 км ф- 3,5 км = 4,5 км.
Упражнение 3
- 1. Пользуясь прямоугольной системой координат, изобразите вектор пере-
мещения, направленный под углом 45° на северо-восток от точки, распо-
ложенной в 1 км к востоку и в 2 км к северу от развилки дорог; модуль
вектора перемещения равен 25 км. Найдите координаты конца вектора.
2. Тело переместилось из точки с координатами х0=1 м и Уо = 4 м в точку с
координатами х=5 м и у=1 м. Найдите вектор перемещения тела и его
проекции на оси координат.
3. Какие векторы называются равными? Что можно сказать о проекциях рав-
ных векторов?
4. Как связан вектор перемещения движущегося тела с его координатами?
5. Определите знаки проекций на ось X векторов перемещения, изображен-
ных на рисунке 14.
§ 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ:
СЛОЖЕНИЕ ВЕКТОРОВ
Ознакомившись с новым видом величин — векторами, мы дол-
жны теперь узнать, как с ними обращаться, как выполнять над ни-
ми математические действия.
Начнем с самой простой из математических операций — со сло-
жения.
15
Рис. 15
Представим себе пешехода на перекрестке двух улиц, которому
надо перейти с угла, обозначенного ЛК (рис. 15), на угол М2. Он
мог бы направиться непосредственно к этому углу по прямой
Тогда мы сказали бы, что перемещение пешехода равно М1М2.
Но на улицах с оживленным движением такой переход запрещен.
Поэтому дисциплинированный пешеход перейдет сначала из точ-
ки в точку А, а затем из точки А в точку Л12. Конечный резуль-
тат будет таким же, как если бы он прошел по прямой ЛКЛ1г- Пе-
ремещение M1M2 достигнуто в результате двух перемещений:
М^А и АМ2. Эти перемещения заменили одно. Естественно считать,
что перемещение МХМ2 есть сумма двух перемещений МГА и АМ2'
М^М2 = М^А + АМ2.
Этот пример ясно показывает, как складываются векторы. На
рисунке 15 векторы-слагаемые расположены так, что конец одно-
го из них примыкает к началу другого. А вектор-сумма, или, как
говорят, результирующий вектор, — это вектор, сое-
диняющий начало одного из слагаемых с концом другого.
Это общее правило сложения любых векторов, а не только век-
торов перемещения.
Чтобы сложить два вектора, нужно их расположить так, что-
бы конец первого вектора примыкал к началу второго. Вектор,
соединяющий начало первого вектора с концом второго, есть сумма
обоих векторов,
16
При выполнении этих построе-
ний векторы можно переносить
параллельно самим себе (напри-
мер, векторы а и b на рис. 16, а).
Их можно также менять местами
(рис. 16, б). От этого ни модуль,
ни направление результирующего
вектора не изменяются.
Есть и другой способ сложе-
ния двух векторов. Вместо того
чтобы располагать складываемые
векторы один за другим, как мы
только что делали, их располага-
ют так, чтобы они исходили из
одной точки (рис. 17). Затем, счи-
тая, что расположенные таким об-
разом векторы образуют две сто7
роны параллелограмма, достра-
ивают параллелограмм (как пока-
зано пунктиром на рис. 17) и про-
водят диагональ из точки, в которой
были совмещены начала складывае-
мых векторов. • Эта диагональ и
Рис. 16
есть результирующий вектор.
Приведенное правило сложения векторов называется прави-
ло м параллелограмма. Оба способа дают, конечно,
один и тот же результат.
Таким образом, в отличие от чисел (скалярных величин) векторы
складываются геометрически и результирующий вектор — это
геометрическая сумма векторов. Модуль этой суммы векторов (как
видно из рассмотренных нами примеров) оказывается меньше сум-
мы модулей этих векторов, так как сумма двух сторон треугольни-
ка больше его третьей стороны.
Если складываются не два, а больше векторов, правило сложе-
в В,
ния остается прежним. Пусть, например, точка
довательно перемещения из О в А, оттуда
(рис. 18). Все эти перемещения могут
быть заменены одним-единственным пе-
ремещением из О в Е по прямой ОЕ.
Перемещение ОЕ и будет геометрической
суммой всех перемещений.
Следовательно, чтобы сложить нес-
колько векторов, надо расположить их
так, чтобы конец первого вектора при-
мыкал к началу второго, конец второго
— к началу третьего и т. д. Результи-
рующим будет вектор, направленный от
начала первого вектора к концу последнего.
совершила
затем в С,
после-
и Е
D
Рис. 18.
17
a b
raijrcwжттпгаии m iw—iwn£l
a+b
Рис. 19
a*b a
«====
b
Рис. 20
Рассмотрим частный случай,
когда векторы направлены вдоль
одной и той же прямой (рис,- 19)
или параллельно друг другу
(рис. 20). Правило сложения ос-
тается и здесь тем же: векторы-
слагаемые надо расположить так,
чтобы конец одного примыкал к
началу другого. Тогда вектор,
соединяющий начало первого
вектора с концом второго, и бу-
дет векторной суммой обоих век-
торов. Что же касается модуля
суммы векторов, то, как видно из
рисунка 19, он равен сумме мо-
дулей складываемых векторов.
Если складываемые параллель-
ные векторы направлены в про-
тивоположные стороны, то из
рисунка 20 видно, что модуль их
суммы равен разности модулей
складываемых векторов, этот ре-
зультирующий вектор направ-
лен в сторону большего по мо-
дулю вектора.
Отсюда следует, что парал-
лельные векторы складываются
так, как будто бы они являются
алгебраическими величинами.
Для этого нужно одному из
направлений приписать знак
«+», а противоположному —
знак «—».
Как найти проекцию векто-
ра, являющегося суммой несколь-
ких векторов? На рисунке 21
приведены векторы а, b и с.
Найдем их результирующий век-
тор /:
f = а 4- b с.
Спроецируем все складывае-
мые векторы и результирующий
вектор на какую-нибудь ось,
например на ось X (см. рис. 21).
Из рисунка видно, что проекции
векторов а и b на ось X положительны, потому что их состав-
► • ►
ляющие по оси X (АВ и ВС) направлены так же, как ось X;
проекция же вектора с отрицательна, так как его составляющая
1 ►
по оси X (CD) направлена против этой оси. Составляющая ре-
зультирующего вектора — это вектор AD, а проекция этого век-
тора fx равна алгебраической сумме проекций ах, Ьх и сх. Сле-
довательно,
fx = ах + Ьх + сх. •
Проекция суммы векторов на данную ось равна алгебраической
сумме проекций слагаемых векторов на ту же ось.
Поэтому, для того чтобы найти проекцию суммы векторов,
нет необходимости приставлять их друг к другу и находить резуль-
тирующий вектор. Надо просто сложить проекции всех векторов,
учитывая их знаки.
§ 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ:
ВЫЧИТАНИЕ ВЕКТОРОВ
Ознакомимся теперь с тем, как выполняют вычитание векторов.
Допустим, что из вектора а надо вычесть вектор Ъ (рис. 22, а),
т. е. найти вектор с, равный разности а — Ь.
Когда мы вычитаем одно число из другого, например 5 из 8,
мы пишем: 8 — 5 = 3. Но можно написать и так: 8 = 5 + 3. Точно
так же равенство а — b = с можно заменить равенством а = b +
+ с. Поэтому, чтобы найти вектор с, равный разности векторов
а и Ь, нужно найти такой вектор, который в сумме с вычитаемым
дает вектор уменьшаемый.
Сделать это можно следующим простым способом. Расположим
векторы а и Ь (не меняя их направления) так, чтобы они
исходили из одной точки (рис. 22, б). Соединим концы обоих век-
торов отрезком, направив его от вычитаемого (вектора Ъ) к
19
Рис. 24
уменьшаемому (вектору а). Это и есть вектор с = а — Ь. Действи-
тельно, как это видно из рисунка, вектор а равен сумме векторов Ъ
и с, а это и значит, что с = а — Ь.
Чтобы найти разность двух векторов а и Ь, нужно расположить
их так, чтобы они исходили из одной точки, и соединить концы обо-
их векторов отрезком, направленным от второго вектора к первому
(от вычитаемого к уменьшаемому). Этот направленный отрезок
и есть вектор-разность.
По этому же правилу можно вычитать и параллельные векторы
(рис. 23, а, b и рис. 24). Анализ этих рисунков показывает, что
параллельные векторы можно вычитать один из другого, как буд-
то бы они являются алгебраическими величинами. Для этого нужно
одному из направлений приписать знак «+», а другому — знак «—».
Если нам. нужно найти проекцию разности двух векторов, то,
так же как и в случае сложения векторов, нет необходимости вы-
полнять геометрические построения.
Действительно, если с = а — Ь, то а = с + &; а так как ах =
= сх + Ьх, то сх = ах — Ьх.
Следовательно, проекция разности векторов на данную ось рав-
на алгебраической разности их проекций на эту ось.
§ 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ:
УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР
Представим себе, что два автомобиля, выехавшие из гаража,
к исходу дня оказались один в 100, а другой в 200 км к северу от
места, где расположен гараж. Что можно сказать о перемещениях
этих двух автомобилей? Очевидно, что одно из них вдвое больше
другого. Если мы обозначим перемещение в 100 км через s, то пе-
ремещение в 200 км будет равно 2s, т. е. вектору s, умноженному на
2. Вектор 2s имеет то же направление, что и вектор s, но его модуль
вдвое больше.
Если бы второй автомобиль отправился не на север, а на юг,
20
то его перемещение было бы равно
—2s, т. е. вектору s, умноженному ~а
на —2. Вектор —2s вдвое больше (по
абсолютной величине) вектора s, но
направлен в противоположную сто-
рону (рис. 25). Рис. 26
При умножении вектора на ска-
лярную величину k изменяется его модуль’, увеличивается при k > 1
или уменьшается при k < 1. Если величина k положительна, то на-
правление вектора ks совпадает с направлением вектора s. Если же
величина k отрицательна, то вектор ks направлен противоположно
вектору s.
Упражнение 4
1. Чем отличаются друг от друга векторные и скалярные величины?
2. Как складываются векторные величины?
3. В чем состоит правило параллелограмма?
4. Сформулируйте правило вычитания векторов.
5. Даны два вектора а и b (рис. 26). Найдите сумму этих векторов, пользуясь
правилом параллелограмма.
6. Найдите разность а — b векторов, изображенных на рисунке 26. Найдите
также разность Ь — а.
7. Бегун на тренировке в парке пробежал 3 км на восток, а затем повернул
к северу и пробежал еще 4 км. Из этой точки он направился по прямой
к месту старта. Пользуясь транспортиром и линейкой, найдите вектор пере-
мещения (модуль и направление) спортсмена от места старта до точки мак-
симального удаления. Какова длина всего пройденного спортсменом пути?
S. Даны два вектора: а, направленный вдоль оси X и по модулю равный 8
единицам длины, и вектор Ь, направленный вдоль оси У и по модулю
равный 6 единицам длины. Найдите сумму этих векторов (модуль и на-
правление результирующего вектора). Найдите также разности векторов:
а — b и b — а.
9. Даны два вектора: а и b (см. рис. 26). При помощи линейки с делениями
постройте векторы 2,5 а-, —3 Ь; —0,5 а.
§ 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ
ДВИЖЕНИЕ
Мы уже знаем, что, для того чтобы найти положение тела в
какой-то момент времени, нужно знать вектор- перемещения, пото-
му что именно он связан с изменением координат движущегося
тела: проекции вектора перемещения точки на координатные оси
просто равны изменениям ее координат.
Как же найти вектор перемещения? Что для этого нужно знать?
Ответ на этот вопрос зависит от того, какой вид движения со-
вершает тело.
Рассмотрим сначала самый простой вид движения — прямо-
линейное равномерное движение.
21
Прямолинейным равномерным движением называют движение,
при котором тело за любые равные промежутки времени совершает
одинаковые перемещения.
При движении тела вдоль прямой в одном направлении пере-
мещение тела непрерывно возрастает. Чтобы найти перемещение
за время t, надо знать, как быстро оно возрастает. Быстрота этого
возрастания определяется отношением перемещения к величине
промежутка времени t, в течение которого оно произошло. Это
отношение называют скоростью движения и обозначают
буквой V. Так как перемещение — величина векторная, а время —
скалярная величина, то скорость тоже векторная величина:
-*• S
v = —.
t
Скоростью равномерного прямолинейного движения тела назы-
вают величину, равную отношению перемещения тела к проме-
жутку времени, в течение которого это перемещение произошло.
Скорость, таким образом, показывает, какое перемещение тело
совершает в единицу времени.
Следовательно, для того чтобы найти перемещение тела, надо
знать его скорость v. Тогда перемещение тела можно вычислить по
формуле
S = vt.
Вектор перемещения направлен, разумеется, так же, как век-
тор скорости, потому что время t — величина скалярная.
При прямолинейном движении траекторией является прямая
линия. Естественно поэтому направить координатную ось вдоль
этой прямой. Если, например, речь идет о движении падающего
тела, то координатную ось следует направить по вертикали; если
рассматривается движение автомобиля по прямой и ровной дороге,
то разумно направить вдоль нее и координатную ось. В этом случае
при движении тела будет изменяться только одна координата, на-
пример координата х, если выбранную ось обозначить через X.
Вдоль этой оси будут направлены и вектор перемещения, и вектор
скорости тела.
Так как векторы s и vt равны, то равны и их проекции
на ось X, т. е.
sx = vxt.
Это позволяет нам найти координату тела в любой момент времени.
Мы знаем, что
х = х0 + sx,
поэтому
X = хо + vxt. (1)
Эта формула показывает, что при прямолинейном равномерном
движении координата тела линейно зависит от времени.
22
^>0 л (^<0 л
G б
Рис. 27
В формуле (1) величины х, х0 и vx могут быть как положитель-
ными, так и отрицательными.
Если вектор скорости v направлен так же, как и ось X (рис. 27, а),
то проекция скорости на ось X будет положительна и поэтому
ox = |o|,
где | v | — абсолютное значение (модуль) вектора скорости. Тогда
х = х0 + |о|А (1а)
Если же направление вектора скорости противоположно на-
правлению оси X (рис. 27, б), то проекция скорости на ось X от-
рицательна и vx=—|uj. Поэтому
х = х0 — | v 11. (16)
Формулы (1а) и (16) удобны тем, что из них сразу видно, как
направлен вектор скорости: по направлению оси Х или противопо-
ложно ему. Когда тело движется по оси, то по значению проекции
его скорости на эту ось можно найти и сам вектор скорости. Ведь
их абсолютные значения совпадают, а знак проекции определяет на-
правление скорости. Поэтому в дальнейшем в таких случаях мы
часто для краткости будем называть скоростью тела значение ее
проекции на эту ось.
Формулы (1а) и (16) позволяют найти положение точки в любой
момент времени при прямолинейном равномерном движении. Для
этого надо знать начальное положение точки (тела) х0 и его
скорость v. Эти же формулы ясно показывают, каков смысл вели-
чины скорости. Модуль скорости v равен абсолютному значению
величины *°. Но х — х0 — это изменение координаты, a t —
это время, за которое такое изменение произошло. Следовательно,
скорость тела равна изменению координаты в единицу времени,
она показывает, как быстро изменяется координата х тела.
Но если известен только модуль скорости, то мы еще не можем
решить задачу механики. Счетчики километров и спидометры, уста-
навливаемые в автомобилях, показывают именно модули величин
перемещения и скорости. Но по их показаниям нельзя узнать ни
23
направления движения автомобиля, ни его положения в любой
момент времени.
Задача. По дороге, идущей с запада на восток, навстречу друг
другу движутся два автомобиля: один — на восток со скоростью
60 км/ч, другой — на, запад со скоростью 90 км/ч. У заправочной
станции автомобили встретились и после этого продолжали свой
путь (рис. 28). Определите положение каждого автомобиля через
30 мин после встречи и расстояние между ними в этот момент.
Решение. Заправочную станцию естественно принять за
начало отсчета координат, а момент встречи автомобилей — за
начало отсчета времени. Условимся считать направление на восток
положительным. Тогда координаты автомобилей через 0,5 ч после
встречи можно вычислить по формулам:
*1 = хо + IЛ1 х2 =Х0—|ц3|^,
где xt — координата автомобиля, движущегося на восток, х2 —
координата встреченного автомобиля, | | — абсолютное значе-
ние скорости 1-го автомобиля, |t)2| — абсолютное значение ско-
рости 2-го автомобиля. Так как начальные координаты у обоих ав-
томобилей равны нулю (х0= 0), то
xi = 1^1 И, х2 = — 1^2 И-
Подставив сюда приведенные в задаче значения, получим:
Xi = 60 — • 0,5 ч = 30 км,
ч
х2 = — 90 — 0,5 ч = —45 км.
ч
Расстояние I между автомобилями равно разности их коорди-
нат: I = хг — х2 = 30 км — (—45 км) = 75 км.
Упражнение 5
1. Следует ли считать величину I, вычисленную в задаче, векторной?
2. В чем различие между перемещением и пройденным путем при прямо-
линейном движении?
3. Объясните, в чем различие между величинами, определяемыми выраже-
s
НИЯМИ V = — И О
и что у них общего?
S
t'
24
4. Какая имеется связь между скоростью тела и изменением его положения в
пространстве?
5. Группа туристов, двигаясь с постоянной по абсолютной величине скоростью
5 км/ч, сначала в течение 1 ч идет на север, затем в течение 0,5 ч идет на
восток (под углом 90° к направлению на север) и, наконец, в течение
1 ч 30 мин на юг (под углом 180°). Где окажется группа после прохождения
этих трех участков? Сколько времени ей потребуется на возвращение в
исходную точку по прямой?
6. Автомобилист, двигаясь со скоростью 30 км/ч, проехал половину пути до
места назначения за 2 ч. С какой скоростью он должен продолжать движе-
ние, чтобы За такое же время достигнуть цели и вернуться обратно?
§ 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
ДВИЖЕНИЯ
Для большей наглядности движение можно описывать с помо-
щью графиков. График показывает, как изменяется одна вели-
чина при изменении другой величины, от которой первая зависит.
Для построения графика обе величины в выбранном масштабе
откладывают по осям координат. Если по горизонтальной оси (оси
абсцисс) откладывать время, прошедшее с начала отсчета времени,
а по вертикальной оси (оси ординат) — значения координат тела,
полученный график будет выражать зависимость координаты тела
от времени (его также называют графиком движения).
Допустим, что тело движется равномерно вдоль оси X (рис. 29).
В моменты времени t = 0, tr — 1 сек, t2 = 2 сек, ts — 3 сек и т. д.
тело находится соответственно в положениях, измеряемых коор-
динатами х0— 3 м (точка Д), хг = 5 м, х2 — 7 м и т. д.
Это значит, что изменяется только его координата х. Для того
чтобы получить график движения тела, будем откладывать зна-
чения х по вертикальной оси, а по горизонтальной оси — значения
времени t. График движения представляет собой прямую линию,
показанную на рисунке 30. Это и значит, что координата линейно
зависит от времени.
График зависимости координаты тела от времени (рис. 30) не
следует путать с траекторией движения тела — прямой, во всех
точках которой тело побывало при своем движении (см. рис. 29).
25
Графики движения дают пол-
ное решение задачи механики в
случае прямолинейного движе-
ния тела, так как они позволяют
найти положение тела в любой
момент времени, в том числе и в
моменты времени, предшествова-
вшие начальному моменту (если
предположить, что тело двига-
лось и до начала отсчета време-
ни). Продолжив график, изобра-
женный на рисунке 29, в сторону,
противоположную положитель-
ному направлению оси времени,
мы, например, найдем, что тело
за 3 сек до того, как оно оказа-
лось в точке А, находилось в на-
чале отсчета координаты (х = 0).
По виду графиков зависимости координаты от времени можно
судить и о скорости движения. Ясно, что скорость тем больше, чем
круче график, т. е. чем больше угол между ним и осью времени
(чем больше этот угол, тем больше изменение координаты за одно
и то же время).
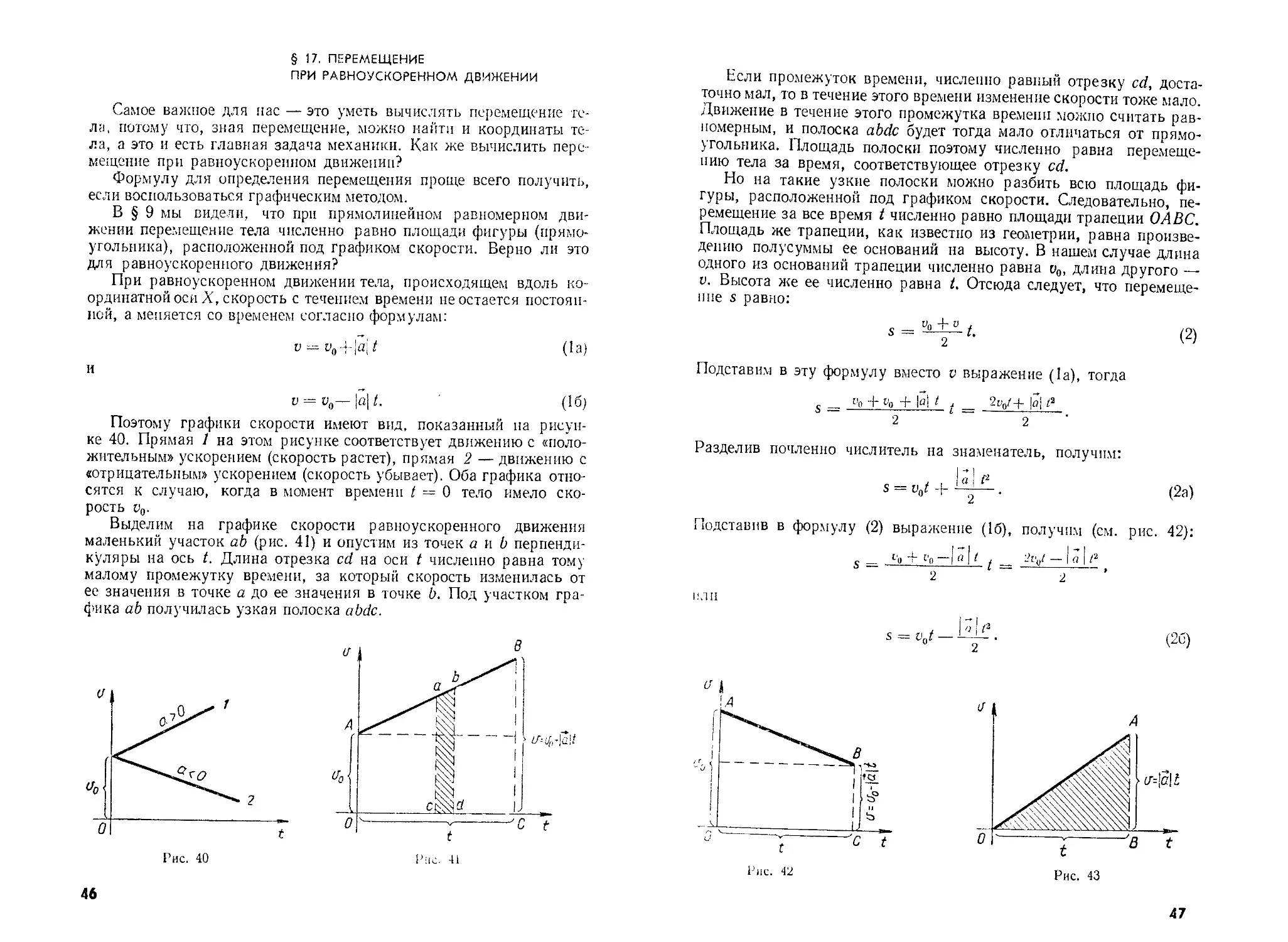
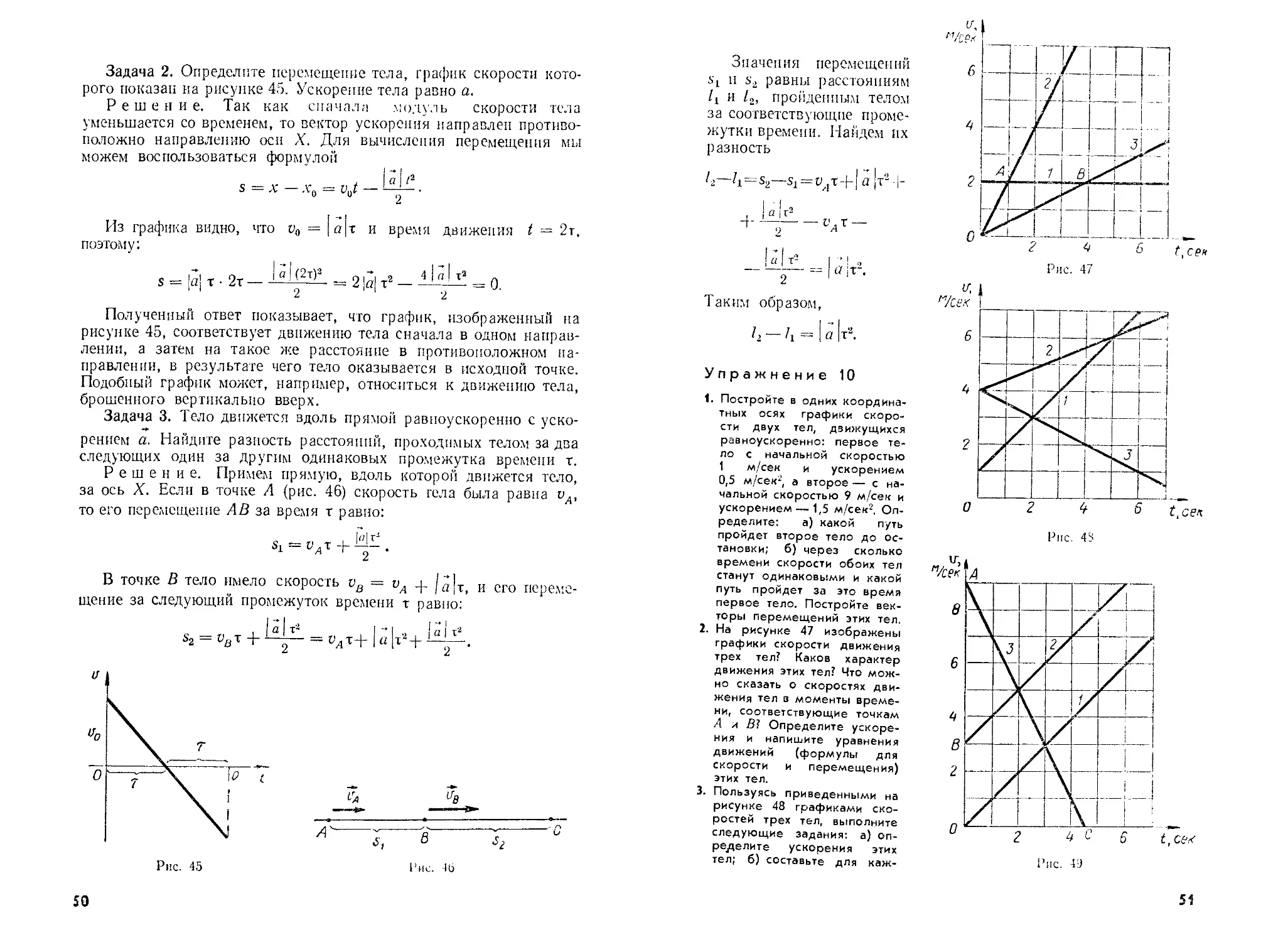
На рисунке 31 показано несколько графиков движений с различ-
ными скоростями. Графики 1, 2 и 3 показывают, что тела движутся
вдоль оси X в положительном направлении. Тело, график движе-
ния которого — прямая 4, движется в направлении, потивопо-
ложном направлению оси X. Из графиков движения можно найти
и перемещения движущегося тела за любой промежуток времени.
Из рисунка 31 видно, например, что тело 3 за время между 1 и
5 сек совершило перемещение в положительном направлении, по
абсолютной величине равное 2 м, а тело 4 за это же время соверши-
ло перемещение в отрицательном направлении, равное по абсолют-
ной величине 4 м.
Наряду с графиками движения часто пользуются графиками ско-
рости. Их получают, откладывая по оси координат проекцию скорости
Рис. 32
t
Рис. 33
26
тела, а по оси абсцисс по-прежнему время. Такие графики показы-
вают, как изменяется скорость с течением времени, т. е. как ско-
рость зависит от времени. В случае прямолинейного равномерного
движения эта «зависимость» состоит в том, что скорость с течением
времени не меняется. Поэтому график скорости представляет собой
прямую, параллельную оси времени (рис. 32). График / на этом
рисунке относится к случаю, когда тело движется в сторону поло-
жительного направления оси X. График // относится к случаю,
когда тело движется в противоположном направлении (так как
проекция скорости отрицательна).
По графику скорости тоже можно узнать абсолютное значение
перемещения тела за данный промежуток времени. Оно численно
равно площади заштрихованного прямоугольника (рис. 33): верх-
него, если тело движется в сторону положительного направления,
и нижнего — в противоположном случае. Действительно, площадь
прямоугольника равна произведению его сторон. Но одна из сторон
численно равна времени t, а другая.— скорости v. А их произведе-
ние как раз и равно абсолютному значению перемещения тела.
Упражнение 6
1. Какому движению соответствует график, изображенный пунктиром на ри-
сунке 31?
2. Пользуясь графиками (см. рис. 31), найдите расстояние между телами 2 и 4
в момент времени t=3 сек.
3. По графику, изображенному на рисунке 30, определите модуль и направ-
ление скорости.
§ 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
В § 2 мы видели, что положение тела (точки) в пространстве
всегда задается относительно какого-то другого тела, выбранного
телом отсчета. Через какую-нибудь точку тела отсчета проводят
оси координат. Принято говорить, что с этим телом отсчета связана
система координат.
Но за тело отсчета мы можем принять любое тело и с каждым из
них связать свою систему координат.
Тогда положение одного и того же
тела мы можем одновременно рассма-
тривать в разных системах координат. д
Ясно, что относительно разных тел
отсчета в разных системах координат
положение одного и того же тела мо-
жет быть совершенно различным. На-
пример, положение автомобиля. на
дороге можно определить, указав,
что он находится на расстоянии 1Г км
к северу от населенного пункта А
(рис. 34). Пункт А служит в данном
Рис. 34
27
случае телом отсчета, а прямая, мысленно проведенная от него к
северу. — координатной осью, связанной с телом отсчета. Но мож-
но выбрать за тело отсчета и какой-нибудь другой населенный
пункт, например В, и сказать, что автомобиль расположен в /2 км
к востоку от него. Это значит, что положение тела относительно', оно
различно относительно разных тел отсчета и связанных с ними
разных систем координат.
Но не только положение тела относительно. Относительно и
его движение. В чем состоит относительность движения?
Часто бывает, что движение одного и того же тела приходится
рассматривать относительно разных тел отсчета, которые сами дви-
жутся друг относительно друга. Так, артиллеристу важно знать,
как движется снаряд не только относительно Земли, на которой его
орудие стоит неподвижно, но и относительно танка, в который он
стреляет и который сам движется относительно Земли; пилот инте-
ресуется движением самолетами относительно Земли, и относительно
воздуха, который в бурную погоду сам движется, и т. д.
Движения одного и того же тела относительно разных тел от-
счета, движущихся одно относительно другого, могут сильно раз-
личаться. Различными могут быть и траектории, и скорости движе-
ния этого тела.
Рассмотрим движения одного и того же тела относительно двух
тел отсчета, движущихся друг относительно друга. Предположим,
что одно тело отсчета неподвижно, а второе движется относительно
первого. Примем для простоты, что оно движется прямолинейно
и равномерно. Выясним, как найти перемещение тела относительно
этих двух тел отсчета (конечно, за одно и то же время).
Вот простой пример. Представим себе человека, плывущего вниз
по течению реки с некоторой скоростью, которую он поддерживает
постоянной, работая руками и ногами (если бы он не работал ру-
ками и ногами, он бы просто лежал на воде и относительно воды
находился в покое). Примем за неподвижное тело отсчета берег, а
за подвижное — воду.
Как же движется пловец относительно берега и относительно
воды? Предположим, что за движением пловца следят два наблю-
дателя: один — на берегу, а другой — на лодке, которая без греб-
ца плывет йо течению реки. Относительно воды лодка покоится,
а относительно берега она движется равномерно с такой же скоро-
стью, как и сама вода.
Проведем мысленно через точку на берегу, в которой располо-
жился наблюдатель, систему координат XOY, причем ось X на-
правим вдоль течения реки (рис. 35). С лодкой (с водой) мы тоже
свяжем систему координат X'0'Y', оси X' и Y' которой параллель-
ны осям X и Y.
Найдем перемещение пловца относительно этих двух систем
координат (систем отсчета).
Для наглядности посмотрим, как движение пловца будет пред-
ставляться наблюдателям в лодке и на берегу. Наблюдатель в лод-
23
ке через некоторое время t отметит, что пловец относительно него
совершил некоторое перемещение sx. Разделив это перемещение
на время, он получит скорость пловца vr:
V1
S1
I
(t»! — это скорость пловца относительно воды (лодки), т. е. в подвиж-
ной системе координат Х'О'У').
Наблюдатель на берегу отметит, что за это же время t перемеще-
ние пловца равно s, а сама лодка совершила перемещение s2 отно-
сительно берега. Из рисунка 35 видно, что перемещение s пловца
относительно берега, т. е. в системе координат X.OY, равно сумме
обоих перемещений:
s = Si s2.
Разделив s на t, наблюдатель на берегу получит скорость v плов-
ца относительно берега:
v — — = 51 +$2 = S1 -J- —
t t t r t ’
Первое слагаемое -— это скорость пловца относительно подвиж-
ной системы координат (воды или лодки). Слагаемое же ~ — это,
Рис. 35
29
очевидно, скорость лодки (воды) относительно неподвижной систе-
мы координат (берега). Обозначим ее через и... Значит, о2 — это
скорость подвижной системы координат относительно покоящейся.
Следовательно,
v = Ci -г V.,. (1)
Эта формула называется формулой сложения скоростей.
Точно такую же формулу сложения скоростей мы получили бы
и в том случае, если бы пловец плыл против течения (рис. 36).
Скорость движения тела относительно неподвижной системы
координат равна геометрической сумме двух скоростей: скорости
тела относительно подвижной системы координат и скорости самой
подвижной системы относительно неподвижной.
Мы видим, что скорости тела относительно различных систем
отсчета, движущихся друг относительно друга, различны. В этом
и проявляется относительность движения.
В рассмотренном нами примере движущееся тело (.пловец)
и подвижная система координат (лодка или вода) движутся вдоль
одной прямой — вдоль осп X. Поэтому вместо векторов v, vt и v2
мы можем воспользоваться их проекциями на ось А'. Тогда формула
сложения скоростей будет иметь вид:
v = vl ф Щ.
Величины v, щ и о, в этой формуле могут быть как положительны-
ми, так и отрицательными в зависимости от направлений векторов и,
и и3 по отношению к осн А.
Рис 38
30
Может случиться и так, что тело, которое движется в одной си-
стеме координат, находится в покое относительно другой. Если
бы тот же пловец перестал работать руками и ногами и просто ле-
жал бы на воде, то относительно лодки ои находился бы в покое, а
относительно берега он двигался бы со скоростью течения. Наобо-
рот, если бы пловец плыл со скоростью течения, нов противополож-
ном направлении, то в покое он находился бы относительно берега,
а относительно воды он двигался бы со скоростью — Vj. Следова-
тельно, относительно не только движение, во и покой. Если тело
относительно какой-то системы координат покоится, то всегда мож-
но найти такие системы координат, относительно которых оно дви-
жется. Это значит, что абсолютно покоящихся тел не существует.
Движение свойственно всем телам и вообще всему, что существует
в природе, т. е. всему материальному миру.
§11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ
(ПРОДОЛЖЕНИЕ)
Не всегда скорости движущегося тела и подвижной системы ко-
с’щднат направлены вдоль одной прямой, как в примере с пловцом,
рж’сюгренном в предыдущем параграфе.
Предположим, что пловцу понадобилось переплыть реку с
гдного берега на другой, так что двигаться он должен все время
перпендикулярно течению, т. е. перпендикулярно оси X (рис. 37).
По-прежнему будем считать движение пловца равномерным.
Каким будет это движение для наблюдателя в лодке (относи-
те тьно подвижной системы координат X'0'Y') и каким оно будет для
наблюдателя на берегу (в покоящейся системе координат XOY)?
Рис. 37
Наблюдатель в ледке видит, что пловец все время удаляется от
него, двигаясь вдоль оси Y'. Oil видит это, находясь и в точ-
ке Л, и в точке В, и в любой другой точке. Через промежуток
времени t, когда лодка будет находиться в точке С, пловец, ока-
жется на противоположном берегу в точке С, совершив перемеще-
ние sx = ССХ (см. рис. 37). Перемещение самого наблюдателя вдоль
оси X равно OC=s2. Разделив перемещение Sj на время t, наблюда-
тель в лодке получит скорость пловца относительно подвижной?
системы координат X'0'Y':
Направлена она вдоль оси У'.
Совсем другим будет представляться движение пловца, переплы-
вающего реку, наблюдателю, находящемуся на берегу. Для этого
наблюдателя перемещаться будет и ось Y'. В «его» системе коорди-
нат перемещение пловца за то же время t представится направлен-
ным отрезком О'С' = s (рис. 37). Пловца отнесло вниз по течению.
Из рисунка 37 видно, что перемещение s равно геометрической
сумме перемещения Sj пловца относительно подвижной системы коор-
динат X'0'Y' и перемещения s, самой системы координат X'0'Y'
относительно неподвижной системы XOY. Следовательно, и теперь
так же, как и в примере, рассмотренном в предыдущем параграфе,
s = sL р s.,.
Скорость пловца v относительно системы ХОУ найдем так:
т. е. -
v = щ -У V,.
Мы видим, что правило сложения скоростей осталось таким же,
как и раньше, но теперь алгебраически скорости складывать нельзя,
так как векторы vt и у2 не параллельны друг другу.
В примере, который мы рассмотрели, не только скорости дви-
жения, но п траектории пловца различны в разных системах коор-
динат. Если для наблюдателя в лодке траекторией движения плов-
ца является прямая, перпендикулярная течению реки, то для наблю-
дателя на берегу траектория движения пловца — это прямая,
наклоненная под некоторым углом (не равным 90) к направлению
течения. Это тоже проявление относительности движения: в раз-
личных системах координат, движущихся друг относительно друга,
и траектории движения различны.
32
Упражнение 7
1. В чем состоит относительность движения?
2. Как в примере с пловцом движутся вода и берег относительно пловца?
3. Двигатель самолета сообщает ему скорость относительно воздуха, рав-
ную 900 км/ч. С какой скоростью движется самолет относительно Земли при
попутном ветре, скорость которого равна 50 км/ч? При таком же встреч-
ном ветре?
4. По двум взаимно перпендикулярным шоссейным дорогам движутся рав-
номерно грузовая и легковая автомашины со скоростями соответственно
54 км/ч и 72 км/ч. На каком расстоянии окажутся друг от друга автомобили
через 10 мин после встречи у перекрестка?
5. Помогает или мешает течение переплыть реку? (Зависит ли время, необхо-
димое пловцу для того, чтобы переплыть реку, от скорости ее течения?)
§ 12. ЕДИНИЦЫ ИЗМЕРЕНИИ ДЛИНЫ
И ВРЕМЕНИ
Из того, что до сих пор говорилось о движении, ясно, что при
его изучении нужно определять по крайней мере две величины:
перемещение и время.
Длины перемещений, как и промежутки времени, выражаются
какими-то числами. Эти числа получают в результате измерений.
Измерить величину — значит сравнить ее каким-нибудь спосо-
бом с однородной величиной, условно принятой за единицу измерения
этой величины.
Можно, например, измерить длину школьного коридора, срав-
нив ее с длиной шага. Сосчитав, сколько шагов укладывается на
длине коридора, мы узнаем, во сколько раз длина коридора больше
длины шага. Это число (во сколько раз) и выражает длину кори-
дора в шагах.
Следовательно, прежде всего необходимо выбрать единицу для
измеряемой величины. Ее можно выбрать совершенно произвольно.
Например, для измерения длины в разные времена и в разных стра-
нах применяли самые разнообразные единицы. Единицей длины
служили и длина шага, и длина ступни человека, и расстояние от
локтя до конца среднего пальца, и расстояние, проходимое пеше-
ходом за день, и т. д. Когда мы читаем в комедии А. С. Грибоедова
«Горе от ума»:
Строжайше б запретил я этим господам
На выстрел подъезжать к столицам,
мы понимаем, что здесь персонаж комедии Фамусов пользуется в
качестве единицы длины расстоянием, которое пролетает снаряд,
выпущенный из пушки, — эту своеобразную единицу длины охот-
но применяли в старину военные.
В настоящее время принята единая для всех стран единица дли-
ны — метр (л«).
1 метр — это расстояние между двумя штрихами, нанесенными
на стержне особой формы, изготовленном из сплава платины и
иридия.
2 Заказ 1126
33
Этот, как говорят, эталон длины хранится в Междуна-
родном бюро мер и весов во Франции. В других странах имеются
точные копии этого эталона (в СССР даже две копии). По ним и
устанавливается длина бесчисленных линеек-метров, которыми
обычно и измеряют длину.
Кроме основной единицы длины — метра, широко пользуются
единицами, которые в 10, 100, 1000 и т. д. раз больше или меньше
метра (километр, сантиметр, миллиметр, мик-
рометр).
Единицу времени тоже можно выбрать произвольно. Но нельзя,
разумеется, изготовить эталон времени в виде какого-то предмета,
вроде линейки-метра. Эталоном времени должна служить продол-
жительность какого-либо правильно повторяющегося процесса, если
она строго постоянна. В настоящее время в качестве такого процес-
са выбрано движение Земли вокруг Солнца: один оборот Земля со-
вершает за год. Но за единицу времени принимают не год, а опре-
деленную часть этого промежутка времени — секунду (сек):
1 год = 31556925,9747 сек (для очень грубых расчетов можно счи-
тать, что 1 год = л • 107 сек).
В быту и технике часто применяют другие единицы времени:
минуту (мин) и ч а с (ч): 1 мин — 60 сек и 1 ч = 3600 сек.
Кроме длины и времени, мы уже имели дело еще с одной величи-
ной — скоростью. Нужно ли и для нее выбирать специальную еди-
ницу?
Этого, оказывается, можно не делать, потому что скорость, как
мы знаем, связана с длиной и временем формулой
S
V = — .
i
Из этой формулы видно, что если за 1 сек какое-нибудь тело со-
вершает перемещение длиной 1 м, то скорость тела окажется равной
единице [ 1-^-1. Скорость такого движения и можно принять за
\ сек )
единицу скорости.
За единицу скорости принимают скорость такого равномер-
ного прямолинейного движения, при котором тело за 1 сек совершает
перемещение в 1 м.
Не выбирают специальной единицы, например, и при измере-
нии объема, так как величина объема связана с величиной длины
и объем можно измерять в кубических метрах. В каких же случа-
ях надо выбирать специальную единицу измерения, а в каких не надо?
Между всеми физическими величинами существует определен-
ная зависимость, потому что все явления природы связаны так или
иначе между собой. Связь между величинами выражают в виде ма-
тематических формул. Эти же формулы будут связывать между со-
бой и единицы измерений физических величии. Поэтому единицы
измерений одних величии можно выразить через единицы измере-
ния других.
34
Можно выбрать небольшое число величин (их называют о с-
н о в и ы м и) и для них произвольным образом установить едини-
цы измерений. Единицы же для всех других величин (производ-
п ы х величии) можно тогда установить на основании математиче-
ских формул, которые связывают нх с основными величинами.
Совокупность установленных таким образом единиц для всех
физических величин называют системой единиц.
Системы единиц могут быть разные. Они зависят как от того,
какие физические величины выбраны в качестве основных, так и
от выбора единиц измерения основных величин.
В настоящее время принята Международная систе-
ма единиц (сокращенно обозначается СИ — Система Интер-
национальная). Она строится на основе семи основных величин,
в число которых входят длина и время. В системе единиц СИ еди-
ницей длины является метр, а единицей времени — секунда. С
остальными основными величинами, па которых основана система
единиц СИ, и с их единицами измерения мы познакомимся позднее.
В физике, кроме системы единиц СИ, пользуются и другой си-
стемой единиц, обозначаемой сокращенно СГС (сантиметр,
грамм, с е к у н д а). В этой системе единиц длина н время тоже
входят в число основных величин. Но за единицу длины в ней принят
не метр, а сантиметр. (Подробности о единицах длины и времени
см. на форзаце.)
Определение единицы скорости, которое мы дали выше (1 м/сек),
очевидно, относится к системе СИ. В системе СГС единицей скорое га
служит 1 см/сек.
Глава 2
Прямолинейное неравномерное
движение
ВВЕДЕНИЕ
Прямолинейное равномерное движение, при котором переме-
щение линейно зависит от времени в соответствии с формулой
s = vt, встречается сравнительно редко. Гораздо чаще приходится
иметь дело с движением, при котором за равные промежутки вре-
мени перемещения тела могут быть различными. Это означает,
что скорость тела с течением времени как-то изменяется. Так, на-
пример, падающие на Землю тела движутся прямолинейно, но с
возрастающей скоростью; тело, брошенное вверх, тоже движется
прямолинейно, но с уменьшающейся скоростью. С переменной ско-
ростью обычно движутся поезда, автомобили, самолеты и т. д.
Движение, при котором скорость с течением времени изменяется,
называют неравномерным движением.
При таком движении формулой s = vt для вычисления переме-
щения пользоваться нельзя. Ведь скорость изменяется во времени
и уже нельзя говорить о какой-то определенной скорости, значение
которой можно было бы подставить в формулу. Как же вычислять
перемещение при неравномерном движении и что для этого нужно
знать?
§ 13. СРЕДНЯЯ СКОРОСТЬ
В некоторых случаях, когда имеют дело с неравномерным дви-
жением, пользуются так называемой средней скоростью.
Если тело совершило некоторое перемещение s за промежуток
времени t, то, разделив s на t, мы получим среднюю скорость:
~ s
fcp = 7 •
Таким образом, средняя скорость показывает, чему равно пере-
мещение, которое тело в среднем совершает за единицу времени.
Если, например, поезд проходит 600 км за 10 ч, то это значит,
что в среднем он каждый час проходит 60 км:
г* । 600 км км
Кр1 = -т— = 60 - .
10 ч ч
36
Но ясно, что какую-то часть времени поезд вовсе не двигался,
а стоял на остановке; трогаясь со станции, поезд увеличивал свою
скорость, приближаясь к ней — уменьшал ее. Все это при опреде-
лении средней скорости мы не принимаем во внимание и считаем,
что поезд каждый час проходит по 60 км, каждые полчаса — по
30 км и т. д. Пользуясь формулой ц,., = р, мы как бы считаем,
что поезд.совершает равномерное движение с постоянной скоростью,
равной vcp, хотя, быть может, за все время движения не было ни
одного такого часа, за который он прошел бы именно 60 км. Но зна-
ние средней скорости позволяет определить перемещение по формуле:
S VCp t.
Но при этом надо помнить, что эта формула дает верный
результат только для того участка траектории, для которого опре-
делена средняя скорость. Если, пользуясь значением средней скорос-
ти в 60 км/ч, вычислять перемещение не за 10 ч, а за 2, 4 или 5 ч, то
мы получим неверный результат. Это объясняется тем, что средняя
скорость за время 10 ч не равна средним скоростям за 2, 4 и 5 ч.
Таким образом, при помощи понятия средней скорости основ-
ную задачу механики — определить положение тела в любой мо-
мент времени — решить нельзя.
Все же во многих случаях знание средней скорости может ока-
заться полезным. Если, например, туристам из их прежнего опыта
или из опыта их товарищей известно, что по горной дороге можно
продвигаться со средней скоростью 2 км/ч, то они, собираясь в новый
поход в горный район, могут воспользоваться этим, чтобы заранее
определить место, куда они придут к исходу дня.
Часто, говоря о средней скорости, подразумевают не вектор
пср = ~ , а скалярную величину, определяемую длиной пути, ко-
торую тело в среднем проходит за единицу времени:
I
Иср — •
Если тело не меняет направления своего движения, то эта сред-
няя скорость совпадает с абсолютным значением вектора оср = — ’
так как в этом случае I = |s|. В случае, когда тело движется по слож-
ной не прямолинейной траектории (например, автомобиль в городе),
эти величины не совпадают. О какой величине идет речь, обычно
бывает ясно из условия задачи. Когда, например, диспетчер в гара-
же определяет, какой запас горючего необходим автомобилю на
день, он пользуется формулой иср — Зная среднюю скорость
автомобиля в городе, т. е. расстояние, которое он в среднем прохо-
дит за 1 ч, можно определить длину пути, которую он пройдет за
37
определенное время, и, следовательно, необходимый запас горюче-
го. В данной задаче нельзя воспользоваться определением средней
скорости как вектора: ведь перемещение s автомобиля за день рав-
но нулю — он выехал из гаража и затем в него вернулся. Поэтому
^Ср “
Задача. Автомобиль двигался в течение 6 ч. В течение первого
часа движение происходило со средней скоростью 110 км/ч, а в
остальные 5 ч — со средней скоростью 50 км/ч. Найдите среднюю
скорость движения автомобиля за все время движения.
Решение. Из условия задачи ясно, что направление движе-
ния здесь не играет роли, так как речь идет не о перемещении, а
о пройденном пути. Общая длина пути I складывается из длин пу-
тей 1Х и 12, пройденных автомобилем со скоростями = 110 км/ч
и и2 = 50 км/ч-.
/ = ^1 + ^2 = + V2^2-
Общее время движения складывается из промежутков времени
tY = 1ч и t2 = 5 ч, в течение которых автомобиль двигался с этими
скоростями:
t = /i -р-12.
Средняя скорость определяется поэтому равенством
_ / _ 4- г2/2
cp~t Ч + Ь
Подставив сюда приведенные в задаче данные, получим:
км км
ПО — • 1 ч+ 50 — - 5 ч
ч ч „пкм
Упражнение 8
1. Что такое средняя скорость?
2. Можно ли, зная среднюю скорость движения тела за определеннь,й про-
межуток времени, найти перемещение, совершенное телом за любую
часть этого промежутка?
3. Половину времени при переезде из одного пункта в другой автомобиль
проехал с постоянной скоростью 60 км/ч. С какой постоянной скоростью
он должен двигаться оставшееся время, если средняя скорость движения
равна 65 км/ч?
4. Первую половину пути до места назначения автомобиль проехал с постоян-
ной скоростью 50 км/ч, а вторую половину — с постоянной скоростью
60 км/ч. Определите среднюю скорость автомобиля.
5. Половину пути до места назначения автомобиль проехал с постоянной ско-
ростью 40 км/ч. С какой постоянной скоростью он должен двигаться
вторую половину пути, чтобы средняя скорость движения была равна
50 км/ч?
38
§ 14. МГНОВЕННАЯ СКОРОСТЬ
Мы сделали попытку свести неравномерное движение к равно-
мерному и для этого ввели среднюю скорость движения. Но это нам
не помогло: зная среднюю скорость, нельзя решать самую главную
задачу механики — определять положение тела в любой момент
времени. Можно ли каким-нибудь другим способом свести нерав-
номерное движение к равномерному?
Этого, оказывается, сделать нельзя, потому что механическое
движение — это процесс непрерывный. Непрерывность движения
состоит в том, что если, например, тело (или точка), двигаясь пря-
молинейно с возрастающей скоростью, перешло из точки А в точку В,
то оно непременно должно побывать во всех промежуточных точках,
лежащих между А и В, без всяких пропусков. Но это еще не
все. Предположим, что, подходя к точке А, тело двигалось равно-
мерно со скоростью 5 м/сек, а после прохождения точки В оно дви-
галось тоже равномерно, но со скоростью 30 м/сек. При этом на
прохождение участка АВ тело потратило 15 сек. Следовательно,
на отрезке АВ скорость тела за 15 сек изменилась на 25 м/сек. Но
так же как тело при своем движении не могло миновать ни одну
из точек на его пути, его скорость должна была принять все значе-
ния скорости между 5 и 30 м/сек. Тоже без всяких пропусков! В этом
и состоит непрерывность механического движения: ни координаты
тела, ни его скорость не могут изменяться скачками. Отсюда мож-
но сделать очень важный вывод. Различных значений скорости в
интервале от 5 до 30 м/сек имеется бесчисленное множество (в ма-
тематике говорят, бесконечно много значений). Но между точками
А и В имеется и бесчисленное множество (бесконечно много!) точек,
а 15-секундный интервал времени, в течение которого тело пере-
местилось из точки А в точку В, состоит из бесчисленного множест-
ва промежутков времени (время тоже течет без скачков!).
Следовательно, в каждой точке траектории движения и в каждый
момент времени тело обладало определенной скоростью.
Скорость, которую имеет тело в данный момент времени и в дан-
ной точке траектории, называют мгновенной скоростью.
При равномерном прямолинейном движении скорость тела опре-
деляется отношением его перемещения к промежутку времени, за
который совершено это перемещение. Что же означает скорость
в данной точке или в данный момент времени?
Допустим, что некоторое тело (как всегда, мы в действительно-
сти имеем в виду какую-то определенную точку этого тела) движет-
ся прямолинейно, но не равномерно. Как вычислить его мгновен-
ную скорость в некоторой точке А его траектории? Выделим неболь-
шой участок 1 на этой траектории, включающий точку А (рис. 38).
Малое перемещение тела на этом участке обозначим через As/,
1 Знак А (греческая буква «дельта») означает «изменение», «кусочек», «про-
межу гок». Следовательно, A — малое перемещение.
39
а малый промежуток времени, в течение которого оно совершено,,
через Д/р Разделив Ast на мы получим среднюю скорость на
этом участке: ведь скорость изменяется непрерывно и в разных
местах участка 1 она различна.
Уменьшим теперь длину участка 1. Выберем участок 2 (см. рис.
38), тоже включающий в себя точку А. На этом меньшем участке
перемещение равно As2 (As2 < AsJ и проходит его тело за проме-
жуток времени Д/2. Ясно, что на участке 2 скорость тела
успевает измениться на меньшую величину. Но отношение
дает нам и для этого меньшего участка все же среднюю скорость.
Еще меньше изменение скорости на протяжении участка 3 (также
включающего в себя точку Л), меньшего, чем участки 1 и 2, хотя,
разделив перемещение Asg на промежуток времени А/3, мы опять
получим среднюю скорость на этом малом участке траектории.
Будем постепенно уменьшать длину участка, а вместе с ним и про-
межуток времени, за который тело проходит этот участок. В конце
концов мы стянем участок траектории, прилегающей к точке А,
в самую точку А, а промежуток времени — в момент времени. Тог-
да-то средняя скорость и станет мгновенной скоростью, потому что
на достаточно малом участке изменение скорости будет настолько
мало, что его можно не учитывать, значит, можно считать, что ско-
рость не изменяется.
Мгновенная скорость, или скорость в данной точке, равна от-
ношению достаточно малого перемещения на малом участке тра-
ектории, прилегающей к этой точке, к малому промежутку време-
ни, в течение которого совершается это перемещение.
Понятно, что скорость равномерного прямолинейного движе-
ния —это одновременно его мгновенная и средняя скорость.
Мгновенная скорость — величина векторная. Ее направленна
совпадает с направлением перемещения (движения) в данной точка
Прием, к которому мы прибегли, чтобы пояснить смысл мгно-
40
венной скорости, состоит, таким образом, в следующем. Участок
траектории и время, в течение которого он проходится, мы мыслен-
но постепенно уменьшаем до тех пор, пока участок уже нельзя от-
личить от точки, промежуток времени — от момента времени, а нерав-
номерное движение — от равномерного. Таким приемом всегда поль-
зуются, когда изучают явления, в которых играют роль какие-ни-
будь непрерывно изменяющиеся величины1.
Нам остается теперь выяснить, что необходимо знать для на-
хождения мгновенной скорости тела в любой точке траектории и в
любой момент времени.
§ 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ
ДВИЖЕНИЕ
При неравномерном движении мгновенная скорость тела не-
прерывно изменяется: от тачки к точке, от одного момента времени
к другому. Как же вычислить скорость в любой момент времени?
Для этого нужно знать, кащ быстро изменяется скорость, или,
другими словами, каково ее изменение в единицу времени.
Для простоты мы будем рассматривать такое неравномерное
движение тела, при котором его скорость за любые равные проме-
жутки времени изменяется одинаково. Такое движение называется
равноускоренным.
Движение, при котором скорость за любые равные промежутки
времени изменяется одинаково, называют равноускоренным дви-
жением.
Если в некоторый начальный момент времени скорость тела
равна v0, а через промежуток времени t она оказывается равной v,
и — v0 .
то за каждую единицу времени скорость изменяется на ----
v — v0
Величина -------характеризует быстроту изменения скорости.
Ее называют ускорениеми обозначают буквой а:
Ускорением движущегося тела называют величину, равную от-
ношению изменения скорости тела к промежутку времени, в течение
которого это изменение произошло.
Если ускорение тела по абсолютному значению велико, го
это значит, что оно быстро набирает скорость (когда тело разгоня-
ется), или быстро теряет ее (при торможении)2.
1 Краткое, но выразительное описание этого приема, составляющего основу
так называемого дифференциального исчисления, можно найти па первой странице
третьей части III тома романа Л, Н. Толстого «Война п мир».
2 Если скорость тела за равные промежутки времени изменяется неодинако-
во, то на одних участках пути скорость может изменяться быстро, на других —
медленно. Тогда и ускорения на разных участках будут различными. В этом слу-
41
Если ускорение а известно, то можно вычислить значение ско-
рости v тела в любой момент времени, если известно еще и значение
начальной скорости и0.
Действительно, из формулы (1) следует, что
v = va ф at.
Ускорение и нужно знать для вычисления скорости о.
Так как ускорение равно произведению векторной величины
1
и — v() на скаляр — оно само является векторной величиной
(СМ. § 7).
В каких единицах измеряют ускорение?
- V — v„
Так как а =---------то абсолютное значение ускорения равно
единице, если равно единице абсолютное значение изменения ско-
рости и равен единице промежуток времени.
За единицу ускорения принимают ускорение такого движения,
при котором за единицу времени скорость изменяется на единицу
скорости.
В системе единиц СИ скорость измеряется в метрах в секунду,
а время — в секундах, так что ускорение измеряется в метрах в
секунду за секунду или в метрах на секунду в квадрате (л/се№).
В системе единиц СГС скорость измеряется в см/сек, а время в се-
кундах, поэтому единицей ускорения является 1 см/сек1.
§ 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ
При прямолинейном движении векторы v0 и v направлены вдоль
одной прямой, которая является в то же время и траекторией дви
жения. Вдоль этой же прямой в направлении движения тела мы
условились направлять и координатную ось (ось X). В таком слу-
чае вектор разности v — v0, а значит и вектор ускорения а, лежш
на той же прямой (см. § 6). Но куда он направлен — в сторону дви-
жения (так же как ось X) или против него?
В § 6 мы видели, что проекция разности двух векторов на ка-
кую-нибудь ось равна разности их проекций на ту же ось. Следо-
вательно, для проекций векторов оо, v и а на ось X можно написать
чае ускорение, вычисленное по формуле (1), должно считаться средним ускоре-
нием за время t.
По применительно к ускорению можно использовать тот же прием, которым
мы воспользовались, когда говорили о мгновенной скорости. Это приведет иас
к выводу, что в каждой точке траектории и в каждый момент времени тело, кото-
рое движется неравномерно, имеет некоторое определенное ускорение, величина
которого может изменяться от точки к точке, от момента к моменту. Ускорение,
с которым тело движется в данной точке траектории или в данный момент време-
ни, называют мгновенным ускорением.
42
Здесь а — проекция вектора а на ось
- • а\
X; v и v0— проекции векторов v и v0
па ту же ось.
Так как все три вектора лежат па
одной прямой (оси X), то абсолютные
значения их проекций равны абсо-
лютным значениям самих векторов. р зд
Рассмотрим 2 случая ускоренного
движения тела.
Первый случай. Скорость тела по абсолютному значе-
нию растет (тело «разгоняется»). Это значит, что v > ид. Тогда из
формулы (I) видно, что проекция ускорения а положительна и
равна | а | . Вектор а, следовательно, направлен так же, как ось X,
т. е. в сторону движения. Когда, например, бронебойный снаряд
движется при выстреле в стволе орудия, его скорость растет и
ускорение направлено так же, как и скорость (рис. 39).
Второй случай. Тело тормозится, т. е. абсолютное зна-
чение его скорости уменьшается (и < у0). Из формулы (1) видно,
что проекция ускорения а в этом случае отрицательна: а —
= —|а| .
Из формулы (1) можно получить выражение для скорости с>:
V = Vo ф at. (2)
В этой формуле, повторяем, v, v0 и а — проекции векторов и, с»,
и а на ось X, которые могут быть как положительными, так и от-
рицательными.
При решении задач выражение для скорости (2) удобно записы-
вать так, чтобы из него сразу было видно, как направлен вектор
ускорения.
Если скорость тела растет (разгон), то а = |а| и
о = и0ф|а|Т (2а)
Когда же скорость тела уменьшается (торможение), а = — |а| и
v = v0—fa ft. (26)
Понятно, что тело, которое тормозится, должно когда-то остано-
виться. Это произойдет, как это видно из формулы (26), тогда, когда
Ц; станет равным |дф, т. е. в момент времени t — Но если
|а|
ускорение остается постоянным (по модулю и направлению) и после
этого момента, то тело, остановившись, начнет двигаться в проти-
воположную сторону. Это видно из того, что при t > — - |а \1
|а|
станет больше,чем т’у; скорость v изменит свой знак на обратный. Так
43
движется, например, тело, брошенное вертикально вверх: долетев до
высшей точки траектории, тело начинает движение вниз.
Если у0 = 0 и вектор ускорения направлен так же, как и ось
координат, то из формулы (2а) следует, что
v = + |а| t.
Если же ось координат выбрана так, что направление вектора
ускорения противоположно направлению оси координат, то из
формулы (26) следует, что
v = — |а| t.
Знак «—» в этой формуле означает, что вектор скорости, так же
как и вектор ускорения, направлен противоположно направлению
оси координат. Модуль скорости, конечно, и в этом случае увеличи-
вается со временем.
Обычно мы называем движение с возрастающей по абсолютной
величине скоростью ускоренным движением, а дви-
жение с убывающей скоростью — з а медленным движе-
ние м. Но в механике любое неравномерное движение является
ускоренным движением. Трогается ли автомобиль с места или
тормозит, в обоих случаях он движется с ускорением. Ускорен-
ное прямолинейное движение отличается от замедленного только
знаком проекции вектора ускорения.
Мы знаем, что и перемещение, и скорость, и траектория движе-
ния различны относительно разных тел отсчета, движущихся друг
относительно друга.
А ускорение? Относительно ли оно?
Ускорение тела, как мы теперь знаем, определяется векторной
разностью двух значений его скорости в различные моменты вре-
мени. При переходе от одной системы координат к другой, движу-
щейся относительно первой равномерно и прямолинейно, изменятся
оба значения скорости. Но изменятся они на одну и ту же величину.
Разность же их останется неизменной. Поэтому и ускорение оста-
нется неизменным.
Во всех системах отсчета, движущихся друг относительно друга
прямолинейно и равномерно, ускорение тела одинаково.
Но ускорения тела будут различными в системах отсчета, дви-
жущихся с ускорением друг относительно друга. В этом случае ус-
корения складываются так же, как скорости (см. § 10).
Задача. Автомобиль проезжает мимо наблюдателя, двигаясь
со скоростью 10 MjceK. В этот момент водитель нажимает на тормоз,
и автомобиль начинает двигаться с ускорением 1 м]сек\ Сколько
времени пройдет с того момента, когда водитель нажал на тормоз,
до остановки автомобиля?
Решение. Выберем за начало отсчета то место, в котором
находится наблюдатель, и направим координатную ось в сторону
движения автомобиля. Тогда проекция скорости автомобиля на
эту ось будет положительной. Так как скорость автомобиля уменьша-
44
ется, то проекция ускорения отрицательна и мы должны восполь-
зоваться формулой (26):
Откуда
у = у0—\a\t.
t —
Подставляя в эту формулу
личин, получим:
численные значения заданных ве-
—о
— = 10 сек.
м
10 —
1 —
сек2
За положительное направление координатной оси можно принять
и направление, противоположное движению. Тогда проекция началь-
ной скорости автомобиля будет отрицательной (у0 — — 10 м/сек),
а проекция ускорения — положительной, и применять тогда нужно
формулу (2а):
Отсюда
v-va
ССК I 1 Л
----------- = 10 сек.
м.
сек2
Результат получился тот же. Да он и не может зависеть от того,
как выбрано направление оси координат!
Упражнение 9
1. Что такое ускорение и для чего его нужно знать?
2. При любом неравномерном движении изменяется скорость. Как ускорение
характеризует это изменение?
3. Чем отличается замедленное прямолинейное движение от ускоренного?
4. Что такое равноускоренное движение?
S. Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/сек 2,
Через сколько времени он приобретет скорость 54 км/ч?
6. Автомобиль, движущийся со скоростью 36 км/ч, останавливается при тор-
можении в течение 4 сек. С каким ускорением движется автомобиль при
торможении?
7. Грузовик, двигаясь с постоянным ускорением, на некотором участке пути
увеличил свою скорость с 15 до 25 м/сек. За какое время произошло это
увеличение скорости, если ускорение грузовика равно 1,6 м/сек2?
8. Какая скорость движения была бы достигнута, если бы тело двигалось
прямолинейно с ускорением 10 м/сек2 в течение 0,5 ч при начальной ско-
рости, равной нулю?
45
§ 17. ПЕРЕМЕЩЕНИЕ
ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ
Самое важное для нас — это уметь вычислять перемещение те-
ла, потому что, зная перемещение, можно найти и координаты те-
ла, а это и есть главная задача механики. Как же вычислить пере-
мещение при равноускоренном движении?
Формулу для определения перемещения проще всего получить,
если воспользоваться графическим методом.
В § 9 мы видели, что при прямолинейном равномерном дви-
жении перемещение тела численно равно площади фигуры (прямо-
угольника), расположенной под графиком скорости. Верно ли это
для равноускоренного движения?
При равноускоренном движении тела, происходящем вдоль ко-
ординатной оси X, скорость с течением времени не остается постоян-
ной, а меняется со временем согласно формулам:
v--=u0-X\a{t (la)
и
v = v0—\a\t. ' (16)
Поэтому графики скорости имеют вид, показанный на рисун-
ке 40. Прямая 1 на этом рисунке соответствует движению с «поло-
жительным» ускорением (скорость растет), прямая 2 — движению с
«отрицательным» ускорением (скорость убывает). Оба графика отно-
сятся к случаю, когда в момент времени t — 0 тело имело ско-
рость п0.
Выделим на графике скорости равноускоренного движения
маленький участок ab (рис. 41) и опустим из точек а и b перпенди-
куляры на ось t. Длина отрезка cd на оси t численно равна тому
малому промежутку времени, за который скорость изменилась от
ее значения в точке а до ее значения в точке Ь. Под участком гра-
фика ab получилась узкая полоска abdc.
46
Если промежуток времени, численно равный отрезку cd, доста-
точно мал, то в течение этого времени изменение скорости тоже мало.
Движение в течение этого промежутка времени можно считать рав-
номерным, и полоска abdc будет тогда мало отличаться от прямо-
угольника. Площадь полоски поэтому численно равна перемеще-
нию тела за время, соответствующее отрезку cd.
Но на такие узкие полоски можно разбить всю площадь фи-
гуры, расположенной под графиком скорости. Следовательно, пе-
ремещение за все время t численно равно площади трапеции ОАВС.
Площадь же трапеции, как известно из геометрии, равна произве-
дению полусуммы ее оснований на высоту. В нашем случае длина
одного из оснований трапеции численно равна в0, длина другого —
V. Высота же ее численно равна t. Отсюда следует, что перемеще-
ние s равно:
S = (2)
2 v '
Подставим в эту формулу вместо v выражение (1а), тогда
с — t'o + ь0 + М Z / — W+ |oj Р
□ — I —• «
2 2
Разделив почленно числитель на знаменатель, получим:
, , | а | Т2 о .
S = vj + • (2а)
Подставив в формулу (2) выражение (16), получим (см. рис. 42):
5 = t'o + с’о ~I I z i = — I « Ь2
2 2
или
47
Формулу (2а) применяют в том случае, когда вектор ускорения
а направлен так же, как и ось координат, а формулу (26) тогда,
когда направление вектора ускорения противоположно направле-
нию этой оси.
Если начальная скорость о0 равна нулю (рис. 43) и вектор
ускорения направлен по оси координат, то из формулы (2а) следует,
что
2
Если же направление вектора ускорения противоположно на-
правлению оси координат, то из формулы (26) следует, что
lak
S = — J.
2
(знак «—» здесь означает, что вектор перемещения, так же как и
вектор ускорения, направлен противоположно выбранной оси
координат).
Напомним, что в формулах (2а) и (26) величины s и о0 могут
быть как положительными, так и отрицательными — это проекции
векторов s и о0.
Теперь, когда мы получили формулы для вычисления переме-
щения, нам легко получить и формулу для вычисления координа-
ты тела. Мы видели (см. § 8), что, для того чтобы найти координату
тела х в какой-то момент времени t, надо к начальной координате
х0 прибавить проекцию вектора перемещения тела на ось коорди-
нат:
X = Хо + S. (3)
Поэтому
X = хо + vof + ’ '3 а>
если вектор ускорения направлен так же, как и ось координат, и
. J Д I /О gf.
x = xf)+vf)t---. (36)
если направление вектора ускорения противоположно направле-
нию оси координат.
Это и есть формулы, позволяющие находить положение тела
в любой момент времени при прямолинейном равноускоренном дви-
жении. Для этого нужно знать начальную координату тела х0,
его начальную скорость v0 и ускорение а.
Задача 1. Водитель автомобиля, движущегося со скоростью
72 км/ч, увидел красный сигнал светофора и нажал на тормоз.
После этого автомобиль начал тормозить, двигаясь с ускорением
48
5 м/сек2. Какое расстояние пройдет
автомобиль за время — 2 сек
после начала торможения? Какое
расстояние пройдет автомобиль до
полной остановки?
Решение. За начало коор-
динат выберем ту точку дороги,
в которой автомобиль начал тор-
мозить. Координатную ось напра-
вим по направлению движения ав-
томобиля (рис. 44), а начало отсчета
в который водитель нажал па тормоз. Скорость автомобиля нап-
равлена так же, как ось X, а ускорение автомобиля противо-
положно направлению этой оси. Поэтому проекция скорости на
ось X положительна, а проекция ускорения отрицательна и коор-
динату автомобиля нужно находить по формуле (36):
Рис. 44
тени отнесем к моменч
х = х» + --------.
Подставляя в эту формулу значения
х0 = 0, t = = 2 сек, v0 = 72 — = 20 — н | а ] = 5 — ,
ч селе сек2,
получим:
м
5 —2 • 4 сек2
х = 20 — • 2 сек------—---------= 40 м—10 м = 30 м.
сек 2
Теперь найдем, какое расстояние пройдет автомобиль до полной
остановки. Для этого нам нужно знать время движения Л2. Его
можно узнать, воспользовавшись формулой v = —| а 11.
Так как в тот момент, когда автомобиль останавливается, его
скорость v равна нулю, то
Щ — |а| t2 = 0
Расстояние, которое пройдет автомобиль до полной остановки,
равно координате автомобиля в момент времени t2.
м
5 —2 • 16 сек2
х = 20 — 4 сек------—------------— 80 м — 40 м = 40 лг.
сек 2
49
Задача 2. Определите перемещение тела, график скорости кото-
рого показан на рисунке 45. Ускорение тела равно а.
Решение. Так как сначала модуль скорости тела
уменьшается со временем, то вектор ускорения направлен противо-
положно направлению осп X. Для вычисления перемещения мы
можем воспользоваться формулой
, I а I /2
S = Л- — Л-О = vot — .
Из графика видно, что о0 = |а|т и время движения t = 2т,
поэтому:
8 = 1а!т.2т-1И^ = 2|ф2-Я1к = 0.
м 2 11 2
Полученный ответ показывает, что график, изображенный на
рисунке 45, соответствует движению тела сначала в одном направ-
лении, а затем на такое же расстояние в противоположном на-
правлении, в результате чего тело оказывается в исходной точке.
Подобный график может, например, относиться к движению тела,
брошенного вертикально вверх.
Задача 3. Тело движется вдоль прямой равноускоренно с уско-
рением а. Найдите разность расстояний, проходимых телом за два
следующих один за другим одинаковых промежутка времени т.
Решение. Примем прямую, вдоль которой движется тело,
за ось X. Если в точке А (рис. 46) скорость гела была равна vA,
то его перемещение АВ за время т равно:
«1 = иАт
2
В точке В тело имело скорость vB = vA /а]т, и его переме-
щение за следующий промежуток времени т равно:
SO
Значения перемещений
s'! u s2 равны расстояниям
1У и /2, пройденным телом
за соответствующие проме-
жутки времени. Найдем их
разность
I,—Zi=s2—S! = wz1t+[ a Jt2 (-
I • I „
, air2
4-_l_-----^T-
Таким образом,
Упражнение 10
1. Постройте в одних координа-
тных осях графики скоро-
сти двух тел, движущихся
равноускоренно: первое те-
ло с начальной скоростью
1 м/сек и ускорением
0,5 м/сек2, а второе — с на-
чальной скоростью 9 м/сек и
ускорением — 1,5 м/сек2. Оп-
ределите: а) какой путь
пройдет второе тело до ос-
тановки; б) через сколько
времени скорости обоих тел
станут одинаковыми и какой
путь пройдет за это время
первое тело. Постройте век-
торы перемещений этих тел.
2. На рисунке 47 изображены
графики скорости движения
трех тел? Каков характер
движения этих тел? Что мож-
но сказать о скоростях дви-
жения тел в моменты време-
ни, соответствующие точкам
А и В? Определите ускоре-
ния и напишите уравнения
движений (формулы для
скорости и перемещения)
этих тел.
3. Пользуясь приведенными на
рисунке 48 графиками ско-
ростей трех тел, выполните
следующие задания: а) Оп-
ределите ускорения этих
тел; б) составьте для каж-
51
дого тела формулу зависимости скорости от времени: в) в “ем сходны и
чем различаются движения, соответствующие графикам 2 и 3?
4. На рисунке 49 показаны графики скорости движения трех тел. По этим
графикам: а) определите, чему соответствуют отрезки ОА, ОВ и ОС
на осях координат; б) найдите ускорения, с которыми движутся тела;
в) напишите уравнения движения для каждого тела.
5. Самолет при взлете проходит взлетную полосу за 15 сек и в момент отрыва
от земли имеет скорость 100 м/сек. С каким ускорением двигался самолет
и какова длина взлетной полосы?
6. Автомобиль остановился у светофора. После того как загорелся зеленый
сигнал, он начинает двигаться с ускорением 1,5 M-lcetC2 и движется так до
тех пор, пока скорость его не станет равной 16 м/сек, после чего он про-
должает движение с постоянной скоростью. На каком расстоянии от свето-
фора окажется автомобиль через 15 сек после появления зеленого сиг-
нала?
7. Снаряд, скорость которого равна 1 000 м/сек, пробивает стену блиндажа за
10'3сек и после этого имеет скорость 200 м/сек. Считая движение снаряда
в толще стены равноускоренным, найдите толщину стены.
8. Ракета движется с ускорением 45 м/сек 2 и к некоторому моменту времени
достигает скорости в 900 м/сек. Какой путь она пройдет в следующие
2,5 сек?
9. На каком расстоянии от Земли оказался бы космический корабль через
30 мин после старта, если бы он все время двигался прямолинейно с ус-
корением 9,8 м/сек2?
§ 18. СРЕДНЯЯ СКОРОСТЬ
ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ
ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ
И СКОРОСТЬЮ
Часто бывает необходимо знать среднюю скбрость при равно-
ускоренном движении. Как ее вычислить? Мы знаем, что
s = оср/. (1)
Но, с другой стороны, как мы видели (см. § 17),
Сравнивая эти формулы, получим:
и =, . (3)
ср 2 4 '
Средняя скорость при равноускоренном движении равна полу-
сумме начальной и конечной скорости.
Такое простое выражение для средней скорости получается
благодаря тому, что график скорости — это прямая линия, т. е.
скорость и время связаны линейной зависимостью.
Иногда бывает нужно вычислить перемещение тела, движуще-
гося равноускоренно, когда неизвестно, сколько времени протекло
от начала движения, но известны значения начальной и конечной
скорости тела. Формулу, позволяющую вычислить перемещение,
можно получить из формулы (2) и формулы
v = ф- at. (4)
Найдем из последней формулы значение t
t = v - v«-
a
52
и подставим его в формулу (2). Получаем:
s = L±A . — (у + ц>) (t> —1>0)
2 а 2а '
с2 —• V?
Отсюда s =---------. (5)
2а
Мы получили, таким образом, формулу, позволяющую вычис-
лить перемещение, если известны начальная и конечная скорость
и ускорение.
Пользуясь формулой (5), можно также найти значение скоро-
сти v тела в любой точке, через которую проходит тело. Из форму-
лы (5) следует;
v2 — vl = 2as,
или v2 = vl 4- 2as.
Откуда | v | + ?as- (6)
Если начальная скорость тела с>0 равна нулю, то
$ = — , | v | = У~2а$.
2а
Задача. При подходе к станции машинист выключил двигатель
локомотива, после чего движение происходило с постоянным уско-
рением, равным 0,1 м!сек2. Какое перемещение поезд совершил до
остановки, если в момент выключения двигателя скорость поезда
была 72 кл/ч? Через сколько времени поезд остановился?
Решение. Направим ось X так же, как направлена скорость
поезда о0. Следовательно, его ускорение будет направлено противо-
положно оси. За начало отсчета времени мы примем момент
выключения двигателя, а за начало отсчета координат — точку,
в которой двигатель был выключен. Перемещение, отсчитанное от
этой точки, вычисляем по формуле
2а
Подставляя в эту формулу
у0 = 72^ = 20--, 1> = 0 и а = —0,1 --,
ч сек сек2
получаем:
! м
— 20 —
\ сек / 400
s = 1-------L. = —. м — 2000 м.
м 0,2
-2-0,1 — .
ce/S
53
Время, протекшее до остановки, находим по формуле
v = v0 — ] a
Так как v = 0, то
Поезд остановился через 3 мин 20 сек после выключения двигателя
в 2 км от места выключения.
Упражнение 11
1. Троллейбус, трогаясь с места, движется с постоянным ускорением 1,5 м/сек2.
Какое он пройдет расстояние к моменту, когда его скорость станет рав-
ной 54 км/ч?
2. Наблюдения показали, что скаковая лошадь достигает своей наибольшей
скорости в 15 м/сек после того, как она, приняв старт, «разгонится» на про-
тяжении 30 м. С каким ускорением скачет лошадь на этом участке?
3. Чтобы оторваться от земли, самолет должен набрать скорость в 180 км/ч.
На каком расстоянии от места старта на взлетной дорожке самолет до-
стигнет этого значения скорости, если его ускорение постоянно и равно
2,5 м/сек 2?
4. Пассажирский поезд тормозит и движется при этом с ускорением
0,15 м/сек2. На каком расстоянии от места включения тормоза скорость
станет 3,87 м/сек, если в момент начала торможения скорость была 54 км/ч?
§ 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ
Простейший способ измерения ускорения состоит в следующем.
На тело, движущееся равноускоренно, помещают капельницу, т. е.
сосуд с окрашенной жидкостью, из которого через определенные
равные промежутки времени вытекают капли (рис. 50). Падающие
капли указывают положение тела через одинаковые и известные про.ме-
Рис. 50
54
9 J
9 е
9 1
9 »
Ф з
ф /о
ф"
ф 12
ф 13
Ф "
Ф’5
ф 16
9 и
жутки времени, которые мы обозначим буквой т. Как
было показано в задаче 3 (см. § 16, стр. 51), раз-
ность расстояний между упавшими каплями за
два любых следующих друг за другом промежут-
ка времени т равна ат2, где а — ускорение. Из-
мерив длины /j и /2 двух соседних промежутков
между каплями, мы и найдем ускорение по фор-
муле L — = ат2, откуда а = -.
X2
Часто пользуются другим, более точным спо-
собом. Это так называемый стробоскопи-
ческий метод. Он состоит в том, что
движущееся тело в темноте освещают через равные
промежутки времени световой вспышкой. Ясно,
что тело будет видно только в тех положениях, в
которых оно оказывается освещенным. Если тело
в процессе его движения фотографировать (затвор
фотоаппарата должен быть открыт в течение всего
времени движения), то на фотографической пленке
будут видны последовательные положения тела че-
рез равные промежутки времени. Измеряя расстоя-
ния между изображениями тела на пленке и зная
промежутки времени между световыми вспышка-
ми, можно вычислить ускорение, если известен
масштаб изображения. Рисунок 51 представляет
собой копию с фотографии падающего шара, полученной мето-
дом вспышек. Рядом помещена шкала для измерения расстояния.
Следует заметить, что изучение прямолинейного равноускорен-
ного движения несколько затруднительно из-за того, что движущее-
ся тело довольно быстро удаляется от наблюдателя. Так, например,
для шарика 3, показанного на цветной вклейке I, б, промежутки
времени между вспышками составляли всего около 0,03 сек, так
что движение, показанное на снимке, длилось всего около 0,5 сек.
§ 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ
Интересным примером прямолинейного равноускоренного дви-
жения является свободное падение тел.
Явление падения тел изучал знаменитый итальянский ученый
Галилео Галилей; им и было установлено, что свободно
падающие тела движутся равноускоренно.
Убедиться в этом и вместе с тем измерить ускорение при свобод-
ном падении можно, воспользовавшись описанным в предыдущем
параграфе методом стробоскопического освещения. Измерения
показали, что это ускорение равно 9,8 м/сек2.
55
Галилео Галилей
(1564—1642)
Особенно удивительно и в течение
долгого времени было загадкой то,
что ускорение свободного падения оди-
наково для всех тел. Но что значит
свободное падение?
Если взять стальной шар, фут-
больный мяч, развернутую газету, .
птичье перо и все эти разнородные
предметы сбросить с высоты в нес-
колько метров и тем или иным спосо-
бом измерить их ускорения, то мы
увидим, что ускорения этих тел ’
различны. Но это объясняется лишь
тем, что на пути к земле телам при-
ходится проходить сквозь воздух, ко-
торый мешает их движению. Если бы
тела падали в трубе, из которой воз-
дух удален, то их ускорения оказа-
лись бы одинаковыми. Такой опыт можно провести с помощью тол-
стостенной стеклянной трубки длиной около 1 м, один конец ко-
торой запаян, а другой снабжен краном (рис. 52, а). Поместим в
трубку три разных предмета, например: дробинку, пробку и пти-
чье перо. Затем быстро перевернем трубку. Все три тела упадут на
дно трубки, но в разное время: сначала дробинка, затем пробка и,
наконец, перо. Но это в том случае, когда в трубке имеется воз-
дух. Стоит только воздух откачать насосом (рис. 52, б) и, закрыв
после откачки кран, снова перевернуть трубку (рис. 52, в), и мы
увидим, что все три тела упадут одновременно. Следовательно, в
вакууме все тела падают с одинаковым ускорением.
Только такое падение в вакууме, падение, которому ничто не
мешает, мы и называем свободным падением.
Свободное падение — это падение в безвоздушном пространстве.
Следует иметь в виду, что ускорение падающего тела не из-
менится, если мы толкнем его вниз, сообщив ему начальную ско-
рость v0. Только нарастание скорости начнется не от нулевого
значения, а от значения ц,.
При рассмотрении движения свободно падающего тела за на-
чало отсчета удобно выбрать ту точку, из которой начинается па-
дение, а координатную ось направить в направлении движения,
т. е. по вертикали вниз (рис. 53). В этом случае направления век-
торов перемещения, скорости и ускорения совпадают, а их проек-
ции на ось координат равны модулям самих векторов.
Формулы для скорости и перемещения свободно падающего
тела ничем не отличаются от формул, полученных нами для прямо-
линейного равноускоренного движения. Но чтобы отличать сво-
бодное падение от всякого другого прямолинейного равноускорен-
ного движения, принято обозначать модуль ускорения свободного
падения буквой g (g ~ 9,8 м/сек2), а модуль перемещения—буквой h.
56
Имея в виду эту замену букв, приведем формулы, описывающие
движение свободно падающего тела.
1. Скорость тела в любой момент времени выражается форму-
лой
v = с,, gt,
где — скорость тела в момент, когда начинается отсчет времени.
Если в этот момент тело покоилось, то
v = gt-
2. Скорость тела в любой точке траектории после прохождения
расстояния h от начала отсчета расстояний определяется выраже-
нием
V = /
Если падение начинается из состояния покоя (о0 = 0), то
v =
3. Модуль перемещения падающе-
го тела за время t находится* по фор-
муле
/г = v.t + ~ .
L 2
Если начальная скорость и0 = 0, то
Пользуясь этими формулами, мож-
но вычислить время падения тела с
заданной высоты, скорость падающего
тела в любой точке и в любой мо-
мент времени и т. д.
Задача. Подъемный кран равномер-
но опускает контейнер. Из контей-
х
Рис. 53
S7
Рис. 54
пера выпал кирпич.
Через сколько времени
кирпич упал на землю,
если в момент его удара
о землю контейнер на-
ходился на высоте 20 м
над землей?
Р е ше н и е. Выбе-
рем в качестве начала
отсчета точку О, в кото-
рой находился контей-
нер в момент, когда вы-
пал кирпич (эту точку
мы считаем неподвиж-
ной относительно земли,
так что телом отсчета
фактически является
земля), и направим ось
X по вертикали вниз.
Обозначим высоту точки
О над землей через И
(рис. .54). Высоту кон-
тейнера в момент паде-
ния кирпича на землю
обозначим h, а скорость
равномерного движения
контейнера через п0.
Тогда можно написать:
(1)
За время I падения кирпича контейнер совершил перемещение
Н — h = vot, откуда Н = h + vot. Подставив это значение Н в
формулу (1), получим:
, , еР
й vQi — vat Т — ,
откуда
Так как h = 20 м, ад — 9,8 — , то
се№
2 . 20 м
м
9,8 —
j/"сек2 = 2 сек.
8
Эгу задачу можно решить короче, если выбрать в качестве тела
отсчета движущийся контейнер. Относительно него скорость кир-
пича в тот момент, когда он выпал из контейнера, равна нулю:
Ц» = 0. Следовательно, перемещение h. кирпича относительно кон-
тейнера определяется по формуле h = — .
Какой результат дает для t эта формула, мы уже видели.
Упражнение 12
1. Камень падал до дна ущелья 4 сек. Какова глубина ущелья?
2. Сколько времени падал бы груз с верхней точки Останкинской телевизион-
ной башни (535 м)? Какова была бы его скорость в момент падения на зем-
лю? Сопротивлением воздуха пренебречь.
3. За какое время тело, начавшее падение вниз из состояния покоя, пройдет
путь, равный 4,9 м? Какова его скорость в конце этого пути?
4. Стоя на краю скалы высотой 180 м над землей, мальчик уронил камень,
а вслед за тем через секунду он бросил вниз второй камень. Какую началь-
ную скорость сообщил он второму камню, если оба камня упали на землю
одновременно?
5. Тело свободно падает с высоты 50 м над землей. Какую скорость имеет
тело в момент удара о землю и на какой высоте его скорость будет вдвое
меньше?
6. На рисунке 51 изображены последовательные положения свободно пада-
ющего шарика через каждые 0,1 сек. Пользуясь рисунком, определите
ускорение свободного падения, если начальная скорость шарика равна
нулю.
§ 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО
ВЕРТИКАЛЬНО ВВЕРХ
Само по себе тело вверх, как известно, не движется. Его нужно
«бросить», т. е. сообщить ему некоторую начальную скорость va,
направленную по вертикали вверх.
Брошенное вверх тело движется, как показывает опыт, с таким
же ускорением, как и свободно падающее тело. Это ускорение рав-
но g и направлено вертикально вниз. Движение тела, брошенного
вверх, — это тоже прямолинейное равноускоренное движение, и
формулы, которые были написаны для свободного падения тела,
годны и для описания движения тела, брошенного вверх. Но при
написании формул надо учесть, что вектор ускорения направлен
против вектора начальной скорости: скорость тела по абсолютному
значению не увеличивается, а уменьшается. Поэтому, если ось коор-
динат направить вверх, проекция начальной скорости v0 будет
положительна, а проекция ускорения g — отрицательна, и форму-
лы примут вид:
v = v0 — gt, (1)
/I = vot - . (2)
59
Так как тело, брошенное вверх, движется с уменьшающейся
скоростью, то наступит такой момент, когда скорость станет рав-
ной нулю. В этот момент тело будет находиться на максимальной
высоте. Подставив в формулу (1) значение и = 0, получим:
Ц» = st-
Отсюда можно найти время, которое требуется для того, чтобы
тело поднялось до максимальной высоты:
t = .
g
Максимальную высоту определяем из формулы (2).
Подставив в формулу (2) t = , получим
После того как тело достигнет высоты /гиакс, оно начнет падать вниз;
проекция его скорости станет отрицательной, а по абсолютной
величине будет возрастать (см. формулу 1), высота же будет умень-
шаться со временем согласно формуле (2) [при t > — |.
Пользуясь формулами (1) и (2), легко убедиться в том, что
скорость тела в момент его падения на землю или вообще туда, от-
куда оно было брошено (при h = 0), равна по абсолютной величине
начальной скорости и0, а время падения тела равно времени его
подъема.
Падение тела можно рассматривать и отдельно как свободное
падение тела с высоты Лмакс. Тогда мы можем воспользоваться
формулами, приведенными в предыдущем параграфе.
Задача. Тело брошено вертикально вверх со скоростью 25 м!сек.
Какова скорость тела через 4 сек? Какое перемещение совершит
тело и какова длина пути, пройденного телом за это время?
Решение. Скорость тела вычисляется по формуле
v = — st.
К исходу четвертой секунды
v = 25 — — 9,8 — • 4 сек — 15 — .
сек сек2 сек
Знак «—» означает, что скорость направлена против координатной
оси, направленной вверх, т. е. в конце четвертой секунды тело уже
двигалось вниз, пройдя через высшую точку своего подъема.
60
Величину перемещения тела найдем по формуле
h = vot — — ,
° 2
9,8—2 • 16 сек2
откуда h = 25 — • 4 сек---------—-----------л; 20 м.
сек 2
Это перемещение отсчитывается от того места, откуда тело было
брошено. Но в этот момент тело уже двигалось вниз. Поэтому дли-
на пройденного телом пути равна максимальной высоте подъема
плюс расстояние, на которое оно успело опуститься вниз:
= ^макс (^чакс “ 2лмакс А.
Значение ймакс вычислим по формуле
/г = —
"макс п •
е 2^
Отсюда I — 2------h =------h.
tg g
Подставив значения с'о = 25 — , h — 20 м, получаем:
Z=-----------20 м .^42,5 м.
м
Упражнение 13
1. Стрела выпущена из лука вертикально вверх со скоростью 30 м/сек. На
какую высоту она поднимется?
2. Тело, брошенное с земли вертикально вверх, упало через 8 сек. Найдите,
на какую высоту оно поднялось и какова была его начальная скорость?
3. Из пружинного пистолета, находящегося на высоте 2 м над землей, выле-
тает вертикально вверх шарик со скоростью 5 м/сек. Определите, на какую
максимальную высоту он поднимется и какую скорость шарик будет иметь
в момент падения на землю. Сколько времени шарик находился в полете?
Каково его перемещение за первые 0,2 сек полета?
4. Тело брошено вертикально вверх со скоростью 40 м/сек. На какой высоте
оно окажется через 3 и 5 сек и какие при этом у него будут скорости?
Принять £=10 м/сек2.
5 Два тела брошены вертикально вверх с различными начальными скоро-
стями. Одно из них достигло вчетверо большей высоты, чем другое. Во
сколько раз его начальная скорость была больше начальной скорости дру-
гого тела?
6. Брошенное вверх тело пролетает мимо окна со скоростью 12 м/сек. С ка-
кой скоростью оно будет пролетать мимо того же окна вниз?
61
Глава 3
Криволинейное движение
ВВЕДЕНИЕ
И в природе, и в технике очень часто встречаются движения,
траектории которых представляют собой не прямые, а кривые ли-
нии. Называют такие движения криволинейными. Но
криволинейным траекториям движутся в космическом пространстве
планеты и искусственные спутники, а на Земле — всевозможные
средства транспорта, части машин и механизмов, воды рек, воздух
атмосферы и т. д.
При криволинейном движении ре-
Рис. 55
шать задачи механики труднее, пото-
му что оно сложнее прямолинейного.
При таком движении уже нельзя ска-
зать, что изменяется только одна коор-
дината тела. Если, например, движе-
ние происходит на плоскости, то,
как это видно из рисунка 55, при
движении изменяются две координа-
ты: хи у. Направление движения, т. е.
направление вектора скорости, так-
же все время изменяется. Изменяет-
ся и направление вектора ускоре-
ния. Если к этому добавить, что мо-
гут изменяться и модули скорости и ускорения, то станет ясно,
насколько сложно криволинейное движение.
Так как для решения задач механики особенно важно уметь
вычислять значения скорости и ускорения, то мы прежде всего
должны выяснить, как изменяются эти величины.
§ 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ
ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ
Мы знаем, что при прямолинейном движении направление век-
тора скорости всегда совпадает с направлением перемещения. Чю
можно сказать о направлении скорости и перемещения при криво-
линейном движении? Чтобы ответить на этот вопрос, мы восполь-
зуемся тем же приемом, которым пользовались в предыдущей главе
при изучении мгновенной скорости прямолинейного движения.
На рисунке 56 представлена некоторая криволинейная траек-
тория. Допустим, что тело движется по ней из точки А в точку Д
62
При этом пройденный телом
путь — это дуга АВ, а его пере-
мещение это вектор АВ. Конечно,
нельзя считать, что скорость те-
ла во время движения направ-
лена вдоль вектора перемещения.
Проведем между точками А и В
ряд хорд (рнс, 57) и представим
себе, что движение тела проис-
ходит именно по этим хордам.
Па каждой из них тело движет-
ся прямолинейно и вектор ско-
рости v направлен вдоль хорды.
Сделаем теперь наши пря-
молинейные участки (хорды)
более короткими (рнс. 58). По-
прежнему на каждом из них век-
тор скорости направлен вдоль
хорды. Но видно, что ломаная
линия на рисунке 58 уже более
похожа на плавную кривую.
Ясно поэтому, что, продолжая
уменьшать длину прямолиней-
ных участков, мы их как бы
стянем в точки и ломаная линия
превратится в плавную кривую.
Скорость же в каждой точке
этой кривой будет направлена
но касательной к кривой в этой
точке (рис. 59).
Скорость движения тела в
любой точке криволинейной
траектории направлена по каса-
тельной к траектории в этой
точке.
В том, что скорость точки
при криволинейном движении
дейстьителыю направлена по
касательной, убеждает нас, нап-
ример, наблюдение за работой
сочила (рнс. 60). Если прижать
к вращающемуся точильному
камню концы стального прутка,
го раскаленные частицы, отры-
вающиеся от камня, будут вид-
ны в виде искр. Эти частицы
летят с той скоростью, которой
63
Рис. 61
они обладали в момент отрыва
от камня. Хорошо видно,
что направление вылета искр
всегда совпадает с касатель-
ной к окружности в той точ-
ке, где пруток касается кам-
ня. По касательной к ок-
ружности движутся и брыз-
ги от колес буксующего авто-
мобиля (рис. 61).
Таким образом, мгновен-
ная скорость тела в разных
точках криволинейной траек-
тории имеет различные нап-
равления, как это показано
па рисунке 62. Модуль же
скорости может быть во всех
точках траектории одина-
ковым (см. рис. 62) или из-
меняться от точки к точке,
от одного момента времени
к другому (рис. 63).
§ 23. УСКОРЕНИЕ
ПРИ КРИВОЛИНЕЙНОМ
ДВИЖЕНИИ
При криволинейном дви-
жении точки направление ее
скорости все время изменяет-
ся, а модуль скорости может
как изменяться, так и оста-
ваться постоянным. Но даже
если модуль скорости не изме-
няется, ее все равно нельзя
считать постоянной. Ведь ско-
рость — величина векторная,
А для векторных величин
модуль и направление оди-
наково важны. Поэтому кри-
волинейное движение всегда
движение ускоренное.
С изменением скорости по
модулю мы уже знакомы. Ведь
при равноускоренном прямо-
линейном движении изменяет-
ся именно модуль скорости.
И мы знаем, что в этом слу-
64
чае вектор ускорения направлен
вдоль вектора скорости пли против
него, а модуль ускорения опреде-
ляется изменением модуля ско-
рости в единицу времени. Так
как нам это уже известно, то в
дальнейшем мы будем рассматри-
вать только такое криволинейное
движение, при котором модуль ско-
рости остается все время постоян-
ным, так что ускорение будет свя-
зано только с изменением направления вектора скорости. Как
направлено и чему равно это ускорение?
И модуль, и направление ускорения должны, очевидно, зави-
сеть от формы криволинейной траектории. Но нам не придется
рассматривать каждую из бесчисленных форм криволинейных тра-
екторий. На рисунке 64 показана сложная траектория, по которой
движется тело. Из рисунка видно, что отдельные участки криво-
линейной траектории представляют собой приблизительно дуги
окружностей, изображенных тонкими линиями. Например, уча-
стки KL или ВМ — это дуги окружностей малых радиусов, уча-
сток EF — это дуга окружности большого радиуса.
Таким образом, движение по любой криволинейной траектории
можно представить как движение по дугам некоторых окружнос-
тей. Поэтому задача нахождения ускорения при криволинейном
движении сводится к отысканию ускорения при равномерном дви-
жении тела по окружности.
Упражнение 14
1. Как направлена мгновенная скорость прк криволинейном движении?
2. Чем различаются изменения скорости при криволинейном и прямолиней-
ном движении?
3. Могут ли совпадать направления скорости к ускорения при криволинейном
движении?
4. Может ли тело двигаться по криволинейной траектории без ускорения?
5. Возможно ли движение тела с постоянной по абсолютной величине ско-
ростью по траектории, представляющей собой ломаную линию?
6. Какая связь между криволинейным движением и движением по окруж-
ности?
§ 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ.
УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ
Движение тела по окружности можно описывать тем же спо-
собом, которым пользуются при описании прямолинейного движе-
ния. Но часто более удобным оказывается другой способ, с кото-
рым мы сейчас ознакомимся.
Представим себе, что некоторое тело движется по окружности
радиусом г (рис. 65). Проведем из центра О окружности радиус
3 Зака. ПОЗ
65
к какой-нибудь точке тела А и будем сле-
дить не только за самим телом, нс и за
радиусом, проведенным к нему. Мы уви-
дим, что, по мере того как тело движет-
ся, радиус поворачивается. Если, напри-
мер, тело за промежуток времени t пере-
местилось из точки А в точку В, то за это
же время радиус повернулся на угол ср.
Этот угол мы будем называть у г л о м
поворота радиуса. О движении тела
можно, следовательно, сказать, во-первых,
что тело за промежуток времени i прешло
путь I по дуге АВ окружности, во-вторых,
Рис- 65 что оно совершило перемещение 6, мо-
дуль которого равен длине хорды АВ,
и, в-третьих, что радиус, проведенный к телу, совершил поворот
на угол <р.
Если бы тело двигалось по окружности другого радиуса > г
(см. рис. 65), то длина пройденного пути была бы больше. Большей
была бы и длина перемещения | s' | = А'В'. Угол же поворота радиу
са в обоих случаях остается одним и тем же. Так, конец минутной
стрелки маленьких ручных часов за 15 мин проходит птть длиной
около 1,5 см. За это же время конец минутной стрелки огромных
башенных часов (например, часов Спасской башни Кремля) про-
Рис. 66
ходит путь длиной в несколько мет-
ров. Но минутные стрелки всех часов
в мире за четверть часа поворачивают-
ся на один и тот же угол — 90°
(рис. 66).
Если мы снова вернемся к рисунку
65, то увидим, что у тел, движущихся
по окружностям с радиусами г и /?,
равны не только углы псвсрста. В
обоих случаях одинаковы и сгношения
длины дуги к радиусу:
1 — L
/ ” R'
По какой бы окружности ни двигало^
тело, при равных углах поворота радиуса
равны и отношения длины дуги к ра-
диусу. Поэтому и сами углы можно из-
мерять величиной этого отношения
1
66
При таком измерении углов за единицу измерения угла удобно
принять не градус, а угол, соответствующий дуге, длина которой I
равна радиусу г, потому что тогда угол <р будет равен единице.
Такая единица измерения угла сейчас общепринята в науке, и на-
зывают ее радианом (сокращенно рад).
Радиан — это угол между двумя радиусами круга, вырезающий
на окружности дугу, длина которой равна радиусу.
Легко установить связь между градусом и радианом.
Когда тело (или точка) совершит один полный оборот по окруж-
ности радиусом г, то длина пройденной дуги будет равна 2лл
Поэтому величина угла в радианах равна:
Ф = — = 2л рад ж 6,28 рад.
Г
Следовательно, один оборот — это поворот радиуса на угол
в 2л рад. В градусной мере этот же угол равен 360э. Отсюда
_ 360’ __ 180“ 180° п701й,
— —• —— □ / 1 о .
2л л 3,14
Таким образом, длина дуги, пройденной телом, и угол поворо-
та радиуса, проведенного к нему, связаны формулой
I = Гф.
Скорость равномерного движения тела по окружности тоже мож-
но выражать в угловых единицах. Для этого используют понятие
угловой скорости.
Под угловой скоростью мы будем понимать отношение угла
поворота радиуса, проведенного к телу, к промежутку времени,
в течение которого совершен этот поворот. Угловую скорость обо-
значают греческой буквой со (омега), так что
Ф
СО — — .
t
Так как здесь угол ф выражен в радианах, а время t в секундах,
то угловая скорость со измеряется в радианах в секунду (рад! сек).
В отличие от угловой скорости скорость v, измеряемую отноше-
нием длины пути I ко времени t и выражаемую в метрах в секунду,
называют линейной скоростью. Между угловой ско-
ростью ю и линейной скоростью v очень простая связь. Если в вы-
ражение для угловой скорости подставить вместо Ф его значение
I 1
—, то мы получим: со= — .
f rt
Так как в свою очередь I = vt, то со = —, или v = cor.
Линейная скорость точки равна произведению угловой скорости
на радиус окружности, по которой происходит движение.
3* 67
Скорость движения тела по окружности часто выражают также
числом оборотов в единицу времени. Легко
связать угловую скорость с числом оборотов в единицу времени.
Действительно, при одном обороте радиус поворачивается на угол
в 2л рад. Значит, совершив в единицу времени, например, п оборо-
тов, радиус повернется на угол 2лп рад. Поэтому угловая скорость
w и число оборотов в единицу времени п связаны выражением
m — 2лн.
Число оборотов в единицу времени (/г) обычно называют также
частотой вращения. Величина, обратная частоте, оп-
ределяет время, за которое тело делает один оборот. Это время на-
зывают периодом вращения и обозначают буквой Т'.
у. 1 2л
п ы
Упражнение 15
1. Что такое угловая скорость? В каких единицах ее измеряют?
2. Как связаны между собой угловая и линейная скорость?
3. Вычислите угловую и линейную скорость движения Земли вокруг Солнца.
Радиус орбиты Земли считать равным 150 000.000 км.
4. Какова линейная скорость конца минутной стрелки часов на Спасской баш-
не Московского Кремля, если длина стрелки 3,5 м? Сравните угловую ско-
рость этой стрелки с угловой скоростью минутной стрелки ручных часов.
§ 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ
ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ
Вернемся теперь к нашей задаче — найти ускорение, с кото-
рым тело движется по окружности с постоянной по модулю скоро-
стью.
Ускорение, как известно, определяется по формуле
где v0 — скорость тела в некоторый начальный момент времени,
a v — его скорость через промежуток времени t. В нашем случае
модули скоростей v и v0 равны друг другу.
Предположим, что тело движется по окружности радиусом
г и что в некоторый момент времени оно находится в точке А
(рис. 67).
Чему равно ускорение в этой точке? Скорость ц, в этой точ-
ке направлена по касательной к окружности в точке А. Через
t сек тело оказывается в точке В, и скорость его v теперь паправ-
68
лена по касательной к окружности в точке В. По модулю ско-
рости v п с0 равны (длины стрелок v и д, одинаковы).
Мы хотим найти ускорение в точке А окружности (мгновен-
ное ускорение). Поэтому точки А и В мы должны взять близкими
друг к другу, настолько близкими, чтобы дуга АВ как бы стяну-
лась в точку.
Выясним сначала, как направлено это ускорение.
Проведем из центра О окружности радиусы к точкам А и В.
Радиус окружности перпендикулярен к касательной в точке каса-
ния, следовательно, радиусы ОА и ОВ перпендикулярны векторам
у() и v. Чтобы узнать направление вектора ускорения, нужно най-
ти вектор, равный разности векторов v и v„. Его направление —
это п есть направление вектора ускорения. Как производят вычи-
тание векторов, мы уже знаем (см. § 6). Чтобы найти разность
v — у0, векторы v п ц, расположим так, чтобы они исходили из
одной точки (рис- 68), и соединим их концы, направив стрелку от
вычитаемого к уменьшаемому (от конца вектора и0 к концу век-
тора у). Вектор CD и есть разность векторов v — v0. Следователь-
— >
но, вдоль вектора CD направлено ускорение. Что можно сказать
об этом направлении?
Треугольник ADC (см. рис. 68) равнобедренный. Угол при вер-
шине А равен углу ф между радиусами ОА и ОВ (рис. 67), так
как они образованы взаимно перпендикулярными сторонами. Точ-
ки А и В расположены близко друг к другу, поэтому угол ф очень
мал (близок к нулю). Каждый из углов при основании треугольни-
ка ADC близок к прямому, так как сумма углов треугольника
равна двум прямым. Это означает, что вектор CD — v — v0 перпен-
69
- дик\,T-:piл вектору скорости. Значит, и ус-
когснне перпендикулярно скорости. Но
д /бд - скорость направлена по касательной к
<7 у с скружностн в точке А, а касательная
[а \ ... перпендикулярна радиусу. Значит, и ус-
а I корение направлено по радиусу к центру
ж \ / \ 1 окружности. Его поэтому называют
2ч Х-- i _ Л т ц е н т р о с т р е м и т е л ь н ы м v с к о-
о кл //17
u X. \ у f рение м.
При равномерном движении тела по
•7 окружности ускорение в любой ее точке
р.,с 59 перпендикулярно скорости движения и
направлено к центру окружности.
Эта интересная особенность ускорения
при движении по окружности с постоянней по модулю скоростью
показана на рисунке 69.
Найдем теперь модуль центростремительного ускорения. Для
этого нужно найти, чему равно абсолютное значение величины
? . Из рисунка 68 видно, что модуль разности векторов
| v — v0 | равен длине отрезка CD. Так как угол ф очень мал, то отре-
зок CD мало отличается от дуги CD окружности (показанной
пунктиром) с центром в течке А. Радиус этой окружности г числен-
но равен v (г — и). Но, как мы знаем (см. § 24), длина такой дуги
равна г<р = Рф. Следовательно, | v — vtt | = CD ~ v<p. Абсолютное
значение ускорения | а | равно -_2ДЛ.1 = Но 2.---это угловая
скорость ®. Поэтому
Н = к4
Ускорение тела, движущегося по окружности, рлоно произведе-
нию его линейной скорости и угловой скорости поворота радиуса,
проведенного к телу.
Формулу для центростремительного ускорения удобнее пред-
ставить в таком виде, чтобы в нее входила величина радиуса ок-
ре жнссти, по которой движется тело. Так как угловая и линейная
скорости связаны соотношением v = сот (г — радиус окружности),
то, подставив это выражение в формулу \а | = |wi , получим:
| а | = | м г& | = сгг.
Но w, поэтому формулу для центростремительного ускоре-
Г
ния можно записать еще и так:
При равномерном движении по окружности тело движется ь
70
ускорением, которое направлено по радиусу к центру окружности
и модуль которого определяется выражением | а| — агг, или|а|= — .
г
Следовательно, верно и обратное: если известно, что скорость
тела равна v и ускорение тела во всех точках перпендикулярно
вектору его скорости и по абсолютному значению равно | а | , то
можно утверждать, что такое тело движется по окружности, радиус
которой г определяется формулой
Значит, если нам известны начальная скорость тела и абсолют-
ное значение его центростремительного ускорения, мы можем изоб-
разить окружность, по которой тело будет двигаться, и найти его
положение в любой момент времени (начальное положение тела
должно быть, конечно, известно). Тем самым будет решена основ-
ная задача механики.
Напомним, что ускорение при равномерном движении по ок-
ружности нас интересует потому, что всякое движение по криво-
линейной траектории представляет собой движение по дугам ок-
ружностей различных радиусов.
Теперь мы можем сказать, что при равномерном движении в
любой точке криволинейной траектории тело движется с ускоре-
нием, направленным к центру той окружности, частью которой
является данная траектория вблизи этой точки. Численное же
значение ускорения зависит от скорости тела в этой точке и от
радиуса соответствующей окружности. На рисунке 70 показана не-
которая сложная траектория и указаны векторы центростремитель-
ного ускорения в различных точках траектории.
Задача, Самолет, выходя из пике, движется по дуге, которая
в нижней своей части является дугой окружности радиусом 500 м
(рис. 71). Вычислите ускорение самолета в наинизшей точке, если
его скорость равна 800 км/ч, и сравните полученное значение с
ускорением свободного падения.
71
Р е uj е н и е. Ускорение самолета вычисляем по формуле
1«1 =
Подставив сюда значения
800 • 103 м ОГ1О м
3600 сек сек
и г = 500 м,
получаем:
л \2
222
сек-
500 Л1
Так как
g = 9,8 — , то | и | л/ 10 g.
° ГРК2
сек-
Упражнение 16
1. Как направлено ускорение тела, движущегося по окружности с постоянной
по модулю скоростью?
2. Если при движении тела по окружности модуль его скорости изменяется,
будет ли ускорение тела направлено к центру окружности?
3. /Ложно ли считать движение по окружности с постоянным по модулю ус-
корением равноускоренным движением?
4. Точильный круг, радиус которого равен 10 см, при вращении делает 1 обо-
рот за 0,2 сек. Найдите скорость точек, наиболее удаленных от оси вра-
щения.
5. Автомобиль движется по закруглению дороги радиусом 100 м со ско-
ростью 54 км/ч. Какова величина центростремительного ускорения авто-
мобиля?
6. Период обращения первого корабля-спутника «Восток» вокруг Земли рав-
нялся 90 мин. Среднюю высоту корабля-спутника над Землей можно счи-
тать равной 320 км. Радиус Земли равен 6 400 км. Вычислите скорость ко-
рабля.
7. Какова скорость движения автомобиля, если его колеса радиусом 30 см
делают 10 оборотов в 1 сек?
8. Два шкива, радиусы которых /1 = 5 см и 10 см, соединены бесконечным
ремнем. Период вращения шкива меньшего радиуса равен 0,5 сек. Какова
скорость перемещения точек ремня? Каков период вращения второго
шкива?
9. Луна движется вокруг Земли на расстоянии 385 000 км от нее, совершая
один оборот за 27,3 суток. Вычислите центростремительное ускорение
Луны.
§ 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА
До сих пор мы изучали поступательное движение тел. При
таком движении все точки тела движутся одинаково. Одинаковы
их перемещения за любой промежуток времени, одинаковы их ско-
рости и ускорения в любой момент времени. И когда мы говорили
о движении тела, будь то прямолинейное, криволинейное движение
или движение по окружности, мы в действительности имели в виду
движение какой-ти одной его точки. Вот почему.мы нигде не интере-
72
совались ни размерами тела,
ни его формой, ин какими-
нибудь другими его свойст-
вами .
Но, кроме поступательно-
го движения, тело (по не
точка!) может совершать еще
один вид движения. Это вра-
щение вокруг некоторой оси.
Когда, например, по дороге
движется автомобиль, то он
движется поступательно. Но
колеса автомобиля, кроме то-
го, что они вместе со всем
автомобилем движутся посту-
пательно, еще н вращаются.
Вращательное движение со-
вершают маховые колеса ма-
шин, крылья ветряной мель-
ницы, винты кораблей, са-
молетов, вертолетов и т. д.
Что же представляет собой
этот вид движения?
Вращательным движени-
ем называют такое движе-
ние, при котором все точ-
ки тела движутся по ок-
ружностям, центры которых
лежат на одной прямой — оси
Рис. 72
Рис. 73
вращения
При таком движении различные точки тела за один и тот же
промежуток времени проходят различные по длине пути: точки,
расположенные ближе к оси вращения, проходят меньшие пути,
чем точки, более отдаленные от нее.
Как же описывать вращательное движение тела, если различ-
ные его точки движутся по-разному?
Ясно, что для этого нужны величины, которые характеризова-
ли бы движение всего тела, а не отдельных его точек.
Такими величинами являются уже знакомые нам величины —
угол поворота ср и угловая скорость со.
Действительно, рассмотрим какое-нибудь тело, которое может
вращаться около неподвижной оси, проходящей через точку О
(рис. 72,а) перпендикулярно плоскости рисунка. Она как бы «про-
тыкает» страницу книги! Опустим из произвольной точки М пер-
пендикуляр МО на ось вращения. При вращении диска точка будет
перемещаться, а перпендикуляр Л-10 — поворачиваться. Ясно,
что, из какой бы точки тела мы ни опустили перпендикуляр на ось
вращения, угол поворота этих перпендикуляров за одно и то же
73
время будет одним и тем же (угол ср на рисунке 72, б). Можно по-
этому считать, что угол ср — это угол поворота тела в целом.
Сказанное можно иллюстрировать следующим простым опытом.
Возьмем диск, укрепленный на горизонтальной оси, и с помощью
ременной передачи приведем его во вращение. Если прижать к
диску в двух его точках мелки, то при повороте диска они прочер-
тят на нем дуги. Легко видеть, что углы поворота одинаковы неза-
висимо от того, прижмем ли мы мелки на одинаковых расстояниях
от оси вращения (рис. 73, а) или на разных (рис. 73, б). Длины же
дуг во втором случае различны (см. рис. 73, б).
Угол поворота ср служит характеристикой движения тела при
вращении. Он дает нам как бы угловое перемещение тела.
Так как тело может вращаться быстро или медленно, то можно
говорить о скорости вращательного движения тела. При описании
вращательного движения следует пользоваться угловой ско-
ростью, которая, как мы уже знаем, определяется выражением
и измеряется в радианах в секунду.
Линейная же скорость о характеризует лишь движение отдель-
ной точки тела, а не всего тела. Если нас интересует линейная ско-
рость движения какой-то точки тела, расположенной на расстоянии
г от оси вращения, то ее можно вычислить по известной нам фор-
муле
о = шг.
При описании вращения твердого тела используют также из-
вестные нам величины: число оборотов в единицу времени п и пе-
риод вращения Т.
Упражнение 17
1. Какая разница между поступательным движением тела по окружности и
вращательным движением тела вокруг неподвижной оси?
2. Какими величинами характеризуется вращательное движение тела?
3. Вычислите угловую скорость патефонного диска при скорости вращения
33 и 78 об/мин.
4. Роторы мощных паровых турбин делают 3 000 об/мин. Найдите угловую
скорость и ускорение конца лопаток ротора, если диаметр рабочего коле-
са 2,7 м.
5. Волчок, вращаясь с угловой скоростью 251,2 рад/сек, свободно падает с
высоты 5 м. Сколько оборотов сделает волчок за время падения?
б. Колесо вращается с угловой скоростью 12,56 рад/сек. Сколько оборотов
оно делает за 30 мин? Какова линейная скорость точек на ободе колеса,
если его радиус 1,8 м? Как расположены точки колеса, движущиеся с ли-
нейной скоростью 9,32 м/сек?
7. Вычислите угловую скорость вращения Земли вокруг ее оси. Сравните еа
с угловой скоростью часовой стрелки. Найдите линейную скорость точек
поверхности Земли на экваторе при этом вращении. Радиус Земли равен
6 400 км.
74
§ 27. СБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ
ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА
В § 10 и 11 мы уже говорили об относительности движения при
прямолинейном движении тел. Мы видели, что движения одного
и того же тела относительно разных систем отсчета, движущихся
прямолинейно друг относительно друга, могут сильно различаться.
Рассмотрим теперь движение тела относительно вращающейся
системы отсчета. Возьмем стержень, вдоль которого может сколь-
еить надетый на него шарик. Закрепим шарик на стержне и
приведем стержень во вращение в горизонтальной плоскости вокруг
одного из его концов (рис. 74, а). В системе координат ХОУ, свя-
ванной с горизонтальной плоскостью, на которой вращается стер-
жень, шарик движется по окружности и его скорость в любой момент
времени направлена перпендикулярно стержню. В то же время в
системе координат Х101У1, связанной с вращающимся стержнем,
шарик покоится.
Предоставим теперь шарику воз-
можность скользить вдоль стержня.
В тот момент, когда стержень нахо- 1
дится в положении / (рис. 74, б),
шарику сообщается скорость
va, перпендикулярная стержню.
Так как шарик не скреплен со
стержнем, то он движется в том
направлении, куда направлен век-
тор его скорости, и через проме-
жуток времени t, когда стержень
будет находиться в положении 11,
шарик окажется в точке В. Его
скорость ьв будет опять направле-
на перпендикулярно стержню, и
поэтому еще через время t, когда г
стержень окажется в положении '
III, шарик будет находиться в точ-
ке С и т. д. Так как гипотенуза
BOj больше катета АОГ прямо-
угольного треугольника АВО}, а
гипотенуза СС\ треугольника СВО1
больше катета ВО± этого треуголь-
ника, то получается, что относи-
тельно неподвижной системы коор-
динат ХОУ шарнкдвижется по сло-
жной траектории, точки которой все
больше и больше удаляются от о
оси вращения стержня. Траекто-
рия движения шарика — это рас-
75
крх чивающаяся спираль. В то же время в системе координат,
связанной с вращающимся стержнем, шарик будет перемещаться
но прямой липин вдоль стержня. Вдоль стержня будет направлена
и скорость шарика. Шарик соскальзывает с вращающегося стержня.
Из рассмотренного опыта следует, что скорости и траектории
тела (шарика) относительно неподвижной п вращающейся систем
отсчета различны.
САМОЕ ГЛАВНОЕ В РАЗДЕЛЕ
«КИНЕМАТИКА»
Основная задача механики состоит в нахождении положения
тела в любой момент времени. Решение этой задачи идет по свое-
образной «цепочке»: чтобы найти координату точки, нужно знать
ее перемещение, а чтобы вычислить перемещение, нужно знать ско-
рость движения. По такой «цепочке» скорость — перемещение —
координата решают задачи механики для прямолинейного равно-
мерного движения. Если движение ускоренное, то нужно знать
ускорение, так что при таком движении задачи решают по «цепоч-
ке»: ускорение — скорость — перемещение — координата. И для
равномерного, и для ускоренного движения должны быть известны
«начальные условия» — начальные координаты и начальная ско-
рость. Мы и рассмотрели три вида движения, различающиеся глав-
ным образом ускорениями.
1. Ускорение равно нулю (а -- 0). В этом случае тело движет-
ся равномерно по прямой линии. Координата тела в любой момент
времени вычисляется ио формуле .v ,vu -У vt.
2. Ускорение постоянно по величине и направлению (а -= const),
а начальная скорость направлена так же, как ускорение. Тело со-
вершает прямолинейное равноускоренное движение,
в любой! момент времени определяется формулой х~
Координата
, , ар
3. Ускорение тела а постоянно по абсолютной величине, но на-
правлено все время перпендикулярно скорости v. Тело движется
по окружности с постоянной по модулю скоростью. Радиус ок-
ружности вычисляется по формуле г -- — ,
Ы '
Зная радиус окружности и начальное положение тела на ней,
можно найти и его положение в любой момент времени.
Перемещение тела, траектория его движения н скорость отно-
сительны в различных движущихся системах отсчета. .Ускорение
тела во всех системах отсчета, движущихся друг относительно дру-
га прямолинейно и равномерно, одинаково. Относительно таких
систем отсчета ускорение имеет абсолютный! характер.
76
s
в
Динамика
Г л 6 в 2 4
Законы движения
ВВЕДЕНИЕ
В предыдущих главах мы видели, что если известно ускорение
тела, то, зная его начальные координаты и скорость, можно вычис-
лить его скорость, перемещение и, наконец, координаты тела в лю-
бой момент времени. Теперь нам нужно научиться находить уско-
рения тел.
Движения тел начинаются и прекращаются, они становятся
более быстрыми или более медленными, изменяются направления
движений. Во всех этих случаях мы имеем дело с изменением ско-
рости, т. е. с появлением ускорения. Понято, насколько важно
знать, при каких условиях возникают ускорения, а при каких те-
ла движутся без ускорений, как определять ускорения (их абсо-
лютные значения и направления). Без этого нельзя решать задачи
механики, без этого нельзя управлять движением. На все эти во-
просы дает ответ основная часть механики —динамика.
Часть механики, в которой изучаются причины появления
ускорения и рассматриваются способы его вычисления, называют
динамикой.
§ 28. ТЕЛА И ИХ ОКРУЖЕНИЕ.
ПЕРВЫЙ ЗАКОН НЬЮТОНА
Чтобы найти причину возникновения ускорений, нужно обра-
титься к опыту, к наблюдениям. Нам будет удобнее сначала выяс-
нить, при каких условиях тело движется без ускорения, т. е.
когда его скорость с течением времени не меняется.
Всякое тело, движется оно или покоится, не одиноко в мире.
Вокруг него есть много других тел — близких и далеких, больших
и малых, покоящихся п движущихся. Естественно предположить,
77
что некоторые из них, а может быть и все, как-то действуют на то
тело, которое мы рассматриваем, как-то влияют на его состояние
движения. Заранее нельзя сказать, какие из окружающих тел су-
щественно влияют, а какие мало влияют на это состояние. Это на-
до исследовать в каждом отдельном случае.
Рассмотрим сначала какое-нибудь покоящееся тело. Такое тело
не обладает ускорением, его скорость постоянна и равна нулю.
На рисунке 75 показан шарик, подвешенный на резиновом шну-
ре. Относительно Земли он находится в покое. Около шарика име-
ется множество различных тел: шнур, на котором он висит, стены
комнаты, множество предметов в ней и в соседних помещениях и,
конечно, Земля. Понятно, что не все эти тела одинаково действуют
на шарик. Если, например, убрать или переставить мебель в комна-
те, то это не окажет какого-либо заметного влияния на шарик. Но
если перерезать шнур (рис. 76), шарик сразу начнет падать вниз,
с ускорением. Хорошо известно, что именно под влиянием Земли
все тела падают вниз. Но пока шнур не был перерезан, шарик все
же находился в покое. Этот простой опыт показывает, что из всех
тел, окружающих шарик, только два заметно влияют на него: ре-
зиновый шнур и Земля, и их совместное влияние обеспечивает со-
стояние покоя шарика. Стоило устранить одно из этих тел — шнур,
и состояние покоя нарушилось. Если бы можно было, сохранив
действие шнура, убрать... Землю, то это тоже нарушило бы покой
шарика: он стал бы двигаться в противоположном направлении.
Это приводит нас к выводу, что действия на шарик двух тел —
шнура и Земли, компенсируют (иногда говорят, уравновешивают)
друг друга.
Когда говорят, что действия двух или нескольких тел компен-
сируют друг друга, то это значит, что результат их совместного
действия такой же, как если бы этих тел вовсе не было.
78
Рассмотренный нами пример и много других подобных примеров
позволяют сделать следующий вывод: если действия тел компенсиру-
ют друг друга, то тело под влиянием этих тел находится в состо-
янии покоя.
Но мы знаем, что движение и покой относительны; и если по
отношению к одной системе отсчета тело покоится, то относительно
других систем отсчета тело может двигаться. Рассмотрим, например,
шайбу, лежащую на льду хоккейного поля (рис. 77). Шайба поко-
ится относительно Земли, потому что действие на нее Земли компен-
сируется действием льда. Но для хоккеиста, движущегося с по-
стоянной скоростью v относительно Земли, а значит и относительно
шайбы, эта шайба движется в сторону, противоположную направ-
лению движения хоккеиста, со скоростью —V. В системе отсчета,
связанной с движущимся хоккеистом, шайба движется равномерно
и прямолинейно.
Ударим по шайбе клюшкой. В результате очень непродолжи-
тельного действия клюшки шайба придет в движение, приобретя
некоторую скорость. Замечательно, что после удара, когда действие
клюшки на шайбу уже прекратилось, шайба продолжает свое дви-
жение. Между тем после удара влияние на шайбу других тел оста-
лось таким же, как и до удара: по-прежнему действие Земли ком-
пенсируется действием льда, а клюшка, как и до удара, никакого
влияния на движение шайбы не оказывает. Шайба же после удара
движется по прямой линии с почти постоянной скоростью, которую
она приобрела в момент удара. Правда, шайба в конце концов оста-
новится, но из опыта известно, что, чем более гладкими будут лед
и сама шайба, тем более продолжительным будет движение шайбы.
Можно поэтому догадаться, что если совсе?! устранить то действие
льда на движущуюся шайбу, которое называется треплем, то шай-
ба продолжала бы двигаться относительно Земли с постоянней
скоростью безостановочно.
Итак, мы видим, что если влияние на тело других тел компенси-
руется, то относительно Земли тело находится или в покое, или
даихсется прямолинейно и равномерно.
Это утверждение справедливо, однако, не для всех систем от-
счета. Например, относительно хоккеиста, бросающегося в атаку
79
и поэтому движущегося относительно Земли с ускорением, шайба
движется тоже неравномерно. Хотя, конечно, и этот хоккеист ска-
жет, что действие Земли и действие льда на шайбу компенсируют
друг друга.
Таким образом, мы приходим к одному из основных законов ме-
ханики, который называется первым законом Нью-
тона.
Существуют такие системы отсчета, относительно которых
движущиеся тела сохраняют свою скорость постоянной, если на
них не действуют другие тела или действие других тел компен-
сируется Г
Само явление сохранения скорости движения тела (в частности,
состояния покоя) при компенсации внешних воздействий на тело
называют и и е р ц и е й. Поэтому первый закон Ньютона часто
называют законом и и е р ц и и.
Те системы отсчета, относительно которых тело при компенса-
ции внешних воздействий движется равномерно и прямолинейно,
называют инерциальными системами отсчета.
В приведенном примере с хоккейной шайбой инерциальными сис-
темами являются система отсчета, связанная с Землей, и система
отсчета, связанная с хоккеистом, движущимся относительно Земли
равномерно и прямолинейно. Но не только они. Ясно, что любая
система отсчета, движущаяся относительно Земли прямолинейно
и равномерно, тоже является инерциальной. Таким образом, если
нам известна из опыта хотя бы одна инерциальная система от-
счета, то инерциальными будут и любые другие системы отсчета,
движущиеся относительно нее прямолинейно и равномерно.
В дальнейшем мы будем пользоваться только инерциальными
системами отсчета.
Закон инерции отнюдь не очевиден, как это может показаться
с первого взгляда. С его открытием было покончено с одним давним
заблуждением. До этого на протяжении веков считалось, что при
отсутствии внешних воздействий на тело (или, что то же самое, при
компенсации всех воздействий) оно может находиться только в со-
стоянии покоя, что покой — это как бы естественное состояние те-
ла. Для движения же тела с постоянной скоростью необходимо,
чтобы на него действовало другое тело. Казалось, что это подтвер-
ждал повседневный опыт: для того чтобы повозка двигалась с по-
стоянной скоростью, ее должна все время тянуть лошадь; чтобы
стол двигался по полу, его нужно непрерывно тянуть или толкать
и т. д.
Великий итальянский ученый Галилео Г а л и л е й был
первым, кто указал, что это неверно, что при отсутствии внешнего
воздействия тело может не только покоиться, по и двигаться пря-
1 Этот закон относится только к материальной точке или к телу, движущему-
ся поступательно. Если действия на тело всех других тел компенсируют друг дру-
га,тело все же может вращаться,а при вращении точки тела движутся с ускорением.
80
молипейно и равномерно. Прямолинейное и равномерное движение
является, следовательно, таким же «естественным» состоянием тел,
как и покой. И если стол, для того чтобы он двигался, нужно тя-
нуть или толкать, то это объясняется тем, что при движении стола
иол не только компенсирует действие Земли, но и создает еще до-
полнительное действие на стол, называемое трением. Воздействие
тех, кто тянет или толкает стол, и нужно, чтобы скомпенсировать
трение. Галилей сделал вывод, что не будь трения стол, приведен-
ный в движение, продолжал бы его с постоянной скоростью и без
воздействия извне.
Гениальный английский физик Исаак Ньютон обобщил
выводы Галилея и включил их в число основных законов движения.
Упражнение 18
1. Приведите примеры тел, находящихся в состоянии покоя. Действие каких
тел компенсируется в этих случаях?
2. Приведите примеры тел, движущихся прямолинейно и равномерно. Ука-
жите тела, действия которых при этом взаимно компенсируются,
3. Гребцы, пытающиеся заставить лодку двигаться против течения, не могут
с этим справиться, и лодка остается в покое относительно берега. Дейст-
вия каких тел на лодку при этом компенсируются?
4. В чем состоит явление инерции?
5. В чем состоит первый закон Ньютона?
6. На столе для игры в настольный теннис лежит мяч. Стол сдвинули с места,
и мяч пришел в движение. Укажите тело отсчета, относительно которого
в этом случае верен закон инерции, и тело отсчета, относительно которого
этот закон не выполняется.
§ 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ
Согласно первому закону Ньютона тело движется без ускоре-
ния, т. е. прямолинейно и равномерно (относительно инерциальной
системы отсчета), если на тело не действуют другие тела или если
воздействия есть, но они скомпенсированы.
Выясним теперь, при каких условиях тела движутся с ускоре-
нием. Опыт показывает, что когда тело движется с ускорением, то
всегда можно указать другое тело или несколько тел, влияние
которых вызвало это ускорение. Так, тела, свободно падающие вниз,
движутся с ускорением. Телом, вызвавшим их ускорение, явля-
ется Земля. Шайба, лежащая на льду, изменила свою скорость
во время удара. Телом, сообщившим шайбе ускорение, является
клюшка.
Приблизим намагниченный стальной стержень (магнит) к же-
лезному шарику. Шарик, до этого покоившийся, начнет двигаться,
у него появится ускорение (рис. 78), вызванное действием магнита.
И до тех пор, пока действует магнит, шарик будет двигаться с уско-
рением, непрерывно увеличивая свою скорость.
Если мы приблизим магнит к движущемуся шарику так, как
показано на рисунке 79, то изменится направление его скорости:
траектория шарика искривится. Это, как мы знаем, означает, что
у шарика появилось центростремительное ускорение. В этом опыте
81
Рис. 78
Рис. 79
мы снова видим, что влияние внешнего тела является причиной имен-
но изменения движения, а не самого движения. Ведь шарик двигал-
ся и до того, как мы приблизили к нему магнит!
Таким образом, причиной ускорения тела является влияние на
него других тел.
§ 30. ВЗАИМОДЕЙСТВИЕ ТЕЛ.
УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ
От чего зависит абсолютное значение и направление ускорения,
которое сообщается телу благодаря влиянию другого тела? Чтобы
найти ответ на этот вопрос, мы опять прибегнем к опыту.
В самом простом случае в опыте должны участвовать два теля:
то, которое влияет, и то, которое подвергается этому влиянию.
Но в действительности оба тела, так сказать, «равноправны».
Каждое из них и влияет на другое тело, и само подвергается влия-
нию. Когда, например, футболист в стремительном беге сталкивает-
ся с другим футболистом, то оба они изменяют свою скорость.
Вообще каждый раз, когда какое-нибудь тело А получает
ускорение из-за того, что на него действует тело В, тело В также
получает ускорение. Происходит, как говорят, взаимодей-
ствие тел, и оба они получают ускорения. Мы теперь должны
выяснить, каковы эти ускорения.
Множество опытов, проведенных с различными телами, показа-
ли, что при взаимодействии двух тел их ускорения направлены
всегда противоположно друг другу. Кроме того, для дв\х данных
взаимодействующих тел отношение абсолютных значений их уско-
рений всегда одно и то же. Это отношение совершенно не зависит
от того, как происходит взаимодействие этих тел. Это может быть
столкновение двух тел; это может быть взаимодействие тех же тел,
связанных между собой пружиной, нитью, проволокой; тела, на-
конец, могут взаимодействовать, не соприкасаясь друг с другом,
как, например, взаимодействуют планеты с Солнцем или Луна
с Землей, магнит с куском железа. Сами же абсолютные вна-
чения ускорений каждого из тел могут быть совершенно различ-
ными при различных взаимодействиях. Одинаково лишь отношение
ускорений.
82
Если бы мы, например, взяли две тележки одинакового разме-
ра — одну алюминиевую, а другую стальную (рис. 80) и заставили
бы их столкнуться, то во время столкновения обе они изменили бы
свою скорость, получили ускорения. Измерения показали бы, что
ускорение at алюминиевой тележки по абсолютному значению в три
раза больше ускорения а., стальной независимо от того, какие ско-
рости имели тележки до столкновения:
-Ы- = з.
к!
Направления ускорений обеих тележек противоположны друг
другу.
Измерять ускорения тележек при столкновении очень трудно,
потому что столкновение длится очень короткое время. Значи-
тельно проще провести опыт, в котором взаимодействующие тела
движутся равномерно по окружности, и измерить центростреми-
тельные ускорения этих тел.
Схема такого опыта показана на рисунке 81. Два одинаковых по
размеру цилиндра — алюминиевый и стальной — с просверленными
по осям отверстиями надеты на стержень, вдоль которого они мо-
гут скользить с малым трением.
Установим стержень с цилиндрами на центробежную машину
и приведем ее во вращение. Цилиндры тотчас же соскользнут к кон-
цам стержня (см. § 27). В этом опыте цилиндры не взаимодейству-
ют друг с другом.
Свяжем теперь цилиндры
тонкой нитью и снова приве-
дем стержень во вращение.
Теперь цилиндры взаимо-
действуют друг с другом пос-
редством связывающей их ин-
ти. При определенных рас-
стояниях цилиндров до оси
вращения стержня они не бу-
дут соскальзывать со стерж-
83
ня, а будут двигаться по окружностям. Радиусы г1 и г2 этих ок-
ружностей — это расстояния цилиндров до осп вращения. Но по
окружности тело движется с центростремительным ускорением,
направленным к центру и равным агг, где ю — угловая скорость
вращения стержня, г — радиус окружности. Отношение абсолют-
ных значений ускорений алюминиевого и стального цилиндров
равно:
к11 =
I oj Г2
Измерив радиусы гг и г2, мы увидим, что для алюминиевого цилин-
дра радиус гг втрое больше радиуса г2 окружности, по которой дви-
жется стальной цилиндр. Это значит, что отношение ускорений ци-
линдров равно трем.
Ускорения обоих цилиндров направлены к оси вращения и поэ-
тому взаимно противоположны. Можно изменить длину нити, свя-
зывающей цилиндры: можно изменять скорость вращения стержня.
Все это изменит ускорение каждого из цилиндров. Но опыт пока-
зывает, что отношение ускорений в любом случае останется равным 3.
Так мы убедились, что при любом взаимодействии двух данных тел
отношение их ускорений одно и то же.
Упражнение 19
1. Что является причиной ускорения?
2. Что можно сказать об ускорениях двух взаимодействующих тел?
3. Найдите скорость алюминиевой тележки, о которой шла речь в этом па-
раграфе, после ее столкновения со стальной тележкой, если начальная
скорость стальной тележки равна 4 м/сек, а ее скорость после столкновения
стала равной 2 м/сек. Алюминиевая тележка до столкновения покоилась.
4. Алюминиевый и стальной цилиндры, опыт с которыми рассматривался в
§ 30, связаны нитью длиной 8 см. На каком расстоянии от центра стержня
расположится каждый из цилиндров?
§ 31. ИНЕРТНОСТЬ ТЕЛ
Из опытов, о которых говорилось в предыдущем параграфе,
следует, что отношение ускорений, получаемых двумя телами при
их взаимодействии, зависит не от способа взаимодействия, а толь-
ко от самих тел. Отсюда следует, что каждое тело обладает каким-то
особым свойством, которое и определяет отношение его ускорения
к ускорению того тела, с которым оно взаимодействует.
Что же это за свойство?
Когда тело движется без ускорения, т. е. так, что оно не меняет
своей скорости, о нем говорят, что оно движется по инерции. При
взаимодействии тел каждое из них изменяет свою скорость. В опы-
тах, рассмотренных в § 30, мы видели, что в результате взаимодей-
ствия телам сообщаются различные ускорения. Так как ускорение
одного из тел сказывалось меньше ускорения другого, можно сде-
84
дать вывод, что за одно и то же
время, в течение которого длится
взаимодействие, одно из тел из-
меняет свою скорость меньше,
чем другое. Напомним, что ус-
корение тела равно отношению
изменения скорости к промежут-
ку времени t, в течение которо-
го произошло это изменение:
И — V.,
а --=-----.
t
Поэтому, чем меньше ускорение
тела, тем меньше меняется его
скорость за заданное время t.
О том теле, которое в результате взаимодействия меньше из-
меняет свою скорость, говорят, что оно более инертно, чем второе.
Если бы оно совсем не меняло свою скорость, то оно двигалось
бы по инерции.
Инертность — это свойство, присущее всем телам. Состоит оно
в том, что для изменения скорости тела на заданную величину
нужно, чтобы действие на него определенного другого тела длилось
некоторое время. Чем это время больше, тем инертнее тело. Из двух
взаимодействующих тел то тело более инертно, которое медлен-
нее набирает скорость.
Следующий опыт особенно ясно показывает, как проявляется
инертность тел и какую роль играет время воздействия одного те-
ла на другое.
На тонкой нити подвешен шар (рис. 82, а). Снизу к нему при-
креплена вторая такая же нить. Если резко дернуть за нижнюю
нить, то она обрывается, а шар продолжает висеть на верхней ни-
ти (рис. 82, б). Но если нижнюю нить тянуть, а не дергать, то
оборвется верхняя нить и шар упадет (рис. 82, в). Это объясняется
тем, что когда за нижнюю нить дергают резко, то время ее действия
на шар оказывается настолько малым, что шар не успевает значи- '
тельно увеличить свою скорость (не успевает набрать скорость) и
совершить заметное перемещение вниз. Поэтому верхняя нить не
обрывается. Нижняя же нить обладает малой инертностью и при
рывке приобретает значительную скорость, поэтому ее перемещение
оказывается достаточным для разрыва. Когда же за нижнюю нить
медленно тянут, она воздействует на шар длительное время, и за
это время шар успевает приобрести такую скорость, что его переме-
щение оказывается достаточным для разрыва и без того растянутой
верхней нити.
85
§ 32. МАССА ТЕЛ
Инертность, которой обладает каждое тело, — одно из важней-
ших его свойств, потому что от нее зависит ускорение тела в резуль-
тате его взаимодействия с другими телами.
Всякое свойство тел выражается определенной величиной. На-
пример, свойство тел занимать часть пространства выражается ве-
личиной его объема. Свойство тел, которое мы назвали инертно-
стью, тоже выражается особой величиной. Такой величиной явля-
ется м а с с а. С этой величиной вы ознакомились в курсе физики
VI класса.
То из двух взаимодействующих тел, которое получает меньшее
ускорение, т. е. более инертно, имеет большую массу. Если обозна-
чить массы взаимодействующих тел через тг и т2, то можно напи-
сать:
т2
т,
Отношение абсолютных значений ускорений двух взаимодействую-
щих тел равно обратному отношению их масс.
Мы, например, видели, что отношение ускорения алюминиево-
го цилиндра к ускорению стального равно трем. Это вызвано тем,
что масса алюминиевого цилиндра в три раза меньше массы сталь-
ного цилиндра.
Таким образом, мы теперь знаем, как найти отношение масс
двух тел. Для этого нужно измерить их ускорения при взаимодей-
ствии. А как найти массу каждого отдельного тела? Здесь поступа-
ют так же, как и при измерении других величин.
Чтобы, например, найти число, выражающее объем тела, мы
сравниваем его с некоторым объемом, условно принятым за едини-
цу, — с кубическим метром. Таким же способом определяют числен-
ные значения масс: чтобы найти число, выражающее массу отдель-
ного тела, нужно сначала выбрать какое-нибудь тело, массу которо-
го условно принимают за единицу, — эталон массы. Затем нужно
провести опыт, в котором тело, масса которого определяется (из-
меряется), как-то взаимодействовало с эталоном массы (см. рис. 81).
Тогда оба они, и тело, и эталон, получат ускорения, которые можно
измерить, и мы сможем написать равенство
тТ а,-
—ПЛИ щт = '-^е- тэт,
тэт м
где тт и от — масса и ускорение тела, а щэт и дэт — масса и уско-
рение эталона. Но масса эталона по условию равна единице, поэ-
тому
[С?эт
щт = единиц массы.
86
Масса тела — это величина, выражающая его инертность. Она
определяет отношение ускорения эталона массы к ускорению тела
при его взаимодействии с эталоном.
Совершенно безразлично, какое именно тело принять за эта-
лон массы. Нужно только условиться, чтобы эталон был одним для
всех стран. На Международном конгрессе в 1889 г. в качестве эта-
лона массы была принята масса специально изготовленного цилин-
дра из сплава платины и иридия. Масса этого цилиндра и есть меж-
дународная единица массы— килограмм (сокращенно: кг).
Эталон массы хранится в Международном бюро мер и весов (во Фран-
ции). В СССР, как и в некоторых других странах, имеется точная
копия этого эталона. С большой точностью можно считать, что
массой в 1 кг обладает 1 л (1 дм3) чистой воды при 153 С.
Масса наряду с такими величинами, как длина и время, входит
в число основных величин систем единиц СИ и СГС. В системе
единиц СГС за единицу массы принимается грамм (сокра-
щенно: г): 1 г = 0,001 кг.
Не следует думать, что каждый раз, когда нужно измерить
массу какого-нибудь тела, его заставляют взаимодействовать с
эталоном массы и измеряют ускорения тела и эталона. Такой спо-
соб практически, конечно, неудобен. Существует, к счастью, дру-
гой способ измерения массы — в звешивание, которым обыч-
но и пользуются. Но в некоторых случаях определение массы по
ускорениям при взаимодействии является единственно возможным
способом. Нельзя, например, взвешиванием измерить массу пла-
нет, звезд и других небесных тел. На весах нельзя также измерять
очень малые массы, например массы атомов и частиц, из которых
они состоят.
Масса тела выражает его собственное свойство (инертность),
которое не зависит ни от того, в каких взаимодействиях тело уча-
ствует, ни от того, как оно движется. Что бы с телом ни происхо-
дило, где бы оно ни находилось, как бы оно ни двигалось, масса
его остается одной и той же.
Об одном интересном и важном свойстве массы можно узнать,
если поставить еще один опыт (рис. 83). Соединим вместе два алю-
миниевых цилиндра и повторим опыт с центробежной машиной (см.
§ 30). Теперь стальной цилиндр
двумя соединенными вместе
алюминиевыми цилиндрами.
Опыт покажет, что отношение
ускорения соединенных вместе
двух алюминиевых цилинд- i
ров к ускорению стального
цилиндра равно не 3, а 3/2.
Это значит, что масса двух
цилиндров, соединенных вмес-
те и ставших как бы одним
телом, вдвое больше массы
взаимодействует не с одним, а о
Сталь И л юми ни а
гг rt
Рис. 83
87
одного из них. Следовательно, когда два или несколько тел сое-
диняются в одно, их массы складываются.
Из-за этого свойства массы иногда говорят, что масса выражает
собой и количество вещества в теле. Ясно ведь, что в двух алюмини-
евых цилиндрах вдвое больше алюминия, чем в одном.
Мы говорили, что масса тела не зависит от того, как движется тело. Но
это не совсем верно. Теория относительности приводит к поразительному вы-
воду, что масса тела все же зависит от того, как оно движется. Оказывается,
масса тела на самом деле растет с увеличением его скорости. Допустим, что
масса некоторого покоящегося тела равна т0. Если измерить массу того же
самого тела, когда оно движется со скоростью о, то окажется, что она равна не
т,., а
где с — скорость света. Масса тела, следовательно, стала больше. Однако замет-
ным это увеличение массы становится только при скоростях, близких к скорости
света (с = 3 • 108 м/сек). С этим нельзя было бы не считаться при скоростях
около 250 000 км/сек. и выше. Но с такими скоростями обычные тела никогда не
движутся. Самые быстрые тела, с которыми приходится иметь дело, — это ис-
кусственные спутники Земли и космические корабли. Но их скорости до сих
пор не превосходили 12 км/сек. К. при таких скоростях массу можно считать
вполне постоянной, не зависящей от скорости.
Упражнение 20
1. Может ли скорость тела изменяться мгновенно?
2. В чем состоит свойство, называемое инертностью тела?
3. Какой величиной характеризуется инертность тела?
4. Какова связь между массами тел и ускорениями, которые они получают
при взаимодействии?
5. Как определяется численное значение массы тела?
6. В каких единицах измеряется масса?
7. Покупатель приобрел в магазине 2 кг хлеба. Что выражает число 2 кг?
8. Тележка движется по горизонтальной поверхности со скоростью 50 смеем.
С ней сталкивается вторая тележка, которая движется в том же направле-
нии со скоростью 150 см/сек. После столкновения обе тележки продолжа-
ют движение в прежнем направлении с одинаковой скоростью 100 см сек.
Найдите отношение масс этих тележек.
§ 33. МАССА ЛУНЫ
В качестве примера того, как определяют массу тел по их уско-
рениям при взаимодействии, мы найдем массу Лупы ио ее взаимо-
действию с Землей.
О том, что Земля влияет на движение Луны, известно всем.
Все знают, что именно под влиянием Земли Луна движется вокруг
Земли по окружности радиусом около 384 000 км.
Обычно считают, что Луна обращается вокруг Земли так, будто
центр Земли есть неподвижный центр лунной орбиты. Если бы это
было так, то это противоречило бы закону взаимодействия, по ко-
торому ускорения получают оба взаимодействующих тела. На са-
88
мом деле и Луна влияет на Землю, заставляя ее двигаться по ок-
ружности и сообщая ей центростремительное ускорение. Но вокруг
какого центра?
Астрономические наблюдения показали, что Луна обращается
не вокруг центра Земли, а вокруг некоторой точки Р (рис. 84),
которая отстоит от центра Земли на 4700 км. (Эта точка находится
внутри земного шара.) Вокруг этой же точки Р движется по окруж-
ности и центр Земли (рис. 85). Значит, радиусы, соединяющие
центры Земли и Луны с точкой Р, движутся с одинаковой угловой
скоростью вокруг точки Р. Центр Земли движется по окружности
радиусом г3«4700 км, а центр Луны — по окружности радиусом
г, х 380 000 км. Выходит, что Земля и Луна ведут себя совершен-
но так же, как алюминиевый и стальной цилиндры в опыте, рассмот-
ренном в § 30. Мы видели там, что отношение центростремитель-
ных ускорений, сообщаемых цилиндрами друг другу, равно отно-
шению радиусов окружностей, по которым они движутся. Точно
так же отношение модулей ускорений Луны | ад | и Земли | а3 |
равно отношению радиусов гл и г3:
__ К>2ГЛ _ г3
Но отношение ускорений взаимодействующих тел равно, как мы
внаем, Обратному отношению их масс, поэтому
г я _ т3
гз т.л
Так как гл л 380 000 км, а г3 4700 км, то
т3 ~ 380000 g
4700
89
Следовательно, масса Луны в 81 раз меньше массы Земли. Если
бы была известна масса Земли, то можно было бы определить мас-
су Луны. Масса Земли действительно была определена (см. гл. 6).
Она оказалась равной 6-10'21 кг. Тогда
... . б-КЯ кг ... 7 1Q23
тл
81
§ 34. СИЛА
Напомним, что наша задача состоит в том, чтобы выяснить, как
вычислять ускорения движущихся тел.
В предыдущих параграфах мы видели, что когда некоторое те-
ло 1, масса которого равна ml( получает ускорение alt то это вызва-
но тем, что на него влияет какое-то другое тело 2 массой т2. Оно
в свою очередь тоже получает ускорение а.2. При этом
mi
Из этой формулы как будто бы следует, что нельзя изучать дви-
жение и вычислять ускорение только одного тела — назовем его
ускоряемым телом. Непременно нужно еще знать массу и ускоре-
ние еще одного тела — ускоряющего тела.
Но обычно нас интересует движение именно одного, ускоряемо-
го тела, а не того тела или тел, которые на него влияют, сообщая
ему ускорение. Когда, например, артиллерийский снаряд посла
выстрела покидает ствол орудия, он взаимодействует с Землей и
воздухом, сквозь который он пролетает. И Земля, и воздух сообща-
ют снаряду ускорения, и сами при этом получают какие-то ускоре-
ния. Но артиллеристу важно знать ускорение только снаряда.
Зачем же ему интересоваться массами и ускорениями Земли и воз-
духа?
Поэтому обычно вычисляют ускорение лишь одного тела — того,
движение которого изучается. Влияние же другого тела, вызываю-
щего ускорение, коротко называют силой, действующей на уско-
ряемое тело. И вместо того чтобы говорить, что ускорение тела вы-
звано влиянием на него другого тела, говорят, что ускорение вызва-
но приложенной к телу (или действующей на него) силой.
Сила, действующая на тело, является причиной его ускорения.
Известно, например, что растянутая пружина, сокращаясь, со-
общает прикрепленному к ней телу ускорение, направленное вдоль
оси пружины. Это значит, что на тело со стороны растянутой пру-
жины действует сила. Ее называют силой упругости
пружины.
Другой пример. Известно, что все тела, свободно падающие или
брошенные вверх, движутся с ускорением. Причиной этого ускоре-
ния является, очевидно, влияние Земли. Но теперь мы будем гово-
рить, что на всякое тело со стороны Земли действует сила, которая и
90
сообщает ему ускорение. Сила эта
Называется силой тяжести.
Точно так же на снаряд, о котором
мы упоминали, действуют силы со
стороны Земли и воздуха.
Сила может быть большой или
малой, т. е. сила — физическая ве-
личина.
►Так как ускорение—величина
векторная, а вызывается оно силой,
приложенной к телу, то ясно, что
и сила — величина векторная.
На ускоряемое тело может дей-
ствовать не одна, а две или несколь-
ко сил, потому что тело может вза-
имодействовать не с одним, а с
несколькими телами.
Если две силы сообщают од-
ному и тому же телу одинаковые по
направлению ускорения, то очевидно,
Отсюда следует, что две силы, равные по абсолютному значению,
но противоположные по направлению, при совместном действии на
тело не сообщают ему никакого ускорения. Если, например, одна
сила сообщает телу ускорение, направленное вверх, а другая —
такое же по абсолютному значению ускорение, но направленное
вниз, то результирующее ускорение тела будет равно нулю.
Что же это за величина — сила? Как она связана с вызываемым
ею ускорением? Как направлен вектор силы? В каких единицах
сила измеряется?
На все эти вопросы отвечает один из важнейших заколов меха-
ники — второй закол Ньютона.
Исаак Ньютон
[1643—1727)
абсолютному значению и по
что они равны между собой.
§ 35. ВТОРОЙ ЗАКОН НЬЮТОНА
Выясним, какой величиной выражается сила, пли, как говорят,
какая величина служит мерой силы, действующей на тело.
На этот вопрос может ответить только опыт. Опыт должен сос-
тоять в том, чтобы одну и ту же силу приложить к различным те-
лам и измерить их ускорения.
При этом ускорения тел могут быть разными. Но если на все
эти тела действует одна и та же сила, то нужно из опыта найти та-
кую величину, характеризующую ускоряемые тела, которая для
всех тел так же была бы одной и той же. Эта величина и будет
выражать действующую на тело силу.
Ускоряющим телом, которое действует на все тела с одной и
той же силой, может служить растянутая пли сжатая пружина.
Это видно из того, что та же пружина в своем нормальном
«1
Рис. 36
сводится к измерению ускорений
состоянии, т. е. иерастяпутая
(и несжатая), вовсе не действует
па прикрепленные к ней тела
какой-либо силой.
Значит, сила упругости, о
которой данная пружина дейст-
вует на прикрепленные к ней
тела, зависит только от ее рас-
тяжения, а не от свойств прик-
репленных к ней тел. Следова-
тельно, растянутая (или сжатая)
на определенную длину пружи-
на действует на все тела с одной
и той же силой.
Упомянутый выше опыт
различных тел, прикрепленных
к пружине, растянутой на определенную длину.
Как уже указывалось в § 30, удобнее всего измерять ускоре-
ние тел, движущихся по окружности, т. е. центростремительное
ускорение. Поэтому мы снова воспользуемся центробежной маши-
ной.
Поместим тело М в виде алюминиевого цилиндра с просверлен-
ным по его оси отверстием на стержень центробежной машины
(рис. 86, а). Прикрепим к цилиндру конец пружины, а другой ее
конец закрепим на раме машины в точке А. Приведем машину во
вращение. Цилиндр Л1, удалившись несколько от оси вращения
(на расстояние х) и растянув при этом пружину, станет двигаться
по окружности (рис. 86, б) радиусом г. Центростремительное уско-
рение цилиндра направлено по радиусу окружности к центру.
Но вдоль радиуса направлена и ось пружины. Следовательно, уско-
рение цилиндра М направлено вдоль оси пружины. Ясно, что это
ускорение сообщает цилиндру сила упругости растянутой пружины.
Ведь не будь пружины цилиндр просто соскользнул бы со стержня
(если бы ему не мешал упор в точке В), как это мы видели в § 27.
Центростремительное ускорение по абсолютному значению
равно, как мы знаем,
где со — угловая скорость вращения машины, аг — радиус окруж-
ности, по которой движется цилиндр, т. е. расстояние от него до
оси вращения.
Измерив угловую скорость со и радиус г, мы найдем модуль уско-
рения а.
При вращении машины пружина с прикрепленным к ней телом
растягивается тем больше, чем больше угловая скорость враще-
ния. И каждому значению угловой скорости соответствует опреде-
92
ленное растяжение пружины и, следовательно, определенное зна-
чение силы упругости.
Заменим теперь алюминиевый цилиндр точно таким же по раз-
мерам стальным цилиндром. Мы уже знаем, что его масса в три ра-
за больше массы алюминиевого цилиндра.
Приведем машину снова во вращение и подберем такую ско-
рость этого вращения, чтобы растяжение пружины было таким же,
каким оно было при вращении цилиндра из алюминия. Тогда и
сила, действующая на стальной цилиндр, будет такой же.
Опыт показывает, что в этом случае угловая скорость вра-
щения машины будет в |/'3 раз меньше. Это значит, что ускорение
стального цилиндра в 3 раза меньше, чем алюминиевого. Направ-
лено это ускорение по-прежнему вдоль оси пружины (по радиусу
окружности к центру). Выходит, что при увеличении массы тела
втрое ускорение, сообщаемое ему одной и той же силой, сохраняет
свое направление, а по абсолютному значению уменьшается в 3
раза.
Отсюда следует, что произведение массы тела на его ускорение
для обоих тел одно и то же.
Можно провести этот опыт со множеством других тел самых раз-
личных масс. Он покажет, что при одном и том же растяжении пру-
жины, т. е. при одной и той же силе, произведение массы тела на
его ускорение для всех тел одно и то же.
Так мы нашли величину, которая одинакова для различных тел,
на которые действует одна и та же сила.
Значит, произведение массы тела на его ускорение выражает си-
лу, действующую на тело.
Если обозначить силу, действующую па тело, через F, ускоре-
ние тела через а, а его массу через т, то можно написать:
F = та.
Но, может быть, это верно только для си-
лы упругости растянутой пружины и к дру-
гим силам не относится? Чтобы ответить и а
этот вопрос, проведем еще один опыт, который
позволит нам сравнить другие силы с силой
упругости. Сравним, например, силу тяжесш
с силой упругости.
Для этого воспользуемся той же пружи-
ной, но расположим ее вертикально, закре-
пив верхний конец неподвижно (рис. 87, а).
К нижнему концу пружины подвесим гр\з
известной массы т (рис. 87, б). Мы увидим,
что пружина растянется, а груз будет нахо-
диться в покое (после нескольких колебаний).
На груз теперь действуют одновременно
две силы: сила тяжести со стороны Земли
Рис. 87
$3
и сила упругости со стороны растянутой пружины. Не будь пружи-
ны, груз под влиянием Земли падал бы свободно вниз с ускоре-
нием g - 9,81 м/сек2, направленным по вертикали вниз. Но раз
ускорение груза равно нулю, это означает, что растянутая пружи-
на сама по себе тоже сообщила бы грузу ускорение а = —g (направ-
ленное вертикально вверх). Значит, сила тяжести F и сила упру-
гости Fynp, действующие на груз, равны по абсолютному значе-
нию и противоположны по направлению: F - —Fytip. Но сила
упругости, действующая на тело, как мы только что выяснили, рав-
на произведению массы на ускорение, которое она ему сообща-
ет, т. е.
Л-„р = — mg.
Значит, сила тяжести F, равная —Fyn?, будет равна:
F = mg.
Так мы установили, что сила тяжести тоже равна произведе-
нию массы тела на ускорение, сообщаемое ему этой силой1.
Опыты, подобные рассмотренным выше, и многие другие позво-
лили Ньютону сформулировать один из важнейших законов меха-
ники — второй закон Ньютона.
Сила, действующая на тело, равна произведению массы этого
тела на сообщаемое этой силой ускорение.
Математически второй закон Ньютона выражается формулой
F = та.
Из формулы, выражающей второй закон Ньютона, видно, в
каких единицах измеряется сила. Сила равна единице, если, дейст-
вуя на тело, масса которого равна единице, она сообщит ему
ускорение, равное единице.
В системе СИ за единицу силы принимается сила, которая массе
в 1 кг сообщает ускорение 1 м/сек2. Эту единицу называют ньюто-
ном (сокращенно: «):
1 н = 1 кг-1 м/сек2 = 1 кгм/сгк2.
В системе СГС за единицу силы принимается сила, сообщающая
массе в 1 г ускорение 1 см/сек2. Эту силу называют диной (сокра-
щенно: дин):
1 дик = 1 г -1 см/сек2 = 1 гем/сек2.
1 Можно на опыте убедиться в том, что растянутая грузом пружина сообщав»
ему ускорение, равное g = 9,81 м/сек?. Для этого надо поместить эту пружину
с грузом в центробежную машину и привести ее во вращение. Скорость вращения
надо подобрать такую, чтобы пружина растянулась на такую же длину, как и под
действием подвешенного груза. Опыт показывает, что произведение сДг, т. е.
ускорение груза, действительно равно 9,81 м/еек?.
94
Легко найти соотношение между ньютоном и диной:
, 1 кгм 10-1 г -102 см ,
1 Н — ------ = -------;--- = Ю5 OUH.
сек'2 сек'2
Например, сила тяжести, действующая на тело массой 1 кг,
вблизи поверхности Земли равна:
F = 1 кг-9,8 — = 9,8 н = 9,8-105 дин.
сек2
§ 36. ВТОРОЙ ЗАКОН НЬЮТОНА
(продолжение)
Из второго закона Ньютона следует, и это важно понять, что
действующие на тело силы определяют его ускорение, т. е. измене-
ние скорости, а не саму скорость движения тела. Поэтому направле-
ние ускорения всегда совпадает с направлением действующей силы.
Направление же скорости, а следовательно, и перемещения может
и не совпадать с направлением действующей силы. Так, например,
сила может быть все время направлена перпендикулярно скорости
движения тела. В этом случае движение происходит по окружности,
а ускорение, так же как и сила, направлено по радиусу, проведен-
ному от движущегося тела к центру. Так двигалось тело под дей-
ствием силы упругости в центробежной машине.
Если тело взаимодействует не с одним, а с несколькими телами,
то на него действует не одна, а несколько сил, причем силы «не ме-
шают» друг Другу сообщать телу, на которое они действуют, свое
ускорение. Поэтому ускорение, которое сообщают телу все совме-
стно действующие на него силы, будет такое же, какое сообщала
бы ему одна сила, равная сумме всех этих сил. Так как сила — вели-
чина векторная, то под суммой всех сил надо понимать векторную
сумму. Такая сумма называется равнодействующей
всех приложенных к телу сил. И в формуле F = та, выражающей
второй еакон Ньютона, под F нужно понимать равнодействующую
всех сил, действующих на тело.
Приведем простой пример. На каче-
лях, известных под названием «гигант-
ские шаги», на человека действуют од-
новременно две силы (рис. 88): сила
Ft — со стороны Земли, направленная
вниз, и сила А — со стороны каната,
направленная вдоль каната. Под дейст-
вием двух сил «пассажир» движется по
окружности вокруг столба, к которому
прикреплен канат. Значит, ускорение
направлено к центру окружности, а не
вдоль силы А или А. Из рисунка видно,
V
Рис. 88
95
Рис. 89 Рис. 90
что к центру окружности направле-
на и сила F, которая равна геомет-
рической сумме сил и F2. «Пас-
сажир», следовательно, движется
так, как будто бы на него действу-
ют не две силы; Fj и F2, а всего од-
на — их равнодействующая F:
F=Pi+K
Векторная сумма сил, действу-
ющих на тело, может быть .равна
и нулю. Тогда ускорение тела тоже
будет равно нулю, и тело будет ли-
бо покоиться, либо двигаться пря-
молинейно и равномерно. Этот слу-
чай мы и имели в виду, когда в
§ 28 говорили о компенсации
действий нескольких тел на данное тело. В примере с подвешенным
на шнуре шариком, который мы там рассматривали, компенсация
состоит в том, что силы, с которыми на шарик действуют шнур и
Земля, противоположны по направлению и равны по абсолютному
значению = —F,), поэтому их равнодействующая равна нулю
(рис. 89).
На рисунке 90 показан случай, когда нулю равна равнодействую-
щая, т. е. векторная сумма, не двух, а трех сил: Flt F2 и F3, дейст-
вующих на тело (фонарь).
Пользуясь понятием силы, мы можем теперь дать другую форму-
лировку первому закону Ньютона.
Существуют системы отсчета, относительно которых тело дви-
жется прямолинейно и равномерно или находится в покое, если
равнодействующая всех сил, действующих на тело, равна нулю1.
Упражнение 21
1. Что такое сила?
2. Как направлено ускорение тела, вызванное действующей на него силой?
3. Может ли тело, на которое действуют силы, двигаться без ускорения? На-
ходиться в покое?
4. Сформулируйте первый закон Ньютона, пользуясь понятием силы.
5. За много лет до Ньютона великий итальянский художник и ученый Леонар-
до да Винчи высказал следующее утверждение: «Если сила перемещает
тело за данное время на определенное расстояние, то та же сила половину
1 На самом деле этот вывод справедлив только для материальной точки или
для тел, движущихся только поступательно. Сумма сил, действующих на тело,
может быть равна нулю, но тело может вращаться. При этом точки тела движутся
о ускорением.
96
I
а) Траектории движения тела, брошенного под углом к горизонту. В отсутствие
сопротивления воздуха снаряд, выпущенный пушкой, летел бы по параболе. Макси-
мальная дальность полета достигалась бы при угле' вылета снаряда, равном 45°. При
углах вылета снаряда 45° — и 45°+ дальность полета снаряда была бы одинаковой,
б) Рисунки сделаны со стробоскопических фотографий движения металлических ша-
риков под действием силы тяжести: шарик 1 был брошен горизонтально: шарики
2 и 3 свободно падали, а шарик 4 был брошен под углом к горизонту.
II
I
а) Рисунок с рентгеновского снимка ноги футболиста и мяча в момент удара по мя-
чу. Видна деформация кости ноги. Упругая сила, действующая на мяч, возникает в
результате деформации бутцы.
б) Рисунок с фотографии ракетки и теннисного мяча в момент удара по мячу.
в) При столкновении двух тел возникают упругие силы, которые приводят к измене-
нию скоростей этих тел.
г) Столкновение упругих шариков (объяснение см. в § 91).
кого тела переместит на такое же расстояние за вдвое меньшее время».
Верно это утверждение или ложно?
б. Сформулируйте второй закон Ньютона.
7. Верно ли утверждение: скорость тела определяется действующей на него
силой?
8. Верно ли утверждение: перемещение тела определяется действующей на
него силой?
9. Верно ли утверждение: тело всегда движется туда, куда направлена дей-
ствующая на него сила?
10. Тело массой 1,5-103 кг движется с постоянным ускорением 50 м/сек2. Най-
дите значение силы, сообщающей телу такое ускорение.
11. Если тело движется по окружности, то как направлена действующая на
него сила? Может ли тело двигаться по окружности равномерно, если
сумма сил, действующих на него, равна нулю?
12. Тело движется с некоторой постоянной скоростью. Квк оно станет дви-
гаться после того, как к нему будут приложены две одинаковые по абсо-
лютному значению и противоположные по направлению силы?
§ 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР
Сила относится к важнейшим величинам в механике. Это потому,
что, зная значение силы F, действующей на тело массой т, можно
вычислить его ускорение а по формуле
tn
А ускорение тела — это та величина, знание которой позволяет ре-
шить основную задачу механики. Но для того чтобы узнать значе-
ние силы, ее надо измерить.
Как же измерить силу, действующую на тело?
Вспомним, как мы измеряли силу тяжести, с которой Земля дей-
ствует на любые тела вблизи ее поверхности.
Для этой цели тело подвешивали к вертикально расположенной
пружине. Пружина растягивалась на такую длину, при которой
сила упругости Купр, направленная по оси пружины вверх, уравно-
вешивала силу тяжести F:
^ynp=- F-
Сила же Купр, с которой растянутая пружина действует на тело,
была известна (см. опыт с центробежной машиной на стр. 92).
Так мы нашли, что сила тяжести, действующая на тело массой
т, равна mg. Значит, измерение силы тяжести заключалось в том,
что ее уравновешивали известной заранее силой.
Таким же способом можно измерить любую другую силу, дей-
ствующую на любое тело. Ее надо уравновесить известной силой,
приложенной к этому же телу.
Пружина особенно удобна для измерения сил потому, что, бу-
дучи растянута (или сжата) на определенную длину, она действует
на все тела с одной и той же силой. Кроме того, при помощи одной
4 Заказ 1126
97
Рис. 91
и той же пружины можно получить различные силы, растягивая
ее на различную длину.
Чтобы пользоваться пружиной для измерения сил, надо заранее
определить значения сил упругости при различных ее растяжениях.
Другими словами, нужно установить, как сила упругости зависит
от удлинения пружины. Для этого можно было бы снова восполь-
зоваться центробежной машиной, поместив туда пружину с прикреп-
ленным к ней телом известной массы и измерив ее удлинение при
различных скоростях вращения.
Но теперь, когда известно значение силы тяжести, действующей
на тело, можно более простым способом установить, какие силы
упругости соответствуют различным удлинениям данной прркины.
Для этого надо к вертикально расположенной пружине подве-
шивать тела различной массы и каждый раз измерять удлинение
пружины. Действительно, мы уже знаем, что на тело массой т дей-
ствует сила тяжести, равная mg. Когда тело подвешено к пружине
и находится в покое, эта сила тяжести уравновешена силой упруго-
сти пружины. Следовательно, и сила упругости пружины по абсо-
лютному значению тоже равна mg.
Поэтому, измерив удлинения пружины при разных значениях
массы подвешенных к ней тел, мы определим значения силы упру-
гости для каждого удлинения пружины. Чтобы измерить удлине-
ние пружины, используют шкалу, вдоль которой перемещается
указатель (стрелка), прикрепленный к подвижному концу пружи-
ны. Если против делений шкалы поставить числа, указывающие в
ньютонах значения силы упругости пружины, то пружина будет
градуирована. Такая градуированная пружина — это уже прибор,
пригодный для измерения различных сил. Называют этот прибор
пружинным динамометром (силомером).
Опыт показывает, что при сравнительно небольших удлинениях
между силой упругости пружины и ее удлинением существует ли-
нейная зависимость.
Эта зависимость была установлена английским физиком Р. Г у-
к о м еще в XVII столетии и называется законом Гука.
Сила упругости пропорциональна удлинению пру-
жины.
Если обозначить силу упругости через Fynp, а удлинение пру-
жины через х, то закон Гука можно выразить формулой
^упр “
93
Рис. 92
Знак «минус» показывает, что сила упругости направлена в сторо-
ну, противоположную удлинению. Коэффициент пропорциональ-
ности k определяет значение силы упругости при удлинении, рав-
ном единице. Этот коэффициент называется жесткостью пру-
жины. Жесткость пружины зависит от ее геометрических размеров
и от материала, из которого она изготовлена. В системе СИ жест-
кость выражается в ньютонах на метр j.
Как измеряют силы динамометром?
Предположим, что на какое-то тело действует горизонтально
направленная сила F, которую нужно измерить (рис. 91).
Прикрепим к этому телу конец горизонтально расположенного
динамометра. Другой его конец закреплен неподвижно. Под дейст-
вием силы F тело получает ускорение и перемещается, увлекая за
собой прикрепленный к нему конец пружины динамометра. Пружи-
на удлиняется. Когда тело остановится, стрелка динамометра ука-
жет на шкале значение действующей на тело силы F.
Заметим, что динамометр вместе с телом, к которому приложена
измеряемая сила, не обязательно должен находиться в покое.
Ничего не изменится, если все они вместе будут двигаться прямо-
линейно и равномерно. Ведь такое движение тоже происходит при
равенстве противоположно направленных сил. На рисунке 92 по-
казано, например, как «на
ходу» измеряют силу, с кото-
рой земля (почва) действует
на плуг, влекомый тракто-
ром. Чтобы измерение было
верным, нужно только, чтобы
трактор двигался с постоян-
ной скоростью.
Примером динамометра
служат домашние пружинные
весы, которыми пользуются
для измерения силы тяжести
(рис. 93).
4*
99
В зависимости от назначения динамометров их внешний вид и
устройство могут быть различны. На рисунке 94 показан динамо-
метр, предназначенный для измерения больших сил. В школьных
лабораториях часто употребляют динамометр, внешний вид кото-
рого показан на рисунке 95. Но как бы ни выглядел динамометр,
основной его частью всегда является какая-нибудь пружина, де-
формация которой и служит мерой силы.
§ 38. ТРЕТИЙ ЗАКОН НЬЮТОНА
Мы много раз указывали на то, что действия тел друг на друга
всегда взаимны, что тела всегда взаимодействуют. Теперь мы мо-
жем сказать, что каждое из взаимодействующих тел действует на
другое с некоторой силой. Именно поэтому каждое из тел и полу-
чает ускорение. В § 30 мы видели, что отношение абсолютных зна-
чений ускорений обоих тел равно обратному отношению их масс:
|ах| _ тг
Отсюда
тх |ах| = т2 |а2|.
Там же указывалось, что ускорения, которые при взаимодей-
ствии сообщаются обоим телам, направлены в противоположные
стороны. Поэтому можно написать:
miai = — /Ц2а2-
Но произведение массы тела на его ускорение определяет силу,
действующую на это тело. Если обозначить силу, приложенную к
первому телу, через Fx, а ко второму — через Р2, то Fx = /лхах и
F2 — т2а2. Следовательно,
Это равенство выражает третий закон Ньютона.
Тела действуют друг на друга с силами, направлен-
ными вдоль одной и той же прямой, равными по абсо-
лютному значению и противоположными по направле-
нию.
Третий закон Ньютона показывает, что силы из-за «взаимного»
действия тел друг на друга всегда появляются парами. Если на ка-
кое-то тело действует сила, то обязательно есть какое-то другое
тело, на которое первое действует такой же по абсолютному значе-
нию силой, но направленной в противоположную сторону. Ускоре-
ния, которые эти силы сообщают телам, тоже имеют противополож-
ные направления.
100
Рис. 9S
Следующий опыт поясняет смысл третьего закона Ньютона.
Возьмем две одинаковые тележки, к одной из которых прикреп-
лена упругая стальная пластинка. Согнем эту пластинку и свяжем ее
ниткой, а вторую тележку приставим к первой так, чтобы она плот-
но соприкасалась с другим концом пластинки (рис. 96). Перере-
жем теперь нить. Пружина начнет выпрямляться, и мы увидим,
что в движение придут обе тележки. Это значит, что обе они по-
лучили ускорение. Так как массы тележек одинаковы (массой пру-
жины можно пренебречь), то одинаковы по модулю и их ускорения,
а следовательно, и скорости, о чем можно судить по одинаковой
длине перемещений тележек за одинаковое время.
Если на одну из тележек положить какой-нибудь груз (рис. 97),
то мы увидим, что перемещения тележек после освобождения пру-
жины будут неодинаковыми. Это значит, что их ускорения тоже
неодинаковы: ускорение нагруженной тележки меньше.
101
В этом примере, как и в любых других, можно отметить еше
одну особенность тех двух сип, которые согласно третьему закону
Ньютона появляются одновременно при взаимодействии двух тел:
силы эти всегда одной природы. Если, например, на одно тело со
стороны другого действует сила упругости, то оно «отвечает» это-
му другому телу тоже силой упругости.
Всегда следует помнить, что силы, появляющиеся при взаимодей-
ствии тел, приложены к разным телам и поэтому они не могут урав-
новешивать друг друга. Уравновешиваться могут лишь силы, при-
ложенные к одному и тому же телу.
Задача. Человек, стоя в лодке, подтягивает к себе вторую лодку
с помощью веревки (рис. 98). Масса первой лодки 400 кг, второй —
200 кг. Каксе перемещение совершит каждая из лодок за 5 сек, если
сила упругости натянутой веревки равна 100 н? Силами трения
пренебречь, а воду считать покоящейся.
Решение. Согласно третьему закону Ньютона па обе лодки
действуют одинаковые пс модулю силы, нс направлены спи в про-
тивоположные стороны — лодки получат противоположные по на-
правлению (знаку) ускорения и двинутся навстречу друг другу.
Направим координатную ось в направлении движения первой лод-
ки. Тогда можно написать:
Л ^2=--m2!«2|,
где Fj — проекция силы, действующей на первую лодку, F2 — про-
екция силы, действующей на вторую лодку, |aj и |я2| — абсолютные
значения ускорений первой и второй лодок. Отсюда
kl = — и |а2| =— .
z/ij т2
Перемещения лодок и s2 вычислим по формулам:
|Дк2 _ fj2 и г. ।
2 2/Я] 2 2 2/я2
Подставляя приведенные в условии задачи данные, найдем:
100 н (5 сек)’-
2 • 400 кг
— 3,125 м, | s21 =—
— 100 н (5 сек)2 г
--------1---- =6,25
2 • 200 кг
м.
102
Упражнение 22
1. Сформулируйте третий закон Ньютона.
2. Компенсируют ли друг друга силы, возникающие при взаимодействии
двух тел?
3. При столкновении легковой автомашины с нагруженным грузовиком по-
вреждения у легковой автомашины всегда больше, чем у грузовой. Объяс-
ните этот факт, исходя из третьего закона Ньютона.
Указание. Подумайте о перемещениях отдельных частей машин.
4. Два человека тянут веревку в противоположные стороны с силой 50 н
каждый. Разорвется ли веревка, если она выдерживает натяжение до 80 н?
5. Два мальчика, массы которых 40 и 60 кг, стоят на коньках на льду катка.
Первый мальчик отталкивается от второго с силой 10 н. Какие ускорения
получат мальчики?
§ 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА
Мы ознакомились с тремя законами движения — законами
Ньютона. Значение законов Ньютона состоит в том, что они позво-
ляют решать основную задачу механики. Первый закон Ньютона
утверждает, что существуют инерциальные системы отсчета. Вто-
рой закон, справедливый для инерциальных систем отсчета, связы-
вает силу, действующую на тело, с вызванным ею ускорением.
И если сила известна, то можно найти ускорение тела в любой
точке траектории.
Так завершается та «цепочка», о которой говорилось в конце
третьей главы: по известным силам и массе тела находят ускоре-
ние, затем вычисляют его скорость и перемещение за любой проме-
жуток времени и, наконец, координаты тела в любой момент вре-
мени. Для этого должны быть известны «начальные условия» —
начальное положение и начальная скорость тела.
Так, например, ученым, которые руководят полетом космиче-
ского корабля, необходимо, конечно, заранее знать положение
корабля в любой момент времени. Они могут узнать его, пользуясь
такой «цепочкой». Им известно начальное положение корабля на
стартовой площадке и его начальная скорость. Им известны и силы,
которые действуют на корабль в любой точке траектории. Пользу-
ясь этими данными, они и решают задачу механики применительно
к космическому полету. Но так как силы, действующие на корабль,
все время изменяются, то вычисления настолько сложны, что при-
ходится привлекать на помощь вычислительные машины.
Мы все время говорили, что .основная задача механики — опре-
деление положения движущегося тела в любой момент времени. Но
не следует думать, что законами движения пользуются исключи-
тельно для определения именно положения тела. На практике ча-
сто требуется вычислять такие величины, как скорость тела, его
ускорение, силы, действующие на него, и т. д. Законы Ньютона
позволяют, разумеется, решать и такие, более простые задачи.
В разделе «Кинематика» мы ознакомились с различными вида-
ми движения. Законы Ньютона позволяют попять, при каких усло-
виях тела совершают то или иное из этих движений. Так, например,
103
согласно первому закону Ньютона тело движется прямолинейно и
равномерно или находится в покое относительно любой инерциаль-
ной системы отсчета, если векторная сумма сил, приложенных к
телу, равна нулю.
Из второго закона Ньютона следует, что равноускоренное дви-
жение тело совершает тогда, когда сила, действующая на него, по-
стоянна, т. е. одинакова во всех точках траектории.
В соответствии с тем же вторым законом Ньютона тело будет
двигаться по окружности, если приложенная к нему сила постоян-
на по своему абсолютному значению и направлена перпендикуляр-
но скорости тела, и т. д.
Третий закон Ньютона утверждает, что силы, действующие на
тела, имеют взаимный характер.
Глава 5
Силы природы
ВВЕДЕНИЕ
Мы уже знаем, что причиной изменения движения, т. е. появле-
ния ускорения у тел, является сила. Сила же возникает при взаимо-
действии тел друг с другом. Но что означает слово «взаимодейст-
вие»? Как именно взаимодействует одно тело с другим? Какие су-
ществуют виды взаимодействий и много ли их?
На первый взгляд может показаться, что различных видов воз-
действий тел друг на друга, а следовательно и различных видов
сил, существует очень много. Ускорение можно сообщить телу,
толкнув или потянув его рукой; с ускорением движется всякое
тело, падающее на землю, с ускорением движутся планеты вокруг
Солнца, Луна и искусственные спутники вокруг Земли; с ускоре-
нием начинает двигаться корабль, когда ветер надувает его паруса;
натянув и отпустив тетиву лука, мы сообщаем ускорение стреле;
автомобиль трогается с места, т. е. получает ускорение, когда вклю-
чают его двигатель, и начинает замедляться, т. е. двигаться с отри-
цательным ускорением, когда водитель выключает двигатель или
нажимает на педаль тормоза. Во всех этих случаях действуют ка-
кие-то силы и все они кажутся совершенно различными. А ведь
можно назвать еще много и других сил. Каждый слышал об элек-
трических и магнитных силах, о силе землетрясений, о силе пружи-
ны, о силе прилива и отлива и т. д.
Но действительно ли в природе существует так много различ-
ных сил? Оказывается, нет.
При рассмотрении механического движения тел приходится
иметь дело всего лишь с тремя видами сил, уже известных из
курса физики VI класса: с силой упругости, силой
трения и силой тяготения. К ним и сводятся все те
как будто бы разнообразные силы, о которых мы только что говорили.
Но и эти три силы являются проявлением всего только двух
действительно различных основных сил природы: электромаг-
нитных- сил и сил всемирного тяготения.
С этими силами и их проявлениями мы и ознакомимся в этой главе.
§ 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ
Из курса физики VII класса известно, что между наэлектри-
зованными телами действует особая сила, которая называется
электрической силой.
105
Напомним, что электрические силы могут быть как силами
притяжения, так и силами отталкивания. В природе существуют
заряды двух видов. Их условились называть положительными и от-
рицательными зарядами. Два тела с одноименными зарядами оттал-
киваются. Если же знаки зарядов различны, то между телами дей-
ствуют силы притяжения.
Электрическая сила зависит от величины зарядов и от расстоя-
ния между заряженными телами, она тем больше, чем больше за-
ряды и чем меньше расстояние между ними
У электрических зарядов есть интересное свойство. Когда за-
ряды движутся друг относительно друга, между ними, кроме элек-
трической силы, возникает еще одна сила, которую называют м а г-
н итной силой.
Обе эти силы — электрическая и магнитная — настолько тес-
но связаны, что их нельзя отделить друг от друга: они дей-
ствуют одновременно. А так как большей частью приходится иметь
дело с движущимися зарядами, то действующие между ними силы
нельзя назвать ни электрическими, ни магнитными. Их называют
электромагнитными силами.
Откуда же берется «электрический заряд», который у тела мо-
жет быть, а может и не быть?
Любое тело состоит из молекул и атомов. В свою очередь атомы,
хотя они и чрезвычайно малы (несколько стомиллионных долей
сантиметра), состоят из еще меньших частиц—атомного ядра и элек-
тронов. Вот они-то, ядра и электроны, обладают электрическими
зарядами. Ядро имеет положительный заряд, электроны — от-
рицательный.
В нормальных условиях в атоме столько электронов, что их об-
щий отрицательный заряд в точности равен положительному заря-
ду ядра, так что атом в целом как бы не имеет заряда. Он, как гово-
рят, электрически нейтрален. Тогда и тела, составленные из таких
нейтральных атомов, электрически нейтральны. Между такими те-
лами нет электрических сил взаимодействия. Заряды, имеющиеся
в одном теле, практически не взаимодействуют с зарядами другого
тела.
Зато в одном и том же твердом (или жидком) теле соседние ато-
мы настолько близко расположены один к другому, что силы взаимо-
действия между зарядами, из которых они состоят, весьма значи-
тельны.
Силы взаимодействия атомов зависят от расстояний между ни-
ми. Зависимость эта сложная и до сих пор еще точно неизвестна.
Но достоверно установлено, что силы взаимодействия между атома-
ми могут изменять свое направление при изменении расстояния меж-
ду ними. Если расстояние между атомами очень мало, то они оттал-
киваются друг от друга. Но если расстояние между ними увеличить,
то вместо сил отталкивания между атомами начинают действовать
силы притяжения. При некотором расстоянии между атомами силы
притяжения и силы отталкивания становятся одинаковыми. Есте-
106
ственпо, что на таких именно расстояниях атомы и располагаются
друг относительно друга (в твердом теле и жидкости). Заметим, что
расстояния эти очень малы. Они приблизительно такие же, как и
размеры самих атомов.
Если растянуть тело, то расстояние между атомами несколько
увеличится и между ними начнут действовать силы притяжения. Эти
силы сообщат атомам ускорения и заставят их снова сблизиться до
прежнего расстояния.
Наоборот, если тело сжать и тем самым сблизить атомы, поя-
вятся силы отталкивания, которые заставят атомы снова разойтись
и занять прежние места.
Таки?,! образом, при растяжении или сжатии тела в нем возни-
кают электрические по своей природе силы, которые восстанав-
ливают прежние размеры тела.
Такие восстанавливающие силы возникают также, когда тела
сгибают (рис. 99) или скручивают (рис. 100), потому что и в этих
случаях изменяется взаимное расположение атомов.
Растяжение и сжатие, изгиб и кручение
называют деформациями тел. Следовательно, при вся-
кой деформации тела возникает сила, которая возвращает тело в
то состояние, в котором оно было до деформации.
§ 41. СИЛА УПРУГОСТИ
Как мы видели, при деформации тела возникает сила, элект-
рическая по своей природе, которая возвращает тело в первона-
чальное состояние.
В § 35 и 37 мы ознакомились с силами, которые возникают при де-
формации пружины. Эти силы мы назвали силами упругости. Те-
перь мы можем сказать, что сила упругости возникает при дефор-
мации любого тела, а не только пружины; всякое тело может играть
роль пружины!
Так как сила упругости возвращает тело к первоначальному
состоянию, то она направлена против направления смещения частиц
тела при деформации. Если, например, стержень, один из концов
107
Рис. 103
Рис. 102
которого закреплен (рис. 101), растянут так, что частицы в нем сме-
щены относительно закрепленного конца вправо (рис. 102), то воз-
никает сила упругости, направленная влево. Если же стержень
сжат, как это показано на рисунке 103, то частицы в нем смещены
влево, а сила упругости направлена вправо.
Сила упругости — это сила, возникающая при деформации тел
и направленная в сторону, противоположную направлению смеще-
ния частиц тела при деформации.
В дальнейшем мы будем рассматривать силы упругости, возни-
кающие только при деформации растяжения или сжатия.
Если бы мы провели опыт, описанный в § 37, не с пружиной,
а, например, с каким-нибудь стержнем, то мы смогли бы убедиться
в том, что при малых деформациях стержня (малых по сравнению с
его длиной) сила упругости деформированного стержня, так же
как и пружины, пропорциональна его удлинению. Следовательно,
закон Гука, выражаемый формулой Fynp = —kx, справедлив для
всякого упругого тела при условии, что эти деформации достаточ-
но малы. Деформация х определяет собой взаимное расположение
частей деформированного тела, т. е. их координаты. Следовательно,
закон Гука показывает, что сила упругости зависит от координат
отдельных частей деформированного тела.
Но как возникает сама деформация тела?
Возьмем две тележки с укрепленными впереди шариками из мяг-
кой резины (рис. 104). Приведем тележки в движение навстречу
друг другу так, чтобы они столкнулись. Когда шарики коснутся
один другого, оба они изменят свою форму, деформируются. Одно-
108
временно скорости тележек, с которыми скреплены шарики, станут
постепенно уменьшаться. В конце концов тележки на мгновение ос-
тановятся, а затем начнут двигаться в противоположных направле-
ниях, т. е. снова получат ускорения. Ясно, что причиной ускорения
является сила упругости, возникающая при деформации шариков.
Из этого опыта видно, что деформация произошла из-за того, что
шарики уже после соприкосновения продолжали еще некоторое
время двигаться в прежнем направлении, пока возникшая из-за
деформации сила упругости не остановила их. После этого дефор-
мированные шарики, восстанавливая свою форму, заставили тележ-
ки двигаться в противоположном направлении. Но как только ша-
рики восстановили свою форму, исчезла и сила упругости. Можно,
следовательно, сказать, что причиной деформации шарика явилось
движение одной его части относительно другой, а следствием дефор-
мации — сила упругости.
Если мы теперь заменим резиновые шарики стальными и повто-
рим опыт, то увидим, что результат будет совершенно таким же.
Тележки столкнутся, на миг остановятся, а затем станут двигаться
в противоположных направлениях. Но мы теперь не увидим изме-
нения формы шариков, их деформации. Это не значит, что дефор-
мации нет. Ведь тележки со стальными шариками ведут себя совер-
шенно так же, как и тележки с резиновыми шариками. Но у сталь-
ных шариков деформации очень малы, и их нельзя заметить без спе-
циальных приборов (это значит, что у стальных шариков жесткость
значительно больше, чем у резиновых).
Часто бывают незаметны не только деформации, но и те движе-
ния, из-за которых деформации возникают. Когда мы, например,
видим лежащую на столе книгу, то, конечно, не можем заметить,
что и книга, и стол слегка деформированы. Но именно деформация
стола, совсем незаметная на глаз, приводит к появлению силы уп-
ругости, которая направлена вертикально вверх и уравновешивает
силу притяжения книги к Земле. Поэтому книга и находится в по-
кое. Когда мы кладем книгу на стол, она под действием притяже-
ния к Земле начинает двигаться вертикально вниз, как всякое па-
дающее тело. Вот при этом-то движении книга и смещает частицы,
из которых состоит соприкасающаяся с ней часть стола. Стол дефор-
мируется, и возникает сила упругости, как раз равная силе притя-
жения книги к Земле, но направленная вверх.
То же можно сказать и о действии подвеса. Когда к свободному
концу шнура АК прикрепляется тело (рис. 105), то в первый момент
оно под действием силы притяжения к Земле F начинает падать
вертикально вниз в направлении, указанном стрелкой. При этом
вместе с телом перемещается вниз и конец шнура К. Вследствие
этого шнур удлиняется, т. е. деформируется. Благодаря деформа-
ции шнура появляется сила упругости Fynp (рис. 106), направлен-
ная вверх. На тело, следовательно, действуют две силы, направлен-
ные противоположно. В начале падения тела удлинение шнура
109
Рис. 105 Рис. 106
мало, мала и сила упругости. По мере
дальнейшего перемещения тела вниз удли-
нение шнура увеличивается, одновременно
увеличивается и сила упругости. Когда
подвешенное тело находится в покое, то
это означает, что сила упругости по свое-
му абсолютному значению равна силе при-
тяжения тела к Земле.
Если шнур АК сделан из мягкой рези-
ны, жесткость которой мала, то его удли-
нение может быть замечено даже на глаз.
Но если этот шнур представляет собой
стальную проволоку большой жесткости,
то удлинение окажется настолько малым,
что его можно обнаружить лишь специа-
льными приборами.
Силу упругости, действующую на тело со стороны опоры или
подвеса, часто называют силой реакции опоры или силой реакции
подвеса (или натяжением подвеса).
Во многих случаях деформации, приводящие к появлению силы
упругости, хорошо заметны. Легко заметить удлинение спиральной
пружины или резинового шнура. С помощью быстрой съемки мож-
но увидеть и деформацию футбольного мяча при ударе футболиста.
На цветной вклейке II, а показано, какую форму принимает этот
круглый предмет в момент удара. Теряет свою сферическую фор-
му и теннисный мяч при ударе ракетки.
Приведенные здесь примеры показывают, что сила упругости
возникает при соприкосновении взаимодействующих тел. Деформи-
руются, разумеется, всегда оба тела.
Важная особенность силы упругости состоит в том, что она на-
правлена перпендикулярно поверхности соприкосновения взаимо-
действующих тел, а если во взаимодействии участвуют такие тела,
как стержни, шнуры, спиральные пружины, то сила упругости на-
правлена вдоль их осей.
Упражнение 23
1. Перечислите существующие в природе виды взаимодействий. К какому
из них относится взаимодействие, приводящее к появлению силы упругости?
2. Какие из перечисленных во введении к этой главе сил являются силами
упругости?
3. Приведите примеры сил упругости.
4. Опишите, как возникают силы упругости в телах, подвешенных на нитях,
и телах, лежащих на опорах.
5. На рисунке 107 изображен стрелок, стреляющий из лука. Как направлены
силы упругости, сообщающие ускорение стреле?
6. На наклонной плоскости неподвижно лежит груз (рис. 108). Действует ли на
него сила упругости? Деформация какого тела вызывает ее? Как направ-
лена сила упругости?
7. Что такое силы реакции опоры?
110
§ 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ
Человеку давно уже известна сила, заставляющая все тела
падать на Землю. Но до XVII в. считалось, что только Земля обла-
дает особым свойством притягивать к себе тела, находящиеся вбли-
зи ее поверхности. В 1667 г. Ньютон высказал предположение,
что вообще между всеми телами действуют силы взаимного притя-
жения. Он назвал эти силы силами всемирного тяготе-
н и я.
Ньютон открыл законы движения тел. Согласно этим законам
движение с ускорением возможно только под действием силы. Так
как падающие тела движутся с ускорением, то на них должна дей-
ствовать сила, направленная вниз, к Земле.
Но нет оснований считать, что только Земля наделена исключи-
тельным свойством притягивать к себе тела.
Почему же мы не замечаем взаимного притяжения между окру-
жающими нас телами? Может быть, это объясняется тем, что силы
притяжения между ними слишком малы?
Ньютону удалось показать, что сила притяжения между телами
зависит от масс обоих тел и, как оказалось, достигает заметной
величины только тогда, когда взаимодействующие тела (или хотя
бы одно из них) обладают достаточно большой массой.
Ускорение свободного падения отличается той любопытной осо-
бенностью, что оно в данном месте одинаково для всех тел, для тел
любой массы. На первый взгляд это очень странное свойство. Ведь
из формулы, выражающей второй закон Ньютона,
F
а = —
т
следует, что ускорение тела должно быть тем больше, чем меньше
его масса. Тела с малой массой должны падать с большим ускоре-
нием, чем тела, у которых масса велика. Опыт же показал (см. § 20),
что ускорения свободно падающих тел не зависят от их масс. Един-
ственное объяснение, которое можно найти этому удивительному
111
факту, заключается в том, что сама сила F, с которой Земля при-
тягивает тело, пропорциональна его массе пг.
Действительно, в этом случае увеличение массы пг, например,
вдвое приведет и к увеличению силы F тоже вдвое, а ускорение,
Р
которое равно отношению —, останется неизменным. Ньютон и
сделал этот единственно правильный вывод: сила всемирного тяго-
тения пропорциональна массе того тела, на которое она действует.
Но ведь тела притягиваются взаимно. А по третьему закону Ньюто-
на на оба притягивающихся тела действуют одинаковые по абсо-
лютному значению силы. Значит, сила взаимного притяжения
должна быть пропорциональна массам каждого из притягивающих-
ся тел. Тогда оба тела будут получать ускорения, которые не за-
висят от их масс.
Если сила пропорциональна массам каждого из взаимодейству-
ющих тел, то это означает, что она пропорциональна произведению
масс обоих тел.
От чего еще зависит сила взаимного притяжения двух тел?
Ньютон предположил, что она должна зависеть от расстояния меж-
ду телами. Из опыта хорошо известно, что вблизи Земли ускорение
свободного падения равно 9,81 м/секл и оно одинаково для тел, па-
дающих с высоты 1, 10 или 100 м. Но отсюда еще нельзя заключить,
что ускорение не зависит от расстояния до Земли. Ньютон считал,
что отсчитывать расстояния надо не от поверхности Земли, а от ее
центра. Но радиус Земли равен 6400 км. Понятно поэтому, что не-
сколько десятков или сотен метров над поверхностью Земли не
могут заметно изменить ускорение свободного падения.
Чтобы выяснить, как влияет расстояние между телами на силу
их взаимного притяжения, нужно знать, с каким ускорением дви-
жутся тела, удаленные от поверхности Земли на большие расстоя-
ния.
Ясно, что измерить ускорение свободного падения по верти-
кали тел, находящихся на высоте в несколько тысяч километров
над поверхностью Земли, трудно. Удобнее измерить центро-
стремительное ускорение тела, движущегося вокруг Земли по
окружности под действием силы притяжения к Земле. Вспомним, что
таким же приемом мы пользовались при изучении силы упругости.
Мы измеряли центростремительное ускорение цилиндра, движуще-
гося по окружности под действием этой силы.
В изучении силы всемирного тяготения сама природа пришла
на помощь физикам и дала возможность определить ускорение тела,
движущегося по окружности вокруг Земли. Таким телом является
естественный спутник Земли — Луна. Ведь если верно предполо-
жение Ньютона, то надо считать, что центростремительное ускоре-
ние Луне при ее движении по окружности вокруг Земли сообщает
сила ее притяжения к Земле. Если бы сила тяготения между Луной
и Землей не зависела от расстояния между ними, то центростреми-
тельное ускорение Луны было бы таким же, как ускорение свобод-
112
ного падения тел вблизи поверхнос-
ти Земли. В действительности цент-
ростремительное ускорение, с кото-
рым движется Луна по орбите, равно,
как мы уже знаем (см. упр. 16, зада-
чу 9), 0,0027 м/сек*. А это приблизи-
тельно в 3600 раз меньше, чем ускоре-
ние падающих тел вблизи Земли. В то
же время известно, что расстояние от
центра Земли до центра Луны равно
384 000 км. Это в 60 раз больше ра-
диуса Земли, т. е. расстояния от цент-
ра Земли до ее поверхности. Таким
образом, увеличение расстояния меж-
ду притягивающимися телами в 60
раз приводит к уменьшению ускоре-
ния в 602 раз. Отсюда можно заклю-
чить, что ускорение, сообщаемое те-
лам силой всемирного тяготения, а
значит, и сама эта сила обратно про-
порциональны квадрату расстояния
между взаимодействующими телами.
К такому заключению и пришел
Ньютон.
Можно, следовательно, написать,
что два тела массами Мит притя-
1
гиваются друг к другу с силой р,
абсолютное значение которой выра-
жается формулой
Tri Мт ,.,
где г — расстояние между телами,
у — коэффициент пропорциональности
Рис. 109
, одинаковый для всех тел
в природе. Называется этот коэффициент постоянной все-
мирного тяготения или гравитационной
постоянной.
Приведенная формула выражает закон всемирного тяготения,
открытый Ньютоном:
Все тела притягиваются друг к другу с силой, пря-
мо пропорциональной произведению их масс и обратно
пропорциональной квадрату расстояния между ними.
Под действием силы всемирного тяготения движутся и планеты
вокруг Солнца, и искусственные спутники вокруг Земли.
Но что надо понимать под расстоянием между взаимодействую-
щими телами? Возьмем два тела произвольной формы (рис. 109).
Сразу возникает вопрос: какое расстояние нужно подставлять в
формулу закона всемирного тяготения? Расстояние гх между
113
самыми дальними точками поверхности обоих тел или же, наоборот,
расстояние г2 между ближайшими точками? А может быть, расстоя-
ние между какими-нибудь другими точками тела?
Оказывается, формула (1), выражающая закон всемирного тя-
готения, справедлива, когда расстояние между телами настолько
велико по сравнению с их размерами, что тела можно считать ма-
териальными точками. Материальными точками при вычислении
силы тяготения между ними можно считать Землю и Луну, планеты
и Солнце.
Если тела имеют форму шаров, то даже в том случае, когда их
размеры сравнимы с расстоянием между ними, они притягиваются
между собой как материальные точки, расположенные в центрах
шаров (рис. ПО). В этом случае г — это расстояние между центра-
ми шаров.
Формулой (1) можно также пользоваться при вычислении силы
притяжения между шаром большого радиуса и телом произвольной
формы небольших размеров, находящимся близко к поверхности ша-
ра (рис. 111). Тогда размерами тела можно пренебречь по сравне-
нию с радиусом шара. Именно так мы поступаем, когда рассматри-
ваем притяжение различных тел к земному шару.
Сила тяготения —это еще один пример силы, которая зависит
от положения (координат) того тела, на которое эта сила действу-
ет, относительно того тела, которое оказывает действие. Ведь сила
тяготения зависит от расстояния г между телами.
§ 43. ПОСТОЯННАЯ ВСЕМИРНОГО
ТЯГОТЕНИЯ
В формулу, выражающую закон всемирного тяготения Ньютона,
входит коэффициент у — постоянная всемирного тяготения (гра-
витационная постоянная). Что это за величина?
Коэффициент у имеет простой и ясный смысл. Если массы обоих
взаимодействующих тел Мит равны единице (Л4 = т = 1 кг)
и расстояние г между ними тоже равно единице (г = 1 м), то, как
это видно из формулы (1),
Постоянная всемирного тяготения численно равна силе притя-
жения между двумя телами (материальными точками) массой 1 кг
каждое, когда расстояние между ними равно 1 м.
В каких единицах выражается постоянная у? Из формулы, вы-
ражающей закон всемирного тяготения, следует, что
у = ^.
Мт
Если сила измеряется в ньютонах (н), расстояние в метрах (л)
и масса в килограммах (кг), то величина, стоящая в правой части
114
чувствительных весов на
Отсюда
должна
значе-
тяготе-
«•м2 ..
равенства, выражается в но в
любой формуле, если она правильна,
величины, стоящие в обоих частях
равенства, должны измеряться в оди-
наковых единицах (5 м, например,
не могут быть равны 5 кг).
следует, что постоянная у
Н'М2
выражаться в —.
кг’-
Что касается численного
ния постоянной всемирного
ния, то оно может быть определено
только из опыта. В таком опыте
нужно, очевидно, каким-нибудь спо-
собом измерить силу F, действую-
щую между двумя телами известных
масс mt и /тг2> расположенными на
известном расстоянии г одно от дру-
гого.
Такие опыты были неоднократно
проделаны. Один из них состоял в
следующем. К одной из чашек
длинной нити подвешивали стеклянный шар, наполненный ртутью
(рис. 112). На другую чашку весов помещали гири, уравновешиваю-
щие весы. После того как весы были тщательно уравновешены, под
шаром с ртутью, как можно ближе к нему, устанавливали шар из
свинца большой массы (около 6000 кг). Вследствие притяжения
ртутного шара к свинцовому равновесие весов нарушалось. Чтобы
снова уравновесить весы, надо на чашку с гирями положить допол-
нительную гирю. Сила притяжения этой дополнительной гири к Зем-
ле, очевидно, равна силе притяжения ртутного шара к свинцовому,
т. е.
тС(;"'рг
л
Здесь тсп — масса свинцового шара, /т?рт — масса ртутного шара
и г — расстояние между их центрами. Отсюда легко вычислить зна-
чение у:
Из этого и из многих других опытов было получено численное
значение постоянной у:
у = 6,67 КГ11
кг'
Это очень малая величина. Именно благодаря тому что она так ма-
ла, мы и не замечаем притяжения между окружающими нас
115
телами. Ведь даже два шара массой каждый в тонну при расстоя-
нии между ними в 1 м притягиваются друг к другу с силой всего в
6,67 стотысячных долей ньютона.
Упражнение 24
1. Как изменится сила притяжения между двумя шарами, если: а) один из
них заменить другим, масса которого вдвое больше; б) заменить и второй
шар шаром вдвое большей массы?
2. Как изменится сила притяжения между двумя шарами, если расстояние
между ними увеличить вдвое?
J. Тела, находящиеся на поверхности Земли, взаимно притягиваются. Почему
они не движутся друг к другу?
4. Вычислите массу Земли, зная ускорение свободного падения тела, значе-
ние гравитационной постоянной и радиус Земли.
5. В опыте, описанном в этом параграфе, масса ртутного шара равна 5 кг, его
радиус 4,5 см, масса свинцового шара 6 т, его радиус 0,5 м. Гирю какой
массы надо добавить на правую чашку весов, чтобы уравновесить силу
притяжения между свинцовым и ртутным шарами?
6. Два корабля массой 50 000 т каждый стоят на рейде на расстоянии 1 км
один от другого. Какова сила притяжения между ними?
7. Вычислите силу притяжения между Луной и Землей. Масса Луны тл «
«7-Ю22 кг, масса Земли т3 6 • 1024 кг, расстояние между Луной и Зем-
лей считать равным 3,84’ 108 м.
8. Космонавт высадился на Луну. Его притягивает и Луна, и Земля. Во сколько
раз сила притяжения космонавта к Луне больше, чем к Земле? Радиус Лу-
ны равен 1730 км.
9. С каким ускорением происходило бы свободное падение тела на Землю,
если бы тело находилось от Земли на таком же расстоянии, как и Луна?
§ 44. СИЛА ТЯЖЕСТИ
Одно из проявлений силы всемирного тяготения — сила тяжес-
ти, т. е. сила притяжения тел к Земле. Обозначим массу Земли М,
ее радиус R, массу данного тела т, тогда сила, действующая на
тело вблизи поверхности Земли, согласно закону всемирного тяго-
тения будет равна:
Мт
I I — Т
Это и есть сила тяжести. Направлена она к центру Земли.
Если на тело действует только эта сила (а все другие уравно-
вешены), то оно совершает свободное падение. Ускоре-
ние этого свободного падения можно найти, применив второй закон
Ньютона,
1Я Мт М ...
g = ~ = У ™ (О
т R2m R2
Отсюда видно, что ускорение свободного падения g не зависит от
массы т тела и, следовательно, оно одинаково для всех тел. Теперь
можно написать, что сила тяжести
\F\=mg.
Это выражение для силы тяжести было получено ранее (см. § 35).
116
Сила тяжести, действующая на тело, равна произведению мас-
сы тела на ускорение свободного падения.
Ускорение свободного падения g одинаково для всех тел, но не-
одинаково в разных местах Земли. Для этого есть несколько причин.
Одна из них состоит в том, что земной шар немного сплюснут у
полюсов. По этой причине ускорение свободного падения у полюса
должно быть больше, чем у экватора. Другая, более существенная
причина — это вращение Земли вокруг ее оси. Оно тоже приводит
к тому, что у полюса ускорение свободного падения больше, чем
на экваторе. В результате у полюсов Земли оно равно 9,83 м/сек2,
а на экваторе — 9,78 м/сек2. Известное уже нам значение ускорения
свободного падения — 9,81 м/сек2 — это его значение на широте 45°.
Приведенные числовые значения показывают, что ускорения
свободного падения в разных районах земного шара различаются
очень мало и очень мало отличаются от величины, вычисленной по
М
формуле g = у — Поэтому именно эту величину часто прини-
мают за ускорение свободного падения тел у поверхности Земли.
В некоторых районах земного шара ускорение свободного па-
дения отличается от приведенных выше значений и по другой при-
чине. Такие отклонения наблюдаются в тех местах, где в недрах
Земли залегают породы, плотность которых больше или меньше
средней плотности Земли. Там, где имеются залежи более плотных
пород, значение g больше. Это позволяет геологам по измерениям
значения g отыскивать месторождения полезных ископаемых.
Наконец, сила тяжести, а значит, и ускорение свободного паде-
ния изменяются при удалении от поверхности Земли. Если тело
находится на высоте h над поверхностью Земли, то выражение для
ускорения свободного падения нужно писать в виде
М
Y (/? -И)3
Так, при подъеме на высоту 300 км ускорение свободного паде-
ния уменьшается на 1 м/сек2. Из приведенной формулы видно, что
при высотах над Землей не только в несколько десятков или сотен
метров, но даже многих километров, сила тяжести может считаться
постоянной, не зависящей от положения тела (см. § 35). Только
поэтому свободное падение вблизи Земли и можно считать равно-
ускоренным движением.
Почему ускорение свободного падения зависит от вращения Земли? По-
чему оно на полюсах больше, чем на экваторе?
Сила притяжения тела к Земле, конечно, не зависит от того, вращается
она или нет! Все определяется тем, чсо полюсы Земли неподвижны, а все
точки экватора движутся по окружности с ускорением
а ----- о>2/?
(со — угловая скорость вращения Земли вокруг своей оси; R—радиус Земли).
(о2 г— эгэ значение центростремительного ускорения. Оно направлено к
центру Земли, т. е. так же, как ускорение свободного падения.
117
На опыте значение ускорения падающего тела получают из наблюдения за
его движением относительно линейки со шкалой (см. стр. 55, рис. 51), кото-
рая служит системой отсчета.
При измерении ускорения тела на полюсах эта система отсчета неподвижна
и значение ускорения g получается в соответствии с формулой (1). На эквато-
ре же система отсчета (та же линейка) движется с ускорением w2/?. Значит,
на экваторе измерение ускорения производится относительно системы отсчета,
движущейся с ускорением. Между ускорениями тела, измеренными относитель-
но неподвижной и движущейся системами отсчета, имеется такое же соотно-
шение, как и для скоростей (см. § 10). Ускорение g тела относительно непод-
вижной системы отсчета равно сумме двух ускорений: ускорения g' тела отно-
сительно движущейся системы отсчета и ускорения a=wv движущейся системы
относительно неподвижной. Следовательно,
g = ф +
Отсюда ускорение, измеренное на экваторе, равно:
g’ = g - - ш27?.
Оно меньше, чем на полюсах, на величину (о2/?.
Упражнение 25
1. Что называется силой тяжести?
2. Вычислите, насколько отличается ускорение свободного падения на эква-
торе от его значения на полюсах.
3. Каково значение ускорения свободного падения на высоте, равной трем
радиусам Земли?
4. На какой высоте над Землей сила тяжести, действующая на тело, умень-
шается в два раза?
5. Вычислите ускорение свободного падения тел вблизи поверхности планеты
Марс. Масса Марса равна 6- кг, его радиус 3 300 км,
§ 45. ВЕС ТЕЛ
Силу тяжести, как и всякую другую силу, можно измерять ди-
намометрами. Динамометры, специально предназначенные для из-
мерения силы тяжести, называют пружинными весами,
потому что с их помощью можно измерить вес тела. Что это за
величина — вес?
Рассмотрим еще раз процесс деформации пружины динамометра,
б
Рис. 113
когда к ней подвешен неко-
торый груз, как это мы дела-
ли в § 36. Но теперь мы об-
ратим внимание не только на
то, что происходит с пружи-
ной, но и на то, что происхо-
дит с самим грузом, подве-
шенным к пружине.
На рисунке 113, а изоб-
ражена пружина динамомет-
ра до того, как к ней был
подвешен груз. Это недефор-
мированная пружина (массой
пружины мы пренебрегаем).
Прикрепим к ее нижнему кон-
цу груз. Груз тотчас же нач-
нет падать под действием си-
118
Рис. 114
лы тяжести mg. При своем падении он увлека-
ет за собой и ниж ний конец пружины, вследст-
вие чего пружина деформируется, как это по-
казано на рисунке 113, б. Возникающая при
этом сила упругости Fynp тоже приложена к
телу, но направлена вверх. При определен-
ном значении удлинения пр ужины сила упру-
гости F,m по абсолютному значению становит-
ся равной силе тяжести mg. Под действием
этих двух сил, равнодействующая которых равна нулю, груз уста-
навливается в состоянии покоя.
Но если пружина динамометра действует на груз, то по третьему
закону Ньютона и груз действует на пружину с такой же по абсо-
лютному значению силой, но направленной в противоположную
сторону, т. е. вниз. Это тоже сила упругости. Возникает она из-за
того, что и груз (а не только пружина) деформируется. В сильно
увеличенном виде эта деформация (удлинение) показана на рисун-
ке 113, б.
Вот эту силу, приложенную не к телу, а к пружине, и называют
весом тела. Вес тела принято обозначать буквой Р.
Если тело не подвешивать, а поместить на горизонтальную опо-
ру (рис. 114), то оно и на опору действует с силой, тоже называемой
весом.
Силу, с которой тело вследствие его притяжения к Земле дейст-
вует на опору или подвес, называют весом тела.
Конечно, не обязательно, чтобы опора или подвес представля-
ли собой спиральную пружину. Тело можно подвесить на нити, на
проволоке или поместить на стол. На нить, проволоку или стол
действовать будет вес тела.
Таким образом, вес тела — это сила, приложенная не к телу, а
к опоре или подвесу.
В тех примерах, которые мы здесь рассмотрели, вес тела, оче-
видно, равен силе тяжести. Но это верно только тогда, когда опора
или подвес находится в покое относительно Земли (или движется
прямолинейно и равномерно).
Надо помнить, что вес и сила тяжести не одно и то же', вес и си-
ла тяжести всегда приложены к разным телам.
§ 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ
В четвертой главе мы узнали, что массу тела можно определить,
измеряя отношение ускорений при взаимодействии этого тела с те-
лом, принятым за эталон массы. Понятно, что этот способ очень
неудобен и на практике обычно не применяется. Теперь мы рассмот-
рим другой, более удобный способ измерения массы. Этот способ
называют взвешиванием. Определение массы методом
119
взвешивания основано на том, что сила тяжести, действующая на
тело, и масса этого тела пропорциональны друг другу:
F = mg.
А силу тяжести можно измерять на весах, так как она равна весу
тела, если весы вместе с взвешиваемым телом покоятся относитель-
но Земли. Поэтому, измерив вес тела Р = F пружинными весами
и зная ускорение свободного падения g в месте, где производится
взвешивание, можно вычислить массу по формуле
Еще удобнее определять массу взвешиванием на рычажных ве-
сах. С этим способом определения массы вы ознакомились в курсе
физики VI класса. На рычажных весах сравнивают веса тела и
гирь. Когда весы уравновешены, можно утверждать, что вес тела
равен весу гирь. Но если равны веса, то равны и массы. Так как на
гирях (разновесках) указаны именно их массы, то массу тела мы
определяем, просто сложив числа, указанные на разновесках.
Рычажные весы — очень чувствительный прибор. Наименьшая
масса, которую можно измерить наиболее чувствительными весами,
составляет несколько миллионных долей грамма.
§ 47. МАССА ЗЕМЛИ
Массу Земли нельзя, конечно, измерить, положив Землю на
весы. Но ее можно вычислить, пользуясь формулой для ускорения
свободного падения:
Отсюда для величины массы Земли получаем:
М =
Численные значения g и у были в свое время определены опыт-
ным путем:
у = 6,67 • 10-“ —
' к#
£=9,81^-
СРК*
Радиус Земли тоже хорошо известен:
R = 6380 км = 6,38 • 10“ м.
по
Подставив численные значения g, Я и у в формулу для Л1, по-
лучаем:
9,81 -^(6,38 10s л)2
М =-------—--------------« 6 • 1024 кг = 6 • 1021 т.
6,67 • Ю-» ^-2
кг2
Масса Земли равна почти шести тысячам миллиардов миллиар-
дов тонн!
§ 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ
Мы уже говорили об одном проявлении электрических взаимо-
действий между телами — силе упругости. Другим проявлением
электрических взаимодействий является сила трения, о
которой мы не раз упоминали. О ней и нельзя не упоминать, потому
что в земных условиях она сопутствует любому движению тел. Имен-
но из-за этой силы всякое движение тела в конце концов прекраща-
ется, если оно не поддерживается какой-нибудь другой силой,
например силой упругости пли силой тяжести.
Сила трения возникает при непосредственном соприкосновении
тел и всегда направлена вдоль поверхности соприкосновения в от-
личие от силы упругости, направленной перпендикулярно этой по-
верхности.
Проследим на опыте за возникновением силы треиия.
На столе помещено некоторое тело (рис. 115). К нему прикре-
плен динамометр, который нитью, перекинутой через блок, связан
с грузом. Тело находится в покое.
На тело действует сила Е, параллельная поверхности соприкосно-
вения его со столом и равная по абсолютному значению весу груза.
Ее и показывает динамометр. Кроме того, на тело действует сила
тяжести и уравновешивающая ее сила реакции, вызванная дефор-
мацией стола, направленная перпендикулярно поверхности сопри-
косновения тела со столом. Если груз недостаточно велик, тело
остается в покое. Это значит, что вместе с силой F на тело дейст-
вует еще одна сила Етр, равная ей численно, но направленная в
противоположную сторону: Frp — —F. Это и есть сила трения,
ее называют силой трения покоя.
Рис. 115
121
Рис. 116
Увеличим груз, прикрепив к нему большую гирю. Динамометр
покажет, что сила F увеличилась. Но тело по-прежнему остается
в покое. Значит, вместе с силой F увеличилась и сила трения покоя,
так что эти две силы, как и прежде, равны и направлены противопо-
ложно друг другу. В этом и состоит главная особенность силы тре-
ния покоя.
Сила трения покоя всегда равна по абсолюпюму значению и
направлена противоположно силе, приложенной к телу параллель-
но поверхности соприкосновения его с другим телом.
Наконец, при некотором определенном значении массы груза
тело сдвинется и начнет скользить. Существует, следовательно,
определенная максимальная сила трения покоя. И толь-
—
ко тогда, когда параллельная поверхности сила F становится
хотя бы немного больше нее, тело получает ускорение.
Сила трения покоя — это и есть та сила, которая -мешает нам
сдвинуть с места тяжелый предмет: шкаф, стол, ящик и т. д.
Но почему важно то, что предмет тяжелый? Ведь двигаем его
мы не вверх, не против силы тяжести!
На этот вопрос отвечает опыт.
Поместим на тело дополнительный груз, чтобы сильнее прижать
тело к столу (рис. 116) (вместо этого его можно прижать рукой,
пружиной и т. д.). Этим мы увеличиваем силу, направленную пер-
пендикулярно поверхности соприкосновения тела и стола. Эту
силу называют силон давления. Если теперь мы снова из-
мерим максимальную силу трения покоя, т. е. силу, которая нуж-
на, чтобы тело начало скользить, то увидим, что опа увеличилась
как раз во столько раз, во сколько раз мы увеличили силу дав-
ления.
Максимальная сила трения покоя пропорциональна силе дав-
ления.
Если обозначить абсолютные значения силы давления через Л',
а максимальной силы трения покоя через FTp. 11акс , то можно на-
писать:
^тр.ма сс ”
где р (греческая буква «мю») — коэффициент пропорциональности
Мы говорили, что сила трепня препятствует началу движения.
Но, с другой стороны, бывают такие случаи, когда именно си-
122
ла трения покоя служит причиной изменения
движения тела. Так, например, при ходьбе
именно сила трения покоя Fit действующая
на подошву, сообщает нам ускорение
(рис. 117). Ведь подошва не скользит на-
зад, и, значит, трение между ней и почвой —
это трение покоя. А если подошва сколь-
зит, то и ходьба невозможна. Сила же F.z,
равная и противоположная Flt сообщает ус-
корение Земле. Таким же образом колеса ав-
томобилей и других самодвижущихся повозок
как бы отталкиваются от земли, и эта тол-
кающая сила есть сила трения покоя.
Когда в ременной передаче ремень застав-
ляет вращаться шкив (рис. 118), то силой,
сообщающей ускорение ободу шкива, тоже
является сила трения покоя между привод-
ным ремнем и шкивом.
§ 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ
В предыдущем параграфе мы выяснили,
что если сила, приложенная к телу парал-
лельно поверхности соприкосновения его с
другим телом, хотя бы немного превосходит
максимальную силу трения покоя, тело по-
лучает ускорение и начинает скользить по
поверхности другого тела. Но и в этом случае
на тело действует сила трения. Только те-
перь это сила трения скольже-
ния. Измерение показывает, что по абсо-
лютному значению она приблизительно рав-
на максимальной силе трения покоя. Направ-
лена же сила трения скольжения (в дальней-
шем мы будем говорить просто сила трения)
противоположную направлению относительной
ющихся тел. Это самая важная особенность силы трения.
Направление силы трения (скольжения) противоположно на-
правлению скорости движения тела относительно соприкасающего-
ся с ним тела.
Ускорение, сообщаемое телу силой трения, также направлено
противоположно направлению его относительной скорости, т. е.
сила трения скольжения всегда приводит к уменьшению относитель-
ной скорости тела.
Так же как и максимальная сила трения покоя, сила трения
скольжения пропорциональна силе давления, действующей па тело:
F\p ~ jxjV.
Рис. 117
всегда в сторону,
скорости соприкаса-
123
F-Юн
Рис. 119
Коэффициент пропорциональ-
ности р. здесь тот же, что и в
формуле для максимальной си-
лы трения покоя.
Из формулы для силы трения
видно, что коэффициент р ра-
вен отношению силы трения к
силе давления:
Значит, коэффициент трения — число отвлеченное (безразмерное).
Обычно коэффициент трения меньше единицы. Эго значит, что
сила трения меньше силы давления. Если, например, коэффициент
трения бруска о поверхность стола (рис. 119) равен 0,5, то это зна-
чит, что при весе бруска в 20 н его можно сдвинуть с места и двигать
по столу, приложив к нему силу в Юн.
Коэффициент трения характеризует не тело, на которое дейст-
вует сила трения, а сразу два тела, трущиеся друг о друга. Зна-
чение его зависит от того, из каких материалов сделаны трущиеся
тела, как обработаны их поверхности, от чистоты поверхностей
и т. д. Опыты показали, что сила трения не зависит от площади со-
прикасающихся поверхностей и от положения одного из тел относи-
тельно другого. Коэффициент трения, например, конька о лед одина-
ков на всем протяжении ледяной дорожки, если, конечно, поверх-
ность льда всюду одинакова. Таким образом, сила трения является
исключением из общего правила, по которому сила, действующая
на тело, зависит от его положения относительно того тела, с которым
оно взаимодействует. Сила трения, оказывается, зависит не от по-
ложения тела, а от его скорости. Впрочем, абсолютное значение
силы трения двух твердых тел от их относительной скорости тоже
мало зависит. Зависимость силы трения от скорости состоит в том,
что при изменении направления скорости изменяется и направле-
ние силы трения. Значения коэффициента трения для некоторых
материалов указаны в приведенной ниже таблице:
Материалы
Коэффициент трепня
Дерево по дереву
Резина по бетону
Сталь по бетону
Сталь по льду
Сталь по стали
0,25
0,75
0,30
0,04
0,20
Эти значения коэффициента трения относятся к случаю, когда
поверхности тел не смазаны. Смазка существенно уменьшает силу
трения. Например, сталь по стали со смазкой скользит так же легко,
как. сталь по льду—коэффициент трения составляет всего 0,04.
124
Почему же возникают силы трения?
Возникновение силы трения связано с яв-
лепиями на поверхностях соприкосновения
тел. Какими бы гладкими ни казались поверх- ННМВ^МН
ности соприкосновения, они на самом деле Ця|^^^И|НН
всегда шероховаты: на них имеются горбики
и впадины, хорошо заметные в микроскоп Рис. 120
(рис. 120). Когда мы пытаемся двигать одно
тело по поверхности другого, эти бесчисленные горбики деформи-
руются и возникают силы, очень похожие на силы упругости. Чем
больше деформация маленьких выступов на поверхности, тем больше
и сила, стремящаяся привести тело в движение. Вот почему сила
трения покоя всегда равна внешней силе. Когда же начинается сколь-
жение, выступы на поверхностях тел разрушаются. Вместо них
образуются новые неровности, которые тоже будут разрушаться
и т. д. Этим объясняется износ трущихся поверхностей.
Заметим в заключение, что трение между соприкасающимися
твердыми телами называют сухим трением.
Упражнение 26
1. При каких условиях возникает сила трения покоя?
2. Действует ли сила трения покоя на стол, стоящий в комнате? Что нужно
сделать, чтобы такая сила появилась?
3. Мальчик толкает книжный шкаф с максимально возможным для него уси-
лием, но не может сдвинуть его. Нет ли здесь нарушения второго закона
Ньютона, согласно которому тело, на которое действует сила, получает
ускорение?
4. Какая сила должна быть приложена к телу, расположенному на горизон-
тальной плоскости, чтобы сдвинуть его на этой плоскости?
S. Вычислите силу, с которой нужно толкать деревянный брус массой 20 кг
по деревянному полу с постоянной скоростью. Как будет двигаться брус,
если к нему будет приложена сила большая, чем вычисленная?
6. К стальному ящику массой 500 кг, стоящему на бетонном полу, приложена
в горизонтальном направлении постоянная сила, равная 1 600 н. Будет ли
под действием такой силы ящик двигаться? Если да, то как он будет дви-
гаться: равномерно или ускоренно?
7. При длительной работе лошадь развивает силу в 600 н. Какой максималь-
ный груз она может везти на санях, масса которых 100 кг, еслй коэффици-
ент трения полозьев саней о снег равен 0,05?
§ 50. СИЛА СОПРОТИВЛЕНИЯ,
ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА
В ЖИДКОСТИ ИЛИ В ГАЗЕ
Мы ознакомились с силой сухого трения между соприкасаю-
щимися твердыми телами. Но часто твердые тела движутся, сопри-
касаясь не с твердыми телами, а с жидкостями или газами, например
самолет в воздухе, корабль на воде. При таких движениях тоже
возникает сила, параллельная поверхности соприкосновения и
125
направленная в сторону, противопо-
ложную относительной скорости тела.
Этим она напоминает силу сухого тре-
ния. Ее часто так и называют: сила
жидкого трения. Но по своему
характеру она заметно отличается от
нее. Поэтому мы и назвали ее силой
сопротивления, а не силой
трения.
При движении твердого тела в жид-
кости или газе сила трения покоя не
возникает. Это значит, что даже самая
малая сила, приложенная к телу, сообщает ему ускорение.
Многие знают по собственному опыту, что, находясь на плоту,
можно сравнительно небольшим усилием оттолкнуться шестом от
берега. Но не стоит и пытаться на том же плоту таким же способом
перемещаться по суше. Отсутствие в жидкостях силы трения покоя
легко наблюдать на следующем опыте. Положим небольшой дере-
вянный брусок на воду в широком сосуде (рис. 121). Брусок легко
привести в движение (изменить его скорость) даже очень малой
силой: достаточно подуть на него или толкнуть бумажной полос-
кой. Но если тот же брусок положить на стол, то его можно при-
вести в движение, только приложив к нему достаточно большую
силу, превышающую максимальную силу трения покоя.
Таким образом, сила сопротивления жидкостей и газов дей-
ствует только при относительном движении, и, как уже указы-
валось, она направлена против относительной скорости.
В отличие от силы сухого трения сила сопротивления в жид-
кости или в газе зависит не только от направления, но и от аб-
солютного значения скорости. При небольших скоростях сила со-
противления пропорциональна скорости, а при больших скоростях
она пропорциональна уже квадрату ско-
рости.
Кроме того, сила сопротивления в
большой мере зависит от формы тел.
На рисунке 122 показаны три тела с
одинаковыми площадями поперечного се-
чения. Но если эти три тела будут дви-
гаться в жидкости или в газе с одина-
ковыми скоростями, то окажется, что
наибольшая сила сопротивления дейст-
вует на плоскую шайбу (верхний рису-
нок), а наименьшая — на тело каплеоб-
разной формы (нижний рисунок).
Геометрическую форму тела, при ко-
торой сила сопротивления мала, называ-
ют обтекаемой формой. Само-
летам, автомобилям и другим машинам,
126
движущимся с большими скоростями в воздухе или в воде, ста-
раются поэтому придать обтекаемую форму, а их поверхности
тщательно заглаживают. Это помогает уменьшить силу сопро-
тивления.
Упражнение 27
1. Сила трения между колесами велосипеда и землей почти не зависит от
скорости. Между тем известно, что, чем большую скорость развивает ве-
лосипедист, тем большую мускульную силу он должен прикладывать к
педалям велосипеда. С чем это связано?
2. Нужно ли придавать обтекаемую форму космическим кораблям? А ракетам,
которые выводят их в космос?
3. Почему обтекаемую форму не придают тракторам, дорожным каткам?
Глава 6
Применение законов движения
ВВЕДЕНИЕ
Зная открытые И. Ньютоном законы движения и умея измерять
или вычислять силы, можно решать основную задачу механики:
по известным силам и начальным условиям определять ускорение,
по ускорению скорость и, наконец, координаты (положение) тела
в любой момент времени.
Сравнительно редко приходится наблюдать, чтобы тело нахо-
дилось под действием только одной силы — силы упругости, силы
трения или силы тяжести. В большинстве случаев на тело действует
сразу несколько сил. В этом случае ускорение определяется равно-
действующей всех приложенных сил.
Но бывает и так, что хотя на тело действует несколько сил, но
только одна из них играет существенную роль. Другие же либо
компенсируют друг друга, либо малы по своему абсолютному зна-
чению.
Мы начнем именно с таких случаев.
§ 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ
СИЛЫ УПРУГОСТИ
Рассмотрим сначала случай, когда начальная скорость тела
равна нулю или направлена параллельно приложенной силе уп-
ругости.
Мы уже знаем, что сила упругости Fynp= — kx. Значит, сила
Fynp изменяется с изменением положения тела, на которое она
действует. Напомним, что удлинение пружины (или любого друго-
го упругого тела) как раз и определяет положение тела относи-
тельно точки, где удлинение равно нулю.
Как движется тело под влиянием такой переменной силы?
Согласно второму закону Ньютона ускорение, которое сила
упругости F = — kx сообщает телу, пропорционально этой силе.
Отсюда следует, что ускорение тела тоже переменная величи-
на, оно зависит от х. Ускорение, так же как и сила, в любой точ-
ке, т. е. при любом значении х, направлено против смещения час-
тей пружины при ее деформации. Этим и определяется характер
движения тела под действием одной только силы упругости. На опы-
те легко увидеть, каково это движение.
128
Ill
а) Космические скорости. Если скорость космического корабля VoPs7,9 км/сек и
направлена параллельно поверхности Земли, то корабль становится спутником Зем-
ли, движущимся по круговой орбите на сравнительно небольшой высоте над Землей.
При скорости, лежащей между 7*9 и 11,1 км/сек, орбита корабля будет эллиптичес-
кой. При скорости 11,2 км/сек корабль будет двигаться по параболе, а при еще боль-
шей скорости — по гиперболе.
б) Старт ракеты.
IV
Вверху фотография плотины крупнейшей в мире Красноярской гидроэлектростанции.
Внизу схематический разрез современной ГЭС.
Потенциальная энергия воды при падении из верхнего в нижний бьеф станции пре-
вращается в кинетическую энергию. При прохождении воды через турбину ее кине-
тическая энергия передается рабочему колесу турбины и связанному с ним генера-
тору. (Цифрами на рисунке обозначены: 1 — камера турбины; 2 — гидротурбина;
3 — гидрогенератор; 4 — отсасывающая труба; 5 — распределительные устройства
(электрические); 6 — трансформатор; 7 — портальные краны.)
Подвесим какой-нибудь груз к
нижнему концу пружины (рис. 123).
Оттянув груз вниз на несколько
сантиметров, отпустим его. Мы уви-
дим, что тело станет периодически
подниматься вверх и опускаться
вниз выше и ниже того положе-
ния, которое оно занимало до того,
как пружина была оттянута. Та-
кое движение называют колеба-
тельным.
В рассмотренном опыте на те-
ло, кроме силы упругости, дейст-
вует еще и сила тяжести. Но она
не влияет на его движение, потому
что сила тяжести сообщает одина-
ковые ускорения при движении те-
ла как вниз, так и вверх. Если бы
пружина была расположена гори-
зонтально (рис. 124), тело тоже
совершало бы колебательное дви-
жение.
Пользуясь вторым законом Нью-
тона, можно найти положение тел:
Рис. 124
в любой момент времени. Но
задача эта трудная, так как сила упругости — величина пере-
менная. Колебательное движение будет подробно рассмотрено в
X классе.
Совсем иначе движется тело, которому сообщена начальная
скорость, перпендикулярная действующей на тело силе упругости.
Мы уже рассматривали подобный случай в § 35. Там мы выяс-
нили, что при таком взаимном направлении силы упругости и ско-
рости тело движется по окружности.
Следовательно, когда сила упругости направлена перпенди-
кулярно начальной скорости движения тела, она сообщает ему
центростремительное ускорение и заставляет тело двигаться по
окружности.
Упражнение 28
1. Какое движение совершает тело под действием силы упругости?
2. Проследите за поведением тела, взвешиваемого на пружинных весах. Сра-
зу ли оно приходит в состояние покоя?
3. Что можно сказать об ускорении тела, на которое действует переменная
сила?
5 Заказ 1126
§ 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ
ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА
РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ
ТЯЖЕСТИ
Силой тяжести мы назвали силу всемирного тяготения, с кото-
рой Земля действует на все тела вблизи ее поверхности.
В отличие от силы упругости, которая в разных положениях тела
различна, сила тяжести может считаться постоянной по крайней
мере до высот в десятки километров над Землей. Поэтому и уско-
рение, которое сила тяжести сообщает телам, тоже одинаково во
всех точках и направлено к центру Земли.
Сила тяжести от силы упругости отличается еще и тем, что уско-
рение, сообщаемое ею, не зависит от массы тела. Поэтому, если на
тело действует только сила тяжести, то, каким бы ни было тело —
большим или малым, легким или тяжелым, оно будет двигаться
с одинаковым ускорением g, равным вблизи поверхности Земли
9,81 м/сек2.
В случае, когда начальная скорость тела равна нулю или на-
правлена параллельно силе тяжести, тело совершает вертикальное
свободное падение. С этим движением мы уже ознакомились в § 20
и 21, которые мы рекомендуем прочитать еще раз.
Упражнение 29
1. Чем отличается ускорение, сообщаемое телам силой тяжести, от ускоре-
ния, которое сообщают им другие силы?
2. В чем причина постоянства ускорения, сообщаемого силой тяжести?
3. Почему ускорение, сообщаемое телу силой тяжести, не зависит от его
массы?
4. Почему время подъема тела на некоторую высоту и время его падения с
этой высоты одно и то же?
5. Если бы тело падало на Землю с высоты в несколько сот или тысяч кило-
метров, было бы его движение равноускоренным? Зависело бы в этом слу-
чае ускорение от массы тела?
§ 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ
С УСКОРЕНИЕМ
В § 45 мы выяснили, что вес тела — это сила, с которой тело
действует на опору или на подвес. Если опора или подвес покоятся
относительно Земли или движутся относительно нее прямолиней-
но и равномерно, то вес тела равен силе тяжести mg. Но вес тела
может существенно отличаться от значения силы тяжести, если
опора или подвес движется с ускорением вверх или вниз. Почему?
Вспомним, что вес — это сила, измеряемая, например, пружин-
ными весами. Посмотрим, что покажут пружинные весы, если они
вместе с подвешенным к ним телом движутся с ускорением вверх
или вниз.
130
Подвесим к пружинным весам ка-
кой-нибудь груз и дадим им возмож-
ность двигаться с некоторым уско-
рением а. Для этого можно взять
весы с грузом в руку и резко опу-
стить их вниз (рис. 125), сообщив
им ускорение, направленное вниз.
Мы увидим, что во время опускания
весов стрелка перемещается вверх.
Это значит, что вес груза во время
опускания стал меньше, чем он был
в случае покоящихся весов. Если,
наоборот, резко поднять весы вверх,
стрелка опустится, показывая, что
вес груза увеличился (рис. 126).
Чем объясняется это уменьшение или
увеличение веса при ускоренном дви-
жении динамометра с грузом?
Ответ на это дает второй закон
Ньютона. Посмотрим, какие силы
действуют на груз. На него дейст-
вуют сила тяжести mg, направленная
вниз, и сила упругости F пружины
весов, направленная вверх. Под дей-
ствием этих двух сил тело и движет-
ся с ускорением а, которое может
быть направлено как вниз, так и
вверх в зависимости от того, будем
ли мы опускать весы или подни-
мать их.
По второму закону Ньютона
та — mg -f- F.
Отсюда
F — та— mg. (1)
С такой же по модулю силой, но
направленной противоположно силе
F, груз действует на пружину. А эта
сила и есть вес груза Р:
Р—Л
Следовательно,
Р = —(та— mg) = m(g — a). (2)
б*
131
Векторы Р, g и а параллельны вертикальной прямой. Напра-
вив координатную ось X по вертикали вниз (см. рис. 125 и 126),
мы можем формулу (2) написать в алгебраической форме для про-
екций этих векторов на вертикальную ось:
Р = т (g - а).
(3)
Если весы движутся с ускорением а вниз, то проекция этого
вектора на координатную ось положительна. Если а < g, то из
формулы (3) следует, что Р < mg.
Вес тела, направление ускорения которого совпадает с направ-
лением ускорения свободного падения, меньше веса покоящегося тела.
Это мы и видели на опыте (рис. 125).
Если же весы движутся с ускорением а вверх, то проекция
вектора ускорения на координатную ось отрицательна и форму-
ла (3) тогда примет вид:
Р= tn[g — (— |а|)] = т (g - 3 'щ),
(4)
т. е. Р Р> mg.
Таким образом, если ускорение тела направлено в сторону,
противоположную ускорению свободного падения, его вес больше
веса покоящегося тела. Это мы и наблюдали на опыте (рис. 126).
Увеличение веса тела, вызванное его ускоренным движением,
называют перегрузкой.
Вес уменьшается или увеличивается не только тогда, когда те-
ло подвешено к пружинным весам. То же самое относится н к любо-
му подвесу, и к любой опоре.
Приведем некоторые примеры изменения веса тела при его ус-
коренном движении.
1. Автомобиль, движущийся по выпуклому мосту, легче того
же автомобиля, когда он стоит на том же мосту (рис. 127).
Действительно, движение по выпуклому мосту — эго движе-
ние по части окружности. Поэтому автомобиль движется с центро-
стремительным ускорением, равным по абсолютной величине:
где v — скорость автомобиля, г — радиус кривизны. В момент,
когда автомобиль находится в высшей точке моста, это ускоре-
ние направлено по вертикали вниз. В таком случае вес автомоби-
ля, т. е. сила, с которой он давит на мост, будет равен:
Р = m(g — а) = т (g — —k Р < mg.
Пассажиры, проезжающие в автомобиле с большой скоростью
по выпуклому мосту, ощущают это уменьшение веса.
122
2. Летчик, выводящий самолет из пикирования (рис. 128), в
нижней части траектории подвергается перегрузке. В самом деле,
в этой части траектории самолет движется по окружности с цент-
ростремительным ускорением, направленным к ее центру по вер-
тикали вверх. Абсолютное значение ускорения по-прежнему равно:
Но его проекция на вертикальную ось, направленную вниз,
отрицательна:
у2
г
Следовательно, вес летчика, т. е. сила, с которой он действует
на опору (сиденье), определяется формулой:
Р = m(.g — а) = m\g — \, Р> mg.
Таким образом, вес летчика больше «нормального» веса, равного
mv2
силе тяжести mg, на величину ~ • Если при выходе из пикирова-
vs
ния центростремительное ускорение ~ превышает по абсолютно-
му2 _ \
му значению ускорение свободного падения g в п раз — пё ) >
то вес летчика
Р = т {g -|- ng) = mg (п + 1),
т. е. он будет в п + 1 раз больше нормального веса летчика.
При перегрузке увеличивают свой вес и внутренние органы
летчика, увеличивается сила, с которой они действуют друг на
друга и на его остов (скелет). Это вызывает болезненные ощущения,
а при чрезмерной перегрузке может стать опасным для здоровья.
Тренированные пилоты выдерживают перегрузку до 10 mg (обыч-
но перегрузку выражают не через величину tng, а через величину g
и говорят, что перегрузка равна, например, 10 g).
U3
Упражнение 30
1. Как изменяется вес тела при его ускоренном движении?
2. Изменяется ли вес тела, если оно движется с ускорением в горизонталь-
ном направлении?
3. Бетонную плиту массой 500 кг подъемным краном равномерно переме-
щают: а) вертикально вверх; 6) горизонтально; в) вертикально вниз. Чему
равны сила тяжести, действующая на плиту, и ее вес в каждом из этих
случаев?
4. На дне шахтной клети лежит груз массой ICC кг. Каков будет вес этого
груза, если клеть: а) поднимается вертикально с ускорением 0,3 м/сек2;
б) двигается равномерно; в) опускается с ускорением 0,4 м/сек2; г) свобод-
но падает?
5. На сколько уменьшится вес автомобиля в высшей точке выпуклого моста?
Радиус кривизны моста 100 м. Масса автомобиля 2 000 кг, скорость его дви-
жения 60 км/ч.
6. Что можно сказать о весе летчика, совершающего фигуру «л«.ертвая петля»,
когда он находится в нижней и верхней точках фигуры?
7. Определите вес тела массой 1 кг на экваторе. Радиус Земли считать рав-
ным 6 000 км.
Указание. При решении задачи учесть, что все тела, находящиеся
вблизи поверхности Земли, участвуют во вращении Земли вокруг своей
оси. Поэтому они движутся с центростремительным ускорением. На эква-
торе центростремительное ускорение направлено к центру Земли
(см. § 44).
§ 54. НЕВЕСОМОСТЬ
Нам осталось еще рассмотреть случай, когда груз вместе с весами
совершает свободное падение, т. е. когда весы просто выпускают из
рук (рис. 129). Опыт показывает, что во время свободного падения
стрелка весов устанавливается на ну-
ле: вес оказывается равным нулю. И
это понятно. Ведь когда груз падает под
действием притяжения к Земле, пру-
жина весов «сама следует за ним»
(см. рис. 129). Поэтому она не дефор-
мируется. Но если пружина не де-
формируется, то на прикрепленный
к ней груз никакая сила с ее сторо-
ны не действует. Груз поэтому тоже
не деформирован и тоже не действу-
ет на пружину. Груз стал невесомым.
То, что при свободном падении
вес тела равен нулю, прямо следует
из формулы
Р = rn(g — а).
При свободном падении тела а — g.
Следовательно,
Р = т (g — g) = о.
При этом условии опора с телом не
взаимодействует.
Рис. 129
134
Рис. 131
Причина невесомости заключается в том, что сила всемирного
тяготения сообщает телу и его опоре одинаковые ускорения. Поэ-
тому всякое тело, которое движется только под действием сил
всемирного тяготения, находится в состоянии невесомости.
Именно в таких условиях и находится свободно падающее тело.
Этот удивительный факт иллюстрируется следующим интерес-
ным опытом (рис. 130). На штативе укреплен блок, через кото-
рый переброшена нить. На конце этой нити подвешена чашка
с двумя грузами достаточно большой массы. Верхний груз
плотно прилегает к нижнему. Другой конец нити прикреплен к
штативу. Между грузами помещена полоска тонкой бумаги. Свободный
ее конец держат неподвижно в руке. Если груз опускать медленно,
то бумага, натягиваясь, разорвется, потому что на зажатый конец
полоски действует сила трения покоя. Теперь заменим полоску
бумаги новой и повторим опыт таким образом, чтобы груз свобод-
но падал. При падении груза полоска бумаги остается в руках
неразорванной. Значит, при падении грузы не давили друг на
друга и сила трения покоя была равна нулю. Это и доказывает,
что грузы при свободном падении находятся в состоянии невесо-
мости.
Упражнение 31
1. Находится ли в состоянии невесомости тело, брошенное вертикально вверх?
Трением в воздухе пренебречь.
2. К рамке, которая может скользить по двум направляющим стержням
(рис. 131), подвешены на двух одинаковых пружинах различные грузы
Если пережечь нить, с помощью которой укреплена рамка, то рамка будет
свободно падать (трение мало, и им можно пренебречь) и при этом де-
формации пружин исчезнут. Объясните, почему исчезают деформации
пружин при свободном падении рамки.
135
ным «метателем» под
§ 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ
ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ
К ГОРИЗОНТУ
Довольно часто приходится иметь дело с движением тел, по-
лучивших начальную скорость не параллельно силе тяжести, а на-
правленную под некоторым углом к ней (или к горизонту). Когда,
например, спортсмен толкает ядро, метает диск или копье, он со-
общает этим «предметам» именно такую начальную скорость. При
артиллерийской стрельбе стволам орудий придается некоторый
угол возвышения, так что вылетевший снаряд тоже получает на-
чальную скорость, направленную под углом к горизонту.
Будем считать, что силой сопротивления воздуха можно пре-
небречь. Как в этом случае движется тело?
Для того чтобы ответить на этот вопрос, рассмотрим следую-
щий несколько искусственный способ бросания тела под углом к
горизонту.
Представим себе автомобиль, движущийся равномерно в гори-
зонтальном направлении со скоростью vx. Пассажир в автомоби-
ле бросает какое-нибудь тело с начальной скоростью vy вертикаль-
но вверх. Это значит, что пассажир видит тело поднимающимся
в вертикальном направлении. А как направлена эта скорость отно-
сительно Земли?
Вспомним, что говорилось в § П об относительности движения.
Ясно, что автомобиль — это подвижное тело отсчета, а Землю мож-
но считать неподвижным телом отсчета. Тогда скорость тела относи-
тельно Земли будет равна векторной сумме скоростей vx и v . Из
рисунка 132 видно, что относительно Земли начальная скорость v
направлена к горизонту под некоторым углом а. Следовательно,
тело, брошенное с движущегося автомобиля вверх, движется от-
носительно Земли так, как будто бы оно было брошено неподвиж-
углом а к горизонту.
Проследим теперь за дальнейшим движе-
нием тела.
Поместим начало неподвижной системы
координат в точку, где автомобиль находил-
ся в момент броска. Направим ось X вдоль
направления движения автомобиля, а ось
У по вертикали вверх (именно поэтому мы
обозначили скорость по горизонтали через
vx, 2l по вертикали через v ). С автомобилем
мы свяжем систему координат X'O'Y', на-
правив оси X' и У' параллельно осям X и
У (рис. 133). Это подвижная система коор-
динат.
Каким будет движение тела относительно
каждой из этих систем координат?
и
Рис. 132
136
Относительно подвижной системы координат, т. е. для пасса-
жира в автомобиле, движение тела — это просто движение по
вертикали вверх вдоль оси У'. Это равноускоренное движение с
ускорением g, которое сообщает телу сила тяжести mg.
Но относительно Земли сама ось У' перемещается вдоль осн X
с постоянной скоростью vx.
Отметим положения тела по оси У' и положения самой этой
оси через равные промежутки времени т (например, через каждую
секунду). Из рисунка 134 видно, что сначала тело удаляется от
наблюдателя на автомобиле вертикально вверх. В некоторый
момент времени tr тело достигнет максимальной высоты ймакс в точ-
ке В, где его скорость по оси У' равна нулю. Для наблюдателя
на Земле тело в этот момент движется горизонтально со ско-
ростью автомобиля vx.
В § 21 мы видели, что время подъема на максимальную высоту
t == ,
g
где р0 — начальная скорость, с которой тело было брошено вверх.
137
В нашем случае v0 — vy, так что тело достигнет точки В по
истечении времени =-1 .
g
Используя полученную в § 21 формулу для максимальной вы-
ж
соты подъема тела, брошенного вертикально вверх (Лмакс = — ,
\ 2g /
, v
найдем, что в нашем случае й.1ачс = — •
2g
Начиная с того момента, в который тело достигло точки В,
наблюдатель на автомобиле будет видеть, что тело падает вниз
все с тем же ускорением g. При этом через такие же последователь-
ные промежутки времени т тело будет занимать на оси Y' те же по-
ложения, что и при подъеме, по в обратном порядке.
В § 21 было показано, что время падения тела равно времени
его подъема. Поэтому еще через промежуток времени, тоже рав-
ный tlt тело снова окажется в автомобиле. Значит, полное время
движения тела
t = 2G = .
g
Относительно Земли за этот промежуток времени сама ось У'
вместе с телом продвинулась вдоль оси X на расстояние ОС = vxt.
ОС — это дальность полета тела. Обозначим ее через I.
Следовательно, I — vxt = —LC'.
g
Соединив точки, через которые последовательно проходит тело,
плавной кривой, мы получим траекторию движения тела относи-
тельно Земли. Эту кривую называют параболой.
Задача. Самоходная зенитная пушка, установленная на авто-
машине, во время испытаний запустила вертикально вверх снаряд
с начальной скоростью 600 м/сек. В момент выстрела автомашина
двигалась со скоростью 21,6 км/ч. После выстрела автомашина оста-
новилась. Как далеко от места выстрела упадет снаряд? До какой
высоты он поднимется? Через какое время он упадет на землю?
Считать, что на снаряд действует только сила тяжести (силой
сопротивления воздуха пренебречь).
Решение. Дальность полета снаряда можно вычислить
по формуле
а максимальную высоту подъема снаряда /iMaKC по формуле
^макс — ~~ ’ (2)
138
Скорость vx — это скорость автомобиля. Следовательно, vx =
= 21,6 км/ч = 6 м/сек, vy = 600 м/сек. Подставив эти значения
в формулы (1) и (2), получим:
м м
2-600 — -6 —
7 СёК СёК *?dr\
I =--------------------ж 720 м
и
/ м \2
600 —
Ймакс — ~--------СвК ~ — 18 000 м = 18 км.
м
Теперь найдем время полета снаряда. Оно равно:
м
2t)i 2-600 —
t= — ’=-------« 120 сек = 2 мин.
Полученные в этом параграфе формулы для дальности и времени полета тела,
брошенного под углом к горизонту, содержат величины vx и иу— проекции на-
чальной скорости на оси X и Y. Между тем обычно бывают известны сама
начальная скорость v и угол а, который вектор v образует с горизонтальной
осью X.
Из рисунков 132 и 134 видно, что
«х
— = cos а,
V
откуда vx ~ о cos а.
Точно так же — = sin а
v
и vу = v sin а.
Пользуясь этими выражениями для vx и vy, можно формулу для дальности
полета написать в таком виде:
ZvxVy 2у2 cos a sin а
Максимальную высоту, на которую поднимется тело, можно теперь выразить
формулой
^2 . .
у v2 sin2 а
Таким образом и дальность, и максимальная высота полета определяются
значениями начальной скорости v и угла а, под которым брошено тело.
Из формулы для дальности полета видно, что дальность полета будет наиболь-
шей при заданной начальной скорости у, когда максимально значение произве-
дения cosa • sina. Можно доказать, что это произведение максимально при
a = 45°.
139
Упражнение 32
При ответах на вопросы этого упражнения считать, что трением можно
пренебречь.
1. По какой траектории движется тело, брошенное под углом к горизонту?
2. Какая сила действует на тело, брошенное под углом к горизонту, во вре-
мя его движения?
3. Можно ли движение тела, брошенного под углом к горизонту, считать
равноускоренным?
4. С каким ускорением движется тело, брошенное под углом к горизонту?
Как направлено ускорение?
5. Постройте траекторию движения тела, брошенного под углом 60° к гори-
зонту. Масштаб чертежа выбрать самостоятельно.
6. Начальная скорость полета спортивного ядра при толкании равна 14 м/сек.
На какую наибольшую высоту над поверхностью Земли поднялось ядро,
если оно выпущено из точки, находящейся на высоте 2 м? Угол, под кото-
рым был сделан толчок, равен 45°.
7. Снаряд, выпущенный из артиллерийского орудия, поразил цель на расстоя-
нии 25 км. Какова начальная скорость снаряда, если известно, что угол
возвышения орудия был равен 45°?
§ 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ
ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО
Теперь нам нетрудно выяснить, как станет двигаться тело, если
ему сообщить начальную скорость, направленную не под произ-
вольным углом к горизонту, а горизонтально. Так движется, на-
пример, тело, оторвавшееся от горизонтально летящего самолета
(или сброшенное с него).
По-прежнему считаем, что на такое тело действует только сила
тяжести. Она, как всегда, сообщает ему ускорение g, направлен-
ное вниз.
В предыдущем параграфе мы видели, что тело, брошенное под
углом к горизонту, в определенный момент времени достигает выс-
шей точки своей траектории (точка В на рисунке 134). В этот мо-
мент скорость тела направлена горизонтально.
Мы уже знаем, как движется тело после этого. Траекторией
его движения является правая ветвь параболы, изображенной на
рисунке 134. Подобную траекторию движения будет иметь и вся-
кое другое тело, брошенное горизонтально. На рисунке 135 изобра-
жена такая траектория. Ее тоже называют параболой, хотя это
только часть параболы.
Тело, брошенное горизонтально, движется по ветви параболы.
Вычислим дальность полета для этого движения тела.
Если тело брошено с высоты h, то время, в течение которого
оно будет падать, мы получим из формулы h = ;
'=/?
Все время, пока тело падает вниз с ускорением g, вертикальная
ось Y' (рис. 133) движется в горизонтальном направлении со ско-
ростью Vx^vu.
149
Поэтому за время падения t она
переместится на расстояние
I = vnt.
Следовательно,
Эта формула позволяет определить
дальность полета тела, брошенного
на высоте h горизонтально с на-
чальной скоростью v0.
Мы рассмотрели несколько примеров движения тела под дей-
ствием силы тяжести. Из них видно, что во всех случаях тело дви-
жется с ускорением g, сообщаемым ему силой тяжести. Это ускоре-
ние совершенно не зависит от того, движется ли еще тело и в гори-
зонтальном направлении или нет. Можно даже сказать, что во
всех этих случаях тело совершает свободное падение.
Поэтому, например, пуля, выпущенная стрелком из ружья в го-
ризонтальном направлении, упадет на землю одновременно с пу-
лей, случайно оброненной стрелком в момент выстрела. Но обронен-
ная пуля упадет у ног стрелка, а вылетевшая из ружейного ство-
ла — в нескольких сотнях метров от него.
На цветной вклейке I, б представлена стробоскопическая фотогра-
фия двух шариков, из которых один падает вертикально, а второ-
му одновременно с началом падения первого сообщена скорость
в горизонтальном направлении. На фотографии видно, что в одни
и те же моменты времени (моменты вспышек света) оба шарика
находятся на одной и той же высоте и, конечно, одновременно до-
стигают земли.
Траекторию движения тел, брошенных горизонтально или под
углом к горизонту, можно наглядно увидеть в простом опыте.
Бутыль, наполненную водой, помещают на некоторой высоте над
столом и соединяют ее резиновой трубкой с наконечником, снаб-
женным краном (рис. 136). Выпускаемые струи непосредственно
показывают траектории частиц воды. Изменяя угол, под которым
выпускают струю, можно убедиться в том, что наибольшая даль-
ность достигается при угле 45°.
Рассматривая движение тела, брошенного горизонтально или
под углом к горизонту, мы считали, что оно находится под дейст-
вием только силы тяжести. В действительности это не так. Наряду
с силой тяготения на тело всегда действует сила сопротивления
(трения) со стороны воздуха. А она приводит к уменьшению ско-
рости.
Поэтому дальность полета тела, брошенного горизонтально или
под углом к горизонту, всегда меньше, чем это следует из формул,
141
Рис. 136
полученных нами в этом парагра-
фе и § 55; высота подъема тела,
брошенного по вертикали, всегда
меньше, чем вычисленная по фор-
муле, приведенной в § 21, и т. д.
Действие силы сопротивления
приводит также к тому, что
траекторией движения тела, бро-
шенного горизонтально или под
углом к горизонту, оказывается
не парабола, а более сложная
кривая.
Упражнение 33
При ответах на вопросы этого упраж-
нения трением пренебречь.
1. Что общего в движении тел, бро-
шенных вертикально, горизонтально
и под углом к горизонту?
1. Можно ли считать движение тела, брошенного горизонтально, равноуско-
ренным движением?
3. Одинаково ли ускорение тела, брошенного горизонтально, во всех точках
его траектории?
4. Находится ли тело, брошенное горизонтально, во время своего движения
в состоянии невесомости? А тело, брошенное под углом к горизонту?
5. Тело брошено горизонтально с высоты 2 м над землей со скоростью
11 м/сек. Через какое время оно упадет? Какое расстояние пролетит тело
в горизонтальном направлении?
6. Тело брошено с начальной скоростью 20 м/сек в горизонтальном направ-
лении на высоте 20 м над поверхностью Земли. На каком расстоянии от
точки бросания оно упадет на землю? С какой высоты его нужно бросить
с такой же скоростью, чтобы дальность полета стала вдвое больше?
7. Самолет летит в горизонтальном направлении на высоте 10 км со скоростью
720 км/ч. На каком расстоянии от цели (по горизонтали) летчик должен
сбросить бомбу, чтобы попасть в цель?
§ 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ.
ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ
В § 56 мы видели, как движется тело, которому на высоте h
над землей сообщена начальная скорость v в горизонтальном на-
правлении, т. е. параллельно поверхности Земли. Тело описывает
особую траекторию — параболу, двигаясь по которой оно падает
на землю.
При рассмотрении такого движения тела мы считали, что по-
верхность Земли плоская. Такое упрощение справедливо при срав-
нительно небольших скоростях v, при которых перемещение тела
в горизонтальном направлении невелико (рис. 137).
Но в действительности Земля — это шар. Поэтому одновремен-
но с продвижением тела по своей траектории поверхность Земли
142
несколько удаляется от него (рис.
138). Ясно, что можно подобрать
такое значение скорости тела v,
при котором поверхность Земли
из-за ее кривизны будет удаляться
от тела как раз на столько, на
сколько тело приближается к Зем-
ле благодаря притяжению к пей.
Тогда тело будет двигаться на пос-
тоянном расстоянии h от поверх-
ности Земли, т. е. по окружности
радиусом R + h, где R — радиус
земного шара (рис. 139).
Какова величина этой скорос-
ти?
Раз тело движется равномерно
по окружности, то его ускорение
равно:
Г’| с2
1 1 R + /г
Это ускорение телу сообщает сила
тяготения к Земле:
Мт
(R + А)2
(здесь М — масса Земли, т —
масса тела).
По второму закону Ньютона
|£| __ М
т — Y + Л)2 *
Следовательно,
о2 __ М
R 4- h ~~ Y (R + Л)2 ’
откуда
v i/za:
г rR-hfi
У
> Поверх ность 'lu
Рис. 13/
Значит, сели телу сообщить в горизонтальном направлении ско-
рость, определяемую формулой (1), то оно будет двигаться по
окружности вокруг Земли, т. е. станет искусственным спутником
Земли.
Спутником Земли может стать тело любой массы, лишь бы ему
была сообщена достаточная скорость. Вычислим эту скорость для
спутника, запускаемого вблизи поверхности Земли (й = 0).
143
В этом случае
Напомним, что Yj^==Sr’ следовательно,
Л1 п
Отсюда v — УgR .
Подставив в эту формулу значение величин g = 9,8 М;сек* и
R = 6,38 • 10° Л1, получаем:
v= 1/э,8 —, • 6,38 -10е м »8 • 103— = 8— .
г сек* сек сек
Такую скорость в горизонтальном направлении нужно сообщить
телу у поверхности Земли, чтобы оно не упало, а стало ее спутни-
ком, движущимся по круговой орбите. Эту скорость называют
первой космической скоростью.
Восемь километров в секунду — это почти 29 тысяч километ-
ров в час! Сообщить такую огромную скорость телу, конечно, не
просто. Только в 1957 г. советским ученым впервые в истории че-
ловечества удалось с помощью мощной ракеты сообщить первую
космическую скорость телу массой около 85 кг. Это тело и стало
первым искусственным спутником Земли.
Движение спутников вокруг Земли происходит под действием
только одной силы — силы всемирного тяготения. Эта сила сообща-
ет спутнику н всем предметам, находящимся в нем, одинаковые уско-
рения. В таком случае, как уже было сказано в § 54, теряет смысл
понятие веса. Ведь в этом случае любое тело и его «опора» друг
друга не деформируют и не могут «давить» друг на друга. Это
означает, что все тела в спутнике, в том числе и пассажиры, на-
ходятся в состоянии невесомости.
Упражнение 34
1. Как должна быть направлена начальная скорость тела, чтобы оно стало ис-
кусственным спутником Земли, движущимся по круговой орбите?
2. Как направлено ускорение искусственного спутника Земли?
3. Можно ли считать движение искусственного спутника Земли равноуско-
ренным?
4. Был ли в состоянии невесомости космонавт А. Леонов: а) в кабине косми-
ческого корабля при полете на орбите; б) при выходе из корабля в от-
крытый космос?
5. Вычислите период обращения спутника Земли (время, за которое спутник
делает один оборот вокруг Земли), если он запущен на высоте 300 км.
6. Вычислите первую космическую скорость для высоты над Землей, равной
радиусу Земли.
7. На какой высоте над Землей первая космическая скорость равна 6 км сек?
8. На какой высоте должен быть запущен искусственный спутник Земли, что-
бы период его обращения был равен 24 ч?
4*4
§ 58. ДВИЖЕНИЕ ПЛАНЕТ
Планеты — это небесные тела, которые движутся вокруг Солнца, каждая
по своей орбите. Всего вокруг Солнца движутся следующие девять сравнительно
больших планет (перечислим их в порядке возрастания радиусов орбит): Мерку-
рий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун и Плутон. Кроме
того, между орбитами Марса и Юпитера движется много малых планет — асте-
роидов.
Орбиты всех планет представляют собой эллипсы, которые, однако, так мало
отличаются от окружностей, что мы в дальнейшем будем для простоты считать
их окружностями.
Движение планет в сущности ничем не отличается от движения спутников
Земли. Как и спутники, планеты движутся по своим орбитам под действием силы
тяготения. Только у планет роль центра тяготения играет Солнце, так что плане-
ты, в том числе и Земля, — это спутники Солнца.
Согласно закону всемирного тяготения планеты должны притягиваться не
только к Солнцу, но и друг к другу. Но массы планет, как ни велики они сами по
себе, малы по сравнению с массой Солнца. Масса всех планет, вместе взятых, при-
мерно в 700 раз меньше массы Солнца. Поэтому обычно пренебрегают притяже-
нием планет друг к другу и учитывают лишь их притяжение к Солнцу. Но все
же воздействие других планет, главным образом соседних, немного изменяет
движение каждой планеты. Эти изменения невелики, но они позволили в свое
время сделать важное открытие, которое явилось триумфом ньютоновского закона
всемирного тяготения.
До середины прошлого века последней самой далекой известной планетой
был Уран. Наблюдения за движением планеты Уран показали, что эта планета
движется не совсем так, как она должна была бы двигаться, если бы на нее дейст-
вовали только силы притяжения к Солнцу и к другим известным планетам. Тогда
астрономы Адамс и Неверье предположили, что существует еще одна
планета, притяжение которой и является причиной того, что Уран движется не
так, как следовало ожидать.
Пользуясь законом всемирного тяготения, можно было вычислить, где
именно нужно искать эту неизвестную планету. В 1846 г. астроном Галле
действительно обнаружил в указанном месте новую планету, получившую наз-
вание Нептун. Как говорят астрономы, Нептун был открыт на кончике пера.
Позже было выяснено, что одного Нептуна недостаточно, чтобы объяснить
искажение движения планеты Уран, что должна существовать еще одна планета.
И опять удалось вычислить место на небесном своде, где нужно искать еще неиз-
вестную планету. В 1930 г. и эта планета, названная Плутоном, была найдена
и опять в том месте, которое было заранее вычислено.
Эти удивительные открытия показывают, насколько точен закон всемир-
ного тяготения.
Упражнение 35
1. Какая сила заставляет планеты двигаться вокруг Солнца?
2. Почему в выражения для ускорений планет и спутников (см. § 55) не вхо-
дят величины их масс?
3. Из наблюдений за движением планет знаменитый астроном Иоганн Кеп-
лер установил, что отношение квадрата периода обращения любой планеты
вокруг Солнца (Г2) к кубу радиуса ее орбиты (г3) одинаково для всех планет
(третий закон Кеплера). Докажите, что этот закон вытекает из закона все-
мирного тяготения Ньютона.
4. Найдите /лассу Солнца, если известны радиус орбиты Марса (7? = 228 млн.
км) и период его обращения вокруг Солнца (7 =687 сут.).
145
§ 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ
СИЛЫ ТРЕНИЯ
Сила трения скольжения отличается от всех других сил тем, что
она направлена в сторону, противоположную направлению отно-
сительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает
движущемуся телу, тоже направлено против относительной ско-
рости. А это значит, что действие силы трения приводит к умень-
шению абсолютного значения скорости тела относительно того
тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности,
никакие силы, кроме силы трения, не действуют, то оно в конце
концов останавливается. Рассмотрим этот часто встречающийся
случай.
Представим себе, что перед движущимся поездом неожиданно
появилось некоторое препятствие и машинист отключил двигатель
и включил тормоз. Начиная с этого момента на поезд действует
только сила трения, так как сила тяжести скомпенсирована реак-
цией рельсов, а сила сопротивления воздуха мала. Через некоторое
время t поезд, - пройдя расстояние L—так называемый тормозной
путь, остановится. Найдем время /, нужное для остановки, и рас-
стояние I, которое поезд пройдет за это время.
Под действием силы трения Атр поезд будет двигаться с уско-
Рп
рением а = —
т
Выберем координатную ось X так, чтобы ее положительное
направление совпадало с направлением скорости движения поезда
(рис. 140). Так как сила трения АТ|) направлена в противополож-
ном направлении, ее проекция на ось X отрицательна. Отрица-
тельна и проекция вектора ускорения на ось X. Поэтому если аб-
.* । I^tpI
солютное значение силы трения равно |гтр |, то ц=— .
Но ускорение определяется также формулой
где ц0 — скорость поезда до начала торможения.
а
Рис. 140
146
Так как нас интересует время t от начала торможения до оста-
новки поезда, то конечная скорость v = 0. Следовательно,
а=—- . t
Таким образом, ДTpl _ ^0_ т t
Отсюда Дтр|
А теперь найдем формулой тормозной путь l. Для этого воспользуемся и2 — = 2nZ.
Так как v — 0, то z=_J. 2а
Но т 2
следовательно, 2 т , mv0
или 1= —. 2|FTp|
Из этой формулы видно, что пройденный до остановки путь
пропорционален квадрату скорости. Если увеличить скорость
вдвое, то потребуется вчетверо больший путь для остановки. Это
следует иметь в виду машинистам поездов, водителям автомашин и
вообще всем, кто управляет транспортными средствами. Об этом
полезно помнить и прохожим, пересекающим оживленную улицу.
Для остановки движущихся тел нужно время и пространство.
Упражнение 36
1. Приведите примеры движения тел под действием одной только силы тре-
ния.
I. Как направлено ускорение, сообщаемое телу силой трения?
3. Можно ли считать движение под действием силы трения равноускорен-
ным?
4. Какие движения в природе происходят без участия сил трения?
5. Можно ли торможением мгновенно остановить тело?
6. От каких величин зависит путь, проходимый при торможении движущимся
телом до остановки? Как изменится этот путь при увеличении каждой из
этих величин вдвое?
147
7. С какой скоростью двигались аэросани, если после выключения двигателя
они прошли до остановки путь 250 м? Коэффициент трения принять рав-
ным 0,02.
8. Шофер автомобиля выключил двигатель и резко затормозил при скорости
72 км/ч. Сколько времени будет двигаться автомобиль до остановки, если
коэффициент трения равен 0,2? Какой путь он при этом пройдет?
§ 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ
НЕСКОЛЬКИХ СИЛ
В предыдущих параграфах этой главы мы выяснили, как дви-
жутся тела, если на них действует одна сила — сила упругости,
сила тяготения или сила трения. Но в действительности с такими
движениями в земных условиях почти никогда не приходится иметь
дело. Наряду с силами упругости и тяготения на тело всегда действует
и сила трения. Как в таких случаях решать механические задачи?
Напомним прежде всего, что в уравнении, выражающем второй
закон Ньютона,
та,
F — это равнодействующая всех сил, приложенных к телу, т. е.
геометрическая сумма векторов этих сил. Поэтому, приступая к ре-
шению какой-нибудь задачи, нужно сначала выяснить, какие силы
действуют на тело, каковы их абсолютные значения и направле-
ния. Затем, изобразив на чертеже действующие на тело силы,
найти их равнодействующую и, пользуясь законами движения
Ньютона, решить задачу.
Но можно и не производить геометрического сложения векто-
ров сил. В § 5 мы узнали, что проекция суммы нескольких векто-
ров на какую-нибудь ось равна сумме проекций этих векторов на
ту же ось. Это позволяет нам заменить геометрическое сложение
векторов алгебраическим сложением их проекций.
В качестве примера рассмотрим движение тела по наклонной
плоскости. Предположим, что по наклонной плоскости с углом
наклона а движется брусок массой т (рис. 141). Найдем его уско-
рение.
На движущийся брусок действуют три силы: сила тяжести
Fi = mg; сила реакции опоры (наклонной плоскости) F2, перпен-
дикулярная плоскости; сила трения F3, направленная против
движения.
Ускорение бруска а по условию направлено параллельно на-
клонной плоскости.
По второму закону Ньютона
+ (1)
148
Направим оси координат X и У вдоль наклонной плоскости и
перпендикулярно к ней, как показано на рисунке 141. Из равен-
ства (1) следует, что проекция вектора та на ось X или У равна
сумме проекций на эти оси векторов F1( F2 и Fs.
Найдем вначале проекции всех векторов на ось X. Ускорение
бруска направлено вдоль оси X, поэтому проекция вектора а рав-
на его модулю | а|. Проекция B6KTopaF2 равна нулю. Вектор F3 па-
раллелен оси X, но его направление противоположно направлению
оси. Поэтому проекция вектора F3 на ось X равна его модулю | F3|,
но взятому со знаком «—».
Проекцию вектора можно найти, воспользовавшись подо-
бием треугольников ABD и ЕОС (оба они прямоугольные, и углы
ADB и ECO равны, как углы, образованные взаимно перпендику-
лярными сторонами). Из подобия этих треугольников следует, что
Zir = Illi
ОЕ ЕС
Но ОЕ = h, а ЕС = L. Поэтому
Теперь, зная проекции всех векторов на ось X, мы можем за-
писать:
ma--ing~-—| F3!. (2)
149
Аналогичное уравнение можно записать и для проекций всех
векторов на ось Y. Проекции векторов а и F3 равны нулю, про-
екция вектора Р2 по модулю равна |F2|, а проекцию вектора мож-
но найти из подобия тех же треугольников ABD и ЕОС:
ВР _ АР
СО ~ ЕС '
Но BD — — Fiy (проекция силы F-i на ось Y отрицательна),
AD — mg, ОС = I и СЕ — L.
Следовательно, Г ?1у_ = FLF. .
Отсюда Fiy — — mg — .
L
Так как проекция ускорения а бруска на ось Y равна нулю, то
равна нулю и сумма проекций на эту ось всех сил, действующих
на брусок. Поэтому
0=-mgl + |/2|. (3)
Рассмотрим вначале случай, когда тело движется без трения
(коэффициент трения ц = 0). В этом случае из уравнения (2) найдем,
что
h
а = g- .
п
Отношение— всегда меньше единицы (катет меньше гипотенузы).
Значит, по наклонной плоскости тело движется с ускорением мень-
шим, чем ускорение g свободного падения. Чем более полога плос-
h
кость, тем меньше отношение — и тем меньше ускорение а.
Но часто силой трения пренебречь нельзя. Найдем поэтому
выражение и для величины j F31.
В § 49 было показано, что сила трения пропорциональна мо-
дулю силы давления N.
Поэтому можно написать, что
1^1 = РЙ.
В нашем случае сила давления равна, но противоположна по
направлению силе реакции опоры Следовательно, модуль силы
N равен просто модулю силы Р2. Из формулы (3) следует, что
|Л|
150
/ h I
a = g[-—^~
\ L>
Отсюда для силы трения |/’3| получаем:
I ЛI = ~ •
Подставив значение |F3| в уравнение (2), мы получим интересую-
щее нас ускорение
/г I
та = mg------ц/ng — ,
или (после сокращения на т)
(4)
Из треугольника ОСЕ видно, что
h I
— = sin а и — = cos а.
L L
Поэтому формулу (4) можно переписать в виде
а = g (sin а — р cos а).
Из этой формулы следует, что когда коэффициент трения равен
нулю (т. е. силой трения можно пренебречь),
а — g sin а.
Упражнение 37
1. Найдите построением геометрическую сумму сил, приложенных к бруску
на наклонной плоскости (по рис. 141). Как направлена равнодействующая
F этих сил относительно наклонной плоскости?
2. С вершины наклонной плоскости высотой 20 см и длиной 1 м соскальзы-
вает брусок. Определите скорость бруска в конце наклонной плоскости.
Трение не учитывать.
3. Санки скатываются с горки длиной 10 м за 2 сек. Найдите угол наклона
горки. Трение не учитывать.
4. Почему в формулы для ускорения тела на наклонной плоскости не входит
масса тела?
5. На наклонной плоскости высотой 5 м и длиной 10 м находится тело массой
50 кг, на которое действует сила
300 н (рис. 142). Определите ускорение
6. Вычислите ускорение тела, скользящего
сота и длина ее основания одинаковы,
а коэффициент трения тела о наклон-
ную плоскость равен 0,2.
7. Приведите примеры использования
наклонной плоскости. В чем ее полез-
ность в этих примерах?
8. Как будет двигаться тело по наклон-
ной плоскости, если проекция силы
тяжести на прямую, параллельную
наклонной плоскости, численно равна
силе трения?
равленная горизонтально и равная
тела. (Трением пренебречь.)
по наклонной плоскости, если вы-
§ 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ
ИЛИ В ЖИДКОСТИ
Интересным случаем прямолинейного движения тела под дей-
ствием двух сил является падение тела в газе или в жидкости. В
этом случае на тело действуют сила тяжести и сила сопротивления
газа или жидкости, с которой мы ознакомились в § 48.
Если пренебречь всеми другими силами, то можно считать, что
в тот момент, когда начинается падение тела (v = 0), на него дей-
ствует только сила тяжести mg. Сила же сопротивления отсутст-
вует. Но как только начнется движение тела, появится сила со-
противления — сила жидкого трения, которая растет вместе со
скоростью и направлена против нее.
Раз сила тяжести остается постоянной, а направленная в про-
тивоположную сторону сила сопротивления растет с увеличением
скорости тела, непременно настанет момент, когда их абсолютные
значения станут равными друг другу. Как только это произойдет,
равнодействующая обеих сил станет равной нулю. Нулю станет
равным и ускорение тела, и тело начнет двигаться с постоянной
скоростью. Так, например, парашютист довольно скоро после
прыжка с самолета начинает падать с постоянной скоростью; с по-
стоянными скоростями падают снежинки и дождевые капли.
Если тело падает в жидкости, нужно учитывать еще одну си-
лу, тоже направленную вверх, архимедову силу. Так как эта сила
Рис. 143
постоянна и не зависит от скорости, то
она не мешает установлению равномерного
движения падающего тела.
Движение тела в жидкости с постоян-
ной скоростью можно наблюдать на прос-
том опыте. Стеклянную трубку длиной
примерно 1 м закрывают снизу пробкой
и наполняют доверху водой или глицери-
ном. Затем в жидкость опускают стальной
шарик (рис. 143). Легко убедиться, что ша-
рик падает в жидкости равномерно. Это
можно увидеть, если на поверхность труб-
ки нанести краской деления и заметить рас-
стояния, проходимые шариком за равные
промежутки времени, отсчитываемые по
ударам метронома.
§ 62. НАКЛОН ТЕЛ
ПРИ ДВИЖЕНИИ
НА ПОВОРОТАХ
Как мы уже не раз видели, для того
чтобы тело двигалось по окружности, не-
обходимо, чтобы сила, приложенная к
152
Рис. 144
нему, была направлена к центру окружности. Если на тело действует
несколько сил, то к центру окружности должна быть направлена
равнодействующая этих сил.
В качестве примера рассмотрим движение железнодорожного
вагона на закруглении горизонтального пути (рис. 144).
Пока поезд движется по прямолинейному участку пути с по-
стоянной скоростью v, на любой вагон, конечно, действует сила
тяжести, но она уравновешивается направленной вверх силой
упругости рельсов. Что же касается силы трения, то она уравно-
вешивается силой тяги локомотива. Но вот вагон дошел до закруг-
ления пути. В этом месте он повернет и начнет двигаться по дуге
окружности. Какая же сила заставляет вагон изменять свою ско-
рость по направлению, т. е. двигаться с ускорением? Этой силой
является сила упругости (сила реакции), действующая на колеса
вагона со стороны рельса.
Колеса железнодорожных вагонов имеют так называемую ре-
борду, соприкасающуюся с рельсами не сверху, а сбоку (рис. 145).
Пока вагон движется по прямолинейному участку пути, реборда
особой роли не играет и деформируется
лишь та часть колеса, которая прилегает к
рельсу сверху. Пройдя точку А (рис. 146),
колесо, продолжая свое движение в преж-
нем направлении, действует на рельс ре-
бордой и деформирует его сбоку—рельс
выгибается наружу (деформируется, ко-
нечно, и сама реборда). При этом возникает
сила упругости F, направленная перпен-
дикулярно боковой поверхности рельса.
Эта сила и заставляет вагон двигаться по
окружности. Если бы колеса вагона не
имели реборд, такая сила не могла бы воз-
никнуть и вагон непременно сошел бы с
рельсов.
Ускорение вагона, движущегося со ско-
ростью v по закруглению радиусом г,
равно —. Поэтому сила упругости F, дейст-
153
вующая на реборду и вызывающая это ускорение, по второму
закону Ньютона должна быть равна:
ти1
г
где т — масса вагона.
Деформация рельса из-за действия реборд достигает как раз
такой величины, при которой сила упругости ^F|, вызванная этой
деформацией, сообщает вагону ускорение Деформация эта
очень мала и на глаз незаметна.
Часто для уменьшения сил давления на боковые поверхности
реборды и рельса и, стало быть, уменьшения их износа полотно
железной дороги на закруглениях делают слегка наклонным в сто-
рону центра закругления (рис. 147). В этом случае сила, направ-
ленная к центру, возникает также из-за того, что равнодействую-
щая Fx силы тяжести mg и силы упругости (реакции рельсов) N,
перпендикулярной верхним поверхностям рельсов, тоже направ-
лена к центру. Это, конечно, «облегчает» поворот в том смысле,
что уменьшается сила упругости F, действующая со стороны рельса
на реборду. Действительно, теперь то же центростремительное
и1
Рис. 147
ускорение ~ вагону сообщают две силы:
F и Flt поэтому
Й + l^tl
— ♦
г т
откуда
|А =7-а-| Al-
Отсюда видно, что сила, действующая на
реборду, теперь стала меньше на величи-
ну (FJ. Поэтому меньшим будет износ
рельса и реборды.
154
Рассмотрим еще, как движется на закруг-
лении пути велосипедист. В этом случае по-
ворот обеспечивается совместным действием
—Э"
силы реакции (силы упругости) N со стороны
дороги, силы трения FTp и силы тяжести
mg велосипедиста (вместе с велосипедом).
Чтобы равнодействующая сила была направ-
лена к центру, велосипедист наклоняется в
сторону поворота (рис. 148. На рисунке
Q = FTp + N). Так как в вертикальном нап-
равлении велосипедист не перемещается, то
N— —mg. Это означает, что равнодействующая
всех сил, действующих на велосипедиста,
равна силе трения Лтр. Умелый велосипедист
инстинктивно наклоняется ровно настолько,
чтобы равнодействующая сила (в данном слу-
чае сила трения покоя FTp) была равна —. Излишний или недо-
статочный наклон приведет к тому, что поворот не удастся и вело-
сипедист упадет;
Наклоняются в сторону поворота мотоциклисты, всадники,
конькобежцы и т. д.
Рис. 148
Упражнение 38
1. Почему спринтер, велосипедист и конькобежец при большой скорости
движения наклоняются при повороте?
2. Равнодействующая каких сил сообщает центростремительное ускорение
железнодорожному вагону, проходящему закругление пути?
3. Какая сила сообщает вагону центростремительное ускорение при отсутст-
вии наклона полотна дороги?
4. Поезд движется по закруглению радиусом 500 м. Ширина железнодорож-
ной колеи 1 524 мм. Наружный рельс расположен на 12 см выше внутренне-
го. При какой скорости движения поезда на закруглении реборды колес
не оказывают давления на рельсы?
5. Конькобежец движется по закруглению ледяной дорожки радиусом 10 м
со скоростью 5 м/сек. Под каким углом к горизонту он наклоняется, про-
ходя этот поворот? (См. таблицу на стр. 124.)
§ 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ
ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС
И ЦЕНТР ТЯЖЕСТИ
Изучая движение тел под действием различных сил, мы пока
не обращали внимания на то, что тела имеют размеры. Определяя
ускорение тел, мы считали их материальными точками.
Такое упрощение верно, если все точки тела перемещаются оди-
наково, т. е. если тело движется поступательно. Надо, однако, выяс-
нить, к какой точке тела должна быть приложена сила для того,
155
Рис. 149
Рис. 152
Рис. 153
чтобы его движение было дей-
ствительно поступательным.
Проведем такой опыт.
Возьмем широкую линейку.
Прикрепим к ее концу в точ-
ке А нить и потянем за эту
нить в направлении, перпен-
дикулярном оси линейки
(рис. 149). Линейка при этом
повернется. При таком пово-
роте разные точки линейки
проходят различные пути и
движутся с различными ско-
ростями, т. е. их движения
неодинаковы и линейка дви-
жется не поступательно.
Изменим теперь направ-
ление силы: будем тянуть
линейку вдоль ее длины
вправо (рис. 150, а). Теперь
линейка движется так, что
все ее точки имеют одинако-
вые скорости и проходят оди-
наковые пути. Такое движе-
ние является поступатель-
ным. Если сила F не урав-
новешена другими силами,
тело движется с ускорением.
Нетрудно убедиться в том,
что если нить прикреплена
к точке А, . то существует
только одна прямая, вдоль
которой должна быть нап-
равлена сила, чтобы она вы-
звала поступательное движе-
ние линейки. При действии
силы в любом другом направ-
лении будет происходить по-
ворот линейки.
Можно изменить направле-
ние силы на противоположное,
прикрепив нить к точке В
(рис. 150, б). Движение линей-
ки опять будет поступатель-
ным. Значит, важно лишь по-
ложение прямой, вдоль кото-
рой сила действует (линия
действия силы).
155
Прикрепим теперь нить в какой-нибудь другой! точке линейки,
например в точке С (рис. 151). Будем опять менять направления
натяжения нити (на рисунке некоторые направления показаны
прямыми, исходящими из точки С). Мы снова убедимся в том, что
линейка совершает поступательное движение только в том случае,
если сила направлена вдоль некоторой определенной прямой. На
рисунке это направление силы показано жирной линией. При всех
других направлениях силы, приложенной к точке С, линейка бу-
дет непременно поворачиваться.
Прикрепляя нить к другим точкам линейки, мы можем убедить-
ся в том, что в каждой точке всегда есть одно направление силы,
при котором линейка движется поступательно, без поворотов. На
рисунке 152 показано, как должны быть направлены силы, прило-
женные в разных точках линейки, чтобы она двигалась поступа-
тельно. Опыт показывает, что прямые, вдоль которых действуют
эти силы, сходятся в одной точке 0.
Подобные опыты с разными телами приводят нас к важному
выводу о том, что в каждом теле существует такая точка, в которой
пересекаются направления действия сил, сообщающих телу посту-
пательное движение. Эта точка получила название центра
масс. Всякая же сила, которая действует вдоль прямой, не
проходящей через центр масс, вызывает поворот тела.
Центром масс называют точку пересечения прямых, вдоль ко-
торых должны быть направлены силы, чтобы тело двигалось по-
ступательно.
В опыте с линейкой легко убедиться в том, что центр масс со-
впадает с точкой пересечения диагоналей. Но это только в том слу-
чае, если линейка однородна (изготовлена из одного материала),
имеет правильную форму и одинаковую толщину. Если бы, на-
пример, она была изготовлена наполовину из дерева, а наполовину
из стали, центр масс находился бы где-то в «стальной» половине,
т. е. ближе к той части, которая имеет большую массу.
Положение центра масс определяется, как показывает опыт,
тем, как распределена масса тела по его объему.
Центр масс может оказаться и вне тела. Ясно, например, что
поступательное движение однородного обруча (рис. 153) возмож-
но только в том случае, если приложенная к нему сила направле-
на по радиусу, Линии действия таких сил сходятся, конечно, в
геометрическом центре обруча. Там и находится его центр
масс.
Если различные части обруча изготовлены из разных материа-
лов, то центр масс может оказаться и в другом месте. Тогда его
нужно искать опытным путем. Существуют, правда, способы вы-
числения координат центра масс, но они трудны, а иногда вычис-
ление и невозможно.
Но зачем нужно знать положение центра масс? Дело в том, что
если тело движется поступательно под действием одной силы Или
нескольких сил, то это значит, что эта сила или равнодействующая
157
всех сил проходит через центр масс тела. Центр масс тела в этом
случае движется так, как будто в нем сосредоточена вся масса
тела и к нему приложены все силы, действующие па тело. Поэтому,
когда мы видим, что тело движется поступательно, то это значит,
что равнодействующая сил, приложенных к телу, проходит через
его центр масс. Как будто в центре масс сосредоточена вся мас-
са тела, а ускорение тела — это ускорение центра масс. Таким
образом, вместо того чтобы рассматривать движение тела, мы
рассматриваем движение материальной точки — центра масс
тела. Так мы и поступали, ничего об этом не говоря, в преды-
дущих главах книги.
Частным случаем поступательного движения является движе-
ние тела под действием силы тяжести, если, конечно, оно не было
приведено во вращение до начала падения. Но сила тяжести дейст-
вует на все точки тела. И если под действием всех этих сил тело
движется поступательно, то это значит, что их равнодействующая
при любом положении тела проходит через его центр масс. Поэто-
му центр масс часто называют и центром тяжести тела.
§ 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ
МЕХАНИКИ НЬЮТОНА
Оглядываясь на все уже изученные темы, мы должны в первую
очередь обратить внимание на основные идеи механики.
Первая идея состоит в том, что если на тело не действуют
силы или равнодействующая всех сил равна нулю, то оно находит-
ся в покое или движется с постоянной по величине и направлению
скоростью. Если же тело движется с ускорением, то это движение
непременно происходит под действием силы. Невозможны покой
или равномерное прямолинейное движение при наличии силы, не-
возможно ускоренное движение без действия силы.
Вторая основная идея механики состоит в том, что сила
создается каким-нибудь телом, далеким или близким, большим
или малым. С этим телом может быть непосредственный контакт,
но может и не быть контакта. Но за каждой силой непременно «скры-
вается» какое-то тело или несколько тел.
В этих двух идеях заключена вся суть механики Ньютона.
Но всегда ли приведенные только что основные утверждения
верны? Чтобы ответить на этот вопрос, рассмотрим мысленный
опыт, который можно было бы провести и на самом деле. (Частич-
но об этом было сказано в § 28.)
На железнодорожной платформе, прицепленной к локомотиву
и имеющей переднюю и заднюю стенки, находится пассажир. До-
пустим, что пол платформы сделан из очень твердого и гладкого
материала, а пассажир стоит на роликах, способных катиться с
очень малым трением (рис. 154). Допустим также, что пассажир
оставил своего приятеля на станции для того, чтобы он наблюдал
за явлениями на платформе. И вот платформа «тронулась», т. е.
158
стала двигаться с ускорением. Оставшийся на станции неподвиж-
ный наблюдатель увидит, что пассажир, после того как платформа
«тронулась», остался стоять на месте, просто пол платформы уходит
из-под него. Зная законы механики, этот наблюдатель скажет, что
так оно и должно быть. Пассажир остается в покое, потому что дей-
ствующие на него силы — сила тяжести и сила упругости плат-
формы — направлены по вертикали и компенсируют друг друга.
И только тогда, когда к пассажиру вплотную придвинется задняя
стенка, он начнет двигаться вместе с платформой. Это тоже согла-
суется с законами механики: стенка при своем движении, придя
в соприкосновение с пассажиром, взаимодействует с ним и деформи-
руется. В результате возникает сила упругости, которая сообщает
пассажиру ускорение, равное ускорению платформы.
Совсем иначе рисуется положение пассажиру, стоящему на ро-
ликах. Пассажир увидит, что он сам вдруг начал двигаться отно-
сительно платформы к задней ее стенке. И движется с некоторым
ускорением. С его точки зрения, это не согласуется с законами меха-
ники. Он просто станет в тупик, если попытается выяснить, какое
тело сообщило ему ускорение. Такого тела он обнаружить не смо-
жет. Кто же из двух наблюдателей прав?
Дело тут, конечно, не в личных особенностях наблюдателей,
а в тех системах отсчета, относительно которых рассматривается
движение. Наблюдатель на остановке говорит о движении относи-
тельно Земли, которую он считает неподвижной системой отсчета.
Пассажир же на платформе имеет в виду движение относительно
системы отсчета, связанной с платформой, которая движется с ус-
корением относительно Земли. Все дело именно в ускоренном дви-
159
женин одной системы отсчета, т. е. платформы, относительно дру-
гой системы отсчета — Земли.
Законы механики Ньютона выполняются только при условии,
что движения рассматриваются относительно некоторых определен-
ных систем отсчета.
В таких системах отсчета тела при отсутствии сил не получают
ускорения (пассажир стоит на месте, к нему приближается стенка
платформы). А если тела в этих системах отсчета получают ускоре-
ние, то на них действуют силы со стороны других
тел (задняя стенка платформы коснулась пассажира, и он стал
двигаться ускоренно вместе с платформой).
В системе же отсчета, связанной с платформой, наоборот, зако-
ны механики неверны. Относительно этой системы пассажир дви-
жется с ускорением, когда на него не действуют другие тела. А
когда сила в действительности появляется (сила упругости задней
стенки), пассажир останавливается и не имеет ускорения. При-
чиной невыполнения в этой системе отсчета законов Ньютона яв-
ляется ее ускоренное движение относительно системы отсчета, в
которой эти законы выполняются, т. е. относительно Земли. Дей-
ствительно, как только платформа, набрав скорость, станет дви-
гаться равномерно, пассажир на роликах уже не будет катиться
назад. Законы механики вступают в силу.
Если законы Ньютона верны при рассмотрении движения от-
носительно одной системы отсчета, то они верны и относительно
любой другой системы отсчета, которая сама движется относи-
тельно первой равномерно и прямолинейно.
Таких систем отсчета бесчисленное множество. Как мы уже зна-
ем из четвертой главы, все они называются инерциальными
системами отсчета. Во всех инерциальных системах отсчета зако-
ны движения одинаковы. Это так называемый принцип
относительности Галилея.
Все системы отсчета, которые движутся относительно инерци-
альной системы ускоренно, называются неинерциальны-
м и, так как в них закон инерции не выполняется, как не выполня-
ется и второй закон Ньютона.
Упражнение 39
1. К потолку вагона подвешен грузик на нити (маятник). Что произойдет с
маятником при торможении вагона? Как это явление объясняют: а) наблю-
датель, находящийся на платформе; б) наблюдатель, находящийся в ва-
гоне?
2. Можно ли, находясь в каюте с закрытым иллюминатором и наблюдая за
грузиком, подвешенным к потолку каюты, определить скорость движения
парохода? Ускорение парохода?
3. Как по углу отклонения маятника, подвешенного в вагоне, определить ус-
корение вагона?
4. Придумайте устройство, которое нужно прикрепить к телу, чтобы оно поз-
волило измерить его ускорение.
5. Проведите рассуждения, аналогичные приведенным в этом параграфе, для
случая, когда платформа движется равномерно по окружности.
160
САМОЕ ГЛАВНОЕ В РАЗДЕЛЕ
«ДИНАМИКА»
Вся динамика содержится в трех законах Ньютона.
Первый закон Ньютона утверждает, что существуют
такие системы отсчета (инерциальные системы), относительно
которых тела движутся прямолинейно и равномерно, если на них не
действуют силы или если сумма всех сил равна нулю.
Ускорение телам сообщают силы, которые являются следствием
действий на них других тел.
Второй закон Ньютона выражает связь между силами
и вызванными ими ускорениями:
а = ? .
т
Сила, действующая на тело, зависит от его положения или ско-
рости относительно тех тел, с которыми оно взаимодействует. За-
висимость эта устанавливается из опыта.
Третий закон Ньютона состоит в том, что силы, с кото-
рыми два тела действуют друг на друга, всегда равны друг другу по
абсолютному значению и противоположны по направлению и явля-
ются силами одной природы.
В механике изучаются три типа сил: силы упругости, силы тре-
ния и гравитационные силы (силы всемирного тяготения).
Сила — величина векторная. Поэтому силы складываются гео-
метрически.
Законы Ньютона выполняются в инерциальных системах от-
счета. Относительно неинерциальных систем отсчета тела мо-
гут двигаться с ускорением и при отсутствии сил, вызванных дей-
ствием каких-либо тел.
Законы Ньютона перестают быть верными, когда скорости тел
становятся близкими к скорости света. Они неприменимы также к
движениям частиц, из которых состоят атомы веществ.
Механика Ньютона — это механика тел, движущихся со ско-
ростями, малыми по сравнению со скоростью света.
6 Злк-n
Равновесие тел
Глава 7
Элементы статики
ВВЕДЕНИЕ
Мы уже знаем, что законы Ньютона позволяют узнать, какие
ускорения получают тела под действием приложенных к ним сил.
Но очень часто бывает важно знать, при каких условиях те-
ла, на которые могут действовать различные силы, не получают
ускорений. О таких телах говорят, что они находятся в состоянии
равновесия. В таком состоянии, в частности, находятся покоя-
щиеся тела.
Знать условия, при которых тела находятся в покое, очень
важно для практики. Это нужно знать, например, при постройке
зданий, мостов, всевозможных опор, подвесов, при изготовле-
нии машин и приборов.
Недопустимо, конечно, чтобы, например, башня телевизионно-
го центра в Останкине (Москва), которая должна незыблемо сто-
ять на своих опорах, могла под порывом ветра получить ускоре-
ние и сместиться с этих опор. И законы Ньютона позволяют нам
выяснить, какие именно условия обеспечивают равновесие, и преж-
де всего состояние покоя тела.
Часть механики, в которой изучается равновесие тел, называют
статикой.
Известно, что всякое тело может двигаться поступательно и,
кроме того, вращаться или поворачиваться вокруг какой-нибудь
оси. Понятно, что при равновесии не должно изменяться ни по-
ступательное, ни вращательное движение тела. В частности, если
требуется, чтобы тело находилось в покое, оно не должно ни дви-
гаться поступательно, ни вращаться или поворачиваться вокруг
какой-нибудь оси.
Рассмотрим условия равновесия тел для этих двух видов воз-
можного движения по отдельности.
162
§ 65. РАВНОВЕСИЕ ТЕЛ
ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ
При поступательном движении все точки тела движутся одина-
ково. Поэтому такое движение можно рассматривать как движение
одной точки тела — его центра масс. При этом мы должны считать,
что в центре масс сосредоточена вся масса тела и к нему приложена
равнодействующая всех сил, действующих на тело. Из второго зако-
на Ньютона следует, что ускорение этой точки равно нулю, если
геометрическая сумма всех приложенных к ней сил — равнодейст-
вующая этих сил — равна нулю. Это и есть условие равновесия
тела при отсутствии вращения.
Для того чтобы тело при отсутствии вращения находилось в
равновесии, необходимо, чтобы равнодействующая сил, приложен-
ных к телу, была равна нулю.
Но если геометрическая сумма сил равна нулю, то и сумма
проекций векторов этих сил на любую ось тоже равна нулю. По-
этому условие равновесия тела можно сформулировать и так:
Для того чтобы тело при отсутствии вращения находилось в
равновесии, необходимо, чтобы сумма проекций приложенных к телу
сил на любую ось была равна нулю.
В равновесии, например, находится тело, к которому, как на
рисунке 155, приложены две равные силы, действующие вдоль
одной прямой, но направленные в противоположные стороны.
Состояние равновесия — это не обязательно состояние покоя.
Согласно второму закону Ньютона при равенстве нулю равнодейст-
вующей всех сил, приложенных к телу, оно может двигаться прямо-
линейно и равномерно. При таком движении тело тоже находится
в состоянии равновесия. Например, парашютист, после того как
он начал падать с постоянной скоростью, находится в состоянии
равновесия.
На рисунке 155 силы приложены к телу не в одной точке. Но
мы уже видели, что важна не точка приложения силы, а прямая,
вдоль которой она действует. Перенос точки приложения силы
вдоль линии ее действия ничего не изменяет ни в движении тела,
ни в состоянии равновесия. Ясно, например,
что ничего не изменится, если, вместо того
чтобы тянуть вагонетку, как это показано на
рисунке 156, а, еестанут толкать (рис. 156, б).
Если равнодействующая сил, приложен-
ных к телу, не равна нулю, то, для того
чтобы тело находилось в состоянии равнове-
сия, к нему должна быть приложена добавоч-
ная сила, равная по модулю равнодействую-
щей, но противоположная ей по направле-
нию.
Поясним это на опыте. Прикрепим к
двум точкам верхней перекладины рамы ди-
6*
163
намометры 1 и 2 (рис. 157).
При помощи нитей в точ-
ке О прикрепим груз. Под действием трех сил Fx, F2 и F3 = mg
точка О будет находиться в равновесии. Теперь заменим силы, дей-
ствующие на точку О со стороны двух динамометров, одной силой.
Для этого прикрепим к точке О еще один динамометр 3 и потянем
его вверх. Когда стрелки динамометров 1 и 2 установятся на нуле
шкалы, на точку О будут действовать только две силы. Одна из
них — сила упругости пружины динамометра 3, измеряемая этим
динамометром, — является равнодействующей сил и F2. Сила
тяжести груза Fs = mg равна этой равнодействующей по абсолют-
ной величине и направлена в противоположную сторону. Поэтому
точка О находится в равновесии.
Рассмотрим еще один пример. Как удержать в равновесии лод-
ку, на которую действуют течение реки и ветер, дующий от берега
(рис, 158)? Найдем равнодействующую F сил и К2, вызванных
ветром и течением воды. Для этогд восполь-
зуемся правилом параллелограмма. Диаго-
наль параллелограмма дает величину и направ-
6= vg
Рис. 157
164
ление равнодействующей F. Для того чтобы лодка была в равнове-
сии, к ней должна быть приложена уравновешивающая сила Fy,
равная этой равнодействующей, но направленная в противополож-
ную сторону. Такой силой, например, может быть сила натяжения
каната, прикрепленного одним концом к носу лодки, а другим к
берегу. Если, например, сила, с которой текущая вода действует
на лодку, равна 150 н, а сила давления ветра равна 100 н, то равно-
действующая этих двух взаимно перпендикулярных сил может
быть вычислена по теореме Пифагора:
| F\ = /(100 н)2 + (150 н)2 « 180 н.
Лодка, следовательно, может быть удержана канатом, способ-
ным выдержать натяжение не менее 180 н.
Задача. Груз массой 100 кг подвешен к кронштейну (рис. 159, а),
который состоит из поперечной балки АВ и укосины ВС. Опреде-
лите силы упругости, возникающие в балке и укосине, если АВ =
= 48 см, АС = 64 см.
Решение. Прежде всего выясним, каково происхождение
сил, действующих па части кронштейна.
Под действием силы тяжести груз начинает падать вертикально
вниз. При этом он увлекает за собой конец В балки. Ясно, что бал-
ка и укосина вследствие этого деформируются: балка удлиняется,
а укосина сжимается (рис. 159, а). В деформированных частях
кронштейна возникают силы упругости, направленные в сторону,
противоположную деформации. Эти силы и нужно определить. На
рисунке 159 вектор изображает силу упругости в сжатой укоси-
165
не, а вектор Р2 — силу упругости в растянутой балке. Эти силы
действуют на точку В, к которой подвешен груз.
Деформации балки и укосины будут увеличиваться до тех пор,
пока равнодействующая сил Fx и F2 не уравновесит силу тяжести
F3 = тё- Тогда точка В будет находиться в равновесии. Следова-
тельно, равнодействующая трех сил, приложенных к точке В:
силы тяжести F3 = mg, силы F2 и силы Fx, равна нулю:
?1+?2+?з = 0.
Равна нулю и сумма проекций этих сил на любую ось.
Направим ось X по горизонтали
вправо (рис. 159, б), а ось Y
по вертикали вверх. Сила f 3 направ-
лена по вертикали, поэтому ее про-
екция на ось X равна нулю. Проекция
силы F2 на ось X равна модулю векто-
ра F2, взятому со знаком «—». Проек-
ция силы F± на ось X равна | Fx | cos а.
Тогда можно записать:
| Fi | cos а — | F21 = О,
или
| F11 cos a — | A|. (1)
Проекции всех сил на ось Y найдем
S
Рис. 153
таким же образом. Проекция силы F2
равна нулю, проекция силы F3 равна
—mg, а проекция силы равна
iFJsina. Поэтому
| f\ | sin a — mg = О,
или
| Fi | sin a = mg. (2)
Из уравнений (1) и (2) нетрудно най-
ти силы Fx и F2.
Значение |FX| найдем непосредст-
венно из уравнения (2):
sin a
Подставив это значение | Fx | в урав-
нение (1), получим:
166
(Aj = -^cosa. (4)
sin a
Из треугольника ABC видно, что
AC AC
sina = — = -r ,
вс УАв2+ас2
AB AB
cos a = — = - r.-~-— —
BC / AB2 + AC2
(согласно теореме Пифагора ВС = /АВ2 -)- ЛС2)-
Перепишем формулы (3) и (4) с учетом этих соотношений:
IАI = mg = mg v Ав' + 4С2-.,
гЮ riG
. -. АВ ВС АВ
|f-l = mgK- x = mgTc-
Подставив значения т, АВ и АС из условия задачи, найдем:
IА | « 100 кг • 10 — — = 750 н,
сек2 64 см
IА I « 100 кг • 10 — . К482_+6Р см = 1250 н_
сек2 64 см
Упражнение 40
1. Груз перемещают с постоянной скоростью по горизонтальной поверхности
двумя канатами, к которым прикладывают силы по 500 н. Канаты образуют
между собой угол 60°, Определите равнодействующую силу. Как изменяет-
ся величина равнодействующей в зависимости от угла между канатами? Рас-
смотрите случаи, когда угол равен 0, 90, 120 и 180°.
2. На кронштейне подвешен фонарь массой 2 кг (рис. 160). Определите силы
упругости, возникающие в горизонтальной балке АВ и в укосине кронштей-
на ВС. Угол 4СВ равен 30°.
3. Шар массой'З кг висит на веревке, прикрепленной к гладкой стене (рис. 161).
Определите силу натяжения веревки и силу давления шара на стену. Нить
образует со стеной угол 15°,
Рис. 160
Рис. 161
167
А. К середине троса длиной 20 м подссшсн светильник массой 3,4 <:г, „след-
ствие чего трос провис на 5 см. Определите силы упругости, возникшие в
тросе.
5. На наклонной плоскости лежит ящик массой 30 кг. Будет ли ящик соскаль-
зывать вниз, если коэффициент трения ящика о наклонную плоскость ра-
вен 0,2? Длина наклонной плоскости 6 м, высота 2 м.
6. Антенная мачта (рис. 162) закреплена оттяжкой АВ, образующей угол 30°
с мачтой. Сила, с которой антенна действует на мачту в точке В (натяжение
антенны), равна 1 000 н. Чему равна сила, сжимающая мачту, и сила, дей-
ствующая на оттяжку?
§ 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ
ОСЬЮ. МОМЕНТ СИЛЫ
В предыдущем параграфе были выяснены условия равновесия
тела при отсутствии вращения. Но как обеспечивается отсутствие
вращения тела, т. е. его равновесие, когда на него действуют силы?
Чтобы ответить на этот вопрос, рассмотрим тело, которое не
может совершать поступательного движения, но может поворачи-
ваться или вращаться. Чтобы сделать невозможным поступательное
движение тела, его достаточно закрепить в одной точке так, как
можно, например, закрепить доску на стене, прибив ее одним гвоз-
дем; поступательное движение такой «пригвожденной» доски ста-
новится невозможным, но доска может поворачиваться вокруг
гвоздя, который служит ей осью поворота.
Выясним, при каких условиях покоящееся тело с закрепленной
осью не будет поворачиваться под действием приложенных к нему
сил. Представим себе некоторое тело, к которому в разных точках
приложены две силы: F\ и F2 (рис. 163, а). Чтобы найти равнодей-
ствующую этих сил, перенесем точки их приложения в точку А
(рис. 163, б), в которой пересекаются линии действия обеих сил.
Построив параллелограмм на силах FY и F2, получим их равнодей-
ствующую F.
Теперь предположим, что в какой-то точке 0 на линии, вдоль
которой направлена равнодействующая F, проходит закрепленная
ось, перпендикулярная плоскости чертежа. Мы можем себе, на-
пример, представить, что в точке О сквозь тело проходит гвоздь,
вбитый в неподвижную стену. Тело в этом случае будет находиться
в покое, потому что равнодействующая F уравновешивается силой
реакции (упругости) со стороны закрепленной оси (гвоздя): обе они
направлены вдоль одной и той же прямой, равны по абсолютной
величине и противоположны по направлению.
Предположим теперь, что одна из сил, например F2, перестала
действовать, так что тело подвергается действию только одной силы
Fr (рис. 163, в). Из рисунка видно, что эта сила заставит тело вра-
щаться вокруг оси О по часовой стрелке. Если, наоборот, устранить
168
Рис. 163
силу F1; то оставшаяся сила F2 вызовет вращение против часовой
стрелки (рис. 163, г). Значит, каждая из сил F± и F2 обладает вра-
щающим действием, причем эти действия характеризуются проти-
воположными направлениями. Но когда обе силы действуют сов-
местно, их вращающие действия взаимно друг друга компенсируют:
вместе они поворота не вызывают. Поэтому следует считать, что,
хотя силы /4 и F2 сами по себе различны как по величине, так и по
направлению, их вращающие действия одинаковы, но противопо-
ложны по направлению.
Попытаемся найти величину, которая характеризует вращаю-
щее действие силы. Мы пока знаем только, что она должна иметь
одинаковые численные значения для обеих сил: Ft и F2.
Обратимся к рисунку 163, д. Силы Fx и F2 неодинаковы по абсо-
лютным значениям: (FJ больше fF2[. Зато расстояние dr от точки О
(оси) до линии действия силы Fx меньше расстояния d2 от оси до
линии действия силы F2. Таким образом, [FJ > |F2[, но dY < d2.
Быть может, равны между собой произведения | FJ dt и | F21 <7.,?
169
Если это так, то можно будет сказать, что величина, равная
произведению силы па длину перпендикуляра, опущенного с за-
крепленной оси на линию действия силы, как раз и характеризует
вращающее действие силы.
Нетрудно доказать, что равенство
| | = | /^2 I ^2
действительно выполняется. Для этого проведем на рисунке 163, д
вспомогательные прямые ОС и ОВ, параллельные силам Ft и Е2-
Из подобия треугольников АВО и АВ'О' следует, что
АВ' _ АВ
В'О' ~ ВО '
Отсюда, учитывая, что АВ — ОС, получаем:
1^1 в0 ’
Рассмотрим теперь треугольники ОВК. и ОСЬ. Эти треугольники
подобны, как прямоугольные с равными углами при вершинах С
и В (они дополняют равные углы АСО и АВО до 180°). Из их подо-
бия следует, что
ОС = OL = Щ 2
ВО OK di '
Сравнивая пропорции (1) и (2), получаем:
। ЛI t
\f\\ dl’
или
Сделанное выше предположение оправдалось.
Приведенное довольно длинное геометрическое рассуждение1 2
позволило нам найти величину, которая одинакова для обеих сил
и характеризует вращающее действие силы. Такой величиной яв-
ляется произведение силы на расстояние от линии ее. действия до
оси вращения. Величина эта носит несколько странное название —
момент силы или вращающий момент* относитель-
но оси, проходящей через точку О.
Если обозначить момент силы F буквой М, а расстояние от оси
вращения до линии ее действия буквой d, то можно написать:
М = | F | d.
1 Статику часто так и называют: «геометрия сил».
2 Слово «момент» в этом названии происходит от латинского слова movi-
mentum, обозначающего «движущая способность». К понятию «момент времени»
это слово отношения не имеет.
170
Заметим, что величина d тоже имеет особое название. Ее назы-
вают плечом силы.
Для новой величины — момента силы — нужно, конечно, найти
единицу измерения. Из выражения
Л4 = |F|d
видно, что момент силы М равен единице, если и сила F равна
единице, и плечо d равно единице. Значит, за единицу вращающего
момента в системе СИ нужно принять момент силы в 1 н, линия
действия которой отстоит от оси вращения на 1 м. Эту единицу
называют ньютон-метром (н • м):
1 н м = 1 н 1 м.
Из курса физики VI класса известно, что в ньютон-метрах выра-
жают работу. Работу, равную 1 н • м, называют джоулем.
Момент силы, следовательно, измеряется в таких же единицах,
как и работа, но единицу момента силы не принято называть джо-
улем, с тем чтобы отличать момент силы от работы силы.
В системе СГС единицей момента силы является дина-сантиметр
(дин • см):
1 дин см — 1 дин 1 см.
§ 67. ПРАВИЛО МОМЕНТОВ
Из того, что было сказано в предыдущем параграфе, становится
ясно, почему тело при условиях, показанных на рисунке 163, б,
находится в равновесии.
Поступательно тело не может двигаться, потому что ось за-
креплена. Поворачиваться же оно не может потому, что моменты
сил F± и F2 равны друг другу по абсолютному значению, но одна си-
ла может повернуть тело по часовой стрелке, а другая — против.
И если приписать моментам сил, вращающим это тело в противо-
положных направлениях, разные знаки, то алгебраическая сумма
этих двух моментов окажется равной нулю.
Тело, способное вращаться вокруг закрепленной оси, находится
в равновесии, если сумма моментов сил относительно закреплен-
ной оси, вращающих тело по часовой стрелке, равна сумме мо-
ментов сил относительно той же оси, вращающих его против ча-
совой стрелки.
Это и есть правило моментов — условие равновесия
тела, имеющего закрепленную ось вращения.
Момент силы зависит от двух величин: от значения самой силы
и длины плеча. Один и тот же момент силы может быть создан ма-
лой силой, плечо которой велико, и большой силой с малым пле-
чом. Если, например, пытаться закрыть дверь, толкая ее поблизо-
171
сти от петель, то этому с успехом смо-
жет противодействовать ребенок, кото-
рый догадается толкать ее в другую сто-
рону, приложив силу поближе к краю,
и дверь останется в покое (рис, 164).
В справедливости правила моментов
можно убедиться на опытах, которые
проводятся с прибором, изображенным
на рисунке 165. Он представляет собой
диск А, укрепленный на оси, проходя-
щей через его центр. На диске нанесены
окружности, радиусы которых последо-
вательно увеличиваются на 1 см, так
что радиус первой, ближайшей к цент-
ру окружности равен 1 см, Второй —
2 см и т. д. На окружностях по нескольким диаметрам диска вбиты
гвоздики, к которым можно привязывать нити с гирями. Нити пе-
реброшены через блоки В и С. Привязывая нити к гвоздикам на
разных окружностях и подвешивая к ним различные грузы, соз-
дают различные моменты сил, действие которых можно уравнове-
сить моментом силы тяжести третьего груза, подвешенного непо-
средственно к диску. При этом легко убедиться, что диск находит-
ся в равновесии, т. е. не поворачивается, когда алгебраическая
сумма моментов всех трех сил равна нулю.
Величина момента силы, с которым действует каждый из гру-
зов, определяется произведением силы тяжести груза на длину пер-
пендикуляра, опущенного из центра диска на нить. Длина же этого
перпендикуляра, выраженная в сантиметрах, равна номеру окруж-
ности, которой касается нить в точке, куда опущен перпендикуляр.
Рис. 165
172
Рис. 166
0,6 м
Нетрудно понять, что из правила моментов следует знаменитое
правило рычага: рычаг находится в равновесии, когдадей-
ствующие на него силы обратно пропорциональны плечам. Но это
не что иное, как другое выражение правила моментов! Не следует
думать, что к рычагу должны быть приложены обязательно парал-
лельные силы. На рисунке 166 показан пример рычага, к которому
приложены взаимно перпендикулярные силы Fr и F2.
Теперь мы можем сформулировать общее условие равновесия
тела:
Для того, чтобы тело находилось в равновесии, необходимо,
чтобы были равны нулю геометрическая сумма приложенных к телу
сил и сумма моментов этих сил относительно оси вращения.
Задача. Однородный стержень массой 2 кг прикреплен своим
нижним концом к шарниру (рис. 167). К другому его концу подве-
шен груз массой 2 кг. Стержень удерживается в равновесии гори-
зонтальной оттяжкой, прикрепленной к неподвижной вертикаль-
ной стойке. Пользуясь числами, указанными на рисунке, найдите
силу натяжения оттяжки.
Решение. На стержень действуют четыре силы: сила тяже-
сти, приложенная к его середине, сила тяжести груза mg, сила FL
упругости оттяжки и сила F2 упругости в шарнире. Осью вращения
служит шарнир у нижнего конца стержня. Из перечисленных сил
только первые три создают вращающие моменты относительно этой
оси. Линия действия силы реакции в шарнире проходит через ось
шарнира, и ее момент равен нулю. Из трех указанных сил только
одна сила упругости оттяжки поворачивает стержень против
часовой стрелки. Две другие вращают его по часовой стрелке. По
правилу моментов
20 н • 0,6 м + 20 н • 0,3 м — | Fx | - 0,8 м = 0.
Решая это уравнение, получаем: ] Fi| = 22,5 н.
173
Упражнение 41
1. На рисунке 168 изображен однородный стержень, ось вращения которого
находится в точке О. На нем в точках А и В подвешены грузы массой
0,2 кг и 0,4 кг соответственно. Какой массы груз должен быть подвешен в
точке С, чтобы стержень находился в равновесии?
2. К однородному стержню, который может вращаться вокруг оси О, прикреп-
лен в точке А груз массой 0,8 кг (рис. 169). Какой массы груз нужно прикре-
пить в точке В, чтобы стержень был в равновесии, если масса стержня
400 г?
3. Приведите примеры практического использования рычага.
4. Покажите, что правило рычага следует из правила моментов.
5. При каком условии рычаг, показанный на рисунке 166, находится в равно-
весии?
§ 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ
ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
Если тело находится в равновесии, то это значит, что сумма
приложенных к нему сил равна нулю и сумма моментов этих сил
относительно оси, вокруг которой тело может вращаться, так-
же равна нулю. Но здесь возникает такой вопрос: а устойчиво ли
равновесие?
С первого взгляда видно, например, что положение равновесия
шарика на вершине выпуклой подставки (рис. 170) неустойчиво:
малейшее отклонение шарика от его равновесного положения при-
ведет к тому, что он скатится вниз. А вот тот же шарик помещен
на вогнутой подставке (рис. 171). Его не так-то просто заставить
покинуть свое место. Положение шарика можно считать устойчи-
вым. В чем тут дело? Ведь в обоих случаях шарик находится в
равновесии: сила тяжести mg равна по абсолютной величине проти-
воположно направленной силе упругости (силе реакции) N, дей-
ствующей со стороны опоры (рис. 172 и 173).
Все дело оказывается именно в том малейшем отклонении, о
котором мы упоминали. При самом малом отклонении, которое
всегда происходит из-за случайных сотрясений, воздушных тече-
ний и других причин, равновесие шарика нарушается. На рисунке
172 видно, что, как только шарик на выпуклой подставке покинул
174
Рис. 170
Рис. 171
свое место, сила тяжести mg перестает уравновешиваться силой N
со стороны опоры (сила N всегда направлена перпендикулярно по-
верхности соприкосновения шарика и подставки). Геометрическая
сумма (равнодействующая) силы тяжести mg и силы реакции N
опоры, т. е. сила F, направлена так, что шарик еще больше удалит-
ся от положения равновесия.
Иное дело на вогнутой подставке (рис. 173). При малом откло-
нении от первоначального положения здесь тоже нарушается рав-
новесие. Сила упругости со стороны опоры и здесь уже не будет
уравновешивать силу тяжести. Но теперь равнодействующая F на-
правлена так, что тело вернется в прежнее положение. В этом и
состоит условие устойчивости равновесия.
Равновесие тела устойчиво, если при малом отклонении от рав-
новесного положения возникает сила, возвращающая тело к поло-
жению равновесия.
Равновесие неустойчиво, если при малом отклонении тела от
положения равновесия возникает сила, удаляющая тело от этого
положения.
Устойчивое и неустойчивое положения равновесия отличают-
ся друг от друга еще и положением центра тяжести тела. Когда
шарик находится в положении неустойчивого равновесия, его центр
тяжести выше, чем когда он находится в любом соседнем поло-
жении. Наоборот, у шарика на вогнутой опоре центр тяжес-
N
Рис. 172
175
- н тл в положении устойчивого рав-
д повесив ниже, чем в любом из со-
I | седних положений. Значит, для
/т устойчивого равновесия центр тя-
нНш жести тела должен находиться в
самом низком из возможных для не-
| го положений. Это определение ус-
,пд тойчивости и неустойчивости тесно
связано с предыдущим.
Рис. 174 Возможно и такое положение
равновесия, когда малые отклоне-
ния от него не приводят к каким-либо изменениям в состоянии
тела. Таково, например, положение шарика на плоской опоре
(рис. 174). Ясно, что при любом изменении положения шарика оно
остается равновесным. Такое равновесие называют безразлич-
н ы м.
Если тело имеет ось вращения, то его устойчивость или неустой-
чивость зависит от того, возникает ли момент силы, возвращающей
тело к положению равновесия или, наоборот, удаляющей тело от
этого положения.
В качестве примера рассмотрим обыкновенную линейку, укреп-
ленную на стержне, проходящем через отверстие вблизи ее конца,
как показано на рисунке 175, а. В таком положении линейка на-
ходится в равновесии, потому что сила тяжести mg, проходящая
через ее центр тяжести, уравновешивается силой реакции N (си-
лой упругости) со стороны стержня
(опоры). Но если отклонить линейку от
вертикального положения (рис. 175, б),
то сила тяжести уже не уравнове-
шивается реакцией опоры. Момент
Рис. 175
176
Рис. 177
Линейка должна
силы тяжести относительно оси теперь не ра-
вен нулю (рис. 175, б). Вследствие этого сила
mg возвратит линейку (после нескольких колеба-
ний) в исходное положение. Поэтому положение
линейки, показанное на рисунке 175, а, устой-
чиво. Но попытаемся подвесить ту же линейку
на стержне так, как это показано на рисунке
176, а. Опыт убедит нас в том, что это сделать
невозможно и нетрудно понять почему. Из ри-
сунка 176, а видно, что при вертикальном поло-
жении линейки сила тяжести mg уравновеши-
вается силой упругости N (реакцией стержня),
действующей на линейку со стороны стержня
находиться в равновесии. Но из рисунка 176, б видно, что при
любом отклонении линейки от вертикального положения возника-
ет момент силы тяжести. Вследствие этого линейка повер-
нется так, чтобы занять положение, показанное на рисунке 176, в.
Значит, равновесие линейки, соответствующее рисунку 176, а,
неустойчиво.
Выходит, что равновесие тела при наличии оси вращения устой-
чиво, если центр тяжести тела находится ниже оси вращения.
Понятно, что линейка, подвешенная на стержне, проходящем
через отверстие в ее центре тяжести, будет находиться в безразлич-
ном равновесии (рис. 177). В этом случае при любом положении
линейки момент силы тяжести, приложенной к ней, относительно
оси вращения равен нулю.
§ 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ
Мы только что рассмотрели условие устойчивости или неустой-
чивости равновесия тел, имеющих точку или ось опоры. Не менее
важен случай, когда опора приходится не на точку (ось), а на не-
которую площадь. Площадь опоры имеет ящик на полу, стакан
на столе, всевозможные здания, башни, фабричные трубы и т. д.
Каковы условия устойчивого равновесия в этом случае?
На тела, имеющие площадь опоры, действуют и уравновешивают
друг друга по-прежнему сила тяжести, которую можно считать
приложенной к центру тяжести, и сила упругости (реакции) со
стороны опоры, перпендикулярная ее поверхности. Как и в ранее
рассмотренных случаях, равновесие будет устойчивым, если при
отклонении от положения равновесия не возникает момент силы,
удаляющей тело от этого положения. Когда, например, цилиндр
стоит на горизонтальной поверхности (рис. 178), он, конечно, на-
ходится в равновесии. Это равновесие устойчивое, потому что, если
отклонить его от этого положения на малый угол, появится момент
силы тяжести относительно оси, проходящей через точку О. Вслед-
ствие этого цилиндр повернется вокруг оси против часовой стрел-
177
ки и займет прежнее положение. Точно так же цилиндр вернется
в положение равновесия, если его отклонить на малый угол в дру-
гую сторону.
Но если еще сильнее отклонить цилиндр, как показано на ри-
сунке 179, то результат будет иным. Направление силы тяжести
теперь проходит вне площади опоры. Поэтому момент силы тяжести
относительно оси, проходящей через точку О, направлен так, что
вращение цилиндра происходит по часовой стрелке. Цилиндр опро-
кинется. Из этого примера видно, что для устойчивости тела необ-
ходимо, чтобы вертикаль, проведенная через его центр тяжести,
пересекала площадь опоры.
Ясно также, что, чем больше допустимый угол отклонения тела,
при котором оно еще возвращается в равновесное исходное положе-
ние, тем более устойчиво тело. Например, из двух цилиндров с
одинаковыми площадями опоры более устойчив цилиндр, у которо-
го центр тяжести ниже. Его можно отклонись на больший угол
без опрокидывания (рис. 180).
Известно, что в городе Пизе в Италии существует наклонная
башня (рис. 181). Несмотря на то что башня наклонена, она не
опрокидывается, хотя ее часто называют падающей. Очевидно, что
при том наклоне, которого башня дос-
тигла к настоящему времени, верти-
каль, проведенная из центра тяжести
башни, все еще проходит внутри ее
площади опоры.
Площадь опоры, от которой зави-
сит равновесие, — это не всегда пло-
щадь, на которой тело действительно
соприкасается с опорой. Стол, напри-
мер, соприкасается с полом только
там, где находятся его ножки. Но
площадь опоры стола — это площадь
внутри контура, который получится,
если соединить прямыми все ножки
стола. Площадь опоры штатива —
178
треноги (рис. 182) — это площадь тре-
угольника, образованного отрезками,
соединяющими концы треноги, и т. д.
Упражнение 42
1, Укажите виды равновесия для следующих
случаев: а) гимнаст делает стойку на брусь-
ях; гимнаст висит на кольцах; б) канатохо-
дец находится на канате; в) колесо надето
на ось; г) шарик висит на нити; д) шарик
лежит на столе.
2. Каким образом обеспечивается хорошая ус-
тойчивость следующих предметов: а) игруш-
ки «ванька-встанька»; б) лабораторного шта-
тива; в) башенного подъемного крана;
г) настольной лампы?
3. Как обеспечивают свою устойчивость боксер
во время боя, матрос во время качки?
4. Грузовик перевозил грузы одинакового ве-
са: в одном случае — стальные листы, в дру-
гом— хлопок и в третьем — дрова. В каком
случае грузовик был более устойчив.
САМОЕ ГЛАВНОЕ В РАЗДЕЛЕ
«РАВНОВЕСИЕ ТЕЛ»
Вопрос о равновесии тела, на кото-
рое действуют силы, важен при расче-
те сооружений, которые должны пос-
тоянно находиться в покое.
Для равновесия тела необходимо вы-
полнение двух условий:
1) гео метрическая сум-
м а приложенных к телу сил долж-
Рнс. 182
на равняться нулю;
2) алгебраическая сумма моментов приложенных
сил должна равняться нулю.
Момент силы относительно какой-нибудь оси — это величина,
характеризующая вращающее действие силы около этой оси. Он
равен произведению силы на плечо.
Не всякое равновесие тела практически осуществимо. Можно
осуществить только устойчивое или безразличное равновесие.
Условие устойчивости равновесия заключается в том, что при
малом отклонении тела от положения равновесия возникают силы,
возвращающие тело в исходное положение.
Законы сохранения
в механике
Глава 8
Закон сохранения импульса
ВВЕДЕНИЕ
В предыдущих главах мы видели, как законы Ньютона позво-
ляют решать задачи о движении тел. Поэтому может показаться,
что на этом мы могли бы и закончить изучение механики. Но во
многих случаях определение значения сил, действующих на тело,
представляет значительные трудности. Когда мы рассматриваем
столкновение двух тел, например двух вагонов, мы знаем, что при
этом они взаимодействуют друг с другом силой упругости. Но оп-
ределить значение этой силы бывает трудно, а иногда и невозможно
из-за того, что деформации соприкасающихся частей вагонов имеют
сложный характер. Даже в простом случае столкновения двух
шаров деформация каждого из них имеет сложный вид, и неясно,
что принять за величину х в формуле закона Гука:
FynP= — kx.
В таких случаях для решения задач механики приходится при-
влекать новые величины и новые законы, которые хотя и выводятся
из законов Ньютона, но не связаны с определением сил, приложен-
ных к телам, а следовательно, с определением ускорений.
К числу таких величин относятся импульс и энергия тел. О них
й пойдет речь в последующих главах. Эти величины важны не толь-
ко для механики. Ими приходится пользоваться во всех разделах
физики. В этом состоит их особая важность.
§ 70. СИЛА И ИМПУЛЬС
Формулу F = та, (1)
которая выражает второй закон Ньютона, можно записать по-
другому, если вспомнить, что ускорение равно изменению скорости
тела в единицу времени:
180
Подставив это выражение в формулу (1), получим:
= и (о —
t ’
илп -J. mv — mva
F =-----t--°. (3)
Формулу (3) можно переписать и в таком виде:
Ft = mv — mv0. (4)
Правая часть этого равенства представляет собой изменение
величины произведения массы тела на его скорость. Эта величина
имеет особое название. Ее называют импульсом тела или
его количеством движения.
Импульсом или количеством движения тела называют произве-
дение массы тела на его скорость.
Импульс тела — векторная величина. Направление вектора
импульса совпадает с направлением вектора скорости.
Очевидно, что за единицу импульса надо принять импульс тела
массой 1 кг, движущегося со скоростью 1 м/сек. Единицей им-
пульса является килограмм-метр в секунду {кг • м/сек}.
Изменение импульса тела равно, как видно из формулы (4),
произведению силы F на время ее действия t. Величина Ft тоже
имеет особое название. Ее называют импульсом силы.
Изменение импульса (количества движения) тела
равно импульсу силы.
Величина импульса замечательна тем, что она изменяется под
действием данной силы одинаково у всех тел, если время действия
силы одинаково. Одна и та же сила, действующая в течение опре-
деленного времени, сообщит одинаковый импульс и тяжело на-
груженной барже и легкой байдарке.
Но вернемся к выражению (3). Отношение
mv — mva
t
представляет собой изменение импульса тела в единицу времени.
Таким образом, сила характеризуется не только произведением
массы тела на его ускорение. Теперь мы видим, что сила — это
величина, измеряемая отношением изменения импульса тела к про-
межутку времени, в течение которого это изменение произошло.
Сила, действующая на тело, равна изменению его импульса
в единицу времени, т. е. быстроте изменения импульса.
Упражнение 43
1. Определите импульс тела массой 5 кг, движущегося со скоростью 2 м/сек.
2. В цистерне поливочной автомашины массой 4 т находится 2 м 3 воды. Чему
равен импульс машины: а) когда машина движется со скоростью 18 км/ч
181
к месту полива; б) когда машина движется со скоростью 54 км/ч после из-
расходования всей воды?
3. Металлический шарик массой 20 г, падающий со скоростью 5 м/сек, уда-
ряется упруго о стальную плиту и отскакивает от нее в прямо противополож-
ном направлении с такой же по абсолютной величине скоростью. Найдите
изменение импульса шарика и среднюю силу, действовавшую на шарик при
ударе, если соударение длилось 0,1 сек.
§ 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Импульсу присуще очень интересное и важное свойство, кото-
рым обладают весьма немногие физические величины. Это — с в о й-
ство сохранения. В чем оно заключается?
Допустим, что два взаимодействующих друг с другом тела, мас-
сы которых и /и2, движутся относительно какой-то системы от-
счета. Обозначим через и v2 их скорости в какой-то момент вре-
мени. В результате взаимодействия скорости тел через некоторое
время / изменятся и станут равными vi и v2. Это означает, что на
тела при их взаимодействии действовали соответственно силы F1 и
F2, равные:
г, 7/1 jVj—
1== - .
II
t
Согласно третьему закону Ньютона силы F\ и F., равны по абсолют-
ной величине и противоположны по направлению, т. е.
Л==— f2.
Следовательно,
туу , — _ m2v2 — т„уг
t t ’
ИЛИ
Л72п2 — ~ m-fV I —
Перепишем последнюю формулу в виде
ВД \-\ -р m2v'2.
В левой части этого равенства стоит сумма начальных импульсов
двух тел, а в правой — сумма импульсов тех же тел через вре-
мя t. Эти суммы равны между собой. Таким образом, хотя импульс
каждого из тел при взаимодействии изменяется, их полный импульс,
т. е. сумма импульсов обоих тел, остается при этом неизменным.
Это и значит, что импульс двух тел при их взаимодействии сохра-
няется.
182
Сохранение полного импульса тел при их взаимодействии —
один из важнейших законов природы. Можно доказать, и опыт это
также подтверждает, что если взаимодействуют не два, а много
тел, то геометрическая сумма импульсов всех тел, или, как гово-
рят, системы тел, остается неизменной. Важно только, чтобы эти
тела взаимодействовали только друг с другом, чтобы па них не
действовали силы со стороны других тел, не входящих в систему
(или чтобы эти внешние силы уравновешивались). Такую группу
тел, которая не взаимодействует ни с какими другими телами, не
входящими в эту группу, называют замкнутой системой.
Когда мы до сих пор говорили о взаимодействии двух тел, то тоже
имели в виду, что эти тела взаимодействуют только друг с дру-
гом, посторонние же тела на них не действуют. Именно для замк-
нутых систем и справедлив закон сохранения им-
пульса.
Геометрическая сумма импульсов тел, составляю-
щих замкнутую систему, остается постоянной при
любых взаимодействиях тел этой системы между
собой.
Импульс — это векторная величина. Поэтому если векторная
сумма импульсов тел сохраняется постоянной, то и сумма проек-
ций этих импульсов на оси координат также остается постоянной.
Вследствие этого геометрическое сложение импульсов можно за-
менить алгебраическим сложением их проекций.
Следующие опыты поясняют закон сохранения импульса.
1. Поставим на рельсы две тележки одинаковой массы т. К тор-
цу одной тележки прикрепим шарик из пластилина. Пусть тележки
движутся навстречу друг другу с одинаковыми по абсолютной вели-
чине скоростями v (рис. 183). При встрече обе тележки остановятся.
Объяснить результаты опыта легко. До встречи импульс левой
тележки равен mv, а правой тележки —mv (тележки двигались
с противоположно направленными скоростями). Значит, до момен-
та встречи тележек их общий импульс был равен нулю:
mv + (— mv) = 0.
После соударения тележки остановились. Следовательно, и
теперь суммарный импульс обеих тележек равен нулю.
Рис. 183
183
I ।
(p © © ©
* —..... №
I - -PM bw'r"7 - 1
® d)
Рис. 184
2. Можно повернуть тележки так, чтобы они были обращены
друг к другу пружинными буферами (рис. 184). Тогда, повторив
опыт, убедимся в том, что после столкновения обе тележки разъ-
едутся в противоположные стороны. При этом взаимодействии ско-
рости тележек изменят свои направления на противоположные,
абсолютные же значения скоростей останутся такими же, какими
они были до взаимодействия. Если до встречи импульс левой те-
лежки равен mv, а правой —mv, то после встречи импульс левой
тележки равен —mv, а правой mv. Поэтому суммарный импульс
обеих тележек равен нулю как до, так и после столкновения, как
этого и требует закон сохранения импульса.
Задача 1. Тележка массой 150 кг движется по рельсам со ско-
ростью 3,6 км/ч. По дороге бежит человек массой 75 кг. Приблизив-
шись к тележке, он вскакивает на нее и прекращает бег. После
этого тележка остановилась. С какой скоростью бежал человек?
Решение. Так как взаимодействие человека и тележки с
землей не влияет на их движение в горизонтальном направлении,
можно к этой системе применить закон сохранения импульса. Это
значит, что суммарный импульс тележки и человека после взаимо-
действия должен быть таким же, как и до взаимодействия.
Обозначим массу тележки через пц и ее скорость до взаимодей-
ствия через vr, массу человека через т2 и его скорость до взаимо-
действия через v2. Полный импульс системы до взаимодействия
равен
В результате взаимодействия тележка и человек остановились.
Следовательно, их общий импульс стал равен нулю. Значит, он
был равен нулю и до того, как человек вскочил на тележку:
т-м + m2v2 = 0.
184
Тележка и человек движутся по одной прямой. Поэтому можно,
направив вдоль этой прямой ось координат, вместо векторной сум-
мы импульсов написать алгебраическую сумму их проекций па
эту ось:
ВД + m2v2 = 0.
Примем направление движения тележки за положительное, тогда
т,с,
v2=-----— ,
т2
или
150 № , м о м
ц2 =--------1 — =—2 — .
75 кг сек. сек
Знак «минус» указывает па то, что вектор скорости движения
человека был направлен противоположно вектору скорости движе-
ния тележки.
Задача 2. Железнодорожный вагон массой 30 tn, движущийся
со скоростью 1,5 м/сек, сцепляется с неподвижным вагоном, масса
которого равна 20 т. Какова скорость вагонов после сцепки? (Ва-
гоны находятся на прямолинейном участке пути.)
Решение. Направим координатную ось вдоль железнодо-
рожного пути. Обозначим массу первого (движущегося) вагона
через «?!, массу второго (неподвижного) через т2, скорость перво-
го вагона до сцепки через а общую скорость обоих вагонов
после сцепки через v. По закону сохранения импульса полный
импульс обоих вагонов до и после сцепки должен быть одинаковым.
До сцепки полный импульс (его проекция на ось) обоих вагонов
был равен
а после сцепки
(/7?! + ff?2) V.
Следовательно,
ffZjOi = (<т?1 + m2) v.
Отсюда
m,v, 3 • 104 кг 1,5 м/сек п л м
V = ----— — , V =--------------------= 0,9 — .
тг + т2 5 • 10’ кг сек
В приведенных задачах мы не знали значений сил взаимодейст-
вия между человеком и тележкой или между сцепляющимися ва-
гонами. Но, пользуясь законом сохранения импульса, мы нашли
скорости интересующих нас тел. Ясно, что если известны их началь-
ные положения, то, зная их скорости, можно найти положения
этих тел в любой момент времени. Вот почему закон сохранения
импульса имеет такое большое значение.
185
Упражнение 44
1. Человек массой 70 кг, бегущий со скоростью 7 м/сек, догоняет тележку
массой 30 кг, движущуюся со скоростью 2 м/сек, и вскакивает на нее.
С какой скоростью станет двигаться тележка после этого?
2. При формировании железнодорожного состава три сцепленных между
собой вагона, движущиеся со скоростью 0,4 м/сек, сталкиваются с непод-
вижным вагоном, после чего все вагоны продолжают двигаться в ту же
сторону с одинаковой скоростью. Определите эту скорость, если массы
всех вагонов одинаковы.
3. Зенитный снаряд взорвался в верхней точке траектории. При этом обра-
зовалось Три осколка. Два осколка разлетелись под прямым углом Друг к
Другу, причем скорость первого осколка массой 9 кг равна 60 м/сек, а
скорость второго массой 18 кг равна 40 м/сек. Третий осколок отлетел со
скоростью 200 м/сек. Определите графически направление полета Третьего
осколка. Какова его масса?
§ 72. РЕАКТИВНОЕ ДВИЖЕНИЕ
Интересный и важный случай проявления закона сохранения
импульса и его практического использования — это реактив-
ное движение. Так называют движение тела, возникающее
при отделении от тела с какой-то скоростью некоторой его чаете.
Реактивное движение совершают, например, ракеты. Всякая
ракета — это система двух тел. Она состоит из оболочки и содер-
жащегося в ней топлива. Оболочка имеет форму трубы, один конец
которой закрыт, а другой открыт и снаб-
жен трубчатой насадкой с отверстием осо-
бой формы — реактивным соплом.
Топливо при запуске ракеты сжигает-
ся и превращается в газ высокого давле-
ния и высокой температуры. Благодаря
высокому давлению этот газ с большой
скоростью вырывается из сопла ракеты.
Оболочка ракеты устремляется при этом в
противоположную сторону (рис. 185).
Перед стартом ракеты ее общий импульс
(оболочки и топлива) в системе координат,
связанной с Землей, равен нулю, вся ра-
кета покоится относительно Земли. В
результате взаимодействия газа и оболоч-
ки выбрасываемый газ приобретает неко-
торый импульс. Будем считать, что влия-
ние силы тяжести пренебрежимо мало,
тогда оболочку и топливо можно рассмат-
ривать как замкнутую систему и их об-
щий импульс должен и после запуска
остаться равным нулю. Поэтому оболоч-
ка из-за взаимодействия с газом приоб-
Рис. 185 ретает импульс, равный по величине
186
импульсу газа, но противоположный по направлению. Вот почему в
движение приходит не только газ, но и оболочка ракеты. В ней
могут быть помещены научные приборы для исследований, всевоз-
можные средства связи и т. д. С ракетой может быть связан и кос-
мический корабль, в котором путешествуют космонавты.
Закон сохранения импульса позволяет определить скорость
ракеты (оболочки).
Действительно, предположим сначала, что весь газ, образую-
щийся при сгорании топлива, выбрасывается из ракеты сразу, а
не вытекает постепенно.
Обозначим всю массу газа, в который превращается топливо
в ракете, через тт, а скорость вылетающего газа через vT. Массу
и скорость оболочки обозначим через тоб и уоб. Согласно закону
сохранения импульса сумма импульсов оболочки и газа после
запуска должна быть такой же, какой была до запуска ракеты,
т. е. должна быть равной нулю. Следовательно,
mtvT + тобуоб = 0, или mc6Do6 = — mvvr
(координатная ось выбрана в направлении движения оболочки).
Отсюда находим скорость оболочки:
Из этой формулы видно, что скорость оболочки ракеты тем
больше, чем больше скорость выбрасываемого газа и чем больше
отношение массы топлива к массе оболочки. Поэтому достаточно
большую скорость оболочка получит в том случае, если масса топ-
лива намного больше массы оболочки. Например, для того чтобы
скорость оболочки была по абсолютному значению в 4 раза больше
скорости выбрасываемого газа, нужно, чтобы масса топлива была
во столько же раз больше массы оболочки, т. е. оболочка должна
составлять одну пятую всей массы ракеты на старте. А ведь «полез-
ной» частью ракеты является именно оболочка.
Мы считали, что весь газ выбрасывается из ракеты мгновенно.
На самом деле он вытекает не сразу, хотя и достаточно быстро.
Это значит, что после выброса какой-то части газа оболочке при-
ходится «возить» с собой еще не сгоревшую и не вылетевшую часть
топлива. Это значительно увеличивает необходимую для достиже-
ния данной скорости массу топлива. Расчет показывает, что, для
того чтобы скорость оболочки была в 4 раза больше скорости газа,
масса топлива на старте должна быть не в 4, а в несколько десятков
раз больше массы оболочки. Если же учесть, что при запуске с Зем-
ли па ракету действуют и сила сопротивления воздуха, сквозь ко-
торый она должна лететь, и притяжение к Земле, то можно будет
сделать вывод, что это отношение должно быть еще больше.
В отличие от всех других транспортных средств ракета может
двигаться, не взаимодействуя ни с какими другими телами, кроме
18?
Константин Эдуардович Циолковский Юрий Алексеевич Гагарин
(1857—1935) (1934—1968)
как с продуктами сгорания содержащегося в ней самой топлива.
Именно поэтому ракеты используются для запуска искусственных
спутников Земли и космических кораблей и для их передвижения
в космическом пространстве, где им не на что опираться и не от
чего отталкиваться, как это делают обычные земные средства
транспорта.
При необходимости ракету можно тормозить. Именно так по-
ступают космонавты, когда, закончив космический полет, они долж-
ны уменьшить скорость своего корабля, чтобы вернуться на Землю.
Понятно, что ракета уменьшит свою скорость, если газ из сопла
ракеты будет вылетать в ту же сторону, куда движется ракета.
Идея использования ракет для космических полетов была пред-
ложена еще в начале нашего века знаменитым русским ученым
К. Э. Циолковским. Эта замечательная идея успешно осу-
ществляется. Уже многие сотни искусственных спутников Земли
и космических кораблей выводились в космическое пространство
с помощью ракет. Благодаря применению ракет люди побывали и
на Луне. С их помощью на Луну доставлены космические лабора-
тории, созданы искусственные спутники Луны.
Первый в истории искусственный спутник Земли был с помощью
ракеты запущен в Советском Союзе 4 октября 1957 г.
Первьш человеком, который на искусственном спутнике совер-
шил полет в космическом пространстве, был гражданин Советского
Союза Юрий Алексеевич Гагарин. 12 апреля 1961 г.
он облетел земной шар на корабле-спутнике «Восток».
Советские ракеты первыми достигли Луны, первыми совершили
облет Луны и сфотографировали ее невидимую, «обратную» сторо-
ну, первыми достигли планеты Венера. СССР занимает ведущее
положение в исследовании космического пространства.
<88
Глава 9
Механическая работа
и мощность
ВВЕДЕНИЕ
В предыдущей главе мы убедились в том, какое важное значе-
ние имеет закон сохранения импульса (количества движения).
Не менее важную роль играет другой закон сохранения — закон
сохранения энергии. Но прежде чем приступить к рас-
смотрению этого закона, нам нужно ознакомиться с величиной,
которую называют механической работой (или про-
сто работой). Эта величина тесно связана с энергией. Она,
кроме того, важна и сама по себе, так как действие всевозможных
машин и механизмов да и трудовая деятельность людей часто сво-
дится именно к совершению механической работы.
Что же это за величина — механическая работа?
§ 73. МЕХАНИЧЕСКАЯ РАБОТА
Величина, которую мы называем работой, появилась в меха-
нике лишь в XIX в. (почти через 150 лет после открытия законов
движения Ньютона), когда человечество все шире стало использо-
вать машины и механизмы. Ведь о действующей машине так и
говорят, что она «работает». Работа совершается, когда трактор
тянет плуг, вспахивающий почву, когда двигатель станка вращает
обрабатываемую деталь, когда подъемный кран поднимает вверх
тяжелый груз, и т. д.
Это не значит, что работа совершается только с помощью машин.
Ведь и до появления тракторов, станков, подъемных крапов паха-
ли землю, обрабатывали изделия, поднимали грузы. И при этом,
разумеется, совершалась работа.
Общим для всех приведенных нами примеров является то, что
тела движутся и к этим движущимся телам приложена сила или
несколько сил. В токарном станке сила приложена к движущемуся
(вращающемуся) обрабатываемому изделию; при вспахивании поч-
вы плугом сила действует на движущийся плуг; в подъемном крапе
сила приложена к движущемуся грузу и т. д. Поэтому говорят,
что работу совершает сила.
С величиной работы вы уже встречались в курсе физики VI
класса. Там говорилось, что если на тело действует постоянная
189
сила F и это тело совершает в направлении действия силы переме-
щение s, то при этом производится работа, равная произведению
абсолютных значений силы и перемещения:
Л==Й’14 (1)
Если к телу приложено несколько сил, то выражение (1) отно-
сится к каждой из них. Л работа, совершенная всеми силами,
приложенными к этому телу, будет равна сумме работ, совершен-
ных каждой из них. В тех примерах, которые мы здесь привели,
на движущееся тело как раз и действует несколько сил. К подни-
маемому грузу, например, приложена не только та сила, которая
его поднимает, но и сила тяжести, сила сопротивления воздуха,
архимедова сила.
Смысл понятия работы в механике не всегда совпадает с пред-
ставлением о работе в обыденной жизни. Обычно считают, что ра-
бота — это что-то такое, от чего устают. Всякий скажет, что дер-
жать длительное время па руках большой груз — очень тяжелая,
утомительная работа. Работой считаете,ч выполнение учебных за-
даний, чтение трудных для понимания книг (хотя чтение занима-
тельной книги никто работой пе назовет) и т. д.
В'физическом же смысле все подобные действия не являются
работой. С точки зрения механики работа совершается только тог-
да, когда сила действует на движущееся тело. Если, например, че-
ловек держит в руках неподвижный груз или толкает тяжелый
шкаф, который ему пе удается сдвинуть с места, то сила, с которой
человек действует на груз пли на шкаф, работу пе совершает. Это
видно и из выражения (1). Ведь если тело не двигается, то переме-
щение s равно нулю, а значит, и работа равна пулю.
Надо также иметь в виду, что когда говорят, что работа силы
равна | Е|-| s |, то это значит, что сила F действует на тело на протя-
жении всего перемещения $, в каждой точке, через которую про-
ходит тело. Поэтому, если, например, камень брошен рукой вверх
с силой F и после броска поднялся на высоту h, это не значит, что
мускульная сила руки, которая действовала на камень во время
броска, совершила работу, равную \F\h. Ведь сила действовала на
камень не на всем пути, а только на том его участке, на котором
камень находился в руке.
Нам остается еще выяснить, в каких единицах выражается ра-
бота.
Из формулы A =|E|-|s| видно, что работа равна единице, если
тело под действием силы, равной единице силы, совершает по на-
правлению силы перемещение, равное единице длины.
За единицу работы принимается работа, совершаемая силой,
равной единице, при перемещении точки приложения силы на еди-
ницу длины в направлении силы.
190
В системе единиц СИ сила измеряется в ньютонах, а перемеще-
ние — в метрах. Поэтому за единицу работы принимается работа
силы в 1 н при перемещении точки ее приложения на 1 м. Эта еди-
ница работы называется джоулем (дж):
I дж = 1 н • 1 м — 1 н • м.
В системе единиц СГС единица работы называется эргом.
1 эрг — это работа силы в 1 дин при перемещении точки ее прило-
жения па 1 см:
1 эрг = 1 дин 1 см = 1 дин • см.
Нетрудно получить соотношение между двумя приведенными
единицами работы.
Так как 1 н = 105 дин, а 1 м — 102 см, то
1 дж — 1н • м — 105 дин • 102 см = 107 эрг.
Следовательно, джоуль в десять миллионов раз больше эрга.
Упражнение 45
1. Гребцам в лодке, несмотря на все их усилия, не удается заставить лодку
двигаться против течения. Но она не движется и вниз по течению. Совер-
шают ли работу гребцы? Совершается ли работа по перемещению лодки?
2 Вычислите работу, совершаемую ребенком, когда он равномерно поднимает
игрушку массой 200 г на высоту 50 см.
3. Вычислите работу, совершаемую тяжелоатлетом, когда он равномерно под-
нимает штангу массой 140 кг на высоту 2 м.
4. Хоккеист ударяет по шайбе клюшкой с силой 50 н, после чего шайба про-
ходит расстояние, равное 50 м. /Ложно ли сказать, что при этом соверше-
на работа, равная 2 500 дж? Можно ли по приведенным данным вычислить
работу?
5. Контейнер с кирпичом, масса которого равна 750 кг, поднимается со ско-
ростью 25 см/сек. Какая работа совершается за 20 сек подъема?
6. На земле лежат 10 кирпичей. Высота каждого из них равна 65 мм, а мас-
са— 3,5 кг. Какую работу нужно совершить, чтобы уложить все кирпичи
един на другой.
7. Подъемный кран равномерно поднимает бетонную плиту размером
320Х1С0Х10 см на высоту 10 м. Вычислите работу, совершаемую при подъ-
еме плиты, если плотность бетона равна 2 400 кг/м3.
§ 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ
КАК ПРОИЗВЕДЕНИЕ | F 11 s'[
Выясним теперь, почему работа силы выражается именно величиной | F 11 s|-
Мы можем это сделать на одном из примеров, приведенных в предыдущем
параграфе. Удобнее всего рассмотреть пример с подъемом груза.
Допустим, что груз массой т нужно поднять па высоту h. Груз, следова-
тельно, должен совершить перемещение s, равное по абсолютной величине h.
На груз действует сила тяжести mg, направленная вниз. Чтобы поднять груз,
к нему нужно приложить некоторую силур, направленную вверх. Если груз вна-
чале покоится, то эта сила по абсолютной величине должна превосходить значение
191
mg (если она будет в точности равна mg, то груз с места
не сдвинется!). Но после того как груз начнет двигаться,
силу F можно уменьшить и сделать ее равной mg, так что
к движущемуся грузу достаточно приложить силу F, по
абсолютному значению равную mg. Груз в таком случае
будет двигаться равномерно. Только, такое движение мы
пока и будем рассматривать. Совершенную силой F ра-
боту подъема груза на высоту /г можно определить по фор-
муле (1):
А = I F h = nigh.
Результатом этой работы будет подъем груза на высо-
ту h.
Но этот же результат может быть достигнут и иначе.
Силу, которая должна совершить работу по подъему гру-
за, можно приложить не к грузу, а к концу рычага (точка А
на рисунке 186), направив ее, конечно, не вверх, а вниз.
Согласно золотому правилу механики
при равновесии рычага отношение перемещений его кон-
цов разно обратному отношению приложенных к ним сил.
Если, например, длина правого плеча рычага (см. рис. 186)
' '^7
Рис. 187
в 3 раза больше дли-
ны левого, то для равномерного движения его концов (при таком движении рычаг
и будет в равновесии) к правому концу нужно приложить силу F, втрое мень-
- mg
шую, чем mg-. ' F | = —Но зато точка, к которой приложена эта сила (правый
конец рычага), совершит перемещение, втрое большее, чем h. Работа силы F на
этом перемещении оказывается равной по-прежнему выражению mgh:
mg
А = — • 3/i = mgh.
Вместо рычага мь’ могли бы воспользоваться системой блоков (п о л и с п а-
с т о м, рис. 187). С помощью этого устройства груз можно поднять, приложив
к концу -нити, перекинутой через блоки (рис. 187), силу, в 6 раз мень-
шую, чем mg. Но точка, к которой приложена эта сила, совершит перемещение,
в 6 раз большее, чем h. Произведение же силы, приложенной к этой точке, на ее
перемещение будет опять равно mgh. Результат во всех трех случаях один
192
и тог же: груз, двигаясь с некоторой по-
стоянной скоростью, поднялся на вы-
соту It- Именно потому работу и выража-
ют величиной mgh, т. е. произведением
силы па перемещение, что эта величина
одинакова при любом способе приложения
силы независимо от того, приложена ли
сила непосредственно к движущемуся те-
лу или посредством другого тела (блока,
рычага, наклонной плоскости, ворота, ле-
бедки и т. д.).
То, что здесь говорилось о работе си-
лы, поднимающей груз, относится и к
другим случаям, К обрабатываемому па токарном станке изделию пли к плугу,
вспахивающему землю, сила может быть приложена и непосредственно, и через
какие-нибудь передаточные устройства. Но при данном перемещении движущего-
ся тела и при данном значении силы произведение силы на перемещение (работа)
и любом случае будет о^но и то же.
Pur 1S8
Упражнение 46
1. Груз массой в 1 г требуется поднять на высоту 1 м. Для этого используется
наклонная плоскость, длина которой больше ее высоты в 5 раз (рис. 183),
Какую по абсолютной величине силу F нужно приложить к грузу, если дви-
жется он при подъеме равномерно, а сила трения о наклонную плоскость
отсутствует?
2. Тяжелый сейф массой 800 кг нужно передвинуть по горизонтальному полу
на расстояние в 2 м. Какая сипа должна быть приложена к сейфу, если
коэффициент трения его о пол равен 0,2 и движется он равномерно? Какая
при этом совершается работа?
3- Для перемещения сейфа (см, задачу 2) используется рычаг, одно из плеч
которого втрое длиннее другого, и сила действует на длинное плечо. Мож-
но ли воспользоваться таким рычагом в комнате размером 4X2 м?
Л, Подумайте над следующим вопросом: является ли работа относительной
величиной, т. е. одинакова она или нет в различных системах отсчета?
§ 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ
В предыдущих параграфах мы рассматривали работу, совер-
шаемую той силой, которая направлена в сторону движения тела,
например силой, поднимающей груз, тянущей плуг. При этом мы
особо отмечали, что тело, при перемещении которого совершается
работа, движется равномерно. Но это означает, что к телу при-
ложены еще какие-то силы, равнодействующая которых направле-
на против его движения.
Только при этом условии геометрическая сумма сил, действую-
щих на тело, может быть равна нулю и тело будет двигаться равно-
мерно. При подъеме груза вверх сила, направленная против дви-
жения, — эго сила тяжести, при перемещении сейфа по полу —
эта сила трения и т. д.
Совершают ли работу и эти силы, направленные противополож-
но перемещению?
Чтобы ответить на этот вопрос, вспомним, что если векторная
сумма сил, приложенных к тел\, равна н\лю, то все должно нро-
11 и?
193
исходить так, как будто на него вовсе не действуют никакие силы.
Но тогда и общая 'работа всех сил, приложенных к телу, должна
быть равна нулю.
Отсюда следует, что силы, направленные против перемещения,
тоже совершают работу, но работа эта имеет знак, противополож-
ный знаку работы, совершаемой силой, направленной ио движению
(перемещению) тела. Значит, работа может быть как положитель-
ной, так и отрицательной.
Естественно считать работу положительной, когда направле-
ние силы и направление перемещения совпадают. Работа, совершае-
мая силой, направленной противоположно перемещению тела,
отрицательна.
Отрицательную работу совершает, например, сила тяжести
при поднятии груза вверх.
Мы говорили здесь только о работе сил, направленных либо по
направлению движения, либо в противоположную сторону. В пер-
вом случае работа силы положительна, во втором — отрицательна.
Но направление силы может и не совпадать с направлением пере-
мещения. На рисунке 189 показаны сани, движущиеся по горизон-
тальной поверхности, а сила F, приложенная к саням, направ-
лена под углом а к горизонту. Как вычислить работу, которую со-
вершает сила F, если перемещение санок по горизонтали равно s?
Силу F можно представить как сумму двух сил Fr и К, (рис. 189, а).
Так как в вертикальном направлении перемещение санок равно
нулю, то работа силы F2 равна нулю. Поэтому работа силы F рав-
няется работе только силы Ft:
Л = |Л1Ы- (1)
Из. рисунка видно, что | Fr | = | F\ cos а, следовательно,
А = |F] jslcosa. (2)
Работа, совершаемая постоянной силой, равна произведению
абсолютных значений силы и перемещения, умноженному на ко-
синус угла между векторами силы и перемещения.
194
Заметим, что произведение |s| cos а равно проекции перемеще-
ния s на направление силы. Поэтому можно сказать, что работа
силы равна произведению абсолютного значения силы и'проекции
перемещения на направление силы.
Если действующая на тело сила не постоянна, а меняется от
точки к точке, то для нахождения работы поступают следующим
образом. Разбивают движение тела на такие малые перемещения
slt s,, s3, ... , что на протяжении каждого из них силу, действую-
щую на тело, можно считать постоянной и равной соответственно
Fr, F.,, F3, ... . На каждом из таких участков работу вычисляют
по формуле (2):
Д = | Л11 si I cos ai» А = | F21 I s21 cos a2, ... .
Полная работа равна сумме работ на этих участках.
Можно поступить и иначе — найти среднюю силу, действую-
щую на тело, и умножить ее на | s| cos а.
Так определяют величину работы в общем случае.
Из формулы (2) видно, что работа — это скалярная величина,
хотя сила F и перемещение s — векторные величины. Нельзя го-
ворить, что работа имеет какое-то направление.
Если направление силы F совпадает с направлением переме-
щения s, го угол а = 0 и cos а = 1. Тогда из формулы (2) следует,
что _
Если угол а тупой (см. рис. 189, б), то cos а принимает отрица-
тельное значение. Это значит, что работа, совершаемая такой си-
лой, отрицательна. В частности, если а = 180°, то cos а = — 1 и
работа А = — |F| |s|.
И наконец, направление силы может оказаться перпендикуляр-
ным перемещению движущегося тела. В этом случае а = 9СР,
cos а = 0 и Д=0. Так, например, при перемещении груза в гори-
зонтальном направлении сила тяжести, действующая на груз,
перпендикулярна направлению перемещения. Поэтому при пере-
мещении тела в горизонтальной плоскости работа силы тяжести
равна нулю. Никакой работы не совершает и сила, вынуждающая
тело двигаться равномерно по окружности, потому что эта сила,
как известно, направлена по радиусу к центру окружности и,
следовательно, в любой точке перпендикулярна направлению пе-
ремещения тела. Например, сила натяжения нити, к которой при-
вязано тело, движущееся равномерно по окружности, не совер-
шает работы. Не совершает работы и сила всемирного тяготения,
под действием которой искусственные спутники Земли движутся
по круговой орбите.
Одна и та же сила, приложенная к телу, может совершать и
положительную, и отрицательную работу. Рассмотрим, например,
?•
195
mg
тело, прикрепленное к пружине и падаю-
щее вниз (рис. 190). Возникающая при
деформации пружины сила упругости со-
вершает отрицательную работу, потому
что эта сила направлена вверх, а тело
движется вниз. В то же время сила тяжес-
ти, тоже действующая на тело, совершает
положительную работу. Но после того как
тело, достигнув определенного наинизшего
положения, начнет двигаться вверх, роли
приложенных к телу сил переменятся: сила
тяжести станет производить отрицательную
работу, а сила упругости, направление ко-
торой теперь совпадает с направлением
движения, будет совершать положительную
работу. Сила упругости и сила тяжести
р jgo могут совершать и положительную, и от-
рицательную работу. Но этого нельзя
сказать о силе трения, действующей
на тело, скользящее вдоль другого, неподвижного тела. В этом
случае сила трения направлена против движения. Работа этой
силы, следовательно, всегда отрицательна. Заметим, что когда
работа какой-нибудь силы отрицательна, то говорят, что совер-
шается работа против этой силы. При подъеме груза, например,
можно сказать, что подъемный кран совершает работу против силы
тяжести, локомотив совершает работу против силы трения колес о
рельсы и против силы сопротивления воздуха и т. д.
Упражнение 47
1. Можно ли говорить о направлении работы?
2. В каком случае сила совершает положительную и в каком — отрицатель-
ную работу?
3. Чему равна работа силы, если эта сила направлена под углом к перемеще-
нию тела?
4. При каких условиях сила, приложенная к движущемуся телу, не совершает
работы?
5. Автомобиль движется по ровной горизонтальной дороге. Совершает ли
работу сила тяжести, действующая на автомобиль?
6. Совершает ли работу сила притяже-
ния Луны к Земле при ее движении
по орбите вокруг Земли? Лунную ор-
биту считать круговой.
7. На рисунке 191 изображено тело, к
которому приложено несколько сил.
Укажите, какие из этих сил соверша-
ют положительную работу, какие —
отрицательную?
8. Тело брошено вертикально вверх.
Укажите, положительную или отрица-
тельную работу совершает сила тя-
жести; а) при подъеме тела, б) при
его падении.
Рис. 191
196
9. На груз, скользящий с трением по плоской горизонтальной поверхности,
действует сила в 200 н, направленная под углом 60‘ к горизонту. Какую
работу совершит сила при перемещении тела на 5 м, если движение про-
исходит с постоянной скоростью? Каков коэффициент трения груза о пло-
скость, если масса груза 20 кг?
10. Тело, масса которого 50 кг, скользит с трением по наклонной плоскости
с углом наклона к горизонту 30°. Двигаясь с постоянной скоростью, тело
проходит всю длину плоскости, равную 6 м. Вычислите работу силы тяжести
при этом движении и силу трения, действующую на тело.
§ 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ,
РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА
НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Мы рассматривали до сих пор сличай, когда на тело действуют
две (или больше) силы, векторная сумма которых равна нулю.
В этом случае тело может либо покоиться, либо двигаться равно-
мерно. Если тело покоится, то общая работа всех приложенных
к нему сил равна нулю. Равна нулю и работа каждой отдельной
силы. Если же тело движется равномерно, то общая работа всех
сил по-прежнему равна нулю. Но каждая сила в отдельности, если
она не перпендикулярна направлению движения, совершает опре-
деленную работу — положительную или отрицательную.
Рассмотрим теперь случай, когда равнодействующая всех сил,
приложенных к телу, не равна нулю или когда на тело действует
только одна сила. В этом случае, как это следует из второго закона
Ньютона, тело будет двигаться с ускорением. Скорость тела бу-
дет меняться, и работа, совершенная силами в этом случае, не рав-
на нулю, она может быть положительной или отрицательной. Мож-
но ожидать, что между изменением скорости тела и работой, совер-
шенной силами, приложенными к телу, существует какая-то связь.
Попытаемся ее установить. Представим себе для простоты рассуж-
дения, что тело движется вдоль прямой линии и равнодействующая
сил, приложенных к нему, постоянна по абсолютному значению;и
направлена по той же прямой. Обозначим эту равнодействующую
силу через F, а проекцию перемещения s на направление силы через s.
Направим координатную ось вдоль направления силы. Тогда
\F\ = F и, как было показано в § 75, совершаемая работа равна А =
~Fs. Направим координатную ось вдоль перемещения тела. Тогда,
как было показано в § 75, работа .4, совершаемая равнодействующей,
равна: A ~Fs. Если направления силы и перемещения совпадают, то
$ положительна и работа положительна. Если равнодействующая F
направлена противоположно направлению движения тела, то ее рабо-
та отрицательна. Сила F сообщает телу ускорение а. По второму
закону Ньютона F = та. С другой стороны, во второй главе мы
нашли, что при прямолинейном равномерно ускоренном движении
197
Отсюда следует, что
2 2
Г2 - V,
S =-----------
2а
2 2 2
v2 — D] mv.2
2а ~ 2
Здесь Vj — начальная скорость тела, т. е. его скорость в начале
перемещения s; t>2 — его скорость в конце этого участка.
Мы получили формулу, связывающую работу, совершенную
силой F, с изменением скорости (точнее, квадрата скорости) тела,
вызванным этой силой.
Половина произведения массы тела на квадрат его скорости
носит специальное название — кинетическая энергия
тела, и часто формулу (1) называют теоремой о кине-
тической энергии.
Работа силы равна изменению кинетической энергии тела.
Можно показать, что формула (1), выведенная нами для силы,
постоянной по величине и направленной вдоль движения, справед-
лива и в тех случаях, когда сила изменяется, а ее направление не
совпадает с направлением перемещения.
Формула (1) замечательна во многих отношениях.
Во-первых, из нее следует, что работа силы, действующей на
тело, зависит только от начального и конечного значений скорости
тела и не зависит от того, с какой скоростью оно двигалось в дру-
гих точках.
Во-вторых, из формулы (1) видно, что ее правая часть может
быть как положительной, так и отрицательной в зависимости от
того, возрастает или убывает скорость тела. Если скорость тела
возрастает (о2 > t»i), то правая часть формулы (1) положительна,
следовательно, и работа А > 0. Так и должно быть потому, что
для увеличения скорости тела (по абсолютной величине) действую-
щая на него сила должна быть направлена в ту же сторону, что и
перемещение. Наоборот, когда скорость тела уменьшается
(п2 < oj, правая часть формулы (1) принимает отрицательное
противоположно перемещению).
скорость тела равна нулю, выраже-
вид:
ffl-.o
А --
2
Формула (2) позволяет вычислить работу, которую нужно со-
вершить, чтобы покоящемуся телу сообщить скорость, равную и2.
Очевидно обратное: для остановки тела, движущегося со ско-
ростью v, необходимо совершить работу
„ mu2
А =---------------------------------.
2
А = Fs =
та
тщ
~2~
(1)
значение (сила направлена
Если в начальной точке
ние для работы принимает
(2)
198
Формула
О 9
mvr^ ти\
2 2
очень напоминает формулу, полученную в предыдущей главе (см. § 59), устанав-
ливающую связи между импульсом силы Ft и изменением импульса тела mv:
Ft — mv, — mvv (3)
Действительно, левая часть формулы (3) отличается от левой части формулы (1)
тем. что в пей сила F умножается не на перемещение, совершаемое телом, а на
время t действия силы. В правой части формулы (3) стоит произведение массы
тела на его скорость (импульс) вместо половины произведения массы тела на квад-
рат его скорости, фигурирующее в правой части формулы (1). Обе эти формулы
являются следствием законов Ньютона (из которых они были выведены), а вели-
те3
чины — и mv являются характеристиками движения.
Но между формулами (1) я (3) имеется и принципиальное различие: формула
(1) устанавливает связь между скалярными величинами, тогда как формула (3) —
эго векторная формула.
Задача К Какую работу надо произвести, чтобы поезд, движу-
щийся со скоростью vt = 72 км/ч, увеличил свою скорость до
v2 = 108 к.м/ч? Масса поезда т = 1000 т. Какая сила должна
быть приложена к поезду, если это увеличение скорости должно
произойти на участке длиной 2 км? Движение считать равноуско-
ренным.
Решение. Работу А можно найти по формуле
Чодставпв сюда приведенные в задаче данные, получим:
I М. \2 I М
10’ кг 30— 10» кг 20—
__ ______\ сек !_________\ сек )
~ 2 2 =
= 250 • 10е дж = 250 000 кдж.
Чо определению А = Fs, следовательно,
Г- А 250- 105 d'K щ-ям 1О-
F = — =--------------= 12о 000 н Ч2-) кн.
s 2000 м
Задача 2, Какой высоты достигнет тело, брошенное вверх а
начальной скоростью о8?
Решение. Тело будет подниматься вверх до тех пор, пока
его скорость не станет равной нулю. На тело действует только сила
тяжести F = mg, где т — масса тела и g — ускорение свободного
падения (силой сопротивления воздуха и архимедовой силой пре-
небрегаем).
199
Применив формул5'
mi2 тиу}
— mgh - --------—t
. получим:
«г£/г = ~ = 0),
ст куда
Л
Это выражение мы уже получили ранее (см. стр. 60) более слож-
ным путем.
Упражнение 48
1. Как связана работа силы с кинетической энергией тела?
2 Как изменяется кинетическая энергия тела, если сила, приложенная к
нему, совершает положительную работу?
3. Как изменяется кинетическая энергия тела, если приложенная к нему сила
совершает отрицательную работу.
4. Тело движется равномерно по окружности радиусом 0,5 м, обладая кине-
тической энергией в 10 дж. Какова сила, действующая на тело? Как она
направлена? Чему равна работа этой силы?
5. К покоящемуся телу массой 3 кг приложена сила в 40 н. После этого тело
проходит по гладкой горизонтальной плоскости без трения 3 м. Затем сила
уменьшается до 20 н, и тело проходит еще 3 м. Найдите кинетическую
энергию тела в конечной точке его движения.
6. Какая работа должна быть совершена для остановки поезда массой 1 000 т,
движущегося со скоростью 108 км/ч?
7. На тело массой 5 кг, движущееся со скоростью 6 м. сек, действует сила в 8 н,
направленная в сторону, противоположную движению. В результате ско-
рость тела уменьшается до 2 м/сек. Какую работу по величине и по знаку
совершила сила? Какое расстояние прошло тело?
8. На тело, первоначально находившееся в покое, начинает действовать сила
в 4 н, направленная под углом 60° к горизонту. Тело движется по гладкой
горизонтальной поверхности без трения. Вычислите работу силы, если тело
прошло расстояние в 1 м.
9. В чем состоит теорема о кинетической энергии? - '
§ 77. РАБОТА СИЛЫ ТЯЖЕСТИ
Полезно ознакомиться в отдельности с работой каждой из ме-
ханических сил, с которыми мы ознакомились в пятой главе: силы
тяжести, силы упругости и силы трения. Начнем с силы тяжести.
Сила тяжести равна F = mg и направлена по вертикали вниз.
Вблизи поверхности Земли ее можно считать постоянной.
При движении тела по вертикали вниз сила тяжести совпадает
по направлению с перемещением. При переходе с высоты h2 над
каким-то уровнем, от которого мы начинаем отсчет высоты, до вы-
соты h2 над тем же уровнем (рис. 192), тело совершает перемеще-
ние, по абсолютной величине равное h2 — h.2. Так как направле-
ния перемещения и силы совпадают, то работа силы тяжести поло-
жительна и равна:
200
A — mg — h2).
Высоты hY и h2 не обязательно отсчи-
тывать ст поверхности Земли. Для нача-
ла отсчета высот можно выбрать любой
уровень. Это может быть пол комнаты, стел
или стул, это может быть и дно ямы, вы-
рытой в земле, и т. д. Ведь в формулу для
работы входит разность высот, а она не
зависит от того, откуда начинать их от-
счет. Мы могли бы, например, условиться
начинать отсчет высоты с уровня В (см.
рис. 192). Тогда высота этого уровня была
бы равна нулю, а работа выражалась бы
равенством
.4 -- mgh,
где h — высота точки .4 над уровнем В.
Если тело движется вертикально вверх, то сила тяжести на-
правлена против движения тела и ее работа отрицательна. При
подъеме тела на высоту h над тем уровнем, с которого оно брошено,
сила тяжести совершает работу, равную
А = —ingh.
Если после подъема вверх тело возвращается в исходную теч-
ку, то работа на таком пути, начинающемся и кончающемся в
одной и той же точке (на замкнутом пути), на пути «туда и об-
ратно», равна нулю. Это одна из особенностей силы тяжести: ра-
бота силы тяжести на замкнутом пути равна нулю.
Теперь выясним, какую работу совершает сила тяжести в слу-
чае, когда тело движется не по вертикали.
В качестве примера рассмотрим движение тела по наклонной
плоскости (рис. 193). Допустим, что тело массой т по наклонной
плоскости высотой h совершает перемещение s, по абсолютной
величине равное длине наклонной плоскости. Работу силы тяжести
mg в этом случае надо вычислять по формуле А = mgs cos а. Но
из рисунка видно, что
h
cos а —
s
Поэтому
, h .
А -- mgs - = mgn.
s
Мы получили для работы то
же самое значение.
Выходит, что работа силы тя-
жести не зависит от того, дви-
жется ли тело по вертикали или
Рис. 193
201
проходит более длинный путь по наклонной плоскости. При одной
и той же «потере высоты» работа силы тяжести одинакова (рис. 194).
Это справедливо не только при движении по наклонной плоско-
сти, но и по любому другому пути. В самом деле, допустим, что
тело движется по какому-то произвольному пути, например по та-
кому, какой изображен на рисунке 195. Весь этот путь мы можем
мысленно разбить на ряд малых участков: АА1Г А1А2, А2А3 и т. д.
Каждый из них может считаться маленькой наклонной плос-
костью, а все движение тела на пути АВ можно представить как
движение по множеству наклонных плоскостей, переходящих одна
в другую. Работа силы тяжести на каждой такой наклонной пло-
скости равна произведению mg на изменение высоты тела на ней.
Если изменения высот на отдельных участках равны hlt h2, h3
и т. д., то работы силы тяжести на них равны mghlt rngli,, tngh3
и т. д. Тогда полную работу на всем пути можно найти, сложив
все эти работы:
А = mghi + tngh., mgh3 -г ... = mg (1^ + h2 д- h3 + ...).
Но
Й! + h.2 -- h3 4-... = h.
Следовательно,
A = mgh.
Таким образом, работа си-
лы тяжести не зависит от
траектории движения тела и
всегда равна произведению
силы тяжести на разность
высот в исходном и конечном
положениях. При движении
вниз работа положительна,
при движении вверх — отри-
цательна.
Почему же в технике и
быту при подъеме грузов
часто пользуются наклонной
202
плоскостью? Ведь работа перемещения груза по наклонной плос-
кости такая же, как и при движении по вертикали!
Это объясняется тем, что при равномерном движении груза по
наклонной плоскости сила, которая должна быть приложена к
грузу в направлении перемещения, меньше силы тяжести. Правда,
груз при этом проходит больший путь. Больший путь — это плата
>а то, что по наклонной плоскости груз можно поднимать с помощью
меньшей силы.
Задача. Шарик массой т скатывается по рельсам, образующим
круговую петлю радиусом г (рис. 196). Какую работу совершает
сила тяжести к моменту, когда шарик достигает высшей точки
петли С, если в начальный момент он находится на высоте Н над
нижней точкой петли?
Решение. Работа силы тяжести равна произведению ее
значения на разность высот начального и конечного положений
шарика. Начальная высота равна Н, а конечная, как это видно из
рисунка, равна 2г. Следовательно,
А = mg (Н — 2r) = mgh.
Упражнение 49
1. Зависит ли работа силы тяжести от длины траектории тела, на которое она
действует? От массы тела?
2. Чему равна работа силы тяжести, если движущееся тело, на которое она
действует, пройдя некоторую траекторию, вернулось к исходной точке?
3. Тело брошено под некоторым углом к горизонту. Описав параболу, тело
упало на землю. Чему равна работа силы тяжести, если начальная и конеч-
ная точки траектории лежат на одной горизонтали?
4. Какая сила совершает работу при движении тела без трения по наклонной
плоскости? Зависит ли эта работа от длины наклонной плоскости?
5. Камень массой т брошен так, что он описал траекторию, показанную на
рисунке 197, а. Какова работа силы тяжести при таком движении камня?
Сравните ее с работой при движении того же камня по траекториям, изо-
браженным на рисунках 197, б и в.
4. Какую работу совершает человек массой 75 иг, когда он поднимается по
лестнице с первого этажа до пятого, если высота каждого этажа равна 3 м.
(Движение человека считать равномерным.)
7. Тепо массой 2 кг брошено вертикально вверх и поднялось на высоту 19 м.
Какая по величине и по знак/ работа совершена силой тяжести?
203
8. Лыжник спускается с горы высотой 60 м. Тотчас после спуска он оказыва-
ется на склоне соседней горы и поднимается по ней на высоту 40 м
(рис. 198), Какую по величине и по знаку работу совершает сила тяжести
при этом движении лыжника? Масса лыжника равна 80 кг.
9. Маятник совершает одно полное колебание. Какова работа силы тяжести
при этом движении маятника?
§ 78. РАБОТА СИЛЫ УПРУГОСТИ
Сила упругости, как мы знаем, возникает при деформации тел.
По своему абсолютному значению она пропорциональна величине
деформации (удлинению), а направлена в сторону, противополож-
ную направлению смещения точек тела при деформации.
На рисунке 199, а показана пружина в ее естественном, недефор-
мированном состоянии. Правый конец пружины закреплен, а к
левому прикреплено тело. Если пружину сжать, сместив левый
204
ее конец на расстояние л у (ряс. 199, б), то возникнет сила упруго-
сти, действующая со стороны пружины на тело, равная:
где k — жесткость пружины.
При перемещении витков пружины сила упругости совершит
работу. Какова величина этой работы?
Предположим, что левый конец пружины переместился из поло-
жения А в положение В (рис. 199, в). В этом положении деформа
ция пружины равна уже не xlt а х2. Значит, конец пружины пере-
местился на расстояние х2 — хг. Чтобы вычислить работу, нужно
это перемещение умножить на силу. Но сила упругости в отличие
от силы тяжести вблизи поверхности Земли при движении тела из-
меняется от точки к точке. Если в начальной точке она была рав-
на —kxlt то в конечной точке (в точке В) она стала равной —kx2.
Для того чтобы вычислить работу силы упругости, нужно взять
среднее значение силы упругости и умножить его на перемещение
х2 —-Vi (см. §75).
Сила упругости пропорциональна деформации пружины. По-
этому среднее значение силы упругости можно найти, используя
метод, который был использован при нахождении среднего значе-
ния скорости при равноускоренном движении (см. § 18).
Для среднего значения скорости при равноускоренном движе-
нии мы получили формулу
_ у, + У„
2 ’
где 1?0 — начальное и — конечное значение скорости. Подобно
этому среднее значение силы упругости можно определить по
формуле
На это-то значение силы упругости и нужно умножить переме-
щение х2 — лу, чтобы получить работу этой силы:
А = _-Ч ±±2 (%2 _ лД.
Так как (лу + х>) (х2 — .vj = х2 — .^, то формула для работы
принимает вид:
Л = |(х, — X'9).
Работа силы упругости равна половине произведения жестко-
сти упругого тела на разность квадратов его начального и конеч-
ного удлинений.
Если конечное удлинение пружины равняется нулю (ту = 0),
т. е. пружина приходит в недеформированное состояние, то она
205
совершает работу
1г 1'3
А = —
2
где .г — начальное удлинение пружины.
Интересно, что работа силы упругости имеет некоторое сход-
ство с работой силы тяжести. Если сравнить выражения для рабо-
ты этих двух сил:
Л = mg (JiL — /г.,)
то можно заметить, что в обоих случаях работа зависит от началь-
ного и конечного положений тела. В первой формуле высота h
определяет положение тела, на которое действует сила тяжести
(например, относительно поверхности Земли). Во второй формуле
удлинение х определяет положение одного конца пружины отно-
сительно другого ее конца.
Работа как силы упругости, так и силы тяжести зависит не от
формы, или длины пути, а только от начального и конечного поло-
жений движущегося тела.
Задача. При столкновении вагонов их буфера (по два на каж-
дом вагоне) сжались на 5 см. Какая работа была при этом соверше-
на силами упругости пружин, если известно, что при сжатии бу-
фера на 1 см возникает сила упругости в 10 000 н?
Р е ш е н и е. Вычислим сначала работу одной из четырех пру-
жин. Для этого воспользуемся формулой
Подставив сюда приведенные в условии задачи значения, по-
лучим:
10я —
А = —[0 — (0,05 ,и)-] = — 1 250 дж.
Так как у сталкивающихся вагонов четыре пружины, то общая
работа сил \ пругости равна — 5000 дж. Знак «минус» означает,
что сила упругости пружин направлена против направления пере-
мещения вагонов.
Упражнение 50
1. Как находится среднее значение сипы упругости?
2, В чем сходство работ, совершаемых силой упругости и силой тяжести?
3. Чему равна работа силы упругости, если тело, на которое она действует,
пройдя какое-то расстояние, вернулось в исходную точку?
4. Мальчик определил максимальную силу, с которой он может растягивать
динамометр. Она оказалась равной 400 н. Какую он совершил при этом
работу, если жесткость пружины k = 10 000 н/м?
206
S. К пружине, верхний конец которой
закреплен, подвешено тело массой
18 кг. При этом длина пружины
равна 10 см. Когда же к ней под-
вешивают тело массой 30 кг, ее
длина становится равной 12 см.
Вычислите работу, которую нужно
совершить, чтобы растянуть пру-
жину от 10 до 15 см.
6. Цирковой артист, масса которого
равна 60 кг, прыгает с высоты
10 м на растянутую сетку. На
сколько прогнется при этом сетка?
Когда артист стоит неподвижно на
сетке, прогиб ее равен 5 см.
7. На рисунке 200 показан график за-
висимости силы, необходимой для
сжатия пружины детского пистоле-
та, от ее деформации. Вычислите
работу, которая совершается при сжатии пружины на 2 см. Докажите, что
эта работа численно равна площади треугольника .4СВ.
§ 79. РАБОТА СИЛЫ ТРЕНИЯ
Нам осталось рассмотреть работу третьей механической силы —
силы трения скольжения. В земных условиях сила трения в той или
иной мере проявляется при всех движениях тел.
От силы тяжести и силы упругости сила трения скольжения
отличается тем, что она от координат не зависит и возникает всегда
при относительном движении соприкасающихся тел.
Рассмотрим работу силы трения при движении тела относитель-
но неподвижной поверхности, с которой оно соприкасается. В этсм
случае сила трения направлена против движения тела. Ясно, что
по отношению к направлению перемещения такого тела сила тре-
ния не может быть направлена под каким-нибудь” другим углем,
кроме угла 180°. Поэтому работа силы трения отрицательна.
Вычислять работу силы трения нужно по формуле
Л = — |^ls,
где F — сила трения, as — длина пути, на протяжении кстсрого
действует сила трения F.
Когда на тело действует сила тяжести пли сила упругости, оно
может двигаться и в направлении силы, и против направления си-
лы. В первом случае работа силы положительна, во втором —
отрицательна. При движении тела «туда и обратно» полная работа
равна нулю.
О работе силы трения этого сказать нельзя. Работа силы тре-
ния отрицательна и при движении «туда», и при движении «обрат-
но». Поэтому полная работа силы трения, после возвращения тела
в исходную точку (при движении по замкнутому пути) неравна
нулю.
207
Задача. Вычислите работу силы трения при торможении поезда
массой 1200 т до полной остановки, если скорость поезда в момент
выключения двигателя была 72 км/ч.
Решение. Воспользуемся формулой
А' -' —— (С1М's7&>-
Здесь т — масса поезда, равная 1 200 000 кг, и., — конечная
скорость поезда, равная нулю, и у, — его начальная скорость,
равная 72 км/ч = 20 м/сек. Подставив эти значения, получим:
А
ти\
2
1,2 Ю3 кг ( 20 —
сек'
2,4 10“ дж.
Упражнение 51
1. На тело действует сила трения. Может ли работа этой силы равняться нулю?
2. Если тело, на которое действует сила трения, пройдя некоторую траекто-
рию, вернется в исходную точку, будет ли работа силы трения равна нулю?
3. Как изменяется кинетическая энергия тела при работе силы трения?
4. Сани массой 60 кг, скатившись с горы, проехали по горизонтальному участ-
ку дороги 20 м. Найдите работу силы трения на этом участке, если коэф-
фициент трения полозьев саней о снег 0,02.
5. К точильному камню радиусом 20 см прижимают затачиваемую деталь с
силой 20 н. Определите, какая работа совершается двигателем за 2 мин,
если точильный камень делает 180 об мин, а коэффициент трения детали
о камень равен 0,3.
6. Шофер автомобиля выключает двигатель и начинает тормозить в 20 м от
светофора. Считая силу трения равной 4 000 н, найдите, при какой наиболь-
шей скорости автомобиля он успеет остановиться перед светофором, если
масса автомобиля равна 1,6 т?
§ 80. МОЩНОСТЬ
Когда идет речь о машинах, двигателях и разных механизмах,
предназначенных для совершения работы, весьма важно знать, как
быстро совершается работа. Ясно, например, что если один подъем-
ный кран поднимает груз в 1 т за 10 мин, а другой делает то же
самое за 0,5 мин, то предпочесть следует второй из них, так как
он выполняет работу в 20 раз быстрее.
Поэтому всякая машина, совершающая работу, характеризуется
особой величиной, называемой мощностью.
Мощность машины или механизма равна отношению совершен’
ной работы ко времени, в течение которого она совершена.
Если мощность обозначить буквой N, то
N.
t
208
Из приведенной формулы видно, в каких единицах измеряется
мощность. В системе единиц СИ, в которой работа измеряется в
джоулях (дж), а время — в секундах, единицей мощности является
I дж!сек (джоуль в секунд у). Такая единица имеет особое
название — ватт (вт):
, 1 дж , дж
1 сек сек
Это сравнительно небольшая единица. В технике часто поль-
зуются единицей, в 1000 раз большей ватта. Это киловатт
(кет). А иногда применяется единица, в миллион раз большая
ватта, — мегаватт (Мет).
В системе единиц СГС работа измеряется в эргах, а время —
в секундах. Поэтому единицей мощности в этой системе единиц
служит 1 эрг (сек.
Приведем пример. На самой крупной в мире Красноярской гид-
роэлектростанции каждую секунду с плотины высотой 100 м низ-
вергается поток воды в 5000 м3, или 5 • 10е кг. Очевидно, что мощ-
ность станнин равна работе, которую сила тяжести совершает над
этой массой воды за 1 сек:
N ='(Lgh'
t t
Учитывая, что у- — 5 10е кгеек, получаем:
N — 5 • 10е кг(сек 9,8 м'сек? 100 м^.5 • 10э — ~ 5 • 10е кет.
сек
Если известна мощность N, то работа А. которая производится
за время t, выражается формулой
А - Nt.
Отсюда следует, что за единицу работы можно принять работу,
которая производится в течение 1 сек при мощности 1 вт. Такая
единица работы называется ватт-секундой (вт сек):
1 вт • сек = 1 дж.
Но джоуль, а значит, и ватт-секунда слишком малые единицы.
Чаще пользуются более крупными единицами — киловатт-часом
(кет ч) и мегаватт-часом (Мет ч):
1 кет ч 1000 вт 360f) сек ~ 3,6 • 10“ вт сек --- 3,6 10“ дчс.
1 Мет ч - 1 000 000 вт 3600 сек ----- 3,6 109 вт сек — 3,6 • 11)!>дж.
Если работа двигателя самолета, корабля, ракеты, автомобиля
равна работе сил сопротивления, то движение будет равномерным,
т. е. оно будет происходить с постоянной скоростью. Но какова
209
величина этой скорости? От чего она зависит? Мы сейчас увидим,
что скорость как раз и зависит от мощности.
Л7 А
В самом деле, Л = —.
Но А = Fs.
>17
Следовательно, JV =
Отношение — = v — это скорость движения тела. Поэтому
N = Fv,
или у = —
F ’
Из этой формулы видно, что при постоянней силе скорость тем
больше, чем больше мощность двигателя.
Поэтому быстроходные поезда и автомобили нуждаются в дви-
гателях большой мощности. Однако на самом деле во многих случа-
ях сила не постоянна, а растет с ростом скорости.
В пятой главе (§ 50) мы видели, что при больших скоростях,
с которыми движутся корабли и самолеты, сила сопротивления
воздуха и воды (жидкое трение) пропорциональна квадрату ско-
рости. Это можно выразить формулой F = р v2, где р — коэффи-
циент пропорциональности.
Подставив в формулу N = Fv вместо F величину 0i>2, для мощ-
ности мы получим выражение
N = Ру3.
Мощность самолетных и судовых двигателей, следовательно, про-
порциональна не первой степени, а кубу скорости. Если, напри-
мер, требуется увеличить скорость самолета вдвое,то мощность его
двигателей нужно увеличить в восемь раз. Вот почему с таким тру-
дом дается каждый новый успех в увеличении скорости самолетов,
кораблей и других средств транспорта.
ТТЛ V N
Из формулы г = — видно также, что если величина мощно-
V
сти N двигателя постоянна, то сила, которая приложена к движу-
щемуся телу благодаря работе двигателя, больше при малых скоро-
стях, чем при больших. Именно поэтому водитель автомобиля при
подъеме в гору, когда нужна наибольшая сила тяги, переключает
двигатель на малую скорость.
Задача 1. Какую среднюю мощность развивает человек массой
70 кг, если лестницу высотой 10 м он пробегает за 15 сек?
Решение. Поднимаясь по лестнице, человек совершает
работу
А = mgh.
210
Следовательно, его мощность
д/ = 'ЛЙ
t ’
Подставив значения т = 70 кг, h = 10 м, t = 15 сгк, получаем:
м
70 « • 9,8 —- 10 м
сек1 2 3 4 5 6 7 8 9
N = -----------------460 вт.
15 сек
Задача 2. Какой массы груз может поднимать со скоростью
90 м[мин подъемный кран с двигателем мощностью 12 квт?
Решение. Из формулы мощности
N = Fv
можно выразить силу, с которой подъемный кран действует на
поднимаемый груз:
F = N-.
V
Но при равномерном подъеме эта сила равна mg. Поэтому
N
mg =
V
или
Подставив в эту формулу значения величин из условия задачи,
получим:
т =
12 000 вт
9,8-----
сек-
м
1,5 —
сек
800 кг.
Упражнение 52
1. Чго такое мощность?
2. К числу каких величин, скалярных или векторных, относится мощность?
3. От чего зависит скорость равномерного движения тела, приводимого в
движение двигателем?
4. Найдите соотношение между единицами мощности в системах единиц СИ
и СГС.
5. Самолет летит прямолинейно и равномерно со скоростью 900 км/ч. Какова
сила тяги моторов, если развиваемая ими мощность равна 1800 кзт?
6. Подъемный кран с двигателем мощностью 8 квт поднимает груз с постоян-
ной скоростью 6 м.мин. Какова масса груза?
7. На токарном станке обрабатывается вал. Мощность, развиваемая двигате-
лем станка, равна 3 квт. Какая совершается при этом работа, если вал обра-
батывается в течение 2 мин?
8. Какую работу совершает гидростанция в течение года, если средняя мощ-
ность ее генераторов равна 2,5 Мвт?
9. Автомобиль массой 200 иг движется по горизонтальной дороге со ско-
ростью 72 км/ч. Сила сопротивления движению составляет 0.05 от его веса.
Определите, какую мощность развивает при этом двигатель?
211
Глава 10
Закон сохранения энергии
ВВЕДЕНИЕ
В предыдущей главе был подробно рассмотрен вопрос о работе,
совершаемой силой, приложенной к движущемуся телу. Сила ха-
рактеризует взаимодействие тел. Поэтому мы часто будем говорить,
что работа совершается не силой, а телом, которое действует с этой
силой на другое тело в направлении его перемещения. Например,
вместо того чтобы говорить о работе, совершаемой силой тяжести
mg, можно говорить о работе, совершаемой Землей (над падающим
телом). Точно так же можно сказать, что растянутая пружина,
сокращаясь, совершает работу над прикрепленным к ней телом,
вместо того чтобы говорить о работе силы упругости, с которой эта
пружина действует на тело.
Вопрос о том, чему приписать произведенную работу — силе
или телу, не имеет большого значения. Но в этой главе, в которой
будет идти речь об очень важной характеристике движения тел —
энергии, будет удобнее считать, что работу совершают тела,
а не силы. Почему? Дело в том, что когда тело совершает работу,
то это не проходит для него бесследно. При этом изменяется то, что
в науке называют состоянием тела. Именно изменение со-
стояния тел при совершении ими работы и будет интересовать пас
в этой главе.
§ 81. ПОНЯТИЕ О МЕХАНИЧЕСКОМ
состоянии
Мы начнем с определения того, что такое состояние тела (или
системы тел). Так как в механике рассматривается движение тел,
то речь у нас пойдет о механическом состоянии.
Вообще состояние какого-нибудь объекта характеризуется ря-
дом величин, или, как их называют, параметров. Например,
физиологическое состояние человека определяется температурой
его тела, частотой пульса, давлением и составом крови и т. д. Со-
стояние атмосферы, от которого зависит погода, определяется тем-
пературой воздуха, атмосферным давлением, влажностью. С тече-
нием времени под влиянием различных причин величины, опреде-
ляющие состояние объекта, или некоторые из них изменяются.
Это означает, что изменяется состояние объекта. При надлежащем
развитии соответствующей науки можно, зная состояние объекта
212
в какой-то начальный момент времени, предвидеть его состояние в
любой другой момент времени. Например, современная метеороло-
гия, т. е. наука о погоде, близка к тому, чтобы с уверенностью пред-
сказывать погоду в будущем, если известно состояние атмосферы
в настоящем.
Чем же определяется состояние движения или механическое
состояние тела? Ясно, что оно определяется теми величинами, ко-
торые нужно знать, чтобы предсказывать (вычислять) положение
тела в любой момент времени. А такими величинами, как мы уже
видели, являются координаты и скорость тела.
Механическое состояние тела определяется его положением
относительно других тел (координатами тела) и его скоростью.
§ 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ
ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ
Выясним, что происходит с телами, когда они совершают рабо-
ту, взаимодействуя друг с другом силами тяготения или силами
упругости. Работу сил трения пока оставим в стороне.
В качестве примера силы тяготения рассмотрим силу тяжести,
с которой взаимодействуют Земля и находящееся вблизи ее поверх-
ности тело. Если это тело переместится так, что его высота умень-
шится, то Земля, действуя на тело силой тяжести, совершит поло-
жительную работу.
Земля п в самом деле производит работу, когда, например, пере-
мещает воду в реках; Земля производит работу, когда гиря стенных
часов («ходиков») опускается вниз. И когда эта работа совершается
(например, когда гиря опускается), изменяется взаимное располо-
жение Земли и тела, т. е. изменяется их механическое состояние.
Примером тела, где проявляются силы упругости, может слу-
жить растянутая (деформированная) пружина, один конец которой
закреплен.
Деформированная пружина тоже способна совершить работу.
В большинстве часовых механизмов пружина применяется для тех
же целей, что и гиря в часах-«ходиках».
При сокращении растянутой пружины, т. е. при перемещении
ее свободного конца, совершается положительная работа (переме-
щение направлено так же, как и сила упругости). Но когда пружи-
на совершает работу, ее механическое состояние изменяется, пото-
му что изменяется взаимное расположение ее витков.
Способностью совершать работу обладает и движущееся тело.
В предыдущей главе мы видели, что когда под действием любых
сил изменяется скорость движения тела, то совершается работа
(теорема о кинетической энергии).
Представим себе тело, движущееся с некоторой постоянной ско-
ростью в горизонтальном направлении. Таким движущимся телом
213
можно воспользоваться, чтобы произ-
вести работу. Можно, например, при-
крепить к телу какой-нибудь груз при
помощи шнура, перекинутого через
блок (рис. 201). Тогда тело, продол-
жая двигаться, поднимет груз на не-
которую высоту h и, следовательно,
совершит работу.
Скорость тела при этом уменьша-
ется, тело тормозится. Значит, дви-
жущееся тело, совершая работу, из-
меняет свое механическое состояние.
Из приведенных примеров видно, что когда тела, способные
совершать работу, в самом деле ее совершают, то их механическое
состояние изменяется. Эти изменения могут быть большими и ма-
лыми. Значит, должна существовать физическая величина, которая
позволила бы выразить числом механическое состояние тела и то
его изменение, которое происходит при совершении работы.
Что это за величина?
Из курса физики VI класса известно, что о телах, способных
совершать работу, говорят, что оии обладают энергией. Значит,
Земля вместе с телом, находящимся над ней, деформированная
пружина, любое движущееся тело обладают энергией.
Энергия тела или системы тел определяется работой, которую
они способны совершить.
Когда о телах говорят, что они способны совершить работу, это
еще не означает, что они ее действительно совершают. Например,
сжатая или растянутая на определенную длину пружина никакой
работы не совершает. Однако энергией такая пружина обладает.
Энергия растянутой пружины равна той работе, которую она со-
вершила бы, если бы ей предоставили возможность сократиться
до нормального состояния (когда ее деформация равна нулю). Ес-
ли пружина сократится только частично, она будет обладать
меньшей энергией. Ее энергия уменьшится как раз на величину
совершенной при сокращении работы. Если же к пружине в про-
цессе ее деформации будет приложена какая-нибудь сила, равная и
противоположная силе упругости пружины, то энергия пружины
увеличится на величину совершенной этой силой работы.
Вот мы и нашли величину, которая характеризует механическое
состояние тел. Это энергия тел.
Энергия — это физическая величина, изменение которой рав-
но совершенной работе.
Так как энергия определяется работой, которую может совер-
шить тело, то измеряют ее в тех же единицах, что и работу, т. е.
в джоулях (в системе единиц СИ) или в э р г а х (в системе
СГС).
214
Упражнение 53
1. Какие величины определяют механическое состояние тела?
2. Одна из двух гирь одинаковой массы помещена на столе, а другая — на
полу. В одинаковых ли состояниях находятся эти гири?
3. Чем характеризуется состояние движущегося тела?
4. Чем характеризуется состояние тела, совершающего свободное падение?
5. В каком случае о теле можно сказать, что оно обладает энергией?
6. Что такое энергия?
§ 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ
ЭНЕРГИЯ
В предыдущем параграфе было выяснено, что когда тела, взаи-
модействующие друг с другом силой упругости или силой тяжести,
совершают работу, то изменяется взаимное расположение тел или
их частей. А когда работу совершает движущееся тело, то изменяет-
ся его скорость. Но при совершении работы изменяется энергия
тел. Отсюда можно заключить, что энергия тел, взаимодействую-
щих силой упругости или силой тяжести, зависит от взаимного
расположения этих тел или их частей. Энергия же движущегося
тела зависит от его скорости.
Энергию тел, которой они обладают вследствие взаимодействия
друг с другом, называют потенциальной энергией. Энергию же
тел, которой они обладают вследствие своего движения, называют
кинетической энергией.
Следовательно, энергия, которой обладает Земля и находящееся
вблизи нее тело, — это потенциальная энергия системы Земля —
тело. Для краткости принято говорить, что этой энергией обладает
само тело, находящееся вблизи поверхности Земли.
Энергия деформированной пружины — это тоже потенциальная
энергия. Она определяется взаимным расположением витков пру-
жины.
Кинетическая энергия — это энергия движения. Кинетиче-
ской энергией может обладать тело и не взаимодействующее с дру-
гими телами.
Тела могут обладать одновременно и потенциальной, и кинети-
ческой энергией. Например, искусственный спутник Земли обла-
дает кинетической энергией, потому что он движется, и потенциаль-
ной энергией, потому что он взаимодействует силой всемирного
тяготения с Землей. Падающий груз тоже обладает и кинетиче-
ской. и потенциальной энергией.
Посмотрим теперь, как можно вычислить энергию, которой
обладает тело в данном состоянии, а не только ее изменение. Для
этой цели нужно из различных состояний тела или системы тел
выбрать одно определенное состояние, с которым будут сравнивать-
ся все остальные.
Назовем это состояние «нулевым состоянием». Тогда энергия
тел в любом состоянии будет равна работе, которая совершается
215
при переходе из этого состояния в нулевое состояние. (Очевидно,
что в нулевом состоянии энергия тела равна нулю.) Напомним, что
работа, совершаемая силой тяжести и силой упругости, не зависит
от траектории движения тела. Она зависит только от его начально-
го и конечного положений. Точно так же работа, совершаемая при
изменении скорости тела, зависит только от начальной и конечной
скорости тела.
Какое состояние тел выбрать за нулевое, безразлично. Но в
некоторых случаях выбор нулевого состояния напрашивается сам
собой. Например, когда речь идет о потенциальной энергии упруго
деформированной пружины, естественно считать, что недеформи-
рованная пружина находится в нулевом состоянии. Энергия неде-
формированной пружины равна нулю. Тогда потенциальная энер-
гия деформированной пружины будет равна той работе, которую
совершила бы эта пружина, перейдя в недеформированноесостояние.
Когда нас интересует кинетическая энергия движущегося тела,
естественно принять за нулевое то состояние тела, в котором
его скорость равна нулю. Кинетическую энергию движущегося
тела мы получим, если вычислим работу, которую оно совершило
бы, двигаясь до полной остановки.
Иное дело, когда речь идет о потенциальной энергии тела, под-
нятого на некоторую высоту над Землей. Эта энергия зависит, ко-
нечно, от высоты поднятия тела. Но тут нет «естественного» выбора
нулевого состояния, т. е. того положения тела, от которого нужно
отсчитывать его высоту. Можно выбрать за нулевое то состояние
тела, когда оно находится на полу комнаты, на уровне моря, на
дне шахты и т. д. Необходимо лишь при определении энергии тела
на разных высотах отсчитывать эти высоты от одного и того же
уровня, высота которого принята равной нулю. Тогда значение
потенциальной энергии тела на данной высоте будет равно работе,
которая была бы совершена при переходе тела с этой высоты на
нулевой уровень.
Выходит, что в зависимости от выбора нулевого состояния энер-
гия одного и того же тела имеет разные значения! В этом нет ни-
какой беды. Ведь для вычисления работы, совершаемой телом, нам
нужно знать изменение энергии, т. е. разность двух значений
энергии. А эта разность никак не зависит от выбора нулевого уров-
ня. Например, для того чтобы определить, на сколько вершина
одной горы выше другой, безразлично, откуда отсчитывается высо-
та каждой вершины. Важно лишь, чтобы она отсчитывалась от од-
ного и того же уровня (например, от уровня моря).
Изменение как кинетической, так и потенциальной энергии тел
всегда равно по абсолютной величине работе, совершенной дейст-
вующими на эти тела силами. Но между обоими видами энергии
имеется важное различие. Изменение кинетической энергии тела
при действии на него силы действительно равно совершенной этой
силой работе, т. е. совпадает с ней как по абсолютной величине,
так и по знаку. Это непосредственно следует из теоремы о кинети-
216
ческой энергии (см. § 76). Изменение же потенциальной энергии
тел равно работе, совершенной силами взаимодействия, только по
абсолютной величине, а по знаку противоположно ей. В самом де-
ле, когда тело, на которое действует сила тяжести, перемещается
вниз, совершается положительная работа, а потенциальная энергия
тела при этом уменьшается. То же относится к деформированной
пружине: при сокращении растянутой пружины сила упругости
совершает положительную работу, а потенциальная энергия пру-
жины уменьшается. Напомним, что изменение величины — это
разность между последующим и предшествующим значением этой
величины. Поэтому, когда изменение какой-нибудь величины со-
стоит в том, что она увеличивается, это изменение имеет положи-
тельный знак. Наоборот, если величина уменьшается, ее измене-
ние отрицательно.
Упражнение 54
1. В каких случаях тело обладает потенциальной энергией?
2. В каких случаях тело обладает кинетической энергией?
3. Какой энергией обладает свободно падающее тело?
4. Как изменяется потенциальная энергия тела, на которое действует сила тя-
жести, при его движении вниз?
5. Как изменится потенциальная энергия тела, на которое действует сила уп-
ругости или сила тяжести, если, пройдя по любой траектории, тело вернет-
ся в исходную точку?
6. Как связана работа, совершаемая пружиной, с изменением ее потенциаль-
ной энергии?
7. Как изменяется потенциальная энергия пружины, когда недеформирован-
ную пружину растягивают? Сжимают?
8. Шарик подвешен к пружине и совершает колебания. Как изменяется по-
тенциальная энергия пружины при ее движении вверх и вниз?
§ 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО
ДЕФОРМИРОВАННОГО ТЕЛА
Вычислим потенциальную энергию упруго деформированного
тела. В предыдущем параграфе было указано, что энергия упруго
деформированного тела, например сжатой или растянутой пружи-
ны, равна работе, которую совершила бы такая пружина, переходя
в недеформированное состояние.
В § 78 мы вычислили работу силы упругости, т. е. работу, кото-
рую совершает упруго деформированная пружина, переходя в не-
деформированное состояние:
А - ix\
2
где k — жесткость пружины, а х — ее начальное удлинение.
Этой величине и равна потенциальная энергия сжатой (или
растянутой) пружины.
В дальнейшем потенциальную энергию мы будем обозначать
буквой П.
217
Итак, потенциальная энергия П деформированной пружины и
вообще любого упруго сжатого пли растянутого тела равна:
77 =
2
Удлинение (деформация) ,v входит в выражение для потенциаль-
ной энергии во второй степени. Поэтому потенциальная энергия не
зависит от знака х. Это значит, что потенциальная энергия зави-
сит только от абсолютного значения деформации и не зависит от?
того, сжато деформированное тело или растянуто.
В § 78 было показано, что если деформация пружины изменяет-
ся от до лц, то при этом совершается работа
7’лд /гл*.,
4 = = 771-Я2 = -(Я2-771),
где П1 и 77., — значения потенциальной энергии пружины соот-
ветственно при деформации л\ и лд. Но П2 — — это изменение
потенциальной энергии пружины. Как и следовало ожидать, совер-
шенная работа равна изменению потенциальной энергии пружины,
взятому с противоположным знаком.
Упражнение 55
3. К пружинным весам подвешен
Рис. 202
1. Чему равна потенциальная энергия упруго сжатого тела?
2. Имеются две пружины с одинаковой жесткостью. Одна из них сжата так,
что она стала короче, чем недеформированная пружина, на 5 см, а вторая
растянута, и ее длина на 5 см больше длины пружины в недеформирован-
ном состоянии. Чем различаются удлинения этих пружин и их потенциаль-
ные энергии?
груз. При этом груз опустился и стрелка ве-
сов остановилась на цифре 3. На сколько
увеличилась потенциальная энергия пружи-
ны весов, если шкала весов градуирована в
ньютонах, а расстояние между соседними
делениями шкалы равно 5 мм?
Две пружины, жесткость которых равна k\
и k2, могут быть соединены как «параллель-
но» (рис. 202, а), так и «последовательноэ
(рис. 202, б). Найдите потенциальную энер-
гию соединенных пружин, если растяжение
в обоих случаях одинаково и равно х.
Сжатая пружина, жесткость которой равна
10 000 н/м, действует на прикрепленное к
ней тело с силой 400 н. Чему равна потен-
циальная энергия пружины? Какая работа
была совершена при сжатии пружины? Ка-
кую работу совершит пружина, если дать ей
возможность разжаться?
?18
§ 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА,
НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ
СИЛЫ ТЯЖЕСТИ
Мы уже знаем, что тело, находящееся на некоторой высоте над
Землей, обладает потенциальной энергией.
Примем поверхность Земли за нулевой уровень, от которого
будем отсчитывать высоту тела. Для того чтобы найти потенциаль-
ную энергию тела на высоте h над Землей, нужно вычислить рабо-
ту, которая была бы совершена телом при его падении на Землю.
В § 77 было показано, что работа А, которую совершит сила тя-
жести при перемещении тела с высоты h на поверхность Земли,
равна:
А = mgh,
где т — масса тела.
Следовательно, потенциальная энергия тела на высоте h равна:
Л = mgh.
Можно было бы принять, что потенциальная энергия тела равна
нулю на высоте h0 над поверхностью Земли. Тогда на высоте h над
поверхностью Земли тело обладало бы потенциальной энергией,
равной
mg (h — /i0).
В этом случае на самой поверхности Земли (h = 0) потенциальная
энергия была бы равна
— mgh0,
т. е. имела бы отрицательное значение.
Если нулевой уровень выбран так, что он находится ниже тела,
то энергия тела положительна. Потенциальная же энергия тела,
расположенного ниже нулевого уровня, отрицательна.
При перемещении тела с высоты до высоты /г2 сила тяжести
совершает работу
А = mg — h2) = — (mgh2 — mghi) = — (1^ — 11^
где и П.2 — значения потенциальной энергии тела соответст-
венно на высотах hr и й2.
Мы снова видим, что совершенная работа равна изменению
потенциальной энергии тела (системы тело — Земля), взятому
с противоположным знаком.
Упражнение 56
1. Чему равна потенциальная энергия тела, поднятого на высоту //?
2. Что происходит с потенциальной энергией тела при его движении вверх?
3. Груз массой 2,5 кг падает с высоты 10 м. Чему равна его потенциальная
энергия через 1 сек после начала падения (начальная скорость груза равна
нулю)?
219
4. Тело массой 5 кг падаег с десятого этажа высотного здания. На сколько
изменится его потенциальная энергия на пути or десятого этажа до пятого
и от пятого до поверхности земли, если все этажи разделены одним и тем
же расстоянием в 3,5 м?
5. Два тела одинаковой массы расположены на одинаковой высоте. Одно из
тел находится в воде, другое — в воздухе. Сравните их потенциальные
энергии.
§ 86. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ
В § 76 мы назвали кинетической энергией величину но
не объяснили, почему ее так называют. Теперь мы можем это сделать.
Напомним, что движущееся тело способно совершить работу.
Если бы это тело действительно совершило работу, то его скорость
уменьшилась бы. Кинетическая энергия тела равна той работе,
которую совершило бы движущееся тело, если бы его скорость
изменила свое значение до нуля.
Как вычислить квиетическую энергию?
Представим себе, что тело массой т, движущееся со скоростью и,
действует с силой F на перекинутую через блок шпь, к которой
прикреплен груз (рис. 203). Направление силы F совпадает с на-
правлением движения. Тогда на само движущееся тело будет дей-
ствовать сила Ft со стороны нити, которая по третьему закону
Ньютона равна силе F по абсолютному значению, но направлена в
противоположную сторону: F1 - — F. Поэтому скорость движуще-
гося тела будет уменьшаться. Предположим, она уменьшилась от
значения vr до значения v.,. Согласно теореме о кинетической энер-
гии (§ 76) работа силы F\ равна:
“ 2
nw~) ти,
А = ---------к
2 2
Нам же нужно найти работу, которую совершает само тело, т. е.
работу силы F. Очевидно, работа силы F равна работе силы Flt
но с противоположным знаком. Следова-
тельно, работа, совершаемая движущимся
телом, равна
’ 2
mej пи1.,
2 ~~ 2 '
При уменьшении скорости тела от зна-
чения до пуля (Oj ~ 0) совершенная те-
лом работа будет равна:
—L--().
Рис. 203 2 2
220
а при уменьшении скорости тела от значения v до нуля совершен-
ная нм работа будет определяться выражением
К = —.
2
Это и есть кинетическая энергия тела массой т, движущегося
со скоростью V.
Упражнение 57
1. Как связаны работа и кинетическая энергия?
2. В чем различие между кинетической и потенциальной энергией?
3. Изменяется ли кинетическая энергия тела при изменении направления
вектора его скорости?
4. Груз массой 1 кг падает с высоты 20 м. Чему равна его кинетическая энер-
гия в середине пути?
5. Тело брошено вертикально вверх со скоростью 16 м/сек. На какой высоте
его кинетическая энергия будет вдвое меньше начальной?
6. Вычислите кинетическую энергию искусственного спутника Земли массой
1300 кг, движущегося по круговой орбите на высоте 100 км над Землей.
§ 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
Рассмотрим энергию, которой обладают тела, взаимодействующие
только друг с другом. Напомним, что такие тела образуют замкну-
тую систему тел (см. гл. 8).
В § 84 и 85 было установлено, что, когда тела взаимодействуют
силой упругости или силой тяжести, совершенная этими силами
работа равна взятому с противоположным знаком изменению по-
тенциальной энергии системы.
Но силы взаимодействия могут вызвать изменение и скоростей
тел, а следовательно, и изменение их кинетической энергии. Со-
гласно теореме о кинетической энергии работа силы, действующей
на тело, равна изменению его кинетической энергии. Следователь-
но, работа сил взаимодействия между телами равна по величине и
совпадает по знаку с изменением кинетической энергии взаимодей-
ствующих тел.
Итак, мы видим, что одна и та же работа сил взаимодействия
равна изменению потенциальной энергии, взятому со знаком «—»,
и изменению кинетической энергии, взятому со знаком «+ ». Это
означает, что изменение кинетической энергии равно взятому с
противоположным знаком изменению потенциальной энергии.
Если потенциальная энергия увеличивается, то кинетическая
на столько же уменьшается и наоборот, когда потенциальная энер-
гия уменьшается, растет кинетическая.
Сумму потенциальной и кинетической энергии тел называют
полной механической энергией. 14з приведен-
ных нами рассуждений следует закон сохранения ме-
ханической энергии замкнутой системы
тел.
221
Полная механическая энергия замкнутой системы тел оста-
ется неизменной при любых движениях тел этой системы, если
между телами действуют силы тяготения или силы упругости.
Превращение потенциальной энергии в кинетическую или кине-
тической в потенциальную — одно из самых замечательных явле-
ний в природе. Это главное отличительное свойство энергии. В даль-
нейшем мы ознакомимся со многими другими примерами превраще-
ний одного вида энергии в другой.
Закон сохранения энергии позволяет лучше понять физический
смысл работы. Из того факта, что одна и та же работа приводит к
увеличению кинетической энергии и такому же уменьшению по-
тенциальной энергии, следует, что работа равна энергии, испытав-
шей превращение из одного вида в другой.
В девятой главе мы ознакомились с законом сохранения им-
пульса замкнутой системы тел. Теперь мы получили второй закон
сохранения—закон сохранения энергии. Эти два закона носят
самый общий характер и являются абсолютно точными даже тогда,
когда законы механики Ньютона перестают быть справедливыми.
Если система тел не является замкнутой, например на одно из
тел этой системы действует внешнее тело, не относящееся к систе-
ме, то полная механическая энергия системы уже не остается по-
стоянной. Когда подъемный кран поднимает груз, на груз действует
не только сила тяжести (сила его взаимодействия с Землей), но и
сила натяжения троса. Поэтому система груз — Земля не является
замкнутой. Если сила натяжения троса равна F, а кран поднял
груз на высоту h, то работа, совершенная обеими этими силами,
равна:
.4 - (F - mg) h.
Эта работа согласно теореме о кинетической энергии равна из-
менению кинетической энергии груза:
9 9
muz mv\
А ----- —------
2 2
где щ— скорость груза в начале, а v, — в конце подъема.
Следовательно,
Отсюда
/ mvz
г li =-= mgh 4- I ~
9
mi>i
Здесь mg/i — изменение потенциальной энергии груза, а —-
1Г
изменение его кинетической энергии.
227
Таким образом, полная механическая энергия этой системы
изменяется на величину работы, совершенной силой натяжения
троса.
Если на тело или тела, образующие систему, действуют внешние
по отношению к той системе силы, полная энергия системы изме-
няется на величину работы, совершенной этими силами.
Если скорость подъема груза, как это часто бывает, остается
постоянной, то
Fh = mgh,
т. е. работа, совершенная силой натяжения троса, равна изменению
потенциальной энергии системы.
Задача. Искусственный спутник Земли движется по эллиптиче-
ской орбите. Найдите скорость v2 движения спутника в апогее,
если его скорость в перигее = 8 км/сек. Перигей орбиты находит-
ся на расстоянии hr = 200 км, а апогей — на расстоянии h2 =
= 400 км от поверхности Земли.
Решение. На спутник действует только сила тяжести —
сила взаимодействия с Землей. Поэтому система тел спутник —
Земля — замкнутая система. Для нее справедлив закон сохране-
ния энергии. Пренебрегая изменением кинетической энергии Зем-
ли, можно написать:
2 9
tnv\ mv2
— + mghi = — + mgh2
(m — масса спутника).
2 9
z-x Vt> V1
Отсюда — + ght — ghz
и v2 = У + 2g — h2).
Подставляя числовые значения, получим:
= ]/б4- 10е—2—2-10—,-2-105ai= 1031/б0-^r^7,7- 103—•
Г сек2 сек2 Г сек2 ’ сек
При решении задачи мы пренебрегли изменением значения g с вы-
сотой над поверхностью Земли.
Упражнение 58
1. Как изменяется с высотой потенциальная и кинетическая энергия свободно
падающего тела?
2. Как изменяется с высотой потенциальная и кинетическая энергия тела, бро-
шенного вверх?
3. Тело подвешено к пружине. Оно начинает падать, и при этом пружина рас-
тягивается. Объясните, какие виды энергии здесь изменяются и как.
223
4. Тело упало с некоторой высоты над Землей. 3 момент падения на поверх-
ность Земли его скорость была равна 39 м сек. Пользуясь законом сохра-
нения энергии, определите, с какой высоты упало тело.
5. Растянутая пружина, сокращаясь, увлекает за собой прикрепленное к ней
тело массой 50 г по горизонтальной поверхности без трения. В тот момент,
когда деформация пружины равна нулю, скорость тела равна 5 м/сек.
На сколько была растянута пружина, если ее жесткость равна 10 000 н/м?
6. Тело массой 2 кг падает с высоты 30 м над Землей. Пользуясь законом
сохранения энергии, вычислите кинетическую энергию тела в момент, когда
оно находится на высоте 15 м. Чему будет равна его кинетическая энергия
в момент падения на Землю?
7. Тело массой 250 г брошено вертикально вверх со скоростью 15 м/сек.
Найдите потенциальную энергию тела в высшей точке его траектории и
наибольшую высоту подъема.
8. Тело массой 400 г прикреплено к сжатой пружине жесткостью 100 н/м.
После освобождения пружины тело совершает такие колебания, что наи-
большая деформация равна 10 см. Какова наибольшая скорость колеблю-
щегося тела? Какова при этой скорости деформация пружины?
§ 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
И СИЛА ТРЕНИЯ
Тело, получив толчок, движется вверх, против силы тяжести.
При этом его кинетическая энергия уменьшается. Достигнув верх-
ней точки траектории, тело на миг останавливается и начинает
обратный путь вниз.
Но вот другой пример. Тело лежит на горизонтальной неглад-
кой поверхности. Получив толчок, оно начинает двигаться. Из-за
действия силы трения кинетическая энергия тела уменьшается.
Пройдя некоторое расстояние, тело останавливается, но не на миг,
как в примере с брошенным вверх телом. Оно остановится совсем
и в обратный путь уже не двинется.
Почему так по-разному ведет себя тело в этих двух как будто
бы похожих случаях? Ведь в каждом из них тело движется против
некоторой силы, которая совершает отрицательную работу, что и
приводит к уменьшению кинетической энергии. Все дело в том, что
в первом примере кинетическая энергия, постепенно уменьшаясь,
превращается в потенциальную энергию взаимодействия тела и
Земли. За счет этой энергии и совершается работа при движении
тела вниз. В случае же движения тела по шероховатой поверхно-
сти кинетическая энергия уменьшается, но не превращается в по-
тенциальную энергию. Поэтому и тело не движется в обратном на-
правлении: нет энергии, за счет которой могла бы быть совершена
работа при таком перемещении.
Выходит, что, когда на тело действует сила трения (сама по
себе или вместе с другими силами), нарушается закон сохранения
энергии: кинетическая энергия уменьшается, а потенциальная
энергия не появляется. Следовательно, полная механическая энер-
гия уменьшается.
Такое уменьшение механической энергии мы наблюдаем даже
при движении падающего на Землю тела, если падение происходит
224
не в вакууме, а в воздухе. При этом движении потенциальная энер-
гия тела уменьшается на величину mgh, как и при движении в пу-
стоте. Но скорость тела, когда оно достигнет поверхности Земли,
будет меньше, чем при свободном падении. Меньшей будет и его
кинетическая энергия, так что она уже не будет равна убыли по-
тенциальной энергии. За счет потерянной энергии была совершена
работа против силы сопротивления воздуха. Хотя мы и знаем,
куда пропала механическая энергия, она все-таки исчезла и за-
izoh сохранения энергии оказывается как будто нарушенным.
Но оказывается, что нарушение закона сохранения энергии
здесь только кажущееся. Дело в том, что трение одного тела о
другое всегда приводит к нагреванию обоих тел, к повышению их
температуры. Из курса физики VII класса известно, что температу-
ра тел определяется кинетической энергией движущихся молекул
или атомов, из которых состоят все тела. Поэтому при нагревании
трущихся тел увеличивается энергия движения молекул тела,
или, как говорят, внутренняя энергия тела. Не
происходит ли это увеличение внутренней энергии как раз за счет
«теряющейся» кинетической энергии движения всего тела? Тщатель-
ные измерения показали, что когда движущиеся тела из-за действия
силы трения уменьшают свою кинетическую энергию, их внутрен-
няя энергия (энергия движения модекул в теле) в самом деле уве-
личивается ровно на столько, на сколько уменьшается механиче-
ская энергия. Следовательно, механическая энергия хотя и умень-
шается, но не теряется бесследно, а только переходит в энергию
движущихся молекул.
Мы приходим, таким образом, к очень важному выводу, что воз-
можно не только превращение энергии из потенциальной в кинети-
ческую и обратно. Кинетическая энергия может превращаться в
немеханическую форму энергии — во внутреннюю энергию движения
частиц, составляющих тело. Энергия и замечательна тем, что она
может иметь различные формы: кинетическую, потенциальную,
внутреннюю и много других форм, с которыми вы ознакомитесь
позже. А закон сохранения энергии означает, что сохраняет-
ся сумма всех видов энергии тела. И всякий
раз, когда при каком-нибудь процессе или явлении наблюдается
«пропажа» какого-нибудь вида энергии, можно быть уверенным,
что в этом процессе появилась энергия какого-нибудь другого вида.
Упражнение 59
1. Как изменяется механическая энергия тела, когда на него действует сила
трения скольжения?
2. На движущееся по горизонтальной плоскости тело на протяжении пути
длиной 15 м действует сила трения, равная 100 н. На сколько изменилась
механическая энергия тела? Какая именно энергия (кинетическая или по-
тенциальная) изменилась?
3. Парашютист массой 70 кг после прыжка с самолета движется сначала
ускоренно, а затем, начиная с высоты /г = 1 ООО м и до приземления, равно-
8 Заказ 1126
225
мерно со скоростью 6 м/сен. Какая работа совершена силой сопротивле-
ния воздуха за время равномерного движения?
4. Тело массой 2 кг падает с высоты 240 м и проникает в грунт на глубину
0,2 м. Сила трения тела о грунт равна 10 000 н. Совершало ли тело свобод-
ное падение или двигалось в воздухе?
5. Существует ли закон сохранения кинетической энергии?
6. Существует ли закон сохранения потенциальной энергии?
7. Пуля массой 10 г, летящая в горизонтальном направлении со скоростью
600 м/сек, попадает в деревянный брус массой 2 кг и застревает в нем. При
этом и пуля, и брус нагреваются. Какая энергия идет на нагревание? Силой
сопротивления воздуха пренебречь.
§ 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ
И ИСПОЛЬЗОВАНИЕ МАШИН
Вот уже около двухсот лет прошло с тех пор, как началось
широкое использование человеком всевозможных машин. Эти ма-
шины приводятся в движение двигателями, которые в свою очередь
получают энергию от того или иного источника.
С механической точки зрения использование машин сводится
к тому, что с их помощью какие-то силы совершают работу. Но
совершить работу — значит затратить энергию, по крайней мере
равную этой работе. В наше время главные виды энергии, за счет
которых совершается работа, — это энергия, освобождающаяся
при сгорании топлива (угля, нефти, газа), энергия падающей воды
и так называемая ядерная энергия, выделяющаяся в ядерных реак-
торах. Ни один из этих видов энергии не подается непосредствен-
но к машинам.
На пути к машинам, в которых совершается работа, энергия
претерпевает ряд превращений из одной формы в другую. Так,
например, энергия взаимодействия частиц горючего и кислорода
(потенциальная энергия) сначала преобразуется во внутреннюю
энергию тех частиц, которые образуются при сгорании. Затем эта
энергия в виде тепла передается водяному пару, а от него к паро-
вой турбине, приводящей в движение электрический генератор.
В нем механическая энергия вращения преобразуется в энергию
электрического тока. Так работает тепловая электростанция. От
генератора электростанции энергия передается по проводам к элек-
трическим двигателям, установленным на бесчисленных станках
и других устройствах. В двигателях энергия снова преобразуется
в механическую энергию и с помощью различных передаточных
механизмов, например рычагов, наклонных плоскостей, винтов,
блоков, подается к станкам и другим машинам.
Мы привели здесь цепь превращений, которые испытывает
энергия «по дороге» от топки тепловой электростанции к машине.
К этому следует добавить, что само топливо появилось на Земле в
результате сложной цепи превращений энергии, цепи, начало ко-
торой находится на Солнце — источнике жизни на нашей планете.
226
Для нас здесь важно то, что все эти прев-
ращения (мы перечислили далеко не все) под-
чиняются закону сохранения энергии, из кото-
рого следует, что при любых превращениях нель-
зя получить энергии одного вида больше, чем
затрачено энергии другого вида. Ни в одном
двигателе нельзя получить больше механической
энергии, чем затрачено электрической или тепло-
вой. Ни один двигатель не может произвести
больше работы, чем затрачено энергии.
Наоборот, в реальных двигателях часть энер-
гии неизбежно теряется из-за сил трения. Теряется
в том смысле, что часть энергии из-за работы сил
трения преобразуется во внутреннюю энергию
и приводит к нагреванию двигателя. Точно так
же и работа, совершенная машиной, всегда нес-
колько меньше затраченной энергии.
Обо всем этом стало известно только тогда,
когда в середине XIX в. был открыт закон
сохранения энергии. До этого времени в тече-
ние столетий упорно делались попытки создать
такую машину, которая могла бы совершить
больше работы, чем тратится энергии. Она даже
заранее получила название «вечного двигателя»
(perpetuum mobile). Но такая машина никогда не была создана, и
она не может быть создана.
На рисунке 204 показана схема одного из бесчисленных проек-
тов «вечного двигателя». Он состоит из двух колес (шкивов), по-
мещенных в верхней и нижней частях башни, наполненной водой.
Через шкивы переброшен бесконечный канат с прикрепленными
к нему через некоторые интервалы полыми легкими ящиками. Из
рисунка видно, что в каждый момент времени часть ящиков по-
гружена в воду, в то время как другая часть находится в воздухе.
Автор проекта уверял, что правые (по рисунку) ящики, всплывая
под действием архимедовой силы, заставят вращаться колеса. На
смену всплывающим ящикам в воду будут входить другие, поддер-
живая «вечное» движение. Вращающиеся колеса могли бы при-
водить в движение электрические генераторы, давая таким обра-
зом «бесплатную» энергию в неограниченном количестве, посколь-
ку устройство действует «вечно».
В действительности, однако, в проекте есть ошибки и такой
двигатель работать не может. Ведь если одни ящики всплывают,
то другие, наоборот, входят в воду. И эти входящие в воду ящики
должны двигаться против архимедовой силы. К тому же входят
они в воду внизу, где на них действует давление всего столба воды.
А сила этого давления всегда больше, чем подъемная сила Архимеда.
Подобные ошибки можно найти в любом проекте «вечного дви-
гателя». Попытки создать такое устройство обречены на неудачу,
227
потому что закон сохранения энергии «запрещает» получение рабо-
ты в количестве, большем затраченной энергии.
Интересно отметить, что и в наше время не перевелись «изобре-
татели», которые не оставляют бесплодных попыток создать веч-
ный двигатель.
Задача техники не в том, чтобы пытаться обойти закон сохра-
нения энергии, а в том, чтобы уменьшить потери энергии в маши-
нах, двигателях, генераторах.
Упражнение 60
1. Попытайтесь объяснить назначение генераторов, двигателей, машин. При-
ведите известные вам примеры этих устройств.
2. В чем состоит идея «вечного двигателя»? Почему эта идея неосуществима?
3. Попробуйте объяснить: какие превращения энергии происходят при выст-
реле из ружья? При запуске ракеты?
§ 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО
ДЕЙСТВИЯ
Когда в какой-нибудь машине совершается работа за счет за-
трачиваемой энергии, то нужно отличать так называемую полез-
ную работу от полной совершенной работы.
Полезная работа — это та работа, для выполнения которой
создана и используется машина. Например, для подъемного кра-
на — это работа подъема груза, для токарного станка — работа
против сил трения изделия о резец и т. д.
Но в любой машине, в любом двигателе полезная работа всегда
меньше полной работы, потому что всегда существуют силы тре-
ния, отрицательная работа которых приводит к нагреванию раз-
личных частей машины или двигателя. А нагревание нельзя считать
полезным результатом работы машины, предназначенной для со-
вершения механической работы. Нагревание приводит к тому, что
часть энергии, подведенной к двигателю, преобразуется не в меха-
ническую энергию, а во внутреннюю, которая обычно не может
быть использована для совершения работы.
Каждая машина, каждый двигатель или механизм характери-
зуется поэтому особой величиной, показывающей, насколько эф-
фективно используется подводимая к ней энергия. Эта величина
называется коэффициентом полезного действия
(сокращенно к.п.д.).
Коэффициентом полезного действия машины или двигателя на-
зывается отношение полезной работы к полной совершенной работе.
Можно также говорить о к.п.д. генератора, в котором один
вид энергии преобразуется в другой. Генератором, например, слу-
жит динамо-машина, в которой механическая энергия превращается
в электрическую. Из-за работы сил трения и некоторых других
причин количество полученной электрической энергии всегда не-
228
сколько меньше затрачиваемой турбиной механической энергии.
В свою очередь механическая энергия турбины меньше затрачен-
ной на ее вращение теплоты и т. д.
Коэффициентом полезного действия генератора называется от-
ношение полученной полезной энергии к затраченной.
К.п.д. никогда не может быть больше единицы. В реальных ма-
шинах, двигателях и генераторах он всегда меньше единицы из-за
неизбежных потерь энергии, вызванных прежде всего отрицатель-
ной работой сил трения. Но есть еще и другие, немеханические при-
чины потерь энергии.
Подчеркнем еще раз, что слово «потеря» не означает исчезнове-
ние энергии. Оно только означает, что часть энергии превращается
не в то, что нужно, и теряется для полезного использования.
Коэффициент полезного действия выражается в процентах.
Если к.п.д. обозначить буквой г] (греческая буква «эта»), полезную
работу (или энергию) через Ап, а затраченную работу (энергию)
через А3, то
П = г 1000/о-
Аз
Задача 1. Подъемный кран приводится в действие двигателем
мощностью 10 квт. Сколько времени потребуется для доставки на
высоту 50 м груза массой 2 т, если к.п.д. двигателя равен 75%?
Решение. С помощью крапа должна быть выполнена по-
лезная работа
А„ = mgh.
Вся произведенная работа А3 выражается формулой
А3 = Nt,
где N — мощность двигателя, a t— время работы крана.
Согласно условию задачи полезно используется только 75%
работы двигателя. Поэтому
Ап = 0,75 Nt.
„ / — Л" — mSh
ОТС1ОДа 0,75Лг 0,75jV ’
2000 кг • 9,8 ~ 50 м
сек t ОЛ
------------------------х 130 сек.
. дж
0,75 • 104 —
сек
Задача 2. Автомобиль массой 2 т с включенными тормозами
спускается с постоянной скоростью по горной дороге и проходит
участок пути, опустившись по высоте на 80 м. Какое количество
энергии Q выделилось в тормозах?
229
Решение. Если бы тормоза не были включены, то убыль
потенциальной энергии была бы равна приросту кинетической
энергии. Но так как автомобиль двигался с постоянной скоростью,
то кинетическая энергия при спуске не увеличилась. Следователь-
но, вся потерянная потенциальная энергия перешла во внутрен-
нюю, т. е.
Q = mg (hi — h2).
Подставив числовые данные, получим
Q = 2000 кг • 9,8 — • 80 м х 16 • 10° дж.
сек2
Упражнение 61
1. Проследите детально за рядом превращений энергии, приводящих к выде-
лению тепла в электрической плитке, если электрическая энергия поступает
в сеть с гидроэлектростанции. Начать нужно с Солнца.
2. Тело упало с некоторой высоты на Землю. Куда делась его потенциаль-
ная энергия?
3. Кузнец поднял молог и ударил им по изделию на наковальне. Проследите
за превращениями энергии, происходящими при этом.
4. Деформированная металлическая пружина опущена в кислоту, растворя-
ющую металл, из которого пружина изготовлена. Куда делась потенциаль-
ная энергия пружины после ее растворения?
§ 91. СТОЛКНОВЕНИЕ ТЕЛ
Закон сохранения энергии позволяет рецдать механические зада-
чи в тех случаях, когда почему-либо неизвестны действующие на
тело силы. Интересным примером именно такого случая является
столкновение двух тел. Этот пример особенно интересен тем, что
при его анализе нельзя обойтись одним только законом сохране-
ния энергии. Нужно привлечь еще и закон сохранения импульса
(количества движения).
В обыденной жизни и в технике не так уж часто приходится
иметь дело со столкновениями тел, но в физике атома и атомных
частиц столкновения — очень частое явление.
Для простоты мы сначала рассмотрим столкновение двух ша-
ров массами и т2, из которых второй покоится, а первый дви-
жется по направлению ко второму со скоростью Будем считать,
что движение происходит вдоль линии, соединяющей центры обоих
шаров (рис. 205), так что при столкновении шаров имеет место
так называемый центральный, или лобовой, удар.
Каковы скорости обоих шаров после столкновения?
До столкновения кинетическая энергия второго шара равна
9
нулю, а первого —%—. Сумма энергий обоих шаров составляет:
230
После столкновения первый шар станет
двигаться с некоторой скоростью Второй
шар, скорость которого была равна нулю,
также получит какую-то скорость и2. Поэтому
после столкновения сумма кинетических энер-
гий двух шаров станет равной
По закону сохранения энергии эта сумма должна быть равна энер-
гии шаров до столкновения:
или
Н - т2и22.
Из этого одного уравнения мы, конечно, не можем найти две
неизвестные скорости: и1 и и2. Вот тут-то на помощь и приходит
второй закон сохранения — закон сохранения импульса. До столк-
новения шаров импульс первого шара был равен т^, а импульс
второго — нулю. Полный импульс двух шаров был равен:
О Д- ТИЛ =/ИЛ.
После столкновения импульсы обоих шаров изменились и стали
равными и m2u2, а полный импульс стал
;/!,«[ -f- Ш2112.
По закону сохранения импульса полный импульс при столкновении
измениться не может. Поэтому мы должны написать:
тЛ=т1“1+т2“2-
Так как движение происходит вдоль прямой, то вместо векторно-
го уравнения можно написать алгебраическое (для проекций ско-
ростей на координатную ось, направленную по скорости движения
первого шара до удара):
= /«!«! -|- mziiz.
Теперь мы имеем два уравнения:
тр2 = т^2 -|- и?2,г2>
231
Такую систему уравнений можно решить и найти неизвестные
скорости и иг шаров после столкновения. Для этого перепишем
ее следующим образом:
т^ — пци] — т2и%,
— ШуПу = т2и2,
или
тх (п* —и~) =
т( (гу — Ну) = т2и2.
Разделив первое уравнение на второе, получим:
01 + щ = и2.
Решая теперь это уравнение совместно со вторым уравнением
mlvl — — tll2U2
(проделайте это самостоятельно), найдем, что первый шар после
удара будет двигаться со скоростью
,,__ (mi — '^k'l
Wj — )
Л'1 + тг
а второй — со скоростью
2zn,t),
U ,= ----i-l— .
+ т2
Если оба шара имеют одинаковые массы (/nt = т2), то их = О,
а и2 = Ор Это значит, что первый шар, столкнувшись со вторым,
передал ему свою скорость, а сам остановился (рис. 206).
Таким образом, пользуясь законами сохранения энергии и импуль-
са, можно, зная скорости тел до столкновения, определить их ско-
рости после столкновения.
А как обстояло дело во время самого столкновения в тот момент,
когда центры шаров максимально сблизились?
Очевидно, что в это время они двигались вместе с некоторой
скоростью и. При одинаковых массах тел их общая масса равна 2т.
По закону сохранения импульса во время совместного движения
обоих шаров их импульс должен быть равен общему импульсу до
2ти = mv.
Отсюда следует, что
столкновения:
Таким образом, скорость обоих шаров при
их совместном движении равна половине
Рис. 206
232
скорости одного из них до столкновения. Найдем кинетическую
энергию обоих шаров для этого момента:
2mu2 „ my2
д==----- =ти ~ —
2 4
А до столкновения общая энергия обоих шаров была равна
mv2
т
Следовательно, в самый момент столкновения шаров кинетиче-
ская энергия уменьшилась вдвое. Куда же пропала половина кинети-
ческой энергии? Не происходит ли здесь нарушения закона сохра-
нения энергии?
Энергия, конечно, и во время совместного движения шаров
осталась прежней. Дело в том, что во время столкновения оба шара
были деформированы и поэтому обладали потенциальной энергией
упругого взаимодействия. Именно на величину этой потенциальной
энергии и уменьшилась кинетическая энергия шаров.
Задача 1. Шар, имеющий массу т,, равную 50 г, движется со
скоростью Di = 10 м/сек и сталкивается с неподвижным шаром, мас-
са которого т2 ~ 1Ю г. Каковы скорости обоих шаров после столк-
новения? Столкновение шаров считать центральным.
Решение. Скорость второго шара вычисляется по формуле
2т, V,
и2 = ---—— .
т, + т2
Подставив значения т1( т2 и р,, получим:
2 • 0,05 кг- 10 —
сек г* Qr- м
и9 ------------------ = 6,25 —.
0,05 кг + 0,11 кг сек
Значение же скорости ut первого шара находим по формуле
т, — т2
—,—-Vi,
+ т2
«1 =
м
(0,05 кг-0,11 кг) - 10 —
. СеК О М
щ = -— ----------------------- =— 3,75—.
0,05 кг + 0,Н кг сек
Знак «минус» показывает, что после столкновения скорость
этого шара изменится не только по абсолютному значению, но и
по направлению (шар станет двигаться в противоположную сторону).
Задача 2. Шар массой т, = 100 г, двигаясь со скоростью
vt — 12 м/сек, сталкивается с неподвижным шаром, масса которо-
го т2 = 50 г. Каковы скорости ut и и2 шаров после столкновения,
если столкновение центральное?
233
Решение. Скорость щ второго шара после столкновения:
2т.v,
Щ =-------LJ— »
«Ч + т2
м
2 -0,1 кг 12-
сек ,,, м
и., ------------------ = 1 о---.
0,1 кг + 0,05 кг сек
Скорость иг первого шара после столкновения:
т. — т.,
«1 = —'----~ П1,
ж
(0,1 кг — 0,0а кг) 12 —
сек . м
и. = ----------------------------- =4 —.
0,1 кг+ 0,05 кг сек
Теперь знак скорости uY такой же, как знак скорости п2. Оба шара,
следовательно, после столкновения движутся по одному направле-
нию — так, как двигался первый шар до столкновения.
§ 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ.
ЗАКОН БЕРНУЛЛИ
В этом параграфе мы применим закон сохранения энергии к
движению жидкости или газа по трубам. Движение жидкости по
трубам часто встречается в технике и быту. По трубам водопровода
подается вода в городе в дома, к местам ее потребления. В машинах
по трубам поступает масло для смазки, топливо в двигатели и т. д.
Движение жидкости по трубам нередко встречается и в природе.
Достаточно сказать, что кровообращение животных и человека —
это течение крови по трубкам — кровеносным сосудам. В какой-то
мере течение воды в реках тоже является разновидностью тече-
ния жидкости по трубам. Русло реки — это своеобразная труба
для текущей воды.
Как известно, неподвижная жидкость в сосуде согласно закону
Паскаля передает внешнее давление по всем направлениям н во все
точки объема без изменения. Однако, когда жидкость течет без тре-
ния по трубе, площадь поперечного сечения которой на разных
участках различна, давление оказывается неодинаковым вдоль
трубы. Выясним, почему давление в движущейся жидкости зависит
от площади поперечного сечения трубы. Но сначала ознакомимся
с одной важной особенностью всякого потока жидкости.
Предположим, что жидкость течет по горизонтально располо-
женной трубе, сечение которой в разных местах различное, напри-
мер по трубе, часть которой показана на рисунке 207.
234
Рис. 207
Если бы мы мысленно провели несколько сечений вдоль трубы,
площади которых соответственно равны S1; S2, S3, S4, и измерили
бы количество жидкости, протекающей через каждое из них за какой-
то промежуток времени t, то мы обнаружили бы, что через каждое
сечение протекло одно и то же количество жидкости. Это значит,
что вся та жидкость, которая за время t проходит через первое се-
чение, за такое же время проходит и через третье сечение, хотя оно
по площади значительно меньше, чем первое. Если бы это было не
так и через сечение площадью S3 за время t проходило, например,
меньше жидкости, чем через сечение площадью Sj, то избыток жид-
кости должен был бы где-то накапливаться. Но жидкость заполня-
ет всю трубу, и накапливаться ей негде.
Как же может жидкость, протекшая через широкое сечение,
успеть за такое же время «протиснуться» через узкое? Очевидно,
что для этого при прохождении узких частей трубы скорость дви-
жения должна быть больше, и как раз во столько раз, во сколько раз
площадь сечения меньше.
Действительно, рассмотрим некоторое сечение движущегося
столба жидкости, совпадающее в начальный момент времени с од-
ним из сечений трубы (рис. 208). За время t эта площадка переме-
стится на расстояние I, которое равно vt, где v — скорость течения
жидкости. Объем V жидкости, протекшей через сечение трубы, ра-
вен произведению площади этого сечения S на длину I:
V = Si, или V = Svt.
В единицу же времени протекает объем жидкости — !
- = Sv.
t
Объем жидкости, протекающей в единицу времени через сечение
трубы, равен произведению площади поперечного сечения трубы на
скорость течения.
Как мы только что видели, этот объем
должен быть одним и тем же в разных
f у,------- сечениях трубы. Поэтому, чем меньше
- A "z: А—' сечение трубы, тем- больше скорость
л 4—•- I । движения.
V — Сколько жидкости проходит через од-
но сечение трубы за некоторое время,
рис. 208 столько же ее должно пройти за такое
235
Даниил Бернулли
(1700—1782)
же время через любое другое сечение.
При этом мы считаем, что данная мас-
са жидкости всегда имеет один и тот же
объем, что она не может сжаться и умень-
шить свой объем (о жидкости говорят, что
она несжимаема). Хорошо известно,
например, что в узких местах реки ско-
рость течения воды больше, чем в широ-
ких. Если обозначить скорость течения
жидкости в сечениях площадями Sn S2,
S3, S4 через vlt v2, v3, vit то можно на-
писать:
Sa = s2y2 = Sa = s4v4.
Отсюда видно, что при переходе
жидкости с участка трубы с большей
площадью сечения на участок с меньшей
площадью сечения скорость течения уве-
личивается, т. е. жидкость движется с ускорением. А это по вто-
рому закону Ньютона означает, что на жидкость действует сила.
Что это за сила?
Этой силой может быть только разность между силами давле-
ния в широком и узком участках трубы. Таким образом, в широком
участке давление жидкости должно быть больше, чем в узком уча-
стке трубы.
Это же следует из закона сохранения энергии. Действительно,
если в узких местах трубы увеличивается скорость движения жид-
кости, то увеличивается и ее кинетическая энергия. А так как мы
приняли, что жидкость течет без трения, то этот прирост кинетиче-
ской энергии должен компенсироваться уменьшением потенциальной
энергии, потому что полная энергия должна оставаться постоян-
ной. О какой же потенциальной энергии здесь идет речь? Если
труба горизонтальна, то потенциальная энергия взаимодействия
с Землей во всех частях трубы одна и та же и не может изме-
ниться. Значит, остается только потенциальная энергия упругого
взаимодействия. Сила давления, которая заставляет жидкость течь
по трубе, — это и есть упругая сила сжатия жидкости. Когда мы
говорим, что жидкость несжимаема, то имеем лишь в виду, что она
не может быть сжата настолько, чтобы заметно изменился ее объем,
но очень малое сжатие, вызывающее появление упругих сил, не-
избежно происходит. Эти силы и создают давление жидкости. Вот
это сжатие жидкости и уменьшается в узких частях трубы, компен-
сируя рост скорости. В узких местах труб давление жидкости долж-
но быть поэтому меньше, чем в широких.
В этом состоит закон, открытый петербургским академиком
Даниилом Бернулли:
Давление текущей жидкости больше в тех сечениях
потока, в которых скорость ее движения меньше, и,
236
наоборот, в тех сечениях, в которых скорость боль-
ше, давление меньше.
Как это ни покажется странным, но когда жидкость «проти-
скивается» через узкие участки трубы, то ее сжатие не увеличива-
ется, а уменьшается. И опыт хорошо это подтверждает.
Если трубу, по которой течет жидкость, снабдить впаянными в
нее открытыми трубками — манометрами (рис. 209), то
можно будет наблюдать распределение давления вдоль трубы.
В узких местах трубы высота столба жидкости в манометрической
трубке меньше, чем в широких. Это означает, что в этих местах
давление меньше. Чем меньше сечение трубы, тем больше в ней
скорость течения и меньше давление. Можно, очевидно, подобрать
такое сечение, в котором давление равно внешнему атмосферному
давлению (высота уровня жидкости в манометре будет тогда равна
нулю). А если взять еще меньшее сечение, то давление жидкости
в нем будет меньше атмосферного.
Такой поток жидкости можно использовать для откачки возду-
ха. На этом принципе действует так называемый водоструй-
ный н а с о с. На рисунке 210 изображена схема такого насоса.
Струю воды пропускают через трубку А с узким отверстием на кон-
це. Давление воды у отверстия трубы меньше атмосферного. Поэтому
Рис. 210
237
газ из откачиваемого объема через трубку В втягивается к кон-
цу трубки А и удаляется вместе с водой.
Все сказанное о движении жидкости по трубам относится и к
движению газа. Если скорость течения газа не слишком велика и
газ не сжимается настолько, чтобы изменялся его объем, и если,
кроме того, пренебречь трением, то закон Бернулли верен и для
газовых потоков. В узких частях труб, где газ движется быстрее,
давление его меньше, чем в широких частях, и может стать меньше
атмосферного. В некоторых случаях для этого даже не требуется
трубы.
Можно проделать простой опыт. Если дуть на лист бумаги вдоль
его поверхности, как показано на рисунке 211, можно увидеть,
что бумага станет подниматься вверх. Это происходит из-за пони-
жения давления в струе воздуха над бумагой.
Такое же явление имеет место при полете самолета. Встречный
поток воздуха набегает на выпуклую верхнюю поверхность крыла
летящего самолета, и за счет этого происходит понижение давления.
Давление над крылом оказывается меньше, чем давление под кры-
лом. Именно поэтому возникает подъемная сила крыла.
Упражнение 62
1. Допустимая скорость течения нефти по трубам равна 2 м/сек. Какой объем
нефти проходит через трубу диаметром 1 м в течение 1 ч?
2. Измерьте количество воды, вытекающей из водопроводного крана за оп-
ределенное время /. Определите скорость течения воды, измерив диаметр
трубы перед краном.
3. Каким должен быть диаметр трубопровода, по которому должно протекать
5 600 м3 водь! в час? Допустимая скорость течения воды 2,5 м/сек.
§ 93. О ЗНАЧЕНИИ ЗАКОНОВ
СОХРАНЕНИЯ
Мы видели, что законы сохранения импульса и энергии позво-
ляют решать задачи механики, когда почему-либо неизвестны зна-
чения сил, действующих на тела.
Но значение законов сохранения этим не ограничивается. За-
коны сохранения импульса и энергии, насколько сейчас извест-
но, абсолютно точны. Этого нельзя, например, сказать о втором
и третьем законах Ньютона. Известно, что если частицы дви-
жутся со скоростями, близкими к скорости света, законы Ньюто-
на выглядят иначе. Законы Ньютона в этом смысле являются
приближенными. Законы же сохранения импульса и энергии не
имеют исключений. Если кто-нибудь, заявит об открытии им яв-
ления или процесса, при котором законы сохранения пе соблю-
даются, то можно смело утверждать, что это ошибка.
Законы сохранения служат путеводной звездой при рассмотре-
нии любых вопросов, связанных с изучением природы. Это своего
рода первичный контроль за правильностью любого утверждения.
Законами сохранения мы будем часто пользоваться во всех разде-
лах курса физики.
238
Заключение
Мы закончили изучение элементов механики Ньютона, или,
как ее часто называют, классической механики.
Мы изучили именно только элементы механики.
Механика — это очень обширная наука, многие вопросы кото-
рой мы вообще не затронули. Например, мы не касались такого важ-
ного вида движения, которое называется колебательным движе-
нием. Этот вид движения будет вами изучаться в X классе. Мы не
изучали вращения тел под действием приложенных к ним сил (вра-
щение тел с ускорением). Эти вопросы более сложны в матема-
тическом отношении по сравнению с вопросами, которые рассмотре-
ны в книге.
Но основой классической механики служат законы Ньютона.
Принципиально при правильном их применении можно решить
любую задачу механики. Но только принципиально. Есть много
задач механики, которые до сих пор пе решены.
Если бы все задачи механики были решены, то не было бы на-
уки механики. Между тем механика — это наука, которая разви-
вается и решает все новые н новые проблемы.
Сведения по механике, полученные из данной книги, послужат
фундаментом для изучения всех остальных разделов курса фи-
зики.
Лабораторные работы
1. Определение ускорения тела
при равноускоренном движении
Работа заключается в измерении ускорения, с которым скатывается шарик
по наклонному желобу. Для этого измеряют длину перемещения s, которое про-
ходит шарик за известное время t. Так как при равноускоренном движении без
начальной скорости
а?
(1)
то, измерив s и t, можно найти ускорение шарика. Оно равно:
2s
а = —. (2)
Приборы и материалы: 1) желоб, 2) шарик, 3) измерительная
лента, 4) метроном (или секундомер), 5) штатив с муфтами и лапкой, 6) металличе-
ский цилиндр.
Порядок, выполнения работы
1. Укрепить желоб с помощью штатива в наклонном положении под неболь-
шим углом к горизонту (рпс. 212). У нижнего конца желоба положить в него
металлический цилиндр.
2. Пустив шарик (одновременно с ударом метронома) с верхнего конца жело-
ба, подсчитать число ударов метронома до столкновения шарика с цилиндром.
Опыт удобно проводить при 120 ударах метронома в минуту.
3. Меняя угол наклона желоба к горизонту,
добиться того, чтобы между моментом пуска ша-
рика и моментом его столкновения с цилиндром бы-
ло 4 удара метронома.
4. Вычислить время движения шарика. Оно
равно 4т, где т — время между следующими друг
за другом ударами метронома.
5. С помощью измерительной ленты определить
Рис. 212
240
6. По формуле (2) найти ускорение шарика.
7. Повторить измерения, передвинув цилиндр вверх по желобу так, чтобы
столкновение шарика с цилиндром происходило на третий или второй удары
метронома.
8. Проведя несколько независимых измерений ускорения шарика, найти
среднее арифметическое значение ускорения аср.
9. Найти разность между аср и измеренным в каждом отдельном опыте уско-
рением шарика. Это ошибка каждого отдельного измерения ускорения Да.
10. Найти среднее арифметическое значение ошибки измерения ускорения
шарика.
11. Составить таблицу результатов опытов:
12. Записать результат измерений в виде а = аСв ± Даср.
2. Определение коэффициента
трения скольжения
Измерение коэффициента трения скольжения необходимо провести двумя
способами.
1-й способ заключается в измерении с помощью динамометра силы, с которой
нужно тянуть брусок с грузами по горизонтальной поверхности, для того чтобы
— "
он двигался равномерно. Эта сила равна по абсолютной величине силе трения Гт(„
действующей на брусок. С помощью того же динамометра можно найти вес бруска
о грузами Р. Этот вес равен силе нормального давления бруска на поверх-
ность, по которой он скользит. Определив таким образом |Етр| и |Р|, можно найти
коэффициент трения. Он равен:
и
2-й способ измерения коэффициента трения позволяет определять на опыте
не силы, а длины отрезков. Для этого используют равновесие бруска, который
находится на наклонной плоскости.
Если брусок находится в равновесии на наклонной плоскости, то сила нормаль-
ного давления бруска на плоскость равна составляющей F, силы тяжести, пер-
пендикулярной наклонной плоскости (рис. 213). А сила трения по абсолютной
- >-
величине равна составляющей FL силы тяжести, параллельной наклонной пло-
скости.
241
Опыт заключается в том, чтобы, уве-
личивая постепенно угол наклона плос-
кости, найти такой угол, при котором бру-
сок только «тронется с места». При этом
сила трения будет равна максимальной си-
ле трения покоя:
_ = и й,
где F2 — сила давления бруска на плос-
кость Так как при этом FTp = —Fv т. е.
Рис. 213 п 1^тр| = Й. то Ц |Р2| = KJ.
Отсюда
Нетрудно показать, что
й А
Это следует из подобия треугольников АВС и OEN. Поэтому коэффициент трения
равен:
h
и=7'
Из этой формулы видно, что для того чтобы найти коэффициент трения, доста-
точно измерить высоту и основание наклонной плоскости, которыми определяется
наклон плоскости, при котором начинается скольжение бруска.
Приборы и материалы: 1) линейка, 2) измерительная лента,
3) динамометр, 4) деревянный брусок, 5) набор грузов, 6) штатив с муфтами и
лапкой.
Порядок, выполнения работы
1. Положить брусок на горизонтально расположенную деревянную линей-
ку. На брусок поставить груз.
2. Прикрепив к бруску динамометр, как можно более равномерно тянуть
его вдоль линейки. Заметить при этом показание динамометра.
3. Взвесить брусок и груз.
iFTpl
4. По формуле р= —— найти коэффициент трения.
|Р|
5. Повторить опыт, положив на брусок несколько грузов.
6. Найти среднее арифметическое значение коэффициентов трения, найденных
в разных опытах.
7. Найти ошибку каждого из опытов — разность между рср и значениями р,
полученными в разных опытах.
8. Определить среднее арифметическое ошибок опытов Дрср.
9. Составить таблицу результатов опытов:
Номер опыта Показание динамометра |ХР| И ^ср Лц=Иср“м А^ср
242
10. Записать результат измерений в виде
|1 = цср ± Арср.
11. Положив линейку на брусок с грузами, медленно изменять ее наклон,
поднимая ее конец, пока брусок не начнет скользить вдоль линейки.
12, Зажать линейку в найденном положении в лапку штатива и убедиться
в том, что брусок движется равномерно.
13. Измерить с помощью измерительной ленты высоту Л и основание I на-
клонной плоскости.
h
14. Определить коэффициент трения по формуле р= —.
15. Повторить опыт несколько раз, меняя количество грузов на бруске.
16. Найти среднее арифметическое найденных значений коэффициента тре-
ния и среднюю ошибку измерений.
17. Составить таблицу результатов:
Р = Рср ± Арср.
19. Сравнить значения коэффициентов трения, найденных 1-м н 2-м спосо-
бами.
3. Изучение движения тела по пара-
боле
Работа состоит в изучении следа, оставленного шариком, которому сообщи-
ли начальную скорость в горизонтальном направлении н который скатывается
затем по наклонной плоскости. Этот след представляет собой траекторию движе-
ния шарика.
Если шарик брошен горизонтально вдоль наклонной плоскости, то он дви-
жется по параболе (рис. 214) (с.м. § 56). При движении точки по параболе про-
екция этой точки па ось X движется равномерно, а ее проекция на ось У дви
жется равноускоренно. В этом можно убедиться, исследовав траекторию движе-
ния шарика.
Проведем оси координат ОХ и ОУ, приняв за начало координат начальное
положение шарика (рис. 215). Выбрав на оси ОХ некоторый отрезок ОА, разобь-
ем его на несколько равных частей Ох,, х,х.,, ... . Из точек деления проведем
перпендикуляры до пересечения с траекторией движения шарика. Затем из
точек, в которых эти перпендикуляры пересекаются с траекторией движения,
опустим перпендикуляры па ось ОУ. Точки у,, у2, ..., В дают координаты
шарика вдоль оси ОУ в те моменты времени, когда координатами шарика вдоль
оси ОХ были точки Xj, л2...А.
243
Вдоль оси ОХ равные между собой отрезки Ох,, хгх2, ... проекция шарика
проходит за одинаковые отрезки времени. Вдоль оси ОУ движение равноус-
коренное, и поэтому разность расстояний, которые проходит проекция шарика
вдоль оси У за последовательные равные промежутки времени, одинакова (см. за-
дачу 3 к § 17). В этом-то и нужно убедиться на опыте.
Приборы и материалы: 1) измерительная лента, 2) штатив с муф-
той и лапкой, 3) лоток для пуска шарика, 4) фанерная доска, 5) шарик, 6) ба-
ночка с вазелином, 7) бумага, 8) кнопки, 9) фильтровальная бумага.
Порядок выполнения работы
1. С помощью штатива укрепить
фанерную доску под углом, составляю-
щим с плоскостью стола примерно 30°.
При этом той же лапкой зажать выс-
туп лотка (рис. 214). Загнутый конец
лотка должен быть горизонтальным.
Рис. 214
Рис. 215
2. Прикрепить к листу кнопками лист бумаги.
3. Смазать шарик вазелином и пустить его по желобу. Скатываясь по бумаге,
он оставит на ней темный след.
4. Вытереть шарик фильтровальной бумагой.
5. Прочертить кривую вдоль следа шарика карандашом.
6. Нанести на лист бумаги оси координат и отметить на них координаты точек
кривой через последовательные равные промежутки времени. Измерить длины
отрезков между последовательными координатами точек па оси У.
7. Убедиться в том, что ytyt — Оу} = у3у2 — = Ву3 — у3у2 = ... .
8. Повторить построение, разбив отрезок ОА на большее число равных
частей.
244
4. Выяснение условия равновесия ры
чага
В работе надо установить соотношение между плечами рычага и приложенны-
ми к нему силами при его равновесии. Для этого к одному из плеч рычага подве-
шивают один или несколько грузов, а к другому прикрепляют динамометр
(рис. 216). С помощью этого динамометра измеряют силу F, которую необходимо
приложить для того, чтобы рычаг находился в равновесии. Длины плеч рычага
к
находятся с помощью линейки. Затем определяют отношения — и
‘2
Р
— (Р—вес
F
грузов). Эти отношения сравнивают друг с другом.
Приборы и материалы: 1) измерительная линейка,
метр, 3) набор грузов, 4) штатив с муфтами, 5) рычаг.
2) динамо-
Порядок выполнения работы
1. Установить рычаг
на штативе и уравновесить
его в горизонтальном по-
ложении с помощью рас-
положенных на его кон-
цах передвижных гаек.
2. Подвесить в неко-
торой точке одного из плеч
рычага груз.
3. Прикрепить к дру-
гому плечу рычага дина-
мометр и определить си-
лу, которую необходимо
приложить к рычагу, для
того чтобы рычаг находил-
ся в равновесии.
4. Измерить с помощью линейки длины плеч рычага,
5. С помощью динамометра определить вес груза Р.
li р
6. Найти отношения — и — .
/2 F
7. Найденные величины занести в таблицу:
Рис. 216
Номер опыта 1, р F 11 ч |*О
„ 11 Р
8. Сравнить отношения — и — .
4 F
9. Повторить опыт несколько раз, прикрепляя к рычагу различное число
грузов и меняя плечи рычага.
245
5. Определение центра тяжести плос-
кой пластины
Если плоскую пластину подвесить в какой-либо точке, то она расположится
так, что вертикальная прямая, проведенная через точку подвеса (рис. 217), прой-
дет через центр тяжести пластины. Это позволяет находить центр тяжести плос-
ких пластин опытным путем. Для этого нужно, подвесив пластину в какой-либо
точке, прочертить иа ней вертикальную прямую,
проходящую через точку подвеса. Затем еще раз
проделать те же операции, подвесив пластину в
другой ее точке. Точка пересечения проведенных
прямых даст положение центра тяжести пластины.
Для того чтобы убедиться в этом, пластину
можно подвесить в третьей точке. Вертикальная
прямая, проходящая через точку подвеса, должна
пройти через точку пересечения двух первых пря-
мых.
Можно также уравновесить пластину на острие
булавки. Пластина будет находиться в равновесии,
если точка опоры совпадает с центром тяжести.
Приборы и материал ы: 1) линейка,
2) плоская пластина произвольной формы, 3) отвес,
4) булавка, 5) штатив с лапкой и муфтой, 6) проб-
ка.
Порядок выполнения работы
1. Зажать в лапку штатива пробку в горизонтальном положении.
2. С помощью булавки, которая вкалывается в пробку, подвесить пластину
и отвес.
3. Остро отточенным карандашом отметить линию отвеса на нижнем и верх-
нем краях пластины.
4. Сняв пластину, провести на ней линию, соединяющую отмеченные точки.
5. Повторить опыт, подвесив пластину в другой точке.
6. Убедиться в том, что точка пересечения проведенных прямых является
центром тяжести пластины.
Ответы к упражнениям
Упражнение 3
1. х = 18,7 км; у — 19,7 км.
2. | s | = 5 м; sx = 4 м; зу = 3 м.
Упражнение 4
7. | s I = 5 км; I = 12 км. 8. |а + = |а — &Т = \Ь — = 10 ед. дл.
Упражнение 5
5. а 3,5 км к юго-востоку; 42 мин. 6. 90 км/ч.
Упражнение 6
2. 7,5 м. 3. 1 м/сек.
Упражнение 7
3. 950 км/ч; 850 км/ч. 4. 15 км.
Упражнение 8
3. 70 км/ч. 4. а 54,5 км/ч. 5. а 60,7 км/ч.
Упражнение 9
5. 10 сек. 6. —2,5 м/сек2. 7. 0,25 сек. 8. 64800 км/ч.
Упражнение 10
1. а) 27 м; б) 4 сек; 8 м. 4. 1 м/сек-; 1 мУек2; Чмуек1. 5. а6,7 м/сек2; 775 м.
6. а 160 м. 7. 0,6 м. 8. а2,4 км. 9. 15876 км.
Упражнение 11
1. 75 м. 2. 3,75 м/сек2. 3. 500 м. 4. 700 м.
Упражнение 12
1. 78,4 м. 2. а 10,4 сек; а 100 м/сёк. 3. 1 сек; 9,8 м/сек.
4. а 11 м/сек. 5. а 31,8 м/сек; 37,5 м.
Упражнение 13
1. 45 м. 2. а 80 м; а 40 м/сек. 3. а 3,25 м; а 8 м/сек;
а 1,3 сек; а 0,8 м. 4. 75 м; 75 м; 10 м/сек; —10 м/сек.
5. В 2 раза. 6. —12 м/сек.
Упражнение 15
3. а 2 • 10'7 рад/сек; а 30 км/сек. 4. «6,1 10'3 м/сек;
а 1,7 • 10~3 рад/сек.
Упражнение 16
4. а 3,14 м/сек. 5. а 2,25 м/сек2. 6. а 7,8 км/сек.
7. -а 67,8 км/ч. 8. 1 сек. 9. а 2,7 10“3 м/сек2.
Упражнение 17
3. а 3,48 рад/сек; а 8,16 рад/сек. 4. 314 рад/сек;
а 425 м/сек; а 1,33 • 105 м/сек2. 5. а 40 об.
6. а 3600 об.; а 22,6 м/сек; а 0,74 м. 7. 7,2 • 10'5 рад/сек; а 467 м/сек.
247
Упражнение 19
3. 6 м/сек. 4. 2 см; 6 см.
Упражнение 20
8. 1.
Упражнение 21
10. к 7,5- 10* н. 11. К центру окружности; нет.
Упражнение 22
4. Да. 5. « 0,25 м/сек1; х 0,16 м/сек2.
Упражнение 23
6. Действует; наклонной плоскости; вертикально вверх.
Упражнение 24
1. а) Увеличится вдвое; б) увеличится в 4 раза. 2. Уменьшится в 4 раза.
pr/
4. М3 = —3 (см. § 47). 5. «0,8 мг. 6. 0,16 н. 7. х 1,9 • IO2» н.
V
8. « в 585 раз. 9. х 2,7 • 10'3- м/сек2.
Упражнение 25 '
2. « 0,03 м/сек2. 4. « 260 км. 5. х 3,7 и.
Упражнение 26
5. « 49 н. 6. Будет двигаться ускоренно, так как FTp. маи = k mg х
х 1500 н. 7. х 1100 кг.
Упражнение 30
3. Во всех случаях х4900 н. 4. а) «1010 н; б) «980 н; в) «940 н; г) 0.
5. Уменьшится на'5600 н. 7. «9,77 н.
Упражнение 32
6. х 7 м. 1. х 5 • 102 м/сек.
Упражнение 33
5. 0,64 сек; 6,9 м. 6. 40 м; 80 .и. 7. « 9 км.
Упражнение 34
5. х 89 мин. 6. х 5,65 км/сек. 7. « 5000 км. 8. « 38000 км.
Упражнение 35
4. 2 • 1030 кг.
Упражнение 37
2. «2 м/сек. 3. «30°. 5. х 10 м/сек2. 6. «5,5 м/сек2.
8. Тело будет покоиться или двигаться равномерно.
Упражнение 38
4. х 70,5 км/ч. 5. а « 76° (tgcc « 0,25).
Упражнение 40
1. «850 н; 1000 н; «700 н; 500 н; 0. 2. «11,6 л; «23,2 н. 3. «31 н; «8 н.
4. 3400 н. 5. Будет. 6. »1730 н; 2000 н.
Упражнение 41
1. 0,1 кг. 2. 0,2 кг.
248
Упражнение 43
1. 10 кг-м/сек. 2. а) 3 Ю4кг • м/сек-, б) 6 I04 кгм/сек. 3. 0,2 кг-м/сек; 2 н.
Упражнение 44
1. 5,5 м/сек. 2. 0,3 м/сек. 3. 4,5 кг.
Упражнение 45
2. «1 дж. 3. «2740 дж. 4. Нет. 5. «37,5 кдж. 6. «11,4 дж. 7.« 77 кдж.
Упражнение 46
1. «2000 н. 2. «1600 я; «3200 дж.
Упражнение 47
9. 500 дж; «3,3. 10. «1500 дж; «250 я.
Упражнение 48
4. 40 я; 0. 5. 180 дж. 6. 4,5 108 дж. 7. 80 дж; 10 м. 8. 2 дж.
Упражнение 49
3. 0. 5. 0. 6. « 9000 дж. 7. »—200 дж. 8. «16 кдж. 9. 0.
Упражнение 50
4. 8 дж. 5. «37,5 дж. 6. 1 м.
Упражнение 51
4. «240 дж. 5. «2700 дж. 6. «36 км/ч.
Упражнение 52
5. 7200 я. 6. 8 т. 7. 360 кдж. 8. 7,8 101' Мдж. 9. 2 кет.
Упражнение 55
k,k2X2 (k. 4- k2) X2
3. 7,5 • 10-? дж. 4. —- 1 „ -------------. 5. 8 дж.
2 + k2) 2
Упражнение 56
3. 127,5 дж. 4. 87,5 дж.
Упражнение 57
4. «100 дж. 5. 9,6 м. 6. «4,16 • 10го дж.
Упражнение 58
4. «45 м. 5. «11,2 см. 6. «294 дж; «588 дж. 7. «28,125 дж; «11,48 м.
8. «1,58 м/сек.'
Упражнение 59
2. Уменьшилась на 1500 дж. 3. «700 кдж. 4. Двигалось в воздухе.
7. «1790 дж.
Упражнение 62
1. «5652 м3. 3. 90 см.
249
Предметно-именной указатель
Бернулли Даниил 236
Бернулли закон 236
Ватт 209
Ватт-секунда 209
Вектор 11
— перемещения 11
— результирующий 16, 17
Вес 118, 130
Весы пружинные 118, 119
— рычажные 120
Вечный двигатель 227
Взаимодействие тел 82
Взвешивание 119
Время 4
Гагарин Ю. А. 188
Галилей Галилео 55, 56, 80
Грамм 87
График движения 25
— скорости 26, 46, 47
Гук Роберт 98
Гука закон 98, 108
Дальность полета 138, 140
Движение вращательное 73
— твердого тела 72
— жидкости 234
— колебательное 129
— криволинейное 62
— механическое 4
— неравномерное 36
— , относительность 27, 75
— планет 145
— по окружности 65, 68
— поступательное 5,156
— прямолинейное 22
— равномерное 22
— равноускоренное 41
— реактивное 186
Деформация 107
— изгиба 107
— кручения 107
— растяжения 107, 108
— сжатия 107, 108
Джоуль (единица работы) 191
Дина 94
Динамика 77
Динамометр 98
Длина пути 9, 63, 66
Единицы измерения 33
— — времени 34
— — дтииы 33
— — импульса 181
— — массы 87
— — момента силы 171
— — мощности 209
— — работы 190
— — силы 94
— — скорости 34
— — угла 67
--- ускорения 42
Жесткость 99, 109
Закон Вернуллн (см. Бернулли закон)
Закон всемирного тяготения 113
— Гука (см. Гука закон)
— Ньютона второй 94
— — первый 80, 96
— — третий 109
— сохранения импульса 183
— — энергии 189, 221, 225, 227
Импульс тела (количество дшокеция)
181
— силы 181
Инертность 85
Инерция 80
Искусщвеппып спутник Земли 143, 188
250
Килограмм 87
Кинематика 9
Количество движения (см. Импульс
тела)
Координата 8, 62
Коэффициент полезного действия
(к.п.д.) 228
— трения 124
Манометр 237
Масса 86, 87
— Земли 120
— Луны 90
Материальная точка 6,114
Материя 3
— , изменчивость 3
Метод стробоскопический 55
Метр 33
Механика 4
Механическое состояние 213
Модуль (абсолютное значение) векто-
ра 11
Момент силы 170
Мощность 208
Насос водоструйный 237
Начало координат 8
— отсчета 8
Невесомость 134
Ньютон Исаак 81, 91
Ньютон (единица силы) 94
Ньютона второй закон (см. Закон
Ньютона второй)
— первый закон (см. Закон Ньютона
первый)
— третий закон (см. закон Ньютона
третий)
Обтекаемая форма тела 126
Оси координат 8
Основная задача механики 4, 9, 76,
103, 128
Перегрузка 132
Перемещение 9, 10, 46, 62
Период 68
Плечо силы 171
Площадь опоры 177
Постоянная всемирного тяготения
(гравитационная постоянная) 113,
114
Правило моментов 171
— параллелограмма 17
— рычага 173
Принцип относительности Галилея 160
Проекция вектора 13
Пространство 4
Прямоугольная система координат 8
Работа 189, 194, 202, 205, 208
Равновесие тел 163, 172, 173, 176, 177
— безразличное 176
— неустойчивое 175
— устойчивое 175
Радиан 67
Ракета 186
Сантиметр 35
Свободное падение 55, 56, 116
Секунда 34
Сила 90, 181
— давления 122
— магнитная 106
— подъемная крыла 238
— равнодействующая 95
— реакции опоры ПО
— сопротивления 126
— трения 121
---покоя 121
— — скольжения 123
— тяготения 111
— тяжести 91, 116, 117, 130
— упругости 90, 108
— уравновешивающая 165
— электрическая 107
— электромагнитная 106
Система единиц измерения 35
---Международная 35
---СГС 35
— замкнутая 183
— отсчета 28
инерциальная 80, 160
--- неииерциальная 160
Скалярная величина (скаляр) 12
Скорость 22,63
— линейная 67, 74
251
Скорость мгновенная 39, 40, 64
— первая космическая 144
— средняя 36, 52
— угловая 67, 74
Составляющая вектора 12
Статика 162
Столкновение тел 230
Тело отсчета 7
Теория относительности 88
Траектория 9, 64, 65
Трение сухое 125
Угол поворота 66, 73
Ускорение 41, 65
— мгновенное 42, 69
— свободного падения 55, 56, 111,
116, 130
— среднее 42
— центростремительное 70
Центр масс 157
— тяжести 157
Циолковский К. Э. 188
Частота 68
Энергия 212, 214
— внутренняя 225
— кинетическая 198, 215, 221
— механическая 221
— потенциальная 215, 218, 219
Эрг 191
Явление 4
ОГЛАВЛЕНИЕ
КИНЕМАТИКА
Глава 1. Общие сведения о движении
Введение ...................................................... 3
§ 1. Поступательное движение тел. Материальная точка . 5
§ 2. Положение точки (тела) в пространстве .......... 6
§ 3. Перемещение ............................. 9
§ 4. Понятие о векторах. Вектор перемещения. Координаты тела. 11
§ 5. Действия над векторами: сложение векторов ........... 15
§ 6. Действия над векторами: вычитание векторов ........... 19
§ 7. Действия над векторами: умножение вектора на скаляр .... 20
§ 8. Прямолинейное равномерное движение ........................ 21
§ 9. Графическое представление движения .......................... 25
§ 10. Относительность движения .................................. 27
§ 11. Относительность движения (продолжение) .................... 31
§ 12. Единицы измерения длины и времени ........................... 33
Глава 2. Прямолинейное неравномерное движение
Введение .......................................................... 36
§ 13. Средняя скорость ............................................. —
§ 14. Мгновенная скорость ......................................... 39
§ 15. Ускорение. Равноускоренное движение ......................... 41
§ 16. Направление ускорения ....................................... 42
§ 17. Перемещение при равноускоренном движении . .................. 46
§ 18. Средняя скорость при прямолинейном равноускоренном движе-
нии. Связь между перемещением н скоростью ....................... 52
§ 19. Измерение ускорения ....................................... 54
§ 20. Свободное падение тел ..................................... 55
§ 21. Движение тела, брошенного вертикально вверх ............... 59
Глава 3. Криволинейное движение
Введение .........................................................' 62
§ 22. Перемещение и скорость при криволинейном движении .... —
§ 23. Ускорение при криволинейном движении ........................ 64
§ 24. Движение по окружности. Угол поворота и угловая скорость. 65
§ 25. Ускорение при равномерном движении тела по окружности ... 68
§ 26. Вращение твердого тела ...................................... 72
§ 27. Об относительности движения тела при вращении системы отсчета 75
ДИНАМИКА
Глава 4. Законы движения
Введение ........................................................ 77
§ 28. Тела и их окружение. Первый закон Ньютона ................ —
§ 29. Почему возникают ускорения .......................... 81
§ 30. Взаимодействие тел. Ускорения тел при взаимодействии .... 82
§ 31. Инертность тел .......................................... 84
253
§ 32. Масса тел ..............................................
§ 33. Масса Луны .............................................
§ 34. Сила ...................................................
§ 35. Второй закон Ньютона ...................................
§ 36. Второй закон Ньютона (продолжение) .....................
§ 37. Измерение сил. Динамометр ..............................
§ 33. Третий закон Ньютона ...................................
§ 39. Значение законов Ньютона ...............................
86
88
89
91
95
97
100
103
Глава 5. Силы природы
Введение .................................................... '05
§ 40. Электромагнитные силы ........................................ —
§ 41. Сила упругости ............................................. 107
§ 42. Сила всемирного тяготения ................................... "1
§ 43. Постоянная всемирного тяготения ............................. "4
§ 44. Сила тяжести ................................................ "5
§ 45. Вес тел ..................................................... "8
§ 46. Измерение массы тел взвешиванием ........................... 119
§ 47. Масса Земли ............................................ • '20
§ 48. Сила трения. Трение покоя .................................. 121
§ 49. Сила трения скольжения ...........................t ... , 123
§ 50. Сила сопротивления, возник., пщ.(я при тинжепни тела в жидко-
сти или в газе ................................................... '25
Глава 6. Применение законов движения
Введение................................................... '28
§ 51. Движение тела под действием силы упругости.................. —
§ 52. Движение под действием силы тяжести: начальная скорость тела
равна нулю пли параллельна силе тяжести ................... 130
§ 53. Вес тела, движущегося с ускорением ......................... —
§ 54. Невесомость .............................................. 134
§ 55. Движение иод действием силы тяжести: тело брошено под углом
к горизонту ............................................... 136
§ 56. Движение под действием силы тяжести: тело брошено горизон-
тально ....................................................... 140
§ 57. Искусственные спутники Земли. Первая космическая скорость. 142
§ 58. Движение планет ......................................... 1-15
§ 59. Движение тела под действием силы трения .................. 146
§ 60. Движение тела под действием нескольких сил ............... 148
§ 61. Падение тела в газе или в жидкости ....<>,<<«>•• 1б2
§ 62. Наклон тел при движении на поворотах . ... t ...... —
§ 63. При каких условиях тела движутся поступательно3 масс
и центр тяжести........................................... 155
§ 64. Всегда ли верпы законы механики Ньютона .................. 158
РАВНОВЕСИЕ ТЕЛ
Глава 7. Элементы статики
Введение .................................................... 162
§ 65. Равновесие тел при отсутствии вращения .................. 163
§ 66. Равновесие тела с закрепленной осью. Момент силы ........... 168
§ 67. Правило моментов ........................................... 17!
§ 68. Устойчивость равновесия тел под действием силы тяжести ... 171
§ 69. Равновесие тел па опорах 177
254
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
Глава 8. Закон сохранения импульса
Введение ........................................................... 180
§ 70. Сила и импульс .............................................. —
§ 71. Закон сохранения и- П)льса ................................ 182
§ 72. Реактивное движение ....................................... 186
Глава 9. Механическая работа н мощность
Введение ..................... ....... ............................. 189
§ 73. Механическая работа ......................................... —
§ 74. Почему работа определяется как произведение |F| js'i .... 191
§ 75. Более общее определение работы ............................ 193
§ 76. Работа, совершаемая силами, равнодействующая которых не
равна нулю. Теорема о кинетической энергии ................ 197
§ 77. Работа силы тяжести ....................................... 200
§ 78. Работа силы упругости ..................................... 204
§ 79. Работа силы трения ........................................ 207
§ 80. Мощность .................................................. 208
Глава 10. Закон сохранения энергии
Введение ........................................................... 212
§ 81. Понятие о механическом состоянии ............................ —
§ 82. Работа тела и изменение его состояния. Понятие об энергии. 213
§ 83. Потенциальная и кинетическая энергия ........ 215
§ 84. Потенциальная энергия упруго деформированного тела......... 217
§ 85. Потенциальная энергия тела, находящегося под действием силы
тяжести ......................................................... 219
§ 86. Кинетическая энергия ...................................... 220
§ 87. Закон сохранения энергии .................................. 221
§ 88. Механическая энергия н сила трения ........................ 224
§ 89. Превращение энергии и использование машин ................. 226
§ 90. Коэффициент полезного действия ............................ 228
§ 91. Столкновение тел .......................................... 230
§ 92. Движение жидкости по трубам. Закон Бернулли ............... 234
§ 93. О значении законов сохранения ............................. 238
Заключение ....................................................... 239
Лабораторные работы ................................................ 240
Ответы к упражнениям ............................................... 247
Предметно-именной указатель ........................................ 250
Исаак Константинович Кикоин
Абрам Константинович Кикоин
ФИЗИКА
Учебное пособие для 8 класса
средней школы
Спецредакторы М. Л. Смолянский
и И. Ш. Слободецкий
Редактор В. А. Обменина
Художник Ю. Л. Сайчук.
Художественный редактор Г. Л. Алябьева
Технический редактор Е. К. Полукарова
Корректоры Т. А. Кузнецова и К. Л. Иванова
Подписано к печати с матриц 8/V 1973 г. 60 x90'/ie-
Бумага тип. № 3. Печ. л. 16,0+иакидка 0,25.
Уч.-изд. л. 16.134-иакидка 0,37. Тираж 3900 тыс.
(2 300 001—3 300 000) экз.
Издательство «Просвещение» Государственного ко«
митета Совета Министров РСФСР по делам изда-
тельств. полиграфии и книжной торговли. Москва,
3-й проезд Марьиной рощи, 4L
Саратовский ордена Трудового Красного Знамени
полиграфический комбинат Росглавполиграфпрома
Государственного комитета Совета Министре н
РСФСР по делам издательств, полиграфии и
книжной торговли. Саратов, ул. Чернышевского.
59. Заказ № 1126.
Цена 35 коп.
Механические единицы
Физическая величина Единица измерения в СИ Единица измерения в системе СГС
Основные единицы
Длина метр (1*) сантиметр (1 см = 10“М
Масса килограмм (1 "?) грамм (1 г = 10-3«г)
Время секунда (1 сея) секунда (1 сек)
Производные единицы
Скорость метр в секунду (1 м/сек) сантиметр в секунду (1 см/сек — Ю-2-и/сея)
Ускорение метр на секунду в квадрате (1 м/сен2) сантиметр на секунду в квадрате (1 см/сек2 = )0~2 м/сек2)
Сила ньютон (1 я «= 1 кг м/сек2) дина (1 дин = 1 г • см/сек2 — 10~ Бя)
Импульс килограмм-метр в секунду (1 я - сек — 1 кг • м/сек) грамм-сантиметр в секунду (1 дин . сея = 1 г • см/сек = = 10~5 я • сея)
Работа, энергия джоуль (1 дм< = 1 к - м) эрг (1 эрг = 1 дин см — ]О~7дж)
Мощность ватт (1 вт = 1 дж/сек) эрг в секунду (1 эрг/сен = Ю-7 ет)
Большие и малые величины
Расстояние
1026 м— расстояние до наиболее удаленного от нас объек-
та, который можно наблюдать с помощью совре-
менного телескопа
10~15 м— диаметр атомных ядер
Скорость
3-108 м/сек — максимальная скорость — скорость света
в вакууме
Ускорение
1027 м/сек2 — с таким ускорением движется электрон в ато-
ме водорода
Время
1018 сек — возраст Земли
10-24 сек — за такое время свет проходит расстояние, рав-
ное диаметру ядра атома водорода
Масса
~ 1030 кг — масса Солнца
«10~3° кг — масса электрона
Плотность
«4-1017 кг/м? — плотность ядерного вещества
10'21 кг/м? — средняя плотность частиц в межзвездном
пространстве
Мощность
6 млн. кет — мощность крупнейшей в мире Красноярской
ГЭС
СОВЕТСКИЕ УЧЕБНИКИ
БОЛЬШОЙ СКЛАД НА САЙТЕ
«СОЕТСКОЕ ВРЕМЯ»
SOVIETIME.RU