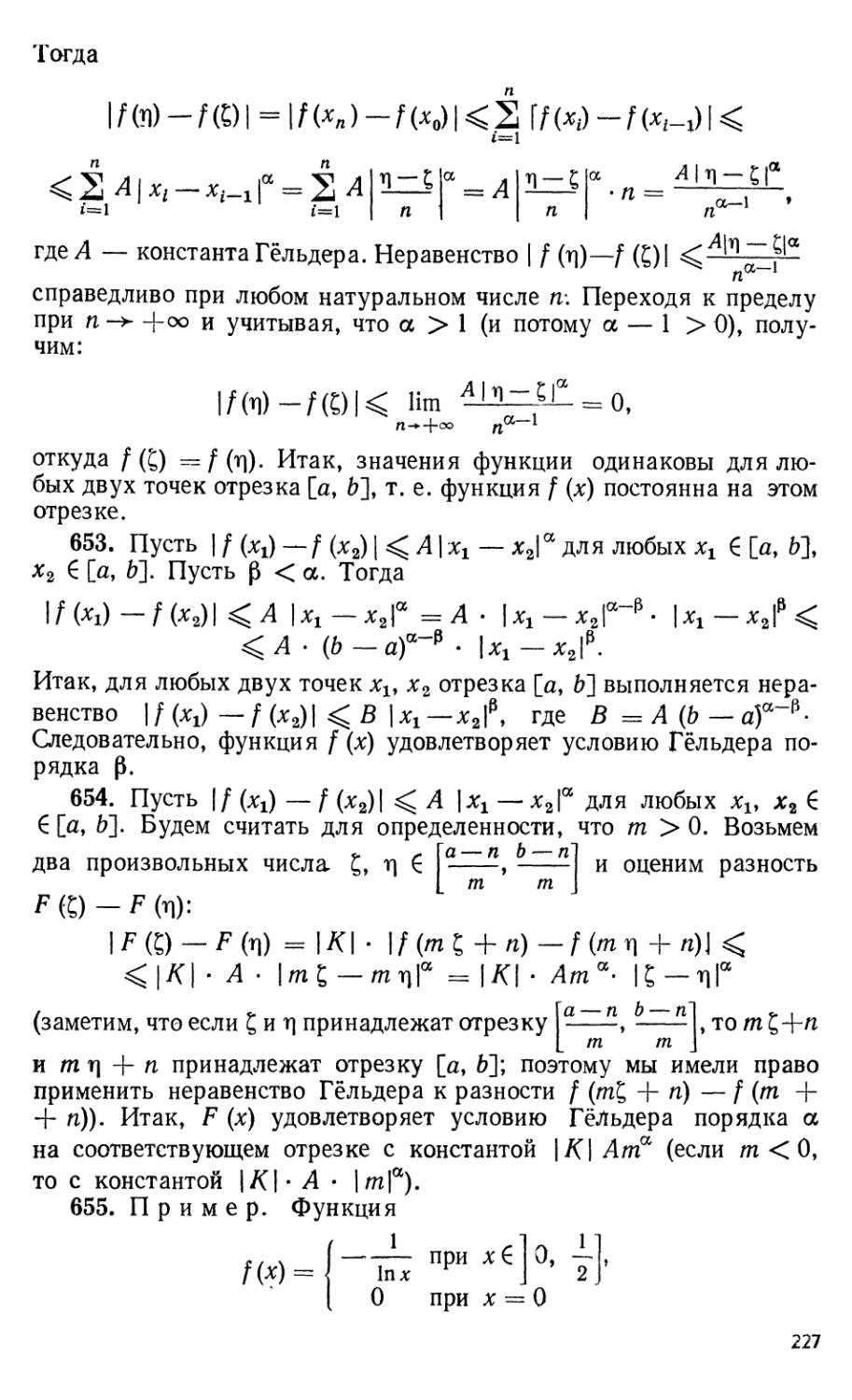«.сочли СБОРНИК ЗАДАЧ
по
МАТЕМАТИЧЕСКОМУ
АНАЛИЗУ
ОБЩАЯ ТЕОРИЯ
МНОЖЕСТВ И ФУНКЦИЙ
ПОД РЕДАКЦИЕЙ
М. Ф. БОКШТЕЙНА
Допущено
Министерством просвещения СССР
в качестве учебного пособия
для студентов
физико-математических факультетов
педагогических институтов
МОСКВА
«ПРОСВЕЩЕНИЕ» 19

ББК 22.16
О-94
Рецензенты:
кафедра математического анализа МГЗПИ
(зав. кафедрой кандидат физико-математических наук Мордкович А. Г.),
доктор физико-математических наук,
профессор Баврин И. И. (МОПИ им. Крупской)
Очан Ю. С.
0-94 Сборник задач по математическому анализу: Общая тео-
теория множеств и фуцкций: Учеб. пособие для студентов физ.-
мат. фак. пед. ин-тов /Под ред. М. Ф. Бокштейна — М.: Про-
Просвещение, 1981.-—271 с.
Сборник состоит из двух частей: теория множеств и теория функций. В нем пред-
представлены тексты задач, а также указания к их решению и ответы; кроме того, перед
каждым разделом приводится необходимый теоретический материал.
60602—862
0 ~26-81 4309020400
юз(оз)-81
Издательство

ПРЕДИСЛОВИЕ
Уже давно ощущается настоятельная необходимость появления
хорошего сборника задач по теории множеств и функций, предназна-
предназначенного для наших педагогических институтов.
Длительное время заслуженной популярностью пользовался
задачник по теории функций действительной переменной, выпущен-
выпущенный издательством «Просвещение» в 1965 г*. Изменения в програм-
программах пединститутов, связанные с прогрессом науки и изменением
взгляда на положение теории функций действительной переменной
внутри математического анализа, привели к необходимости созда-
создания нового задачника, более современного.
Настоящий сборник является результатом предпринятой авто-
автором коренной переработки названной выше книги, в которой после
его смерти принимали участие его друзья-математики, а также его
дочь Н. Ю. Очан.
Многие задачи и примеры, помещенные в настоящем пособии,
носят учебный характер. Однако наряду с элементарными задачами
сборник содержит также ряд задач повышенной трудности; решение
таких задач требует от учащегося известной изобретательности и
некотррых навыков математического исследования. Эти более труд-
трудные задачи (или циклы задач, объединенные общей темой) могут
служить материалом для спецсеминаров и кружков; их можно пред-
предлагать также в качестве тем для курсовых работ,
Несколько слов о построении книги.
Ввиду того что в различных учебниках употребляется различ-
различная терминология и различные обозначения, перед каждой главой
автор дает сводку основных определений и обозначений, а также
формулировку тех теорем, которые предполагаются известными и
на которые следует опираться при решении задач.
Книга разбита на две части. Вся теория множеств, начиная с
общей теорий (операции над множествами, вопросы взаимно од-
однозначного соответствия и мощности) и кончая теорией меры Ле-
Лебега, заключен^ в первой части. Вторая часть посвящена теории
функций, начиная с общих вопросов, связанных с отображениями
множеств, и кончая теорией интеграла Лебега в евклидовом про-
пространстве.
М. Ф. Бокштейн
* О ч а н Ю. С. Сборник задач и теорем по теории функций действительно-
действительного переменного. М., Просвещение, 1965.

ЧАСТЬ ПЕРВАЯ
ТЕОРИЯ МНОЖЕСТВ
Глава !.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
И ОБОЗНАЧЕНИЯ
Если а является элементом множества Л (или а входит в Л, принадлежит
Л), то пишут а £ Л, а если а не является элементом множества Л, то а £ Л (или
а $ Л). Элементы множества Л мы будем иногда называть точками этого множе-
множества.
Множество, не содержащее ни одного элемента, называется пустым множе-
множеством и обозначается 0.
Если все элементы множества Л являются также элементами множества В,
то говорят, что Л включается я В или Л содержится в В; говорят также, что В
включает или содержит Л. Это обозначают так: j4c5 или В id Л.
Если ЛсВи Бег Л, то говорят, что Л равно В или Л совпадает с В, пи-
пишут: А = В. Если Л не равно В, то пишут: Л Ф В.
Если ЛсиВ, то говорят, что А является подмножеством множества В. Если
при этом Л = В, то говорят, что Л является собственным подмножеством мно-
множества В.
Действия над множествами
1. Объединением множеств Л и В называется множество, составленное из
тех и только тех элементов, которые входят хотя бы в одно из данных множеств.
Объединение множеств Л и В обозначается Л U В.
Объединением семейства множеств {Аа}а,А (где индекс а пробегает не-
некоторое непустое множество индексов А) называется множество, составленное из
всех элементов, входящих хотя бы в одно из множеств Аа (а £ А). Объединение
семейства множеств {Аа }а,А обозначается U Л .
С6£А
2. Пересечением (или общей частью) множеств Л и В называется множество,
составленное из всех тех элементов, которые входят как в Л, так и в В. Пересе-
Пересечение множеств Л и В обозначается Л П В. Два множества называются непере-
непересекающимися, если их пересечение пусто.
Пересечением (или общей частью) семейства множеств {Аа }а^А называется
множество, составленное из всех элементов, входящих одновременно во все
множества Аа(а £ А). Пересечение множеств Аа обозначается П Аа.
а£А
Для объединения и пересечения справедливы переместительный и сочета-
сочетательный законы:
А\]В=В\]А,А[\В=*В[\А\
А[)(В[)С)=(А {) В){)С, А ()(В ()С)=(А [)В)()С,
Кроме того, справедливы распределительные законы:
л П (U*a)= U Ип ва), а и (ляа)= (](А ияа)
а^А а$А а€А а^А
(распределительность пересечения относительно объединения и объединения
относительно пересечения).

3. Разностью множеств А и В называется множество, элементами которого
являются те и только те элементы множества Л, которые не входят в В. Разность
множеств Л и В обозначается А \ Я-
4. Симметрическая разность А Д В множеств А и В определяется равен-
равенством
АЬВ=(А\В)[}(В\А).
Ясно, что А Д В = В Д А.
5. Произведением множеств А и В называется множество всевозможных пар
(х, у) таких, что х 6 Л, у £ В, Произведение множеств А и В обозначается
АХ В.
Если, в частности, А — множество чисел на оси Ox, a В — на оси Оу, то
А X В — множество всевозможных пар чисел (я, у), где х £ А, у (; В. Так как
пару чисел можно рассматривать как точку на плоскости Оху, то А X В можно
считать множеством всех точек (х, у) плоскости Оху таких, что х £ А, у £ В.
По аналогии с произведением двух множеств можно говорить о произведе-
произведении трех и большего числа множеств. В частности, если А — множество на оси
Оху В — на оси Оу> С — на оси Oz, то А X В X С — множество всех таких
точек (я, у, z) пространства Oxyz, что х € А, у € В, z £ С.
6. Верхним пределом последовательности множеств Е1у Еъ.,. называется
множество lim Ею определяемое равенством
НшЕл= П U Em.
п=\ т—п
Нижним пределом этой последовательности называется множество lim ЕП9
определяемое равенством
-f-oo -f-°°
НтЯл= U П Ет.
7. Пространство. Если все множества, фигурирующие в некоторой за»
даче, являются подмножествами некоторого множества X", то X называется
пространством.
Разность X \ Е (где Е СИ X) называется дополнением к множеству Е (от-
(относительно пространства X) и обозначается СХЕ или, короче, СЕ:
СЕ = X \ £.
8. Закон двойственности. Для любого семейства множеств {^a}a^Al
каждое из которых является подмножеством пространства X, справедливы сле-
следующие равенства:
С ( U Ла) -= П СЛа, С (Г) Аа) - U СЛа.
а£А а:А а£А а€А
В частности, для двух множеств А и В законы двойственности запишутся так:
С (Л U В) = СЛ П С£, С (Л П В) = СЛ U СБ.
Задачи
1. Доказать равносильность следующих трех соотношений:
A cz В, А () В =А, А [} В =В
(т. е. доказать, что из выполнения любого из них вытекает спра-
справедливость остальных двух).
2. Доказать, что А \ В = A f| СВ.
3. Доказать включения:
а) (А () С) {} (В ft D)cz(A {) В) () (С () D);
б) (В \ С) \ (В \ А) а А \ С;
в) А \ С а (А \ В) U (В \ С).

4. Доказать равенства:
а) А \ (В \ С) = (Л \ В) U (А П С);
б) (Л \ В) \ С = (А \ С) \ (В \ С);
в) (Л \ В) U (В \ С) U (С \ Л) U (^4 П В П С) = Л U
г) (Л \ В) П С = (Л П С) \ (В П Q = (Л П Q \ В;
д) (Л U В) \ С = (Л \ С) U (В \ С);
е) (Л П В) \ С = (Л \ С) П (В \ С).
5. Вытекает ли из Л \ В == С, что Л = В [) С?
6. Вытекает ли из Л = В U С, что Л \ В = С?
7. Верны ли равенства: а) Л \ (В U С) = (Л \ В) \ С;
б) Л U (В \ С) = (Л U В) \ С; в) (Л \ В) и С= (Л U Q \ В?
Если нет, то в какую сторону имеет место включение?
8. Доказать равносильность включений Л \ В cz С и
Л cz В U С1.
9. Доказать, что равенство Л \ (В \ С) = (Л \ В) U С вер-
верно, если Л =э С, и неверно, если С \ А ф 0.
10. Доказать включение
= U (Ak\Bky
k
Показать на примере, что в общем случае здесь нет равенства.
п -f оо -f°°
11. Доказать, что: а) если Вп == U Аи то U Ап = U Вл;
б) если С„= П Л то ПI 4= Л Сй.
t=l «=1 й=1
12. Доказать, что ЛАВ = (Л (J В) \ (Л fl В).
13. Пусть Л — заданное множество. Доказать, что множество X
пусто тогда и только тогда, когда А АХ = Л.
14. Доказать равенства: а) ЛД (BAD) =(ЛДВ) AD; б) Л П
П (BAD) = (Л П В) А (Л П D); в) ЛАЛ = 0.
15. Доказать включения: а) ЛАВ с= (ЛАС) U (ВАС); б) (Л |J
U В) AF cz (ЛAF) U (BAF); в) (А [) В) А (С \J D) a (AAC) U
(J (BAD). Показать на примере, что в общем случае здесь нет ра-
равенства.
16. Доказать равенства: а) С (А\В) = СЛ U В; б) С (С (СЛ U
U В) U (Л U СВ)) =В\А; в) (А {] В) [j (А (] СВ) [} (СЛ П
П В) == Л U В.
17. Используя закон двойственности, упростить выражение
С (С (X U Y) П (СХ U СУ)).
18. Доказать, что lim En состоит из тех и только тех точек, ко-
которые входят во все множества последовательности множеств {Еп},
начиная с некоторого номера. Доказать, что lim En состоит из тех
и только тех точек, которые входят в бесконечное число членов этой
последовательности.

19. Доказать, что если последовательность множеств {Еп} мо-
монотонно убывает (т. е. Еп id Еп+г при любом п) или монотонно воз-
возрастает (т. е. Еп а Еп+1 при любом я), то lim En = lim En.
20. Доказать, что для любой последовательности множеств
имеют место включения Q En a lim En a lim Еп а [} Еп. По-
п п
строить пример такой последовательности множеств, для которой
ни один из этих знаков включения не может быть заменен знаком
равенства.
21. Доказать, что для любых множеств Е> Ft G справедливы ра-
равенства:
a) Ex(F[)G)=(ExF)[)(ExG); б) (F[}G)xE=(FxE)[){GxE);
в) Ex(F(]G) = (ExF)f](ExG); г) (F(]G)xE=(FxE)(](GxE).
22. Справедливы ли равенства:
а) (А X В) П (С X D) = (А (] С) X (В f] D)\
б) (А X В) U (С X D) = (A U С) X (В U D)?
23. Доказать, что (А \ В) X С = (А X С) \ (В X С).
24. Доказать, чт<* (Р х Q) \ (А X В) = ((Р \ Л) X Q) U
U (Р X (Q \ В)).
25. Пусть множества Л и С непусты. Доказать, что, для того
чтобы А а В, С a D, необходимо и достаточно, чтобы было А X
X С с: В х D. Остается ли в силе это утверждение, если А или С
пусто?
26. Доказать, что если А а Р, В cz Q, то
А X В = (Л X Q) П (В X Р).
Глава II.
ВЗАИМНО ОДНОЗНАЧНОЕ
СООТВЕТСТВИЕ
Если каждому элементу а множества Л по некоторому закону поставлен в
соответствие один и только один элемент Ь множества В, причем различным эле-
элементам множества А отвечают различные элементы множества В, и если при этом
соответствий использованы все элементы множества В, то говорят, что между
множествами Л и В установлено взаимно однозначное соответствие.
Так, например, можно установить взаимно однозначное соответствие между
множеством всех рациональных чисел и множеством всех натуральных чисел.
Если между некоторым множеством Е и множеством N всех натуральных
чисел установлено взаимно однозначное соответствие, то говорят, что элементы
множества Е занумерованы с помощью натуральных чисел.
Целью задач настоящей главы является установление взаимно однозначного
соответствия между двумя заданными множествами (т. е. построение функции,
определенной на одном из заданных множеств и взаимно однозначно отображаю-
отображающей это множество на другое заданное множество).
Среди множеств, с которыми мы будем иметь дело, особенно важными яв-
являются числовые множества, т. е. множества, элементами которых являются
действительные числа. Важны следующие примеры числовых множеств (проме-
(промежутков): 1) множество всех действительных чисел (числовая прямая ]—оо, +CX)[)i
2) множество всех чисел х> удовлетворяющих неравенству х ^ а (луч [а, +°°[)
или неравенству х > а (луч ]а, +оо[); аналогично определяются лучи ]—оо, а]

и ]—оо, а[ (здесь а — заданное число); 3) множество всех чисел х, удовлетворяю-
удовлетворяющих неравенствам а < х < Ьу где а и Ь — заданные числа, причем а < Ъ (замк-
(замкнутый промежуток, или отрезок [а, bj); 4) множество всех чисел *, удовлетво-
удовлетворяющих неравенствам а < х < b (открытый промежуток, или интервал^, Ь\)\
5) множество всех чисел, удовлетворяющих неравенствам а ^ х < b или нера-
неравенствам а < х ^ b (полуоткрытый промежуток [а, Ь\_ или ]а, &]).
Числовое множество £ называется ограниченным сверху, если существует
такое число Ь, что для всех х £ Е выполняется неравенство х < Ь. Число Ь,
удовлетворяющее этому условию, называется верхней границей множества Е.
Наименьшая из верхних границ непустого ограниченного сверху множества
называется верхней гранью этого множества. Каждое непустое множество, огра-
ограниченное сверху, имеет верхнюю грань, притом единственную. Верхняя грань
множества Е обозначается символом sup Е. Если множество Е не является ог-
ограниченным Сверху, то, по определению, полагают sup Е = +оо.
Числовое множество Е называется ограниченным снизу, если существует
такое число а, что х ^ а для всех х £ Е. Число а, удовлетворяющее этому усло-
условию, называется нижней границей множества. Наибольшая из нижних границ
множества называется нижней гранью множества и обозначается inf E. Каждое
непустое множество, ограниченное снизу, имеет нижнюю грань, притом един-
единственную. Есди множество не ограничено снизу, то полагают, по определению,
inf £= —оо.
Числовое множество Е, которое ограничено и сверху, и снизу, называется
ограниченным. Верхней и нижней гранями непустого ограниченного множества
являются конечные числа (причем inf Е < sup Е)щ Примерами ограниченных
числовых множеств являются отрезок, интервал, полуоткрытый прЬмежуток*.
Наряду с числовыми множествами мы будем рассматривать также плоские
множества, т. е. множества точек на плоскости. Примеры: 1) множество всех
точек плоскости; 2) множество всех тех точек плоскости, координаты которых
удовлетворяют неравенству х2 + у2 ^ а2 (замкнутый круг) или неравенству
х2 + у2 < а2 (открытый круг) и т. д.
Кроме того, мы будем иметь дело с пространственными множествами, т. е.
с такими, которые расположены в трехмерном пространстве (например, сфера).
В некоторых случаях для установления взаимно однозначного соответствия
между числовыми множествами бывает полезно числа, входящие в эти множества,
записывать с помощью систематических дробей.
Если положительное число а может быть представлено в виде суммы сходя-
сходящегося ряда:
где р >• 1 — целое положительное число, А — целое неотрицательное число, а
fti» пъ Пз> Щ> ••• — целые неотрицательные числа от 0 до р — 1, то говорят, что
а разложено в систематическую дробь с основанием р (или в р-ичную дробь). Это
записывают следующим образом:
а — А у
А называется целой частью числа а\ мь я2, ^з» ••• — р-ичными знаками числа а.
Если все р-ичные знаки я#, начиная с некоторого номера k, равны нулю, то дробь
называется конечной, в противном случае — бесконечной.
При заданием р > 1 всякое положительное число а может быть представле-
представлено в виде-бесконечной р-ичной дроби, причем каждому числу а соответствует
* Наряду с верхней и нижней гранями числового множества нередко при-
приходится встречаться с верхней и нижней гранями функции (одной или нескольких
переменных). Если функция / (М) определена на множестве Е и принимает число-
числовые значения, то под символом sup / (M) (inf / (М)) подразумевается верхняя
М{Е М$Е
(нижняя) грань множества тех значений функции, которые соответствуют все-
всевозможным значениям независимой переменной М из множества £•

только одна бесконечная р-ичнаяидробь и, обратно, каждой бесконечной р-ичной
дроби отвечает единственное положительное число а. Вместе с тем некоторые ра-
рациональные числа а (не все!) допускают, наряду с разложением в бесконечную
р-ичную дробь, также разложение в виде конечной р-ичной дроби; например, при
р i= 10
— = 0,63000... (конечная дробь); -—=0,629999... (бесконечная дробь).
Числа, которые могут быть разложены в конечную р-ичную дробь, назы-
называются р-ично рациональными.
Все остальные числа называются р-ично иррациональными.
Систематическая дробь с основанием р = 10 называется десятичной дробью;
с основанием р = 2 — двоичной дробью; с основанием р = 3 — троичной дро-
дробью и т. д.
Задачи
27. Установить взаимно однозначное соответствие между множе-
множеством N всех натуральных чисел и множеством S всех четных по-
положительных чисел.
28. Установить взаимно-однозначное соответствие между мно-
множеством N всех натуральных чисел и множеством Т всех четных
чисел.
29. Установить взаимно однозначное соответствие между мно-
множеством Q+ всех неотрицательных рациональных чисел и множе-
множеством N всех натуральных чисел.
30. Существует ли функция вида /(д)^ <
&0 + М + —+ bmxm
(где коэффициенты а0, ..., ап9 &0, ..., bm — целые числа), обладающая
следующим свойством: для любого рационального числа г найдется
целое число &, такое, что / (k) = г?
31. Найти взаимно однозначное отображение отрезка [0, 1]
на отрезок [а, Ъ~].
32. Найти взаимно однозначное отображение интервала ]0, 1[
на всю числовую прямую.
33. Найти взаимно однозначное отображение числовой прямой
на интервал ]а, Ь[.
34. Найти взаимно однозначное соответствие между промежут-
промежутком [0, 1[ и лучом [0, +оо[.
35. Построить взаимно однозначное отображение отрезка [0, 1]
на интервал ]0, 1[.
36. Построить взаимно однозначное отображение отрезка [0, 1]
на всю числовую прямук).
37. Найти взаимно однозначное соответствие между отрезком
[0, 1] и лучом [0у +оо[.
38. Установить взаимно однозначное соответствие между лучом
[0, +оо[ и интервалом ]а, Ь[.
39. Отобразить взаимно однозначно луч [0, +оо[ на всю число-
числовую прямую.
40. Существует ли непрерывная функция, взаимно однозначна
отображающая отрезок [а; Ь] на всю числовую ось?

41. Существует ли непрерывная функция, взаимно однозначно
отображающая отрезок [а, Ь~\ на интервал ]с, d[?
42. Существует ли непрерывная функция, взаимно однозначно
отображающая отрезок [a, ft] на множество, состоящее из двух от*
рез ков [0, 1] и [3, 4]?
43. Построить взаимно однозначное отображение окружности
единичного радиуса на отрезок [0, 1].
44. Установить взаимно однозначное соответствие между от-
открытым единичным кругом и множеством точек плоскости, являю-
являющихся дополнением к замкнутому единичному кругу.
Примечание. Открытым единичным кругом называется множество
таких точек М (х, у) плоскости Оху, для которых выполнено неравенство х2 +
+ у2 < 1; замкнутым единичным -кругом — множество точек, для которых вы-
выполнено Соотношение х2 + у2 ^ 1.
45. Установить взаимно однозначное соответствие между от-
открытым единичным кругом и замкнутым единичным кругом.
46. Найти взаимно однозначное соответствие между замкнутым
единичным кругом и дополнением к открытому единичному кругу.
47. Найти взаимно однозначное соответствие между замкнутым
единичным кругом и дополнением к нему.
48. Установить взаимно однозначное соответствие между ок-
окружностью и прямой.
49. Установить взаимно однозначное соответствие между сферой
с одной выколотой точкой й плоскостью.
50. Установить взаимно однозначное соответствие между сфе-
сферой и плоскостью.
51. Установить взаимно однозначное соответствие между про-
произвольным замкнутым кругом и произвольной замкнутой звездной
областью.
Примечание. Плоское множество Л называется замкнутой звездной
областью относительно точки О, если на каждом луче, выходящем из точки О,
найдется та"кая точка М, отличная от О, что замкнутый прямолинейный отрезок
ОМ включается в Л, а остальная часть этого луча не содержит ни одной точки
из А.
52. Установить взаимно однозначное соответствие между мно-
множеством всех иррациональных чисел и множеством всех действи-
действительных чисел.
53. Установить взаимно однозначное соответствие между:
а) точками открытого квадрата I——, — X ——, — и точками
открытого прямоугольника ]а, b[_ X ]c, d[;
б) точками открытого квадрата ——, —| х , — и точками
J 2 2 i ] 2 2 l
плоскости; в) точками открытого прямоугольника ]а, ft[X]c, d[ и
точками плоскости.
54. Запишем в виде бесконечной десятичной дроби координаты
точки М (х, у) из квадрата ]0, 1] X ]0; 1]: абсцисса х =0, nxntnz ...,
ордината у =§,тхтгтъ ... . Поставим в соответствие
to

дой точке М @, пхщпъ ..., О, т1т2тэ ...) из квадрата точку
Р (О, п1т1п2т2п3т3 ...) из промежутка ]0, I]. Все ли точки промежут-
промежутка J), 1] получатся при этом соответствии? Будет ли это соответствие
взаимно однозначным соответствием между точками квадрата
]0, 1] X ]0, 1] и точками промежутка ]0, 1]?
55. Установить взаимно однозначное соответствие между мно-
множеством всех рациональных чисел отрезка [О, 1] и множеством всех
точек с рациональными координатами квадрата [0, 1] х [0, 1].
56. Установить взаимно однозначное соответствие между мно-
множеством всех рациональных точек числовой прямой и множеством
тех точек плоскости, у которых обе координаты рациональны.
57. Установить взаимно однозначное соответствие между мно-
множеством всех многочленов с рациональными коэффициентами и мно-
множеством всех натуральных чисел.
58. Установить взаимно однозначное соответствие между мно-
множеством всех конечных подмножеств натурального ряда чисел и
множеством всех натуральных чисел.
59. Установить взаимно однозначное соответствие между мно-
множеством всех последовательностей натуральных чисел и множеством
всех строго возрастающих последовательностей нату-
натуральных чисел.
60. Установить взаимно однозначное соответствие между мно-
множеством всех строго возрастающих последовательностей натураль-
натуральных чисел и множеством всех тех бесконечных двоичных дробей,
которые соответствуют числам промежутка ]0, 1].
ГлаЪа III.
МОЩНОСТЬ МНОЖЕСТВ
Два множества называются эквивалентными, если между ними можно уста-
установить взаимно однозначное соответствие. Если множества А и В эквивалентны,
то пишут: Л ~ В.
Легко видеть^ что если А ~ В, В ~ С, то А ~ С.
Признаки эквивалентности множеств (теоремы Кантора — Бернштей-
на):
1. Если А а В а С, причем А ~ С, то А ~ В,
2. Если А эквивалентно подмножеству множества В, а В эквивалентно под-
подмножеству множества А, то А ~ В.
Множество Е называется конечным, если оно эквивалентно множеству всех
натуральных чисел п, удовлетворяющих неравенствам 1 ^ п ^ N для некото-
некоторого фиксированного натурального числа N.
Пустое множество мы также причисляем к конечным множествам.
Множество, не являющееся конечным, называется бесконечным.
Два конечных множества эквивалентны тогда и только тогда, когда они
имеют одинаковое число элементов.
Для бесконечных множеств нельзя говорить о числе элементов множества;
количественной характеристикой любого множества, обобщающей понятие числа
элементов, является мощность множества; говорят, что два множества имеют
одинаковую мощность, если они эквивалентны.
Мощность множества А обозначается символом А.
Если множества А и В имеют одинаковую мощность (т. е. если они эквива-
эквивалентны), то пишут: А = В.

Если два множества неэквивалентны (т. е. между ними нельзя установить
взаимно однозначного соответствия), то пишут: А Ф /Гили (A rjj В).
Если множество В эквивалентно какому-либо подмножеству множества Ау
то говорят, что мощность множества В не превосходит мощности множества А.
Это записывают так: В ^ А или А ^ В.
Если множества А и В неэквивалентны, но множество А эквивалентно не-
некоторому подмножеству множества /^ тог^оворят^что^ножество В мощнее, чем
множество А. Это записывают так: В > А или А < В.
__ Из^теорем Кантора — Бернштейна вытекает, что если А ^ В и В ^ Ау то
А = В~.
Если же А ^ В, но А г£, В, то А < В.
Для доказательства эквивалентности множеств А н В можно: либо непо-
непосредственно установить взаимно однозначнре соответствие между множествами
А и В; либо, если это сделать трудно, установить эквивалентность множества А
подмножеству множества В и множества В подмножеству множества Л, а затем
применить вторую теорему Кантора — Бернштейна.
Если множество А конечно и HMeejr_/z элементов, то пишут: *7 = п\ в частно-
частности, если А — пустое множество, то Л~= 0.
Множество А, эквивалентное множеству всех натуральных чисел, называет-
называется счетным.
Примеры счетных множеств: множество всех целых чисел; множество
всех рациональных чисел; множество всех полиномов с рациональными коэф-
коэффициентами; множество всех алгебраических чисел и т. д.
Если множество имеет мощность, большую, чем множестйо натуральных
чисел, то оно называется несчетным множеством. Так, например, отрезок [0, 1]
является несчетным множеством.
Всякое множество, эквивалентное отрезку [0, 1], называется множеством
мощности континуума или множеством континуальной мощности. Если мно-
множество А имеет мощность континуума, то пишут: Л~= с.
Если множество имеет мощность континуума, то иногда для краткости гово-
говорят, что оно имеет континуум элементов.
Примеры множеств, имеющих мощности континуума (т. е. ту же мощ-
мощность, что и отрезок [0, 1]): отрезок [at ft] и интервал ]а, Ь\_ (при любых а и Ь,
где а < Ь)\ числовая прямая; множество всех бесконечных десятичных дробей;
множество всех иррациональных чисел; множество всех точек любого круга;
множество всех точек квадрата [0,1] X [0,1] (и вообще любого прямоугольни-
прямоугольника); множество всех точек плоскости; множество всех точек пространства Oxyz;
множество всех непрерывных функций, заданных на отрезке [0, 1], и т. д.
Если задано некоторое множество Е, то множество $, элементами которого
являются все подмножества множества Е, имеет мощность, большую, чем
Е : Г>Ш
Если Е — конечное множество мощности п, то $ — конечное множество
мощности 2п.
Если Е — бесконечное множество мощности а, то мощность множества Е
обозначается 2а.
В том случае, когда Е является счетным множеством, S имеет мощность кон-
континуума.
Всякое множество, мощность которого равна 2е (с — мощность континуу-
континуума), называется множеством мощности гиперконтинуума.
Примеры множеств мощности гиперконтинуума: множество всех под-
подмножеств отрезка [0, 1]; множество всех подмножеств числовой прямой; множе-
множество всех подмножеств плоскости; множество всех (не только непрерывных)
числовых функций, заданных на отрезке [0, 1], и т. д.
В заключение отметим некоторые свойства счетных множеств:
1. Любое подмножество счетного множества либо конечно, либо счетно.
12

2. Всякое бесконечное множество содержит счетное подмножества (говорят:
«Счетная мощность является наименьшей из бесконечных мощностей»).
3. Объединение конечной или счетной совокупности счетных множеств есть
счетно^ множество.
4. Если к несчетному множеству Е добавить или из него вычесть конечное
или счетное множество М, то мощность множества Е не изменится:
Задачи
61. Какова мощность множества всех треугольников на пло-
плоскости, вершины которых имеют рациональные координаты?
62. Какова мощность множества всех рациональных функций
с целыми коэффициентами в числителе и знаменателе?
63. Доказать, что множество всех окружностей на плоскости,
радиусы которых рациональны и координаты центра которых —
рациоцальные числа, счетно.
64. Какова мощность множества всех конечных десятичных
дробей? Какова мощность множества всех конечных р-ичных дробей
при заданном р > 1?
65. Какова мощность множества всех многочленов, коэффициен-
коэффициентами которых служат алгебраические числа?
66. Дано бесконечное множество Е неотрицательных чисел.
Обозначим через s верхнюю грань сумм чисел для любых конечных
подмножеств множества Е. Доказать, что если s < +оо, то в Я име-
имеется не более счетного множества чисел, отличных от нуля.
67. Доказать, что множество точек разрыва монотонной функ-
функции, заданной на отрезке [a, ft], конечно или счетно.
68. Доказать, что множество точек разрыва монотонной функции,
определенной на всей числовой прямой, конечно или.счетно.
69. Пусть Е — какое-либо несчетное множество положи-
положительных чисеЛ; доказать, что найдется такое число т > 0, что мно-
множество Е Г) ]т, +оо[ несчетно.
70. Верно ли утверждение: «Если Е — бесконечное множество
чисел, расположенное на луче ]0, +<х>], то найдется такое число
т > 0, что множество Е (] ]т, +оо[ бесконечно»?
71. Пусть Е — счетное множество точек на прямой. Можно ли
сдвинуть это множество на величину а (т. е. заменить все точки х €
£ Е точками х + а) так, чтобы получившееся в результате сдвига
множество Еа не пересекалось с Е?
72. Пусть Е — счетное множество точек на окружности. Можно
ли повернуть окружность вокруг центра на некоторый угол <р
так, чтобы множество Е , получившееся из £ в результате поворота,
не пересекалось с Е?
73. Доказать, что если расстояние между любыми двумя точка-
точками множества Е на прямой больше единицы, то множестве^ Е ко-
конечно или счетно.
74. На плоскости задано множество Е такое, что расстоя-
расстояние между любыми двумя точками этого множества больше, чем а
13

(где а —данное положительное число). Доказать, что множество Е
не более чем счетно (т. е. либо счетно, либо конечно).
75. Доказать с помощью теоремы Кантора — Бернштейна эквива-
эквивалентность замкнутого круга и открытого круга того же радиуса
на плоскости.
76. Доказать с помощью теоремы Кантора — Бернштейна экви-
эквивалентность плоскости и замкнутого квадрата на плоскости.
77. Доказать с помощью теоремы Кантора — Бернштейна экви-
эквивалентность квадрата ]0, 1] X ]0, 1] и промежутка ]0, 1] (исполь-
(использовать результат задачи 54).
78. Доказать, что множество всех конечных подмножеств счет-
счетного множества счетно.
79. Какова мощность множества всех строго возрастающих
последовательностей натуральных чисел?
80. Какова мощность множества всех последовательностей на-
натуральных чисел?
81. Показать, что множество всех перестановок натурального
ряда N имеет мощность континуума.
Примечание. Перестановкой множества называется всякое его вза-
взаимно однозначное отображение на себя.
82. Какова мощность множества всех конечных последователь-
последовательностей действительных чисел?
83. Доказать, что множество Е всех стационарных последова-
последовательностей натуральных чисел счетно.
Примечание. Последовательность {ап} называется стационарной,
если для нее существует номер по такой, что ап = аПо для всех п > по.
84. Доказать, что множество Е всех стационарных последова-
последовательностей действительных чисел имеет мощность континуума.
85. Какова мощность множества всех последовательностей на-
натуральных чисел, не содержащих числа 7?
86. Какова мощность множества всех последовательностей на-
натуральных чисел, содержащих число 7?
87. Какова мощность множества всевозможных последователь-
последовательностей рациональных чисел?
88. Какова мощность множества всевозможных многочленов
(с произвольными действительными коэффициентами)?
89. Какова мощность множества всех отрезков на числовой
прямой?
90. На прямой задано множество попарно не пересекающихся
отрезков. Что можно сказать о мощности этого множества?
91. Какова мощность множества всех кругов на плоскости?
92. На плоскости построено некоторое множество попарно не
пересекающихся окружностей. Может ли это множество быть не-
несчетным?
93. На плоскости построено некоторое множество попарно не
пересекающихся букв Т (размеры этих букв могут быть и различ-
различными). Может ли множество этих букв быть несчетным?
14

94. На плоскости построено некоторое множество попарно
не пересекающихся букв Г. Может ли это множество быть несчет-
несчетным?
95. Какова мощность множества всех последовательностей дей-
действительных чисел?
96. Какова мощность множества всех конечных и счетных под-
подмножеств множества £, если Е имеет мощность континуума?
97. Доказать, что множество всех числовых функций, определен-
определенных на отрезке [а, 6], имеет мощность гиперконтинуума.
98. Доказать, что множество всех непрерывных функций на
отрезке [а, Ь~\ имеет мощность континуума.
99. Какова мощность множества всех функций, определенных
на отрезке [а, 6] и разрывных хотя бы в одной точке этого отрезка?
100. Какова мощность множества всех строго возрастающих не-
непрерывных функций, заданных на отрезке [я, 6]?
101. Какова мощность множества всех монотонных функций на
отрезке [а, Ь] (не только непрерывных)?
102. Какова мощность множества всех функций, определенных
на отрезке [а, 6] и представимых в виде предела сходящейся после-
последовательности непрерывных функций?
103. Доказать, что существуют разрывные функции, опреде-
определенные на [я, Ь"] и не представимые в виде предела сходящейся по-
последовательности непрерывных.
104. Какова мощность множества всех действительных чисел,
заключенных между 0 и 1, в разложении которых в бесконечную
десятичную дробь отсутствует цифра 7?
105. Какова мощность множества всех действительных чисел,
заключенных между 0 и 1, в разложении которых в бесконечную
десятичную дробь цифра 7 находится на третьем месте?
106. Какова мощность множества всех действительных чисел,
заключенных между 0 и 1, в разложении которых в бесконечную
десятичную дробь имеется цифра 7?
107. Какова мощность множества всех чисел, заключенных
между 0 и 1, в разложении которых в бесконечную троичную дробь
отсутствует цифра 1?
108. Пусть А и В — эквивалентные бесконечные множества.
Существует ли подмножество множества Л, отличное от А, эквива-
летное В?
109. Доказать, что если А \ В ~ В \ А, то А ~ В.
110. Доказать, что если Л с= В и Л ~ Л [} С, то В ~ В {) С.
111. Верно или нет утверждение: «Если А ~ С, В ~ D, при-
чем A zd В, С zd D, то А \ В ~ С \ D»?
112. Пусть А =э С, В zdD, C\j В ~ С. Доказать, что
A UD-A
113. Верно ли утверждение: «Если А ~ В, С =э А, С =э В,
то С \ А ~ С \ В»?
114. Верно ли утверждение: «Если А ~ В, А =э С, В =э С,
то А \ С - В \ С»?
1*5

115. Доказать, что множество всевозможных равномерно схо-
сходящихся на [а, 6] последовательностей непрерывных функций име-
имеет мощность континуума.
116. Какова мощность множества всевозможных последова-
последовательностей непрерывных функций (на отрезке [а, Ь])?
117. Доказать следующее утверждение: «Если множество Е
на плоскости несчетно, то найдется такой круг с центром в начале
координат, который содержит несчетное множество точек из £».
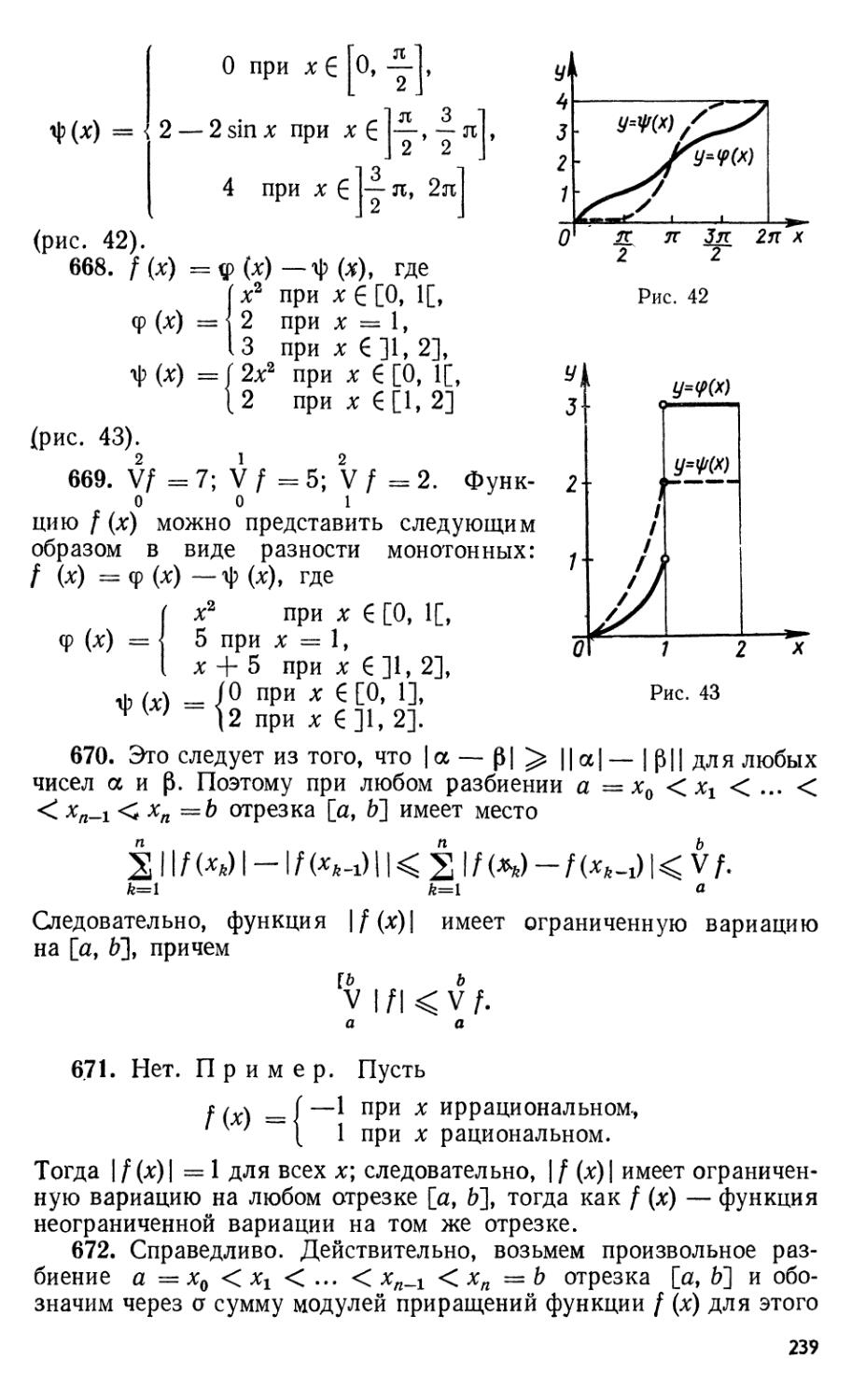
Глава IV.
МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
Говорят, что множество X снабжено метрикой, если каждой паре его эле-
элементов х, у поставлено в соответствие неотрицательное число р (х, у) («расстоя-
(«расстояние между х и у»), удовлетворяющее следующим аксиомам («аксиомы метрики»):
1) Р (х> У) — 0 тогда и только тогда, когда х = у («аксиома тождества»),
2) Р (х, У) = Р (У, х) для любых х £ X, у £ X. («аксиома симметрии»),
3) Р (х, у) < р (х, г) + р (г, у) для любых х, у, г £ X («аксиома треуголь-
треугольника»).
Множество X с введенной в нем метрикой р называется метрическим про-
пространством и обозначается (X, р). При этом множество X называют носителем
метрического пространства (X, р).
Метрическое пространство (X, р) мы часто будем обозначать той же буквой,
что и его носитель (т. е. только X, опуская букву р), если по смыслу ясно, какая
метрика введена в X.
Примеры метрических пространств:
1. Числовая прямая, где в качестве расстояния принято
р(#, у) = \х — у\.
2. Евклидово /г-мерное пространство Rn, носителем которого является
множество всевозможных упорядоченных наборов из п чисел (эти наборы назы-
называют также «кортежами длины w> или «точками п-мерного пространства»), а
расстояние вводится па формуле
P (x, У) =
где х — набор п чисел (alt ..., ап), ay — набор п чисел (by, ..., bn).
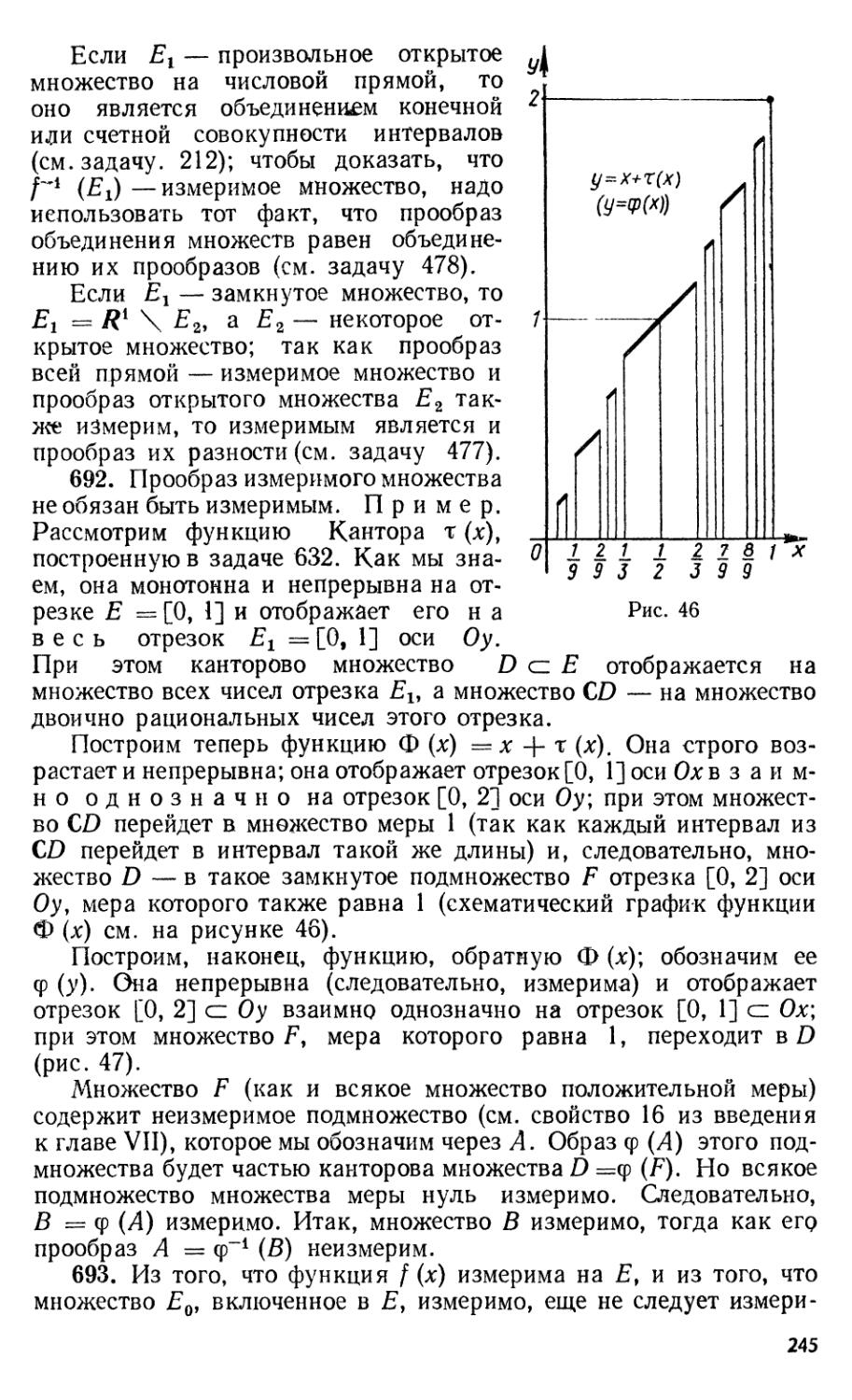
Числовая прямая является частным случаем евклидова пространства (при
* = 1).
3. Пространство С [а, Ь]9 носителем которого является множество всех не-
непрерывных функций на отрезке [a, Ь], a метрика вводится по формуле
Р (х, у) — max | / (х) — g (x) |,
х£1а, Ь\
где / и g — непрерывные функции на [а, Ь].
Для того чтобы проверить, что то или иное множество с введенным в нем рас-
расстоянием р (х, у) является метрическим пространством, надо убедиться в том, что
р (х, у) удовлетворяет всем трем аксиомам метрики. В частности, для того чтобы
доказать, что RH является метрическим пространством, используется неравен-
неравенство Коши — Буняковского, которое заключается в том, что для любых кортежей
(аь ..., ап) и фх, ..., РЛ) длины п имеет место соотношение
16
l
l*=l

Если р — метрика на множестве X, то сужение р на каждое множество
Е d X также есть метрика (будем обозначать ее той же буквой р). Метрическое
пространство (£, р) называется подпространством метрического пространства
(X, р).
Пример. Множество рациональных чисел с метрикой р (я, у) = \х—у\
является подпространством числовой прямой.
Последовательности в метрическом, пространстве. Полные простланства.
Говорят, что последовательность хъ х2, ..., хПУ ... (короче: {хп} ) элементов мет-
метрического пространства X сходится к элементу Ъ 6 X, если для любого числа
е > О существует такой номер N, что для всех номеров я > N выполняется не-
неравенство р (хп, Ь) < е.
Ьсли последовательность {хп} сходится к 6, то Ь яазывается пределом этой
последовательности; пишут: Ь = lim xn.
П-*+оо
Последовательность {хп} элементов пространства X называется фундамен-
фундаментальной, если для любого е > 0 существует такой номер N, что р (хп, хт) <е
для всех п > N, т > N.
Всякая сходящаяся последовательность фундаментальна; однако обратное
верно не. во всяком пространстве.
Пространство X называется полным, если всякая фундаментальная после-
последовательность его элементов сходится (к элементу этого пространства).
Примеры полных пространств: числовая прямая, евклидово простран-
пространство, пространство С [а, Я. Пример неполного пространства — множество
всех рациональных чисел (с обычным расстоянием).
Изометрия и гомеоморфизм. Метрические пространства (X, рх) и (У, pY)
называют изометричными, если между их носителями существует взаимно одно-
однозначное соответствие у = f (х) {х £ X, у G Y) такое, что для любых хг 6 X,
х% 6 X имеет место
Рх (*i> *а) = Ру (/ (*ib
Метрические пространства (X, р^) и (К, pY) называют гомеоморфными, если
между их носителями существует взаимно однозначное соответствие у = / (х)
(х 6 X, у б У), сохраняющее сходимость (т. е. из того, что рх (хп, а) ->■ 0, сле-
следует, что рк (/ (хп), f (а)) -> 0 и обратно)*
Изометричные пространства гомеоморфны. Однако обратное неверно; на-
например, интервалы ]0,1[, ]0,2Ци луч ]0, +оо[ (рассматриваемые как подпростран-
подпространства числовой прямой) гомеоморфны, но не изометричны.
Если пространство (X, р^) изометрично некоторому подпространству про-
пространства (У, рк), то говорят, что (X, рх) изометрично вкладывается в (У, ру).
Например, Rm изометрично вкладывается ц Rn при т < п.
Пусть в одном и том же множестве X введены две метрики: рг и р2. Если
для любой последовательности {хп} из рх (хп, а) ->■ 0 следует, что р2 (хп, а) -*0
и обратно, то говорят, что метрики рг и р2 эквивалентны. Ясно, что если метрики
р! и р2 эквивалентны, то пространства (X, Pi) и (X, р2) гомеоморфиьь
Задачи
118. Является ли метрическим пространством множество всех
действительных чисел, если под расстоянием между х и у понимать
sin2 (x — >')?
119. Показать, что рх (х, у) = arctg \x — у\ является метрикой
в множестве всех чисел. Эквивалентна ли она метрике р (х, у) =
=1 х —у|? Является ли полным пространством числовая прямая с
метрикой рх?
17

12Q. Будет ли метрическим пространством множество всех
действительных чисел, если расстояние между х и у определить так:
Р(*,У) =V\x-y\?
121. Пусть X —множество всех пар чисел (а, Ь). Для любых
двух его элементов х (аъ Ьг), у (а2, Ь2) положим:
Pi (*i У) = max {\а2 — аг\9 \Ь2 — Ь1\}\
Р2(*. У) = ka —ail + \Ъ% — Ьг\\
р3 (я, у) z=Y\a2 — аг\2 + \Ь2 — Ьг\2 (евклидова метрика).
Доказать, что рх и р2 удовлетворяют аксиомам метрики и что все
три метрики рх, р2, Рз эквивалентны.
Доказать полноту пространств (X, pt), (X, pg), (X, р3).
122. Пусть X — множество всех точек окружности С; примем
в качестве расстояния между точками х € X, у 6 X длину кратчай-
кратчайшей дуги окружности С, соединяющей х и у. Удовлетворяет ли это
расстояние аксиомам метрики?
123. Пусть X — множество всех прямых на плоскости, не про-
проходящих через начало координат. Определим расстояние между
двумя прямыми
1г: х cos аг + у sin ax — рх = 0, /2: х cos a2 + у sin аг — р2 =0
(где 0 ^ at < 2д, 0 ^ а2 < 2д, рх > 0, р2 > 0) формулами:
) Pii 2) V(Pa — PiJ+ (sin a2~ sin axJ+ (cos a2 —cos axJ;
б) p2 Сь '2) = IP2 — Pi I + lsin a2— sin aj +|cos a2 — cos axf;
в) Рз (/i, к) = lp2 — Pil + |sina2 — sinotjl.
Являются ли px, p2, Рз метриками? Если (X, pi), или (X, p2), или
(X, рз) — метрическое пространство, то полно ли оно?
124. Будет ли метрическим пространством семейство всех не-
непустых подмножеств метрического пространства X, если расстояние
между множествами Е а X и F а X определить равенством
р (£, F) = inf p (х, у)?
хгЕ
У F
125. Пусть X — произвольное непустое множество. Введем в
нем следующую метрику: р (х; у) = 1 при х ф у\ р (х, у) = 0 при
х = у. Будет ли пространство (X, р) полным?
126. Доказать, что множество всех числовых последовательно-
Н-оо
стей х {аъмъ ...), таких, что ряд 2 \ai I сходится, образует метри-
ческое пространство (оно обозначается /j), если за расстояние меж-
между х (аъ а21 ...) и у (Ьъ Ь2, ...) принять число
P(*f y) = Slft/-a/l.
127. Пусть хп (хп1, ...,^, ...)(п =1,2, ...) и а {аъ ..., aif ...) —
элементы пространства llf и щ = 1im x^ для любого натурального/.
Следует ли из этого, что р (хя1 а) -ИЗ?
18

128. Доказать полноту пространства 1г (см. задачу 126).
129. Доказать, что множество М (Е) всех ограниченных функций
на множестве Е образует метрическое пространство, щш за рас-
расстояние между функциями фиф принять число
Р(Ф,Ф) =sup |ф@—Ф@1.
Доказать полноту этого пространства.
Замечание. Частным случаем пространства М (Е) — когда Я есть
натуральный ряд — является пространство т всех ограниченных числовых по-
последовательностей, в котором за расстояние между х (аъ а2, •••) и у (bt, &*, ...)
принято число
р (х, у) = sup | bi — сц |.
i
130. Доказать полноту пространства С [а, Ь].
131. Доказать, что множество всех числовых последователь-
последовательное
ностей х (йъ а2, ...), для которых ряд 2 а?сходится, являетсяметри-
ческим пространством (оно обозначается /2), если за расстояние
между х (аъ а2, ...)иу фъ Ьъ ...) принять
f i=i
Доказать, что пространство /2 полно.
132. Доказать, что множество всех непрерывных функций на
[а, Ь~] образует метрическое пространство (обозначим его С [а, Ь]),
если за расстояние между ф (х) и я|> (х) принять число
ь
Эквивалентны ли метрики пространств С[а> &] и С; [а, &]?
133. Является ли метрическим пространством множество всех
непрерывных функций на [а, Ь], если за расстояние между ф (х)
и я|> (#) принять число
Р(Ф, Ф)
' a
Указание. Предварительно вывести неравенство Коши —
Буняковского для интегралов:
* < 1/ I (Ф (*)J ^ • I (Ф WJ
) ф (х) ф (х) d* < 1/ I (Ф (*)J ^ • I (Ф WJ
а г а а
его можно получить предельным переходом из неравенства Коши —
Буняковского для конечных сумм (см. введение к этой главе), если
принять щ = ф (*,.) КА^Г, Pi =*Ф (^)КА^.
134. Доказать, что множество F [а, &] всех пар непрерывных
функций на [а, Ь] является метрическим пространством, если за рас-
19

стояние между парами (Д, gx) и (/2, g2) принять число
xz\a, b]
Доказать полноту этого пространства.
135. Доказать неполноту пространства С [а, Ь] (см. задачу 132).
136. Доказать неполноту пространства, рассмотренного в за-
задаче 133.
137. Доказать, что подпространство Е пространства С [я, &],
составленное из всех непрерывных функций /, удовлетворяющих
условию А ^ / (х) ^ В для всех х £ [я, Ь] (где А и В — заданные
числа), является полным пространством.
138. Пусть F и G — фиксированные непрерывные функции на
[а, 6], такие, что F (x) ^ G (х) всюду на [а, 6]. Доказать, что под-
подпространство пространства С [а, Ь], состоящее из всех непрерывных
функций / таких, что F (х) ^ / (х) ^ G (х), полно.
139. Пусть рх и р2 — эквивалентные метрики на множестве X.
Следует ли из полноты пространства (X, р±) полнота пространства
(X. Р2)?
140. Доказать, что для эквивалентности метрик рх и р2 на множе-
множестве Е достаточно, чтобы существовали такие два числа А > 0 и
В > 0, что для любых х € Е, у € Е выполняются неравенства
^Pi (х, у) < р2 (х, у) < Вр! (*, у).
Показать, что это условие не является необходимым для экви-
эквивалентности метрик pi и р2.
141. Пусть Cj — множество всех непрерывных функций на
[а, 6], имеющих непрерывную производную (под производной в
точке а или в точке Ь подразумевается соответствующая односторон-
односторонняя производная). Введем в Сх две различных метрики:
Pl(/,g) =sup \f(x)-g(x)\ -fsup If (*)-g'(*)l;
p2 (/, gf = sup (]/ (*) -g (x)f + If (x) -g' (jc)|).
Доказать, что эти метрики эквивалентны. Доказать полноту
пространств (Сь рг) и (Сх, р2).
142. Пусть каждой паре элементов (х, у) множества X поставле-
поставлено в соответствие неотрицательное число р (х, у), удовлетворяющее
всем аксиомам метрики, кроме первой, которая выполняется в сле-
следующем ослабленном виде: если х = у, то р (х, у) = 0. Назовем
классом, содержащим х0 (где х0 € X) множество всех х 6 X таких,
что р (х, х0) = 0. Ясно, что классы попарно не пересекаются и их
объединением является все множество X. Доказать, что множество
всех классов образует метрическое пространство, если под расстоя-
расстоянием между двумя классами А и В подразумевать р (а, 6), где
а 6 A, b 6 В.
143. Будет ли метрическим пространством(Х, р), гдеХ —множе-
—множество всех функций с непрерывной производной на [a, ft], a p(/, g) =
1П)'I?
20

Произвести разбиение множества X на классы так, чтобы множе-
множество классов стало метрическим пространством.
144. Пусть X — множество всех последовательностей непре-
непрерывных на [a, ft] функций /ь /2, ..., /л, ... со сходящимся рядом
-foo
2 sup \fn(x)l Доказать, что (X, р), где
п=1 х:[а. Ь]
Р ({/«}, W) = 2 «up |/, (х) - ft (*) |,
1=1 хЦа, b]
является полным метрическим пространством.
145. Пусть А я В — полные подпространства метрического про-
пространства X. Доказать, что А [} В и А {] В также являются пол-
полными пространствами. Показать на примере, что А \ В может
оказаться неполным пространством.
146. Пусть (X, рх) и (Y; pY) — полные пространства. Дока-
Доказать, что пространство X X Y, снабженное метрикой
PXXY ((*Ь У1>. (*«« У Я» = У (Рх (*!' Х2)J + (Ру (У1, У2)J! О)
является полным пространством.
147. То же, если
Pxxy ((*i» У1>. (*2. У2)) - Рх (*ь *«) + Ру (Уь b)> B)
148. Доказать, что для сходимости последовательности{(хп, уп)}
к (а, Ь) в пространстве X X F, снабженном метрикой по фор-
формуле A) или B), необходимо и достаточно, чтобы {хп} сходилась к а
в пространстве X, а {уп} — к Ъ в пространстве Y.
Глава V.
ЗАМКНУТЫЕ И ОТКРЫТЫЕ МНОЖЕСТВА
Пусть X — какое-либо метрическое -пространство. Элементы этого простран-
пространства называют точками.
Окрестности. Окрестностью (или е-окрестностью) точки Хо 6 X называется
множество V (хо, е) всех точек х С X, удовлетворяющих условию р (xt Хо) < е.
При этом число 8 > 0 называют радиусом окрестности, точку Хо — ее центром.
Окрестность V (хо, е) называют также открытым шаром радиуса е с центром в
точке лго. Если знание радиуса окрестности точки хо несущественно, мы будем
вместо V (лго, е) писать просто V (лсо).
Если основное пространство X — числовая прямая, то е-окрестностью точ-
точки хо является интервал ]*о — е, хо + е[. Если X — плоскость, то V {хо, е) —
открытый круг радиуса 8 с центром в точке xq.
Важное свойство окрестностей: если у£ V (х0, е), то существует число
6 > 0 такое, что V (>', 6) а V (#о, е).
Классификация точек метрического пространства по отношению к данному
множеству. Пусть Е — какое-либо множество метрического пространства X.
Точка а:о 6 X называется точкой прикосновения множества £, если в любой ее
окрестности имеется хотя бы одна точка из Е. Легко видеть, что для этого необ-
необходимо и достаточно, чтобы в Е существовала последовательность точек {xn}f
сходящаяся в X к точке Хо. Множество всех точек прикосновения множества Е
называется замыканием множества Е и обозначается Е. Ясно, что Е cz E.
Пример. Замыканием интервала ]д, 6[ на прямой служит отрезок [а, 6].
Точка хо 6 X называется внутренней точкой множества Е, если существует
окрестность V (хо), содержащаяся в Е.
Множество всех внутренних точек множества Е называется его внутрен-
внутренностью и обозначается Е°. Ясно, что Е° а Е.
21

Предельной точкой множества Е называется точка хо £ X, в любой окрест-
окрестности которой имеется хотя бы одна точка из JE", отличная отхо. Легко видеть, что
для этого необходимо и достаточно, чтобы в любой окрестности точки хо содержа-
содержалось бесконечно много точек из Е.
Множество всех предельных точек множества Е называется его производным
множеством и обозначается Е'. Множество всех предельных точек множества Е'
называется вторым производным множеством множества Е и обозначается Е",
Аналогично определяются производные множества более высокого порядка
(производное множество порядка п обозначается Е^п)).
Точка хь 6 X называется изолированной точкой множества £, если Хо 6 Е,
причем в некоторой ее окрестности V (хо) нет других точек из Е (кроме самой
точки хо).
Точка #о С X называется граничной точкой множества Е, если в любой ок-
окрестности этой точки имеются как точки, принадлежащие Е, так и точки, не
принадлежащие Е.
Множество всех граничных точек множества Е называется границей мно-
множества Е и обозначается Fr E.
Легко видеть, что Е — Е' U Е — Е° {J Fr E.
Замкнутые множества. Множество Е в метрическом пространстве X назы-
называется замкнутым, если оно содержит все свои точки прикосновения (иначе
говоря, множество Е замкнуто, если оно совпадает со своим замыканием: Е = Е).
Примеры замкнутых множеств: пустое множество; все пространство Х\
любое конечное множество в Х\ замкнутый шар В (хо, е) в X радиуса е > 0 с
центром в точке лго, т. е. множество всех точек х 6 Х% для которых р (х> хо) ^ е.
Свойства замкнутых множеств: а) объединение конечного числа замк-
замкнутых множеств замкнуто; б) пересечение любой совокупности замкнутых мно-
множеств замкнуто.
Если множество замкнуто и не содержит изолированных точек, то оно на-
называется совершенным.
Примеры совершенных множеств на прямой: вся прямая, пустое мно-
множество, отрезок. Важным примером совершенного множества является также
канторово множество D, которое строится следующим образом: из отрезка
1 2Г
[0, 1] исключается интервал —, — ; затем из оставшихся двух отрезков («от-
J 3 3 I
резков первого ранга») исключаются интервалы длины — с центрами в середи-
о
нах этих отрезков; затем из оставшихся четырех отрезков («отрезков второго
ранга») выбрасываются интервалы длины -j с центрами в серединах этих отрез-
отрезков и т. д. до бесконечности. Множество D, оставшееся после исключения всех
этих интервалов, является совершенным. Его называют канторовым множеством.
Точки канторова множества разделяются на точки первого рода — концы вы-
выбрасываемых интервалов (их — счетное множество) и точки второго рода (все
остальные точки множества D\ их — множество мощности континуума). Множе-
Множество D имеет следующую арифметическую структуру: оно включает те и только те
точки отрезига [0, 1], которые могут быть записаны в виде троичной дроби (ко-
(конечной или бесконечной), не содержащей единицы в числе своих троичных
знаков.
Каждое непустое совершенное множество на прямой имеет мощность конти-
континуума (см. задачу 253).
Открытые множества. Множество Е в метрическом пространстве X назы-
называется открытыму если все его точки являются внутренними, т. е. Е совпадает
со своей внутренностью Е°.
Примеры открытых множеств на прямой — интервал, объединение
любой совокупности интервалов, вся прямая; на плоскости — открытый круг,
вся плоскость.
В любом метрическом пространстве X открыты пустое множество и все про-
пространство; открытым множеством в X является также каждый открытый шар.
22

Свойства открытых множеств: а) пересечение конечного числа открытых
множеств есть открытое множество; б) объединение любой совокупности откры-
открытых множеств есть открытое множество.
Между открытыми и замкнутыми множествами существует следующая связь:
1) дополнение к любому открытому множеству есть замкнутое множество; 2) до-
дополнение к любому замкнутому множеству есть открытое множество. Здесь (и
всюду в дальнейшем) имеется в виду дополнение до всего пространства.
Множества типа Fo и множества типа G$ . Множество, которое может быть
представлено как объединение счетной совокупности замкнутых множеств, на-
называется множеством типа Fo (типа «эф-сигма»).
В частности, множествами типа Fo являются: любое замкнутое множество;
любое открытое множество (задача 205); любое счетное множество и т. д.
Очевидно, объединение любой конечной или счетной совокупности множеств
типа Fo есть множество типа Fo .
Множество, которое может быть представлено как пересечение счетной со-
совокупности открытых множеств, называется множеством типа G$ (типа «же-
дельта»).
В частности, множествами типа G6 являются все замкнутые и все открытые
множества на числовой прямой; кроме того, множествами типа G6 являются все
полуоткрытые промежутки, множество всех иррациональных точек и т. д.
Очевидно, пересечение любой конечной или счетной совокупности множеств
типа G6 есть множество типа G6.
Расстояние от точки до множества, раоотояние между множествами. Диа-
Диаметр множества.. Расстоянием от точки х £ X до множества Е cz X (где X —
метрическое пространство) называется нижняя грань чисел р (х, у), где у пробе-
пробегает множество Е:
d (х, Е) = inf p (х, у).
УНЕ
Для того чтобы d (х, Е) было равно нулю, необходимо и достаточно, чтобы х
была точкой прикосновения для Е. Отсюда следует, что если Е замкнуто, то
d (х, Е) = 0 тогда и только тогда, когда х £ Е. Если же х £ Е (где Е замкнуто),
то d (х, Е) > 0.
Расстояние d между множествами А я В в метрическом пространстве X
определяется равенством
d{A,B)= infp (*,*/).
x'zA
Диаметром множества Е в метрическом пространстве называется верхняя
грань расстояний между всевозможными парами его точек:
diam E = sup p (х, у).
х:е, у:Е
Плотные и нигде не плотные множества. Множество Е cz X называется
плотным в множестве А, если Ё zd А. Если, в частности, Е плотно в простран-
пространстве X (т. е. Е = X), то Е называется всюду плотным.
Множество Е, лежащее в метрическом пространстве X, называется нигде
не плотныму если оно не плотно ни в каком открытом шаре этого пространства.
Это определение равносильно следующему: множество Е нигде не плотно в X,
если любой открытый шар пространства X содержит открытый шар, полностью
свободный от точек множества Е.
В частности, множество Е нигде не плотно на числовой прямой R1, если
любой интервал ]а, Ь\_ содержит интервал ]а, |S[, полностью свободный от точек
множества Я. Примеры нигде не плотных множеств на прямой: любое ко-
конечное множество; множество всех целых чисел; канторово совершенное множе-
множество.
Множество, являющееся объединением конечной или счетной совокупности,
нигде не плотных множеств, называется множеством первой категории. Множе-
Множество, не представимое в виде объединения: счетной совокупности нигде не плот-
плотных множеств, называется множествам второй категории,
23

Задачи
149. Показать, что V (х0, е) с: В (xQi г). Привести примеры ме-
метрических пространств, в которых V (х0, е) Ф В (х0, е) для некото-
некоторых х0 и е, и метрических пространств, в которых V (xQy в) =
= В (xQ% е) для всех х0 и е.
150. Доказать, что замыкание объединения двух множеств
равно объединению их замыканий. Доказать, что для бесконечного
семейства множеств {Аг} справедливо включение (JA <= [}А ,
It It
но не всегда верно равенство.
151. Доказать равенства С (Е°) ^ С£, С (Ё) = (С£)°.
152. Верно ли утверждение: «Внутренность пересечения двух
множеств равна пересечению их внутренностей»? Верно ли анало-
аналогичное утверждение для бесконечной совокупности множеств?
153. Верно ли утверждение: «Внутренность объединения двух
множеств равна объединению их внутренностей»? Если нет, то
имеется ли в какую-либо сторону включение?
154. Построить множество, для которого производное множество
непусто, а второе производное пусто.
155. Привести примеры: а) множества на плоскости, не имею-
имеющего граничных точек; б) множества Е на плоскости такого, что
Fr Е Ф 0, Е П Fr Е = 0; в) несчетного множества Е на плоско-
плоскости такого, что Е == Fr E.
156. Доказать, что Fr Е = Ё\Е° для любого множества Е.
157. Доказать, что граница объединения двух множеств со-
содержится в объединении их границ. Показать на примере, что ана-
аналогичное утверждение для бесконечной совокупности множеств не
всегда верно.
158. Доказать, что замыкание каждого множества замкнуто.
159. Доказать, что производное множество каждого множества
замкнуто.
160. Доказать, что граница каждого множества замкнута.
161. Доказать, что для эквивалентности метрик р{ и р2 в про-
пространстве X необходимо и достаточно, чтобы совокупность всех
подмножеств пространства X, замкнутых в смысле метрики р1э
совпадала с совокупностью всех~ подмножеств, замкнутых в смысле
метрики р2.
162. На плоскости дана последовательность концентрических
окружностей радиусов гг < г2 < ... < гп < ... Является ли их
объединение замкнутым множеством?
163. На плоскости дана последовательность замкнутых кон-
концентрических кругов радиусов г± < г2 < ... < гп < ... Является
ли их объединение замкнутым множеством? Является ли оно от-
открытым множеством?
164. Будем считать Землю идеально гладким шаром. Рассмот-
Рассмотрим множество Е всех тех точек М на поверхности Земли, которые
24

обладают следующим свойством: если из М пройти 7 км на север,
затем 7 км на запад и, наконец, 7 км на юг, то окажешься снова в
точке М. Является ли Е замкнутым множеством? Если нет, то ка-
какое множество является его замыканием? Его производным множе-
множеством?
165. Пусть / — непрерывная функция, определенная всюду на
оси Ох. Доказать, что множество Еа тех точек оси 0ху где / (х) ^ а%
замкнуто.
166. Пусть /0 — фиксированная непрерывная функция на [0, 1];
доказать, что множество Е всех непрерывных функций / на [0, 1],
удовлетворяющих неравенству / (х) ^ /0 (л;) для всех х € [0, 1],
замкнуто в пространстве С [О, 1].
167. Доказать равносильность следующих определений замкну-
замкнутого множества: а) множество называется замкнутым, если оно
включает все свои точки прикосновения; б) множество называется
замкнутым, если оно включает все свои предельные точки; в) мно-
множество называется замкнутым, если оно включает все свои граничные
точки.
168. Доказать, что замыкание Е множества Е есть пересечение
всех замкнутых множеств, содержащих Е.
169. Доказать, что для любого множества Е справедливы вклю-
включения £" id EfriD ... г> £<л> => ...
170. Доказать, что если Е замкнуто, то Fr Е = Fr (Fr E). Для
любого же множества Е Fr £ id Fr (Fr E) = Fr (Fr (Fr £)).
171. Доказать, что всякое замкнутое подпространство Е пол-
полного метрического пространства X есть полное метрическое про-
пространство.
172. Доказать, что незамкнутое подпространство Е метрического
пространства X не является полным пространством.
173. Пусть X — множество всех, функций на [a, f?], имеющих
непрерывную производную. Введем в нем метрику
P(f,g) =sUp \f(x)-g(x)\.
Будет ли пространство (X, р) полным?
174. Является ли совершенным множеством гиперболическая
спираль р = — @ < ф < +°°) на плоскости? Является ли совер-
Ф
шенным множеством замыкание этой спирали?
175. Всегда ли объединение конечного семейства совершенных
множеств является совершенным множеством? А объединение счет-
счетного семейства совершенных множеств?
176. Доказать, что внутренность любого множества есть от-
открытое множество.
177. Доказать, что внутренность Е° множества Е есть объеди-
объединение всех открытых множеств, содержащихся в Е.
178. Доказать, что для любого множества А в метрическом про-
пространстве и любого числа е > 0 множество Е всех тех точек х, для
которых имеет место неравенство d (х, Л) < е, открыто.
25

179. Пусть / — непрерывная функция, определенная всюду
на оси Ох. Доказать, что множество Еа тех точек оси Ох, где
/ (л:) > а, открыто.
180. Доказать, что множество Е всех непрерывных функций /
на [0, 1], удовлетворяющих для всех х € [0, 1] неравенствам
A <f(x) < В (где А < В — заданные числа), является открытым
множеством в пространстве С [0, 1].
181. Пусть F — фиксированная непрерывная функция на [0, 1].
Доказать, что множество всех функций /, удовлетворяющих для
всех х € [0, 1] неравенству f (х) > F (х), открыто в С[0, 1].
182. Построить последовательность открытых множеств, пере-
пересечение которых не является открытым.
183. Верно ли утверждение: «Если Е — замкнутое множест-
множество, то замыкание внутренности Е совпадает с Е (т. е. Е = £°)»?
Если это утверждение неверно, то имеет ли место одно из включе-
включений Е zd £°, E d E° и какое именно?
184. Верно ли утверждение: «Если Е — открытое множест-
множество, то внутренность замыкания Е совпадает с Е (т. е. E^^iEH)»?
Если это утверждение неверно, то имеет ли место одно из включе-
включений Е zd (£)°, E d (E)° и какое именно?
185. Доказать, что для любого множества А имеют место
включения: а) (Л)° cz Л, б) (А°)° =э Л°, но равенства не всегда
имеют место.
186. Пусть / — непрерывная функция на [а, Ь~\ и Еп — множе-
множество тех точек отрезка [а, 6], где п ^ f (х) ^ п + 1. Доказать, что
множество Ех U E3 (J Еь Q ... U Я2ь-1 U ••• замкнуто на число-
числовой прямой.
187. Пусть / — конечный интервал ]а, Ь[ на прямой, Ех а
а Е2а ... —возрастающая последовательность замкнутых мно-
множеств, в объединении дающих /. Верно ли, что любое замкнутое
множество f с/ содержится хотя бы в одном из Еп? Если верно —
доказать, если Het — построить противоречащий пример.
188. Построить на прямой такое множество Еу что 1) все его
точки изолированные; 2) нижняя грань расстояний между различ-
различными его точками равна нулю; 3) оно не имеет предельных точек
на прямой.
189. Доказать, что любое множество £, все точки которого
изолированные, является множеством типа Fa.
190. Пусть 1Е — множество всех изолированных точек про-
произвольного множества Е. Доказать, что IE есть множество типа Fa.
191. Привести пример несчетного множества, все точки кото-
которого изолированные.
192. Пусть X—метрическое пространство, Z—его подпро-
подпространство и Е cz Z. а) Доказать, что Ег = Ех[) Z, где Ег и Ех—
замыкания Е соответственно в Z и в X. б) Доказать, что, для того
чтобы Е было замкнуто в Z, необходимо и достаточно, чтобы суще-
26

ствовало замкнутое в X множество F такое, что Е = F (] Z.
193. Пусть X — метрическое пространство, Z — его подпро-
подпространство. Доказать, что, для того чтобы множество Е cz Z было
открыто в Z, необходимо и достаточно, чтобы существовало откры-
открытое в X множество G такое, что Е = G f| Z.
194. Пусть Z — подпространство метрического пространства X,
Е с Z и Е замкнуто (или открыто) в X. Доказать, что Е замкнуто
(соответственно открыто) в Z.
195. Пусть Е замкнуто (или открыто) в замкнутом (соответ-
(соответственно открытом) подпространстве Z метрического пространства X.
Доказать, что Е аамкнуто (соответственно открыто) в X.
196. Пусть X и У — метрические пространства, X X У — их
произведение. Пусть в X введена метрика, рассмотренная в задаче
146 (или 147). Доказать, что если Е — замкнутое множество в X,
a F — замкнутое множество в У, та £ X F — замкнутое множество
в X X У.
197. Доказать, что если В — замкнутое подмножество метриче-
метрического пространства X, то (Л° [) В)° — (Л [} ВH для любого
А сгХ.
198. Верно ли, что для любой точки х0 метрического простран-
пространства X и любого множества A a X
d(xQiA) = d(xQ,A)?
199. Верно ли, что для любой точки xQ метрического простран-
пространства X и любого множества A a X
d(xeiA) =d(xQiA°)?
200. Доказать, что для любых двух множеств А и В в метриче-
метрическом пространстве X имеет место
d (Л, В) = inf d (х, В) = inf d (Л, у).
201. Доказать, что для любых двух множеств А и В в метриче-
метрическом пространстве справедливы равенства
d (Ау В) = d (Л, 5) = d (J, В) = d (Л, В).
202. Для всяких ли двух множеств Л и 5 в метрическом про-
пространстве имеет место равенство
d(A,B) =d(A\ET).
203. Доказать, что для любых двух непересекающихся замкну-
замкнутых подмножеств Fx и F2 метрического пространства X существу-
существуют непересекающиеся открытые множества Gx cz X и G2 cz X та-
такие, что Gx =э Fly G2 =з F2.
204. Доказать, что дополнение ко всякому множеству типа G6
является множеством типа Fa, а дополнение ко всякому множеству
типа Fo — множеством типа G6.
205. Всякое замкнутое множество в метрическом пространстве
есть множество типа G6, а всякое открытое—типа Fa. Дока-
Доказать это.
27

206. Доказать, что множество Е всех точек плоскости, у кото-
которых обе координаты иррациональны, есть множество типа G6.
207. Пусть {Еп} — последовательность замкнутых множеств.
Доказать, что lim En есть множество tnna Fo. Сформулировать и
доказать аналогичное утверждение для верхнего предела.
208. Доказать, что убывающая последовательность замкнутых
множеств Ех zd E2 id ... в полном метрическом пространстве такая,
что lim diam En =0, имеет непустое пересечение.
г?-»-оо
209. Верно ли утверждение, что всякая убывающая последо-
последовательность замкнутых шаров Ех z> E2 => ... в любом полном
метрическом пространстве имеет непустое пересечение?
210. Верно ли утверждение, что убывающая последователь-
последовательность открытых шаров Ех zd E2 zd ... в полном метрическом про-
пространстве имеет непустое пересечение, если lim diam En = 0?
ГС-»-ОО
21К Пусть Ег id Е2^> ... —такая последовательность от-
открытых шаров в полном метрическом пространстве, что
a) lim diam En = 0; б) £л+1 cr En для каждого м. Доказать, что
П-+ОО
(]Еп непусто.
п
212. Доказать, что любое непустое открытое множество на пря-
прямой представляет собой объединение конечной или счетной сово-
совокупности попарно не пересекающихся интервалов (конечных или
бесконечных).
Примечание. Такое представление открытого множества в виде объе-
объединения интервалов единственно (эти интервалы называются составляющими
интервалами открытого множества на прямой, а также смежными интервалами
замкнутого множества, служащего дополнением к этому открытому).
213. Доказать: «Для того чтобы замкнутое множество на пря-
прямой было совершенным, необходимо и достаточно, чтобы никакие
два его смежных интервала не имели общих концов».
214. Доказать, что отрезок [а, Ь] нельзя представить в виде
объединения двух непустых непересекающихся замкнутых мно-
множеств.
215. Доказать, что отрезок [а, Ь} нельзя представить в виде
объединения счетной совокупности попарно не пересекающихся не-
непустых замкнутых множеств.
216. Доказать, что интервал ]а, Ь[ нельзя представить в виде
объединения счетной совокупности попарно не пересекающихся
замкнутых множеств.
217. Доказать, что числовая прямая R1 не может быть пред-
представлена в виде объединения счетной совокупности попарно не пе-
пересекающихся непустых замкнутых множеств.
218. Можно ли представить канторово множество в виде объе-
объединения счетной совокупности попарно не пересекающихся непу-
непустых замкнутых множеств?
219. На прямой даны отрезок [а, Ь] и совершенное множество Е%
28

причем концы отрезка не принадлежат Е. Доказать, что [a, fr] П
П Е — совершенное множество.
220. Доказать; «Для того чтобы замкнутое множество Е на пря-
прямой было нигде не плотным, достаточно, чтобы любой интервал со-
содержал хотя бы одну точку, не принадлежащую £».
221. На прямой даны интервал ]сс, р[ и нигде не плотное совер-
совершенное множество Е. Доказать, что их пересечение является либо
совершенным множеством, либо объединением счетной совокупно-
совокупности попарно не пересекающихся непустых совершенных множеств.
222. На прямой даны два нигде не плотных совершенных мно-
множества Р и Q. Доказать, что Р \ Q является либо совершенным мно-
множеством, либо объединением счетной совокупности попарно непере-
непересекающихся совершенных множеств.
223. Доказать, что объединение счетной совокупности нигде
не плотных совершенных множеств на прямой можно представить в
виде объединения счетной совокупности попарно не пере-
пересекающихся нигде не платных совершенных множеств,
224. Доказать, что канторово множество D является нигде не
плотным совершенным множеством на прямой.
226. Известно, что канторово множество имеет следующую ариф-
арифметическую структуру: оно состоит из тех и только из тех точек
отрезка [0, 1], которые могут быть записаны в виде троичной дроби,
не содержащей единицы в числе своих троичных знаков. Дока-
Доказать это.
226. Какова арифметическая структура множества точек пер-
первого рода (т. е. концов смежных интервалов) канторова множества?
Какова арифметическая структура точек второго рода (т. е. осталь-
остальных точек канторова множества)?
227. Найти в канторовом множестве какую-либо точку первого
рода, заключенную между десятичными дробями 0,1 и 0,2.
228. Найти в канторовом множестве какую-либо точку второго
рода, заключенную между десятичными дробями 0,05 и 0,1. Можно
ли выбрать эту точку так, чтобы она была рациональной?
229. Построить непустое совершенное подмножество канторовй
множества D, не включающее ни одной его точки первого рода.
230. Существует ли интервал, содержащий хотя бы одну точку
первого рода канторова множества Ь, но не содержащий ни одной
точки второго рода?
231. Доказать, что для любой точки х (i D (где D — канторово
множество) существует точка у € D такая, что р (х, у) иррацио-
иррационально.
232. Пусть Е — произвольное счетное множество на прямой.
Построить непустое совершенное множество на прямой, не содер-
содержащее ни одной точки множества Е.
233. Пусть Е — нигде не плотное совершенное множество, а
]аь PiC» •••» lat» P*[» •••—его смежные интервалы. Построим на
каждом интервале ]at., Pt.[ нигде не плотное совершенное множе-
множество Е{ d ]aif Р£. Доказать, что множество F == Е \j Ег \} ...
29

— U Е. U ••• совершенно, нигде не плотно и что все интервалы,
на которые распадаются множества ]ccf., P,[ \ Е. (i = 1, 2, ...),
и только они являются смежными интервалами для F.
234. Доказать, что множество Е на прямой, содержащее более
одной точки, не может удовлетворять одновременно трем условиям:
а) для любых а € £, р € Е (а < Р) существует у € Е такое, что
а < У < Р; б) Е замкнуто; в) Е нигде не плотно. Однако суще*
ствуют непустые множества на [а, Ь], удовлетворяющие любым двум
из этих условий (без третьего).
Для дальнейшего (задачи 235—241) нам понадобятся понятия предельной
точки и предельного множества последовательности точек метрического про-
пространства. Предельной точкой последовательности {ап} называется точка, яв-
являющаяся пределом какой-либо ее сходящейся подпоследовательности. Множе-
Множество всех предельных точек последовательности называется предельным множе-
множеством этой последовательности.
235. Построить последовательность, предельное множество ко-
которой пусто.
236. Доказать, что если предельное множество некоторой число-
числовой последовательности пусто, то последовательность модулей чле-
членов этой последовательности сходится к + оо.
237. Построить числовую последовательность, для которой пре-
предельным множеством служит вся прямая.
238. Доказать, что предельное множество любой последователь-
последовательности замкнуто.
239. Доказать, что, каково бы ни было замкнутое множество F
на прямой, можно построить числовую последовательность, для
которая F служит предельным мйожеством.
240. Доказать, что для сходимости числовой последовательно-
последовательности необходимо, а в случае ее ограниченности — и достаточно, что-
чтобы ее предельное множество было одноточечным.
241. Привести пример расходящейся последовательности, у
которой предельное множество состоит всего из одной точки.
242. Пусть Е —- множество точек квадрата [0, 1] X [0, 1], у
которых обе координаты иррациональны. Доказать, что существу-
существует непустое совершенное подмножество множества Е.
243. Представить замкнутый квадрат в виде объединения конти-
континуума нигде не плотных пояарно непересекающихся непустых со-
совершенных множеств на плоскости.
244. Построим на плоскости множество А следующим образом:
I 2 1
разделим квадрат [0, 1] X [0, 1] прямыми х = —, х = —, у =—,
2 3 3 3
у = — на девять одинаковых квадратов и выкинем центральный
открытый квадрат (т. е. квадрат —, — X —, — ). Затем каждый
J3 з[ J3 3[
из оставшихся восьми замкнутых квадратов делим на девять оди-
одинаковых квадратиков и выбрасываем все центральные открытые
квадратики; далее продолжаем этот процесс неограниченно. Мно-
Множество, оставшееся после счетного числа шагов, обозначим А (оно
30

и
§§§
и
называется «ковром Серпинского»), Доказать,
что А — нигде не плотное совершенное
множество.
245. Построим на плоскости множество
В следующим образом: разделим замкну-
замкнутый квадрат [0, 1] X [0, 1] прямыми
12 12
х =Т х =з~' у = "з' у ^7 на девять
одинаковых квадратов. Четыре замкну-
замкнутых квадрата, примыкающих к вершинам
основного квадрата, назовем квадратами
первого ранга, а их объединение обозна-
обозначим Вг (на рисунке 1, а множество В1 не зашт-
риховано). Затем каждый из квадратов пер-
первого ранга разделим на девять одинаковых
замкнутых квадратиков, и те из них, кото-
которые примыкают к вершинам соответствую-
соответствующего квадрата первого ранга, назовем
квадратами второго ранга; объединение
всех шестнадцати замкнутых квадратов
второго ранга обозначим В2 (на рисун-
рисунке 1, б множество В2 не заштриховано).
Далее, делим каждый квадрат второго
ранга на девять одинаковых замкнутых
квадратов и назовем квадратами третьего
ранга те из них, которые примыкают к
вершинам соответствующих квадратов вто-
второго ранга; объединение всех шестидесяти
четырех замкнутых квадратов третьего ранга обозначим В3 и т. д.
Ясно, что Bxzd В2 id B3zd ... Общую часть всех Вк назовем «клад-
«кладбищем Серпинского» и обозначим через В:
Рис. 1
к
Доказать, что В — нигде не плотное совершенное множество.
Исследовать его арифметическую структуру.
246. «Канторовой гребенкой» называется множество Е на пло-
плоскости Оху, состоящее из всех тех точек М(х-, у), координаты которых
удовлетворяют следующим условиям: х 6 [О, 1], у € D, где D —
канторово множество на оси Оу. Доказать, что Е — нигде не плотное
совершенное множество, и исследовать его арифметическую струк-
структуру.
247. Можно ли множества А («ковер Сер пи не кого»), В («кладби-
(«кладбище Серпинского») и Е («канторову гребенку») выразить через кан-
канторово множество с помощью действий дополнения (до отрезка [0, 1])
и произведения?
248. Пусть G — открытое множество, плотное в метрическом
пространстве X. Доказать, что для любого открытого шара So ci
с= X найдется открытый шар S такой, что S с: So (] G.
31

249. Доказать, что пересечение счетной совокупности открытых
множеств, плотных в полном пространстве X, является плотным в
X множеством.
250. Показать на примере, что предыдущее утверждение ста-
становится неверным, если пространство X неполно.
251. Пусть X — полное пространство без изолированных то-
точек. Доказать, что пересечение счетной совокупности открытых
плотных в X множеств имеет мощность, не меньшую мощности кон-
континуума.
252. Представить отрезок [0, 1] в виде объединения двух непе-
непересекающихся всюду плотных на нем множеств Л и В, обладающих
тем свойством, что для любых а и § таких, что 0 <J a < р <^ 1,
пересечения ]а, |3[ f| А и ]а, р[ (] В имеют мощность континуума.
253. Доказать, что непустое совершенное множество Е в пол-
полном пространстве X имеет мощность, не меньшую мощности конти*
нуума.
254. Доказать, что пересечение конечной или счетной совокуп-
совокупности множеств типа G6, каждое из которых плотно в подном про-
пространстве X, является множеством типа G6, плотным в X.
255. Привести пример убывающей последовательности {Еп}
всюду плотных множеств на прямой, имеющей пустое пересечение.
256. Построить счетную совокупность попарно не пересекаю-
пересекающихся всюду плотных множеств на прямой.
257. Доказать^ что множество всех рациональных чисел на пря-
прямой есть множество типа Fa, но не является множеством типа Ьб.
258. Доказать, что множество всех иррациональных чисел на
прямой есть множество типа G6, но не является множеством типа Fa .
259. Пусть Е — счетное всюду плотйое множество на прямой;
доказать, что оно не является множеством типа G6.
260. Пусть Е — дополнение к счетному всюду плотному мно-
множеству на прямой; доказать что Е не является множеством ти-
типа FQ.
261. Доказать, что множество всех рациональных чисел, рас-
расположенных на полуинтервале [а, |3[, не является множеством
типа G6.
Доказать, что множество всех иррациональных чисел, лежащих
на том же полуинтервале, не является множеством типа Fa.
262. Построить пример множества на прямой, не являющегося
ни множеством типа Fa, ни множеством типа G6.
263. Пусть А — нигде не плотное множество; доказать, что его
замыкание также нигде не плотно.
264. Доказать, что дополнение к нигде не плотному множеству
всюду плотно. Справедливо ли утверждение, что дополнение к
всюду плотному множеству нигде не плотно?
265. Доказать, что дополнение к открытому всюду плот-
плотному множеству Е нигде не плотно.
32

266. Доказать, что объединение Е конечного числа нигде не
плотных множеств в метрическом пространстве X является нигде
не плотным множеством в X. Сохраняется ли это утверждение в силе
для объединения счетной совокупности нигде не плотных множеств?
267. Доказать, что полное пространство X не может быть пред-
представлено в виде объединения счетной совокупности множеств, ни-
нигде не плотных в X (т. е. что полное пространство есть множество
второй категории) (теорема Бэра).
268. Показать на примере, что существуют неполные простран-
пространства, являющиеся множествами первой категории.
269. Канторово множество D замкнуто на прямой; следователь-
следовательно, оно является полным пространством. Вместе с тем оно нигде не
плотно и, следовательно, является множеством первой категории.
Нет ли здесь противоречия с теоремой Бэра (задача 267)?
270. Доказать, что всякое метрическое пространство, имеющее
хотя бы одну изолированную точку, является множеством второй
категории.
271. Привести пример неполного пространства без изолирован-
изолированных точек, являющегося множеством второй категории.
272. Доказать, что в полном пространстве дополнение к множе-
множеству первой категории есть множество второй категории.
273. Какой категории на плоскости является множество Е
всех точек, обе координаты которых иррациональны? Какой катего-
категории его дополнение?
274. Доказать, что множество DE всех точек второй категории
для Е замкнуто и содержится в £".
Примечание. Точка х0 метрического пространства X называется
точкой второй категории для множества Е а X, если для любой окрестности
V (х0) множество V (х0) fl E есть множество второй категории.
275. Доказать, что если Е — нигде не плотное (или всюду плот-
плотное) множество на прямой, то множество Еа всех точек вида х + а,
где а — фиксированное число, а х пробегает £, также нигде не плот-
плотно (или всюду плотно) на прямой.
276. Пусть Е — всюду плотное открытое множество на прямой
/J1. Доказать, что любая точка а (i Z?1 предстазима в виде
а = хг + х2, где хг (: Е, х2 6 Е.
277. Пусть Е — всюду плотное множество на прямой и Л —
какое-либо его конечное подмнбжество. Доказать, что Е \ А
всюду плотно на прямой.
278. Построить на прямой счетную совокупность всюду плот-
плотных попарно не пересекающихся несчетных множеств {£",}.
279. В этой и двух следующих задачах X и У — метрические
пространства, X X Y — их произведение с метрикой, введенной в
задаче 146. Пусть Е — нигде не плотное множество в X, F — про-
произвольное множество в Y. Доказать, что Е X F нигде не плотно в
X X Y.
280. Пусть Е и F — замкнутые множества соответственно в X
33

и У, причем одно из них совершенное. Доказать, что Е х F —
совершенное множество в X X У.
281. Пусть Е —множество, плотное в X, F — множество, плот-
плотное в У. Доказать, что Е X F плотно в X X У.
282. Найти замыкание множества всех точек вида—, где р и
q — всевозможные целые числа, причем q Ф 0.
283. Найти замыкание множества всех точек вида Ъ , где р и
q — всевозможные натуральные числа. 2
284. Найти замыкание множества всех точек вида —-—
4р2 + ?2
где р й q — всевозможные целые числа, отличные от нуля.
285. Пусть £ — иррациональное число. Доказать, что множе-
множество всех чисел вида т + л£, где тип — всевозможные целые чис-
числа, плотно на прямой.
286. Пусть £ — иррациональное число. Является ли множество
всех чисел вида т + п£, где тип — всевозможные четные
числа, плотным на прямой?
287. Доказать, что множество М точек, расположенных на еди-
единичной окружности Г с центром в начале координат и имеющих
полярные углы 1, 2, ..., п, ... радиан, плбтно на Г.
288. Доказать, что множество всех точек (#, у) с рациональными
координатами плотно на плоскости.
289. Построим множество Е на отрезке [0, 1] следующим обра-
образом: зададим произвольную последовательность положительных
чисел {ап}> образующую сходящийся ряд, сумма которого меньше 1.
Исключим из [0, 1] интервал длины ах с центром в середине отрезка;
далее, из оставшихся двух отрезков удалим интервалы длины —
с центрами в серединах этих отрезков; затем из оставшихся четырех
отрезков удалим интервалы длины 2? с центрами в серединах этих
отрезков, и т. Д.; множество, оставшееся после счетного числа ша-
шагов, обозначим Е. Доказать, что оно нигде не плотно на [0, 1] и
совершенно.
290. Доказать, что множество Е точек отрезка [0, 1], десятич-
десятичное разложение которых возможно без цифр 4 и 5, является нигде
не плотным совершенным множеством.
291. Замкнуто ли множество Е тех иррациональных чисел
отрезка [0, 1], в десятичном разложении которых отсутствует циф-
цифра 5? Если нет, то что представляет собой его замыкание? Содержит
ли это множество изолированные точки? Является ли оно нигде не
плотным?
292. Построить счетное подмножество канторова множества D,
плотное в D.
293. Доказать, что любое замкнутое множество F на прямой
обладает конечным или счетным подмножеством Е таким что
~Ё =F.
34

Для решения некоторых из последующих задач нам понадобится следующая
аппроксимационная теорема Вейерштрасса:
Теорема. Если функция f (х) непрерывна на отрезке [а, 6], то для лю-
любого 8 > 0 существует такой многочлен Р (х), что для всех х 6 [я, И справедливо
неравенство \f(x) — Р {х) \ < 8.
294. Доказать, что множество всех многочленов. плотно в-про-
в-пространстве С [0, 1].
295. Доказать, что множество всех многочленов с рациональ-
рациональными коэффициентами плотно в С [0, 1].
296. Пусть / (х) — четная (нечетная) непрерывная функция на
отрезке [—1, 1]. Доказать, что для любого е >0 существует мно-
многочлен Р (х)> содержащий лишь четные (нечетные) степени л;, та-
такой, что |/ (х) — Р (х)\ < е для всех х 6 [—1, 1].
297. Доказать, что для любой функции / (х)у непрерывной на
всей оси Оху существует последовательность многочленов, сходя-
сходящаяся к / (х) в каждой точке х ё 0%.
298. Доказать, что если для функции / (л;), определенной на
всей оси Оху существует последовательность многочленов, равно-
равномерно на Ох сходящаяся к / (х)у то / (х) — многочлен.
299. Привести пример последовательности множеств {Еп}>
каждое из которых плотно в С [0, 1], а их пересечение пусто.
Могут ли все Еп быть открытыми в С£0, 1]?
300. Доказать, что множество Е всех многочленов степени не
выше N, где N — фиксированное натуральное число, нигде не плот-
плотно в С[0, 1].
301. Доказать, что множество Е всех числовых последователь-
последовательностей (х19 х2, ...), у которых лишь конечное число членов отлично
от нуля> плотно в пространстве /2.
302. Доказать, что множество Е всех числовых последователь-
последовательностей (хъ х2, ..., хп9 ...), у которых хп = 0 для всех п > N (где W —
фиксированное натуральное число), нигде не плотно в /2.
Глава VI.
КОМПАКТНОСТЬ, СЕПАРАБЕЛЬНОСТЬ,
СВЯЗНОСТЬ
Компактные множества. Пусть X — метрическое пространство, Е а X.
Если из каждой последовательности {хп}, все элементы которой принадлежат Е,
можно выделить сходящуюся в X подпоследовательность {xnk}, то множество Е
называется относительно компактным.
Если из каждой последовательности {хп}, все элементы которой принадле-
принадлежат Е, можно выделить подпоследовательность {xnk}> сходящуюся к точке из Е,
то множество называется компактным (или компактом).
Ясно, что любое компактное множество Е относительно компактно, но не
наоборот. Для того чтобы множество Е в метрическом пространстве, X было
компактным, необходимо и достаточно, чтобы оно было относительно компактным
и замкнутым (задача 304).
Множество Е в метрическом пространстве называется ограниченным, если
его диаметр есть конечное число: diam Е < + оо.
35

Всякое относительно компактное множество в метрическом пространстве
ограничено, всякое компактное — ограничено и замкнуто (задача 303); обратные
утверждения, вообще говоря, неверны (задача 309).
Теорема Кантора. Пусть Аъ А2, ... — непустые компактные мно-
жества в метрическом пространстве X, причем Ах id Л2 =э ... Тогда пересечение
[\Ап непусто. Если, кроме того, lim diam An=* 0, то [\Ап состоит из единст-
П П-+оо п
венной точки (задача 317).
Укажем один критерий относительной компактности множества в метриче-
метрическом пространстве. Предварительно дадим несколько определений, Пусть 8 > 0;
множество М называется г-сетью для множества Е, если для каждой точки х 6 Е
существует точка у £ М такая, что р (х, у) < 8. Множество Е называется вполне
ограниченным, если для него при любом 8 > 0 существует конечная е-сеть.
Теорема Хаусдорфа. Для того чтобы множество Е в метриче-
метрическом пространстве X было относительно компактным, необходимо, а в случае,
если X — полное пространство, то и достаточно, чтобы Е было вполне ограни-
ограниченным (задача 325).
Из теоремы Хаусдорфа вытекают важные признаки относительной компакт-
компактности и компактности множества в евклидовом пространстве.
Теорема Больцан о— Вейерштрасса. Если множество Е в
евклидовом пространстве Rn ограничено, то оно относительно компактно, а
если Е a Rn ограничено и замкнуто, то оно компактно (задачи 329, 330).
Следствие 1. Всякая ограниченная последовательность точек евкли-
евклидова пространства имеет входящуюся подпоследовательность.
Следствие 2. У всякого бесконечного ограниченного множества Е в ев-
евклидовом пространстве существует хотя бы одна предельная точка (не обяза-
обязательно принадлежащая Е).
Пусть Е — какое-либо множество в метрическом пространстве X. Семейство
открытых множеств {Ga} (о& £ А) называется открытым покрытием множества
Е, если U GaZD E.
Открытое покрытие множества Е называется конечным, если оно состоит из
конечного числа множеств.
Множество Е называется бикомпактным (или бикомпактом), если из любого
открытого покрытия {Ga} множества Е -можно выделить конечное покрытие этого
множества (т. е. отбросить все множества из Покрытия {Ga}, кроме конечного
их числа, так, чтобы оставшиеся множества также покрывали множество Е).
Примеры. Любое конечное множество бикомпактно. Множество
{ 1 1 1 }
{1, —, -г-, ..., —, ..., 0> бикомпактно в R1.
Теорема. Для того чтобы множество Е в метрическом пространстве
было бикомпактным, необходимо и достаточно, чтобы оно было компактным (за-
(задача 336).
Следствие. Если множество Е в евклидовом пространстве Rn замкнуто
и ограничено, то из любого его открытого покрытия можно выделить конечное
покрытие.
Сепарабельность. Счетный базис. Метрическое пространство X называется
сепарабельным, если существует не более чем счетное множество Е cr X, плотное
Примеры сепарабельных пространств: любое метрическое пространст-
пространство, состоящее из конечного числа точек; любое евклидово пространство Rn\
С (а, ЬУ, 12 (задачи 345—347), любой компакт (задача 350); пространство М [а, 6]
(задача 351); здесь М [я, 6] есть М ([а, Ь~\) (см. задачу 129).
Базисом открытых множеств (или просто базисом) метрического простран-
пространства X называется всякое семейство открытых множеств, обладающее тем свой-
* Очевидно, что множество Е конечно тогда и только тогда, когда X конеч-
конечно (в этом случае Е = X); для бесконечного сепарабельного пространства Е
всегда счетно.
36

ством, что любое открытое множество пространства X является объединением
некоторой совокупности множеств из этого семейства.
Примеры базисов: 1) все открытые множества метрического простран-
пространства X образуют базис этого пространства; 2) все интервалы на числовой прямой
R1 образуют базис в Z?1; 3) все интервалы с рациональными концами образуют
базис в R1.
Пространство X называется пространством со счетным базисом, если оно
обладает хотя бы одним счетным базисом (т. е. базисом, образованным счетной
совокупностью открытых множеств).
Теорема 1. Для того чтобы метрическое пространство имело счетный
базис, необходимо и достаточно, чтобы оно было бесконечно и сепарабельно (см.
задачу 355).
Теорема 2. Мощность совокупности всех открытых (всех замкнутых)
множеств сепарабельного пространства не превосходит мощности континуума
(задачи 358—359).
Теорема 3. Мощность любого сепарабельного пространства не превос-
превосходит мощности континуума (задача 360).
Точки конденсации. Точка Мо 6 X называется точкой конденсации множе-
множества Е d X, если в каждой ее окрестности содержится несчетное множество точек
из Е.
Теорема 4 (Линделёфа). Если множество Е в сепарабельном
пространстве X не имеет точек конденсации, принадлежащих Е, то Е не более
чем счетно (задача 366).
Теорема 5. Множество точек конденсации произвольного множества Е
в сепарабельном пространстве совершенно (задача 367).
Теорема 6 (Кантора — Бендиксон а). Любое замкнутое
множество F в сепарабельном пространстве предстаъимо в виде объединения двух
множеств: совершенного и не более чем счетного (задача 368).
Теорема 7. Замкнутое множество в полном сепарабельном пространстве
либо не более чем счетно, либо имеет мощность континдума (задача 371).
Связнооть. Множества А и В в метрическом пространстве X называются
разъединенными, если они непусты и ни одно из них не содержит точек прикос-
прикосновения другого.
Ясно, что разъединенные множества не пересекаются (хотя обратное невер-
неверно). Ясно также, что если А и В разъединены и Аг а А, Вг с: В, причем Аг и В±
непусты, то Аг и Вг также разъединены.
Множество Е называется связным, если оно не может быть представлено
в виде объединения двух разъединенных множеств. Если же Е представи-
мо в виде объединения двух разъединенных множеств, то оно называется не-
несвязным.
Призеры. Пустое и одноточечные множества связны в любом метриче-
метрическом пространстве. На числовой прямой JR1 связны, кроме того, любые проме-
промежутки, и только они (задача 395).
Задачи
303. Доказать, что любое относительно компактное множество
ограничено, а любое компактное — ограничено и замкнуто.
304. Доказать, что для компактности множества Е~в метриче-
метрическом пространстве X необходимо и достаточно, чтобы оно было от-
относительно компактно и замкнуто в X.
305. Доказать, что любое замкнутое подмножество компакта
есть компакт.
306. Пусть Е — относительно компактное подмножество про-
пространства X. Доказать, что Е компактно.
37

307. Доказать, что множество Е функций у = kx2, где k пробе-
пробегает отрезок [0, 3], компактно в С [0, 1].
308. Доказать, что множество Е всех функций у = kx + Ь
@<fe<l,0<ft<l) компактно в С [0, 1].
309. Доказать, что множество Е всех непрерывных на [0, 1]
функций таких, что \f(x)\ ^ А (где А—фиксированное положи-
положительное число), ограничено и замкнуто в С [0, 1], однако не ком-
компактно (и даже не относительно компактно).
310. Привести пример замкнутого ограниченного множества
в /2, не являющегося компактом.
311. Пусть А и В—непустые относительно компактные мно-
множества в пространстве X. Доказать, что числа р (х, у) (где х 6 Л,
у £ В) образуют ограниченное числовое множество.
312. Доказать, что объединение конечного числа компактов есть
компакт, а объединение конечного числа относительно компактных
множеств — относительно компактное множество.
313. Доказать, что пересечение любой совокупности компактов
есть компакт; доказать аналогичное утверждение для отйоситель-
но компактных множеств.
314. Пусть Л с X и В с У, причем А и В непусты. Доказать,
что для компактности множества А X В в пространстве X X У,
наделенном метрикой, указанной в задаче 146, необходимо и доста-
достаточно, чтобы А и В были компактами.
315. Доказать, что для относительной компактности непустого
множества А X В в X X Y необходимо и достаточно, чтобы А
было относительно компактно в X, а В — в У.
316. Доказать, что всякий компакт есть полное пространство.
317. Пусть Аъ Л2, ...—непустые компактные множества в
метрическом пространстве X, причем Ах =э А2 id ... Доказать, что
П Ап непусто, причем если diam Ап ->■ 0, то f] Ап состоит из един-
п
ственной точки (теорема Кантора).
318. Пусть Alf А2, ...—убывающая последовательность ком-
компактов и К — П Ап. Доказать, что для каждого е > 0 найдется та-
п
кой номер N, что Ап а V (/С, г) для всех п > N (где V (/С, в) =
= U V (х, е).
х'-К
319. Пусть Аъ А2, ...—убывающая последовательность ком-
компактов, пересечением которых является одноточечное множество.
Доказать, что diam Ап ->• 0 при п ->• +оо.
320. Пусть {Et}—последовательность множеств в метриче-
метрическом пространстве X таких, что a) Et — компакт для каждого /;
б) Ег cz Ег-г для каждого / > 1. Доказать, что Q Еь непусто. По-
i
казать на примере, что это утверждение становится неверным, если
условие б) заменить на б'): Ег с: Ег-х для каждого i > 1.
321. Пусть Glf G2, ... —возрастающая последовательность от-
открытых множеств такая, что замыкание G их объединения G есть

компакт. Доказать, что для каждого е > О существует номер N
такой, что для всех п > N имеет место включение
Fr Gn cz V (Fr G, e).
322. Привести пример последовательности непустых замкну-
замкнутых ограниченных множеств {Еп} в полном пространстве X таких,
что 1) Еп+1 cz Еп для всех пу 2) f] En пусто.
п
323. Пусть {Еп} — последовательность компактов такая, что
пересечение любой конечной совокупности этих компактов непусто.
Доказать, что пересечение f] En всех этих компактов также непусто.
п
324. Остается ли в силе результат предыдущей задачи, если,
все Еп лежат в полном пространстве X, а условие компактности
множеств Еп заменить условием их замкнутости и ограниченности?
325. Доказать, что, для того чтобы множество Е в метрическом
пространстве X было относительно компактным, необходимо, а
в случае полноты X и достаточно, чтобы Е было вполне ограничен-
ограниченным {теорема Хаусдорфа).
326. Доказать, что для относительно компактного множества
в метрическом пространстве можно при любом е > О выбрать ко-
конечную е-сеть так, чтобы она содержалась в этом множестве.
327. Доказать, что, для того чтобы множество Е в метрическом
пространстве X было компактно, необходимо, а в случае полноты X
и достаточно, чтобы Е было замкнуто и вполне ограничено.
328. Пусть Е — множество в полном метрическом пространстве
X. Доказать, что если при любом е > О существует относительно
компактная е-сеть для £, та Е относительно компактно. Верно ли
это утверждение, если X неполно?
329. Доказать, что в евклидовом пространстве Rn любое огра-
ограниченное множество Е относительно компактно (теорема Больца-
но — Вейерштрасса).
330. Доказать, что в евклидовом пространстве Rn любое зам-
замкнутое ограниченное множество компактно.
331. Доказать, что любое относительно компактное (а следо-
следовательно, и любое компактное) множество в /2 нигде не плотно в /2.
332. Доказать, что любое относительно компактное (а следо-
следовательно, и любое компактное) множество в С [a, ft] нигде не плот-
плотно в С [а, ft].
333. Будем говорить, что множество Е в метрическом простран-
пространстве X обладает свойством Я, если его пересечение с любым замкну-
замкнутым шаром компактно. Доказать, что любое компактное множество
обладает свойством Н и что любое множество, обладающее свой-
свойством Я, замкнуто.
334. Показать, что в евклидовом пространстве Rn класс всех
замкнутых множеств совпадает с классом множеств, обладающих
свойством Н (см. предыдущую задачу). Построить пример полного
метрического пространства и замкнутого множества в нем, не обла-
обладающего свойством Я.
39

335. Доказать, что множество Е, обладающее свойством Н
(см. задачу 333) в С [а, 6], нигде не плотно в С [а, Ь].
336. Доказать, что, для того чтобы множество Е в метрическом
пространстве X было бикомпактным, необходимо и достаточно,
чтобы оно было компактным.
337. Дано счетное компактное множество £ = |0, 1, —, —,...,
—,...}. Его покрывает система интервалов ]1—е, 1 + я[,
где е — заданное положительное число, меньше чем —. Выделить
из этой системы интервалов конечную систему, покрывающую мно-
множество Е. 1 1 1 1 F
338. Дано счетное множество Е = [1, —, —• '"' —п9 '"]-
покрывает система интервалов: \ 2 4 2 J
1 i±[ lizzf L±i[
где 0 < е < —. Можно ли из этого покрытия выделить конечное
покрытие множества Е?
339. Дано замкнутое счетное множество Е = {1, 2, 3, ..., п, ...}.
Его покрывает бесконечная система интервалов:
]1-е, 1+е[, ]2 — е, 2 + е[, ]3 —е, 3 + е[, ...,]л —е, л + е], ....
где е — произвольное положительное число. Можно ли из этого
покрытия выделить конечное покрытие?
340. Рассмотрим на плоскости открытый круг Е единичного ра-
радиуса с центром в точке О; проведем концентрическую окружность С
радиуса — и построим семейство всевозможных открытых кругов
о
2
радиуса —, центры которых лежат на окружности С. Эти открытые
3
круги образуют бесконечное покрытие множества Е. Доказать, что
из этого покрытия нельзя выделить конечного покрытия.
341. Можно ли из того покрытия круга £, которое рассмотрено
в задаче 340, выделить счетное покрытие?
342. Совокупность открытых кругов, рассмотренная в задаче
340, покрывает замкнутый круг радиуса 1 — ее центром в точке О,
где 0 < е < —, Как из этого покрытия выделить конечное покры-
покрытие? 2
343. Построить пример ограниченного открытого множества
на прямой, покрытого интервалами так, что из этого покрытия
нельзя выделить конечного покрытия.
344. Верна ли теорема: «Из любого покрытия компакта замы?
каниями открытых множеств можно выделить конечное покрытие»?
345. Доказать сепарабельность евклидова пространства Rn.
о

346. Доказать сепарабельность пространства С [а, 6].
347. Доказать сепарабельность пространства /2.
348. Доказать сепарабельность пространства пар непрерывных
функций на [а, 6] с метрикой
Р (tfi, &)> (/2» g2)) = max |/2 (д) — /х (х)\ + max |g2 (д) —gl (x)\.
xt [а, Ь] хг ia> b]
349* Для того чтобы пространство X было сепарабелыго
необходимо и достаточно, чтобы при любом г > О для X существо-
существовала не более чем счетная е-сеть. Доказать это.
350. Доказать, что любой компакт является сепарабельным про-
пространством.
351. Доказать, что пространство М [a, b~] несепарабельно.
352. Доказать, что любое множество Е, лежащее в сепарабель-
ном пространстве X, обладает не более чем счетным подмножеством
Аь плотным в £, т. е. таким, что А =э Е. (Рассматривая Е как под-
подпространство пространства X, мы можем это утверждение сформу-
сформулировать также следующим образом: любое подпространство сепа-
рабельного метрического пространства сепарабельно.)
353. Построить какой-либо счетный базис на плоскости Ох)
354. Пусть А и В — два семейства открытых множеств в метр1 -
ческом пространстве X такие, что для каждого Л из А найдется В
из В, содержащееся в Л, и для каждого В из В найдется А из А,
содержащееся в В. Пусть В — базис в X. Можно ли утверждать,
что А также базис?
355. Доказать, что для того чтобы метрическое пространство X
было сепарабельным, необходимо и достаточно, чтобы оно имело
счетный (или конечный) базис.
356. Доказать, что из любого бесконечного семейства {Ga} от-
открытых множеств в пространстве X со счетным базисом можно вы-
выделить счетное подсемейство с тем же объединением.
357. Верно ли утверждение: «Если из любого бесконечного се-
семейства {Ga} открытых множеств в пространстве X можно выделить
счетное подсемейство с тем же объединением, то X есть пространство
со счетным (или конечным) базисом»?
358. Доказать, что мощность совокупности всех открытых под-
подмножеств сепарабельного метрического пространства не превосхо-
превосходит мощности континуума.
359. Доказать, что мощность совокупности всех замкнутых под-
подмножеств сепарабельного метрического пространства не превосхо-
превосходит мощности континуума.
360. Доказать, что мощность любого сепарабельного простран-
пространства не превосходит мощности континуума.
361. Доказать, что если X — сепарабельное пространство, имею-
имеющее мощность континуума, то совокупность всех его замкнутых
множеств также имеет мощность континуума.
362. Доказать, что непустой компакт без изолированных точек
имеет мощность континуума.
41

363. Обозначим через SE множество всех точек конденсации
множества Е в метрическом пространстве X. Доказать, что для лю-
любых множеств А и В имеет место: SA\jB~ SA [} SB.
364. Справедливо ли утверждение, что SyA = [}SA для про-
п п п
п
п
извольного счетного семейства множеств {Ап\>
365. Доказать, что, для того чтобы х0 была точкой конденсации
для множества Е в метрическом пространстве X, необходимо и до-
достаточно, чтобы любое множество G из базиса пространства X,
содержащее х0У включало несчетное множество точек из Е.
366. Доказать теорему Линделёфа (с. 37).
367. Доказать, что для любого множества Е в сепарабельном
пространстве X множество точек конденсации SE совершенно.
Привести пример несепарабельного пространства X и множе-
множества Е в нем такого, что множество SE Qro точек конденсации не-
несовершенно.
368. Доказать теорему Кантора — Бендиксона (с. 37).
369. Доказать, что если пространство X не только сепарабель-
но, но и полно, то любое замкнутое множество F а X един-
единственным образом разбивается на два непересекающихся мно-
множества: совершенное и не более чем счетное.
370. Показать на примере, что единственность разбиения замк-
замкнутого множества на совершенное и не более чем счетное множества
может нарушиться, если пространство X не полно.
371. Доказать, что замкнутое множество F в полном сепарабель-
сепарабельном пространстве X либо не более чем счетно, либо имеет мощность
континуума.
372. Доказать, что если все точки множества Е в сепарабельном
пространстве X изолированы, то Е не более чем счетно.
373. Показать на примере, что предыдущее утверждение не-
неверно, если пространство X несепарабельно.
374. Может ли множество Е на плоскости, имеющее мощность
континуума, содержать лишь конечное или счетное множество
своих предельных точек?
375. Доказать существование хотя бы одной точки конденса-
конденсации у несчетного множества Е на конечном отрезке методом после-
последовательного деления отрезка на две равные части, отмечая каждый
раз ту половину отрезка, которая содержит несчетное множество
точек из Е.
376. Пусть Е — связное множество, содержащее более одной
точки. Доказать, что оно не имеет изолированных точек.
377. Доказать, что, для того чтобы непустые множества А и В
были разъединены, необходимо и достаточно, чтобы выполнялось
равенство
ГА П В) U {А П В) =0.
378. Доказать, что если А и В — оба замкнутые или оба откры-
42

тые непустые множества, причем А () В = 0, то Л и В разъеди-
разъединены.
379. Пусть Е — несвязное замкнутое множество. Доказать, что
его можно представить в виде объединения двух непересекающихся
непустых замкнутых множеств.
380. Пусть Е — несвязное открытое множество. Доказать, что
его можно представить в виде объединения двух непересекающихся
непустых открытых множеств.
381. Пусть Е и F — замкнутые множества. Доказать, что если
Е U F и Е П F связны, то Е и F связны.
382. Показать на примере, что утверждение предыдущей задачи
становится неверным, если отказаться от требования замкнутости
хотя бы одного из множеств £, F.
383. Доказать, что если Е связно, то его замыкание Е тоже
связно. Показать на примере, что обратное утверждение неверно.
384. Доказать, что если Е связно и Е cz Н а Е, то Н также
связью.
385. Доказать, что если для любых двух точек множества Ё
существует связное множество Q, содержащее эти точки и включаю-
включающееся в £, то Е связно.
386. Доказать, что множество точек плоскости, у которых обе
координаты иррациональны, несвязно.
387. Доказать связность отрезка, соединяющего две точки пря-
прямой, плоскости, трехмерного евклидова пространства.
388. Доказать связность замкнутого круга на плоскости и замк-
замкнутого шара в трехмерном евклидовом пространстве.
389. Пусть Ех и Е2 — связные множества с непустым пересече-
пересечением. Доказать, что Е = Ех \] Е2 связно.
390. Пусть Еъ Е2У ...—возрастающая последовательность
связных множеств. Доказать, что их объединение Е = [) Et связно.
391. Пусть {Ei) — последовательность связных множеств та-
такая, что Et f] £h-i непусто для каждого номера i. Доказать, что
-foo
U Et связно.
i=\
392. Пусть {Et} — последовательность непустых множеств та-
такая, что Et U Ег+х связно для каждого номера i. Доказать, что
у Еь связно.
393. Доказать, что множество точек плоскости, у которых хотя
бы одна координата рациональна, связно.
394. Доказать, что множество Е на прямой связно в том и толь-
только в том случае, если вместе с любыми двумя своими точками оно
содержит и весь соединяющий их отрезок.
395. Доказать связность следующих множеств на прямой:
а) [а, &]; б) ]а, 6[; в) ]а, &]; г) [а, Ь[; д) [а, +^[; е) ]а, +оо[;
ж) ]—оо, а]; з) ]—оо, а[; и) ]—оо, +оо[; к) одноточечное множе-
множество {а}\ л) 0.
43

Доказать, что никакое множество на прямой, кроме множеств
вида а) — л) (при всевозможных а и Ь, а < о), не является связным.
396. Доказать связность евклидова пространства Rn.
397. Пусть X — связное метрическое пространство. Доказать,
что в нем, кроме пустого множества и всего пространства X, не су-
существует множества, которое было бы одновременно замкнутым и
открытым.
398. Можно ли открытый круг на плоскости представить в виде
пересечения двух открытых множеств, отличных от всей плоскости,
объединение которых есть вся плоскость?
399. Пусть X и У — метрические пространства. Доказать, что
для связности непустого множества Е X F в пространстве X X Y,
наделенном метрикой, указанной в задаче 146, необходимо и доста-
достаточно, чтобы Е и F оба были связны.
400. Доказать, что любые две точки связного открытого множе-
множества G на плоскости можно соединить ломаной, каждое звено кото-
которой параллельно одной из осей координат.
401. Пусть {Аа} (а € А) — некоторое семейство связных мно-
множеств с непустым пересечением. Доказать, что объединение всех
множеств семейства, т. е. множество Е = [) Ап, связно.
402. Доказать, что для любой точки х0 (: Е существует, и при-
притом единственная, компонента множества Е, содержащая х0.
Примечание. Непустое множество Л называется компонентой мно-
множества Е, если: 1) A cz E; 2) А связно; 3) любое связное множество В, такое, что
А а В а £, совпадает с А.
403. Доказать, что каждая компонента А замкнутого множества
Е есть замкнутое множество.
404. Доказать, что любое непустое множество Е разбивается
на компоненты, и притом единственным образом.
405. Множество называется всюду разрывным, если оно содер-
содержит более одной точки и все его компоненты — одноточечные мно-
множества. Привести примеры несчетных всюду разрывных множеств.
406. Пусть F ci E, F связно и непусто. Доказать, что существует,
и притом единственная, компонента множества Е, включающая F.
Глава VII.
МЕРА МНОЖЕСТВ (В ЕВКЛИДОВОМ
ПРОСТРАНСТВЕ)
Параллелепипеды и их объемы. Пусть Rn — евклидово пространство. Во
всем дальнейшем изложении будем считать п фиксированным натуральным
числом.
Пусть А (а1у .,., ап), В (Ьъ ..., Ьп) — две точки из Rn такие, что щ <J Ъ{
при i = 1, 2, ..., п. Множество всех точек М (хи ..,, хп) 6 Rn таких, что щ <
< xi < bi при любом i, называется открытым п-мерным параллелепипедом
о
D (Л, В). Множество всех точек М (xlt ..., хп) таких, что а/ ^ x-t ^ bi, назы-
называется замкнутым п-мерным параллелепипедом D (Л, В). Наконец, п-мерным
параллелепипедом с вершинами в точках А и В называется любое множество
44

D (At B)t удовлетворяющее включениям
D (Л, B) a D (A, B) czD (Л, В).
Ясно, что D (Л, В) и D (А, В) — частные случаи параллелепипеда D (А, В).
Если хотя бы одна координата точки А равна соответствующей координате точки
В, то параллелепипед D (А, В) называется вырожденным, в противном случае —
невырожденным.
п-мерным объемом параллелепипеда D (Л, В) с вершинами А (а1г ..., ап),
В (Ь±, ..., Ьп) называется число
liD= (b1 — а^ ... (Ьп — ап).
Если D — вырожденный параллелепипед, то \iD — 0; в противном случае
\xD > 0. Частными случаями /t-мерного объема являются: при п = 1 — длина
отрезка, при п — 2 — площадь прямоугольника, при п — 3 — обычный объем
трехмерного параллелепипеда.
Внешняя мера множества. Пусть Е a Rn. Внешней п-мерной мерой (или
просто внешней мерой) тЕ множества Е называется нижняя грань сумм /г-мер-
ных объемов открытых параллелепипедов, объединение которых покрывает Е
(нижняя грань берется до всевозможным таким покрытиям {Da }):
тЕ = inf 2j \iD.
а
Свойства внешней меры: 1) тЕ определена для любого множества
Е a Rnt причем 0 ^ тЕ ^ + оо; 2) для любой системы {Da }, покрывающей Е,
имеет место 2\iDa ^ тЕ; 3) если Е а Яп и тЕ < + оо, то для любого е > 0
существует покрытие Фа} множества Е открытыми параллелепипедами такое,
что 2jx£>a ^ тЕ + е; 4) если Е cz F> то тЕ ^ mF\ 5) для любой конечной или
счетной системы множеств {Еп} справедливо неравенство т {\] Еп) ^ 2тЯя;
п п
6) внешняя мера конечного или счетного множества точек равна нулю; 7) внеш-
внешняя мера параллелепипеда D (Л, В) равна его я-мерному объему: mD — jxD;
8) конгруэнтные множества имеют равные внешние меры.
Измеримые множеотва. Мера Лебега. Множество Е a Rn называется из-
измеримым по Лебегу (или просто измеримым), если для любого множества Л dRn
справедливо равенство
т~А = т(А (] Е) + in (А П С_£),
т. е. если Е рассекает любое множество Л cz Rn на такие две^асти, сумма внеш*
них мер которых дает внешнюю меру всего Л.
Если Е измеримо, то его внешняя мера называется мерой Лебега (или про-
просто мерой) множества Е и обозначется тЕ.
Свойства измеримых множеств и их мер:
1. Если Е измеримо, то и СЕ измеримо.
2. Если тЕ — 0, то Е измеримо. Такие множества называются множества-
множествами меры нуль. Любое подмножество множества меры нуль измеримо и имеет
меру нуль.
3. Добавление к измеримому множеству или изъятие из него множества
меры нуль не нарушает его измеримости и не изменяет его меры.
4. Любой параллелепипед измерим, и его мера равна его я-мерному объему.
5. Если Е и F — измеримые множества такие, что Е с: Ft то
тЕ ^ mF («монотонность меры»).
6. Объединение любой конечной или счетной совокупности измеримых мно-
множеств {Еп} есть измеримре множество, причем
т ([}Еп) ^ 2>тЕп («полуаддитивность меры»),
п п
45

7. Для объединения любой конечной или счетной совокупности попарно не
пересекающихся измеримых множеств {Еп} справедливо равенство
т (U Еп)~ 2>тЕп («счетная аддитивность меры»).
п п
8. Если Е и F измеримы, то Е \ F также измеримо; если при этом Ezd F
и тЕ < + оо, то т (Е \ F) = тЕ — mF.
9. Пересечение любой конечной или счетной совокупности измеримых мно-
множеств измеримо.
10. Любое замкнутое и любое открытое множество пространства Rn изме-
измеримо.
11. Для любого измеримого множества Е и любого числа 8 > 0 существует
замкнутое множество FaE такое, что
12. Мера всякого измеримого множества EczRn является верхней гранью
мер замкнутых множеств F, включающихся в Е, и нижней гранью мер открытых
множеств G, включающих Е:
тЕ = sup mF = inf mG.
FCZE GZDE
13. Если {En} — возрастающая последовательность -измеримых множеств
то т (U Еп) — lim mEn.
14. Если {Еп} — убывающая последовательность измеримых множеств,
причем тЕ1 < +оо, то
15. Если Е измеримо, то всякое конгруэнтное ему множество также изме-
измеримо и имеет ту же меру, что и Е.
16. В пространстве Rn существуют неизмеримые множества. Более того,
всякое измеримое множество, мера которого больше нуля, содержит неизмери-
неизмеримое подмножество.
Если /i= 1, т. е. если рассматриваемое пространство является числовой
прямой, то измеримые множества в нем называются линейно измеримыми, а
мера в R1 называется линейной мерой. Для отрезков она сводится к обычной
длине. Желая подчеркнуть, что речь идет именно о линейной мере, мы пишем
внизу индекс 1: m*Ji.
Если п — 2, т. е. если речь идет о множествах на плоскости, то мера назы-
называется плоской, а измеримые множества— множествами, измеримыми в смысле
плоской меры. Плоская мера множества Еа R2 обозначается т2Е. Для прямо-
прямоугольников она сводится к обычной площади.
Аналогично обстоит дело для множества в R3. В этом случае мы говорим о
трехмерной мере и обозначаем ее т3Е. Для трехмерных параллелепипедов она
сводится к обычному объему.
В дальнейшем индекс, обозначающий размерность меры, будет, как правило,
опускаться.
В заключение отметим одно свойство линейной меры: если G — открытое
множество на прямой, то mG = 2т/й, где /# — составляющие интервалы мно-
множества G.
Задачи
407. Доказать, что всякое множество Е9 расположенное на оси
Ох (даже если оно является неизмеримым множеством на прямой),
измеримо на плоскости Оху и его плоская мера равна нулю.
408. Доказать, что совокупность всех измеримых множеств
46

на прямой (а также на плоскости) имеет мощность 2е (гиперконти-
(гиперконтинуум).
409. Построить на отрезке [0, 1] нигде не плотное совершенное
множество, линейная мера которого равна 0,9.
410. Построить на отрезке [0, 1] нигде не плотное совершенное
множество заданной меры а < 1.
411. Можно ли построить на отрезке [0, 1] нигде не плотное со-
совершенное множество меры 1?
412. Построить на квадрате [0, 1] X [0, 1] нигде не плотное со-
совершенное множество, плоская мера которого равна заданному
неотрицательному числу а < 1.
413. Какова плоская мера множества, построенного в задаче
244 («ковер Серпинекого»)?
414. Какова плоская мера множества, построенного в задаче
245 («кладбище Серпинского»)?
415. Какова плоская мера множества, построенного в задаче
246 («канторова гребенка»)?
416. Доказать, что любое ограниченное измеримое множество
Е на прямой, имеющее положительную линейную меру р, содер-
содержит измеримое подмножество меры q, гдед — произвольное заданное
положительное число, меньшее, чем р.
417. Доказать, что любое измеримое множество Е на прямой
(не обязательно ограниченное) такое, что 0 < тЕ = р ^ +оо,
содержит ограниченное измеримое подмножество меры q> где q —
произвольное заданное положительное число, меньшее, чем р.
418. Пусть Е—измеримое множество на прямой такое, что
0 < тЕ = р ^ -\- оо, a q — какое-либо положительное число,
меньшее, чем р. Доказать, что существует ограниченное совер-
совершенное множество М а Е такое, что тМ = q.
419. Доказать, что всякое измеримое множество Е положитель-
положительной линейной меры имеет мощность континуума.
420. Доказать, что любое измеримое множество Е на плоскости,
имеющее положительную плоскую меру р, содержит измеримое
подмножество М плоской меры q, где q — произвольное заданное
положительное число, меньшее, чем р.
421. Доказать, что плоское множество М cz E (см. предыдущую
задачу) можно выбрать совершенным.
422. Может ли равняться нулю мера множества, которое содер-
содержит хотя бы одну внутреннюю точку?
423. Можно ли построить на отрезке [а, 6] замкнутое множество
линейной меры Ь — а, отличное от всего отрезка?
424. Может ли пересечение Е = [\ En убывающей последова-
п
тельности {Еп} измеримых множеств бесконечной меры иметь бес-
бесконечную меру? Конечную меру, отличную от нуля? Меру нуль?
425. Может ли объединение Е = [)Еп возрастающей после-
п
довательности измеримых множеств конечной меры иметь конечную
меру? Бесконечную меру?
47

426. Пусть Е — множество всех тех точек отрезка [0, 1], в раз-
разложении которых в бесконечную двоичную дробь на всех
четных местах стоят нули. Доказать, что Е нигде не плотно и что
мера Е равна нулю.
427. Может ли неограниченное измеримое множество на прямой
иметь конечную положительную меру?
428. Доказать, что всякое непустое замкнутое множество меры
нуль на прямой нигде не плотно. Решить аналогичную задачу
для плоскости и для трехмерного пространства.
429. Пусть множество Е на отрезке [0, 1] имеет меру нуль. Дол-
Должно ли и его замыкание Е быть множеством меры нуль?
430. Пусть Е — нигде не плотное множество меры нуль на от-
отрезке [0, 1]. Должно ли и его замыкание Е быть множеством меры
нуль?
431. Доказать, что если Е — измеримое множество положи-
положительной меры на прямой, то в нем найдутся точки, расстояние меж-
между которыми иррационально.
432. Доказать, что если Е — измеримое множество положи-
положительной меры |я, расположенное на отрезке [а, 6], то в нем найдется
хотя бы одна пара различных точек, расстояние между которыми
рационально.
433. Доказать, что если Е — неограниченное измеримое мно-
множество положительной меры на прямой, то в нем найдется Хотя бы
одна пара различных точек, расстояние между которыми рацио-
рационально.
434. Каково строение и какова мера множества Е тех точек от-
отрезка [0, 1], которые допускают разложение в десятичную дробь
без использования цифры 7?
435. Каково строение и какова мера множества тех точек от-
отрезка [0, 1], десятичное разложение которых невозможно без
цифры 7?
436. Каково строение и какова мера множества Н всех тех то-
точек прямой, которые допускают разложение в десятичную дробь
без использования цифры 7 после запятой?
437. Каково строение и какова мера множества точек отрезка
[0, 1], в разложении которых в бесконечную десятичную
дробь фигурируют все цифры от 1 до 9?
438. Каково строение и какова мера множества тех точек от-
отрезка [0, 1], которые допускают десятичное разложение без комби-
комбинации стоящих рядом цифр 2, 2, 2?
439. Около каждой точки канторова множества описан интер-
интервал длины 0,1 с центром в этой точке. Чему равна мера объединения
всех этих интервалов?
440. Пусть "]аъ Ьг[, ..., ]аЛ, Ьл[, ... — смежные интервалы нигде
не плотного совершенного множества Е меры 0,6, расположенного
на отрезке [0, 1] и такого, что inf E = 0, sup E = 1. Опишем около
каждой точки а1% как около центра, интервал щ длины l ~~ai ;
4
А*

такие же интервалы vt длины ——~ опишем около каждой точки
4
Ьг Покроет ли множество ([} и.) [} ([) vt) все множество £? Что
i i
можно сказать о мере множества (\}и) И (Uvf)?
i l i
441. Можно ли представить отрезок [0, 1] в виде объединения
двух непересекающихся измеримых множеств А и В так, чтобы
для каждого интервала ]а, Ь[ £ [О, 1] имело место:
т (]а, Ь[ П А) > О и т (]а, 6[ П В) > О?
442. Может ли объединение счетной совокупности нигде не
плотных совершенных множеств на отрезке [a, ft] иметь меру, рав-
равную Ь — а?
443. Может ли объединение счетной совокупности попарно
не пересекающихся нигде не плотных совершенных
множеств на отрезке [а, Ь~\ иметь меру, равную b — а?
444. Существует ли на отрезке [0, 1] несчетное множество меры
нуль, плотное на этом отрезке?
445. Пусть {Еп} — Последовательность измеримых множеств
на отрезке [0, 1], обладающая тем свойством, что для любого е>0
найдется такое ky что mEk > 1 — в. Доказать, что мера объедине-
объединения Е этих множеств равна 1.
44 Д Е
446. Доказать, что если
евклидовом пространстве, то
тЕх + тЕ2 = т
Ег
(Ег
и
и
£2-
Е2)-
- измеримые
f т (Ег П Е<
множества
г)-
447. Доказать, что для любой конечной или счетной совокупно-
совокупности {Et } измеримых множеств в евклидовом пространстве имеет
место неравенство
IimEl^m(\jEl)+ 2 т(^П^у).
448. В замкнутом параллелепипеде / с ребрами единичной дли-
длины заданы п измеримых множеств Аъ А2, ..., ЛЛ, сумма мер которых
больще чем п — 1:
тАг + тА2 + ... + tnAn > п *— 1,
Доказать, что f| At имеет положительную меру.
449. Пусть {Еп} — убывающая последовательность измеримых
множеств в евклидовом пространстве и г — заданное положитель-
ног число. Доказать, что существует убывающая последователь-
последовательность замкнутых множеств {Fn} такая, что для каждого п имеет
место
Fn cz Eni mFn > тЕп — г.
450. Пусть Е — измеримое множество на прямой, k — про-
произвольное действительное число. Обозначим через kE множество
всех точек вида kx, где х пробегает Е. Доказать, что множество kE
измеримо и
m{kE) = \k\ • тЕ.

451. Пусть измеримое множество Е на прямой обладает тем
свойством, что при любом б > 0 множество Е [\ ]—6, б[ имеет
положительную меру. Пусть, кроме того, О (: Е. Доказать,
что существует совершенное множество Q а Е такое, что
m(Q [\ ]—б, б[) > 0 при любом б > 0.
Пусть Е — измеримое множество в Rn и х0 £ Rn.
т(Е {]У(х0, г))
Если hm— существует, то его значение а называется
е-о mV(xOt г)
плотностью множества Е в точке лго. Ясно, что 0 ^ а ^ 1. Если а = 1, то хо
называется точкой плотности для Е, если а = 0, то хо называется точкой раз-
разрежения.
452. Какова плотность круга х2 + у2 ^ 1 в различных точках
плоскости /?2? Каковы его точки плотности и точки разрежения?
453. Какова плотность множества Е = ]—1, 0[|J]0, 1[(J {2}
на прямой? Каковы его точки плотности и точки разрежения?
454. Построить множество на плоскости, имеющее в данной
точке Мо € R2 плотность, равную заданному числу а £ ]0, 1[.
455. Построить множество на прямой, имеющее в данной точке
х0 плотность, равную заданному числу а £ ]0, 1[.
456. Пусть Е — измеримое множество на прямой и пусть точка 0
принадлежит Е и является его точкой плотности. Доказать, что су-
существует совершенное множество F cz £, для которого 0 также яв-
является точкой плотности.
457. Пусть Е — неизмеримое множество на прямой, А — мно-
множество меры нуль на той же прямой. Доказать, что множество
Е {] СА неизмеримо.
458. Пусть Л, В — открытые множества конечной линейной
меры на осях Ох и Оу соответственно. Доказать, что т2 (А X В) .=
= тгА • mJB.
459. Пусть А — множество линейной меры нуль на оси Ох,
В — произвольное множество на оси Оу. Доказать, что множество
А X В имеет плоскую меру нуль.
460. Доказать утверждение задачи 458 для случая, когда А а
а Ох, В cz Оу — произвольные измеримые множества конечной
линейной меры.
461. Пусть A ci Ox, В а Оу линейно измеримы, причем тгА =
= +°°, 0 < тхВ <^ +°о. Доказать, что А X В измеримо в смыс-
смысле плоской меры, причем
т2 (А X В) = +оо.
462. Обозначим через Е множество всех, тех точек квадрата
[0, 1] X [0, 1], у которых обе координаты иррациональны. По-
Построить совершенное множество М cz E положительной плоской
меры.
В задачах 463—469 _под X подразумевается произвольное евклидово про-
пространство, а под т (или т) — мера (или внешняя мера) множества в этом про-
пространстве,
50

463. Доказать, что при добавлении к произвольному множеству
Е а X или при изъятии из него множества Н меры нуль внешняя
мера множества Е не меняется.
464. Доказать, что для любого множества Е а X конечной
внешней меры и любого числа г > О существует такое открытое
множество A zd Еу что тА — г < ТпЕ ^ пгА.
465. Доказать, что для любого множества Е а X существует
такое содержащее его множество В типа G6, что mB = m£.
466. Пусть Е — ограниченное множество в X, / — какой-либо
замкнутый параллелепипед, включающий Е. Доказать, что если
ml = mE + m (I \ Е)у то Е измеримо.
467. Пусть Е с: X. Доказать равносильность следующих ут-
утверждений:
1) Е измеримо.
2) Для каждого е > 0 существует открытое множество G такое,
что G =э Е и m (G \ Е) < е.
3) Для каждого е > 0 существует замкнутое множество F такое,
что F а Е -и m (£ \ F) < 8.
4) Существует множество Л типа G6 такое, что A zz E и
m (Л \ Е) = 0.
5) Существует множество В типа Fa такое, что В а Е и
m (E \ В) = 0.
Иначе говоря, любое из условий B) — E) равносильно изме-
измеримости множества Е.
468. Доказать, что для измеримости множества Е cz X необхо-
необходимо и достаточно выполнение любого из следующих условий:
а) Для каждого 8 > 0 существуют замкнутое множество F
и открытое G такие, что F си Е cz G и m (G \ F) < 8.
6) Существуют множество Л типа G6 и В типа Fo такие, что
ВаЕаАит(А\В)=0.
469. Доказать следующий признак Валле-Пуссена: «Для того
чтобы множество £ cz X конечной внешней меры было измеримо,
необходимо и достаточно, чтобы для каждого 8 > 0 существовало
такое множество Я, составленное из конечного числа открытых
параллелепипедов, что т (£ДЯ) < 8».

ЧАСТЬ ВТОРАЯ
ТЕОРИЯ ФУНКЦИЙ
Глава VIII.
ОБЩАЯ ТЕОРИЯ ОТОБРАЖЕНИЙ
Если каждой точке х множества R поставлена в соответствие некоторая точ-
точка у множества L, то говорят, что задано отображение R в L; это отображение
называется также функцией, отображающей R в L (или определенной в R и
принимающей значения в L). При этом R называется областью определения функ-
функции, a L — ее областью прибытия.
Обозначим через / какую-либо функцию, отображающую R в L. Если эта
функция ставит в соответствие точке х £ R точку у 6 t, то у называется значе-
значением функции f в точке х и обозначается / (х). Пусть A a R- Тогда через / (А)
обозначается множество всех тех точек у 6 L, которые являются значениями
функции / хотя бы для одного х £ А. Множество / (А) называется образом мно-
множества А. В частности, образ всей области определения (т. е. множество / (R) d
d L) называется областью значений или множеством значений функции /.
Пусть В — какое-либо подмножество множества L. Обозначим через f~x (В)
множество тех и только тех точек х £ R, для которых значения функции принад-
принадлежат В. Множество f'1 (В) называется прообразом множества В.
Если область значений функции / совпадает со всем множеством L, то / на-
называется отображением множества R на множество L.
Если прообраз каждого одноточечного множества из области значений функ-
функции / есть одноточечное множество, т. е. если из / (Xi) = f (x2) (хг 6 R, x2 <E R)
следует хг == х2, то / называется взаимно однозначным отображением к на f (R).
Если при этом функция / отображает R на L, т. е. / (R) = L, то / будет взаимно
однозначным отображением множества R на множество L (в этом случае говорят
также, что / осуществляет взаимно однозначное соответствие между множест-
множествами R и L); для такой функции однозначно определяется обратная функция,
ставящая в соответствие каждой точке у £ L ту единственную точку х 6 R> Для
которой / (х) = у. Ясно, что обратная функция взаимно однозначно отображает
L на R.
Часто функцию / обозначают через / (л:), считая л: переменной точкой обла-
области определения R функции /. Если R а Х± X ... X Хп, то функцию / обозна-
обозначают также через / (xlt ..., хп) и считают ее зависящей от п переменных хъ ...,
хп, принимающих значения в соответствующих множествах Х±9 ..., Хп так,
что при этом (*ь ..., хп) 6 R-
Задачи
470. Пусть А — произвольное множество из области определе-
определения функции /. Верно ли равенство /-1 (/ (А)) = Л?
471. Пусть В — произвольное множество из области значений
функции /. Верно ли равенство / (/-1 (В)) = В?
472. Верны ли утверждения
/ (A U В) = / (A) U / (В),
f(A(\B)=f{A)(\f (В)?
52

Если какое-либо из этих утверждений неверно, то привести проти-
противоречащий пример.
473. Доказать, что если / является взаимно однознач-
однозначным отображением множества R на множество / (R), то для любой
последовательности множеств Alf Л2, ..., Aki ... (Ak cz R) справед-
справедливы равенства:
1) f(\]Ak) = у f{Ak\
2)f((]Ak) = hf(Ah).
к к
474. Какие из равенств, рассмотренных в предыдущей задаче,
перестают быть верными, если отображение / не является взаимно
однозначным?
475. Верно ли, что f (R \ A) =f(R)\f (Л), где R — область
определения функции?
476. Пусть А и В — множества из области прибытия функ-
функции /. Верны ли равенства:
Г1 (А П В) =Г»(Л) П Г1 (В),
Г1 (Л и в) =Г*(Л) и Г1 E)?
477. Пусть функция / отображает множество R в множество L
и A cz L. Справедливо ли равенство
ri(L\A) =ГЩ\Г(А)?
478. Пусть / — какая-либо функция и множества Аъ Л2, ...
..., Aki ... являются подмножествами ее области прибытия. Верны
ли равенства
Г1 ([)Ак) = иГ1 (Л,), Г1 (ПД*) = ПГ1 (Л,)?
к к к к
Глава IX.
НЕПРЕРЫВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ В
МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ
Числовой функцией называется функция, принимающая числовые значения^
т. е. имеющая областью значений некоторое множество действительных чисел.
Только такие функции рассматриваются в настоящей главе, где они называются
просто функциями.
Пусть областью определения числовой функции / (х) является подмножест-
подмножество А метрического пространства X, и пусть Е — произвольное множество, рас-
расположенное в X. Дадим определение непрерывности функции f (х) в точке хо
относительно множества Е.
Определение! (Кош и). Функция f (x), определенная на множест-
множестве А, называется непрерывной в точке хо относительно множества Е, если
1) хо е А П Е;
2) для любого е > 0 существует такая окрестность U (хо) точки xq, что для
всех х 6 А П Е П U (хо) имеет место неравенство
Отсюда, в частности, следует, что если хо является изолированной точкой
области определения функции / (х), то эта функция непрерывна в точке лго отно-
относительно любого множества Е, содержащего точку хо.
Из определения 1 следует также, что если хо является изолированной точкой
53

множества Е, то любая функция / (х), определенная в точке л:о; непрерывна в
этой точке относительно Е.
Если функция / (л:) непрерывна в точке хо относительно некоторой ее окрест-
окрестности, то она называется полностью непрерывной в точке xq. В тех случаях, когда
это не будет приводить к неясности, мы будем опускать слово «полностью» и
называть функцию, полностью непрерывную в точке Хо, просто непрерывной в
этой точке.
Ясно, что если функция полностью непрерывна в точке лго, то она непрерыв-
непрерывна в этой точке также относительно любого множества Е, содержащего точку *о.
Примеры. 1) Функция / (х) = х2, определенная всюду на R1, непрерыв-
непрерывна в каждой точке хо 6 R1-
2) Функция Дирихле
f /х\ __ П при х рациональном,
' * * ~~~ \0 при х иррациональном,
определенная всюду на Z?1, непрерывна в точке хо = "К 2 относительно множества
всех иррациональных чисел; однако она не является полностью непрерывной в
этой точке.
3) Функция
5, если х2 + у2 > 1,
непрерывна в точке Мо -—, -— ) относительно замкнутого единичного круга
£ с центром в начале координат; однакр она не является полностью непрерывной
в этой точке. Та же функция полностью непрерывна в любой точке Мг (х1% уг),
лежащей внутри круга £; следовательно, она непрерывна в точке Мг также от-
относительно какого угодно множества, содержащего точку Мг.
Для функций одной переменной (т. е. функций, область определения кото-
которых лежит на прямой R1) можно говорить также об односторонней непрерывно-
непрерывности.
Функция / (я), определенная на числовой прямой или на ее части, называется
непрерывной справа в точке лго, если она непрерывна в этой точке относительно
некоторого промежутка [хо, b\_t где Ь > Хо', эта функция называется непрерывной
слева в точке хо, если она непрерывна в этой точке относительно некоторого про-
промежутка ]а, *о], где а < хо.
Легко видеть, что если функция непрерывна в точке ха справа и слева, то
она полностью непрерывна в этой точке.
Дадим теперь другое определение непрерывности функции, эквивалентное
определению Коши.
Определение 2 (Гейне). Функция f (x), определенная на множе-
множестве А, называется непрерывной в точке хо относительно множества Е, если
1) хо 6 А П Е;
2) для любой последовательности точек {##} из А (] Е, сходящейся к Хо
(т. е. такой, что lim р (х^, Хо) = 0), имеет место равенство
lim / (xk) = / (*о).
Колебание функции на множестве и в точке. Пусть функция / (л:) определена
на множестве Л. Кожбанием о/ функции f (x) на этом множестве называется раз-
л
ность между верхней и нижней гранями этой функции на множестве А:
о/ = sup / (*) — inf / (х).
A xtA XzA
Заметим, что мы не требуем, чтобы функция / (х) была ограничена на множестве
Л. Поэтому sup / (х) может равняться либо конечному числу (если / (х) ограни-
ограничена сверху на множестве Л), либо +оо (если эта функция не ограничена сверху
на Л). Точно так же и inf / (л:) может равняться либо конечному числу, либо
— оо. Следовательно,
0 < со/ < +оо.
54

Если Аг CZ Аъ то sup / (л:) < sup / (х), inf / (х) > inf / (х).
х$Ах х$А2 xiAt х£Аг
Поэтому ®f ^ ©/.
Пусть функция / (х) определена на множестве Л, расположенном в метриче-
метрическом пространстве; пусть Е — какое-нибудь множество, лежащее в том же про-
пространстве, и пусть лго б Л f] Е. Колебанием функции f (х) в точке хо относитель-
относительно множества Е (обозначается (о [f, л:о, £]) называется предел, к которому стре-
стремится колебание этой функции на множестве Е f]V (хо, Ьп) при бл ->■ 0. Этот
предел (конечный или равный + °°) всегда существует и не зависит от выбора
последовательности окрестностей {V (х0, бЛ)} (лишь бы радиусы этих окрестно-
окрестностей стремились к нулю при п -+■ + оо). Итак,
© [Л х0, Е-] = lim о /.
60E[]V(x6)
Если, говоря о колебании функции / (х) в точке хо, мы не указываем, относи-
относительно какого множества Е рассматривается это колебание, то подразумевается,
что речь идет о колебании в точке хо относительно некоторой окрестности этой
точки. В этом случае колебание функции / (х) в точке хо обозначается о [/, хо].
С помощью понятия колебания функции в точке можно дать третье опреде-
определение непрерывности функции, эквявалентное первым двум.
Определение 3 (Бэра). Функция f (х), определенная на множестве
Л, называется непрерывной в точке хо относительно множества Е, если хо 6 Л (] Е
и колебание функции в этой точке относительно множества Е равно нулю:
со [/, хо, Е] = 0.
Точки разрыва. Пусть функция / (х) определена на множестве Е (Е а X);
точкой разрыва этой функции называется всякая точка из Е, в которой колеба-
колебание функции (относительно множества Е) не равно нулю, а также любая пре-
предельная точка ее области определения Е, не входящая в Е.
Пример. Функция sgn x (читается «сигнум икс»), определенная равен-
равенствами sgn х = 1 при х > 0, sgn х — —1 при х < 0, sgn 0=0, разрывна в точ-
точке хо = 0.
Точка лго называется точкой устранимого разрыва, если можно изменить
значение функции только в этой точке (или доопределить функцию в этой точ-
точке, если она в ней не определена) так, чтобы функция стала непрерывной в точ-
точке *о.
Точка хо, являющаяся точкой разрыва функции / (х), называется точкой
разрыва первого рода, если существуют оба односторонних предела при х -* хо\
/(*0 —0)= lim / (*) и / (*0 + 0) = lim /(*),
х-+хо—0 *->*0+0
и они оба конечны. При этом разность / (х0 + 0) — / (х0 — 0) называется скачком
функции f (х) в точке х0. Если функция определена в точке х0, то разности
/ (хо + 0) — / (хо) и f (хо) — / (хо — 0) называются соответственно правым, скач-
скачком и левым скачком функции / (х) в точке хо.
Ясно, что точка устранимого разрыва является частным случаем точки раз-
разрыва первого рода и скачок функции в этой точке равен нулю.
Точка разрыва, не являющаяся точкой разрыва первого рода, называется
точкой разрыва второго рода.
Свойства функций, непрерывных в точке. 1) Если функции ф (х) и ф (х) не-
непрерывны в точке лго относительно множества Е, то сумма и произведение этих
функций непрерывны в этой точке относительно Е. Если, кроме того, ф (хо) ф 0,
ф(ЛГ)
то частное — также непрерывно в этой точке относительно Е.
* (х)
2) Пусть функция ф (л:) непрерывна в точке хо относительно множества Е,
причем ф (хо) = уо. Пусть, кроме того, функция "ф(у), определенная на число-
числовом множестве, непрерывна в точке уо относительно некоторого множества
F a R1. Тогда суперпозиция этих функций, т. е. сложная функция г|? (ф (#)),
непрерывна в точке Хо относительно множества Е fj ф (/*")•
55

3) Если функция / (х) определена на множестве А и непрерыв на в точке хо
относительно Е, то она ограничена в некоторой окрестности этой точки (точнее
говоря, на пересечении множества А (] Ё с некоторой окрестностью точки хо).
4) Если функция / (л:) определена на множестве А и непрерывна в точке хо
относительно множества Е, причем / (хо) > 0, то существует такая окрестность
V (хо) точки хо, что / (х) > 0 для всех х £ А (] Е [\ V (хо); аналогичное утверж-
утверждение справедливо и тогда, когда f (хо) < 0. Другими словами: «Непрерывная
в точке хо функция сохраняет свой знак в некоторой окрестности этой точки».
5) Если Ei а Е и в некоторой точке лго 6 /^функция / (х) непрерывна отно-
относительно Е, то в этой же точке она непрерывна и относительно Е± (обратное ут-
утверждение неверно: функция может оказаться непрерывной в точке хо относи-
относительно Eit но не быть непрерывной в этой точке относительно множества Е и> Ег).
Свойства функций, непрерывных на компактном множестве.
Определение. Пусть функция f (x) определена на множестве Е. Если
она непрерывна во всех точках множества Е относительно этого множества, то
она называется непрерывной на Е.
Мы рассмотрим некоторые свойства функций, непрерывных на компакте.
Теорема 1, Если функция f (x) непрерывна на компактном множестве Е,
то множество f (E) также компактно. Другими словами: «Непрерывный образ
компакта есть компакт» (см. задачу 505).
Непосредственными следствиями этой теоремы являются теоремы 2 и 3 (за-
(задачи 514, 515).
Теорема 2. Если функция f (x) непрерывна на компактном множестве Е,
то она ограничена на нем (т. е. существует такое число С > 0, что | / (х) \ < С для
всех х £ Е).
Теорема 3. Если функция f (x) непрерывна на компактном множестве Е,
то она достигает своей верхней и своей нижней грани на этом множестве, т. е.
существуют такие точки хг £ Е, х2 6 Е, что
Для того чтобы сформулировать теорему 4, дадим определение равномерно
непрерывной функции.
Функция / (л:), определенная на множестве £, называется равномерно непре-
непрерывной на Е, если для любого 8 > 0 существует б > 0 такое, что для всяких
х' 6 Е vt x" £ E, таких, что р (х'\ х") < 6, выполняется неравенство
|/<•)-/(*") К «.
Легко видеть, что если / (х) равномерно непрерывна на £, то она непрерывна
на Е', обратное утверждение, вообще говоря, неверно; однако если Е — компакт-
компактное множество, то справедлива и обратная теорема (задача 540):
Теорема 4. Если функция непрерывна на компактном множестве Е, то
она равномерно непрерывна на нем.
Свойства функций» непрерывных на связном множестве.
Теорема 5. Если функция f (x) непрерывна на связном множестве Е,
то множество f (E) также связно. Другими словами: «Непрерывный образ связ-
связного множества есть связное множество» (см. задачу 535).
Непосредственными следствиями этой теоремы являются теоремы 6 и 7 (за-
(задачи 536 и 537).
Теорема 6. Если функция f (x) непрерывна на связном множестве Е,
причем f (а) = A, f (Ь) = В, где а £ Е, b £ Е, то для любого числа С, заключен-
заключенного между А и В, существует точка с £ Е такая, что f (с) = С.
В частности, если на Е найдутся две точки, в которых / (х) принимает зна-
значения разных знаков, то существует точка с £ Е такая, что / (с) == 0.
Теорема 7. Если функция f (x) непрерывна на связном компактном мно-
множестве Еу причем inf f (х) = A, sup / (х) — В, то f (Е) — [Л, Б] (или, jb част-
частое я xfE
ности, одноточечное множество, если А = В).
56

Характеристическая функция. Пусть Е — произвольное множество в мет-
метрическом пространстве X. Характеристической функцией множества Е назы-
называется функция %Е (х), определенная на X и задаваемая следующими равенст-
равенствами:
ХЕ (х) = 1 при х f £, хЕ (х) = 0 при х £ £.
Так, например, функция Дирихле % (дс), равная 1 для- всех рациональных
чисел и 0 для всех иррациональных чисел, является характеристической функ-
функцией множества рациональных чисел на прямой.
Задачи
479. Пусть функция / (х) определена в метрическом простран-
пространстве X. Доказать, что множество Е всех ее точек разрыва есть мно-
множество типа Fa в X.
480. Пусть функция / (х) определена в метрическом простран-
пространстве X. Доказать, что множество всех ее точек непрерывности есть
множество типа Ge в X.
481. Пусть Е — произвольное счетное множество точек х от-
отрезка [а, 6]. Построить функцию, разрывную во всех точках мно-
множества Е и непрерывную в остальных точках отрезка [a, ft].
482. Пусть ф (л:) —функция, заданная всюду на числовой пря-
прямой, ограниченная на ней и непрерывная во всех точках, кроме
точки х = 0; пусть 2аЛ — сходящийся числовой ряд с положи-
п
тельными членами, а {хъ хъ -•} — счетное всюду плотное множе-
множество точек на прямой. Найти множество точек разрыва и множество
точек непрерывности функции
483. Доказать, что функция, определенная на всей прямой,
не может быть непрерывной на счетном всюду плотном множестве Е
и разрывной в остальных точках прямой.
484. Построить функцию, определенную во всех точках число-
числовой прямой, разрывную всюду, кроме точек х = 1 и х =—1,
и непрерывную в этих точках.
485. Построить функцию, разрывную во всех точках числовой
прямой, кроме точек х =0, ±1, ±2, ...
486. Каковы точки разрыва у функции, имеющей значение 1
в точках канторова множества и значение 2 во всех остальных точ-
точках числовой прямой. Будут ли эти точки разрыва первого или вто-
второго рода?
487. Построить функцию, определенную на отрезке [0,-3],
разрывную в каждой точке, изображаемой конечной десятичной
дробью, и непрерывную в точках, которые не могут быть изобра-
изображены с помощью конечной десятичной дроби.
488. Найти точки разрыва и точки непрерывности функции
f (х), определенной на отрезке [0, 1] условиями:
f (х) = 0 в точках канторова множества,
/ (х) = 1 в серединах его смежных интервалов,
57

f (x) линейна на участках \ani пп и Гя п, Ьп , где
]аЛ, Ьл[ — га-й смежный интервал канторова множества (п = 1, 2, ...).
489. Исследовать на непрерывность функцию, заданную на
отрезке [0, 1] следующими условиями:
f (x) =0в точках канторова множества,
f (х) =спв середине п-ro смежного интервала ]аЛ, ЬЛ[,
f(x) линейна на участках \ап% fl» + 4, \ал±_^^ Ьп\
(п =1, 2, 3, ..,). При этом предполагается, что смежные интер-
интервалы канторова множества перенумерованы в порядке убывания их
длин:
Рассмотреть случаи: а) последовательность {сЛ} такова, что
lim сп = 0; б) lim сЛ существует и отличен от нуля.
490. Найти все точки разрыва и точки непрерывности функции
f /гч __/ сп во всех интервалах /г-го ранга канторова множества D;
' w ~@ €D
(р
Рассмотреть случаи: 1) сп ->• 0 при я ->• +оо; 2) сп->~ q (q Ф
Ф 0) при п ->• +оо; 3) {сп} не имеет предела.
491. Построить функцию, непрерывную во всех иррациональных
точках отрезка [0, 1] и разрывную во всех его рациональных точках.
492. Существует ли функция, непрерывная во всех рациональ-
рациональных точках отрезка [0, 1] и разрывная во всех его иррациональных
точках?
493. Построить функцию, непрерывную во всех точках канторова
множества и разрывную во всех точках его смежных интервалов.
494. Построить функцию, непрерывную во всех точках смежных
интервалов канторова множества и разрывную всюду на канторо-
вом множестве.
495. Исследовать на непрерывность функцию, равную хг в
рациональных точках числовой прямой и —х2 в иррациональных.
496. Функция / (х) определена на отрезке [0, 1] следующим
образом: она равна нулю во всех точках некоторого нигде не плот-
плотного совершенного множества; на каждом смежном интервале этого
множества / (х) положительная и имеет своим графиком полуокруж-
полуокружность, диаметром которой служит этот смежный интервал. В каких
точках эта функция непрерывна?
497. Доказать, что для любой функции, определенной на мно-
жертве А, имеет место равенство:
<о/= sup |/(i)
58

498. Доказать, что для любых двух функций / (х) и g (x), опре-
определенных на множестве Л, справедливо неравенство
°> if + ё) < ©/ + cog;
А А А
если же хотя бы одно из чисел со/, cog конечно, то, кроме того, име-
А А
ет место неравенство
/
А А А
499. Пусть {fk} — последовательность функций, определенных
4-оо
в метрическом пространстве X, такая, что ряд ^fk (x) равномерно
о
сходится на X. Доказать, что для любого множества Е а X и
любой точки х0 (: X имеет место неравенство
[-f-"oo "I
*-t *• x<" J
0>
500. Доказать, что если функция f (х) непрерывна в точке х0
то и функция |/ (х)\ непрерывна в этой точке.
501. Привести пример функции / (х) такой, что / (х) разрывна
во всех точках отрезка [0, 1], а |/ (х)| непрерывна на [0, 1].
502. Функция / (х) определена на числовой прямой следующим
образом:
f (х) = 0 в иррациональных точках,
/ (x) =1—L в рациональных точках, представимых в виде ре-
ц
сократимой дроби ~ Ф 0 (где q > 0),
Я
f (x) =1 при х = 0.
Найти все ее точки разрыва и точки непрерывности.
503. Построить функцию / (х, у), разрывную во всех точках
квадрата [0, 1] X [0, 1], но непрерывную как функция от х при
любом постоянном у.
504. Функция двух переменных / (х, у) определена на квадра-
квадрате [0, 1] X [0, 1] следующим образом: в точках, где обе координаты
иррациональны или обе рациональны, / (х, у) = 0; кроме того,
/ (х, у) =^ 0 там, где л: =0 или у = 0; в точках, где абсцисса равна
рациональному числу — > 0 (— — несократимая дробь, q > 0),
я ч i
а ордината иррациональна, / (х, у) = —; в точках, где абсцисса ир-
иррациональна, а ордината записывается в виде несократимой дроби
— > 0 (q > 0), / (ху у) = . В каких точках эта функция раз-
q •?
рывна и где она непрерывна?
505. Доказать, что непрерывным образом компактного множе-
множества является компактное множество.
59

Примечание. Непрерывным образом множества Е называется множе-
множество / (£"), где f — какая-либо функция, определенная и непрерывная
нз Е.
506. Показать на примере, что непрерывный образ неограничен-
неограниченного замкнутого множества на числовой прямой не обязательно
является замкнутым множеством.
507. Показать на примере, что непрерывный образ открытого
множества не обязан быть открытым множеством.
508. Пусть / (х) — непрерывная функция, определенная » мет-
метрическом пространстве X, a F — произвольное замкнутое множе-
множество на числовой прямой. Доказать, что множество/ (F) замкнуто
в X.
509. Пусть / (л:) — непрерывная функция, определенная в мет-
метрическом пространстве X, a G — произвольное открытое множество
на числовой прямой. Доказать, что множество Z" (G) открыто в X.
510. Может ли прообраз компактного множества при непрерыв-
непрерывном отображении быть неограниченным?
511. Доказать, что функция / (х), определенная на всей числовой
прямой, непрерывна тогда и только тогда, когда прообразы всех
интервалов ]а, Ь\_ являются открытыми множествами.
512. Доказать, что если функция / (х) определена на всей число-
числовой прямой и прообразы множеств ]— оо, а] и [а, +°°[ замкнуты при
любом действительном а, то функция / (л:) непрерывна во всех точ-
точках числовой прямой.
513. Пусть функция / (х), определенная на всей числовой пря-
прямой, принимает только целые значения. Доказать, что множество
точек непрерывности такой функции является открытым множест-
множеством, а множество точек разрыва замкнуто.
514. Доказать, что любая непрерывная на компакте Е функция
ограничена на Е.
515. Пусть / (х) — числовая функция, непрерывная на ком-
компакте Е. Доказать, что существует точка а € Е такая, что / (а) =
= inf f (х), и точ-ка Ь € Е такая, что / (b) = sup / (х).
xtE х$Е
516. Привести пример числовой функции, непрерывной на замк-
замкнутом ограниченном множестве Е некоторого полного метрического
пространства и не ограниченной на Е.
517. Привести пример числовой функции f (х), непрерывной на
замкнутом множестве Е некоторого полного метрического про-
пространства, такой, что / (Е) ограничено, но в Е не существует такого
элемента а, что / (а) = inf / (х).
х$Е
518. Доказать, что р (л:, у0) (где у0—фиксированная точка
метрического пространства X) есть непрерывная функция от х.
519. Доказать, что d (х, Е) (где Е — заданное непустое множе-
множество в метрическом пространстве X) есть непрерывная функция
от х.
520. Пусть Е — компактное множество в пространстве X и
х0 € X. Доказать, что существует точка у0 € £ такая, чтор (хо,уо) —
60

= d (x0, E) (т. е. расстояние от х0 до компакта Е достигается в
некоторой точке этого компакта).
521. Доказать, что если множество Е в метрическом простран-
пространстве X обладает свойством Н (см. задачу 333) и х0 б X, то существу-
существует точка у0 € Е такая, что р (*0, у0) == d (х0У Е).
522. Доказать, что для любых двух множеств £, F в метриче-
метрическом пространстве X имеет место равенство
d (£, F) = inf d (у, Е).
523. Пусть Е и F — множества в метрическом пространстве X,
причем Е обладает свойством Я, a F компактно. Доказать, что су-
существуют точки х0 € £, у0 € F такие, что
Р (*о> Уо) = d (£, F)
(расстояние между множествами Е и F достигается в точках этих
множеств).
524. Доказать, что расстояние между двумя компактными мно-
множествами метрического пространства достигается в точках этих
множеств.
525. Доказать, что в евклидовом пространстве Rn расстояние
между замкнутым множеством Е и замкнутым ограниченным множе-
множеством F достигается в точках этих множеств.
526. Показать на примере, что расстояние между двумя замк-
замкнутыми непересекающимися множествами в евклидовом простран-
пространстве может равняться нулю (если эти множества не ограничены).
527. Привести пример замкнутых неограниченных множеств А нВ
на плоскости таких, что d (Л, В) =1 и что не существует точек
а (: Л, b € В таких, что р (а, Ь) = 1.
528. Привести пример двух замкнутых ограниченных множеств
в некотором полном метрическом пространстве, расстояние между
которыми не достигается в точках этих множеств.
529. Пусть (X, р) — метрическое пространство, (X X X, R) —
множество пар (х> у) (х б X, у б X), метризованное по формуле
R ((*i. Ух)> (*» У2» = V(p(*i> *2)J + (Р (Уь У2)J-
Доказать, что р (х, у) является непрерывной функцией на
(X X X, R).
530. Пусть Е — непустой компакт в метрическом пространстве
X. Доказать, что в нем найдутся точки х0 € £, у0 б Е такие, что
Р (*о> Уо) = diam E.
531. Пусть хг и х2—две точки метрического пространства X,
хг Ф х2. Построить непрерывную в X функцию / (х) такую, что:
1) / (х) 555= 0 в некоторой окрестности точки лу, 2) / (х) = 1 в неко-
некоторой окрестности точки х2; 3) 0 <[ / (х) ^ 1 для всех х 6 X.
532. На прямой даны п попарно не пересекающихся замкнутых
множеств Е19 Е2^ ..., Еп\ построить функцию f (х), непрерывную
всюду на прямой и такую, что / (х) = pk при х € Ek (k = 1, 2, ...
..., п), где Pi, p2, ..., рп — заданные числа.
61

533. На прямой дана счетная совокупность попарно не пере-
пересекающихся замкнутых множеств Ek(k=\, 2, ...), причем ни одно
из этих множеств не содержит точек прикосновения объединения
всех остальных множеств. Построить функцию / (х) непрерывную
всюду на прямой и такую, что для любого натурального числа k
имеет место / (х) = pk при х (: Ek, где pk — заданные числа, такие,
что ряд 2р& абсолютно сходится.
k
k
534. На прямой дана счетная совокупнрсть попарно не пере-
пересекающихся замкнутых множеств Ek (k = 1, 2, ...), причем Е1
содержит хотя бы одну точку прикосновения объединения остальных
множеств. Пусть ^pk — абсолютно сходящийся ряд, причем рхф
k
Ф 0. Доказать, что не существует функции / (я), непрерывной на
всей прямой и такой, что/ (х) — pk при х £ Ek для любого натураль-
натурального числа k.
535. Доказать, что непрерывный образ связного множества есть
связное множество.
536. Доказать теорему Больцано — Коши: «Если числовая функ-
функция f (х) непрерывна на связном множестве Е, причем f (а) = Л,
f (Ь) = В, где а (: Е, Ь (: Е, то для любого числа С, лежащего меж-
между числами Л и В, найдется точка с € Е такая, что / (с) = С».
537. Пусть / (х) — числовая функция, непрерывная на связ-
связном компактном непустом множестве Е. Доказать, что / (Е) —
либо отрезок, либо одноточечное множество.
538. Говорят, что функция / (х), определенная на [а, 6], обладает
Свойством Дарбу на отрезке [a, ft], если для любых хг £ [а, 6],
х2 € [а, Ь] (хг < х2) и для любого числа С, лежащего между / (л^)
и / (я2), найдется точка 1 € (хъ х2) такая, что / (|) = С. Является
ли выполнение свойства Дарбу достаточным условием для непре-
непрерывности функции / (л:) на [а, &]?
539. Являются ли равномерно непрерывными на указанных мно-
множествах следующие функции, непрерывные на этих множествах:
1) sin— на интервале ]0, 1[; 2) х sin — на луче ]0, +оо[; 3) Зх
X X
на всей числовой прямой; 4) х2 на всей числовой прямой; 5) s-^
х
на луче ]0, +оо[?
540. Доказать, что если функция / (х) непрерывна на компакт-
компактном множестве Е метрического пространства, то она равномерно
непрерывна на Е.
541. Доказать, что если функция равномерно непрерывна на
относительно компактном множестве Е метрического пространства,
то она ограничена нд» Е.
542. Пусть f (х) и g (x) — функции, равномерно непрерывные
на Е. Является ли их сумма равномерно непрерывной на Е функ-
функцией?
543. Пусть f (х) и g (x) — функции, равномерно непрерывные
62

на множестве Е. Всегда ли их произведение является равномерно
непрерывной функцией на £?
544. Является ли произведение двух функций f (х) и g (х),
равномерно непрерывных на относительно компактном множестве Е
метрического пространства, равномерно непрерывной функцией
на £?
545. Доказать, что если функция / (х) определена и непрерывна
на луче [0, +оо[и lim / (х) существует, то она равномерно непрерыв-
ЛГ-*+оо
на на этом луче.
546. Верно ли, что функция / (х), непрерывная и ограниченная-
на луче [0, +°°[, равномерно непрерывна на этом луче?
547. Является ли функция / (х)у построенная в задаче 488,
равномерно непрерывной на множестве Е, где Е — дополнение к
канторову множеству до всего отрезка [0, 1]?
548. Зададим / (х) на [0, 1] следующим образом: f (х) =0 всюду
на канторовом множестве D\ f (х) = — на смежном интервале пер-
первого ранга, т. е. на I—, — ; / (х) = — на смежных интервалах вто-
J 3 3 I 22
рого ранга, т. е. на —, — и —, — ; вообще f (х) =— на всех
J9 9|_J9 9l
смежных интервалах й-го ранга. Найти все точки разрыва функ-
функции / (*).
Является ли эта функция равномерно непрерывной на допол-
дополнении CD к канторову множеству до всего отрезка [0, 1]?
549. Доказать, что если функция / (х) равномерно непрерывна
на множестве Е метрического пространства, то она может быть
продолжена с сохранением непрерывности на его замыкание Е
и притом единственным образом (т. е. существует одна и только одна
непрерывная функция ф (х), определенная на £ и такая, что ср (х) =
г= / (х) для всех х € Е). Показать, что ф (х) равномерно непрерыв-
непрерывна на Е.
550. Доказать, что если функция / (х) равномерно непрерывна
на множестве Е числовой прямой, то она может быть продолжена на
всю прямую с сохранением непрерывности.
551. Привести пример функции / (jc), непрерывной и ограничен-
ограниченной на ограниченном множестве Е числовой прямой, которую нель-
нельзя продолжить на всю числовую прямую с сохранением непрерыв-
непрерывности.
552. Доказать, что если функция / (х) непрерывна, но не рав-
равномерно непрерывна на ограниченном множестве Е числовой пря-
прямой, tq она не может быть продолжена на всю числовую прямую с
сохранением непрерывности.
553. Пусть / (х) — функция, равномерно непрерывная на всей
числовой прямой. Доказать, что существуют два неотрицатель-
неотрицательных числа А и В такие, что |/ (х)\ < А • \х\ + В для всех х € R*
554. Привести пример числовой функции / (х)% непрерывной на
63

замкнутом ограниченном множестве Е некоторого полного метриче-
метрического пространства, но не равномерно непрерывной на Е.
1
555. Доказать, что функция / (х) = [х (t)dt, определенная для
всех х (: С [0, 1], равномерно непрерывна на С [О, 1].
556. Показать на примере, что функция, равномерно непрерыв-
непрерывная на ограниченном множестве Е некоторого метрического про-
пространства, может оказаться неограниченной на Е.
557. Пусть Е — произвольно заданное множество типа FG на
числовой прямой Z?1. Построить функцию/ (я), определенную всюду
на Л1, разрывную во всех точках множества Е и непрерывную в
остальных точках.
558. Пусть %Е (х) — характеристическая функция множества Е.
Доказать, что для любых множеств £, Еъ Е2 имеют место равен-
равенства:
X£tU£2 (*) = %Bl (*) + Х£, (х) — %Ei (x) - %Ei (*),
ХС£ (*)=!— %Е (*)•
559. Пусть М =Ег f] ... П Еп9 N = Ег[) ... [) Еп. Выразить
tM (х)и х^ W чеРез х^ W» -э х£/г W-
560. Доказать, что характеристическая функция любого мно-
множества Е разрывна в граничных точках этого множества и непре-
непрерывна во всех остальных точках пространства.
561. Доказать, что если ф (х) и г|) (х) непрерывны на £, то функ-
функции F (х) = max {ф (х), i|) (x)}t G (х) = min {ф (х), г|) (х)} также
непрерывны на Е.
562. Доказать, что если f (х) — непрерывная функция на Е,
то для произвольно заданных чисел a, b (а < Ь) функция
(f(x)y если а</(*)<Ь,
U (х)Уа = а, если / (х) < а,
{ bt если f (х) > b
также непрерывна на Е.
563. Пусть функция / (х) определена всюду на числовой прямой
J?1. Доказать, что для того чтобы f (х) была непрерывна на /J1,
необходимо и достаточно, чтобы при всяком а > 0 определенная в
предыдущей задаче функция [/ (яI_2 была непрерывна на /J1.
564. Построить пример функции / (х), определенной на [0, 1],
у которой как множество точек непрерывности, так и множество
точек разрыва всюду плотны на [0, 1] и имеют мощность контину-
континуума в любом интервале ]а, |3[ cz [0, 1].
565. Зададим функцию / (я, у) на квадрате [0, 1] X [0, 1] сле-
следующим образом:
f (ху у) = 0 в точках множества Л, где А — «ковер Сер пи не кого»
(см. задачу 244);
64

/ (я, у) = 1 в центрах всех выбрасываемых квадратов;
/ (л:, у) линейна в каждом из четырех треугольников, на которые
делится диагоналями всякий выбрасываемый квадрат.
Является ли функция / (х, у) непрерывной на квадрате [0, 1] X
X [0, 1]? Является ли она непрерывной на множестве Е == {[0, 1] X
х [0> Ш \ А^ Является ли она равномерно непрерывной на £?
566. Зададим функцию / (х, у) на квадрате [0, 1] X [0, 1] так:
f (ху у) = 0 в точках множества Л, где Л — «ковер Серпинского»;
/ (х9 у) = — в центрах всех квадратов, выбрасываемых на п-м
п
шаге;
/ (х, у) линейна в каждом из четырех треугольников, на которые де-
делится всякий выбрасываемый квадрат своими диагоналями.
Является ли функция / (х, у) непрерывной на квадрате [0, 1] X
X [0, 1]? На множестве Е == {[0, 1] х [0, 1]} \ Л? Является ли
она равномерно непрерывной на квадрате? На множестве Е?
Oyv
567. Функция —— непрерывна на открытом множестве 0 <
х2+ у2
< х + у2 < 4 (открытый круг с выколотым центром); является ли
эта функция равномерно непрерывной на указанном множестве?
Является ли она равномерно непрерывной в открытом кольце
1 < хг + у2 < 4?
568. Построить функцию / (х)г определенную на всей прямой,
непрерывную в некоторой точке х0 относительно канторова множе-
множества D, но не являющуюся полностью непрерывной в этой точке.
569. Верно ли утверждение: «Если / (х) непрерывна в точке
х0 относительно любого счетного множества, содержащего точку х0,
то она полностью непрерывна в этой точке»?
570. Пусть функция двух переменных / (х, у) определена в не-
некоторой окрестности точки Мо (х0У у0). Верно ли утверждение: «Для
того чтобы функция / (х, у) была полностью непрерывна в точке Мо,
необходимо и достаточно, чтобы она была непрерывна по любому
лучу, исходящему из точки Мо»?
571. Пусть функция / (х, у, г) определена во всем трехмерном
пространстве R3 и непрерывна в точке Мо б /Г относительно лю-
любой плоскости, проходящей через эту точку. Можно ли утверждать,
что эта функция полностью непрерывна в точке Мо?
572. Пусть функция / (я, у) определена всюду на плоскости и
непрерывна в точке @, 0) относительно любой архимедовой спирали
р = а (ф — а) (при любых значениях постоянных a > 0 и а). Мож-
Можно ли утверждать, что эта функция полностью непрерывна в точ-
точке @, 0)?
Глава X.
НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ
Пусть / — отображение множества А метрического пространства X в метри-
метрическое пространство Y, так что A cz X есть область определения отображения /,
а / (A) cz Y — его область значений (при этом метрическое пространство X
65

называют областью отправления, а метрическое пространство Y—областью при-
прибытия отображения /). Частный случай такого отображения — когда простран-
пространством Y является числовая прямая — был рассмотрен в предыдущей главе. Рас-
Распространим теперь данные там определения на случай, когда Y — произвольное
метрическое пространство.
Отображение / множества А а X в пространство Y мы будем называть не-
непрерывным в точке хо 6 X относительно множества Е cz X, если хо £ A f| E и
для любого 8 > 0 существует окрестность V (хо) такая, что для всех х 6 А (\ Е [\
р| V (хо) имеет место неравенство р (/ (#), / (хо)) < е (определение Коши).
Это определение равносильно следующему: отображение / множества А а X
в пространство Y называется непрерывным в точке *о£ X относительно множества
Е d X, если хо £ А {] Е и для любой последовательности точек {хп} из Л f) Et
сходящейся к хо, имеет место lim / (хп) — f (хо) (определение Гейне).
Если отображение непрерывно во всех точках множества Е относительно Е,
то оно называется непрерывным на Е.
Теорема 1. Если отображение f непрерывно на компактном множестве
Е cz X, то f (E) также есть компактное множество (коротко: «Непрерывный
образ компакта есть компакт», см. задачу 575).
Теорема 2. Если отображение f непрерывно на связном множестве
Е а X, то f (E) также есть связное множество (коротко: «Непрерывный образ
связного множества есть связное множество», см. задачу 579).
Отображение f, определенное на Е cz X, называется равномерно непрерывным
на Е, если для любого числа в > 0 существует б > 0 такое, что для любых
х' £ Е, х" 6 Е, таких, что р (*', х") < б, имеет место р (/ (*'), / (*")) < е.
Теорема 3. Если отображение f равномерно непрерывно на Е, то оно
непрерывно на Е.
Теорема 4. Если отображение f непрерывно на компактном множестве
Е, то оно равномерно непрерывно на Е.
Сжимающее отображение. Отображение / метрического пространства X в
метрическое пространство Y называется сжимающим (или сжатым), если суще-
существует такое число /С, 0 < /С < 1, что для любых х' 6 X, х" 6 X имеет место
Р W, f(x"))<K9(x',x").
Ясно, что сжимающее отображение непрерывно (и даже равномерно непре-
непрерывно) на X.
Теорема 5 (Банаха). Если отображение f полного метрического про-
пространства X в себя является сжимающим, то существует, и притом единствен-
единственная, точка #о 6 X такая, что xq = / (хо) (такая точка называется неподвижной
точкой отображения f).
Гомеоморфизм. Если отображение / множества Е cz X на множество G cz Y
является взаимно однозначным и непрерывным и если обратное отображение /-1
множества G на множество Е также непрерывно, то / называется гомеоморфным
отображением или гомеоморфизмом.
Если для множеств Е и G существует гомеоморфизм, отображающий Е на G,
то говорят, что множества Е и G гомеоморфны.
Всякое свойство множества Е, сохраняющееся при гомеоморфизме, назы-
называется топологическим свойством. Уточним это: пусть А — класс всех множеств,
обладающих некоторым свойством; это свойство называется топологическим,
если из того, что Е £ А, / — гомеоморфизм, заданный на Е, следует, что
/ (Е) е а.
Отображения евклидовых пространств. Важным частным случаем отображе-
отображения является отображение, у которого областью отправления и областью при-
прибытия являются евклидовы пространства.
Непрерывное отображение / множества Е cz Rm в евклидово пространство
Rn может быть задано с помощью п непрерывных на Е числовых функций от т
переменных:
Уг = Ф1 (*г. •••> хт), .,., уп = фл (*ь ..., хт),
где Xi, ..., хт — числовые переменные (координаты точки х), а Ух,..*%Уп —
координаты точки у = / (#).
66

Кривая Жордана. Непрерывное отображение отрезка Е числовой оси R1
в я-мерное евклидово пространство Rn называется я-мерной кривой Жордана или
жордановой кривой (в частности,- при п = 2 — плоской кривой Жордана, при
п = 3 — пространственной).
Образ отрезка Е при этом отображении называется носителем этой жорда-
жордановой кривой. Носитель жордановой кривой — всегда связное множество. Иног-
Иногда — в тех случаях, когда это не будет вызывать недоразумения, — мы будем
называть жордановой кривой не только непрерывное отображение отрезка, но
и образ отрезка при этом отображении.
Ясно, что жорданова кривая может быть задана непрерывными числовыми
функциями одной переменной х1 = фх (/), ..., хп = цп (t), где t £ Е (Е — отре-
отрезок на оси Of).
Важным примером жордановой кривой является кривая Пеано, носителем
которой является замкнутый квадрат на плоскости. Первый пример такого не-
непрерывного отображения был приведен итальянским математиком Пеано в 1890 г.
(см. ниже, задачу 594).
Проектирование. Рассмотрим еще один способ непрерывного отображения —
проектирование множества, расположенного на плоскости, на какую-либо ось.
Проекцией точки М cz Оху на ось Ох называется пересечение с осью Ох пря-
прямой линии, проходящей через точку М под заданным углом а к оси Ох.
Проекцией множества Е а Оху на ось Ох называется множество проекций
всех точек множества Е на ось Ох; при этом проектирование всех точек множест-
множества Е проводится под одним и тем же углом а к оси Ох.
Проекция множества, проведенная под углом 90° к оси, называется ортого-
ортогональной (или прямоугольной) проекцией.
Проекция множества, проведенная под углом, отличным от прямого, назы-
называется косоугольной проекцией.
Арифметическая сумма множеств. Для решения некоторых задач нам пона-
понадобится понятие арифметической суммы множеств.
Арифметической суммой двух множеств Е и F, расположенных на числовой
прямой, называется множество всевозможных сумм вида х + у, где х 6 Е, у 6 F.
Арифметическая сумма множеств Е и F обозначается Е ^ F.
Так, например, арифметической суммой отрезка [4,2] и интервала ]4, 6[
является интервал ]5, 8[.
Задачи
573. Доказать, что если / — непрерывное отображение множе-
множества Е метрического пространства X в метрическое пространство Y
и Е1 cz Е плотно в £, то / (Ех) плотно в f (E).
574. Доказать, что множество точек In (г2 + 1) числовой оси,
где г пробегает все рациональные числа, плотно на луче [0, +°°[.
575. Доказать, что непрерывный образ компакта есть компакт.
576. Пусть / — отображение метрического пространства X в
метрическое пространство Y. Доказать, что для непрерывности это-
этого отображения необходимо и достаточно, чтобы прообразом лю-
любого замкнутого множества пространства Y являлось замкнутое
множество пространства X.
577. Пусть / — отображение пространства X в пространство Y.
Доказать, что для непрерывности этого отображения необходимо
и достаточно, чтобы прообразы всех открытых множеств простран-
пространства Y были открытыми множествами пространства X.
578. Доказать, что если при отображении / пространства X в
пространство Y прообразы всех открытых шаров пространства Y
являются открытыми множествами в X, то отображение / непре-
непрерывно.
67

579. Доказать, что непрерывный образ связного множества есть
связное множество.
580. Доказать, что любое линейно сзязное множество Е связно.
Примечание. Множество Е в евклидовом пространстве называется
линейно связным, если для любых двух точек xt £ Е, х2 6 Е существует жорда-
нова кривая, носитель которой включается в Е и содержит точки xlt x2-
581. Привести пример компактного множества, являющегося
связным, но не линейно связным.
582. Доказать, что если открытое множество G евклидова про-
cfpancTBa связно, то оно и линейно связно.
583Ч Пусть / — взаимно однозначное непрерывное отображение
множества Е метрического пространства X на множество Ег метри-
метрического пространства У. Обязано ли обратное отображение Ег на
Е быть непрерывным? Если да — доказать, если нет — привести
противоречащий пример.
584. Пусть / — взаимно однозначное непрерывное отображение
компактного множества Е на множество Ег. Доказать, что обратное
отображение Ег на Е также непрерывно (т. е. что / является гомео-
гомеоморфизмом).
585. Пусть / — взаимно однозначное непрерывное отображение
множества Е на Ег. Доказать, что если Е не имеет изолированных
точек, то Ег также не имеет изолированных точек. Остается ли в
силе это утверждение, если / — непрерывное, йо не взаимно одно-
однозначное отображение?
586. Верно ли утверждение: «Если / — непрерывное отображение
множества Е на Ег и если Ег не имеет изолированных точек, то Е
также не имеет изолированных точек»? Будет ли верно аналогичное
утверждение, если / — взаимно однозначное непрерывное отобра-
отображение Е »а Ег?
587. Пусть / — взаимно однозначное непрерывное отображение
компактного множества Е на Ег. Доказать, что если Ег не имеет
изолированных точек, то и Е не имеет их.
588. Доказать, что компактность и связность являются тополо-
топологическими свойствами.
589. Доказать, что отсутствие изолированных точек у множе-
множества является топологическим свойством.
590. Доказать, что свойство множества быть полным простран-
пространством не является топологическим свойством.
591. Доказать, что если некоторое свойство является топологи-
топологическим, то его отрицание также является топологическим свойством.
592. Доказать, что не существует взаимно однозначного непре-
непрерывного отображения отрезка [0, 4] на замкнутый квадрат [0, 1] X
X [0, 1] (т. е. чтоютрезок и квадрат не гомеоморфны).
593. Пусть Sm —m-мерная единичная сфера в т+ 1-мерном
евклидовом пространстве /?m+1, т. е. множество всех точек
+2
(xlt..., xm+1)czRm+i9 для которых 2*1 = 1, и а — какая-либо точка
этой сферы. Доказать, что Sm \ {а} гомеоморфно Rm.
68

2
1
3
4
6
5
4
1
7
8
3
2
W
9
14
15
If
12
13
16
6)
22
21
20
17
16
15
2
J
23
24
19
16
#.
/4
J
4
26
25
SO
31
12
9
в
5
27
26
29
32
11
10
7
6
38
37
36
33
54
55
5&
59
39
40
35
54
53
56
57
60
42
41
46
47
52
51
62
61
43
44
45
48
49
50
63
64
2 3 4567 в 9Ю111213Ц151В
Рис. 2
594. Пусть / (x) — непрерывное отображение отрезка [0; 1]
оси Ot на весь квадрат [0, 1] X [0, 1] плоскости Оху («кривая Пеано»).
Это отображение осуществим следующим образом. Разделим отре-
отрезок [0, 1] на четыре равных отрезка первого ранга, а заданный
квадрат — на четыре равных замкнутых квадрата первого ранга;
отрезки первого ранга занумеруем слева направо, а квадраты пер-
первого ранга — в том порядке, как указано на рисунке 2, а. Далее
каждый отрезок первого ранга разбиваем на четыре равных отрез-
отрезка второго ранга, а каждый квадрат первого ранга — на четыре рав-
равных замкнутых квадрата второго ранга; получившиеся в резуль-
результате шестнадцать отрезков второго ранга нумеруем слева направо,
а квадраты второго ранга нумеруем так, чтобы два квадрата с со-
соседними номерами имели общую сторону (см. рис. 2, б). Далее раз-
69

бйваем каждый отрезок второго ранга на четыре отрезка третьего
ранга и нумеруем все отрезки третьего ранга слева направо, а
каждый квадрат второго ранга — на четыре квадрата третьего ранга
и нумеруем все квадраты третьего ранга по тому же правилу, что
и квадраты второго ранга (см. рис. 2, в). Далее продолжаем этот
процесс неограниченно.
Поставим в соответствие каждому отрезку я-го ранга с номером i
квадрат того же ранга п с тем же номером /. Так мы установим
взаимно однозначное соответствие между отрезками и квадратами
одного и того же ранга; заметим, что это соответствие обладает
следующим свойством: если отрезок я-го ранга 8г соответствует
квадрату я-го ранга Уъ а отрезок я + 1-го ранга б2 — квадрату
п + 1-го ранга V2 и если 8г zd б2> то Уг id V2.
Теперь устанавливаем отображение отрезка [0, 1] оси Ot на за-
заданный квадрат следующим образом. Пусть t0 — какая-либо точка
отрезка [0, 1]. Построим последовательность отрезков {8п} (где
бх — отрезок первого ранга, б2 — отрезок второго ранга и т. д.),
содержащих точку tQ\ этой последовательности отрезков соответ-
соответствует последовательность квадратов {Vn}\ при этом так кад 8г id
=> б2 id ... id 8n id ..., то Vi id V2 id ... id Vn id ... Так как
diam Vn ->■ 0 при n -> +oo, то существует единственная точка Мо,
принадлежащая всем Vn. Ее мы и ставим в соответствие точке t0,
т. е. полагаем / (/0) = Мо.
Доказать, что: а) каждой точке /0 £ [О* 1] отвечает только одна
точка Мо из данного квадрата; б) при этом отображении получаются
все точки квадрата; в) это отображение непрерывна на [0, 1]; г) оно
не является взаимно однозначным.
595. Доказать, что проектирование на ось Ох множества £,
лежащего на плоскости Оху, является непрерывным отображением.
596. Всегда ли проекция на ось Ох плоского открытого множе-
множества является открытым множеством на прямой?
597. Всегда ли проекция на ось Ох плоского замкнутого множе-
множества является замкнутым множеством на прямой?
598. Даны две пересекающиеся оси на плоскости. Доказать,
что при ортогональном проектировании каждое несчетное множе-
множество проектируется по крайней мере на одну
из этих осей в несчетное множество.
599. Доказать, что арифметическую
сумму множеств Е и F (т. е. множест-
множество Е © F) можно построить следующим
образом: поместим Е на оси Ox, F на оси
v +*- Оу и построим множество Е X F на плос-
плоскости Оху\ затем спроектируем Е х F на
ось Ох с помищью косоугольной проекции
Рис-3 с углом проектирования, равным 135°;
полученная проекция и будет множеством Е © F (рис. 3).
600. Доказать, что арифметическая сумма двух ограниченных
замкнутых множеств является ограниченным замкнутым множеством.
70

601. Что представляет собой арифметическая сумма двух кан-
торовых совершенных множеств?
602. Доказать, что если множество А на прямой открыто, то,
каким бы ни было множество 5, арифметическая сумма А ф В
является открытым множеством.
603. Доказать, что если Ех и Е2 — непустые числовые множества,
то sup (Ег © Е2) = sup Ег + sup £2,
inf (Ег © Е2) = inf Ег + inf Е2.
604. Пусть Е и F — связные множества на прямой. Доказать,
что Е ® F также связно.
605. Что представляет собой множество всевозможных расстоя-
расстояний между точками канторова множества?
606. Пусть А — открытое множество на оси Ох, В— произвольное
множество на той же оси. Доказать, что множество всевозможных
расстояний между точками § 6 А и т] € В является либо открытым
множеством, либо объединением открытого множества и одноточеч-
одноточечного (начала координат).
607. Пусть / (х) — числовая функция, определенная на всей
оси Ох, имеющая производную для всех х, причем \f (x)\ ^ /С,
где К — заданное число, 0 < К < 1. Доказать, что уравнение
х = f (x) имеет решение, и притом единственное.
608. Пусть / (х) — числовая функция, определенная на всей
оси- Ох, имеюща-я производную для всех я, причем \ff (x)\ ^ /С,
где К — фиксированное число, К > 1. Доказать, что уравнение
х = f (x) имеет решение, и притом единственное.
609. Рассмотрим бесконечную систему уравнений:
где 2 с\< 1, 2^ < +°°- Доказать, что данная система имеет одно
i, к i
и только одно решение (хъ х2> ...) в пространстве /2.
610. Рассмотрим функцию f(x) — — In х на участке 1 ^ х < + оо.
Для любых хг^11у +°°С> ^2^[1> +°° С имеем: | / (х2) —
— f(xd\ = \F (с) (*2 — Xi)\^-\x2 — x1\, где с б ] хъ х2[. Следова-
Следовательно, данное отображение сжимающее. Однако оно не имеет
неподвижной точки (уравнение х = — In x не имеет действительных
решений). Нет ли здесь противоречия с теоремой Банаха?
611. Функция f (х) = не имеет неподвижной точки, хотя
2\х\
для любых хг € £, х2 6 Е, где Е — область определения функции
/ (х), имеет место неравенство | / (х2) — / (хг) I ^ — \х2 — jcxI-
Нет ли здесь противоречия с теоремой Банаха?
71

Глава XI.
ЧИСЛОВЫЕ ФУНКЦИИ ОДНОЙ
ПЕРЕМЕННОЙ (МОНОТОННОСТЬ,
ОГРАНИЧЕННАЯ ВАРИАЦИЯ)
Монотонные функции. Функция / (х) от одной действительной переменной
называется возрастающей на множестве £, если она определена всюду на Е и
если для любых хх £ Е, х2 6 Е, таких, что хг < х2, выполнено неравенство
/ (*i) < / (*2).
Если же для всех Хх £ Е, х2 (: Е, хг < х2 выполнено неравенство / (*i) <
< / (x2)t то функция называется строго возрастающей.
Аналогично определяются убывающая и строго убывающая функции.
Если функция возрастает на множестве Е или убывает на множестве £, то
она называется монотонной на £; аналогично определяется строго монотонная
функция.
Если функция монотонна на отрезке [а, 6], то множество ее точек разрыва
не более чем счетно и все ее точки разрыва — первого рода (см. выше, задача 67).
Вариация функции. Пусть функция f (х) задана на [а, Ь~\\ разобьем [а, 6] на
п отрезков точками *3 < х2 < ...< хп^.г\ обозначим, кроме того, а== хо, Ь = хп.
Рассмотрим следующую сумму:
Эта сумма зависит от способа разбиения отрезка [а, Ь\ Если для всевозможных
разбиений отрезка [а, Ь] эта сумма не превосходит некоторого положительного
числа, то говорят, что функция / (я) имеет ограниченную вариацию (или ограни-
ограниченное изменение) на [а, Ь]. При этом верхняя грань сумм б при всевозможных
разбиениях [а, Ь] называется вариацией функции / (х) (или полным изменением
ь
функции / (х)) и обозначается V/:
2
a t=l
где sup берется по всевозможным разбиениям отрезка [а, Ь].
Если множество сумм а не ограничено, то функция / (х) называется функ-
функцией неограниченной вариации; это записывается с помощью символического ра-
ь
венства V/ = +оо.
а
Функции, имеющие ограниченную вариацию, коротко называют функциями
ь
ограниченной вариации. Для функций ограниченной вариации V/ < +оо.
а
Примеры функций ограниченной вариации: 1) всякая монотонная на
[а, Ь] функция (в частности, и любая разрывная монотонная функция); 2) вся-
всякая непрерывная функция, имеющая ограниченную на [а, Ь] производную.
Следует заметить, что далеко не всякая непрерывная функция имеет ограни-
ограниченную вариацию (см. задачу 645).
Теорема 1. Если функция имеет ограниченную вариацию на [а, 6], то
она является разностью двух возрастающих функций.
В частности, всякую функцию f (x) ограниченной вариации на [а, Ь] можно
представить в виде следующей разности:
f (*) = ф W - * (Г),
X X
где ф (х) = V/ (вариация функции / (х) на [а, *]), а а|) (х) = V/ — / (х); ф (х) и
а а
if (x) являются возрастающими функциями на [а, Ь].
72

Из теоремы, сформулированной выше, в частности, следует, «что множество
точек разрыва функции ограниченной вариации не более чем счетно и что все
точки разрыва такай функции являются точками разрыва первого рода.
Теорема 2. Если функция непрерывна и имеет ограниченную вариацию
на [а, 6], то она представима в виде разности двух непрерывных возрастающих
функций.
Производная. Для функции одной переменной, определенной в некоторой
окрестности точки х, можно определить обычным образом производную в точ-
точке х. Известно, что если производная функции / (х) в точке х существует:, то
/ (х) непрерывна в этой точке; обратное утверждение неверно.
Если производная функции / (я) существует всюду на ]а, Ы и, кроме того, в
точке а существует правая производная
а в точке b — левая производная
f' /м г f(b + h)-f(b)
^^Л
то говорят, что / (я) имеет точную производную на [а, 6], в этом случае функцию
/' (х) называют точной производной функции f (x). Если [а, Ь] есть область опре-
определения функции / (х), то вместо /п'р(а) и /лев (Ь) пишут просто /' (а) и f (b).
Точная производная не обязана быть непрерывной функцией (см. задачи 612—614).
Однако точная производная обладает рядом важных свойств:
ТеоремаЗ (Дарбу). Если f (х) имеет точную производную на [а, Ь\
причем f (а) = A, f (b) = В, то для любого числа С, заключенного между А и В,
существует точка с £ [а, Ь] такая, что /' (с) = С (т. е. точная производная
обладает свойством Дарбу).
Теорема 4. Точная производная f (x) не может иметь разрывов первого
рода.
Условие Гёльдера. Функцию / (х) называют удовлетворяющей условию Гель-
дера порядка а (где а ^ 0 задано) на отрезке [а, 6], если существует такое К > О,
что для любых хг 6 [^, Wi *2 6 [^, И выполняется неравенство
l/(*2)-/(*i)l < /С- U2-*iK
Число К называется константой Гёльдера, а — показателем Гёльдера. Легко
видеть, что если функция удовлетворяет на [а, Ь] условию Гёльдера порядка
а > 0, то она непрерывна (и даже равномерно непрерывна) на [а, Ь]. В случае
а = 1 условие Гёльдера называется условием Липшица (с константой Липши-
Липшица К).
Спрямляемые кривые. Пусть жорданова кривая (т. е. непрерывное отобра-
отображение отрезка [а, Ь] оси Oi в Rn) задана непрерывными на [а, Ь} функциями
*;=Ф1(О,.».*Л=ФЯ (О- О)
Разобьем произвольным образом [а, Ь] точками t-t\
а = *о < h < ... < tk^ <tk = b. B)
Шагом этого разбиения называется число X = max (^ — ti-л)- С разбиением
\<i<k
B) мы можем связать следующее число /лом («длина вписанной ломаной»):
k
'лом = 2 PWl.Mi-J,
t=l
где Mi — образ точки t-t при отображении A). Если при стремлении шага раз-
разбиения к нулю существует конечный предел длин ломаных, то этот предел назы-
называется длиной кривей A), а сама кривая называется спрямляемой на [а, Ь]. Уточ-
Уточним это определение: если при любом е > 0 существует 6 > 0 такое, что при
73

любом разбиении [а, Ь] с шагом, меньшим, чем б, выполняется неравенство
| ^лом — ^ I < £, то число / называется длиной данной кривой.
Теорема 5. Для спрямляемости кривой A) необходимо и достаточно,
чтобы множество чисел /лом (при всевозможных разбиениях отрезка [а, Ь])
было ограничено сверху, при этом
I = sup /лом.
Теорема 6. Для спрямляемости кривой A) необходимо и достаточно,
чтобы все функции (ft (t) (I ^ i ^ n) имели ограниченную вариацию на [а, 6].
Задачи
612. Построить функцию, имеющую производную во всех точ-
точках оси Ох, причем эта производная разрывна в начале координат и
не ограничена в любой окрестности начала координат.
613. Построить на отрезке [0, 1] функцию, имеющую производ-
производную во всех точках, причем эта производная разрывна на заданном
непустом нигде не плотном замкнутом множестве, и только на нем.
614. Построить на отрезке [0, 1] функцию, имеющую производ-
производную во всех точках, причем эта производная не ограничена в любой
окрестности любой точки некоторого множества положительной
меры.
615. Существует ли функция / (л:), имеющая во всех точках про-
производную, совпадающую с функцией Дирихле (т. е. /' (х) = 1 в
рациональных точках, /' (х)=0в иррациональных точках)?
616. Функция f (x) имеет производную во всех точках числовой
прямой. Может ли производная /' (х) быть разрывной и монотон-
монотонной?
617. Пусть ъо всех точках отрезка [а, Ь] существуют и правая,
и левая производные функции / (х). Верно ли, что /'лев (х) прини-
принимает все промежуточные значения (т. е. обладает свойством Дарбу)?
618. Построить непрерывную на всей прямой функцию, имеющую
производную во всех точках, кроме точек заданного ограниченного
счетного множества £, в которых производная не существует.
619. Пусть ф (t) — функция, возрастающая на [а, &], a / (х) —
функция, монотонная на [Л, В], где А = <р (а), В = ф (Ь). Явля-
Является ли монотонной функция / (ф (/))?
620. Рассмотрим монотонные функции ср (/) и / (х) из предыдущей
задачи. Пусть ф (/) разрывна в точке /0 (а < t0 < b). Обязана ли
быть разрывной функция / (<р (/))?
621. Доказать, что если функция f (x) строго монотонна на от-
отрезке [а, &] и если lim / (xn) =f (Ь), где хп € [я„6] (п = 1, 2, ...),
П~>оо
то lim хп = Ъ.
П->со
622. Доказать, что если f (х) — непрерывная на отрезке [а, Ь]
функция, то функции т (х) = inf / (г) и М (х) = sup / (г) моно-
zz [а, х] Zc [а, х]
тонны и непрерывны на [_а> Ь].
623. Доказать, что если / (х) — произвольная возрастающая
функция, заданная на [а, Ь], то функция М (х), определенная в
74

предыдущей задаче, совпадает с f (х). Если же определить М (х)
равенством
М{х) = sup /(г),
^ zQa, х[
то М (х) может не совпасть с функцией / (х) в ее точках разрыва.
624. Доказать, что если функция / (х) определена и монотон-
монотонна на [а, Ь~\ и если она принимает в качестве своих значений все
числа отрезка [inf / (x)\ sup / (jc)], то она непрерывна на [а, Ь].
х [а, Ь] х [а, Ь]
625. Пусть на множестве Е cz [а, Ь] задана ограниченная функ-
функция / (х), удовлетворяющая условию: / (хг) ^ / (jc2) для всех х1 £
€ Е, х2 £ £", #i < х2. Можно ли ее доопределить на всем отрезке
[а, Ь~] так, чтобы она была монотонной на всем отрезке?
626. Пусть на множестве Е cz [a, &] задана неограниченная функ-
функция / (jc) такая, что / (хг) ^ / (х2) для всех хг 6 £, х2 6 £, Xi < jc2.
Можно ли ее продолжить на весь отрезок [а, Ь] тад, чтобы она стала
монотонкой на всем отрезке?
627. Доказать, что если функция / (х) непрерывна на [а, Ь\
то для существования обратной функции необходимо и достаточно,
чтобы / (х) была строго монотонна.
628. Может ли сумма двух монотонных функций быть немоно-
немонотонной функцией? Может ли произведение двух возрастающих функ-
функций быть немонотонно? Привести соответствующие примеры.
629. Пусть функция / (х) определена на [а, Ь] и имеет в каждой
точке интервала ]а, Ь[_ предел слева и предел справа. Доказать, что
множество точек разрыва такой функции не более чем счетно.
630. Построить пример строго монотонной функции, определен-
определенной на всей числовой прямой и разрывной во всех рациональных точ-
точках, и только в них.
631. Доказать, что для любого счетного множества точек на оси
Ох можно построить строго возрастающую функцию, у которой мно-
множеством всех точек разрыва является это счетное множество.
632. Построим на отрезке [0, 1] канторово совершенное множе-
множество D. Зададим функцию т (х) следующим образом: на смежном
интервале первого ранга* т (х) =-—; на смежных интервалах вто-
1 3
рого ранга т (х) = — на левом ит(х)=- на правом интервале;
вообще на смежных интервалах fe-ro ранга полагаем: т (х) = — на
самом первом интервале &-го ранга (если двигаться слева направо),
3 5
т (х) =—k на втором интервале fe-ro ранга, х (х) = — на Третьем
* Интервалами &-го ранга мы называем те смежные интервалы канторова
множества, длина которых равна —г.
75

II
2
J
7 X
Рис. 4
и т. д.; на последнем интервале
k-то ранга т (х) == —^—. Таким
образом, функция т (я) опреде-
определена на всем дополнении CD к
множеству D относительно от-
отрезка [0, 1]. Она монотонна на
CD, и множество ее значений
всюду плотно на [0, 1] (значени-
(значениями функции т (х) на CD явля-
являются все двоично рациональные
числа между 0 и 1).
Теперь доопределим функцию
на D, положив для х б D т (х) =
= sup т (£) (т. е. в качестве
1 &CD
1, &
значения в точке х€ D принима-
принимаем верхнюю грань значений этой функции на той части множества
CD, которая лежит слева от х). Полагая, кроме того, т @) =0,
мы определим функцию т (х) на всем отрезке [0, 1]. Эта функция
называется функцией Кантора (схематический график этой функ-
функции см. на рисунке 4). Доказать, что т (х) — возрастающая функ-
функция, непрерывная во всех точках отрезка [0, 1].
633. Может ли монотонная непрерывная на отрезке
[а, Ь~] функция*, отличная от постоянной, иметь производную, рав-
равную нулю почти всюду в области определения (говорят, что какое-
либо свойство имеет место почти всюду на множестве Е, если оно
выполняется во всех точках этого множества, кроме точек некото-
некоторого подмножества меры нуль).
634. Доказать, что если функция / (х) монотонна, ограничена
и непрерывна на конечном интервале ]а, Ь[, то она равномерно не-
непрерывна на этом интервале.
635. Справедливо ли предыдущее утверждение, если заменить
конечный интервал ]а, &[ бесконечным промежутком ]—оо, +оо[?
636. Пусть / (х) — произвольная непрерывная функция, опре-
определенная на [0, 1], и пусть е — произвольное положительное число.
Доказать, что существует непрерывная функция ф (х), определенная
на [0, 1] и такая, что: а) <р @) = / @), <р A) = / A); б) q/ (x) = 0
почти всюду на [0, 1]; в) |ф (х)—/ (я)| < 8 для всех х (Е [0> 1].
637. Пусть Е — нигде не плотное замкнутое множество на отрез-
отрезке [а, Ь]. Построить на этом отрезке строго возрастающую функцию
/ (#), имеющую непрерывную производную всюду на отрезке [а, &],
причем /' (х) = 0 во всех точках множества Е.
638. Имеет ли решение предыдущая задача, если отказаться от
требовани.я, что Е является нигде не плотным множеством?
639. Доказать, что если f (х) —монотонная функция, удовлет-
удовлетворяющая равенству / (х) + f (у) = / (х + у) для всех х и у, при-
причем /A) =а, то f(x) =ax.
76

640. Вариация функции f (x) на [а, Ь]равна Л. Чему равна вариа-
вариация функции kf (х) + т на [а, &]?
641. Чему равна вариация функции
•к О при х == О,
/(*) = | 1—х при 0 <х < 1,
E при л: == 1
на отрезке [0, 1]?
642. Чему равна вариация функции
(х — I для х < 1,
/(*) =| 10 для х = 1,
[ X2 ~~ ДЛЯ X > 1
йа отрезке [0, 2]?
643. Если изменить значение функции из предыдущей задачи
в точке разрыва (при х = 1), то вариация функции изменится. Как
изменить значение этой функции в точке х = 1, чтобы вариация
стала наименьшей?
644. Доказать, что функция
0 при х = 0,
{0 при х = 0,
*2cos — при хфО
X
имеет ограниченную вариацию на отрезке [0, 1].
645. Доказать, что функция
О при х — О,
I х sin — при 'х Ф О
X
имеет неограниченную вариацию на отрезке 0, —
646. Функция f(x) имеет ограниченную вариацию на [0, 1];
доказать, что функция F (х) = f {ах + Ь), где а>0, имеет ограни-
1—b
г г » 1 -1 1а
ченную вариацию на отрезке , , причем V/—V F
[а а \ о _ ь_
а
647. Обобщить результат предыдущей задачи, доказав, что если
/ {х) имеет ограниченную вариацию на [0, 1], а ф (х) — строго воз-
возрастающая непрерывная функция на [а, (}] такая, что ф (а) = О,
ф (Р) = 1, то функция F (х) = f (ф {х)) имеет ограниченную вариа-
вариацию на [а, р], причем V/ = V/7.
О а
648. Доказать, что функция, имеющая во всех точках отрезка
[а, &] производную, ограниченную на [а, 6], является функцией
ограниченной вариации.
649. Доказать, что характеристическая функция %Е {х) множе-
множества Е а [а, Ь~\ имеет ограниченную вариацию на [а, Ь] тогда и
77

m
только тогда, когда множество Е имеет лишь конечное число гра-
граничных точек.
650. Обязательно ли сумма равномерно сходящегося ряда не-
непрерывных функций ограниченной вариации является функцией
ограниченной вариации?
651. Доказать, что если функция удовлетворяет условию Лип-
Липшица на отрезке [а, Ь], то она имеет на этом отрезке ограниченную
вариацию.
652. Доказать, что если функция f (х) удовлетворяет условию
Гёльдера порядка а > 1 на отрезке [а, &], то / (х) постоянна на этом
отрезке.
653. Доказать, что если функция / (х) удовлетворяет условию
Гёльдера порядка а на отрезке [а, &], то она удовлетворяет на этом
отрезке также условию Гёльдера порядка р, где р — любое неотри-
неотрицательное число, меньшее чем а.
654. Пусть функция / (х) удовлетворяет условию Гёльдера по-
порядка а на [а, &]; доказать, что тогда F (х) = К f (тх + п)
удовлетворяет условию Гёльдера порядка а на отрезке
(если т > 0) или на отрезке -:==^, ^—Ч (если т < 0).
I т т \
655. Построить на каком-нибудь отрезке [а, Ь] непрерывную
функцию, которая имеет на этом отрезке ограниченную вариацию
и не удовлетворяет на нем условию Гёльдера ни при каком а > 0.
656. Построить на каком-нибудь отрезке [а, Ь] непрерывную
функцию, которая имеет на этом отрезке неограниченную вариа-
вариацию и удовлетворяет условию Гёльдера некоторого порядка а,
где а — заданное число, 0 < а < 1.
657. Построить на каком-нибудь отрезке [я, &] непрерывную
функцию, которая имеет на этом отрезке неограниченную вариа-
вариацию и не удовлетворяет на нем условию Гёльдера ни при каком
и >0.
658. Пусть функции / (х) и g (x) имеют ограниченную вариацию
на [а, &]. Доказать, что их сумма и произведение также имеют огра-
ограниченную вариацию на [а, &], причем
ь ь ь
V(/ + gKV/ + Vg,
а а а
VtfgK sup |/(*)|-Vg+ sup \g(x)\-Vf.
a x £ [a, b) a x € [a, b] a
659. Пусть / (x) — функция ограниченной вариации на [a, fe],
причем f (x) ^ c> 0 всюду на [a, &]. Доказать, что также име-
имеет ограниченную вариацию на [а, Ь]. ' М
660. Пусть / (х) определена на [а, &] и а < с < Ь. Доказать
b с b
равенство V/ = V/ + V/.
а а с
661. Пусть f (х)—функция ограниченной вариации на [а, &],
х
F (х) = V/ — вариация функции / на [а, х].
78

Доказать, что для непрерывности / (х) в точке х0 б [а, Ь] необ-
необходимо и достаточно, чтобы функция F (х) была непрерывна в этой
точке.
662. Пусть функция / (х) определена на [а, +оо[ и имеет огра-
ограниченную вариацию на любом отрезке [а, £] (£ > а). Доказать, что
если lim V/ существует, то и lim / (х) существует. Показать на при-
мере, что из существования конечного предела lim / (х) еще не сле-
t ЛГ->-|-оо
дует существования lim V/.
663. Доказать, ,что если / (х) — разрывная функция ограничен-
х
ной вариации на [а, Ь], то F (х) = V/ также разрывна на [а, 6],
а
причем разрывы обеих функций находятся в одних и тех же точках.
Доказать, что в каждой точке разрыва х0 имеют место равенства:
(о 0) - / (х0) \=F(xo+O)-F (*0),
(х0) -f(xo-O)\=F (x0) -F(Xo-O).
664. Доказать, что множество V (а, Ь) функций ограниченной
вариации на {a, fe] является метрическим пространством, если за
расстояние между / б V (а; Ь) и g $ V {а, Ь) принять число
Доказать, что это пространство полно.
665. Объединим в один класс все функции ограниченной вариа-
вариации на^а, &], отличающиеся друг от друга на постоянное слагаемое.
Доказать, что множество этих классов является метрическим про-
странством V (а, Ь), если за расстояние между двумя классами / и
g принять число
где / — какая-либо функция из класса /, ag — какая-либо функция
из класса g. ^
Доказать полноту пространства V (а, Ь).
666. Представить функцию ограниченной вариации cos2 x на
отрезке [0, я] в виде разности двух возрастающих функций.
667. Представить функцию ограниченной вариации sin x на
[0, 2я] в виде разности двух возрастающих функций.
668. Представить функцию ограниченной вариации на £0, 2]
(— хг при х б [0, 1[,
f (х) = 10 при х = 1,
11 при х 6]1, 2]
в виде разности двух монотонных функций.
669. Чему равна вариация функции
79

х2 при х € [0, 1[,
f (х) = 5 при х = 1,
* + 3 при л: €]1, 2]
2 1 2
на отрезке [0, 2]? Проверить, что V/ = V/ + V/. Представить f(x)
о о 1
в виде разности двух возрастающих функций.
670. Доказать, что если функция f (х) имеет ограниченную ва-
вариацию на [а, 6], то ее абсолютная величина \f (х)\ также имеет
ограниченную вариацию на этом отрезке.
671. Справедливо ли утверждение: «Если \f (х)\ имеет ограничен-
ограниченную вариацию на [а, &], то и / (х) имеет ограниченную вариацию-на
этом отрезке»?
672. Пусть f (х) — непрерывная на Га, &] функция.
Справедливо ли утверждение: «Если \f {х)\ имеет ограниченную ва-
вариацию на [а, Ь], той / (х) имеет ограниченную вариацию на этом
отрезке»?
673. Доказать теорему: «Для того чтобы функция / (х) имела
ограниченную вариацию на [а, Ь], необходимо и достаточно, чтобы
существовала такая возрастающая функция ер (х), что для
любого х 6 [а, &] и для любого h > 0 (такого, что х + h б [а, &])
имеет место [/ (х + /i) — / (я)| <; ф (я + Ь) — ф (я)».
674. Доказать, что кривая
_ J*asin— при
[ 0 при х = 0
спрямляема на [0, 1].
675. Доказать, что кривая
_ f л: sin — при х =£0,
У j %
[ 0 при х = 0
не спрямляема на [0, 1].
676. Доказать, что функции х = ф (/), У =Ф @ @ <J * <J 1),
задающие кривую Пеано (см. задачу 594), не могут иметь ограничен-
ограниченной вариации.
677. Рассмотрим жорданову кривую:
_ j/sin— при гфО, __ f^sin— при t=£0,
(О при/-0, (О при f = 0 (<€[0f 1]).
Так как обе функции, задающие эти параметрические уравне-
уравнения, не имеют ограниченной вариации на отрезке [0, 1] (см. задачу
645), то, согласно теореме 6 введения к настоящей главе, эта кривая
не спрямляема. С другой стороны, кривая, определяемая этими урав-
уравнениями, является отрезком прямой у =х от точки (а, а) до точ-
точки (Ь, Ь), где а= min [/sin— j b = max (/sin—]; но конеч-
* e ]o, i] \ ' ' * € ] o, l ] V / /
ный отрезок прямой всегда имеет конечную длину. Чем объяснить
кажущееся противоречие.
80

678. Доказать, что если функции ф (f) и я|> (f) имеют всюду на
[О, 1] производную, причем q/ (?) и яр' (t) ограничены на [0, 1], то
кривая х = ф @, у =я|? (/), @<: / <! 1) спрямляема.
Глава XII.
ИЗМЕРИМЫЕ ФУНКЦИИ, ИНТЕГРАЛЫ
РИМАНА И ЛЕБЕГА
Измеримые функции. Числовая/ функция / (х), определенная на множестве
£, где £ — подмножество евклидова пространства Rn (в частном случае — под-
подмножество числовой прямой), называется измеримой, если измеримы множество
Е и все множества Е (f (х) > а) для любых а, —оо < а < + оо.
Здесь, как и всюду дальше, Е (/ (я) > а) (или £ (/ > а)) — множество всех
тех точек х из £, в которых имеет место неравенство / (х) > а. Аналогичный
смысл имеют обозначения: Е (f (х) !> а), Е (f (х) < а), Е (f (х) ^ а), Е (/ (я) =
= а), £ (а < / (*) < 6) и т. д. (или £ (/ > а), £ (/ < а) и т. д.).
Для измеримости функции / (я), заданной на измеримом множестве £, не-
необходимо и достаточно, чтобы были измеримы все Е (/ (я) !> а), или чтобы были
измеримы все Е (f (х) < а), или чтобы были измеримы все Е Ц (х) ^ а).
Свойства измеримых функций.
1. Если две функции /х (*) и /2 (х) измеримы, то измеримы также их сумма,
произведение, частное (последнее — при условии /2 М ¥= 0 на £).
2. Если дана последовательность измеримых на множестве Е функций
h (х)> /г (■*)> •••» /« (*)t •••» сходящаяся всюду на £ к функции F (я), то F (х) из-
измерима на Е. Даже если соотношение- lim fn (x) = F (х) выполняется не всюду,
а лишь почти всюду* на Е, То и тогда F (х) измерима на £.
3. Если две функции, определенные на Е, отличаются друг от друга на
множестве меры нуль, то они либо обе измеримы, либо обе неизмеримы.
Функции, отличающиеся друг от друга только на множестве меры нуль,
называются эквивалентными.
4. Если / (я) измерима на £ и если измеримое множество А является
подмножеством множества £, то f-fcc) измерима на Л.
Примеры измеримых функций.
1. Функция, принимающая постоянное значение С во всех точках измери-
измеримого множества Е, измерима на Е.
2. Всякая функция, непрерывная на отрезке [а, И, измерима на нем.
3. Функция, непрерывная почти всюду на отрезке [а, &], измерима на нем.
4. Функция, являющаяся пределом сходящейся последовательности не-
непрерывных на [а, Ь] функций, измерима на [а, Ь].
Не всякая функция измерима. Так, например, если Е — неизмеримое мж>
жество на прямой, то функция, имеющая значение 1 на £ и 0 вне £, неизмерима.
Сходимость по мере. Пусть £ — измеримое множество конечной меры. По-
Последовательность {fn (x)} измеримых на £ функций называется сходящейся по
мере к измеримой функции ср (я) на £, если для всякого числа б > 0 имеет место:
Hmm£(|q>(x)-fe(*)| > б) = 0.
Теорема 1 (Лебега). Если последовательность функций {fn (x)},
* Напомним, что термин «некоторое свойство выполняется Почти всюду на £»
означает, что это свойство выполняете» во всех точках множества £, кроме точек
некоторого подмножества меры нуль.
31

измеримых на множестве Е конечной меры, сходится почти всюду на Е к функции
Ф (х), то она сходится к этой функции и по мере на Е.
Таким образом, сходимость по мере является обобщением сходимости почти
всюду. Вместе с тем эти понятия не совпадают: существуют последовательности
измеримых функций, сходящиеся по мере на множестве Е конечной меры, но не
сходящиеся в обычном смысле ни в одной точке множества Е (см. задачу 699).
Теорема 2. Из всякой сходящейся по мере на Е последовательности
{fn (x)} можно выделить подпоследовательность, сходящуюся почти всюду на
Е (где Е — множество конечной меры).
Теорема 3 (Егорова). Если последовательность {fn (x)} сходится
по мере к ф (х) на множестве Е конечной меры, то для любого б > 0 существует
такое измеримое подмножество Ех с Е, что
а) mEi > тЕ — 6;
б) последовательность {fn (x)} равномерно на Е± сходится /с ф (я).
Интеграл Римана. Пусть функция / (х) задана на [а, Ь"]. Разобьем [а, Ь~\
точками а = хо < Х\ < ... < хп = Ь и назовем шагом Я этого разбиения макси-
максимальную длину интервалов l*/_lf ;ty[ Я = max (xi — Xi-i)-
Далее построим суммы
где
&xi = x-t — #z_ii m-t = inf / (x), Mi = sup / (x).
Эти суммы называются соответственно нижней и верхней суммами Дарбу. Если
существует общий предел верхних и нижних сумм Дарбу при стремлении шага
разбиения к к нулю, то этот предел называется интегралом Римана от / (я) на
отрезке [а, Ь"]:
Ь п п
(R) J7 (#) dx = lim 2 Щ^Ч — lim 2 MAxi*
Если для функции / (я) на отрезке [а, И существуют пределы нижних и верхних
сумм Дарбу и эти пределы равны друг другу, то говорят, что / (я) интегрируема
на [а, Я /го Риману.
Теорема. Для того чтобы функция f (x) была интегрируема по Риману
на [а, Я» необходимо и достаточно, чтобы она была ограничена на [а, Ь~\ и мера
множества ее точек разрыва равнялась нулю (т. е. чтобы функция / (я) была почти
всюду на [а, Я непрерывна).
Свойства интеграла Римана.
1. Если ф (я) Ъ i|? (я) интегрируемы по Риману на [а, Ь], то для любых чисел
а, Р имеет место
2. Если / (я) интегрируема на [a, b~\ и на [Ь, с], то она интегрируема и на
[а, с], причем
j ] ]l
a a b
3. Если т ^ f (х) ^ М всюду на [a, b~] и / (я) интегрируема по Риману на
la, W, то
ь
т . ф — а) < J / (x) dx < М . (Ь — а).
а
82

Интеграл Лебега от ограниченной функции. Пусть / (/; — ограниченная
измеримая функция, определенная на измеримом множестве* Е евклидова про-
пространства и принимающая значения строго между А и В: А < / (х) < В для всех
х £ Е. Разобьем отрезок [Л, J3] оси Оу точками А = у0 < ух < у2 < ... < уп =
= В и построим следующие суммы:
t=i t
где e-t = £ (у/_х ^ / (а:) < у/). Эти суммы называются соответственно нижней
и верхней суммами Лебега. Наибольшая длина отрезков [уг_ь у{] при данном
разбиении называется шагом разбиения и обозначается X.
Если существует общий предел верхних и нижних сумм Лебега при стрем-
стремлении шага разбиения Я к нулю, то функция / (я) называется интегрируемой
по Лебегу на множестве Е и этот общий предел сумм Лебега называется интегра-
интегралом Лебега от / (я) по множеству Е:
п п
(L) f / (x) dx = lim У\ yi^mei = lim У\ ytmei
Е ^-0Й ^«Ы
(когда ясно, что речь идет об интеграле Лебега, то знак (L) перед обозначением
интеграла часто опускают).
Множество Е называется при этом областью интегрирования. Если, в ча-
частности, областью интегрирования является отрезок [а, Ь\ то интеграл Лебега
по этому множеству записывают в виде
Ь ъ
(L)$f(x)dx, или \f(x)dx.
а а
Теорема. Всякая ограниченная измеримая на Б функция интегрируема
по Лебегу на этом множестве (предполагается, что Е — множество конечной
меры).
Свойства интеграла Лебега.
1. Если функция f (х) интегрируема по Риману на отрезке [а, Я, то она
интегрируема и по Лебегу на этом отрезке, причем эти интегралы равны друг
другу:
(R)]f(x)dx = (L)]f(x)dx.
а а
Таким образом, интеграл Лебега на отрезке является обобщением интеграла
Римана.
2. Если k < / (х) < К всюду на Е, то
k • тЕ < (L) j / (*) dx < К • тЕ.
Е
3. Если множество Е конечной меры разбито на конечную или счетную сово-
совокупность попарно не пересекающихся, измеримых множеств £#, то для любой
измеримой ограниченной на Е функции / (я) имеет место
(это свойство интеграла Лебега называется «полной аддитивностью»).
4. Если ф (я) и \f> (я) ограничены и измеримы на £, то для любых чисел аир
имеет место
J (аФ (х) + Р« (*)) ^ - /х J ф (х) dx +P J г|) (х) dx.
5. Если / (х) и ф (л) ограничены и измеримы на £, причем почти вс-юду
* Здесь и всюду в дальнейшем мы считаем, что Е — измеримое множество
конечной меры, если специально не оговорено противное.
83

(*) < ф (Х), Тб
\f(x)dx<\y(x)dx.
'Е Е
В частности, если / (х) = ф (х) почти всюду на £, то
6. Если f (x) — неотрицательная измеримая ограниченная функ-
функция на £, причем J / (я) dx = 0, то / (х) = 0 почти всюду на Е.
7. Если / (х) измерима и ограничена на £, то
\$f(t)dx\<$lf(x)ldx.
8. Если дана последовательность измеримых ограниченных на Б функций
/i (*)t ^ W. •••» fk (*)t •••» сходящаяся почти всюду на Е к функции Т7 (#), и если
существует такое число Л, что \fa (х) | ^ А для всех kt то
Hm [ fk (x) dx = [ F (x) dx.
fc + +0O £ £
Интеграл Лебега от неограниченной функции. Пусть / (я) — неограничен-
неограниченная измеримая функция постоянного знака, например всюду на Е (f (x)^ 0).
Построим вспомогательную функцию [/ (x)~}t («срезка» функции / (х) числом t),
которая определяется следующим образом:
_ Г / (х) при 0 < / (х) < /,
\ t при / (х) > t.
Зта функция измерима и ограничена (числами 0 и 0-
Интеграл Лебега от неограниченной неотрицательной функции
/ (*) по множеству Е определяется равенством
(L) j / (х) dx = ^ lirn^ (L) J U {xIt dx.
Указанный здесь предел всегда существует; однако он не обязательно равен
конечному числу (он может равняться и +°°)- Если (L) J f (x) dx конечен, то
Е
функция называется суммируемой на Е (или интегрируемой по Лебегу на Е);
если этот интеграл бесконечен, то функция называется несуммируемой (или He-
интегрируемой по Лебегу).
Интеграл от знакопеременной измеримой неограниченной функ-
функции / (я) на Е определяется равенством
где
(L) j / (х) dx = (L) J /+ (x) dx - (L) J /_ (x) dx,
E E E
f (x)- Sf (*) при / (x) > 0,
'+ W - \ 0 при / (x) < 0f
-1\H*)\
- \ 0
0 при / (x) > (У,
т.е.
Функция / (х) называется суммируемой, если /+ (д:) и /_ (х) обе суммируемы.
Тогда интеграл от / (х) равен конечному числу,, определенному указанной выше
формулой.
Функция / (х) несуммируема, если хотя бы одна из неотрицательных функ-
функций /+ (х) или /_ (х) несуммируема,
84

Свойства интеграла Лебега от неограниченных функций.
1. Если ф (а:) и \|) (я) суммируемы на £, то для любых чисел а, р функция
омр (я) + Р\|) (х) также суммируема, причем
(L) J (оир (х) + Ря|з (*)) dx=a.(L)$<p(x)dx + ?>. (L) j> (x) dx.
Е ЕЕ
2. Если / (х) суммируема на Е и множество Е разбито на конечную или
счетную совокупность попарно не пересекающихся измеримых множеств £#, то
f (x) суммируема, на всех Е^ и
(L)
(«полная аддитивность» интеграла Лебега). Для неотрицательной на Е измеримой
функции / (я)) это равенство сохраняется и в том случае, когда f (x) несуммируема
на Е (в обеих частях равенства тогда стоит +оо).
3. Если / (х) и ф (х) суммируемы на Е и f (х) <! ф (я) почти всюду на £, то
Jq>
В частности, если / (х) = ф (х) почти всюду на £, то их интегралы равны.
4. Если/ (я) — измеримая на Ефункция, то из суммируемости / (я) вытекает
суммируемость |/ (*)|, а из суммируемости |/ (*)| вытекает суммируемость / (x)i
при этом имеет место неравенство
\(L)$f(x)dx\<(L)$\f(x)\dx.
Е Е
5. Если f (х) и g (х) измеримы на Е, причем почти всюду на Е имеет место
неравенство | / (*)| ^ | g (x)\t и если g (х) суммируема на £, то и / (я) суммируема
на Е.
6. Если / (х) !> 0 на Е и (L) | / (я) dx == 0, то / (х) = 0 почти всюду на /?.
7. Если последовательность {fn(x)} измеримых на Е функций сходится по
мере на £ к функции F (х) и если существует такая суммируемая на Е неотрица-
неотрицательная функция G (х), что | fn (x)\ ^ G (х) для всех п и почти всех к 6 £, то
функции fn (х) и F (х) суммируемы на £, причем
lim ^pn(x)dx
Задачи
679. Доказать, что если функция (/ (x)f измерима на Е> то и
/ (х) измерима на £.
680. Показать, что из того, что (/ (х)J измерима на Е, еще не
следует, что / (х) измерима на Е.
681. Доказать, что если f{x) измерима на Е, то и \f(x)\ измери-
измерима на Е. Показать на примере, что обратное утверждение неверно.
682. Доказать, что если функции f (х) и g (x) измеримы на Е9
то функции
т (х) = min {/ (л:), g {х)}, М (х) = max {/ (х), g (x)}
также измеримы на Е.
683. Доказать, что если функция / (х) измерима на всяком от-
отрезке [а, р], где a < а < р < &, то она измерима и на всем отрезке
[а, Ь1
85

684. Измерима ли функция / (х), равная х2 во всех точках пе-
пересечения канторова множества и некоторого неизмеримого множе-
множества Е и равная г5 во всех остальных точках отрезка [0, 1]?
685. Доказать, что если / (х) имеет производную во всех точках
отрезка [а, Ь], то эта производная /' (х) является измеримой функ-
функцией на отрезке [а, &].
686. Доказать, что если Е — измеримое множество, то харак-
характеристическая функция %Е (х) измерима. Если же £ — неизмеримое
множество, то %Ё (х) — неизмеримая функция.
687. Построить измеримую функцию, определенную на всей
прямой, разрывную во всех ее точках и обладающую тем свойством,
что, как бы ни изменять значения этой функции на любом множестве
меры нуль, она остается разрывной во всех точках прямой.
688. Доказать, что если функция / (х) измерима на множестве Е9
то функция [/ (х)~]а также измерима на Е (определение функции
U (х)% гДе а <Ь, см. в условии задачи 562).
689. Пусть х М — характеристическая функция множества
рациональных чисел. Доказать, что ее произведение на любую функ-
функцию есть функция измеримая.
690. Доказать, что всякая функция ограниченной вариации на
[а, 6] есть измеримая функция на [а, Ь].
691. Пусть функция / (х) измерима на множестве Е и пусть Ег —
произвольное открытое или замкнутое множество на числовой пря-
прямой. Доказать, что прообразом множества Ех во всех этих случаях
является измеримое подмножество множества Е.
692. Пусть функция / (х) измерима на множестве £; пусть Ег —
произвольное измеримое множество на числовой прямой. Обязано
ли множество /-1 (Е%) быть измеримым?
693. Пусть функция / (х) измерима на множестве Е\ пусть Ео —
измеримое подмножество множества Е. Обязано ли множество
f(E0) быть измеримым? Если нет—привести соответствующий пример.
694. Пусть ф (t) —измеримая на множестве Е функция, Ег =
= ф (Е) — ее множество значений. Пусть f. (x) — функция, не-
непрерывная на Ег. Доказать, что суперпозиция этих функций
/ (ф @) является измеримой функцией на Е.
695. Пусть ф (/) — функция, непрерывная на отрезке Е =
= [«» Р]> и £i = Ф {Щ — ее множество значений. Пусть / (х) —
функция, измеримая на Ег. Обязана ли быть измеримой суперпози-
суперпозиция этих функций, т. е. функция / (ф (£))?
696. Пусть Е — измеримое множество положительной меры,
{/„} и {gn} —две последовательности измеримых функций, сходя-
сходящиеся по мере на множестве Е соответственно к функциям / (х) и
g(x). Доказать, что последовательности {fn+gn}> {fngn}> (—)
сходятся по мере соответственно к функциям / + g, /g, — (послед-
g
нее — в случае, если g (х) Ф 0 почти всюду на Е).
86

697. Пусть {fn(x)} сходится по мере на £ к функции / (х). До-
Доказать, что если для всех х ^£и всех п имеет место неравенство
fn (х) < а, то / (х) < а почти всюду на Е.
698. Понятие сходимости последовательности {fn(x)} по мере
к ф (х) на множестве Е можно обобщить (не меняя определения)
на тот случай, когда Е измеримо, но имеет бесконечную меру.
Верны ли для случая тЕ=+ оо теоремы 1 и 2 (с. 81—82) о схо-
сходимости по мере из введения к настоящей главе?
699. Привести пример последовательности измеримых функций,
сходящейся по мере на отрезке [0, 1], но не сходящейся в обычном
смысле ни в одной точке этого отрезка.
700. Выделить из последовательности, построенной в предыду-
предыдущей задаче, подпоследовательность, сходящуюся почти всюду на
[0, 1].
701. Пусть Е — измеримое множество конечной или бесконеч-
бесконечной меры, б > 0 — заданное число. Можно ли из всякой последо-
последовательности {fn} измеримых на Е функций, сходящейся почти всю-
всюду на Еу извлечь подпоследовательность, сходящуюся равномерно
на некотором подмножестве Ег а Е таком, что т (Е \ Ег) < 8?
702. Доказать, что любая функция ограниченной вариации на
[а, й] интегрируема по Риману на [а, й].
703. Может Ли быть интегрируемой по Риману на [а, й] функция,
разрывная во всех точках некоторого непустого открытого множе-
множества G cz [а, й]?
704. Показать на- примере, что из интегрируемости по Риману
функции / (х) на всяком отрезке [а, р], где а < а < (J < й, еще
не следует, что она интегрируема по Риману на [а, й].
705. Доказать, что если / (х) интегрируема по Риману на вся-
всяком отрезке [а, E] таком, что а < а < |5 < й, и если она ограниче-
ограничена на [а, й], то она интегрируема по Римайу на всем отрезке [а, й].
706. Пусть последовательность функций {/„(*)}, каждая из
которых интегрируема по Риману на [а, й], сходится всюду на [а, 6]
к ф (х); пусть, кроме того, существует такое А > 0, что \fn(x)\ ^
^ А для всех х € [а, 6] и всех. д. Следует ли из этого, что функция
Ф (х) интегрируема по Риману на [а, &]?
707. Доказать, что предел равномерно сходящейся последо-
последовательности функций, интегрируемых по Риману на отрезке [а, £],
является функцией, интегрируемой по Риману на [а, й]. Доказать,
что интеграл от функции, являющейся пределом, равен пределу
интегралов от функций данной последовательности.
708. Верно ли утверждение: «Если Е — множество меры нуль
на [а, й], то %Е (х) интегрируема по Риману на [а, &]»?
709. Верно ли утверждение: «Если Е — нигде не плотное мно-
множество на [а, й], то 1Е (х) интегрируема по Риману на [а, Ь]»?
710. Верно ли утверждение: «Если Е — нигде не плотное мно-
множество меры нуль на [а, й], то %Е (х) интегрируема по Риману на
[а, й>?
87

711. Пусть Е — замкнутое множество меры нуль, расположен-
расположенное на отрезке [а, 6]. Интегрируема ли функция %Е (х) на [а, &]
по Риману?
712. Верно ли утверждение: «Если Е — множество на [a, ft],
замыкание которого имеет меру нуль, то %Е (х) интегрируема по
Риману на [а, Ь]»?
713. Интегрируемы ли по Риману на отрезке [0, 1] функции при-
примеров 486, 488, 489, 495, 502?
714. Доказать, что все функции, рассмотренные в этих примерах,
интегрируемы по Лебегу на отрезке [0, 1]. Вычислить их интегралы
на этом отрезке.
715. Функция / (х) равна х2 в точках канторова множества и
равна — на тех смежных интервалах, длина которых равна -j.
1
Вычислить (L)lf(x)dx.
о
716. Интегрируема ли по Риману функция из предыдущей за-
задачи? Если да, то чему равен ее интеграл Римана?
717. Интегрируема ли по Риману функция
в иррациональных точках,
1 в рациональных точках
на отрезке [0, 1]? Интегрируема ли она по Лебегу? Чему равен ее
интеграл на отрезке [0, 1]?
718. Доказать, что если Е — измеримое множество на [а, &],
то его характеристическая функция %е (х) интегрируема по Лебегу
на множестве [а, Ь], причем ее интеграл равен мере множества Е:
(L)j%B(x)dx=mE.
а
719. На отрезке [0, 1] построено нигде не плотное совершенное
множество Е меры —; смежные интервалы этого множества перену-
перенумерованы в порядке убывания их длин ]аь рх[, ]а2, р2[, ..., ]ал, рл[,
... . Затем на [0, 1] задана функция / (х)9 определенная следую-
следующим образом:
f(x) = 0 на Е,
f (х) = 1 в серединах интервалов ]оьл, рл[,
f(x) линейна на отрезках ал,
Интегрируема ли эта функция по Риману? Интегрируема ли она
по Лебегу? Чему равен ее интеграл Лебега на отрезке [0, 1]?
720. Пусть / (х) — неотрицательная ограниченная измеримая на
Е функция и мера множества тех точек из Е, где / (х) ^ с, равна а.
Доказать, что (L) J/ (x)dx ^ ас.
721. Чему равен интеграл Лебега на множестве [0, 1] от функции
88

f (x), равной х2 во всех точках пересечения канторова множества и
некоторого (даже и неизмеримого) множествами равнойл^ в осталь-
остальных точках отрезка [0, 1]?
722. Вычислить интеграл Лебега от функции / (х) на отрезке
[О, 1], если / (х) = 10 в точках канторова множества, а на смежных
интервалах графиком функции служат верхние полуокружности,
опирающиеся на эти интервалы, как на диаметры.
723. Вычислить (L) J/ (x)dxt если
fix) =
х2 для х иррациональных, больших, чем —,
о
чем —,
3
для х иррациональных, меньших,
0 в рациональных точках.
724. Вычислить с точностью до 0,01 интеграл Лебега от функ-
функции Зх2 на множестве £, которое получится, если из отрезка
[0, 1] выбросить интервалы 1-, if, I lf -if 1i, if ...,
1-i -if
\2n 2n —
если
725. Вычислить (L) j/ (x)dx,
sinnx для х €
f(x) =
cos ял: для х €
2'
х2 для *€D,.
где D — канторово множество, a CD — его дополнение до всего
отрезка [0, 1].
726. Обозначим через $k (x) функцию, значение которой в каж-
каждой точке х € [0, 1] равно &-му знаку в разложении числа х в
бесконечную двоичную дробь. Доказать, что
1 1
727. Обозначим через yk (x) функцию, определенную на отрез-
отрезке [0, 1] следующим образом: если на k-м месте в двоичном разложе-
разложении точки х в бесконечную двоичную дробь стоит 1, то <рл (х) = 1,
а если на fe-м месте стоит 0, то yk (х) = —1. Доказать, что система
функций {фх, ф2, ..., фл, ...} ортонормирована на отрезке [0, 1],
т. е. что
t 1
(L)|q>,(х)ф,(х)dx = 0 при iФ/, (L) J
dx=\.
728. Доказать, что если ф (х) имеет производную почти всюду
на [а, Ь] и если ф' (х) ограничена на [а, 6], то ф' (х) интегрируема по
Лебегу на [а, 6].
89

729. Пусть {fn(x)} — последовательность измеримых на Е
ограниченных неотрицательных функций. Пусть (L) yn (x)dx->0
при п-+ +°°. Следует ли из этого, что fn(x)->0 при п-+ +°°
всюду или хотя бы почти всюду на £?
730. Пусть на [а, Ь] задана измеримая ограниченная функция
с
f (х). Доказать, что если U(x)dx = 0 при любом с £ [а, &], то f(x)
а
почти всюду на [а, Ь] равна нулю.
731. Вычислить интеграл Лебега от функции ъ на интер-
■/* — 1
вале ]1, 2[.
732. Суммируемы ли функции — и — на интервале ]0, 1[?
X X
1
733. Вычислить (L)^f(x)dxy если
о
0 для x£D9
3/--
/x
Для
где D — канторово множество.
1
734. Вычислить (L) lf(x)dxy если
о
1
для х иррациональных,
х3 для х рациональных.
735. Если ограниченная функция f (х) интегрируема по Лебегу
на множестве £, то будут ли интегрируемы по Лебегу на этом мно-
множестве функции (f(x))iot \f (х)\, —?
/W
736. Доказать, что если / (х) = 0 в точках канторова множества D
1
и / (х) = п на его смежных интервалах ранга п, то (L) Г/ (x)dx = 3.
737. Доказать: «Для того чтобы неотрицательная функция / (х),
измеримая на множестве Е конечной меры, была суммируема на Е>
+ 0О
необходимо и достаточно, чтобы сходился ряд ^k • mEk, где Ек =
= £(*</(*) <£ + 1)».
738. Доказать: «Для того чтобы неотрицательная функция / (х),
измеримая на множестве Е конечной меры, была суммируема на £,
необходимо и достаточно, чтобы сходился ряд ^mEk, где Ek =
= Etf (x) > *>.
90

739. Доказать: «Если функция f(x) суммируема на отрезке
[О, а], то при любом положительном k функция / (kx) суммируема на
О, |] и $f(x)dx = j§ f(kx)dx».
740. Доказать, что функция — cos — не суммируема на ]0, 1[
X X
ни при каком k > 0.
741. Пусть на [а, 6] расположены п измеримых множеств Е1%
£2» •••, Еп\ пусть каждая точка отрезка [а, &] принадлежит по
меньшей мере q из этих множеств. Доказать, что хотя бы одне из
множеств Еъ £2, ..., £й имеет меру, большую или равную (Ь — а)—.
742. Пусть функция / (х) измерима на множестве Е конечной
меры- Доказать, что существует измеримая функция ф (х), поло-
положительная при всех х € Е и такая, что произведение / (х)у (х)
суммируемо на Е.
743. Построить на каком-нибудь множестве Е конечной меры
последовательность ограниченных измеримых функций {/„(*)}>
сходящуюся к несуммируемой на Е функции ер (х).
744. Построить на каком-нибудь множестве Е конечной ме-
меры последовательность суммируемых функций {fn{x)}> сходя-
сходящуюся почти всюду на Е к суммируемой функции ер (х) так, что
lim [fn(x)dx ф Г ф (x)dx.
745. Построить на каком-нибудь множестве Е конечной меры
последовательность суммируемых функций {fn (x)} такую, что
а) {fn (x)} сходится почти всюду к некоторой суммируемой функ-
функции ф (х);
б) lim $fn(x)dx = $<p(x)dx;
п-++оо Е Е
в) не существует суммируемой неотрицательной функции G (х)
такой, что \fn(x)\ ^ G (х) для всех п и почти всех х €■ Е.
746. Построить на како^-нибудь множестве Е конечной меры
последовательность суммируемых функций {fn (x)} такую, что
а) {fn (x)} сходится по мере к некоторой суммируемой функции
Ф (*), но не сходится к ней в обычном смысле ни в одной точке мно-
множества Е\
б) J^co[fn(x)
в) не существует суммируемой неотрицательной функции G (х)
такой, что | fn (x)\ ^ G (х) для всех п и почти всех х (£.
747. Пусть функция / (х) непрерывна всюду на отрезке [а, Ь],
91

кроме точки а. Назовем эту функцию С-интегрируемой на [а, &],
если существует конечный предел интеграла
U(x)dx <1)
при t-+a + O; если функция f (х) С-интегрируема на [а, Ь], то
предел интеграла A) называется С-интегралом (или несобственным
ь
интегралом Коши) от функции / (х) и обозначается (С) J/ (x)dx.
а
Ь Ъ
(C)lf{x)dx= lim §f(x)dx.
a f-*a+0 t
Доказать, что если непрерывная функция на ]a, b] суммируема
по Лебегу на [а, £], то она и С-интегрируема на [а, &], причем оба
интеграла равны друг другу.
748. Показать на примере, что существуют функции, непре-
непрерывные всюду на [а, &], кроме точки а, которые С-интегрируемы на
[а, 6], но не суммируемы по Лебегу на этом отрезке.

ОТВЕТЫ И УКАЗАНИЯ
К РЕШЕНИЮ
ЧАСТЬ ПЕРВАЯ
ТЕОРИЯ МНОЖЕСТВ
Глава I.
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
5. Не вытекает. Из А \ В = С вытекает лишь, что А а В [)
и с.
6. Нет; из А = В \j С вытекает лишь, что А \ В с С (рис. 5).
7. а) Равенство справедливо; б) не верно; справедливо включе-
включение A U (В \ С) =э (A U В) \ С; в) не верно; справедливо вклю-
включение (А \ В) U С =) (A U С) \ В.
10. См. рис. 6. (Аг U Л2) \ (Вг U 52) —область, заштрихо-
заштрихованная квадратной штриховкой; (Аг \ Вг) (J (Л2 \ В2) —вся
заштрихованная область. Здесь (Ах [) Л2) \ (Вг \] В2) Ф
^iAtXBJ U (А2\В2).
13. Л АХ = А означает, что (А \ X) [} (X \ А) = А. Сле-
Следовательно, X \ А = 0, т. е. та часть X, которая не входит в Л,
пуста. С другой стороны, А \ X = А, т. е. X (] А = 0, так что
та часть X, которая входит в Л, также пуста. Итак, X = 0.
15. Для случая б) см. рис. 7. Здесь (Л (J B)AF — множество,
заштрихованное квадратной штриховкой, а (ЛA/7) (J (бД^7) —
все заштрихованное множество, так что (Л |J B)&F ф (AAFy \j
U (BAF).
17. С (С (X U У) П (СХ U СГ)) - С (С (X U Y)) U С (СХ U
U ск) = (х и У) U (ccx n ссу) = (X и У) U (а: П П =
= Хи^таккакХиКэХП^.
21. а) Пусть (х, у) 6 £ X (F U G); тогда Н£, у 6 /* U G;
следовательно, у £ F или у £ G; значит, (х, у) б Е X F или
Рис. 5
Рис. 6
93

(xf у) € E X G; но в таком случае
(xy у) 6 (Е х F) U № х G),
т. е.
£x(FUG)c(£xF)U(£x G). A)
Точно так же доказывается, что
(£xf)U(£xG)c£x(FU G). B)
Сравнивая включения A) и B), получим
равенство а).
Остальные равенства доказываются
аналогично.
22. а) Справедливо для любых множеств Л, В, С, D (доказа-
(доказательство,, как в задаче 21; см. рис. 8).
б) Справедливо не для любых множеств А, В, Су D (см., напри-
например, рис. 9); однако всегда справедливо включение
(А X В) U (С X D) с: (А X С) U (В X D),
которое доказывается так же, как в задаче 21.
25. При пустом СизЛхСсибхОне следует, что А а В.
Глава II.
ВЗАИМНО ОДНОЗНАЧНОЕ
СООТВЕТСТВИЕ
27. Взаимно однозначное соответствие между множествами N
и S можно установить с помощью функции у = 2х9 где х б ТУ,
у 6S.
28. Расположим все четные числа (т. е. элементы множества
Т) в последовательность следующим образом:
О, 2, —2, 4, —4, 6, —6, ..., 2/5, — 2k, ...,
и затем каждому четному числу поставим в соответствие тот номер,
который это число занимает в данной последовательности.
29. Запишем каждое число г € Q+ в виде несократимой дроби и
назовем высотой числа г сумму числителя и знаменателя; ясно, что
Уи
Ш
A»B
(AuC)x(BuD)
АхВ
C*D
) X
94

имеется лишь конечное множество неотрицательных рациональных
чисел данной высоты. Расположим теперь все неотрицательные ра-
рациональные числа в последовательность в порядке возрастания их
высот: на первое место поместим число 0 = — (это — число высо-
высоты 1), затем — единственное число высоты 2 (число —j, далее —
/ 1 2 \
числа высоты 3 числа — и —) и т. д.; если какую-либо высоту име-
имеют несколько различных рациональных чисел, мы их располагаем
в порядке возрастания. Таким образом, все элементы множества Q+
расположатся в виде следующей последовательности:
О 1 1 2 - 3 ' 2^4151 2А*
Поставим теперь в соответствие каждому рациональному числу г
из Q4" тот номер д, который это число занимает в нашей последова-
последовательности; это соответствие является взаимно однозначным соот-
соответствием между множествами Q+ и N.
30. Не существует. Всякая функция / (х)> представимая в виде
частного от деления двух многочленов, имеет конечный или беско-
бесконечный предел при #->+оо. Если lim / (x) — q (конечное число),
#-►+00
то существует такое N, что для всех k > N имеют место неравенства:
q — 1 < f (k) < q + 1. Но тогда тем рациональным числам, ко-
которые лежат вне интервала ] q —1, q + 1[, может соответствовать
лишь конечное число номеров k (только те номера k, которые пред-
предшествуют числу ЛО- Следовательно, не все рациональные числа по-
получатся в виде значений / (k).
Если lim / (х) = оо, то рассуждения аналогичны (в этом случае
X -J.-J-OO
рациональным числам, принадлежащем фиксированному интерва-
интервалу ]—Л, Л[, может соответствовать лишь конечное число номеров k).
31. Линейное преобразование х = (b — a)t + a.
32. Функция х =dgnt.
33. Функция х = а-\- ——^arcctg/.
я
35. Выделим на интервале ]0, 1[ какукх-либо последователь-
последовательность попарно различных точек, например: хг = —, х2 = —, х3 =
Z о
== —, ... , хп = , .... Установим следующее соответствие: точ-
4 п -\- 1
ке 0 отрезка ставим в соответствие точку хх интервала; точке 1 €
1] —точку #2€] 0, 1[; точке *i=f-e[O, 1] —точку хь€
1[; точке ^2=i-g[0f 1] —точку д:4€Р, 1[; и, вообще, точ-
ке #„€[(), 1] — точку а:л+2^]0, 1[ ... . Всем остальным точкам
*€[0» 1] ставим в соответствие саму эту точку х. Полученное со-
соответствие взаимно однозначно (рис. 10).
95

Рис. 10
36. Отобразить [0, 1] на]0, 1[ (задача 35) и затем]0, 1[ на
]—оо, +оо[ (задача 32).
37. Использовать метод, которым решена задача 35.
38. Отобразить ]а, Ь[ на [а, Ь[ тем методом, каким решена зада-
задача 35, затем [а, Ь[ на [о, —Г с помощью линейной функции; наконец,
0, — на [0, +°°[ с помощью функции у = tg х.
40. Нет, так как непрерывная функция, определенная на отрез-
отрезке [а, &], должна быть ограниченной.
41. Нет; если бы существовала непрерывная функция х = ф (f),
отображающая [а, Ь]на]£, d[, то на [а, Ь~\ не нашлось бы точки t0
такой, что ш (L) =d (тогда как sup ф (t) = d). Это противоречило
к [а, щ
бы теореме о том, что непрерывная на отрезке функция достигает
на нем своей верхней грани.
42. Нет*, так как для непрерывной функции ф (t)> определенной
на [а, &], верна теорема о промежуточных значениях (в частности,
пусть ф (*х) = 1, ф (t2) = 3, где tx С [а, &], t2 б [я, 6]; тогда должна
была бы найтись точка t0 б [а, Ь] такая, что ф (£0) = 2).
43. Отображаем окружность на промежуток [0, 2я[, ставя в
соответствие каждой точке окружности численное значение угла,
составленного радиус-вектором этой точки с некоторым фиксиро-
фиксированным радиусом. Затем промежуток [0, 2я[ линейным преобразова-
преобразованием отображаем на промежуток [0, 1[; наконец, последний про-
промежуток отображаем на [0, 1] методом, рассмотренным в задаче 35.
44. Сначала отображаем открытый круг х2 + у2 < 1 на круг с
выколотым центром 0 < х2 + у2 < 1. Для этого выделяем в от-
открытом круге какую-либо последовательность попарно различных
точек Мо, Мъ Мъ ..., Mkf ..,, где Мо — центр круга, и устанавли-
устанавливаем следующее соответствие: каждой точке Mk из круга х2 + у1 <
< 1 ставим в соответствие точку Mk+1 из круга с выколотым цен-
центром. Остальные точки обоих кругов (т. е. точки, отличные от всех
Mk) ставим в соответствие по принципу идентичности (т. е. каждой
точке N (х, у) из первого круга ставим в соответствие точку N'
с теми же координатами из второго круга) (рис. И).
Затем открытый круг с выколотой точкой отображаем на до-
дополнение к замкнутому кругу с помощью инверсии: через произ-
96

Рис. 11
вольную точку М из круга и центр О Проводим луч ОМ и на его
продолжении находим точку М* такую, что ОМ • ОМ' = 1. Тогда
точке М из круга с выколотым центром ставится в соответствие точ-
точка М' из дополнения к замкнутому кругу (рис. 12). Это соответствие
взаимно однозначно.
45. Использовать метод решения задачи 35 для каждого отрез-
отрезка, являющегося радиусом круга.
46. См. задачу 44.
47. Отобразить замкнутый круг на открытый (см. задачу 45),
затем открытый — на дополнение к замкнутому (задача 44).
48. См. решение задачи 43 или задач 49 и 50.
49. Отображение производится с помощью так называемой
«стереографической проекции». Обозначим через Ро выколотую точ-
точку на сфере, а через Мо диаметрально противоположную ей точку
на сфере. Построим плоскость, касающуюся сферы в точке Мо.
Далее проведем прямую через точку Ро и произвольную точку М
сферы. Точку N, в которой эта прямая пересечет плоскость, ставим
в соответствие точке М. Полученное соответствие взаимно однознач-
однозначно (рис. 13).
Рис. 12
Рис. 13
97

50. Отобразим сначала всю сферу на сферу с выколотой точкой
(это можно сделать тем же способом, каким круг отображался на
круг с выколотым центром, см. решение задачи 44). Затем сферу с
выколотой точкой отображаем на плоскость с помощью стереографи-
стереографической проекции.
51. Помещаем центр круга в точку О и устанавливаем взаимно
однозначное соответствие между точками отрезка ОМ (где М —
произвольная точка границы звездной области) и точками того ра-
радиуса ОБ, который лежит на луче ОМ\ соответствие устанавливаем
так, чтобы точка О соответствовала самой себе.
52. Выделим в множестве А иррациональных чисел какую-либо
последовательность попарно различных чисел, например У~2,
2]/г2> 3 ]/!2, ..., п ]/2, ..., рассмотрим множество R всех действи-
действительных чисел и множество Q всех рациональных чисел; рациональ-
рациональные числа занумеруем: гъ г2, г3, ..., гп, ...; множество всех чисел
вида д]/г2 обозначим через L; множество всех иррациональных
чисел, не представимых в виде п \^2 (п > 0, целое), обозначим че-
через С. Тогда
А = С U U R = С U (L U Q)>
Элементы множества L ставим %во взаимно однозначное соответствие
элементам множества L [] Q, например, следующим способом:
L: FT 2J/T ЗК2" 4J/T... Bk — \)Уг 26J/2"..
L{]Q: г, V2 r2 2/2~... rk kV2 ...
Точки множества С ставим в соответствие сами себе. В итоге полу-
получится взаимное однозйачное соответствие между А и JR.
53. а) Каждой точке (£, ц) прямоугольника ]а, Ь[ х ]с, d[ ста-
ставим в соответствие точку (х, у) квадрата! — —, — | х I — —, —
следующим образом:
2 ^ Ь-а * 2 ^ d—c
б) Каждой точке (х, у) квадрата — —* — х — —; — I
J 2 2[J 2 2 [
ставим в соответствие точку (X, Y) плоскости следующим образом:
X = tg xy Y = tg у.
в) См. а) и б).
54. Не все: не получится ни одной точки, разложение которой
в бесконечную десятичную дробь содержит нули на всех четных
местах, начиная с некоторого номера; например, не получится точ-
точка 0,35703070... Итак, это не будет взаимно однозначным соответ-
соответствием между Точками квадрата ]0, 1] X ]0, 1] и промежутка ]0, 1].
Однако это соответствие является взаимно однозначным между точ-
п

ками квадрата и точками некоторого подмножества промежутка
30,1].
55. Перенумеруем все рациональные числа отрезка [0, 1];
Гц r2t ..., гп9 ... A)
Все точки квадрата с рациональными координатами расположим в
следующую таблицу:
(>i> гг) (Гъ r2) (rl9 г3) .,.
{Гъ П) (>*2. Г*) fo. Гз) ...
(г89 гх) (г,, г2) (г3, г3) ...
^4> rl) (U. Гг) (Г4, Г3) ...
Выпишем все точки из этой таблицы в одну последовательность в
следующем порядке; сначала (гъ rt)y затем точки, у которых сумма
индексов абсциссы и ординаты равна 3; точки, у которых сумма
индексов равна 4, и т. д., т. е.
(>ъ гг), (гх, г2), (г* гг), (гъ г3), (г2, Гз), (r3, /i), (rlf r4), (r2, r3), ... B)
Теперь устанавливаем взаимно однозначное соответствие между
членами последовательности A) и членами последовательности B)
обычным способом: п-му члену последовательности A) ставим в со-
соответствие п-й член последовательности B).
56. Указание. Установите взаимно однозначное соответ-
соответствие между множеством всех квадратов ]га, т + 1] X ]я, п + 1] и
множеством всех промежутков ]р, р + 1] (где т, nf p — всевозмож-
всевозможные целые числа). Затем установите взаимно однозначное соответ-
соответствие между множеством точек квадрата ]ту т + 1] X ]л, п + 1]
с рациональными координатами и множеством рациональных тачек
соответствующего промежутка.
57. Указание. Всякий многочлен с рациональными коэф-
коэффициентами можно представить в виде частного от делений много-
многочлена с целыми коэффициентами на натуральное число.
58. Установим сначала взаимно однозначное соответствие между
совокупностью всех конечных подмножеств натурального ряда м
множеством всех двоично рациональных точек промежутка [0; 1[:
каждому конечному множеству {п19 п2, ..., nk} (где пг <й% < ...
••• < nk) ставим в соответствие двоичную дробь, у которой на ме-
местах с номерами nlt пг, ..., nk после запятой стоят единицы, а на
остальных местах —нули; например, множеству {2t 3, 5} соответ-
соответствует двоичная дробь 0,01101, т. е. двоично рациональная точка
1 + 1 + 1= L3
22 2* 25 32'
После того как такое соответствие установлено, остается только
перенумеровать все двоично рациональные точки промежутка [0, 1[.
Это можно сделать, например, следующим образом:
oj L 1 1 А А 1 J i-i! LJLii ii
' 2* 22 ' 22 ' 23 ' 23 ' 23 ' 23 f 24 * 24 ' 24 ' 24 ' ~2*9 24 ' 24 ' **"
99

Тем самым множество двоично рациональных чисел промежутка
[0; 1[ поставлено во взаимно однозначное соответствие с множе-
множеством всех натуральных чисел.
59. Каждой последовательности натуральных чисел
ставим в соответствие возрастающую последовательность натураль-
натуральных чисел
тг < т2 < т3 < ... < тл < ...,
где
тг = пъ т2 =пг + п2, т3 = пг + п2 + п3, ..., mk = пг + ...
... + nk9 ...
Это соответстрие взаимно однозначно.
60. Последовательности пг < п2 < п3 < ... < nk < ... ставим
в соответствие бесконечную двоичную дробь, у которой после запя-
запятой на местах с номерами пъ пъ п3, ..., nk> ... стоят единицы, а на
остальных местах — нули (ср. с решением задачи 58).
Глава ПК
МОЩНОСТЬ МНОЖЕСТВ
61. Множество счетно.
62. Множество счетно.
64. Множества счетны (см. для случая р = 2 решение задачи 58).
65. Множество счетно.
66. Обозначим через Еп(п^ 1) множество тех элементов из £,
которые превосходят —, а через В — множество всех отличных от
п
нуля элементов из Е. Ясно, что ЦЕп = В. Если бы В было несчет-
п
ным, то хотя бы одно из Еп, например Еп , тоже было бы несчет-
несчетным. Но тогда конечные суммы из Е будут сколь угодно велики
(так как сумма р элементов из Е превосходит —, а — стремится
п0
nQ п0
к бесконечности при р->+оо). Итак, В не может быть несчетным.
Значит, оно конечно или счетно.
67. Заметим, что каждая точка разрыва х0 монотонно возрастаю--
щей функции / (х) является точкой разрыва первого рода. Действи-
Действительно, так как функция / (х) монотонна и ограничена на [а, #0[,
то она имеет предел при х -> х0 — 0; аналогично этому проверяется,
что функция / (х) имеет предел и при х -> х0 + 0.
Назовем скачком функции в точке разрыва х0 разность / (х^ +
+ 0) — f (х0 — 0) этих пределов. В каждой точке разрыва моно-
монотонно возрастающей функции скачок положителен. Легко прове-
проверить, что множество точек разрыва, в которых скачок больше а
(где а — какое-либо положительное число), конечно, а число этих
точек не больше чем' * ' ~~ ^ . Обозначим через Ек множество точек
100

разрыва со скачком, большим чем —. Множество Е всех точек раз-
k
рыва равно объединению всех Ek\
Е = Ег U E2 U Е3 U - U Ek U ...
Так как все Ek конечны, то Е не более чем счетно.
Для монотонно убывающей #а [а, 6] функции доказательство
аналогично.
68. Обозначим через At множество точек разрыва функции на
отрезке [—/, /]. Множество А всех точек разрыва (на всей числовой
прямой) равно объединению всех At:
А =Аг U A2 U - U At U ...;
каждое At tie более чем счетно (см. задачу 67). Объединение счетного
числа таких слагаемых также является не более чем счетным множе-
множеством. Итак, А не более чем счетно.
69. Положим Еп= Е п]-^-, +<*>[. Ясно, что [)Еп = Е, так
J п I
[
I
как
]
=£ПЗО,
Если бы все Еп были не более чем счетны, то и их объединение, т. е.
множество С, было бы не более чем счетно; но Е по условию несчет-
несчетно. Следовательно, по крайней мере одно из Еп несчетно.
70. Неверно. Пример. Е = И, 1,1,1, ..., 1, ... ]. Са-
[234 п )
мо множество Е бесконечно; однако для любого т > 0 множество
Е П ]т> +°°С конечно.
71. Можно. В качестве а можно взять любое положительное
число, отличное от всех чисел | xt — Xj \ (где {х1у х2, х3у ..., хь ...} —
данное множество Е). Различных чисел \xt — Xj \ счетное множество.
Поэтому всегда найдется число а > 0, отличное от всех | xt — Xj\.
72. Можно. См. решение задачи 71.
73. Разобьем прямую на счетное множество отрезков точками 0,
±1, ±2, ±3, ... Каждый отрезок содержит не более одной точки
данного множества; следовательно, между точками множества Е
и некоторой совокупностью построенных отрезков существует вза-
взаимно однозначное соответствие. Значит, множество Е не более чем
счетно.
74. Указание. Разбейте плоскость прямыми х = const и
у = const на счетное множество квадратов со стороной -тг=. Да-
Далее см. решение задачи 73.
75. Обозначим замкнутый круг радиуса г буквой Л, открытый
круг с тем же центром и того же радиуса буквой £, а замкнутый
круг радиуса — с тем же центром буквой С. Тогда A id В zd С
Множества А я С эквиваленты (взаимно однозначное соответствие
101

между ними устанавливается с помощью преобразования подобия.
Из эквивалентности множеств А и С вытекает (на основании тео-
теоремы Кантора — Бернштейна), что А эквивалентно В.
76. Если А — вся плоскость, В — замкнутый квадрат, С —
включенный в него открытый квадрат, то A zd В :э С. Но А экви-
эквивалентно С (см. задачу 53, в). Следовательно, А эквивалентно В.
78. См. задачу 58.
79. Мощность континуума (см. задачу 60).
80. Мощность континуума (см. задачи 79 и 59).
81. Перестановка натурального ряда есть последовательность
натуральных чисел, элементы которой попарно различны и в сово-
совокупности исчерпывают весь натуральный ряд. Поэтому множество
всех перестановок натурального ряда, как часть множества всех
последовательностей натуральных чисел, имеет мощность, не пре-
превосходящую мощность континуума (см. задачу 80).
Докажем теперь, что мощность множества всех перестановок на-
натурального ряда не меньше мощности континуума. Назовем пере-
перестановку множества полной, если при ней не остается «неподвижным»
ни один элемент множества. Как легко видеть, каждое множество
натуральных чисел, содержащее более одного элемента, допускает
полную перестановку. Поставим в соответствие каждому множеству
М а N \ {1, 2} (где N— множество всех натуральных чисел)
перестановку натурального ряда, оставляющую все элементы из М
на месте и подвергающую N\ M какой-либо полной перестановке
(множество N\ M допускает полную перестановку, так как оно
состоит более чем из одного элемента). Тогда разным М будут со-
соответствовать разные перестановки, поскольку у этих перестановок
различны множества их неподвижных элементов. Поэтому мощность
множества всех перестановок натурального ряда не меньше мощно-
мощности множества всех подмножеств счетного множества N \ {1,2},
т. е. не меньше мощности континуума.
82. Мощность континуума. Действительно, множество всех ко-
конечных последовательностей действительных чисел есть объединение
-foo
[}Ani где Ап—множество всех последовательностей длины я.
Так как Ап = В X ... х В, где В — множество всех действитель-
п раз
ных чисел, и так как В ~ ]0, 1], то Ап эквивалентно множеству
]0, 1] X ... X ]0, 1]. Но последнее множество эквивалентно ]0, 1]
(это получается по индукции, см. задачу 77). Значит, Ап имеет мощ-
мощность континуума и потому эквивалентно промежутку ]/г — 1, я].
-foo
А тогда [)Ап(т- е- множество всех конечных последовательностей
п=1
действительных чисел) эквивалентно множеству ]0, 1]1)]1» 2] U
=]0, +оо[ и, следовательно, имеет мощность континуума.
83. Обозначим через Ek множество всех тех стационарных после-
последовательностей натуральных чисел, у которых члены, начиная с
102

некоторого номера, равны к. Множество Ek счетно. Действительно,
каждая последовательность из Ek> отличная от (fe, fe, ...), предста-
вима в виде (аъ аъ ..., ат, k, fe, ...), где ат Ф k\ но такой последо-
последовательности можно поставить в соответствие конечную последова-
последовательность из натуральных чисел (аъ а2, ..., ат)\ множество же таких
конечных последовательностей, как легко видеть, счетно. Теперь
остается заметить, что Е = [}Ek.
к
84. См. решение задачи 83 (использовать задачу 82).
85, 86. Мощность континуума.
87. Мощность континуума. Указание. Установите взаимно
однозначное соответствие между множеством всех рациональных
чисел и множеством всех натуральных чисел. Тем самым установит-
установится взаимно однозначное соответствие между множеством всех по-
последовательностей натуральных чисел. Далее см. задачу 80.
88. Мощность континуума.
89. Мощность континуума (каждому отрезку [а, Ь~\ соответствует
точка с координатами а, Ь на полуплоскости у > х\ это соответствие
взаимно однозначно, а множество точек полуплоскости у > х име-
имеет мощность континуума).
90. Мощность этого множества конечна или счетна.
91. Мощность континуума. Указание. Каждому кругу
(х — аJ + (у — bJ ^ #2 поставьте в соответствие точку трехмер-
трехмерного пространства с координатами a,b,Rn затем найдите мощность
полученного множества точек пространства.
92. Может; например, множество всех окружностей, имеющих
общий центр.
93. Любое множество попарно не пересекающихся букв Т будет
не более чем счетным. Докажем это. Поставим в соответствие каждой
букве Т из данного множества тройку рациональных точек М, N, Р
на пдоскости так, чтобы отрезок MN пересекал ножку буквы Т,
а отрезки МР и NP пересекали боковые отростки этой буквы {ркс.
14). Тогда одаой и той же тройке рациональных точек М, N, Р
может соответствовать не более одной буквы Т (легко доказать, что
если бы этой тройке соответствовали две различные буквы Т, то
они бы пересекались). Итак, между заданным множеством букв Т
и некоторым множеством троек рациональных точек на плоскости
установлено взаимно однозначное соответ-
соответствие. Так как множество таких троек не
более чем счетно, то и множество попарно ^
не пересекающих букв Т не более чем
счетно.
94. Такое множество может иметь лю-
любую мощность, меньшую или равную мощ-
мощности континуума. Для того чтобы в, этом
убедиться, построим произвольное мно- ^..
жество Е на прямой у = —х и через каж-
каждую точку этого множества проведем бук- Рис. 14
УОЗ

ву Г, приняв эту точку за вершину угла
буквы Г и направив отрезки буквы Г парал-
параллельно осям координат (рис. 15). Все пост-
построенные буквы будут попарно не пересека-
пересекающимися, и множество этих букв имеет
мощность, равную мощности множества Е.
95. Мощность континуума. Действитель-
Действительно, пусть х19 хъ х3, ... —произвольная пос-
последовательность действительных чисел. В
силу результата задачи 80, каждому числу
р 1С ^„(л =1, 2, 3, ...) соответствует после-
ис' довательность натуральных чисел сп , сп ,
сп , ... Перенумеруем Множество всех пар натуральных чисел \п, т)\
(пъ mi), (n2t /п2), (/г3, т3), ... (это возможно, так как множество таких
пар счетно и поставим в соответствие последовательности хъ x2ix3i ...
последовательность натуральных чисел спт, спт, спт, ... Как
легко видеть, тем самым устанавливается взаимно однозначное со-
соответствие между множеством всех последовательностей действи-
действительных чисел и множеством всех последовательностей натуральных
чисел. Значит, в силу результата задачи 80, рассматриваемое мно-
множество имеет мощность континуума.
96. Мощность континуума.
97. Мощность этого множества не меньше мощности гипер-
гиперконтинуума. Действительно, множество функций на [а, &], прини-
принимающих всего два значения: 0 и 1, уже имеет мощность гиперконти-
гиперконтинуума, так как множество этих функций находится во взаимно одно-
однозначном соответствии с множеством всех подмножеств отрезка
[а, Ь] (каждой такой функции ставим в соответствие множество всех
тех точек отрезка [а, &], в которых она равна нулю).
С другой стороны, каждой числовой функции Д определенной
на [а, &], соответствует ее график, т. е. множество точек плоскости
вида (jc, / (*)), где х пробегает отрезок [а, &]; при этом разным функ-
функциям соответствуют разные графики.Следовательно, мощность мно-
множества всех числовых функций на [а, Ь] не больше мощности множе-
множества всех подмножеств ллоскости, т. е. не больше мощности гипер-
гиперконтинуума.
Применяя теорему Кантора — Бернштейна, получаем требуемый
результат.
98. Рассмотрим множество Q рсех рациональных точек отрезка
[а, &], занумерованное каким-либо образом: Q = {гъ г2, ...}. По-
Поставим в соответствие каждой непрерывной на [а, &] функции /
последовательность действительных чисел / (гх), / (г2), ... Так как
непрерывная функция на [а, Ь~] полностью определяется своими зна-
значениями в точках множества Q, татем самым устанавливается вза-
взаимно однозначное соответствие между множеством всех непрерывных
функций на£а, Ь~] и частью множества всех последовательностей дей-
действительных чисел. Значит, в силу результата задачи 95, мощность
104

множества всех непрерывных функций на [а, Ь] не больше мощности
континуума. С другой стороны, она и не меньше мощности контину-
континуума, так как все функции, постоянные на отрезке [а, &], уже обра-
образуют множество мощности континуума. Остается применить теорему
Кантора — Бернштейна.
99. Мощность гиперконтинуума.
100. Обозначим через А множество всех функций вида kx,
где k > 0; через В множество всех строго возрастающих непрерыв-
непрерывных функций; через С множество всех непрерывных функций. Тогда
А а В а С. Но Л и С имеют мощность континуума; следователь-
следовательно, В также имеет мощность континуума.
101. Мощность континуума. Указание. Учтите, что мно-
множество всех точек разрыва монотонной функции не более чем счет-
счетно и что у такой функции все точки разрыва являются точками раз-
разрыва первого рода (см. решение задачи 67), а также то, что множе-
множество всех счетных подмножеств отрезка [а, Ь] имеет мощность кон-
континуума (задача 96).
102. Мощность континуума.
104. Мощность континуума. Для доказательства установим
взаимно однозначное соответствие между множеством А всех беско-
бесконечных десятичных дробей, в десятичном разложении которых от-
отсутствует 7, и множеством В всех бесконечных девятирич-
ных дробей на отрезке [О, 1]: каждой десятичной дроби из А
ставим в соответствие дробь из В, которая получится из первой дро-
дроби, если в ней повсюду цифру 9 заменить цифрой 7. Это соответствие
взаимно однозначно. Но В = [0, 1] = с; следовательно, А = с.
105. Мощность континуума. Взаимно однозначное соответствие
между множеством А десятичных дробей указанного вида и множе-
множеством В всех десятичных дробей устанавливаем следующим обра-
образом: каждой бесконечной дроби из А ставим в соответствие беско-
бесконечную дробь, получающуюся из лее вычеркиванием цифры, стоя-
стоящей на третьем месте, например: дроби х =0,257361... 6 А соот-
соответствует дробь у := 0,25361... е В] дроби х = 0,237758... С А
соответствует дробь у =0,23758... € В. Множество В имеет мощ-
мощность континуума; следовательно, А также имеет мощность конти-
континуума.
106. Мощность континуума.
107. Мощность континуума (см. задачу 104).
108. Да; любое множество А \ С, где С — какое-либо конечное
подмножество множества Л, эквивалентно В.
109. А = (А \ В) U (А П Я); В = (В \ А) [] (А (] В). При
этом А \ В и А П В не имеют общих точек, так же, как и множе-
множества В \ А и А П В. Так как А\ В ~ В\ А по условию и
А П В ~ А П В, то А — £.
110. В условии задачи имеют место легко проверяемые соот-
соотношения:
В =А {) (В\А), A)
В U С = (A U (С \ В)) U (В \ А). B)
105

Объединяемые множества в правой части равенства (I) не имеют
общих точек; то же верно и для правой части равенства B). Множе-
Множества А и A U (С \ В) эквивалентны; это следует из того, что А а
си A U (С \ В) с= A U Си что по условию А ~~ A U С. Итак,
А ~ A U (С \ В). Из этого соотношения, а также из равенств A)
и B) вытекает, что В — В [} 'С.
111. Неверно. Пример:
А = {1, 2, 3, 4, ...}, В « {2, 3, 4, ...}, С = Л, D - {3, 4, 5, ...}.
Здесь А — С, В — D, Л =э В, С =э D, но А \ В не эквивалентно
С \ D (Л \ В состоит из одного элемента, а С \ D — из двух).
ИЗ, 114. Не верньк
116. Мощность континуума.
117. Обозначим через С круг радиуса п с центром в начале ко-
координат. Ясно, что
Если бы все Сп {] Е были не более чем счетны, то таким же было
бы и множество Е; но, по условию, Е несчетно; следовательно, хотя
бы одно из множеств Сп [\ Е несчетно.
Глава IV.
МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
118. Нет, не является (не выполнена уже аксиома тождества:
из равенства sin2 (х — у) = 0 не вытекает, что х = у; нетрудно ви-
видеть, что не выполнена и аксиома треугольника).
119. Выполнение первых двух аксиом метрики очевидно. Чтобы
проверить третью, надо сначала доказать, что для любых а ^ О,
р ^ 0 имеет место неравенство arctg a + arctg p ^ arctg (а + Р)
(для этого достатрчно доказать, что при фиксированном р > 0 функ-
функция f (a) = arctg а + arctg р — arctg (а + Р) возрастает: так как
f @) = 0, то при а >0 / (а) > 0). Метрики рх и р эквивалентны, так
как из arctg \хп — а\ -> 6 следует: \хп — а\ -> 0, и обратно.
Покажем, что числовая прямая с метрикой рх является полным
метрическим пространством. Пусть\хп\ — фундаментальная после-
последовательность в этом пространстве. Для произвольного е > 0 вы-
выберем 6 > 0 так, чтобы при | х\< 6 было tg \x\ < е. Далее для это-
этого б выберем номер N такой, что при nt m ^ N выполняется нера-
неравенство arctg \хп — хт\ < б (это можно сделать, так как последова-
последовательность {хп} фундаментальна). Тогда
для любых nt т^ N. Следовательно, {хп} фундаментальна и в
метрике р, а потому имеет предел lim xn = а. Число а будет преде-
П-+оо
лом данной последовательности и в метрике рх, поскольку метрики
pt и р эквивалентны.
106

120. Да. Выполнение аксиомы треугольника следует из нера-
неравенства Va + Р < Кос + Кр, которое имеет место при любых а >
^ 0, р ^ 0 (проверяется это неравенство извлечением квадратного
корня из обеих частей очевидного неравенства а + р<^а + Р +
121. Эквивалентность метрик ръ р2 и р3 следует иа неравенств
|я2 ~ «il + \b2 — fell < 2 max {[a2 — aj, |62 — fej} <
< 2 /|aa - atf + |6, - fexl2 < 2 (|a2 - аг\ + \b2 - b±\)9 A)
справедливых для любых действительных чисел аъ a2i Ьъ Ь2.
Пространства (X, р3) полно, так как это евклидово пространство
/?2. Если последовательность {xn(ani bn)} фундаментальна в мет-
метрике р! (или р2), то из неравенств A) следует, что {хп } фундамен-
фундаментальна в метрике р3, а значит, {хп } сходится в метрике р3. Тогда
{хп } будет сходиться к тому же пределу и в метрике рг (соответ-
(соответственно и в метрике р2) в силу эквивалентности метрик.
122. Да.
123. (X, рх) и (X, р2) — метрические пространства. (X, р3) не
является метрическим пространством; здесь не выполнена аксиома
тождества: прямые
1г: х cos а + у sin а — р = 0; /2: х cos (я—а) + у sin (я—а)—р =0
не совпадают, тогда как р3 (/ь /2) = 0; с другой стороны, прямые
Ьг\ х cos а + у sin а = 0; L2: x cos (я + а) + у sin (я + а) =0
совпадают, хотя р3 (Ьъ L2) =2 | sin a|=£0 (при 0 < а < я).
Пространства (X, рг) и (X, р2) полны. Действительно, если
{1п (ап , рп)} — фундаментальная последовательность в (X, рг)
(или в (X, р2)), то {ап } и {рп } — фундаментальные числовые после-
последовательности. Пусть аоирв — их пределы и
/в: х cos а0 + у sin а0 — р0 = 0.
Тогда рх Aп , /0) -> 0 (соответственно р2 Aп , /0) -> 0).
124. Это семейство не является метрическим пространством,
если X состоит более чем из одной точки. Действительно, тогда най-
найдутся Е cz Хи F а Xтакие, чтоЕ П F ф 0(и, значит, р (Е, F) =
= 0), но Е ф F.
125. Пространство (X, р) полно, так как любая фундаментальная
последовательность в нем стационарна (т. е. все члены ее, начиная
с некоторого номера, совпадают).
126. Прежде всего докажем, что для любых последовательно-
последовательностей х (аъ аъ ...) и у {Ьъ Ь2, ...)> У которых ряд из модулей членов
сходится, расстояние р (х, у) будет определено. Действительно,
ряд 2 Iai — bi\ сходится, так как | а{ — bL\ < | aj + Ibt\, а ряды
2 1^1 и 2 1^1 сходятся по условию.
1=1 1=1
Для проверки выполнения аксиомы треугольника (выполнение
первых двух аксиом очевидно) заметим, что для любого номера i
107

и любого числа с.
к — М < I at — ci\ + \°i —
а потому
т. e. p (x, y) < p (*, г) + p (z, у), где 2: ^ z (q, c2t ...).
127. Условие задачи не является достаточным для сходимости в
пространстве lv Пример. Пусть а = @, 0, ..., О, ...) и хп =
= fo,O, -, О, |. £, .... ^ ..Л Тогда \хп.-а£\ = 0 при я > *
п раз
и, следовательно, at. = Hm x . для любого /. Однако р (х , а) =
tt-»-foo Л
4-оо -j-oo
^ ~01 =2^ =! при любом п-
il k=l
128. Пусть {xn(xnVxn2, ..., лгт., ...)}— фундаментальная после-
последовательность элементов пространства /1# По определению, для лю-
любого е > 0 найдется номер N такой, что при любых п^ N, m ^ N
имеет место:
4-О0
2 \хпк — хтк\<в. A)
fe=l
Из неравенства \хы —xmt\ ^ 2 Кл —^1 слеДУет> что числовая
последовательность {xni}+^ при любом t фундаментальна и, зна-
значит, сходится. Пусть at = lim хпГ Покажем, что а (аъ ..., an,...)^'i
и хп-> а в 11и
к
Действительно, из неравенства A) следует, что 2 \xnk —
k=i
— xmk\ < 8 Для любого /С и всех п, т^ N. Переходя в этом нера-
неравенстве к пределу сначала при т~>- +оо, а затем при К -> +оо.
получим:
S|^*-a*|<e B)
для всех п^ N. Так как \ak\ ^\xnk —ak\ + \xnk\, то из нера-
венства B) и сходимости ряда 2 1#/гл1слеДУет» что РЯД S \ак\ сх0"
дится, т. е. а € /х. А тогда B) показывает, что хп*+ а.
129. Выполнение первых двух аксибм в М (Е) очевидно. Про-
Проверим выполнение аксиомы треугольника. Для любых ограниченных
функций ф, я|) и % на Е имеем:
108

р(Ф,г|)) =su| 1Ф(О—Ф@1<
< sup (|Ф @ - X @1 + IX @ -♦ Ml) <
< sup | Ф (t) - х @1 + sup | х @ —Ф @1 = P (Ф, X) + P (X, Ф).
HE t*E
Докажем, что пространство М (Е) полно. Пусть {$п} —фунда-
—фундаментальная последовательность функций из М (£). Тогда в каждой
точке t б Е числовая последовательность {фл@} фундаментальна
и, следовательно, стремится к некоторому пределу ф (/). Для задан-
заданного 8 > 0 найдем номер N такой, что sup |фя@ — фт @1 < 8
НЕ
для всех я, т > N. Переходя к пределу при т ->- +°° в неравен-
неравенстве | фЛ @ — Фт @1 < s, получаем:
1ФЛ0-ФЧ0К*
для всех п > N и t € Е. Отсюда легко следует, что ф€ М (£);
а так как 8 > 0 произвольно, то отсюда же следует, что фЛ сходится
к <р по метрике пространства М (Е).
130. Пусть {фЛ} — фундаментальная последовательность в
С [а, Ь]. Тогда в каждой точке х € [а, Ь] существует lim фя (х);
обозначим его ф (х). Для каждого 8 > 0 существует N такое, что
1фл (*) — Фт (х)\ < е Для всех Л1 tn > N к всех я б [а, Ь]. Беря
здесь /п~> +оо, получим в пределе |фя(я) — ф (jc)| ^ 8 для всех
п > N и всех х € [а, ft]. Тем самым Фя-^ ф равномерно на [a, ft].
Taii как все фл непрерывны, то отсюда заключаем, что ф также не-
непрерывна. Следовательно, ф б С [a, ft] и фл->ф по метрике про-
пространства С [a, ft].
131. Если ряды 2#? и 2^? сходятся, то и ряд 2 (а* — ^iJ схо-
i i i
дится; это следует из того, что
(а* — Ь^ = aui— 2a-pt + ft? <а? + (а? + ft?) + ft? - 2 (а? + ft?).
Выполнение первых двух аксиом метрического пространства оче-
очевидно. Третья аксиома проверяется так: для я-мерного евклидова
пространства справедливо неравенство
1/
f
2j (at — by ^ I/ 2j {a-t — CiY +1/ JL (Ci — ftz) .
Переходя в этом неравенстве к пределу при п -> +оо, получаем*
/-f-oo / -f-oo / -f-oo
Sta-ад^У 2(^-^J+1/ 2(^-^J.
t=i ^ t=i r 1=1
Доказательство полноты пространства /2 аналогично доказатель-
доказательству полноты пространства /х (см. решение задачи 128); только на
последнем шаге цадо вместо неравенства | ah\ ^ \xnk — ak\ + \xnk\
воспользоваться неравенством
10?

132. Аксиома треугольника проверяется интегрированием (в
границах от а до Ь) неравенства
I Ф (х) -ф (х)\ < |Ф (х) - Х Ml + Ix (х) -гр (х)\.
Метрики в пространствах С [а, Ь] и С7 [а, Ь] не эквивалентны.
Например, последовательность функций
заданных на [0, 1], сходится к ф(л:) = 0 в метрике пространства
С [О, 1], но не сходится вообще в пространстве С[0,1]- Аналогично
строится пример для произвольного отрезка [а, 6].
133. Да. Действительно, умножая в неравенстве Коши —Буня-
козского обе части на 2 и затем прибавляя к обеим частям
ь ь
I (ф (*)J dx + I (Ф (x))*dx, получим после преобразований:
Пусть теперь и, v и w — произвольные непрерывные функции на
[а, &]; подставляя в последнее неравенство ф = и —1>, ty =v — w,
получим:
p (и, ш)< р (a, v) + р (а, ш),
т. е. аксиома треугольника выполнена. Выполнение аксиомы сим-
симметрии очевидно. Легко проверяется и выполнение аксиомы тож-
тождества.
134. Выполнение первых двух аксиом метрики очевидно. Спра-
Справедливость аксиомы треугольника вытекает из неравенств
sup (]/х (х) -h (х)\ + |ft (х) -g2 (х)\) <
< SUg (Jf, (X) - /, (Х)\ + \f$ (X) - f% (Х)\ + |ft {X) ~g3 (X)] +
+ T£E) -«. wd <^suP ад (x) - f3 wi + igi (x) - g3 wo -f
+ sup (I/, W -Ш\\ \8г (х) -g, Ml).
*£ [a. 6]
Далее, если {(/„, grt)}—фундаментальная последовательность а
F\_a, b\ то {/я} и (gn) —фундаментальные последовательности в
С [а, Ь\ а стало быть, сходятся в С [а, Ь]. Обозначим предельные
функции соответственно / и g. Из неравенства
р ((/«, в«). (/, е)) < sup |/я w - / WI + sup \gn (х) -g(x)\
лге [a. b] xz [а. Щ
следует, что р ((fnf gn)y (/, g)) -► 0 при п -* оо. Таким образом,
Z7^, Ь] —ь полное пространство.
135. Вот пример фундаментальной последовательности функций
из С [а, 6], не имеющей предела & этом пространстве:
ив

о
линейна при ^i^ b—ji < х < 'Lkl.
г 2 л 2 ^ 2
136. См. решение задачи 135.
137. Пусть {fn} — фундаментальная последовательность функ-
функций из Е и / — ее предел в С [а, 6]. Так как А ^ fn (x) ^ В для
всех п и всех х d[a, ft], a / (х) =\\mfn (x) в каждой точке
л: € [а, 6], то и Л ^ / (#)<!£ в каждой точке X 6 [а, &], т. е. / 6 £.
Следовательно, £ тюлно.
138. См. решение задачи 137.
139. Не следует. Например, в промежутке т= , — обыч-
J 2 2 (^
ная метрика рг (х, у) = \х — у\ и метрика р2 (х, у) = \tgx — tg y|
эквивалентны, однако пространство (т, pj) не полно, тогда как (т, р2)
изометрично числовой прямой и потому полно.
140. Достаточность неравенств для эквивалентности метрик рг
и р2 очевидна. То, что эти неравенства не являются необходимыми,
показывает пример, построенный в решении задачи 139.
141. В соответствий с задачей 140 эквивалентность метрик рг
и р2 в пространстве Сг следует из неравенств
jjup6j|/ (x) -g(x)\+\f (x) -g' Ml) < sup \f(x)-g(x)\ +
+ sup I/' (x) -g' Wl< 2 sup (\f(x)-g (x)\ + I/' (x) -g' Ml).
л£[а, fc) x£[a, b]
Докажем полноту пространства (Ci, Pi). Пусть {/я} — фундамен-
тальная последовательность в (Clf Pi). Тогда {/л} и {/^} — фун-
фундаментальные и, значит, сходящиеся последовательности в С [а, Ь].
Пусть /и g — их пределы, т. е. {fn } равномерно сходится к / на
[а, Ь], а {/^} — Kg. Как известно из курса анализа, в этом случае
g =f'. Следовательно, {/„} сходится к /в (С1э р^ и тем самым
(Clf pi) полно.
Полнота пространства (Съ р2) доказьгеается аналогично.
142. Докажем, что расстояние между классами Л и В не зависит
от выбора точек а 6 А и b € В. Пусть а1 6 Л и 6' € В. Тогда
Р (я', Ь') < Р (я\ я) + Р (а, Ъ) + р F, &') = р (а, ft).
Аналогично р (а, Ь) ^ р (а', 6') и, значит, р {а, Ъ) = р («', Ь').
Далее, )если а € Л и & € В, А ф В, то по определению р (а, Ь) ф 0.
Следовательно, аксиома тождества выполняется. Выполнение осталь-
остальных аксиом метрики очевидно.
143. Не будет (не выполняется первая аксиома метрики). Раз-
Разбиение множества X на классы следует произвести так, чтобы функ-
функции из одного класса отличались друг от друга на постоянную.
144. Выполнение аксиом метрики проверяется так же, как в
111

задаче 126. Полнота пространства (X, р) доказывается по тому же
плану, что и полнота пространства 1г в задаче 128.
145. Полнота пространства А (] В очевидна. Докажем полноту
пространства А [} В. Пусть {хп } — фундаментальная последова-
последовательность точек из A U Б. Тогда либо Л, либо В содержит беско-
бесконечную подпоследовательность \хп } из {хп }. Последовательность
{хп } также фундаментальна (в пространстве Л, для определенно-
определенности}. Так как Л полно, то {хп } сходится. Пусть р (хп , хо)->О.
Из фундаментальности последовательности {хп } легко следует тог-
тогда, что и р (*я, хо)->О, т. е. последовательность {хп } сходится.
Пространство А \ В может оказаться неполным. Пример.
Л —числовая прямая, В — отрезок [—1, 1] с обычной метрикой.
146. Если последовательность {(хп, уп)} фундаментальна в X X У,
то, как видно из формулы A), {хп} и {уп} фундаментальны (и, зна-
значит, сходятся) соответственно в X и Y. Пусть х0 = lim \иуо=<
= Нтуя; тогда (х0, y0) =\\т(хп, уп) в пространстве XxY с
данной метрикой.
147. См. решение задачи 146.
148. Это непосредственно следует из формул A) или B).
ГЛава V.
ЗАМКНУТЫЕ И ОТКРЫТЫЕ МНОЖЕСТВА
149. Если х 6 V (х0, е), то х = lim хп, где хп € V (х0У е). Из
/1->оо
неравенств р (х, х0) < р (х, хп) + р (хп , х0) < р (х, хп) + г полу-
получаем (переходя к пределу при п -> оо), что р (х, х0) ^ е. Но это и
означает, что х ё В (х09 е). Таким образом, V (х0, г) а В (х0, г).
Примером пространства, в котором V (х0, е) Ф В (х0, е), может
служить непустое множество X, наделенное метрикой задачи 125
(т. е. р (х, у) = 1 при х ф у и р (х9 у) =0 при х = у). Для любой
точки х0 € X имеем: V (хо> 1) = V (х09 1) = {х0}, а В (х09 1) = X.
Поэтому, если X содержит более одной точки, то V (х0, 1) ф В (х0, 1).
С другой стороны, для таких пространств, как /?*, llf /2, С [a, fe],
при всех хои г будет 5 (xQ9 г) = V (хо> е). Докажем это, напри-
например, для пространства С [а, &]. Пусть /65 (/0, е); положим
/л = A - ±)f + 1/0. Тогда fn б F (/о, е) и / = lim /л, так что
/ € V (/0, e).
150. Пусть {A^} — произвольное (конечное или бесконечное)
семейство множеств и U — его объединение. Так как Л^ cz U,
то Ar cz U для каждого £ и, значит, {) Ar a U. В частности,
_ L L_ —
Л U В cz Л U В. Пусть теперь с б Л U В. Если бы с б Л U В,
112

то существовали бы гА > 0 и ев > 0 такие, что V (с, ел) не пересека-
пересекается с Л, а V (с, ев) — с В. Но тогда V (с, е), где е = min {ел, ев},
не пересекалось бы с Л (J б, а это противоречит тому, что с —
точка прикосновения для Л U В. Таким образом, Л U В а ~А \}~В
и, значит, А {] В = А [} В~.
Для бесконечного семейства множеств равенство не всегда име-
имеет место. Пусть, например, Ап = \ , —1 (п = 1, 2, ...).
___ [п + 1 п\ _
Тогда [}Ап = U Лл =]0, 1], a U 4Я =[0, 1], так что [} АпФ
ф U Лл. Другой пример: множество всех рациональных точек
п
отрезка [0, 1] есть объединение последовательности одноточечных
(и потому замкнутых) множеств, а его замыканием служит весь от-
отрезок [0, 1].
151. Утверждение х 6 С (Е°) означает, что х не есть внутренняя
точка множества £, т. е. что никакая окрестность точки х не содер-
содержится в £. Но это равносильно тому, что всякая окрестность точки х
содержргт точку из СЕ, т. е. х 6 СЕ. Таким образом, х (: С (Е°)
тогда и только тогда, когда х б СЕ, т. е. С (Е°) = СЕ. Заменив в этом
равенстве Е на СЕ и перейдя к дополнениям, получим второе ра-
равенство.
152. Равенство Л° f| В° = (Л П В)° всегда верно. Для беско-
бесконечного семейства множеств {Л^} верно включение П А\ => (Г\Л^)°,
однако равенство справедливо не всегда (пример:
Л„=]-±, 1+1Г („=1,2, ...))•
153. Включение А° [] В0 cz (А \} В)° очевидно. Однако ра-
равенство не всегда имеет место (пример: Л = [0, 1], В = [1, 2]).
154. Этому условию удовлетворяет, например, множество £х
» t 1 И 1 1 л
точек на прямой: 1, ■—, —, —, ..., —, ..., 0.
2 3 4 п
Здесь £\ = {0} (одноточечное множество), Е\ =* 0.
155. а) Пустое множество и вся плоскость; б) любое непустое
открытое множество на плоскости, отличное от всей плоскости;
в) прямая х = 0.
156. Точка а — граничная для Е тогда и только тогда^когда
каждая ее окрестность содержит как точку из Е (т. е. а б £), так
и точку из СЕ (т. е. а б Е°). Таким образом, Fr Е = Е \ Е°.
157. Согласно задаче 156, Fr (Л U В) =» Л Ц Д \ (Л Ц В)°,
Но,__очевидно, (Л U ВH эЛ° U В°, а по задаче 150 Л U В с:
cz Л U В. Следовательно, ___ _^__ _
(л и в) d (л и в) \ (^4° ив°)с(л\ л°) и (в \ 5°) =
РЛ FrB.
113

Если же Е является объединением бесконечной совокупности
множеств, та аналогичное утверждение уже неверно. Напри-
Например, возьмем на числовой прямой множества Е' = —, 1
[л п \
(л = 1, 2, ...). Тогда Е = [}Еп = ]0, 1[, так что Fr Е = {О, 1};
п
но тачки 0 и 1 не содержатся в [}¥т Еп = [] \-~, \ L
158. Пусть а — точка прикосновения для Е и V (а) — произ-
произвольная ее окрестность. Тогда V (а) содержит точку Ь 6 Е, Рассмот-
Рассмотрим окрестность V (Ь) точки Ь, включающуюся в V (а). Так как
b € Еу то V (Ь) (а значит, и V (а)) содержит точку из Е. Итак, про-
произвольная окрестность V (а) точки а содержит точку из Е, т. е.
а €Е. Таким образом, Е содержит все свои точки прикосновения,
т. е. Е замкнуто.
159. Пусть а 6 £" и У (а) — произвольная окрестность точки а.
В V (а) найдется точка b € Е'. Возьмем какую-либо ее окрестность
V (Ь) а V (а). Так как b — предельная точка для Ег то в V (Ь)
(а значит, и в V (а)) содержится бесконечно много точек из Е. Сле-
Следовательно, а б Е'. Тем самым Ег а £", т. е. Е' замкнуто.
160. Это вытекает из легко проверяемого равенства Fr Е =
= £ 0 СЕ и из того, что множества Е и СЕ замкнуты (задача 158).
Замкнутость Fr E можно доказать также непосредственно — та-
таким же способом, как и утверждение задачи 158.
161. Необходимость. Пусть метрики р2 и р2 эквива-
эквивалентны и Е замкнуто в (X, рг). Если х0—точка прикосновения
для Е в (X, р2), то существует последовательность (хп } точек из
Е такая, что р2 (хп , х0) -> 0. Тогда и рх (хп , х0) -> 0, т. е. хе — точка
прикосновения для Е в (X, рг) и, значит, х0 £ Е; тем самым Е замк-
замкнуто в (X, р2). Аналогично, если F замкнуто в (X, р2), то F замкну-
замкнуто в (X, рх).
Достаточность. Пусть совокупности замкнутых мно-
множеств в (X, рх) и в (X, р2) совпадают, и пусть рх (хп , х0) -> 0 при
п -> оо. Если {хп } не сходится к х0 ь (X, р2), то существуют подпо-
подпоследовательность {хп } и число е > 0 такие, что р2 (хп , х0) > е
при любом fe. Пусть Е—множество, образованное точками х , и
Е — его замыкание в метрике рг. Ясно, что х0 € Е. Но так как Е
замкнуто в (X, р2) (задача 158), то по условию оно замкнуто также
в (X, рх)и, значит, должно содержатьхп (поскольку p~t (хп , х0) -> Q).
Полученное противоречие показывает, что р2 (хп, 0) -> 0. Анало-
Аналогично из р2 (уп, у0) -> 0 вытекает рх (ул, у0)->0, т. е. метрики рх
и р2 в X эквивалентны.
162. Объединение этих окружностей замкнуто, если последова-
последовательность гъ г2, ..., гя, ... не ограничена, и не замкнуто, если она
ограничена; в последнем случае замыкание объединения окружнб-
114

стей получится, если к ним добавить пре-
предельную окружность радиуса а =* lim rn.
п-+оо
163. Это множество замкнуто, если
lim rn = +оо (в этом случае оно совпадает
со всей плоскостью); оно не замкнуто, ес-
если lim rn — а < +оо. В обоих случаях
это множество является открытым.
164. Обозначим через Сп окружность
радиуса — км с центром на земной оси,
2пп
расположенную в северном полушарии на
поверхности Земли; длина этой окружнос-
окружности равна — км (рис. 16). Через Вп обозначим окружность, рас-
п
положенную на поверхности земного шара на 7 км южнее, чем
Ся. Тогда искомое множество £ таково:
\ \j 2 U * * * \J О'
где Ро — одноточечное множество, образованное Южным полюсом.
Множество £ не замкнуто. Кроме точек окружностей Ви В2, ...,
предельными являются также все точки окружности Л, отстоящей
на 7 км южнее Северного полюса (окружность А не входит в £).
Поэтому
F W A Fr IF 11 A\ \ P
165. Пусть ^ —точка прикосновения множества Еа1 т. е. в Еа
существует последовательность {хп }, сходящаяся к £. Тогда / (£) =
= limf(xn) (в силу непрерывности функции /). Так как
/ (хп) > а для всех п, то также f (Q J> а. След<жателъно, С € Еа и,
значит, Еа замкнуто.
166. Пусть ф € £. Тогда в £ существует последовательность
{fn}, сходящаяся в С[0, 1] к ф. Так как fn(x) ^/0 (х) для всех
х б [0, 1] и всех п, а ф (х) = \imfn (х) в каждой точке х € [О, I],
то и / (х) ^ /д (х) для всех х € [0, 1], т. е. ф € £. Следовательно, Е
замкнуто.
167. Требуется доказать равносильность включений а) £ и £,
б) £ Z) £', в) £ zd Fr £. Так как всегда справедливы включения
£' с £ и Fr £ cz £, то из а) следует б) и из а) следует в). С другой
стороны, так как £ cz £ U £', то из б) следует а); а так как £ =
~ £° (J Fr £ и £° cz £, то из в) следует а).
168. Согласно задаче 158, £ замкнуто. С другой стороны, если
£ cz F и F замкнуто, то £ cz F = F. Тем самым £ — наименьшее
замкнутое множество, содержащее £.
115

169. Так как £" замкнуто (задача 159), то Е' zd Е' zd E". Со-
Совершенно так же Е" zd Еш и т. д.
170. Так как для любого Е множество Fr E замкнуто (задача
160), то Fr (Fr E) cz Fr Е (задача 167). Если же Е замкнуто, то
Fr E cz E; следовательно, (Fr E)° с£° и потому, согласно зада-
задаче 156, Fr (Fr Ё) = Fr E \ (Fr Е)° = (Е \ Е°) \ (Fr E)° =
= Е \ Е° = Fr £.
Для произвольного £ равенство Fr (Fr £) = Fr (Fr (Fr E)) сле-
следует теперь из замкнутости множества Fr E.
171. Если {хп} — фундаментальная последовательность точек
из £, то {хп} фундаментальна и в X, а значит, сходится в X к неко-
некоторой точке х. Так как Е замкнуто, то х 6 Е\ поэтому {хп} сходится
к х и в £. Следовательно, Е полно.
172. Так как Е незамкнуто, то существуют последовательность
{хп} точек из Е и дочка х 6 X такие, что хп -+- х> но х ТЕ. Тогда
\хп} фундаментальна, но не сходится в Е. Следовательно, Е не-
неполно.
173. Нет, не будет, так как X незамкнуто в пространстве
Л1[а, Ь] (см. задачу 129). Например, положим fn(x) =
= у (х—?L±_| -|—. Тогда fn£X при каждом п, но {/„} схо-
сходится в М [а, Ь] к функции f(x)~ х — 5L±_ ? не имеющей про-
производной в точке - ■ g [fl, Ь].
2
174. Это множество не является совершенным. Но добавление к
нему одной точки (начала координат) делает его совершенным.
175. Объединение конечного семейства совершенных множеств
всегда является совершенным множеством. Объединение же счетного
семейства совершенных множеств не всегда совершенное множество
(см. примеры в решении задачи 150).
176. Пусть Е — данное множество и х0 € Е°. Надо доказать, что
х0 — внутренняя точка множества £°. Для этого опишем около х0
окрестность V (х0), входящую в Е (что возможно, так как х0 —
внутренняя точка множества £). Каждая точка х 6 V (х0) также бу-
будет внутренней точкой множества Е (так как около х можно описать
окрестность V (х), входящую в V (х0) и тем самым входящую в £).
Итак, всякая точка х € V (х0) является точкой из £°. Значит, х0 —
внутренняя точка множества £°. Таким образом, каждая точка
множества Е° является его внутренней точкой, т. е. Е° — откры-
открытое множество.
177. Согласно предыдущей задаче, Е° — открытое множество.
С другой стороны, если G cz Е и G — открытое, то G = G° cz E°.
Тем самым Е° — наибольшее открытое множество, содержаще-
содержащееся в Е.
178. Это следует из того, что Е =± \] V (ху е).
116

179. Указание. Используйте свойство непрерывной функ-
функции: если непрерывная функция положительна в точке х0, то она
положительна и в некоторой окрестности этой течки.
180* Пусть ф € £, т. е. А < <р (х) < В всюду на [0, 1]. Обозна-
Обозначим sup ф (х) = р, inf ф (х) = а. Ясно, что sup ф (х) не может рав-
*с[о, 1] *;[о, 1] дг:[о, 1]
няться В, так как по свойствам функций, непрерывных на отреаке,
sup ф (х) достигается в некоторой точке х' отрезка [0, 1]: р == ф (х').
Так как ф (х1) < В, то р < В. Аналогично а > А. Обозначим через
е наименьшее из чисел а — А и В — р. Тогда все функции х»
удовлетворяющие для каждого х 6 [0, 1] неравенствам ср (х) — е <
<Х W < ф (х) + е, принадлежат множеству £. С другой стороны,
эти функции х образуют е-окрестность функции ф, так как все эти
функции, и только они, удовлетворяют условию: р (ф, х) <е-
Итак, вместе с функцией ф в множество Е входит также некоторая
ее окрестность, а это и означает, что Е — открытое множество в
С [0, 1].
181. См. решение задачи 180.
182. Пусть Ek — открытый круг на плоскости с центром в на-
J СЮ
чале координат и радиусом —. Тогда П Ek является одноточечным
к k=\
множеством (образованным началом координат). Оно не является
открытым множеством.
183. Неверно. Пример. Е — множество на плоскости, яв-
являющееся объединением Замкнутого круга D и одноточечного мно-
множества, лежащего вне D. Тогда Е° =D° и Е° =D, но Е Ф D.
Однако для всякого замкнутого множества Е имеет место вклю-
включение £°с£.
184. Нет. Пример. Е — открытый круг на плоскости с вы-
выколотым центром; здесь (Е)° ф Е. Однако для всякого открытого
множества Е справедливо включение (Е)° zd E.
185. Указание: примените результаты задач 183, 184.
186. Каждое из множеств Еп замкнуто (см. задачу 165). Так как
f — непрерывная функция на отрезке, то существует N такое, что
|/ {х)\ ^ N для всех х € [а, Ь]; следовательно, все Еп при п > N
пусты. Поэтому множество Ег [} Е3 U ••• U ^2a-i U ••• есть объе-
объединение конечного числа непустых замкнутых множеств и, следо-
следовательно, замкнуто.
187. Неверно. Пример. Пусть
[■+£. ~i] U [
(тогда и £,= ]—!, 1[) и ? = [_!, 11 с: и Я,: здесь р не
содержится в Еп ни при каком п.
188. Пример. Множество Е всех чисел вида 1 + -• +— + •••
1 2 о
...+-i (n =1, 2, ...)■
п
117

189. Ясно, что £ П Е' = 0. Если Е' пусто, то £ замкнуто.
Если же £' непусто, то опишем около каждой точки множества £'
открытый шар радиуса —, а объединение этих шаров (при фикси-
п
рованном п) обозначим Ап; далее, положим Вп = Е \ Ап . Тогда
каждое Вп замкнуто (оно не имеет предельных точек), и [} Вп = £.
п
Следовательно, £ есть множество типа Fa.
190. 1Е есть множество, все точки которого изолированные;
следовательно, в силу предыдущей задачи, 1Е — множество типа Fa.
191. Такой пример можно привести не в любом пространстве
(например, на прямой или в евклидовом пространстве любое множе-
множество изолированных точек не более чем счетно). Однако, например,
в пространстве М ([0, 1]) (см. задачу 129) множество функций
при 0 < х < 1,
при |<х<1,
где | пробегает интервал ]0, 1[, является несчетным, а все его эле-
элементы изолированные.
Другой пример см. в решении задачи 373.
192. е-окрестностью точки х € Z в Z для каждого е > 0 служит
V (ху е) fl Z, где V (х, е)-окрестность этой точки в X. Поэтому х €
€ £z тогда и только тогда, когда 1) х € Z; 2) {V (х, t) (] Z) (] Е не-
непусто для каждого е > 0. А так как (V (х, е) f) Z) П Е = V (х, г) f)
Г) £, то условие 2) означает, что V (х, е) f| £ непусто для каждого
е > 0, т. е. что л: б £*. Таким образом, х d Ez тогда и только тогда,
когда х 6 £х П 2. Тем самым утверждение а) доказано. Утвержде-
Утверждение б) легко следует из него. Действительно, пусть £ замкнуто в
Z; тогда £ == Ez = Ех {] Z, причем Ех замкнуто в X (задача 158).
Обратно, пусть £ = F Г) 2, где F — замкнутое множество в X;
так как £ d F, то £xcz F (задача_168); поэтому Е = F [] Z^
zd £* П ^ = £z ;з £, откуда £ = £z, т. е. £ замкнуто в Z.
193. Это следует из равносильности следующих утверждений
относительно множества £ с: Z:
1) £ открыто в Z;
2) Z \ £ замкнуто в Z;
3) Z \ £ = F П Z, где F — замкнутое множество в X;
4) £ = G П 2, где G = X \ F — открытое множество в X
(второе и третье утверждения равносильны согласно пункту б)
задачи 192, а третье и четвертое равносильны, поскольку из вклю-
включений Z с= X и F cz X следует, что Z \ (F П 2) - <Х \ F) П 2).
194. Это следует из задач 192 и 193.
195. Согласно задаче 192 (или 193), £ = F f] Z, где F замкнуто
^соответственно открыто) в X. Но тогда £ замкнуто {соответственно
открыто) в X, как пересечение двух замкнутых (соответственно от-
открытых) множеств.
не

196. Пусть (#0, у0) — точка прикосновения множества Е X F.
Каждая ее окрестность V ((xQt y0), е) содержит хотя бы одну
точку (лг, у) из Е X F. Но тогда х € V (х0% е) и у € J/ (я0, е), так что
хоиуо — точки прикосновения множеств Б и F соответственно и,
в силу замкнутости этих множеств, принадлежат им. Поэтому
(х0, у0) £ Е X Л
197. Пусть # € (Л U 5)°, т. е. V (#, г) с A U В при некотором
г > 0. Тогда У (я, г) \ В си Л. Но У (я, г) \ В открыто; следова-
следовательно, V (х, г) \ В cz Л°, откуда V {х, г) cz А° U В. Значит,
х € (A0 U В)°. Тем самым (Л U В)° с (Л° U В)°; обратное включе-
включение очевидно. ___ __
198. Верно. В самом деле, так как ЛсЛ, Tod (хй$ A) ^d (xa, Л).
С другой стороны, для каждого е > 0 существует элемент а% i A9
для которого р (хо,"а8) < d (х0, А) + --, а для этого \ —
элемент а6 € Л такой, что р (ае, ае) < ~. Отсюда р (х0, ав) <
< Р (*0. ^) + Р К аг) < Р &<» «в) + f • Тогда
= d(x0, А) + г.
Так как е произвольно, Tod (х0, Л) ^ d (#0, Л).
199. Неверно. Например, если на прямой взять х0 s= 2 и
Л == [0, 1] U {2 }, то d (я0, Л) = 0, в то время как d (х0, Л°) =1,
поскольку Л° = ]0, 1[.
200. Вообще для любой числовой ограниченной снизу функции
/, определенной на произведении А X В любых двух множеств А
и S, имеет место:
ш^в^*' У) =1^{Ыр{х, у)) =inj(mj/(xf у)). A)
Действительно, так как, очевидно, inf f{x, y)^inf/(A:t у) для
каждого х 6 Л, то
inf ^/(х, yXinJ ^/(x, у)).
С другой стороны, для каждого е > 0 существует пара (xs> ye)
такая, что
Так как inf (inf/(л;, у))^ inf/(*е, у)</(^е, уе), та
inf j(inf / (л:, y))^inf f(xf y)-f-e.
119

Это неравенство верно для каждого е > 0, поэтому
inf(inf/(x, y))<inf/(x, у).
х^А у±В х^А, у^В
Следовательно, inf/(х, у) ~inf(inf f(x, у)). Совершенно так же
х$А, у$В х$А у£В
доказываем второе из равенств A).
Взяв в A) множества А к В из метрического пространства (X, р)
и положив / = р, получим требуемые соотношения.
201. В силу задач 198 и 200, имеем:
d (Л, В) = inf d (х, В) = inf d(xyB) =d (Л, Б).
х^А х£А
Аналогично доказываются остальные равенства.
202. Не для всех. Пример. Возьмем на прямой А = [0, 1] U
U {2}, В = {2} U [3, 4]; тогда Ло=] 0, 1[, 5° = ]3, 4[ и
d (Л°, В0) = 2, в то время как d (Л, В) =-0.
203. Для каждой точки х € Fx положим гх = — d (x, F2).
«з
Аналогично для каждой точки у € F2 положим гу = —d (у, Fj).
Докажем, что множества вг = []V (x, гх) и G2 = [)V (у, е )
x$Ft xiFt
обладают требуемыми свойствами. Ясно, что они открыты, причем
Gx zd Fjl и G^zd F2. Предположим, что существует точка z ^ Gx П
П G2. Тогда найдутся точки х б Flf у б F2 такие, что z 6 V (х, е^),
z € V (у, еу). Для них будем иметь:
P(^t У)<Р(*. г) + р(г, у) < —d(x, /72) + ^d(>f' fiX
<-jp(-«. y)+ -p(*. y) = -jp(-«. y),
2
т. e. p (л:, у) <—p (x, у); но этого не может быть, поскольку
о
Р (^» У) > 0- Следовательно, Gx {] G2 = 0.
204. Пусть Л —множество типа G6, т. е. Л =Г)ГЛ> где Гя —
п
открытые множества. Тогда СЛ = С (f| FJ = 1)СГЛ, где СГЯ замк-
п п
нуты. Итак, СЛ есть множество типа Fa.
Пусть В — множество типа Fa, т. е. В = U #я, где firt — замкну-
п
тые множества. Тогда СВ =С([)Вп) = ПСВЛ, где СВ^—откры-
тые множества. Итак, СВ есть множество типа G6.
205. Пусть F — замкнутое множество. Рассмотрим для каждого
натурального числа п открытое множество Gn = (J V 1х9 —). Оче-
оо оо
видно, что F a [}Gn. С другой стороны, если у € П Gw, то для
каждого п найдется точка хп € Z7 такая, что р ^сл, у) < — . Следо-
п
120

вательно, у — точка прикосновения для F\ а так как F замкнуто, то
оо
у € F. Таким образом, F = (] Gn, т. е. F — множество типа G6/
/1=1
Справедливость второго утверждения задачи Вытекает отсюда
по двойственности (см. задачу 204).
206. В силу результата задачи 204, достаточно доказать, что
СЕ — множество типа Fa. Но СЕ есть объединение счетного числа
прямых* =rk(k = 1,2, ...)иу =rk(k-^ Г, 2, ...), где гьг2, ... —
множество рациональных чисел, занумерованное произвольным
образом. Так как каждая прямая является замкнутым множеством
на плоскости, то СЕ — множество типа Fa.
207. Доказательство вытекает непосредственно из определения
нижнего предела.
208. Выберем в каждом Еп по точке х. Последовательность {хп }
обладает тем? свойством, что каждое Еп содержит все члены этой
последовательности, начиная с хп . Поэтому р(хт, хп )^ diam Em[n{m п)
и, значит, р (хт, хп)-*0 при т, п->-оо. Следовательно, {хп }—
фундаментальная последовательность. Так как пространство пол-
полно, то существует л: =iim xn . Покажем^ что х есть точка прикоснове-
прикосновения для каждого Ет. Действительно, произвольная окрестность
V (х, е) точки х содержит зсе члены последовательности, начиная с
некоторого N; при этом все члены с номерами п ^ max (m, Af).
входят в Ет. В силу замкнутости каждого Ет> точка х всем им при-
принадлежит, т. е. П Ет ¥* 0-
т
209. Нет. Пример. Пусть {а.} — строго убывающая число-
числовая последовательность, сходящаяся к 1, и X — счетное множество
точек хъ х2, ... , в котором метрика введена формулами:
p(xl9xj) =amWtj) при 1Ф1
Р (*„ xt) = 0.
Так как каждая фундаментальная последовательность в X ста-
стационарна, то X полно. Замкнутые шары В (х., at) =z{xpxi+v
А'.+2, ...} образуют убывающую последовательность, имеющую
пустое пересечение.
210. Нет. Например, в jR1 последовательность интервалов
0, — \(п = 1, 2, ...) имеет пустое пересечение.
J n L —
211. Выберем по точке хпв каждом Еп . Как и в задаче 208, убе-
убедимся в том, что существует точка х, общая для всех Еп. В силу
условия б) задачи, она будет принадлежать и всем Еп.
212. Пусть Е — непустое открытое множество на прямой, хо£Е.
Обозначим через а нижнюю грань левых концов интервалов,
содержащих х0 и включающихся в £, а через р верхнюю грань пра-
правых концов таких интервалов (не исключено, что а = —оо или
Р = +оо). Тогда ]at р[ € Е, а~£Е, plf £ (если бы, например, бы-
было р £ Еу то, в силу открытости £, некоторый интервал ]E — е,
121

P 4- e[ также включался бы в Е\ но тогда интервал ]а, р + е[ вклк>
чался бы в 5, что противоречит выбору Р).
Итак, каждая точка х0 € Е входит в некоторый интервал, вклю-
включающийся в Еу концы которого не принадлежат £. Докажем, что
такой интервал (для данной точки х0) единственный. Если бы наш-
нашлись два таких интервала ]аь EХ[ и ]а2, |$2[, причем, например,
хо < Pi < р2> то Pi принадлежало бы интервалу ]а2, Р2[ и, значит,
входило бы в Е вопреки предположению. Аналогично не может быть
аг < а2 или а2 < аг. Единственность доказана. Интервал, входя-
входящий в £, концы которого не принадлежат £Г, и будет составляющим
интервалом для Е. Множество составляющих интервалов не более
чем счетно: фиксируя в каждом составляющем интервале по одной
рациональной точке, мы получаем взаимно однозначное соответ-
соответствие между множеством всех составляющих интервалов и некото-
некоторым подмножеством рациональных чисел (а это подмножество ко-
конечна или счетно).
213. Необходимость очевидна. Докажем достаточ-
достаточность. Пусть ]аь &!,[, ... — смежные интервалы множества Е
причем они не имеют попарна общих концов. Допустим, что Е
имеет изолированную точку х0. Тогда существует такое е > 0, что
]*о — е» *&[<=€£ и ]х0> х0 + е[ с: СЕ. Но тогда ]х0 — 8, х£ н
]х0, х9 + е[ включаются в некоторые смежные интервалы с общим
концом х^ чта противоречит условию. Итак, Е не имеет изолирован-
изолированных точек; кроме того, Е замкнута. Значит, Е — совершенное мно-
множество.
214. Допустим, что [а, 6] = F (J Ф, где F и Ф замкнуты, не-
непусты w не пересекаются. Каждое из множеств F, Ф, будучи замкну-
замкнутым* непустым № ограниченным а§изу числовым мйожеством, обла-
обладает наименьшей точкой. При этш у одного из них, скажем*, у мно-
множества F, этой точкой служит а. Пусть с — наименьшая точка мно-
множества Ф. Тогда с > а (так как F {] Ф = 0); значит, [а, г[с: F,
а потому и [а, с] си F (так как F замкнуто). Следовательно,
с 6 F О Ф; вопреки тому, что F и ф не гтересекаются.
215. Допустим, что [a, bj = Ft [} F2 Ц ..., где Ft- (*' = 1, 2,
...) — непустые попарно не пересекающиеся замкнутые множества.
Пусть Fnt— множество с наименьшим номером, для которого^
]#> Ь [П Fn Ф 0- Так как Fn не совпадает со всем отрезком [а, &]/
то и ]а,' b [ П CFn =т^ 0. Поэтому на интервале ]а, Ь[ найдется
точка а^ являющаяся концом некоторого смежного интервала мно-
множества Fn . Обозначим через 1г интервал, одним из концов которого
служит эта точка, и такой, что /х с: CFn , lx cz ]af fe[.
Далее, среди множеств Fn+l* ^+2» ••• найдем множество Fnj
с нтшеньшим номером, для которого 1г [\ Fn ф 0 (назначит, 1г fj
П (^i U— U pnt<-\) = &)- Легко видеть, что тогда и It [\ СРп^Ф
Ф 0. Действительно, если бы интервал 1Х целиком содержался в
Fn , то и тачка аг входила бы в F (в силу замкнутости Fn^] но
122

(Xj € Fn , а множества Fw и Fn не пересекаются. Итак, Ix (] F Ф
Ф 0 и /x П CFn =#= 0. Поэтому на интервале 1г найдется точка*а2,
являющаяся концом смежного интервала множества Fn . Но тогда
существует интервал /2, одним из концов которого служит точка а2,
и такой, что /2 cz С/7 , /2 cz 1г.
Продолжая таким же образом далее, получим в результате убы-
убывающую последовательность интервалов /0=]а, Ь[, /1э /2, ...
такую, что /~Л cz 1к__ъ и строго возрастающую последовательность
номеров #!, п2, ... такую, что
/* П (Fx U ... U Fn^) =0(k=l,29 ...).
Тогда должна существовать точка, принадлежащая всем интер-
интервалам Ik (а именно общая точка отрезков /Л, k = 1, 2, ...). Эта
точка не принадлежит ни одному из множеств Fn, хотя принадлежит
оо
отрезку [а, Ь]. Следовательно, [а, Ь~]ф [) Fh что противоречит до-
t=i
пущению.
216. Если ]а, &[ = у Fiy где Ff — попарно не пересекающиеся
i
непустые замкнутые множества, то [а, Ь] = {а} [) {b} [} (\jFt},
что противоречит результату задачи 215. *
217. Утверждения задач 216 и данной равносильны, поскольку
]а, Ь[ и /f1 гомеоморфны.
218. Можно, например, следующим образом: пусть сг —середина
смежного интервала первого ранга (т. е. сг =— ], с2 — середина
смежного интервала второго ранга, лежащего справа от сх (т. е
середина интервала —, -— ), и вообще ch+1 —середина смежного
J 9 9 |_/
интервала (k + 1)-го ранга, лежащего справа от ск. Тогда канторово
множество/) разбивается на следующие попарно не пересекающиеся
непустые замкнутые множества:
0={1>иФП[0, cj) U (D П [А, с2]) и .- U
и (d n [^, ^+i3) и ...
219. Множество [a, b] fl E замкнуто. Докажем, что оно не со-
содержит изолированных точек.
Пусть х0 € [а, Ь] П Е- Так как а € £*, b € £, то л:0 — внутрен-
внутренняя точка отрезка [я, Ь]. Опишем произвольную окрестность V (хо)а
cz[a, b]. В этой окрестности найдется точка х € £, <яличная от jc0.
Но jc € [а, Ь] П £*• Следовательно, в произвольной окрестности
точки х0 нашлась отличная от х0 точка х £ [а, Ь] {] Е\ значит, х%
не является изолированной точкой множества [a, b~] fl E. Итак,
[а, Ь] П Е — совершенное множество.
220. Рассмотрим любой интервал А на прямой. По условию су-
существует х £ Д f| СЕ. Так как СЕ открыто, то Л [} СЕ тоже откры-
открыто и существует интервал А', содержащий точку х, такой, что A' cz
cz А П СЕ. Отсюда A' cz А, А' [\ Е = 0 и, значит, Е нигде не плотно,
123

221. Рассмотрим два случая: 1) концы интервала аир оба не
принадлежат Е\ 2) хотя бы один из этих концов принадлежит Е.
В первом случае имеет место равенство ]а, р[ A Е = [а, р] П Е\
в правой части этого равенства стоит совершенное множество (см.
задачу 219); следовательно, и множество ]а, р [fl E является совер-
совершенным.
Рассмотрим второй случай: пусть а € Е, р £ Е (если бы только
одна из точек а, р принадлежала Е, доказательство было бы ана-
аналогичным). Так как Е нигде не плотно, то на любом интервале
]а, а'[ найдутся трчки, не принадлежащие Е. Отсюда следует, что
существует последовательность точек аг > а% > ... > ап > ..., не
принадлежащих £, сходящаяся к а. Из тех же соображений выте-
вытекает, что найдется последовательность точек Ьх < Ь2 < ...< Ьп< ...,
не принадлежащих £, сходящаяся к Р; при этом всегда можно счи-
считать, что аг < bj (рис. 17). Но тогда ]а, p[f| E является объедине-
объединением следующих множеств:
Tfih, h СП Е% ]а2, аг СП Е, ]а3, а2 СП £, К, ^з СП £, ...
У>1,Ь2Н) Е, ]й2, йзЕП £, ]*з. &4[П Я, ...
Все эти множества совершенные (см. первый случай). Если сре-
среди них лишь конечное число непустых, то их объединение, т. е.
За> РЕП Е, также совершенное множество; в противном же случае
]а, р [ П Е есть объединение счетной совокупности попарно не пере-
пересекающихся непустых совершенных множеств.
222. Заметим сначала, что Р \ Q = Р (] CQ, где CQ — от-
открытое множество. Пусть CQ = U]af, pt[, где ]af, РД — состав-
i
ляющие интервалы. Тогда Р \ Q = у (]ol, Pt. [П ^)- Согласно
предыдущей задаче, каждое множество ]at7 pt. [П Р либо совер-
совершенное, либо есть объединение счетной совокупности попарно не
пересекающихся непустых совершенных множеств; но тогда и их
объединение Р \ Q является либо совершенным, либо объедине-
объединением счетной совокупности попарно не пересекающихся непустых
совершенных множеств.
223. Пусть А = U Еп , где Еп — нигде не плотные совершенные
п
множества. Множество А можно записать следующим образом:
A=EiU(E,\ £J U (Е, \ (Ег U EJ) U ... U (Еа \ (Й,)) U -О)
l
Слагаемые правой части попарно не пересекаются; каждое из них
является либо нигде не плотным совершенным множеством, либо
непустой разностью двух нигде не плотных совершенных; во втором
#а Qj й2 a, bji
ос
Рис. 17
124

случае на основании предыдущей задачи оно представимо в виде
объединения счетной совокупности попарно не пересекающихся
непустых совершенных множеств.
Отсюда следует (в силу равенства A)), что и множество А пред-
представимо в виде объединения счетной совокупности попарно не пере-
пересекающихся нигде не плотных совершенных множеств.
224. Множество D замкнуто (как дополнение к открытому),
и никакие два его смежных интервала, по построению, не имеют
общих концов. Следовательно, О—совершенное множество (см.
задачу 213).
Докажем, что D нигде не плотно на прямой. Возьмем произ-
произвольный интервал / =]а, (J[. Если он не содержит точек из £>,
то в качестве интервала, содержащегося в / и полностью свобод-
свободного от точек множества D, берем сам этот интервал. Если же име-
имеется точка х0 €D, содержащаяся в /, то мы можем найти отрезок
какого-либо достаточно высокого ранга д, содержащий х0 и вклю-
включающийся в / (такой найдется, так как длина каждого отрезка
п-то ранга равна -Л. Возьмем интервал длины -^ С центром в
о J о
середине этого отрезка (рис. 18). Этот интервал не содержит точек
из D и вместе с тем содержится в /.
225. Смежный интервал первого ранга состоит из всех чисел,
в троичном разложении которых первый знак обязательно равен
единице*. Каждый смежный интервал второго ранга состоит из
всех чисел, в троичном разложении которых (при фиксированном
первом знаке, отличном от единицы) второй знак обязательно ра-
равен единице. Вообще каждый смежный интервал &-го ранга состо-
состоит из всех чисел, в троичном разложении которых (при фиксиро-
фиксированных первых k — 1 знаках, отличных от единицы) на /е-м месте
обязательно стоит единица. Отсюда вытекает, что множество, остав-
оставшееся после иеключения из [0, 1] всех смежных интервалов, со-
состоит из тех и только тех чисел отрезка [0, 1], которые могут быть
* Слово «обязательно» надо понимать в том смысле, что если х допускает два
различных разложения в троичную дробь — одно с единицей на первом месте, а
другое без единицы на первом месте (например, х — —), то мы х не включаем
в интервал первого ранга; иными словами, в интервал первого ранга войдут те и
только те числа х> которые при любом разложении в троичную дробь имеют на
первом месте после запятой единицу.
125

записаны в виде троичной дроби, не содержащей единицы в числе
своих троичных знаков.
226. Точки первого рода канторова множества состоят из всех
тех чисел, которые являются троично рациональными (т. е. могут
быть представлены в виде конечной троичной дроби) и вместе с тем
допускают хроичное разложение, не содержащее единиц в числе
своих троичных знаков.
Точки второго рода — это те точки, в троичном разложении
которых отсутствуют единицы и которые являются троично ирра-
иррациональными (т. е. в их разложении имеется и бесконечно много
нулей, и бесконечно много двоек).
227. Между десятичными дробями 0,1 и 0,2 имеется бесконечное
множество точек первого рода; одна из них к = — (ее разложение
в троичную дробь таково: х =0,0100...; следовательно, эта точка
троично рациональна; ее троичное разложение может быть записа-
записано без единиц: х =0,00222...; следовательно, эта точка принадле-
принадлежит канторову множеству).
228. Между этими числами имеется бесконечно много точек
второго рода; например, одной из них является точка х, троичное
/ 2
разложение которой имеет вид: 0,00202020202... (так как х = — +
2 2 11 1 \
Н 1 Ь ... = —f то — < х <— ; х является точкой вто-
З5 З7 12' 20 10/
рого рода канторова множества, так как ее троичное разложение
содержит бесконечно много двоек, бесконечно много нулей и не
содержит единиц; притом она рациональна.
229. В качестве Н можно взять множество точек, разложение
которых в троичную дробь состоит лишь из чисел 0 и 2, причем на
местах с номерами вида Зп + 1 стоят только нули, а на местах с
номерами вида Зп + 2 — только двойки. Ясно, что Я содержится в
D, не содержит его точек первого рода, замкнуто и не имеет изо-
изолированных точек.
230. Не существует. Докажем это. Возьмем точку х0 первого
рода канторова множества D и опишем около нее произвольную
окрестность /. Так как D не имеет изолированных точек, го 1 (] D
также не имеет изолированных точек. Следовательно, / fl D —
совершенное множество. Но непустое совершенное множество (а
оно непусто, так как содержит точку х0) имеет мощность контину-
континуума (задача 253). Тогда и / (] D имеет мощность континуума (оно
отличается от своего замыкания не более чем на две крайние точ-
точки). Следовательно, / f| D не может состоять только из точек
первого рода (их всего счетное множество), но должно содержать
также точки второго рода. Таким образом, всякий интервал /,
содержащий хотя бы одну точку первого рода множества D, со-
содержит бесконечно много точек второго рода.
Заметим, что это рассуждение верно не только для канторова
множества, но и для любого совершенного множества на прямой.
126

231. Так как множество D несчетно, то различных расстояний
от данйой точки х <L D до точек у € D должно быть также несчетное
множество (для каждого числа а > О множеству D принадлежит
не больше двух точек уг и у2, отстоящих от х на расстоянии а).
Значит, среди всевозможных расстояний р (х, у) (у € D) найдутся
иррациональные (так как рациональных чисел имеется только счет-
счетное множество).
232. Перенумеруем все точки множества Е\
Xiy Х2у •♦♦> Xk9 ...
Рассмотрим всевозможные расстояния р (xh xj) между точка-
точками хь Xj множества Е. Их счетное множество. Опишем произволь-
произвольным радиусом еь отличным от каждого р (xh yj) (такое число обя-
обязательно найдется, так как всего чисел на прямой несчетное множе-
множество), окрестность около хх\ назовем ее 1г. Далее, среди точек х2,
х3у ..., хкУ ... найдем первую, не вошедшую в 1г; пусть это будет
xk ; она не совпадает ни с одним из концов интервала /ь так как
£i Ф Р (хъ %д Для любого хг. Опишем около .^окрестность радиу-
радиуса е2, отличного от каждого р (xh Xj), не пересекающуюся с 1г и не
имеющую с ним общих концов; обозначим ее /2.
Следующим шагом находим среди точек ^ +р xk , 2, ... первую,
не входящую ни в 1Ъ ни в /2; пусть это будет xk; она не совпадает
ни с одним из концов как 1Ъ так и /2; поэтому около нее можно опи-
описать окрестность радиуса е3, отличного от всех р (xh x}), не пере-
пересекающуюся ни с /ь ни с /2 и не имеющую с ними общих концов;
обозначим ее /3.
Продолжая далее таким же образом, мы построим последова-
последовательность попарно не пересекающихся интервалов /ь /2, ... . До-
Дополнение F к объединению этих интервалов является искомым со-
совершенным множеством. Действительно, F замкнуто, как допол-
дополнение к открытому множеству (к объединению интервалов Ik).
Оно не пусто, так как содержит, например, концы всех интервалов
]k. Оно не имеет изолированных точек, так как по построению его
смежные интервалы /1э /2, ... не имеют общих концов. Следователь-
Следовательно, множество F совершенно и непусто.
233. Множество F не имеет изолированных точек, так как ни
одно из множеств Е, Еъ £2, £3» ••• не имеет изолированных точек.
Множество F замкнуто, так как его дополнением является
открытое множество у (]а, & [\^])| отсюда также следует, что
все интервалы, на которые распадаются множества ]с^, & [\Et
(i = 1, 2, ...), и только они, являются смежными интервалами к F.
Докажем, что F нигде не плотно. Пусть ]а, Ь[_ — произвольный
интервал; в силу того что Е нигде не плотно, ]я, Ь\_ содержит интер-
интервал /, полностью свободный от точек множества Е\ но тогда / cz
с ]ая , EП [ для некоторого п 0- Интервал / полностью свободен
от точек множеств Еъ Е2, ..., En__v £п+1 ...; а так как Е^ —
нигде не плотное множество, то в / найдется подинтервал /0, сво-
свободный также и от точек множества ЕПо. Итак, интервал /0 свобо-
127

ден от точек всех множеств £, Еъ £2, ..., т. е. от точек множества F.
234. Докажем, что если выполнены условия б) и в), то а) выпол-
выполняться не может. Действительно, по предложению Е содержит две
различные точки #, у; пусть, скажем, х < у. Так как Е замкнуто и
нигде не плотно, то существует смежный к Е интервал ]а, |J[ c=
с=- Iх* УС- Тогда а € Е9 Р £ Е, но ни одна точка у$ заключенная
между а и р, не принадлежит Ех т. е. условие а) не выполняется.
Примером множества, для которого выполняются а) и б), может
служить любой отрезок. В качестве примера, в котором выполня-
выполняются а) и в), можно взять множество, получающееся из канторова
множества D выкидыванием концов смежных интервалов; оно со-
содержит более одной точки, так как D имеет мощность континуума,
а концы смежных интервалов образуют счетное множество. Нако-
Наконец, примером множества, удовлетворяющего условиям б) и в),
служит D.
235. Натуральный ряд (и вообще всякая неограниченная моно-
монотонная последовательность).
236. В любом отрезке с центром в начале координат имеется
лишь конечное число членов данной последовательности (если бы
их было бесконечно много, то, ш теореме Больцано — Вейерштрас-
са, из них можно было бы выделить сходящуюся подпосле-
подпоследовательность). Следовательно, для любого М >6 существует та-
такое N > О, что \ап\ > М для всех номеров п > N, а это и озна-
означает, что
lim \ап\ = +00,
237. Примером может служить последовательность, составлен-
составленная из всех рациональных чисел, занумерованных произвольным
образом.
238. Пусть F — предельное множество последовательности
{ап } и | — точка прикосновения множества F. Тогда существует
последовательность {л^} точек из F, сходящаяся к |. Так как хх —
предельная точка последовательности {ап}, то найдется номер пх
такой, что р (ап , хг) < 1. Далее, так как и х2 — предельная точка
заданной последовательности, то существует номер п2, больший,
чем пъ и такой, что р (ап , х2) < —. Если теперь уже выбраны но-
номера пъ я2, ..., nh,1 такие, что пг < п2 < ... < nk__x и р (ал/| xt) <
<— для / =1,2, ..., k — 1, то в качестве п возьмем номер
nk > пк_ъ для которого р (ап. xk) < —.
« k
По индукции получим подпоследовательность ап f ап, ... ис-
исходной последовательности {ап}у сходящуюся к |.
128

Действительно,
p(ank, 9л
откуда следует, что ank -*»-1 при k -> оо. Но это означает, что
Итак, любая точка прикосновения | множества F принадлежит
этому множеству; следовательно, оно замкнуто.
239. Случай F = 0 рассмотрен в задаче 235. Если F непусто
и конечно, F = {аъ ..., ak}, то требуемым свойством будет обладать
последовательность аъ ..., аЛ, аъ ..., аЛ> аь ..., аЛ, ...
Пусть теперь F бесконечно. Тогда существует счетное множе-
множество Е, замыкание которого равно F. А именно в качестве Е можно
взять объединение следующих двух множеств: множества Ег всех
концов смежных интервалов к F и множества Е2 всех рациональных
точек, являющихся внутренними точками множества F (конечно,
Е2 может оказаться и пустым; это будет в том случае, когда F нигде
не плотно). Легко видеть, что каждая точка х0 множества F явля-
является точкой прикосновения для Е: если х0 — внутренняя точка
множества F, то в любой ее окрестности V (х0) найдутся точки из
Еч\ если же х0 — граничная точка множества F, то в любой ее
окрестности V (х0) найдутся точки из Et. Таким образом, F с= Е.
С другой стороны, так как Е a F и F замкнуто, то Е с= F. Тем
самым F = Е\
Расположим теперь точки множества Е произвольным образом
в последовательность {ая}. Если Е не имеет изолированных точек,
то эта последовательность и будет искомой. Но в любом случае
требуемым свойством будет обладать последовательность аь аи
а2, аи аъ аэ, аи а2, a3t а±, ...
240. Необходимость. Пусть {хп} — последователь-
последовательность, сходящаяся к точке х. Очевидно, х — предельная точка для
{хп}. С другой стороны, пусть у — любая точка, отличная от х.
Отделим х и у друг от друга непересекающимися окрестностями
V (х) и V (у). В CV (х), а значит, и в V (у) может находиться лишь
конечное число членов из {хп}, т. е. у — не предельная точка для {хп}.
Достаточность. Пусть {хп} — ограниченная последо-
последовательность с предельным множеством, образованным одной точ-
точкой х0, и пусть V (х0) — произвольная окрестность точки х0. Если
бы в CV (хъ) находилось бесконечное число членов из {хп}, то, в
силу теоремы Больцано — Вейерштрасса, из них можно было бы
выделить подпоследовательность {хп }, сходящуюся к некоторой
точке х. Так как хПк £ CF (х0} и CV (х0) замкнуто, то х( CV (х0),
т. е. х ф Xq\ следовательно, у {хп} существовали бы по крайней мере
две предельные точки (х0 и х)у что противоречит условию. Итак,
вне любой окрестности точки х0 лежит не более чем конечное мно-
множество точек из {хп}> т. е. х0 = lim xn.
241. {ап}у где a2k = Л, a2*-i = 1-
242. Пусть А — совершенное подмножество множества ирра-
иррациональных точек отрезка [0, 1]. Такое множество можно построить
129

Рис. 19
по схеме! решения задачи 232, если в качестве гк брать иррацио-
иррациональные числа, меньшие единицы, удовлетворяющие принципам
выбора в решении задачи 232. Тогда искомым совершенным множе-
множеством будет А X А. Заметим, что А X А нигде не плотно, так как
оно замкнуто, и его дополнение всюду плотно.
243. Квадрат [и, ft] X [с, d] (a < ft, с < d) есть объединение
попарно не пересекающихся вертикальных отрезков: х = ky
с ^у ^ d (a ^ k ^ ft). Множество этих отрезков имеет мощность
континуума. Каждый из них является непустым совершенным мно-
множеством.
244. Назовем Замкнутыми квадратами первого ранга те восемь
замкнутых квадратов, которые остаются на плоскости после вы-
выбрасывания центрального открытого квадрата, а сам этот выбрасы-
выбрасываемый квадрат назовем открытым квадратом первого ранга
(рис. 19, а). Аналогично определим замкнутые квадраты второго
ранга (их число равно 82, сторона каждого из них равна
З2
см.
рис.
19, б) и открытые квадраты второго ранга (их число равно 8,
сторона каждого равна — ]. Продолжая так дальше, мы определим
открытые и замкнутые квадраты всех рангов.
Ясно, что А = П Рп> где Рп — объединение всех замкнутых
п
квадратов ранга п. Так как каждое множество Рп замкнуто, то и
их переселение (т. е. А) тоже замкнуто.
Чтобы доказать, что А нигде не плотно, рассмотрим произволь-
произвольный открытый круг J. Этот круг либо полностью свободен от точек
множества Л, либо содержит хотя бы одну его точку М\ докажем,
что и в этом последнем случае в круге / найдется меньший круг,
полностью свободный от точек множества А. Для того чтобы убе-
убедиться в этом, рассмотрим замкнутый квадрат Кп ранга п, содер-
содержащий точку М и такой, чтобы его диагональ была меньше расстоя-
расстояния от точки М до границы круга / (это можно сделать, так как
диагонали замкнутых квадратов стремятся к нулю при стремлении
130

Рис. 2 0
Рис. 21
их ранга п к бесконечности). Этот квадрат целиком лежит внутри
круга J (рис. 20). Тогда открытый квадрат п + 1-го ранга, ле-
лежащий в середине квадрата Кп, полностью свободен от точек множе-
множества А (и тоже лежит внутри круга J). Следовательно, круг Vy впи-
вписанный в этот открытый квадрат, будет лежать внутри круга /
и не будет содержать Точек множества А. Итак, А — нигде не плот-
плотное множество на плоскости.
Подобным же путем доказывается, что А не имеет изолирован-
изолированных точек. Пусть Мо€ А\ опишем около Мо произвольную окрест-
окрестность J и рассмотрим замкнутый квадрат Кп, содержащий Мо
и включающийся в J (рис. 21). Границы этого квадрата будут при-
принадлежать А и содержаться в J. Значит, Мо не является изолирован-
изолированной точкой.
Так как А замкнуто и не содержит изолированных точек, то
А — совершенное множество.
Выясним арифметическую структуру множества А. На первом
этапе мы исключаем из основного квадрата такие точки М (ху у),
у которых разложение и абсциссы, и ординаты в троичную дробь
обязательно содержит единицу на первом месте. На втором этапе
исключается, кроме того, все такие точки, у которых и абсцисса,
и ордината содержат единицу на втором месте, и т. д. Таким обра-
образом, в множестве А останутся те и только те точки М (х, у)у у ко-
которых абсциссу и ординату можно разложить в троичные дроби
х = 01а1а2а3...1 у = 0, Ь{Ь2Ь3... так, чтобы ни при каком k
не выполнялось равенство ak = bk = 1. Так, например,
Aft @,212121..., 0,121212...) g Л; М2 @,202020..., 0,202020...К А\
М3 @,1000..., 0,1111...) € А (в последнем случае, хотя а4 =
= bt = 1, абсциссу этой точки можно переписать так: 0,02222...)*.
С другой стороны, М4 @,1010..., 0,1021...) £ А (эта точка исклю-
исключается уже на первом шаге; она входит в открытый квадрат первого
ранга).
* Здесь и далее координаты точек Мъ М2, М3} М± заданы с помощью троич-
троичных дробей.
131

245. Исследование аналогично проведенному в решении зада-
задачи 244. Арифметическая структура множества В такова; в него вхо-
входят те и только те точки М (х, у) основного квадрата, у которых как
абсцисса х> так и ордината у могут быть записаны в виде троичных
дробей, не содержащих единицы среди своих троичных знаков.
246. Исследование проводится аналогично. Арифметическая
структура множества Е такова: оно состоит из всех точек М (х, у)
основного квадрата, абсциссы которых произвольны @ ^ х ^ 1),
а ординаты могут быть записаны в виде троичной дроби, не содер-
содержащей единицы среди своих троичных знаков.
247. А = {[0, 1] X [0, 1]} \ {CD X CD}, где CD —допол-
—дополнение к канторову множеству D до всего отрезка [0, 1]; В = D X
XD;£- [0, 1] X D.
248. Так как G плотно в X, то So содержит точку х0 € G. Но х0 —
внутренняя точка множества G. Поэтому некоторая ее окрестность
V (xOi 80) также входит в G. Эту окрестность можно выбрать столь
малого радиуса, чтобы она содержалась в So и G вместе со своим
замыканием: V (х^ е0) с So f| G.
249. Пусть G4, G2, G3, ..., Gny ... — последовательность открытых
множеств, плотных в X, и So — произвольный открытый шар. Со-
Согласно задаче 248, найдется открытый шар Si Такой, что S4 с: So f]
П Gi, причем 5i можно выбрать так, чтобы diam Si < 1. Согласно
той же задаче, найдется открытый шар S2 такой, что S2 с: Si П
П G2, причем S2 можно выбрать так, чтобы diam S2 < —; далее,
найдется открытый шар S3 с diam 53 < — такбй, что S3 с= S2 П
о
О G3, и т. д. В итоге у нас получится последовательность откры-
открытых шаров {Sn} такая, что ^Л+1 с Sn (п = 1, 2, ...), причем все
они содержатся в ранее выбранном шаре So. Следовательно, со-
согласно задаче 211, существует точка £, общая для всех этих шаров
и, значит, тоже содержащаяся в So. С другой стороны, £ содержится
в каждом Gk (так как | £ Sk с: Sfe_i f) G^). Таким образом, в про-
произвольном шаре So нашлась точка | С f]Gh. А это и означает, что
f\Gk плотно в X.
k
250. Пусть р — обычное расстояние на прямой, X = {ги г2, ...}
— множество рациональных точек на прямой, занумерованных
произвольным образом. Тогда (X, р) — неполное метрическое про-
пространство. Множества Fn = {ги ..., гп) (п = 1, 2, ...) замкнуты в
(X, р), и, значит, множества Gn = X \ Fn открыты. Кроме того,
оо
Gn плотны в X. Но (]Gn = 0.
/1=1
251. Пусть G|, G2, ..., Gnt ... — открытые множества, плотные в
X, н Е = f\Gk. Согласно задаче 249, Е плотно в X.
k
132

Возьмем в X какие-либо два непересекающихся шара So и St
и в каждом из них выберем шары б0 и 6t так, чтобы б0 cz So f| Gtl
6^1 cz Si П Gu причем diam б0 < 1, diam 6t < 1 (см. задачу 248).
Назовем б0 и 6j шарами первого ранга.
Для дальнейшего заметим, что в каждом шаре S а X можно
выбрать два непересекающихся шара. Действительно, в S суще-
существуют две различные точки х и у, так как X не имеет изолированных
точек. Точки х и у можно отделить друг от друга непересекающими-
непересекающимися шарами, причем столь малых радиусов, чтобы эти шары вхо-
входили в S.
Используя этот результат, рассмотрим теперь какие-либо два
непересекающихся шара 500 и SOi> включающиеся в б0, и два непе-
непересекающихся шара Slo и Sh, включающиеся в 8{. В каждом из
них найдем по шару б00, бОь б10, би так, чтобы
б00 cz Soo П G2, _6Oi <= Sqi р G2, б10 cz Slo П G2,
би cz Sh П G2,
и диаметр каждого из этих шаров был меньше —. Шары б00, б01,
б1а, би назовем шарами второго ранга. Вообще, если построены шары
k-YQ ранга, то для построения шаров k + 1-го ранга поступаем
следующим образом: пусть б.( . (где iu i2, ..., ik —нули или
единицы) — какой-либо шар /г-го ранга, причем diam б . <
V* - 1ь
< —. Выделим в нем два непересекающихся шара S.. и
k h^t ••• *£°
S.. . , ив каждом из них найдем по шару б.. . л и б.. . ,
так, чтобы
\iz... ik о c Sij2 ... iko П Gk+ii \tt ^ ik { cz SMi >м ^ П G^x
и
diam6... . n < , diam6.. . , ^ .
Все полученные таким образом шары назовем шарами k + Uean
ранга. Их вдвое боЛьше, чем шаров fe-ro ранга. Ясно, что: а) раз«
личные шары &-го ранга (при фиксированном к), и даже их замука-
ния, не пересекаются друг с другом; б) с возрастанием номера k
диаметры шаров стремятся к 0; в) для любой последовательности
нулей и единиц iu i2, ..., ik> ••• имеем:
б. id б.., б.. zd б.. . , ...
Из свойств б) и в) вытекает, что для любой последовательности
нулей и единиц iu i2i ... существует единственная точка х. . { ,
общая для всех шаров б^, б.^, б.^, ... (см, задачу 211); вмеете
с тем из свойства а) следует, что двум различным последовательно-
последовательностям iu гъ i3, ... и i'v i'v i'v ... соответствуют две различные точки
133

x, , ? ... нх.' .' ./ •..следовательно, множество Л всех таких точек
хт ••• будет иметь ту же мощность, что и множество всевозмож-
всевозможных последовательностей из нулей и единиц, т. е. мощность конти-
континуума.
Докажем, что А а £. Пусть iu i2, i3t ... — произвольная после-
последовательность нулей и единиц; ^ля любого номера k имеем:
Следовательно, х.,, £[\Gk = £, т. е. любая точка множест-
4*2*3 £ К
ва А является элементом множества Е. Так как, по доказанному,
А имеет мощность континуума, то мощность множества Е не мень-
меньше мощности континуума.
252. Построим на отрезке [0, 1] последовательность совершен-
совершенных множеств Аи А2> ASt ... следующим образом. В качестве А\
возьмем канторово множество D. Для построения Ап при п > 1
разобьем [0, 1] на п равных отрезков и на каждом из них построим
нигде не плотное совершенное множество тем же процессом, каким
строилось D на [0, 1]; объединение этих п множеств примем за Ап.
Положим теперь А = [)Ап, В = [О, 1] \ А. Каждый интервал
п
]а, Р[ с= [0, 1] содержит отрезок вида U-, 1-^—\ с достаточно боль-
[п п \
шим п. По построению Ап(][ — > 1 ] есть совершенное множе-
п п
ство, подобнее канторову, и потому имеет мощность континуума.
А так как [0, 1] id А[\ ]а, Р[ •=> Ап [\ \L9 L±i], той А П ]а, Р[
[п п J
имеет мощность континуума.
Докажем теперь, что В (] ]а, р[ имеет мощность континуума.
Возьмем произвольный отрезок [у, б] cz ]a, р[ Имеем:
в п Ст. б] - п {Ст, в] \ К }.
Но [у, 6] — замкнутое и потому полное подпространство числовой
прямой (наделенной обычной метрикой), а [у, б] \ Ап — откры-
открытые в нем множества (см. задачу 193). Так как они всюду плотны
в [?» 6]» то> в силу результата задачи 251, В {] [у, б] имеет мощ-
мощность, не меньшую мощности континуума. А так как [0, 1] id В f|
П ]а, р [ id В П [у, б]» то В П ]<*, PC имеет мощность континуума.
253. Это непосредственно вытекает из задачи 251, если учесть,
что совершенное множество Е само является полным пространством
без изолированных точек и что Е = (] Еп9 где Еп == Е при п =
п
= 1,2, ..., так что каждое Еп открыто и плотно в Е.
254. Пусть Въ В2, ..., Bk> ... — плотные множества типа G6
в X и В — их пересечение. Тогда для любого k Bh = f| Cw, где
Ghi — открытые множества. Так как Gki id ВкУ то все Gki также
плотны в X. Следовательно, В = f]((]Ghi) =f\Gkl есть пересече-
/г i k, i
134

ние конечной или счетной совокупности плотных открытых мно-
множеств Gki. Но тогда В является множеством типа G6, плотным в X
(см. задачу 249).
255. В качестве множеств Еп можно взять множества Gn из
решения задачи 250.
256. Как известно, множество всех простых чисел бесконечно
и, значит, счетно. Перенумеруем их: рх = 2, р2 = 3, р3 = 5, р^=7,
ръ = 11, ...и обозначим через Ek множество всех чисел вида
г + У ркУ где г пробегает все рациональные числа, a pk фиксиро-
фиксировано. Тогда каждое Ек счетно и всюду плотно на прямой (оно полу-
получается из множества всех рациональных чисел сдвигом на Урк).
Докажем, что множества Ек попарно не пересекаются»
Пусть k ф i и, следовательно, ркф рг Возьмем произвольный
элемент % = гг + Урл из множества Ek и произвольный элемент
т| == г2 + У Pi из множества Et и докажем, что § ф rj. Допустим
что 1 = х\\ тогда гг + Урк = г2 + Kft, откуда (гх — г2J =
2 или У PiPk = Pt" +Р/г~ (;i~r2)^ мы П0ЛуЧИЛИ за-
заведомо неверный результат (квадратный корень из произве-
произведения двух различных простых чисел оказался рациональным
числом). Следовательно, наше допущение, что | =т|, неверно; зна-
значит, Et П Ek = 0 при любых различных ink.
257. Множество Е всех рациональных чисел, как всякое счет-
счетное множество, есть объединение счетной совокупности одноточеч-
одноточечных и, значит, замкнутых множеств. Следовательно, Е — множе-
множество типа FQ.
С другой стороны, Е всюду плотно на прямой. Если бы оно
было множеством типа G&, то множество Еъ полученное из Е сдви-
сдвигом на V~2 (т. е. множество всех чисел вида г + У~2, где г £ £),
также было бы всюду плотным множеством типа G6. Но в этом слу-
случае и их пересечение было бы всюду плотным множеством (см. за-
задачу 254), тогда как на самом деле Ег (] Е = 0. Следовательно,
допущение, что Е является множеством типа G6, неверно.
258. Для доказательства надо использовать результаты задач
204 и 257.
259. См. решение задачи 257. Указание. Сдвиг надо произ-
производить на число а, выбранное так, чтобы множество точек вида
х + а (где х € Е) не пересекалось с Е (это возможно в силу счет-
ности Еу см. задачу 71).
Требуемый результат можно получить и другим способом —
Как следствие задачи 251.
260. См. задачу 259.
261. Если бы множество [0, 1[ЛА где /—множество всех
иррациональных чисел, имело тип Fo, то любое множество вида
[k9 k + 1 [П Л гДе k — целое, также имело бы тип Fdi так как оно
135

конгруэнтно данному. Но тогда объединение |J {[ft, k + 1 [f\I},
к
где k пробегает все целые числа, также было бы множеством типа
Fo, что невозможно, так как оно совпадает со всем множеством /
(см. задачу 258).
Доказательство того, что [а, {5[П / при любых а и р, где а < р,
не есть множество типа Fa, проводится аналогична; только сдвиги
производятся не на целые числа, а на целые кратные какого-либо
фиксированного рационального чисЛа г £ ]0, р — а].
Чтобы доказать, что [a, p [f| £, где Е — множество всех рацио-
рациональных чисел, не есть множество типа G6, достаточно заметить,
что его дополнение [a, p [f| / до полуинтервала [а, р[ не есть мно-
множество типа Fa.
262. Например, множество М, составленное из всех отрица-
отрицательных рациональных и всех положительных иррациональных
чисел. Если бы М имело тип G6, то его часть, попавшая в промежу-
промежуток [—1, 0[, также имела бы тип G6, что неверно (см. задачу 261);
если бы М имело тип Fo, то его часть, попавшая в промежуток
[1, 2[, Также имела бы тип Fo, что тоже неверно.
263. Пусть А нигде не плотно, V — какой-либо шар, а ^ —
открытый шар, содержащийся в V, свободный от точек множе-
множества А. Тогда Vx не содержит также точек множества Л, и тем са-
самым А нигде не плотно.
264. Прямое утверждение доказывается без труда. Обратное
утверждение неверно. Пример. Множество рациональных
чисел всюду плотно на прямой, но и его дополнение всюду плотно.
265. Пусть S — любой открытый шар. Согласно задаче 248,
S О Е содержит вместе с замыканием некоторый шар 50, очевидно
свободный от точек СЕ. Значит, СЕ нигде не плотно.
п
266. Пусть Е = U Eif где Еъ Е2> ..., Еп — нигде не плотные
1=1
множества и S — произвольный шар. Так как Ег нигде не плотно,
то найдется шар Si в S, свободный от точек Ег. Далее, так .как Е2
нигде не плотно, то в Sx найдется шар 52, свободный от точек Е2;
а так как S2 cz Sl9 то S2 не содержит также точек множества Ег.
Продолжая этот процесс, мы получим, после п шагов, шар Sn,
Свободный от точек множеств Е1у Е2, ..., Еп и, значит, свободный
от точек множества Е, причем Sn cz S. Следовательно, Е нигде
не плотно. Для объединения счетной совокупности множеств это
утверждение опровергается примером множества рациональных
точек на прямой, которое всюду плотно, но является объединением
счетной совокупности одноточечных и, значит, нигде не плотных
множеств.
267. Пусть X = у Е1$ Где Et нигде не плотны в X. Пусть
i
V (хъ г±) — шар, свободный от точек множества Ег\ V (х2> г3) —
шар, свободный от точек множества Е%, включающийся вместе со
136

своим замыканием в V (хъ ех) и такой, что е2 < ~; V (л:3, е3) —
шар, свободный от точек множества £3, включающийся вместе
с замыканием в V {хъ е2) и такой, что е3 < —, и т. д. Последова-
о
тельность хъ х2, х3у ...фундаментальна и, следовательно, в силу
полноты пространства, имеет предел: £ = lim xn (£ £ X). Так
кдк С С V (*,+1, е/+1) для всех /, а У(*т> е/+1) с: У (xit ef), то
£ С Et для всех Л Значит £ £ у ££, что противоречит тому, что
X = [)Et. Итак, X —множество второй категории.
268. Множество Е всех рациональных точек на прямой, наде-
наделенное обычным расстоянием, есть неполное метрическое простран-
пространство, являющееся объединением счетной совокупности нигде не
плотных (а именно одноточечных) множеств; следовательно, Е —
множество первой категории.
269. Противоречия нет. Канторово множество D нигде не плот-
плотно как подмножество пространства /?*, но не является таковым в
самом себе, где оно, наоборот, всюду плотно.
270. Пусть х0 — изолированная точка метрического простран-
пространства X. Одноточечное множество {х0} открыто в X. Если Е —
какое-либо нигде не плотное множество в X, то существует непу-
непустое открытое множество {/с: {х0} такое, что U {] Е = 0. Но
единственное непустое подмножество в {х0} есть оно само. Поэтому
U = {х0} и х0 (; Е для каждого нигде не плотного множества Е.
Значит, X не представимо в виде объединения любогог в том числе и
счетного, семейства нигде не плотных множеств.
271. Пусть X — числовая прямая с выколотой точкой, напри-
например, X = Z?1 \ {0}; р — обычное расстояние на X. Тогда (X, р) —
неполноз метрическое пространство без изолированных точек.
Любое множество Е> нигде не плотное в X, нигде не плотно и в Z?1.
Действительно, для любой точки х (; R1 и любой ее окрестности
V (х\ найдется интервал I а V (х)у не содержащий точки 0 и, зна-
значит, вхбдящий в X. Talc как Е нигде не плотно в X, то в / содер-
содержится интервал 1Ъ не пересекающийся с Е, Но 1г а V (х) a R1.
А это и доказывает, что Е нигде не плотно в Z?1.
Если теперь предположить, что X = U ЕПУ где все Еп нигде
п
не плотны в X, то R1 представится в виде объединения счетного
числа нигде не плотных множеств:
Я' = U Еп 0 {0}.
п
Но это невозможно, поскольку /?* — полное пространство (см. за-
задачу 267). Следовательно, X — множество второй категории.
272* Пусть X — полное метрическое пространство и Е —
множество первой категории в X, так что Е = U ЕПУ где все Еп
п
нигде не плотны в X. Предположим, что СЕ — множество первой
137

категории, т. е. СЕ = (J Sn, где 5Л — нигде не плотные множества
п
в X. Тогда X = ([}Еп) [) (US/*)> что противоречит теореме Бэра.
п п
Значит, СЕ — множество второй категории.
273. Множество СЕ — первой категории, так как оно является
объединением прямых х = rk (k =1,2, ...) и у = rk (k = 1, 2, ...),
где rk пробегает все рациональные числа (каждая прямая — нигде
не плотное множество на плоскости). Следовательно, Е — множе-
множество второй категории (см. задачу 272).
274. Пусть х € DЕ. В любой окрестности V (х) найдется точка
х0 £ DE. Возьмем окрестность V (х0) с: V (х). Так как V (xQ) (] Е —
множество второй категории, то и V (х) {] Е — множество второй
категории, т. е. х £ DE. Следовательно, DE замкнуто.
Пусть теперь х0 (: DE. Так как для любой окрестности V (х0)
множество V (xQ) fl E второй категории, и, следовательно, бес-
бесконечно, то V (х0) содержит бесконечное число точек из Е. Значит,
х0 €£'.
275. Пусть Е нигде не плотно и / — произвольный интервал
на прямой. Интервал I_aJ полученный из / сдвигом на —а, содер-
содержит подинтервал /, свободный от точек множества Е. Но тогда
интервал Ja> который получится из I сдвигом на а, включается в /
и не содержит ни одной точки из Е. Следовательно, Еа #игде не
плотно.
Если же Е всюду плотно и / — произвольный интервал, то 1а
содержит точку xQ б Е\ а тогда xQ + а £ I (] Еа и, следовательно,
Еа всюду плотно.
276. Пусть Еа — множество всех точек вида а — х, гд$ х про-
пробегает Е. Как легко проверить, Еа — открытое всюду плотное
множество на прямой. Поэтому из задачи 249 следует, что Е [\ ЕаФ
ф 0. Пусть х1 £ Е Г) Еа\ тогда хг € Е и хг = а — х2, где х2 £ Е.
Следовательно, а = х1 + х2У где хъ хъ ^ Е.
277. Если множество Е всюду плотно на прямой, то любой
интервал ]а, р[ содержит бесконечно много точек из Е, так как в
противном случае на ]а, (i[ нашелся бы интервал, полностью сво-
свободный от точек множества Е. Если теперь из Е исключить конеч-
конечное подмножество Л, то на произвольном интервале ]а, |3[ все же
останется бесконечно много точек из Е \ А. Значит, Е \ А всюду
плотно на прямой.
278. В задаче 256 была построена последовательность Еъ £2, ...
попарно не пересекающихся всюду плотных счетных множеств
на прямой. Обозначим дополнение к объединению этих множеств
через / (его пересечение с любым интервалом несчетно) и рассмот-
рассмотрим счетную совокупность множеств:
Ek U (/ П ]*-!,*[)(* =1,2, ...).
Ясно, что эти множества попарно не пересекаются, а каждое из
них всюду плотно на прямой и несчетно.
138

279. Пусть (#0, у0) — произвольная точка пространства X х Y
и V ((х0У у0), г) — произвольная ее окрестность. Так как Е нигде
не плотно в X, то окрестность V (х0У -^= J содержит шар V (z0, 6)
радиуса б ^ —у=-$ свободный от точек множества Е. Но тогда шар
У ((^о» Уо)» *) содержится в V ((х0, у0), г) и свободен от точек мно-
множества Е X F.
280. Согласно задаче 196, множество Е X F замкнуто. Предпо-
Предположим теперь, что оно имеет изолированную точку (х0, у0), т. е.
существует г > 0 такое, что V ((х0, у0), е) не содержит ни одной
точки из Е X F, отличной от (хо> у0). Но тогда V (х0, е) не содер-
содержит ни одной точки из Е, отличной от х0 (если бы нашлась точка
х ф х0 такая, что х € V (х0, е) П Е, то мы имели бы (х, у0) £
€ V ((*о' Уо)» 8) П (£" X F) и (х, у0) =7^= (а:0, у0)). Аналогично
V (у0, е) не содержит ни одной точки из F. Но это противоречит
тому, что Е или F — совершенное множество.
281. Пусть (*0, у0) — произвольная точка из X X Y и
V ((xQ9 у0), е) — произвольная ее окрестность. Существуют х из Е
такое, что рх (х, х0) < -?т, и у из F такое, что ру(у, уо)< -р=.. Но
тогда (jc, у) € V ((jc0, y0), e) f| (Е X F). Тем самым Е X F плотно
в X х Y.
282. Луч [0, +оо[. Действительно, любой интервал ]а, fj[, где
0 <; а < р, содержит число вида р— (это число легко найти:
сначала найдем рациональное число —, заключенное между ]Ах и
Я
а затем возведем его в квадрат).
283. Луч [1, +оо[.
284. Отрезок [0, 1].
285. Для каждого натурального числа k существует такое це-
целое число пкУ что nk < kt < nk + 1; положим xk = —nk + Щ>\
ясно, что 0 < xk < 1. Покажем теперь, что произвольный интер-
интервал и содержит число вида т + я£ с целыми т и п. Пусть i — на-
натуральное число такое, что — <|ы|, где \и\ — длина интервала и.
Тогда среди чисел хъ х2, ..., xt+x найдется по меньшей мере два
таких, расстояние между которыми меньше, чем —:
I — 1^-1
или, считая, что, например, xk > xk :
0<хь —л- <-.
Положим б = xk — xk и разобьем прямую точками, кратными б:
..., -36, -26, —6,0,6,26,36, ...
139

Так как 0 < б < | и\, то по крайней мере одна из этих точек, ска-
скажем рб, где р — целое число, попадет в интервал и. Но
nR П (Y Y \ П (( VI I Ъ Т\ / И I h f*X\ *п I *^Т~
UU fj \Ab Л. f U II II. -]— /vj^Lj/ I fly -]— KaUf) =5 III -j— lLL,i
где m = pnk^ — pn^ n n = pkx — pk2 — целые. Таким образом,
любой наугад выбранный интервал и содержит по меньшей мере
одну точку вида m + я£, т. е. множество этих точек всюду плотно
на прямой.
286. Да. Это следует из результата предыдущей задачи. Дейст-
Действительно, пусть ]а, §[ — произвольный интервал. Так как —, —
содержит число вида пг + я£ (где тип — целые), то ]а, р[ содер-
содержи! число 2т Аг
287. Допусти^, что существует дуга До с: Г, свободная от
точек множества М. Обозначим через ДЛ дугу, которая получает-
получается в результате поворота дуги До на k радиан по часовой стрелке.
Ясно, что ДЛ при любом целом k ^ 0 также свободна от точек из М.
Дуги До, Alf ..., ДЛ> ... , имеющие одинаковую длину и рас-
расположенные на окружности Г конечной длины, не г^огут все по-
попарно не пересекаться. Пусть, например, Д,Г|А,+||1 ф 0.
При этом А, ф Л/о+т, поскольку угол т не может быть кратным
углу 2я в силу иррациональности числа я. Из того, что Д£. f| At. , т ф
Ф 0, вытекает, что при повороте любого ДЛ по часовой стрелке на
угол т мы получим дугу Д#+т, пересекающуюся с ДЛ по непустому
множеству. В частности, по непустому множеству пересекаются
любые две соседние дуги из последовательности
О У ffl9 ZfTl9
Но тогда эти дуги покрывают всю окружность Г, что невозможно,
поскольку ни одно ДА не содержит точек из М (рис. 22).
Итак, на окружности Г не существует дуги, свободной от точек
множества М, т. е. М плотно на Г.
Уо
Рис. 22
Мп
Хо Г1
Рис. 23
С X
140

288. е-окрестность произвольной точки М (#0, у0) плоскости
Оху содержит рациональную точку Р (г\ г"), где
(рис. 23).
289. См. решение задачи 224.
290. Это множество строится следующим образом: делим от-
отрезок на десять равных частей и выбрасываем интервал ]0,4, 0,6[.
Затем каждый из оставшихся отрезков первого ранга:
[0, 0,1], ... ,[0Д 0,4], [0,6, 0,7], ..., [0,9, 1] делим на десять
равных частей и выбрасываем в каждом из них два средних интер-
интервала вместе с разделяющей их точкой, т. е. из отрезка [0, 0,1] —
интервал ]0,04, 0,06[, из отрезка [0,1, 0,2] — интервал ]0,14, 0,16[
и т. д. Затем каждый из оставшихся отрезков второго ранга делим
на десять равных частей и выбрасываем два средних интервала
Вместе с разделяющей их точкой и т. д.
Доказательство того, что Е нигде не плотно и совершенно,
проводится так же, как для канторова множества.
291. Это множество не замкнуто. Его замыкание состоит из
всех (в том числе и рациональных) точек отрезка [0, 1], обладаю-
обладающих десятичным разложением, не содержащим цифры 5. Как само
заданное множество, так и его замыкание не содержат изолиро-
изолированных точек. Как заданное множество, так и его замыкание нигде
не плотны на прямой.
292. Такое множество образуют концы смежных интервалов к
D. Его плотность в D легко следует из описания арифметической
структуры точек первого и второго рода множества D (см. решение
задачи 226).
293. См. решение задачи 239.
294. Пусть ф — произвольный элемент пространства С [0, 1].
Согласно определению расстояния в С [0, 1], окрестность V (ф, е)
состоит из всех функций % £ С [0, 1] таких, что ф (х) — е < % (х) <
< ф (х) + е для всех х £ [0, 1]. Но согласно аппроксимационной
теореме Вейерштрасса, существует такой многочлен Р, что ф (х) —
— е < Р (х) < ф (х) + е для всех х d [0, 1]; таким образом, мно-
множество всех многочленов плотно в С [0, 1].
295. Пусть 8 — произвольное положительное число. Для лю-
любой функции ф £ С [0, 1] существует такой многочлен Р, что
р (ф, Р) < — (теорема Вейерштрасса). Пусть Р (х) = а0 + а^х +
+ ... + апхП* Заменим все щ рациональными числами bt такими,
что ] щ — bt | < , и обозначим через Q получившийся много-
многочлен с рациональными коэффициентами bt:
Q(x) - bo + btx+ ... + bnxn.
14)

Тогда для всех х £ [0, 1],
\P(x)-Q (х)\ = |(Оо - бе)
+ @« - &„)*" К I «о - Ьо\ + I
т. е. р(Р, Q) < —. Но тогда
Итак, множество многочленов с рациональными коэффициентами
плотно в С [0, 1].
296. Пусть / (—х) = —/ (х) для всех х £ [—1, 1]. По теореме
Вейерштрасса, для любого е > 0 найдется многочлен Q (х) такой,
что
|/ (х) — Q(x)\<e для всех х £ [—1, 1]. A)
Так как вместе с х также —-х £ [—1, 1], то и |/ (—х) — Q (—х)\ <
< е для всех х £ [—1, 1]. Но
|/ <-*) - Q (-х)\ = | -/ (х) - Q (-х)\ = \f(x)-(-Q (-x))\.
Следовательно,
I/ (х) - (-Q (—х))\ < е для всех х € [—1, 1]. B)
Из неравенств A) и B) получаем:
Q(x)-Q(-x)
< 8.
Многочлен Р {х) ==■ ^ ^~~ является искомым. Действитель-
но, пусть
Q (х) = а0 + aix + а2х2 + а3х3 + ... + апхп.
Тогда
—Q (—х) = — aQ + flljc — агх* + а3х* — ... + (—\)п+1апхп и
Р (х) содержит лишь нечетные степени х.
Для случая, когда / (х) — четная функция, рассуждение ана-
аналогично.
297. Для любого натурального числа k найдем многочлен Pk
такой, что | Pk (х) — / (х) | < — для всех х £ [—Л, Л]. Последова-
Последовательность {Pk} будет искомой.
298. Пусть {Рд,}—данная последовательность многочленов,
сходящаяся к / равномерно на Ох. Тогда существует номер jV та-
такой, что для всех пгу п > N и всех вещественных х выполняется
неравенство
\Рт(х)-Рп(х)\< 1.
142

Зафиксируем номер п0 > N. Многочлены Рт (х) — РПд (х) ограни-
ограничены на всей прямой, что возможно, лишь когда Рт (х) — Рщ (х) =
= ат, где ат — постоянные. Отсюда / (х) — Р„в (х) = lim am
для всех х, так что / (х) — Рщ (х) = с, где с — постоянная. Следо-
Следовательно, / (х) = РПй (х) + с, т. е. / (х) — многочлен.
299. Пусть Ei — множество всех многочленов с рациональ-
рациональными коэффициентами. Оно счетно (см. задачу 62 или 65). Распо-
Расположим его как-нибудь в последовательность £4 = {gu g2t ...} и
положим Еп = {gn, gH-i» ...} (п = 2, 3, ...). Из результата задачи
295 следует, что Ех плотно в С [0, 1]. Остальные множества плот-
плотны в С [0, 1], так как отличаются от Ei только на конечные мно-
множества точек. Поскольку С [0, 1] полно (задача 130), никакая по-
последовательность его плотных подмножеств с пустым пересече-
пересечением не может состоять из одних открытых множеств (см. зада-
задачу 249).
300. Докажем сначала, что Е замкнуто. Пусть Pk -> f, где
Рл € £ (ft = 1, 2, ...), / € С[0, 1]. Выберем в [0, 1] какие-нибудь
N + 1 попарно различных точек хи ..., xN+x- Тогда для i = 1, ...,
N + 1 будем иметь: Pk (xt) -> / (xt), или Pk (xt) = f (xt) + ylk%
N
где yik-> 0 при ft-> +oo. Обозначим Pk (x) = 2 аы х"
0
шим (при фиксированном ft) систему линейных уравнений
= / (xi) + lik (l == ^ •••» N + *) относительно аЛя. Так как
lim 7/л = 0, то, как легко видеть, akn-+an при ft->+oo, где
(аь ..., aN , j) — решение системы линейных уравнений
2 V? - /to) (t = 1, .-, ЛГ + 1). Тогда lim Pk (x) =
N N
=? lim 2 аЛлхл =2 а/2х/г Лля всех *€[0, 1],
Л/
т. e.f(x)= 2 ал^Л и* значит /6£. Следовательно £" замк-
нуто, так что С£ открыто.
Но тогда, в силу результата задачи 265, нам достаточно для
любого Р 6 Е и любого е > 0 найти элемент из С [0, 1], входя-
входящий в V (Pt г) и не принадлежащий £. Таким элементом будет,
например, функция ср (х) = Р {х) + — xN^1. Итак, Е нигде не
плотно в С [0, 1].
301. Пусть £ (аь а2» •••) — произвольная точка из /2. Так как
+ОО
ряд 2#? сходится, то для каждого г > 0 существует N такое, что
143

+00
2 a? < g2r- Обозначим через z последовательность (аи аъ ..., а*,,
О, ...). Ясно, что z £ Е и р (£, г) < 8. Итак, £ плотно в /2-
302. Пусть U — произвольный шар в /2. Этот шар либо пол-
полностью свободей от точек множества Ег либо содержит точку £ € Е$
£ == (zly ..., zN, 0, 0, ...). В последнем случае возьмем е > 0 та-
такое, что V (£, е) a U, и рассмотрим точку r\ (zit ..., zN% —, 0, ...).
Тогда для любой точки х £ Е имеем: р (х, г\) ^ —, т. е. V 1% —\ а
2 \ 2 /
с СЕ. Кроме того, 1/ /tj, ~\ a V (S, е) с (/. Таким образом,
в £/ всегда найдется шар, свободный от точек множества £, т. е. Е
нигде не плотно.
Г л а в а VI.
КОМПАКТНОСТЬ, СЕПАРАБЕЛЬНОСТЬ,
СВЯЗНОСТЬ
303. Если множество Е не ограничена, т. е. diam Е = sup p(x, у) =
= +°°» то, какова бы ни была точка хо€ Еу sup р (х0, х) =
Х';Е
= +°о (так как если р (х0, х) ^ УИ для всех х € £", то р (я, у) ^
^ Р (х, х0) + р (л:0, у) ^ 2М для всех х, у £ Е). Поэтому, зафикси-
зафиксировав какую-нибудь точку х0 € Е> можно найти в Е последователь-
последовательность точек {хп}, для которой р (х0, хп)-г- +оо. Тогда р (хо> хт^->
-v + оо и для любой ее подпоследовательности {хПк}> а потому
последняя не будет фундаментальной и, значит, сходящейся. Сле-
Следовательно, Е не является относительно компактным.
Точно так же, если Е не замкнуто, то найдется последователь-
последовательность его точек, сходящаяся к точке прикосновения множества Е,
не принадлежащей Е\ но из такой последовательности нельзя
выделить подпоследовательности, сходящейся к точке из £, так
что Е некомпактно.
304. Достаточность очевидна, так же как и относительная
компактность любого компактного множества. Замкнутость ком-
компактного множества установлена в решении предыдущей задачи:
305. Вытекает из результата предыдущей задачи.
306. Пусть {хп} — последовательность точек из Е. Рассмотрим
последовательность {уп} точек из Е такую, что р (ул, хп) < —.
п
Так как Е относительно компактно, то {уп} обладает подпоследо-
подпоследовательностью {ynk}, сходящейся к точке с £ X. Тогда последова-
последовательность {хп } сходится к той же точке с, а так как Е замкнуто,
то с б Е. Итак* Е компактно.
144

307. Указание. Построить конечную е-сеть.
308. См. указание к дредыдущей задаче.
309. Последовательность функций
fn(x) = Asm2nnx(n= 1, 2, ...),
где А > 0, удовлетворяет условию \fn (х)\ < А для всех х £ [0, 1]
и всех п. Вместе с тем не только сама эта последовательность, но и
никакая ее подпоследовательность не может сходиться в С [0, 1],
так как расстояние между любыми двумя различными членами
этой последовательности не меньше числа Л. Чтобы убедиться в
этом, заметим, что функция ft (x) = A sin 2lnx равна А при х =
= .*+1 , а функция ffjix) = A sin 2knxy где k > i, равна 0 при
том же значении х. Поэтому
Следовательно, никакая подпоследовательность данной последова-
последовательности не является фундаментальной и, значит, не сходится.
310. Рассмотрим счетное множество точек е4 A, 0, 0, 0, ...),
е2 @, 1, 0, 0, ...),... из /2 (у еп единица стоит на я-м месте, а на
остальных местах — нули}; Оно ограничено и замкнуто, но ни-
никакая подпоследовательность последовательности {еп} не фунда-
фундаментальна и, значит, не сходится, поскольку р (ei9 ek) = Y% при
i фк.
311. Относительно компактные множества А и В ограничены
(задача 303). Выберем в каждом из них по точке а £ А> Ь £ В.
Тогда для любых точек х £ Л, у £ В будем иметь: р (х, у) ^
^ р (хУ а) + р (а, Ь) + р (Ь, у) <Г diam A + p (а, b) + diam В <
< + оо.
312. Пусть {хп} — произвольная последовательность точек из
к
U At. Так как число членов этой последовательности бесконечно,
то хотя бы одно из множеств Аи ..., Ак содержит ее бесконечную
подпоследовательность {хПк}. Тогда {хПк} (а значит, и {хп}) со-
содержит сходящуюся подпоследовательность, если множества
Аи ..., Ak относительно компактны, и подпоследовательнрсть, схо-
k
дящуюся к точке из \] Ач если эти множества компактны.
313. Очевидно, всякое подмножество относительно компактного
множества относительно компактно. Поэтому пересечение любой
совокупности относительно компактных множеств относительно
компактно. Если же рассматриваемые множества компактны, то
они замкнуты (задача 303) и потому замкнуто также их пересече-
пересечение. Так как это пересечение, кроме того, относительно компактно,
то оно компактно (задача 304).
314. Необходимость. Пусть А X В компактно, а {хп} —
145

произвольная последовательность точек из Л. Последова-
Последовательность {(хп, у)}, где у — какая-либо точка из В, обладает под-
подпоследовательностью {(хПк, у)}, сходящейся к некоторой точке
(*, у') € А X В (так что х £ А). Так как р ^Wft, x) ^
Р ((хп > У)л(х* У'))» то *nk ""*" х- Значит, Л компактно. Аналогич-
Аналогично доказывается компактность J5.
Достаточность. Пусть А и В компактны, а {(хПУ уп)} —
произвольная последовательность точек из А X Й. Последова-
Последовательность {хп} обладает подпоследовательностью ixnk}> сходя-
сходящейся к некоторой точке х £ А\ далее, последовательность {уПк}
обладает подпоследовательностью {уПк}, сходящейся к некото-
некоторой точке х € В. Тогда подпоследовательность {(хПк» Упк )}
последовательности {(хп, уп)} будет сходиться к точке (х> у) €
€ А X £.
315. См. решение предыдущей задачи.
316. Пусть Е — компакт, {хп} — фундаментальная последова-
последовательность его точек. Она обладает подпоследовательностью {хПк}9
сходящейся к некоторой точке с £ Е. Тогда и хп -> с, так как
Р (*п> С)<Р (*п> Xnk) + Р (xnk> С)<\ + \ = г
при п > N, k > N (а значит, и nk > АО, где W выбрано так, чтобы
было р (хп, хт) <~ при т > N, п > N и р (хч, с) < — при
k > N.
317. Выберем в каждом Ап по точке ал. Так как все эти точки
лежат в компактном множестве Аи то последовательность {ап}
обладает подпоследовательностью {аПк}, сходящейся к некоторой
точке а £ Alt Отбрасывая в {аПк) первые k — 1 членов, получим
последовательность ап , ап , ап ..., сходящуюся к той же
точке а и состоящую из точек, содержащихся в АПк. Так как АПк
замкнуто (см. задачу 303), то заключаем, что а £ Ап для любого
k и, значит а £ П Л = П Ап. Следовательно, (]Ап ф 0.
k п п
Если diam Ап -> 0, то для всякой другой точки b £ [\ Ап будем
п
иметь р (а, Ь) ^ diam Ап при всех пу а потому р (а, Ь) = 0, т. е.
318. Допустим, что это не так; тогда существует г > 0 такое,
что для каждого п найдется точка хп С Лл, не содержащаяся в
V (/С, е). Так как все эти точки принадлежат компакту Ль то по-
последовательность {хп} обладает сходящейся подпоследователь-
подпоследовательностью {хПк}\ так как для любого п все члены этой последователь*
ности с номерами k ^ п принадлежат Лл, а Ап замкнуто, то и £ =•
= lim #Лл 6 Ап для всех /г, т.че. % € /С- А так как, с другой сторо-
146

ны, хПк е V (/С, е), то р (хПк, £) > е для всех k. Это противоречит
тому, что хПк -> £.
319. Это непосредственно следует из результата предыдущей
задачи. _ _ _ __
320. Так как Ei+1 с Et с Я], то П £/+i с: П £;<= Л £*• Край-
ние члены последних включений непусты (теорема Кантора) и
совпадают. Следовательно, fl Et = [\ЕьФ0. Недостаточность
i i
условия 60 для справедливости утверждения задачи видна на при-
примере последовательности интервалов ]0, ![,, о — » Р» — » •••»
J 2 L 3 L
V. %....
321. Обозначим Кп = G \ Gn. Ясно, что /Сл — компакты, при-
причем П Кп = Fr G и Fr &„ с; /£я. Так как {/СЛ} — убывающая по-
п
следовательность компактов, то, в силу результата задачи 318,
для каждого г > 0 найдется такой номер N, что Кп cz У (Fr G, г)
при n > N; но тогда и Fr Gn cz У (Fr G, г).
322. Пусть / (х) = , а Еп — множество всех функций
1 + пх2
f € С [—1, 1], удовлетворяющих неравенству 0 ^ / (х) ^ fn (x) для
всех х g[—1, 1] и условию /@) = 1. Множества Еп замкнуты,
ограничены (р (/, g) < 1 для всех /, g £ Еп) и En+l cz En. Однако
(Е 0
п
Другой пример см. в решении задачи 209.
323. Положим Ап = Ei f| ... f| En(n = 1,2,...). Множества
An непусты по условию, компактны (см. задачу 313) и Ai zd Аг id
zd Л3 =э ..., а потому, в силу теоремы Кантора, (]Еп = (] Ап Ф 0.
п
324. Нет (см. задачу 322).
325. Необходимость. Пусть Е — относительное ком-
компактное множество и б — произвольное положительное число. Обо-
Обозначим через Xi произвольный элемент из Е. Если все точки дз Е
отстоят от Xi меньше чем на г, то искомая г-сеть построена (она
состоит из одного х^. Если же это не так, то найдется х2 £ Е такое,
что р (*i, х2} ^ £. Если точки хи хг в свою очередь не образуют
е-сети, то найдется х3 £ Е такое, что р (хи *з) ^ е» Р (Х2, %з) ^?-
Если и точки #1, х2, х3 не образуют^ г-сети, то найдется х± £ Е
такое, что р (xiy х4) ^ г при i = 1, 2/3. Этот процесс обязательно
оборвется на некотором номере пОу так как если бы он продолжался
неограниченно, то из последовательности {хп} нельзя было бы
выделить сходящейся подпоследовательности (любая ее подпосле-
подпоследовательность не фундаментальна). Итак, множество хи ..., хПо
образует искомую г-сеть, а значит, Е вполне ограничено.
Достаточность. Пусть Е — вполне ограниченное мно-
множество в полном метрическом пространстве X и {хп} — последо-
147

вательность точек из Е. Докажем, что у нее существует сходящая-
сходящаяся подпоследовательность.
Возьмем какую-нибудь конечную сеть для г^ = 1 и около каж-
каждого ее элемента опишем шар радиуса 1. Хотя бы один из этих
шаров — обозначим его Vi — включает бесконечное число членов
последовательности {хп} (под этим мы подразумеваем, что имеется
бесконечно много номеров таких, что члены последовательности
с этими номерами содержатся в рассматриваемом шаре). Пусть
хПх — один из этих членов. 1
Далее, возьмем конечную сеть для е2 = — и около каждого
1
ее элемента опишем шар радиуса —^ Хотя бы один из этих шаров —
назовем его V2 — включает бесконечно много элементов последо-
последовательности {хп} из числа тех, которые попали в V±. Обозначим
через хПг какой-либо из них, с единственным условием, что п2 > «i.
Вообще, пусть уже построены элементы хПхУ ... , хПк% где
Щ < ... < Яь хп. 6 Vt (I = I, ..., k) и Vi — шар радиуса е, = —,
включающий бесконечно много членов последовательности {хп}
из числа содержащихся в шаре Fj—i. Тогда строим конечную сеть для
ek+i ^ и около каждого ее элемента описываем шар ра-
k+ 1
диуса . Тот шар, который включает бесконечно много членов
k-\-1
последовательности {хп} из числа входящих в Vk, обозначим Vk+1
и примем за xnk+i какой-либо из этих членов, с единственным
условием, чтобы было nk+1 > nfc. Неограниченно продолжая
этот процесс, мы получим подпоследовательность {хпЛ последо-
последовательности {хп}. Она фундаментальна, так как при i ;> k, j ^ k
имеем: хП{ ^ Vk, хп. 6 Vk и, значит, р (хп.у хП]) < —. В силу
полноты пространства X, она сходится. Значит, Е — относительно
компактное множество.
326. См. доказательство необходимости в решении предыдущей
задачи.
327. Это непосредственно следует из теоремы Хаусдорфа (зада-
(задача 325) и результата задачи 304.
328. Пусть г — произвольное положительное число, А — отно-
относительно компактная — сеть для £, а В — конечная — -сеть
для относительно компактного множества А (существующая в силу
теоремы Хаусдорфа). Множество В является конечной е-сетью
для Е; следовательно, Е относительно компактно.
Если X неполно, то утверждение задачи становится неверным.
Пример. X —множество всех рациональных чисел с обычной
метрикой, Е—множество рациональных чисел х из [0, ^.Множест-
^.Множество Е не является относительно компактным, хотя для него при любом
148

e > 0 существует относительно компактная (даже конечная) е-сеть.
329. Так как Е ограничено, то оно включается в некоторый па-
параллелепипед [alf bi] X [а2, b2] X ... х Оя» Ьл]. Зададим произ-
произвольное 8 > 0 и разобьем каждый отрезок [aiy bj, точками aL =
= xtp < 42> < ... < #(£г-!> < x{f0=bi так, чтобы расстояние между
о
любыми двумя соседними точками было меньше ■ __ . Тогда мно-
Vn
жество всех точек из Rn вида (x\s*\ х^\ ..., *£«>), где sb s2, .,., sn
принимают, независимо друг от друга, значения st = 1, 2, ...,
Pi, s2 = 1, 2,..., /?2fM s* = 1, 2, ..., /7Л, является конечной е-сетью
для £ в пространстве /?л. Следовательно, £" вполне ограничено, а
значит, в силу полноты Rn и первой теоремы Хаусдорфа, относи-
относительно компактно.
330. Это следует из задач 329 и 304.
331. Пусть Е —относительно компактное множество в /2. Если
бы оно не было нигде не плотным, то его замыкание Е включало бы
некоторый шар V а 1г. Пусть а = (ai, а2, ...) — центр этого ша-
шара. Построим последовательность {bt} {bt £ 12) следующим обра-
образом: bi = (ai + 1-9 а2, а3, ...), Ьъ = (аи а2 + ^-, а3, ...), Ь3 =-
= (^i, ^2, % + —• ...). •-., где 6 —радиус шара V. Все Щ содер-
жатся в V, а значит, и в Е. Но так как р (bt, bj) = 1/ (—) + (—-) =«
g r \2/ \2 /
= —у=г при I Ф /, то никакая подпоследовательность последова-
последовательности {Ьп} не фундаментальная и, следовательно, не сходится,
что. противоречит компактности Е (см. задачу 306).
332. Доказательство аналогично приведенному в решении пре-
предыдущей задачи. Если центр фигурирующего там шара V радиуса
б есть функция /0, то за Ъь можно принять функции /0 + //» ГДО ft —
функции из решения задачи 309, в которых А заменено на 6, а
отрезок [0, 1] линейно преобразован в отрезок [а, Ь].
333. Если множество Е компактно, то оно обладает свойством
Я, так как любое замкнутое подмножество компакта есть компакт
(см. задачу 305).
Пусть теперь множество Е обладает свойством Я. Докажем,
что оно замкнуто, Пусть х0 £ Е, так что х0 = Пт хп, где {хп} —
М->-оо
некоторая последовательность точек из Е. Пусть, далее, V (х0) и
В (хъ) — открытый и замкнутый шары одинакового радиуса с цент-
центром в х0. Так как, начиная с некоторого номера, хп € Е f| V {х0) а
c£f)B (х0), а Е П В (х0) замкнуто, то х0 £ Е ft В (х<>) и, зна-
значит, х0 € Е. Следовательно, Е замкнуто.
334. Утверждение следует из результата задачи 330. С другой
стороны, пространство С [0, 1] полно (задача 130), а замкнутый
единичный шар в нем не обладает свойством Я, так как он не-
некомпактен в С [0, 1] (см. задачу 309).
149

_ 335. Пусть V — произвольный открытый шар в С [а, 6]. Тогда
V П Е компактно в С [а, Ь~] и, значит, нигде не плотно (см. задачу
332). Следовательно, найдется шар Vi a F, свободный от точек
множества V (] Е, а значит, и от точек множества Е.
336. Необходимость. Пусть Е бикомпактно. Рассмот-
Рассмотрим произвольную последовательность {хп) точек из Е. Допустим,
что ни одна ее подпоследовательность не сходится к точке из Е.
Тогда каждая точка z £ Е обладает окрестностью V (г), содержа-
содержащей лишь конечное (быть может, пустое) число членов последова-
последовательности. Эти окрестности V (г) образуют открытое покрытие
множества Е. Так как Е бикомпактно, то существует конечное число
точек ги ..., th d Е такое, что Е а V (г{) [} ... U V (zn). Но это
невозможно, поскольку множество, стоящее справа, содержит
конечное число членов последовательности, тогда как Е содержит
все ее члены. Полученное противоречие показывает, что каждая
последовательность точек из Е обладает подпоследовательностью,
сходящейся к точке из Е, т. е. Е компактно.
Достаточность. Пусть Е компактно. Допустим, что су-
существует открытое покрытие {Ga} множества £", из которого нель-
нельзя выделить конечного покрытая. Зададим убывающую последо-
последовательность чисел {еп}, стремящуюся к 0. Построим конечную
ггсеть для Е (задача 325) и около каждой ее точки опишем шар
радиуса е4. Замыкание каждого из этих шаров имеет с Е компакт-
компактное пересечение (см. задачу 305) с диаметром не больше чем 2е4;
следовательно, Е представляется в виде объединения конечного
числа компактов с диаметрами не больше чем 2е4. Если, как мы
предположили, Е не может быть покрыто конечным числом мно-
множеств Ga, то по крайней мере один из этих компактов также не
имеет такого конечного покрытия. Обозначим его £i.
Далее, построим конечную г2-сеть для Е{ и, описав около каж-
каждой точки этой сети шар радиуса г2, представим Е, как и в преды-
предыдущем случае, в виде объединения конечного числа компактов с
диаметрами не больше чем 2г2. Тот из них, который не покрывает-
покрывается конечным числом множеств Ga, обозначим £2.
Продолжая неограниченно этот процесс, получим убывающую
последовательность компактов Е zd £\ zd E2 =э ..., ни один из
которых не может быть покрыт конечным числом множеств Ga,
причем diam Еп -> 0. Пусть g — их общая точка (задача 317). Так
как I £ £\ то найдется множество Ga из нашего открытого покры-
покрытия такое, что I £ Ga . Пусть V (£, б) cz Ga и 2гп < б. Тогда £п с=
cz Ga . Мы пришли к противоречию: с одной стороны, по построе-
построению, ни одно из Еп не может юыть покрыто конечным числом мно-
множеств семейства {Ga}; с другой стороны, множество Еп включается
в одно из множеств этого семейства (в G ). Полученное противоре-
противоречие доказывает, что Е бикомпактно.
150

337. Пусть k0 таково, что -£- < е. Тогда точка 0, а также
точки
£-,
1' ~Vf2' '" ПОКРЫТЫ интервалом ]—8, е[; остальные
же точки покрыты интервалами 1—^, —j4t где £ = О, 1, 2f ...f
* 1
ь .
338. Нельзя, поскольку каждая точка множества Е покрыта
только одним интервалом из данной системы.
339. Нельзя, поскольку Е не ограничено, а объединение лю-
любого конечного числа интервалов из данной системы — ограничен-
ограниченное множество.
340. Допустим, что из данного покрытия можно выделить ко-
конечное покрытие круга Е\ пусть его образуют круги Clf C2, ..., Ся.
п п •—• п .
Тогда U Ct zd Е и, значит, (J Сь = [} С, => Е (см. задачу 150).
i=l 1=Л i=l _
Но это невозможно, так как каждый замкнутый круг Ct содержит
лишь одну точку окружности, ограничивающей круг Е, И, значит,
п _
U Ct не покрывает всего круга £.
i=i
341. Можно. Для этого достаточно из всего покрытия выделить
те круги, центры которых лежат в рациональных точках окружнос-
окружности С (мы называем точку окружности рациональной точкой, если ее
радиус-вектор составляет угол гп с фиксированным неподвижным
радиусом, где г — рациональное число).
Докажем, что Е покрывается этой счетной системой кругов.
Рассмотрим произвольную точку Р £ Е (рис. 24). Пусть она от-
отстоит от О на расстоянии d (d < 1) и луч ОР пересекает С в точке
Ро при этом | РР0\ =
d__l_
< —). Если Ро—рациональная
точка, то круг с центром в Ро содержит Р. Если же Ро — иррацио-
иррациональная точка, то, в силу плотности множества рациональных то-
точек на С, найдется рациональная точка Pi € С такая, что \P0Pi\ <
1
Тогда круг с центром в
у Р, та]
. Л)) + р(Л» Pi)<
Jl ^ _
о о
содержит точку Р, так как
р(Л Л)<
з ' и " з
342. Окружности радиуса — с центра-
о
ми в точках окружности С пересекают
окружность радиуса 1 — г (с центром О)
в двух точках каждая, отсекая от нее дуги
одной и той же длины. Пусть п — нату-
Рис. 24
151

ральное число, превосходящее отношение длины всей окруж-
окружности радиуса 1-ек длине этих дуг. Если на С взять п равно-
равноотстоящих точек и принять их за центры открытых кругов радиуса
2
—, то мы и получим конечное покрытие, выделенное из заданного
о
бесконечного.
343. Пример 1. Открытое множество ]0, 1[ покрыто интер-
интервалами , —I (п =1,2, ...). Если из этого покрытия выбро-
]я + 2 п\_
сить хоть один интервал, то оставшаяся система не будет покры-
покрывать всего множества ]0, 1[. Тем более из этой системы интервалов
нельзя выделить конечного покрытия.
Пример 2. Интервалы —, 1 (п = 1, 2, 3, ...) образуют
открытое покрытие открытого множества ]0, 1[, не содержащее
конечного покрытия.
344. Нет. Пример. Компактное множество [0, 1] покрыто
Г1 ,] Г1 п Г1 11 Г 1 п
системой отрезков --, 1 , —, — , Т'Т > •••» ~Т7' ~~ ' ••• и
12 J [о 2JL4 3 ] \п -\- \ п \
[—1, 0], из которой нельзя выделить конечного покрытия (более
того, из этой системы нельзя исключить ни одного отрезка, не
оставив хотя бы одну точку отрезка [0, 1] непокрытой).
345. Счетное множество всех точек (хъ ..., хп) (: Rn с рацио-
рациональными координатами хъ ..., хп плотно в Rn.
346. Счетное множество, плотное в С [а, Ь], можно построить
так. Для каждого натурального числа п разобьем отрезок [а, Ь] на
п отрезков точками
/ = а, *{"> = а + ^=^, х^ = а + 2.^у ... , *<?> = b
и рассмотрим множество Ан всех функций ф на {a, b], принимаю-
принимающих в точках х[п) (i =0,1, ..., п) рациональные значения и ли-
линейных на отрезках [яй, х^"] (/ = 1, ..., я), т. е. определенных
условиями:
х х(п)
Ф<х) = Ф(х^) + ( ^ (Ф(*<«>)-Ф Щ%)) при *<!>,<х<х\п)
Xi ~~xi-\
(i = 1, ..., п)у
где ф (*on)), •••» Ф (Лп)) — рациональные числа.
оо
Рассмотрим далее множество А = [) Ап. Мощность этого
п—\
множества функций счетна (доказать!), и все они принадлежат про-
пространству С [а, &].
Покажем, что А плотно в С [я, &]. Пусть / ( С [а, 6] и е > 0.
Так как / равномерно непрерывна на [а, Ь], то существует б > 0
такое, что | / (х1) — / {х") | <~ для любых точек/, х" (: [а, Ь], удов-
5
152

летворяющих неравенству \х'— х"\ <Ь. Возьмем натуральное
число п, для которого-^ <б, и рассмотрим функцию ф € Ап> при-
принимающую в точках хоп\ xin), ..., х{^ рациональные значения такие,
что | ф (*{«>) — / (х[п^)\ < ~ (I = 0, 1, ..., /z). Для всякой точки
5
х € [а, Ь] найдется i такое, что х € [я}^, хИ]. Тогда
|ф(х)-Ф(хй)|<|ф(^)-фD1\I<
< I ч>да -/да I + If Htt)) -/Di}i) I +
и, следовательно,
Таким образом, р (ф, /) = max | ф (x) — f (x)\ < e; значит, счетное
хйа, b]
множество А плотно в С [а, 6].
Замечание. Другим примером счетного множества, плот-
плотного в С [а, &], является множество всех многочленов с рацио-
рациональными коэффициентами (см. задачу 295).
347. Счетным множеством, плотным в /2, будет, например, мно-
множество всех точек (х\, хъ ...) € /2, у которых лишь конечное число
координат х1у хъ ... отлично от нуля, причем все эти координаты
рациональны. Доказательство счетности этого множества предо-
предоставляем читателю. Покажем, что оно плотно в /2. Пусть а (а1у
а2, ...)£/2и е>0 Найдемтакое п, что для точки a'(#i, ...,ал, 0^ 0, ...)
будет р (а, а') <— (см. решение задачи 301). Пусть
х1у ..., хп — рациональные числа такие, что \at —xt\ <г-т= ПРИ
i = 1, ..., п\ обозначим через х точку из /2 с координатами
(*ь ..., хп, 0, 0, ...). Тогда
р(а,
что и доказывает наше утверждение.
348. Счетным множеством, плотным в этом пространстве, бу-
будет, например, множество всех пар функций из счетного множе-
множества, плотного в пространстве С [a, b] (например, из множества Л,
построенного в решении задачи 346).
349. Необходимость очевидна: если X сепарабельно,
153

то плотное в нем конечное или счетное множество является е-сетью
для X при Любом е > 0.
Достаточность. Пусть для каждого е > 0 существует
не более чем счетная е-сеть Ме. Тогда не более чем счетное множе-
оо
ство Е = {J М 1 плотно в X. Значит, X сепарабельно.
350. Для компакта при любом е > 0 существует конечная
е-сеть (задача 327); остается применить результат предыдущей
задачи.
351. Покажем, что никакое счетное множество £ = {/ь /2, /3, ...}
ограниченных функций на [а, Ъ] не плотно в М [а, Ь]. Отметим на
отрезке [а, Ь] какое-нибудь счетное множество точек х1у х2, х3, ...
и определим функцию / С М [а, 6] условиями: f (х) = Q, если х
не совпадает ни с одной из точек хъ х2, х3, ..., и
f(x\ = ( — 1, если fk (xk) > 0,
ю [ 1, если fk (xk) < 0
(k = 1, 2, 3, ...). Тогда р (/, /,) = sup I/ (x) - fk (x)\ > 1, а по-
тому / не является точкой прикосновения множества Е. Следова-
Следовательно, Е не плотно в М [а, Ь]. Итак, пространство М [я, Ь] не-
сепарабельно.
352. Можно считать, что X бесконечно, так как в случае конеч-
конечного X утверждение тривиально. Возьмем счетное множество
В = {хъ хъ х3, ...}, плотное в X, и последовательность положи-
положительных чисел е1у е2, е3, ..., стремящуюся к нулю (например, гк =
= —). Для каждой точки хь € В выберем в каждой из окрестно-
окрестному
стей V (xh ek), которые имеют непустое пересечение с £, по точке
хш € Е. Множество А всех таких точек xik € V (xt, гк) р] Е не
более чем счетно. Покажем, что A zd Е. Пусть х0 € Е и е > 0 —
произвольное число. Возьмем k столь большим, чтобы было гк < — .
Так как В плотно в X, то V (хо> гк) содержит некоторую точку
хг € В. Тогда х0 ^ V (xt, гк), так что V (xh гк) f] В ф 0, и по-
потому V (xl9 гк) содержит некоторую точку xlk € А* Но К (xt, гк) а
cz V (х0, е); действительно, если х £ V (xh гк)у то р (xQy x) ^
^ р (*о> хд + Р (xi> х) < 8д? "Ь гк < 8- Значит, каждая окрест-
окрестность У (х0, е) точки л:0 содержит точку из Л, т. е. л:0 6 Л. Таким
образом, A id £.
353. Назовем рациональным кругом на плоскости всякий круг,
у которого координаты центра и радиус рациональны. Множество
всех рациональных кругов счетно (задача 63). Докажем, что оно
образует базис открытых множеств на плоскости. Для этого сна-
сначала докажем, что любой круг включает рациональный круг, со-
содержащий его центр. Пусть Е — круг радиуса R с центром С
154

(рйс. 25), Возьмем внутри концентричес-
кого круга радиуса — точку Сх с рацио-
3
нальными координатами. Тогда круг с
центром Сг и рациональным радиусом г,
заключенным между — и —, обладает тре-
буемым свойством: он содержит точку С
(R \
так как р (С, Сх) < — < г и включается
3 /
в £, так как для любой точки Р, для кото-
рой р(Р, С^)^, будем иметь:
, С)<р(Р,
Рис. 25
<!+!=*•
Пусть теперь G — произвольное открытое множество на пло-
плоскости. Опишем вокруг каждой точки х £ G какой-нибудь откры-
открытый круг V (х) a G и построим какой-нибудь рациональный круг
Е (х)> включающийся в V (х) (а значит, и в G) и содержаний точ-
точку X. Очевидно, тогда будем иметь: G = U Е (х). Таким образом,
каждое открытое множество на плоскости является объединением
некоторого семейства рациональных кругов.
354. Нет. Пример. Пусть А — семейство следующих интер-
интервалов на числовой прямой: rk —, rk -\—-— \{k = 1, 2, ...),
где rk — все рациональные числа, занумерованные каким-либо
способом; и пусть В — семейство всех интервалов с рациональ-
рациональными концами. Очевидно, семейства А и В удовлетворяют усло-
условиям задачи, причем В — базис. Однако А не является базисом,
так как объединением интервалов из семейства А, во всяком слу-
случае, нельзя получить никакого интервала, длина которого больше
двух. Действительно, пусть такой интервал нашелся. Возьмем
какой-нибудь содержащийся в нем отрезок длины 2. Тогда интер-
интервалы семейства А образуют его открытое покрытие, из которого, в
силу компактности отрезка, можно выделить покрытие конечным
числом этих интервалов. Но это невозможно, поскольку сумма
длин любого конечного числа интервалов из А меньше суммы длин
всех интервалов из А, т. е. меньше 2.
355. Если X имеет счетный базис, то, взяв в каждом из множеств
этого базиса по точке, получим не более чем счетное множество
точек, которое, как легко видеть, плотно в Х\ значит, X сепара-
бельно.
Обратно, пусть X сепарабельно и А = {хг, х2, х& ...}—счетное
плотное в X множество (случай конечного А тривиален). Тогда
155

семейство открытых шаров lv{xt, -Ml (t = I, 2, 3...) счетно. По-
Покажем, что оно образует базис пространства X. Для этого пока-
покажем сначала, что для каждого шара V(x0, e) существуют ink
такие, что x^V [хь — \czV(xQ, е). Действительно, пусть k столь
V kl
велико, что ~-<~. ШаР V\xo> —\ содержит некоторую точку
k 2 \ k)
^£Л, откуда xo£V(xi9 4); кР°ме того, vlxi9 ^)czV(xot e), так
\ kj \ k]
как если x£v(xlt ~\ то р(*0, х) <р(лг0, ^)+р(^, *)< ~ +
-\— = — < е. Если теперь G — произвольное открытое множество
k k
в X, то каждая точка xo(zG обладает окрестностью V (х0, е), ле-
лежащей в G; следовательно, некоторый открытый шар V\xi9 —) ле-
жит в V (xQ, e), а значит, и в G и содержит точку jca. Объедине-
Объединением таких шаров V(xi9 — 1, построенных для всех точек xo£G,
\ k)
очевидно, служит G. Тем самым семейство /W^-, —Н есть базис
открытых множеств в X. I \ kJ)
356. Пусть Е = U G , и {Гл} — счетный базис пространства X.
а
Для каждого а и каждой точки л: € Ga выберем множество -из ба-
базиса, включающееся в Ga и содержащее эту точку. Пусть отобран-
отобранные таким способом множества базиса (расположенные, например
в порядке возрастания их номеров) будут ГЯ,ГД| ..., Гял, ...;
ясно, что Е = U Гп . Далее, для каждого k выберем одно из под-
k k
множеств семейства {Ga}, содержащее Г„ ; обозначим его Ga/j.
Тогда, очевидно, Е = U Ga..
к
357. Верно. Если X не имеет счетного или конечного базиса,
то для некоторого 8 > 0 оно не имеет счетной или конечной е-сети
(см. задачи 349 и 355). Зафиксируем это 8 и опишем около каждой
точки х € X 8-окрестность V (х, е). Тогда X = (J V (х, г). Семей-
х£Х
ство открытых множеств {V (х, г)} несчетно, и из него нельзя
выделить счетного семейства с тем же объединением, так как если
бы было U V (хп, г) = X, то счетцое множество {хъ х2, ...} явля-
/г=1
лось бы е-сетью для X, что противоречит выбору числа 8. Итак,
если X не имеет конечного или счетного базиса, то существует се-
семейство открытых в X множеств, из которого нельзя выделить
счетного подсемейства с тем же объединением.
358. Сепарабельное метрическое пространство есть пространство
со счетным (или конечным) базисом, скажем, Ех, Г2, ... (задача 355).
156

Каждое открытое множество G пространства есть объединение хотя
бы одной совокупности {Г , ..., Гп , ...} множеств из базиса.
Тем самым каждому открытому множеству G пространства можно
поставить в соответствие множество {пъ ..., nk, ...} натуральных
чисел, причем разным открытым множествам, очевидно, будут
соответствовать разные множества натуральных чисел. Поэтому
мощность совокупности всех открытых множеств пространства не
превосходит мощности множества всех подмножеств натурального
ряда, т. е. мощности континуума.
359. Это вытекает из результата предыдущей задачи, поскольку
между совокупностью всех замкнутых и совокупностью всех от-
открытых множеств пространства можно установить взаимно одно-
однозначное соответствие, относя каждому замкнутому множеству
открытое множество, являющееся его дополнением.
360. Пусть А = {хъ x2r x3i ...} — не более чем счетное плот-
плотное множество в сепарабельном пространстве X. Если А конечно,
то и X конечно (А не может иметь других точек прикосновения,
кроме точек из Л). Пусть А счетно. Выберем для каждой точки
х € X некоторую сходящуюся к ней последовательность хп , х , ...
точек из А. Так как множество всех последовательностей пъ я2, ...
натуральных чисел имеет мощность континуума (задача 80) и
так как разным точкам из X в силу однозначности предела будут
отвечать разные сходящиеся к ним последовательности точек из А,
то мощность X не превосходит мощности континуума.
361. Согласно результату задачи 359, мощность совокупности
всех замкнутых множеств пространства X не превосходит мощности
континуума.. С другой стороны, все одноточечные множества из X
замкнуты, а они уже образуют множество мощности континуума;
для доказательства утверждения остается применить теорему
Кантора — Бернштейна.
362. Компакт есть сепарабельное пространство (задача 350),
а потому имеет мощность, не превосходящую мощности континуума
(задача 360). С другой стороны, компакт есть полное пространство
(задача 316), а так как п« условию это пространство не содержит
изолированных точек, то, согласно результату задачи 253, мощ-
мощность его не меньше мощности континуума.
363. Ясно, что каждая точка конденсации множества А, как
и каждая точка конденсации множества В, есть вместе с тем точка
конденсации для объединения А [] В. Следовательно, Sa[JBzd
id SA U SB. Докажем обратное включение. Пусть xQ € SA[jBt
Если х0 £ SA, то существует е0 > 0 такое, что V (xQi e0) содержит
конечное или счет*ное множество точек из Л. Тем же сёойством об-
обладают тогда и все окрестности V (х0, б) с б < е0. Так как всякая
окрестность точки xQ содержит несчетное множество точек из A (J 5,
то каждая из указанных окрестностей V (х0, 6) должна содержать
несчетное множество точек из В (если бы V (х0, б) имела конечное
157

или счетное множество точек как из Л, так и из 5, то она имела бы
не более чем счетное множество точек и из A (J В). Но всякая
окрестность точки х0 включает окрестность V (х0, б) с достаточно
малым б < е0; поэтому каждая окрестность V (xOi г) содержит не-
несчетное множество точек из В, т. е. х0 £ SB, Итак, для произволь-
произвольной точки х0 € SA u в справедливо по крайней мере одно из соот-
соотношений: х0 € SA или xQ € SB. Значит, SAUB cz SA U SB. Срав-
Сравнивая это с полученным ранее включением SA и в =э SA U SB ,
заключаем, что SAU в = SA (J SB.
364. Нет. Пример. Рассмотрим на плоскости последователь-
последовательность концентрических окружностей Ап радиусов — (п= 1, 2, ...).
п
Множество Sa точек конденсации каждого множества Ап совпа-
совпадает с самим Ап. Однако множество S\jAn точек конденсации
объединения [) Ап не совпадает с U Ап — U Sa , а получается
п п п п
добавлением к нему еще одной точки — общего центра окружно-
окружностей Ап. Итак, в данном случае Su лп =э [j Sa , но S\j лп Ф U 5ля-
п п п п
Включение Su л =э U S. , очевидно, всегда имеет место,
п
п п
поскольку точка конденсации каждого Ап является вместе с тем
точкой конденсации объединения [)Ап.
п
365. Справедливость утверждения легко следует из того, что,
какова бы ни была точка х0 (: X, каждая ее окрестность V (х0, е)
(будучи отбытым множеством) включает некоторое множество
из базиса, содержащее xOi и, обратно, каждое множество из бази-
базиса, содержащее точку х0, включает все ее окрестности V (х0, г)
достаточно малого радиуса е.
366. Сепарабельное метрическое пространство есть пространство
со счетным (или конечным) базисом (задача 355). Пусть {Gn} —
не более чем счетный базис пространства X. Если ни одна точка
множества Е не является его точкой конденсации, то в силу ре-
результата предыдущей задачи, для каждой точки х € Е найдется
множество Gnx из базиса, в котором содержатся эта точка х и не
более чем счетное множество других точек из Е. Таким образом,
множество Е в этом случае складывается из не более чем счетной
совокупности не более чем счетных множеств, а потому само не
более чем счетно. Следовательно, хотя бы одна точка несчетного
множества Е должна быть его точкой конденсации (в частности,
множество SE непусто).
367. Замкнутость SE доказывается легко (причем в любом мет-
метрическом пространстве X, а не только в сепарабельном). Докажем
отсутствие изолированных точек у множества SE. Пусть #D€SE;
тогда для произвольной окрестности V (х0, г) множество
isa

(E \ {x0}) П V (x0, г) несчетно; значит, по теореме Линделефа, су-
существует точка конденсации х1 этого множества, принадлежащая
ему (и, значит, отличная от х0). Но тогда х± будет точкой конден-
конденсации и для £. Итак, в произвольной окрестности точки х0 € SE
нашлась точка из SE, отличная от х0. Значит, SE не имеет изоли-
изолированных точек.
оо
Приведем пример. Пусть X = {а} [) [U Еп\ где Еп —
1
попарно не пересекающиеся несчетные множества, а а — точка,
не принадлежащая ни одному Еп . Метрику в X введем следующим
образом: р (а, х) = — при х 6 Еп , р (х, у) = щах (—, —1 при
п [ п т )
х d Еп> у £ Ет и хФу. Полученное метрическое пространство
несепарабельно; все его точки, кроме а, изолированы. Если те-
теперь взять Е = X, то SE есть одноточечное множество {а}\ оно
замкнуто, но несовершенно.
368. Так как трчки конденсации любого множества являются
его точками прикосновения, а множество F замкнуто, то SFa F.
Поэтому F == SF U (F \ SF). Согласно предыдущей задаче, Sp
совершенно. Остается показать, что F \ SF конечно или счетно.
Но это следует из теоремы Линделефа (задача 366), так как если
бы F \ SF было несчетно, то одна из его точек была бы его точ-
точкой конденсации, а значит, и подавно точкой конденсации множе-
множества F, т. е. принадлежала бы SF, что невозможно.
369. Пусть F = Р U N — какое-нибудь представление мно-
множества F в виде объединения совершенного множества Р и не более
чем счетного множества N = F \ Р. Докажем: а) Р cz SF. Пусть
х € Р и е — произвольное положительное число. Множество
»"") П Р не имеет изолированных точек. Действител: нэ, лю-
бая его изолированная точка, будучи внутренней для V (х, — ,
являлась бы изолированной для Р\ а это противоречит тому, что
Р — совершенное множество. Поэтому Vlx, — Л Р также не
— .
х> — П Р
замкнуто, оно совершенно и, следовательно, несчетно (см. задачу
253). Но V(x, г) id V (х, ~) => V fx, -J] П Р- Таким образом,
V (х, е) при любом е > 0 содержит несчетное множество точек из
Р, а значит, и из F, т. е. х k SF. б) SF cz P. Действительно, если
х € Р, то некоторая окрестность V (х, г) точки х не пересекается с
Р. Тогда V (х, г) f| F а N, т. е. V (х, е)_содержит не более чем
счетное множество точек из F и потому х € SF.
159

Таким образом, Р = SF , а значит, N = F \ SF.
370. Пусть X — множество рациональных точек на прямой с
обычной метрикой и F = X. Тогда множества Р = F Г) (А Ь] и
N ~ F \ Р при произвольных а и Ь, а < Ь дают разбиение F на
два множества, из которых Р совершенно, а N счетно.
371. По теореме Кантора — Бендиксона (задача 368) F есть
объединение совершенного множества Р и не более чем счетного
множества N. Если Р пусто, то F не более чем счетно. Если же Р
непусто, то, как следует из результатов задач 253 и 360, оно имеет
мощность континуума. А так как N не более чем счетно, то и мно-
множество F = Р U N имеет в этом случае мощность континуума.
372. Согласно результату задачи 352, Е, рассматриваемое как
подпространство пространства X, сепарабельно. Но единственным
плотным множеством в пространстве, все точки которого изолиро-
изолированные, является само пространство. Следовательно, Е не более
чем счетно.
373. Пусть X — несчетное множество, наделенное метрикой,
введенной в задаче 125, т. е, определенной следующим образом:
о(х V) _ { 0, если х = у,
Если за Е принять само X, то все его точки будут изолированы,
хотя оно и несчетно.
374. Не может. Действительно, в противном случае несчетное
множество Е \ Е\ не пересекающееся с £", не содержало бы ни
одной своей предельной точки, а значит, и ни одной своей точки
конденсации. Но, в силу сепарабельности плоскости (задача 345),
это противоречит теореме Линделёфа (задача 366).
375. Метод доказательства указан в условии задачи.
376. Если бы точка х0 € Е была изолированной, то Е было бы
объединением двух разъединенных множеств {х0} и Е \ {xQ}t что
противоречит связности Е.
377. Равенство (А [) В){] (А (} В) = 0 равносильно тому,
что АПВ=0пА(}13=0,т. е. что В не содержит точек
прикосновения множества Л и Л не содержит точек прикосновения
множества В. _
378. а) Если Л и В оба замкнуты, то (Л П Щ (J (Л П В) =
== Л П В = 0, так как Л = Л, В = В. б) Если Л и В оба от-
открыты, то Л П В = 0, так как все точки множества В внутрен-
внутренние, а потому не могут быть точками прикосновения множества Л;
точно так же Л П В = 0.
379. Так как Е несвязно, то Е = Л U В, где Л и В — разъеди-
разъединенные множества; тогда, в частности,^ f| В = 0. Так как Е
замкнуто, то 1с Е. Таким образом, A d Е \ В = Л, т. е. Л
замкнуто. Аналогично проверяется замкнутость В.
380. Так как Е несвязно, то Е = Л U В, где Л и В — разъеди-
160

ненные множества. Каждая точка х0 € Л обладает окрестностью
V (хю? е) с: Е (поскольку Е открыто). Так как х0 не является точ-
точкой прикосновения для В, то найдется окрестность V (xQi 6) cz
cz V (xQi e), не содержащая точек из В\ но V (xQi e) cz E\ поэтому
V (xOi б) d Е \ В = Л, т. е. х0 € Л°. Таким образом, Л открыто.
Аналогично доказывается, что В открыто.
381. Допустим, что Е несвязно. Тогда Е = А [} В, где Л и В —
непересекающиеся непустые замкнутые множества (см. задачу 379).
При этом хотя бы одно из множеств А (] F, В (] F пусто (если
бы! они оба были непусты, то множество Е (] F = (А (] F) []
\J(Bf]F) было бы несвязно). Пусть, например, А Л F = 0- Тогда
Е [j F =(А [} В) [) F =А [} (В [] F),
причем А и В [} F замкнуты, непусты и не пересекаются (так как
А П (В U F) = (Л П в) U (А П F) = 0); но это противоречит
связности Е {) F. Полученное противоречие доказывает связность
множества Е. Аналогично проверяется связность F.
382. Пример в пространстве 7?1 : Е = [0, 1] U [2, 3],
F=[0,2[.
S33. Допустим, что £ — несвязное множество, так что Е =
— Л U В, где Л и В — непересекающиеся непустые замкнутые
множества (см. задачу 379). Тогда множества Е (] А и Е (] В
непусты (если бы, например^ Е (] А было пустым, то имело бы
место включение Е cz В cz £, где В замкнуто и отлично от Е;
а это невозможно в силу результата задачи 168. Следовательно,
множества Е (] А и Е (] В разъединены (поскольку разъединены
Л и В). Но это противоречит связности £, так как Е = (Е [\ А) [)
U (Е П В). Итак, допустив, что Е несвязно, мы пришли к проти-
противоречию. Значит, Е связно.
Пример. Пусть Е — множество всех рациональных чисел
на прямой. Тогда Е несвязно, а Е связно.
384. Это следует из результата задачи 383, если учесть, что Н
является замыканием множества Е в пространстве Н (см. задачу
192).
385. Если бы Е было несвязным, то его можно было бы предста-
представить в виде объединения двух разъединенных множеств Л и В.
Пусть х £ Л, у £ В. По условию задачи существует связное мно-
множество Q cz £, содержащее точки хну. Тогда Q = (Q f| A) U
U (Q Г) В), где Q Г) A* Q Л # — разъединенные множества; но
это невозможно в силу связности множества Q.
386. Пусть Е — рассматриваемое множество. Обозначим через
£\ множество точек из Е с-отрицательными абсциссами, через £2 —
с положительными. Тогда £-= £\ (J £2> причем (£i f| £2) U
U (£\ П Е2) = 0, т. е. множества £\ и £2 разъединены (см. зада-
задачу 377).
387. Пусть X — прямая, плоскость или трехмерное евклидово
161

пространство с обычной метрикой и пусть точки а и b принадлежат
X. Прямолинейный отрезок с концами а и Ь будем обозначать [а, 6].
Если а = by то отрезок [а, Ь~] состоит из одной точки и потому
связен. Пусть а Ф Ь и [а, ft] == F [] Ф, где F и Ф — непустые
замкнутые множества. Докажем, что F П Фф 0. Для этого раз-
разделим отрезок [а, Ь] пополам и обозначим через [аь Ь4] какую-
нибудь его половину, содержащую как точки из F, так и точки из Ф;
по крайней мере одна половина отрезка [а, &] обладает этим свой-
свойством (если, например; середина отрезка принадлежит множеству
F, то в качестве [аи Ь{\ берем ту половину [а, &], которая содержит
хотя бы одну точку множества Ф). Аналогично поступим с отрез-
отрезком \_аи Ь{\: разделим его пополам и обозначим через [а2, 62] ка"
кую-нибудь его половину, содержащую как точки из F, так и точ-
точки из Ф. Неограниченно продолжая этот процесс, мы получим убы-
убывающую последовательность отрезков {[аЛ, йЛ]}, длины (т. е. диа-
диаметры) которых стремятся к нулю, причем каждый из этих отрез-
отрезков содержит как точки из F, так и точки из Ф. Пусть С — общая
точка всех этих отрезков (см. задачу 208). Каждая ее окрестность
содержит \_аю Ьп~] с достаточно большим номером п и, следователь-
следовательно, точки и из F, и из Ф. Поэтому С — точка прикосновения и для
F, и для Ф. Так как оба эти множества замкнуты, то С £ F (] Ф,
т. е. f П Фф0. Применяя результат задачи 379, заключаем,
что отрезок [а, 6] связен.
Заметим, что для случая отрезка на прямой утверждение на-
настоящей задачи следует также из задачи 214.
388. Любые две точки замкнутого круга (шара) соединяются
содержащимся в нем прямолинейным отрезком на плоскости (в
трехмерном евклидовом пространстве). Утверждения задачи выте-
вытекают поэтому из результатов предыдущей задачи и задачи 385.
389. Предположим, что Е несвязно, т. е. Е = А [) В, где Л и
В — разъединенные множества. Хотя бы одно из множеств Eit
Е2 имеет непустое пересечение и с Л, и с В (в самом деле, если, на-
например, Е2[\А = 0, то Bid Е2 и E^zd Л; поэтому £4 П В =э Е^{\
ft Е2ф 0 и Ei П А Ф 0). Пусть, скажем, £4 П А ф 0 и
£i П Вф 0. Тогда Ei *■ (Et f] A) [} (£i П В), и множества
Ei () А к Ei 0 В разъединены, так как А и В разъединены. Но
это противоречит условию связности Ei. Итак, предположение,
что Е несвязно, привело к противоречию; значит, Е связно.
390. Для любых двух точек jc, у £ Е имеем х € ЕпУ у £ £^ ;
тогда х € Ею у £ ЕПУ где п = max {nu п2), т. е. существует связ-
связное множество, включающееся в £ и содержащее х w у. Поэтому,
согласно результату задачи 385, множество Е связно.
391. Из результата задачи 389 следует (после применения ин-
п
дукции), что для любого номера п множество Fn = U Et связно.
А тогда {Fn}y как возрастающая последовательность связных
162

множеств, имеет связное объединение (см. предыдущую задачу).
оо оо оо
Но (J Fw = U Et\ следовательно, (J Et также связно.
392. Множества Нь = Et*[) E^ связны и удовлетворяют усло-
условию
Hi П Я<+1 = (Ег U £|+1) Л (£*+i U Е1+2) гэ Ei+1 = 0
для каждого номера i. Согласно результату предыдущей задачи
оо оо оо
связно и их объединение \]Ht= U {Et \] £h-i) = U £/.
393. Любые две точки данного множества можно соединить
ломаной, входящей в это множество и состоящей не более чем из
трех звеньев, параллельных осям координат; но ломаная есть
связное множество (см. задачи 387 и 389). Значит, в силу резуль-
результата задачи 385, рассматриваемое множество связно.
394. Пусть Е — связное множество на прямой и хи хг — любые
две различные его точки. Если бы какая-нибудь точка с, заключен-
заключенная между х{ и х2, не принадлежала £, то Е можно было бы пред-
представить в виде объединения двух разъединенных множеств А =
= ]—оо, с [П Е и В = ]с, +°°[П Е\ но это противоречит связно-
связности Е. Итак, если множество Е связно, то вместе с любыми двумя
своими точками оно содержит и весь отрезок, соединяющий эти
точки.
Обратно, пусть множество Е на прямой таково, что каковы
бы ни были точки Xi £ £, Х2 € Еу где Xi < a;2, отрезок \_хи х{\ пол-
полностью входит в Е. Тогда множество Е связно в силу результатов
задач 385 и 387.
395. Связность каждого из этих множеств вытекает из резуль-
результатов предыдущей задачи.
Докажем, что этими множествами исчерпываются все связные
множества на прямой.
Пусть Е — связное непустое и неодноточечное множество на
прямой, а = inf E, b = sup £. Рассмотрим сначала тот случай,
когда а и b — конечные числа (а < Ь). Тогда любое число с, за-
заключенное между а и Ь, входит в Е. Действительно, так как b —
=sup Е, то существует точка Ъ^ £ Е такая, что с< b^ ^ b. Точно
так же устанавливается, что существует аА £ £, где а ^ а4 < с.
Но тогда, в силу связности Е9 на основании результата предыду-
предыдущей задачи заключаем, что [аь b^\ cz E и, значит, с £ Е. Итак,
интервал ]а, Ь[ включается в £, а точки, лежащие за пределами
отрезка [а, Ь], не принадлежат Е. Следовательно, Е является од-
одним из следующих множеств: ]а, 6[, ]а, ft], [a, b[, [а, &].
Если а = —оо, a b конечно, то Е равно]—оо, Ь\_ или ]—op, b];
если а конечно, a b = +оо, то £ равно ]я, +°°[ или [а, +<*>[; на-
наконец, если а = —оо, Ь = +оо, то Е = ]—оо, +оо[. Во всех
этих случаях доказательство проводится так же, как и в том слу-
случае, когда а и b конечны.
163

СЕ
396. Доказательство проводится так
же, как при решении задач 387 и 388.
Под отрезком в пространстве Rnt соеди-
соединяющим точки а = (аь ..., ah) и b =
(bu ..., bn), понимается совокупность точек
с координатами ck = A — К) ak + kbk
(k=l9 ..., n)f где к пробегает отрезок [0, 1]
числовой прямой.
397. Если бы в X было такое множест-
множество £, то его допрлнение СЕ= X \ Е так-
также было бы непустым множеством, одно-
одновременно открытым и замкнутым. Но тог-
тогда все пространство X было бы объединением двух непересе-
непересекающихся непустых замкнутых множеств Е и С£, что, в силу
результата задачи 378, противоречит связности X.
398. Нельзя. В самом деле, допустим, что открытый круг Е
можно представить в виде Е = Gi f] G2, где GA и G2 — открытые
множества, отличные от всей плоскости и вместе составляющие
всю плоскость. Тогда мы имели бы (в силу закона двойственности):
Рис. 26
СЕ =
U CG2,
где CGi и CG2 — непересекающиеся непустые замкнутые множе-
множества, т. е. множество СЕ было бы несвязным.
На самом же деле СЕ связно. Действительно, любые две его
точки а и b можно соединить ломаной, принадлежащей СЕ (рис. 26),
а ломаная является связным множеством (см. задачи 387 и 389);
поэтому связность СЕ вытекает из результата задачи 385.
399. Необходимость. Пусть Е X F связно. Так как
по условию Е X F непусто, то множества Е и F также непусты.
Докажем, что эти множества связны. Если бы одно из них, напри-
например £, было несвязным, то его можно было бы представить в виде
объединения Е = A U В, где А и В — разъединенные множества.
Тогда, как легко видеть, множества А х F и В X F также разъе-
разъединены (они непусты, так как F непусто). Но Е X F = (А X F) U
U (В X F); поэтому Е X F было бы несвязным, что противоречит
условию.
Достаточность. Пусть множества Е и F связны. Возь-
Возьмем Две любые точки (xi} у4) и (х2, у2) из £ X F\ рассмотрим мно-
множества {xi} X F и Е X {у2}* Пересечение этих множеств непусто:
оно состоит из точки (хи у2). Кроме того, каждое из этих множеств
связно, так как {xi} X F изометрично F, Е X {у2} изометрично Е,
а множества F и Е связны. Значит, объединение ({#i} X F) [}
U(£x{y2}) связно (задача 389). Но это объединение содержит
обе точки (xi9 yi) и (х2у у2). Следовательно, в силу результата за-
задачи 385, Е X F связно.
Замечание. Вместо метрики для Е X F из задачи 146
можно взять метрику из задачи 147 — важен лишь тот факт, что
164

подпространства {х} X F и Е X {у} пространства Е X F изомет-
ричны исходным пространствам F и £.
400. Пусть л;0 — произвольная точка из G. Рассмотрим мно-
множество А всех точек множества G, которые можно соединить с
точкой хОу лежащей в G ломаной, каждое зв^но которой парал-
параллельно одной из осей координат. Множество А непусто, так как
оно содержит точку х0. Покажем, что множества А и G \ А от-
открыты.
Пусть х £ Л. Так как G открыто, то существует круг V (х, е),
лежащий в G. Каждую его точку х' можно соединить с точкой х
ломаной, лежащей в V (х9 е) и состоящей не более чем из двух
звеньев, каждое из которых параллельно одной из осей коорди-
координат. Дополнив этими звеньями ломаную, соединяющую х с х0,
мы получим в G ломаную, соединяющую точки х0 я х\ звенья ко-
которой параллельны осям координат. Значит, х' £ Л, т. е. V (х, г) с:
cz Л. Следовательно, А открыто.
Пусть теперь х £ G \ Л. Так как х £ G, то существует круг
V (х, г) a G. Если бы некоторая его точка х' принадлежала Л,
то мы получили бы, вопреки предположению, что и х £ А (по-
(поскольку х можно соединить с х ломаной, лежащей в V (х, е),
звенья которой параллельны осям координат). Таким образом,
V (х9 е) cz G \ Л и G \ А открыто.
Итак, множества Л и G \ Л открыты, причем Л непусто. Так
как <j связно, то G \ Л пусто (см. задачу 378). Но это и означает,
что утверждение задачи справедливо.
401. Докажем, что любые две точки х £ Е и у £ Е можно со-
соединить связным множеством, включающимся в Е. В качестве
такого множества можно взять А (х) [} А (у), где Л (л:) и Л (у) —
какие-либо множества из семейства {Ла}, содержащие соответст-
соответственно точки л: и у. Так как Л (л:) и Л (у) связны, а Л (х) П Л (у) Ф
Ф 0, то Л (х) U Л (у) связно (задача 389). Поэтому, в силу ре-
результата задачи 385, Е связно.
Замечание. Иа доказательства видно, что достаточно тре-
требовать, чтобы множества Аа (а £ А) попарно пересекались, пере-
пересечение же всех этих множеств может быть и пустым.
402. Этой компонентой является объединение всех связных
подмножеств множества £, содержащих х0 (оно непусто, так как,
во всяком случае, включает множество {х0}; связность объедине-
объединения вытекает из результата задачи 401). Единственность компонен-
компоненты легко доказывается.
403. Согласно результату задачи 383, Л вместе с Л связно.
А так как Л с Л с £, то, по определению компоненты, А = А9
т. е. Л замкнуто.
404. Это вытекает из результатов задач 389 и 402.
405. Множество всех иррациональных точек на прямой; кан-
торово совершенное множество; множество из задачи 191.
165

406. Такой компонентой является объединение всех связных
подмножеств множества £, содержащих какую-нибудь фиксиро-
фиксированную точку х0 £ F. Единственность легко доказывается.
Глава VII.
МЕРА МНОЖЕСТВ (В ЕВКЛИДОВОМ
ПРОСТРАНСТВЕ)
407. Ось. О* имеет плоскую меру нуль. Следовательно, все
подмножества оси Ох измеримы на плоскости Оху и их плоская
мера равна нулю.
408. Канторово совершенное множество D имеет линейную
меру нуль. Следовательно, каждое его подмножество также имеет
линейную меру нуль и поэтому измеримо. Но совокупность всех
подмножеств канторова множества имеет мощность гиперконтину-
гиперконтинуума B*), так как D = с. Значит, совокупность U всех измеримых
множества числовой прямой имеет мощность большую или рав-
равную 2е: D > 2е.
С другой стороны, так как совокупность всех вообще множеств
на прямой имеет мощность 2е, то п<; 2е. Следовательно, U = 2е.
409. В качестве примера можно взять совершенное множество,
построенное в задаче 289, приняв Иап = 0,1. Тогда сумма длин
п
выброшенных интервалов равна 0,1, а значит, мера оставшегося
совершенного множества равна 1 —0,1 = 0,9.
410. В задаче 289 взять ^ап =1 — а.
п
411. Нет. Дополнение СЕ к нигде не плотному совершенному
множеству Е cz [0, 1] до всего отрезка [0, 1] содержит интервалы и^
значит, имеет положительную меру, так что тЕ =1 — т (СЕ) < 1.
412. Построение этого примера проводится примерно так же,
как и построение совершенного множества в задаче 289. Зададим
произвольный сходящийся ряд с положительными членами
#i + а2 + а3 + ..., сумма которого равна 1 — а. Проведем теперь
в основном квадрате [0, 1] х [0, 1] две вертикальные и две гори-
горизонтальные прямые так, чтобы площадь креста, вырезаемого этими
прямыми, равнялась а4 и чтобы четыре четырехугольника, ос-
оставшиеся после отбрасывания этого креста, были замкнутыми
квадратами (рис. 27, а). Эти замкнутые квадраты назовем квадра-
квадратами первого ранга; их объединение обозначим Pi (P4 — замкну-
замкнутое множество). Далее, в каждом из квадратов первого ранга про-
проведем по две вертикальные и по две горизонтальные прямые так,
чтобы каждый крест, вырезаемый этими прямыми, имел площадь
— и чтобы после отбрасывания этого креста в каждом квадрате
первого ранга осталось по четыре замкнутых квадрата; назовем
последние квадратами второго ранга, их объединение обозначим
Р2\ число квадратов второго ранга равно 42 (рис. 27, б). Вообще,
если построены квадраты fe-ro ранга (их число равно 4*), то даль-
166

iill
22
21
20
17
16
2
1
23
24
19
18
13
14
J
4
26
<25
30
31
12
9
в
5
27
28
29
32
n
W
7
6
38
37
36
33
54
55
58
59
39
40
35
34
53
56
57
60
42
41
46
47
52
51
62
61
43
44
45
48
49
50
63
64
7
tun
64
Рис. 27
нейшее построение проводится так: в каждом из квадратов &-го
ранга проводим по две вертикальные и по две горизонтальные
прямые так, чтобы крест, вырезаемый этими прямыми, имел пло-
площадь -ak+1 и чтобы оставшиеся четырехугольники были замкну-
замкнутыми квадратами; назовем их квадратами (k + 1)-го ранга; обо-
обозначим их объединение Pk+1 (число всех квадратов (k + 1)-го
ранга равно 4Л+Х).
Если взять теперь пересечение всех Pk> то мы получим совер-
совершенное множество меры а. Последнее следует из того, что допол-
дополнением к этому множеству является объединение всех выброшед-
ных крестов; а мера этого объединения равна 1 — а:
■_...= 1—а.
Итак, дополнение к построенному совершенному множеству
до квадрата [0,1] X [0, 1] имеет меру 1 — а, значит, само оно
имеет меру а.
16/

413. Мера дополнительного множества равна сумме площадей
выбрасываемых квадратов всех рангов, т. е.
]_
"~ 9
Следовательно, тА = 0.
414* Мера дополнительного множества равна сумме площадей
всех выбрасываемых «крестов», т. е.
A + i4 +42+ + А4*+ 1
9 ' 9* ' g» ' ' 9*+1 '
Следовательно, тВ =?= 0.
415. Мера дополнительного множества равна сумме площадей
всех выбрасываемых прямоугольников, т. е.
тСЕ = 1 + 1-2 +1.22 + ... + —L.-2* + ... = 1.
3 З2 З3 3k+1
Следовательно, тЕ = 0.
416. Пусть Е cz [а, &]. Рассмотрим функцию / (#) на [я, 6],
определенную формулой
f {х) = m ([а, л:] П £)•
Очевидно, что f (а) = 0, / (b) = т£ = /? и f (х) монотонно возрас-
возрастает (хотя не обязательно строго). Докажем, что функция / (х)
непрерывна. Пусть х> х + h £ [#, 6] и ft > 0. Тогда
/ (х + ft) - / (х) = m ([а, ^ + ft] П £) - т ([а, *] П
П Е) = m (>, х + h] П £) < /и >, * + Л] = h.
Следовательно, / (jc-+ h) — f (jc)-^O при h -> +0, т. е. / (x) непре-
непрерывна справа во всех точках х £ [а, Ь[. Аналогично доказывается,
что / (jc) непрерывна слева во всех точках # ^ ]а, Ь\
Итак, / (х) непрерывна на [а, &]. Поэтому ее значения заполня-
заполняют весь отрезок [/ (а), / (Ь)]< В частности, так как f (a) < q < / (b),
то найдется £ £ ]а, fe[ такое, что f (£) = ^. Но / (£) = т ([а, £] f] f).
Следовательно, множество [сц £] П Е, включающееся в £, имеет
меру, в точности равную q.
417. Случай, когда множество Е ограничено, рассмотрен в
решении предыдущей задачи. Если же £ — неограниченное мно-
множество на прямой, то поступаем следующим образом. Положим
Еп = Е П [—л, л].
Ясно, что Ei cz E2 cz ... cz £Л с: ..., причем (J £Л= £. Тогда
/п£ = Пт тЕпу т. е. lim тЕп = р. Так как по условию q < р,
П-+ОО П-
то существует такой номер п0, что m£n > 9. Обозначим тЕп — г.
Множество Е ограничено и имеет меру г > q. Согласно предыду-
168

щей задаче, оно обладает измеримым подмножеством Л, мера ко-
которого равна qK Остается заметить, что А с Е.
418. Пусть q' — какое-либо число, заключенное между р и
Ц (Я < Я' < р)- Согласно предыдущей задаче, существует ограни-
ограниченное измеримое множество A cz E такое, что тА = q'. Пусть
A cz [a, ft]. Так как тА > qy то существует замкйутое множество
В cz А такое, что тВ > q (см. свойство 11, с. 46).
Наконец, так же, как это было сделано в решении задачи 416,
устанавливаем, что на отрезке [a, ft] имеется точка £ такая, что
т ([а, И П В) = q.
Множество [а, Q (] В замкнуто, как пересечение двух замкну-
замкнутых множеств. Обозначим его через С:
С = [а, И П В, тС = ц.
Как всякое замкнутое множество на прямой, С разбивается на
совершенное множество D и не более чем счетное множество N
(см. задачу 368). Так как мера N равна нулю, то mD = тС = q.
Остается заметить, что D а Е.
419. Так как тЕ > 0, то, в силу предыдущей задачи, Е обла-
обладает ограниченным совершенным подмножеством D положитель-
положительной меры. Поскольку D непусто, его мощность не меньше мощно-
мощности континуума (см. задачу 253). Поэтому Е ^ с. Но, с другой
стороны, Е — подмножество числовой прямой, которая также
имеет мощность континуума, и потому Е ^ с. Следовательно,
420. Если Е — ограниченное плоское множество, то поступаем
следующим образом-. Пусть Е проектируется на ось Ох в отрезок
[a, ft]. Рассмотрим множество Ех тех точек из £, абсциссы которых
не превосходят х, и определим на [a, ft] функцию /\ положив
/ (#) = тЕх . Тогда / (а) = 0, f (ft) = р. Легко доказать, что / —
непрерывная функция на [a, ft]. Так как / (а) < q < f (ft), то,
следовательно, на [a, ft] найдется точка £ такая, что / (£) = q.
Тогда М = Е^ и будет искомым множеством: М cz £, причем
тМ =f q.
Если Е не ограничено, мы поступаем так же, как в задаче 417.
421. Опираясь на результат задачи 420, поступаем так же, как
в аналогичном случае при решении задачи 418.
422. Не может. Если множество Е содержит внутреннюю точку
х0, то в £ входит и некоторая окрестность V (х0) этой точки. Но
тогда тЕ ^ mV (х0) > 0.
423. Нельзя. Если бы мера замкнутого множества Е с [a, ft],
отличного от [а, ft], равнялась ft — а, то [а, 6] \ Е содержало бы
внутренние точки и имело бы меру нуль. А это невозможно (см.
предыдущую задачу).
424. Все три возможности осуществимы. Примеры:
а) если Еп = , + оо[, то Е == [0, +оо[, так что тЕ == + оо;
L я
169

б) если Еп = [—1, 0] U [я, +<*>[> то Е = [—1, 0], так что
тЕ = 1;
в) если £Л = [л, +оо[, то Е = 0, так цто тЯ ?= 0.
425. Обе возможности осуществимы. Примеры:
а) если Еп = [о, 1 — -1, то £ = [0, 1[, *ак что т£ < + оо;
б) если Еп = [0, я], то Е = [0, + оо[, так что тЕ = +оо.
426. Обозначим через Ei множество всех тех точек отрезка
[0, 1], в разложении которых в бесконечную двоичную дробь на
втором месте стоит нуль; через Е2 — множество всех тех точек, в
разложении которых на втором и четвертом местах стоят нули;
через Е3 — множество всех тех точек, в разложении которых на
втором, четвертом и шестом местах стоят нули и т. д. Ясно, что
Ei zd Е2 :э Е3 z5 ... и что mEk ~ —г при любом k (каждое мно-
жество Е есть объединение 2k попарно не пересекающихся полу-
1 \ п
открытых промежутков длины -г . Так как Е = fl Ek, то
4*/ fe=i
А
тЕ = lim mEft = lim -- = 0.
To, что £ нигде не плотно, доказывается так же, как для кан-
торова множества (задача 224).
427. Может; например, множество Е == U fe, fe + — не
k=\ J 2AJ[_
ограничено, а его мера равна единице.
428. Пусть / — произвольный интервал на прямой. Он не
может содержаться в Е, так как в противном случае тЕ ^ ml > 0.
Таким образом, / П СЕ Ф 0. Так как Е замкнуто, то СЕ откры-
открыто. Следовательно, / (] СЕ — непустое открытое множество; но
тогда существует интервал, включающийся в / и свободный от
точек множества Е. Тем самым Е — нигде не плотное множество
на прямой.
Доказательство для плоскости и трехмерного пространства
аналогично.
429. Нет. Пример. Пусть Е — множество всех рациональ-
рациональных чисел на отрезке [0, 1]. Тогда тЕ = 0, а тЕ = 1.
430. Нет. Пример. Пусть F — нигде не плотное совершен-
совершенное множество положительной меры на отрезке [0, 1] (см., напри-
например, задачу 410), а £ — множество его точек первого рода (т. е.
множество концов всех смежных интервалов). Тогда Е — нигде
не плотное счетное множество, а всякое счетное множество есть
множество меры нуль. В то же время £г= F и, следовательно,
тЕ «= mF > 0.
431. Так как Е — множество положительной меры, то оно
имеет мощность континуума (задача 419). Пусть х0 — произволь-
170

ная точка из Е. Тогда множество всевозможных чисел вида
р (xQi х), где х £ £, имеет мощность континуума; следовательно,
не все эти числа могут быть рациональными. Иначе говоря, най-
найдется такая точка х £ £, что р (лг0, х) иррационально.
432. Занумеруем все рациональные числа интервала ]0, 1[:
rit Г2> •••> rk> •••
и для каждого натурального числа k обозначим через Ek множест-
вб, получившееся из Е сдвигом на rki т. е. множество всех точек
вида х + rk, где rk фиксировано, ах(£, Множества Ek конгру-
конгруэнтны Е и потому все имеют меру \i. Если бы они попарно не пере-
пересекались, то, положив Н = U Eki мы имели бы тН = E
k
k
+ тЕ2 + ... +• mEk +...== \i + \i + ... + |^ + ... = + oo, что
невозможно, так как Яс[а, b + 1] и, значит, тН ^ fr + 1 —
— а. Итак, существуют такие два различных номера i и /, что
Е. ft Ej== 0. Пусть £ € £, П £У Tor^a S = л; + г, = у + гу,
где *, у € £, откуда \х — у\ = \г. — гу| ^= 0, так что р (*, у) ра-
рационально.
433. В силу результата задачи 417, Е содержит ограничен-
ограниченное подмножество £0, мера которого также положительна; остает-
остается применить к множеству Ео результат предыдущей задачи.
434. Е — нигде не плотное совершенное множество на отрезке
[О, X] (см., например, задачу 290). Мера дополнительного множе-
множества равна сумме длин смежных интервалов:
+ i + + + £+ L
Следовательно, тЕ = 0.
435. Это множество является дополнительный (до отрезка
[0, 1]) к тону, которое рассмотрено в предыдущей задаче; поэтому
оно всюду плотно на отрезке [0, 1] и открыто; его мера равна 1.
436. Часть этого множества, расположенная на отрезке
[п, п + 1] (п — целое), получается из множества Е задачи 434 сдви-
сдвигом на пи потому имеет меру нуль. Все множество Я представляет
собой объединение этих частей:
Я = U {Я П [л, п + 1]},
п
и потому также имеет меру нуль.
437. Обозначим через Ak множество всех чисел отрезка [0, 1],
в бесконечном десятичном разложений которых фигурирует циф-
цифра k. Множество Ak можно получить, если к множеству точек,
десятичное разложение которых невозможно без цифры й, доба-
добавить те точки, которые допускают два различных способа разложе-
разложения ив бесконечном разложении которых имеется цифра k.
Таким образом, Ak есть объединение открытого и счетного множеств;
следовательно, Ak — множество типа Fa. Указанное открытое
множество, а с ним и Ak, плотно в [0, 1]; mAk = 1 (см. задачу 435).
171

Интересующее нас множество Е является пересечением всех
А^ (k = 1, 2, ..., 9). Следовательно, Е — множество типа Fa ,
Чтобы найти меру Е> найдем сначала меру его дополнения отно-
относительно отрезка [0, 1]:
но mCAk =0(k~ 1, ..., 9); следовательно, mC£=0-, так что тЕ=1.
Отсюдд, в частности, следует, что Е ллотно на отрезке [0, 1].
43& Это — совершенное нигде не плотное множество. Оно
содержится в множестве Л, получающемся следующим образом:
разделив отрезок [0, 1] на 1000 отрезков длины 0,001 и удалив из
него интервал ]0,222, 0,2,23[, получим множество Ль составленное
из 999 отрезков; замениб каждый из них содержащимся в нем
множеством, получающимся подобным сжатием множества А{
в 1000 раз, получим множество Л2, составленное из 9992 отрезков
длины 0,0012; заменив каждый из них содержащимся в нем множе-
множеством, получающимся подобным сжатием множества Ai в 10002
раз, получим множество Л3, составленное из 9998 отрезков длины
0,0013, и т. д.; за А принимаем пересечение Л^^гП^зП--*
всех этих множеств. Так как тА = 1 — @,001 + 999 • 0,0012 +
+ 9992 • 0,0013Ч- ...) = 0, то и рассматриваемое Множество тоже
имеет меру нуль.
439. Объединение всех этих интервалов представляет собой
открытое множество
("То' ^ + ^)U(?~~io' i + ^o)UU 2~о' 9" +
Его мера равна 4 • ( 1—) = —.
v v V1Q 9/ 45
440. Мера объединения всех интервалов щ и vt не превосходит
суммы их длин; поэтому
Но 2(bi—ai) = mCE = 1 — 0,6 = 0,4. Итак,
Так как мера множества (Uty) U (U^) меньше меры множества
i i
Е, то это множество не может покрыть всего Е.
172

441. Можно. Пусть {yt} — какая-либо последовательность по-
со
ложительных чисел, такая, что ряд 2v* сходится и его сумма мень-
ше 1. Пусть, кроме того, {ц^ — какая угодно убывающая после-
последовательность положительных чисел, стремящаяся к нулю.
Впишем* в отрезок [0, 1] нигде не плотное совершенное множе-
множество At меры уь каждый смежный интервал которого имеет длину
меньше чем r]i.
Далее, в каждый смежный интервал ]а, р[ множества Ах впи-
впишем нигде не плотное совершенное множество меры (Р — а )у2,
каждый смежный интервал которого, расположенный на ]а, р[,
имеет длину < rj2. Объединение всех этих совершенных множеств
обозначим А2\ ясно, что тА2 = у2тСАх < у2 (здесь и дальше до-
дополнения берутся до всего отрезка [0, 1]). В силу результата зада-
задачи 233, Ai U A z — нигде не плотное совершенное множество и
каждый его смежный интервал имеет длину меньше t]2; при этом
О < т (Ах U А2) < Yi + 72.
Пусть уже построены нигде не плотные совершенные множества
Аг, ..., Ап на [0, 1] с нигде не плотным совершенным объедиие-
п
нием (J Аг В каждый смежный интервал ]а, р[ этого объединения
впишем нигде не плотное совершенное множество меры (Р —а) уп+19
каждый смежный интервал которого, расположенный на ]«, Р£,
имеет длину меньше чем т]/г+1. Объединение всех этих совершенных
множеств обозначим Ап+1; ясно, что
i = Уп+iM (С (U At)) < уя+1.
Тогда U Л. — нигде не плотное совершенное множество; его мера
я+1
меньше чем ^yt\ каждый его смежный интервал имеет длину мень-
ше т|я+1.
оо
Покажем, что множества В = U А{ и А = СБ удовлетворяют
1=1
требованиям задачи. Пусть ]а, Ь[_ — произвольный интервал, вхо-
входящий в [0, 1], и п таково, что t\n <-^=^. Так как [}А{ —нигде
3 t=i
не плотное совершенное множество и длины всех его смежных ин-
интервалов меньше чем х\п, то внутри ]а, Ь\_ найдется хотя бы один
смежный интервал этого множества; обозначим его/.
Тогда/ {] Ах = 0 для i = 1, 2, ..., п\
* Влисать в отрезок [а, 6] или в интервал ]а, &[ совершенное множество —
это значит построить совершенное множество, включающееся в [а, 6] или э ]я, &[.
173

m (/ П An+l) =|/|уя+1* где |/| — длина интервала /; далее,
т V П >W < I /IYh+2. m G П Л„+3) <1ЛуЛ+3и т. д. Так как Bid An+1
и ]а, b[ id /, то ]а, 6 [f| 5 id / (*] ЛЛ+1; следсжательно
Чтобы доказать теперь, что /n (]a, b [ f] Cfl) > 0, напомним,
что множества А. попарно не пересекаются. Поэтому
2
1=1
Но т (I П СБ) = | /| — m (/ П 5). Следовательно, m (/ (] СВ) >0.
А так как I a]a, b[, то и подавно
т (]ау Ъ [ П СВ) > D.
442. Может. Пример. Построим для каждого натурально-
натурального числа п нигде не плотное совершенное множество Еп на [а, Ь]
такое, что тЕп =Ь — а (см. задачу 410), и положим Е =
п
= U Еп. Так как Еп а Е с [а, &], то & — а = т£л <
м=1 /г
^ тЕ ^ b — а для любого п и, следовательно, mJ? = Ь — а.
443, Да. Проведем соответствующее построение на отрезке
Го, п.
Прежде всего построим на отрезке [0, 1] нигде не плотное со-
совершенное множество Ех меры —. Далее, в каждый смежный ин-
интервал "}ацу PiiC множества Ег впишем нигде не плотное совершен-
совершенное множество Elh мера которого равна половине длины интерва-
оо 1
ла ]аи, $ц [. Тогда m([}Elt) = —. Множество Е2 =Et\J
со
U (U Еи) совершенно и нигде не плотно (см. задачу 233). В каж-
1
дый его смежный интервал ]a2i, E2£ впишем нигде не плотное со-
совершенное .множество Е21, мера которого равна половине длины
интервала ]a2i, р2£. Тогда m([}E2i) = —, а множество Е3 =
ОО
= Е2 U A1^2/) совершенно и нигде не плотно. Продолжая этот
процесс неограниченно, мы получим счетную совокупность по-
попарно не пересекающихся нигде не плотных совершенных множеств
174

При этом
и) = 1, ... , m(y£fti) = -L-, ....
и потому
т(Е1 U (\JEU) U ... U (\)ЕЫ) U •••) =
= ± + 1 + +-!-ч- =1
2 ' 22 2ft+1
Таким образом, счетная совокупность множеств Ех и
£^. (k = 1, 2, ..., / = 1, 2, ...) удовлетворяет всем условиям за-
задачи.
444. Существует; в качестве такого множества можно взять
[О, 1] \ £» гДе £ — объединение всех множеств, построенных
при решении предыдущей задачи.
445. Так как 1 — е < тЕк ^ тЕ ^ 1, ае можно взять произ-
произвольно малым, то тЕ = 1.
446. По свойству аддитивности меры имеем:
тЕг + тЕ2 = тЕх + т(Е2\ Ег) + т (Ег (] Е2) =:
= т (Ег U £«) + т (Ег (] Е2).
447. Для совокупности из двух измеримых множеств Ег и Е2
это соотношение доказано в предыдущей задаче, причем в этом
случае имеет место равенство. Для любой конечной совокупности
множеств {Et} докажем неравенство по индукции. Пусть
/n(U£/)+ ^ m(Ei()Ej). A)
Тогда
fe+i k k
2 mEt =^тЕ, + mEk+1 < m (U Et) + 2 m (Et П £y
l1 t
(
t=l t=l l==1
k+\ k
= m (U £,) + m ((U ^) П £^+i)+ S m (^ П ^y)
^=1 *=1 \<i<f<k
<m(U £г)+ 2 " ^
1=1 \<i<k
Для счетной совокупности множеств требуемое неравенство
получается предельным, переходом в неравенстве A) при k -> ею
(при этом надс* использовать свойство 13 из введения к данноц
главе).
448. Так как П Л£ =С (UC^), то
i-i t=i
175

m(b^=\-m(UCA^ A)
Но
m(U CAt) <2тСЛ, =ilA— тАй=п — ^
l==1 t=i t=i t=i
А так как по условию 2mA > п — Ь то п —
Следовательно,
m(jjCAd<l.
Сопоставляя A) и B), получим окончательно:
449. Выберем сначала замкнутое множество Fx си Ег такое,
что mF1 > тЕ1 (см. свойство 11 из введения к этой главе).
Дальнейшее построение ведем по индукции. Пусть для всех k < п
построены замкнутые множества F* Такие, что Fk c= Ek9 mFk >
> mEk —-—- и Fx zd F2 zd ... id Fn^. Выберем в качестве
Fn замкнутое множество, удовлетворяющее условиям
FnczEn{] Fn^ и mFn>m (En(] Fn^) - ±.
Так как m (En f] Fn^) = mEn + mFn_x - m (En U Fn_x)
(см. задачу 446), то тогда
mFn > mEn + mF^ ~ m (En [} Fn^) - i.
Учитывая теперь, что Еп [} Fnmml cz En_l и потому
m (En U Fn^) ^ mEn_x и что, по индуктивному предположению,
п^г < tnFn^.1 + ——J^ ' 9 получим окончательно:
mFn > тЕп
2« i
= mEn — 8 • ——.
Итак, Fnd En, mFn>мЕп-г- ^—^>mEn-8, Fncz Fn^. Ис-
Искомая последовательность замкнутых множеств построена.
450. Если k = 0, то kE = {0}, и утверждение задачи очевидно.
Пусть теперь k ф 0. Докажем сначала, что для любого множест-
множества А на прямой имеет место:
т (kA) =5 \k\ • тЛ.
176

Действительно, любому покрытию множества А системой интер-
интервалов {/а} отвечает покрытие множества kA системой интервалов
{kla} и, обратно, любое покрытие множества kА имеет вид {kla},
где {/а} — некоторое покрытие множества Л. Отсюда и из равен-
равенства (л {kl) = \k\ • |л/, справедливого для любого интервала /,
получаем: rn(kA) = inf 2 У (^а) — in* 21
21
= |А| • inf S jx/a = |ft|
а
Поэтому если Е и kE оба измеримы, то
m (&£) = m(kE) =
Осталось доказать, что из измеримости Е следует измеримость
kE. Пусть А — произвольное множество на прямой. Так как Е
измеримо, то для множества —А имеем:
m - л = m -
т (j (Л П *£)) + т A (Л П С (Ы-))) =
1*1
откуда
\k | • m Ц A) = m (Л П &£)+ m (Л П С (fe£)).
А так как I fe | • т (— А) = т (k • — Л) = /пЛ, то
= m (Л П *£) + m (Л П С (££)).
Но это и означает, в силу произвольности множества Л, что kE
измеримо.
451. Для каждого натурального числа п обозначим через Fa
совершенное множество такое, что
(если т \Е{\\\ , [U | , — [))>0, то существование
\ \ \\ п п+\\ [п+Х пЦ)
такого множества Fn следует из результата задачи 418; если же
т(Е(](]-±, L-]u Г—|—t — J^ =0, то в качестве Fn меж-
177

со
но взять пустое множество). Положим Q = (U Fn)[){0}. Ясно, что
Q — совершенное множество. Кроме того, для любого б>0 имеем:
где N — натуральное число, такое, что — < 6. Поэтому
n=N
452. Все внутренние точки круга х2 + у2 ^ 1 являются точ-
точками плотности, а все точки его дополнения — точками разреже-
разрежения. Плотность круга в точках границы х2 + У2 = 1 равна —.
454. В качестве такого множества можно взять круговой сек-
сектор с центром в точке MQ и центральным углом 2яа.
455. Построим множество, имеющее в точке 0 плотность, рав-
равную а.
Для каждого натурального числа п рассмотрим объединение
двух промежутков
и возьмем такое измеримое множество Ап с= 1п, что тАп = а • mln\
например, можно взять Ап ~\ , \-а( —ч U »
J п п \п п+\)\ [п+1
—- + а( I • Докажем, что множество Е = \\ Ап имеет
в точке 0 плотность, равную а.
Рассмотрим произвольное положительное число б < 1; пусть
п —такое натуральное число, что ^ б <—.
п + \ п
Тогда v@, ——V=K(O, б) czV fot -In потому
\ n + lj \ n)
, б)) . i
A)
mv(<
178
т
v\o,
V@, .
1\
1 \
+ ч
б) ^ ,( 1 \
2
a • —
2 a \ ~* м J ^
я+1

(последнее неравенство следует из того, что — ^ —— < 26).
п п + 1
С другой стороны,
т (Е()V @, Ь)) ^ т\ П \ ' п + 1// _ а' m^\Q> n+ i) ^
^ / 1 \ ~~ / l \ ~
mV 10. — 1 mV\Q. —I
B)
I n + 1
Из неравенств A) и B) получаем, что lim т^ ———- —а.
6->o mV@, 6)
Итак, множество Е имеет в точке 0 плотность, равную а. Если
же х0 Ф 0, то в качестве искомого множества можно взять множе-
множество всех точек вида х0 + у, где у 6 £.
456. Для каждого натурального числа п положим
и обозначим через Fn совершенное множество такое, что Fn cz Еп и
-)тЕп. Пусть F =(UFJ U {0}. Очевидно, F —
совершенное множество, содержащееся в £. Возьмем произволь-
произвольное б > 0. Обозначая через Af целую часть числа —, получим:
о
m(FnV@, 6))
26 1
Л/
1 \ iV
2
n=N+\
iV
Предел последнего выражения при б -> 0 равен 1. Следовательно,
lim HLJ]—lj—L =1 т. е. 0 является точкой плотности для F.
6->0 26
457. Представим Е в виде объединения двух множеств: Е =
179

=s= {E П A) U (E П СЛ). Множество £ fl Л измеримо (как часть
множества Л меры нуль). Если бы было измеримо и множество
Е П СЛ, то было бы измеримо и их объединение £, что противо-
противоречит условию. Следовательно, Е (] СЛ неизмеримо.
458. Если А и В — интервалы, то утверждение задачи очевид-
очевидно. Если А и В — произвольные открытые множества, то Л X В
также открыто; при этом А = (J Аь В = у By, где Л£, равно
как и By, — попарно не пересекающиеся интервалы. Тогда
Л X В = U (Л* X Ву)
И
m2 (Л X В) = 2 /иа (Л; X By) = 2 (щА1 • т^у) =
*= 2 ^гЛ/ • 2/%В/ = тз.Л • тхВ.
i 1
459. Пусть е — произвольное положительное число и Ап (п =
= 1,2,...) — открытые множества на прямой, содержащие Л и
такие, что т1Ап < —. Так как Л X В с U (Лл X ]—пгп[),
то
т2 (Л х В)< m2 (U (Лл X ] - я, я[)) <
i
(см. предыдущую задачу).
Следовательно, т2 {А X В) — 0.
460. Если А и В — множества типа G6, то
Л = Q Ац В = П By, где Аг =э Л2 => ..., Вх zd В2 =э ... —
открытые множества на прямой. Тогда Л X В = f] (Л^ X Bf),
где {At X Bf} — убывающая последовательность открытых мно-
множеств на плоскости. Следовательно, Ах В измеримо и т2 (Л ХВ)=
= lim m2(Ai x Bt) = lim mxAt • m^ = тгА - mji.
i -> со t -»• oo
Если Л и В — произвольные измеримые множества конечной
меры, то существуют множества А я В типа G6 такие, что Л => А,
Bzd В и тх (А\ А) =т1 (В\ В) = 0
(см. ниже, задачу 465). Так как
Л Х'В = (А X В) U (И\ Л) X В) U (А X (В \ В)) U
11((Л\Л) X (В\В)),
180

то, согласно результату предыдущей задачи, А X В отличается
от измеримого множества Л X В лишь на множество меры нуль.
Следовательно, А X В измеримо и
т2 (А X В) —т2(А X В) = тхА'• тхВ ^
= mi Л • ШхВ.
461. Положим Лл — Л Л С—л, /г], Вл = В f| [—п, п]. Тогда
{Лл X Вл}—возрастающая последовательность измеримых мно-
множеств. Применяя результат предыдущей задачи, будем иметь:
т2(А X В) =ma(U (Ап X Вп)) =
= lim m2 (Лл X Вп) == lim (m^ • тхВ^ = +о°.
П->ОО П->С5О
462. В качестве такого множества М можно взять множество
Л X Л, построенное в решении задачи 242, если выбирать ek
удовлетворяющими дополнительному условию
е^ < ^^- Тогда тх([0, 1] \ Л)< 2 V е < ±
и, значат, т1А> -. Следовательно, т2(АхА) = (т1АJ>— > 0.
463. Используя свойства внешней меры, получаем:
Ъ m (£ U Н) ^~тЕ +1пН =тЕ
/й"((£ \ Я) U Я)< m"(£ \ Я)
Отсюда ~тЕ =~т (Е [} Н) = m"(£ \ Я).
464. По определению внешней меры, существует покрытие
{Dn }множества Е открытыми параллелепипедами такое, что
^mDn < тЕ + е. Положив Л = и^я» получим: Л открыто,
п п
A zd Е, тЕ ^ тА, тА ^ ^raDn < m£ ~fc- е, т. е.
тЛ — е < т£" ^ тА.
465. Если тЕ = +оо, то полагаем В =Х. Если же т£ < +оо,
то, в силу результата задачи 464, для каждого п существует от-
крытое множество Ап такое, что AnZD Е и тАп — — < тЕ ^
оо
^ тАп . Положим В = f) Лл . Тогда Bid Е,В —множествотипа
Об и тЕ ^ тВ ^ тАп < т£ Н— для каждого /г, откуда тВ =
п
181

466. Согласно результату предыдущей задачи, существуют мно-
множества В и С типа Об такие, что
В zd Е, С =) / \ Е, тВ =тЕ, тС = m(I \ E). A)
Не ограничивая общности, можно считать, что В cz /, С cz / (если
это не так, возьмем вместо В и С их пересечения с /; это будут
тоже множества типа G&, включающие соответственно Е и / \ Е,
и для них также выполняются равенства A)). Так как I = В [} С,
то, в силу результата задачи 446 и равенств A),
т (В Г) С) = тВ + тС — т (В [} С) = тЕ + т (I \ E) —
—ml -О
(мы воспользовались равенством ml = тЕ + т (I \ £), данным
по условию). Отсюда следует, что множество В \ Е измеримо (как
подмножество множества В (] С, имеющего нулевую меру). Но
тогда и Е измеримо, как разность измеримых множеств В и В \ Е.
467. а) Покажем сначала, что из условия A) следует условие
B) гA) =* B). Положим Еп = Е (\D ((-^-я, ..., —п), (/г, ..., /г));
оо
тогда Е = П Еп. Если Е измеримо, то все Еп измеримы. В силу
результата задачи 464, при заданном г > 0 для каждого п суще-
существует открытое множество Gn =э Еп такое, что mGn < тЕп + ~ ,
откуда т (Gn \ Еп) < -^. Тогда G = (J G — открытое мно-
оо
жество, содержащее Е. Так как G \ E cz U (^Л \Еп), то,
m(G\£) <
б) B)=>-D). Пусть выполнено условие B). Для каждого п
существует открытое множество Ghzd Е такое, что т (Gn \Е)< —.
п
оо
Тогда для множества А = f) Gn типа Об будем иметь: A zd E,
п—\
т (А\Е)^т (Gn\E) < — при люйом я, и, значит, т(А\Е) = 0.
п
в) D)=^A). Если существует множество А типа Gt такое, что
А =э Е и m (Л \ £) = 0, то Е измеримо, как разность измери-
измеримых множеств — множества А типа (?б и множества А\ Е меры
нуль.
г) A)=>C). Пусть Е измеримо. Тогда измеримо и СЕ. Следо-
Следовательно (в силу пункта а)), для каждого е > 0 существует
открытое множество G zd СЕ такое, что т (G\ СЕ) < е. Положив
182

P = CG (F — замкнуто), получим: F с £, E \ F = CF \ C£ =±
= G \ C£; следовательно,
m(E\ F) =m(G\CE) < e.
д) C)=>A). Пусть для каждого^ >0 существует замкнутое
множество F cz Е такое, что т (Е \ F) < е. Тогда и
m (С/7 у СЕ) < е, где CF => С£ и CF открыто.
Следовательно (в силу пунктов б) и в)), множество СЕ измеримо;
но тогда измеримо и Е.
е) Эквивалентность условий A) и E) доказывается аналогично.
468. Эквивалентность измеримости множества Е выполнению
любого из условий а) и б) непосредственно следует из результатов
предыдущей задачи.
469. Необходимость. Пусть Е измеримо, тЕ < +оо.
Для каждого е > 0 существует покрытие множества Е счетным
оо
семейством {DJ открытых параллелепипедов такое, что
< тЕ +—. Так как ряд 2 m^i сходится, то найдется номер N
со
такой^ что ^mDi <~. Тогда Н — OiU---U^a/ будет искомым
2
множеством: оно состоит из конечного числа параллелепипедов и
т (Е А Н) < ~ + - = е.
Достаточность. Для произвольного е > 0 построим
множество Я, составленное из конечного числа открытых парал-
параллелепипедов и такое, чтот (Е А Н) < — , тогда подавно т (£\Н)<
о
<— . Покроем множество Е\ Н семейством открытых парал-
лелепипедов {Dn} так, чтобы 2 т&п < т (Е \ Н) + — <— ♦
п 3 3
Множество G = Н [} (\jDn) открыто, G => Е (так как
EczH [}"(Е\Н)<=Н {) (\}DH) = G),
_
m(G\E) =
£) U (иОл))< ^|
Но тогда, в силу результата задачи 467, множество Е измеримо.
183

ЧАСТЬ ВТОРАЯ
ТЕОРИЯ ФУНКЦИЙ
Глава VIII.
ОБЩАЯ ТЕОРИЯ ОТОБРАЖЕНИЙ
470. Неверно. Прообраз множества / (Л) может включать точ-
точки, лежащие за пределами множества Л; например, если / (х) =
= х\ А = [0, 2] a R\ то / (А) = [0, 4], а /"' (/ (Л)) =
= [—2, 2]. Здесь jM (/ (Л)) ф А. Однако включение /-1 (/ (A))zdA
верно всегда.
471. Равенство / (f~l (В)) = В справедливо для любого В из
множества значений функции /.
472. Равенство f (А [} В) =f(A)[}f(B) справедливо для
любых множеств Л и В из области определения функции /.
Равенство / (Л f) Щ = / (Л) f| / (В) справедливо не всегда.
Так, например, если Л = |"о, — 1, В=[-, — 1, f (x) = sin xy то
/(Л) =[0, 1], f(B) =[-lf 1],
= [0, 1].
Однако всегда верно включение / (Л П В) cz f (Л) П )
473. Первое справедливо для любого, а не только взаимно
однозначного отображения f.
Докажем второе.
а) Пусть у0 € / (П Ak)\ тогда в множестве f) Ak найдется точка
к к
хд такая, что у0 = / (д:0); значит, х0 (: Ak для всех k, откуда у0 =
= / (*о) € / (Лл) для всех Л, т. е. у0 € П / ИЛ). Итак, / (П ЛЛ) с
с fl / (^л)- При доказательстве этого включения мы не пользо-
пользовались тем, что отображение / взаимно однозначно; следователь-
следовательно, это включение справедливо для любого отображения /.
б) Пусть у0 € П f(Ak). Тогда у0 € / (Ak) для любого k. Так
как отображение / является, взаимно однозначным отображением
R на / (/?), то Существует, и притом только одна, точка х0 € R
такая, что f (х0) =у0- Значит, эта точка х0 принадлежит всем Л^,
т. е. х0 С ПЛЛ. Поэтому у0 =/(х0) ^/(ПЛЛ). Итак,
184

Объединяя результаты, полученные в а) и б), получим нужное
равенство.
474. Равенство A) справедливо для любого отображения f.
Равенство B) перестаёт быть верным, если отображение / не яв-
является взаимно однозначным.
475. Равенство / (R \ А) = / (R)\ f (А) справедливо для
взаимно однозначного отображения /. Для произвольных отобра-
отображений / справедливо лишь включение / (R \ A) id f (R) \ f (A).
Так, например, если f (x) = х2, R =] — оо, 4-°°[> А = [0, +°°[,
то / (R \ А) = f (]-oof 0[) = ]0, +оо[, a f{R)\f (A) = 0.
476. Верны.
477. Справедливо.
478. Верны.
Г л а в а IX.
НЕПРЕРЫВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ В
МЕТРИЧЕСКИХ ПРОСТРАНСТВАХ
479. Обозначим через Ah множество всех тех точек х простран-
пространства X, в которых о (/, х) ^ —. Покажем, что Ап замкнуто.
п
Пусть а — точка прикосновения множества Ап. Во всякой окре-
окрестности V (а, е) найдется точка х (: Ап\ при этом некоторая ок-
окрестность V (х, б) точки х включается в V (а, е). Колебание функ-
функции /в V (ху б), а значит, и в У (а, е) больше или равно со (/, х) ^
^ — . Устремляя е к нулю, найдем, что колебание в точке а также
п
не меньше —, т. е. а € Ап. Итак, Ап замкнуто.
п
Далее, Е = Аг {} А2 \] ...; следовательно, Е является мно-
множеством типа Fo в X.
480. Это следует из предыдущей задачи и из того, что дополне-
дополнение к множеству типа Fa есть множество типа Ge (задача 204).
481. Пусть Е = {г1у г2, г3, ...}. Построим следующую функ-
функцию:
\\ ПРИ х = г*' где k = *' 2> 3» -• •
10 при х £ Е.
Эта функция разрывна в каждой точке rk\ действительно, в любой
окрестности V (rk) найдутся точки, не принадлежащие заданному
счетному множеству Е\ в этих точках функция равна нулю; по-
поэтому (of^— для любой окрестности V (rk) точки rk\ следова-
k
тельно, колебание функции в точке rk также ^ —ц значит, функ-
k
ция разрывна в точке rk.
1В5

Пусть теперь х0 € Е. Для каждого г > О найдется окрестность
точки х0, не содержащая ни одной точки rk с номерами k < —
8
(таких точек rk лишь конечное число). Для всех точек х, попавших
в эту окрестность, имеет место неравенство |/(х)| < 8> т- е-
I/ (х)—/(л:0)|<8. Следовательно, функция / непрерывна в
точка х0.
оо
482. Так как ряд 2#&ф (х — xk) равномерно сходится на всей
/г=1
числовой прямой, то его сумма непрерывна в тех точках, в которых
все функции ak = ф (х — xk) непрерывны; следовательно, сумма
ряда непрерывна во всех точках х, отличных от хъ x2t х3, ...В каж-
каждой же из точек xl9 х2, xs сумма ряда терпит разрыв.
483. Это следует из того, что множество всех точек разрыва
любой функции, определенной на всей прямой, является множе-
множеством типа Fa (задача 479). Множество же С£, дополнительное к
счетному всюду плотному множеству £, не может быть множеством
типа Fa (см. задачу 260).
484. Пример. / (х) = (х2 — 1) % (х), где % (х) — функция
Дирихле, т. е.
/ (х) z=z[x^ — I» если х РаВД°нально,
/v ; ~"~ \ 0, если х иррационально.
485» Пример, f (х) =%{х) - sin ял:, где % (х) — функция
Дирихле.
486. Все точки, принадлежащие смежным интервалам канто-
канторова множества, являются точками непрерывности этой функции.
Все точки канторова множества — ее точки разрыва (так как в
любой окрестности каждой точки канторова множества имеются
точки из смежных интервалов). Все эти точки являются точками
разрыва второго рода.
487. Пример.
—- для точек х = —., где —. Ф0—несократимая дробь,
10* 10й 10й
/(*) =
р
0 для точек х, не представимых в виде ~
10*'
1 при х = 0.
Исследование этой функции проводится так же, как в задаче 481.
488. Заданная функция непрерывна во всех точках смежных
интервалов и разрывна во всех точках канторова множества.
489. Если lim сп = 0, то эта функция непрерывна во всех точ-
точках отрезка [0, 1]. Если lim cn существует и отличен от нуля, то
эта функция разрывна во всех точках канторова множества и не-
непрерывна во всех точках смежных интервалов.
490. В случае 1) функция / (я) разрывна в концах смежных
интервалов канторова множества и непрерывна в остальных точ-
точках отрезка [0, 1].
186

В случаях 2) и 3) функция / (х) разрывна во всех точках канто-
рова множества D и непрерывна на [О, 1J \ D.
491. Пример.
— при х = —, где —ФО—несократимая дробь,
а а а
fix) ==|
w | 0 при х иррациональном,
1 при х = 0.
Исследование этой функции проводится так же, как в задаче 481.
492. Не существует (см. задачу 483).
493. Такой будет, например, функция F (х), равная произведе-
произведению функции / (л:), построенной в задаче 489 (при сп -> 0), на функ-
функцию Дирихле:
F(X) =/(*)• Х(х).
494. Такой будет, например, функция, имеющая значение 1
в точках канторова множества, и 0 вне его.
Другим примером может служить функция, построенная в
задаче 488.
495. Данная функция разрывна во всех точках числовой пря-
прямой, кроме точки х = 0; в этой точке функция непрерывна.
496. Данная функция непрерывна во всех точках отрезка [0, I].
497. Если функция f (х) не ограничена на Л, то равенство
очевидно: обе его части равны +оо. Пусть теперь / (х) ограничена
на Л и sup / (я) = М, inf / (я) = т. Так как для любых § £ А и
ц 6 Л имеем: т ^ / (£) ^ М, М ^ / (rj) ^ m, то
I/ F) — / (Т|)|< Af — /я = соД
А
откуда
sup 1/A) -/(л) 1< со/. A)
I, ЩА А
Для доказательства обратного неравенства возьмем произ-
произвольное е > 0 и найдем в множестве Л такие две точки хх и г2,
что
/ (хг) < т + е, / (х2) >М—г.
Тогда
I/ (*2) - / (%I > / (xj - f (хг) >М-т-2г,
и, следовательно sup |/ (g) — f (ц)\^ М — т — 2е. В силу про-
извольности 8 > 0, вытекает, что
sup|/F)-/(r|)|>Af-mf т. е.
^A B)
p\f(l)fm>f
Сравнивая неравенства A) и B), получаем требуемое равенство.
187

498. В силу результата предыдущей задачи, для любых двух
точек |, т] £ А имеем:
К/ (!) + S {%)) ~ (/ ft) + g ft))l < I/ A) - / (Ц)\ +
+ \g (Ъ) - ё Ш < f
л л
Беря в левой части верхнюю грань по всем |, г\ £ Л, получим:
о) (/ + g)< о)/ + cog. A)
л л л
Пусть теперь хотя бы одно из чисел со/, cog конечно; предполо-
Л А
жим, что cog ^ со/ (и, значит, cog < + оо). Так как /=(/ + £) +
л л л
+ (—£)» то из неравенства A), примененного к функциям / + g и
—g, следует;
ю/ < (о (/ + g) + о> (—g) = со (/ + g) + o)g.
Л Л А А А
Поскольку cog конечно, получаем:
© (/ + Я) > <°/ — cog = |(о/ — cog|.
Л Л А А А
-{-оо
499. Так как ряд 2 /л (*) равномерно сходится, то для любого
6
е > 0 существует такой номер
Ч-i 4
— для всех
Выберем такую окрестность V(x0) точки х0, что
« /А<(о[/„ х0, Е-} + £-
для k ^ 1, 2, ..., N. Тогда
i
< 2 е0 С/л
Так как е > 0 произвольно, то
0)
500. Так как для любых | € Е и т] € £" имеет место неравенство
II/FI - I/(ч)И < 1/F)-
то, в силу результата задачи 497, <й|/| < о/ для любого множе-
л а
188

ства А а Е. Отсюда вытекает, что (о[|/|, #0] ^ аз [/, х0]. А так
как функция / непрерывна в точке #0, то со [/, хо~\ = О, и, значит,
00 [1Л» хо] = О) н0 это означает, что функция \f\ Также непрерывна
в точке х0.
501. Пример.
f (х\ _ ( 1 Для рациональных х € [0, 1],
1^-1 Для иррациональных х ё [0, 1].
502. Эта функция непрерывна во всех иррациональных точках
и разрывна во всех рациональных точках; ее исследование прово-
проводится примерно так же, как исследование функции в аадаче 481.
503. Пример. / (я, у) = 0 в тех точках (х, у), где у ирра-
иррационально (при любом х), / (х, у) = 1 в тех точках (х, у), где у
рационально (при любом х).
504. Функция / (х, у) непрерывна во всех тех точках квадрата
[0, 1] X [0, 1], где обе координаты иррациональны; она непре-
непрерывна также в точках, где одна из координат иррациональна, а
другая равна 0; кроме того, она непрерывна в точке @, 0). Во всех
остальных точках квадрата функция разрывна.
Докажем, например, разрывность функции / (я, у) в точке
(—,—), где — > 0, — > 0 — рациональные числа, записан-
\я Я\) я Я\
ные в виде несократимых дробей с положительными знаменателя-
знаменателями. В этой точке значение функции равно нулю. В любой окрест-
окрестности этой точки найдутся точки с иррациональной абсциссой и с
ординатой р±\ значение функции в таких точках равно ,
Ях Ях
а потому колебание функции в любой окрестности точки (—, —)
больше или равно —. Значит, эта точка является точкой разрыва.
Я\
Исследование функции в остальных точках проводится ана-
аналогично.
505. Пусть / — функция, определенная и непрерывная на
компактном множестве Е. Рассмотрим произвольную последова-
последовательность {уп} точек из /(£"). Для каждого п существует точка
хп € Е такая, что f (хп) =уп> В силу компактности £, последо-
последовательность {хп} обладает подпоследовательностью {хПк}% сходя-
сходящейся к некоторой точке а € Е. Так как функция / непрерывна в
точке а и lim хПь = а, то lim / (хп ) = / (а), т. е.
Итак, всякая последовательность {уп} точек из / (Е) обла-
обладает подпоследовательностью, сходящейся к точке из /(£").
Значит, / (Е) — компакт.
506. Примеры, а) Пусть / (я) = ех; эта функция непрерыв-
непрерывна на замкнутом множестве ]—оо, 0] числовой прямой. Однако
образом этого множества является незамкнутое множество ]0,1}.
189

б) Пусть f(x) -arctgx, Е =]-оо, +оо[, /(£) = J-|,||\
Множество Е замкнуто, тогда как / (Е) незамкнуто.
507. Пусть fix) =sinx, E = ]0, 2я[. Тогда / (£) = [—1, 1],
а это множество не является открытым на числовой прямой.
508. Пусть xlf x2, ... — последовательность точек из /-1 (F),
сходящаяся к точке § ё X. Функция / (я) непрерывна всюду на X,
и в частности в точке |; поэтому
Так как / ixn) €F, а множество F замкнуто, то и / (|) $ /% т. е.
I (: f^1 iF). Итак, каждая сходящаяся последовательность точек
из /-* (F) сходится к точке из f*1 (F); следовательно, множество
/~* (F) замкнуто.
509. Пусть х0 С Г1 (О); тогда у0 = /(*0) € G*. Пусть V (у0) =
= ]Уо — 8» Уо + 8[ — окрестность точки у0, включающаяся в G.
В силу непрерывности функции в точке х0, существует окрест-
окрестность V (х0, б) такая, что для всех х € V (х0, б) имеем: |/(x) —
— уо| < е, т. е. / (*) 6 У (у0) с: G. Следовательно, 1/ (х0, б) с:
с: Z (G), т. е. вместе с точкой х0 ё f (G) в это множество входит
и некоторая окрестность точки х0. Значит, /-1 (G) — открытое
множество.
Заметим, что этот результат можно получить также из резуль-
результата предыдущей задачи переходом к дополнениям.
510. Может. Примеры: a) f ix) = с; здесь прообразом
компактного одноточечного множества {с} является вся числовая
прямая; б) fix) = sin х\ здесь прообразом отрезка [—1,1] являет-
является вся ось Ох.
5Н. Необходимость условия доказана в задаче 509.
Докажем его достаточность. Возьмем произвольную точ-
точку х0 числовой прямой и рассмотрим произвольную окрестность
]Уо — 8» Уо + 8С точки Уо = / (*о)> прообразом этой окрестности
является по условию некоторое открытое множество G, причем
х0 (: G. Пусть ]#0 — б, х0 + б[ — окрестность точки х0, входящая
в G. Тогда / (х) б ]у0 — е, у0 + е[ для всех х € >0 — б, х0 + б[;
но это и означает, что функция / (д:) непрерывна в точке х0.
Так как х0 — произвольная точка числовой прямой, то функ-
функция fix) непрерывна на всей числовой прямой.
512. Пусть ]а, Ь[ — произвольный интервал на числовой пря-
прямой. Он является дополнением к множеству ]—оо, a] U [Ь, +оо[,
а прообраз этого множества замкнут, как объединение двух замк-
замкнутых множеств (см. задачу 476). Поэтому прообраз интервала
]а, Ь[ открыт (см. задачу 477).
Итак, прообразы всех интервалов открыты; но тогда, на осно-
основании результата предыдущей задачи, функция / ix) непрерывна.
513. Пусть х0 — точка непрерывности функции / ix), причем
/ (д:0) — я0; докажем, что существует окрестность этой точки, все
190

точки которой являются точками непрерывности функции f (х).
Пусть V (х0) — такая окрестность точки х0, что для всех х (: V (х0)
выполняются неравенства f(x0) < f(x) < f(xo)-\—, т. е.
no—j<f(x)<no +i.
Так как функция, по условию, принимает только целые значения,
то это означает, что / (х) = п0 для всех х € V (х0). Таким образом,
функция Постоянна на V (х0), а значит, непрерывна во всех точках
этой окрестности*
Итак, если х0 (: Е, где Е — множество точек непрерывности
функции / (х)у то некоторая окрестность V (х0) этой точки также
входит в Е\ а это означает, что Е — открытое множество.
Множество точек разрыва функции f (х) замкнуто, как допол-
дополнение к открытому множеству.
514. Множество / (Е) компактно (см. задачу 505), а всякое
компактное множество ограничено (см. задачу 303).
515. Непустое множество / (Е) компактно и, следовательно,
замкнуто (см. задачу 303). Но тогда оно содержит все свои точки
прикосновения, и в частности точку А = inf / (х) и точку В =
XZE
= sup / (х) (то, что, например, А есть точка прикосновения для
f (£), следует из того, что в любом интервале ]Л — е, А + е[ най-
найдется ^сотя бы одна точка из / (£); в противном случае число А + е
было бы одной из нижних границ функции / (х) на £, а это противо-
противоречит тому, что А есть наибольшая из нижних границ).
516. Пусть Е — множество всех непрерывных функций х (t)
да [0, 1] таких, что х @) ^ 1, 0 <; х (t) ^ 1 при / ё [0,1]. Множе-
Множество Е ограничено и замкнуто в С [0, 1], которое является полным
пространством (см. задачу 130). Поставим в соответствие каждому
элементу х ё Е число / (л:) = . Функция / (х) непрерывна
]x(t)dt
на Е, но не ограничена на нем (непрерывность следует из того, что
J х (t)dt непрерывно зависит от х в С [0, 1] и не обращается в нуль
1
на Е\ неограниченность следует из того, что \х (t)dt может быт»
о
сделан сколь угодно малым для надлежащим образом подобран-
подобранных х (t) из Е.
517. В качестве Е можно взять то множество в С [0, 1], которое
было построено в предыдущей задаче, а в качестве / (х) — функ-
функцию / (х) = \ х (t) dt. Непрерывность и ограничейность / (х) на Е
о
очевидны. Однако нет такой непрерывной функции a (t)f принад-
принадлежащей Е, для которой / (a) = inf / (х), так как inf / (х) = 0,
Х£Е xiE
191

1
а для любой функции х (t) из Е имеет место / (х) = j x (t) dt > 0.
о
518. Для любых х £ X, х' 6 X имеют место неравенства:
Р (*', Уо) - Р (*", Уо) < Р (*', х*), р (х\ yQ) - р (*', у0) <
< Р (х\ х")у откуда | р (*', уо) — Р (*", УоI < Р (V, х), а это оз-
означает, что функция р (ху уо) равномерно непрерывна в X (и,
следовательно, непрерывна в X).
519. Пусть у € £• Тогда для любых х' ( X и х" ( X имеем:
d (*', £) < р (*', у) < р (х\ х") + р (jc*. у),
P(*",y)>d(*'f£)-p(*'f Л-
Переводя в этом неравенстве к нижней грани по всем у € £, по-
получим:
d (/', £) - inf р (У, у) > d (x'f £) - р (х\ х"),
УкЕ
ИЛИ
d{x\E)-d{x\E)^9{x\x").
Меняя ролями х1 и х\ получим: d (х", Е) —d (х', Е) ^
< р (х', х)у откуда \d (x\ E)—d(x\ Е)\ < р {х\ х"). Следова-
Следовательно, функция d (x, E) равномерно непрерывна и, значит, не-
непрерывна в X.
520. Рассмотрим р (xOt у) как функцию от у на компакте Е.
В силу ее непрерывности (см. задачу 518), существует точка у0 g E
такая, что р (х0, у0) = inf р (х0, у) (см. задачу 515), т. е. р (х0, у0) =
у:б
«= d {х0, Е).
521. Построим в пространстве X замкнутый шар В = В (хОу г)
такой, что множество Е (] В непусто. В силу компактности этого
множества, в нем найдется точка у0 такая, что р (х0, у0) = d (xOf
Е (] В) (см. предыдущую задачу). Тогда р (х0, Уо) = d (х0, Е),
так как для любого у € Е выполняется неравенство р (#о, у) ^
^ Р (^о» Уо): Для у € £" П В это следует из выбора точки у0» а Для
у € £ \ (Е П В) — из того, что р (хо, у) > г > р (д:0, у0).
522. Для любых х £ Е, у ^ F имеем: р (#, у) ^ d (у, £) ^
> inf d (у, £), т. е.
р(х, у) > infif (у, £);
переходя в этом неравенстве к нижней грани по всем х € Е, у € F,
получим: inf p (х, у) ^ inf d (у, £), или
x£E,y:F yzF
d(E, f)>infd(yf £). A)
С другой стороны, при фиксированном у € J7 имеем:
inf р (я, г) < inf р (х, у), т. е. d (E, F) < d (у, Я).
192

Так как это неравенство справедливо при любом )/ (F, то оно
сохранится и для нижней грани (по всем у £ F), т. е.
d (£, F) < inf d (у, Е). B)
yiF
Сравнивая неравенства A) и B), получаем искомое равенство.
523. Согласно задаче 519, d (у, Е) есть непрерывная функция
от у. Поэтому в компакте F найдется точка у0 такая, что d (у0, Е) =
= inf d (у, £), т. е. d (у0, Е) = d (£, F) (см. задачи 515 и 522).
Так как Е обладает свойством //, то, в силу результата задачи
521, существует 1ючка х0 € Е такая, что р (х0, у0) =*= d (£, у0). Сле-
Следовательно, р (лг0, Уо) = d (E, F).
524, 525. Это следует нейосредственно из задачи 523 (если
учесть также результат задачи 334).
526. Пример. Гипербола на плоскости и ее асимптота,
527. Пример. Кривая у
и прямая у=—1.
528. Пусть Е = {fи /2, ...}, где fn (п = 1, 2, ...) — непрерыв-
непрерывная на [0, 1] функция, определенная следующим образом:
при х 6 0,1
линейна на 1 , 1 ,
L п п + \\
О при лег е Г1 —.—* l|
[ я + 1 J
(см. рис. 28). Множество Е ограничено и замкнуто в полном
пространстве С [0, 1] (замкнутость Е следует из того, что
PifJ) >
НА*)
В качестве множества F возь-
возьмем одноточечное множество, со-
состоящее из функции уо (х), тож-
тождественно равной нулю на [0, 1].
Тогда р (fn, уо) = 1 + -1^ > j,
d = (£, f) = d(E, уо) ==
= inf р (/„, у0) = -, так что
п 2.
d(E, F) =^p (fn, уо) ни для какого
элемента fn множества Е.
529. Это следует из неравенств
Р (Уь
Рис. 28
193

(первое из них легко выводится из неравенства треугольника, вто-
второе следует из неравенства а + b ^1^2 У а2 + Ь2, справедливого
для любых чисел а ^ 0, b ^ 0).
530. р {ху у) — функция, непрерывная на компакте Е X Е
(см. задачи 314 и 529). Следовательно, в силу результата задачи
515, найдется точка (х0, у0) € Е X £, в которой эта функция до-
достигает своей верхней грани, т. е.
Р (хо, У о) = sup р (х, у) = diam E.
xiE, y£E
531. Пусть р (xiy х2) = а. Рассмотрим окрестности У4 =
= V (xi9 — ], Уг = V (х2у — \ Искомая функция может быть зада-
задана равенством / (х) = —— >.
F W d(xV) + d(xV)
A) + B)
532. В качестве искомой функции можно взять, например,
следующую:
p(x,\)Et) p(*, \}Ei)
= Pl +/?
P(x. EJ + p(x, [)Et) +/?2 p(x, E2) + p(x, [}Et)
Р(х, \}Et)
Легко видеть, что / (л:) = pk при х £ Ek (k = 1, ..,, п).
Покажем, что эта функция определена и Непрерывна на всей
числовой прямой. Действительно, множество U Et замкнуто,
как сумма конечного числа замкнутых множеств E2t Е3, ..., Еп\
поэтому множества Ei и у Ег не имеют общих точек прикосновения
и, следовательно, знаменатель первой дроби ни в одной точке не
равен нулю; это же справедливо и для знаменателей всех осталь-
остальных дробей. Но тогда из непрерывности функций р (х, Ek) и
р (л:, U Et) (k = 1, ..., п) вытекает непрерывность функции / (х).
533. Искомую функцию можно задать следующим образом:
~ р(х, \j^Ei)
f(x) = 2d Pk 9{x, Ek) + p(x, U EiY
534. Допустим, что такая функция / (х) существует. Пусть
х0 £ Ei — точка прикосновения для U Et. Тогда в любой окрест-
окрестности V (х0) точки х0 найдутся точки из Et со сколь угодно больши-
большими номерами i (так как объединение конечного числа множеств Et
замкнуто); следовательно, в этой окрестности найдутся точки, в
которых значения' функции / (х) сколь угодно близки к нулю (так
как Pi~>0 при г -> +оо); но тогда в любой окрестности точки хо
194

колебание функции f (x) больше или равно |/(лго)| =s |pi|, а это
означает, что функция / (рс) разрывна в точке х0.
535. Пусть / (х) — функция, непрерывная на связном множе-
множестве Е. Допустим, что / (Е) несвязно. Тогда f (Е) =• А [} В, где
А я В — разъединенные множества. Рассмотрим множества At =
= f~x (А) и Вх = f (В). Они непусты, их объединение равно Я,
и ни одно из них не содержит точек прикосновения другого: если
бы, например, а £ Ai была точкой прикосновения для Ви то не-
некоторая последовательность {хп} точек из 54 сходилась бы к а;
но тогда, в силу непрерывности функции / (х), последовательность
{/ (хп)} точек из В сходилась бы к / (а) £ Л, что противоречит разъ-
разъединенности множеств А и В. Итак, At и В4 — разъединенные
множества, объединение которых равно Е. Но это противоречит
связности Е.
536. Согласно результату предыдущей задачи, / (Е) — связное
множество на прямой. Поэтому вместе с точками А и В множество
/ (Е) содержит и весь соединяющий их отрезок (см. задачу 394).
Следовательно, С £ / (£), т. е. существует точка с £ Е такая, что
/ (с) = С.
537. В силу результатов задач 505 и 535, / (Е) — непустое
компактное связное множество на прямой. Но такими являются
только отрезки и одноточечные множества (см. задачи 303 и 395).
538. Нет, не является. Например, функция
sin — при х Ф 0,
х
0 при х = 0
обладает свойством Дарбу на отрезке [—1, 1], но разрывна в точке
х0 = 0. (Однако можно легко доказать, что функция, обладающая
свойством Дарбу, не может иметь точек разрыва первого рода.)
539. 1) Функция sin— не является равномерно непрерывной
на интервале ]0, 1[, так как для всякого б > 0 колебание этой
функции на интервале 0, — min (б, 1) , длина которого меньше
чем б, равно 2.
2) Функция х sin — равномерно непрерывна на ]0, +оо[. До-
Докажем это. Доопределим данную функцию в точке 0, положив
/(*)=;
х sin— при хф 0,
х
О при х = 0.
Полученная функция / (х) непрерывна на луче[0, +оо[.
Зададим произвольное б > 0. Так как / (х) ->• 1 при #->- +оо,
то найдется х0 такое, что |/ (х) —1| < — для любого х ^ х0. На
195

отрезке [0, лг0] функция / (х) равномерно непрерывна как функция,
непрерывная на отрезке. Значит, найдется тадое б > 0, что для
всех х\ х" € [О, х0], для которых \х' —х"\< б, будет
Тогда для всех точек/, х" € ]0, +°о[, / < Этаких, что*" — х' <
< б, имеем: \f{x')-f {х")\< е; если *', У € ]0, хо1 то |/@
/ () -1 < 8; если *-', х" ё >о, +«>[, то |/ {x')-f {x")\ <
< I/ №)— И + II—/<Л1 < j + j < е; наконец, если
х' € Ю, хо1 х" € >о, +оо[, то |/ (*') - / {х")\ <| / (У) -/ (*0)| +
+ I / W - И + I 1 - / (ЛI < f +f +7 = 8' Итак* функ"
ция / (л), а значит, и совпадающая с ней на луче ]0, +оо[ функция
х sin — равномерно непрерывны на этом луче.
3) Функция Зд: равномерно непрерывна на числовой прямой.
Действительно, поставив в соответствие каждому е > 0 число б =
= —, получим, что из | х — х"\ < б следует: |3/ — Зх"\ < е.
4) Функция х2 не равномерно непрерывна на всей числовой
прямой.
5) Функция ^^ равномерно непрерывна на луче ]0, +оо[.
540. Допустим, что функция / (х) не является равномерно не-
непрерывной на Е. Тогда существует такое е0 > 0, чтр для любого
б > 0 найдутся точки х' и х" из £", расстояние между которыми
меньше чем 6, тогда как |/ (xr) —f {x")\ > е0. В частности, для
бл == -L (п = 1, 2, ...) найдутся точки хп, хп $.Е такие, что
п
р (ХП, Хп) < ^ , I / (Хп) — f (Хп)\ > в0.
Рассмотрим последовательность {х'п}. В силу компактности Е,
из нее можно выбрать подпоследовательность {хп^ сходящуюся
к некоторой точке хо£Е. Тогда х0 является пределом также для
подпоследовательности {xnj- Действительно, р (х*п , х0) ^
< Р (*L« x'nJ + Р (*nb> xo)< - + Р (x'f х0) и ~ + Р (х', хо)-+О при
« « « Му^ « fife R
k -> 00; ПОЭТОМУ р (JC* , Хо) -> 0 НрИ k-><X).
В точке д:0 функция / непрерывна относительно £. Но тогда
Шп / (д:^ ) = / (д:0) и lim f(x"n ) = /(x0)- Следовательно,
А эта противоречит тому, что |/ (хп ) — / (х'п )| ^ г0 для любого
196

номера nk. Полученное противоречие доказывает, что функция /
равномерно непрерывна на Е.
541. Пусть функция / (х) равномерно непрерывна на Е. Найдем
такое число б > 0, что |/ (#')— / (V)| < 1 для любых х' € Е,
х" £ Е таких, что р (х\ х ) < б. В силу задачи 326, существует
конечная б-сеть xl9 ..., хп для множества £, содержащаяся в са-
самом Е. Пусть А — наибольшее, а В — наименьшее из чисел
/ (), -..» / (#Л). Тогда для любого х £ Е получим:
542. Да. Это следует из неравенства
I if (xf) + g (*')) - (/ (хГ) + g (x"))\ < |/ (/) - / (x")i +!*(**)-
-g(x")l
543. He всегда. Например, функции f (x) = x и g (x) = x рав-
равномерно непрерывны на всей числовой прямой, однако tox произ-
произведение / (х) g (х) = j? не является равномерно непрерывной
функцией на]—оо, +оо[.
544. Да. Это следует из неравенств
1/ (*') 8 (х') - f (х") g{x")\ < |/ (x')g (x') - f (x')g {x")\ +
+ \f{x')g{x")-f{x")g{x")\= |/(*')|.|g(*')-g (*")!
(ЛI I/ (*') - / (ЛI < A • |g (л;') - g (/')| + В . |/
где Л = sup |/ (x)|, В = sup| g (#)| (ограниченность функций, рав-
номерно непрерывной на относительно компактном множестве,
была доказана в задаче 541).
545. Зададим произвольное е > 0 и найдем такое N, что для
всех х > N имеет место |/ (х) — Ь\ < —, где Ь = lim / (х). Тогда
для любых точек х{ ^ N, х2 ^ N справедливо неравенство
На отрезке [О, ЛГ] функция непрерывна-; следовательно, она
равномерно непрерывна на нем. Найдем б > 0 такое, что для всех
*' € [О, N1 х" € [О, ATI, \xr — х"\ < б имеет место |/ (xf) —
— / (х")\ < ~- окажем, что это число б «годится» для всего луча
[О, +оо[. Пусть xi, х2 ё [0, +°°[ и \Xi — х2\ < б. Если хх €[0, ЛГ)
и х2 € [0, ЛЯ, то |/ (*4) —/ (х2)\ < -1 < е; если Xi > Л^, х2 > Л^,
то L/ (*i)— / (л:2I < ~<е; наконец, если одна из этих точек,
например хи принадлежит [0, Л/], а другая больше чем N, то
197

Итак, из I*!—х2\ <б всегда следует: I / (агх)—f (х2)\ < е. В си-
силу произвольности числа е > 0, это означает, что функция f (x)
равномерно непрерывна на луче [0, +оо[.
546. Неверно. Например, функция sin x2 непрерывна и огра-
ограничена на всей числовой прямой, однако она не равномерно не-
непрерывна на ней. Действительно, каким бы малым ни взять поло-
положительное число б > 0, всегда найдется интервал вида "\УШ1
У (k + 1)я[, длина которого меньше чем б (так как длины этих
интервалов стремятся к нулю при k -> +°о). Вместе с тем колеба-
колебание функции sin х2 на этом интервале равно 1. Следовательно, для
е = 1 не существует такого б > 0, чтобы на всяком интервале
длины, меньшей чем б, колебание функции было бы меньше чем 8.
547. Не является (хотя, как следует из результата задачи 488,
она непрерывна во всех точках множества Е).
548. Эта функция разрывна во всех точках первого рода мно-
множества D и непрерывна во всех точках множества CD, а также во
всех точках второго рода множества D. На множестве CD функция
не является равномерно непрерывной.
549. Пусть х € Е. В силу равномерной непрерывности функции
/ на Е, для каждого е > 0 найдется такое б > 0, что из х\ х" ё Е,
р (х', х") <б следует: \f(x')—f {х")\ < е. В частности, если х\
х" € v(x, ~\ П £> то |/(*')— f{x")\ <e. Поэтому для всякой
последовательности {xk} точек из Е, сходящейся к х, последова-
последовательность чисел {/ (xk)} фундаментальна и, в силу полноты число-
числовой прямой, имеет предел \imf(xk). Этот предел не зависит от вы-
бора последовательности точек множества Е> сходящейся к х:
если бы для каких-либо двух сходящихся к х последовательностей
{xk} и {xk} мы имели lim / (х'ь) ф lim / (xl), то последовательность
{хп}, где хи_г =x'kt x2k = xl, также сходилась бы к х, однако
последовательность {/ (хп)} не имела бы предела.
Положив теперь ф (х) = lim / (xk), где {xk} — какая-нибудь
k-+-\-oo
последовательность точек из Е, сходящаяся к точке х, мы получим
функцию ф, определенную на множестве Е. На множестве Е она
совпадает с функцией /, так как если х € Е, то можно положить
хк = х для всех k.
Докажем, что функция ф равномерно непрерывна на Е. Зада-
Зададим произвольное е > 0 и возьмем б > 0 такое, что из х> у (: Е,
Р {х, у) < б следует: | / (х) — /(у)|< —, Пусть х' и х" — произ-
произвольные точки из Е такие, что р (х\ х") <б и {xl}, {xl} —
какие-нибудь последовательности точек из Е, сходящиеся соот-
соответственно кх'и х". Выберем k столь большим, чтобы выполнялись
следующие неравенства:
198

(неравенству р (х'к, х"к) < б можно удовлетворить, если взять
x'k£V(x', *i)> x"k£V{x", ц), где т)= у(° — Р(*'« х")); Действитель-
Действительно, при этом р (*;, д$ < р (x'k, х') + р (*', х") + р (х", х'к)< 2т| +
Тогда получим:
^ + | + ~ = в.
Таким образом, для любых точек х\ х" из Е таких, что р (х1, х") <
<б, имеем: |ф(х')— ф(#")| < е. В силу произвольности числа
е > О, это означает, что ф равномерно непрерывна на Е. Тем более
она непрерывна на Е.
Условием непрерывности функция ф определена на Е одно-
однозначно. Действительно, пусть ^ — какая-либо непрерывная на Е
функция, совпадающая с / на множестве Е. Тогда для любой точки
х € Е и любой последовательности {хк} точек из Е, сходящейся
к х, имеем:
г|)(л:) = lim ф(д:Л) = lim f(xk) = ф(х).
ft-*-}0 fc-*-f-oo
550. Продолжим сначала функцию / с сохранением непрерыв-
непрерывности на замкнутое множество Ег как это сделано в предыдущей
задаче. Чтобы продолжить полученную функцию ф на всю прямую,
достаточно продолжить ее линейно на всех смежных интервалах
множества Е: если смежный интервал ]а, р[ конечен, то для точек
# € ]а» PC полагаем ф (х) = ф (а) + х~~а (ф ф) — ф (а)); если же
р — а
смежный интервал бесконечен, т. е. имеет вид ]—сю, а[ или
]а, +оо[, то на нем можно положить функцию постоянной, ф (х) =в=
ess ф (а). Построенная таким образом функция ф определена на
всей числовой прямой. Покажем, что она непрерывна во всех точ-
точках прямой.
Ясно, что ф непрерывна на всех смежных интервала^множества
Е, Пусть теперь х0 6 Е. В силу непрерывности ф на Е9 для каж-
каждого е > 0 найдется такое б > 0, что при х € Jx0 — б, xQ + б [f| E
имеем: | ф (л:) — ф (д:0I < е. Если интервал ]х0, х0 + б[ не содер-
содержит точек множества Е, то на отрезке [л:0, х0 + б] функция ф
линейна, а потому непрерывна справа в точке х0. Если же интер-
интервал ]х0, х0 + б[ содержит точки из £, то__ положим хг =
sup(>0, хо+б [(!"£). Так как~Е замкнуто, то х^ Е. Покажем, что
|ф(л:) — ф(л'0)|<е для всех х € ]х0, х&. Если х € £, то это
199

следует из того, что >0, х£ а >0—б, хо+б[. Если же_* лежит в
каком-нибудь смежном интервале ]а, р[ множества Et то ср (х)
заключено между числами ср (а) и ф (р) (в силу линейности ф на
]а, р[). А так как]а, р[ с;>0, хг [ cz >0 — б, х0 + б[ и а € Я, Р€ £,
то Ф (%) — е < ф (а) < ф (х0) + е и хр (л;а) — 8 < ф (р) <
<Ф (х0) + е- Поэтому и ф (л;0) — е < ф (л:) <: ф (л:0) + е, т. е.
1ф(*)—ф(*оI < Е- Следовательно, функция ф непрерывна спра-
справа в точке #0. Точно так же доказывается- ее непрерывность слева
в этой точке.
Таким образом, ф (х) непрерывна во всех точках числовой
прямой и совпадает с / (х) на множестве Е.
551. Пример. Функция sin — непрерывна и ограничена
на ]0, 1[, однако ее нельзя продолжить с сохранением непрерыв-
непрерывности даже на отрезок [0, 1], так как она не имеет предела при
х-+ +0.
552. Действительно, если бы такая функция / могла быть про-
продолжена с сохранением непрерывности на всю числовую прямую,
то продолженная функция была бы непрерывна на Е. Но Е замк-
замкнуто и ограничено и, следовательно, компактно (см. задачу 330).
Поэтому, согласно задаче 540, продолженная функция была бы
равномерно непрерывна на £, а значит, и на Е. Но на Е она сов-
совпадает с /; поэтому / была бы равномерно непрерывна на Е, что
противоречит условию.
553. Возьмем такое б >0, чтобы для всевозможных х\ Xя
таких, что \х'—х"\ <б, было |/(#')—f (х*)\ < 1; такое б най-
найдется в силу равномерной непрерывности функции f. Пусть х —
произвольное число. Разобьем отрезок [0, я] (при х > 0) или
[х, 0] (при х < 0) точками
1 J2 П--1
л, Х9 ,•. у ■ Xf
п п п
где п подобрано так, что — | х | < б <^ 1 х |. Тогда
п п — 1
Так как, в силу выбора числа б, каждая разность в правой части
неравенства меньше чем 1, то
откуда | / (х) | < | / @) | + л; далее, так как — - \ х \ > б, та
п — 1
п < !■—* + !; поэтому
о
200

l/WK
±1*1 + 1 =
где
/ t
Л = 1,Б=
554. Пусть Е — множества
тех непрерывных функций х (f)
на tO, 1], для которых л: @) = 1
и 0 < х @ < 1 при / € [0, 1].
Это множество замкнуто и ог-
ограничено в пространстве С [0, 1].
Функция /(л:), заданная на
этом множестве равенством
/(*)=- , непрерывна на Е.
$x(t)dt
о
Вместе с тем она не является равномерно непрерывной на Е9 так
как не существует б > 0 такого, что из р (хъ х2) < б (хг € Ег
х2 (: Е) вытекает: \f(xx)—f (х2)\ < 1. В самом деле, допустим,
что такое б > 0 существует; не ограничивая общности, можно
считать б ^0,4. Беря в качестве хг (t) и х2 (t) функции» графики
которых даны на рисунке 29, будем иметь:
Рис. 29
но IftXjW
вопреки выбору б. Итак, / (х) не является равномерно непрерыв-
непрерывной на Е.
555. Для любых хг € С [0, 1], х2 6 С [0, 1] имеем:
I/ (*i) - / (х*)\ = lj*i (t) dt-$QX2 (t) dt | < j \xx (t) -x% (Old/ <
l
p(xltx2)dt =p(*x, x2),
откуда и следует равномерная непрерывность / (л:) (для любого
е > 0 в качестве б можно взять б == е).
556. Пусть Е — множество всех точек пространства 12> у кото-
которых одна из координат равна единице, а все остальные — нулю
(т. е. точек вида @, ..., 0, 1,0, ...). Это множество ограничено.
Зададим на Е функцию /, положив f (хп) = п\ где хп —* точка из
Еу у которой 1 стоит на п-ж месте. Эта функция равномерно не-
непрерывна на множестве Е, но не ограничена на нем.
557. Представим Е в виде объединения счетного семейства замк-
замкнутых множеств:
Е - Fx U /Ч U ^з U ... U Fk U ...;
201

всегда можно считать, что Fx с: Ft a Fs с: ... (в противном слу-
случае мы заменили бы Р2 на Ft [) F2, F3 на Fx [) F2 \J F3 и т. д.;
тогда новая последовательность замкнутых множеств возраста-
возрастает; объединением же этих множеств по-прежнему является множе-
множество Е).
Построим теперь на /f1 последовательность функций {/Л}, опре-
определенных условиями:
— в рациональных точках, принадлежащих множеству /у,
2
— в иррациональных точках множества Fk\
О в точках, не принадлежащих Fk,
Функция fk (x) разрывна во всех точках множества Fk и не-
непрерывна на CFk (действительно, около каждой точки х0 6 CFk
можно описать окрестность V (х0), которая входит в CFk; всюду
в этой окрестности функция постоянна и, значит, непрерывна).
Положим теперь
J
Этот ряд равномерно сходится на 7?1, так как \fk (^)f ^— для
всех к и всех х € /?*. В любой точке 1 € СЕ каждая функция fk (x)
непрерывна; поэтому из равномерной сходимости ряда 2/дМ вы-
вытекает непрерывность функции / (х) в этой точке.
Пусть теперь | ё Е. В этом случае найдется такой номер к,
что 1 € Fkf но | С /v^ (здесь мы полагаем Fo = 0). Тогда |
является точкой разрыва для функций /л, /л+1, ... и при fe > 1 точ-
точкой непрерывности для функций /i, ...»/*_i. При этом
(О
9 • Ю*
(см. задачу 499). Поэтому, в силу результата задачи 498, имеем:
1 2
Следовательно, функция / (х) разрывна в точке 1.
Итак, / (х) непрерывна всюду на множестве Е и разрывйа всюду
на СЕ.
558. Доказательство сводится к непосредственной проверке
формул.
202

559. Хл1 (*) = %gXx) %Б (x) ... %E (x)\
1 * ft
2 xB(*)xB(*)xB («)-
i<j<k i i k
ia(x) ...%еп(*).
56ft. Если точка х0 является граничной для множества Е% то
в любой окрестности этой точки колебание характеристической
функции равно 1, и, следовательно, функция разрывна в точке х0.
Если же точка х0 не является граничной, то она является внут-
внутренней либо для Еу либо для СЕ. Значит, найдется окрестность
точки х0, в которой колебание функции %Е (х) равно нулю; следо-
следовательно, в этой точке функция непрерывна.
561. Непрерывность этих функций вытекает из тождеств
max{ф(х),
min{Ф(х), ф(х)} =
2
и результата задачи 500.
562. Обозначим
Tfirii9 _ 17 М, если / (*) < Ь9
Ясно, что [/(д:)]?_оо = min {f (л:), &}. На основании результатов
предыдущей задачи [/ (*)]Loo непрерывна на £. Далее, [/ (*)]£ =
= max {а, [/(я)]-»}. Следовательно, и [/ (л:)]а непрерывна на £.
563. Необходимость этого условия доказана в пре-
предыдущей задаче. Докажем его достаточность.
Допустим, что на прямой нашлась точка разрыва х0 функции
/ (л:). Если колебание у функции f (x) в точке х0 конечно, то функ-
функция [/ (х)Х-а при а> \ f (хо)\ +7 совпадает с / (х) в некоторой
окрестности точки х0. Но тогда и функция [/ (*)]!1д разрывна в
точке х0.
Если же в точке разрыва х0 колебание функции / (х) равно +оо,
то в любой окрестности точки х0 колебание функции [/ (лг)]^.а при
а> 1/Ч*оI не меньше чем а—1/(#0I- Следовательно, и в этом
случае функция [/ (лг)]1а разрывна в точке xQ.
Итак, разрыв функции / (х) в какой-либо точке х0 влечет за
собой разрыв функции [f (x)~f-a в той же точке для достаточно
больших а, что противоречит условию.
564. Разобьем отрезок [0, 1] на два непересекающихся множе-
множества: множество А типа Fa, всюду плотное на [0, 1], и множество
В типа G6, также всюду плотное на [0, 1], причем каждое из них
203

имеет мощность континуума в любом интервале ]а, (}[ с: [0, 1]
(пример такого разбиения см. в решений задачи 252). После этого
построение искомой функции / (я) может быть проведено так же,
как в задаче 557.
565. Эта функция разрывна во всех точках множества А и
непрерывна во всех точках множества Е. Равномерно непрерывной
на множестве Е -функция / (х, у) не является. Исследование этой
функции аналогично исследованию функции в задаче 488.
566. Эта функция непрерывна (а следовательно, и равномерно
непрерывна) на замкнутом квадрате [0, 1] X [0, 1], а значит, и
на Е. Исследование этой функции аналогично исследованию функ-
функции в задаче 489.
567. На множестве 0 < х2 + у2 < 4 функция непрерывна, но
не равномерно непрерывна. В кольце 1 < х2 + у2 < 4 эта функ-
функция равномерно непрерывна: действительно, она непрерывна,, а
следовательно, и равномерно непрерывна в замкнутом кольце
1 ^х2 + у2 ^ 4. Значит, она равномерно непрерывна и на любом
его подмножестве, в частности в открытом кольце 1 < х2 + у2 < 4.
568. Так как функция / (х) по условию непрерывна в точке х0
относительно множества D, то х0 ё D. В качестве / (х) можно взять,
Например, функцию
1 6
.0 при х €D.
569. Верно. Для доказательства достаточно воспользоваться
определением непрерывности по Гейне.
570. Неверно. Пример. Обозначим через а замкнутую
область, ограниченную первым завитком архимедовой спирали
р = щр @ ^ ф ^ 2я) и отрезком [0, 2ла] на оси абсцисс (рис. 30)»
Пусть
11 \ Г1 при х £ а,
/(*'У)={опри,ёа.
Эта функция в точке @, 0) непрерывна по любому лучу, исхо-
исходящему из начала координат; однако она не является полнос-
полностью непрерывной в точке @, 0).
571. Нет. Пример. Пусть L —
винтовая линия, расположенная в трех-
трехмерном евклидовом пространстве:
х = a cos /, у = a sin /, z = bt\
пусть Мо— точка с координатами (а, 0, 0).
Определим функцию / (х, у, г) следующим
образом:
0 всюду на L, кроме точ-
точки Мо;
v __ § 1 в точке MQf а также во
/ (х9 у у z) == i всех точках пространства
Л3, не принадлежащих
Рис. 30 i кривой L.
204

Эта функция непрерывна относительно любой плоскости, про-
проходящей через точку Мо, но не является полностью непрерывной
в этой точке.
572. Нет. Пример.
11 во всех точках плоскости с координатами (х, 0),
где х > 0;
0 во всех остальных точках плоскости (включая
и начало координат).
Функция / {х, у) непрерывна в точке @, 0) относительно любой
архимедовой спирали, однако она не является полностью непре-
непрерывной в этой точке.
Глава X.
НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ
573. Пусть у € / (£), т. е. у = f (х), где х € Е. Так как Ег
плотно в £, то х = lim хп, где {хп} — некоторая последователь-
П-»-оо
ность точек из Ег. Но тогда, в силу непрерывности отображения /,
у =lim уп, где уп = f (xn) € f (Ег) для всех п. Следовательно,
f (Ег) плотно в / (£).
574. In (х2 + 1) — непрерывная функция, определенная на Е =
= Л1, принимающая неотрицательные значения, равная 0 при
х = 0 и стремящаяся к +оо при *-> оо. Поэтому множеством ее
значений служит луч [0, +°°[- Так как множество Ег всех рацио-
рациональных чисел всюду плотно в Е, то остается применить результат
предыдущей задачи.
575. См. решение задачи 505.
576. Необходимость доказывается так же, как в за-
задаче 508.
Достаточность. Если прообраз замкнутого множества
F a Y замкнут в X, то прообраз его дополнения Y \ F открыт в
X, так как
f-i (Y \ F) = Г (Y) \ Г (F)=X\ Г1 (F).
Но любое открытое множество в Y является дополнением к не-
некоторому замкнутому; следовательно, прообраз любого открытого
множества в Y есть открытое множество в X; в частности, прообраз
любой окрестцости точки пространства Y открыт.
Докажем, что отображение / непрерывно в любой точке х0 6 X.
Возьмем произвольную окрестность V (/ (х0), е) точки / (л:0). Ее
прообраз /-1 (V (/ (x0), e)) открыт в X. Значит, точка
хо€ Z (V (f (xo)f e)) является внутренней точкой этого прообраза,
т. е. найдется такая ее окрестность V (xQ, 6), что V (х0, б) с:
с= Г1 (V (/ (х0), е)); тогда / (V (х0, б)) с: V (/ (х0), е). Но это озна-
означает, что для всех точек х € V(x0, б) будет выполняться неравенство
Р (/ W» / W) <£- Таким образом, отображение / непрерывно
во всех точках пространства X, т. е. на всем пространстве.
205

577. Необходимость
доказывается так же, как в
задаче 509.
Достаточность до-
доказывается, повторением второй
половины доказательства до-
достаточности из решения пре-
предыдущей задачи.
578. Доказывается повторе-
повторением второй половины доказа-
доказательства достаточности из реше-
решения задачи 576.
579. См. решение задачи 535.
580. Это следует из связнос-
связности жордановой кривой (см. пре-
предыдущую задачу и задачу 387) и
результата задачи 385.
581. Множество А на плоскости, являющееся объединением
графика функции sin -I на [—1, 0[ (JP, 1] с отрезком, соединяю-
соединяющим точки @, —1) и @, 1) (см. рис. 31). Так как А — ограничен-
ограниченное замкнутое множество на плоскости, то оно компактно,
Докажем, что А связно. Обозначим через С множество всех
точек вида (х9 sin—], где х €]0, 1], а через D —множество всех
У
. IP
"Jf
Г.
hi > '
Рис. 31
точек вида
х, sin-
где х € [—1, 0[. Множества С и D оба связ-
связны, так как они линейно связны. Значит, множества С и D также
связны (задача 383). Но их пересечение непусто (оно состоит из
«предельного» отрезка, соединяющего точки @, —1) и @,1). По-
Поэтому множество А = С U D связно (см. задачу 389).
Но вместе с тем множество А не является линейно связным.
Действительно, рассмотрим произвольную плоскую жорданову
кривую / (t) (t € [a, b]), носитель которой включается в Л и со-
содержит точку A, sin I). He ограничивая общности, можно считать,
что A, sin 1) = / (а). Докажем, что носитель этой кривой не может
содержать, например, точки @, 0).
Функция / (f) непрерывна на компакте [а, Ь] и, значит, равно-
равномерно непрерывна на нем. Следовательно, для е = 1 найдется
б > 0^ такое, что при \Г — f | < 6 (Г, f 6 [а, 6]) имеем:
Р if (О, / (О) < 1. Разобьем отрезок [а, Ь] на п частей точками
t0 = a, tl9 t2, ..., tn=b так, чтобы было tt — t^ < S (i = 1, ..., n).
Тогда Tt =/e([^_1, tj) — связное подмножество множества Л,
причем diam Ft < 1. Покажем, что каждое Ft (i =1, ..., п) вклю-
включается в С. Действительно, если бы Fx не включалось в С, то орто-
ортогональная проекция F* множества Fx на ось Ох содержала бы не-
некоторую точку а <; 0. Но отображение проектирования на ось
206

непрерывна (см. ниже, задачу 595); поэтому F* — связное множе-
множество на [—1, 1]. Так как A, sin 1) € Flf то 1 6 F*\ но тогда р, 1] cz
d[a, 1] с: F\ (см. задачу 394). Значит, Ft содержало &* все точки
графика функции sin —, абсциссы которых принадлежат ]0, 1]э
т. е. бесконечное число «волн» этой «синусоиды». Но это невозмож-
невозможно, поскольку diam Ft < 1, а амплитуда волны равна 2» Следова-
Следовательно, Fi включается в С.
Далее, F2 содержит хотя бы одну точку из С (а именно точку
/ (tt), принадлежащую Fx f| F2). Но тогда точно также убеждаем-
убеждаемся, что F2 с С и т. д. п
Таким образом, множество / ([а, Ь]) = [) Ft целиком включа-
включается в С и, значит, не может содержать точки @, 0). Итак, точки
A, sin 1) и @, 0) нельзя соединить никакой жордановой кривой,
т. е. А не является линейно связным.
582. Для множества G на плоскости это следует из результата
задачи 400, если учесть, что ломаная g конечным числом звеньев
является носителем жордановой кривой. Для G cz Rn при любом
п > 2 доказательство аналогично.
583. В силу взаимной однозначности отображения /, обратное
отображение существует; покажем на примерах, что оно не обяза-
обязано быть непрерывным, а) Занумеруем все рациональные числа
на оси Оу. Эту нумерацию можно рассматривать как непрерывное
взаимно однозначное отображение множества Е всех натураль-
натуральных чисел оси Ох на множество Ег всех рациональных чисел оси
Оу. Однако обратное отображение разрывно в каждой точке мно-
множества Ех. б) Пусть Е — промежуток [0,2я[ оси Ох, Ех — окруж-
окружность на плоскости Оху с центром в точке 0. Поставим в соответ-
соответствие каждой точке х (: [0, 2я[ ту точку М окружности, радиус-
вектор которой составляет с положительным направлением оси
абсцисс угол х (рис. 32). Ясно, что это отображение непрерывно и
взаимно однозначно. Однако обратное отображение терпит разрыв
в той точке окружности УИ0, которая соответствует точке х = 0.
584. Согласно задаче 575, множество Е± компактно. Обозна-
Обозначим через ф функцию, обратную для функции /. Докажем, что
функция ф непрерывна в каждой точке
у0 (: £\ относительно множества El9
т. е. что для всякой окрестности
V (х§, е) точки х0 = ф (у0) найдется такая
окрестность V (у0, б) точки у0, что для
всех точек у £ V (у0, б) П Ег имеет мес-
место ф (у) 6 V (х0, е).
Для этого заметим, что множество
Е\ V (х0, г) замкнуто, а потому ком-
компактно (см. задачу 305); следовательно,
его непрерывный образ F =/ (E\V(x0, e))
является" компактным (см. задачу Рис. 32
207

575ft а потому замкнутым (см. задачу 303) подмножеством множе-
множества^. При этом (в силу взаимной однозначности отображения /)
у0 € F. Следовательно, точка у0 обладает окрестностью V (у0, 6),
не содержащей ни одной точки из F. Но тогда ф (F(y0, б) f) Et)
не содержит ни одной точки из ср (£), т. е. из Е \ V (х0, е). Значит,
Ф (V (у0, б) П £i) d V (*0, е), т. е. для всех у € V (у0, б) П £i
имеет место ф (у) € V (#0, е). Так как у0 — произвольная точка из
El9 то ф непрерывна на множестве Ev
585. Допустим, что Ег имеет изолированную точку, например
точку у0; пусть х0 ё Е — прообраз точки у0. Обозначим через
V (Уо» е) ту окрестность точки у0, которая не содержит других
точек из Ег. В силу непрерывности отображения /, найдется ок-
окрестность V (х0, б) такая, что f (V (xQ1 б) fl Е) а V (у0, е). Но
тогда, в силу взаимной однозначности отображения /, множество
У (*o» б) П £" состоит только из одной точки л:0; поэтому х0 являет-
является изолированной точкой множества Е, Но это противоречит ус-
условию задачи.
Итак, допущение, что Ех имеет хотя бы одну изолированную
точку, приводит нас к противоречию; значит, множество Ех не
может иметь изолированных точек.
Это утверждение теряет силу, если отображение / не взаимно
однозначно. Так, например, функция, определенная на отрезке
Е = [0, 1] равенством / (х) =3 для всех х 6 Я, непрерывна на Е;
при этом множество Е не имеет изолированных точек, а Ех содер-
содержит изолированную точку у == 3 (оно само состоит из одной толь-
только этой точки).
586. Неверно. Пример. Отображение множества Е всех
натуральных чисел оси Ох на множество Ех всзх рациональных
чисел оси Оу (см. например, пункт а), приведенный в решении за-
задачи 583); это отображение к тому же и взаимно однозначно.
587. В этом случае обратное отображение множества Ех на Е
также непрерывно и взаимнр однозначно (см. задачу 584). Так
как Ег не имеет изолированных точек, то, согласно результату
задачи 585, их не имеет и Е.
588. Это следует из задач 575 и 579.
589. Это вытекает из задачи 585.
590. Пример, показывающий, что полнота пространства не
является топологическим свойством: непрерывная функция е
отображает всю числовую ось Z?1 взаимно однозначно на промежу-
промежуток ]0, +оо[ и имеет непрерывную обратную функцию In у; однако
метрическое пространство R1 полно (см. введение к главе IV), тогда
как промежуток ]0, +оо[ (рассматриваемый как подпространство
пространства /J1, т. е. снабженный обычной метрикой) не является
полным, так как фундаментальная последовательность |— | в нем
не сходится.
591. Пусть т — некоторое топологическое свойство. Если мно-
множество Е не обладает свойством т и / — гомеоморфизм Е на Е19
208
X

то Ег также не обладает свойством т. Действительно, из определе-
определений гомеоморфизма видно, что отображение, обратное гомеоморф-
ному, тоже будет гомеоморфным. Следовательно, отображение,
обратное /, является гомеоморфизмом Ег на Е. Поэтому, если бы
Ех обладало свойством т, то и Е обладало бы этим свойством.
592. Предположим, что существует взаимно однозначное непре-
непрерывное отображение / отрезка [0, 1] на замкнутый квадрат Ег =
= [О, I] X [0, 1]. Тогда обратное отображение ф также непрерыв-
непрерывно (см. задачи 330 и 584). Пусть Мо € Ег — образ точки — € [0,1]
при отображении /:
()
Множество Ег \ {Мо} связно, так как любые две его точки можно
соединить ломаной, лежащей в Е19 а лом&ная является связным
множеством (см. задачи 387 и 389). Но тогда множество ф (Ег \
\ {Мо}) = [0, 1] \ |—| должно быть связным (см. задачу 579),
а оно несвязно. Полученное противоречие показывает, что не су-
существует непрерывного взаимно однозначного отображения отрез-
отрезка на квадрат.
593. Без ограничения общности можцо считать, что а =
= @, 0, ..., 0,1). Гомеоморфное отображение множества Sm \ {а}
на пространство Rm осуществляется с помощью равенства
Ь= 7-^—0=1, .-, т).
594. а) Если t0 не двоично рациональна, или если /0 есть 0
или 1, то это очевидно. Если же t0 — двоично рациональная точка
отрезка [0, 1], отличная от 0 и 1, то ей соответствуют две различные
последовательности отрезков, содержащих эту точку: бх id б2 ^э ...
и б! id 62 id ...; им отвечают две различные последовательности
вложещшх квадратов: Vt id У2 id ... и V[ id V2 => ... Однако, на-
начиная с того номера, когда эти последовательности становятся
различными, Ьп и б„ будут соседними отрезками; а тогда, согласно
построению, квадраты Vn и Vn имеют общую сторону и, стало
быть, вместе образуют Прямоугольник Vn [) V'n = Wn. Очевидно,
Wn zd Wn+1 (начиная с того номера я, для которого Ьп Ф Ь'п )
и diam Wn = J^£ -> 0, а потому [\Wn состоит из одной точки,
т. е. [\Vn = [\v'n = {(\Wn).
п п п
б) Каждая точка квадрата [0, 1] X [0, 1] входит в некоторый
квадрат первого ранга Уь в некоторый квадрат второго ранга V2
(содержащийся в 1^), в некоторый квадрат третьего ранга V3 (со-
(содержащийся в V2) и т. д. и является единственной точкой пересе-
пересечения этой убывающей последовательности квадратов. В силу
построения, эта последовательность соответствует убывающей по-
209

следовательности отрезков бх zd 62 :Эб3 => ..., единственная точка
пересечения которых имеет своим образом взятую точку квадрата.
в) Пусть t0 £ [0, 1] и {tk} — произвольная последователь-
последовательность точек отрезка [0, 1], сходящаяся к t0. Если t0 не двоично ра-
рациональна или если t0 равна 0 или 1, то для всякого содержащего
эту точку отрезка 8п (произвольного ранга) найдется такой номер
N, что при k > N все tk попадут в бл; а значит, / (tk) б Vny f (t0) 6
6 Vn, где Vn — квадрат n-го ранга, отвечающий 6Л. Если же t0 —
двоично рациональна и отлична от 0 и 1, то t0 (при достаточно
большом п) будет попадать не внутрь, а на границу отрезка Ьп и
соседнего с ним отрезка 6^; но тогда найдется такой номер N, что
при k > N все tk попадут в Ьп [} 6^, а значит, каждое / (tk) по-
попадет либо в Vn, либо в Vn> тогда как / (/0) € V*n Г) Уп (см. пункт
а)). Таким образом, в обоих случаях при k > N будем иметь:
Р (/ ('*)• / {t0)) < diam vn> так «ак diam Vn = ^f ->• 0 при n ->
-> +оо, то отсюда следует, что limf(tk) =f (t0). Это и доказы-
вает непрерывность построенного в задаче отображения /.
г) То, что отображение / не является взаимно однозначным,
следует из задачи 592. В этом же можно убедиться и непосредст-
венйо. Действительно, прообраз всякой точки УИ0, лежащей на
общей стороне двух квадратов некоторого ранга, занумерованных
несоседними номерами, содержит по крайней мере две различные
точки (эти точки лежат в двух несоседних отрезках, которые отве-
отвечают взятым квадратам); если точка Мо лежит в общей вершине
четырех квадратоб некоторого ранга, то ее прообраз состоит даже
из трех различных точек.
595. Если проектирование проводится под углом а к оси Ох, то для
любых двух точек Мг и М2 множества Е имеет место соотношение
^ sin a
где Рг и Р2—проекции точек Мг и М2 на ось Ох (рис. 33). Отсюда сле-
следует, что проектирование является не только непрерывным, но даже
равномерно непрерывным отображением множества Е на ось Ох,
596. Да, проекция плоского открыто-
открытого множества всегда открыта на прямой.
597. Если Е'— ограниченное замкну-
замкнутое множество на плоскости, то его про-
проекция на ось всегда ограничена и замкнута
(см. задачи 330, 595, 575 и 303). Если же £ —
неограниченное замкнутое множество на
плоскости, то его проекция может оказа-
оказаться и незамкнутым множеством; так,
например, график функции tg x является
замкнутым множеством на плоскости, а
его ортогональная проекция на ось абс-
Рис. 33 цисс не замкнута.
210

M0(x0)
.Ч\
598. Допустим, что проекции некоторо-
некоторого плоского множества^ на обе оси явля-
являются счетными множествами. Проведем
через каждую точку множества Е прямые,,
перпендикулярные первой оси, и прямые,
перпендикулярные второй оси; таких пря-
прямых окажется лишь счетное множест- ° y°eF x°eE zoeE*F x
во; следовательно, и точек пересечения
перпендикуляров на первую ось с пер- Рис- 34
пендикулярами на вторую ось будет
лишь счетное множество. Но Е содержится в этом множестве точек
пересечения; значит, и Е — счетное множество, что противоречит
условию.
599. Непосредственно проверяется что каждая точка z0 той
косоугольной проекции, о которой идет речь в условии задачи,
изображает сумму двух чисел: х0 ё Е и уа ё F, и, обратно, любая
сумма указанного вида изображается некоторой точкой z0 из этой
косоугольной проекции (рис. 34).
600. Если Е и F ограничены и замкнуты, то множество Е X F
очевидно, тоже ограничено и, согласно задаче 196, замкнуто. Чтобы
получить £0F, надо (см. предыдущую задачу) спроектировать
Е х F на ось Ох под углом 135°; следовательно, множество Е © F
тоже ограничено и замкнуто (см. решение задачи 597).
601. Арифметическая сумма D@D двух касторовых совер-
совершенных множеств совпадает с отрезком [0, 2]. Докажем это.
Произведение D X Z> совпадает с «кладбищем Серпинского»
(см. задачу 245). Проведем через произвольную точку z0 отрезка
[0, 2] оси Ох прямую, наклоненную к оси абсцисс под углом 135°,
Ясно, что эта прямая пересечет по крайней мере один из квадратов
первого ранга (рис. 35); обозначим этот квадрат через Сг. Далее,
та же прямая пересечет по меньшей мере один квадрат второго
ранга из числа квадратов, входящих в Сг\ обозначим его С2. В нем
найдется квадрат третьего ранга С3, с которым эта прямая пересе-
пересечется по непустому множеству, и т. д.
Обозначим общую часть прямой и квадрата Ck через uk\ мно-
множества uk замкнуты, ограничены, и каждое последующее вложено
в предыдущее: ал+1 <= uk. Но тогда f| ик непусто; оно состоит из
к
одной.точки, так как diam ик -> 0. Эта точка принадлежит множе-
множеству D X D, и ее косоугольная проекция совпадает с точкой zb,
а потому, в силу результата задачи 599, z0 $ D © D.
Итак, каждая точка z0 £ [0, 2] принадлежит арифметической
сумме D(BD. С другой стороны, непосредственно ясно, что ни
одна точка, лежащая вне Отрезка [0, 2], не может принадлежать
этой арифметической сумме. Следовательно, D © D ^= [0, 2].
602. Пусть с — произвольная точка множества А Ф В\ тогда
с = а + Ь, где а 6 Л, Ь € В. Так как А открыто, то существует
окрестность У (а), целиком входящая в А. Но тогда множество
всех точек вида х + Ь, где х (: V (а), образует окрестность точки
211

\
\
hi
Рис. 35
с = a + b\ это множество входит в А © В* Следовательно, для
любой точки с £ А Ф В существует ее окрестность, входящая в
А® В. Значит, множество А® В открыто.
603. Пусть sup Ег = a, sup Е2 = 6; тогда если z £ Ег® £2,
то г = х + У, где х € £"г, у 6 £2; следовательно, г =д: + У<^ +
+ Ь. С другой стороны, для всякого е > 0 найдутся такие х € Elf
у € £2, что а; > а — ~, у > 6 — ~, а тогда * + у € £х © £ и
х-+у >а + Ь — е. Это доказывает первое равенство;, второе
равенство доказывается аналогично.
604, На основании результата задачи 599 множество Е (В F
можно получить, проектируя множество Е X F па ось Ох с углом
проектирования, равным 135°. Но если множества Е и F связны,
то и множество Е х F тоже связно (см. задачу 399); а так как
проектирование является непрерывным отображением (см. задачу
595), то оно переводит связное множество в связное (см. задачу
579).

605, Отрезок [0, 1]. Доказательство проводится так же, как
в задаче 601.
606, Доказательство аналогично тому, которое проводилось
при решении задачи 602.
607, Теорема Лагранжа дает для любых x',#" € Л1:
(для некоторого с между х' и я"), откуда
Так как /С < 1, то выполняются условия теоремы Банаха (теоре-
(теорема 5 введения к настоящей главе), из которой и следует утвержде-
утверждение задачи.
608, Указание. В силу теоремы Дарбу (см. ниже, теорему
3 введения к главе XI), /' (я) не меняет знака; следовательно,
/ (х) строго монотонна. Далее, в силу теоремы Лагранжа, |/ (х) —
— / @)| = |/' (с)\ • \х\ > К • |*| > \х\, откуда следует, что функ-
функция / (я) принимает значения на всей числовой оси (так как она
монотонна и не ограничена ни снизу, ни сверху). Следовательно,
для функции / (я) существует обратная функция <р (у), определен-
определенная на всей числовой оси и такая, что |q/ (у)| = , <^ — <1.
I /'(*)' К
После этого пишется уравнение <р (у) = у, эквивалентное данному,
и к нему применяется теорема Банаха.
оо
609. Пусть х(хг х2> ...)€/2, т. е. ряд 2 х\ сходится. Пока-
жем, что тогда z(zlt z2, ...)€/2, гДе 2/ = 2 cikxk. Действительно,
применение неравенства Коши—Буняковского (см. введение к гла-
главе IV) дает
\k=l
оо
а значит, ряд 2 ^Л сходится (даже абсолютно) и
/ оо \2 оо оо
г\ = B cikxk < 2 с*ь - 2 х\. Следовательно,
2
т. е. г 6 /2-
Рассмотрим теперь точку у (ух, у2, ...), где yt. = ^ + Ьг Так
как z (zl9 z& ...) € /2 и Ь Flf &2, ...) € /2, то и у € /2 (см. решение
задачи 131).
Таким образом, отображение, переводящее точки х (xlf хъ ...)
в точки у (ух, у2> •••)» есть отображение пространства /2 в себя.
213

Покажем, что это отображение сжимающее. Пусть х' {х\, х2>...) €/2
и х" (х[, xv ..w) € /2, а у' (у;, y'v ...), у" (у';, у'2, ...) — точки, полу-
получаемые в результате нашего отображения, т. е.
оо оо
у\ = 2 cikxk + bit y[ = 2 cikXk + bt.
Имеем:
/оо I оо / оо
2 Ы — у'J = V 2 2 %(^ —^
t=l Г 1=1 \/е=1
оо
Если положить xk —x"k = л:Л, 2 ^а^а = гь то выражение,
fe=i
оо
стоящее под корнем в правой части, есть 2 2Ь Выше мы показа-
оо оо
ли, что 2z?< 22 с% -2 х\. но 2^2 = 2(^-^J =
1=1 \г=1 Лг=1 / fe=l fe=l fe=l
= р(д:', л:"). Поэтому последнее неравенство дает:
оо
р(у'. Ж 2 сЪ-Р(х', х").
i, *=1
оо
Так как по условию 2 £#< 1» то это означает, что наше ото-
i, k=l
бражение сжимающее, а тогда, по теореме Банаха, для него суще-
существует одна и только одна неподвижная точка. Но это равносильно
утверждению задачи.
610. Нет, так как область определения отображения есть
Е = [1, +оо[, а значения / (х) выходят за пределы Е.
61К Пространство Е> в котором определена функция / (х),
является неполным (ось Ох за вычетом точки О); следовательно,
к данному случаю теорема Банаха неприменима.
Глава XL
ЧИСЛОВЫЕ ФУНКЦИИ ОДНОЙ
ПЕРЕМЕННОЙ (МОНОТОННОСТЬ,
ОГРАНИЧЕННАЯ ВАРИАЦИЯ)
612.
0 при х = Ос
Здесь
~!х • sin cos — при
X2 X Хг
О при х = 0.
214

613. Пусть Е а [О, 1] — заданное непустое нигде не плотное
замкнутое множество, ]ал, РЛ[— его смежные интервалы, содер-
содержащиеся в [0, 1] (п = 1, 2, 3 ...), ро = inf £, а0 = sup E.
Искомую функцию определим условиями:
( (х — апJФп — *Jsin- -L при *£]<*„, ря[,
'v ' | 0 при л: € F,
I 0 при х < ро и при л: > а0.
Функция / (х) определена на всей числовой оси и имеет производ-
производную ъо всех точках числовой оси, в частности во всех точках от-
отрезка [0, 1], а именно:
V
О при x£E,
О при x < po и при я > a0.
Производная /' (л:) непрерывна всюду вне множества Е и разрывна
во всех точках этого множества.
614. Построим на отрезке [0, 1] нигде не плотное совершенное
множество положительной меры (см. задачу 410). Пусть ]ал, рл[
(п = 1, 2, 3, ...) —смежные интервалы этого множества. Тогда
функция, построенная в предыдущей задаче, будет удовлетворять
всем предъявляемым требованиям.
615. Нет. Точная производная /' (л:) должна обладать свойством
Дарбу, т. е. принимать все промежуточные значения. Этим свой-
свойством не обладает функция Дирихле.
616. Нет^ так как точная производная может иметь точки раз-
разрыва только второго рода, тогда как разрывная монотонная функ-
функция имеет точки разрыва только первого рода.
617. Нет. Пример. Функция / (х) = \х\ имеет во всех точ-
точках как правую, так и левую производную; однако ни та, ни дру-
другая не обладают свойством Дарбу. Например:
t' /v\ _ Г —1 при х <0,
fre»(*)-( ! при х^0
оо
618. Например, функция fix)—^ '*"""**', где х19 х2, ...,%,...—
k=l 2й
все возможные точки множества £, занумерованные натуральными
числами. Эта функция непрерывна, как сумма ряда непрерывных
функций, равномерно сходящегося на любом отрезке. Найдем про-
производную от / (х) при х\Е.

Имеем:
— xk\ _ \x — xk\\
)
ft U\ \ 2k
1"— xk I — I x —k xk I
' 2d
2kh ' 2d 2% э ()
где сумма 2' распространена на те значения k> для которых
\х — xk\ > |Л|, а сумма 2" — на остальные значения k. В первой
из этих сумм х + h — xk и х — xk имеют одинаковый знак; по-
поэтому в этой сумме l* + *-**l-l*-**Lea <°(^Ч
Если л: £ £, то при достаточно малом \h\ вторая из этих сумм ста-
становится сколь угодно малой по модулю, а первая — сколь угодно
оо
близкой к сумме ряда V S *^~ "» в самом Деле» для вся-
2
кого натурального числа Af можно найти такое б > 0, чтобы в
окрестность ~]х — б, х + б[ не попали те xki для которых k t^ N;
тогда при |Я| < б
2*A
|
2*
Поэтому, переходя в равенстве A) к пределу при h -> 0, полу-
получим, что при х £ £
л=1 _
Итак, /' (л:) существует во всех точках х ^ Е. Убедимся теперь
в том, что ни в одной точке множества Е производная f'(x) не су-
существует.
Пусть хк — какая-либо точка множества Е. Представим / (х)
в виде суммы двух функций:
il
2*0 Й0
Тем же способом, которым мы доказывали существование произ-
производной у функции / (л:) в точках х 6 £, проверяется, что функция
X~Zbk им^ет производную в точке хк; функция же '*"""
2 °
не имеет производной в этой точке. Следовательно, сумма этих
функций, т. е. функция / (л:), не имеет производной в точке xk.
216

619, Да, функция / (ф (/)) монотонна на отрезке [а, &]; при
этом, если / — возрастающая функция, то и суперпозиция / (ф (/))
возрастает, а если / — убывающая функция, то и суперпозиция
убывает.
620. Нет. Пример. Пусть ф (t) определена на отрезке [0, 2]
равенствами:
(t при t € [0, 1[,
и ^2
Эта функция разрывна при / = 1 и для нее ф @) = 0, ф B) = 3.
Определим теперь на отрезке [0, 3] оси Ох монотонно возрастаю-
возрастающую функцию
(х при х (: [0, 1],
/(*)= 1при* 6]1,2[,
Ух — 1 при X €[2, 3].
Легко видеть, что суперпозиция / (<р (t)) тождественно равна /
при 0 ^ t ^ 2; следовательно, она непрерывна всюду, и в частно-
частности в точке / = 1.
Заметим, однако, что если функция / {х) строго монотонна,
а функция ф (t) разрывна в точке tQ, то суперпозиция / (<р (/)) обя-
обязательно терпит разрыв в точке tQt
621. Для определенности будем считать, что f (х) строго воз-
возрастает на [а, 6]. Возьмем произвольное положительное е, не пре-
превосходящее Ь — а. В силу строгого возрастания функции, имеем:
f (Ъ — е) </(&). Найдем такое N, что для всех п > N имеет ме-
место: f (хп) > / (Ь — е); это можно сделать, так как lim / (хп) =
/г-»-оо
= / (Ь). В силу строгого возрастания функции, из / (хп) > f (b — e)
вытекает, что хп > Ь — е; следовательно, для всех п > N имеем:
Ь — е < хп ^ Ь, откуда \хп — Ь\ < е. Но это и означает, в силу
произвольности числа е > 0, что lim хп — Ь.
П-*-оо
622. Функции т (х) у. М (х) определены на всем отрезке [а, Ь]
(если считать, что отрезок [а, х\ при х —а есть одноточечное
множество {а}). Какова бы ни была функция / (х), функция М (х) =
= sup / (г) возрастает на отрезке [а, &], так как если h > 0,
z-:[a, x]
то [а, х] а [а, х + ft], и, следовательно, sup / B) ^ sup / (г).
г[а, х+Щ z£[a, *]
Если функция / (х) непрерывна, то М (х) также непрерывна.
Для того чтобы доказать это, покажем сначала, что для любых
чисел с, d 6 [а, &], с < d имеет место неравенство
sup /(г)< sup /(г) + со/ . A)
z; [a, d] 2c [а, с] [с, d]
Действительно, sup f(z) равен наибольшему из чисел sup f(z) и
z£ [о, d] z£ [а, с]
sup f(z). Если наибольшим является sup /(z)> то
гс'[с, d] г^[а, с]
syp /(г)= sup /(г)< sup /(г)+ ю/.
2£ [a, d] zi [а, с] zi [а, с} [с, d]
217

так как оз/ !^0. Если же наибольшим является sup /(г), то
{с, d\ г е {с, d]
sup f(z)= sup /(г) + ( sup /(г)— sup /B));
г£ [а, tf] ге [a, c] ze[c, tf] гб[а, с]
но sup f{z)^f(c)> inf /(г); поэтому
zi [a, c] z£ [c, d]
sup /(z)< sup f(z)+( sup /(г)- inf /(z)) =
z£ [a, d] z£ [a, c] z£ [c, d] z£ {c, tf\
= sup f(z) + со/ .
26 [a, с] [с, d]
Таким образом, неравенство A) доказано. Из него, в частности,
следует, что при х ё [а, Ь] и при 0 <h ^Ь — х
sup /(г)< sup /B)+ оз /.
г£ [а, *+А] г£ [а, х] [к, k+h]
Отсюда, принимая во внимание, что М (х) — возрастающая функ-
функция, получаем:
О < М (х+ К) — М (х) < оз /.
[х, x+h]
При h -> 0 правая часть неравенства стремится к нулю, так как
/ (г) непрерывна; но тогда и М (х + К) -> М (х); значит, М (х)
непрерывна справа в точке х.
Для того чтобы доказать непрерывность М (х) в точке х с л е-
в а, применим неравенство A) к точкам x~—hf x отрезка [a, b]
(h > 0):
sup /(z)< sup f(z)+ со f,
z£ [a, x] zi [a, x-h] [x-h, x]
откуда
[x—h, x]
Следовательно, M (x — h) -> M (x) при /i -> 0; значит, М (х) не-
непрерывна и с л е в а в точке х.
Итак, если функция / (х) непрерывна всюду на [а, 6], то и М (х)
непрерывна всюду на [а, Ь~].
Аналогично доказываются монотонность и непрерывность функ-
функции т (х).
623. Если / (х) — возрастающая функция на [а, &], то
sup / (z) = / (я), т. е. М (х) = f (х) для всех х £ [а, &].
Для функции М (х) = sup / (z) аналогичное равенство не
всегда имеет место. Пример. Пусть / (л;) =/ J J J ^^ 2
Эта функция возрастает (и даже строго возрастает) на отрезке [0,2].
Для нее М (х) = f x f^€]°i];1ol
^ v ' \х + 1 для л; 6 ]1,2].
Как мы видим, f (х) =^= М (х) в точке х = 1.
218

Обобщая этот пример, можно построить такую монотонную
функцию / (х), для которой равенство f (х) =М (х) не выполняется
на счетном множестве точек.
624. Пусть, для определенности, / (х) возрастает на отрезке
[а, ft]. Тогда inf f(x)=f(a)y sup / (х) = f (b). Допустим,
x [a, b] x^[a, b]
что эта функция разрывна в точке с, где а ^ с ^ Ь\ тогда по край-
крайней мере на одном из интервалов ]/ (с — 0), / (с)[, ]/ (с), f (с + 0)[
оси Оу нет значений функции. Но это значит, что функция f (х)
принимает в качестве своих значений не все числа отрезка
Следовательно, если функция возрастает на [а, ft] и принимает
на этом отрезке в качестве своих значений все числа из
[/ (я). / (&)]. то она непрерывна на [а, ft]. Случай убывшощей
функции аналогичен.
625. Можно; достаточно положить
/ (х) при х € Е,
sup / (£) при х € [а, ft] \ £, х > х0,
inf / (£) при х € [а, ft] \£, * < *0%
где х0 = inf E.
Ясно, что ф (я) — монотонно возрастающая функция, опреде-
определенная всюду на [а, ft] и совпадающая с / (х) на множестве Е.
626. Нельзя. Если, например, / (я) не ограничена сверху, то
она не определена в точке b (иначе было бы / (х) ^J (b) всюду на Е.
Но тогда и доопределить ее в точке b с сохранением монотонности
нельзя. Если же / (я) не ограничена снизу, то ее нельзя доопреде-
доопределить с сохранением монотонности в точке а.
627. Достаточностъ очевидна: если f (x) строго моно-
тоцна, то она взаимно однозначно отображает свою
область определения [а, &] на свою область значений Ег = f ([a, 6]);
а это есть необходимое и достаточное условие существования об-
обратной функции, отображающей Ег на [a, ft] и ставящей в соответ-
соответствие каждой точке у 6 Ег ту единственную точку х (: [а, 6], для
которбй f (х) = у.
Необходимость. Пусть функция / (х) непрерывна на
[a, ft] и имеет обратную функцию, т. е. взаимно однозначно отобра-
отображает [a, ft] на Z?! = / ([a, ft]). Тогда / (а) Ф f (ft), так как равенство
f (а) = / (ft) противоречит взаимной однозначности этого отобра-
отображения. Положим для определенности, что / (а) < f (ft). Тогда в
точке а функция достигает наименьшего значения на [a, ft]. Дейст-
Действительно, если бы в некоторой точке #0 € ]а, ft[ было / (#0) < / (а),
то, в силу теоремы о промежуточных значениях непрерывной
функции, между точками х0 и ft нашлась бы точка £ такая, что
/(£)=/ (а) (так как / (*0) <f(a)<f (ft), см. рис. 36); но это про-
противоречит тому, что / (я) взаимно однозначно отображает отрезок
[а, 6] на множество Ег.
219

6 X
1
Рис. 36
а 71 х1 хг b x
Рис. 37
Докажем теперь, что функция / (л:) строго возрастает на [а, &].
Допустим, что это не так; тогда найдется хотя бы одна пара точек
xlf х2 (: [а, &], хх < х2 такая, что / (xj ^ / (х2). Равенство здесь
исключено из-за взаимной однозначности отображения /; зна-
значит, / (х^ >f(x2). Но тогда на участке [а, хг2 найдется точка г\
такая, что f (ц) =f (х2) (так как f (a) < f (х2) < f (л^)) (см. рис. 37).
А это также противоречит взаимной однозначности отображения f.
Значит, для любых точек хг < х2, лежащих на отрезке [а, &], имеет
место неравенство / (хг) <f(x2), т. е. функция / (х) строго воз-
возрастает на [а, Ь].
628. Если обе функции возрастают или обе убывают, то их
сумма монотонна. Однако если одна из этих функций возрастает,
а другая убывает, то сумма может оказаться немонотонной. На-
Например, обе функции ф (х) = х, ty (х) = —х2 монотонны на [0, 1],
однако их сумма f (х) = х + (—х2) не монотонна на [0, 1}.
Произведение двух неотрицательных возрастающих
функций монотонно. В общем случае это це так. Например, обе
функции ф (х) — xf ty (х) == х — 1 возрастают на [0, 1], однако
их произведение f (х) = х (х — 1) не монотонно на этом отрезке.
629. Сначала докажем, что для любого натурального п множе-
множество Еп тех точек, где колебание функции больше или равно —,
п
не более чем счетно. Для этого опишем около каждой точки #(:]а, Ь{_
окрестность ~\х — б, х + б[ (б зависит от х) такую, что колеба-
колебание функции на ус—б, х[_ и на ]*, лг+ б[ м е н ь ш е чем —. Далее,
п
из покрытия интервала ]а, Ь[_ интервалами ~\х — б, х + б[ выбе-
выберем не более чем счетное покрытие усг — 619 хг + бх[, ..., "]xs—б5,
xs + $Л> ••• (см- задачи 345, 355 и 356). Ясно, что ни в одной точ-
точке | интервала ]а, Ь[, отличной от точек xlf ..., xs1 ..., колебание
не может превзойти числа —, так как любая такая точка % являет-
п
ся внутренней либо для некоторого интервала ~]xt — 6^, х^ либо
для некоторого интервала ]дгр xi + 6£. Следовательно, Еп а
220

с: {xlt ..., xsf ...}, и, значит, Еп не более чем счетно. Но тогда и
множество всех точек разрыва Е = [} Еп не более чем счетно.
п
630. Пусть rl9r2frB9...—все рациональные точки числовой
прямой К}1, занумерованные каким-либо способом; построим функ-
функцию / (х) следующим образом: для любого х € R1 положим
n*r= 2 i
где суммирование производится по всем номерам k таким, что-
rk < х. Эта функция определена для всех х, так как ряд ^ —
rk<x2
всегда сходится; она строго возрастает, так как для любых чисел
хг < х2 найдется рациональное число rk такое, что хг < rk < х21
откуда / (х2) ^ / (хг) + -^о > / (xj). Эта функция разрывна в каж-
каждой рациональной точке гп; действительно, для любого х > гп
2 + S
переходя в этом неравенстве к пределу при х-+гп-\- 0, получим:
f (гп+ 0) ^ f (rn) + —п. Значит, в каждой точке гп функция / (х)
разрывна справа и ее правый скачок / (гп + 0)—/ (гп) больше
или равен —.
2п
Докажем, что функция / (я) не имеет разрывов в других точках
и что в рациональных точках гп скачки равны в точности —п.
Это вытекает иэ следующих соображений: для монотонно
возрастающей функции разность между ее верхней и ее
нижней гранью больше или равна сумме s всех скачков; но
sup / (х) = 5 -г = 1, inf f (x) =0; следовательно, s< 1. С
х$ц* ** 2й XZR*
k
другой стороны, сумма всех скачков больше или равна сумме пра-
правых скачков в точках тп; поэтому s ^ ^— = L Сравнивая это с
п
полученным выше неравенством, находим, что s = 1. Следователь-
Следовательно, правые скачки в точках гп исчерпывают все возможные скачки
функций (т. е. в остальных точках функция непрерывна); при этом
в самих точках гп скачки равны в точности — (в противном елу-
чае было бы s > 1).
221

631. Эта задача является обобщением предыдущей; построение
такой функции проводится так же, как в предыдущей задаче.
632. Возрастание функции т (х) на отрезке [0, 1] вытекает из
самого построения функции. Чтобы доказать, что т (х) непрерывна
на [0, 1], достаточно заметить, что если бы она была разрывна в
какой-то точке х0 ё [0, 1], то (в силу монотонности функции) хотя
бы один из интервалов ]т (х0 — 0), т (*0)[, ]т (x0), т (х0 + 0)[ не
содержал бы ни одного значения функции. Однако это невозмож-
невозможно, так как значениями функции являются, в частности, все двоич-
двоично рациональные числа отрезка [0, 1], а они расположены всюду
плотно на этом отрезке.
633. Может. В качестве примера такой функции можно взять
функцию Кантора т (х), построенную в предыдущей задаче. Она
монотонна и непрерывна всюду на отрезке [0, 1] и отлична от по-
постоянной; вместе с тем ее производная х'(х) существует всюду на
CD и во всех точках множества CD она равна нулю. Следователь-
Следовательно, т' (х) = 0 почти всюду на [0, 1] (так как т CD =1).
634. Пусть f (x) возрастает на ]а, Ь[, непрерывна и ограничена
на этом интервале. Доопределим ее на концах интервала, положив
f (а) = / (а + 0), f (Ь) = / (Ь — 0) (пределы функции f (x) при
х -»- а + 0 и при х -»- Ъ — 0 существуют, так как эта функция
монотонна и ограничена на ]а, Ь[). Теперь функция определена и
непрерывна на всем отрезке [а, Ь\ в том числе также в точках а
и Ь. Но тогда она равномерно непрерывна на [а, Ъ~\ (см. задачу 540),
а значит, и на любом подмножестве отрезка [а, Ь], 6 частности на
интервале ]а, &[. В случае, когда / (х) убывает на ]а, &[, доказа-
доказательство аналогично.
635. Справедливо. Если функция / (х) ограничена и монотонна
на ]—оо, +оо[, то она имеет конечные пределы lim / (х) и lim / (х).
Но тогда равномерная непрерывность функции на всей прямой
]—оо, +оо[ доказывается тем же методом, которым мы решали
задачу 545.
636. Разделим отрезок [0, 1] точками
0 =х0 < хх < ...,< хп_г < хп = 1
так, чтобы на каждом отрезке [_хкт.ъ xk~\ колебание функции / (х)
было меньше чем —. Далее, на каждом отрезке [_хк_ъ xk~\ опре-
определим функцию ф (х) так, чтобы выполнялись условия:
Ф (х) монотонна и непрерывна на [_хк_ъ хк~], ф' (х) = 0 почти всюду
на [*ft_lf xkl
Функцию, удовлетворяющую этим условиям, можно построить
так же, как строилась функция Кантора в задаче 632.
Построенная таким способом функция ф (х) определена и не-
непрерывна на всем отрезке [0, 1] и удовлетворяет условиям а) и б).
222

Нетрудно также проверить, что для любого х € [0, 1] она удовлет-
удовлетворяет неравенству |/ (х) — ф (х)| < е.
637. Построим непрерывную функцию ф (х), равную нулю
на множестве Е и положительную вйе его (например, ф (х) =
х
= d(x,E), см. задачу 519). Далее обозначим / (х) = |ф (t) dt.
а
Тогда /' (х) = ф (х) для всех х € [а, &]; в частности, /' (х) = О
для всех х £ Е. Кроме того, / (х) является строго возрастающей
функцией; для проверки этого возьмем две точки хг и х2 (а <; хх <
< х2 ^ Ь) и найдем между этими точками отрезок [а, р], свободный
от точек множества Е. Тогда
= Ф (с)ф-а),
хх а
где с£ [а, р]; так как с £ £, то ф (с) > 0; следовательно, / (х2) >
638. Нет. Пусть ]а, р[ — интервал, целиком содержащийся
& Е (если £ замкнуто и не является нигде не плотным, то такой
интервал наверняка найдется. Если для некоторой функции / (х)
ее производная равна нулю всюду на Е, то, в частности, /' (х) = 0
всюду на интервале ]а, р[, и, значит, на этом интервале функция
/ (х) постоянна. Следовательно, она не может быть строго моно-
монотонной на [a, ft].
639. Сначала докажем, что / @) = 0; действительно, / @ + 0) =
= / @)+ f @) = 2/ @), т. е./ @) ^ / @), откуда / @) = 0.
Далее, для любого целого k >0 имеет место f(kx) = k -f(x)\
поэтому /A) =f[k -\)-k • /(-i), откуда ffy = f-R = ±t где
a = f(\). Наконец, /Ш =р ./Ш = p . ^ = a . £, т. е. f(x) =
\q I \q I q q
= ax для любого рационального л;>0.
Пусть теперь х — положительное иррациональное число; по-
построим возрастающую последовательность рациональных чисел
Т\ <г2 <г3 < ..., сходящуюся к л:, и убывающую последова-
последовательность рациональных чисел г[ > г'2 > т'ъ > ..., также сходя-
сходящуюся к х. Тогда, в силу монотонности / (я), / (rk) ^ f (х) ^ / (г* )
для любого k, т. е. ark ^ / (х) ^ ar'k. Устремляя теперь k к беско-
бесконечности, получим: ах ^ / (х) ^ ах, откуда f(x)=ax. Значит,
/ (я) = ах при любых положительных х (как рациональных, так
и иррациональных).
Наконец, если х < 0, то f (х) + f (—х) = / @), т. е. / (*) =
= / @) — / (—х) = —/ (—х)\ но в этом случае — х > 0; поэтому
/ (—х) = а • (—л:). Следовательно,
/ (х) = -f (-х) = -а (-х) = ах.
Итак, / (я) = ах для всех я.
640. Вариация этой функции равна \ k\ • А.
223

641. Вариация функции равна 7. В этом убеждаемся следую-
следующим образом: разобьем отрезок [0, 1] точками 0 =х0 <хг < ...
... <xn-i <хп = 1- Тогда
2
При этом 2 I / (хд — / (#i-i) I может быть сделана сколько
п
угодно близкой к числу 7. Поэтому sup 2 I / (хд — / {Х;Л | = 7,
т. е. вариация функции / (х) на отрезке [0, 1] равна 7.
642. Вариация функции равна 23.
643. Для этого следует положить / A) = а, где а — какое
угодно число, заключенное между f A — 0) и / A + 0) (т. е.
O^an^l). В этом случае вариация функции на [0, 2] будет равна 5.
644. Эта функция непрерывна и имеет производную во всех
точках отрезка [0, 1]:
2л: • cos [-яsin.— при хФ0,
0 при х = 0.
На участке [0, 1] производная ограничена:
2xcos—
п
2xcos —
я
Jisin —
А непрерывная функция с ограниченной производной является
функцией ограниченной вариации (см. ниже,, задача 648).
645. Пусть k — произвольное натуральное число. Разобьем
[2 I
0, — точками
п\
о< 2 < 2 <...<-3-<-1
я B/е + 1) я B/е — 1) Зя я
на fe + 1 отрезок и составим сумму аЛ модулей приращений функ-
функции на этих отрезках:
2fe + 1) /TUBfe+l) tBfel)j^
, 2 N /4 Wf
я Bfe 3)j ^ '" \5n Зп) ^ \3я
В квадратных скобках стоит k-я частная сумма расходящегося
2 2 2 2
ряда 1 +-Т-Н 1— + ...Н h ...'» ПРИ достаточно большом
3 5 7 2fe + 1
224

k эта сумма делается сколь угодно большой. Следовательно, для
любого А > О можно найти такое число k (и, следовательно, такое
разбиение отрезка 0, — }, что ak > А. Но это означает, что сумма
ok модулей приращений функции может быть сделана сколь угод-
угодно большой, т. е. что функция / (х) имеет неограниченную вариа-
вариацию на отрезке 0, — .
646. Допустим, что F (х) = f (ах + Ь) имеет неограниченную
вариацию на отрезке , —^l. Тогда для любого натурально-
[ а а \
го числа N можно найти такое разбиение отрезка , "Г
I а а \
h 1 h П
точками = £0 < £i < ... < ^ < Ъп = -=^-, что 2 IF СУ —
a a k—\
— F(£ft_iI > N. Разобьем теперь отрезок [0, 1] точками цк = аСл+
+ b (fe = 0, 1, ..., п). Тогда
= 2 IF^-F^-i)^^. A)
Итак, если бы функция F(x) имела неограниченную вариацию
на , -=— I то /(х) также имела бы неограниченную вариа-
[ а а \
цию на [0, 1]. Следовательно, функция F(x) имеет ограниченную
Г ь I — hi
вариацию на , .
L а а \
Переходя теперь к верхним граням в равенстве A), убеждаем-
1—b
СЯ, ЧТО V f =•• V /\
О __6_
а
647. Решение этой задачи аналогично предыдущей.
648. Пусть |/' (#)| ^А всюду на [а, Ь\ тогда при любом раз-
разбиении отрезка [а, Ь] точками
имеем, в силу формулы Лагранжа:
I/ (С*) - / (ЬмI = 1/' (Ч) (Ik ~ tk-J\ <А- К* - C*-il
(здесь тл — некоторая точка, лежащая между ^_х и £л).
Поэтому
225

Итак, при любом разбиении отрезка [а, Ь~\ сумма модулей прира-
приращений не превосходит числа А (Ь — а). Значит, функция f(x) имеет
ограниченную вариацию на [а, &].
649. Если Е имеет лишь конечное число граничных точек, то
ХЕ(х) имеет ограниченную вариацию на [а, &], —это утверждение
тривиально. Если же Е имеет бесконечное множество граничных
точек, то %Е (х) имеет неограниченную вариацию на отрезке
[а, &]. Докажем это. Зададим произвольное натуральное число N
и из множества всех граничных точек, лежащих внутри ]а, &[,
выберем N точек, расположив их в порядке возрастания:
а <хг <х2 < ... <х^< Ь.
Около этих точек построим попарно не пересекающиеся окрестно-
окрестности V (xi)f V (x2), ..., V (xN) и в каждой из этих окрестностей возь-
возьмем по две точки ££ и r]f такие, что ^ ё £, т]г (: £. Тогда
1=1
Итак, вариация функции %Е (х) на отрезке [а, Ь] больше любого
наперед заданного натурального числа Af; следовательно, она рав-
равна бесконечности.
650. Не обязательно. Пример. Пусть
(*+1)-1) на отрезке
о вне этого отрезка.
Ряд S /*W равномерно сходится на отрезке [0, 1]; каждая из функ-
функций fk (x) имеет ограниченную вариацию на этом отрезке, однако
сумма ряда представляет собой функцию неограниченной вариа-
вариации на [0, 1].
651. Пусть \f(x) — f(y)\ < А \х — у\ для всех х € [а, &],
У €[а> &]• Тогда для любого разбиения а = £0 < £х < ... <
< ^л_1 < £,п = ^ отрезка [а, Ь~] имеет место
Следовательно, функция / (х) имеет ограниченную вариацию на
[а, Ь].
652. Возьмем две произвольные точки £ и г) (£ < т]) отрезка
[а, Ь] и разделим отрезок[£, ц] над равных частей, где п — произ-
произвольное натуральное число:
226

Тогда
1=1
A
• n =
где Л — константа Гёльдера. Неравенство | / (r\)—f (£)| <Л|\_ра
справедливо при любом натуральном числе п\ Переходя к пределу
при п ->• +оо и учитывая, что а > 1 (и потому а — 1 > 0), полу-
получим:
1/D)-ШК Ит 4bf^£ = 0,
откуда / (£) г^/(г]). Итак, значения функции одинаковы для лю-
любых двух точек отрезка [а, &], т. е. функция f (x) постоянна на этом
отрезке.
653. Пусть | / (*!)—/ (х2) | < Л | хх — х2\а для любых ^ ё [а, &],
л:2 € [а, &]. Пусть р < а. Тогда
\f(xi)-f(x2)\<A \х1-х2\а =А . Ui-^r^. |^-^a|p<
<Л • F-а)а-р • I*!-*/.
Итак, для любых двух точек хъ х2 отрезка [а, &] выполняется нера-
неравенство | / (Xl) - / (х2)\ < В Ux -х2|р, где В = Л (Ь - аГ~р-
Следовательно, функция / (х) удовлетворяет условию Гёльдера по-
порядка р.
654. Пусть |/ (хх) — f (х2)\ < Л \хг—х2\а для любых хъ х2 £
(: [а, Ь]. Будем считать для определенности, что т > 0. Возьмем
два произвольных числа £, г) б fl"^"^, ~~| и оценим разность
[ m m J
f Й) - F (Л):
m
m
Л
^1^
(заметим, что если ^и г\ принадлежат отрезку р
I т т
п тц + п принадлежат отрезку [а, 6]; поэтому мы имели право
применить неравенство Гёльдера к разности / (т£ + п) — f (т +
+ п)). Итак, F (х) удовлетворяет условию Гёльдера порядка a
на соответствующем отрезке с константой \К\ Ата (если т < 0,
то с константой \К\- А • \т\а).
655. Пример. Функция
]
0 при х = 0
227

непрерывна на отрезке!О, —I и строго возрастает на этом отрезке,
а следовательно, имеет на нем ограниченную вариацию. Докажем,
что эта функция не удовлетворяет условию Гёльдера ни при ка-
каком а > 0. Пусть а — какое-либо числа заключенное между ну-
нулем и единицей. Покажем, что для люоого А >0 найдутся две
точки xlf х2 £ 0, — I такие, что |/ (х2) — f (хг)\ > А \х2 — хг\а.
В качестве хх возьмем точку хг = 0; для того чтобы подобрать х2
проверим, что а ->• + °° при х -> 0; действительно,
Iх — I
применяя правило Лопиталя, находим:
In л: ,. — х
lim
~а
|/(*) —/@I . In л: ,. — х к -а ,
lim и-^-1—Ц-^-1 = lim — = lim = hm ax = + оо.
х^о ]х — 0|а *^о ха х^о \пх х+о
Но тогда для любого А > 0 можно подобрать такое х2, что ILx^l—lLII ^
I Х2 — 0|
> Л, откуда | / (х2) — / @) \ > А | д:2 — 0|а. Следовательно, / (х)
не удовлетворяет условию Гёльдера при 0 <а <1, а значит, в
силу результата задачи 653 и при любом а > 0.
656. Пусть аг + а2 + ... + ап + ... — произвольный сходя-
сходящийся ряд с убывающими положительными членами; пусть его
сумма равна s. Построим на [0, s] функцию / (х) следующим обра-
образом:
/ (х) =0 в точках х = 0, alt ах + а2, ах + а2 + Яз» •••'»
/(*)=— в точках х= ах + а2+ ... +ал-1 + ^(л=1, 2, 3, ...);
П 2,
f(x) линейна на каждом отрезке вида \аг + ... + ал-1» ai + ••• +
+ ал-1 + ^| и на кажА°м отрезке вида \ах + ... + ап_х + °~> ах+
+ ...+ал-1+-ал (в частности, на отрезках 0, ■&-1 J-^-, aij);
схематический график этой функции см. на рисунке 38. Эта функ-
функция непрерывна на отрезке [0,s] и имеет на нем неограниченную
вариацию, каков бы ни был исходный ряд % + а2 + ...+ал + ...
Чтх>бы убедиться в последнем, разобьем отрезок [0, s] точками
где k — произвольно взятое натуральное число; вычислим сумму
ok модулей приращений функции для этого разбиения:
228

+ 1+1 + 1 + 1 + 1
0\ а, п?п2 п/шм^нц. s x
Отсюда видно, что, выбрав дос-
достаточно большое k, можно сде-
сделать сумму ok сколь угодно
большой. Следовательно,
s
V/ = + оо.
о
Подберем теперь ряд0!+а2+
+ ...+«„+... так, чтобы функ- Рис. 38
ция / (х) удовлетворяла усло-
условию Гёльдера заданного порядка а. Пусть Мг (х1у ух) и
Л^г fe» Уг)—Аве точки графика функции / (л:), принадлежащие
одному и тому же прямолинейному отрезку графика (см. рис. 38).
Если, например,
^ ап . !
5 — хг\, где К = — =»—. Следовательно, в этом случае
7
Л—a
X, — Хл
«ал пап
\Л2 Л1 Г ■— М
То же самое верно и для случая, когда
а, + ... + ам +^ < *х < х2
Возьмем в качестве {ап } последовательность f — |; это можно
сделать, так как — > 1 и, следовательно, Т!
2 2
ряд с убывающими положительными членами. Тогда — = —■
па
/г п . —
П
229

«= 2; поэтому, согласно предыдущему, для любых двух точек хг и
х2, для которых соответствующие точки графика принадлежат од-
одному и тому же прямолинейному отрезку графика, имеет место
\f(x2)-f(xl)\^2\x2-x1\a.
Пусть теперь хх й х2 — два числа на отрезке [0, s], для которых соот-
соответствующие точки графика Мх и М2 не лежат на одном и том
же прямолинейном отрезке, причем хг < х2. Тогда найдутся точки
М\ (х'\, f (xj) и М'2 (х'2, f (х2)), лежащие на одном прямолинейном
отрезке графика, у которых ординаты совпадают с ординатами
точек Мг и М2, а абсциссы удовлетворяют неравенствам:
*i < х[ < х2 < х2. A)
Действительно, точки Мх и М2 расположены на боковых сторонах
некоторых равнобедренных треугольников Gt и G2, каждый из ко-
которых образован двумя соседними прямолинейными отрезками гра-
графика и отрезком оси Ох (в частности, Gx и G2 могут совпадать).
Если / (хг) ^ / (х2), то в качестве М[ и М'2 берем точки, располо-
расположенные на правой стороне треугольника Gx и имеющие те же орди-
ординаты, что и точки Мг, М2 соответственно (рис. 39, а).
Если же / (Xi) < / (*а), то берем в качестве М[ и М'2 точки, рас-
расположенные на левой стороне треугольника G2 и имеющие те же
ординаты, что и точки Мъ М2 соответственно (рис. 39, б).
Легко видеть, что в каждом из этих случаев абсциссы точек
удовлетворяют неравенствам A). Так как точки М'{ и М'2 лежат
на одном прямолинейном отрезке графика, то, согласно предыдуще-
предыдущему,
Итак, неравенство | / (х2) — / (хг) ^ 2 \х2 — j^l* выполняется
для любых двух чисел xlt х2 отрезка [0, s]; значит, функция / (х)
удовлетворяет на этом отрезке условию Гёльдера порядка а.
Заметим, что / (х) не удовлетворяет на отрезке [0, s] условию
230

Гёльдера порядка р ни для какого р > а. Это следует из того, что
Urn »/<»«>-'<ggH = со,
М->оо \Ьп — Сп\Р
где Ьп = ах + ... + ал_х + ая, сл = ах + ... + ап__х + а-&\ дейст-
действительно,
\f(bn)-f(cn)\ = _л_ = я = 2Р -I- - 1
а последнее выражение стремится к бесконечности при п->оо.
657. Обозначим через фа (х) функцию / (х)> построенную в ре-
решении предыдущей задачи для заданного числа а. Она удовлет-
удовлетворяет условию Гёльдера порядка а, но не удовлетворяет условию
Гёльдера порядка р ни для какого р > а. Обозначим, кроме того,
черезап сумму ряда ^-.
&i
Построим теперь искомую функцию / (х). Для этого нанесем
на отрезок [0, 1] последовательность точек |2, |3» %4» •••»
О =и <1з <14 <-.. <!«<-.
где|/г->1 при д-^оо, и на каждом отрезке [|я, |я+1] зададим
/ (д:) следующим образом:
а) если /г четное, то полагаем f(x) = — <р . fq/t' ^""^ЯМ (гра-
п ±\ Ъп+1 — Ъп I
фик этой функции получается из графика <рг сжатием в /г раз по
п
оси ординат, сжатием в отношении ——— по оси абсцисс и пе-
реносом вдоль оси абсцисс вправо на величину £л).
б) если п нечетное, то полагаем f(x) = —q>l уп' ^*+1"~*' \
П — \ 6/1+1— 6л /
(график этой функции получается аналогично графику предыдущей
с добавлением зеркального отражения от вертикальной прямой).
Таким образом, функция / (х) определена всюду на [0, It; до-
доопределив ее в точке х = 1 равенством / A) = 0, мы получим функ-
функцию / (л:), определенного и непрерывную всюду на отрезке [0, 1].
Функция / (х) имеет неограниченную вариацию на этом отрезке
и даже на отрезках[|л, |я+1] (схематический график этой функции
см. на рисунке 40).
Функция / (х) на отрезке [|я, |я+1] не удовлетворяет условию
Гёльдера порядка —— (хотя она удовлетворяет на нем условию
п — I
231

1 \
Гёльдера порядка — ; след ова-
овалу
тельно, на всем отрезке [0, 1]
она не удовлетворяет условию
Гёльдера ни для какого а > 0.
658. Рассмотрим произволь-
произвольное разбиение отрезка [а, &]:
а = хо< хг< ...<*„_! <хп =Ь.
Имеем:
2 I/W -
= Sl(/W-/(;
П
-i)) + (g (xt) -
b b
a
n
11
< sup \f(x)\-Vg+ sup
Xz [a, b] a x- [a, b] a
Таким образом, суммы, стоящие в левых частях, ограничены
для всевозможных разбиений отрезка [а, &] числами, стоящими в
правых частях этих неравенств, т. е. функции / (х) + g (x)nf(x)x
X g (x) имеют ограниченную вариацию на [а, &]. Переходя к верх-
верхним граням этих сумм по всевозможным разбиениям отрезка [а, &],
ь ь
получаем указанные неравенства для V (/ + g) и V (/ • ^).
а а
659. Рассмотрим произвольное разбиение отрезка [а, &]
хг < ... < #„_! < л:л = &,
а = х0
и оценим сумму модулей приращений функции для Выбранного
разбиения:
f ta-i
& \f(*i)\
S \f(xi)-f(*i-i)\
<— 7,
232

так как |/ (xj| ^ с, |f (a:£_i)| ^ с. Неравенство
f(Xi) f(ti-
справедливо для любых разбиений отрезка [а, &]. Беря верхнюю
грань (по всевозможным разбиениям) от правой и левой частей
этого неравенства, получим:
откуда следует ограниченность вариации функции .
660. Для произвольных разбиений а = х0 < хг < ... < хг_г <
<хг = с и с = хг < хГ+г < ... < xr+5_i < хГ^ = & отрезков
[а, с] и [с, Ь] имеем:
S
2
Переходя в левой части к верхним граням по всем разбиениям
отрезков [а, с\ и [с, &], получаем:
с 6 6
vf+v/<v/.
аса
Чтобы получить теперь неравенство противоположного знака,
рассмотрим произвольное разбиение а = х0 <хг < ... < х„_г <
< лл — & отрезка [а, &]. Тогда точка с попадет в один из отрезков
Oj_i, х{\\ пусть, например, с € [хг-х, хг\
Так как
то будем в этом случае иметь:
Переходя в левой части к верхней грани по всем разбиениям от-
отрезка [я, &], получим неравенство
v /
233

Из двух найденных неравенств вытекает искомое равенство:
661. а) Достаточность. Пусть функция F (х) непре-
непрерывна в точке х0; докажем непрерывность функции / (х) в точке
х0. Пусть h > 0; тогда
но, в силу результата предыдущей задачи,
xo+ti xo+h x0
V/= V f-Vf = F(xo + h)-F(xo).
х0 а а
Значит, |/ (х0 + h) — / (л:0)| < F (xQ + h) — F (х0). В силу непре-
непрерывности функции F (х) в точке хо> отсюда следует, что / (х0 + К) —
— / (*о) ~^ 0 при h -> + 0, т. е. функция / (х) непрерывна справа
в точке х0. Аналогично доказывается, что f (x) непрерывна слева
в точке х^.
б) Необходимость. Пусть / (х) непрерывна в точке
х0 €[а, Ь[. Докажем непрерывность справа функции F (х) в этой
точке. Возьмем произвольное г > 0 и докажем, что найдется
/i > 0 такое, что \F A) — F (хо)\ < г при х0 <1 <х0 + h. Для
этого построим такое разбиение отрезка [#0, й] точками л:0 < хх <
< ... < *„.! < хп =6, при котором сумма модулей приращений
Ъ g
функции f (х) отличается от вариации V /меньше чем на—■; при этом
всегда можно считать точку хг столь близкой
— / (^оI <~~ (если бы точка хг не удовлетворяла этому условию,
мы бы добавили к точкам деления отрезка еще одну точку, доста-
достаточно близкую к хо\ добавление этой точки к точкам деления отрез-
отрезка может только увеличить нашу сумму). Итак,
т. е.
234

Поэтому
b b
V/-V/<8,
x0 xx
xx xx x0
т. e. V/< e, откуда V/—Vf< e (см. предыдущую задачу). Обо-
х0 а а
значив теперь хг — х0 + h> получим:
F (х0 + ft) - F (*о) < е.
Так как F (х) — возрастающая функция, то для любого |,
х0 < | < х0 + h, имеет место
\F(l)-F(xo)\ <е,
откуда и следует непрерывность справа функции F (х) в точке х0.
Непрерывность слева в точке х0 ё ]а, &] доказывается анало-
аналогично.
662. Пусть функция F (/) = V/ имеет предел при /-> + оо.
Тогда, в силу критерия Коши существования предела функции, для
каждого 8 > 0 найдется t0 € [а, + °°[ такое, что для любых t\
Г, удовлетворяющих условиям t" > f > /0, выполняется нера-
неравенство |F (О —^@1 <8> т- е- IV/ —V Л <е. Но V/ — V/ =
а а а а
t" t"
= V/, и, значит, V/<8. Тогда и подавно |/(О—/@1<8-
Следовательно, для функции / также выполнен критерий Коши,
т. е. lim / (x) существует.
ДС-+-+ОО
Таким образом, если lim V / существует, то и lim / (х) сущест-
вует.
Обратное утверждение неверно. Пример. Пусть / (х) =
= — sin х. Тогда
X
пл
я
-00
при п->+оо, так как ряд V расходится. Однако li
^ 2П 1 Х\
^
= lim ^j? существует (этот предел равен нулю).
663. Первое утверждение является непосредственным след-
следствием результата задачи 661.
235

Докажем первое из приведенных в задаче равенств. Сущест-
Существование предела F (х0 + 0) ==lim F (х) вытекает из монотонно-
х х^хо+О
сти функции F (х) = V /. Существование предела / (х0 + 0) =
а
= lim / (х) доказывается так же, как в предыдущей задаче. Пе-
реходя теперь в неравенстве | / (хо+ ft) — / (*0)| <J F (х0 + ft) —
— F (х0) к пределу при ft -^ + 0 (доказательство этого неравенства
см. в решении задачи 661), получим:
I / (Хо + 0) - / (*o)l <F(xo + O)-F (x0). A)
Чтобы доказать неравенство противоположного знака, зададим
произвольное е > 0 и для всякого отрезка [>0, х0 + ft] a [a, ft]
построим такое его разбиение х0 <хг < ... < хп = х0 + /г, что
Тогда
*о
(см. задачу 660). Так как х0 <хг^х0+ h, то, переходя к пределу
в неравенстве | / (хг) — f (х0) \ > F (хг) — F (х0) — г при h -> + 0,
получим:
I / (*0 + 0) - / (х0) \>F(xo + O)-F (х0) - е.
В силу произвольности числа 8 > 0, имеем: | / (л:0+ 0) — / (л:0)| ^
^ F (х0 + 0) — F (#0). Сравнивая это неравенство с ранее дока-
доказанным неравенством* A), получим:
\t(x0 + 0) - f (*0)| = F (x0 + 0) - F (x0).
Второе приведенное в задаче равенство доказывается аналогично.
664. Проверим, что р удовлетворяет аксиомам метрики:
1) р (/,/)== 0 для любого / 6 V (а, Ь). Если р (/, g) = 0, то V (/ —
а
— g) = 0 и | / (а) — g" (й)| =0, откуда следует, что функция f — g
постоянна на отрезке [а, Ь~\ и эта постоянная равна нулю, т. е.
/=g;2) p(/,g)=pfe, f), так как V (/ - g) = V (g - /);
3) (
так
э (/» h) ^ р (/, g) + р
как
\f(a) —ft (a)\
ь ь
Vtf — ft)<V(/ — g)
а а
(ё> л),
<1/(«)-вГ
+ V(ff-A)
а
ш ■
(см.
-Ь \g(a) —ft
задачу 658).
236

Докажем полноту пространства V (а, Ь). Пусть /lf /2, /3, ... —
произвольная фундаментальная последовательность из этого мет-
метрического пространства. Имеем при т < п и х € [а, &]:
1/Л (*) - /« WK 1 (/„ М - /« (*)) - (/„ W - fm (а))| +
+ 1/я(а) -/« (а)К V (/«-U + 1/я W -L (а)\ -
а
= Р (/я » /т)«
Значит, для каждого я € [а, Ь] последовательность чисел fx (л;),
/2 М» /з (х)у ••• тоже будет фундаментальной. Поэтому существует
предел Нт/т(л:), который мы обозначим через f (х).
т-*оо
Покажем, что функция / принадлежит пространству V (а, &),
т. е. Является функцией ограниченной вариации на [а, &], и что
fm -> / в смысле метрики этого пространства.
Зададим произвольное е > 0. Пусть Л^ — такое число, что при
т > Ыъ п > Nx будет: р (/т, /Л) < —. Рассмотрим произвольное
4
разбиение
а =х0 <хг < ...< xSmml <xs =b
отрезка [а, &]. Пусть п > Л^х столь велико, что |/л (д:.) — / (x.)| < —
для всех I =0, 1, ..., s. Тргда для произвольного т > Nt будем
иметь:
- fn Ы I + I (/« (*|) - /
Значит,
s
2л \ V/ \xlh Im \Л0) \l \xl-l) Im \xi-V/ I <^
4 У 4 4 4 4 ~~ 4"
Так как это верно для всех разбиений отрезка [а, 6], то функция
/ — fm при т > Nx есть функция ограниченной вариации на
Ь 38
[а, Ъ\ для которой V (/ — fm) < -. Так как f = (f — fm)+ /m, a
fm ^ V (a, b), то и / — функция ограниченной вариации на [а, Ь]
(см. задачу 658), т. е. / £ У (а, Ь).
Пусть теперь N2 таково, что при т> N2 будет: | / (а) —
— fm(a)\<~- Тогда при m>N, где N = max(Nv N2)> будем
4
237

иметь:
Зе
в силу Произвольности е > 0, это означает, что lim fm—f в смыс-
т-*-оо
ле метрики пространства V (а, Ь). Итак, каждая фундаментальная
последовательность пространства V (а, Ь) сходится в этом про-
пространстве, т. е. V (а, Ь) полно.
665. Доказательство можно провести аналогично тому, кото-
которое дано в решении предыдущей задачи.
Можно также выбрать из каждого класса /по одному элементу/,
удовлетворяющему условию / (а) =0. Тем самым мы отобразим прост-
ранство V (ау Ь) на некоторое подпространство Vo (a, b) метрического
пространства V (а, Ь) из предыдущей задачи. При этом значение
функции рх для любых двух элементов /, g пространства V (а, Ь)
будет равно расстоянию междулх образами в Vo (a, b). Следова-
Следовательно, V (а> Ь) — метрическое пространство с метрикой рь изо-
метричное Vo (а, Ь). Так как Vo (a, b) замкнуто в V (а, Ь) и, значит,
полно, то и У (а, Ь) — полное пространство.
666. Функция / (х) = cos2 х представима в виде разности воз-
возрастающих функций следующим образом:
/(*) = V7-<p(*)f
0
где
= V f—f{x). Здесь
x i 1 — cos2 x при x
О
О, у],
и, значит,
cos2 х при х 6 ] —, я],
1 — 2 cos2 x при х 6
1 при х 6
(см. рис. 41).
667. sin х = ф (х)
[* т\
Ж
2
Рис. 4JL
Я X
г|) (х), где
sin л: при х 6 Го, —1,
2 — sin л; при х 6 —, — я ,
4 + sin я при д: 6 К-*, 2я,
J 2 J
238

о при xehyl
2 — 2 sin л; при л: 6 —, — л; ,
J 2 2 J
13 1
— л, 2я
(рис. 42).
668. f(x) =
где
()
х2 при *6[0,
Функ-
; 2
Рис. 43
Ф (х) =\2 при х = 1,
,3 при л: €]1, 2],
я|) (лг) = Г 2л;2 при х (: [0, 1[,
[2 при х €[1,2]
(рис. 43).
669. V/ =7; V/ =5; V/ =2.
О О 1
цию / (л:) можно представить следующим
образом в виде разности монотонных:
/ (х) ==ф (*) — г|) (*), где
( х2 при л: € [0, 1[,
Ф (х) = I 5 при х = 1,
I л;+ 5 при х €]1, 2],
ф (г) = /0 при * € [0, 1],
Y v ; |2 при л: €]1, 2].
670. Это следует из того, что | а — р| > || а| — | $\\ для любых
чисел аир. Поэтому при любом разбиении а = х0 < хг < ... <
< л:л_1 < л:л =Ь отрезка [а, Ь~\ имеет место
« rt h
К
Следовательно, функция |/(л:)| имеет ограниченную вариацию
на [а, &], причем
V |/| < V /.
а а
671. Нет. Пример. Пусть
/ (х\ __ Г —1 при х иррациональном-,
( 1 при х рациональном.
Тогда \f(x)\ =1 для всех х\ следовательно, |/ (д:)| имеет ограничен-
ограниченную вариацию на любом отрезке [а, &], тогда как / (я) — функция
неограниченной вариации на том же отрезке.
672. Справедливо. Действительно, возьмем произвольное раз-
разбиение а = х0 < хг < ... < хп_х < хп = Ь отрезка [а, &] и обо-
обозначим через а сумму модулей приращений функции / (х) для этого
239

разбиения. Если на каком-либо участке \_хктт1, xk~] этого разбиения
функция / (х) не меняет знака, то на этом участке приращение функ-
функции равно по абсолютной величине приращению модуля функции.
Если же на участке \_xk_ly xk~\ функция / (х) меняет знак, то в силу
непрерывности она обращается в нуль в некоторой точке £Л, хк_х <
<lk <*k (см. задачу 536). Так как на участках [xk_lt £Л] и [£Л, xk]
приращение функции равно по абсолютной величине приращению
ее модуля, то
Итак, сумма а модулей приращений функции / (х) для заданного-*
разбиения не превосходит суммы а*' модулей приращений функции
\f(x)\ для некоторого разбиения отрезка [a, b] (a именно для того
разбиения, которое получится, если к точкам хк добавить точки
£Л, выбранные выше). Но а* не больше вариации функции |/(*)|
(по условию |/(x)|—функция ограниченной вариации). Поэтому
ъ
а ^ сг* <^V |/|. Итак, для любого разбиения отрезка [а, Ъ~\ сумма
а Ъ
а не превосходит числа V|/|; следовательно, f (х) —функция ог-
а
раниченной вариации, причем
ь ь
V/ < VI Л.
а а
Ь
Замечание. Из рещения задачи 670 вытекает, что V |/| ^
а
ь
^ V /. Сравнивая это неравенство с полученным выше, заключаем,
а
что для непрерывной функции / (х) имеет место равенство
ь ь
V/ =V |/|.
а а
673. а) Необходимость. Пусть / (х) — функция огра-
х
ничейной вариации на [а, &]; функция ф (х) = V / является возра-
а
стающей на [а, Ь] функцией; очевидно, что она удовлетворяет задан-
заданному неравенству при любом h > 0, так как
x+h x+h x
\f(x + h)—f(x)\^ Vf= V/ —V/-
x a a
= ф (x + h) — ф (x)
(см. задачу 660).
б) Достаточность. Пусть / (x) — функция, заданная на
[а, 6], и ф (х) —такая возрастающая на [а, &] функция, что для
любого х € [а, &] и любого h > 0 (при условии, что х + h € [а, &])
выполнено неравенство
\f(x + h)—f (х)| < ф (* + ft) — Ф (х).
240

Разобьем отрезок [а, Ь] точками а = xQ < хх< ... < хп^х< хп = b
и оценим сумму а модулей приращений функции / (х):
Итак, а не превосходит числа ф (Ь) — ф (а) при любом разбиении
отрезка [а, &]; следовательно, / (х) — функция ограниченной ва-
вариации, причем
<
а
674. Спрямляемость этой кривой следует из того, что функция
О при х = О
имеет ограниченную вариацию на отрезке [0, 1] (последнее дока-
доказывается так же, как при решении задачи 644).
675. Неспрямляемость этой кривой вытекает из того, что функ-
функция, графиком которой она является, не имеет ограниченной ва-
вариации на отрезке [0, 1] (последнее доказывается таким же методом,
как при решении задачи 645).
676. Покажем, например, что функция ф (t) имеет неограничен-
неограниченную вариацию на отрезке [0, 1]. Рассмотрим для произвольного
п разбиение квадрата [0, 1] X [0,1] на 4п замкнутых квадратов л-го
ранга. Пусть эти квадраты занумерованы по правилу, указанному
в условии задачи 594, и точка Mt (xit yt) является центром квад-
квадрата n-го ранга с номером i (i = lr2, ..., 4й). Выберем для каждо-
каждого i на отрезке [0, 1] оси Ot один из прообразов tt точки M-t (при
отображении, задающем кривую Пеано). Тогда tt является точкой
f-го отрезка n-го ранга, соответствующего /-му квадрату п-то
ранга, причем все tt попарно различны. Так как отрезки зануме-
занумерованы слева направо, то отсюда следует, что 0 = £0< tx < /2 <
< ... < t4n < 1, т. е. точки tt задают некоторое разбиение отрезка
[0, 1]. Оценим для этого разбиения сумму оп модулей приращений
функции ф (t). Для этого возьмем разбиение квадрата [0, 1] X
X [0, 1] на замкнутые квадраты (п — 1)-го ранга и рассмотрим
/-й квадрат (п — 1)-го ранга. В силу построения, составляющие
его квадраты п-го ранга будут занумерованы числами 4/—3,
4/ — 2, 4/ — 1, 4/ и квадраты с соседними номерами имеют общую
сторону. Ясно, что из них хотя бы два квадрата с соседними но-
номерами имеют общую вертикальную сторону. Пусть это
будут, например, квадраты с номерами 4/ -— 1 и 4/. Тогда
|Ф (<4у) — Ф 0W-i)l = 1*4/ — *4y-il = ^
241

г
—i
Рис. 44
А
т
(см. рис. 44). Поэтому на отрезке [/4у_4, t±j\
сумма модулей приращений функции
Ф (/) не меньше —. Так как число таких от-
резков равно 4я, то для суммы оп моду-
модулей приращений функций ф (/) на всем
отрезке [0, 1] получим:
оя>А*-*.±=2*-*.
Следовательно, оп -> оо при п -> оо,
т. е. функция ф (/) имеет неограниченную
вариацию на [0, 1].
Аналогично проверяется, что функция
'ф (/) имеет неограниченную вариацию.
Замечание. Из полученного ре-
результата и из теоремы 6 введения к этой
главе следует, что кривая Пеано не спрям-
спрямляема.
677. Когда параметр / пробегает зна-
значения от 1 до 0, точка М (х, у) на плос-
плоскости, действительно, движется по отрез-
отрезку, соединяющему точки (а> а) и (Ь, Ь).
Но при этом точка М совершает колеба-
колебательные движения по этому отрезку; таким
образом, кривой, заданной этими парамет-
параметрическими уравнениями, является не ука-
указанный выше отрезок, а ломаная АВгВ%В3 ... С с бесконечным чис-
числом звеньев, которые все лежат на этом отрезке (см. рис. 45). Эта
ломаная не спрямляема.
678. Функции ф @ и "ф (/) имеют ограниченную вариацию на
[О, 1] (см. задачу 648); следовательно, кривая *=ф (t), y = ty (t)
(О ^ / ^ 1) спрямляема.
Глава XII.
ИЗМЕРИМЫЕ ФУНКЦИИ, ИНТЕГРАЛЫ
РИМАНА И ЛЕБЕГА
679. Пусть а — произвольное число. Легко видеть, что
Е ((/ (x)f >a) =E{f (x) > ^а).
Так как по условию / (х) — измеримая функция, то множество
Е (f (х) > У а) измеримо; следовательно, множество Е ((/ (х)K > а)
также измеримо при любом а\ значит, функция (/ (x)f измерима.
680. Пример. Пусть
1 на каком-либо неизмеримом множестве Af
Рис. 45
242

Функция / (х) неизмерима, тогда как функция {/ (л:)J, тождественно
равная единице, измерима.
681. Если функция / (х) измерима, то измеримость функции
\f [х)\ следует из равенства, справедливого при любом а > 0:
Е ([/ (х)\ > а) = Е (/ (х) <-п)[) Е (/ (*) > а).
Пример, построенный в предыдущей задаче, показывает, что
из измеримости \f {х)\ не вытекает, вообще говоря, измеримость
fix).
682. Измеримость функций т {х) и М (х) следует из результата
задачи 681 и равенств
max {/(л:),
2
J(x)+g(x)+\f(x)—g(x)\
683. Построим последовательность точек at > а2 > а3 > ...,
сходящуюся к а, и последовательность $± < |32 < f53 < •••> сходя-
сходящуюся к &. Ясно, что
]а, &[ = U [ов„ PJ-
1=1
Так как функция / (л:) по условию измерима на любом [а^ PJ, то
для всякого числа с множество
Et =[«,.&] П E(f(x) >c)
измеримо. Но 0 Et =]а, Ь[(] Е (/ (х) >с).
Следовательно, и множество ]а, Ь[ П Е (/ (л:) > с) измеримо при
любом с; значит, / (х) измерима на интервале ]а, Ь[. А так как от-
отрезок [а, Ь] отличается от интервала ]а, &[ лишь множеством меры
нуль, то функция / (х) измерима и на отрезке [а, 6].
684. Измерима; она отличается от функции ф (х) = х? только
на множестве меры йуль (на подмножестве канторова множества).
Значит, функции / (х) и ф (х) эквивалентны. Но ф (х) измерима на
отрезке [0, 1]; следовательно, и / (х) измерима на этом отрезке.
685. Рассмотрим функцию ц>п (х) = — ; она опре-
п
делена и измерима на а, Ь 1. Предел Нтфл (х) = ff (x) су-
ществует для всех #ыа> Ь ; следовательно, функция f\x) из-
измерима на отрезке а, Ь .
А так как промежуток [а, Ь[ является объединением промежутков
а, 6 \ (п = 1, 2, ...), то /' (л:) измерима на промежутке [а, &[
L nj
243

(в этом мы убеждаемся так же, как и в задаче 683). Но тогда /' (х)
измерима и на всем отрезке [а, Ь].
686. Если ХЕ (х) — характеристическая функция множества £,
то
(R, если а <0 (здесь R—все пространство),
Е AЕ(х)>а) = Е, если 0 < а < 1,
[ 0 если а ^ 1.
Отсюда видно, что если Е— измеримое множество, то функция
%Е{х) измерима, а если Е — неизмеримое множество, то функция
1Е (!t) неизмерима.
687. Построим функцию / (х) следующим образом: пусть Е —
измеримое множество на прямой, обладающее тем свойством, что
для любого интервала ]а, р[ мера множества Е Г) ]а, |3[ отлична
от нуля и мера множества СЕ f] ]а> |3[ также отлична от нуля
(пример такого множества можно получить, взяв арифметическую
сумму множества В, построенного при решении задачи 441, с мно-
множеством всех целых чисел). В качестве искомой функции / (х)
возьмем характеристическую функцию ХЕ (х) множества Е\ она
разрывна в любой точке х0 (так как колебание функции на любом
интервале, содержащем эту точку, рзвно 1). Если изменить значе-
значения этой функции на множестве меры нуль, то на каждом интерва-
интервале ее колебание может только увеличиться; следовательно, и после
изменения значений этой функции на каком угодно множестве меры
нуль она остается разрывной в любой точке.
688. Обозначим [/ {x)~fa = ср (х). Ясно, что
{Е при с < я,
Е if (х) > с) при а < с < fe,
0 при с ^ Ь.
Так как / (х) — измеримая функция, то множества Е(ц>(х) > с)
измеримы при любом с. Значит, функция ср (х) измерима.
689. Пусть / (х) — произвольная функция; произведение
% (х) • / (х) почти всюду равно нулю. Следовательно, функция
X (х) • f (х) эквивалентна функции, тождественно равной нулю,
т. е. измеримой функции. Значит, сама функция 1 (х) - f (x) изме-
измерима.
690. Очевидно, всякая монотонная функция измерима; а любая
функция ограниченной вариации есть разность двух монотонных;
следовательно, она также измерима.
691. Пусть Ех — интервал ]а, р[ на числовой прямой. Тогда
]а, р[ =]—оо, р[ f] ]а, +оо[. В силу измеримости функции/ (х),
прообразы бесконечных интервалов ]—оо, р[ и ]а, +оо[ измеримы,
а так как прообраз пересечения двух множеств равен пересечению
их прообразов (см. задачу 476), то
ГО, К) =Г1а-°°, Ю П Г1 (X +<*>[);
следовательно, прообраз интервала —измеримое множество.
244

Ill 1 Z 7 в 1
9 9 3 2 3 9 9
Рис. 46
Если Ег — произвольное открытое
множество на числовой прямой, то
оно является объединением конечной
иди счетной совокупности интервалов
(см. задачу. 212); чтобы доказать, что
/~~* (Ej) —измеримое множество, надо
использовать тот факт, что прообраз
объединения множеств равен объедине-
объединению их прообразов (см. задачу 478).
Если Ел — замкнутое множество, то
Ег = R{ \ Еъ а Е2 — некоторое от-
открытое множество; так как прообраз
всей прямой — измеримое множество и
прообраз открытого множества Е2 так-
также измерим, то измеримым является и
прообраз их разности (см. задачу 477).
692. Прообраз измеримого множества
не обязан быть измеримым. Пример.
Рассмотрим функцию Кантора т (лс),
построенную в задаче 632. Как мы зна-
знаем, она монотонна и непрерывна на от-
отрезке Е = [0, 1] и отображает его н а
весь отрезок Ег = [О, 1] оси Оу.
При этом канторово множество D а Е отображается на
множество всех чисел отрезка Еъ а множество CD — на множество
двоично рациональных чисел этого отрезка.
Построим теперь функцию Ф (х) = х + т (х). Она строго воз-
возрастает и непрерывна; она отображает отрезок [0, 1] оси Охвз аи м*
но однозначно на отрезок [0, 2] оси Оу; при этом множест-
множество CD перейдет в множество меры 1 (так как каждый интервал из
CD перейдет в интервал такой же длины) и, следовательно, мно-
множество D — в такое замкнутое подмножество F отрезка [0, 2] оси
Оу, мера которого также равна 1 (схематический график функции
Ф (х) см. на рисунке 46).
Построим, наконец, функцию, обратную Ф (х)\ обозначим ее
Ф (у). Она непрерывна (следовательно, измерима) и отображает
отрезок [0, 2] с: Оу взаимно однозначно на отрезок [0, 1] cz Ox\
при этом множество F, мера которого равна 1, переходит в D
(рис. 47).
Множество F (как и всякое множество положительной меры)
содержит неизмеримое подмножество (см. свойство 16 из введения
к главе VII), которое мы обозначим через А. Образ ср (А) этого под-
подмножества будет частью канторова множества D =cp (F). Но всякое
подмножество множества меры нуль измеримо. Следовательно,
В = ф (А) измеримо. Итак, множество В измеримо, тогда как егр
прообраз А = ф (В) неизмерим.
693. Из того, что функция f (х) измерима на Е, и из того, что
множество Ео, включенное в Е> измеримо, еще не следует измери-
245

1 t
Рис. 47
мость множества / (Ео). Пример» Рассмотрим функцию Ф (х) =
= х + т (л:), где т (я) — канторова функция (см. решение преды-
предыдущей задачи). Функция Ф (л:) переводит (взаимно однозначно и
непрерывно) отрезок [О, 1] оси Ох в отрезок [0, 2] оси Оу, а канто-
рово множество Dc[0, 1] — в некоторое подмножество/1 cz [0,2],
причем mF = 1. Пусть А — неизмеримое подмножество множест-
множества F, а В = ф-1 (А) — прообраз множества Л. Тогда множество
В измеримо (как часть канторова множества, которое имеет меру
нуль).
Итак, В измеримо, а Л = Ф (В) неизмеримо. Функция, с по-
помощью которой осуществляется отображение, измерима (даже
непрерывна).
694. Пусть а — произвольное число. Тогда множество тех
х € Еъ для которых выполнено неравенство / (х) > а, есть прооб-
прообраз открытого множества ]я, +оо[ числовой оси, а потому открыто
в Ех (см. задачу 509), т. е. является пересечением множества Ег
с некоторым открытым множеством Г числовой оси (см. задачу 193).
Поэтому условие / (ф (t)) > а равносильно условию <р (t) € Ех {} Г,
т. е. условию ф @ € Г (поскольку условие ср (/) 6 Ег выполняется
для всех t£E). Следовательно, множество всех тех / €Е, для кото-
которых / (ф @) > а, есть прообраз ф-* (Г) множества Г. Но если ф —
измеримая функция, а Г — открытое множество, то множество
ф-^Г) измеримо (см. задачу 691). Итак, для любого а множество
всех тех /, для которых / (ф (/)) > а, измеримо. Значит, функция
/ (ф @) измерима.
695. Из того, что ф (t) непрерывна на Е = [а, Д, a / (x) измери-
измерима на Ег = ф (£), еще не следует, что суперпозиция / (ф (/)) изме-
измерима на Е. П р и м е р. Пусть ф (/) — функция, обратная к функ-
функции Ф (х) =х + х(х), где т (х) канторова функция <р (/), рас-
рассмотренная в задаче 692. При решении этой задачи было по-
показано, что ф (/) взаимно однозначно и непрерывно отображает от-
отрезок [0, 2] на отрезок [0, 1] и что на отрезке [0, 1] имеетея измери-
измеримое множество В, прообраз которого А = ф-1 (В) является неиз-
неизмеримым множеством на отрезке [0, 2].
246

В качестве измеримой функции f (х) примем теперь характери-
характеристическую функцию множества В. Она измерима, так как измеримо
множество В.
Однако функция / (ф (/)) неизмерима. Для того чтобы в этом
убедиться, достаточно доказать, что множество всех тех t, для ко-
которых / (ф (t)) > О, неизмеримо. Но неравенство / (ф (t)) > 9
равносильно тому, что ф (/) £ В; а множество тех t, для которых
Ф @ £ В, есть множество Л, т. е. неизмеримое множество.
Итак, множество А тех точек t, для которых / (ф (/)) > 0, неиз-
неизмеримо. Значит, эта функция неизмерима.
696. Для любого а > О справедливо соотношение
Действительно, если x~eE(\f — fn\>-^)[) E(\g—gn\>^\
то |/(д)-/я(*)|<|. teW-foWKf и
1 (/ (х) + g (х)) - {fn (х) + gn (х))\ < |/ (х) - fn (x)\ + \g (x) -
-gn(x)\<~2 +f = <*> т.е. x
Из полученного включения следует:
при п ->■ oo для любого фиксированного а > 0. Следовательно,
ifn + £«} сходится по мере к функции/ + g.
Заметим далее, что тЕ (| ф| > t) -► 0 при £ -► + оо для любой
измеримой функции ф на множестве Е конечной меры (это следует
из свойства 14 введения к главе VII). Поэтому для произвольного
е > 0 найдется такое t > 0, что
mE{\f\ >t) <e, mE(\g\ > t) < е.
Из тождества
Ы-Ып-f- (g-gn)+g- (f-D-if-U- (g-gn)
следует неравенство
\fg-Un\<\f\- \g-Sn\+ \g\- I/-/J+ \Mn\-\g-gJ'
247

Отсюда получаем включение, справедливое при любом а > 0>
(проверяется аналогично предыдущему включению). Тогда имеем
следующую оценку по мере:
tnE (\fa —
Переходя к верхнему пределу при п ->• оо, получим:
^-fngn\ >a)<2e,
откуда, в силу произвольности е > О,
UmmE(\fg-fngn\ >a) =0.
П-*-оо
Следовательно, {/„g,J сходится к fg по мере.
Для доказательства последнего утверждения задачи доста-
достаточно показать, что 1—1 сходится к — по мере. Так как# (л:) Ф 0
почти всюду на £*, то тЕ (|g|< /) ->- 0 при / ->- + 0 (см. свойство
14 из введения к главе VII). Зададим произвольное s>0 и выберем
/ > 0 такое, что тЕ (| g\< t) < е. При любом а > 0 и любом п
справедливо включение
U
Действительно, если х не входит в правую часть этого включения,
то из неравенств | g (x) |< t, J g(x) — gn (x) | > ~ следует, что |#я(*)| >
не
?AB
t m
2'
ВХОДИТ
тогда
1
£(*)
и в левую
1
часть.
*)пп
п (х)
(X)
^ 2
' 2
= а, т. е. х

Из этого включения получаем:
откуда следует, что
П-+оо \\ g gn
при любом е > Q; значит,
limm£f|- — 1
П-+оо \\ g
■)-
>о\=0
и/1]
сходится по мере к —.
я
697. Предположим, / (х) > а на множестве положительной ме-
меры. Тогда, в силу свойства 13 из введения к главе VII, для некото-
некоторого натурального п0 будем иметь:
/ (х) > а -\— на некотором множестве £" положительной меры;
пусть тЕ' = а > 0. Но /я (х) < а, так что Е (\f —fn\ > -) =>
\ "о/
zd i: ; следовательно,
при любом пу т. е. последовательность {fn (x)} не сходится по ме-
мере к / (х). Получим противоречие.
698. Если тЕ = 4-°°, to теорема 1 (теорема Лебега), вообще
говоря, неверна. Пример. Пусть Е == [0, + оо[ и
f (х\ __( 1 ПРИ X $.{Пу П + 1[,
1п { } "\0 при х € [0, л [ U Е« + 1, +оо[.
Последовательность {/^ (x)} почти всюду на Е сходится к функции
Ф (х), тождественно равной нулю. Однако тЕ (| ф — fn\ > —) = 1
при любом /г, т. е. {/„} не сходится к ф по мере.
Теорема 2 остается верной и при тЕ = +°°- Докажем это.
Пусть Ek = £ f] У @, fe) (У @, /г) — шар радиуса к с центром в
начале координат). Если последовательность {fn} сходится по ме-
мере на Е, то она сходится по мере и на Ег\ но тогда из нее можно из-
извлечь подпоследовательность {fni}, сходящуюся почти всюду на
Ех- Далее, так как последовательность {fn.} сходится по мере на
Е9 то она сходится по мере и на Е2; извлечем из нее сходящуюся
почти всюду на Е2 подпоследовательность {fni}. Аналогично на-
находим подпоследовательность {/.. }, сходящуюся почти всюду на
249

fy и т. д. Выделяя теперь из таблицы
/f!t '«, 1пх '
lnii 1щ2 1щз
\nijx fnlj% fnih'
диагональную последовательность / , fni^ /„.., ..., получим
подпоследовательность последовательности {/„}, сходящуюся почти
всюду на Е.
699. Заметим сначала, что любое натуральное число п может
быть представлено, и притом единственным образом, в виде п =
= 2* + /, где k = 0, 1, 2, ..., О < i < 2*. Зададим теперь на Е =
= [0, 1] следующую последовательность функций {/„ (*)}:
,0 в остальных точках отрезка [0, 1],
где ink — числа, соотнесенные числу п указанным выше образом
(рис. 48).
Ясно, что эта последовательность сходится по мере к функ-
функции ф (х), тождественно равной нулю, так как
0 при а^ 1,
/л£(|ф-/л|>а) =
- при 0<а< 1.
С другой стороны, {fn (x)} не сходится к нулю ни в одной точке мно-
множества Е = [0, 1].
У i
1
0
У
1
0
1
;
4
) ■
Tc(Xj
У\
7
x" 0
У
1
\ x 0
j
т i
1
1 x 0
У
> J
w
1 ± / x 0
r
г
ш
1
4 ^
0
2 J
% 4
yt
x ^
; x i?
■НШВ
н
<
1 L 1 f X
/ 1 X
Рис. 48
2513

700. Подпоследовательность функций fl9 /2, /4, /s, /16, ... из по-
последовательности {/Л}, построенной в решении задачи 699, сходит-
сходится к функции ф (х) =0 всюду на Е = [0, 1], кроме точки х = 0.
701. Если мера множества £ конечна, то это утверждение
верно; оно сразу следует из теоремы Егорова (с. 82), если учесть,
что сходящаяся почти всюду на Е последовательность функций схо-
сходится на £ и по мере.
Если же тЕ = +оо, то данное утверждение неверно. При-
мер. Последовательность функций /л (х) = — сходится почти
п
всюду (и даже всюду) на £ = ]— оо, + оо[ к функции <р (х) = 0.
Однако ни для какого подмножества Ег а Е бесконечной меру нель-
нельзя извлечь из {fn (x)} подпоследовательность, равномерно сходя-
сходящуюся на Ег.
702. Всякая функция ограниченной вариации на [а, 6] ограни-
ограничена и имеет не более счетного множества точек разрыва на [а, И]
(см. следствие из теоремы 1, с. 73); следовательно, мера множест-
множества точек разрыва равна нулю. Поэтому такая функция интегрируе-
интегрируема по Риману на [а, Ь] (см. введение к настоящей главе, с. 82).
703. Нет. Если функция разрывна всюду на непустом открытом
множестве G cz [а, Ь], то множество ее точек разрыва имеет поло-
положительную меру. Такая функция не может быть интегрируемой
по Риману на отрезке [я, Ь] (см. введение к настоящей главе).
704. Функция
— при х Ф О,
0 при х = 0
не интегрируема по Риману на отрезке [0, 1] (в силу неограничен-
неограниченности), однако она интегрируема на любом отрезке [а, Р], где
0 <а <р < 1.
705. Так как функция интегрируема по Риману на любом от-
отрезке [а, р] таком, что а < а < р < Ь, то она, в частности, инте-
интегрируема на отрезках \а+ —, b — — L где с =-^2., п — 1, 2,
3, ...; следовательно, на каждом таком отрезке множество точек
разрыва имеет меру нуль. Обозначим через Еп множество точек
[с с Л
а Л , Ь ; тогда множество всех то-
п п \
чек разрыва на отрезке [а, Ь~] равно объединению всех Еп% к кото-
которому, может быть, добавлены точки аи b (или одна из них)> Но так
как тЕп = 0 при любом п, то и т (U Еп) = 0. Добавление к мро-
п
жеству [) Еп одной или двух крайних точек отрезка [_а, Ь~] не из-
п
менит меры этого множества. Итак, множество всех точек разрыва
функции на отрезке [а, Ь] имеет меру нуль, Так как функция по ус-
условию ограничена аа [а, Ь], то она интегрируема по Риману на
[а, Ц.
251

706. Функция ф (л:) может оказаться неинтегрируемой по Ри-
ману (хотя <р (х) всегда будет интегрируемой по Лебегу (см. свой-
свойство 8 на с. 84). Пример.
/ (х) =il ПРИ х =Г1» т^ •••' г">
ln v ' [0 в остальных точках [а, Ь]
(здесь rv г2, ... —все рациональные числа отрезка [а, Ь], перену-
перенумерованные произвольным образом). Функция ф (х) есть харак-
характеристическая функция множества рациональных чисел отрезка
[а, Ь]. Она всюду разрывна и поэтому не интегрируема по Риману
на [а, 6].
707. Пусть функции ц>п (х) интегрируемы по Риману на отрез-
отрезке [а, Ь~] и последовательность {уп (х)} равномерно сходится к / (х)
на этом отрезке. Докажем, что / (х) интегрируема на [а, Ь].
а) Функция / (л:) ограничена. Действительно, если последова-
последовательность {фл (х)} равномерно сходится к / (x)t то для любого е>0,
и в частности для г = 1, найдется N такое, что для всех п ^ N
имеет место
При п =^N это неравенство принимает вид |/ (л:) — ф^ (х)\ < 1,
или ф^ (х) — 1 < / (л:) < yN (х) + 1. Так как функции ф^ (л:) —
— 1 и ф^ (х) + 1 ограничены на [а, &], то и / (х) ограничена на
U 6].
б) Множество точек разрыва функции / (х) имеет меру нуль.
Действительно, обозначим через Еп множество точек разрыва
функции фл (х)\ тогда тЕп = О, а значит, и т ([} Еп) = 0. В каж-
п
дой точке #0, принадлежащей множеству [a, b] \ U Еп, все функ-
п
ции фл (х) непрерывны; но тогда и функция f (лс), являющаяся их
пределом, непрерывна в точке х0 (в силу равномерной сходимости
последовательности {сря (х)}). Значит, функция может бы^гь раз-
разрывна только в точках множества [} ЕпУ т. е. только на множестве
п
Меры нуль.
Итак, функция / {х) ограничена на [а, Ь], и мера множества ее
точек разрыва равна нулю. Следовательно, / (х) интегрируема по
Риману на [а, Ь].
ь ь
Равенство Г f(x) dx = lim f фя (дг) dx доказывается так же, как
а ~ а
и аналогичное равенство для равномерно сходящихся последова-
последовательностей непрерывные функций, т. е. исходя из того, что
b b
[yn(x)dx — U (x) dx < е при | фл (х) — f (х) \ < ——.
J ^ О — CL
а л
252

708. Неверно. Например, если Е — множество рацао-
нальных чисел на [0, 1], то тЕ = 0, однако %Е (х) не интегрируема
на [0, 1] (множество точек разрыва этой функции совпадает со всем
отрезком [0, 1]).
709. Неверно. Пример. Пусть Е — совершенное нигде не
плотное множество меры —, расположенное на отрезке [0, 1].
Тогда %Е (х) разрывна во всех точках множества Еу т. е. на мно-
множестве положительной меры; следовательно, функция ИЕ (х) не
интегрируема по Риману на [0, 1].
710. Неверно. Пример. Пусть F—совершенное нигде не пло-
плотное множество меры — на отрезке [0, 1]и£ — множество концов
всех его смежных интервалов. Тогда Е — нигде не плотное множе-
множество меры нуль (так как Е — счетное множество). Однако харак-
характеристическая функция %Е (х) разрывна не только в точках множе-
множества Еу но и всюду на F, т. е. на множестве положительной меры.
Следовательно, она не интегрируема по Риману.
711. Интегрируема. Это следует из того, что -все граничные
точки замкнутого множества включаются в это множество. Следо-
Следовательно, мера множества граничных точек множества Е равна
нулю. А характеристическая функция Х£ (я) разрывна только в гра-
граничных точках множества Е.
712. Верно. В этом случае функция Х^ (х) разрывна во всех
точках множества Е и непрерывна во всех точках дополнения
[я, &] \ Е- Следовательно, множество точек разрыва функции
%Е (х) имеет меру нуль. Так как эта функция, кроме того, ограни-
ограничена на [а, Ь], то она интегрируема по Риману на этом отрезке.
713. Функции примеров 486, 488, 489У 502 интегрируемы по Ри-
Риману на отрезке [0, 1]; они все ограничены; функция примера 489
при сп -> 0, кроме того, непрерывна; для функций из примеров
486, 488 и 489 при lim сп =# 0 множество точек разрыва — КаНТО-
рово множество, т. е. множество меры нуль; для функции примера
502 множество точек разрыва есть множество рациональных чисел,
которое также имеет меру нуль.
Функция примера 495 не интегрируема по Риману на [0, 1];
она ограничена, но множество ее точек разрыва — промежуток
]0, 1] — имеет положительную меру.
714. Все эти функции ограничены и измеримы на отрезке [0, 1]
и, следовательно, интегрируемы по Лебегу. Вычислим их инте-
интегралы:
а) для вычисления интеграла от функции из примера 486 разо-
разобьем область интегрирования на два непересекающихся множе-
множества: [0, 1] =D U CDr где D — канторово множество, a CD —
дополнение к нему до всего отрезка [0, 1]. Используя аддитивность
253

интеграла Лебега, получим:
(L) j / (х) dx = (L) J / (x) dx + (L) j / (x) rix.
0 D
CD
Интеграл по множеству D равен нулю, так как mD = 0. На CD
функция постоянна, поэтому
(L) ) / (х) dx = 2 • mCD -
CD
1
Следовательно,
б) Для вычисления интеграла от функции задачи 489 разобьем
область интегрирования на счетную совокупность попарно не пе-
пересекающихся множеств:
[0, 1] =D U X, &х[,и ]аа, &2[ U ... U >л, bn[ U ....
гдеО — канторово множество, а ]ая, Ь„[ — его смежные интервалы,
занумерованные в порядке убывания их длин, т. е. ]alt bx[ — ин-
интервал длины — ,]а2, &2Ги]Яз» &з[ — интервалы длины —, ]а4, &4С» ...
..., jo,, 67[ — интервалы длины — и т. д. При этом интервалы оди-
«з
наковой длины нумеруем слева направо. Используя полную адди-
аддитивность интеграла Лебега, получим:
f(x)dx
Рис. 49
Так как mD === 0, то первый ин-
интеграл равен нулю. Остальные
интегралы вычисляются легко:
на каждом интервале ]а„, bji
функция интегрируема по Рима-
ну и поэтому
{L)
Интегралы Римана в данном
случае равны площадям соответ-
соответствующих треугольников (см.
график функций, рис. 49):
254

1 fc 1
x)J 3
j/ (x) dx = -Ц2., (/?) j/<
2
Co • ^4 О • -1-
2 ' "■ '
«3
f (R)
Суммируя, получим формулу, дающую искомый интеграл Лебега:
(так как функция / (х) интегрируема по Лебегу на отрезке [0, 1],
то ряд, стоящий в правой части равенства, сходится; впрочем, в
этом можно убедиться и непосредственно, исходя из того, что по-
последовательность {сп} сходится и потому ограничена).
В частности, для функции задачи 488 имеем: сп == 1 для всех
п, поэтому здесь
З3
в) Функция / (х) из задачи 495 эквивалентна функции —х2.
Поэтому
(L) f/(x)dx - (L) f (-x2) dx - (R) j(-*V* =-|.
oo Ь
г) Функция / (jc) из задачи 502 эквивалентна функции, тождест-
тождественно равной нулю. Поэтому здесь
1 1
(L) ^f(x)dx = (L) JO .d* = 0.
6 о
715. Разс^ьем область интегрирования на попарно не пересе-.
кающиеся множества Р, Аъ Л2, ..., Ak, ..., где D — канторово
множество, Ak (k = 1, 2, ...) —объединение всех смежных интер-
интервалов &-го ранга [т. е. интервалов длины — j. Используя полную
аддитивность интеграла Лебега, получим:
255
(L) f/(x)dx = (L) f S

Так как mD = 0, то (L) \ f (x) dx = 0. На каждом из остальных
Ь
множеств функция постоянна. Поэтому для каждого номера k имеем:
(L) f f(x)dx = \ • mAk = \ * 2*-1. 1 = —ь.
Следовательно,
(L) [f(x)dx - y—L-=l.
v ; J ' v ; ^ 2 . 3* 4
о k=i
716. Интегрируема по Риману на отрезке [0, 1], так как она ог-
ограничена на этом отрезке [0, 1] и множество ее точек разрыва (мно-
(множество D) имеет меру нуль. Интеграл Римана от этой функции ра-
равен вычисленному выше интегралу Лебега. Следовательно,
717, Эта функция не интегрируема по Риману на отрезке [0, 1]
(она разрывна на множестве положительной меры — ее точками
разрыва являются все точки отрезка [0, 1], кроме точки х = 1).
По Лебегу эта функция интегрируема, так как она измерима и
ограничена. Для вычисления интеграла Лебега от / (х) заменим
подынтегральную функцию эквивалентной ей функцией ц>(х)=х3,
которая интегрируема по Риману на [0, 1]. Получим:
о
о
1 1
о
718, Функция Х£ (х) измерима и ограничена; следовательно,
она интегрируема по Лебегу. Для вычисления ее интеграла, разо-
разобьем [а, Ь] на два множества: Е и СЕ (где СЕ = [a, b~] \ E). Тогда
ь
J ХЕ (x) dx = J %E(x) dx + J ХЕ {x) dx = тЕ + 0 = тЕ.
а Е СЕ
719, Функция / (х) не интегрируема по Риману (она разрывна
на множестве Е положительной меры), но интегрируема по Лебегу.
Вычислим ее интеграл на [0, 1]:
(L) Г / (х) dx = (L) \ f (x) dx -j- \] (L) Г / (х) dx.
О Е n=i an
На множестве Е функция постоянна (равна нулю); поэтому
256

(L) J / (x) dx = 0 • mE = 0. На интервале ]ля, prt[ — функция ин-
интегрируема по Риману; поэтому
dx = (R) р (х) dx = b=^L . L
Итак,
о п==1
оо
Но 21 (Р/г — ал) — зта сумма длин смежных интервалов; она равна
мере множества СЕ (т. е. — J. Следовательно, окончательно
(L)
720. Разобьем Е на два множества: множество А тех точек,
где / (х) ^ с, и множество В тех точек, где 0 ^ / (х) < с. Тогда
(L) j / (x) dx = (L) f / (x) dx + (L) J / (x) dx > (L) J / {x) dx,
E А В А
так как (L) J / (x) dx^O (в силу неотрицательности подыйтеграль-
в
ной функции). На множестве А имеет место / (х) ^ с; мера Л по ус-
условию равна а. Поэтому
(L) I / (х) dx > (L) J / Ос) dx > с • тЛ = с • а.
721. Данная функция почти всюду на [0, 1] равна х3. Следователь-
Следовательно, интегралы Лебега от / (х) и от х3 равны друг Другу; поэтому
(L) j / (x) dx = (L) j x3 dx - (R) J x3 dx = ^p
722. Обозначим смежные интервалы канторова множества D,
расположенные в порядке убывания их длин, через ]ап> рл[. Тогда
(L) f /(x)dx - (L) f/(x) dx + S (L) f /(x)dx.
Интеграл noD равен нулю, так как mD — 0; интегралы же по про-
промежуткам ]ал, Prt [ могут быть вычислены как интегралы Римана;
25/

следовательно, каждый из них равен площади соответствующего
полукруга. Поэтому
(L)
£
8
Но для канторова множества имеем: ра — ах = —, jj2 —а2 = рз —
о
ft /v • ___ Q ~. (К <п# ft
— CXi* — — И Т. Д.
15 34
Поэтому
1
~ 8 \32 З4 Зв" '" ' 32/I "^ "у ~~ 8 7 ~~ 56*
о
723. Разобьем отрезок [0, 1] на два отрезка: 10, —1 и —, 1 ;
L 3 J 3 J
на первом из них функция / (х) эквивалентна функции х3, на вто-
втором — функции х2; поэтому
f/(*)dx= {x3dx+ f
о о i
4 . 34 ^ \ 3 3. 33 / 108
3
724. Множество Е является объединением отрезков —, — ,
[3 2 J
[—,— ,—,— , ... , ,— , ... , а также множества меры
5 4j [7 6J L2/1 + 1 2n\ ¥
нуль, состоящего из двух точек: 0 и 1. На каждом из этих от-
отрезков функция интегрируема по Риману; поэтому
J_ JL L
2 Т 2п
U(x)dx^ \3x2dx+ \3x*dx + ...+ f
Е J JL 'i
5
2з 33^43 53^ ^ Bnf Bn + \f
Этот ряд абсолютно сходится, и его сумма с точностью до 0,01
равна 0,10.
725.
1
1 Т 1
(L) f / (*) dx = (sin nxdx-\- f cos nxdx = 0t
258

У-
г
А2(*)
;■
Z
1x0
Ill
4 2 4
Рис. 50
О 1 2 3 ± 5 6 7 1
в в в в д 8 8
726. Функция ft (x) является характеристической функцией мно-
множества Е1 —
—, 1 , Р2(дг) — характеристической функцией мно-
—, — U —, lL Рз(#) — характер!1стнческой функ-
цией множества *, = ] j.|] U ] f. {] U ]{.{] U ]{, l] и т. д.
( 50) Д |ЗД) р)
жества Е2 =
] ] ] ] ]] ] ]
(см рис. 50). Далее, произведение |ЗДл:) • ру-(л:) является характе-
характеристической функцией множества £/П£;- (см. задачу 558); в част-
частности, (&(я)J есть характеристическая функция множества Et,
т. е. ф1 (х)J = рг (х). Легко видеть, что все множества Еь имеют ме-
меру —, а множества
при 1 ф U
имеют меру — (при i
4
). Поэтому
dx
727. Функции фй (а:) легко выражаются через функции $k (х),
рассмотренные в предыдущей задаче: фй (х) = 2 рй (л:) — 1.
Поэтому
1 1
1
фу (х) d* = J Bft (x) -
= 4 f ft (л:) p; (x) dx — 2 \^(x)dx — 2 f py(x)dx+ f dA; = 0
s i £ £
при г =t^= /. Аналогично получаем:
259

728, Производная <р' (х) измерима на отрезке [а, Ь] (см. задачу
685) и, кроме того, по условию ограничена; следовательно, <р' (х)
интегрируема по Лебегу на отрезке [а, Ь].
729, Не следует. В качестве примера возьмем последова-
последовательность функций {fn (jc)}, построенных в решении задачи 699.
Ясно, что
fn (x) dx з= —■ (см. рис. 48). Так как при п -> + оо
также и k ->■ + оо, то
lim $ f»(*)dx=O-
Л-*-+оо О
Однако {/я (х)} не стремится к нулю ни в одной точке отрезка [0, 1].
730. Этот результат легко получается из теоремы о том, что
с
функция от с (L) J / (x) dx имеет производную для почти всех
а
с £[а, Ь"] и эта производная почти всюду равна значению подын-
подынтегральной функции в точке с. Из тождества
вытекает, что производные от обеих его частей равны друг другу,
т. е; что для почти всех с €[а, Ь] имеет место равенство / (с) = О,
731. Для вычисления интеграла от функции / (х) = 3
/х— 1
построим ее срезку числом / > 1 (рис. 51):
/ при х
I >' * — 1
Вычислим интеграл от срезки:
[/(A:)lrfx= \ tdx+ - ==
11. 2[
41-/U fA_lU2_l.
Чтобы вычислить интеграл от / (а:), на-
надо найти предел интеграла от срезки при
Рис. 51
11.21
260

732. Вычисляя аналогично предыдущему, найдем1.
(L) j" Id* = + «>;(L) J" id* =+оо.
]0. i[ ]6, i[*
Следовательно, обе эти функции не суммируемы на интервале
]0, 1[.
733. Функция / (л:) эквивалентна функции ф (я), равной ^-^
на промежутке ]0, 1] и нулю в точке х — 0; следовательно,
(L) J / (х) dx - (L) I Ф (х) dx -
[0. 1] [0, 1J
= (L) f * dx.
Вычисляя последний интеграл как предел интеграла от срезки
подынте
тельно,
(L)
[Oil]
(а:) на пром
следовательно,
о
подынтегральной функции, находим, что он равен —. Следова-
(L) \ / (х) dx = |.
734. Здесь fix) на промежутке ]0, 1] эквивалентна функции -т= ;
(L) j" f(x)dx=(L) [ -kd.v.
[б. i] ]6, i]^ x
Последний интеграл легко вычисляется (он равен 2). Следова-
Следовательно,
(L) J / (х) dx = 2.
[0,1]
735. Если f {x) ограничена и измерима на множестве Я, то
(f (x))i0 и |/ (#)| также ограничены и измеримы на этом множестве
и, следовательно, интегрируемы. Функция может оказаться
и неограниченной, а неограниченная функция может быть неин-
тегрируемой; например, функция / (л:) = х2 ограничена и изм'ерима
на Е = [0, 1], тогда как функция — не ограничена и не интегриру-
интегрируема на этом отрезке (см. задачу 732).
736. Найдем срезку функции / (л:) числом t > 0:
0 для х £D,
Д^ х € Ек A < к < /I),
для а: £ Мл,
где £"д, — объединение смежных интервалов ранга k (очевидно,
п — целая часть числа tf Mn —объединение
261

всех смежных интервалов рангов больших чем п (мера множества
Мп равна
£ 2*-*
£? 2*-* = 2*\
2d У 3я/'
Вычислим интеграл от срезки;
2\«
Чтобы вычислить интеграл от / (х), надо найти предел интеграла
от срезки при /-> + <». Заметим, что если / -> + оо, то и п->+ оо,
Так как t (-Y ^ (п + 1) • (—) , а предел последнего выражения
при я -> + оо равен нулю, то / • (—] -> 0 при / -^ + оо. Следо-
\ 3/
вательно,
f / (х) dx - lim f [/ (х)\dx = lim
о /">+0° о /1""f0
*-i
Сумма последнего ряда находится следующим образом: обозна-
оо
чим сумму более общего ряда 2 k * Qk~* через ф (q). Этот ряд явля-
является степенным; следовательно, его можно почленно интегрировать
на любом отрезке, лежащем внутри интервала сходимости, в частно-
частности на отрезке [0, q], где | q \ < 1. Поэтому
б
т. е.
я
Ф (я) dq =
1-Я
О
Беря теперь производную от обеих частей равенства, получим:
1
(lrt»' Следовательно»
262

В частности,
Итак, окончательно:
737. Необходимость. Пусть ряд ^k • mEk расходится.
fe=O
Из определения множеств £Л следует, что \f{x)dx^k- mEk.
Ek
Поэтому для любого натурального числа N справедливы нера-
неравенства
j[/(xINdx > ^ j / (*) d* > %k ■ mEk.
E k=0 Ek fe=0
N~{
Так как 2 * * m Ek->- + oo при Af -> + <*>, той J[/ (х)]^Лс-^ 4 °o
при Л/'-^ + оо; следовательно, функция f (x) не суммируема ла
множестве Е.
Достаточность. Пусть ряд V ft • т£"й сходится. Тогда и
Й=0
ряд ^ (^ + \)tnEk сходится, так как он может быть разбит на
два сходящихся ряда: "V й • mEk и ^V /^£"^. Отсюда, очевидно,
следует, что функция g{x) = k-\-\ при x£Ek(k ■-= 0, 1, 2, ...)
суммируема на £ и ее интеграл равен !?(&+ 1)юЕЛ. Тогда из
fe0
неравенств O^/(jc)^g(A:) при д:6£" вытекает, по свойству 5) ин-
интеграла Лебега от неограниченных функций (с. 85), что и f (х)
суммируема на Е.
738. Используя обозначения предыдущей задачи, легко убе-
убедиться в том, что для любого натурального числа k имеет место
равенство
откуда (так как Et П Ej = 0 при i ф '])
k= тЕ„ -f m£ft+1 + tnEk+% + ...;
263

полагая здесь k = 1, 2, 3, ..., имеем:
пгЕ2 ■= тЕ2 + mEs + ... + гпЕп
% = тЕ3 + ... + тЕп
Суммируя почленно эти равенства от первого до iV-ro, где N
какое-нибудь натуральное число, получим:
mEk = тЕг -\- 2тЕ2 -f 3mEs -f ... + Л^
+ N • mEN+l + N • mEN+2 + ...
Если ряд 2 * ' т£* сходится, то 2
мы получаем:
k=l /2=1
оо
т. е. ряд 2 тЕп сходится (как ряд с неотрицательными членами,
частичные суммы которого ограничены постоянным числом).
оо ^
Обратно, если сходится ряд 2 т ^л» то
^k.mEk = ^mEk— |j Л^. тЯл < 2 ^ ^
оо
а значит, сходится и ряд ^ ^ Е
Итак, сходимость ряда ^j m^k равносильна сходимости ряда
оо
2 k • mEk. Но тогда из результатов предыдущей задачи вытекает,
что для суммируемости неотрицательной функции / (а:) необходимо
и достаточно, чтобы ряд 2 m^k сходился.
k
739. Пусть f (х) — ограниченная функция, примем
264

sup / (л:) = В, inf f (x) =A. Разобьем произвольным образом
x'z [0, а\ х i [0, а]
отрезок [Л, В] оси Оу на части: А =у0 <уг < ... < уПтЛ < уп =*
5= 5. Обозначим
*i = Я (Ум < / (*) < У*). <• = Я (Ум < / (**) < У*)-
Ясно, что л: € et тогда и только тогда, когда—х £е\, т. е. е\ = — et.
k k
Следовательно, me'i =—mei (см. задачу 450).
k
Вычислим теперь для этого разбиения нижние суммы Лебега
s и $' для функций f (х) и f (kx) соответственно;
п
с Х^ \i win
п п 1
V ~—" ^^ V /77 Р —— ^^ V • — tTi P —— - о
^>i-\ i j^Ji-\ k i k '
Аналогично получаем, что S' = —S, где S и S; — верхние суммы
k
Лебега для функций f (x) ъ f (kx). Отсюда легко следует, что если
/ (х) суммируема на [0, а], то / (kx) суммируема на |0, — и имеет
место равенство
Если /(л:) не ограничена на [0, а] и неотри цате-
льна, то мы пишем сначала равенство A) для срезок [/ (х)\ и
[/ (*х)]/» а затем переходим к пределу при /-> + оо.
Если же f (х) — знакопеременная функция, не огра-
ограниченная на [0, а], то хМы пишем сначала равенство^) для функций
/, (Х) _(/ (х) при / (х) > 0, Г 0 при / (х) > 0,
А+ w "~1 0 при / (х) < 0 и /- W =[ —/ (х) при / (jc) < 0,
а затем почленно вычитаем из равенства A), написанного для /ц. (л:),
аналогичное равенство для функции /_ (х).
740. Заметим прежде всего, что если функция — cos — не
X X
суммируема на ]0, 1[ при каком-либо £ > 0, то она не суммируема
на этом интервале и при любом другом k > 0 (это легко вытекает
из результата предыдущей задачи).
1 2
Докажем, что —cos несуммируемая функция на ]0,1[.
Если бы она была суммируема на этом интервале, то была бы
суммируема и функция —cos—; но тогда, согласно свойству 5)
X X
265

интеграла Лебега от неограниченных функций (с. 85), была бы
cos2
суммируема и функция — cos2—t потому что
XX
icosl
XX
)
— • cos2 —
XX
2 1 1
А так как cos — = 2 cos2 1 и, значит, — =
XX XX X
= 2» —cos2 cos—, то отсюда вытекала бы суммируемость
X X X X
функции — на ]Q,1[, что неверно (см. задачу 732).
1 2
Полученное противоречие показывает, что функция — cos —
X К
1 k
несуммируема на ]0,1[. Но тогда и любая функция вида — соз —
X X
также несухммируема на ]0, 1[.
741. Пусть %Е (х), %Е (х), ..., хЕ (х) — характеристические
12 п
функции множеств Еъ E2t ..., Еп\ рассмотрим интеграл / от суммы
этих функций:
ь
1 = \ (%Et М + %Е$ W + ... + Хяд {X)) dx =»
а
Ъ Ь
= f 1Е (х) dx + ,„ + f 1E (x) dx = тЕ1 + ... + гпЕп. A)
а а
Заметим теперь, что хЯ| (х) + %Ег (х) + ... + %Е (х) > q в любой
точке л: $ [a, fc] (это следует из того, что любая точка х $ [a, fc]
принадлежит по меньшей мере q из заданных множеств Еь\ поэто-
поэтому по меньшей мере q слагаемых суммы %Е (х) + %Е (х) + ... +
+ ХЕ (х) в точке х равны 1). Поэтому
ь
= q(b—a). B)
Сравнивая A) и B), получаем:
тЕ1 + тЕ2 + ... + тЕп > q (b — а). C)
Если бы для всех i было тЕ1 < q^ ~~^ , то мы бы имели V тЕ1 <
п t=i
<g (b—а), что противоречит неравенству C). Итак, хотя бы для од-
одного из Et имеет место
тЕ. > -^ ^ .
п
742. Обозначим через Ft множество тех точек х из £, где £ — 1 ^
< I / Wl</ (/ = 1, 2, ...>. Тогда Е = Fx U F2 [}... . Ясно, что
функция / (а;) суммируема на множествах Ft. Возьмем какой-ни^
будь ряд Za. с положительными членами и зададим функцию
266

(х) на Е следующим образом:
при x£Ft, если
1 при л;б/7., если
Л>0,
0=1, 2, ...).
Тогда ф (л:) — измеримая функция, принимающая положительные
значения при всех х 6 Е, и
следовательно, функция |/(#)ф(л;)| суммируема на £. Но тогда
и функция / (х) ф (я) суммируема на £ в силу свойства 4) интеграла
Лебега от неограниченных функций (с. 85).
743. Пример. Пусть <р (х) =~ На Е =]0, 1[ и /я (а:) =*
= [ф WL* Последовательность {/я (х)} сходится всюду на Е =
= ]0, 1[ к несуммируемой функции ф-(х) = —.
а:
744. Пример. Пусть Е = [0, 1] и
/. (х) =
п на 0, - ,
О на
ъ ']•
Тогда lim fn (x) = 0 для всех а: ^ ]0, 1]. Однако предел интегралов
отличен от нуля:
lim J f(x)dx =1 ^=0,
n-*+oc [0, 1]
745. Пример. Пусть Е = [0, 1] и
iO в остальных точках отрезка [0,1].
Тогда limfn(x) = 0 всюду на [0,1] и
lim f/«
""+О°[0Л]
Однако не существует суммируемой на [0, 1] функции G (х), кото-
которая превосходила бы все функции /я (х) почти всюду на [0, 1]. Дей-
Действительно, любая функция Q (х), удовлетворяющая неравенству
G (x) ^ \fn (x)\ для всех п и почти всех х, будет удовлетворять
267

неравенству G (х)^— почти всюду на [0, 1]; а такая функция не сум-
суммируема на [0, 1], так как — не суммируема (см. свойство 5 ин-
интеграла Лебега от неограниченных функций, с. 85).
746. Пример. Для п = 2* + /, где k = 0, 1, 2, ..., О <
^ i < 2kr положим
k при ~ ^ х < , ,
0 в остальных точках отрезка [0,1]
(т. е. фл (х) = k • /л (х), где /л (л:) — функции, построенные в ре-
решении задачи 699).
Так же, как в задаче 699, убеждаемся, что последовательность
функций {фл (л:)} сходится по мере на Е =[0, 1] к функции, тож-
тождественно равной нулю (так как пгЕ (фя > а) ^ ~ при любом
а > О), но не сходится к ней в обычном смысле ни в одной точке
этого отрезка. Легко видеть, что
[6, U
Так как из п -> + оо следует k ->■ + °°, то последовательность
этих интегралов сходится к нулю при п -> + оо. Однако не суще-
существует суммируемой функции (и вообще конечнозначной функции)
G (я) такой, что \fn (x)\ ^ G (х) для всех п почти всюду на [0, 1].
747, Пусть сначала функция /(х) неотрицательна на
[а, &]. Надо Доказать, что
ъ ь
lim \f(x)dx = (L) \f(x)dx, (I)
т. е. что разность
(L)$f(x)dx-p(x)dx B)
a t
может быть сделана сколь угодно малой по модулю при t, доста-
достаточно близком к а. Пусть е > 0 — произвольное положительное
ь ь
число, а N — такое число, что (L) J / (х) dx — (L) J[/(*)]dx<
а а N
Преобразуем разность B) следующим образом:
|(L) \f(x)dx-{L) \f(x)dx\= (L) f f(x)dx
a t a
\ C)
26a

под знаком каждого из интегралов в последней части равенства
стоит неотрицательная функция; поэтому здесь знаки модуля мо-
могут быть отброшены. Оценим теперь каждый интеграл в отдель-
отдельности:
(L) j (/ (х) - [/ (*)]„) dx < (L) j (/ (x) - С/ (х)У) dx =
a a
= (L)\f (x) dx - (L) j [/ (*)]„ <**<■§;
Ho N (t—a) <— при 0< t — a< —. Итак для всех /, удовле-
удовлетворяющих неравенству 0</ — а<—, имеем, согласно равен-
равенству C):
\(L)Sf(x)dx-^f(x)dx\ <е,
a t
откуда следует, что
Если теперь суммируемая функция / (л:) принимает на [я, Ь]
значения разных знаков и непрерывна всюду на ]a, ft],
то мы представляем ее в виде
f(x) =/+(*)_/_(*),
где
/+(*)= 1-{\П*)\+Нх)), /-W = »-(l/W|-/W).
Функции /+ (л:) и /_ (х) обе непрерывны на промежутке ]я, ft] и не-
неотрицательны. Поэтому
(I) J / (х) dx = (I) j /+ (x) dx- (I) j /. (x) dx =
s= lim f /+ (a:) d^: — lim Г /. (jc) dx = lim f / (jc) dx.
/->a+oJ /-*^+oJ <->a+oJ
Итак, для любой суммируемой функции / (х), непрерывной всюду
на [a, ft], кроме точки а, несобственный интеграл Коши равен ин-
интегралу Лебега.
26?

748. Пусть
1 l
О при х = О.
Эта функция интегрируема по Коши на [0, 1]. Действительно,
1 1 1
(С) Г-i cos— dx = lim f — cos- dx = lira [z • cosz • (—-) dz =
' 1
!. f cos 2 , С cos г л
5= hm I — dz = \ — dz,
*-*■+(> J Z J 2
а несобственный интеграл f ^^-dz, как известно из анализа, су-
1 г
ществует.
Что же касается интеграла Лебега от функции —cos— на
X X
участке [0, 1], то он не существует (см. задачу 740).

УКАЗАТЕЛЬ ОБОЗНАЧЕНИИ
7 d
0
АаВ
AzdB
A=B
A[}B
{Aa }a<A
Af]A^
I
Лх£
lim An
lim Л„
C£
]-oof6[,
[a, b[
]a, 6]
4
—
—
I
e
D
—
—
oo[ 7
0
0
sup E
inf £
sup / (ЛГ)
inf / (M)
A^B
АфВ
7
£>J
T
2a=C
2C
P (x, y)
(Xn P)
С [a, b]
'A
С [a, b]
V (*0, 8)
V (л:0)
E°
8
—
11
12
—
—
16
—
—
—
17
18—19
19
21
—
E\E
Fr E
В (xOi
Fa
Gb
d \Ar
diam
{*nk)
Ъ (Л,
D (A,
D (A,
mE
mE
f (A)
f—1 (/
f V
A^
со [/,
sgn x
If (x)
b
V/
a
", E(")
£)
B)
E
B)
B)
B)
\\
V
x9, E]
x9)
1
22
23
—
—
35
44
—
45
—'■
52
54
55
57
64
67
72
J (a) * f
'np v**/' 'лев
E(f>a),
b
(R)j
a
b
V Ml*
/+ (*)- /- W
6