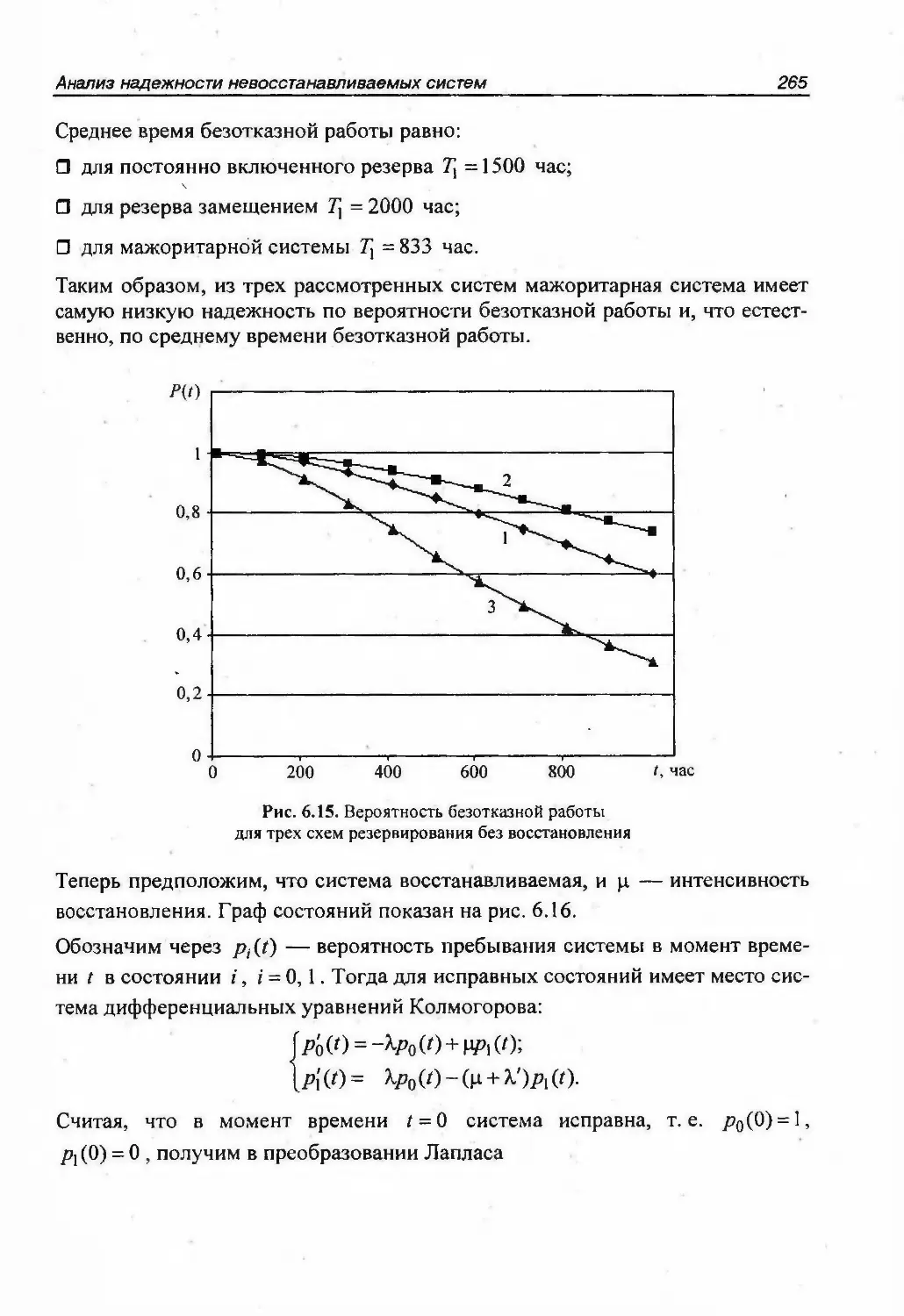
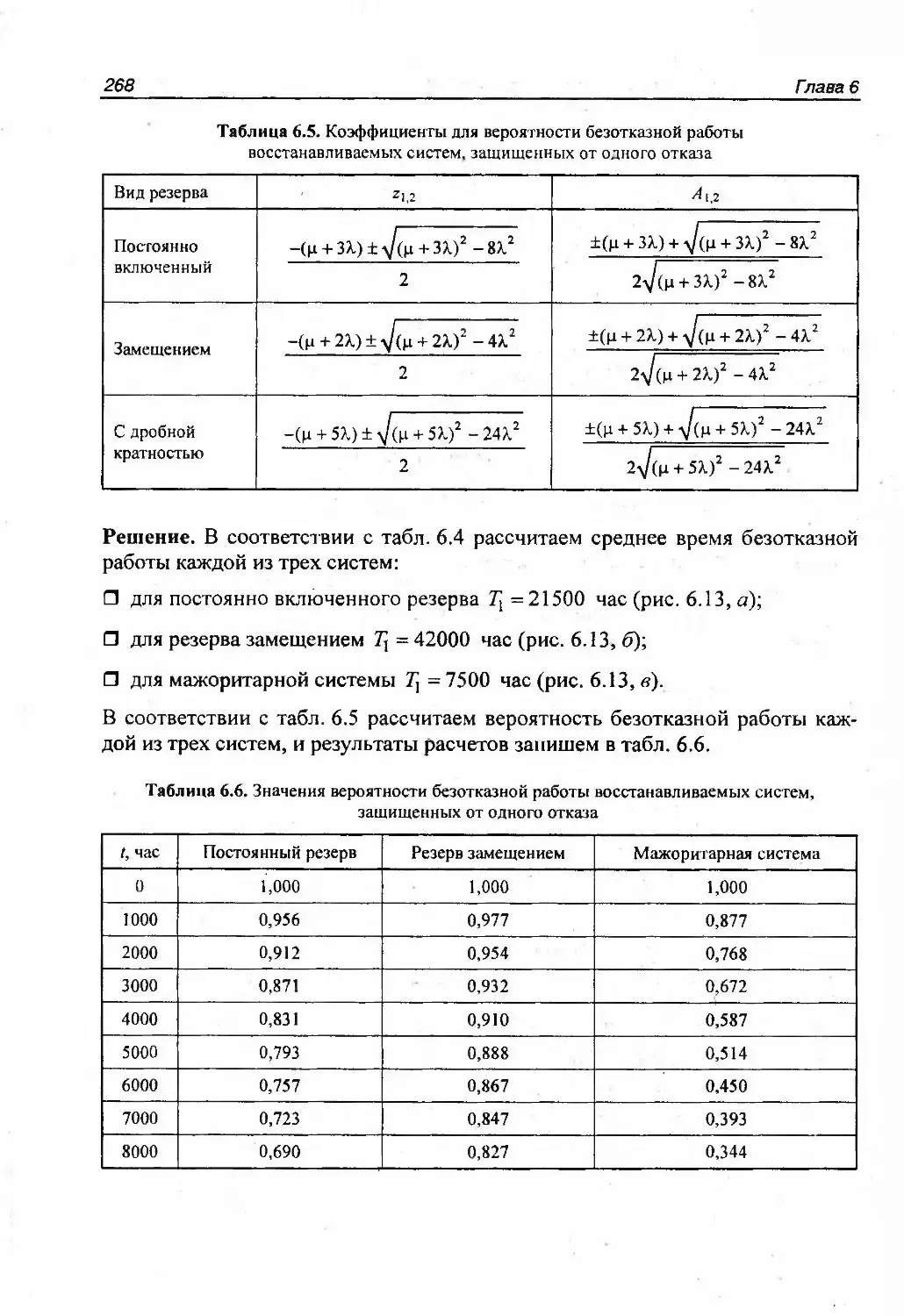
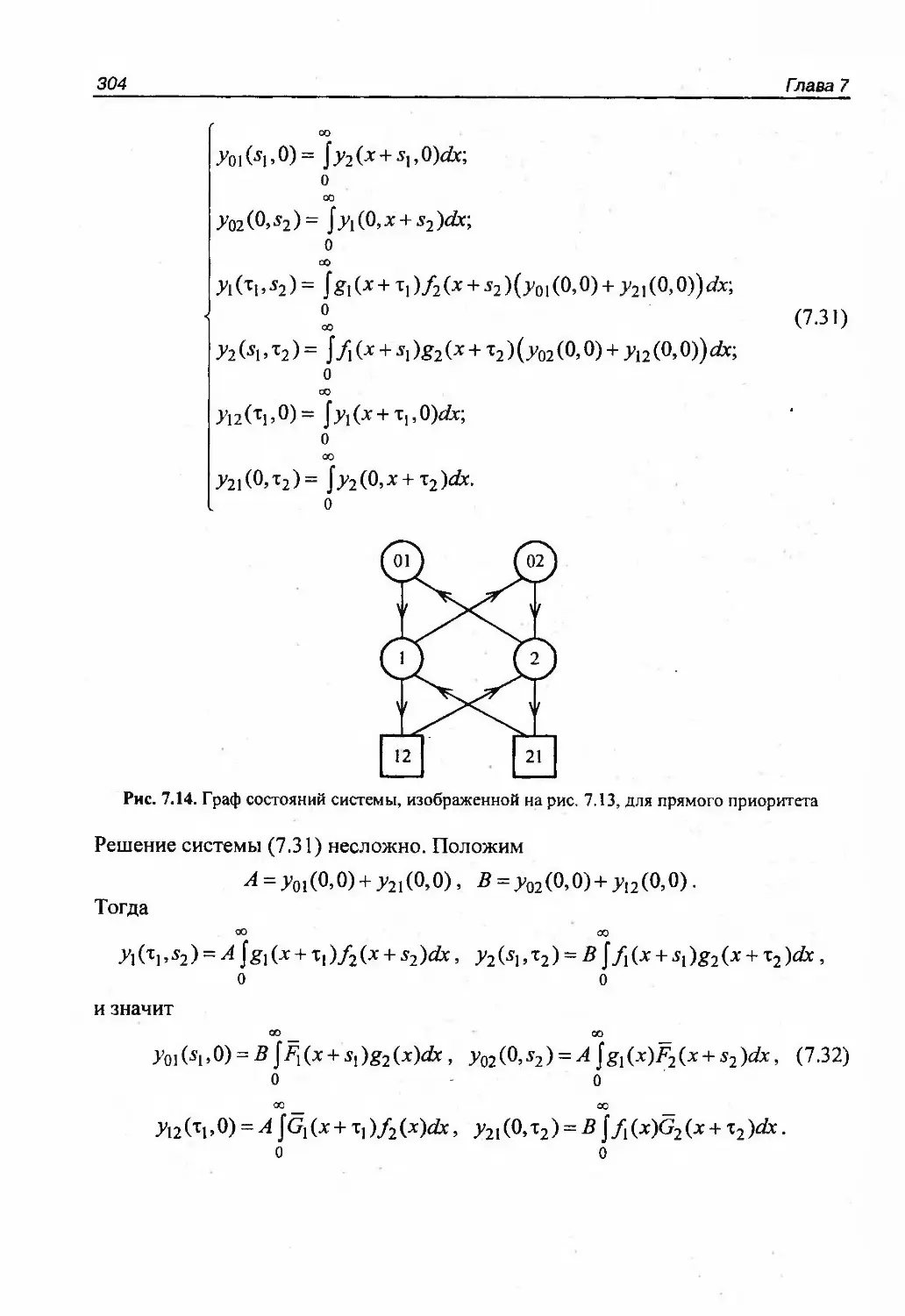
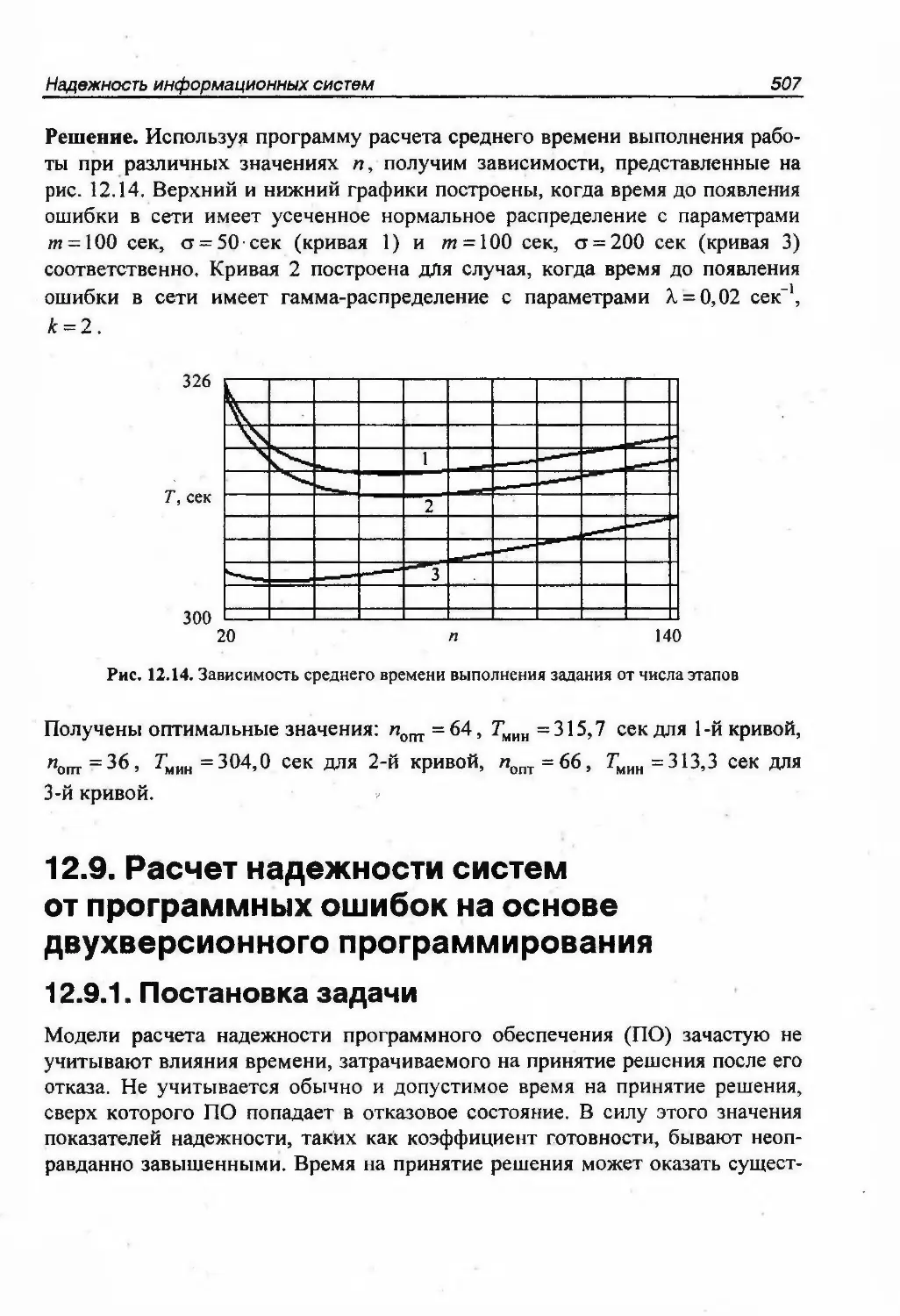
Автор: Половко А.М. Гуров С.В.
Теги: компьютерные технологии вычислительная математика численный анализ учебники и учебные пособия математика статистика математическая статистика
ISBN: 5-94157-541-6
Год: 2006
А. М. Половко, С. В. ГуровОСНОВЫТЕОРИИНАДЕЖНОСТИКритерии и показатели
надежности технических
и информационных системМетоды анализа и синтеза
сложных системСпособы обеспечения
и повышения надежности,
оценка их эффективностиНаучные методы эксплуатации
технических системНадежность и рискАбсолютно надежные системы
А. М. Половко
С. В. ГуровосновыТЕОРИИ
НАДЕЖНОСТИИздание 2-е, переработанное и дополненноеРекомендовано УМО вузов
по университетскому политехническому образованию
в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по направлению подготовки 230100 (654600)
«Информатика и вычислительная техника»Санкт-Петербург«БХВ-Петербург»2006
УДК 681.3.06+519.6(075.8)
ББК 32.973я73
П52Половко А. М., Гуров С. В.П52 Основы теории надежности. — 2-е изд., перераб. и доп. — СПб.:
БХВ-Петербург, 2006. — 704 с.: ил.ISBN 5-94157-541-6Теория надежности излагается как наука и учебная дисциплина. Содержатся
критерии, методы анализа и синтеза технических и информационных систем,
методы обеспечения и повышения их надежности, научные методы эксплуата¬
ции. Рассматриваются невосстанавливаемые и восстанавливаемые, нерезерви¬
рованные и резервированные системы длительного и короткого времени суще¬
ствования. Описаны методы анализа надежности технических и информацион¬
ных систем при произвольных законах распределения времени отказа и
восстановления. Предлагается ряд методов, неизвестных ранее в теории надеж¬
ности. Практическая реализация методов приводится в пособии "Основы теории
надежности. Практикум", дополняющем данную книгу.Для ученых, инженеров, аспирантов и студентов технических вузовУДК 681.3.06+519.6(075.8)
ББК 32.973я73Группа подготовки издания:Главный редактор Екатерина КондуковаЗам. главного редактора Людмила ЕремеевскаяЗав. редакцией Григорий ДобинРедактор Нина СедыхКомпьютерная верстка Ольги СергиенкоКорректор Зинаида ДмитриеваДизайн обложки Инны ТачинойЗав. производством Николай ТверскихРецензенты:Смагин В. А., заслуженный деятель науки РФ, д. т. н.,
профессор кафедры "Эксплуатация автоматизированных систем управления"
Военно-космической академии имени А. Ф. Можайского
Богатырев В. А., д. т. н., профессор кафедры вычислительной техники Санкт-Петербургского
государственного университета информационных технологий, механики и оптики
Андреев А. М., к. т. н., доцент кафедры "Компьютерные системы и сети”МГТУ им. Н. Э. БауманаЛицензия ИД Г* 02429 от 24.07.00. Подписано в печать 15.02.06.
Формат 70х 100’/,9. Печать офсетная. Уел. Печ. л. 56,76.Тираж 3000 экз. Заказ Nt 3094
"БХВ-Петербург", 194354, Санкт-Петербург, ул. Есенина, 55.Санитарно-эпидемиологическое заключение на продукцию
Ng 77.99.02.953.Д.006421.11.04 от 11.11.2004 г. выдано Федеральной службой
по надзору в сфере защиты прав потребителей и благополучия человека.Отпечатано с готовых диапозитивов
в ГУП "Типография "Наука"199034, Санкт-Петербург, 9 линия, 12ISBN 5-94157-541-6О Половко А. М., Гуров С. В., 2006О Оформление, издательство "БХВ-Петербург”. 2006
ОГЛАВЛЕНИЕВВЕДЕНИЕ 13Надежность техники и ее теория 13Особенности книги 14Для кого эта книга..... 15ГЛАВА 1. ТЕОРИЯ НАДЕЖНОСТИ И ЕЕ ФУНДАМЕНТАЛЬНЫЕ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 171.1. Теория надежности как наука и научная дисциплина 171.2. Определение понятия "надежность" 191.3. Понятие "отказ". Классификация и характеристики отказов 201.4. Надежность и сохраняемость 221.5. Терминология теории надежности 221.6. Классификация технических систем ' 26ГЛАВА 2. КРИТЕРИИ НАДЕЖНОСТИ. ЗАКОНЫРАСПРЕДЕЛЕНИЯ ВРЕМЕНИ ДО ОТКАЗА 292.1. Что такое критерий и показатель надежности 292.2. Критерии надежности невосстанавливаемых систем 302.2.1. Вероятность безотказной работы 312.2.2. Плотность распределения времени безотказной работы (частота отказов).... 322.2.3. Интенсивность отказов 322.2.4. Среднее время безотказной работы 342.3. Критерии надежности восстанавливаемых систем 372.3.1. Среднее время работы между отказами и среднее время восстановления 382.3.2. Параметр потока отказов 382.3.3^ Функция готовности и функция простоя .....402.4. Законы распределения времени до отказа, наиболее часто используемыев теории надежности л 412.5. Преобразование Лапласа .....502.6. Специальные показатели надежности элементов и систем 522.6.1. Показатели надежности элемента 522.6.2. Стационарные значения показателей надежности элемента 612.6.3. Показатели надежности невосстанавливаемой и восстанавливаемой
техники 632.6.4. Основное уравнение функционирования системы 64
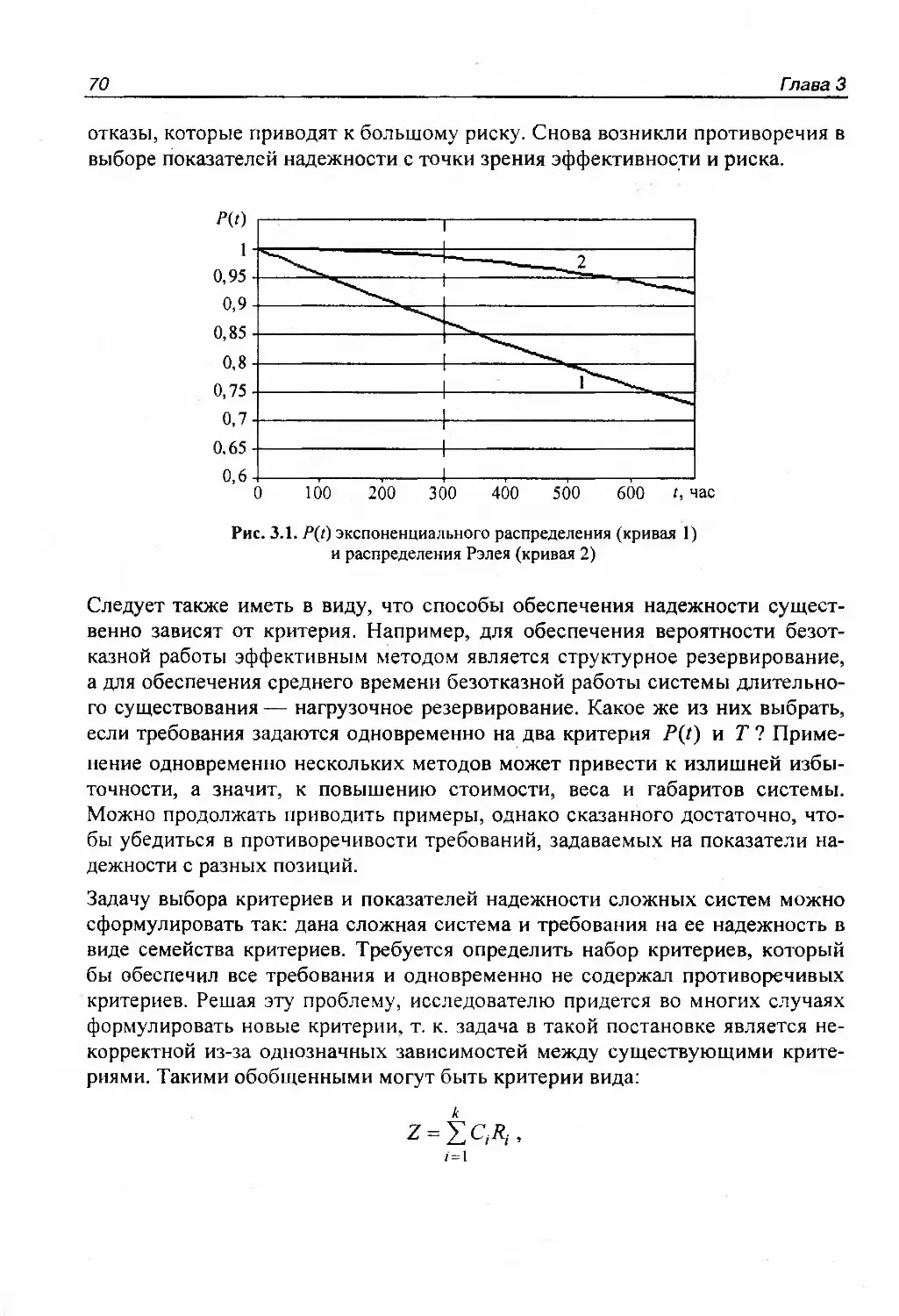
ОглавлениеГЛАВА 3. ПРОБЛЕМЫ АНАЛИЗА НАДЕЖНОСТИСЛОЖНЫХ ТЕХНИЧЕСКИХ СИСТЕМ 683.1. Научное обоснование критериев и показателей надежности 693.2. Разработка моделей функционирования сложной системы 713.3. Методы анализа надежности технических систем 733.3.1. Обзор существующих методов расчета надежности сложных систем 733.3.2. Причины неэкспоненциальности случайных параметров, отказов и
восстановлений технических систем 773.3.3. Зависимость показателей надежности от законов распределения и
дисциплины восстановления элементов 803.3.4. Критичное влияние произвольных распределений отказов и
восстановлений на нестационарные показатели надежности 843.3.5. Методы и проблемы расчета надежности систем с большим числом
состояний . 883.3.6. Проблемы расчета надежности реконфигурируемых систем 893.4. Проблемы создания высоконадежных систем 913.4.1. Основная проблема надежности технических систем 913.4.2. Технические проблемы обеспечения надежности сложных систем 933.5. Краткие замечания, касающиеся проблем анализа надежности систем 96ГЛАВА 4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ФУНКЦИОНИРОВАНИЯ ТЕХНИЧЕСКИХ ЭЛЕМЕНТОВ
И СИСТЕМ В СМЫСЛЕ ИХ НАДЕЖНОСТИ 984.1. Общая модель надежности технического элемента 984.2. Общая модель надежности систем в терминах интегральных уравнений 1034.2.1. Основные обозначения и допущения 1034.2.2. Матрица состояний 1044.2.3. Матрица переходов 1064.2.4. Выражения для вероятностей состояний и параметров переходов между
состояниями : 1104.2.5. Правило составления системы интегральных уравнений 1144.3. Общая модель функционирования системы в смысле надежности в терминах
дифференциальных уравнений в частных производных 1164.4. Модель надежности стационарного режима ' 1194.5. Модели надежности невосстанавливаемых систем 1224.6. Модели надежности систем при экспоненциальных законах распределения
отказов и восстановлений элементов 125ГЛАВА 5. МЕТОДЫ АНАЛИЗА НАДЕЖНОСТИТЕХНИЧЕСКИХ СИСТЕМ 1325.1. Способы описания функционирования технических систем ^смысле
их надежности 1325.1.1. Структурная схема системы 1335.1.2. Функции алгебры логики 1345.1.3. Матрица состояний системы. 136
Оглавление55.1.4. Граф состояний системы 1365.1.5. Формализованный способ построения графа состояний системы 1415.1.6. Описание функционирования системы с помощью уравненийтипа
массового обслуживания 1455.1.7. Описание функционирования системы с помощью интегральных
уравнений 1495.2. Методы анализа надежности технических систем, основанныена применении теорем теории вероятностей 1545.2.1. Метод перебора гипотез 1545.2.2. Метод, основанный на применении классических теорем теории
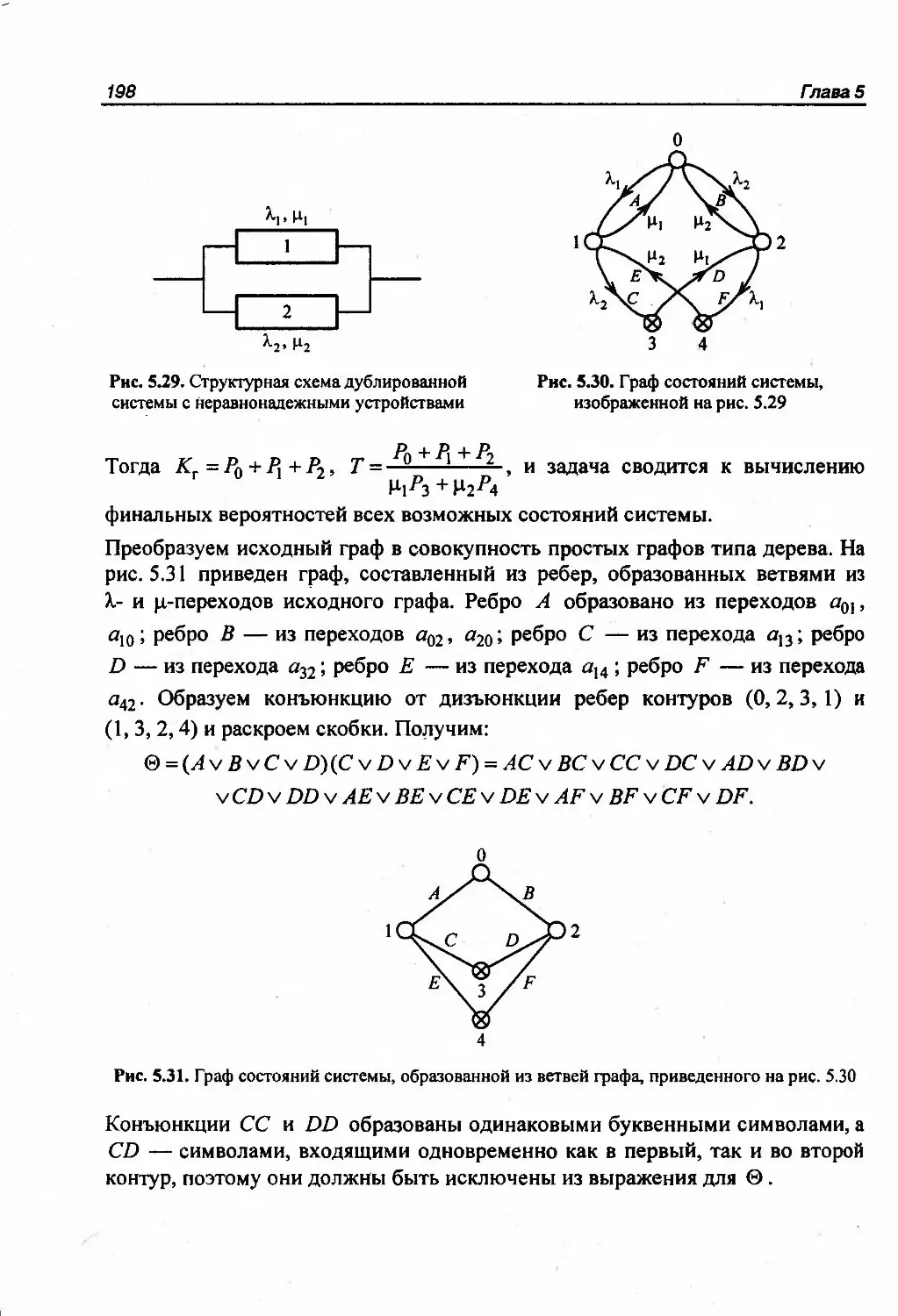
вероятностей 1555.2.3. Метод минимальных путей и минимальных сечений 1585.3. Логико-вероятностные методы анализа надежности 1615.3.1. Сущность логико-вероятностных методов 1615.3.2. Метод кратчайших путей и минимальных сечений л 1645.3.3. Алгоритм разрезания 1675.3.4. Алгоритм ортогонализации 1705.4. Топологические методы анализа надежности 1735.4.1. Определение вероятностей состояний системы 1745.4.2. Определение финальных вероятностей состояний системы 1815.4.3. Определение вероятности попадания системы в г'-е состояниев течение времени t 1845.4.4. Определение количественных характеристик надежности по графу
состояний 1865.4.5. Определение количественных характеристик надежности систем,
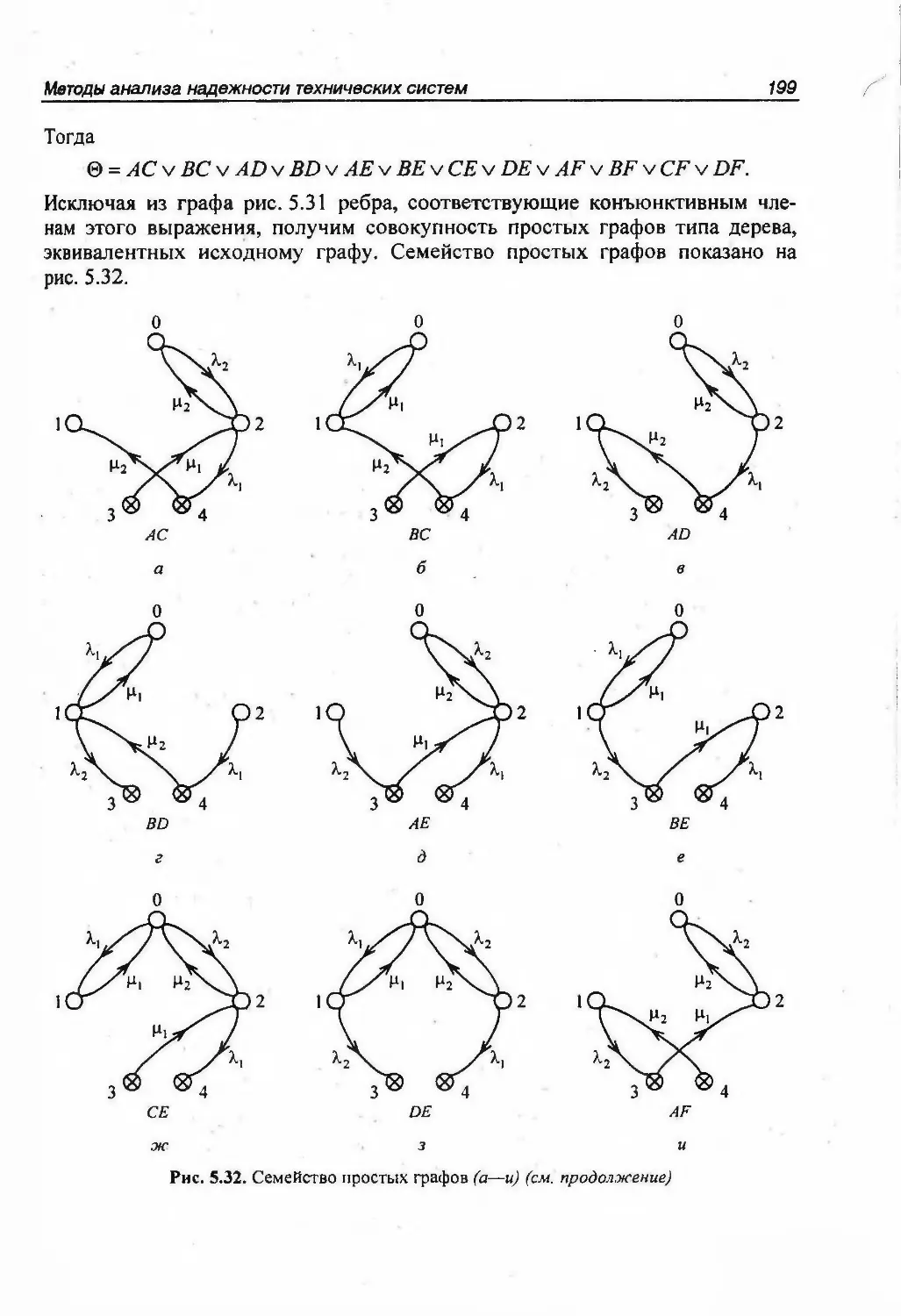
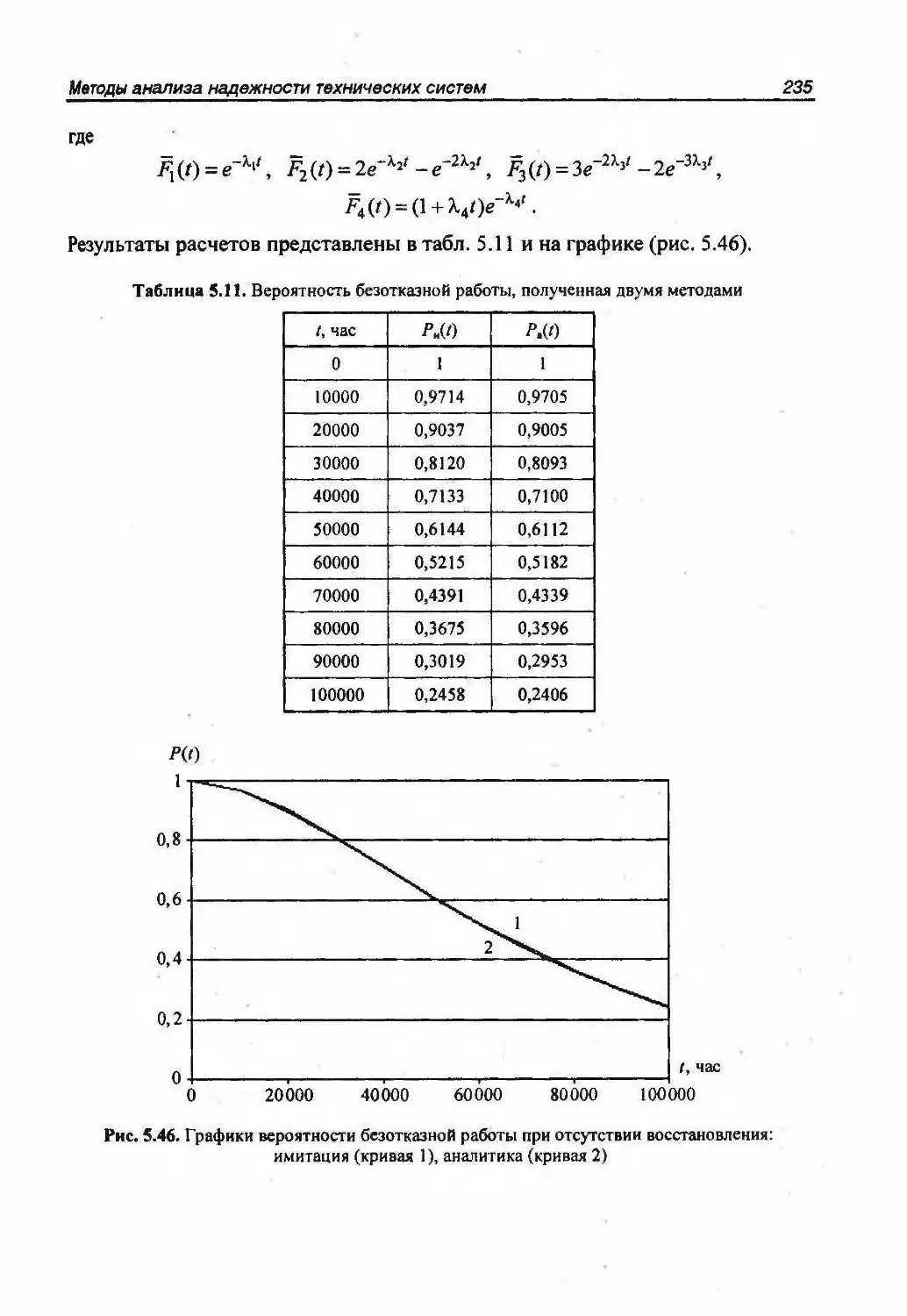
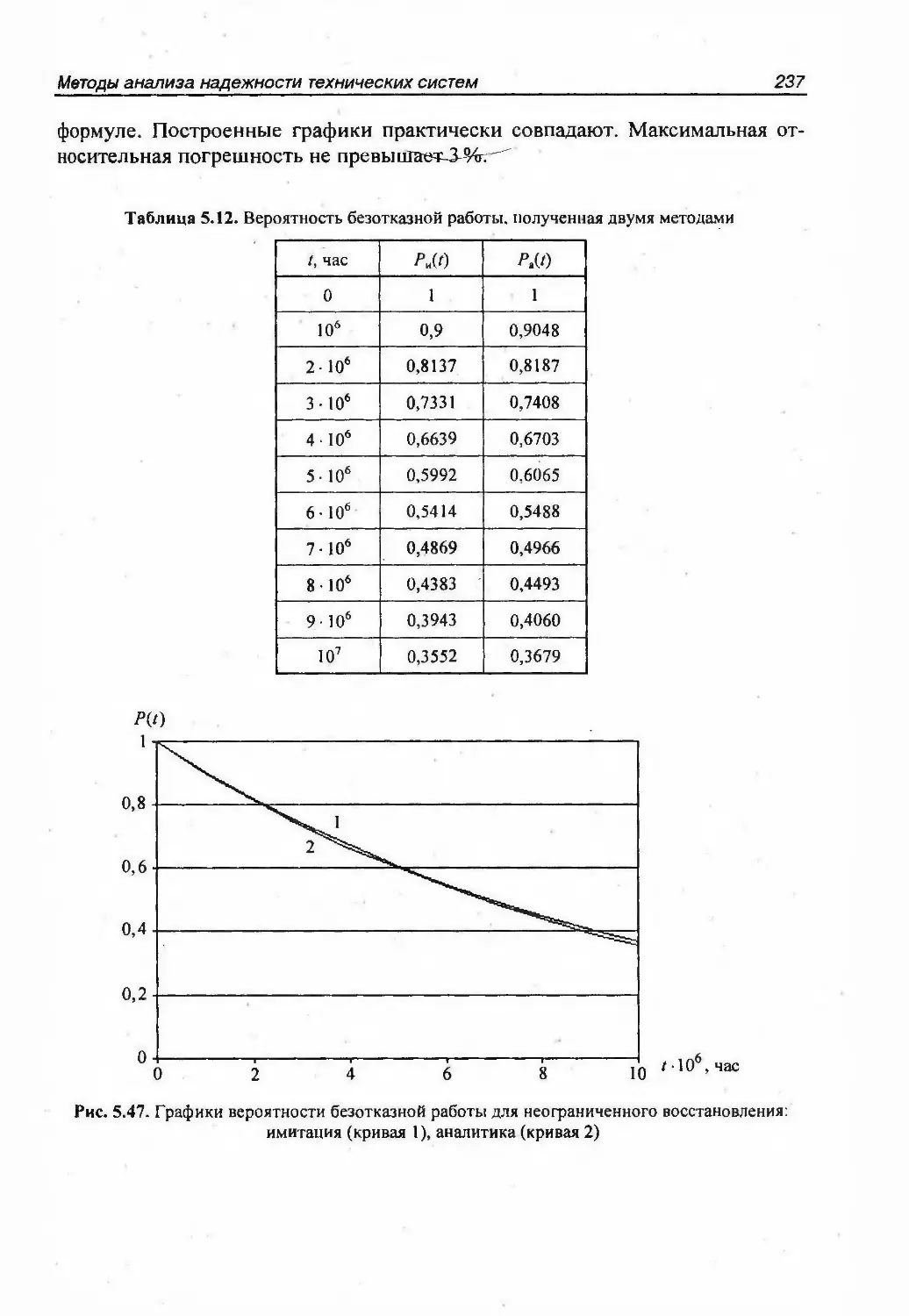
описываемых многосвязными графами 195Разложение графа на деревья 195Преобразование сложного многосвязного графа в совокупностьпростых графов 195Вычисление вероятностей состояний, соответствующих узлам простыхграфов 196Вычисление вероятностей состояний исходной системы 197Непосредственное вычисление стационарных показателей надежности 2015.5. Методы, основанные на теории марковских процессов 2065.5.1. Однородный марковский процесс 2065.5.2. Инженерная методика расчета показателей надежности 2105.5.3. Пример расчета показателей надежности методом марковскихпроцессов 2135.5.4. Особенности анализа надежности систем при законах распределения
отказов и восстановлений, отличных от экспоненциального 2165.6. Метод статистического моделирования „ 2175.6.1. Сущность и обоснование метода статистического моделирования 2185.6.2. Разыгрывание случайных величин 220Разыгрывание дискретной случайной величины 222Разыгрывание непрерывной случайной величины 223
6ОглавлениеРазыгрывание равномерно распределенной случайной величины
на многомерном симплексе..., 2265.6.3. Сравнение метода статистического моделирования с аналитическимиметодами расчета надежности 228ГЛАВА 6. АНАЛИЗ НАДЕЖНОСТИ ^ВОССТАНАВЛИВАЕМЫХ
СИСТЕМ 2416.1. Надежность нерезервированной системы 2416.2. Надежность простейших резервированных систем 2446.2.1. Постоянно включенный резерв 2446.2.2. Резервирование с дробной кратностью 2476.2.3. Резерв замещением 2516.2.4. Скользящее резервирование 2536.3. Надежность систем при общем и раздельном резервировании 2566.4. Надежность резервированных систем, защищенных от одного отказа 261ГЛАВА 7. АНАЛИЗ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ
СИСТЕМ 2727.1. Анализ надежности восстанавливаемых систем с основным соединением
элементов . 2727.2. Расчет надежности восстанавливаемых систем с основным соединением
элементов и произвольных законах распределения отказов и восстановлений 2767.2.1. Стационарные показатели надежности неизбыточных систем v 2767.2.2. Нестационарные показатели надежности неизбыточных систем 2797.3. Расчет резервированных восстанавливаемых систем при экспоненциальных
законах распределения отказов и восстановлений 2867.3.1. Общее постоянное резервирование 2867.3.2. Общее резервирование замещением 2897.4. Расчет резервированных восстанавливаемых систем при произвольных
законах распределения отказов и восстановлений 1 2937.4.1. Дублированная система с постоянно включенным резервом 293Прямой приоритет 294Обратный приоритет 298Назначенный приоритет 299Неограниченное восстановление .'...3017.4.2. Дублированная система с ненагруженным резервом 303Прямой приоритет 303Обратный приоритет 306Назначенный приоритет 307Неограниченное восстановление 308ГЛАВА 8. АНАЛИЗ НАДЕЖНОСТИ СЛОЖНЫХ СИСТЕМ
С УЧЕТОМ ИХ ФИЗИЧЕСКОЙ РЕАЛИЗУЕМОСТИ 3108.1. Приближенные методы анализа надежности 3108.2. Описание функционирования системы графом типа дерева 313
Оглавление78.3. Анализ надежности восстанавливаемой системы по усеченномуграфу состояний 3188.4. Метод эквивалентных схем 3228.5. Системы с дробной кратностью резервирования 3258.5.1. Системы т/п с нагруженным резервом и неограниченным
восстановлением 328Модель функционирования системы 329Расчетные соотношения для характеристик надежности 332Исследование конкретных схем 3338.5.2. Системы т/п с нагруженным и ненагруженным резервоми произвольным восстановлением 336Модели функционирования для нагруженного и ненагруженного резерва(идентичные элементы) 336Приближенное решение и оценка погрешности 338Исследование конкретных схем 339Свойства систем с дробной кратностью резервирования 3418.5.3. Надежность систем т/п при отказе группы смежных элементов 342Модель функционирования для системы 1/4 343Быстрый алгоритм расчета функции готовности 3468.6. Системы с автоматом контроля и коммутации 3498.6.1. Невосстанавливаемая система с абсолютно надежным переключателем 3508.6.2. Невосстанавливаемая система с ненадежным переключателем 3558.6.3. Анализ восстанавливаемой системы с переключателем 3578.7. Системы с последействием отказов 3618.7.1. Система с переменными законами распределения времени безотказной
работы 3618.7.2. Дублированная система с последействием отказов 3638.7.3. Сравнительный анализ надежности систем с последействием при
отсутствии и наличии "памяти" 3658.7.4. Обобщение результатов на случай любого числа элементов 3668.8. Анализ надежности системы с учетом неодновременности работы.ее
элементов 367ГЛАВА 9. МЕТОДЫ ОБЕСПЕЧЕНИЯ И ПОВЫШЕНИЯ
НАДЕЖНОСТИ ТЕХНИКИ 3719.1. Классификация методов 3719.2. Методы обеспечения и повышения надежности техникив процессе проектирования ; 3739.3. Обеспечение надежности техники в процессе производства и эксплуатации 3779.4. Свойства структурного резервирования 3779.4.1. Выигрыш надежности по вероятности отказа 3789.4.2. Выигрыш надежности по среднему времени безотказной работы 3799.4.3. Выигрыш надежности по интенсивности отказов 3799.4.4. Выигрыш надежности по коэффициенту простоя 3819.4.5. Выигрыш надежности по наработке на отказ 382
8Оглавление9.5. Инвариантность надежности одного класса технических систем к законам
распределения отказов и восстановлений 3829.5.1. Математическое описание системы . ,3839.5.2. Оценка надежности восстанавливаемых мажоритарных систем
последовательно-параллельной структуры 3859.6. Влияние резервирования на интенсивность отказов системы 3889.7. Эффективность восстановления при различных законах распределения 3939.8. Сравнение надежности системы при общем и раздельном резервированиях 3969.9. Сравнительный анализ нагрузочного и структурного резервирований 3999.10. Надежность систем с временной избыточностью 4029.10.1. Описание функционирования системы с произвольным распределением
временной избыточности в терминах интегральных уравнений 4029.10.2. Распределение суммарных наработок 4099.10.3. Обесценивающие отказы 4119.11. Определение функции оперативной готовности системы 4129.12. Надежность систем из элементов с несколькими состояниями 415ГЛАВА 10. НАУЧНЫЕ МЕТОДЫ ЭКСПЛУАТАЦИИ ТЕХНИКИ 41710.1. Два вида эксплуатации техники. 41710.2. Способы поддержания надежности техники в процессе ее технической
эксплуатации 42110.2.1. Свойства и показатели критичности элементов системы 42110.2.2. Анализ данных по критичным элементам 42310.2.3. Планирование восстановления элементов системы 42410.3. Профилактика и ее эффективность 42510.4. Анализ надежности техники при наличии системы контроля 43310.4.1. Надежность аппаратуры контроля с двумя типами отказов 43310.4.2. Модель надежности системы с периодическим контролем 43810.4.3. Надежность системы с контролем во время хранения 44010.5. Оптимизация резервных элементов и ремонтных органов 44110.5.1. Проблемы оптимального резервирования и ремонта 44110.5.2. Математическая модель и решение 44510.5.3. Численные результаты 448ГЛАВА И. ОЦЕНКА НАДЕЖНОСТИ ТЕХНИКИ ПО ОПЫТНЫМ
ДАННЫМ И ДАННЫМ ЭКСПЛУАТАЦИИ 45311.1. Оценка надежности техники по опытным данным 45311.2. Сбор и обработка данных об отказах техники в процессе эксплуатации 45511.3. Методика анализа надежности систем и их элементовпо данным эксплуатации 456ГЛАВА 12. НАДЕЖНОСТЬ ИНФОРМАЦИОННЫХ СИСТЕМ 46412.1. Фундаментальные понятия теории надежности информационных систем 46412.2. Критерии надежности информационных систем 466
Оглавление912.3. Методы анализа надежности информационных систем 46712.4. Анализ многоканальной системы массового обслуживания с отказами 46812.5. Готовность многоканальной системы массового обслуживания 47912.6. Надежность диспетчерского пункта системы управлениявоздушным движением : 48312.7. Методы расчета моментов распределений в задачах надежности 48612.7.1. Поглощающие состояния отказа 48812.7.2. Отражающие состояния отказа 48912.7.3. Алгоритмы определения моментов распределений для процесса"гибели и размножения" 4931217.4. Численная оценка временных показателей надежности процессов
"гибели и размножения" 49712.8. Распределение работ по этапам в дискретных системах 49912.8.1. Постановка задачи 49912.8.2. Описание системы графом состояний 50112.8.3. Математическая модель 50212.8.4. Распределение времени выполнения работы 50312.8.5. Среднее время выполнения работы 50512.9. Расчет надежности систем от программных ошибок на основе
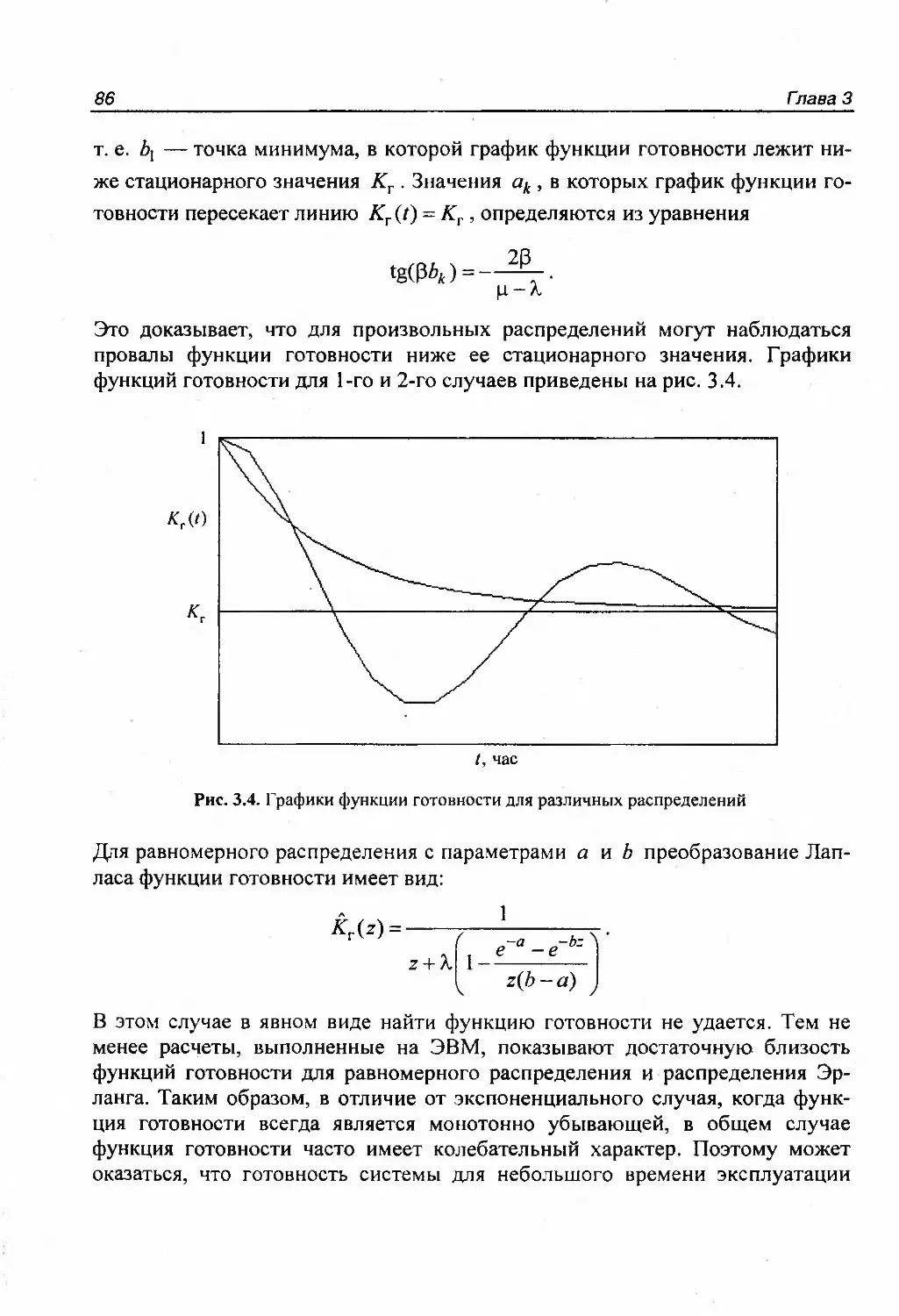
двухверсионного программирования 50712.9.1. Постановка задачи ; 50712.9.2. Модель функционирования вычислительной системы с двухверсионным
прикладным программным обеспечением 50812.9.3. Алгоритм решения и показатели надежности ПО 51112.9.4. Численные результаты 51712.10. Анализ надежности многофункциональных систем 51912.10.1. Формулировка задачи 51912.10.2. Описание работы двухфункциональной системы 52212.10.3. Решение системы уравнений и оценка коэффициента готовности 52512.10.4. Численный пример 52712.11. Анализ эффективности систем управления при многофазном режиме
функционирования - 52912.11.1. Модель функционирования системы 53012.11.2. Критерий эффективности 53112.11.3. Описание функционирования системы в нормальном режиме
эксплуатации 53312.11.4. Описание модели функционирования системы при возникновении
аварийной ситуации ., 53612.11.5. Оценка готовности объекта 54112.11.6. Вопросы технического обслуживания 54412.11.7. Модель функционирования системы на одном периоде жизненного
цикла 54512.11.8. Анализ системы управления в течение всего жизненного цикла 54812.11.9. Установление оптимальных сроков проведения профилактическихработ и длительности жизненного цикла 549
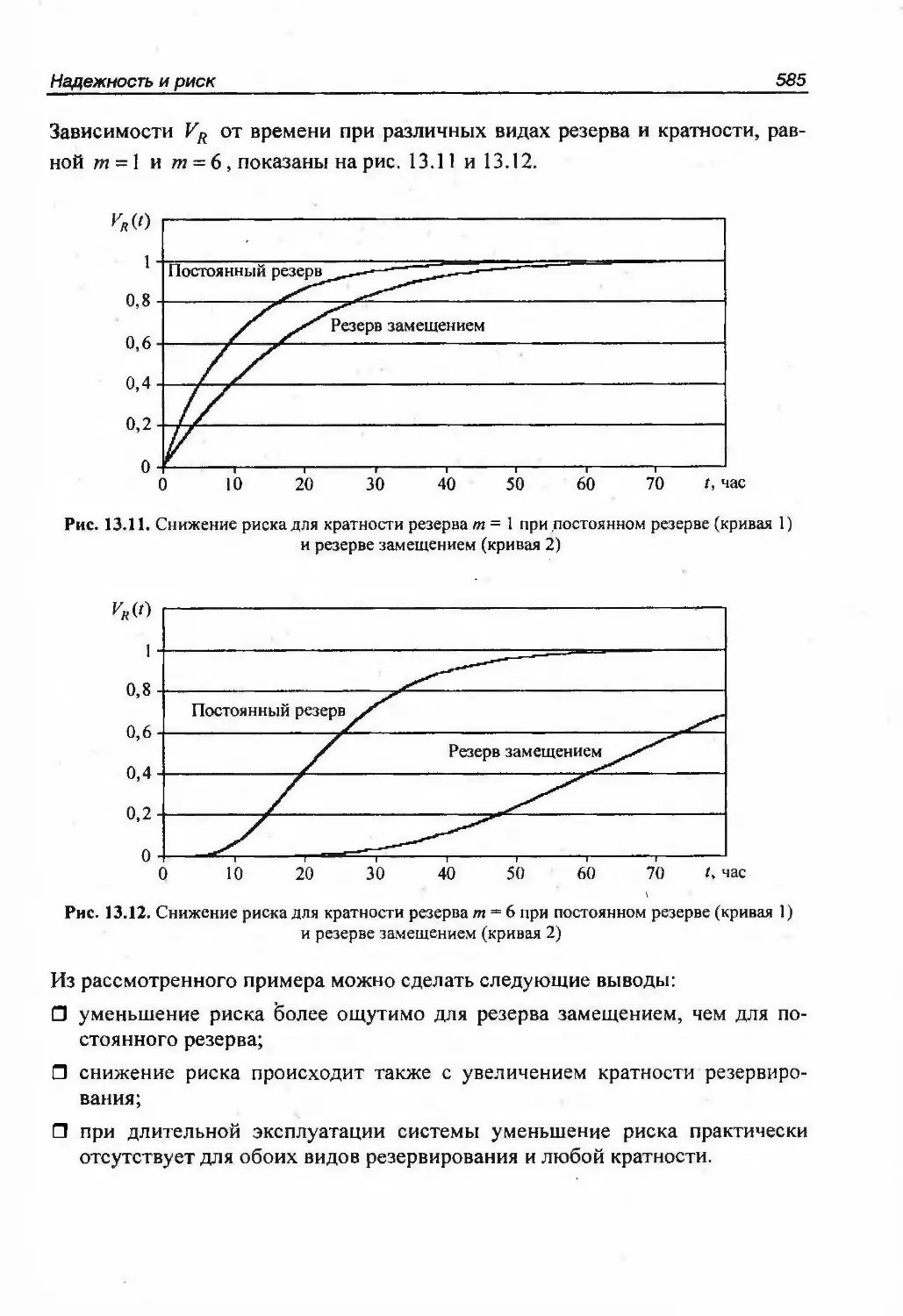
10ОглавлениеГЛАВА 13. НАДЕЖНОСТЬ И РИСК 55313.1. Определение понятия "риск" 55313.2. Оценка техногенного риска 55413.2.1. Риск системы с двумя состояниями 55413.2.2. Формула техногенного риска 55713.2.3. Кумулятивный техногенный риск 56113.2.4. Непосредственное вычисление техногенного риска 562Нерезервированная неремонтируемая система 1 563Нерезервированная ремонтируемая система : 56513.2.5. Асимптотическое поведение функции риска 572Неремонтируемая система 572Ремонтируемая система 57413.3. Полезность системы 57613.4. Зависимость риска от частоты неблагоприятных событий 58013.5. Методы снижения риска 583ГЛАВА 14. АБСОЛЮТНО НАДЕЖНЫЕ СИСТЕМЫ 58814.1. Понятие "абсолютно надежная система" 58814.2. Качественные критерии надежности '. 59514.2.1. Кратность резервирования системы при общем резервированиис постоянно включенным резервом 59814.2.2. Кратность резервирования абсолютно надежной системы при общем
резервировании замещением 59814.3. Способы создания абсолютно надежных систем 59914.3.1. Разработка качественных критериев и их выбор из условий реализации ... 60014.3.2. Разработка структурной схемы системы 60014.4. Анализ абсолютно надежных технических систем .". 601ГЛАВА 15. ГРАНИЧНЫЕ ОЦЕНКИ НАДЕЖНОСТИ СИСТЕМ
В УСЛОВИЯХ НЕПОЛНОЙ ИНФОРМАЦИИ О ЗАКОНАХ
РАСПРЕДЕЛЕНИЯ ОТКАЗОВ ЭЛЕМЕНТОВ 60515.1. Класс непараметрических распределений H(r, s) 60615.2. Свойства распределений из класса H(r, s) ^..60915.3. Принадлежность классу H[r, s) некоторых параметрических распределений... 61415.4. Двусторонние ограничения для показателей надежностиневосстанавливаемых систем в классе H(r, s) 61615.4.1. Интервальные оценки среднего времени безотказной работы
нерезервированной и резервированной систем 61615.4.2. Интервальные оценки среднего времени безотказной работы для системс монотонной структурой и элементами из класса H(r, s) 61815.5. Граничные оценки среднего времени безотказной работы монотонных
систем для независимых и однотипных по надежности элементовс функциями распределения из класса H{r, s) 62115.5.1. Интервальные оценки среднего времени безотказной работы 62115.5.2. Нерезервированная система 623
Оглавление1115.5.3. Резервированная система с постоянно включенным резервом 62415.5.4. Мажоритарная система т/п 62515.5.5. Мостиковая система 62615.5.6. Последовательно-параллельная система 62715.6. Некоторые экстремальные задачи при оценке показателей надежностисистем 62815.7. Интервальные средние наработки на отказ восстанавливаемой
дублированной системы 63215.7.1. Резерв замещением : 63215.7.2. Постоянно включенный резерв 63715.7.3. Сравнительная характеристика интервальных средних наработокна отказ дублированной системы с различными типами резервирования 63915.7.4. Интервальные оценки в классе систем с быстрым восстановлением
элементов 64215.8. Функция готовности элемента при неполной информации о законах
распределения 64615.9. Двусторонние оценки коэффициента оперативной готовности в классе
функций ограниченного роста Н{г, 5) ; 64815.10. Определение параметров г и s по статистическим данным об отказах 650ГЛАВА 16. АНАЛИЗ НАДЕЖНОСТИ ПРОГРАММНОГО
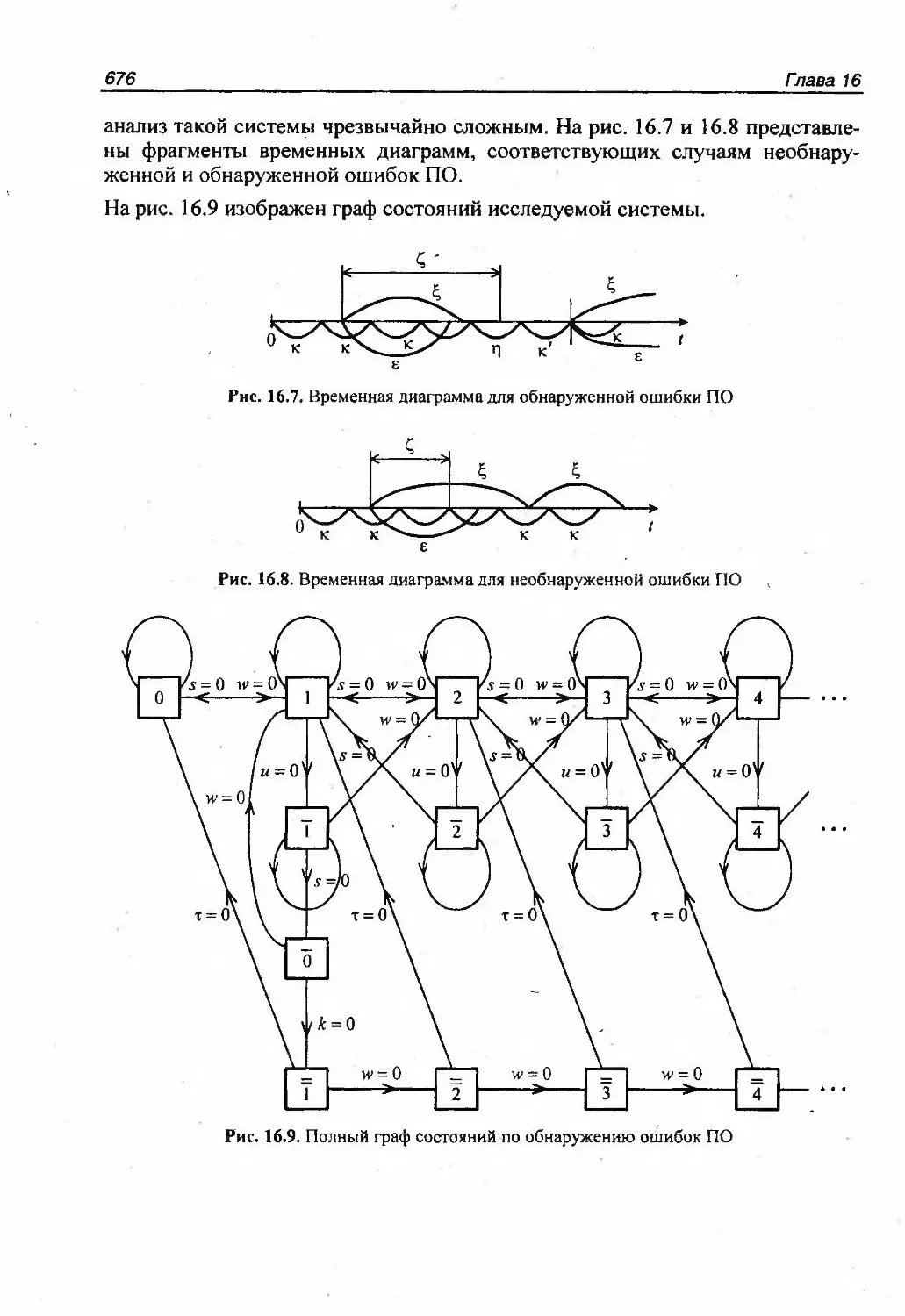
ОБЕСПЕЧЕНИЯ .....65316.1. Модель работы программы с изменяющимся распределением временидо проявления ошибки 65516.1.1. Режимы функционирования ПО и их математическое описание 655Отсутствие "памяти" 657Наличие "памяти" : 65916.1.2. Временные характеристики эффективности программных средств 66216.1.3. Вероятностные характеристики эффективности ПО 66516.2. Модель чередования интервалов решения задачи и интервалов контроля 66616.2.1. Описание работы системы 66716.2.2. Закон распределения случайной величины ст 66816.2.3. Математическая модель функционирования 66916.2.4. Оценка надежности ПО для стационарного режима 67116.3. Анализ эффективности ПО как системы массового обслуживания 67416.3.1. Описание работы системы 67416.3.2. Отсутствие очереди на обслуживание 677Граф состояний 677Система интегральных уравнений 678Критерий качества системы 67916.3.3. Независимость от предыстории моментов начала решения задачи 68016.4. Учет других особенностей функционирования ПО 684СПИСОК ЛИТЕРАТУРЫ .689ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ 699
ВВЕДЕНИЕНадежность техники и ее теорияНадежность является одним из самых важных показателей современной тех¬
ники. От нее зависят такие показатели, как качество, эффективность, безо¬
пасность, риск, готовность, живучесть. Техника может быть эффективной
только при условии, если она имеет высокую надежность.Надежность техники определяется при ее проектировании и производстве.
Чтобы создать техническую систему, удовлетворяющую требованиям надеж¬
ности, необходимо уметь рассчитать ее надежность в процессе проектирова¬
ния, знать методы обеспечения высокой надежности и способы их техниче¬
ской реализации. Необходимо также доказать экспериментально, что показа¬
тели надежности спроектированной системы не ниже заданных. И это еще не
все. Нужно также разработать методы, обеспечивающие высокую безотказ¬
ность техники в процессе ее эксплуатации. Все это невозможно реализовать,
если не владеть основами теории надежности. Ее должен знать инженер, про¬
ектирующий технику, инженер-технолог, инженер-эксплуатационщик.Необходимость знания теории надежности широкому кругу специалистов —
одна из особенностей теории надежности как науки и научной дисциплины.Теория надежности — это наука, изучающая закономерности отказов техни¬
ческих объектов. Она изучает:□ критерии и показатели надежности различных видов технических объ¬
ектов;□ методы анализа и синтеза техники по критериям надежности;□ методы обеспечения и повышения надежности техники;□ научные методы эксплуатации, обеспечивающие ее эксплуатационную
надежность.Теория надежности является научной дисциплиной, относящейся к числу
общетехнических дисциплин. Она изучается во всех технических вузах стра¬
ны под разными названиями. На основании теории надежности в специаль¬
14Введениеных технических дисциплинах изучаются вопросы надежности конкретных
технических объектов.Один из законов развития науки гласит: для обеспечения роста производства
необходимо, чтобы скорость роста научных исследований опережала ско¬
рость роста техники, а скорость роста техники опережала скорость роста
производства. Если же роста научных исследований нет, наука о надежности
не будет востребована, то техника не будет высоконадежной. Это мы наблю¬
даем в нашей действительности.Теория надежности как наука и техническая дисциплина имеет ряд особен¬
ностей:□ теория надежности — трудный для изучения, предмет. Это объясняется
широким использованием математики при изучении теории надежности, в
частности таких дисциплин, как теория вероятностей и математическая
статистика, решение интегральных, алгебраических и дифференциальных
уравнений (с постоянными и переменными коэффициентами, линейных и
нелинейных), математическая логика, теория систем массового обслужи¬
вания, элементы теории графов, методы статистического моделирования,
методы оптимизации и многое другое;□ необходимость применения компьютерных технологий решения практи¬
ческих задач;□ случайный характер отказов и восстановлений. Эта особенность приводит
к тому, что любые решения задач надежности имеют вероятностный ха¬
рактер;□ трудность математического моделирования объектов из-за отсутствия дос¬
товерных данных о надежности элементов системы, в частности, данных о
законах распределения отказов и восстановлений;□ трудность, а во многих случаях невозможность статистических испытаний
из-за технических и экономических ограничений;□ сложность современных систем и, как результат, большие размерности
уравнений, решение которых во многих случаях невозможно даже при ис¬
пользовании компьютерных технологий.Эти особенности требуют глубокого изучения теории надежности и серьез¬
ных научных исследований в этой области знаний.Особенности книгиУникальность книги определяется ее научным содержанием, объемом и ме¬
тодикой изложения теории. Далее излагаются основные особенности книги.
Введение15□ Основное внимание уделяется вопросам анализа надежности техники при
законах распределения отказов и восстановления, отличных от экспонен¬
циального, с использованием математического аппарата интегральных
уравнений.□ Наличие большого числа примеров, в которых четко ставится задача и
приводятся результаты ее решения. Само решение отсутствует, т. к. оно
реализуется с помощью компьютерных технологий по программам авто¬
ров, которые в книге не приводятся. Этот недостаток методов расчетов
только кажущийся. Вместе с этой книгой издательство "БХВ-Петербург"
выпустило вторую нашу книгу "Основы теории надежности. Практикум",
в которой описаны компьютерные технологии решения задач надежности.□ Значительное внимание уделяется проблемным вопросам теории и прак¬
тики надежности, а также изложению методов, которые не публиковались
в широкой печати. К таким вопросам относятся следующие:• анализ надежности информационных систем (глава 12);• надежность и риск (глава 13);• абсолютно надежные системы (глава 14);• сравнительный анализ эффективности различных методов введения из¬
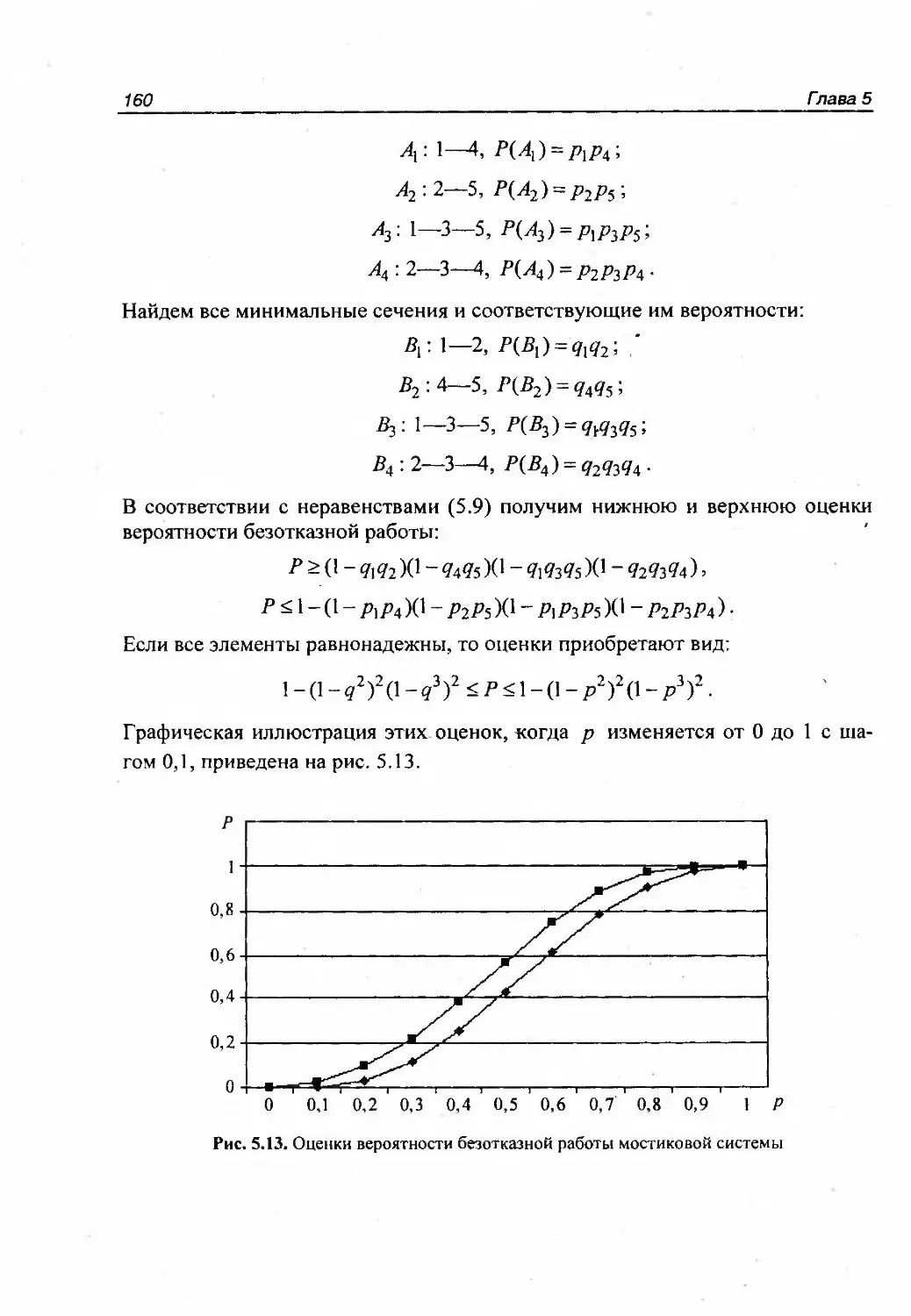
быточности (структурной, нагрузочной, временной);• интервальные оценки показателей надежности систем при неполной
информации о законах распределения отказов (глава 15);• топологические методы анализа надежности;• надежность программного обеспечения (глава 16).Для кого эта книгаКнига конкретного адресата не имеет. Это не учебник для студентов, не
сборник инженерных методов расчета показателей надежности в процессе
проектирования техники, не набор инструкций по научным методам эксплуа¬
тации техники с целью поддержания ее высокой надежности.Эта книга для всех, кому нужна теория надежности как наука и научная дис¬
циплина.Ученый в ней найдет проблемы и задачи, решение которых требует серьез¬
ных научных исследований. Научный руководитель и аспирант найдут тема¬
тику диссертационных исследований.Инженер, проектирующий и создающий высоконадежные технические сис¬
темы, изучит методы обеспечения и повышения надежности, их свойства и
16Введениесравнительный анализ, области применения. Инженер по эксплуатации най¬
дет советы по научным методам, обеспечивающим высокую эксплуатацион¬
ную надежность техники.Преподаватель и студент получит пособие по теории надежности.Книга будет полезной также лицам, занимающимся изучением показателей
техники, в которых надежность — лишь один из параметров более общего
показателя. К таким показателям относятся: качество и эффективность, безо¬
пасность и риск, готовность, живучесть и сохраняемость.Надеемся, что книга будет способствовать созданию высоконадежных объек¬
тов техники.
ГЛАВА 1ТЕОРИЯ НАДЕЖНОСТИ
И ЕЕ ФУНДАМЕНТАЛЬНЫЕ
ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ1.1. Теория надежности как наука
и научная дисциплинаТеория надежности— наука, изучающая закономерности отказов техниче¬
ских систем. Основными объектами ее изучения являются:□ критерии надежности технических систем различного назначения;□ методы анализа надежности в процессе проектирования и эксплуатации
технических систем;□ методы синтеза технических систем;□ пути обеспечения и повышения надежности техники;□ научные методы эксплуатации техники, обеспечивающие ее высокую на¬
дежность.Особенности этой дисциплины таковы:□ теория надежности — общетехническая дисциплина;А математическое моделирование — основа изучения дисциплины;□ комплексный характер;□ высокая значимость и глубокая связь с другими техническими пред¬
метами;□ трудность моделирования и изучения процессов, протекающих в сложных
технических системах (в смысле их надежности).Рассмотрим более подробно эти особенности.Процессы, протекающие в сложных технических системах, в смысле их на¬
дежности, закономерны и не зависят от вида техники. Это дает возможность
18Глава 1их изучения общими для любых технических средств методами. Разработан¬
ные в теории надежности методы анализа, синтеза, способы повышения на¬
дежности и научные методы эксплуатации техники являются общими для
любых технических систем. Этим определяется общетехнический характер
теории надежности и ее научность. Особенности отдельных видов техники
изучаются в специальных технических дисциплинах, в которых на основании
общей теории решаются конкретные задачи надежности.Математическое моделирование является основой изучения функционирова¬
ния сложных систем в смысле их надежности. При этом у исследователя воз¬
никают значительные трудности в связи со следующими особенностями ре¬
шаемых задач:П случайный характер явлений;□ многокритериальность;□ высокая размерность уравнений;□ многовариантность;□ необходимость обеспечения высокой точности.Эти особенности требуют применения в процессе моделирования объемного
математического аппарата: теории вероятностей и математической статисти¬
ки, решения алгебраических, дифференциальных, интегральных уравнений,
теории графов, интегральных преобразований, вычислительной математики,
методов оптимизации, статистического моделирования и др.Надежность является важнейшим параметром любой технической системы.
Она во многом определяет такие характеристики системы, как качество, эф¬
фективность, безопасность, живучесть, риск, которые изучаются в специаль¬
ных предметах. Глубокая связь с этими предметами — еще одна особенность
теории надежности как науки.Теория надежности — дисциплина комплексная. В ее разделы входят пред¬
меты, которые могут быть самостоятельными дисциплинами. К ним относят¬
ся:О математическая теория надежности;□ физическая теория надежности ("физика отказов");□ прогнозирование;□ диагностика;□ теория контроля;□ теория восстановления (управление запасами).Надежность техники зависит от многих факторов; критерии и показатели на¬
дежности устанавливаются в зависимости от вида техники и ее применения;
Теория надежности и ее фундаментальные понятий и определения19обеспечение надежности в процессе эксплуатации определяется дисциплиной
обслуживания, квалификацией обслуживающего персонала, экономическими
соображениями. Отсюда ясно, что техника с позиции надежности — это объ¬
ект системного анализа.Любая наука развивается из основных понятий и определений. В теории на¬
дежности такими понятиями являются "надежность" и "отказ". Сформулиру¬
ем эти понятия и дадим им научные определения.1.2. Определение понятия "надежность"Надежностью называется свойство технического объекта сохранять свои
характеристики (параметры) в определенных пределах при данных условиях
эксплуатации.Из этого определения следует, что надежность — понятие объективное, неза¬
висимое от нашего сознания.В природе все, что имеет начало, имеет и конец. В течение жизни объект рас¬
ходует свои ресурсы и, наконец, погибает. Так же происходит и с надеж¬
ностью. Создается техническое средство с определенным ресурсом. В про¬
цессе эксплуатации оно приносит человеку пользу за счет потери этого ре¬
сурса. Оно отказывает (болеет), его ремонтируют (лечат). Этот процесс длит¬
ся до тех пор, пока эксплуатация технического средства целесообразна.Этот процесс и все, что с ним связано (применительно к техническим средст¬
вам), и изучает теория надежности.В литературе и даже в некоторых стандартах приводятся определения поня¬
тия "надежность", существенно отличающиеся по смыслу от сформулирован¬
ного ранее. Иногда это понятие отождествляется с его численной оценкой:
"надежностью называется вероятность безотказной работы системы в течение
времени /". Численные показатели не могут быть определениями физических
явлений, подобные определения ошибочны.Часто понятие "надежность" связывают со временем работы технического
объекта. Следует иметь в виду, что время — лишь аргумент показателей на¬
дежности, такой же, как число элементов системы п, интенсивность отказов
элементов. Манипулируя временем, можно прийти к ложным выводам. Вот
типичный пример. Имеются две системы, их вероятности безотказной работы
имеют значения Рх(100) = 0,95, Р2(200) = 0,92. Какая из систем более надеж¬
на? Очевидный ответ, что первая, т. к. Р{> Р2, ошибочен. В ответе не учтено,
что системы работают разное время. Правильный ответ здесь неизвестен.
Ошибочны также определения, в которых понятие "надежность" трактуется
как совокупность свойств безотказности, ремонтопригодности, сохраняемо¬
20Глава 1сти, долговечности. В подобных определениях содержатся две принципиаль¬
ные ошибки. Во-первых, безотказность, ремонтопригодность и долговечность
не являются физическими свойствами техники. Во-вторых, физическое свой¬
ство не может быть совокупностью других физических свойств. Приведен¬
ные нами определения понятия "надежность" не научны, их часто называют
монтерскими.1.3. Понятие "отказ".
Классификация и характеристики отказовОтказом называется событие, после возникновения которого характеристики
технического объекта (параметры) выходят за допустимые пределы.Это Понятие субъективно, т. к. допуск на параметры объекта устанавливает
пользователь. Вот один из примеров. Математическая система Maple имеет в
своем составе около 3000 функций. Предположим, что перестала функциони¬
ровать одна из них, например функция вычисления логарифма действитель¬
ного числа. Является это отказом компьютера или, вернее, системы Maple
или нет? Ответ здесь не однозначный, субъективный.Отказ— фундаментальное понятие теории надежности. Критерий отказа —
отличительный признак или совокупность признаков, согласно которым ус¬
танавливается факт возникновения отказа.По типу отказы подразделяются на:□ отказы функционирования, при которых прекращается выполнение объек¬
том основных функций (например, поломка зубьев шестерни);□ отказы параметрические, при которых параметры объекта изменяются в
недопустимых пределах (например, потеря точности измерения напряже¬
ния вольтметром).По своей природе отказы могут быть:□ случайные, обусловленные непредусмотренными перегрузками, дефектами
материала, ошибками персонала, сбоями системы управления и т. п.;□ систематические, обусловленные закономерными явлениями, вызываю¬
щими постепенное накопление повреждений: усталость, износ, старение,
коррозия материалов и т. п.Основными признаками классификации отказов являются:□ характер возникновения;□ причина возникновения;□ последствия отказов;
Теория надежности и ее фундаментальные понятия и определения21□ дальнейшее использование объекта;□ легкость обнаружения;□ время возникновения.Рассмотрим подробнее каждый из классификационных признаков.По характеру возникновения отказы могут быть внезапные, постепенные и
перемежающиеся. Внезапный отказ— это отказ, проявляющийся в резком
(мгновенном) изменении характеристик объекта. Постепенный отказ— от¬
каз, происходящий в результате медленного, постепенного ухудшения харак¬
теристик объекта из-за износа и старения материалов. Внезапные отказы
обычно проявляются в виде механических повреждений элементов (поломки,
пробои изоляции, обрывы и т. п.) и не сопровождаются предварительными
видимыми признаками их приближения. Внезапный отказ характеризуется
независимостью момента наступления от времени предыдущей работы. Пе¬
ремежающимся называется отказ самоустраняющийся (возникающий/исче-
зающий). Типичным примером перемежающегося отказа является сбой ком¬
пьютера.По причине возникновения отказы могут быть конструкционные, производст¬
венные и эксплуатационные. Конструкционный отказ появляется в результа¬
те недостатков и неудачной конструкции объекта. Производственный отказ
связан с ошибками при изготовлении объекта по причине несовершенства
или нарушения технологии. Эксплуатационный отказ вызывается нарушени¬
ем правил эксплуатации объекта.По признаку дальнейшего использования объекта отказы могут быть полные
или частичные. Полный отказ исключает возможность работы объекта до его
устранения. При возникновении частичного отказа объект может частично
использоваться.По признаку легкости обнаружения отказы бывают очевидные (явные) и
скрытые (неявные).По времени возникновения отказы подразделяются на приработочные, возни¬
кающие в начальный период эксплуатации, отказы при нормальной эксплуа¬
тации, износовые отказы, вызванные необратимыми процессами износа де¬
талей, старения материалов и т. п.Анализ сведений об отказах оборудования при эксплуатации сложных систем
показывает, что с течением времени происходит старение элементов и увели¬
чение их отказов, что приводит к значительному росту затрат (материальных,
временных, финансовых) ресурсов. Многолетняя практика эксплуатации
сложных систем показывает, что важной задачей при поддержании объектов
в состоянии работоспособности является организация и проведение техниче¬
ского обслуживания и различных видов ремонтов (восстановлений) элемен¬
22Глава 1тов систем. Исключительно важна проблема продления ресурса стареющих
систем с учетом критериев надежности и уменьшения техногенного риска.1.4. Надежность и сохраняемостьСуществуют технические объекты, основным режимом функционирования
которых является хранение. К таким объектам относятся системы разового
использования, например: системы вооружения, системы с малым коэффици¬
ентом использования, запасные элементы, приборы, устройства, хранящиеся
на складе, и т. п.Понятие "надежность", сформулированное ранее, в полной мере относится и
к таким объектам. Вводится только новое название "сохраняемость".Сохраняемостью называется свойство технического объекта сохранять свои
характеристики (параметры) в процессе хранения.Из этого определения следует, что понятия "надежность" и "сохраняемость"
тождественны. Их отличие лишь в условиях эксплуатации.Критериями и показателями сохраняемости могут быть все критерии и пока¬
затели, применяемые для оценки надежности техники в процессе ее работы.
Однако методы анализа надежности и сохраняемости по этим показателям
существенно различны.В процессе хранения техника не работает. В связи с этим основным видом ее
отказа является отказ постепенный, возникающий вследствие старения мате¬
риалов. Время возникновения такого отказа— величина случайная. Полу¬
чить экспериментальным путем ее распределения чрезвычайно трудно. В свя¬
зи с этим прогнозировать показатели сохраняемости в процессе проектирова¬
ния и создания техники вряд ли возможно.1.5. Терминология теории надежностиНадежность — один из самых важных параметров техники. Ее показатели
необходимы для оценки качества техники, ее эффективности, безотказности,
живучести, риска. Надежность зависит от многих внешних и внутренних
факторов и оценивается многими критериями и показателями. Все это приве¬
ло к появлению в теории надежности большого числа различных терминов и
их определений. Далее приводятся некоторые из них, часто применяемые на
практике и в теории.Элемент — объект (материальный, энергетический, информационный), об¬
ладающий рядом свойств, внутреннее строение (содержание) которого значе¬
ния не имеет.
Теория надежности и ее фундаментальные понятия и определения23В теории надежности под элементом понимают элемент, узел, блок, имею¬
щий показатель надежности, самостоятельно учитываемый при расчете пока¬
зателей надежности системы. Понятия элемента и системы трансформируют¬
ся в зависимости от решаемой задачи. Например, станок при оценке его на¬
дежности рассматривается как система, состоящая из элементов — деталей,
механизмов, узлов и т. п. При оценке надежности технологической линии
станок является элементом системы.Система— совокупность связанных между собой элементов, обладающая
свойством (назначением, функцией), отличным от свойств отдельных ее эле¬
ментов.Практически любой объект с определенной точки зрения может рассматри¬
ваться как система. Системой с точки зрения механики являются, например,
собранная из стержней стрела крана или труба газопровода. Элементами по¬
следней будут ее участки между сварными швами или опорами. Связи в дан¬
ном случае имеют силовой (энергетический) характер— каждый элемент
действует на соседний.Структура системы — взаимосвязи и взаиморасположение составных час¬
тей системы, ее устройство. Расчленение системы на группы элементов мо¬
жет иметь материальную (вещественную), функциональную, алгоритмиче¬
скую и другую основу. Структура сборного моста состоит из его отдельных,
собираемых на месте секций. Грубая структурная схема укажет только эти
секции и порядок их соединения. Последнее и есть связи, которые здесь но¬
сят силовой характер. Пример функциональной структуры — это деление
двигателя внутреннего сгорания на подсистемы питания, смазки, охлажде¬
ния, передачи силового момента.Обычно понятие структура связывают с ее графическим отображением.
В зависимости от связей между элементами различают следующие виды
структур: последовательные, параллельные, с обратной связью, сетевые и
иерархические.Процесс — это набор состояний системы, соответствующий упорядоченному
(непрерывному или дискретному) изменению некоторого параметра, опреде¬
ляющего характеристики (свойства) системы.Процесс изменения системы во времени называется динамикой системы. Па¬
раметрами процесса могут также выступать температура, давление, линейные
и угловые координаты и другие физические величины, которые, однако, сами
зависят от времени.Технический объект в процессе функционирования может находиться в раз¬
личных состояниях, оцениваемых численными показателями. Приведем тер¬
мины состояния объекта и их оценки.
24Глава 1Исправность — состояние объекта, при котором он соответствует всем тре¬
бованиям, установленным нормативно-технической документацией (НТД).Работоспособность — состояние объекта, при котором он способен выпол¬
нять заданные функции, сохраняя значения основных параметров, установ¬
ленных НТД.Основные параметры характеризуют функционирование объекта при выпол¬
нении поставленных задач.Понятие исправности шире, чем понятие работоспособности. Работоспособ¬
ный объект обязан удовлетворять лишь тем требованиям НТД, выполнение
которых обеспечивает нормальное применение объекта по назначению. Та¬
ким образом, если объект неработоспособен, то это свидетельствует о его не¬
исправности. С другой стороны, если объект неисправен, то это не означает,
что он Неработоспособен.Предельное состояние — состояние объекта, при котором его применение по
назначению недопустимо или нецелесообразно. Применение (использование)
объекта по назначению прекращается в следующих случаях:□ при неустранимом нарушении безопасности;□ при неустранимом отклонении величин заданных параметров;□ при недопустимом увеличении эксплуатационных расходов.Для некоторых объектов предельное состояние является последним в его
функционировании, т. е. объект снимается с эксплуатации, для других объек¬
тов — определенной фазой в эксплуатационном графике, требующей прове¬
дения ремонтно-восстановительных работ.В связи с этим, объекты могут быть:□ невосстанавливаемые, для которых работоспособность в случае возник¬
новения отказа не подлежит восстановлению;□ восстанавливаемые, работоспособность которых может быть восстанов¬
лена, в том числе и путем замены.К числу невосстанавливаемых объектов можно отнести, например, подшип¬
ники качения, полупроводниковые изделия, зубчатые колеса и т. п. Объекты,
состоящие из многих элементов, например станок, автомобиль, электронная
аппаратура, являются восстанавливаемыми, поскольку их отказы связаны с
повреждениями одного или немногих элементов, которые могут быть заме¬
нены.В ряде случаев один и тот же объект в зависимости от особенностей, этапов
эксплуатации или назначения может считаться восстанавливаемым или не-
восстанавливаемым.
Теория надежности и ее фундаментальные понятия и определения25Восстановление может быть полностью ограниченным, когда обслуживание
системы производится одной ремонтной единицей, ограниченным, если име¬
ется более одной ремонтной единицы, но при этом может образоваться оче¬
редь на обслуживание вследствие нехватки ремонтных единиц. Восстановле¬
ние может быть неограниченным, если ремонтных единиц достаточно для
одновременного обслуживания всех отказавших элементов.Наработка — продолжительность или объем работы объекта, измеряемые
единицами времени, числом циклов нагружения, километрами пробега и т. п.Наработка до 'отказа — наработка объекта от начала его эксплуатации до
возникновения первого отказа.Наработка между отказами — наработка объекта от окончания восстанов¬
ления его работоспособного состояния после отказа до возникновения сле¬
дующего отказа.Технический ресурс — наработка объекта от начала его эксплуатации (или ее
возобновления после ремонта) до перехода в предельное состояние. Техниче¬
ский ресурс может быть также регламентирован, например, от начала экс¬
плуатации до среднего или капитального ремонта, или от среднего до капи¬
тального ремонта, после которого требуется продление технического ресурса.
Если регламентация отсутствует, то имеется в виду ресурс от начала эксплуа¬
тации до достижения предельного состояния после всех видов ремонтов.Для невосстанавливаемых объектов понятия технического ресурса и наработ¬
ки до отказа совпадают.Назначенный ресурс — суммарная наработка объекта, при достижении кото¬
рой эксплуатация должна быть прекращена независимо от его состояния.Срок службы — календарная продолжительность эксплуатации (в том числе
хранение, ремонт и т. п.) от ее начала до наступления предельного состояния.Для большинства объектов электромеханики в качестве критерия долговеч¬
ности чаще всего используется технический ресурс.Время восстановления работоспособного состояния — продолжительность
восстановления работоспособного состояния объекта.В теории надежности важную роль играют такие понятия, как безотказность,
долговечность, ремонтопригодность, сохраняемость. Часто ошибочно счита¬
ют эти понятия — составляющие надежности и определяют их как физиче¬
ские двойства. Уточним эти понятия.Безотказность — это способность объекта непрерывно сохранять работо¬
способность в течение некоторого времени или некоторой наработки.Часто безотказность отождествляют с понятием "надежность" и характери¬
зуют теми же показателями: вероятностью безотказной работы, средней на¬
26Глава 1работкой до отказа, средней наработкой на отказ, интенсивностью отказов,
параметром потока отказов,Долговечность — способность объекта сохранять работоспособное состояние
до наступления предельного состояния при установленной системе техниче¬
ского обслуживания и ремонта.Долговечность определяется следующими показателями:□ средний ресурс — математическое ожидание технического ресурса;□ гамма-процентный ресурс — наработка, в течение которой объект не дос¬
тигнет предельного состояния с заданной вероятностью у, выраженной
в процентах;П средний срок службы — математическое ожидание срока службы;□ гамма-процентный срок службы — календарная продолжительности от
начала эксплуатации объекта, в течение которой он не достигнет предель¬
ного состояния с заданной вероятностью у, выраженной в процентах.Ремонтопригодность — способность объекта, заключающаяся в его приспо¬
собленности к предупреждению и обнаружению причин возникновения отка¬
зов, поддержанию и восстановлению работоспособного состояния путем про¬
ведения ремонтов и технического обслуживания.К показателям ремонтопригодности относятся вероятность восстановления
работоспособного состояния в течение заданного времени и среднее время
восстановления работоспособного состояния.1.6. Классификация технических системТехнические системы могут быть невоестанавливаемыми и восстанавливае¬
мыми, длительного и короткого времени работы, резервированными и нере¬
зервированными.Техническая система называется невосстанавливаемой (перемонтируемой),
если ее отказ приводит к неустранимым последствиям и систему нельзя ис¬
пользовать по своему назначению. Работа после отказа невосстанавливаемой
системы считается невозможной или нецелесообразной. Типичными приме¬
рами не восстанавливаемых систем являются полупроводниковые приборы,
управляемые снаряды, система управления воздушным судном в процессе
полета и т. п.Под восстанавливаемой (ремонтируемой) понимается система, которая мо¬
жет продолжать выполнение своих функций после устранения отказа, вы¬
звавшего прекращение ее функционирования. Работа восстанавливаемой сис¬
темы после отказа может быть возобновлена в результате проведения необ¬
Теория надежности и ее фундаментальные понятия и определения27ходимых восстановительных работ. При этом под восстановлением системы
понимается не только ремонт тех или иных элементов системы, а также пол¬
ная замена отказавших элементов на новые.Существуют системы смешанного типа, у которых часть элементов может
восстанавливаться, а другая — нет.В зависимости от выполняемых функций различаются системы длительного
существования и системы короткого существования.Резервированием называют способ повышения надежности путем включения
резервных единиц, способных в случае отказа основного устройства выпол¬
нять его функции. Этот метод обладает большими возможностями получения
заданных уровней надежности и имеет широкое практическое применение.Разнообразные методы резервирования и способы включения резерва могут
быть сведены к трем методам: общему, раздельному (поэлементному) и ком¬
бинированному (смешанному) резервированию. Общим называется такое ре¬
зервирование системы, при котором параллельно включаются идентичные
системы. Раздельным называется резервирование системы путем использова¬
ния отдельных резервных устройств. При комбинированном резервировании
в одной и той же системе применяется общее и раздельное резервирование.Отношение числа резервных устройств к числу основных называется крат¬
ностью резервирования. Если это отношение — число целое, то такое резер¬
вирование называется резервированием с целой кратностью, иначе — с дроб¬
ной кратностью.Резервирование может быть с восстановлением, если основные и резервные
элементы ремонтируются в процессе эксплуатации, и без восстановления
в противном случае. Классификация методов резервирования показана на
рис. 1.1.Главными^способами включения резервных устройств при отказах основных
являются следующие:□ постоянное, при котором резервные объекты соединены с основными в
течение всего времени работы;□ замещением, при котором резервные объекты замещают основные только
после отказа последних.При этом в обоих случаях резервные объекты могут находиться в трех режи¬
мах работы:□ нагруженном, при котором резервные объекты находятся в тех же услови¬
ях, что и основные;□ непогруженном, при котором резервные объекты не включены и не могут
отказывать;
28Глава 1Рис. 1.1. Классификация методов резервирования□ облегченном, при котором резервные объекты включены, но работают не
на полную нагрузку, т. е. их надежность в резервном состоянии выше, чем
в рабочем. Однако отказ элементов возможен.
ГЛАВА 2КРИТЕРИИ НАДЕЖНОСТИ.
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
ВРЕМЕНИ ДО ОТКАЗА2.1. Что такое критерий
и показатель надежностиКритерием называется признак (мерило), по которому оценивается надеж¬
ность. Например, вероятность безотказной работы P{t), интенсивность отка¬
зов X(t), средняя наработка на отказ Т .Основными характеристиками критериев являются:□ научность;П полнота оценки надежности технического объекта;□ вычисляемость;□ наглядность;□ непротиворечивость иным критериям качества объекта;□ возможность применения для оценки других, более общих показателей
технического объекта (например, эффективность, безопасность, живу¬
честь, риск).Показателем надежности называется численное значение критерия. Напри¬
мер, вероятность безотказной работы в течение 1000 часов равна 0,95, т. е.
Р(1000) = 0,95, или средняя наработка на отказ равна 687 часов, Т = 687 час.Показатели задаются в технических требованиях на изделие, рассчитываются
в процессе проектирования, оцениваются в процессе испытания и эксплуата¬
ции технического объекта.Разработка критериев, методов анализа техники по критериям надежности,
методов испытания и обработки их результатов — это задачи глубоко науч¬
30Гпава 2ные. Расчеты показателей надежности, способы их обеспечения в процессе
проектирования и создания, сбор данных об отказах техники в процессе ис¬
пытания и эксплуатации — это инженерное дело.Надежность является сложным физическим свойством, поэтому не существу¬
ет одного обобщенного критерия и показателя, который бы достаточно полно
характеризовал надежность техники. Только семейство критериев позволяет
оценить надежность сложной технической системы. Выбор критериев зави¬
сит от типа технического объекта, его назначения и требуемой полноты
оценки надежности.Между показателями надежности существуют однозначные математические
зависимости в виде формул. Поэтому при разработке семейства показателей
надежности нельзя их задавать в виде равенств. Например, нельзя формули¬
ровать требования на надежность в таком виде: вероятность безотказной ра¬
боты в течение 150 часов должна быть равна 0,97, а среднее время безотказ¬
ной работы Т = 650 час. Такие требования могут оказаться противоречивыми.Рассмотрим критерии надежности невосстанавливаемых и восстанавливае¬
мых систем.2.2. Критерии надежности
невосстанавливаемых системОтказ элемента является событием случайным, а время Ь, до его возникнове¬
ния — случайной величиной. Основной характеристикой надежности эле¬
мента является функция распределения продолжительности его безотказной
работы F(t) = Р(£, < t) , определенная при t > 0. На ее основе могут быть по¬
лучены следующие показатели надежности невосстанавливаемого элемента:□ P(t) — вероятность его безотказной работы в течение времени t;□ Q(t) = 1 - P(t) — вероятность отказа в течение времени t;□ 7] — среднее время безотказной работы (средняя наработка до отказа);□ /(0 — плотность распределения времени безотказной работы;□ \{t) — интенсивность отказа в момент времени t;□ А(0 — функция ресурса;□ ty — у-процентный ресурс— наработка, в течение которой элемент неУдостигает состояния отказа с вероятностью .
Критерии надежности. Законы распределения времени до отказа31Рассмотрим эти показатели более подробно. Дадим вероятностные и стати¬
стические определения, укажем на их свойства, достоинства и недостатки.Вероятностью-безотказной работы называется вероятность того, что техниче¬
ский объект не откажет в течение времени t или что время £ работы до отка¬
за технического объекта больше времени его функционирования t:Вероятность безотказной работы является убывающей функцией времени,
имеющей следующие свойства:По статистическим данным об отказах, полученным из опыта или эксплуата¬
ции, P(t) определяется следующей статистической оценкой:где N0 — общее число образцов, находящихся на испытании, N(t) — число
исправно работающих образцов в момент времени t, n{t) — число отказав¬
ших образцов в течение времени t. Здесь и далее звездочкой обозначаются
величины, полученные по статистическим данным.Вероятность безотказной работы имеет следующие достоинства:О характеризует надежность во времени, являясь интервальной оценкой;.□ определяет многие важные показатели техники, например эффективность,
безопасность, живучесть, риск;□ сравнительно просто вычисляется и определяется по статистическим дан¬
ным об отказах техники;□ достаточно полно характеризует надежность невосстанавливаемой тех¬
ники.Основной недостаток этого критерия— ограниченность применения. Веро¬
ятность безотказной работы характеризует надежность невосстанавливаемой
техники или восстанавливаемой до первого ее отказа.2.2.1. Вероятность безотказной работы(2.1)О < P(t) < 1, />(0) = 1, Р(+оо) = 0.(2.2)
32Глава 22.2.2. Плотность распределения времени
безотказной работы (частота отказов)*Плотность распределения времени безотказной работы /(/) — это плотность
распределения случайной величины £,. Она наиболее полно характеризует
надежности техники в данный момент (точечная характеристика). По ней
можно определить любой показатель надежности невосстанавливаемой сис¬
темы. В этом основное достоинство плотности распределения времени безот¬
казной работы.Статистически /(/) определяется отношением числа отказавших образцов
техники в единицу времени к числу испытуемых образцов при условии, что
отказавшие образцы не восполняются исправными:где n{t, t + ДО — число отказавших образцов за промежуток времени
[/, t + Аг], N0 — число образцов, первоначально поставленных на испытания.Действительно, т. к. /(/) = Q'{t) = -P'(t), то для малых значений At имеемПусть N(/) — число исправно работающих образцов к моменту времени t,
N(t + At) — число образцов, исправно работающих к моменту 1 + At. По¬
сколькучто совпадает с выражением (2.3), т. к. N(t) - N(t + At) = n(t, t + At).2.2.3. Интенсивность отказовИнтенсивностью отказов называется отношение плотности распределения
к вероятности безотказной работы объекта:, л(М + Д0
N0At(2.3), P{t) - P{t + At)то♦ N{t)-Nit + At)
N0At(2-4)
Критерии надежности. Законы распределения времени до отказа33Статистически интенсивность отказов есть отношение числа отказавших об¬
разцов техники в единицу времени к среднему числу образцов, исправно ра¬
ботающих на интервале [/, t + А/]:где Ncp(t) = ——— — среднее число исправно работающих образ-N(t) + N(t + At)2цов на интервале [/, t + А/]. Соотношение (2.5) для малых At следует непо¬
средственно из (2.2) и (2.3).На основе определения интенсивности отказов (2.4) имеет место равенство= (2.6)
Р{ ОИнтегрируя (2.6), получимt\\(t)dt = -\nP{t),оилиArndtP(t) = e 0Интенсивность отказов X(t) является основным показателем надежности
элементов сложных систем. Это объясняется следующими обстоятельствами:□ надежность многих элементов можно оценить одним числом, т. к. интен¬
сивность отказа элементов — величина постоянная;□ по известной интенсивности X(t) наиболее просто оценить остальные по¬
казатели надежности как элементов, так и сложных систем;□ k(t) обладает хорошей наглядностью;□ интенсивность отказов нетрудно получить экспериментально.Опыт эксплуатации сложных систем показывает, что изменение интенсивно¬
сти отказов k(t) большого количества объектов описывается {У-образной
кривой (рис. 2.1).Время можно условно разделить на три характерных участка:1. Период приработки.2. Период нормальной эксплуатации.3. Период старения объекта.2 Зак. 3094
34Гпава 2X(t), время 1УПериод Период нормальной Периодприработки' эксплуатации старенияОРис. 2.1. (7-образный вид кривой интенсивности отказовПериод приработки объекта имеет повышенную интенсивность отказов, вы¬
званную приработочными отказами, обусловленными дефектами производст¬
ва, монтажа и наладки. Иногда с окончанием этого периода связывают гаран¬
тийное обслуживание объекта, когда устранение отказов производится изго¬
товителем. В период нормальной эксплуатации интенсивность отказов
практически остается постоянной, при этом отказы носят случайный характер
и появляются внезапно, прежде всего из-за случайных изменений нагрузки,
несоблюдения условий эксплуатации, неблагоприятных внешних факторов и
т. п. Именно этот период соответствует основному времени эксплуатации
объекта. Возрастание интенсивности отказов относится к периоду старения
объекта и вызвано увеличением числа отказов из-за износа, старения и дру¬
гих причин, связанных с длительной эксплуатацией.Средним временем безотказной работы 7J называется математическое ожи¬
дание времени безотказной работы технического объекта:По статистическим данным об отказах 7] определяется следующей зависи¬
мостью:2.2.4. Среднее время безотказной работыТХ=М(£).(2.7)(2.8)где N0 — число испытуемых образцов техники, — время безотказной ра¬
боты /-го образца.
Критерии надежности. Законы распределения времени до отказа35Как математическое ожидание случайной величины с плотностью f(t),
среднее время безотказной работы вычисляется по формуле:Т\ = °\tf{t)dt. (2.9)оИнтегрируя (2.9) по частям, получимГ, = \f(l)dt = -\tP\t)dt = ~tP(t)\™ + ]p(t)dt.0 0 оПервое слагаемое равно нулю, т. к. Р(0) = 1, Р(+оо) = 0, и тогда выражениедля 7} будет иметь вид:007] = \P(t)dt. (2.10)оСреднее время безотказной работы является интегральным показателем на¬
дежности. Его основное достоинство— высокая наглядность. Недостаток
этого показателя в том, что он, будучи интегральным, характеризует надеж¬
ность техники длительного времени работы.Итак, между показателями надежности существуют следующие зависимости:p{t)=m=\-F{t), (2.11)
-}мо<*P(t) = e 0 =<ГЛ(/), (2.12)f{t) = -P\t), (2.13)P{t)^\f{t)dt^\f{x + t)dx, (2.14)t оЦ() = 1Ш (2.15)P(t)Т\ = °\P(t)dt = °^tf(t)dt, (2.16)о оtЛ(0 = - In P(t) = jk(x)dx, (2.17)оP(ty) = Т~. (2-18)100
36Гпава 2ПРИМЕР 2.1. На испытании находилось jV0 = 100 образцов техники. Данные
об их отказах приведены в первых трех строках табл. 2.1.Таблица 2.1. Исходные данные об отказахИнтервал, час0—100100—
200200—300300—400400—500500—600600—700700—800Длина At, час100100100100100100100100Число
отказавших
образцов
n(t, t + At)12132213P{t)0,990,970,960,930,910,890,880,85ДО-КГ4, час'112132213Я#)'КГ4, час-11,012,031,043,172,202,221,123,47Необходимо вычислить показатели надежности: P(t), f(t), М0> Тх.Решение. Вычислим P(t). Будем иметь в виду, что нам достоверно неизвес¬
тен момент отказа на промежутке длины At. Поэтому будем предполагать,
что отказы происходят в середине этого промежутка, т. е. в моменты време¬
ни: t = 50, 150, 250 и т. д. На первом интервале произошел один отказ. Тогда
согласно (2.2) вероятность безотказной работы будет:На втором участке произошло 2 отказа, а всего за два периода длины At —
3 отказа. ТогдаРезультаты расчетов приведены в четвертой строке табл. 2.1.
Вычисления значений /(t) выполним по формуле (2.3):
Критерии надежности. Законы распределения времени до отказа37и т. д. В данном случае число отказов на промежутке длины At не суммиру¬
ется с числом отказов на предыдущих участках, т. к. функция /(/) является
точечной. Результаты расчетов приведены в пятой строке табл. 2.1.Вычислим значения X(t), воспользовавшись выражением (2.5). На первом
участке произошел один отказ, при этом в начале участка число исправных
образцов Щ0) = N0= 100, а в конце участка N(100) = N0 -1 =99. Тогда2Аналогично на втором участке^150>= = 2,03 10-* час'1- - • 1002и т. д. Значения X(t) приведены в последней строке табл. 2.1.Вычислим среднее время безотказной работы по формуле (2.8):„ 1 £ 1-50 + 2-150 + 1- 250 + 3 • 350 + 2 ■ 450 + 2 • 550 +1 • 650 + 3 • 750' 'Nh‘‘ 15 == 437 час.В данном случае испытания закончены при отказе 15 из 100 образцов.Очевидно, что полученный результат существенно ниже действительного
значения среднего времени безотказной работы как математического ожида¬
ния случайной величины.2.3. Критерии надежности
восстанавливаемых системПоказателями надежности восстанавливаемых элементов и систем могут
быть также показатели надежности невосстанавливаемых элементов. Это
имеет место в тех случаях, когда система, в состав которой входит элемент,
является неремонтируемой по условиям ее работы (необитаемый космиче¬
ский аппарат, аппаратура, работающая в агрессивных средах, самолет в про¬
цессе полета, отсутствие запчастей для ремонта и т. п.). Надежность восста¬
навливаемых объектов оценивают следующими показателями:ПТ — среднее время работы между отказами (средняя наработка на отказ);□ Гв — среднее время восстановления;
38Глава 2□ со(0 — параметр потока отказов;□ Kr(t) — функция готовности — вероятность того, что система исправна в
момент t;□ Кп (/) — функция простоя— вероятность того, что в момент t система
неисправна и восстанавливается;□ Кг — коэффициент готовности— вероятность того, что система будет
исправной при длительной эксплуатации (стационарный режим);□ Кп — коэффициент простоя — вероятность того, что система будет неис¬
правной при длительной эксплуатации.Рассмотрим эти показатели несколько подробнее.2.3.1. Среднее время работы между отказами
и среднее время восстановленияСреднее время между отказами Т определяется отношением средней сум¬
марной наработки к среднему числу отказов при длительной работе объекта.
Среднее время восстановления Тв определяется отношением среднего сум¬
марного времени восстановления к среднему числу восстановлений при дли¬
тельной работе объекта. Данные определения обсуждаются далее в разд. 2.6.По статистическим данным среднее время между отказами вычисляется по
формуле:* 1 N°Г= —ЕЛ, (2-19)/=1где — время между отказами /-го образца, полученное при условии, что
испытания ведутся с восстановлением отказавших образцов техники или их
заменой. В этом случае число испытуемых образцов техники N0 остается
постоянным.2.3.2. Параметр потока отказовПараметром потока отказов со(() называется производная (скорость измене¬
ния) среднего числа отказов объекта в момент t.Статистически параметр потока отказов определяется как отношение числа
отказавших образцов техники в единицу времени к числу образцов, постав¬
ленных на испытание при условии, что отказавшие образцы заменяются ис¬
правными или отремонтированными:
Критерии надежности. Законы распределения времени до отказа39(2.20)где n(t, t + АО — число отказавших образцов за промежуток времени
[/, t + А/], Лц — число образцов, первоначально поставленных на испытания.Параметр потока отказов обладает следующими свойствами:□ в случае экспоненциального закона времени работы объекта (см. разд. 2.4)
с параметром X и мгновенного восстановления со(/) = А,;□ при мгновенном восстановлении предел, к которому стремится параметр
потока отказов при t -> оо, равен величине, обратной среднему временибезотказной работы, т. е. lim со(/) = — ;/-*00 Т□ при мгновенном восстановлении параметр потока отказов и плотность
распределения времени до отказа связаны следующим интегральным
уравнением Вольтерра второго рода:Это уравнение устанавливает зависимость между показателями надежно¬
сти восстанавливаемой и невосстанавливаемой техники. Оно позволяет
определить по статистическим данным об отказах восстанавливаемой тех¬
ники в процессе ее эксплуатации показатели надежности невосстанавли¬
ваемой техники (см. гл. 11).ПРИМЕР 2.2. Время до отказа объекта имеет нормальное распределение с
математическим ожиданием Т = 1000 час и средним квадратическим откло¬
нением о = 300 час. Привести графическую иллюстрацию плотности распре¬
деления /(0 и параметра потока отказов сo(t).Решение. Графики функций изображены на рис. 2.2. Параметр потока отка¬
зов co(t) получен путем численного решения уравнения Вольтерра.Для относительно небольшого времени функционирования объекта параметр
потока отказов близок к плотности распределения, но при длительной работе
плотность распределения стремится к нулю, тогда как параметр потока отка¬
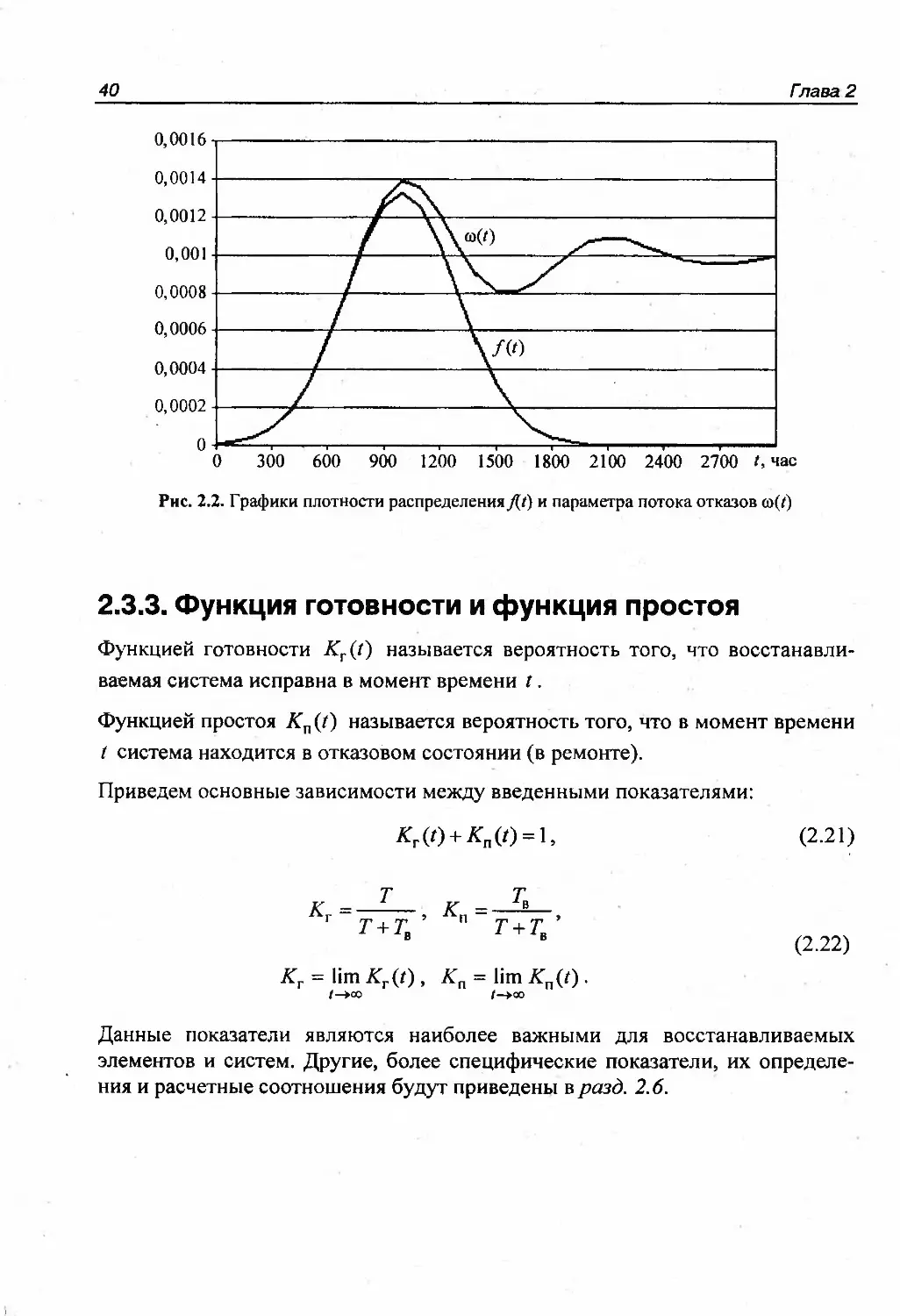
зов приближается к своему стационарному значению, равному — = 0,001 час-1./ю(0 = /(0 + /со(т)/(/ - x)dx.оТ
40Глава 2Рис. 2.2. Графики плотности распределения ДО и параметра потока отказов <а(/)2.3.3. Функция готовности и функция простояФункцией готовности Kr(t) называется вероятность того, что восстанавли¬
ваемая система исправна в момент времени t.Функцией простоя Kn(t) называется вероятность того, что в момент времени
t система находится в отказовом состоянии (в ремонте).Приведем основные зависимости между введенными показателями:Кг(0 + Кп(0 = \, (2.21)г Т v - Т"г гг . гг 9 Л-пТ + Т1 " т + твв в (2.22)Кг = lim Kr(t), Кп = lim Kn(t)./-+00 /->00Данные показатели являются наиболее важными для восстанавливаемых
элементов и систем. Другие, более специфические показатели, их определе¬
ния и расчетные соотношения будут приведены в разд. 2.6.
Критерии надежности. Законы распределения времени до отказа412.4. Законы распределения
времени до отказа, наиболее часто
используемые в теории надежностиПриведем наиболее часто используемые в теории надежности параметриче¬
ские семейства распределений случайной величины т. е. распределений,
зависящих от одного или нескольких параметров.ФункцияF(t) = 1 - e~kt при t > Озадает экспоненциальное (или показательное) распределение. Экспоненци¬
альным законом распределения можно аппроксимировать время безотказной
работы большого числа элементов. В первую очередь это относится к эле¬
ментам радиоэлектронной аппаратуры, а также к машинам, эксплуатируемым
в период после окончания приработки и до существенного проявления посте¬
пенных отказов. Экспоненциальное распределение применяется в областях,
связанных с "временем жизни": в медицине— продолжительность жизни
больных, в надежности — продолжительность безотказной работы устройст¬
ва, в психологии — время, затраченное на выполнение тестовых задач. Оно
используется в задачах массового обслуживания, в которых речь идет об ин¬
тервалах времени между телефонными звонками, или между моментами по¬
ступления техники в ремонтную мастерскую, или между моментами обраще¬
ния клиентов.Это распределение имеет один параметр X-—, где Тх — средняя наработкат\элемента до отказа. Таким образом, параметр X характеризует число отказов
элемента в единицу времени и называется интенсивностью отказов, он имеет
размерность (время)-1, например, час"1 или лет-1. Плотность экспоненциаль¬
ного распределения задается как:m=xe~xt.Функция надежностиP(t) = е~Х1определяет вероятность безотказной работы за время t (рис. 2.3).В данном случае интенсивность отказов есть величина постоянная X(t) - X.
Функция ресурса для экспоненциального распределения является линейной
Л(/) = Xt.
42Глава 2Величина у-процентного ресурса определяется по формулет
10,8
0,6
0,4
0,2
00 20 40 60 80 t, часРис. 2.3. Функция надежности при А. = 0,02 час'1ПРИМЕР 2.3. Время безотказной работы элемента подчинено экспоненци¬
альному распределению с параметром к = 0,02 час"’. Найти вероятность того,
что элемент проработает безотказно в течение 10 часов и в течение 50 часов.Решение. Используя функцию надежности P(t) = e~fd, получимР(10) = е~0’02'10 = е~0'2 = 0,8187,Р( 50) = е-0’02'50 = е~\ - 0,3679.Экспоненциальное распределение выделяется среди других распределений
свойством "отсутствия памяти". Пусть X — время службы некоторого из¬
делия с экспоненциальным законом распределения. "Отсутствие памяти" оз¬
начает, что изделие, проработавшее время t, имеет такое же распределение,
что и новое, только что начавшее работу. Математически это свойство выра¬
жается в виде следующего равенства:Р(Х > t + х/Х > 0 = Р(Х > х)Iдля любых t, х > 0. Данное свойство как бы исключает износ и старение из¬
делия.t =~ In- -
у Я. 100
Критерии надежности. Законы распределения времени до отказа43Числовые характеристики экспоненциального распределения выражаютсячерез его параметр: математическое ожидание М(Х) = —, дисперсияА,D{X) = Дг, среднее квадратическое отклонение о(Х) = — .X А.Итак, при экспоненциальном законе отказов, на основании формул (2.11)—
(2.18), между показателями надежности невосстанавливаемых систем суще¬
ствуют следующие зависимости:P{t) = e~Xt, Г = |, f{t) = Xe~u.КДля характеристики постепенных отказов обычно используют другие законы
распределения.Нормальное распределение (распределение Гаусса) определяется плотностьюI ('-"О2f(t) = —т=е 2°2 , -со <t <+оо
а\/2пи зависит от двух параметров m и ст, которые являются соответственно ма¬
тематическим ожиданием и средним квадратическим отклонением времени
безотказной работы элемента. График плотности нормального распределения
(кривая Гаусса) изображена на рис. 2.4.Рис. 2.4. Плотность нормального распределения с параметрами m = 80 час, ст = 20 час
44Гпава 2Согласно закону больших чисел, распределение всегда подчиняется нор¬
мальному закону, если на изменение случайной величины оказывают влияние
многие примерно равнозначные факторы. Нормальному распределению под¬
чиняются ошибки измерения деталей, дальность полета снарядов и т. п. При
большом времени работы элемента и наличии восстановления среднее число
отказов имеет асимптотически нормальное распределение.Для нормального распределения функция надежности вычисляется по фор¬
муле:' t — mСО J (*-"0 /,P(0=J—-j=e 2°2 dx = 0,5-Ф0
, ctv 2 яI _5где Ф0(/) = —т= fe 2 dx— функция Лапласа, значения которой сведеныV 2п оов таблицы.ПРИМЕР 2.4. Время безотказной работы элемента подчинено нормальному
распределению с параметрами т = 80 час и ст = 20 час. Найти вероятность
того, что элемент проработает безотказно в течение 60 часов.Решение. Так как для нормального распределения функция надежности
равнаР(/) = 0,5-Ф0тоР{Щ = 0,5 -Ф0 = 0,5 -Ф0(-1) = 0,5 + Ф0(1) = 0,8413 .Отметим важное свойство нормального распределения: сумма независимых
случайных величин, имеющих нормальное распределение, также распределе¬
на по нормальному закону. При этом параметры суммы выражаются через
параметры слагаемых, а именно: математическое ожидание суммы равно
сумме математических ожиданий, дисперсия суммы равна сумме дисперсий.На рис. 2.5 представлены графики интенсивности отказов X(t) для следую¬
щих параметров нормального распределения:От- 200 час и ст = 100 час (кривая 1);□ т = 200 час и ст = 80 час (кривая 2).
Критерии надежности. Законы распределения времени до отказа45Рис. 2.5. Интенсивность отказов для нормального распределения при разных параметрахУсеченное нормальное распределение получается из нормального при огра¬
ничении интервала изменения случайной величины на промежуток [0, + оо).
Плотность распределения записывается так же, как для нормального распре¬
деления, но с коэффициентом пропорциональности с :(t-mо)2С/(0 =сУо"^2тгУсеченное нормальное распределение зависит от двух параметров т0 и ст0,
где т0 — значение случайной величины, соответствующее максимальному
значению fit) и называемое модой. Коэффициент с определяется из усло¬
вия нормировки:откудас = ■10,5 + Ф0Математическое ожидание и среднее квадратическое отклонение усеченного
нормального распределения определяются через параметры т0 и ст0 по
формулам:
46Глава 2где к--т=-те 2а°
ы2пВ логарифмически нормальном распределении логарифм случайной величи¬
ны подчиняется нормальному закону с плотностью:где ц и j — параметры распределения. Математическое ожидание и среднее
квадратическое отклонение определяются в соответствии с формулами:Логарифмически нормальное распределение применяют, например, для опи¬
сания наработки подшипников качения. Вообще, оно удобно для описания
случайных величин, представляющих собой произведение достаточно боль¬
шого числа случайных величин, подобно тому, как нормальное распределе¬
ние описывает сумму большого числа случайных величин.Распределение Вейбулла является достаточно универсальным, благодаря воз¬
можности варьирования двух его параметров. Оно характеризуется плот¬
ностью распределения вероятностей:с параметром формы а и параметром масштаба р. Математическое ожида¬
ние и среднее квадратическое отклонение выражаются через эти параметры
следующим образом:Вейбулла объясняется следующим: при а = 1 распределение превращается в
экспоненциальное; при а<1 функции плотности и интенсивности отказов
убывающие; при а > 1 интенсивность отказов возрастающая; при а = 2гдеm = РГ(1 + 1/а) , а = Р^/Г(1 + 2/а) -Г2(1 + 1/а) ,1 „е dx — гамма-функция. Универсальность распределенияо
Критерии надежности. Законы распределения времени до отказа47функция А.(О линейная и распределение Вейбулла превращается в распреде¬
ление Рэлея с плотностью:m = 2-kte-xt\при а = 3,3 распределение Вейбулла близко к нормальному. Наряду с лога¬
рифмически нормальным распределением, оно хорошо описывает наработку
деталей по усталостным разрушениям, наработку до отказа подшипников, а
также используется для оценки надежности деталей и узлов машин, в част¬
ности автомобилей, подъемно-транспортных и других машин.Зависимости между показателями надежности в случае распределения Вей¬
булла имеют вид:/>(0 = Лр) , 7i=pr|l + ij, X = pta~l.На рис. 2.6 представлены графики интенсивности отказов X(t) для следую¬
щих параметров распределения Вейбулла:□ а = 2 и Р = 200 час (кривая 1);□ а = 3 и Р = 200 час (кривая 2).Рис. 2.6. Интенсивность отказов для распределения Вейбулла при разных параметрах
Галша-распределение имеет плотность:
48Глава 2с параметрами аир. Математическое ожидание и среднее квадратическое
отклонение связаны с этими параметрами соотношениями:т = ар, ст = >/ар.Вероятность безотказной работы элемента, имеющего гамма-распределение,
выражается через интеграл® а-1 _£P(t) = Г— е рdx.i Р“Г(а)Параметр а, характеризующий асимметрию гамма-распределения, опреде¬
ляет вид характеристик надежности. При а > 1 интенсивность отказа возрас¬
тает, при а < 1 убывает, а при а = 1 становится постоянной, т. е. гамма-
распределение превращается в экспоненциальное.При целом а гамма-распределение называется распределением Эрланга по¬
рядка а . Сумма а случайных величин, имеющих экспоненциальное распре¬
деление с параметром X, имеет распределение Эрланга с параметрами а иР = —. Вероятность безотказной работы элемента, имеющего распределение
XЭрланга, равнаа-1 #' ~/=0/!РЗависимости между показателями надежности в случае гамма-распределения
имеют вид:-i-d-1 А .а-1Р(0 = е —, Т = ар, Х = W "о/.ч’ а-1nR'/l а-1.=°Pl. par(a)£_L_/=оР'/!Смесь распределений определяется как линейная комбинация других распре¬
делений, например распределение с плотностью" -ht/(0 = Zc,Vv,/=1где Xе/ =Ь образует смесь и экспоненциальных распределений. Такое рас-<=1пределение называется гиперэкспоненциальным.
Критерии надежности. Законы распределения времени до отказа49Смесь гамма-распределенийn fa/-l яДО - I с, — е р' при условии X с,,=1 р,Т(а,) ,=1= 1образует плотность обобщенного гамма-распределения и т. п.Перечень полезных параметрических распределений можно продолжить. На¬
пример, если параметр А экспоненциального распределения является слу¬
чайной величиной, имеющей гамма-распределение с параметрами а и (3, то
в результате получается семейство распределений Парето с плотностью:/(0 =—-—•0 + Р0“При расчете надежности ряда изделий (рессор, подшипников и т. п.) приме¬
няют семейства распределений с дополнительным параметром сдвига или
смещения. Так обобщением распределения Вейбулла является трехпарамет¬
рическое семейство распределений с плотностью:Д0 =a-lt-t0РР“, при t>t0;О,при t<t0.Параметр сдвига t0 интерпретируется как гарантированное время безотказ¬
ной работы.Если элемент имеет перерывы в работе, то закон распределения времени до
его отказа изменяется. Пусть F0(t) — вероятность безотказной работы эле¬
мента, если бы он работал непрерывно. Предположим далее, что на непересе-
кающихся интервалах \ak; А* ], k = 1, 2,..., п элемент простаивает, причемвремя простоя не влияет на его надежность. Тогда вероятность безотказной
работы элемента при наличии интервалов простоя характеризуется парамет¬
рами смещения и выражается равенством:F{t) =к-1 *-1
1=1 /=1V
(кпри bk_\ <t <ak, к = \, 2,..., и+ 1;к-11чс=1 (=i
Здесь принято, что Ь0 = О , а„+1 = со .при ak<t<bk, к = 1,2,, п.
50Глава 2ПРИМЕР 2.5. Предположим, что график вероятности безотказной работы
элемента у = F0(t) имеет вид, изображенный на рис. 2.4. Пусть этот элемент
работает только на временных интервалах [0; 10], [30; 40], [60; 70],..., а на
остальных интервалах элемент простаивает. Требуется определить вероят¬
ность безотказной работы элемента у = F(t) с учетом простоя.Решение. График искомой функции y = F(t) изображен на рис. 2.7. На ин¬
тервалах простоя вероятность безотказной работы не уменьшается (функция
постоянна), а на интервалах простоя график у = F0 (/) смещается вправо на
величину, равную суммарному времени простоя элемента.Рис. 2.7. Закон распределения времени до отказа при наличии перерывов в работеЗаметим, что интервалы простоя могут быть как детерминированными, так и
случайными. В последнем случае необходима информация о законах распре¬
деления ак и Ьк. Учет перерывов в работе элементов может существенно
повлиять на надежность системы, образованной этими элементами.2.5. Преобразование ЛапласаМногие числовые показатели надежности элементов и систем выражаются
через функции типа свертки или бесконечными рядами, члены которых яв¬
ляются свертками функций. Для исследования таких показателей большую
помощь может оказать преобразование Лапласа. Оно удобно также при рас¬
четах предельных значений функций, лежит в основе операционного метода
решения дифференциальных уравнений и систем. Преобразование Лапласа
Критерии надежности. Законы распределения времени до отказа51позволяет преобразовать любую систему обыкновенных дифференциальных
уравнений в систему линейных алгебраических уравнений.Пусть функция /(/) кусочно-непрерывна при ^0 и имеет ограниченный
рост, т. е.\т\йСем,где С и а — некоторые постоянные. Тогда она называется оригиналом, а
функция+0°/(*)= J f(t)e~zldtо— ее изображением. Переход от оригинала к изображению называется пре¬
образованием Лапласа, а переход от изображения к соответствующему ори¬
гиналу — обратным преобразованием Лапласа. В дальнейшем вместо f(z)
будем иногда писать f(s).Перечислим некоторые полезные свойства преобразования Лапласа.1. Изображение линейной комбинации функций равно линейной комбинацииП А Пизображений: если f(t) = (/), то /(г) = Y*ciMz) •/=1 ; = 12. Изображением производной /'(/) является функция zf(z)-f(0).3. Изображение свертки функций равно произведению изображений сомно-А Ажителей: если h(t) = то h(z) = f(z)g(z).4. При вычислении предельных значений функций можно использовать ра-Авенство lim /(/) = lim zf(z). Заметим, что данное свойство не всегда вер-/->оо г->0но. Так, например, если /(/) представляет собой сумму 5-функций, т. е.00/(/) = Y, &кт(0 > т0 предел вообще не существует. Однако:к=0lim zf (z) = lim —7-=- = —.
z_»0 o\-e~Tz T5. Если f(t) — плотность распределения вероятностей неотрицательнойслучайной величины X, то ее изображение f(z) удовлетворяет соотно¬
шениям:
52Глава 2/<*>(0)= \{-t)kf(t)dt.В частности, /(0) = 1, /'(0) = -Т, /"(0) = а2 , где Т — математическое
ожидание, а а2 — второй начальный момент случайной величины X .Решение системы алгебраических уравнений, полученной по системе линей¬
ных дифференциальных уравнений, образуют дробно-рациональные функции
вида2.6. Специальные показатели надежности
элементов и систем2.6.1. Показатели надежности элементаРаботу восстанавливаемого элемента с двумя состояниями можно предста¬
вить в виде последовательности интервалов исправной работы %к и интерва¬
лов восстановления щ, чередующихся друг за другом, как показано на
рис. 2.8.причем т<п. Если знаменатель дроби N{z) имеет только простые корни
2,,Zi,..., z„, то оригинал определяется равенствомЕсли знаменатель дроби N(z) имеет кратные корни: zx кратности rx, z2
кратности г2,..., zk кратности гк (гх +г2 + ... + гк =п), то оригинал определя¬
ется равенствомгде коэффициенты Ау находятся по формулам:
Критерии надежности, Законы распределения времени до отказа53Рис. 2.8. Временная диаграмма восстанавливаемого элементаПредположим, что случайные величины Ъ,к и г\к независимы и имеют плот¬
ности fk(t) и gk(t) соответственно. Обозначим через Fk(t) и Gk(t) функ-к кции распределения сумм и ^ Г|, соответственно, а через Fk г(() —/=1 <=1к Iфункцию распределения суммы случайных величин V ^ + ]Г Г|#. Предполо-(=1 /=1жим также, что F0(f) = G0(t) = 1.Рассмотрим следующие случайные процессы C,(t) и С,Я(1), равные соответст¬
венно числу отказов и числу восстановлений элемента за время [0; /]. Это
дискретные случайные процессы с непрерывным временем. Обозначим через
M{t) = М(^(/)) и Мв (t) = M(ClB (t)) их математические ожидания (в предпо¬
ложении, что они существуют). Функции M(t) и Ma(t) характеризуют сред¬
нее число отказов и среднее число восстановлений элемента за время [0; t\.
Если в момент времени t = О элемент был исправен, то очевидно, что
M(t) > Мв (/) для любого t.Определим скорости изменения среднего числа отказов со(/) = М'Щ и сред¬
него числа восстановлений (x>B(t) = . Функции со(/) и сов(0 называются
параметрами потоков отказов и восстановлений соответственно. Принимая во
внимание, что М(0) = Мв(0) = 0, получимМ(?) = |<о(т>/т , Мв(0 = JcoB(x)cft; .
о оРассмотрим случайный процесс х(0> как суммарное время работы (наработ¬
ка) элемента, и случайный процесс у_в(/), как суммарное время восстановле¬
ния элемента за время [0; /]. Это есть непрерывные случайные процессы с
непрерывным временем (на самом деле функции распределения в одной точ¬
ке терпят разрыв). Обозначим через m(t) = и mh(t) = —ма¬
54Гmm 2тематические ожидания этих случайных процессов. Функции m{t) и mB(t)
показывают среднюю наработку и среднее суммарное время восстановления
элемента в течение времени [0; /]. Функция готовности Kr(t) и функция
простоя K„(t) элемента определяются как вероятности того, что в момент t
элемент находится в состоянии работоспособности и в состоянии восстанов¬
ления. Далее в этом разделе будет показано, что Kr(t) = m'(t), Kn(t) = m's{t).Разделив среднюю наработку на среднее число отказов элемента за время
j 0; /], получим среднее время работы элемента между отказами, или нара¬
ботку на отказ. Тогда среднее время работы элемента между отказами в тече¬
ние времени [0;/] определится отношением:Г(/)=т<')M(t)Аналогично определяется среднее время восстановления элемента в течение
времени [0; г], как отношение среднего суммарного времени восстановления
элемента на среднее число восстановлений:М,«)Интенсивности потоков отказов и восстановлений в момент t определим ра¬
венствами®(0 1|ГЛ ®в(0т~КЛ,У АГ„(0’Получим представление введенных характеристик через плотности и функ¬
ции распределения случайных величин и г\к .Любое сечение случайного процесса £,(t) есть случайная величина дискрет¬
ного типа с возможными значениями к = 0,1,2,... и вероятностями рк(t).
Поскольку РкО) — вероятность того, что за время [0; l] произошло ровно к
отказов, тогPk(t)=pк *~1 &+1 к
y/=i i=i /=1 ;=1- ^к,к~\ (0 - Fk+l,k (0 •
Критерии надежности. Законы распределения времени до отказа55Поэтому математическое ожидание случайной величины C,(t) равнооткуда(2.23)Параметры потоков со(t) и coB(t) были определены как производные от ма¬
тематических ожиданий числа отказов и числа восстановлений элемента за
промежуток времени [0; I j. Дадим теперь иное, локальное в некотором смыс¬
ле, но эквивалентное первоначальному, определение этих параметров.Пусть p(t, t + At) — вероятность отказа элемента за время [/; t + А?], а
pb(t, t + ДО — вероятность того, что за промежуток времени [/; t + А/] эле¬
мент будет восстановлен. Тогдат. е. параметры потоков отказов и восстановлений равны соответственно ве¬
роятностям отказа и восстановления за малый промежуток времени, отнесен¬
ным к длине этого промежутка. Эквивалентность определений видна из сле¬
дующих соотношений:Аналогично для случайного процесса (0 математическое ожидание равно(2.24)
56Гпава 2Из этих формул следует, что интенсивность потока отказов есть вероятность
отказа за малый промежуток времени [/; / + Д/] при условии, что в момент tэлемент находится в исправном состоянии, отнесенная к длине этого проме¬
жутка. Интенсивность потока восстановлений есть вероятность восстановле¬
ния в течение времени [/; t + А/] при условии, что в момент t элемент нахо¬
дится в состоянии восстановления, отнесенная к длине этого промежутка.
Перейдем к изучению случайных процессов х(0 и Хв(0 • Рассмотрим слу¬
чайный процесс х(0 > равный суммарному времени работы элемента в тече¬
ние времени [0; /]. Зафиксируем момент времени t0 и найдем закон распре¬
деления случайной величины х(Уо ) •Пусть F(t) — функция распределения случайной величины x(t0) ■ Очевидно,
что F(t) = О при t < 0 и F(t) = 1 при t>t0. Из временной диаграммы, изо¬
браженной на рис. 2.8, следует, что при 0 < t < t0Используя (2.12), получим:что и доказывает равносильность двух определений функции со(t). Подобные
рассуждения справедливы и для функции сов (/).Из определения интенсивностей потоков отказов и восстановлений, а также
из равенств (2.24) получаются следующие выражения для Х(() и со(t) :
Критерии надежности. Законы распределения времени до отказа57График функции F(() представлен на рис. 2.9.Рис. 2.9. Закон распределения случайной величины x(h)Функция F(t) имеет в точке /0 разрыв, поскольку F(t0 -0) = Fl(t0), и вели¬
чина скачка равна 1 - F| (;0). Вычислим математическое ожидание случайной
величины х(/о) ■ Д™ случайной величины смешанного типаИз принятых ранее обозначений следует, чтоПреобразуя эти выражения, получимТаким образом, средняя суммарная наработка системы за время [0; / ] равна(2.25)
58Глава 2Рассмотрим случайный процесс хв(0> равный суммарному времени восста¬
новления элемента в течение времени [0; /]. Можно показать, что при
0</</0 закон распределения случайной величины Хв(*о) характеризуется
функцией распределенияРис. 2.10. Закон распределения случайной величины х»(*о)Математическое ожидание случайной величины %в(/0) равноСкладывая ряды (2.25) и (2.26), убеждаемся в том, что m(t) + mB(t) = t.
Вычислим функции готовности и простоя. Очевидно, что(2.26)Полученная зависимость иллюстрируется графиком на рис. 2.10.и, значит, среднее суммарное время восстановления элемента за время [0; /]
составляет
Критерии надежности. Законы распределения времени до отказа59где Pk{t) — вероятность того, что момент времени t приходится на к-й ин¬
тервал исправной работы элемента. ПосколькуТО(2.27)— вероятность безотказной работы элемента в течение(2.31)(2.30)(2.29)(2.28)Для функций готовности и простоя из (2.27) и (2.28) будем иметьоткуда следуют зависимостиВ частности, если законы распределения времени исправной работы на каж¬
дом интервале одинаковы и имеют плотность /(/), а законы распределения
времени восстановления имеют плотность g(t), то соотношения для введен¬
ных характеристик можно записать в более компактном виде. Будем обозна¬
чать через f*{K} ^-кратную свертку функции / . Тогда из (2.23) получим сле¬
дующие выражения для параметров потоков:Дифференцируя функции m(t) и тв ({) и сравнивая производные с выраже¬
ниями (2.27) и (2.28), видим, чтоТаким же образом доказывается формулагдевремени i, ане будет восстановлен.— вероятность того, что за время t элемент
60Глава 2Из (2.31) следует, чтоКг(/) = F(t) + сов * F{t), Kn(t) = a>* G(t).(2.32)ПРИМЕР 2.6. Время до отказа элемента имеет нормальное распределение с
параметрами а = 1000 час, 5 = 300 час. Время восстановления имеет нор¬
мальное распределение с параметрами 6 = 10 час, г = 30 час. Требуется оп¬
ределить функцию готовности.Решение. Вычислим функцию готовности по формуле (2.27). По свойству
нормального распределения функции Fkk(t) и Fk+l, k{t) также являютсяфункциями нормального распределения с параметрами mk = k(a + b),Расчеты, выполненные по этой формуле, позволяют построить график функ
ции готовности (рис. 2.11).соответственно. Поэтому, используяфункцию Лапласа, получим0,9980,9960,9940,9920,990,9880,9860,9840 120 240 360 480 600 720 840 /.часРис. 2.11. Функция готовности для нормальных (кривая 1)
и экспоненциальных (кривая 2) распределенийДля сравнения на этом же рисунке изображен график функции готовности,
если время до отказа и время восстановления элемента имеют экспоненци¬
альные распределения со средними а и Ъ соответственно.
Критерии надежности. Законы распределения времени до отказа61Различие двух кривых очевидно. Функция готовности для случая нормально¬
го распределения имеет колебательный характер, отсутствующий у системы
с экспоненциальным законом распределения отказов и восстановлений. Ста¬
ционарный режим в первом случае долго не наступает, во втором он наступа¬
ет практически мгновенно.2.6.2. Стационарные значения показателей
надежности элементаПолучим предельные значения для показателей надежности восстанавливае¬
мого элемента, предполагая, что с течением времени процесс функциониро¬
вания элемента устанавливается и приобретает стационарный характер. Бу¬
дем считать в дальнейшем, что fk = /, gk= g, k = 1, 2,... с математическими
ожиданиями Т и Гв соответственно.Наиболее удобным способом вычисления предельных соотношений является
представление характеристик в виде преобразования Лапласа.Из равенств (2.29) следует, что параметры потоков отказов и восстановлений
в изображениях имеют вид:Ш-, <ш=. /(z)*w1-/(*)£(*) 1 -/(z)g(z)Следовательно, по свойствам (4) и (5) преобразования Лапласа (см. разд. 2.5)
получим:V г • -v ч г zf(z) г z(l - 7z) 1(о = lim со(/) - Ijiti zco(z) = lim = lim- -f~»«> z-> о z-»o i - f (z)g(z) z~>° 1 - (1 - Tz)( 1 - TBz) T + TBАналогичноюв = lim со. (t) = —-—.
t->=0 BW T + TbТаким образом, стационарные значения параметров потоков отказов и вос¬
становлений одинаковы и равны1со = со. = .в Т + ТъИз (2.32) следует, что4(2) = Ь/Ё(1 + йв(:)), Ka(z)*^Q&(z).
62Глава 2Коэффициент готовности определяется только средним временем работы
элемента до отказа и средним временем восстановления вне зависимости от
законов распределения. Это означает, что Кг нельзя применять для оценки
надежности технических систем кратковременного использования. Более
полная информация о работе такой системы содержится в функции готовно¬
сти (см. рис. 2.11).Получим предельные соотношения для среднего числа отказов и восстанов-Применяя свойство (5) преобразования Лапласа, получимгде а2 и Р2 — вторые начальные моменты случайных величин с плотностя¬
ми /(/) и g(t) соответственно. Отсюда следует асимптотическая оценка
среднего суммарного числа отказов:Аналогично при / -» оо имеет место асимптотическая оценка среднего сум¬
марного числа восстановлений:Похожие рассуждения позволяют найти асимптотические оценки для средней
суммарной наработки и среднего суммарного времени восстановления эле¬
мента:Следовательно, коэффициенты готовности и простоя равны соответственнолений. Вычислим предел разности
Критерии надежности. Законы распределения времени до отказа63Как и следует ожидать, для стационарного режима средняя наработка между
отказами равна среднему времени безотказной работы элемента.2.6.3. Показатели надежностиневосстанавливаемой и восстанавливаемой техникиВ разд. 2.6.1 были введены показатели надежности элементов. Определим
теперь показатели надежности системы. Пусть Е — множество состояний
системы, к,1 еЕ — любые два состояния множества Е . Введем в рассмот¬
рение следующие случайные процессы и свяжем с ними определенные функ¬
ции.О Са,/(0 — число переходов системы из состояния к в состояние / в тече¬
ние времени [0;Л, — математическое ожидание С,к /(7) ,
со^ ДО = — параметр перехода системы в момент времени t из со¬
стояния к в состояние /;О Хк(0 — суммарное время пребывания системы в состоянии к в течение
времени [0;/], mk(t)—математическое ожидание х*(0» Рк(О~т'к(0 —
вероятность пребывания системы в момент времени t в состоянии к ,Определим теперь случайные процессы и некоторые производные от их
функции для подмножеств состояний множества Е, где ей/ — любые
непересекающиеся подмножества множества состояний Е :Теперь легко найти предельные соотношения для интенсивностей потоков
отказов и восстановлений:Вычислим стационарные значения средней наработки межцу отказами и
среднего времени восстановления:
64Глава 2□ С,е j-(t) — число переходов системы из состояний множества е в состоя¬
ния множества / в течение времени [0;?], Ме j-(t) — математическое
ожидание C,ej(t), a>ej{t) = M'ej(t) — параметр перехода в момент вре¬
мени t из множества состояний е в множество состояний / ;□ Хе(0 — суммарное время пребывания системы в состояниях множества е
в течение времени [0; /], me(t)— математическое ожидание %e{t),
pe{t)-m’e(t) — вероятность пребывания в момент времени t в каком-
либо состоянии множества е .Случайные процессы Се,/(О и Хе(0 являются базовыми, поскольку черезних может быть получена вся информация о работе системы с позиции тео¬
рии надежности. Так, например, математические ожидания этих процессов
позволяют определить среднее время Tej(t) пребывания системы в множе¬
стве е до перехода в множество / в течение времени [0; /]:me(t)Те,А‘) =Интенсивность перехода системы в момент времени t из множества е в
множество / определяется отношением:РАО ■Укажем формулы связи между показателями, характеризующими множества
состояний из Е и отдельные состояния множества Е :MeJ(t)= 2 Mkj{t), юе>/(0= I <М0,кее,1е / кее,1е /me{t) = Е тк(*)» А (О =1Л (0 ■кее кее2.6.4. Основное уравнение
функционирования системыПредположим, что процесс функционирования системы состоит из случай¬
ных времен пребывания в некоторых состояниях и мгновенных переходов из
одного состояния в другое. Случайное время пребывания в состоянии г ха¬
рактеризуется вероятностью а переход из состояния / в состояние j
Критерии надежности. Законы распределения времени до отказа65характеризуется параметром перехода а>,;У(0- Тогда имеет место система
уравнений:Л'(0 = -£ со,.у(0+ £ со,, до, ieE. (2.33)Уе£ _/е£Для доказательства обозначим через v*(f) число входов в состояние i излюбого другого состояния, а через v~(t) — число выходов из состояния i влюбое другое состояние в течение времени [0; t]. При фиксированном I этослучайные величины, принимающие целочисленные значения. Рассмотрим2 случая.Случай 1. Состояние г не является начальным состоянием процесса функ¬
ционирования.Процесс не может выйти из состояния /, если он не оказался в этом состоя¬
нии, поэтому vj (0 < v+ (0 ■ После пребывания процесса в состоянии i в это
состояние нельзя войти вновь до тех пор, пока процесс не выйдет из этого
состояния, поэтому vt(t) < v~(t) +1. Отсюда следует, что случайная величина
v+(/)-v-(0 принимает только два значения: 0 или 1. При этом
V/40~V~(0 = 1, если процесс пребывает в состоянии /. Вероятность этогособытия равна p,(t). Аналогично v*(t) - v~(t) - 0, если процесс вышел из
состояния /, но вновь еще не вошел в это состояние. Вероятность этого со¬
бытия равна 1 - pt(t). Следовательно, математическое ожидание случайнойвеличины v+(/)-vT(0 равно P/(t).Так какv+(0 = £ Су.,(О и v“(/) = £ С,)7(0>jeE jeETO£ - £ Mij(0=MO • (2-34)jeE jeEСлучай 2. Состояние i является начальным состоянием процесса функцио¬
нирования.Очевидно, что здесь выполняется неравенство v*(0 ^ v” (t) < v* (t) +1, поэто¬
му случайная величина v~(t)-v*(t) может принимать только два значения О3 Зак. 3094
66Гпава 2и 1 с вероятностями pt(jt) и 1 - pt(t) соответственно. Математическое ожи¬
дание этой случайной величины равно 1 - /?, (/), следовательно,I S М;. i(t) = \-pi(t). (2.35)jeE jeEВыражения (2.34) и (2.35), а также определения параметров переходов дока¬
зывают требуемое утверждение (2.33).Из уравнений (2.33) и значений интенсивностей переходов получаем сле¬
дующую систему уравненийp'i (0 = ~ X Чу (О А(0 + X ^j,i(t)Pj(t), г е /1. (2.36)уе£ уе£Система уравнений (2.36), полученная в самом общем виде, является обоб¬
щением системы дифференциальных уравнений Колмогорова [7, 28] для слу¬
чая, когда интенсивности переходов из состояния в состояние постоянные.Расчленим множество всех состояний системы Е на два непересекающихся
подмножества: Е+ — множество работоспособных и Е_ — множество отка-
зовых состояний. Тогда функционирование системы можно рассматривать
как функционирование одного (укрупненного) элемента, для которого в
разд. 2.6.2 уже получены соотношения для показателей надежности. Так, ис¬
пользуя обозначения разд. 2.6.3, получим:□ M(t) - МE+(t), MB(t)~ME_(t) — среднее число отказов и среднее число
восстановлений системы в течение времени [0; ?];□ со(/) = (оЕ+ (J), (ов(1)-(йЕ■ (t) — параметр отказа и параметр восстановле¬
ния системы в момент времени t;□ m(f) = mE (0, — средняя суммарная наработка и среднее
суммарное время восстановления системы в течение времени [0; /];□ Kr(t) = рЕ (t), Kn(t) = рЕ (t) — функция готовности и функция простоя
системы в момент t;□ T(t) = ТЕ■ (/), TB(t) = ТЕ (t) — средняя наработка на отказ и среднее время
восстановления системы в течение времени [0; /],□ X(t) = Х£ (/), ц(Г) = \iE (t) — интенсивность отказов и интенсивность вос¬
становления системы в момент t.
Критерии надежности. Законы распределения времени до отказа67Суммируя равенства (2.33) по всем состояниям ie Е+, получимZ P'i(0 = ~ Z Z Z ®«,/0 + Z Z»/,/W+Z Z ®y./(0 =ieE+ ieE+jeE+ ieE+j<=E_ ieE+jeE+ ieE+jeE_=-Z Z®u(0+Z Z wy,/(0-ieE+jeE_ ieE+jeE_Воспользовавшись формулами связи различных показателей, содержащихся в
разд. 2.6.3, получим соотношениеед=-со(0+сов(0,устанавливающее зависимость между параметрами потоков отказов и восста¬
новлений и функцией готовности системы.В теории надежности обычно предполагается, что каждый элемент системы
может находиться только в двух возможных состояниях: состоянии работо¬
способности и состоянии отказа. Однако на практике это не всегда справед¬
ливо. Подобно тому, как это было сделано в настоящей главе, можно опреде¬
лить характеристики надежности для случая разбиения множества всех
состояний на три и большее число подмножеств, а полученные здесь теоре¬
тические результаты естественным путем могут быть распространены на сис¬
темы, элементы которых имеют несколько возможных состояний.
ГЛАВА 3ПРОБЛЕМЫ АНАЛИЗА
НАДЕЖНОСТИ СЛОЖНЫХ
ТЕХНИЧЕСКИХ СИСТЕМСовременные технические и информационные системы являются системами
человеко-машинными, в состав которых входят технические средства, сред¬
ства математического обеспечения и люди, занимающиеся их созданием,
технической эксплуатацией и эксплуатацией по назначению. Такие системы
относятся к классу сложных систем, обладающих следующими свойствами:□ большое количество элементов, функционально связанных между собой;□ наличие естественной и искусственной избыточности;□ многофункциональность;□ восстанавливаемость;□ неоднозначность понятия "отказ";□ неодновременность работы элементов.Характеристиками таких систем являются: качество, эффективность, безо¬
пасность, живучесть, риск, готовность и долговечность. Все эти характери¬
стики в той или иной степени зависят от надежности системы.Практика эксплуатации сложных технических систем ставит перед теорией
надежности такие задачи, решение которых— сложная научная проблема.
К таким задачам можно отнести следующие:□ научное обоснование критериев и показателей надежности сложных сис¬
тем;□ разработка математических моделей функционирования сложных систем
(в смысле надежности) и алгоритмов их практической реализации;□ разработка инженерных методов анализа надежности систем на всех эта¬
пах их жизненного цикла;□ способы практического решения проблем надежности.Рассмотрим эти задачи более подробно.
Проблемы анализа надежности сложных технических систем693.1. Научное обоснование критериев
и показателей надежностиНе существует единственного критерия, достаточно полно характеризующего
надежность сложной системы. Это объясняется ее многофункциональностью.
От надежности сложной системы зависят такие ее показатели, как качество,
эффективность, долговечность, готовность, безопасность, живучесть и риск.
При этом для обеспечения высоких показателей необходимо, чтобы сложная
система была высоконадежной и удовлетворяла требованиям по множеству
критериев, таких как вероятность безотказной работы, среднее время безот¬
казной работы, наработка на отказ, функция и коэффициент готовности и др.Так, например, для достижения заданной эффективности системы необходи¬
мо гарантировать определенное значение вероятности безотказной работы,
для обеспечения долговечности— среднее время безотказной работы, для
обеспечения готовности — коэффициент готовности.Между тем, все критерии надежности связаны между собой однозначными
математическими зависимостями. Поэтому, задавая требования на множество
критериев, в большинстве случаев обнаруживается их противоречивость и
физическая нереализуемость. Например, для обеспечения эффективности
сложной системы задается требование на вероятность безотказной работы
P(t) = 0,97 в течение 300 часов, а для обеспечения долговечности— нара¬
ботка на отказ Т = 2200 час. Эти критерии связаны зависимостьюООТ - | P(t)dt, т. е. при задании требований на P(t) наработка на отказ уже бу-одет однозначно определена. Например, если время до отказа системы имеет
экспоненциальное распределение, то наработка на отказ не будет удовлетво¬
рять требуемому значению. Если время до отказа системы подчинено распре¬
делению Рэлея, то наработка на отказ соответствует заданному требованию
на долговечность (рис. 3.1).Техногенный риск системы R(t) вычисляется по формуле:Я(0=Е^(0,с=1где rt — риск при возникновении отказа /-го типа, — вероятность отка¬
за /-го типа.Из формулы видно, что для обеспечения заданного риска не обязательно
иметь систему с высокой вероятностью безотказной работы P{t). Достаточ¬
но, чтобы система имела высокую вероятность того, что не возникнут такие
70Гпава 3отказы, которые приводят к большому риску. Снова возникли противоречия в
выборе показателей надежности с точки зрения эффективности и риска.Рис. 3.1. P(t) экспоненциального распределения (кривая 1)
и распределения Рэлея (кривая 2)Следует также иметь в виду, что способы обеспечения надежности сущест¬
венно зависят от критерия. Например, для обеспечения вероятности безот¬
казной работы эффективным методом является структурное резервирование,
а для обеспечения среднего времени безотказной работы системы длительно¬
го существования — нагрузочное резервирование. Какое же из них выбрать,
если требования задаются одновременно на два критерия P(t) и Т ? Приме¬
нение одновременно нескольких методов может привести к излишней избы¬
точности, а значит, к повышению стоимости, веса и габаритов системы.
Можно продолжать приводить примеры, однако сказанного достаточно, что¬
бы убедиться в противоречивости требований, задаваемых на показатели на¬
дежности с разных позиций.Задачу выбора критериев и показателей надежности сложных систем можно
сформулировать так: дана сложная система и требования на ее надежность в
виде семейства критериев. Требуется определить набор критериев, который
бы обеспечил все требования и одновременно не содержал противоречивых
критериев. Решая эту проблему, исследователю придется во многих случаях
формулировать новые критерии, т. к. задача в такой постановке является не¬
корректной из-за однозначных зависимостей между существующими крите¬
риями. Такими обобщенными могут быть критерии вида:z = Z CjRj,<=i
Проблемы анализа надежности сложных технических систем71где Z — обобщенный критерий надежности; Л, — /-й критерий; С, — ко¬
эффициент значимости z'-го критерия; к — число критериев, полностью ха¬
рактеризующих систему с точки зрения ее надежности.3.2. Разработка моделей функционирования
сложной системыРазработанные в теории надежности модели функционирования сложных
систем часто являются слишком абстрактными, а поэтому не адекватны ори¬
гиналам. Они не учитывают неодновременность работы элементов, наличие
последействия отказов и естественной избыточности, физической реализуе¬
мости структурного резервирования, а также не обеспечивают требуемой
точности расчетов.Элементы сложной системы, являющейся многофункциональной, работают
не одновременно. При этом набор элементов, одновременно функционирую¬
щих, существенно зависит от внешних факторов, а поэтому является величи¬
ной случайной. В моделях, реализованных на практике, в большинстве случа¬
ев не учитывается человек как активный элемент информационной системы.
Анализ надежности таких систем требует моделирования собственного вре¬
мени функционирования системы. В большинстве практических случаев вы¬
числение показателей надежности осуществляется по формулам:P(t) = e~X‘<, Гс=-Ь.При этом интенсивность отказов системы равна сумме интенсивностей отка-пзов ее элементов, т. е. Хс = . Здесь не учитывается то обстоятельство, что»=1число одновременно работающих элементов является функцией времени:
« = /(0-В резервированных структурах имеют место последействия отказов, т. к. от¬
каз резервных элементов неизбежно приводит к увеличению интенсивностей
отказов исправных элементов. Последействия имеют место также в ремонти¬
руемых системах, потому что после-ремонта показатели надежности элемен¬
тов, подвергшихся ремонту, иные, чем до ремонта.Применение резервирования на практике требует учета его физической реа¬
лизуемости: наличия автоматов контроля и коммутации при резервировании
замещением, наличия двух характеров отказов элементов электроники, изме¬
нения параметров элементов при раздельном резервировании с постоянно
включенным резервом и т. д.
72Гпава 3Неодновременность работы элементов и наличие последействия отказов яв¬
ляются основанием утверждать, что интенсивность отказов сложной системы
не может быть величиной постоянной, если даже интенсивности отказов эле¬
ментов постоянны. Отсюда вытекает важный вывод: экспоненциальный закон
надежности к сложным системам не применим.В сложных системах могут возникать внезапные, постепенные и переме¬
жающиеся отказы. Существующие модели предполагают независимость этих
отказов. Это допущение для случая сложных систем сомнительно. Изменение
параметров системы по причине ее старения изменяет коэффициенты нагруз¬
ки, а значит, и вероятность возникновения внезапных отказов и сбоев.К сложным системам предъявляются высокие требования надежности. Необ¬
ходимо, например, чтобы вероятность безотказной работы или коэффициент
готовности имели значение несколько девяток после запятой. Между тем,
интенсивности отказов элементов, получаемые из эксплуатации, содержат,
как правило, только одну или две значащие цифры. Тогда расчеты показате¬
лей надежности, выполняемые в процессе проектирования, принципиально
не могут иметь значения большие, чем одна или две цифры после запятой. Из
сказанного ранее можно сделать следующий важный вывод: разработка ма¬
тематических моделей функционирования сложных систем является матема¬
тической и технической проблемой; ее решение следует искать в разработке
приближенных моделей и методов их реализации, учитывающих необходи¬
мость моделирования собственного времени системы, наличие последействия
отказов, физическую реализуемость системы, обеспечение погрешностей
расчета.Существующие модели, в частности экспоненциальная, позволяют выпол¬
нить лишь сравнительную оценку надежности различных схемных решений и
выбрать наилучшую. Они практически не дают возможности с необходимой
для практики точностью получить ответ в виде числа.Проблема анализа надежности столь сложна, что возникает мысль отказаться
от численных показателей надежности и разработать показатели качествен¬
ные. При наличии качественных показателей расчеты не требуются. Такие
показатели должны быть научно обоснованны, при этом они будут уникаль¬
ными для данной системы. Эта проблема будет обсуждаться в гл. 14.В следующих пунктах настоящей главы подробно рассматриваются пробле¬
мы анализа надежности технических систем. Дается обзор существующих
методов, их возможности, достоинства и недостатки. Главное внимание уде¬
ляется вопросам анализа надежности сложных систем при неэкспоненциаль¬
ных законах распределения отказов и восстановлений.
Проблемы анализа надежности сложных технических систем733.3. Методы анализа
надежности технических систем3.3.1. Обзор существующих методов расчета
надежности сложных системАнализ надежности технических систем производится, как правило, на осно¬
ве известных методов с привлечением данных об отказах и восстановлениях
элементов, полученных в результате эксплуатации или испытаний систем и
их элементов. На практике обычно используют аналитические методы, а так¬
же методы имитационного и статистического моделирования. Математиче¬
ский аппарат теории надежности сложных систем состоит из большого числа
аналитических методов. Прежде всего, это логико-вероятностные методы,
методы, основанные на теории случайных процессов, декомпозиции, асимп¬
тотические и эвристические, аналитико-статистические.Основой аналитических методов для решения задач надежности служит тео¬
рия случайных процессов (марковских, полумарковских, многомерных мар¬
ковских). При помощи однородных марковских процессов с конечным или
счетным множеством состояний [20, 26, 28, 45] описывается эволюция сис¬
тем при максимальных ограничениях: время безотказной работы, восстанов¬
ления и подключения резервных элементов, временной резерв, время между
сеансами контроля, проведения контроля, существования скрытых отказов
и т. д. Они не должны зависеть от предшествующей истории, а значит, имеют
экспоненциальные распределения. Экспоненциальные законы распределения
можно использовать только в том случае, когда потоки отказов и восстанов¬
лений являются простейшими, т. е. обладают свойствами ординарности, ста¬
ционарности и отсутствия последействия. Вообще говоря, потоки отказов
элементов технических систем можно считать ординарными. Потоки восста¬
новлений могут быть неординарными, когда одновременно восстанавливают¬
ся несколько элементов. Свойство стационарности должно быть подвергнуто
сомнению, т. к. в системе возможно старение или омоложение элементов, и
за равные промежутки времени вероятности появления тех или иных собы¬
тий могут быть различны. Наличие последействия проявляется постоянно,
например, после любого ремонта или любого отказа резервированного эле¬
мента.Случайные процессы, с которыми приходится встречаться в теории надежно¬
сти, далеко выходят за пределы марковских процессов. Попытка отказаться
от предположения об "экспоненциальности" отказа или восстановления хотя
бы одного элемента приводит к появлению значительных трудностей в связи
с необходимостью составлять системы интегродифференциальных уравне¬
ний. Эти уравнения в теории массового обслуживания впервые рассматрива¬
74Гпава 3лись Р. Форте, Д. Коксом, Б. А. Севастьяновым [102] для простейшего вхо¬
дящего потока и произвольного распределения длительности обслуживания
заявок. Ю. К. Беляев [13] ввел в рассмотрение класс линейчатых марковских
процессов, составил для них интегродифференциальные уравнения и исполь¬
зовал их для решения некоторых задач теории надежности.Математическое описание функционирования системы с произвольными
распределениями (Эрланга, нормальное и т. д.) часто удается получить с по¬
мощью теории полумарковских процессов, когда процессы исправной работы
и обслуживания рассматриваются в специально подобранные моменты вре¬
мени [13, 34, 41, 59, 60, 64] или марковскими процессами восстановления со
специально построенным фазовым пространством [55, 56, 93]. Эти приемы
использовал еще А. Я. Хинчин, а позднее Д. ,Кендалл. Однако поведение
сложной системы с восстановлением лишь в нескольких исключительных и
довольно тривиальных случаях удается описать полумарковским процессом.
Для расширения круга решаемых задач применяются процессы с вложенны¬
ми точками, которые также используются для оценки надежности достаточно
простых восстанавливаемых систем. Методы, основанные на полумарковских
процессах, применяются в тех случаях, когда только некоторые распределе¬
ния (часто одно или небольшое их количество) являются произвольными, а
остальные — экспоненциальными. Кроме того, эти методы, как правило, по¬
зволяют определять лишь стационарные значения показателей надежности, а
для исследования переходных процессов функционирования системы здесь
возникают непреодолимые трудности. Возможности применения методов
ограничены, поскольку в общем виде на их основе не удается разработать
математическую модель восстанавливаемой технической системы с учетом
структурной избыточности и любой дисциплины ремонта.Известно [25], что любой случайный процесс может быть дополнен до мар¬
ковского соответствующим расширением фазового пространства. Следуя
этому теоретическому положению, в настоящее время выполнен анализ на¬
дежности класса систем, описываемых суперпозицией независимых полу¬
марковских процессов [65, 105]. Основные недостатки этих работ— невоз¬
можность исследования более сложных зависимых процессов и известные
трудности в исследовании нестационарных характеристик.В более общих ситуациях приходится рассматривать марковские процессы с
континуальным множеством состояний, т. е. многомерные марковские про¬
цессы [45, 53, 56]. На их основе удается описать эволюцию технической сис¬
темы при произвольных распределениях времен безотказной работы и вос¬
становления элементов с учетом структурной и временной избыточности, с
учетом контроля технических средств, с учетом нескольких видов отказов
и т. д. Инженерная реализация метода многомерных марковских процессов в
простейших случаях осуществляется с помощью статистического моделиро¬
Проблемы анализа надежности сложных технических систем75вания на ЭВМ, требующего колоссальных затрат машинного времени и па¬
мяти. Даже ускоренные методы статистических испытаний часто не позво¬
ляют произвести расчет надежности с требуемой точностью в реальном мас¬
штабе времени.Среднее время восстановления элементов технических систем обычно в
несколько раз меньше среднего времени между соседними отказами. Это об¬
стоятельство позволяет использовать для оценки их надежности асимптоти¬
ческие методы. Исследование надежности систем с помощью асимптотиче¬
ских методов является важной задачей, т. к. точные формулы для характери¬
стик надежности удается получить лишь в редких случаях, и они, как
правило, сложны для практического использования. Распределения исходных
характеристик элементов обычно заранее не известны, а их оценка требует
большего труда, чем оценка некоторых числовых параметров.В практическом плане интерес представляют результаты, в которых доказы¬
вается асимптотическая независимость показателей надежности от исходных
распределений. Примером могут служить исследования А. Д. Соловьева и
Б. В. Гнеденко [7], в которых установлено, что распределение длительности
безотказной работы резервированных систем в условиях "быстрого" восста¬
новления асимптотически экспоненциально. Асимптотический анализ слож¬
ных систем, основанных на сочетании аналитического метода и метода
статистического моделирования, проводился в работах И. Н. Коваленко,
В. А. Ивницкого, Н. М. Акулиничева [52, 53, 54].В настоящее время работы, посвященные изучению свойств восстанавливае¬
мых систем на основе асимптотического метода, носят в основном теорети¬
ческий характер и могут использоваться для систем с малым числом состоя¬
ний. Эти методы не определяют предельное значение параметра, начиная с
которого можно использовать асимптотические формулы. С помощью этих
методов затруднен также анализ переходных процессов. И, наконец, погреш¬
ность характеристик надежности может быть достаточно высокой.Перечисленные методы имеют наибольшее распространение в практике ин¬
женерных расчетов. Тем не менее для анализа надежности систем с неэкспо¬
ненциальными распределениями иногда применяются и другие методы. Это
прежде всего методы логико-вероятностные, графовые, укрупнения состоя¬
ний, эвристические, аналитико-статистические, декомпозиции, метод разло¬
жения на фазы, диффузионных процессов, Кендалла и метод аппроксимации
интенсивностей.Логико-вероятностные методы основаны на непосредственном применении
теорем теории вероятностей для анализа надежности технических систем.
Дифференциальный метод разложения на фазы, а также метод Кендалла,
применяемый в задачах массового обслуживания с одним пуассоновским
76Гпава 3случайным процессом, позволяют сводить немарковскую модель к марков¬
ской. Практически эти методы позволяют использовать лишь распределения
Эрланга и приводят к значительному увеличению числа состояний. Подоб¬
ные трудности встречаются при оценке надежности систем с большим чис¬
лом равнонадежных элементов методом диффузионных процессов, как не¬
прерывного аналога уравнений Колмогорова. Эти методы могут использо¬
ваться для расчета стационарных характеристик надежности и вероятности
безотказной работы для систем кратковременного действия. При этом "не¬
экспоненциальные" компоненты, как правило, состоят из нескольких фаз и
имеют распределение Эрланга. С помощью введения промежуточных со¬
стояний, соответствующих моментам окончания фаз, модель сводится к мар¬
ковской. Методы ступенчатой аппроксимации интенсивностей отказов и вос¬
становлений элементов можно применять для оценки надежности систем,
имеющих незначительное число состояний и медленно изменяющиеся интен¬
сивности. Определение погрешностей расчетов на основе этих методов —
сложная задача.Более общей для описания технической системы является графовая модель,
учитывающая влияние практически любых факторов, влияющих на систему,
например средств контроля и системы обслуживания. Существенным недос¬
татком описания системы графом состояний является сложность ввода дан¬
ных и методов определения характеристик надежности, если количество
состояний системы велико. Здесь могут использоваться методы укрупнения
состояний [59] с недостатками, присущими методам полумарковских про¬
цессов.Сущность эвристического метода оценки надежности восстанавливаемых
систем состоит в объединении групп элементов этой системы в один эквива¬
лентный элемент, который характеризуется альтернирующим процессом вос¬
становления. Тем самым происходит уменьшение числа элементов в системе.
Метод применяется исключительно для случая высоконадежных элементов и
систем и не позволяет установить погрешность вычислений.Метод декомпозиции сложных систем основан на построении оценочных ма¬
тематических моделей, позволяющих получать простые и достаточно точные
верхнюю и нижнюю границы для оцениваемого показателя надежности. Ос¬
новные сложности метода связаны с его точностью.Методы машинного моделирования в целом являются универсальными
и допускают рассмотрение систем с большим количеством элементов
[21,29,53, 144]. Однако их использование в качестве метода исследования
задач надежности целесообразно лишь тогда, когда трудно или невозможно
получить аналитическое решение. Основными этапами такого исследования
являются: построение формальной модели, разработка программ имитации
траекторий модели, проведение имитационных экспериментов.
Проблемы анализа надежности сложных технических систем77При анализе высоконадежных систем с помощью имитационной модели воз¬
никают проблемы, связанные с очень большими затратами машинного вре¬
мени, необходимого для вычислений с требуемой точностью. Для увеличения
скорости расчетов применяются методы ускоренного моделирования, искус¬
ственного введения моментов регенерации, "взвешенного" моделирования,
в частности метод малого параметра, а также комбинированные методы ана¬
лиза с приложениями методов статистического моделирования. С увеличени¬
ем надежности элементов эффективность моделирования уменьшается
[52, 54], и оно становится практически не реализуемым. Часто используется
методика уменьшения дисперсии, которая базируется на применении допол¬
нительной информации относительно системы [132, 144]. Однако этот метод
не может быть использован для разработки универсальных прикладных про¬
грамм оценки надежности. Здесь проявляется противоречие между основны¬
ми требованиями, предъявляемыми к математическим моделям, а именно: с
требованиями адекватности и универсальности с одной стороны и высокой
экономичности с другой. Методы статистического и имитационного модели¬
рования не позволяют в полном объеме определять надежность системы, если
учесть большое количество сопутствующих факторов, влияющих на ее функ¬
ционирование. Поэтому следует подчеркнуть исключительную важность про¬
ведения исследований по надежности систем аналитическими методами [7].3.3.2. Причины неэкспоненциальности
случайных параметров, отказов и восстановлений
технических системВ настоящее время большинство практических расчетов в области надежно¬
сти предполагает использование экспоненциального закона распределения
времени между отказами элементов и параметров функционирования систе¬
мы, таких как время принятия решения, время перерыва в работе элементов,
время существования скрытого отказа и т. д. Это обусловлено, с одной сто¬
роны, известным положением о сходимости суммарных независимых пото¬
ков отказов к пуассоновскому потоку и, с другой стороны, сравнительной
простотой аналитических расчетов. Известно, однако, что использование
экспоненциального закона, как правило, приводит к существенному расхож¬
дению аналитических и экспериментальных данных о надежности сложных
систем.Если не учитывать неэкспоненциальность распределений времени безотказ¬
ной работы и времени восстановления элементов сложной системы, то это
может привести к чрезвычайно большим ошибкам [97, 108, 109].Элементы электроники, как правило, имеют экспоненциальное распределе¬
ние времени безотказной работы. Однако устройства, содержащие непосле¬
78Гпава 3довательно соединенные в смысле надежности элементы, уже не обладают
экспоненциальными распределениями. Поэтому включение этих устройств в
систему в качестве ее элементов приводит к необходимости исследовать на¬
дежность системы при неэкспоненциальных распределениях.Покажем, что при нагруженном резерве вероятность безотказной работы уст¬
ройства подчиняется гиперэкспоненциальному распределению, а при нена-
груженном или смешанном резервировании— обобщенному гамма-распре¬
делению.Экспоненциальное распределение обладает следующим свойством: свертка
(см. разд. 2.5) плотностей = есть плотность, подчиненная обоб¬щенному гамма-распределению, причем если все А,, различны, то свертка
указанных плотностей дает гиперэкспоненциальное распределение. Действи¬
тельно, свертка всех плотностей ft(t) с одинаковыми параметрами А,, обра¬
зует плотность гамма-распределения, а свертка гамма-распределений с раз¬
ными параметрами, как известно, приводит к плотности обобщенного гамма-
распределения. В частности, если все различны, то имеем линейную ком¬
бинацию плотностей экспоненциальных распределений:
л И n g~VП /(О^П^Етг гт “ — —/=1 /•=1 »=l(A,i-А,,-).../ -A.JФункционирование невосстанавливаемого устройства, элементы которого
имеют экспоненциальные распределения, описывается графом состояний, в
ветви которого проставлены параметры этих распределений. На рис. 3.2 при¬
веден фрагмент графа, содержащий вершину /0, предшествующую ей верши¬
ну /_] и вершины i\, i2,..., , следующие из данной вершины за один пере¬
ход.Рис. 3.2. Фрагмент графа, включающий вход и выходы для состояния /0
Проблемы анализа надежности сложных технических систем79Тогда для вероятности р,г) (?) состояния г0 справедливо равенствоPio (0 = К^Рц (0 * е_(Ч'/| +Чл +"+Х'0'")Г •Это значит, что вероятность пребывания системы в любом состоянии равна
свертке экспоненциальных функций, и, в силу сделанного ранее замечания,
она представляет собой линейную комбинацию гамма-распределений. Отсю¬
да следует, что вероятность безотказной работы также равна линейной ком¬
бинации гамма-распределений.Заметим, что эта линейная комбинация гамма-распределений превращается в
линейную комбинацию экспоненциальных распределений, если все суммар¬
ные интенсивности переходов для любого пути графа различны. Поскольку
для основного соединения и нагруженного резерва суммарная интенсивность
при переходе на более низкий уровень графа убывает, то плотность распре¬
деления времени безотказной работы всей системы имеет гиперэкспоненци-
альное распределение. Ненагруженное и скользящее резервирование отме¬
ченным свойством не обладает, а поэтому плотность распределения времени
безотказной работы системы имеет обобщенное гамма-распределение. По¬
добные заключения можно сделать и для элемента с экспоненциально рас¬
пределенным резервом времени, и для элементов, обладающих экспоненци¬
альным распределением, но в которых учитываются дополнительные свойст¬
ва, такие как возможность накопления нарушений, встроенный контроль, два
вида отказов и др. Еще в большей степени это относится к механическим
элементам, которые принципиально являются стареющими. Как показывают
проводимые исследования [8, 105], время безотказной работы механических
элементов имеет распределение Вейбулла или усеченное нормальное распре¬
деление. Значит, экспоненциальная модель не адекватна физическим процес¬
сам, протекающим в системе. Для ремонтируемых систем время восстанов¬
ления практически никогда не является экспоненциальным, т. к. оно склады¬
вается из времени обнаружения, времени локализации и времени устранения
неисправности, т. е. равно сумме (зависимых или независимых) обычно не-
экспоненциапьных распределений случайных величин. Причинами неэкспо¬
ненциальных распределений также могут быть: неодновременность работы
элементов, наличие восстановления большого числа механических устройств,
наличие искусственной и естественной избыточности.Таким образом, проблема анализа надежности восстанавливаемых систем с
произвольными распределениями отказов и восстановления является не толь¬
ко научной, но главным образом технической проблемой, вытекающей из
свойств сложных систем.
80Гпава 33.3.3. Зависимость показателей надежности
от законов распределения и дисциплины
восстановления элементовВ теории надежности важное место отводится нахождению простых прибли¬
женных расчетных формул для показателей надежности. В то же время эти
формулы должны иметь достаточно высокую точность, удовлетворяющую
инженера-практика. Как показывают исследования, даже в случае простей¬
ших резервированных систем не удается найти простых аналитических соот¬
ношений для вычисления показателей надежности с требуемой точностью.
Исключение составляют некоторые системы специального вида, показатели
надежности которых зависят только от математических ожиданий времени
безотказной работы и времени восстановления элементов и не зависят от за¬
конов распределения. Так бывает, например, в следующих случаях:□ элементы системы независимы по отказам и восстановлению (параллель¬
ное соединение с неограниченным восстановлением);□ при вычислении стационарных показателей надежности, когда отсутствует
очередь на работу исправных элементов и очередь на восстановление от¬
казавших элементов системы.Однако при вычислении показателей надежности, как правило, недостаточно
знать лишь первые моменты соответствующих распределений. Если даже
предположить, что среднее время восстановления элементов значительно
меньше среднего времени их исправной работы, то и в этом случае сущест¬
вующие расчетные формулы дают весьма грубые приближения к истинным
значениям показателей надежности. При надлежащем выборе законов рас¬
пределения относительная погрешность может быть очень высокой и даже
неограниченной. Кроме того, эти формулы не учитывают приоритета обслу¬
живания отказавших элементов. Как известно, для экспоненциальных рас¬
пределений дисциплина восстановления элементов незначительно влияет на
показатели надежности всей системы, особенно если ее функционирование
протекает при дополнительном условии "быстрого" восстановления. Однако
если законы распределения неэкспоненциальны, то дисциплина восстановле¬
ния может оказать существенное влияние на надежность системы. В этом
можно убедиться на примерах некоторых резервированных систем.ПРИМЕР 3.1. Дано: восстанавливаемая дублированная система, составлен¬
ная из равнонадежных элементов с ограниченным восстановлением. Оценить
влияние дисциплины восстановления элементов на среднюю наработку на
отказ системы.
Проблемы анализа надежности сложных технических систем81Решение. Предположим, что время безотказной работы элементов экспонен¬
циальное с параметром X, а время восстановления имеет произвольное рас¬
пределение с плотностью g(t) .В гл. 7 будет показано, что средняя наработка
на отказ для прямого, обратного и назначенного приоритетов выражается
формулами:уЧпр) _ 2 - g(X) ^(обр) _ Т2 + ^(наз) _ (2 — g(A.))(l + ХТЪ)2Х{\ -g{X)Y 2Тв ’ ^(l-i(^)) + A.2(2- g(X))rB 'Здесь и далее g(X) — преобразование Лапласа (см. разд. 2.5) функции g(t),
Тв — среднее время восстановления элементов. Предположим, что
g(t) = сце~^‘ +(1 -c)ve~vl и имеет место "быстрое" восстановление элемен--1 (V —1)цтов, например: Т = 100 час, Тв =1 час. Тогда X = 0,01 час , с = . Пу-v-цтем простых преобразований легко показать, что Г<пр) -> оо, если ja —> 0 ,V—>оо, тогда как Г(обр) =5100 час. Например, полагая ц = 0,001 час-1,v = 10, получим Г(пр)= 27 577 час,Т(наз) =8565 час. Таким образом, средняя
наработка на отказ системы существенно зависит от приоритета обслужива¬
ния элементов. Сопоставим полученные результаты с асимптотической фор-мулой 7^ас) = , справедливой при условии "быстрого" восстановления2ТВэлементов и любой дисциплины восстановления. Видим, что Г(ас) = 5000 час
и существенно отличается от ее точного значения. Следовательно, простота
асимптотических формул не может служить основанием для возможности их
применения при оценке надежности резервированных систем.ПРИМЕР 3.2. Дано: восстанавливаемая дублированная система из равнона¬
дежных элементов, обслуживаемая одним ремонтным органом с прямым
приоритетом. Установить зависимость среднего времени восстановления сис¬
темы от закона распределения времени восстановления ее элементов.Решение. Пусть распределение времени безотказной работы каждого эле¬
мента экспоненциальное с параметром X, а время восстановления имеет^a-l -Lгамма-распределение с плотностью g(t) = ^ац' ^е ^ ’ сРедним = оф и ве- : 00роятностью невосстановления G(t)= Jg(;t)c£t.
82Гпава 3Тогда среднее время восстановления системы может быть найдено по форму¬
ле (см. гл. 7)г _ Тв -G(X)и, значит,XG(X)JBCт■L О/XT1+1ЦВа у*а ХТаИсследуя это отношение в зависимости от а, получим графики, представлен¬
ные на рис. 3.3.ГВСГ.Рис. 3.3. Зависимость — от а при значениях ХГ = 0,001 (кривая 1),
Тв0,1 (кривая 2), 1 (кривая 3)Таким образом, в зависимости от параметра а, а в общем случае — от закона
распределения, можно получить характеристики надежности системы, изме¬
няющиеся в достаточно широком диапазоне. При а = 1 имеем экспоненци¬
альный случай, при котором Твс - Тъ.Для неэкспоненциальных распределений некоторые показатели надежности
не полно характеризуют систему и нечувствительны к ее изменениям.
Проблемы анализа надежности сложных технических систем83ПРИМЕР 3.3. Дано: невосстанавливаемая резервированная система при об¬
щем резервировании с кратностью m -1. Определить выигрыш в надежности
ТGT = — для распределений: экспоненциальное, Вейбулла, вырожденное,
Торавномерное.Решение. Пусть F(t) — вероятность безотказной работы, а Т0 — наработка
до отказа одного элемента. Тогда для системы вероятность безотказной рабо¬
ты и средняя наработка до отказа вычисляются соответственно по формуламFC(0=1-(1-F(/))"; тс = J(i-(1 -mr)dt.оДля вырожденного распределения очевидно, что Тс = Т0 для любых значений_ -UJm . Для распределения Вейбулла F(t) = e имеемТ m . -
-'О / = 1В частности, при а = 1 получаем экспоненциальное распределение, для кото¬
рогоm /_ lV-l f'i m 1Gr = iL-Ь-Хт-
,=i i ы \lДля равномерного распределения с параметрами а и b^ Тс 2{mb + о)\JT — — 1г Г0 {m + \\a + b)2mВ частности, при a = 0 получим GT = . Результаты расчетов по приве-m +1денным формулам сведем в табл. 3.1.Как следует из таблицы, для вырожденного распределения наработка до от¬
каза Тс совершенно не чувствительна к числу резервных элементов. Для рав¬
номерного распределения резервирование также дйет незначительный выиг¬
рыш (не более чем вдвое). Распределение Вейбулла при достаточно большом
значении параметра а не оказывает существенного влияния с ростом m на
изменение наработки до отказа. В то же время для распределения Вейбулла
при молодеющем распределении можно получить любой сколь угодно боль-
84Гпава 3той выигрыш. Заметим, что для ненагруженного резерва GT есть величина
постоянная, равная т.Таблица 3.1. Выигрыш в надежности Gj для различных распределенийmВырожд.распред.Распределение ВейбуллаЭкспон.распред.Равном.распред.а « 0а = 0,5а = 211,001,001,001,001,001,0021,002,001,751,291,501,3331,003,002,361,461,831,5041,004,002,881,572,081,6051,005,003,341,652,281,67со1,00оооо2,00Приведенные примерь! доказывают необходимость количественной оценки
надежности систем при распределениях, отличных от экспоненциальных: она
продиктована существенной зависимостью показателей надежности от зако¬
нов распределения и дисциплины восстановления отказавших элементов,3.3.4. Критичное влияние произвольных
распределений отказов и восстановлений
на нестационарные показатели надежностиПрактические задачи, возникающие в теории надежности, показывают важ¬
ность расчета и анализа нестационарных характеристик, которые часто не
принимаются во внимание, хотя, как показывают вычислительные экспери¬
менты, продолжительность переходного процесса может быть довольно
большой. Более того, существуют системы, стационарное состояние которых
вообще не наступает.Пусть /(t) и g(t) — плотности распределения времени безотказной работы
и времени восстановления элемента. Как было показано в разд. 2.6.1, функ¬
ция готовности системы удовлетворяет уравнениюKr(t) = F(t) + J{db(t)F(> - x)dx,
о
Проблемы анализа надежности сложных технических систем85Численное решение этих уравнений для многих распределений не представ¬
ляет затруднений. Получим аналитические выражения функции готовности
для некоторых часто встречающихся распределений.В преобразовании Лапласа выражение функции готовности имеет вид:(3.1)Случай 1. Если законы распределения экспоненциальные с параметрами X и
и, то, как известно,Случай 2. Закон распределения времени безотказной работы экспоненциаль¬
ный, а времени восстановления — Эрланга 2-го порядка с параметром ц. Из(3.1) следует, чтоТочки экстремума Ьк получаются в результатерешения уравнения:Тем самыми функция Kr(t) имеет бесконечное число точек экстремума, а это соответ¬
ствует колебательному процессу. Для значения А, имееми функция готовности находится в явном виде:где функция юв находится из уравнения
86Гпава 3т. е. 6] — точка минимума, в которой график функции готовности лежит ни¬
же стационарного значения Кг. Значения ak , в которых график функции го¬
товности пересекает линию Kr(t) = Кг, определяются из уравненияЭто доказывает, что для произвольных распределений могут наблюдаться
провалы функции готовности ниже ее стационарного значения. Графики
функций готовности для 1-го и 2-го случаев приведены на рис. 3.4.Для равномерного распределения с параметрами а и Ъ преобразование Лап¬
ласа функции готовности имеет вид:В этом случае в явном виде найти функцию готовности не удается. Тем не
менее расчеты, выполненные на ЭВМ, показывают достаточную близость
функций готовности для равномерного распределения и распределения Эр¬
ланга. Таким образом, в отличие от экспоненциального случая, когда функ¬
ция готовности всегда является монотонно убывающей, в общем случае
функция готовности часто имеет колебательный характер. Поэтому может
оказаться, что готовность системы для небольшого времени эксплуатацииI, часРис. 3.4. Графики функции готовности для различных распределений
Проблемы анализа надежности сложных технических систем87меньше, чем при ее длительной эксплуатации. Этот факт часто игнорируется
на практике, что может привести к нежелательным результатам.Можно показать, что с уменьшением дисперсии времен безотказной работы
элементов усиливается колебательный характер функции Kr(t) и значитель¬
но увеличивается время наступления стационарного режима системы.Случай 3. Законы распределения вырожденные со средними Т и Тв соответ¬
ственно. В этом случае из (3.1) получим:Из этого выражения следует, что функция Kr(t) тождественно равна единице
на интервалах [к(Т + ГВ), к(Т + ГВ) + Г], к = 0,1, 2,..., и равна нулю вне этих
интервалов, т. е.Стационарный режим здесь вообще не наступает, и коэффициент готовности
не существует.1 оо1~е e~k(T+Te)z =2 к=ОКг«)Ооt, час20Рис. 3.5. Г рафик функции готовности для вырожденных распределений
88Гпава 33.3.5. Методы и проблемы расчета
надежности систем с большим числом состоянийПри разработке математической модели технической системы с большим
числом состояний, как правило, сталкиваются со следующими препятствия¬
ми, существенно затрудняющими анализ ее надежности:□ неоднозначность понятия отказа системы;□ взаимовлияние отказов элементов и частей системы;□ неопределенность исходных данных;□ многокритериальность;□ восстанавливаемость;□ наличие избыточности (естественной или искусственной, введенной с
целью повышения надежности);□ наличие контроля состояний;□ возможность перестройки структуры системы.Одной из центральных проблем теории надежности больших систем следует
считать разработку математического аппарата для ее расчета, анализа и про¬
гнозирования. Сложность технической системы и большое число состояний
ее функционирования приводит к необходимости решения систем уравнений
весьма больших размерностей. Так, например, в системе из п элементов раз¬
личной надежности с нагруженным резервом, обслуживаемой одним ремонт-П .ником, насчитывается N - ^ А'п >п\ состояний, где А‘п — число размеще¬
ноний из п по /. Даже для простейших схем (типа дублированной системы
элементов) могут быть сотни состояний, если учитывать контроль состояний,
переключение на резерв и другие особенности реальной системы.В настоящее время для анализа надежности больших систем, как правило,
используется общеизвестный математический аппарат, основанный на мето¬
дах имитационного моделирования, асимптотического анализа, случайных
процессов и связанных с ними интегродифференциальных уравнений. На ос¬
нове этих методов расчеты характеристик надежности больших систем, обла¬
дающих значительной сложностью, достаточно редко могут быть доведены
до численных результатов с требуемой точностью. Таким образом, отсутст¬
вие традиционных методов для анализа сложных технических систем с
большим числом возможных состояний (порядка сотен тысяч и более) требу¬
ет разработки нестандартных подходов к оценке их надежности и эффектив¬
ности. При рассмотрении надежности технических устройств обычно пред¬
полагается, что они могут пребывать в двух возможных состояниях: работо¬
Проблемы анализа надежности сложных технических систем89способном и отказовом. Значение любого показателя надежности зависит от
того смысла, которое вкладывается в понятие "отказовое" состояние. Иссле¬
дование сложных систем ставит перед теорией надежности новые задачи. Ес¬
ли для исследуемой сложной системы определено понятие отказа, то прин¬
ципиально можно найти требуемые характеристики надежности. Однако да¬
леко не всегда очевидно, какое состояние системы можно считать отказовым.
При появлении отказов отдельных частей лишь частично ухудшаются харак¬
теристики системы, но она продолжает выполнять свои функции. Возникает
вопрос об оценке меры целесообразности применения данной системы.В существующих методах расчета надежности технических систем обычно
предполагается, что отказы элементов независимыми система попадает в со¬
стояние отказа при отказе определенного числа элементов. Для сложных сис¬
тем эти допущения часто бывают неприемлемыми. Между характеристиками
отдельных частей системы имеется тесная взаимосвязь, и отказы отдельных
частей системы являются зависимыми событиями. Возникает проблема изу¬
чения суммарных потоков отказов элементов большой системы и учета их
влияния на надежность системы в целом.В вопросах анализа надежности сложных систем с большим числом состоя¬
ний существенным препятствием служит неопределенность начальных ис¬
ходных данных по надежности и ремонтопригодности элементов. Как прави¬
ло, характеристики времен безотказной работы и восстановления элементов
являются случайными величинами, имеющими некоторые распределения ве¬
роятностей. Одной из особенностей моделирования сложной системы являет¬
ся также учет неопределенности данных.3.3.6. Проблемы расчета надежности
реконфигурируемых системОсобой спецификой обладают системы с переменной структурой. В общем
случае к ним можно отнести системы, характеристики надежности которых
изменяются, например, из-за изменения нагрузки на систему или ее элемен¬
ты, модификации структуры системы, наличия временных интервалов про¬
стоя элементов системы, изменения условий функционирования системы
и т. д.Указанные технические системы относятся к системам с реконфигурацией их
структуры. Модификации в системе могут происходить как через постоян¬
ные, так и через переменные промежутки времени; они могут быть детерми¬
нированными или случайными, периодическими и непериодическими.
Структура системы может изменяться потому, что меняются функции, вы¬
полняемые системой, а также с целью повышения ее надежности. Большое
90Гпава 3количество технических систем может быть интерпретировано как системы
с модификациями или с переменной структурой [139].Например, многопроцессорные системы могут изменять свою структуру в
зависимости от исходных данных. То же относится и к производственным
линиям, узлы которых могут выполнять различные операции в зависимости
от условий их применения. Анализ подобных систем показывает, что, как
правило, их модификации являются периодическими. Например, период для
производственных линий может быть равен 24 часам или продолжительности
производства цикла. Все модификации происходят в фиксированные момен¬
ты времени, между которыми характеристики надежности не меняются.Анализ надежности систем со статической и динамической реконфигурацией
структуры представляет собой новое направление в теории надежности
сложных технических систем. Различаются системы, когда в момент измене¬
ния структуры информация о времени работы или восстановления элементов
"забывается", и после момента реконфигурации система с измененной струк¬
турой начинает функционировать как новая. Это условие может быть вполне
естественным для системы типа "черного ящика", о которой лишь известно,
что она имеет два состояния и определены законы распределения вероятно¬
стей перехода между состояниями. Для таких систем предполагается, что до¬
пустимыми являются лишь переходы между исправными состояниями и ме¬
жду отказовыми состояниями. Иначе обстоит дело с системой, имеющей не¬
сколько уровней возможных состояний, а в процессе перестройки структуры
системы имеются переходы между состояниями одного уровня. При этом
может оказаться, что из исправного состояния система переходит в отказовоеи, наоборот, из отказового — в исправное. Таким свойством как раз обладают
системы типа /и/и с нагруженным и ненагруженным резервом.Сложная техническая система с позиций надежности характеризуется такой
специфической особенностью функционирования, как многофункциональ¬
ность. Количество выполняемых системой функций может достигать не¬
скольких десятков. При этом в реализации одной функции может участвовать
большое число модулей (элементов). Один и тот же модуль может быть за¬
действован в выполнении нескольких функций. Поэтому модули, образую¬
щие систему, имеют различную длительность эксплуатации. Так, некоторые
из них работают непрерывно, поскольку участвуют в выполнении всех функ¬
ций, а некоторые модули включаются только на время выполнения какой-
либо одной или нескольких функций. Многофункциональность накладывает
определенный отпечаток на саму постановку задачи анализа надежности та¬
кой системы.При изучении надежности систем, выполняющих несколько функций, как
правило, применяется функциональный подход, при котором описание на¬
Проблемы анализа надежности сложных технических систем91дежности производится по каждой функции в отдельности, а поэтому надеж¬
ность системы характеризуется вектором показателей надежности всех ее
функций. Таким образом, сравнительная оценка различных систем одного и
того же назначения часто является затруднительной, а то и вовсе невыполни¬
мой. Основной сложностью в исследовании многофункциональных систем,
на наш взгляд, является то обстоятельство, что исследования проводятся без
учета потока задач, поступающих в систему. В этом случае анализ надежно¬
сти системы, функционирующей по нескольким функциям, неоднозначен, а
возникающая при этом неопределенность без какой-либо дополнительной
информации не поддается измерению. Выходом из этой тупиковой ситуации
может служить исследование системы вместе с потоком задач, поступающих
на обслуживание. Без учета потока задач можно говорить о временах исполь¬
зования системы по каждой функции и исследовать ее надежность с учетом
времени выполнения системой всех ее функций.Основным вопросом анализа систем с переменной структурой является раз¬
работка моделей и методов расчета характеристик их надежности, а также
управление процессом модификаций с целью получения наибольшей надеж¬
ности систем в соответствии с выбранными критериями.3.4. Проблемы создания
высоконадежных систем3.4.1. Основная проблема надежности
технических системСложные технические системы должны длительное время работать безотказ¬
но. Это требование диктуется необходимостью обеспечения высокой их эф¬
фективности, безопасности, живучести, готовности и других показателей ка¬
чества.Сложные системы состоят из десятков и сотен тысяч элементов, а время их
работы исчисляется тысячами часов.К таким системам предъявляются высокие требования по надежности. На¬
пример, вероятность безотказной работы P(t)> 0,99, коэффициент готовно¬
сти Кг > 0,98.Удовлетворяют ли таким требованиям современные технические системы?Пусть система состоит из и = 1000 элементов, длительность ее работы —
2000 час, элементы, из которых состоит система, высоконадежны, имеют по¬
стоянную интенсивность отказов, среднее значение которой X = 0,2 • 10-6 час 1,
92Гпава 3Вероятность безотказной работы такой системы будет:Pc(2000) = e~nXl =e'°A =0,67.Такая система эксплуатироваться не может по причине низкой надежности:
вероятность ее отказа превосходит требуемую ((7 = 0,01) в 33 раза. Для по¬
вышения ее надежности применим структурное резервирование. Расчеты по¬
казывают, что для обеспечения вероятности безотказной работы системы
Рс(2000) = 0,99 необходимо иметь 5 резервных систем в случае резервирова¬
ния с постоянно включенным резервом и две резервные системы в случае ре¬
зервирования замещением при условии, что автомат контроля и коммутации,
обеспечивающий подключение резервной системы при отказе основной, иде¬
альный в смысле надежности.Существенно повысить работоспособность системы может восстановление
резервированной системы при условии, что ремонт осуществляется без вы¬
ключения системы. Расчеты показывают, что вероятность безотказной рабо¬
ты системы Рс (2000) = 0,99 можно обеспечить при восстановлении дублиро¬
ванной системы со средним временем восстановления Гв<100 час. При
Гв=100 час Рс(2000) = 0,993.Однако такой метод не всегда возможен. Нельзя ремонтировать двигатель
или систему управления самолета в полете, спутника связи на орбите, океан¬
ский лайнер в плавании. Нельзя осуществлять ремонт техники в ее рабочем
состоянии, если ремонт должен осуществляться в специальных мастерских.
Следует также иметь в виду, что техническая реализация этого способа тре¬
бует наличия системы диагностики отказов, что может привести к пониже¬
нию надежности резервированной системы. Не следует также забывать, что
резервирование существенно повышает стоимость системы, ее вес и габари¬
ты. В нашем случае при применении резервирования стоимость системы воз¬
растет в 6 раз при общем резервировании и в 3 раза при резервировании за¬
мещением. На практике резервирование с восстановлением применяется ред¬
ко. Причин для этого достаточно.Надежность элементов непрерывно увеличивается. Появление материалов
высокой прочности, защищенных от коррозии, твердых схем, не требующих
большой энергии для их питания, существенно уменьшили интенсивность
отказов элементов. Однако сложность технических систем и требования к
показателям их надежности растут с такой же скоростью, как и надежность
элементов. Поэтому надежность многих сложных технических систем прак¬
тически не растет. В этом основная проблема надежности техники.
Проблемы анализа надежности сложных технических систем933.4.2. Технические проблемы обеспечения
надежности сложных системОсновным способом повышения надежности является структурное резерви¬
рование. При этом наиболее эффективным считается раздельное (поэлемент¬
ное) резервирование. Такой вывод следует из теории. Он безусловно верен,
но без учета практической реализуемости раздельного резервирования.Пусть необходимо защитить систему управления от отказа дифференцирую¬
щей цепи, обеспечивающей устойчивость системы. Схема цепи приведена на
рис. 3.6.С, ,RРис. 3.6. Дифференцирующая цепьПередаточная функция дифференцирующей цепи имеет вид:W(z) = -^- (3.2)Tz + \где Т = RC —постоянная времени цепи.Применим поэлементное резервирование для повышения надежности цепи.
Резистор наиболее часто отказывает из-за обрыва. Тогда для повышения на¬
дежности необходимо включить параллельно еще один (резервный) резистор.
Какой же величины должно быть сопротивление резервного резистора? Если
его сопротивление равно R (резистор такой же, как и основной), то общее
сопротивление цепи с двумя параллельно включенными резисторами будет
R/2, т. е. постоянная времени дифференцирующей цепи уменьшится вдвое и
не обеспечит устойчивости системы. Если же оба резистора будут иметь со¬
противление 2R, то цепочка будет иметь общее сопротивление R, но при
отказе одного из резисторов (основного или резервного) сопротивление воз¬
растет в 2 раза и вновь постоянная времени цепи выйдет за допустимые пре¬
делы. Наступит отказ системы управления. Таким образом, дублирование
резистора привело к понижению надежности. В подобных случаях применя¬
ется резервирование с дробной кратностью.Предположим, что устойчивость системы управления будет обеспечена, если
сопротивление резистора изменится не более чем на 1/3. При таком условии
защитить систему от одного отказа можно, включив параллельно 3 резистора,
94Гпава 3каждый из которых имеет сопротивление 3R. Кратность резервирования бу¬
дет т = 1/2.Конденсатор имеет два вида отказов — обрыв и короткое замыкание (про¬
бой). Поэтому его резервирование можно осуществить только путем после¬
довательно-параллельной схемы (рис. 3.7).Рис. 3.7. Резервирование конденсатораТаким образом, дифференцирующая цепь повышенной надежности будет
иметь вид, показанный на рис. 3.8.С, , Cj , 3R 3R 3RРис. 3.8. Резервированная схема цепи обратной связи системы управленияОбратим внимание на то, что схема защищена только от одного отказа. При
отказе любых двух элементов постоянная времени Т может измениться на
недопустимую величину, и устойчивость системы не будет обеспечена. Более
того, эта схема не защищена от короткого замыкания конденсатора. Действи¬
тельно, при коротком замыкании любого конденсатора емкость цепи увели¬
чивается вдвое, т. е. вдвое увеличится постоянная времени Т .Таким образом, мы создали схему, которая защищена лишь от одного отка¬
за— типа обрыв, увеличив число элементов в 3,5 раза. При этом надежность
схемы от короткого замыкания уменьшилась.Подобные эффекты имеют место при резервировании любого электротехни¬
ческого элемента и даже схемы, например: фильтра, реле, предохранителяит. д.Применить здесь общее резервирование (всей дифференцирующей цепи)
вряд ли возможно, т. к. для этого потребуется автомат контроля и коммута¬
ции, который будет более сложным, чем цепочка RC, а значит, менее надеж¬
ным, чем дифференцирующая цепь.
Проблемы анализа надежности сложных технических систем95Приведем еще один пример. Для повышения надежности энергетической
системы решено использовать дублирование генераторов. Пусть основной
генератор имеет мощность W . Если резервный генератор будет иметь такую
же мощность, то постоянное резервирование приведет к большому избытку
мощности. Поэтому генераторы (основной и резервный) берут меньшей
мощности, но тогда при отказе одного из них другой будет работать с пере¬
грузкой. Экономически является более целесообразным применить резерви¬
рование с дробной кратностью пг = 1/2, т. е. использовать три генератора,
каждый из которых имеет мощность W/2. Тогда при отказе одного из них
энергетическая система будет исправной, т. к. ее общая мощность станет рав¬
ной W . При отказе двух генераторов наступит отказ системы, возникший из-
за перегрузки системы. Однако такое резервирование приведет к снижению
надежности энергетической системы длительной непрерывной работы, т. к.
ее среднее время безотказной работы Т = 5/6 ■ Т0, где Т0 — среднее время
безотказной работы нерезервированного генератора. Такая схема позволяет
повысить надежность энергетической системы короткого времени работы.
Система может иметь большой выигрыш в надежности при возможности ее
ремонта без выключения из работы на период ремонта отказавшего генерато¬
ра. Заметим, что в данном случае существенным является наличие последей¬
ствия отказов, которое мы не учли при расчете среднего времени безотказной
работы.Из приведенных примеров следует, что методы анализа надежности сложных
систем должны учитывать:□ наличие последействия отказов энергетических систем и систем с восста¬
новлением;□ два характера отказа электротехнических элементов;□ изменение основного параметра электрической схемы при отказе элемен¬
тов структурно резервированной системы;□ структуру сложной системы при ее физической реализуемости (наличие
системы контроля, автоматов коммутации и т. д.);□ неодновременность работы элементов.Математические модели функционирования сложных систем, в смысле их
надежности, полученные без учета перечисленных выше факторов, не могут
быть адекватными реальным системам.Методы анализа надежности сложных систем с учетом их физической реали¬
зуемости будут рассматриваться в гл. 8.
96Гпава 33.5. Краткие замечания, касающиеся проблем
анализа надежности систем1. Существующие в настоящее время аналитические методы расчета и ана¬
лиза надежности технических систем с произвольными распределениями
отказов, случайных параметров и восстановлений элементов обладают
следующими недостатками:• методы сложные, не доведены до машинных алгоритмов и программ;• позволяют анализировать системы только простой структуры;• отсутствует единая математическая модель надежности функциониро¬
вания систем;• невозможность исследования зависимых процессов;• трудности исследования нестационарных характеристик надежности;• сложность, а часто и невозможность учета таких особенностей функ¬
ционирования систем, как наличие структурной и временной избыточ¬
ности, контроль состояния элементов, наличие нескольких видов отка¬
зов, существование скрытых отказов и т. д.;• невозможность анализа систем с переменной структурой.В связи с указанными обстоятельствами оценка надежности и эффектив¬
ности функционирования сложных систем требует разработки новых под¬
ходов и методов анализа, учитывающих сложность системы и все много¬
образие ее отличительных особенностей.2. Известные в настоящее время методы расчета надежности технических
средств не позволяют оценить погрешности вычисления показателей на¬
дежности с необходимой для практики точностью. Более того, при надле¬
жащем выборе законов распределения показатели надежности, получен¬
ные асимптотическими методами, могут совершенно исказить истинное
значение показателей даже при дополнительном условии "быстрого" вос¬
становления элементов.3. Аналитические методы являются исключительно важными для исследова¬
ния надежности реальных технических систем, поскольку для большого
количества факторов, влияющих на надежность систем, высокая досто¬
верность имитационного моделирования практически не достижима.4. Использование экспоненциальных законов при анализе надежности реаль¬
ных технических систем длительного функционирования в принципе не¬
правомерно, т. к. исходные посылки в моделях не адекватны физическим
процессам, протекающим в системах. При решении практических задач
Проблемы анализа надежности сложных технических систем97указанная идеализация реальных процессов отказов и восстановлений мо¬
жет приводить к существенным ошибкам.5. При разработке математической модели функционирования сложной тех¬
нической системы и методов ее анализа, как правило, сталкиваются с не¬
обходимостью учета важных особенностей ее функционирования, таких
как контроль состояния элементов, последействие отказов, переключение
на резерв, возможность реконфигурации системы во время ее эксплуата¬
ции, введение различных видов резервирования, наличие интервалов про¬
стоя элементов и т. д. Случайные параметры, характеризующие указанные
особенности, обычно являются "неэкспоненциальными".6. Традиционные методы ограничены возможностью анализировать надеж¬
ность и эффективность функционирования технических систем с малым
числом состояний (несколько десятков). Решение задач в случае систем с
большим числом состояний (порядка сотен тысяч и более) требует разра¬
ботки нестандартных подходов.7. В настоящее время отсутствуют не только инженерные методы, но и тео¬
ретические разработки анализа надежности технических систем с пере¬
менной структурой, обусловленной ее многофункциональностью. Анализ
надежности систем со статической и динамической реконфигурацией
структуры представляет собой новое направление в теории надежности
сложных технических систем.8. Отсутствие инженерных методов анализа надежности сложных систем,
учитывающих их свойства и особенности функционирования, объясняется
следующими причинами: неадекватностью моделей физическим процес¬
сам, математическими трудностями, отсутствием статистических данных
по надежности элементов.4 Зак. 3094
ГЛАВА 4МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ФУНКЦИОНИРОВАНИЯ
ТЕХНИЧЕСКИХ ЭЛЕМЕНТОВ
И СИСТЕМ В СМЫСЛЕ
ИХ НАДЕЖНОСТИРасчет надежности сложных технических систем часто базируется на пред¬
положении о том, что время безотказной работы и время восстановления
элементов имеют экспоненциальные распределения вероятностей. Как было
показано в гл. 3, это допущение приводит к существенным ошибкам при вы¬
числении показателей надежности. Более реальным является анализ надеж¬
ности технических систем, если снять ограничения об экспоненциальности
распределений времени до отказа, восстановления и случайных параметров,
сопутствующих функционированию системы. К таким параметрам относятся:
время между очередными сеансами контроля и время его проведения, момент
подключения в работу резервных элементов, время между очередными про-
филактиками и время их проведения и т. п.4.1. Общая модель надежности
технического элементаНапомним, что под элементом в теории надежности понимается любой тех-'
нический объект, имеющий показатель надежности, самостоятельно учиты-'
ваемый при расчетах.Элемент с восстановлением имеет два возможных состояния:□ (0) — элемент работает;□ (1) — элемент восстанавливается.
Математические модели функционирования технических элементов и систем99Пусть Y0(s,t) — вероятность того, что на интервале [?; t + s] элемент нахо¬
дится в исправном состоянии, a Yx{x,t) — вероятность того, что на интервале
[f; t + т] элемент восстанавливается. Продифференцируем эти функции:яМ~Я£!>.OS отФункция yo(s,t) представляет собой плотность распределения вероятностей
исправной работы элемента на интервале [r;/ + i], а функция ^(т,/) —
плотность распределения вероятностей времени восстановления элемента на
интервале [?; t + т].Предположим, что в начальный момент времени t = О элемент находится в
исправном состоянии, тогдаr0(J,O) = F(j), Yx(т,0) = 0,и потому>>о(5>0) = /(*)> л('с»°) = °-Момент перехода из состояния восстановления в состояние исправной рабо¬
ты показан на рис. 4.1.О t — х t t + s tРис. 4.1. Фрагмент диаграммы, поясняющий образование интегральных уравненийНа рис. 4.1 приняты следующие обозначения:□ 4 — случайное время исправной работы элемента;□ — случайное время восстановления элемента;□ / — момент времени, при котором элемент исправен;□ х — произвольный момент времени, взятый на промежутке от 0 до t;□ t — х —момент окончания восстановления отказавшего элемента;□ 5 — время, в течение которого элемент исправен.Вероятность того, что элемент исправно работал в течение времени x + s при
условии, что в момент времени t-x произошло его восстановление, равна
>>,((),/-x)/(x + s).
100Гпава 4Так как х — любой момент времени из интервала [0; (], то в результате ин¬
тегрирования этой функции от 0 до t получим уравнениеIУ о (з>0= \/{х + s)_y, (0 ,t- x)dx + f(t + s),
ов котором слагаемое f(t + s) обусловлено началом процесса функциониро¬
вания и означает, что при отсутствии отказа до момента t элемент работает
безотказно в течение времени (t + s). Аналогичное уравнение имеет место и
для второй функции но уже без свободного члена. Это позволяет за¬писать следующую систему интегральных уравнений относительно функций
Уо и У\ '■tу о (■*> 0 = J/C*+•у)>;1 (°> * - +fit+5);° (4-1)JVl('t,0= Jg(* + 1)Уо (0 ,t- x)dx.
оСистема уравнений (4.1) связывает между собой две функции, содержащие
предысторию процесса функционирования элемента. Это обусловлено нали¬
чием в аргументах функций jv0 (^,/) и У|(т,/) дополнительных переменных
s и х , которые соответствуют остаточному времени работы и восстановле¬
ния элемента.Если остаточное время работы и восстановления равно нулю, то функции
ю(0 = Уо(0,0 и сов(/) = v, (0,0 являются параметрами потока отказов и вос¬
становления соответственно. Обозначая cps(t) = cp(t + s), получим:yQ(s,t) = (0B*fs(t) + fs(t), ^i(T,0 = co*gT(0, (4.2)r0(s,/) = coB * Fs(t) + Fs(t), Yt(T,t) = co*Gt(/).Последние формулы дают возможность выразить вероятности Y0 при малых
5 и Yx при малых х через важнейшие характеристики элемента: функции
готовности и простоя и параметры потока отказов и восстановлений. Выра¬
жения имеют вид:Г0 (5,0 = Кг (0 - a(t)s + o(s2), Ц(т,0 = Кп (0 - сов (От + о(х2 ).ТогдаKr(t) = F0(0,O = ]y0(s,t)ds, Ka(t) = 7,(0,0 = Ь(T,t)dx.
о о
Математические модели функционирования технических элементов и систем 101Полагая в (4.2) s = 0 и х = 0, получимсо(0 = сов * ДО + ДО, со„ (0 = ® * g(0 • (4.3)Отсюда следует, чтою(0 = ДО + / * / * giO +f*f*f*g* gif) + ..;=£ /*(*+1) * g{k) (О,k=0“в (О=/ * g(o+f*f*g* gif)+... = z /*(4) * g*w(o ■*=1Вероятности /?0 (/) и (0 пребывания элемента в исправном и отказовом
состояниях, очевидно, совпадают соответственно с функциями готовности и
простоя. Нетрудно показать, что эти вероятности удовлетворяют уравнениям,
аналогичным уравнениям Эрлангаj р'о (О=-40 Ро (0+ц(0 ру (0; м 4)\р{ (0 = 40Ро (0 - Ц(0Pi (О-Здесь X(t) и ц(0 — интенсивности потоков отказов и восстановлений, опре¬
деленные в разд. 2.6. Отсюда следует, что работу элемента можно описать
простейшим графом состояний (рис. 4.2), в ветвях которого находятся функ¬
ции А.(О и р(0. Этому графу соответствует система обыкновенных диффе¬
ренциальных уравнений (4.4).©п И(0
v МО□Рис. 4.2. Граф состояний восстанавливаемого элементаСогласно принятому ранее допущению вероятности p0(t) и Р\(0 удовле¬
творяют начальным условиям: /?0(О) = 1> Р\ (0)= 0 > означающим, что в мо¬
мент времени t = 0 элемент исправен.Следует иметь в виду, что решить систему уравнений (4.1) проще, чем внача¬
ле определять интенсивности X(t) и ц(0, а затем решать систему дифферен¬
циальных уравнений (4.4). Наоборот, указанные интенсивности могут быть
определены в результате решения системы (4.1).
102Глава 4Аналогичные рассуждения позволяют записать для оценки надежности мате¬
матическую модель функционирования любой сложной системы. В следую¬
щем разделе мы получим такую модель в достаточно общей ситуации, однако
для ее составления применим несколько иной способ.ПРИМЕР 4.1. Предположим, что время безотказной работы и время восста¬
новления элемента имеют экспоненциальные распределения с параметрами
X и ц соответственно. Требуется получить выражения для параметров пото¬
ков отказов и восстановлений, среднего суммарного числа отказов и восста¬
новлений в течение времени [0; /], функций готовности и простоя, средней
суммарной наработки и суммарного времени восстановления элемента в те¬
чение времени [0; /].Решение. Из соотношений (4.3) на основании разд. 2.5 параметры потоков
отказов и восстановлений в преобразовании Лапласа имеют вид:_Л£>—= , &.U). ДеШ- А!-/0)£00 z(z + n + X) 1 -f(z)g(z) z(z + ii + X)отсюдаю(/)=JfL+JL-e-(n+xx 5 Юв(0=J^ \Л_е-ЫХ)<ц +А, ц + А- р, + X- |д. + А,На основе формул разд. 2.6 определим среднее суммарное число отказов и
среднее суммарное число восстановлений в течение времени [0; f]:0J ц + Х (ц + ^V /Мв (0 = JcoB (x)dx = ^(l - ) •0 (j. + А, (ц + X,)Из соотношений (2.32) и (4.3) функции готовности и простоя в преобразова¬
нии Лапласа имеют вид:ад _ - IzM . (£±м) , (г).. Ml- iML z[\-f(z)g{zj) z(z + [L + X)’ " z(l-/(z)g(z>) z(z + ^l + X)Отсюда
Математические модели функционирования технических элементов и систем103На основе формул разд. 2.6 определим среднее суммарное время безотказной
работы и среднее суммарное время восстановления в течение времени [0; /]:m(t) = )кт (x)dx = -V-t + —- е-(^+Х)'),
о li + A' (Ц + Л.) VmB(0 = )Kn(x)dx = -e_("+X)<) •0 V + ^ (Ц + ^) V ’Приведенные соотношения будут часто использоваться в дальнейшем. Для
распределений, отличных от экспоненциального (за редким исключением), не
удается получить явных соотношений для рассмотренных показателей на¬
дежности.4.2. Общая модель надежности систем
в терминах интегральных уравнений4.2.1. Основные обозначения и допущенияПредположим, что техническая система состоит из m элементов с известны¬
ми распределениями времени безотказной работы и времени восстановления,
а ее функционирование осуществляется в соответствии с заданной схемой
расчета надежности. Все элементы условно разделим на рабочие и резервные.
К первому классу отнесем также все элементы нагруженного и облегченного
резерва, а ко второму— только элементы, находящиеся в ненагруженном
состоянии. При отказе рабочего элемента и при наличии резервного он заме¬
няется резервным, причем эта замена осуществляется мгновенно и абсолютно
надежным устройством. Как будет показано в гл. 8, ограничение о мгновен¬
ной замене можно снять. При наличии нескольких резервных элементов по¬
рядок замены отказавшего рабочего элемента резервным будем считать из¬
вестным. Контроль состояния элементов является непрерывным, и отказ лю¬
бого элемента обнаруживается немедленно после его возникновения. Это
условие также может быть снято (см. гл. 10). Предполагается, что число ре¬
монтных бригад и порядок восстановления отказавших элементов известны,
т. е. имеется указание о том, какие элементы и в какой последовательности
будут приняты на обслуживание. Разумеется, этот порядок необходимо знать
только в том случае, когда речь идет об ограниченном восстановлении и мо¬
жет появиться очередь на восстановление. Восстановление элемента начина¬
ется сразу же после его отказа или после обнаружения отказа контролирую¬
щим устройством при наличии свободной бригады или по очереди, согласно
принятому приоритету обслуживания. В процессе ремонта элементов проис¬
ходит полное восстановление их надежности.
104Гпава 4На функционирование и на ремонт каждого элемента могут оказывать влия¬
ние остальные элементы системы. В связи с этим, любой элемент может пре¬
бывать в нескольких возможных состояниях: в состоянии работоспособности,
в состоянии восстановления или в состоянии простоя. Причем состояние
простоя элемента может быть обусловлено следующими причинами:□ произошло прерывание работы элемента, что может быть в том случае,
если данный элемент находится в составе узла, соединенного последова¬
тельно с отказавшим элементом или узлом;□ произошло прерывание восстановления элемента, что может быть в том
случае, когда дисциплина обслуживания системы такова, что ремонтные
органы, восстанавливающие данный элемент, прекращают его восстанов¬
ление и приступают к ремонту некоторого другого элемента (восстановле¬
ние с приоритетом);□ элемент исправен, но по условиям функционирования он находится в оче¬
реди на работу, что может произойти, например, в случае ненагруженного
резервирования;□ элемент находится в отказовом состоянии, но по условиям обслуживания
он не ремонтируется и находится в очереди на восстановление, что воз¬
можно, например, в случае ограниченного восстановления с прямым или
назначенным приоритетом.Указание возможных состояний каждого элемента системы существенно при
описании ее функционирования в целом. Будем считать, что переход каждого
элемента из одного состояния в другое осуществляется мгновенно вследствие
отказа или восстановления данного элемента или какого-либо другого эле¬
мента системы. Дополнительно предложим, что отказ или восстановление
любого элемента не влияет на законы распределения остальных элементов и
время простоя элемента (если не оговорено особо) не сказывается на его ха¬
рактеристиках надежности, т. е., находясь в состоянии простоя, элемент со¬
храняет эти характеристики такими же, как и в момент прерывания работы
или восстановления.4.2.2. Матрица состоянийМножество всех состояний системы обозначим через Е , а через п — число
этих состояний. В соответствии с заданным понятием отказа все состояния
системы разбиваются на два класса: множество работоспособных состояний
Е+ и множество отказовых состояний Е_. В каждый фиксированный момент
времени t и для каждого к-го состояния определяются шесть подмножеств
множества всех элементов:
Математические модели функционирования технических элементов и систем 105□ Rk — множество номеров работающих элементов;□ Wk — множество номеров ремонтируемых элементов;□ R'k — множество номеров элементов, находящихся в состоянии простоя
вследствие прерывания их функционирования;□ W'k — множество номеров элементов, находящихся в состоянии простоя
вследствие прерывания их восстановления;□ — множество номеров элементов, образующих очередь на работу;□ Wk — множество номеров элементов, образующих очередь на восстанов¬
ление.С каждым к-м состоянием (к е Е) свяжем вектор Ак = (alk, a2k,..., amk), ха¬
рактеризующий состояния всех элементов системы в момент времени t.Компоненты вектора Ак предполагаются равными:«Л =S,, если isRkuRk;
х,, если ieWku Wk;
О, если ieRk u Wk .Если /е R’k (ieWk), то соответствующую компоненту будем иногда снаб¬
жать штрихом и писать s' ( х ■). Если ajk = 0, то соответствующую компонен¬
ту будем называть "нулевой" и для различия состояний будем писать
alk = OR, если г-й элемент находится в очереди на работу, или aik = OW, ес¬
ли /-й элемент находится в очереди на восстановление. "Нулевая" компонента
должна содержать также четкое указание о порядковом номере очереди на
работу или очереди на восстановление, если таких компонентов более одной.
В некоторых случаях, когда это не может вызвать недоразумений, "нулевые"
компоненты мы будем опускать.Таким образом, функционирование любой восстанавливаемой системы пол¬
ностью определяется матрицей состояний S размерности m х п, столбцами
которой служат векторы Ак .Для удобства матрица состояний дополняется верхней строкой, содержащей
коды (или номера) соответствующих состояний, например совокупностью
(упорядоченной или неупорядоченной) отказавших элементов, и нижней
строкой, показывающей, к какому классу ( Е+ или Е_ ) относится состояние с
номером к : 1, если кеЕ+, или 0, если к<вЕ_.
106Глава 44.2.3. Матрица переходовПри изучении процесса функционирования систем часто бывает удобно ис¬
пользовать понятия теории графов. Введем некоторые определения.Графом [96] называется тройка (E,D,T), где Е и D — конечные множест¬
ва, а Г — отображение из множества D в декартово произведение ЕхЕ.
Элементы множества Е называются узлами (вершинами) графа, а элементы
множества D — ветвями (дугами) графа. Отображение Т каждой ветви гра¬
фа deD сопоставляет упорядоченную пару его узлов (кх,к2), кх,к2& Е,
первый из которых называется началом ветви d, а второй — концом ветви
d . Граф может быть изображен с помощью рисунка, на котором узлам соот¬
ветствуют точки, а ветвям — линии со стрелками, идущими от начала к кон¬
цу. Пусть заданы последовательность узлов к0, кх, к2,..., кг графа и последо¬
вательность ветвей dx,d2,..., dr. Будем называть эту пару последовательно¬
стей путем, если узел kj_x является началом, а узел kj является концом
ветви dj, j -1, 2,..., г. Узел к0 называется началом пути, а узел кг — кон¬
цом пути, число г называется длиной пути.Функционирование восстанавливаемой (и невосстанавливаемой) системы
может быть описано графом состояний. Множество всех состояний системы
Е отождествим с множеством узлов графа. Возможным переходам системы
из одного состояния в другое сопоставим множество всех ветвей графа D.
Будем считать, что все переходы системы за один шаг вызваны или отказом,
или восстановлением некоторого элемента системы. Тем самым исключается
возможность одновременного отказа или восстановления более чем одного
элемента системы.Информация о всевозможных переходах системы за один шаг содержится в
матрице переходов Р размерности тхп . Каждый элемент bjk этой матрицы
представляет собой код состояния, в которое имеется непосредственный пе¬
реход из состояния с номером к вследствие изменения состояния (отказа или
восстановления) /-го элемента. Если из состояния к отсутствует переход,
вызванный изменением состояния /-го элемента, то соответствующее место
матрицы Р не заполняется. Таким образом, элементам матрицы Р соответ¬
ствуют ветви графа с началом в узле с кодом, соответствующим состоянию с
номером к и с концом в узле с кодом bik . При этом в силу принятой нумера¬
ции состояний в матрице Р дается указание о номере элемента, отказ или
восстановление которого вызвало данный переход.При изучении свойств технической системы с точки зрения надежности нет
необходимости задавать множество всевозможных переходов, т. к. они пол¬
Математические модели функционирования технических элементов и систем107ностью определяются состояниями системы и списком аргументов, связан¬
ных с этими состояниями. Тем самым матрица Р может быть построена по
матрице S программно. Для построения матрицы переходов надо определить
допустимые переходы для каждого элемента. Допустимыми являются пере¬
ходы вида:s-+s,s', x,OW ;x->5,x,t',OR ;s's,s';x'->x,x';OR —> s,OR jOW —> x,OW .Значения s,s',t,t', OR,OW представляют собой характеристики состояния
каждого элемента системы (см. разд. 4.2.2). При этом переходы s-»x или
s -> OW будем называть отказовыми, а переходы х -> s или х -» OR — вос¬
станавливающими.Чтобы определить существование перехода из состояния к в состояние /,
надо сопоставить между собой компоненты векторов Ак = (alk, а2к,..., атк)
и Ai =(au, a2i,..., cimi). Непосредственный переход к ->/ существует вслед¬
ствие отказа или восстановления элемента /0, если переход а^к —> аи явля¬
ется отказовым или восстанавливающим, а остальные поэлементные перехо¬
ды aik -* afl допустимы, но не являются отказовыми или восстанавливающи¬
ми. В этом случае Ь^к равен коду состояния с номером /. Таким путемможет быть сформирована матрица Р. Если переход к -»/ не существует, то
соответствующий элемент матрицы Р не заполняется.ПРИМЕР 4.2. Составить матрицу и граф состояний для основного соедине¬
ния трех элементов в предположении, что при отказе 1 -го или 2-го элемента
остальные элементы выключаются, а при отказе 3-го элемента остальные
продолжают функционировать. Восстановление отказавших элементов про¬
изводится одной ремонтной бригадой с обратным приоритетом.Решение. Система имеет следующие состояния и соответствующие им век¬
тора:□ (0) — все элементы исправны, Aq = (5],52,^з);□ (1)— отказал и восстанавливается 1-й элемент, другие элементы про¬
стаивают вследствие прерывания их работы, Aj = (xt,s2,s^);
108Гпава 4□ (2) — отказал и восстанавливается 2-й элемент, другие элементы простаи¬
вают вследствие прерывания их работы, Л2 = (, т2, Л’з);□ (3) — отказал и восстанавливается 3-й элемент, другие элементы продол¬
жают работать, Ai = (sj, s2, т3);П (31) — отказали 3-й, а затем 1-й элементы, восстанавливается 1-й элемент,
2-й простаивает вследствие прерывания работы, 3-й простаивает вследст¬
вие прерывания восстановления, Л4 = (Tj,4»^3);□ (32) — отказали 3-й, а затем 2-й элементы, восстанавливается 2-й элемент,
1-й простаивает вследствие прерывания работы, 3-й простаивает вследст¬
вие прерывания восстановления, Л5 = (s{,t2,x3) •Таким образом, матрица состояний имеет вид:01233132*1*14*1*1s{s2s2*2s2s2Ъs3s34bx3*3100000Граф состояний представлен на рис. 4.3. Он имеет нумерацию узлов, приня¬
тую ранее.Рис. 4.3. Граф состояний системы из примера 4.2В соответствии с общими принципами построения матрицы переходов она
имеет вид:
Математические модели функционирования технических элементов и систем10901 233132103132032330ПРИМЕР 4.3. Составить матрицу и граф состояний резервированной систе¬
мы при общем постоянном резервировании кратности т = 2. Обслуживание
отказавших элементов осуществляют два ремонтных органа с прямым при¬
оритетом.Решение. Система имеет следующие состояния:□ (0) — все элементы исправны;□ (к) — отказал и восстанавливается к-й элемент, другие элементы рабо¬
тают;□ (kl) — отказали и восстанавливаются элементы с номерами к и /, ос¬
тавшийся элемент работает;□ (klm) — отказали и восстанавливаются элементы с номерами к и /, ос¬
тавшийся элемент находится в очереди на восстановление.Матрица состояний имеет вид:Граф состояний представлен на рис. 4.4.По графу легко составляется следующая матрица переходов:01231213231231322311012132323123232122311323113313231231211212
110Гпава 4Рис. 4.4. Граф состояний системы из примера 4.34.2.4. Выражения для вероятностей состояний
и параметров переходов между состояниямиФункционирование технической системы с произвольными законами распре¬
деления элементов может быть описано системой интегральных уравнений
или эквивалентной системой дифференциальных уравнений в частных произ¬
водных. Эти системы уравнений строятся непосредственно по матрице со¬
стояний S и матрице переходов Р.Сначала получим явные соотношения для вероятностей состояний системы
pk(t) и параметров перехода из состояния в состояние со^Дг), k,l е Е. Пустьк0 — начальное состояние процесса функционирования технической систе¬
мы. Обозначим через множество всех путей графа состояний длины г сначалом в узле к0 и концом в узле к . Двигаясь по пути у е , можно по¬
пасть из состояния к0 в состояние к за г шагов (некоторые ветви при этом
могут повторяться). Напомним, что за один шаг принимается переход, обу¬
словленный или отказом, или восстановлением какого-либо одного элемента
системы. Предположим, что путь у проходит через состояния с номерамиkQ, кх, к2,..., кг =к . Обозначим через х, время пребывания системы в со¬
стоянии kj, а через л: = (л0, хх, ..., хг) — вектор с компонентами X:.
Математические модели функционирования технических элементов и систем111Рассмотрим изменение состояний /-го элемента на пути у и определим
функции ф^(х) = ф^(л:0, х1з..., *,), характеризующие плотность распреде¬
ления вероятностей пребывания /-го элемента в состоянии kj в течение вре¬
мени Xj, 7 = 0,1, 2,..., г. Каждому узлу kj отвечает значение /-й компонен¬
ты aik , равной одной из величин: s,j',t,t',OR,OW , при этом указанные ве¬
личины чередуются в следующем порядке: OR (очередь на работу), s или
s' (работа или прерывание работы), OW (очередь на восстановление), т или
х' (восстановление или прерывание восстановления). Некоторые из приве¬
денных величин могут быть опущены. Множество индексов {0,1, 2,..., г}
представимо в виде объединения непересекающихся подмножеств, состоя¬
щих из индексов, следующих в порядке возрастания:«о{0,1, 2,..., г} - U eal uea2 u еа3 иea4,а=1где= {у •• a,kj = or} , ea2 = {у: aikj = s или aikj = sj, eal = {у e ea2 : aikj = s j,
ea3 = {У: aikj =Ow}, ea4= jy : aikj = x или aikj = xj , e'a4= {; e ea4 : aik. = xj.
Тогда функция ф^ определяется равенством“о40'а = 1ф5,'ЧДС6,л„...,хг)= Y\fiIхjKj-ea2^e'ail )gi\J е<гЛ 'еа4 Jгде f(t) и gj(t) — плотности распределения времени безотказной работы и
времени восстановления /-го элемента. С точностью до бесконечно малой
величины Ax0Axj ...Ахг функция ф^ равна, очевидно, мгновенной вероятно¬
сти того, что /-й элемент пребывает в состоянии kj время х},
j = 0,1, 2,..., г .Предположим, что последнее состояние к = кг является состоянием работы
или восстановления /-го элемента. Тогда имеет смысл говорить о мгновенной
вероятности того, что /-й элемент в каждом состоянии к}, кроме последнего,пребывает время х^, а в последнем состоянии — время, не меньше хг.
112Гпава 4Совершенно ясно, что эта вероятность равна00Фу Оо> Х1> •" > Хг) ~ /фу (Х0’ х1> ••• > xr ^ik )dQjk •ПРИМЕР 4.4. Пусть /-й элемент системы пребывает в состояниях s, х, OR ,
s, х, х', х, s, как показано на временной диаграмме (рис. 4.5). Требуетсясоставить выражения для функций <р^ и <р^ .О Л| А 2 Л3 Лу *Рис. 4.5. Временная диаграмма функционирования /'-го элементаРешение. На рис. 4.5 х0, хх, х2, х3, х4, х5, х6, х7 — времена пребывания г'-го
элемента в соответствующих состояниях. Из диаграммы следует, чтоФ?} = fi (*0)Si (х\ )fi Оз )Si (х4 + *6 )/(*7) ,Фу ' = /г(>0)2, (*1 )fi(*3)Si(*4 +Хб)Ц(х7) •Вероятность pk(t) пребывания системы в момент времени t в состоянии к
находится по формуле полной вероятности. Пусть Hy(t) — событие, со¬
стоящее в том, что в момент t система достигла состояния к, двигаясь из
начального состояния к0 по пути у е . Вероятность этого события равна/ \ т
р(ну(о)= J...J Yltf\x)dx,or(X)=t <=1Ггде cr(X) = t обозначает гиперплоскость ]>] = / в (г + 1)-мерном эвклидо¬
вовом пространстве. Искомая вероятность равна сумме вероятностей событий
Hy(t), вычисленной по всем путям у, ведущим из состояния к0 в состоя¬
ние к, т. е.00 т
Рк( 0=1 I J...J Пф?даг- (4-5)г=0 or(X)=t i=i
Математические модели функционирования технических элементов и систем113Рассмотрим переход системы из состояния к в состояние /. Пусть этот пе¬
реход вызван отказом или восстановлением элемента с номером /0 = /0 (&,/).
Параметр перехода со* /(0 представляет собой мгновенную вероятность пе¬
рехода в момент t из состояния к в состояние /, отнесенную к единице вре¬
мени, т. е.col ,(t) = lim —2 .*■' At-*o AtПоэтому для получения параметра перехода необходимо в формуле (4.5) все
функции при / * /0 оставить без изменения, а функцию ф^ — заменить
на выражениеj А/Hm-Jcp^o)(x0, ДС|, , xr + ak>k)daiok =$°\х0, хи ..., хг).Таким образом,со m®*,/(0=S S Н Пф?)(^)ф?о)(^)^' (4-6)
гв0 у<\к <-!Выражения (4.5) и (4.6) похожи по форме записи, поэтому их можно рассмат¬
ривать совместно. С этой целью обозначим через Yk(Ak,t) =
= Yk(alk, a2k,..., amk, t) вероятность пребывания системы в момент времени
t в состоянии к в предположении, что после момента t »‘-й элемент системы
сохранит свое состояние работоспособности или восстановления в течение
времени aik (i = 1, 2,..., m ). Предположим, что функции Yk имеют частные
производные по всем переменным вида s и т . Обозначим через ук смешан¬
ную производную по этим переменным порядка a = |i?*. ^Wk\ со знаком "+"
или определяемую формулойук(Ак,0 = (-1)а^2*(у.П daikieRkvWkФункции ук представляют собой плотности распределения вероятностей и
являются неизвестными в системе интегральных уравнений.Посколькуо° mYk(Ak>0=Ё Е f -1Пф?\xQ, хь , xr + aik)dX, (4.7)
Г=°Г6Г%\kor(X)=t Ы1
114Гпава 4то00 т
Ук(Ак>0='Ё, Z J -Щфу)(x0,xu...,xr+aik)dX. (4.8)r=0y6 dlro>kar(X)=t /=1Вероятности состояний и параметры переходов находятся по функциям ^ с
помощью единообразных соотношений. Действительно, как следует из (4.8),
а также из (4.5) и (4.6), имеют место равенства:00Pk(0= jyk(Ak’OdAk, (4.9)оt»kJ(0 = ]yk(Akiio\t)dAk(i°\ (4.10)Огде /0 =i0(k,l) — номер элемента, вызвавшего переход к —*1, а вектор Ак0^
получается из Ак , если положить в нем компоненту с номером /0 равной ну¬
лю, т. е. Ако) =(alk,..., Ojok,..., amk). Интегрирование в (4.9) и (4.10) распро¬
страняется на все "ненулевые" значения переменных aik . В некоторых случа¬
ях удобно вычислять неизвестные функции прямо через вероятности Yk в
соответствии с формулами:pk(t) = Yk(0,t), cokl(t) = Yk(О,/),8%кгде 0 = (0, 0,..., 0) — нулевой вектор. Отсюда, в частности, следует, что при
малых значениях параметров aik справедливо разложениеYk(Ak,t) = pk(t)~ £ (£>kj(t)ai k +о(Ак).
к->1Суммирование в правой части распространяется на все состояния к и /, ме¬
жду которыми имеются переходы & -»/.4.2.5. Правило составления
системы интегральных уравненийДля каждого состояния к е Е интегральное уравнение составляется следую¬
щим образом. Определяются все состояния, из которых имеется одношаго¬
вый переход в состояние к . Пусть j — одно из таких состояний, и переход
из j в к вызван отказом или восстановлением элемента с номеромI
Математические модели функционирования технических элементов и систем 115i0 =i0(j,k) . Обозначим через Xjk = (jcb х2,..., xm) вектор, в котором компо¬
ненты Xj принимают два значения: х (переменная интегрирования) или 0.
Если в состоянии к элемент с номером /' работает или восстанавливается, то
xj=x. Если в состоянии к элемент с номером i находится в состоянии про¬
стоя, то х, = 0.Пусть для /-го элемента А, есть плотность распределения времени безотказ¬
ной работы f,, если aik = s,, или плотность распределения времени восста¬
новления g,, если aik = Т;. Тогда справедливо уравнение:У к (Ак >•0 = £ /П + aik )У] (xjk + Aj° ]’t-x)dx. (4.11)j-*k o iСуммирование в правой части производится по всем состояниям j, из кото¬
рых имеется непосредственный переход в состояние к. Произведение под
знаком интеграла распространяется на все индексы i, для которых векторАк \ имеет "ненулевые" компоненты. Для начального состояния к0 кправой части соответствующего интегрального уравнения (4.11) добавляется
слагаемое£>к0(\>0= П h,(t+“ik0)>ieRk^Wkoобусловленное началом функционирования системы.В справедливости системы (4.11) можно убедиться путем подстановки в нее
функций (4.8). Эта система описывает функционирование технической сис¬
темы с произвольными законами распределения времени безотказной работы
и времени восстановления элементов при заданных плотностях распределе¬
ния вероятностей. Она содержит в себе всю вероятностную информацию о
работе и восстановлении технической системы.Решение системы (4.11) позволяет определить по формулам (4.9) и (4.10) со¬
ответственно вероятности пребывания системы во всех состояниях и пара¬
метры переходов из состояния в состояние. Далее по известным соотношени¬
ям рассчитываются любые характеристики надежности.Описание с помощью системы интегральных уравнений является универ¬
сальным и при сделанных ранее допущениях может служить математической
моделью функционирования любого сложного устройства с конечным или
счетным множеством состояний. В частности, эта система пригодна для опи¬
сания невосстанавливаемых и восстанавливаемых устройств при любом виде
резервирования. Она может быть использована для описания стационарного
116Гпава 4и нестационарного режимов эксплуатации. Кроме того, в ряде случаев систе¬
ма (4.11) позволяет получить некоторые качественные свойства функциони¬
рования системы.4.3. Общая модель функционирования
системы в смысле надежности
в терминах дифференциальных уравнений
в частных производныхСистема (4.11) может быть представлена также в виде эквивалентной систе¬
мы дифференциальных уравнений в частных производных, каждое из кото¬
рых является уравнением первого порядка. Для доказательства этого утвер¬
ждения рассмотрим соотношение/у(А, 0 = \и(Х + A,t- x)dx + 9(А + Т), (4.12)огде А - (о,, а2,..., am), X = (х, х,..., х), Т = (/, t,..., t) — /w-мерные векторы,
у и и — дифференцируемые функции, зависящие от (m +1) аргумента, 0 —
дифференцируемая функция т аргументов. Применяя к обеим частям (4.12)т д доператор дифференцирования L = + —, получим:,=1<Эа, dt' d т ЯLy(A, t) = - f— и(Х + A, t - x)dx + и(Т + А, 0) - У— в(А + Т) +
о cbc i=\dajm л+X 0(Л + T) = и(А, Т) - и(Т + А, 0) + и(Т + А, 0) = и(А, Г).,=|3а,Таким образом, из равенства (4.12) следует, чтоy(A,t) = u(A,t). (4.13)Очевидно также, что из (4.12) при t = 0 определяется начальное условие:ХЛ,0) = е(Л). (4.14)Верно и обратное. Из соотношений (4.13) и (4.14) следует (4.12).
Математические модели функционирования технических элементов и систем117Действительно, для этого достаточно от обеих частей равенства (4.13) вычис¬
лить криволинейный интеграл вдоль прямой, определяемой параметрически¬
ми уравнениями:(0:В результате будем иметь\А' = А + Х;
[t' = t-x,где 0<хй(.(/)Г-У—i—] dat dty{A,t)dl= J u(A,t)dl<0Произведя замену переменных, получим>( м д эЛили| — + — у(А + X,t-x)dx = \u{A + X,t -x)dx
o\ dtJ оt d 1
- f—y{A + X,t-x)dx= [u(A + X,t-x)dx.
JQdx 0JОтсюда следует, чтоy(A,t)~ y(A + T,0)= fu(A + X,t- x)dx,Используя начальное условие (4.14), получим (4.12).Из равносильности соотношений (4.12) и (4.13)—(4.14) следует эквивалент¬
ность системы интегральных уравнений (4.11) и следующей системы диффе¬
ренциальных уравнений:г- XieRkuWk daik dtд д
+ —с дополнительными начальными условиямиЛ(Л>0= I (4.15)J-*k iУк0(Ак0> °)= П hi(aik0), л (Л. °)=0(4.16)Произведение в правой части (4.15) распространяется на те множества индек¬
сов /, что и в (4.11), а суммирование производится по всем номерам состоя¬
ний j, из которых существует одношаговый переход в состояние к .
118Гпава 4ПРИМЕР 4.5. Составить систему интегральных и дифференциальных урав¬
нений для описания функционирования основного соединения 3-х элементов
из разд. 4.2.3.Решение. Поскольку устройство имеет 6 возможных состояний, то неизвест¬
ными в системах уравнений являются 6 функций, аргументами которых слу¬
жат столбцы матрицы состояний S и время t: ^0(л1952,Яз,/), y\{t\,s'2,s'2,t),y2(s[,T2,53,0» Уз(лг1>52»тз>0» ^3i(Ti’J2>T3>0> Система инте¬гральных уравнений составляется в соответствии с общей методикой по фор¬
муле (4.11), считая, что в момент времени t = О все элементы исправны:tyb(sx,s2,s-i,t)=\f(x + s\)y^,x + s2,x + s2,t-x)dx +0t i
+ \f2(.x + s2)y2(x + sx,0,x + STt,t-x)dx + \fi(x + s3i)yT)(x + sx,x + s2,0,t-x)dx +о 0
+/l (t + 5| )/2 (l + s2 )/з 0 + s3 XIyx (Tj, s2,53,.t) = Jg, (x + x, )y0 (0, s2,s3,t- x)dx,01y2 (Sj', t2 ,s'3,t) = jg2(x + t2 )^0 (J,, 0, S3, / - x)dx-
0t>3(j1,s2,t3,0= Jg3(^ + 'c3)^0(x + s1,x4-52,0,f-jc)£6: +0t t
+ J/i(jc + j1)^31(0,x + s2,^ + t3,/-j:)<ix+ \f2{x + s2)yi2{x + sx,0,x + ^,t-x)dx,
о 0tУз 1 (*1»■*2 >T3 >0 = J#i О + T, )>>3 (0,s2,t3,,t - x)dx,0tУ32 (S1 >T2>T3 »0 = jg2(x + *2 )Уз 0s!. 0,t3,f - x)dx.0Система дифференциальных уравнений составляется исходя из равенств
(4.15):f д д д длds} ds2 ds3 dtyQ(sx,s2,s2,t) = fx(sx)yx(0,s2,si,t) +
+/2(^2 )Уг (*i ,0,53,O + /3 («3 ХУз^МгД 0.
Математические модели функционирования технических элементов и систем 119У\ (*i»s2 ,,s3,,t) = g, (t i )>'0 (0, s2, s3, t),\У 2 O'l ,t2,53,0 = g2 (x2 )л (J2 ’ °> S3 ’ 0,V%(*1>Я2»*Э>0 = ft(T3)^0(sl>s2!°»O +/dsx ds2 dx3 dt+f\ (Ji )Уг l (0, , x3, /) + /2 02 ).y32 C*i, 0, x3, / ),'_J_+^ dtj Э/a s•4- —^3 l(tl,s2^3>0 = gl(^l )Уз (°. *2»■T3»0.JV32 (*1 ,*2 > T3 > 0 = &2 (x2 )^3 (S1 >°> T3 ’ 0,dx2 dtа начальные условия — исходя из равенств (4.16):У о (s],s2,s3,0) = fi(sl )/2 (s2 )/з (Л'з).Остальные функции при t - 0 равны нулю.4.4. Модель надежности
стационарного режимаВ процессе эксплуатации технической системы ее многие временные харак¬
теристики стремятся к некоторым постоянным значениям. В этом случае го¬
ворят, что система работает в установившемся или стационарном режиме.
Предположим, что функции yk(Ak,t), описывающие функционирование сис¬
темы, имеют предельные значения, и yk(Ak) = lim yk(Ak,t). Тогда формаль-ный переход к пределу в уравнениях (4.11) показывает, что относительно
функций yk(Ak), k е Е имеет место следующая система интегральных урав¬
нений:+00Ук(Ак)= Z Ш¥*+a&)yj(xjk+ Aj )<&•j-*k 0 i(4.17)Система уравнений (4.17) описывает стационарный режим восстанавливае¬
мой системы. В ней приняты те же обозначения, что и в уравнениях (4.11).
Заметим, что добавочное слагаемое Qk(j(Aka,t), характеризующее начальное
120Глава 4распределение вероятностей, стремится к нулю при и система (4.17)его не содержит. Поэтому система уравнений (4.17) является однородной и
всегда имеет тривиальное решение ук = 0. Таким образом, если ук — какое-
либо ненулевое решение системы (4.17), то функции сук (с = const) также
образуют решение этой системы. Поэтому решение системы (4.17) обычно
определяется при дополнительном нормировочном условии: сумма вероятно¬
стей всех состояний равна единице.Система дифференциальных уравнений (4.15) также может быть формально
преобразована для описания стационарного режима, а именно предельный
переход при t -> со приводит к следующей системе уравнений:" I "Л(4)=1П^КЖ4'о))' (4-18)i€RkuWk 0aik j-*k iСистема (4.18) эквивалентна системе (4,17). Решение систем для установив¬
шегося режима обычно проще, чем решение аналогичных систем, описы¬
вающих нестационарный режим, и в некоторых случаях оно может быть по¬
лучено в конечном виде. Решение приведенных систем уравнений дает воз¬
можность найти вероятности состояний в установившемся режиме, а также
параметры перехода из состояния к в состояние / (k,l е Е):ооРк = к&Е, (4.19)о®*./ = b(4/0V4/0)> (4-20)Огде i0=i0(k,l) -— номер того элемента, отказ или восстановление которого
вызвал данный переход.ПРИМЕР 4.6. Составить систему интегральных уравнений, описывающую
стационарный режим функционирования основного соединения 3-х элемен¬
тов из разд. 4.2.3.Решение. В примере 4.5 приведена математическая модель функционирова¬
ния рассматриваемой системы для любого момента времени t. Предельный
переход при со дает математическую модель функционирования в ста¬
ционарном режиме:ооy0(sl,s2,s3)= J/] (* + 5, )>>,((), x + s2,x +53)й?Х +0со 00+ I flix + s2)y2(x + su0,x + s2)dx + J/з (x + -s3 )уъ (x + s,, x + s2, Q)dx,
о о
Математические модели функционирования технических элементов и систем12100Л(*1.Л2»дз)= J #10 + Т1 Х^О (0, ^2 ,s3)dx = G, (т, )у0 (0,S2, *3 )>
о00у2 (s(, х2, s3 ) = J g2 (х + х2 )у0 (st, 0,53 )dx = G2 (т2 )у0 (5,, 0,53 ),
о00-V3 (^1. »тз) = fg3(* + T3)>,o(* + si>-x + s2>())£& +000 00
+ J/i (х + s, )у3, (О, X + s2,X + х3 )dx + { /2 (х + s2 )у32 (х + 5,, 0, * + х3 )dx,
о о00•У31(Т1>52>Т3)= J^l(^ + 'Cl)j3(0»-s2>T3)^ = A('tl)>'3(0»-s2»T3)>
о00^32 (51 Лг. ■тз) = \ё2 (х + Ь )Уз (S1>°> тз уь = G2 (х2 )Уз (Л1»°> тз )•оНепосредственной подстановкой легко проверить, что данная система имеет
следующее решение:У о (•*! ,s2 ,S3 ) = Fi О, )F2 (s2 )F3 (s3 ),= ^1 (^1 )^*2 (s2 )-^3 (s3 ) >y2 (j,, x2, s3 ) = F, (s, )G2(x2)F3 (s3 ),Уз (51 >s2 > Ъ > = ^1 (s\ )*2 (s2 )G3 (b) »
y3, (Tj, s2, x3 ) = Gj (Tj )F2 (s2 )G3 (x3 ),>'32(51’х2’тз) = -^1 (^l )^2 (T2 )^3 (T3 ) •Теперь не представляет труда определить стационарные вероятности состоя¬
ний и параметры перехода из состояния в состояние с точностью до постоян¬
ного множителя С :Ро - стхт2т3, рх = СТъХТ2Т3, р2 = СТ{Гй2Т3, р3 = ст{т2тв3,Рз 1 - СТъ\Т2ТъЗ» Р32 = СТ{Гъ2Т,3 ,Ю01 =со10 =с^2^3> ю02 = со20 ~с^1^3’ ^03 “ ®30 = с^1^2 ’®3,31 = “31,3 = сТ2ТъЗ > ®3,32 = ®32,3 = сТ\ТъЗ ■
122Гпава 4Постоянное число С находится из условия нормировки:Ро + Pi + Рг + Рз + + Ръг =1»откудаС = + Тв1Т2Т3 + 7’,Гв2Г3 + г,г2гвз + гв1г27;з + 717;2гвз )~1.На основе полученных базовых показателей определяются основные показа¬
тели надежности, например средняя наработка на отказj Ро та©01 + ®02 + ш03 ^2^3 + Щ +
и среднее время восстановленият Р\ + Рг + Рг + Рз1 + Ръ2 тв\т2тз + + + ТъХТ2Тй, + Г|Гв2Гв3
®10 + ©20 + ©ЗО ^2^3 +Т{Г3+ТТ24.5. Модели надежности
невосстанавливаемых системОценка надежности технической системы без восстановления является зна¬
чительно более простой задачей по сравнению с оценкой восстанавливаемой
системы. Описание функционирования такой системы представляет собой
частный случай математической модели системы при наличии восстанов¬
ления.Пусть Е — множество состояний невосстанавливаемой системы. Тогда для
любого состояния к е Е естественным образом определяются множества Rk,R'k, R®, характеризующие соответственно номера работающих элементов,
элементов, находящихся в состоянии простоя по причинам прерывания их
функционирования, и элементов, образующих очередь на работу. При этом
условно будем считать, что отказавшие элементы становятся в очередь навосстановление, и номера этих элементов образуют множество W£ . Множе¬
ства Wk и W[, характеризующие процесс восстановления элементов, являют¬
ся пустыми. Таким образом, аргументы искомых функций ук равны s,, либо
s'j, либо нулю. В графе состояний отсутствуют все переходы, соответствую¬
щие восстановлению, и все пути графа имеют конечную длину, не превы¬
шающую количество уровней графа. Соотношения (4.9) и (4.10) для вероят¬
ностей состояний и параметров переходов, а также правила составления сис¬
тем интегральных и дифференциальных уравнений при этом сохраняются, но
по своей форме они значительно упрощаются.
Математические модели функционирования технических элементов и систем123ПРИМЕР 4.7. Описать функционирование невосстанавливаемой системы
для основного соединения 3-х элементов из разд. 4.2.3.Решение. Как и прежде, устройство имеет 6 возможных состояний и 6 неиз¬
вестных функций: 70(^,52,53,0, л(°>52^3>0, Jb(s{>0,3$,0, 7з(5,,52Д0,
^31 (0,^2 >0)0 > ^32 (^[, 0,0,0. Считая, что в момент времени t = 0 все элементы
исправны, будем иметь следующую систему интегральных уравнений:y0{sx,s2,s3,t) = fx{t + sx)f2(t + s2)f3(t + s3),
tyx (0, s’2, S3, it) = jy0 (0, s2, s3 ,t - x)dx,0ty2 (s(, 0, S3,0 = JVo (^l >10.'*3 - x)dx>0ty3 (s,, s2,0,0 = jy0 (x + > •* + s2 > °>' - x)dx,0ty3, (0, s'2,0,0 = jy3 (0,S2,0,t - x)dx,0tУ32 0[>0,0,0 - j)>3 (^1,0,0,t - x)dx.0Все неизвестные функции определяются последовательной подстановкой:•Vo(s\ >s2 >'*3>0 = Л 0 + sl )fl (t + s2 )/з (t + s3 )>
ty, (0, s2, s3,0 = Jfi (x)f2 (X + S2)f3(x + S3 )dx,0ty2 (Si, 0,s3,0 - J/i (X + Ji )/2 (x)fi (X + s3 )dx,0Уз Ol > s2,0,t) = f](t + s] )f2 (t + s2 )F3 (0,
tУз 1 (0» 52 A 0 = J/i (x)ft(x + S2 )F3 (x)dx,0tУ32 О!> °»°> 0 = ]f\ (x + Si )f2 (x)F3 (x)dx .0
124Гпава 4Далее находим вероятности состояний:ро (о=Ц (0^2 (о^з (о > Pi (о= !л о)^> (хщ (*>& >ор2(0 = jF,(х)/2(x)F3(x)dx, р3(О = Ц(t)F2(t)F3(t),
оP3iO)=\fx(x)F2(x)F3(x)dx, Рзг(0= р1М/2М^(Л'>&-
о оНетрудно видеть, что сумма вероятностей равна единице, что может служить
контролем правильности вычислений.ПРИМЕР 4.8. Описать функционирование невосстанавливаемой резервиро¬
ванной системы при постоянном резервировании кратности т = 2 из разд. 4.2.3.Решение. В графе состояний невосстанавливаемой системы отсутствуют все
переходы с нижнего уровня на верхний. Мы не будем выписывать полностью
систему интегральных уравнений, приведем только те уравнения, которые
отвечают состояниям: 0, 1, 12, 123. Остальные уравнения составляются ана¬
логично.~Mt + sx)f2(t + s2)f3(t + s3),Iyx(0,s2,s3,t) = ly0(0,x + s2,x + s3,t-x)dx,
оt t
J12(0,0,s3,0= jj1(0,0,x + s3,/-x)c&+ ^(ОДх + ^з,
о 0tym (0,0,0,0 = jyl2 (0,0,0,t - x)dx.
оНепосредственной подстановкой найдем решение этой системы:д>0 О, ,s2,s3,t) = fx(t + sx)f2{t + s2 )/3 (t + s3),У\ (0, s2,s3,t) = Fx (0/2 (t + s2 )/3 (t + s3 ),t t
У12 (0,0, S3,t)= jF, (x)f2 (x)dxf3 (t + s3) + J/j (x)F2 (x)dxf3 (t + s3) =
о 0= Fx(t)F2(t )f3 (t + s3 ),
Математические модели функционирования технических элементов и систем125*ш(0,0,0,о = jFl(x)F2(x)f3(x)dx.
оОпределим вероятности соответствующих состояний:Po(t) = Ft(t)F2(t)F3(0, Pl(t) = F,(t)F2(t)F3(t),
Pn{t) = Fx(t)F2(t)F3{t), pm(0 = \Fx{x)F2{x)f^x)dx .оВыписывая вероятности остальных состояний, можно показать, что сумма
вероятностей всех состояний равна единице.Вычислим вероятность отказа системы:Q(t) = /7] 23 (0 + Р132 (0 + Р2Ъ1 (0 >ИЛИQ(t) - ‘\F{{x)F2{x)Ux)dx + J'Fi(x)f2(x)F3(x)dx + )fx(x)F2(x)F3(x)dx =О 0 0= F[(t)F2(t)F3(t).Следовательно, вероятность безотказной работыР(0 = 1 - ^1(0^2 (О^з (0 •4.6. Модели надежности систем
при экспоненциальных законах
распределения отказов
и восстановлений элементовРассмотрим частный случай системы уравнений (4.15), когда времена безот¬
казной работы и восстановления элементов имеют экспоненциальные законыраспределения вероятностей. Пусть h, (0 = Aie~A‘t, где А, — интенсивность
отказа или восстановления /-го элемента в зависимости от того, какой смысл
вкладывается в плотность распределения /г, (время безотказной работы или
время восстановления). Будем искать решение системы дифференциальных
уравнений (4.15) в видеЛ(4>0 = ПА<(%)Л(0. к&Е, (4.21)
126Гпава 4где произведение распространяется на все индексы i е Rk u RkuWk и Wk, а
pk(t) — некоторые функции времени. Подставляя это решение в левую часть
(4.15) и используя равенство -hj(x) = ЛД(д), получим:S Л< № (aik )Рк (О+П h, (atk )Рк (О=Пи> (aik)ieRk'uWk i i iZ AiPk(.o+p'kioieRkuWkПреобразуем теперь правую часть уравнения (4.15). Так как(^У° \о=т («у )л/0 pj (о»iгде произведение вычисляется для всех i е i?? и и и , i * /0» то пРа‘
вая часть (4.15) принимает видX П hi (aik )П hi (aij Pj СО./' iпричем первое произведение распространяется на все индексы Mi, для кото¬
рых вектор Л* \Aij°) имеет "ненулевые" компоненты, поэтому оба произве¬
дения под знаком суммы дополняют друг друга, и после их объединения по¬
лучим [ JЛ, (ajk), в котором индексы / являются номерами "ненулевых" ком-
iпонент вектора Ак, т. е. i<=RkuR'kuWkuWk. Тем самым правая часть
дифференциального уравнения равнаШ(%) X \Pj(О-
/ jf->ArПриравнивая левую и правую части, получим:X Л,л (0+^(0= X AioPj(t)ieRkvWk j~*kилиРк(0 = - X Л/Л(0+ X \Р/(0- (4.22)ieRkufVk j->kВ соотношении (4.22) i = i(j,k) — номер элемента, вызвавшего переход из
состояния j в состояние к. Это уравнение показывает, что функции pk(t)
удовлетворяют уравнениям Колмогорова, справедливым для экспоненциаль¬
ных распределений, и, следовательно, pk(t) есть вероятность пребывания
системы в момент t в состоянии к . Таким образом, функции (4.21), в кото¬
рых вероятности pk(t) определяются системой (4.22), являются искомым
Математические модели функционирования технических элементов и систем127решением системы дифференциальных (и интегральных) уравнений, описы¬
вающих функционирование технической системы с экспоненциальными рас¬
пределениями.Заметим также, что если какой-либо компоненте вектора Ак с номером ц
соответствует плотность hj экспоненциального распределения, а остальные
плотности А, произвольные, то число аргументов функций ук уменьшается,
т. к.00Ук(Ак,0 = \ (aiok )\ук{Ак, t)daiok.
оЭто значит, что необходимость введения дополнительной компоненты в
функции ук отпадает. Этим фактом можно пользоваться для уменьшения
количества неизвестных, если время до отказа или время восстановления не¬
которых элементов системы имеет экспоненциальное распределение.Предположим, что техническая система состоит только из элементов элек¬
троники, имеющих экспоненциальные распределения времени безотказной
работы и любые распределения времени восстановления. Тогда математиче¬
ская модель в виде системы интегральных уравнений значительно упрощает¬
ся. Наибольшее упрощение системы уравнений происходит при полностью
ограниченном восстановлении, когда неизвестные функции содержат лишь
одну дополнительную компоненту.ПРИМЕР 4.9. Описать функционирование восстанавливаемой системы из
примера 4.2 при следующих условиях: время до отказа элемента имеет экс¬
поненциальное распределение с параметром Я,, / = 1, 2, 3, а восстановление
отказавших элементов производится одной ремонтной бригадой с прямым
приоритетом.В примере будет показано принципиальное отличие анализа надежности сис¬
темы в общей ситуации от случая, когда все законы распределения времени
до отказа и времени восстановления элементов являются экспоненциальны¬
ми. Так, например, количество состояний системы зависит от приоритета
восстановления отказавших элементов. Для прямого приоритета количество
возможных состояний увеличивается по сравнению с рассмотренным ранее
случаем обратного приоритета обслуживания, поскольку каждое из состоя¬
ний (1) и (2) приходится разбивать на два состояния.Решение. Перечислим все состояния системы:□ (0) — все элементы исправны, Aq = (sl,s2,s3);□ (1)— отказал и восстанавливается 1-й элемент, другие элементы про¬
стаивают вследствие прерывания их работы, Ах -;
128Глава 4П (1) — восстанавливается 1-й элемент, 2-й элемент простаивает из-за пре¬
рывания его работы, 3-й элемент исправен, но не включен в работу,
Лг=(т1,4,0);□ (2) — отказал и восстанавливается 2-й элемент, другие элементы простаи¬
вают вследствие прерывания их работы, Л2 = (s{,T2,.s3);□ (2) — восстанавливается 2-й элемент, 1-й элемент простаивает из-за пре¬
рывания его работы, 3-й элемент исправен, но не включен в работу,
A2=(s'l,x2,0);□ (3) — отказал и восстанавливается 3-й элемйнт, другие элементы продол¬
жают работать, А3 = (sus2,x3); *'*'□ (31) — отказал 3-й, а затем 1-й элементы, 1-й элемент находится в очереди
на восстановление, 2-й элемент простаивает из-за прерывания работы, 3-й
элемент восстанавливается, Л4 = (0,s2,x3);□ (32) — отказал 3-й, а затем 2-й элемент, 1-й элемент простаивает вследст¬
вие прерывания работы, 2-й элемент находится в очереди на восстановле¬
ние, 3-й элемент восстанавливается, Л5 = (jf, 0,т3 ) .В связи с принятой дисциплиной обслуживания, когда при наличии очереди
сначала восстанавливается первый отказавший элемент, граф состояний
(рис. 4.6) будет другим по сравнению с графом, изображенным на рис. 4.3 для
обратного приоритета.Рис. 4.6. Граф состояний системы из примера 4.9Система интегральных уравнений также изменяется и приобретает следую¬
щий вид:
Математические модели функционирования технических элементов и систем129y0(sl,s2,s3,t) =
t t
= j/i (х + sx )yl (0,x + s2 ,x + s3 ,t - x),dx + J/i О + sx )/3 (x + s3 )y^ (0,x + s2 0,t - x)dx +
о 0t t
+1/2 (x + s2 )y2 (x + sx,0,x + s3,t- x)dx + J/2 (x + s2 )f3(x + 53 )yj (x + Л|, 0,0, / - x)dx +
о 0I+ J/3 (x + s3 )>-3 (x + s,,jc + s2,(U- x)dx +f(t + Sj )f2(t + s2 )/3 {t + s3 ),0}>i(T,,S2,s3,0= JgiO + ь )y0 (0, S2,s3,t- x)dx,0t>T(xi, s'2,0,t)= jg\(x + xx)y3l(0,s2,0,t-x)dx,0ty2(s[,x2,s3,t)= jg2(x + x2)y0(s,,0,s3,t- x)dx,
0
tj^(j(,t2,0,0 = \g2(x + x2)y32(sx,0,0,t ~ x)dx,
0ty3(sx,s2,x3,t) = Jg3 (x +13)^0 + +0ty3 J (0, s2, т3, /) = \y3 (0, s2, x + x3, / - x)dx,y32 (s(, 0, x3,0 = \y3 (s 1,0, x + x3, t - x)dx.0Согласно принятому допущению об экспоненциальное™ времен до отказа
элементов, искомые функции можно представить в виде:у0 о, ,s2,s3,t) = V~Vl Уо (0,ух (т,, s2, s'3, /) = \2е~Хл X3e~hS3 yx(xx,t),yr(xj,S2,0,O = he~klS2У~\ (Ti»0»
y2(s'x,x2,s'3,t) = 'kxe~x's' Я.3е“ ^ У2 (x2>0»5 Зак. 3094
130Глава 4yj (s{ ,т2,0,/) = V~Vl Уг (T2.0»Уз 0] ,s2,x3,t) = V“V| Л,2е_хл J73 (x3,0,>>31 (0, s'2, x3, /) = Х2е~х**2 y3 , (x3,/),732(5,',0,t3,0 = V~Vl РзгСМХ
где функции у получены из функций у путем интегрирования по всем ком¬
понентам, соответствующим экспоненциальным распределениям, например:ОООООО ' СО 00Уо(0= J J J(si>^2»>Ods\ds2ds3, 7,(т,,0= J lyl(TUs2,s3,t)ds2ds3ООО 00ИТ. д.С учетом этого замечания получим следующую систему уравнений:5Ш == |е-(х1+х2+А-з)^^](о,г-х) + 7Г(0,/-х) + 72(0,Г-х) + >^(0,/-х) + y3(Q,t-x))dx +
оtУ\ (Х1,0 = h Jgi (X + т, )У0 (t - x)dx,
оtУ\ (* 1 ><0 = \g\(х + Xi)у31 (О,/-x)dx,
оIу2 (т2,0 = Х2 J82 (X + т2 )у0 (t - x)dx,
оtУг (х2 .■О = jg2 (х + х2 )?32 (0,г - x)dx,
оУз (т3,0 = Хз +kz)xg3 (х + т3 )у0(г - x)dx,о/Уз iCM) = (Л + *з>' - x)dx,У32(хз,0 = ^2 jy3(x + T3,t-X)dx
о
Математические модели функционирования технических элементов и систем131Если ограничиться стационарным режимом, то получим_ у, (0) + уг(0)+МП + ^(°>+У0 1 *1 *1 >A.J Ч* Л.2 А*^л (xi)=ЗД (xi )7о» Ут (Ti) = G\ (Ti )Ъ 1 (°)>У2(х2) = ^2 (х2 )7о > Уг (х2) = &2 (х2)Рз2(0),.Уз(тз)= ^з£з,т3 (^i + ^-г)Уо»00 оо3731('С3) = ^1 \ЫХ+Хз)^^ Д'з2(тз) = ^2 j%(* + T3)*-
О оВыразим все искомые функции через у0 :Ji(xi) = >>r(xi) = ^i^'3^i(Ti)^:3(^i +^г)Уо’Уг(х2) = ^2^2{хг)Уо ’ >^(Х2) = ^2^-3^2(Х2)^3(^1 + ^-2)>’о»Уз (х3 ) = ^3&3,Тз (^1 + ^2)*0 >А А*з 1 (хз)= ^*i^з^з.тз(^i +^г)Уо> Узг(тз)= ^2^-з^з,х}(^1 + ^-г)Уо-Выразим теперь вероятности всех состояний через вероятность р0 = у0 на¬
чального состояния:Р\ =^i^biPo> Pi =^\hTB\G3(h +^г)Ро’Ар2 =к2ТЪ2Ро> Рг =^2^з7в2<^з(^1 + ^2)Ро>Рз ~+ ^2)Ро ’Р31 = ^ ^ |^вЗ-адц +^2)|р0> Р32 = jJT+x”(^в3 +^2))р0 •Используя условие нормировки, найдем вероятность начального состояния,
являющегося в данном случае коэффициентом готовности системы:Ро =(l + (№ +^2^в2)^ + ^3^з(^1 +^2)| + ^З^вЗ j •Таким образом, показатели надежности зависят не только от моментов перво¬
го порядка, но и от закона распределения времени восстановления элементов.
ГЛАВА 5МЕТОДЫ АНАЛИЗА НАДЕЖНОСТИ
ТЕХНИЧЕСКИХ СИСТЕМРассчитать надежность сложной системы — это значит определить ее по¬
казатели надежности по известным показателям надежности элементов.Существует большое количество методов расчета надежности. Основными из
них являются:□ метод, основанный на применении классических теорем теории вероят¬
ностей;□ логико-вероятностные методы;□ топологические методы;□ методы, основанные на теории марковских процессов;□ методы интегральных уравнений;□ методы статистического моделирования.Опишем эти методы, укажем их достоинства и недостатки.5.1. Способы описания функционирования
технических систем в смысле их надежностиСуществуют следующие способы описания функционирования технической
системы в смысле ее надежности:□ структурная схема;□ функции алгебры логики;□ граф состояний;□ дифференциальные и алгебраические уравнения;□ интегральные уравнения.Опишем эти способы и приведем примеры их использования.
Методы анализа надежности технических систем1335.1.1. Структурная схема системыКаждый элемент сложной системы изображается в виде геометрической фи¬
гуры, чаще всего прямоугольника. Прямоугольники соединяют линиями та¬
ким образом, чтобы полученная структурная схема отображала условия рабо¬
тоспособности. В качестве примера на рис. 5.1 приведены соответственно
структурные схемы нерезервированной системы, состоящей из п элементов,
и системы с раздельным (поэлементным) резервированием.2яm = 1/2бРис. 5.1. Структурные схемы нерезервированной (а) и резервированной (б) системРезервирование элементов осуществляется методами постоянно включенного
резерва, замещением и с дробной кратностью m = 1/2 .Из структурных схем наглядно видны условия работоспособности. Система
на рис. 5.1, а работоспособна, если все ее элементы исправны. Отказ любого
элемента нарушаем работоспособность системы, наступает ее отказ. Система
на рис. 5.1,6 работоспособна, если исправным является элемент 1 и любой
один элемент дублированных пар, а также два любых элемента из трех резер¬
вированных с дробной кратностью m = 1/2 .Высокая наглядность— основное достоинство этого метода. Его недостат¬
ком является далеко не полная информация о функционировании системы.
Например, из рис. 5.1 не ясно: ремонтируемая или неремонтируемая система,
дублирование осуществлено равнонадежными элементами или нет, какова
дисциплина обслуживания системы, если она ремонтируемая (количество
ремонтных бригад, приоритетность обслуживания), какова кратность резер¬
вирования в случае резервирования с дробной кратностью.Эти и ряд других недостатков требуют дополнительных описаний условий
работоспособности системы. Только при этих условиях можно выполнить
134Глава 5анализ системы по критериям надежности. Следует также иметь в виду, что
структурная схема не является математической моделью функционирования
системы.5.1.2. Функции алгебры логикиЗакодируем состояния каждого из элементов структурной схемы двоичными
переменными: 1 (элемент исправный), 0 (элемент в отказовом состоянии).Тогда функционирование системы можно описать с помощью функций ал¬
гебры логики (ФАЛ), используя операции конъюнкции, дизъюнкции и инвер¬
сии. В качестве примера составим ФАЛ, соответствующую работоспособно¬
сти системы с последовательным соединением элементов. Система находится
в работоспособном состоянии при условии, что все ее элементы исправны.
Обозначим Xj — исправное состояние i-го элемента, xt — отказовое состоя¬
ние, /' = 1, 2,... ,п. Тогда ФАЛ будет иметь вид:у(х1,х2,...,хп) = ххх2...х„.Приведем еще один пример. Структурная схема системы имеет вид, пред¬
ставленный на рис. 5.2.*3Рис. 5.2. Структурная схема системы с неравнонадежными элементамиСистема будет в работоспособном состоянии в следующих случаях: все эле¬
менты исправны, исправными являются элементы 1 и 2 или 1 и 3. Тогда
ФАЛ, соответствующая функции работоспособности, будет иметь вид:у(хх,x2,xi) = xlx2x3v ххх2хъ vххх2хг .Процедура получения ФАЛ может быть формализована. Одним из способов
формализации является получение совершенной дизъюнктивной нормальной
формы (СДНФ), получаемой из таблицы истинности, соответствующей рабо¬
тоспособному состоянию системы.Пусть, например, структурная схема системы имеет вид, показанный на
рис. 5.3.Таблица истинности приведена в табл. 5.1.
Методы анализа надежности технических систем135х2Рис. 5.3. Структурная схема системы со смешанным соединением элементовТаблица 5.1. Таблица истинностиXI*2*3ХА,У00000000100010000110010000101001100011111 ’00001001о101001011111000110101110011111Функция y(xl,x2,xi,x4) имеет значение 1 лишь на трех наборах двоичных
аргументов:□ 0111 (исправными являются элементы х2, х3, х4);□ 1011 (исправными являются элементы xt, jc3, jc4);□ 1111 (все элементы исправны).
136Гпава 5Тогда следующая СДНФ будет функцией алгебры логики, описывающей ра¬
ботоспособное состояние системы:у(хх,х2,хт1,х^) = ХгХ2Х}Х4 V ХХХ2Х$Х4 V X1X2X3JC4 .Функция алгебры логики может быть математической моделью функциони¬
рования системы в смысле ее надежности.Способы получения ФАЛ, достоинства и недостатки метода более подробно
описаны в разд. 5.3.5.1.3. Матрица состояний системыВ матрице состояний содержится вся информация о функционировании сис¬
темы в смысле ее надежности. Каждая строка матрицы представляет собой
вектор, компонентами которого служат признаки о том, в каком состоянии
пребывает каждый элемент, когда сама система находится в состоянии i,
ieE, где Е — множество всех состояний системы. Элемент может нахо¬
диться не только в двух состояниях: работает или восстанавливается. Эле¬
мент системы может находиться в состоянии простоя, которое вызвано раз¬
личными причинами. Для дальнейшей работы системы необходимо знание
того, вызван ли указанный простой элемента очередью на восстановление
или отказом других элементов, или элемент является резервным и находится
в ненагруженном состоянии и т. д. Задание матрицы состояний системы было
подробно описано в гл. 4. Вместо матрицы состояний информация о функ¬
ционировании системы может находиться в аргументах функций, являющих¬
ся неизвестными в системе интегральных уравнений. Достоинством описания
системы с помощью матрицы состояний является удобство ее хранения в па¬
мяти ЭВМ или на внешнем носителе информации. При этом матрица может
иметь практически любую размерность. Другое дело — использование этой
матрицы для построения системы интегральных уравнений. Данный вопрос
достаточно сложный и требует серьезного изучения.5.1.4. Граф состояний системыВосстанавливаемая система, состоящая из п элементов, может находить¬
ся в большом числе состояний. Например, z-e устройство отказало
(/' = 1, 2,..., п), а остальные исправны; z-e и j-e устройства отказали, а осталь¬
ные исправны, и т. д. Из-за отказов и восстановлений система в дискретные
моменты времени переходит из одного состояния в другое. В процессе дли¬
тельной эксплуатации она может побывать в каждом из возможных состоя¬
ний многократно. Тогда ее функционирование может быть описано графом,
узлам которого приписываются состояния системы, а ветвям — возможные
Методы анализа надежности технических систем137переходы из состояния в состояние. Если в графе имеется п узлов, то среди
них будет к узлов, соответствующих отказовым состояниям, и (п-к) —
исправным.Если оценивать функционирование системы до некоторого /'-го состояния,
например до первого ее отказа, то /-е состояние считается поглощающим.
Система, попавшая в /-е состояние, уже не может перейти в другое, и в графе
отсутствуют ветви переходов из этого состояния (говорят, что в такие ветви
ставится жран).Вид графа зависит от структуры системы (схемы расчета надежности), числа
обслуживающих бригад и дисциплины обслуживания. Обычно узлы графа
нумеруются и отмечаются (например, крестом) те, которые соответствуют
отказовым состояниям системы. На графе также указываются все интенсив¬
ности переходов.Рассмотрим примеры графов, описывающих функционирование системы в
смысле ее надежности.ПРИМЕР 5.1. Схема расчета надежности нерезервированной системы при¬
ведена на рис. 5.4, где приняты обозначения:□ п — число элементов системы;□ Х' — интенсивность отказа /-го элемента;□ ц, — интенсивность восстановления /-го элемента, / = 1, 2,..., п .Рис. 5.4. Структурная схема нерезервированной восстанавливаемой системыГраф состояний рассматриваемой нерезервированной восстанавливаемой
системы приведен на рис. 5.5.(Л12пРис. 5.5. Граф состояний нерезервированной восстанавливаемой системы
138Гпава 5Исправное состояние обозначено (0), а отказовые пронумерованы от 1 до и
и изображены квадратами. В любом i-м отказовом состоянии система не ра¬
ботает, а /-й элемент находится в ремонте. Очевидно, что система в г-е отка-
зовое состояние может попасть с интенсивностью отказа г-ro элемента, т. е.
Xj, и может быть восстановлена (возвращена в состояние (0)) с интенсив¬
ностью Ц; .Указанные интенсивности приведены на графе. В рассматриваемом случае
вид графа и интенсивности переходов не зависят от числа обслуживающих
бригад, т. к. предполагается, что после возникновения отказа одного элемента
вся система не работает и отказы элементов в процессе ее восстановления не
возникают.Если необходимо проанализировать поведение системы до первого отказа, то
следует считать, что состояния (1), (2),..., (п) являются поглощающими
(система, попав в эти состояния, больше не возвращается в исправное со¬
стояние (0), экран на графе состояний).ПРИМЕР 5.2. Необходимо описать графом функционирование дублирован¬
ной системы, схема расчета надежности которой приведена на рис. 5.6.Рассмотреть следующие случаи:а) систему обслуживают две бригады;б) обслуживание осуществляется одной бригадой с прямым приоритетом;в) обслуживание осуществляется одной бригадой с обратным приоритетом;г) обслуживание осуществляется одной бригадой, причем первый элемент
имеет высший приоритет по сравнению со вторым.^•1»^2> ^2Рис. 5.6. Структурная схема дублированной системы с неравнонадежными элементамиРешение. Из рис. 5.6 видно, что дублированные устройства неравнонадежны
и обладают различной ремонтопригодностью. Предполагается также, что по¬
следействие отказов отсутствует.Графы состояний системы для всех случаев приведены на рис. 5.7.
Методы анализа надежности технических систем139Рис. 5.7. Граф состояний дублированной системы при различных дисциплинах обслуживанияСистема может находиться в следующих состояниях:□ (0) — состояние, когда оба устройства исправны;□ (1) — состояние, когда первое устройство отказало и находится в ремонте,
а второе исправно;□ (2) — состояние, когда второе устройство отказало и находится в ремонте,
а первое исправно;□ (3)— отказовое состояние системы, когда оба устройства неисправны;
при этом в случае (а) ремонтируются и первое, и второе устройства; в слу¬
чае (б) и (г) ремонтируется первое, а второе находится в очереди на ре¬
монт; в случае (в) ремонтируется второе, а первое находится в очереди;□ (4)— отказовое состояние, когда оба устройства неисправны, при этом
в случае (б) ремонтируется второе устройство, а в случаях (в) и (г) —
первое.Рассмотрим первоначально случай (о) (рис. 5.7, а). В дублированной системеможет отказать либо первое, либо второе устройство. Поэтому из исходного
140Гпава 5состояния (0) возможны два перехода: в состояние (1) с интенсивностью А,] и
в состояние (2) с интенсивностью Х2 . Отказавшее устройство может быть
восстановлено до отказа системы, т. е. система из состояний (1) и (2) может
возвратиться в исходное нулевое состояние. Может также оказаться, что до
восстановления отказавшего устройства откажет еще одно, и система перей¬
дет в отказовое состояние (3), показанное на графе квадратом. В это состоя¬
ние она может попасть либо из состояния (1) с интенсивностью к2 (второе
устройство отказало), либо из состояния (2) с интенсивностью А, (первое
устройство отказало). Так как восстановлением системы занимаются две об¬
служивающие бригады, то в состоянии (3) оба устройства ремонтируются
независимо от того, какое из них отказало первым. Если в состоянии (3) пер¬
воначально будет отремонтировано первое устройство, то система перейдет с
интенсивностью ц, в состояние (2), а если второе — то с интенсивностью \х2
в состояние (1).Случаи (б), (в), (г) отличаются от рассмотренного тем, что ремонтом дубли¬
рованной системы занимается лишь одна обслуживающая бригада. При та¬
ком обслуживании в отказовом состоянии дублированной системы ремонти¬
руется только одно из отказавших устройств, а второе находится в очереди на
ремонт. А это значит, что дублированная восстанавливаемая система имеет
два разных отказовых состояния, которые объединить в одно в общем случае
невозможно. На рис. 5.7, б—г эти состояния обозначены (3) и (4) и показаны
квадратами.При обслуживании дублированной системы с прямым приоритетом (случай
(б)) в отказовом состоянии (3) ремонтируется первое устройство, а в состоя¬
нии (4) — второе. Если будет отремонтировано первое устройство, то систе¬
ма перейдет в исправное состояние, когда первое устройство работает, а вто¬
рое находится в ремонте, т. е. в состояние (2). Интенсивность перехода будет
равна интенсивности восстановления Ц| первого устройства. Если будет от¬
ремонтировано второе устройство, то система перейдет в исправное состоя¬
ние, когда второе устройство работает, а первое находится в ремонте, т. е. в
состояние (1). Интенсивность перехода будет равна интенсивности восста¬
новления \х2 второго устройства.При обслуживании системы с обратным приоритетом (случай (в)) в состоя¬
нии (3) ремонтируется второе устройство, а в состоянии (4) — первое, поэто¬
му из отказовых состояний (3) и (4) возможны переходы соответственно в
состояние (1) с интенсивностью \12 и в состояние (2) с интенсивностью р.].В случае (г) первое устройство имеет приоритет в обслуживании, поэтому в
отказовых состояниях (3) и (4) оно ремонтируется первым. А это означает,
Методы анализа надежности технических систем141что переход системы из отказовых состояний (3) и (4) возможен лишь в ис¬
правное состояние (2), когда первое устройство работает; а второе находится
в ремонте. Интенсивность перехода равна интенсивности восстановления Ц}
первого устройства.Из примера следует, что вид графа зависит не только от структуры системы,
но также от числа обслуживающих бригад и дисциплины обслуживания.Из приведенных примеров видно, что граф состояний восстанавливаемой
системы полностью определяется ее структурой (схемой расчета надежно¬
сти), надежностью устройств, их ремонтопригодностью, числом ремонтных
бригад, дисциплиной обслуживания и видом восстановления. В нем содер¬
жится вся информация о функционировании системы. Поэтому граф состоя¬
ний можно рассматривать как один из способов описания поведения^ системы
в смысле ее надежности. Основным преимуществом такого описания являет¬
ся наглядность и сравнительная простота.Граф состояний сложной системы может иметь большое число узлов. В этом
случае при построении графа приходится просматривать большое число воз¬
можных сочетаний отказавших элементов. Это можно выполнить при усло¬
вии формализации построения графа.5.1.5. Формализованный способ
построения графа состояний системыКаждому узлу графа соответствует определенное состояние системы. Сово¬
купность состояний, когда в системе отказало / устройств, будем называть
i-м уровнем графа. Тогда при / = 0 (нулевой уровень) все устройства исправ¬
ны, при / = 1 (первый уровень) одно любое устройство отказало, а остальные
исправны, при / = 2 (второй уровень) два любых устройства отказали, а ос¬
тальные исправны, и т. д.Исходными данными по построению графа являются: структурная схема сис¬
темы, интенсивности отказов и восстановления, дисциплина обслуживания,
вид восстановления. Для удобства построения графа целесообразно элементы
структурной схемы нумеровать и указывать значения их интенсивностей от¬
казов и восстановления.Сущность формализованного способа построения графа состояний системы
заключается в следующем.Проводятся горизонтальные линии, которым присваиваются номера О,1, 2,...
Линия с номером / соответствует /-му уровню графа. Их целесообразно рас¬
142Глава 5полагать в последовательности возрастания номеров. Первой из них присваи¬
вается номер 0 (нулевой уровень системы).Далее строится граф состояний с переходами от верхних к нижним уровням.
Назовем их ^.-переходами. Для этого на нулевой горизонтальной линии отме¬
чается точкой или кружком нулевой узел графа, соответствующий состоянию
системы, когда все устройства исправны. Затем на линии с номером 1 обо¬
значаются все узлы, соответствующие первому уровню графа. Число узлов
первого уровня всегда равно числу устройств (элементов) структурной схе¬
мы. Соединяя узел нулевого уровня со всеми узлами первого уровня и отме¬
чая стрелками направление переходов, получим неполный граф состояний
системы, который назовем графом первого уровня с ^-переходами. Все узлы
первого уровня нумеруются в соответствии с номерами элементов (уст¬
ройств) структурной схемы, а возле ветвей записываются соответствующие
интенсивности переходов. Все узлы первого уровня, которые соответствуют
отказовым состояниям системы, необходимо отметить (например, квадратом
или крестом). Из этих узлов ^-переходы в узлы более высокого уровня графа
отсутствуют.Для построения графа состояний второго уровня с л-переходами на линии с
номером 2 наносятся узлы графа, соответствующие всем возможным состоя¬
ниям системы, когда отказали два ее устройства. Все узлы нумеруются двух¬
разрядными числами. Двухразрядное число показывает номера отказавших
элементов структурной схемы и последовательность их отказов. Например,
если узел второго уровня имеет номер 31, то это значит, что в данном состоя¬
нии система оказалась в результате отказа первого и третьего элементов
структурной схемы, причем первым отказал третий элемент, а вторым —
первый. Соединяя ветвями соответствующие узлы первого и второго уровня
и отмечая стрелками направления переходов, получим граф состояний систе¬
мы, который называется графом второго уровня с ^.-переходами.Узлы, соответствующие отказовым состояниям системы отмечаются квадра¬
тами или крестами. Из этих узлов переходы в узлы более высокого уровня
отсутствуют. Возле ветвей графа записываются соответствующие интенсив¬
ности переходов.Построение графа состояний с Х-переходами заканчивается тогда, когда все
узлы в данном уровне будут соответствовать отказовым состояниям системы.ПРИМЕР 5.3. Необходимо построить граф состояний системы, схема расче¬
та надежности которой приведена на рис. 5.8. Предполагается, что восста¬
новление неограниченно, последействие отказов элементов отсутствует, а
элемент 5 находится в ненагруженном резерве и до отказа элемента 4 его ин¬
тенсивность отказа равна нулю.
Методы анализа надежности технических систем143Х.5> ц5Рис. 5.8. Структурная схема резервированной восстанавливаемой системы
с неравнонадежными элементами1,4,2 1,4,3 1,4,5 2,4,1 2,4,3 2,4,5 4,1,2 4,1,3 4,1,5 4,2,1 4,2,3 4,2,5
Рис. 5.9. Граф состояний системы, изображенной на рис. 5.8Решение. Граф состояний системы приведен на рис. 5.9.Граф имеет четыре уровня. В исходном нулевом состоянии система исправна
и ни один из ее элементов не отказал. Все состояния последнего третьего
уровня соответствуют отказовым состояниям системы. При простейшем по¬
токе отказов, удовлетворяющем условиям ординарности, система может пе¬
рейти из начального нулевого состояния в состояния, когда отказал один лю¬
бой ее элемент. Эти состояния отмечены на линии уровня 1 цифрами 1, 2, 3,4
в соответствии с отказавшими элементами структурной схемы. На линии
первого уровня отсутствует узел с номером 5. Это объясняется тем, что пя¬
тый элемент находится в ненагруженном резерве и по условию задачи отка¬
зать до замещения основного четвертого элемента не может. Из структурной
схемы видно, что отказ элемента 3 приводит к отказу всей системы. Поэтому
узел 3 первого уровня помечен крестом и из этого узла отсутствуют переходы
144Гпава 5в узлы второго уровня. Отказ одного из элементов 1, 2, 4 не ведет к отказу
системы, поэтому из узлов 1, 2, 4 первого уровня имеются переходы в узлы
второго уровня.Из состояния (1) первого уровня возможны переходы в состояния, когда
вслед за отказом элемента 1 отказывает либо элемент 2, либо элемент 3, либо
элемент 4. Эти состояния на линии второго уровня отмечены соответственно(1.2), (1,3), (1,4), Так как отказ элементов 1, 2 или 1, 3 ведет к отказу системы,
то состояния (1,2) и (1,3) отмечены крестами и из этих состояний отсутству¬
ют переходы в состояния уровня 3. При отказе элементов 1 и 4 отказ системы
не наступает, поэтому из состояния (1,4) возможны переходы в состояния
третьего уровня. Вслед за отказами элементов 1 и 4 могут отказать элементы
либо 2, либо 3, либо 5. Соответствующие состояния расположены на линии
уровня 3 и обозначены (1,4,2), (1,4,3), (1,4,5). Так как отказ элементов 1, 4, 2,
или 1, 4, 3, или 1, 4, 5 ведет к отказу системы, то все узлы отмечены крестами.
Остальная часть графа строится аналогично.Для окончательного построения графа необходимо на графе состояний
с ^-переходами изобразить ветви переходов из узлов нижних уровней в узлы
верхних уровней. Эти переходы возникают из-за восстановления отказавших
элементов. Узлы, соединенные между собой ветвями ц-переходов, легко оп¬
ределить, если известен приоритет в обслуживании отказавших элементов.Пусть, например, система попала в состояние, отмеченное на линии уровня 3
графа состояний как (1,4,3). И пусть установлен прямой приоритет в обслу¬
живании отказавших элементов (обслуживание элементов осуществляется в
порядке их отказов). Тогда первым будет восстановлен элемент 1 и система с
интенсивностью р.] перейдет в состояние (4,3) второго уровня. Состояние(4.3) является отказовым, поэтому, пока ремонтируется элемент 4, новых от¬
казов не возникает. После ремонта элемента 4 система перейдет с интенсив¬
ностью р4 в состояние (3) первого уровня, затем с интенсивностью ц3 в ну¬
левое состояние. Указанные переходы показаны на рис. 5.9.Пусть теперь отказавшие элементы обслуживаются с обратным приоритетом,
т. е. восстановление элементов осуществляется в порядке, обратном очеред¬
ности поступления их в ремонт. Тогда из состояния (1,4,3) возможен переход
с интенсивностью Х,3 в состояние (1,4), потом с интенсивностью Х4 — в со¬
стояние (1) и затем с интенсивностью — в нулевое состояние.Описание функционирования системы с помощью графов позволяет сформу¬
лировать ряд важных общих свойств графов состояний.1. Граф состояний полностью описывает функционирование восстанавли¬
ваемой системы, как системы массового обслуживания. Вид графа зависит
от структурной схемы системы, надежности и ремонтопригодности эле¬
Методы анализа надежности технических систем145ментов, а также от дисциплины обслуживания. На основании этого свой¬
ства можно утверждать, что все количественные характеристики надежно¬
сти восстанавливаемой системы могут быть определены непосредственно
из графа состояний системы.2. Число узлов графа может быть больше или меньше возможного числа со¬
стояний восстанавливаемой системы. Это объясняется тем, что граф опи¬
сывает поведение системы совместно с функционированием обслужи¬
вающего органа, т. е. он описывает функционирование системы массового
обслуживания.3. Граф, не содержащий поглощающих состояний, описывает поведение вос¬
станавливаемой системы при неограниченном ремонте, т. е. описывает по¬
ведение системы, функционирующей бесконечно долго.4. Функционирование восстанавливаемой системы с одним ремонтным орга¬
ном и обратным приоритетом в обслуживании отказавших элементов опи¬
сывается графом типа дерева.Составить систему дифференциальных уравнений типа массового обслужи¬
вания для определения количественных характеристик надежности восста¬
навливаемой системы можно по виду графа состояний системы.Сформулируем первоначально правило составления уравнений для определе¬
ния вероятности пребывания системы в /-м состоянии в момент времени t.Часть произвольного графа с состояниями / —1, /, i +1 показана на рис. 5.10.Дифференциальное уравнение для вероятности pt(t) пребывания системы в
г'-м состоянии в момент времени t будет иметь вид:Из уравнения видно, что слева пишется производная по времени от вероятно¬
сти пребывания системы в i-м состоянии в момент времени /, а справа —5.1.6. Описание функционирования системы
с помощью уравнений типа массового
обслуживанияРис. 5.10. Фрагмент графа состояний= k,-iA-i(0-(^ + Ц/)#(0 + H,+iA+i(0 •at
146Глава 5сумма произведении интенсивностей переходов из всех соседних состоянии в
/-е состояние и из /-го во все состояния на соответствующие вероятности со¬
стояний. Знаки в правой части уравнения определяются по направлению
стрелок в ветвях графа. Если стрелка направлена в /-е состояние, то при соот¬
ветствующей интенсивности перехода ставится знак "+", в противном слу¬
чае — знак Это правило справедливо при любом числе соседних с i-м
состояний.ПРИМЕР 5.4. Составить систему дифференциальных уравнений, описы¬
вающих функционирование системы, граф состояний которой приведен на
рис. 5.7, г.Решение. На основании сформулированного правила и в соответствии с гра¬
фом состояний система дифференциальных уравнений будет иметь вид:Фо(0dt
dpi (t)dtФ2(0dt= ~{\x + k2 )p0 (о+ц, pi (о+ц2р2 (0;= A,,p0-(^2+Hi)/7i(0;
= x2p0 -04 +Ц2>Р2(0+Ц1Рз(0+Ц1А(0; (5-1)~^- = k2pi(t)-[Lip3(t);at)=>'lP2(0-^lP4(0-dtНаписанные ранее уравнения позволяют найти вероятность того, что система
в данный момент времени находится в i-м состоянии.На практике часто приходится определять вероятность того, что в течение
времени t система попадает в /-е состояние. Для определения этой вероятно¬
сти необходимо считать z'-e состояние поглощающим и запретить, путем по¬
становки экранов, переходы из /-го состояния во все остальные. Преобразовав
таким образом граф состояний, записываются дифференциальные уравнения
по сформулированному выше правилу.Для нашего случая состояния (3) и (4) являются отказовыми. Для определе¬
ния вероятности безотказной работы дублированной системы запретим пере¬
ход из состояния (3) в состояние (1), а также из состояния (4) в состояние (2).
Тогда система (5.1) преобразуется в следующую систему дифференциальных
уравнений:
Методы анализа надежности технических систем147dp°}^ = ~(h + ^2 )Ро (О+Hi Pi (О+М2Р2 (О;
at^р- = \Ро (О - (Ч + Hi )Р\ (О;at- ”3” - ^-гРо (О - (^i +Цг)л(0;
а/(5.2)^М!atУкажем на одно важное свойство уравнений функционирования системы. Так
как сумма всех вероятностей состояний системы равна единице, т. е.А это значит, что сумма правых частей системы уравнений всегда равна
нулю.Это свойство полезно иметь в виду при проверке правильности составления
уравнений функционирования системы.Дифференциальные уравнения типа массового обслуживания позволяют оп¬
ределить вероятности состояний системы или вероятности попадания в эти
состояния в Течение времени t. По известным вероятностям pf(t) можно
найти любую другую количественную характеристику надежности системы.
А это означает, что система уравнений достаточно полно описывает функ¬
ционирование восстанавливаемой системы.В установившемся режиме функционирования вероятности состояний явля¬
ются величинами постоянными. Тогда все производные равны нулю и систе¬
ма дифференциальных уравнений превращается в систему линейных алгеб¬
раических уравнений.Для случая, рассмотренного в примере 5.4, система дифференциальных урав¬
нений (5.1) превращается в следующую систему алгебраических уравнений:-(X, + Х2)р0 + + ц2р2 = 0;
^■lPo(0~(^2 + Hl)/’l = Ф
■ hPo - (h + v-i)P2+И1Р3 + HiA = о;
^гР\-У*-\Рг=Ь
Л^2-Н1/?4=0-(5.3)
148Глава 5Эта система является однородной (ноль в правой части каждого уравнения) и
имеет бесконечное множество решений. Для получения однозначного реше¬
ния системы следует использовать нормировочное уравнениеРо (0 + Р\ (0 + Рг (0 + Ръ (0 + Ра (0 =1»
которым заменяется одно любое уравнение системы (5.3).Анализ способов описания функционирования технических систем позволяет
сделать ряд важных выводов.Существуют, по крайней мере, следующие три способа описания функциони¬
рования восстанавливаемых систем:□ схема расчета надежности (структура системы);□ граф состояний;□ система дифференциальных уравнений типа массового обслуживания.Схема расчета надежности не позволяет в полной мере описать функциони¬
рование восстанавливаемой системы, т. к. она не дает возможности учесть
дисциплину обслуживания отказавших элементов. Однако она является ис¬
ходной для построения графа и для составления дифференциальных уравне¬
ний функционирования системы.Описание функционирования восстанавливаемой системы с помощью графа
состояний обладает высокой наглядностью. В этом основное преимущество
данного способа перед всеми остальными. Граф состояний в ряде случаев
дает возможность качественно сравнить различные схемные решения, вы¬
брать наиболее приемлемую дисциплину обслуживания, наметить пути по¬
вышения надежности систем. Он существенно облегчает процедуру записи
дифференциальных уравнений функционирования системы.Граф состояний достаточно полно описывает функционирование восстанав¬
ливаемой системы. По графу состояний наиболее просто найти финальные
вероятности пребывания системы в любом /-м состоянии, а также интеграль¬
ные показатели надежности — наработку на отказ и среднее время восста¬
новления системы. Он позволяет определить также показатели надежности
невосстанавливаемых систем.Функционирование восстанавливаемой системы можно наиболее полно опи¬
сать системой дифференциальных уравнений. Решая уравнения известными в
классической математике методами, можно вычислить любую количествен¬
ную характеристику надежности. Наличие программ решения системы диф¬
ференциальных уравнений на ЭВМ существенно расширяет возможности
метода. Однако описание функционирования восстанавливаемой системы с
помощью дифференциальных уравнений имеет существенные недостатки.
Методы анализа надежности технических систем149Метод не обладает наглядностью и требует громоздких вычислений при оп¬
ределении количественных характеристик надежности даже сравнительно
простых систем.Сложные системы имеют большое число состояний (сотни и тысячи). Анализ
надежности таких систем путем решения уравнений типа массового обслу¬
живания практически невозможен.Интенсивности отказов элементов в большинстве практических случаев не
являются величинами постоянными. Имеет место старение элементов и, как
следствие, ХД/)^const. В таких случаях описание функционирования систе¬
мы с помощью дифференциальных уравнений типа массового обслуживания
невозможно. В этом основной недостаток метода дифференциальных уравне¬
ний. На смену им приходит метод, который в теории надежности называется
методом интегральных уравнений.5.1.7. Описание функционирования системы
с помощью интегральных уравненийОписание функционирования системы с произвольными законами распреде¬
ления времени до отказа и времени восстановления элементов состоит в сле¬
дующем:□ определяются все состояния системы и переходы между состояниями;□ для каждого состояния определяется вектор состояний элементов сис¬
темы;□ вводится неизвестная функция, соответствующая каждому состоянию сис¬
темы;□ составляется система интегральных уравнений.ПРИМЕР 5.5. Составить систему интегральных уравнений, описывающую
функционирование системы, граф состояний которой приведен на рис. 5.7, г.
Плотность распределения времени до отказа i-ro элемента равна аплотность распределения времени восстановления /-го элемента— gt(t).
В момент времени t = О система считается полностью исправной.Решение. Состояния системы и переходы между состояниями показаны на
графе на рис. 5.7, г. Рассмотрим каждое состояние системы. В состоянии (0)
оба элемента являются исправными, и этому состоянию соответствует вектор
>4о = (л1,, ) - Аргументы Sj и s2 означают, что, когда система пребывает в
состоянии (0), оба элемента являются работоспособными. В состоянии (1)
первый элемент восстанавливается, а второй работает. Этому состоянию со¬
150Глава 5ответствует вектор Ах = (xx,s2), в котором аргумент xt соответствует восста¬
новлению первого элемента, В состоянии (2) второй элемент восстанавлива¬
ется, а первый работает. Этому состоянию соответствует вектор Л2 = (sx,x2),
в котором аргумент т2 соответствует восстановлению второго элемента.
В состоянии (3) оба элемента являются не рабочими, причем согласно приня¬
той дисциплине обслуживания первый элемент восстанавливается, а второй
находится в очереди на восстановление. Этому состоянию соответствует век¬
тор А3 =(Т|,0). Нулевой аргумент означает простой второго элемента в ожи¬
дании, пока не освободится ремонтная бригада, занятая восстановлением пер¬
вого элемента. В состоянии (4) оба элемента также являются не рабочими.
В силу принятой дисциплины обслуживания восстанавливается первый эле¬
мент, но при этом не было закончено восстановление второго элемента, и ре¬
монтная бригада переключилась на восстановление первого элемента. Этому
состоянию соответствует вектор Л4 = (xj,x2). Аргумент х2 означает, что вто¬
рой элемент восстанавливался, однако восстановление было прервано отка¬
зом первого элемента.Указанные векторы поместим в матрицу состояний:01234sx*1s\Ч*2s2х20т211100Верхняя строка матрицы содержит номера состояний системы, а нижняя
строка состоит из нулей и единиц. Значение нижней строки равно 1, если со¬
ответствующее состояние системы является работоспособным, и 0, если со¬
стояние системы является отказовым.Каждому и му состоянию системы сопоставим неизвестную функцию у,, ар¬
гументами которой служат компоненты z'-го столбца матрицы S и время t:
Ы*1»*2>0» _У4(Х15Х2,0, Уз (X) ,0,0, У4(Х1,Х2,0- функцияyo(si>s2>0 есть плотность распределения вероятностей времени пребывания
системы в момент t в состоянии (0) при условии, что после момента t пер¬
вый элемент будет работать время ^, а второй элемент — время s2. Функция
yx(x{,s2,t) есть плотность распределения вероятностей времени пребывания
системы в момент t в состоянии (1) при условии, что после момента t пер¬
вый элемент будет восстанавливаться время х,, а второй элемент будет рабо¬
тать в течение времени s2. Функция y2(sx,x2,t) есть плотность распределе¬
Методы анализа надежности технических систем151ния вероятностей времени пребывания системы в момент t в состоянии (2)
при условии, что после момента t первый элемент будет работать время 5], а
второй элемент будет восстанавливаться в течение времени х2. Функция
.УзС^ДО есть плотность распределения вероятностей времени пребывания
системы в момент t в состоянии (3) при условии, что после момента t пер¬
вый элемент будет восстанавливаться время х,. Функция y^{xx,x'2,t) есть
плотность распределения вероятностей времени пребывания системы в мо¬
мент t в состоянии (4) при условии, что после момента t первый элемент
будет восстанавливаться время т,, а остаточное время восстановления второ¬
го элемента равно х2 . Таким образом, аргументы функций у, характеризуют
остаточные времена работы или восстановления элементов.На основании формулы (4.11) система интегральных уравнений будет иметь
вид:1y0(sus2,t)^ jfi(x + s,)yl(0,x + s2,t-x)dx +0I+ \f2(x + s2 )y2 (x + 5,,0,/-x)dx + /,(/ + sx )f2 (t + s2 );
оiyl(xl,s2,t)= Jgi(x + T,)jHo(0;x + ^2,/- x)dx;
о
t- y2(sx,x2,t)= \g2(x + x2)y0(x + sxAt-x)dx+ (5.4)+ fe (* + Ъ )f\(x + s\ )Уг (0,0,/—x)dx + J/, (x + 5, )y4 (0, x + x2 , t - x)dx;о оt/y3 (x, , 0,0 = Jy, (x + X,, 0,/-x)dx;
оiy4 (Tl. Ь у0 = jg\ (x + Tl )У2 x)dx.0При составлении системы надо учитывать следующее: если аргумент s, или
xt не содержит "штрих", то в правой части под знаком интеграла к такому
аргументу добавляется переменная интегрирования; если в аргументах s, или
х, имеется "штрих", то к данному аргументу переменная интегрирования не
152Гпава 5добавляется. После этого "штрихи" над аргументами могут быть опущены,
как это сделано в последнем уравнении.Решение данной системы уравнений позволяет найти вероятности пребыва¬
ния системы в каждом состоянии, которые определяются интегрированием
соответствующих функций по всем "ненулевым" аргументам:0000 00 00
А)(0= { \yQ(sx,s2,t)dsxds2 , pi(t)= j jyx(xx,s2>t)dxxds2 ,0 0 0 0
00 00 00
Рг(0= | \yi(sx,x2,t)dsxdx2 , /?3(/)= \yj,{xx,Q,t)dxx,0 0 0
00 00p4(t)= J jy4(xx,x2,t)dxxdx2 .о 0Решение системы интегральных уравнений позволяет найти также параметры
перехода из одного состояния в другое. Чтобы найти параметр перехода из
состояния / в состояние j, в функции yt надо положить нулю аргумент, со¬
ответствующий элементу, который вызвал данный переход, и проинтегриро¬
вать функцию yt по остальным аргументам. Например, параметр перехода из00состояния (0) в состояние (1) равен со01(7) = ^yQ(0,s2,t)ds2 , а параметр пере-охода из состояния (3) в состояние (2) равен a>32(t) = y3(0,0,t).Здесь указан способ получения вероятностей pt (/) того, что в момент време¬
ни t система будет находиться в состоянии i. Если нас интересует вероят¬
ность первого попадания системы в состояние i, то это состояние надо сде¬
лать поглощающим. Например, чтобы найти вероятность безотказной работы
системы, запретим выходы из состояний (3) и (4). Тогда изменяются аргу¬
менты функций уj и у4: уз(т',,0,г), y4(x\,x'2,t), а система интегральных
уравнений преобразуется к виду:
tУо (5, ,S2,t)= j/]0 + Si )>>] (0 ,x + s2,t- x)dx +
о
t+ \f2(x + s2 )y2 (x + sx, 0, t — x)dx + f(t + sx )f2 (t + s2 );
оyx (t, , s2,0 = Jgi (*+ Ti )y0 (0, д; + s2,t- x)dx;о (5.5)
Методы анализа надежности технических систем153у2 (л,, т2,0 = fg2 (х + т2 )yQ (x + sx,0,t-x)dx;
оtУз (t,, 0,0= [yx(ixt0,t-x)±biУ4 (*1. х2.0 = 8\ (Х1) \У2 (°> Ъ >t - x)dx-
ОВ результате решения данной системы и интегрирования функций yt полу¬
чим вероятности исправных состояний и вероятность безотказной работы
системы в течение времени t:P(t) = Ро(0 + Pi(0 + Р2(?) ■По известным вероятностям p^t) и параметрам переходов соу(/) можно най¬
ти любую другую количественную характеристику надежности системы. Это
значит, что система интегральных уравнений полностью описывает функ¬
ционирование восстанавливаемой системы с произвольными законами рас¬
пределения.В установившемся режиме функционирования система уравнений (5.4) уп¬
рощается незначительно и по-прежнему остается системой интегральных
уравнений:ОО 00J/iU + ^i)Ji(0^ + ^2)^+ \f2(x + s2)y2(x + s{,0)dx\о о00О00 00
|.т2>“ Jft(;,t + 'I2)>'ot* + sl’0)* + Js2<-t + x2)/l(;t + sl)73(0.0)‘* +° 0 (5.6)00+ J/1(jc + j1)^4(0,jt + x2>&;осоУз('с1’°)= /л(дс+т1,°>&;.оООУ4 (Т1»■*2 ) = Jgl (х + Т1 )У2 (О, Ъ )dx-О
154Глава 5Вероятности состояний и параметры переходов вычисляются так же, как для
нестационарного режима.Система (5.6) имеет бесконечно много решений, и ее следует решать вместе с
условием нормировки:Р0+Р1+Р2+Рз+Р4=1-5.2. Методы анализа надежности
технических систем, основанные
на применении теорем теории вероятностей5.2.1. Метод перебора гипотезПусть невосстанавливаемая система состоит из п элементов и имеет произ¬
вольную структуру. Предположим, что каждый элемент может находиться в
двух состояниях: состоянии работоспособности и состоянии отказа. Пусть
Pj — вероятность работоспособного, a qi — вероятность отказового состоя¬
ния i-го элемента, р{ + #, =1. Тогда система может находиться в 2" состоя¬
ниях:□ Н0 — все п элементов работоспособны;□ Ht — отказал /-Й элемент, остальные работоспособны;□ Hj j — отказали /-й иу'-й элементы, остальные работоспособны;□ Я, 2 „ — отказали все элементы.Предполагая, что отказы элементов события независимые, можно найти ве¬
роятность каждой гипотезы:P(HQ) = pxp2...p„,P(Hi)=P\P2-q<-Pn’P(Hu) = p1p2...qi...qj...pn,Р(Н\,2 п) = Я\Я2-Чп-Вероятность безотказной работы системы определяется суммированием ве¬
роятностей тех гипотез, которые соответствуют работоспособным состояни¬
ям системы, т. е.
Методы анализа надежности технических систем155Р= Z РШо).as Е+Последняя запись означает, что суммирование производится по всем гипоте¬
зам, соответствующим работоспособным состояниям системы.В силу очень большого числа состояний системы метод прямого перебора
гипотез является достаточно трудоемким и редко применяется на практике.ЗамечаниеОбычно системы обладают свойством монотонности, которое заключается в том, что
если Яа — состояние отказа системы и (3 => a, то Hf — также состояние отказа. Длямонотонных систем после достижения некоторого состояния отказа На перебор гипо¬
тез с большим количеством индексов прекращается. Часто это приводит к существен¬
ному сокращению вычислений.5.2.2. Метод, основанный на применении
классических теорем теории вероятностейМетод удобно применять для расчета надежности последовательных, парал¬
лельных, последовательно-параллельных и других систем в предположении
взаимной независимости длительностей безотказной работы элементов сис¬
темы. В этом случае, основываясь на теоремах сложения и умножения теории
вероятностей, а таюке на формуле полной вероятности легко найти явные
выражения для вероятности безотказной работы системы.ПРИМЕР 5.6. Требуется оценить надежность систем, структурные схемы
которых изображены на рис. 5.11. Вероятности безотказной работы элемен¬
тов соответственно равны pt, i = 1, 2,3, 4.aбРис. 5.11. Структурные схемы для раздельного (я) и общего (5) резервирования
156Гпава 5Решение. Обозначим через А, — событие, состоящее в том, что /-Й элемент
исправен. Тогда At — событие, состоящее в том, что й элемент отказал. Ве¬
роятности этих событий соответственно равны P(Aj) = pj, P(Ai) = qi,i = 1, 2,3,4.Для схемы на рис. 5.11, а вероятность отказа узла 1—2 равна Р(А1А2), а ве¬
роятность отказа узла 3—4 равна Р(А3А4). По теореме умножения вероят¬
ностейР(А,А2) = Р(А)Р(А2) = q,q2, Р(А3А4) = Р(А3)Р(А4) = q3q4.Отсюда следует, что вероятности безотказной работы этих узлов соответст¬
венно равны\~P(AlA2) = \~qiq2, 1 - Р(А3А4) =1 - q3q4 .Вероятность безотказной работы системы равна произведению вероятностей
этих узлов, т. е.Р = (У-Ч\Ч2)(1~ЬЯа)-Рассмотрим схему на рис. 5.11, б. Вероятность безотказной работы узла 1—3
равна Р(А\А3) = р\р3, а вероятность безотказной работы узла 2—4 равна
Р(А2А4) - р2р4. Вероятности отказов этих узлов равны соответственно1 - р\р3 и 1 - P2P4 , а вероятность отказа системы равна произведению веро¬
ятностей этих узлов, т. е.£?=0-лаХ1-лл)-Вероятность безотказной работы системы определяется как вероятность до¬
полнительного события Р -1 - Q, отсюдаР = \-{\-рхр3)(\-р2р4).Довольно часто при расчете надежности используется формула полной веро¬
ятности. Пусть события Hj образуют полную группу попарно несовместных
событий (гипотезы), а А — любое событие. Тогда имеет место формула пол¬
ной вероятностиР(Л) = ХР(Я,.)Р(Л/Я,.),iгде Р(А/Н{) — вероятность события А, вычисленная при условии, что гипо¬
теза Я, осуществилась.
Методы анализа надежности технических систем157ПРИМЕР 5.7. Требуется оценить надежность мостиковой системы, струк¬
турная схема которой изображена на рис. 5.12. Вероятности безотказной ра¬
боты элементов соответственно равны Pj, / = 1, 2, 3, 4, 5 .Решение. Пусть //, — гипотеза, состоящая в том, что элемент 3 является
работоспособным, а Н2—- гипотеза, что элемент 3 отказал, Р(Нх)-р3,Пн2) = яз-Определим вероятность безотказной работы системы при условии, что 3-й
элемент работоспособен. В этом случае мостиковая схема имеет структуру
раздельного резервирования, как показано на рис. 5.11, а, а поэтомуP(A/Hx) = (\-qiq2)(\-q4q5).Определим теперь вероятность безотказной работы системы при условии, что
3-й элемент находится в состоянии отказа. При этом мостиковая схема имеет
структуру общего резервирования, как показано на рис. 5.11, б, а поэтомуP(A/H2) = \~(l-Plp4)(l-p2p5).По формуле полной вероятностиР(А) = Р{НХ)Р{А/НХ) + Р(Н2)Р(Л/Н2).Следовательно, вероятность безотказной работы системы равнар = Рзо - Я\<12X1 - Я4Я5) + Чз 0 - 0 - Р\Р\X1 - PiPs)) •Рассмотренный метод называется методом разложения относительно особого
элемента.
158Глава 55.2.3. Метод минимальных путей
и минимальных сеченийВведем два необходимых понятия.Минимальный путь — такой набор элементов в структуре, при котором сис¬
тема исправна, если исправны все элементы этого набора; отказ любого из
элементов ведет к отказу системы.Минимальное сечение— такой набор элементов в структуре, при котором
система неисправна, если неисправны все элементы этого набора; исключе¬
ние любого элемента из набора переводит систему в исправное состояние.У систем с произвольной структурой может быть несколько минимальных
путей и минимальных сечений. Последовательное соединение из п элемен¬
тов имеет один минимальный путь и п минимальных сечений, проходящих
через каждый элемент. Параллельное соединение из п элементов имеет п
минимальных путей, проходящих через каждый элемент, и одно минималь¬
ное сечение.Пусть Ах, А2,..., Аг — множество всех минимальных путей. Событие, со¬
стоящее в том, что все элементы пути At исправны, будем также обозначать
Aj. Можно показать, что объединение событий At совпадает с множествомГвсех исправных состояний системы jj At = Е+, и поэтому для вероятности/=1безотказной работы справедливо равенствоР = Рг \и 4
1=1= I P(A,AjAt)-...+; = 1 к j i<j<k \?-')+ (-1 )r~xP(AxA2...Ar).Пусть Вх, В2,..., Bs — множество всех минимальных сечений. Событие, со¬
стоящее в том, что все элементы сечения 2?, неисправны» обозначим также
через Bj. Можно показать, что объединение событий Bt совпадает с множе-Sством всех отказовых состояний системы (J Bt = Е_, и поэтому для вероят-/=1ности отказа системы справедливо равенствоQ = Pv/=iых UJ j i<j<k J (5.8)+ (-1 rx P(BXB2...BS).
Методы анализа надежности технических систем159Каждая из вероятностей, стоящих в правой части (5.7) и (5.8), легко вычисля¬
ется. Однако если число путей или число сечений велико, то вычисление по
этим формулам становится весьма сложной задачей.ПРИМЕР 5.8. Методом минимальных путей и минимальных сечений требу¬
ется рассчитать надежность системы, структурная схема которой изображена
на рис. 5,11, а.Решение. Найдем минимальные пути: 1—3, 1—4, 2—3, 2—4. По форму¬
ле (5.7)Р = рхрг + р{рЛ + р2р3 + р2р4 - р{р3р4 - Р\Р2Ръ - РхРгРл ~-Р2Р3Р4 + Р\РгРъР\-
Найдем минимальные сечения: 1—2, 3—4. По формуле (5.8)Q = 4\Я2 + ЯгЯ4~Я\ЯгЯъЯА-Нетрудно показать, что эти выражения равносильны выражению, полученно¬
му ранее:р = (}-Я\Я2)([-ЯзЯ4)-Формулы (5.7) и (5.8), применяемые непосредственно для вычисления пока¬
зателей надежности, все-таки достаточно громоздки и неудобны для расче¬
тов. Тем не менее на них базируются приближенные оценки вероятности без¬
отказной работы.Верхняя оценка вероятности безотказной работы определяется как вероят¬
ность безотказной работы параллельного соединения минимальных путей.Верхняя оценка вероятности отказа системы определяется как вероятность
отказа последовательного соединения минимальных сечений.Отсюда получаются двусторонние оценки вероятности безотказной работы:П(1 - P(Bt)) < Р < 1 - П(1 - Р(Л,)) . (5.9)/=1 (=1ПРИМЕР 5.9. Требуется оценить надежность мостиковой системы, струк¬
турная схема которой изображена на рис. 5.12.Решение. Найдем все минимальные пути и соответствующие им вероят¬
ности:
160Гпава 5Ах: 1—4, Р(Ах)-рхр4;А2: 2—5, Р(А2) = р2р5 -
А3: 1—3—5, Р(Л3) = рхр3р5;Аа : 2—3—4, Р(А4) = р2р3р4 .Найдем все минимальные сечения и соответствующие им вероятности:Вх: 1—2, P(Bx) = qxq2; 'В2 : 4—5, Р(В2) = q4q5;В3 : 1—3—5, P(B3) = qvq3q5;В4 : 2—3—4, Р(В4) = q2q3q4 ■В соответствии с неравенствами (5.9) получим нижнюю и верхнюю оценки
вероятности безотказной работы:Р > (1 - qxq2)(1 - q4q5 )0 - X1 ~ ЯгЯгЯ*)»Р < 1 - (1 - рхр4 )(1 - р2р5 )(1 - P\PiPs XI - Р2Р3Р4) •Если все элементы равнонадежны, то оценки приобретают вид:1-(1-92)2(1-93)2 <Р<1-(1-р2)2(1-р3)2.Графическая иллюстрация этих оценок, когда р изменяется от 0 до 1 с ша¬
гом 0,1, приведена на рис. 5.13.Рис. 5.13. Оценки вероятности безотказной работы мостиковой системы
Методы анализа надежности технических систем1615.3. Логико-вероятностные методы
анализа надежности5.3.1. Сущность логико-вероятностных методовЛюбой метод анализа надежности требует описания условий работоспособ¬
ности системы. Такие условия могут быть сформулированы на основании:□ структурной схемы функционирования системы (схемы расчета надеж¬
ности);□ словесного описания функционирования системы;□ граф-схемы;□ функции алгебры логики.Логико-вероятностный метод анализа надежности позволяет формализовать
определение и смысл благоприятных гипотез. Сущность этого метода состо¬
ит в следующем.□ Состояние каждого элемента кодируется нулем и единицей:{О, если элемент в отказовом состоянии;1, если элемент в исправном состоянии.В функциях алгебры логики состояния элементов представляются в сле¬
дующем виде:• х( — исправное состояние элемента, соответствующее коду 1;• х. — отказовое состояние элемента, соответствующее коду 0.□ Записывается с помощью функций алгебры логики условие работоспособ¬
ности системы через работоспособность (состояние) ее элементов. Полу¬
ченная функция работоспособности системы является двоичной функцией
двоичных аргументов.П Долученная ФАЛ преобразуется таким образом, чтобы в ней содержались
члены, соответствующие благоприятным гипотезам исправной работы
системы.□ В ФАЛ вместо двоичных переменных jc, и х,- подставляются вероятности
соответственно безотказной работы /?, и вероятности отказа q,. Знаки
конъюнкции и дизъюнкции заменяются алгебраическими умножением и
сложением.Полученное выражение и есть вероятность безотказной работы системыад.6 Зак. 3094
162Гпава 5Рассмотрим логико-вероятностный метод на примерах.ПРИМЕР 5.10. Структурная схема системы представляет собой основное
(последовательное) соединение элементов (рис. 5.14).*1 *2 Х„2Рис. 5.14. Структурная схема системы с основным соединением элементовНа структурной схеме х,, i = 1, 2,..., п — состояние /-го элемента системы,
кодируемое 0, если элемент находится в отказовом состоянии, и 1, если он
исправный. В данном случае система исправна, если исправны все ее элемен¬
ты. Тогда ФАЛ является конъюнкцией логических переменных, т. е.
у = Х\Х2-..хп, представляющей собой совершенную дизъюнктивно нормаль¬
ную форму системы.Подставляя вместо логических переменных вероятности исправных состоя¬
ний элементов и заменяя конъюнкцию на алгебраическое умножение, по¬
лучим:РЛО = Р\0)Р2(.0-Рп(1)-ПРИМЕР 5.11. Структурная схема системы представляет собой дублирован¬
ную систему с неравнонадежными, постоянно включенными подсистемами
(рис. 5.15).На рис. 5.15 Х\ и х2 — состояния элементов системы. Составим таблицу ис¬
тинности двух двоичных переменных (табл. 5.2).Таблица 5.2. Таблица истинности двух двоичных переменныхх,*2У000011101111В таблице 0 — отказовое состояние элемента, 1 — исправное состояние эле¬
мента. В данном случае система исправна, если исправны оба элемента (1,1)
Методы анализа надежности технических систем163или один из них ((0,1) или (1,0)). Тогда работоспособное состояние системы
описывается следующей функцией алгебры логики:у = х{х2 V х{х2 V х{х2.Эта функция является совершенной дизъюнктивной нормальной формой.*iх2Рис. 5.15. Структурная схема дублированной системыЗаменяя операции дизъюнкции и конъюнкции на алгебраические операции
умножения и сложения, а логические переменные— на соответствующие
вероятности состояния элементов, получим вероятность безотказной работы
системы:Рс (0 = Я\ (0Р2 (0 + Р\ (0Я2 (0 + Pi (ОРг (0 ■ПРИМЕР 5.12. Структурная схема системы имеет вид, показанный на
рис. 5.16.*2*3Рис. 5.16. Структурная схема системыСоставим таблицу истинности (табл. 5.3).В данном примере система исправна, если исправны все ее элементы или ис¬
правным является элемент х, и один из элементов дублированной пары
(х2, л:3) . На основании таблицы истинности СДНФ будет иметь вид:у = ххх2х3 v X\X2X3 v ххх2х3.
164Гпава 5Таблица 5.3. Таблица истинности*1*2•*3У00000010010001101000101111011111Подставляя вместо двоичных переменных соответствующие вероятности, а
вместо конъюнкций и дизъюнкций— алгебраические умножение и сложе¬
ние, получим вероятность безотказной работы системы:ад = Р\ 0)<72 (Орз (0 + Р\ (t)P2 (О^з (0 + A (Opi (Орз (0 •Функцию алгебры логики можно представить в минимальной форме, если
воспользоваться следующими преобразованиями:□ вынос за скобки: у - ххх2 + *]*3 = хх (х2 + х3);□ поглощение: у = jcj + ххх2 = ;□ склеивание: у-ххх2 +х1х2 =лг,.Операции поглощения и склеивания в алгебре не применимы. В связи с этим
нельзя полученную ФАЛ минимизировать, а затем вместо логических пере¬
менных подставлять значения вероятностей. Вероятности состояний элемен¬
тов следует подставлять в СДНФ, а упрощать по правилам алгебры.Недостатком описанного метода является необходимость составления табли¬
цы истинности, что требует перебора всех работоспособных состояний сис¬
темы.5.3.2. Метод кратчайших путей
и минимальных сеченийЭтот метод был рассмотрен ранее в разд. 5.2.3. Изложим его с позиции алгеб¬
ры логики.
Методы анализа надежности технических систем165Функцию работоспособности можно описать с помощью кратчайших путей
успешного функционирования системы и минимальных сечений ее отказа.Кратчайшим путем называется минимальная конъюнкция работоспособных
состояний элементов, образующих работоспособную систему.Минимальным сечением называется минимальная конъюнкция неработоспо¬
собных состояний элементов, образующих неработоспособное состояние
системы.ПРИМЕР 5.13. Необходимо образовать функцию работоспособности систе¬
мы, структурная схема которой приведена на рис. 5.17, используя метод крат¬
чайших путей и минимальных сечений.*3 *4Рис. 5.17. Структурная схема системы с неравнонадежными элементамиРешение. В данном случае кратчайшими путями, образующими работоспо¬
собную систему, будут: ххх2 , х3х4 , ххх5х4, х3х5х2 ■ Тогда функция работо¬
способности запишется в виде следующей функции алгебры логики:У = х{х2 V XjX4 V X]Х5Х4 V х3х5х2 .В соответствии с этой ФАЛ структурная схема системы рис. 5.17 может быть
представлена структурной схемой рис. 5.18.Минимальными сечениями, образующими неработоспособную систему, бу¬
дут: Х|Х3, х2х4, ххх5х4, хъх5х2. Тогда функция неработоспособности запи¬
шется в виде следующей функции алгебры логики:у - ХхХг V *2*4 V ДГ,JC5JC4 V Х3Х5Х2 .В соответствии с этой ФАЛ структурная схема системы будет представлена в
виде, показанном на рис. 5.19.
166Гпава 5х, х2Рис. 5.18. Структурная схема работоспособной системы, соответствующая ФАЛх\ *з*2Рис. 5.19. Структурная схема неработоспособного состояния системыСледует иметь в виду, что структурные схемы рис. 5.18 и рис. 5.19 не явля¬
ются схемами расчета надежности, а выражения для ФАЛ работоспособного
и неработоспособного состояний не являются выражениями для определения
вероятности безотказной работы и вероятности отказа:Pc(t) * P\Pi + Р3Р4 + Р1Р5Р4 + Р3Р5Р2 (ФАЛ для кратчайших путей),Qc(t) * PiP3 + P2P4 + PiР5Ра + Р3Р5Р2 (ФАЛ метода минимальных сечений).Основные достоинства ФАЛ в том, что они позволяют получить формально,
не составляя таблицы истинности, СДНФ и СКНФ (совершенная конъюнк¬
тивная нормальная форма), которые дают возможность получить вероятность
безотказной работы (вероятность отказа) системы путем подстановки в ФАЛ
вместо логических переменных соответствующих значений вероятностей
безотказной работы, заменив операции конъюнкции и дизъюнкции на алгеб¬
раические операции умножения и сложения.Для получения СДНФ необходимо каждый дизъюнктивный член ФАЛ умно¬
жить на (X/ vx)), где xt — недостающий аргумент, и раскрыть скобки. Отве¬
том будет СДНФ. Рассмотрим этот способ на примере.
Методы анализа надежности технических систем167ПРИМЕР 5.14. Необходимо определить вероятность безотказной работы
системы, структурная схема которой приведена на рис. 5.17. Вероятности
безотказной работы элементов равны рх, р2, р3, р4, р$.Решение. Воспользуемся методом кратчайших путей. Функция алгебры ло¬
гики, полученная методом кратчайших путей, имеет вид:у - ХхХг v х3х4 V Х1Х5Х4 V *3*5*2 •Получим СДНФ системы. Для этого умножим дизъюнктивные члены на не¬
достающие (х, v Xj):у = ХХХ2 Оз V *3 )(х4 V Х4 )(х5 V *5 ) V *з*4 (х, V X, )(х2 V Х2 )(х5 V Х5 ) V
VX]XjX4(х2 V х2 )(х3 V х3) V Х3Х5Х2 (X! V Xj )(х4 V Х4 ).Раскрывая скобки и выполняя преобразования по правилам алгебры логики,
получим СДНФ:У - Х[Х2*3X4X5 V Х|Х2Х3Х4Х5 V XiX2X3X4X5 V Х]Х2ХзХ4Х5 V Х]Х2Х3Х4Х5 V
VХ[Х2Х3Х4Х5 V Х1Х2Х3Х4Х5 V Х1Х2Х3Х4Х5 V Х1Х2ХзХ4Х5 V Х1Х2Х3Х4Х5 V
V*lX2X3X4X5 V xix2x3x4x5 V xjx2x3x4x5 V Х,Х2ХзХ4Х5 V Х!Х2Х3Х4Х5 Vvxjx2x3x4x5.Подставляя в СДНФ вместо ^ , х2, х3, х4, х5 вероятности безотказной ра¬
боты р^, р2, р3, р4, р$ и используя соотношения qi = 1 - р\,, получим сле¬
дующее выражение для вероятности безотказной работы системы.Pc(t) = 2p\p2p3p4p5-
-(PiPiPiPs + Р1Р3Р4Р5 + Р1Р2Р3Р4 + Р2Р1Р4Р5 + PxPiPaPs ) ++Р2Р3Р5 + P\PaPs + P1P2 + РзРл-Из приведенного примера видно, что метод кратчайших путей освободил нас
от определения благоприятных гипотез. Тот же результат можно получить,
если воспользоваться методом минимальных сечений.5.3.3. Алгоритм разрезанияАлгоритм разрезания позволяет получить ФАЛ, подставляя в которую вместо
логических переменных вероятности безотказной работы (вероятности отка¬
за) элементов можно найти вероятность безотказной работы системы. Полу¬
чения для этой цели СДНФ не требуется.
168Гпава 5Алгоритм разрезания основан на следующей теореме алгебры логики: функ¬
ция алгебры логики }>(*), х2, ..., *„) может быть представлена в следующей
форме:у(*1, х2,..., *,-,..., х„) = х,у(хих2,..., 1,..., x„)v^„ х2,..., 0,..., хп).
Покажем применимость этой теоремы на трех примерах:1. у = *] V х2 V*3 =*1(1 V х2 V*3) V*,(0 V х2 V*3) = *i V*i(*2 V*3) .Применяя второй распределительный закон алгебры логики, получим:У = *] V *](*2 V *3) = (*j V V х2 V *3) = JCj V х2 V *3 .2. у- *1*2*3 = х\ (1*2*3 ) v *1 (0*2*3 ) = *1*2*3 •3. у-Х !*2 V *3*4 = *] (1*2 V *3*4 ) V *! (0*2 V*3*4) = *]*2 V *1*3*4 V ^*3*4 == *1*2 V *3*4 (*, V *]) = *1*2 V *3*4 .ПРИМЕР 5.15. Определить вероятность безотказной работы системы, струк¬
турная схема которой представлена на рис. 5.16, воспользовавшись алгорит¬
мом разрезания.Решение. Используя метод кратчайших путей, получим следующую ФАЛ:у = *,*2 v *!*3 .Применим алгоритм разрезания:у-Х1*2 V*1*3 = *2 (*j 1 V *1*3 ) V *2 (*10 V *1*3 ) = *1*2 V *i*2*3 V *i*2*3 == *1*2(1 V *з) V *1*2*3 = *1*2 v *1*2*3■Подставляя теперь вместо логических переменных вероятности и заменяя
операции конъюнкции и дизъюнкции на алгебраические умножение и сложе¬
ние, получим:Ро =Р\Р2+Р\ЯгРъ = P\Pi+ Р\Ръ(У~Рг) = Р\Рг+ Р\Ръ ~РхРгРъ-ПРИМЕР 5.16. Определить вероятность безотказной работы системы, струк¬
турная схема которой приведена на рис. 5.17. Воспользоваться алгоритмом
разрезания.Решение. Функция алгебры логики, полученная методом минимальных сече¬
ний, имеет вид:у - *1*2 V *3*4 V *1*5*4 V *3*5*2 .
Методы анализа надежности технических систем169Реализуем алгоритм разрезаний относительно *5:у = JC5 {Х\Х2 V *3*4 V *, 1*4 V *31*2 ) V *5 (*)*2 V *3*4 V *[ 0*4 V *3 0*2 ) == *5 (*!*2 V *3*4 V *,*4 V *3*2 ) V *5 (*]*2 V *3*4).Упростим полученное выражение, пользуясь правилами алгебры логики. Вы¬
ражение в первых скобках упростим, используя правило выноса за скобки:*]*2 V *3*4 V *,*4 V *з*2 = *i (*2 V *4 ) V *3 (*2 V *4 ) = (*, V *3 )(*2 V *4 ).Тогда ФАЛ будет иметь вид:у = *5 (*! V *3)(*2 V *4 ) V *5 (*,*2 V *3*4 ).Этому выражению соответствует структурная схема рис. 5.20.х\*2 *4Рис. 5.20. Структурная схема иллюстрации алгоритма разрезанияПолученная схема является также схемой расчета надежности, если логиче¬
ские переменные заменить вероятностями безотказной работы р{, р2, р3,
р4, р5, а переменную *5 — вероятностью отказа q$. Из рис. 5.20 видно, что
структурная схема системы сведена к последовательно-параллельной схеме.
Вероятность безотказной работы вычисляется по следующей формуле:ре=1-(1-(1-(1-АлХ1-ЛА)Х1-л))-(1-(1-(1-лХ1-л))-•(l-(l-ftXl-A))ft)-Формула в объяснении не нуждается, она записана непосредственно по
структурной схеме.
170Гпава 55.3.4. Алгоритм ортогонализацииАлгоритм ортогонализации, как и алгоритм разрезания, позволяет формаль¬
ными процедурами образовать функцию алгебры логики, подставляя в кото¬
рую вместо логических переменных вероятности, а вместо дизъюнкции и
конъюнкции — алгебраические сложение и умножение, получить вероят¬
ность безотказной работы системы. Алгоритм основан на преобразовании
функций алгебры логики в ортогональную дизъюнктивную нормальную
форму (ОДНФ), которая существенно короче СДНФ. Прежде чем излагать
методику, сформулируем ряд определений и приведем примеры.Дее конъюнкции называются ортогональными, если их произведение тожде¬
ственно ноль. Дизъюнктивная нормальная форма называется ортогональной,
если все ее члены попарно ортогональны. СДНФ является ортогональной, но
самой длинной из всех ортогональных функций.Ортогональную ДНФ можно получить с помощью следующих формул:□ если >-(*,,*2,..., *„) = *,*2...*„, тоу =■ хх vххх2 v*,*2X} v ...v ххх2хъ...хп_{хп', (5.10)□ если у(хх,х2* ••• > хп) = х1 v х2 v•••vхп, т0Я*1>*2> ..., *„) = *! v *,*2 V*,*2*3 v-v *1*2 "ХП-1ХП- (5Л ОЭти формулы легко доказать, если воспользоваться вторым распределитель¬
ным законом алгебры логики и теоремой де-Моргана. Алгоритмом получения
ортогональной дизъюнктивной нормальной формы является следующая про¬
цедура преобразования функции у(хих2,..., хп) в ОДНФ:□ функция у(хьх2, ...,*„) преобразуется в ДНФ с помощью метода крат¬
чайших путей или минимальных сечений;□ находится ортогональная дизъюнктивно-нормальная форма с помощью
формул (5.10) и (5.11);□ минимизируется функция путем приравнивания к нулю ортогональных
членов ОДНФ;□ логические переменные заменяются вероятностями безотказной работы
(вероятностями отказов) элементов системы;□ окончательное решение получается после упрощения выражения, полу¬
ченного на предыдущем шаге.Рассмотрим методику на примере.
Методы анализа надежности технических систем171ПРИМЕР 5.17. Определить вероятность безотказной работы системы, струк¬
турная схема которой приведена на рис. 5,17. Применить метод ортогонали¬
зации.Решение. В данном случае функционирование системы описывается сле¬
дующей функцией алгебры логики (метод минимальных сечений):у = *,*2 V х3х4 V *,*5*4 V *3*5*2 .Обозначим К\ =*|*2, К2 = *3*4, К3=ххх5х4, К4 = х3х5х2. Тогда ОДНФ за¬
пишется в следующем виде:y = Kxw КХК2 v КхК2Кг v КХК2КЪК4 . (5.12)Значения Кп / = 1, 2, 3, на основании формулы (5.10) будут иметь вид:Кх = *| V *1*2 , К2 - *3 V *з*4 , К3 = *, V *!*5 V *,*5*4 .ТогдаКХК2 = (*, V *,*2)*з*4 = *]*з*4 V *,*2*3*4,, КХК2К3 = (*, V *,*2)(*з V *3*4) = *,*2*з*4*5,KxK2KjK4 = (*, V *,*2Х*3 v *3*4Х*1 V *,*5 V *,*5*4)*2*з*5 = *,*2*з*4*5 .
Подставляя эти выражения в (5.12), получим:у = *,*2 V *1*3*4 V *,*2*з*4 V *,*2*з*4*5 V *,*2*з*4*5 .Заменяя в этом выражении логические переменные соответствующими веро¬
ятностями и выполняя алгебраические операции сложения и умножения, по¬
лучим вероятность безотказной работы системы:Рс = 2Р\Р2РзР*Р5 - (Р\РгРъР* + Р1Р2Р3Р5 + РхРгРьРь + РхРъРаРъ +
+ЛЛЛЛ) + Р\РаРь + РгРъРь + Р\Рг + РзР4-
Ответ совпадает с полученным в примере 5.14.Из примера видно, что алгоритм ортогонализации более производительный,
чем способы, рассмотренные ранее. Более подробно логико-вероятностные
методы анализа надежности изложены в [72, 99]. Логико-вероятностный ме¬
тод, как и любой другой, имеет свои достоинства и недостатки. О его досто¬
инствах было сказано ранее. Укажем его недостатки.Исходными данными в логико-вероятностном методе являются вероятности
безотказной работы элементов структурной схемы системы. Однако во мно¬
гих случаях эти данные не могут быть получены. И не потому, что надеж¬
ность элементов неизвестна, а потому, что время функционирования элемен¬
172Гпава 5та является случайной величиной. Это имеет место в случае резервирования
замещением, наличия последействия отказов, неодновременности работы
элементов, наличия восстановления с различной дисциплиной обслуживания
и во многих других случаях.Приведем примеры, иллюстрирующие эти недостатки. Структурная схема
системы имеет вид, показанный на рис. 5.21, где приняты следующие обозна¬
чения: Xj — логические переменные, имеющие значения 0 и 1, соответст¬
вующие отказу и исправной работе элемента, i = 1, 2, 3 .*1 *2*3Рис. 5.21. Структурная схема системы с резервированием замещениемВ данном случае логическая переменная х3 является 0 до момента времени т
отказа основного элемента и 1 в течение времени (/ - т), где t — время,
в течение которого определяется вероятность безотказной работы системы.
Время т является величиной случайной, поэтому значение р(т) неизвестно.
В данном случае составить ФАЛ и тем более СДНФ невозможно. Ни один из
рассмотренных нами логико-вероятностных методов не позволяет найти ве¬
роятность безотказной работы системы.Вот еще один типичный пример. Энергетическая система состоит из регуля¬
тора напряжения RH и двух параллельно работающих генераторов Г, и Г2.
Структурная схема системы показана на рис. 5.22.Г,Рис. 5.22. Структурная схема энергетической системыПри отказе одного из генераторов оставшийся исправным работает один на
общую нагрузку. Его интенсивность отказов увеличивается. Если до момента
Методы анализа надежности технических систем173х отказа одного из генераторов интенсивность его отказа была равна X, то
после отказа Я] > А,. Так как время х является величиной случайной, то Р(т)
неизвестно. Здесь, как и в случае резервирования замещением, логико¬
вероятностные методы бессильны. Таким образом, указанные недостатки ло-
гико-вероятностных методов снижают их практическое применение при рас¬
чете надежности сложных систем.5.4. Топологические методы
анализа надежностиТопологическими будем называть методы, которые позволяют определить
показатели надежности либо по графу состояний, либо по структурной схеме
системы, не составляя и не решая уравнений. Топологическим методам по¬
священ ряд работ [84, 147], в которых описаны различные способы их прак¬
тической реализации. В настоящем разделе излагаются методы, позволяющие <
определить показатели надежности по графу состояний.Топологические методы дают возможность вычислять следующие показатели
надежности:□ P(t) — вероятность безотказной работы в течение времени t;□ 7] — среднее время безотказной работы;□ KT(t) — функцию готовности (вероятность того, что система исправна в
любой произвольный момент времени t);□ Кг = lim Kr(t) — коэффициент готовности;/->00ПТ — наработку на отказ восстанавливаемой системы.Топологические методы имеют следующие особенности:□ простота вычислительных алгоритмов;О высокая наглядность процедур определения количественных характери¬
стик надежности;□ возможность приближенных оценок;□ отсутствие ограничений на вид структурной схемы (системы восстанавли¬
ваемые и невосстанавливаемые, нерезервированные и резервированные с
любым видом резервирования и любой кратностью).В настоящей главе будут рассматриваться ограничения топологических ме¬
тодов:□ интенсивности отказов и восстановления элементов сложной системы яв¬
ляются величинами постоянными;
174Гпава 5□ временные показатели надежности, такие как вероятность безотказной
работы и функция готовности, определяются в преобразованиях Лапласа;D трудности, в ряде случаев непреодолимые, при анализе надежности слож¬
ных систем, описываемых многосвязным графом состояний.Идея топологических методов состоит в следующем.Граф состояний является одним из способов описания функционирования
системы. Он определяет вид дифференциальных уравнений и их количество.
Интенсивности переходов, характеризующие надежность элементов и их вос¬
станавливаемость, определяют коэффициенты дифференциальных уравне¬
ний. Начальные условия выбираются кодированием узлов графа.В графе состояний содержится вся информация о надежности системы. А это
является основанием считать, что показатели надежности могут быть вычис¬
лены непосредственно по графу состояний.5.4.1. Определение вероятностей
состояний системыВероятность застать восстанавливаемую систему в состоянии i в фиксиро¬
ванный момент времени t в преобразовании Лапласа может быть записана в
следующем виде:Д Д(*) s [Л» s""1 + A s”~2 + -+Л-i 1 ’где A(s) — главный определитель системы дифференциальных уравнений,
записанной в преобразованиях Лапласа; Д, (s) — частный определитель сис¬
темы.Из выражения (5.13) видно, что P,(s) будет определена, если из графа со¬
стояний будут найдены степени тип полиномов числителя и знаменателя,
а также коэффициенты 5,, ( j = 0,1, 2,..., т ) и Л, (/ = 0,1, 2,..., п -1).Первоначально рассмотрим методику определения Pj(s) графа состояний
только таких систем, в графе состояний которых отсутствуют переходы через
состояния. К ним относятся все неизбыточные системы, резервированные
системы при общем резервировании с целой и дробной кратностью, резерви¬
рованные системы любой структуры с обслуживанием отказавших устройств
в последовательности, обратной их поступлению в ремонт. К указанному
классу систем относятся также некоторые резервированные системы с равно¬
надежными устройствами при различной дисциплине их обслуживания.
Методы анализа надежности технических систем175Функционирование системы описывается дифференциальными уравнениями,
число которых равно числу узлов графа. Это значит, что главный определи¬
тель системы A(s) в общем случае будет полиномом п-й степени, где п —
число узлов графа состоянии. Легко показать, что полином знаменателя не
содержит свободного члена. Действительно, т.к. lim^Cs) =;= const, тоS-* Ознаменатель функции Pt(s) должен содержать s в качестве сомножителя,
в противном случае финальная вероятность Pt(оо) будет равна нулю. Исклю¬
чением являются случаи, когда число ремонтов ограничено.Степень полинома числителя А, находится из выражения:mi=n-\-ii, (5.14)где п — число узлов графа состояний; — число переходов из начального
состояния системы, определенного начальными условиями ее функциониро¬
вания, в состояние г по кратчайшему пути.Если начальным состоянием системы является состояние, когда все устрой¬
ства исправны, то — номер уровня состояния /', т. е. равно минималь¬
ному числу отказавших устройств системы в состоянии /. Таким образом,
степень полинома числителя вероятности Pt(s) пребывания системы в /-м
состоянии зависит от номера состояния / и от начальных условий. Так какчисло переходов £j может быть 0,1, 2 п-1, то степень полинома A,(s)на основании (5.14) также может принимать значения т,, = 0,1, 2,..., п -1.Коэффициенты А,■ и Bj, зависящие от интенсивностей переходов, определя¬
ются из графа состояний по следующим правилам.Коэффициент при s"-1 всегда равен единице, т. е. А$ = 1. Коэффициент Ах
равен сумме всех интенсивностей переходов в графе состояний. Коэффици¬
ент А2 равен сумме всех попарных произведений интенсивностей переходов,
за исключением членов вида а, у • cij t и -ai k. Интенсивности переходов
atj и djj находятся в ветвях, образующих контуры, а интенсивности а,; и
at k — в ветвях, исходящих из /'-го узла. Коэффициент At (/' = 3, 4,..., и-1)равен сумме произведений интенсивностей переходов, взятых по /', за ис¬
ключением тех произведений, в которые входят одновременно интенсивно¬
сти переходов ветвей, образующих контуры и исходящих из одного и того же
узла. Такие члены легко определить по графу состояний.Следует иметь в виду, что главный определитель системы A(s) не зависит от
начальных условий, а поэтому сформулированное правило определения ко¬
176Гпава 5эффициентов Aj полинома знаменателя справедливо при любых начальных
условиях решения задачи.Коэффициенты полинома числителя В7 (у = 0,1,, т) находятся из выра¬
жений для коэффициентов А, полинома знаменателя при соответствующих
степенях s. Коэффициент BJt при sm~J равен сумме только тех слагаемых
коэффициента А{ при s той же степени, у которых:□ содержатся произведения всех интенсивностей переходов из начального
состояния системы, определенного начальными условиями решения зада¬
чи, в состояние / по кратчайшему пути;□ отсутствуют интенсивности переходов из /-го состояния.ПРИМЕР 5.18. Необходимо определить вероятности всех состояний системы
(рис. 5.23). Систему обслуживают две бригады. Предполагается также, что
начальными условиями функционирования системы являются: Р0(0) = 1,
?,(()) = Р2(0) = Р3(0) = 0.К цК |ДРис. 5.23. Структурная схема системыРешение. Граф состояний системы изображен на рис. 5.24.Рис. 5.24. Граф состояний системы, изображенной на рис. 5.23
Методы анализа надежности технических систем177Определим сначала полином знаменателя вероятностей Pi (s) (/ = О,1, 2, 3 ),
т. к. он является общим и не зависит от i.Из графа рис. 5.24 видно, что система может находиться в четырех состояни¬
ях, поэтому п - 4 . ТогдаA (s) = s(AqS3 + Ах s2 + A2s + А3).На основании сформулированного выше правила находим коэффициенты
полинома.Коэффициент Aq = 1. Коэффициент А1 равен сумме всех интенсивностей пе¬
реходов, указанных на рис. 5.24, поэтому Ах = 5А. + 4ц .В выражении для коэффициента А2 будут отсутствовать члены a02a20,
а01а10, ciua3l, т.к. они являются произведениями интенсивностей, находя¬
щихся в ветвях, образующих контуры. Не будет также членов вида ci02a0],
al0a 13, являющихся произведениями интенсивностей переходов из одного и
того же узла (0 или 1). ТогдаА2 - a02al0 + a02a]3 + a02a3l + a01a20 + a01al3 + a0ia3i + a\3a20 ++a31a10 + a31a20 + al0a20 = 6X2 +1 lAp + 5(I2.В выражении для коэффициента А3 будут отсутствовать слагаемые вида
a02a20, a(nal0, a]3a3j, a02a0x, al0aX3,... Перебор всех возможных комбина¬
ций интенсивностей переходов по три показывает, что коэффициент А3 име¬
ет лишь четыре слагаемых:А3 = сгзха10а02 + a20aX0a3X + a20aQXa3l + <^20^01^13 = 2Х3 + 6Ац2 + 4Х2ц.
Найдем теперь полиномы Д,.Степень полинома Д0 будет: m0=n-1 — = 4 — 1 — 0 = 3.Т ЛТогда A0(s) = B00s + Bl0s + B20s + B30. Так как степень полинома A0(s)совпадает со степенью полинома , то коэффициент В(М определяется изsкоэффициента Aq, В10 — из Ах, В20 — из А2, В30 — из А3. На основании
сформулированного выше правила коэффициенты Ву0 не должны содержатьслагаемых, в которые входят в качестве сомножителей интенсивности пере¬
ходов из состояния 0, т. е. интенсивности а01 и а02. Исключая эти слагаемые
из выражений для А,, получим:
178Гпава 5*оо ~ А) ~ 1 > *ю - ^20 + °ю +а\г+аз\ - 2Л. + 4ц;*20 = ai3°20 + аъ\а\й + a3ia20 + ^ю^го = 5ц2 + 2Ац; В30 = я2оаюа31 = ^М3 •Подставляя значения коэффициентов в выражение для определителей, по¬
лучим:р лл AqQs) 53 + (2Х + 4ц)д2 + (5р.2 + 2Я,ц)5 + 2ц3 ■° Л(л') 5[j3+(5Х + 4р)52+(6Х2+11Хц + 5р2)5 + (2ц3+6Л.Ц2+4А.2(х)]ЛСтепень полинома А, будет тх =п-\ = 4-1 -1 = 2, т. е. А1=50,^ +
+j5u5 + В2[. Тогда коэффициент Вох определяется из коэффициента Ах,
Вх! — из А2, S21 — из А3.Коэффициенты BjX не должны содержать слагаемых, в которые входят в ка¬
честве сомножителей интенсивности переходов из состояния (1), т. е. интен¬
сивности а10 , ахз. Коэффициенты В]Х должны содержать только те слагае¬
мые, соответствующие At, которые содержат в качестве сомножителя интен¬
сивность перехода из начального состояния (0) в состояние (1), т. е.
интенсивность <з01. Исключая указанные слагаемые из выражений для At, по¬
лучим:*oi=aoi=2X, Вхх =a0i<ar2o +аъ\аъ\ =6Хц, В2Х=а0Ха2оа31=4Хц.2.ТогдаА[ (д) _ 2As2 + бцАл + 4Хц21 Ms) 5[л3+(5Я. +4ц)л2+(6Л,2 +11А.ц. + 5|а2)5+ (2ц3 + 6ц2Х+ 4Я,2р.)]•уСтепень полинома Д2С0 будет т2=п-1-£ 2 = 4 -1 -1 = 2, т. е. А2 = B02s +
+B]2s + В22 . В данном случае коэффициенты BJ2 не должны содержать сла¬
гаемых, в которые входит интенсивность перехода из состояния (2), т. е. ин¬
тенсивность а2о, кроме того, Bj2 должны содержать только те слагаемыекоэффициентов Ап которые содержат в качестве сомножителя интенсив¬
ность а02. Исключая из As указанные слагаемые, получим:*02=а02=^> *12 =а02а10+а02°13+а02а31 + ЗХц ,*22 = °31а10а02 = 2Хц2 .Тогдар (л _ Аг(s) Ал2 + (2Х2 + 3 цХ).? + 2Х-ц2 2 5 ~ А(л) _5[53+(5Х + 4|л>2+(6Х2+1ац + 5|а2> + (2ц3+6Яц2+4Х2|х)]'
Методы анализа надежности технических систем179Степень полинома A3(j) будет шъ = п-\-£3 =4 — 1 — 2 = 1, т. е. A3(j) =
= B03s + В13- Коэффициенты 503 и 2?13 не должны содержать слагаемых, в
которые входит интенсивность перехода из состояния (3) в состояние (1), т. е.
интенсивность а31, кроме того, они должны иметь только те слагаемые ко¬
эффициентов А/, которые содержат в качестве сомножителя произведение
интенсивностей перехода из состояния (0) в состояние (3) по кратчайшему
пути, т. е. произведение a0ial3 .Исключая указанные слагаемые из А/, получим:*03 = а01а13 = 4Х2 , 513 = «20°01°13 = 4Х2Ц .Тогдар.. А3(д)_ 4X2s + 4\2\l 3 A (s) 5[л3+(5Х + 4ц)52+(6Х2+1ац + 5ц2)5 + (2ц3+6Хц2+4Х2ц)]'ПРИМЕР 5.19. Необходимо определить вероятности всех состояний системы
(рис. 5.23). Предполагается, что начальными условиями функционирования
системы являются:Р](0) = 1, />0(0) = />2(0) = Р3(0) = 0.Отличие примера 5.19 от примера 5.18 состоит в том, что здесь изучаются
закономерности функционирования системы с момента, когда отказал один
из резервных элементов, т. е. с момента, когда система находится в состоя¬
нии 1.Решение. Так как главный определитель системы не зависит от начальных
условий, то полином знаменателя будет тем же, как и в примере 5.18. Опре¬
делим полиномы A ,(s). Степень полинома A0(s) будет
т0 =п-\-£0 =4-1-1 = 2. Здесь £0 =1 потому, что из состояния (1), в кото¬
ром находится система в начале функционирования, в состояние (0) она пе¬
реходит в результате однократного изменения состояния. ТогдаА0(5) = 5о0^2+*10^*20-Коэффициенты Bj0 здесь не должны содержать слагаемых, в которые в видесомножителя входят интенсивности перехода из состояния (0), т. е. интен¬
сивности а01 и а02, кроме того, они должны иметь только те слагаемые ко¬
эффициентов А/, в которые входит в качестве сомножителя интенсивность
перехода из состояния (1) в состояние (0), т. е. интенсивность а10 .
180Глава 5Исключая указанные сомножители из соответствующих коэффициентов At,
получим:Тогда*00 - °10 - М- 5 *10 “ al0a20 + а10а31 ~ Зр2» *20 ~ а20а31а10 ~ ^Ц3 .A0(s) = рл2 + 3|А + 2ц3,Л«Степени остальных полиномов будут:ml =п-1-£1 = 4 — 1 — 0 = 3;
т2 — п — \ — (.2 = 4 — 1 — 2 = 1;
т3=и-1-^3=4-1-1 = 2.ТогдаA](5) = *01£3 + *i i^2 + *21, АгС^) = *02s + *12 ’ A3(s) - B03s2 + Bi3s + В23.
Коэффициенты BjX полинома А| (s) не должны содержать слагаемых, в ко¬
торые в качестве сомножителя входят интенсивности а10, а]3.Коэффициенты Bj2 полинома Л2(^') не должны содержать слагаемых, в ко¬
торые в качестве сомножителя входит интенсивность а20 • Кроме того, коэф¬
фициенты Bj2 должны содержать только те слагаемые соответствующих ко¬
эффициентов , в которые входит произведение интенсивностей а10а02.
Коэффициенты Bj3 полинома A3(s) не должны содержать слагаемых, в ко¬
торые в качестве сомножителей входят интенсивности a3J. Кроме того, ко¬
эффициенты Bj3 должны содержать только те слагаемые коэффициентов Ai,
в которые входит в качестве сомножителя интенсивность а13.Выполнив очевидные преобразования над коэффициентами полинома знаме¬
нателя функции Pj(s) и элементарные вычисления, получим:п/ ч 53 + (ЗХ, + Зц)^2 +(8Хц + 2ц2)5 + 4Я.ц2mW" 7ГТ »ДО)^ + 2Хц2*2\s) ~ 7ТТ >A (s)
Методы анализа надежности технических систем181„/ч 2Ъ2 +(2Х(д + 6Х2)5 + 4?12ц
з W - 77Т •Д($)5.4.2. Определение финальных вероятностей
состояний системыФинальные вероятности пребывания системы в i-м состоянии можно вычис¬
лить, воспользовавшись соотношениемPj = Y\msPi(s). (5.15)i->0Подставляя в это выражение вероятность Pj(s) из (5.13), получим:Р,= (5.16)Ап-1Таким образом, для вычисления финальных вероятностей достаточно опре¬
делить свободные коэффициенты полиномов A(-(s) и A(s) по приведенным
выше правилам. Однако коэффициенты Bmj и А„_х можно получить значи¬
тельно проще непосредственно из графа состояний, если предположить, что в
графе отсутствуют переходы через состояния.Вероятность Рг является величиной безразмерной, поэтому каждое из сла¬
гаемых коэффициентов Bmi и Ап_х имеет одно и то же число сомножителей,
равное (и-1). Так как слагаемые не должны содержать сомножителей вида
djjdjj, то для графа типа дерева в каждое из них должна входить только одна
из этих интенсивностей перехода.На основании сформулированных выше правил коэффициент Bmi не имеет
интенсивностей переходов из /-го состояния и содержит только такие члены,
в которые входят произведения интенсивностей переходов из начального со¬
стояния в i-e по кратчайшему пути.Все это позволяет сделать следующий вывод: коэффициент Bmi имеет только
один член, который представляет собой произведение всех интенсивностей
переходов из крайних свободных узлов графа в i-e состояние.л-1 л-1Так как 2] /) = 1, то ^ Вш = Ап_х, а это означает, что коэффициент Ап_х
1=0 1=0имеет столько членов, сколько узлов в графе состояний. Каждое из слагаемых
равно соответствующему коэффициенту Bmi и определяется по сформулиро¬
ванному выше правилу определения коэффициента Bmi для /-го состояния.
182Гпава 5Таким образом, финальную вероятность пребывания системы в /-м состоянии
по графу типа дерева можно определить по формуле:(5|7>IX,1=0где п — число узлов графа, Bmi — произведение интенсивностей переходов
из всех крайних свободных узлов в узел, соответствующий i-му состоянию
системы, при перемещении по кратчайшему пути в направлении стрелок.ПРИМЕР 5.20. Необходимо определить финальные вероятности пребыва¬
ния системы во всех возможных состояниях, схема расчета надежности
которой приведена на рис. 5.25. Восстанавливает систему одна бригада об¬
служивания.X, ц X, цX, ц X, цРис. 5.25. Структурная схемапоэлементно-резервированной системыРешение. Из графа на рис. 5.26 видно, что система может находиться в пяти
состояниях в соответствии с числом узлов графа, причем узлы 0, 2 и 4 явля¬
ются крайними.Рис. 5.26. Граф состояний системы, изображенной на рис. 5.25
Методы анализа надежности технических систем183Перемещаясь из узлов 2 и 4 в узел 0 по направлению стрелок и перемножая
все встречающиеся интенсивности переходов, получим:Bm0 ~ a2)a\Qa43ai\ ~ М4 •Перемещаясь в узел 1 из крайних узлов 0, 2 и 4, получим:Вт1 = а01а21Л43а31 =4Я.Ц3 .Аналогично,АиЗ = a01°!3a21a43 = 8Х,2Ц2 ,*/я2 = a01a12a43a3I = 4Х,2Ц2 ,Вт4 ~ £*01<а13<аг34<я21 = 1 ■Тогда£ Bmi = ц4 + 4Хц3 + Ш2\х2 + 16Х3ц1=0и на основании (5.17) получим:Р = £ ° ц4 + 4А.Ц3 +1 2Х2\х2 +16Я.3ц ’р= 4^ ‘ ц4+4Хц3+12Х2ц2+16?13ц’4Х2ц22 ц4 + 4Х|а3+12Х2ц2+16Х3|д’___8ХУ__3 ц4 + 4 А,ц3 +12Х2ц2 +16Х,3ц ’р = 16*-3Ц4 ц4 + 4Хц3 +12Х.2ц2 +16Х3ц.Из описания способа вычисления и приведенного примера видно, что оп¬
ределение финальных вероятностей по графу состояний значительно проще,
чем путем решения уравнений функционирования системы.
184Глава 55.4.3. Определение вероятности попадания системы
в he состояние в течение времени tДля определения преобразования Лапласа искомой вероятности по графу со¬
стояний достаточно во всех ветвях, выходящих из состояния /, поставить
экраны и выполнить те же действия, что и в случае определения вероятности
пребывания системы в г-м состоянии в данный момент времени.Вероятность попадания системы в состояние г в течение времени t в преоб¬
разовании Лапласа может быть представлена в следующем виде:, (5,8)А (■*) S [A^jS + AiS +-.+ А„_ 1 Лгде A(s) — главный определитель системы дифференциальных уравнений,
записанной в преобразовании Лапласа; АДл) — частный определитель сис¬
темы.Выражения (5.18) и (5.13) принципиально отличаются друг от друга, несмот¬
ря на их внешнее сходство. Основные их отличия состоят в следующем:□ полином знаменателя выражения (5.13) не зависит от начальных условий и
состояния i, в то время как коэффициенты полинома знаменателя выра¬
жения (5.18) зависят от состояния i, вероятность попадания в которое вы¬
числяется по формуле (5.18);В□ в отличие от (5.13), Pt = lim sP^s) = —mL- = 1, т. e. Bmi = A ,,.*->° 4ri,iДействительно, какова бы ни была структура системы и дисциплина обслу¬
живания при / ->оо (j -» 0 ), система обязательно попадет в состояние /.ПРИМЕР 5.21. Необходимо определить вероятность попадания во все воз¬
можные состояния в течение времени t системы, схема расчета надежности
которой и граф состояний приведены на рис. 5.23 и 5.24 соответственно. Ус¬
ловия функционирования системы те же, что и в примере 5.18.Решение. Из графа видно, что система может находиться в четырех состоя¬
ниях, поэтому п = 4, и на основании (5.18)+ Aus2 + A2is + A3i]
Методы анализа надежности технических систем185Сначала найдем вероятность попадания системы в состояние (0), для чего
запретим переходы из состояния (0) в состояния (1) и (2), т. е. будем считать,
что а0! = я02 =0.Вычисляя коэффициенты Ар по описанной ранее методике, получим:4)0 =1 ,4 о - аю + а20 + «13 + a3i = 2А, + 4ц,420 = а\За20 + а31а10 + а31а20 + а10°20 = + ^Ц2 ,4?0 ~ а20а10а31 = .Степень полинома числителя на основании (5.14) будет иметь значение:т0=я-1-^0=4 — 1 — 0 = 3.Тогда коэффициент В00 можно вычислить из коэффициента А00, В10 — из
А10, В20 — из А20 и В30 — из А30. На основании сформулированного в
разд. 5.4.1 правила коэффициенты BJ0, вычисляемые из соответствующих
коэффициентов Aj0, не должны содержать в качестве сомножителей интен¬
сивности переходов из состояния (0). Однако в данном случае коэффициенты
Aj0 не содержат этих интенсивностей, т. к. состояние (0) является погло¬
щающим. Тогда В00 = Aq0 , В10 = А10, В20 = А20, В30 = А30, а значит P0(s) = -,sт. е. B0(t) = 1, что и следовало ожидать, т. к. по условию задачи при t = 0 сис¬
тема находится в состоянии (0) с вероятностью, равной единице.Определим вероятность попадания системы в состояние (1), полагая, что это
состояние является поглощающим и а10 = ai3 - 0. При этом условии коэффи¬
циенты Ajl будут иметь значения:4)1 =1* 4l =а02+а20+ай\+аЪ\ =ЗА. + Зц,^21 ~ а02а31 + «01«31 + °01°20 + °31°20 ~ ,^31 = а20а01а31 = 4А,Ц^ .Степень полинома числителя будет:гпу=п-1-^1=4-1-1 = 2.Тогда Aj(s) = BQls2 + Bus + В21, т. e. коэффициент B0l вычисляется из коэф¬
фициента Ап, Вп — из А21 и В2] — из А31. Коэффициенты BJt должны
186Гпава 5содержать только те слагаемые, у которых в качестве сомножителя имеется
интенсивность перехода из начального состояния (0) в состояние (1), т. е.
а01. Исключая из коэффициентов Ajf члены, не содержащие интенсивностьа01, получим:*01 =CtQ\=2X, = «01°31 + й01а20 = , *21 = а20°01а31 = ,Подставляя значения коэффициентов в полиномы числителя и знаменателя
искомой вероятности, получим:р. ч 2Xs2 + бцАл + 4Х]л2 2X(s + ц) 1 s [s3 + (ЗХ + 3p.)s2 + (8Я.ц + 2ц2 )s + 4Яц2 ] s[.s2+(ЗХ + р.).я-2Я,ц]Вычисления -P|(s) можно было бы упростить, рассматривая граф рис. 5.24 без
состояния (3). Действительно, если состояние (1) является поглощающим, то
при начальных условиях Р0(0) = 1, Р{ (0) = Р2 (0) = Р3 (0) = 0 система в состоя¬
ние (3) перейти не может, а значит, это состояние является лишним.Выполнив аналогичные вычисления, можно получить следующие выражения
для вероятностей попадания системы в состояния (2) и (3):р ^ ч _ Xs2 + (2Х2 + ЗЛ.ц)л + 2А,ц2 2 s|>3 + (5Х + Зц)52 + (6А? +1X\x + 2\x2)s + 2X\i2}p(s) = 4А.25 + 4Я2ц 3 5[^3 + (5Х + 2\x)s2 + (6Х2 + 5Х(д. + ц2)5 + 4Х2ц]Из полученных выражений видно, что полиномы знаменателей /•($) различ¬
ны, a Pj; = lim sPt(s) = 1 для каждого состояния,о5.4.4. Определение количественных характеристик
надежности по графу состоянийВ предыдущих разделах были описаны правила, позволяющие из графа со¬
стояний найти в преобразованиях Лапласа вероятности пребывания восста¬
навливаемой системы в данный момент времени в любом состоянии и веро¬
ятности попасть в любое состояние в течение времени t. Эти вероятности
позволяют найти основные количественные характеристики надежности сис¬
темы, например: функцию и коэффициент готовности, вероятность безотказ¬
ной работы, среднее время безотказной работы, наработку на отказ, а также
среднее время восстановления. Рассмотрим особенности определения основ¬
ных характеристик.
Методы анализа надежности технических систем187□ Вычисление функции готовностиФункция готовности Kr(t) является вероятностью застать систему в ис¬
правном состоянии в любой момент времени, поэтому для ее определения
необходимо найти сумму вероятностей всех исправных состояний систе¬
мы. Для определения Kv(t) из графа состояний по методике, изложенной
в разд. 5.4.1, находятся преобразования Лапласа вероятностей всех ис¬
правных или всех отказовых состояний и определяется преобразование
Лапласа функции готовности по одной из следующих формул:(5-19)г=0вд=--1ад, (5-2°)s i=kгде Pj(s) — преобразование Лапласа вероятности пребывания системы в
данный момент времени в исправном (или отказовом) состоянии, соответ¬
ствующем /-му узлу графа;и — общее число узлов графа, равное числу всех возможных состояний
системы;к — число узлов графа, соответствующих исправным состояниям сис¬
темы.Если число отказовых состояний системы меньше числа исправных, то
следует пользоваться формулой (5.20), в противном случае— форму¬
лой (5.19).Знаменатели функций Pt(s) одинаковы, поэтому целесообразно искать
оригинал Kr(t), осуществив предварительно все возможные преобразова¬
ния суммы слагаемых.□ Вычисление коэффициента готовностиКоэффициент готовности является финальной вероятностью пребывания
системы в исправном состоянии, поэтому его можно найти из (5.19), вы¬
числив один из следующих пределов:k-1КГ = Urn sKJs) = Т limsR(s), (5.21)s~»0 j=os~* 0AV=1-S limsP,(s). (5.22)i=ks~>°
188Гпава 5Наиболее просто можно вычислить коэффициент готовности для графа
типа дерева непосредственно по графу состояний, если просуммировать
выражение (5.17) по всем /, соответствующим исправным состояниям
системы. В результате суммирования получим:где п — общее число узлов графа;к — число узлов графа, равных числу исправных состояний системы;Вmj — произведение всех интенсивностей переходов графа, которые
встречаются при движении по стрелкам из крайних свободных состояний
в состояние i по кратчайшему пути.□ Вычисление вероятности безотказной работыВероятность безотказной работы является вероятностью того, что восста¬
навливаемая система в течение времени / не попадет ни в одно из ее отка¬
зовых состояний. Поэтому искомая вероятность может быть вычислена по
формулегде Pj(t) — вероятность того, что система в течение времени t попадет
в i-e исправное состояние;к — число узлов графа, соответствующих числу исправных состояний
системы.Для вычисления Pt(t) необходимо все отказовые состояния считать по¬
глощающими и запретить все переходы из этих состояний в предотказо-
вые. Только после постановки экранов следует вычислять по графу со¬
стояний преобразования Лапласа функций Pt{t) в соответствии с методи¬
кой, изложенной в разд. 5.4.3.Следует иметь в виду, что вероятность безотказной работы резервирован¬
ной системы зависит от начальных условий ее функционирования. В зада¬
чах надежности вероятность безотказной работы обычно вычисляется в
предположении, что при t = О все элементы системы исправны.к-1(5.23)к-\рс(о=тт,(5.24)
Методы анализа надежности технических систем189□ Вычисление среднего времени безотказной работыСреднее время безотказной работы системы вычисляется по формуле:где Pc(s) — преобразование Лапласа вероятности безотказной работы,
вычисленной в предположении, что при / = О все элементы системы ис¬
правны.где Tj — среднее время пребывания системы в /-м исправном состоянии.□ Вычисление наработки на отказНаработка на отказ может быть вычислена по формулегде Тв — среднее время восстановления системы. Этой формулой целесо¬
образно пользоваться тогда, когда среднее время восстановления системы
известно из опыта или может быть легко вычислено. Тогда задача сводит¬
ся к определению КГ из графа состояний одним из описанных ранее спо¬
собов.При неизвестном Гв следует использовать формулу:При вычислениях по этой формуле необходимо определять по графу фи¬
нальные вероятности пребывания системы во всех возможных состояниях.
Формула является наиболее общей, т. к. позволяет вычислять Т при лю¬
бом числе отказовых состояний и при любой дисциплине обслужива¬
ния [57].(5.25)Так как Pc(s) = £ Pt(s), то*-1i=0или/с-1(5.26)i=0(5.27)Т -ieE+(5.28)£ pi £ v-ij 'ie.E^ JeE+
190Гпава 5ПРИМЕР 5.22. Необходимо найти основные количественные характеристики
надежности энергетической системы, схема расчета надежности которой
приведена на рис. 5.27. Определить функцию и коэффициент готовности,
вероятность безотказной работы, среднее время безотказной работы, нара¬
ботку на отказ и среднее время восстановления системы при следующихисходных данных: Я = 1-1(Г2 час-1, X,1=2-10’i час-1, Х2 =0,01 -10 час-1,ц = 0,1 час-1, ц2 = 1 час-1.Рис. 5.27. Структурная схема энергетической системыРешение. Предполагается, что схема функционирует следующим образом.
Три генератора Г j, Г2 и Г3, каждый из которых работает с интенсивностью
отказов X, питают нагрузку мощностью несколько меньшей, чем суммарная
мощность трех параллельно работающих генераторов. При отказе одного из
генераторов каждый из двух оставшихся исправных работает с небольшой
перегрузкой с интенсивностью Я, > X. Если откажут два любых генератора
из трех, то наступает отказ энергетической системы. Регулирующая аппара¬
тура (РА) работает с интенсивностью Х2, ее отказ ведет к отказу системы.
Предполагается, что систему обслуживает одна бригада, причем обслужива¬
ние происходит с приоритетом, обратным поступлению заявок (в данном
случае это означает, что регулирующая аппаратура имеет более высокий
приоритет обслуживания, чем генераторы).При указанных условиях функционирования граф состояний системы имеет
вид, приведенный на рис. 5.28.Из графа состояний наиболее просто определить коэффициент готовности и
наработку на отказ. Состояния (0) и (1) являются исправными, поэтому
КГ=Р0 + Р1, На основании формулы (5.23) и в соответствии с методикой
разд. 5.4.2, получим:JT а20аЮа31а41 +а20а01а31а4) а20а10а31а41 + а20°0!а31°41 + а02а10а31а41 + а20а01а13а41 + а20а01а31а14
Методы анализа надежности технических систем191Рис. 5.28. Граф состояний энергетической системы
Подставляя значения интенсивностей переходов, получим:Кг =Ц2Ц2+ЗХ|Л|Д2+^2^2^2+3^2№2+6^1^2 1 + 3 - + ^ + ^hh, + 6MlЦ Р-2 ^ И2 Н-
1 + 0,3 1,31 + 0,3 + 0,001+ 0,3 0,001+ 0,6-0,2 1,4213= 0,915 .Наработку на отказ вычислим по формуле (5.28). В нашем случае в область
исправных состояний Е+ входят состояния (0) и (1). В область отказовых
состояний входят состояния (2), (3) и (4). Тогдаpo+piPlV-2 +Р^2 + />Подставляя в это выражение значения финальных вероятностей, которые мо¬
гут быть записаны непосредственно из выражения для Кг, получим:т = Ц2Иг +ЗЛ.ЦЦ2 Ц + ЗХХ2ц2ц2 + ЗХХ,2р.р2 + 6ХХ,]|лр.2 + 3^2 + ^^10,1 + 3-Ю’2 Q7_- =97,7 час.0,1-Ю-2 -0,1 + 3-Ю-2 -0,1-10“2 +6-10-2 -2-10-2По известным коэффициенту готовности и наработке на отказ легко найти
среднее время восстановления системы, воспользовавшись формулой:1-Кг 1-0,915
192Гпава 5Из трех оставшихся характеристик надежности (функция готовности, ве¬
роятность безотказной работы и среднее время безотказной работы) пер¬
вой необходимо вычислять функцию готовности. Это объясняется тем
обстоятельством, что вероятность безотказной работы может быть полу¬
чена формально из выражения для функции готовности. Будем предполагать,
что система начинает эксплуатироваться, когда все устройства исправны.
Тогда Kr(t) и Pc(t) будем находить при начальных условиях Р0(0) = 1,
Р,(0) = Р2(0) = ,Р3(0) = Р4(0) = 0.Так как число исправных состояний системы меньше, чем число отказовых,
то для вычисления Кг($) целесообразно воспользоваться формулой (5.19).
Тогда*r(j)= Ё pi(s)=W+р\ (s)=Ар(^ f1 ^ ■,'=0 ЛС0В графе состояний имеются пять состояний, поэтомуA(s) = + Axs3 + A2s2 + A3s + A4).Коэффициенты этого полинома получим из графа состояний по методике,
изложенной в разд. 5.4.1. Из графа видно, что в выражениях для коэффици¬
ентов будут отсутствовать слагаемые, в которые входят произведения интен¬
сивностей вида: а01й(|0, aQ2a2о> ai3a3i’ а\4а4\> a02a0i > аюа13 ■> aioai4 » а\за14 ■В эти произведения входят интенсивности переходов, находящиеся в ветвях,
образующих контуры или исходящих из одного и того же узла. Записывая
выражения коэффициентов через интенсивности переходов и производя вы¬
числения в соответствии с исходными данными, получим:Aq=1,Ах = а02 + а01 + а20 + а10 + а!3 + а31 + а14 + о41 == ЗА. + 2A.J + Тк2 + 2ц + 2ц2 — 2,272,-а02(а14 +а4! +а31 +а\3 +a10) + £i!0l(a14 +°41 + а3\ + а\3 + а2о) +
+а14(а31 + а2о) + a4l(a31 + а\3 + а\0 + а2о) + а3\(а\0 + а2С>) + а13а20 + а10а20 == Я,2(2А.| + Х2 + 2ц + ц2) + ЗА.(2А,1 + Х2 + ц + 2ц2) + 4Я.]Ц2 + ц(А-2 2ц2)+ц2(А,2 + 2ц + ц2) = 1,557,Ay = «02a14a31 +fl02a14(a31 +af10 +fif13) + a02a31a10 +а01а14(а31 +а2<)) +
+a01a4l(°31 +a13 +a20) + a0la31a20 +а01а13а20 +а14а31а20 + a41a3l(a10 + а2о) +
+a4Ia13°20 + a41«10a20 + «31аЮа20 = 2Х.,Я.2Ц2 + Я2Ц(Ц2 + Ц + ^2) + ^2^2 + 12АД.,Ц2 +
+ЗА,ц(2ц2 + Я,2) + ЗХц2 + ЗАХ2Ц2 + 2Х]Ц2 + цц2(ц + ц2) + цХ2ц2 + ц ц2 + Ц2Ц = 0,3,S
Методы анализа надежности технических систем193А4 - Д02а31а10а41 + а20а\0аЪ\а4\ +а20а01й31а41 + а20а01°13а41 + а20а01а31о14 ~= ц2ц2^2 +М-2|^2 +ЗХ.ЦЦ2 + ЗЯ-Х2Р.Р-2 +6ХХ]Ц2 =0,0142.Степень полинома AqCs) будет:пг0 = п-1 — ^0 = 5 — 1 — 0 = 4,поэтому A0(s) - B00s4 + 5,0s3 + B20s2 + B30s + B40. Коэффициенты Bi0 не
должны содержать интенсивностей перехода из состояния (0), т. е. интенсив¬
ностей а0] и а02. Исключая слагаемые, содержащие указанные интенсивно¬
сти, из коэффициентов At при соответствующих степенях s получим:% = 1 j 510 — д?2о + О]q + + й]4 + Я41 = 2/Ц + Х,2 + 2ц + 2jll2 = 2,242,^20 =au(a31 +a2o) + a4l(fl3! +а13 + а10 + а2о) + °3l(a10 +а20) + а13а20 +а10°20 == 4А.,ц2 +Ц(2Ц2 +^2 +M-) + li2(^'2 + 2Ц + Ц2) = 1,49,*30 “а14а31а20 +°41a3l(a10 +а20) + а41а13°20 +а41й10а20 + °31°10а20 ~= 2Х, ц2 + цц2 (ц + Ц2)+ ^2^2 + V^V-i + М-21-1 = 0,:26,*40 = = 0» 01 •Степень полинома А] (я) будет:mx=n — l — ^i = 5-1-1 = 3,
поэтому A! (i) = 50153 + вх 1 52 + B2\S + ВЪ\ .Коэффициенты Вп не должны содержать интенсивностей перехода из со¬
стояния (1), т. е. интенсивностей а10 , а13, а14 , Кроме того, каждое слагаемое
должно содержать сомножителем интенсивность перехода из начального со¬
стояния (0) в состояние (1), т, е. ci0!. Исключая соответствующие слагаемые в
коэффициентах Ai, получим:*oi ~aoi = ЗА, = 0,03, ВХ] =aoi(a4j +a3i + а2о) = ЗА,(ц + 2ц2) = 0,063,*21 =a01a4l(a31 + af20) + a01a31a20 = 6А,ЦЦ2 + ЗА,Ц2 = 0,036,*31 = a20a01a31a41 =ЗА.ЦЦ2 =0,003.Подставляя полученные значения коэффициентов полиномов в выражения
для вероятностей состояний (0) и (1), получим:AqOQ + A^) И+2,272s3 +1,553s2 +0,2965 + 0,013
г 5 ~ A(s) s(s4 + 2,27s3 +1,56лг2 + 0,35 + 0,014)’7 Зак. 3094
194Глава 5Найдем преобразование Лапласа вероятности безотказной работы системы
Pe(s), для чего запретим переходы из поглощающих состояний (2), (3) и (4)
(экраны в виде пунктирных линий на рис. 5.28), и вычислим значения коэф¬
фициентов полиномов Д(s), A0(s), Д](s), полагая, что а20 = <я3! = а41 = 0.Исключая слагаемые, в которых содержатся интенсивности йг2о> «31 * «41 >
получим следующие выражения для коэффициентов А( и BJ::Aq = 1, А] — 0q2 «oi «ю «13 «14 = ЗА. + 2Х] + ц = 0,172,А2 = «02 («14 + «13 + «10) + «0l(°l4 +«1з) == к2 (2 Ц + Х2 + й) + Щ2Хх + Х2 ) = 1.37 • 10'3,А3 = 0, А4=0, Bqq = 1, Лю =Ojo +0)3 +Я|4 = ц + А,2 +2Х| =0,141,*20 =*зо =*40 =0» *oi = ЗА, = 0,03, В1Х = B2i = B3j =0.Подставляя значения коэффициентов в выражение для Kr(s) и выполняя
очевидные преобразования, получим преобразование Лапласа вероятности
безотказной работы:р = 54 + (ц + А.2 + 2А-! )53 + ЗА^3 =5 [5** + (ЗА. + 2А.| + 2А,2 + ц)53 + Х2 (2A.J + А,2 + ц)52 +3A,(2Xj + А,2)52]
s + ЗА. + 2A.j + X2 + ц
s + (ЗА, + 2 А,, + 2А,2 + ц)5 + А>2 (2X.j + А.2 + ц) + ЗА,(2А.[ + Х2 )£+ 0,171 5 + 0,171 1,05 0,05” s2 +0,1725 + 0,137-10~2 ~(s + 0,0085)(s + 0,1635)” 5 + 0,0085 5 + 0,1635' ,Вероятность безотказной работы системы в течение времени t, являясь ори¬
гиналом функции Pc(s), имеет вид [57]:Рс(0 = 1,05е~°'т51 - 0,05е"°’1635'.Среднее время безотказной работы наиболее просто вычислить, воспользо¬
вавшись формулой (5.25):Г,=РС(5)| = U + 2-!+-2 + ^ = —------7 = 125 час.и=0 Х2(2А.1+А,2+|л) + ЗА,(2Х1+Х2) 0,137-10Из приведенного примера видно, что методика определения количественных
характеристик надежности по графу состояний сравнительно проста. Наибо¬
лее просто вычисляются коэффициент готовности, наработка на отказ и сред¬
нее время восстановления. Наибольшие трудности возникают при о пределе-
Методы анализа надежности технических систем195НИИ функции готовности. Если Kr(s) получено, то вычислить преобра¬
зование Лапласа вероятности безотказной работы Pc(s) и среднее время без¬
отказной работы можно путем формальных преобразований функции Kr(s).5.4.5. Определение количественных характеристик
надежности систем, описываемых
многосвязными графамиРазложение графа на деревьяФункционирование восстанавливаемых систем часто описывается много¬
связными графами, в которых имеются переходы через состояния. Такими
являются системы с приоритетным обслуживанием, многие резервированные
системы с неравнонадежными элементами, избыточные системы, которые
ремонтируются после отказов нескольких элементов и др. В этих случаях в
графе может быть большое число кратчайших путей в i-e состояние из на¬
чального и конечных отказовых состояний. Поэтому методика определения
количественных характеристик надежности по графу состояний, приведенная
в предыдущих разделах, непосредственно не может быть применена.Излагаемая здесь методика анализа надежности восстанавливаемых систем,
описываемых многосвязным графом, состоит из следующих этапов:О преобразование сложного многосвязного графа в совокупность простых
графов типа дерева;О вычисление вероятностей состояний, соответствующих узлам простых
графов;□ вычисление вероятностей пребывания исходной системы во всех возмож-- ных ее состояниях;□ вычисление количественных характеристик надежности исходной сис¬
темы.Рассмотрим методику по этапам.Преобразование сложного многосвязного графа
в совокупность простых графовСовокупность ветвей из X- и ц-переходов между двумя соседними узлами на¬
зовем (обобщенным) ребром или ветвью графа. Тогда в графе типа дерева
ребра не образуют контуров. Контуры образуются из ребер только тогда, ко¬
гда система описывается многосвязным графом. При этом может оказаться,
что ребро будет образовано лишь X- или ц-переходом. Пусть в графе состоя¬
ний имеется А, В,..., Н контуров. Причем контур А образован ребрами
4, А2,..., АпХ, контур В — ребрами Вх, В2,..., Вп2,..., контур Н — реб¬
196Гпава 5рами Нх, Н2,..., Нпт. Тогда для образования графов типа дерева необхо¬
димо в каждом из контуров исключить одно ребро. Из контура А можно ис¬
ключить либо ребро А}, либо Аг,..., либо Ani; из контура В — либо ребро
2?], либо В2 ,..., либо Вп2; из контура Н —либо ребро Нх, либо Н2,...,
либо Нпт . Тогда число простых графов типа дерева и их вид можно опреде¬
лить следующим образом. Ребрам графа, обозначенным буквенными симво¬
лами, приписываются свойства двоичных переменных. Образуется дизъюнк¬
ция из буквенных символов ребер, принадлежащих контуру. Записывается
конъюнкция из дизъюнкций буквенных символов ребер выбранных контуров,
и раскрываются скобки. Число простых графов, содержащихся в сложном
исходном, будет равно числу конъюнктивных членов в полученном выраже¬
нии. Причем каждый из буквенных символов конъюнктивного члена соответ¬
ствует тем ребрам, которые должны быть исключены одновременно из ис¬
ходного графа для получения соответствующего простого графа типа дерева.В сложных многосвязных графах контуры могут иметь общие ребра. Тогда в
выражении для дизъюнкции конъюнкций после раскрытия скобок необходи¬
мо исключить конъюнктивные члены, содержащие два и более одинаковых
буквенных символа, а также члены с разными буквенными символами, но
встречающиеся в конечном выражении несколько раз.Вычисление вероятностей состояний,
соответствующих узлам простых графовВероятности состояний, соответствующих узлам простых графов, можно вы¬
числять любым из известных способов, однако наиболее просто их получить
непосредственно по графу состояний в соответствии с методикой, изложен¬
ной ранее.Обозначим за Р\к^ финальную вероятность пребывания системы в состоянии
/ при условии, что ее функционирование описывается простым ^-графом.
Тогда на основании соотношения (5.14) имеем:д(*)(5-29)Л-iгде В^} — произведение интенсивностей переходов из всех конечных узлов
к-то простого графа в г'-й узел при перемещении в направлении стрелок по
кратчайшему пути; п — число узлов графа;Лк) _ у1 в(к)
лп-1 - Zj mi ■/=0
Методы анализа надежности технических систем197Вычисление вероятностей состояний исходной системыФинальная вероятность пребывания системы в г'-м состоянии равна взвешен¬
ной сумме финальных вероятностей пребывания системы в каждом из г-х уз¬
лов всех простых графов, причем весами служат вероятности того, что функ¬
ционирование системы описывается к-м простым графом:Если в исходном графе имеются ребра, состоящие только из X- или
ц-переходов, то в совокупности простых графов, полученных указанным ра¬
нее способом, будут такие, которые не используются при вычислении данной
i-й финальной вероятности. Эти графы легко распознать, т. к. в них невозмо¬
жен переход в i-e состояние из свободных узлов по направлению стрелок. По
этой причине некоторые простые графы вообще не используются при вычис¬
лении финальных вероятностей, а некоторые используются при вычислении
всех или только некоторых вероятностей.Из выражения (5.31) видно, что задача определения финальных вероятностей
исходной системы, описываемой сложным многосвязным графом, свелась
к определению финальных вероятностей множества простых графов типа
дерева.По известным финальным вероятностям вычисляются коэффициент готовно¬
сти, наработка на отказ и среднее время восстановления. Методика их опре¬
деления не отличается от описанной ранее для случая графов типа дерева.ПРИМЕР 5.23. Необходимо определить коэффициент готовности и наработ¬
ку на отказ дублированной системы, схема расчета надежности которой при¬
ведена на рис. 5.29. Предполагается, что обслуживает систему одна бригада, а
ремонт отказавших элементов осуществляется в последовательности их отка¬
зов (прямой приоритет).(5.30)кОтсюда и из (5.29) получим(5.31)Решение. Из графа состояний, приведенного на рис. 5.30, видно, что состоя¬
ния (0), (1) и (2) являются исправными, а состояния (3) и (4) отказовыми.
^2» Иг3 4Рис. 5.29. Структурная схема дублированной
системы с неравнонадежными устройствамиРис. 5.30. Граф состояний системы,
изображенной на рис. 5.29Pq + Pi+P2и задача сводится к вычислениюфинальных вероятностей всех возможных состояний системы.Преобразуем исходный граф в совокупность простых графов типа дерева. На
рис. 5.31 приведен граф, составленный из ребер, образованных ветвями из
X- и ц-переходов исходного графа. Ребро А образовано из переходов а0],
а10; ребро В — из переходов а02, а20; ребро С — из перехода <я13; ребро
D — из перехода <я32; ребро Е — из перехода ан ; ребро F — из перехода
о42. Образуем конъюнкцию от дизъюнкции ребер контуров (0, 2, 3, 1) и
(1, 3, 2,4) и раскроем скобки. Получим:® = (Av BvCv D)(Cv Dv Ev F) = AC v BC v CC v DC v AD v BD v
v CD v DD v AE v BE v CE v DE v AF v BF v CF v DF.Рис. 5.31. Граф состояний системы, образованной из ветвей графа, приведенного на рис. 5.30Конъюнкции СС и DD образованы одинаковыми буквенными символами, а
CD — символами, входящими одновременно как в первый, так и во второй
контур, поэтому они должны быть исключены из выражения для ©.024
Методы анализа надежности технических систем199Тогда0 = AC v ВС v AD v BD v АЕ v BE v СЕ v DE v AF v 2?F v CF v DF.Исключая из графа рис. 5.31 ребра, соответствующие конъюнктивным чле¬
нам этого выражения, получим совокупность простых графов типа дерева,
эквивалентных исходному графу. Семейство простых графов показано на
рис. 5.32.00'2K/fХ>21 ОСТ JD 21 CL 'Э 2\'''4sL2 /Ч /\‘13 ® -43^ 4ВСAD6в00BDАЕBEгде000J V А<2^7 2\ 723 ®Ъ® 43 (Е> ® 4СЕDEAFж3иРис. 5.32. Семейство простых графов (а—и) (см. продолжение)
200Гпава 5ООО3 >су чу 4 3 ^ 4 3 ^ 42BFCFDFклРис. 5.32. Семейство простых графов (к—м)мВычислим теперь по совокупности простых графов финальные вероятности
состояний исходной системы. Так как в исходном и во всех простых графах
содержатся пять узлов, то числители и знаменатели финальных вероятностей
будут состоять из суммы слагаемых, каждое из которых состоит из четырех
сомножителей. Каждое слагаемое представляет собой произведение интен¬
сивностей переходов из свободных узлов в узел, соответствующий состоя¬
нию дублированной системы при перемещении по кратчайшему пути в на¬
правлении стрелок. Для их определения необходимо всякий раз перемножать
четыре интенсивности перехода, расположенные в четырех разных ветвях
соответствующего графа. Выберем из семейства простых графов такие, кото¬
рые необходимо взять для определения финальных вероятностей PQ, Рх, Р2,
Р3, Р4. Для определения финальной вероятности Р0 необходимо взять графы
ВС, AF и CF, т. к. только в этих графах возможен переход из свободных
узлов в узел 0 по четырем ветвям в направлении стрелок.По этому же признаку определение вероятности Рх необходимо осуществить
по графам АС, ВС, CF ; вероятности Р2 — по графам AF, BF, CF ; веро¬
ятности Р3 — по графам AD, BD, DF; вероятности РА — по графам АЕ,
BE, СЕ. Тогда на основании формулы (5.31) по методике, изложенной ра¬
нее, получим:к 1=0к 1=0
Методы анализа надежности технических систем201*32 + -®}2^ + ^32^ ^1^-2 Ml М-2 + ^2MlM2 + ^2М?М2
2 “ “к С=Ок 1 = 0п ^23 + -®23D) + ^2^F) ^1^2М-2 + ^-?^2М-2 + ^АгМг
_ _ .к » = О* г = 0„ B[f> + 5<f > + s££) х^ц, + XjVi + Х,Х2ц?г4 - “А ( = 0А 1=0Так как знаменатель финальных вероятностей равен сумме всех их числите¬
лей, то финальные вероятности всех возможных состояний дублированной
системы определены.Заметим, что при определении финальных вероятностей граф CF использо¬
вался трижды (при определении вероятностей Р0, Рх и Р2), графы ВС и
AF — дважды, а граф DE вообще не использован. В графе DE свободные
узлы 3 и 4 являются поглощающими состояниями, а поэтому не существует
такого узла, в который возможен переход из свободных узлов в направлении
стрелок по четырем ветвям.Подставляя полученные выражения вероятностей в формулы для Кт и Т,
получим искомые коэффициент готовности и наработку на отказ.Непосредственное вычисление
стационарных показателей надежностиПриведем теоретические основы топологического метода для расчета ста¬
ционарных показателей надежности восстанавливаемой системы, описывае¬
мой произвольным графом. Метод позволяет рассчитывать показатели на¬
дежности, не используя разложение графа на подграфы типа дерева. Так как
все стационарные показатели надежности системы выражаются через ста¬
ционарные вероятности, то для расчета искомых показателей достаточно оп¬
ределить лишь вероятности пребывания системы в каждом состоянии.Вероятность пребывания системы в состоянии S',, i- 0,1, 2,... ,п, определя¬
ется по формуле(5.32)
202Главз$где Д, — сумма всех возможных произведений п интенсивностей переходовиз каждого состояния Sj, j * i графа в соседнее состояние, за исключениемтех произведений, в которые входят интенсивности ветвей, образующих на
графе элементарные контуры,Д=£а,.. (5.33)/=ОПРИМЕР 5.24. Требуется определить стационарные показатели надежности
системы, структурная схема которой изображена на рис. 5.33. Интенсивности
отказов и восстановлений дублированной подсистемы равны соответственно
А-! и р.,. Интенсивности отказов и восстановлений элемента 2 равны соответ¬
ственно Х2 и (J-2 • Обслуживает систему одна ремонтная бригада, приоритет
обслуживания — прямой, т. е. восстановление отказавших элементов осуще¬
ствляется в порядке их отказов.*■!> И|Рис. 5.33. Структурная схема системыРешение. Граф состояний системы изображен на рис. 5.34. Узлам поставле¬
ны в соответствие следующие состояния:□ (0) — все элементы исправны;□ (1) — отказал и восстанавливается один из элементов дублированной под¬
системы, остальные элементы исправны;□ (2)— отказал и восстанавливается элемент 2, остальные элементы ис¬
правны;□ (3) — отказали оба элемента дублированной подсистемы, причем первый
отказавший элемент находится в ремонте, второй — в очереди на обслу¬
живание, элемент 2 исправный;□ (4) — отказал и восстанавливается один из элементов дублированной под¬
системы, отказал и находится в очереди на обслуживание элемент 2.В данном случае граф не является графом типа дерева.
Методы анализа надежности технических систем20302V13®Рис. 5.34. Граф состояний системы, изображенной на рис. 5.33Узлы 0 и 1 соответствуют исправным, а узлы 2, 3 и 4 — отказовым состояни¬
ям. Дугам графа приписаны интенсивности отказов и восстановлений atj,с которыми происходят переходы из состояния в состояние.Определим стационарные вероятности состояний системы по формуле (5.32).
Для этого предварительно составим табл. 5.4.Таблица 5.4. Таблица переходовСостояния системыПереходы из данного состояния
во все другие состоянияСуммарная интенсивность
выхода(0)«01 ~ 2^1 > «02 = ^2«01 + «02О)«ю = И| > аи = X,, а14 = А.г«10 + «13 + «14(2)«20 = Н-2«20(3)«31 “Ц|«31(4)«42 = И|«42Для вычисления Д, надо составить произведение суммарных интенсивностей
выхода из всех состояний, кроме состояния 5,. Затем в полученном произве¬
дении раскрыть скобки и выкинуть все слагаемые, содержащие интенсивно¬
сти ветвей, образующих на графе контуры.Для состояния S0 получим произведение(°10 +а13 +аи)а20а31а42 =а10а20а31а42 + а!3а20а31а42 + а14а20а31а42 •
204Гпава 5Поскольку во второе слагаемое входит произведение а13а31 интенсивностей
ветвей, образующих контур, то такое слагаемое следует опустить, и тогдаА0 = a\0a20a3\aA2 + а14а20а31а42 = М-?Р-2 + ^2Hl М-2 •Для состояния «S'] получим произведение(а01 + °02)а20а31а42 ~ а01а20а31°42 + а02а20а31а42 •Во второе слагаемое входит произведение a02a20 интенсивностей ветвей, об¬
разующих контур, поэтомуД} = <3oia20a31a42 = •Для состояния S2 получим произведение(°01 +а02)(а10 + а\3 +й,и)а31а42 =“ aQ\a\0a3\aA2 + а01а13°31а42 + a01a14a31a42 + а02°10й31а42 +
+а02а13а31а42+а02а14а31а42-
Контуры образуются в первом (а01а10), втором (а13а31) и пятом (а13а31) сла¬
гаемых, поэтому эти слагаемые исключаются из рассмотрения:2 3 2 2^2 = aQ\a\Aa3\aA2 + a02a\0a3\aA2 + а02а14а3!а42 = ?^1^2Ml + ^2Ml + ^-гМ-1 •Для состояния 53 получим произведение(а01 + а02)(а10 + а13 + °14)а20а42 == а01а10°20а42 + a0\ana20aA2 + а01а14а20а42 + a02al0a20aA2 ++°02а13°20а42 + a02alAa20aA2-Контуры образуются во всех слагаемых, за исключением второго, следова¬
тельно,2Д3 = aoiai3a20a42 - 2Хх \хх\х2 ■Для состояния S4 получим произведение(а01 + «02 )(«ю +а13 +ан)а20а31 == a0\a\0a20a3\ +О01а13а20а31 + а01а14а20°31 + О02°10°20а31 ++a02a\3a20a3\ + a02alAa20a3\-Контуры образуются во всех слагаемых, за исключением третьего, следова¬
тельно,Д4 = «01а14°20а31 = 2X.JA.2M-lM-2 ■
Методы анализа надежности технических систем205По формуле (5.33) получимА — Ag + Aj + А2 + А3 + А4 =- Ц?Ц2 + + 2Х[Ц^ц2 + 2A.tX2nf +Х2ц^+Х2ц^ + 2А.^ц1ц2 +2А.1Х2р.||л,2-Следовательно,И-?f-^2 +^2Р-?М-2 _ 2A.1|4.fn2 „ _ 2Х,Х2Ц^ + Х2Ц^ +РО- - . Р\ д . й- д .2A,fpjp2 2Я.1А.2Ц|р.2Рг ——, Л- д •Определяем показатели надежности системы:□ коэффициент готовности:*r=Po+Pi = (М-i +2Х.] + Л,2)ц^ц2 (д.]Ц2 +Х2ц^ц2 +2Х[Ц^Ц2 +2Л,,Х2ц^ +Х2ц^ +А,2р.? + 2Х{г|л.1ц2 + 2А,1А.2ц1ц2□ наработка на отказ:■г _ Ро + Р\ 0*1 + 2Хх + Я.2)ц^ц2 _^-гРо +(^-1 + ^-г)Р\ Х2(Ц[ + Х2)ц^(Д.2 -t-(A.J + Л,2)2Я.1(д.^(Д2
_ (И-! +2Xt +X2)PjX2 + X2 + 2A,j* + 2XjX2□ среднее время восстановления:j _ Рг + Рг + Pa _ + ^2M? + + 2А,1А,2ц1ц2 _^-гРо +(^-l + ^”2 )iPl ^2(^1 +^"2)M'12M'2 + (^-1 ^-2)2Я-1 ц.22 . л 2„ , ,,2.2Х,Х.2ц1 + А,2 jutj + Х2|Д| + 2Х| ц2 + 2Х}Х2ц2
(p,jX2 + Я-2 + 2Xj *+■ 2XjA*2 )Ц.|Ц2Как следует из рассмотренных примеров, топологический метод целесооб¬
разно использовать лишь для расчета стационарных характеристик надежно¬
сти систем с небольшим числом возможных состояний. В силу трудоемкости
поиска контуров на графе, что представляет собой сложную комбинаторную
задачу, предпочтительнее использовать методы, основанные на теории мар¬
ковских процессов. Эти методы годятся для расчета надежности невосста-
навливаемых и восстанавливаемых систем. Так для расчета стационарных
206Глава 5характеристик лучшим методом является составление и решение системы
алгебраических уравнений, а для нестационарных характеристик — системы
обыкновенных дифференциальных уравнений.5.5. Методы, основанные на теории
марковских процессов5.5.1. Однородный марковский процессСлучайный процесс X{t) называется марковским или процессом без после¬
действия, если для любых двух моментов t0 и t{, где t0<tx, распределение
вероятностей ^(/]) при условии, что заданы все значения X(t) при t^t0,
зависит только от X(t0).Марковские процессы являются математической схемой, пригодной для опи¬
сания эволюции физической системы, которая после любого заданного мо¬
мента времени /0 не зависит от эволюции, предшествовавшей /0 при усло¬
вии, что значение процесса в этот момент фиксировано.Рассмотрим три последовательных момента времени т < t0 < tx. Пусть
X(t0) = i — значение, фактически принятое процессом для данной реализа¬
ции. Тогда можно считать известным закон распределения процесса, соответ¬
ствующего моменту ; при этом совсем не обязательно знать, какое значение
имел процесс в момент х . Для марковского процесса зависимыми являются
только два соседних сечения. Если под моментом /0 понимать настоящее
время, под х — прошедшее и под tx — будущее, то можно сказать, что для
марковского процесса прошедшее не влияет на будущее, если известно на¬
стоящее (рис. 5.35).Рис. 5.35. К определению марковского случайного процессаМарковские процессы могут быть процессами как с дискретным, так и с не¬
прерывным временем. Приведем примеры марковских процессов.1. X(t) — число частиц радиоактивного вещества в данном объеме. Знаяскорость распада вещества и зная, что в момент /0 имеется N частиц
Методы анализа надежности технических систем207(X(t0) = N), можно вычислить вероятность того, что в момент tx, близкий
к t0, в объеме будет (N + S) частиц.2. X{t) — число живых бактерий в данном объеме. Если известно
X(t0) = N, то, зная скорость деления и продолжительность жизни бакте¬
рии, можно сделать прогноз о количестве бактерий в момент tx = t0 + At.
Знать состояние процесса до момента t0 не нужно.3. X(t) — число вызовов, поступивших на телефонную станцию за время t.
Зная вероятности поступления вызовов за время At и число N вызовов в
данный момент t0, можно вычислить вероятность того, что в момент
t0 + At на станции число вызовов будет больше N. Очевидно, что при
этом не нужно знать, сколько вызовов было до момента t0 .Важным частным случаем марковского процесса является процесс Пуассона.
Процессом Пуассона называется процесс X(t) с непрерывным временем,
удовлетворяющий условиям:1. Каждое сечение процесса имеет возможные значения: 0, 1,2,....2. С течением времени состояние процесса может только увеличиваться:
X(t + At)ZX(t).3. Р(АХ(/) = 1) = ХАt + о(Д0. Здесь АХ(t) = X(t + At) - X(/) — приращение
процесса за время At; At — бесконечно малая величина; X — постоянное
для данного процесса число; o(At) — сумма всех членов, имеющих поря¬
док малости выше чем At.4. Р(АХ(0 = 5) = о(А/), где s £ 2.Третье условие означает, что вероятность изменения состояния на единицу за
бесконечно малое время At есть бесконечно малая величина того же порядка,
что и At. Четвертое условие означает, что вероятность изменения состояния
за At на две единицы и больше есть величина более высокого порядка мало¬
сти, чем At. Из 3-го и 4-го условий следует, что процесс Пуассона является
марковским.Можно доказать, что каждое сечение процесса Пуассона есть случайная ве¬
личина, распределенная по закону Пуассона с параметром Xt:P(X(t) = m) = ^^-e~x‘, m = 0,1,2,...
m\Математическое ожидание сечения при любом фиксированном t будетM(X(t)) = Xt.
208Гпава 5Если положить t = 1, то М(Х( 1)) = X — среднее число событий потока в еди¬
ницу времени.Выделение марковских процессов вызвано рядом причин, важнейшими из
которых являются относительная простота случайного процесса, описываю¬
щего эволюцию системы, наличие возможности использовать хорошо разра¬
ботанный математический аппарат для аналитического исследования марков¬
ских процессов, возможность получения аналитических выражений для пока¬
зателей качества систем и, наконец, возможность сведения к указанным
моделям более общих моделей.Марковский процесс называется однородным, если для любых возможных
значений г и к и произвольного т>0 вероятность события X(t + x) = k при
условии X(t) = / не зависит от t. Условная вероятностьpik{x) = P(X(t + x) = klX(t) = i)называется вероятностью перехода из состояния i в состояние j за время х .
Для любых состояний / и j вероятности перехода обладают свойствами:Pik (О ^ °> Z Pik ОО = 1. Pik (*1 + Ъ ) = Е Pij (Т1 )Pjk (*2 > ’
к jПоследнее соотношение, называемое иногда уравнением Чэпмана — Колмо¬
горова, лежит в основании всех исследований о марковских процессах.В теории надежности обычно исследуются случайные процессы двух видов:
моментов отказов и моментов окончания ремонтов системы. Если предполо¬
жить, что все распределения времени безотказной работы и времени восста¬
новления отдельных элементов системы являются экспоненциальными и все
состояния системы пронумерованы, то случайный процесс X(t), равный но¬
меру состояния в момент времени t, является однородным марковским про¬
цессом. Если процесс X(t) характеризует число отказов или число произве¬
денных ремонтов в течение времени /, то он также является однородным
марковским процессом.Однородный марковский процесс X(t) с дискретным множеством состояний
S0, S\, S2,..., Sm определяется постоянными интенсивностями переходаv.hWlMSH,J Д/-+0 Д tиз состояния Sj в состояние Sj, а также начальным вектором распределения
вероятностейPi(0) = P(X(0) = i), / = 0,1, 2,..., т.
Методы анализа надежности технических систем209Событие X(t) = i означает, что в момент времени t процесс X(t) находится
в состоянии Sj. Если переход из состояния S,■ в состояние Sj отсутствует, тоЧ/ = 0-Обозначим через Pi(t) вероятность пребывания системы в момент времени t
в состоянии Sj, i = 0,1,2,..., m . Эти вероятности удовлетворяют системе
обыкновенных дифференциальных уравнений Колмогорова:Р\(0 = KjPi(О + Z\jPj(*)’ * = 0,1, 2,..., да. (5.34)J jСистема уравнений составляется по следующему правилу: для каждого со¬
стояния Sj записывается уравнение, в левой части которого стоит производ¬
ная от Pj(t), а в правой — сумма произведений вероятностей всех состояний,
умноженных на интенсивности перехода из этих состояний в состояние St,
причем произведения, соответствующие выходам из состояния S,•, берутся со
знаком а произведения, соответствующие входам в состояние S,, берутся
со знаком "+".Из системы уравнений Колмогорова можно получить модель функциониро¬
вания системы при длительной ее эксплуатации, т. е. при / -> со. В этом слу¬
чае p,(t) —> р, и /?'(/)-> 0. Вероятности pt называются стационарными или
финальными вероятностями. Относительно этих вероятностей имеет место
система линейных алгебраических уравнений:\jPi + £ KjPj = °» * = °Л 2,..., да, (5.35)j Jткоторая должна решаться вместе с условием £ р, = 1 •с=оПРИМЕР 5.25. На рис. 5.36 представлен граф состояний системы, ветвям
которого приписаны постоянные интенсивности перехода из состояния в со¬
стояние. В момент времени t = 0 система находилась в состоянии S0. Требу¬
ется составить математическую модель для нестационарного и стационарного
режима функционирования системы.Решение. Приведенное ранее правило позволяет записать следующую систе¬
му дифференциальных уравнений:Po(0 = ~(hi + ^-02)Ро(0 + ^ioPi(0'>■ Pi (0 = hiPo(0 - hoPi(0 + 4iPi(0;(0 = ^02 A)(0“^2lft(0-
210Глава 5^•oiЯ-21Рис. 5.36. Граф состояний системыТак как при t = 0 система находилась в состоянии S0, то />0(0) = 1,
Р\ (0) = (0) = 0. Решение системы при заданных начальных условиях по¬
зволяет найти вероятности pt(t) пребывания системы в каждом состоянии,
/ = 0,1,2.При длительной эксплуатации системы вероятности состояний становятся
постоянными, а их производные равны нулю. Тогда математическая модель
функционирования системы будет иметь вид:-(Л,01 + Х02)Р0 + XjoPj = 0;• ^oiPo _^ioPi +^2\Р2 =0;Л02Р0 ~^2lP2 = 0-Полученная система является неопределенной и должна решаться при допол¬
нительном условии: р0 + р{ + р2 -1, которое заменяет одно любое уравнение
системы.5.5.2. Инженерная методика
расчета показателей надежностиОсновными допущениями метода, основанного на теории марковских про¬
цессов, являются:□ время безотказной работы и время восстановления каждого элемента, вхо¬
дящего в систему, имеют экспоненциальное распределение вероятностей;□ функционирование системы контролируется непрерывно, т. е. момент от¬
каза обнаруживается немедленно после его возникновения;□ восстановление элемента начинается сразу после его отказа при наличии
свободной бригады, обслуживающей данный элемент; при отсутствии
свободной ремонтной бригады отказавший элемент становится в очередь
на обслуживание.
Методы анализа надежности технических систем211Метод позволяет рассчитать надежность невосстанавливаемых и восстанав¬
ливаемых, нерезервированных и структурно-резервированных технических
систем при любом состоянии резерва (ненагруженном, облегченном, нагру¬
женном), при любом количестве ремонтных бригад и произвольной дисцип¬
лине обслуживания с учетом сделанных ранее допущений. Метод позволяет
вычислять следующие характеристики надежности систем: вероятность без¬
отказной работы, среднее время безотказной работы, функцию и коэффици¬
ент готовности, наработку на отказ, среднее время восстановления.Инженерная методика анализа надежности технической системы, осно¬
ванная на теории марковских процессов, состоит из следующих этапов:1. Формулировка понятия "отказ" и представление исходных данных.Отказ является понятием субъективным, поэтому его определение для
конкретной системы согласуется с заказчиком. Исходными данными для
расчета показателей надежности являются: структурная схема системы
(схема расчета надежности), интенсивности отказов и восстановлений
каждого элемента, количество ремонтных бригад, приоритет обслужива¬
ния, время непрерывной работы, начальное состояние процесса функцио¬
нирования системы.2. Построение графа состояний.Порядок построения графа состояний приведен в разд. 5.1. В соответствии
с принятым понятием отказа множество всех состояний Е разбивается на
множество работоспособных состояний Е+ и множество отказовых со¬
стояний Е_. Если система работает только до первого отказа и вычисля¬
ются показатели P{t) и 7j, то в графе отсутствуют ветви из всех отказо¬
вых состояний.3. Составление по графу системы линейных дифференциальных и/или алгеб¬
раических уравнений.По виду графа формально записывается система линейных дифференци¬
альных уравнений (5.34) для вероятностей /?,(/) пребывания системы в
момент времени t в состоянии /. Проверяется правильность составления
системы дифференциальных уравнений: если сумма правых частей равна
нулю, то считается, что система составлена правильно.Для определения вероятности безотказной работы следует ограничиться
составлением уравнений только для исправных состояний системы.4. Решение систем уравнений и определение вероятностей состояний сис¬
темы.Вероятности состояний р,(/) определяются путем решения системы (5.34)
любым из известных математических методов. Часто бывает удобно
212Гпава 5использовать метод преобразования Лапласа (см. разд. 2.5). Для этого
в уравнениях (5.34) вместо вероятностей />Д0 необходимо поставить
их изображения Pi(z), а вместо производных p\(t) — выражения
(zp^z)-pj(0)). Тогда система дифференциальных уравнений (5.34) в пре¬
образовании Лапласа записывается в виде системы алгебраических урав¬
нений:zpi (z) - Pi (0) - -]Г Xjjp; (z) + Xijpj (z), / = 0,1, 2,...,m. (5.36)j jtВероятности pt(0) определяются начальными условиями функциониро¬
вания системы. В большинстве случаев при / = 0 все элементы системы
находятся в исправном состоянии, тогда /;0(0) = 1, Р\(0) =... = рт{0) = 0.В результате решения системы алгебраических уравнений (5.36) опреде¬
ляются Pj(z). Оригиналы Pj(t) находятся по любому известному методу.5. Вычисление требуемых показателей надежности системы.Решение систем уравнений (5.34) и (5.35) позволяет определить любые
показатели надежности невосстанавливаемых и восстанавливаемых сис¬
тем.Рассмотрим случаи невосстанавливаемой и восстанавливаемой систем.Случай 1. Система работает только до первого отказа. Вероятность безотказ¬
ной работы технической системы за время t вычисляется по формуле:т=2>«(о-/е£+Среднее время безотказной работы вычисляется по одной из следующих
формул:ООТх= \P(t)dt или ТХ=Р{0).оПервой формулой целесообразно пользоваться в том случае, когда вероят¬
ность безотказной работы представлена в явном виде, а второй — когда веро¬
ятность безотказной работы вычислена с помощью преобразования Лапласа.
Для определения среднего времени безотказной работы 7] при неизвестныхвыражениях для P(t) или P(z) составляется система линейных алгебраиче¬
ских уравнений относительно среднего времени пребывания технической
системы в исправных состояниях:" Z Чут« + £ Ч'ту = “A(0)> i е Е+ .jeE jeE
Методы анализа надежности технических систем213Последняя система формально получается из системы (5.36) при z-0 и с
использованием очевидных равенств:QOт( = jPi(t)dt, i<=E+.
оТогда среднее время безотказной работы находится суммированием средних
времен пребывания системы в исправных состояниях:ieE+Случай 2. Система восстанавливается после наступления отказа. Функция
готовности системы вычисляется по формуле:ад=Ей(0. (5-37)ieE+Решение системы алгебраических уравнений (5.35) позволяет определитьстационарные значения вероятностей pt = lim Pj(t), ieE, а по ним— сред-/->00нюю наработку на отказ, среднее время восстановления и коэффициент го¬
товности системы:£ Pi Z Pirrt гг* ^ /€/£_" I Pi I Чу ’ B=bIV/e£+ ys£_ ieE+ je E_Существенным недостатком метода, основанного на теории марковских про¬
цессов, является ограниченность его применения. Он применим только в слу¬
чае экспоненциальных распределений времени безотказной работы и восста¬
новления элементов.5.5.3. Пример расчета показателей надежности
методом марковских процессовПРИМЕР 5.26. Вычислить показатели надежности системы, структурная
схема которой представлена на рис. 5.33. Элементы дублированной подсис¬
темы равнонадежны с интенсивностью отказов Х]=0,02 час-1 и интенсив¬
ностью восстановления ц, =0,5 час-1. Интенсивности отказов и восстанов¬
лений нерезервированного элемента равны соответственно Х2 =0,01 час”1 и
ц.2=1 час'1. Обслуживает систему одна ремонтная бригада с прямым при¬
оритетом. В начале функционирования все три элемента находятся в исправ¬
ном состоянии. Время непрерывной работы системы t = 10 час.*г=ЕРг/е£+т+та(5.38)
214Глава 5Решение. Будем следовать приведенному ранее алгоритму.Отказ системы наступает в том случае, когда откажут оба элемента, входя¬
щие в дублированную подсистему, или произойдет отказ нерезервированного
элемента. Граф состояний изображен на рис. 5.34. Дугам графа приписаны
интенсивности переходов, равные интенсивностям отказов и восстановлений
тех элементов, из-за которых происходят эти переходы.Состояния (0) и (1) являются состояниями работоспособности, а состояния
(2), (3), (4) — отказовыми.Система дифференциальных уравнений для определения P(t) имеет вид:| Ро (0 = —(2Я., + Х2 )р0 (/) + ц,/?, (/);I Р\ (О = 2Х,а>(0 - (X, + Х2 + ц, )рх (/).Вычислим вероятности исправных состояний p0(t) и px(t) при условии, что
все элементы при / = 0 исправны, т. е. />0(0) = 1, /7, (0) = 0 . В преобразовании
Лапласа система уравнений имеет вид:f zp0 (z) -1 = -(2Х, + Х2 )р0 (z) + (z);[Pi (*) = 2Xxp0(z) - (X, + \2 + ц, )рх (z).Решая эту систему алгебраических уравнений, получим:Ро ^ z + + Х2 + ц, z + (ЗА.| + 2"К2 + Ц] )z + 2X.J + ЪХхХ2 + Х2 + Х2Ц12Ххpx(z) = — ^ .z + (3Xj + 2Я<2 + Ц] )z + 2Хх + 3 А.|\2 + \2 +Вероятность безотказной работы в преобразовании Лапласа имеет вид:P(z) = p0(z) + px (z) = -s L+2hlh..+ Mi .z + (3Xl + 2X2 "Ь + 2A#j И- 3A.jA/2 + ^2 ^2MiПодставляя числовые значения интенсивностей, получим:P(Z)=— Z-1^- .z2 + 0,58z+ 0,0065Переходя от изображения к оригиналу, определим вероятность безотказной
работы как функцию времени:Р(0 = 1,002е~°'°1 и - 0,002е-0’569'.Для / = 10 час Р(10) = 0,898.
Методы анализа надежности технических систем215Найдем среднее время безотказной работы:Тх = Р(0) = 87,69 час.Система дифференциальных уравнений для определения функции готовности
имеет вид:>0 (0 = —(2Л., + Х2 )Ро (0 + Mi Pi (0 + V2P2 (0;
p\(t) = 2Xxp0(t) - (Хх + Х2 + ц, )рх (0 + ц,/?3(0;' P2(0 = ^2Po(0-M2/J2(0 + MlP4(0;/>з(0=Ча(0-шл(0;
p\(t) = X2px(t)-\xxp4(t).Так как по условию задачи при / = 0 все элементы исправны, тор0(0) = 1, Р\(0) = р2(0) = /73(0) = />4(0) = 0.Запишем систему уравнений в преобразовании Лапласа:zp0(z)-\ = -(2Xx +X2)p0(z) + nxpx(z) + n2p2(z);
zpx(z) = 2Xxp0(z)-(Xl+X2+Lil )Р\ (z) + р, рг (z);< zp2(z) = X2p0(z)-\x2p2(z) + iixp4(z);
zpi(z) = Xxpi(z)-ixxp3(z);
zp4(z) = X2px(z)-iixp4(z).Решая эту систему для заданных значений интенсивностей переходов, по¬
лучим:. , ч z4 + 2,53z3 + 2,3z2 + 0,8975z + 0,1275Pa (Z) — z г ,z(z + 2,58z + 2,3965z + 0,9572z + 0,139475)
0,04z3+0,08z2+0,05z + 0,01p\ (Z) — * : г г .z(z4 + 2,58z3 + 2,3965z2 + 0,9572z +0,139475)Найдем изображение функции готовности:^ z4 + 2,57z3 + 2,38z2 + 0,9475z + 0,1375r Z ~~ z(z4 + 2,58z3 +2,3965z2 +0,9572z + 0,139475)Чтобы перейти от изображения Kr(z) к оригиналу, найдем корни знамена¬
теля:z,=0, z2 =-0,436, z3=-0,5, z4 =-0,632, z5 =-1,012.
216Гпава 5Тогда оригинал имеет вид:Kr(t) = 0,986 + 0,017е“°'436' -0,014е“°’632' +0,011<Г!’012'.
Для 1 = 10 час АГг(10) = 0,98619.Определим коэффициент готовности системы:*г = Шп/:г(О = 0,986.
<->00Определим стационарные вероятности исправных состояний:Ро = I™ РоО) = Hm zpQ (z) = = 0,914,t-yco z-> о 0,139475р, = lim Рх (0 = lim zpx (z) = - °’01 = 0,072 ./-><» z-> о 0,139475Наработку на отказ и среднее время восстановления определим по формулам
(5.38):т = Ро±Р} _ 0,072 = 87,26 час,^Po+iK+^Pi 0,01-0,914 + 0,03-0,072т _ 1 -iPo + Pi) _ 1-(0,914+ 0,072) . 24 час
в Х2р0+(Х1+Х2)р1 0,01-0,914 + 0,03 0,072 ’Поскольку коэффициент готовности, наработка на отказ и среднее время вос¬
становления связаны между собой соотношениемгК=-Т + Твто это равенство может служить проверкой правильности расчетов.5.5.4. Особенности анализа надежности систем
при законах распределения отказов
и восстановлений, отличных от экспоненциальногоКак известно, экспоненциальные распределения обладают свойством "отсут¬
ствия памяти". Поэтому для прогнозирования развития процесса в будущем
достаточно знать поведение системы лишь в данный момент времени и не
важно, как протекал процесс до этого. Если хотя бы одна случайная величи¬
на, входящая в процесс функционирования системы, имеет неэкспоненциаль¬
ный закон распределения, то для описания эволюции системы уже необходи¬
мы знания о всей предыстории системы. В этом и состоит основная особен¬
ность расчета надежности при неэкспоненциальных распределениях. Для
Методы анализа надежности технических систем217каждого состояния системы информация о прошлом может запоминаться в
виде компонент вектора состояний всех элементов или, по крайней мере,
элементов, имеющих неэкспоненциальные распределения.Безусловно, расчет показателей надежности и анализ таких систем представ¬
ляет собой достаточно сложную задачу для инженера. Выход из этого поло¬
жения состоит в разработке программных средств с дружеским интерфейсом,
позволяющий производить расчеты в реальном масштабе времени и с прием¬
лемой точностью. В настоящее время методики доведены до практической
реализации, а разработанные программные средства дают возможность ин¬
женеру выполнить расчеты всех показателей надежности сложной системы.
Ограничениями являются лишь недостаточно высокие характеристики ис¬
пользуемых разработчиком ЭВМ.В последующих главах будут рассматриваться методы анализа надежности и
большое число примеров при произвольных распределениях времени до от¬
каза и восстановления элементов. В ряде случаев получаются законченные
аналитические выражения для оценки показателей надежности систем,
позволяющие довести значения требуемых показателей до числового резуль¬
тата.5.6. Метод статистического моделированияОпределение закона распределения времени безотказного функционирования
сложной системы по известным характеристикам надежности составляющих
ее элементов является очень важной задачей в теории и практике надежности.
Эта задача изучалась многими авторами [29, 53, 36, 123], но она еще далека
до своего окончательного практического решения. Достаточно сказать, что в
настоящее время отсутствует хороший алгоритм для вычисления вероятности
безотказной работы дублированной восстанавливаемой системы с постоянно
включенным резервом и произвольными законами распределения элементов.
Справедливости ради следует отметить, что имеются простые по форме запи¬
си аналитические модели, описывающие функционирование технических
систем при произвольных распределениях времени исправной работы и ре¬
монта их элементов, которые, к сожалению, оказываются весьма сложными
для их реализации на ЭВМ. Эти модели представляют собой системы инте¬
гральных или дифференциальных уравнений в частных производных относи¬
тельно функций с большим числом аргументов [33]. Расчет надежности ана¬
литическими методами может быть выполнен для восстанавливаемых систем
только следующего вида:□ резервированная система из п элементов с постоянно включенным резер¬
вом, обслуживаемая п ремонтными бригадами (нестационарный и ста¬
ционарный режимы) по критериям Т , Тв, Кг, T(t), TB(t), Kr(t);
218Глава 5□ дублированная система с резервом замещением для полностью ограни¬
ченного восстановления (стационарный режим) по критериям Т , Тв, Кг;□ последовательно-параллельная система с нагруженным или ненагружен-
ным резервом, обслуживаемая одной ремонтной бригадой с обратным
приоритетом (стационарный режим) по критериям Т , Тв, Кг.Такая важнейшая характеристика надежности системы, как вероятность без¬
отказной работы P{t), может быть вычислена для ряда частных систем путем
решения некоторых относительно несложных интегральных уравнений (типа
свертки).Известные в настоящее время подходы (полумарковские и асимптотические
методы, методы регенерирующих процессов и многомерных марковских
процессов и т. д.) позволяют оценивать вероятность безотказной работы
только для систем с всевозможными допущениями относительно их функ¬
ционирования и обслуживания. Основными допущениями, как правило, яв¬
ляются экспоненциальность некоторых компонент или быстрое восстановле¬
ние элементов системы. В общем случае вычисление P(t) системы при про¬
извольных распределениях времени безотказной работы и восстановления
элементов сопряжено с большими вычислительными трудностями. Тем не
менее существует всеобъемлющий метод статистического моделирования,
который, в принципе, позволяет решать перечисленные и другие аналогич¬
ные задачи. Метод, несмотря на его универсальность, имеет существенные
недостатки: большое время решения задачи, сложность оценки погрешностей
расчетов, отсутствие явных выражений показателей надежности. Однако в
некоторых случаях он вполне может использоваться.5.6.1. Сущность и обоснование
метода статистического моделированияМетод статистических испытаний (Монте-Карло) базируется на использова¬
нии значений случайных величин с заданным распределением вероятностей.
Сущность метода статистического моделирования состоит в построении ал¬
горитма, имитирующего поведение системы, и реализации этого алгоритма
на ЭВМ. В результате статистического моделирования системы получается
серия частных значений искомых показателей надежности. Эти значения об¬
рабатываются и классифицируются методами математической статистики,
что позволяет получить сведения о надежности реальной системы в произ¬
вольные моменты времени. Если количество реализаций N достаточно вели¬
ко, то результаты моделирования системы приобретают статистическую ус¬
тойчивость и могут быть приняты в качестве оценок искомых показателей
надежности.
Методы анализа надежности технических систем219Теоретической основой метода статистического моделирования на ЭВМ яв¬
ляются предельные теоремы теории вероятностей. Принципиальное значение
предельных теорем состоит в том, что они гарантируют высокое качество
статистических оценок показателей надежности при весьма большом числе
испытаний (реализаций). Практически приемлемые количественные оценки
показателей надежности систем могут быть получены уже при сравнительно
небольших значениях N.Предположим, что требуется вычислить неизвестную величину m. Это мо¬
жет быть, например, математическое ожидание некоторой случайной величи¬
ны \, т. е. = m. Пусть при этом среднее квадратическое отклонение
случайной величины ^ равно а.Рассмотрим N независимых случайных величин распределе¬ния которых совпадают с распределением \. Если N достаточно велико, то,
согласно центральной предельной теореме, распределение величины— 1 ^ СУ£ = — V 4/ будет приблизительно нормальным с параметрами m и —в=.
N i=\ y/NПри этом имеет место приближенное равенство:1 N<8sVtV(5.39)где Ф0(О — функция Лапласа.Это чрезвычайно важное для метода Монте-Карло соотношение. Оно дает
нам и метод расчета m , и оценку погрешности. В самом деле, из (5.39) видно,
что среднее арифметическое значений случайной величины £ будет прибли¬
женно равно m. С большой вероятностью ошибка такого приближения непревосходит величины Очевидно, эта ошибка стремится к нулю с рос-y/Nтом N. Уже при числе реализаций N>20 это равенство дает хорошее при¬
ближение.Если доверительная вероятность у = 2Ф0, то для обеспечения точно-/сти в количество испытаний должно быть равно величине N =-Фо18\2 j j
220Гпава 5f 2 бет ^Так, например, при у = 0,99 имеем N = —— . Конечно, N зависит отV. S усреднего квадратического отклонения случайной величины которое ино¬
гда заменяется соответствующим выборочным значением.5.6.2. Разыгрывание случайных величинПри решении различных задач надежности методом статистического модели¬
рования приходится моделировать различные случайные величины. В мате¬
матическом обеспечении современных ЭВМ имеются специальные програм¬
мы генерирования случайных чисел с различными законами распределения.
Наиболее употребительны равномерно распределенные на отрезке [0; 1] слу¬
чайные числа %п. Для их получения в алгоритмических языках есть специ¬
альные функции: Rnd — в языке Basic, Randu — в языке Fortran, Random —
в языках Clipper, Pascal, C++, СЛЧИС () — в Excel, Rand— в Php, Perl и т. д.
Все машинные датчики дают псевдослучайные числа, т. к. вследствие конеч¬
ности разрядной сетки наблюдается их повторение.Этими функциями располагают также все универсальные программные сред¬
ства символьной математики (Mathematica, Maple, Derive и др.)Поскольку "качество" используемых случайных чисел проверяется с по¬
мощью специальных тестов, можно не интересоваться тем, как эти числа по¬
лучены, лишь бы они удовлетворяли принятой системе тестов. Можно даже
попытаться вычислять их по заданной формуле. Числа, получаемые по какой-
либо формуле и имитирующие значения случайной величины £, называются
псевдослучайными.В качестве примера в табл. 5.5 приведены равномерно распределенные (псев-
до) случайные числа (РРСЧ) на промежутке [0; 1], полученные в Excel с по¬
мощью функции СЛЧИС ().Таблица 5.5. Псевдослучайные числа0,33330,23800,91670,25330,46110,08250,04350,45900,74510,8787Почти все стандартные библиотечные программы вычисления последова¬
тельностей псевдослучайных чисел основаны на конгруэнтных методах. Од¬
ним из наиболее известных является мультипликативный конгруэнтный ме¬
тод. Его основная формула выглядит следующим образом:£л+1 =^„(modm),
Методы анализа надежности технических систем221где а и m — неотрицательные целые числа. Очевидно, что выполняются
неравенства < m. Согласно этому выражению, мы должны взять последнее
число , умножить его на постоянный коэффициент а и взять модуль по¬
лученного числа по m , т. е. разделить на m , и найти остаток. В резуль¬
тате получаем последовательность псевдослучайных чисел, равномерно рас¬
пределенных от 0 до m -1. Для того чтобы из нее получить последователь¬
ность псевдослучайных чисел, равномерно распределенных от 0 до 1, нужно
каждый из членов полученной последовательности разделить на m . В каче¬
стве примера приведем один из достаточно "хороших" коротких алгоритмов
разыгрывания РРСЧ, который по начальному числу из промежутка [0; 1]
позволяет найти новое число £„+] из этого промежутка:а = 16807-Ю10, /я = 2147483647, у = а£и, у = у-У_mЬп+\= — ■
mСледует еще раз подчеркнуть, что программные генераторы дают последова¬
тельность псевдослучайных чисел, которые не являются случайными по сво¬
ей сути, но в силу огромной длины последовательности псевдослучайных
чисел само появление их в этой последовательности воспринимается нами
как появление случайных чисел.Достоинства метода псевдослучайных чисел очевидны. Во-первых, на полу¬
чение каждого числа затрачивается всего несколько простых операций, так
что скорость генерирования случайных чисел имеет тот же порядок, что и
скорость работы ЭВМ. Во-вторых, программа генерирования обычно очень
проста. В-третьих, любое из случайных чисел может быть легко воспроизве¬
дено. В-четвертых, нужно лишь один раз проверить "качество" такой после¬
довательности, затем ее можно много раз использовать при расчете сходных
задач.Единственный недостаток метода — ограниченность "запаса" псевдослучай¬
ных чисел. Однако существуют способы, позволяющие получать гораздо
больше чисел, меняя начальное число. Подавляющее большинство расчетов
по методу Монте-Карло в настоящее время осуществляется с использованием
псевдослучайных чисел.По числам 5 равномерно распределенным на [0; 1], получают числа, рас¬
пределенные по любому другому закону с функцией распределения F(x).Процесс нахождения значения какой-либо случайной величины X путем
преобразования одного или нескольких значений % называется разыгрывани¬
ем случайной величины X.
222Глава 5Разыгрывание дискретной случайной величиныДопустим, что нам нужно получить значения случайной величины X с рас¬
пределениемXхх х2 ... х„рPi Pi - PnРассмотрим интервал 0 < у < 1 и разобьем его на п интервалов, длины кото¬
рых равны р{, р2,, рп. Координатами точек деления, очевидно, будутУ-Р\ъ У = Р\+Рг» y = Pi+P2+Pi>-’ У = Р\ + Р2+-+ Pn-i- Полученные
интервалы пронумеруем числами 1, 2,..., п, как показано на рис. 5.37.О Р\ Р\+Рг Р\+Рг+ Рг Р\ + Рг+~ + Рп-\ 1 у
Рис. 5.37. Получение дискретной случайной величиныКаждый раз, когда нам надо разыграть значение X, мы будем выбирать слу¬
чайное число \, имеющее равномерное распределение на [0; 1]. Если число
\ попало в /-й интервал, то будем считать, что X = х{. Законность такой
процедуры достаточно очевидна. В самом деле, т. к. случайная величина £,
равномерно распределена в [0; 1], то вероятность того, что % окажется в не¬
котором интервале, равна длине этого интервала. Значит,P(0<$<Pi) = P\>Р(.Р\ ^Z,<Pl+P2) = P2»P(Pi +р2+ - + Рп-\ <^<\) = рп.Согласно нашей процедуре X = х, тогда, когда рх + р2 + — + Pi-\ £%<
рх + р2 +... + Pj_\ <£,</?!+ р2 +... + Pj с вероятностью р,.ПРИМЕР 5.27. Требуется разыграть 10 значений случайной величины, за¬
данной таблицейX3 5P0,64 0,36
Методы анализа надежности технических систем223Решение. В качестве значений £ берем числа из табл. 5.5, ограничиваясь
двумя цифрами после запятой:0,33; 0,24; 0,92; 0,25; 0,46; 0,08; 0,04; 0,46; 0,75; 0,88.По нашей схеме значениям, меньшим 0,64, отвечает значение X = 3, а значе¬
ниям, большим или равным 0,64 — значение X = 5 . Следовательно, мы по¬
лучим значения: X = 3, 3, 5, 3, 3, 3, 3, 3, 5, 5 .Если случайная величина X имеет геометрическое распределение с пара¬
метром р, то процедура разыгрывания упрощается. Случайная величина X
может принять одно из значений /и = 1,2,3,... с вероятностьюр(Х = m) = qm~lр. Для разыгрывания случайной величины, подчиненной
геометрическому распределению, применяется формулаIn £,Л -1п(1-/?)где £, — равномерно распределенное случайное число из промежутка [0; 1].Разыгрывание непрерывной случайной величиныПредположим, что случайная величина X непрерывна, а ее функция распре¬
деления вероятностей F(x) монотонно возрастает. Тогда искомое распреде¬
ление имеют числа хп =F~’(^„), где — равномерно распределенные слу¬
чайные числа на промежутке [0; 1]. Указанный метод получения (разыгрыва¬
ния) случайных чисел носит название метода обратных функций. Он имеет
простой геометрический смысл, представленный на рис. 5.38.
224Гпава 5Указанный метод можно применять только в том случае, если существует
обратная функция.Рассмотрим метод для получения случайных чисел, имеющих показатель¬
ное распределение. Для показательного распределения F(х) = \-е~1'л при*>0, а обратная функция имеет вид F~\x) = —-Infl -х). ПоэтомуА,х„ = 1п(1 -%п)— случайное число, распределенное по показательному
Xзакону. Заметим, что вместо можно писать просто .Нормально распределенные случайные числа нельзя получить методом об¬
ратных функций, т. к. для этого необходимо решать уравнение с неизвест¬
ным, являющимся верхним пределом интеграла. Здесь мы рассмотрим другой
способ получения случайных чисел, имеющих нормальное распределение с
параметрами т и а.Сначала получим случайные числа, имеющие нормальное распределение с
параметрами 0 и 1. Эти числа находят парами. Пусть г]j и т]2 — два случай¬
ных числа, имеющие нормальное распределение с параметрами 0 и 1, полу¬
ченные по паре случайных чисел и §2, равномерно распределенных наотрезке [0; 1]. Построим вектор r(r|,,г|2)» как показано на рис. 5.39.Угол а имеет равномерное распределение на промежутке [0;2тс], т. е,"Уa = 2л£,. Квадрат длины вектора г имеет показательное распределение
с параметром 1/2. Действительно,_ 1 *1 +х2 1 2% <ю 1-2 ■ _1_F(f) = P(rfi + til > t) = — IT e 2 dxldx2=-—j dcp (re 2dr = e2.2Пх?+хЫ 2n 0 ftРис. 5.39. К получению нормально распределенных случайных чисел
Методы анализа надежности технических систем225Поэтому г2 = -21п(£2) • Отсюда г = л/-21п(£2) • В результате получили пару
чисел, имеющих нормальное распределение с параметрами 0 и 1:Г)! = rcosa = yj-21п(42) cos(2n^),r)2 = г sin a = ^/-2ln(42)siri(2rc^2).Теперь легко получить нормально распределенные случайные числа с пара¬
метрами m и a. Они вычисляются по формулам:= m + стгц, С2 = m + CTTl2 •Формулы для разыгрывания рассмотренных и некоторых других случайных
величин непрерывного типа помещены в табл. 5.6.Таблица 5.6. Формулы разыгрывания непрерывных распределенийРаспределениеФормулы для разыгрыванияРавномерное U(a,b)iy = a + (b-a)$Экспоненциальное1п£Ехр(Х) Iл XЭрланга Е(к,к)л1/=1 лНормальное N(/n,a)г\ = m + OyJ-2 In cos(27t^,),
r\ = m + Gy]-2 in^2 sin(27i5,)Логнормальное LN(a,.s)ri = exp(o + Syj-2 In\г cos(27t^)),
r) = exp(a + syj-2ln^2 sin(2ii£,))Вейбулла W(a,p)1n = P(— in 4)“Величины \ и E,j представляют собой равномерно распределенные случай¬
ные числа из промежутка [0; 1].8 Зак. 3094
226Глава 5Разыгрывание равномерно распределенной
случайной величины на многомерном симплексеРассмотрим способ разыгрывания важной многомерной случайной величины.
Пусть, например, я-мерная случайная величина X = (Хх, Х2,..., Хп) распре¬
делена равномерно на симплексе: xx+x2+... + xn<t, л, > 0, х2>0,...,
хп*0.Разыгрывание этой случайной величины можно осуществить следующим об¬
разом. Разыграть я РРСЧ на [0; f] %\,^2,..., и проверить, выполняется ли
неравенство jct + х2 + ...+ хп <t. Если выполняется, то тем самым будет полу¬
чена реализация многомерной случайной величины X. В противном случае
разыгрывается другой набор РРСЧ на [0; /] ^\,%2,... и т. д. Такой подходявляется абсолютно неприемлемым, поскольку вероятность попадания в
я-мерный симплекс очень мала, особенно при больших значениях п. Дейст-tnвительно, объем я-мерного симплекса Vn = —, следовательно, вероятностьл!1попадания в него равна рп= —.и!Поэтому надо иметь алгоритм, который бы на каждой своей реализации да¬
вал значения случайной величины X.Распределение Х{ на отрезке [0;/] должно быть таким, чтобы соответст¬
вующая функция распределения была равна отношению объема я-мерной
фигуры, которая проектируется на отрезок [0; jcj ] к объему всего я-мерного
симплекса. Это значит, чтоV tn tyn,l t \ 1Пояснением этому при я = 2 служит рис. 5.40.Методом обратных функций разыграем случайную величину с функцией
распределения (atj ):
Методы анализа надежности технических систем227Рис. 5.40. Генерирование случайных точек, равномерно распределенных на симплексе (я = 2)
Отсюда( 1 "l( ^X, =t, или xx-ti-sf4 /V /где — РРСЧ на [0; 1].Распределение случайной величины Х2 зависит от Хх. Ее значение получа¬
ется по формулеi-sr1где — РРСЧ на [0; 1].
Далее получим:*3 =(*-*1 -х2)( j_
\-ц-2где — РРСЧ на [0; 1], и т. д.Формула разыгрывания случайной величины Хп имеет видx„=(t~xl —лг2 ——Jc„_i)(l —
где ^ — РРСЧ на [0; 1].В частности, при п = 2 алгоритм получения случайных точек, равномерно
распределенных на симплексе х + y<t, х>0, у> 0, дается формулами:[y = (t-x)^2.
228Гпава 55.6.3. Сравнение метода
статистического моделирования
с аналитическими методами расчета надежностиБудем сравнивать эти методы на примерах решения задач.ПРИМЕР 5.28. Требуется определить долю времени K(t) = f в течениеtкоторого система находится в исправном состоянии при ее функционирова¬
нии в течение времени t. Здесь m(t) — средняя суммарная наработка. Функ¬
ционирование системы представляет собой альтернирующий процесс с двумя
состояниями: исправная работа и восстановление после возникновения отказа
системы. Пусть /(*) —- плотность распределения времени исправной рабо¬
ты, a g(x) — плотность распределения времени восстановления системы.Решение. Произведем разыгрывание случайных чисел isi, имеющих распре¬
деление вероятностей с плотностью f(x), и , имеющих распределение ве¬
роятностей с плотностью g(х). Один из возможных вариантов расположения
чисел и Г|; показан на рис. 5.41., *■ | Ч, | $2 | П, | $3 | >О I' t, часРис. 5.41. Диаграмма, иллюстрирующая определение функции K(t)Число проводимых опытов заранее неизвестно, оно определяется моментом
времени t и значениями чисел ^ и Г|,.Для решения задачи должно быть предусмотрено накопление двух сумм:
суммарной наработки S,, равной сумме 4,, и S, равной сумме и г|;.
Опишем алгоритм метода статистического моделирования:1. 5 = 0, 5, =0.2. Пока S < t, выполнить:• разыгрывание ^ и г|,;• если S + £,•>/, то 51, = Sx + / - S , и выйти из цикла;• иначе, если S + ^i+r\i>t, то Sx = Sx + , и выйти из цикла.3.
Методы анализа надежности технических систем2294. S=S+^+ л,--5. K(t) = Sjt.В результате работы этого алгоритма будет получена одна из реализаций
функции K(t). Выполнив этот алгоритм многократно, получим множество
реализаций, и тогда за истинное значение требуемой величины можно при¬
нять среднее арифметическое этих реализаций.Рассмотрим поведение функции K(t) для следующих исходных данных:
время безотказной работы имеет экспоненциальное распределение с пара¬
метром X = 0,001 час-1, время восстановления также имеет экспоненциальное
распределение с параметром ц = 0,04 час-1. В табл. 5.7 получены значения
функции K(t) для N = 20 опытов (реализаций), для N = 500 опытов и точ¬
ное значение, рассчитанное по формулец XK(t) = -^1 + Х (ц + А.)2*Таблица 5.7. Значения доли времени пребывания системы в исправном состоянииt, часW= 20ОО•о11Точное01111000,9740,9760,9812000,9750,980,9793000,9870,9780,9784000,9620,980,9775000,970,9750,9776000,9780,9750,9777000,9580,9740,9768000,9710,9760,9769000,9840,9770,97610000,9640,9770,976Соответствующая графическая иллюстрация приведена на рис. 5.42 в виде
трех графиков.Из рис. 5.42 следует вывод о существенной зависимости K(t) от числа опы¬
тов. При малом числе опытов (N = 20) наблюдается значительное отклоне¬
230Глава 5ние кривой K(t) от истинной. При большом числе опытов (N = 500) график
функции K(t) оказывается очень близким к истинному.тРис. 5.42. Доля времени пребывания в исправном состоянии для N = 20 (кривая 1),
для N = 500 (кривая 2), точное значение (кривая 3)ПРИМЕР 5.29. Структурная схема системы приведена на рис. 5.43.Рис. 5.43. Структурная схема системы с резервом типа "замещение"Времена безотказной работы Хх, Х2, Хг элементов системы являются слу¬
чайными и распределены по нормальному закону. Параметры распределений
содержатся в табл. 5.8.Таблица 5.8. Значения параметров распределенийПараметры**2х3т, часНО150260а, час283040I
Методы анализа надежности технических систем231Требуется оценить надежность системы методом статистического моделиро¬
вания и сравнить полученные результаты с аналитическим методом.Решение. Проведем имитацию работы системы. Согласно схеме, отказ пары
элементов 1 и 2 произойдет тогда, когда откажет первый, а затем второй эле¬
мент, т. е. время до отказа этой пары равно сумме Хх + Х2. Считая пару эле¬
ментов 1 и 2 одним элементом, имеем последовательное соединение с эле¬
ментом 3. Время до отказа этой пары равно минимальному из времен до от¬
каза составляющих ее частей. Значит, время до отказа системы
r = min(^ +Х2,Х3).Поставленную задачу удобно решить с помощью программного средства
Microsoft Excel. На лист Excel (табл. 5.9) в блок ячеек А1 : D4 помещаются
законы и параметры заданных случайных величин.Таблица 5.9. Разыгрывание случайных величин в ExcelАВСDЕF1СлучайнаявеличинаЗаконраспределенияmа2XIНорм.110283Х2Норм.150304ХЗНорм.2604056РРСЧРРСЧXIХ2ХЗY70,1470,425132,127181,255291,610291,61080,8920,183150,090115,224317,272265,3141060,0270,781129,429153,549287,756282,979В ячейки шёстой строки А6—F6 помещаются заголовки таблицы. В ячейки
А7 и В7 заносятся равномерно распределенные случайные числа из проме¬
жутка [0; 1] в соответствии с формулами:А7 = СЛЧИС (),В7 = СЛЧИС ().В ячейки С7, D7, Е7 помещаются значения случайных величин Хх, Х2, Х3,
имеющие нормальное распределение, в соответствии с формулами разыгры¬
вания, приведенными в табл. 5.6:
232Гпава 5С7 = 110 + 28*KOPEHb(-2*LN(B7))*COS(2*ПИ()*А7)),D7 = 150 + 30*КОРЕНЬ(-2*LN(В7))*SIN(2*ПИ()*А7)),Е7 = 260 + 40*KC>PEHb(-2*LN (В7) ) *COS (2*ПИ() *А7) ).Колонка F служит для значений случайной величины Y:F7 = МИН (С7 + D7; Е7).В результате этих действий будут заполнены ячейки седьмой строки А 7—F7.
Получим 100 значений данных случайных величин. Для этого содержимое
ячеек А7—F7 копируется в следующие строки вплоть до 106 строки, как по¬
казано в табл. 5.9.В результате получены статистические данные, характеризующие время до
отказа системы. Эти данные содержатся в ячейках F7—F106.Вычислим выборочное среднее:F108 = СРЗНАЧ(F7 : F106) = 246,64.Это значит, что среднее время безотказной работы по методу статистическо¬
го моделирования составляет 7]и = 247 час.Полученные статистические данные с помощью функции "Частота" позволя¬
ют определить статистическую функцию распределения F(t) в виде значе¬
ний накопленных относительных частот, как показано в табл. 5.10, а по
ней — вероятность безотказной работы PH(t) = 1 - F(t) .Таблица 5.10. Расчет вероятности безотказной работы двумя методамиГруппаГраницыСере¬динаЧастотаНак.частотаНак. отн.
частотаР( 0ЛеваяПраваяИмитацияАналитика102010000,0001,0001,0002204030000,0001,0001,0003406050000,0001,0001,0004608070000,0001,0001,00058010090000,0001,0001,0006100120110000,0001,0001,0007120140130000,0001,0000,9998140160150000,0001,0000,9939160180170220,0200,9800,97410180200190790,0900,9100,918
Методы анализа надежности технических систем233Таблица 5.10 (окончание)ГруппаГраницыСере¬динаЧастотаНак.частотаНак. отн.
частотапоЛеваяПраваяИмитацияАналитика1120022021014230,2300,7700,7951222024023026490,4900,5100,5941324026025018670,6700,3300,3571426028027016830,8300,1700,162152803002907900,9000,1000,053163003203107970,9700,0300,012173203403302990,9900,0100,0021834036035011001,0000,0000,0001936038037001001,0000,0000,0002038040039001001,0000,0000,000Для сравнения в табл. 5.10 приведены расчеты P(t) аналитическим методом
в соответствии с формулой:Г , \РЛ0=*з(0-!- J f\ * h(x)dx\ -00 уГрафики P(t), построенные методом статистического моделирования и ана¬
литическим методом, приведены на рис. 5.44. Они достаточно близки друг к
другу.Точное значение среднего времени безотказной работы составляет Ц а = 260 час.Заметим, однако, что в примере легко можно применить аналитические мето¬
ды, т. к. свертка нормальных распределений снова дает нормальное распре¬
деление. В общем случае аналитический метод далеко не всегда может быть
применен для расчета надежности сложной системы, тем более если отсутст¬
вуют аналитические выражения видов распределений случайных величин, а
имеются только статистические данные об их отказах.ПРИМЕР 5.30. Рассмотрим структурную схему расчета надежности, состоя¬
щую из 4-х подсистем, включающих типичные виды резервирования
(рис. 5.45). Интенсивности отказов элементов каждой подсистемы предпола¬
гаются постоянными и равными Л.х, Х2, Х,3 и Я.4 соответственно.
234Глава SРО)Рис. 5.44. Сопоставление расчетов двумя методами: имитация (кривая 1),
аналитика (кривая 2)Х3Постоянный Дробная Резерврезерв кратность замещением1/2Рис. 5.45. Структурная схема расчета надежностиПроанализируем работу системы для следующего варианта интенсивностей
отказов элементов (в час-1): А.,=1(Г7, А,2=5-10~6, А.3=1(Г5, Х4=4-1(Г6.
Рассмотрим случаи невосстанавливаемой и восстанавливаемой систем.Решение. Предположим сначала, что рассматривается система без восста¬
новления. Вероятность безотказной работы системы определяется двумя спо¬
собами: по программе имитационного моделирования и по точной аналити¬
ческой формуле:
Методы анализа надежности технических систем235гдеFx(t) = e~Xi‘, F2(0 = 2е~х* - е^‘, F3(t) = Ъе~гх* - 2е~зх>‘,F4(0 = (1 + M«~W-Результаты расчетов представлены в табл. 5.11 и на графике (рис. 5.46).
Таблица 5.11. Вероятность безотказной работы, полученная двумя методамиt, часЛ,(0Р.0)011100000,97140,9705200000,90370,9005300000,81200,8093400000,71330,7100500000,61440,6112600000,52150,5182700000,43910,4339800000,36750,3596900000,30190,29531000000,24580,2406РО)Рис. 5.46. Графики вероятности безотказной работы при отсутствии восстановления:
имитация (кривая 1), аналитика (кривая 2)
236Гпава 5Из примера видно, что результаты расчетов методом имитационного модели¬
рования и по известным аналитическим формулам практически совпадают.
Относительная погрешность не превосходит 2 %, причем на начальном уча¬
стке функционирования системы она намного ниже.Решим ту же задачу при наличии восстановления. Определение вероятности
безотказной работы ремонтируемой системы является более сложной зада¬
чей. Чтобы упростить ее аналитическое решение, предположим, что каждый
узел структурной схемы (см. рис. 5.45) имеет свою ремонтную бригаду. Тогда
эти подсистемы являются независимыми, и в этом случае для P(t) всей сис¬
темы легко выписывается аналитическое выражение:P(t) = Px(t)P2(t)P3(t)PA(t),в которой вероятности безотказной работы узлов выражаются равенствами:Px(t) = e~^,р ^ _ zi + ^2 + 3^2 Qzxt z2+^2+ 3^-2 Cz-,I
Z\ -Z2 Z] - z2-(Й2 + 3^-2 ) - >/(М-2 +3X,2)2 -%k\
где zX2 - — ,p ф _ zi + + SX3 cz,t z2 + ц3 + 5X,3 ^,Z\ Z2 — Z2_ _(йз + 5A,3)±л/(М-з + 5^з)2 “ 24Я,3
где 2, 2 - - ,p _ Z[ + Ц4 + 2A.4 _2lt Z2+\i4 + 2A.4
z\ —Z2 zx—z2_-(»4+2Х4)±^+2Х4)2 -4X24
где Zj 2 — — •2Эти формулы будут получены в гл. 6.Интенсивности восстановления элементов подсистем примем равными сле¬
дующим значениям: (i]=0,l час"1, |л2=0,5 час-1, ц3=0,3 час-1, ц4=1 час-1
соответственно. Результаты расчетов представлены в табл. 5.12 и на графике
(рис. 5.47).Один из графиков (Имитация) получен программным путем для 10000 реали¬
заций, а другой график (Аналитика) рассчитан по точной аналитической
Методы анализа надежности технических систем237формуле. Построенные графики практически совпадают. Максимальная от¬
носительная погрешность не превышаеч^-З^п"'Таблица 5.12. Вероятность безотказной работы, полученная двумя методами1, часР»0)Р.0)01110s0,90,90482 ■ 1060,81370,81873 1060,73310,74084 ■ 10б0,66390,67035 - Ю60,59920,60656- 10б0,54140,54887 - 1060,48690,49668 ■ 1060,43830,44939 -10б0,39430,40601070,35520,3679РО)Рис. 5.47. Графики вероятности безотказной работы для неограниченного восстановления:
имитация (кривая 1), аналитика (кривая 2)
238Глава 5Для упрощения использования аналитических формул мы рассмотрели слу¬
чай неограниченного восстановления. Если восстановление является ограни¬
ченным, то необходимо использовать общие методы анализа систем, осно¬
ванные на теории марковских процессов. Так, например, если все элементы
системы обслуживает один ремонтный орган с прямым приоритетом, то это
потребует составления и решения системы дифференциальных уравнений
65-го порядка. Метод, основанный на имитации, не изменяется; меняются
только исходные данные. Результаты расчетов, полученные методом имита¬
ционного моделирования и путем решения системы дифференциальных
уравнений, практически такие же, что и для неограниченного восстановления.ПРИМЕР 5.31. Методом статистического моделирования требуется полу¬
чить функцию готовности элемента с плотностями распределения времени до
отказа /(/) и времени восстановления g(t). Сравнить полученные результа¬
ты с аналитическим методом.Решение. Функцию готовности можно получить аналогично примеру 5.28.
Однако здесь мы хотим продемонстрировать другой прием, основанный на
применении метода статистического моделирования к вычислению кратных
интегралов типа "свертки". Расчет функции готовности выполним по форму¬
ле (2.31), раскрывая которую получим:Kr(t) = F(t) + JJ f(xl)g(x2)F(t-xx-x2)dxldx2 +ДС|+ДС2<,t+ ffi \f(xx)g(x2)f(x3)g(x4)F{,t-xx-x2-x3-xA)dxxdx2dx7>dx4+...+XAZtИспользуя теорему о среднем, проведем N опытов и заменим интегрирова¬
ние на симплексах генерированием на них равномерно распределенных слу¬
чайных точек с последующим усреднением подынтегральной функции. Тогда
получим:*г(0 = т + ^ I («1 -?2,„>) +|/Wi,»)S('?2,„)/№j,»)sW4,„)P(<0-5u -$2.»-?3.„ -?4,,)) + ■••Здесь в первой сумме (§i „, £2 л) — случайная точка двумерного единичного
симплекса, во второй сумме (^, „, £,2„, \Ъ п, „) — случайная точка четы¬
рехмерного единичного симплекса, и т. д.Формулы для разыгрывания случайной точки л-мерного единичного сим¬
плекса следуют из разд. 5.6.2:
Методы анализа надежности технических систем2391( 1 1( 1 1*!=!-£", x2=(l-x,)l-sr1, х3 =(1-*,-х2)1-4з"-2Ч Ухп = (1 — *! - х2 -...-х„_х )(1 - %п).Для удобства сопоставления методов в качестве /(t) и g(t) примем экспо¬
ненциальные законы распределения с параметрами А. = 0,001 час-1 и
ц = 0,04 час-1. В табл. 5.13 получены значения функции Kr(t) для Т = 10000
реализаций метода статистического моделирования на многомерных сим¬
плексах. Число' слагаемых в сумме соответствует разыгрыванию случайных
точек десятимерного симплекса. Точное значение функции готовности рас¬
считывается по формулеJCr(0—lV+—Ц-е-"1*1".
ц+л ц+лТаблица 5.13. Значения функции готовности, полученные
методом статистического моделирования и аналитическим методомt, часКг.иМ*г,.(0011100,9920,992200,9860,986300,9830,983400,9800,980500,9790,979600,9780,978700,9770,977800,9760,977900,9760,9761000,9770,976НО0,9760,9761200,9760,9761300,9750,9761400,9760,9761500,9760,976
240Гпава 5Соответствующая графическая иллюстрация табличных данных приведена на
рис. 5.48.К«)Рис. 5.48. Графики функции готовности, полученные двумя методами: имитация (кривая 1),аналитика (кривая 2)Совпадение графиков Kr(t) достаточно хорошее, причем оно лучше на пере¬
ходном участке времени, чем на стационарном, для которого' как раз и требу¬
ется большое число реализаций метода статистического моделирования.
ГЛАВА 6АНАЛИЗ НАДЕЖНОСТИ
НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМПредположим, что невосстанавливаемая система состоит из элементов, вре¬
мена до отказа у которых являются независимыми случайными величинами
Хг Пусть Pj(t) и fj(t) — вероятность безотказной работы и плотность рас¬
пределения времени до отказа /-го элемента соответственно.Определим следующие характеристики надежности системы: вероятность
безотказной работы Pc(t), среднее время безотказной работы 7j, плотность
распределения времени до отказа fc(t), интенсивность отказа А,с(/). Рас¬
смотрим случаи нерезервированной и структурно резервированной системы
при общем и раздельном резервировании с постоянно включенном резервом
и по методу замещения.6.1. Надежность
нерезервированной системыСтруктурная схема (схема расчета надежности) нерезервированной системы,
состоящей из п элементов, приведена на рис. 6.1.Рис. 6.1. Структурная схема нерезервированной системыТакое соединение в теории надежности называется основным. В данном слу¬
чае отказ системы происходит при отказе элемента с минимальным временем
исправной работы, т. е.Хс = min(Ar|, Х2, —, Хп},где Хс — время работы системы до отказа. При этом остальные элементы
прекращают работу.
242Глава 6По теореме умножения вероятностей получим:Р(ХС >0 = Р(minCT,,X2,...,X„)>t) == P(Xt >t,X2> t,... ,Xn>t) = fl P(Xj > t),7=1здесь t — время функционирования системы.Отсюда следует, что вероятность безотказной работы системы равна произ¬
ведению вероятностей безотказной работы ее элементов:(6.1)/=1Так как /(/) = -P'(t), то/с(о=1ад.../,(о...ад.j=1Среднее время безотказной работы, являясь математическим ожиданием вре¬
мени до отказа системы, вычисляется по формуле:Г, =]tfc(t)dtилиTx = \Pc(t)dt. (6.2)оОпределим интенсивность отказов системы Xc(t). По определению, интен¬
сивности отказовкт.жш&— ±ш.поэтомуj=1М0=1М0- (6.3)7=1Таким образом, интенсивность отказов системы с основным соединением
элементов равна сумме интенсивностей отказов ее элементов, независимо от
их законов распределения времени до отказов.
Анализ надежности невосстанавливаемых систем243ХМ)Если элементы имеют одинаковую надежность, то —— = п. Последнее оз-МОначает, что интенсивность отказов системы, составленной из равнонадежных
элементов, в п раз превышает интенсивность отказов элемента.Получим формулы показателей надежности системы для случая постоянных
интенсивностей отказов элементов. В данном случае Xj (t) = Xj = const,7 = 1, 2,... ,n .Тогдаn n , X XjJ’cW-rWo-n* e 7=17 = 1 7=1т. e.где Xc = £ Xj .7 = 1Среднее время безотказной работыт. е.Тх = \PQ(t)dt= \e~4dt,о оТ\ =т—• (6.5)ПРИМЕР 6.1. Время исправной работы каждого элемента нерезервирован¬
ной системы имеет распределение Вейбулла с одинаковым параметром фор¬
мы а и параметром масштаба 0у , j = 1, 2,..., п . Найти закон распределениявремени до отказа системы.Решение. Отказы элементов системы имеют распределение Вейбулла, по-/ \ос ._этому Pj(t) = e ^ ' . Тогда зависимость Pc(t) будет иметь вид:Рс(0 = ПРА»=Пе7=1 7=1( I Y "1
— -2—/“
244Глава 6Это значит, что время безотказной работы системы также имеет распределе-1 " 1ние Вейбулла с параметрами аир, где -— = У — .Р“ 7 = 1Р“6.2. Надежность
простейших резервированных системОсновным способом повышения надежности и снижения техногенного риска
является структурное резервирование, которое реализуется путем введения в
систему дополнительных элементов, узлов, блоков.Рассмотрим системы с постоянно включенным резервом и с резервом заме¬
щением.6.2.1. Постоянно включенный резервСтруктурная схема системы с постоянно включенным резервом изображена
на рис. 6.2. Элемент с номером 0 является основным, а элементы с номерами1, 2,..., т — резервными. Общее число элементов в системе rt = т +1, где
т — кратность резервирования — отношение числа резервных элементов к
числу основных.В данном случае отказ системы наступает при отказе элемента с максималь¬
ным временем работы, т. е.Xc=m&x(XQ,Xx,...,Xm).Рис. 6.2. Резервированная система с постоянно включенным резервомПо теореме умножения вероятностей имеем:P(XQ <0 = р{rnax(X0, Хь ... ,Xm)<t) =т= Р(Х0 <t,xx< t,..., хт Z 0 = П Р(Х, * 0-1=0
Анализ надежности невосстанавливаемых систем245Отсюда следует, что вероятность отказа системы равна произведению веро¬
ятностей отказов ее элементов:m&(0 = 1Ш0/=оилиmРс( o=i-по-ад). (6.6)/=0На практике наиболее часто имеют место случаи, когда основная система и
все резервные одинаковы и имеют вероятность безотказной работы P(t).
ТогдаPc(t) = \-(\-P(t))n. (6.7)Так как /(t) = Q'(t), тоm/с(о=Ебь(о.../,(о-а,(о,/=0тогдаmл (о=I (1 - ад)... мо ... о - рт( о) •(=0Определим интенсивность отказов Хс(г) резервированной системы с посто¬
янно включенным резервом. По определению интенсивности отказов имеем:т ттЕшо-жо-одо z/,(ona(oЯ. с(/)=М)=м = i^/ с w р (f\ т тcU i-naw i-naw
( = 0 ( = 0Получим расчетные формулы для случая равнонадежных систем и постоян¬
ной интенсивности отказов элементов Х,0 =Хх = ... = Хт . В этом случае
вероятность безотказной работы системы определяется по формуле:Рс (0 = 1 - (1 - P(t))m+I = 1 - (1 - е~х< )т+]. (6.8)Выражение для интенсивности отказов системы легко получить из соотно¬
шения:
246Глава 6Подставляя в это соотношение Pc(t) из (6.8) и его производную P^(t), по¬лучим:1-(1 —е )-Xt\m(6.9)Из выражения (6.9) видно, что А,с(0) = 0 и с ростом t увеличивается. Пре¬
дельное значение равно lim Xc(t) = А.. Зависимость интенсивности отказов от/->00времени приведена на рис. 6.3.Рис. 6.3. Зависимость интенсивности отказа резервированной системы от времениПолучим выражение для среднего времени безотказной работы системы. Из
выражения (6.8) следует, чтотх ==](i -(1 _«-*')"+» yt.о оВычислим вспомогательный интеграл:1{тп +1) = J(l - (1 - е~х‘ )Л+1) dt = J(l - (1 - e'Xt )m (1 - e~Xt)) dt =(m + 1)A.1(w + l)?iОтсюда следует, что
Анализ надежности невосстанавливаемых систем247Таким образом,1 «1+11
Н?,!'то=Т’тоТак как среднее время безотказной работы нерезервированной системы
Xm+1 1ТХ=Т^~. (6.10)*=1*Из формулы видно, что с ростом кратности резервирования среднее время
безотказной работы системы растет медленно.6.2.2. Резервирование с дробной кратностьюСуществуют технические системы, часто называемые мажоритарными, сдробной кратностью резервирования —т , где т — число резервных эле-п-т.ментов, п — общее число элементов.Мажоритарная система будет работоспособной в течение времени t (собы¬
тие А ) при отказе не более чем т элементов. Пусть At — событие, состоя¬
щее в отказе любых i (0<i<m) элементов за время t. ТогдатЛ=£Л,./=оСобытие А, произойдет, если откажут любые i элементов, а остальные n-i
элементов останутся работоспособными. Вероятность этого события выража¬
ется формулой Бернулли:P(Ai) = ClnQi(t)P"~'(t).Поскольку события Aj попарно несовместны, то вероятность суммы событий
равна сумме вероятностей этих событий, т. е.т тР(А) = Z РШ = I C'nQ\tyPn-\t).(=0 ;=0Таким образом, вероятность безотказной работы мажоритарной системы при
условии, что все элементы имеют одинаковую надежность, равнатPc(t)=I1C,nQ‘(t)Pn-,(t). (6-11)( = 0
248Гпава 6В частности, при т = О получаем основное соединение элементов, для кото¬
рого P0(t) = Pn(t), при m = n-1 —резервное соединение элементов, для ко¬
торого Pc{t) = \-Qn(t). При т = 1 получаем систему, отказ которой наступа¬
ет при отказе двух любых ее элементов. В этом случаеPQ(t) = P\t) + nQ(t)P"-\t).Формулу для вероятности безотказной работы символически можно предста¬
вить следующим образом:(/>(/)+ *2(0")Рс(»=Т- 1i=Оitaьс'*=0Справедливо также рекуррентное соотношение, выражающее вероятность
безотказной работы мажоритарной системы PQ(t) = Pc(t,n,m) через вероятно¬
сти аналогичной системы меньшей размерности:Рс (t,n,m) = Q(t)Pc (t,n-\,m-\)+ P(t)Pc(t,n-\,m).Определим интенсивность отказа Хс (t) мажоритарной системы и исследуем
ее свойства.Так как плотность распределения /сЦ) = -Рё(.0» то> используя формулу
(6.11), получим:т. . т/с(0--Z СЖ (0рП~‘(0/(0 + I ся(И-i)Q‘(t)Pn-‘-x(0/(0 •/=о /=оПреобразуем это выражение:/с(0 = -Z- ~&-\t)PH-\t)m + £ —g'(0^”~'-'(0/(0 =t=1 (/ —1)!(« —z)! /=0г!(«-г-1)!»»-l „I . , m n\=-1 r;—— e' (o^-'-1 (o/(o +1 ——— q' (op"—' (0/(0=/=0г!(и-/-1)! ,=o г!(« — / — 1)!Найдем теперь интенсивность отказа мажоритарной системы:. /с(о _ (и - т)се'п(0Рп-от-'(/)/(/>*с(0 =ад ^с'ечо^-чо/=0
Анализ надежности невосстанавливаемых систем249или£с;е'(<)/■"■'(о
/ = 0Вычислим, во сколько раз интенсивность отказов системы больше интенсив¬
ности отказов одного элемента:МО (л my C"Qfa(t)Pn~m(t)40 'ZcnQ‘(t)Pn4(t)ы оРассмотрим случай наличия резерва (/и>1). Тогда в начальный момент вре-Хс(0) лмени t = О получим - - = 0, а при t -> оо имеет место равенство:к МО , ч,- 1lim —= (п - т) Ига — = п-т./->оо Х(0 /->» (У f Р(() ‘У —/=О'-'птТаким образом, наличие резерва приводит к изменению отношения интен¬
сивности отказов системы к интенсивности отказов элемента от нуля до по¬
стоянной величины, равной количеству основных элементов системы
Оп-т).ПРИМЕР 6.2. Пусть система состоит из трех одинаковых устройств. При
этом ее отказ наступает при отказе любых двух или всех трех устройств.
В данном случае имеет место мажоритарное резервирование с кратностью
1/2, т. е. одно резервное устройство и два основных. Необходимо определить
показатели надежности Рс (t), 7j, Хс (/), предполагая, что интенсивности от¬
каза постоянны.Решение. Воспользуемся формулой (6.11). В нашем случае т = 1, и = 3.
ТогдаРс (0 = р3 (0 + C\Q(t)P2 (0 = Рг (0 + 3(1- Р(0) Р2 (/) = ЗР2(0 - 2Р3 (0 •Сравним надежность мажоритарной и нерезервированной системы. Для этого
решим неравенство:Рс(t) > Р(0, или 3P2(t) - 2Р3(0 > P(t) .
250Глава 6Отсюда следует, что P(t)> 0,5. Таким образом, мажоритарное резервирова¬
ние позволяет повысить надежность системы при условии P(t) > 0,5.Для постоянных интенсивностей отказов P(t) = е м, и, значит,Pc(t) = 3e~2Xt -ге-На рис. 6.4 приведены зависимости вероятности безотказной работы нерезер¬
вированной и резервированной систем при X = 0,01 час"'.„-ЗХ/Рис. 6.4. Зависимости вероятности безотказной работы системы от времениИз рисунка видно, что Рс(() > Pit), если P(t) > 0,5.Вычислим среднее время безотказной работы системы:3 2- = -Г0.2Х ЗХ 6Х 6 07J = jPc(t)dt= ](Зе~2Х1 -2 e~3Xt)dt=-
о оРезультат вычислений показал, что среднее время безотказной работы систе¬
мы с кратностью резервирования 1/2 ниже, чем нерезервированной.Вычислим интенсивность отказа:К(0 = -тРс(0•2 Xt __Зе~2Х‘ -2е~ъи) »(-2 XI -3X1 ■
е —е3e~2Xi -2е~ъиГрафик этой функции показан на рис. 6.5.График подтверждает приведенные ранее свойства интенсивности отказов
мажоритарной системы. В частности, Xc(t) с течением времени приближает¬
ся к 2Х = 0,02 час-1.
Анализ надежности невосстанавливаемых систем251Рис. 6.5. Зависимости интенсивности отказов мажоритарной системы от времени6.2.3. Резерв замещениемСтруктурная схема системы приведена на рис. 6.6. Отказ системы наступает
при отказе нулевого элемента, затем первого, второго и т. д., т. е. всех (m +1)
элементов.Рие. 6.6. Резервированная система с резервом замещением
Это значит, что общее время до отказа системы равно сумме времен до отказатэлементов Хс = £ Xt. Из теории вероятностей известно, что плотность сум-
1=0мы независимых случайных величин равна свертке плотностей слагаемых,
поэтому/c(0 = /o*/iОпределим вероятность безотказной работы системы в течение времени t.
Пусть сначала т = 1. Система проработает безотказно в течение времени /
при наступлении одного из двух несовместных событий:
252Гпава 6ПА — элемент с номером 0 проработает безотказно в течение времени (;П В — элемент с номером 0 откажет в некоторый момент времени х < t, а
элемент с номером 1 проработает безотказно в течение оставшегося вре¬
мени (t-x).Вероятность события А равна Pq(0- Вероятность события В, полученная поIформуле полной вероятности, равна $f0(x)Px(t - x)dx = /0 *Px(t). По теоремеосложения вероятностей получим:рс(о=ад+/0*ад-Эта формула обобщается на систему, содержащую произвольное число эле¬
ментов:рс(о=р0(о+л*т+л*л* р2 со+...+/о * л *... * fm-1 * рт(о,илитРАО = Z Л *Л* ■■■*/'-!*№■ (6.12)i=ОНа практике в большинстве случаев резервирование замещением осуществ¬
ляется однотипными системами, когда основная система и все резервные
равнонадежны. В этом случае из формулы (6.12) следует, чтот ...Рс(‘)=Е/'0)*Р(».1=0где /(О — плотность распределения времени безотказной работы,/ (0 = /*/*•••*/(0 — /-кратная свертка плотностей, P(t) — вероят-i у -/ность безотказной работы каждой системы.Преобразуем полученное выражение, используя соотношениеP(t) = 1 - )f(x)dx = 1 - / * 1(0,отогдаРс (0 = 1-/*1(0 +/*(!-/*i)(0 + -+/*(m) *(i-/*i)(0i= 1-/*(т+1)* КО-Таким образом,Pc(t) = l-]f{m+'\x)dx.о
Анализ надежности невосстанавливаемых систем253Получим формулу для вероятности безотказной работы при условии, что ин¬
тенсивность отказов X является величиной постоянной. Так как сумма слу¬
чайных величин из (ш + 1)-го слагаемого, каждое из которых имеет экспо¬
ненциальное распределение с параметром X, подчинена распределению Эр¬
ланга с параметрами а = m +1 и j3 = -^~ (см. разд. 2.4), тоА,(6.13)/=о J'-Формулу для среднего времени безотказной работы можно получить из соот¬
ношенияTx = \Pc{t)dt.В результате интегрирования получим:1Тх =(m +1)— = (/я + 1)Г0,(6.14)где Т0 — среднее время безотказной работы основной системы. Это соотно¬
шение понятно из физических соображений.6.2.4. Скользящее резервированиеРассмотрим мажоритарную систему m/п с резервом замещением (ненагру-
женным резервом). Такое резервирование называется еще скользящим
(рис. 6.7).п-т\А N/*n-m+l —'Г 1Рис. 6.7. Скользящее резервированиеСначала работают (и - т) основных элементов системы, а остальные т эле¬
ментов не работают (находятся в очереди на работу). При отказе любого ос¬
новного элемента он заменяется новым из числа резервных, который теперь
254Глава 6выполняет функции основного элемента. При этом количество резервных
элементов уменьшается. При отказе следующего основного элемента он
опять заменяется новым из числа резервных и т. д. Отказ системы наступает,
когда будут израсходованы все резервные элементы и откажет любой из ос¬
новных элементов.Определим вероятность безотказной работы системы со скользящим резер¬
вом при условии, что все элементы системы имеют одинаковую надежность,
а именно случайное время до отказа каждого элемента имеет плотность /(()
и вероятность безотказной работы P(t).Система будет работоспособной в течение времени t при отказе не более чем
т элементов. Событие Ак , состоящее в отказе любых к (0<к <т) элемен¬
тов за время t, может произойти в том случае, когда произойдет хотя бы од-(к к к )но из несовместных событий Ак 2’' "~т , которое состоит в том, что ос¬
новной элемент системы, стоящий на i-м месте, будет заменен kt резервными
элементами, j = 1, 2,..., п — т. При этом kt> 0 и такие, что
кх +к2 + ... + кп_т = к. Поскольку событие Ак является суммой несовместных(к к к )событий Акь ъ '"> "~т , то по теореме сложения вероятность суммы событий
равна сумме вероятностей этих событий:Р(Ак)= £ )•к1+к2+...+к„_т=кСобытие Акк',к2 к"~т^ равно произведению событий Акк/\ состоящих втом, что один основной элемент будет замещен kt резервными элементами,(к )находящимися в ненагруженном состоянии. Вероятность события Ак рав¬
на, очевидно, /*^ * P(t), и, значит, по теореме умножения вероятностей для
независимых событий получим:р/А(к, ,кг,..., к„_т)\ Yy plAp \ = "fj /*(*,) * P(t).
i=i (=1Тем самым вероятность безотказной работы системы т/п с ненагруженным
резервом равнаад = £ £ f*{k[) * pw'(ki) * p(t)... * p(t). (6.15)k=0 k]+k2+...+k„_m=kЭта формула очевидным образом может быть обобщена на общий случай,
когда все элементы системы имеют разную надежность.
Анализ надежности невосстанавливаемых систем255Пусть элементы системы имеют экспоненциальное распределение вероятно¬
стей времени до отказа с параметром X. Вычислить вероятность безотказной
работы и интенсивность отказов системы со скользящим резервом.Так как /(/) = Xe~Kt, P(t) = e~Xt, тоkjiи поэтому по формуле (6.15) вероятность безотказной работы системы равнаk = 0 к1+к2+...+кп_т=к 'М кп-т•(^0 -(n-m)Xt V'к=О к1+к2+.:+к„.т=к • ••• •к=о ' ' *to.Последнее означает, что вероятность безотказной работы системы со сколь¬
зящим резервом имеет распределение Эрланга с параметрами а = т + \ иР=- .(и - т)ХНайдем интенсивность отказов:((n-tn)X)m+l tm e-{n-m)xt (Сn-m)Xt)mМО = ^- = г = (п-т)Х ^ ,W " ((n-m)Xt) A {(n-m)Xt)к=о ' Л! *to *!Если резерв существует ( т > 1), то в момент времени t = 0 имеем —s— = 0,Xа при длительной работе системы, когда t -* оо получимМОlim —£- - = п-т./->» А(0Таким образом, как и для постоянно включенного резерва, для резерва заме¬
щением при длительном функционировании системы отношение интенсив¬
ности отказов системы к интенсивности отказов одного элемента равно числу
основных элементов системы.
256Гпава 6 f*Скользящее резервирование высокоэффективно. Система, состоящая из п
элементов с одним резервным, имеет такую вероятность безотказной работы,
как и дублированная система, число элементов которой равно 2(и -1). Дей¬
ствительно, при т = 1что совпадает с вероятностью безотказной работы дублированной системы.6.3. Надежность систем
при общем и раздельном резервированииОсновными видами структурного резервирования являются общее и раздель¬
ное (поэлементное) при постоянно включенном резерве и по способу заме¬
щения. Метод резервирования, когда резервируется вся система в целом, на¬
зывается общим, а в случае, когда резервируются отдельные элементы систе¬
мы, называется раздельным. Структурные схемы этих видов резервирования
(схемы расчета надежности) приведены на рис. 6.8—6.11. На рисунках при¬
няты следующие обозначения: гг — число элементов нерезервированной сис¬
темы, т — число резервных систем.Рис. 6.8. Общее резервирование с постоянно включенным резервомРис. 6.9. Общее резервирование замещением
Анализ надежности невосстанавливаемых систем257Рис. 6.10. Раздельное (поэлементное) резервирование с постоянно включенным резервомl_t L,ьLiГ 1Г 1Рис. 6.11. Раздельное резервирование замещениемНайдем зависимость времени безотказной работы системы от времени рабо¬
ты ее элементов. Пусть XtJ — случайное время до отказа элемента, стоящегов i-м ряду и j-й колонке, т. е. элемента с номером (/,/'), Хс — случайное
время до отказа системы. Получим выражения, связывающие Хс с Ху для
различных схем расчета надежности.□ При общем резервировании с постоянно включенным резервом (см.
рис. 6.8) элементы /-го ряда (/ = 0,1, 2,..., т) образуют последовательное
соединение элементов, поэтому время до отказа подсистемы, составлен¬
ной из элементов z'-го ряда, равно X: = min Хи. Так как вся система7=1,2,...,л Jпредставляет собой параллельное соединение этих подсистем, то время до
отказа системы равно Хсmax X., отсюда( = 0,1,2,...,»!X' = max min Хи./'=0,1,2 mj=l,2,-,n J(6.16)□ При общем резервировании замещением (см. рис. 6.9) элементы /-го ряда
(/ = 0,1, 2,..., т) образуют последовательное соединение элементов, по¬
этому время до отказа подсистемы, составленной из элементов /-го ряда,9 Зак. 3094
258Глава 6равно X/ = min Хи. Время до отказа всей системы равно, очевидно,тсумме времени до отказа этих подсистем, следовательно, Хс = £ Xt, от-1=0сюдатXC = Z min XtJ, (6.17)/=07 = '.2 п "□ При раздельном резервировании с постоянно включенным резервом (см.
рис. 6.10) элементы у- й колонки (J = 1, 2,..., п) образуют параллельное со¬
единение элементов, поэтому время до отказа подсистемы, составленной
из элементов й колонки, равно XJ = max Хи. Так как вся система/=0,1,2...., т Jпредставляет собой последовательное соединение этих подсистем, то вре¬
мя до отказа системы равно Хс = min XJ, отсюдаj=\,2,-,nХс= min max Хи. (6.18)у=1,2,...,и /=0,1,2,...,т□ При раздельном резервировании замещением (см. рис. 6.11) время до отка¬
за подсистемы, образованной элементамиу'-й колонки (J = 1, 2,..., п), рав-тно сумме времени до отказа элементов, т. е. XJ = £ Хи . Так как вся сис-1=0тема представляет собой последовательное соединение этих подсистем, то
время до отказа системы равно Хс = min XJ , отсюдаУ=1.2 птХс= min %Ху. (6.19)у=1,2 л/=0Пусть Ру (/) — вероятность безотказной работы элемента с номером (/,_/), а
fjj(t) — плотность распределения времени до отказа этого элемента,i = 0,1, 2,..., т, j = 1, 2,..., и . Вычислим вероятность безотказной работы
системы Pc(t) в зависимости от схемы резервирования, используя результаты
разд. 6.2 и соотношения (6.16)—(6.19):□ общее резервирование с постоянно включенным резервом:f \тw=i-n1=0i-nwV 7 = 1(6.20)
Анализ надежности невосстанавливаемых систем259□ общее резервирование замещением:m(6.21)/=огде Р, (О = П ро (О» /< (0 = ~р№'»7 = 1□ раздельное резервирование с постоянно включенным резервом:ЗД)=П i-n(i-vo)y=n i=О□ раздельное резервирование замещением:я mад=п s Лу Ч\, * • дУ(о7=1'=0(6.22)(6.23)Расчет вероятности Рс(0 по формулам (6.20)—(6.23) требует привлечения
соответствующих программных средств, особенно при больших значениях m
и п. Для наглядности приведем эти соотношения для малых значений пара¬
метров.ПРИМЕР 6.3. Для частного случая: m = 1, п = 2 представить формулы веро¬
ятности безотказной работы систем при различных видах резервирования че¬
рез вероятности безотказной работы элементов.Решение:□ общее резервирование с постоянно включенным резервом:Рс(0=1 ■- (1 - /*01 (О^щ(О)О - PniOPniO);□ общее резервирование замещением:РАО = P0l(t)P02(t)-/(/>0.(х)/»02(х)) Рп«-Т)Px2(t-х)dx;
оО раздельное резервирование с постоянно включенным резервом:рс(0=(1 -(1 - Ро, (0)0 - Рх, (0))(1 - (1 - р02(0)(1 - Рх2(0));□ раздельное резервирование замещением:\/РА0 =^01 (0+ J^oi (х)^ 1 (/ - х)£/т Р02(0+/ч
260Гпава 6Каждая из рассмотренных схем резервирования имеет одинаковое количество
элементов, по-разному соединенных между собой. Важной задачей при про¬
ектировании сложных технических систем является определение наиболее
надежной системы. Сравнение различных видов резервирования по вероят¬
ности безотказной работы будет проведено в гл. 9, посвященной методам по¬
вышения надежности.Методика анализа надежности невосстанавливаемых систем, рассмотренная
ранее, позволяет рассчитать показатели надежности системы сложной струк¬
туры. Задача при этом формулируется так: дана структурная схема системы
(схема расчета надежности) и показатели надежности ее элементов, необхо¬
димо рассчитать показатели надежности системы.Рассмотрим методику на примере.ПРИМЕР 6.4. Структурная схема системы представлена на рис. 6.12.Рис. 6.12. Структурная схема сложной системыВероятности безотказной работы ее элементов (в некоторый фиксированный
момент времени) приведены в табл. 6.1.Таблица 6.1. Данные о надежности элементов№ элемента1234567Вероятность р0,980,960,950,990,940,950,97Необходимо вычислить вероятность безотказной работы системы Рс.Решение. При расчете показателей надежности сложной системы целесооб¬
разно решение получить в аналитическом виде. Такое решение позволяет
легко вычислить показатели надежности системы при любых значениях пока¬
зателей надежности ее элементов.Представим нашу систему в виде последовательного соединения ее подсис¬
тем. Первой подсистемой является совокупность элементов 1, 2, 3, образую¬
щих резервированную подсистему с неравнонадежными элементами. Эле¬
менты 1, 2 соединены в смысле надежности последовательно, поэтому
Анализ надежности невосстанавливаемых систем261Р\2~ Р\Рг или Q2=l- P\Pi. Тогда вероятность безотказной работы первой
подсистемы будет равна^1,2,3 =1 “0 -Р\Рг)<У-Рг)-
%Элементы 5 образуют дублированную систему с резервированием методом
замещения. Вероятность ее безотказной работы определяется выражениемp5,s = PsO~lnPs)-Элементы 6 образуют общее резервирование с постоянно включенным резер¬
вом. Вероятность безотказной работы подсистемы имеет вид:Р6,6=1-(\-р6)2.Элементы 7 образуют подсистему с дробной кратностью резервирования,
равной 1/2 . Вероятность ее безотказной работы*7,7,7 = 3Pi ~ 2Pi ■Считая отказы подсистем событиями независимыми, на основании теоремы
умножения вероятностей получим:*с = Р,2,3 ■ *4 • *5,5 ■ *65,6 ' *7,7,7ИЛИPQ =(\-{\-pxp2\\-p3))-p4-p5-(\-\np5)-{\-(\-p6)2y^p^j-2р1).
Подставляя в это выражение значения вероятностей, получим: Рс = 0,98.
ЗамечаниеВ задаче было сделано допущение о постоянстве интенсивности отказов элемента 5.6.4. Надежность резервированных систем,
защищенных от одного отказаПолучим значения показателей надежности некоторых простых, но важных в
практическом отношении резервированных систем, отказ которых наступает
при отказе двух элементов системы. В качестве таких систем могут быть
дублированные системы с постоянно включенным резервом (рис. 6.13, а) и
резервом замещением (рис. 6.13, б), мажоритарные системы кратности 1/2
(рис. 6.13, в) и т. п.
262Глава 6X, ц К цПостоянный резерв Резерв замещениемa бК ИДробная кратность 1/2
вРис. 6.13. Структурные схемы систем, защищенных от одного отказаПриведенные здесь системы, а также другие системы, защищенные от одного
отказа, будем рассматривать совместно. Для расчета надежности таких сис¬
тем применим два метода. Первый метод основан на классических теоремах
теории вероятностей, а второй использует теорию марковских процессов.Сначала предположим, что система является невосстанавливаемой. Граф со¬
стояний представлен на рис. 6.14.©х мОх'\>ИРис. 6.14. Граф состояний невосстанавливаемой системы,
защищенной от одного отказа
Анализ надежности невосстанавливавмых систем263На рисунке приняты обозначения:О А, — интенсивность перехода с нулевого на первый уровень графа;□ А' — интенсивность перехода с первого на второй уровень графа.Система проработает безотказно в течение времени t, если до момента t
первый элемент не откажет. Вероятность этого события равна рх = е~х‘. Сис¬
тема также проработает безотказно в течение времени t, если первый эле¬
мент откажет в любой момент времени т < t, а в течение времени (t - т)
больше не произойдет отказов. По формуле полной вероятности вероятность
этого события равнар2 = ]xe-kxe-x'(t-T)dz = Ae"v' )e(X'~X)%dx.Если А * А', тоа если А = А', то. е( }-1 Ае х‘-Хе х‘Рг-Хе —1 = i'-X Х'-Хр2 = Xte Xt.Поскольку P(t) = pj + р2, то вероятность безотказной работы системы, за¬
щищенной от одного отказа, определяется формулой:Хе~х'‘ -Х'е~х‘P(t) =если А*А';А-А' . ’ (6.24)(1 + Аt)e~Xl, если А = А'.Средняя наработка системы до отказа очевидно равнаТ;=1 + 1 = А±Л:. (6.25)1 А А' АА'Результаты расчетов показателей надежности по формулам (6.24) и (6.25) для
трех схем, изображенных на рис. 6.13, приведены в табл. 6.2.ПРИМЕР 6.5. Требуется сравнить надежность резервированных невосста-
навливаемых систем, представленных на рис. 6.13. Интенсивности отказов
элементов одинаковы и равны А = 0,001 час-1.Решение. На основе табл. 6.2 получим значения вероятности безотказной
работы, когда t изменяется от 0 до 1000 час. Результаты сведены в табл. 6.3.
264Глава 6Таблица 6.2. Показатели надежности невосстанавливаемых систем,
защищенных от одного отказаВид резерваXX'Т,Р( оПостоянно включенный2ХX3- -XI -2XI2е - е2ХЗамещениемXX2X(1 + Xt)e^С дробной кратностьюзх2Х5Ъе~2и - 2еГЪХ16ХТаблица 6.3. Значения вероятности безотказной работы для невосстанавливаемых систем,защищенных от одного отказа1, часПостоянный резервРезерв замещениемМажоритарная система01,0001,0001,0001000,9910,9950,9752000,9670,9820,9133000,9330,9630,8334000,8910,9380,7465000,8450,9100,6576000,7960,8780,5737000,7470,8440,4958000,6970,8090,4249000,6480,7720,36110000,6000,7360,306Соответствующая графическая иллюстрация приведена на рис. 6.15. Кривая 1
отвечает системе с постоянно включенным резервом, 2 — системе с резервом
замещением, 3 — мажоритарной системе.Резерв замещением обеспечивает наибольшую надежность системы по срав¬
нению с другими видами резервирования, при этом для трех рассмотренных
систем наблюдается существенное различие по критерию P(t).
Анализ надежности невосстанавливаемых систем265Среднее время безотказной работы равно:□ для постоянно включенного резерва Тх =1500 час;□ для резерва замещением 7] = 2000 час;□ для мажоритарной системы 7] = 833 час.Таким образом, из трех рассмотренных систем мажоритарная система имеет
самую низкую надежность по вероятности безотказной работы и, что естест¬
венно, по среднему времени безотказной работы.Рис. 6.15. Вероятность безотказной работы
для трех схем резервирования без восстановленияТеперь предположим, что система восстанавливаемая, и ц — интенсивность
восстановления. Граф состояний показан на рис. 6.16.Обозначим через pt(t) — вероятность пребывания системы в момент време¬
ни t в состоянии i, i = 0,1. Тогда для исправных состояний имеет место сис¬
тема дифференциальных уравнений Колмогорова:j/>o(0 = -*Po(0 + HPi(0;1д'(0 = Vo (0- (и+ *>').Р\ со¬
считал, что в момент времени t = 0 система исправна, т. е. /?0(0) = 1,
р1 (0) = 0 , получим в преобразовании Лапласа
266Глава 6илиГ zp0(z) = -Ap0(z) +1фх (z) +1;
\zpx(z)f Ар0(г)-(ц + А'Хр,00\(z + X)p0(z) ~m(z) = 1;
[ -Ap0(z) + (z + H + A')£,0O = 0-©Ц' i I
к WoХ’ИШРис. 6.16. Граф состояний восстанавливаемой системы,
защищенной от одного отказаРешение этой системы уравнений дается равенствамиЛ . . z + u + A' ... X
Л)00 = 7 » Р\(г) = ~,Л Лгде А == z + (ц + X + X')z + XX' — главный определительz + X -ц
—A. z + ц + Xсистемы. Отсюда следует, что преобразование Лапласа вероятности безот¬
казной работы имеет видz + ц + А + A z + ц. + А + АР(г) = p0(z)+ px(z)=-z + (ц + X + X )z + ААПредставим полученную дробь в виде суммы простейших дробей. Полагая, ,,, , —a± yja2 -4Ь
а = ц + А + А , Ь = ХХ , найдем корни знаменателя z1>2 - — • Тогда
Анализ надежности невосстанавливаемых систем267где коэффициенты Ах и Л2 определяются из системы уравнений\АХ + А2 — 1;
[Axz2 + A2zx = -a,откудаZ\ +aг-, + aZ\ 2^2 Z| Z2Переходя от функции P(z) к оригиналу, получим окончательное выражение
для вероятности безотказной работы системы:P(t) = AxeZl‘ + A2eZ2‘. (6.26)Вычислим среднюю наработку до первого отказа системыz2+a _ а _ ц + А + А'71="zx + a(zx-z2)zx (zx—z2)z2 zxz2XX'(6.27)Рассматриваемая система является обобщением систем, защищенных от од¬
ного отказа, со структурными схемами, изображенными на рис. 6.13. Для
этих систем в табл. 6.4 приведены значения интенсивностей переходов X, X'
графа состояний и выражение для среднего времени безотказной работы.Таблица 6.4. Средняя наработка до отказа восстанавливаемых систем,
защищенных от одного отказаВид резерваXX'г,Постоянно включенный2ХXц + ЗХ
2Х2ЗамещениемXXц + 2Х
X2С дробной кратностьюЗХ2Хц + 5Х
6Х.2В табл. 6.5 содержатся коэффициенты zx 2 и АХ2, стоящие в выражении ве¬
роятности безотказной работы (6.26).ПРИМЕР 6.6. Требуется сравнить надежность резервированных восста¬
навливаемых систем, представленных на рис. 6.13. Исходные данные:
А, = 0,001 час-1, ц = 0,04 час-1.
268Гпава 6Таблица 6.5. Коэффициенты для вероятности безотказной работы
восстанавливаемых систем, защищенных от одного отказаВид резерваZl,2Л 1,2Постоянновключенный-(ц + ЗХ) ± v1(р+ЗХ)2 -SX2±(|i *4* ЗА.) + ^kn + 3X)2 -SX222\/(ц + ЗХ)2 -SX2Замещением-(ц + 2Х) ± \i(|i + 2Х) + ^I& + 2X)2 -4Х21(ц + 2Х)2 - 4Х222у)'(ц + 2Х)2 - 4Х2С дробной
кратностью-(ц + 5 X)±J±(ц + 5 X) + yj(ц + 5Х)2 - 24Х2(ц + 5Х)2-24Х22W(ц + 5Х)2 - 24Х2Решение. В соответствии с табл. 6.4 рассчитаем среднее время безотказной
работы каждой из трех систем:□ для постоянно включенного резерва 7} =21500 час (рис. 6.13, а);□ для резерва замещением 7] = 42000 час (рис. 6.13, б);□ для мажоритарной системы 7] = 7500 час (рис. 6.13, в).В соответствии с табл. 6.5 рассчитаем вероятность безотказной работы каж¬
дой из трех систем, и результаты расчетов запишем в табл. 6.6.Таблица 6.6. Значения вероятности безотказной работы восстанавливаемых систем,
защищенных от одного отказаt, часПостоянный резервРезерв замещениемМажоритарная система01,0001,0001,00010000,9560,9770,87720000,9120,9540,76830000,8710,9320,67240000,8310,9100,58750000,7930,8880,51460000,7570,8670,45070000,7230,8470,39380000,6900,8270,344
Анализ надежности невосстанавливаемых систем269Таблица 6.6 (окончание)I, часПостоянный резервРезерв замещениемМажоритарная система90000,6580,8070,301100000,6280,7880,263Расчеты проведены на интервале от 0 до 10 ООО час.
Иллюстрация соответствующих графиков показана на рис. 6.17:□ кривая 1 — для постоянно включенного резерва;□ кривая 2 — для резерва замещением;□ кривая 3 — для мажоритарной системы.Рис. 6.17. Вероятность безотказной работы для трех схем резервирования
при наличии восстановленияХарактер графиков для систем с восстановлением несколько отличается от
графиков невосстанавливаемых систем: во-первых, P(t) на рис. 6.15 имеет
при t = 0 касательную, параллельную оси абсцисс, а на рис. 6.17 это свойство
отсутствует; во-вторых, восстановление обеспечивает примерно одинаковый
уровень надежности, но в течение намного (в 10 раз) большего времени.В то же время видна и значительная разница как в средней наработке, так и в
вероятности безотказной работы* Наибольшую надежность дает резервиро¬
вание замещением, а наименьшую — резервирование с дробной кратностью.
270Глава 6ПРИМЕР 6.7. Требуется сравнить надежность систем при отсутствии и на¬
личии восстановления. Оценить выигрыш в надежности от восстановления.Решение. Рассмотрим системы, представленные на рис. 6.13, и для каждой из
них вычислим отношение P(t) восстанавливаемой к P(t) невосстанавливае¬
мой системы. Это отношение будем называть выигрышем от восстановления
W(t). Для этой цели воспользуемся табл. 6.2 и 6.5. Результаты расчетов по¬
местим в табл. 6.7.Таблица 6.7. Выигрыш от восстановления по вероятности безотказной работы
систем, защищенных от одного отказаt, часПостоянный резервРезерв замещениемМажоритарная система01,0001,0001,0001001,0061,0031,0152001,0261,0141,0693001,0581,0321,1564001,1021,0561,2755001,1571,0871,4276001,2221,1231,615700Г. 1,2981,1661,8468001,3841,2142,1249001,4821,2682,46010001,5911,3282,863Безусловно, что с течением времени величина выигрыша fV(t) увеличивает¬
ся. Но, кроме того, расчеты и рис. 6.18 показывают, что наибольший выиг¬
рыш восстановление дает для мажоритарной системы (кривая 3), а наимень¬
ший — для резервирования замещением (кривая 2).Таким образом, чем более надежной является система, тем меньший выиг¬
рыш для нее оказывают восстановительные мероприятия.
Анализ надежности невосстанавливаемых систем271Рис. 6.18. Выигрыш в надежности, полученный от восстановления
ГЛАВА 7
АНАЛИЗ НАДЕЖНОСТИ
ВОССТАНАВЛИВАЕМЫХ СИСТЕМОсновными особенностями восстанавливаемых систем по сравнению с не-
восстанавливаемыми являются:□ большое число состояний;□ наличие последействия отказов элементов;П зависимость показателей надежности от большого числа факторов (интен¬
сивности восстановления, дисциплины обслуживания).Расчет показателей надежности восстанавливаемых систем — задача более
трудная, чем невосстанавливаемых. Инженерные методы существуют лишь
для случая экспоненциальных законов распределения времени безотказной
работы и времени восстановления.В случае неэкспоненциальных законов аналитических формул и тем более
инженерных методик не существует (за редким исключением). Приходится
использовать численные методы расчета и компьютерные технологии.В данной главе рассматриваются методы анализа надежности восстанавли¬
ваемых систем при экспоненциальных и неэкспоненциальных законах отка¬
зов и восстановлений. Основное внимание уделяется последним.7.1. Анализ надежности
восстанавливаемых систем
с основным соединением элементовГраф состояний системы, состоящей из п элементов, представлен на рис. 7.1.Математической моделью функционирования системы в смысле надежности
является следующая система дифференциальных уравнений:
Анализ надежности восстанавливаемых систем273~р- = -Кро(0 + X нМО;■ dt '=> (7.1)= А,р0(О -ц,/?,(/), / = 1, 2,..., я,.■ atгдеK = lh (7-2)»=1— интенсивность отказа системы.1Рис. 7.1. Граф состояний системы с основным соединением элементовРешение системы уравнений обычно осуществляется при начальных усло¬
виях:Р0(°) = 1 > Pl(°) = Р2(°) = - = Рп(°) = 0 •Показатели надежности восстанавливаемых систем, такие как функция го¬
товности, коэффициент готовности, наработка на отказ и среднее время вос¬
становления, могут быть получены из системы (7.1) в аналитическом виде.
Однако наиболее просто их получить непосредственно из графа состояний
топологическим методом.□ Вычисление коэффициента готовностиКоэффициент готовности является финальной вероятностью того, что сис¬
тема исправна в произвольный момент времени /. На графе это состояние
помечено цифрой 0. Тогда КГ = р0. На основании топологического метода
получаем:
274Глава 7Сокращая на ц,, получим/=1«г- . (7-3)1 + Ёр,/=1\ ' .где р,- =□ Вычисление среднего времени между отказамиНаработку на отказ Т наиболее просто определить по формуле (5.38):Елj _ 'б£+ Ро£ Pi £ ^!/ р УхieE+ jeE_ PoL,Kt
т. к. система имеет одно исправное состояние с номером 0. Тогда(7.4)2>|/=1Из полученного выражения следуют два важных вывода:• наработка на отказ нерезервированной системы не зависит от восста¬
новления;• наработка на отказ и среднее время безотказной работы совпадают.□ Вычисление среднего времени восстановленияТ \ — кТак как КГ =———, то Тв = ^ Г Т . Подставляя в это выражение значе¬
ния Кг и Т из (7.3) и (7.4), получим:Г.-7-ip,. (7.5)АС 1 = 1где л.с определяется формулой (7.2).□ Вычисление функции готовностиВычисление функции готовности требует решения системы дифференци¬
альных уравнений (7.1). В преобразовании Лапласа она имеет вид:
Анализ надежности восстанавливаемых систем275(s + \)p0(s)-X^Pi(s) = \;(=1 (7-6)(s + p,)p,(s) = XiP0(s) = 0, i = 1, 2,..., n.Так как Kr(t) = p0(/), то достаточно найти Po(s), а затем обратное преоб¬
разование Лапласа p0(t).ПРИМЕР 7.1. Восстанавливаемая система состоит из двух подсистем, обра¬
зующих основное соединение элементов. Интенсивности отказов и вос¬
становлений имеют значения: ^=0,1 час-1, Х2 =0,15 час-1, jj.t = 1 час'1,
ц2 -1,2 час-1. Определить Kr(t) и вычислить значение Кг(t) в диапазоне
t = 0 +10 час с шагом h = 1 час.Решение. Граф состояний показан на рис. 7.1, он имеет три состояния: (0), (1)
и (2).Получим выражение для Kr(s) из графа состояний, не решая системы урав¬
нений (7.6). В нашем случае число узлов п = 3. Тогда степень многочлена
знаменателя будет равна 3, а степень числителя w0=«-l-/0=3-l-0 = 2.
На основании разд. 5.4.1 функция готовности в преобразовании Лапласа име¬
ет вид:ЛГгМ- B«S\*B'S*Bг .s(A$s + A}s + A2)В соответствии с топологическим методомAq= \ , Ах = + Х2 + Ц| + И2 = 2,45, А2 = Ц1Ц2 + ^1^2 + ^2^1 = Ь47,= Ц1 + Й2 = 2,2, В2 = (Д.1И.2 = 1,2.Подставляя эти значения в выражение для Kr(s), получим52+2,25 + 1,2Kr(s) =г s(s2 + 2,45s+ 1,47)Обратное преобразование Лапласа имеет вид:Kr(t) = 0,816 + 0,163е-1,4' + 0,0204е-1’05'.Оно было получено с помощью программной системы Mathcad.
Результаты табулирования приведены в табл. 7.1.
276Глава 7Таблица 7.1. Результаты табулирования функции KT(t)t, час0123456кг(п10,8630,8280,8190,8170,8160,816Результаты расчетов показали, что техническая система имеет низкий коэф¬
фициент готовности Кг =0,816, при этом установившийся режим наступает
через весьма короткое время ее работы (5—6 часов).Определение KT(t) с помощью преобразования Лапласа при большом п вы¬
зывает большие трудности, а при и >10 — непреодолимые, т. к. найти об¬
ратное преобразование даже с помощью компьютерных технологий в боль¬
шинстве случаев не удается.При неэкспоненциальных законах отказов и восстановлений расчет надежно¬
сти даже для основного соединения элементов значительно усложняется.
Рассмотрим этот случай более подробно.7.2. Расчет надежности восстанавливаемых
систем с основным соединением элементов
и произвольных законах распределения
отказов и восстановлений7.2.1. Стационарные показатели надежности
неизбыточных системВо многих задачах надежности, возникающих на практике, наибольший ин¬
терес представляют вероятностные характеристики надежности системы, ра¬
ботающей достаточно длительное время. Показатели надежности такой сис¬
темы могут быть вычислены из системы интегральных или дифференциаль¬
ных уравнений, составленной для стационарного режима функционирования,
т. е. при t —> со.Будем следовать общим правилам составления математической модели
(см. гл. 4), описывающей стационарный режим функционирования.Граф состояний основного соединения п элементов представлен на рис. 7.2.Будем предполагать, что при отказе некоторого элемента системы все ис¬
правные элементы не работают, и на время ремонта отказавшего элемента
они сохраняют свои показатели надежности.Пусть fj(t) — плотность, a Ft(t) — функция распределения вероятностей
времени безотказной работы г-го элемента, Fl(t) = l-Fl(t)\ gt(t) — плот¬
Анализ надежности восстанавливаемых систем277ность, a Gj(t) — функция распределения вероятностей времени восстановле¬
ния z'-го элемента, (?,-(*) = ! Tt и ГВ) 1—соответствующие средние.Рис. 7.2. Граф состояний основного соединенияСистема имеет (и +1) состояние:□ (0) — состояние работоспособности;□ (к) — состояние отказа, вызванное отказом к-го элемента, к = 1,2,..., п.
Матрица состояний основного соединения имеет вид012. n*1*1s[ .■ s'\s2x2 .. s'2sns'n .•100 .. 0Символ Sj, стоящий в столбце с номером 0, означает, что во время пребыва¬
ния системы в состоянии (0) i-й элемент исправно функционирует. Символ sj,
стоящий в столбце с номером к, означает, что во время пребывания системы
в состоянии (к) i-й элемент исправен, но он выключен на время ремонта отка¬
завшего элемента. Символ т, означает, что i-й элемент восстанавливается.В соответствии с разд. 4.4 запишем систему интегральных уравнений. Аргу¬
ментами неизвестных функций ук являются компоненты k-io столбца мат¬
рицы S (без верхней и нижней строк):п 00>>0(s,, s2,...,sn)=X j/k(x + sk)yk(x + s „ ..., 0к,..., x + sn)dx;Г *=1° (7-7)' ООyk(su ..., т k,...,sn)= jgA(x + T^oCsi,..., 0к,..., s„)dx, к = 1,2,..., и.о
278Глава 7Для удобства в системе (7.7) опущены "штрихи" у аргументов sj. Составлен¬
ная система уравнений имеет ненулевое решение:В этом можно убедиться непосредственной подстановкой (7.8) в систе¬
му (7.7). Таким образом, для основного соединения соответствующая система
интегральных уравнений допускает точное решение. Решение (7.8) определя¬
ется с точностью до постоянного множителя С, который можно найти из
условия нормировки, так, чтобы сумма вероятностей состояний была равна
единице.По формулам (4.19) определим стационарные значения вероятностей состо¬
яний:i*kа по формулам (4.20) найдем параметры перехода из состояния в состояние:Полученные соотношения для основного соединения элементов позволяют
определить стационарные показатели надежности: наработку на отказ Т,
среднее время восстановления Тв и коэффициент готовности Кг системы:Пy0(.Sl,S2,...fSH)=YlFk(.skyi<п(7.8)Ук(^1 ’ •••> 5„)= П *i(Si)Gk(тк).»=1,р0=с j...jy0(sx, s2,..., s„)dsxds2 ...dsn =С\\Тк,оо oo nPk=C J... J^(jlf..., xk, ...,sn)dsx...dxk...dsn =С1\Т?вк,®o,k С JVoOi. ••• > •••» sn)^i —dsk •••dsn — CY\ Tj\о 0/=1,
i*k®*,o =C J-fjfcfai» - > 0*..... sn)dsx ...dxk ...dsn =СЦТ<.о 0/=1,i*kPoАша u,#c JLa rp
k = \ k = \*k
Анализ надежности восстанавливаемых систем279Л,U гр* = 1 к = \1кт 1Т + 1 I у Zb*/mU rp
к = 1Из полученных соотношений следует, что для стационарного режима значе¬
ния показателей надежности при основном соединении не зависят от законов
распределения времени безотказной работы и времени восстановления эле¬
ментов. Они полностью определяются математическими ожиданиями соот¬
ветствующих случайных величин и выражаются такими же формулами, как и
для экспоненциальных распределений. При этом интенсивности переходов
Хк и Цд. также определяются только средними значениями соответствующих
распределений:Это означает, что при большом времени работы системы в ветви графа
(см. рис. 7.1) могут быть поставлены интенсивности переходов, равные об¬
ратным значениям соответствующих математических ожиданий.7.2.2. Нестационарные показатели надежности
неизбыточных системПоказатели надежности систем при неэкспоненциальных и невырожденных
распределениях времени до отказа и времени восстановления элементов даже
для основного соединения могут быть получены лишь численными метода¬
ми. В данном разделе рассматривается метод вычисления двухсторонних
границ для функции готовности основного соединения при произвольных
распределениях времени до отказа и времени восстановления элементов.
Этот метод эффективен с вычислительной точки зрения и дает достаточнолитическое выражение для погрешности, возникающей при расчете функции
готовности. На числовых примерах показывается отличие в характеристиках
надежности систем при различных распределениях, а также важность анализа
нестационарных характеристик, которые часто не принимаются во внимание.
Однако, как показывают вычислительные эксперименты, продолжительность
переходного процесса может быть довольно большой.ю0,* _ 1ю*.О _ 1Рк Тъкточные с инженерной точки зрения характеристики. Приводится точное ана-
280Гпава 7Особая трудность в анализе надежности систем с произвольными распреде¬
лениями времени безотказной работы и времени восстановления элементов
наблюдается тогда, когда система имеет большое количество элементов, как,
например, в электронных системах, в многофункциональных системах с мно¬
гоступенчатыми производственными линиями и т. д. В этом случае невоз¬
можно определить функцию готовности традиционными методами даже в
том случае, когда все законы распределения экспоненциальные. Предлагае¬
мый подход дает возможность определения верхней и нижней границ для
функции готовности системы, состоящей практически из любого числа эле¬
ментов. При этом система из 10а элементов рассчитывается за время, мень¬
шее 1 минуты, а система из 107 элементов анализируется на современных
компьютерах в среднем за 4—5 минут.Одна из проблем анализа надежности больших систем — неопределенность
начальных данных относительно надежности и ремонта элементов. Очень
часто параметры времен безотказной работы и ремонта элементов представ¬
ляются случайными величинами с некоторыми распределениями вероятно¬
стей на определенном интервале. Предлагаемый здесь подход позволяет при¬
нять во внимание и это обстоятельство. Таким образом, важность данного
пункта определяется тремя факторами:□ возможность анализа систем с большим количеством элементов;□ возможность анализа характеристики надежности переходных процессов;□ возможность учесть неопределенность данных о надежности элементов.Рассмотрим систему, состоящую из и последовательно соединенных в смыс¬
ле надежности элементов при условии, что при отказе любого элемента ос¬
тальные временно отключаются. Система интегральных уравнений, состав¬
ленная по матрице состояний S и полному графу (см. рис. 7.1) при условии,
что в момент времени t = 0 все элементы исправны, имеет вид:n t}>o(si, s2,..., s„, 0 = 2 {/<(* + St)y,(x+®i, s2,..., 0,,..., x + sn, t — x)dx +/=10+ + si)\
i = It^(Sj,..., T,.,..., s„, 0= Jg/Cs + ^Xtyfai* s2> - > - » S„,t-x)dx, / = 1, 2, ...,n.
0(7.9)Система (7.9) полностью характеризует функционирование основного соеди¬
нения п элементов, а ее решение позволяет найти показатели надежности как
Анализ надежности восстанавливаемых систем281функции времени. Например, функция готовности выражается и-кратным
интегралом от функции у0 :00 00*г(0“ s2,, sn,t)dsxds2 ... ds„ .о оОчевидно, что использование системы (7.9) для вычисления Kr(t) представ¬
ляет значительные вычислительные трудности, и требуется разработка при¬
ближенных методов ее решения с оценкой погрешности. Указанные трудно¬
сти можно преодолеть, если выразить функции у0 и yt через характеристики
элементов. В качестве такого приближенного решения системы (7.9) примемy0(su s2,..., sn, 0 = C(0flK)i(‘si>0;i=lJ’/C^is ■— г-Т/г ••• i $n> О С(/)©B(-(xj5011 k(‘^a >0» i 2,..., n,(7.10)k = 1
k*tгде co,(s(,/) и coB((ij,0 — обобщенные параметры потоков отказов и восста-1новлений /-го элемента, a C(t) = -П^гДО/=!Ы *п(0,раемая из условия нормировки так, чтобы сумма вероятностей пребывания во
всех состояниях была равна единице для любого значения t. Функции
соj(Sj,t) и сов,(т,,0 определяются из сравнительно простой системы уравне¬
ний:Г<о, <Л = + s,) + /<л * совг (0;[ЮвДт,-, О = £/,,,Отсюда следует приближенное соотношение для функции готовности основ¬
ного соединения п элементов:1*г(0 =! , f ЫйKri(t)(7.11)Решение (7.10) позволяет найти и другие временные характеристики надеж¬
ности системы, в частности параметры и интенсивности потоков отказов и
восстановления:
282Гпава 7у Д0/(0 у toB, (Q
_ ,ti*r,(0 _ /=1^г/(0“(0 = „ ^ „ч , сов(0 =х, f Ащ(0 * 1 + у«0’/=i ^п(о £i^„(oу Юв/(0M0 = z-^, ц(/) = ——-■■(^).£*„(/) f *„/(0
й^п(0Это, в свою очередь, дает возможность включения основного соединения в
качестве подсистемы в более сложную систему для анализа надежности по¬
следней.Без учета нормировочного коэффициента функции (7.10) представляют собой
точное решение первого уравнения системы (7.9), т. е. имеет место соотно¬
шение:n n t пП®/(л<»о=Х1/(*+я<»*"*)Пт*(*+4*»,-*)Л+П/<(*+*/)- (7.12)i=l / = 1о кФ4 / = 1Доказательство этого утверждения содержится в [135].Оценим теперь погрешность, возникающую при подстановке функций (7.10)
в систему (7.9) с учетом нормировочного множителя C{t). На основании ра¬
венства (7.12) для абсолютной погрешности, вычисленной по интегральной
метрике, имеют место оценки:Ао(0* £ p,(*)|C(f-х)-С{фь($- *)П Кгк(t-x)dx + |l-С(/)|ПFt(0,
/=10 k*i /=1А,(/)< jG((x)co,(/-x)оC(t -х)П KTk{t -х)- С(/)П Krk(0
k*i кфidx, / = 1,2,..., n,A(t)~ max A At) . (7.13)/=0,1 nЗаметим, что оценка погрешности достаточно эффективна при t —> 0 и при
/->оо, т. к. при этом Д(/)-*0. Учет погрешности позволяет также указать
двухсторонние оценки функции готовности системы.Таким образом, получены простые аналитические зависимости для нестацио¬
нарных показателей надежности основного соединения, и при этом сущест¬
вует оценка погрешности.
Анализ надежности восстанавливаемых систем283Используя программное средство Conspz (http://www.gurov.spb.ru/isant
/isant.html), определяются стационарные и нестационарные характеристики
надежности основного соединения элементов, таких как средняя наработка на
отказ, среднее время восстановления, параметры и интенсивности потоков
отказов и восстановлений, функция готовности и др. Все характеристики оп¬
ределяются как функции времени. При этом расчет характеристик сопровож¬
дается графической иллюстрацией. Программа позволяет производить каче¬
ственное и количественное исследование влияния законов распределения и
их параметров на выходные характеристики системы. Следует отметить, что
использование программы позволяет достаточно оперативно исследовать ха¬
рактеристики надежности основного соединения элементов, имеющих раз¬
личные распределения вероятностей.Для иллюстрации влияния параметров и видов законов распределения слу¬
чайного времени до отказа X, и времени восстановления XBi элементов на
функцию готовности системы рассмотрим ряд числовых примеров.ПРИМЕР 7.2. Восстанавливаемая система имеет следующие данные: число
элементов о = 100, случайные величины и XBj имеют гамма-рас¬
пределения с параметрами 7] е [1000,1500] час, Гв, е[5, 6] час. Параметры 7]
и Гв< генерируются в указанных интервалах случайным образом по равно¬
мерному закону, среднее квадратическое отклонение времени до отказа а
принимает значения 300, 500 и 900 часов, среднее квадратическое отклонение
времени восстановления ств = 1 час.Необходимо выполнить анализ влияния дисперсии D = a2 распределения
случайных величин X, на Kr(t).Решение. Расчеты функции готовности проведены с помощью программы
Conspz. На рис. 7.3 показаны графики функций Кг (/), соответствующие сле¬
дующим значениям дисперсии:□ кривая 1 — а = 300 час;□ кривая 2 — а = 500 час;□ кривая 3 — a = 900 час.Из графиков видно, что при увеличении ст уменьшается колебательный ха¬
рактер функции готовности системы и значительно уменьшается время на¬
ступления стационарного режима системы.ПРИМЕР 7.3. Необходимо оценить влияние вида законов распределения
случайных величин X, и XBi на Kr(t) для случая трех систем с распределе¬
ниями:
284Глава 7*ь3 ><ч—АV—
J^/О t, час 4000Рис. 7.3. Влияние дисперсии на функцию готовности1. Xj —гамма-распределение, Хы —гамма-распределение;2. Xj — распределение Рэлея, Хв, — равномерное распределение;3. Xj —гамма-распределение, Хш —усеченное нормальное распределение.Известны также следующие данные по системам: число элементов « = 100,
параметры распределений для всех элементов 7) е [1000,1500] час,
Тт е [5, 6] час, ств = 1 час.Решение. На рис. 7.4 и 7.5 показаны графики функций Kr(t) при ст = 625 час
и a - 300 час соответственно. Выбор <т = 625 час обусловлен тем, что это
значение является средним квадратическим отклонением для однопарамет¬
рического распределения Рэлея и позволяет корректно сопоставить графики
функций готовности систем.0 t, час 4000Рис. 7.4. Влияние видов законов распределения на функцию готовности, ст = 625 час
Анализ надежности восстанавливаемых систем285Рис. 7.5. Влияние видов законов распределения на функцию готовности, с = 300 часИз графиков видно существенное различие характера кривых в зависимости
от видов распределений случайных величин X, и Хы, особенно с уменьше¬
нием дисперсии времени до отказа.ПРИМЕР 7.4. Необходимо определить функции готовности для сложной
системы, состоящей из трех подсистем. Каждая подсистема содержит по
100 элементов. Виды законов распределений и их параметры представлены в
табл. 7.2.Таблица 7.2. Законы распределения и параметры подсистемПодсистема 1Подсистема 2Подсистема 3Распределения X,ГаммаУ сеченно-нормальноеРэлеяРаспределения ХыРавномерноеРэлеяУ сеченно-нормальноеТ, час[1000, 1500][500, 900][5000, 6000]Т„ час[5, 6]П,3][5, Ю]ст, час300100300ств, час10,12Проведенные расчеты дают возможность построить график функции готов¬
ности системы (рис. 7.6).Предложенный метод является очень эффективным с вычислительной точки
зрения и позволяет исследовать системы с большим числом элементов. По¬
грешность, возникающая при определении функции готовности, как показы¬
вают эксперименты, достаточно мала.
286Гпава 71ад0,40 U час 7000Рис. 7.6. Функция готовности основного соединения трех подсистемИспользуемый здесь метод оценки надежности систем с произвольными рас¬
пределениями элементов может быть реализован и для избыточных систем, а
также для систем, обладающих некоторыми дополнительными условиями
функционирования (наличие контроля, учет переключения на резерв и т. д.).7.3. Расчет резервированных
восстанавливаемых систем
при экспоненциальных законах
распределения отказов и восстановленийОсобенностями расчета резервированных восстанавливаемых систем по
сравнению с нерезервированными являются:□ необходимость учета дисциплины обслуживания;□ наличие последействия отказов, вызванного не только фактом обслужива¬
ния, но также отказами элементов;П большое число состояний системы;□ сложность структурной схемы и графа состояний системы.Рассмотрим первоначально методы расчета надежности резервированных
систем при экспоненциальных законах отказов и восстановления.7.3.1. Общее постоянное резервированиеСтруктурная схема и граф состояний системы приведены на рис. 7.7 и 7.8.На рис, 7.7 и 7.8 приняты следующие обозначения:□ X и ц — интенсивности отказа и восстановления элемента системы;Пт — кратность резервирования.\{\■I*/*-V
Анализ надежности восстанавливаемых систем287X, цРис. 7.7. Структурная схема резервированной системыИ Ц ИaЦ 2ц (/я + 1)цбРис. 7.8. Графы состояний резервированной системы: одна бригада обслуживания (в),(m + 1) бригада обслуживания (б)Получим расчетные формулы при следующих допущениях:□ резервирование целой кратности;□ последействие отказов отсутствует.Для случая одной обслуживающей бригады определим коэффициент готов¬
ности, наработку на отказ и среднее время восстановления.□ Вычисление коэффициента готовностиОпределим сначала вероятность пребывания системы в отказовом состоя¬
нии т, т. е. коэффициент простоя.Пользуясь топологическим методом и графом на рис. 7.8, а, получим
288Гпава 7После сокращения на (т + l)!Am+i получимк,1! 2! (т -ь 1)!Цгдеу=-..Коэффициент готовности и коэффициент простоя связаны зависимостью
КТ = 1 - Кп . Тогда после очевидных преобразований получимm+\X-
Й г!<7Л4>XI-
/=0□ Вычисление среднего времени восстановленияВ соответствии с формулой (5.38) и графом на рис. 7.8, а получимХат _ ieE- _ Prn+1 _ 1£ Pi £ Ч Art# Ц '|'е£_Впрочем, это и так очевидно, поскольку интенсивность восстановления
элементов одинакова. Поэтому среднее время восстановления системы Гв
равно среднему времени восстановления элемента.□ Вычисление наработки на отказКВ силу соотношения Т = —-Гв и формул для Кп, КГ и Гв получимкп1 m+yjц /=1илиОТ+1г=го £ ~г ’ <7Л5)/=1где Г0=-~ — наработка на отказ нерезервированной системы. Тем самымустановлена зависимость наработки на отказ системы от кратности резер¬
вирования.
Анализ надежности восстанавливаемых систем 289В случае неограниченного восстановления (число бригад обслуживания равно
т +1) процедуры получения формул те же, что и в случае одной бригады
обслуживания. Они очевидны и просты, если пользоваться топологическим
методом. Поэтому приведем лишь конечные результаты:Л/л+1КГ =1-Т - тг(1+рУ(1+р)
m+1т+1т+1Т -* R(W + l)pw 1_(т + 1)ц(7.16)(7.17)(7.18)В формулах р = —.ЦАнализ полученных формул позволяет сделать ряд важных выводов об эф¬
фективности резервирования, как средства повышения надежности восста¬
навливаемых систем. Этот анализ будет проведен в гл. 9.7.3.2. Общее резервирование замещениемСтруктурная схема и граф состояний системы приведены на рис. 7.9 и 7.10.Рис. 7.9. Структурная схема резервированной системыГрафы состояний резервированной системы настолько просты, что топологи¬
ческими методами показатели надежности вычисляются в одну строку.При одной обслуживающей бригаде определим коэффициент готовности,
среднее время восстановления и наработку на отказ.ЮЗак. 3094
290Глава 7т Ь т + \
V-т 1- т + \■ZXXZX^S(от + 1)цРис. 7.10. Графы состояний резервированной системы: одна бригада обслуживания (а),
(т + 1) бригада обслуживания (б)□ Вычисление коэффициента готовностиц'л+1+Хцт+Х2ц'"-,+...ииц
г Р0+Р\+Р2+- + Рт цт+1+Хц/и+ЯД1'»-1+>+V-ц+ *."*!1 + Р + Р2 +... + рт1 + Р + р2+...+ рт+рт+1ИЛИк =IP'1=0г т+1Ер'( = 0Коэффициент готовности можно вычислить также по формуле:(7.19)КГ =т+11у'<=i
г т+1Ег'/=0□ Вычисление среднего времени восстановленияJ_Ц□ Вычисление наработки на отказК т+1Т = -^-Тъ=Тв'£у‘ ,т =—в/=1
Анализ надежности восстанавливаемых систем291илиmТ = Т0Ху‘ ■ (7.20)/=оРассмотрим случай неограниченного восстановления (число ремонтных бри¬
гад равно числу подсистем, т. е. т +1).На основании графа состояний рис. 7.10, б и правил топологического метода
запишем выражение для коэффициента простоя:л т+1■ЦТ _ ^(т +1)!^+1 + 1)! *1)! ц'*4?,2 +... + (от + 1)цА/” + Хт+хр т+1(от + 1)I! 2! от! (от + 1)!
Тогда коэффициент готовности будет иметь вид:р р2 рт1 + —+ — + ... + —АГг = I - АГ„ = -—— «LI! 2! от! (от + 1)!
илит niZir^==7- <7-21)X —/=0 />!Среднее время восстановления выражается формулойГ»"—!—. (7.22)(от + 1)цНаработку на отказ вычислим, воспользовавшись формулой Т = —-Тв :К
292Глава 7или«itТ = Т0Х-—.-У', (7.23)/=о(/и_г)!где Т0 =- наработка на отказ нерезервированной системы, у =— .А. А,ПРИМЕР 7.5. Вычислить коэффициент готовности и наработку на отказ вос¬
станавливаемой резервированной системы с постоянно включенным резер¬
вом и по методу замещения. Сравнить результаты расчетов. Исходные дан¬
ные: наработка на отказ нерезервированной системы Т = 500 час, среднее
время восстановления Тв = 50 час. Решение необходимо получить при крат¬
ности резервирования m = 1, 2, 3, 4, 5 . Рассмотреть случаи одной бригады
обслуживания и независимого восстановления.Решение. Решение получено с помощью универсального программного сред¬
ства символьной математики Derive 5 по полученным ранее формулам. Ре¬
зультаты приведены в табл. 7.3.Таблица 7.3. Результаты решения примера 7.5ВидвосстановленияРезервирование постоянноеРезервирование замещениемтГ, частКгТ, часОграниченное,
п = 100,90950000,90950010,9836300010,991550020,99561133320,9995,55-10430,99843216730,99995,55- 10s40,99937393340,999995,55-10650,99971432785.0,9999995,55107Неограниченное,
n = m + 100,90950000,90950010,9917300010,9955550020,99922216720,999851,105-10530,99991,8310s30,9999963,3155-10640,999991,6Ы06411,326-10950,9999991,476-107516,63-109Из табл. 7.3 видно, что резервирование с восстановлением позволяет сущест¬
венно повысить коэффициент готовности системы и особенно наработку на
Анализ надежности восстанавливаемых систем293отказ. Значительное повышение надежности получается уже при кратности
резервирования m = 1. При дублировании с восстановлением среднее время
работы между отказами повысилось в 6 раз в случае постоянного резервиро¬
вания и в 11 раз при резервировании замещением. Анализ данных таблицы
показывает, что показатели надежности системы тем выше, чем выше крат¬
ность резервирования и число обслуживающих бригад. Однако нетрудно за¬
метить, что эффективность резервирования убывает с ростом кратности m .Рассмотрим теперь функционирование резервированных систем при законах
распределения отказов и восстановлений, отличных от экспоненциального.
Изложим методы расчета для различных методов резервирования и приори¬
тетов обслуживания.7.4. Расчет резервированных
восстанавливаемых систем
при произвольных законах распределения
отказов и восстановленийОценка надежности резервированных систем для определенных стратегий
обслуживания представляет собой достаточно сложную задачу, поскольку
соответствующая система интегральных уравнений не допускает точного ко¬
нечного решения, удобного для инженерных расчетов. Показатели надежно¬
сти выражаются лишь приближенными соотношениями, погрешность кото¬
рых зависит от законов распределения времен безотказной работы и восста¬
новления элементов.В данном разделе производится расчет только стационарных показателей на¬
дежности восстанавливаемых резервированных систем, состоящих из двух
элементов различной надежности.7.4.1. Дублированная система
с постоянно включенным резервомОценим надежность пары элементов с нагруженным резервом. Структурная
схема и граф состояний представлены на рис. 7.11, а и б соответственно.При полностью ограниченном восстановлении система имеет 5 возможных
состояний:□ (0) — оба элемента системы исправно работают;□ (1) — элемент 1 отказал и восстанавливается, элемент 2 исправен;
294Глава 7□ (2) — элемент 2 отказал и восстанавливается, элемент 1 исправен;□ (12) — отказал сначала элемент 1, а затем — элемент 2;□ (21) — отказал сначала элемент 2, а затем — элемент 1.Рассмотрим различные случаи функционирования системы в зависимости от
дисциплины восстановления отказавших элементов.Рис. 7.11. Схема (а) и граф состояний (б) дублированной системы с нагруженным резервоми прямым приоритетомПрямой приоритетПрямой приоритет означает, что при отказе двух элементов первым восста¬
навливается первый отказавший элемент. В этом случае состояние (12) ха¬
рактеризуется тем, что элемент 1 восстанавливается, а элемент 2 находится в
очереди на обслуживание. Аналогично состояние (21) таково, что элемент 1
стоит в очереди на восстановление, а элемент 2 восстанавливается. Матрица
состояний системы имеет вид:5 =0121221*1*1*1h0*2s2*20ь11100Неизвестные функции, соответствующие указанным состояниям, имеют сле¬
дующие аргументы: У2(Ч>Ъ)> Уп(х1’0)> Jbi(0,t2).Составим систему уравнений для описания стационарного режима функцио¬
нирования:
Анализ надежности восстанавливаемых систем295= J/l(* + «l)M°»* + 's2)<& + 1/2(л + ^2)^2(л + 51>°)^О о00 соMT1»*2) = lgl(x + x])y0(0,x + s2)dx+ \gx(x + x{)f2(x + s2 )у2, (0,0)dx\
о о00 00y2(sl,T2) = fg2(* + х2).Уо(* + S1 >0)dx + J&2 (* + т2)/l(* + 51 )>,12(°>О)'*; (7-24)
О О00Л2(т1>°)= \y\(x + xx,0)dx\о00J^21 (°»"^2 > = |^2(°>л + т2)сЬ:-ОПри произвольных распределениях точное ненулевое решение системы (7.24)
представляется бесконечной суммой ряда, члены которого— многомерные
кратные интегралы, и это решение не пригодно для расчетов. Мы ограничим¬
ся отысканием приближенного решения и соответствующей ему относитель¬
ной погрешности. Возьмем за приближенное решение системы (7.24) набор
функций:УоС*1>52) = Жл'1)^2(52);00У\ O’! >^2> = Jgl(* + Ti)F2(* + S2)<&;(7.25)У 2 (^1 > ^2 ) = J^2(^ + 'c2)Fl(;t + 'sl)^О00>'12(т1.°)= |<5,(дс + т, )£,(*>&;
о
00J2i(°^2)= \G2(x + x2)Fx(x)dx.Поясним, из каких соображений выбираются именно эти функции. В предпо¬
ложении, что система работает до первого отказа, имеем основное соедине¬
ние двух элементов, и поэтому yo(sx,s2) = Fx(sx)F2(s2). Подставляя функцию
у0 во второе и третье уравнения системы (7.24) и пренебрегая слагаемыми,
соответствующими переходам "снизу", получим функции ух, у2, а затем,
следуя тому же способу, получим функции у12 и у21.
296Гпава 7Для дальнейших вычислений будут полезны следующие обозначения:00 00
Ф,(/)= \Ц(Х + 1)(Ы, ¥,(0= \Gj(x + t)dx.
о оМожно доказать, что относительная погрешность функций (7.25) и стацио¬
нарных показателей надежности Т, Тв, Кг оценивается величиной8<5р - maxZk I Zb2
71 T2Тв2 JG1 (x)7<2 (*)<& Tai JG2 (*)F, (*)<&jGi(Af)02(^)<3& JG2(x)Oi(x)6&. (7.26)Эта погрешность зависит не только от средних 7] и Гв,, но и от самих зако¬
нов распределения. В частности, если распределения времен безотказной ра¬
боты являются экспоненциальными или молодеющими (время жизни элемен-- 1 00 -тов не меньше их остаточного времени жизни, т. е. F(t) < — jF(.x)dx), тоТ tоценка погрешности зависит только от средних значений и удовлетворяет
неравенству2 (Тв1 Тв2
5 < max -6i- + -aA.I тх Т2Из соотношений (7.25) определяются вероятности состояний системы00 00
Ро=СТ\Т2, px=C\Gx(x)<b2(x)dx, p2=C \G2(x)<&x(x)dx,
о оРп -C^x(x)F2(x)dx, plx = C°\'¥2(x)Fx{x)dx
о ои параметры переходов из состояния в состояние®о,1 =СТ2, со0>2 = C7J, озХХ2=С \Gx(x)F2(x)dx, со2 21 = С\G2(x)Fx(x)dx,о ’ осо 00 00«>1,о = С \gx(x)<b2(x)dx, со2 0=С|я2(л:)Ф1(л:)сйс, со12>2 =СlGx(x)F2(x)dx,“21,1 - С jG2(x)Fx(x)dx,
о
Анализ надежности восстанавливаемых систем297где С — постоянный сомножитель, определяемый из условия нормировки.
Отсюда получаются значения требуемых показателей надежности:□ наработка на отказ:т Рь+Р\+Pi .®1,12 +(02,21□ среднее время восстановления:т Р\г+Рг\ .СО, 12+02,21□ коэффициент готовности:ТКГ = .Т + ТвЗначения полученных показателей можно несколько уточнить, если опреде¬
лить интенсивности переходов из одного состояния в другое для графа, изо¬
браженного на рис. 7.11, б, в соответствии с их определениями:Составляя и решая систему алгебраических уравнений с коэффициентами
Xkl, можно определить показатели надежности с точностью более высокой,
чем (7.26). Относительную погрешность можно записать в более удобном
виде:5<тах(А.01Гв1+Я.02Гв2, \i2^B2> ^2,2i^bi)- (7.27)Неравенство (7.27) можно трактовать следующим образом: относительная
погрешность стационарных показателей надежности, полученных описанным
способом, не превышает наибольшей из сумм произведений интенсивностей
Л-переходов и средних времен восстановления элементов, вызвавших данные
переходы. Нетрудно показать, что погрешность показателей надежности су¬
щественно уменьшается, если определить значения интенсивностей перехо¬
дов по приближенным значениям рк и соы с последующим решением систе¬
мы линейных уравнений. Например, для экспоненциальных распределений
времени безотказной работы и произвольных распределений времени восста¬
новления соотношения, полученные в результате решения системы уравне¬
ний, являются точными, а без решения системы уравнений— приближенны¬
ми. Приведем для сравнения эти формулы.
298Гпава 7Приближенные соотношения выглядят следующим образом:1+ад(*2)+*24(х,) „ ^(^2-4^1))я.]А,2|(о,р.2)+о2(х,))а.,я2|(A(X2)+4(^i))1а точные:1(1 + Я.Д(Х.2))(1 + Х2С2(^))1*1*21[G1(X2) + G2(X1) + (^1+?12)G1(X2)G2(X1))*ll(rB, - 6, (^2))(l + Я.2«32(X,)) ч- ^2 1(^в2-4(^))(1 + ЗД(Ч))*1*21[g,(x2)+g2(a.i)+(x1.+• *2 )Gj (^-2 )G2 (\j) j1Рассмотрим теперь функционирование дублированной системы с постоянно
включенным резервом для других дисциплин обслуживания. На рис. 7.12
изображены соответственно графы состояний для обратного и назначенного
приоритетов обслуживания, а также для случая неограниченного восстанов¬
ления. В следующих разделах мы приводим лишь запись соответствующих
систем уравнений и результаты точного или приближенного их решения.Рис. 7.12. Графы состояний дублированной системы
с постоянно включенным резервом для обратного приоритета (а),
назначенного приоритета (б), неограниченного восстановления (в)Обратный приоритетСостояниям системы соответствуют функции ,s2 ), л(т1>52) > Уг (51 > т2) >
yi2('ci,'c2), Уг\(х\->х'г) ■> относительно которых имеет место система инте-
гральных уравнений, описывающая стационарный режим:
Анализ надежности восстанавливаемых систем299Уо(51>52)= J/|(* + *i)^(0»* + j,2)<&+ |/2(л + 52)^2(л + 51’°)^;О о00 00Л(Х1,^2)= J Si (.х )Уо (®> х + s2 )dx + \f2(x + s2)yx2(x + xx,0)dx\о о
оо оо■ У2 С^2)= Jg2(* + x2b'o(* + 'si>0)‘&: + J/l(x + sl)y2l(°^ + T2)^ (7-28)О О00Л2(т1>т2)= \g2i.x + x2)y\(xx,0)dx-,о00^2l(Tl.T2)= J^Tl + Т1 )^2 (°? т2 )^-0Решение системы (7.28) дает возможность с точностью до постоянного мно¬
жителя определить вероятности состояний системы и параметры перехода из
одного состояния в другое:Ро = СТ{Г2, рх - СТвХТ2, р2 = СТхТв2, рХ2 = р2Х - СТв1Тв2,Ю01 = ю10 -СТ2 , <002 =С020 =СТХ, ©[ 12 =С012 1 =СГв1 , (В2 21 =®21,2 ~^Тв2 .Через эти показатели определяются наработка на отказ, среднее время вос¬
становления, коэффициент готовности:J _ Т\Т2 + ЗД + Т\Тъ2 т 2ТвХТв2 ^ _ Т{Г2 + Тк]Т2 + 7]Гв2т*1+тв2 ’ 8 твХ+тв2’ г тхт2 + твхт2+тхтв2+2твхтв2'Таким образом, стационарные показатели надежности в случае указанной
дисциплины восстановления полностью определяются своими математиче¬
скими ожиданиями и не зависят от вида распределений. Интенсивности пере¬
ходов Xkl очевидно равны здесь величинам, обратным математическим ожи¬
даниям тех элементов, из-за отказа или восстановления которых происходят
эти переходы.Назначенный приоритетПредположим, что дисциплина обслуживания дублированной системы тако¬
ва, что при отказе обоих элементов первым восстанавливается элемент 1 вне
зависимости от порядка номеров отказавших элементов. Для дальнейшего
исследования введем пять функций, соответствующих указанным состояни¬
ям: УоСад). .V2(si>*2)> Уп^хМ’ у2](т,,т2). По общей методике
составления системы интегральных уравнений* стационарный режим форма¬
лизуется следующим образом:
300Гпава 7y0(slts2)= |/1(х + ^)^1(0,л: + 52)бйс+ ^(х + а^^Сл+^.О)*;
о оСОJi(*i^2) = Jgi(* + JSi)^o(°*x + 's2)<fe»о00У2 (5i j ^2)= \g2(x + i2)y^{x + sx,Q)dx+ jg2 (х + т2 )/,(* +s, )>-12 (0,0>& +° ° . (7.29)+ J/i (* + .sj )y2\(0, х + х2 )<&',О00Л2('с]»°)= \yx(x + xx,Q)dx-,Ун (xi»'Ь) = \g\ (* + Ti )Уг (°»‘Ь )<*•
оНе проводя подробных выкладок по решению этой системы уравнений, ука¬
жем приближенные значения средней наработки на отказ и среднего времени
восстановления:. Т{Г2 + ]ад Ф2(х)сЬс + Т1Тв2 °J 'f', (x)F2 (x)dx + Тв1Тв2Т = 2 ———, Т=^ .00 7 В 00j Gi (x)F2 (л:)dx + Тв2 JG, (x)F2 (x)dx + Tn2о 0Можно показать, что относительная погрешность не превосходит величины5< —.ТхКак и в случае прямого приоритета, более точные формулы могут быть полу¬
чены, если по графу состояний составить и решить систему линейных урав¬
нений, коэффициенты которых равны соответствующим значениям интен-сивностеи переходов кы = —*=-.РкЕсли времена безотказной работы элементов имеют экспоненциальные рас¬
пределения вероятностей, то нетрудно получить точное решение системы
(7.29), которое определяет и точные значения стационарных характеристик
надежности:
Анализ надежности восстанавливаемых систем301Т =1(l + A1G,(A;2)j(l + A.2rB2)Тъ\ ~ G\ (*2 ) + *27в17в2 |Т1 _[l + XjG,^))*1*2 1(rB2+(l + *,7;2)Gi(*2))!’ ‘в *2!(rB2+(l + X17;2)G1(*2))IНеограниченное восстановлениеПредположим, что каждый из элементов дублированной системы обладает
своим ремонтным органом, и тогда при отказе двух элементов очереди на
восстановление не возникает. Функционирование системы описывается инте¬
гральными уравнениями относительно функций yofai»^)» >> Уп(х\-‘х1) '•со ооy0(sx,s2) = |/,(л: + 51)^1(0,д: + 52)Л+ jf2(x + s2)y2(x + sx,0)dx;О оОО 00>i(Ti»J2) = Jgi(* + Ti):>;o(0>* + -s'2>3&: + jf2(x + s2)yl2(x + T],0)dx;Уг^и^~ \8г(х+ 'сг)>’о(л: + S\,Q)dx + J>i(* + *1)>i1(O.Jc + T2)dc;
о 0(7.30)00 00Л2(т1»0)= Jg2(* + T2).>’i(* + i:i>0>& + \g\(,x + xx)y2(0,x + T2)dx.
о 0Система (7.30) имеет точное решение, на основе которого определяются ста¬
ционарные показатели надежности:j _ т\тг + ЗД + Т\Тв2 ^ ТвХТв2 ^ Т{Г2 + твХт2 + тхт%2Тй\ + тв2 8 ТЛ + Тв2 г ТХТ2 + ТвХТ2 + ТхТъ2 + ТвХТв2Вероятности состояний, параметры и интенсивности переходов, а также по¬
казатели надежности стационарного режима не зависят от законов распреде¬
ления, а зависят лишь от математических ожиданий.ПРИМЕР 7.6. Требуется получить стационарные показатели надежности
дублированной системы с постоянно включенным резервом для рассмотрен¬
ных ранее дисциплин обслуживания при следующих исходных данных: вре¬
мя безотказной работы элементов имеет экспоненциальное распределение с
параметрами X, =0,001 час-1 и Х2 =0,002 час-1. Время восстановления обо¬
их элементов имеет равномерное распределение на интервале от 5 до 9 часов.
302Глава 7Решение. Математические ожидания времени до отказа элементов соответ¬
ственно равны 7j =1000 час, Т2 =500 час, Гв1 =Гв2 =7 час. В расчетах ис¬
пользуется соотношение:G(X) =X XДля равномерного закона распределения времени восстановления на интер¬
вале [а;6] величина G(A.) принимает вид:1 —1b — a
G(X) = а\e~x*dt1X. (b-a)X2Для приведенных ранее дисциплин восстановления отказавших элементов мы
имеем точные значения показателей надежности, приведенные в табл. 7.4.Таблица 7.4. Стационарные показатели надежности
для различных дисциплин обслуживанияДисциплинаобслуживанияСредняя наработка
на отказ, часСреднее время
восстановления, часКоэффициентготовностиПрямой приоритет362823,60,99990Обратный приоритет3646470,99981Назначенный приоритет354705,30,99985Неограниченное восста¬
новление364643,50,99990Наблюдается высокая зависимость показателя Тв от дисциплины восстанов¬
ления. В этом легко убедиться, сопоставив результаты для прямого и обрат¬
ного приоритетов. Кроме того, надежность системы, обслуживаемой одним
ремонтником с прямым приоритетом, близка к надежности системы с двумя
ремонтниками.
Анализ надежности восстанавливаемых систем3037.4.2. Дублированная система
с ненагруженным резервомСтруктурная схема дублированной системы с ненагруженным резервом пред¬
ставлена на рис. 7.13.Рис. 7.13. Схема дублированной системы с ненагруженным резервомЕсли систему обслуживает только один ремонтный орган, то она имеет
6 возможных состояний:О (01)— оба элемента исправны, причем элемент 1 работает, а элемент 2
находится в очереди на работу;□ (02) — оба элемента исправны, причем элемент с номером 1 находится в
очереди на работу, а элемент 2 работает;□ (1) — элемент 1 отказал и восстанавливается, элемент 2 работает;□ (2) — элемент 1 работает, элемент 2 отказал и восстанавливается;□ (12) — отказал сначала элемент 1, а затем — элемент 2;О (21) — отказал сначала элемент 2, а затем — элемент 1.В зависимости от вида приоритета обслуживания отличие будет лишь в ха¬
рактеристике состояний (12) и (21), когда отказали оба элемента системы.Прямой приоритетВ состоянии (12) восстанавливается элемент 1, а элемент 2 находится в оче¬
реди на восстановление, в состоянии (21) восстанавливается элемент 2, а эле¬
мент 1 находится в очереди на восстановление. Граф состояний системы
представлен на рис. 7.14. Составим соответствующую матрицу состояний0102121221s\0*1*1*100*2*2*20*2111100и систему уравнений для описания стационарного режима функциониро¬
вания:
304Глава 7•VoiC^l»0) = +О00У02 (°>s2 ) = \у\ (О, Л + S2 )dx;О00У\ (*1 >s2) = J g\ (X + т, )/2 (л: + s2 )(У01 (0,0 ) + Уг\ (0,0)) dx;
осоУ2 (*,*2 ) = J f\(* + sx )g2 (х + т2 ) (,у02 (0,0) + уХ2 (0,0)) dx;ОооЛ2(т1>°)= j.Vi(* + ti,0)A;(7.31)У21(°>х2)= jy2(0,x + x2)dx.оРис. 7.14. Граф состояний системы, изображенной на рис. 7.13, для прямого приоритета
Решение системы (7.31) несложно. ПоложимТогда^ ~ -^01 СО, 0) ч- ^2i(0>0), В - >’о2(0>0) + ^i2-(0»0) ■yi(xus2) = A jgx(x + xx)f2(x + s2)dx, y2(sl,x2) = B jfl(x + sl)g2(x + x2)dx,
о ои значитJta (*1.0) = Д pi (* + $1 )&(*)&, yO2(0,s2) = A jgx(x)F2(x + s2)dx, (7.32)
о о00 00
У12(хи°) = А\G\(х + Ti)/2(x)dx, у21 (О,т2) = В \f (x)G2(x + x2)dx.
Анализ надежности восстанавливаемых систем305Из обозначений коэффициентов А, В и выражений (7.32) следует, что
A-В. Функции (7.32) позволяют с точностью до постоянной А найти веро¬
ятности пребывания системы во всех состояниях, а также параметры перехо¬
да из состояния в состояние:оО ОО 00рох= A \FX (x)G2(x)dx, Л)2 =AjGl (x)F2(x)dx, px= A \GX (x)F2(x)dx,
о oooo oo ooPi = A JF,(x)G2(x)dx, pl2 = A \Gx(x)F2(x)dx, p2, = A j>,(x)G2(x)dx,
o o о00 00
©01,1 =со2,01 =Л pi(x)g2(x)dx, to02)2 =co102 = A \gx(x)F2(x)dx,0 0со 00©1,12 = ©12,2 = A jGi(x)/2(x)dx, 0)2 21 = co2i , = A\fx(x)G2(x)dx.
о 0Постоянный множитель А определяется из условия нормировки:АРо\ + Рог +Р\ + Рг + Р\г + РгО =1»
а затем находятся значения стационарных показателей надежности:□ наработка на отказ:г._ .J G\ (*)/2 (x)dx + J /, (x)G2 (x)dx
о 0□ среднее время восстановления:00 00
j G, (x)F2 (x)dx + jF] (x)G2 (x)dxт _0 0 .■* о »J G, (x)f2 (x)dx + J/j (x)G2 (x)dx
о 0□ коэффициент готовности системы:Ъ+Т2Kr =■тх +Т2+ \Gx(x)F2(x)dx + ]Fx{x)G2{x)dx
о оНа рис. 7.15, а, б и в изображены соответственно графы состояний дублиро¬
ванной системы для обратного и назначенного приоритетов обслуживания,
306Глава 7Рис. 7.15. Графы состояний дублированной системы с ненагруженным резервом
для обратного приоритета (а), назначенного приоритета (б),
неограниченного восстановления (в)а также для неограниченного восстановления. Оценим надежность системы
для каждого случая.Обратный приоритетЗапишем систему уравнений для стационарного режима:оОУо1 (si >°)= fy2(x + si’ °№*
оооУ02 (О, S2) = JVi (О, х + s2 )dx;ОСО 00' Ж*1^2) = J^i(-^-f-)./2+ -^2)>^о 1 (°>0)йЬс + jf2(x + s2)yx2(x + x{,0)dx; (7.33)
о ооо ооУг(*\,Ъ)= ) f\(х + s\ )#2 (* + х2 )Уо2 (°> + \f\(x + sx)y2x(0,x + x2)dx\°_ оУп(.хиЪ) = О2(х2)у1(хи0);.У21(х\^2) = Ох(хх)у2(0,х2).В результате решения системы (7.33) и вычисления показателей надежности
получим среднюю наработку на отказ и среднее время восстановления:оо 00Ту ^7bx(x)G2(x)dx + T2 j52(^)G](j:)fl!t
J __ о о оо oo 9J©i(x)G2 (.*)<&+ fa2{x)Gx(x)dx
Анализ надежности восстанавливаемых систем307Тш1 Jco,(x)G2(x>& + 7;2 jco2(x)Gl(x)dxр = о о В 00 00J<0[(x)G2(x)<£c + Jco2(x)G[(x)afccгде со, (х) = X f*{k) (*), (*) = 5(х) + со, (х), / = 1,2.
к=1Для некоторых распределений функции ю,(х) можно получить в явном виде.
Например, для экспоненциального времени безотказной работы с параметром
X, имеем оо,(х) = Xt.Назначенный приоритетСоответствующая система интегральных уравнений имеет вид:о00>'02(°^2)= \y\{0,x + s2)dx\
оооУ\ ("Г] ,s2 ) = f gi (.X + х, )/2 (х + s2 )^01 (О, О )dx;(7.34)У2 (*1 > т2 ) = j f\ (х + S{ )g2 (х + ь ){У02 (°> °) + У\2 (°> °))dx +О
00+ J/i (х + )у2х (0, х + т2 )dx;
о00оy2i(t\>t2) = Gi(h)y2(0’x2)-Решение системы (7.34) дает следующие значения стационарных показателей
надежности:Г = -7] |©j (x)G2 (x)dx + Т2 о 00JcOj(x)G2(x)<ix:+ jGl(x)f2(x)dx
о оГ„ JcO](x)G2(x)a&c + jGl(x)F2(x)dx
р _ о о 5 в оо 00 Jco1(x)G2(x)<it + jGj(x)/2(x)cfe
о о
308Гпава 7Неограниченное восстановлениеПусть у каждого элемента резервной группы имеется свой ремонтный орган,
тогда состояния отказа (12) и (21) можно объединить в одно состояние, кото¬
рое будем обозначать (12). В этом случае система имеет 5 состояний
(рис. 7.15, в), из которых первые четыре состояния такие же, как и при огра¬
ниченном восстановлении, а состояние (12) характеризуется восстановлением
обоих элементов. Составим систему интегральных уравненийИи(я1»°) = Jj2(x + 5,,0)A;
о00У02 (°> 52) = \У\ (О,X + .v2 )dx;о00 00
л(т1»^)= Jgi(* + *i)/2(* + *2X>'oi(0»0)flfr + \f2(x + s2)yn(x + xbQi)dx-, (7.35)о00УгЬ i.*2)= \Mx + s\)Si(x + x2 )Уо2 (0,0>& + \fx(x + s{)yn(0,x + x2)dx\о о00 00У\г(хьЧ)= |g'2(x + 'C2)^i(x+^,0)^+ Jgi(x + T,)^2(0,x + T2)^.
о оРешая систему (7.35) приближенно и исходя из условия высокой надежности
элементов, получим:00 00
т\ \b\\(x)G2(x)dx + T2 Jc5b2(x)G1(x)<^Т = — ^,J®1(x)G2(x)g£c+ Jco2(x)G1(jx:)atc
о о00 00
\KnX(x)G2(x)dx+ \Kn2{x)Gx(x)dxТ =-*в_ о 0_JcO](x)G2(x)c6c+ J со2 ( jc)G| (д:)<Я[хго оПри этом относительная погрешность не превышает^00 00 "N6<2max \KnX(x)g2(x)dx, \Kn2(x)gx(x)dx
\о о
Анализ надежности восстанавливаемых систем309которая мала, если элементы системы достаточно надежны. В частности, если
элементы имеют неубывающие функции простоя, то8 < 2 шахIkЛ'в2Приведенные ранее способы математического описания технических систем
могут быть распространены на схемы с большим числом элементов. Конечно
же, решение получающихся при этом интегральных уравнений и установле¬
ние его точности представляет собой более сложную вычислительную за¬
дачу.
ГЛАВА 8АНАЛИЗ НАДЕЖНОСТИ
СЛОЖНЫХ СИСТЕМ С УЧЕТОМ
ИХ ФИЗИЧЕСКОЙ РЕАЛИЗУЕМОСТИ8.1. Приближенные методы
анализа надежностиВ большинстве практических случаев расчет надежности сложных систем
с помощью точных аналитических методов невозможен в связи со следую¬
щими особенностями решаемых задач:□ большая размерность систем уравнений;□ сложность структурной схемы (схемы расчета надежности) системы из-за
наличия избыточности и восстановления с различной дисциплиной об¬
служивания;О субъективность определения понятия "отказ";□ большие погрешности показателей надежности элементов сложной сис¬
темы.Одним из возможных способов решения этой проблемы является создание
приближенных аналитических методов и компьютерных технологий решения
задач надежности.Большинство существующих приближенных методов основаны на допуще¬
нии о справедливости экспоненциальных законов распределения времени до
отказа и времени восстановления. Это объясняется следующими причинами:1. В настоящее время отсутствуют статистические данные о законах распре¬
деления времени до отказа элементов электроники и Механики. Неизвест¬
ны не только их параметры, но даже вид закона. Элементы могут работать
в различных условиях, при различной нагрузке (электрической, механиче¬
ской, тепловой и т. д.). В этих условиях определить опытным путем пара¬
метры законов распределения, если даже вид их известен, практически не¬
Анализ надежности сложных систем с учетом их физической реализуемости 311возможно. И не потому, что нельзя создать реальные условия эксплуата¬
ции, а потому, что необходим слишком большой объем и время испыта¬
ний. Разработчик сложных систем такие испытания не может выполнить
физически, не говоря уже о материальных затратах. В случае экспоненци¬
ального закона распределения данные об интенсивностях отказов элемен¬
тов системы получить значительно легче, особенно по данным эксплуата¬
ции. Такие данные о многих элементах разработчикам сложных систем
известны.2. Методы анализа надежности технических систем при постоянных интен¬
сивностях отказов элементов в теории надежности хорошо разработаны.
Многие из них доведены до инженерных. Существуют инструкции и даже
стандарты.3. Время безотказной работы любой технической системы во много раз
больше времени ее восстановления от возникшего отказа, т. е. —«1.ЦВ этом случае вид закона распределения времени восстановления и дис¬
циплина обслуживания слабо влияют на значения показателей надежно¬
сти. Достаточно при расчетах знать лишь среднее время восстановления.
В случае восстанавливаемых систем может быть принято допущение об
экспоненциальном законе.4. Если не учитывать периода приработки техники после ее изготовления, то
интенсивность ее отказов при любом законе распределения времени до
отказа (Рэлея, Гаусса, гамма-, Вейбулла) является возрастающей функцией
времени (рис. 8.1).Рис. 8.1. Интенсивность отказов элемента во времениДо момента х X(t) < А.. А это значит, что расчеты показателей надежности
при допущении об экспоненциальном законе распределения времени до
312Глава 8отказа дают заниженные результаты. Если такие расчеты удовлетворяют
требованиям заказчика, то можно быть уверенным, что показатели надеж¬
ности системы в процессе эксплуатации не ниже расчетных.После т показатели надежности могут быть ниже расчетных. Однако если
система ремонтируется, то в результате профилактики и ремонта она воз¬
вращается в стационарный режим эксплуатации, что позволяет предполо¬
жить постоянство интенсивности отказов.Конечно, эти рассуждения не совсем верны. Почему, например, считается
допустимым более высокая надежность системы, чем требуемая? Ведь
любое улучшение надежности имеет цену: увеличиваются вес, габариты,
стоимость. Профилактика и ремонт могут восстановить систему до ее
прежнего состояния, но неизвестно, когда их проводить. Значение х не
определено. Также можно привести и другие возражения.И все же в подобных рассуждениях есть доля правды. Если нельзя выпол¬
нить анализ надежности системы при реальных законах распределения от¬
казов, то лучше вычислить показатели надежности системы приближен¬
ными методами при Я. = const, чем вовсе их не рассматривать.Если практически невозможно выполнить анализ надежности сложной сис¬
темы при реальных законах распределения отказов и восстановления, то это
вовсе не значит, что не следует и разрабатывать такие методы. Как раз на¬
оборот. Математические модели позволяют:□ исследовать свойства систем при произвольных законах распределения
отказов;□ исследовать влияние неэкспоненциальности на надежность сложных сис¬
тем;□ разработать рациональные пути повышения надежности системы;□ разрабатывать научные методы эксплуатации;□ вводить коррективы на результаты анализа надежности системы, выпол¬
ненные при допущении о экспоненциальных законах отказов и восстанов¬
лений.В книге уделяется много внимания этим вопросам. В разд. 8.2—8.4 рассмат¬
риваются способы и методы анализа надежности при экспоненциальных за¬
конах распределения времени до отказа и времени восстановления, хотя идеи
этих методов общие и во многих случаях могут использоваться при любых
законах отказов и восстановлений.
Анализ надежности сложных систем с учетом их физической реализуемости 3138.2. Описание функционирования системы
графом типа дереваИдея этого способа проста: функционирование системы в смысле надежно¬
сти, описываемое многосвязным графом, приводится к такой модели, при ко¬
торой многосвязный граф преобразуется в граф типа дерева. Это может су¬
щественно упростить вычисления показателей надежности восстанавливае¬
мой системы, таких как коэффициент готовности, наработка на отказ, среднее
время восстановления.Одним из способов преобразования графа в граф типа дерева является выбор
дисциплины обслуживания системы. При дисциплине обслуживания с обрат¬
ным приоритетом и любом виде резервирования функционирование системы
часто описывается графом типа дерева. Основанием для такого преобразова¬
ния является слабая зависимость показателей надежности системы от при¬
оритета обслуживания. Убедимся в этом на примерах.ПРИМЕР 8.1. Пусть имеется дублированная система с неравнонадежными
элементами, имеющими интенсивности отказов A,j и Я2 и интенсивности
восстановления Ц] и ц2 ■ Необходимо определить коэффициент готовности
Кг при дисциплинах обслуживания с прямым, обратным и назначенным
приоритетами. В результате расчетов оценить влияние приоритетов на на¬
дежность системы.Решение. Функционирование системы в каждом из трех случаев описывается
системой алгебраических уравнений, состоящей из пяти уравнений. Их ре¬
шение дает следующие выражения для коэффициента готовности:□ прямой приоритет обслуживания:v М-1 М-2 (^-1 +*2 + MlX*l +*2 + Мг) .^*1 (X 2 (Ml + М2 ) + М1М2 ) + *1 (*2 + Ml )(*2 + М2 )(Ml + М2 ) + M1M2 (*2 + Ml )(*2 + М2 )О обратный приоритет обслуживания:g М?М2 +*lMlM2 +*2М^М2 .М?М2 + *iMiM2 + *2М?Мг + 2A.1A.2MiM2□ приоритет в обслуживании элемента с интенсивностью Xj:£ Ml(*l +*2 +Ml)(*2 +M2)(*1 + Ml X*l*2 + (*2 + MlX*2 + М2))
314Гпава ВРезультаты расчетов приведены в табл. 8.1.Таблица 8.1. Значение коэффициента готовности дублированной системыПриоритетобслуживанияХ|, час 1\ъ час 1Hi, час 1йг, час'1ктПрямой0,10,1110,9840,10,5110,9410,10,51100,9690,50,1110,9410,50,11100,969Обратный0,10,1110,9840,10,5110,9410,10,51100,9910,50,1110,9410,50,11100,993Назначенный0,10,1110,9840,10,5110,9490,10,51100,9670,50,1110,9310,50,11100,965Из таблицы видно, что коэффициент готовности зависит от интенсивностей
отказов и восстановления и практически не зависит от приоритета обслужи¬
вания.ПРИМЕР 8.2. Структурная схема системы приведена на рис. 8.2. Граф со¬
стояний представлен на рис. 8.3, а в случае обратного приоритета в обслужи¬
вании, на рис. 8.3, б — в случае прямого приоритета в обслуживании.Необходимо оценить влияние приоритета обслуживания на наработку на
отказ.Решение. Из графов видно, что состояния (0) и (1) являются исправными.
Тогда на основании формул разд. 2.6.2 имеем:□ прямой приоритет обслуживания:
Анализ надежности сложных систем с учетом их физической реализуемости 315К Й1X|,HiРис. 8.2. Структурная схема системыРис. 8.3. Графы состояний системы: случай обратного приоритета обслуживания (а),
случай прямого приоритета обслуживания (б)□ обратный приоритет обслуживания:Т-■Ро+Р\V-lPl + V-2P3 + ЩР4В результате решения системы уравнений получим значения вероятностей
состояний системы. Подставляя эти значения в выражения для Т , получим:□ прямой приоритет обслуживания:2Л.] + Я-2 + Ц]Т=-□ обратный приоритет обслуживания:Т = -2Я,Ml2X.J + 2Я]А.2 + Я2М]Результаты расчетов по приведенным формулам представлены в табл. 8.2.Из таблицы видно, что наработка на отказ практически не зависит от дисцип¬
лины обслуживания в широком диапазоне изменения интенсивностей отказов
элементов и интенсивностей обслуживания.
316Гпава 8Таблица 8.2. Значение наработки на отказчас-1Х2, час 1Hi, час-1Гпр, час7'об, час0,010,00118238365958961109789800,0010,00119969985999999,610999,6999,80,010,00011335533775713071501083228336Обратим попутно внимание на следующий факт. Из формул для Т видно,
что наработка на отказ не зависит от интенсивности восстановления ц2 нере¬
зервированного элемента. Объяснение этому явлению было дано в гл. 5.Описание функционирования системы графом типа дерева существенно уп¬
рощает расчеты показателей надежности, особенно топологическим методом.
Теперь не нужно искать прадеревья графа. Решение можно получить в анали¬
тическом виде непосредственно по графу состояний в одну строку. Покажем
это на следующем примере.ПРИМЕР 8.3. Структурная схема системы представлена на рис. 8.4. Требует¬
ся составить граф состояний, предполагая, что обслуживание осуществляется
одной бригадой с обратным приоритетом, вычислить коэффициент готовно¬
сти системы.Рис. 8.4. Структурная схема системы
Анализ надежности сложных систем с учетом их физической реализуемости 317Решение. Граф состояний будет иметь вид, показанный на рис. 8.5.Коэффициент готовности вычислим по графу состояний, пользуясь методи¬
кой, изложенной в разд. 5.4.4: 'Л„Кг =г д„+\где Ар — члены, соответствующие исправным состояниям системы, Aq —
члены, соответствующие отказовым состояниям системы.Ь-р =MlM-2M3 -Ь И-2И-3 +*2filM2M-3 + 2*1*2М-?М2М'3 +2Я1А.2Ц?Р2Мз >Aq - ^-зМ-f М2И-3 + 2*?(j-?P'2M'3 + 2A,jA-3|x^И-гМ-з + *2н|м1м| + *2*зМ?М-2Цз ++ 2^Х2ц]*р.2Мз + 2A.1X-2|J.fМ-2И-3 ч- 2A,1X.2X,3|j.fр.2И-з + 2&?*2Н?Н2Н-з +
+2*i*2M-f М2Мз + 2*i*2*3M-fM-2M-3 •Исследуемая система имеет 16 состояний. Для определения показателей ее
надежности с учетом приоритета в обслуживании необходимо решать систе¬
му уравнений 16-го порядка. При сделанном нами допущении об обратном
приоритете обслуживания решение получается в одну строку непосредствен¬
но из графа состояний.Рис. 8.5. Граф состояний системы с обратным приоритетом обслуживания
318Глава 88.3. Анализ надежности
восстанавливаемой системы
по усеченному графу состоянийСущность метода состоит в следующем.Пусть граф состояний состоит из N узлов и к уровней. Укоротим граф до
уровня п<к, сохранив во всех переходах интенсивности отказов и восста¬
новлений. Уровень п выберем таким, чтобы в нем был хотя бы один узел,
соответствующий отказовому состоянию системы. Укорочение графа эквива¬
лентно предположению, что все элементы, которые в результате отказов пе¬
реводили систему на уровень п +1, являются идеальными (Я = 0) . Тогда по¬
казатели надежности, вычисленные по укороченному графу, будут верхней
оценкой надежности системы.Если предположить, что все исправные состояния уровня п являются отказо¬
вым и, то расчеты дадут нижнюю оценку надежности.Расчет показателей надежности по укороченному графу состояний системы
выполняется в следующей последовательности:□ строится укороченный граф состояний до уровня п, в котором имеется
хотя бы одно отказовое состояние;О вычисляются показатели надежности по укороченному графу, которые
будут верхними оценками надежности системы;□ все состояния уровня п принимаются за отказовые и вновь вычисляются
показатели надежности, которые будут нижними оценками надежности
системы;□ результаты вычислений сравниваются между собой, если окажется, что
они значительно отличаются друг от друга, то граф состояний увеличива¬
ется на один уровень и вновь выполняются расчеты верхней и нижней
оценок.Процедуры повторяются до тех пор, пока разность между верхней и нижней
оценками не будет удовлетворять необходимой точности расчетов.ПРИМЕР 8,4. Система состоит из 100 последовательно соединенных эле¬
ментов, каждый из которых дублирован с постоянно включенным резервом
(рис. 8.6). Все элементы равнонадежны, интенсивности отказов и восстанов¬
ления имеют значения: А. =.0,01 час-1, ц = 1 час-1. Систему обслуживает одна
бригада. Необходимо определить коэффициент готовности системы и нара¬
ботку на отказ.
Анализ надежности сложных систем с учетом их физической реализуемости 319X, ц X, ц X, цРис. 8.6. Структурная схема системыРешение. Система состоит из 201 состояния (рис. 8.7). Определить точные
значения Кт и Т не просто из-за вычислительных трудностей. Воспользуем¬
ся методом усечения графа.Укоротим граф до второго уровня, в котором находится узел 101, соответст¬
вующий отказовому состоянию системы. Граф будет иметь вид, показанный
на рис. 8.8.Рис. 8.8. Укороченный граф до второго уровняПользуясь топологическим методом, определим коэффициент готовности и
наработку на отказ:' ц3 + 200Яц2 + 200 • 198Я2цкг =Ро + Р\ + Pi = ~5— о— ^ —Т~>ц3 + 200Яц2 + 200 • 1 98Я2ц + 200Я2цj. _ Ро + Р\ + Рг М3 + 200Л.Ц2 + 200 • 198А,2ц
ВД01 200Я2ц2
320Гпава 8Подставляя в эти выражения значения Яиц, получим оценку показателей
надежности сверху:Кг =0,997, Т = 332 час.Принимая состояние (2) за отказовое, получим нижнюю оценку показателей
надежности:К-г=Ро + Р\ =
Т =р.3 + 200Яц2ц3 + 200Яц2 + 200 ■ 198Я2ц + 200Я2ц
Ро + Р\ц3 + 200Яц2\лр2 + M^ioi 200-198Я2ц2 + 200Я2ц2Подставляя в эти выражения значения Яиц, получим:Кг= 0,43, Г = 50 час.Диапазон значений Кг и Т слишком большой. Укоротим граф до состояния
третьего уровня. Тогда граф состояний будет иметь вид, показанный на
рис. 8.9.101<102 <xi1 р 2ХА200Х. '
>t / 198Х \1 / 196Х03Рис. 8.9. Укороченный граф до третьего уровня
Выражения для Кг и Т в случае верхней оценки будут иметь вид:Кг=Ро+Р\+Р2+Ръ =
ц5 + 200Яц4 + 200 • 198Я2ц3 + 200 198 196ЯУц3 + 200Яц4 + 200-198Я2ц3 + 200 • 198 • 196ЯУ + 200Я V + 200 • 198 • 2Я V3..2I 3. ,2у, Pq + Pi + Р2 + Р3 + 200Яц4 + 200 • 198Я2ц3 + 200 • 198 ■ 196Я^ ц
№101 + №102 200Я2ц4 + 200 • 198; 2Я3ц3Подставляя в эти выражения значения Яиц, получим:Кг =0,993, Г = 148 час.I 3, ,2
Анализ надежности сложных систем с учетом их физической реализуемости321Нижнюю оценку вычислим следующим простым способом. Предположим,
что последействие отказов дублированных элементов отсутствует. Тогда их
отказы являются событиями независимыми и коэффициент готовности сис¬
темы равен произведению коэффициентов готовности дублированных эле¬
ментов. При X = 0,01 час-1, ц = 1 час-1. Коэффициент готовности будет иметьзначение:Кглоо1,021,0202slOO= 0,98.Наработку на отказ вычислим по формуле:Кг „ 0,98Т = -1 -кг-Т =■х D1-0,98• 1 = 49 час.Из полученных результатов видно, что при усечении графа до третьего уров¬
ня оценки коэффициента готовности достаточно близки, однако оценки нара¬
ботки на отказ отличаются значительно. Если укоротить граф до четвертого
уровня, то Кг =0,9889, Т = 89 час, а при пятом уровне АГг= 0,982,
Г = 55 час. Этот ответ можно считать окончательным.Коэффициент готовности и наработка на отказ находятся в следующих диа¬
пазонах:Кг =0,98 + 0,982, Т = 49-55 час.При этом укороченный граф состояний ймеет 10 узлов вместо 201 в полном
графе состояний.Из приведенного примера видно, что разница между верхней и нижней оцен¬
ками при укорочении графа быстро убывает с увеличением уровня п. Этообъясняется следующим свойством графа состояний при условии — «1: ве-Цроятность пребывания системы в п-м состоянии выше суммы вероятностей
пребывания системы во всех остальных состояниях выше п.Вычислительные процедуры метода укорочения графа просты, особенно если
пользоваться топологическим методом. Расчет новых значений коэффициен¬
та готовности и наработки на отказ осуществляется с использованием вычис¬
лений на предыдущем уровне. В приведенном примере каждое уточнение
верхней оценки коэффициента готовности требует вычисления только двух
новых членов.11 Зак. 3094
322Глава 88.4. Метод эквивалентных схемИдея метода состоит в следующем.Из физических соображений путем качественного анализа исходной струк¬
турной схемы анализируемой системы находятся две эквивалентные струк¬
турные схемы, которые должны удовлетворять следующим условиям:□ одна из структурных схем по сравнению с исходной более надежна, дру¬
гая — менее надежна;□ расчет показателей надежности эквивалентных схем можно легко выпол¬
нить известными методами;□ эквивалентные структурные схемы должны позволять определять диапа¬
зон значений показателей надежности, удовлетворяющий требованиям
точности.В качестве конечного (итогового) показателя надежности можно взять сред¬
нее значение. Таким средним может быть среднее гармоническое Я , среднее
геометрическое G, среднее арифметическое А, среднее квадратическое К .
Эти типы средних получаются из формулы степенной средней1/X =1 ”zгде z — показатель степени, определяющий тип средней; п — число вели¬
чин X;.На основании степенной средней формулы средних имеют вид:□ среднее гармоническое, z = -1:иЯ = -□ среднее геометрическое, z = 0:G =□ среднее арифметическое, z = 1:I-/=1 Xi1/ \“
П ППлi=i
Анализ надежности сложных систем с учетом их физической реализуемости323□ среднее квадратическое, z = 2:К =i=1Средние удовлетворяют условию:Н <G<A<K.Это условие может быть полезным при определении итогового значения по¬
казателя надежности.Рассмотрим методику эквивалентных схем на примере.ПРИМЕР 8,5. Структурная схема рис. 8.6 состоит из двух элементов, каждый
из которых дублирован. Восстановление осуществляется одной бригадой с
обратным приоритетом и постоянной интенсивностью обслуживания ц.X XПредполагается, что р, = —- = 0,1 и р2 - — = 0,05 .ц цНеобходимо определить коэффициент готовности системы и наработку на
отказ.Решение. Эта система имеет 11 состояний. Метод эквивалентных схем по¬
зволяет более чем в 2 раза сократить их число и существенно упростить вы¬
числения, обеспечив необходимую точность расчетов.В качестве эквивалентных выберем две структурные схемы с постоянным
раздельным резервированием, предполагая, что элементы равнонадежны, т. е.
Л-! = Х2 = X. Тогда при ц = const р, = р2 = р . При этом в более надежной схе¬
ме р! = р2 = 0,05, а в менее надежной pj = р2 = 0,1.При этих условиях граф состояний будет иметь вид, показанный на рис. 8.7
с числом состояний, равным 5, и с постоянными интенсивностями переходов
X и (Л. Из графа состояний топологическим методом получаем следующие
выражения для коэффициента готовности и наработки на отказ:к 1 + 4р + 8р2 1 1 + 4р + 8р2г 1 + 4р + 12р2 +16р3 ’ X 4р + 16р2
Расчеты по этим формулам дают следующие результаты:Кг = 0,9635 при р = 0,1,
iCr=0,99 прир = 0,05,Кт = 0,978 при рср = 0) ’°5 = 0,075 .
324Гпава 8Точная формула для коэффициента готовности исходной системы имеет вид:
^ . 1 + 2р| + 2р2 + 8Р[Р2 1 + 2р| + 2р2 + 8pjp2 + 2pf + 2р| + 8pf р2 + 8р,р|Способ получения этой формулы из графа состояний исходной системы оче¬
виден, поэтому здесь не приводится. Подставляя в формулу значения pj и
р2, получим Кг - 0,977 .Сравнивая точное значение коэффициента готовности и его среднее значе¬
ние, видим, что в данном случае решение методом эквивалентных схем полу¬
чено практически с нулевой погрешностью. Расчеты наработки на отказ дают
следующие результаты:Г 2’64 А IТ = —— при р = 0,1,А,Тпри р = 0,05,Лг„ 3,45 0,1 + 0,05 ЛА„Г
Г = — при рср — = 0,075.Выражение для наработки на отказ исходной схемы имеет следующий вид:j 1 + 2р] +2р2 +8pjp2 2*iPi +2Я2р2 н- 8Я.1р1р2 + 8X2PjP2
Подставляя в формулу значения pj и р2, получим:г=—«_.12A.J +7Я2Из расчетов значений Г видим, что в конечных выражениях при заданных р
содержатся интенсивности отказов элементов. Характерным также является
то, что при расчете методом эквивалентных схем получается большой диапа¬
зон значений Г, что может быть источником ошибок при определении сред¬
него значения Т. В нашем примере этого не случилось. Значение Т при
Я] = 0,1 и Х2 ~ 0,05, что соответствует исходным данным при р = 1, на осно¬
вании точной формулы будет равноТ = 52 = 43,2 час.12A.J + 1Х23 45Наработка на отказ Т при среднем р = 0,075 имеет значение Т - ——.ЕслиА.+ Х-)теперь X - —J = 0,075 , то Т = 46 час, что близко к точному значению.
Анализ надежности сложных систем с учетом их физической реализуемости325Существует большое число приближенных методов расчета надежности
сложных технических систем, как восстанавливаемых, так и невосстанавли¬
ваемых. Это методы укрупнения состояний, объединения ветвей графа со¬
стояний, последовательного дифференцирования, разложения в степенной
ряд и т. п. Эти и другие методы будут рассмотрены в дальнейших главах.Описанные нами в настоящей и в предыдущих главах точные и приближен¬
ные методы анализа надежности не учитывают физической реализуемости
структурной схемы. Это может привести к существенным ошибкам расчетов.
Более того, математическая модель может быть не адекватна истинной струк¬
турной схеме. В следующих разделах настоящей главы излагаются методы
анализа надежности сложных систем с учетом их физической реализуемости.8.5. Системы
с дробной кратностью резервированияВ разд. 6.2 были рассмотрены невосстанавливаемые системы с дробной крат¬
ностью резервирования, или системы типа m/п. Для расчета характеристик
надежности таких систем были приведены конечные формулы и получен ряд
интересных свойств. В этом разделе будут рассмотрены системы т/п с вос¬
становлением. Эти системы могут иметь как нагруженный, так и ненагру-
женный резерв. Восстанавливаемые системы с дробной кратностью могут
также классифицироваться по числу ремонтных органов, участвующих в ре¬
монте отказавших элементов и дисциплине их обслуживания. Если элементы
системы имеют разную надежность, то для ненагруженного резервирования
является важным также и порядок включения в работу резервных элементов.
Восстановление вносит значительные сложности в анализ таких систем.Предположим, что техническая система состоит из п элементов, каждый из
которых имеет свои характеристики безотказности и ремонтопригодности.
Предполагается также, что известны законы и параметры распределения вре¬
мени безотказной работы и времени восстановления каждого элемента, а
также число ремонтных органов, обслуживающих систему. Будем считать,
что система попадает в состояние отказа, если произойдет отказ ее любого
(т + 1)-го элемента. Расчет надежности восстанавливаемых технических сис¬
тем с дробной кратностью резервирования представляет собой сложную за¬
дачу, решение которой в общем случае может быть дано только в виде опре¬
деленного алгоритма. Сложность определения показателей надежности сис¬
темы объясняется следующими причинами:□ лавинообразный рост числа состояний системы, являющихся функцией от
исходных параметров;
326Глава 8□ работа в реальном масштабе времени (поэтому часто оказываются неудов¬
летворительными методы статистического моделирования);□ наличие технического обслуживания, состоящего в восстановлении отка¬
завших элементов;□ существенная зависимость надежности от числа обслуживающих органов;□ различное состояние резерва (нагруженный, ненагруженный);□ произвольные законы распределения времени безотказной работы и вре¬
мени восстановления элементов;□ выбор критерия (скалярного или векторного), по которому необходимо
производить оценку качества системы.Системы с нагруженным и ненагруженным резервом привлекают большое
внимание благодаря тому, что многие технические системы моделируются на
их основе. Система с нагруженным резервом состоит из таких п элементов,
что она находится в работоспособном состоянии до тех пор, пока, по крайней
мере, т элементов функционируют исправно. Система с ненагруженным
резервом состоит из (п-т) основных и т элементов в холодном резерве.
Обслуживание систем осуществляется г ремонтниками или ремонтными
службами.В разд. 8.5.1 будут описаны в общем виде системы т из п с нагруженным
резервом и неограниченным восстановлением. В разд. 8.5.2 рассматриваются
т/п системы как с нагруженным, так и с ненагруженным резервом в услови¬
ях ограниченного восстановления элементов. При этом математические мо¬
дели, расчетные соотношения для показателей надежности и оценка погреш¬
ности приводятся только для случая одинаковых по надежности элементов.
Также приводится ряд числовых примеров и исследуются интересные свой¬
ства рассматриваемых систем. В разд. 8.5.3 исследуется надежность систем
т/п при особом понятии отказа, а именно: отказ системы т/п наступает
только при отказе (т+ 1)-го элемента, образующих группу смежных эле¬
ментов.Сделаем следующие допущения:□ время до отказа элементов имеет произвольное распределение;□ восстановленное устройство является новым;□ время восстановления отказавшего элемента может иметь произвольное
распределение;□ во время ремонта системы исправные элементы не работают;□ все отказы статистически независимы;
Анализ надежности сложных систем с учетом их физической реализуемости 327□ в резервированных системах замещением восстановленный элемент воз¬
вращается в резерв или в работу;□ механизм переключения из состояния резерва в активное состояние явля¬
ется абсолютно надежным и мгновенным;□ используется прямой приоритет обслуживания.В дальнейшем приняты следующие обозначения:□ п — количество элементов в системе;П m — количество избыточных элементов в системе;□ г — число ремонтных бригад;□ N = (1, 2,..., п) — множество номеров элементов;□ 0 — пустое множество;□ |м| — число элементов множества М с N ;□ М — упорядоченное множество М без последнего элемента;□ /иЛ/ — упорядоченное множество М , дополненное слева элементом /;□ (А, В, С, D) -— разбиение множества N на дизъюнктные подмножества,
где А — множество номеров работающих элементов, В — множество
номеров ремонтируемых элементов, С — множество номеров элементов,
образующих очередь на работу, D — множество номеров элементов, об¬
разующих очередь на восстановление. Если какое-либо из перечисленных
здесь подмножеств пусто, то оно может быть опущено;^ SA = Сsi )ieA ’ = (Of )feC » ХВ = (т/ )jeB > ®Z> ~ (0/)уе£> ;□ уА в с d(sA’0c’xb>0d’*) — плотность распределения вероятностей, что в
момент времени t каждый элемент is А работает и будет исправен в те¬
чение времени s,•, каждый элемент j е В восстанавливается и будет вос¬
станавливаться в течение времени ту, а элементы с номерами /еС и
j е D находятся в очереди;□ х + $А —вектор с компонентами (х + )ieA ;□ (sA)j — вектор, полученный из sA , если i'-ю компоненту положить равной
нулю;□ Вк — множество упорядоченных наборов номеров , /2,..., ik длины к ;
328Гпава 8□ В 'к — подмножество Вк, наборы которого не содержат в себе (т +1) по¬
следовательный номер (исправное состояние &-го уровня);□ Вк — подмножество Вк , наборы которого содержат в себе (т +1) после¬
довательный номер (отказовое состояние к-го уровня);□ Вк^ — подмножество Вк , в каждом наборе которого существует т по¬
следовательных номеров (исправное граничное состояние к-го уровня);□ ВТ/ — подмножество Вк , в каждом наборе которого существует в точно¬
сти (т +1) последовательный номер (отказовое граничное состояние Л-гоуровня);□ /(0, g(0 — плотности распределения времени безотказной работы и
времени восстановления элемента соответственно;QO 00□ F(t) = \f(t + x)dx , G(t) = Jg(f + x)dx — вероятности безотказной работы ио оневосстановления элемента за время t;□ сo(s,0) сов(т,0 — обобщенные параметры потока отказов и восстановле¬
ний соответственно;□ Kr(t), Kn(t) — функции готовности и простоя элемента соответственно;Г-. , ч Knit)п р(0=——;Kr(t)00 00□ U{x,t)~ Jco(x+ £,?-*)<& , UB(x,t)= Jcob(x + x,?-x)c/t;о 0□ С™, A™ — число сочетаний и число размещений из п по т соответст¬
венно;□ Ki sys(t), Kn sys(t) — функции готовности и простоя системы соответст¬
венно.8.5.1. Системы т/п с нагруженным резервом
и неограниченным восстановлениемСистемы т/п изучались достаточно интенсивно [7,32,93, 134, 143], благо¬
даря их широкому применению. Однако в большинстве работ предполагает¬
ся, что время до отказа и время восстановления элементов являются экспо¬
Анализ надежности сложных систем с учетом их физической реализуемости329ненциально распределенными, что существенно ограничивает применение
предлагаемых методов анализа. Учет произвольности распределений делает¬
ся только для ряда частных случаев. В общем случае анализ надежности сис¬
тем m/п при произвольных распределениях отказов и восстановлений эле¬
ментов выполняется, как правило, с использованием статистического моде¬
лирования [21,29,145]. Задача усложняется, если необходимо вычислить
показатели надежности как функции времени, например вероятность безот¬
казной работы или функцию готовности системы.В этом разделе предлагается метод вычисления двусторонних границ для не¬
стационарных характеристик надежности систем с дробной кратностью ре¬
зервирования при произвольных распределениях времени до отказа и време¬
ни восстановления элементов. Предполагается, что восстановление системы
неограниченное, т. е. при отказе любого элемента начинается немедленное
его восстановление. Метод дает точное решение при вычислении стационар¬
ных показателей надежности и приближенное при вычислении функций вре¬
мени. Он достаточно эффективен с вычислительной точки зрения и дает ре¬
зультаты с необходимой для практики точностью.Модель функционирования системыФункционирование рассматриваемой системы в общем виде можно описать
интегральными уравнениями:□ для начального состояния:i;М%.0= X (8-0ie/V о ieJV□ для состояний k-го уровня (|i?| = А;, |л| = и - А:, 1 <к<т):tУл,в(*Л’*в>0 = Z \sj(* + )Ул^j,B\j (о + SavjЪ>х + xB\j,t-x)dx +t jeB° ; (8.2)+ S \fi(* + si)yA\i,B^i (x + sA\i>(X + *Bul)i,t-x)dxieA о□ для состояний (w + 1)-го уровня (р| = /и + 1, |^| = n-m-\):tyA,B(sA>zB’0= z \sj(x + Xj)yA^j ^j((<sAKJj)j,x + xBXj,t-x)dx. (8.3)
jeBoДля наглядности построения модели на рис. 8.10 приведен неориентирован¬
ный граф состояний системы 1/4.
330Глава ВО уровень1 уровень2 уровеньРассмотрим приближенный способ решения системы уравнений (8.1)—(8.3).
Для каждого состояния системы т/п определим функции7а/(%.0 = Псо/(‘у/>0ieN (8.4)Уа,в^л^в**) = ГК(М)П юв/(ху>0,ieA jeBи установим некоторые их свойства. Доказательства справедливости свойств
содержатся в [137] и здесь не приводятся.Свойство 1. При любых т и п (0<т<и-1) функции (8.4) удовлетворяют
уравнению (8.1) и каждому уравнению (8.2). При т~п-\ (один рабочий
элемент, остальные резервные) функции (8.4) удовлетворяют также уравне¬
нию (8.3).Таким образом, при т = п-1 функции (8.4) являются точным решением сис¬
темы интегральных уравнений (8.1)—(8.3), из них могут быть получены точ¬
ные значения временных характеристик надежности.К сожалению, при т<п-1 функции (8.4) не могут служить даже прибли¬
женным решением системы (8.1)—(8.3), поскольку сумма вероятностей пре¬
бывания во всех состояниях, вычисленных по этим функциям, не равна еди¬
нице. Действительно, для нулевого уровня pN(t) = ]~[ Kri(t), а для состоянийieNк-го уровня (|i?| = A:, \а\ = п-к, \<k<m + \) pAtB(t) = ГКгЛОП Кп/(0 • По‘teA jeBэтому сумма всех вероятностей равна/ . „ ,л/я+1р(0 = Ы0+£ Z Ра,в(0= П^п(0
к = \\в\=к ieNт+\ К (t)1+Z I П-fjp:k=\\B\=k jeB KriV) у
Анализ надежности сложных систем с учетом их физической реализуемости331Определим далее нормировочный коэффициент1с(/) =р(0и положим приближенное решение системы интегральных уравнений (8.1)—
(8.3) в видеУ а, в (*л >хв >■0 - С(0П'®/ СЬ у0 П ®вj (xj> 0. (8-5)ieA jeBгде (А,В) —любое разбиение N, Q<\B\<m + \.Свойство 2. Для стационарного режима функции (8.5) представляют собой
точное решение системы интегральных уравнений (8.1)—(8.3).Как следует из свойства 2, функции (8.5) "хорошо" ведут себя при длитель¬
ной эксплуатации системы. Однако в нем не говорится о поведении этих
функций для переходного процесса. Поэтому возникает задача оценки по¬
грешности при замене точного решения системы уравнений (8.1)—(8.3) при¬
ближенным решением (8.5) при любых значениях /. Следующее свойство
устанавливает величину разности между левой и правой частями каждого
интегрального уравнения, если в качестве решения приняты функции (8.5).Свойство 3. Справедливы следующие соотношения:□ для начального состояния:twn(sn у0 = Щ <*>»О + si >•(- х)C'(t ~ X)dx;О ieN□ для состояний k-го уровня (|i?| = к , \а\ = п - к, 1 <,к<т):Iwa, в (sa ’хв >0 = Щ ®< (х + Sj ,t - х) П “в/ (x + Xj,t- X) C\t - х) dx;0 ieA jeB□ для состояний (т + 1)-го уровня (|5| = т +1, \а\ = п - т -1):1 d ( \WA,B(sA’XB’t) = ~\— Il0)i^V-*)C(/-l) Пв>^(Х + ТУ>/-дс)йЬс*0 Vie Л ) jeBНа основании свойства 3 легко вычисляются абсолютная и относительная
погрешности»» |а^ в(о|^a,b(0 = J lwA,B(sA’XB’0dsAdxB ’ 8А,в(0= (8-6)о о Ра, в (О
332Глава 8где00 ООРл,в(0~ J \уa,b(sB’OdsAdxв •(8.7)о оИнтегралы в (8.6) и (8.7) вычисляются по всем s,, ieA и всем , jeB.Относительная погрешность приближенного решения (8.5) рассчитывается
по формуле 8(г) = max5- B(t), где максимум распространяется на все воз-л о *можные состояния системы т/п. Эта погрешность определяется программ-Расчетные соотношения для характеристик надежностиНа основании полученного приближенного решения (8.5) можно записать
формулы для характеристик надежности системы т/п. Определим сначала
стационарные характеристики Г и Г, системы. Согласно свойству 2, указан¬
ные характеристики точны, они зависят лишь от начальных моментов рас¬
пределений первого порядка, а именно:Выпишем теперь приближенные значения нестационарных характеристик.
Функции готовности и простоя системы:ным путем в зависимости от исходных данных исследуемой системы.£ = 1|Д| = £ /ей Т: IflUm+l (ей Ti‘-г Z. Z,к=\\В\=к jeB ■‘'•Ir/vUпараметры потока отказов и восстановлений системы:
Анализ надежности сложных систем с учетом их физической реализуемости 333На основе этих характеристик и разд. 2.6 определяются интенсивности пото¬
ков отказов и восстановлений системы X(t), fx(t), плотности распределения
времени безотказной работы /(/) и времени восстановления g(t) системы.Расчет по приведенным здесь формулам при больших значениях пит (по¬
рядка нескольких десятков) требует колоссальных затрат машинного време¬
ни. Поэтому необходима разработка методов, существенно упрощающих вы¬
числение по указанным формулам. Рассмотрим суммы<*к = £ ПРу > vk = X ПР jT.aj> *“1,2,..., л,\B\ = kjeB \B\=kjeB JeBв которых суммирование осуществляется по всем сочетаниям из п элементов
по т . Получим простые и удобные правила вычисления этих сумм. Через т:
обозначим "моменты" 1-го порядкаv 1щ = Ъ р j ■7=1Свойств 4. Элементы последовательности удовлетворяют следующим
равенствам:к ы 1где ст0 равно нулю. Элементы последовательности удовлетворяют сле¬
дующим равенствам:vk = Z «/р/4-i>ieNгде cj^ вычисляются так же, как и ак, только применительно к массиву
{ру}, из которого исключен i-й элемент.Свойство 4 упрощает расчет характеристик надежности, поскольку позволяет
организовать быстрые вычисления для любых значений тип. Для нерезер¬
вированной системы ( т = 1) полученные выражения полностью совпадают с
результатами разд. 7.2.Исследование конкретных схемАнализ характеристик надежности осуществляется программным путем.
Программа Magor (http://www.gurov.spb.ru/isant/isant.html) предназначена
для вычисления стационарных и нестационарных характеристик надежности
т из п систем, таких как среднее время между отказами, среднее время вое-
334Гпава 8становления, интенсивности отказов и восстановлений, функция готовности
и т. д. Все характеристики являются функциями времени. Использование
программы позволяет оперативно исследовать характеристики надежности
систем при достаточно больших значениях тип.ПРИМЕР 8.6. Рассмотрим систему с параметрами: « = 100, т~6. Вре¬
мя безотказной работы и восстановления элементов имеет усеченное
нормальное распределение, причем 7) е [1000; 1500] час, TBj е [20; 30] час,
г = 1, 2,..., п. Для каждого элемента параметры Tt и TBj являются равномерно
распределенными числами из указанных интервалов. Среднее квадратическое
отклонение времени безотказной работы элементов равно 300 часов, а време¬
ни восстановления элементов — 5 часов. Требуется получить двусторонние
границы функции готовности системы.Решение. Результаты расчетов приведены на рис. 8.11 (кривая 2— точное
значение Kr(t), кривые 1 и 3 — граничные значения).Рис. 8.11. Функция готовности и двусторонние границыПо программе получены также значения стационарных показателей: на¬
работка на отказ Т = 1201 час, среднее время восстановления Тв =3,6 час,
коэффициент готовности системы Кг =0,99703, максимальная погрешность
Атах (0 = 0,002049.
Анализ надежности сложных систем с учетом их физической реализуемости335ПРИМЕР 8.7. Для иллюстрации влияния различных распределений на функ¬
цию готовности возьмем три системы со следующими распределениями вре¬
мени безотказной работы и времени восстановления элементов: экспоненци¬
альные распределения, усеченные нормальные распределения, гамма-распре¬
деления. Известны параметры систем: п = 100, m-2, Tt е[1 ООО; 1500] час,Ttj 6[20; 30] час, 1 = 1, 2,среднее квадратическое отклонение временибезотказной работы элементов равно 300 часов, а времени восстановления
элементов — 5 часов.Решение. Результатами расчетов является функция готовности каждой сис¬
темы, графики которых приведены на рис. 8.12 (кривая 1 — экспоненциаль¬
ное распределение, кривая 2 — нормальное распределение, кривая 3 — гам¬
ма-распределение).Рис. 8.12. Зависимость функции готовности от трех различных распределенийЗначения стационарных показателей соответственно равны: наработка на от¬
каз Т- 31,6 час, среднее время восстановления Гв = 8,4 час, коэффициент
готовности Кг = 0,79077.В заключение этого раздела еще раз отметим, что предложенный метод ана¬
лиза надежности m из п систем при вычислении стационарных характери¬
стик дает точные значения. При вычислении нестационарных характеристик
мы получаем двусторонние оценки показателей надежности. В частном слу¬
чае, для систем с нагруженным резервом значения нестационарных характе¬
336Гпава 8ристик— точные. Метод позволяет организовать быстрые вычисления для
любых значений тип.8.5.2. Системы т/п с нагруженным и ненагруженным
резервом и произвольным восстановлениемВ данном разделе рассматривается общий случай систем т/п с нагруженным
и ненагруженным резервами при различных условиях восстановления. Будем
считать, что обслуживание системы осуществляется г ремонтниками или
ремонтными службами. Одной из основных причин трудоемкости расчета
показателей надежности таких систем является высокая размерность соответ¬
ствующей математической модели. Например, для ненагруженного резервачисло уравнений в системе равно А™^ 1 п-гk=0k\ r\и поэтому естествен¬ным является желание уменьшить порядок системы. В общем случае, когда
элементы разнонадежны или порядок выбора элементов из очередей назна¬
ченный, уменьшить количество состояний в системе невозможно. Однако для
идентичных элементов система уравнений существенным образом упрощает¬
ся. Ее можно представить в компактном виде, уменьшив число состояний до
(т + 2). Соответствующий граф состояний изображен на рис. 8.13.Рис. 8.13. Укрупненный граф состояний для системы из идентичных элементовМодели функционирования для нагруженного
и ненагруженного резерва (идентичные элементы)Для нагруженного резервирования имеет место система уравненийЛ(^^в>Оо.О = Фо“)(^,тд,Од,0 + П/(/ + -5«);ieA• yk(sA’XB’°D’O = 4>(k)(sA’'cB’0D’t) + <?kl\sA’'tB>()D’O, 1 ^ к < (Щ (8.8)
Ут+\ (sA>xB,0D,t) = ф(^,(sA,xB,0D,t),где функции <p(f)(sA,xB,0D,t) соответствуют переходам сверху вниз с
(к - 1)-го уровня графа на к-й уровень, а функции q>^\sA,xB,0D,t) соответ¬
Анализ надежности сложных систем с учетом их физической реализуемости 337ствуют переходам снизу вверх с (к + 1)-го уровня на к-й. Данные функции
вычисляются по следующим далее формулам.Функция ^k\sA,xB,0D,t) равна:
tX \g(x + xj)yk_l(x + sA'<jQj,x + xBXj,QD,t-x)dx при к = \, 2,..., г,jeB о/jyk-i(x + sA^°D\D’X + xB,0Q,t-x)dx при к = г + \,, m,оt\yk_i(sA'u0D\Q,x + xB,0j2,t-x)dx при r<m, k = m +1,оtX lg(x + xJ)yk_l(sAu0j,x + xBXj,0D,t-x)dx при т — m + \, k = m +1.
jeBoФункция \sA,xB,0D,t) равна:
tX + + + u0i,0D,t-x)dx при Л: = 0,1,, Л- — 1,ieA ОIieA jeBoпри к = r,..., т.Для ненагруженного резервирования и идентичных элементов имеет место
система уравнений:yo(sA’®C’XB’®D’t) ~ ФоМ)(^’ ®C’XB’®D’0+ Yl fit + Sj);ieA• ykisA^C’XB>^D’t) = (?(jf\sA,0c,XB,0D,t) + ^k\sA,0c,XB,0D,t), (8 9-)1 <k<m;Ут+l isA>0c>xB>®D>t) = Фт+l isA>0c,XB,0D,t),где (pjjf\sA,0c,xB,0D,t) соответствуют переходам сверху вниз с (к - 1)-гоуровня графа на к-й уровень, a <p<ku}(sA,0c,xB,0D,t) соответствуют переходамснизу вверх с (к+ 1)-го уровня на к-й, и эти функции вычисляются по сле¬
дующим далее формулам.
338Гпава 8Функция ф^)(54>Ос,тд,0£).,0 равна:X X lf(x + si)g(x + xJ)yk_](x + sA\i^0j,0^c,x + xB\J,0D,t-x)dxieA jeBoпри к = 1, 2,..., г,tX J/(* + Xv*-i (* + ^\, U 00Vfi, Оюс, JC + тд, 0£, f - -x)otc при А: = г +1,..., тп,ieA Оt+ при к = т + \, г<т,оX \s(x + xj)ym(sA u0j,0c,x+TBXj,0D,t-x)dx при£ = т + 1, г-т + \.
jeBoФункция <p(£\sA,0c,xB,0D,t) равна:1 tlyk+i(x + sA>QQ’x + xB'J0C£,02,t-x)dx при к = 0,1,о/X J^+xy)^+l(JC + ^>°C’Ji: + TB\y U°C\C>°/uD’'-■*)<& ПРИ 1Я-1,yefiO/X X J/(*. + Ж* + x7 ХУ«+1 (* + SA\i>0C>x + xB\j V 0/»'°£)uy >' - *)d*/еЛ jeB опри k = m, r <m,tX \f(x + si)ym+\(x + sA\i’QC’x + xB ^~>Oi,0D,t-x)dx при k = m, r = m +1.ieA оСоставленные системы уравнений имеют сравнительно невысокую размер¬
ность, однако их нельзя решить в конечном виде, за исключением лишь неко¬
торых отдельных случаев. Поэтому мы ограничимся нахождением прибли¬
женного решения системы и оценкой погрешности, возникающей от замены
точного решения приближенным.Приближенное решение и оценка погрешностиБудем искать приближенное решение систем уравнений в виде следующего
набора функций:yk(sA’0C’XB’°D’0 = C{t)Mk П СО,(*,,/)Г1 Кп(ОП °V(ту >О П Knj(0 (810)ieA ieC jeB jeD
Анализ надежности сложных систем с учетом их физической реализуемости 339при к = 0,1,..., m +1, где постоянные коэффициенты Мк определяются для
нагруженного и ненагруженного резервов соответственно равенствами—п~, при к<г;
к\при к >гг\гк-г(п - mfк\(п - т)кг\гк-гпри к<г;
при к>г,1£ мк(кг(/))п (кМk=Q— нормировочный множитель. Безусловно, это приближенное решение в не¬
которых случаях может иметь высокую погрешность. Тем не менее мы его
используем в связи со следующими обстоятельствами:□ существует оценка погрешности;□ решение можно уточнить, применяя итерационную процедуру и беря ука¬
занное решение за начальное; правда, для этой цели необходимо исполь¬
зовать компьютер с высоким быстродействием;□ решение простое, поэтому из него получаются достаточно простые соот¬
ношения для характеристик надежности.Приближенные значения функций готовности и простоя системы для равно¬
надежных элементов с прямым приоритетом обслуживания имеют вид:I мкшУKr.vJt) = — r.sysv > т+\I мкШ)кк=О*n,sys(0 = l-*r,sys(0-(8.11)Так как нас интересуют лишь вероятностные характеристики надежности
системы, то, как показано в [137], погрешность приближенного решения
(8.10) оценивается по интегральной метрике, т. е. для каждого состояния по¬
грешность вычисляется как интеграл от разности между левой и правой час¬
тями соответствующего уравнения.Исследование конкретных схемПРИМЕР 8.8. Рассмотрим систему 4/100 с ненагруженным резервом. Время
до отказа элементов имеет гамма-распределение с математическим ожидани¬
ем 1000 часов и средним квадратическим отклонением 300 часов. Время вое-
340Гпава 8становления элементов имеет гамма-распределение с математическим ожи¬
данием 20 часов и средним квадратическим отклонением 10 часов. Требуется
оценить влияние числа ремонтников г на функцию готовности.Решение. На рис. 8.14 изображено 5 кривых функции готовности системы
при г = 1,2, 3,4, 5.Конечно же, с увеличением числа г функция готовности возрастает.Рис. 8.14. Функция готовности для системы с ненагруженным резервом
при различном числе ремонтниковПРИМЕР 8.9. Рассмотрим две системы 4/20 с нагруженным и ненагру¬
женным резервами соответственно. Время до отказа элементов имеет гамма-
распределение с математическим ожиданием 1 ООО часов и средним квад¬
ратическим отклонением 350 часов. Время восстановления элементов имеет
гамма-распределение с математическим ожиданием 30 часов и средним квад¬
ратическим отклонением 15 часов. Каждую систему обслуживают две ре¬
монтные бригады. Требуется оценить влияние типа резерва на функцию го¬
товности.Решение. На рис. 8.15 изображены две кривые функций готовности для раз¬
личных систем.Из графиков следует, что функция готовности системы с ненагруженным ре¬
зервом выше, чем системы с нагруженным резервом.ПРИМЕР 8.10. Требуется определить функцию готовности и ее двусторон¬
ние границы для системы 4/10 с ненагруженным резервом. Систему обслу¬
живают две ремонтные бригады. Время до отказа элементов имеет гамма-
распределение с математическим ожиданием 1000 часов и средним квадрати¬
ческим отклонением 350 часов. Время восстановления элементов имеет гам-
Анализ надежности сложных систем с учетом их физической реализуемости341Рис. 8.15. Функция готовности для системы с ненагруженным (кривая 1)
и нагруженным (кривая 2) резервомма-распределение с математическим ожиданием 30 часов и средним квадра¬
тическим отклонением 15 часов.Решение. Рис. 8.16 показывает кривую функции готовности и ее двусторон¬
ние границы, иллюстрируя возникающую при этом погрешность метода, из¬
ложенного в разд. 8.5.2.Рис. 8.16. Функция готовности и ее граничные оценки для системы с ненагруженным резервомСвойства систем с дробной кратностью резервированияОтметим без доказательства некоторые свойства функции готовности, выте¬
кающие из расчетной формулы (8.11). Рассмотрим две системы m/п, одна из
которых имеет нагруженный, а другая — ненагруженный резерв, с функция¬
ми готовности Kr pai(t) и Kr c0\(t) соответственно при прочих одинаковыхусловиях. Если р(/) = 0, то, согласно (8.11), Kr pai(t) = Krco](t) = 1. Если
р(0 > 0, то эти величины являются, очевидно, бесконечно малыми при
342Гпава 8и-»оо, а функции Krpa[(t) и Krco{(t) эквивалентны при «->оо, т. е.lim*г,раг (О”^°°^r,col(0Рассмотрим вопрос о возможности достижения функцией готовности значе¬
ния, равного единице, в зависимости от числа т резервных элементов. Число
основных элементов системы (п-т) и число ремонтных единиц г счи¬
таются постоянными величинами. Предположим, что момент времени t,
для которого вычисляется функция готовности, зафиксирован и р = р(/).
Тогда в зависимости от состояния резерва справедливы два свойства систем
т/п [137].□ При фиксированном значении г за счет увеличения числа резервных эле¬
ментов нельзя получить значение функции готовности системы с нагру¬
женным резервом, равное единице, т. е. lim Krsys(t)<\. Однако еслиг — т + \, то lim Кг sys (t) = 1./я-юо□ Если г <(п-т)р, то за счет увеличения числа резервных элементов нель¬
зя получить значение функции готовности системы с ненагруженным ре¬
зервом, равное единице, т. е. lim Кг sys(t) < 1. Если г>(п-т)р, тот—ко ’lim К s (t) — 1.m—><жЭти свойства систем т/п полностью подтверждаются проведенными расче¬
тами. Указанный здесь подход для вычисления функции готовности и дву¬
сторонних оценок может быть полезен для решения проблемы оптимизации
надежности, которая будет рассмотрена в разд. 10.5.8.5.3. Надежность систем т/п
при отказе группы смежных элементовРассмотрим систему т/п при следующей трактовке понятия отказа: отказ
системы наступает при отказе определенных, заранее фиксированных групп
из (т +1) элементов. Если, например, все элементы системы упорядочены, то
такие группы могут состоять из (т + 1)-го элемента со смежными номерами
[127]. Такими системами могут моделироваться фазированные антенные ре¬
шетки, телекоммуникационные системы и т. д.В общем случае анализ надежности таких систем при произвольных законах
распределений отказов и восстановлений элементов может быть выполнен
посредством имитационного моделирования [21, 29]. Однако этот подход яв¬
ляется чрезвычайно сложной вычислительной задачей для больших и высо¬
Анализ надежности сложных систем с учетом их физической реализуемости 343конадежных систем. Проблема значительно усложняется при анализе неста¬
ционарных характеристик надежности.Далее будем использовать метод интегральных уравнений, позволяющий вы¬
числять стационарные и нестационарные характеристики надежности. Для
существенного сокращения времени вычислений получим двусторонние гра¬
ницы функции готовности. Сделаем при этом следующие допущения:□ отказ системы из п элементов наступает при отказе (m +1) соседнего
элемента;□ при отказе группы из (т + 1 )-го элемента система продолжает работать,
расходуя свой ресурс;□ восстановление системы неограниченное;□ элементы могут иметь разную надежность при произвольном распределе¬
нии отказов и восстановлений.В качестве показателя надежности системы примем функцию готовности.
Аналогичным образом можно рассмотреть также и другие показатели.Модель функционирования для системы 1/4Граф состояний исследуемой системы для частного случая п = 4, т = 1 при¬
веден на рис. 8.17. Круги соответствуют состояниям исправной работы сис¬
темы, а квадраты — состояниям отказа. Отказ системы происходит при отка¬
зе группы из любых двух смежных элементов.На основе рисунка запишем множества, смысл которых раскрыт в начале
разд. 8.5:Вх ={1, 2,3, 4}, В2 = {(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)},Въ ={(1,2,3),(1,2,4),(1,3,4),(2,3,4)}, Вх = {(1,2,3,4)},B+=B;f =ВХ, Bx=Bxf=0,В\ = Я2+/ = {(1,3),(1,4),(2,4)}, Я2 = B-2f = {(1,2),(2,3),(3,4)},53+ =53+/ =0, В1 =53_/ =В3, й4+ = 54+/ = 0, В'А = B~f =В4.Согласно общим правилам, функционирование рассматриваемой системы с
разнонадежными элементами можно описать следующей системой инте¬
гральных уравнений:□ для начального состояния (5 = 0):IydsN’0= X \М* + )yNXiJ(x + sNXi,(T,.)i,t-x)dx + П ft(.t + Si); (8.12)ieN о ieN
344Глава 8Рис. 8.17. Граф состояний системы l/4
□ для состояний к-го уровня (|5| = к ):/•Ув (SN\B ’ ТВ > 0 - X \sj(x+xj )Уы\Ви j,B\ j ((•*• + sN\Bui )j’x + XB\j’t ~ x)dx +(8.i3)+ Z Jfi(x+si)yn\B\t,iui(x + Sn\B\i>(x + *evi)irI-X)dx;
ieN\B о□ для состояний п-го уровня (В = N):/» (тл.■0 = X Jgj(x + xj )yj,N\j(С*/ )j>x + 1N\J,t - x)dx . (8.14)jeN оПри сделанных ранее предположениях система уравнений (8.12)—(8.13) до¬
пускает следующее простое решение:>'й(5Л'\В>тВ> 0 - П ш,(М)П<°в/(*,,0, (8.15)ieN\B jeBсправедливое для любого состояния В, в том числе и для случая, когда
5 = 0 или В = N. Доказательство этого утверждения можно получить непо¬
Анализ надежности сложных систем с учетом их физической реализуемости 345средственной подстановкой функций (8.15) в уравнения (8.12)—(8.14). Из
(8.15) легко определяются вероятности состоянийРв(0= П ВДПКп/(0. (8.16)ieN\B jeBРешение (8.15) позволяет найти стационарные и нестационарные характери¬
стики надежности. Функция готовности, например, равна*r(0=i- X X Рв(о»£ = /я+1 ВеВка подставляя значения вероятностей в соответствии с формулами (8.16), по¬
лучим" К (t)К,(0 = 1-пад £ I П-Г7ГГ- (8|7>ieN k=m+\ BeBk jeB •‘'■г/v>Для определения параметра потока отказов системы следует рассмотреть ис¬
правные граничные состояния £-го уровня (m<k <п) и для каждого из них
найти сумму параметров перехода во все отказовые состояния (k + 1 )-го
уровня:= X X X ПМ0«а(0П^(0. (8-18)k=rn ВеВ^ а ieA jeBВиаеВ*и i*aПараметр потока восстановлений системы определяется как сумма парамет¬
ров переходов из отказовых граничных состояний к-го уровня (т<к<п)
в исправные состояния (к — 1)-го уровня:®в(0= XXX П^п(ОП^пу(Осовр(0- (8.19)к=т+\ ВеВк* Р ieA jeBВ\реВ*+_, J* РСтационарные значения этих характеристик Кг и со = сов определяются ана¬
логично, например, коэффициент готовности рассчитывается по формуле*г=!-П± I п^- <8'20)ieN Л' ' ■‘в/ А=/и+1 ВеВк jeB * jПоэтому наработка на отказ и среднее время восстановления системы равны
соответственноК 1 — кТ = ^-, Тв =-——(8.21)
со ю
346Глава 8Быстрый алгоритм расчета функции готовностиРасчет по формулам (8.17), (8.20) требует очень больших временных затрат.альному алгоритму исправных или отказовых состояний. Для существующей
вычислительной техники такая задача является неразрешимой уже при
п = 100 . Для преодоления указанных сложностей рассмотрим суммы видаДля значений т = п-1 и т = п-2 суммы sk вычисляются очевидным обра¬
зом. Если т-п-\, то к = п и sk =sn =р, ... р„. Если т = п-2, то при
к = п-1 sk =s„_{ =р, ...р„_, +р2 ...р„, а при к = п sk=s„=px ...р„. Поэтому
интерес представляет случай, когда т<п-3. Рассмотрим особый подход к
вычислению сумм sk . С этой целью введем суммыв которых суммирование осуществляется по всем сочетаниям из п элементов
Pi,... ,рп по к элементам. Эти суммы рассмотрены в разд. 8.5.1, и для них
получены весьма простые и удобные для вычислений рекуррентные формулы
(свойство 4):Так, на к-м уровне требуется перебор С* состояний и определение по специ-ВеВк jeBa(;)(p„...,pj= £ ПРу >ВеВк jeBгде = 1, а mj — "моменты" /-го порядка:V I
mi = L Pj ■Можно показать, что при т<>п-Ъ имеет место соотношениеп-т<h,j) = X <*У U(Pi - Рj.\)^k-m-h°(ру+т+2 - р»). ПРИ 2<j<n-m-2\при j = 1;CT*-m-l(Pl ••• Py-l)>при j = п-т-1, или j = п-т.
Анализ надежности сложных систем с учетом их физической реализуемости 347Таким образом, суммы sk выражаются через суммы с^и), для которых име¬ется простой вычислительный алгоритм. Это обстоятельство позволяет про¬
изводить расчет намного быстрее, чем непосредственно по формулам (8.17),Заметим также, что расчет по указанным формулам будет ускорен, если вос¬
пользоваться двусторонними оценками для функции и коэффициента готов¬
ности. Действительно, из (8.17) следует верхняя оценка для функции готов¬
ности системы, если ограничить суммирование по к от (m +1) до п', где
п' — любое целое число между (т +1) и п:Значение п' выбирается на основании необходимой точности расчетов. Как
показывают многочисленные примеры, п', взятое в пределах от т 'т(п,т + 6)
до min(«,m + ll), дает совпадение верхней и нижней границ с точностью
до 5-ти знаков после запятой.ПРИМЕР 8.11. Рассмотрим систему 5/40, отказ которой наступает при отка¬
зе смежных элементов. Время до отказа элементов имеет гамма-
распределение с параметрами 7} е [200; 300] час, / = 1, 2,..., п. Для всех эле¬
ментов математические ожидания Tt являются равномерно распределенными
в интервале [200; 300]. Среднее квадратическое отклонение времени до отка¬
за равно 90 часов. Время восстановления элементов имеет гамма-
распределение с параметрами TBj е [50; 60] час, i =1, 2,..., п, среднее квадра¬
тическое отклонение равно 30 часов. Требуется определить функцию готов¬
ности системы и проиллюстрировать влияние величины п' на точность дву¬
сторонних оценок KT(t).Решение. На рис. 8.18 показаны двусторонние границы при различных зна¬
чениях п': и'= 10 (кривые 1, 2), п' = 12 (кривые 3, 4), «' = 16 (кривые 5, 6).Максимальные значения абсолютных ошибок равны 5 • 10_3, 6-10-4 и 410-6(8.20).ieN к = т+\ ВеВк jeB ^rj (0Нетрудно получить также и нижнюю границу для KT(t):-п ад i sк<‘\o=n*r,<oi ~р.)-
348Гпава 8соответственно. Из рис. 8.18 можно заключить, что максимальная ошибка
имеет место в переходном режиме.Рис. 8.18. Двусторонние границы функции готовности при различных значениях п'(гамма-распределения)Для сравнения на рис. 8.19 показаны двусторонние границы Kr(t) для анало¬
гичной системы с экспоненциально распределенными временем до отказа и
временем восстановления.Рис. 8.19. Двусторонние границы функции готовности при различных значениях я'
(экспоненциальные распределения)
Анализ надежности сложных систем с учетом их физической реализуемости 349Из рис. 8.19 видно, что ошибка значительно меньше, чем для предыдущей
системы. Для тех же значений п' = 10 (кривые 1, 2), «' = 12 (кривые 3, 4),
и'= 16 (кривые 5, 6) максимальные значения абсолютных ошибок равны3,4• 10-4, 2,4-10-5 и 2-10-7 соответственно. Этот факт объясняется различ¬
ной продолжительностью переходного процесса для двух систем.8.6. Системы с автоматом контроля
и коммутацииМодели расчета надежности зачастую не учитывают влияния переключаю¬
щих устройств. Поэтому значения показателей надежности, таких как веро¬
ятность безотказной работы или коэффициент готовности, бывают неоправ¬
данно завышенными. В действительности время подключения резервных
элементов может оказать существенное влияние на надежность систем, что
необходимо учитывать при их проектировании [19,38,55,90]. Существую¬
щие в настоящее время методы оценки надежности систем при наличии пе¬
реключающих устройств, как правило, обладают следующими недостатками:□ пригодны только для систем, состоящих из сравнительно небольшого чис¬
ла элементов, например для дублированных систем;П распределение времени безотказной работы элементов предполагается
экспоненциальным;□ время переключения на резерв обычно считается постоянным;□ методы являются эвристическими и не позволяют указать оценку погреш¬
ности.Одним из путей анализа описанных выше систем с произвольными распреде¬
лениями времени до отказа переключателя, элементов системы и времени
переключения на резерв является составление и решение системы интеграль¬
ных уравнений (см. гл. 4). Подход, основанный на составлении математиче¬
ской модели в виде системы интегральных уравнений, не только позволяет
учесть в резервированных системах время переключения на резерв, но также
дает возможность избежать перечисленных выше недостатков. Основной це¬
лью данного раздела является поиск аналитического решения получаемых
систем интегральных уравнений. Приводятся численные примеры, демонст¬
рирующие влияние различных типов переключателей на надежность системы
в целом.Дополнительно к обозначениям разд. 8.5 введем следующие:□ £ — время безотказной работы элементов, f(t), F(t) — соответственно
плотность и функция распределения %, F(t) = 1 - F(t);
350Гпава 8□ г| — время восстановления элементов, git), G(t) — соответственно
плотность и функция распределения r|, G(t) = 1 - G(t) ;□ Z — время переключения на резерв, h(t), H(t) — соответственно плот¬
ность и функция распределения Z, H{t) = 1 - H(t);□ — время безотказной работы переключателя, u(t), £/(/)-— соответст¬
венно плотность и функция распределения £р > U(t) = l-U(t);□ rip — время восстановления переключателя, v(t), V(t) — соответственно
плотность и функция распределения t|p, V(t) = 1 - V(t) .8.6.1. Невосстанавливаемая система
с абсолютно надежным переключателемРассмотрим схему резервирования, в которой имеется один основной и т
резервных элементов, пребывающих в ненагруженном состоянии. Все эле¬
менты считаются равнонадежными. При отказе основного элемента он заме¬
няется резервным не сразу, а через случайное время Z. Это время может
быть также и постоянным, если его плотность является 8-функцией Дирака.
Определим вероятность того, что в момент времени t система находится в
исправном состоянии. Сначала предположим, что переключатель является
абсолютно надежным и не может отказывать.Все состояния такой системы делятся на состояния исправной работы, когда
работает основной элемент (состояния с четными номерами), и отказовые
состояния, когда совершается процедура подключения резервного элемента
(состояния с нечетными номерами). Это соответствует графу состояний,
представленному на рис. 8.20.Рис. 8.20. Граф состояний при n = т+ 1 (надежный переключатель)Каждому состоянию системы поставим в соответствие функцию у, аргумен¬
ты которой характеризуют поведение в момент времени t как элементов в
Анализ надежности сложных систем с учетом их физической реализуемости351системе, так и переключателя. Относительно этих функций справедлива сле¬
дующая система интегральных уравнений:yo(s,0 = f(t + s);IУгк-\ (z>0 = JaO+г)У2к-2 (°>t ~ x)dx'>
оty2k(s^)= \f(x + s)y2k-\i0,t-x)dx, k = l,
о
tУ2т+1 (0 = Jy2m (0> t ~ x)dx.(8.22)Решение системы (8.22) элементарно и дается формулами:Уо(*,*) = /50),
y2k-X(z,t) = fik)*h-(k-X)*hz{t),У2кМ = Г(к)*11*{к)*т,
y2w+1(0 = r(m+1)^*(w)^(0.Из полученных соотношений следует, что вероятности состояний, как функ¬
ции времени, определяются формулами:Po(0 = F(0,Р2к-\0) = Г(к)**(к-Х)*Н«),P2k0)=f’(k)*h*w*m,
P2m+i0) = ft{m+l)*h*^*l(t).Можно выполнить проверку на справедливость условия нормировки:тРо 0)+ Z {Р2к-\ (О + Ргк (0) + Р2т+1 (0 = 1.
к = 1Это условие вытекает из представления вероятностей в видеРоО)=т,P2k-\0)~Fk *h*^k~X\t)-Fk *h,(k)(t),
352Гпава 8P2k(t) = Fk*h'(k\t)-Fk+lP2m^) = Fm+x*hKm\t),где Fk = f*(k) * 1(0 .Отказовыми являются состояния с нечетными номерами, когда происходит
подключение некоторого резервного элемента или отказали все элементы
системы. Тогда для рассматриваемой системы отказовые состояния (кроме
последнего) не являются поглощающими, т. е. имеет место "частичное вос¬
становление". Следовательно, сумма вероятностей исправных состояний ха¬
рактеризует не вероятность безотказной работы, а готовность системы. Таким
образом, функция готовности системы равна*r(0 = Ро(0 + I Р2к(0 = 1 /*(к) * h'M * (0.
к=1 к=0Остановимся на одном частном случае последней формулы. Пусть время пе¬
реключения на резерв постоянно, т. е. h(t) = Ът (/), тогда получим:*г(0 =X /*(*) *F(t — kTp) при /Гр </<(/ + 1)71, / = 0,1,..., т-1;к=0
т /I \ —X / * F(t -кТр) при mTp<t.к = 0Это соотношение позволяет провести исследование зависимости Kr(t) от
различных параметров, например: от числа резервных элементов, от закона
распределения времени безотказной работы элементов, от времени Тр под¬
ключения резервных элементов.ПРИМЕР 8.12. Предположим, что m = 3 , вероятность безотказной работыкаждого элемента имеет гамма-распределение с параметрами а = к и р = -,Xгде Л. = 0,01 мсек-1. Определить функцию готовности в зависимости от пара¬
метров к и Тр.Решение. На рис. 8.21—8.23 приведены графики функций готовности при
различных значениях к и времени Тр подключения резервных элементов.
Анализ надежности сложных систем с учетом их физической реализуемости353Рис. 8.21. Случай к = 2, Г = 0 (кривая 1), 10 (кривая 2), 20 (кривая 3), 30 (кривая 4) мсекРис. 8.22. Случай к = 10, Г = 0 (кривая 1), 200 (кривая 2), 400 (кривая 3), 600 (кривая 4) мсекРис. 8.23. Случай к = 2, Т = 0 (кривая 1), 200 (кривая 2), 400 (кривая 3), 600 (кривая 4) мсек
12 Зак. 3094
354Глава 8ПРИМЕР 8.13. Предположим, что т = 20, вероятность безотказной работы„ _ 1каждого элемента имеет гамма-распределение с параметрами а = 2 и р = —,Xгде >. = 0,01 мсек"1. Требуется рассчитать функцию готовности системы, ко¬
гда резервные элементы подключаются мгновенно или через определенное
время.Решение. На рис. 8.24 приведены графики функций готовности для случаев
Гр =0 (кривая 1) и Гр =300 мсек (кривая 2).Рис. 8.24. Графики функций готовности для данных примера 8.13ПРИМЕР 8.14. Предположим, что т = 10, вероятность безотказной работы_ _ 1каждого элемента имеет гамма-распределение с параметрами а = 3 и Р = —,Xгде X = 0,03 мсек-1. Необходимо определить функцию готовности при разном
времени подключения резервных элементов.Рис. 8.25. Графики функций готовности для данных примера 8.14
Анализ надежности сложных систем с учетом их физической реализуемости 355Решение. На рис. 8.25 приведены графики функций готовности для случаев
Гр = 150 мсек (кривая 1) и Гр = 300 мсек (кривая 2).Результаты последних примеров показывают, что частота колебаний функции
готовности увеличивается при увеличении времени подключения резервных
элементов.8.6.2. Невосстанавливаемая система
с ненадежным переключателемПредположим теперь, что в процессе включения в работу резервного элемен¬
та сам переключатель может отказать. Время безотказной работы переключа¬
теля является произвольным с плотностью распределения u(t). Времяремонта переключателя г|р тоже имеет произвольное распределение с плот¬
ностью v(/). На время переключения на резерв может приходиться, вообще
говоря, несколько циклов исправной работы и ремонта переключателя. При
этом после очередного ремонта переключателя возможны две ситуации:1. Прошедшее время переключения на резерв "забывается", и включение ре¬
зервного элемента может произойти только при условии £р > Z на неко¬
тором интервале исправной работы переключателя.2. Прошедшее время переключения на резерв накапливается.Фрагменты соответствующих временных диаграмм изображены на рис. 8.26
и 8.27.Рис. 8.27. Фрагмент временной диаграммы (случай 2)
356Глава 8Здесь мы ограничимся вычислением надежности лишь для случая 2, когда
прошедшее время переключения на резерв не "забывается". Соответствую¬
щий граф состояний представлен на рис. 8.28.Рис. 8.28. Граф состояний при п = т + 1 (ненадежный переключатель)В связи с ненадежностью переключателя изменяются аргументы функций у
в системе (8.22) и надлежащим образом изменяется сама система уравнений:4(^0=/('+*);
tУгк-\ (p,z,t)= \u(x + p)h(x + z)y2k_2 (О, t - x)dx +Оt+ Jm(jc + p)y2k_\(0,x + z,t - x)dx\
о' (8.23)У2к-\ (<l,z,t)= J v(x + q)y2k-i (0, z, / - x)dx;
оI COy2k(s’0= jf(x + s)jy2k-\(pAt-x)dpdx, k = 1, 2,, m;0 о1У2т+\(*)= \У2т(°’*-х)Лс-0Решение системы (8.23) несложно, хотя и громоздко [140]. Ограничимся
формулировкой основного результата.Нестационарные значения вероятностей состояний, определяемые на основе
решения системы уравнений (8.23), имеют вид:Ро( 0 = ^(0.
Анализ надежности сложных систем с учетом их физической реализуемости 357Ри-i (о = Z (u*U) *ин) * v*U) * * /*w(0.7=0Pik-i (0 = Z («*0+,) * Я) * v*0) * F * a*(*-1) * f*{k) (/),7=0p2k«) = aW*fik)*m,где ст(/) = ) * t/Л) * v*^ (t).7 = 0Можно доказать, что сумма вероятностей всех состояний системы равна еди¬
нице:mРо (О + Z СО + Pik-1 (0 + Pik (0) + р2т+1 (0 = 1-
*=1Считая, как и раньше, исправными все состояния с четными номерами, опре¬
делим функцию готовности системы с ненадежным переключателем:m m _*r(0= Z Л*(0= Z a (*> */*w *F(/). (8.24)*=0 A=0По формуле (8.24) можно провести исследование надежности системы в за¬
висимости от законов распределения времени безотказной работы и восста¬
новления переключателя, а также от их параметров.8.6.3. Анализ восстанавливаемой системы
с переключателемРассмотрим систему из двух разнотипных по надежности элементов. Пред¬
положим, что в начале функционирования первый элемент является основ¬
ным, а второй находится в ненагруженном резерве. В процессе отказов и ре¬
монтов роль этих элементов (как основного, так и резервного) может изме¬
няться, т. е. второй элемент может стать основным, а первый — резервным.
При отказе основного элемента системы и исправном резервном элементе
первый элемент начинает восстанавливаться (время восстановления — слу¬
чайная величина г|), и требуется некоторое время Z для подключения ре¬
зервного элемента. Если Z < г|, то в работу включается резервный элемент, а
первый элемент продолжает восстанавливаться. Если Z > г|, то в работу
включается первый элемент, а второй по-прежнему находится в резерве. Бу¬
358Глаза 8дем считать, что систему обслуживает один ремонтный орган с прямым при¬
оритетом. Тогда при отказе обоих элементов сначала восстанавливается пер¬
вый из отказавших элементов. Временная диаграмма и граф состояний резер¬
вированной системы с переключателем представлены на рис. 8.29 и 8.30 со¬
ответственно.Рис. 8.29. Временная диаграмма резервированной системы с переключателемРис. 8.30, Граф состояний для разнотипных элементовНа графе указаны следующие возможные состояния:□ (0) — первый элемент работает, второй находится в очереди на работу;□ (1)— первый элемент восстанавливается, второй находится в очереди на
работу; переключатель включен;□ (2) — первый элемент восстанавливается, второй работает;□ (3) — первый элемент восстанавливается, второй находится в очереди на
восстановление.Состояния (0)—(3) аналогичны состояниям (0)—(3) с заменой первого эле¬
мента на второй, а второго — на первый. Переключатель представляет собой
некий третий элемент с двумя состояниями (включен, выключен).
Анализ надежности сложных систем с учетом их физической реализуемости359Для элементов, одинаковых по надежности и ремонтопригодности, граф со¬
стояний укрупняется (рис. 8.31) и количество уравнений в системе уменьша¬
ется вдвое.Рис. 8.31. Граф состояний для идентичных элементовКаждая функция, входящая в систему интегральных уравнений, имеет три
аргумента (не считая t), характеризующих состояние двух элементов и со¬
стояние переключателя на резерв. Аргументы функции ^(^,0,0,/) означают,
что работает один элемент, а второй элемент и переключатель находятся в
резерве; аргументы функции xx,0,z,t) означают, что один элемент восста¬
навливается и расходуется время переключения на резерв, другой еще не
включен в работу; аргументы функции у2(х[,s2,0,/) означают, что один эле¬
мент восстанавливается, а другой включен в работу, переключатель выклю¬
чен; аргументы функции у3(тх,0,0,/) означают, что один элемент восстанав¬
ливается, а другой находится в очереди на восстановление, переключатель
выключен. Относительно этих функций справедлива следующая система
уравнений:toо Iу0 (^,, 0,0,0 = J/(x + sx) j Ух (0,0, z, t - x)dzdx + \у2 (0, * + sx, 0, / - x)dx + f(t + sx);0 0 о1yx (x J, 0, z, t) = Jg(x + X, )h(x + z) y0 (0,0,0, t - x)dx;оi■ y2(xx,s2,0,t) = l/(x + s2)yx(x + xx,0,0,t-x)dx +0I+ JgO + *1 )/(* + «2 )Уз (°> 0 >0, f -
0ty3 (x,, 0,0,/) = jy2 (x + x,, 0,0, t - x)dx.о
360Гпава 8Решение этой системы может быть получено аналитически, и тогда можно
рассчитать любые нестационарные характеристики надежности. Однако для
нахождения числовых значений характеристик надежности, а также для по¬
лучения эквивалентных плотностей распределения предпочтительнее исполь¬
зовать непосредственное решение системы на ЭВМ.Стационарные характеристики получаются в результате предельного перехо¬
да при / -»оо и решения соответствующей системы уравнений:>>оО,0,0)= \f(x + s)\yx(Q,0,z)dzdx + J>>2(0,x + .y,0)rfr,
оо о00У\(Л 0,z)- |g(x + x)h(x + z)dxy0 (0,0,0);о00 00
у2 (Т, 5,0) = j/(x + (х + х, 0,0 )dx + jg(x + x)f(x + s)dxy3 (0,0,0);(8.25)од>3(х,0,0,/) = \y2(x + xAQ)dx.
оОтсюда определяются стационарные значения вероятностей пребывания сис¬
темы в каждом состоянии и все характеристики надежности системы для ста¬
ционарного режима. Например, коэффициент готовности с учетом переклю¬
чающего устройства равенf '’О со Лкг=:\fGdx + \f*hGdx
Vo о"\. (8.26)jjGdx Т+ ]GHdx+ jGF*hdx + \f*hGdx T+ \GFdxо v о 0 Jo VOИз системы уравнений (8.25) нетрудно получить также выражения для нара¬
ботки на отказ и среднего времени восстановления системы.ПРИМЕР 8.15. Техническая система представляет собой дублированную
систему однотипных по надежности устройств, одно из которых является ра¬
бочим, а второе— резервным (резерв ненагруженный). Время безотказной
работы имеет усеченное нормальное распределение с математическим ожи¬
данием m-Ю час и средним квадратическим отклонением и-5 час. Время
восстановления имеет распределение Эрланга второго порядка с параметром
ц = 1 час-1. Время переключения на резерв постоянное и равно 0,5 час. Тре¬
буется определить коэффициент готовности системы с учетом времени пере¬
ключения на резерв.
Анализ надежности сложных систем с учетом их физической реализуемости 361Решение. Расчеты по формуле (8.26) показывают, что для приведенных дан¬
ных Кг =0,926 . Заметим, что для мгновенного подключения резервного уст¬
ройстваТ+ \GFdxочто дает завышенную оценку, и относительная погрешность, вычисленная по
коэффициенту простоя, составляет 21 %.8.7. Системы с последействием отказов8.7.1. Система с переменными законами
распределения времени безотказной работыС течением времени в технической системе могут происходить какие-либо
внутренние или внешние изменения, влияющие на длительность ее жизни.
Внешние изменения связаны, как правило, с изменением условий эксплуата¬
ции резервированной системы, когда отказы одних элементов вызывают из¬
менение нагрузки на другие элементы системы. При этом моменты времени,
когда меняется нагрузка, могут быть как детерминированными, так и случай¬
ными. Поэтому поведение системы после произошедшего изменения ее на¬
грузки заранее может быть не известно, т. к. оно зависит от моментов време¬
ни изменения нагрузки. С математической точки зрения это может означать,
что с течением времени в системе изменяется закон распределения времени
жизни системы. Будем в этом случае говорить, что система имеет перемен¬
ный закон распределения времени безотказной работы.Пусть Z — случайный момент времени изменения нагрузки на систему с
плотностью h(t), X — время безотказной работы системы до изменения на¬
грузки (до момента Z ) с плотностью /(t), X' — время безотказной работы
системы после изменения нагрузки (после момента Z) с плотностью f'(t).
Требуется найти закон распределения времени безотказной работы Хс сис¬
темы. При изучении случайной величины Хс могут встретиться две принци¬
пиально разные ситуации:□ после момента Z система становится новой и не учитывается время ее
работы до этого момента, т. е. система не имеет "памяти";□ после момента Z учитывается ресурс, выработанный системой до этого
момента, т. е. эта система с "памятью".
362Глава 8Далее будут рассмотрены обе указанные ситуации. В первом случае будем
обозначать вероятность безотказной работы системы через P(t), а во вто¬
ром— через Рп(/).Предположим, что отсчет случайного времени X' начинается после измене¬
ния нагрузки, тогда\Х, если 2>Х\IZ + X', если Z<X.'хс ='Хс =Используя формулу полной вероятности, получим:P(t) = P(Z > X, X > t) + P(Z <,X,Z + X'>t) =00 / 00
= jf(x)H(x)dx+ jh(x)F(x)F'(t-x)dx + jh(x)F(x)dx,t о tили' _ _ _ _ _ _P(t) = H{t)F(t) + \h(x)F(x)FXt - X)dx =H(t)F(t) + (hF) * F\t). (8.27)оРассмотрим второй, более важный в практическом отношении случай. Счи¬
тая, что ресурс случайной величины X расходуется с самого начала функ¬
ционирования системы, а не с момента изменения нагрузки, получим:X', если Z <X,Z <Х'\Z, если X'<Z <Х;X, если Z > X.Отсюда следует, чтоPn(t) = P(Z<X,Z<X', X’>t) + P(X'<Z<X,Z>t) + P(ZZX,X>t) == \f\x)dx\h(y)F(y)dy + \h{x)F'(x)F(x)dx+ jf(x)H(x)dx.i о t tПроизводя в первом слагаемом интегрирование по частям и упрощая полу¬
ченное выражение, будем иметь:Pn(0 = H(t)F(t) + J h(x)F(x)dxF\t). (8.28)оВ силу убывания функции F' из соотношений (8.27) и (8.28) следует, что
Pn(t) < P(t), а это вполне согласуется с интуитивным представлением о на¬
дежности системы при наличии и отсутствии "памяти". Возможно, что для
Анализ надежности сложных систем с учетом их физической реализуемости363решения реальных задач оценки надежности систем с переменными условия¬
ми нужно выбирать нечто среднее между этими функциями.Рассмотренные положения являются отправными при исследовании надеж¬
ности систем с последействием.8.7.2. Дублированная система
с последействием отказовРассматривается пара элементов с нагруженным резервом и случайным вре¬
менем безотказной работы Хх и Х2 с плотностями распределения времени
безотказной работы fx(t) и f2(t) соответственно. При отказе элемента с но¬
мером 1 может произойти изменение нагрузки на элемент с номером 2, после
чего расходуется ресурс времени Х4 с плотностью распределения /4(() .
Аналогично при отказе элемента с номером 2 может произойти изменение
нагрузки на элемент с номером 1, в результате чего будет расходоваться ре¬
сурс времени Х3 с плотностью распределения f3(t). Требуется найти закон
распределения времени безотказной работы системы Хс в целом. Как и
раньше, мы можем рассмотреть две ситуации в зависимости от наличия или
отсутствия "памяти".Предположим сначала, что после отказа любого элемента, другой элемент
начинает функционировать, имея новый закон распределения отказов. По¬
скольку(Хх+Х4, если X] <Х2;+ Х3, если Х2 ^Хх,то, используя формулу полной вероятности, получим:Pit) = Р(Хх <Х2, Х,+Х4 >/) + Р(Х2 <Хх, Х2+Х3 >t),
следовательно,Р( 0 = jfi 0)^4 (' “ х)Жс + \f\(x)F2 (x)dx +О t+ Р, (x)f2 (x)F3 (t - x)dx + J (д;)f2 (x)dx.
о tПреобразуя полученное выражение, будем иметь:P(t) = Fx(t)F2(t)+ ]fx(x)F2{x)F4(t-x)dx+ \Fx(x)Ux)W-x)dx.
о о
364Гпава 8Хс =В частности, если элементы равнонадежны и имеют плотности распределен
ния до и после отказа другого элемента /(t) и /'(0 соответственно, то_ tP(t) = F2(t) + 2 Jf(x)F(x)F'(t - x)dx. (8.29)оТеперь предположим, что система обладает "памятью". Это допущение несо¬
мненно является более корректным с инженерной точки зрения. Тем самым
мы считаем, что ресурсы времен Х3 и Х4 начинают расходоваться с момен¬
та включения системы в работу, т. е. вместе с временами Хх и Х2 .Легко видеть, что в зависимости от условий время безотказной работы сис¬
темы может принимать одно из четырех значений:Хх, если Х4< Хх < Х2;Х2, если Х3 <Х2<Хх;Х3, если Х2 < Хх, Х2 < Х3:Х4, если Хх < Х2, Хх < Х4.Для определения закона распределения вероятностей случайной величины
Хс применим формулу полной вероятности, тогда получим:Pn(t) = P(X4<X]<X2, Xj >t) + P(X3 <Х2 <ХЬ Х2 >t) ++Р(Х2 <Xj,X2 < Х3, Х3 >t) + P(Xj < Х2, Х{ < Х4, Х4 > ().Отсюда следует, чтоРп( 0 = ]f,(x)F4(x)F2(x)dx + ]/2(x)F3(x)^ (x)dx +/ i+ f/з ^dx 00^ (y)dy + J/4 (x)dx\fj (y)F2 (y)dy.
to toПреобразуя, получим:Pn(t) = Fj(t)F2(t) + )f2(x)Fj(x)dxF3(t)+)fj(x)F2(x)dxF4(t).о 0В частности, если элементы равнонадежны, тоРЛ0 = F\t) + 2]f(x)F(x)dxF'{t) = F\t) + (1 - F2(t))F\t). (8.30)о
Анализ надежности сложных систем с учетом их физической реализуемости 3658.7.3. Сравнительный анализ надежности систем
с последействием при отсутствии
и наличии"памяти"ПРИМЕР 8.16. Проведем сравнительную оценку формул (8.29) и (8.30) для
распределения Эрланга различного порядка. Пока в системе работоспособ¬
ными являются оба элемента, то параметры распределений равны а и Р = —.А,При отказе одного из элементов на другой элемент ложится большая нагруз¬
ка, и параметры его распределения становятся равными а' и р' = . Рас-Xсмотрим 3 варианта исходных данных:1. а = 1, А. = 0,001 час"1, а' = 1, А,' = 0,1 час-1 (экспоненциальный случай).2. а = 2, А. = 0,002 час"1, а'= 2, X' = 0,2 час-1.3. а = 5, X = 0,005 час-1, а'= 5, Я'= 0,5 час-1.Эти параметры берутся так, чтобы было совпадение математических ожида¬
ний соответствующих случайных величин. Необходимо определить вероят¬
ности безотказной работы системы при отсутствии и наличии "памяти".Решение. На рис. 8.32 представлено 3 графика вероятности безотказной ра¬
боты P(t) при отсутствии "памяти" и 3 графика вероятности безотказной ра¬
боты Pn(t) при наличии "памяти". Графики соответствуют трем вариантам
исходных данных.Рис. 8.32. Вероятность безотказной работы дублированной системы
при отсутствии и наличии "памяти”
366Глава 8Указанные графики сливаются, образуя "жирные" линии, и визуально нераз¬
личимы. Чтобы определить различие между функциями P(t) и Рп (/), на
рис. 8.33 для этих же трех вариантов исходных данных изображены графики
разностей (P(t)-Pn(t)), характеризующие отличие при использовании соот¬
ношений (8.29) и (8.30).Рис. 8.33. Графики, характеризующие превышение Р(1) над Р (/)Как ни парадоксально, наибольшая погрешность наблюдается для экспонен¬
циального распределения, причем на начальном этапе функционирования
системы.8.7.4. Обобщение результатов
на случай любого числа элементовМетоды нахождения закона распределения и анализа систем с последействи¬
ем отказов, рассмотренные в разд. 8.7.2, обобщаются на любое число элемен¬
тов. Мы приведем здесь эти обобщения только для идентичных по надежно¬
сти элементов.Рассмотрим невосстанавливаемую систему, состоящую из п элементов, ра¬
ботающих одновременно. После отказа одного из них исправные элементы
системы меняют свой закон распределения. Обозначим через плот¬ность распределения времени безотказной работы, а через FM(t) — вероят¬
ность безотказной работы каждого элемента после отказа i элемента?.,
/ = 0,1, 2,..., я -1. Отказ системы наступает при отказе всех ее элементов.
Определим вероятность безотказной работы системы. Как и раньше, могут
встретиться две различные ситуации, характеризующиеся отсутствием и на¬
личием "памяти".
Анализ надежности сложных систем с учетом их физической реализуемости 3671. Если в момент отказа некоторого элемента все исправные элементы начи¬
нают заново расходовать свой ресурс надежности (с новыми законами
распределения), то это система без "памяти" и для нее вероятность безот¬
казной работы выражается равенством2. Если в момент отказа некоторого элемента все исправные элементы про¬
должают расходовать свой ресурс надежности (с новыми законами рас¬
пределения), то это система с "памятью" и для нее вероятность безотказ¬
ной работы выражается равенствомПолученные соотношения являются обобщением формул (8.29) и (8.30) на
системы с произвольным числом элементов. Можно также показать, что для
любых законов распределения имеет место неравенство8.8. Анализ надежности системы с учетом
неодновременности работы ее элементовПрактически в любой сложной системе элементы работают не одновременно.
Поэтому в расчетах необходимо моделировать время функционирования сис¬
темы. Введем новое в теории надежности понятие: собственное время рабо¬
ты системы и определим его влияние на надежность.Предположим, что элементы системы могут работать лишь часть календар¬
ного времени и простаивать в течение остальной его части. Интервалы про¬
стоя могут быть как детерминированные, так и случайные. Мы ограничива¬
емся здесь рассмотрением только детерминированных интервалов простоя.
Моменты времени изменения интенсивностей отказов для части элементов
являются моментами реконфигурации всей системы. Между моментами ре¬
конфигурации системы все элементы имеют постоянные интенсивности отка¬
зов и восстановлений. Предполагается, что интервалы простоя повторяются
через определенный период функционирования системы Т. Однако это не
означает, что система в начале каждого периода становится новой. Надеж¬
ность системы зависит от ее предыдущего функционирования, и в начале
каждого периода она имеет другой ресурс по сравнению с началом предыду¬
щего периода. В каждый момент времени, соответствующий началу и концу
простоя, приходится перестраивать граф состояний и получать новые значе¬
368Гпава 8ния для интенсивностей переходов. Однако на каждом таком интервале про¬
цесс функционирования системы может рассматриваться как марковский.
Начальные условия в каждом из интервалов образуются из расчетов для пре¬
дыдущего интервала, что обеспечивает непрерывность перехода через мо¬
мент реконфигурации системы.Пусть 0 = /0< tx<t2<...< tn=T — моменты реконфигурации системы, а
Aj, Л2,..., Ли — интенсивности отказов системы на 1-м, 2-м,..., п-м интер¬
валах времени соответственно. Тогда, считая, что при t = t0 система исправ¬
на, вероятность безотказной работы будет очевидно равна:□ для 1-го интервала P{t) = е_Л‘',□ для 2-го интервала P(t) = ,□ для 3-го интервала P(t) = P{t2)e~K^t~t'^,□ для и-го интервала P(t) = P(tn_x .Преобразуя эти выражения, получим соотношение для вероятности безотказ¬
ной работы системы на интервале tm_{ <t<tm :Р(0 = ,-I л,Л/,где am =е ,=t , Att = /,- -/м, m = l, 2,и.Интегрируя P(t) от нуля до бесконечности, найдем выражение для среднего
времени безотказной работы:ПРИМЕР 8.17. Требуется определить показатели надежности основного со¬
единения трех элементов, интенсивности отказов которых равны соответст¬
венно А.] =2-10-5 час-1, Я.2=410-5 час-1 и А.3=81(Г5 час-1. Время работы
системы Т = 1 ООО час. Первый элемент простаивает на интервале от 100
до 500 часов, второй элемент — на интервале от 300 до 700 часов, а третий —
на интервалах от 400 до 600 и от 700 до 1000 часов. Сравнить полученные
значения P(t) и 7] со случаем, когда система работает непрерывно.
Анализ надежности сложных систем с учетом их физической реализуемости369Решение. Моменты времени реконфигурации системы, т. е. моменты, в кото¬
рые изменяется интенсивность отказа, имеют значения:/0 = 0, tx =100, t2 = 300, t3= 400, t4 = 500,t5 = 600, t6 = 700, f7 =1000.Составим табл. 8.3, в которую поместим интенсивности отказов и соответст¬
вующие выражения для вероятности безотказной работы системы для каждо¬
го промежутка времени.Таблица 8.3. Интенсивность отказов и вероятность безотказной работы системыкак функции времениПромежуток
времени, часИнтенсивность отказов
системы Л, час-1Вероятность i
безотказной работы P(t)0—100А, = Xj + Х2 + Х^ — 14 -10-Л./е100—300Л2=Х2+Х3 = 12 • 10 5-Л, (/-100)ate 2300-^00Л3 = Х3 = 8 10-5-А.0-300)°2е400—500>А.НО-Л. (/-400)а3е ;500—600Л5 =\, = 2 • 10~5-Л, (/-500)але 5 |600—700Л6 =х, + а.3 = 10 • 10~5-Л, (/-600)а5е700—1000Л7 =Х, +Х2 = 6 • 10~5-Л, (/-700)а6еБез учета простоя элементов имеемp(j) = е~(^1+^2+^з)<На рис. 8.34 изображены графики функций P(t):□ кривая 1 — с учетом простоя;□ кривая 2 — без учета простоя элементов.Естественно, что с течением времени расхождение между кривыми увеличи¬
вается.Наработка до отказа, полученная с учетом простоя элементов, равна
Ту = 11763 час, а без учета простоя— 7] =7143 час. При этом относительная
погрешность составляет 39,3 %.
370Глава 8Рис. 8.34. Вероятность безотказной работы системы
с учетом и без учета собственного времени
ГЛАВА 9МЕТОДЫ ОБЕСПЕЧЕНИЯ
И ПОВЫШЕНИЯ НАДЕЖНОСТИ
ТЕХНИКИ9.1. Классификация методовМетоды обеспечения и повышения надежности техники можно сформулиро¬
вать и научно обосновать, если проанализировать функциональные связи ме¬
жду показателями надежности и расчетные соотношения для показателей на¬
дежности сложных систем.Обратимся к языку формул. Вероятность безотказной работы невосстанавли-
ваемой системы Pc(t) с основным соединением элементов выражается фор¬
мулой-\Xz(t)dtРй{!) ~ е 0Пгде А.с(0 = X ^/(0 — интенсивность отказов системы, состоящей из п эле-
/=1ментов. Из этого соотношения следует, что надежность системы Н является
функцией t, п, Xt, i = 1, 2,..., п, т. е. Н = /(и, t). Отсюда очевидно, что
для обеспечения надежности необходимо: упрощать систему (уменьшать
число элементов п), снижать интенсивность отказов элементов Х:, сокра¬
щать время непрерывной работы системы t.Показателями надежности восстанавливаемых систем являются: функция го¬
товности Kr(t), коэффициент готовности Кг, наработка на отказ Г, пара¬
метр потока отказов со(t). Основной формулой определения коэффициента
готовности являетсяТкт= ,
т + тв
372Гпава 9где Тв — среднее время восстановления системы. Наработка на отказ Т зат
висит от показателей надежности, таких как интенсивность отказов элемен¬
тов и сложность системы. Среднее время восстановления зависит от интен¬
сивности восстановления элементов ц(, числа обслуживающих бригад к й
дисциплины обслуживания (до). Таким образом, готовность системы являет¬
ся функцией тех же параметров, что и вероятность безотказной работы, а
также параметров восстановления , к , до. Тогда Н = /(и, A.,, t, ц,, к, до).Отсюда очевидно, что для повышения готовности системы необходимо по¬
вышать ее ремонтопригодность (увеличивать ) и выбирать рациональную
дисциплину обслуживания (число ремонтных органов, приоритетность об¬
служивания).Современные технические системы настолько сложны, а требования их на¬
дежности столь высокие, что перечисленные ранее методы часто недостаточ¬
ны для удовлетворения требований на показатели надежности.Приходится прибегать к крайним мерам — вводить избыточность в структу¬
ру системы. Избыточность может быть структурная, нагрузочная, временная,
информационная. Тогда надежность системы будет зависеть от объема избы¬
точности (кратность резервирования m ), вида резервирования (общее, раз¬
дельное), способа реализации (постоянное, замещением). Дополним нашу
функциональную связь новыми параметрами (параметрами избыточности),
такими как m , вид резервирования (вр), способ реализации (ср). Тогда функ¬
ция надежности будет иметь вид:Н = f{n, Л., , /, ц„ к, до, т, вр, ср).И это не все, т. к. мы не учли эксплуатацию системы, в процессе которой и
расходуется надежность. В целях поддержания высокой надежности техники
в процессе ее эксплуатации проводятся такие мероприятия, как профилакти¬
ка, ремонт, доработка, продление ресурса. Назовем эти мероприятия усло¬
виями эксплуатации (ус). Тогда функция надежности примет вид:Я = fin, Л.,, t, Ц;, к, до, т, вр, ср, ус). (9.1)Таким образом, функция надежности зависит от десяти параметров (при же¬
лании их количество можно несколько увеличить), имеющих разное влияние
на надежность техники. Поэтому целесообразно классифицировать их по ря¬
ду признаков. Одним из признаков может быть период реализации', в процес¬
се проектирования, изготовления, эксплуатации.Рассмотрим методы обеспечения и повышения надежности более подробно.
Укажем на их возможности, достоинства и недостатки.
Методы обеспечения и повышения надежности техники3739.2. Методы обеспечения
и повышения надежности техники
в процессе проектированияБудем разрабатывать методы, решая конкретную задачу.Пусть проектируемая система состоит из « = 1350 элементов, средняя интен¬
сивность отказов которых Я. = 1,2 ■ 10-6 час-1. Система предназначена для
длительной эксплуатации. Требованием на ее надежность является
Р(250) > 0,97. Предположим, что справедлив экспоненциальный закон рас¬
пределения времени до отказа. Тогда вероятность безотказной работы систе¬
мы (если не принимать мер по ее повышению) будет иметь значение:/>(250) = e-nXt = g-' 350-1,2-10'6 -250 = е-0,405 = ^Надежность системы низкая, она не соответствует требованию. Какие же ме¬
тоды повышения надежности следует использовать для удовлетворения тре¬
бований?Обратимся к функции надежности (9.1). Так как система не восстанавливаема
и не резервирована, то Н - f(n,X,,t). Тогда вероятность безотказной работысистемы будет обеспечена при условии: е > 0,97 , или nXt < 0,03.Обеспечить это условие можно, если n, X, t будут иметь, при прочих рав¬
ных условиях, значения:^ 0,03 0,03п < = 7 = 100,Xt 1,2-10 -250Х< — = - 0,03 ■ =0,88-10~7 час"1,
nt 1350-2500,03 0,03t<—— = 2 г = 18>5 час.пХ 1350-1,2-10-6Из этих расчетов видно, что упрощение системы, повышение надежности
элементов или сокращение времени непрерывной работы системы не могут
обеспечить необходимую вероятность безотказной работы, т. к. из 100 эле¬
ментов вместо 1350 создать систему невозможно, уменьшить на порядок ин¬
тенсивность отказов всех элементов нельзя, сократить время работы системы
с 250 до 18,5 часов невозможно по техническим условиям. Какой же выход?
Применение избыточности в процессе проектирования — единственный спо¬
соб обеспечения требуемой надежности. Для нашей системы это использова¬
ние нагрузочной или структурной избыточности.
374Глава 9Если средняя интенсивность отказа элементов, приведенная в условии зада¬
чи, относится к номинальным нагрузкам, то теоретически путем облегчения
режимов работы интенсивность отказов можно уменьшить на порядок (ре-—7 1жим хранения). Тогда при X = 1,2 ■ 10 час вероятность безотказной работы
системы будет:Р(250) = e~nXt = е-13501>210"7'250 = е-0,0405 _ 0j96Вероятность безотказной работы не удовлетворяет требованиям даже в ре¬
жиме хранения системы.Применим структурное резервирование. При постоянном включении резерва
Pc(t) = 1 - (1 - р)т+х. Так как Pc(t) = 0,97 , а р = 0,667, то0,97 = 1 -(1 -0,667)m+1 или да = 03 -1 = 2,19.In 0,333При резервировании замещением и т = 1
при т-2рс(/) = e~Xl(1 +Л./) = 0,667(1-In0,667) = 0,937 ,Pci 0 = е~Х12!= 0,667= 0,992.Таким образом, для обеспечения вероятности безотказной работы системы
Рс>0,91 необходимо применить резервирование замещением кратностит = 2.Из этого краткого примера видно, что такие методы, как упрощение системы
(уменьшение числа элементов) и сокращение времени непрерывной работы
мало эффективны. Только благодаря применению резервирования удалось
обеспечить требования на надежность системы.При этом увеличение вероятности безотказной работы с 0,667 до 0,992 стоит
слишком дорого. К основной системе нужно прибавить две резервные. Стои¬
мость, вес, габариты возросли в 3 раза.Из примера следует, что для повышения надежности системы целесообразно
подходить комплексно и одновременно использовать многие методы повы¬
шения надежности. В нашем примере это может быть одновременное приме¬
нение нагрузочного и структурного резервирования. Пусть, например, в ре¬
зультате облегчения режимов работы элементов удалось уменьшить среднюю
интенсивность отказов элементов в 2 раза.
Методы обеспечения и повышения надежности техники375Тогда вероятность безотказной работы системы будет:riktPc(t) = e 2 =е“0’2025 = 0,8 1 7.Применим теперь общее резервирование с постоянно включенным резервом
кратности m = 1. ТогдаРс(250) = 1 - (1 - 0,817)2 =0,97.Теперь требования удовлетворены при меньшей кратности резервирования и
более простой его реализации (постоянно включенный резерв).Пусть теперь анализируемая система является восстанавливаемой со средним
временем восстановления Та = 55 час, а коэффициент готовности должен
удовлетворять условию: Кг > 0,97. Необходимо разработать способы обес¬
печения коэффициента готовности.Первоначально вычислим коэффициент готовности системы, воспользовав-Тшись формулой Кг =Т + ТвИсследуемая система является нерезервированной и имеет экспоненциальные
законы распределения отказов и восстановления. В таких системах наработка
на отказ и среднее время безотказной работы совпадают, т. е. Т = 7J. ТогдаТ = — = г = 617 час,\ 1350-1,2 -10-6Кг =—— = 617 =0,92.
г Т + Тв 617 + 55Так как Кг не удовлетворяет требованиям, то будем искать пути его повы¬
шения. Для повышения надежности имеются два принципиально различных
способа: повышение надежности системы путем увеличения среднего време¬
ни безотказной работы Т или повышение ремонтопригодности системы
снижением среднего времени восстановления.Пойдем по первому пути. Для обеспечения коэффициента готовности, равно¬
го 0,97, необходимо повысить среднее время безотказной работы до вели-
376Гпава 9.Тогда средняя интенсивность отказа элементов должна быть:Х = — = = 0,42-10_6 час-1.пТ 1350-1778Для обеспечения Кг необходимо уменьшить среднюю интенсивность отка¬
зов в 3 раза. Для сложной системы длительной работы и большим числом
элементов это вряд ли можно реализовать.Пойдем по второму пути. Повысим ремонтопригодность системы. Для обес¬
печения коэффициента готовности Кг > 0,97 необходимо, чтобы при
Т = 617 час среднее время восстановления было не меньше следующего зна¬
чения:^ 1-*г„ 1-0,97 1Л71 = -Т = 617 = 19 час.в Кг 0,97Это почти в 3 раза меньше, чем получено в процессе проектирования. Повы¬
шение в 3 раза ремонтопригодности — большая техническая проблема. Для
ее решения необходимо менять технологию восстановления в направлении
автоматизации этого процесса, что потребует дополнительного оборудова¬
ния, которое должно передаваться заказчику. Вряд ли такой способ можно
реализовать на практике.Воспользуемся структурным резервированием.При дублировании системы с постоянно включенным резервом и одной об¬
служивающей бригаде коэффициент готовности определяется выражением:1 2Г + гУкг= г 1 + 7 + — 72
2В нашем случаеT-L.«Z-,1.22.Г. 55Подставляя это значение в формулу для Кг, получим11,2 +—11,22
Кг = 2. = 0,99.1 + 11,2 + —11,22
2Проблема обеспечения готовности системы низкой надежности и ремонто¬
пригодности решена путем дублирования системы без увеличения числа ре¬
монтных бригад.
Методы обеспечения и повышения надежности техники3779.3. Обеспечение надежности техники
в процессе производства и эксплуатацииИз (9.1) видно, что параметров производства в Н функции нет. Это объясня¬
ется тем, что производство реализует результаты проектирования, в процессе
которого разрабатывается техника, удовлетворяющая требованиям надежно¬
сти. Производство должно доказать, что изготовленная техника удовлетворя¬
ет требованиям надежности, заложенным в процессе ее проектирования. Для
этого в процессе производства должны проводиться ее испытания на надеж¬
ность.Известно, что на начальной стадии эксплуатации техники (период приработ¬
ки) возникает большое количество отказов за счет ошибок технологии произ¬
водства, недоброкачественных элементов, человеческого фактора. Для обес¬
печения надежности техники в процессе ее эксплуатации целесообразно уча¬
сток приработки пройти на предприятии изготовителя. Однако это
мероприятие слишком дорогое, поэтому изготовитель в большинстве случаев
выпускает технику, не прошедшую этапа приработки. Взамен этого он дает
пользователю гарантию на срок, близкий к периоду приработки, который
проходит у потребителя.Изготовитель проводит еще одно важное мероприятие, обеспечивающее тре¬
бования надежности. Он выполняет доработку техники, если в процессе экс¬
плуатации обнаружены явные дефекты производства.Повысить надежность техники в процессе эксплуатации нельзя. Ее можно
только обеспечить и поддерживать на необходимом уровне. Для этого прово¬
дятся следующие мероприятия: профилактика, контроль состояния, восста¬
новление и ремонт. Целью всех этих мероприятий является продление перио¬
да нормальной эксплуатации, когда интенсивность отказов является величи¬
ной постоянной.Подробно об этих мероприятиях будет рассказано в гл. 10.Способы обеспечения надежности, рассмотренные в разд. 9.1—9.3, действи¬
тельны при любых законах распределения отказов и восстановления.Вид законов распределения оказывает существенное влияние на численные
оценки и эффективность методов. В последующих разделах этому вопросу
уделяется основное внимание.9.4. Свойства структурного резервированияСвойства структурного резервирования и его эффективность можно сформу¬
лировать путем анализа выигрыша надежности по вероятности отказа Gq (t),
378Глава 9среднему времени безотказной работы GT , интенсивности отказов Gx(t),функции и коэффициенту готовности GKr(t) и GKr , наработке на отказ GT.Будем анализировать функции выигрыша надежности, предполагая, что
справедливым является экспоненциальный закон распределения отказов и
восстановления. Это допущение оправдано тем, что общие свойства струк¬
турного резервирования не зависят от вида законов распределения. Законы
распределения оказывают существенное влияние лишь на эффективность ре¬
зервирования. Допущение здесь полезно еще тем, что при экспоненциальном
законе отказов и восстановлений наиболее просто иллюстрировать свойства
структурного резервирования путем численных оценок выигрышей надеж¬
ности.9.4.1. Выигрыш надежности по вероятности отказаВыигрыш надежности по вероятности отказа есть отношение вероятности
отказа нерезервированной системы к вероятности отказа системы с резервом.
Это отношение для случая постоянного резервирования имеет вид:°о= Кг- • (9.2)4 (\-е-х,)тЗависимость Gq{Xt,m) приведена в табл. 9.1.Таблица 9.1. Зависимость выигрыша надежности Gq от Xt
и кратности резервирования тXtт12340,110,5110,41160121940,33,914,957,4221,60,52,56,516,441,70,72,03,97,815,60,91,72,84,88,11,11,52,23,45,0Анализ таблицы позволяет сформулировать следующие свойства структурно-*
го резервирования:□ эффективность резервирования тем выше, чем более надежна основная
система и чем короче время ее непрерывной работы;
Методы обеспечения и повышения надежности техники379□ чем выше кратность резервирования, тем выше выигрыш надежности, од¬
нако он резко убывает с ростом Xt.9.4.2. Выигрыш надежности
по среднему времени безотказной работыДля случая постоянного резервирования выигрыш GTf имеет вид:т m+1 1От,=?=!,-■ (М)^0 1 = 1 1Из формулы (9.3) очевидно следующее свойство структурного резервирова¬
ния с постоянно включенным резервом: значительное повышение кратности
резервирования ведет к несущественному повышению среднего времени без¬
отказной работы. Например, для увеличения среднего времени безотказной
работы в 2 раза требуется резервирование с кратностью т-3, т. е. должно
быть четыре системы, при необходимости увеличения 7J в 3 раза систем
должно быть 11 (т = 10). В случае резервирования замещением среднее вре¬
мя безотказной работы растет пропорционально т :Тс = (т + 1)Г0 .9.4.3. Выигрыш надежности
по интенсивности отказовИнтенсивность отказов резервированной системы выражается формулой:Р&)Рс(0Анализ этой формулы показывает, что при любом т и любом виде струк¬
турного резервирования А,с(0) = 0 и с увеличением t стремится к интенсив¬
ности отказов нерезервированной системы. Это свойство позволяет в процес¬
се проектирования сложной системы выбрать вид резервирования, сравнить
по надежности структурные схемы.ПРИМЕР 9.1. Структурные схемы систем показаны на рис. 9.1, a—б. Какаяиз этих систем имеет более высокую надежность, если ]ГД,- < ХЛ/ •/ /Зависимости интенсивностей отказов от времени приведены на рис. 9.2.
380Гпава 9Я»| Х>2 Х,| Xjт = 1/2aХ2 *3 ^4 ^5бРис. 9.1. Структурные схемы системРис. 9.2. Зависимость интенсивностей отказов систем от времениРешение. В случае системы, изображенной на рис. 9.1, а, функция Хс(?)
(кривая 1 на рис. 9.2) при t = 0 равна сумме интенсивностей отказов нерезер¬
вированных элементов, т. е. ^с(0) = Я,2 + Х,4. С увеличением времени A,с(()будет увеличиваться, стремясь к своему пределу ]Г А.у .iВ случае с системой на рис. 9.1, б Яс(0) = 0 (кривая 2 на рис. 9.2), т. к. все
элементы структурной схемы зарезервированы. С ростом t Хс(/) будет рас¬
Методы обеспечения и повышения надежности техники381ти, стремясь к своему пределу, равному сумме интенсивностей отказов нере¬
зервированной системы £ А.'-./Так как ^А,,- > ХЛ; ’ то графики функций А,с(/) структурных схем будут пе-
/ iресекаться. Из рисунка следует очевидный факт, что при t < т более надеж¬
ной является система на рис. 9.1, б, при t > х — система на рис. 9.1, а. Кри¬
тическое время т можно найти, если известны численные значения интен¬
сивностей отказов элементов.9.4.4. Выигрыш надежности
по коэффициенту простояКоэффициент простоя нерезервированной системы равенК - 1п0“7+у ’резервированной при постоянном включении резерва —К 1"Р m+\ J 'Z-h«Тогда выражение выигрыша надежности по коэффициенту простоя будет
иметь вид:т+1 yi
1.1г _ ^по /=• 1'~‘-пО _ i=Кпо 1 + УпрРезультаты расчетов выигрыша приведены в табл. 9.2.Таблица 9.2. Выигрыш надежности от коэффициенту простоя и наработке на отказт123У151010015101001510100°к.1,253,085,5550,51,336,5620,717001,3510,958,64,3-104GT1,53,56511,77,722,717171,7112,964,34,34-104Из таблицы следует, что выигрыш надежности по коэффициенту простоя тем
выше, чем выше кратность резервирования т и значение у. При этом чем
382Гпава 9.выше у, тем выше выигрыш надежности в случае одной и той же кратности
резервирования. При небольшом значении у увеличение кратности резерви¬
рования ведет к несущественному повышению выигрыша.9.4.5. Выигрыш надежности
по наработке на отказНа основании формулы (7.15) имеем:Результаты расчетов по этой формуле также приведены в табл. 9.2. Из табли¬
цы видно, что выигрыш надежности по среднему времени безотказной рабо¬
ты растет с ростом т и у . Однако при малом у увеличение кратности резер¬
вирования не приводит к существенному увеличению наработки на отказ.
Эффективность резервирования значительно возрастает при больших значе¬
ниях у.Из табл. 9.2 можно сделать следующий вывод: основным методом обеспече¬
ния надежности систем является резервирование с восстановлением. При
этом нет необходимости иметь высокую кратность резервирования. При дуб¬
лировании системы можно снизить коэффициент простоя и увеличить нара¬
ботку на отказ в десятки раз. При этом должно выполняться условие-<0,1 (у >10).ЦОписанные ранее свойства резервирования справедливы для любых видов
резервирования и произвольных законов распределения отказов и восстанов¬
лений. Отличия состоят лишь в численных оценках.9.5. Инвариантность надежности
одного класса технических систем
к законам распределения
отказов и восстановленийВ сложных энергетических системах, локальных вычислительных сетях, сис¬
темах защиты атомных электростанций и ряде других технических систем с
целью повышения надежности применяется глубокое резервирование от¬
дельных устройств, узлов и элементов. Как правило, такие системы являются
Методы обеспечения и повышения надежности техники383восстанавливаемыми, и их надежность существенно зависит от законов рас¬
пределения времени функционирования и восстановления элементов, входя¬
щих в систему.В связи со сложностью анализа этих систем, возникающей из-за большого
числа их состояний, важным является выявление класса систем, для которых
показатели надежности зависят только от математических ожиданий времени
функционирования и восстановления и не зависят от видов законов распре¬
деления.9.5.1. Математическое описание системыРассмотрим класс восстанавливаемых систем, имеющих только нагруженный
резерв, обслуживаемых одной ремонтной бригадой с обратным приоритетом.
Опишем любое состояние системы вектором из m компонент, каждая из ко¬
торых соответствует текущему состоянию /-го элемента. Для данного класса
систем любой ее элемент может находиться в одном из четырех состояний:□ состояние работоспособности;О состояние простоя, вызванного прерыванием его исправной работы из-за
отказа другого элемента, который сделал невозможным нормальное функ¬
ционирование данного работоспособного элемента;□ состояние восстановления;□ состояние простоя, вызванного перерывом в его обслуживании вследствие
переключения восстанавливающих органов на восстановление другого
элемента с более высоким приоритетом обслуживания.Обозначим через s,, s', т(, т' время пребывания i-го элемента в каждом из
отмеченных состояний. Тогда состоянию А исходной системы можно поста¬
вить в соответствие функциюУ А (т/, > » V, ’ Ч ’ sik+] ’ - ’ V SiM > - ’ Sim ) ’в которой аргументы отсчитываются от произвольного достаточно большого
момента времени пребывания системы в этом состоянии.Из начального состояния, когда все элементы исправны, в состояние А сис¬
тема перешла вследствие последовательного отказа элементов с номерами
i|, /2,..., /* • При этом остальные элементы с номерами ik+i, ik+2,..., im рабо¬
тоспособны. Из них элементы с номерами ik+15..., i/ работают, а с номерами
//+1,..., im простаивают из-за предыдущих отказов. Так как обслуживание
осуществляется одним органом с обратным приоритетом, то восстанавлива¬
ется только последний из отказавших элементов с номером ik .
384Глава 9Из некоторого состояния В0 в состояние А имеется один переход, вызван¬
ный отказом элемента с номером ik , и поэтому аргументы функции, соответ¬
ствующей состоянию В0, будутУв0 (т/, > ->Vг5 Ч-i ’ sk > ’ - ’ s‘i5 s‘i+1 ’ - * ■Ч, ) •Знак "+" над символом означает, что /-й элемент исправен (работает или
простаивает).Из состояния А в состояния ,..., В[ есть (1-к) переходов вследствие
отказов элементов с номерами ik+x,...,it. Каждому состоянию Вп
(п = к + \,...,/) отвечает функцияУвп (х/, * - > xik » sik+1 > - > т/„» » sil+l > - » ) >аргументы которой показывают, что в течение времени пребывания системы
в состоянии Вп элемент с номером /„ находится в состоянии отказа и вос¬
станавливается, у элемента с номером ik прервано восстановление, а все ис¬
правные элементы или работают, или простаивают на время восстановления
отказавших элементов. В силу принятой дисциплины обслуживания, система
может перейти в состояние А только из состояний В0, Вк+Х,..., Bt.Для /-го элемента системы (/ = 1, 2,..., т ) вероятность безотказной работы и
вероятность невосстановления обозначим через F, и Gt соответственно, а
через fj - —F/ и g, = -G- — плотности распределения вероятностей. Пусть
7] — наработка на отказ и Тш — среднее время восстановления /-го эле¬
мента.Согласно общей методике описания функционирования системы с произ¬
вольными законами распределения (см. гл. 4) справедлива следующая систе¬
ма интегральных уравнений:У A(Ti, > - > \» sik+l * - ’ sii,» sfM ’ - >SiJ~00- К (* •+ч )yBo Ц* °*. ■*+ ’~>x+s‘, ’ SL > ■"’ SL ^+0/ ®+ I \fiSx+sOyBS^->4-,’x+x*>’V>*+sh’SL>->O-л=*+10(9.4)Если состояние Л является начальным, то в соответствующем уравнении от¬
сутствует слагаемое, вызванное отказом некоторого элемента; если А — от-
Методы обеспечения и повышения надежности техники385казовое состояние системы, то в уравнении отсутствуют слагаемые, обуслов¬
ленные восстановлением элементов.Система уравнений (9.4) имеет следующее решение:(9.5) в правую часть системы (9.4). При этом штрихи над аргументами х и s
в функции уА опущены.Интегрирование функций (9.5) позволяет найти вероятности рА пребывания
системы в произвольном состоянии Аи параметры перехода со из любого состояния в некоторое смежное с ним:где С — постоянный множитель, который находится из условия нормиров¬
ки. Из этих выражений следует, что интенсивности переходов независимы от
законов распределения и имеют вид:Таким образом, независимость показателей надежности рассмотренного
класса систем от законов распределения отказов и восстановления элементов
доказана.9.5.2. Оценка надежности
восстанавливаемых мажоритарных систем
последовательно-параллельной структурыРассмотрим применение свойства, установленного в разд. 9.5.1, к оценке на¬
дежности основного соединения п резервированных узлов (раздельное ре¬
зервирование), i-й узел которого состоит из mi идентичных элементов
(рис. 9.3) с произвольными распределениями времени безотказной работы и
времени восстановления. Отказом системы будем считать состояние, при ко¬kmЭто может быть доказано непосредственной подстановкой функций видаk mк-1 m kmj*n<&AB„ _ 113 Зак. 3094
386Глава 9тором отказывают lt из mi элементов в каком-либо из г'-х узлов. Изобразим
любое состояние системы вектором (кх, к2,..., кп), в котором /-я компонента
(/ = 1, 2,..., п) означает, что в i-м узле отказало ровно ki элементов.Рис. 9.3. Структурная схема расчета надежностиОчевидно, что при ki < /, -1, г = 1, 2,..., п соответствующие состояния явля¬
ются работоспособными. Состояние отказа наступит в том случае, когда для
некоторого j (j = 1, 2,..., п) выполняются соотношенияkj=lj, к' й 1,-1, i*j.Число работоспособных состояний вида (кх, к2,..., кп) удовлетворяет сле¬
дующему функциональному уравнению:J(kx, к2,... ,к„)= ]Г J(kx, к2,..., kj-1,..., kn)(mj-kj+1), (9.6)j=iрешением которого служат функцииfJ(kx,k2,...,kn)~(к\ + к2 + - + ^)!ПСт, •<=1(9.7)Число возможных отказовых состояний, появившихся в результате отказа
у'-го узла, определяется из соотношения:J j 1 J ^2 9 9 fj9 ••• 9 к/г ) — *^(^1 5 ^2 9 ••• 9 ^ ,м > ^71 у 7у +1),откудаJ°(£„ *2,..., lj,... ,кп) = {кх+к2+... + /, +... + - 1)!/Д П с; • (9.8)J i=i
i*J‘ГПоложим р, = , / = 1,2,..., и, где 7] и Гв; — среднее время работы и
среднее время восстановления элементов /-го узла. Выражения (9.7) и (9.8)
Методы обеспечения и повышения надежности техники387позволяют определить отношения суммарной вероятности всех работоспо¬
собных и всех отказовых состояний к вероятности р0 пребывания системы в
начальном состоянии. Вероятность р+ всех работоспособных состояний с
точностью до множителя р0 получается суммированием числа состоянийА квида (&|, к2,..., кп), умноженных на вероятности таких состояний J |р,' ./=1Вероятность р_ всех отказовых состояний определяется суммированием чис¬
ла отказовых состояний вида (кх, к2,..., /у,..., кп), умноженных на их веро-” к I
ятности ПР/'Ру ■»=1i*JИз каждого работоспособного состояния вида (£,, к2,..., /у -1,..., кп) суще¬
ствует переход в отказовое состояние за счет отказа nij - lj+1 элементов j- гоузла с интенсивностью —, что позволяет определить параметр потока отка¬
зузов системы со.Выражения для р+, р_ и со можно представить в следующем удобном для
вычислений виде:ОО пР+=А>Щоо „О /=1У к кkt =0е Xdx,0 7 = 1 J i=1i*j4*1=0® - M i ^ (py*)7'"1 ft ( z c; (p^0 y = l ' /=1^=0i*,/e Xdx.(9.9)(9.10)(9.11)Из соотношений (9.9)—(9.11) определяются показатели надежности системы:т-£±. т -Р- v - Т1 ) -*в 9 гСОСОт+т,:Таким образом, стационарные значения показателей надежности выражаются
только через р, и полностью определяются математическими ожиданиями 7J
и TBi элементов /-го узла, / = 1, 2,..., п.
388Глава 9Заметим, что приведенные формулы позволяют также найти общее число ра¬
ботоспособных и отказовых состояний системы. Соответствующие значения
получаются при р, = 1, /' = 1, 2,..., и. Точные выражения для числа состояний
представляют и самостоятельный интерес, т. к. в некоторых случаях это чис¬
ло надо знать заранее, еще до начала расчетов количественных характеристик
надежности системы. Такая необходимость может возникнуть, например, при
динамическом распределении памяти ЭВМ.9.6. Влияние резервирования
на интенсивность отказов системыПредположим, что система представляет собой последовательное в смысле
надежности соединение резервированных подсистем, элементы которых
имеют различную надежность. Тогда имеют место следующие свойства сис¬
тем с постоянно включенным резервом и произвольными законами распреде¬
ления элементов:□ в начальный момент эксплуатации надежность системы равна надежности
нерезервированной части;□ в любой момент времени интенсивность отказов системы не превышает
интенсивности отказов нерезервированной системы, составленной из наи¬
худших элементов каждой подсистемы;□ при длительной эксплуатации надежность системы стремится к надежно¬
сти нерезервированной системы, составленной из наиболее надежных
элементов каждой подсистемы.Если система является неизбыточной и состоит из п независимых подсистем,
то, согласно разд. 6.1, интенсивность отказов системы равна сумме интен¬
сивностей отказов подсистем, т. е.У = 1поэтому приведенные свойства автоматически выполняются.Перейдем к рассмотрению избыточных систем. Возьмем любую подсистему
кратности резервирования т . Согласно разд. 6.2, интенсивность отказов под¬
системы определяется выражением:т1/,(0ГН(0Хс(,) = /=° J+J . (9.12)i-п т
1=0
Методы обеспечения и повышения надежности техники389Покажем, что интенсивность отказа подсистемы не превосходит интенсивно¬
сти отказа самого ненадежного элемента, т. е.Xc(t) < max Xk(t)с OZkim *для любого момента t. Для фиксированного момента времени t упорядочим
интенсивности отказов элементов по возрастанию, т. е. (?) < ^(f) <... < Xm{t) .
Установим требуемое неравенство методом математической индукции. При
m = О оно очевидно. Пусть неравенство верно для к элементов. Докажем его
справедливость для (к + 1)-го элемента, т. е. покажем, что£■//(0114(07=0'*71-П4(0/=0<ШПреобразуя это неравенство, получим искомый результат:. / , \Z//(onw*(o^/*xo7 = 0>*Ji-П m/= 0I /У(0П ■WW)Fki»+Л(0П WW) * Л(0j=0 j i=0к-11-П4(0(1-^(0)/=ок-1Z /А0ПЪ№№(')*Л(07=0 i*j*-1i-пад/ = 0z/Aonm „л f*J -Fk(t)<^к-11-П4(0/=0^(0Согласно предположению метода математической индукции, неравенство
А-о (0 < X, (0 <... < (0 доказано.Докажем теперь, что интенсивность отказов системы Xc(t) эквивалентна ин¬
тенсивности отказа наиболее надежного элемента. Пусть при (-> со самым
надежным является элемент с номером 0. Тогда для всех элементов с номе¬
рами / ^ m имеет место соотношение:
390Глава 9С течением времени элементы не становятся абсолютно надежными, т. е. их
интенсивности отказов при /->а> не приближаются к нулю. Тогда А,0(/)^6
при всех достаточно больших t.Из (9.13) следует, что для всякого s>0 существует такое Г, что при t>T
выполняется неравенствоМО-МО Непо¬
следовательно,f (t\ -[(ХДт)-Х0(х))Л -|(ХДт)-?.0(т))Л -е|Х,(т)Лlim -=г— = lim е 0 < lim е 0 е т = 0 .(-»со Fftit) /->« /->00Аналогичное соотношение имеет место и для плотностей, поскольку/до = йот л,МО xo(0F„(O 6 'а, значит,'-**>/о(0Отсюда и из (9.12) следует, чтоlim ЛЮ- = о .lim-^£^= lim 7—т = |im—= j.t->«>X0(t) t-xafi-nO-m)V '=04(0 1+I^Таким образом, интенсивность отказов системы эквивалентна интенсивности
отказов наиболее надежного элемента.ПРИМЕР 9.2. Рассмотрим дублированную невосстанавливаемую систему в
двух вариантах исполнения. В первом варианте законы распределения эле¬
ментов экспоненциальные с параметрами >.,=0,01 час-1 и Х2 = 0,02 час-1.
Во втором варианте время безотказной работы элементов подчинено распре¬
делению Рэлея с параметрами X, =0,01 час-2 и Х2 =0,02 час-2. Для этих двух
случаев требуется определить интенсивности отказов системы.Решение. На основе (9.12) запишем выражения интенсивностей отказов дуб¬
лированной системы для экспоненциальных распределений отказов и распре¬
делений Рэлея:
Методы обеспечения и повышения надежности техники391X (;) 0 ~ е~^> + 0 ~ б~Х|/}с 1 - (1 - )(1 - )2уе~Х|<2 (1 - е~х*2) + 2\г1е~х^ (1 - е~х^)1 - (1 - е~х'‘2 )(1 - е~Х2‘2)Проводя расчеты по этим формулам, получим графики, изображенные на
рис. 9.4 и 9.5 соответственно.)//О t, час 300Рис. 9.4. Интенсивность отказов системы (случай экспоненциальных распределений)Рис. 9.5. Интенсивность отказов системы (случай распределений Рэлея)Из сопоставления этих графиков следует, что кривая интенсивности отказов
системы близка к кривой интенсивности отказов наиболее надежного эле¬
мента. Разница между ними в стационарном режиме не превышает 10%, и
только на начальном этапе получается ощутимый выигрыш в надежности.
392Глава 9Предельное поведение интенсивности отказов, справедливое для любых за¬
конов распределения при постоянно включенном резерве, перестает быть
верным при некоторых распределениях для резерва замещением.В этом случае время X до отказа системы равно сумме времени безотказной
работы подсистем, т. е.т/=0где X, — случайное время работы до отказа /-й подсистемы. Поэтому плот¬
ность распределения величины X равна свертке плотностей слагаемых/(0 = /o*/i*~*/w(0,
и, значит, интенсивность отказа системы равна1-л*/,♦-*/„♦1(0Рассмотрим сначала экспоненциальные распределения. Пусть fi(t) = Xje~Xi,>
причем будем для определенности считать, что все параметры X, различны.
Тогдат ./(0=Sc,V'v,/=оП^утгде с, = —— и со(Х.) = ]""[ (Я. - X,). Следовательно,“(^/) (=0fW’*lim ХМ) = lim — = min Xt.о /->qo i . 0<i<,m( = 0Таким образом, для экспоненциальных распределений имеет место предель¬
ное свойство.Рассмотрим теперь нормальные распределения. Пусть f^t) — плотность
нормального распределения с математическим ожиданием /и, и дисперсиейjа, . Тогда /(0 также является плотностью нормального распределения ст 2 т 2
математическим ожиданием тс = ^ т, и дисперсией сс = X ст/ ./=0 1=0
Методы обеспечения и повышения надежности техники393Интенсивность отказов для нормального распределения при больших значе--п
~2г t-m ^ниях t ведет себя так же, как —г—. Отсюда следует, что для всякого элемен-стта с номером / имеет место соотношениеlim с = lim - ^ < 1,/-»» (t) f-*» (t - tttj )стр acкоторое означает, что интенсивность отказа системы неэквивалентна интен¬
сивности отказа никакого элемента, в том числе и наиболее надежного. От¬
сюда вытекает также важное свойство нормального распределения: при дли¬
тельной работе надежность избыточной системы с резервом замещением
по критерию интенсивности отказов выше надежности любого элемента сис¬
темы.9.7. Эффективность восстановления
при различных законах распределенияВосстановление является важнейшим средством, влияющим на улучшение
показателей надежности технических систем. Однако следует сказать, что это
влияние существенным образом зависит от самой системы, точнее от законов
распределения отказов и восстановлений ее элементов. Проведем сравни¬
тельную оценку надежности систем при экспоненциальных и неэкспоненци¬
альных распределениях.ПРИМЕР 9.3. Рассмотрим восстанавливаемую систему при следующих ис¬
ходных данных:□ распределения времени безотказной работы и времени восстановления
экспоненциальные с математическим ожиданием Т = 1 ООО часов и
Тв = 2 часа;□ распределения времени безотказной работы и времени восстановления
нормальные с параметрами Г = 1000 часов, a = 300 часов и Гв = 2 часа,
<тв =0,5 часа.Требуется оценить влияние восстановления на надежность систем.Решение. Для сравнения проведем оценку надежности по двум критериям:
вероятности безотказной работы, когда восстановление не играет роли, и
функции готовности, когда восстановление весьма существенно.На рис. 9.6 изображены графики вероятностей безотказной работы P{t) для
обоих случаев. Характер этих графиков различен. Для нормальных распреде¬
394Гпавадлений (кривая 2) система оказывается более надежной на начальном периоде
работы и менее надежной при длительной ее эксплуатации.Для тех же случаев на рис. 9.7 представлены графики функции готовностиKT(t).Рис. 9.6. Влияние видов распределения на вероятность безотказной работыО I, час 3000Рис. 9.7. Влияние видов распределения на функцию готовностиЗдесь особенно ярко проявляется зависимость от законов распределения.
Укажем на самые важные отличия. Для экспоненциального распределения
(кривая 1) наблюдается быстрое вхождение в стационарный режим по срав¬
нению с нормальным распределением (кривая 2). Для приведенного примера
система входит в стационарный режим уже через 10 часов эксплуатации для
первого случая и через 3000 часов — для второго. Это значит, что нельзя ха¬
рактеризовать систему, имеющую неэкспоненциальные распределения, ко¬
эффициентом готовности; очень важным является учет переходных процес¬
сов и поведение системы во времени.
Методы обеспечения и повышения надежности техники395Для неэкспоненциальных распределений может наблюдаться колебательный
характер функции готовности. Особенно характерным в этом смысле являют¬
ся нормальное и гамма-распределения. На некоторых интервалах времени
график функции готовности может опускаться ниже своего стационарного
значения. А это означает, что коэффициент готовности не отражает истинно¬
го значения готовности системы в данный момент времени. При этом провал
функции готовности может быть весьма большим. Его величина определяет¬
ся дисперсией времени безотказной работы системы, а именно: чем меньше
дисперсия, тем выше колебания функции готовности.Оценим влияние восстановления на надежность системы, пользуясь показа¬
телем выигрыша надежности.Под выигрышем от восстановления в момент времени t будем понимать от¬
ношениеP{t)Как известно, для экспоненциальных распределений восстановление является
исключительно эффективным при оценке надежности, а функция выигрыша
Vit) с течением времени возрастает.Это утверждение остается справедливым и для неэкспоненциальных распре¬
делений. Однако следует иметь в виду, что для неэкспоненциальных распре¬
делений график Krit) может иметь провалы и в особых случаях опускаться
вплоть до P(t). Поэтому важно определить, когда указанный эффект от вос¬
становления будет больше. На рис. 9.8 представлены зависимости отношения
Vit) от времени работы системы для приведенных ранее случаев.
396Глава 9Из рис. 9.8 видно, что на начальном этапе выигрыш от восстановления V(t)
больше, хотя и незначительно, при экспоненциальном распределении (кри¬
вая 1). При длительном времени работы выигрыш V(t) становится значи¬
тельно больше при нормальном распределении (кривая 2).Следует иметь в виду, что здесь сравниваются показатель надежности P(t) и
показатель готовности Кг (/). Первый характеризует надежность невосста-
навливаемой системы, а второй — восстанавливаемой. Поэтому из рис. 9.8
делать какие-либо выводы о влиянии восстановления на надежность не сле¬
дует. Функция V{t) лишь иллюстрирует свойства резервирования, как метода
повышения надежности.9.8. Сравнение надежности системы
при общем и раздельном резервированияхУровень резервирования, на котором производится добавление резервных
элементов, может быть различным: резервировать можно отдельные элемен¬
ты, подсистемы, а также систему в целом. Масштаб резервирования считает¬
ся более мелким, если меньшая часть системы резервируется как единое
целое.Известно [57], что надежность системы тем выше, чем мельче масштаб ре¬
зервирования. Рассмотрим этот вопрос более подробно на сопоставлении
систем при различных видах резервирования.Резервирование, являющееся одним из эффективных методов повышения на¬
дежности систем, делится на общее и раздельное. При этом раздельное резер¬
вирование дает больший эффект для повышения надежности, чем общее. Это
утверждение справедливо как для постоянно включенного резерва [107], так
и для резерва замещением. Доказательство опирается на следующее свойство
из теории вероятностей: если для случайных величин X и Y имеет место
неравенство X й Y, то для соответствующих распределений выполняется
неравенство Рх(t) < PY(t) для любого момента времени t, т. е.X <Y => Px(t)<PY(t) V t. (9.14)Действительно, для событий X > t и Y > t имеет место включение
(X > /) с (У > t), отсюда вытекает требуемое неравенство.Рассмотрим сначала резервирование с постоянно включенным резервом. Со¬
гласно (6.16) и (6.18), для времени безотказной работы систем при общем и
раздельном резерве справедливо неравенствошах min Хи < min шах Хи./=0,1,2,...,/и у'=1,2,...,л /=1,2,...,п/ = 0,1,2 т
Методы обеспечения и повышения надежности техники397Поэтому на основании (9.14) вероятность безотказной работы системы при
общем резервировании не превышает вероятности безотказной работы сис¬
темы при раздельном резервировании, т. е. надежность раздельного резерви¬
рования выше, чем общего.Аналогично обстоит дело и с резервом замещением. Согласно (6.17) и (6.19),
для общего и раздельного резервирования имеет место неравенствоm m£ min Ху< min ]Г XtJ.£0j=\,2,...,n J 7=1,2 nflyJ JТогда на основании (9.14) вероятность безотказной работы системы при об¬
щем резервировании не превышает вероятности безотказной работы системы
при раздельном резервировании.Таким образом, с точки зрения увеличения вероятности безотказной работы
раздельное резервирование более эффективно, чем общее. Оценим на част¬
ных примерах выигрыш, получаемый от раздельного резервирования по
сравнению с общим.ПРИМЕР 9.4. Рассмотрим случай дублирования (т = 1) и предположим, что
все элементы идентичны по надежности и имеют экспоненциальные распре¬
деления времени до отказа с параметром А, = 1(Г5 час-1. Определим величину
выигрыша для постоянно включенного резерва и резерва замещением при
числе элементов п = 10 и п = 20. Сравним полученные результаты.Решение. Для постоянно включенного резерва величина выигрышау (2e~Xt-e~2Xt)n (2-e~u)n" 1_(1 -e~nUf ~ 2e~nXt -e~lnXt ~ 2-e~nXl ’
а для резерва замещением((l + ?g)g~x<) _ (1 + Xt)n(1 +nXt)e~nXl ~ 1 + rihtK(0 = -Ha рис. 9.9 и 9.10 представлены зависимости выигрыша от времени для этих
двух способов резервирования при п-10 и « = 20 элементов.Из рисунков видно, что выигрыш существенно возрастает с увеличением ко¬
личества элементов в системе. При этом для постоянно включенного резерва
величина выигрыша больше, чем для резерва замещением.Сопоставим теперь величину выигрыша при одном и том же числе элемен¬
тов. На рис. 9.11 и 9.12 изображены графики выигрышей для постоянно
398Глава9Рис. 9.9. Выигрыш для постоянно включенного резерваРис. 9.10. Выигрыш для резерва замещениемРис. 9.11. Выигрыш при л = 10 элементов
Методы обеспечения и повышения надежности техники399Рис. 9.12. Выигрыш при и = 20 элементоввключенного резерва и резерва замещением при и = 10 и « = 20 элементов
соответственно. При этом на рисунках кривая 1 соответствует постоянно
включенному резерву, а кривая 2 — резерву замещением.Из рис. 9.11 следует, что большим выигрышем обладает система с постоянно
включенным резервом, если продолжительность ее использования не велика,
а для систем длительного использования больший выигрыш имеет система с
резервом замещением.9.9. Сравнительный анализ
нагрузочного и структурного
резервированийРезультатом нагрузочного резервирования является уменьшение отказов эле¬
ментов в « раз. Физически этот вид резервирования реализуется путем об¬
легчения режимов работы элементов (электротехнических, тепловых, меха¬
нических и др.). Так же, как и при структурном резервировании, он приводит
к увеличению объема оборудования (повышение мощности элементов, уста¬
новка вентиляторов, демпфирование колебаний и т. д.). Какой же из этих ме¬
тодов более эффективен?Для ответа на этот вопрос выполним анализ выигрыша надежности, пред¬
ставляющего собой отношение показателя надежности системы при нагру¬
зочном (или структурном) резервировании к показателю надежности при
структурном (или нагрузочном) резервировании. За критерий надежности
можно взять любой, который достаточно полно характеризует надежность
данной системы. Во многих случаях удается сравнить эти методы качествен¬
но, без математического анализа.
400Гпава 9Пусть, например, интенсивность отказов некоторой системы Я. = 0,01 час'1.
В результате применения нагрузочного резервирования интенсивность отка¬
зов уменьшилась и стала X- 0,006 час-1. Сравним этот вид резервирования
со структурным при общем постоянном резервировании с кратностью т = 1.
На рис. 9.13 показаны интенсивности обеих систем как функций времени.Рис. 9.13. Интенсивность отказов системы
На рисунке обозначены:□ кривая 1 — интенсивность отказов системы без резервирования;□ кривая 2 — интенсивность отказов системы с нагрузочным резервом;□ кривая 3 — интенсивность отказов дублированной системы.Так как интенсивность отказов структурно резервированной системы при
t = 0 также равна нулю и асимптотически приближается в области больших t
к интенсивности отказов исходной системы, имеющей интенсивность отказов
X = 0,01 час'1, то кривая пересечет прямую X = 0,006 час-1. Очевидно, что
при t < х более надежной будет система со структурным резервированием, а
при t > х — с нагрузочным. Значение х легко найти. Воспользуемся выиг¬
рышем надежности по вероятности отказа системы. Так как вероятность от-XIказа при нагрузочном резервировании Q\(t) = l-e ", а при структурном
Qi (0 - 0 _ e~Xt)m+l, то выигрыш надежности имеет вид:Xt1-е п
Методы обеспечения и повышения надежности техники401Определим зависимость т = /(«) при значениях Xt, при которых Gq(t) = 1,т. е. оба метода обеспечения надежности равноценны. Задача сводится к ре¬
шению трансцендентного уравнения:X1-е” -(1 -e~x)m+l = 0,где x-Xt.Результаты решения приведены в табл. 9.3.Таблица 9.3. Результаты определения критического значения Xtп2510m123123123Xt0,961,892,530,250,71U0,110,430,720,620,390,280,950,870,80,9890,9570,93В таблице также приведены критические значения вероятности безотказной
работы системы в случае применения резервирования. Критическое значение
Xt позволяет установить время t, при котором оба метода равноценны.
Пусть, например, X = 0,01 час-1, кратность резервирования m-1, п - 2 .В этом случае Xt - 0,96. Тогда критическое = ^ час‘ ^то значит>что структурное резервирование с кратностью т = 1 более эффективно при
времени работы системы t < 96 час. При t > 96 час более целесообразным
является нагрузочное резервирование при п > 2 .Из табл. 9.3 видно, что область целесообразности структурного резервирова¬
ния уменьшается с увеличением п и увеличивается с ростом т .Определим выигрыш надежности по среднему времени безотказной работы.Среднее время безотказной работы системы с нагрузочным резервированиемТ = —, при структурном резервировании
XGT= ПТ /л+1 1I1
/ = 1 *Из этого выражения видно, что выигрыш надежности по среднему времени
безотказной работы растет линейно с ростом п и медленно убывает с ростом
402Глава 9m+1 jm. Выигрыш GT = 1, если - = n . Отсюда следует, что уменьшение интен-/=1 1сивности отказов системы в 2 раза (и = 2) эквивалентно системе с крат¬
ностью общего резервирования т = 3 , при и = 3 т = 10, а при п = 4 т = 30.При резервировании замещением выигрыш надежности по среднему времени
безотказной работы определяется какИз этого выражения следует, что уменьшение интенсивности отказов систе¬
мы в п раз эквивалентно структурному резервированию кратности т (об¬
щему числу систем (т +1) ).Из приведенного анализа можно сделать следующий вывод: структурное ре¬
зервирование более эффективно для систем с коротким временем работы.
Для систем длительного использования более целесообразным является на¬
грузочное резервирование, особенно в случае, если надежность оценивается
средним временем безотказной работы.9.10. Надежность систем
с временной избыточностьюВажным способом повышения надежности систем является временное резер¬
вирование. Говорят, что система обладает временным резервом, если для
устранения отказа система имеет определенный запас времени. Временной
резерв может быть как постоянной, так и случайной величиной. Возникает
другое понятие отказа системы, а именно: если отказ системы устранен в те¬
чение временного резерва, то соответствующее состояние не является отказо-
вым, Безусловно, временное резервирование способствует повышению веро¬
ятности безотказной работы, но техника при этом не становится более на¬
дежной. Оценке влияния временного резерва на надежность системы и
посвящен данный раздел.9.10.1. Описание функционирования системы
с произвольным распределением временной
избыточности в терминах интегральных уравненийНаличие временного резерва может рассматриваться как существование в
системе еще одного элемента, который включается в работу на период неис¬
правности системы (расходуется резервное время) и простаивает во время
Методы обеспечения и повышения надежности техники403исправной работы системы (резерв времени не расходуется). При этом в за¬
висимости от пополняемости временного резерва дополнительный элемент
может находиться в очереди на работу или в состоянии прерывания работы.Таким образом, за счет увеличения числа элементов анализ надежности сис¬
темы с временной избыточностью может быть выполнен по той же методике,
что и без резерва времени.Пусть £ характеризует время работы системы с плотностью fit), г| — вре¬
мя восстановления с плотностью g(t). Пусть X — случайная величина с
плотностью h(t), представляющая собой резерв времени на предотвращение
отказа системы. Рассмотрим две модели функционирования системы в зави¬
симости от того, является ли резерв X пополняемым или нет. Предположим
сначала, что резерв времени X пополняется таким образом, как показано на
временной диаграмме (рис. 9.14).Очевидно, возможны три состояния системы:□ (0) — система исправна, резерв времени не расходуется;□ (1)— система восстанавливается (г| — время восстановления) и расходу¬
ется временной резерв;□ (2) — система восстанавливается, но временной резерв исчерпан (г| > X).
Соответствующий граф состояний представлен на рис. 9.15.Рис. 9.15. Граф состояний для пополняемого временного резерваС каждым состоянием свяжем функцию для составления системы интеграль¬
ных уравнений: состоянию (0) отвечает функция _y0(s,,0,O, состоянию (1) —
404Глава 9функция yx(xx,s2,t), а состоянию (2) — функция д>2(т1>0,/) • Все эти функции
содержат по два аргумента (не считая t), из которых первый относится к изу¬
чаемой системе, а второй соответствует "функционированию" резерва време¬
ни. Система интегральных уравнений имеет вид:Заметим, что переход из состояния (1) в состояние (0) связан с восстановле¬
нием системы за время, не превосходящее X, поэтому в системе (9.15) сла¬
гаемое, отвечающее указанному переходу, интегрируется по всем s2 от нуля
до бесконечности в силу того, что резерв пополняемый и величина его остат¬
ка безразлична.Аналитическое решение полученной системы уравнений находится путем
несложных преобразований и имеет вид:Из этого решения определяются следующие вероятности состояний, а также
параметры потоков отказов и восстановлений:y0(s{,0,t) = lf(x + sl)jyl(0,s2,t-x)ds2dx+lf(x + sl)y2(0,0,t-x)dx +ооо+ /(/ + Si);t(9.15)у{ (tj ,s2,t) = Jg(x + xl )h(x + s2 )y0 (0,0,( - x)dx;оty2 (Tj, 0,/) = [y, (x + x,, 0, / - x)dx.оУо(^,0,0 = Л, *g*(o(t) + f(t + sl),
yi(Tl,s2,t) = (gxhS2)*G>(t),
y2(xx,0,t) = (ghH)*G)(t).Po(0 ~ F * g * co(0 + F(t), p{(/) = oGH) * co(0, p2(0 = (GH) * co(0,OO®c(0= 1л(т1,0,/)йГт, = (Gh)*co(t), (oBC(t) = y2(0,0,t) = (gH)*a(t).оФункция co(0 удовлетворяет соотношениям (4.3).Отсюда находим, например, функцию готовности системы с пополняемым
резервом времени:Кг (/) = F(t) + (F*g + GH) * со(0 .(9.16)
Методы обеспечения и повышения надежности техники405Стационарные вероятности, параметры и показатели надежности определя¬
ются из нестационарных путем предельного перехода при t —> оо. Они имеют
следующий вид:□ коэффициент готовности:Т+ jG(t)H(t)dt+ Р\ =□ средняя наработка на отказ:Кг=Ро + Р1= ; (9.17)Т+ \G{t)H(t)dtт Ро+Р 1 = о (918)со 00 -с \G{t)h{t)dtо□ среднее время восстановления:\G(t)H(t)dtГ..= — = 1 • (919)О) 00 с \G{t)h{t)dt
оС помощью соотношений, связывающих параметры потоков и плотности (см.
разд. 4.1), можно определить эквивалентные плотности распределения вре¬
мени до отказа и времени восстановления системы с резервом времени как
явные функции времени.Если нас интересует работа системы только до первого отказа, то в графе,
изображенном на рис. 9.15, следует запретить выход из отказового состояния
(сделать состояние (2) поглощающим) и соответствующим образом изменить
систему уравнений (9.15):t <Ю>>0 (s,, 0,0 = f/(x + л,) J ух (0, s2, / - x)ds2dx + f(t + sx)\о оtyl(T,,s2,0= 1г(* + т,)й(л: + Я2)У0(0,0,Г-дс)Л; (9.20)оу2 (т;, 0,0 = Jj! (т,, 0, t - x)dx.
406Глава* 9Можно показать, что решение системы (9.20) образуют функции:>-0(j,, 0,/) = Д * (gH) * ОД + /(/ + j,),>'l(Ti>-s2»0 = (gTA2)*Q(0,у2(ъм=^н)*п*т,где Q(0 удовлетворяет уравнению:O(0 = /*(gtf)*Q(0 + /(/).Вероятность безотказной работы для системы с пополняемым временным
резервом является решением простого интегрального уравнения:Pit) = P*f* (gH)(t) + F(t) + f * (GH)(t). (9.21)ПРИМЕР 9.5. Требуется определить вероятность безотказной работы для
технического устройства при отсутствии и наличии временного резерва.
Время безотказной работы имеет распределение Рэлея с параметром
А. = 0,1 час'2, а время восстановления— распределение Эрланга второго по¬
рядка с параметром ц = 1 час'1. Резервное время постоянно и равно 1 часу.Решение. Для принятых данных результаты расчетов вероятности безотказ¬
ной работы при наличии и отсутствии временного резерва, выполненные по
формуле (9.21), приведены в табл. 9.4.Таблица 9.4. Вероятность безотказной работы/, часБез резерва времениС резервом времениУвеличение надежности,отн. ед., %01,00001,00000,020,98020,99701,740,92310,96965,060,83530,91729,880,72610,844916,4100,60650,759725,3120,48680,668637,3140,37530,578054,0160,27800,492877,3180,19790,4162110,3200,13530,3496158,4
Методы обеспечения и повышения надежности техники407На рис. 9.16 дана соответствующая графическая иллюстрация вероятности
безотказной работы.Рис. 9.16. Вероятность безотказной работы при отсутствии и наличии временного резерваКак и должно быть, результаты расчетов свидетельствуют о существенной
зависимости вероятности безотказной работы от наличия резерва времени.
В последнем столбце табл. 9.4 содержатся значения, характеризующие уве¬
личение надежности системы. С течением времени эффект от наличия вре¬
менного резерва возрастает от 0 до 158,4 %.Если резерв времени непополняемый, то случайная величина X попадает на
несколько интервалов длины Г|, причем последний интервал может быть не¬
полным (рис. 9.17).Опишем состояния системы (рис. 9.18) и укажем соответствующие этим со¬
стояниям функции:□ (0) — система работает, временной резерв не включен, _у0 , 0, г);□ (1) — система восстанавливается, включен временной резерв, ^|(Tj,52.0 ;□ (2) — система работает, временной резерв выключен на время работы сис¬
темы, y2(sx,s'2,t);
408Гпава 9.□ (3) — система работает, временной резерв исчерпан полностью, ^(^,0,/);□ (4) — система восстанавливается, временной резерв исчерпан, y4(xl,0,t).Рис. 9.18. Граф состояний для непополняемого временного резерва
Составим систему интегральных уравнений:'y0(sbO,t) = f(t + sO;
iУ\ Оч, Щ>О - Jg(* + х\ Ж* + ^2 )^о (°> 0, t - x)dx +
о+ lg(x + ^)y2(0,x + s2,t- x)dx;01 (9.22)
y2(si’s2’0= j/O + s, )>», (0, s2,t- x)dx;0/Уз (S\ ,0,0= ff(x + S, )y4 (0,0, t - x)dx;01 iy4 (ti, 0, /) = j^i (x + Tj, 0, / - x)dx + Jg(x + Tj )уъ (0,0, t - x)dx.
о 0Все характеристики надежности полностью определяются эквивалентными
плотностями распределения вероятностей, которые находятся из уравнений
по параметрам потоков отказов и восстановлений:ОО<0(0= !у1(^,0,О^1+Уз(0,0,О, 6)В(0 = У4(0,0,0.
оЕсли требуется найти вероятность безотказной работы, то в графе, изобра¬
женном на рис. 9.18, следует запретить выход из отказового состояния, изме¬
нить и решить систему уравнений (9.22). Тогда вероятность безотказной ра¬
боты будет равна сумме вероятностей работоспособных состояний системы.
Методы обеспечения и повышения надёжности техники409Для непополняемого резерва стационарные характеристики системы будут
такие же, как и без резерва времени.ПРИМЕР 9.6. Определить стационарные показатели надежности для систе¬
мы с пополняемым и непополняемым временным резервом. Время безотказ¬
ной работы имеет распределение Рэлея с параметром >. = 0,1 час'2, а время
восстановления — распределение Эрланга второго порядка с параметром
ц = 1 час-1. Резервное время постоянно и равно 1 часу.Решение. Без временного резерва имеем среднюю наработку на отказ1 [л 2Т = — . — =2,802 часа и среднее время восстановления Тв = — -2 часам, по-2 V А. цэтому коэффициент готовности Кг = 0,584 .При наличии пополняемого резерва времени с учетом формул (9.17)—(9.19)
для стационарных показателей надежности получим коэффициент готовности
Кт =0,770, наработку на отказ Тс =5,024 часа, среднее время восстановле¬
ния Твс =1,5 часа. По всем трем показателям надежность системы заметно
возросла.9.10.2. Распределение суммарных наработокДля задач временного резервирования существенное место занимают вопро¬
сы нахождения законов распределения суммарных наработок. Эти вопросы
также легко поддаются математическому описанию с помощью систем инте¬
гральных уравнений.Пусть функционирование технической системы описывается процессом сме¬
ны работоспособных состояний и состояний восстановления с плотностями
/ и g соответственно. Обозначим через <^(/0) суммарную наработку систе¬
мы за заданное время t0 и определим закон распределения этой случайной
величины, т. е. найдем вероятность того, что C,(t0)>t для любого t. Вероят¬
ность P{tQ,t) = P{^(tQ)>t) может быть истолкована следующим образом.
Предположим, что на вход системы поступает заявка, которая обслуживается
во время исправной работы системы. Пусть t = ?зад — заданное время обслу¬
живания заявки, тогда P(tQ,t) — вероятность того, что заявка будет обслу¬
жена за время [0,/0]. Если время обслуживания заявки X случайно с плот¬
ностью fx(0, то P(t,(t0)> X) — вероятность того, что за время [0,/0] заяв¬
ка со случайным временем будет обслужена. При этом считается, что заявка
410Глава 9обслуживается в течение всего времени работы системы и ее отказы сказы¬
ваются на задержке обслуживания.Будем считать, что заявка на обслуживание является вторым элементом с
плотностью распределения времени безотказной работы /х и плотностью
распределения времени восстановления 8М. На рис. 9.19 и 9.20 представлены
диаграмма и граф состояний для нахождения закона распределения суммар¬
ной наработки в случае необесценивающих отказов.Рис. 9.20. Граф состояний для случая необесценивающих отказовОпишем состояния всей системы вместе с заявкой:□ (0) — система работает, заявка обслуживается;П (1) — система восстанавливается, обслуживание заявки прервано;□ (2) — система работает, заявка обслужена.Этим состояниям отвечает система уравнений:tу о (5i >s2 >О = J A*+si )л (0, * + *2 J ~ xtf* + А* + s\ )fx 0+s2);оt■ Мт i,s2,t)= \g(x + x])y0(0,s2,t-x)dx; (9.23)о/y2 (5,, 0,0 = J_v0 (*i . 0, t - x)dx.
оВероятность того, что суммарная наработка за время [0,/0] превосходит ве¬
личину X, равна вероятности попадания системы в момент t0 в состоя¬
Методы обеспечения и повышения надежности техники411ние(2), т. е. P(C,{t0)^X) = p2(t0). Поэтому надо решить систему уравне-00ний (9.23), найти функцию и вероятность р2(0 = \y2(s\^,t)dsx.о9.10.3. Обесценивающие отказыМы рассмотрели случай, когда отказы не обесценивают проделанную работу
(обслуживание заявки). Однако возможен вариант, когда отказ системы при¬
водит к прекращению обслуживания и после восстановления системы заявка
начинает обслуживаться заново (рис. 9.21).При этом меняется смысл состояний системы:□ (0) — система работает, заявка обслуживается;□ (1)— система восстанавливается, обслуживание заявки прервано, и в
дальнейшем оно будет начинаться сначала;□ (2) — система работает, заявка обслужена.Система уравнений приобретает вид:tУо (s{, s2, t) = J/(x + S\ )fx (x + *2 )У\ (0,0, t - x)dx + f(t + s, )fx (t + s2)\оI 00• я(т„ 0,0= Jg^ + Xj) \y0 (0,s2, t-x)ds2dx; (9.24)о оty2 (sj, 0,0 = Jj>0 (*1 >1“ x)dx-оОпределение закона распределения суммарной наработки при обесцениваю¬
щих отказах, как и ранее, связано с нахождением вероятности p2(t).Используя решения систем (9.23) и (9.24), можно определить также и некото¬
рые другие характеристики, например среднее число интервалов работоспо¬
собности системы, достаточное для обслуживания заявки. Для этого надо оп¬
412Глава 9ределить среднее число переходов из состояния (0) в состояние (1), а оно рас¬
считывается по формуле:I I СоЩ\0) = J®01 (x)dx = I $yo(0,s2,x)ds2dx.О ООДля систем более сложной структуры, обладающих временным резервом,
можно определить эквивалентные плотности распределения и затем приме¬
нить результаты, полученные ранее. Можно изменить граф состояний. Его
необходимо дополнить переходами, ведущими из каждого работоспособного
состояния в дополнительные поглощающие состояния. Эти переходы обу¬
словлены случайной величиной X с плотностью fx. Тогда вероятность со¬
бытия, состоящего в том, что суммарная наработка системы С(*о) за время /0
превысит случайную величину X, равна вероятности попадания в любое до¬
полнительное состояние.9.11. Определение функции
оперативной готовности системыОдним из важнейших показателей эффективности работы восстанавливаемой
технической системы является функция оперативной готовности R(t,s),
представляющая собой вероятность исправной работы системы на промежут¬
ке времени от t до / + s. Это значит, что система должна находиться в мо¬
мент времени t в исправном состоянии и не должна отказать после этого мо¬
мента в течение времени s . Обычно такие системы длительное время нахо¬
дятся в состоянии простоя и используются кратковременно, в случае
необходимости. При s = 0 R(t,s) совпадает с функцией готовности Kr(t), апри t- 0 — с вероятностью безотказной работы системы на интервале [0,s|.Функция оперативной готовности достаточно полно характеризует надеж¬
ность технической системы. Она используется также для анализа эффектив¬
ности вычислительных систем, обслуживающих потоки задач, поступающих
на решение. В этом случае R(t,s) представляет собой вероятность правиль¬
ного решения задачи за заданное время и служит показателем эффективности
работы технической системы.В обозначениях разд. 4.1 функция оперативной готовности совпадает с функ¬
цией Yq^sJ) . Согласно формуле (4.2)R(t,s) = a>B*Fs(t) + Fs(t)
Методы обеспечения и повышения надежности техники413илиR(t,s) = Fs (/) + J /(**> * (0. (9.25)A = lВ преобразовании Лапласа по аргументу t функция оперативной готовности
имеет вид:R(z,s) = . (9.26)1 -Az)g(z)По формулам (9.25) или (9.26) можно аналитически или численно рассчитать
функцию R(t,s) для целого ряда известных распределений.ПРИМЕР 9.7. Получить выражение для функции оперативной готовности,
если fit) = \e~Xl, g(t) = ре“ц'.Решение. По формуле (9.26) получим:1 -в-**откудаилиR(t,s) =(z + X)iz + ц)' и- | Ъ.р. + А. р + я.F(s)Rit,s) = Krit)Fis). (9.27)Таким образом, функция оперативной готовности равна произведению функ¬
ции готовности в момент времени t и вероятности безотказной работы в те¬
чение времени s .Заметим, что равенство (9.27) имеет место тогда и только тогда, когда время
до отказа системы имеет экспоненциальное распределение. Для всякого дру¬
гого распределения соотношение (9.27) является неверным.Получим теперь некоторые асимптотические оценки для вероятности Rit,s).
Пусть ak — начальный момент распределения с плотностью f * g к-го по¬
рядка. В частности, a{ = Т + Тв, а2 = а2 + 27ТВ + р2 > где а2 и р2 — вторые
начальные моменты распределений с плотностями fug соответственно.
414Глав,a-'SТогда коэффициент оперативной готовности равенR(s) = lim R(t,s) = lim zR(z,s) = lim —'.г->0 z->o l — f (z)g(z) T + TBТаким образом, для стационарного режима вероятность безотказной работы
элемента в течение времени s равнаВД = ~~-, (9.28)оогде Ф($) = jF(f + s)dt. Аналогично вероятность невосстановления элемента воЧЧт) 00 —течение времени т равна —, где ’•F(x) = j\G(t + x)dt.т + тв 0Без доказательства отметим, что в общем случае имеют место соотношения:ОJf Y0(s,t) Ф(5) dt = \Pk+x{t)F(t + s)df,V a\ J/О}tk Y{{x,t) - -вд)л =]qm (t)G(t + x)dt,о У °i Joгде Pk+\(t), Qk+\(t) —некоторые полиномы степени (к + 1). В частности,* * . \ dm- 1 ,2 . «2 , , 2а,а3-За|Pi (0-—1+~2 ’ Р2(0-~-—t +—~jt +a\ 2а, 2а, 2а, 12а,В реальной технической системе, особенно на стадии проектирования, очень
трудно прогнозировать точное время начала операции и ее продолжитель¬
ность. Например, длительность выполнения операции сложной компьютер¬
ной системой зависит как от начальных данных, так и от используемых про¬
граммных средств. Начальные данные могут быть произвольными, и, следо¬
вательно, время выполнения программы также произвольно. Поэтому
возникает задача определения вероятности исправной работы системы на ин¬
тервале времени со случайными концами. Назовем эту вероятность функцией
готовности системы на случайном интервале и обозначим через R.Предположим, что левый конец интервала а и длительность интервала р
представляют собой двумерную случайную величину (а,Р) с плотностью
распределения <p(t,s). Тогда функция готовности системы на случайном ин¬
тервале задается равенством:
Методы обеспечения и повышения надежности техники415R = J jR(t,s)q>(t,s)dtds .о оИз этого представления очевидным является следующее свойство: для вы¬
пуклой функции R(t,s) имеет место оценка снизуRZR(t,s), (9.29)где 7 и J — математические ожидания случайных величин аир соответ¬
ственно. Это свойство является следствием неравенства Йенсена, характери¬
зующего выпуклые функции.При длительной работе системы пессимистическая оценка (9.29) всегда спра¬
ведлива, поскольку предельное значение функции оперативной готовности,
согласно (9.28), пропорционально функции Ф($), которая является выпук¬
лой, т. к. Ф*(а) = /(s) > 0 . Для малых значений t неравенство (9.29) может
быть неверным. Например, в предположении, что случайный параметр s
имеет равномерное или нормальное распределение для систем m/п справед¬
лива как раз противоположная оценка.9.12. Надежность систем из элементов
с несколькими состояниямиСуществующие методы позволяют вычислять показатели надежности техни¬
ческих систем, как правило, при условии, что каждый элемент системы мо¬
жет пребывать лишь в двух возможных состояниях: работоспособном и нера¬
ботоспособном. Однако в реальных условиях функционирования техниче¬
ской системы некоторые или все ее элементы могут иметь промежуточные
состояния, определяемые условиями эксплуатации системы [28].Так, например, при переменных условиях эксплуатации нагрузка на рабо¬
тающие элементы системы может изменяться с течением времени, что влияет
на изменение законов распределения времени безотказной работы элементов
(или только их параметров) и может восприниматься как наличие у элемен¬
тов нескольких работоспособных состояний. Эти состояния естественным
образом упорядочены.Состояние обслуживания отказавшего элемента также может представляться
в виде нескольких упорядоченных отказовых состояний. Так, например, по¬
сле отказа элемента необходимо сначала обнаружить и локализовать отказ,
затем доставить запасной элемент и лишь потом приступить к его восстанов¬
лению. Время обнаружения неисправности, время доставки запасного эле¬
416Глава 9,мента и время непосредственного восстановления отказавшего элемента рас¬
пределены обычно по различным законам.Время пребывания элемента в каждом своем состоянии будем считать неза¬
висимыми случайными величинами с произвольными распределениями.
Предполагается, что переход от одного состояния к другому мгновенный.Рассмотрим систему, образованную из элементов с несколькими состояния¬
ми. Во время нахождения элемента в каком-либо состоянии другие работо¬
способные элементы могут отказывать, а отказавшие — восстанавливаться,
если имеются свободные ремонтные единицы. Используя аппарат интеграль¬
ных уравнений, можно показать, что функционирование описанной системы
эквивалентно функционированию аналогичной системы, элементы которой
имеют только два состояния. Эти состояния получаются в результате объ¬
единения всех работоспособных состояний и всех отказовых состояний. При
этом плотности распределения времени пребывания в укрупненных состоя¬
ниях равны сверткам плотностей отдельных состояний. Значения показателей
надежности, вычисленные для системы с несколькими состояниями, такие
же, как и для системы с укрупненными состояниями.Приведенное свойство дает возможность существенно сократить общее число
состояний технической системы. Так, например, для дублированной системы
с постоянно включенным резервом и полностью ограниченным восстановле¬
нием, каждый элемент которой обладает п состояниями, общее число со-'Устояний уменьшается с (3п + 2п) до 5.
ГЛАВА 10
НАУЧНЫЕ МЕТОДЫ
ЭКСПЛУАТАЦИИ ТЕХНИКИ10.1. Два вида эксплуатации техникиСуществует два вида эксплуатации техники: по назначению и техническая.
Они оказывают разное влияние на надежность. Надежность техники в про¬
цессе ее эксплуатации по назначению зависит от условий эксплуатации.
Большие нагрузки, неумелое управление, плохие условия хранения, не свое¬
временное проведение профилактик и другие факторы сокращают период
нормальной эксплуатации, увеличивают интенсивность отказов техники.
Причиной отказа в таких случаях часто называют человеческий фактор.Неумелая эксплуатация техники по назначению нередко приводит к сниже¬
нию ее эффективности. Вот типичный пример.Самолет не вылетел по назначению из-за того, что экипаж, по условиям его
труда, должен отдыхать определенное время после посадки самолета. Воз¬
душное судно в исправном состоянии, пассажиры ожидают вылета, а его нет.
Коэффициент готовности системы невысокий. Наличие резервного экипажа
может существенно его повысить. При наличии нескольких самолетов такой
резерв является скользящим: один экипаж может заменить любой другой из
общего их числа.Методами обеспечения и повышения надежности техники в процессе экс¬
плуатации по назначению являются:□ повышение квалификации пользователя;□ облегчение режимов эксплуатации;□ обеспечение нормальных условий хранения;□ резервирование объектов эксплуатации, в частности организация много¬
канальной системы эксплуатации по назначению.Техника и система ее эксплуатации по назначению образуют единую систему
с основным соединением элементов. Она допускает применение структурно¬14 Зак. 3094
418Гпава 10го раздельного резервирования, которое может существенно повысить пока¬
затели надежности системы.ПРИМЕР 10.1. Пусть в эксплуатации находится п однотипных объектов (на¬
пример, самолетов), обслуживаемых по назначению п эксплуатационниками
(п экипажами самолета). Для повышения надежности системы введен один
резервный экипаж. Необходимо оценить эффективность такого резервирова¬
ния по коэффициенту простоя и наработке на отказ.Сделаем следующие допущения:□ все экипажи самолетов равноценные;□ справедлив экспоненциальный закон отказов экипажей.Коэффициент готовности и наработка на отказ системы с основным (после¬
довательным) соединением имеют вид:к 1 r=_L1 я,. х2 К К’1 н—— н—— +... + —— сгде Хс = ]£ Xj.На основании принятого допущения о равноценности экипажей
Я, = Х2 =... = Х„ = X. Предполагая также, что Щ = Ц2 ~ = Н-« = М- ’ получим:Кг =—-—, 7" = —,1 + ир пХXгде р = —.ЦТогда коэффициент простоя нерезервированной системы будет иметь вид:*„=1-^=7“-
1 + прРезервированная система представляет собой систему со скользящим резер¬
вом, реализованным по принципу замещения. Коэффициент готовности и на¬
работка на отказ такой системы имеют вид: ^
Научные методы эксплуатации техники419Тогда коэффициент простоя выражается формулой:кп=-(яр)1 + пр + (пр)Выигрышем надежности по коэффициенту простоя Gn будем называть от¬
ношение коэффициента простоя нерезервированной системы к коэффициенту
простоя резервированной системы. ТогдаGn =1 + пр + (пр)
пр(\ + пр)Выигрышем надежности по наработке на отказ называется отношение на¬
работки на отказ резервированной системы к наработке на отказ нерезерви¬
рованной системы:Gj = 1 + —у .
пФункция Gn в зависимости от пр представлена графически на рис. 10.1 ив
форме табл. 10.1.Таблица 10.1. Выигрыш надежности по коэффициенту простояпрСп0,110,090,25,170,33,560,42,790,52,330,62,04°>71,840,81,690,91,5811,50Из рисунка и таблицы видно, что выигрыш по коэффициенту простоя убыва¬
ет с ростом пр, стремясь к единице. Физически это означает, что выигрыш
надежности тем меньше, чем сложнее система (больше п), чем менее надеж¬
ны ее элементы (экипаж самолета) и хуже ремонтопригодность (меньше ц).
420Глава 10Рис. 10.1. Зависимость выигрыша надежности от прПод интенсивностью восстановления ц здесь понимается интенсивность
восстановления рабочего состояния экипажа.Выигрыш надежности по наработке на отказ тем выше, чем меньше п, более
надежны ее элементы (меньше X ) и выше интенсивность восстановления ц.Учет надежности техники приведет к уменьшению эффективности резерви¬
рования. Физически это очевидно.Выигрыш надежности от резервирования экипажей будет тем выше, чем вы¬
ше надежность самолетов.Техническая эксплуатация предназначена для поддержания высокой надеж¬
ности техники в процессе ее работы. Она не призвана повышать ее надеж¬
ность. Надежность техники в процессе эксплуатации часто называют экс¬
плуатационной надежностью. Для поддержания высокой надежности и уве¬
личения периода нормальной работы проводятся следующие мероприятия:
профилактика, контроль состояния, восстановление элементов, отказавших
или ухудшивших свои характеристики.Следующие разделы посвящены вопросам технической эксплуатации.
Научные методы эксплуатации техники42110.2. Способы поддержания
надежности техники в процессе ее
технической эксплуатации10.2.1. Свойства и показатели критичности
элементов системыПри анализе надежности сложных систем значительное внимание уделяется
вопросам определения слабых звеньев систем. Эта проблема особенно акту¬
альна при анализе надежности систем в условиях ограниченных ресурсов.
Поскольку системы содержат большое количество элементов, то в условиях
ограниченных ресурсов обеспечить повышение надежности путем улучшения
качества одновременно всех элементов не представляется возможным. Одна¬
ко подсистемы играют при функционировании объекта далеко не одинако¬
вую роль, и отказы их компонентов могут приводить к разным последствиям.
Поэтому необходимо сосредоточить усилия на совершенствовании критич¬
ных элементов и узлов, играющих наиболее важную роль в обеспечении на¬
дежности и уменьшении риска.Свойство критичности элемента отражает возможность возникновения отка¬
за, определяет степень влияния элемента на работоспособность системы в
целом и учитывает тяжесть последствий отказа. В инженерной практике сис¬
темы с различным функциональным назначением, такие как энергетические
установки, трубопроводы, электрические кабели, космические системы и
т. д., характеризуются набором частных показателей критичности. Эти пока¬
затели могут выражаться как количественными значениями, так и принимать
значения лингвистических переменных.Показателями критичности являются:□ возможность отказа;□ тяжесть последствий отказов;П устойчивость элемента к воздействию внешних неблагоприятных факто¬
ров среды;□ моменты возникновения и величина риска вследствие отказа;□ возможность локализации отказа;□ контролируемость состояния элементов в ходе эксплуатации;□ резервирование и др.Степень влияния на эти показатели, как правило, выражаются на основе не¬
которых порядковых лингвистических шкал. Перечислим возможные состоя¬
ния этих шкал в зависимости от показателя критичности элемента.
422Гпава 10Возможность отказа элемента может принимать, например, следующие зна¬
чения:□ элемент обладает относительно высокой вероятностью отказа в течение
времени эксплуатации;□ отказ считается возможным и вероятным, если конструкция не прошла
достаточный объем испытаний, обеспечивающий приемлемый уровень ве¬
роятности безотказной работы;□ отказ считается возможным, но маловероятным, если отказов данного эле¬
мента на предшествующих аналогах не наблюдалось;□ отказ возможен, но почти невероятен, если при проектировании приняты
меры для исключения отказа, обеспечен высокий показатель безотказно¬
сти, достигнута стабильность характеристик, отсутствуют предельные
температурные, радиационные, вибрационные и другие нагрузки;□ отказ считается невозможным, если отсутствуют логические условия для
возникновения отказа.Тяжесть последствий отказов может принимать значения:□ отказ приводит к катастрофической ситуации;□ в результате отказа возникает необходимость в принятии экстренных мер
для предотвращения катастрофической ситуации;□ отказ приводит к потере некоторых эксплуатационных свойств, в резуль¬
тате чего время эксплуатации может сократиться;□ отказ приводит к потере некоторых эксплуатационных свойств, не влияю¬
щих на продолжительность эксплуатации;□ отказ изменяет режимы работы зависимых элементов, что увеличивает
вероятность их отказов.Устойчивость к воздействию внешних неблагоприятных факторов может ха¬
рактеризоваться следующими факторами:□ из опыта эксплуатации известно, что в условиях воздействия внешних
факторов ресурс меньше, чем проектный;□ опыт эксплуатации в условиях воздействия внешних факторов отсутству¬
ет, но анализ предсказывает, что ресурс меньше проектного;□ фактический ресурс в реальных условиях эксплуатации близок к проект¬
ному;□ известно, что реальный ресурс больше проектного;□ отсутствуют неблагоприятные факторы внешнего воздействия в период
эксплуатации.
Научные методы эксплуатации техники423Моменты возникновения и величина риска вследствие отказа могут класси¬
фицироваться следующим образом:П риск существует от начала функционирования до окончания эксплуа¬
тации;□ риск существует от начала функционирования до завершения второго эта¬
па функционирования;П риск существует от начала функционирования до завершения первого эта¬
па функционирования.Возможность локализации отказа может принимать значения:□ локализация нужна, но технически невозможна в данной конструкции;□ предусмотрены меры к локализации отказа;□ специальные меры к локализации отказа не нужны.Контроль состояния элемента в ходе эксплуатации может быть следующим:□ состояние элемента не контролируется;□ предусмотрен контроль без прогнозирования;□ предусмотрен прогнозирующий контроль.Резервирование может принимать, например, такие состояния:□ резервирование невозможно;□ резервирование возможно, но отсутствует;□ однократное резервирование без контроля состояния резерва;□ однократное резервирование и состояние резерва контролируется;П двукратное и более резервирование без контроля состояния резерва;П двукратное и более резервирование, состояние резерва контролируется.Операция ранжирования элементов по степени критичности может осущест¬
вляться на разных уровнях структурирования объектов систем, агрегатов и
узлов, частей конструкций и отдельных элементов на основе анализа морфо¬
логических блоков и структурных взаимосвязей. Чем больше вес элемента,
тем он важнее для обеспечения безопасности объекта.10.2.2. Анализ данных по критичным элементамДля организации нормативно-технического обеспечения и сопровождения
данными критичных элементов на различных этапах восстановления необхо¬
димо создание баз данных о дефектах и их расположениях, размерах, резуль¬
татах испытаний и диагностики, проблемах восстановления, структурных
схемах систем, деревьях отказов и т. д. Эти данные являются важными как
для оценки вероятности проявления дефектов, так и для более тщательного
424Глава 10их изучения. Ведение "информационного паспорта" исследуемых критичных
элементов с данными о технико-экономических показателях и операциях, ко¬
торые выполнялись с элементами на предыдущих периодах восстановления,
позволяют реализовать наиболее рациональные пути и способы устранения
дефектов.На основе анализа информационного паспорта элемента для различных пе¬
риодов восстановления можно контролировать развитие дефекта, сравнивать
обнаруженные дефекты с определенными эталонами для их ранжирования,
проводить классификационный анализ, принимая к вниманию аспекты, свя¬
занные с безотказностью и ресурсами для системы. Информационный пас¬
порт элементов — это также основа для выбора и построения принципов
контроля с учетом технических характеристик и экономических показателей.Отсутствие эксплуатационных данных и материалов диагностики и контроля
не позволяет рационально организовывать эксплуатацию систем таким обра¬
зом, чтобы расходовать технический ресурс как можно дольше, не снижая
при этом уровень надежности в целом.Проблема рационального использования технического ресурса для отдельных
элементов и агрегатов системы ставит задачи исследования моделей и меха¬
низмов деградации элементов систем. Актуальной задачей является построе¬
ние моделей развития дефектов различного типа элементов (кабелей, труб,
двигателей и т. д.) с учетом условий окружающей среды и возмущений.Отметим также задачу выбора инструментов или комплекса методов нераз¬
рушающего контроля для проведения диагностики технического состояния
как отдельных элементов, так и их совокупности с учетом технико¬
экономических показателей. Инженерная практика выдвигает ряд требова¬
ний, которым должны удовлетворять методы, например: возможность визуа¬
лизации дефектов, высокая вероятность определения дефектов, чувствитель¬
ность приборов, компактность и практичность оборудования. Для различных
работ применяются как отдельные методы неразрушающего контроля, так и
их комбинации. Однако их совместное сочетание позволяет получить более
достоверную информацию о качестве элементов. Например, в космосе соче¬
тание визуального и вихретокового контроля дает более достоверные сведе¬
ния о качестве металлоизделий.Важная роль уделяется методам неразрушающего контроля для обеспечения
надежности и долговечности систем с высокой ценой отказа.10.2.3. Планирование
восстановления элементов системыПри решении задач восстановления актуальными являются модели и методы
планирования восстановления элементов систем, которые учитывают воз¬
Научные методы эксплуатации техники425можности совмещения отдельных операций технического обслуживания, ре¬
монта и технологических процессов, методы совершенствования расписаний
обслуживания с учетом различных критериев и т. д. Для подготовки техниче¬
ского обслуживания критичных элементов необходимо также планировать
обеспечение их различного рода ресурсами и разработать модели расходова¬
ния ресурсов на основе теории управления запасами. Важными являются за¬
дачи планирования объемов и сроков проведения технического обслужива¬
ния, разработки оптимальных стратегий ремонтов по различным показателям
готовности, стоимости и т. д. Основанием для назначения того или иного ви¬
да ремонта является выработка технологическим оборудованием техническо¬
го ресурса, при котором создается угроза безопасности объекта.При разработке таких моделей необходимо формировать показатели крите¬
риев и учитывать ограничения на ресурсы: численность специалистов, участ¬
вующих в проведении эксплуатационных процессов, объем оборудования,
финансовые затраты, временные ограничения на восстановление.Объемы ремонтно-профилактических работ для каждого агрегата или систе¬
мы зависят от экспертной информации о величине его остаточного ресурса,
интенсивности отказов, результатов контроля систем, выделенных ресурсов и
т. д. При проведении работ могут быть задействованы различное число бри¬
гад, ремонтных органов, оборудование разного типа и т. д. От этих затрат за¬
висит качество и сроки проведения работ, что и определяет время достиже¬
ния предельного состояния системы после восстановления.10.3. Профилактика и ее эффективностьВ процессе функционирования сложной технической системы ухудшаются
характеристики ее элементов, происходит разрегулировка узлов, наблюдается
явление старения техники. Профилактика предназначена для устранения этих
дефектов.При постоянной интенсивности отказов система в профилактике не нуждает¬
ся. Она проводится лишь частично в процессе восстановления отказавших
элементов.Профилактика нужна как средство продления периода эксплуатации систе¬
мы, когда интенсивность отказов — величина переменная. В процессе старе¬
ния системы она необходима для снижения скорости роста Ц/).Периодичность профилактики можно научно обосновать по статистическим
данным об отказах техники и известным требованиям на показатели ее на¬
дежности. Однако такие способы обоснования периодичности профилактики
имеют следующий недостаток.
426Гпава 10Время между отказами элементов при любых законах распределения имеет
большую дисперсию. А это означает, что могут возникнуть большие ошибки
в выборе периодичности профилактики данного конкретного образца техники.Поэтому целесообразно проводить профилактику техники по ее состоянию.
Для этого необходим непрерывный контроль ее состояния.Надежность элементов сложной системы (узлов, подсистем) различна. По¬
этому и период их профилактики должен быть различным. Однако если про¬
водить профилактику по состоянию элементов, то это потребует большого
общего времени за счет увеличения частоты профилактики.Возникают сложные математические и технические проблемы, связанные с
выбором оптимальной частоты и глубины профилактики для обеспечения
высокой надежности техники и ее анализа с учетом профилактики.Математическая модель системы с профилактикой может быть представлена
по-разному в зависимости от условий ее функционирования.Ограничимся рассмотрением только одного из возможных вариантов матема¬
тического описания работы системы с учетом профилактики.Предположим, что случайное время работы системы распределено по закону
с плотностью /(О - В течение времени х, пока профилактика не проводи¬
лась, система потеряла часть своего ресурса. Если t > т, то без проведения
профилактики плотность распределения времени до отказа осталась бы рав¬
ной /(t). При наличии профилактики время до отказа будет иметь другую
плотность распределения; равную Это значит, что с точки зрениянадежности система "забывает" свое прошлое — обновляется.Ниже в этом разделе дается математическое описание функционирования
системы с учетом ее профилактики на основе интегральных уравнений. По¬
лучаемые при этом соотношения позволяют определять не только показатели
надежности системы, но и рассчитывать оптимальную периодичность и сро¬
ки проведения профилактик с целью поддержания максимальной надежности
системы.Предположим, что время функционирования технической системы распада¬
ется на интервалы работы, которым соответствуют значения случайной вели¬
чины ^, и интервалы восстановления, которым соответствуют значения слу¬
чайной величины r|j. Профилактические работы проводятся через случайные
промежутки времени длительностью время проведения профилактик обо¬
значим через Г|2. Будем считать также, что во время ремонта системы про¬
филактика не проводится. Временная диаграмма работы системы изображена
Научные методы эксплуатации техники427на рис. 10.2, из которой следует невозможность отказа системы во время про¬
ведения профилактики.Рис. 10.2. Временная диаграмма работы системы с профилактикойВозможность получения расчетных соотношений, удобных для инженерного
использования, требует изучения стационарного режима. Система имеет сле¬
дующие возможные состояния и соответствующие им искомые функции
(рис. 10.3):□ (0)— устройство исправно и работает, профилактика не проводится,□ (1)— устройство отказало и восстанавливается, момент профилактики не
наступил, л(т1,52);□. (2) — устройство исправно, проводится профилактика, у2(0,х2);□ (3)— устройство восстанавливается, профилактика не проводится,
3>з(т1>0)-Рис. 10.3. Граф состояний системы с профилактикойИсправным является состояние (0), когда идет нормальная работа основного
устройства, вне зависимости от того, проводится профилактика или нет. Со¬
стояния (1), (2) и (3) являются отказовыми.
428Гпава 10Представим математическую модель функционирования в виде системы ин¬
тегральных уравнений:.Уо(51>52)= j/l(^ + 5l)^l(0,x + 52)dx +000+ J f\(* + 5] )/2 о + s2 )dx (у 2 (О,0) + у3 (0,0));
о00Mxi>s2) = Jgi(x + t,)y0(0,x + j2)c&;
оСО 00 00у2 (0, т2) = jg2 (х + т2) \у0 (5,, 0)dsxdx = G2 (т2) J у0 (^, ())<&,;оо о00.Уз(т1>0) = Jj'i(* + Ti»°)<fe-оВыполним некоторые преобразования уравнений. Из первого и второго урав¬
нений следует, чтосо 00 00У о Cv*2)= j J А (х + si )S’i (“)^0 (О, х + ос + s2 )dadx + A J/, (х + s, )/2 (х + s2)dx,
оо огде А = у2(0,0) + ^3(0,0).Перепишем это уравнение в другом виде:00 XЛ)(51>52)= J/м, *g\(x)y0(0,x + s2)dx + Ajfl(x + sl)f2(x + s2)dx.
о оПрименяя итерационную процедуру, видим, что решением этого уравнения
является функцияУ о С*1 ^2 ) = А 11® 1 (■*! ’ x)fi (х + s2 )dx,где со,(5[,д:)= ]Г * f\ s {х) — обобщенный параметр потока отка-к=о ’ 1зов устройства.Далее последовательно находим все искомые функции:00 ОО 00y\(x\,S2) = A\g{(x + T.\)\(i>x(Q,a)f2(x + a. + s2)dadx = A\(£>bX(xx,x)f2{x + s2)dx,
оо о
Научные методы эксплуатации техники429У2 (0. Ч) = ас2 (т2 ) J^ri (*)/а (*>** >
о00 00у3 (х,, 0) = A J Jюв! (а + т,,х)/2(x)dadx .
о оЗдесь и далее используются обозначения:mB, (х j, х) = X fi(k+i) * g\ik) * g\,Xl (*)» °>i (*) = ®i (°> х)» ®в1 (*)= ®в1 (°>*) >к=О00\|/] (0 = JGj (х + t)dx .
оОпределим вероятности состояний:00 00
PQ = A\KrX(x)F2(x)dx, рх = A \Knl(x)F2(x)dx,Р2 = АТв2 \KvX{x)f2(x)dx,ръ=А\щ*ых (x)f2 (д:)dx - А
оТвХ ]ax(x)F2(x)dx- \Knl(x)F2(x)dx
Vo оПараметры потоков отказов и восстановлений равны(оо оо ^jco x(x)F2(x)dx+ \KrX(x)f2(x)dx
Vo оС0с =со01 + ®02 = А®вс _ сою + <°20 + юзо _ АJ(DBi(x)F2(x>fc + lVO= А{со, (x)F2 (*)<& + jKrX(x)f2(x)dx
Vo оПолученные показатели выражаются через постоянный коэффициент А, ве¬
личина которого определяется из условия нормировки.Находим показатели надежности системы с учетом проведения профилак¬тики:
430Глава W□ коэффициент готовности:ООfKrl(x)F2(x)dxлгс Ро —'О(Kn(x)F2(x)cfc + 7^ [(0\(x)F1(x)tfc + rs2 [КЛ(х) f2(x)dxО□ средняя наработка на отказ:jX,(x)F2(x>ftт _£о о .со 00° |сО[(х)Р2(х)гйс+ ji^rl(x)/2(x)fl?x
о о□ среднее время восстановления:00 соГв1 |со,(х)^2(х)с/х + :Гв2 |ЛГг1(х)/2(х)Л
_ Р] + Р2 + Рз _ о о вс со _ 00вс J со, (x)F2 (x)dx + Jxrl (х)/2 (x)dxо оДалее будем считать, что профилактика проводится через определенное вре¬
мя Т2 (частота профилактики) и продолжается время (глубина профилак¬
тики). Тогда закон распределения времени между профилактиками является
детерминированным с плотностью /2(0 = 5т (/). Для коэффициента готовно¬
сти получим следующее выражение:Т2| KrX(x)dxКг= * илигс т2 Тг ’\Kvl(x)dx + Ts] ](£>х(х)сЬс + Тв2КгХ(Т2)
о окГС= ВISL , (юл)т1(Т2) + Тв]Мх(Т2) + Тв2КгХ(Т2)где тх(Т2) — средняя суммарная наработка системы в течение времени Г2;
МХ(Т2) — среднее суммарное число отказов системы в течение времени Т2 .Наработка на отказ и среднее время восстановления соответственно будут
равны:
Научные методы эксплуатации техники431J _ т\(7г) Т _ (Т2) + Тъ2Кг](Т2) (102)с МХ(Т2) + КГХ(Т2)’ вс МХ(Т2) + КгХ(Т2)На основе полученных соотношений установим два свойства системы с про¬
филактикой.Свойство 1. Если Т2 -» оо, что означает отсутствие профилактики, то коэф¬
фициент готовности, наработка на отказ и среднее время восстановленияТсовпадают со своими обычными значениями: - - , Тх и Гв).т\ + тъ1Установим это свойство для коэффициента готовности. Аналогично его мож¬
но доказать и для других показателей надежности. Из (10.1) получимв1 тх(Т2) 82 тх(Т2)млт2) 1 кглт2) .В пределе при Т2-*<х> имеем ——> —, ———-—> 0, откуда и следуетт\(Т2) Т\ тп\(Т2)данное свойство.Свойство 2. Если интенсивность отказа устройства постоянна, то профилак¬
тика не дает выигрыша в надежности, а, напротив, коэффициент готовности
системы уменьшается по сравнению с отсутствием профилактики.Для постоянной интенсивности отказа mx(t) = TxMx(t) для любого момента
времени t. Тогда из (10.1) следует:Кг<-Щ (Т2) Тхгс ГПХ(Т2) + ТВХМХ(Т2) Тх+ТвхТаким образом, проведение профилактики может лишь уменьшить коэффи¬
циент готовности системы, если время до отказа имеет экспоненциальное
распределение.Посмотрим, как влияет профилактика на надежность, если время до отказа
неэкспоненциально.ПРИМЕР 10.2. Время безотказной работы системы имеет гамма-
распределение с математическим ожиданием Тх = 200 час и средним квадра¬
тическим отклонением О] = 20, 50 и 80 час. Время восстановления имеет
экспоненциальное распределение со средним Гв1 =10 час. Время между оче¬
редными профилактиками постоянно и равно Т2 =150 час. Время проведения
432Глава 10профилактики составляет Тв2 = 2 час. Определить показатели надежности
системы без учета и с учетом профилактики.Решение. Без учета профилактики наработка на отказ, среднее время восста¬
новления и коэффициент готовности системы соответственно равны 200 час,
10 час и 200/210 = 0,9523.В соответствии с формулами (10.1)—(10.2) расчет аналогичных показателей
с учетом профилактики требует вычисления суммарного числа отказов,
суммарной наработки и функции готовности системы в зависимости от
времени. Воспользуемся для этой цели программой Prevention (http://
www.gurov.spb.ru/isant/isant.html). В результате получим значения, приве¬
денные в табл. 10.2.Таблица 10.2. Показатели надежности системы с учетом и без учета профилактикиПоказателинадежностиБез профилактикиС профилактикой(Т) = 20 часСт! = 50 часа, = 80 часК'0,95230,98660,97720,9683тс, час200149,8134,2118,7Тк ’ час102,033,123,88Видим, что для гамма-распределения наличие профилактики повышает зна¬
чение коэффициента готовности системы, причем это повышение зависит от
среднего квадратического отклонения времени до отказа системы. Чем
меньше ст,, тем больше значение Кг. Наработка на отказ при этом меньше,
чем без профилактики.Понятия "профилактика" и "контроль" существенно различны. Контроль про¬
водится с целью установления состояния техники в смысле ее надежности.
Он часто необходим для установления глубины профилактики.Профилактика является средством поддержания надежности на заданном
уровне. Эффективность профилактики определяется величиной снижения
интенсивности отказов техники в периоды между профилактиками. При на¬
личии статистических данных об отказах и величине периодов расчеты эф¬
фективности профилактики достаточно просты.
Научные методы эксплуатации техники43310.4. Анализ надежности техники
при наличии системы контроля10.4.1. Надежность аппаратуры контроля
с двумя типами отказовПредположим, что техническое устройство снабжено аппаратурой контроля,
функционирование которой представляет собой альтернирующий процесс с
двумя составляющими: ожидание контроля и его проведение. Аппаратура
контроля не является абсолютно надежной и может выходить из строя как во
время работы, так и в то время, когда она не используется по назначению.За счет возможных отказов контролирующего органа могут появляться си¬
туации, приводящие к снижению качества работы системы в целом.Рассмотрим сначала только аппаратуру контроля без учета работы техниче¬
ского устройства. Будем считать, что отказы аппаратуры контроля, возни¬
кающие во время работы и во время хранения, независимы, имеют разную
природу и требуют разного восстановления.Сначала предположим, что эти отказы являются необесценивающими. Про¬
цесс функционирования, временная диаграмма которого изображена на
рис. 10.4, включает в себя:□ ожидание очередного сеанса контроля Ъ,х ;□ собственно проведение контроля т]];□ два типа временных интервалов, соответствующих работе аппаратуры:
безотказная работа во время проведения контроля £,2 и восстановление
аппаратуры контроля, отказавшей во время работы, г|2;□ два типа интервалов времени, соответствующих хранению аппаратуры:
аппаратура исправна £,3 и проводится восстановление аппаратуры кон¬
троля, отказавшей во время хранения, г|3 .Плотности распределения случайных величин £,• и г), обозначим соответст¬
венно через fj и gj, / = 1, 2, 3 . Граф состояний, отвечающий временной диа¬
грамме, представлен на рис. 10.5.
434Глава 10Рис. 10.5. Граф состояний аппаратуры контроляРассматриваемый процесс разбивается на попарно непересекающиеся интер¬
валы, соответствующие времени ожидания очередного сеанса контроля и
времени его проведения, включающего в себя также интервалы восстановле¬
ния аппаратуры контроля (АК). Это есть альтернирующий процесс, опреде¬
ляемый случайными величинами и г|(^ с плотностями и g^ соот¬
ветственно.Требуется найти законы распределения времени пребывания на этих интер¬
валах, т. е. выразить плотности и g('k) через ft и g,, i = 1, 2, 3 . С этой
целью опишем возможные состояния системы и укажем соответствующие
этим состояниям функции, относительно которых составляется математиче¬
ская модель переходного процесса:□ (0) — расходуется ресурс во время хранения АК, контроль не проводится
и ранее не проводился, ^(.s^O,^,/) ;□ (1)— расходуется ресурс во время работы, проводится контроль, ранее
расходовался ресурс АК при хранении, >',(х1,л2,^з,^);□ (2) — расходуется ресурс во время хранения, контроль не проводится, хо¬
тя ранее он проводился, ;□ (3) — отказ АК во время работы и ее восстановление, уъ{;□ (4)— отказ АК во время хранения без восстановления (скрытый отказ),
ранее расходовался ресурс АК во время работы, ^(^..s^AO;П (5) — восстановление АК после обнаружения скрытого отказа, ранее рас¬
ходовался ее ресурс во время работы, ^(О,^,^^) 5□ (6) — расходуется ресурс АК во время работы, проводится контроль, ре¬
сурс АК при хранении не расходовался, у6(х,,52!0,0;
Научные методы эксплуатации техники435□ (7)— восстановление АК после отказа, возникшего в процессе работы,
контроль не проводится, _у7 (т,, т2,0,f);□ (8)— отказ АК во время хранения без восстановления (скрытый отказ),
ресурс АК во время работы не расходовался, у8(5],0,0,0;□ (9) — восстановление АК после обнаружения скрытого отказа, ресурс АК
во время работы не расходовался, _у9(0,0,т3,/).Заметим, что по описанию некоторые состояния близки между собой, напри¬
мер состояния (4) и (8), однако их следует различать, т. к. в состоянии (4) ап¬
паратура контроля ранее была включена в работу и уже частично израсходо¬
вала свой ресурс (второй аргумент функции у4 снабжен штрихом), а в со¬
стоянии (8) аппаратура контроля в работу не включалась и ресурс не
расходовала (второй аргумент функции у8 равен нулю). То же относится к
состояниям (0) и (2), (1) и (6), (3) и (7), (5) и (9). Указанные пары состояний
действительно могут быть объединены между собой, если случайные вели¬
чины £,2 и имеют экспоненциальные распределения.Состояния множества Е+ = {0, 2, 4, 8}, соответствующие ожиданию в прове¬
дении контроля, отнесем к работоспособным состояниям, а состояния мно¬
жества Е_ = {1, 3, 5, 6, 7, 9}, соответствующие или сеансу контроля, или вос¬
становлению аппаратуры контроля в результате ее отказа, отнесем к отказо-
вым состояниям. Система интегральных уравнений для нестационарного
режима функционирования АК имеет вид:+ jg’i(x + 't1)>'2(0,x + .s2>.s3,f-x)dx + \fi(x + 8г)Уг(х + ~x)dx',y0 (J,, 0, s3,0 = fx (/ + 5, )/3 (t + s3);tyx (t, , s2, Sj, 0 = jgx (x + T, )/2 (x + s2 )y0 (0,0, s3, t - x)dx +оооty2(st,s'2,53,0 = \f\ (x + 5, )yx (0, s2, X + s3, t - x)dx +0t+ j/, (x + sx )f3 (x + s3 )y6 (0, s2,0, t - x)dx;0tУз (т| ,x2,s3,t)= Jg2(x + T2)y,(x„0,j3,/- x)dx;(10.3)
436Гпава 10t (10.3)У4 («1> s'l»°>0 = ]У2 (* + s\>s2.0.* - x)dx;
оУь (О, 4>Ъ’0 = |£з(* + х3 )Уа (°> s2’0’t- x)dx;
о
t76(ti^2,0,O= Jg1(x + x1).y5(0,x + ,s2,0,/-x)<& +0t+\f%(x + S2)y7(x + Xj.0,0,/ - x>& + Jg](x + Tj)/2(x + s2)yg(0,0,0,t - x)dx;
о 0У1 (xj, X2,0,0 = Jg2 (x + x2 )y6 (xt, 0,0, t - x)dx;
оtJbCsj, 0,0,0 = jy0 (x + 5), 0,0, / - x)dx;
о
ty9 (0,0, x3,0 = J g3 (x + x3 )>'g (0,0,0,/ - x)dx.Для получения результатов в аналитическом виде предположим, что время
исправности аппаратуры контроля в процессе функционирования и во время
хранения распределены экспоненциально с параметрами Х2 и А.3 соответст¬
венно. В результате решения системы (10.3) получим:Ло-жо,f\(z)гдеФ) = Mz + h) + £i (z)(fi (z) ~Mz + h))-Выражение (10.4) представляет собой преобразование Лапласа эквивалент¬
ной плотности распределения времени контроля с учетом восстановления
АК.Отсюда легко найти математические ожидания времени ожидания и проведе¬
ния контроля (с учетом восстановления АК), которые равны:7-ю =7i, 7f) = -g; (0)=7в3 (1 - /,(Х3 ))+Гв, (1 + Х2Тв1) .Предположим теперь, что отказы аппаратуры контроля являются обесцени¬
вающими, т. е. ранее проведенный контроль "забывается" и после восстанов-
Научные методы эксплуатации техники437ления аппаратуры контроль начинается заново. Отличие от предыдущего
случая состоит в том, что изменяются аргументы у функций у3 и уп, а имен¬
но: вместо аргумента т, ставится 0. При этом соответствующим образом из¬
меняется система уравнений (10.3). В результате решения системы инте¬
гральных уравнений, составленной при условии обесценивающих отказов
аппаратуры контроля и экспоненциальных распределений %2 и £з > получим:/да(0 = Ж0,gw(z) = - (10,5)Математические ожидания времени ожидания и времени проведения контро¬
ля (с учетом восстановления АК) выражаются соотношениями:<„ (Н15 в blglMЗаметим, что для последующего анализа обращение формул (10.4)—(10.5) не
потребуется.Обратимся теперь к оценке надежности самого технического устройства,
имеющего два возможных состояния: работоспособности и отказа. Пусть
время пребывания устройства в этих состояниях случайно и имеет плотности
распределения /,(/) и g] (t) со средними 7] и Гв1 соответственно. Предпо¬
ложим, что указанные состояния устройства могут быть обнаружены только
в результате аппаратурного контроля и контроль дает правильное обнаруже¬
ние отказа.Контролирующий орган, как и выше, представляется в виде технического
устройства с двумя состояниями: ожидание контроля и его проведение. При
этом аппаратура контроля может отказать, когда она находится в выключен¬
ном или во включенном состоянии, а все состояния ее ремонта предполага¬
ются содержащимися в состоянии проведения контроля. Пусть %2 = 4^ и
г)2 = — случайные* величины, образующие альтернирующий процессфункционирования аппаратуры контроля с плотностями f{k> и g{k> соответ¬
ственно, вычисляемыми в соответствии с (10.2) или (10.3). В зависимости от
работы технического устройства в течение времени проведения контроля
рассмотрим следующие две ситуации:□ устройство не выключается на время проведения контроля;□ устройство включается только во время контроля.
438Глава 1010.4.2. Модель надежности системы
с периодическим контролемПредположим, что в течение времени проведения контроля техническое уст¬
ройство не выключается и соответствующее состояние всей системы является
работоспособным. При этом во время проведения контроля может произойти
отказ основного устройства. Для описания нестационарного режима функ¬
ционирования системы с периодическим контролем перечислим ее возмож¬
ные состояния:□ (0) — устройство исправно и работает, контролирующая аппаратура нахо¬
дится в состоянии ожидания контроля, y0(sl,s2,t);□ (1)— устройство отказало, но отказ не обнаружен, поскольку контроли¬
рующая аппаратура находится в состоянии ожидания контроля, ^(0,^,0;□ (2) — устройство отказало и простаивает, но факт отказа не установлен,
проводится контроль, y2(0,x2,t);□ (3) — устройство восстанавливается,, контролирующая аппаратура выклю¬
чена, у3 (tj, 0,0;□ (4) — устройство работает во время проведения контроля, y4(s{,x2,t).Математическая модель функционирования представляется системой инте¬
гральных уравнений:tу0(sus2,t) = J/lO + $1 )ЛО + s2)УЗ(°»°>1 ~ х+0t+ \f2(x + s2 )у4 (х + S,, 0, t - x)dx + /,(/ + sx )f2 (t + s2 );0t^i(0,52,O= \y0(0,x + s2,t-x)dx\0 (10.6)t t72(°»t2»0= \g2(x + x2)y\{Q),0,t-x)dx+ jy4(0,x + x2,t-x)dx;
о 0y3 (x,, 0,0 = Jg| (x + x, )y2 (0,0, t - x)dx;0tУ4 C*1. ■T2»■0 = 182 (* + X2 )Уо (x + su0,t- x)dx.0
Научные методы эксплуатации техники439Система уравнений (10.6) носит общий характер. По полученному из нее ре¬
шению можно определить различные временные характеристики надежно¬
сти. Плотность распределения времени безотказной работы контролируемого
устройства находится в явном виде: f(t) = f\(t). Плотность распределения
времени восстановления находится из интегрального уравнения:f*g(0 = (№в2 )*fl* 82- ^1®в2 ) * gl (0 »где сов2 — решение уравнения®в2 =S + /2*g2 *®в2-В качестве примера приведем еще формулу для вычисления коэффициента
оперативной готовности устройства R(s) в течение любого фиксированного
времени s для установившегося режима:00Jir1(x + 5)dx:ад= £- ,(Г2 + Тъ2 ) JF\ М®в2 {ХУЬ + Тя1Оа также правило для нахождения плотности распределения вероятностей
времени скрытого отказа: эта плотность определяется в результате решения
интегрального уравненияCO0i(O + <042 (/) = /с.о.(0 + /с.о. * £23 (0 ’где00 со®oi(0 = \yo(0,s2,t)ds2 , (a42(t)= \y4(0,x2,t)dx2, 0)23(t) = y2(0,0,t).
о оТаким образом, решение системы уравнений (10.6) позволяет найти не только
среднее время пребывания технической системы в состоянии скрытого отка¬
за, но также определить закон распределения этой случайной величины.Приведем формулы для стационарных показателей надежности системы.
Средняя наработка на отказ, среднее время восстановления, коэффициент
готовности равны соотвественно:00Тй=Т\, Гвс =(Т2 +TB2)\coB2(x)Fl(x)dx-Tl +Гв1,о*гс=-Т\(Т2 + Гъ2 ) 1® в2 (*)*i (X)dx + Тв 1
440Глава 10Среднее время пребывания системы в состоянии скрытого отказаООТс.о. =(т2 +7’в2)|®в2(*)^С*№-71 •ОФормулу для коэффициента готовности можно представить в виде:К„=- ^ Ц + Тс.о. + ?в1
При мгновенном обнаружении отказаКг=~-^-Т\ +ТЪ\Таким образом, эффективность контроля определяется временем существо¬
вания скрытого отказа. Чем меньше это время, тем выше коэффициент готов¬
ности системы.10.4.3. Надежность системы с контролем
во время храненияПодобно тому, как было показано в разд. 10.4.2, можно составить математи¬
ческие модели, а затем найти эквивалентные плотности распределения и
необходимые стационарные и нестационарные характеристики для других
условий эксплуатации устройства с контролем.Так, например, можно получить характеристики надежности устройства со
следующими условиями эксплуатации. В промежутках времени между со¬
седними интервалами проведения контроля устройство выключено (находит¬
ся в состоянии хранения). Устройство включается в работу только на время
проведения сеанса контроля. Если отказ устройства произошел во время хра¬
нения, то он обнаруживается во время очередного сеанса контроля и начина¬
ется его восстановление. При возникновении отказа устройства во время его
работы, а значит, и во время проведения контроля, отказ мгновенно обнару¬
живается и сразу начинается восстановление отказавшего устройства.ПРИМЕР 10.3. Время безотказной работы технической системы имеет экс¬
поненциальное распределение с параметром ^[=0,05 час-1, время восста¬
новления имеет распределение Эрланга 4-го порядка с параметром
щ=2 час"®. В системе один раз в смену (Tik' =8 час) проводится функцио¬
нальный контроль. Длительность контроля составляет Т^к> =0,1 час. Система
контроля может отказать во время работы с интенсивностью Хк =0,1 час"1,
Научные методы эксплуатации техники441время восстановления имеет распределение Эрланга 2-го порядка с парамет¬
ром =1 час-1. Требуется найти коэффициент готовности технической сис¬
темы, которая не выключается на период контроля для случаев необесцени¬
вающих и обесценивающих отказов.Решение. Для оценки стационарных показателей в системе (10.6) следует
перейти к пределу при / —> со, найти решение соответствующей системы
уравнений, вычислить вероятности пребывания системы во всех возможных
состояниях и определить коэффициент готовности. Не проводя этих вычис¬
лений, приведем лишь окончательный результат:к hM±Шh(Т2 + Тв2) + Х{ГвХ[\-}2(X,)&(*.,)) ’где /2 — плотность распределения времени между очередными сеансами
контроля; g2 — плотность распределения длительности контроля с учетом
возможных отказов аппаратуры контроля. Используя соотношения (10.4)—
(10.5) и подставляя численные данные, получим, что для необесценивающих
отказов Кг =0,762, для обесценивающих отказов Кг =0,622. Заметим, что
для случая непрерывного контроля Кг =0,909. Завышенная оценка коэффи¬
циента готовности объясняется тем, что не учтен аппаратурный контроль.
При этом относительная погрешность коэффициента готовности для необес¬
ценивающих отказов составляет 19,3 %, а для обесценивающих — 46,1 %.10.5. Оптимизация резервных элементов
и ремонтных органов10.5.1. Проблемы оптимального резервирования
и ремонтаОдним из наиболее распространенных методов повышения надежности тех¬
нических систем является введение структурной избыточности. Как правило,
это либо постоянно действующие дополнительные элементы, либо запасные
элементы. При этом для обеспечения максимально возможной надежности
или достижения заданной надежности при минимальных затратах возникает
задача оптимального распределения ресурсов. В настоящее время имеется
огромное количество публикаций по данному вопросу [7, 143, 145, 150, 151].На наш взгляд, одной из наиболее сложных проблем здесь является создание
простых с вычислительной точки зрения методов расчета надежности систе¬
мы, являющихся обязательным элементом оптимизационного процесса. Мы
442Гпава 10рассматриваем достаточно общий класс восстанавливаемых систем, состоя¬
щих из последовательно соединенных подсистем. Каждая подсистема состо¬
ит из одинаковых элементов и представляется как система типа т из п с на¬
груженным или ненагруженным резервом. Кроме того, каждая подсистема
может обслуживаться некоторым количеством ремонтников. Все законы рас¬
пределений времени до отказа и времени восстановления элементов произ¬
вольные. Для такой системы возникают следующие вопросы:□ сколько избыточных элементов необходимо иметь в резерве для обеспече¬
ния требуемой надежности;□ сколько ремонтников необходимо иметь для обслуживания в каждой ре¬
зервной группе.Для ответа на эти вопросы нужно решать оптимизационные задачи. Вопрос
выбора критерия является в какой-то степени субъективным и зависит от раз¬
работчика системы. В качестве критерия могут быть приняты: наработка на
отказ, вероятность безотказной работы системы за заданное время или функ¬
ция готовности системы в заданный момент времени. Ограничимся только
одним, наиболее важным, на наш взгляд, критерием надежности восстанав¬
ливаемой системы, таким как значение функции готовности в заданный мо¬
мент времени.Анализ надежности описанной выше системы выполняется на основе резуль¬
татов гл. 8 (см. также [134—-138]), в которых рассмотрены и доведены до
практического использования эффективные методы анализа надежности ти¬
повых систем, таких как т из п, систем с ненагруженным резервом, после¬
довательных систем при произвольных распределениях времени до отказа и
времени восстановления элементов и при заданном количестве ремонтников.
Данные методы основаны на приближенном решении системы интегральных
уравнений, полностью описывающих работу с точки зрения ее надежности.
Способы вычисления погрешности приближенного решения, рассмотренные
в указанных работах, позволяют определить погрешность и для оптимизаци¬
онной проблемы.Следует отметить, что поставленная оптимизационная проблема полностью
доведена до практического инженерного применения и реализована в виде
соответствующего программного средства.Введем следующие обозначения:□ п — количество последовательно соединенных подсистем;□ пj — количество элементов в j-й подсистеме;□ kj — количество основных элементов в j- й подсистеме;
Научные методы эксплуатации техники443□ rrij — максимально возможное количество избыточных элементов в j-й
подсистеме;D х, — количество избыточных элементов в j- й подсистеме, 0 < Xj < ntj;□ rj — максимально возможное количество ремонтных единиц, которые
могут обслуживать j-ю подсистему;□ у j — количество ремонтных единиц, которые могут обслуживать j-ю
подсистему, 0 < у j < rj;□ Pj — стоимость одного резервного элемента j- й подсистемы;□ qj — стоимость одной ремонтной единицы, обслуживающей j-ю подсис¬
тему;□ fj (/), gj (/) — плотности распределения времени безотказной работы и
времени восстановления элементов j-й подсистемы;Gj(t) — вероятность безотказной работы и вероятность невосста-
новления за время t элементов j- й подсистемы;□ KTJ(t), Knj(t) — функция готовности и функция простоя для элементовК (t)j-й подсистемы, р(7) = J ;ГУ (О□ Kffit), K„j\t) — функция готовности и функция простоя для у'-й подсис¬
темы;□ Kr(t), Кп (0 — функция готовности и функция простоя для всей сис¬
темы;□ ta, Кд — заданный момент времени и требуемый уровень функции го¬
товности соответственно.Сделаем следующие предположения:1. Время безотказной работы элементов имеет произвольное распределение.2. Восстановление элементов осуществляется заменой новыми элементами.3. Время восстановления отказавших элементов имеет произвольное распре¬
деление.4. Во время восстановления системы все остальные элементы выключаются
из работы и не расходуют свой ресурс.5. Все отказы статистически независимы.
444Глава 106. При восстановлении элемента из подсистемы с ненагруженным резервом
он становится в ненагруженный резерв.7. Переключающее на резерв устройство является абсолютно надежным.8. Восстановление отказавших элементов производится по прямому приори¬
тету.9. Отказавшие элементы из разных подсистем могут ремонтироваться одно¬
временно.Рассматривается последовательная система, состоящая из технических уст¬
ройств типа подсистем т из (т + к) (т резервных и к основных элемен¬
тов), элементы которых идентичны.Система содержит п устройств, соединенных в виде последовательной схе¬
мы. Для у'-го устройства системы (у = 1, 2,..., п) известно количество kj ос¬
новных элементов, максимально возможное число т , резервных элементов,находящихся в нагруженном или ненагруженном состоянии, максимально
возможное число /у ремонтных органов, обслуживающих данное устройство,законы fj, gj и параметры распределения времени безотказной работы ивремени восстановления элемента, а также стоимостные характеристики од¬
ного элемента pj и одного ремонтного органа qj .В зависимости от выбора управляющих переменных может рассматриваться
одна из трех задач оптимизации в соответствии с тремя проблемами.Проблема 1. Требуется определить фактическое количество резервных эле¬
ментов Xj при заданном числе ремонтников rj, чтобы надежность системыдостигла требуемого значения, а ее стоимость приняла бы минимальное зна¬
чение.Проблема 2. При заданном количестве резервных элементов ntj требуется
определить фактическое количество ремонтников y>j, чтобы надежность сис¬
темы достигла требуемого значения, а ее стоимость, включающая в себя оп¬
лату обслуживающего персонала, приняла бы минимальное значение.Проблема 3. Требуется определить фактическое количество резервных эле¬
ментов Xj и фактическое количество ремонтников у;, чтобы надежностьсистемы достигла требуемого значения, а ее стоимость вместе с оплатой об¬
служивающего персонала приняла бы минимальное значение.Далее рассматривается общая идея приближенного решения этих проблем с
указанием его точности. Фактически эта идея реализована в виде программ¬
Научные методы эксплуатации техники445ного средства Redopt (http://www.gurov.spb.ru/isant/isant.html). При этом
делается предположение (хотя и не принципиальное) о прямом приоритете
выборки элементов из очереди на работу и из очереди на восстановление.10.5.2. Математическая модель и решениеПриведем вывод математической модели только для третьей (самой общей)
проблемы.В разд. 7.2 было получено приближенное выражение (формула (7.11)) для
функции готовности системы=, (10.7)где K^\t) — соответственно функция готовности и функция про¬стоя j-й подсистемы в последовательной цепочке. Поскольку каждая подсис¬
тема является системой типа и из и с нагруженным или ненагруженным
резервом, то для оценки ее надежности можно использовать результаты
разд. 8.5, согласно которымХ±мл(р/оУ
> 4s)(o=i-4f)(o.t MjApAO?Тогда*;+1К - (О *'w £м,,(р/0У(=]Постоянные коэффициенты М 7 определяются формулами:□ для нагруженного резерва(10.8)
446Гпава 10'iVII2?i\J*/yJJ□ для ненагруженного резерваki-при г<уу;—> ПРИ {>Урyj'-yгде 0 <Xj <itij, 0 < у j < Vj.Неравенство КГ(1Д)>КЛ согласно (10.7) эквивалентно неравенствуf , i ,>,4*>(»д) х, ’а согласно (10.8) оно эквивалентно также неравенствуу (р>^Д^) < _1 J7 = 1Х»А>)'Кп«■=1В других обозначениях получим:гдеФу^лу>А)) 'I» /»«>)'
( = 0■, 6.=-—1.
Д *дСуммарная стоимость резервных элементов и yj ремонтных единиц равнаП'L(pJxj+4jyJ)-
j=iТаким образом, речь идет об отыскании оптимальных значений Xj и у;.
j —1, 2,..., n, для которых целевая функция достигает наименьшего значенияz = Ё (Pjxj + Qjyj) min
J=i(10.9)
Научные методы эксплуатации техники447при ограничениях'Z(pJ(Xj,yJ)<ba, 0 <Xj<mj, 0< у j <rj. (10.10)J=iРешение задачи (10.9)—(10.10) может быть выполнено разными путями. Пе-n mJребор требует большого количества действий, равного £ min(x + l,r7 ).j=1х=0Например, для одинаковых подсистем при m = 10, г = 1 требуется перебрать10", а при ш = 10, г = 11 — 66” вариантов. А если п велико, то простой пе¬
ребор становится практически невозможным. Перебор вариантов можно реа¬
лизовать в виде короткой рекурсивной процедуры, что хотя и сокращает объ¬
ем текста программы, однако не уменьшает количества операций. Вид моде¬
ли удобен для использования метода динамического программирования,
который требует больше памяти для хранения промежуточных данных, но
значительно повышает скорость оптимизации.Мы не будем приводить здесь подробного алгоритма метода динамического
программирования, поскольку он является общеизвестным. Ограничимся
лишь записью функциональных уравнений, лежащих в основе метода.На первом шаге решается задача целочисленной оптимизации с двумя пере¬
менными JC[ и у^:Z\(b) = P\X\+qxyx^mmпри ограниченияхФ1(л:1,.У1)<6, 0<я, < w,, 0<=у, <г,
для всех значений b, 0 < b < Ьд.На последующих шагах при j = 2,3,..., п решается задача целочисленной
оптимизации с двумя переменными хj и у -:г jib) = pjXj + q jyj + г}_х [b - cp jixj.yj)) -> min
при ограниченияхq>J{xj,yJ)<b, 0<Xj <irij, 0<yj<rj
для всех значений b, 0 <Ь<ЬД.В результате решения этих задач получаются условные оптимальные реше¬
ния x*j(b) и У*{Ь) и соответствующие минимальные значения целевых
448Глава 10функций z*(b) • На этом завершается прямой ход метода динамического про¬
граммирования.Минимальная стоимость системы равна^min ~ zn (ba ) 'Обратный ход позволяет найти безусловные оптимальные решения, а имен¬
но: оптимальное решение на и-м шаге х* = х*п(Ьд), у* = у*п(Ьд). Затем нахо¬
дится значение Ь = ЬД ~(рп(х*п,у*), по которому определяются безусловные
оптимальные решения на (и - 1)-м шаге х*_) =х*_1(й), у*п_] =у*п_\(Ь) и т.д.На к-м шаге находится значение Ь = ЬЛ- <р, (х* ,у*), по которому опреде-' V-1ляются безусловные оптимальные решения х*к =х*к(Ь), у*к =у*к(Ъ), соответ¬
ствующие этому шагу {к-п-\,..., 1).Свойства систем т/п, приведенные в разд. 8.5, показывают, что далеко не
всегда можно достичь требуемой надежности. Поэтому задача может не
иметь оптимального решения при соответствующем задании требуемого
уровня надежности КД или заданного момента времени /д.10.5.3. Численные результатыИспользование программы Redopt позволяет достаточно оперативно исследо¬
вать характеристики надежности большого класса систем. Программа позво¬
ляет решать три проблемы оптимизации, рассмотренные в этом разделе.
В качестве исходных данных могут быть приняты общеизвестные функции
распределения типа нормального, гамма-, показательного, Рэлея и т. д.ПРИМЕР 10.4. Для иллюстрации решения сложной оптимизационной про¬
блемы рассмотрим систему 1, состоящую из 5 подсистем. Все данные для
этой системы, в соответствии с введенными обозначениями, представлены в
табл. 10.3.Для этой системы заданы ограничения на функцию готовности Кд= 0,99
в моменты =2000 час и /д =850 час.Решение. Результаты оптимизации представлены в табл. 10.4.Графики функций готовности системы 1 после оптимизации показаны на
рис. 10.6 (кривая 1 —для /д =2000 час, кривая 2 —для tA =850 час).
Научные методы эксплуатации техники449Таблица 10.3. Исходные данные для оптимизации системПодсистема12345ТипНе нагруж.Не нагруж.Нагруж.Нагруж.Не нагруж.kJ241103mj581010404310155Pj2015122040Ь84151022fjнормал.нормал.гаммаРэлеяРэлеяМат. ожид.1000150070020002500Ср. кв. откл.35050015010001250Sjравномер.нормал.нормал.гаммаРэлеяМат. ожид.10010012014080Ср. кв. откл.4545705040Таблица 10.4. Результаты оптимизации системы 1ПроблемаW*)Стоимость
системы, zРезервные
элементы, хРемонтные
бригады, у18500,99346722243 128500,9977789113 1138500,990435122 5 3 12 23 3 1120000,99256952 3 3 4 1220000,99637691112 1320000,9905404232422 33 4 1Обратим внимание на 3-ю подсистему, являющуюся самой ненадежной.
"Спад" функции готовности на начальном участке обусловлен как раз пове¬
дением этой подсистемы. Из рис. 10.6 (кривая 2) видно, что для "поднятия"15 Зак. 3094
450Гпава 10функции готовности на начальном участке /д = 850 час. Для третьей подсис¬
темы используется максимальный ресурс = 5, _уз = 3 (табл. 10.4).10,99ад0,950 850 2000 /, час 4000Рис. 10.6. Функции готовности системы после оптимизации для t = 2000 час (кривая 1)
и для /д = 850 час (кривая 2) с ограничением Кл = 0,99В то же время при /д = 2000 час основное влияние на функцию готовности
оказывает 2-я и 4-я подсистемы. Из табл. 10.4 видно, что максимальный ре¬
сурс расходуется на 2-ю и 4-ю подсистемы х\=2>, у\ = 3 , х\=А, у\ = 4. Из
данного примера можно заключить, что алгоритм оптимизации достаточно
чувствителен к колебательности функции готовности.ПРИМЕР 10.5. Для иллюстрации неправомерности замены произвольных
распределений на экспоненциальные для простоты расчетов рассмотрим сис¬
тему 2, имеющую те же параметры, что и система 1, но законы распределения
времени до отказа и времени восстановления для всех элементов приняты
экспоненциальные.Решение. Результаты оптимизации системы 2 представлены в табл. 10.5.Таблица 10.5. Результаты оптимизации системы 2 при экспоненциальных распределенияхПроблема^дтСтоимость
системы, zРезервные
элементы, *Ремонтныебригады,)'18500,99346802234 i28500,99777691112 138500,9904372223422223 1
Научные методы эксплуатации техники451Таблица 10.5 (окончание)ПроблемаK(QСтоимость
системы, zРезервные
элементы, хРемонтные
бригады, у120000,99086802234 1220000,99727691112 1320000,99023722 2 3422223 1Табл. 10.4 и 10.5 показывают различие результатов оптимизации этих двух
систем. Графики функций готовности для системы 1 (кривая 1) и системы 2
(кривая 2) показаны на рис. 10.7.Рис. 10.7. Функции готовности системы после оптимизации при произвольных (кривая 1)
и экспоненциальных (кривая 2) распределениях вероятностейПРИМЕР 10.6. Для сравнения систем с нагруженным и ненагруженным ре¬
зервом рассмотрим системы 3 и 4, имеющие те же параметры, что и систе¬
ма 1, но в системе 3 все подсистемы представлены как системы с нагружен¬
ным, а в системе 4 — как системы с ненагруженным резервом.Решение. Результаты оптимизации систем 3 и 4 содержатся в табл. 10.6.Из таблицы следует, что стоимость системы 4 меньше, чем системы 3. Так,
для момента времени /д = 800 час стоимости систем соответственно равны310 и 374 ед., а для момента Гд = 2000 час стоимости равны 354 и 407 ед. Этологично, т. к. надежность системы с ненагруженным резервом выше, чем на¬
дежность системы с нагруженным резервом.Интересные результаты получаются для /д = 800 час (начальный этап функ¬
ционирования). Как видно из рис. 10.8, надежность системы 3 выше, чем на¬
452Гпава 10дежность системы 4 на начальном участке функционирования. Однако после
t = /д надежность системы 3 резко падает по сравнению с системой 4. На
рис. 10.8 показана функция готовности после оптимизации (кривая 1 — сис¬
тема 4, ta = 2000 час; кривая 2 — система 3, /д = 2000 час; кривая 3 — сис¬
тема 4, /д = 800 час; кривая 4 — система 3, /д = 800 час).Таблица 10.6. Результаты оптимизации при всех подсистемах с нагруженным резервом
и всех подсистемах с ненагруженным резервомПроблемаТип резерва^дСтоимость
системы, гРезервные
элементы, хРемонтные
бригады, у3Нагруженный(система 3)80037422 5 3 13 243 13Не нагруженный
(система 4)8003102243 12 12213Нагруженный
(система 3)20004073 3 3 4 22 22 3 13Не нагруженный
(система 4)20003542 3 3 4 12 2 13 2Рис. 10.8. Функции готовности систем после оптимизации для /д = 800 час и /д = 2000 час
с ненагруженным (кривые 1, 3) и нагруженным (кривые 2, 4) резервом подсистемИз данного примера можно сделать вывод, что представленный путь оптими-;
зации должен быть усовершенствован, если необходимо обеспечить надежд
ность системы не в отдельной точке, а на заданном интервале времени. ЭЩ,
обстоятельство является чрезвычайно важным для обеспечения требуемоп|
уровня функции оперативной готовности.
ГЛАВА 11
ОЦЕНКА НАДЕЖНОСТИ ТЕХНИКИ
ПО ОПЫТНЫМ ДАННЫМ
И ДАННЫМ ЭКСПЛУАТАЦИИ11.1. Оценка надежности техники
по опытным даннымОсновными целями испытания элементов и систем на надежность являются:□ подтверждение соответствия данных анализа, полученных в процессе про¬
ектирования системы, с требуемыми показателями надежности;□ разработка рекомендаций по технической эксплуатации системы;□ получение показателей надежности элементов с целью их использования
при расчетах надежности технических систем в процессе проектирования.Анализ надежности сложной системы осуществляется путем расчетов. Рас¬
считать надежность системы это значит определить ее показатели по извест¬
ным показателям надежности элементов структурной схемы, которые можно
получить лишь путем статистических экспериментов. Наука еще не разрабо¬
тала методов определения интенсивностей отказов элементов методами рас¬
четов.В большинстве случаев разработчик технической системы не имеет данных о
надежности элементов. Поэтому результаты расчетов во многих случаях не
достоверны. Часто они выполняются тогда, когда система уже спроектирова¬
на, и делаются для того, чтобы удовлетворить требованиям заказчика.Отсутствие достоверных статистических данных об отказах техники затруд¬
няет разработку научно обоснованных методов эксплуатации. В технических
описаниях нередко отсутствуют указания о дисциплине обслуживания, опти¬
мальном объеме ЗИП, штатной численности обслуживающего персонала.
Частота и глубина профилактики часто не обосновываются. Опыт эксплуата¬
ции техники показывает, что они далеки от оптимальных. Получить данные о
454Глава 11надежности элементов путем лабораторных испытаний — задача исключи¬
тельно трудная. Ее техническая реализация в большинстве случаев не выпол¬
нима.Элементы сложных технических систем имеют интенсивности отказов по¬
рядка 1(Г5 -И (Г7 час-1. Требования на надежность систем, состоящих из та¬
ких элементов, представляют собой численные показатели с двумя значащи¬
ми цифрами после запятой. Например, вероятность безотказной работы
в течение времени / должна удовлетворять условию P(t)> 0,97 или коэффи¬
циент готовности Kr(t)> 0,99.Нередко, особенно в системах с высоким риском и в системах вооружения,
требования задаются с тремя значащими цифрами после запятой. Для обеспе¬
чения этих требований в процессе проектирования необходимо иметь данные
о показателях надежности элементов с такой же или более высокой точ¬
ностью.Получить такие данные путем лабораторных испытаний в большинстве слу¬
чаев невозможно. Пусть, например, необходимо получить значение интен¬
сивности отказа элемента, если X ~ 10-6 час-1. При постановке такого опыта
необходимо провести испытание миллиона элементов в течение одного часа
или тысячи элементов в течение тысячи часов; чтобы получить один отказ.
При этом достоверность такого испытания до первого отказа будет практиче¬
ски нулевой. Для получения данных об интенсивности отказа элемента с не¬
обходимой точностью объем и время испытаний должны быть значительно
выше.В целях сокращения объема и времени испытаний разрабатывались ускорен¬
ные методы. Технически такие испытания реализуются путем повышения
нагрузок на элементы и создания тяжелых условий работы.Авторы этих методов делают много допущений. Вот одно из них: законы
распределений отказов элементов при увеличении нагрузки не меняются, из¬
меняются лишь моменты законов, например среднее значение и дисперсия.
Подобные допущения не доказываются и не проверяются. Поэтому получае¬
мые модели неадекватны объекту.Следует также иметь в виду, что в лаборатории создать реальные условия
эксплуатации чрезвычайно трудно.Анализируя современные методы испытания, убеждаемся, что в большинстве
случаев в лабораторных условиях практически невозможно получить данные
о надежности элементов, которые бы позволили с требуемой точностью оп¬
ределить законы распределения отказов и их параметры. Подобные испыта¬
ния требуют такого объема и времени проведения, которые разработчик фи¬
зически и экономически реализовать не может.
Оценка надежности техники по опытным данным и данным эксплуатации455Где же выход из создавшегося положения?Решить эту важнейшую техническую задачу можно лишь при анализе потока
отказов технических систем в процессе их эксплуатации, когда функциони¬
рует большое количество техники в течение длительного времени в реальных
условиях эксплуатации.11.2. Сбор и обработка данных
об отказах техники в процессе эксплуатацииВ настоящее время в нашей стране отсутствует единая система сбора и обра¬
ботки информации о надежности техники. Это является одной из причин ее
сравнительно низкой надежности. Без таких данных практически невозможно
спроектировать новую систему на заданные показатели надежности.Сбор статистических данных об отказах техники трудно автоматизировать.
Эту работу должен выполнять обслуживающий персонал. В таких условиях
получить из эксплуатации необходимые и достоверные статистические дан¬
ные о надежности и ремонтопригодности техники трудно. Это объясняется
следующими обстоятельствами.Статистические данные об отказах часто не отражают физической сущности
надежности, а поэтому не могут быть обработаны для получения ее количе¬
ственных характеристик.Случайными величинами для оценок надежности техники являются время
между отказами и длительность ремонта. Если техника работает непрерывно,
то для получения этих данных достаточно фиксировать лишь дату отказа и
длительность ремонта. Сложные системы работают с перерывами, вызван¬
ными профилактиками, ремонтами, отсутствием необходимости использова¬
ния техники и многими другими причинами. При этом для получения чис¬
ленных показателей надежности необходимо фиксировать не только дату от¬
каза, но также время работы между отказами, исключив время нерабочего
состояния техники.Ремонтируемые системы работают в режиме смены отказавших элементов.
При таком режиме работы нужно учитывать возможность замены элемента
данного типа в прошлом.Отсутствие единой системы сбора и обработки статистических данных об
отказах и ремонтах техники приводит к тому, что во многих случаях сбор
статистических данных (если он ведется) ведется не квалифицированно. По¬
этому разработчик не может с необходимой точностью оценить надежность
техники в процессе ее проектирования. Более того, анализ надежности при
недостоверных данных о надежности элементов может привести к ложным
выводам.
456Гпава 11Система сбора данных об отказах должна удовлетворять следующим требо¬
ваниям:□ статистические данные, получаемые из эксплуатации, должны позволять
подтвердить характеристики надежности системы, полученные в процессе
проектирования (расчета);□ статистические данные должны позволять получить показатели надежно¬
сти не только системы, но также ее элементов;□ методика сбора данных должна быть предельно простой, не требующей
больших усилий эксплуатационника системы.Этим требованиям удовлетворяет карта отказов, приведенная в табл. 11,1,
которую должен вести эксплуатационник.Таблица 11.1. Карта отказов техникиТипотказав¬шейсистемыИз-за какого
элемента
произошел
отказВремяначалаэксплуа¬тациисистемыДатаотказаСуммарное
время на¬
работки
системы
от начала
эксплуатации,
часСуммарное
время
наработки
от последнего
восстановле¬
ния до дан¬
ного отказа,
часВремявосста¬новле¬ния,часПККлавиатура20.10.199611.03.199711563284,5СамолетТУ-154МСистемауправления04.05.199503.07.200148000328Табл. 11.1 является предельно простой. Статистические данные, указанные в
ней, позволяют определить с помощью непосредственных вычислений пока¬
затели надежности восстанавливаемых систем. Однако по данным таблицы
невозможно определить показатели надежности невосстанавливаемых сис¬
тем: вероятность безотказной работы, среднее время безотказной работы, ин¬
тенсивность отказов, закон распределения времени до отказа. Для получения
этих показателей необходимо знать время до первого отказа, которое в таб¬
лице отсутствует.Ниже приводится методика, позволяющая по данным таблицы получить так¬
же показатели надежности невосстанавливаемых систем и их элементов.11.3. Методика анализа надежности систем
и их элементов по данным эксплуатацииЗависимость между показателями надежности невосстанавливаемых и вос¬
станавливаемых систем можно получить путем решения следующего инте-
Оценка надежности техники по опытным данным и данным эксплуатации457трального уравнения, устанавливающего связь между параметром потока от¬
казов со(0 и законом распределения отказов f(t)\Возможны два способа решения этого уравнения: аналитический и числен¬
ный. При определении показателей надежности невосстанавливаемых систем
по данным об отказах восстанавливаемых систем применять численный ме¬
тод нецелесообразно.Ниже излагается инженерная методика анализа надежности техники по дан¬
ным ее эксплуатации, основанная на аналитическом решении интегрального
уравнения.1. По данным эксплуатации определяется параметр потока отказов со{7). Ре¬
зультаты расчетов представляются в виде таблицы и вычисляются погде n(At) — число отказов за промежуток времени At, N0 — количество
систем, находящихся в эксплуатации.2. Параметр потока отказов представляется в виде формулы. Задача решается
методами аппроксимации, приближенными в узлах. Вид функции интер¬
поляции со = ср(0 выбирается на основе анализа исходных данных, воз¬
можностей универсальных математических программных средств и физи¬
ческой сущности случайных процессов — отказов исследуемой техники.3. Функция со(0 записывается в виде преобразования Лапласа a>(s).4. Определяется преобразование Лапласа плотности распределения времени
до отказа f(s). Получение функции f(s) осуществляется путем решения
интегрального уравнения (11.1). Уравнение представляет собой свертку
функций и в преобразовании Лапласа имеет вид:5. Находится обратное преобразование Лапласа функции /(s). Полученное
выражение закона распределения времени до отказа используется для оп¬
ределения основных показателей надежности системы./(11.1)оформуле:(11.2)ф) = f(s) + (o(s)f(s)или(11.3)
458Гпава 116. Определяются основные показатели надежности системы. Вероятность
безотказной работы P{t), среднее время безотказной работы Тх и интен¬
сивность отказов X(t) определяются по формулам:О О “'■*)Наиболее эффективным способом реализации предложенной методики явля¬
ется применение универсальных математических программных средств сим¬
вольной математики. Наиболее популярными из них являются: Mathematica,
Maple, Derive, Mathcad, Matlab. Применение двух последних пакетов не целе¬
сообразно ввиду их невысокой интеллектуальности, затрудняющей эффек¬
тивно реализовать методику. Использование системы Derive 5 может быть
эффективным, если оригинал функции f(s) определить с помощью других
перечисленных систем. Анализ показывает, что реализация методики в пол¬
ном объеме возможна лишь с помощью универсальных программных средств
Mathematica и Maple. Мы отдаем предпочтение пакету Mathematica как наи¬
более удобному в общении, имеющему превосходные графические возмож¬
ности и простые способы решения задач при большом числе вариантов, на¬
пример при анализе надежности системы и большого числа ее подсистем.Наибольшие трудности при практической реализации методики возникают
при выборе функции интерполяции со = ср(/). Возможности пакетов здесь
крайне ограничены: построение графиков и выбор функции интерполяции по
их виду, определение степени многочлена по табличным разностям (Matlab),
аппроксимация одновременно функциями семи видов (Derive):y = a + bx, у = aebx, у = axb, y = a\nx + b,b a axy = a + ~, y = - , y=- .x b + cx b + cxСущественную помощь здесь могут оказать программные средства автомати¬
зации интерполяции: Formula, CurveExpert, TableCurve, которые предлагают
пользователю сотни различных функций. Выбранная функция интерполяции
должна удовлетворять следующим требованиям: иметь преобразование
Лапласа, а функция f(s), полученная путем решения уравнения (11.3),должна иметь обратное преобразование Лапласа и удовлетворять уело-00вию J /(t)dt = 1.
оЭти трудности в ряде случаев могут быть непреодолимыми, и тогда остается
попытаться решить уравнение численными методами. Однако такое решение
имеет свои недостатки:
Оценка надежности техники по опытным данным и данным эксплуатации459□ численное решение не является математической моделью изучаемого объ¬
екта или явления, в данном случае надежности системы;□ для обеспечения высокой точности определения со(/) необходим настоль¬
ко малый шаг интегрирования, что внутри интервала At отказы отсутст¬
вуют. Приходится увеличивать интервал At, что приводит к недопустимо
большим погрешностям определения co(t). Выручает исследователя то об¬
стоятельство, что при аналитическом решении задачи в соответствии с
предложенной методикой не нужно добиваться выполнения условиясоjf(t) = 1. Это объясняется тем, что показатели надежности P(t) и X(t)
оопределяются при ограниченном времени t. Нет необходимости опреде¬
лять эти показатели при больших значениях /, т. к. функция P(t) быстро
убывает и lim P(t) = 0. Решение множества задач показало, что почти все-гда удается подобрать вид функции интерполяции, при которой определе¬
ние показателей надежности системы и ее элементов в достаточно широ¬
ком диапазоне значений t удовлетворяет заданной точности.В качестве примера ниже приводится расчет надежности самолета ТУ-154 М
по данным его эксплуатации с помощью приведенной выше методики.В табл. 11.2 приведены статистические данные об отказах самолета ТУ-
154 М и его систем. Данные получены из эксплуатации восьми самолетов в
течение двух лет их эксплуатации, отказы обобщались поквартально.Таблица 11.2. Число отказов самолета по годам и кварталамЧисло отказов260431421306351369546363Налет в часах23514066459633812630366545853158По данным табл. 11.2 определяются параметр потока отказов со(7), вероят¬
ность безотказной работы P{t), плотность распределения времени до отказа
ДО, интенсивность отказов X(t). Расчеты выполнены с помощью универ¬
сального программного средства символьной математики Mathematica. Ниже
приводятся вычислительные процедуры анализа надежности воздушного
судна.Параметр потока отказов со(/) вычисляется по формуле (11.2) вручную, без
обращения к системе Mathematica. Данные расчета приведены в табл. 11.3.На основании табл. 11.3 получена функция со(t) в виде табл. 11.4, которая
является исходной для определения показателей надежности самолета по
описанной выше методике.
460Глава 11Таблица 11.3. Значение параметра потока отказов самолетап(Ы)260431421306351369546363(, час23514066459633812630366545853158ш(0-0,001, час-113,813,211,411,316,612,514,914,4Таблица 11.4. Исходные данные для расчета <й(/)t, час01175438387141270215708188552298026858о)(/), час00,01380,01320,01140,01130,01660,01250,01490,0144В табл. 11.4 значения со(0 отнесены к середине интервала At. Из физических
соображений принято со(0) = 0.Ниже приводится решение задачи с помощью системы Mathematica. Решение
сопровождается комментариями. В процедурах применяются символы:□ In [п] — обозначение на экране строки введенных данных;□ Out [п] — обозначение на экране строки отклика программы;□ п — номер строки данных или отклика программы.Ввод данных и отклик функции оз(/) (табл. 11.4):1п[1]:={{0,0},{1175, 0.0138},{4383, 0.0132},{8714,0.0114},{12702, 0.0113},{15708, 0.0166},{18855,0.0125},{22980, 0.0149},{26858, 0.0144}}Out [1]={{0,0},{1175, 0.0138},{4383, 0.0132},{8714,0.0114},{12702, 0.0113},{15708, 0.0166},{18855,0.0125},{22980, 0.0149},{26858, 0.0144}}лАппроксимация данных полиномом второй степени a + bt + ct :In [2] :=Fit [Out [1] , {a, t, t2}, t]Out [2]=0.00687391 + 7 . 947 4 8-10~7t-2 . 00 4 23-10_11t2Построение графика функции со(/):In[3]:=Plot[Out[2], {t, 0, 28000}]Out[3]=-Graphics-Откликом системы является график функции co(f) в диапазонеt = 0-j-28000 час.
Оценка надежности техники по опытным данным и данным эксплуатации461Преобразование Лапласа функции со(0 :In[4 ] : =«Calculus ' LaplaceTransform' LaplaceTransform[Out [2] , t, s]4 . 0084610-11 7 . 94710’7 0.00687391
Out [5] = + + S S SПреобразование Лапласа функции /(л) по формуле (11.3):In[6]:=Factor[Out[5]/{1+Out[5])]0.00687391(-0.0000379683 +s) (0.000153586+ s)Out [ 6 ] = (-0.0000379269 + s) (0.0001564 52 + s) (0.00675539 + s)Обратное преобразование Лапласа функции f(s):In[7]:=Factor[InverseLaplaceTransform[Out[6],s t]Out [7] =0.00687694 e"°-006911S4 t (e0-000156452 ‘-0 . 000434134 e0-00675539 ‘-6
.0078 10“6 e0'00694977 t)Построение графика функции /(/) :In[8]:=Plot[Out[7], {t, 0, 28000}]Out[8]=-Graphics-Определение интенсивности отказов X(t):In[9]:=Out[7]/(l-Integrate[Out[7], {t,0,t}0ut[9]=(0. 00687694 e'0-00691184 t (eo.oooi56452 t-o . 0004 34134 e0-00675539 t-
6.0078 10'6 e°-0069497 t) )/(-2.22045 10'16+1.01799 e'°-00675539 c-
0.0190826 e'°-00015645+ 0 . 00108934 e0'0000379269 t)Построение графика функции X(t):In[10]:=Plot[Out[9], {t,0,600}]Out[10]=-Graphics-Определение вероятности безотказной работы:In[11]:=1-Integrate[Out[7], {t,0,t}]Out [ll]=-2.22045 10'16+1. 01799 e'0-00675539 ‘-0. 0190826 e-°-000i56452 t+0.00108934 e0'0000379269 tПостроение графика функции P(t):In[12]:=Plot[Out[11], {t,0,600}]Out[12]=-Graphics-
462Гпава 11Расчет показателей надежности с помощью описанной программы позволяет
получить решение в аналитическом виде, дает возможность сопроводить ре¬
шение графическими образами. Решение для пользователя является предель¬
но простым. Отметим еще одно важнейшее свойство этой программы. Для
определения показателей надежности систем самолета достаточно внести из¬
менения в первую строку программы, введя новые значения со(t). Программа
выдаст показатели надежности системы.Расчеты по приведенной программе и данным из табл. 11.2 позволили полу¬
чить показатели надежности самолета в диапазоне функционирования
t = 5 -И00 час. Результаты расчетов приведены в табл. 11.5.Таблица 11.5. Вероятность безотказной работы самолетаt, час510205070100P(t)0,9660,9330,8710,7080,6170,5Анализ надежности самолета ТУ-154 М и его систем позволяет сделать сле¬
дующие важные выводы.Надежность анализируемых самолетов не удовлетворяет требованиям, кото¬
рые предъявляются или должны предъявляться к воздушным судам граждан¬
ской авиации. Вероятность безотказной работы самолета в течение 100 часов
налета всего лишь 0,5, т. е. 50% самолетного парка будет иметь отказы тех¬
ники. Конечно, большинство отказов не будут приводить к авариям и катаст¬
рофам, однако среди них могут быть и такие. Часто причинами аварий и ка¬
тастроф считается человеческий фактор. Данный анализ показывает, что ве¬
лика доля в этом и низкой надежности техники. Интенсивность отказов
самолета ТУ-154 М является возрастающей функцией времени, что свиде¬
тельствует об интенсивном старении техники. Резкое увеличение X(t) начи¬
нается после 400 часов его функционирования с момента наблюдения.Предложенная методика анализа надежности техники по данным эксплуата¬
ции, несмотря на свои достоинства, имеет и недостатки.Реализация методики на практике возможна лишь в том случае, если пара¬
метр потока отказов со(/) имеет преобразование Лапласа, а частота отказов
/(s) имеет обратное преобразование Лапласа. Эти условия выполняются,
если со(0 является полиномом и-й степени. Но они могут не выполняться при
многих других видах функции со(/). В настоящее время не существует мето¬
дики выбора вида такой функции интерполяции, которая удовлетворяла бы
этим требованиям.
Оценка надежности техники по опытным данным и данным эксплуатации463Функция f(t), характеризующая случайную величину— время до отказа
системы, должна удовлетворять также следующему условию:]/№=Л.оЕсли это условие не выполняется, то функция fit) не является плотностью
распределения случайной величины — времени до отказа. А это означает, что
следующие формулы, применяемые в нашей методике, несправедливы:Pit) = 1 - \f{t)dt, МО = Ш, -7J = ]tfit)dt.
о “V) оВернее, они могут использоваться лишь для случая узкого диапазона времени
функционирования системы.В теории надежности наиболее часто используются следующие законы рас¬
пределения времени до отказа: экспоненциальный, Рэлея, гамма-, Вейбулла.
Анализ этих законов показывает, что их, к большому нашему сожалению,
использовать нельзя, если применять методику анализа надежности сложных
систем по данным об их отказах в процессе эксплуатации с использованием
перечисленных выше программных пакетов. Это объясняется тем, что преоб¬
разование Лапласа для этих законов в указанных пакетах отсутствует.Таким образом, основная проблема в вопросе совершенствования методики
состоит в выборе вида функции интерполяции со(0, которая должна удовле¬
творять следующим условиям:1. lim со(0 = — ■/-*» Т2. ю(0 должна иметь преобразование Лапласа.3. Плотность распределения времени до отказа fit), вычисленная через
ю(0 по формуле (11.3), должна иметь обратное преобразование Лапласа и
удовлетворять условию:]/(0Л = 1.оОпределение оо(0, удовлетворяющей этим условиям, возможно при компью¬
терных технологиях автоматизации интерполирования. Такими программами
являются TableCurve, CurveExpert и SIMPLE FORMULA.
ГЛАВА 12
НАДЕЖНОСТЬ
ИНФОРМАЦИОННЫХ СИСТЕМ12.1. Фундаментальные понятия теории
надежности информационных системЛюбая наука развивается, исходя из основных понятий и определений. Таки¬
ми понятиями в теории надежности являются "надежность" и "отказ".Надежностью называется физическое свойство технического устройства со¬
хранять свои характеристики в процессе эксплуатации. Это определение яв¬
ляется объективным фундаментальным понятием. Оно не вызывает возраже¬
ний и каких-либо уточнений, если речь идет о надежности техники.Отказом называется событие, после возникновения которого характеристики
технического устройства выходят за допустимые пределы. Это понятие явля¬
ется субъективным, т. к. допустимые пределы зависят от нашего сознания и в
большинстве случаев не могут быть установлены объективно.В классической теории надежности нетехнические системы, например ин¬
формационные, не рассматривались. Более того, считалось, что понятие на¬
дежность к таким системам, как производство, диспетчерский пункт, эконо¬
мическое предприятие и т. п., не применимо. Функционирование этих объек¬
тов с позиции теории надежности должно было оцениваться показателями их
эффективности. Указанное ограничение в теории надежности необходимо
снять. Теория надежности должна развиваться не только вглубь, но и вширь.
Ее понятия и методы полезно использовать для оценки функционирования не
только технических объектов.Понятие "надежность" в том виде, как оно было сформулировано ранее, не
применимо для нетехнических объектов. Надежность функционирования не¬
технической системы не является ее физическим свойством. Это лишь спо¬
собность системы выполнять определенные функции. Этому понятию можно
дать следующее определение: надежностью называется способность объекта
выполнять свои функции в процессе эксплуатации.
Надежность информационных систем465Дадим следующее определение понятию "отказ". Отказом нетехнического
объекта называется событие, после возникновения которого его показатели
выходят за допустимые пределы.По аналогии с техническими объектами, видами отказов нетехнического объ¬
екта могут быть: внезапные, постепенные и перемежающиеся. При внезапном
отказе функционирование объекта либо прекращается, либо становится мало¬
эффективным. При постепенном отказе характеристики объекта с течением
времени ухудшаются до наступления полного отказа, когда функционирова¬
ние объекта становится нецелесообразным. Перемежающимся отказом назы¬
вается событие, после возникновения которого функционирование объекта
лишь временно становится неэффективным.Отказы нетехнического объекта являются событиями случайными, т. к. в
большинстве случаев предсказать время их возникновения практически не¬
возможно, хотя прогнозирование отказа здесь более вероятно, чем в техниче¬
ских системах.Типичными примерами информационных систем являются: информационно¬
поисковые системы, базы данных, диспетчерские системы, банкоматы, биб¬
лиотеки, телефонные сети, справочные системы и т. д. Заявками на обслужи¬
вание в этих системах являются люди — потребители информации, обслужи¬
вающими органами— базы данных, диспетчерские пункты, библиотеки,
справочники, банки данных и т. п. Все эти системы можно отнести к систе¬
мам массового обслуживания (СМО).Широкое распространение СМО требует серьезных научных исследований
по оценке их эффективности, одним из показателей которой является надеж¬
ность. Рассмотрим функционирование СМО с позиции ее надежности и уточ¬
ним понятия "надежность" и "отказ".Существуют два класса СМО: системы с отказами и системы с очередью. Как
те, так и другие могут быть одноканальные и многоканальные с различными
приоритетами обслуживания. Системы массового обслуживания с отказами
наиболее часто бывают многоканальными. В этих системах очередь на об¬
служивание не образуется. Если все каналы заняты, то очередной заявке от¬
казывают в обслуживании. Примерами таких систем являются: больница с
ограниченным числом мест для больных, диспетчерский пункт системы
управления воздушным движением, платная стоянка автомобилей, телефон¬
ный узел и т. п.Для заявок на обслуживание наиболее важным показателем функционирова¬
ния СМО является возможность обслуживающего органа принять заявку на
обслуживание в любой произвольный момент времени /. Тогда отказом
СМО является событие, при котором заявка не будет принята на обслужива¬
ние в момент ее поступления.
466Глава 12Системы массового обслуживания с очередью в обслуживании не отказыва¬
ют. Можно подумать, что эти системы отказов не имеют. Однако это далеко
не так. Если, например, очередь на обслуживание длинная, а заявка ограни¬
чена во времени, то последняя покинет обслуживающий орган и для нее та¬
кая СМО является ненадежной. Для СМО с очередью отказом является собы¬
тие, при котором заявка покидает очередь. В данном случае отказ СМО явля¬
ется понятием субъективным, зависящим от мнения заявки. Для заявки
наиболее важным показателем функционирования такой СМО является дли¬
тельность обслуживания.12.2. Критерии надежности
информационных системАнализ функционирования информационных систем позволяет утверждать,
что критериями их надежности могут быть те же критерии, которые в теории
надежности применяются для анализа надежности невосстанавливаемых и
восстанавливаемых технических систем. Отличие состоит лишь в их физиче¬
ском смысле. Основными из них являются:□ P{t) — вероятность безотказной работы;□ Тх — среднее время безотказной работы;□ Kr(t)—функция готовности;□ Кг — коэффициент готовности;ПТ — наработка на отказ.Дадим определение этим критериям.Вероятностью безотказной работы информационной системы будем
называть вероятность того, что ни одной из заявок не будет отказано в об¬
служивании в течение времени t. Вероятность безотказной работы является
функцией, убывающей во времени и им€ющей следующие свойства: Р(0) = 1,
Дао) = 0. Вероятность безотказной работы есть интервальная характеристика
надежности информационной системы.Средним временем безотказной работы называется математическое ожида¬
ние времени до отказа. Эта характеристика является интегральной. Ее приме¬
нение целесообразно в тех случаях, когда информационная система длитель¬
ного функционирования без перерывов в работе.Информационную систему следует рассматривать, как систему с восстанов¬
лением. Действительно, при возникновении отказа в обслуживании заявки
Надежность информационных систем467система не прекращает функционирование. Спустя время, равное времени
обслуживания одной заявки, она будет готова обслуживать очередную заявку.Функцией готовности информационной системы называется вероятность
того, что в произвольный момент времени t информационная система готова
принять заявку на обслуживание. Функция готовности может иметь вид, по¬
казанный на рис. 12.1.Коэффициент готовности является предельным значением функции готов¬
ности и определяется выражением:КГ = lim КТ (t).t-> 00Рис. 12.1. Функция готовности информационной системыНаработкой на отказ Т называется математическое ожидание времени ме¬
жду отказами системы.Ни один из рассмотренных показателей не может в полной мере характеризо¬
вать надежность функционирования информационной системы. Только сово¬
купность этих критериев позволит оценить надежность системы массового
обслуживания.12.3. Методы анализа надежности
информационных системВесь объем информации, хранящейся в системе, можно представить как со¬
вокупность п независимых, отличных по содержанию частей. Тогда функ¬
ционирование информационной системы, в смысле ее надежности, можно
описать в виде последовательного (основного) соединения элементов. Источ¬
ников информации может быть несколько (например, несколько компьюте-
468Глава 12ров с базами данных). Тогда для потребителя информации такая система яв¬
ляется структурно резервированной. При этом резерв может быть постоян¬
ный (если системы работают одновременно) или замещением (если резервная
система подключается только при отказе основной).Информационная система является, как правило, восстанавливаемой. Однако
ее надежность иногда полезно оценивать до первого отказа.Заявки на обслуживание— это потребители информации. При этом время
между заявками есть величина случайная, аналогично времени между отка¬
зами технической системы. Будем считать, что поток заявок на обслуживание
является простейшим.Время обслуживания заявки зависит от множества факторов: объема необхо¬
димой информации, квалификации обслуживающего органа и т. п. Это время
также является величиной случайной. Будем считать, что время обслужива¬
ния заявки имеет экспоненциальное распределение вероятностей.Из сказанного ранее видно, что с точки зрения надежности функционирова¬
ние информационной системы аналогично технической. А это дает нам право
утверждать, что методы анализа надежности, разработанные в теории надеж¬
ности технических систем пригодны также для анализа надежности инфор¬
мационных систем.12.4. Анализ многоканальной системы
массового обслуживания с отказамиИзвестны три основных способа описания функционирования технических
систем в смысле их надежности: структурная схема, граф состояний и систе¬
ма дифференциальных или алгебраических уравнений. Эти способы приме¬
нимы и для случая надежности функционирования СМО.Эффективным способом описания функционирования СМО в смысле ее на¬
дежности является граф состояний. Узлам графа приписываются состояния
системы, а ветвям, их соединяющим, интенсивности переходов из состояния
в состояние. Функционирование многоканальной СМО с отказами описыва¬
ется графом, приведенным на рис. 12.2.Рис. 12.2. Граф состояний многоканальной СМО'
Надежность информационных систем469Далее и на рис. 12.2 используются следующие обозначения:□ А.— интенсивность потока заявок на обслуживание;□ ц — интенсивность обслуживания заявки;□ п — число обслуживающих органов;□ S0 — состояние системы, при котором заявок на обслуживание нет;□ г = 1,2,..., и-1 — состояние системы, при котором обслуживаются i
заявок;□ Sn — состояние отказа системы, когда все каналы заняты и очередная за¬
явка получит отказ в обслуживании.Предположим сначала, что система работает до первого отказа. В этом случае
отсутствует переход из отказового состояния Sn в исправное состояние .
В этом случае говорят, что на соответствующей ветви графа ставится экран.
Математическая модель функционирования системы массового обслужива¬
ния с отказами представляется следующей системой дифференциальных
уравнений:dP°(0 =-lPQ(t) + liP:(t);dt= ХРЫ(0 -(X + щ)Р,(() + (/ + 1)цР<+1 (/), / = 1, 2,... , и -2;Ш (12.1)
= ХРп_2 (/) -(*. + (*- 1)ц)Р„_, (0;*Ml = XPn_x(t).В уравнениях системы (12.1) обозначения имеют следующий смысл:□ P0(t) — вероятность того, что в момент времени t система находится в
состоянии отсутствия заявок;□ Pj(t), i-1, 2,..., п-1 — вероятность того, что в момент времени t систе¬
ма находится в состоянии обслуживания i заявок;□ Рп (t) — вероятность того, что в момент времени t система находится в
отказовом состоянии, т. е. в таком состоянии, когда на обслуживании на¬
ходится предельное число заявок и очередной заявке будет отказано в об¬
служивании. Pn(t) является вероятностью отказа системы в течение вре¬
470Глава 12мени t. Тогда вероятность безотказной работы системы Pc(t) будет вы¬
ражаться следующей зависимостью:рс(0=1-ад. (12.2)Получим математическую модель системы при условии отсутствия экрана из
состояния S„ в исправное состояние Sn_j. Такая модель аналогична модели
технической системы с восстановлением отказов. Она позволит оценить на¬
дежность СМО по критериям KT(t), Кг, Т. В этом случае система диффе¬
ренциальных уравнений будет иметь вид:^Ш = -и»0(О + ц/»,(О;at■ шр- = (0-a + iц)/}(0 + (/ +1)цРм(/), i = 1, 2,..., п-1; (12.3)
atВероятность Р„(/) имеет смысл неготовности системы принять очередную
заявку в момент времени t (коэффициент простоя). Тогда функцией готовно¬
сти Kr(t) будет следующее выражение:Kr(t) = \-Pn(t). (12.4)При t-> оо вероятности Р0, Рп стремятся к постоянным величинам, и
система дифференциальных уравнений (12.3) превращается в следующую
систему линейных алгебраических уравнений:-Щ + = Oi• ХРЫ ~(Х + Щ)Р, + (/ + 1)ц^+1 =0, i = 1, 2,..., я -1; (12.5)XPn_x-n\iP„ =0.Эта система имеет бесчисленное множество решений. Однако имеет место
уравнениеР0 +Р\ + ... + Рп =1,которое замещает одно любое уравнение системы (12.5). Тогда система будет
иметь единственное решение.В системе (12.5) вероятность Рп имеет смысл коэффициента неготовности
системы. Тогда коэффициент готовности, как предельное значение функции
готовности, определяется выражением:Кг=\-Рп. (12.6)
Надежность информационных систем471Вычисление вероятности безотказной работы системы требует решения сис¬
темы дифференциальных уравнений (12.1). Возможны два способа решения:
численный и аналитический.Аналитический метод предпочтительнее, т. к. он дает решение в виде форму¬
лы. Сущность аналитического метода состоит в следующем:□ система (12.1) записывается в виде преобразования Лапласа;П система алгебраических уравнений в преобразованиях Лапласа решается с
помощью универсальных математических программных средств символь¬
ной математики (Mathematica, Maple, Derive, Mathcad, Matlab);□ находится обратное преобразование Лапласа с помощью тех же систем
символьной математики;□ по вероятности безотказной работы находится среднее время безотказной
работы, используя соотношение:7] = НтРс($).S-* ОСистема (12.1) в преобразовании Лапласа имеет вид:(5 + ЭД(5)-|^(5) = 1;(5 + Х + /|а)РД^)-Л.^_1(5)-(/ + 1)ц^+1(5) = 0, / = 1, 2,..., и-2;(s + А + (и - 1)ц)Р„_1 (S) - АР„_ 2 (s) = 0;
sP„(s)-XP„_l(s) = 0.Предполагается, что начальными условиями являются: i^(0) = l,
Р,(0) = Р2(0) = ... = Р„(0) = 0.Решение этой системы уравнений нами было выполнено с помощью матема¬
тической системы Derive 5. Далее приводятся результаты вычисления веро¬
ятности отказа Pn(s) в диапазоне гг = 1 н- 7 :ад=тттг>j(s + Л)1 2Р2С*) =—^s(s + (2А + jj,)s + А )т, 3Р rs\ — 3 s (s3+ (ЗА + Зц)52 + (ЗА,2 + 3Ац + 2ц2 )s + А3) ’
472Глава 12А4АСО = 2 , 7 ,s(s + (4А + 6ц)5 + (6А +12Ац +11ц )s +
X4P5(s)+(4А3 + 6А2ц + бАц-" + 6ц3)5 + X4) ^ ф5 + 5s4 (X + 2ц) + 5s3 (2Х2 + 6Ац + 7ц2 ) + А^ +5.у2 (2А3 + 6А2ц +11Ац2 +1 Оц3 ) + ^ +s(5A4 +10А3ц + 20А2ц2 + ЗОАц3 + 24ц4) + X5) ’РбЮ*X6ф° + 3 s> (2А + 5ц) + 5s4 (ЗА1 +12Ац +17ц^) +А,6+55 (4А +18А ц + 42Ац +45ц ) + А* +52 (15 А4 + 60А3ц +165А2ц2 + ЗООАц3 + 274ц4 ) + - А6 +5(6А6 +15А4ц + 40А3ц2 + 90А2ц3 +144Ац4 +120ц5) +А5)I1р ^ — 7 ф7 + 756(А + Зц) + Is5 (ЗА2 +16Ац + 25ц2) ++35i (А + 6А ц + 17Ац + 21ц ) + а7 +753(5А4 +ЗОА3ц + Ю5А2ц2 +225Ац3 +232ц4) + а7 +7s2 (ЗА5 +1 5А4ц + 55А3ц2 +150А2ц3 + 274Ац4 + 252ц5) +_ а7 +5(7 А6 + 21 А5ц + 70А 4ц2 + 210А3ц3 + 504А2ц4 + 840Ац5 + 720ц6) +А7)
Надежность информационных систем473Полученные выражения являются предметом дальнейшего анализа. Они по¬
зволяют определить основные показатели надежности системы: вероятность
и среднее время безотказной работы.Формулы для вероятностей отказа в течение времени / были нами получены
в результате вычисления оригиналов функций Pn(s). Обратное преобразова¬
ние Лапласа получено с помощью математической системы Mathematica.
Аналитические выражения система Mathematica позволяет получить при
п<4 . При этом уже при и = 3 выражение для P3(t) настолько сложно, что
им трудно воспользоваться при практических расчетах. Далее приводятся
оригиналы функций Px(t) и P2(t) в символьном виде:Расчетные соотношения при п> 2 легко получить для конкретной системы
массового обслуживания, когда значения Аир. известны. Далее приводится
такой пример. Расчетные формулы для Pn(t) получены при А = 3,7, |i = 4,7 .Формулы имеют вид:р2 (0 = 1- e~6,05t (1,264 sinh(4,79/) + cosh(4,79/)),Р3 (/) = 50,65 (0,02 - 0,02e~°’2U + 0,00043 е~12’5' cos(9,33/) ++ 0,000123«T12,5'sin(9,33/)),Р4 (0 = 187,4(0,0053 + 0,000164е“3’82' -0,0055е~°’104' ++ 3,16-10-6 е-7’54' cos(20,43/) + 3,845 • 10_6 е-7’54' sin(20,43/)),
р5 (0 = 693,4 (0,00144 - 2,06 • 10-7 е~30’2' + 2,2 • 10-6 е-19’1' --8,72-10-6е~х 1,121 + 0,0000184е-5’036' -O^OMSe-0,214'),Р6 (/) = 2565,73 (0,00039 + 4,063 • 10-9 е~36,33' -5,64-10~V24’9' ++ 2,88-10"7 <Г16’57' - 7,36 • 10-7е-10’07' +1,103 • 10“V4’79' -- 0,0003 9 е-0’0035'),Px(t) = \-e~Xt,\р2(0 = 1-вV/Р1(/) = 1-е~3’7'
474Глава 12Р1 (0 = 9493,2 (О, ООО 105 +1,24 • 10~9 е~30,7/ - 7,96 • 10-9 е~22,09‘ ++ 2,58 • 10-6<Г15’2' - 4,63 • 10~8 е~9’6' + 5,18 • 10-8е~4,72' -- О, ООО 105 е-°’00048'),Получим теперь формулы для среднего времени безотказной работы. Ис¬
пользуем для этой цели выражения для вероятности безотказной работы в
преобразовании Лапласа. Преобразование Лапласа вероятности безотказной
работы системы Pc(s) будет равно:ед=Д-р„(5).5Среднее время безотказной работы легко вычислить, воспользовавшись пре¬
дельным соотношением:7j = limPc(S). (12.8)s-+0В результате вычислений получим следующие выражения для среднего вре-мени безотказной работы:п = 1:нп = 2:7]=1(2 + у),п- 3:7]=1(3 + 3у + 2у2),п = 4:Т\ =1(4 + 6у + 6у2 + 6у3),п = 5:7] =—(5 +1 Оу -ь 20у2 +З0у3 + 24у4),А,п = 6:7] = - (6 +15у + 40у2 + 90у3 +144у4 +120у5 ),А,п-1:Тх = 1(7 + 21у + 70у2 + 21 Оу3 + 504у4 + 840у5 + 720у6),А,Цгде у = —.Эти выражения позволяют получить общую формулу для среднего времени
безотказной работы.
Надежность информационных систем475Формула имеет вид:?1=4 Х^СУ- (12.9)кы оВ табл. 12.1 приведены значения среднего времени безотказной работы приц и. 4,7п = \, 2,..., 7 и при следующих значениях у: у = — = 1, у = — = —— = 1,27 .А. А, 3,7Таблица 12.1. Значения среднего времени безотказной работып1234567Т\, час, у = 113822894152372Т\, час, у = 1,270,270,8842,719,95472962077Из таблицы видно, что среднее время безотказной работы существенно воз¬
растает с увеличением числа обслуживающих органов.Анализ надежности системы по критериям вероятности и среднему времени
безотказной работы можно выполнить путем построения графиков и табули¬
рования функций Pn(t) в широком диапазоне t.На рис. 12.3 и 12.4 приведены графики зависимостей вероятности отказа сис¬
темы для случаев п = 2 и п = 7 соответственно и двух значениях у = 1 (кри¬
вая 1) и у = 1,27 (кривая 2). Результаты табулирования содержатся в
табл. 12.2—12.4. В табл. 12.2 приведены зависимости вероятности отказа
P2{t) в обслуживании системы при п = 2 и двух вариантах значений интен¬
сивностей отказов и восстановления (у = 1 и у = 1,27). В табл. 12.3 приведе¬
ны зависимости P1(t) при и = 7 и (у = 1, у = 1,27 ). В табл. 12.4 содержатся те
же данные, что и в табл. 12.3, но в более широком диапазоне t.Рис. 12.3. Вероятность отказа системы при п ~'2
476Глава 12Рис. 12.4. Вероятность отказа системы при п = 7Таблица 12.2. Значения вероятности
отказа Р2(0Таблица 12.3. Значения вероятности
отказаt, часPi(t)У= 1У =1,2700,0000080,0210161000,0402380,0434312000,0797140,0881113000,1175650,1306974000,1538600,1712875000,1886620,2099756000,2220320,2468507000,2540300,2819978000,2847120,3154969000,3141320,34742610000,3423420,377859t, часPi(t)у = 1у= 1,2710,2132730,67986820,4554590,90946530,6277990,97439640,7459340,99275950,8265980,99795260,8816540,99942170,9192290,99983680,9448740,99995490,9623770,999987100,9743230,999996Анализ полученных математических моделей надежности функционирования
СМО позволяет сделать важные выводы:1. Вероятность безотказной работы системы существенно зависит от време¬
ни t, числа заявок п, одновременно обслуживаемых диспетчером, интен¬
сивностей потока заявок X и обслуживания ц. С увеличением времени
работы системы и интенсивности потока требований вероятность безот¬
казной работы убывает. С увеличением п и ц вероятность безотказной
работы возрастает.
Надежность информационных систем477Таблица 12.4. Значения вероятности отказа Р7(/) (в другом диапазоне)t, часР-МУ “ 1У = 1,2700,0000080,02101610000,3423420,37785920000,5678880,61380430000,7160820,75980240000,8134530,85014450000,8774300,90604660000,9194660,94063770000,9470850,96204280000,9652320,97528690000,9771560,9834821040,9849900,9885532. Вероятность отказа в обслуживании существенно зависит от числа заявок
п, одновременно обслуживаемых системой. Так, например, при интенсив¬
ности потока заявок X = 1 час*' и п - 2 система откажет в обслуживании
заявки с вероятностью 0,83 уже в течение времени / = 5 час ее функцио¬
нирования, в то время как при п = 7 вероятность отказа в обслуживании
в течение времени функционирования / = 100 час составляет всего лишь0,04.Система при п = 2 и интенсивности потока заявок X > 1 час-1 практически
не может работать.3. При больших значениях п вероятность отказа в обслуживании слабо зави¬
сит от интенсивности X . Это видно из табл. 12.3. Так, например, при уве¬
личении интенсивности потока с 1 час-1 до 3,7 час-1 вероятность отказа в
обслуживании в течение времени / = 1000 час изменяется с 0,34 до 0,38.
При малых п эта зависимость более существенна, что видно из табл. 12.2
и рис. 12.3.4. Надежность функционирования системы должна оцениваться по двум ос¬
новным критериям: вероятность того, что система в течение времени / не
откажет в обслуживании (критерий надежности), и вероятность того, что
система в любой произвольный момент времени готова к обслуживанию
(критерий готовности).
478Глава 12Наглядным критерием надежности является среднее время безотказной
работы. Из табл. 12.1 видно, что среднее время безотказной работы весьма
существенно зависит от п и у. При п - 7 среднее время безотказной ра¬
боты в 2372 раза выше, чем при п = 1, когда среднее время безотказной
работы равно 1 час.Из табл. 12.1 видно также, что с ростом у среднее время безотказной ра¬
боты убывает. В общем случае такой вывод будет ошибочным. Все зави¬
сит от интенсивности потока заявок X. Если интенсивность потока заявок
одинакова, то с ростом у будет увеличиваться и среднее время безотказ¬
ной работы.Полученные нами результаты являются общими в теории надежности. Дело в
том, что аналогом функционирования многоканальной системы массового
обслуживания с отказами является резервированная восстанавливаемая сис¬
тема с резервированием по методу замещения с кратностью, равной числу п
одновременно обслуживаемых заявок. Структурная схема такой системы и
граф ее состояний приведены на рис. 12.5, а и б соответственно.На рисунке приняты следующие обозначения:□ X — интенсивность отказов нерезервированной системы;□ р — интенсивность восстановления системы;Пт — кратность резервирования, равная в данном случае числу резервных
элементов.aбРис. 12.5. Структурная схема (а) и граф состояний (б) системы
Надежность информационных систем479Сравнивая графы состояний рис. 12.2 и 12.5, б, видим, что при кратности ре¬
зервирования m = п они являются идентичными.Таким образом, с позиции теории надежности многоканальная система мас¬
сового обслуживания — это резервированная система, интенсивность отказов
элементов которой является интенсивностью потока заявок X, а интенсив¬
ность восстановления отказавших элементов есть интенсивность обслужива¬
ния заявки. Полученные ранее формулы в полной мере относятся к надежно¬
сти резервированных восстанавливаемых систем при общем резервировании
замещением.12.5. Готовность многоканальной системы
массового обслуживанияФункционирование многоканальной СМО можно описать графом рис. 12.2,
при этом экран перехода из состояния п в состояние п -1 отсутствует.Математической моделью функционирования такой системы является систе¬
ма дифференциальных уравнений (12.3).В этой системе Pn(t) является вероятностью того, что все каналы в данный
момент времени t заняты и очередной заявке будет отказано в обслужива¬
нии. Тогда выражение (12.6) является функцией готовности системы.Анализ функционирования, в смысле надежности, технической системы и
решение системы дифференциальных уравнений (12.3) показывают, что ве¬
роятности состояний Pj(t) имеют вид, приведенный на рис. 12.6.Из рис. 12.6 видно, что в СМО имеют место переходные процессы, длитель¬
ность х которых мала и зависит от интенсивности потока заявок, интенсив¬
ности их обслуживания, числа обслуживающих каналов. При / > т вероятно¬
сти состояний — величины практически постоянные.Системы массового обслуживания являются системами длительной работы,
поэтому имеет смысл оценивать готовность системы коэффициентом готов¬
ности Кг.Анализ готовности системы— задача чрезвычайно важная. Критерии го¬
товности во многом определяют показатели эффективности системы, риск,
безопасность.Систему дифференциальных уравнений (12.3) будем решать при следующих
начальных условиях: Р0(0) = 1, Р/(0) = 0, / = 1, 2,..., и. Выбранные нами на¬
чальные условия наиболее физичны и просты в практической реализации.
Так как стационарное решение системы уравнений не зависит от начальных
480Глава 12условий, то определять финальные вероятности можно при любых начальных
условиях.Рис. 12.6. Графики вероятностей состояний системыС учетом принятых нами начальных условий система уравнений (12.3) в пре¬
образовании Лапласа будет иметь вид:(5 +А.)Р0(5)-цР1(5) = 1;(s + X + i[x)Pt(s) - АРМ (s)(i + 1)ц^+1 (s) = 0, i = 1, 2,..., л -1; (12.10)
(s -f n\x)Pn(s) - APn_x (s) = 0.Относительно неизвестных /qCs), P\(s),, Pn(s) данная система является
системой линейных алгебраических уравнений с постоянными коэффициен¬
тами. Главный ее определитель М 0. Поэтому она имеет единственное ре¬
шение.Решение системы (12.10) нами было получено с помощью универсального
математического программного средства символьной математики Derive 5.
Далее приводятся результаты решения системы уравнений для случаев
п = 1, 2, 3.п = 1: P0(s) =S + jds(s + А + ц)Pl(s) =s(s + А + ц)
Надежность информационных систем481где Д = s[s2 + (2А + 3|i)s + А2 + 2Ац + 2|i2],,2« = 3: P0(s) =s3 + 2s2(A + Зц) + s(A2 + 4Ац +11ц2) + 6ц3где Д = s[.s3 + 3s2(A + 2ц) + s(3A2 + 9Ац. +11ц2) +А3 + ЗА2|д. + бАц2 + 6|j.3].Для получения аналитических выражений вероятностей состояний во вре¬
менной области необходимо найти обратные преобразования Лапласа при¬
веденных ранее выражений. Решение нами получено с помощью системы
Mathcad 2001. При п = 1,2 значения вероятностей имеют вид:Решение задачи показало, что при п> 2 выражения для вероятностей столь
сложны, что по их виду практически невозможно установить закономерности
изменения функций Pt(t). При п> 2 определение функций Pj(t) с помощью
компьютерных технологий наиболее эффективно тогда, когда функции Pj(s)
записаны с числовыми значениями переменных А и ц. В этом случае P,(t)
представляют собой сумму экспоненциальных функций, легко поддающихся
анализу. Далее приводятся формулы Pt(t) для п = 3 со значениями интен¬
сивностей А = |! = 1 час-1 и А = 3,7 час-1, ц = 4,7 час-1.В формуле приняты следующие обозначения:ПП ос = ~ + Зц3 + 7^ \П р — + 2Х.ц + 2ц^ 5
□ у = Цл/Я .16 Зак. 3094
482Глава 12При п=3:1. А = ц = 1 час-1Р0(О = 0,375 + 0,457е"из9' +7,43-КГ3 е"5’115' +0,161еГ2’746',Р,(0 = 0,375-0,0637<Г,Д39' -0,03Обе-5’115' -0,281 е"2’746',Р2(0 = 0,1875-0,256e_U39' +0,0439e"5’115' +0,0243g~2-746',Р3(0 = 0,0625-0,137е-1,139' -0,0208<Г5'115' +0,0957е"2’746';2. Я. = 3,7 час"1, ц = 4,7 час-1Р0 (0 = 0,0044 +0,000224 <Г5’097' + 1,89е-22’22' -0,896е~12',Р, (0 = 0,361-0,122 е"5’^7' -0,0208е~22’22' -0,218<Г12/,Р2(О = О,142-0,205е~5’097' + 0,0286<Г22’22' -0,034е"12',Рг (0 = 0,03 73 - 0,0841 е-5’097' - 0,013 е“22’22' + 0,9598 е~12‘.Полученные формулы для вероятностей состояний позволяют исследовать
динамику СМО, в частности, определить длительность переходных процес¬
сов. Теперь для этого не нужно решать систему уравнений численными мето¬
дами. Достаточно протабулировать одну из функций в широком диапазоне
времени функционирования системы.□ Вычисление коэффициента готовностиКоэффициент готовности наиболее просто определить топологическим
методом, воспользовавшись выражением Кг = \-Рп. Значение Рп, полу¬
ченное топологическим методом непосредственно из графа состояний на
рис. 12.2, имеет вид:р = " X" + + п(п - 1)Г-2ц2 + п{п - 1)(и - 2)АИ-У +... + л !ц"Разделив числитель и знаменатель на я!ц”, получим следующую формулу:и И-1 п'*г=1г-^7^4. (12.11)у pL у £1
/То '! /=о i-
Надежность информационных систем483□ Вычисление наработки на отказНаработка на отказ рассчитывается по формуле:л-1г 5Йсо Хрп_\ 'Поскольку pi=—p0,TO
ЛЛ-1 П'Z —, /to»4 1 Y (и~1)!Л—1 у 2*0 .. и-,’-1 ’^_Р А- / = о /!р(и-1)!или окончательно^ /=0цгде у = ~ •12.6. Надежность диспетчерского пункта
системы управления воздушным движениемВ качестве примера выполним анализ надежности диспетчерского пункта
системы управления воздушным движением (УВД). Диспетчерский пункт —
это обслуживающий орган системы УВД, потоком заявок которой являются
воздушные суда, прибывающие в аэропорт. Диспетчер при этом может об¬
служивать несколько самолетов одновременно. Промежутки времени между
прибытиями самолетов являются случайными. Это объясняется многими
причинами: опозданием вылета самолета из пункта отправления, отказами
техники, метеорологическими условиями и т. д. По этим причинам возможны
случаи отказа системой УВД в приеме самолета с отправлением воздушного
судна на второй круг, или в зону ожидания, или на запасной аэродром. Таким
образом, диспетчерский пункт системы УВД является многоканальной СМО
с отказами.Анализ надежности этой системы требует знания интенсивности воздушных
судов и интенсивности их обслуживания.Анализ функционирования аэропорта Пулково показал, что интенсивность
потока воздушных судов является величиной постоянной и равной 3,7 судов
484Глава 12в час, т. е. X = 3,7 час1. Интенсивность обслуживания воздушного судна
диспетчером равна ц = 4,7 час-1. Так как интенсивность обслуживания
ц>А, то обслуживание воздушных судов было бы абсолютно надежным,
если бы самолеты летали по расписанию. Какова же надежность системы
УВД в условиях случайности потока самолетов?Определим показатели надежности системы P{t), 7j и показатели готовности
Kr(t), Кг, Т .□ Вероятность безотказной работыПодставляя в выражения для вероятности отказа Pn(s) (см. разд. 12.3)
значения X = 3,7 час-1 и ц = 4,7 час4 и определяя оригиналы Pn(t), по¬
лучим выражения для вероятности безотказной работы системырс(0=1-ед.Формулы имеют вид:• п = 1/>,(/) = 1-<Г3’7';• п - 2Р2 (/) = 1 - <Г6-05' (1,264 sinh(4,79/) + cosh(4,79/));• п-3Ръ (0 = 50,65(0,02 - 0,02е~°’2и + 0,00043е“12’5' cos(9,33/) ++ 0,000123e_12’5'sin(9,33/));• п = 4Р4 (/) = 187,4(0,0053 + 0, ООО 164е-3’82' -0,0055<Г°’104' ++ 3,16 ■ 10-6 e~1Ml cos(20,43/) + 3,845 ■ 10-6 <Г7>54' sin(20,43/));• п = 5Р5 (/) = 693,4 (0,00144 - 2,06 • 10-7 е~30’2' +2,2-10_6 е~19’и -- 8,72 • 10-6 е~11,12/ + 0,0000184 е-5,036' -0,00145<Г°’214');• п = 6Р6(/) = 2565,73 (0,00039 + 4,063 ■ 10"9е-36’33' - 5,64 • 10“8 е~24’9' ++ 2,88 ■ 10“7 е~16’511 - 7,36 • 10-7 <Г 10’07/ +1,103 • 10-6И’79' -- 0,00039 е-0’0035');
Надежность информационных систем485• п — 7Р70) = 9493,2(0,000105 + 1,24• 10-9е-30’7' -7,96-l(rV22’09' ++ 2,5 8 • 10“V15’2' - 4,63 • 10-8 е'9’6' + 5,18 • 10~8 е-4’72' -
-0,0001 Обе-0’00048').В табл. 12.2—12.4 приведены значения вероятностей отказа системы УВД
при п = 2 и и = 7 в широком диапазоне времени работы системы
/ = 0-^-10000 час. Из таблиц, в частности, видно, что при малом п надеж¬
ность системы низкая, при п = 2 она практически неработоспособна.□ Среднее время безотказной работы4 7Подставляя в выражение (12.9) значение у = —^— = 1,27 , получим среднее3,7время безотказной работы в функции числа одновременно обслуживаемых
самолетов диспетчером системы УВД. Данные приведены в табл. 12.1. Из
таблицы видно, что среднее время безотказной работы существенно зави¬
сит от п. При п< 5 аэропорт практически является неработоспособным
по причине его низкой надежности.□ Функция готовностиАнализ функции KT(t) показывает, что переходные процессы в системе
скоротечны. Установившийся режим функционирования диспетчерского
пункта УВД наступает в течение нескольких часов. Это позволяет утвер¬
ждать, что основным критерием готовности системы УВД является коэф¬
фициент готовности Кг = lim Kr(t)./->00□ Коэффициент готовностиX 3 7Подставляя значение р = — = -2— = 0,787 в формулу (12.11), получим зна-ц 4,7чения коэффициента готовности (табл. 12.5).Таблица 12.5. Значения коэффициента готовностип1234567Кг0,560,850,960,9930,9990,99980,99998Из таблицы видно, что коэффициент готовности существенно зависит от
числа самолетов, одновременно обслуживаемых диспетчером. При и<3 и
интенсивности потока воздушных судов Я. = 3,7 час-1 аэропорт практиче¬
ски не может функционировать по причине его низкой надежности.
486Глава 12□ Наработка на отказПодставляя в выражение (12.12) значение у = 1,27, получим значение на¬
работки на отказ в зависимости от п. Значения наработки на отказ приве¬
дены в табл. 12.6.Таблица 12.6. Значения наработки на отказп1234567Т, час0,270,611,837,24372351794Из анализа надежности системы УВД аэропорта Пулково можно сделать сле¬
дующие важные выводы:□ установившийся режим функционирования системы УВД наступает после
нескольких часов ее работы, поэтому готовность системы целесообразно
оценивать по коэффициенту готовности;□ надежность системы УВД высокая при п > 5, т. е. при условии возможно¬
сти диспетчера обслуживать одновременно не менее 5 самолетов;□ система УВД аэропорта Пулково высоконадежна: ее коэффициент готов¬
ности при п £ 5 не менее 0,999, а вероятность безотказной работы в тече¬
ние 100 часов не менее 0,96.12.7. Методы расчета моментов
распределений в задачах надежностиДанный раздел посвящен обобщению некоторых формул для оценки надеж¬
ности информационных систем, математическими моделями которых явля¬
ются многоканальные СМО с очередью. Здесь излагается также метод расче¬
та не только математических ожиданий времени функционирования системы
до отказа, между отказами, времени восстановления, но и моментов более
высоких порядков. При этом для СМО, описываемых процессом "гибели и
размножения" (см. разд. 12.6.3), получены аналитические выражения или по¬
следовательность вычисления указанных ранее характеристик.Сначала рассмотрим алгоритм расчета моментов распределений с общих по¬
зиций теории надежности применительно к системам произвольной струк¬
туры.Большое количество работ в теории надежности посвящено вопросам оценки
численных характеристик надежности систем. Чаще всего рассматриваются
такие показатели, которые связаны с первым моментом случайной величины,
характеризующей процесс функционирования системы, например: средняя
Надежность информационных систем487наработка на отказ, среднее время восстановления и т. д. Однако эти характе¬
ристики не всегда дают полное представление о надежности. Мало того, если
опираться только на них, они могут привести к ошибочному решению, свя¬
занному с обеспечением надежности. Поэтому, наряду с первым моментом,
очевидна необходимость рассматривать и моменты более высоких порядков,
например дисперсию.Моменты могут иметь различное применение в анализе надежности. Так в
работе [24] предлагаются гарантированные оценки надежности, основанные
на использовании математического ожидания и дисперсии. Эти оценки наи¬
более полезны, когда точно не известен закон распределения вероятности
безотказной работы системы. При этом отмечается, что знания одного мате¬
матического ожидания недостаточно для определения гарантированной
оценки. В работе также рассматривается проблема выбора методов резерви¬
рования и влияние дисперсии на ее решение. В работе [114] предлагается ис¬
пользовать первые два момента при решении задач обеспечения запасными
элементами. В частности, когда ожидаемое число запасных элементов вели¬
ко, можно не иметь информацию о законе распределения случайной наработ¬
ки до отказа, а достаточно знать лишь среднее значение и дисперсию. Еще
одним полезным использованием моментов является прогнозирование и
оценка функции (или плотности) распределения случайных величин, таких
как время работы системы до первого отказа, между отказами и время вос¬
становления. Знание моментов в данном случае позволяет существенно со¬
кратить время вычислений, связанных с расчетом функции распределения.
При этом следует отметить, что моменты должны вычисляться не через эти
распределения, а какими-либо другими способами.В данном разделе рассматривается общая процедура определения моментов
любого порядка в предположении, что интенсивности отказов и восстановле¬
ний элементов являются постоянными.Методы вычисления моментов распределения основаны на решении системы
линейных алгебраических уравнений с матрицей, представляющей собой
матрицу переходов, описывающую стационарный режим функционирования
системы. При этом для расчета момента к-го порядка применяется система
уравнений, в правые части которой подставляются результаты решения сис¬
темы, полученные на предыдущем (к - 1)-м шаге. Отличительной особен¬
ностью данного подхода является использование в качестве исходных дан¬
ных только стационарных характеристик системы, что значительно облегчает
расчеты.Как известно (см. гл. 7), функционирование технической системы с позиций
надежности описывается системой линейных дифференциальных уравнений
Колмогорова:р'к (0=Zaik Pi (О - XakiPk (О > (12.13)i i
488Глава 12где ajk — постоянные интенсивности переходов из состояния i в состояние
к , i, к <=Е. Суммирование распространяется на все i, из которых возможен
переход в состояние к (для первой суммы) или в которые возможен переход
из состояния к (для второй суммы).Предполагается, что все множество состояний системы Е разбито на два
подмножества Е+ и Е_, соответствующие подмножествам исправных и от-
казовых состояний.В зависимости от типа состояний отказа (поглощающие или отражающие)
используются хотя и близкие, но все же различные подходы.12.7.1. Поглощающие состояния отказаВ этом случае вероятность пребывания системы в каждом исправном состоя¬
нии к е Е+ стремится к нулю, т. е. lim рк (t) = 0./-» 0000 00Величины x<m) = - j tmp'k (t)dt = т \tm~Xрк (t)dt при т-1, 2,... представляюто особой начальные моменты m-го порядка времени пребывания системы в мо¬
мент времени t в состоянии к . Заметим, что при т = 0 эти величины обра¬
зуют начальное распределение вероятностей, т. е. = рк(0).Умножим обе части уравнения (12.13) на mtm4 и проинтегрируем от нуля до
бесконечности, тогда получимp'k(t)dt = ][>,* m\tm~xpi(t)dt - pk(t)dt0 i 0 i 0илиZ » = 1.2,... (12.14)i iСистема уравнений (12.14) представляет собой итерационную процедуру для
последовательного вычисления чисел ткт^ на основе полученных на преды¬
дущем шаге значений . На каждом шаге должна решаться система ли¬
нейных алгебраических уравнений с одной и той же матрицей при неизвест¬
ных. Эта система составляется только для исправных состояний системы.
При этом на первом шаге правыми частями системы уравнений являются ве¬
роятности пребывания = рк(0) в соответствующих состояниях в момент
Надежность информационных систем489времени / = 0. На последующих шагах правыми частями служат величины
, рассчитанные на предыдущем шаге.Рассмотрим теперь способ определения моментов наработки до первого отка¬
за . Начальный момент этой характеристики т-го порядка равенх(«) = JjtmP'(t)dt = m\tm~xP{t)dt,о огде P(t) — вероятность безотказной работы системы, определяемая по вы¬
ражению:Р{0= Z рк(0- (12.15)кеЕ+Суммирование в (12.15) производится по всем исправным состояниям. Отсю¬
да следует, чтот(") = £ т£") . (12.16)кеЕ+Таким образом, все начальные моменты случайной величины X, могут быть
вычислены с помощью решения системы линейных алгебраических уравне¬
ний, составленной для исправных состояний и последующему использова¬
нию формул (12.16).В частности, средняя наработка до первого отказа равна7] = т(1) = X xjP, (12.17)кеЕ+а дисперсия рассчитывается по формулеЕ\ =T(2)-7i2 = £ т*2) ~Т\ ■ (12-18)кеЕ+12.7.2. Отражающие состояния отказаВ этом случае вероятность пребывания системы в каждом состоянии к е Е с
течением времени стремится к своему стационарному значению рк, т. е.
lim pk(t) = рк. Стационарные вероятности рк удовлетворяют однороднойсистеме линейных уравнений:Y.axkPi~lLakiPk =°- (12.19)
490Глава 12При этом выполняется условие нормировкикеЕПредположим, что решение системы (12.19) получено. Тогда моменты перво¬
го порядка вычисляются по формулам:Т = —L, Тв=^-, (12.20)со совгде Кг = Е Pi — коэффициент готовности; ЛТП = £ р, — коэффициентieE+ ieE_простоя; со = Е aijPi и сов = Е aijPi — стационарные значенияieE+, jeE_ ieE_, jeE+параметров потока отказов и восстановлений (они равны между собой). Та¬
ким образом, далее речь пойдет о нахождении начальных моментов, начиная
со второго порядка.Вычитая из (12.13) равенство (12.19), получим:/(Pk(O-Pk) = £ aik (Pi (О-Pi)~Z ah (Pk if) -Pk)-i iУмножая обе части последнего уравнения на mtm~{ и интегрируя его от нуля
до бесконечности, получим:m К-1 (PkiO-Pk)' dt = (Piif)~ Pi)dt-0 i 0(Pki 0 - Pk)dt.i 0Отсюдаm = 1,2,.../ (12.21)i iгдеxkm) =-ltm(Pk(0-Pk) dt = mjtm~l(pk(t)-pk)dt, m = l,2,... (12.22)
о оОчевидно, что при т-0 = pk(0)-pk.Как и ранее, многократное решение системы (12.21) позволит рекуррентно
определить величины х[т*. Из равенств (12.22) в силу условия нормировки
следует, что2><">=о.кеЕ
Надежность информационных систем491Начальные моменты времени безотказной работы и времени восстановления00 00
обозначим соответственно через = jtmf(()dt и Р(от) = jtmg(t)dt. Здесьо о/(О и SiO — плотности распределения времени безотказной работы и вре¬
мени восстановления системы. Плотности связаны с параметрами потоков
отказов и восстановлений с помощью соотношений:ю(0 = /(0 + /*“в(0, (oB=g*(o(t). (12.23)Положимф(0 = со(0-со, 9в(0 = сов(0-ю.Тогда из равенств (12.23) получим:ф(0 = ДО-coF(0 + /*срв(/), Фв(t) = g*ф(/)-oG(0. (12.24)
Для этих функций "начальные моменты"Ф(т) = m\t™~\®(t)-<is)dt = m\tm~x £ ^(p^t)-pt)dt = £ а^х\т),
О 0 ieE+,jeE_ ieE+, jeE.Фвт) =wJ/m_1(coB(/)-co)^ = m°J/m"1 £ aiJ(pi(t)-pl)dt= £ Ojx\m)
О 0 /s£_, jeE+ ieE_, jeE+могут быть вычислены на основе решения системы уравнений (12.21). А че¬
рез них рассчитываются искомые моменты а^ и Р(т) с помощью следую-ж—1щих преобразований. Умножив первое выражение из (12.24) на mt и ин¬
тегрируя его от нуля до бесконечности, получим:00 00ф(,п) =/жх(т-1) -ооа(т) + /и | J(jc -f- >’)'”-1 У*(jc)(сов (jy) — со) csfccc/y,о оилиttl~~ 1Ф(и) = та{т~Х) -соа(т) + £ CJmau\[m'J) .j=оОтсюда для наработки системы находим начальный момент т-го порядка:Г _ . Л(12.25)а(т)=1сот~—\пш{т~Х) -ф(от> + t CJmauW”-J)
о
492Глава 12Аналогично из второго соотношения (12.24) для среднего времени восста¬
новления получим начальный момент т-го порядка:f . лР(т) = j.
СОЪФиЧт-лУ=о(12.26)Таким образом, моменты рассчитываются рекуррентно по формулам (12.25) и(12.26), причем на каждом шаге требуется решение системы линейных алгеб¬
раических уравнений (12.21) с одной и той же матрицей коэффициентов.В частности, из равенств (12.25) и (12.26) следует, что средняя наработка на
отказ и среднее время восстановления равны соответственно:г цш 1-фИ+фУ>, Г. = Р<|> = ф(1) ф*')СО ШДисперсии наработки на отказ и времени восстановления вычисляются поформулам:,Л2Ь 9Гт(1)Р = - Г2 = 2r ~ Ф + Ф‘ + 2Г<Р‘ - Т2 .СОВ, ■ Р<2) - Г.2 ■ ф<2> + 2Г,<|>11> - <Р<*2) - т1.СО(12.27)(12.28)ПРИМЕР 12.1. Для иллюстрации применения методов вычисления моментов
выполним анализ восстанавливаемой системы, состоящей из 9 элементов,
структурная схема которой показана на рис. 12.7.Рис. 12.7. Структурная схема системыРешение. Все элементы обслуживаются тремя ремонтниками и имеют оди¬
наковые значения интенсивностей отказов 0,1 час"1 и восстановлений 1 час"1.
Элементы 6 и 7 являются резервными к элементу 2 (резерв нагруженный),
элемент 8 является резервным к элементу 4 (резерв нагруженный), а элемент
Надежность информационных систем4939 — резервный к системе, образованной остальными элементами (резерв не-
нагруженный).Данная система имеет 1867 состояний, поэтому определение моментов может
быть выполнено только с помощью соответствующих программных средств.
Система уравнений- была решена при помощи программной системы Relass
(http://www.gurov.spb.ru/isant/isant.html), а характеристики надежности,
такие как математические ожидания и дисперсии наработок и времени вос¬
становления, получены с помощью приведенного ранее алгоритма. Результа¬
ты расчетов представлены в табл. 12.7.Таблица 12.7. Моменты наработок и времени восстановления системыХарактеристикаМатематическое
ожидание, часДисперсия, час2КоэффициентвариацииНаработка до отказа52,727080,9873Наработка на отказ51,325600,9863Время восстановления0,460,19500,953212.7.3. Алгоритмы определения
моментов распределений
для процесса "гибели и размножения"Приведенные в разд. 12.6.1 и 12.6.2 соотношения для расчета математических
ожиданий, дисперсий и начальных моментов более высоких порядков требу¬
ют решения систем линейных алгебраических уравнений, размерность кото¬
рых определяется числом возможных состояний. Количество состояний мо¬
жет быть весьма большим, и тогда решение системы уравнений будет прак¬
тически не выполнимым. Однако в частном случае, когда функционирование
технической системы описывается процессом "гибели и размножения", ре¬
шение указанных систем уравнений значительно упрощается, и для расчета
моментов могут быть выписаны законченные выражения, не использующие
решения систем уравнений. К таким процессам относятся процессы функ¬
ционирования всевозможных систем нагруженного, облегченного или нена-
груженного резервирования, мажоритарных систем и систем со скользящим
резервом с однотипными по надежности элементами. При этом обслужива¬
ние таких систем может быть самым произвольным.Рассмотрим систему, которая описывается процессом "гибели и размно¬
жения".Графически модель функционирования такой системы представлена на
рис. 12.8.
494Глава 12< > fl W->l 2 ) < > ( 3 )— • • • —6»-2) < > Q»~ j) < >Рис. 12.8. Граф состояний процесса "гибели и размножения"Предполагается, что состояния (0), (1),..., (и-1) на графе являются исправ¬
ными, а состояние (п) — отказовым.1Введем обозначения: рi=—L, г~ 1, 2,Для определения характеристик системы, работающей только до первого от¬
каза, необходимо получить решение системы уравнений следующего вида:-^iTo +M-iTi =^о>' ^кхк-\ “О1* + ^*+i)T* + M*+it*+i =h> к = \,2,..., п-2; (12.29).^■л-1^л-2 (М'п—1 ~^п-\-Система формально составляется по графу в предположении, что = 0 (со¬
стояние (и) является поглощающим). Правые части системы (12.29)— про¬
извольные числа. Решением системы (12.29) служит следующий набор зна¬чениих?} = -"Х Ъо+- + ьш (12.30), = 0 Pk+l---Pk+ikk+i+lдля всех к = 0,1,2,..., и-1.Формулы (12.30) дают решение системы (12.29) при любых правых частях.
Полагая в (12.30) b0 = -1, Ьк = 0, к = 1, 2,..., п — 2 , получим решение систе¬
мы в виде:T(i) "f-1 |1=0 Р*+1 •"?£+/л/Ы-й-1
Тогда по формуле (12.17) средняя наработка до первого отказа равнал-1 л-1 п-к~ 1 171 = S = I I г • (12.31)к = 0 к=0 Г=0 Р/Ы-1"-Р*+/^'£+;+1Если положить теперь в системе (12.30) ^ = ~2т^1), к = 0,1, 2,..., п -1, то по¬
лучим решение этой системы на втором шаге:/-.ч л-А-1 «ДО _l. 4. «ДО
т(2) _ о V Т0 +- + Xk+i, = 0 P/t+l— Pk+i^k+i+l
Надежность информационных систем495и в соответствии с формулой (12.18) дисперсию наработки до первого отказа:л-1a “I*?’-?;2-
к=0Для нахождения характеристик времени работы системы между отказами и
времени восстановления надо решить трехдиагональную систему вида:+ц,*, =Ь0\' hxk-1 - + *-*+1 )** + К*+Л+1 = h, к = 1, 2,..., и -1; (12.32)~ М'ПЛ'« = ^л •Система составляется по графу, изображенному на рис. 12.2 в предположе¬
нии, что состояние (п) является отражающим. При этом должно быть вы-пполнено соотношение £ £>, = 0. Решение системы (12.32) определяется фор-( = 0муламихк = р,...р*х0 + f к = 1, 2,..., и. (12.33)/=1 Ц/Для вычисления моментов первого порядка система (12.32) решается в пред¬
положении, что правые части равны нулю, но при этом выполняется условиеянормировки: Е хк = ^ •к=0Тогда в результате решения получим значения стационарных вероятностей:_ Pi —РД:Рк ~Хк ~ п£ Pi*-Рк
к=0Отсюда, а также из соотношений (12.20) следует, что средняя наработка на
отказ равна:л-1 п-1Е а X pi-p*Т = —— = — , (12.34)№пРп Pl’-'Pn-l^nа среднее время восстановления:Рп 1
496Глава 12Для вычисления моментов второго порядка система (12.32) решается в пред¬
положении, что правые части равны Ьк = рк -рк{0). Тогда согласно (12.33)
получим:Хр =Pi-P^0 + f p.ai--PA.^Q-+-.t-Pi-l-V (12.35)/=1 Рчпри условии, что в момент ( = 0 система находилась в состоянии (0). Значе¬
ние х^ на втором шаге определяется из условия = 0 . Тогдак = 0^ ^ Pi+1 •••Pfr 0 ~Ро ~ — ~Pi-\)^ . (12.36)Z Pi-P*к = оДисперсия наработки на отказ и дисперсия времени восстановления опреде¬
ляются теперь по формулам (12.27)—(12.28):D = 2{T + ТЬ)(Т + {Трп+\)хУ)-Т2, DB=T2.При этом используется соотношение:0,(2) _ш(2) „(2) _и (2) __2v(l)Ф Фв “ Кпхп-1 tхпхп - АХп ■Полученные в настоящем разделе аналитические соотношения для математи¬
ческих ожиданий и дисперсий могут быть использованы для исследования
систем с произвольным числом элементов, что позволяет разрешить пробле¬
му размерности в системах, описываемых процессом "гибели и размно¬
жения".Рассмотрим один важный частный случай многоканальный СМО с отказами,
когда очередь на обслуживание заявок не возникает. Тогда Хк=Х, =&ц,
к = 1, 2,..., п. Ограничимся лишь средними значениями. По формуле (12.31)
среднее время безотказной работы равно:л-1 п-к-\ 1 1 и-1 л—1 1 л-1 л-1-1= 2 Z -—-г-г—=у2>' I (Аг+1)...(^+о4елу' Z cL,к = 0 ; = 0 Рк+\ ■■•Р^+/ЛАг+|+1 i—О к = 0 ^ i=0 к=0ИЛИ(12.37)^1 = о
Надежность информационных систем497где у = — . По формуле (12.34) средняя наработка на отказ равна:Ат = \ S«Ci_,y'. (12.38)А «=оИз полученных соотношений следует, что 7j > Т.Для многоканальной СМО с очередью аналогично могут быть выписаны вы¬
ражения для 7], Т, Гв и , а также для дисперсий соответствующих слу¬
чайных величин.12.7.4. Численная оценка временных показателей
надежности процессов "гибели и размножения"Как следует из разд. 12.3, аналитические выражения для P(t) и Кг (/) слиш¬
ком сложны. Более простой способ состоит в численном решении систем
дифференциальных уравнений одним из известных методов, например мето¬
дом Рунге — Кутты. При этом для решения системы уравнений не требуется
обращения преобразования Лапласа и привлечения математических пакетов.Простейший вариант программы Rungekutt, реализующий метод Рунге — Кут¬
ты, можно найти в Интернете по адресу http://www.gurov.spb.ru/isant
/isant.html. Здесь рассмотрен случай п-1, А = 3,7 час”1, ц = 4,7 час"1. Про¬
грамма позволяет рассчитать P(t) и /Г, (/), а также вероятности пребывания
СМО в каждом состоянии. Вероятности состояний системы, работающей до
первого отказа, показаны на рис. 12.9. Их особенность состоит в том, чтоРис. 12.9. Вероятности состояний СМО, работающей до первого отказа
498Глава 12основной вклад в P(t) вносят вероятности нулевого, первого и второго со¬
стояний. Остальные вероятности практически равны нулю.График вероятности безотказной работы, рассчитанный на интервале от нуля
до 10000 час, показан на рис. 12.10.Рис. 12.10. Вероятность безотказной работы СМОНа рис. 12.11 показаны графики вероятностей состояний системы, которая
может выходить из состояния отказа за счет восстановления системы. Здесь
также видно, что, во-первых, основную роль в функции готовности играют
Р0(О, Р\(О, Рг(О > и, во-вторых, все графики довольно быстро входят в ста¬
ционарный режим. Переходной процесс продолжается менее 1 час.Рис. 12.11. Вероятности состояний СМО
498Глава 12основной вклад в P(t) вносят вероятности нулевого, первого и второго со¬
стояний. Остальные вероятности практически равны нулю.График вероятности безотказной работы, рассчитанный на интервале от нуля
до 10000 час, показан на рис. 12.10.Рис. 12.10. Вероятность безотказной работы СМОНа рис. 12.11 показаны графики вероятностей состояний системы, которая
может выходить из состояния отказа за счет восстановления системы. Здесь
также видно, что, во-первых, основную роль в функции готовности играют
Р0(1), P\(t) , P2(t), и, во-вторых, все графики довольно быстро входят в ста¬
ционарный режим. Переходной процесс продолжается менее 1 час.Рис. 12.11. Вероятности состояний СМО
500Глава 12Задержки возникают из-за ошибок в результатах, которые вызываются в ос¬
новном сбоями технических средств и помехами вследствие шумов и затуха¬
ний сигналов в информационных цепях и сетях. Основной путь устранения
ошибок — это повторное выполнение работы. Поскольку частота сбойных и
помеховых ошибок близка к частоте выполнения самих работ, то проблема
снижения потерь в пропускной способности из-за воздействия этих возму¬
щающих факторов относится к числу наиболее актуальных в дискретных
системах.Для достижения приемлемых уровней пропускной способности и надежности
в работе [126] предложено регулировать пропускную способность дискрет¬
ной системы по установленному оптимальному правилу. При ее снижении
появляется некоторый расчетный резерв времени, который можно использо¬
вать для повторного выполнения (рестарта) части работы на глубину, опреде¬
ляемую рамками этого резерва времени. При необходимости повышения
пропускной способности вследствие роста информационной нагрузки в тече¬
ние случайного времени предыдущий резерв времени либо сокращается, либо
полностью исключается, затем возможны управления в сторону его повыше¬
ния и т. д. Этот подход может быть эффективным при условии рационально¬
го разбиения работы на составные части (этапы). Чем больше этапов в соста¬
ве одной работы, тем меньше глубина рестарта, тем меньше требуемый ре¬
зерв времени и потери в пропускной способности даже при интенсивной
информационной нагрузке. С другой стороны, для организации каждого эта¬
па работы необходимо сформировать "контрольную точку" предыдущего
этапа, запомнить начальный адрес и установить в исходное состояние таймер
длительности данного этапа. Эти операции требуют определенного времени и
по сумме всех этапов работы могут привести к существенному снижению
пропускной способности системы.Задаче оптимального распределения работ по этапам посвящено много пуб¬
ликаций [47, 118, 124 и др.]. Однако решения предлагались только для неко¬
торых частных случаев, таких как: времена выполнения этапов постоянные,
времена между ошибками в выполнении работ экспоненциальные, нет при¬
вязки к пропускной способности системы [124] или к работам, выполняемым
дискретными системами [47, 118], решения имели либо весьма приближен¬
ный характер, либо не доведены до численного алгоритма.Здесь проблема распределения работ по этапам в дискретных системах реша¬
ется в интересах достижения разумного компромисса между пропускной спо¬
собностью и надежностью, сняв все упомянутые ограничения и доведя до
численных алгоритмов и машинной реализации математические результаты,
полученные при произвольных распределениях длительностей работы, эта¬
пов, ошибок и назначаемых временных резервов.
Надежность информационных систем501Пусть требуется выполнить в дискретной системе одну определенную рабо¬
ту, которую можно распределить на п этапов одинаковой или различной
продолжительности. Результаты решения, полученные после каждого этапа,
служат входными данными для следующего этапа, что означает последова¬
тельное выполнение всех этапов работы.Длительности этапов работы и длительности тактов, отведенных на органи¬
зацию соответствующих этапов, считаются независимыми случайными вели¬
чинами с плотностями к-го этапа и к-то такта равными соответственно hk и
gk , к = 1, 2,..., п. Если работа выполняется безошибочно, то плотность рас¬
пределения времени работы представляет собой свертку Т\ *...*hn * gx *■■■* gn
плотностей отдельных этапов и тактов. Ошибки в работе с плотностью / и
время, связанное с их устранением путем рестарта отдельных этапов, могут
вносить существенные коррективы как на время выполнения соответствую¬
щих этапов, так и на время выполнения всего задания в целом.Задача состоит, во-первых, в построении и решении модели времени выпол¬
нения работы в дискретной системе при общих условиях длительностей эта¬
пов, тактов, ошибок. Во-вторых, нужно распределить работу на такое коли¬
чество этапов пот, при котором достигается минимальное время работы из
всех возможных с учетом временных затрат на устранение ошибок.12.8.2. Описание системы графом состоянийВозможные состояния исследуемой системы и переходы между ними показа¬
ны на графе, изображенном на рис. 12.13. Так состояние с номером к
(к = 1, 2,..., п) означает выполнение к-го этапа работы, в состоянии (к) осу¬
ществляется организация этого этапа. Циклический переход из состояния (к)
в состояние (к) вызван проявлением нарушений при выполнении к-го этапа
и его рестартом. Состояние с номером п +1 характеризует завершение вы¬
полнения многоэтапной работы.Рис. 12.13. Граф состояний при выполнении многоэтапной работыВремя выполнения работы складывается из длительностей этапов и длитель¬
ностей тактов, предназначенных для организации соответствующих этапов,
502Глава 12причем соответствующие случайные величины независимы. Поэтому вероят¬
ность выполнения работы за время t определяется какF(t) = gi*-*gn*Pn+i> (12.39)где pk(t), к = \, 2,..., п + \ — вероятность пребывания системы в момент
времени t в состоянии (к), вычисленная при условии отсутствия состояний
вида (к). Среднее время выполнения работы определяется, очевидно, суммойТ=±Тк+Т, (12.40)к=100где Tk = \pk{t)dt— среднее время пребывания системы в состоянии к,
оа Т — средняя суммарная длительность тактов.12.8.3. Математическая модельБудем предполагать, что:□ при появлении ошибки на каком-либо этапе выполнения работы этот этап
начинается заново, и время, уже затраченное на его выполнение, в даль¬
нейшем не учитывается;□ наличие переходов от одного этапа к другому не влияет на величину вре¬
мени до появления очередной ошибки.Каждому состоянию системы поставим в соответствие функцию, аргументы
которой показывают величину остаточного времени выполнения операций.
В состоянии (к) может быть завершено выполнение А>го этапа работы или
может произойти ошибка, требующая возврата к началу этапа, значит этому
состоянию соответствует функция yk(st,s2>0> в которой аргумент s, равен
остаточному времени по выполнению к-го этапа, а аргумент s2 — остаточ¬
ному времени непоявления ошибки.Вероятности пребывания в состояниях выражаются через функции ук по
формулам00 00Pk(0= J /^(^1^2>t)dsxds2 . (12.41)о оПо общей методике описания функционирования системы при произвольных
распределениях (см. гл. 4) функции yk(sx,s2,t) удовлетворяют системе инте¬
гральных уравнений:
Надежность информационных систем503yl(sus2,t)= \hx{x + л, )f(x + s2 ) J Ух (s, 0, / - x)dsdx + hx(t + sx )f{t + s2);0 01 COyk (5, ,s2,t)= J hk (x + sx )f(x + S2)\yk (s, 0, t - x)dsdx + (12.42)+ + + к = 2,3,..., n.оЭти уравнения составлены для всех состояний, соответствующих выполне¬
нию некоторого этапа работы. Для последнего поглощающего состояния, со¬
ответствующего окончанию работы, имеем:IУп+i(0,-s2»0= jyn(0,s2,t-x)dx . (12.43)о12.8.4. Распределение
времени выполнения работыВ результате решения системы уравнений (12.42) получим:Л(*1.*2»0 = ®1 *(hu/s2 ХО (12.44)Ук (5, ,s2,0 = jhk (х + 5, )ук_х (0,ЛГ + s2 ,t - x)dx +
о
/ _+5* * (hk^fs2) * \Hk(x)yk_x(0,x,t-x)dx, к = 2,3,..., п.
о(12.45)Здесь принято обозначение®*(0 =t(Hkn*U)(0- (12.46)у=оВыражения (12.44) и (12.45) представляют собой рекуррентные соотноше¬
ния для вычисления функций yk(sx,s2,t), к = 1,2,, п . Однако они весьма
сложны для расчетов функции распределения времени выполнения всей ра¬
боты. Поэтому далее формулы (12.44) и (12.45) будут преобразованы к более
простому виду.ОбозначимУк(3>0-Ук(°>я>0>
504Гпава 12ak(t) =©j(0, при к-1;_ 1 — (12.47)®к * jHk(x)\\Jk_l(x,t-x)dx, при к = 2,3,..., п.оТогда из (12.44) и (12.45) вытекает, чтоVl(^0 = «i *(ЛЛ)(0.tVk(5>0 = \hk(x)Vk-1 (X + S,t~ x)dx + ctk* (hkfs)(t), к = 2,3,..., n .0Можно показать, что явное представление функций через коэффици¬енты ak{t) дается равенствамиVk(s>0='Zai*(hi*-*hkfsW- О2-48)(=iТеперь нетрудно получить способ вычисления коэффициентов ak(t). При
к = 2,3,..., п согласно (12.47) и (12.48) имеем:' - *-1ак(0 = * \нк WE ai * <hi * - * hk-\№-x)dx,
о c=iа используя равенствоjh(x)a*(gfx+s)(t-x)dx = a*(g*hfs)(t), (12.49)0получим:ak(t) = (bk*'£ai**...*hk_x *Hkf)(t). (12.50)i=iВ заключение запишем достаточно простое выражение для решения системы
интегральных уравнений (12.42) через коэффициенты ak(t). В силу (12.44),
(12.45) и (12.48)1 к-\У к (sx,s2,t) = \hk (х + Sl )Х a, *(ht *...* hk_xfx+S2 )(t -x)dx + ak* (hkS] fh )(t).
о fc=lПрименяя (12.49) и выполняя несложные преобразования, получим;yk(sl,s2,t) = 'Zai*(hi*...*hk_i *hksifs ХО- (12.51)/=1
Надежность информационных систем505Из (12.51) по формулам (12.41) находятся вероятности пребывания системы
во всех состояниях, а именно:Рк (О = !>;* ОЦ *... * Л*_, * НкЁШ к = 1, 2,..., п. (12.52)
»=1Используя также (12.43), а затем (12.48), получим:Л.+1 (0 = f\^n(s2^~x)ds2dx = 'Lai *Уч * — *hnF)*\{t). (12.53)
оо »=•Сумма всех вероятностей равна единице, что может служить контролем пра¬
вильности проведенных выкладок. Таким образом, как следует из (12.53),
распределение времени выполнения работы с учетом возможных ошибок и
повторного счета, а также наличия тактов для подготовки к выполнению эта¬
пов, вычисляется по формулеFit) = * (A, *...*hnF)*g{*...*gn* 1(0. (12.54)i=iДля большого класса распределений соотношение (12.54) представляет собой
сравнительно простую в вычислительном отношении процедуру.12.8.5. Среднее время выполнения работыИз (12.40) и (12.52) следует, чтоT=t £ a<lhi * - * h-\ * Hk(0F(t)dt + T ,A = 1 i = l оилиT = ±a"\H^(t)F(t)dt + T, (12.55)( = 1 оCO Iгде dt = jat(t)dt, tfw(0 = l- jht * ...* hn(x)dx. Далее, интегрируя (12.50), по-
o олучим:° к = J®* (0 dt £ a JA, *. V *hk-\*Hk (t)f(t)dt.
о <=1 оИз соотношения (12.46) следуют рекуррентные формулы для расчета коэф¬
фициентов ак:
506Глава 12Z (*i fa Hk(t)f(t)dt=— . — » • (12-56)l-]я,(0/(0А 1-|ВД)/(0<*о оТаким образом, значение Г определяется формулой (12.55), в которой коэф¬
фициенты ак находятся рекуррентно по формулам (12.56). Очевидно, что для
большого класса распределений времени выполнения этапов задача (12.55)—-
(12.56) с вычислительной точки зрения не представляет никаких трудностей.
К этому классу относятся, например, гамма-распределение, нормальное и вы¬
рожденное распределения.Рассмотрим только постоянные длительности этапов, для которых
hk(t) = bx (t). В этом случае функция А, *...*hk_x *Hk(t) равна 1 только напромежутке [х,(+ + ,+...+ х*], а для остальных значений х она рав¬
на 0. Поэтому из (12.56) следует, чтоV Qi (F(x, +... + xk_i) - F(xi +... + xk ))°1 = F^)’ °k= T(.^) ’Преобразуя (12.55), получим:n Xj+...+Xft т = ^ J F(t)dt + T.
i~ 1 0Эти простые формулы для вычисления коэффициентов ак и Т вполне при¬
годны даже для ручных вычислений.Для иллюстрации полученных результатов вычислим среднее время выпол¬
нения работы при произвольных распределениях времени появления ошибок
и постоянных временах выполнения каждого этапа.ПРИМЕР 12.2. Необходимо передать сообщение, требующее непрерывной
работы сети передачи данных в течение 5 мин. Сообщение может быть пере¬
дано полностью или разбито на п частей, которые передаются последова¬
тельно как самостоятельные сообщения. При этом время передачи каждой
части сообщения увеличивается на 0,1 сек. При нарушении работоспособно¬
сти сети часть не полностью принятого сообщения передается заново. На
сколько частей следует разбить передаваемое сообщение, чтобы среднее вре¬
мя его успешной передачи было бы минимальным?
Надежность информационных систем507Решение. Используя программу расчета среднего времени выполнения рабо¬
ты при различных значениях п, получим зависимости, представленные на
рис. 12.14. Верхний и нижний графики построены, когда время до появления
ошибки в сети имеет усеченное нормальное распределение с параметрами
т = 100 сек, ст = 50 сек (кривая 1) и т = 100 сек, о = 200 сек (кривая 3)
соответственно, Кривая 2 построена для случая, когда время до появления
ошибки в сети имеет гамма-распределение с параметрами \ = 0,02 сек'1,
к-2.Рис. 12.14. Зависимость среднего времени выполнения задания от числа этаповПолучены оптимальные значения: иопт=64, Гмин =315,7 сек для 1-й кривой,
лопт = 36, Гмин =304,0 сек для 2-й кривой, иопт = 66, Гмин =313,3 сек для
3-й кривой.12.9. Расчет надежности систем
от программных ошибок на основе
двухверсионного программирования12.9.1. Постановка задачиМодели расчета надежности программного обеспечения (ПО) зачастую не
учитывают влияния времени, затрачиваемого на принятие решения после его
отказа. Не учитывается обычно и допустимое время на принятие решения,
сверх которого ПО попадает в отказовое состояние. В силу этого значения
показателей надежности, таких как коэффициент готовности, бывают неоп¬
равданно завышенными. Время на принятие решения может оказать сущест¬
508Глава 12венное влияние на надежность системы, что необходимо учитывать при ее
проектировании. Существующие в настоящее время методы оценки надежно¬
сти ПО для двухверсионного программирования обладают следующими не¬
достатками:□ программы, как правило, считаются однотипными с одинаковыми распре¬
делениями до отказа;□ распределения времен безотказной работы программ предполагаются экс¬
поненциальными;□ время на принятие решения или вообще не учитывается, или предполага¬
ется постоянным;□ не учитывается допустимое время, выделяемое на принятие решения;□ не учитывается дисциплина обслуживания программ и порядок их восста¬
новления при отказе обеих программ и возможном образовании очереди;□ методы являются эвристическими и не позволяют указать оценку погреш¬
ности.Одним из путей анализа ПО с произвольными распределениями времени до
отказа программ, времен на принятие решения и допустимого времени явля¬
ется составление и решение системы интегральных уравнений. Подход, осно¬
ванный на составлении математической модели в виде системы интеграль¬
ных уравнений, позволяет избежать для двух версий программ перечислен¬
ных ранее недостатков. Заметим, что время принятия решения может быть
как постоянным, так и случайным с известным законом распределения.Отметим, что анализ надежности ПО в задачах двухверсионного программи¬
рования должен учитывать тип восстановления: полностью ограниченное или
неограниченное. При полностью ограниченном восстановлении необходимо
учитывать также приоритет обслуживания программ: прямой, обратный, на¬
значенный или случайный. Здесь мы разбираем только случай полностью ог¬
раниченного восстановления с прямым приоритетом, хотя все изложение ма¬
териала может быть с соответствующими изменениями распространено и на
другие стратегии обслуживания.12.9.2. Модель функционирования
вычислительной системы с двухверсионным
прикладным программным обеспечениемРаботу программ для случая полностью ограниченного восстановления с
прямым приоритетом можно пояснить временной диаграммой, представлен¬
ной на рис. 12.15.
Надежность информационных систем509Рис. 12.15. Временная диаграмма для двух версий программ
для одного оператора-программиста с прямым приоритетомНа диаграмме введены следующие обозначения:□ 4/ — время безотказной работы /-й программы с плотностью распределе¬
ния fj(t), вероятностью безотказной работы Ft(t) и наработкой до отказа
Т„ / = 1,2;□ г), — время восстановления i-й программы с плотностью распределениявероятностью невосстановления G,(/) и средним временем восста¬
новления TBi, i = 1, 2;□ tpi — время принятия решения по г'-й программе с плотностью распреде¬
ления вероятностью непринятия решения Fpi(t) и средним време¬
нем принятия решения Tpi, i = 1, 2;□ tД(- — допустимое время для принятия решения по i-й программе с плот¬
ностью распределения fai (t), вероятностью, что допустимое время превы¬
сит t, F^it) и средним ТЯ1, i = 1, 2.Восстановление любой из отказавших программ начинается только после
принятия решения по ней. Отказ наступает только в следующих двух ситуа¬
циях: произошел отказ обеих программ или время принятия решения после
отказа некоторой программы оказалось больше, чем допустимое, т. е. если
tpi > ?д/. На временной диаграмме отсутствуют интервалы, соответствующиедопустимому времени принятия решения, т. к. они не влияют на дальнейшую
эволюцию процесса. Действительно, если tpj > tai или tpi < tai восстановле¬
ние i-й программы начинается после окончания принятия решения, т. е. после
момента времени tpi.Согласно диаграмме мы имеем следующие состояния функционирования ПО:□ (0) — работает первая программа;□ (1) — произошел отказ первой программы, расходуется время на принятие
решения по первой программе, расходуется допустимое время;
510Гпава 12□ (2) — произошел отказ первой программы, расходуется время на принятие
решения по первой программе, допустимое время полностью израсходо¬
вано;□ (3) — происходит восстановление первой программы после принятия ре¬
шения, работает вторая программа;П (4) — произошел отказ второй программы, расходуется время на принятие
решения по второй программе, расходуется допустимое время, первая
программа восстанавливается;□ (5) — произошел отказ второй программы, расходуется время на принятие
решения по второй программе, допустимое время полностью израсходо¬
вано, первая программа восстанавливается;□ (6)— обе программы отказали, восстанавливается первая программа по¬
сле принятия решения (в силу принятого приоритета обслуживания).Аналогичные состояния имеют место при замене первой программы на вто¬
рую, а второй — на первую:□ (0) — работает вторая программа;□ (1) — произошел отказ второй программы, расходуется время на приня¬
тие решения по второй программе, расходуется допустимое время;□ (2) — произошел отказ второй программы, расходуется время на приня¬
тие решения по второй программе, допустимое время полностью израсхо¬
довано;□ (3) — происходит восстановление второй программы после принятия
решения, работает первая программа;□ (4) — произошел отказ первой программы, расходуется время на приня¬
тие решения по первой программе, расходуется допустимое время, вторая
программа восстанавливается;□ (5) — произошел отказ первой программы, расходуется время на приня¬
тие решения по первой программе, допустимое время полностью израсхо¬
довано, вторая программа восстанавливается;□ (6) — обе программы отказали, восстанавливается вторая программа по¬
сле принятия решения.Состояния (2), (5), (6), а также состояния (2), (5) , (6) являются отказовы-ми. Граф состояний работы ПО представлен на рис. 12.16.
Надежность информационных систем511Рис. 12.16. Граф состояний работы ПО для одного оператора-программиста
с прямым приоритетом12.9.3. Алгоритм решения
и показатели надежности ПОИз приведенного графа следует, что рассматриваемая система имеет 14 воз¬
можных состояний, и система уравнений, описывающая работу ПО, будет
содержать 14 интегральных уравнений.Мы ограничимся здесь изучением только стационарного режима функциони¬
рования. По графу, изображенному на рис. 12.16, составим систему уравне¬
ний для описания стационарного режима функционирования:00^o(Ji)= J>>3 (О, X+ *,)<&;
о00 00У\ (sp\ > 5д1) = \fp\ (* + sp\ )/д1 (* + 5д1 )Уо (°№ + \у* (°’х + spi >х + 5д1
о о00 00Уг^Р\)= + f>t(°»Jf + ,pi)dr»уъ(т 1,J2)= ^1 )/2 (JC + -^2 ) /л(0.^д1)*д1 У 2 (°) Ув (°)о Чоdx;
512Глава 1?У4 (Х1»sp2 > sn2 )= jfp2(x + s p2 )fp2 (x + sm2 )Уз (x + Ti » 0)dx;
оoOMxl>sp2)= fy4(x + 'tl’x + sp2’°)dx'’0OO 00 OOУ6 (Ti) = J 1У4 (x + h> 0, 5д2 )dxdsД2 + j>5 (x + X,, 0 )dx.0 0 0Похожие уравнения имеют место и относительно других функций.00•УоС*2)= |7з(0,л + ^2)^;о ■'*'00 00■Уу (sp2»^д2 ) = jfP2(x + Sp2)fja(x + Sa2)y0^dx+ Iy4(°’x + Sp2’x + Sa2.)dx’
О 0СО 00Уг (Sp2 ) = 1у\ (* + sp2>°)dx + f >>5 (°> * + sp2 )dx\OO GO>^(T2.sl)= Ja(* + x2)/l(* + sl) |>г(0'5д2)Лд2 +^(°) + >;б(0)0 U00У4 (x2 » spl. 5д1) = j /pi (* + )/д1 (* + ^д] )У$ С* + *2>0)dr,000^(^2^/71)= |^(х + т2,дс + Spl,0)dx;000 00 00
>*6(^2) = J ]>*(* +*2 + Jyj(x + b’°)dx-dx;Решение приведенной системы уравнений несложно. Положим00 00А= /л(0,5д1)Лд1 +^2(0) + ^(0), В= J^T (0, 5д2 )<*д2 + ^2 (0) + (0).о оТогда из системы получим:00 00ЖХ1>Ъ) = А \gx(x + xx)f2(x + s2)dx, y1(x2,sl) = B jg2(x + x2)f{(x + sl)dx,о о
Надежность информационных систем513и значит:00 00= )&2 (x)dx» Уо (s2 ) = А р2 (* + *2 )Sl С■О оДалее последовательно находим:ООООУ4 (Ti»■sp2 >s&) = А J Ml (х + « +1] )fP2 (X + sp2 )/д2 (дг + s# )/2 (a)dxda,О о00 00 00У5 (Ti»'sp2 ) = А JJJsi Сх + а + р+ т, )fp2 (* + а + sp2 )/д2 (а)/2 ($)dxdad$,
ООО00 00 ооооУ в (Ti) = А J J J J#i (х + а + (3 + т, )fp 2 (а)/д2 (х + )/2 (р )dxdad^>dsB2 +ОООО00 00 00 00+ЛШ l&(x + a + P + Y + ti)/p2(a + Р)/д2 (Р)/г (y)dxdadpdy =ООООсо оо оо= Al\ Jgi(* + a + P+Ti)//>2(а)^д2(а)/г(V)dxdad$ +ОООоооооо+А (х + а + Y + h )fP2 (а)^д2 (а)/г (y)dxdady =ООО= АТJ А (а + Р+ Ti )fP2 («)/2 i$)dxdad$,
О ОилиУ6 (Т1) = А JG1С* + Х1 )/г * fp2 ix)dx.
оНайдем теперь функцию у1:ОО 'yi(.spl>sjKl)~ \fP\(x + sP\)/д 1 (* + 5Д1 )>0(°>*е +оОООО+ J J Л>1 (* + a + spi )/Д1^ + а + 5д1 )^з (a, 0)afo/ct =о о00г \ооdx.17 Зак. 3094
514Глава 12ПосколькуX СО СОУо(0) + j>3 (а,0)</а = B\Fx (x)g2(x)dx + В \(G2{ а + x)-G2(a))fl (a)da =0 0 оОО СО 00= B\FX (x)g2 (x)dx -B\(g2(a + x)-g2 (a)) Fx (a)da = В-В \g2( а + x)Fl (a)da =
оо оOO 00 00= В + В J/<j (a)dG2 (а + x)da = В - В JG2 (а + x)fx (a)da = В |С2(а + x)fx (a)da,о ooTOooУ\ (^l. 5д1) = B \fp\ (X + Sp 1 )/д1 (x + sM )G2 (a + *)/, (a)dadx .
оНайдем функцию y2:У2 (spi ) = BYf)fp\(x + a + sp\)/д! (a)G2 (« + P)/i (P)AJaJp +0 0 000 00 00+B\\jg2(* + a + ©fy (* + a + «pi )/Д1 (a)/i (p)^a^p.0 0 0Первый интеграл равенA JFP\ (« + SP\ )/Д1 (a)G2 (« + P)/i (p)rfajp,
ooа второй:оооо-Я J f ^,1 (a + Spx )G2( a + Р)/д1 (a)/i (руай?р +
о о00 00 00+B J J f/pi + a + )G2 (* + a + Р)/д1 (a)/l (Р>ЙИ/СИ/Р =ОООоооо= BWfp\(X + Sp\ )G2 (* + Э)^д1 (*)/l (Р«Ф
0 0ЗначитУ г (spi) = 5 J J /pi (* + sPi )G2 (x + a)Fa, (jc)/, (a)dxda .
о оТаким же образом определяются и остальные неизвестные функции в системе
интегральных уравнений. Здесь они не выписываются.
Надежность информационных систем515Интегрируя полученные функции по всем аргументам, определим вероятно¬
сти пребывания системы в каждом состоянии:00 00
р0 = В JF, (x)G2(x)dx, A \F2(jc)G, (x)dx,• о оР\~В lG2(x)(FplFax)*fx(x)dx, PY = A JG,)* f2(x)dx,
о 000 COp2 = В \G2(x)(FpXFaX)* fx(x)dx, p^=B \Gx(x)(Fp2Fn2)*f2(x)dx,
о о
00 00
ръ = A jGx (x)F2 (x)dx, />3 = 5 JG2 (jc)/; (x)fifr ,
о о
p4 = ^JG, (x\Fp2Fд2 ) * /2 (*)<&, Pt = В |G2 W(Fpl ) * /, (*)<&,
о оp5 = AjG^xXFp^)* f2(x)dx, p-5=B]G2(x)(FplFal)*Mx)dx,
о 000 oop6=AjGl (x)f2 *Fp2 (x)dx, pl=B\G2 (*)/, * FpX (x)dx.
о 0Из обозначений для А и В с помощью несложных преобразований следует,
что А = В. Таким образом, с точностью до постоянного сомножителя А по¬
лучены значения вероятностей состояний. Величина А определяется из ус¬
ловия нормировки:Кл+лО-1-/=оИз этого условия получим:_ N f - ЛАTBl + J(F, + fx *Fp0(x)G2(x)dx + А Тв2+ j(F2+f2*Fp2Xx)Gl(x)dxV о=1,\о )и, следовательно,/ ' ■ v-iОП 00А =Ть1+Тл+ j(Fx+fx *FpX)(x)G2(x)dx + j(F2+f2*Fp2Xx)Gx(x)dx\
516Глава 12Нетрудно показать, что для коэффициента А справедливо также и другое
выражениег со соА = Ту+ТрХ +Т2 + Тр2 + J(/, *FpX)(x)G2(x)dx + |(/2*^2)(*)ВДЛ
Vo о jИсходя из полученного решения системы интегральных уравнений, найдем
параметр потока отказов:СО = С0,2 + С045 + 0)4б + C0f2 + «45 + (0^ •Так каксо оо®12 = = А $G2(xXFp\fai)*Z(x)dx,О о00 00 00®45 = j \yA^\’Sp2Wdx\dsp2 =AjG\ (x){Fp2fja)* fi{x)dx,0 0 0
00 00 00
©46 = I J^Ov0,sn2)dxxdsa2 = A jG^xXf^Ftf)* f2(x)dx,0 0 0
00 00WT2 = \y-\(sp2^)dsp2 =AjGi(xXFp2fja)*f2(x)dx,
о 00000 00®45 = I \n(x2>sp\> °)d bdspl=A! G2 (x)(Fp! /д,) * /, (x)dx,0 0 000 00 OO®46 = 1 |>^(х2,0,5д! )dx2dsdl = A JG2(xXfpiFaX)*f\(x)dx ,о 0TO(° = A \Fp2(х)/д2 (x)dx + A \Fpl0)/д, (x)dx + A JG, (хХ/р2*д2) * f2 (x)dx -
о о 000+AlG2(x)(fplFAl)*fl(x)dx.оЗаметим, что для параметра потока восстановлений справедливо равенство:00шв = СО2з + ш6з + (023 + Ш63 = А 1G2 (x)(fp\Fa\) * f\(*)*& +о00 00 00
+A\GX(x)f2 * fp2(x)dx + A JG, (x)(fp2Fjg) * f2(x)dx + A JG2(x)f * fpX (x)dx,o o оа это, как нетрудно видеть, совпадает со значением со.
Надежность информационных систем517Теперь по определению показателей надежности находим наработку на отказ:
Т_. Ро + р1+рг + р4+Ро+Р\+Рг+Р4соТ\ + Т2 + [FplFja + \Fp\Fa\ о о \Pp2U + J^/д! + jG,(/2 •(/Р2^2))+ 1G2(/i *(/^д>))
О о о осреднее время восстановления:т : Р2 + Р5+Рб+Р2+Р5+Рб _вЮОО ОО ОО 00+ \Fp2Fu2 + JGl(/2/+^2)+ JG2(/,*^i)_ о о о о J W* + JfyAl +lgl(/2 *(Л.2^)) + ]о2(/, *(/,Л,))ООО ои коэффициент готовности:^ +72 + Р^д, + |^2-^д2К = Т П п• 7’ + 7; 7J+r2+rpl+r(,2+]Gl(/2.FJl2)+]G2(/,.f,1)12.9.4. Численные результатыПолученные аналитические результаты позволяют провести анализ надежно¬
сти ПО для двухверсионного программирования по любому из вычисленных
критериев. Мы ограничимся рассмотрением лишь коэффициента готовности
ПО. Будут рассмотрены два численных примера, рассчитывающих значение
коэффициента готовности в соответствии с приведенной ранее формулой.
В примерах предполагается, что время принятия решения одинаково для обе¬
их программ. То же предположение относится и к допустимым временам.
Тогда коэффициент готовности вычисляется по формуле:Т\+Т2+2 \FpFaКг=-Т1+Т2+ 2Тр + }G,(/2 * Fp) + |G2(/, * Fp)о о
518Глава 12Пусть случайные величины ^ и г|, имеют нормальное распределение веро¬
ятностей со средними 7] = 50 сек и Гв1 = 1 сек и средними квадратическими
отклонениями О] =0,5 сек и ав1 =0,3 сек соответственно; случайные вели¬
чины и Лг имеют нормальное распределение вероятностей со средними
Г2 = 100 сек и Тъ2 =0,5 сек и средними квадратическими отклонениями
о2 =1 сек и ств2 =0,1 сек соответственно. Далее в зависимости от изменения
времени принятия решения и допустимого времени мы рассмотрим следую¬
щие численные примеры.ПРИМЕР 12.3. Допустимое время принятия решения для обеих программ
одинаково и постоянно со средними Тл = 1—15 сек. Время принятия решения
для обеих программ также одинаково и имеет нормальное распределение с
математическим ожиданием Тр =10 сек и средним квадратическим отклоне¬
нием ор = кТр, где коэффициент к принимает одно из трех значений:
к = 0,1; 0,2; 0,3. Определить коэффициент готовности ПО.Решение. На рис. 12.17 представлена зависимость коэффициента готовности
от допустимого времени принятия решения для трех значений средних квад¬
ратических отклонений, а именно: 10% (кривая 1), 20% (кривая 2) и 30%
(кривая 3) от соответствующих математических ожиданий, что отвечает раз¬
личным значениям параметра к .1 ^д>сек '5Рис. 12.17. Зависимость коэффициента готовности
от допустимого времени принятия решенияКак и следовало ожидать, коэффициент готовности возрастает при увеличе¬
нии допустимого времени принятия решения, причем, начиная с некоторого
Надежность информационных систем519значения Гд, зависящего от к , величина коэффициента готовности не изме¬
няется (явление насыщения).ПРИМЕР 12.4. Допустимое время принятия решения для обеих программ
одинаково и постоянно со средним Тд =1, 5, 10, 20, 40 сек. Время принятия
решения для обеих программ также одинаково и имеет нормальное распреде-Тление с математическим ожиданием Тр = -—(это условие означает, что95% площади под кривой нормального распределения расположено левее
значения Гд ) и средним квадратическим отклонением ор = кТр . Таким обра¬
зом, имеет место одновременное увеличение как допустимого времени, так и
времени принятия решения. Определить коэффициент готовности ПО.Решение. Из рис. 12.18 следует, что при одновременном увеличении указан¬
ных времен коэффициент готовности уменьшается.Рис. 12.18. Взаимное влияние Тл и Тр на коэффициент готовностиОтметим также, что коэффициент готовности становится больше с увеличе¬
нием степени разброса случайных величин. Так, для кривых 1, 2, 3 средние
квадратические отклонения составляют 10, 20 и 30% от соответствующих
математических ожиданий.12.10. Анализ надежности
многофункциональных систем12.10.1. Формулировка задачиСложные технические системы с позиций надежности, как правило, характе¬
ризуются многофункциональностью [57, 115]. Количество выполняемых сис¬
520Глава 12темой функций может достигать нескольких десятков. При этом в реализации
одной функции может участвовать большое количество модулей (элементов).
Один и тот же модуль может быть задействован в выполнении нескольких
функций. Поэтому модули, образующие систему, имеют различную длитель¬
ность эксплуатации. Так, некоторые из них работают непрерывно, поскольку
участвуют в выполнении всех функций, а некоторые модули включаются
только на время выполнения какой-либо одной или нескольких функций.Многофункциональность накладывает определенный отпечаток на форму
постановки задач анализа надежности такой системы. При изучении надеж¬
ности систем, выполняющих несколько функций, обычно применяется функ¬
циональный подход, при котором описание надежности производится по
каждой функции в отдельности, и поэтому надежность системы характеризу¬
ется вектором показателей надежности всех ее функций. Таким образом,
сравнительная оценка различных систем одного и того же назначения часто
является затруднительной, а то и вовсе невыполнимой. Основной слож¬
ностью в исследовании многофункциональных систем, на наш взгляд, явля¬
ется то обстоятельство, что исследования проводятся без учета потока задач,
поступающих в систему. В этом случае анализ надежности системы, функ¬
ционирующей по нескольким функциям, неоднозначен, а возникающая при
этом неопределенность без какой-либо дополнительной информации не под¬
дается измерению. Выходом из этой тупиковой ситуации может служить ис¬
следование системы вместе с потоком задач, поступающих на обслуживание.
Без учета потока задач можно говорить о временах использования системы
по каждой функции и исследовать ее надежность с учетом времен выполне¬
ния системой всех ее функций.Будем говорить, что некоторая функция активна, если работают или восста¬
навливаются модули, обеспечивающие работу данной функции. Остальные
функции будем называть пассивными, несмотря на то, что некоторые модули,
отвечающие за эту функцию, при наличии восстанавливающего органа могут
ремонтироваться.Задача анализа надежности многофункциональной системы может быть
сформулирована следующим образом. В систему поступает поток задач п
различных типов. Система предназначена для обслуживания данного потока
задач и может выполнять п функций, соответствующих приходящим заяв¬
кам. Все оборудование, имеющееся в системе, может быть разбито на моду¬
ли, которые включаются в работу по мере необходимости для выполнения
соответствующей функции. Предположим, что модуль с номером
(1 < к < п) задействован только в выполнении функций с номерами
/[, /2,..., ik и не участвует в i-й функции, если i отлично от ij, i2,..., . Та¬
ким образом, общее количество модулей, предназначенных для обслужива¬
ния заявок п типов, может достигать (2" -1). Фактически это значение мо¬
Надежность информационных систем521жет быть гораздо меньше. Так, если в системе имеются модули, предназна¬
ченные для выполнения каждой функции в отдельности, а один модуль уча¬
ствует в выполнении всех функций, то эти модули могут быть обозначены
номерами /2,..., > и общее число модулей равно (я +1).Будем считать, что времена выполнения каждой функции детерминированы
или случайны с известными законами распределения. Пусть /« — время вы¬
полнения системой i-й функции перед переходом на выполнение j-й функции.
При этом будем считать, что указанный переход может происходить как во
время исправной работы всех модулей, отвечающих за работу г'-й функции,
так и во время восстановления некоторых модулей. Обозначим через Тусреднее время выполнения системой i-й функции до перехода к выполнению
j-й функции, а через fy(t) — соответствующую плотность распределения ООвероятностей, Fу (t) = j fy (J + x)dx.0Обратим внимание на большое разнообразие особенностей функционирова¬
ния и обслуживания многофункциональных систем. Возможны, например,
следующие варианты поступления заявок в систему:□ заявки поступают строго по очереди; таким образом, имеет место после¬
довательное чередование заявок разных типов;П заявки поступают и обслуживаются системой случайным образом в про¬
извольном порядке.Далее мы ограничимся изучением ситуации только первого вида. Модули,
отвечающие за работу той или иной функции, могут иметь различную струк¬
турную схему расчета надежности. Мы рассмотрим только случай, когда
структура каждой функции представляет собой основное соединение. После
выхода системы из работы по некоторой функции все модули, ответственные
за работу по следующей функции, могут:□ "забыть" прошлое и начать работать сначала;□ продолжить работать с того состояния, в котором была прервана их ра¬
бота.Мы рассматриваем здесь случай, когда система "не забывает" прошлое свое
состояние. Возможна также различная дисциплина обслуживания заявок, по¬
ступивших в систему, а в случае образования очереди также и различный
приоритет их обслуживания.Законы распределения времени безотказной работы и времени восстановле¬
ния модулей могут быть, вообще говоря, произвольными, однако для просто¬
522Глава 12ты мы рассмотрим только случай экспоненциальных распределений. Времена
переходов с выполнения одной функции на другую могут иметь любые рас¬
пределения вероятностей.Многофункциональная система с учетом времени выполнения каждой функ¬
ции может быть проанализирована по различным критериям, общепринятым
в теории надежности. При этом может рассматриваться как стационарный,
так и нестационарный режимы функционирования. Здесь мы ограничимся
расчетом коэффициента готовности системы.12.10.2. Описание работы
двухфункциональной системыДалее рассмотрим только случай п = 2. Предположим, что в двухфункцио¬
нальную систему (рис. 12.19) поступает поток заявок двух типов, каждая из
которых обслуживается своей функцией. В первой функции задействованы
модули с номерами 0 и 1, а во второй — модули с номерами 0 и 2.Рис. 12.19. Структурная схема двухфункциональной системыТаким образом, при поступлении любой заявки в систему модуль с номе¬
ром 0 работает постоянно, а модули с номерами 1 и 2 включаются лишь при
поступлении заявки соответствующего типа, при этом заявка первого типа
обслуживается первой функцией, а заявка второго типа — второй функцией.
Интенсивность отказов и интенсивность восстановления /-го модуля обозна¬
чены через Xj и ц, соответственно, / = 0,1, 2.Опишем работу двухфункциональной системы в случае ее обслуживания од¬
ним ремонтником с назначенным приоритетом, а именно: при возникновении
очереди первыми восстанавливаются модули, входящие в состав активной
функции; если в очереди оказались модули активной функции, то первым
восстанавливается модуль с номером 0, участвующий в выполнении обеих
функций. На рис. 12.20 приведен граф состояний, левая часть которого соот¬
ветствует случаю, когда активной является первая функция, а правая часть —
случаю, когда активной является вторая функция.
Надежность информационных систем523Рис. 12.20. Граф состояний двухфункциональной системыНа графе проставлены переходы из каждого возможного состояния первой
функции в соответствующие состояния второй функции, а также обратные
переходы. Перечислим все состояния графа для активной первой функции:□ (0) — модули 0, 1 и 2 исправны;□ (1)— восстанавливается модуль 0, модуль 1 выключен из работы, модуль
2 исправен;□ (2)— восстанавливается модуль 1, модуль 0 выключен из работы, модуль
2 исправен;□ (3) — модули 0 и 1 исправны, модуль 2 восстанавливается;□ (4) — восстанавливается модуль 0, модуль 1 выключен из работы, модуль
2 неисправен;□ (5)— восстанавливается модуль 1, модуль 0 выключен из работы, модуль2 неисправен;□ (6)— неисправны модули 0 и 1, восстанавливается модуль 0, модуль 2
исправен.Аналогичные состояния (обозначаемые теми же номерами, но с чертой свер¬
ху) имеют место и для второй активной функции.Между состояниями / и i имеются следующие двусторонние переходы:0<-»0, lo 1 , 2<->3, 3<-»2, 4<-»6, 5<->5, 6<-»4. Эти переходы показаны
на графе. Если предположить, что заявки поступают и обслуживаются систе¬
524Гпава 12мой в произвольном порядке, то тогда существуют также переходы из каждо¬
го состояния / в состояние i , обусловленные повторным выполнением пер¬
вой функции, а из каждого состояния i имеется переход в состояние i, обу¬
словленный повторным выполнением второй функции. Эти переходы отсут¬
ствуют на графе, но их необходимо учитывать при составлении системы
уравнений.Примем следующие обозначения. Пусть уДл) (y-t(s))— плотность распре¬
деления вероятностей, что при длительной эксплуатации система будет нахо¬
диться в состоянии / (/•), и, начиная с произвольного момента времени, для
перехода на новую функцию остается время s . Тогда стационарные вероят¬
ности пребывания системы в состояниях / и i вычисляются как
00 00Pi = \yi(s)ds и р-. = соответственно. Положим также, что 6, =j,(0),о оЬ-.=у.( 0).Используя общую идею описания функционирования системы частично
с произвольными, а частично с экспоненциальными распределениями (см.
разд. 4.6), получим уравнения, соответствующие активной первой функции:GOУо СО = J е~а°+Х| )JC (р07, (х + s) + ц, у2 (х + s) + \х2уг (x + s) + b^fx2(x + 5)) dx\
о00Ж5) = je~Ц(>Х (k0y0(x + s) + bjfl2(x + 5))й6с;
о00У2& = КЦ|ДГ (Vo(*+s)+шлО+s)+bifni*+■*))<&;о• Уз(*)= K(X°+X|+,i2)"r(po^4(^ + -!f) + lIiJ;5(JC + s) + ^/i2(;v: + s))^ (12.57)о00У4 О) = КИоДС (^0^3 О + 5) + 2 (* + s)) dxr,
о00У5 (5) = J е^'х (^1 Уз (x + s) + b-5fl2(x + s)) dx;О00.УбО)= le~^xb-4fn(x + s)dx.
о
Надежность информационных систем525Аналогичные уравнения имеют место, когда активной является вторая функ¬
ция. Запись этой части системы уравнений мы опускаем.12.10.3. Решение системы уравнений
и оценка коэффициента готовностиРешение системы уравнений будем искать в виде6 ®.У/00= X bj \aij(x)fn(x + s)dx,
7=0 о^(■s) = £ bj \alj(x)f2X{x + s)dx,j=о о(12.58)(12.59)где ay(x) и atj(x) — вычисляемые функции. Можно показать, что коэффи¬
циенты ау(х) разложения (12.58) являются элементами матрицы:Ф ЦоФо*Ф ЦгФ * Ф Hi9i*VА.0Фо*Ф ^“оМ'оФо(2) * Ф + Фо ^-о^гФо *Ф*Ф >-оШФо*Ф1*ФХ,Ф,*Ф А.,ЦоФо * ср, * Ф ^ц2ф,*ф*ф ^щф^+ф + ф,
о 0 Ф о0 0 Я0ф0 * ф 0О 0 Я,[ф] *ф о0 0 0 0Цо1^1Фо*Ф1*Ф^оИФо(2)*Ф1*Ф^ЦоШФо * Ф1(2) * Ф + ЦоФо * Ф1
ОООФоЦ1(12Ф1*Ф*Ф ЦоЦгФо * ф * ф
^оМ-1Ц2Фо*Ф1 *Ф*Ф ^о^2Фо2) *Ф*Ф?ч№Ф1(2)*Ф*Ф ^Ц0Ц2Ф0*Ф1 *Ф*Фц,Ф1*Ф Р0Фо*Ф^1Фо*Ф1*Ф ^оФо2)фФ + Фо^1Ц,ф|(2) *Ф + Ф, ?ЦЦ0Ф0*Ф,*Фооздесь используются обозначения: ф0(х) = е Ф1 (д:) = е ^, а функции ф и
ф в изображениях имеют вид:
526Гпава 12ф(г) = •1Z + А,0 + + fj_21--1z + X,q + A,j + \х2
1^OM’O\ ’l^Z + Цо Z+jljZ + “t" A,1z + A.0 + A/|^z + p0 z + ViJАналогично мы можем найти также и все функции а^(х), являющиеся эле¬
ментами матрицы А . Полагая затем в (12.58) и (12.59) 5 = 0, получим од¬
нородную систему уравнений относительно коэффициентов 6, и Ь-:Ъ1 - X Ь-. !ау(х)/12(х)сЬ;
У=о оbj = X bj l^ij(x)f2\(x)dx.
7 = 0 О(12.60)Сумма элементов матрицы А (а также и матрицы А) в каждой строке равна
единице:6 6 _ .X aij = X aij =1 при J = 0,1,..., 6 ./=о/ = 0Поэтому следствием из системы (12.60) является равенствоб 6I *.,= 167=4.
j.o ;.оОтсюда вытекает, что система (12.60) имеет ненулевое решение, которое оп¬
ределяется с точностью до постоянного множителя, определяемого из усло¬
вия нормировки (сумма вероятностей всех состояний равна 1). Интегрируя
теперь соотношения (12.58) и (12.59), получим с точностью до того же посто¬
янного множителя значения вероятностей состояний двухфункциональной
системы:6 со _ 6 ооPi - X bj ja,j(x)Fn(x)dx, pT=Ydbj \aiJ(x)F2x{x)dx.7=0 0 7=0 0
Надежность информационных систем5276 6При этом Yj Pj =ЬТп, X Pj =ЪТгх. Поскольку исправными являются со-/=0 ы остояния (0), (3), (0), (3), то отсюда следует, что коэффициент готовности
системы выражается отношением:2 bj J(%W + a3yW)^i2W^ + S bj J(%W + 53yW)^2iW^K ^ j = о 0 7=0 0 b(Tl2+Tn)12.10.4. Численный примерПроведем расчеты коэффициента готовности двухфункциональной системы
с последующим его анализом и установлением зависимости от параметров
А,0, А1, Я,2, ц0’ М-i» Й2 и распределений случайных величин /12 и f2i-ПРИМЕР 12.5. Коэффициент готовности системы вычислим для следующих
данных: Д.0 =0,05 час-1, Xj = 0,1 час-1, Х2 = 0,2 час-1, ц0 = щ = ц2 = 1 час'1
при постоянных временах Тп и Г21 выполнения функций. Установим зави¬
симость Кт от Тп для трех фиксированных значений Г21, равных 0,1 час,0,5 час и 0,9 час соответственно. Установим зависимость Кг от Г21 для трех
фиксированных значений Тп, равных 0,2 час, 0,8 час и 1,6 час соответст¬
венно.Решение. Соответствующие графики приведены на рис. 12.21 и 12.22.Рис. 12.21. Зависимость коэффициента готовности от Тц
528Гпава 12Рис. 12.22. Зависимость коэффициента готовности от 721Получены также оптимальные значения параметра Тп (Т21) и максимальные
значения коэффициента готовности, которые приведены в табл. 12.8 и 12.9
соответственно.Таблица 12.8. Оптимальные Таблица 12.9. Оптимальныезначения Г|2 значения ТгхТ21, часУ/Yr, макс7*12, опт, час0,10,8860,470,50,8891,310,90,8861,86Т\ г, час*г, макс721. опт, час0,20,8840,080,80,8900,381,60,8880,60Программа, разработанная авторами на основе приведенного ранее алго¬
ритма, позволяет также решать оптимизационные задачи по критерию
, Г21) —> шах. Установлено, что для принятых ранее исходных данных
наибольшее значение коэффициента готовности, равное 0,890256, достигает¬
ся при 7)2 = 0,83 час и *21 = 0,36 час.Таким образом, исследование надежности многофункциональных систем
может проводиться подобно системам с одной функцией. На основе метода
интегральных уравнений можно проводить анализ надежности этих систем
при произвольных распределениях времени перехода между состояниями,
отвечающими за работу каждой функции.L
Надежность информационных систем52912.11. Анализ эффективности
систем управления при многофазном
режиме функционированияПри проектирований сложных управляющих комплексов встает задача обес¬
печения требований как по точности и качеству управления, так и по надеж¬
ности и эффективности их функционирования. При этом анализ надежности
и эффективности систем в большинстве случаев осуществляется на основе
синтезированной структуры системы без учета всего жизненного цикла ее
функционирования. Трудности анализа обусловлены отсутствием в настоя¬
щее время общепризнанных критериев оценки эффективности систем с уче¬
том всего жизненного цикла их функционирования. Полный жизненный цикл
систем составляет множество повторяющихся периодов эксплуатации. При
этом для большого класса систем любой ремонт или восстановление возмож¬
ны только между периодами эксплуатации. Во время эксплуатации восста¬
новление не допускается, и система функционирует по своему прямому на¬
значению.Особенность функционирования систем обеспечения безопасности и проти-
воаварийных систем состоит в том, что, находясь в режиме постоянного
функционирования, они контролируют состояние объекта управления, не
производя на него никаких воздействий до возникновения аварийных ситуа¬
ций. При возникновении аварийной ситуации они должны оперативно ее рас¬
познать и сформировать управляющие воздействия по ее предотвращению.Для выполнения возложенных на систему функций она должна периодически
получать сигналы с датчиков физических параметров объекта, на их основе
оценивать вектор состояния объекта и область его допустимых значений, оп¬
ределять принадлежность вектора состояния области допустимых значений и
только при его выходе из допустимой области формировать противоаварий-
ные воздействия.Каждый период эксплуатации таких систем — это последовательность чере¬
дующихся между собой фаз по опросу и оценке состояния объекта, а сами
системы — это сложный комплекс взаимосвязанных подсистем и устройств,
каждая из которых удовлетворяет определенным техническим требованиям и
обладает собственными показателями надежности, контролируемости и вос-
танавливаемости на каждой из фаз. Основной целью функционирования та¬
ких систем является формирование управляющего воздействия при возник¬
новении аварийной ситуации. В этих условиях за критерий оценки эффектив¬
ности функционирования системы, учитывающий весь ее жизненный цикл,
может быть принята вероятность выдачи противоаварийного воздействия при
выходе вектора состояния объекта из допустимой области в любой момент
времени на периоде эксплуатации системы.
530Глава 1212.11.1. Модель функционирования системыРассматриваемый класс систем представляет собой сложный комплекс взаи¬
мосвязанных подсистем и устройств, среди которых можно выделить как ми¬
нимум три подсистемы: подсистему сбора информации (с,), подсистему об¬
работки информации и формирования сигналов управления (с0) и подсисте¬
му выдачи управляющих воздействий (с2) ■ Подсистема сх включает в свой
состав набор датчиков, коммутаторов, блоков кодирования информации
и т. д., обеспечивающих формирование вектора наблюдений 7(0 за состоя¬
нием управляемого объекта. Подсистема с0 представляет собой вычисли¬
тельный комплекс, который управляет процессом опроса и приема информа¬
ции о векторе Y(t), на его основе оценивает вектор состояния управляемого
объекта X(t) и область его допустимых значений Q(x,t). При значениях
X(t), принадлежащих Q(x,t), никаких управляющих воздействий на объект
не производится, и подсистема с2 в работу не включается. При выходе
Хкр(0 из Q(x,t) подсистема с0 формирует вектор управлений Um, посту¬
пающий на подсистему с2 . Подсистема с2 служит для формирования проти-
воаварийных управляющих воздействий на объект управления и в ее состав
входят исполнительные механизмы, вспомогательные подсистемы (электро¬
снабжения, гидравлики и т. п.), датчики положения исполнительных органов,
локальные регуляторы и т. д. Обобщенная функциональная схема данного
класса систем управления приведена на рис. 12.23.Рис. 12.23. Функциональная схема системы управленияОсобенностью функционирования рассматриваемого класса систем является
то, что их жизненный цикл представляет собой последовательность чере¬
дующихся между собой однотипных фаз длительностью (?J+, - г,) (рис. 12.24).
На каждой из фаз можно выделить как минимум два этапа. На первом этапе
определяется текущий вектор наблюдений состояния объекта управления Y(,
Надежность информационных систем531При этом в функционировании системы задействованы только две из трех
подсистем, а именно с0 и с1. На втором этапе подсистема с0 на основе век¬
тора наблюдений Y(t) оценивает состояния управляемого объекта Xt , а
подсистема с2 находится в режиме готовности к приему UKp и началу функ¬
ционирования при достижении Xt, критических значений Хкр с целью из¬
менения состояния исполнительных органов для предотвращения аварийной
ситуации.у,,4 -tt-.С0> СI С0> с2 у 1опрос управлениеК Уlo (\ h li *i+iРис. 12.24. Многофазный двухэтапный жизненный цикл системыОтличительной чертой данных систем является то, что подсистема с0 нахо¬
дится в постоянной работе, подсистема с, периодически включается в работу
под управлением с0, а подсистема с2 , находясь практически весь свой жиз¬
ненный цикл в состоянии готовности, может так и не вступить в работу. Вме¬
сте с тем при возникновении аварийной ситуации подсистема с2 должна не¬
медленно включиться в работу, что накладывает на нее высокие требования с
точки зрения надежности ее функционирования.Мы предполагаем, что каждая из подсистем удовлетворяет требуемым техни¬
ческим показателям по точности, качеству, быстродействию и т. п., но обла¬
дает собственными показателями надежности, возможностью контролируе¬
мости и восстанавливаемости на каждом из этапов. В этих условиях актуаль¬
ной является разработка критерия оценки эффективности функционирования
системы, учитывающего весь ее жизненный цикл как последовательность
чередующихся между собой фаз, что позволит проводить сравнительный
анализ различных вариантов структур построения систем данного класса.12.11.2. Критерий эффективностиПериод эксплуатации системы состоит из чередующихся этапов, каждый из
которых на временной диаграмме (см. рис. 12.24) занимает некоторый интер¬
вал времени. Интервалы с нечетными номерами будем называть интервалами
опроса, а интервалы с четными номерами — интервалами управления. Пусть
интервалы Vx, V2,..., V„ — это интервалы опроса, а Wx, W2,..., Wn — интер-%±•оJLопрос управлениеУ, W,С0> С1'<1iхн_±_С0> С2опрос управлениеV, W,
532Глава 12валы управления. Сумма Т = Vx + V2 +... + V„ + Wx + W2 +... + Wn является пе¬
риодом эксплуатации системы. Случайные величины Vt и Wt предполагают¬
ся независимыми, их законы распределения считаются известными, а Л,,i -1, 2,..., 2п — соответствующие плотности распределения вероятностей.Рассматривается следующая модель функционирования системы управления.
В начальный момент времени она полностью исправна, а затем в процессе
эксплуатации отдельные подсистемы могут отказывать и восстанавливаться.
Обозначим через f,(t) и (t) — плотности распределения времени безот¬
казной работы и времени восстановления подсистемы с,, i = 0,1, 2. Подсис¬
тема с0 находится в постоянном функционировании, а подсистема сх функ¬
ционирует только на нечетных интервалах. Подсистема с2 находится в ре¬
жиме постоянной готовности к выдаче управляющих воздействий на объект.
Эти подсистемы могут восстанавливаться только по истечении текущего пе¬
риода эксплуатации.Эффективность системы управления может оцениваться по целому ряду по¬
казателей, среди которых мы выберем лишь тот, который в наибольшей сте¬
пени отвечает поставленной цели. А именно, предположим, что целью про-
тивоаварийной системы управления является локализация аварийной ситуа¬
ции путем формирования противоаварийных воздействий на каком-либо из
интервалов управления.Исходя из этого, мы будем рассматривать следующий критерий эффективно¬
сти (Г): вероятность, что в течение периода эксплуатации объекта любая
аварийная ситуация будет успешно устранена, т. е. при возникновении ава¬
рийной ситуации подсистемы с0 и с, будут исправны, а подсистема с2 смо¬
жет успешно функционировать в течение времени, достаточном для предот¬
вращения аварийной ситуации.Величина критерия зависит от надежности подсистем, составляющих систему
управления, и способов их комплектования в единое целое, а также от веро¬
ятностных характеристик случайных времен пребывания системы в состоя¬
ниях опроса и управления. Критерий Г можно считать обобщенным, по¬
скольку он учитывает как надежность системы, так и условия ее эксплуа¬
тации.Анализ функционирования системы в соответствии с выбранным критерием
зависит от следующих факторов:□ условия соединения или условия совместной работы оборудования на всех
этапах жизненного цикла;□ понятия отказа системы;
Надежность информационных систем533□ дисциплины обслуживания отказавших устройств;П законов распределения времен нахождения объекта на интервалах опроса
и управления.Для получения численных оценок критерия Г мы сначала определим законы
распределения времени безотказной работы подсистем с0 и сх на одном пе¬
риоде эксплуатации.12.11.3. Описание функционирования системы
в нормальном режиме эксплуатацииПри нормальном функционировании объекта период эксплуатации состоит из
этапов опроса и управления. На каждом этапе опроса совместно с с0 функ¬
ционирует подсистема с,, а с2 находится в состоянии простоя. При повтор¬
ном включении оборудования сх на очередном этапе его функционирование
начинается с того состояния, которое было достигнуто на предыдущем этапе.
Оборудование С] работает только на нечетных интервалах, поэтому из со¬
стояний (1), (3),..., (2и-1) с нечетными номерами может произойти переход
в отказовое состояние. В состояниях (2), (4),..., (2п) с четными номерами
оборудование с, простаивает. Граф состояний представлен на рис. 12.25.Рис. 12.25. Граф состояний для нормального режима функционирования (п = 2)Пусть ha и hb — плотности распределения времени пребывания объекта со¬
ответственно на всех интервалах опроса и управления в течение периода экс¬
плуатации системы. Очевидно, что ha=hl*hi*... * h2n_x, hb = * h4 *... * h2„,
обозначим h = ha*hb.Введем неизвестные функции: .УгыС5»5]»*) (j2((5’sl’0)» » = 1,... ,и — плот¬
ность распределения вероятностей времени пребывания системы в момент t
534Гпава 12на i-м интервале опроса (управления) при условии, что после момента ( дли¬
тельность этого интервала будет больше, чем s, и оборудование сх будет
исправно еще в течение времени s,.Исходя из описания процесса функционирования и графа состояний, можно
составить следующую систему интегральных уравнений относительно этих
функцийIУ\ (s, ,0 = рг, (х + s)^,, (0,* + s,, t - x)dx + hx(t + s)fx(t + Sj);
оt' >j2m(-s»si»0= + + / = 2,3,..., n; (12.61)0/yu(s,s 1,0= \h2i(x + s)y2i_x(d,sx,t-x)dx, / = 1,2,..., n.0Докажем, что система уравнений (12.61) имеет следующее решение:i,0= f, (K[k)*h\ 2k=0V ’^2<(J. Ji.O = X (ha(k) * W-*h2i_xfx ) * h*b(k) *h2* ...*h2is(t).* =0 ’Обозначим для краткости через А свободный член первого уравнения систе¬
мы (12.61). В результате последовательного исключения из этой системы
всех функций, кроме функции ух, получим следующую цепочку равенств:/ t-xЛ(5,ли0= J J hxs(x)h2n(a)y2n_x(0,x + sx,t-x-a)dadx + А =
о оtt-x t-x-a= JJ J y2n-2(0,x + $ + sx,t-x-a-p)d$dacbc + A =0 0 оtt-x t-x-a= J J^U*^2«-l(*)^2n(a) j h2n_2($)y2n_i(0,x + sx,t-x-a-$)d$dadx + A =0 0 0
tt-x= J J Ks *h2n^(x)h2n*h2n_2(a)y2n_3(0,x + sx,t-x-a)dadx + A =
о 0t t-x= J J Ks *^2«-i *-*h3(x)h2n *h2n_2 *...*h1(a.)yx(b,x + sx,t-x-a)dadx + A.
о 0
Надежность информационных систем535Таким образом,У\ (s,s{,t) = || hls * Л3 *... * *2„_! (x)Ji2 *... * /*2„(a)y{ (0 ,x + sXtt-x- a)dadx +Решение последнего уравнения можно получить, например, методом итера¬
ций с доказательством справедливости бесконечного перехода методом ма¬
тематической индукции. Тогда получим решение в виде:В справедливости полученной функции можно убедиться также с помощью
подстановки. Зная ух, из системы (12.61) определяются и все остальные
функции.Полученное решение позволяет записать формулы для вероятностей пребы¬
вания системы в каждом исправном состоянии:Особенно важным является частный случай, когда все распределения времен
пребывания на этапах опроса и управления детерминированы, т. е.функция Хевисайда. Обозначим через a - хх+ х3 +... + x2n+i сумму длитель¬
ностей интервалов опроса, через Ь = х2+х4+...+ х2п — сумму длительностей
интервалов управления, к = 0,1, 2,... —порядковый номер периода эксплуа¬
тации системы. Можно показать, что функция распределения времени до от¬
каза системы, состоящей из оборудования сх, включаемого в работу только
на нечетных интервалах, представляется следующим образом:х+ай1+hx(t + s)fx(t + s,).к = оFx(t-kb-х2 —— x2i_2 ),при к(а + Ь) + хх +... + x2i_2 к(а + b) + jc, +... + x2j_x;(12.62)Fx(ka + xx +... + x2j_x),при k(a + b) + xx +... + x2j_x < t < k(a + b) + xx + ... + x2i.
536Гпава 12Теперь нетрудно определить распределение времени жизни системы, состоя¬
щей из оборудования с0 и с,. Поскольку эта система образует основное со¬
единение, то вероятность безотказной работы равнаF°(t) = F0(t)F{l)(t).Соответствующую плотность распределения будем обозначать через /°(0.12.11.4. Описание модели функционирования
системы при возникновении аварийной ситуацииВ произвольный момент времени £ поступает сообщение о наступлении ава¬
рийной ситуации. В этот же момент включается подсистема с2, предназна¬
ченная для локализации аварийной ситуации в течение некоторого времени
г) и возвращения объекта в нормальный режим функционирования. Длитель¬
ности £ и т] предполагаются случайными с плотностями распределения
/(/) и g(t) соответственно. Плотность распределения времени X безотказ¬
ной работы подсистемы с2 обозначим через f2(t), а вероятность безотказной
работы— через F2{t). Для удобства последующего математического описа¬
ния введем еще одну случайную величину — длительность периода эксплуа¬
тации объекта Т с плотностью ff(t) и вероятностью безотказной работыFT( t).Согласно принятому ранее критерию качества системы предполагается, что
на одном периоде Т может не быть ни одной аварийной ситуации, а может
быть и несколько аварийных ситуаций.Опишем возможные состояния системы:□ (0) — сообщение об аварийной ситуации не поступило, все оборудование
исправно, причем с0, сх функционирует, а с2 находится в ненагруженном
резерве;□ (1) — поступило сообщение об аварийной ситуации, оборудование с0, сх,
с2 исправно функционирует;□ (2) — сообщение об аварийной ситуации не поступило, произошел отказ
оборудования с0 или Cj, с2 находится в ненагруженном резерве;□ (3) — закончен период эксплуатации объекта в то время, когда он нахо¬
дился в состоянии (0);□ (4) — закончен цикл эксплуатации объекта в то время, когда он находился
в состоянии (1);
Надежность информационных систем537□ (5) — закончен цикл эксплуатации объекта в то время, когда он находился
в состоянии (2);□ (6) — произошел отказ оборудования с0 или Cj во время устранения ава¬
рийной ситуации;□ (7) — поступило сообщение об аварийной ситуации после отказа оборудо¬
вания с0 или с{;□ (8)— произошел отказ оборудования с2 во время устранения аварийной
ситуации.Граф состояний приведен на рис. 12.26.Будем считать, что отказ объекта наступает при следующих обстоятельствах:
или произошел отказ любого вида оборудования во время устранения ава¬
рийной ситуации, или наступила аварийная ситуация после выхода из строя
какого-нибудь оборудования. Отказовыми являются состояния (6), (7) и (8).В качестве математической модели объекта рассмотрим систему интеграль¬
ных уравнений:Рис. 12.26. Граф состояний функционирования объектаty0(s,s0,s2,sT,t) = jf(x + s)yl(0,x + s0,s2,x + sT,t-x)dx +о+f(t + s)f° (/ + 50 )fl (s2 )/t (t + ST );yl(x,s0,s2,sT,t)= lg(x + T)y0(0,x + s0,x + s2,x + sr,t-x)dx;0ty2 (s, 0, s2 ,sT, t) = JjFo (X + s, 0, s2, x + sT ,t - x)dx;
о(12.63)
538Глава 12y3(s,s0,s2,0,t) = ly0(s,s0>s2,0,t-x)dx-, (12.63)0
tУ A (T> so»s2»0» 0 = J^l (T> so >s2>0 ,t- x)dx\0ty5(s,0,s2,0,0 = jy2(s,0,s2,0,t -x)dx;
о1y6(x,0,s2,sr,t)= lyl(x,0,s2,sT,t-x)dx;
о
tyn (0,0, s2, sT, t) = jy2 (0,0, s2, sT ,t - x)dx;
о
t^8 (t, So, 0, ST ,it) = \yx (x, s0 ,0, sT,.t - x)dx.0Введем обозначения:k=04>(s,s2,t) = fs(t)*<pQ(s2,t),фо(0 = ]фо(^2»0^2 = I f'(k) *(gHk)F2)(t), (12.64)0 k=0ооооф(0 = J j(p(s,s2J)dsds2 =F*y0{t),
о 04>(T,s2,t)= 5 fHM)*(g4k)*gJ2,s2)(0,
k = 0Ф(0= jj4>(t^2»0^2 = S /*(i+1) *(g'{k]*GF2)(t). (12.65)
0 0 * = 0Чтобы найти решение системы (12.63), подставим ух в первое уравнение:t t-xy0(s,s0,s2,sT,t)= |/(x + 5) | g(a)>'0(0,Ar + a + 50,a + 52,^ + cc + 57’,/-^-a)<i(X£& +0 0+/Q + s)f°(t + s0)f2(s2 )fT (t + sT).
Надежность информационных систем539Это уравнение имеет решениеy0(s,s0,s2,sT,t) = (p(s,s2,t)f°(t + s0)fT(t + sT) ,что проверяется непосредственной подстановкой. Найдем теперь остальные
функции:Д>,(Т,.У0,52,5Г,0 = Jg(* + т) f] f(k+V> * (g’{k)f2>x+s2 + SQ)fT(t + ST)dx =0 A=0= £ JgT (x) j f*(k+l) (a )g'w (t-x- a)flsi (t - a)/0 (t + s0 )fT (t + sT )da.dx =
k= 00 0= Z I f(k+X)(a)^*U) *gxO-a)f2,s2 (' ~ a)/°(f + s0)/r 0 + ST)da =k = Oq- t /*<M> • * g,/2j! )wAt+s0)M,+Sr)=
i=0= y(x,s2,t)f°(t + s0 )fT (t + sT ),
ty2(s,0,s2,sT,t)= fax+ s,s2,t-x) f° (t-x) fT(t + sT)dx =
оt= /Л-м * Фо(S2-x)f°(t - x)/t(t + ST)dx-
0t t-x= J 1 а)Фо (s2 > CL)daf° (t - x)fT (t + sT)dx =о 0t t-a= lfs(t-a)y0(s2,a)da { f°(t-x)dxfT(t + sT) =
о 0= if At ~ а)Фо (s2>a) (f° (a) - F° (t))dafT (t + sT) =
о= (fs (0 * (ф0 (s2 > t)F° (/)) - fs (/) * Фо (>2»t)F° (/)) fT (t + ST ),ty3 (s, s0 ,s2,0,0 = }ф(.у, s2, x)f° (x + 50 )fT (x)dx,0/y4 (t,sq,s2, 0, t) = JV(T, s2 , x)f° (x + sQ )fT (x)dx,
540Глава 12y5(s,0,s2,0,t) = jf fs(x) * (ф0(s2,x)F°(x)\ - fs(лг) * фо(s2,x)F°(*)) fT(x)dx,
о/ye(x,Q,s2,sT,t) = j\|/(x, 52, x)/° (x)fT (x + sT )dx,0y1 (0,0,s2, sT, t) = jf f(x) * (ф0(s2, x)F° (л)) - f(x) * Ф0(s2,x)F° (x))fT(x + sT )dx,
о/,y8(t,,0,sT,t) - Jv|/(X,0,x)f°(x + s0)fT(.x + sT)dx.
оНайдем вероятности состояний:Po(t)=mF°(t)FT(t),Pl(o=mF°(t)FT(t),
p2(t) = (f * (фо^°ХО ~(F * ф 0)F°(t))FT(t),Рг (0 = * Фо (X)F° (*)/r (*)«**>
оP4(t) = \y(x)F°(x)fT(x)dx,
оPs (0 = J(^ * (Фо^° X*) - (F * Фо )^° С*)) /т (x)dx.0Рб(0 = .ОPi (0 = I(/ * (Фо^° X*) - (/ * Фо )^° (x))Fr (x)dx,0Ps(0= J°J4>(*> 0. x)dTF° (x)FT (x)dx .
ooВ качестве контроля правильности выполненных преобразований можно по¬
казать, что сумма всех вероятностей равна 1.
Надежность информационных систем54112.11.5. Оценка готовности объектаБудем считать, что период эксплуатации объекта Т является на самом деле
детерминированной величиной, т. е. fT(t) = 8T(t). Согласно принятому ранее
критерию качества Г мы можем считать, что все вероятности вычисляются
при t = T, и тогдаГ = А(0 + р4(t)ps(t) = F * (фо^°)(Г) + WW\T), (12.66)где функции ф0(О и ф(/) определяются формулами (12.64) и (12.65) соот¬
ветственно. Таким образом, готовность объекта может быть оценена с по¬
мощью формулы (12.66). Однако, как видно из соотношений для функций
ф0(О и ф(0, задача получения удобных вычислительных процедур для Г
является достаточно сложной.Остановимся на наиболее важном в практическом отношении случае, когда
на периоде эксплуатации объекта аварийная ситуация может возникнуть не
более одного раза. В этом случае выражение для критерия Г значительно
упрощается. Чтобы получить требуемое выражение, при построении матема¬
тической модели в виде системы интегральных уравнений нужно принять
различный характер распределений между соседними аварийными ситуация¬
ми, т. е. считать, что время до первой аварийной ситуации имеет распределе¬
ние с плотностью /^(0> Д° второй аварийной ситуации— /*2Ч0> и т- Д-Полагая затем f('2\t) = 8o0(t), что физически означает невозможность насту¬
пления второй аварийной ситуации, запишем, не проводя подробных выкла¬
док, окончательное выражение для Г:г = m + J / * (gF2)(t)F\t)dt + / * (GF2W)F\T), (12.67)ов котором индекс "единица" опущен. Очевидно, соотношение (12.67) ком¬
пактно и удобно для расчетов.Разработанная модель многофазного режима эксплуатации противоаварий-
ных систем в процессе их жизненного цикла позволяет с учетом предложен¬
ного критерия качества проводить их всесторонний анализ:1. На основе характеристик отдельных подсистем, длительности их функ¬
ционирования на каждой фазе и заданного периода эксплуатации системы
появляется возможность определения характера изменения качества
функционирования системы в течение всего жизненного цикла. Если ве¬
личина критерия качества задана, то можно определить и предельное зна¬
542Глава 12чение жизненного цикла системы, после которого система должна быть
выведена из эксплуатации или капитально отремонтирована.2. Можно получить зависимость качества функционирования системы от
длительности периода ее эксплуатации, исходя из характеристик подсис¬
тем и режима их многофазной работы. Так как для данного класса систем
восстановление в период эксплуатации не возможно, то этот подход по¬
зволяет определить обеспечивающий заданное качество максимальный
период эксплуатации до проведения текущих ремонтно-восстановитель¬
ных работ.3. Можно исследовать, какое влияние на качество функционирования систе¬
мы оказывает различная длительность локализации аварийной ситуации
при заданных характеристиках подсистем и режиме эксплуатации сис¬
темы.4. Исходя из длительности периодов эксплуатации и интервалов профилак-
тико-восстановительных работ, можно получить характер изменения каче¬
ства системы на всем ее жизненном цикле. При этом может быть опреде¬
лено наилучшее соотношение между этими интервалами, обеспечивающее
заданное качество системы в течение всего жизненного цикла.Заметим, что анализ качества системы в соответствии с разд. 12.10.1 и 12.10.4
может быть проведен, если снять допущение о полном восстановлении на¬
дежности оборудования после каждого периода эксплуатации, и здесь такой
анализ не рассматривается.ПРИМЕР 12.6. Требуется рассчитать готовность системы Г при следующих
исходных данных: жизненный цикл изделия — 3 года, период эксплуата¬
ции — 8 час. Время простоя изделия между соседними периодами, в течение
которого производится восстановление оборудования, равно 16 час. Времена
опроса одинаковы и равны 0,5 сек, времена управления одинаковы и равны
1,5 сек. Вероятность возникновения аварийной ситуации на любом периоде
эксплуатации равна р = 0,01. Распределение момента возникновения ава¬
рийной ситуации на периоде равномерное. Время устранения аварийной
ситуации Тй = 20 сек. Распределение времени безотказной работы обору¬
дования с0, С), с2 экспоненциальное с параметрами А,0 = 1/800 час'1,
Я, =1/1600 час4, Х2 =1/^00 час ' соответственно.Требуется выяснить зависимость Г от следующих факторов:□ от длительности каждого периода эксплуатации Т ;□ от времени устранения аварийной ситуации Тв.
Надежность информационных систем543Решение. Прежде всего заметим, что случайное время £ равномерно распре¬
делено на интервале [0; А], где А = Т/р. Действительно, если F(x) — функ¬
ция распределения £, то вероятность возникновения аварийной ситуации на
к-м периоде равнаР((к -1 )Т<%< кТ) = F(kT) - F((k - 1)Г) = р .Отсюда, очевидно, следует, что F(kT) = kp, и поэтому F(x) = рх/Т. Тем са¬
мым F(jc) — линейная функция на [0; А], где А таково, что рА/Т -1, а это
и требуется доказать.Поскольку время устранения аварийной ситуации детерминировано, то из
(12.65) следует, чтоТшХ-UMl + \F2(t)dt.А А у. А оНа основе изложенной ранее методики авторами была разработана програм¬
ма по исследованию эффективности многофазного режима функционирова¬
ния рассматриваемого класса систем для различных режимов функциониро¬
вания оборудования. Далее приведены результаты исследований, проведен¬
ные по этой программе.Значение критерия, вычисленное для приведенных данных, составляет
Г = 0,9999438. Зависимости Г от Г и Г, для фиксированных значений ос¬
тальных переменных представлены графически на рис. 12.27 и 12.28 соответ¬
ственно.8 Т, час 800Рис. 12.27. Зависимость готовности системы
от длительности периода эксплуатации
544Глава 12fРис. 12.28. Зависимость готовности системы
от времени устранения аварийной ситуации12.11.6. Вопросы технического обслуживанияРанее был проведен анализ качества функционирования системы в предпо¬
ложении, что имеет место полное восстановление надежности оборудования
после каждого периода эксплуатации. Фактически каждый период работа
оборудования приводит к расходованию его ресурса и ухудшению надежно¬
стных характеристик, поэтому указанное допущение может вносить некото¬
рое загрубление модели. Здесь мы снимаем это допущение и предполагаем,
что после каждого периода эксплуатации происходит старение всех видов
оборудования. В качестве основной решается задача определения жизненного
цикла системы, после которого система должна быть выведена из эксплуата¬
ции, и при этом в течение всего жизненного цикла критерий эффективности
системы управления остается не ниже допустимого уровня.Весьма важным на стадии проектирования системы является вопрос выбора
стратегии обслуживания и проблема организации профилактических меро¬
приятий. Правильная организация технического обслуживания систем играет
большую роль и в процессе их эксплуатации, поскольку современные по глу¬
бине и объему профилактические работы позволяют повышать технические
характеристики систем и сокращать эксплуатационные расходы. Профилак¬
тику целесообразно применять также для повышения безопасности работы
систем, отказы которых ведут к опасным последствиям или когда устранение
последствий оказывается дороже, чем замена еще исправных элементов. При
выборе стратегии обслуживания важным фактором является планируемый
интервал времени использования системы, а также выбор меры надежности.
Надежность информационных систем54512.11.7. Модель функционирования системы
на одном периоде жизненного циклаБудем рассматривать процесс функционирования системы на одном т-м пе¬
риоде эксплуатации длительности Т, протекающий следующим образом.
Оборудование с0 работает постоянно, оборудование сх работает только нанечетных интервалах, и пусть F0m(t) и Flm(/) — вероятности безотказнойработы оборудования с0 и с) соответственно.Совместное оборудование с0 и сх будем обозначать через с0, а вероятностьего безотказной работы — через (/) . Закон распределения оборудованияс0 определяется формулой (12.62), и для постоянных длительностей отдель¬
ных этапов он имеет вид:В произвольный момент времени поступает сообщение о наступлении ава¬
рийной ситуации. В этот же момент включается подсистема с2, предназна¬
ченная для локализации аварийной ситуации в течение некоторого времени и
возвращения объекта в нормальный режим функционирования. Время до на¬
ступления сообщения об аварийной ситуации и длительность ее устранения
случайны с плотностями распределения /(?) и g(t) и вероятностями F(t) и
G(t) соответственно. Вероятность безотказной работы подсистемы с2 обо¬
значим через Fffait).Будем считать, что в начале каждого периода эксплуатации системы обору¬
дование с0 и с2 полностью исправно, хотя его ресурс ниже, чем на преды¬
дущем периоде.Предполагая, что время до наступления аварийной ситуации имеет равно¬
мерное распределение на промежутке [0;Л], где А = Т/ р и р — вероят¬
ность ее возникновения на каждом периоде, а время устранения аварийной
ситуации постоянно и равно Тъ, и повторяя рассуждения разд. 12.10.5, най¬
дем вероятность безаварийной работы системы для m-го периода:2/-2F\,m t- Z X2j > при Z Xj ^ X */>V 7 = 1 J J = l J =1\2 iF\ m Z x2j-\ > при £ Xj < t < £ Xj, i =1, 2,..., n.
\j=i У J=1 J=118 Зак. 3094
546Глава 12А А т. А оПРИМЕР 12.7. Требуется найти изменение величины Тm в зависимости от
номера периода на интервале 1 < m < М = 3285, что соответствует трем годам
функционирования изделия при следующих исходных данных: период экс¬
плуатации 8 час; время простоя изделия ^ежду соседними периодами, в тече¬
ние которого производится восстановление оборудования, равно 16 час; вре¬
мена опроса одинаковы и равны 0,5 сек, времена управления одинаковы и
равны 1,5 сек; вероятность возникновения аварийной ситуации на любом пе¬
риоде эксплуатации равна /? = 0,01. Распределение момента возникновения
аварийной ситуации на периоде равномерное. Время устранения аварийной
ситуации Тв = 20 сек. Распределение времени безотказной работы оборудо¬
вания с0, С], с2 экспоненциальное с параметрами Х,0 = кт/800 час-1,
А.] =кт/\600 час"1, л2 =кт/800 час'1 соответственно.Решение. Рассмотрим четыре случая изменения коэффициента к в зависи¬
мости от номера периода т, причем так, чтобы во всех случаях были выпол¬
нены граничные условия: кх = 1, а км принимает одинаковые значения:1. Линейная зависимость:£ = 1 + 0,01(/и-1).2. Квадратическая зависимость:£ = 1 + 0,01 1)2 .М-13. Экспоненциальная зависимость:т-1к = (1 + 0,01(М-1))М-*.4. Кусочно-линейная зависимость вида:1, при т<т0;к =1 + 0,01 (Л/-1)-——при т>т0,
М -т02где т0 — количество периодов, соответствующих —М- 2190.
Надежность информационных систем547Готовность рассматриваемого класса систем при различных режимах функ¬
ционирования оборудования представлена на рис. 12.29 в виде графиков 4-х
функций.Рис. 12.29. Графики готовности системы для четырех различных зависимостейПРИМЕР 12.8. В условиях примера 12.7 для квадратичной функции измене¬
ния интенсивностей отказов оборудования требуется выяснить зависимость
Гт от старения только какого-нибудь одного вида оборудования.Решение. На рис. 12.30 представлены графики Тт для случаев, когда стареет
только оборудование с0, или сх, или с2, или, для сравнения, все три вида
оборудования с0, с,, с2 .1 т 3285Рис. 12.30. Сравнение эффективности систем
при условии старения одного и всех видов оборудования
548Глава 12Отсюда следует, что наибольшая доля в эффективности системы приходится
на оборудование с0, а другие виды оборудования оказывают незначительное
влияние на величину эффективности Гт .12.11.8. Анализ системы управления
в течение всего жизненного циклаЭффективность работы системы в течение всего жизненного цикла характе¬
ризуется вероятностью предотвращения аварийной ситуации в случае ее воз¬
никновения на любом периоде эксплуатации. Следовательно, по формуле
полной вероятности эта вероятность равна произведению вероятности выбо¬
ра j-го периода и вероятности предотвращения аварийной ситуации на j-м
периоде, т. е.где т — число периодов жизненного цикла системы, 1 < т < М . Гт пред¬
ставляет собой среднее значение эффективностей на всем интервале жизнен¬
ного цикла изделия.ПРИМЕР 12.9. При тех же исходных данных, что и в примере 12.7, требует¬
ся найти зависимость средней эффективности Тт от номера периода на ин¬
тервале 1 <т<М = 3285 .Решение. Графическая иллюстрация функции Гш для указанных ранее че¬
тырех зависимостей приведена на рис. 12.31.Рис. 12.31. Изменение критерия средней эффективности в зависимости от числа периодов
Надежность информационных систем549В табл. 12.10 приведены, в частности, значения критерия Гт в конце жиз¬
ненного цикла.Таблица 12.10. Значения для четырех видов зависимостей кт№ЗависимостьГм1Линейная0,9990942Квадратичная0,9993733Экспоненциальная0,9995064Ломаная0,999660Наименьшее значение эффективности достигается для линейной зависимо¬
сти, а наибольшее — для ломаной линии.12.11.9. Установление оптимальных сроков
проведения профилактических работ
и длительности жизненного циклаКритерий эффективности Г зависит от числа проводимых профилактик п в
течение жизненного цикла изделия М, а также от временных интервалов
тх,т2,..., тп между профилактиками, выраженных через количество перио¬
дов. Таким образом, Г = Г(и, М, тх, т2,..., тп). Требуется найти параметры
п, /И], т2,..., тп, а также продолжительность жизненного цикла изделия, в
течение которого значение критерия эффективности Г было бы не ниже за¬
данного критического значения Гкрит. При этом моменты профилактикдолжны быть, во-первых, кратны определенным значениям dx,d2, ...,dp
(месяц, квартал, полгода, год и т. д.), и, во-вторых, каждому значению dj
приписывается коэффициент у j (0 < уу < 1), характеризующий уменьшениеинтенсивностей отказов оборудования после /-Й профилактики. Продолжи¬
тельность жизненного цикла изделия выбирается из условия совпадения мо¬
ментов ближайших профилактик. В качестве исходной информации будем
считать известным поведение интенсивностей отказов оборудования с0, q,
с2 без учета профилактических работ в течение достаточно большого числа
периодов М . Интенсивности отказов выражаются функциями , к^\х,к^Х2, где к^у> — некоторые монотонно возрастающие функции аргумента
550Глава 12т, а А.0, л,, Х2 — интенсивности отказов оборудования на первом периоде.
В соответствии с (12.47), не принимая во внимание проводимые профилакти¬
ки, мы можем определить значение критерия для каждого периода т(1 йт<М).Математически поставленная задача может быть записана следующим обра¬
зом: найти длительность жизненного цикла М, количество проводимых
профилактик в течение жизненного цикла и моменты проведения профилак¬
тик тх,т2,..., тп, такие, чтобы:1. О <т1<т2<...<тп<М;2. для каждого / = 1, 2,..., п существовало dj, такое, что т, кратно dj;3. Г = Г(и, М, /и,, т2, ...,тп)> Гкрит .При этом значение п должно быть минимальным.Это есть задача дискретной оптимизации с неизвестным заранее количеством
неизвестных величин. Далее приводится алгоритм решения поставленной
задачи, состоящий из следующих пунктов:1. Если при всех т (1 < т < М) > Гкрит, то профилактик проводить не
нужно, т. к. предельный уровень эффективности системы сохраняется на
всем жизненном цикле изделия М = М.2. Если уровень эффективности даже на начальном этапе эксплуатациименьше критического, т. е. Г|0) < Гкрит, то это означает, что система имеетслишком малую надежность, и речь не может идти о проведении каких-
либо профилактик. Жизненный цикл должен быть равен нулю.3. Пусть Г(^ < Гкрит < Г[0). Полагается / = 0, т0 = 1.4. По функции на промежутке [от^М] определяется значение
т = ткрш, для которого = Гкрит .5. Значение i увеличивается на 1, т. е. полагается / = / +1.6. Среди всех чисел, кратных dj, 7=1,2,..., р, определяется зна¬
чение ml - kdj (к — целое), удовлетворяющее неравенству
kdj <пгкрт <(k + \)dj, для которого разность (ткрит - kdj) минимальна.
Тем самым будет определен номер j, характеризующий вид профилакти¬
ки и соответствующий коэффициент уу.
Надежность информационных систем5517. Если /и, = /ям, то число проводимых профилактик полагается равнымГО, при / = 1;п = <[i - 2, при / > 2,
длительность жизненного цикла беретсяГО, при /=1;[/»,_!, при / > 2и осуществляется выход из алгоритма.8. На промежутке [/и,; М] берутся новые интенсивности переходов обору¬
дования с0, сх, с2, равные соответственно *14. *i%> где(km ^ j ■ Эти интенсивности однозначно определяюткритерий эффективности объекта. Производится переход к шагу 4 ал¬
горитма.ПРИМЕР 12.10. Требуется найти времена проведения профилактических
работ без учета их дискретизации, чтобы на протяжении всего жизненного
цикла, равного М = 3285, эффективность изделия была бы не ниже
Г^ит= 0.999. При этом имеем следующие условия функционирования:=1, км одинаковы.Решение. Для четырех различных выпуклых кривых, отражающих зависи¬
мость к от m, в соответствии с описанным алгоритмом получены значения
оптимальных моментов профилактик, которые помещены в табл. 12.11.Таблица 12.11. Оптимальные моменты проведения профилактик№ЗависимостьМоменты проведения профилактик1Линейная59712281858248831182Квадратичная140220092472286032023Экспоненциальная210025952884308932484Ломаная23882599280930193229Заметим, что для линейной зависимости в отличие от других оптимальные
моменты идут с постоянным шагом.
552Глава 12лПРИМЕР 12.11. Для квадратичной зависимости вида к = \ + а(т-\) , где
а = 10-6, и Гкрит = 0,9999 требуется получить моменты проведения профи¬
лактик с учетом их дискретизации и величину жизненного цикла изделия.
При этом рассматриваются следующие четыре вида дискретности:□ 0 — через месяц (90 периодов);□ 1 — через квартал (3 * 90 периодов);□ 2 — через полгода (6 * 90 периодов);□ 3 — через год (12*90 периодов).Для каждого вида дискретности определены коэффициенты у j, j = 0,1, 2, 3.Решение. В табл. 12.12 для трех различных наборов коэффициентов у j при¬
ведены моменты проведения профилактик в месяцах и вид дискретности.
В верхней строке стоят коэффициенты улучшения качества системы после
месячной, квартальной, полугодовой и годовой профилактик. В нижней части
таблицы указано значение жизненного цикла.Таблица 12.12. Моменты проведения профилактикоIIIIк>IIII70 = 0,9,71 = 0,9,72= 1,уз= 1Уо = 0,7, Yi = 0,8, ъ = 0,9, у3 = 1Моменты,мес.ВиддискретностиМоменты,мес.ВиддискретностиМоменты,мес.Виддискретности919191130130123160151151182170170200182182220190190243200250211220470230483243Жизненный цикл = 48 мес.Жизненный цикл = 24 мес.Жизненный цикл = 19 мес.
ГЛАВА 13
НАДЕЖНОСТЬ И РИСК13.1. Определение понятия "риск"Отказ технической системы неизбежно ведет к потерям: производство оста¬
навливается или сокращается, отказавшая система ремонтируется, последст¬
вия аварий или катастроф ликвидируются. Кроме того, эксплуатация техники
может оказывать негативное влияние на окружающую среду. Безопасность
стала одной из самых актуальных для человека проблем. Потери могут быть
так велики, что возникает сомнение в целесообразности эксплуатации техни¬
ки из-за низкой ее надежности.Отказы являются событиями случайными. При этом потери зависят от вида
отказа. Например, отказ двигателя автомобиля ведет к потерям, которые пре¬
восходят потери от отказа фары. Величина потерь также зависит от условий,
в которых возник отказ. Например, отказ двигателя самолета на стоянке и в
полете приводит к разным потерям. Потери, так же как и отказы, являются
событиями случайными.В процессе эксплуатации человек рискует. Автомобилист рискует при выезде
на трассу, потребитель электроэнергии атомной электростанции рискует быть
облученным.Риск является неизбежным атрибутом эксплуатации техники. Он является
одним из важнейших показателей безопасности. Риск, возникающий в ре¬
зультате отказов техники, называется техногенным.Риск имеет место не только при эксплуатации техники. Он присутствует при
любых аномалиях: неблагоприятные условия среды (метеорологический
риск), неблагоприятная экономическая ситуация (экономический риск) и т. д.При изучении риска возникают проблемы, требующие для их решения серь¬
езных научных исследований и их практической реализации. К таким про¬
блемам относятся:□ создание научной терминологии риска;□ разработка критериев и показателей риска;
554Глава 13□ разработка математических моделей риска;□ разработка методов снижения риска.В настоящее время научной/теории риска не существует: не сформулированы
фундаментальные понятия и определения, не разработаны математические
модели, отсутствуют инженерные методы расчета. В данной главе рассмат¬
риваются эти проблемы только применительно к техногенному риску, как
результату отказов техники. Нашей основной целью является исследование
влияния надежности техники на величину риска.Что же такое риск?Риском называется возможность потерь вследствие внутренних аномалий в
системе или аномалий среды.Такое определение слишком общее, а поэтому может вызывать различные
толкования, если его применять к техногенному риску и надежности. Поэто¬
му сузим это понятие и дадим ему следующее определение.Техногенным риском называется возможность потерь из-за отказов техники.
Это определение имеет следующие особенности:□ определение конкретно;□ отражает случайный характер риска;□ не учитывает вредного влияния техники на окружающую среду;□ применимо лишь для случая потерь от отказов техники.В большинстве случаев риск оценивается денежными единицами, хотя могут
быть случаи, когда потери носят такой характер, что оценить их деньгами
трудно или даже невозможно. Из определения следует, что риск является
случайной величиной, вызванной двумя причинами: случайностью события
"отказ" и случайностью величины потерь. При расчетах используется его ха¬
рактеристика — математическое ожидание риска.13.2. Оценка техногенного риска. \13.2.1. Риск системы с двумя состояниямиРаботоспособность технических систем (деталей машин, валов, зубчатых пе¬
редач, станков, тракторов и др.) характеризуется рядом критериев: безотказ¬
ностью, прочностью, износоустойчивостью, жесткостью,- теплостойкостью,
виброустойчивостью, точностью.Расчет по этим критериям сводится к сопоставлению расчетных параметров с
их предельными (допустимыми) величинами. Такими предельными величи-
Надежность и риск555нами служат: вероятность отказа, пределы прочности, текучести, выносливо¬
сти, предельная нагрузка, ресурс, несущая способность, теплостойкость мас¬
ла и материалов, предельные частоты и амплитуды колебаний, динамическая
устойчивость. Предельные величины выбирают по нормативным или спра¬
вочным данным, а также устанавливают путем испытаний или наблюдений
при эксплуатации.Работоспособность системы по заданному критерию обеспечена, если рас¬
четный параметр X не превышает его предельного значения X*. В общемслучае параметр X не должен выходить за X*. Это условие представим в
следующем виде:где п — коэффициент безопасности, задаваемый из условий работоспособ¬
ности.Величины X и X* часто рассматриваются как детерминированные, однако,
на самом деле, они являются случайными, поэтому условие (13.1) может вы¬
полняться лишь с некоторой вероятностью. При этом мерой работоспособно¬
сти системы служит вероятность выполнения условия (13.1):Если выполняется неравенство, противоположное (13.1), то это означает
свершение неблагоприятного события с вероятностьюЭто неблагоприятное событие (по терминологии теории надежности это от¬
каз) может привести к некоторым убыткам или даже к потере работоспособ¬
ности системы. Пусть с — максимально возможные убытки, если расчетныйX*параметр X превысил предельную величину .Значение фактических потерь представляет собой случайную величину, ко¬
торая может принимать два значения: 0 или с с вероятностями р и q соот¬
ветственно. Тогда произведение(13.1)иR = cq(13.2)характеризует средние потери или средний риск системы.
556Гпава 13Вероятность неблагоприятного события q может быть вычислена, если из¬
вестны законы распределения случайных величин X и X*. Если плотности
этих случайных величин равны fx(j) и fx>(t) соответственногоq= J F A- fx(t)dt,где Fx,(t)= J f t (x)dx .Предположим, что случайные величины X и X* являются нормально рас¬
пределенными с параметрами (т, а) и (т*,а*) соответственно. Поскольку
алгебраическая сумма случайных величин, имеющих нормальное распреде¬
ление, сама имеет нормальное распределение, то<7 - 0,5 + Ф01но рассчитать величину среднего риска.1где Ф0(О = —f= Je 2 dx — функция Лапласа. Далее по формуле (13.2)л/2л омож-ПРИМЕР 13.1. Нагрузка на подшипник является нормально распределенной
случайной величиной со средним значением т = 80 Ни средним квадратиче¬
ским отклонением сг = 10 Н. Предельная нагрузка также имеет нормальноераспределение со средним т* = 80 Ни средним квадратическим отклонени¬
ем а* =2 Н. Величина максимально возможных убытков вследствие превы¬
шения предельной нагрузки составляет 106 руб. Требуется определить сред¬
ний риск системы.Решение. Вычислим вероятность отказа подшипника (превышения предель¬
ной нагрузки):д = 0,5 + Ф0' 80-100 4
л/lO2 +22= 0,02493
Надежность и риск557Тогда величина среднего риска равнаR = с■q = \06 -0,02493 = 24930 руб.Если расчетный параметр X и его предельное значение X* зависят от вре¬
мени, то вероятность неблагоприятного события, а следовательно, и средний
риск системы также являются функциями времени, т. е.q(t) = PП, R(t) = c q(t).Таким образом, средний риск технической системы может быть получен как
произведение потерь при наступлении неблагоприятного события на вероят¬
ность этого события.13.2.2. Формула техногенного рискаВ предыдущем разделе был рассмотрен лишь простейший случай, когда сис¬
тема имеет только одно неблагоприятное состояние. Предположим теперь,
что техническая система имеет несколько неблагоприятных состояний.Множество всех состояний системы Sx, S2, , Sm обозначим через Е . Это
множество разбивается на два непересекающихся подмножества:
Е = Е+и Е_, где Е+ — множество благоприятных, а Е_ — множество не¬
благоприятных состояний. В этом разделе будем считать, что отсутствуют
переходы из состояний множества Е_ в состояния множества Е+. Такое
множество Е_ называется эргодическим.Пусть Pj(t) — вероятность пребывания системы в состоянии Sj,
j = 1, 2,..., m, Cj — величина потерь от перехода системы из множества бла¬
гоприятных состояний Е+ в неблагоприятное состояние Sj е Е_. Предпола¬
гается, что эта величина одна и та же для каждого перехода из множества Е+
в состояние Sj е Е_. В противном случае состояние Sj следует разбить на
подсостояния, для которых требуемое условие будет выполнено.В качестве примера рассмотрим движение автомобиля, у которого неблаго¬
приятное состояние Sj вызвано двумя причинами: отказ тормозов и поломказадней двери. Эти причины могут сопровождаться соответственно крупной
аварией и небольшими неприятностями для водителя. Величина потерь су вэтом случае просто не может быть определена. Однако, если состояние Sjразбить на два подсостояния и (рис. 13.1, а—б), соответствующие
558Гпава 13указанным причинам, то величины потерь cJi и для них могут быть оп¬
ределены.О оCJ\Ch ShРис. 13.1. Разбиение неблагоприятного состояния (а) на подсостояния (б)Благоприятным состояниям на рис. 13.1 соответствуют круги, а неблагопри¬
ятным — квадраты.По формуле полной вероятности получим выражение для среднего техноген¬
ного риска системы:т= s cjpjit). (1з.з)Sj€E_Суммирование в формуле (13.3) производится по множеству всех неблаго¬
приятных состояний технической системы.Предположим, что система имеет три состояния: /Sls S2, S3 (рис. 13.2), из
которых состояние Sl — благоприятное, а состояния S2, S3 — неблагопри¬
ятные. На графе указаны вероятности каждого состояния и потери системы,
вызванные переходом в неблагоприятные состояния.Рис. 13.2. Граф состояний системы и параметры этих состоянийОбщий риск системы определяется в соответствии с формулой (13.3):R(t) = c2p2(t) + c^p3(t).
Надежность и риск559Дадим несколько иную интерпретацию техногенного риска. Из формулы
(2.33) следует, что между вероятностями пребывания системы в состояниях и
средним числом переходов между состояниями имеется зависимость:pj(t)= I Ми(0- £ Му><(/). (13.4)Sj —> Sj Sj —*SjЭто означает, что вероятность pj(t) состояния Sj равна сумме двух вели¬
чин. Первое слагаемое, равное общему числу переходов М, у из всех состоя¬
ний S’, в данное состояние Sj, берется со знаком Второе слагаемое, рав¬
ное общему числу переходов из данного состояния S.- во все другие состоя¬
ния Sf, берется со знаком
Рассмотрим два случая работы системы.Случай 1. Система работает до первого попадания в неблагоприятное со¬
стояние. Это значит, что, попав в любое неблагоприятное состояние, система
навсегда в нем остается (поглощающее состояние).Если Sj — неблагоприятное состояние, из которого нет выходов в другиесостояния, то соотношение (13.4) для его вероятности упрощается и прини¬
мает вид:Pj(t)= £ £ MtJ(t). (13.5)Sj —>Sj Sj € E+Здесь суммирование производится по всем благоприятным состояниям
Sj е Е+, из которых имеется непосредственный переход в состояние Sj еЕ_. )В результате подстановки выражения (13.5) в равенство (13.3) получаем
формулу техногенного риска, эквивалентную формуле (13.3):m= I cj I (13.6)SjeE_ S,eE+В соответствии с (13.6) средний риск системы равен сумме произведений по¬
терь от перехода в каждое неблагоприятное состояние, умноженных на общее
среднее число переходов в данное состояние.Случай 2. Система, попав в какое-либо неблагоприятное состояние, может
переходить в другие неблагоприятные состояния, но никогда не попадет в
благоприятное состояние. Это значит, что возможны переходы между со¬
стояниями множества Е_, но отсутствуют переходы из множества Е_ в мно¬
жество Е+.
560Глава 13Используя (13.3) и (13.4), получим следующее выражение для среднего тех¬
ногенного риска системы:т= 2 £ (cj . (13.7)Sj€E_ SieE_SJeE_Первое слагаемое в (13.7) совпадает с выражением (13.6), а второе обуслов¬
лено переходными процессами в множестве неблагоприятных состояний Е_.
Это слагаемое обращается в нуль, если потери системы для каждого неблаго¬
приятного состояния одинаковы: с, = Cj для любых , Sj <= Е_. Следова¬
тельно, если все неблагоприятные состояния системы равноправны по отно¬
шению к потерям, то для техногенного риска и в этом случае справедлива
формула (13.6).Однако если неблагоприятные состояния системы дают различные потери, то
для расчета техногенного риска необходимо' использовать выражение (13.7).
Это обстоятельство может иметь место, когда вслед за состоянием с неболь¬
шими последствиями наступает состояние с серьезными последствиями, как
показано на рис. 13.3.Рис. 13.3. Граф с двумя последовательными неблагоприятными состояниямиТак, если за неблагоприятным состоянием S2 может последовать другое не¬
благоприятное состояние S3, несущее в себе большие потери (с3 >с2), то по
формуле (13.3)Л(0 = С2Р2 (0 + с3Рз (0 + С4Р4(0 •Тогда согласно формуле (13.7) получим:R(t) = с2М\ 2(0 + (с3 -c2)M2 j(t) + c4Mi 4(0.
Надежность и риск561Заметим, что в формулах (13.6) и (13.7) учитываются только переходы в не¬
благоприятные состояния системы, и для них вычисляются средние значения
числа переходов.13.2.3. Кумулятивный техногенный рискВ предыдущем разделе было сделано предположение о том, что множество
неблагоприятных состояний эргодическое, т. е. из них невозможны переходы
в благоприятные состояния. Это справедливо для случая невосстанавливае-
мых технических систем. В случае восстановления система становится рабо¬
тоспособной и вновь возникает опасность перехода в неблагоприятное со¬
стояние с возможностью новых потерь. В результате суммарный риск систе¬
мы может накапливаться с течением времени. Такой риск будем называть
кумулятивным, или неоднократным, или риском с накоплением.Таким образом, в этом разделе мы снимаем все ограничения на возможные
переходы системы из одного состояния в другое. Из каждого состояния име¬
ется некоторый переход в другое состояние, возможно не за один шаг. По
определению такие состояния называются отражающими.Сразу отметим, что выражение (13.3) теряет смысл, поскольку в этом выра¬
жении отсутствует накопление функции риска. Однако полученные выше
формулы (13.6) и (13.7) имеют смысл, т. к. среднее число переходов из со¬
стояния в состояние с течением времени непременно возрастает. Тем самым
во время функционирования системы происходит накопление риска.Для расчета техногенного риска эти формулы принимаются в качестве ос¬
новных. Следовательно, величина риска, накопленного в течение времени /
работы системы, определяется по формуле (13.7). В частности, если отсутст¬
вуют переходы между неблагоприятными состояниями, то величина риска
определяется формулой (13.6).Пусть в графе, изображенном на рис. 13.2, появился переход из неблагопри¬
ятного состояния S2 в благоприятное состояние , как это показано на
рис. 13.4.Рис. 13.4. Граф состояний для определения кумулятивного риска системы
562Гпава f3В соответствии с формулой (13.6) накопленный риск системы будет равенR(t)=с2м1Л(0+с3ми(0=С2м1>2(0+Cjft (0 •Очевидно, что первое слагаемое в функции риска монотонно возрастает и
с течением времени может принять сколь угодно большое значение.13.2.4. Непосредственное вычисление
техногенного рискаС позиций теории надежности системы могут задаваться графически в виде
своих структур или структурных схем. Понятие отказа системы в этих схемах
обычно определяется по умолчанию. Так, например, основное соединение
элементов представляется в виде последовательной схемы, отказ которой на¬
ступает при отказе любого ее элемента. Из структурной схемы резервирован¬
ной системы также нетрудно определить понятие отказа.Будем считать, что каждое исправное состояние системы является благопри¬
ятным и принадлежит множеству Е+, а каждое отказовое состояние — не¬
благоприятным с точки зрения потерь и является элементом множества Е_.
Предположим, что переход из исправного состояния Sj е Е+ в отказовое со¬
стояние Sj е Е_ вызван отказом элемента системы с номером к = k(i,j) . При
этом для к-го элемента системы будем считать известными потери гк, кото¬
рые понесет система в результате такого перехода. Эти потери будем назы¬
вать также риском системы вследствие отказа к-то элемента.Трудности использования формул типа (13.6) или (13.7) для расчета риска
безусловно связаны со сложностью нахождения величин потерь системы в
результате ее перехода из исправного состояния в отказовое. Для облегчения
использования указанных формул сделаем предположение, что для каждого
состояния Sj е Е_ величины су равны потерям системы из-за того элемента,который обусловил переход в состояние Sj. Таким образом, если переходЕ+ -» Sj вызван отказом к-го элемента, то Cj = гк.Сделаем еще одно непринципиальное допущение: из состояния отказа систе¬
мы возможен переход только в ее исправное состояние. В этом случае для
вычисления техногенного риска можно пользоваться только формулой (13.6),
представив формулу для риска в следующем виде:m= z I ■ (13.8)Ste.E+ Sj е Е_Вычисление риска системы по формуле (13.8) требует определения среднего
числа переходов из каждого исправного состояния во все отказовые. Для сис¬
Надежность и риск563темы с произвольной структурой, произвольными распределениями времени
до отказа и времени обслуживания это можно осуществить путем составле¬
ния и решения системы интегральных уравнений в соответствии с гл. 4.Рассмотрим один важный частный случай, когда для вычисления среднего
числа переходов Mf j(t) не требуется составления системы интегральныхуравнений. Предположим, что функционирование системы описывается мар¬
ковским случайным процессом. Тогда среднее число переходов из состояния
Sj в состояние Sj рассчитывается по формуле/ IMjjit) = /соij(x)dx = Xjj jpj(x)dx,о огде Xjj — интенсивность указанного перехода. Поэтому для величины риска
имеет место выражениеW)= £ Xk(ijfk(i,j) \p,(x)dx. (13.9)/б£+, j(zE_ ОРасчеты по формуле (13.9) требуют составления и решения системы обыкно¬
венных дифференциальных уравнений относительно вероятностей pt{f), что
также сопряжено с вычислительными трудностями. Естественным является
желание выделить определенные классы систем, для которых техногенный
риск рассчитывается более простыми способами.Рассмотрим частные случаи систем, для которых соотношение (13.8) значи¬
тельно упрощается.Нерезервированная неремонтируемая системаОбозначим через m число элементов в системе, fk(t), ^t(0 — плотность и
функцию распределения времени до отказа &-го элемента, Fk{t) = \-Fk(t),Среднее число переходов из исправного состояния с номером 0 в k-е состоя¬
ние отказа, вызванное отказом к-го элемента, равномо,к (О = (*)■••/* (x)...Fm (x)dx,Опоэтому в соответствии с (13.8) величина риска системы вычисляется по фор¬
мулеm 1 _ _R(.t)=YlrkjFl(x)...fk(x)...Fm(x)dx. (13.10)k = l 0
564Глава 13В частности, для экспоненциальных распределений получимт 1 _ р~К‘*(0=S hnt-т—. (13.11)к=\ Лстгде Хс = Z Хк — интенсивность отказа системы.*=1Для вырожденных распределений со средними Тк, к = 1, 2,..., m, получимГ 0, при / <Тк ;
т=\ ° (13.12)[%> при (-\-где к0 — номер элемента с минимальным средним.ПРИМЕР 13.2. Нерезервированная система состоит из четырех элементов,
интенсивности отказов которых соответственно равны: А,, =3-10~5час-1,Х2 - 5 ■ Ю-4 час-1, Х3 = 7 • 10~5 час-1, Х4 = 2•10"7 час-1. Величины риска систе¬
мы из-за отказа элементов составляют: гх =650 ден. ед., г2 =1430 ден. ед.,
гг = 800 ден. ед., гА = 920 ден. ед.Определить риск системы как функцию времени. Найти самый критичный
элемент в системе.Решение. Воспользуемся соотношением (13.11). Вычислим интенсивность
отказа системы:Хс = 3-10~5 + 5-10-4 + 7-10-5 + 2-10-7 =0,0006002 час-1.*Вычислим суммуm£ V* = 3 10 -650 + 5-10-4 -1430 + 7-10-5 -800 + 2-10-7 -920 =
к=\= 0,0195 + 0,715 + 0,056 + 0,000184 = 0,790684.Теперь рассчитываем риск системы:, -0,0006002/R(t) = 0,790684 • — = 1317,4 • (1 - е-°-0006002') .0,0006002С течением времени функция риска возрастает от 0 до 1317,4 ден. ед.Из расчетов также следует, что из четырех элементов самым критичным яв¬
ляется второй элемент, т. к. слагаемое Х2г2 =0,715 максимально.
Надежность и риск565Если бы время до отказа каждого элемента было постоянным, то согласно(13.12) величина риска системы была бы равна риску наименее надежного
элемента, т. е. 1430 ден. ед.Нерезервированная ремонтируемая системаВ силу (13.8) имеем:где М0 k (t) — среднее число переходов из исправного состояния в состояниеотказа, вызванное отказом k-го элемента. Даже в случае экспоненциальных
распределений нельзя получить выражение для среднего числа переходов
М0 k(t) в конечном виде, поэтому мы рассмотрим некоторые приближенныеоценки и частные случаи расчета риска нерезервированной системы с восста¬
новлением.Приближенная оценкаВоспользуемся приближенной оценкой для вычисления М0 k(t), приведен¬
ной в разд. 7.2.2, согласно которойгде (ok(t) — параметр потока отказов; Kvk (t) — функция готовности;
Knk(t) — функция простоя &-го элемента. Подставляя это значение в форму¬
лу для R(t), получим:Чтобы применить равенство (13.13), необходимо для каждого элемента сис¬
темы знать функцию готовности и параметр потока отказов.Двусторонняя оценкаВ случае экспоненциальных распределений можно получить несколько более
удобные для расчетов выражения. Интеграл от функции р() по промежуткуmRif) - Цгкм0к(о,(13.13)
566Гпава 13М есть средняя суммарная наработка системы за время t, которая, оче¬
видно, находится в пределах [Krt\ /]. Следовательно, согласно (13.9) для
риска системы имеют место двусторонние оценкит то<1 V/-j=i у=1Случай одинаковых интенсивностей восстановленийЕсли интенсивности восстановления каждого элемента одинаковы и равны
ц,тоЛ) (0 = ,^“с + Iх + И-и поэтомут KXc+^t + Xc(\~e-iX^‘)R(t)=ThrJ ~—Ц 1• (13-14)7 = 1 (^с + М')При больших значениях t из (13.14) получим асимптотическую оценку для
риска системытR(t)=£XjrjKr(t+KnTB).7 = 1Если интенсивности восстановления элементов различны, то для определения
функции p0(t) и функции риска R(t) надо решать систему дифференциаль¬
ных уравнений.ПРИМЕР 13.3. Нерезервированная система состоит из четырех элементов,
имеющих те же характеристики надежности и риска, что в примере 13.2. Ин¬
тенсивность восстановления каждого элемента д = 1 час-1.Определить риск системы и сравнить его с риском невосстанавливаемой сис¬
темы.Решение. Интенсивность отказа системы Хс = 0,0006002 час”1. На основании
примера (13.2)т=0,790684.k = 1
Надежность и риск567Тогда на основании формулы (13.14) риск системы будет:R(t) = 0,7906841,0006002? + 0,0006002(1 - еГ1’0006002')или1,0006002R(t) = 0,79021 • t + 0,000474 • (1 - е-1’0006002 ').Сравним теперь риск системы с восстановлением и риск системы без восста¬
новления. Результаты расчетов сведем в табл. 13.1.Таблица 13.1. Риск систем без восстановления и с восстановлениемt, часРиск системы
без восстановленияРиск системы
с восстановлением00050034239510005957901500782118520009211580250010241976300011002371350011562766400011983161450012293556500012523951На основе полученных данных можно сделать важный вывод: восстановле¬
ние удлиняет время работы системы, но приводит к значительному увеличе¬
нию риска в силу возможности повторных отказов. Особенно отчетливо этот
результат виден на рис. 13.5.Кривая 1 соответствует риску невосстанавливаемой системы. С течением вре¬
мени кривая приближается к своему стационарному значению, равному
1317,4 ден. ед. Кривая 2 соответствует риску восстанавливаемой системы.
Со временем она ведет себя линейно с угловым коэффициентомmI VA =0,79021.У=1
568Глава 13Рис. 13.5. Риск систем без восстановления (кривая 1) и с восстановлением (кривая 2)Относительное увеличение риска от восстановления в случае нерезервиро¬
ванной системы определяется отношением риска, вычисленного по формуле(13.14), к риску, вычисленному по формуле (13.11):|aA.c(^c+^4-^(l-e-(W)Р (Хс+ц)2(1-е-^)Результаты расчетов увеличения риска от времени приведены в табл. 13.2.
График функции Vp(t) показан на рис. 13.6. Из графика следует, что функция
Vp(t) практически является линейной.Таблица 13.2. Влияние восстановления на риск системыt, часvP(t)01,01000' 1,320001,730002,240002,650003,260003,770004,380004,890005,4100006,0
Надежность и риск569Основное соединение подсистем при отсутствии ремонтаПусть система состоит из п подсистем. Все элементы к-й подсистемы иден¬
тичны по надежности и риск системы вследствие их отказа равен гк. Из
(13.8) следует, чтоR(t)=±rkM{k\t),
к=1где M^k\t) — среднее число переходов из исправных состояний в отказо-
вые, вызванных отказом какого-либо элемента £-й подсистемы. Определим
это число.Положим pk(t) — вероятность безотказной работы, a qk(t) = \- pk(t) — ве¬
роятность отказа k-vi подсистемы, к = 1, 2,..., п . Введем в рассмотрение слу¬
чайную величину X, равную числу переходов из исправных состояний в от-
казовые вследствие отказа элементов к-й подсистемы. Случайная величинаX может принимать значения 0 и 1 с вероятностями р^ (О и p\k\t) соот¬
ветственно. Указанный переход произойдет, если за время t к-я подсистема
откажет раньше, чем другие подсистемы с номерами I *к. Вероятность этого
события равнаР\к)(0 = Щ PiMkW* ■Ol*k
570Глава 13Среднее число переходов M^k\t) есть математическое ожидание случайной
величины X, и значитM(k\t) = p[k\t).ОтсюдаЛ(0 = £ rk \Y[Pi^)q'k^)dx • О3-15)£ = 1 01*кФормула (13.15) очень удобна для расчетов. Чтобы рассчитать риск по этой
формуле, достаточно знать лишь вероятности безотказной работы каждой
подсистемы.ПРИМЕР 13.4. Рассчитать риск системы, состоящей из трех подсистем,
структурная схема которой изображена на рис. 13.7.^-з/я = 1/2Рис. 13.7. Структурная схема системыРешение. Интенсивности отказов элементов во всех подсистемах являются
величинами постоянными. При этом они одинаковы в элементах подсистемы.
Данные об интенсивностях отказов элементов и значения риска подсистем
приведены в табл. 13.3.Таблица 13.3. Исходные данные для расчета риска системыПодсистемаРезервИнтенсивность отказов
Хк, час-1Риск rh ден. ед.1Нагруженный5 • 10"4202Ненагруженный6-1СГ41В3Дробная кратность4-КГ410
Надежность и риск571В разд. 6.4 приведены формулы для вероятности безотказной работы pk(t)
каждой рассматриваемой здесь подсистемы. Вычисляя производные q[(t),
получим:д (0 = 2е~Х'1 - е~2х'1, q[(t) = 2 ~ 2 V"2*1',p2(t) = (1 + X2t)e-^‘, q'2(t) = Х\te~^,p3(t) = 3e~2x>‘ - 2e~3X}‘, q'3(t) = 6X3e~2Xi' - 6X3e~3X}l.Согласно (13.15) получим выражение для риска системы:R(t) = rx j(2V~V -2^e"2XlTXl + X2x)e~Xl\3e~2XiT -2eT3X^)dx +о+r2 J(2e~x,r -e~2x,r)Xjxe~X2T(3e~2X}T -2e~3X}X)dx +оt+r3 J(2e_x,T - e~2X'x )(1 + X2x)e~X2\6X3e~2X^ -6X3e~3X}X)dx.оРезультаты вычислений сведены в табл. 13.4.Соответствующий график функции риска изображен на рис. 13.8.Как следует из рисунка, риск неремонтируемой системы с течением времени
приближается к постоянной величине, равной 14,7 ден. ед.Таблица 13.4. Изменение риска системы во времениt, час№00.05002,010006,215009,7200012,1250013,4300014,1350014,5400014,6450014,7500014,7
572Гпава 13Рис. 13.8. Изменение риска системы13.2.5. Асимптотическое поведение
функции рискаРассмотрим возможные упрощения формулы (13.8) при большом времени
работы системы.Неремонтируемая системаИз (13.8) следует, что для предельного значения риска системы при t —>оо
имеет место равенствоR= lim R(t)= X rk(,j)Pj - (13.16)SteE+,SjeE_где pj — стационарное значение вероятности состояния Sj. Таким образом,для неремонтируемой системы ее риск— ограниченная величина, опреде¬
ляемая формулой (13.16).Разберем один частный случай, при котором указанные вероятности состоя¬
ний вычисляются относительно просто. Предположим, что система состоит
из п последовательно соединенных подсистем, причем система резервирова¬
на и защищена от одного любого отказа. Пусть Л, — интенсивность первого
отказа, а Л' — интенсивность второго отказа /-Й подсистемы. Тогда нетрудно
получить алгоритм для вычисления стационарных значений вероятностей
состояний отказа Sj е Е_.Поскольку система является неремонтируемой, то стационарная вероятность
каждого исправного состояния равна нулю. Среднее время пребывания сис¬
темы в состоянии (0), при котором все элементы исправны, равно:
Надежность и риск5731т0 = .и п2>,/=1Для каждого состояния первого уровня, вызванного отказом элемента под¬
системы с номером ij, среднее время пребывания системы в состоянии пер¬
вого уровня равно:\Xi' Е л, + л' т°Для каждого состояния второго уровня, вызванного последовательным отка¬
зом элементов различных подсистем с номерами ix и i2, среднее время пре¬
бывания равно:^ £ Л.+Л'+А'^'1и т. д. Для каждого состояния к-го уровня, вызванного последовательным от¬
казом элементов различных подсистем с номерами i{, i2,..., , среднее время
пребывания равно:Л/,Th.h.~.b £ Л.+ £ AJ 4-1-'*'|.'2 '* ' = '1.'2 '*Отказ системы произойдет, когда система будет находиться в состоянии вида
/) , /2,..., ik, и при этом откажет еще один из элементов подсистемы с номе¬
ром г), где I = 1,2,..., к . Соответствующее состояние обозначим через
/j, i2,..., ik, if. Вероятность такого состояния равна:Piui2,...,ik,i, =\Xihi2 '* ‘Определяя по этой формуле вероятность каждого отказового состояния и
применяя формулу (13.16), можно рассчитать стационарное значение риска
неремонтируемой системы.ПРИМЕР 13.5. Вычислить стационарное значение риска системы из приме¬
ра 13.4, структурная схема которой представлена на рис. 13.7.Решение. Прежде всего, на основе табл. 13.3 определим значения интенсив¬
ностей первого и второго отказов каждой подсистемы:
574Глава 13□ для нагруженного резерва Aj = 20,0005 = 0,001 час"1, Aj - 0,0005 час'1;□ для ненагруженного резерва Л2 =0,0006 час-1, Л2 =0,0006 час-1;□ для резерва с дробной кратностью А3 =3 0,0004 = 0,0012 час-*,
Аз = 2 • 0,0004 = 0,0008 час'1.С учетом принятых выше обозначений выражение (13.16), записанное в раз¬
вернутом виде, имеет вид:i? = rjA|(Ti +х12 +т13 + Т21 + х31 +х123 + т132 +т213 +т231 +т312 +T32l) +
+^2-^2(т2 + т12 + х23 + Т21 + т32 + т123 + т132 + х213 + т231 + х3!2 + т321) +
+Г3Лз(т3 +Т13 + Т23 +Х31 +Х32 +Т)2з +t132 +Т213 +t23i +х312 +T32l)-Вычислим среднее время пребывания системы во всех состояниях:1 1т0 = = — — = 357,1 час,0 Л] + Л2 + Л3 0,001 + 0,0006 + 0,0012Ai 0,001 ^сп , 1СС ,,т. = * тп = 357,1 = 155,3 час,1 Л',+Л2+Л3 0 0,0005 + 0,0006 + 0,0012Л2 0,0006 Kt, Лп сх 1 т 155,3 = 40,5 час,12 а;+Л^+Л3 0,0005 + 0,0006 + 0,0012лз 0,0012 ... __ ,х _ =—■ —— 40,5 = 25,6 час123 л;+А^ + А^ 12 0,0005 + 0,0006 + 0,0008ит. д.Аналогично вычисляются остальные средние.В результате расчетов получим стационарное значение риска системы, рав¬
ное 14,7 ден. ед. Это значение совпадает с тем, что было получено в приме¬
ре 13.4.Ремонтируемая системаТеперь будем считать, что система является ремонтируемой. Пусть ю(; —
стационарное значение параметра перехода из состояния £,• в состояние Sj.
Так какIMij (0 = °Ч/ + 00 - ®/,у )dx >
Надежность и риск575то асимптотой для М, у (/) является функция(OtJ + b'j,гдеооbiJ = l((Oij(x)-G>u)dx .
оСледовательно, асимптотически при больших значениях t имеет место при¬
ближенное равенствоЛ(0* Z + (13.17)геЕ+, /е£_Из (13.17) видно, что при наличии ремонта риск системы увеличивается во
времени.Рассмотрим случай экспоненциальных распределений времени безотказной
работы элементов. В этом случае формула (13.17) приобретает вид:Л(/)« Z rk(iJ)^k{iJ) (Pi1 + ^<) > (13.18)ieE+,jeE_где Pj — стационарное значение вероятности пребывания системы в состоя¬
нии Sj, а00= l(Pi(x)-pj)dx.
оПРИМЕР 13.6. Требуется получить асимптотическое поведение риска нере¬
зервированной ремонтируемой системы, рассмотренной в примерах 13.2 и 13.3.Решение. Асимптотическая формула (13.18) для нерезервированной системы
представляется в этом случае в следующем виде:4Л(0« Z V*OV + Ao)>
k = 14где сумма ]Г Xkrk =0,790684 была получена в примере 13.2.*=1Так как функция готовности системыu X. _fu+>
576Глава 13то коэффициент готовностир0 - —= = О,999400.]х + 1с 1 + 0,0006002Подставляя значение /»0 в выражение для 6,, получим:Ъ0 = ] (р0 (0 - р0 )Л = = = 0,0006002 = 0()05990 0JViP0W ц + Хс 0J (Ц + Яс)2 1,0006002Теперь воспользуемся формулой риска:R(t) » 0,790684(0,999400/ + 0,000599) = 0,79021 • / + 0,000474.Такая же асимптотика была получена в примере 13.3.13.3. Полезность системыЛюбая созданная человеком система должна обеспечивать некоторый эффект
(выигрыш) от своего функционирования, т. е. должна быть полезной. Поня¬
тие ценности и пользы не имеют универсального характера, даже когда они
отражают интересы больших групп людей. Индивидуальные представления о
них из-за весьма различных мотивов и взглядов сильно различаются. Это
различие может быть ограничено, если рассматривать полезность принимае¬
мых решений в инженерной и хозяйственной деятельности. Однако и здесь
остается возможность субъективной оценки полезности небольшими группа¬
ми и отдельными людьми.На полезность, в конечном счете, оказывают влияние и такие плохо оцени¬
ваемые свойства, как наглядность, удобство в эксплуатации и некоторые фак¬
торы, просто не поддающиеся учету. Пользу в этом случае трудно оценить, и
ее приходится описывать только рядом желаемых свойств.Полезность системы во время ее эксплуатации может оцениваться величиной
"выигрыша" W(t), который приносит система в момент времени /. Общий
выигрыш системы складывается из выигрыша пребывания системы в состоя¬
ниях и из выигрыша, который получается вследствие мгновенных переходов
из состояния в состояние.Если /-е состояние является состоянием исправной работы системы, то обо¬
значим через а, стоимость продукции, производимой в единицу времени.
Если z'-e состояние классифицируется как состояние отказа системы, то через
аг можно обозначить штраф за недовыпуск продукции или затраты на прове¬
дение ремонта в единицу времени (в этом случае будем считать, что а, < 0).
Надежность и риск577Аналогично переходам из состояния в состояние также могут быть сопостав¬
лены числа а, у, имеющие следующий смысл: если переход из состояния / всостояние j вызван отказом некоторого элемента системы, то я, j характе¬
ризует потери или убытки, связанные с этим отказом (считаем, что а, ,■ < 0);
если переход из состояния i в состояние j вызван ремонтом некоторого
элемента системы, то качество системы улучшается, и а,- • характеризует
прибыль или доход, связанный с восстановлением.Средний выигрыш от пребывания системы в состоянии /, очевидно, равен
произведению а, на среднее время пребывания системы в этом состоянии/я,(О. т. е. а,тиДО.Средний выигрыш, обусловленный переходом из состояния i в состояние j,
очевидно, равен произведению atJ на среднее число таких переходов
Mjj(t), т. е. ajjMjjO) • Общий средний выигрыш системы в момент t опре¬
деляется тогда следующим образом:W(t)= X «*«,(') + I (13.19)■ S,eE SnSj<EEФормула (13.19) представляет собой функцию полезности системы, учиты¬
вающую как время пребывания системы в каждом состоянии, так и число пе¬
реходов из состояния в состояние.Формула техногенного риска (13.6), определенная выше, является важным
частным случаем формулы (13.19). Она получается, если все коэффициенты
а, и а( j положить равными нулю, за исключением коэффициентов а( /, со¬
ответствующих переходам из исправных в отказовые состояния, для которых
Si е Е+, Sj е Е_.ПРИМЕР 13.7. Пусть-ремонтируемая система имеет только два состояния:
состояние работоспособности и состояние отказа. Получим средний выиг¬
рыш системы.Решение. Из (13.19) следует, что средний выигрыш равенW(t) = a0m0(t) + axm{(t) + a0]M0l(t) + al0Ml0(t).Временные характеристики m0(t), M01(0, M|0(O определяются noметодике, изложенной в разд. 4.1. Они имеют следующие значения:19 Зак. 3094
578Гпава 13т0 =—!=—? + :Ц + X (ц + Х)‘X2г(1_е-(^)/)) =^01=—' +W(t) = a0
(+а01-/ + ■Ц + X (ц + X)х (1-е-(^+Х),)| + а,цА.t + -Ц + А. (ц + А.):+ <3ю1: +
d.(ц + А)2 1\ix tцА.ц + X(ц + Х)2( ЬХ (+ Х(ц+Х)Л]хХ^ .(1-(ц+Х)/)»'О"*-(Ц+».)/'~{\i+X)t'Ц + X (ц + А,)Вычислим средний выигрыш системы при следующих значениях экономиче¬
ских показателей: а0 = 16 ден. ед./час, ах = -5 ден. ед./час, а01 = -7800 ден. ед.,
а]0 =100 ден. ед. Вычисления выполним при (1 = 0,5 час-1 и трех значениях
X: X = 0,005 час-1, А. = 0,001 час-1, А, = 0,0005 час-1.Результаты расчетов приведены в табл. 13.5.Таблица 13.5. Средний выигрыш системы с двумя состояниямиt, часВыигрыш системы, ден. ед.X, час-10,0050,0010,0005000010-2258312120-44816524330-67124836440-89433148550-111841460760-134149672870-156457984980-1787662. 97190-20117441092100-22348271213
Надежность и риск579Изменение функции выигрыша W(t) во времени для А, = 0,005 час"1 (кри¬
вая 1), А. = 0,001 час-1 (кривая 2), А = 0,0005 час-1 (кривая 3) приведено на
рис. 13.9.Относительный выигрыш системы является стабильным. Асимптотическоезначение среднего выигрыша равно:ГГ(0- ao^ + aik + (0oi +Qio)^f-
ц + XДля нашего случая относительный выигрыш составляет:□ Щ) =-22,34 при А = 0,005 час'1;□ кр. = 8,27 при А = 0,001 час"1;□ = 12J3 при А = 0,0005 час-1.
tПо результатам расчетов можно сделать следующие выводы:О повышение надежности системы (уменьшение А) приводит к повышению
выигрыша, при недостаточно высокой надежности техники выигрыш ста¬
новится отрицательным; в нашем примере существенный проигрыш имеет
место при А = 0,005 час"1;
580Глава 13□ общий выигрыш системы растет с течением времени практически линейно
(рис. 13.9);□ цена выпускаемой продукции из-за отказов техники может существенно
снижаться. Например, при отсутствии отказов стоимость выпускаемой
продукции в единицу времени равна 16 ден. ед., однако фактически, в ос¬
новном вследствие риска из-за отказа системы, стоимость продукцииW(t) 0в единицу времени уменьшается и составляет всего —-— = 8,27 ден. ед.,
если интенсивность отказов системы А, = 0,001 час-1.13.4. Зависимость риска
от частоты неблагоприятных событийАномалии являются редкими явлениями. При этом, чем сильнее аномалия,
тем реже она встречается. Например, отказ авиационного двигателя (сильная
аномалия) является более редкой, чем отказ лампы накаливания в салоне воз¬
душного судна (ВС), а катастрофа на атомной электростанции — событие
еще более редкое. Эти наблюдения в природе и обществе позволяют предпо¬
лагать, что зависимость величины риска от частоты возникновения аномалий
представляет собой гиперболический закон Парето. Аналитически этот закон
представляется в виде:»(*)=^г> (13-2°)где п(х) — число элементов множества, встречающихся ровно х раз в дан¬
ной их совокупности; А, а — параметры распределения.Этому закону подчиняются многие явления в природе и обществе, например:
распределение богатства в обществе, количество жителей в городах, знания
студентов в зависимости от контингента и т. п.В табл. 13.6 приведены данные о частоте неблагоприятных событий и вели¬
чине потерь (стоимости возмещения ущерба) в авиации.Таблица 13.6. Данные о величине потерь и частоте неблагоприятных событий№п/пСобытиеУщерб(У-е.)Частота событий
за время t1Уход ВС на второй круг10 '122Уход ВС на запасной аэродром15233Отказ двигателя на взлете502
Надежность и риск581Таблица 13.6 (окончание)№п/пСобытиеУщерб(У-е.)Частота событий
за время t4Отказ двигателя в полете6035Отказ двигателя при заходе на посадку4036Пожар двигателя на взлете7017Пожар двигателя в полете8028Пожар двигателя при заходе на посадку6519Ошибка техники пилотирования при взлете20410Ошибка техники пилотирования при заходе
на посадку30611Потеря ориентирования экипажем в полете10112Потеря радиосвязи экипажем в полете25313Отказ пилотажно-навигационного оборудования35514Полет в опасных метеорологических условиях154815Выполнение вынужденных посадок ВС
вне аэродрома20216Грубые посадки на аэродроме25717Террористический захват ВС40118Выход из строя члена экипажа в полете30219Отказ техники в полете30720Влияние человеческого фактора на полет ВС1014Для получения математической модели явления риска систематизируем дан¬
ные табл. 13.6. Результаты систематизации проведены в табл. 13.7, где х —
число событий за время t, у — ущерб.Таблица 13.7. Зависимость величины ущерба от числа событийX4923111У, У-е.215190170105Статистические данные, приведенные в табл. 13.6, лишь приближенно оце¬
нивают ущерб от случайных событий, вызванных аномалиями. Поэтому для
сглаживания неточностей данных используем для получения математической
582Глава 13модели интерполяцию, приближенную в узлах. Предположим, что функцией
интерполяции является закон Парето (13.20).Линеаризуем эту функцию и воспользуемся полиномиальной интерполяцией.Линеаризацию можно осуществить путем логарифмирования гиперболиче¬
ской функции. Пусть п(х) = у, 1 + а = -Ь, тогда функция (13.20) будет иметь
вид:у = Ахь или In у = In А + Ъ In х .Обозначая In у = Y, In х = X , получим линейную функцию вида:Y=a+bX.Преобразуем обобщенную таблицу, представив узлы интерполяции jc и зна¬
чения функции у в логарифмических масштабах. Получим табл. 13.8.Таблица 13.8. Данные таблицы 13.7 в логарифмическом масштабеX1,3862,1973,1354,710Y5,3715,2475,1364,654Задача интерполяции нами решена с помощью универсального математиче¬
ского средства символьной математики Derive 5. Ответ компьютер выдал в
следующем виде:У = 5,71530-0,21471*.Из этого решения получаем:А = е5’71530 =303,5 , Ъ = -0,21471.Тогда закон Парето для случая нашей задачи риска имеет вид:303,5у=.0,21471(13.21)Об адекватности модели можно судить по результатам табулирования функ¬
ции (13.21). В табл. 13.9 приведены исходные данные (функция f{x)) и зна¬
чения функции интерполяции ф(х).Таблица 13.9. Сравнение исходных данных с результатами интерполяцииX4923111Ах)215190170105<р(х)225,4189,3154,8110,4
Надежность и риск583ЧастотаРис. 13.10. Зависимость ущерба от частоты событийИз сравнения данных таблицы и рис. 3.10 можно утверждать, что явление
риска по данным о потерях в авиации подчиняется закону Парето.Этот результат имеет важное практическое значение. Он позволяет:□ предсказывать величину риска по данным об интенсивности воздушного
движения;□ вычислять величину риска при известных показателях частоты неблаго¬
приятных событий;□ оценить влияние внешних факторов, качества техники и человеческого
фактора на величину риска.13.5. Методы снижения рискаПовышение надежности системы путем введения избыточности влечет за со¬
бой уменьшение риска из-за отказов ее элементов. Рассмотрим этот вопрос
для следующих видов резервирования:□ постоянно включенный резерв;□ резерв с дробной кратностью;□ резерв замещением.Для нерезервированной системы с функцией распределения времени до отка¬
за F(t) риск рассчитывается по формуле:Ro(t) = rF(t),
584Глава 13где г — риск вследствие ее отказа. Повысим надежность системы путем
структурного резервирования. Тогда риск системы будет равен:R(t) = rq(t),где q(t) — вероятность отказа резервированной системы. Будем считать, что
резервирование осуществляется однотипными по надежности системами.Для постоянно включенного резерва кратности т вероятность отказа равна
q(t) = Fm+l (t). Значит, уменьшение риска в момент t составит:ВД=-^ = Г“«).Для системы с дробной кратностью резервирования, состоящей из п элемен-П _тов, из которых т резервных, q(t)= £ C'nF‘(t)Fn~‘(t). Тогда уменьшениеi~m+\риска составит:£ С‘пР1 (t)Fn~‘(t)= = у C'Fi-1(t)Fn-i(t).ад т ,~m+1Для резерва замещением q(t) = /* F(t). ТогдаR(t) /*(т) * F(t)VR( t) =ПРИМЕР 13.8. Необходимо получить зависимость VR{t) от кратности резер¬
вирования и определить уменьшение величины риска VR в случае постоян¬
ного резерва и резерва замещением. Элементы системы имеют экспоненци¬
альные распределения с параметром X - 0,1 час-1.Решение. Получим зависимости VR от кратности резервирования:□ для постоянного резерваVR(t) = ( 1-е~и)т;□ для резерва замещениемXm+ltm и
Я<)‘ l-e-" “ 1-<г"
Надежность и риск585Зависимости VR от времени при различных видах резерва и кратности, рав¬
ной m = 1 и т = 6, показаны на рис. 13.11 и 13.12.Рис. 13.11. Снижение риска для кратности резерват = 1 при постоянном резерве (кривая 1)и резерве замещением (кривая 2)Рис. 13.12. Снижение риска для кратности резерва т = 6 при постоянном резерве (кривая 1)и резерве замещением (кривая 2)Из рассмотренного примера можно сделать следующие выводы:□ уменьшение риска более ощутимо для резерва замещением, чем для по¬
стоянного резерва;□ снижение риска происходит также с увеличением кратности резервиро¬
вания;□ при длительной эксплуатации системы уменьшение риска практически
отсутствует для обоих видов резервирования и любой кратности.
586Глава 13ПРИМЕР 13.9. Определить уменьшение величины риска VR от применения
резервирования, если элементы системы имеют нормальное распределение с
математическим ожиданием а = 10 час и средним квадратическим отклоне¬
нием а = 2 час. Рассмотреть случаи постоянного включения резерва и резер¬
ва замещением.Решение. Функция нормального распределения с параметрами а и с имеет
вид:, IFN(t,a,c) = —т= \е 2°2 dx.
стл/2лТогда для постоянного резерва уменьшение риска в момент t будет равноVRit) = Ftf(t,a,a).Поскольку * F(t) есть функция нормального распределения с парамет¬
рами (т +1 )а и cr-s/m+T , то f*^ *F(t) = ,(m + \)a,Gy/m + \). Отсюда
следует, что для резерва замещением уменьшение риска в момент t равно:V (t)= FN(.^(m + \)a,GyJm + \)R FN(t,a,a)Графики функций VR{t) для постоянного резерва (кривая 1) и резерва заме¬
щением (кривая 2) кратности т = 1 и т-6 изображены на рис. 13.13 и 13.14.Из графиков видно, что все свойства, справедливые для экспоненциального
распределения, имеют место и для нормального распределения. Однако вРис. 13.13. Снижение риска для кратности резерва т = 1 (нормальное распределение)
Надежность и риск587Рис. 13.14. Снижение риска для кратности m = 6 (нормальное распределение)данном случае наблюдается более существенное уменьшение риска системы
для резерва замещением (особенно высокой кратности), чем в случае экспо¬
ненциального распределения.Отметим, что снижение риска имеет место только для систем непродолжи¬
тельного действия. Функция VR(t) имеет предел. В стационарном режиме
величина риска остается постоянной, не зависящей от времени работы сис¬
темы.
ГЛАВА 14
АБСОЛЮТНО НАДЕЖНЫЕ
СИСТЕМЫ14.1. Понятие
"абсолютно надежная система"Термин "абсолютно надежная система" и проблемы, с ним связанные, не слу¬
чайны. Многие технические системы, призванные решать важные для людей
задачи, не должны отказывать. К ним относятся системы энергетики (особен¬
но атомной), космические аппараты, ракеты с атомными зарядами, информа¬
ционные, транспортные и многие другие системы. Их отказ приводит к ката¬
строфам. Цена отказа столь велика, что часто нет смысла создавать такие
системы, если не обеспечить их абсолютную надежность. Для уменьшения
техногенного риска к таким системам предъявляются высокие требования по
надежности. Нередко в технических требованиях на их разработку предъяв¬
ляются требования практически абсолютно надежной системы. Например,
вероятность безотказной работы в течение выполнения системой задания
должна быть не менее 0,999 или коэффициент готовности Кг > 0,995.Разработчик такой сложной системы, стремясь удовлетворить требования
надежности, сталкивается с рядом трудностей, которые в большинстве случа¬
ев не преодолимы.Первая трудность: Рассчитать показатели надежности сложной системы с
точностью три знака невозможно по следующим причинам:П точность исходных данных (интенсивностей отказов элементов) ниже тре¬
буемой точности расчета показателей надежности системы;□ математические модели, разработанные в теории надежности, не адекват¬
ны функционированию реальной системы;□ размерность уравнений, описывающих функционирование сложных сис¬
тем, столь высока, что точное решение получить невозможно.
Абсолютно надежные системы589Вторая трудность'. Определить показатели надежности приведенных выше
систем методами испытаний практически невозможно из экономических, фи¬
зических соображений и соображений безопасности.Возникла идея создания абсолютно надежной системы, которая не требует
расчетов показателей надежности и статистических испытаний по их опреде¬
лению, но удовлетворяет высоким требованиям безотказности.Абсолютно надежной называется система, которая удовлетворяет качест¬
венным критериям надежности. Качественными будем называть такие крите¬
рии, которые обеспечивают заданные показатели, не требуя расчетов и испы¬
таний по определению численных показателей надежности.Смысл этих терминов покажем на примере.ПРИМЕР 14.1. Пусть релейное устройство включения энергетической сис¬
темы разового действия имеет постоянную интенсивность отказов элементовА, = 2,4-10-6 час-1. Время его работы равно времени включения системы,
длительность которого исчисляется секундами и не превышает 5 минут.
Тогда вероятность безотказной работы релейного устройства в течение вре-J -2,4-10”®-^-мени t будет иметь значение: P(t) = e =е 60 =0,9999976.Надежность релейного устройства за счет короткого времени работы столь
высока, что практически оно удовлетворяет требованиям абсолютной надеж¬
ности. Однако его нельзя назвать абсолютно надежным по следующим двум
причинам.Во-первых, вероятность безотказной работы P(t) Ф1; во-вторых, мы не учли
того обстоятельства, что реле может отказать в момент включения.Применим для обеспечения его показателя надежности P(t) = 1 резервирова¬
ние с кратностью т-\. Тогда можно утверждать, что наша система абсо¬
лютно надежна, и вовсе не потому, что ее вероятность безотказной работы
равна 1 (с точностью 10 знаков). Если интенсивность отказа релейной систе¬
мы X является величиной постоянной, то имеет место ординарность потока
отказов. А это значит, что в момент времени t два отказа произойти не мо¬
гут. Получим зависимость интенсивности отказа резервированного реле от
времени, воспользовавшись формулой:Р'(0
Решение было получено с помощью математической системы Derive 5. На
экране монитора оно имеет следующий вид:#1: р = е#2: 1 - (1 - e"X't )2#3: — (l-(l-e'vt)2)
dt#4:#5: X = -2-(2 . 4-10 )-ё6, ~-2-(2. 4-10~в)-(5/60)— 2• (2 . 4 -10 )-ё,-6. д-(2.4-10"6)-(5/60)#6: Л = -■10-е)-(5/60) \2- {2 . 4■ 10-в)-(5/ 60)#7: Л = 9 . 599994240 ■ 1(Г13В строке #1 представлено выражение для вероятности безотказной работы
нерезервированного реле, в строках #2, #3, #4— вероятность безотказной
работы и ее производная резервированного реле. В строке #5 приведено вы¬
ражение для интенсивности отказов резервированного реле. В строках #6 и
#7 находятся результаты вычисления значения интенсивности отказа дубли¬
рованного реле при t = 5 мин (5/60 час).Интенсивность отказа дублированной системы показана на рис. 14.1.Из рисунка видно, что интенсивность отказа реле от времени в случае дубли¬
рования при t = 0 равна нулю и асимптотически приближается к интенсивно¬
сти отказа нерезервированного реле (2,4 • 10~6 час-1).Из полученных результатов можно сделать следующий вывод: релейную
дублированную систему можно считать абсолютно надежной, т. к. время ее
функционирования мало (вероятность безотказной работы практически равна
единице), а вероятность отказа одновременно двух элементов системы в одно
и то же время равна нулю. Качественным критерием надежности релейной
системы может быть следующий: релейная система абсолютно надежна, если
отказ ее любого элемента не ведет к отказу системы.Нельзя отождествлять понятие "абсолютно надежная система" с системой,
которая никогда не отказывает, имея вероятность безотказной работы, рав¬
ную единице, т. е. P(t) = 1 при любом t.
Абсолютно надежные системы591МО, * М-* час'1Технических систем, которые никогда не отказывают, нет и не может быть.
Из теории вероятностей известно, что случайное событие может случиться
даже в том случае, если вероятность его возникновения равна нулю. Следует
иметь в биду, что вероятность безотказной работы является убывающей
функцией времени t, имеющей следующие свойства: Р(0) = 1, Р(оо) = 0. Из
этого следует, что определение понятия "абсолютно надежная система" тре¬
бует ограничения на время ее функционирования. Время t, в течение которо¬
го система должна удовлетворять условиям абсолютной надежности, следует
ограничивать временем выполнения ею задачи, которое не может превышать
ее срока службы. Например, двигатель самолета не должен отказывать в те¬
чение времени полета. Но, будучи на земле после посадки, над ним могут
выполняться регламентные работы и даже ремонты. Таким образом, авиаци¬
онный двигатель должен быть абсолютно надежным в течение времени поле¬
та самолета.Из теории вероятностей известно, что если справедлив нормальный закон
распределения случайной величины, то вероятность ее появления, равная
0,997, соответствует трехсигмовому диапазону изменения случайной величи¬
ны, и это событие считается практически достоверным. Интерпретируя слу¬
чайные события как отказы, можно утверждать, что если вероятность безот¬
казной работы технической системы в течение времени выполнения задания
не менее 0,997, то такая система является абсолютно надежной.При расчете надежности сложной системы исходными данными являются
интенсивности отказов элементов, которые получают по результатам их ис¬
592Глава 14пытаний или данным эксплуатации техники. Так как статистические испыта¬
ния по определению показателей надежности дорогостоящие, то число об¬
разцов и время испытания ограничены. По этим причинам данные об интен¬
сивностях отказов элементов получают с точностью, не превышающей две
значащие цифры. По данным об отказах элементов в процессе эксплуатации
техники также не удается получить X с более высокой точностью. Это объ¬
ясняется малой достоверностью данных и некорректностью алгоритмов их
обработки. Показатели надежности системы, рассчитанные по данным интен¬
сивностей отказов элементов, не могут быть получены с точностью выше,
чем точность исходных данных, т. е. с точностью двух значащих цифр. Если,
например, в результате расчета вероятность безотказной работы P(t) = 0,997 ,
то для получения верного результата необходимо это число округлить до
двух значащих цифр. После округления получим P(t) = 1, т. е. система абсо¬
лютно надежна.Требования на показатели надежности системы формулируются в виде чис¬
ленных показателей, таких как вероятность безотказной работы P(t), среднее
время безотказной работы, функция и коэффициент готовности, наработка на
отказ. Для удовлетворения заданных требований разработчик должен в про¬
цессе проектирЬвания вести расчет надежности, разработать методы ее обес¬
печения и подтвердить достоверность расчетов испытаниями. При этом он
встречается с непреодолимыми трудностями.Расчеты надежности сложных систем по указанным критериям не дают воз¬
можности получить численные оценки с необходимой для инженерной прак¬
тики точностью. Это объясняется следующими основными причинами:□ неадекватность математических моделей, широко известных в теории на¬
дежности, физическим моделям функционирования технических систем;□ высокая размерность уравнений, описывающих функционирование техни¬
ческих систем;□ недостоверность исходных данных.Рассмотрим эти вопросы более подробно. Обратимся к экспоненциальной
модели надежности. Она предполагает, что поток отказов является простей¬
шим со свойствами стационарности, ординарности и отсутствия последей¬
ствия.В сложной технической системе поток отказов не удовлетворяет этим усло¬
виям. Элементы, узлы и устройства работают, как правило, не одновременно.
При взлете самолета работают одни органы управления, в полете — другие,
при посадке — третьи. Из-за отсутствия полного контроля работоспособно¬
сти техники состояния ее элементов в каждый момент времени не определе¬
ны. Во всех этих и других случаях вероятность возникновения п отказов за
Абсолютно надежные системы593время At зависит от того, где на оси времени находится Ы, а это означает,
что поток отказов сложной системы не стационарный, если даже интенсивно¬
сти элементов постоянны.В процессе функционирования сложной системы нагрузки на исправные эле¬
менты при отказах техники меняются. Это значит, что имеет место последей¬
ствие отказов.Нестационарность и последействие отказов особенно четко проявляются в
восстанавливаемых системах. В таких системах отказавшие элементы ремон¬
тируются. После их ремонта система уже не возвращается в доотказовое со¬
стояние. Если предположить, что интенсивность отказов системы после ее
ремонта остается постоянной, но другой по величине, то граф функциониро¬
вания системы будет иметь вид, показанный на рис. 14.2.0 2 4 пРис. 14.2. Граф состояний системы в случае ремонта элементовПосле отказа система переходит из состояния (0) в состояние (1) с интенсив¬
ностью К. После восстановления она не возвращается в состояние (0), а пе¬
реходит с интенсивностью ц в новое состояние (2), т. к. теперь ее интенсив¬
ность отказа после ремонта равна ^ > к. Из состояния (2) при новом отказе
она перейдет в состояние (3) с интенсивностью А., и т. д. Граф функциониро¬
вания системы представлен в предположении, что интенсивность восстанов¬
ления постоянна и равна ц. Из описания функционирования системы и графа
состояний видно, что в системе нет установившегося режима и коэффициент
готовности, как показатель надежности восстанавливаемой системы, не имеет
смысла. Если теперь учесть нестационарность от неодновременной работы
элементов и наличие последействия отказов, то математическая модель
функционирования системы будет такой сложности, что ею невозможно бу¬
дет воспользоваться для оценки надежности сложной системы даже с исполь¬
зованием современных средств вычислительной техники.Число состояний сложной системы велико и может превосходить значение
2", где п — число элементов системы.Существующие методы расчета, содержащиеся в различных руководящих
материалах и стандартах, всего сказанного не учитывают.
594Гпава 14Важным условием необходимой точности расчетов является точность исход¬
ных данных. Обычно расчеты показателей надежности ведутся по данным
интенсивностей отказов элементов. Эти данные получают из опыта. Погреш¬
ность опыта такова, что интенсивности отказов имеют точность, не превы¬
шающую двух значащих цифр, причем вторая цифра является сомнительной.Приведем простой пример. Пусть интенсивность отказа некоторого устрой¬
ства X = 0,0001 час-1, время непрерывной работы / = 100 час. Тогда абсолют¬
ная погрешность определения X равна половине единицы последнего разря¬
да, т. е. ех = 0,00005 . Абсолютная погрешность произведения Xt будет:ех/ = ех/ + е А >где г, — абсолютная погрешность времени t. Так как s, = 0, тоs\i = = 0> 00005 * 100 = 0,005 .Тогда относительная погрешность произведения8^ = /Xt * 100 = 50 %.Так как вероятность безотказной работы P(t) = e~lt, то P(t) = е~0-0001*100 = о,99
вычислено с относительной погрешностью 8 = 50 %. В нашем примере ин¬
тенсивность отказа X вычислена с одной значащей цифрой, поэтому по пра¬
вилам приближенных вычислений величина P{t) должна быть округлена до
одной значащей цифры, т. е. расчетное значение будет P(t) = 1. Это означает,
что система абсолютно надежна. .Показатели надежности элементов можно получить с высокой точностью по
данным эксплуатации сложных систем. Это объясняется двумя обстоятельст¬
вами — возможностью большого объема испытаний и реальными условиями
работы элементов. Однако в настоящее время в стране не существует единой
системы сбора информации об отказах техники, а там, где она ведется, дан¬
ные недостоверны (см. гл. 11).Подтвердить расчетные показатели надежности опытным путем по результа¬
там испытаний крайне трудно. Причины этого следующие:□ невозможно по экономическим соображениям провести испытания нуж¬
ного объема;□ отсутствуют инженерные методики ускоренных испытаний;П не разработаны неразрушающие методы испытаний.Из сказанного выше вытекает следующий важный вывод: рассчитать пока¬
затели надежности сложной системы методами современной теории
практически невозможно, как невозможно их подтвердить путем испытания
Абсолютно надежные системы595техники. Причинами этого являются: неадекватность математических моде¬
лей физическим, сложность расчетов из-за большой размерности уравнений,
отсутствие достоверных данных о надежности элементов сложных систем.Уточним понятие абсолютно надежной системы.Абсолютно надежной называется система, надежность которой не менее
заданной и для которой одновременно удовлетворяются качественные крите¬
рии надежности. За заданную вероятность безотказной работы рекомендуется
принимать P(t) = 0,997 .Полезность такого определения состоит в следующем:□ используя качественные критерии, исчезает необходимость расчетов пока¬
зателей надежности в процессе проектирования техники;□ не нужно подтверждать достоверность результатов расчета дорогостоя¬
щими испытаниями.Из сказанного выше очевидно, что при создании высоконадежных систем
целесообразно пользоваться качественными критериями, которые не требуют
расчетов надежности.Качественные критерии должны удовлетворять следующим условиям:□ непротиворечивость численным показателям;О независимость от численных показателей при проектировании техниче¬
ской системы;□ физичность и легкая реализуемость на практике;□ достоверность результатов.14.2. Качественные критерии надежностиНепротиворечивость качественных и количественных критериев означает
выполнение следующего условия:К >Лгр,т. е. количественный показатель надежности системы должен быть выше тре¬
буемого.Независимость качественных показателей означает, что вести расчеты пока¬
зателей надежности, таких как вероятность безотказной работы, коэффициент
готовности, наработка на отказ и др., в процессе создания системы нет необ¬
ходимости. Разработчик должен лишь доказать, что система удовлетворяет
качественным критериям.Качественные критерии легко сформулировать, если не думать о их практи¬
ческой реализации. Вот один из таких критериев: система абсолютно надеж-
596Гпава 14на, если отказ ее пяти элементов не ведет к отказу системы. Критерий физи-'
чен, но не реализуем, т. к. требует пятикратного резервирования. Здесь не
учтены ограничения на вес, габариты и стоимость системы.Создание абсолютно надежной системы требует знания методов повышения
надежности и способов их практической реализации.Надежность системы зависит от ее сложности (числа элементов), интенсив¬
ности отказов элементов, времени непрерывной работы системы, интенсив¬
ности восстановления и дисциплины обслуживания. Из этого следует, что
путями повышения надежности являются упрощение системы (уменьшение
числа элементов), снижение интенсивности отказов элементов, сокращение
времени непрерывной работы, улучшения качества обслуживания путем по¬
вышения интенсивности восстановления. Если этих способов недостаточно
для создания абсолютно надежной системы, то применяется резервирование
(структурное, нагрузочное или временное).Выбор критериев абсолютно надежной системы зависит от используемого
метода обеспечения надежности. При этом возможны два типа критериев:
одинарные и комплексные.Одинарным называется критерий, позволяющий создать абсолютно надеж¬
ную систему путем применения одного метода повышения надежности. При¬
мерами таких критериев могут быть следующие:□ система абсолютно надежна, если число ее элементов п<т;П система абсолютно надежна, если время ее непрерывной работы t < т ;□ система абсолютно надежна, если время ее восстановления Гв не превы¬
шает заданное Т3.При применении таких критериев должны быть оговорены некоторые другие
условия, например тип элементов, на которых создается система, и условия
ее эксплуатации.Комплексным называется критерий, позволяющий создать абсолютно надеж¬
ную систему путем применения двух и более методов повышения надежно¬
сти. Примерами таких критериев могут быть следующие:□ система абсолютно надежна, если она состоит из числа элементов N <т
и отказ одного любого элемента не ведет к отказу системы;□ система абсолютно надежна, если время ее непрерывной работы не пре¬
вышает Т3 и все ее элементы работают с нагрузкой, не превышающей к%
от номинальной;□ система абсолютно надежна, если время ее восстановления не превышает
заданного и отказ одного любого механического элемента не ведет к ееотказу.
Абсолютно надежные системы597Критериев надежности абсолютно надежных систем может быть много. Их
приходится формулировать путем анализа надежности проектируемой систе¬
мы традиционными вероятностными методами. Рассмотрим этот вопрос бо¬
лее подробно на примерах.ПРИМЕР 14.2. Проектируемая система будет состоять из числа элементов
п >675 со средней интенсивностью отказов Я. = 1,2 • 10-6 час-'. Время непре¬
рывной работы системы t = 300 час. Требуется разработать критерий надеж¬
ности абсолютно надежной системы. Предполагается, что абсолютно надеж¬
ная — это такая система, вероятность безотказной работы которой превыша¬
ет 0,997, т. е. Р(300) > 0,997.Решение. Прежде всего, определим вероятность безотказной работы системы
без применения методов ее повышения:P(t) = е~пХ‘ = е~675'1,2 ’ 10‘6-300 = 0,784.Теперь определим, существует ли одинарный критерий. Для этого вычислим
значение rikt и его проанализируем.Так как по условию задачи Р(ЗОО) > 0,997, то e~nXt > 0,997, т. е.rikt < - 1п(0,997) = 0,003.Тогда по условию задачи абсолютно надежная система должна иметь число
элементов п = 0,003/(1,2-10-6 • 300) = 8.Система, которая по предварительным расчетам должна иметь 675 элементов,
не может быть создана на восьми элементах.Определим, какой должна быть средняя интенсивность отказов элементов
абсолютно надежной системы:к = 0,003/nt = 0,003/(675 * 300) = 1,48 * 10"8.Из расчета видно, что для создания абсолютно надежной системы необходи¬
мо снизить интенсивность отказов элементов примерно на два порядка. Фи¬
зически это реализовать невозможно. Опыт показывает, что снизить интен¬
сивность отказов элементов путем облегчения режимов их работы можно не
более чем в 10 раз, т. е. только на один порядок. Вычислим теперь, в течение
какого времени функционирования систему можно считать абсолютно на¬
дежной:/ = 0,003/(675*1,2*10~6) = 3,7 час.Система будет абсолютно надежной, если снизить время ее функционирова¬
ния с 300 час до 3,7 час, что практически невозможно.
598Глава 14Из выполненного анализа видно, что не существует одинарного критерия аб¬
солютно надежной системы. Вернее, он может быть сформулирован даже в
трех видах, но не может быть реализован путем упрощения системы, или по¬
вышения надежности элементов, или сокращения времени ее работы.Попытаемся создать абсолютно надежную систему, используя структурное
резервирование. Первоначально определим кратность общего резервирования
абсолютно надежной системы. Рассмотрим два случая: общее резервирование
с постоянно включенным резервом и по методу замещения.14.2.1. Кратность резервирования системы
при общем резервировании
с постоянно включенным резервомВ данном случае вероятность безотказной работы системы при кратности ре¬
зервирования т вычисляется по формуле: Рс(/) = 1-(1--?о(ОУ”> гДе ^(0 —
вероятность безотказной работы исходной нерезервированной системы. Из
формулы получаем следующее выражение кратности резервирования:т = —^с(О) _ 1 в нашем случае PJt) = 0,997, P0(t) = 0,784 . Подставляя
In(l-P0(O) cw . 0Wэти данные в формулу, получим: т = 2,78, т. е. т = 3 . Сформулируем каче¬
ственный критерий абсолютно надежной системы: система абсолютно на¬
дежна, если отказ трех ее любых элементов не ведет к отказу системы.14.2.2. Кратность резервирования
абсолютно надежной системы
при общем резервировании замещениемВ этом случае вероятность безотказной работы системы при кратности резер¬
вирования т выражается формулой:i = 0В данном случае получить в явном виде выражение для кратности резервиро¬
вания т нельзя. Решение было нами получено численными методами с по¬
мощью универсальной математической системы Derive 5. Ответом является
т = 2.Сформулируем качественный критерий абсолютно надежной системы: сис¬
тема абсолютно надежна, если она дублирована по принципу замещения.
Абсолютно надежные системы599ПРИМЕР 14.3. Дана нерезервированная восстанавливаемая система, состоя¬
щая из « = 5 устройств. Интенсивности отказов "X. и интенсивности восста¬
новления ц приведены в табл. 14.1.Таблица 14.1. Параметры системы№ устройства12345X, час"10,030,0240,010,0140,01ц, час-11,51,211,41Необходимо разработать качественные критерии абсолютно надежной систе¬
мы, коэффициент готовности которой Кг =0,997 .Решение. Определим сначала коэффициент готовности исходной системы:1 1*г=‘ "А
1 + 1^
»=1 h, 0,03 0,024 0,01 0,014 0,01
1 + _?—+ +-1—+ — += 0,935.1,5 1,211,41Результат расчета показал, что система не удовлетворяет требованиям на¬
дежности.Облегчим режимы работы элементов до максимально возможных, уменьшив
интенсивность их отказа на порядок. Рассчитав вновь коэффициент готовно¬
сти, получим Кг =0,993. Применение нагрузочного резервирования методом
облегчения режимов работы элементов не позволило создать абсолютно на¬
дежную систему. Увеличим вдвое интенсивность восстановления системы за
счет повышения качества диагностики и улучшения дисциплины обслужива¬
ния. Повторяя расчеты при новых значениях ц, получим: Кг = 0,997 . По ре¬
зультатам расчетов можно сформулировать следующий критерий абсолютно
надежной системы: система абсолютно надежна, если применено нагрузоч¬
ное резервирование с облегчением режимов работы элементов до предельно
возможных и вдвое увеличена интенсивность восстановления элементов.14.3. Способы создания
абсолютно надежных системЭтапами создания абсолютно надежных систем являются:1. Разработка качественных критериев.2. Выбор качественных критериев из условий физической реализуемости.
600Глава 143. Разработка структурной схемы системы.4. Создание абсолютно надежной системы.14.3.1. Разработка качественных критериев
и их выбор из условий реализацииИз рассмотренных примеров видно, что для разработки качественных крите¬
риев надежности абсолютно надежных систем необходимо знать методы
обеспечения и способы анализа надежности сложных систем. При этом в пе¬
реборе вариантов большую роль имеет интуиция и знание свойств различных
методов повышения надежности. Однако этого недостаточно. Необходимо
еще хорошо знать анализируемую систему. Только при этих условиях из
множества критериев можно выбрать тот, который легко реализуем при про¬
ектировании и создании системы. Разработчик критериев должен быть весь¬
ма квалифицированным специалистом, хорошо знающим теорию надежности
и инженерное дело. Процесс выбора качественных критериев можно автома¬
тизировать. Для этого достаточно построить номограммы зависимостей пока¬
зателей надежности P{t), 7j, Кг(/), Кг, Т от времени, средней интенсивно¬
сти отказов элементов, числа элементов при различных методах резервирова¬
ния и характеристик обслуживания ремонтируемой системы. Безусловно,
можно разработать программу, по которой компьютер при заданных п, К, t,
ц и виду резервирования выдаст все возможные варианты критериев.14.3.2. Разработка структурной схемы системыСхема расчета надежности необходима для самопроверки правильности вы¬
бранного критерия. Проверка осуществляется путем расчета показателей на¬
дежности по методикам, известным в теории. При наличии структурной схе¬
мы можно рассчитать надежность системы не только по тем показателям, по
которым получены качественные критерии, но и по другим показателям.
Структурная схема также нужна для разработки научных методов эксплуата¬
ции, в частности при расчете оптимального ЗИП.Абсолютно надежная система имеет свои особенности, которые необходимо
учитывать при ее создании. Она не требует проверки вероятностных показа¬
телей надежности в процессе эксплуатации. Но зато она требует проверки
выполнения условий обеспечения качественных критериев. Пусть, например,
за качественный принят следующий критерий: система абсолютно надежна,
если отказ одного любого элемента не ведет к отказу системы. В этом случае
разработчик должен предусмотреть возможность проверки в любой момент
времени состояния основных и резервных элементов системы. Если отказал
Абсолютно надежные системы601хотя бы один из них, то система уже не абсолютно надежна. Она требует вос¬
становления отказавшего элемента.Приведем еще один пример. Пусть качественным критерием является сле¬
дующий: система абсолютно надежна, если нагрузка на элементы в к раз
меньше номинальной. В этом случае должны быть предусмотрены средства
проверки в любой момент времени реальной нагрузки каждого элемента, и
если она не соответствует условиям абсолютно надежной системы, то преду¬
смотреть способы ее восстановления.14.4. Анализ
абсолютно надежных технических системАнализ абсолютно надежных технических систем необходим на этапах раз¬
работки требований и в процессе эксплуатации.Целью анализа на этапе разработки требований является установление крите¬
риев абсолютно надежной системы. Если такие критерии установлены, то на
этапе проектирования расчеты надежности не нужны. В процессе эксплуата¬
ции абсолютно надежной системы должны проводиться два вида испытаний:
качественные и количественные. Качественные испытания необходимы для
установления факта: является ли в данный момент система абсолютно на¬
дежной. Если она удовлетворяет качественным критериям, то этого доста¬
точно для продолжения дальнейшей эксплуатации. Если не удовлетворяет, то
должны проводиться профилактические работы или ремонты до доведения ее
до абсолютно надежной. Статистические испытания необходимы для полу¬
чения данных о надежности элементов системы и проверки соответствия аб¬
солютно надежной системы качественным критериям. Данные о надежности
элементов необходимы для расчета показателей надежности системы при
разработке качественных критериев систем, подобных эксплуатируемой.
Сбор и обработка данных об отказах абсолютно надежных систем — задача
более трудная, чем в случае обычных систем. Отличие состоит в том, что в
обычных системах время отказа фиксируется по факту, который очевиден.
Задача заключается лишь в том, чтобы данные об отказе занести в журнал
отказа техники. В абсолютно надежных системах факт отказа зафиксировать
трудно. Это объясняется тем, что отказ элемента в абсолютно надежной сис¬
теме еще не означает, что отказала вся система. Она может быть работоспо¬
собной, но потеряла свойство абсолютно надежной системы. Это может быть
при случайном изменении нагрузки на элементы, отказе резервного элемента
и т. п. Пусть, например, качественным критерием является следующий: сис¬
тема абсолютно надежна, если нагрузка на любой ее элемент не превышает
40%. Такой критерий означает, что если нагрузка на любой из элементов
602Глава 14превысит 40%, то наступит отказ системы. Чтобы его зафиксировать, необ¬
ходима специальная диагностическая система.Обработка данных об отказах элементов абсолютно надежной системы долж¬
на вестись по методике обработки данных об отказах обычной восстанавли¬
ваемой системы. Это объясняется тем, что любые отказы элементов абсолют¬
но надежной системы фиксируются, как ее отказ, т. к. система при таком от¬
казе потеряла свойство абсолютно надежной системы. Здесь мы сталкиваемся
с двойственным понятием "отказ" абсолютно надежной системы. По первому
определению, отказ — это событие, после возникновения которого система
потеряла свойство абсолютно надежной системы. По второму определению,
отказ— это событие, после возникновения которого характеристики (пара¬
метры) системы вышли за допустимые пределы. Первое определение означа¬
ет, что при таком отказе система работоспособна, она может выполнять свои
функции, но потеряла свойство абсолютно надежной системы. Второе опре¬
деление не отличается от понятия "отказ" обычной системы.Понятие "отказ" определяет вид структурной схемы, а следовательно, и метод
ее анализа. Проблемы анализа надежности покажем на примере.ПРИМЕР 14.4. Пусть абсолютно надежная система состоит из п элементов и
удовлетворяет следующему критерию: отказ одного любого элемента не ве¬
дет к отказу системы. Реализован этот критерий путем раздельного резерви¬
рования. Необходимо вычислить вероятность безотказной работы системы в
течение времени t.Решение. Сформулируем понятие "отказ" системы: отказом будем называть
событие, после возникновения которого система потеряла свойство абсолют¬
но надежной системы. В данном случае отказ системы наступает при отказе
любого элемента системы, а это значит, что ее структурная схема представ¬
ляет собой основное (последовательное) соединение элементов (основных и
резервных). Тогда вероятность безотказной работы системы Pc(t) вычисляет¬
ся по формуле:Pc(t) = e~2nX‘.В данном случае Pc(t) есть вероятность того, что в течение времени t систе¬
ма будет абсолютно надежной, а при возникновении отказа она не потеряет
работоспособности, но в дальнейшем будет функционировать как обычная
система, т. е. не будет удовлетворять критерию абсолютно надежной си¬
стемы.Сформулируем теперь следующее понятие отказа: отказом будем называть
событие, после возникновения которого характеристики системы выходят за
допустимые пределы. При такой формулировке отказа схема расчета надеж¬
Абсолютно надежные системы603ности представляет собой поэлементно резервированную систему с числом
элементов, равном п. Тогда вероятность ее безотказной работы вычисляется
по формуле:^(o=nn-(i-^v)2]-1=1В результате расчетов может оказаться, что абсолютно надежная система не
удовлетворяет требованиям надежности, хотя и отвечает критерию абсолют¬
но надежной системы. Такой вывод может будет сделан в том случае, когда
мала вероятность того, что система абсолютно надежна.Пусть число элементов п = 10, время непрерывной работы системы
t = 120 час, а значения интенсивностей отказов элементов соответствуют
данным, приведенным в табл. 14.2.Таблица 14.2. Значения интенсивностей отказов№ элемента12345678910X- 1(Г5, час-111.21.11,52,10,51,80,22,51,3Расчеты по приведенным выше формулам дают следующие результаты: ве¬
роятность безотказной работы системы в случае раздельного резервирования
равна 0,999, т. е. Р(120) = 0,999, что удовлетворяет требованиям абсолютно
надежной системы. Вероятность безотказной работы абсолютно надежной
системы, когда под отказом понимается событие, после возникновения кото¬
рого система теряет свойство абсолютно надежной системы, Рс (120) = 0,98.В заключение укажем на достоинства и недостатки абсолютно надежных
систем.Достоинства-.□ абсолютно надежные системы не требуют расчетов показателей надежно¬
сти в процессе их проектирования;□ нет необходимости в определительных испытаниях с целью доказательст¬
ва того, что показатели надежности системы соответствуют требуемым.Недостатки:□ абсолютно надежные системы требуют разработки для каждой конкретной
системы качественных критериев;□ эксплуатация системы требует непрерывной диагностики ее состояния с
целью определения статуса абсолютно надежной системы;
604Глава 14□ расчет показателей надежности в процессе эксплуатации системы более
сложный, чем в традиционных системах в связи с многовариантностью
понятия "отказ".Разработка и создание абсолютно надежных систем является сложной науч¬
ной проблемой. Для ее решения необходимо разработать теорию надежности
таких систем, а также инженерные методы и технологии их создания. В на¬
стоящей главе были изложены лишь идеи создания абсолютно надежных
технических систем. Для их реализации требуются серьезные исследования
ученых и инженеров, занимающихся исследованиями и созданием высокона¬
дежных технических систем.
ГЛАВА 15ГРАНИЧНЫЕ ОЦЕНКИ
НАДЕЖНОСТИ СИСТЕМ
В УСЛОВИЯХ НЕПОЛНОЙ
ИНФОРМАЦИИ О ЗАКОНАХ
РАСПРЕДЕЛЕНИЯ ОТКАЗОВ
ЭЛЕМЕНТОВЗадачи надежности технических систем сопровождаются, как правило, огра¬
ниченностью или отсутствием достоверных данных о надежности их элемен¬
тов. Следствием неполноты информации является отсутствие законов рас¬
пределения времени до отказа элементов, а для систем с восстановлением —
отсутствие законов распределения времени восстановления элементов. Для
расчета надежности обычно используется информация или о средних значе¬
ниях времени безотказной работы и времени восстановления, или о значени¬
ях функции распределения в некоторых точках. Неполнота информации ха¬
рактеризуется также возможным отсутствием сведений о независимости эле¬
ментов системы.Все приведенные ранее семейства распределений определяются заданием ко¬
нечного числа параметров. Эти семейства, как правило, используются для
аппроксимации неизвестной функции распределения F(t). Наряду с пара¬
метрическими распределениями в теории надежности используются классы
так называемых непараметрических распределений. Любую функцию из этих
классов нельзя полностью задать с помощью конечного числа параметров.
Таковыми служат, например, классы стареющих или классы стареющих в
среднем распределений [7, 9]. Такие классы распределений достаточно вели¬
ки, получаемые в них оценки показателей надежности слишком широки, а
поэтому практически бесполезны.По мере получения новой информации об отказах и восстановлении элемен¬
тов классы распределений могут быть сужены, причем весьма значительно.
606Глава 15Выделение более узких классов распределений ведет к тому, что в рамках
этих классов верхние и нижние оценки показателей надежности сближаются.
Такими классами могут служить, например, классы H(r,s) [31]. Кроме того,
использование функций класса H{r,s) удобно, а иногда и незаменимо при
отсутствии информации о законах распределения. Примером может служить
известное двустороннее неравенство, справедливое для любого стареющего в
среднем распределения со средним Т и функцией распределения F(t):, Как будет показано далее в этой главе, в классе распределений H(r,s) это
неравенство может быть существенным образом уточнено.15.1. Класс непараметрических
распределений H(r, s)Пусть г и s — любые числа, такие что 0 < г < s < +а>. Определим класс рас¬
пределений H(r,s) следующим образом: в него включаются те и только тераспределения F(t) = е~А(1>, для которых функция —^ является возрастаю-trщей, а функция — убывающей. При этом будем писать FeH(r,s) иtsAeA(r,i).Таким образом, класс H{r,s) состоит из тех распределений, для которых
функция ресурса А(/) имеет степенной порядок роста с граничными показа¬
телями г и S .Такими классами распределений, в частности, могут быть следующие:□ Я(1,+ю) — класс всех стареющих в среднем распределений;□ H(r,s), 1 <r<s — подкласс всех стареющих в среднем распределений,
рост которых ограничен показателями г и s ; интенсивности отказа для
функций из этого подкласса являются возрастающими;□ #(0,1) — класс всех молодеющих в среднем распределений;□ H(r,s), г <s< 1 — подкласс всех молодеющих в среднем распределений,
скорость убывания которых ограничена показателями г и s ; интенсивно¬
сти отказа для функций из этого подкласса являются убывающими.
Граничные оценки надежности систем607Функции класса H(r,s) при г < 1 < s таковы, что соответствующие интен¬
сивности отказа могут не быть монотонными. Заметим, что функции этого
класса являются наиболее популярными в теории надежности, когда в про¬
цессе эксплуатации изделия присутствуют интервалы приработки и старения.Очевидно, что для, вложенных интервалов [г; s] классы распределений
H(r,s) также являются вложенными, т. е. H(rx,s{) cz H(r2,s2), если
Г2 й rx < 5] <: s2 .Рассмотрим примеры распределений из классов H(r,s) при различных зна¬
чениях показателей г и s .ПРИМЕР 15.1. Интенсивность отказов X(t) — неубывающая функция. Тогда
функция ресурса A(t) выпуклая. Так как nA(t)< A(nt) при п> 1, то функцияявляется возрастающей, и поэтому е_Л(/) € Я(1,+оо).tПРИМЕР 15.2. Интенсивность отказов Xit) — невозрастающая функция.
Тогда функция ресурса А(^) вогнутая. Так как nA(t) > A(nt) при п > 1, тофункция является убывающей, и поэтому е_Л(/) е Н(0,1).ПРИМЕР 15.3. Интенсивность отказов задана функцией2при 0^/<1;X(t) = • 1, при 1 < / < 2;
t, при t> 2.
График функции представлен на рис. 15.1.Рис. 15.1. График немонотонной функции интенсивности отказа
608Глава 15Тогда функция ресурса Л(0 имеет вид:лА (/) =21-—, при 0</<1;
1/ +—, при \<t<2\
t2 +1, при t >2.Она является вогнутой на промежутке [0; 1] и выпуклой на промежутке[2;+оо). Легко показать, что функция ~~~ - является убывающей, а функцияГ— возрастающей при г = 2/3 и не является таковой для всякого поло-trжительного г <2/3, поэтому е~А(Г> е Н(2/3,2).ПРИМЕР 15.4. Пусть А(/) = (/ — I)3 +1. График функции X(t) изображен на
рис. 15.2.Рис. 15.2. Непрерывная функция интенсивности отказа
Можно показать, что е S(!> е Я(0,4), причем число s = 4 нельзя уменьшить.Принадлежность функции распределения классу H(r,s) можно определить
на основе статистических данных. При этом увеличение-объема выборки не¬
избежно приводит к сближению между собой параметров г и 5 .
Граничные оценки надежности систем 60915.2. Свойства распределений
из класса Н(г, s)Перечислим некоторые свойства распределений класса H{r,s). Пусть
F{t) = е H(r,s). Тогда имеют место следующие свойства [31].Свойство 1. Функция ^—-)) является возрастающей, а функцияtr— убывающей.tsСвойство 2. Имеют место неравенства:^A{t)<X{t)<-A{t).Свойство 3. Функция y{t) = F{t) удовлетворяет системе неравенств:) + sy(t) In yit) < 0;[-^'(O + O'W In 7(0^0.Свойство 4. Равенство г = s имеет место тогда и только тогда, когда F(t)
есть распределение Вейбулла с параметром формы г (или s ).Свойство 5. Имеют место равенства:-tf{t) -tfit)г = min—— , s - max———— .г Fit) ln(F(/)) / F{t)\niFit))Свойство 6. Если функция ресурса А(/) является строго возрастающей, тое~М0 е Hir,s) тогда и только тогда, когда е~А ^ е Я(1/^,1/г).Свойство 7. Если функция А^г (Г) выпуклая, а функция Л^s(t) вогнутая, то
е~Л(<) е H{r,s).Свойство 8. Функции класса H{r,s) при г > 0 и s < оо непрерывны.Свойство 9. Пусть FeH{r,s) с математическим ожиданием а, и пусть
b > 0 — любое число. Тогда задача оптимизации F{b) -» max имеет опти¬
мальное решение Fmax(х) = , где:20 Зак. 3094
610Глава 15Лтах(*) С\и у
f-v
л, при х<,Ь;, при х > Ь,а постоянная с = cmax(a,b,r,s) есть корень уравненияje~a dx+ je~cx dx = —.
о l *Свойство 10. Пусть FeH(r,s) с математическим ожиданием а, и пусть
6 > 0 — любое число. Тогда задача оптимизации F{b) —> min имеет опти¬
мальное решение Fmjn(x) = , где:\Ъ, при л:<Ъ\— | , при х > Ъ,а постоянная c = cm^n(a,b,r,s) есть корень уравненияJe~cxr (tx+ Je-cx dx~ —.
о 1 *Из свойств 9 и 10 следует, что функцииF(t) = е~а и F(t) = е“Р,гдеJe <//+ Je а' б?/ = — и Je Л+ je р‘ dt = — ,0 1 { о 1 1(15.1)являются соответственно верхней и нижней огибающими функций класса
H(r,s) с математическим ожиданием а. При этом сами огибающие уже не
принадлежат указанному классу. Графическая иллюстрация этого следствия
приведена на рис. 15.3.Следующие свойства играют основную роль в определении интервальных
средних для распределений классов H(r,s).
Граничные оценки надежности систем611Рис. 15.3. Огибающие класса Н( 1,2) с математическим ожиданием a = 105 часСвойство 11. Пусть c(t) — монотонная функция. Тогда задача оптимизацииьz = jc(t)e~A^dt —> maxabна множестве распределений AeA(r,i), таких что |е-д(,)Л = с/, разрешима.aПри этом если функция c(t) возрастающая, то максимум достигается нафункции ctr, а если убывающая, то максимум достигается на функции cts,
где с = const.Следствие. Задача оптимизации00z = ^c{t)e~h^dt —> max
о00при условиях АеЛ(r,s), |е_Л(/)Л = а имеет решение:А (ОНГ 1 + -, если функция c(t) — возрастающая;ЛГ\ 1 + -г/ “уiVv, если функция c(t) — убывающая.Свойство 12. Пусть с(0 — монотонная функция. Тогда задача оптимизацииьz = Jc(t)e~A^dt -> min
612Глава 15на множестве распределений Л е Л(/%л), таких что je KU)dt = d, разрешима.При этом если функция c(t) возрастающая, то минимум достигается нафункции cts, а если убывающая, то минимум достигается на функции ctr,
где с = const.Следствие. Задача оптимизации00z — jc(t)e~A^dt —> min
о00при условиях Л е A(r,s), je~A^dt -а имеет решение:, если функция c(t) — возрастающая;, если функция c[t) — убывающая.л (/) =Г, 0гГ1+-11 sjя,fГ,\г1+-чя,Свойство 13. Предположим, что промежуток [0; оо) разбит на непересекаю-
щиеся интервалы вида [?у_,, t-), j = 1,2,, т (t0= 0, tm = °о ), и на j-м ин-fc .тервале функция А(/) равна Cjt ]., причем r<kj<s. Если функция А(0 не¬
прерывна на промежутке [0; оо) , то она принадлежит классу H(r,s).Свойство 14. Определим экстремальные функции в классе распределений
H(r,s) с конечным числом заданных значений.Обозначим через H(r, s, {?,}, {/^}, / = 1, т) подмножество распределений
F-1-F класса H(r,s), таких, что F(tt) = Ft, i = 1, 2,..., т .Тогда в классе H(r, s, {/,}, {/^},./ = 1, т) существуют максимальный и мини¬
мальный элементы, т. е. в этом классе существуют функции Fmin, Fmax, та¬
кие, чтоFmin<F<Fmax, = (15.2)Действительно, пусть А, = — 1п(1 — /*}) = — ln(l - F(tt)) . Из определения классаH(r, s, {tj}, {Fj}, i = \, т) следует, что числа ti, А/ удовлетворяют нера¬
венствам:
Граничные оценки надежности систем613Л,1+1А,- л, t — 1, m-l.tr tr
4 1*(15.3)Рассмотрим интервал Из принадлежности функции F(/) классу7/(r, 5, {/,}, {/'’I, 1 = 1, т) следует, что для функции A(/) = -ln(l-F(0) имеют
место неравенства:Л ^ Л(р ^ л/+1tr tr tr ’'/ * ‘/+1А(0>^<±1‘l+lОткуда вытекают двусторонние оценки для функции ресурса:/• \
А) ^ А;+|
с >Amin (О = max/ \
^L(r '+1tr ’V '/ */+]:£ A(/) < minАщах (0 ■Пусть теперь t<tx. Тогда для функции Л(/) = - ln(l - F(t)) выполняются не¬
равенства:Л(р Л!.'ГМ£)>А
ts t* ’из которых следуют оценки:Amin (0 = ■^ts < А(0 <V = Amax (0.hНа интервале t>tm для функции Л(0 = -ln(l-F(0) выполняются нера¬
венства:Л(р ^Л№*Л(0 < Amоткудал„|„(!)=—■!' £ Л(Г) £ = л„„ (ос с
614Глава 15Таким образом,Amin (ОшахАтах (ОK<iАт frtrlmЛ] г
'!‘мттf \
А/ ^ А,+1 ^’ tr\ Ч li+1 у-HLts
4s ' ’t^tm,t<tx\(15.4)(15.5)(15.6)и неравенства (15.2) имеют место для функций распределения^min (0 = 1 - e_Amin (/), Fmax (0 = 1 - е‘Лт“(0.В силу (15.3) функции (15.4) и (15.5) непрерывны, и потому функции (15.6)
принадлежат классу #(r, s, {/,}, {/-}}, / = 1, т). Тем самым требуемое утвер¬
ждение полностью доказано.Укажем на частный случай полученных оценок. Пусть г = О, s = оо. Тогда
искомые функции ресурса являются ступенчатыми функциями вида:0,1ЛAi»i<h-,Amin (0 = •A max(0 = -A,+i >ti<tZti+.А т>°°,что соответствует результатам работы [50].15.3. Принадлежность классу H(r, s)
некоторых параметрических распределенийОпределим классы H(r,s), к которым принадлежат некоторые известные
распределения теории вероятностей. Соответствующие доказательства при¬
ведены в [31].
Граничные оценки надежности систем6151. Равномерное распределение принадлежит классу Н( 1,°о).2. Гамма-распределение с параметром формы а при а >1 принадлежит
классу 7/(1, а), а при а < 1 — классу 7/(а,1).3. Для усеченного нормального распределения с параметрами т0 и а0 зна¬
чения г и s зависят только от отношения d = ^-. Графики зависимости
г и s от d приведены на рис. 15.4.ОРис. 15.4. Иллюстрация зависимостей г и s от d = —Так, например, если d = 1, то г = 0,67 , s = 2,12, и распределение относит¬
ся к классу /7(0,67; 2,12).4. Рассмотрим систему, элементы которой имеют распределения из класса
H(r,s). Предположим, что /-й элемент относится к классу //(^,5,),
/ = 1, 2,...,«. Тогда распределение нерезервированной системы относится
к классу H(r,s), где r=m\nri, 5 = maxs/? распределение резервирован-\<iin 1 <,i<nной системы с постоянно включенным резервом— к классу H(r,s), гдеИг = min s = Yssi [31]'
i-'-" i=\Эти свойства позволяют проводить декомпозицию сложных систем последо¬
вательно-параллельной структуры и определять, к какому классу распределе¬
ний относится распределение их времени безотказной работы.
15.4. Двусторонние ограничения
для показателей надежности
невосстанавливаемых систем в классе Н(г, s)15.4.1. Интервальные оценки среднего времени
безотказной работы нерезервированной
и резервированной системПредположим, что й элемент системы принадлежит классу H^r^Sj) и а, —
среднее время его безотказной работы, / = 1, 2,..., п.Тогда для системы с основным соединением элементов имеют место сле¬
дующие нижняя и верхняя оценки среднего времени безотказной работы:Т = , Т = ,О /=1 0' = 1гдеf ( \\t'kA(t,a,k) =(Г, 0£г1+-ч1 Ь)ауДействительно, среднее время безотказной работы системы равноО <=1 0 < = 1Коэффициент при каждой функции е“л'^ является монотонно убывающей
функцией, поэтому данное утверждение следует из свойств 11 и 12 класса
Я(Г,5).В частности, если все элементы системы принадлежат одному и тому же
классу распределений H(r,s), то справедливы оценкиТ=-1Т = -1/ \
1 " 12-7гf \
\ п 1
i-Vч, = 1 ai J<'-* °i ;(15.7)Если г = 1, s = +оо (класс стареющих распределений), то1 ™
Гоаничные оценки надежности систем617Если г = О, 5 = 1 (класс молодеющих распределений), тот = о, т=——.— П 1(=1 aiДля резервированной системы с постоянно включенным резервом справед¬
ливы следующие нижняя и верхняя оценки среднего времени безотказной
работы:Т = J 1 - П(! - e'W**'))dt, Т = } 1 -П(1 -e-AU'a^)oV. <=iOV i=ldt.Действительно, среднее время безотказной работы системы равнот - Ъ1- ПО - т)\л=]( 1 ■- п(| ■- o_v,))OV i=1OV »'=1dt.Для элемента с номером j выделим в этом выражении член с функциейi=i»=iФункция 17^1-e Л,(,) j под знаком второго интеграла является монотонно/=1i*Jвозрастающей. Поэтому нижняя и верхняя оценки Т следуют из свойств 11
и 12 класса H(r,s) .В частности, если все элементы резервированной системы принадлежат од¬
ному и тому же классу распределений H{r,s), то справедливы оценки11л-11=1i<jг .
1\11 S/< j<k111 \11 S< \
Я 12-тatJSJ«/п-I1+ 11•+НГ1i111(=1»</г11I гVV(11j >1j- 1гСп 1к'-1 i /гКU“к-,(15.8)
618Глава 15Если г = 1, s — +оо (класс стареющих распределений), тоOj Oj Qfc1StЕсли г = 0, 5 = 1 (класс молодеющих распределений), тоПРИМЕР 15.5. Система состоит из и = 10 элементов. Известно среднее вре¬
мя безотказной работы каждого элемента в часах: ^=10800, a2 = 10000,
а3 =9750, аА = 9000, а5 =10300, <з6 =8800, а7 =9500, я8 =9300,
а9 =11000, а,о = 10400. Для всех элементов распределение времени безот¬
казной работы принадлежит классу Н(4,5). Требуется определить границы
среднего времени безотказной работы системы для нерезервированной и
структурно резервированной системы с постоянно включенным резервом.Решение. На основе формул (15.7) находим нижнюю и верхнюю оценки
среднего времени безотказной работы нерезервированной системы:На основе формул (15.8) и (15.9) определяем нижнюю и верхнюю оценки
среднего времени безотказной работы резервированной системы:Для проведения расчетов по указанным формулам использовались математи¬
ческие пакеты.15.4.2. Интервальные оценки среднего времени
безотказной работы для систем с монотонной
структурой и элементами из класса Mr, s)Пусть система состоит из п элементов, каждый из которых может пребывать
только в двух состояниях: исправном или неисправном. Положим х, = 1, если
i-й элемент исправен, и xt = 0, если /-й элемент неисправен. Состояние сис¬
темы характеризуется функцией g(x) = g(xt, х2,..., х„), зависящей от
состояния ее элементов; она также принимает значение 1, если системаГ = 5698 час, Г = 6310 час.Г = 13487 час, Г = 14318 час.
Граничные оценки надежности систем619работоспособна, и значение 0, если система отказала. Функция
g(x) = g(x,, х2,..., хп) называется структурной функцией системы. Система
имеет монотонную структуру, если выполняются следующие естественные
условия:□ система работоспособна, если все ее элементы исправны, т. е.
g{ 1,1, —, 1) = 1;□ система отказала, если все ее элементы неисправны, т. е. g(0, 0,..., 0) = 0;□ если система неисправна, то дополнительные отказы элементов не могут
перевести ее в работоспособное состояние; это условие может быть запи¬
сано в виде g(x,, х2,..., х„) <, g(yx, у2,..., у„), если xi < yi, i = 1, 2,..., п.Сформулированные в разд. 15.2 свойства позволяют получить оценки сред¬
него времени безотказной работы систем с монотонной структурой. Восполь¬
зуемся методом минимальных путей и сечений. Тогда получим:Т = max 7^, bmin^, (15.10)j - kгде — нижнее среднее для последовательного соединения, входящего в^(2)j-и путь, а Тk — верхнее среднее для параллельного соединения, входящего
в k-е сечение. Заметим, что интервальные оценки средних не являются точ¬
ными.ПРИМЕР 15.6. Пусть система состоит из трех элементов, как показано на
рис. 15.5. При этом г'-й элемент системы входит в класс H(rt,st) и имеет
среднее время безотказной работы я,, / = 1, 2, 3 .0*2 > ^2 )(r3,s3)a3Рис. 15.5. Система из элементов класса H(r,s)Требуется получить выражения для оценок среднего времени безотказной
работы системы.
620Глава 15Решение. Среднее время безотказной работы системы равноТ = ]%)(! -(1 -F2(0X1 - F3(t)))dt.оОднако, поскольку функции распределения Ft(t) не известны, воспользуемся
формулами (15.10) и свойствами 9 и 10. Тогда получим требуемые оценки:лТ = maxА )+Л(Л<з2 ,r2 ))jt |е-(Л((,а, ,г, )+Л(/,а3 Л))$
V0 0Т = min а, ,](l - (l - в-А(^л))(i -е-М'^з))1где K{t,a,r) =оА / , \ л'1 + -V VСледствия из свойств 9 и 10 позволяют также высказать следующее утвер¬
ждение. Пусть /-й элемент системы с монотонной структурой принадлежит
классу #(/,,£,) и имеет математическое ожидание времени до отказа at,i = 1, 2,, п . Тогда вероятность безотказной работы системы удовлетворяет
неравенствам:g(^l,min СО» ^2, min СО» •••» ^j,min СО j — ^с(0 ^ g(^*l,max СО» ^*2, max СО» •■•» ^.тахСО),где ^ mi„, тах — соответственно нижняя и верхняя огибающие класса
), g(wj, и2» •••» ми) — структурная функция системы.ПРИМЕР 15.7. Мостиковая система состоит из пяти одинаковых по надеж¬
ности элементов. Распределения времени безотказной работы элементов при¬
надлежат классу #(1;2) и имеют математические ожидания а = 105 час.
Требуется определить оценки вероятности безотказной работы системы.
Решение. Структурная функция мостиковой системы выглядит так:g(u) — 2и5 - 5и4 + 2и3 + 2и2,и имеют место оценкиgC^min (0) * рс СО * s(Fmax (0) ,где Fmin(0, -/maxСО — соответственно нижняя и верхняя огибающие класса
Я(1;2). На рис. 15.6 дана графическая иллюстрация указанных оценок.
Граничные оценки надежности систем621Рис. 15.6. Нижняя и верхняя оценки вероятности безотказной работы
мостиковой системыГрафики получены на основе расчетов огибающих класса Н{ 1;2) в соответ¬
ствии с формулами (15.1) и вычислении нижней и верхней оценок вероятно¬
сти безотказной работы системы:P(t) = g(Fmin(t)) и P(t) = g(Fmax(t)).15.5. Граничные оценки среднего времени
безотказной работы монотонных систем
для независимых и однотипных
по надежности элементов с функциями
распределения из класса Щг, s)15.5.1. Интервальные оценки
среднего времени безотказной работыВ работе [31] доказано следующее утверждение. Пусть g(u) — неубываю¬
щая на промежутке [0; 1] функция, для которой существует конечный пределlim — — . Пусть далее 0 = х0 < хх <... < хт_х < хт = со — разбиение промежут¬
ков ика [0, оо) на интервалы монотонности функции — . Тогда задача опти-е хмизации00z = Jg(e~AW)<#-> max(min)
о
622Глава 15GOна множестве распределений H{r,s), таких что fe~A^dt = a, разрешима.оПри этом максимальное (минимальное) значение достигается на функциигдеkj =A*(t) = CjtJ, при tj_x<,t<tj, j = 1, 2,, т,g(e'x)(15.11)г, если функция —-— возрастающая на [*, |,х.] в задачее *максимизации и убывающая в задаче минимизации;
g(e~x)s, если функция _х убывающая на [х7_,,д:у] в задачемаксимизации и возрастающая в задаче минимизации.
Коэффициенты Cj и границы интервалов tj (t0 = 0, tm=<x>) связаны между
собой равенствамиxj = c/j = с]+$*' ’ J = 2> - > т (15.12)00 .и такие, что выполняется условие je~A ^dt = a .оОтметим один частный случай этого утверждения. Если функцияg(e-x)возрастает на промежутке [0, jcj] и убывает на промежутке [xl5co], то макси¬
мальное и минимальное значения z достигаются на функциях:Лтах(0 = *1/ V
t_), при/ V
t_\h)Amin (0 = *1, при />/,,'iv
KhjГ1У\hj, при(15.13), при t>t\,где параметр tx выбирается из условия (15.12). Экстремальные значения
функции z соответственно равны1z =а—Jg(e Х'Г )dt + jg(e х'1' )dt jg(e *>'' )dt + jg(e ^ )dtle-x',rdt + ]e-x'r'dt(15.14)fe~x,,'dt+ Je Х',Г dt
Граничныв оценки надежности систем623Рассмотрим применение соотношений (15.13) на примерах получения интер¬
вальных оценок среднего времени безотказной работы различных систем.15.5.2. Нерезервированная системаСтруктурная функция нерезервированной системы с равнонадежными эле¬
ментами имеет вид g(w) = un, поэтому - un~l s и функцияj[(£—1 = е (” *)* является монотонно убывающей. Согласно утверждениюе хразд. 15.5.1, максимальное значение z достигается на функции A*(t) = cts.00Так как должно выполняться равенство je~A^dt = a, тоо( t уЛ*(/)= Г(1 + \/s)— , и потому верхняя граница среднего времени работыV а)системы равнаz= je-nA(0dt= je [ a)dt=-^j.Аналогично минимальное значение z достигается на функцииV, и потому нижняя граница среднего времени ра-A\t) = ctr = Г(1 + 1/г)-I ajботы системы равнаz= \е~пА ®dt= \е ^ a)dt = -?J7.
о о п гВ частности, для класса Н(0,оо) имеем:z = 0, 1 = а.ПРИМЕР 15.8. Система представляет собой основное соединение из трех
элементов со средним временем безотказной работы а = 3000 час. Требуется
оценить среднее время безотказной работы системы Тс.Решение. Рассмотрим два случая:1. Какая-либо информация о работе системы отсутствует. Тогда г = 0,
s = +оо , и можно заключить, что 0 < Тс < а . Это значит, что среднее время
работы системы до отказа находится в интервале от 0 до 3000 часов.
624Глава 152. Известно, что каждый элемент имеет гамма-распределение с показателем
формы, изменяющемся от 1 до 2. Тогда по свойству гамма-распределенияиз разд. 15.3 имеем: г = 1, s = 2 , и поэтому —<ТС< . Отсюда следует,3 >/3что среднее время работы системы до отказа находится в интервале
от 1000 до 1732 часов, что существенно уточняет границы Тс.15.5.3. Резервированная система
с постоянно включенным резервомСтруктурная функция резервированной системы с равнонадежными элемен-, . , ,, „ , g(w) 1 - (1 - и)" t;1 ктами имеет вид g{u) = 1 - (1 - и) , и функция —— = — — = 2^ (* “ и>и и k-Qубывает на промежутке [0; 1], следовательно, функция ^ ^ является мо-нотонно возрастающей.Максимальное значение z достигается на функции( t УA\t) = ctr= Г(1 + 1/г)— .V а)Поэтому верхняя граница среднего времени работы системы равнаМинимальное значение z достигается на функцииА*(/) = cts = |г(1 + l/s)—j .Поэтому нижняя граница среднего времени работы системы равнап ь 1 СкВ частности, для класса Н{0, оо) имеем:z = a, J = па.ПРИМЕР 15.9. Система представляет собой параллельное соединение трех
элементов, работающих одновременно, со средним временем безотказной
Граничные оценки надежности систем625работы а = 3000 час. Требуется оценить среднее время безотказной работы
системы Тс.Решение. Рассмотрим два случая:1. Какая-либо информация о работе системы отсутствует. Тогда г = 0,
s = +оо , и можно заключить, чтоa<Tc<3a.Это значит, что среднее время работы системы до отказа находится в ин¬
тервале от 3000 до 9000 часов.2. Каждый элемент имеет гамма-распределение с неизвестным показателем
формы, находящимся в пределах от 1 до 2. Тогда имеем г = 1, 5 = 2, и по¬
томуг 3 1Го зГ\а<>Тс <3 — +a) °1 2ЗуОтсюда следует, что среднее время работы системы до отказа находится в
интервале от 4368 до 5500 часов. Таким образом, при наличии дополни¬
тельной информации мы вновь получаем намного более узкие граничные
оценки.15.5.4. Мажоритарная система т/пОтказ системы наступает при отказе любых (т + 1 )-го элемента
(0 < т < п -1). Структурная функция системы с равнонадежными элементами
имеет вид:*(»)-'£ с; о
к = 0Функция у = имеет на промежутке [0; 1] единственную точку макси¬
мума и,, которая определяется из уравненият u( U \т~к£С* UL. = С™ (п-т).
к=оОбозначим jcj=-lnw|, тогда функция — возрастает на промежуткее х[0,*,] и убывает на промежутке [jcj, оо). Поэтому справедливы формулы(15.14).
626Глава 15В частном случае при т = 1 решением приведенного уравнения будетп{п - 2)
и\ ~ Т’(«-1)2/ 1 \ 2и, значит, хх = In ————. При этом g(u) = им"-1 - (п -1 )ип .п(п - 2)ПРИМЕР 15.10. Система представляет собой мажоритарную систему типа 1
из 3. Среднее время безотказной работы каждого элемента a = 3000 час. Тре¬
буется оценить среднее время безотказной работы системы Тс.Решение. Рассмотрим два случая.1. Какая-либо информация о работе системы отсутствует. Тогда г = 0,
5 = +со . Можно показать, что в этом случае 0 <ТС < 1,124а. Это значит, что
среднее время работы системы до отказа находится в пределах от 0
до 3372 часов.2. Каждый элемент имеет гамма-распределение с показателем формы, за¬
ключенным между 1 и 2. Тогда имеем г = 1, s = 2, и потому граничныезначения представляются в виде выражений (15.14), где g(u) = 3u2 -2и3, а4л:, = In—. Вычисляя интегралы в (15.14), получим, что среднее время рабо¬
ты системы до отказа будет находиться в интервале от 1074 до 1827 часов.15.5.5. Мостиковая системаСтруктурная функция мостиковой системы, состоящей из 5 равнонадежныхэлементов, равнаg(u) = и5 + 5(1 - и)и4 + 8(1 - и)2 и3 + 2(1 - м)3 и2 = 2м5 - 5и4 +2иг + 2и2.Функция — — = 2ц4 - 5и3 + 2и2 + 2и имеет на промежутке [0; 1] единствен-иную точку максимума и,, которая определяется из уравнения8и3 -15м2 + 4и + 2 = 0.Обозначим х, =-In м,, тогда функция —- возрастает на [0, jc, ] и убываете хна [дГ], да]. Поэтому справедливы соотношения (15.14). Результаты проведен-
Граничные оценки надежности систем627ных расчетов показывают зависимость нижних и верхних интервальных
средних от значений параметров г и s .ПРИМЕР 15.11. Система представляет собой мостиковую систему из 5 эле¬
ментов. Среднее время безотказной работы каждого элемента а = 3000 час.
Требуется оценить среднее время безотказной работы системы Тс.Решение. Рассмотрим два случая:1. Какая-либо информация о работе системы отсутствует. Тогда г = 0,
s = +00 . Можно показать, что 0<,ТС < 1,149а. Это значит, что среднее вре¬
мя работы системы до отказа находится в интервале от 0 до 3447 часов.2. Каждый элемент имеет гамма-распределение с показателем формы, за¬
ключенным между 1 и 2. Тогда имеем r = 1, s = 2, и потому граничные
значения представляются в виде выражений (15.14), гдеg(u) = 2u5 -5и4 +2и3 +2и2, а хх =0,3044. Вычисляя интегралы в (15.14),
получим, что среднее время работы системы до отказа находится в интер¬
вале от 2406 до 2967 часов.15.5.6. Последовательно-параллельная системаСистема представляет собой последовательное соединение п резервирован¬
ных участков, каждый из которых содержит m параллельно соединенныхэлементов. Структурная функция системы равна #(и) = (1-(1-и)"!)”. Функ¬
ция имеет на промежутке [0; 1] точку максимума щ , определяемую из
иуравнения g'(u)u = g(u), или=1-(1 -u)m.Я(е~х)Обозначим лг1=-1пм], тогда функция — возрастает на промежуткее х[0, ] и убывает на промежутке [дг15 со). Поэтому справедливо соотношение(15.14).ПРИМЕР 15.12. При т = 20, « = 100 имеем щ =0,284, х{ =1,259. Результа¬
ты расчетов, проведенные по формулам (15.14), показывают зависимость
нижних и верхних интервальных средних от значений параметров г и s . Эти
результаты для a = 1 приведены в табл. 15.1.
628Глава 15Таблица 15.1. Значения нижних и верхних интервальных средних
Последовательно-параллельной системы\5
г \0,20,51510500,20,076—0,0760,076—1,2300,076—2,0050,076—2,5750,076—2,6380,076—2,6860,51,152—1,1521,061—1,7490,888—2,1040,854—2,1370,822—2,16211,504—1,5041,123—1,7111,056—1,7260,998—1,73751,180—1,1801,094—1,1811,019—1,180101,094—1,0941,019—1,093501,019—1,019Из табл. 15.1 видно, как расширяется диапазон интервального среднего вре¬
мени безотказной работы с расширением множества [г, s].Отметим также, что при отсутствии информации о законах распределений
этот диапазон равен [0; 3,106], что значительно превышает фактические диа¬
пазоны, приведенные в таблице.15.6. Некоторые экстремальные задачи
при оценке показателей надежности системАналитические выражения показателей надежности в качестве своих состав¬
ляющих часто содержат интегралы видаогде /(/) — плотность распределения вероятностей некоторой случайной ве¬
личины. Например, средняя наработка на отказ дублированной системы с не-
нагруженным резервом и идентичными по надежности элементами выража¬
ется соотношением:С 00 \G(t)f(f)dxоДля дублированной системы с постоянно включенным резервом, обслужи¬
ваемой одной ремонтной бригадой с прямым приоритетом и экспоненциаль¬
Гоаничные оценки надежности систем629ным распределением времени безотказной работы, средняя наработка на от¬
каз равна2 2\G(t)f{t)dtои т. п. Это позволяет получить двусторонние граничные оценки соответст¬
вующих показателей в произвольном классе распределений F :ОО 00А = inf \ty{t)f(t)dt, А = sup \y(t)f(t)dt.
fsFо f*FоТем самым возникают две экстремальные задачи по определению плотностей
распределений в классе F. Предположим, что класс F образован всеми рас¬
пределениями с известным математическим ожиданием Т. Непосредствен¬
ное решение этих задач оптимизации не просто. Лучше перейти к соответст¬
вующим двойственным задачам и воспользоваться известными теоремами
теории двойственности.В табл. 15.2 представлены исходная задача максимизации и двойственная за¬
дача минимизации.Таблица 15.2. Задача максимизации и двойственная задачаЗадача I (шах)Задача IIсоz - |сp(t)f(t)dt -» max
0w = с0 + с,Г —> min00\f{()dt -1
0с0 — любого знака00\tf(t)dt = т
0с, — любого знака/(0 ^ о, V/2:0с0 + с,/ £ ф(/), VtZ 0В табл. 15.3 представлены исходная задача минимизации и двойственная за¬
дача максимизации.Если перейти к соответствующему дискретному аналогу, то задачи I и II об¬
разуют пару несимметричных двойственных задач линейного программиро¬
вания. Этот подход к решению экстремальных задач имеет своим источником
известную теорему продолжения [66, 152].
630Глава 15Таблица 15.3. Задача минимизации и двойственная задачаЗадача I (min)Задача IIz = |cp(0/(0<* -> min
0w-cQ+ с,Г -» шах00\mdt = i0с0 — любого знакаОСW(t)dt = Г0с, — любого знака/(/)> 0, V/ > 0с0 + с,/ й ср(/), V/ S 0Свойства составленных задач очень похожи на свойства конечномерных за¬
дач линейного программирования. Ограничимся лишь формулировкой
свойств для двойственных задач из табл. 15.2. Обозначим через / любое до¬
пустимое решение задачи I, а через с = (с0,с]) — любое допустимое решение
задачи II. Значения целевых функций для соответствующих допустимых ре¬
шений будем обозначать через z(/) и w{c).Свойство 1 (неравенство двойственности). Для допустимого решения /
задачи I и допустимого решения с задачи II справедливо неравенствоz(/) < w(c).Свойство 2 (теорема двойственности). Если для допустимого решения /
задачи I и допустимого решения с задачи II имеет место равенство
z(f) ~ w(c), то / и с являются оптимальными решениями соответствую¬
щих задач.Свойство 3. Если для допустимого решения / задачи I и допустимого ре¬
шения с задачи II в каждой строке приведенной схемы хотя бы одно из усло¬
вий является равенством, то / и с — оптимальные решения соответствую¬
щих задач.Двойственные задачи, записанные в табл. 15.2 и 15.3, обобщаются на задачи
с многомерными плотностями распределения (табл. 15.4 и 15.5).Мы рассматриваем вопросы, связанные с экстремальностью, применительно
к теории надежности при условии отсутствия какой-либо информации о зави¬
симости или независимости элементов, входящих в систему. В предположе¬
нии о независимости элементов системы также формально можно составить
Гоаничные оценки надежности систем631пару двойственных задач, однако эти задачи существенно видоизменяются
[31]. Они становятся бесконечномерными задачами нелинейной оптими¬
зации. IТаблица 15.4. Задача максимизации с многомерной плотностью и двойственная задачаЗадача IЗадача II00 00г = ..., f,,)/(',> - > t„)dti- dtn -*• max
0 0пw = c0 + 2 (bjC'i - alci) -> mini = IJ—J/(*!» — » *„)dt\= 10 0 4c0 —любого знака00 00- > <„)/(<!» --0 0с, >0, /' = I, 2,..., m00 00/...Jф.(/,, ..., /„)/(#,,..., tH)dtr..din <b,
0 0c] SO, i = 1, 2,..., m4IV
©
<
J»IVоmc0 + S (< - с, )ф, (г, ф(^,1 = 1Таблица 15.5. Задача минимизации с многомерной плотностью и двойственная задачаЗадача IЗадача II00 ооz = J...Jф(/|,..., <„)/(', t„)dtv..dtH -> min0 0пW = с0 + £ {а,с, - Ь{с]) -> max
i=i00 00
о 0с0 — любого знака00 00J...f ф((/р ..., /,)/(/„ ..., t„)dtydt„ > a,
0 0ct >0, /' = 1, 2, ..., m00 00J ...J Ф, (/,,..., /„)/(/,,..., t„)dtv..dtn <> b,
0 0с] SO, /' = 1, 2, ... ,mIVо<-Г*-.*ч*IV1 оmco + H(CI -с/)ф/(,р - > О 5 4>(fi. - > '„)i = l
632Глава 1515.7. Интервальные средние наработки
на отказ восстанавливаемой
дублированной системы15.7.1. Резерв замещениемДля дублированной системы с резервом замещением, обслуживаемой одной
ремонтной бригадой с прямым приоритетом, стационарная наработка на от¬
каз вычисляется по формуле:т_ а\ +а2 00 со 5\Gx(t)f2(t)dt + \G2{t)f{t)dt
о огде ft(t) — плотность распределения времени до отказа /-го элемента,
G,-(t) — вероятность восстановления /-го элемента за время t, / = 1, 2.Получим верхнюю и нижнюю оценки интеграла00 00 00
z = JG(0/(t)dt при условиях \tf(t)dt = а , |G(t)dt = Ъ .
о ооПокажем, что точная верхняя грань интеграла равна 1. Очевидно, что
supz < 1. Найдем функции, для которых достигается равенство. Положим-() fl, np[О, при t>b.Если а < Ъ , то fit) = 5a(f) и:ю=1.Если а > Ъ , то fit) = аЪь it) + (1 - а)5с it), причем 0 < а < 1, а параметр с вы¬
берем так, чтобыi/i \ a-abab + i\-a)c = a, или с .1 -аПолучимz = ]G{t)fit)dt = )fit)dt = a.
о оТак как а можно взять сколь угодно близким к единице, то supz = 1.Точная нижняя грань интеграла равна 0. Это следует из доказанного ранее и
из того, что:
Граничные оценки надежности систем633z= \G{t)f{t)dt = -\G(t)dF(t) = 1 - \F(t)g{t)dt.
о о оОтсюда получаем граничные значения наработки на отказ:inf Г = ~ 2 ’ sup Т = +со.Эти оценки могут быть улучшены, если наложить некоторые дополнитель¬
ные ограничения на распределения времени безотказной работы и восстанов¬
ления элементов.Предположим, что время восстановления элементов вырожденное, т. е.fl, при t <bj\где I = 1, 2.Тогда наработка на отказ равнаО, при t>bt,т a\+a2 (i\ + а2о , оПолучим интервальные значения наработки на отказ, когда распределения
вероятностей времени безотказной работы принадлежат классу H(r,s).Если распределение времени до отказа элементов принадлежит классу
H(r,s), а время восстановления вырождено, то из свойств 9 и 10 интерваль¬
ные средние наработки на отказ системы с резервом замещением имеют вид:Q\ +а2 Т =1 _ е_сши (д2 А >'•>•0 + I _ е~стах («1 A,r,s) ’f = . а\+а21 _ g~cmin (О2 A ’r’*) + J _ е~стт (°1 A >r>s) 'Функции cmBX(a,b,r,s) и cmin(a,b,r,s) были определены в свойствах 9 и 10.Если элементы идентичны по надежности и ремонтопригодности, то в этом
случае имеют место следующие оценки:а — лТ = " г, Т =■- 1 _ g-W (a,b,r,s) ’ J _ g-cmm (a,b,r,s) "Зависимость интервальных средних от различных характеристик элементов, а
также от параметров г и s легко устанавливается программным путем.
634Гпава 15ПРИМЕР 15.13. Среднее время безотказной работы элементов дублирован¬
ной системы a = 5000 час. Требуется получить граничные значения средней
наработки на отказ системы в зависимости от времени восстановления b.Решение. Результаты расчетов при различных значениях показателей г и s
приведены в табл. 15.6 и 15.7.Таблица 15.6. Интервальные средние наработки на отказ при г = 1, s = 4b, час7minТтахЬ, част ■1 minЛлах102,5 1064,6 10142001,3 10s2,9-109201,3 • 10е2,9-10133008,6 1045,7-108308,4-1055,7 Ю124006,5 -1041,8 10s406,3 • 1051,8 10125005,2 1047,4 • 107505,0-1057,4 • 10"6004,4 1043,6 107604,2-1053,6-ю"7003,8 ■ 1041,9 107703,610s1,910й8003,4-1041,1 107803,1-1051,1 Ю119003,0-1047,110s902,8 1057, МО1010002,7-1044,6 10s1002,5-1054,6 -Ю10Таблица 15.7. Интервальные средние наработки на отказ при г = 2, S = 3b, часT’minT* maxb, час7'minТ'ш.Х101,6 1098,8 10"2004,0 10s1,1 • 108204,0 10s1,110"3001,8 1063,3-107301,8 10s3,3-io104001,0-1061,4 107409,9 • 1071,4-10105006,4 10s7,0 • 106
Граничные оценки надежности систем635Таблица 15.7 (окончание)Ь, часTmiBт1 maxb, част1 minт* max506,4 -1077,0 1096004,4 Ю54,1-Ю6604,4-1074,1 -109'7003,3-Ю52.6-106703,2-1072,6 1098002,5-1051,7 • 10б802,5 • 1071,7-10*9002,0 • 1051,2 • 106902,0 -1071,2 • 10910001,6 ю58,8 1051001,6-1078,8 10sИз таблиц следует, что диапазон между нижней и верхней оценками средней
наработки на отказ слишком велик, особенно при быстром восстановлении
элементов. Поэтому использовать эти оценки следует с осторожностью. Од¬
нако в условиях отсутствия информации о законах распределения предло¬
женный метод позволяет, хотя и с широким диапазоном, но все же указать
точные оценки наработки на отказ. Если использовать экспоненциальные
законы времени до отказа и времени восстановления, то для 6 = 100 час по¬
лучим:. | 100т _ 1 +..Р. 5000 _л 55.]о5 часьр 1 100 • ’5000 5000что вообще не укладывается в диапазон оценок, приведенный в табл. 15.7.
Табл. 15.6 и 15.7 показывают явное сближение граничных оценок средней
наработки на отказ с уменьшением диапазона вложенных интервалов [г, л ].Очень важными являются нижние оценки наработки на отказ. Так, если нет
информации о том, какому классу принадлежит распределение времени без¬
отказной работы элементов, то Гт|П = 5000 час и оно совсем не зависит от
времени восстановления. Пусть время восстановления постоянно и равно
10 час. Тогда, если F еН( 1; 4), то Гт)п =2,5-106 час, а если F е /7(2; 3}< тоrmjn =1,6-109 час. Как видно, эта новая информация существенно влияет на
оценки показателей надежности дублированной системы.
636Глава 15Пусть теперь время безотказной работы элементов экспоненциальное, а вре-В частности, для идентичных по надежности и ремонтопригодности элемен¬
тов имеют место следующие интервальные оценки:Этот результат кажется парадоксальным, однако наработка на отказ действи¬
тельно может принять любое сколь угодно большое значение, если специаль¬
ным образом подобрать закон распределения времени восстановления с ма¬
тематическим ожиданием Ъ. Здесь уместно сказать, что лучше иметь широ¬
кие оценки наработки на отказ, полученные на основании имеющейся
информации, чем одно значение, которому нельзя доверять и которое было
получено, например, в предположении экспоненциальности распределения
времени восстановления.Посмотрим, как изменятся эти оценки, если ограничить множество распреде¬
лений времени восстановления элементов классом G е H(r,s).мя восстановления произвольное. Если f(t) = Xe и, то нам следует решить
следующую задачу оптимизации:ОО00оос0 H-qjc^l-e Vx>0,где b — математическое ожидание времени восстановления.
Оптимальное решение этой задачи очевидно. Оно таково, чтос0 + схЪ = 1 — е хь ._ьСледовательно, zmax = 1 - e~xb = \~е a . Вполне очевидно также, что zmin = 0.
Таким образом, интервальные оценки имеют вид:1-е “2 +1-е а’Т =aТ = +со.ь ’1-е а
Граничные оценки надежности систем637В этом случае надо решить задачу:ОО 00z = \G(t)f(t)dt = jke~XlG(t)dt -» max .
о оПоскольку функция e~Xt убывающая, то на основе следствий из свойств 11
и 12 целевая функция достигает максимальное значение на функцииG(t) = e ' , а минимальное значение—на функции G{t) = е v г> 1 .Таким образом, с учетом дополнительной информации интервальные оценки
наработки на отказ имеют вид:Т a\+a2 J dt+ fe ^ sJb>J dtT =о оax + a200 J rf 1+lW) -I oo- -frfI-t
Je ')*>■ Л+Je^ dtо оДля идентичных по надежности и ремонтопригодности элементов получим
следующие интервальные оценки:Т = , т=- a<=0 -I rl l+-]-t I -/ =0-1 r| i+- P-t1 -ts )b0 0
Численное сравнение этих оценок с аналогичными оценками, но без требова¬
ния G е H(r,s), приведено далее в разд. 15.7.3.15.7.2. Постоянно включенный резервДля дублированной системы с постоянно включенным резервом, обслужи¬
ваемой одной ремонтной бригадой с прямым приоритетом, отсутствует явное
выражение для средней наработки, как это имеет место для резерва замеще¬
нием. Поэтому мы ограничимся здесь рассмотрением случая экспоненциаль¬
ного времени безотказной работы, для которогоТ =I[и-\Д(Х2))|^1 + A,2Cj2(^i)|1А,,Х,2 |(g, (Я,2 ) + G2 (^i) + (Я,, + Л2 )G, (Я-2 )G2 (^i))
638Глава 15А 00 |где Gj(X)= [Gt(t)e~Xrdt — преобразование Лапласа функции G,(0, А.,- =—,
о а,/ = 1,2.Ясно, что наработка на отказ — это убывающая функция по Gj(X2) и G2(Xj).
Поэтому для нахождения интервальных оценок достаточно найти наиболь¬
шее и наименьшее значения указанных выражений.Решим следующую задачу:л 00 _ 001 — р~^z = G(X) = jG(f)e~x,efr = J g(t)dt -> max(min).ооЗадача на максимум может быть решена путем перехода к двойственной за¬
даче:с0 + схЬ —» minпри ограничениях-Хх1 — ес0 + схх> , Vx^O.1 —е-иОптимальное решение этой задачи очевидно, и zmax . Нетрудно ви-А,деть, что zmjn = 0. Таким образом,т _/ах + а2( -А/l-eVга2+ах\' -ЬА1-е а>< ) А'«2г _о1-еч J+ ах' -к)
1-еУ+ (а, +а2)(1-е °2V /( .к)
1-еV У, Т = +оо.В частности, для идентичных по надежности и ремонтопригодности элемен¬
тов имеют место следующие интервальные оценки:( ±\2-е аТ = -r h\ь т = +ъ,1-е а
Граничные оценки надежности систем639Предположим теперь, что время восстановления принадлежит классу распре¬
делений с функцией ресурса степенного роста, т. е. G е H(r,s). Определение
интервальных оценок в этом случае связано с решением следующей задачи:z = G(X) = §G(t)e dt -» max(min)
ов классе распределений G е H{r,s). Как было показано в разд. 15.2, имеют
место следующие экстремальные значения:» - Г 1+- -/ -I
2тах(°>й) = й|е dt’ zmm(a’b) = aleсо -I г| ulYt | -idt.0Следовательно,
T =<¥Ъ(Л + zmax(а2,Ьх))(а2 +-max (Р|Л))a\a2 (^max (^2 ) “*" ^max (al»^2 )) ^2 )^inax (a2 ’^1 )гтах (®1 >^2 )•^min (q2>^l)Xa2 + ^min (Д|Л))ala2 (zmin («2 A ) + zmin («1Л » + (al + a2 )zmin (%>A>min («IЛ )а для идентичных по надежности и ремонтопригодности элементов справед¬
ливы оценки:Т =оо JpfiA/T-r 4
1+ Je ^ dtо«> -jrfl+Л-Н-/
2je ^ ' dt
0r = -2°Je_'' J 4 dtВ следующем разделе приводятся числовые примеры оценок, полученных по
приведенным формулам.15.7.3. Сравнительная характеристика
интервальных средних наработок на отказ
дублированной системы с различными типами
резервированияПроведем сопоставление интервальных средних наработок на отказ дублиро¬
ванной системы при следующих допущениях:
640Глава 15□ элементы системы являются однотипными;□ время до отказа элементов имеет экспоненциальное распределение;□ время восстановления произвольное.Для сравнения полученные оценки сведены в табл. 15.8 и 15.9.Таблица 15.8. Интервальные оценки наработки на отказ в случае резерва замещениемКласс распределенийНижняя оценка ТВерхняя оценка ТaG е #(0,оо)ь+оо1-е “aaG е H(r,s)fe 1 1 Л* ' dt» -(r(i+-)-«) -1
\е 1 ' 'I*' dt00Таблица 15.9. Интервальные средние наработки на отказ
в случае постоянно включенного резерваКласс распределенийНижняя оценка ТВерхняя оценка TG 6 Я(0,оо)a— + —2' 2af\-e a\ у-■+00G s Н(г,$)a aa a2je0if*)-tdt2 ‘ « -frf1+‘hV-r2je [ 1 dt0ПРИМЕР 15.14. Пусть среднее время до отказа каждого элемента дублиро¬
ванной системы о = 5000 час. Вычислить нижнюю границу средней наработ¬
ки на отказ для резерва замещением и постоянно включенного резерва. Про¬
вести сравнение полученных оценок.Решение. Результаты расчетов нижней оценки средней наработки на отказ
для различных видов резервирования приведены в табл. 15.10.Из таблицы следует, что сужение класса распределений времени восстанов¬
ления элементов ведет к значительному изменению наработки на отказ. Эф¬
фект особенно ощутим для систем с быстрым восстановлением элементов.
Граничные оценки надежности систем641Таблица 15.10. Нижняя оценка средней наработки на отказ
дублированной системы Т, часЬ, часПостоянный резервРезерв замещениемG е Я(0,оо)G e tf(l;4)Getf( 0,qo)G e tf(l;4)101,3 -1061,9-10672,5 -1063,7 -1067206,3 - 10s2,9 • 103s1,3 -1065,8-1035304,2 • 10s7,2 • 10248,4-10s1,4 1025403,2 - 10s3,6-10196,3 10s7,2-1019502,5 -10s2,4-10165,0-10s4,8-1016602, МО51,8 • 10144,2 10s3,61014701,8 10s5,5-10123,6 -10s1,1-!013801,610s4,0-10"3,2-10s8,010n901,4 10s5,3-Ю102,8-10s1,110"1001,3 10s1,0 -10102,5 10s2,1-1010Нижняя граница наработки на отказ определяется только значением показа¬
теля s , а параметр г никак на нее не влияет. Поэтому нижняя граница зави¬
сит только от величины старения распределения G(t).При одинаковых условиях надежность системы (по наработке на отказ) для
резерва замещением всегда выше надежности системы для постоянно вклю¬
ченного резерва.На рис. 15.7 показано, как нижняя граница наработки на отказ зависит от
среднего времени восстановления элементов системы. Кривая 1 соответству¬
ет резерву замещением, а кривая 2 — постоянно включенному резерву. Эти
кривые построены при отсутствии какой-либо информации о законах распре¬
деления времени восстановления; известно лишь среднее время восстанов¬
ления.Аналогичные кривые имеют место и при наличии информации о скорости
старения распределения G(t), только соответствующие значения будут на2! Зак. 3094
642Глава 15несколько порядков выше, чем в рассмотренном случае. Дополнительная ин¬
формация, как видно из табл. 15.10, существенно уточняет нижнюю границу
средней наработки на отказ системы.Рис.15.7.4. Интервальные оценки в классе систем
с быстрым восстановлением элементовПроведем анализ влияния скорости восстановления элементов на близость
граничных оценок показателей надежности системы. Ограничимся рассмот¬
рением дублированной системы (резерв замещением) из двух равнонадежных
элементов, обслуживаемых одной ремонтной бригадой с прямым приорите¬
том. Пусть /(/) — плотность распределения времени безотказной работы
элементов с математическим ожиданием a, g(t) — плотность распределе¬
ния времени восстановления элементов с математическим ожиданием Ъ.
Сделаем следующее важное допущение: функция g{t) имеет ограниченный
носитель supp(g) с [0, Tg ], причем Tg«a (насколько Tg меньше а будет
рассмотрено далее).Посмотрим, как скорость восстановления элементов влияет на сближение
оценок средней наработки на отказ системы. Как известно, наработка на от¬
каз системы вычисляется по формулеООоразличных видов100резервирования010 Ь, час15.7. Нижняя граница наработки на отказ для
Гоаничные оценки надежности систем643В связи с этим будем решать оптимизационные задачи вида:ОО ООz= \G(t)f{t)dt = fF(t)g(t)dt -> max(m in)
о опри условияхJg(0<* = 1, \g(t)dt = b, g(t)> 0.о оВ силу ограниченности носителя плотности g(t) соответствующие двойст¬
венные задачи формулируются следующим образом: найти числа с0 и с,
(любого знака), для которыхw = c0+ctb—> min(max)при ограниченияхc0+cxt> F(t), (c0+c^<F(O), Vt :0 <t <Tg .Графическая интерпретация двойственной задачи показана на рис. 15.8.Д'1F(b)ОО ь Tg ‘Рис. 15.8. Пояснение к решению двойственной задачи (функция F(t) вогнутая)Среди всех прямых линий, огибающих кривую F(t) на промежутке 0<t <Tgсверху (снизу), надо найти такую линию, для которой ее значение в точке
t = b было бы наименьшим (наибольшим).Рассмотрим некоторые частные случаи, допускающие точное решение. Пусть
время до отказа имеет равномерное распределение:
644Глава 15Очевидно, что оптимальные решения задач на максимум и минимум совпа¬
дают и равны с0 = 0, С] = —. Поэтому zmax = zmin - —, и2 a 2aТ = Т =—.Пусть F(/) — вогнутая функция при 0<t<Tg. Тогда в задаче на минимум
искомая прямая должна касаться кривой F(t) в точке t = b, т. е.
с0 + С] 6 = /г(6), и, значит, wmin = F(h). В задаче на максимум искомая прямая
должна проходить через две точки с координатами (О, F(0)) и (Tg,F(Tg)).F(TS)-F(0) F(T )-F(0)
Отсюда c0 = F(0), с, = , и, значит, wmax = F(0) + b .Если F(t) — выпуклая функция на интервале 0 < t < Т„, то^min =F(0) + bF(Tg)-F( 0)wmax =F(b).Пусть время до отказа одного элемента имеет показательное распределение:F(t) = 1-е “ .
Так как функция F(i) вогнутая, тоТ =a_ь
l-e aТ=-аТ„g1-е аСчитая отношение — малым, получим приближенные равенства:
ааL N »
1-А|
2а)Т Л '
1--«-
2 аОтсюда явно видна близость интервальных оценок при условии быстрого
восстановления элементов, если время до отказа элементов экспоненциально.Если время до отказа элемента имеет нормальное распределение, то функция
F(t) выпуклая при t < а . Если время до отказа имеет распределение Вейбул-!!
Гоаничные оценки надежности систем645ла с параметрами (а, р), то при а > 1 функция F(t) выпуклая при
(а-1)аt <—£ a. Поэтому для этих распределении имеют место следующие- ( па“Г 1 + —^ а)нижняя и верхняя оценки средней наработки на отказ:oTg — аL = (Tg-b)F(Q) + bF{Tgy T=~mпри условии, что Tg находится на интервале выпуклости функции F(t).ПРИМЕР 15.15. Для дублированной системы (резерв замещением) опреде¬
лить оценки средней наработки на отказ. Среднее время безотказной работы
каждого элемента а = 50 час. Закон распределения времени восстановления
неизвестен, среднее время восстановления Ь = 4 час. Элемент не может вос¬
станавливаться более Tg = 8 час.Решение. Результаты вычислений в зависимости от закона распределения
времени безотказной работы элементов приведены в табл. 15.11.Таблица 15.11. Нижняя и верхняя оценки средней наработки на отказЗакон и параметры распределенияТ, часТ , часЭкспоненциальный (50)650676Нормальный (50; 20)41544662Вейбулла (2; 44,3)31186161Для распределения Вейбулла значения нижней и верхней оценок средней на¬
работки на отказ различаются почти в 2 раза. Если показатель формы а уве¬
личить, то эта разница возрастет еще больше. Так, при а = 3 превышение
верхней оценки над нижней будет уже более чем в 4 раза. Поэтому даже бы¬
строе восстановление элементов не гарантирует близости этих оценок, как
это происходит для показательного распределения.Таким образом, для заданной функции F(0 и произвольной функции g(t)
с ограниченным носителем существует достаточно хороший алгоритм полу¬
чения двусторонних оценок наработки на отказ резервированной системы.Укажем еще возможный путь получения интервальных оценок среднего вре¬
мени восстановления дублированной системы.
646Глава 15Среднее время восстановления вычисляется по формуле00 I\G(t)F(t)dt {\F(x)dxg(t)dt
j4 _ _о о о]o(t)f(t)dt ]F(t)g(t)dt
о оДля определения интервальных оценок следует решить следующие задачи
оптимизации:J \F(x)dxg(t)dtТв =— > max(min)J F(t)g(t)dt
опри условиях]g(t)dt = 1, jtg(t)dt = b, g(O>0.
о оДля решения этих задач следует перейти от дробно-линейной к линейной це¬
левой функции, а затем составить двойственные задачи:w = с2 —> min(max)при ограниченияхt ' Ic0+clt + c2F(t)>jF(x)dx (с0 +cxt + c2F(t)< fF(x)dx), Vt:0<t<Tg;о 0c0 + cxb < 0 (c0 + сф > 0).Решение двойственных задач позволяет найти экстремальные значения целе¬
вой функции wmin и vvmax , а затем оценки среднего времени восстановления:Т-w Т — wхв "min 5 _f_B KVmax ■15.8. Функция готовности элемента
при неполной информации
о законах распределенияДля расчета функции готовности воспользуемся соотношениемKr(t) = F(t) + (oB*F(t),
Граничные оценки надежности систем647где юв(0 —параметр потока восстановлений, удовлетворяющий уравнениююв СО = f * £(0 + / * g * со, (/).Предположим, что время безотказной работы принадлежит семейству рас¬
пределений H(r,s) , т. е. FeH(r,s), и Т — среднее время безотказной ра¬
боты. Обозначим через F* и F** соответственно верхнюю и нижнюю оги¬
бающие класса H(r,s). Указанные огибающие были определены в разд. 15.2.При замене F на F* или на F** получим верхнюю и нижнюю границы
функции готовности соответственно.В частности, если время восстановления имеет равномерное распределение
на промежутке [0; Ъ\, то'тf*g{ о =F{t)-F{t-Ь)при t<b;
при / > b.ПРИМЕР 15.16. Время до отказа имеет произвольное распределение из клас¬
са #(0,5;2). Среднее время безотказной работы Т = 100 час. Время восста¬
новления имеет равномерное распределение на промежутке [0; 4]. Привести
оценки функции готовности.Решение. Среднее время восстановления Тв= 2 час. Результаты расчетов
верхней и нижней оценок функции готовности представлены на рис. 15.9.
648Глава 15Совершенно аналогично, основываясь на свойстве 14 класса H(r,s), могут бытьполучены границы функции готовности в классе H{r, s, {^}, {Fj}, i = 1, т).
Это связано с существованием в этом классе верхней и нижней функций рас¬
пределений.15.9. Двусторонние оценки коэффициента
оперативной готовности в классе функций
ограниченного роста Н(г, s)Пусть F е H(r,s), GeH(0,оо) с математическими ожиданиями Т и Гв соот¬
ветственно. Тогда коэффициент оперативной готовности удовлетворяет нера¬
венствам1T + Taе 4'Мdt.(15.15)10 в 1оДействительно, достаточно применить следствия из свойств 11 и 12 о нахож¬
дении экстремумов интегралаООjc(t)F(t)dtо 'в классе функций F е H{r,s), где c(t) = Н,о (t) — функция Хевисайда.Частный случай неравенства (15.15) для стареющих распределений #(1,оо)
имеет вид:1 Jo
ТT + Ta(15.16)‘в V •* / ‘ 1 'вчто совпадает с известными двусторонними оценками [57].ПРИМЕР 15.17. Пусть математические ожидания соответственно равны
Т = 10000 час и Г8=1 час соответственно. Провести сравнение оценок коэф¬
фициента оперативной готовности в классе всех стареющих распределений
#(1;со) и в подклассе стареющих распределений 7/(2; 3).Решение. Двусторонние граничные оценки коэффициента оперативной го¬
товности в классе всех стареющих распределений получим по формуле
Граничные оценки надежности систем649(15.16), а в классе #(2;3) — по формуле (15.15). Соответствующие кривые
для сравнения изображены на рис. 15.10.0 t0, час 17200Рис. 15.10. Двусторонние граничные оценки коэффициента оперативной готовности
в классе #(!;<») (кривые 1 и 4) и в классе Я(2;3) (кривые 2 и 3)Отметим, что по формуле (15.15) можно получать оценки также и в более
широких классах распределений, например при r<\, s>l. На рис. 15.11
представлены двусторонние граничные оценки коэффициента оперативной
готовности в классе #(0,8;2) (кривые 2 и 3) и в более широком классе
#(0,5; 20) (кривые 1 и 4).Рис. 15.11. Двусторонние граничные оценки коэффициента оперативной готовности
в классе #(0,8; 2) (кривые 2 и 3) и в классе #(0,5; 20) (кривые 1 и 4)В узком классе распределений #(0,8; 2) оценки коэффициента R(t0) явля¬
ются более близкими друг к другу, чем в классе #(0,5; 20).
650Глава 1515.10. Определение параметров г и s
по статистическим данным об отказахРассмотрим вопрос об установлении принадлежности распределения времени
до отказа классу H(r,s) на основе статистических данных об отказах.Предположим, что на испытании находится п однотипных по надежности
элементов со средним временем безотказной работы, равным a. Пусть
tx,t2,...,tn — моменты времени отказов элементов. Требуется определить
параметры г и s, для которых распределение выборочной совокупности
оказывается принадлежащим классу H(r,s). Число а есть среднее время
безотказной работы элемента, поэтому разумно положить его равным сред¬
нему арифметическому выборочной совокупности t\,t2, , tn .Применение функции правдоподобия связано с требованием иметь функцию,
подобную плотности распределения вероятностей времени до отказа. Будем
исходить из того, что основу класса H(r,s) образуют распределения Вейбул¬
ла с параметрами, принадлежащими промежутку [г; s]. Как известно, плот¬
ность распределения Вейбулла с параметром формы а и параметром мас¬
штаба р имеет вид:-f1!'/(;,а,Р) = —— е W , 0<IS-Ko.Выражая параметр Р через математическое ожидание, получим:Г(1 + 1/а)Функцию правдоподобия можно получить, если для каждого элемента вы¬
борки tm произвести разыгрывание случайной величины £т, равномернораспределенной на промежутке [/*; s], и положить” aЩ, t2,.г, s)= П/('«»$«• Эи)» где Pm =— ; 777 :■т=1 1 О "I" V S/n )Таким образом, значения параметров г и s могут быть получены в результа¬
те решения следующей задачи оптимизации:и 1Щ, t2,..., t„, Г, S) = аП —хт(*т> $т)е -> ШЭХт = 1
Граничные оценки надежности систем651при ограничениях 0 < г <, s < +00. Здесь xm (tm, £,m) =tjnni+VUaАлгоритм позволяет по заданной выборке определить значения параметров г
и s методом максимального правдоподобия. Решение можно получить на ПК
с помощью программных средств, разработанных по данному алгоритму.ПРИМЕР 15.18. Проведено 16 независимых опытов, в которых объем стати¬
стических данных п изменялся от 100 до 1500 с шагом 100. Выборка объема
п была извлечена из распределения Вейбулла с параметром формы а = 4,6 и
математическим ожиданием а = 1000 час. Требуется установить значения
показателей класса распределений H(r,s), которому принадлежит выбороч¬
ная совокупность.Решение. Методом максимального правдоподобия по разработанной нами
программе получены оптимальные значения г и s как функции от объема
выборочной совокупности. Графическая зависимость показателей класса
H(r,s) от значения п представлена на рис. 15.12.Рис. 15.12. Зависимость г и s от объема статистических данныхПолученные результаты численных экспериментов позволяют сделать сле¬
дующие выводы:□ для случайных чисел, сгенерированных по распределению Вейбулла с
произвольными параметрами значения г и s оказываются соответственно
левее и правее показателя формы а ;□ при увеличении объема выборки наблюдается явное сближение г и s к
показателю а;
652Глава 15□ параметр г оказывается в среднем ближе к показателю а, чем пара¬
метр s;□ наблюдается достаточно быстрое вхождение в стационарный режим.Таким образом, принадлежность случайных величин классу распределенийH(r,s) может быть установлена на основе получения и обработки статисти¬
ческих данных.В заключение укажем на основные недостатки методов, рассмотренных вданной главе:1. Необходимо знать статистические данные о законах распределения отка¬
зов элементов сложных систем.2. Получение параметров г и s по статистическим данным требует допол¬
нительного более широкого изучения.3. Теория интервальных оценок надежности систем не доведена до инженер¬
ной методики.4. Диапазон получаемых оценок показателей надежности в ряде случаев
слишком велик.5. Для инженера-практика может оказаться сложным используемый матема¬
тический аппарат; эта сложность преодолима с помощью компьютерных
технологий.
ГЛАВА 16
АНАЛИЗ НАДЕЖНОСТИ
ПРОГРАММНОГО ОБЕСПЕЧЕНИЯВ компьютерных системах компьютер, как часть системы, обычно выполняет
функции управления и должен работать в режиме реального времени. В ти¬
повых компьютерных системах компьютер выполняет бесконечный цикл, в
котором сначала считываются сигналы и показания датчиков и сенсоров, за¬
тем затрачивается определенное время, чтобы вычислить или спланировать
некоторый отклик или реакцию на воздействие, и в конце цикла компьютер
выполняет эту реакцию. Очевидно, что структура одного периода цикла
управления может быть и гораздо сложнее. Однако укрупнение различных
операций обычно сводится к описанным этапам. Надежность компьютерной
системы может определяться как последовательное соединение статистиче¬
ски независимых аппаратной и программной компонент системы. Но наибо¬
лее подходящей мерой надежности является вероятность того, что система
выполняет свою миссию или справляется с функциями управления в течение
заданного времени при условии взаимодействия аппаратуры и программы.
Надежность такой системы определяется надежностью аппаратной и про¬
граммной частей в их взаимодействии. Отказы аппаратуры происходят
вследствие многих причин: износ компонентов, сбои, короткое замыкание,
обрывы и т. п. Причинами отказов программного обеспечения являются:□ наличие ошибок в программе;□ использование неоптимальных и несовершенных алгоритмов, таких как
эвристические, приближенные, численные;□ ограничения на функционирование в реальном времени.Остановимся подробнее на некоторых факторах, влияющих на надежность
компьютерной системы:1. Надежность элементов аппаратуры. Компоненты аппаратной части ком¬
пьютерной системы имеют самые различные механизмы отказов. Некото¬
рые из них могут быть вызваны воздействием программной части системы.
Например, чрезмерное "стрессовое" использование каких-либо компонен¬
654Глава 16тов аппаратуры, особенно имеющих механические элементы функциони¬
рования. Примерами этого являются: длительное и непрерывное исполь¬
зование принтера, интенсивные чтение и запись на жесткий диск, частое
изменение режимов работы дисплея. Таким образом, можно утверждать,
что во многих случаях отказы программного обеспечения и техники ком¬
пьютера являются событиями зависимыми.2. Влияние программы на надежность аппаратуры. Например, рассмотрим
двухфункциональную систему. Один план управления требует, чтобы обе
функции были активными для расчета реакции на входные данные, в то
время как другой требует, чтобы только одна функция была бы активной.
Когда программа влияет на надежность аппаратуры таким образом, мы
можем говорить только об условной статистической независимости аппа¬
ратной и программной частей.3. Отказы в программе. Если программное обеспечение не модифицируется,
то интенсивность его отказов остается постоянной вследствие оставшихся
в ней необнаруженных ошибок.4. Внутренние отказы программы. Такие отказы обусловлены фундамен¬
тальными ограничениями алгоритма, используемого в программном обес¬
печении. Например, использование эвристик может привести к случайным
отказам, даже если в программе отсутствуют ошибки.5. Отказы, обусловленные ограничением на функционирование в реальном
времени. В рассматриваемых системах среда может изменяться динамиче¬
ски. Поэтому если время планирования или расчета отклика слишком ве¬
лико, то к моменту выполнения отклика среда может быть уже изменен¬
ной так сильно, что вычисленный или спланированный отклик не будет
иметь требуемого эффекта. Эти отказы часто характеризуются неспособ¬
ностью системы функционировать в ограничениях на реальное время.Следует отметить, что перечисленные факторы влияют друг на друга. На¬
пример, имеется противоречие между устранением внутренних отказов и от¬
казов, обусловленных ограничением на функционирование в реальном вре¬
мени. Использование оптимального и высокоточного алгоритма решения
какой-либо задачи требует значительных затрат времени для получения ре¬
шения, что может привести к нарушению ограничений, связанных с реаль¬
ным временем функционирования системы. В то же время, использование
рационального (но не оптимального) или приближенного эвристического ал¬
горитма позволит преодолеть проблему реального времени, однако может
привести к внутренним ошибкам. Таким образом, анализ надежности компь¬
ютерной системы является достаточно сложной задачей, на которую влияет
большое количество факторов. И очевидно, что ее решение необходимо вы¬
полнять поэтапно: сначала рассмотреть аппаратную часть, затем программ¬
Анализ надежности программного обеспечения655ную в отдельности и только после этого анализировать надежность с учетом
взаимодействия всех компонентов.16.1. Модель работы программы
с изменяющимся распределением времени
до проявления ошибкиАнализ надежности программного обеспечения (ПО) состоит, как правило, из
двух основных этапов: этап испытаний и тестирования ПО и этап эксплуата¬
ции ПО. На первом этапе обычно по результатам выборочных данных или
субъективных наблюдений строится математическая модель, при помощи
которой можно выполнить прогноз надежности программы на этапе эксплуа¬
тации. Анализ поведения на этапе эксплуатации предусматривает учет раз¬
личных факторов и ограничений работы программы, таких как используемые
аппаратные средства, способы обнаружения ошибок, времена исправления
ошибок, многократность выполнения программы, допустимая область исход¬
ных данных, параллельное или последовательное совместное использование
других программ, возможное использование избыточности (многоверсионное
программирование). Для повышения надежности программного обеспечения
предлагается jV-версионное программирование, использование временной
избыточности и просто оперативное исправление ошибок в программе.Имеется большое количество работ по разработке модели надежности про¬
граммного обеспечения. В ряде работ предлагается подход к построению мо¬
дели, согласно которому поведение программного обеспечения в смысле на¬
дежности является нечетким по природе, т. к. каждая программа является
уникальной. Обзор как вероятностных, так и иных методов анализа про¬
граммного обеспечения показывает, что все модели предусматривают изме¬
нение характеристик ошибок в программе по мере их исправления, т. е. время
до возникновения очередной ошибки увеличивается. При этом предлагались
различные возрастающие функции, связывающие времена между последова¬
тельными ошибками: линейная, логарифмическая и т. д.16.1.1. Режимы функционирования ПО
и их математическое описаниеВ настоящем разделе рассматривается программная система, состоящая из
нескольких подпрограмм, которая обеспечивает контрольные функции и ра¬
ботает в бесконечном цикле. При этом в случае проявления ошибки в одной
из подпрограмм осуществляется ее исправление, и данная подпрограмма сно¬
ва выполняется. Так как после исправления мы имеем новую улучшенную
656Глава 16подпрограмму, то ее характеристики надежности изменяются. Можно рас¬
смотреть два режима функционирования программы:1. После выполнения очередного цикла время до ошибки накапливается с
учетом предыдущих циклов.2. Начало каждого нового цикла определяет начало времени до ошибки.Мы рассмотрим оба эти случая, т. к. они могут иметь место в реальных про¬
граммных системах.Одним из основных вопросов является выбор показателей надежности. Здесь
мы рассчитываем следующие характеристики программы:□ среднее число правильно решенных задач (количество полностью завер¬
шенных циклов) до заданного момента времени;□ среднее число ошибок до заданного момента времени;□ вероятность решения заданного количества задач к некоторому моменту
времени;□ вероятность появления заданного количества ошибок к некоторому мо¬
менту времени;□ распределение длительности заданного количества циклов.Далее рассматривается следующая ситуация по отысканию ошибок ПО. Вы¬
полняется некоторая задача с использованием программы, время решения
которой £ случайно с плотностью распределения /(() . Если задача решена и
ошибка ПО не проявилась (время до появления первой программной ошибки
е, случайно с плотностью hx(t)), то по этой же программе запускается на
решение следующая задача, длительность которой имеет то же распределе¬
ние, что и у предыдущей задачи. Этот процесс продолжается до тех пор, пока
не проявится ошибка ПО. При обнаружении ошибки задача прекращает свое
выполнение, и начинаются поиск и устранение проявившейся ошибки. Время
восстановления программы г\ случайно с плотностью g(t). После устране¬
ния ошибки задача снова запускается на решение. Если ошибка не прояви¬
лась, то снова начинается процесс решения задачи. Если проявилась вторая
ошибка, время до которой е2 имеет плотность распределения /^(0, то начи¬
нается поиск и устранение этой ошибки. Таким образом, при постепенном
устранении ошибок закон распределения времени проявления новой ошибки
изменяется. Для &-й ошибки длительность ее обнаружения гк имеет плот¬
ность распределения hk(t). Граф состояний представлен на рис. 16.1. Он бес¬
конечен и имеет счетное множество состояний, поскольку, по крайней мере,
теоретически число ошибок ПО может быть бесконечным.
Анализ надежности программного обеспечения657Рис.' 16.1. Граф состояний по обнаружению ошибок ПОВ данной постановке могут встретиться два случая, связанные с отсутствием
или наличием "памяти" у случайных величин ек :□ для каждой задачи, решение которой начинается заново в некоторый мо¬
мент t, время до обнаружения очередной ошибки также начинает идти,
начиная с момента t, т. е. время по обнаружению ошибки, которое расхо¬
довалось для предыдущей задачи, как бы забывается (отсутствие "памяти");□ для каждой задачи, решение которой начинается заново в некоторый мо¬
мент t, время обнаружения ошибки, которое расходовалось для предыду¬
щей задачи, продолжается (наличие "памяти").Далее мы рассмотрим оба указанных случая. Заметим, что на графе эти слу¬
чаи неразличимы, и для их математического описания необходимо изобра¬
зить временные диаграммы (рис. 16.2 и 16.3 соответственно). Выше оси вре¬
мени расположено время решения задач, а ниже оси времени — время до об¬
наружения ошибок и длительности их устранения.Отсутствие "памяти"На диаграмме, изображенной на рис. 16.2, приведен первый случай.Для каждого состояния системы определим неизвестные функции yk(s,u,t) и
zk(x,t), к = 1,2,... Функция yk(s,u,t) есть плотность распределения вероят¬
ности пребывания системы в момент времени / в состоянии к при условии,
что остаточное время решения задачи равно 5 и время до проявления оче¬
редной ошибки равно и. Функция zk{x,t) есть плотность распределения ве¬
роятности пребывания системы в момент времени t в состоянии к при ус¬
ловии, что остаточное время устранения ошибки равно т .Рис. 16.2. Временная диаграмма при отсутствии "памяти"
658Глава 16Относительно этих функций имеет место следующая система уравнений:I ООyx(s,u,t) = J/(x + s)hx(x + и) \yx(0,u,t -x)dudx + f (t + s)hx(t + u);
о оt 00
yk(s,u,t) = j/(x + s)hk(x + и) jyk(0,u,t - x)dudx +° ° (16.1)+ }/(* + s)hk(x + u)zk_x(0,t -x)dx, к = 2,3,...;
оzk(x,t)= \g(x + x)\yk(s,0,t-x)dsdx, k = l, 2, ...Для решения системы (16.1) положим (р*(0= \ykW>u’t)du и перепишем ееов более компактном виде:Ух (s, и, t) = fshXu* ф, (0 + fs (t)hXu (/);
yk(s,u,t) = fshku*<$>k{t) + fshku*zk_x(Q,t), к = 2,3,...;(!6.2)zkM = gT* \yk(s,0,t)ds, к = 1,2,...
оИз второго уравнения системы (16.2) получим уравнение относительно
функции ф*(/):q>k(t) = JHk * ц>к (t) + fHk * zk_x (0,/). (16.3)Из (16.3) можно получить выражение для функции ф*(0 через функциюz*_i(0,O:Фл(О = ®л*^_1(0,О, (16.4)гдеЩ (0 = Е )*(,)(0, йк(t,s, и) = fshku * &к (0 + fsЬы (0 .i=iДействительно, подставляя функцию (16.4) в правую часть уравнения (16.3),
получимR = JHk*(hk* zk_x (0, t) + JHk* zk_x (0,0-ю* * 2к-1 (°> 0 = Флг (0 >
что и требовалось доказать.
Анализ надежности программного обеспечения659Из (16.2) и (16.4) следует, чтоук(s,u,I) = fshku *&к *z*_,(0,/) + fshku *z*_,(0,O,илиyk(s,u,t) = ak(t,s,u)*zk_l (0, t). (16.5)ОбозначимОО4>к(0= J% (/, 5,0)ds = Fhk * (0 + Fhk (/).
оТогда на основании уравнения (16.5) и последнего равенства системы (16.2)
получим:ООyk(s,u,t) = &k(t,s,u)*g* jyk_^s,0,t)ds.оОтсюда следует рекуррентное соотношение00 00
J У к (s > °> 0ds = Ук*8*\Ук-1 (*> °> Ods,о ои, следовательно,yk(s,u,t) = &k{t,s,u)*yj * \\i2 *...*Wk-i *g,(k~l)(0 >а значит,гкМ = g,*4ii * V2 * - * Vk * g*ik~l)(0 ■Решение системы (16.2) получено.Наличие "памяти"На диаграмме, изображенной на рис. 16.3, приведен второй случай.2 ь3Рис. 16.3. Временная диаграмма при наличии "памяти"Относительно функций yk(s,u,t) и zk(z,t) справедлива следующая система
уравнений:
660Глава 16yx(s,u,t) = J/0 + s)j>, (0,x + u,t - x)dx + f(t + s)h{ (t + u);
о
/yk (s, u, t) = J f(x + s)yk (0 ,x + u,t- x)dx +° (16.6)+ ff(x + s)hk(x + u)zk_i($,t -x)dx, к = 2,3,...;
оt 00z*(V)= ]#(* + *) -*)<&<&, k = 1,2,...о 0Решим систему (16.6). Представим второе уравнение системы (16,6) в виде:
tyk(s,u,t)= jf(x + s)yk(0,х +и,t-x)dx + fshku*zk_l(0,t). (16.7)
оДокажем, что имеет место равенствоyk(s,u,t) = a(t,s)hku (0 * гкЛ (0,0, (16.8)гдеш(М) = со*/5(0 + /ДО= + (16.9)к=1Действительно, преобразуем сначала равенство (16.8), используя обозначение
(16.9):/ук (5, и, Г) = /оэ(/ - a, s)/?b (t - а)zk_x (0, а)dа =
оt= J(® * fs if ~ а) + Л 0 " а))Ль 0 - (0, аУ а.
оПодставим полученное выражение в правую часть уравнения (16.7), тогда
получим:I t-xR= |/(x + j) J (ю* f(t-x-a) + f(t-x-a))hku(t-a)zk_l(0,a)d(xdx +
о 0+fshku ***4 (0,0 =/ /-a= J/7b(r-a)z*_,(0,a)rfa J f(x + s)(co* f{t -x-a) + fit -x-a))dx +
о о+fshku*zk-1(0,0 =
Анализ надежности программного обеспечения661= \hku(?-a)zk-\(°>а)ю*fs(t-o.)da+fshb *zk_x(0,t) =о= (°>* fshku)*zk-1 (°»0■+fshku *zk-1(°>0 = <t>s)hku(0*zk-1 №Требуемое утверждение доказано.На основе установленного свойства (16.8) и третьего уравнения системы
(16.6) получим рекуррентную формулу для определения неизвестных функ¬
ций ук:00yk(s,u,t) = a(t,s)hku(t)*g* J^_i(j,0,0^- (16.10)о -Последовательно используя формулу (16.10), из системы уравнений (16.6)
получим все искомые функции:yl(s,u,t) = G)(t,s)hlu(t),00z\M = gx* \y\(sAt)ds = g^*hx(t),оу2 (s, u, 0 = (со(t, s)h2U (0) * g * hi (0,COz2M = gx * jy2(sAt)ds = gx*h2*g*hl(t)0и т. д. В общем случаеyk(s,u,t) = (co(/,s)Ab(0) *hi*h2*...*hlc_]* g*{k~[)(t);zkM = gz*hi*h2*...*hk*gHk~])(0.Проведем контроль правильности расчетов, проверив справедливость усло¬
вия нормировки. Для этого найдем вероятность каждого состояния:pk(t) = hl*h2*...* *Нк* g*(*4)(0,qk(t) = hl*h2*...*hk*G* g*(*_1) (t).Просуммировав вероятности, получим:Z (рк(О + Як(0) =£(V-*hk-1 *g*(*_,) * 1(0-hy* — *hk*g*{k~X) * 1(0 +
k=1 *=1+/?! *... *hk* g*(A-1) * 1(0 - h[ *... * hk * g*w * 1(0) = 1 •
662Глава 1616.1.2. Временные характеристики эффективности
программных средствВведем две характеристики надежности программ, имеющих, на наш взгляд,
важное прикладное значение. Пусть N3(t) — среднее число задач, решенных
за время [0;/], a N0(t) — среднее число ошибок, обнаруженных в течение
времени [0; /].Нетрудно видеть, что среднее число решенных задач равно сумме числа пе¬
реходов M^t) из каждого к-го состояния в к-е состояние по всем к = 1, 2,...,
а это число связано с соответствующим параметром перехода по формулеIMkk(0= \tokk{x)dx.0Следовательно,N3(t)= ^№^(1) = X jcokk(x)dx = X f\yk(0,u,x)dudx. (16.12)£ = 1 * = 10 A: = 10 ОСреднее число ошибок ПО равно сумме числа переходов Mkk(t) из каждого
£-го состояния в состояние к нижележащего уровня по всем к = 1, 2,..., а это
число связано с соответствующим параметром перехода по формуле1Mkk(t)= jakk(x)dx.
оСледовательно,N0(t) = ЕМуг(0= £ {«**(*>& = Е \\yk(s,0,x)dsdx. (16.13)* = 1 Лг = 1 о А: = 10 ОВычислим введенные характеристики для двух случаев функционирования
системы.Получим значения характеристик для первого случая, когда ошибки не име¬
ют "памяти". Из соотношенияyk(s,u,t) = &k(t,s,u) * у! * ц/2 *... * * g*(i_1)(О
Анализ надежности программного обеспечения663следует, что00= /л(0,и,ОА* = Ч>1*Ц>2* -*ц>к-1 * % * g4*~l}(0>О00®*jf(0 = 7л (*,0,/)<й = V)/, * \\12 *... * ц,к_, * у* * g*(lt_1)(0 •оТогда 00 t^*(0 = S Jvi * V2 * - * V*-I * * £*( _1) (*>&.*=Ю оэ t*o(0«S -,)(x)&.*=юПолучим значения характеристик для второго случая, когда ошибки облада¬
ют "памятью". Как следует из формул (16.11)00®«(0 =\Ук('0,u,t)du = (<вЯ*)*hl*h2*...*hk_l* g'{k~l)(0,О00(Okk(0= fyk(s,0,t)ds = hx *h2*...*hk_l*hk*g*(k~l\t),
оследовательно,N3(t)= X J(cotf*)*/?, *h2*...*hk_l*gt{k~l)(x)dx,
к=Ю^о(0= S
*=ЮДля сопоставления полученных результатов предположим, что, во-первых,
все ошибки в программе устранены за п шагов и, во-вторых, рассматривает¬
ся установившийся режим работы программы.Тогда в случае отсутствия "памяти" среднее число решенных задач равно
— — " 00iV3 = limtf3(0= £ (Vi *(bk *g*( ~\x)dx =,->0° k = \ 0„= EKwa=z^ .*=,0 k=h-jjHk(x)dx0
664Глава 16При наличии "памяти" среднее число решенных задач равноN3 = lim N3(0=1 J(^Нк)*hl*h2*...*hk_l*g*(kA){x)dx = £ J•
'->0° k = \ о * = ЮНетрудно видеть, что среднее число ошибок в обоих случаях оказывается
равнымN0 = lim N0(t) = п.1-> соЭто число, рассчитанное в установившемся режиме, справедливо для любых
распределений.ПРИМЕР 16.1. Сравнить количество решенных задач при отсутствии и
наличии "памяти" у возможных ошибок программы. Пусть п = 3, время
решения задачи имеет экспоненциальное распределение с параметром
X = 0,02 час-1, время до возникновения к-й ошибки имеет:1. Экспоненциальное распределение.2. Постоянно с математическим ожиданием Ток = 100 часов.Решение.00 А,1. Так как jjHk(x)dс = —, то при отсутствии "памяти"О Х + —ТокК=1™ок=6.
к=1Поскольку оз(0 = X, то при наличии "памяти" получим:й3 = ±хток=б.
к = 1ОО2. Так как fjHk(x)dx = F(Tok) = 1 -е~'кТ<Л , то при отсутствии "памяти"о_ П 1 _ р~*-Ток^3=1—^F- = 19-
k=i е °*Поскольку ш(0 = X, то при наличии "памяти" получим: •N3 = 'ZXTok =6.
k=l
Анализ надежности программного обеспечения665Видно, что среднее число решенных задач зависит от законов распределения
моментов возникновения ошибок в программе. Оно зависит также и от рас¬
пределения длительности решения задачи. Для экспоненциальных распреде¬
лений результаты двух рассмотренных случаев полностью совпадают.16.1.3. Вероятностные характеристики
эффективности ПОГраф, представленный на рис. 16.1, содержит лишь укрупненные состояния
системы, а именно: состояние к характеризуется обнаружением (к - 1)-й
ошибки ПО, при этом остаются неизвестными вероятностные показатели то¬
го, что было решено i задач без проявления очередной ошибки. Обозначимчерез Pk\t) — вероятность того, что в течение времени t будет решеноровно i задач после обнаружения и устранения (к - 1)-й ошибки ПО, а черезPk\t) — вероятность того, что в течение времени / будет решено не менееi задач после обнаружения и устранения (к - 1)-й ошибки ПО. Очевидно,1'№ю-J=iОграничимся лишь случаем наличия "памяти". Из формулы полной вероят¬
ности и диаграммы, изображенной на рис. 16.3, следует, что вероятностьpk\t) представляется в следующем виде:Рк ] (0 = J4t_i (0, x)P(t - x)dx.
оP(t) — вероятность того, что момент времени t приходится на интервал ре¬
шения задачи с номером (/ +1), причем к-я ошибка возникнет после момен¬
та /:Р(0=Р' I ■ м Л£$><*<£$>» е*>/
и-» >-iВ силу (16.11) получим:pf{t) = hx *[(f{i)*F)Hk)(t), i = 0,1, 2,Суммируя вероятности pk\t) по числу решенных задач, получим:Рк(0 = W •••* К-\ *Нк* ,
666Глава 16что совпадает с ранее найденным выражением для вероятности пребывания
системы в к-м состоянии.Далее по "локальным" вероятностным показателям можно определить и со¬
ставные вероятностные показатели надежности ПО. Например, среднее время
решения точно / задач до проявления £-й ошибки равно4° (о = М°(ол=]/*(0 - тнк(1)л.ПРИМЕР 16.2. В условиях примера 16.1 определить среднее время решения
точно i задач до проявления к-й ошибки.— X't' — 1
Решение. Поскольку / *F(t) = и Нк(t) = e~v*‘, где vk= =г! Ток= 0,01 час-1, тооо л i ЛVt' -V./ V\~e-Xle-v*‘dt =
о *'В частности, среднее время, когда на интервале проявления £-й ошибки не
будет решена ни одна задача, равноmf\t)=—^— = = 33,3 час,* \ + 0,02 + 0,01среднее время решения точно одной задачи равноm.. Я 0,02m\’{t)= - = г-= 22,2 час(X + vk) (0,02 +0,01)2и т. д. Общее среднее время пребывания системы в состоянии к равно]я*(/)Л = Го*=100час./=о о16.2. Модель чередования интервалов
решения задачи и интервалов контроляВ следующих разделах рассмотрим некоторые модели анализа надежности
программного обеспечения. Возможно, некоторые из них не всегда адекват¬
ны существующим в настоящее время инженерным подходам. Однако разра¬
ботанные математические модели и оценки показателей надежности, возни¬
Анализ надежности программного обеспечения667кающие на их основе, способствуют проведению перспективных исследова¬
ний в этой области.16.2.1. Описание работы системыФункционирование системы состоит из чередующейся последовательности
интервалов решения задачи случайной длительности £, и интервалов контро¬
ля случайной длины к, как показано на временной диаграмме (рис. 16.4).
Ниже оси времени показано случайное время до появления скрытой ошибки8, которая может возникнуть на любом интервале решения задачи. Предпо¬
ложим, что ошибка возникла на некотором интервале £ в момент време¬
ни t0.►tРис. 16.4. Фрагмент диаграммы при отсутствии ошибок ПОПосле возникновения ошибки она сначала не проявляется, т. е. имеет место
скрытая ошибка, и ее существование может быть установлено только после
проведения очередного или последующих сеансов контроля. Возможные
продолжения временной диаграммы после возникновения ошибки могут
происходить в соответствии с временными диаграммами (рис. 16.5, a—в).На диаграммах и в последующем изложении материала приняты обозна¬
чения:П £, — случайное время решения задачи, /(i) — плотность, F(t) — функ¬
ция распределения, Т — математическое ожидание \, F(t) = 1 - F(t);□ к — случайное время проведения контроля, h(t) — плотность, H{t) —
функция распределения, Тк — математическое ожидание к, H(t) = 1 - H(t);П е — случайное время до появления скрытой ошибки, e(t) — плотность,
E(t) — функция распределения, ТЕ — математическое ожидание е,
E(0 = \-E(t);□ г) — случайное время восстановления системы, g(t) — плотность,
G(t) — функция распределения, Тв — математическое ожидание г|,
G(/) = l-G(/);
668Глава 16Рис. 16.5. Ошибка ПО обнаружена после первого (а), второго (б) и третьего (в)сеансов контроля□ К[ — случайное время проведения контроля после восстановления,
h'(t) — плотность, H'(t) — функция распределения, Т'к — математиче¬
ское ожидание Kj, H'(t) = 1 - H'(t).Заметим, что количество диаграмм бесконечно велико, поскольку скрытый
отказ (со) может быть выявлен после любого интервала контроля: после 1-го,
как показано на рис. 16.5, а, или после 2-го, как показано на рис. 16.5, б, по¬
сле 3-го, как показано на рис. 16.5, в, или после любого количества интерва¬
лов длины £ + к . Чтобы описать функционирование данной системы в виде
некоторой математической модели, необходимо определить функцию рас¬
пределения времени скрытого отказа без учета остаточного времени случай¬
ной величины \. Будем обозначать эту случайную величину через а.16.2.2. Закон распределения случайной величины аПусть известна вероятность правильного обнаружения ошибки при одно¬
кратном контроле а . Тогда очевидно, что вероятность обнаружения ошибкина п-м интервале контроля равна (1~«х)"а, п = 0,1,2,...' Найдем функцию
распределения для величины а. Обозначим через P{t) вероятность обнару¬
жения ошибки за время t (без учета остаточного времени случайной величи¬
ны \ ), а через pit) — соответствующую плотность распределения вероятно-
Анализ надежности программного обеспечения669стей. Пусть Нп — гипотеза, состоящая в том, что ошибка будет выявлена на
п-м интервале контроля. Тогда по формуле полной вероятности/ лР(О = Р(ст < 0=i P(Hn)P(a < t/H„)= £ (1 - а)"аР к + £ (£ + к) < fw=0 л=0 1=0 у00\*(л)= а X (1 - а)" (/ * А)Пи> * Я (0и=0и, значит,р(0 = аХ(0-а)/*Л)*(”)+Л(0-л=0Выразим математическое ожидание а через Т и Тк . Так как в преобразова¬
нии Лапласаp(z) =ah(z)то№> =l-(l-a)/(z)A(r)
ah'(z) + a(\-a)h2(z)f\z)(l-(l-a )Мг)|_ 71 + (1 - а)ГСледовательно, = — .a16.2.3. Математическая
модель функционированияДля определения надежности системы по любым критериям построим граф
состояний (рис. 16.6) при условии, что законы распределения перечисленных
выше случайных величин известны.Рис. 16.6. Граф состояний по обнаружению ошибок ПО
670Глава 16Узлы графа соответствуют следующим возможным состояниям функциони¬
рования системы:□ (0) — решение задачи, скрытой ошибки не произошло;□ (1) — контроль ПО, скрытой ошибки быть не может;П (2) — решение задачи при условии наличия скрытой ошибки;□ (3) — контроль ПО при условии наличия скрытой ошибки;□ (4) — восстановление системы;□ (5) — контроль ПО после восстановления системы.Математическая модель функционирования системы может быть описана в
рамках интегральных уравнений относительно специальных функций, свя¬
занных с каждым состоянием: y0(s,u,t), yx(k,u,t), >>2(.s,0,0, j>3(v,0,0,
y4(x,0,t), y5(k,0,t). Аргументы этих функций показывают остаточное время
выполнения операций после момента времени t. Система интегральных
уравнений представляется в виде:tу0 (5, и, t) = \f{x + $)>>, (0, X + и, t - x)dx +
о
t+ Jf(x + s)e(x + u)ys (0,0, / — x)dx + f(t + s)e{t + u);
о
tУ] (к, и, t) = \h(x + k)y0 (0, u, t - x)dx;0t• y2(s,0,t)= Jy0(* + s,0,/-.*)<&; (16.14)о
ty3 (v, 0, t) =\p(x + v)y2 (0,0, t - x)dx;
о
ty4 (x, 0,0 = jg(* + t)>>3 (0,0, t - x)dx;01y5 (k, 0 ,()= \h'(x + k)y4 (0,09t — x )dx.
оНетрудно показать также, что система (16.14) сводится к системе из трех ин¬
тегральных уравнений:
Анализ надежности программного обеспечения671У0 (s, и, 0 = j/О + (О,x + u,t- x)dx ++ J/(* + s)e(x + u)y5 (0,0, / - x)dx + f(t + s)e(t + u);
о
/yx(k,u,t)= fh(x + k)y0(0,u,t-x)dx;(16.15)t-xy5(k,0,t)= \h'k *g*p(x) J y0(a,0,t-x-a)dadx0 0или даже к одному интегральному уравнению относительно функции
yo(s,u,t):1 t-xy0(s,u,t)= ff(x + s) J h(a)y0(0,x + u,t-x-a)dadx +0 0 (16.16)I t-x+ \(fseu)*h'*g*p(x) I y0(a,0,t-x-a)dadx + f(t + s)e(t + u).
о 0Нетрудно получить численное решение данного уравнения и затем опреде¬
лить необходимые показатели надежности во временной области функциони¬
рования системы. Однако ограничимся решением уравнения (16.16) только
для стационарного режима, при котором оно значительно упрощается.16.2.4. Оценка надежности ПО
для стационарного режимаВ результате предельного перехода имеем следующее уравнение для неиз¬
вестной функции _у0:00 ОО ОО ООy0(s,u) = J/(* + s) |/г(а).У0(0,я: + u)dadx + \(fseu )*h'*g* p(x) jy0(a,0)dadx,или.y0(j,w) = J/O + sXv^O,* + «)<&+ \f{x + s)e(x + u)dxjj>0(a,0)cfa. (16.17)Обозначим a= Jjy0(a,0)<ia, тогда, полагая в уравнении (16.17) u = О и ин-
отегрируя его по s , получим
672Глава 16'ои оиa— fF(x)yQ($,x)dx + a |^(д:)е(дс)<Л:. (16.18)о оОтсюда находим выражение коэффициента а через функцию _у0 :00р(*).Уо(0>*>&
о = ^~ • (16.19)1- |F(j:)e(jc)Jjc
оС учетом коэффициента а уравнение (16.17) преобразуется к виду:00 00
у0(5, и) = J/(x + s)^(0,х + u)dx + a jf(x +s)e(x + u)cbc.
о оЛегко показать, что решением последнего уравнения является00yQ(s,u) = а Jco(.s,Jc)e(;t + w)c£c, (16.20)огдеa(s,x) = fs(x) + f*fs(x) + f*f* fs(x) +...Таким образом, с точностью до постоянного сомножителя найдено решение
уравнения (16.17), и это решение дается формулой (16.20). Теперь можно по¬
следовательно найти выражения для остальных неизвестных функций в ста¬
ционарном режиме. Так как00У\ (к, и) = J h(x + к)у0 (0, u)dx = Н(к)у0 (0,и),
о00 00
у2 (s, 0) = jy0 (х + s, 0)dx, уг (к, 0) = Jр(х + к)у2 (0,0)dx = Р(к)у2 (0,0),о о00У4 (т, 0) = J g(x + х)у3 (0,0 )dx = G(x)y3 (0,0),
оу5 (к, 0) = J И(х + к)у4 (0,0 )dx = Н\к)уЛ (0,0),ТО00 0000
ух(к,и) = аН(к) fo(x)e(x + u)dx, y2(s,0) = a J f<o(x + s,a)e(a)da.dx,о oo
Анализ надежности программного обеспечения673>>з(£,0) = aP(k) | J co(jc, a)e(a)dccdx =аР(к) fe(a)da = аР(к),0 0 оу4 (т, О) = aG(x), у5 (к, 0) = аН'(к).Отсюда находятся стационарные вероятности пребывания системы во всех
состояниях:ОО ООр0 = a jE(x)dx = аТв, рх = аТк Jco(jc)£'(a:)c£x: ,
о оОООО 00Pi~a\ \x®(x,a)e(a)dadx = a Jj£’(jc)(Z’<o(jc) — 1), р3 =аТс,
оо ор4=аТв, р5 = аТк .Коэффициент а определяется из условия нормировки Po+ P\+ Pj+ Ръ ++Р4 + Ps - 1 и Равен1 .а--(Т + Тк) /со(х)ЕШх + Га + Тъ + Т'коПодставляя выражение для Та, получим:а-(Г + Тк) J <о(х )E(x)dx + ^+(1 + ГВ+ГА<хТеперь можно найти любые стационарные характеристики системы. В част¬
ности, если исправными состояниями системы являются состояния (0) и (1);
то стационарная вероятность исправной работы равна00тг + тк \a{x)E(x)dx
Р+^Ро + Р\ = 5 (Т + Tk)]co(x)E(x)dx + Г*+0 а)Г + Тв+ТкаПолученное аналитическое выражение позволяет установить влияние раз¬
личных параметров на вероятность исправной работы.ПРИМЕР 16.3. Определить вероятность исправной работы ПО и безошибоч¬
ного решения задачи для следующих данных: длительность решения задачи22 Зак. 3094
674Гпава 16имеет экспоненциальное распределение с параметром Х = 2 час ', среднее
время проведения контроля Тк =0,1 часа, среднее время до появления скры¬
той ошибки Тъ =1 час, среднее время восстановления Тв =0,5 часов, среднее
время проведения контроля после восстановления Тк =0,1 часа. ВероятностьНа вход системы поступает поток заявок на решение определенного класса
задач. Время между заявками случайно и равно С,. Под обслуживанием заяв¬
ки понимается решение задачи с помощью некоторого программного средст¬
ва. Время решения каждой задачи £, также является случайной величиной.Программа может содержать ошибки, которые проявляются только в резуль¬
тате проведения периодического контроля. Моменты проведения контроля
представляют собой случайный процесс, а длительности интервалов между
ними равны к. В частности, если плотность случайной величины к является
функцией Дирака ЬГк, то длительность контроля постоянная. Наличие про¬
граммной ошибки проявляется следующим образом. Предположим, что каж¬
дый раз в момент начала решения задачи возникает случайная величина s,
равная времени до появления скрытой ошибки. Если за время решения задачи
ошибки не произойдет (е < , то, решая новую задачу, величина £ как бы
обновляется и появляется вновь с тем же распределением вероятностей. Еслиправильного обнаружения ошибки при однократном контроле а = 0,8 .ООтЕ0 + ътк)те(\+хтк)+Подставляя числовые данные, получим:Р+ =1-(1 +2-0,1)= 0,59.(0,5+ 0,1)-2-1Если программные ошибки отсутствуют, то Тъ —> оо, и тогда р+ -»1.16.3. Анализ эффективности ПО
как системы массового обслуживания16.3.1. Описание работы системы
Анализ надежности программного обеспечения675за время решения задачи произойдет ошибка (е >£,), то она может обнару¬
житься только в момент окончания очередного такта контроля t0, следующе¬
го сразу после окончания решения задачи. В этом случае могут возникнуть
две ситуации.Ситуация 1. Если до момента t0 больше не поступило задач на решение, то
после этого момента начинается восстановление системы, которое имеет слу¬
чайную длительность г), а потом проводится функциональный контроль слу¬
чайной длительности к,. После указанных операций обнаружения и устране¬
ния ошибки функционирование системы продолжается, при этом в интервал
ожидания задачи г| входит его часть, которая была до момента времени (0 .-4-Ситуация 2. Если очередная задача поступила на решение до момента /0, то
контролирующее устройство начинает тестировать новую задачу, и проявив¬
шаяся ошибка оказывается необнаруженной.Далее приняты следующие обозначения:□ 4 — случайное время решения задачи, /(/) — плотность, F(t) — функ¬
ция распределения, Т — математическое ожидание %, F(t) = 1 - F(t);□ С, — случайное время ожидания задачи, q(t) — плотность, Q(t) — функ¬
ция распределения, Т0 —математическое ожидание £, Q(t) = 1 - Q(t);П к — случайное время проведения контроля, h(t) — плотность, H(t) —
функция распределения, Тк — математическое ожидание к, H{t) = 1 - H(t);□ s — случайное время до появления скрытой ошибки, e(t) — плотность,
E(t) — функция распределения, Тъ — математическое ожиданце е,
£(0 = 1-£(0;□ г| — случайное время восстановления системы, g(t) — плотность,
G{t) — функция распределения, Гв — математическое ожидание ц,
G(t) = l-G(t);□ К| — случайное время проведения контроля после восстановления,
h'(t) — плотность, H'(t) — функция распределения, Т'к — математиче¬
ское ожидание Kj, H'(t) = 1 - H\t).В описанной системе массового обслуживания теоретически может скапли¬
ваться любое число задач, требующих решения. Кроме того, само обслужи¬
вание поступивших задач зависит от работы системы, т. к., если обнаружена
ошибка в ПО, требуется время на ее устранение и на последующий функцио¬
нальный контроль. Это приводит к счетному множеству состояний и делает
676Глава 16анализ такой системы чрезвычайно сложным. На рис. 16.7 и 16.8 представле¬
ны фрагменты временных диаграмм, соответствующих случаям необнару¬
женной и обнаруженной ошибок ПО.На рис. 16.9 изображен граф состояний исследуемой системы.Рис. 16.9. Полный граф состояний по обнаружению ошибок ПОРис. 16.8. Временная диаграмма для необнаруженной ошибки ПО
Анализ надежности программного обеспечения677В следующих разделах остановимся на способах упрощения модели и поиску
численного алгоритма.16.3.2. Отсутствие очереди на обслуживаниеЧтобы свести граф к конечному, предположим, что очередь на решение задач
отсутствует. С этой целью допустим, что рассматривается альтернирующий
процесс, состоящий из последовательности интервалов решения задачи слу¬
чайной длительности £, и интервалов ожидания задачи случайной длительно¬
сти С,. В остальном работа системы и обозначения случайных величин оста¬
ются без изменения.Описанная ситуация, на первый взгляд, представляется очень похожей на си¬
туацию, рассмотренную выше. Однако если раньше поступление заявок было
(.независимо от работы всей системы, то теперь процесс поступления задач
чередуется с промежутками ожидания этих задач и очереди на обслуживание
не возникает.Функционирование системы для случая необнаруженных и обнаруженных
ошибок в ПО соответствует временным. диаграммам, представленным на
рис. 16.10 и 16.11.№ки8<= >ч_/ч 'П к'Рис. 16.10. Обнаруженная ошибка ПО.—СГч^^Т'Рис. 16.11. Необнаруженная ошибка ПОГ раф состоянийВ соответствии с приведенными на рис. 16.10 и 16.11 временными диаграм¬
мами опишем возможные состояния системы и укажем функции, отвечающие
этим состояниям:□ (0) — решение задачи, ожидание сеанса контроля; ошибка не произошла
(время до появления скрытой ошибки активно), y0(s,k,u,t);
678Глава 16□ (1) — ожидание задачи, ожидание сеанса контроля; ошибка не может про¬
изойти (время до появления скрытой ошибки пассивно), yx(w,k,0,t) ;□ (2) — решение задачи, ожидание сеанса контроля; ошибка произошла, но
является скрытой, y2(s,k,0,t);□ (3) — ожидание задачи, ожидание сеанса контроля; ошибка произошла, но
является скрытой, y3(w,k,0,t);□ (4)— простой в ожидании задачи, устранение обнаруженной ошибки,
y4(w,x,0,t);□ (5) — простой в ожидании задачи, проведение функционального контроля
после устранения ошибки, y5(w,&',(),/).На графе, изображенном на рис. 16.12, представлены все перечисленные со^
стояния и показаны переходы из одного состояния в другое. В частности, для
некоторых состояний имеется переход (возможно многократный) в то же са¬
мое состояние. Таковыми являются состояния (0), (1) и (2). Этот переход обу¬
словлен тем, что аргумент к обращается в нуль.Рис. 16.12. Граф состояний по обнаружению ошибок ПОСистема интегральных уравненийМатематическая модель функционирования системы может быть описана
системой интегральных уравнений относительно введенных функций. Аргу¬
менты этих функций показывают остаточное время для выполнения операций
после момента времени t.
Анализ надежности программного обеспечения679Система интегральных уравнений записывается в следующем виде:/ 00
у0 (s, k,u,t) = ff(x + s)h( х + к)е(х + u)fy{ (0, k,0,t- x)dkdx +0 оt+ jh(x + k)y0(x + s,0,x + u,t-x)dx +
о/ 00
+ jf(x + s)h(x + k)e(x + u) J_y3 (0, k,0,t- x)dkdx +
о 0+ f (t + s)h(t + k)e(t + u);1 <».y, (w, k, 0, t) = j q(x + w) |_y0 (0, x + k,u,t - x)dudx +0 оt t
+ \h(x + k)yx(x + w, 0,0, t - x)dx + j7?(x + k)y5 (jc + w, 0,0,1 - x)dx;
о о1 iy2 (s, k, 0, t) = jy0 (x + s, x + k, 0, / - x )dx + J h(x + k)y2 (x + s, 0,0, t - x)dx;
о о(16.21)_V3 (w, k, 0, t) = fq{x + w)y2 (0, x + k, 0,t — x)dx;01у4(w,x,0,0= Jg(x + x)y3(w,0,0,t -x)dx;
о
/y5 (w, к, 0,0 = J h'(x + k)y4 (и», 0,0, t - x)dx.Система (16.21) составлена во временной области функционирования при
самых общих условиях. Для упрощения решения этой системы уравне¬
ний сделано одно дополнительное предположение о том, что с приходом но¬
вой задачи контроль начинается заново и ранее проведенный контроль "за¬
бывается". Это предположение нашло отражение при составлении систе¬
мы (16.21).Критерий качества системыПосле решения системы (16.21) можно получить некоторые характеристики
качества или эффективности функционирования. Если нас интересует коли¬
чество обнаруженных и количество необнаруженных программных ошибок,
680Глава 16то надо найти функцию y3(w,k,0,t), по ней определить параметры переходов
из состояния (3) в состояния (0) и (4):00 00
®зо(0 = \yi(0,k,0,t)dk, со34(0 = \y3{w,Q,0,t)dw,
о оа затем найти следующие характеристики:□ среднее число переходов из состояния (3) в состояние (0) в течение време¬
ни [0; /], т. е. среднее число необнаруженных ошибок из числа тех, кото¬
рые произошли во время решения задачи:tМ30(О = Jco30 (*)*&;;
о□ среднее число переходов из состояния (3) в состояние (4) в течение време¬
ни [0; /], т. е. среднее число обнаруженных ошибок из числа тех, которые
произошли во время решения задачи:tМЪА (0 = |ю34 (x)dx.
оТогда доля обнаруженных ошибок из числа тех, которые произошли во время
решения задачи, составляету(0 = ■ (16.22)м30(о+м34(оАналогично можно записать формулы для расчета и других нестационарных
и стационарных характеристик.16.3.3. Независимость от предыстории моментов
начала решения задачиБудем исходить из конечной цели, а именно получение оценок для доли об¬
наруженных и необнаруженных ошибок при условии проявления ошибки во
время решения задачи. Введем три события:□ А — во время решения задачи ошибка не проявилась;□ В — во время решения задачи ошибка проявилась и обнаружена;□ С — во время решения задачи ошибка проявилась и не обнаружена.Временные диаграммы, демонстрирующие эти события, изображены на
рис. 16.13—16.15 соответственно.
Анализ надежности программного обеспечения681Рис. 16.13. Временная диаграмма
для события А0\кК Г| + КРис. 16.14. Временная диаграмма
для события ВНетрудно видеть, чтоР(А) = Р(е>$),j=о V 1=1 i=1/ Р(С) = \-Р(А)-Р{В).Тогда для стационарного режима доля обнаруженных ошибок из числа тех,
которые произошли во время решения задачи, составляетР(В)У Р(В) + Р(С)'Вычислим вероятности событий А, В:p(A)=]m/m,О00 СОР(В) = £ J/»(e <£,./<§</ + к < Qh'U)(t)dt =7 = 0 Ооо °0 со= S J <х, к>x-t, t^>t + к)f(x)h*('J\t)dxdt =7 = 0 0 /00 оо 00 00= X J f /(x)E(x)dx J h{a)P(t, > t + a)dah*^ (t)dt =7 = 0 о t x-t~ X 1 J/(x)£(x)<ic | h(a)Q(t + a)dah*(J\t)dt.7=0 0 I x-f
682Глава 16Делая во внутреннем интеграле замену переменной Р = а +1 - х , получимооР(В)= I J Jf(x)E(x)dx jA(p - / + х)б(р + x)d$h*u)(t)dt
j=О О I оТеперь во втором интеграле сделаем замену у = x—t, получимПв)= 1 T\f(y + OE(y + t)dy]h® + y)QW+y + t)dph*V\t)dt =7 = 0 О О о= ]/(0£(0]ё(Р,+ t№P,t)d$dt.О осоПоложим a(t)= |£>(а + /)ю(а,/)с/а, тогдаР(В)= f f (t)E(t)a(t)dt,
ои, очевидно, что вероятность события С равна:P(C) = Xjf(t)E(t)(]-a(t))dt.оПо известным вероятностям состояний получим долю обнаруженных ошибок:]f(t)E(t)a(t)dt
у = ^ . (16.23)]твтоЕсли интервалы между сеансами контроля постоянны и равны Тк, то нетруд-00но найти функцию a(t). Так как h(j) = 6Tk(t) и co(a,0 = X 5(у+1)^_а(0 при7=0а < Тк , то в этом случае функция a(t) равна00 Тк _ да Tk+t _0(0= X J 2(а + *)^(у+1)г* -а (t)dcL= X 1 б(а)§(7+1)г* (а)с?а ,7=0 0 7 = 0 tИЛИa{t) = Q{{j + \)Tk) при jTk <t <(j + \)Тк . (16.24)
Анализ надежности программного обеспечения683Очевидно, что a(t) является убывающей кусочно-постоянной функцией
(рис. 16.16).a(t) m) Q{2Tk) 6(37*) Q(4Tk) 0 Tk 2Tk 3 Тк 4 ТкРис. 16.16. График функции a{t)Время до появления ошибки s неизвестно, оно вносит неопределенность в
формулу (16.23). В связи с этим можно считать, что эта случайная величина
имеет равномерное распределение, и тогда доля обнаруженных ошибок среди
проявленных может быть рассчитана по формуле:/(WHOA дау = JL_ = \tf{t)a(t)dt. (16.25)0оПРИМЕР 16.4. Пусть время ожидания задачи С, равномерно распределено на
интервале от 0 до 12 мин. Время решения задачи \ случайное, имеющее
нормальное распределение с математическим ожиданием 10 мин и средним
квадратическим отклонением 1 мин. Интервалы между сеансами контроля
одинаковы и равны Тк. Требуется определить долю обнаруженных отказов,
которые произошли во время решения задачи.Решение. Так как интервалы между сеансами контроля постоянны, то функ¬
ция a(t) рассчитывается по формуле (16.24), а доля обнаруженных отказор,
которые произошли во время решения задачи,— по формуле (16.25). На
рис. 16.17 приведена зависимость величины у от длительности Тк .График показывает, что не всегда увеличение частоты контроля приводит к
увеличению доли обнаруженных ошибок ПО. Большую роль играют здесь
684Глава 16остальные параметры процесса. Ошибки могут совсем не обнаруживаться
при определенных сочетаниях параметров.Рис. 16.17. Зависимость доли обнаруженных ошибок ПО
от времени между сеансами контроля16.4. Учет других особенностей
функционирования ПОВ этом разделе мы приведем несколько другие, на наш взгляд, более реаль¬
ные условия функционирования системы. Например, представляется сомни¬
тельным сформулированное в разд. 16.2 следующее допущение: в случае
возникновения ошибки ПО она может быть обнаружена только после окон¬
чания решения задачи в момент очередного сеанса контроля. Предположим,
что ошибка может обнаружиться также и во время решения задачи в момент
очередного сеанса контроля, следующего за возникновением ошибки. Таким
образом, будут учтены случаи возникновения "обнаруженных" ошибок, ко¬
торые влекут за собой прекращение решения задачи сразу после их возник¬
новения, но в момент ближайшего сеанса контроля. Кроме того, предполо¬
жим, что после выявления и устранения ошибки, а также после проведения
функционального контроля задача без какого-либо ожидания запускается на
повторное решение. Временная диаграмма для описанной ситуации пред¬
ставлена на рис. 16.18.Система имеет следующие состояния и искомые функции, связанные с этими
состояниями:□ (0) — решение задачи, ожидание сеанса контроля; ошибка не произошла
(время до появления скрытой ошибки активно), y0(s,k,u,t);
Анализ надежности программного обеспечения685Рис. 16.18. Временная диаграмма обнаружения ошибок ПО□ (1) — ожидание задачи, ожидание сеанса контроля; ошибка не может про¬
изойти (время до появления скрытой ошибки пассивно), yx(w,k,0,t);□ (2) — решение задачи, ожидание сеанса контроля; ошибка произошла, но
является скрытой, y2(s,k,0,t);□ (3) — ожидание задачи, ожидание сеанса контроля; ошибка произошла, но
является скрытой, y3(w,k,0,t);□ (4) — устранение обнаруженной ошибки, y4(0,x,0,t);□ (5)— проведение функционального контроля после устранения ошйбки,
у5 (0, к', О, О-Все эти состояния, а также переходы из одного состояния в другое изображе¬
ны на графе (рис. 16.19).Рис. 16.19. Граф состояний обнаружения ошибок ПОВ отличие от разд. 16.2 здесь имеются следующие особенности:П может быть несколько переходов между состояниями (2) и (3), что соот¬
ветствует возможности решения нескольких задач вместе с ожиданиями
их поступления на одном интервале ожидания контроля;
686Глава 16□ наличие перехода из состояния (2) в состояние (4), что соответствует слу¬
чаю обнаружения возникшей ошибки ПО в момент очередного сеанса
контроля и прерыванию решения задачи;О наличие перехода из состояния (5) в состояние (0), что соответствует по¬
вторному решению задачи без ожидания поступления следующей задачи.Результатом решения системы интегральных уравнений, составленной по
данному графу, является набор функций ук, к = 0,1, 2, 3, 4, 5. По этим функ¬
циям можно определить вероятности состояний и параметры перехода из
одного состояния в другое. Затем можно получить необходимые характери¬
стики качества или эффективности функционирования средств контроля по
обнаружению программных ошибок. Такая характеристика, как доля обнару¬
женных ошибок, сейчас не подходит, поскольку любая возникшая ошибка
рано или поздно будет обнаружена. В связи с этим возникает задача выбора
критерия качества изучаемой системы.Дополнительно предположим, что:□ за каждым интервалом ожидания очередного сеанса контроля к следует
интервал его проведения кг, на время которого приостанавливается ре¬
шение (или ожидание) задачи;□ после возникновения ошибки ПО и завершения интервалов ожидания и
интервала проведения сеанса контроля могут возникнуть две ситуации,
когда произошедший ранее отказ ПО обнаруживается с вероятностью а и
когда отказ не обнаруживается с вероятностью (1 - а) .В этом случае временная диаграмма функционирования системы имеет вид,
изображенный на рис. 16.20.сс,\Ак,£к, к кг к/£Рис. 16.20. Временная диаграмма для измененных условийПо сравнению с графом, представленным на рис. 16.19, появляется несколько
новых состояний. Перечислим все возможные состояния системы для новых
условий функционирования:□ (0) — решение задачи, ожидание сеанса контроля; ошибка не произошла
(время до появления скрытой ошибки активно), y0(s,k,u,t);
Анализ надежности программного обеспечения687□ (0) — проведение сеанса контроля, задержка в решении задачи и в воз¬
можности появления ошибки, y^is',kr,u',t) ;□ (1) — ожидание задачи, ожидание сеанса контроля; ошибка не может про¬
изойти (время до появления скрытой ошибки пассивно), yx(w,k,0,t);□ (1) — проведение сеанса контроля, задержка в ожидании сеанса Контро¬
ля; ошибка не может произойти (время до появления скрытой ошибки пас¬
сивно), yj(w',kr,0,t)-,П (2) — решение задачи, ожидание сеанса контроля; ошибка произошла, но
является скрытой, у2 (5, к,0,/);□ (3) — ожидание задачи, ожидание сеанса контроля; ошибка произошла, но
является скрытой, y3(w,k,0,t);□ (4) — проведение сеанса контроля с прерыванием решения задачи; ошибка
произошла, но является скрытой, y4(s',кг,0,();□ (5)— проведение сеанса контроля с прерыванием времени ожидания за¬
дачи; ошибка произошла, но является скрытой, y5(w',kr,0,t);□ (6) — устранение обнаруженной ошибки, у6(0,т,0,0;□ (7)— проведение функционального контроля после устранения ошибки,у7(0,к'Л0 •Все эти состояния, а также переходы из одного состояния в другое изображе¬
ны на графе (рис. 16.21).Рис. 16.21. Граф состояний для измененных условий
688Глава 16По этому графу может быть составлена система интегральных уравнений от¬
носительно введенных функций, решение которой позволит определить веро¬
ятности состояний, параметры перехода системы из одного состояния в дру¬
гое и прочие составные характеристики работы ПО.Таким образом, надежность ПО во многом может быть проанализирована с
помощью традиционных вероятностных подходов, в основе которых лежат
математические модели немарковских процессов.
СПИСОК ЛИТЕРАТУРЫ1. Афанасьев В. Г., Зеленцов В. А., Миронов А. Н. Методы анализа надеж¬
ности и критичности отказов сложных систем. — М.: Мин-во обороны,
1992, 100 с.2. Базовский И. Надежность. Теория и практика. — М.: Мир, 1965, 373 с.3. Байхельт Ф., Франкен П. Надежность и техническое обслуживание. Ма¬
тематический подход. — М.: Радио и связь, 1988, 389 с.4. Барзилович Е. Ю., Каштанов В. А. Некоторые математические вопросы
теории обслуживания сложных систем. — М.: Сов. радио, 1971, 272 с.5. Барзилович Е. Ю. Модели технического обслуживания сложных сис¬
тем. — М.: Высшая школа, 1982, 231 с.6. Барзилович Е. Ю., Павленко М. И., Тиньков Л. А. Оптимальное обслужи¬
вание систем с зависимыми элементами. Изв. АН СССР. Сер. Техниче¬
ская кибернетика, № 3, 1979, с. 80—85.7. Барзилович Е. Ю. и др. Вопросы математической теории надежности
/ Под ред. Б. В. Гнеденко. — М.: Радио и связь, 1983, 376 с.8. Барлоу Р., Хантер Л., Прошан Ф. Оптимальные планы проверки. — В кн.:
Оптимальные задачи надежности / Под ред. И. А. Ушакова, 1968, с. 271—
283.9. Барлоу Р., Прошан Ф. Математическая теория надежности /Пер. с англ.
под ред. Б. В. Гнеденко. — М.: Сов. радио, 1969, 488 с.10. Барлоу Р., Прошан Ф. Статистическая теория надежности и испытания на
безотказность. — М.: Наука, 1984.11. Баскин Э. М. Приближение законов надежности обобщенными полино¬
мами Лаггера. Изв. АН СССР. Техническая кибернетика, № 5, 1978.12. Белецкий В. В. Теория и практические методы резервирования радио¬
электронной аппаратуры. — М.: Энергия, 1977, 360 с.13. Беляев Ю. К. Линейчатые марковские процессы и их приложение к зада¬
чам теории надежности. Тр. МШ Всесоюзного совещания по теории ве¬
роятностей и математической статистике. Вильнюс, 1962.
690Список литературы14. Бердичевский Б. Е. Вопросы обеспечения надежности радиоэлектронной
аппаратуры при разработке. — М.: Сов. радио, 1977, 384 с.15. Берс Л., Джон Ф., Шехтер М. Уравнения с частными производными.—
М.: Мир, 1966.16. Бессонов А. А., Мороз А. В. Надежность систем автоматического регули¬
рования. — Л.: Энергоатомиздат, 1984, 216 с.17. Болотин В. В. Прогнозирование ресурса машин и конструкций.— М.:
Машиностроение, 1984, 312 с.18. Большие системы. Теория, методология, моделирование / Под ред.
Б. В. Гнеденко. — М.: Наука, 1971, 328 с.19. Броди С. М., Власенко О. Н. Надежность систем со многими режимами
работы. — В кн.: Теория надежности и массовое обслуживание / Под ред.
Б. В. Гнеденко. — М.: Наука, 1969, с. 165—171.20. Бусленко Н. П., Калашников В. В., Коваленко И. Н. Лекции по теории
сложных систем. — М.: Сов. радио, 1973.21. Бусленко В. Н. Автоматизация имитационного моделирования сложных
систем.—М.: Наука, 1977. *22. Варжапетян А. Г. Техническая эффективность и надежность судовых сис¬
тем управления. — Л.: Судостроение, 1969, 268 с.23. Гаскаров Д. В., Голинкевич Т. А., Мозгалевский А. В. Прогнозирование
технического состояния и надежности радиоэлектронной аппаратуры. —
М.: Сов. радио, 1974, 223 с.24. Гермейер Ю. Б. Методологические и математические основы исследова¬
ния операций и теории игр. Вып. 1—5. — М.: Изд. МГУ, 1967.25. Гихман И. И., Скороход А. В. Теория случайных процессов. — М.: Наука,
1973, т. 2,639 с.26. Глазунов Л. П., Грабовецкий В. П., Щербаков О. В. Основы теории на¬
дежности автоматических систем управления. — Л.: Энергоатомиздат,
1984, 208 с.27. Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д. Математические методы в
теории надежности. Основные характеристики надежности и их стати¬
стический анализ. — М.: Наука, 1965, 524 с.28. Гнеденко Б. В., Коваленко И. Н. Введение в теорию массового обслужи¬
вания. — М.: Наука, 1966.29. Горский Л. К. Статистические алгоритмы исследования надежности. —
М.: Наука, 1970.30. ГОСТ 27.002-89. Надежность в технике. Термины и определения.
Список литературы69131. Гуров С. В., Уткин JI. В. Надежность систем при неполной информа¬
ции. — СПб.: Любавич, 1999, 160 с.32. Гуров С. В., Хабаров С. П. Оценка надежности восстанавливаемых сис¬
тем последовательно-параллельной структуры с произвольными закона¬
ми распределения.— СПб.: Изв. ВУЗов, Приборостроение, т. XXX11I,
Т. 12, 1988.33. Гуров С. В. Анализ надежности технических систем с произвольными за¬
конами распределений отказов и восстановлений. Качество и надежность
изделий. Т. 2 (18). — М.: Знание, 1992.34. Демьянчук В. С. Надежность систем управления воздушным движени¬
ем. — Киев: Вища школа, 1979, 150 с.35. Дзиркал Э. В. Задание и проверка требований к надежности сложных из¬
делий.— М.: Радио и связь, 1981, 176 с.36. Диллон Б., Сингх Ч. Инженерные методы обеспечения надежности сис¬
тем.— М.: Мир, 1984, 318 с.37. Доманицкий С. М. Построение надежных логических устройств.— М.:
Энергия, 1971, 279 с. _38. Дружинин Г. В. Надежность автоматизированных производственных сис¬
тем. — М.: Энергоатомиздат, 1986, 480 с.39. Дядков В. К., Северцев П. А. Основные вопросы эксплуатации сложных
систем. — М.: Высшая школа, 1976, 406 с.40. Журавлев Ю. П., Котелюк Л. А., Цикланский Н. Н. Надежность и кон¬
троль ЭВМ. — М.: Сов. радио, 1978, 412 с.41. Збырко М. Д., Кузнецов В. Н., Турбин А. Ф. О полумарковской модели
для анализа надежности систем с восстанавливаемой защитой. — М.: Ав¬
томатика и телемеханика, 1980, № 6, с. 175—185.42. Зеленцов В. А., Гагин А. А. Надежность, живучесть и техническое об¬
служивание сетей связи. — Мин. обор. СССР, 1991, 169 с.43. Золотарев В. М. Метрические расстояния в пространствах случайных ве¬
личин и'их распределений. Математ. сб. 101 (143), вып. 3.— М.: Наука,1976, с. 416—454.44. Зубова А. Ф. О холодном резервировании с восстановлением. — М.: Ав¬
томатика и телемеханика, № 10, 1965.45. Ивченко Г. И., Каштанов В. А., Коваленко И. Н. Теория массового об¬
служивания. — М.: Высшая школа, 1982.46. Иыуду К. А. Надежность, контроль и диагностика вычислительных ма¬
шин и систем. — М.: Высшая школа, 1989, 214 с.
692Список литературы47. Какубава Р. В., Кукава Р. К., Курцер М. III., Микадзе И. С. Распределение* времени выполнения задания на ЭВМ с учетом ее надежности. — М.: Ав¬
томатика и телемеханика, 7, 1981.48. Канарчук В. Е. Основы надежности машин. — Киев: Наукова думка,
1982, 248 с.49. Капур Е., Ламберсон Л. Надежность и проектирование систем. — М.:
Мир, 1980, 604 с.50. Каштанов В. А. Оптимальные задачи технического обслуживания. — М.:
Знание, 1981, 50 с.51. Коваленко И. Н. Асимптотический метод анализа надежности сложных
систем. В кн.: О надежности сложных технических систем. — М.: Сов.
радио, 1967.52. Коваленко И. Н. Исследование по анализу надежности сложных сис¬
тем. — Киев: Наукова думка, 1975, 209 с.53. Коваленко И. Н. Аналитико-статистический метод расчета характеристик
высокоответственных систем. — Кибернетика, Т. 6, 1976.54. Коваленко И. Н. Анализ редких событий при оценке эффективности и на¬
дежности систем. — М.: Сов. радио, 1980, 208 с.55. Коваленко И. Н., Кузнецов Н. Ю. Построение вложенного процесса вос¬
становления для существенно многомерных процессов теории массового
обслуживания и его применение к получению предельных теорем: Пре¬
принт 80.12. — Киев: Ин-т кибернетики АН УССР, 1980, 61 с.56. Коваленко И. Н., Кузнецов Н. Ю. Методы расчета высоконадежных сис¬
тем. — М.: Радио и связь, 1988.57. Козлов Б. А., Ушаков И. А. Справочник по расчету надежности аппарату¬
ры радиоэлектроники и автоматики. — М.: Сов. радио, 1975, 472 с.58. Кокс Д., Смит В. Теория восстановления. — М.: Сов. радио, 1967, 420 с.59. Королюк В. С., Турбин А. Ф. Полумарковские процессы и их приложе¬
ния. — Киев: Наукова думка, 1976, 182 с.60. Королюк В. С., Лебединцева Е. П. Предельная теорема для времени пре¬
бывания полумарковского процесса в подмножестве состояний. — Киев:
Укр. мат. журн., 1978, 30 № 5, с. 671—674.61. Костецкий Б. И. и др. Надежность и долговечность машин. — Киев: Тех¬
ника, 1975, 408 с.62. Креденцер Б. П. Прогнозирование надежности систем с временной избы¬
точностью. — Киев: Наукова думка, 1978, 240 с.
Список литературы69363. Кугель Р. В. Надежность машин массового производства.— М.: Маши¬
ностроение, 1981, 244 с. S64. Кузнецов В. Н. О полумарковской модели для нагруженного дублирова¬
ния. — М.: Кибернетика, 1980, № 4, с. 91—98.65. Кузнецов В. Н., Турбин А. Ф., Цатурян Г. Ж. Полумарковские модели
восстанавливемых систем. Препринт 81.11. — Киев: Ин-т математики АН
УССР, 1981,44 с.66. Кузнецов В. П. Интервальные статистические модели. — М.: Радио и
связь, 1991, 352 с.67. Леонтьев Л. П. Надежность технических систем.— Рига: Зинатне, 1969,
266 с.68. Ллойд Д., Липов М. Надежность: организация, исследования, методы, ма¬
тематический аппарат. — М.: Сов. радио, 1964, 686 с.69. Лонгботтом Р. Надежность вычислительных систем. — М.: Энергоатом¬
издат, 1985, 383 с.70. Маньшин Г. Г. Управление режимами профилактик сложных систем. —
Минск: Наука и техника, 1976, 255 с.71. Математическая теория надежности систем массового обслужива¬
ния / Под ред. проф. В. И. Зубова — М.—Л.: Энергия, 1966.72. Мендельсон Э. Введение в математическую логику.— М.: Наука, 1976,
320 с.73. Мозгалевский А. В., Гаскаров Д. В. Техническая диагностика.— М.:
Высшая школа, 1975, 207 с.74. Моломин В. П. Модели управления надежностью авиационной техни¬
ки. — М.: Машиностроение, 1981, 200 с.75. Надежность в машиностроении. Справочник / Под ред. В. В. Шашкина,
Г. П. Карзова. — СПб.: Политехника, 1992, 718 с.76. Надежность технических систем /Под ред. Е. В. Сучака, Н. В. Василен¬
ко. — Красноярск: МГП "Раско", 2001, 600 с.77. Надежность технических систем. Справочник / Под ред. И. А. Ушако¬
ва. — М.: Радио и связь, 1985, 606 с.78. Нечипоренко В. И. Структурный анализ и методы построения надежных
систем. — М.: Сов. радио, 1968, 255 с.79. Оре О. Теория графов. — М.: Наука, 1980, 336 с.80. Панфилов И. В., Половко А. М. Вычислительные системы.— М.:
Сов. радио, 1980.
694Список литературы81. Песоцкий В. М., Кузнецов В. Н., Левинский Б. Г. Оценка надежности
функционирования АСУ ТП при воздействии импульсных помех. — Ки¬
ев: Электронное моделирование, № 1, 1981, с. 55—59.82. Пирс У. Построение надежных вычислительных машин. — М.: Мир,
1968,270 с.83. Половко А. М. Основы теории надежности. — М.: Наука, 1964.84. Половко А. М., Гурович Б. Н. Метод расчета надежности резервирован¬
ных восстанавливаемых устройств. — М.: Известия академии наук СССР.
Техническая кибернетика, № 4, 1971.85. Половко А. М. Принципы построения абсолютно надежных технических
устройств, О-во "Знание", РСФСР. — Л., 1993.86. Половко А. М., Гиндин С. И. Надежность программного обеспечения в
специализированных цифровых вычислительных комплексах.— СПб.:
ЦНИИ Румб, 1988, 80 с.87. Половко А. М., Гуров С. В. Надежность технических систем и техноген¬
ный риск. — СПб.: Знание, 1998, 119 с.88. Проников А. С. Надежность машин. — М.: Машиностроение, 1978, 592 с.89. Прохоренко В. А. Надежность радиоэлектронных средств сложных тех¬
нических систем. — Минск, МВИЗРУ, 1975, 215 с.90. Прошан Ф., Цатурян Г. Ж. Многозначные монотонные системы. — М.:
Надежность и контроль качества, Т 1, 1990, с. 6—16.91. Путинцев Н. Д. Аппаратный контроль управляющих цифровых вычисли¬
тельных машин. — М.: Сов. радио, 1966, 157 с.92. Райкин А. Л. Вероятностные модели функционирования резервирован¬
ных устройств. — М.: Наука, 1971, 303 с.93. Райкин А. Л. Элементы теории надежности технических систем/Под
ред. И. А. Ушакова. — М.: Сов. радио, 1978.94. Райншке К., Ушаков И. А. Оценка надежности систем с использованием
графов. — М.: Радио и связь, 1988, 209 с.95. Решетов Д. Н., Иванов А. С., Фадеев В. С. Надежность машин. — М.:
Высшая школа, 1988, 240 с.96. Романовский И. В. Алгоритмы решения экстремальных задач. — М.: Нау¬
ка, 1977, 352 с.97. Рябинин И. А., Рубинович В. Д. О влиянии типа законов распределения
времени исправной работы и времени восстановления на характеристики
надежности резервированной системы. В кн.: Теория надежности и мас¬
совое обслуживание. — М.: Наука, 1969, с. 46—54.
Список литературы69598. Рябинин И. А. Основы теории и расчета надежности судовых электро¬
энергетических систем. — Д.: Судостроение, 1971, 456 с.99. Рябинин И. А., Черкесов Г. Н. Логико-вероятностные методы исследо¬
вания надежности структурно-сложных систем. — М.: Радио и связь,
1981,264 с. ■100. Рябинин И. А. Надежность и безопасность структурно-сложных сис¬
тем. — СПб.: Политехника, 2000, 247 с.101. Сборник задач по теории надежности / Под ред. А. М. Половко,
Н. М. Маликова. — М.: Сов. радио, 1972, 407 с.102. Севастьянов Б. А. Эргодическая теорема для марковских процессов и ее
приложение к телефонным системам с отказами. — М.: Теория вероят¬
ностей и ее применения, 1957, т. 11, № 1, с. 106—116.103. Северцев Н. А. Надежность сложных систем в эксплуатации и отработ¬
ке. — М.: Высшая школа, 1989, 432 с.104. Седякин Н. М. Об одном физическом принципе надежности. — Изв. АН
СССР. Техническая кибернетика, 1966, № 3, с. 80—87. __105. Сильвестров Д. С. Полумарковские процессы с дискретным множеством
состояний. — М.: Сов. радио, 1980, 289 с.106. Смагин В. А. Немарковские задачи теории надежности. — Мин. обор.
СССР, 1982,269 с.107. Смолицкий X. J1., Чукреев П. А. О сравнении надежности систем при
поэлементном и общем резервировании. — Изв. АН СССР, ОТН, Энер¬
гетика и автоматика, №3,1959.108. Соловьев А. Д. Резервирование с быстрым восстановлением. — Изв. АН
СССР. Сер. "Техн. кибернетика", Т 1, 1970, с. 56—70.109. Соловьев А. Д. Основы математической теории надежности. В кн.: Ма¬
териалы лекций, прочитанных в Политехническом музее на семинаре по
надежности и прогрессивным методам контроля качества продукции.
Вып. 1. — М.: Знание, 1975, 64 с.110. Сотсков Б. С. Основы теории и расчета надежности элементов и уст¬
ройств автоматики и вычислительной техники. — М.: Высшая школа,1970, 272 с.111. Судаков Р. С. Испытания технических систем. — М.: Машиностроение,
1988, 271 с.112. Турбин А. Ф., Збырко М. Д., Кузнецов В. Н. Анализ надежности систем
с защитой посредством полумарковских процессов со сложным фазо¬
вым пространством. В кн.: Надежность и эффективность автоматизиро¬
696Список литературыванных систем управления технологическими процессами и производст¬
вами.— Киев: май 1976, Тез. докл. М.: ЦНИИТЭИ приборостроения,
1978, с. 8-—9.113. Труханов В. М. Методы обеспечения надежности изделий машино¬
строения. — М.: Машиностроение, 1995, 304 с.114. Ушаков И. А. Вероятностные модели надежности информационно¬
вычислительных систем. — М.: Радио и связь, 1988.115. Ушаков И. А. Эвристический метод оптимизации резервирования мно¬
гофункциональных систем. — Изв. АН СССР. Сер. "Техн. кибернетика",№4,1972.116. Фанаржи Г. Н. Оценка надежности восстанавливаемых систем. Про¬
блемные вопросы теории и практики надежности. — М.: Сов. радио,1971.117. Червонный А. А., Лукъяшенко В. И., Котин Л. В. Надежность сложных
систем. — М.: Машиностроение, 1976, 304 с.118. Черкесов Г. Н. Надежность технических систем с временной избыточ¬
ностью / Под ред. А. М. Половко. — М.: Сов. радио, 1974, 295 с.119. Черкесов Г. Н. Методы и модели оценки живучести сложных систем. —
М.: Знание, 1987, 56 с.120. Чернышев А. А. Основы надежности полупроводниковых приборов и
интегральных микросхем. — М.: Радио и связь, 1988, 256 с.121. Хазов Б. Ф., Дидусев Б. А. Справочник по расчету надежности машин на
стадии проектирования. — М.: Машиностроение, 1986, 224 с.122. Хенли Э., Кумамото X. Надежность технических систем и оценка рис¬
ка. — М.: Машиностроение, 1984, 528 с.123. Шор Я. Б. Статистические методы анализа и контроля качества и на¬
дежности промышленной продукции. — М.: '3нание, 1968, 284 с.124. Шаракшанэ А. С., Шахин В. П., Халецкий А. К. Испытания программ
сложных автоматизированных систем. — М.: Высшая школа, 1982.125. Шишонок В. А., Репкин В. Ф., Бравинский Л. Л. Основы теории надеж¬
ности и эксплуатации радиоэлектронной техники. — М.: Сов. радио,
1964,551 с.126. Шубинский И. Б., Николаев В. И., Колганов С. К., Заяц А. М. Активная
защита от отказов управляющих модульных вычислительных систем. —
СПб.: На^ка, 1993, 284 с.127. Шубинский И. Б., Гуров С. В., Уткин Л. В. Методы оценки надежности
восстанавливаемых систем с возможными нарушениями групп состав-
Список литературы697ных элементов // Известия Санкт-Петербургской лесотехнической ака¬
демии. Вып. 3(161). — СПб.: 1995.128. Шубинский И. Б., Гуров С. В., Уткин JI. В. Распределение работ по эта¬
пам в дискретных системах//Известия Санкт-Петербургской лесотех¬
нической академии. Вып. 4. — СПб.: 1997.129. Ястребенецкий М. А. Надежность невосстанавливаемых изделий при
внешних воздействиях. — Изв. АН СССР. Технич. кибер., № 3, 1970.130. Ястребенецкий М. А. Надежность восстанавливаемых изделий при
внешних воздействиях. — Изв. АН СССР. Технич. кибер., № 4, 1970.131. Ястребенецкий М. А. Надежность технических средств в АСУ техноло¬
гическими процессами. — М.: Энергоиздат, 1982,228 с.132. Ayyub, Н. RASCS for risk assessment. Software for Engineering Work¬
station. Vol. 5, no. 1, 1989, pp. 45—50.133. Barlow R. E., Wu A. S. Coherent Systems with Multi-State Components.
Math. Oper. Res. № 3, 1978.134. Gurov S. V., Utkin L. V. A new method to compute reliability of repairable
m-out-of-n systems by arbitrary distributions, Microelectron.Reliab., Vol. 34,
No. 12, 1877—1889, 1994.135. Gurov S. V., Utkin L. V. A new method to compute relibility of repairable
series systems by arbitrary distributions. Microelectron. Reliab. Vol. 35,
No. l,pp. 81—85, 1995.136. Gurov S. V., Utkin L. V., Shubinsky I. B. Two-sided bounds of reliability for
large systems, Microelectron. Reliab. Vol. 35, No. 5, pp. 841—845, 1995.137. Gurov S. V., Utkin L. V. The time-dependent availability of repairable m-out-
of-n and cold standby systems by arbitrary distributions and repair facilities,
Microelectron. Reliab. Vol. 35, No. 11, pp. 1377—1393, 1995.138. Gurov S. V., Utkin L. V., Shubinsky I. B. Optimal reliability allocation of re-'
dundant units and repair facilities by arbitrary failure and repair distributions,
Microelectron. Reliab. Vol. 35, No. 12, pp. 1451—1460, 1995.139. Gurov S. V., Utkin L. V. Reliability of repairable systems with periodic
modifications, Microelectron. Reliab. Vol. 36, No. 1, pp. 27—35, 1996.140. Gurov S. V., Utkin L. V. Cold standby systems with imperfect and noninstan-
taneous switch-over mechanism, Microelectronics and Reliability Vol. 36,
No. 10, pp. 1425—1438, 1996.141. Gurov S. V., Utkin L. V. Reliability and optimization of systems with peri¬
odic modifications in the probability and possibility contexts, Microelectron.
Reliab. Vol. 37, No. 5, pp. 801—808, 1997.
698Список литературы142. Gurov S. V., Habarov S. P., Utkin L. V. Safety analysis of a multi-phased
control system, Microelectron. Reliab. Vol. 37, No. 2, pp. 243—254, 1997.143. Dhillon B. S., Singh G. Engineering Reliability. New Techniques and Appli¬
cations. John Wiley. Sons, New York, 1981.144. Henlej E. J., Kumamoto H. Reliability engineering and risk assessment.—
No. 4: Prentice-Hall Inc., 1981.145. Kleijnen J. P. C. Statistical techniques in simulation. Part 1. Marcel Pekker,
Inc., New York, 1974.146. Misra К. B., On optimal reliability design: A review, SystemScience, 12, 5—30, 1986.147. Satyanarayana A., Prabhakar A. New topological formula and rapid algorithm
for reliability analysis of complex networks. IEEE Transactions on Reliabil¬
ity, v. 27, no. 2, pp. 82—100, 1978.148. Somani A. K., Ritcey J. A., Au S. H. L. Computationallyefficient phased-
mission reliability analysis for systems with variable configurations, TREE
Trans.Reliab. R-41 504—510, 1992.149. Toshiyuki Inagaki and Koichi Inoue, Adaptive choice of a safety management
scheme upon an alarm ujider supervisory control of a large-complex system,
Reliab.Engng Syst. Safety, 39 81—87, 1993.150. Tillman F. A., Hwang C. L,, Kuo W. Optimizationtechniques for system reli¬
ability with redundancy— a review, IEEETrans.Reliab., R-26(3), 148—155,1977.151. Trafestas S. G. Optimization of system reliability; asurvey of problems and
techniques, Int. J. Syst. Sci., 11(4), 455—486, 1980.152. Walley P. Statistical Reasoning with Imprecise Probabilities. Chapman and
Hall, London, 1991,706 р.'153. Who Kee Chung, Reliability and availability analysisof cold standby system
with repair and multiple non-critical andcritical errors, Microelectron. Re¬
liab., 34, 1891—1896, 1994.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬлХ-переход 142м(х-переход 144ААлгоритм:О ортогонализации 170
0 разрезания 167
Аппаратура контроля (АК) 434ББезотказность 25ВВероятность:0 безотказной работы 31
0 безотказной работы информационной
. системы 466
0 отказа 30
0 состояний 110
0 стационарная 209
Выигрыш надежности:0 от восстановления 270, 395
0 по вероятности-отказа 378
0 по интенсивности отказов 379
0 по коэффициенту простоя 381,419
0 по наработке на отказ 382, 4190 по среднему времени безотказной,
работы 379ГГраничные оценки надежности 605
Граф 76, 106, 136
0 ветвь 1950 процесса "гибели и размножения"
4930 типа дерева 313
0 усеченный 318дДвойственные задачи 629
Динамика системы 23
Долговечность 26ЖЖизненный цикл 529ИИзбыточность 372
0 структурная 441
Интенсивность отказа 32
Исправность 24
Испытания:0 качественные 601
0 статистические 601
700Предметный указательККлассы распределений 605
Коэффициент готовности
информационной системы 467
Критерий надежности 29
Критичность 421мМатрица:0 переходов 106
0 состояний 105, 136
Метод:0 декомпозиции 76
0 логико-вероятностный 75, 161
0 машинного моделирования 76
0 мультипликативный конгруэнтный2200 обратных функций 223
0 перебора гипотез 154
0 разложения относительно особого
элемента 157
0 статистических испытаний (Монте-
Карло) 218
0 статистического моделирования 218
0 эвристический 76
Минимальное сечение 158
Многофункциональность 520
Множество, эргодическое 557
Модель надежности:0 невосстанавливаемых систем 122
0 общая 98, 1030 при экспоненциальных законах
распределения 125
0 стационарного режима 119нНадежность 19
0 критерий 290 многофункциональных систем 519
0 показатель 290 программного обеспечения 507, 653
0 сложной системы 132
0 эксплуатационная 420Наработка 25
0 до отказа 25
0 между отказами 25
0 на отказ информационной системы
467ООтказ 200 абсолютно надежной системы 602
0 смежных элементов 342
Отсутствие памяти 42пПамять 361
Параметр:0 переходов 110
0 потока отказов 38
Переключатель:0 надежный 350
0 ненадежный 356
Переключение на резерв 349
Период реализации 372
Плотность распределения времени
безотказной работы 32
Показатель надежности 29
Полезность системы 576
Последействие отказов 593
Преобразование Лапласа 50
Профилактика 425
Процесс 23
0 марковский 206
0 однородный марковский 208
0 Пуассона 207
Псевдослучайные числа 220
Путь 106 <0 кратчайший 165
0 минимальный 158РРаботоспособность 24
Разыгрывание случайной величины221Распределение:0 Вейбулла 46
Предметный указатель701О гамма- 47О логарифмически нормальное 46
О нормальное (Гаусса) 43
О усеченное нормальное 45
О экспоненциальное 41, 78
Резерв:О временный 402
О замещением 251,397
О постоянно включенный 244
Резервирование 27
0 временное 402
0 нагрузочное 70, 374
О общее 256
О раздельное 256
О с дробной кратностью 247
О скользящее 253
О структурное 70, 244, 378
Ремонтопригодность 26
Ресурс:0 назначенный 25
0 технический 25
Риск 554О кумулятивный (с накоплением) 561
О средний 555
О техногенный 69, 554ССистема 23О абсолютно надежная 589, 595
О дифференциальных уравнений 110
О интегральных уравнений 110
О информационная 468
О мажоритарная 247
О массового обслуживания (СМО)
465О нерезервированная 241
О пропускная способность 500
О резервированная 244
О релейная 589
О с дробной кратностью
резервирования 247, 325
О с монотонной структурой 619
О с переменной структурой 89О с последействием отказов 361
О сбора данных об отказах 456
О собственное время работы 367
0 техническая 26
О управления 529
Смесь распределений 48
Соединение, основное 241
Состояние:0 восстановления 104
0 отражающее 489, 561
0 поглощающее 488, 559
0 предельное 24
0 промежуточ ное 415
0 простоя 104
0 работоспособности 104
Сохраняемость 22
Среднее время:0 безотказной работы 34
0 безотказной работыинформационной системы 466
0 восстановления 38
0 между отказами 38
Структура системы 23
Схема:0 структурная 133
0 эквивалентная 322тТеория надежности 17УУравнение Чэпмана — Колмогорова
208ФФункции алгебры логики (ФАЛ) 134
Функция:0 верхняя огибающая класса 610
0 готовности 40
0 готовности информационной
системы 467
702Предметный указательФункция (проб.):О надежности 371О нижняя огибающая класса 610О оперативной готовности 4120 полезности системы 5770 простоя 400 ресурса 606эЭкран 469
Эксплуатация:О по назначению 417
О техническая 420
Элемент 22О с восстановлением 98
основыТЕОРИИо ^P(t) = 0,997НАДЕЖНОСТИПоловко Анатолии Михайлович, доктор технических наук, профессор, зас¬
луженный деятель науки и техники РФ, профессор Санкт-Петербургской
государственной лесотехнической академии. Автор более 160 научных и
методических работ. Один из основоположников теории надежности как
науки. Его книга «Основы теории надежности» переведена на многие языки
мира.Гуров Сергей Владимирович, доктор технических наук, профессор кафедры
«Математические методы и моделирование в экономике и управлении»
Санкт-Петербургской государственной лесотехнической академии. Автор
более 100 научных и методических работ по надежности, математическому
моделированию и использованию компьютерных технологий.Книга посвящена изложению теории надежности как науки и научной дисци¬
плины. Значительный вклад в теорию внесли авторы, и в настоящее время
книга является наиболее полным изложением теории надежности. Благода¬
ря научности и одновременно практической направленности книги, наибо¬
лее полному описанию применяющихся и наличию новых методов анализа
и синтеза сложных технических систем, а также использованию компьютер¬
ных технологий, книга может быть полезна различным категориям читате¬
лей. Она является учебным пособием для студентов технических вузов,
изучающих теорию надежности и ряд смежных дисциплин. В ней есть необ¬
ходимые сведения для ученых и инженеров, занимающихся исследования¬
ми проблем надежности и созданием высоконадежных технических и ин¬
формационных систем. Аспиранты и соискатели ученых степеней найдут
здесь тематику кандидатских и докторских диссертаций.Книгу дополняет пособие «Основы теории надежности. Практикум», содержа¬
щее задачи, примеры, лабораторный практикум и курсовое проектирование.(bhyБХВ-ПЕТЕРБУРГ
194354,
ул. Есенина, 5Б
E-mail: mail@bhv.ru
internet: www.bhv.ru
тел./факс: (812) 591-6243ISBN 5-94157-541-6