УДК 681.3.06+519.6(076.1)
ББК 32.973я73
П52
Половко А. М., Гуров С. В.
П52 Основы теории надежности. Практикум. — СПб.: БХВ-Петербург,
2006. — 560 с: ил.
ISBN 5-94157-542-4
Основы теории надежности излагаются путем решения практических задач,
выполнения лабораторных и курсовых работ и проектов. Рассматриваются
вопросы надежности иевосстаиавливаемых и восстанавливаемых,
нерезервированных и резервированных систем. Проводятся расчеты показателей
надежности систем разной структуры при различных законах распределения отказов и
восстановлений. Лабораторные работы носят исследовательский характер. В
процессе их выполнения изучаются особенности критериев надежности, свойства и
эффективность различных методов повышения надежности. Расчеты проводятся
с использованием средств символьной математики Mathematica, Derive 5, Excel,
а также авторских программных средств. Теоретические сведения, необходимые
при решении задач практикума, содержатся в книге "Основы теории надежности".
Для ученых, инженеров, аспирантов и студентов технических вузов
УДК 681.3.06+519.6(076.1)
ББК 32.973я73
Группа подготовки издания:
Главный редактор ЕкатеринаКондукова
Зам. главного редактора Людмила Еремеевская
Зав. редакцией Григорий Добин
Редактор Нина Седых
Компьютерная верегка Ольги Сергиенко
Корректор Зинаида Дмитриева
Дизайн обложки Инны Тачиной
Зав. производством Николай Тверских
Рецензенты:
Смагин В. А., заслуженный деятель науки РФ, д. т. н.,
профессор кафедры "Эксплуатация автоматизированных систем управления"
Военно-космической академии имени А. Ф. Можайского
Богатырев В. А., д. т. п., профессор кафедры вычислительной техники Санкт-Петербургского
государственного университета информационных технологий, механики и оптики
Андреев А. М., к. т. н., доцент кафедры "Компьютерные системы и сети"
МП'У им. Н. Э. Баумана
Лицензия ИД № 02429 от 24.07.00. Подписано в печать 15.02.06.
Формат 70x400Vie. Печать офсетная. Усл. печ. л. 45,15.
Тираж 3000 экз. Заказ Ns 553
"БХВ-Петербург", 194354, Санкт-Петербург, ул. Есенина, 5Б.
Санитарно-эпидемиологическое заключение на продукцию
№ 77.99.02.953.Д.006421.11.04 от 11.11.2004 г. выдано Федеральной службой
по надзору в сфере защиты прав потребителей и благополучия человека.
Отпечатано с готовых диапозитивов в ОАО «Техническая книга»
190005, Санкт-Петербург, Измайловский пр., 29
ISBN 5-94157-542-4 © Половко А. М., Гуров С. В.. 2006
© Оформление, издательство "БХВ-Петербург", 2006

ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 13
ЧАСТЬ I. УПРАЖНЕНИЯ 17
ГЛАВА 1. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
НЕРЕЗЕРВИРОВАННЫХ ^ВОССТАНАВЛИВАЕМЫХ СИСТЕМ 19
1.1. Методы расчета показателей надежности 19
1.2. Примеры решения задач 21
1.3. Задачи для самостоятельного решения.... 33
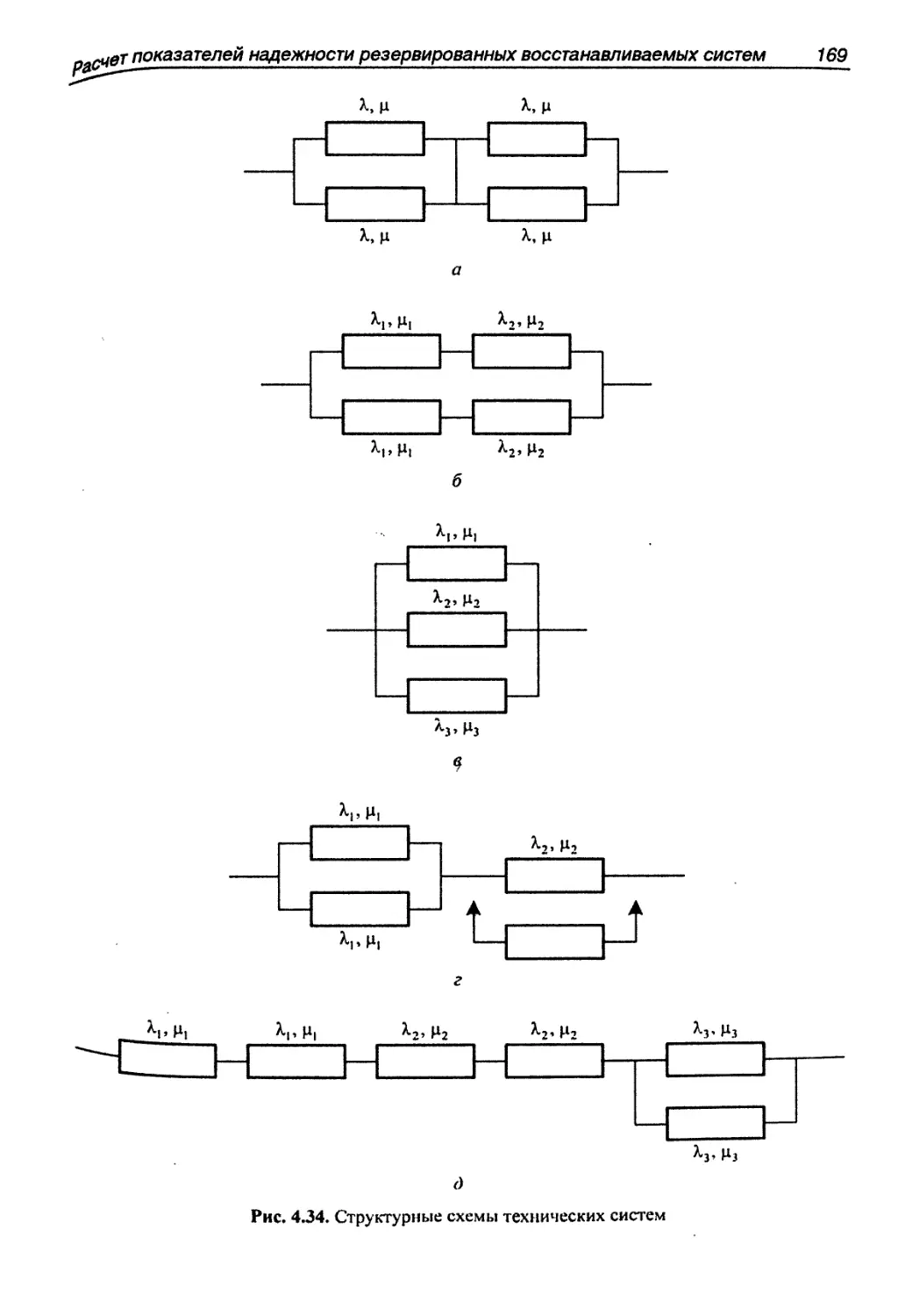
ГЛАВА 2. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ РЕЗЕРВИРОВАННЫХ
НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ 37
2.1. Методы расчета показателей надежности 37
2.1.1. Общее резервирование с постоянно включенным резервом 37
2.1.2. Общее резервирование замещением 39
2.1.3. Раздельное резервирование 40
2.1.4. Резервирование с дробной кратностью 41
2.1.5. Скользящее резервирование 41
2.2. Примеры решения задач 42
2.3. Задачи для самостоятельного решения 68
ГЛАВА 3. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
НЕРЕЗЕРВИРОВАННЫХ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ 72
3.1. Сведения из теории 72
3.1.1. Надежность восстанавливаемой системы как одного элемента 73
Постоянные интенсивности отказа и восстановления 73
Нормальные законы распределения времени до отказа и времени
восстановления 74
Произвольные интенсивности отказа и восстановления 74
3.1.2. Показатели надежности восстанавливаемой системы, состоящей из п
элементов 76
Экспоненциальный закон распределения времени до отказа и времени
восстановления элементов 76
Экспоненциальный закон распределения времени до отказа
и произвольный закон времени восстановления элементов 77

4
Оглавление
Произвольные законы распределения времени до отказа
и времени восстановления элементов 78
3.2. Примеры решения задач 80
3.3. Задачи для самостоятельного решения 103
ГЛАВА 4. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
РЕЗЕРВИРОВАННЫХ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ 108
4.1. Методы расчета надежности систем при экспоненциальных законах
распределения отказов и восстановлений 109 .
4.2. Методы расчета надежности систем при произвольных законах
распределения отказов и восстановлений 112
4.2.1. Дублированная система с постоянно включенным резервом 112
Ограниченное восстановление. Прямой приоритет 113
Ограниченное восстановление. Обратный приоритет 117
Ограниченное восстановление. Назначенный приоритет 118
Неограниченное восстановление 122
4.2.2. Дублированная система с резервом замещением 122
Ограниченное восстановление. Прямой приоритет 123
Ограниченное восстановление. Обратный приоритет обслуживания 124
Ограниченное восстановление. Назначенный приоритет обслуживания 126
4.2.3. Дублированная система с облегченным резервом 128
4.2.4. Нестационарные показатели надежности 134
4.3. Примеры решения задач 135
4.4. Задачи для самостоятельного решения 167
ГЛАВА 5. АНАЛИЗ НАДЕЖНОСТИ СИСТЕМ СЛОЖНОЙ СТРУКТУРЫ 174
5.1. Методы расчета показателей надежности сложных систем 174
5.2. Оценка надежности сложных систем по данным о надежности подсистем,
независимых по восстановлению 175
5.2.1. Экспоненциальные распределения 175
5.2.2. Произвольные распределения 178
5.3. Примеры решения задач 179
5.4. Задачи для самостоятельного решения 196
ЧАСТЬ II. ЛАБОРАТОРНЫЙ ПРАКТИКУМ 201
ЦЕЛИ И ЗАДАЧИ ЛАБОРАТОРНОГО ПРАКТИКУМА 203
ЛАБОРАТОРНАЯ РАБОТА 1. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ ЭЛЕМЕНТОВ ПО ОПЫТНЫМ ДАННЫМ 205
1.1. Постановка задачи 205
1.2. Сведения из теории 205
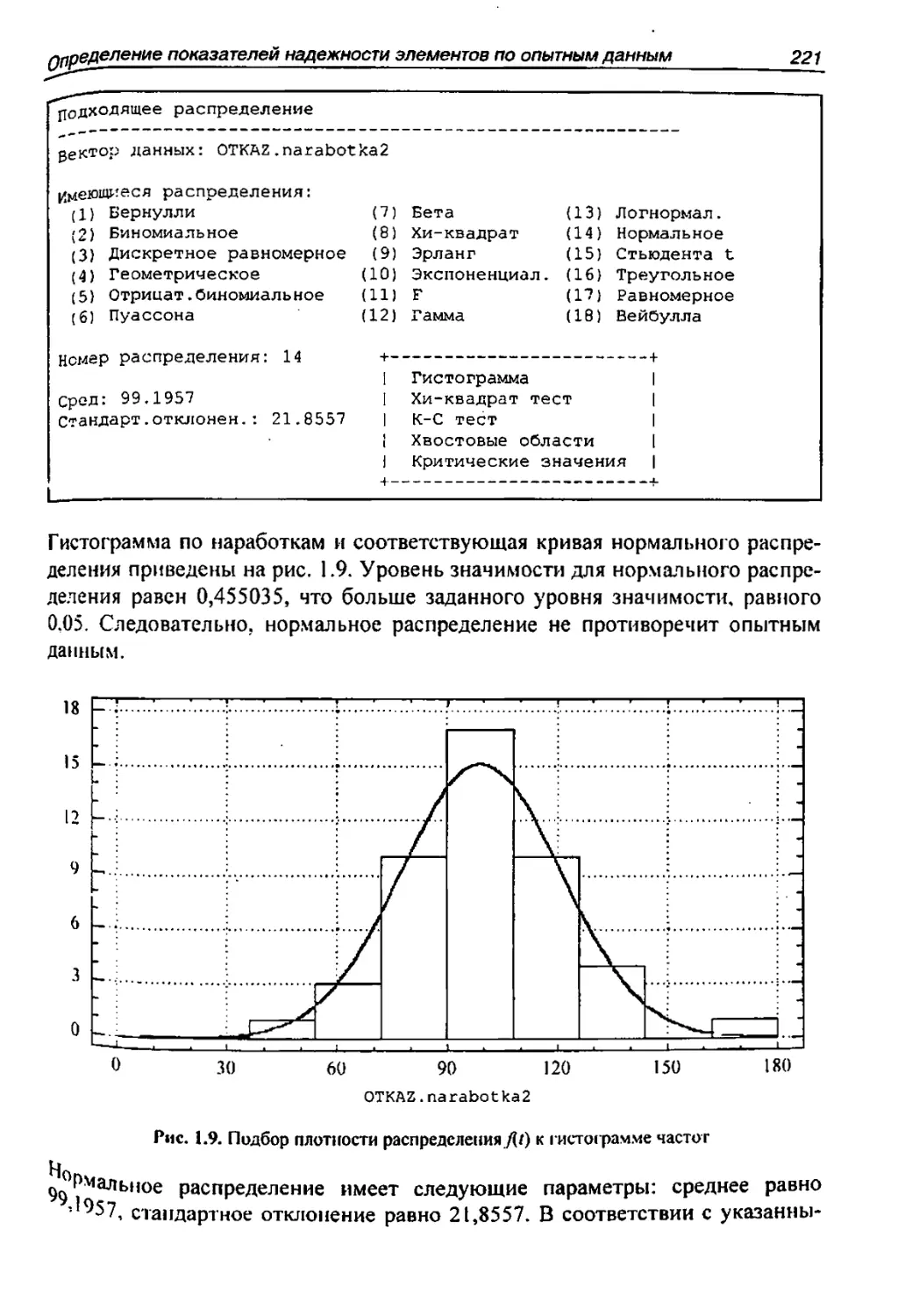
1.3. Пример выполнения лабораторной работы 213
1.3.1. Постановка задачи 213

,OrnasneHue
. .


5


1.3.2. nOCJJeIlOBaTenbHocTb BblnonHeHH
 pa60Tbi C Hcnonb30BaHMeM nporpaMMbl


S ta tG fa phi c s .. · · · · . · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · . . . . . . . . . . . . .. ? 1 4


1.3.3. OnpeJleneHHe nOKa3aTcneH Hane)f(I
OCTH I-lepeMoHTHpyeMoro 3neMeHTa........ 2) 7
1.3.4. OnpeneneHHe nOKa3aTeneH Hane)f(HOCTI1 peMoHTi1pyeMoro 3neMeHTa............ 220


1.4. <1>0 pM a OTlf eTa · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · . · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · . · · · . . . . . . . . . .. 223


""'",. u 6 1
1.5
 BapHaHTbl 3analiHI1 K naoopaTopHoH pa OTe ...........................................................223
. , . . .


JlAJ;OPATOPI*IA}I PA60;r:\ 2. HCCJ1EL{OBAHME HAL{EIKHOCTM
H PHCKA HEPE3EPBHPOBAHHOA TEXHHlfECKOM CHCTEMbl.................. 249
.


2. :1,
 n OCTaH 0 B K a 3 ana If It ..................................................................................................... 249


2.2. Csene H M
 li3 Teo p
f if ........... · · · . · · · · · · · · · · · · · · · · · · · · · · · · · · .. · · · · · · · · · · · · · · · · · · · . · . . .. . . . .. .. . . . . . . . . . . . . . . . . . . . . . . .. ? 5 0


2.3. I1ocnenoBaTenbHOCTb BblnOnHeHJf
 .. pa6oTbl............................................................. 250
. .
2i4
 npHMep BbinonHeHHSI na6opaTopHoH pa60Tbl ............................................................251
2.4.1. OnpeneneHHe nOKa3aTeneH Hane)J(HOCTI1 CHCTeI\.1bl............................... ....... ....252
2.4.2. Onpel1eneHI'fe p
lcKa CHCTeMbJ no TOlfHOH QJopMyne........................................ 252
2.4.3. H C C n en 0 B a H 11 e QJ y H K U 1111 P
f C I( a ....................................................................... 2 5 4
n on)"-l e H He rp a QJ 11 K a QJ y H I( UH 11 P 1-1 C K a ........ II . .. II .. . .. . .. .. . .. . . . .. . . . . .. . eo .. .. . II . . . .. .. . . . . . . .. . II 25 4
npe.L1 CT aBneH lie QJYHKUI.t
t pl-fCKa B BMne Ta6nHUbi ..........:.. eo II eo.. II... ...................... 255
OnpeneneHl-te KpJ.fT
1lfecKoro BpeMeHH pa60Tbi CI1CTeMbi .....................................257
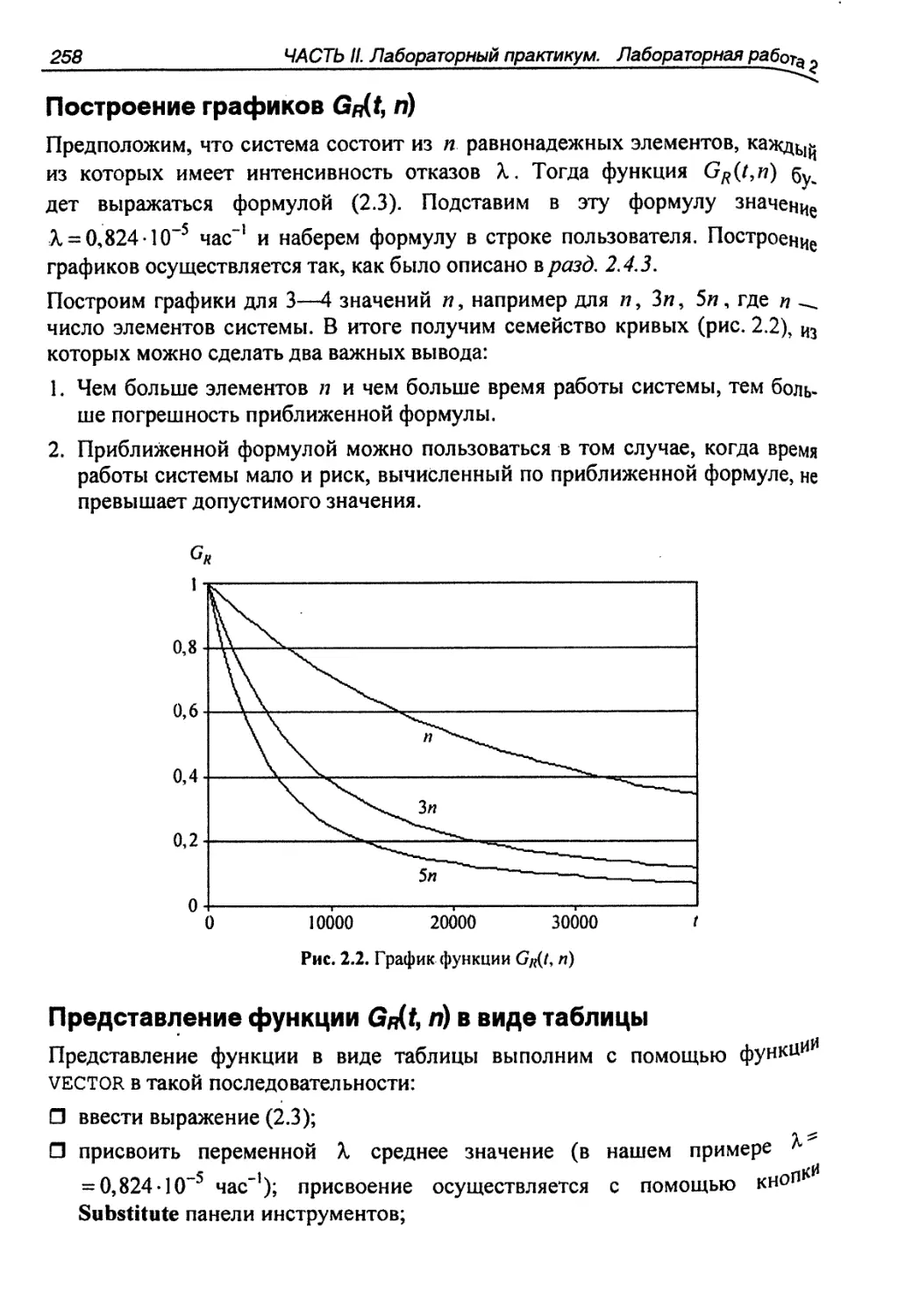
2.4.4. HccnenoBaHI1e 3aBHCI.tMOCTI1 Gu(/., 11) ..............................................................257
n oc TP 0 e H Me rp a q) I-I K 0 B G u( I, n)............................................................................. 25 8
npellcTaBneHI'le ct)YHKUJ1
t Gu(t, 1'1) B BHne Ta6nliubl.............................................. 258
aio5
. BapHaHTbl 3a11aHliH K J1a60paTopHoH pa60Te 2............... ....................... ..................... 260
.



IJOPATOPIIA» PAIJOTA 3. HCCJ1EL{OBAHHE CBOMCTB
CfpYKTYPHO PE3EPBHPOBAHHbIX CHCTEM nPH 06ll1.EM
ft3EPBHPOHAHHH C nOCTORH HO HKJ1I01JEHHbIM PE3EPBOM .............263


. , .
. '


;$..I
. nOcTaH OBKa 3a.na tr Ii .................................................................................................... 263
.
 - Il " ,
.: .;.
.
,
 CRe 264
-.
 . , , .n. e H H SI H 3 Te 0 p H H . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.'. nOCJ1e110BaTeJ1bHOCTb BblnOJIHeHIiSf pa60TbI .. ......... .............. ..... ....... ..... ..................... 265
3.3.1. HCCJIe.noBaHue 3QJQJeKTHBHocni CTpYKTypHoro pe3epBMpoBaHMSf.................... 266
Ou.eHKa BblMrpblwa HaneIKHOCTM no cpenHeMY BpeMeHH 6e30TKa'3HOH pa60Tbi ...266
OueHKa BblMrpblwa Hane)l{I-IOCTH no BepOjiTHOCTM OTKa3a cHcTeMbl..................... 267
I1cCJ1e.ll.OBaHHe CBOtfcTB HHTeHCHBHOCTM OTKa3a pe3epBHpoBaHHoH CHCTeMbl ...... 268
3.3.2. CpaBHHTeJ1bHbIH aHaJUI3 3QJQJeKTMBHOCTH HarpY304Horo H CTPYKrypHoro


pe3e p B M P 0 B a 1-1 H$I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . .. 27 I


. 3.3.3. Jifccnel!OnaHI'Ie BnliSi H It
 nocneneMcTBMSI OTKa30B........... II............................... 273
3
4. BapHaHTbl 3a.ll.aHHH K J1a60paTOpHbJM pa60TaM 3 H 4................................................. 275
JlA60PATOPHA» PA60TA 4. HCCJlEL{OBAHHE CBOHCTH
CTPYKTYPHO PE3EPBHPOBAHHbIX CHCTEM nPH 06ll1.EM
P£3EPBHPO HAH H H 3AM E llI. E H HEM ..................................................................... 276


4.1. n aCTa HOB Ka 3 all a 4 H .................................................................................................... 276
4.2. C Be !l e H H Sf Ii 3 Teo p H Ii ........ .. . .. . . . . . .. .. . .. . .. .. .. .. . .. .. . . . . .. . .. .. .. .. . .. .. . .. .. . .. .. . .. . .. . .. .. . .. .. . . . .. .. .. ... .. 2 76




6 Оглавление
4.3. Последовательность выполнения работы 277
4.3.1. Исследование эффективности структурного резервирования
замещением при идеальном автомате контроля и коммутации 278
Оценка выигрыша надежности по вероятности отказа 278
Оценка выигрыша надежности по среднему времени безотказной
работы системы 282
4.3.2. Исследование влияния автомата контроля и коммутации на
эффективность резервирования замещением 284
4.3.3. Исследование свойств интенсивности отказа резервированной
системы 288
ЛАБОРАТОРНАЯ РАБОТА 5. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ И РИСКА
ВОССТАНАВЛИВАЕМОЙ НЕРЕЗЕРВИРОВАННОЙ СИСТЕМЫ 292
5.1. Постановка задачи 292
5.2. Сведения из теории 292
5.3. Последовательность выполнения работы 295
5.4. Пример выполнения лабораторной работы 296
5.4.1. Определение наработки на отказ системы 296
5.4.2. Исследование функции и коэффициента готовности системы 296
5.4.3. Анализ риска системы 301
5.5. Варианты заданий к лабораторной работе 302
ЛАБОРАТОРНАЯ РАБОТА 6. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ И РИСКА
РЕЗЕРВИРОВАННОЙ ВОССТАНАВЛИВАЕМОЙ СИСТЕМЫ 304
6.1. Постановка задачи 304
6.2. Сведения из теории 305
6.3. Последовательность выполнения работы 306
6.4. Пример выполнения лабораторной работы 307
6.4.1. Постановка задачи 307
6.4.2. Определение наработки на отказ Т и коэффициента готовности К,
системы 307
6.4.3. Определение вероятности безотказной работы резервированной
системы 311
6.4.4. Определение среднего времени безотказной работы системы 312
6.4.5. Определение риска системы 313
6.5. Варианты заданий к лабораторной работе 6 314
ЛАБОРАТОРНАЯ РАБОТА 7. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
ИНФОРМАЦИОННОЙ ВОССТАНАВЛИВАЕМОЙ СИСТЕМЫ 316
7.1. Постановка задачи 316
7.2. Сведения из теории 316
7.3. Пример выполнения лабораторной работы 318
7.4. Варианты заданий к лабораторной работе 7 322

Оглавление 7
ЛАБОРАТОРНАЯ РАБОТА 8. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
ТЕХНИЧЕСКИХ СИСТЕМ С УЧЕТОМ ИХ ФИЗИЧЕСКОЙ
РЕАЛИЗУЕМОСТИ 325
8.1. Влияние неодновременной работы элементов на надежность системы 325
8.1.1. Постановка задачи 325
8.1.2. Сведения из теории 326
8.1.3. Пример выполнения работы 328
8.1.4. Варианты заданий к лабораторной работе 332
8.2. Влияние последействия отказов элементов на надежность системы 335
8.2.1. Постановка задачи 335
8.2.2. Сведения из теории 336
Экспоненциальные распределения времени до отказа 336
Произвольные распределения времени до отказа 336
8.2.3. Пример выполнения работы 341
. 8.2.4. Задания к лабораторной работе., 345
ЛАБОРАТОРНАЯ РАБОТА 9. АНАЛИЗ ВЛИЯНИЯ ПРОФИЛАКТИКИ
НА НАДЕЖНОСТЬ ТЕХНИЧЕСКОЙ СИСТЕМЫ '. 347
9.1. Постановка задачи 347
9.2. Сведения из теории 348
9.3. Пример выполнения работы 350
9.4. Варианты заданий к лабораторной работе 9 357
ЛАБОРАТОРНАЯ РАБОТА 10. ИССЛЕДОВАНИЕ ВЛИЯНИЯ ВРЕМЕННОГО
РЕЗЕРВИРОВАНИЯ НА НАДЕЖНОСТЬ ТЕХНИЧЕСКОЙ СИСТЕМЫ 359
10.1. Постановка задачи 359
10.2. Сведения из теории 360
10.3. Пример выполнения лабораторной работы 363
10.4. Варианты заданий к лабораторной работе 10 367
НАСТЬ ПТ. КУРСОВОЕ ПРОЕКТИРОВАНИЕ ....371
ЦЕЛИ И ЗАДАЧИ КУРСОВОГО ПРОЕКТИРОВАНИЯ 373
ГЛАВА 1. ТЕМАТИКА КУРСОВОГО ПРОЕКТИРОВАНИЯ 376
Тема I. Синтез оптимальной структуры технической системы по обеспечению
^надежности 376
1.1. Постановка задачи 376
1.2. Методика решения задачи синтеза структуры системы 377
1.2.1. Анализ надежности исходной системы 377
1.2.2. Определение кратности общего резервирования 378
1.2.3. Определение кратности раздельного резервирования 379
1.2.4. Определение показателей надежности оптимальной системы 380

8
Оглавление
1.3. Алгоритмы анализа и синтеза оптимальной структуры системы 380
1.4. Компьютерные технологии анализа и синтеза оптимальной структуры
системы '. 382
1.5. Индивидуальные задания на проектирование 383
Тема 2. Проектирование технической системы по заданным показателям
надежности и риска 385
2.1. Задание на курсовой проект 385
2.2. Методические указания по выполнению курсового проекта 387
2.2.1. Показатели надежности и риск нерезервированной системы 387
2.2.2. Вероятность безотказной работы резервированных подсистем 388
2.2.3. Надежность и риск резервированной системы, состоящей
из независимых подсистем 389
2.2.4. Надежность и риск резервированной системы, состоящей
из зависимых по восстановлению подсистем 390
2.3. Пример выполнения курсового проекта 392
2.3.1. Определение показателей надежности исходной системы и
суммарного риска из-за ее отказа 392
2.3.2. Разработка структурной схемы системы, риск которой в от раз
меньше риска исходной 393
2.3.3. Расчет показателей надежности усовершенствованной системы 394
2.3.4. Расчет показателей надежности новой системы для резерва
замещением 396
2.3.5. Вычисление показателей надежности и риска системы при наличии
восстановления 396
2.3.6. Определение показателей надежности и суммарного риска
усовершенствованной системы 398
2.3.7. Определение показателей надежности и суммарного риска
усовершенствованной системы (резерв замещением) 402
2.3.8. Выводы по работе 402
2.4. Варианты заданий на курсовой проект 403
Тема 3. Анализ надежности системы по данным эксплуатации 406
3.1. Задание на курсовой проект 406
3.2. Сведения из теории 407
Тема 4. Разработка структурной схемы системы длительного использования,
удовлетворяющей требованиям надежности и ограничениям на техническую
реализацию 409
ГЛАВА 2. ТЕМАТИКА КУРСОВЫХ РАБОТ 411
Тема 1. Оценка влияния дисциплины обслуживания на надежность
дублированной восстанавливаемой системы 411
Тема 2. Оценка влияния дисциплины обслуживания на надежность
энергетической системы 412
Тема 3. Анализ влияния законов распределения отказов на переходные процессы
при оценке показателей надежности и готовности восстанавливаемой системы 413

Оглавление д
Тема 4. Влияние параметров резервированной восстанавливаемой системы
на длительность переходных процессов при оценке ее готовности 413
Тема 5. Влияние параметров резервированной восстанавливаемой системы на
длительность переходных процессов при оценке ее готовности (случай
резервирования замещением) 414
Тема 6. Установление закона распределения времени безотказной работы
системы по известным законам распределения элементов 415
6.1. Задание на курсовую работу 415
6.2. Алгоритм статистического моделирования 417
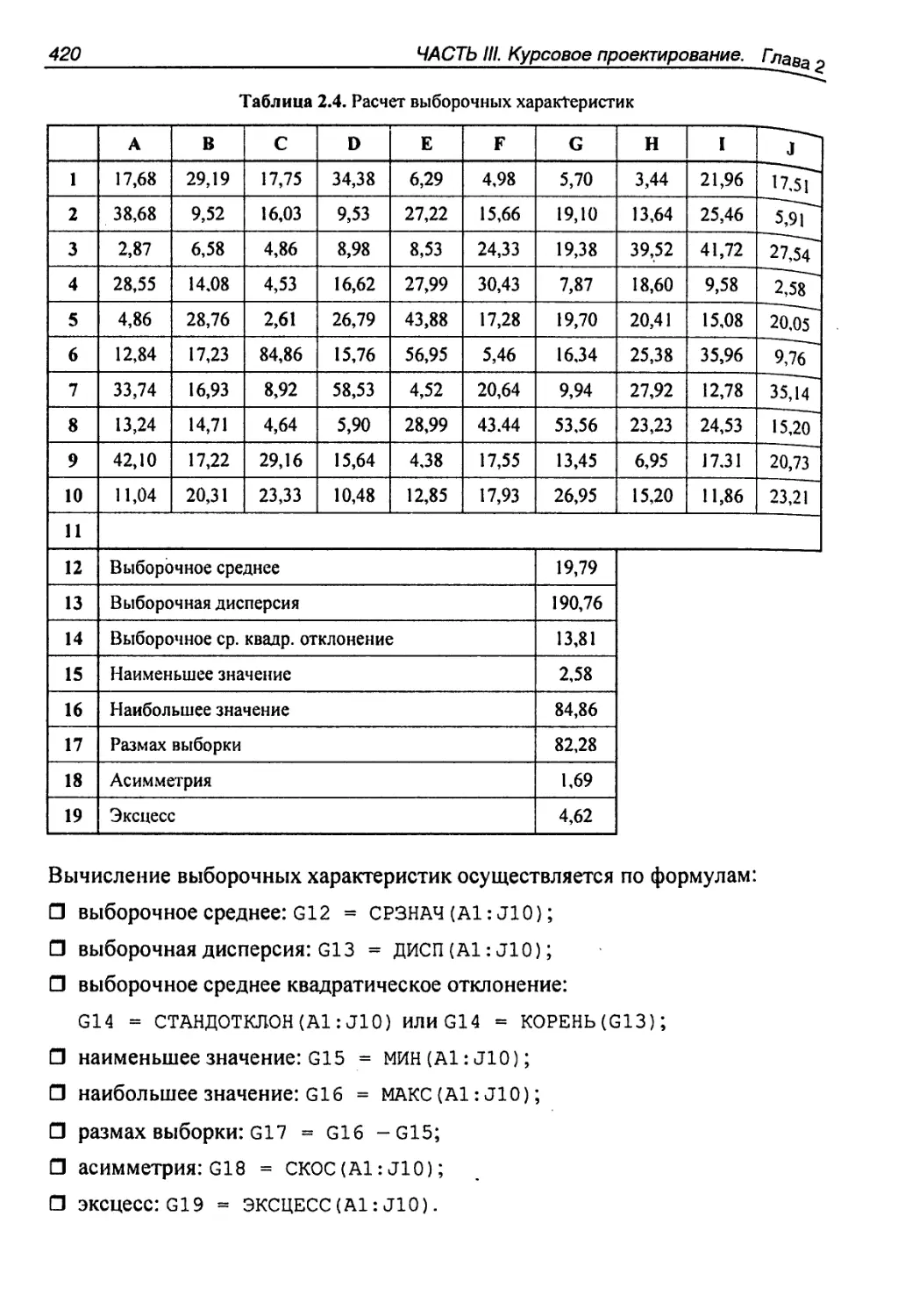
6.3. Статистическая обработка данных 419
6.3.1. Вычисление основных характеристик выборки 419
6.3.2. Формирование статистического ряда и графическое представление
данных 421
6.3.3. Подбор подходящего закона распределения вероятностей 424
6.4. Определение характеристик надежности системы 430
6.5. Варианты заданий на курсовую работу 432
Тема 7. Сравнение надежности систем при различных видах структурного
резервирования 435
7.1. Задание на курсовую работу 435
7.2. Методика сравнения надежности систем последовательно-параллельной
структуры 436
7.3. Расчет вероятности безотказной работы системы
последовательно-параллельной структуры 440
7.4. Варианты заданий на курсовую работу 446
ЧАСТЬ IV. КОМПЬЮТЕРНЫЕ ТЕХНОЛОГИИ РЕШЕНИЯ
ЗАДАЧ НАДЕЖНОСТИ 449
ГЛАВА 1. УНИВЕРСАЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СИСТЕМЫ
СИМВОЛЬНОЙ МАТЕМАТИКИ И РЕШЕНИЕ ЗАДАЧ НАДЕЖНОСТИ 451
Ы. Основы работы в системе Derive 452
1.1.1. Derive 5 как универсальная система символьной математики 452
1.1.2. Основное окно системы 453
1.2. Ввод выражений 456
1.3. Вычисление математических выражений 457
Ь4. Преобразование выражений 458
1.5. Специальные вычисления 460
1.5.1. Табулирование функций 460
1.5.2. Команда Table 462
1.6. Разложение функций в ряд Тейлора 463
1.7. Вычисление пределов 464
1.8. Вычисление суммы ряда 464
1.9. Вычисление произведения ряда 465

10 Оглавление
1.10. Вычисление производных.. ......466
1.11. Вычисление интегралов 466
1.12. Решение уравнений с одним неизвестным 467 .
1.13. Решение систем линейных алгебраических уравнений 470
1.14. Решение систем нелинейных уравнений 473
1.14.1. Метод Ньютона — Рафсона 473
1.14.2. Метод итераций 474
1.15. Решение дифференциальных уравнений 475
1.16. Интерполяция 476
1.16.1. Интерполяция точная в узлах 476
1.16.2. Сплайн-интерполяция 478
1.16.3. Интерполяция приближенная в узлах (аппроксимация) 479
1.16.4. Паде-аппроксимация 483
1.17. Визуализация вычислений 484
1.18. Функциональные возможности табличного процессора Excel 487
ГЛАВА 2. СПЕЦИАЛИЗИРОВАННЫЕ ПРОГРАММНЫЕ СРЕДСТВА
АНАЛИЗА НАДЕЖНОСТИ СЛОЖНЫХ СИСТЕМ 491
2.1. Требования, предъявляемые к интегрированной системе 491
2.2. Структура интегрированной системы 492
2.3. Методика и алгоритм программы Relass 493
2.3.1. Возможности и ограничения программы 494
2.3.2. Представление и формализация структуры исследуемой системы 495
2.3.3. Описание системы графом состояний 498
2.3.4. Алгоритм уменьшения размерности графа состояний системы 500
2.3.5. Анализ систем при наличии интервалов простоя элементов 502
2.4. Методика программы Kasm 504
2.5. Возможности программы Redopt 507
2.6. Программные средства анализа надежности сложных систем
с произвольными распределениями отказов и восстановлений элементов..:. 508
2.7. Программные средства расчета и прогнозирования надежности систем
с переменной структурой 510
2.8. Другие программные средства 511
2.8.1. Анализ показателей надежности системы при различных законах
распределения времени до отказа 511
2.8.2. Анализ надежности резервированной системы при наличии
подключающего устройства 512
2.8.3. Оценка последействия отказов и его влияния на надежность
невосстанавливаемой дублированной системы 512
2.8.4. Анализ надежности невосстанавливаемой системы
при неодновременной работе ее элементов 513
2.8.5. Анализ надежности системы с временным резервированием 513
2.8.6. Оценка влияния профилактики на надежность системы 514
2.8.7. Оценка вероятности безотказной работы
последовательно-параллельных схем 515

Оглавление ; ц
2.8.8. Анализ надежности структурно резервированных восстанавливаемых
систем с постоянными интенсивностями отказов и восстановлений
элементов 516
2.8.9. Решение систем линейных дифференциальных уравнений
методом Рунге — Купы с автоматическим выбором шага 517
2.9. Выводы 517
ГЛАВА 3. РЕШЕНИЕ ЗАДАЧ НАДЕЖНОСТИ С ПОМОЩЬЮ
УНИВЕРСАЛЬНЫХ И СПЕЦИАЛИЗИРОВАННЫХ ПРОГРАММНЫХ
СРЕДСТВ 519
3.1. Решение задач надежности на основе Derive 5 519
3.1.1. Определение среднего времени безотказной работы 519
3.1.2. Определение вероятности безотказной работы системы 525
3.1.3. Определение показателей надежности восстанавливаемых систем 530
3.2. Использование специализированных программ для решения задач
надежности 540
3.2.1. Программное средство Relass 540
3.2.2. Программа Conspz 547
3.2.3. Программа Posl_par : 550
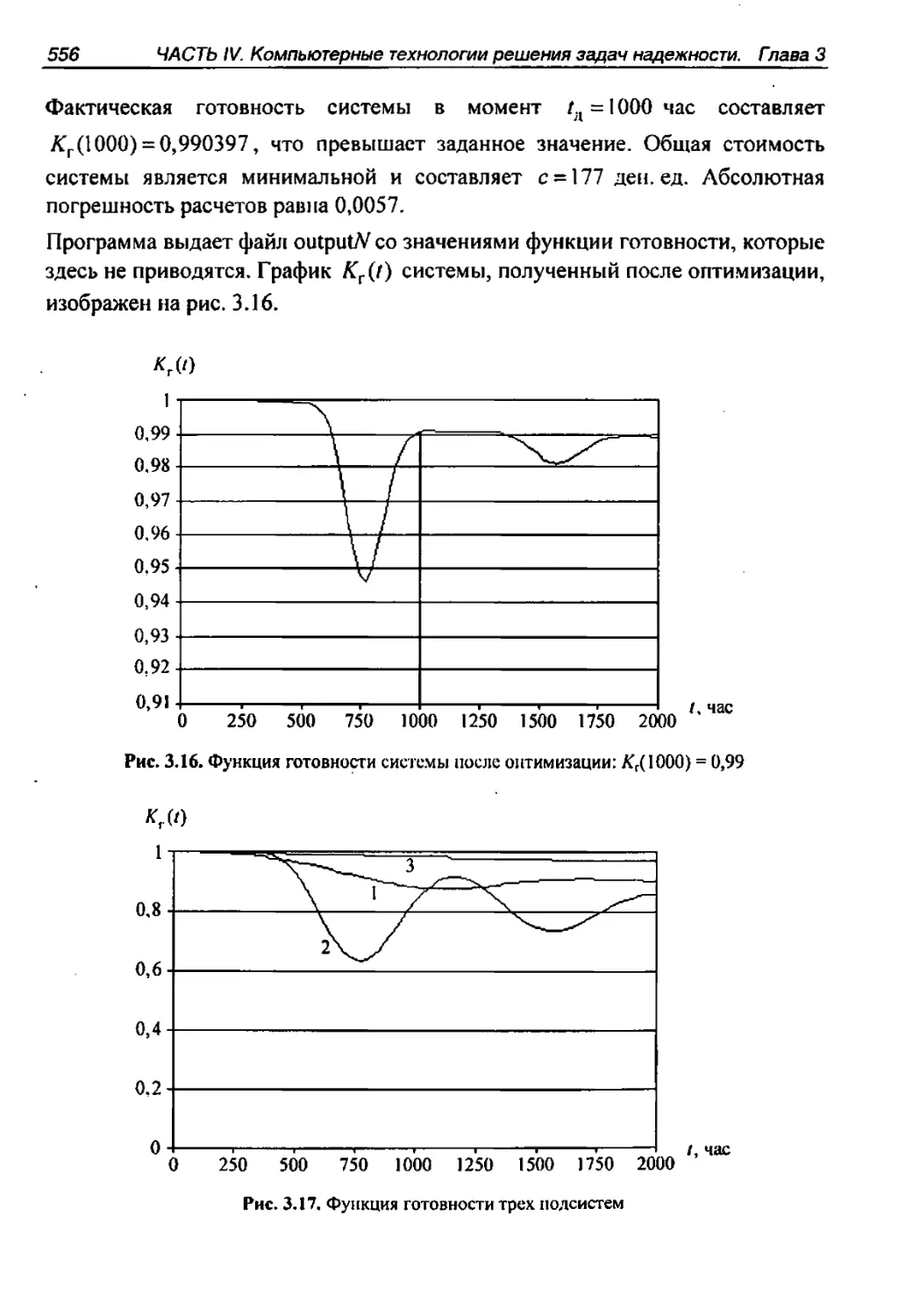
3.2.4. Программное средство Redopt 553
СПИСОК ЛИТЕРАТУРЫ 559
/

ВВЕДЕНИЕ
i
i
i
Учебные курсы "Основы теории надежности, "Надежность и
отказоустойчивость информационных систем", "Надежность технических систем и
техногенный риск" и другие предметы технических вузов, близкие по названию и
содержанию, состоят из лекций, практических занятий, лабораторных работ и
курсового проектирования. Однако учебных пособий по практическим
занятиям, лабораторному практикуму и курсовому проектированию в настоящее
время не существует. Имеются лишь методические указания для студентов,
составленные преподавателями кафедр и в лучшем случае изданные малым
тиражом для студентов данного вуза.
Теория надежности является достаточно трудным для студентов предметом.
Она требует хороших знаний математики, компьютерных технологий
решения математических задач, твердых знаний предметной области, в которой
решаются задачи надежности.
Процессы, протекающие в технических и информационных системах и
связанные с отказами техники, являются сложными случайными процессами. Их
моделирование требует составления и решения алгебраических и
дифференциальных уравнений высокого порядка. При этом в результате их решения
получают показатели надежности, имеющие вероятностный смысл, который
трудно понять, если нет опыта решения подобных задач.
Надежность сложных технических и информационных систем оценивается
многими показателями. Определение каждого из них осуществляется по
уникальной методике. Вычисление вероятности безотказной работы и функции
готовности связано с решением дифференциальных уравнений. Вычисление
среднего времени безотказной работы требует знания интегрального
исчисления. Определение параметра потока отказов невозможно без знания
методов решения интегральных уравнений и т. п. В результате в теории
надежности имеется большое число методов анализа и синтеза технических и
информационных систем по различным критериям надежности.
Однако, изучив теорию на отлично, можно не решить задачу надежности.
Для этого недостаточно теоретических знаний, необходимо также иметь опыт
решения задач.

14
Введение
Книга призвана помочь читателю хорошо понять теорию надежности и
получить навыки решения практических задач. '
В части I книги приводятся без доказательства необходимые сведения; из
теории надежности, решаются типичные практические задачи. В каждой Ыа-
ве приводятся задачи для самостоятельного решения. i
Часть II посвящена лабораторному практикуму. В ней дано описание девяти
лабораторных работ, большинство из которых внедрено авторами в учебный
процесс. Каждая из работ рассчитана на 2—4 академических часа. Вариантов
заданий вполне достаточно для проведения индивидуального обучения. Для
облегчения выполнения лабораторных работ приводятся примеры, которые
доведены до конечных результатов.
Все лабораторные работы рассчитаны на их выполнение с помощью
компьютерных технологий. При этом могут использоваться любые математические
системы компьютерной алгебры. В книге приводятся технологии решения
задач с помощью систем Derive 5 и Microsoft Excel.
Особенностью всех лабораторных работ является их научное содержание.
Студент получает математическую модель системы в смысле ее надежности
и исследует ее свойства.
Часть III книги посвящена курсовому проектированию. Тематика курсовых
работ и проектов различна. Приводится большое число вариантов в каждой
теме, что обеспечивает индивидуальность ее выполнения. Некоторые темы
сопровождаются примерами. Выполнение курсовых проектов и работ также
требует использования компьютерных технологий.
В части W книги излагаются компьютерные технологии решения задач
надежности. В конспективной форме дается описание систем Derive 5 и Excel,
которые используются при решении задач, при выпблнении лабораторных
работ и курсовых проектов. Описаны уникальные программные средства,
предназначенные для решения задач надежности, которые не могут быть
выполнены с помощью универсальных программных средств. Программы
позволяют вычислять показатели надежности систем сложной структуры при
различных законах распределения времени до отказа и восстановления
элементов системы.
Компьютерные технологии решения задач иллюстрируются многими
примерами.
Книга необходима не только преподавателям и студентам вузов, Она также
может быть использована специалистами, проектирующими и создающими
любые технические и информационные системы, которые должны
удовлетворять высоким требованиям надежности. В книге инженер найдет
методики, компьютерные технологии анализа и синтеза систем по критериям на-

Введение 75
■Г
дежиости, доведенные до численных решений. Аналог своей задачи он
обязательно найдет в книге. Основанием для такого утверждения является
достаточная широта и глубина решаемых здесь задач.
В книге анализируются не восстанавливаемые и восстанавливаемые,
нерезервированные и резервированные системы со всеми видами избыточности:
структурной, нагрузочной и временной. Рассматриваются случаи общего и
раздельного резервирования, с постоянно включенным резервом и по методу
замещения, с различными видами обслуживания: с ограниченным и
неограниченным восстановлением при прямом, назначенном и обратном
приоритетах.
Анализируются системы с учетом возможностей физической реализуемости
структурного резервирования: неодновременность работы элементов, учет
последействия отказов, влияние автомата контроля и коммутации. Во всех
этих случаях надежность системы анализируется при различных законах
распределения отказов и восстановления системы и ее элементов:
экспоненциальном, Рэлея, гамма-, нормальном, Вейбулла и др.
Книга нужна также специалистам, занимающимся вопросами эффективности,
безопасности, живучести и риска. Эти показатели технических и
информационных систем существенно зависят от их надежности.
Авторы надеются, что их труд, воплощенный в эту книгу, будет использован
преподавателями и студентами, учеными и инженерами, а также
соискателями ученых степеней.

• ЧАСТЬ I
УПРАЖНЕНИЯ
Глава 1. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
НЕРЕЗЕРВИРОВАННЫХ ^ВОССТАНАВЛИВАЕМЫХ
СИСТЕМ
Глава 2. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
РЕЗЕРВИРОВАННЫХ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ
Глава 3. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
НЕРЕЗЕРВИРОВАННЫХ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
Глава 4. РАСЧЕТ ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
РЕЗЕРВИРОВАННЫХ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
Глава 5. АНАЛИЗ НАДЕЖНОСТИ СИСТЕМ СЛОЖНОЙ СТРУКТУРЫ

ГЛАВА 1
РАСЧЕТ
ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
НЕРЕЗЕРВИРОВАННЫХ
НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ
1.1. Методы расчета
показателей надежности
Критериями надежности невосстанавливаемых систем являются:
О Pc(t) — вероятность безотказной работы системы в течение времени t;
□ Тс — среднее время безотказной работы системы;
^ ^с(0 — интенсивность отказа системы в момент /;
^ /с (0 ~ плотность распределения времени до отказа.
Между этими показателями существуют следующие зависимости:
Tlc=)pc(t)d(,
о
с Рс<0
М0 = &(*) = -№*
о

20
ЧАСТЬ I. Упражнения. Глава 1
Замечание
Следует иметь в виду, что среднее время безотказной работы является
неудовлетворительным показателем надежности систем с коротким временем работы.
Структурная схема нерезервированной системы, состоящей из п элементов,
приведена на рис. 1.1.
Рис. 1.1. Структурная схема нерезервированной системы
При отказе любого элемента наступает отказ системы. При этом остальные
элементы системы прекращают свою работу.
Показатели надежности такой системы вычисляются по формулам:
/>с(о=П/у(о,
оо
Tlc = \Pc(t)dt,
о
*с С) =!>,(')'
/с(0 = /,(0^2(0.../>Л(0 + ^|(0/2(0^Д0 + ...+ Л(0/>2(0.-^(/),
где:
□ Pj{t) — вероятность безотказной работыу-го элемента, j = 1, 2,..., и;
О fj(t) — плотность распределения времени до отказа у'-го элемента,
j = 1, 2,..., и;
□ А,у(/) — интенсивность отказау'-го элемента, j = 1, 2,..., п .
Для случая постоянных интенсивностей отказов элементов имеют место
соотношения:
ад=<гх<',
п
\ = Z *7 '
У=1
т —1-
/C(/) = VV-

Расчет показателей надежности нерезервированных невосстанавливаемых систем 21
1.2. Примеры решения задач
ПРИМЕР 1.1. Нерезервированная система состоит из 5 элементов.
Интенсивности их отказов приведены в табл. 1.1.
Таблица 1.1. Интенсивности отказов элементов
Номер элемента
Х>, час"1
1
0,00007
2.
0,00005
3
0,00004
4
0,00006
5
0,00004
Определить показатели надежности системы: интенсивность отказа, среднее
время безотказной работы, вероятность безотказной работы, плотность
распределения времени безотказной работы. Показатели надежности P(t) и
/(/) получить на интервале от 0 до 1000 часов с шагом 100 часов.
Решение. Вычислим интенсивность отказа и среднее время безотказной
работы системы:
Хс = £ Xj = 0,00007 + 0,00005 + 0,00004 + 0,00006 + 0,00004 = 0,00026 час"1,
/=1
т;= —= ! = 3846 час.
1с Хс 0,00026
Получим значения вероятности безотказной работы и плотности
распределения времени до отказа, табулируя функции
/>(,) = «TV = e-o.ooo2fr/ и /с(/) = Ке-К< = о,00026е-°'00026/
на интервале от 0 до 1000 часов. Результаты табулирования представлены
в табл. 1.2.
Таблица 1.2. Вероятность безотказной работы и плотность
распределения времени до отказа
/, час
0
100
200
300
400
500
ад
1
0,974335
0,949329
0,924964
0,901225
0.878095
m
0,00026
0,000253
0,000247
0,000240
0,000234
0.000228

22
ЧАСТЬ I. Упражнения. Глава 1
Таблица 1.2 (окончание)
t, час
600
700
800
900
1000
Рс(0
0,855559
0,833601
0,812207
0,791362
0,771052
МО
0,000222
0,000217
0,000211
0,000206
0.000200
Графическая иллюстрация Pc{t) и fc(t) показана на рис. 1.2 и 1.3.
Рис. 1.2. Вероятность безотказной работы системы
Интенсивность отказа системы в данном случае есть величина постоянная,
равная Хс = 0,00026 час"1, ее графиком является прямая, параллельная оси
времени.
ПРИМЕР 1.2. Нерезервированная система состоит из 5 элементов, имеющих
различные законы распределения времени работы до отказа. Виды законов
распределения и их параметры приведены в табл. 1.3.
Таблица 1.3. Законы распределения времени до отказа
Номер элемента
Закон распределения
времени до отказа
1
W(2; 1800)
2
Г(7; 300)
3
R(8 10'8)
4
Ехр(0,002)
5
TN(2000; 90)

Расчет показателей надежности нерезервированных невосстанавливаемых систем 23
Рис. 1.3. Плотность распределения времени до отказа
В табл. 1.3 и в дальнейшем приняты следующие обозначения законов
распределения:
О W — Вейбулла;
О Г — гамма;
□ R —Рэлея;
О Ехр — экспоненциальный;
О TN — усеченный нормальный;
ON — нормальный;
□ U — равномерный.
В скобках указаны параметры распределений.
Определить показатели надежности каждого элемента и всей системы:
вероятность безотказной работы, среднее время безотказной работы,
интенсивность отказа, плотность распределения времени безотказной работы. Для
показателей, зависящих от времени, получить решение в виде таблиц и
графиков.
Решение. В табл. 1.3 заданы параметры законов распределения времени до
отказа. Вычислим начальные моменты распределений: математические
ожидания и средние квадратические отклонения. Для этого воспользуемся
формулами связи моментов с параметрами распределений, которые приведены в
табл. 1.4.

24
ЧАСТЬ I. Упражнения. Глава 1
Таблица 1.4. Связь параметров распределений с первыми двумя моментами
Распределение
Экспоненциальное Ехр(Я.)
Равномерное U(a,b), а^О
Гамма Г(а,Р)
Усеченное нормальное
TN(m0,a0) ч
Рэлея R(k)
Вейбулла W(a,p)
Нормальное N(w.a) от > За
т
1
a + b
2
ар
от0 + кс0
V4X
рг(1 + 1/а)
т
а
1
к
b-a
2л/з
V^P
| "'»
о. 1 + А-2--Г, А = -7=е 2°°,
V °о V2ti
1
с~ г „, ^
0,5+ Ф0 -i
ЧаоУ
/4-я
V 4Х
Р>/г(1 + 2/а)-Г2(1 + 1/а)
с
В таблице введены следующие обозначения:
□ Фо(0 = -7= Je 2 лбе — функция Лапласа;
л/2л 0
00
О Г(а) = jxa~le~xdx — гамма-функция,
о
Простым способом вычисления значений этих функций является обращение
к системе Microsoft Excel, что будет показано в разд. 1.19 части IV.
Определим математическое ожидание и среднее квадратическое отклонение
времени до отказа элементов.
□ Элемент 1. Распределение Вейбулла с параметром формы a = 2 и
параметром масштаба |3 = 1800 :
w = 1800• Г(1,5) = 1595 час, a = 1800-^(2)-Г2(1,5) =834 час.

расчет показателей надежности нерезервированных невосстанавливаемых систем 25
О Элемент 2. Гамма-распределение с параметром формы а = 7 и
параметром масштаба р = 300:
т = 7-300 = 2100 час, cr = V7-300 = 794 час.
□ Элемент 3. Распределение Рэлея с параметром X = 8 • 10~8:
т = А ^-=3133 час, а= / ^-=1638 час.
V4-8-10"8 V4-8-10"8
О Элемент 4. Экспоненциальное распределение с параметром X = 0,0002 :
т- = 5000 час, а = /« = 5000 час.
0,0002
О Элемент 5. Усеченное нормальное распределение с параметрами
ю0=2000, a0=900:
_Щ_ 20002
k = —r ! -?е 2ст° = ? -Ц -^в"2.9002 =о,0342.
{ l°oJJ V К 900 J J
Значит,
т = 2000 + 0,0342 • 900 = 2029 час,
a = 90oJl + 0,0342-^^-0,03422 =931 час.
V 900
Полученные значения сведены в табл. 1.5
Таблица 1.5. Параметры законов распределения времени до отказа элементен
Номер элемента
Среднее время безотказной работы, час
Среднее квадратическое отклонение
времени безотказной работы, час
1
1595
834
2
2100
794
3
3133
1638
4
5000
5000
5
2029
931
Для вычисления вероятности безотказной работы и плотности распределения
времени до отказа элементов нам потребуются аналитические выражения,
которые приведены в табл. 1.6.
В гамма-распределении функция 7(a,/) = \xa~le~xdx есть неполная
П«) о
гамма-функция.

26
ЧАСТЬ I. Упражнения. Глава 1
Таблица 1.6. Некоторые законы распределения вероятностей
Распределение
Экспоненциальное Ехр(Х)
Равномерное \J(a,b), a £ 0
Гамма Г(сс,Р)
Усеченное нормальное
TN(m0,a0)
mt 1,33a
Рэлея R(X)
Вейбулла W(a,p)
Нормальное Щт,о), т > Зст
АО
\е-Ь
Г 1
, a<t£b;
ib-a
[О, t<a,t>b
раГ(а)
С г°1
1-е
о0у12п
\
С= ( \
0,5 + Ф0 -JL
\aoJ
Ihe^
С-»')2
ол/2п
ДО
-X/
е
[l, ><я;
< , a<t<,b\
b-a
0, />6
1-/ а,-
t-mQ
С 0,5-Ф0 ^
-3U2
е
Д
0,5-Ф0
Равномерное и нормальное распределения имеют ограничения на параметры
для того, чтобы их можно было использовать для решения задач надежности
в неотрицательной временной области (/ > 0).
Вычислим вероятность безотказной работы элементов.
□ Элемент 1. Распределение Вейбулла:

Расчет показателей надежности нерезервированных невосстанавливаемых систем 27
CJ Элемент 2. Гамма-распределение:
00 г"-1 -4 ( Л ( t \
P(t)= f— е Vdx = \-I a,- =1-/ 7,— .
/раГ(а) I Pj I 300 J
О Элемент 3. Распределение Рэлея:
Р,(,) = е-Х'2 =е-ш"'2.
О Элемент 4. Экспоненциальное распределение:
Р4(0 = е-х'=е-°'0002'.
О Элемент 5. Усеченное нормальное распределение:
. (W 0,5-Ф0^1 о,5-Ф0Г^ООО]
?5(0= с ]е *5 л= Ui= \ ш )
°о&! 0 5 + Ф0Ы <>,5 + Ф0 ~
°UoJ boo J
Табулируя эти функции от 0 до 2000 часов с шагом 100 часов, получим
табл. 1.7.
Таблица 1.7. Вероятность безотказной работы элементов
/, час
0
100
200
300
400
500
600
700
800
900
1000 .
1100
1200
/МО
1
0,980199
0,960789
0,941765
0,923116
0,904837
0,886920
0,869358
0,852144
0,835270
0,818731
0,802519
0,786628
/МО
1
1
0,999994
0,999917
0,999532
0,998321
0,995466
0,989932
0,980612
0,966491
0,946799
0,921097
0,889326
Л(0
1
0,995696
0,990256
0,983464
0,975087
0,964883
0,952605
0,938013
0,920884
0,901022
0,878275
0,852542
0,823788
ад
1
0,9992
0,996805
0,992826
0,987282
0,980199
0,971611
0,961558
0,950089
0,937255
0,923116
0,907738
0,891188
Ps(t\
1
0,996918
0,987730
0,972604
0,951817
0,925741
0,894839
0,859646
0,820755
0,778801
0,734444
0,688351
0,641180
ПО
1
0,972194
0,936745
0,894281
0,845456
0,790895
0,731242
0,667280
0,600058
0,530939
0,461577
0,393774
0,329303

28
ЧАСТЬ I. Упражнения. Глава 1
t, час
1300
1400
1500
1600
1700
1800
1900
2000
ЛС)
0,771052
0,755784
0,740818
0,726149
0,711770
0,697676
0,683861
0,670320
ад
0,851793
0,809123
0,762184
0,712001
0,659674
0,606303
0,552922
0,500461
РАО
0,792053
0,757456
0,720202
0.680578
0,638951
0,595754
0,551479
0,506654
Таблица 1.7 (окончание)
PaU)
0,873541
0,854875
0,835270
0,814810
0,793581
0,771669
0,749162
0,726149
P*(t)
0,593567
0,546108
0,499352
0,453789
0,409845
0.367879
0,328179
0,290960
РАО
0,269727
0,216247
0,169613
0,130105
0,097577
0,071540
0,051268
0,035911
В последнюю колонку записаны значения вероятностей безотказной работы
системы, которые определяются произведением вероятностей безотказной
работы элементов:
Pc(t) = P](OP2(t)P3(t)P4(t)P5(t).
На рис. 1.4 показаны графики функций Р)(1), / = 1,2,3,4,5,
соответствующих вероятностям безотказной работы элементов. Номера графиков
соответствуют номерам элементов. На рис. 1.5 изображен график вероятности
безотказной работы системы Pc(t).
Рис. 1.4. Вероятности безотказной работы элементов

Расчет показателей надежности нерезервированных невосстанавливаемых систем 29
Из графиков видно различное поведение вероятностей.безотказной работы
элементов. Скорость убывания вероятностей зависит от вида и параметров
закона распределения. В нашем случае медленнее всего убывает P(t) для
экспоненциального распределения и распределения Рэлея, т. е. при большом
времени работы наиболее надежными оказываются третий и четвертый
элементы системы.
Вычислим среднее время безотказной работы системы:
7j =)pc(t)dt = )pl(t)P2(t)P3(t)P4(t)P5(t)dt
о о
по формуле Симпсона:
7i=7 \+io+(-vk)wm(M)p3(kh)p4(kh)p5(kh),
-ч *=i )
где n — число точек, h — шаг интегрирования, выбираемый из условия
обеспечения требуемой точности. Расчеты показывают, что для данных
табл. 1.7 7J =976,3 час.
"а рис. 1.6 изображены графики интенсивностей отказов элементов.
Кривая 4, соответствующая экспоненциальному закону, параллельна оси време-
Ни> т. к. имеет постоянную интенсивность отказа. Все остальные кривые ин-
тенсивностей отказов являются возрастающими функциями времени.
На рис. 1.7 показан график интенсивности отказа системы, равной сумме ин-
енсивностей отказов ее элементов:
^с(0 = Л.,(/) + Х2(/) + Л.3(/) + А.4(/) + Л.5(/).
Рис. 1.5. Вероятность безотказной работы системы

30
ЧАСТЬ I. Упражнения. Глава 1
Интенсивность отказа системы также является возрастающей функцией
времени, что говорит о том, что система является стареющей, а закон
распределения времени до ее отказа не экспоненциальный.
Вычислим плотности распределения вероятностей времени безотказной
работы элементов.
□ Элемент 1. Распределение Вейбулла:
1 ра 18002
Рис. 1.7. Интенсивность отказа системы
Рис. 1.6. Интенсивности отказов элементов

Расчет показателей надежности нерезервированных невосстанавливаемых систем 31
О Элемент 2. Гамма-распределение:
,а-1 -1 ,6 _J_
/,(/) = —- е р= - е 300
|ЗаГ(а) 3007Г(7)
О Элемент 3. Распределение Рэлея:
/3(0 = 2А,^-Х/2 =2-8-10"8te"810_8/2.
□ Элемент 4. Экспоненциальное распределение:
/4(/) = ^-^=0,0002^0002/.
О Элемент 5. Усеченное нормальное распределение:
С-/по)2 (/-2000)2
л (о=-4=* 2G° = т—-—т—^~ 290°2 -
I Ч 900 ))
Табулируя плотности распределения от 0 до 2000 часов с шагом 100 часов,
получим табл. 1.8.
Таблица 1.8. Плотности распределения времени безотказной работы элементов
/, час
0
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
МО
0,0002
0,000196
0,000192
0,000188
0.000185
0,000181
0,000177
0,000174
0,000170
0,000167
0,000164
0,000161
0,000157
0,000154
МО
0
0
0
0,000002
0,000007
0,000019
0,00004
0,000072
0,000116
0,000168
0,000227
0,000288
0,000347
0,000402
МО
0,000038
0,000048
0,000061
0,000075
0,000092
0,000112
0,000134
0,000158
0,000185
0,000213
0,000242
0,000272
0,000303
0,000332
МО
0
0,000016
0,000032
0,000048
0,000063
0,000078
0,000093
0,000108
0,000122
0,000135
0,000148
0,000160
0,000171
0,000182
МО
0
0,000062
0,000122
0,000180
0,000235
0,000286
0,000331
0,000371
0.000405
0,000433
0,000453
0,000467
0,000475
0,000476

32
ЧАСТЬ I. Упражнения. Глава 1
Таблица 1.8 (окончание)
/, час
1400
1500
1600
1700
1800
1900
2000
МО
0,000151
0,000148
0,000145
0,000142
0,000140
0,000137
0.000134
МО
0,000450
0,000487
0,000514
0,000530
0,000535
0,000531
0,000517
МО
0,000360
0,000385
0,000407
0,000425
0,000438
0,000446
0,000449
МО
0,000191
0,000200
0,000209
0,000216
0,000222
0,000228
0,000232
МО
0,000472
0.000462
0,000448
0.000430
0.000409
0,000385
0,000359
Графики, построенные по данным табл. 1.8, приведены на рис. 1.8.
Рис. 1.8. Плотности распределения времени до отказа элементов
Плотность распределения времени до отказа системы /с(/) изображена на
рис. 1.9. Для ее изображения вычисления выполнялись по формуле:
/С(/) = А.С(/)РС(/).
Из графика отчетливо видна неэкспоненциальность распределения времени
до отказа нерезервированной системы, если законы распределения времени
до отказа ее элементов не являются экспоненциальными.

Расчет показателей надежности нерезервированных невосстанавливаемых систем 33
1.3. Задачи для самостоятельного решения
ЗАДАЧА 1.1. Техническая система состоит из п = 3 подсистем, которые
могут отказать независимо друг от друга. Отказ каждой подсистемы приводит к
отказу всей системы. Вероятность того, что в течение времени / первая
подсистема проработает безотказно, равна 0,7, вторая — 0,9, третья — 0,8. Найти
вероятность того, что в течение времени / система проработает безотказно.
Найти вероятность отказа системы за время /.
Ответ: 0,504; 0,496. .
ЗАДАЧА 1.2. Известно, что серийно выпускаемая деталь имеет
экспоненциальное распределение времени до отказа с параметром X = 10" час-1. Деталь
используется конструктором при разработке нового прибора. Назначенный
ресурс прибора Тн=\04 час.
Определить следующие показатели надежности детали:
О вероятность отказа детали до момента Г„;
О вероятность того, что деталь безотказно проработает в течение
времени Гн;
О вероятность того, что деталь безотказно проработает в интервале времени
от 103до 104час.
Ответ: 0,0952; 0,9048; 0,0852.
2 Заг553
Рис. 1.9. Плотность распределения времени до отказа системы

34
ЧАСТЬ I. Упражнения. Глава 1
ЗАДАЧА 1.3. Проектируется нерезервированная система, состоящая из
элементов четырех групп. Количество элементов каждой группы, а также
интенсивности их отказов приведены в табл. 1.9.
Таблица 1.9. Данные о числе элементов системы и интенсивности их отказов
Номер группы
I
2
. 3
4
Число элементов
10
15
32
8
Интенсивность отказа элемента, час"1
2-Ю-6
4-Ю"6
2,5-Ю-6
5-КГ6
Определить:
□ интенсивность отказа системы;
О среднее время безотказной работы;
□ вероятность безотказной работы системы в течение времени /, =100 час,
/2 = 1000 час и в интервале указанных наработок;
□ плотность распределения времени безотказной работы системы при
наработке t2 =1000 час.
Ответ: Л.с =2-10~4 час-1; Гс=4800 час; />(/,) = 0,9792; P(t2) = 0,8106;
Pft;/2) = 0,1686; /(/2) = 1,7-.10~4 час-1.
ЗАДАЧА 1.4. Система состоит из пяти элементов. Данные о их надежности
приведены в табл. 1.10.
Таблица 1.10. Законы распределения времени до отказа элементов и их параметры
Вариант
1
2
3
4
5
Элементы
I
TN(390; 100)
R(l • Ю-5)
Г(10;70)
TN(380; 100)
W(6; 195)
2
Г(9;65)
W(4,5; 180)
Ехр(5-Ю~5)
RO.6-10"5)
TN(410;95)
3
Ехр(8-10-5)
Г(8; 77)
TN(375; 86)
W(7;210)
Ехр(2-10-5)
4
R(2-10_s)
TN(400; 92)
R(3 • 10-5)
Ехрсг-ю-4)
Г(8; 75)
5
W(5; 200)
Ехр(1 • Ю-4)
W(4,8; 190)
Г(9; 85)
R(2,5-10"5)

расчет показателей надежности нерезервированных невосстанавливаемых систем 35
Определить:
О вероятность безотказной работы системы;
О среднее время безотказной работы системы;
О интенсивность отказов системы;
О плотность распределения времени до отказа системы.
Решение представить в аналитическом виде, в виде графиков и таблиц.
ЗАДАЧА 1.5. Система состоит из пяти элементов с экспоненциальными
законами распределения времени до отказа. Показателями их надежности
являются: /j(100) = 0,99, >-2 =0,00001 час"1, Т3 =8100 час, Г4 =7860 час,
Х5 =0,000025 час-1.
Определить время /, в течение которого система будет исправна с
вероятностью 0,92.
Ответ: / = 215 час.
ЗАДАЧА 1.6. Система состоит из пяти элементов с постоянными интенсив-
ностями отказов. Вероятности безотказной работы элементов в течение / часов
имеют следующие значения: Р,(100) = 0,99, Р2(200) = 0,97, />3(157) = 0,98,
Р4(350) = 0,95, Р5(120) = 0,98.
Определить вероятность безотказной работы системы в течение 625 часов ее
функционирования, а также среднее.время безотказной работы.
Ответ: Рс(625) = 0,4611; 7] =807 час.
ЗАДАЧА 1.7. Время работы до отказа серийно выпускаемой детали
распределено по нормальному закону с параметрами: ш = \000 час, а = 250 час.
Определить:
О вероятность того, что деталь проработает безотказно более 1200 часов;
Е вероятность того, что наработка до отказа будет находиться в интервале
[т-За, т + Зо];
О вероятность того, что безотказно проработав до момента времени
1200 часов, деталь безотказно проработает и до 1500 часов.
°твет: 0,2119; 0,9973; 0,1074.
3АДАЧА 1.8. Комплектующая деталь, используемая при изготовлении
устройства, по данным поставщика имеет нормальное распределение времени до

36
ЧАСТЬ I. Упражнения. Глава 1
отказа с параметрами т = 4000 час, а = 1000 час. Определить следующие
показатели надежности детали:
□ наработку до отказа, соответствующую 90 % надежности детали;
П вероятность того, что деталь имеет наработку, лежащую в интервале
[2000; 3000];
□ вероятность того, что деталь имеет наработку, большую чем 4000 часов.
Ответ: 2718 часов; 0,1359; 0,5.

ГЛАВА 2
РАСЧЕТ
ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
РЕЗЕРВИРОВАННЫХ
НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ
2.1. Методы расчета
показателей надежности
Критерии надежности резервированных невосстанавливаемых систем те же,
что и нерезервированных невосстанавливаемых систем.
Основными видами резервирования являются: общее постоянное, общее
замещением, раздельное постоянное, раздельное замещением. Структурные
схемы резервированных систем приведены на рис. 2.1.
Приведем основные соотношения для показателей надежности
резервированных систем.
2.1.1. Общее резервирование
с постоянно включенным резервом
Пусть />.(/) — вероятность безотказной работы /-го элемента за время /,
0(0 — вероятность отказа /-го элемента за время t, /•(/) — плотность
распределения времени до отказа /-го элемента в момент времени t. Тогда
вероятность безотказной работы, плотность распределения времени безотказной
работы и интенсивность отказов системы с кратностью резервирования т
определяются соотношениями:
т
ЗД=1-П0-^(О), <21>
/=0

38
ЧАСТЬ I. Упражнения. Глава 2
Рис. 2.1. Структурные схемы резервированных систем: общее резервирование
с постоянно включенным резервом (а), раздельное резервирование с постоянно включенным
резервом (б), общее резервирование замещением (в),
раздельное резервирование замещением (г)

Расчет показателей надежности резервированных невосстанавливаемых систем 39
m
Л(0= Z0-W))...//(/)...(l-/,m(O), (2.2)
/=0
m m
I//on aw
\(') = J"° J*J • (2.3)
1-П0О)
7 = 0
В частности, для экспоненциальных распределений времени до отказа
элементов с одинаковыми параметрами X имеют место равенства:
Pc(t) = \-(\-e~Xt)m+l, (2.4)
fc(t) = (m + \)Xe-kt(\-e-Xl)m, (2.5)
(m + \)\e-x'(\-e-x')m
W- x-Q-e-by* ■ . (26)
Среднее время безотказной работы системы определяется выражением:
1 WI+1 1 >
Формулы справедливы для случая, когда нерезервированная система
рассматривается как один элемент, показатели надежности которого известны.
В действительности любая система состоит из большого числа элементов,
каждый из которых имеет показатель надежности, самостоятельно
учитываемый при расчете. В таком случае формула для вероятности безотказной
работы имеет вид:
1(0=1-П 1-пр > (2-8)
где n — число элементов нерезервированной системы, Py(t) — вероятность
безотказной работы элемента с номером (/,у).
2-1.2. Общее резервирование замещением
Вероятность безотказной работы, плотность распределения времени до отка-
За и среднее время безотказной работы системы определяются выражениями:
/и
/,с(0 = /Ь(0+1/о*/*...*/м*^(0, (2-9>
/=1

40
ЧАСТЬ I. Упражнения. Глава 2
/c(0 = /o*/i *•..*/«(/), (2.Ю)
°о т
7j = p>c(0<//=l7j,.. (2.11)
о /=о
Если все элементы равнонадежны, то
т I
W) = Z /Ч/) * ПО = 1 - \f{m+X\x)dx. (2.12)
/=о о
Формулы содержат свертки функций, обозначенные символом (*). Свертка
функций /(/) и g(t), заданных при t > 0, определяется соотношением:
/ * £(0 = J/(/ - *Ж Jf )Л = J/(*)g(f - х)Л.
о о
Выражение /*( (0 = /*/* —*/(0 представляет собой /-кратную свертку
4 '
/
функции /(0.
Еслишнтенсивность отказов элементов постоянна и равна А, то формулы для
вероятности и среднего времени безотказной работы системы имеют вид:
^с(0=£^Л (2ЛЗ)
Гс=|(/и + 1).
2.1.3. Раздельное резервирование
Пусть исходная система состоит из п элементов. Тогда вероятность
безотказной работы системы при раздельном резервировании выражается
следующими формулами:
П раздельное резервирование с постоянно включенным резервом:
п ( т ^
^с(0=П i-nO-W) > (2Л4)
j=\\ /=о ;
□ раздельное резервирование замещением:
п т
W = ni.foj*fij*-*fi-ij*W). (2-15)
у = 1/=0

Расчет показателей надежности резервированных невосстанавливаемых систем 41
В формулах приняты следующие обозначения: Py(t) — вероятность
безотказной работы элемента с номером (/,./), /у(0 — плотность распределения
времени до отказа элемента, / = 0,1, 2,..., m, j-1, 2,..., n.
2.1.4. Резервирование с дробной кратностью
Приведем формулы для показателей надежности мажоритарных систем
(систем с дробной кратностью резервирования), в которых и — общее число
элементов, (n-m) основных и m резервных элементов. Отказ такой системы
наступает при отказе (т + 1)-го элемента.
Показатели надежности мажоритарной системы при условии, что все
элементы имеют одинаковую надежность, вычисляются по формулам:
т
Pcit)=YJC,„Ql{t)Pn-l{t), (2.16)
MO = (n-m)C'nnQm(t)Pn-m-\t)f(t), (2.17)
^.Mlgg'^m. (2.18)
Xcje'co^-'co
2.1.5. Скользящее резервирование
Скользящее резервирование представляет собой резервирование замещением
с кратностью т/(п - т), где п — общее число элементов, т — число
резервных элементов, (п-т) — число основных резервируемых элементов.
Вероятность безотказной работы системы со скользящим резервом при
условии, что все элементы системы имеют одинаковую надежность, равна
pc(')=Z. I f{kl)*P(t)f*{k*)*P(t)..JHk"-»)*P(t). (2.19)
А=0 kt+k2 +-+k„_m =k
Если элементы системы имеют экспоненциальное распределение
вероятности времени до отказа с параметром X, то вероятность безотказной работы,
интенсивность отказов и среднее время безотказной работы системы
соответственно равны:
/>(/) = £ (("-™Я0*с-(я-т)Х/ 9 (2.20)

42
ЧАСТЬ I. Упражнения. Глава 2
{{n-m)Xt)m
Xc(t) = (n-m)X —^ т, (2.21)
» ((n-m)Xtf
7JC=—7j. (2.22)
n-m
2.2. Примеры решения задач
Примеры и задачи для самостоятельного решения требуют использования
компьютерных технологий. Применение универсальных математических
программных средств позволит получить решение в короткое время без особого
труда. В некоторых случаях решение удается получить в аналитическом виде.
В примерах приводятся компьютерные технологии решения задач с
применением систем Derive 5 и Excel. В части IV книги приведено в
конспективной форме описание системы Derive 5. Рекомендуем ознакомиться с
этой системой прежде, чем решать задачи. Использовать эту систему
необходимо всегда, где требуется получить решение в аналитическом виде.
ПРИМЕР 2.1. Дана резервированная система с постоянным резервом
кратности т-2. Элементы системы имеют постоянную интенсивность отказа
А, = 0,05 час-1. Найти показатели надежности системы: вероятность
безотказной работы, плотность распределения времени до отказа, интенсивность
отказа, среднее время безотказной работы.
Решение. Воспользуемся формулами (2.4)—(2.6). Тогда получим:
рс (0 = 1-(1- e~Xt )m+1 = 1 - (1 - e~mi )3,
/с (/) = (//7 +1) Xe~Xt (\-е~)а)т=3-0,05е-°'05' (1 - <Г0'05' )2,
(/и + О^-^О-^Г 0>15^054l-g"0>05/)2 _ 0,15(1-в"0'05')2
с (0 1 _ (1 _ е-х/)-+! i _ (, _ в-о.05/ )3 з - 3<Г°'05/ + е~ои '
Табулируя функции, найдем искомые показатели надежности,
представленные в табл. 2.1.
Наиболее просто табулирование выполнить с помощью функции VECTOR
системы Derive. Технология табулирования на экране монитора имеет вид:

Расчет показателей надежности резервированных невосстанавливаемых систем 43
#1: l-d-e-^r1
#2: — (l-d-e-^r1)
dt
#3: A-e •(m + l)-(e -1)
•e -(m + l)-(e -1)
44 •
l-d-r^r1
#5: VECTOR( [t, l-CL-e"^)^1, A-e"X-t-(ra + 1) -(т + 1)-(еХ'с -1)т,
А-ё'х'''(т + 1)-(т + 1)-(ёл"с-1)га
;I -] , t, 0, 100, 5)
l-u-r^r1
#6: VECTOR([t,l-(l-e-0-05-t)2+1,0.05-e-°-05-t-(2+1)-(2 + l)-(e0-05-t-l)2,
0i05.e-o.05.f(2+i, eo.o5.t_ 2
>-o os-t 2+1 ]' fc' °' 100' 5)
l-(l-e °-05t)2+1
Пользователь вводит выражение вероятности безотказной работы (строка #1).
Функции /(/) и \(t) получены в соответствии с формулами:
Производная получена с помощью кнопки Find Derivative панели
инструментов (строки #2 и #3). Интенсивность отказа (строка #4) получена в
результате выполнения операции #3/#1. Функция табуляции представляется в
следующем виде:
VECTOR([t,#1,#3,#4],t, 0,100, 5)
С помощью кнопки Sub панели инструментов вводятся исходные данные
задачи. После щелчка мыши по кнопке Approximate на экране появится
решение в виде табл. 2.1.
Таблица 2.1. Показатели надежности резервированной системы
с постоянно включенным резервом и кратностью резервирования m = 2
/, час
0
5
10
15
РАО
1
0,989177
0,939084
0,853108
МО
0
0,005716
0,014085
0,019726
Ш
0
0,005778
0,014999
0,023122

ЧАСТЬ I. Упражнения.
Таблица 2.1 (окончание)
/, час
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
РМ
0,747420
0,636777
0,531138
0,435977
0,353538
0,284042
0,226594
0,179785
0,142048
0,111871
0,087884
0,068907
0,053947
0,042185
0,032958
0,025731
0,020078
МО
0,022049
0,021878
0,020200
0.017794
0,015177
0,012653
0,010374
0,008402 •
0,006743
0,005374
0,004260
0,003364
0,002648
0.002079
0.001630
0,001275
0,000997
КС)
0,029501
0,034357
0,038031
0,040814
0,042930
0,044546
0,045784
0,046736
0,047469
0,048036
0,048475
0,048815
0,049079
0,049283
0,049442
0,049566
0,049662

расчет показателей надежности резервированных невосстанавливаемых систем 45
Рис. 2.3. Интенсивность и плотность распределения времени до отказа
Графическая иллюстрация результатов дана на рис. 2.2 и 2.3.
Согласно (2.7), среднее время безотказной работы системы будет равно:
1 ОТ+1 1 / 1 1 \
ПРИМЕР 2.2. Требуется определить кратность резервирования системы с
постоянным резервом, обеспечивающим вероятность безотказной работы
0,96 в течение времени / = 150 час. Элементы системы равнонадежны и
имеют экспоненциальное распределение со средним временем безотказной
работы Г = 300 час. Найти также кратность резервирования для системы,
элементы которой имеют распределение Рэлея с тем же средним.
Решение. Кратность резервирования может быть определена по формуле:
^ino-^))
ln(l-/>(/))
где Р(г) — вероятность безотказной работы элемента в течение времени t,
^(0 = 0,96 — вероятность безотказной работы системы в течение
времени /.
Для экспоненциального распределения ^(0 = е~Х'', где X, =— —
интенсивность отказа элемента.

46
ЧАСТЬ I. Упражнения. Глава 2
-X /2 Я
Для распределения Рэлея P2(t) = e 2 , где Х2 =—j — параметр
распределения.
В течение времени t = 150 час получим:
О для экспоненциального закона:
P,(/) = e"V =е~т =е 300 =0,606531;
□ для закона Рэлея:
Tit2 я-1502
р2 (г) = е-V2 = е at2 = e 4-зоо2 = о, 821725 .
Подставляя значения Р,(/) и P2{i) в формулу для кратности резервирования
m ,получим:
□ для экспоненциального распределения:
ln(l-0,96) t
/w, = - -—- 1 = 2,45;
1 1п(1-0,606531)
О для распределения Рэлея:
'"(1-0.96) _, = М7.
2 1п(1-0,821725)
Округляя до целых чисел в большую сторону, получим тх =3, т2 = 1. Таким
образом, для достижения заданной надежности в первом случае потребуется
3 резервных элемента, а во втором случае — только один.
Из примера видно, что надежность системы определяется не только ее
структурой и временем работы, но также законом распределения времени до
отказа элементов.
ПРИМЕР 2.3. В условиях предыдущего примера необходимо обеспечить
заданную надежность системы в течение времени t = 450 час.
Решение. Определим вероятность безотказной работы элемента в течение
времени / = 450 час для экспоненциального распределения и распределения
Рэлея:
_t_ 450
/>(f) = e-V=e т =е зоо=0}22313,
Ш2 п-4502
P2(t) = e-^'2 =e «г2 =е 4™2 =0,17082.

расчет показателей надежности резервированных невосстанавливаемых систем 47
Найдем кратность резервирования:
О для экспоненциального распределения:
41-0,96)
1 1п(1-0,22313)
О для распределения Рэлея:
Ш(1-0,96)
2 ln(l-0,17082)
Округление до целых чисел дает требуемую кратность Wj =12, m2=\l.
Если система работает время t = 450 час, то для достижения заданной
надежности необходимо иметь 12 резервных элементов в первом случае и
17 резервных элементов во втором случае.
Из расчета следует, что структурное резервирование не может обеспечить
вероятность безотказной работы системы 0,96 в течение 450 часов. Кратность
резервирования настолько высока, что ее практическая реализуемость вряд
ли возможна.
ПРИМЕР 2.4. Структурная схема системы представляет собой
дублированную систему с постоянно включенным резервом. Элементы системы имеют
разные законы распределения времени до отказа: экспоненциальный с
интенсивностью отказа Я = 2• 10-3 час"1 и Вейбулла с параметрами ос = 4,
Р = 500 час. Необходимо определить: вероятность безотказной работы
системы Pc(t), среднее время безотказной работы 7|с, интенсивность отказов
Хс(/). Решение получить в виде формул, таблиц и графиков.
Решение. Задачу будем решать с помощью системы Derive. Процедуры
решения и результаты выглядят следующим образом:
#1: e~x-fc
#2: £-(2"10~3)-t
#3: r!t/f5f
#4: 4~(t/500)4
#5: (i-i-«2-io-3K).(1_r(t/sooy)
#6: !_(!_£- (2-icf 3)-t). (! _ £- (t/500)4}

48
ЧАСТЬ I. Упражнения. Глава 2
#7: ±U1^-i2-l0-3,ty{1_^it/b00)i))
dt
#8. £-tV62500000000 ( t3 e^500 -(t3 + 31250000)} ( e"t/50°
15625000000 15625000000 500
#9: }(l-(l-e-(2xl0"3,xt)x(l-e-(t/500)4))dt
о
#10: 661.8659584
--tVezsoooooooo .( t3 _ e"t/500-(t3+31250000)) + e"t/50°
#11. 15625000000 15625000000 500
1-(1-ё-(2'10"3к)-(1-е-(с/500>4)
#12: VECTOR([t,l-(l-e~<2'10 к).(1-е~и/500)4) ] , t, 0, 700, 100)
" 0 1
100 0.9997102011
200 0.9916673067
300 0.9451565831
#13 *
400 0.8149281452
500 0.6004235991
600 0.3890566915
700 0.2627644198_
В строках #1 и #2 представлены выражения вероятности безотказной работы
системы при экспоненциальном законе распределения времени до отказа, а в
строках #3 и #4 — при распределении Вейбулла. В строках #5 и #6 находятся
выражения вероятности отказа и вероятности безотказной работы системы
при общем резервировании с постоянно включенным резервом в виде
следующих формул: Qc(t) = (\-Pl(t))0-P2(t)), />c(0 = l-ft(0.
В строке #7 находится производная от вероятности отказа системы, а в
строке #8 — плотность распределения времени до отказа, полученная по формуле
/О = £'(').
В результате интегрирования вероятности безотказной работы (строка #9)
получено среднее время безотказной работы системы (строка #10), которое
равно примерно 662 часам.

Расчет показателей надежности резервированных невосстанавливаемых систем 49
В строке #11 находится выражение для интенсивности отказа системы,
полученное по формуле: Xc(t) = ——.
Табулирование функции Pc(t) осуществлено в строке #12, а его результаты
сведены в таблицу (строка #13).
На рис. 2.4 приведены зависимости от времени вероятностей безотказной
работы элементов. Из графиков видно, что вероятность безотказной работы
системы с законом распределения времени до отказа Вейбулла больше в
области малых значений / и меньше при больших /.
Рис. 2.4. Вероятность безотказной работы элементов системы с законом распределения
времени до отказа: экспоненциальным (кривая I) и Вейбулла (кривая 2)
Интересным, с точки зрения теории надежности, является график
интенсивности отказов резервированной системы, построенный системой Derive по
выражению #13 (рис. 2.5). Согласно теории интенсивность отказа
резервированной системы при t = 0 равна нулю и с ростом / приближается к
интенсивности отказа наиболее надежного элемента резервированной системы.
° нашем случае при больших / более надежной является система с экспо-
Ненциальным законом распределения времени до отказа, имеющей
интенсивность отказа Х = 0,002 час"1. Из рис. 2.5 видно, что это условие идеально вы-
"олняется.
ПРИМЕР 2.5. Дана резервированная система с постоянным резервом кратно-
сти m, все элементы которой равнонадежны и имеют усеченный нормальный
акон распределения времени до отказа с параметрами т0 = 400 час и

50
ЧАСТЬ I. Упражнения. Глава 2
Рис. 2.5. Интенсивность отказа системы
а0 = 200 час. Определить все показатели надежности системы. Результаты
представить в виде таблиц и графиков. Принять т = 0,1, 2.
Решение. Для равнонадежных элементов формулы (2.1)—(2.3) показателей
надежности принимают вид:
Pc{t) = 1 -(1 -P(t))m+], /с(/) = (ш +1)/(/)(1 -/»(/))",
XU)_(ni + \)f(Q(\-P(t))m
i-(i-A/))w+1
Плотность распределения времени до отказа и вероятность безотказной
работы для усеченного нормального распределения равны соответственно:
С-»'о)г 0,5-Ф0 е-
/(0= Н—Тъ* 2°1 ' >(0= Т^Т'
a0V2^ 0,5 + Фор^ 0,5+ Ф0-^
V lCToJJ Vao;
где Ф0(0 — функция Лапласа. Для исходных данных задачи получим:
nc ^ ff-400^
J/-40Q)2 0,5-Ф0 ——-
/■(/) = ! е 2-2002 р(/) = I 20Q J
200^(0,5+ Ф0 (2)) ' 0,5 + Ф0(2)

Расчет показателей надежности резервированных невосстанавливаемых систем 51
Значения вероятности безотказной работы системы Pc(t) для кратности
резервирования m = О, I, 2 содержатся в табл. 2.2. Соответствующие графики
приведены на рис. 2.6.
Таблица 2.2. Вероятность безотказной работы резервированной системы
/, час
0
50
100
150
200
250
300
350
400
450
500
550
600
650
700
750
800
850
900
950
1000
ш = 0
1,00000
0,98229
0,95492
0,91517
0,86093
0,79138
0.70756
0,61264
0,51164
0,41064
0,31572
0,23190
0,16235
0,10811
0,06836
0,04099
0,02328
0,01251
0,00635
0,00305
0,00138
w=l
1,00000
0,99969
0,99797
0,99280
0,98066
0,95648
0,91448
0,84996
0,76150
0,65265
0,53176
0,41003
0,29834
0,20453
0,13205
0,08030
0,04602
0,02486
0,01267
0,00609
0,00276
m — 2
1,00000
0.99999
0,99991
0,99939
0,99731
0,99092
0,97499
0,94188
0,88353
0,79528
0.67959
0,54684
0,41225
0,29053
0,19139
0,11800
0,06823
0,03706
0,01894
0,00912
0,00414
Следует иметь в виду, что при больших значениях / вероятность безотказной
работы настолько мала, что нет смысла эксплуатировать систему. Таблица
необходима только для иллюстрации результатов решения задачи,
представления решения в графическом виде и вычисления среднего времени
безотказной работы системы методом Симпсона.

52
ЧАСТЬ I. Упражнения. Глава 2
Рис. 2.6. Вероятность безотказной работы при различной кратности резервирования
Из графиков следует, что Pc(t) возрастает при увеличении кратности
резервирования, причем этот эффект тем сильнее, чем меньше т.
На основе данных табл. 2.2 приближенно вычислим среднее время
безотказной работы системы для значений /и = 0,1,2. Воспользуемся формулой
Симпсона:
П=- i+I(3+H)Vc(M) ,
в которой шаг интегрирования примем равным Л = 50 час, и = 20. Расчеты
показывают, что при т = 0 7] «411 час, при т = \ 7] «518 час, при /и = 2
7] « 573 час.
В табл. 2.3 содержатся значения плотности распределения вероятностей /с(/)
для той же кратности резервирования. Графики fc(t) приведены на рис. 2.7.
Таблица 2.3. Плотность распределения времени до отказа
/, час
0
50
100
150
200
ет = 0
0,00028
0,00044
0,00066
0,00093
0,00124
т=\
0,00000
0,00002
0,00006
0,00016
0,00034
т = 2
0,00000
0,00000
0,00000
0,00002
0,00007

Расчет показателей надежности резервированных невосстанавливаемых систем 53
Таблица 2.3 (окончание)
t, час
250
300
350
400
450
500
550
600
650
700
750
800
850
900
950
1000
/и = 0
0,00154
0,00180
0,00198
0,00204
0,00198
0,00180
0,00154
0,00124
0,00093
0,00066
0,00044
0,00028
0,00016
0,00009
0,00005
0,00002
т=\
0,00064
0,00105
0,00153
0,00199
0.00233
0,00247
0,00237
0,00207
0,00167
0,00123
0,00085
0,00054
0,00032
0,00018
0,00009
0,00005
/л = 2
0,00020
0,00046
0,00089
0,00146
0,00206
0,00253
0,00273
0,00261
0,00223
0,00173
0,00122
0,00079
0,00048
0,00027
0,00014
0,00007
рис. 2.7. Плотность распределения времени до отказа при различной кратности резервирования

54 ЧАСТЬ I. Упражнения. Глава 2
При т = О имеем график плотности усеченного нормального распределения
времени до отказа основной системы. С увеличением кратности
резервирования увеличивается среднее время безотказной работы и уменьшается
дисперсия. Указанные факторы более ощутимы для системы с меньшей кратностью
резервирования.
Интенсивности отказа системы для различных кратностей т имеют
значения, приведенные в табл. 2.4. Соответствующие графики показаны на
рис. 2.8.
Таблица 2.4. Интенсивность отказа резервированной системы
/, час
0
50
100
150
200
250
300
350
400
450
500
550
600
650
700
750
800
850
900
950
1000
ш = 0
0,00028
0,00045
0,00069
0,00102
0,00144
0,00195
0,00255
0,00323
0,00399
0,00482
0,00571
0,00664
0,00763
0,00864
0,00969
0,01077
0,01187
0.01298
0,01411
0,01526
0,01641
т=\
0,00000
0,00002
0,00006
0,00016
0,00035
0,00067
0,00115
0,00180
0,00262
0,00357
0,00464
0,00577
0,00695
0,00815
0,00935
0,01054
0,01173
0,01290
0,01407
0,01524
0,01640
т = 2
0,00000
0,00000
0,00000
0,00000
0,00002
0,00007
0,00020
0,00047
0,00095
0,00165
0,00259
0,00372
0,00499
0,00632
0,00768
0,00902
0,01032
0,01159
0,01282
0,01402
0,01521
Из графиков следует, что большей кратности резервирования соответствует
меньшая интенсивность отказов.

Расчет показателей надежности резервированных невосстанавливаемых систем 55
Рис. 2.8. Интенсивность отказа системы при различной кратности резервирования
ПРИМЕР 2.6. Определить вероятность безотказной работы и плотность
распределения времени до отказа мажоритарной системы, состоящей из /? = 5
элементов с постоянной интенсивностью отказа X = 0,004 час"1 при числе
резервных элементов m = 1, 2, 3 .
Решение. Для постоянной интенсивности отказов элементов P(i) = e~J,
Q{t) = 1 -e~Xt. В соответствии с формулами (2.16) и (2.17) получим
/MO-ICiO-e^ye-*"^, M) = {n-m)\Cnn{\-e~Xl)me-^-m)t.
/ = 0
Формула для Pc(t) представляет собой накопленные суммы биномиального
распределения вероятностей с параметрами и = 5 и p = \-e~Xt. Вычисления
по этим формулам в системе Derive настолько просто, что нет надобности
приводить здесь решение. Такие формулы также удобно программируются в
Excel. В колонку А запишем значения t от 0 до 500 часов с шагом 20 часов.
В ячейки В1 : F1 поместим кратность резервирования m. В ячейку В2
запишем формулу:
В2 « БИНОМРАСП(В$1;5;1-ЕХР(-0,004*$А2);1),
которую скопируем на остальные ячейки блока В2 : F27. В результате
получим табл. 2.5.

56
ЧАСТЬ I. Упражнения. Глава 2
Таблица составлена при т = 0,1, 2, 3, 4. Следует при этом иметь в виду, что
при т - 0 и т = 4 схема не является мажоритарной.
Таблица 2.5. Вероятность безотказной работы системы
с дробной кратностью резервирования
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
А
/, час
' 0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
320
340
360
380
400
420
440
460
480
500
В
0
1
0,6703
0,4493
0,3012
0,2019
0,1353
0,0907
0,0608
0,0408
0,0273
0,0183
0,0123
0.0082
0.0055
0,0037
0,0025
0,0017
0,0011
0,0007
0,0005
0,0003
0,0002
0,0002
0,0001
0,0001
0,0000
с
1
1
0,9495
0,8391
0,7097
0,5826
0,4681
0,3702
0,2891
0,2235
0,1714
0,1305
0,0989
0,0745
0,0560
0,0419
0,0312
0,0232
0,0172
0,0128
0,0094
0,0070
0,0051
0,0038
0,0028
0,0020
0,0015
D
2
1
0,9960
0,9744
0,9313
0,8697
0,7955
0,7145
0,6317
0,5511
0,4752
0,4056
0,3433
0,2883
0,2406
0,1995
0,1647
0,1353
0,1107
0,0902
0,0733
0,0594
0,0480
0,0387
0,0311
0,0250
0,0200
Е
3
1
0,9998
0,9979
0,9914
0,9780
0,9565
0,9266
0,8890
0,8448
0,7955
0,7428
0,6881
0,6329
0,5782
0,5251
0,4742
0,4262
0,3812
0,3396
0,3014
0,2666
0,2351
0,2067
0,1813
0,1586
0,1384
F
4
1
1,0000
0,9999
0.9996
0,9985
0,9961
0,9919
0,9855
0,9764
0,9644
0,9494
0,9314
0,9105
0,8870
0,8612
0,8334
0,8039
0,7730
0,7413
0,7089
0,6762
0,6434
0,6109
0,5788
0,5474
0,5167

Расчет показателей надежности резервированных невосстанавливаемых систем 57
Рис. 2.9. Вероятность безотказной работы мажоритарной системы
Графики Pc(t) при различном числе резервных элементов приведены на
рис. 2.9 (номера кривых соответствуют числу резервных элементов).
Из рисунка следует, что с ростом кратности резервирования надежность
системы существенно увеличивается.
Плотность /с(/) без постоянного коэффициента (n-m)X есть формула Бер-
нулли для вычисления вероятностей биномиального распределения в
зависимости от кратности резервирования с параметрами и = 5 и р-\-е~ '.
Поместим в колонку G время, а кратность резервирования в ячейки HI : L1.
В ячейку Н2 запишем формулу:
Н2 = (5-Н$1)*0,004*БИНОМРАСП(Н$1; 5; 1-ЕХР(-0,004*$А2); 0),
которую скопируем на остальные ячейки блока Н2 : L27. В результате
получим табл. 2.6, которая содержит значения плотности /с(/) при различных m
и /.
Табулирование функции /с(/) в системе Derive осуществляется с помощью
Функции VECTOR, которая представляется в следующем виде:
VECTOR([t,fl(t),f2(t),f3(t),f4(t)],t,0,500,20).
Это наиболее простой способ представления решения в табличном виде.
Графики плотностей изображены на рис. 2.10.

58 ЧАСТЬ I. Упражнения. Глава 2
Таблица 2.6. Плотность распределения времени безотказной работы системы
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
G
Л час
0
20
40
60
80
100
120
140
160
180
200
220
240
260
280
300
320
340
360
380
400
420
440
460
480
500
Н
0
0,02000
0,01341
0,00899
0,00602
0,00404
0,00271
0,00181
0.00122
0,00082
0,00055
0,00037
0,00025
0,00016
0,00011
0,00007
0,00005
0,00003
0,00002
0,00001
0,00001
0,00001
0,00000
0,00000
0,00000
0,00000
0,00000
1
1
0,00000
0,00447
0,00624
0,00654
0,00609
0,00532
0,00447
0,00365
0,00292
0,00230
0,00180
0,00139
0,00106
0,00081
0,00061
0,00046
0,00035
0,00026
0,00019
0,00014
0,00011
0,00008
0,00006
0,00004
0,00003
0,00002
J
2
0,00000
0,00056
0,00162
0,00266
0,00345
0,00393
0,00413
0,00411
0,00393
0,00365
0,00330
0,00293
0,00257
0,00222
0,00189
0,00160
0,00134
0.00112
0,00093
0,00077
0,00063
0,00051
0,00042
0,00034
0,00028
0,00022
К
3
0,00000
0,00003
0,00019
0,00048
0,00087
0,00129
0,00170
0,00206
0,00235
0,00256
0,00270
0,00276
0,00276
0,00270
0,00260
0,00248
0,00233
0,00216
0,00200
0,00183
0,00166
0,00150
0,00134
0,00120
0,00107
0,00095
L
4
0,00000
0,00000
0,00001
0,00003
0,00008
0,00016
0,00026
0,00039
0,00053
0,00068
0,00083
0,00097
0,00111
0,00124
0,00134
0,00144
0,00151
0,00157
0,00161
0,00163
0,00164
0,00163
0,00162
0,00159
0,00156
0,00151
Кривая 0 соответствует плотности распределения времени до отказа
нерезервированной системы, состоящей из 5 элементов. Кривая 4 представляет собой

Расчет показателей надежности резервированных невосстанавливаемых систем 59
плотность распределения времени до отказа резервированной системы с
одним основным и четырьмя резервными элементами.
Рис. 2.10. Плотность распределения времени безотказной работы мажоритарной системы
ПРИМЕР 2.7. Дана резервированная система с резервом замещением
кратности т = 2. Элементы системы имеют постоянную интенсивность отказа
А, = 0,05 час-1. Определить вероятность безотказной работы и среднее время
безотказной работы системы. Сравнить Pc(t) с постоянно включенным
резервом.
Решение. По формуле (2.13) получим:
J=o У' I 2 J
Рассчитанные Pc(t) при различных значениях t сведены в табл. 2.7. Для
сРавнения в таблицу помещены также значения Pc(t) для постоянно
включенного резерва.
* Рафик вероятности безотказной работы для обоих видов резервирования
"оказан на рис. 2.11.
вреднее время безотказной работы для резерва замещением по формуле
(2-П) равно Г1с = 37] =3-20 = 60 час. Для постоянного резерва, как было
показано в примере 2.1, это время составляет 36,7 часа.

60
ЧАСТЬ I. Упражнения. Глава 2
Таблица 2.7. Вероятность безотказной работы системы
при различных видах резервирования
/, час
0
10
20
30
40
50
60
70
80
90
100
ПО
120
130
140
150
160
170
180
Резерв замещением
1
0,985612
0.919699
0,808847
0,676676
0,543813
0,42319
0,320847
0,238103
0,173578
0,124652
0,088376
0,061969
0,043036
0,029636
0,020257
0,013754
0,009283
0,006232
Постоянный резерв
1
0,939084
0,74742
0,531138
0,353538
0,226594
0,142048
0,087884
0,053947
0,032958
0,020078
0,01221
0,007418
0,004504
0,002733
0.001658
0,001006
0,00061
0,00037
ПРИМЕР 2.8. Даны 3 системы с кратностями резервирования т = 0, 2, 4
(резерв замещением). Элементы системы равнонадежны и имеют гамма-
распределение времени до отказа с параметрами а = 3, р=100 часам.
Определить показатели надежности систем: вероятность безотказной работы,
плотность и среднее время безотказной работы. Привести таблицы и
графики.
Общее число элементов в системах равно п = 1,3, 5 соответственно.
Решение. Воспользуемся формулами (2.10)—(2.12). Если /(/) — плотность
гамма-распределения с параметрами а и р,то п — кратная свертка /*(и)(')

Расчет показателей надежности резервированных невосстанавливаемых систем 61
Рис. 2.11. Вероятность безотказной работы для резерва замещением (кривая 1)
и для постоянно включенного резерва (кривая 2)
также имеет гамма-распределение с параметрами woe и р. Поэтому
плотность распределения времени до отказа и вероятность безотказной работы
выражаются равенствами:
/с(0 = /Чл)(0 = — е К
/ ла-1 --
cW 0JPmr(Wa)
Плотность и функция гамма-распределения легко вычисляются в Excel. Для
этого на листе Excel в графе А поместим время /, изменяющееся от О
До 2000 часов с шагом 100 часов. Вторую строку таблицы заполним
формулами:
В2 = ГАММАРАСП(А2;1*3;100;0),
С2 = ГАММАРАСП(А2;3*3;100;0),
02 = ГАММАРАСП(А2;5*3;100;0),
Е2 = 1 - ГАММАРАСП($А2;1*3;100;1),
F2 а 1 - ГАММАРАСП($А2;3*3;100;1),
G2 = 1 - ГАММАРАСП($А2;5*3;100;1).

62
ЧАСТЬ I. Упражнения. Глава 2
В ячейках В2 : D2 содержатся значения плотности гамма-распределения
(последний аргумент равен 0) с параметром формы, соответствующим числу
элементов 1, 3, 5. В ячейках Е2: G2 содержатся значения функции гамма-
распределения (последний аргумент равен 1) с такими же параметрами
формы.
Копируя эти формулы на блок ячеек ВЗ : G22, получим табл. 2.8.
Таблица 2.8. Плотность и вероятность безотказной работы
для различной кратности резервирования
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
А
t
0
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
1800
1900
2000
В
Д/), »' = о
0
0,00184
0,00271
0,00224
0,00147
0,00084
0,00045
0,00022
0,00011
0,00005
0,00002
0,00001
0,00000
0,00000
0.00000
0,00000
0,00000
0,00000
0,00000
0,00000
0,00000
с
АЧт = 2
0
0,00000
0,00001
0,00008
0,00030
0,00065
0,00103
0,00130
0,00140
0,00132
0,00113
0,00089
0,00066
0,00046
0,00030
0,00019
0,00012
0,00007
0,00004
0,00002
0,00001
D
Мт = А
0
0,00000
0,00000
0,00000
0,00000
0,00000
0,00002
0,00007
0,00017
0,00032
0,00052
0,00073
0,00090
0,00102
0,00106
0,00102
0,00093
0,00080
0,00065
0,00051
0,00039
Е
/>(/), т = 0
1
0,9197
0,6767
0,4232
0,2381
0,1247
0,0620
0,0296
0,0138
0,0062
0,0028
0,0012
0,0005
0,0002
0,0001
0.0000
0,0000
0,0000
0,0000
0,0000
0,0000
F
P{t),m = 2
1
1,0000
0,9998
0,9962
0,9786
0,9319
0,8472
0,7291
0,5925
0,4557
0,3328
0,2320
0,1550
0,0998
0,0621
0,0374
0,0220
0,0126
0,0071
0,0039
0,0021
G
P(t),m = 4
I
1,0000
1,0000
1,0000
1,0000
0,9998
0,9986
0,9943
0,9827
0,9585
0,9165
0,8540
0,7720
0,6751
0,5704
0,4657
0,3675
0,2808
0,2081
0,1497
0,1049
По колонкам Е, F, G таблицы можно построить графики вероятности
безотказной работы для кратностей резервирования т = 0, 2, 4 (рис. 2.12).

расчет показателей надежности резервированных невосстанавливаемых систем 63
Рис. 2.12. Вероятность безотказной работы системы с резервом замещением
По колонкам В, С, D можно построить графики плотности распределения
времени безотказной работы для тех же кратностей резервирования
(рис. 2.13).
Рис. 2.13. Плотность распределения времени до отказа системы
с резервом замещением
вреднее время безотказной работы резервированной системы вычислим
По формуле (2.11): 7]с = пТх, где 7] = а|3 = 300 час — среднее время
безотказной работы одного элемента. Для системы с заданными кратностями ре-

64
ЧАСТЬ I. Упражнения. Глава 2
зервирования соответственно получим 7]с=7]=300 час, 7]с =37] =900 час,
7]с =57] =1500 час.
ПРИМЕР 2.9. Вычислить среднее время безотказной работы системы при
общем резервировании с постоянно включенным резервом и нормальном
законе распределения времени до отказа нерезервированной системы.
Решение получить в аналитическом виде и в виде таблицы при следующих
значениях исходных данных: кратность резервирования к = 1 ■*-10, параметры
нормального закона распределения w = 100, a = 20.
Решение. Далее приведена технология решения задачи в системе Derive.
#1: m :e Real (0,oo )
#2: a :e Real (0,оо )
# з : I . е~(t-ra)2/f 2'°2'
a-V(2-n)
#4: J ^=.e-(t-ra)/l2o,dt
0o-V(2-n)
л/i-m V2-(m-t)
ERF (- ) - ERF (-— -)
#5: ^ ^
2
Vi-m \/2-(m-t)
ERF ( ) - ERF ( - -)
#6: l-( 2lS Ъо }k+l
2
Vi-m Vi-(m-t)
t ERF ( ) - ERF ( -)
#7: f(l-( ^ && )kTl)dt
2
о /L
Vi-ioo Vi-(ioo-t)
«o ERF( )-ERF( -)
#8: f(l-( ^ 2l20 ^i)dt
2
>/i-ioo Vi-(ioo-t)
ERF( )-ERF( - )
#9: VECTOR([k, f(l-( ^^ 2j-2-2 )k+1) dt] , k, 0, 10)
2
0 Z

Расчет показателей надежности резервированных невосстанавливаемых систем 65
0
1
2
3
4
5
6
7
8.
9
10
126
164
196
226
255
284
312
340
367
395
422
4763203
2363726
3545833
4926806
.6407902
2017309
.3772958
.2821222
.9866182
5376220
6830879
В строках #1 и #2 определены области изменения переменных. В строке #3
приводится выражение плотности нормального закона распределения
времени до отказа. Интеграл (строка #4) от плотности является вероятностью
отказа системы (строка #5). В строке #6 определяется выражение вероятности
безотказной работы резервированной системы с кратностью к . В строках #7
и #8 находятся выражения среднего времени безотказной работы
резервированной системы. Табулирование функции осуществлено с помощью функции
VECTOR (строка #9), а ее результаты приведены в строке #10.
ПРИМЕР 2.10. Дана резервированная система со скользящим резервом,
состоящая из 4-х элементов: два основных и два резервных (и = 4,m = 2).
Время безотказной работы каждого элемента имеет нормальное распределение с
математическим ожиданием Т - 500 час и средним квадратическим
отклонением о* = 100 час. Найти вероятность безотказной работы, сравнить Pc(t) с
аналогичным показателем для экспоненциального распределения.
Решение. Раскрывая формулу (2.19) при п = 4, m = 2, получим
Рс (0 = Р2(0 + 2/ * P(t)P(t) + 2/*(2) * P(t)P(l) + (/ * P(t)f,
гДе P(t) — вероятность безотказной работы, а /(/) — плотность распреде-
ления времени до отказа одного элемента.
Поскольку сумма к независимых нормально распределенных случайных
еличин имеет нормальное распределение с параметрами кТ и -Jka, то:
3 Зак. 553
#10:

66
ЧАСТЬ I. Упражнения. Глава 2
\ yjk(5 J \ yjk+lG J
где Ф0(О — функция Лапласа. Тогда:
□ при к = 0
(t-тЛ
/>(/) = 0,5-Ф0 — ;
v cj ;
□ при к = \
/*Р(/) = Ф0 Ф0 п^~ ;
V су У Л V2a у/
□ при А; = 2
/(2)*Р(/) = Ф0 -7=- -Ф0 -г- .
Функция Лапласа совсем просто вычисляется в Excel. Оформим рабочий
лист, как показано в табл. 2.9. В колонку А запишем значения / от 0 до 1800
часов с шагом 100 часов. Значения Г и а поместим в ячейки G1 и HI
соответственно.
В ячейки В2 : Е2 запишем формулы, соответствующие вычислению функций
P(t),f*P(t),f{2)*P(t)nPc(t):
В2 = 1 - НОРМРАСП((А2 - $G$1)/$H$1; 0; 1; 1),
С2 = НОРМРАСП((А2 - $G$1)/$H$1; 0; 1; 1) - НОРМРАСП((А2 -
2*$G$l)/(KOPEHb(2)*$H$l); 0; 1; 1),
D2 = НОРМРАСП((А2 - 2*$G$1)/(КОРЕНЬ(2)*$Н$1); 0; 1; 1) -
НОРМРАСП((А2 - 3*$G$1)/(КОРЕНЬ(3)*$Н$1); 0; 1; 1),
Е2 = В2Л2 + 2*С2*В2 + 2*D2*B2+C2A2.
Из (2.20) получим вероятность безотказной работы резервированной системы
с элементами, имеющими экспоненциальное время до отказа:
^с,э(0 = 0 + 2^ + 2(^)2 )e~2Xt,
где X - — . В ячейку F2 поместим соответствующую формулу:
F2 = (1 + 2*А2/$М$1 + 2*(А2/$М$1)Л2) * ЕХР(-2*А2/$М$1).
В результате копирования формул на ячейки ВЗ : F20 получим табл. 2.9.

расчет показателей надежности резервированных невосстанавливаемых систем 67
Таблица 2.9. Расчеты вероятности безотказной работы
для нормального и экспоненциального распределений
1
2
3
4
5
6
7
8
9
10
11
12
13»
14
15
16
17
18
19
20
А
/
0
100
200
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
1600
1700
1800
В
/>(/)
1 •
0,999968
0,99865
0,97725
0,841345
0,5
0,158655
0,02275
0,00135
3,17Е-05
2.87Е-07
9,9Е-10
1,29Е-12
0
0
0
0
0
0
С
/*Р(0
2.87104Е-07
3,16859Е-05
0,001349959
0,02274969
0,158644207
0,499796482
0,839005810
0,960302572
0,920000380
0,760218327
0,499999713
0,239749986
0,078649653
0,016947366
0,002338930
0,000203518
1.10526Е-05
3,72109Е-07
7,73015Е-09
D
/(2) * P(t)
8J4349E-13
8J4349E-13
8,14238Е-13
8,13349Е-13
8,07798Е-13
7,93920Е-13
7,80154Е-13
7,74825Е-13
7J3936E-13
7J3936E-13
7.73936Е-13
7,73936Е-13
7,73936Е-13
7,73936Е-13
7J3936E-13
7,73936Е-13
7.73936Е-13
7,73936Е-13
7,73936Е-13
Б
PUQ
1,0000
1,0000
1,0000
1,0000
1,0000
0,9996
0,9953
0,9664
0,8489
' 0,5780
0,2500
0,0575
0,0062
0,0003
0,0000
0,0000
0,0000
0,0000
0,0000
F
PU0
1,0000
0,9921
0,9526
0,8795
0,7834
0,6767
0,5697
0,4695
0,3799
0,3027
0,2381
0,1851
0,1425
0,1088
0,0824
0,0620
0,0463
0,0344
0.0255
Из таблицы видно, что функция /*(2) * P{t) практически не влияет на
надежность всей системы. На основе колонок Е и F построены графики
вероятностей безотказной работы -PCtH(t) и ^>э(/) для нормального и
экспоненциального случаев. Они представлены на рис. 2.14.
Рафики вероятностей безотказной работы системы со скользящим резервом
^я рассмотренных законов распределения очень сильно отличаются друг от
Друга. В случае нормального распределения (с малой дисперсией) в течение
Отельного времени работы система практически абсолютно надежна, но в
Учение короткого времени она теряет ресурс и быстро становится нена-
Де*ной.

68
ЧАСТЬ I. Упражнения. Глава 2
Рис. 2.14. Вероятность безотказной работы системы при нормальном (кривая I)
и экспоненциальном (кривая 2) распределениях
2.3. Задачи для самостоятельного решения
ЗАДАЧА 2.1. Техническая система представляет собой дублированную
систему с постоянно включенным резервом. Вероятность безотказной работы
основной и резервной подсистем в течение / = 200 час равна 0,8. Найти
вероятность безотказной работы и вероятность отказа системы в течение времени
/. Найти среднее время безотказной работы системы при условии, что ее
подсистемы имеют постоянную интенсивность отказа.
Ответ: Рс(/) = 0,96, g.(/) = 0,04, 7|c=1344 час.
ЗАДАЧА 2.2. Интенсивность отказа элементов системы Я, = 0,0025 час".
Требуется определить кратность резервирования системы с постоянно
включенным резервом, построенную из этих элементов, которая обеспечивает
среднее время безотказной работы системы 7]с = 800 час.
Ответ: т = 3 .
ЗАДАЧА 2.3. Найти показатели надежности резервированной системы
с постоянным резервом кратности /и = 3, элементы которой имеют
интенсивности отказа Х0 =0,004 час"1, Х{ =0,007 час-1, Х2 =0,002 час",
Х3 =0,001 час-1. Время непрерывной работы системы / = 120 час.

Расчет показателей надежности резервированных невосстанавливаемых систем 69
ЗАДАЧА 2.4. Определить показатели надежности мажоритарной системы,
состоящей из 6 равнонадежных элементов, время до отказа которых
равномерно распределено на интервале от 0 до 1000 часов. Количество резервных
элементов равно 2. Получить аналитическое и графическое представления
показателей надежности системы.
ЗАДАЧА 2.5. Получить формулу для вероятности безотказной работы
мажоритарной системы, состоящей из элементов разной надежности при л = 4,
/и = 2.
ЗАДАЧА 2.6. Интенсивность отказа одного элемента А. = 0,0035 час"1.
Требуется определить кратность резервирования системы (резерв замещением),
построенную из этих элементов, которая обеспечивает среднее время
безотказной работы системы 7]с = 800 час.
Ответ: т = 2.
ЗАДАЧА 2.7. Найти показатели надежности Pc(t), Tc, Xc(t)
резервированной системы (резерв замещением) кратности w = 3, элементы которой имеют
интенсивности отказа Х0 =0,04 час-1, X,j =0,07 час"1, Х2 =0,02 час-1,
Х3 = 0,1 час"1. Решение получить в виде формул, таблиц и графиков.
ЗАДАЧА 2.8. Для резерва замещением кратности m получить формулу
вероятности безотказной работы, если элементы системы равнонадежны и
имеют гамма-распределение времени до отказа с параметрами аир.
ЗАДАЧА 2.9. Для резерва замещением кратности m получить формулу
плотности распределения времени безотказной работы при условии, что элементы
системы равнонадежны и имеют нормальное распределение с параметрами
'« и о (а < т/3):
ЗАДАЧА 2.10. Даны две системы со скользящим резервом. Первая система
состоит из п = 7 элементов, из которых т = 3 резервных. Вторая система
состоит из п = 5 элементов с т = 2 резервными. Определить более надежную
систему по критерию вероятности безотказной работы. Элементы обеих сис-
ем имеют постоянную интенсивность отказа X = 0,01 час"1.
Чцача 2.11. Дана последовательно-параллельная система размером ЗхЬ
^5 элементов нерезервированной системы, 3 резервных подсистемы) с посто-

70
ЧАСТЬ I. Упражнения. Глава 2
янно включенным резервом. Все элементы имеют одинаковую надежность,
время до отказа элементов имеет распределение Рэлея с математическим
ожиданием Т = 50 час. Требуется определить вероятность безотказной
работы системы при общем и раздельном резервировании. Провести сравнение по
критерию Pc{t).
Указание: воспользоваться формулами (2.8) и (2.14).
ЗАДАЧА 2.12. Дана последовательно-параллельная система размером 3x5
(5 элементов нерезервированной системы, 3 резервных подсистемы),
резервированная методом замещения. Все элементы имеют одинаковую
интенсивность отказа А, = 0,02 час-1. Требуется определить вероятность безотказной
работы системы при общем и раздельном резервировании. Провести
сравнение по критерию Pc(t).
Указание: воспользоваться формулами (2.9) и (2.15).
ЗАДАЧА 2.13. Элементы резервированной системы с постоянно
включенным резервом имеют распределение Вейбулла времени работы до отказа.
Найти выражение для среднего времени безотказной работы системы при
кратности резервирования m = 0,1, 2, 3, 4, 5 . Вычислить среднее время
безотказной работы при параметрах закона распределения а = 2,5, р = 20.
Решение представить в виде таблицы.
ЗАДАЧА 2.14. Элементы резервированной системы с постоянно
включенным резервом имеют усеченно-нормальное распределение времени до отказа.
Найти выражение для среднего времени безотказной работы системы при
кратности резервирования m = 0,1, 2, 3, 4, 5 . Вычислить значение среднего
времени безотказной работы при параметрах закона распределения mQ =380,
сг0 = 200. Решение представить в виде таблицы.
Указание: воспользоваться программными средствами символьной
математики, например Derive 5.
ЗАДАЧА 2.15. Даны две системы с постоянно включенным резервом с
дробной кратностью резервирования m = 1/2 и m - 2/3 соответственно.
Определить показатели надежности систем Pc(t), Tc, А-с(0- Решение представить в
виде формул, графиков и таблиц. Известны следующие исходные данные для
числового анализа: время работы системы / = 0^-500 час, среднее время
безотказной работы нерезервированной системы Г = 550 час, основная и все

Расчет показателей надежности резервированных невосстанавливаемых систем 71
резервные системы равнонадежны и имеют экспоненциальное распределение
времени до отказа. Определить, какая из систем имеет более высокие
показатели надежности.
ЗАДАЧА 2.16. Даны две системы, описанные в задаче 2.15. Определить
критическое время /кр, свыше которого резервирование с дробной кратностью
не целесообразно. Определить значение вероятности Д'кр)- Решение
получить в аналитическом и численном виде.
ЗАДАЧА 2.17. Даны две системы, описанные в задаче 2.15. Определить
аналитические выражения интенсивностей отказов резервированных систем и
найти предел lim Xc(t). Представить функцию \c(t) в виде графика и объяс-
нить полученный результат.
Ответ: 2Х и ЗА,.
ЗАДАЧА 2.18. Резервированная система с постоянно включенным резервом
состоит из двух подсистем, имеющих различные законы распределения
времени до отказа. Необходимо вычислить Pc(t), Tlc, Xc(t). Решение получить в
аналитическом виде, в виде графиков и таблиц. Графики представить в
диапазоне t = 0 ч- 500 час. Исходные данные содержатся в табл. 2.10.
Таблица 2.10. Законы распределения времени до отказа
козание: решение целесообразно получить с помощью систем символьной
Математики, например Derive 5.
Вариант
1
2
3
4
5
Законы
распределения
Ехр(0,005)
R(0,0002)
Ехр(0,004)
N(400; 120)
Ехр(0,007)
Г(4; 120)
W(3; 50)
R(0,0005)
W(l,5; 150)
Г(2,5; 145)
Вариант
6
7
8
9
10
Законы
распределения
W( 1,2; 200)
TN(400; 180)
N(360; 110)
Г(4;95)
N(410; 130)
R(0,0006)
R(0,0004)
Г(3,2; 220)
Ехр(0,001)
W(l,l; 160)
Вариант
11
12
13-
14
15
Законы
распределения
Ехр(0,0015)
TN(350; 180)
R(0,0001)
TN(390; 190)
W(2; 100)
N(360; 100)
N(420; 140)
TN(380; 200)
TN(400;215)
Exp(0,002)

ГЛАВА 3
РАСЧЕТ
ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
НЕРЕЗЕРВИРОВАННЫХ
ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
3.1. Сведения из теории
Критериями надежности нерезервированных восстанавливаемых систем
являются:
□ Kr(t) — функция готовности (вероятность того, что система готова к
работе в произвольный момент времени /);
□ Кг — коэффициент готовности (финальная вероятность того, что система
исправна в произвольный момент времени /);
□ Т — наработка на отказ (среднее время между отказами);
□ Тв — среднее время восстановления системы;
□ со(0 — параметр потока отказов.
Между этими показателями существуют следующие зависимости:
Т
Кг = ,
т+тв
Kr = \\mKr(t).
Показатели надежности восстанавливаемых и невосстанавливаемых систем
связаны между собой следующим интегральным уравнением:
<o(/) = /(/)+Jco(t)/(/-t)</t,
о

Расчет показателей надежности нерезервированных восстанавливаемых систем 73
где /(0 — плотность распределения времени до отказа невосстанавливае-
м0й системы.
решение этого интегрального уравнения не позволяет получить в явном виде
зависимость функции готовности от таких показателей надежности системы,
как вероятность безотказной работы, интенсивность отказов, наработка на
отказ, среднее время восстановления и др.
Простых расчетных соотношений в виде формул для определения функции
готовности не существует даже для простейших случаев. Рассмотрим этот
вопрос более подробно на примере системы как одного элемента.
3.1.1. Надежность восстанавливаемой системы
как одного элемента
Пусть /(/) — плотность распределения времени до отказа, P{t) —
вероятность безотказной работы, Т — математическое ожидание времени до
отказа, g(t) — плотность распределения времени восстановления системы, Гв —
математическое ожидание времени восстановления.
Основная сложность расчета показателей надежности состоит в вычислении
функции готовности Kr(t).
Из теории известно [5, гл. 2], что функция готовности удовлетворяет
интегральному уравнению:
A:r(/)=/*g*A:r (о+/>(/). (3.i)
Решением уравнения (3.1) является функция
Kr(0 = P(0+tfHk)*gHk)*nO- (3.2)
Функция Kr(t) представлена в аналитическом виде, но в общем случае
непригодна для инженерных расчетов. Рассмотрим частные случаи,
допускающие аналитическое или численное решение уравнения (3.1).
Постоянные интенсивности отказа и восстановления
Пусть X — интенсивность отказа, а ц — интенсивность восстановления
системы. Тогда
^1.(0 = -Ё-+-^-^(Х+ц)'. <3-3>
Х + р. А, + р.
fro следует из решения системы дифференциальных уравнений, а также из
Формулы (3.1).

74
ЧАСТЬ I. Упражнения. Глава 3
Нормальные законы распределения времени до отказа
и времени восстановления
Пусть время до отказа и время восстановления имеют нормальные
распределения с параметрами соответственно Т и а, Тв и ств.
Члены ряда (3.2) представим в виде разности двух функций распределения:
/*(*) * g*<*> * р(() = /*(*) * g4*> * i(^) _ /*(*+1> * g*(*> * i(/).
Так как /** '(f) — плотность нормального распределения с параметрами кТ
и yflcG, a g*^k\t) — плотность нормального распределения с параметрами
кТв и у[къв, то /**** * g**** * 1(/) — функция нормального распределения
с параметрами кТ + кТв и <Jka + кхув . Аналогично /** +,)*g-*( '*1(/) —
функция нормального распределения с параметрами (к + \)Т + кТв и
yj(k + \)о2 + key] . Тогда:
( Л ( Л
r*ik\ *(кл гч. ч ^ t-kT-kTn ^ t - (к + \)Т - кТЛ
f{k)*gik)*P(0=% I , ! -Фо / , .
ykG2+kG2B) {yj(k + l)cj2+kGl)
где Ф0(/) —функции Лапласа.
На основании (3.2), получим следующую формулу для коэффициента
готовности:
( ( \ ( \\
#Г(0 = 0,5-Фо +S фо / -Фо , = •
Произвольные интенсивности отказа и восстановления
Самый простой способ решения интегрального уравнения (3.1) для случая
разных интенсивностей отказов и восстановлений элементов состоит в
использовании численных методов. По определению свертки из (3.1) получим:
Кг (/) = J/ * g(t - x)Kr(x)dx + PQ).
о
Для вычисления интеграла применим формулу трапеций:
( *-i "I
Kr{kh) = h 0,5*f*g(kh)+I,f*g((k-i)h)Kr(ih) +P(kh), * = 1,2,...,л,
(3.4)

где h —шаг интегрирования; п —требуемое количество значений функции
готовности.
Выбор формулы трапеций связан с тем, что на каждом шаге значение Kr(t)
зависит только от значений, вычисленных на предыдущих шагах. Точность
вычислений обеспечивается надлежащим выбором шага интегрирования.
Пусть время восстановления системы постоянное, т. е. g(t) = дт (/). Тогда
f*g(t) = f*bT(t) = \
в [0, при /<ГВ.
Аналогично можно получить формулы свертки, а значит, и алгоритм
вычисления Kr(t) для некоторых других распределений времени до отказа и
восстановления. Но в общем случае рассчитывать значения функции f*g(J)
приходится на основе численных методов с применением квадратурных
формул Симпсона, Котеса и др. Если плотности распределения являются
непрерывными функциями и время восстановления системы невелико по
сравнению со временем ее работы, то можно применить формулу Гаусса. Для
функции ф(/) = / * g(t) формула Гаусса с к узлами имеет вид:
\ф)ск = - j<p -* + - <& = -Хс/Ф т*/+т >
где Cj и Xj — соответственно веса и узлы квадратурной формулы Гаусса.
В табл. 3.1 приведены веса и узлы для случая к = 7.
Таблица 3.1. Веса и узлы формулы Гаусса
/
1
2
3
4
5
6
7
с,
0.129484966168870
0,279705391489277
0,381830050505119
0,417959183673469
0,381830050505119
0,279705391489277
0,129484966168870
х,
-0,949107912342759
-0,741531185599394
-0,405845151377397
0,000000000000000
0,405845151377397
0,741531185599394
0,949107912342759
Расчет показателей надежности нерезервированных восстанавливаемых систем 75

76
ЧАСТЬ I. Упражнения. Глава 3
3.1.2. Показатели надежности
восстанавливаемой системы,
состоящей из л элементов
Схема расчета надежности системы очевидна. Она представляет собой
последовательное, в смысле надежности, соединение Элементов.
Приведем расчетные соотношения для показателей надежности системы,
состоящей из п элементов. Стационарные показатели надежности
восстанавливаемой системы выражаются через среднее время безотказной работы и
среднее время восстановления элементов [5, гл. 7]. При этом наработка на
отказ Т, среднее время восстановления Тв и коэффициент готовности Кг
системы определяются по формулам:
« т
I Т 1
Т = , г =ilLJ_ к ! . (3.5)
у± yi. 1 + yiaL
i-U rp i—l rp Z_i rp
1=1*1 i=\li /=1 Ji
В большинстве практических случаев при расчетах показателей надежности
невосстанавливаемых и восстанавливаемых систем известными являются
интенсивности отказов Х{ и интенсивности восстановления Ц; элементов,
/ = 1, 2,..., и. Тогда формулы для показателей надежности имеют вид:
I n 1 n 5l T 1
л ' С £-* I ' В л Z-i ' Г T.I-T » }
лс /=1 лс/=1^/ у +iB ] + y^L
Для функции готовности системы простые расчетные соотношения
отсутствуют. Рассмотрим способы и алгоритмы вычисления Kr(t).
Экспоненциальный закон распределения времени до отказа
и времени восстановления элементов
Математической моделью функционирования системы является система
обыкновенных дифференциальных уравнений:
р'о(0 = -KPoiO+£и,а(0; „ „
/=1 (З.о)
/?,'(/) = X,p0(0-ViPiO)> i = l 2,..., n,

Расчет показателей надежности нерезервированных восстанавливаемых систем 77
где-'
О X/ —интенсивность отказа /-го элемента;
р Хс = Y, ^/ — интенсивность отказа системы;
О ц,- — интенсивность восстановления /-го элемента;
О Л)(0 = ^г(0 — вероятность того, что в момент / система исправна;
О /?/(/) — вероятность того, что в момент / система находится в
неисправном состоянии вследствие отказа /-го элемента.
Систему (3.6) линейных дифференциальных уравнений с постоянными
коэффициентами можно решить двумя способами: аналитическим и численным.
Однако получить решение в виде формулы для произвольного и можно лишь
для случая ограниченного числа элементов или при фиксированных
значениях интенсивностей их отказа и восстановления.
Существуют приближенные методы, позволяющие получить решение в
аналитическом виде. Однако при этом возникают проблемы с оценкой
погрешностей результатов вычисления показателей надежности.
Проще всего решить систему (3.(5) численным методом, например, методом
Рунге — Купы.
Экспоненциальный закон распределения времени до отказа
и произвольный закон времени восстановления элементов
Математической моделью является система интегральных уравнений
[5, гл. 7]. Если время безотказной работы /-го элемента имеет
экспоненциальный закон распределения с параметром А,,, то из системы интегральных
Уравнений следует, что функция готовности удовлетворяет интегральному
Уравнению:
КГ(() = Xce~Kt *g*Kr(t) + е~х*', (3.7)
1 "
гДе g(/) = — Y,^i8i(0 — плотность распределения времени восстановления
К 1=1
системы; g,(/) — плотность распределения времени восстановления /-го
элемента.
Согласно (3.7) функционирование нерезервированной системы с
постоянными интенсивностями отказов с позиций надежности эквивалентно функцио-

78
ЧАСТЬ I. Упражнения. Глава 3
нированию системы, имеющей интенсивность отказов Xc = '£\i и закон рас-
/=1
1 Л
пределения времени восстановления g(t) = — 2^/ЯДО- Плотность g(/)
представляет собой среднее взвешенное плотностей распределения времени
восстановления элементов.
Пусть интенсивность восстановления /-го элемента постоянна й равна jn,.
Тогда g(t) = — J] ^/Ц,е Ц// , и функция готовности нерезервированной
системе /=1
мы с любым числом элементов совпадает с функцией готовности одного
элемента, имеющего гиперэкспоненциальную плотность распределения времени
восстановления. Способ нахождения Kr(t) в этом случае был описан ранее в
разд. 3.1.1. Применение численного метода связано с определением свертки
функций /(/) = Хсе~Хс' и g(t). В предположении, что ц, ф Хс , получим:
/*^=iw"M*^4^T(^c'-^'). (3.8)
1 = 1 / = lM-/~^C
Пусть время восстановления элементов системы постоянное, т. е.
1 "
ЯДО = 87- (0. / = 1,2,..., W. Тогда g(t) = — Х^б^/), и,значит,
"-с /=1
/*g(0 = I^(0^-v = E^r ' при/.у , (39)
/=1 /=1 [0, при /<ГВ/.
Аналогично можно получить формулы свертки, а следовательно, и алгоритм
вычисления Kr(t) для некоторых других распределений времени
восстановления.
Произвольные законы распределения времени до отказа
и времени восстановления элементов
В общем случае функция готовности нерезервированной системы, состоящей
из п элементов, имеет вид:
/, =0/4=0 /л=0
(З.Ю)

Расчет показателей надежности нерезервированных восстанавливаемых систем 79
где:
0 /•(/) — плотность распределения времени безотказной работы;
О Л-(0 — вероятность безотказной работы у'-го элемента;
О gj(0 — плотность распределения времени восстановления у'-го элемента,
j = 1, 2,..., я.
формула (3.10) не годится для вычислений. Однако на ее основе для ряда
распределений могут быть получены конечные выражения. Предположим,
что время восстановления элементов постоянное g (t) = 5r (/). Тогда
J в/
x,w= 11Л(ащ)*^-/2{'2)*р2----/:ы*рЛ'-1',-тЛ (з.п)
i,=0/2=0 /„=0 \ k = \ J
причем слагаемое, соответствующее набору (/,, /2,..., /я), обращается в нуль,
п
если / < X 4 • 71/, •
А = 1
Рассмотрим два частных случая.
Случай 1. Время безотказной работы у-го элемента имеет нормальное
распределение вероятностей с параметрами Tj и ау . Тогда
И*аУ J I ** + 1аУ J
где Ф0(/) — функция Лапласа. В результате из (3.11) получим следующую
формулу для функции готовности системы:
. . . J ('-w-ii-^l ('-('y+^y-ii^l
*<'>=! Z-..Z п Фо г^ ф0 —-7=^ •
/,=0,2=0 /„=0y=I д/'уО/ >/'У+1оУ
< V ) \ ')
(3.12)
Случай 2. Время безотказной работы у-го элемента имеет гамма-распре-
Деление вероятностей с параметрами oty и |3у. Тогда
( Л ( t)
fj{lj)*Pj(0 = f ijaj,{- -I Су+ !)*>. «- •
V рУУ V pJ J

80
ЧАСТЬ I. Упражнения. Глава 3
f ( n } ( " V
*r(')=E Z-Z П / ijbj*—^ 1 (О+^у—4 .
/,=0/2=0 /Я=0У=1 Py Py
ч V ) V J)
(3.13)
где I(k,t) —неполная гамма-функция.
Несмотря на то, что (3.12) и (3.13) выражаются многократными рядами,
слагаемые в них являются совсем несложными для разработки быстро
работающего алгоритма.
Существенным недостатком полученных выражений является, во-первых,
отсутствие общности законов распределения и, во-вторых, возможность
использования этих формул только для систем с числом элементов, не
превышающих нескольких десятков.
Функция готовности нерезервированной системы с большим числом
элементов, подчиненных не экспоненциальным законам распределения времени
до отказа, может быть получена только приближенно в соответствии с
формулой:
*г(0 = , (3.14)
х, у *п,(0
Ы*г/С)
где Kni(t) — функция простоя, a Kri(t) — функция готовности /-го
элемента. Вопрос о погрешности формулы (3.14) рассмотрен в [5, гл. 7].
Для расчета надежности нерезервированных систем можно использовать
программное средство Conspz.exe, описание которого приведено в части. IV.
3.2. Примеры решения задач
ПРИМЕР 3.1. Нерезервированная система состоит из 8 элементов.
Интенсивности их отказов приведены в табл..3.2.
Номер
элемента
Х„ час"1
1
0,0003
2 3 4 5 6
0,0002
0,0009
0,0006
0,0004
0,0003
7
0,0005
8
0,0007
Таблица 3.2. Интенсивности отказов элементов

расчет показателей надежности нерезервированных восстанавливаемых систем 81
Интенсивности восстановления элементов одинаковы и равны ц. = 0,4 час-1.
Требуется определить показатели надежности системы.
решение. Вычислим интенсивность отказа системы:
Я.с = £ А., = 0,00Q3 + 0,0002 + 0,0009 + 0,0006 + 0,0004 +
+0,0003 + 0,0005 + 0,0007 = 0,0039.
Тогда наработка на отказ, среднее время восстановления и коэффициент
готовности равны соответственно:
Т = — = —!— = 256,4 час,
Хс 0,0039
•/„= — = = 2,5 час,
Ц 0,4
Кг=—^—= 25М =0,9903.
г Т + Тъ 256,4 + 2,5
Поскольку интенсивности восстановления элементов одинаковы, то систему
можно рассматривать как один элемент с интенсивностью отказов Хс и
интенсивностью восстановления р.. Согласно (3.3) получим:
г Лс+ц Xc+ii 0,4039 0,4039
Табулируя функцию от 0 до 40 часов с шагом 2 часа, получим значения,
приведенные в табл. 3.3.
/, час
0
2
4
6
8
10
12
Kr(t) /, час АГг(0 /, час
1
0,994649
0,992263
0,9912
0,990726
0,990514
0,99042
14
16
18
20
22
24
26
0,990378
0,990359
0,990351
0,990347
0,990345
0,990345
0,990344
28
30
32
34
36
38
40
КМ
0,990344
0,990344
0.990344
0,990344
0,990344
0,990344
0,990344
Таблица 3.3. Функция готовности системы

82
ЧАСТЬ I. Упражнения. Глава 3
График функции готовности изображен на рис. 3.1.
Из рис. 3.1 видно, что время переходного процесса мало ^составляет
примерно 10 часов. Это значит, что в случае высоконадежной системы
(Кг >0,99) и большой длительности ее работы готовность системы
целесообразно оценивать коэффициентом готовности.
Рис. 3.1. Функция готовности системы для одинаковых интенсивностей восстановления
ПРИМЕР 3.2. Нерезервированная система состоит из 8 элементов. Их
интенсивности отказов те же, что и в табл. 3.2. Интенсивности восстановления
различны и приведены в табл. 3.4.
Таблица 3.4. Значения интенсивностей восстановления элементов
Номер элемента
ц„ час"1
1
0,5
2
0,2
3
0,1
4
0,4
5
0,9
6
0,7
7
0,6
8
0,8
Требуется определить показатели надежности системы.
Решение. По формулам (3.5) находим стационарные показатели надежности:
г-— т -tlh. к 1
/-1*1/

Расчет показателей надежности нерезервированных восстанавливаемых систем 83
Как и в предыдущем примере, интенсивность отказа системы
X =0,0039 час"1. Вычислим сумму
ДА., 0,0003 0,0002 0,0009 0,0006 0,0004 0,0003
~1Ц/ 0,5 0,2 0,1 0,4 0,9 0,7
+М005 + 010007= '
0,6 0,8
Тогда
Т = —-— = 256,4 час, Т.в = 0,0147=3,77 час, Кг = ! = 0,9855.
0,0039 в 0,0039 г 1 + 0,0147
Определим функцию готовности системы следующими способами:
О решение системы дифференциальных уравнений аналитическим методом;
□ решение системы дифференциальных уравнений численным методом;
□ решение интегрального уравнения;
О приближенный способ объединения узлов графа состояний системы.
Решение системы дифференциальных уравнений аналитическим методом
Составим систему дифференциальных уравнений типа (3.6):
Ро(0 = "А: А) (0 + V-\P\ (О + ViPi (0 + Из/Ъ(0 + ^4 МО + VsPsiO +
+ РвРбО)+v-iPi (О+^ А$(0;
/?2(0 = а.2ро(0-Ц2Р2(0;
^(О^зРоСО-ЦзРзСО;
Р4(0 = я.4/?0(/)-ц4/?4(0;
Р5(0 = ^5Ро(0-ц5Р5(0;
Рб(0 = ^бА)(0-ц6А>(0;
Р7(0 = ^7Ро(0-ц7Р7(0;
.Р8(0 = ^8Ро(0-ц8/?8(0-

84 ЧАСТЬ I. Упражнения. Глава 3
Система дифференциальных уравнений в преобразовании Лапласа имеет вид:
О + Xc)p0(s) - u,/?, О) - [i2p2(s) - \x3p3(s) - \i4p4(s) - \isp5(s) -
-y-6P6(s)-^Pi(s)-^Ps(s) = ^
(s + ^\)P\(s)-Xlp0(s) = 0;
(s + ii2)p2(s)-\2p0(s) = 0;
(s + \i3)p3(s)-X3p0(s) = 0;
(s + \x4)p4(s)-X4p0(s) = Q;
(s + li5)p5(s)-X5pQ(s) = 0;
(s + V>6)P6(s)-hPo(s) = °>
(s + \i7)p7(s)-X7p0(s) = 0;
(s + ^)ps(s)-X^po(s) = 0.
Решение этой системы алгебраических уравнений выполнено с помощью
функции SOLVE системы Derive 5. Выражение функции готовности в
аналитическом виде здесь не приводится в связи с его громоздкостью. После
подстановки значений интенсивностей X и ц функция готовности принимает
следующий вид:
58 + 4,2s7 + 7,44s6 + 7,218s5 +4,1619s4 + l,44468s3 +
г Ро s(s + 0,2002)0 + 0,6005)0 + 0,100893)0 + 0,5003)0 + 0,8007) •
+0,290276s2+0,0301872s +0,0012096
О + 0,7003)0 + 0,9004)(s + 0,4006)
Обратное преобразование Лапласа получено с помощью системы Mathcad.
Оно имеет вид:
АГГ(/) = 0,98553 +- 0,001 е-0 2002/ + 0,000833 «f0*6005' + 0,00878 е-0'10089' +
+0,000598 е-0'5003' +0,000884 е-0'8007' + 0,00043 е-0'7003' +
+0,000456е-0'9004/+0,00148е-°'4006/.
Результаты табулирования функции Kr(t) приведены в табл. 3.5.
Метод обладает высокой точностью. Погрешности могли возникнуть только
при получении оригинала функции Kr(s), когда в функцию уже были
подставлены численные значения интенсивностей отказов элементов.

Расчет показателей надежности нерезервированных восстанавливаемых систем 85
Таблица 3.5. Результаты табулирования функции готовности
/, час
0
4
8
12
16
20
км
1
0,9923778877
0,9897343737
0,9882552613
0,9873246720
0.9867196419
/, час
24
28
32
36
40
ад
0,9863214638
0,9860579091
0,9858829003
0,9857664582
0,9856888839
Решение системы дифференциальных уравнений численным методом
Наиболее популярным, обладающим высокой точностью, является метод
Рунге — Кутты.
Алгоритм метода Рунге— Кутты с автоматическим выбором шага
реализован авторами в программном средстве rungekutt.exe, описание которого
содержится в разд. 2.8.9 части IV.
Программа выдает решение на экране монитора и в виде файла rungekutt.txt,
содержащего значения времени / и девяти функций /?0(0> А(0» •••» Ря(0 •
Значения функции готовности Kr(t) = p0(t) помещены в табл. 3.6 в столбце
И*Р(/) PK".
Метод Рунге — Кутты реализован в любой системе компьютерной алгебры,
в том числе и в системе Derive 5 (см. часть IV).
Составление и решение интегрального уравнения
Функционирование системы из 8 элементов можно заменить
функционированием одного элемента с постоянной интенсивностью отказов
^с =0,0039 час-1 и переменной интенсивностью восстановления. Плотность
распределения времени восстановления является гиперэкспоненциальной
g(t) = __ £ х.^.е~М Поэтому для определения функции готовности системы
Достаточно решить одно интегральное уравнение (3.7).
Уравнение (3.7) решим численным методом с использованием формул (3.4) и
0.8). Расчеты по указанным формулам нетрудно выполнить вручную, но
быстрее это сделать программным путем. Результаты решения содержатся
в табл. 3.6 в столбце " Kr(t) ИУ".

86
ЧАСТЬ I. Упражнения. Глава 3
Таблица 3.6. Значения коэффициента готовности системы
/, час
0
2
4
6
8
10
12
14
16
18
20
К&) РК
1,0000
0,9949
0,9924
0,9908
0,9897
0,9889
0,9883
0,9877
0,9873
0.9870
0,9867
Kr{t) ИУ
1,0000
0,9948
0,9922
0,9907
0,9896
0,9887
0,9881
0,9876
0,9872
0,9868
0,9866
t, час
22
24
26
28
30
32
34
36
38
40
К,{1) РК
0,9865
0,9863
0,9862
0,9861
0,9860
0,9859
0,9858
0,9858
0,9857
0,9857
Kr(t) ИУ
0,9863
0,9862
0,9860
0,9859
0,9858
0,9857
0,9856
0,9856
0,9855
0,9855
Способ объединения узлов графа состояний системы
Граф состояний системы из 8-ми элементов имеет 9 узлов, один из которых
соответствует исправному состоянию системы, восемь — отказовым.
Интенсивность отказа системы равна сумме интенсивностей отказов элементов.
Поэтому ветви переходов из исправного состояния системы в отказовое
можно объединить. Определим теперь эквивалентную интенсивность
восстановления системы. Предположим, что интенсивность восстановления есть
величина постоянная и определяется выражением:
1
^с=7~'
где Гвс — среднее время восстановления системы. При принятом допущении
интенсивность, восстановления вычисляется на основании следующих
очевидных соотношений:
гв=Ь^г, г=-!-, кГ=—Ц-.
Подставляя эти выражения в выражение цс = —, получим:
•*вс
Цс = — •
у Ь.

Расчет показателей надежности нерезервированных восстанавливаемых систем 87
п Х-
По условиям задачи Хс = 0,0039 час" , £ — = 0,0147. Тогда цс = 0,2656.
ы\ И/
Получим функцию готовности, воспользовавшись выражением (3.3).
Подставляя в это выражение значения ^ X и ц, получим искомое выражение
функции готовности:
JCr(0 = 0,985 + 0,015 е-°'2695/.
Результаты табулирования функции приведены в табл. 3.7.
Таблица 3.7. Результаты табулирования функции готовности
t, час
0
4
8
12
16
20
КМ
1
0,9901041309
0,9867368101
0,9855909937
0,9852011006
0,9850684296
t, час
24
28
32
36
40
Kr(t)
0,9850232849
0,9850079232
0,9850026960
0,9850009174
0,9850003121
Анализ результатов решения задачи позволяет сделать следующий вывод: все
рассмотренные методы дали возможность получить решение с допустимой
Для практики точностью, в том числе и приближенный метод, который
позволил получить решение с точностью два знака после запятой.
Наиболее точным является аналитический метод решения
дифференциальных уравнений. Это объясняется тем, что в этом методе только на этапе
получения обратного преобразования Лапласа выполнялись численные расчеты.
На остальных этапах получались точные аналитические решения.
По этой же причине высокой точностью обладает интегральный метод.
Менее точное решение задачи этим методом по сравнению с аналитическим и
методом Рунге — Кутты получено лишь потому, что шаг интегрирования из
Условий точности не выбирался и был равен одному часу. Метод Рунге —
Кутты реализован при заданной точности вычисления с автоматическим
выбором шага.
На рие. 3.2 приведены графики функций готовности, полученные
интегральным методом и методом Рунге— Кутты. Из графиков рисунка видно, что
^^тоды дают практически одинаковые результаты.

88
ЧАСТЬ I. Упражнения. Глава 3
/, час
Рис. 3.2. Функция готовности системы для различных интенсивностей восстановления
ПРИМЕР 3.3. Нерезервированная система состоит из трех элементов
(подсистем). Законы распределения времени до отказа и времени восстановления
элементов, а также параметры этих законов приведены в табл. 3.8.
Таблица 3.8. Характеристики элементов системы
Номер элемента
Время до отказа
Время восстановления
1
Г(5; 40)
Ехр(2)
2
N(120; 30)
Ехр(0,5)
3
W(3; 200)
Ехр(1,5)
Требуется определить показатели надежности системы.
Решение. Для этого вычислим математические ожидания времени до отказа
и времени восстановления элементов (соответствующие формулы приведены
в табл. 1А гл. 1 части I):
П для гамма-распределения:
т;=оф = 5-40 = 200 час, о, =7оф = >/5 -40 = 89,4 час;
□ для нормального распределения:
Т2 = m = 120 час, а2 = 30 час;
□ для распределения Вейбулла:
Г3 = |ЗГ(1 + 1/а) = 200 • Г(1,333333),
а3 = р7г(1 + 2/а)-Г2(1 + 1/а) = 200-у/г(1,666667)-Г2(1,333333).

расчет показателей надежности нерезервированных восстанавливаемых систем 89
Значения гамма-функций найдем в Excel. В ячейки А1 и А2 поместим
формулы:
А1 = ЕХР(ГАММАНЛОГ(1, 333333) ),
А2 = ЕХР(ГАММАНЛОГ(1,666667)).
Тогда получим Г(КЗЗЗЗЗЗ) = 0,89298, Г(1,666667) = 0,902745 .
Следовательно,
Ту = 200• 0,89298 = 178,6 час, а3 = 200>/о,902745-0,892982 = 64,9 час.
Математические ожидания среднего времени восстановления соответственно
равны:
^в1 =^- = — = 0,5 час,
Г„2 = — = — = 2 час,
в2 Х2 0,5
7U = — = — = 0,6667 час.
в3 Х3 U5
Стационарные показатели надежности определим по формулам (3.5).
Результаты расчетов, выполненные в Excel, приведены в табл. 3.9.
Таблица 3.9. Показатели надежности элементов системы
1
2
3
4
5
А
N
1
2
3
В
т,
200
120
178,6
С
Ты
0,5
2
0,6667
Сумма
D
»л
0,005
0,00833
0,00560
0,01893
Е
т.1т
BI / 1
0,0025
0,01667
0,00373
0,02290
F
Кп
0,99751
0,98361
0,99628
Данные колонок D, Е и F получены по формулам:
02 - 1/В2,
Е2 = С2/В2,
Р2 = 1/(1 + Е2)
с Последующим протягиванием ячеек.

90 ЧАСТЬ I. Упражнения. Глава 3
В ячейках D5 и Е5 располагаются итоговые суммы:
D5 = CYMM(D2 : D4),
Е5 = СУММ(Е2 : Е4).
Найдем стационарные показатели надежности системы:
п т
у1 IBi
Т = = = 52,8 час, 71 = = = 1,2 час,
"\_ 0,0189 в ^J_ 0,0189
К= ! = ]- = 0,9776.
1 + yZk l + 0>0229
Решать задачи такого класса более рационально с помощью математических
систем компьютерной алгебры, например, Derive 5. Их преимущества состоят
в следующем:
□ возможность получить решение в аналитическом виде;
□ не нужны промежуточные вычисления;
□ простота вычислений и возможность анализа зависимостей показателей
надежности системы от параметров законов распределения отказов и
восстановлений ее элементов.
Далее приведены процедуры и результаты вычислений значения а с
помощью системы Derive 5:
( Л
#1: 3-Г 1 + -
V а/
( Л
#2: 200-Г 1 + -
#3: 178.5959023
\{ ( 2) ( I]2)
#4: р- Г 1+ Г 1 + -
уУ \ ос J V а/ у
К ( 2\ ( iVl •
#5: 200- Г 1+- \-Г 1 + -
\\{ { з) v з; J
#6: 64.91005618

Расчет показателей надежности нерезервированных восстанавливаемых систем 91
В строке #1 находится результат ввода выражения математического
ожидания времени безотказной работы. В это выражение с помощью кнопки Sub
панели инструментов вводятся значения параметров а = 3 и р = 200.
Результатом решения является число в строке #3 (кнопка Approximate).
Аналогично вычисляется а (строки #4, #5, #6).
Далее приводятся процедуры вычисления коэффициента готовности системы.
При этом используется выражение:
К- = .
г п у
1
#1:
Xl-al-pi
1
#2:
m-X2
1
#3: . ,
(3-ХЗ-Г 1 + -
#4: К = 1
1 1 1
1+Xl-al.Pl + m.A2 + p.A3>^1 + Ij
(Л
al-p-|Jl-Xl-X2-X3-m- - !
#5- к- ±2*1
к : щ
0-X3-(al-pi-Xl-(X2-m + l) + X2-m)- - ! + al-pl-Xl-X2-m
\ocJ
(А
5-200-40-2-0.5-1.5-120- - !
#6: К = Ш .
(Л
200-1.5-(5-40-2-(0.5-120 + 1) + 0.5-120Ы - !+ 5-40-2-0 . 5-120
\з)
#7: Т = 0.9776131588
п^рвых трех строках находятся выражения -^- для элементов системы.
■*/
ь
строке #4 определяется коэффициент готовности. С помощью команды ме-
** Simplify | Factor оно преобразуется в формулу #5.

92 ЧАСТЬ I. Упражнения. Глава 3
С помощью кнопки Sub панели инструментов в формулу подставлены
исходные данные (выражение #6) и после нажатия кнопки Approximate
получено значение коэффициента готовности (строка #7).
Наиболее интересным результатом наших расчетов является формула в
строке #5. Она позволяет исследовать влияние законов распределения и их
параметров на показатели готовности системы.
Определим функцию готовности системы по приближенной формуле (3.14).
Функция готовности Krj(t) каждого элемента, входящего в систему,
определяется по формуле (3.4). В эту формулу входит свертка функций /*g(0»
которая для постоянной интенсивности восстановления рассчитывается по
формуле:
f*g{t)=\f{t-x)\xe-^dx.
о
Для вычисления интеграла применим формулу Гаусса с тем, чтобы
уменьшить количество арифметических действий. Пусть а таково, что Ц£~ца = 8,
1 е
где £ —точность вычислений. Тогда a- — In—.Верхний предел интегри-
рования b(t) равен наименьшему из чисел / или а, т. е.
( 1 Л
b(t) = m\n(t; fl) = min /; —In— . (3.15)
Применяя формулу Гаусса с 7 узлами и полагая е = 10" , получим
b(t) 7
/*S(0= J f(t-x)vLe~i3Xdx = 0,5b(t)yZcif(t-0,5b<<t)(xl: +1))ц*-^('к*<+,).
о *=i
(3.16)
Таким образом, алгоритм вычисления функции готовности одного элемента
включает в себя формулы (3.15), (3.16) и (3.4), которые целесообразно
оформить в виде отдельных модулей. Расчеты, проведенные по данному
алгоритму, а также соотношение (3.14) позволяют найти функцию готовности
каждого элемента и системы в целом. Результаты расчетов приведены в табл. 3.10.
Из табл. (3.9) и (3.10) видна сходимость функций готовности элементов и
всей системы к своим предельным значениям. Для наглядности данные
зависимости представлены на рис. 3.3 и 3.4. На рис. 3.3 кривая 1 соответствует
гамма-распределению, кривая 2 — нормальному распределению, а кривая 3 —'
распределению Вейбулла.

Расчет показателей надежности нерезервированных восстанавливаемых систем 93
Таблица ЗЛО. Функции готовности системы и ее элементов
/, час
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
500
525
550
575
600
*г.<0
1
1,0000
0,9997
0,9991
0,9984
0,9978
0,9975
0,9974
0,9974
0,9974
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
КйС)
1
0,9998
0,9985
0,9921
0,9796
0,9732
0,9811
0,9893
0,9879
0,9825
0,9800
0,9821
0,9850
0,9852
0,9834
0,9823
0,9828
0,9838
0,9841
0,9835
0,9830
0,9831
0,9834
0,9836
0,9834
Кгз(')
1
0.9999
0.9994
0.9987
0,9978
0.9969
0,9961
0,9957
0,9956
0,9958
0,9961
0,9964
0,9965
0,9965
0,9964
0,9962
0,9962
0.9962
0,9962
0,9962
0,9963
0,9963
0.9963
0,9963
0,9962
КМ
I
0,9996
0,9975
0,9899
0.9759
0.9682
0,9750
0,9825
0.9811
0.9759
0,9739
0,9763
0,9793
0,9794
0.9775
0,9763
0,9767
0,9777
0,9780
0,9775
0,9770
0,9771
0,9775
0,9776
0,9774
Ьсе функции, изображенные на рис. 3.3, имеют колебательный характер. Это
уличительная особенность неэкспоненциальных распределений. При этом
аМплитуда" колебаний различна. Наибольшие колебания функции
готовности соответствуют нормальному распределению. Это объясняется тем, что
Ремя до отказа 2-го элемента имеет наименьшую дисперсию по сравнению с
Тугими элементами.

94
ЧАСТЬ I. Упражнения. Глава 3
Рис. 3.3. Функции готовности элементов системы
Рис. 3.4. Функция готовности системы
ПРИМЕР 3.4. Нерезервированная система состоит из трех элементов с теми
же законами распределения времени до отказа, что и в примере 3.3. Однако
время восстановления каждого элемента предполагается не случайным, а
постоянным и равно соответственно: Тв1 = 0,5 час, Гв2 =2 час, Гв3 =0,6667 час.
Они взяты такими же, что и математические ожидания времени
восстановления элементов. Требуется определить показатели надежности системы.

расчет показателей надежности нерезервированных восстанавливаемых систем 95
решение. Так как стационарные показатели надежности не зависят от
законов распределения, а зависят лишь от средних значений, то согласно
формулам (35) они совпадают с аналогичными показателями примера 3.3:
Т = 52,8 час, Гв=1,2час, Кг =0,9776.
Вычислим функцию готовности элементов и системы. Поскольку время
восстановления элементов постоянно, то выражение для свертки функций имеет
вид:
f*g(<) = At-TB) при/>Гв.
функцию готовности элементов определим по формуле (3.4), а функцию
готовности системы— по формуле (3.14). Результаты расчетов приведены в
табл. 3.11.
Таблица 3.11. Функция готовности системы и ее элементов
Л час
0
25
50
75
100
125
150
175
200
225
250
275
300
325
350
375
400
425
450
475
*г.(0
I
1,0000
0.9996
0,9990
0,9983
0,9978
0,9975
0,9973
0,9974
0,9974
0,9975
0,9975
0,9975
0,9975
0,9975
0,9975
0.9975
0,9975
0,9975
0,9975
*й(0
1
0,9998
0,9984
0,9918
0,9791
0,9732
0,9816
0,9894
0,9878
0,9823
0,9800
0,9823
0,9852
0,9852
0,9834
0,9823
0,9829
0,9839
0,9841
0,9836
А'гз(0
1
0,9998
0,9994
0,9987
0,9978
0,9969
0,9961
0,9957
0,9956
0,9958
0,9962
0,9964
0,9965
0,9965
0,9964
0,9963
0,9962
0,9962
0,9962
0,9963
«0
1
0,9996
0,9974
0,9895
0,9754
0,9681
0,9754
0,9826
0,9809
, 0,9758
0,9739
0,9765
0,9794
0,9794
0,9775
0,9763
0,9768
0,9778
0,9781
0,9776

96
ЧАСТЬ I. Упражнения. Глава 3
Таблица 3.11 (окончание)
t, час
500
525
550
575
600
Knit)
0,9975
0,9975
0,9975
0,9975
0,9975
*й(0
0,9831
0,9832
0,9836
0,9837
0,9835
Kri{t)
0,9963
0,9963
0,9963
0,9963
0.9963
Kr(t)
0,9771
0,9772
0,9776
0,9777
0,9775
Значения функций готовности почти не изменились по сравнению с
аналогичными значениями для экспоненциального закона распределения времени
восстановления. Это говорит о том, что в случае элементов с быстрым
восстановлением функция готовности слабо зависит от законов распределения.
То же подтверждают и графики функций готовности, изображенные на
рис. 3.5.
/, час
Рис. 3.5. Функции готовности элементов и всей системы
(время восстановления постоянное)
Из рисунка следует, что 1-й и 3-й элементы более надежны, чем 2-й, а
надежность системы ниже надежности каждого элемента.
ПРИМЕР 3.5. Рассмотрим систему, состоящую из двух элементов,
соединенных последовательно. Отказ любого из них приводит к отказу системы-

расчет показателей надежности нерезервированных восстанавливаемых систем 97
При этом если произошел отказ первого элемента, то второй не выключается
и расходует свой ресурс. Если произошел отказ второго, то первый
выключается и ресурс не расходует. Элементы имеют разную надежность с
постоянными интенсивностями отказов 7^=0,05 час-1 и А,2=0,01 час-1
соответственно. Обслуживает систему одна ремонтная бригада с прямым приоритетом.
Закон распределения времени восстановления имеет плотность g(t).
Требуется определить стационарные показатели надежности системы при двух
законах распределения времени восстановления: экспоненциальном и
нормальном со средним временем восстановления Тв = 10 час и средним квадратиче-
ским отклонением ав = 1 час.
Решение. Представим функционирование системы графом состояний,
который изображен на рис. 3.6.
Рис. 3.6. Граф состояний нерезервированной системы
На рисунке следующие обозначения:
О (0) — оба элемента системы исправны;
^ 0)— элемент 1 отказал и восстанавливается, элемент 2 исправен и
продолжает работать;
" (2) — элемент 2 отказал и восстанавливается, элемент 1 выключен из
работы;
а О) — отказали оба элемента, первый восстанавливается;
u л-i, Х2 — интенсивности отказа элементов;
*Ч» М-2» М-з — интенсивности восстановления элементов,
•^я вычисления показателей надежности системы необходимо определить
Интенсивности Ц|, ц2» М-з * Введем функции, соответствующие состояниям
СИсгемы: -Уо(^2)> У^х^г) * Уг(*\Ъ)* ^^„О). Тогда система интеграль-
4 3»к. 553

98
ЧАСТЬ I. Упражнения. Глава 3
ных уравнений для описания стационарного режима функционирования
будет иметь вид:
г
оо оо
yo(s\,s2) = \fl(x + sl)yl(Q,x + s2)dx + \f2(x + s2)y2(x + s]t0)dx;
о О
оо
y\(.i\>s2)= fg(x + Tl)y0(0,x + s2)dx;
0 (3.17)
оо оо
У2 C*h Ч ) = jg(x + т2 )У0 (* + sl> °)^ + J #(* + т2 )/l (* + *1 ХУз (°> °№
О О
оо
д^зСх,»0>= Jy, (* + т,,0)<&.
о
Вычислим интенсивности восстановления щ, \х2, Из •
Согласно [5, гл. 4] из системы (3.17) получим:
_со10+со20
Ро-"^—:—»
л,, + а2
со оо
о о
оо оо
1У2(з\>Ъ№\ = lg(x + T2)e-x*xdx(hPo+y3WM>
о ' о
00
у3(т1,0) = Х1Х2 JGix + x^e'^dxpo.
о
Тогда
СО
*i jg(x)e-^xdxp0 ■
Ц1 = ^ = -£- = #^, (3.18)
А A.,]G(^e-^x^p0 G^)
О
00
Jg(*)e_4k(?,2A) + ^(0,0))
„ _ш20__о _ 8(л\) И 19)
Р2 lG(x)e-^xdx(X2p0 + y3(0M G<M
о

Таблица 3.12. Значения функций g(k) и G(k)
*М
G(X)
X, = 0,05
0,607289
7,854214
Х2 = 0,01
0,904883
9,511734
В
соответствии с формулами (3.18)—(3.20) и данными табл. 3.12 получим:
^1 =0,0951 час"1, ц2 =0,0773 час""1, ц3 =0,1948 час-1. Интенсивности вос-
Тан°вления достаточно сильно отличаются от аналогичных интенсивностей
*1я случая экспоненциального закона времени восстановления.
расчет показателей надежности нерезервированных восстанавливаемых систем 99
00
X{k2\G(x)e-^xdxpts
,3=^ = ^Н = ±^Ы.. (3.20)
Ръ A,, \G{x){\ - e~x*x)dxp0 Г* ~ G^2)
о
В формулах (3.18)—(3.20) введены обозначения:
U g(W — преобразование Лапласа плотности g(t);
А,
О 5(k)— преобразование Лапласа функции G(/) = l-G(/), где G(t) —
функция распределения времени восстановления.
Из полученных формул видно, что интенсивности ц,, \х2, Ц.3 зависят не
только от закона распределения времени восстановления, но и от
интенсивностей отказов элементов.
Для экспоненциального распределения времени восстановления Ц| = ц2 = Цз =
=-L = 0,l час"1.
Г
Для нормального распределения с параметрами Тв и ав преобразования
Лапласа функций g(t) и G(t) соответственно равны:
i 2 2 f l22\
g(X) = e 2 9 G(X) = 1 x_e 2 .
ч )
Результаты вычисления значений g(X) и G(k) приведены в табл. 3.12.

100 ЧАСТЬ I. Упражнения. Глава 3
Вычислим вероятности состояний системы топологическим методом.
В табл. 3.13 приведены интенсивности переходов графа, изображенного на
рис. 3.6.
Таблица 3.13. Таблица иитенсивностей переходов
Состояния
системы
0
1
2
3
Переходы из данного
состояния во все другие
°01 = V а02 = ^2
аю = И,, я,з = К
°20 = ^2
Я32=^3 ■
Суммарная
интенсивность перехода
aoi + аог
а10 + ап
°20
°32
В соответствии с топологическим методом [5, гл. 5] получим:
А0 = а10а20^32 + а13а20а32 = (Ш + ^) 1*2^3 »
А1 = а01а20а32 =^1И-2М-3>
А2 = ата13а32 + а02а10а22 + а02апа22 = (А,2 + й + ^) А.2Из,
А3 = «oi«i3fl20 = ^1^-2^2 •
Тогда выражения наработки на отказ, среднего времени восстановления и
коэффициента готовности будут иметь вид:
т.—Si—-_!_,
(Х,+А.2)А) ^1+^-2
Т = П + Р2 + Р* = fo + ^2>^lM-2 + (h + Щ + h)h^3
к Т ОЧ + Ш^З
Т + Тв (Х2 +^l)H2J^3 +(^3 + h)hV2 + (Х\ +Ml +^2)^2М-3
Расчеты по этим формулам дают следующие результаты:
П при экспоненциальном законе времени восстановления:
Т = 16,7 час, Гв =10,8 час, КГ = 0,6077 ;
О при нормальном законе времени восстановления:
Г = 16,7 час, Гв= 11,5 час, £г=0,5914.

расчет показателей надежности нерезервированных восстанавливаемых систем 101
црИМЕР 3.6. Рассмотрим сложную нерезервированную систему,
составленную из 80 разнородных элементов, отличающихся законами распределения и
их параметрами, а также случайностью исходных данных. Система состоит
из ДВУХ грУпп элементов. Данные по этим группам содержатся в табл. 3.14.
Номер
группы
1
2
Таблица 3.14. Показатели надежности элементов
Число
элементов
50
30
Время
до отказа
ТЫ
W
г
нижнее
10000
5000
Т
верхнее
15000
7000
с
2000
2000
Время
восстановления
Г
Г
Т
24
24
\
о-в
10
10
В каждой группе элементы имеют различное среднее время безотказной
работы. Первая группа состоит из элементов, имеющих среднее время
безотказной работы, равномерно распределенное на промежутке от 10 000
до 15 000 часов. Вторая группа состоит из элементов, имеющих среднее
время безотказной работы, равномерно распределенное на промежутке от 5000
до 7000 часов.
Время непрерывной работы системы / = 80000 часов. Определить показатели
надежности системы.
Решение. Воспользуемся для расчетов программой Conspz.exe, описание
которой приведено в разд. 3.2.2 части IV. Результатом работы программы
являются следующие показатели надежности системы:
О наработка на отказ;
О среднее время восстановления;
П коэффициент готовности;
О Функция готовности (нижняя граница, верхняя граница, среднее значение).
В Основе алгоритма лежит приближенное равенство (3.14). Для данных
рассматриваемого примера получим следующие показатели надежности
системы:
Т = 1*11,1 час, Гв=24час, £г =0,8224.
Результаты расчетов функции готовности (средние значения) содержатся в
Табл.3.15.
^Относительная погрешность, рассчитанная по формуле
s 2-(^г)Верх(0-^г,ниж(0) .
о = max 100%,
' ^г.верхСО + ^г.нижСО
вставляет 0,17%.

102
ЧАСТЬ I. Упражнения. Глава 3
Таблица 3.15. Средние значения функции готовности
/, час
0
2000
4000
6000
8000
10000
12000
14000
16000
18000
20000
22000
24000
26000
28000
30000
32000
34000
36000
38000
40000
Kr(t)
1,0000
0,9791
0,9161
0,8695
0,8716
0,8236
, 0,7394
0,7655
0,8540
0,8848
0,8667
0,8243
0,7841
0,7829
0,8211
0,8579
0,8604
0,8346
0,8062
0,7980
0,8147
/, час
42000
44000
46000
48000
50000
52000
54000
56000
58000
60000
62000
64000
66000
68000
70000
72000
74000
76000
78000
80000
км
0,8398
0,8501
0,8390
0,8200
0,8100
0,8159
0,8311
0,8417
0,8392
0,8280
0,8192
0,8197
0,8280
0,8364
0,8378
0,8322
0,8257
0,8239
0,8279
0,8337
На рис. 3.7 изображен график функции готовности системы.
График построен по данным табл. 3.15. Результирующий файл содержит
1001 значений Kr(t). Построение графика по всем рассчитанным значениям
лишь улучшит его качество.

расчет показателей надежности нерезервированных восстанавливаемых систем 103
О 12000 24000 36000 48000 60000 72000 /, час
Рис. 3.7. Функция готовности сложной системы
3.3. Задачи для самостоятельного решения
ЗАДАЧА 3.1. Нерезервированная восстанавливаемая система состоит из
п = 10 элементов. Необходимо определить наработку на отказ, среднее время
восстановления и коэффициент готовности системы. Предполагается, что
справедлив экспоненциальный закон отказов и восстановлений элементов.
Варианты заданий приведены в табл. 3.16.
п
Та, час
/, час
Таблица 3.16. Исходные данные задачи 3.1
1
4
40
Вариант 1
P(t)
0,97
Вариант 2
Ь10-\час-'
1,2
Вариант 3
Г, час
480
Вариант 4
Кг
0,99
2
6,5
21
3
8,5
20
4
12
18
0,99
0,98
0,95
1,8
1
1,5
540
860
820
0,98
0,98
0,95
5
3,8
19
6
7,3
18
7
2,4
16
0,96
0,99
0,94
1,75
1,35
1,2
320
900
500
0,97
0,99
0,94
8
8
18
0,95
0,9
380
0,98
9
7
21
0,99
1,84
420
0,99
10
7,5
23
0,98
1,6
400
0,97

104 ЧАСТЬ I. Упражнения. Глава 3
В таблице приняты следующие обозначения:
О п — номер элемента;
□ Гв — среднее время восстановления элемента;
□ t — время работы элемента;
П P(t) — вероятность безотказной работы элемента в течение времени t;
□ X — интенсивность отказа элемента;
□ 7] — среднее время безотказной работы элемента;
О Кг — коэффициент готовности элемента.
В каждом из вариантов одно и то же значение среднего времени
восстановления элементов.
ЗАДАЧА 3.2. Нерезервированная восстанавливаемая система состоит из
« = 10 элементов. Среднее время восстановления элементов— величина
постоянная и равна Гв=5 час-1. Значения интенсивностей отказов элементов
приведены в табл. 3.17.
Таблица 3.17. Интенсивности отказов элементов
№ элемента
ЫО^час"1
1
0,5
2
0,55
3
0,47
4
0,58
5
0,5
6
0,47
7
0,6
8
0,52
9
0,52
10
0,5
Определить коэффициент готовности системы по точной и приближенной
формулам. Вычисления выполнить при значениях X, приведенных в
табл. 3.17, уменьшенных в 10 и в 100 раз. По результатам расчетов сделать
выводы о возможности использования приближенной формулы для оценки
коэффициента готовности системы.
и
Приближенная формула имеет вид Кгс = ]~[ £п , т. е. коэффициент готовно-
сти системы равен произведению коэффициентов готовности ее элементов.
ЗАДАЧА 3.3. Нерезервированная восстанавливаемая система имеет
интенсивность отказа X = 0,003 час-1, среднее время восстановления Гв=60 час
Необходимо определить время работы Г, при котором функция готовности
будет равна: 0,997; 0,99; 0,95; 0,9; 0,85.
Указание: воспользуйтесь формулой функции готовности, подставьте в нее
исходные данные и определите корни трансцендентного уравнения.
А

расчет показателей надежности нерезервированных восстанавливаемых систем 105
ЗдДАЧА 3.4. Исследовать влияние безотказности и восстанавливаемости на
длительность переходных процессов системы при оценке ее надежности
функцией готовности. Рассмотреть два случая:
1. Среднее время восстановления Гв=10 час, варианты интенсивностей
отказов X приведены в табл. 3.18.
Таблица 3.18. Интенсивности отказов системы
X, час '
т, час
0,1
0,05
0,01
0,005
0,001
0,0005
0,0001
2. Интенсивность отказа системы X = 0,01 час , варианты значений
среднего времени восстановления приведены в табл. 3.19.
Таблица 3.19. Варианты среднего времени восстановления системы
Гв, час
т, час
1
5
10
15
20
26
30
Определить длительность переходного процесса т, заполнив пустые строки в
табл. 3.18 и 3.19. Вычисления выполнить по формуле (3.3). Переходный
процесс считать законченным, если выполняется условие:
|*г(0-*гР0»001-
По результатам расчетов сделать выводы о влиянии безотказности и
восстанавливаемости на длительность переходных процессов.
ЗАДАЧА 3.5. Нерезервированная система состоит из п подсистем, одинако-
Вь1Х по надежности и восстанавливаемости, п = 1, 2, 3, 4, 5. Закон распреде-
Ления времени до отказа и его параметры известны (табл. 3.20). Время
восстановления подсистем постоянно и равно Тв.
Таблица 3.20. Характеристики элементов системы
Вариант
1
2
3
Время до отказа
TN(300; 100)
Г(4; 60)
N(250;80)
Время восстановления ТЛ. час
20
5
6

106 ЧАСТЬ I. Упражнения. Глава 3
Таблица 3.20 (окончание)
Вариант
4
5
6
Время до отказа
W(2; 180)
ВДООООб)
Ехр(0,005)
Время восстановления Гв, час
10
15
12
Вычислить показатели надежности системы. Установить зависимость
показателей надежности от числа п.
ЗАДАЧА 3.6. Нерезервированная система состоит из двух подсистем. При
отказе одной подсистемы другая не выключается и продолжает расходовать
свой ресурс. Интенсивности отказов подсистем равны \ и Х2. Обслуживает
систему одна ремонтная бригада с обратным приоритетом. Закон
распределения времени восстановления имеет плотность g(t). Требуется вычислить
стационарные показатели надежности системы. Доказать независимость
показателей надежности системы от вида закона распределения времени
восстановления. Варианты заданий содержатся в табл. 3.21.
Таблица 3.21. Характеристики элементов системы
Вариант
1
2
3
4
5
6
Х\, час-1
0,004
0,007
0,0008
0,005
0,0004
0,0002
Х2, час-1
0,008
0,003
0,0005
0,007
0,0007
0,0006
Время восстановления
TN(30; 10)
Г(4; 6)
N(25; 8)
W(2; 18)
R(0,006)
Ехр(0,5)
ЗАДАЧА 3.7. Определить показатели надежности нерезервированной
системы, состоящей из трех групп разнородных элементов, отличающихся
законами распределения и их параметрами, а также случайностью исходных
данных. Данные по этим группам приведены в табл. 3.22.
Элементы каждой группы имеют среднее время безотказной работы,
равномерно распределенное на интервале между нижним и верхним значениями-
Время непрерывной работы системы / = 10000 час.
Указание: воспользоваться для расчетов программой Conspz.exe.

расчет показателей надежности нерезервированных восстанавливаемых систем 107
Таблица 3.22. Показатели надежности элементов
Номер
группы
1
2
3
Число
элементов
45
20
35
Время
до отказа
Г
W
TN
Г
нижнее
3000
4000
3500
Т
верхнее
4000
6000
5000
a
2000
3000
2500
Время
восстановления
Ехр
Ехр
Ехр
тш
24
36
20
ЗАДАЧА 3.8. Техническая система представляет собой основное соединение
двух подсистем. Первая подсистема является восстанавливаемой, а вторая —
не восстанавливаемой. Интенсивности отказов и восстановлений подсистем
соответственно равны: Х{ =0,01 час"1, Х2 =0,001 час"1, ц, =2 час-1.
Определить показатели надежности системы с частичным восстановлением: Т, Гв,
Kr,P(t),Kr(t).
Получить аналитические и численные выражения для всех показателей
надежности.

ГЛАВА 4
РАСЧЕТ
ПОКАЗАТЕЛЕЙ НАДЕЖНОСТИ
РЕЗЕРВИРОВАННЫХ
ВОССТАНАВЛИВАЕМЫХ СИСТЕМ
Методы расчета показателей надежности резервированных
восстанавливаемых систем, как правило, являются сложными с точки зрения инженерного
применения. Однако при определенных допущениях можно выделить классы
систем, имеющих достаточно простые алгоритмы для вычисления
показателей надежности. Такими допущениями обычно являются:
О относительная простота структурных схем расчета надежности;
О независимость элементов по отказам и по восстановлению;
О экспоненциальные законы распределения времени безотказной работы и
времени восстановления элементов;
О определенные стратегии обслуживания отказавших элементов;
□ стационарный характер показателей надежности системы.
При оценке надежности стационарных и нестационарных показателей
надежности восстанавливаемых систем чаще всего используются методы
одномерных и многомерных марковских случайных процессов. Далее в этой главе
будут рассматриваться примеры расчета надежности с помощью этих
методов.
В некоторых случаях удается получить точные значения показателей
надежности. В общем случае значения показателей надежности являются
приближенными и рассчитываются программным путем.

Рис. 4.1. Граф состояний системы
На рисунке приняты следующие обозначения:
О А,, — интенсивности переходов, соответствующие отказам элементов
системы;
□ ц, — интенсивности переходов, соответствующие восстановлениям
элементов системы;
О и+1 — общее число состояний.
Состояния с номерами 0,1, 2,..., п-\ являются исправными, а состояние
с номером п — отказовым.
Коэффициент готовности, наработка на отказ, среднее время восстановления
и среднее время безотказной работы вычисляются по формулам:
п-\ п-\
i+Zpi-p* i+Epi-p*
Кг=—^ , Г = —^ , Г.= —, (4.1)
i+Ipi-p* ^pi-p«-» ц"
*=1
Т - У 1 + Y*-! +4k-\1k-i +- + Ук-1"У\ 9 (4.2)
*=i ^к
рДер.=Ь. У.=Ь-
7^ли все элементы системы идентичны по надежности и ремонтопригодно-
~Ти» то графом рис. 4.1 описывается функционирование систем с постоянно
•^Юченным резервом и резервом замещением, мажоритарные системы и
расчет показателей надежности резервированных восстанавливаемых систем 109
4.1. Методы расчета надежности систем
при экспоненциальных законах
распределения отказов и восстановлений
Предположим, что функционирование системы описывается графом,
изображенным на рис. 4.1.

110
ЧАСТЬ /. Упражнения. Глава 4
системы со скользящим резервом, обслуживаемые любым количеством
ремонтных бригад.
Пусть X — интенсивность отказа, a ji — интенсивность восстановления
каждого элемента системы. В зависимости от условий функционирования и
обслуживания системы интенсивности переходов \ и ц, принимают
различные значения. Значения X,- содержатся в табл. 4.1.
Таблица 4.1. Интенсивности отказов
Вид резервирования
Постоянное
(1 основной, т резервных элементов)
Замещением
(1 основной, т резервных элементов)
Мажоритарное
((л - т) основных, т резервных элементов)
Скользящее
((л - т) основных, т резервных элементов)
h
(л + 1 -/)Х, /= I, 2,... , л
X, /= 1,2,... ,л
(л + 1-/)Х,1 = 1,2,... ,т+ 1
(л - т) X, i = 1, 2,..., т + 1
Интенсивности восстановления ц, вычисляются по формуле:
Г/ц, при i<n ,Л„
[гц, при i>r,
где г — число ремонтных бригад.
Приведем частные случаи резервированных систем, показатели надежности
которых вычисляются по соотношениям (4.1):
□ Система с постоянно включенным резервом
Структурная схема резервированной системы с кратностью т приведена
на рис. 4.2.
В этом случае для полностью ограниченного восстановления (одна
обслуживающая бригада) показатели надежности вычисляются по формулам:
/и+1«,'
Е-
*г=^ГГ, ТЛ^!-, ТШЛ, (4.4)
/=о /!
где у = -.

расчет показателей надежности резервированных восстанавливаемых систем щ
Рис. 4.2. Структурная схема резервированной системы
(постоянно включенный резерв)
Для неограниченного восстановления (число бригад обслуживания равно
т +1) справедливы формулы:
*г=1—2—i-, Г = (1 + р) -р , Тв=—]—. (4.5)
□ Система с резервом замещением
Структурная схема системы кратности m приведена на рис. 4.3.
О
L, yi ,
• • •
t-i J
1 ' m
Рис. 4.3. Структурная схема резервированной системы (резерв замещением)
В случае полностью ограниченного восстановления, показатели
надежности определяются так:
m
X, =■*=!-. тЛ±у>, т;=1, (4.6)
ур/ л/=0 М-
/=0

112 ЧАСТЬ I. Упражнения. Глава 4
а в случае неограниченного восстановления:
т J
у, £_
X^iil, Г = 1£-!=!-т'.Г.=—L-. (4.7)
/=0 /!
Нестационарные показатели надежности, такие как вероятность безотказной
работы или функция готовности, определяются путем составления и решения
систем дифференциальных уравнений.
4.2. Методы расчета надежности систем
при произвольных законах распределения
отказов и восстановлений
В этом разделе будем предполагать, что все или некоторая часть элементов
системы имеют неэкспоненциальные законы распределения времени до
отказа или времени восстановления. Тогда функционирование системы
описывается интегральными уравнениями. Вопросы составления и решения систем
интегральных уравнений для структурных схем с небольшим числом
элементов в каждом случае будут рассматриваться индивидуально.
4.2.1. Дублированная система
с постоянно включенным резервом
Структурная схема системы показана на рис. 4.4.
Рис. 4.4. Структурная схема дублированной системы с постоянным резервом
На рисунке введены следующие обозначения:
D fi(t) — плотность распределения времени безотказной работы /-го
элемента;

расчет показателей надежности резервированных восстанавливаемых систем 113
О %№ — плотность распределения времени восстановления /-го элемента,
/ = 1,2.
исследование надежности системы зависит от дисциплины обслуживания
отказавших элементов.
Ограниченное восстановление. Прямой приоритет
Граф состояний системы, обслуживаемой одной ремонтной бригадой с
прямым приоритетом, представлен на рис. 4.5.
Рис. 4.5. Граф состояний дублированной системы (ограниченное восстановление,
прямой приоритет)
Система имеет 5 возможных состояний:
О (0) — оба элемента системы исправны;
0(1) — элемент 1 отказал и восстанавливается, элемент 2 исправен;
О (2) — элемент 2 отказал и восстанавливается, элемент 1 исправен;
О (3) — отказал сначала элемент 1, а затем элемент 2, элемент 1
восстанавливается;
О (4) — отказал сначала элемент 2, а затем элемент 1, элемент 2
восстанавливается.
Предположим, что элементы системы имеют постоянные интенсивности от-
^ов Хх и Х2. Тогда X4=Xl9 Х3=Х2.
ь,числим интенсивности восстановлений. На графе они обозначены щ, ц2»
^з > Ц4 • Для этого введем функции, соответствующие указанным состояниям:
*оЦ,*2), ^(т„.?2), y2(sbx2), Л(*1>0). У№г)> и составим следующую
Истему уравнений для описания стационарного режима функционирования:

114 ЧАСТЬ I. Упражнения. Глава 4
00 00
yo(si,s2)= jfl(x + sl)yl(Q,x + s2)dx + lf2(x + s2)y2(x + su0)dx;
о о
оо оо
У\ (Ti>s2) = JVi С* + т1 )Уо (О, * + *2 )<& + j*£i (* + х, )/2 (л + $2 ) j/4 (0,0)dx;
о о
оо оо
* У2(^Ъ)= ig2(x + x2)yo(x + si>°)dx+ jg2(x + b)fi(x + s\)y3(°>°)cix> (4.8)
о о
оо
Уз(Ъ°) = jy\(x + xltO)dx;
о
оо
У*ФЛг) = ^2(°^ + т2)^-
О
Так как время безотказной работы элементов имеет экспоненциальное
распределение, то из уравнения для функции ух системы (4.8) получим:
оо оо
©1,0 = jyi(0,s2)ds2 = lgl(x)e-^xdx(XlPo +y4(0,Q)),
о о
оооо оо
Л = Jfr(*i>2)rfM*2 = \Gx{x)e-^xdx{^Po + у,(0,0)).
00 О
Тогда интенсивность перехода ц, будет равна:
Pi G,(?i2)'
Функцию ^(х^О) можно представить в следующем виде:
оо
Ji(x„0) = A.2 Jg^ + x^^iA) +^4(0^)).
О
Из 4-го уравнения системы (4.8) найдем функцию у2 :
оо оооо
Уз (ti, 0) = j>, (х + х,, 0)^ = Х2 J Jg, (jc + a + x, )e-^xdadx(XlPo + yA (0,0))
0 00
или
00
7з(*1,0)= М1(* + х,Х1-е"Х2Х>&(А.1Л)+Л(0,0)).
0

расчет показателей надежности резервированных восстанавливаемых систем 115
Тогда
со3 2 =Л(М) = ]*1 (*)0 -e-k>xWhPo +Л(0,0)) = (1 -g,04))(Vo + *(0,0)),
о
со оо
А = Ь^.О^т, = /G,(xXl-e"V>&(^iPo + *(0,0)) =
о о
= №i-G,(X2)XA.Ijp0+>'4(0,0)).
Следовательно,
ц юз.2= l-ii(A>2)
А Гв1-^(Я.2)'
Аналогично получаются и другие интенсивности восстановления:
„ -ЫЫ. „ __ЫгЛ)_
Зная все интенсивности переходов в графе, можно составить систему
линейных алгебраических уравнений для стационарного режима
функционирования и в результате ее решения определить вероятности состояний рк и
параметры переходов coft f. После этого вычисляются значения требуемых
показателей надежности. Наработка на отказ, среднее время восстановления и
коэффициент готовности системы вычисляются по формулам:
TssPo + Pi+Pi9 Тв= Рз+Р* ^ Кг=^—. (4.9)
hPi+ ^Pi hPi+ КР2 т + тв
Оценим надежность системы для переменных интенсивностей отказов
элементов. В [5,разд. 7.4] получены следующие приближенные значения
вероятностей состояний системы и параметров перехода из одного состояния
в Другое:
Ро -CqTiT29
00 00 _
Pl = С, |Ф2 (*)G, (x)dx, p2 = С2 /Ф, (x)G2 {x)dx,
о о
Pi=C~\F2{x)4x{x)dxt p4 =C4)Fl(x)V2(x)ax,
о о

116 ЧАСТЬ I. Упражнения. Глава 4
00 оо
©ко = с\ 1ф2(*)#1 (x)dx, со2,о = с2 /ф1 (x)g2(x)dx,
о о
оо оо ""
Ю] з = С, JF2 (x)G] (x)dx, со2,4 = Q J^i (*)^2 (*№ >
о ' о
оо оо
С03)2 = С3 1^2(*Х?1 (*)<&, ©4,1 = Q J^ (JC)^2(*)*** •
о ' о
В выражениях приняты следующие обозначения:
□ /*}(0 = 1-/^(0, /*}(0 — функция распределения времени до отказа /-го
оо
элемента, Ф,-(/)= ^Fj(x + t)dx;
о
□ G,(/) = l -G,(/), G,(0 — функция распределения времени восстановления
00
/-го элемента, ¥,-(/) = JG, (х + t)dx.
о
Здесь и далее 7J — среднее время безотказной работы, а Гв/ — среднее время
восстановления /-го элемента, / = 1,2.
Постоянные коэффициенты определяются с учетом следующих условий:
О сумма вероятностей всех состояний равна единице:
Po+Pl+Pl+P3+P4=l>
П для каждого состояния сумма параметров переходов в другие состояния
равна сумме параметров переходов из всех состояний в данное:
©0,1+©0,2 =©1,0+©2,0»
©1,0+©1,3 =©0,1+©4,1 >
©2,0+©2,4 =©0,2+©3,2 >
©3,2= ©1,3 >
©4,1 = ©2,4-
Найдем интенсивности переходов из одного достояния в другое по формуле
©/ /
Pi

расчет показателей надежности резервированных восстанавливаемых систем 117
ца основании графа, изображенного на рис. 4.5, получим:
00 00
J<t>2(*)gi(*)d* 1Фх(х) g2(x)dx
Л1 - т ' А2 - т ' Ц| ~ « ~ » ^2 - „ ~ »
1 2 \02(x)Gl(x)dx /Ф,(*)а2(*)А
о о
оо оо оо
j F2(x)Gl(x)dx j Fl(x)G2(x)dx ^F2(x)Gx{x)dx /
)ф2(хЩ(х)с1х }ф,(*)<32(;фЬ: ]/?2(jc) ¥,(*)<&
0 0 0
^ •
0
Показатели надежности системы определяются стандартным способом,
путем составления и решения системы линейных алгебраических уравнений,
описывающей стационарный режим функционирования, и использования
формул (4.9).
Ограниченное восстановление. Обратный приоритет
Предположим, что элементы дублированной системы имеют произвольные
законы распределения отказов и восстановлений. Обслуживание
осуществляет одна ремонтная бригада с обратным приоритетом. Граф состояний
системы изображен на рис. 4.6.
Рис. 4.6. Граф состояний дублированной системы (ограниченное восстановление.
обратный приоритет)

118
ЧАСТЬ I. Упражнения. Глава 4
Так как показатели надежности инвариантны к законам распределения и
зависят только от математических ожиданий [5, гл. 9], то интенсивности
переходов в графе состояний равны соответствующим интенсивностям отказов и
восстановлений элементов. Тогда:
1 i _ 1 - ] '- 1
В соответствии с формулами (4.9) стационарные показатели надежности
определяются по формулам:
т= 1 + Pi+P2_ т = 2 к I + P1+P2
(Ц1+Ц2)р1р2 ' " Щ+Ц2' Г l + Pl+P2+2PlP2 '
где р,- = —^-, / = 1,2.
Ограниченное восстановление. Назначенный приоритет
Пусть элементы системы имеют постоянные интенсивности отказов. В
соответствии с принятой дисциплиной обслуживания при отказе двух элементов
первым восстанавливается элемент 1, независимо от порядка номеров
отказавших элементов. Тогда граф состояний имеет вид, изображенный на
рис. 4.7.
Рис. 4.7. Граф состояний дублированной системы
(ограниченное восстановление, назначенный приоритет)
Введем функции, соответствующие состояниям графа: y0(sl,s2), y\(*i>si)'
JbC5!»*^)» ^12(х1>0), >*21 (Ti»т2)> и составим систему интегральных уравнении
для стационарного режима:

Расчет показателей надежности резервированных восстанавливаемых систем 119
\
. ' ' 00 00
y0(si,s2) = J7i (x + s[)yl (0,x + s2)dx + \f2(x + s2)y2(x + su0)dx;
о 0
с»
Л(*1»*2)= Igiix+x^y^x + s^dx-
о
ao oo
. ° ° (4.10)
oo '
+ lfl(x + sl)y4(09x + x2)dx;
о
00
о
oo
У A, (*1 >*2 ) = \g\ (x + Tl )^2 (°> T2 )^ = Gl (xl )^2 (0» x2 )•
0
Так как время до отказа элементов имеет экспоненциальное распределение
с параметрами А,, и Х2, то из уравнения для функции ух системы (4.10)
получим:
оо оо
©1,0 = \y\^i)ds2 = \g\(x)e~XlXdx\xpQ,
о о
оооо оо
Р\ = 1 \y\^bsi)dx\ds2 = \Gx{x)e~^xdxXxp^.
оо о
Тогда интенсивность перехода \хх будет равна:
„ _(ui.o_gi(^2)
м- -"z •
Л G,(X2)
полагая в функции ух аргумент s2 - О, получим:
00
^(т,,0) = Я2 \gx{x + xx)e~^xdxk{p0.
о
3 4-го уравнения системы (4.10) найдем функцию у3:
00 0000
Уз (Ti, 0) = j>, (х + т,, 0)dx = Х2 J \gx (х + а + х, )e~u-x dadx\{ p0
О 00

120 . ЧАСТЬ I. Упражнения. Глава 4
или
оо
ЯС*|.0)= \g\{x + xx)(\-e-x>x)dx\xPo.
о
Тогда
со
со3,2 =^з (0,0)= lg](x)0-e-^x)dxXlPo=0-gl(K2))XlPo,
о
оо оо А
А = ЫъМЪ = JGiW-e-^dxbiPii =(Гв1 -G,(X2))A.,/^.
о о
Следовательно,
ft ^-G,^)'
Таким образом, интенсивности jij и ц.3 получились такими же, как и для
прямого приоритета обслуживания. Вычислим теперь интенсивности ц2 и ji4.
Из выражений для функций у2 и у4 получим:
оо оо
У2(°>Ъ)= lg2(x + b)yo(x,0)dx+ jg2(x + x2)fl(x)y3(0,0)dx +
о о
оо
+ \fl(x)y2(0,X + X2)dx
О
или
оо оо
y2(0,x2) = Xl \g2(x + x2)e-^xdx(X2p0+y3(0M+ \Mx)y2{^x + x2)dx.
о о
Получено интегральное уравнение, имеющее вид:
оо
^2(0»Т2) = Ф(Х2)+ SMx)y2(0,x + T2)dx,
\ о
где
оо
Ф(т2) = \{Аjg2{x + x2)e~^xdx, A = Х2р0 + у3(0,0).
о
Решением этого уравнения является функция
оо
у 2 (О, т2) = ф(т2) + Jco(x)q>2 (х + x2)dx,
о

расчет показателей надежности резервированных восстанавливаемых систем 121
00
где <о(х)= Yj f\ (*)• В этом можно убедиться, подставив решение в
исходам
ное уравнение. Для случая экспоненциального закона распределения отказов
&{х) = ^i • Следовательно,
оо ос
y2(0}x2) = (?(x2) + Xl\(p2(x + x2)dx = XlA\g2(x + x2)e~^xdx +
о о
оооо оо
+XJA J jg2(x + а + x2)e~XlXdadx = ХХА \g2{x + x2)e~X{Xdx +
оо о
0000 ОО
+X, A J \g2 (дг + т2 XI - е"М )Л = h A \g2 (х + х2 )dx.
00 О
Таким образом,
j>2(0,t2) = ^G2(t2).
Отсюда находим
йз2>0=Х,Л, р2=Х]АТв2.
Тогда интенсивность перехода ц,2 будет равна
°>2,о 1
/>2 Л»2
Из выражения для функции у4 следует:
оо оо
Щ,2 = J^4(0,x2)^t2 = \y2(0,x2)dx2,
о о
0000 00
Ра = \ \уа(?\^2)dxxdx2 = Г„ \y2{^x2)dx2 ,
00 0
поэтому
со4>2 1
Интенсивности ц2 и ц4 получились такими же, как и для обратного приори-
^а обслуживания.
ТаЦионарные показатели надежности системы определяются по
формулам (4.9).

122
ЧАСТЬ /. Упражнения. Глава 4
Неограниченное восстановление
Предположим, что обслуживание системы осуществляют две бригады. Граф
состояний системы изображен на рис. 4.8.
Рис. 4.8. Граф состояний дублированной системы (неограниченное восстановление)
Поскольку для неограниченного восстановления очередь не образуется, то
для любых законов распределения времени до отказа и восстановления
интенсивности переходов в графе равны соответствующим интенсивностям
отказов и восстановлений элементов, т. е.:
i _ * 1 _ 1 - 1 - 1
М J2 Ув1 Ув2
Стационарные показатели надежности определяются по формулам:
г= 1 + Р!+р2 т = 1 к = l + Pi+Рг
(И +Ц2)Р1Р2 ' В to+^г' Г I + P1+P2+P1P2'
где р,= —, / = 1,2.
to
4.2.2. Дублированная система
с резервом замещением
Структурная схема дублированной системы с резервом замещением
представлена на рис. 4.9.
Плотности распределения времени безотказной работы элементов
обозначены через fj(t), а плотности распределения времени восстановления — через
g,(0, ' = 1,2.

расчет показателей надежности резервированных восстанавливаемых систем 123
Проведем анализ надежности системы для различных приоритетов
обслуживания.
Рис. 4.9. Структурная схема дублированной системы с резервом замещением
Ограниченное восстановление. Прямой приоритет
Граф состояний системы, обслуживаемой одной ремонтной бригадой с
прямым приоритетом, изображен на рис. 4.10.
Рис. 4.10. Граф состояний дублированной системы
(ограниченное восстановление, прямой приоритет)
° [5, гл. 7] получены точные соотношения для вероятностей состояний и
параметров переходов при любых законах распределения времени до отказа и
вРемени восстановления элементов. Эти соотношения имеют вид:
оо оо оо
Рох = АЩмЩхуЬ, р02 = A\Gl(x)F2(x)dx, рх = A \Gx(x)F2{x)dx,
ооо
00 00 °0
P2^A\Fl(x)G2(x)dx1 р3 = A\Gx{x)F2(x)dx, р4 = A\Fx{x)G2{x)dx,
ооо
оо оо _
<°о\Л =<o2)oi =A\F{{x)g2{x)dx, со02>2 =«i,02 =A\g\(x)F2(x)dxt
о о

124 ЧАСТЬ I. Упражнения. Глава 4
00 СО
Щ,з =соз,2 = AJGl(x)f2(x)dx, а>2,4 =©4,i = Л\fl(x)G2(x)dx,
о о
где Л = const.
Ha основе этих формул легко найти интенсивности переходов в графе
состояний для стационарного режима функционирования системы. Искомые
интенсивности имеют вид:
]Ц(х)Я2(*№ )F2(x)gl(x)dx )Gl(x)f2(x)dx
л _ 0 л _ 0 1 _0
А,- — 1 A2-^— , Aq- — - >
\FX (x)G2(x)dx \F2(x)G] (x)dx fa {x)F2{x)dx
ooo
)G2(x)Mx)dx )gl(x)F2(x)dx )ё2(х)Ц(х)4х
X,4=_ _ 1 Hi=^ - » M-2=^ - »
JG2 (jc)F, ( jc)& |Gj (^)F2 (x)dx \G2 (хЩ (x)dx
0 0 0
"jGtWMxydx )G2(x)Mx)dx
.. _ 0 .. 0
v-3—^2 ' ^ ^Z '
fa (x)F2 (x)dx \G2 (jc)Fj (x)dx
о о
Из этих соотношений следует, что для случая экспоненциального времени
безотказной работы элементов интенсивности переходов при резервировании
замещением и при постоянно включенном резерве совпадают.
Полученные интенсивности переходов позволяют определить стационарные
вероятности состояний рк, на основе которых вычисляются наработка на
отказ, среднее время восстановления и коэффициент готовности системы.
Соответствующие формулы имеют вид:
Т=Р01+Р02+Р\+Р2 т ___ РЗ+Р4 К = Т (4.10
hP\+X4P2 ' В hP\+X4P2i ' Т + Тв
Ограниченное восстановление.
Обратный приоритет обслуживания
Рассмотрим только случай постоянных интенсивностей отказов элементов-
Граф состояний системы изображен на рис. 4.11.

Расчет показателей надежности резервированных восстанавливаемых систем 125
Из А
3
ЛЙ4
4
Рис. 4.11. Граф состояний дублированной системы
(ограниченное восстановление, обратный приоритет)
Для оценки надежности составим следующую систему интегральных урав- i
нений:
со
УоМ,0)= \y2(x + s],0)dx;
о
00
Уо2(°^2)= jy](0,x + s2)dx;
о
оо оо
' У1(?\>*2)= lgi(x + xl)f2(x + s2)y0](0J0)dx+ //2(* + 52)й(* + *1 »<>)*; (4.12)
о о
со оо
У2 С*1 >Ъ ) = \f\ (* + sl )S2 (* + х2 )У02 (°> °)dx + \f\ (* + *1 )У4 (°»* + Т2 №
О О
>'3(t„x2) = G2(x2)^1(t„0);
U(x1,t2) = G1(x1)^2(0,t2).
Преобразуем третье уравнение, соответствующее функции у1:
со оо
о о
Методом последовательных приближений найдем
оо
гДе
k=\

126
ЧАСТЬ I. Упражнения. Глава 4
Так как ю,(.х) = А,,, то У\(х{,0) = ^2G|(X}Xy01(0,0) . Следовательно,
Аналогично,
y2(sl,x2) = XlG2(x2)e-x^y02(0,0).
Определим функцию нулевого уровня:
оо
УоМ,0) = \у2(х + Sl,0)dx = <Т^'.у02(0,0).
о
Определим функцию второго уровня:
y3(xl,x2) = G2(x2)yl(xb0)=X2Gl(xl)G2(x2)ym(0,0).
Тогда
Ю01 1 Ю1 3
А01,1 - ~Л1» Л1,3 - -A2'
Poi Р\
т. е. интенсивности отказов совпадают с соответствующими интенсивностя-
ми отказов элементов. Определим интенсивности восстановлений:
_ ю1,02 _ 1 _ _0)3.1 _ 1
^1 - Ш,02 ~ ~ 7Г"' М-3 _ И-3,1 - - ТГ~ •
Pi Гв1 РЪ Гв2
Таким образом, интенсивности переходов равны значениям, обратным
математическим ожиданиям. Стационарные показатели надежности определяются
по формулам (4.11).
Ограниченное восстановление.
Назначенный приоритет обслуживания
Рассмотрим лишь случай постоянных интенсивностей отказов элементов.
Граф состояний изображен на рис. 4.12.
Рис. 4.12. Граф состояний дублированной системы
(ограниченное восстановление, назначенный приоритет)

расчет показателей надежности резервированных восстанавливаемых систем 127
искомые функции удовлетворяют следующей системе интегральных
уравнений [5, гл. 7]:
со
.Koi(*i.0) = J>2(* + 5i>0№
о
00
Уо2(0^г) = ly\(0,x + s2)dx;
о
00
У\(Ь^2)= jS\(x + xl)f2(x + s2)y0](0,Q)ch;
о
' У2^,Ъ)= lfi(x + sl)g2(x + x2)(y02(0,0) + y3(0i0))dx+ (4.13)
о
00
+ JMx + Sl)y4(0,x + x2)dx;
о
00
Д>з(хь°) = jy\(x + x]yQ)dx;
о
>'4(Tl»x2) = ^l(xl)>'2(0»x2)-
Для экспоненциального времени безотказной работы решение этой системы
имеет вид:
y0l(s[>0) = e-k*(y02(0,0) + y]2(0M,
yo2(0^2) = ^]G,W^2(x+52)^oi(050).
о
00
yl(Tbs2) = X2lgl(x + Tl)e-X^x+s*)y0l(0,0)ctx,
о
y2(Sl,x2) = XxG2{x2)e-}^ (yQ2(0,0) + yl2(0t0)),
y3(xli0) = \2)Gl(x + xl)e-x>xdxy<n(0,0),
о
Уа(Ь^2) = ^А(ьШч)(У02(^) + У12(0,0)).

128
ЧАСТЬ I. Упражнения. Глава 4
Определяем интенсивности отказов:
. _®0U 1 л _ ю02,2 _ 1
Н\,1~ -ЛИ Л02,2 - ~Л2>
Р01 А)2
«3
<i 't-J 0 л л ~>z_ 1
A,l3-——-— - -Л2, Л24--— -Aj,
о
и интенсивности восстановлений:
ос
„_®1.02__о _g|(^2) „ _Ю2,01 1
щ_ __ __ t ц2 _ ~ — >
Рх \G{{x)F2{x)dx G^D Л Г*
о
оо
JG,(*)/2(*)<& А
„ _Ш3,2_^ l~g\(h) „ _Ш4,2 1
ЦЗ — — ~ — ~£ , Ц.4 ~" ~~ •
й lG,(x)F2(x)dx T«-<h<M P* Г"
О
Как и для других приоритетов обслуживания, стационарные показатели
надежности определяются по формулам (4.11).
Заметим, что для неограниченного восстановления простые формулы для ин-
тенсивностей переходов найти не удается. Это объясняется тем, что функция,
определяющая отказовое состояние, зависит от двух аргументов,
соответствующих неэкспоненциальным компонентам.
4.2.3. Дублированная система
с облегчённым резервом
Дублированная система с постоянно включенным резервом состоит из рав-
нонадежных элементов. Однако один из них работает в облегченном режиме,
при котором его интенсивность отказов равна кХ, где к < 1. При отказе
любого из элементов интенсивность отказа исправного элемента становится
равной X. Структурная схема системы представлена на рис. 4.13.
Рассмотрим две возможные стратегии обслуживания системы с облегченным
резервом.

расЧ#гпоказателей надежности резервированных восстанавливаемых систем 129
Рис. 4.13. Дублированная система с облегченным резервом
Стратегия 1. Система функционирует следующим образом: сначала
работают оба элемента (состояние (0)), при этом первый (основной) элемент имеет
интенсивность отказа X, а второй (резервный) — кХ, где к < 1. Второй
элемент работает с меньшей нагрузкой (в облегченном режиме), и
интенсивность его отказа меньше, чем у первого элемента. На графе рис. 4.14
состоянию (0) соответствует функция y$(s) •
Рис. 4.14. Граф состояний дублированной системы с облегченным резервом
(предыстория "забывается")
При отказе любого элемента он восстанавливается. Второй элемент работает
с максимальной нагрузкой и может отказать с интенсивностью X. Это
состояние (1), которому соответствует функция y\(x,s).
Отказ другого элемента приводит к отказу системы. Система обслуживается
°Дним ремонтником, причем после восстановления одного из элементов дру-
г°и элемент начинает восстанавливаться заново, даже тогда, когда он ранее
Уже восстанавливался. Это состояние (2), которому соответствует функция
*2(т).
Ри этой стратегии отсутствует зависимость показателей надежности от
дисциплины восстановления. Время ранее проводимого восстановления "забыва-
°я". Время восстановления для обоих элементов имеет один и тот же закон
Распределения с плотностью g(t).
5 За* 553

130
ЧАСТЬ I. Упражнения. Глава 4
Функционирование системы в стационарном режиме описывается
следующей системой интегральных уравнений:
оо оо
Л>СО = \Mx + s)jyl(0,s)dsdx;
о о
оо со
< yl(x,s) = \f(x + s)g(x + x)y0(0)dx + lf(x + s)g(x + x)y2(0)dx-i
о о
СО
I о
При экспоненциальном законе времени до отказа плотности /0(/) и /(/)
имеют параметры (1 + к)Х и X. Тогда решение системы уравнений
определяется достаточно просто. Из первого уравнения получим:
00
yo(s) = F0(s)lyl(0,s)ds.
о
Из второго уравнения следует, что
со
yl(x,s) = CJf(x + s)g(x + x)dxi
о
где С = у0 (0) + у2 (0) = const.
Тогда
оо
у0 (s) = CF0 (s) \F(x)g(x)dx,
о
со
y2W = C\g(x + z)F(x)dx.
о
Определим интенсивности д-гсереходов:
оо ' оо
1^(0,5)^ lF(x)g(x)dx
„ _со1,о__о __о _£(*■)
Pl jyi(x,s)dxds \F(x)G(x)dx G^
0 0
оо
\F(x)g(x)dx
„ _*2Л МО) о _ l-gft)
м _ — = — — т: ' .
•^ _ 00 ОО
\М№ JF(x)G(x)dx Тв-°(х)
о о

расчет показателей надежности резервированных восстанавливаемых систем 131
Зная интенсивности переходов, легко найти вероятности состояний и
параметры переходов из одного состояния в другое. Однако в данном случае
можно найти эти характеристики непосредственно. Определим вероятности
состояний:
Ро = CJ^» Л = C\F{x)G{x)dx = CGiX),
р2 = С JG(x)F(x)dbc = С(ТВ - G(X)).
о
Определим параметры переходов:
«0.1 = Уо(°) = Cg(X), coIj0 = c)F(x)g(x)dx = Cg(X),
о
®i.2 = с J/W G(*)^ = C^W> <°2,! = Уг (0) = С* Jg(*)F(*)^ = С (1 - g(A,)).
о о
Отсюда находим наработку на отказ, среднее время восстановления и
коэффициент готовности системы:
r=Po + A = 0 + ^ W = g(^) + (l + A:)A.G(A,)_ l + £(l-g(?t))
«01.2 Хб(Я.) (1 + *)X2G(A.) (1 + *)М1-£(*.))'
' _ р2 _T,-G(X)^XTB-(\-g(X))
в со2Л \-g(X) X(\-g(X)) '
^ = l + *(l-g(A,)) l + *(l-g(A.))
r ] + k(\-g(X)) + (\ + k)(XTB-(\-g(X))) 0 + k)XTB+g(X)'
Рассмотрим теперь стратегию, при которой уже прошедшее время восстанов-
ления элементов не "забывается". В этих случаях необходимо учитывать
дисциплину обслуживания отказавших элементов. Время восстановления
элементов может иметь произвольный закон распределения.
Стратегия 2. Случай назначенного приоритета: при отказе двух элементов
еРвьщ восстанавливается основной с номером 1. Опишем возможные со-
т°яния системы:
состояние (0) — работают оба элемента, при этом первый элемент имеет
Интенсивность отказа Х{ = X, а второй — Х2 = кХ, где к < 1;

132
ЧАСТЬ I. Упражнения. Глава 4
О состояние (г)— отказ и восстановление первого элемента. Плотность рас-
пределения времени восстановления есть gl (/). Второй элемент работает
и может отказать теперь с интенсивностью Х{;
□ состояние (2) — отказ и восстановление второго элемента. Плотность
распределения времени восстановления есть g2(0- Первый элемент
продолжает работать с интенсивностью А.,;
□ состояние (3) — отказ второго элемента во время восстановления первого,
первый элемент продолжает восстанавливаться, а второй элемент
находится в очереди на восстановление;
О состояние (4) — отказ первого элемента во время восстановления второго,
начинает восстанавливаться первый элемент, а второй становится в
очередь на восстановление.
Граф состояний изображен на рис. 4.15.
Рис. 4.15. Граф состояний дублированной системы с облегченным резервом
(назначенный приоритет обслуживания)
Этот граф очень похож на граф, изображенный на рис. 4.7, описывающий
работу дублированной системы с постоянно включенным резервом и
назначенным приоритетом обслуживания. Отличие состоит в интенсивности перехода
из состояния (I) в состояние (3), равной Х] вместо Х2. Из-за этого
изменяется система интегральных уравнений. Однако ее решение практически не
меняется. Ограничимся указанием новых интенсивностей ц-переходов:
_liM _ 1 1-iifl.j) _ 1
<?■(*.,) Г*2 7-Bl-G,(A,) T*i
Стационарные вероятности состояний определим, используя результата
[5, разд. 5.4.5]. Для этого составим таблицу интенсивностей переходов меЖДУ
всеми состояниями (табл. 4.2).

расчет показателей надежности резервированных восстанавливаемых систем 133
Таблица 4.2. Таблица интенсивностей переходов
Состояние
системы
0
1
2
3
4
Переходы из данного состояния
во все другие
°0\ = \ ' °02 = *"2
аю - V>\. а\г = К
fl20 = ^2 ' fl24 = ^1
а32=Н3
Л42=^4
Суммарная интенсивность
выхода
Д01 + Д02
°ю + а\з
аго + агл
flJ2
й42
Вычислим значения, пропорциональные вероятностям состояний:
А0 = аЮа20а32а42 + а\Ъа20аЪ2аА2 = (^ + М^ШШ »
Л1 = а01а20а32а42 =^lM-2^3^4»
А2 = a0la13°32a42 + а02а10а32й42 + й02й13а32а42 = (^1 + ^2^1 + ^-1 ^-2 ) ИзИ-4'
А3 = а01а13д20а42 = ^1 Ц2М-4 »
Д4 = аЫа\Ъа24аЪ2 + ^02^10^24^32 + %2а\Ъа2ЬаЪ2 = (^1 + *А^1 + ^1 ^2^3 •
Определим показатели надежности системы:
О наработка на отказ:
T=Po+Pl+P2 =W2 + 2M2'<-^+^2Hl+^2.
\Р\+\Р2 X,(X,^2+Xf+А,2Ц|+Я.,Я,2)
^ среднее время восстановления:
г РЗ + Р4 _ ^f^2^4 + 0J + *Ч^1 + ^2)ИЗ ■
ig — " — Г >
hP\ +hP2 MhV-2 + M + ^i +^i *-г)УзЙ4
а коэффициент готовности:
Г
Яг=—— =
т+тв
= (ЩЦ2 + 2^2 + ^f + *-2^1 + ^2 ) 1*3^4
Иг^зМш + *i) + ^ЦгМйз + ^1 ) + (*•? + Я.2Ш + ^1^2)^3(^4 + *ч)

134
ЧАСТЬ I. Упражнения. Глава 4
В результате преобразований получим:
к 2-g(X) + XTB2(k + \-g(X))
г (\ + \TBl)(\ + XTa(k + \-g(X)))'
4.2.4. Нестационарные показатели надежности
Расчет нестационарных показателей надежности систем с
неэкспоненциальными законами распределения времени до отказа и восстановления
элементов — трудная задача с вычислительной точки зрения. Это объясняется
необходимостью решения системы интегральных уравнений с различным числом
аргументов, зависящих от предыстории функционирования системы. В
настоящее время математический аппарат для решения таких классов
интегральных уравнений в общем виде не разработан. Анализ надежности может
быть выполнен лишь для частных случаев.
Рассмотрим систему, все элементы которой работают непрерывно и
независимо друг от друга, а восстановление является неограниченным. Отказ
наступает при отказе всех элементов системы. Тогда система интегральных
уравнений, являющаяся математической моделью работы технической
системы, допускает точное решение:
J4*fo.w)=n®/(v)nVV),
ieA jeB
где:
О А — множество номеров работающих элементов;
П В — множество номеров восстанавливающихся элементов;
□ уАВ — неизвестная функция системы уравнений, отвечающая разбиению
множества номеров всех элементов на два подмножества (А, В);
П sA — вектор, составленный из компонентов si,, / е А ;
□ хв — вектор, составленный из компонентов Ту, j e В;
О <uj(sht) — обобщенный параметр потока отказов /-го элемента;
О сову(ту,/) — обобщенный параметр потока восстановленийу'-го элемента.
Отсюда следует, что функция готовности выражается равенством:
*г(о=1-по-*г,(0),
где п — общее число элементов в системе; KTj(t) — функция готовности
у'-го элемента, j = 1, 2,..., п.

распет показателей надежности резервированных восстанавливаемых систем 135
4.3. Примеры решения задач
ЛрИМЕР 4.1. Дана резервированная система с постоянно включенным
резервом кратности m = 5 . Интенсивности отказов и восстановлений являются
величинами постоянными: Л. = 0,3 час"1, \х = 2 час"1. Определить зависимость
коэффициента готовности; наработки на отказ, среднего времени
восстановления и среднего времени безотказной работы системы от числа
обслуживающих бригад г = 1, 2, 3, 4, 5, 6.
решение. Для постоянного резерва, согласно табл. 4.1, находим:
Х{ =6^ = 1,8 час-1, А,2 = 5А- = 1,5 час"1, А,3 =4А, = 1,2 час-1,
Х4=ЗХ = 0,9 час"1, ^5=2Х = 0,6 час"1, Х6 =Я = 0,3 час"1.
По формуле (4.3) при г = 1 находим щ = ц2 =ц3 =М-4 =Мо ~Иб = 2 час"1.
Тогда
Pi = 0,9, р2=0,75, р3=0,6, р4=0,45, р5=0,3, р6 =0,15.
Для расчета среднего времени безотказной работы необходимо знать
величины обратные р,. В нашем примере они имеют значения:
у, =1,111, у2 = 1,333, Уз =1,667, у4 =2,222, у5 =3,333, у6= 6,667.
Показатели надежности, вычисленные по формулам (4.1) и (4.2) для одной
ремонтной бригады (г = 1), приведены в первой строке табл. 4.3.
Аналогичные расчеты выполнены и для всех остальных значений г . Результаты
расчетов приведены в табл. 4.3.
г
1
2
3
4
5
6
Таблица 4.3
Кт
0,997457
0,999892
0,999978
0,999991
0,999994
0,999995
Показатели надежности системы
Т
196,1
2306,9
7625,1
13538,4
16922,2
16922,2
тш
0,5
0,25
0,17
0,13
0,1
0,08
г,
238,4
2512,8
8051,7
14091,4
17475,2
17475,2
Из к
таблицы видно, что показатели надежности сильно зависят от числа
рентных бригад. Так, например, при трех и более ремонтных бригадах
г * 1, т. е. система является практически абсолютно надежной. Значительно

136
ЧАСТЬ I. Упражнения. Глава 4
увеличиваются также наработка на отказ и среднее время безотказной рабо>
ты. Соответствующие зависимости показаны на рис. 4.16 и 4.17.
Рис. 4.16. Зависимость коэффициента готовности системы от числа обслуживающих бригад
Рис. 4.17. Зависимость средней наработки и среднего времени безотказной работы
от числа обслуживающих бригад
Отметим следующую особенность системы при общем постоянном резервИ'
ровании: наработка на отказ для случая шести ремонтных бригад такая ж6,
как и для пяти ремонтных бригад. Для экспоненциальных распределений это
свойство имеет место в общем случае, когда ремонтных бригад г. Наработк
на отказ системы одинакова при г = т и г = т + \ ремонтных бригадах. Э?°

I
расчет показателей надежности резервированных восстанавливаемых систем 137
свойство справедливо также для среднего времени безотказной работы
системы-
ЛРЙМЕР 4.2. Восстанавливаемая резервированная система (резерв
замещением кратности т) состоит из одинаковых по надежности элементов.
Интенсивности их отказов X = 0,1 час-1, интенсивности восстановления
и = 0,5 час-1. Определить кратность резервирования, при которой наработка
на отказ системы удовлетворяет требованию надежности: Т ^9000 час.
Рассмотреть случаи полностью ограниченного и неограниченного
восстановления.
Решение. Случай ограниченного восстановления (одна ремонтная бригада)
Наработка на отказ резервированной системы кратности m вычисляется по
формуле (4.6):
т = тТу''. где у = -г = 5-
В результате расчетов получим:
О при m = 1 Т = 10(1 + 5) = 60 час;
Опри/и = 2 Г = 10(1 + 5 + 25) = 310 час;
О лри w = 3 Г = 10(1 + 5 + 25 + 125) = 1560 час;
П при /и = 4 Г = 10(1 + 5 + 25 + 125 + 625) = 7810 час;
П при от = 5 Г = 10(1 + 5 + 25 +125 + 625 + 3125) = 39060 час.
Требуемая надежность обеспечивается только при кратности резервирования
В случае неограниченного восстановления наработка на отказ вычисляется по
Формуле (4.7):
Т = — 2L, Y •
Результате расчетов получим:
а при щ = \ Г = 10(1 + 5) = 60 час;
1:1 при т = 2 Г = 10(1 + 2-5 + 2-1-25) = 610 час;
Q при w = 3 Г = 10(1 + 3-5 + 3-2-25 + 3-21125) = 9160 час.
ь
Данном случае требуемая надежность достигается уже при кратности ре-
жирования т = 3 .

138
ЧАСТЬ I. Упражнения. Глава 4
Таким образом, за счет увеличения ремонтных бригад можно добиться
существенного увеличения надежности системы, используя 3 резервных элемента
вместо 5.
ПРИМЕР 4.3. Восстанавливаемая резервированная система со скользящим
резервом кратности 1/2 состоит из различных по надежности элементов.
Структурная схема системы показана на рис. 4.18.
Рис. 4.18. Скользящий резерв
Данные по надежности и ремонтопригодности элементов приведены в
табл. 4.4.
Таблица 4.4. Данные о надежности и ремонтопригодности элементов
Номер элемента
Интенсивность отказа Х„ час-1
Интенсивность восстановления, Ц/, час"'
1
0,04
2
2
0,08
1
3
0,1
4
Восстановление элементов осуществляет одна ремонтная бригада с обратным
приоритетом. Требуется определить показатели надежности системы: Кг, Т,
Т
в"
Решение. Представим функционирование системы графом состояний (рис. 4.19).
На нулевом уровне находятся три состояния, которые соответствуют
исправной работе всех элементов системы:
О (03)— работающими являются 1-й и 2-й элементы, 3-й элемент находится
в резерве;
П (02) — работающими являются 1-й и 3-й элементы, 2-й элемент находится
в резерве;
□ (01) — работающими являются 2-й и 3-й элементы, 1-й элемент находится
в резерве.
Внутри кружков и квадратов находятся упорядоченные номера состоянии-
Числа, стоящие слева от вершин графа, показывают номера отказавши

расчет показателей надежности резервированных восстанавливаемых систем 139
элементов. Например, число I означает отказ 1-го элемента и работу
элементе с номерами 2 и 3. Если элемент 1 будет восстановлен, то система
перейдет в состояние, когда все элементы исправны, но рабочими являются
элементы 2 и 3.
Рис. 4.19. Граф состояний системы со скользящим резервом
* Состояния второго уровня являются отказовыми. Согласно принятой
дисциплине обслуживания из этих состояний возможен переход только в свои
предотказовые состояния.
Видим, что даже при обслуживании системы одной ремонтной бригадой с
обратным приоритетом при наличии очереди на работу граф не является
графом типа "дерева". Поэтому анализ надежности проще всего провести
универсальными методами, основанными на теории марковских процессов.
Вычислим стационарные показатели надежности системы Кг, Т и Гв. Для
этого составим систему линейных алгебраических уравнений относительно
стационарных вероятностей pt, / = 0,1, 2,..., 11:
-Ф| +h)Po+\ъра =°;
-(kl+X3)pl+ti2p5=0;
-(h+h)P2+\x\P3=°'>
hPo + hP\ — (M-i + h + хз)Рз + V2P6 + ^з/>7 = 0;
hPi + hPi ~(Из + *-i + h)PA + Hi/* + V2P9 =.°;
X2Po+hP2 -0*2 + ^i +h)Ps +V\P\o + Ц3А1 =0'
^3-^2^6=°;
^з/?з-цз/?7=°;
hP4-V-\Ps=b

140
ЧАСТЬ I. Упражнения r„
hP4-V2P9=fy
hPs~liiPiQ=b
hPs-^3P\\=°-
Система уравнений является однородной, и должна решаться вместе с vo
11 усл°-
вием нормировки: J] pi, = 1. Ее можно упростить, однако мы не будем это
/=о г°
делать, а воспользуемся для решения системы программным средство
Microsoft Excel. Подготовим исходные данные, как показано в табл. 4.5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
А
рО
-0,12
0,04
0,08
1
0,418
В
р!
-0,14
0,04
0,1
1
0,335
С
р2
-0,18
0,1
0,08
1
0,167
D
РЗ
2
-2,18
0,08
0,1
1
0,015
Е
р4
4
-4,12
0,04
0,08
1
0,013
F
р5
1
-1,14
0,04
0,1
1
0,047
G
рб
1
-1
1
0,001
н
р7
4
-4
1
0,000
I
р8
2
-2
1
0,000
J
р9
1
-1
1
0,001
к
р10
2
-2
1
0,001
L
pll
4
-4
1
0,001
м
0
0
0
0
0
0
0
0
0
0
0
0
1
N
0
0
0
0
0
0
0
0
0
0
0
0
1
В первой строке укажем обозначения для вероятностей состоянии, о ..
ячеек А2 : L13 содержатся коэффициенты системы уравнений. В блок .,
N2 : N13 содержатся правые части системы (нули). В 14-й строке за
ются коэффициенты условия нормировки (единицы). ^
Строка 15 остается пока пустой, она предназначена для записи реше
темы, которое получит компьютер.
Таблица 4.5. Исходные данные для решения задачи

Рис. 4.20. Решение системы алгебраических уравнений
Результате в ячейках А15 : L15 будет получено решение системы
уравнений:
Ро =0,418442, Р] =0,334754, р2 =0,167377, р3 =0,015064,
/>4 =0,012553, р5 =0,046866, р6 =0,001205, р7 =0,000377,
^8=0,000251, р9=0,001004, рх0 =0,000937, ри =0,001172.
8табл 4<:о
On " вписано решение, округленное до трех знаков после запятой.
^ ЛИм показатели надежности системы:
эФфициент готовности:
S n Kv = Po + Pi+P2+P3+P4+P5 =0,995055;
РаМетР потока отказов:
<° * (А.2 + Х3 )р3 +(\Х+Х2 )р4 + (Я., + Х3 )/?5 = 0,010779 час-1;
--гелей надежности резервированных восстанавливаемых систем 141
""""^ до записываются формулы левых частей системы. В ячейку М2
В ^«формула
. сУММПРОИЗВ(А2:Ъ2; $А$15:$L$15),
„ „ппируется на ячейки МЗ : Ml4.
которая копиру
подготовки данных следует обратиться к процедуре Поиск решения
^°°1] меню Сервис, заполнить надлежащие поля, как показано на рис. 4.20,
ПУН ь кнопку Выполнить. Заметим, что первое уравнение системы, ко-
ИжАиииенты которого находятся во 2-й строке, не вошло в систему ограниче-
- поскольку оно заменено условием нормировки.

142 ЧАСТЬ i Упражнения. Глава 4
□ наработка на отказ:
r=£L=01995055
со 0,010779
П среднее время восстановления:
_ К„ 1-0,995055 ЛАЛ
Т-— = 0,46 час.
со 0,010779
Вычислим функцию готовности системы АГГ(/). Составим систему линейных
дифференциальных уравнений относительно переходных вероятностей pt{t)t
1 = 0,1, 2, ...,11:
>о(0 = ~ih + *>г)Ро + ЦзА;
p'\(t) = -(\l+Xi)pl+\X2p5;
/4(0=-(^2+а-з)л+жл;
Рз(0 = Х1Ро + hP\ -(Hi + h + h)Pi + №б + РзРГ>
p'4(0 = hPi +hPi -(Из + *•! +h)P4 +V\P& +M2P9;
а Р5^) = Х2Р0+Х2Р2 ~(»2 +h +h)Ps +ЩР\0 + \ЪРП>
РбО^ЬгРз-ЪРб*
p'7(t) = X3p3-p.3p7;
Pb0) = hP4-»iPii
PioiO^hPs-PiPio*
Решим систему методом Рунге — Купы с автоматическим выбором шага по
программе rungekutt.exe. Описание этой программы содержится в частик-
Результатом решения системы является набор функций /?о(0> Pi0)>-*
Р\\(0 > графики которых представлены на рис. 4.21.
На рисунке видны только первые 4 функции, которые максимальным образом
влияют на готовность системы. Функция готовности получается
суммированием вероятностей /?,-(/), соответствующих исправным состояниям системы:
/=0
Чтобы найти вероятность безотказной работы системы Р(/), надо в граф
запретить все переходы из отказовых состояний, а затем для исправных с°'
стояний составить систему дифференциальных уравнений:

расчет показателей надежности резервированных восстанавливаемых систем 143
P\(0 = -fr\+h)P\+\i2P5>
p2(t) = -(X2 + X3)p2+^p3;
P3(t) = hPo+hP\-(Vi+h + h)P3'>
P\ (0 = hP\ + hPi ~ (^з + h + h )Pa '■>
P5{t) = X2pQ + X2P2 -ito+h +h)P5-
^га система также решается с помощью программы rungekutt.exe. В
результате будут получены функции p0(t), /7j(/), p2(t), /73(0, МО, Ps(0,
соответствующие исправным состояниям. Вероятность безотказной работы равна
сумме полученных вероятностей:
/40=i>/(0.
/=0
Рис. 4.21. Вероятности состояний переходного процесса
На Рис. 4.22 изображено два графика: Kr(t) и P(t).
0 сравнению с вероятностью безотказной работы, функция готовности
Изка к 1. При этом время переходного процесса мало. Это говорит о том,
° готовность системы вполне можно оценивать коэффициентом
готовности.

144
ЧАСТЬ I. Упражнения. Глава 4
Рис. 4.22. Функция готовности и вероятность безотказной работы системы
Вычислим среднее время безотказной работы системы. С этой целью
запретим выходы из отказовых состояний и составим систему линейных
алгебраических уравнений относительно времени пребывания в исправных
состояниях т,, / = 0,1, 2, 3, 4, 5 :
'-(Xl+X2)x0 + ii3x4=-\;
-(Xl+X3)xl+\i2x5=0;
-(X2 + X3)x2+\ilx3=0;
Xlx0 + Xlx[ -(ц, +Х2 + Х3)х3 = 0;
hx\ + hb ~ (И^з + Х{+Х2 )т4 = 0;
Х2х0 + Х2х2- Qi2 + Х1+Х3)х5=0.
Решение системы уравнений выполним в Excel с помощью процедуры Поиск
решения. Рабочий лист имеет вид, показанный в табл. 4.6.
В 8-й строке получим среднее время пребывания системы в исправных
состояниях:
т0 =46,20 час, т, =31,05 час, х2 =15,75 час, т3=1,42 час, т4=1,14 час
т5 =4,35 час.
Значит, среднее время безотказной работы системы равно:
7] = т0 + tj + х2 + х3 + х4 + т5 = 99,9 час.
ПРИМЕР 4.4. Три различные по показателям надежности генератора o6paj
зуют энергетическую систему. Такая система является восстанавливаемой

^показателей иадежнооп^езервированиыхвосотанавливаемых систем
145
1
2
3
4
5
6
7
8
А
то
-0,12
0,04
0,08
46,20
В
*1
-0,14
0,04
0,1
31,05
С
*2
-0,18
0,1
0,08
15,75
D
Ь
2
-2,18
1,42
Е
т4
4
-4,12
Ы4
F
т5
1
-1,14
4,35
G
-1
0
0
0
0
0
н
-1
0
0
0
0
0
е дробной кратностью резервирования (т = 1/2) при разной надежности ее
подсистем. Значения интенсивностей отказов и восстановлений подсистем
приведены в табл. 4.4 примера 4.3. Требуется определить:
О коэффициент готовности и наработку на отказ системы при одной бригаде
Ь и обратном приоритете обслуживания;
О коэффициент готовности и наработку на отказ системы при одной бригаде
и прямом приоритете обслуживания;
О функцию готовности Kr(t) при прямом приоритете обслуживания;
О вероятность и среднее время безотказной работы системы.
Решение. Функционирование системы при прямом и обратном приоритетах
обслуживания описывается графами состояний, приведенными на рис. 4.23.
Определение коэффициента готовности системы при обратном приорите-
те обслуживания
° случае обратного приоритета обслуживания граф состояний системы
являли графом типа "дерева" (рис. 4.23, а), поэтому наиболее просто коэффици-
Нт готовности вычислить топологическим методом.
°стояния (0), (1), (2), (3) соответствуют исправным состояниям системы,
Оэтому коэффициент готовности равен сумме вероятностей этих состояний,
соответствии с топологическим методом выражение коэффициента готов-
°сти имеет вид:
*т = Pq + Р\ + Р2 + Рг = =-т-= 5~Т"5 322»
А + 2А., \2Щ \&\4 + 2\{къ\х\ д^з + 2А.2Д.3Ц, Ц2^з
Таблица 4.6. Результаты решения системы уравнений

146
ЧАСТЬ I. Упражнения. Глава 4
где
А = И?МгНз + *#? H2V3 + ^1^3 + ^з^М^з ■
*"' 1 *2
Разделив числитель и знаменатель на |j.fц2Цз' получим:
^ = l + Pi+Рг+Рз
1 + р, + р2 + р3 + 2р,р2 + 2р,р3 + 2р2р3 '
где р/ = —, i = 1, 2, 3 .
На основании исходных данных р, = 0,02, р2 = 0,08, р3 = 0,025 . Подставляя
эти значения в выражение для Кс, получим: Кг = 0,99276 .
о
Рис. 4.23. Граф состояний энергетической системы при прямом (а) и обратном (б)
приоритете обслуживания

Расчет показателей надежности резервированных восстанавливаемых систем 147
Определение наработки на отказ системы при обратном приоритете об-
сяуживанш
0 соответствии с графом состояний выражение наработки на отказ имеет вид;
Т = P0+Pl+P2 + P3 ^
где
„ _ PlP2 p _PlP3 р _PlP2 p _P2P3 p _PlP3 p _Р2РЗ
'•* Д А А А А ■ А
А = 1 + pj + р2 + рз + 2p^2 + 2pjp3 + 2р2р3.
Подставляя эти вероятности в выражение для Т, получим:
т== 1 + Р1+Р2+РЗ
PlP2(^1 +^2) + PlP3(M-l +Цз) + Р2Рз(^2 +М-3>
Вычисления по этой формуле очевидны, они дают следующий результат:
Т = 59,84 час.
Определение коэффициента готовности и наработки на отказ системы при
прямом приоритете обслуживания
В случае прямого приоритета обслуживания граф состояний системы не
является графом типа "дерева" (рис. 4.23, б). Поэтому воспользуемся
классическим способом описания функционирования системы алгебраическими
уравнениями и решим их с помощью системы Derive 5. Технология решения
задачи и ее результаты имеют вид:
#i= p0 + pl-rp2 + p3 + pl2 + pl3 + p21 + p23 + p31 + p32 = 1
#2: Л1-рО-(Л2 + ЛЗ+111)-р1 + ц2-р21 + цЗ-р31 = 0
1з: Л2-р0-(М + ЛЗ + 112)-р2+|Л-р12'+уЗ-р32 = 0
*4: ЛЗ-рО-(Л1 + Л2 + цЗ)-рЗ + ц1-р13+1а2-р23 = 0
#5: А2.р1-ц1.р12 = 0
#6: Л3-р1-ц1.р13 = 0
#7: А1.р2-р2-р21-0
с: Л3-р2-ц2-р23 = 0
#ч.
■ Л1-рЗ-рЗ-р31=0
10: А2-рЗ-цЗ-р32 = 0

148
ЧАСТЬ I. Упражнения. Глава 4
~рО + pi + р2 + рЗ+ р12 + р13 + р21 + р23 + р31 + р32 = Г
Л1-р0-(Л2 + ЛЗ+у1)-р1+у2-р21 + цЗ-р31 = 0
Л2-р0-(Л1 + ЛЗ + и2)-р2 + р1-р12 + рЗ-р32 = 0
ЛЗ-р0-(Л1 + Л2 + уЗ)-рЗ + р1-р13 + р2-р23 = 0
Л2-р1-р1-р12 = 0
#11:
Л3'р1-р1-р13 = 0
Л1-р2-р2-р21=0
Л3-р2-р2-р23 = 0
Л1-рЗ-уЗ-р31 = 0
Л2'рЗ-рЗ-р32 = 0
*p0+pl + p2 + p3 + pl2 + pl3 + p21 + p23 + p31 + p32 = l~
0. 04-рО-(0.08 + 0.1 + 2)-pl + l-p21 + 4-p31 = 0
0.08-рО-(0.04+0.1 + 1)-р2+2-р12 + 4-р32 = 0
0.1-р0-(0.04 + 0.08 + 4)-рЗ + 2-р13+1-р23-0
0.08-р1-2-р12 = 0
#12 •
0.1ф1-2-р13 = 0
0.04-р2-1-р21-0
0.1-р2-1-р23-0
0.04-рЗ-4-р31=0
0.08-рЗ-4'р32=0
ТрО + pi + р2 + рЗ + pi 2 + р 13 + р21 + р23 + рЗ 1 + р32 = 1*
0. 04 ■ рО -(0.08 + 0.1+2)- pi +1 • р21 + 4- рЗ 1 = 0
0.08-р0-(0.04 + 0.1 + 1)-р2 + 2-р12 + 4-р32 = О
0.1-рО-(0.04+0.08 + 4)-рЗ + 2'р13 + 1-р23 = 0
0.08-pl-2-Dl2 = 0
#13: SOLVE * , [рО,
0.1-pl-2-pl3 = 0
0.04-р2-1-р21 = 0
0.1-р2-1-р23 = 0
0.04-рЗ-4-р31=0
J_ 0.08-рЗ-4-р32 = 0
pi, р12, р13, р2, р21, р23, рЗ, р31, р32] , ReaJ
J

расчет показа гелей надежности резервированных восстанавливаемых систем 149
#14: [рО = 0.8 82 5508 534 л pi -0 . 01781294 030 л р12 = 0. 000712517 6123
А р13 = 0.0008 90 64 70154 Л р2=0.06482742210лр21=
0.002593096884 лр23 = 0.006482742210 АрЗ = 0.02342697125
л р31 = 0.0002342697125 лр32 = 0.0004685394251]
#15: 0.9886181870
102968
#1б: р12 =
* 144512919
128710
#17: р13 =
144512919
124912
#18: р21=
48170973
312280
#19: р23 =
48170973
11285
#20: р31=
48170973
22570
#21: р32 =
48170973
„ 0.9886181870
( 102968 ^ л ( 128710 ^ ( 124912 ^
р12 = -2+ о13 = -2+ р21= -1 +
V 144512919J Г 144512919J ^ 48170973J
J ^ 312280 ^ ( 11285 ^ ( ^ 22570 ^ Л
+ Р23 = -1+ р31= -4+ р32 = -4
V 48170973; V 48170973J ^ 48170973^
#2V 0.9886181870 ^г гплл,ллл
^•5: = 65.50001099
2-р12 + 2-р13 + р21 + р23 + 4-р31 + 4-р32
#24- г!+г2+гЗ+1
1 + г1 + г2 + гЗ + 2-г1т2 + 2-г1-гЗ + 2-г2-гЗ
#25: - 0.02 + 0.08 + 0.025 + 1 ___^_
1 + 0. 02+ 0.08+ 0.025+ 2'0.02-0.08+ 2-0, 02-0.025 +2-0. 08-0.025
#2р.
D> 0.9927638545
Строках #1—#10 находятся уравнения системы, а в строке #11 — система
раеНений, образованная из исходных уравнений кнопкой Sub панели инст-

150
ЧАСТЬ I. Упражнения. Глава 4
рументов. В строке #12 показана система уравнений с численными
значениями X и ц. Подстановка исходных значений переменных осуществлена с
помощью кнопки Sub панели инструментов. В строке #13 образована функция
SOLVE решения системы уравнений. После нажатия кнопки Approximate на
экране появляется ответ, показанный в строке #14. В строке #15 находится
значение коэффициента готовности, представляющее собой сумму
вероятностей Р0+Р]+Р2 + Р3 из строки #14.
Наработка на отказ вычисляется по формуле:
т = Р0 + Рх+Р2 + Р3
Эта формула реализована в строках #22 и #23. При образовании формулы нет
надобности набирать многозначные числа. Следует пользоваться номерами
строк #16—#21.
Из результатов расчета видно, что исследуемая система имеет низкую
надежность: наработка на отказ системы равна всего лишь 65,5 часа. Сравнительно
высокий коэффициент готовности системы обеспечивается высокой
интенсивностью ее восстановления. Отметим, что при прямом приоритете
обслуживания коэффициент готовности системы (АГГ = 0,9886) несколько ниже
коэффициента готовности при обратном приоритете (Кг =0,99276), а
среднее время безотказной работы наоборот ниже у системы при обратном
приоритете обслуживания (Т = 59,8 час против Т = 65,5 час).
Определение функции готовности системы
Функцию готовности получим в численном виде, воспользовавшись методом
Рунге — Кутты. Рассмотрим случай прямого приоритета обслуживания.
Технология решения задачи в системе Derive 5 проста и имеет следующий вид:
#1: LOAD(C:\DfW5Trial\DfW\MATH\ODE_APPR.MTH)
#2: -(А1 + А2+АЗ)-р0 + р1-р1 + у2-р2 + цЗ-рЗ
#3: Al-p0-(A2 + A3 + pl)-pl + ]i2-p21 + p3-p31
#4: А2-р0-(А1 + АЗ + у2)-р2 + р1-р12 + цЗ-р32
#5: A3-p0-(Al + A2 + p3)-p3 + ]il-pl3 + u2-p23
#6: А2-р1-р1-р12
#7: А3-р1-ц1-р13
#8: А1-р2-ц2-р21
#9: А3-р2-р2-р23
#10: А1-рЗ-рЗ-р31

Расчет показателей надежности резервированных восстанавливаемых систем 151
|-Ц: А2-рЗ-цЗ-р32
#12: RK([-(Al + A2 + A3)-p0 + ]il-pl + p2-p2 + p3-p3,Al-p0-
-(А2 + АЗ + )Л)-р1 + р2-р21 + рЗ-р31, А2-рО-(А1 + АЗ + р2)-р2 +
+ р1-р12 + цЗ-р32, АЗ-р0-(А1 + А2 + рЗ)-рЗ + у1-р13 + ц2-р23,
A2-pl-pl-pl2, A3-pl-iil-pl3, Л1-р2-ц2-р21, А3-р2-
-у2-р23, А1-рЗ-рЗ-р31, А2-рЗ-цЗ-р32] , [t, рО, pi, р2, рЗ,
р12, р13, р21,р23, р31, р32],[0, 1,0, 0, 0, 0, 0, 0, 0, 0,0],
0.2,40)
#13: RK([-(0.04 + 0.08 + 0.1)-p0 + 2-pl + l-p2 + 4-p3,0.04-p0-
-(0. 08 + 0.1 + 2)-pl + l-p21+ 4-р31, 0.08-рО-(0. 04+ 0.1+1 )-р2 +
+ 2-р12 + 4-р32,0.1-р0-(0.04+0.08 + 4)-рЗ + 2-р13 + 1-р23,
0.08-pl-2-pl2,0.1-pl-2-pl3,0.04-p2-l-p21,0.1-p2-
-1-р23,0.04-рЗ-4-р31,0.08-рЗ-4-р32] , [t, pO, pi, р2, рЗ,
р12, р13, р21, р23, р31, р32] , [0, 1,0, О, О, О, О, О, О, 0,0],
0.2,40)
"О 1
0.2 0.999550325
0.4 0.9986584211
0.6 0.9976398692
0.8 0.9966198161
,-„ 1 0.9956506945
#14:
1.2 0.9947551772
" • • • • ■
7.4 0.9886429493
7.6 0.9886385389
7.8 0.9886349052
8 0.9886319133_
Первой строке находится процедура вызова утилиты ODEAPPR.MTH ре-
ения системы дифференциальных уравнений. В строках #2—#11 находятся
нРавь,е части дифференциальных уравнений, описывающих функционирова-
е системы. Ввод этих уравнений — основная трудность для пользователя
определении функции готовности с помощью Derive 5.

152 ЧАСТЬ I. Упражнения. Глава 4
В строке #12 находится функция RK решения системы дифференциальных
уравнений. При ее вводе нет необходимости набирать и вводить уравнения.
Достаточно указать номера строк, в которых находятся уравнения. В
функции RK указываются также шаг интегрирования h и число строк решения п.
В нашем случае h = 0,2, п = 40.
Теперь для получения решения достаточно нажать кнопку Approximate на
панели инструментов. Получим решение в виде таблицы, в которой число
столбцов равно числу неизвестных, а число строк п = 40. Решение содержит
вероятности всех состояний системы. Для определения функции готовности
необходимо знать лишь вероятности исправных состояний /q(/), P\(t),
/г(0» ^з(0- Выделить эти вероятности из общего решения можно с
помощью функции
EXTRACT_2_COLUMNS(A, i, j ),
где А — матрица решения системы уравнений, i — /-й столбец матрицы, j —
у'-й столбец матрицы. Выделив с помощью этой функции P0(t), /j(/)> P2(t),
P3(t) и просуммировав их, получим функцию готовности системы, которая
приведена в строке #14.
Из полученного решения видно, что исследуемая система имеет высокую
готовность и весьма короткий переходный процесс. Уже через 8 часов Kr(t)
совпадает с коэффициентом готовности с точностью 4 значащих цифры после
запятой.
Определение вероятности и среднего времени безотказной работы системы
Вычислим вероятность безотказной работы численным и аналитическим
методами. Для этого составим систему дифференциальных уравнений
функционирования системы. Из графа состояний, изображенного на рис. 4.23,
видно, что исправными состояниями являются (0), (1), (2) и (3). Переход в
них из отказовых состояний запрещается (ставится экран). Тогда система
дифференциальных уравнений будет иметь вид:
>0' = -(Л.| + Х2 + Яо) + ц,/? + \х.2Р2 + V>3P3',
р; = Х{Р0-(Х2+ 1^1x0^;
' Р1=Х2Р0-(Х1+\3+112)Р2>
Pi = Мо~ (Я.1+Я.2 +йз)^з-
Технология определения вероятности безотказной работы численным
методом Рунге — Кутты имеет вид:

расчет показателей надежности резервированных восстанавливаемых систем 153
#l: LOAD(C:\DfW5Trial\DfW\MATH\0DE_APPR.MTH)
#2: -0.22-p0 + 2-pl + p2 + 4-p3
0: 0.04-р0-2.18-р1
|4: 0.08-р0-1.14-р2
#5: 0.1-рО-4.12-рЗ
#б: RK([-0.22-p0 + 2-pl + p2 + 4-p3,0.04-p0-2.18-pl,0.08-p0-
-1.14-р2,0.1-рО-4.12-рЗ] ,[t, рО, pi, р2, рЗ] ,
[О,1,0,0,0],0.2,100)
0 1 О О О
0.2 0.9658413465 0.006351747413 0.01402956970 0.01326291898
0.4 0.9443633026 0.01028786987 0.02481583860 0.01876718231
0.6 0.92968067-03 0.01272055612 0.033151744^2 0.02096529744
0.8 0.9189001690 0.01421357827 0.03960984065 0.02177023368
1 0.9105216661 0.01511834015 0.04461635900 0.02199983475
1.2 0.9037165010 0.01565503702 0.04849481783 0.02200081738
f7. 1.4 0.8979949245 0.01596203228 0.05149374669 0.02191800996
1.6 0.8930482774 0.01612633677 0.05380549180 0.02181029241
19 0.6871459076 0.01269285587 0.04884385825 0.01673737837
19.2 0.6851502081 0.01265599161 0.04870199949 0.01668876747
19.4 0.6831603047 0.01261923441 0.04856055274 0.01664029776
19.6 0.6811761807 0.01258258397 0.04841951679 0.01659196881
19.8 0.6791978193 0.01254603997 0.04827889047 0.01654378024
_ 20 0.6772252036 0.01250960211 0.04813867256 0.01649573161_
ft
° строке #1 производится вызов утилиты решения системы
дифференциальных уравнений методом Рунге— Купы. В строках #2—#5 система
уравнений с численными значениями коэффициентов, которая вводится
пользователем. В строке #6 вызывается функция Рунге — Кутты. После нажатия кнопки
Pproximate на панели инструментов на экране появляется решение в виде
аблицы, показанной в строке #7.
ак как вероятность безотказной работы системы равна сумме вероятностей
Се* исправных ее состояний, т. е.

154
ЧАСТЬ I. Упражнения. Глава 4
то из общего решения эти вероятности нужно выделить и просуммировать.
Выделение столбцов осуществляется функцией:
EXTRACT_2_C0LUMNS(A, i,j ).
В результате суммирования получается решение, приведенное в следующей
табл. 4.7.
Таблица 4.7. Зависимость вероятности безотказной работы системы от времени
Л час
0
0,2
0,4
0,6
0,8
I
1,2
1,4
1,6
...
19
19,2
19,4
19,6
19,8
20
ГЦ)
1
0,9994855825
0,9982341933
0,9965182681
0,9944938216
0,9922561999
0,9898671732
0,9873687134
0,9847903983
...
0,76542
0,7631969666
0,7609803896
0,7587702502
0,7565665299
0,7543692098
Теперь получим решение в виде формулы, воспользовавшись методом
преобразования Лапласа. Компьютерные технологии в системе Derive 5 имеют
следующий вид:
#1: (s + 0.22)-p0-2-pl-p2-4-p3 = l
#2: -0.04-p0 + (s + 2.18)-pl = 0
#3: -0.08-p0 + (s + 1.14)-p2 = 0
#4: -0.1-p0+(s + 4.12)-p3 = 0

расчет показателей надежности резервированных восстанавливаемых систем 155
~(s + 0.22)-p0-2-pl-p2-4-p3 = l~
-0.04-p0 + (s + 2.18)-pl = 0
#5: -0.08-p0 + (s + l Л4)-р2 = 0
-0.1-p0 + (s + 4.12)-p3 = 0
T(s + 0.22)-p0-2-pl-p2-4-p3 = ll ^
-O.04-p0 + (s + 2.18)-pl = 0
й6: SOLVE , [pO, pi, p2, p3], Real
* -0.08-p0 + (s + 1.14)-p2 = 0
K[_ -0.1-p0 + (s + 4.12)-p3 = 0 J ;
50-{25-s + 103)-(50-s + 57)-{50-s + 109)
|7: p0 =
3125000- sA + 23937500-s3+53876250-s" +36069425 -s + 513229
100 •( 1250-s2 +6575- s + 5871)
#8. pl = . - -
3125000-s" +23937500-S- + 53876250-s^+36069425-S + 513229
200-(25-s + 103)-(50-s + 109)
|9: p2 = ;
3125000-s +23937500-S + 53876250-S-+36069425-S + 513229
125-(50-s + 57)-(50-s + 109)
#10: P3 = -
3125000-s + 23937500-S +53876250-s^+36069425-s +513229
..,, • 6.088899886-s3+46.64097312-s2+104.7899670-s+
#11:
6.088899884-s" +46.64 097311-s3+104.9750695-s2 +
69.37658432
70.27939766-s+l
*12: s = -0.01454278653vs = -2.217497055 v
s = -1. 206346238 vs = -4. 221613919
Первых четырех строках представлены уравнения в преобразовании
Лапласа, а в строке #6 образована функция solve решения системы уравнений.
Поле нажатия кнопки Approximate на экране появляется решение (строки #7—
Щ- В строке #11 находится вероятность безотказной работы системы в пре-
у ковании Лапласа, полученная в результате суммирования строк #7—#10.
Рощение выражения получено в результате выполнения команды главного
Нк) Simplify. В строке #12 приведены корни уравнения знаменателя, полу-
ИоНиь,е с помощью функции SOLVE. Они необходимы при проверке правиль-
Ти получения обратного преобразования Лапласа.
те р^ятность безотказной работы как функция времени вычислена в
результаты 1Гратного преобразования Лапласа. Решение получено с помощью систе-
fathead. Результаты выглядят следующим образом:

156 ЧАСТЬ I. Упражнения. Глава 4
#1: р =-7. 460923-Ю-4-ё'-4-2216^-!. 5226988-Ю"3-e("2-217497)t-
6. 7540381-Ю-3-e(-1-206346,t+1.0090228-e,-1-4542'78-10"2,-t
#2: -7.460923-Ю-4-e("4-2216,t-l.5226988-10-3:ё("2-217497)с-
6.7540381-10-3.e,-1-206346,-t+1.0090228.e,"1-454278'10"8)-t
#3: ](-7. 460923-Ю"4-e(-4-2216,t-l.5226988-Ю"3.е("2-217497к-
о
6. 7540381-Ю-3 •ef-1-206346)c+1.0090228-e(-1-454278-10"Z,c)dt
#4: 69.37661314
В строке # 1 находится выражение вероятности безотказной работы, в строке
#2 — то же выражение, только без его левой части. Это необходимо для
удобства интегрирования выражения. В строках #3 и #4 находятся результаты
вычисления среднего времени безотказной работы, полученного в результате
интегрирования вероятности безотказной работы.
Значения вероятности безотказной работы приведены в табл. 4.8. Таблица
получена в результате табулирования функции P{t).
Таблица 4.8. Вероятность безотказной работы системы в функции времени
/, час
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
...
19
19,2
19,4
19,6
19,8
20
Р{0
1,0000068
0,9994949518
0,9982467078
0,9965357454
0,9945178926
0,9922880244
0,9899074838
0,9874179270
0,9848487160
...
0,7660424735
0,7638241684
0,7616122871
0,7594068110
0,7572077215
0,7550150000

0яСцет показателей надежности резервированных восстанавливаемых систем 157
ца рис 4.24 решение представлено в виде графика.
По результатам расчетов можно сделать следующие важные выводы:
0 энергетическая система не удовлетворяет требованиям, предъявляемым к
таким системам: ее вероятность безотказной работы в течение 25 часов
равна примерно 0,75, а среднее время безотказной работы не превышает
70 часов;
0 достаточно высокий коэффициент готовности системы (примерно 0,99)
обеспечивается ее высокой ремонтопригодностью (среднее время
восстановления системы немного больше 0,5 часа);
О численные и аналитические методы дают практически одинаковые
результаты;
О при обратном приоритете обслуживания наиболее эффективным методом
вычисления коэффициента готовности, наработки на отказ и среднего
времени восстановления является топологический метод.
Рис. 4.24. Вероятность безотказной работы системы
ИМЕР 4.5. Дана дублированная система с постоянно включенным резер-
°м при прямом приоритете обслуживания и следующих исходных данных:
чтенсивности отказов элементов равны X, =0,001 час-1 и Х2 =0>002 час •
л?ем* Установления обоих элементов одинаково и имеет одно из распреде-
Кий: экспоненциальное, равномерное, гамма, усеченное нормальное, Рэлея,
ибулла, нормальное с математическим ожиданием Гв = 7 час и средним
^Ратическим отклонением ав = —?= час.
Т ^
^Уется определить показатели надежности: Т, Тв, Кг.

158 ЧАСТЬ I. Упражнения. Глава 4
Решение. Результаты вычислений, выполненные на основе описанной ранее
методики, учитывающей любые распределения, приведены в табл. 4.9.
Таблица 4.9. Стационарные показатели надежности
для различных законов распределения времени восстановления
Закон
распределения
Экспоненциальный
Равномерный
Гамма
Усеченный нормальный
Рэлея
Вейбулла
Нормальный
Средняя наработка
на отказ, час
36464
36282
36282
36282
36329
36282
36284
Среднее время
восстановления, час
7
3,6
3,6
3,6
4,5
3,6
3,6
Коэффициент
готовности
0,99981
0,99990
0,99990
0,99990
0,99988
0,99990
0,99990
Для экспоненциального времени восстановления имеем: Т = 36464,5 час,
Тъ =7 час, а точные значения равны: Г = 36464,3 час, Тв =7 час. Как видим,
совпадение идеальное.
В случае равномерного распределения времени восстановления с
параметрами a = 5 час, Ь = 9 час показатели надежности, полученные по точным
формулам [5, разд. 7.4], также полностью совпадают с данными табл. 4.9. Такое
сравнение возможно, т. к. значение ав соответствует указанным параметрам
равномерного распределения.
Однако расчет по точным формулам можно выполнить только при условии
экспоненциальных законов времени до отказа. При этом используется
преобразование Лапласа для плотности времени восстановления, вычисление
которого для многих законов имеет известные трудности. Описанный здесь метоД
снимает эти трудности, и позволяет произвести расчеты показателей при лЮ*
бых распределениях с помощью стандартных процедур.
Данные табл. 4.9 показывают, что Т и Гв, вычисленные для двухпараметр*1'
ческих законов распределения, отличаются от аналогичных показателей, №
лученных для однопараметрических законов — экспоненциального и Рэле ^
При этом наибольшее отличие проявляется для экспоненциального распреД
ления. Этот факт еще раз подчеркивает необходимость исследования наДе
ности при законах распределения, отличных от экспоненциального.

расчет показателей надежности резервированных восстанавливаемых систем 159
*0>0МЕР 4.6. Определить надежность системы, если закон распределения
времени до отказа совпадает с законом распределения времени
восстановления. Исходные данные те же, что и в примере 4.5. Для двухпараметрических
распределений дополнительно предположим, что время безотказной работы
казкдого элемента имеет среднее квадратическое отклонение ст = 300 час.
решение. Результаты вычислений приведены в табл. 4.10.
Таблица 4.10. Стационарные показатели надежности
(одинаковые распределения времени до отказа и восстановления)
Закон
распределения
Экспоненциальный
Равномерный
Гамма
Усеченный нормальный
Рэлея
Вейбулла
Нормальный
Средняя наработка
на отказ, час
36464
36151
36085
36109
36086
36089
36122
Среднее время
восстановления, час
7
3,6
3,6
3,6
4,5
3,6
3,6
Коэффициент
готовности
0,99981
0,99990
0,99990
0,99990
0,99988
0,99990
0,99990
Значение средней наработки на отказ в зависимости от законов
распределения изменяется, хотя и незначительно (рис. 4.25). Это говорит о высокой
чувствительности метода.
Нс> 4.25. Средняя наработка на отказ дублированной системы с постоянным резервом

160
ЧАСТЬ I. Упражнения. Глава 4
Таким образом, если закон распределения времени до отказа не известен, то
замена его на экспоненциальный часто неоправдана, поскольку надежность
по наработке на отказ может оказаться завышенной.
ПРИМЕР 4.7. Определить влияние законов распределения времени до отказа
и времени восстановления на наработку на отказ. Математические ожидания
и среднее квадратическое отклонение такие же, как и в примерах 4.5 и 4.6.
Решение. Результаты расчетов содержатся в табл. 4.11.
Таблица 4.11. Наработка системы в зависимости от законов распределения элементов
Закон распределения
времени до отказа
Ехр
и
Г
TN
R
W
N
Закон распределения времени восстановления
Ехр
36465
36210
36084
36130
36089
36097
36119
и
36282
36151
36085
36109
36087
36089
36120
Г
36282
36151
36085
36109
36087
36089
36120
TN
36282
36151
36085
36109
36087
36089
36120
R
36329
36166
36085
36115
36087
36091
36120
W
36282
36151
36085
36109
36087
36089
36120
N
36284
36153
36088
36112
36089
36091
36122
Иллюстрация данных табл. 4.11 приведена на рис. 4.26.
Рис. 4.26. Средняя наработка на отказ для различных распределений
времени до отказа и времени восстановления

рясчвт показателей надежности резервированных восстанавливаемых систем 161
Из гистограммы на рис. 4.26 можно сделать следующие выводы:
rj для фиксированного закона распределения времени до отказа имеется
зависимость наработки на отказ от законов распределения времени
восстановления (группа примыкающих друг к другу столбиков);
0 наибольшей наработкой на отказ обладает система с экспоненциальными
распределениями времени до отказа и времени восстановления;
0 наименьшая наработка на отказ наблюдается для гамма-распределения
времени до отказа, при этом весьма близкими оказываются наработки и
для других распределений, особенно для Рэлея и Вейбулла.
расчеты показывают также, что относительная погрешность показателей
надежности не превышает 2,1 %.
ПРИМЕР 4.8. Для экспоненциального и гамма-распределений установить
зависимость показателей надежности системы от среднего времени
безотказной работы Т2 и от среднего квадратического отклонения а2.
Характеристики элементов те же, что и в примерах 4.5 и 4.6. Время восстановления имеет
усеченное нормальное распределение.
Решение. Предположим, что время безотказной работы второго элемента Т2
^изменяется от 500 до 1500 часов. Тогда результаты вычислений по средней
наработке на отказ системы содержатся в табл. 4.12.
Таблица 4.12. Зависимость средней наработки на отказ
от времени безотказной работы одного из элементов
3(*. 553
Г2, час
500
600
700
800
900
1000
поо
1200
1300
1400
1500
Наработка на отказ
Ехр
36465
43657
50850
58043
65236
72429
79622
86815
94008
101201
108394
Г
36085
43253
50421
57589
64757
71925
79093
86261
93429
100596
107764
5,%
2,10
1,87
1,70
1,58
1,48
1,40
1,34
1,28
1,24
1,20
1,17

162
ЧАСТЬ I. Упражнения. Глава 4
Для рассматриваемых распределений имеет место примерно равномерное
увеличение надежности системы по наработке на отказ одного элемента.
В последнем столбце табл. 4.12 приведено значение относительной
погрешности средней наработки на отказ.
На рис. 4.27 показано увеличение коэффициента готовности системы.
Рис. 4.27. Зависимость коэффициента готовности системы от средней наработки
одного из элементов
Готовность системы в случае гамма-распределения выше, чем при
экспоненциальном распределении.
Среднее время восстановления системы равно Гв = 7 час для
экспоненциального распределения и Тъ =3,6 час для гамма-распределения.
Теперь предположим, что среднее квадратическое отклонение ст2 времени
безотказной работы второго элемента изменяется от 300 до 1500 час.
Результаты вычислений по средней наработке на отказ системы для трех распред6'
лений (экспоненциальное, гамма и Вейбулла) представлены в табл. 4.13.
Из таблицы следует, что для небольших значений а2 < Т2 экспоненциальное
распределение дает некоторый выигрыш в средней наработке на отказ, а ДЛ
а2 > Т2 имеет место существенное увеличение средней наработки на откз3
для гамма-распределения и распределения Вейбулла. Это особенно хоро^
видно из рис. 4.28. В этом случае по критерию наработки на отказ экспоне
циальное распределение может служить нижней границей надежности среД
рассмотренных распределений.

p&e&L
показателем надежности резервированных восстанавливаемых систем
163
Таблица 4.13. Зависимость наработки от ст2
сь, час
300
400
500
600
700
800
900
1000
1100
1200
1300
1400
1500
Ехр
36282
36282
36282
36282
36282
36282
36282
36282
36282
36282
36282
36282
36282
Г
36085
36099
36216 i
36573
37225
38144
39276
40576
42018
43589
45289
47117
49076
W
36089
36121
36216
36393
36645
36962
37330
37737
38176
38641
39126
39628
40143
Рис. 4.28. Зависимость средней наработки на отказ системы от ст2
4VK^P 4*9, тРебУется установить зависимость показателей надежности
Жированной системы от среднего времени восстановления второго эле-
Нта 7в2» изменяющегося от 1 до 20 часов. Время безотказной работы обоих

164
ЧАСТЬ I. Упражнения. Глава 4
элементов подчинено гамма-распределению, а время восстановления имеет
усеченное нормальное (случай I) и экспоненциальное (случай 2) распредели
ния. Параметры этих распределений такие же, как и в примерах 4.5 и 4.6.
Решение. На основании проведенных расчетов получены зависимости ста.
ционарных показателей надежности Г, Гв, Кг от Тв2. Эти зависимости
представлены на рис. 4.29—4.31.
Из рис. 4.29 следует, что среднее время восстановления элементов сильно
влияет на среднюю наработку на отказ системы. Однако практически
отсутствует влияние закона распределения времени восстановления.
Рис. 4.29. Зависимость Гот среднего времени восстановления элементов
Из рис. 4.30 и 4.31 следует, что среднее время восстановления элементов
также сильно влияет на среднее время восстановления и на коэффициент
готовности системы. Однако, в отличие от наработки, здесь существенное
влияние оказывает и вид закона распределения. Если время восстановления
второго элемента имеет распределение, отличное от экспоненциального, то
среднее время восстановления системы оказывается меньше, а коэффициент
готовности больше, чем для экспоненциального распределения.
Как видно из последующих расчетов, имеется, причем весьма существенная-
зависимость показателей надежности от среднего квадратического
отклонения времени восстановления второго элемента ав2. Предположим, что это
параметр изменяется также от 1 до 20 часов. Время безотказной работы ооо
их элементов подчинено гамма-распределению. Время восстановления име
гамма-распределение (случай 1) и экспоненциальное распределение (с^У
чай 2). Параметры этих распределений такие же, как и в примерах 4.5 и 4.6.

расчет показателей надежности резервированных восстанавливаемых систем 165
Рис. 4.31. Зависимость Кг от среднего времени восстановления элементов
ависимости показателей надежности Т и Гв от ств2 представлены на
Рис 4.32 и 4.33.
онечно, для экспоненциального распределения данные зависимости отсут-
вУЮт. Но для гамма-распределения увеличение разброса времени восста-
°вления одного из элементов уменьшает надежность системы как по нара-
Тке на отказ, так и по среднему времени восстановления.
Рис. 4.30. Зависимость Гв от среднего времени восстановления элементов

166
ЧАСТЬ I. Упражнения. Глава 4
Рис. 4.32. Зависимость Гот среднего квадратичсского отклонения
времени восстановления элемента
Рис. 4.33. Зависимость Тв от среднего квадратичсского отклонения
времени восстановления элемента
ПРИМЕР 4.10. Дана дублированная система с резервом замещением при
прямом приоритете обслуживания и следующих исходных данных:
интенсивности отказов элементов равны X.j =0,001 час-1 и *А,2 =0,002 час" . Врем*
восстановления обоих элементов одинаково и имеет одно из распределении-
экспоненциальное, равномерное, гамма-, усеченное нормальное, Рэлея, ВеИ'

pae&L
показателей надежности резервированных восстанавливаемых систем
167
булла, нормальное с математическим ожиданием Тв = 7 час и средним квад-
2
оатическим отклонением ств = —т= час.
Р л/3
Требуется определить показатели надежности Т, TR, Кг.
решение. Результаты вычислений, выполненные по приведенным ранее
формулам, сведены в табл. 4.14.
Таблица 4.14. Показатели надежности в зависимости от законов распределения
времени восстановления (резерв замещением)
Закон
распределения
Экспоненциальный
Равномерный
Гамма
Усеченный нормальный
Рэлея
Вейбулла
Нормальный
Наработка на
отказ, час
72261
71857
71857
71857
71960
71857
71861
Среднее время
восстановления, час
7
3,6
3,6
3,6
4,5
3,6
3,6
Коэффициент
готовности
0,99990
0,99995
0,99995
0,99995
0,99994
0,99995
0,99995
Легко убедиться в том, что для экспоненциального распределения времени
восстановления имеем точное значение показателей надежности.
Для неэкспоненциальных распределений, как и в случае постоянного резерва,
получаем близкие между собой значения показателей. Однако эти значения
по средней наработке на отказ почти вдвое превышают значения показателей
Для постоянного резерва.
Чуднее время восстановления практически не изменилось.
4.4. Задачи для самостоятельного решения
ЧЦАЧА 4.1. Дана резервированная система с постоянным резервом крат-
°Сти m, состоящая из одинаковых по надежности элементов.
Интенсивности отказов элементов X = 0,08 час-1, интенсивности восстановлений
^М час"1. Определить кратность резервирования, чтобы было выполнено
Ребование по ее надежности: коэффициент готовности системы должен быть
е Менее Кг >0,98. Рассмотреть случаи полностью ограниченного и неогра-
ЧеНного восстановлений.

168
ЧАСТЬ I. Упражнения. Глава 4
ЗАДАЧА 4.2. Определить кратность резервирования системы (резерв заме-
щением), состоящей из одинаковых по надежности и ремонтопригодности
элементов. Интенсивности отказов элементов А, = 0,2 час"1, интенсивности
восстановлений ц = 0,9 час-1. Должно быть выполнено условие: Г>900 час.
Рассмотреть два случая: полностью ограниченное и неограниченное
восстановление.
ЗАДАЧА 4.3. Определить вероятность и среднее время безотказной работы
резервированной системы с постоянным резервом кратности т = 7.
Обслуживание осуществляется двумя ремонтными бригадами. Интенсивности
отказов и восстановлений элементов соответственно равны: Х = 0,0006 час-1,
ц = 0,05 час"1.
ЗАДАЧА 4.4. Определить вероятность и среднее время безотказной работы
резервированной системы с ненагруженным резервом кратности т = 7.
Обслуживание осуществляется двумя ремонтными бригадами. Интенсивности
отказов и восстановлений элементов соответственно равны: А. = 0,0006 час-1,
ц = 0,05 час""1.
ЗАДАЧА 4.5. Структурные схемы (схемы расчета надежности) пяти систем
приведены на рис. 4.34. Интенсивности отказа элементов X и восстановления
\i указаны на структурных схемах.
Определить в виде формул показатели надежности: Кг — коэффициент
готовности, Т — наработку на отказ, Гв — среднее время восстановления.
Вычислить показатели надежности при значениях интенсивностей отказов,
приведенных в табл. 4.15.
Таблица 4.15. Интенсивности отказов элементов систем
X, час"'
0,001
Хь час"1
0,005
\ъ час"'
0,008
Х3, час '
0,002
И, час '
0,3
|ii, час"1
0,36
ц2- час '
0,7
Из* ча(
0,5
Указания:
П решение во всех вариантах получить в виде формул топологическим ме'
то дом;
□ при изображении графа стремитесь уменьшить число узлов путем их объ
единения;

0йСцвт показателей надежности резервированных восстанавливаемых систем 169
Рис. 4.34. Структурные схемы технических систем

170
ЧАСТЬ I. Упражнения. Глава 4
□ восстановление осуществляется одной ремонтной бригадой с обратные
приоритетом;
О в целях упрощения формул используйте обозначения:
А. Л] Лт А,э
р=-, р, =-Ч p2=-S р3= —•
Ц Hi ^2 Цз
ЗАДАЧА 4.6. Структурные схемы двух систем представляют собой общее
постоянное резервирование с дробной кратностью. Кратность
резервирования первой системы т = 1/2 (один элемент резервный на два основных),
второй — т - 2/3 (два элемента резервных на три основных). Интенсивности
отказа и восстановления постоянны и равны X и р..
Определить показатели надежности системы: Кг, Т, Гв. Найти численные
показатели надежности, если Л. = 0,01 час-1, а среднее время восстановления
Гв =1,5 час. Определить, какая из систем более надежна и каков выигрыш
надежности по коэффициенту готовности и наработке на отказ. Рассмотреть
случаи одной и двух бригад обслуживания.
ЗАДАЧА 4.7. Система состоит из пяти элементов, каждый из которых
дублирован с постоянно включенным резервом. Интенсивности отказов элементов
имеют следующие значения: A.j =0,001 час"1, Х2 =0,002 час"1,
Х3 =0,004 час"1, Х4 =0,0028 час"1, Х5 =0,005 час"1. Среднее время
восстановления элементов постоянно и равно Г = 4,2 час. Систему обслуживает
одна бригада. Определить методом эквивалентных схем диапазон значений
Кг и Т системы.
ЗАДАЧА 4.8. Восстанавливаемая дублированная система с постоянно
включенным резервом состоит из элементов разной надежности.
Необходимо определить коэффициент готовности и наработку на отказ
системы при двух дисциплинах обслуживания: при приоритете более и менее
надежного элемента. Значения интенсивностей отказов элементов приведены
в табл. 4.16.
Таблица 4.16. Варианты интенсивностей отказов элементов системы
Вариант
kh час"1
А.2, час-'
1
0,01
0,035
2
0,005
0.0075
3
0,001
0,005

ря&ют показателей надежности резервированных восстанавливаемых систем 171
Средние времена восстановления элементов постоянны и равны Гв1 = 4 час,
Гв2=10час.
решение получить в аналитическом виде и в виде таблицы. Сделать вывод о
целесообразности применения назначенного приоритета (какой из
приоритетов с позиции надежности более эффективный).
ЗАДАЧА 4.9. Структурные схемы пяти систем приведены на рис. 4.34.
Определить показатели надежности Кг, Т, Тъ для случая двух вариантов
обслуживания:
о) прямой приоритет с одним обслуживающим органом;
б) восстановление не ограниченное.
Решение получить в аналитическом и численном виде. Значения интенсивно-
стей отказов и восстановлений элементов приведены в табл. 4.17.
Таблица 4.17. Интенсивности отказов и восстановлений элементов
Xj, час '
0,01
Ци час"1
1
Х2, час"1
0,025
ц2, час-1
0,5
X}, час '
0,008
Цз, час-1
0,34
Х4, час"1
0,035
щ, час"1
0,25
%s, час"1
0,05
|!5, час"1
0,17
ЗАДАЧА 4.10. Интенсивности отказов и восстановлений элементов
дублированной системы с постоянно включенным резервом имеют значения:
^ = 0,0076 час"1, ц = 0,15 час"1.
Необходимо найти аналитические выражения для вероятности безотказной
Работы и функции готовности системы. Путем табулирования функций
представить решения в виде таблиц и графиков.
10 известным аналитическим выражениям определить среднее время безот-
^ной работы и коэффициент готовности системы.
казание: для получения P(t) и Яр(0 воспользуйтесь решением
дифференциальных уравнений с помощью преобразования Лапласа.
/ЧцАЧА 4.11. Структурные схемы систем приведены на рис. 4.34. Необхо-
мо определить в виде таблиц и графиков показатели надежности: /£(/)<•
г^> /с(0. МО- Данные об интенсивностях отказов и восстановлений

172
ЧАСТЬ I. Упражнения. Глава 4
приведены в табл. 4.17. Решение получить методом Рунге— Кутты с
помощью компьютерных технологий.
ЗАДАЧА 4.12. Интенсивность отказов элементов дублированной системы
равна А. = 0,02 час-1. При отказе одного из элементов увеличивается
интенсивность отказа второго элемента А/= 0,04 час"1. Восстановление
производится одним ремонтником, время восстановления подчинено закону Эрланга
2-го порядка с параметром ц = 1 час"1. Определить коэффициент готовности
системы.
ЗАДАЧА 4.13. Структурная схема системы изображена на рис. 4.35.
Рис. 435. Структурная схема системы, состоящей из трех групп элементов
Все элементы разбиты на три группы. Элементы, входящие в одну группу,
имеют одинаковые показатели надежности и восстановления, содержащиеся
в табл. 4.18.
Таблица 4.18. Показатели надежности и восстанавливаемости элементов
Номер группы
Номера элементов
Время до отказа
Время восстановления
1
1,2
N(60; 15)
U(2; 14)
2
3
Г(4; 16)
R(0,01)
3
4,5,6
W(2; 56)
Ехр(0,1)
Элементы 3-й группы образуют мажоритарную систему кратности 1/2.
Восстановление отказавших элементов производится одной бригадой с обратным
приоритетом. Требуется определить показатели надежности системы: Кг, '
иГв.
Указание: используйте свойство независимости стационарных показателе
надежности от законов распределения элементов.

расчет показателей надежности резервированных восстанавливаемых систем 173
^дДАЧА 4.14. Определить функцию готовности дублированной системы.
Время до отказа элементов имеет распределение Вейбулла с математическим
^киданием ^ = 280 час и средним квадратическим отклонением а = 100 час.
Зремя восстановления элементов имеет равномерное распределение на
промежутке от 0 до 24 часов. Результаты представить в виде таблиц и графиков.
ЗАДАЧА 4.15. Дана система с постоянно включенным резервом кратности
# = 2, работающая в стационарном режиме. Интенсивности отказов
постоянные, а время восстановления произвольное с плотностью распределения
g(t). Определить интенсивности переходов графа, соответствующие
восстановлению элементов. Рассмотреть случаи полностью ограниченного
восстановления для прямого и обратного приоритетов обслуживания.
ЗАДАЧА 4.16. Дана резервированная система (резерв замещением)
кратности m = 2, работающая в стационарном режиме. Интенсивности отказов
постоянные, а время восстановления произвольное с плотностью распределения
g(t). Восстановление производится одной ремонтной бригадой с прямым
приоритетом обслуживания. Определить интенсивности переходов в графе
достояний, соответствующие восстановлению элементов.

ГЛАВА 5
АНАЛИЗ НАДЕЖНОСТИ СИСТЕМ
СЛОЖНОЙ СТРУКТУРЫ
5.1. Методы расчета показателей надежности
сложных систем
При анализе надежности сложных систем возникают трудности, часто
непреодолимые. Их основными причинами являются:
□ отсутствие достоверных данных о надежности элементов;
□ слишком большие размерности уравнений, описывающих
функционирование сложной системы в смысле ее надежности;
П недостаточные математические знания разработчика сложных
высоконадежных технических и информационных систем.
Сложные системы состоят из большого числа простых элементов, из которых
конструируются узлы и блоки. Из узлов и блоков образуются подсистемы, из
которых затем создается сложная система. Законы распределения времени до
отказа элементов часто бывают известными, но созданные из них узлы, блоки
и, тем более, подсистемы имеют произвольные законы распределения
времени до отказа, параметры которых исследователю неизвестны. Знания лишь
показателей надежности узлов, блоков и подсистем недостаточно для
определения показателей надежности сложной системы.
Сложные восстанавливаемые технические и информационные системы часто
бывают избыточными с различными видами резервирования и дисциплинами
обслуживания. Число состояний таких систем настолько велико, что
определить их показатели надежности точными методами практически невозможно-
В таких случаях приходится применять приближенные методы, делать
обоснованные допущения, выбирать необходимый математический аппарат. Кр0'
ме того, необходимо глубоко понимать физическую сущность задачи.
Специалист, который ведет анализ надежности сложной системы, должен иметь
большие знания в различных областях науки. Он должен также владеть коМ

Af^jW3 надежности систем сложной структуры 175
пькугерной технологией решения математических задач. Вот почему анализ
наДежности сложной системы в большинстве случаев требует научных
исследований.
Трудности анализа надежности в ряде случаев можно преодолеть, если
хорошо владеть теорией и глубоко знать физическую сущность задачи. Такими
случаями являются:
О сравнительная оценка вариантов структурных схем с целью выбора
наилучшего;
О оценка границ показателей надежности системы;
О приближенные расчеты, основанные на допущениях, не противоречащих
физической сущности задачи и обеспечивающих допустимую точность
вычисления показателей надежности.
В настоящей главе будут показаны способы оценки надежности сравнительно
сложных систем, которые не поддаются расчетам точными методами.
Описать эти способы, доведя их до инженерных методик, вряд ли возможно, т. к.
в каждом конкретном случае они имеют особенности.
5.2. Оценка надежности сложных систем
по данным о надежности подсистем,
независимых по восстановлению
5.2.1. Экспоненциальные распределения
Рассмотрим сложную восстанавливаемую техническую систему, структурная
схема которой представляет собой основное соединение г подсистем
типовых структур. Под типовой структурой понимается техническое устройство,
°бслуживаемое независимо от остальных подсистем, т. е. имеющее свои
ремонтные органы и свою дисциплину восстановления. Будем считать, что при
отказе системы из-за отказа какой-либо типовой структуры остальные под-
Системы не работают и поэтому не могут отказать в течение периода ремонта
Системы. Однако в подсистемах могут восстанавливаться отказавшие ранее
лементы. Такими системами являются автоматизированные системы управ-
ения технологическими процессами и многие информационные системы.
^ли система состоит из большого числа подсистем, то применение извест-
Ь1Х методик вызывает вычислительные трудности, обусловленные чрезвы-
***но большим количеством состояний системы. Но для стационарных пока-
телей надежности можно привести достаточно близкие между собой ниж-
^•Ою и верхнюю оценки. Здесь описывается способ получения этих оценок и
РИводятся простые расчетные формулы, позволяющие по заданным показа-

176
ЧАСТЬ I. Упражнения. Глава s
телям надежности типовых структур определить показатели надежности всей
системы.
Для получения таких, оценок анализируются две другие системы, показатели
надежности одной из которых выше, а другой — ниже аналогичных
характеристик надежности исходной системы, причем эти характеристики
сравнительно легко могут быть вычислены. Такие системы образуются из исходной,
если сделать следующие допущения относительно ее функционирования:
1. После отказа какой-либо подсистемы другие подсистемы полностью
отключаются, т. е. даже при наличии свободных ремонтных бригад
элементы этих подсистем не могут восстанавливаться и к моменту окончания
ремонта данной подсистемы сохраняют все свои вероятностные
характеристики такими же, как и в начале ремонта.
2. Если какая-либо подсистема пришла в предотказовое состояние, из
которого обязательно последует переход в отказовое состояние, то все
остальные подсистемы отключаются и сохраняют свои вероятностные
характеристики на время пребывания системы в соответствующем предотказовом
состоянии. При этом предотказовое состояние считается состоянием
работоспособности всей системы.
Очевидно, что если система удовлетворяет первому допущению, то, получив
для нее коэффициент готовности и наработку на отказ, будем иметь нижние
оценки Kf' и Т^ для соответствующих показателей надежности исходной
системы. Второе допущение позволяет найти верхние оценки К^ и Г(в) для
коэффициента готовности и средней наработки на отказ исходной системы.
Для каждой /-и типовой структуры (/ = 1,2,..., г) должны быть
предварительно получены следующие показатели надежности: коэффициент
готовности Krj, наработка на отказ 7] и вероятность P0j. Коэффициент готовности и
наработка на отказ вычисляются в соответствии с методикой, изложенной в
[5, гл. 5]. Вероятность Р0/ вычисляется по формуле:
J Kj+Vj
где pj — стационарная вероятность /-го предотказового состояния; Xj -"
суммарная интенсивность переходов из/-го предотказового состояния во все
состояния отказа; цу — суммарная интенсивность переходов из/-го предо1""
казового состояния во все исправные состояния. Суммирование в формул
(5.1) производится по всем предотказовым состояниям, за исключением
начального.

лияпиз надежности систем сложной структуры 177
Нижняя и верхняя оценки коэффициента готовности рассчитываются по
формулам:
1 i У Kri ~ Ро'
4Н) ! , *г(,) = '■' Р<" . (5.2)
Г 1 _ Jf Г Г \ п
/=1 ^п /=I POi
За истинное значение коэффициента готовности принимается среднее
арифметическое нижней и верхней оценок:
Кг= r r . (5.3)
Относительная погрешность расчета определяется по коэффициенту простоя
системы. Эта погрешность (для высоконадежных систем) более наглядно по
сравнению с погрешностью по Кг отражает физическую сущность расчетов.
Относительная погрешность вычисляется по формуле:
&-(в) _ Ин)
5 = ,х,1 '100%- (5-4)
Нижняя и верхняя оценки наработки на отказ рассчитываются по формулам:
1 i У Кг' ~ Р°'
j(h) _ 1 j(b) _ /=l POi ,$ 5ч
У- \ + У-^-
/=1 Л i=l ЛА)/
За истинное значение наработки на отказ принимается среднее
арифметическое нижней и верхней оценок:
т(и) т(в)
Т = - ——. (5.6)
2
относительная погрешность расчета не превышает
г(в) _ тМ
s =' \.\om. (5.7)
у(в) + у(н)
РеДнее время восстановления системы вычисляется по известным коэффи-
НтУ готовности и наработке на отказ:
r=Iz*L.r. (5.8)
В «г

178 ЧАСТЬ I. Упражнения. Глава s
5.2.2. Произвольные распределения
В предыдущем разделе была показана возможность приближенного расчета
показателей надежности систем, представляющих собой последовательное
соединение типовых структур в случае, когда законы распределения времени
безотказной работы и времени восстановления элементрв каждой типовой
структуры экспоненциальные. Однако формулы (5.2) и (5.5) получены без
учета экспоненциальности распределений и, следовательно, справедливы в
общем случае.
Описанный ранее метод применим и в том случае, когда система
представляет собой последовательно-параллельное соединение типовых структур
(резерв нагруженный). Для этого резервированные узлы следует рассматривать
как самостоятельные типовые структуры. Покажем, как можно найти
показатели Кг, Т и Р0 для резервированных узлов по аналогичным показателям
типовых структур. Функционирование резервированного узла, элементы
которого имеют независимое обслуживание, можно описать графом состояний,
в ветви которого ставятся величины, обратные наработке на отказ и среднему
времени восстановления соответствующих элементов. В данном случае под
элементом подразумевается типовая структура.
Предположим, что резервированный узел имеет кратность резервирования
m, т. е. он состоит из m +1 типовой структуры, причем /-я типовая структура
имеет коэффициент готовности Kri, наработку на отказ 7J, среднее время
восстановления Гш, / = 0,1, 2,..., m . Тогда коэффициент готовности и
наработка на отказ всего узла определяются по формулам:
m к
jcr=i-no-Jcrt). r= ^— • (5-9)
/=0 /в/
Теперь для узла в целом вычислим вероятность Р0. Узел окажется ву-м пред-
отказовом состоянии (у* = 0,1, 2,..., т), если все его типовые структуры*
кромеу'-й, откажут и будут восстанавливаться, ау-я структура будет исправна-
Следовательно, вероятностьу-го предотказового состояния равна:
т
Pj = YlO-Kri)KrJ.
/=о,
Суммарная интенсивность переходов из состояния у в отказовое состояни
равна X i; =—, а суммарная интенсивность переходов из состояния у* во вс
Tj

диализ надежности систем сложной структуры 179
иСправные состояния равна Цу = J] —. Подставляя найденные выражения в
формулу для вероятности PQ, получим:
m m m f.
/Ь=1-П0-^г/)-Е ПО^п)^-]—J—r- (5-ю)
/=o j=oi=o, _L+v_L
По формулам (5.9) и (5.10) находятся требуемые показатели Кг, Т и Р0 для
каждого резервированного узла. После этого определяются нижние и верхние
оценки коэффициента готовности и наработки на отказ всей исследуемой
системы.
5.3. Примеры решения задач
Убедимся на примерах в справедливости двусторонних оценок показателей
надежности по формулам (5.2) и (5.5).
ПРИМЕР 5.1. Структурная схема системы состоит из двух устройств
(рис. 5.1). Первое устройство представляет собой дублированную систему, а
второе — один элемент. Интенсивности отказов и восстановлений всех
элементов одинаковы и равны X и у. соответственно. Каждое устройство
обслуживается одной ремонтной бригадой. Требуется определить нижние и
верхние оценки коэффициента готовности и наработки на отказ.
Рис. 5.1. Схема расчета надежности
^ение. Граф состояний системы представлен на рис. 5.2.
° П^афу составим систему уравнений для определения стационарных значе-
** вероятностей состояний системы:

180
ЧАСТЬ I. Упражнения. Глава
Рис. 5.2. Граф состояний системы
2Хр0 - (ц + 2Х)рх + \хр3 + ц/?4 = 0;
<Xp0-\xp2+\ip4=0;
Хрх-\хръ=0;
A,/?, -2|ip4 =0.
Из решения этой системы найдем:
2 + р 4р
2 + 7р + 9р2 2 + 7р + 9р2
Я.
где р = —.
Следовательно, коэффициент готовности будет равен
2 + 7p + 9pz
Так как параметр потока отказов
со = Хро + 2Хрх = г-,
2 + 7р + 9р2
то наработка на отказ равна
т = кг= 2+5р
со Я.(2 + 9р)'

лиализ надежности систем сложной структуры
181
хш получения нижних и верхних оценок рассмотрим оба устройства в
отдельности и вычислим для каждого из них коэффициент готовности Kri,
сумму вероятностей всех исправных состояний, за исключением
вероятностей последних предотказовых состояний p0i и наработку на отказ 7J. Эти
характеристики определяются по графам состояний каждого из устройств,
которые представлены на рис. 5.3, а и б соответственно.
©
И А
О 0
Ц А Ц А •
Л. V X \f '
2 1
а б
Рис. 5.3. Графы состояний подсистем
Из первого графа находим показатели надежности первого устройства:
К . 1 + 2р X 1+Зр г=1±2р
Г! 1 + 2р + 2р2 Г' ^ + /° (14-р)(1 + 2р + 2рУ ' 2^р •
Для второго устройства эти характеристики равны:
^г2=^02=7—' 72=Т"
1 +р А,
Иижние и верхние оценки находим по формулам (5.2), (5.5):
*-(») - * + 2Р Ив) _ 1 + Зр + 2р2
l + 3p + 4p2 l + 4p + 7pz+2pJ
у(») = 1 + 2Р г(в) = 1 + 3р + 2р2
М1 + 4р)' Х(1 + 5р + 2р2)'
^РУДно проверить, что К{г11) <КГ<К(гв), Т{н) <Т<Т{в). Численные значе-
я Показателей для р = 0,01 приведены в табл. 5.1.

182
ЧАСТЬ I. Упражнения. Глава s
Таблица 5.1. Значения показателей при р = 0,01
Показатель
надежности
Кг
Т
Оценки
Нижняя
0,9899068
0.980769Д
Верхняя
0,9899087
0,98095бД
Точное
0,9899077
0,98086 ,Д
Относительная
погрешность
0,00019
0,00019
ПРИМЕР 5.2. Требуется определить коэффициент готовности, наработку на
отказ и среднее время восстановления системы, структурная схема которой
приведена на рис. 5.4. Система представляет собой основное соединение
четырех независимо обслуживаемых технических устройств (ТУ). Законы
распределения времени безотказной работы и времени восстановления каждого
элемента экспоненциальные.
A.|.Mi I h< Mi '
I 1 h-»2 I 1 1 V *'$ *■(•■• Й6
Г Я,|'Ц' 1 ] г- *ч.И4 \-\ П J J
I4ZZH l|4ZZH It, Л1
i и, 2J 3 J L^-^Tj
Рис. 5.4. Схема расчета надежности
Интенсивности отказов и восстановлений элементов, а также дисциплина
обслуживания каждого устройства различны:
□ структура 1: X, =0,02 час"1, ц., = 0,5 час-1, А.2=0,01 час"1, и2=1 час",
одна ремонтная бригада, прямой приоритет обслуживания;
□ структура 2: Х3 =0,03 час-1, ц3 =0,6 час"1, ХА =0,04 час-1, ц4 =0,8 час ,
одна ремонтная бригада, обратный приоритет обслуживания;
О структура 3: Л,5 =0,01 час-1, ц5=1 час-1, одна ремонтная бригада;
О структура 4: Хе =0,02 час"1, ц6 =0,2 час"1, одна ремонтная бригада,
прямой приоритет обслуживания.
Решение. Определим характеристики Kri, 7}, P0i для каждой типовой
структуры. Как следует из примера 5.1, требуемые характеристики для
типовой структуры 1 имеют следующие значения: •
/Сг1=0,986, Г, =87,26 час, P0l=Krl-pt X*+X2 =0,982.
Х1 +Х2 +Ц|

Анализ надежности систем сложной структуры
183
ддя других подсистем эти характеристики вычисляются аналогично.
Результаты расчетов представлены в табл. 5.2.
Таблица 5.2. Показатели надежности типовых структур
Номер типовой
структуры
I
2
3
4
к«
0.986
0,995
0,990
0,99!
Т„ час
87,26
314,28
100
550
Р*
0,982
0,991
0,990
0.983
В соответствии с формулами (5.12)—(5.18) и с учетом характеристик,
помещенных в табл. 5.2, получим:
О оценки коэффициента готовности:
/Сг(и) = 0,9630, *<в) = 0,9634, Кг = 0,9632;
□ оценки средней наработки на отказ:
Т(н) =37,79 час, Т(в) =38,30 час, Т = 38,04 час;
П оценка среднего времени восстановления:
Тв =1,45 час.
Относительные погрешности расчетов составляют:
Ьк =0,54%, 5Г=0,67%.
ПРИМЕР 5.3. Рассмотрим сложную систему, структурная схема которой
изображена на рис. 5.5.
Рис. 5.5. Структурная схема расчета надежности

184
ЧАСТЬ I. Упражнения. Глава s
Система состоит из пяти типовых структур, причем структуры 1, 2, 3 нере-
зервированы, а типовые структуры 4 и 5 образуют дублированную систему
(резерв нагруженный).
Структура 1 представляет собой дублированную систему с облегченным
резервом. Время безотказной работы обоих элементов имеет экспоненциальное
распределение с параметрами А, = 0,01 час"1 для основного и 0,5А, для
резервного элемента. Время восстановления каждого элемента имеет
распределение Эрланга 2-го порядка с параметром ц = 0,5 час-1. Обслуживание
структуры осуществляет одна ремонтная бригада.
Структура 2 представляет собой дублированную систему с ненагруженным
резервом. Время безотказной работы основного и резервного элементов
имеет распределение Эрланга третьего порядка с параметрами Xj =0,05 час-1 и
Х2 =0,08 час"1 соответственно. Время восстановления каждого элемента
подчинено распределению Эрланга второго порядка с параметрами
Ц] =0,2 час"1 и ц2 =0,25 час"1 соответственно. Ремонт отказавших
элементов осуществляет одна ремонтная бригада с прямым приоритетом.
Структура 3 состоит из трех элементов. Законы распределения времени
безотказной работы экспоненциальные с параметрами X, =0,005 час"1,
Х2 =0,0025 час"1, Х3 =0,0004 час-1. Время восстановления каждого
элемента имеет распределение Эрланга второго порядка с параметрами
р., =0,2 час"1, \х2 =0,25 час"1, ц3 =4 час"1. Обслуживание структуры
осуществляет одна ремонтная бригада с обратным приоритетом.
Структура 4 представляет собой дублированную систему с нагруженным
резервом. Время безотказной работы обоих элементов экспоненциальное с
параметрами Xj=0,02 час"1, А.2=0,04 час"1 соответственно. Времена
восстановления имеют распределения Эрланга 2-го порядка с параметрами
ц, =0,2 час"1, |х2 =0,25 час"1 соответственно. Восстанавливает структуру
одна ремонтная бригада с прямым приоритетом.
Структура 5 состоит из одного элемента. Время безотказной работы и время
восстановления имеет экспоненциальное распределение с параметрами
Х = 0,01 час"1, ц = 0,25 час"1 соответственно.
Требуется определить коэффициент готовности, наработку на отказ и средне
время восстановления всей системы.
Решение. Показатели надежности типовых структур рассчитываются обы4'
ными методами путем графического изображения состояний и переход0
между ними, составления и решения системы интегральных уравнений и оП'
ределения требуемых показателей. Можно использовать также программ^

диализ надежности систем сложной структуры 185
предназначенные для расчета надежности типовых структур, элементы
которых имеют произвольные законы распределения времени безотказной работы
й восстановления.
вычислим показатели надежности Кг, Т и Р0 для типовых структур I, 2, 3.
для типовой структуры I имеем:
к k + \-kg(X) T= k + \-kg(X)
г (k+\)XTB+g(xy (*+dmi-£(*.))'
(* + 1)А.
р-к -р-±-=к к Ь-=к (*+'>0-gft»2
Г°~ г ^Ч + ц, r (к + \)Х (k + ])X2X + vn r (к + \)ХТЛ+§(к)*
1 Н 1
где к = 0,5 . Для структуры 2 имеем:
*г=_ 5_±5 ,
](1 - Fx{t)G2{t))dl + ](1 - F2(t)Gx(t))dt
о о
' *, 21+72
Г = - !—^ ,
р^ОлСОЛ + ^С'ЫОЖ
о о
г» ы ^-3 ^4
^ А,3+ц, A.4+H2J
Й (Oft (0* Jfl «)G2 {t)dt + ]f2 (/)g, (/)Л JF2 (Об, (ОЛ
_£ __0 0 0 0 -
}(1 - Fx(t)G2(t))dt + ](1 - F2(t)Gx (t))dt
о о
Усмотрим структуру З. Ее дисциплина обслуживания такова, что стацио-
аРные характеристики не зависят от законов распределения, поэтому
*г=А+А+А. Т = Po+Pi+Pi ,
hPo + (^2 + ^з )Р\ + (М + ^з )Р2
f \
P-V ^2+^3 ■ _ h + ^3
/0=л-г_ Р\ — + Р2 Р •
^2+^3+^Г~ ^1+^3+^Г-
А Ув1 1ъ2 /

Номер типовой „ ,„ _
Кг ■ Г, час Р0
структуры u
1
2
3
4и5
0,9982
0,9942
0,9979
0,9976
1751,55
1089,38
1638,59
1055,85
0,9960
0,9858
0,9958
0,9922
В соответствии с формулами (5.2)—(5.5) определяются нижние и верхние
оценки коэффициента готовности и наработки на отказ всей системы. Они
имеют значения:
К(гн) = 0,9880, Г(и) = 328,29 час,
^в) =0,9881, Г(в) =332,61 час.
Поэтому принимаем Кг= 0,988, Г = 330,45 час. При этом относительная
погрешность не превышает Ък =0,0042 по коэффициенту простоя
Ът =0,0065 по наработке на отказ. Среднее время восстановления равн
Гв=4,01 час.
ПРИМЕР 5.4. Восстанавливаемая система представляет собой систему с р
дельным (поэлементным) резервированием и прямым приоритетом обслу*
186 ЧАСТЬ I. Упражнения. Глава s
Для структуры 4 определим значения интенсивностей переходов в графе
состояний:
1 i-g,(*2)' 2 1-&(*.,)' ^Bi-O-ii(^))'
а затем обычным способом, например путем решения системы линейных
уравнений или непосредственно по- графу, определить требуемые
характеристики Т, Тв и Кг. Для структуры 5 эти характеристики находятся
непосредственно по исходным данным.
Требуемые показатели Кг, Т, Р0 для узла, объединяющего типовые
структуры 4 и 5, определяются по формулам (5.9) и (5.10).
Необходимые для дальнейших расчетов показатели сведены в табл. 5.3.
Таблица 5.3. Показатели надежности типовых структур

fi>0!!!!l
надежности систем сложной структуры
187
ания. Структурная схема (схема расчета надежности) системы приведена на
рис 5.6.
Рис. 5.6. Структурная схема системы
Значения интенсивностей отказов и восстановления элементов приведены в
табл. 5.4.
Таблица 5.4. Интенсивности отказов и восстановления элементов
№ элемента
X, I0'24ac-'
ц, час-1
Р
Кг
1
6
1,5
0,04
0,997
2
0,1
1
0,001
0,999
3
7
3,5
0,02
0,9996
4
7,5
1
0,075
0,99975
5
1
2
0,005
0,99479
По техническим условиям система должна удовлетворять следующим
требованиям надежности: коэффициент готовности Кг > 0,97.
Необходимо определить, удовлетворяет ли система этим требованиям.
Решение. Число состояний системы более 100. Составить и решить систему
Уравнений такой размерности очень трудно, хотя и возможно при использо-
Вании компьютерных технологий.
Однако обратимся к теории. Известно, что нижняя оценка коэффициента
годности Кгс системы может быть вычислена по следующей формуле:
п
1=1
„ лг/ — коэффициент готовности /-го элемента; п — число элементов сис-
^ элементом понимается любая часть системы, имеющая показатель на-
Реч °Сти' самостоятельно учитываемый при расчетах. В нашем примере это
еРВированные элементы.

188
ЧАСТЬ I. Упражнения. Глава s
Таким образом, проверить условие Кг > 0,97 можно путем вычисления
коэффициентов готовности элементов системы с последующим их
перемножением. Если окажется, что полученное значение больше 0,97, то система удов-
летворяет требованиям.
Выражения для Krj элементов нашей системы просты и имеют вид:
v - 1 + 2Pi v -_!_ v - 1 + Рз v 1 + Р4
l + 2p,+2pf l + p2 1+Рз+Рз 1 + Р4+Р4
_ 1+Зр5
1 + Зр5 + 6pJ
Значения р, и коэффициентов готовности элементов приведены в табл. 5.4.
Коэффициент готовности системы, вычисленный как произведение
коэффициентов готовности элементов, имеет значение: Кгс =0,9865. Результат
расчета показывает, что система удовлетворяет требованиям надежности.
Действительные значения ее надежности будут несколько выше расчетных. Итак,
мы решили поставленную задачу достаточно простым способом, не составляя
и не решая систему, состоящую из более 100 уравнений.
ПРИМЕР 5.5. Разработчик предложил два варианта структурной схемы
системы: схему, изображенную на рис. 5.6, и схему с основным соединением
элементов с использованием нагрузочного резервирования, при котором
интенсивности отказов элементов уменьшились в и, раз. Значения п(: щ-2,
«2=2,5, /?3 =3, п4=\,5, Щ =2.
Необходимо установить, какая из предложенных структурных схем имеет
более высокую надежность. Критериями надежности являются вероятность и
среднее время безотказной работы. Необходимо рассмотреть два случая:
система невосстанавливаемая и восстанавливаемая с одной ремонтной бригадо*1
и прямым приоритетом обслуживания. Интенсивности отказов и
обслуживания элементов приведены в табл. 5.5.
Таблица 5.5. Интенсивности отказов и обслуживания элементов системы
№ элемента
Ксх- Ю"\ час-1
п
^обл-Ю"3, час"1
ц, час"1
1
1,4
2
0.7
0.5
2
1
2,5
0,4
0,25
3
2,1
3
0,7
0,3
4
2
1,5
1,33
0,3
5
1,5
2
0,75
0,2

/l/^ff
надежности систем сложной структуры
189
решение. Обратим внимание на то обстоятельство, что в задаче не указано
время работы системы. Поэтому решим задачу, не вычисляя вероятностей
состояний и вероятности безотказной работы системы.
0з теории известно, что интенсивность отказа резервированной системы
% (0 при / = 0 также равна 0 и с ростом / увеличивается, стремясь к своему
пределу — интенсивности отказа нерезервированной системы.
На рис. 5.7 изображены графики интенсивностей отказа трех систем.
Цифрой 1 обозначена интенсивность отказа исходной нерезервированной систе-
мы, равная сумме интенсивностей отказов элементов, приведенных в
табл. 5.5, и равная Хнсх =0,008 час-1. Цифрой 2 обозначена интенсивность
отказа системы с нагрузочным резервированием, равная 0,00388 час-1.
График структурно резервированной системы обозначен цифрой 3. При / = 0
интенсивность отказа системы равна интенсивности отказа
нерезервированного элемента Х2 =0,001 час-1 и с ростом t возрастает, стремясь к
интенсивности отказа исходной нерезервированной системы.
Рис. 5.7. Интенсивности отказа исходной системы (кривая 1),
системы с нагрузочным резервированием (кривая 2)
и системы структурно резервированно_й (кривая 3)
Рис. 5.7 видно, что интенсивность отказа структурно резервированной
темы при / < т ниже интенсивности отказа системы с нагрузочным резер-
• Это значит, что вероятность ее безотказной работы P(t) при / <, т, выше
я™ости безотказной работы системы с нагрузочным резервом.

190
ЧАСТЬ I. Упражнения. Глава $
Определим критическое значение т., при котором вероятности безотказное
работы обеих систем одинаковы. Это значение не будет совпадать с т h;i
рис. 5.7, т. к. критерии разные.
Рассмотрим случаи иевосстанавяиваемой системы. Выражение вероятности
безотказной работы структурно резервированной системы имеет вид:
/>(/) = (1 -(1 _e-V)2)<r?.2/ e-V(1 + x}()e~Xil(\ + X^)(3e~2kst -2<Г3^5').
Вероятность безотказной работы системы с нагрузочным резервированием
определяется выражением:
5 ^.
где XQ - ^]—'-. В нашем случае А,с =0,00388 час"1.
Технология определения т с помощью системы Derive имеет вид:
#1: 1-(1-е"Л1'сГ
#2: ё"Л^
#3: е"ЛМ-(l+A3-t)
#4: e"M,t-(l + A4-t)
#5: з-ё-^-г-ё-3*5*
#6: e_Xct
#7: (l-(l-e~'41'tn^e"x?','-(e"A3't-(l+A3-t))-(e"M't-(l + A4-t))-
.(3-e"2'Xb-t-2.e"3'A5'L) = e-Ac-t
#8: {l-d-e^-^-^^.e^-^^-te"0-0021^-(1 + 0. 0021-1) )■
чё-0-002с-(1+о.оо2^))-(з-ё-2-0-0015-ь-2-ё-3'0-с015М=ё-0-00388'
#9: ЫЗОЬУЕ((1-(1-ё-0-0014'сГ)-ё-Э'С01'с-(ё-0-0021-г-(1 + 0.0021-1))-
(e-0.002.ti(1+0>002.t)).(3.i^0.001S.t_2.r3.0.0015.t)!S
= e-°-00388c/t/0.1/500)
#10: t = 372.8926679
В строках #1—#5 находятся введенные выражения вероятностей безотказна
работы элементов структурно резервированной системы. В строке #6 пРе
ставлено выражение вероятности безотказной работы с нагрузочным ре-* ^
вированием, в строке #7 — исходное уравнение для определения т. Это ур'

шз надежности систем сложной структуры
191
нце с подставленными исходными данными находится в строке #8. В стро-
#9 представлена функция NSOLVE решения уравнения из диапазона
_- 0.1 -ь500 час. После нажатия кнопки Approximate на панели
инструментов получаем ответ, который находится в строке #10.
Критическое значение т = 373 час. При этом времени вероятность
безотказной работы системы равна />(373) = 0,235. Таким образом, система со
структурным резервированием является более надежной в течение времени работы
/=373 час. При г > 373 более надежной станет система с нагрузочным
резервом. Но при этом ее надежность будет достаточно низкой.
Зависимости Pc(t) для обеих схем показаны на рис. 5.8. Из рисунка видно,
что вероятность безотказной работы системы со структурным
резервированием (кривая I) в диапазоне времени /<373 час существенно выше
вероятности безотказной работы системы с нагрузочным резервированием
(кривая 2).
Рис. 5.8. Вероятность безотказной работы резервированных систем
Ринятие решения о наилучшем варианте структурной схемы существенно
висит от выбранного критерия надежности. Покажем это на нашем
примере
Кть наша система— это система длительного использования, и се крите-
41 надежности является среднее время безотказной работы. Вычислим 7j
Г,° Формуле:
00
T^\Pc(l)d(.

192 ЧАСТЬ I. Упражнения. Глава s
Интегрируя выражения вероятностей безотказной работы рёзервированнь^
систем, получим: среднее время безотказной работы структурно резервиро.
ванной системы 7] =263,7 час, а системы с нагрузочным резервированием -^
7] =257,7 час. В этом случае структурное резервирование малоэффективно.
Большой объем резервных элементов приводит к незначительному повыше,
нию среднего времени безотказной работы системы.
Рассмотрим случай системы с восстановлением. При этом сделаем следую,
щие допущения:
□ на время восстановления подсистемы элементы других подсистем не
могут восстанавливаться;
□ приоритет в обслуживании слабо влияет на вероятность безотказной
работы системы.
Первое допущение означает, что при отказе системы восстанавливается
только тот элемент, из-за отказа которого произошел отказ системы. На период
его ремонта восстановление других элементов запрещено. Это допущение
снижает эффективность восстановления. В действительности вероятность
безотказной работы системы будет выше, чем при таком допущении.
Второе допущение обосновано нами ранее при решении ряда примеров и
задач в предыдущих главах книги.
При принятых допущениях вероятность безотказной работы структурно
резервированной системы равна произведению вероятностей безотказной рабо-
ты ее элементов, т. е. Pc(t) = ]Г[/}(/).
/=|
В нашем примере граф состояний любого дублированного элемента имеет
вид, приведенный на рис. 5.9.
Вероятность безотказной работы такого элемента можно получить из
решения следующей системы уравнений (переход из состояния (2) в состояние (D
запрещен — экран):
Р{=-аР0+тР{,
P{ = aPQ-{b + m)P,.
При начальных условиях /q(0) = 1, /](0) = 0 система уравнений в преобраз0
вании Лапласа имеет вид:
(j + a)P0-i»i/5=l,
-aPQ + (s + Ъ + т)Р] = 0.

fif&am
надежности систем сложной структуры
193
Рис. 5.9. Граф состояний элементов системы
Из этой системы уравнений получим:
s + (a + b + m)s + ab
№)=-2 г г-
s + (a + b + m)s + ab
Так как состояния (0) и (1) соответствуют исправным состояниям элемента,
то выражение для вероятности безотказной работы в преобразовании Лапласа
имеет вид:
s +(a + b + m)s + ab
"ервый элемент структурной схемы на рис. 5.6 — это дублирование с
постоянно включенным резервом. В этом случае a = 2X{, b = X{, m = \ix. Третий и
четвертый элементы образуют дублирование замещением. Тогда а = \$,
b — \
~~ ^з» m = М-з и> соответственно, для схемы 4 а = Х4, b = X4, m = \x4. Пятый
лемент структурной схемы— это резервирование с дробной кратностью
? s 1/2. В этом случае а = ЗХ5, Ь = 2Х5, т = р.5.
Аставляя в выражение P(s) численные значения интенсивностей перехо-
0в из табл. 5.5, получим следующие выражения Pj(s) каждого резервиро-
анНого элемента:
/>(-) 5 + 0,5042
, ' s2+0,5042*+ 0,00000392'
3«с553

194
ЧАСТЬ I. Упражнения. Глава s
5 + 0,3042
3 S s2 +0,30425 + 0,00000441'
5 + 0,304
4 s2+ 0,3045 + 0,000004'
p 5 + 0,2075
5 * 52+0,20755 + 0,0000135'
Второй элемент системы нерезервирован, его вероятность безотказной
работы равна:
Теперь нужно найти оригиналы функций P{(s), /3(5), Р4(5)' ^sCO»
образовать их произведение и получить вероятность безотказной работы системы,
сравнив ее с вероятностью безотказной работы системы с нагрузочным
резервированием.
Так как система с нагрузочным резервированием представляет собой систему
с основным соединением элементов и экспоненциальным законом времени до
отказа, то ее вероятность безотказной работы не зависит от восстановления и
равна/>с(О = е-°'О0388/.
Далее приводятся результаты расчетов, выполненные с помощью системы
Derive 5.
#1: е~°-2Ь2'1 -SINH (0. 252- t) + e"°-252'c -COSH (0. 252-1)
#2: е°-001<
#3: e"0-152't-SINH(0.152-t) + e"0-152't -COSH (0.152-1)
#4: e"°-152't-SINH(0.15198-t) + e"°-152'c -COSH (0.15198-1)
#5: e"0'10375't-SINH(0.*1036849-t) + e"0-10375't-COSH(0.1036849-t)
„,- --0.00388-t
#6: e
#7: (e"°-252't-SINH(0.252-t) + e"°-252-t-COSH(0.252-t) ).£"°-001-t •
(е-0-15^ •SINH(0.152-t) + e"0,152't-COSH(0.152-t) He"0,152'1 •
SINH(0.15198-t) + e"0,152't-COSH(0.15198-t) ).(e~°-l031b't ■
SINH(0.1036849-t) + e"°-10375'c -COSH (0 .1036849-1) )

...рпиз надежности систем сложной структуры
195
а строках #1—#5 находятся выражения вероятностей безотказной работы
лементов системы. Выражения получены путем обратного преобразования
Яапласа функций Pt{t) с помощью системы Mathcad.
п етроке $6 находится выражение вероятности безотказной работы системы с
аГрузочным резервированием, в строке #7 — вероятность безотказной
работы структурно резервированной системы в виде произведения вероятностей
безотказной работы элементов. По выражениям #6 и #7 построены графики
вероятностей безотказной работы систем, рис. 5.10.
Рис. 5.10. Вероятности безотказной работы резервированных систем
"арис. 5.10 приняты следующие обозначения:
а кривая 1 — вероятность безотказной работы структурно резервированной
системы;
кривая 2— вероятность безотказной работы системы с нагрузочным
резервированием;
кривая 3 — вероятность безотказной работы второго нерезервированного
элемента структурно резервированной системы.
вИду графиков можно сделать следующие выводы:
НаДежность структурно резервированной системы выше надежности
системы с нагрузочным резервированием во всем диапазоне времени их
работы;

196 ЧАСТЬ I. Упражнения. Глава s
П вероятность безотказной работы структурно резервированной системы
определяется главным образом вероятностью безотказной работы ее нере.
зервированного элемента (кривые 1 и 3 почти совпадают);
П восстановление отказавших резервированных элементов существенно по„
вышает надежность системы.
Большой выигрыш дает структурное резервирование с восстановлением, если
надежность системы оценивать средним временем безотказной работы. Рас-
00
четы по формуле 7j = jPc(l)dt дают следующие результаты:
о
□ среднее время безотказной работы системы с нагрузочным
резервированием 7j =257,7 час;
П среднее время безотказной работы структурно резервированной
восстанавливаемой системы 7] =921 час;
□ среднее время безотказной работы структурно резервированной
восстанавливаемой системы без учета нерезервированного элемента 2
Г, =11750 час.
Универсальные программные средства компьютерной алгебры позволяют
решать задачи надежности технических систем, содержащих сотни
резервированных элементов. В этом можно убедиться на нашем примере.
Пусть система состоит из 10 и 20 систем нашего примера, соединенных
последовательно в смысле надежности. Тогда число элементов в системах будет
соответственно 50 и 100. Derive 5 вычислила среднее время безотказной
работы этих систем соответственно за 40 секунд и 12 минут. Среднее время их
безотказной работы равно 53 часам и 31,6 часа.
Вероятность безотказной работы любой системы является убывающей
функцией времени, быстро стремящейся к нулю. Поэтому при вычислении среД"
него времени безотказной работы можно вычислять интеграл не до
бесконечности, а руководствуясь видом функции Р(1). Это позволит сократить врем*
вычисления 7j.
5.4. Задачи для самостоятельного решения
пЯ'
ЗАДАЧА 5.1. Структурная схема восстанавливаемой системы состоит из »
ти элементов, каждый из которых дублирован идентичным элементом. ПР
менено резервирование с постоянно включенным резервом. Последейств
отказов отсутствует. Варианты интенсивностей отказов и восстановлен
элементов приведены в табл. 5.6.

лиализ надежности систем сложной структуры
197
Необходимо установить, удовлетворяет ли система требованиям надежности.
Критериями надежности могут быть: вероятность безотказной работы P(t),
среднее время безотказной работы 7], коэффициент готовности Кг,
наработка на отказ Т . Значения этих показателей приведены в табл. 5.6.
Таблица 5.6. Интенсивности отказов и восстановления элементов
и требования на надежность системы
Исходные
данные
?ч,час~'
Х2, час"1
А.3, час-1
Х4, час-1
Х5, час-1
Hi, час-1
ц2, час-1
Из, час"1
щ, час"1
Ms, час"1
/>(/)
Ts
*г
Г
1
0,002
0,001
0,007
0,005
0,003
0,1
0,5
0,4
0,2
0,4
0,95
450
0,95
860
2
0,008
0,003
0,004
0,002
0,007
0,4
0,4
0,3
0,4
0,2
0,97
570
0,97
790
Л
3
0.01
0,003
0,003
0,006
0,005
0,3
0,3
0,2
0,3
0,3
0,94
780
0,9
1000
г« варианта
4
0,005
0,004
0,006
0,005
0,002
0,2
0,3
0,5
0,5
0,1
0,97
520
0,98
970
5
0,007
0,006
0,002
0,003
0,003
0,4
0,1
0,1
0,3
0,5
0,96
1200
0,97
760
6
0,005
0,002
0.007
0,004
0.003
0,3
0,2
0,3
0,2
0,3
0,9
630
0,98
680
7
0,006
0,005
0,002
0,007
0,004
0.5
0,3
0,4
0.5
0.2
0,95
580
0,97
920
Указание: сделайте допущение о равнонадежности элементов системы,
составьте граф состояний и определите все показатели надежности, воспользо-
авШись топологическим методом.
JvjAMA 5.2. Структурная схема восстанавливаемой системы приведена на
Рис. 5.Ц.
ь ные об интенсивностях отказов и восстановлений элементов приведены
Втабл.5.7.
Ределить вероятность и среднее время безотказной работы системы в
РеДположении, что отказы элементов являются событиями независимыми.

198
ЧАСТЬ I. Упражнения. Глава $
Решение представить в виде формул, графиков и таблиц. Определить верояг.
ность и среднее время безотказной работы системы, состоящей из 20 таких
подсистем, соединенных последовательно в смысле надежности.
Рис. 5.11. Структурная схема резервированной системы
Таблица 5.7. Интенсивности отказов и восстановлений элементов
№ элемента
ХЮЛчас-'
и-!(Г\ час"'
1
I ; 2
1.5
0,2
1
03
3
2
0,5
ЗАДАЧА 5.3. Структурная схема восстанавливаемой системы и данные о
надежности ее элементов приведены в задаче 5.2.
Необходимо установить, удовлетворяет ли система требованиям надежности,
если по техническим условиям коэффициент готовности должен быть не
ниже 0,98.
ЗАДАЧА 5.4. Структурные схемы пяти восстанавливаемых систем
приведены на рис. 5.12. Для каждых двух схем необходимо определить, какая из ни*
имеет более высокий показатель надежности. Показателями надежности
являются: P(t), 7J, Kr, T.
Исходные данные задачи приведены в табл. 5.8.
Число вариантов можно существенно увеличить, если в каждом из них иесТ
расчет только по одному или двум критериям надежности.

цвап»1
надежности систем сложной структуры
199
Рис. 5.12. Структурные схемы технических систем

200 ЧАСТЬ I. Упражнения. Глава
Таблица 5.8. Исходные данные решения задачи
Исходные
данные
Х,-10~2, час4
Л.2-10 2, час-1
МО"2, час"1
Ць час"1
ц2. час-1
из. час"1
№ схем
№ варианта
1
0,1
0.2
0,8
0.5
0,8
0,4
а, б
2
0,07
0,15
.0,5
0,5
0,8
0,3
а, в
3
0,15
0.25
0,7
0,8
0,2
0,4
а, г
4
0,1
0.15
0.15
0,2
0,5
0,3
а, д
5
0,2
0,1
0,3
0,3
0,5
0,3
б. в
6
0,6
0.2
0,2
0,3
0,5
0,7
б, г
7
0,5
0,2
0,4
0,5
0,3
0,4
б,д
8
0,3
0,1
0,6
0,4
0,2
0,6
в, г
9
0,2
0,2
0,1
0,3
0.2
0,3
в,д
10
0,6
0,2
0,2
0,7
0.3
0.4
лд

ЧАСТЬ II
ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ЦЕЛИ И ЗАДАЧИ ЛАБОРАТОРНОГО ПРАКТИКУМА
Лабораторная работа 1. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ ЭЛЕМЕНТОВ ПО ОПЫТНЫМ ДАННЫМ
Лабораторная работа 2. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ И РИСКА
НЕРЕЗЕРВИРОВАННОЙ ТЕХНИЧЕСКОЙ СИСТЕМЫ
Лабораторная работа 3. ИССЛЕДОВАНИЕ СВОЙСТВ
СТРУКТУРНО РЕЗЕРВИРОВАННЫХ СИСТЕМ ПРИ ОБЩЕМ
РЕЗЕРВИРОВАНИИ С ПОСТОЯННО ВКЛЮЧЕННЫМ РЕЗЕРВОМ
Лабораторная работа 4. ИССЛЕДОВАНИЕ СВОЙСТВ
СТРУКТУРНО РЕЗЕРВИРОВАННЫХ СИСТЕМ ПРИ ОБЩЕМ
РЕЗЕРВИРОВАНИИ ЗАМЕЩЕНИЕМ
Лабораторная работа 5. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ И РИСКА
ВОССТАНАВЛИВАЕМОЙ НЕРЕЗЕРВИРОВАННОЙ СИСТЕМЫ
Лабораторная работа 6. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ И РИСКА
РЕЗЕРВИРОВАННОЙ ВОССТАНАВЛИВАЕМОЙ СИСТЕМЫ
Лабораторная работа 7. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
ИНФОРМАЦИОННОЙ ВОССТАНАВЛИВАЕМОЙ СИСТЕМЫ
^бораторная работа 8. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
ТЕХНИЧЕСКИХ СИСТЕМ С УЧЕТОМ ИХ ФИЗИЧЕСКОЙ
РЕАЛИЗУЕМОСТИ
^бораторная работа 9. АНАЛИЗ ВЛИЯНИЯ ПРОФИЛАКТИКИ
НА НАДЕЖНОСТЬ ТЕХНИЧЕСКОЙ СИСТЕМЫ
аб°раторная работа 10. ИССЛЕДОВАНИЕ ВЛИЯНИЯ ВРЕМЕННОГО
РЕЗЕРВИРОВАНИЯ НА НАДЕЖНОСТЬ ТЕХНИЧЕСКОЙ СИСТЕМЫ

ИвЮЯЙЮЯЯЯЯЯЯЯВИВ
ИЕМ"М"""**МЖ'"»ИИ*«">'*">МИ»*М'МЧ">МН»«и«М1^ИИИШМНИ1^ИМЦя1|11«Д|ив
ЦЕЛИ И ЗАДАЧИ
ЛАБОРАТОРНОГО ПРАКТИКУМА
Источник знаний, и притом единственный, — это наука. Лабораторные
работы являются тем источником, который содержит начальные элементы
научных исследований. Можно хорошо изучить теорию надежности и даже уметь
решать задачи, доведя их решение до численного ответа, но не видеть
проблем в теории и практике надежности, не уметь формулировать задачу.
Всему этому учит лабораторный практикум.
Студент, выполняя лабораторную работу, учится ставить задачу, выбирает
метод и компьютерные технологии ее решения. Анализ полученных
результатов позволяет выяснить физическую сущность процессов, протекающих в
^следуемой системе.
Лабораторный практикум преследует следующие цели:
П подтверждение теоретических положений, высказанных преподавателем
на лекциях;
О ознакомление студента с методами научных исследований;
О изучение компьютерных технологий и приобретение навыков решения
задач надежности, которые не могут быть изложены на лекциях;
^ изложение физической сущности процессов, в смысле надежности,
протекающих в технических и информационных системах.
Лабораторный практикум состоит из 10 лабораторных работ
исследовательского характера.
"■ сновные особенности данного практикума:
исследовательский характер всех лабораторных работ;
компьютерные технологии решения задач с использованием
универсальных программных средств и программ, разработанных авторами;
^следование надежности технических и информационных систем при
Произвольных законах распределения отказов и восстановлений;
Широкий класс исследуемых систем (невосстанавливаемых и восстанавли-
Ваемых, нерезервированных и резервированных) при различных видах из-

204 ЧАСТЬ II. Лабораторный практику^
быточности (структурной, нагрузочной, временной) и способах включения
резерва (общее, раздельное, с постоянно включенным резервом и замеще-
нием);
□ исследование показателей надежности системы с учетом физической pea.
лизуемости структурной схемы;
О многовариантность задач в каждой лабораторной работе, обеспечивающих
индивидуализацию обучения;
□ необходимость представления решений в аналитическом, численном и
графическом виде;
□ наличие в описании каждой лабораторной работы примера ее выполнения.
Реализация описанных ниже лабораторных работ невозможна без
использования компьютерных технологий. Для этого рекомендуется использовать
универсальные математические системы. В примерах задачи решаются с
помощью таких систем, как Derive 5, Mathcad, Excel, Statgraphics. Решать задачи
надежности при законах распределения отказов, отличных от
экспоненциального, рекомендуется с помощью программ, описанных в части IV книги.
Там же излагается в конспективной форме одна из наиболее
интеллектуальных систем символьной математики Derive 5.
По каждой выполненной лабораторной работе студент представляет отчет,
который должен содержать следующие пункты:
О постановка задачи;
□ модели и алгоритмы решения задачи;
П краткое изложение методики выполнения работы;
□ решение задачи в виде формул, таблиц, графиков;
□ анализ полученных результатов и основные выводы.
Решение задач, сформулированных в лабораторных работах, целесообразно
не только студентам, изучающим теорию надежности, но также
специалистам, занимающимся разработкой и эксплуатации технических и информацй'
онных систем и нуждающихся в повышении знаний в области теории наде#"
ности.

ЛАБОРАТОРНАЯ РАБОТА 1
ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ
НАДЕЖНОСТИ ЭЛЕМЕНТОВ
ПО ОПЫТНЫМ ДАННЫМ
1.1. Постановка задачи
Дано:
D N — число элементов, находящихся на испытании;
О /, — время исправной работы /-го элемента, / = 1, 2,..., п;
О и — число отказавших элементов за время испытания /.
Определить показатели надежности элемента:
О \{t) — интенсивность отказа как функцию времени;
О f(t) — плотность распределения времени исправной работы элемента;
□ <о(г) — параметр потока отказов как функцию времени.
Эти показатели надежности необходимо определить при следующих двух
видах испытания:
а) с выбрасыванием отказавших элементов;
) с заменой новыми или отремонтированными.
случае (а) число элементов в процессе испытания убывает, в случае (б) —
бается постоянным.
Рианты заданий приведены далее в разд. 1.5.
1-2. Сведения из теории
Ч1ий°РИИ наДежности П°Д элементом понимают элемент, узел, блок, имею-
4 Показатель надежности и входящий в состав системы. Элементы бывают

206 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа ;
двух видов: невосстанавливаемые (резистор, конденсатор, подшипники и т. п.)
и восстанавливаемые или ремонтируемые (генератор тока, колесо автомоби-
ля, телевизор, ЭВМ и т. п.). Отсюда следует, что показателями надежности
невосстанавливаемых элементов являются только такие показатели, которые
характеризуют надежность техники до ее первого отказа. Показателями на-
дежности восстанавливаемых элементов являются показатели, которые
характеризуют надежность техники не только до первого отказа, но и между
отказами.
Показателями надежности невосстанавливаемых элементов являются:
□ P(t) — вероятность безотказной работы элемента в течение времени /;
П 7J — среднее время безотказной работы (наработка до отказа);
□ /(/) — плотность распределения времени до отказа;
□ X(t) — интенсивность отказа в момент /.
Между этими показателями существуют следующие зависимости:
-\\{t)dt
P(t) = e° , (1.1)
Д0 = -П0, Р(/) = ]/(0Л, (1.2)
/>(/)
00
Tx = jP(t)dt. (1.4)
о
Интенсивность отказа многих элементов, особенно элементов электроники,
является величиной постоянной: X(t) = X. В этом случае зависимости межДУ
показателями надежности имеют вид:
Д/) = А.е-Х/,
X(t) = X = const.

Oflj&g.
тение показателей надежности элементов по опытным данным 207
Показателями надежности восстанавливаемых элементов являются:
rj ©(/) — параметр потока отказов в момент времени /;
j-j f — среднее время работы между отказами (наработка на отказ).
Показателями надежности восстанавливаемых элементов могут быть также
показатели надежности невосстанавливаемых элементов. Это имеет место в
тех случаях, когда система, в состав которой входит элемент, является нере-
монтируемой по условиям ее работы (необитаемый космический аппарат,
аппаратура, работающая в агрессивных средах, самолет в процессе полета,
отсутствие запчастей для ремонта и т. п.). Между показателями надежности
невосстанавливаемых и восстанавливаемых элементов имеют место
следующие зависимости:
©(/) = /(/)+Цх)/(/-т)£/т, (1.5)
о
Птсо(/) = ^. (1.6)
Из выражений для показателей надежности невосстанавливаемых и
восстанавливаемых элементов можно сделать следующий важный вывод: основным
показателем надежности элементов сложных систем является интенсивность
отказов X(t). Это объясняется следующими обстоятельствами:
О надежность многих элементов можно оценить одним числом, т. к. их
интенсивность отказа — величина постоянная;
О по известной интенсивности X(t) наиболее просто оценить остальные
показатели надежности элементов и сложных систем;
" Mt) обладает хорошей наглядностью;
и интенсивность отказов нетрудно получить экспериментально.
бедует, однако, иметь в виду, что плотность распределения наиболее полно
^растеризует случайное явление — время до отказа. Остальные показатели,
том числе и X(t), лишь в совокупности позволяют достаточно полно оце-
Ить надежность сложной системы.
сНовным способом определения показателей надежности элементов слож-
* систем является обработка статистических данных об их отказах в
прочее эксплуатации систем или при испытаниях в лабораторных условиях.
"и этом возможны следующие два случая:
Сказавшие элементы в процессе испытания или эксплуатации системы
н°выми не заменяются (испытания без восстановления);

208 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа j
О отказавший элемент заменяется новым того же типа (испытания с восста-.
новлением).
В процессе эксплуатации системы или при испытаниях в лабораторных уело,
виях фиксируется дата возникновения отказа. По этим данным путем
статистической обработки и определяются показатели надежности элементов.
Как следует из определений показателей надежности невосстанавливаемого
элемента, все они могут быть вычислены, если известен закон распределения
времени работы элемента до отказа в виде плотности /(/). Если элемент мо-
жет ремонтироваться, то все показатели надежности выражаются через закон
распределения времени безотказной работы /(/). Поэтому важным
обстоятельством является умение находить /(/) с помощью проведения и
обработки результатов эксперимента.
Предположим, что в результате проведения испытаний над N элементами в
течение времени Т получены некоторые статистические данные о
распределении количества отказавших элементов. Возможны три принципиально
различных способа регистрации отказов элементов.
□ Первый способ регистрации
Элементы, поставленные на испытания, являются невосстанавливаемыми.
При возникновении отказа некоторого элемента фиксируется момент
времени его отказа. В результате испытаний статистической информацией
является последовательность /}, /2> ■•• >',» — > tN моментов времени отказов
элементов (рис. 1.1).
Рис. 1.1. Временная диаграмма моментов отказов невосстанавливаемых элементов
О Второй способ регистрации
Элементы, поставленные на испытания, являются восстанавливаемым ^
После отказа какого-либо элемента он заменяется новым. В результате и

определение показателей надежности элементов по опытным данным 209
пытаний исходной статистической информацией является последователе
ность моментов времени отказов /-го элемента //у (j: = \, 2,..., л,,
/ = 1, 2,..., N) в течение периода наблюдений Т (рис. 1.2). Реализациями
наработок элемента в этом случае служат разности х,, • = ttj - tt y_j
(предполагается, что /, 0 =0).
Рис. 1.2. Временная диаграмма моментов отказов восстанавливаемых элементов
с известными номерами
Второй способ регистрации отказов, очевидно, сводится к первому, если
фиксируются номера отказавших элементов. В качестве статистических
данных берется совокупность разностей т, у, представляющих собой
времена работы элементов до первого отказа.
и Третий способ регистрации
Элементы, поставленные на испытания, являются восстанавливаемыми.
После отказа какого-либо элемента он заменяется новым, однако не
известен номер отказавшего элемента. В результате испытаний исходной
статистической информацией является последовательность /,, t2,..., /,-,..., tn
моментов отказов элементов, где п — число отказавших элементов.
Таким образом, в отличие от второго способа, здесь регистрируются
моменты отказов элементов без указания их номеров.
^смотрим статистические определения показателей надежности элемента.
°°тветствующий статистический аналог показателя надежности будем
обожать тем же символом, что и раньше, но со знаком (Л) сверху.

210
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа /
Невоссшанавлаваемые элементы
Исходными статистическими данными является время работы элементов до
первого отказа: /h /2,..., /,,..., tN . Тогда среднее время работы элемента д0
отказа равно среднему арифметическому времени tt, т. е.
- 1 Д
Обозначим через v(/) число элементов, для которых отказ произошел не
позднее момента времени /. Тогда вероятность отказа элемента равна
а вероятность безотказной работы —
P(t) = \-Q(t).
Пусть последовательность /^,/^2)>•••■>'(/)>•••> *(Л') получена упорядочением
А
исходной последовательности. Функция Q{t) представляет собой
эмпирическую функцию распределения, и если все t^ различны, то
0, при /</(1);
Q(t) = \i/N, при /(/)</</{/+1);
1, при t>t(N).
Величина всех скачков равна \/N, а типичный график функции Q{t)
приведен на рис. 1.3.
Рис. 1.3. График статистической вероятности отказа элемента

определение показателей надежности элементов по опытным данным 211
другим наглядным способом представления статистических данных является
дртограмма. Область значений [/(]);/(#>] разбивается на равные интервалы
д / = 1,2,..., к длины h = —, где R = t^N^-t^, и называется размахом вы-
борки. Гистограмма представляет собой примыкающие друг к другу
прямоугольники, основанием которых являются указанные интервалы, а высоты
оавны плотностям относительных частот —-, где N, — число выборочных
v Nh
значений, попавших в данный интервал (рис. 1.4). Гистограмма является
статистической плотностью распределения времени работы до отказа. Для
оценки плотности иногда используется также полигон относительных частот,
который представляет собой ломаную линию, построенную по точкам,
абсциссами которых являются середины интервалов А,, / = 1, 2,... ,к, а ординаты
N-
соответствуют плотностям —L (рис. 1.4).
Nh
Рис. 1.4. График статистической плотности распределения
в виде гистограммы и полигона частот
•интенсивность отказа элемента рассчитывается как отношение плотности
Распределения к вероятности безотказной работы.
Останавливаемые элементы
исходными статистическими данными являются моменты времени отказов
Элементов: /.,£>,...,/;, ...,/„, где п— число отказавших элементов, N —
C\f\
"ОЩее число элементов, участвующих в испытаниях. Информация об отказах
Цементов может быть представлена в виде табл. 1.1. Весь период испытаний
Сбивается на интервалы времени определенной длины, и подсчитывается
°личество отказавших элементов на каждом интервале.

212
ЧАСТЬ //. Лабораторный практикум. Лабораторная работа 1
Таблица 1.1. Таблица отказов элементов
д/
Ал
Д/,
ДЛ|
Д/2
Ап2
...
...
Atk
Дл*
Табличные данные означают, что на интервале времени А/, было
зафиксировано точно Aw, отказов элементов, / = 1, 2,..., к. Тогда имеет место
следующее статистическое определение параметра потока отказов элемента:
Л, ч Ал.
«(0=—-
ЛТД/,
для всех /, принадлежащих /-му интервалу времени:
А/! +... + Д/м < / < А/, +... + Д/,._, + А/,-.
Определение плотности распределения /(/) путем решения интегрального
уравнения (1.5) связано с некоторыми трудностями, которые вызваны
скачкообразным изменением параметра потока отказов. Один из возможных
подходов к определению функции /(/) состоит в следующем. Будем искать
функцию, /(/) в виде кусочно-постоянной функции
|Л> если ак-\<{^ак> к = \,2,...,щ
[О, если t>an.
Здесь а0 = 0, ап = Т, /к — искомые величины, которые можно определить
из условия выполнения уравнения (1.5) в среднем по интегральной метрике
т( t Л2
J <в(0 - /(/) - |/(х)ю(/ - х)dx dt -> min
о\ о )
при ограничениях
lf№ = \, д/)>о.
о
Полученная задача нелинейной оптимизации может быть сведена к задаче
линейного программирования и решена симплексным методом с некоторым1*
дополнительными условиями, что составляет предмет специального исследи"
вания.

ррределение показателей надежности элементов по опытным данным 213
1.3. Пример выполнения
лабораторной работы
1.3.1. Постановка задачи
Требуется определить показатели надежности элемента без восстановления и
с восстановлением соответственно для двух вариантов исходных данных:
р Первый набор исходных данных
На испытания поставлено N = 100 элементов. Моменты отказов
элементов представлены в табл. 1.2. Все элементы работают до своего отказа
и после отказа не ремонтируются. Требуется определить статистические
и теоретические показатели надежности элемента: 7], P(t), Q{t), /(/),
ад.
Таблица 1.2. Моменты отказов элементов, в часах
455
129
151
32
171
95
88
90
334
315
552
81
85
217
86
97
291
162
203
57
109
221
4
90
36
54
70
162
78
4
340
35
17
210
180
50
1
155
72
59
103
318
7
39
61
127
642
139
51
133
152
180
20
74
3
176
89
27
137
77
62
20
79
71
47
21
266
11
216
142
163
37
50
57
578
122
260
9
35
103
•35
26
41
106
23
109
136
30
43
63
5
18
51
14
131
89
2
77
12
13
Второй набор исходных данных
На испытаниях находится N = 10 элементов. В течение периода Т = 500 час
Регистрируются моменты времени отказов элементов (табл. 1.3).
Предполагается, что отказавшие элементы заменяют идентичными по надежности
элементами. Требуется определить показатели надежности элемента,
характеризующие время его работы между соседними отказами: Т, /(()■>
Щ, МО.
Обработка статистических данных предусматривает их группировку в
*0 частичных интервалах (классах). Уровень значимости принять
равным 0,05.

214 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа 1
Таблица 1.3. Моменты времени отказов элементов
Номер элемента, /
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 500 часов, час
114; 209; 293; 405
136; 217; 308; 479
73: 184; 289; 378; 478
63;162:257; 365; 484
54; 169; 301; 378; 462
114; 213;343: 408
96;162;271; 374; 468
106: 198; 273; 385; 499
95; 229; 308; 403
77; 179; 292; 387; 477
1.3.2. Последовательность выполнения работы
с использованием программы StatGraphics
Статистический графический пакет StatGraphics (Statistical Graphics System)
предназначен для статистического анализа и обработки данных на
персональном компьютере. Он является наиболее полной интегрированной
статистической и графической системой, объединяющей профессиональные методы
обработки больших объемов данных, качественную графику и дружественный
пользовательский интерфейс. StatGraphics позволяет выполнять
статистический анализ экспериментальных данных, полученных в результате
исследования сложных стохастических (вероятностных) систем. Начальные сведения
по работе с системой версии 2.6 можно найти в книге: Тюрин Ю. Н.,
Макаров А. А. Анализ данных на компьютере. — М.: ИНФРА-М, Финансы и
статистика, 1995.
Главное меню системы содержит 22 подменю, помеченных буквами от А
до V и логически сгруппированные под шестью основными заголовками. При
первом появлении главного меню курсор установлен на первом пункте
А. Управление данными.
Для определения показателей надежности для двух вариантов исходных ДаН
ных необходимо выполнить последовательность действий:
1. Подготовка исходных данных к статистической обработке для двух нао
ров одновременно. С этой целью в пункте меню А. Управление даннь

определение показателей надежности элементов по опытным данным
215
ми | 2. Операции с файлами создадим файл StatGraphics с именем
OTKAZ, а в этом файле создадим две переменные (2 столбца) с именами
narabotkal и narabotka2. В переменную (столбец) narabotkal
поместим первый набор исходных данных непосредственно из табл. 1.2. Для
исходных данных, содержащихся в табл. 1.3, вычислим разности между
последующими и предыдущими значениями моментов времени отказов
каждого элемента, в результате чего получим набор чисел, приведенный в
табл. 1.4.
Таблица 1.4. Время между отказами элементов
Номер элемента, /
1
2
3
4
5
6
7
8
9
10
Время между отказами, час
114; 95; 84;112
136;81;91;171
73; 111; 105; 89; 100
63; 99; 95; 108; 119
54; 115; 132; 77; 84
114; 99; 130; 65
96; 66; 109; 103; 94
106; 92; 75; 112;114
95; 134; 79; 95
77; 102; 113; 95; 90
Полученные разности из табл. 1.4 поместим в переменную (столбец)
narabotka2. На экране компьютера должна получиться следующая
заставка:
Курсор на стр: 1 Редак. дан. Максим. Стр.: 46
Колон.: 1 File: OTKAZ Число колонок : 2
стр narabotkal narabotka2
+ +
1 I 455. 114. I
2 I 552. 95. I
3 I 109. 84. I
4 I 340. 112. I
5 I 103. 136. I
6 I 152. 81. I
7 I 62. 91. I
8 I 163. 171. I
,9 I 35. 73. I
10 I 5. 111. I

216 ЧАСТЬ //. Лабораторный практикум. Лабораторная работа 1
11 1
12 1
13 |
14 |
Длина
Тип/Шир
129.
81.
221.
35.
100
N/13
105.
89.
100.
63.
46
N/13
1
1
1
1
Заметим, что длины переменных narabotkal и narabotka2
соответственно равны 100 и 46, что соответствует количеству чисел в табл. 1.2 и 1.4.
Определение статистических показателей для каждого набора данных,
содержащихся в переменных OTKAZ.narabotkal и OTKAZ.narabotka2.
Для этого следует войти в пункт меню F. Описательные методы |
1. Суммарные статистические показатели. В поле Векторы данных
надо ввести имя файла (нажать <Ctrl>+<F7> и выбрать файл OTKAZ) или
имена двух переменных narabotkal и narabotka2 (нажать <F7> и
выбрать переменные OTKAZ.narabotkal и OTKAZ.narabotka2). С
помощью клавиши <ТаЬ> следует перейти в поле Статистики. Используя
клавиши управления курсором и клавишу <Del>, в этом поле надо
оставить буквы, означающие требуемые характеристики. На экране
компьютера должна получиться следующая заставка:
Суммар. Статистика
Векторы данных: OTKAZ
Статистики: AFHIJ
(а)Среднее (f)Стан.отклонен
(Ь)Медиан (д)Стан.ошиб.
(с)Мода (h)Минимум
(d)Геометр.средн.(i)Максим.
(е)Дисперсия (j)Размах
(к)Нижн.квартиль (р)Эксцесс
(1)Верх.квартиль (q)Коэф.эксцесса
(т)Внутрикв.размах
(п)Асимметрия
(о)Коэф.асимметрии
Нажатие клавиши <F6> приведет к расчету требуемых характеристик и
выводу их на экран в следующем виде:
Отсюда следует, что для первого набора исходных данных средняя нара
ботка до первого отказа приближенно равна 7] =116 час, а для втор°г
Variable: narabotkal narabotka2
Разм.выборки 100 46
Среднее 116.06 99.1957
Стандарт.отклонен. 121.427 21.8557
Минимум 1 54
Максимум 642 171
Размах 641 117

определение показателей надежности элементов по опытным данным
217
набора средняя наработка на отказ равна Т = 99 час. Заметим также, что в
первом случае стандартное отклонение з:1 =121 достаточно близко к
средней наработке до отказа, что свидетельствует о возможной близости
распределения к экспоненциальному. Во втором случае распределение
времени работы элемента между отказами явно отличается от
экспоненциального, т. к. стандартное отклонение s2 = 22 существенно отличается от
средней наработки на отказ.
Видим также, что для первого набора данных все реализации случайной
наработки до отказа находятся в интервале [1; 642], и размах выборки
равен 641 час. Для второго набора данных все выборочные значения
содержатся в интервале [54; 171] длиной 117 часов.
3. Показатели надежности элемента, зависящие от времени, определяются
в пункте меню Н. Функции распределения. Этот вопрос рассматривается
в разд. 1.3.3 и 1.3.4 для случая первого и второго набора исходных
данных.
1.3.3. Определение показателей надежности
неремонтируемого элемента
В пункте меню Н. Функции распределения | 1. Подбор распределения
произведем перебор 5 различных непрерывных распределений и выберем
наиболее подходящее по уровню значимости.
В качестве примера для переменной narabotkal подберем
экспоненциальное распределение. Заполнение поля Вектор данных переменной
OTKAZ. narabotkal, поля Номер распределения числом 10 и двойное
нажатие клавиши <F6> приведет к появлению следующей заставки:
Подходящее распределение
Вектор данных: OTKAZ.narabotkal
Имеющиеся распределения:
(1) Бернулли (7) Бета (13) Логнормальное
(2) Биномиальное (8) Хи-квадрат (14) Нормальное
(3) Дискретное равномерное (9) Эрланг (15) Стьюдента t
(4) Геометрическое (10) Экспоненциальное (16) Треугольное
(5) Отрицат. биномиальное (11) F (17) Равномерное
<б) Пуассона (12) Гамма (18) Вейбулла
Номер распределения: 10 + +
с I Гистограмма I
Р6Д: 116.06 | Хи-квадрат тест I
| К-С тест I
| Хвостовые области I
| Критические значения I
— + +

218
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа 1
В появившемся вспомогательном меню следует выбрать пункт Гистограмма,
тогда на экране получим гистограмму частот и выравнивающую ее функцию
плотности экспоненциального распределения (рис. 1.5).
Рис. 1.5. Подбор плотности распределения к гистограмме частот
Выбор пункта Хн-квадрат тест вспомогательного меню приведет к
вычислению уровня значимости для экспоненциального распределения. В результате
расчетов уровень значимости равен 0,817099. Так как это значение больше
требуемого 0,05, то экспоненциальное распределение хорошо согласуется
с экспериментальными данными.
В пункте меню Н. Функции распределения | 2. Графики распределений
строятся графики требуемых показателей надежности в соответствии с
рассчитанными ранее параметрами. Для экспоненциального распределения
задается только среднее значение, равное 7J =116,06 час. В результате
появляется следующая заставка:
График распределения
Имеющиеся распределения:
(1) Бернулли
{2) Биномиаль ное
(3) Дискретное равномер.
(4) Геометрич.
(5) Отрицат. биномиал.
(б) Пуассона
(7)
(8)
(9)
(10)
(11)
(12)
Бета
Хи-квадрат
Эрланга
Экспоненциал.
F
Гамма
(13)
(14)
(15)
(16)
(17)
(18)
Логнормал.
Нормальное
Стьюдента t
Треугольное
Равномерное
Вейбулла

пп0еделение показателей надежности элементов по опытным данным
219
номер распределения:
Сред.': 116.06
10
Density function
Cumulative d.f.
Survivor function
Log survivor function
Hazard function
-+
Пункты вспомогательного меню означают следующее:
р Density function — плотность распределения /(/);
О Cumulative d.f. — функция распределения Q{t);
О Survivor function — вероятность безотказной работы Р(/);
О Log survivor function — логарифм вероятности безотказной работы;
О Hazard function — интенсивностцотказов %{t).
В результате выбора того или иного пункта меню получим графики,
изображенные на рис. 1.6—1.8.
Средняя наработка до отказа равна 7} =106,06 час.
Рис. 1.6. Вероятность безотказной работы элемента P{i)

220
ЧАСТЬ //. Лабораторный практикум. Лабораторная работа j
Рис. 1.7. Вероятность элемента Q{t)
Рис. 1.8. Интенсивность отказов элемента Х.{1)
1.3.4. Определение показателей надежности
ремонтируемого элемента
В пункте меню Н. Функция распределения | 1. Подбор распределеии
производим перебор 5 различных распределений и выбираем наиболее и0-3
ходящее по уровню значимости. В качестве примера рассмотрим нормалы'0
распределение. На экране появится соответствующая заставка:

/определение показателей надежности элементов по опытным данным
221
подходящее распределение
Вектор данных: OTKAZ.narabot
имеющееся распределения:
(1) Бернулли
(2) Биномиальное
(3) Дискретное равномерное
(4) Геометрическое
(5) Отрицат.биномиальное
(б) Пуассона
Номер распределения: 14
Сред: 99.1957
Стандарт.отклонен.: 21.8557
L
ка2
(7)
(8)
(9)
(10)
(11)
(12)
1
1
1
1
1
Бета
Хи-квадрат
Эрланг
Экспоненциал
F
Гамма
Гистограмма
(13)
(14)
(15)
[. (16)
(17)
(18)
Хи-квадрат тест
К-С тест
Хвостовые области
Критические
Логнормал.
Нормальное
Стьюдента t
Треугольное
Равномерное
Вейбулла
значения |
Гистограмма по наработкам и соответствующая кривая нормального
распределения приведены на рис. 1.9. Уровень значимости для нормального
распределения равен 0,455035, что больше заданного уровня значимости, равного
0.05. Следовательно, нормальное распределение не противоречит опытным
данным.
Рис. 1.9. Подбор плотности распределения Д/) к гистофамме частот
Рмальное распределение имеет следующие параметры: среднее равно
''957, стандартное отклонение равно 21,8557. В соответствии с указанны-

222
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа
ми параметрами в пункте меню Н. Функции распределения | 2. График
распределения строятся графики требуемых показателей надежности. На
рис. 1.10 и 1.11 изображены графики функции распределения и интенсивно»
сти отказов соответственно.
Средняя наработка на отказ элемента равна Г = 99,1957 час.
Рис. 1.10. Функция распределения времени работы элемента между отказами F(t)
Рис. 1.11. Интенсивность отказов элемента X(t)

давв2
тение показателей надежности элементов по опытным данным 223
\£. Форма отчета
По результатам выполненной лабораторной работе представляется отчет, в
котором должны содержаться следующие пункты:
1 Постановка задачи с конкретным содержанием, сформулированном для
своего варианта. Исходные данные должны быть представлены в виде
табл. 1.2 и 1.3.
2 Представление второго набора данных в виде табл. 1.4.
3. разбиение статистических данных на группы вручную и построение
гистограммы частот без использования программы StatGraphics.
4. Выполнение задания в программе StatGraphics. Для этого необходимо
указать имя файла и имена переменных, в которых содержатся
"экспериментальные" данные, привести формулы для расчета требуемых
статистических показателей, числовые значения и смысл этих показателей,
представить результаты группировки данных в виде таблицы распределения
частот, привести гистограммы частот, полученные в StatGraphics.
5. Перебор пяти распределений, включая заданное, и выбор среди них
наиболее подходящего к "экспериментальным" данным по критерию хи-
квадрат, графическое изображение гистограммы и всех рассмотренных
кривых распределений.
6. Выводы по результатам исследований.
В работе следует указать названия процедур StatGraphics, используемых при
выполнении каждого пункта.
1-5. Варианты заданий
к лабораторной работе 1
Дано:
Два набора исходных данных об отказах элементов;
№ — число элементов в каждом наборе;
3акон распределения времени до отказа в первом варианте;
закон распределения времени между отказами во втором варианте;
Моменты отказа элементов.
пРеделить:
Показатели надежности элемента, работающего до первого отказа (первый
Набор исходных данных): 7j, P(t), Q(t), f(t), *.(/);

224 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа i
D показатели надежности элемента, характеризующие время его работы
между отказами (второй набор исходных данных): Т, /(f), F(t), X(t).
Решение получить в виде таблиц и графиков.
При обработке данных вручную и на компьютере их следует разбить на
10 групп (классов). Подбор подходящего распределения необходимо осуще.
ствить для уровня значимости, равного 0,05.
ВАРИАНТ 1
Первый набор исходных данных (Нормальное распределение):
155
142
140
140
136
166
147
119
128
163
147
143
145
149
146
137
148
145
123
112
126
138
169
149
140
147
153
137
139
126
139
144
148
123
130
137
146
149
134
146
137
149
121
141
147
126
128
163
154
147
132
145
135
164
108
143
145
141
149
149
120
157
152
145
122
114
135
137
144
146
165
152
138
131
133
109
147
137
166
127
163
145
128
157
115
147
151
146
152
143
156
140
161
123
165
135
151
133
159
154
Второй набор исходных данных (Экспоненциальное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 700 часов
37; 90; 279; 355; 360; 420; 466; 488: 627; 671
26; 77; 141; 532; 642; 661
53; 59; 164; 183; 316; 568; 607
22; 26; 134; 287; 356; 470; 472; 481
24; 40; 152; 412; 431; 486; 567; 630; 649
193; 216; 474;488; 538;616
86; 355; 415; 451
117; 157; 358; 462; 527; 673
74; 89; 356; 356; 420; 492; 497; 512; 548; 601
204; 276; 327;515; 516;544

пг.рбделение показателей надежности элементов по опытным данным
0Лр0АНТ 2
Первый набор исходных данных (Гамма-распределение):
225
27
98
388
332
75
246
288
96
103
454
162
226
389
263
120
321
425
100
318
286
131
234
229
116
292
509
64
737
68
197
111
416
161
85
363
547
610
396
57
236
414
79
94
562
151
424
140
258
28
313
191
213
182
44
50
456
88
510
312
115
166
210
41
268
400
102
171
37
232
111
222
323
79
272
89
404
163
246
333
138
268
103
148
370
308
323
108
166
130
216
168
392
528
502
116
122
84
258
151
268
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 600 часов
107; 201; 295; 397; 515
95; 213; 320; 403; 483; 568
97; 196; 282; 399; 504;584
109; 216; 328; 422; 528
112; 226; 310; 417; 524
103; 195; 300; 392;480 570
93; 178; 268; 375; 494
93; 203; 312; 393; 488 581
119; 210; 293; 408; 518
102; 220; 334; 439; 537
3«* 553

226 ЧАСТЬ II. Лабораторный практикум. Лабораторная работу
ВАРИАНТ 3
Первый набор исходных данных (Гамма-распределение):
221
282
107
91
369
204
80
277
86
559
370
97
37
255
305
306
466
155
161
138
84 ! 97
321
176
169
209
163
93
83
397
405
315
197
149
227
159
60
67
508
187
196
107
182
256
475
108
467
53
276 j 351
221
123
298
334
229
235
706
168
252
107
426
156
146
283
244
126
112
30
582
167
151
597
97
103
216
106
236
210
24
519
72
241
244
468
382
670
298
178
427
226
133
210
54
38
430
72
49
275
139
247
Второй набор исходных данных (Нормальное распределение):
Помер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
нремени 600 часов
ПО; 211; 296; 408; 512; 584
80; 167; 239; 336; 435; 523
113; 206; 292: 370; 466; 588
123; 211; 301; 397; 502
79; 197; 296; 377; 457; 538
132;224;302;383; 486; 570
86; 185; 312; 390; 471; 576
106; 195; 265; 350; 431; 537
83; 176; 253; 328; 407; 511; 595
130; 232; 371; 442; 539

овделение показателей надежности элементов по опытным данным 227
1ДГЙАНТ 4
[ервый набор исходных данных (Нормальное распределение):
156
135
176
165
148
169
157
175
149
158
161
156
155
175
133
163
182
167
148
140
145
176
165
153
154
174
174
141
150
152
122
160
140
131
149
135
162
163
154
162
180
163
165
180
152
154
173
142
149
163
1
190
150
160
168
150
183
191
143
178
148
153
157
138
149
188
172
165
167
145
184
174
156
181
156
163
136
146
149
168
159
163
136
183
173
145
166
151
142
176
143
133
168
182
156
142
157
163
173
170
163
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
7
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 500 часов
105; 208; 323; 414
113; 216; 331; 433
111;192; 272;363;453
ПО; 209; 314; 426
85; 192; 301; 393; 480
87;174;292; 381; 479
102;195; 314; 404
94;190;275; 363; 449
118; 230; 331; 433
105;219;310; 408

228 ЧАСТЬ II. Лабораторный практикум. Лабораторная работу
ВАРИАНТ 5
Первый набор исходных данных (Гамма-распределение):
65
106
54
550
220
426
174
23
361
223
266
231
243
210
29
212
142
200
409
345
138
169
702
124
270
395
374
35
393
79
87
219
245
293
481
199
170
286
20
98
219
387
128
209
499
412
97
352
296
51
466
82
153
473
854
182
52
53
409
25
71
63
260
114
533
153
434
544
42
188
286
92
448
228
606
109
392
198
73
194
107
104
220
194
133
156
197
111
138
88
349
96
326
334
174
65
356
93
515
106
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 700 часов
86; 194; 299; 406; 505; 619
119; 221; 333; 438; 528; 643
86;200; 295; 389; 496; 600
107; 188; 286; 385;501;612
82; 185; 294; 392: 510: 591; 675
117; 234; 340; 425; 516; 613; 695
ПО; 202; 318; 414; 503; 597
104; 197; 310; 429; 534; 622
109; 196: 289; 395; 510; 619
83; 193; 309; 419; 507; 592; 683

ппределение показателей надежности элементов по опытным данным 229
ВЛРЙАНТ 6
гтер0ЫЙ набор исходных данных (Гамма-распределение):
188
191
95
199
403
139
171
163
292
240
27
332
164
227
ПО
104
8
355
221
77
604
98
78
118
224
728
189
307
254
149
136
177
182
124
163
129
381
10
93
18
78
132
115
112
93
197
50
241
253
30
194
127
67
96
9
241
177
256
515
344
312
100
165
196
90
282
98
29
44
54
389
137
113
150
158
152
156
128
58
71
38
224
244
319
377
161
37
82
434
127
153
104
84
39
77
228
277
100
167
271
Второй набор исходных данных (Нормальное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 500 часов
94; 181; 278; 365: 478
87; 168; 261; 353; 468
ПО; 211; 336; 412
93;194; 280; 357; 459
80; 175; 266; 365; 493
113;230;346;430
88; 191; 295; 400
74;187;286; 405; 478
79; 187; 308; 400; 476
123; 206; 333; 464

230
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа 1
ВАРИАНТ 7
Первый набор исходных данных (Гамма-распределение):
226
295
583
191
416
538
233
134
205
199
649
323
72
40
293
14
700
478
495
243
453
61
60
404
290
363
223
180
508
77
304
257
476
755
112
594
466
658
134
790
340
54
281
61
138
116
380
149
314
41
321
226
1395
23
44
369
532
643
244
1102
50
277
230
219
ПО
127
230
155
287
733
497
97
203
125
176
68
141
296
579
63
149
222
122
300
90
219
256
280
343
1412
293
764
29
124
547
175
996
346
272
354
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 900 часов
98; 209; 295; 392; 502; 592; 691; 806
111; 197; 292; 405; 509; 590; 704; 788;877
105; 218; 313; 397; 485; 570; 656; 766; 870
105; 218; 335; 419; 532; 618; 698; 792
95; 196; 292; 372; 452; 534; 653; 745; 829
99; 208; 293; 390; 478; 561; 669; 773; 860
103; 211; 326; 406; 515; 624; 722; 822
108; 205; 299; 412; 501; 612; 731; 812; 892
88; 191; 278; 360; 443; 539; 644; 750; 854
80; 177; 277; 365; 476; 564; 661; 775;887

определение показателей надежности элементов по опытным данным 231_
ВАРИАНТ8
Первый набор исходных данных (Гамма-распределение):
93
142
173
149
80
78
253
151
326
38
28
233
123
574
116
119
234
85
20
140
116
105
111
131
208
87
135
155
381
195
300
99
161
70
369
132
106
90
279
15
247
298
111
33
69
119
220
301
49
166
207
180
269
200
190
259
22
429
535
206
40
229
87
41
76
94
198
165
94
60
155
440
245
60
295
48
412
304
51
120
141
150
390
41
108
155
449
207
158
57
17
124
129
16
234
139
186
124
48
225
Второй набор исходных данных (Нормальное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 900 часов
73; 169; 282; 341; 425; 540; 663; 777
73; 147; 213; 305; 372; 461; 569; 666; 768; 873
109; 200; 286; 402; 480; 575; 718; 797; 871
112; 197; 286; 380; 486; 564; 665; 782; 889
92; 187; 260; 355; 476; 567; 668; 760; 865
88; 191; 313; 419; 533; 609; 700; 797
110; 221; 369; 448; 529; 643; 772;887
94; 182; 280; 340; 436; 534; 638; 750; 875
99; 202; 274; 365; 441; 526; 643; 742; 825; 899
101; 193; 288; 419; 542; 635; 716; 799; 881

232 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабрщ
ВАРИАНТ 9
Первый набор исходных данных (Гамма-распределение):
350
226
206
147
143
228
191
377
136
331
244
118
257
71
60
37
14
319
224
83
69
219
181
219
119
296
392
258
174
97
234
204
104
361
190
51
157
37
601
178
145
120
130
162
281
254
16
68
35
328
196
180
341
112
437
44
203
235
71
194
389
406
245
67
226
190
89
385
345
ПО
23
182
9
182
307
143
346
128
132
120
251
74
226
34
41
795
303
111
197
106
127
240
161
76
148
117
40
640
35
109
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 600 часов
104; 200; 287; 373; 477; 586
96; 198; 314; 399; 513
81; 165; 277; 375; 475; 562
111; 226; 312;413; 530
111; 209; 322; 406; 516; 596
83; 198; 288; 384; 468 565
99; 215; 317; 415; 506
84;200; 316; 431; 516
109; 218; 330; 435; 536
85;172; 271; 386; 496

ние показателей надежности элементов по опытным данным
233
[Т10
рДРИАН'
Первый набор исходных данных (Экспоненциальное распределение):
55
106
173
165
96
116
341
412
162
176
87
42
119
395
468
211
0
362
7
137
105
186
41
185
37
243
23
120
117
49
18
113
57
382
19
225
41
346
304
190
386
147
86
67
263
77
89
29
73
133
187
306
59
351
58
108
486
34
4
598
118
202
38
16
267
200
137
21
123
115
227
168
151
0
3
702
18
123
32
4
65
44
348
41
20
634
55
10
82
178
89
0
41
31
130
436
139
89
113
167
й набор исходных данных (Нормальное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 1000 часов
115; 222; 328; 406; 486; 594; 696; 801; 896; 977
91; 215; 316; 411; 484; 603; 687; 797; 878
89; 175; 266; 360; 468; 604; 695;813;895
85; 170; 258; 382; 470; 579; 658; 739; 819; 920
115; 222; 327; 436; 550; 634; 732; 811; 933
86; 164; 247; 366; 495; 588; 713; 816; 939
105; 205; 290; 409; 473; 580:680; 773; 869; 969
99; 199; 315; 430; 527; 650; 762; 844; 945
105; 220; 311; 389; 478; 563; 661;734;855;968
106; 184; 284; 395; 490; 593; 697; 779; 922

234 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабоТя
ВАРИАНТ 11
Первый набор исходных данных (Равномерное распределение):
134
119
130
89
175
142
105
165
80
154
126
95
121
116
163
111
172
82
126
165
130
123
121
88
150
174
132
86
84
160
98
173
155
94
100
108
125
117
170
172
172
122
144
110
128
122
150
165
106
162
140
150
124
131
148
118
115
147
ИЗ
114
99
88
127
169
133
83
177
103
92
168
141
104
140
81
121
118
93
169
96
82
91
170
150
86
128
109
141
88
154
128
111
137
139
121
97
176
133
138
114
95
Второй набор исходных данных (Экспоненциальное распределение):
I (омер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 700 часов
1; 1:63; 75; 133; 356; 363; 403; 417
126; 240; 557
40; 72; 216; 220; 267; 305; 313;474; 493
43;234;248;431; 433; 583; 668; 680
35; 56; 70; 81; 225; 558; 568
18; 93; 121; 130; 229; 313; 461; 474; 532; 572; 603; 610
ИЗ; 375; 401; 479; 659
138; 163; 421; 479; 500; 636; 638; 671
222; 261; 404; 533; 568
55; 96; 111: 148;252; 281;633

?ние показателей надежности элементов по опытным данным
235
ВАРИАНТ 12
первый набор исходных данных (Нормальное распределение):
97
127
124
121
139
ИЗ
119
122
119
132
120
124
117
113
118
98
126
129
136
113
102
133
135
124
120
113
113
140
120
127
100
137
120
123
120
120
116
140
93
143
124
132
107
127
106
114
ПО
95
120
124
146
111
92
103
121
97
107
113
96
103
113
138
130
108
130
130
128
128
114
108
ПО
112
137
99
118
124
141
121
113
118
112
126
130
ПО
128
130
129
113
119
89
119
133
97
116
117
121
122
103
129
116
Второй набор исходных данных (Экспоненциальное распределение):
11омер элемента
1
2
3
4
5
6
7
8
9
10
i
Моменты отказа на периоде
времени 800 часов
112; 193; 247; 249; 284; 439
162; 255; 290; 317; 388: 456; 460; 661; 765
53; 335; 390; 401; 445; 610; 623; 792
73: 139; 140; 188; 204; 332: 555; 631
103; 165; 227; 513; 592; 718; 791
43;158;688; 792
17; 26; 339; 484; 529
27; 71; 203: 253; 281
216; 318; 669
146: 146; 240; 315; 543; 648

236 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабоГя
ВАРИАНТ 13
Первый набор исходных данных (Гамма-распределение):
120
123
120
247
128
232
239
378
56
422
221
130
14
197
130
186
45
289
87
255
151
235
120
62
15
93
216
76
357
360
212
87
309
25
462
146
55
310
260
360
40
147
432
40
34
518
239
413
79
82
57
31
243
71
294
24
560
351
58
114
411
61
649
69
120
177
263
141
243
242
415
74
158
267
30
84
144
29
39
396
152
201
300
99
165
127
139
319
61
166
750
319
9
32
215
198
261
96
14
224
Второй набор исходных данных (Экспоненциальное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 700 часов
204; 221; 345; 376; 537; 697
2; 39; 71; 104; 118; 213: 544; 596; 608; 657
138; 314; 387; 467; 471; 556; 699
8; 11; 52; 94; 192; 476; 491; 527; 655
106; 168; 325; 360; 690
192; 207; 217; 362; 426
225; 440; 618:657; 667
371; 420; 500
85; 371; 568; 579: 611; 625; 663
80; 111; 152; 162; 369; 394; 462; 551

>ние показателей надежности элементов по опытным данным 237
^РЙАНТ 14
^рвый набор исходных данных (Равномерное распределение):
102
126
171
108
164
ПО
105
82
170
138
133
177
159
161
111
120
120
83
163
119
104
128
159
106
145
173
91
95
112
98
136
118
136
169
106
136
129
97
145
91
109
127
105
151
151
126
95
90
170
113
171
82
142
116
103
160
95
167
99
139
167
107
96
80
148
83
96
142
95
84
159
120
98
125
103
124
127
89
115
150
176
155
176
119
112
139
92
93
119
86
153
165
127
178
158
101
80
157
134
175
второй набор исходных данных (Нормальное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 700 часов
106; 208; 279; 390:488; 582; 656
98; 186; 304; 377; 477; 539; 622
100; 217; 337; 467; 584; 670
121; 217; 290; 397; 473; 595
100; 212; 301; 385; 480; 605; 694
131: 213; 292; 393; 481; 564; 688
130; 229; 309; 440: 521:601; 690
87; 196; 297; 403; 499; 610
117; 236; 351; 428; 507: 594
103; 205; 295; 402; 516; 603

238 ЧАСТЬ II. Лабораторный практикум. Лабораторная работу
ВАРИАНТ 15
Первый набор исходных данных (Нормальное распределение):
99
109
88
79
100
95
99
100
115
90
91
98
99
100
90
98
93
98
113
94
104
119
99
111
102
97
104
93
94
102
114
84
104
103
91
107
90
104
ПО
ПО
97
102
103
89
89
90
90
107
93
90
91
120
ПО
92
95
112
109
98
94
99
99
107
96
109
98
85
89
104
82
93
101
97
85
99
87
101
95
112
100
87
99
ПО
109
91
117
94
102
100
94
115
95
102
89
86
100
87
88
105
102
9*7
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 600 часов
104; 197; 304; 422; 511; 597
86; 184; 300; 382; 492; 595
106; 218; 312; 395:493; 573
94; 200; 302; 409; 498; 589
117; 213; 316;433; 516
94; 186; 293; 401; 507
90; 188; 272; 379; 478; 577
104; 210; 309; 412; 506; 588
99; 194; 300; 419;530
109; 227; 331; 426; 524

022222
ение показателей надежности элементов по опытным данным
239
0ДРИАНТ 16
Первый набор исходных данных (Равномерное распределение):
164
118
176
148
101
112
172
88
150
91
82
176
105
133
106
85
93
153
162
141
90
118
85
145
116
107
144
108
81
112
157
142
126
127
85
124
112
161
86
94
102
101
N3
146
165
164
156
162
128
177
~ 1
106
102
94
139
123
116
144
96
108
106
i
92
177
109
155
87
125
98
167
89
80
163
155
159
144
147
166
111
148
120
101
165
175
83
98
170
139
137
90
133
132
92
131
96
90
102
115
128
127
120
92
Второй набор исходных данных (Нормальное распределение):
1 Ьмер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени Ю00 часов
118; 202; 326; 434; 505; 610; 712; 791; 901; 984
96; 173; 304; 405; 524; 643; 741; 853; 940
116; 197; 269; 381; 483; 587; 687; 804; 923
111; 182; 293; 438; 545; 639; 751; 845; 978
76; 185; 286; 390; 492; 579; 664; 748; 822; 898
111; 239; 360; 469; 555; 652; 739; 824; 923
131; 223; 344; 444; 551; 674; 792; 917
92; 185; 283; 372; 499; 585; 711; 808; 904
95; 186; 273; 353; 447; 568; 689; 793; 865; 944
79; 190; 324; 408; 485; 591; 665; 776; 855; 930

240 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабрТа
ВАРИАНТ 17
Первый набор исходных данных (Равномерное распределение):
102
147
127
105
111
151
86
108
167
170
164
146
132
98
115
80
141
139
138
121
ПО
136
139
88
151
106
105
81
158
130
176
81
167
119
100
150
119
141
156
108
161
176
150
103
154
138
176
178
117
80
142
153
107
104
107
98
144
92
136
123
123
118
106
111
133
96
159
163
90
136
81
87
103
117
176
87
122
81
139
118
119
150
137
172
150
134
91
113
111
136
99
82
174
104
84
171
111
109
96
157
Второй набор исходных данных (Экспоненциальное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 1000 часов
8; 135; 196; 273; 291; 466; 697; 703; 854; 862; 872
124; 164; 203; 320; 370; 411; 448; 486; 619; 704; 719; 810
45; 50; 249; 257; 409; 483; 535; 572; 592; 678; 701; 802
96; 126; 193; 388; 417; 724; 889;989
255; 427; 911
12; 35; 39; 137; 204; 349; 372; 379; 452; 455; 456; 539
151; 215; 513; 526; 546; 674; 694
104; 170; 247; 340; 609; 754; 759; 782; 904
71; 80; 128; 411; 910
19; 240; 280; 308; 576; 739; 781; 881

огределение
показателей надежности элементов по опытным данным
241
0ДРИАНТ 18
Первый набор исходных данных (Нормальное распределение):
136
158
118
131
129
148
130
154
147
118
167
162
136
140
143
114
125
150
151
118
127
125
140
125
125
142
137
132
120
133
149
129
141
170
133
123
162
136
132
161
127
135
127
142
135
168
140
158
137
172
144
127
145
156
136
152
128
127
161
141
141
155
116
139
122
149
128
116
124
142
124
143
128
147
120
124
139
135
125
127
121
138
140
138
166
162
122
137
124
142
148
133
133
117
116
137
148
160
129
125
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 600 часов
108; 214; 329; 423; 509
94; 200; 311; 423; 538
94; 195; 307; 393; 486; 569
94; 195; 279; 373; 465; 565
86; 201; 303; 417; 524
80; 161; 271; 363; 478; 592
115; 218; 308; 395; 501
112; 213; 318;423; 523
108;201; 302; 383; 475; 557
92;184;272;358; 463; 559

242 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа 1
ВАРИАНТ 19
Первый набор исходных данных (Нормальное распределение):
125
122
141
120
162
129
162
137
145
166
150
131
123
153
133
135
124
139
148
107
160
121
132
157
127
150
122
165
148
148
127
125
121
132
150
137
138
151
144
158
159
142
147
151
137
151
127
125
116
152
130
128
112
151
164
125
149
124
105
115
151
156
142
149
150
134
147
135
142
138
116
126
149
140
137
150
151
90
134
129
150
127
175
142
106
135
144
127
134
128
155
146
140
135
145
129
140
153
151
192
Второй набор исходных данных (Гамма-распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 1000 часов
68; 368; 709; 867
64; 255
389; 718; 989; 999
326; 540; 643
385; 486; 494; 609; 724; 756; 772; 872
212; 278; 370; 579; 818; 998
195; 451; 656; 676; 819; 841; 991
95; 239; 277; 320; 516; 543; 606; 675; 709; 1000
57; 262;587; 755; 904
395; 494; 569; 637

определение показателей надежности элементов по опытным данным 243
вдРИАНТ 20
Первый набор исходных данных (Гамма-распределение):
168
50
86
143
87
350
126
25
352
28
71
16
35
197
40'
210
73
165
145
96
358
116
162
54
384
236
396
80
284
383
250
91
125
164
42
270
142
78
80
168
42
229
54
29
237
28
60
74
82
173
134
41
135
40
186
107
194
151
128
80
27
128
179
79
159
75
107
137
37
163
203
151
177
70
316
147
156
47
314
118
178
215
77
ПО
195
64
167
488
186
216
109
96
90
404
44
331
190
119
58
106
Йторой набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
. 5
6
7
8
9
10
Моменты отказа на периоде
времени 1000 часов
114; 212; 296; 406; 504; 593; 673; 780; 861; 977
117; 201; 282; 388; 469; 576; 675; 771; 854; 969
105; 202; 316; 412; 504; 619; 729; 809; 928
95; 198; 290; 370; 478; 561; 659; 770; 871; 968
117; 204; 309; 390; 504; 604; 696; 811; 924
104; 186; 293; 388; 484; 596; 702; 820; 929
119; 199; 301; 405; 497; 585; 687; 798; 911
96; 186; 304; 422; 538; 657; 751; 859;954
101; 218; 305; 392; 489; 573; 660; 753; 836; 941
99; 204; 307; 422; 541; 652; 766;875;964

244
ЧАСТЬ //. Лабораторный практикум. Лабораторная работа 1
ВАРИАНТ 21
Первый набор исходных данных (Нормальное распределение):
137
145
166
180
147
158
170
172
166
160
140
156
156
193
162
179
162
153
162
169
184
141
179
152
170
166
178
156
153
180
143
136
163
150
162
144
148
176
174
135
167
154
152
136
172
161
146
134
138
133
187
146
171
148
181
165
144
176
164
168
160
148
140
167
130
162
173
167
201
181
169
160
131
158
167
121
165
159
171
152
187
145
153
149
180
137
177
168
158
198
170
158
171
143
193
139
165
161
141
178
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 600 часов
89; 169; 264; 344; 433; 547
95; 179; 275; 359; 440; 526
85; 166; 274; 372; 487; 585
105; 221; 308; 391; 489; 587
115; 196; 296; 413; 503; 583
86; 192; 275: 361; 455; 574
91; 183; 263; 356; 472; 572
НО; 195; 280; 362; 481; 566
105; 195; 296; 381; 475; 562
113; 198; 293; 409; 517

(Определение показателей надежности элементов по опытным данным
0АРИАНТ 22
Первый набор исходных данных (Гамма-распределение):
408
173
277
337
240
54
207
928
494
140
438
288
58
352
266
515
137
400
103
138
218
529
515
603
127
123
21
12
232
306
80
621
125
331
491
54
249
116
569
329
253
73
200
682
194
494
284
152
93
27
447
416
265
327
433
914
191
74
718
217
160
734
53
289
326
81
400
139
379
292
394
438
165
252
250
13
18
720
296
34
193
285
251
82
436
226
153
77
103
589
167
164
115
242
173
527
325
185
242
159
Второй набор исходных данных (Равномерное распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 600 часов
119; 232; 341; 427; 529
106; 206; 300; 406; 499
98; 187; 297; 389; 487; 570
88: 185; 285; 397; 506
91; 173; 266; 376; 476;595
106; 213; 293; 381; 469; 565
83; 173; 278; 370; 478; 572
117; 201; 319; 418; 524
94; 211; 325; 429; 509
97; 203; 299; 417; 498

246
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа 1
ВАРИАНТ 23
Первый набор исходных данных (Экспоненциальное распределение):
116
10
148
155
20
250
100
140
437
627
326
99
63
67
23
91
444
7
38
137
19
524
33
8
425
266
70
67
25
196
565
46
171
23
120
124
125
167
175
246
456
99
10
194
159
55
24
33
404
303
9
1055
189
2
20
92
484
275
81
87
17
187
56
101
223
73
192
867
184
25
50
31
166
70
4
59
68
173
198
39
21
946
31
153
403
1
14
7
11
11
118
81
160
310
282
16
49
88
7
94
Второй набор исходных данных (Гамма-распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 1000 часов
277; 397; 420; 797; 861
108; 352; 792; 943
146; 240; 289; 427; 494; 542; 863; 918
21; 177; 396; 654; 755; 958; 976
23; 209; 452; 561; 936
335; 508; 811; 950
90; 336; 457; 769
48; 139; 252; 279; 449; 500; 885
162; 343; 496; 551; 589; 765; 776; 844
164: 533; 722; 891

Определение показателей надежности элементов по опытным данным 247
ВАРИАНТ 24
0ервый набор исходных данных (Экспоненциальное распределение):
285
128
496
253
32
71
80
57
411
29
12
46
169
73
311
95
365
61
26
378
23
27
5
24
108
107
659
227
30
23
182
43
345
673
141
92
13
112
153
278
63
733
69
66
0
91
242
18
543
15
92
120
469
281
68
96
309
55
519
70
132
211
546
12
17
349
0
71
229
95
36
157
445
18
45
47
44
14
284
248
21
208
472
392
' 47
116
116
27
36
441
386
435
137
546
7
177
30
289
105
222
Второй набор исходных данных (Гамма-распределение):
Номер элемента
1
2
3
4
5
6
7
8
9
10
Моменты отказа на периоде
времени 800 часов
164; 736
111; 249; 370; 384; 465; 517
41; 99; 575;716
247; 399; 493
31; 380; 721; 757
137; 280; 380; 671
19;468; 501
216; 286; 440; 509; 681
173; 298; 394; 670;759
47;142;523; 636; 679; 757

248
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа f
ВАРИАНТ 25
Первый набор исходных данных (Равномерное распределение):
100
85
154
119
112
120
94
136
123
108
124
92
155
168
165
122
93
155
142
168
168
149
141
165
179
101
124
96
135
132
143
104
175
111
152
170
168
82
170
170
155
124
85
81
126
107
109
173
116
98
137
141
146
98
124
174
85
114
123
159
144
118
146
171
128
103
152
154
100
174
ПО
168
177
88
102
143
160
114
112
124
107
148
149
122
92
174
159
119
100
134
85
163
161
125
86
92
139
107
173
138
Второй набор исходных данных (Гамма-распределение):
Номер элемента
1
2
3
4
5
6
7 -
8
9
10
Моменты отказа на периоде
времени 700 часов
376; 488; 522; 626
369
306; 459; 656
192;553
417;685
40; 176
101; 291: 430
519; 635
64; 202; 467
134; 255; 507

ЛАБОРАТОРНАЯ РАБОТА 2
ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
И РИСКА НЕРЕЗЕРВИРОВАННОЙ
ТЕХНИЧЕСКОЙ СИСТЕМЫ
2.1. Постановка задачи
Дано:
О структурная схема системы в виде основного (последовательного в смысле
надежности) соединения элементов;
On — число элементов системы;
О А,; — интенсивность отказа /'-го элемента системы, / = 1, 2,..., п;
П Г; — риск из-за отказа /-го элемента системы, i = 1, 2,..., п;
^ Л — допустимый риск;
ОТ — суммарное время работы системы.
Определить:
О показатели надежности системы:
* ^с(0 — вероятность безотказной работы системы в течение времени /,
а также ее значения при t = Т и / = 7|;
• Тх — среднее время безотказной работы системы;
^с(0 — риск системы как функцию времени; значение риска при t = T и
8°зможность расчета риска по приближенной формуле.
Рианты заданий приведены далее в разд. 2.5.

250 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа о
2.2. Сведения из теории
Основными показателями надежности нерезервированной невосстанавливае-
мой системы являются: Рс(/) — вероятность безотказной работы системы в
течение времени t, 7j — среднее время безотказной работы. При постоянных
интенсивностях отказов элементов
п
где А,с = Y, ^/ — интенсивность отказа системы.
Риск системы Rc(t) и Я*(f) вычисляются по следующим формулам:
*c(0 = ^LV/. (21)
\ / = 1
^(0 = 1^/(0'}, (2.2)
где Qc(t) = \-Pc(t) — вероятность отказа системы в течение времени /;
qt{t) — вероятность отказа /-го элемента системы в течение времени t.
Формула (2.1) является точной, формула (2.2)— приближенной. Если
элементы системы равнонадежны, то отношение i^.(/) к B^(t) имеет вид:
Gs(M)=M)=Jz£^. (2,)
£(0 л(1-<ГХ')
GR(t,ri) является убывающей функцией времени, при этом:
\imGR(t,n) = \, limG^(/,«)=—.
/->0 /->оо п
Это означает, что с увеличением длительности времени работы системы
погрешность приближенной формулы увеличивается.,
2.3. Последовательность
выполнения работы
Лабораторную работу следует выполнять в такой последовательности:
1. Вычислить показатели надежности системы PQ(t) и 7]. Значение веро*
ности безотказной работы Pc(t) следует получить при / = Т и / = 7J.

глггледование надежности и риска нерезервированной технической системы 251
2 Исследовать функцию риска системы по точной формуле (2.1), для чего:
• получить формулу риска для заданных п, Xj} r,;
• исследовать зависимость ЯД/), представив функцию в виде графика и
таблицы;
• вычислить значение риска для исходных данных своего варианта при
t = Т и / = 7J.
3. Исследовать зависимость GR(t,ri) при допущении, что элементы системы
равнонадежны и интенсивность отказа каждого элемента равна их средней
1 "
интенсивности отказов, т. е. X = — ]|Г А., .
4, Сделать выводы.
По результатам лабораторной работы представляется отчет, в котором
обязательными являются следующие пункты:
1. Постановка задачи.
2. Расчетные формулы.
3. Численные значения показателей надежности и риска исследуемой
системы.
4. Значение времени непрерывной работы системы, при котором
обеспечивается требуемое значение риска.
5. Графики и таблицы функций риска.
6. Выводы по результатам исследований.
2.4. Пример выполнения
лабораторной работы
*Усть дана система со следующими исходными данными:
число элементов системы /7 = 10;
вРемя непрерывной работы Г = 1000 час;
Допустимый риск R = 5000 усл. ед.
ачения риска и интенсивностей отказов элементов приведены в табл. 2.1.
алее приводится последовательность выполнения работы. Исследования
ku^M пР°в°Дить с помощью универсальной системы символьной
математики Derive 5.

252 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа р
Таблица 2.1. Исходные данные примера
Номера
элементов
Х-10"5,-час"1
г, усл. ед.
1
1,2
2000
2
0,8
300
3
0,5
8000
4
1
1000
5
1,5
1200
6
0,6
60
7
0,09
5000
8
0,05
6000
9
1
100
10
1,5
120
2.4.1. Определение
показателей надежности системы
Интенсивность отказов системы равна Хс = £ %i. Подставляя в это выраже-
/=1
ние значения интенсивностей отказов элементов из табл. 2.1, получим:
Хс = 8,24-10~5 час-1 (технология вычисления А,с с помощью системы
Derive 5 приведена далее в разд. 2.4.2).
Тогда вероятность и среднее время безотказной работы будут равны:
Рс(/) = е"Хс'=е~8'24'10~$/, 7;= —= 12136 час.
При / = Г=1000 час Рс(1000) = е"8'2410"5103 =0,918.
2.4.2. Определение риска системы
по точной формуле
Для образования вектора интенсивностей отказов и вектора риска г в
системе Derive 5 необходимо выполнить следующие действия:
О выбрать пункт меню Author | Vector, на экране появится окно Vector
Setup;
П ввести размер вектора (в нашем случае 10), нажать кнопку ОК, на экране
появится окно ввода элементов вектора Auhor 10 element vector;
О ввести интенсивности отказов элементов (для ускорения процедуры ввоДа
значения X не умножаются на 10-5), после нажатия кнопки ОК на экран6
в строке #1 отобразится вектор интенсивностей отказов элементов.
Аналогично образуется вектор риска г. Пусть он находится в строке #2.
Вычисление интенсивности отказов системы Хс осуществляется с помоШь
следующих действий:

исследование надежности и риска нерезервированной технической системы 253
rj набрать в строке пользователя функцию:
ELEMENT (#1,11),
после нажатия клавиши <Enter> на экране появится функция element
с вектором интенсивностей отказов;
Внимание
В функции element первым аргументом должен быть номер строки с вектором X,
определенным ранее, а вторым аргументом — символ п, а не его численное значение.
О щелкнуть на кнопке Find Sum панели инструментов, на экране появится
новое окно Calculus Sum. На вкладке Variable установить значение п, на
вкладке Sum установить переключатель в положение Definite, на вкладке
Definite Sum определить область суммирования (в нашем случае от 1
(Lower Limit) до 10 (Upper Limit)). После нажатия ОК на экране
отобразится выражение суммы элементов вектора Хс;
О нажать кнопку Approximate панели инструментов, на экране появится
искомое значение суммы интенсивностей отказов элементов. В нашем
случае с учетом масштаба (10~5) Хс =8,24-10"5 час-'.
п
Для вычисления суммы Х^/7/ необходимо получить скалярное произведе-
/=1
ние векторов X и г, которые в нашем примере находятся соответственно под
номерами #1 и #2. Для этого в строке пользователя набирается выражение
■■#1 #2, нажимаются клавиши <Enter> и кнопка Approximate панели
инструментов, на экране появляется ответ 1,0506 • 104. В нашем случае с учетом
масштаба интенсивностей отказа (Ю-5) искомая сумма равна 0,10506.
Процедуры решения на экране монитора имеют следующий вид:
*1: [1.2,0.8,0.5,1,1.5,0.6,0.09,0.05,1/1-5]
#2: [2000, 300, 8000, 1000,1200,60,5000,6000,100,120]
13: ELEMENT([1.2, 0.8, 0.5, 1,1.5, 0.6, 0.09, 0.05,1,1.5],п)
4: £ ELEMENT([1.2, 0.8, 0.5, 1,1.5, 0.6, 0.09, 0.05,1, 1.5], п)
П = 1
8.24
*6: 8.24-10-5
• [1.2,0.8,0.5,1,1-5,0.6,0.09,0.05,1, 1. 5]-[2000, 300, 8000,
1000,1200,60,5000,6000,100,120]

254 ЧАСТЬ //. Лабораторный практикум. Лабораторная работа ?
#8: 1.0506-Ю4
#9: 0.10506
Так как Qc(t) = \-Pc(t) = \-e~K*, Хс = 8,2410~5, £*,// =0,10506, то в соот.
/=1
ветствии с (2.1) функция риска будет равна:
1 -8,24-10"5 г
j?(/) = l_r —-0,10506,
8,24-Ю-5
или
7^(0 = 1275-(1-е-8,2410"5')-
Вычисление /^(Z) для заданного значения времени непрерывной работы
/ = Г и среднего времени безотказной работы t = 7J выполняется с помощью
кнопок Variable Substitute и Approximate панели инструментов. Для нашего
примера при / = 1000 час риск /^(1000) = 100,848.
Для t = T{ =12136 час значение риска Д,(/) = 805,953 . Из полученных
значений Rc(t) видно, что риск исследуемой системы ниже допустимого значения,
равного 5000 условных единиц.
2.4.3. Исследование функции риска
Предполагая, что все элементы системы равнонадежны, а интенсивность от-
каза каждого элемента Х = —— = 0,824- Ю-5 час"1, получим следующее выра-
п
жение риска:
]-p-nXt п 1 -0,82410"5 я/ , -0,824-10"s я/
^(/) = 1_1 Y\r-LJ. — 10506-Ю-5 =12750-— •
пХ Д 0,824-10"5и и
Найдем зависимость R^(t) при различных значениях п в виде графиков и
таблиц, используя возможности пакета Derive 5.
Получение графика функции риска
Построим графики функции риска, выполнив следующие действия:
П ввести выражение риска i^(/,w):
12750-Q -г-0'824'10'5"')
n

i следование надежности и риска нерезервированной технической системы 255
<\ получить выражение риска для различных значений п путем подстановки
в выражение риска численных значений п с помощью кнопки Sub панели
инструментов, на экране появится выражения риска (в нашем случае при
„ = 10,30,50);
г\ щелкнуть мышью на кнопке 2D-plot window панели инструментов, на
экране появится окно 2D-plot с сеткой координат;
г\ настроить с помощью клавиш <F5>—<F10> оси координат на нужный
диапазон времени (ось*) и риска (ось>>);
О после нажатия кнопки Plot Expression панели инструментов на экране
появится график функции риска при данном п;
р щелкнуть мышью на кнопке Algebra window панели инструментов
графического окна, на экране появится главное окно системы;
О выделить формулу риска при новом значении п (в нашем случае при
и = 30) и построить график описанным ранее способом и т.д. На экране
образуется семейство графиков (в нашем случае три графика при и = 10,
30, 50).
J)pee приводятся процедуры образования функций риска и соответствующих
им графиков (рис. 2.1):
ютил ,-, "-0.824-10"5-n-t.
.». t 12750-(l-e )
п
12. 12750-(1-е )
10
#3: i2750-(l-e )
30
#4:- 1275СН1- е-0-824"10"5-50^)
50
Из п
рисунка видно, что с увеличением времени / работы системы техноген-
,и риск функционирования системы увеличивается и при / -> оо стремится
°стоянной величине, равной среднему значению риска.
Оставление функции риска в виде таблицы
§~* выполнении предыдущих действий для построения графика на экране
^° получено выражение риска. Предположим, что оно находится в строке

256
ЧАСТЬ //. Лабораторный практикум. Лабораторная рабрТя
Л.
Рис. 2.1. Зависимость риска от времени при различных значениях п
#1. Тогда функцию риска в виде таблицы можно получить путем
табулирования функции Rc(t).
В строке пользователя набирается функция табулирования:
TABLE([t,#1] , t, tn, tk, dt),
где t — аргумент функции риска; tn, tk, dt— соответственно начальное,
конечное значения времени t и шаг изменения /. В нашем случае tn = 0, tk
выбираем равным среднему времени безотказной работы tk = Т= 12136 час.
Выберем шаг таблицы dt = 1500. Тогда функция будет иметь вид:
TABLE{[t,#l], t, 0, 12136, 1500).
После ввода функции нужно нажать кнопку Approximate панели
инструментов. Процедуры табулирования и итоговая таблица при « = 10 на экране
монитора имс'ют следующий вид:
12750-(l-e~n'At)
#1:
п
12750-(1-а-10'(0-824-10"Ь^)
#2:
10
fl2750.(l-e-10!0-82','lo5)'t)
#3: TABLE - 4^1000,10000,1000
10
V )

„едование надежности и риска нерезервированной технической системы 257
О О
1500 148.2400890
3000 279.2447867
4500 395.0179957
6000 497.3306315
7500 587.7477110
9000 667.6522918
1.05-Ю4 738.2666278
1.2-104 800.6708653_
Из строки #4 видно, что риск возрастает с увеличением времени
функционирования системы t. Так, например, с увеличением t с 1500 до 12 000 часов
риск увеличивается примерно с 150 до 800 условных единиц.
Определение критического времени работы системы
Так как R^it) возрастает с ростом /, то представляет интерес предельное
время, выше которого риск будет превышать допустимое значение. Решение
задачи сводится к определению корня уравнения
Так как в рассматриваемом случае £*./;= 10506-10"5, Хс =8,24-Ю-5 час-1,
i = \
5000, то, подставляя эти значения в последнее выражение, получим:
5000 = 1275(1-<Г8Д4'!оЛ).
еШая это уравнение с помощью функции SOLVE, получим критическое зна-
Ние т. В нашем примере вещественного корня нет. Это значит, что при
"°м / риск системы не превосходит допустимого значения..
•4.4. Исследование зависимости Gf^t, n)
анализа зависимости GR(t,n) представим эту функцию в виде графиков
"лиц. Графики позволят сделать качественный анализ, а таблицы — ко-
гр ^СТвенный. Далее описываются процедуры представления функций в виде
^фИков и таблиц с помощью системы Derive 5.

258
ЧАСТЬ II. Лабораторный практикум. Лабораторная рабрГд
Построение графиков G^t, n)
Предположим, что система состоит из п равнонадежных элементов, каждые
из которых имеет интенсивность отказов X. Тогда функция GR(t,n) §у.
дет выражаться формулой (2.3). Подставим в эту формулу значение
X = 0,824-КГ5 час"1 и наберем формулу в строке пользователя. Построение
графиков осуществляется так, как было описано в разд. 2.4.3.
Построим графики для 3—4 значений п, например для и, Зи, 5п, где я ^
число элементов системы. В итоге получим семейство кривых (рис. 2.2), из
которых можно сделать два важных вывода:
1. Чем больше элементов л и чем больше время работы системы, тем
больше погрешность приближенной формулы.
2. Приближенной формулой можно пользоваться в том случае, когда время
работы системы мало и риск, вычисленный по приближенной формуле, не
превышает допустимого значения.
Рис. 2.2. График функции Gj&t, n)
Представление функции Gnit, n) в виде таблицы
Представление функции в виде таблицы выполним с помощью функии
VECTOR в такой последовательности:
О ввести выражение (2.3);
П присвоить переменной X среднее значение (в нашем примере **"
= 0,824-Ю-5 час-1); присвоение осуществляется с помощью кноП
Substitute панели инструментов;

следование надежности и риска нерезервированной технической системы
259
* прйсвоить переменной п значения и = 10, 30, 50. На экране появятся три
сражения. Пусть эти выражения находятся на строках #2, #3, #4;
j-j рвести функцию:
VECTQR([t,#2,#3,#4], t, tn, tk, dt).
3 нашем примере tn = 1000, tk = T\ - 10000, dt = 1000, тогда команда
будет иметь вид:
VECTOR*[t,#2,#3,#4], 1000, 10000, 1000);
О нажать кнопку Approximate, на экране появится решение в виде таблицы.
Вычислительные процедуры и итоговая таблица имеют следующий вид:
П: Ml-**-')
, «-10-(0.824-10"5)-t
1-е
#2*
ю-(1-ё-(0-824-10"5)-ь)
, «-30-(0.824-lCf5)-t
i3. JtZl
30-(i-e-<0-824-10"s,-t)
, »-50-(0.824-10"5)-t
#4: Jtl®
50-(1-ё-(0-824-10"5)-ь)
, --10-(0.824-10"5)-t , »-30-{0.824-lCf5)-t
*5: VECTOR([t, , ,
lO-d-e'10-824'10" K) 30-(l-e~{0-824-10 K)
, »-50-(0.824-10"5)-t
—], t, 1000, 10000, 1000)
50.(1_е-(0.824.10-К)
"1000 0.9638689494 0.8896403810 0.8229826665"
2000 0.9295636973 0.7954817751 0.6868502286
3000 0.8969810018 0.7148703099 0.5811172570
4000 0.8660238341 0.6456139387 0.4981476918
#6. 5000 0.8366009899 0.5858989249 0.4323514074
6000 0.8086267264 0.5342218372 0.3796132168
7000 0.7820204206 0.4893341167 0.3368857825
8000 0.7567062512 0.4501968454 0.3018984066
9000 0.7326129002 0.4159437960 0.2729479655
_104 0.7096732736 0.3858512133 0.2487482452_

260 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабрТа
Из таблицы видно, что функция GR(t,n) является убывающей. Это означает
что с увеличением времени и увеличением числа элементов погрешность
приближенной формулы возрастает.
Определим предельные значения функции GR(t,n), воспользовавшись кноп*
кой Find Limit (lim) панели инструментов.
Пределы существуют, если переменные п и X положительны и значение п
конечно. Укажем это программе с помощью пункта меню Declare | Variable
Domain. Процедуры решения имеют вид:
, »-n-X-t
1-е
#1: ГГ
#2: Л :е Real[0,oo)
#3: n :e Realfl, 1000]
#4: lim
t-»o+ п-П-е~К'*)
#5: 1
- «-п-Л-t
1-е
#6: lim —
t-« n-(l-e c)
#7: I
n
Таким образом, предельное значение погрешности приближенной формулы
равно 1/«.
2.5. Варианты заданий
к лабораторной работе 2
В заданиях приняты следующие обозначения:
П Т — суммарное время работы системы, час;
П R — допустимый риск, усл. ед.;
□ Xj —интенсивность отказов/-го элемента, час-1;
П /; — риск системы из-за отказа /-го элемента, усл. ед.

..рпедование надежности и риска нерезервированной технической системы
261
„дРИАНТ 1
Номера элементов
х. Ю-5, час""1
Л усл. ед.
1
1,1
2500
2
0,5
6000
3
3
3000
4
4,2
2850
5
3,6
6180
6
2,1
4200
7
4,4
680
8
4,8
1000
у* 1500 час, R = 8000 усл. ед.
ВАРИАНТ2
Номера элементов
Ы0"5, час"1
г, усл. ед.
I
2,6
6800
2
3,2
9200
3
6,4
2000
4
1,2
20000
5
3
9200
6
1,8
1000
7
5,1
2100
8
4,2
600
Г= 1200 час, R = 5000 усл. ед.
ВАРИАНТ 3
Т§омера элементов
Ы О""5, час'1
''.усл. ед.
1
0,5
12000
2
0,2
8000
3
1
6000
4
1,2
560
5
0,6
3200
6
2,1
7600
7
1,2
10000
8
0,7
770
Г* 2500 час, R = 3200 усл. ед.
ВАРИАНТ 4
Номера элементов
^Лчас"1
''Усл. ед.
1
0,2
1200
2
0,8
2600
3
2,3
3000
4
0,1
14000
5
0,5
4500
6
1,2
9000
7
3,4
3500
8
0,7
2750
Г*
3800 час, R = 5000 усл. ед.
]*^ИАНТ5
--^^Раэлементов
l^ycjue^
1
1,1
2500
2
2,3
2600
3
4,7
1800
4
0,6
16000
5
5
4000
6
4.8
2600
7
3,2
1200
8
2.6
860
* 4000 час, R = 4800 усл. ед.

262
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа
ВАРИАНТ 6
Номера элементов
Х-Ю-5, час'1
г, усл. ед.
1
1,2
6800
2
0,8
2400
3
1,6
3200
4
0,2
670
5
0,1
5000
6
0,05
20000
7
6,2
360
8
2,4
780
Т= 4200 час, Л = 3850 усл. ед.
ВАРИАНТ 7
Номера элементов
Х-10'5, час"1
г, усл. ед.
1
3,2
368
2
0,1
680
3
1
12000
4
0,7
7000
5
1,2
3200
6
0,3
1200
7
0,1
590
8
1,2
1050
Т= 5000 час, R = 860 усл. ед.
Далее приводятся варианты заданий с 8 по 25, в которых указано, из каких
приведенных ранее вариантов с 1 по 7 берутся значения А,,, rit T, R.
ВАРИАНТЫ 8—16
Номер варианта
Номер варианта для X,
Номер варианта для r„ T, R
ВАРИАНТЫ 17—25
Номер варианта
Номер варианта для Xt
Номер варианта для r„ T, R
8
1
7
17
3
4
9
2
6
18
5
1
10
3
5
19
5
1
11
4
3
20
6
3
12
5
2
21
7
5
13
6
1
22
1
2
14
7
4
23
3
6
15
1
6
24
3
7
16
2
5
25
4
1

ДАБОРАТОРНАЯ РАБОТА 3
ИССЛЕДОВАНИЕ СВОЙСТВ
СТРУКТУРНО РЕЗЕРВИРОВАННЫХ
СИСТЕМ ПРИ ОБЩЕМ
РЕЗЕРВИРОВАНИИ С ПОСТОЯННО
ВКЛЮЧЕННЫМ РЕЗЕРВОМ
3.1. Постановка задачи
Дано:
О техническая система с основным соединением элементов;
О и — число элементов системы;
О \. — интенсивность отказа элемента /-го типа, i -1, 2,..., п;
О t — текущее время работы системы, не превосходящее допустимого
времени из условия старения; "
" т — кратность резервирования, т < 4.
Необходимо:
1:1 оценить эффективность структурного резервирования как метода
повышения надежности;
выполнить сравнительный анализ надежности системы при структурном и
нагрузочном резервировании;
исследовать влияние последействия отказов на эффективность
структурного резервирования.
°Дные данные для индивидуальных заданий приведены далее в разд. 3.4.

264 ЧАСТЬ II. Лабораторный практикум. Лабораторная работ* 0
3.2. Сведения из теории
Показателями эффективности различных методов обеспечения и повыше^
надежности могут быть выигрыш надежности по вероятности отказа G (/) и
выигрыш по среднему времени безотказной работы GT. Выигрышем наде^.
ности называется отношение показателя надежности резервированной систе.
мы к соответствующему показателю надежности нерезервированной сие.
темы.
Так как для резервированной системы с постоянно включенным резервом
вероятность и среднее время безотказной работы выражаются формулами
от+11
Рс(/) = 1-(1-е-х'Г+1, ТС=Т^-, (3.1)
то соответствующие выигрыши имеют вид:
G„(,) = M)= 1 , (3.2)
т in+l t
GT=f=ZL. (3.3)
В формулах приняты обозначения:
Е Quit), Tq — вероятность отказа и среднее время безотказной работы
исходной (основной) системы;
О бс(0» ТС — вероятность отказа и среднее время безотказной работы
резервированной системы;
О Л. = 2] А,, = const — интенсивность отказа исходной нерезервированной
системы.
Анализ выигрышей надежности позволяет сформулировать следующие
важные свойства структурного резервирования:
О чем более надежна система и чем меньше время ее работы, тем выше эф*
фективность резервирования;
О чем выше кратность резервирования, тем выше выигрыш надежности
любому из критериев, однако с ростом кратности резервирования скоро0
роста выигрыша убывает;
□ при резервировании с постоянно включенным резервом значительное
вышение кратности резервирования ведет к несущественному повышен1
среднего времени безотказной работы;

л^пеДОвание свойств структурно резервированных систем 265
f\ интенсивность отказа резервированной системы
X(/) = __£l2 (3.4)
/>с(0
является возрастающей функцией времени. При / = 0 Яс(/) = 0 и с ростом
t Xc(t) асимптотически стремится к интенсивности отказа
нерезервированной системы.
Существенное повышение надежности может достигаться путем применения
нагрузочного резервирования. В процессе проектирования сложных
технических систем конструктор не может уменьшить нагрузку на элементы более,
чем в 10 раз по сравнению с номинальной. При этом интенсивность отказов
остается постоянной во времени и для многих элементов линейно убывает с
уменьшением коэффициента нагрузки.
Сравнительный анализ надежности резервированных систем показывает, что
нагрузочное резервирование может быть более эффективным в системах,
предназначенных для длительной работы. Во многих практических случаях
существует критическое время работы т, после которого более
целесообразным оказывается нагрузочное резервирование.
Указанные свойства резервирования полезно знать не только конструктору,
но и инженеру, занимающемуся эксплуатацией техники, обеспечивая
безопасность жизнедеятельности. Данная лабораторная работа позволит численно
оценить эффективность резервирования, как средства повышения
надежности и снижения риска.
3.3. Последовательность
выполнения работы
Лабораторную работу следует выполнять в такой последовательности:
'• Исследование эффективности структурного резервирования.
*• Сравнительный анализ структурного и нагрузочного резервирования.
• Исследование влияния последействия отказов на эффективность
структурного резервирования.
отчете о лабораторной работе должны быть следующие пункты:
• Постановка задачи.
' Результаты исследований в виде формул, графиков и таблиц по каждому
Ъразд. 3.3.1—3.3.3.
• Выводы по результатам исследований.

266
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа а
3.3.1. Исследование эффективности
структурного резервирования
Оценка выигрыша надежности
по среднему времени безотказной работы
Оценить выигрыш GT можно, если представить зависимость GT=GT{m)
в виде таблицы. Воспользуемся для этой цели системой Derive 5. Для реше-
ния задачи нужно выполнить следующие действия:
1
О ввести выражение -;
i
О образовать выражение £- с помощью кнопки Find Sum панели ин-
струментов;
□ протабулировать это выражение с помощью функции vector, имеющей
вид:
VECTOR([m,#2], m, mn, mk, dm),
/И+1 1
где #2— номер выражения У- (в данном случае предполагается, что
м *
выражение находится в строке #2); mn, mk — начальное и конечное
значения кратности резервирования; dm — шаг таблицы.
Выберите mn = 0 (резервирование отсутствует), mk = 9 (в системе 10
подсистем, из которых 9 резервных), dm = 1. Тогда функция будет иметь
вид:
VECTOR([m/#2]/ m, 0, 9, 1).
После выполнения функции на экране монитора появится решение в виде
табл. 3.1.
Таблица 3.1. Выигрыш надежности системы
по среднему времени безотказной работы
m
0
1
2
...
9
G,(m)
1
1.5
1,83333
...
2,92896

.^следование свойств структурно резервированных систем
267
Рис. 3.1. Выигрыш надежности резервированной системы
°лучим зависимость G(x,m) в виде таблицы, воспользовавшись функцией
£Ctor следующего вида:
EctOR([x,#2,#3,#4,#5], х, xn, xk, dx),
^таблицы следует важный вывод: с увеличением кратности резервирования
м среднее время безотказной работы увеличивается незначительно.
Проанализируйте данные таблицы и сделайте более конкретные выводы.
Оценка выигрыша надежности
по вероятности отказа системы
Выигрыш Gq(0 надежности резервированной системы по вероятности отказа
является функцией времени, зависящей от интенсивности отказа исходной
системы и кратности резервирования.
Представим эту функцию в виде:
G(x,m) = , (3.5)
(\-e'x)m
где х = Xt.
Зависимости G = G(x,m) приведены на рис. 3.1.

268 ЧАСТЬ II. Лабораторный практикум. Лабораторная работу д
где #i — номера выражений для G(x,m) на экране монитора, соответственно
для /я = 1, /w = 2, w = 3, /w = 4. С позиции полноты анализа результатов и
удобства их представления на экране выберем: хп = 0,1, хк = 2
dx = 0,2. Тогда функция будет иметь вид:
VECTOR([х,#2,#3,#4,#5], х, 0.1, 2, 0.2).
Выражения выигрышей G(x,m) для m = \, w = 2, /w = 3, /и = 4 можно полу,
чить из формулы (3.5). Для этого необходимо в (3.5) подставить поочередно
значения /и, используя кнопку Sub панели инструментов. В результате на
экране монитора будут выведены 4 выражения с присвоенными номерами, в
нашем случае это строки #2, #3, #4, #5. После исполнения команды vector
на экране появляется табл. 3.2
Таблица 3.2. Результаты табулирования функции G(x,m)
Шапка таблицы на экране отсутствует, ее можно составить самостоятельно.
Спишите данные таблицы и сделайте выводы. Обратите внимание на главное:
с ростом х выигрыш надежности G(x,m) убывает, т. е. чем более надежна
резервируемая система и чем меньше время ее работы, тем выше
эффективность резервирования.
С увеличением кратности резервирования выигрыш увеличивается, причем
увеличение тем значительней, чем меньше произведение Xt. Делая выводы,
проиллюстрируйте их числовыми данными таблицы.
Исследование свойств интенсивности
отказа резервированной системы
Исследуем свойства интенсивности отказа, воспользовавшись зависимостью
(3.4). Исследования целесообразно выполнить в такой последовательности:
□ ввести выражение для вероятности безотказной работы резервированной
системы Рс (/) = 1 - (1 - e~u )m+l;

исследование свойств структурно резервированных систем 269
q нажать кнопку Find Derivative панели инструментов, на экране появится
окно Calculus Differentiate;
0 установить на вкладке Variable переменную дифференцирования /, на
вкладке Order установить порядок производной— 1, после нажатия
кнопки ОК на экране отобразится обозначение производной;
0 нажать кнопку Simplify или Approximate — на экране появится
выражение для производной;
0 ввести выражение интенсивности отказа системы— #3/#1
(предполагается, что в строке #1 находится выражение вероятности безотказной работы,
а в строке #3 — производная), на экране появится выражение
интенсивности отказов системы;
О определить диапазон изменения переменной m с помощью пункта меню
Declare | Variable Domain (переменная m положительна в диапазоне от О
до оо), на экране появится запись:
m :e Real (0,оо )
О после нажатия кнопки Find Limit панели инструментов на экране
отобразится окно Calculus limit;
О установить на вкладке Variable переменную t, а на вкладке Limit Point
задать 0, после нажатия кнопки ОК на экране отобразится выражение
предела;
О после нажатия на кнопку Simplify или Approximate на экране появится
значение предела — 0;
О выделить выражение для Я,с(/) и повторить предыдущих три пункта для
случая /->оо, на экране появится значение предела— X. Предел будет
получен только после замены переменной m любым ее численным
значением.
Процедуры вычисления пределов имеют следующий вид:
*1: l-(l-e-Vt)m+1
#2: Ац-ц-ё^Г1)
dt
#3: -A-e-^-'^'-dn + lHe^-lf
#4: -Х-ё'х-№41'-(т + 1)-(еи-1)т
1-(1-е"Л'п)т+1
*5: т :е Real (0,oo )

270
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа щ
. -л-е -(m + lHe -1)
#6: lim ——
t-o^ l-(l-e"X,t)m+1 J
#7: 0
-A-e-^^-il + lMe^-l)1
#8:
l-d-e"^)1*1
( -A.e^^-d + D-le^^l)1)
#9: lim rTTI
t-»*^ l-(l-e ) )
#10: X
-A-e"x-t-(4fl).(4+l).(ex-t-l)4
#11:
1-(1-е-л,с)4+1
„10 ,. -A-e -(4 + l)-(e -1)
#12: lim
t—^ l-(l-e"x,t)4+1 J
#13: X
Изобразим графики функции Xc(t) при различных значениях m и одном
значении X. Для этого создадим выражения для \c(t) при /и = 1, ю = 2, m = 3,
m-A и последовательно, один за другим, построим семейство графиков,
предварительно подобрав необходимые масштабы по осям координат (рис. 3.2).
Рис. 3.2. Зависимости интенсивностей отказов системы от времени

фслеДование свойств структурно резервированных систем 271
Зависимости А,с(/) получены для случая А,с = 0,1, m = 1, 2, 3, 4.
u3 графиков видно, что при постоянной, отличной от нуля интенсивности
отказов исходной системы, интенсивность отказа резервированной системы
при t - 0 равна нулю и увеличивается с течением времени, стремясь к
постоянной величине, равной интенсивности отказов нерезервированной системы.
Объясните это явление физически на основании ваших знаний теории
надежности.
3.3.2. Сравнительный анализ эффективности
нагрузочного и структурного резервирования
Вероятность отказа Qc(t) и среднее время безотказной работы Тс системы
при нагрузочном резервировании выражаются формулами:
где п — число, показывающее, во сколько раз уменьшается интенсивность
отказа системы при наличии нагрузочного резервирования.
Тогда выигрыш надежности при структурном резервировании по сравнении с
нагрузочным будет равен:
2±
1-е "
GJt)= г. (3.6)
Представим эту функцию в виде:
х
1-е "
G„(jt,w,w)= г. (3.7)
Исследование выполним в такой последовательности:.
" построим график функции Gq(x,m,ri)\
•J определим критическое значение т, характеризующее эффективность
структурного резервирования по сравнению с нагрузочным.
Рафики функции Gq(x,m,n) построим с помощью кнопки 2D-plot window
Панели инструментов. На рис. 3.3 показаны графики для случаев /м = 1,

272
ЧАСТЬ II. Лабораторный практикум. Лабораторная работу д
Рис. 3.3. Графики выигрыша надежности
Из графиков можно сделать следующие важные выводы:
□ при малом времени работы системы целесообразно использовать
структурное резервирование;
□ область применения структурного резервирования тем шире, чем
меньше и;
О критическое значение целесообразности структурного резервирования
зависит от его кратности m и величины нагрузочного резервирования п.
Для определения критического значения времени х целесообразности
структурного резервирования решим следующее уравнение:
1-е "-(\-e~x)m+l = 0.
Решение получим с помощью системы Derive 5 (функция solve). Результаты
решения при различных значениях п и m приведены в табл. 3.3.
Таблица 3.3. Критическое значение Хт целесообразности
структурного резервирования
п
m
Хх
1
0,96
2
2
1,89
3
2,53
1
0,25
5
2
0,71
3
1,1
1
0,11
10
' 2
0,43
3
0,72

исследование свойств структурно резервированных систем 273
лероятности безотказной работы структурно резервированных систем могут
быть вычислены по данным последней строки таблицы.
0з графика рис. 3.3 видно, что критическое значение т тем больше, чем
меньше п.
3.3.3. Исследование влияния
последействия отказов
рассмотрим следующую задачу: дана дублированная система; интенсивности
отказа основной и резервной систем одинаковы и равны X. При отказе одной
из них нагрузка на исправную увеличивается и интенсивность отказа
становятся равной A,j > X. Необходимо найти показатели надежности и оценить
влияние последействия отказов.
Задачу решим с помощью пакета Derive 5 в такой последовательности:
О получим формулы для вероятности и среднего времени безотказной
работы, для чего введем формулу
Pc{t) = P2{t) + 2\Q'(x)P(x)Px{t-x)dx, (3.8)
о
где P(t) = e~Xl-, />(т) = е~Ял; Q'{x) — производная от вероятности отказа
Q(x) = 1 - Р(х); Рх (/ - х) = е-Х| (/_т).
Рекомендуется ввести первоначально составляющие формулы (3.8), а
затем образовать саму формулу, оперируя номерами строк, которые
присвоены составляющим;
Q получим решение для Рс(/) с помощью кнопки Approximate;
" найдем среднее время безотказной работы, вычислив интеграл от
полученного выражения для Рс(/) с помощью кнопки Integrate:
т=)рс№.
о
" результате решения задачи получим следующие формулы:
^(0=^—^4-^—^',
Т__Х{+2Х

274 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа л
Обратим внимание на формулу для Pc{t). Если \ =2Х, то формула не
имеет смысла;
□ найдем аналогично предыдущему решение для (3.8), подставив А., ~2\
в составляющую Рх (/ - т);
□ найдем новое значение среднего времени безотказной работы.
В результате решения получим следующие формулы:
Рс(/) = в-2Х,(1 + 2Х/), Г = 1.
Далее показаны процедуры решения задачи и конечные результаты.
#1: ё"*"'
#2: е_х'т
#3: e'xut-x)
#4: Л-е~х"х
#5: л-е"х"т-Гх'х-е*Х1'а_г)
#6: /А-ё^-ё"^-^1^!
о
t
#7: (e ) +2-JX-e -e -e di
о
Xl.e'2Xt 2-X-e_xlt
#8: +
Л1-2-Л 2-А-Л1
#9: A :<= Real(0,oo)
#10: Л1 :€ Real (0,oo)
"°f \ i A-2-X-t 0 ч i-Xl-t \
#11: f + dt
J0{ Л1-2-А 2-A-A1 ,
„10 0.5-(2-Л + Л1)
#12:
A-Al
#13: (е"х'')2+2-|А-ё"х'т-ё"х-т-е-(2ХН,:-т^1
о
#14: e~2x-t+2-A-t-e"2Xt

исследование свойств структурно резервированных систем
275
00
#15: f(e~2Vt+2-A-t-e"2-A't)dt
о
#16= X
Днализ формул показывает, что последействие отказов может существенно
снизить эффективность структурного резервирования. Так, например, если
%. = 2%, то среднее время безотказной работы резервированной системы
будет равно среднему времени безотказной работы нерезервированной
системы, т. е. резервирование не будет иметь смысла.
3.4. Варианты заданий
к лабораторным работам 3 и 4
В заданиях X — интенсивность отказа нерезервированной системы, час-1.
.ВАРИАНТЫ 1—8
Номер варианта
Х-Ю-5, час-1
ВАРИАНТЫ 9—16
Номер варианта
_ Х10-5,час-'
варианты п—25
.^Номер варианта
.. Х-10-5,час-'
1
3,8
9
5,9
17
4,7
2
4
3
1.5
4
2,7
5
1,9
6
3,2
7
4,1
10
3,7
11
7,5
12
2,6
13
6,8
14
5
15
4,4
18
6,5
19
3,5
20
8,4
21
2,9
22
2,8
23
4,6
24
4.3
8
1,2
16
3,3
25
6,2

ЛАБОРАТОРНАЯ РАБОТА 4
ИССЛЕДОВАНИЕ СВОЙСТВ
СТРУКТУРНО РЕЗЕРВИРОВАННЫХ
СИСТЕМ ПРИ ОБЩЕМ
РЕЗЕРВИРОВАНИИ ЗАМЕЩЕНИЕМ
4.1. Постановка задачи
Дано:
□ техническая система с основным соединением элементов;
п
П X = £ Xj — интенсивность отказа нерезервированной системы, состоящей
из п элементов;
□ / — текущее время работы системы;
П т — кратность резервирования, не превосходящая по условиям
физической реализуемости четырех, т. е. т < 4.
Необходимо:
□ провести сравнительный анализ надежности однотипных систем при оо-
щем постоянном резервировании и при резервировании замещением;
О исследовать влияние надежности автомата контроля и коммутации на
эффективность резервирования замещением;
□ исследовать свойства интенсивности отказа резервированной системы.
Для индивидуальных заданий следует использовать исходные данные из
лабораторной работы 3 (см. разд. 3.4).
4.2. Сведения из теории
Основными показателями надежности невосстанавливаемых систем явля*0
ся: Рс(/)— вероятность безотказной работы в течение времени /, 'I

.^лвдование свойств структурно резервированных систем 277
оеднее время безотказной работы. Формулы для Pc{t) иГ,в случае
резервирования замещением имеют вид:
РЛ0 = е->->1{^-, (4.1)
71=Г0(/н + 1), (4.2)
где Tq = среднее время безотказной работы нерезервированной
системы; м — кратность резервирования.
формулы справедливы для случая, когда основная и все резервные системы
одинаковы и автомат контроля и коммутации, физически реализующий
подключение резервной системы при отказе работающей, абсолютно надежен.
Анализ формул (4.1) и (4.2) показывает, что эффективность резервирования
замещением выше, чем при постоянно включенном резерве, а расход ресурса
ниже. Однако резервирование замещением по сравнению с постоянно
включенным резервом имеет ряд недостатков, основными из которых являются:
О необходимость автоматов контроля и коммутации для подключения
резерва при отказе работающей системы;
'Щ снижение производительности системы из-за того, что резервные системы
не работают при исправной основной системе.
Учет надежности автомата контроля и коммутации снижает эффективность
резервирования: при определенных условиях оно может оказаться
нецелесообразным.
Показателями эффективности резервирования замещением могут быть
выигрыши надежности по вероятности отказа GM) и по среднему времени
безотказной работы GT. Наибольший выигрыш по сравнению с постоянным
резервом система имеет по среднему времени безотказной работы. Интенсив-
ность отказа системы с увеличением времени работы растет и при /-»оо
Щемится, как и при постоянном резервировании, к интенсивности отказа
Нерёзервированной системы.
ь
процессе выполнения данной лабораторной работы студент должен убе-
иться в справедливости указанных ранее теоретических положений.
£•3. Последовательность
*Ь|полнения работы
оораторную работу целесообразно выполнять в такой последовательности:
Исследовать эффективность структурного резервирования замещением
При идеальном автомате контроля и коммутации.

278 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа л
2. Исследовать влияние автомата контроля и коммутации на эффективность
структурного резервирования замещением.
3. Исследовать свойства интенсивности отказа резервированной системы.
(Зтчет о лабораторной работе должен содержать следующие пункты:
1. Постановка задач.
2. Расчетные формулы.
3. Таблицы и графики.
4. Выводы по результатам исследований.
4.3.1. Исследование эффективности
структурного резервирования замещением
при идеальном автомате контроля и коммутации
Эффективность резервирования замещением по сравнению с постоянно
включенным резервом можно оценить по показателям выигрыша G?(/), Gr,
которые имеют вид:
_w + l
£?
где Q\(t) — вероятность отказа системы при резервировании с постоянно
включенным резервом; Q2{t) — вероятность отказа системы при
резервировании замещением.
Оценить эффективность резервирования можно, если функции выигрыша
представить в виде таблиц и графиков. Выполним исследования с помошью
компьютерных технологий, используя систему Derive 5.
Оценка выигрыша надежности по вероятности отказа
Представим функцию Gq(t) в виде таблицы и графика. Обозначим УЛ~**
тогда Gq (t) будет иметь вид:
G (х, т) = .
4 т у.1

.следование свойств структурно резервированных систем 279
задача решается в следующей последовательности:
х1
f\ ввести выражение -7-;
rj образовать выражение X — с помощью кнопки Find Sum панели инст-
/=о '•
рументов (пусть это выражение на экране монитора находится в
строке #2);
{\-е~х)т+х
CJ образовать выражение , на экране появится выражение выиг-
рыша Gq(x,m)\
О получить выражение для выигрыша Gq(x,m) при /и = 1, /я = 2, т = 3,
т = 4, воспользовавшись командой Variable Substitution (пусть эти
выражения на экране имеют номера #4, #5, #6, #7);
О протабулировать выигрыши с помощью функции:
t*VECTOR([x,#4,#5,#6,#7], x, xn, xk, dx).
В целях наглядности табличного представления выигрыша выберем
следующий диапазон изменения аргумента х:хп = 0.1;хк = 2; dx=0.2.
После выполнения команды на экране появится таблица выигрышей для
четырех значений кратности т.
Процедуры образования таблицы Gq(x,m) имеют вид:
#1: *1
i!
*2: ±±
i-oi!
13: Jl-e"x)m+1
m vi
iT0i!
#4: Jl-e~x)1+1
1 x1
iToi!

280
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа л
2 х1
1-ё-х-Е —
,, »-х .3+1
1-е )
#6: —
3 х1
i-e-x-I-
, , <• -X А +1
#7: ч- )
4 *
1-е-х-Х-
i-oi!
(l-e'x)1+1 (l-e"x)2+1 (1-е"х)3+1
#8: VECTOR ( [x, — -, — r, r,
1 1 2 1 3 V1
., *-x V"1 x , A-x v4 x о *-x V"
1-е • 2L,— 1-е -2-— 1-е • 2,—
i=oi! i>oi! i=oi!
(l-e_>:)4+1
— H/X, 0.1,2,0.2)
4 х
l-e-x-I^
i-oi!
"0.1 1.935504675 5.572372046 21.31873640 101.7797845"
0.3 1.818676231 4.836954987 16.97636131 74.09291250
0.5 1."716310849 4.233913517 13.68368472 54.79414754
0.7 1.626561298 3.736749640 11.16283853 41.15889064
0.9 1.547834087 3.324727415 9.214572854 31.39557328
#9:
1.1 1.478751769 2.981542171 7.694844901 24.31228785
1.3 1.418121073 2.694311361 6.498672094 19.10685924
1.5 1.364905963 2.452806455 5.548917070 15.23318075
1.7 1.318204853 2.248866066 4.788443216 12.31522561
_1.9 1.277231347 2.075945815 4.174588855 10.09115727.
Шапка таблицы #9 на экране отсутствует, создайте ее сами в отчете о лабор
торной работе. Числа в таблице округлите до двух значащих цифр после
пятой, как это сделано в табл. 4.1.
Представьте таблицу в отчете и сделайте соответствующие выводы. Обрати
внимание на главную особенность структурного резервирования: с росТ

MCLi/l*'?*'""" """ -'-"'"--■■— — •г--у--7Г""~ . . .
^атности т эффективность резервирования возрастает, причем она тем
значительней, чем выше надежность (меньше интенсивность отказов)
нерезервированной системы и чем меньше длительность ее работы. Выводы в отчете
подтверждайте цифровыми данными таблицы.
Таблица 4.1. Выигрыш надежности GAx,m)
0,1
0,3
...
1,9
1
1.94
1,82
...
1,28
2
5,57
4,84
...
2.08
3
21,32
16.98
...
4,17
4
101,78
74,09
...
10,09
Представим функции Gq(x,m) в виде графиков, воспользовавшись командой
2D-plot window панели инструментов (рис. 4.1).
Представьте графики в отчете и дайте им объяснения.
Рис. 4.1. Выигрыш надежности G<J(x. m) при различных значениях т

282
ЧАСТЬ //. Лабораторный практикум. Лабораторная работа л
Оценка выигрыша надежности по среднему времени
безотказной работы системы
Технология решения задачи состоит в выполнении следующих процедур:
П ввести выражение 1//;
m+l л
О образовать с помощью кнопки Sum сумму ]Г- (пусть это выражение
имеет на экране номер #2);
□ образовать выражение —г—;
zj
□ протабулировать функцию GT(m) с помощью функции:
VECTOR([m, #2], m, mn, mk, dm),
приняв параметры таблицы равными mn = l;mk = 9; dm = 1.
Процедуры решения задачи на экране будут иметь вид:
#1: ±
i
m + l л
#2: I-
i-l i
m + 1
#3: ——
m + l -l
I1
i-ll
#4: VECTOR ([т,^Ц—], 111,1,10)
m + l -I
I1
" 1 1.333333333"
2 1.636363636
3 1.92
4 2.189781021
#5: 5 2.448979591
6 2.699724517
• • ■ • • •
9 3.414171521
10 3.642532044_

исследование свойств структурно резервированных систем
283
Зависимость GT{m) близка к линейной. Убедимся в этом, решив задачу ин-
^рполяции. Применим полиномиальную интерполяцию, приближенную в
узлах. В Derive 5 она реализуется функцией FIT (строки #6 и #7). В стро-
ке #6 (в тексте отсутствует) находится матрица строки #7 без слова fit
(строка #7). Результатом решения будет линейная функция GT = 0,25m + 1,14
(строка #8).
m a + b-m
1 1.333333333
2 1.636363636
3 1.92
4 2.189781021
#7: FIT 5 2.448979591
6 2.699724517
7 2.943495400
8 3.181371861
9 3.414171521
10 3.642532044_
£8: 0.2548253997-m+l.139435594
На рис. 4.2 показаны графики линейной функции (сплошная линия) и
табличные значения функции (семейство точек). Графики построены с помощью
кнопки 2D-plot window панели инструментов.
В строках #11 и #12 приведены результаты табулирования линейной функции
с помощью функции TABLE. Сравнение таблиц #5 и #12 показывает, что
погрешность интерполяции не велика и линейная функция может быть
математической моделью выигрыша надежности GT{m).
#11: TABLE(0.2548253997-m + l.139435594, m,I,10,1)
"l 1.394260993"
2 1.649086393
3 1.903911793
4 2.158737192
#12: 5 2.413562592
6 2.668387992
7 2.923213391
8 3.178038791
9 3.432864191
10 3.687689591_

284
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа a
Рис. 4.2. Зависимость Gj(m)
4.3.2. Исследование влияния
автомата контроля и коммутации
на эффективность резервирования замещением
При наличии автомата контроля и коммутации структурная схема
резервированной системы с кратностью /и = 1 будет выглядеть так, как показано на
рис. 4.3.
Рис. 4.3. Структурная схема резервированной системы
с автоматом контроля и коммутации
На рис. 4.3 приняты следующие обозначения:
□ 1,2 — основная и резервная системы соответственно;
□ АКК — автомат контроля и коммутации;
□' X, "к{ — интенсивности отказа системы и автомата соответственно.

.^следование свойств структурно резервированных систем 285
Вероятность безотказной работы системы Pc(t) можно представить в
следующем виде:
Pc(t) = P(t) + )QbW (x)P(t - x)dx, (4.4)
о
где:
£ % — момент времени отказа основной системы;
0 P(t) — вероятность безотказной работы основной системы в течение
времени t;
Р P(t - х) — вероятность безотказной работы резервной системы в течение
времени (/ - т), т. е. с момента замещения до /;
О Р\ (т) — вероятность безотказной работы автомата контроля и коммутации
в течение времени т, т! е. до момента отказа основной системы;
□ .&(%)■ — производная от вероятности отказа основной системы в момент т .
При X = const выражения для составляющих в формуле (4.4) имеют вид:
Л P(t) = e-lt, P(t-T) = e-4'-x\ Q(x) = \-e~k\ Р1(х) = е^т. (4.5)
Получим, расчетные формулы с помощью Derive 5. Решение получим в такой
последовательности выполнения команд:
О ввести правые части выражений (4.5); пусть этим выражениям присвоены
номера: #1, #2, #3 и #4;
О получить производную от Q(t) с помощью кнопки Find Derivative панели
инструментов (пусть производной присвоен #5);
а ввести выражение #5 * #2 * #4;
" образовать интеграл от последнего выражения с помощью кнопки Find
Integral, не вычисляя первообразной (пусть интегралу присвоен #6);
а ввести выражение #1 + #6;
получить решение с помощью кнопки Simplify или Approximate.
пРощая полученное решение по переменной / с помощью кнопки Expand,
_ к°Нчательно получим формулу для вероятности безотказной работы в сле-
^Щем виде:
Р(0=^е^_Ае-(^)'.

286 ЧАСТЬ II. Лабораторный практикум. Лабораторная работ* .
Интегрируя Pc(t) от 0 до оо с помощью кнопки Find Integral, получим ф0^
мулу для среднего времени безотказной работы системы. При этом следу^
иметь в виду, что интеграл от Pc(t) существует лишь при условии, что \ и
А-j действительны и положительны. Установим с помощью меню Declare)
Variable Domain эти значения и проинтегрируем Pc(t). В результате интег.
рирования будет получена следующая формула для среднего времени безот.
казной работы системы:
IX + Х]
1 Х(Х + Х{)
Процедуры получения формул на экране монитора имеют вид:
#1: Гл',:
#2: e-Mt'T)
#3: 1-е"*'1
#4: ё"Л1-х
#5: —(1-ё~х"х)
dT
#б: А-ё"хЛ
#7: \.e-x-K.eXVx-e-K-{t-x)
#8: Jx-e^-e^.e'^'^di
о
#9: e-Kt+)x-e-x-K.eK1-x-eK-{t-x)dT
о
#10: ё-x-t/Al^.iLl^l'
< XI XI J
«-. е •(Л + А1) л-е
Л1 Л1
#12: X :е Real (0,оо )
#13: Al :e Real(0,oo)

Рис. 4.4. Зависимость Pc(t) с учетом автомата контроля и коммутации
при различных значениях X)
^ графиков видно, что автомат контроля и коммутации снижает вероятность
безотказной работы резервированной системы.
ФОанализируйте полученные формулы для Pc(t) и 7J и сделайте выводы о
Лес°образности резервирования замещением. Установите, при каком соот-
°Щении X и \{ резервирование замещением менее эффективно, чем резер-
Рование с постоянно включенным резервом, объясните ваши выводы фи-
Некими соображениями. Обратите внимание, что при X = Х1 среднее время
4vR°TKa3H0^ Ра^оты системы равно среднему времени безотказной работы
лированной системы с постоянно включенным резервом. Вычислите вы-
^ ение (4.4) "вручную" и убедитесь, что формулы, полученные с помощью
er,ve, верны.
.^ёдование свойств структурно резервированных систем 287
r e -(A + Al) А-е
^- I м —Jdt
2-А + А1
#l5' A-(A + A1)
Ларис 4.4 приведены графики Pc(t) для случая А, = 0,1 и Х\ =0; 0,1; 0,2.

288 ЧАСТЬ II. Лабораторный практикум. Лабораторная раб0т
4.3.3. Исследование свойств интенсивности отказа
резервированной системы
Интенсивность отказа системы при любой ее структуре имеет вид:
Исследуем свойства интенсивности отказа системы, построив графики фуцк.
ции А,с(/) и определив предельные значения Xc(t) при / = 0 и /-»«>. Полу.
чим функцию Хс((), воспользовавшись формулой (4.1).
Построение графика функции A.c(f) выполняется следующим образом:
□ ввести выражения —;— и е ;
ГО ПА'
□ образовать выражение £ с помощью кнопки Sum панели инстру-
ментов;
П образовать выражение для Рс(() как е "' £ ;
О образовать производную с обратным знаком от последнего выражения,
пользуясь кнопкой Find Derivative;
П получить на экране выражение для Хс((), пользуясь номерами строк, в
которых находятся выражения для Pc(t) и -/£(/);
□ построить графики Лс(/) при т-\, т = 2, т = 3, т = 4 и при одном
значении А,, например при X = 0,1.
Графики изображены на рис. 4.5, а процедуры их получения имеют вид:
#1: ё~Л'<
(A-t)1
#2: -
i!
iTo i!
#4: e-.I^^
i-0 i!

^пеДОвание свойств структурно резервированных систем 289
.t- ■— е ' 2-
*3' dt^ iTo i! J
4 J
r»_л^е_ >
-A.c l-Q(i-l)! m xi.ti
e • A'2,
*7: : ;
.-o.i.t i-o (i"D! n . f.O.l'-t1
e • o.1'2j
t i-o i!
18: ^ 1
-o.i-t y(O.l-t)1
e . ^
i-o l!
e • 0.1-2,
S9: V I
.-o.i-t 4-<°-1't)i
e 'I Г"
i-o i!
..0.1,:. »-0(i-D! Q i 20>1l.tl
t " iTi i!
#10: V >.
_o.it ^ (0.1-t)1
^ак SS3 i=0 ! •

Рис. 4.5. Интенсивность отказов системы Хс(() при различных значениях т
290 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабп>
-!^<
е . 0.1-2.
t i=o i!
#11:
»-o.i-t ^-i {0.1 • t)
i = 0 -L •
"^O.l^t1 '
-o.i-t i-o(i-l)i n , ^0Л^
e . 0.1-2.
t i-o i!
#12: —
-c.i.i. A(O.i-t)1
e -Z—-—
i-0 l!
e • 1-2,
#13: ^ '-
..i.t ^(1-t)1
e "I——
i-o l!

педование свойств структурно резервированных систем 291
-Златите внимание на то, что независимо от кратности резервирования m
флк функции Хс(0 начинается с нуля и асимптотически стремится к
тенсивности отказа нерезервированной системы, в данном случае к
- ;=0,1 час-1. Пользуясь кнопкой Find Limit, определите предельные
значения КО при '->° и '->с0-
приведите графики в отчете о лабораторной работе (в качественном виде) и
-делайте соответствующие выводы.

ЛАБОРАТОРНАЯ РАБОТА 5
ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
И РИСКА ВОССТАНАВЛИВАЕМОЙ
НЕРЕЗЕРВИРОВАННОЙ СИСТЕМЫ
5.1. Постановка задачи
Дано:
О п — число элементов нерезервированной системы;
О Xj, ц, — интенсивности отказа и восстановления элемента /-го типа,
/ = 1,2,...,«;
□ Гя — общее время работы системы;
О rt — риск системы из-за отказа 1-го элемента, / = 1, 2,..., п;
П Лд — допустимый риск.
Определить:
□ Г — наработку системы на отказ;
□ Kr(t), Kr —функцию и коэффициент готовности системы;
□ R — техногенный риск системы.
Необходимо также исследовать свойства нерезервированной
восстанавливаемой системы.
Исходные данные и индивидуальные задания приведены далее в разд. 5.5.
5.2. Сведения из теории
Основными показателями надежности восстанавливаемых технических с
тем являются: наработка на отказ Т, функция готовности Kr(t) и коэфФи
ент готовности £г.

чередование надежности восстанавливаемой нерезервированной системы 293
g общем случае эти показатели зависят от интенсивностей отказов и восста-
0влений элементов системы, времени ее непрерывной работы, вида и
кратности резервирования. В случае нерезервированной системы они вычисляют-
я по следующим формулам:
*г(/) = —^- + -А_ е~(К^с)^ (5.1)
А.с+цс Xc+\ic
Kr = \imKr(t) = --&—, (5.2)
/-*» А.с+цс
Kr=—\—t (5.3)
1 + 1^
Т = -±~, (5.4)
п
где \с = £ А,, — интенсивность отказа системы; \хс — интенсивность вос-
/=1
становления системы, вычисляемая по формуле:
M.-VT-. (5-5)
Следует иметь в виду, что формула (5.1) является приближенной,
погрешность которой зависит от исходных данных.
Граф состояний нерезервированной восстанавливаемой системы имеет вид,
приведенный на рис. 5.1.
Рис. 5.1. Граф состояний нерезервированной восстанавливаемой системы
Ункцию готовности системы можно определить следующими двумя
спорами.
«особ 1. Обозначим через /?,(/) вероятность пребывания системы в момент
РеМени / в состоянии /, / = 0,1, 2,..., п. Тогда функционирование восста-

294
ЧАСТЬ II. Лабораторный практикум. Лабораторная работ* *•
навливаемой нерезервированной системы описывается следующей системой
дифференциальных уравнений, составленной по графу состояний (рис. 5.1):
at ,=l
(5.6)
^Р- = Ъ.,РоО)-ЩМ*), ' = 1, 2,..., п.
. at
Система дифференциальных уравнений решается численными методами при
следующих начальных условиях: р0(0) = 1, /?|(0) = р2(0) -... = рп(0) = 0. То-
гда функция готовности системы равна вероятности ее исправного состояния,
т.е. Kr(t) = pQ(t).
Способ 2. Будем рассматривать нерезервированную систему как один
элемент, имеющий интенсивность отказа Хс и интенсивность восстановления
цс. Тогда функционирование системы можно описать графом,
изображенным на рис. 5.2.
Рис. 5.2. Обобщенный граф состояний системы
Из графа следует, что система может находиться лишь в двух состояниях:
исправном (0) и отказовом (1). Тогда ее функционирование можно описать
следующей системой дифференциальных уравнений:
. л (5.7)
^> = ХвЛ(/)-цеЛ(/)
I at
с начальными условиями: Po(Q) = \, /?j(0) = 0 . Решением этой системы
является функция (5.1).
Восстанавливаемые системы — это системы многократного использовани •
В течение времени "жизни" они могут отказывать и ремонтироваться. ТогД
общий риск системы можно вычислить по формуле:
Л(/) = ]рСг(т)л£х,Г/. (5-Ю
о /=i

***пеДОванив надежности восстанавливаемой нерезервированной системы 295
сЧет функции готовности Kr(t) является сложной задачей. Поэтому целе-
ообразно пользоваться следующими двусторонними оценками для
вычисления риска системы:
*rr£V/£*(/)£/.iVi. (5,9)
/=i /=1
где Кг — коэффициент готовности системы.
Восстанавливаемые нерезервированные технические системы в смысле
надежности имеют следующие важные свойства:
1. Наработка на отказ системы не зависит от восстановления и численно
равна среднему времени ее безотказной работы. Это свойство присуще лишь
таким системам, элементы которых имеют постоянные интенсивности
отказов.
2. Функция готовности является убывающей функцией времени, при / = 0
АГГ(0) = 1 и с ростом / убывает и стремится к постоянной величине,
равной коэффициенту готовности. Это свойство также справедливо для
систем, элементы которых имеют постоянные интенсивности отказов.
3. Коэффициент готовности зависит от отношений —L, / = 1,2,..., и; чем
меньше эти отношения, тем выше функция и коэффициент готовности.
4. Риск высоконадежной системы линейно возрастает со временем,
определяется только надежностью техники и практически не зависит от
интенсивности ее восстановления.
При выполнении этой лабораторной работы студент должен убедиться в
истинности этих положений.
5-3. Последовательность
выполнения работы
вдораторную работу целесообразно выполнять в такой последовательности:
• Определить наработку на отказ системы.
• Исследовать функцию и коэффициент готовности системы.
Выполнить анализ риска системы.
Чет о лабораторной работе должен содержать следующие пункты:
• Постановка задачи.
Уравнения и расчетные формулы.

296
ЧАСТЬ II. Лабораторный практикум. Лабораторная рабп>
■—'5;
3. Таблицы и графики.
4. Выводы по каждому пункту и по результатам работы в целом.
5.4. Пример выполнения
лабораторной работы
Пусть нерезервированная система имеет следующие исходные данные:
О число элементов системы « = 10;
□ время жизни (долговечность) системы Тп -1000 час;
□ допустимый риск системы Л < 2500 усл. ед.;
□ значения риска, интенсивностей отказов и восстановления элементов
системы приведены в табл. 5.1.
Таблица 5.1. Исходные данные задачи
Номера элементов
Х- Ю-4, час"1
г, усл. ед.
ц-10"', час'1
1
1
20
0,2
2
0,23
50
0,3
3
0,36
40
0,5
4
0,054
104
2
5
0,72
600
1
6
0,83
250
1,2
7
0,08
103
7
8
0,25
10
0,5
9
0,6
80
1
10
1,2
100
1
5.4.1. Определение наработки на отказ системы
Определим интенсивность отказа системы. Суммирование интенсивностей
отказов элементов с помощью пакета Derive 5 наиболее просто и удобно
выполнить с помощью функции element и кнопки Sum панели инструментов,
предварительно образовав вектор элементов /, / = I, 2,..., п. Подробно этот
способ был описан в лабораторной работе 2. В результате вычислений по-
лучим: Хс = £А,, =5,324-10 час"1. Тогда на основании формулы (5.4) нара*
/=1
ботка на отказ будет равна Т = — = 187,8 час.
5.4.2. Исследование функции
и коэффициента готовности системы
Определить коэффициент готовности с помощью системы Derive 5 наиоо
просто следующими способами:

derпеДОвание надежности восстанавливаемой нерезервированной системы 297
XX X
л пбраз°вать вектор значений —, —-,..., —- с помощью кнопки Author
Vector, при этом операцию деления нужно только обозначить, но
вычисления не делать;
« х.
rt вычислить значение суммы элементов вектора У]— с помощью кнопки
Find Sum панели инструментов;
р вычислить Кг = 1/(1 + #к), где #к— номер выражения суммы.
для исходных данных нашей задачи получаем:
Е^ = Ю2,367.10-3, Цс=-А-= 5-324-10"33 =0,052,
ы\Щ yh. 102,367-Ю-3
^=-4т-=о'907»
1 + Е^
или
_^= 0,052
г Я, + ц 0,0053 + 0,052
Значения коэффициента готовности, вычисленные по формулам (5.2) и (5.3),
полностью совпадают.
%нкцию готовности определим двумя способами.
Способ 1. Решим систему дифференциальных уравнений (5.6) методом Рун-
rfc Кутты с помощью Derive в такой последовательности:
а Установить режим ввода переменных с индексами, выбрав пункт главного
меню Declare | Input и щелкнув мышью на вкладке Word;
ввести уравнения системы (5.6) в аналитическом виде;
подставить в уравнения численные значения X• и \if с помощью команды
Variable Substitution (кнопка Sub); на экране отобразятся 11 уравнений,
не объединенных в систему;
Вызвать утилиту решения дифференциальных уравнений методом Рун-
Ге -— Кутты: пункт меню File | Load | Utility File;
ввести имя утилиты: ODE_appr.mth;

298 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабрТя _.
□ набрать и ввести выражение функции решения дифференциальных урав^
нений методом Рунге — Купы:
RK([#1,#2,#3,#4,#5,#6,#7,#8,#9,#10,#11], [t,РО,Р1,Р2,РЗ,Р4,р5
Р6,Р7,Р8,Р9,Р10], [0,1,0,0,0,0,0,0,0,0,0,0], 1, 500).
В первых квадратных скобках записаны номера, которые присвоены ураВч
нениям на экране монитора. Во вторых квадратных скобках перечислены
аргумент / и все искомые вероятности. В третьих квадратных скобках
указаны начальные условия, за начальными условиями указывается шаг
интегрирования (в нашем случае h -1) и конечное значение аргумента /
(в нашем случае 500).
В нашем примере состояние (0) соответствует исправному состоянию
системы (см. рис. 5.1). Тогда KT(t) = pQ(t), а Кг = lim p0(0 •
Описанные ранее процедуры на экране монитора имеют вид:
#1: -Аф0 + р1ф1 + р2-р2 + рЗ-рЗ + р4-р4 + р5-р5 + 1аб-р6 + р7-р7 + р8-р8+
р9-р9 + р10-р10
#2: А1-р0-р1-р1
#3: А2-р0-р2-р2
#4: АЗ-рО-рЗ-рЗ
#5: А4-р0-р4-р4
#6: А5-р0-р5-р5
#7: Аб-рО-рб-рб
#8: А7-р0-р7-р7
#9: А8-р0-р8-р8
#10: А9-р0-р9-р9
#11: АЮ-рО-рЮ-рЮ
#12: -(5.324-10"3)-рО + 0.02-р1 + 0.03-р2 + 0.05-рЗ + 0.2-р4 + 0.1-р5 +
0.12-рб + 0.7-р7 + 0.05-р8 + 0.1-р9 + 0.1-р10
#13: 10"3-р0-0.02-р1
#14: (0.23-10~3)-р0-0.03-р2
#15: (0.3б-10"3)-р0-0.05-рЗ
#16: (0.054-10"3)-р0-0.2-р4

..^следование надежности восстанавливаемой нерезервированной системы 299
^7: (0.72-10"3)-р0-0.1-р5
#18: (0.83-10"3)-р0-0.12-рб
#19: (0.08-10~3)-р0-0.7-р7
#20: (0.25-10"3)-р0-0.05-р8
#21: (0.6-10"3)-р0-0.1-р9
#22: .(1.2-10"3)-р0-0.1-р10
#23: LOAD(С:\DfW5Trial\DfW\MATH\0DE_APPR.MTH)
#25: RK([-(5.324-10~3)-р0+ 0.02-pi+ 0.03-р2 + 0. 05-рЗ + 0.2-р4+
Q.l-p5 + 0.12-p&+0.7-p7 + 0.05-p8 + 0.1-p9 + 0.1-pl0,
10~3-р0-0.02-р1,(0.23-10~3)-р0-0.03-р2,
(0.36-10~3)-p0-0.05-p3,(0.054-10~3)-p0-0.2-p4,
(0.72-10"3)-pO-0.1-p5,(0.83-10"3)-pO-0.12-p6/
(0.08-10~3)-р0-0.7-р7,(0.25-10~3)-р0-0.05-р8,
(0.6-10~3)-p0-0.1-p9,(1.2-10~3)-p0-0.1-pl0],[t,p0,pl,p2,p3,
р4,р5,р6, р7,р8,р9, р10],[0,1,0,0,0,0,0,0,0,0,0,0],
1,500)
В табл. 5.2 приведены результаты решения задачи при шаге интегрирования
Л = 0,5 и конечном значении аргумента, равном пяти (третий столбец
таблицы).
Способ 2. Будем рассматривать нерезервированную систему как один эле-
Мент, имеющий интенсивность отказа А,с и интенсивность восстановления
К- Тогда справедлива система дифференциальных уравнений (5.7), решени-
ей которой является функция (5.1). Для сравнения результатов расчетов дву-
Мя способами представим Kr(t) в виде таблицы. Решение легко получить,
Аудируя (5.1) с помощью функции
VEGTOR([t, Kr(t)], t, tn, tk, dt).
щ нашем случае tn = 0, tk = 5, dt = 0,5. Результаты табулирования приведе-
bI в табл. 5.2 (второй столбец таблицы). Из анализа данных таблицы следуют
4*а важных вывода:
^ оба способа вычисления функции готовности в данном примере дали
Практически одинаковые результаты;

300
ЧАСТЬ II. Лабораторный практикум. Лабораторная работ*
^——«^у
О приближенная формула (5.1) дает несколько заниженные значения ЛГг(л
является ее нижней оценкой.
Таблица 5.2. Функция готовности
системы
Таблица 5.3. Оценка длительности
переходного процесса системы
/, час
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
прибл.
1
0,99737
0,994825
0,992347
0,989939
0,987599
0,985325
0,98311
0,980969
0,978882
0,976855
Рунге — Кутты
1
0,99739
0,994915
0,992538
0,990263
0,988083
0,985991
0,98398
0,982057
0,980205
0,978425
/, час
0
10
20
30
40
50
60
70
80
90
100
прибл.
1
0,95947
0,93664
0,923766
0,916510
0,912420
0,910115
0,90881
0,908084
0,907671
0,907438
Рунге — Кутты
1
0,96387
0,946047
0,935725
0,928954
0,924133
0,920533
0,91776
0,915615
0,913918
0,912574
Определим теперь длительность переходного режима системы. Для этого
увеличим диапазон табулирования функции (5.1), выбрав tn = 0, tk-100»
dt = 10. Данные табулирования приведены в табл. 5.3.
В третьем столбце таблицы приведены данные решения дифференциальны*
уравнений методом Рунге — Кутты. Из табл. 5.3 видно, что переходный про'
цесс в системе длится короткое время. Так, например, в течение 100 часо
работы системы функция готовности совпадает с коэффициентом готовност
с точностью три знака после запятой. При t = Т = 188 час функция и коэфф
циент готовности совпадают с точностью пять знаков после запятой. Из эт
исследований вытекает важный для практики вывод: в течение времени »
равного наработке на отказ, переходный режим функционирования восс
навливаемой системы заканчивается и функция готовности практически с
падает с коэффициентом готовности.

,1гГпвДОвание надежности восстанавливаемой нерезервированной системы 301
б 4.3. Анализ риска системы
вычисляя составляющие в неравенстве (5.9), получим:
10
isTr =0,907, 2^ =1475,9-10"3.
Так как
Л:г/Х^=0,907-1000-1475,910~3=1339,
/=1
^^т;. = 1000-1475,9-10"3<1476,
то
1339<ЗД000)<1476.
Риск системы можно считать приближенно равным среднему арифметиче-
п,. 1339 + 1476 ,-._
скому из полученных оценок: /^(z) = = 1407 усл. ед.
laac как техногенный риск меньше допустимого, равного 2500, то такая
система пригодна для эксплуатации.
По работе можно сделать следующие выводы:
1- Наработка на отказ восстанавливаемой нерезервированной системы не
зависит от восстановления и равна среднему времени безотказной работы
аналогичной ^восстанавливаемой системы.
*• Риск восстанавливаемой нерезервированной системы может быть легко
получен на основе простых двусторонних оценок. Анализируемая система
Удовлетворяет требованиям риска.
• Длительность переходных процессов в системе мала, при времени ее
Функционирования, равном наработке на отказ, функция и коэффициент
готовности совпадают.
4 р
' ^ достаточной для практики точностью функцию готовности можно
вычислять по простой приближенной формуле, полученной при замене
системы, состоящей из п элементов, одним элементом, имеющим
эквивалентные исходной системе интенсивности отказов Хс и восстановле-

302
ЧАСТЬ II. Лабораторный практикум. Лабораторная ра6рГя
5.5. Варианты заданий
к лабораторной работе
В вариантах приняты обозначения:
ОТ — время жизни (долговечность) системы, в часах;
□ R — допустимый риск, в усл. ед.;
□ Xj — интенсивность отказа элемента /-го типа, в час-1;
□ rt — риск системы из-за отказа /-го элемента, в усл. ед.;
О цу — интенсивность восстановления /-го элемента системы, в час-1.
ВАРИАНТ!
Номера элементов
MO-4, час4
ц-КГ\ час-1
г, усл. ед.
1
0,2
0,2
65
2
0,25
0,16
38
3
0,05
0,07
3000
4
0,06
0,08
12000
5
0,1
0,8
800
6
0,7
1
340
7
0,34
0,85
640
8
0,08
0,6
830
Г= 1200 час, R = 2600 усл. ед.
ВАРИАНТ2
Номера элементов
Х-КГ4, час"1
ц-КГ'.час'1
г, усл. ед.
1
0,2
1
1000
2
0,3
2,5
780
3
0,7
1,6
10000
4
0,4
1,6
700
5
0,1
0,8
900
6
0,25
7
380
7
0,8
3,2
1000
•*
8
0,9
0,4
600
Т = 2000 час, R = 3000 усл. ед.
ВАРИАНТ 3
Номера элементов
Х- Ю-4, час-1
ц- КГ'.час-1
г, усл. ед.
1
0,1
2
600
2
0.3
3,1
700
3
0,25
1,6
580
4
0,6
1,2
1200
5
0,7
2,1
2100
6
0,35
1,5
820
7
0,8
1
340
8
0^
1
160
Т= 2500 час, R = 1850 усл. ед.

^следование надежности восстанавливаемой нерезервированной системы
0ДРИАНТ4
303
Номера элементов
х.10Лчас"'
и. 10"', час"1
г;усл. ед.
1
0,7
1
650
2
0,3
1,2
720
3
0,1
0,9
1900
4
0,65
1,8
680
5
0,2
2,6
1080
6
0,1
1,8
608
7
0,12
1
732
8
0,4
1,6
2000
Т~ 2200 час, R = 720 усл. ед.
ВАРИАНТ 5
Номера элементов
ЫО^час-'
ц..Ю"*1, час-1
г, усл. ед.
1
0,15
0,8
850
2
1
1,2
830
3
0,3
2,1
780
4
0,25
3,1
1200
5
0,2
2,5
1180
6
0,7
1
340
7
0,34
0,85
640
8
0,8
1,6
830
Т= 1200 час, R = 2600 усл. ед.
Далее приводятся варианты заданий с 6 по 25. В таблицах указаны номера
вариантов, из которых следует взять значения А,,, ц,, rn T, R.
ВАРИАНТЫ 6—15
Номер варианта
Номер варианта для X,
Номер варианта для ц,
J°Mep варианта для r„ T, R
^РИАНТЫ 16—25
JJP^epBapHaHTa
^^°^€р^вариантадля X/
Л^^Р^иачта для ц,
.^^варианта для r„ T, R
6
1
5
4
16
1
3
4
7
2
4
3
17
2
1
5
8
3
1
4
18
3
5
1
9
4
2
5
19
4
1
2
10
5
1
1
20
5
3
2
11
1
2
3
21
1
2
4
12
2
3
4
22
2
5
3
13
3
4
5
23
3
2
5
14
4
5
2
24
4
3
1
15
5
2
1
25
5
4
2

ЛАБОРАТОРНАЯ РАБОТА 6
ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
И РИСКА РЕЗЕРВИРОВАННОЙ
ВОССТАНАВЛИВАЕМОЙ СИСТЕМЫ
Целью настоящей лабораторной работы является изучение влияния
восстановления (ремонта) на надежность и риск технической системы.
6.1. Постановка задачи
Дана техническая система, имеющая следующие показатели:
О Тс — срок службы (долговечность), лет;
□ / — время непрерывной работы, час;
П X — интенсивность отказов, час-1;
□ ц — интенсивность восстановления, час-1;
П /и — допустимая кратность резервирования;
□ г — риск из-за отказов системы, усл. ед.;
□ R(t) — допустимый риск в течение времени /, усл. ед.
Определить:
П показатели надежности и риска исходной нерезервированной системы;
О показатели надежности и риска резервированной системы с заданно
кратностью резервирования m;
□ эффективность резервирования и восстановления как средств повышен
надежности и снижения риска техники.
Варианты заданий приведены в разд. 6.5.

„„едование надежности и риска резервированной восстанавливаемой системы 305
б 2. Сведения из теории
ровными показателями надежности восстанавливаемых систем являются:
работка на отказ Г, функция готовности ЯД/), коэффициент готовности
• Эти показатели зависят от следующих основных факторов: вид и
кратность резервирования, дисциплина обслуживания.
ггдя повышения надежности техники наиболее часто применяются два вида
оезервирования: с постоянно включенным резервом и по методу замещения.
При этом обслуживание системы может осуществляться с двумя видами
приоритета— прямым и обратным. При прямом приоритете техника
обслуживается в порядке ее поступления в ремонт. При обратном приоритете первой
обслуживается система, поступившая в ремонт последней. Структурное
резервирование с возможностью восстановления отказавших элементов в
процессе функционирования системы является наиболее эффективным способом
обеспечения и повышения надежности техники и снижения техногенного
риска. Однако применение резервирования удорожает технику и ее
эксплуатацию. Поэтому кратность резервирования ограничена, и в большинстве
случаев применяется резервирование с кратностью т = \ (дублирование). Из
деух указанных видов резервирования наибольший выигрыш надежности
Цетигается при резервировании замещением. Однако это резервирование
имеет два существенных недостатка:
О для его физической реализуемости требуется автомат контроля состояния
системы и коммутации при отказе работающей системы;
О снижается производительность системы, т. к. резервные системы до
замещения не работают.
По этим причинам на практике наиболее часто применяется резервирование с
постоянно включенным резервом.
Наработка на отказ и коэффициент готовности резервированных
восстанавливаемых систем при одной обслуживающей бригады вычисляются по сле-
%ЮЩим формулам:
Q) Для системы с постоянно включенным резервом:
ОТ J J
Т = Tq 2^ , Кг = —;
/=о(/ + 1)!р 74-
Для резервированной системы замещением:
т j j
Т = ТоИ~^ Кг= Г-
/=ор 74-

306
ЧАСТЬ II. Лабораторный практикум. Лабораторная работ *
В формулах приняты обозначения: р= —, Т0 =—. Показатели надежности т
и Кг зависят от числа обслуживающих бригад. Формулы для любых видов
обслуживания легко получить топологическими методами расчета надежно,
сти. Приведем формулы для двух обслуживающих бригад:
а) для системы с постоянно включенным резервом:
fm-\ 2' 2m~] 1 Т
Т = То У, гн , Кг = —;
[/to(/ + l)!pf (/>* + l)!pwJ T + ±
б) для резервированной системы замещением:
fm-\ о' о'"-1 ^ Т
v<-=op р. ; т+—
2\х
Исследования свойств структурного резервирования показывают, что для
случая высоконадежных систем, когда р < 0,001, дисциплина обслуживания
не оказывает существенного влияния на надежность резервированных
восстанавливаемых систем.
Риск системы определяется по формуле:
R{t) = rM{t) = rX\pm{x)dx, (6.1)
о
где M{t) — среднее число отказов системы в течение времени /, pm(i) —
вероятность пребывания системы в предотказовом состоянии в момент т.
Для расчетов можно использовать простую приближенную формулу
R{t) = r\pmt, (6-2)
где рт — стационарная вероятность пребывания системы в предотказовом
состоянии.
6.3. Последовательность
выполнения работы
Лабораторную работу целесообразно выполнять в такой последовательност
1. Определить наработку на отказ Т и коэффициент готовности Кг систе
при двух видах резервирования, одной и двух бригадах обслуживания.

,лг/У1вДОвание надежности и риска резервированной восстанавливаемой системы 307
» Найти вероятность безотказной работы резервированных систем.
* Вычислить среднее время безотказной работы резервированных систем.
а Определить техногенный риск исходной системы и резервированных
систем при различных характеристиках обслуживания.
результаты расчетов необходимо сопровождать выводами.
Отчет о лабораторной работе должен содержать следующие пункты:
1. Постановка задачи.
2. результаты расчетов в виде формул и таблиц.
3. Выводы по результатам работы.
6.4. Пример выполнения
лабораторной работы
6.4.1. Постановка задачи
Дано:
О срок службы системы Тс = 5 лет;
О время непрерывной работы / = 1000 час;
О интенсивность отказа системы А, = 10 час"1;
п **
и интенсивность восстановления системы, определяемая значением р = —,
которое может быть равно 1; 0,1; 0,05; 0,01;
G кратность резервирования m -1;
^ риск из-за отказа системы г = 150000 усл. ед.;
а Допустимый риск в течение времени непрерывной работы
^(1000) = 360 усл.ед.
пРеделить показатели, указанные в разд. 6.3.
6'4.2. Определение наработки на отказ Г
и Коэффициента готовности Кт системы
На
а Рис. 6.1 и 6.2 приведены структурные схемы и графы состояний систе-
! при общем постоянном резервировании (а) и резервировании замеще-

308
ЧАСТЬ II. Лабораторный практикум. Лабораторная работа о
Рис. 6.1. Структурные схемы резервированных систем
Рис. 6.2. Графы состояний резервированных систем
Расчетные формулы для случая дублированной системы {тп = 1) имеют вид:
а) дублированная система с постоянно включенным резервом:
• одна обслуживающая бригада (и = 1):
Т = 7q 1 + —— , Кг = г-;
V 2р; l + 2p + 2pz
• две обслуживающие бригады (и = 2):
Т = Tq 1 + —— , Кг = г-;
I, 2p; l + 2p + pz
б) дублированная система замещением:
• одна обслуживающая бригада (и = 1):
f 1 ^ „ 1 + р
V р; i + p+pz

^следование надежности и риска резервированной восстанавливаемой системы 309
• две обслуживающие бригады (« = 2):
rer0(i+ll, Kr=-^;
v р' 1+р+-р2
2
л нерезервированная система:
r = 7i=7o=7' ^г=7— •
А, 1 + р
Из приведенных формул видно, что наработка на отказ и коэффициент готов-
X
ности дублированной системы являются функциями р= —. Это позволяет
автоматизировать расчеты, используя математическую систему Derive 5.
Методика состоит в следующем:
D создается матрица формул размерностью 8x1 по числу формул для Т и
Кг дублированной системы (кнопка Author Matrix);
О в формулы подставляются значения р (кнопка Variable Substitution);
О выполняются расчеты (кнопка Approximate).
Решение выдается в виде таблицы. Для удобства чтения целесообразно
принять следующие обозначения:
О ТР1, ТР2— наработка на отказ системы с постоянно включенным
резервом с одной и двумя обслуживающими бригадами соответственно;
О TZ1, TZ2— наработка на отказ системы, резервированной по принципу
замещения с одной и двумя обслуживающими бригадами соответственно;
Q KP1, КР2— коэффициент готовности системы с постоянно включенным
резервом с одной и двумя обслуживающими бригадами соответственно;
^ KZ1, KZ2— коэффициент готовности системы, резервированной по
принципу замещения с одной и двумя обслуживающими бригадами
соответственно.
6зУльтаты расчетов для нашего примера сведены в табл. 6.1.
^3 приведенных формул видно, что наработка на отказ нерезервированной
пистемы не зависит от восстановления и равна среднему времени безотказной
Работы системы.
^ нашего примера Т0 = — = 10000 час. Для сравнения в табл. 6.1 приведены
ачения коэффициента готовности Кг нерезервированной системы при всех
данных значениях р.

310 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа
Таблица 6.1. Результаты решения задачи
р
ТР1/Г0
ТРЭД
КР1
КР2
TZl/Го
Т2ЭД
KZ1
KZ2
Кг
1
1,5
1,5
0,6
0,75
2
2
0,667
0,8
0,5
0,1
6
6
0,984
0,992
11
11
0,991
0,995
0,91
0,05
11
11
0,995
0,9977
21
21
0,9976
0,9988
0,95
0,01
51
51
0,9998
0,9999
101
101
0,9999
0,99995
0,99
Анализ данных таблицы позволяет сделать следующие важные выводы:
О наработка на отказ резервированной системы с кратностью m -1 не
зависит от числа ремонтных бригад;
□ при малых значениях р наработка на отказ дублированной системы
замещением практически вдвое больше, чем при дублировании с постоянно
включенным резервом;
□ резервирование с восстановлением является мощным средством
повышения наработки на отказ системы: так, например, в случае резервирования
замещением при р = 0,01 наработка на отказ TZ1 =TZ2 = 7о * 101 =
= 1 010000 час, что составляет примерно 115 лет и в 23 раза превышает
срок службы системы (5 лет);
□ число ремонтных бригад оказывает незначительное влияние на коэффиии"
ент готовности дублированной системы, если р мало: так, например,
коэффициент готовности дублированной системы с постоянно включенным
резервом и р = 0,05 при одной и двух бригадах обслуживания составляет
0,995 и 0,9977 соответственно;
□ при малых р вид резервирования практически не влияет на величину к°"
эффициента готовности: например, коэффициент готовности системы пр
одной бригаде обслуживания составляет 0,9998 и 0,9999 соответствен^
для случая резервирования с постоянно включенным резервом и замеШ
нием.
Следует иметь в виду, что приведенные расчеты наработки на отказ ли
иллюстрируют эффективность резервирования с восстановлением, но не

исследование надежности и риска резервированной восстанавливаемой системы 311
ляются достоверными, т. к. в течение 115 лет работы системы интенсивность
ejp отказов не может быть величиной постоянной, как это принято при
расчетах-
5.4.3. Определение вероятности
безотказной работы резервированной системы
для определения вероятности безотказной работы необходимо составить и
решить систему дифференциальных уравнений функционирования системы.
Система дифференциальных уравнений с учетом экранов (см. рис. 6.2) имеет
вид:
О для схемы (а):
^l = -2Xp0(t) + m(t);
< dt (6.3)
^ = 2^0(/)-(А. + ц)/71(О;
I at
P для схемы (б):
'^ = -Ал(0+ми(0;
< dt (6.4)
^ = Яя>(/)-(А. + ц)Л(/).
I at
За начальные условия примем р0(0) = 1, р1(0) = 0.
Методика решения уравнений методом Рунге — Купы была описана в
лабораторной работе 5. Решение для / = 1000 час было получено с помощью
Derive. Удовлетворительная точность решения получается при шаге Л = 10.
*°гда функция будет иметь вид:
RK([#1,#2]/ [t,p0,pl], [0,1,0Ы0,100),
— правые части дифференциальных уравнений. Так как состояния
* ' и (1) соответствуют исправным состояниям системы, то вероятность без-
^Казной работы будет равна Pc(t) = Po(t) + P\(t). Результаты решения задачи
с**Лены в табл. 6.2.
^Роятность безотказной работы нерезервированной системы не зависит от
Сстановления и равна:
Pc0000) = e-Ki=e-w~4 l°3 =0,9048.

312
ЧАСТЬ II. Лабораторный практикум. Лабораторная работ
36
Таблица 6.2. Результаты решения задачи
Постоянное резервирование
Р
Рс(1000)
Я( 1000), усл. ед.
1
0,9912
10000
0,1
0,9932
2500
0,05
0,9947
1364
0,01
0,9982
294
Резервирование замещением
Р
/>с(1000)
/?(1000), усл. ед.
1
0,9955
7500
0,1
0,9965
1364
0,05
0,9973
714
0,01
0,999
149
По данным табл. 6.2 можно сделать следующие важные выводы:
резервирование с восстановлением позволяет существенно повысить надежность
системы. Так, например, выигрыш надежности по вероятности отказа системы,
резервированной по методу замещения, при р = 0,01 по сравнению с
нерезервированной системой будет:
G(1000) = b» = 95,2,
* 1-0,999
т. е. почти в 100 раз.
6.4.4. Определение среднего времени
безотказной работы системы
Среднее время безотказной работы можно определить одним из следующих
способов.
Способ 1. Найти аналитическое выражение для вероятности безотказной ра"
да
боты системы Pc(t) и воспользоваться формулой 7] = \PG{t)dt. Можно так*6
о
найти вероятность безотказной работы системы в преобразовании Лаплас
00
P(s) = $P(t)e~tsdt и воспользоваться соотношением 7] = Рф).
о
Способ 2. Составить систему линейных алгебраических уравнений 0TH°/1i
тельно среднего времени т0 и zx пребывания системы в состояниях (0) и
соответственно (см. рис. 6.2):

^следование надежности и риска резервированной восстанавливаемой системы 313
0 для схемы (а):
\-2XTfi + цх, = -1;
(6.5)
2Я.т0-(Х + ц)х,=0;
0 для схемы (б):
Г-А.т0 + цт,=-1;
< (6.6)
Яд0-(Х + ц)т, =0.
Далее нужно решить полученные системы уравнений и определить среднее
время безотказной работы по формуле 7] = х0 + т}.
формулы для среднего времени безотказной работы имеют следующий вид:
О для схемы (а):
( 1 )
7]=Г0 1,5 + — ;
О для схемы (б):
( Л
v р;
где Г0 = среднее время безотказной работы нерезервированной сис-
к
темы.
Сравнивая полученные значения среднего времени безотказной работы и
наработки на отказ, полученной в разд. 6.4.2, видим, что они практически оди-
X
наковы при малых значениях р = —, что характерно для высоконадежных
V-
систем.
6*4.5. Определение риска системы
Иск системы определим по приближенной формуле (6.2). Для исходной
нерезервированной системы при р = 0,01 получим:
p/innm rXt 15'104-НГ*-1000 НК1
Л(1000) = = = 14851 усл. ед.,
1 + р 1,01
0 выше допустимого.
Иск резервированной системы с кратностью т = \ определяется по
формам:

314 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа
О для постоянно включенного резерва:
1 + 2P+2P_
п
О для резерва замещением:
Результаты расчетов техногенного риска системы R{t) при / = 1000 час при
различных видах резервирования и дисциплинах обслуживания сведены в
табл. 6.2. Из таблицы видно, что риск может быть меньше допустимого,
равного 360 усл. ед., при условии, что использован любой вид резервирования с
кратностью т-\ при р<0,01 и применяется обслуживание с любым
приоритетом. Для нашего случая обеспечить заданный риск можно при условии,
что среднее время восстановления не будет превышать 100 часов.
Определим теперь величину риска в течение всего срока службы системы,
равного 5 годам. По сравнению с R(\ 000) техногенный риск системы
увеличится в = 43,8 раз и превысит требуемый риск, равный 360 усл. ед.
В заключение можно отметить, что исходная нерезервированная система
недостаточно надежна и не может обеспечить требуемый риск. Вероятность ее
безотказной работы в течение 1000 часов равна 0,9, а риск равен
14851 усл. ед., что значительно выше требуемого (360 усл. ед.). В течение
этого времени риск будет допустимым, если применить структурное
резервирование любого вида кратности т = 1 и обеспечить обслуживание со средним
временем восстановления не выше 100 часов.
6.5. Варианты заданий
к лабораторной работе 6
В заданиях приняты обозначения:
П Т — время жизни (долговечность) системы, лет;
П X — интенсивность отказа системы, час-1;
О t — время непрерывной работы системы, час;
□ m — кратность резервирования;

следование надежности и риска^ резервированной восстанавливаемой системы 315
* г — риск из-за отказа системы, усл. ед.;
rj Щ) — допустимый риск в течение времени /, усл. ед.
ЗДРИАНТЫ 1—8
Номер варианта
/,час
Тг нас
•ЗНеЛчас"1
г- Ю3, усл. ед.
R(t), усл. ед.
ВАРИАНТЫ 9-
Номер варианта
А час
Г, час
%.• Ю-4, част1
г- 103, усл. ед.
ЖО» усл. ед.
1
600
4
1,2
100
400
-16
9
380
3
0,8
90
525
2
700
3,5
2,1
90
520
10
900
2,6
1,2
ПО
480
3
650
5
U
120
360
11
820
3,5
1,6
210
360
4
1000
2,5
0,8
68
420
12
630
4
0,7
180
720
5
960
3
1,6
93
516
13
1000
2
2,1
68
800
6
810
2,7
1,3
120
180
14
750
2,5
1,8
87
495
7
380
4,2
1,5
85
275
15
600
3,5
1
100
470
8
750
5
1
120
500
16
500
4
1,2
80
390
варианты п—25
ВАРИАНТЫ 9—16
^°мер варианта
'«час
г,час
i^Viac"1
^^У» усл. ед.
.Лусл. ед.
17
350
2,8
0,8
120
500
18
460
3,5
2,1
90
490
19
750
5
1,8
85
450
20
820
4,3
2
150
380
21
680
3,8
0,75
165
525
22
1000
2,5
1,5
92
475
23
800
3
1,8
87
600
24
700
4
0,9
115
380
25
720
3 2
1
126
725

ЛАБОРАТОРНАЯ РАБОТА 7
ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
ИНФОРМАЦИОННОЙ
ВОССТАНАВЛИВАЕМОЙ СИСТЕМЫ
7.1. Постановка задачи
Дано:
D информационная система с п обслуживающими органами;
□ Р — вероятность того, что заявка в произвольный момент времени /
будет принята на обслуживание;
□ X — интенсивность потока заявок на обслуживание;
О \х — интенсивность обслуживания заявки.
Определить:
□ число обслуживающих органов п, обеспечивающих заданное значение Р',
D длительность переходных процессов в информационной системе;
О функцию готовности системы Kr(t) для найденных значений п.
Решение задачи выполнить в предположении, что время между заявками и
время обслуживания подчиняются экспоненциальному закону.
Численные значения Р, X, \х приведены в индивидуальных заданиях в
разд. 7.4.
7.2. Сведения из теории
ли'
Показателями надежности информационной восстанавливаемой системы
ляются:
□ Kr(t) — вероятность того, что заявка будет принята на обслуживани
произвольный момент времени / (функция готовности);

исследование надежности информационной восстанавливаемой системы 317
q Кт — коэффициент готовности;
0 Т — среднее время между отказами в обслуживании (наработка на отказ).
функционирование информационной восстанавливаемой системы можно
описать структурной схемой функционирования резервированной системы
с замещением кратности m при числе обслуживающих органов п = т.
Структурная схема и граф состояний системы изображены на рис. 7.1 и 7.2
соответственно.
В состоянии я все каналы обслуживания заняты и очередной заявке будет
отказано в обслуживании. Тогда pn(t) — вероятность отказа системы, а
\-рп(0 — функция готовности. Коэффициент готовности определяется
следующей формулой:
п
Кг=\-Рп=\ Г'
.V Р
ту —
/to /1
А,
гдер = —.
#fe этой формулы следует, что определение числа обслуживающих бригад
сводится к решению трансцендентного уравнения при разных значениях Кг
«р.
Представим уравнение для коэффициента простоя в следующем виде:
п п
/.о''!
Рис. 7.1. Структурная схема
системы
Рис. 7.2. Граф состояний системы

318
ЧАСТЬ //. Лабораторный практикум. Лабораторная работа у
В соответствии с заданием решение уравнения необходимо представить ь
виде таблицы n = f(pnip). Решение задачи легко получить, если воспо.1ь3о
ваться системой Derive 5.
7.3. Пример выполнения
лабораторной работы
Пусть интенсивность потока заявок Х. = 5,1 час-1, интенсивность
обслуживания заявки р. = 1,5 час"'. Определить, сколько необходимо иметь обслужи,
вающих органов, чтобы готовность системы была Кг = 0,8; 0,9; 0,95; 0,997.
Процедура решения задачи имеет вид:
п!
»
р"
#2: —
i!
#3: I*-
Pi
п о1
i-0 1 !
3.4n
#5: 0.2 = —^~—
#6: NSOLVE 0.2 = ^ , n, Real
villi
k i-0 i! J
#7: n-4.634988307
В строках #1 и #2 задаются составляющие трансцендентного уравнения (/• ■

^следование надежности информационной восстанавливаемой системы
319
а строке #3 образовала сумма выражения #2 с помощью кнопки Find Sum
ацели инструментов. В строке #4 записано конечное уравнение, полученное
0f введения выражения /? = #]/#3. В строке #5 приведено трансцендентное
.-равнение, полученное в результате подстановки в уравнение (7.1)
численны* значений исходных данных Х-5,\ час"1, ц = 1,5 час"', р = 0,2 с по-
мошью кнопки Variable Substitution.
3 строке #6 и #7 происходит вызов функции NSOLVE решения алгебраических
уравнений численным методом и результат решения для случая /;„ = 0,2.
результаты решения при заданных значениях вероятности Кг приведены в
табл. 7.1.
Таблица 7.1. Результаты определения числа обслужипающих органов
А',.
"
0.8
4.6
0,9
5,7
0.95
6.6
0.997
9,5
Из физических соображений ясно, что результаты определения числа
обслуживающих органов п должны быть округлены до ближайшего целого в
сторону увеличения.
Полученные решения будут иметь смысл лишь в том случае, если
длительность переходных процессов мала. В противном случае результаты могут
быть существенно завышены.
Исследуем длительность переходных процессов на основании анализа
функции готовности Кг(1).
Процедура решения задачи с помощью системы Derive 5 имеет вид:
1; InputKode := Word
*2: -A-p0+p-pl
*3: Л-рО-(Л + р)-р1 + 2-р-р2
н- Л-р1-2-ц-р2
°: LOAD(C:\DfW5Trial\DfW\MATH\ODE APPR.MTH)
#6- ^ ~
' RK{ [-Л-pO + u-pl, Л-рО-(А + }д)-р1 + 2-р-р2, А-р1-2-р-р21,
[t,pO,pl, р2] , ГО, 1,0,0 3,0.1,50)
«7.
1 RK( [-5.1-p0 + 1.5-pl, 5.1-р0-(5.1 + 1. 5)-pl+ 2-1.5-р2, 5.1-р1-
2-1.5-р2] , [t, pO, pi, р2],[0, 1, 0, 03,0.1, 50)

320 ЧАСТЬ II. Лабораторный практикум. Лабораторная раб0>а
"1.7 0.09858396772 0.3341327357 0.5672832965"
1.8 0.09845676311 0.3340805370 0.5674626998
1.9 0.09837550949 0.3340471894 0.5675773010
2 0.09832360732 0.3340258862 0.5676505064
#8: 2.1 0.9829045376 0.3340122777 0.5676972684
2.2 0.09826927622 0.3340035847 0.5677271390
2.3 0.09825574859 0.3339980318 0.5677462195
2.4 0.09824710751 0.3339944847 0.5677584077
2.5 0.09824158782 0.3339922189 0.5677661932_
В строке #1 находится отклик настройки системы на прием переменных с
индексами (пункт главного меню Declare | Input).
В строках #2—#4 задается система дифференциальных уравнений (правые
части) для случая п - 2.
Вызов утилиты ODE_APPR.MTH решения отражен в строке #5. В строке #6
вызывается функция:
RK([#2,#3,#4], [t,p0,pl,p2], [0,1,0,0],' 0.1, 50)
решения системы дифференциальных уравнений методом Рунге— Кутты
с шагом h = 0,1 и числом точек 50. Уравнения представлены в
аналитическом виде. В строке #7 вызывается функция RK с численными
значениями X = 5,1 час-1 и ц = 1,5 час"1 и начальными условиями р^Ф)-^
д(0) = А(0) = 0.
Результаты решения системы уравнений приведены в таблице в строке #8 в
диапазоне / = 1,7-5-2,5 час. Из таблицы видно, что длительность переходного
процесса составляет примерно 2,4 часа, вычисленного с точностью четыр6
знака после запятой. Так как длительность переходных процессов мала, f°
данные табл. 7.1 можно считать достоверными.
Функцию готовности целесообразно вычислить, воспользовавшись выра*
нием Kr(t) = 1 - pn{t). В этом случае достаточно вычислить вероятность то
что система находится в состоянии п в произвольный момент времени t.
Для получения решения в аналитическом виде воспользуемся преобразова
ем Лапласа.
Процедуры вычисления функции простоя с помощью системы Derive 5
ют вид:

,гГпеДОвание надежности информационной восстанавливаемой системы 321
-. InputMode := Word
2. (s + A)-pO-ypl = l
#3: -A-p0 + (s+A + p)-pl-2-p-p2 = 0
f4. A-pl-(s + 2-p)-p2 = 0
(s + A)-pO-p-pl = l
|5.: -A-p0 + (s + A + p)-pl-2-y-p2 = 0
A-pl-(s + 2-p)-p2 = 0
T (s + A)-pO-ypl = l 1 ^
#6: SOLVE -A-p0 + (s + A + u)-pl-2-y-p2 = 0 , [pO, pi, p2] , Real
^L A-pl-(s + 2-vi)-p2 = 0 J J
A-s + (y + s)-(2-p + s)
#7: P0 = ; ^ f—^—= ■ ЛР1 =
s-(A"+2-A-(p + s) + (p + s)-(2p + s) )
i—= - лр2 =
s-(A^+2-A-(p + s) + (p + s)-(2p + s))
A^ "
s-(A2+2-A-(p + s) + (|i + s)-(2p + s))_
#8: p2 = *L
s-(A2+2-A-(p + s) + (p + s)-(2-ii + s))
*9: P2 = ;
s-(s2+s-(2-A + 3-p) + A2+2-A-p + 2-p2)
no: p2= : ?^oi ; .
s-(100-s2+1470-s + 4581)
tll^0.444.e-10-2-t-1.012.e"4-484-t +0.568
Сроках #2, #3, #4 представлены уравнения в преобразованиях Лапласа.
v Строке #5 отображается система уравнений, образованная кнопкой Author
*atrix.
кЛ(еНие системь1 уравнений получено с помощью функции solve (стро-
6) и представлено в строке #7. Из общего решения выделено выражение
| ^образования Лапласа коэффициента простоя РгС5) (строка #8).

322
ЧАСТЬ II. Лабораторный практикум. Лабораторная рабпг
С помощью пункта главного меню Simplify | Factor выражение p2{s) факт
ризовано по переменной jc для получения решения в привычном для нас щй
(строка #9)
В строке #10 находится выражение преобразования Лапласа коэффициент
простоя при исходных данных нашего примера X = 5,1 час-1 и р. = 1,5 час4
Подстановка выполнена с помощью кнопки Sub панели инструментов.
В строке #11 находится выражение функции простоя, полученное путем
обратного преобразования Лапласа выражения #10 с помощью математической
системы Mathcad 2000.
График функции р2(0 приведен на рис. 7.3.
Рис. 7.3. График функции простоя системы
7.4. Варианты заданий
к лабораторной работе 7
Выполнить анализ надежности информационной восстанавливаемой сие**
мы, определив:
О п — необходимое число обслуживающих органов, обеспечивающие
данный коэффициент готовности системы;
О т —длительность переходных процессов;
□ АГГ(/) — функцию готовности системы.
Использовать приведенную ранее методику и компьютерные технологии V
шения задачи.

к, час"1
ц, час"1
МЙГК
10
1
0,2; 0,1; 0,05;
0,003
5
1
0,2; 0,1; 0,05;
0,003
3
1
0,2:0,1; 0,05;
0,003
1
1
0,2; 0,1; 0,05;
0,003
ВАРИАНТ 2
К час"1
й, час"1
Р
'отк
1
0,2
0,5; 0,1; 0,05;
0,003
1
0,5
0,5; 0,1; 0,05;
0,003
1
1
0,5; 0,1; 0,05;
0,003
1
2
0,5; 0,1; 0,05;
0,003
ВАРИАНТ 3
К час"1
Мае"1
«их
5
2
0,2; 0,1; 0,05;
0,003
3
2
0,2; 0,1; 0,05;
0,003
2
2
0,2; 0,1; 0,05;
0,003
1
2
0,2; 0,1; 0,05;
0,003
?^ИАНТ 4
^час4
7
1
0,2; 0,1; 0,05;
0,003
3
1
0,2; 0,1; 0,05;
0,003
1
1
0,2; 0,1; 0,05;
0,003
0,5
1
0,2; 0,1; 0,05;
0,003
следование надежности информационной восстанавливаемой системы 323
«юн определении числа обслуживающих бригад могут возникнуть
следующие трудности:
{% программа выдает решение, которое противоречит физическому смыслу
задачи;
г) прогРамма не ВЬ1Дает значение п.
о таких случаях следует попытаться решить трансцендентное уравнение,
указав область изоляции корня. Если это также не даст результата, то следует
функцию (7.1) протабулировать в области искомого корня и по результатам
табулирования найти п (по равенству левой и правой частей уравнения (7.1)).
Далее приводятся варианты заданий. В таблицах Р0ТК — вероятность отказа в
обслуживании заявки.
ВАРИАНТ 1

324
ВАРИАНТ 5
X, час"1
ц, час"1
р
1 отк
5
0,5
0,2; 0,1; 0,05;
0,003
5
1
0,2; 0,1; 0,05;
0,003
5
2
0,2; 0,1; 0,05;
0,003
5 "^^i
10 ^
0,2;0,1;0Д)5>
0,003 '
ВАРИАНТ6
X, час"'
ц, час"'
р
' отк
10
1
0,2; 0,1; 0,05;
0,003
10
5
0,2; 0,1; 0.05;
0,003
10
10
0,2; 0,1; 0,05;
0,003
10 ""
20
0,2; 0,1; 0,05;
0,003
ВАРИАНТ 7
X, час"'
ц, час"'
1 отк
10
1
0,2; 0,1; 0,05;
0,003
5
1
0,2; 0,1; 0,05;
0,003
1
1
0,2; 0,1; 0,05;
0,003
0,5
1
0,2; 0,1; 0,05;
0,003
ВАРИАНТ 8
X, час-1
\х, час"1
р
' отк
10
1
0,2; 0,1; 0,05;
0,003
10
2
0,2; 0,1; 0,05:
0,003
10
5
0,2; 0,1; 0,05;
0,003
10
10
0,2; 0,1:0.05:
0,003
ВАРИАНТ 9
X, час"1
ц, час"'
р
* отк
10
1
0,2; 0,1; 0,05;
0,003
10
5
0,2; 0,1; 0,05;
0,003
10
10
0,2; 0,1; 0,05;
0,003
10
20^
0,2;0,1:0,05:
0,003_^J
ВАРИАНТ 10 ^^^
X, час"1
ц, час"'
* отк
8
1
0,2; 0,1; 0,05;
0,003
8
5
0,2; 0,1; 0,05;
0,003
8
10
0,2; 0,1; 0,05;
0,003
JL—-^
20^_^
0.2:0,1:0.05:
о,ооз_^
ЧАСТЬ II. Лабораторный практикум. Лабораторная рабг»

ЛАБОРАТОРНАЯ РАБОТА 8
ИССЛЕДОВАНИЕ НАДЕЖНОСТИ
ТЕХНИЧЕСКИХ СИСТЕМ С УЧЕТОМ
ИХ ФИЗИЧЕСКОЙ РЕАЛИЗУЕМОСТИ
Целью настоящей лабораторной работы является изучение влияния на
показатели надежности системы следующих факторов:
О различных видов законов распределения времени до отказа;
О неодновременности работы элементов системы;
О последействия отказов.
8.1. Влияние неодновременной работы
элементов на надежность системы
8.1.1. Постановка задачи
Дано:
в структурная схема технической системы;
™ п — количество элементов системы;
^ т — период работы системы;
fl(0 — вероятность безотказной работы элементов, / = 1, 2,..., п;
[#/,£,] — интервал времени работы элементов на периоде т, / = 1, 2,..., п;
1 — время работы системы.
Определить:
вероятность Pjfip(t) и среднее время 7], пр безотказной работы элементов
с Учетом времени их простоя;
в^роятность безотказной работы системы без учета и с учетом времени
простоя элементов: Pc(t) и Pcrip(t) соответственно;

326 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабпт
П вероятности безотказной работы Pc(t), РСчПр(0 в виде таблиц значение
графиков;
□ среднее время безотказной работы системы без учета и с учетом времен
простоя элементов 7] и 7] пр .
Варианты заданий приведены в разд. 8.1.4.
8.1.2. Сведения из теории
На периоде т элементы системы работают не одновременно. Рассмотрим
функционирование одного элемента. Пусть на интервале времени от а до b
элемент работает, а вне этого интервала — простаивает. На следующем
периоде длительностью т элемент работает на интервале от х + а до х + Ь и
простаивает вне этого интервала, и т. д. Выключение элемента не влияет на
его надежность. Пусть P(t) — вероятность безотказной работы элемента в
случае, когда он работает непрерывно. Оценим его надежность при условии,
что элемент может простаивать на заданных интервалах времени. В [5, гл. 2]
было приведено общее выражение вероятности безотказной работы элемента
Pnp(t) при наличии интервалов простоя. Для нашего случая получим:
1, при 0<t<a;
Pnp(t) = < P(t-k(x-b + a)-a), при kx + a<t<kx + b, k = 0,1, 2,...; (8.1)
P(k(b - a)\ при (k - \)x + b < t < kx + a, k = \, 2,...
Соотношение (8.1) определяет новый закон распределения времени работы
элемента с учетом его простоя. Закон Pnp(t) имеет на три параметра больше,
чем ?(/).
Среднее время безотказной работы вычислим на основе формулы (8.1).
Интегрируя Pnp(t), получим:
со оо kx+b
Ti,np = \PnpWt = а + X J P(t-k(x-b + a)-a)dt +
О *=0 кх+а
оо кх+а со (к+\)(Ь-а)
+ Е J P(k(b-ay)dt = a+ft J P(t)dt +
k = \ (k-\)x+b * = 0 k(b-a)
00 CO 00
+(x -b + a) £ P{k{b - a)) = \P{t)dt + a + (x-b + a)Z P(k(b - a)).
Л = 1 О k = l

нежность технических систем с учетом их физической реализуемости 327
0#ЮДа
Т1пр=Т1+а + (х-Ь + а)^Р(к(Ь-а)), (8.2)
ще Т\ — сРеДнее время безотказной работы элемента в случае его
непрерывной работы,
о частности, для экспоненциального распределения с параметром X получим:
7i,np4^+(T-*+«)l:«-U(6-',)=Y+«+4(^rT> <8-3)
к д=1 л е v ' -1
из формулы (8.3) следует, что повысить среднее время безотказной работы
элемента можно не только путем уменьшения интенсивности отказа X, но
также и путем увеличения времени его простоя за счет уменьшения величины
Ь-а. Полагая а = 0, получим, что выигрыш по среднему времени
безотказной работы равен:
г -^'"Р 1 ■ Ч*~Ь + а)
\Jt — — 1т Г"77 С •
l\ 7J еЧЬ-а) _ j
%сленное значение выигрыша по критерию 7j при х = 10 час приведено в
табл. 8.1.
Таблица 8.1. Выигрыш по среднему времени безотказной работы
в зависимости от А, и времени работы элемента Ь-а
X, час-1
0,1
0,01
0,001
0,0001
Ь-а, час
10
1,00
1,00
1,00
1,00
8
1,16
1,24
1,25
1,25
6
1,49
1,65
1,66
1,67
4
2,22
2,47
2,50
2,50
2
4,61
4,96
5,00
5,00
ц таблицы следует, что на величину 7] пр оказывает влияние не только на-
е)кность элемента, но и увеличение времени его простоя, когда элемент не
асХодует свой ресурс надежности.
ссмотрим систему, состоящую из п элементов, имеющих интервалы про-
°я. Для каждого элемента системы эти интервалы имеют различную про-
^Жительность на периоде х. Тогда время до отказа элементов всегда имеет
Экспоненциальное распределение, выражаемое формулой (8.1).

328
ЧАСТЬ II. Лабораторный практикум. Лабораторная работ*
Оценка надежности такой системы осуществляется методами, учитывают.,
ми произвольный характер времени до отказа элементов. Эти методы ра
смотрены в [5, гл. б]. Вероятность безотказной работы нерезервированной
и
системы, состоящей из п элементов равна Рс(/) = П/}(0» вероятность безот.
казной работы резервированной системы кратности m с постоянным резеп.
m
вом равна Pc(t) = 1 - ЦО -/}(0)» и т. д.
/=о
8.1.3. Пример выполнения работы
Структурная схема расчета надежности изображена на рис. 8.1. Она состоит
из и = 4 элементов и представляет собой общее резервирование с постоянно
включенным резервом.
I
3
2
4
Рис. 8.1. Схема расчета надежности
Время работы элементов до отказа является случайным и подчинено
экспоненциальному закону распределения с параметром А, = 0,002 час"1. Период
работы, состоящий из интервалов работы и простоя каждого элемента, равен
х = 10 час. Время работы элементов на каждом периоде приведено в табл. 8.2.
Таблица 8.2. Время работы элементов
Номер элемента
Интервал работы
1
[0;5]
2
[2;3]
3
[5; 8]
4
[0;7]
На остальной части периода т элементы выключены из работы.
Решение. Вероятность безотказной работы каждого элемента имеет &и
P(t) = e~ '. Поэтому, если бы все элементы системы работали непрерывно,
вероятность безотказной работы системы была бы равна:
Pc(t) = \-Q-e-2Xt)2. (8'4)

.ыявжность технических систем с учетом их физической реализуемости 329
йо фоРмУле (8-1) найдем вероятность безотказной работы элементов с учетом
простоя:
[P{t-5k\ при \0k<t<\0k + 5, £ = 0,1, 2,...;
Я „„(ОН (8-5)
1>пр [Р(5к), при 10(*-1) + 5</<И0*, £ = 1,2,...,
1, при 0</<2;
P2np(t) = < P(t-9k-2), при 10£ + 2</£10А: + 3, fc = 0,1, 2,...; (8.6)
/>(£), при 10(£-1) + 3</<10£ + 2, А: = 1,2,...,
1, при 0</^5;
p3np(t) = <P(t-7k-5), при 10А: + 5 < Г < 1 ОЛг -н 8, к = 0,1, 2,...; (8.7)
|/(3*), при 10(£-1) + 8<><10А: + 5, А: = 1,2,...,
_1>(/-3£), при \0k<t<\0k + 7, k = 0,1, 2,...;
4'пр [Р(7А:), при 10(£-1) + 7</<;10А:, А: = 1,2,.;.
На основе структурной схемы определим вероятность безотказной работы
шстемы с учетом простоя элементов. Вероятность безотказной работы
нерезервированной подсистемы, состоящей из элементов 1 и 2, равна
произведению их вероятностей безотказной работы. Тогда />i>2,np(0 = jPi,np(0 ^2,пр(0-
Вероятность безотказной работы резервной подсистемы равна
^,4,1ф(0 = /з,пр(0*А,пр(0' Поэтому вероятность безотказной работы всей
системы с учетом времени простоя элементов равна:
Таблицу значений и графики вероятностей безотказной работы элементов и
систем получим в Microsoft Excel. В ячейках А1 : II записываются заголовки
^олбцов. В колонке А помещается время t, изменяющееся от 0 до 500 часов
[| ^агом 5 часов. В ячейку В2 записывается отношение текущего времени ра-
°ты системы к периоду х = 10:
52 * А2/10.
ь
ячейку С2 помещается значение к как целое от деления / на х :
°2 * ЦЕЛОЕ(В2).
ь
ячейках D2 : G2 содержатся формулы (8.5)—(8.8) для вычисления
вероятий безотказной работы элементов:
Do
Q * ЕСЛИ(В2 <= С2 + 0,5; ЕХР(-0,002*(А2 - 5*С2));
^(-О,002*5* (С2 + 1) ) ),

330 ЧАСТЬ II. Лабораторный практикум. Лабораторная работ*
Е5 = ЕСЛИ(В5 > С5 + 0,2 & В5 <= С5 + 0,3;
ЕХР(-0,002*(А5 - 9*С5 - 2)); ЕХР(-0,002*(С5 + 1))),
F8 = ЕСЛИ(В8 > С8 + 0,5 & В8 <= С8 + 0,8;
ЕХР(-0,002*(А8 - 7*С8 - 5)); ЕХР(-0,002*3*(С8 + 1))),
G2 = ЕСЛИ(В2 <= G2 + 0,7; ЕХР(-0,002*(А2 - 3*С2));
ЕХР(-0,002*7* (C2 + 1))).
Заметим, что для 2-го и 3-го элементов расчетные формулы записываются
начиная с ячеек Е5 и F8, поскольку в предыдущих ячейках значения функций
равны единице.
Ячейки Н2 и 12 содержат формулы (8.9) и (8.4) для вычисления вероятностей
безотказной работы системы при наличии и отсутствии интервалов простоя
элементов:
Н2= 1 - (1 - D2*E2)*(1 - F2*G2),
12 = 1 - (1 - ЕХР(-0,004*А2)}л2.
Затем полученные формулы протягиваются на весь блок рассчитываемых
ячеек. Результаты табулирования функций содержатся в табл. 8.3.
1
2
3
4
•••
102
Таблица 8.3. Расчет вероятностей безотказной работы элементов и системы
А
/
0
5
10
...
500
В
//10
0
0,5
1
...
50
С
к
0
0
1
...
50
D
Р\
1,00000
0,99005
0,99005
...
0,60653
Е
Р1
1,00000
1,00000
1,00000
...
0,90303
F
РЪ
1,00000
1,00000
1,00000
...
0,73639
G
/Ч
1,00000
0,99005
0,98610
...
0,49659
Н
РСП
1
0,999901
0,999862
...
0,713106
I
PC
1
0,999608
0,998463
...
0.252355
R2
Графическая иллюстрация таблицы приведена на рис. 8.2 и 8.3. На рис °-
показаны графики вероятностей безотказной работы элементов.
Обратим внимание на то, что надежность элементов по критерию P{t) oflPe
деляется временем их работы. Чем меньше это время, тем более надежны ^
оказывается элемент. Самым надежным является второй элемент, работа
щий на периоде 1 час, третий элемент работает 3 часа, первый элемент
5 часов, а четвертый — 7 часов.
бе3
На рис. 8.3 приведены графики вероятностей безотказной работы системы
простоя элементов и при наличии простоев.

аяаежность технических систем с учетом их физической реализуемости
331
Рис. 8.3. Вероятность безотказной работы системы для случаев
непрерывной и неодновременной работы элементов
13 графиков следует, что Рс(/) значительно меньше, чем /£эПр(0> т- е- нали-
йе простоя у элементов повышает надежность системы.
&»^ЧИСЛИМ среднее время безотказной работы элементов и системы. Среднее
^Мя безотказной работы элементов без учета времени простоя равно
4*^ = 500 час.
Рис. 8.2. Вероятности безотказной работы элементов

332 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабо-^
Используя формулу (8.4), найдем среднее время безотказной работы систем
без учета времени простоя элементов:
Т1с = ]/> {t)dt = ](1 - (1 - e~2Xt ? )dt = )(2e-2Xl - е^1 )dt =
0 0 0
21 3 п<
= = — = 375 час.
2Х АХ АХ
Среднее время безотказной работы элементов с учетом времени их простоя
определим из соотношения (8.3):
т^=1 +^=500+7йЬт=997'5 час>
т*-*~{ +2+^rrm+7^rrm7'5 час'
т*-п' = х +~^ГШ+7П>Ш~\=1П'*часа'
Среднее время безотказной работы системы с учетом времени простоя
элементов определим на основе табличных данных, по формуле трапеций:
Гспр «1030 час.
На основе полученных результатов можно сделать следующие выводы:
О закон распределения времени безотказной работы элементов и системы
существенно зависит от того, как долго элементы пребывают в
выключенном состоянии;
□ надежность системы по вероятности P(t) значительно выше, если на
определенных интервалах времени элементы простаивают, причем с
течением времени разница PnM)-P(t) будет увеличиваться;
□ наличие интервалов простоя элементов повышает также среднее вре^,
безотказной работы системы, которое в нашем случае увеличилось с 3
до 1030 часов, т. е. почти в 3 раза.
8.1.4. Варианты заданий к лабораторной работе
Выполнить анализ надежности элементов и системы при непрерывной и ^
одновременной работе элементов. Структурные схемы приведены на рис-
Период работы для всех вариантов т = 10 час.

Рис. 8.4. Схемы расчета надежности
.ы/гежность технических систем с учетом их физической реализуемости 333

334
ЧАСТЬ II. Лабораторный
f практикум. Лаборатории
1 Работа Л
■—-^о
Вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Схема
рис. 8.4, е
рис. 8.4, в
рис. 8.4, а
рис. 8.4, б
рис. 8.4, г
рис. 8.4, д
рис. 8.4, г
рис. 8.4, б
рис. 8.4, а
рис. 8.4, е
рис. 8.4, в
рис. 8.4, д
рис. 8.4, б
рис. 8.4, в
рис. 8.4, а
рис. 8.4, е
рис. 8.4, г
рис. 8.4, <)
рис. 8.4, а
рис. 8.4, г
рис. 8.4, б
рис. 8.4, е
рис. 8.4, в
рис. 8.4, д
рис. 8.4, а
рис. 8.4, д
рис. 8.4, е
рис. 8.4, в
рис. 8.4, г
рис. 8.4, б
Закон
распределения
Ехр(0,005)
N(300; 50)
U( 100; 200)
Ехр(0,007)
Ехр(0,001)
TN(200; 70)
Г(3; 150)
Ехр(О.ООЗ)
W( 1,8; 220)
R(0,00018)
Ехр(0,004)
TN(160;50)
U(300; 500)
TN(220; 80)
N(300; 90)
Г(2; 270)
Exp(0,002)
W(2,3; 240)
U(340; 400)
Exp(0,003)
N(190; 60)
Г(3; 180)
Exp(0,008)
W(3; 200)
U( 150; 200)
TN(280; 60)
N(150; 40)
Г(2; 230)
Г(2; 100)
W(2,4; 250)
Интервалы работы элементов "*
1
[3;9]
[0;8]
П;6]
Р;5]
[5; 7]
[2; 6]
[0;9]
[8; 9]
[1;4]
[3;6]
[2; 5]
[3;7]
[4; 9]
[8; 9]
[0;7]
[3;7]
[8; 9]
[0;5]
[3;4]
[0;8]
[7; 9]
[2; 6]
[5; 9]
[4; 7]
[3;9]
[5; 8]
[6; 8]
[8; 9]
[0;9]
[3;6]
2
[6; 10]
[5; 6]
[2; 8]
[5; 10]
[0;8]
[0;71
[4; 7]
[6; 7]
[4; 10]
[6; 8]
[0;6]
[7; 10]
[0;6]
[5; 8]
[7; 8]
[0;5]
[6; 9]
[2; 4]
[0;5]
[5; 8]
[6; 10]
[0;3]
[0;5]
[6; 7]
[0;4]
[5; 8]
[0;8]
[0;3]
[0;5]
[0;6]
3
[0;3]
[0;2]
Р;3]
[3;6]
[0;3]
[U5]
[i;3]
[0;4]
[i;3]
[0;8]
[0;3]
[3;5]
[3; 8]
[0;8]
[5; 9]
[0;5]
[1;3]
[0;6]
[2;3]
[i;3]
[U5]
П;3]
[2; 8]
[2; 8]
[0;7]
[0;7]
[»;б]
[2;3]
[3:4]
[0;6]
4
[0;4]
[3;4]
[0;7]
[0;5]
[2; 4]
[i;4]
[3;4]
[3;8]
[0;4]
[3;4]
[i;4]
[0;6]
[3;4]
[0;8]
[0;7]
[i;4]
[0;7]
[0;6]
[8; 10]
[0;6]
[0;5]
[0;9]
[3;4]
[0;5]
[2; 4]
[0;8]
[2; 4]
[6; 8]
[5; 8]
[2; 4]
5
""ТгТтР
"iTi^
~12Т4Г
^^~~~~~~
[0;7]
[2; 81
[0;3]
[1;9]
[2:3]
[6; 8]
[3;5]
___———
________^
[1;6]
J22JL
J3J^L
[0^

.мдежность технических систем с учетом их физической реализуемости 335
$ таблице приняты следующие обозначения законов распределения:
г\ Бхр — экспоненциальный;
f\ V— равномерный;
0 р — гамма;
(j TN — усеченный нормальный;
0 R —Рэлея;
|-j W — Вейбулла;
0 N — нормальный.
В скобках указаны параметры распределений.
формулы вероятностей безотказной работы элементов для приведенных в
задании распределений содержатся в табл. 1.6 гл. 1.6 части I.
8.2. Влияние последействия отказов
элементов на надежность системы
8.2.1. Постановка задачи
Дано:
О структурная схема технической системы (система 1);
,0 X — интенсивности отказов элементов до отказа какого-нибудь одного из
них;
О V — интенсивности отказов элементов после отказа любого одного
элемента;
^ Дублированная система с постоянно включенным резервом (система 2);
а вид закона распределения времени до отказа элементов системы 2,
отличный от экспоненциального;
Математическое ожидание и среднее квадратическое отклонение времени
безотказной работы элементов:
* до отказа т, а любого элемента;
• после отказа т', а' любого элемента;
вРемя работы систем /.
Оделить:
Вероятность безотказной работы системы 1 при отсутствии и при наличии
Последействия отказов Рс(/), Рс,поел (0 в виде формул, таблиц и графиков;

336 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабрТл
□ среднее время безотказной работы системы при отсутствии и при наличии
последействия отказов: Тс и Тстюсл;
П вероятность безотказной работы дублированной системы (системы 2) при
отсутствии и при наличии последействия отказов: Pac(t) и Рж,посп(()',
П среднее время безотказной работы дублированной системы при
отсутствии и при наличии последействия отказов: Тлс и Гдс посл.
Варианты заданий приведены в разд. 8.2.4.
8.2.2. Сведения из теории
Практически в любой технической системе отказы одних элементов приводят
к увеличению нагрузки на остальные элементы. В результате интенсивности
отказов работающих элементов возрастают. Этот эффект носит название
"последействие" отказов. Любая техническая система в той или иной степени
подвержена этому явлению.
Экспоненциальные распределения времени до отказа
Расчет надежности систем с последействием, элементы которых имеют
экспоненциальные распределения времени до отказа, изменяется незначительно
по сравнению с расчетом надежности систем без последействия.
Общий подход к анализу надежности таких систем состоит в следующем:
□ описание функционирования системы графом состояний;
О составление по графу системы алгебраических уравнений относительно
среднего времени пребывания системы т, в каждом исправном состоянии,
решение системы и определение среднего времени безотказной работы-
7] = Xх/' где Е+ — множество исправных состояний;
П составление по графу системы дифференциальных уравнений
относительно вероятностей пребывания системы /?,(/) в исправных состояния »
решение системы и определение вероятности безотказной работь-
/40= Z АС).
Произвольные распределения времени до отказа
Проведем анализ надежности системы с последействием отказов, если э
менты имеют неэкспоненциальные законы распределения времени до откз

и^лежность технических систем с учетом их физической реализуемости 337
Докажем, что и в этом случае при вычислении показателей надежности сис-
^jibi эффект последействия можно учесть.
рассмотрим дублированную систему с постоянно включенным резервом.
Введем следующие обозначения:
0 /,(/) и P{(t) — плотность распределения времени до отказа и вероятность
безотказной работы элемента 1;
О h (О и ^2 (О — плотность распределения времени до отказа и
вероятность безотказной работы элемента 2;
0 /з(0 и ^з(0 — плотность распределения времени до отказа и вероятность
безотказной работы элемента 1 после отказа элемента 2;
0 /ДО и А(0 — плотность распределения времени до отказа и
вероятность безотказной работы элемента 2 после отказа элемента 1.
Определим закон распределения времени до отказа системы. По формуле
полной вероятности получим:
Pc(t) = Pl(OP2(t)+lfl(x)P4(t-i-x2-x)dx+lf2(x)P3(t + xl-x)dx. (8.10)
о о
Появление параметра сдвига х2 в аргументе функции P4(t + x2 -x)
обусловлено тем, что элемент 2 уже проработал время х, и теперь до отказа он
должен проработать время t-x, но с законом распределения Р4(0 * причем не с
самого начала, а с момента времени х2, обеспечивающего продолжение
Функционирования элемента 2. Момент времени х2 берется так, чтобы
вероятность остаточного времени работы элемента 2 после момента х была
одинаковой для законов P4(t) и P2{t). Это значит, что должно выполняться
рабство Р4(х2) = Р2(х) (условие сохранения остаточного ресурса). Таким
образом, момент времени х2 в формуле (8.10) является функцией момента х.
Аналогичный смысл имеет аргумент *j в функции Р3^ + х{ -*), который
Определяется уравнением Р3(х1) = />,(*).
Усмотрим частный случай экспоненциальных заколов распределения, когда
*)(/) = e-Vs / = i)2, 3,4.
^° Формуле (8.10) получим:
^с(0 = е~(Х>+х*>' + )\хе-^хе-х<('+JC*~x)dx + jV^2*^3('+А''"^ ■
о о

338 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабоГя _
Из соотношения Р4(х2) = Р2(х) следует, что Х4х2=Х2х, а из соотношения
P3(*i) = Р] (х) — что Х3х{ = h\x • Следовательно:
рс(/) = e-^i+W + e-U jXie-^xeXAX~^xdx + e~h' \Х2е~^х еХгХ~^х dx =
о о
= е-Ъ+Ъ)< + х^ — + V 3' — .
А] + Х2 ~ ^-4 ^*1 ~^ ""2 ~ ^3
Для одинаковых по надежности элементов с первоначальной интенсивностью
отказа X и интенсивностью отказа X' после возникновения отказа другого
элемента получим:
2Х 2Х _г/ X' -2xt
cW ОХ-У V / 7Х-Х'
LK — А, ^ 2.А, — А* 2.К — А.
Для неэкспоненциальных распределений расчет по формуле (8.10) является
более сложной вычислительной задачей.
Если элементы дублированной системы имеют одинаковую надежность, то
Pc(t) = P2(t) + 2\f(x)PXt + x'-x)dx, (8.11)
о
где:
□ /(/) и P(t) — плотность распределения и вероятность безотказной
работы элемента до наступления отказа другого элемента;
□ P\t) — вероятность безотказной работы после отказа другого элемента;
О х' — корень уравнения Р'(х') = Р(х).
Исследование надежности дублированной системы с последействием отказов
элементов можно провести на основе программного средства aftereffect.exe,
рассчитывающего вероятность безотказной работы в соответствии с формУ"
лами (8.10) или (8.11). Описание программы содержится в части IV.
В [5,разд. 8.7] получены вероятности безотказной работы дублированной
системы с последействием отказов для случаев отсутствия и наличия
"памяти". Приведем соответствующие формулы:
О отсутствие "памяти". Вероятность безотказной работы системы выра#а'
ется формулой:
/>(/) = Р, (t)P2(/) + )f, (х)Р2(х)Р4(/ - x)dx + J/», (*)/2(х)Р3(/ -x)dx. (8-12)

иадежность технических систем с учетом их физической реализуемости 339
В частности, если элементы равнонадежны, то
Р«) = Р2 (/) + 2 jf(x)P(x)P'(t -x)dx; (8.13)
о
р наличие "памяти". Вероятность безотказной работы системы вычисляется
по формуле:
P„{t) = Pl(t)P2(t)+ )Mx)P2(x)dxP4(t) + )ых)Р{{х)ахРъ{1). (8.14)
о о
В частности, если элементы равнонадежны, то
Pn(t) = P2(t) + 2\f(x)P(x)axPy) = pHt) + Q-P2(t))nt)- (8.15)
о
докажем, что выражения (8.12) и (8.14) являются соответственно нижней и
верхней оценками вероятности безотказной работы системы, вычисленной по
формуле (8.10).
Для этого сделаем два естественных допущения:
CJ распределения P((t) — "стареющие", т. е. вероятность остаточного
времени "жизни" элемента в течение времени х не превышает вероятности
безотказной работы за это же время:
^-^■<Р{(х), или />(* + *)£/?(/)/}(*);
О эффект последействия может только ухудшить показатели надежности
элементов:
Р3(0^,(') и P4{t)<P2{t).
° силу первого допущения:
P4(t + x2-x)<P4(x2)P4(t-x) = P2(x)P4(t-x),
и> значит:
J/, (х)Р4 (t + x2- x)dx <, J/, (х)Р2 (х)Р4 (t - x)dx.
о о
^сюда следует, что Рс (/) £ P{t).
Гласно второму допущению, Р2(х) = Р4(х2)<Р2(х2), и в силу убывания
%Нкции Р2(t), получим х > х2. Тогда:
P2(x)P4(0<P4(0<P4(t + x2-x),

Рис. 8.5. Структурные схемы систем с последействием отказов
для случаев отсутствия (а) и наличия "памяти" (б)
340 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа я
значит:
\Mx)P2(x)dxPA(t)< |/,(х)Р4(Л-х2 -x)dx.
о о
Отсюда следует, что Pn(t) < Pc(t).
Таким образом, получена двусторонняя оценка вероятности безотказной
работы системы с последействием отказов:
Pn(t)<Pc(t)<P(t). (8.16)
В [5,разд. 8.7] получены формулы для вероятности безотказной работы
резервированной системы кратности «-1 с последействием отказов для
случаев отсутствия и наличия "памяти":
р(о=1-п(+)о-^+1"')'*ко, р„(о=1-П(1-^Г,"'хо. (8.П)
где fj+i(t) — плотность распределения времени безотказной работы, а
Pj+i(t) — вероятность безотказной работы каждого элемента после отказа /
элементов, i = О,1, 2,..., п -1.
Соотношения (8.17) являются обобщением формул (8.13) и (8.15) на системы
с произвольным числом элементов. Они имеют простой смысл. Вероятности

Надежность технических систем с учетом их физической реализуемости
341
f(t) и Рп(0 равны вероятностям безотказной работы схем общего
резервирования замещением (рис. 8.5, а) и с постоянным резервом (рис. 8.5, б).
Элементы каждой нерезервированной подсистемы равнонадежны, а элементы
различных подсистем имеют разную надежность.
рремя до отказа системы в случае отсутствия "памяти"
*,=£"Ч*М° *&и)
соответствУет резервированию замещением, а в случае наличия "памяти"
Хс „ = max ттЫ'*, Xf,..., хЩм)
— резервированию с постоянным резервом. Отсюда, в частности, следует
fнеравенство P(t) £ Pn{t).
8.2.3. Пример выполнения работы
Структурная схема системы 1 (схема расчета надежности) изображена на
рис. 8.6. Она состоит из четырех элементов и представляет собой общее
резервирование с постоянно включенным резервом.
Рис. 8.6. Схема расчета надежности
Время работы до отказа каждого элемента имеет экспоненциальное
распределение с параметром X = 0,002 час-1. После отказа любого элемента
интенсивность отказа резервных элементов увеличивается и равна X' = 0,003 час" .
Элементы дублированной системы (системы 2) с постоянно включенным
резервом имеют усеченно нормальный закон распределения времени до отказа
е Математическим ожиданием w = 500 час и средним квадратическим
отклонением а = 200 час. После отказа одного из элементов исправный элемент
с°храняет вид закона, но в 2 раза уменьшается среднее время до отказа:
**' = 250 час.
ft
°ремя работы обеих систем / = 400 час.
Необходимо определить вероятность и среднее время безотказной работы
сИстем 1 и 2 при отсутствии и при наличии последействия отказов.

342 ЧАСТЬ II. Лабораторный практикум. Лабораторная рабоТя a
—————— ~^5о
Решение. Определим вероятность безотказной работы системы 1 при отсу^.
ствии последействия отказов. Вероятность безотказной работы нерезервир0.
ванной системы равна P(t) = е~ ', вероятность ее отказа Q{t) = 1 - е~ '. n0w
этому вероятность отказа резервированной системы равна £?c(0 = (l-e~2^]
а вероятность ее безотказной работы:
Pc(t) = \-(\-e-™f=2e-m-e-4*. (8.18)
Определим вероятность безотказной работы системы 1 при наличии
последействия отказов. На рис. 8.7 представлен граф состояний системы.
О Ы 1 2Х> 2
О—> О—>—<Е>
Рис. 8.7. Граф состояний системы с последействием отказов
Система дифференциальных уравнений для определения P^mcn(t) имеет вид:
>J(/) = -4^0(0;
\p{(t) = 4\p0(t)-2X'Pl(t).
Найдем решение системы аналитически. Из первого уравнения получаем
Po(0 = e~4kt ■ Тогда из второго уравнения p{(t) + 2X'p[(t) = 4\e'~4Xt. Это
линейное дифференциальное уравнение первого порядка, которое можно пред-
ставить в виде: ip\{t)e2Xt\ = 4А,е~4Х'е2Х/. Интегрируя обе части, получим:
Таким образом,
^спосл(0 = Ро(0 + А(0 = -^Це-2Х''-^-7е-4Х'. (8-19)
с поелw ™w FWJ 4Я.-2А.' 4A.-2V
Графики вероятностей безотказной работы Pc(t) и PcaoGa(t) строятся п°
формулам (8.18) и (8.19). Они изображены на рис. 8.8.
Как следует из графиков, если не учитывать эффект последействия отказов
вероятность безотказной работы системы будет завышенной. ОтносительН
погрешность в момент времени / = 400 час составляет 33,7 %.

и^дежность технических систем с учетом их физической реализуемости
343
Рис. 8.8. Вероятность безотказной работы системы 1 без последействия (кривая 1)
и с последействием отказов (кривая 2)
Определим среднее время безотказной работы системы 1 при отсутствии
последействия отказов на основе формулы (8.18):
Г1=>е(/)й = ](2е-*-е^)л=^-^г = ^- = 375ч«!.
q qv ' 2А. 4>. 4А,
Среднее время безотказной работы системы при наличии последействия
определим на основе формулы (8.19):
Подставляя численные значения, получим 7|посл =292 час. Таким образом,
по среднему времени безотказной работы без учета последействия оценка
также является завышенной.
Проведем анализ надежности дублированной системы (системы 2) с
усеченными нормальными законами распределения отказов элементов.
в&роятность безотказной работы дублированной системы при отсутствии и
П£? наличии последействия отказов определим с помощью программы after-
er»ect.ex:e, описание которой содержится в части IV. Результаты расчетов
Риведены в табл. 8.4 и в виде графиков на рис. 8.9.
_ езУльтатом работы программы является также среднее время безотказной
^ботЬ1 дублированной системы при отсутствии и при наличии последействия
Указов:
Гдс=608час, ГДС(Посл=554 час- -

344
ЧАСТЬ II. Лабораторный практикум. Лабораторная рабрщ
Таблица 8.4. Значения P{t) дублир<
/. час
0
40
80
120
160
200
240
280
320
360
400
Л.с«)
1
0,9997
0,9989
0,9968
0,9927
0,9854
0,9734
0,9544
0,9261
0,8860
0,8320
званной системы
* дс. послЧ*)
1
0,9999
0,9998
0,9995
0,9985
0,9964
0,9919
0,9832
0,9679
0,9432
0,9058
Рис. 8.9. Вероятность безотказной работы дублированной системы
без последействия (кривая 1) и с последействием отказов (кривая 2)
На основе полученных расчетов можно сделать следующие выводы:
D эффект последействия отказов отрицательно влияет на показатели наде>к
ности систем;
О определение вероятности безотказной работы системы при наличии п
следействия отказов элементов — более сложная вычислительная зада
чем при его отсутствии;

Надежность технических систем с учетом их физической реализуемости 345
0 имеет место существенное различие в графиках вероятностей безотказной
работы двух систем, а именно: для системы с экспоненциальными
распределениями времени до отказа элементов наблюдается достаточно быстрое
снижение надежности по сравнению с неэкспоненциальными
распределениями.
8.2.4. Задания к лабораторной работе
Выполнить анализ надежности двух систем без последействия и с
последействием отказов: система 1 задана структурной схемой, представленной на
рис. 8.4, a—е, система 2 — дублированная. Для системы 2 последействие
выражается уменьшением математического ожидания в 2 раза.
Указание: для элементов дублированной системы известны закон и
параметры распределения времени до отказа элементов. Определить математическое
"ожидание m и среднее квадратическое отклонение о*.
Вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
Номер схемы
рис. 8.4, а
рис. 8.4, б
рис. 8.4, в
рис. 8.4, г
рис. 8.4, д
рис. 8.4, е
рис. 8.4, а
рис. 8.4, б
рис. 8.4, в
рис. 8.4, г
рис. 8.4, д
рис. 8.4, е
рис. 8.4, а
рис. 8.4, б
рис. 8.4, в
рис. 8.4, г
рис. 8.4, д
X
0,01
0,02
0,015
0,03
0,02
0,01
0,025
0,02
0,01
0,03
0,011
0,02
0,013
0,021
0,007
0,01
0,015
X'
0,02
0,04
0,03
0,042
0,027
0,015
0,033
0,029
0,018
0,041
0,014
0,026
0,019
0,032
0,011
0,013
0,022
Распределение времени
до отказа элементов
дублированной системы
R(0,00005)
N(300; 5)
U( 100; 200)
TN(460; 100)
R(0,00002)
TN(200; 70)
Г(3; 250)
N(540; 100)
W(l,8; 220)
R(0,00008)
Г(3; 500)
TN(160;50)
U(300; 500)
TN(220; 80)
N(300; 90)
Г(2; 270)
R(0,00002)

346 ЧАСТЬ II. Лабораторный практикум. Лабораторная ра6рт^
(продолжение)
Вариант
18
19
20
21
22
23
24
25
26
27
28
29
30
Номер схемы
рис. 8.4, е
рис. 8.4, a
рис. 8.4, б
рис. 8.4, в
рис. 8.4, г
рис. 8.4, д
рис. 8.4, е
рис. 8.4, a
рис. 8.4, 6
рис. 8.4, в
рис. 8.4, г
рис. 8.4, д
рис. 8.4, е
X
0,022
0,006
0,011
0,01
0,02
0,02
0,009
0,012
0,018
0,02
0,019
0,015
0,011
X'
0,031
0,01
0,016
0,014
0,025
0,033
0,018
0,017
0,024
0,028
0,03
0,022
0,018
Распределение времени
до отказа элементов
дублированной системы
W(2,3; 240)
U(340; 400)
Г(3; 400)
N(190; 60)
Г(3; 180)
R(0,00004)
W(3; 200)
U( 150; 200)
TN(280; 60)
N(150; 40)
Г(2; 300)
Г(2; 100)
W(2,4; 250)

ЛАБОРАТОРНАЯ РАБОТА 9
АНАЛИЗ ВЛИЯНИЯ
ПРОФИЛАКТИКИ НА НАДЕЖНОСТЬ
ТЕХНИЧЕСКОЙ СИСТЕМЫ
9.1. Постановка задачи
Дано:
□ закон распределения времени безотказной работы системы и его
параметры;
D закон распределения времени восстановления системы и его параметры;
О Т2 — среднее время между очередными профилактиками, в часах;
О Гв2 — среднее время проведения профилактик, в часах.
Определить:
U математическое ожидание 7] и среднее квадратическое отклонение с{
времени безотказной работы системы без профилактики;
™ математическое ожидание Тв] и среднее квадратическое отклонение ав1
времени восстановления системы без профилактики.
Определить показатели надежности системы без профилактики:
Функцию готовности системы Krl(t);
среднее суммарное число отказов системы Mx(t);
сРеднюю суммарную наработку системы mx(t) за время /.
РеДелить для системы с профилактикой:
коэффициент готовности А"гс, наработку на отказ Тс и среднее время
восстановления Твс;

348 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа a
П зависимость коэффициента готовности системы от частоты профилактики
для различных значений времени ее проведения в виде таблицы и графцКа.
О оптимальное значение частоты профилактики Г2опт, при которой коэф.
фициент готовности системы Кгс превышает коэффициент готовности
Кг1 системы без профилактики и имеет при этом наибольшее значение.
Варианты заданий приведены далее в разд. 9.4.
9.2. Сведения из теории
Профилактика применяется с целью продления периода эксплуатации
системы. Теоретические вопросы изложены в [5,разд. 10.3]. Там же приведены
соотношения для расчета стационарных показателей надежности системы
с учетом проведения профилактик. Средняя наработка на отказ Гс, среднее
время" восстановления Гвс и коэффициент готовности Кгс вычисляются по
формулам:
*££
с М,{Т2) + КгХ{Т2)
т _^ЩТ2)+тв2кг1(т2)
Мх{Т2) + КгХ{Т2) '
Кгс = 3^2) (9.3)
/"1(г2)+7;1м1(г2)+гв2а:г1(г2)
где:
□ Т2 — время между профилактиками;
О Тв2 —время проведения профилактики;
□ КгХ(Т2) — функция готовности системы в момент времени Т2;
О /И{(Г2) — средняя суммарная наработка системы в течение времени Т2 \
П Mi (Т2) — среднее суммарное число отказов системы в течение времени п •
Из приведенных соотношений следует, что для системы с постоянной инте
сивностью отказов проведение профилактики оказывается лишним, °о
того, оно даже уменьшает коэффициент готовности системы. Поэтому пр°
дение профилактик в этом случае вредно. Профилактические работы м°
быть выгодны только для систем с неэкспоненциальным законом распр
ления времени до отказа. Критерием такой выгоды является выполнение
равенства:

лиализ влияния профилактики на надежность технической системы
349
Кгс>-^—. (9.4)
Если для заданных значений Т2 и Тв2 неравенство (9.4) имеет место, то
проведение профилактики целесообразно. Если это неравенство оказывается
неверным, то профилактика лишь уменьшает готовность системы. В этом
случае надо выяснить два вопроса:
(3 существует ли частота профилактики, для которой справедливо
неравенство (9.4);
О при положительном ответе на первый вопрос определить оптимальное
время между профилактиками Т2 опт, для которого коэффициент
готовности системы достигает максимального значения.
По формулам (9.1)—(9.3) можно рассчитать показатели надежности без
использования математических пакетов только для случая постоянных интен-
сивностей отказов и восстановлений системы. Однако как раз при этом
применять профилактику и не нужно. В общем случае для расчетов необходимо
иметь соответствующее программное средство. Будем использовать для
анализа надежности системы с профилактикой программу prevention.exe,
описание которой содержится в части IV.
Исходными данными являются параметры распределений. Для применения
программы требуется знание математического ожидания и среднего квадра-
тического отклонений этих распределений. Соответствующие формулы
содержатся в табл. 9.1.
Таблица 9.1. Связь параметров распределений с первыми двумя моментами
Распределение
Экспоненциальное Ехр(Х)
Равномерное Ща, b), a > 0
Гамма Г(а,(3)
Усеченное нормальное
TN(m0,a0)
т
1
к
а + Ь
2
аР
т0 + ка0
а
1
X
Ь-а
2л/з
V^P
1
i _"'"
1 Шп , С 2а2
*г4* ■ к"^е
( (т Yf'
С= 0,5+ Ф0 —
V Ч сто ))

350
ЧАСТЬ II. Лабораторный практикум. Лабораторная работ*
-——^ff 9
Таблица 9.1 (окончание)
В таблице Ф0(/) —функция Лапласа, Г(0 —гамма-функция.
9.3. Пример выполнения работы
Предположим, что время работы системы до отказа подчинено
распределению Вейбулла с параметрами а = 3, Р = 100 час. Время восстановления
системы имеет экспоненциальное распределение с параметром X = 0,05 час-1.
Среднее время между очередными профилактиками Г2=120 час, среднее
время проведения профилактик Гв2=1, 3 и 5 часов (рассмотреть три
варианта).
Решение. Для проведения расчетов воспользуемся формулами связи
начальных моментов с параметрами распределений. По табл. 9.1 находим
математическое ожидание времени безотказной работы системы:
m = рГ(1 + 1/а) = 100 • Г(1 +1/3) = 100- Г(1,3333).
Среднее квадратическое отклонение времени безотказной работы:
ст = р\/г(1 + 2/ос) - Г2 (1 + 1/а) = 100у]щ + 2/3) - Г2 (1 +1/3) =
= 1 OO-y/ni, 6667) - Г2 (1,3333).
Вычисление значений гамма-функции легко выполнить в программе Ех°е •
Для этого в ячейки А1 и А2 запишем выражения:
А1 = ЕХР(ГАММАНЛОГ(1,3333)),
А2 = ЕХР(ГАММАНЛОГ(1,6667)).
Тогда в этих ячейках получим:
Г(1,3333) = 0,8930, Г(1,6667) = 0,9028.
Распределение
Рэлея R(X)
Вейбулла W(a,P)
Нормальное N (/и, а) т>Ъа
т
<ы
РГ(1 + l/a)
т
а
U-it
V 4Х
р>/г(1 + 2/а)-Г2(1 + 2/а)
а

ливлиз влияния профилактики на надежность технической системы 351
лдедовательно,
7J = 100■ Г(1,3333) = 89,3 час, а, =100^(1,6.667)-Г2(1,3333) =32,5 час.
еще проще гамма-функцию вычислить в системе Derive 5. Для этого доста-
^чно в строке пользователя набрать выражение Г(1,3333) и, не выводя его
^ экран, нажать кнопку (=) слева от строки пользователя. На экране получим
0твет.
Среднее время восстановления системы равно Гв1 = — = 20 час. Таково же и
А.
значение ав1.
Вычислим коэффициент готовности системы без профилактики:
Кг1 = —^— = y,J =0,8170.
rl 7J+7;, 89,3 + 20
Для расчетов остальных характеристик воспользуемся программой
prevention.exe. После запуска программы необходимо ввести следующие
исходные данные:
О по времени безотказной работы системы:
• математическое ожидание 7] =89,3 час;
• среднее квадратическое отклонение о1 =32,5 час;
• выбрать из списка распределение Вейбулла;
О по времени восстановления системы:
• математическое ожидание Гв1 =20 час;
• среднее квадратическое отклонение aai = 20 час;
• выбрать из списка экспоненциальное распределение;
а время между очередными профилактиками Т2 = 120 час;
время проведения профилактик Тв2 = 1 час.
^Ультатами решения являются:
Показатели надежности системы без учета и с учетом профилактики;
Файл prevention.txt, содержащий требуемые по заданию характеристики
Надежности системы в зависимости от времени ее работы;
таблицу значений и график зависимости коэффициента готовности
системы от частоты профилактики.

352
ЧАСТЬ II. Лабораторный практикум. Лабораторная работ*
Показатели надежности системы при различном времени проведения профй
лактики приведены в табл. 9.2.
Таблица 9.2. Стационарные показатели надежности системы
Показатели
надежности
А'г
Гс, час
Твс, час
Без профилактики
0,8170
89,3
20
С профилактикой
Тв2 = 1 час
0,8540
64,6
11,05
Тл = 3 час
0,8435
64,6
11,99
Тв2 = 5 час
0,8332
64,6
12,93
Из таблицы следует, что профилактика заметно повышает коэффициент
готовности системы для широкого диапазона времени ее проведения. Если
время профилактики равно 1 часу, то выигрыш составит:
= 0,8540-0.8170, 5%
*г1 0,8170
Наработка на отказ не зависит от времени профилактики. Это ясно из
физических соображений, а также из таблицы и из формулы (9.1). Поскольку
после профилактики система обновляется, то время ее восстановления
сокращается, а за счет этого происходит увеличение коэффициента готовности.
Уменьшение времени восстановления системы Твс следует из формулы (9.2),
если Гв2 меньше ГВ|.
Программа создает файл prevention.txt, в котором содержится информация об
обобщенных показателях надежности системы, таких как параметр потока
восстановлений сов1(/), среднее суммарное число отказов Mx(t), средняя
суммарная наработка m{{t), функция готовности Krl(t). Все эти показатели
являются функциями времени и содержатся в табл. 9.3. Обобщенные
показатели присутствуют в расчетных формулах (9.1)—(9.3).
Таблица 9.3. Переходные характеристики надежности системы
/, час
0
6
12
18
24
Wel(0
0
0
0
0,0002
0,0005
мт
0
0,0002
0,0017
0,0058
0,0138
«КО
0
5,99969
11,99533
17,9777
23,93337
KrlO
1
0,999797
0,99849
0,995255
0,989514

шапиз влияния профилактики на надежность технической системы
Таблица 9.3 (окончание)
353
t, час
30
36
42
48
54
60
66
72
78
84
90
96
102
108
114
120
юВ|(/)
0,0009
0,0015
0,0022
0,0031
0,0041
0,0051
0,0062
0,0073
0,0083
0,0093
0,01
0,0106
0,011
0,0112
0,0112
0,011
то
0,0267
0,0458
0,0717
0,1051
0,1463
0,1953
0,2515
0,3141
0,3819
0,4535
0,5271
0,6012
0,6742
0,7447
0,8117
0,8747
«,(/)
29,84612
35,6982
41,47155
47,14902
52,71562
58,15974
63,4742
68,65719
73,71261
78,65047
83,48615
88,23987
92,93492
97,59615
102,2481
106,9129
*п(0
0,980908
0,969282
0,954687
0,937382
0,917827
0,89668
0,87476
0,853007
0,832417
0,813962
0,798505
0,786715
0,778996
0,775441
0,775821
0,779606
Рис. 9.1. Функция готовности системы

Рис. 9.2. Среднее суммарное число отказов системы
Рис. 9.3. Средняя суммарная наработка системы
354 ( ЧАСТЬ II. Лабораторный практикум. Лабораторная работ-
На рис. 9.1—9.3 изображены графики обобщенных показателей. Функш,
готовности (рис. 9.1) имеет колебательный характер. За время 120 часов 0цЯ
еще не вошла в стационарный режим и достаточно далека от коэффициенте
готовности, равного А"г1 =0,8170. В момент времени 120 часов кривая нах0
дится ниже своего предельного значения.
Среднее суммарное число отказов (рис. 9.2) и средняя суммарная наработка
(рис. 9.3) имеют возрастающий характер. Отношение 7] (/) = —'— характе
ризует среднюю наработку системы в течение времени /. Предельное
значение 7] (/) совпадает с наработкой на отказ 7].

Анализ влияния профилактики на надежность технической системы
определим зависимость коэффициента готовности системы от частоты
профилактики. Для этого пересчитаем строки табл. 9.3 по формуле (9.3).
Получим табл. 9.4.
Таблица 9.4. Коэффициент готовности системы при различных значениях Тг и Гв2
Тг, час
0
6
12
18
24
30
36
42
48
54
60
66
72
78
84
90
96
102
108
114
120
Гв2 = 1 час
0
0,856672
0,920747
0,941785
0,949779
0,951695
0,949837
0,945539
0,939441
0,932039
0,923721
0,914891
0,905861
0,896932
0,88836
0,880408
0,873225
0,866947
0,861658
0,857369
0,854029
Гв2 = 3 час
0
0,666404
0,798369
0,852854
0,880618
0,895665
0,903248
0,906094
0,905612
0,90274
0,89814
0,892388
0,88592
0,879123
0,87232
0,865826
0,859836
0,854528
0,850019
0,846358
0,843523
Тв2 = 5 час
0
0,545294
0,704705
0,779268
0,820846
0,845867
0,861015
0,869808
0,874135
0.875228
0,873937
0,870965
0,866837
0,862008
0,85685
0,85172
0,846853
0,842459
0,83869 ,
0,835625
0,833272
Рафическая иллюстрация табл. 9.4 дана на рис. 9.4.
/^Дая кривая, изображенная на рисунке, имеет точку максимума. Это зна-
1гр» что существует оптимальная точка, в которой коэффициент готовности
аКсимален. Для различного времени профилактики оптимальная точка
2.огтг и наибольшее значение Кг1 приведены в табл. 9.5.
355

356
ЧАСТЬ II. Лабораторный практикум. Лабораторная работ*
Рис. 9.4. Коэффициент готовности системы в зависимости
от частоты и глубины профилактики
Таблица 9.5. Оптимальный план профилактики
Время проведения профилактики
Тл = I час
Гв2 = 3 час
Тв2 = 5 час
7*2, о™ час
30
42
54
Кт\ (макс.)
0,9517
0,9061
0.8752
Оптимальная частота профилактики получена здесь приближенно, поскольку
табл. 9.4 рассчитана с шагом 6 часов. Используя файл prevention.txt, можно
более точно получить Т2 опт и максимальное значение Ку].
Проведенные расчеты и полученные результаты позволяют сделать следу10"
щие выводы:
□ система, имеющая экспоненциальное время до отказа, в профилактике н
нуждается; профилактика оказывает негативное влияние на коэффииие
готовности системы;
□ для систем с переменной интенсивностью отказа профилактика м°*
дать ощутимый выигрыш по среднему времени восстановления и коэфФ
циенту готовности;
□ профилактика ведет к сокращению наработки на отказ;
О на основе 'известных законов распределения времени до отказа и вое
новления можно определить частоту и глубину профилактики. Су^

Анализ влияния профилактики на надежность технической системы 357
венную помощь в этом вопросе может оказать компьютерная программа
prevention.exe.
9.4. Варианты заданий
к лабораторной работе 9
Требуется оценить влияние профилактики на надежность системы в
соответствии со своим вариантом.
В таблице вариантов заданий приняты следующие обозначения законов
распределения времени до отказа и времени восстановления:
О R — Рэлея;
(3N — нормальный;
Я U — равномерное;
О W — Вейбулла;
П Г — гамма;
О TN — усеченно нормальный;
О Ехр — экспоненциальный.
В скобках указаны параметры закона для данного варианта задания.
Вариант
1
2
3
4
5
6
7
8
9
10
И
12
Закон распределения
Времени до отказа
R(0,006)
N(300; 15)
U(200; 250)
W(2; 220)
Г(3,5;110)
UN(200; 12)
Г(3; 125)
R(0,002)
W( 1,8; 220)
R(0,008)
Г(3,2; 150)
TN(320; 30)
Времени восстановления
Ехр(0,1)
Exp(0,06)
Exp(0,13)
Exp(0,16)
Exp(0,025)
Exp(0,08)
Exp(0,l)
Exp(0,06)
Exp(0,08)
Exp(0,ll)
Exp(0,08)
Exp(0,12)
T2
60
200
200
180
300
190
270
100
170
50
400
320
ТЛ
1,3,5
1,3,5
1,3.5
1,3,5
1,3,5
1,3,5
1,3,5
1,3.5
1,3,5
1,3,5
1.3,5
1,3,5

358 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа
(окончание)
Вариант
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Закон распределения
Времени до отказа
11(300; 400)
UN(220; 10)
N(300; 14)
Г(2; 270)
TN(270; 15)
W(2,3; 240)
U(340; 400)
R(0,004)
N(190; 6)
Г(3; 170)
N(400; 20)
W(3; 200)
U( 150; 200)
TN(280; 12)
N(150; 7)
Г(2; 300)
Г(2; 100)
W(2,4; 250)
Времени восстановления
Exp(0,04)
Exp(0,07)
Exp(0,09)
Exp(0,06)
Exp(0,03)
Exp(0,l)
Exp(0,05)
Exp(0,03)
Exp(0,08)
Exp(0,ll)
Exp(0,085)
Exp(0,15)
Exp(0,075)
Exp(0,06)
Exp(0,U)
Exp(0,075)
Exp(0,2)
Exp(0,07)
Тг
290
340
230
400
290
200
310
80
160
500
350
150
160
210
110
430
230
220
Ta2
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5
1,3,5

ЛАБОРАТОРНАЯ РАБОТА 10
ИССЛЕДОВАНИЕ ВЛИЯНИЯ
ВРЕМЕННОГО РЕЗЕРВИРОВАНИЯ
НА НАДЕЖНОСТЬ ТЕХНИЧЕСКОЙ
СИСТЕМЫ
10.1. Постановка задачи
Дано:
□ восстанавливаемая система с пополняемым временным резервом;
|J закон распределения времени безотказной работы системы;
□ закон распределения времени восстановления системы;
О /рез — величина пополняемого временного резерва, в часах.
Определить:
О математическое ожидание т и среднее квадратическое отклонение а
времени безотказной работы нерезервированной системы;
О математическое ожидание тъ и среднее квадратическое отклонение ств
времени восстановления нерезервированной системы;
О показатели надежности системы с временным резервом:
• наработку на отказ Грез;
• среднее время восстановления Гврез ;
• коэффициент готовности Кг ^ ; <
• вероятность безотказной работы /^.(О;
u показатели надежности системы без учета временного резерва:
• наработку на отказ Т ;
• среднее время восстановления Тв;

360 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа iq
• коэффициент готовности Кг;
• вероятность безотказной работы P(t);
□ выигрыш надежности системы от введения временного резерва.
Варианты заданий приведены в разд. 10.4.
10.2. Сведения из теории
Временное резервирование (временная избыточность) является важным
способом повышения надежности технических и особенно информационных
систем. Система обладает временным резервом, если для устранения отказа
она имеет определенный запас времени. Временной резерв может быть как
постоянной, так и случайной величиной.
Если после любого отказа системы временной резерв имеет один и тот же
запас времени, то резерв является пополняемым. Если в результате отказа
система продолжает "расходовать" резервное время, оставшееся после
предыдущего отказа, то резерв является непополняемым. В зависимости от этого
различают системы с пополняемым или с непополняемым резервом времени.
Предположим, что система обладает пополняемым резервом времени. Тогда
стационарные показатели надежности, такие как наработка на отказ, среднее
время восстановления и коэффициент готовности, определяются
следующими соотношениями:
оо оо со
Т+ \G{t)H{t)dt \G(t)H(t)dt T+ \G{t)H{t)dt
тс=—°- , твс=£ , кг=—°- лм.\)
Cqo 'ВС оо 'Г Т А-Т
\G(t)h(t)dt \G{t)h{t)dt B
о о
где:
□ Г — наработка на отказ системы при отсутствии временного резерва;
О Тв — среднее время восстановления системы при отсутствии временног
резерва;
О G(t) — функция распределения времени восстановления систем*»-
G(/) = l-G(0;
О H(t) — функция распределения резерва времени, H{t) = 1 - #(/) •
-•tO
В частности, при постоянном резерве времени, равном /рез, имеют ме°
формулы:

таблице Ф0(/) — функция Лапласа, Г(0 — гамма-функция, /(а,/) —
нежная гамма-функция.
Влияние временного резервирования на надежность технической системы 367
т Т + Ъ-М^) vftpcJ v Т + Тв-ц,(^)
I— _ i =__ д = (lU.Z)
где
oo
y(/) = |G(/+ *)<&.
о
Выражения функции \y(t) для различных распределений вероятностей
приведены в табл. 10.1.
Таблица 10.1. Функция ц/(/) для различных распределений
Распределение
Экспоненциальное Ехр(Х)
Равномерное U(a, b\ a 2.0
Гамма Г(а,(3)
Усеченное нормальное TN(/»0,ct0)
Рэлея ЩХ)
Вейбулла W(cc,p)
Нормальное N(m, a), m > За
00
ц/(0= l<3(t+x)dx
0
1 -и
—е
1 '
( Ь + а
/, К а:
2
(b-i)2
<- —, a$t<b;
2(6-а)
0, t>b
V
( ( t\\ f ( t\\
ар 1-/ а + 1. - -/ 1-/ а,-
c20g{l)-{t-m0)G(t)
J-(0,5-O0(V2X/))
Prf4_/i,fAYll
а ЧаД ^а VP/ ))
a2g(t)-(i-m)GU)

362 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа iq
Показатели надежности системы зависят от закона распределения времени
восстановления системы и величины временного резерва и не зависят от
закона распределения времени безотказной работы. Это следует из формул
(10.1) и (10.2). Насколько велика данная зависимость, предстоит выяснить в
лабораторной работе.
Функция готовности системы с пополняемым резервом времени определяется
выражением:
Kr(t) = F(t) + (F*g + GH)* co(0, (10.3)
где:
□ F(t) — функция распределения времени безотказной работы системы,
F(/) = 1-F(0;
□ g(/) — плотность распределения времени восстановления системы;
□ со(/) — параметр потока отказов нерезервированной системы:
<о(0=1/,(*+"*Л);
□ * — обозначение свертки функций:
f*g(0=\f(t-x)g(x)dx;
о
О у*( +1)(/) — (k+ 1)-кратная свертка функции f{t);
□ g*^k\t) — ^-кратная свертка функции g(t).
Вероятность безотказной работы системы с пополняемым резервом времени
есть решение следующего интегрального уравнения:
P(t) = P*f* (gH)(t) + F(t) + f * (GH)(t). (10-4)
Заметим, что временные показатели надежности зависят от закона распреД6'
ления времени безотказной работы.
Интегрируя (10.4), получим выражение для среднего времени безотказно»
работы системы:
)(F(t) + f*(GH)(t))dt ■ T + ™\G{t)H{t)dt
т _о о
1 |с — —
\-)(gH)(t)dt ™\G{t)h(t)dt
о о

Влияние временного резервирования на надежность технической системы 363
Йз формулы (10.1) следует, что среднее время безотказной работы равно
наработке на отказ: Г1с = Тс.
faKHM образом, расчетные соотношения для всех основных показателей
надежности системы с пополняемым временным резервом у нас есть. Однако
Проведение вычислений без использования компьютерных средств
затруднительно, да и нецелесообразно. Воспользуемся программой timerezerve.exe,
описание которой дано в части IV. Программа рассчитывает показатели
надежности системы с временным резервом на основе соотношений (10.1)—
(10.4).
10.3. Пример выполнения
лабораторной работы
Исходными данными задачи являются:
О время до отказа имеет гамма-распределение с параметрами а = 16,
{3 = 12,5 час;
О время восстановления имеет распределение Рэлея с параметром
X = 0,007854 час"1;
□ временной резерв составляет fpe3 = 5 час.
Вычислим начальные моменты для гамма-распределения и распределения
Рэлея по формулам из табл. 9.1.
Математическое ожидание времени безотказной работы системы равно:
т = сф = 16-12,5 = 200 час.
Среднее квадратическое отклонение времени безотказной работы равно:
CT = VaP = 4-12,5 = 50 час.
Математическое ожидание времени восстановления системы равно:
ПГ J 3,14159
тЛ=А—= = 10 час.
в V4X V40^07854
вреднее квадратическое отклонение времени восстановления равно:
/4^Г /4-3,14159 _.
aB = J = / = 5,2 час.
Указатели надежности системы с временным резервом и без временного
^езерва вычислим по программе timerezerve.exe. После запуска программы
^Изводится ввод законов распределения времени безотказной работы, вре-

Таблица 10.2. Показатели надежности системы
при наличии и отсутствии резерва времени
Временной резерв
Есть
Нет
Т& час
249,1
200
Ты час
6,4606
10
Кг
0,9747
0,9523
Таблица 10.3. Вероятность безотказной работы системы
при наличии и отсутствии резерва времени
/, час
0
8
16
24
32
•40
48
56
64
72
80
88
96
104
112
120
128
vw
1
1
1
1
0,9999
0,9999
0,9999
0,9999
0,9999
0,9998
0,9995
0,9988
0,9973
0,9935
0,9877
0,9787
0,9635
РЦ)
1
1
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9996
0,999
0,9974
0,9942
0,9884
0,9787
0,9637
0,9424
/, час
136
144
152
160
168
176
184
192
200
208
216
224
232
240
248
256
264
/wo
0,9442
0,9195
0,8896 '
0,8549
0,7992
0,7474
0,6933
0,6383
0,5841
0,5318
0,4827
0,4375
0,3967
0,3606
0,3291
0,2946
0,269
Pit)
0,9136
0,877
0,8326
0,781
0,7234
0,6614
0,5967
0,5312
0,4667
0,4047
0,3465
0,2929
0,2447
0,202
0,1649
0,1331
0,1064
/, час
272
280
288
296
304
312
320
328
336
344
352
360
368
376
384
392
400
Л«.(0
0,2474
0,2292
0,214
0,2011
0,1902
0,1808
0,1724
0,1647
0,1576
0,1508
0,1441
0,1375
0,131
0,1243
0,1П7
0,111
0,1043
Pit)
0,0841
0,0659
0,051!
0,0393
0,03
0,0226
~~однГ
0,0126
0,0093
0,0068
0^005^
00^
0.0026^
о.оо|^
^^
Рассчитаем выигрыш надежности системы от введения временного ^р
За показатель выигрыша примем относительный процент повышени
364 ЧАСТЬ II. Лабораторный практикум. Лабораторная сяк
_ . С5?ОГа ,
мени восстановления, рассчитанных значений начальных моментов:
тв, ств, а также резерва времени. Нажатие кнопки Расчеты приводит * °'
числению показателей надежности. Стационарные показатели приведи **"
табл. 10.2, а вероятность безотказной работы — в табл. 10.3. bI в
Графики вероятности безотказной работы показаны на рис. 10.1.

а временного резервирования на надежность технической системы 365
надежности системы от введения временного резерва. Согласно
ф® |Q о относительное превышение надежности будет иметь следующее
л по наработке на отказ:
т т
q =_ьт—L. юо% = 24,6%;
'с т*
*с
0 среднему времени восстановления:
Т -Т
G =_вс—2SE£i..ioo% = 35,4%;
'ВС f
$ по коэффициенту готовности:
2(Кг „л., — Кг)
G„ =—X-IiEHi Li.ioo% = 2,3%;
Лг,рез. "г Лг
О по коэффициенту простоя:
G„ = - 2iE!il.ioo% = 61,4%.
Лп,рез. ^ Лп
Результаты аналогичных расчетов по вероятности безотказной работы в
соответствии с формулой:
G = РезЛ UL. 1 оо%
( ^рез. (0 + ^(0
сведены в табл. 10.4.
«•I. Вероятность безотказной работы системы с резервом времени (кривая 1).
без резерва времени (кривая 2)

366 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа m
Таблица 10.4. Выигрыш от временного резерва по />(/)
/, час
0
8
16
24
32
40
48
56
64
72
80
88
96
104
112
120
128
GPd)
0
0
0
0
0
0
0
0
0
0,0
0,1
0,1
0,3
0,5
0,9
1,5
2,2
/, час
136
144
152
160
168
176
184
192
200
208
216
224
232
240
248
256
264
Gp(t)
3,3
4,7
6,6
9,0
10,0
12,2
15,0
18,3
22,3
27,1
32,9
39,6
47,4
56,4
66,5
75,5
86,6
/, час
272
280
288
296
304
312
320
328
336
344
352
360
368
376
384
392
400
Gp«)
98,5
110,7
122,9
134,6
145,5
155,6
164,1
171,6
177,7
182,7
186,6
189,8
192,2
194,3
195,6
196,8
197,7
Графическая иллюстрация выигрыша по показателю P(t) показана на
рис. 10.2.
Выполненные расчеты и графики позволяют сделать следующие выводы:
□ временное резервирование, как и другие виды резервирования, повышает
надежность системы по всем показателям надежности;
О количественная оценка увеличения надежности от введения временног
резерва может быть получена численными методами на основе вариаШ1
законов распределения, их параметров и величины временного резерва;
□ выигрыш от временного резерва для различных показателей различнь
но он особенно высок для коэффициента простоя системы;
□ выигрыш по вероятности безотказной работы возрастает с течением &Р
мени и приближается к стационарному значению, равному 200 %.

сияние временного резервирования на надежность технической системы
367
Jp(i)
Рис. 10.2. Выигрыш от временного резервирования по вероятности
безотказной работы системы
Следует иметь в виду, что большой выигрыш по вероятности безотказной
работы достигается тогда, когда вероятность безотказной работы системы
мала и нет смысла ее эксплуатировать даже при наличии временного резерва.
При практически допустимой вероятности безотказной работы выигрыш не
большой и составляет единицы процентов.
Полезно оценивать эффективность временного резервирования выигрышем
надежности по вероятности отказа:
г <,л ]-рУ
где 1-Р(г) — вероятность отказа нерезервированной системы, 1-^3.(0 —
вероятность отказа резервированной системы.
Расчеты показывают, что для данного примера выигрыш надежности слабо
зависит от t и практически Gq(t)<2. С увеличением резерва времени выиг-
РЫщ существенно возрастает.
ь
° лабораторной работе исследуйте зависимость выигрыша надежности от
^личины временного резерва.
1°.4. Варианты заданий
к Лабораторной работе 10
^Мполните анализ влияния временного резервирования на надежность сис-
**Ь1 в соответствии со своим вариантом задания.

368 ЧАСТЬ II. Лабораторный практикум. Лабораторная работа 1д
В таблице приняты следующие обозначения законов распределения времени
до отказа и времени восстановления:
П R — Рэлея;
О N ^— нормальный;
DU — равномерное;
О W — Вейбулла;
О Г— гамма;
О TN — усеченно нормальный.
В скобках указаны параметры закона для данного варианта задания.
Вариант
I
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Закон распределения
Времени до отказа
R(0,006)
N(300; 15)
U(200;250)
W(2; 220)
Г(3.5;110)
. TN(200; 12)
Г(3; 125)
R(0,002)
W( 1,8; 220)
R(0,008)
Г(3,2; 150)
TN(320; 30)
U(300; 400)
TN(220; 10)
N(300; 14)
Г(2; 270)
TN(270; 15)
W(2,3; 240)
U(340; 400)
R(0,004)
Времени восстановления
N(30;8)
U(20; 25)
W(2; 22)
l(3,5;ll)
TN(20; 12)
Г(3: 12)
R(0,02)
W(K8;22)
R(0,08)
1(3,2; 15)
TN(32; 10)
U(30; 40)
TN(22; 10)
N(30; 4)
Г(2; 27)
TN(27; 5)
W(2,3;24)
U(34; 40)
R(0,04)
N(19; 6)
Резерв
времени
6
10
4
4
22
7
5
10
8
6
9
6
17
11
12
9
20
8
15
21

йрияние временного резервирований на надежность технической системы 369
(окончание)
Вариант
21
22
23
24
25
26
27
28
29
30
Закон распределения
Времени до отказа
N(190; 6)
Г(3; 170)
N(400; 20)
W(3; 200)
U( 150; 200)
TN(280; 12)
N(150; 7)
Г(2; 300)
Г(2; 100)
W(2,4; 250)
Времени восстановления
Г(3; 17)
N(40; 13)
W(3; 20)
U(15;20)
TN(28; 12)
N(15; 5)
Г(2; 30)
fixp(0,l)
W(2,4; 25)
R(0,06)
Резерв
времени
11
7
10
8
10
12
7
12
3
11

• ЧАСТЬ III
КУРСОВОЕ ПРОЕКТИРОВАНИЕ
ЦЕЛИ И ЗАДАЧИ КУРСОВОГО ПРОЕКТИРОВАНИЯ
Глава 1. ТЕМАТИКА КУРСОВОГО ПРОЕКТИРОВАНИЯ
Глава 2. ТЕМАТИКА КУРСОВЫХ РАБОТ

ЦЕЛИ И ЗАДАЧИ
КУРСОВОГО ПРОЕКТИРОВАНИЯ
В учебных планах дисциплин, содержащих основы теории надежности,
планируется курсовой проект или курсовая работа.
Основными целями и задачами курсового проектирования являются:
О более глубокое изучение теории надежности;
□ приобретение умений и навыков применения теории надежности при
проектировании высоконадежных технических систем.
Для достижения этих целей студент в курсовом проекте должен разработать
структурную схему системы, удовлетворяющую требованиям надежности.
При этом система может быть задана как невосстанавливаемая или
восстанавливаемая, длительного или короткого времени существования,
допускающая или не допускающая структурное резервирование и т. д.
Исходными данными для проектирования оптимальной структуры должны
быть:
О сложность системы (число элементов);
О вид системы (восстанавливаемая или не восстанавливаемая, длительного
или короткого времени работы);
О показатели надежности элементов (вид законов распределения до отказа,
численные значения показателей надежности каждого элемента);
^ время работы системы;
^ показатели восстановления: число обслуживающих бригад, приоритет в
обслуживании, показатели ремонтопригодности элементов (интенсивность
или среднее время восстановления);
^ ограничения на практическую реализацию: возможность использования
структурного, нагрузочного, временного резервирования, допустимая глу- -
бина структурного резервирования, максимально допустимая степень
нагрузочного резервирования, возможность реализуемости структурного
резервирования, наличие последействия отказов элементов;
Требования на показатели надежности элементов.

374 ЧАСТЬ III. Курсовое проектировав
По этим исходным данным студент должен разработать оптимальную струк.
турную схему системы. Оптимальной считается такая структурная схема, к0„
торая имеет минимальное число элементов и удовлетворяет требованиям
надежности. Для достижения этой цели необходимо выполнить следующее
процедуры синтеза оптимальной структуры:
□ рассчитать показатели надежности исходной системы;
□ разработать алгоритм синтеза оптимальной структуры, в простейшем
случае — алгоритм последовательного повышения надежности элементов;
□ разработать математические модели синтеза структуры, представляющие
собой формулы показателей надежности элементов и системы на
различных этапах синтеза;
□ разработать компьютерные технологии решения задачи синтеза;
□ решить задачу синтеза оптимальной структуры.
Если в учебном плане имеется курсовая работа, то тематика проектирования
должна быть иной, чем при курсовом проектировании. Она должна носить
исследовательский характер. Темами курсовой работы могут быть:
□ сравнительная оценка различных методов анализа надежности;
□ исследование влияния законов распределения отказов и восстановления
элементов на надежность системы;
□ анализ эффективности различных методов обслуживания техники
(влияние приоритетности обслуживания);
□ сравнительная оценка различных методов повышения надежности
техники;
□ оценка надежности техники с учетом физической реализуемости
резервирования;
□ компьютерные технологии анализа надежности сложных систем.
В качестве рекомендаций по содержанию и оформлению курсовой работы
можно отметить следующее.
Курсовая работа должна содержать такие разделы, как:
О титульный лист;
О задание на курсовую работу;
□ оглавление;
□ введение;
П постановку задачи;

1ШИ и задачи курсового проектирования . 375
0 решение задачи аналитическими или численными методами;
0 результаты решения задачи на ЭВМ с анализом результатов;
0 графическое представление результатов;
д численные расчеты требуемых характеристик надежности элементов и
системы;
0 библиографический список.
курсовую работу следует оформлять по ГОСТ 2.105-95 ЕСКД на одной
стороне листа бумаги формата А4 (210x297 мм) со следующими полями вокруг
текста: слева — 25 мм, справа — 10 мм, сверху — 20 мм, снизу — 25 мм.
Первым листом курсовой работы является титульный лист. За титульным
листом следует лист задания, на курсовую работу, далее — оглавление.
Разделы и подразделы, если таковые предусмотрены, обозначаются арабскими
^фрами: первая цифра обозначает номер раздела, вторая — номер
подраздела (разделяются точкой).
Наименования разделов в тексте курсовой работы всегда пишутся
прописными (большими) буквами, а подразделов— строчными (малыми). Номера
страниц в оглавлении проставляются только после того, как работа
составлена и сброшюрована.
Нумерация страниц в тексте начинается с титульного листа. Номера ставятся
на полях над текстом в верхнем правом углу. На титульном листе номер
страницы не ставится.
Остальные разделы курсовой работы следует выполнять по образцу,
указанному в соответствующих разделах книги.

ГЛАВА 1
ТЕМАТИКА
КУРСОВОГО ПРОЕКТИРОВАНИЯ
В этой главе приводятся четыре темы курсового проекта с большим числом
вариантов в каждой теме. В первой теме ставится задача, описывается
методика ее решения, приводятся алгоритмы анализа и синтеза оптимальной
структуры системы, излагаются компьютерные технологии решения задачи.
Вторая тема посвящена вопросам проектирования технической системы по
заданным показателям надежности и риска, приводится пример выполнения
курсового проекта. Третья тема посвящена разработке компьютерных
технологий анализа надежности системы по данным ее эксплуатации. Решается
практическая задача оценки надежности систем самолета ТУ-154М. В
четвертой теме определяется структурная схема системы длительного
использования, которая удовлетворяет требованиям надежности и ограничениям на
техническую реализацию.
Тема 1. Синтез оптимальной структуры
технической системы по обеспечению
ее надежности
1.1. Постановка задачи
Дано:
□ структурная схема системы, представляющая собой основное
(последовательное) соединение элементов;
□ п — число элементов;
□ / — время непрерывной работы системы;
□ %i, / = 1, 2,..., п — интенсивность отказа элементов исходной системы,
□ /в;, / = 1,2,..., п— среднее время восстановления элементов исхоДн
системы;
□ R^ — коэффициент оперативной готовности.

Хематика курсового проектирования 377
Для всех вариантов задания и = 10, / = 10 час, R^. =0,95. Значения А,, и tBj
приведены далее в разд. 1.5.
Определить:
р оптимальную структурную схему системы, удовлетворяющую
требованиям надежности;
0 показатели надежности системы: вероятность безотказной работы Pc(t),
среднее время безотказной работы Т1с, коэффициент готовности Кгс,
наработку на отказ Тс.
Оптимальной считается структурная схема, удовлетворяющая требованиям
надежности и имеющая минимальное число резервных элементов.
Предполагается, что справедлив экспоненциальный закон распределения
отказов и восстановления отказавших элементов.
1.2. Методика решения задачи синтеза
структуры системы
Для обеспечения требуемой надежности R^ =0,95 используется структурная
избыточность. Допускается применение любого ее вида. При этом
рекомендуется следующая последовательность решения задачи:
П анализ надежности исходной системы;
О определение кратности общего резервирования, обеспечивающего
требования надежности;
О определение кратности раздельного резервирования, обеспечивающего
требования надежности при минимальном числе резервных элементов;
О определение показателей надежности системы оптимальной структуры.
1-2.1. Анализ надежности исходной системы
коэффициент оперативной готовности определяется выражением:
WO = ^)pc(t + x)ck = Krc~)pc(t + x)dx,
1 +/в 0 1 0
°Торое, по крайней мере, для экспоненциального распределения можно
забить приближенной оценкой:
^(/) = *геРс(/).
УДем анализировать надежность исходной системы по критерию
/* ^гс^сСО > гДе ^гс — коэффициент готовности системы, PG(t) — вероят-
^ть безотказной работы системы в течение времени /.

378
ЧАСТЬ III. Курсовое проектирование. Глаь*
Коэффициент готовности системы вычисляется по формуле:
Вероятность безотказной работы системы при условии независимости отка-
зов ее элементов определяется по формуле:
где Pj(t) — вероятность безотказной работы /-го элемента.
Предполагается, что интенсивность отказов элементов есть величина
постоянная. Тогда
п
где A,C = £A.,..
Одновременно с расчетом коэффициента оперативной готовности системы
рассчитываются коэффициент готовности и вероятность безотказной работы
элементов системы. Это необходимо для установления влияния надежности
элементов на надежность системы и принятия решения об их
резервировании. Расчеты целесообразно свести в следующую таблицу:
По данным таблицы находятся показатели надежности системы 'сЛ''
1.2.2. Определение кратности общего резервирования
Определение кратности m общего резервирования с постоянно включен
резервом и по методу замещения осуществляется путем решения следу10
трансцендентных уравнений:
X/, час"1
г* час
Р,
Р,«)
Kri
1
2
3
4
5
6
7
8
9
10

Тематика курсового проектирования
379
0 постоянно включенный резерв:
( \
^=(l-(l-Pc(/))'-1) l-_-ir_ ;
{ /=i<!PcJ
р резервирование замещением:
/-о <• 1 + ZJ_
V '=1 Рс )
В формулах приняты следующие обозначения:
О Pc(t) — вероятность безотказной работы нерезервированной системы;
п
О Rf. = 0,95 — заданное значение коэффициента оперативной готовности.
1.2.3. Определение кратности раздельного резервирования
Методика определения кратности раздельного резервирования состоит в
следующем: по данным расчета надежности исходной системы выбирается
наименее надежный элемент (у которого рс наименьший) и дублируется таким
же элементом методом постоянного резервирования.
Выполняется расчет надежности системы новой структуры, т. е. структуры с
°Дним дублированным элементом. Если надежность новой системы не
удовлетворяет требуемой (i^.>0,95), то выбирается следующий наименее
надежный элемент, который также дублируется, и вновь ведется расчет надеж-
^ти системы теперь уже с двумя резервными элементами. Вновь
проверяли условие Rc > 0,95 и т. д., до тех пор, пока условие не будет выполнено.
сли в процессе такого последовательного приближения окажется, что наи-
еНее надежным является уже дублированный элемент, то его резервируют
ец*е раз.
Ли условие Rf. > 0,95 выполнено, то считается, что оптимальная структура
Нцена. Теперь следует определить число ее элементов и вычислить
показали надежности.

380 ЧАСТЬ HI. Курсовое проектирование. Глаяа
Аналогичные расчеты следует выполнить, применяя раздельное резервироВа
ние замещением.
В результате расчетов будут получены две структуры, удовлетворяющие тре.
бованиям надежности. Выполнив их сравнительный анализ, следует выбраТь
оптимальную с позиции минимума числа элементов.
1.2.4. Определение показателей надежности
оптимальной системы
Вероятность и среднее время безотказной работы оптимальной системы
рассчитываются по методам, известным в теории надежности [5].
Коэффициент готовности и наработка на отказ восстанавливаемой системы при
большой кратности резервирования могут быть вычислены одним из
приближенных методов. Предпочтительным является метод, основанный на допущении
независимости восстановления элементов системы.
1.3. Алгоритмы анализа и синтеза
оптимальной структуры системы
Алгоритмы анализа и синтеза оптимальной структуры системы представляют
собой совокупность математических выражений и формул, позволяющих
рассчитать показатели надежности исходной системы и определить кратность
различных видов резервирования, обеспечивающих требования надежности,
а также позволяющих рассчитать показатели надежности оптимальной
системы.
Алгоритмы анализа надежности исходной системы выглядят следующим
образом:
я
лс = 2* ^;»
/=1
р/:
РЛО--
Kri-
~ /в/» — ' »•••
п
л
=Пл('),1(')=
/=1
1 10
, i = 1, 2,.
1 + Р/
,и,
-е с
..,и,

фматика курсового проектирования
381
к l - ]
i + Zp/
1=1
^=АГгеРс(0.
Алгоритмы определения кратности общего резервирования следующие:
р постоянно включенный резерв:
V /=w!PcJ
О резерв замещением:
С CV //-, ., от+1 «
,=о '• 1+Х-у
< /=1 Рс >
Кратность раздельного резервирования оптимальной системы определяется
так:
О раздельное постоянное резервирование:
^=(l-(l-pIГ+,,l-(l-p2Г+1,...,l-(l-/?и)'"»+,,
(1-(1-/71Г"+1)(1-(1-/72Г^1)...(1-(1-рл)'»^!)),
v = 1 ] 1—!_ 1 '
^г от,+1 1 ' ш2+1 1 ''"' т„+\ 1 '
I, /=1 /!Р| /=1 Ф2 /=1 Ф„
( V \ ( V
1 ' , ! ... I ! .
^ /=1 /!р, Д ,=i /!р2 ) \ ы\ i\pn))
Значение коэффициента оперативной готовности определяется как
произведение последних элементов векторов Vp и VK ;

382
ЧАСТЬ III. Курсовое, проектирование. Глаь
О раздельное резервирование замещением:
VP= P\(OL т. >P2(0L т. >->/w)2- 7. ,
[ /=0 '! 1=0 '! /=0 *!
^c(of:("ln;?/(0)/£(~ln/?2(0)/.-. x("ln/?/,(0)'l
/=o '! /=o '! "*/=o '! J'
F = i-—i— i-—L_ i__L_
^г /wh-1 i ' m2+I i ' '"' mn+\ i '
V ' = 1 Pi ' = 1 P2 ' = 1 P«
( Y ^ f Yl
, !_ , !_ ... , L_ .
w(+l i ffb+1 i /м„+1 i
^ ,=i pj Д ,=i p2 J { /=i p„ J J
Значение коэффициента оперативной готовности определяется как
произведение последних элементов векторов Vp и VK .
1.4. Компьютерные технологии анализа и синтеза
оптимальной структуры системы
Реализация на ЭВМ описанного ранее алгоритма синтеза оптимальной
структуры системы по критериям надежности требует решения следующих задач:
□ представление данных А,,-, /в/ в виде векторов;
□ умножение векторов для получения вектора рс;
О вычисление суммы элементов вектора для получения Хс и рс;
□ вычисление произведения элементов вектора для получения значен
D табулирование функции для получения значений Pt(t) и Kri;
О вычисление по формулам для получения значений Pc(t), Кгс, /^ •
Решение перечисленных задач обеспечивает все расчеты по анализу над
ности исходной системы. Л
Определение оптимальной структуры системы при использовании ои -
резервирования связано с определением оптимальной кратности m о

гаилатика курсового проектирования
383
резервирования с постоянно включенным резервом и по методу замещения,
решение этой задачи требует вычисления корней двух трансцендентных
уравнений.
Определение оптимальной кратности раздельного резервирования по
приведенным ранее алгоритмам требует многократных вычислений элементов
вектора, представляющих собой формулы вероятностей безотказной работы и
коэффициентов готовности каждого из элементов исходной системы,
резервированного m раз.
Выполнять расчеты студент может с помощью любых программных средств.
Наиболее эффективными из них являются универсальные программные
средства символьной математики, хорошо описанные в литературе.
1.5. Индивидуальные задания на проектирование
В этом разделе приводятся задания на проектирование. Студент выбирает
вариант, номер которого соответствует его номеру в групповом журнале.
Для всех вариантов число элементов исходной системы « = 10, время
непрерывной работы / = 10 час, требуемый коэффициент оперативной готовности
оптимальной системы R^. =0,95 . Значения интенсивностей отказов и среднее
|§емя восстановления элементов приведены в табл. 1.1.
Вар. 1
Вар. 2
Вар.з
Вар. 4
Вар. 5
Ц>.6
h
'в,
h
t«
К
'в,
Л*
'в,
к
'в/
к
'в,
1
1,2
10
4
2,5
0,7
14
5
2,4
2,5
12,5
1,5
11,5
2
5
2
1,4
9
2,5
2,5
1,4
12
1,6
7,8
6
2,4
Таблиц:
3
2
5
3
3,2
5*,4
г4,5
0,6
18,5
0,7
18
2,5
6,5
а 1.1. Варианты
заданий
№ элемента
4
0,8
20
0,5
2
3
7,5
2,2
5,4
2,5
5,4
0,7
18,5
5
1,5
8
0,8
12
2,5
10
2,4
11
6
2,8
2,5
11,5
6
2,5
12
5
6
2
8,5
1,6
8,5
1,5
11,5
1,8
9
7
3,2
8
2,5
10
0,8
19,6
5
5
0,9
16,5
3,5
9
8
5,6
5
2,7
10
2,5
5,5
3
7,6
2,5
3,4
5,2
4,8
9
2,4
3
3
2,5
4
2,5
0,7
14
4,8
6,5
2,2
3,7
10
0,8
15
1,5
8
1,5
9
2,5
3,2
3
7,8
0,6
13

384 ЧАСТЬ III. Курсовое проектирование. Главя
Таблица 1.1 (продолжещ
Вар. 7
Вар. 8
Вар. 9
Вар. 10
Вар. 11
Вар. 12
Вар. 13
Вар. 14
Вар. 15
Вар. 16
Вар. 17
Вар. 18
Вар. 19
Вар. 20
h
'■/
h
'а/
К
'«
h
1ы
h
'в/
h
'в,
К
'в/
х,
Ь
h
t*i
h
*Ml
h
t«
h
t*
h
to,
к
hi
№ элемента
1
0,6
14
0,7
14
1,6
10
1,4
12,3
1,8
3
1,2
8,5
1
10
10
1,2
1
8,6
1
10
7
4,8
1
9
1
10
2
5,2
2
2,6
4
2
4
6,5
2,2
5,5
7,8
6
2,8
6,5
3,4
7,2
3,2
1
12
2
7,3
0,8
17
0,8
15
8,5
3
9
1,2
1
9,8
3
4,8
4,5
5
4,5
1,5
4,8
1,8
15
1,4
4,1
1,2
8,3
1,2
8,5
1
8,7
11
1,5
12
2
1
8,5
1,3
9
0,8
13,5
11
1,2
4
3,8
7,3
4
7,3
0,6
21
0,9
17,2
1
10
0,7
20
0,9
15,4
0,9
18,5
0,4
25,2
0,6
18,6
11
2,5
0,6
18,5
5
2,1
2,5
4,3
5
2,2
12,5
2,5
12,5
2
6,2
2
7,5
1,8
8,2
2,1
5,4
1,4
5,3
3
2,1
6
4
10
2,5
1,2
7
7
7
1,2
8,5
1,5
6,7
6
1,7
7,9
1,9
7,9
3
12,5
3
6,5
3,2
6,5
3,8
6,8
2
4
8
3
0,3
18,3
1
9,8
0,2
25
1,5
7,5
0,5
18,6
9,5
1,1
7
0,5
22,3
0,6
22,3
3
8,2
2,8
5,8
2
7,4
1,9
12,3
3
2,3
0,7
20
8
3,2
1,2
8,6
0,6
20
12
2,3
1,4
7,5
0,6
15,5
8
2,4
4,6
2
4,6
4,6
6,1
5,1
3,2
6,5
3,2
6
2,3
2,2
3,1
1
9,3
6
4,5
5
3,6
1
8,5
0,7
15
7,7
2,1
1,8
6,2
9
4,5
2,3
4
2,3
2,5
2,9
2,4
2,4
2,1
5
2,5
5,2
7
4,2
1,4
6,5
0,3
20,6
1,2
8,6
1,1
7,3
0,8
18
1,4
6,8
8
1,3
Ю
1,4
9,6
1,5
9,6
0,7
16,5
0,8
18
0,7
20
1
10
0,5
19,3
9,2
2,5
1
7
3
9
3,2
0,5
20
0,6
J5^
0^

Тематика курсового проектирования
385
Таблица 1.1 (окончание)
'
Вар. 21
Вар. 22
Вар. 23
Вар. 24
Вар. 25
Вар. 26
V
i -
Вар. 27
К
t*
К
/«
h
'в,
к
'»
X,
/в/
ъ
'«
х,
'■.
№ элемента
1
11
1,2
0.5
20
3,1
3,5
0,8
13
9
1,2
0,5
21
6,5
1,7
2
1,2
8,6
9,5
1,2
0.7
14
1.5
7,4
10
1
5
2
1,5
7
3
1
9,5
2
5,1
1
9,8
11
I
0,7
16
2
5,2
2
5,2
4
2
4,8
3,5
2,6
0,8
12
3,5
3
1
10,3
11
1
0,8
12
5
1,3
6,7
0,7
15
7.5
1,3
1
9,8
8
1,3
0,7
14
7,5
1,3
6
8
1.4
1
10
8,5
1.2
2,2
5
2
4,8
7
1,5
0,2
35
7
2.5
4
И
9;7
1,5
7,5
1
10,2
1,5
6,5
1
10
1
10
8
3
3,3
0,8
12
2
4.8
9,5
1,2
7
1,5
1,2
9,6
9
1,2
9
1,6
6,2
7
1,5
2,5
4
1,6
6.2
2,6
4,6
1,5
7
0,7
14
10
9,8
1,3
0.2
20,5
10
1,1
0.7
14
0,2
25
1
9,8
5
10
Интенсивность отказов элементов представлена в таблице в масштабе
А,-10" час"1, размерность /в/ — в часах.
Тема 2. Проектирование технической
системы по заданным показателям
Надежности и риска
2*1. Задание на курсовой проект
Ребуется разработать структурную схему технической системы, отказ кото-
РОи приводил бы к риску, не более заданного.
Годными данными для расчетов являются:
структурная схема системы в виде последовательного (основного)
соединения элементов, как показано на рис. 1.1;
13 Зад 553

386 ЧАСТЬ III. Курсовое проектирование. Глад-,
□ п — число элементов системы;
□ Т( — среднее время безотказной работы /-го элемента, i = 1, 2,..., п;
П г, — риск из-за отказа /-го элемента, / = 1, 2,..., п;
О t — время непрерывной работы системы;
□ m — коэффициент уменьшения риска в результате повышения
надежности системы;
О Гв; — среднее время ремонта /-го элемента, / = 1, 2,..., и;
О приоритет обслуживания отказавших элементов, который может быть
прямым, обратным и назначенным (с заданным порядком номеров
ремонтируемых элементов).
п
Рис. 1.1. Структурная схема системы
В результате расчетов необходимо:
□ определить показатели надежности исходной системы и суммарный риск
из-за ее отказа;
□ разработать структурную схему системы, риск которой в m раз меньше
исходной, применяя структурную избыточность с постоянно включенным
резервом;
□ определить показатели надежности и суммарный риск новой системы;
□ определить показатели надежности и суммарный риск новой системы,
заменяя постоянно включенный резерв на резерв замещением;
□ провести сравнительный анализ рассмотренных методов введения стрУк*
турной избыточности;
П вычислить вероятность безотказной работы, среднее время безотказн
работы и риск из-за отказа ремонтируемой системы, считая восстанови
ние неограниченным;
П оценить влияние восстановления на надежность и риск системы с на Р
женным резервом;
О построить граф состояний для полностью ограниченного восстановлен
заданного приоритета обслуживания, составить и решить систему ДИ(Р) ^
ренциальных уравнений, определить вероятность безотказной рабо
техногенный риск системы;

•Тематика курсового проектирования 387
0 составить и решить систему алгебраических уравнений, определить
наработку на отказ;
0 сделать выводы по работе.
варианты заданий приведены далее в разд. 2.4.
2.2. Методические указания
по выполнению курсового проекта
2.2.1- Показатели надежности
и риск нерезервированной системы
Основными показателями надежности, характеризующими случайное время
до первого отказа неремонтируемой или ремонтируемой системы, являются:
О вероятность безотказной работы P(t) в течение заданного времени /;
О среднее время безотказной работы 7j.
Вероятность безотказной работы представляет собой закон распределения
времени до первого отказа, а среднее время безотказной работы — среднее
|ремя функционирования системы до первого отказа.
Обозначим через Я,, =— интенсивность отказов /-го элемента системы. Если
после наступления отказа /-й элемент может ремонтироваться, то через
Ц/ =— обозначим его интенсивность восстановления, / = I, 2,..., п.
*в/
Для нерезервированной системы, состоящей из п элементов, вероятность
безотказной работы и среднее время безотказной работы определяются по
Формулам:
Р(0 = е"Л', 7J=l, (1.1)
Л
и
гДе Л = ]Г X,- — интенсивность отказа системы. Суммарный риск системы за
Ремя / вследствие отказа какого-либо элемента определяется по формуле:
ад=£зд(о, (1-2)
^е Р,(0=—(1 -e~At) — вероятность отказа /-го элемента системы в момент
^Мени /.

388 ЧАСТЬ III. Курсовое проектирование. /лала
Замечание
Формулы (1.1) и (1.2) даже для нерезервированной системы справедливы только в с*
чае, когда время до отказа каждого элемента случайно и имеет экспоненциальное па
пределение вероятностей. В общем случае эти формулы являются приближенными.
2.2.2. Вероятность безотказной работы
резервированных подсистем
Неремонтируемая резервированная система
Предположим, что некоторый элемент зарезервирован m -1 раз
однотипными по надежности элементами с интенсивностью отказа А..
Тогда при постоянно включенном резерве вероятность безотказной работы
P(t) и среднее время безотказной работы системы 7J выражаются форму-
лами:
/>(/) = 1-(1-е-Х/)'\ (1.3)
?i=7£ }. "• 0-4)
В случае резерва замещением формулы вероятности P(t) и среднего времени
безотказной работы системы 7] имеют вид:
/л-1 у * Д ,
7,=^. (1-6)
1 А,
Ремонтируемая резервированная система
Определение вероятности безотказной работы ремонтируемой системы
является более сложной задачей, и мы ограничимся здесь случаем только дубл*1"
рованной системы. Пусть А, — интенсивность отказа, ц — интенсивное*
восстановления каждого элемента дублированной системы. Тогда веро
ность безотказной работы системы для постоянно включенного резерва в
ражается равенством:
p(f) = *i+H + 3A,c..,, *2+ц + ЗХс..,^ (1.7)
z\ ~z2 z\~ z2
где
-(ц. + ЗА.) ± У(ц + ЗА,)2 - %Х2
\2 ~ i '

-тематика курсового проектирования
средняя наработка до отказа равна:
гг, М. + ЗА
Для резерва замещением вероятность безотказной работы системы
выражается равенством:
/.(0=i±ii±^e-v_i±M^^) (1.9)
2, - 22 2, - 22
где
_ -(Ц + 2Х) ± >/(ц + 2А)2 - 4А2
а среднее время безотказной работы равно:
U + 2A
7]=-^-. (1.10)
А2
Оценим выигрыш от восстановления GT дублированной системы по
среднему времени безотказной работы. Так как среднее время безотказной работы
дублированной системы 7] =1,5— для случая постоянно включенного резер-
А
ва и 7j = 2— для случая замещения, то этот выигрыш соответственно равен
А
Gr=-^ + l и От =-^- + 1.
' ЗА ^ 2А
2-2.3. Надежность и риск резервированной системы,
состоящей из независимых подсистем
Рассмотрим метод определения показателей надежности и риска резервиро-
ванной системы. Предположим, что /-й элемент зарезервирован /и,--1 раз
Однотипными по надежности элементами, /' = 1, 2,..., п, причем вид
резервирования произвольный (нагруженный, ненагруженный, облегченный). На
pv,c- 1.2 показан случай раздельного резервирования с постоянно включен-
Ь,М резервом.
истема может быть неремонтируемой или ремонтируемой, но при этом от-
ельные ее подсистемы должны быть независимы по обслуживанию.
Позднее означает, что имеет место неограниченное восстановление, т. е. каж-
я подсистема имеет такое число ремонтных органов, чтобы не возникала
ередь на восстановление отказавших элементов.

390
ЧАСТЬ III. Курсовое проектирование. Г/jaa^
Рис. 1.2. Структурная схема системы с раздельным резервированием
Обозначим через /}(/) — вероятность безотказной работы, а через
0(/) = 1-/?(/)— вероятность отказа i-й подсистемы, / = 1,2,..., л. Тогда
вероятность безотказной работы и средняя наработка до отказа всей системы
соответственно равны:
Л0 = ПА(0, ?i = pW. (l.ii)
/=i о
Риск из-за отказа системы определяется по формуле:
m=tn /ад - #(*)». PMdx. (i.i2)
/=i о
2.2.4. Надежность и риск резервированной системы,
состоящей из зависимых по восстановлению подсистем
Для систем, образованных из зависимых по восстановлению подсистем, не
существует простых соотношений типа (1.11) и (1.12) для расчета ее
показателей надежности и риска. Здесь необходимо учитывать дисциплину
обслуживания отказавших элементов, а именно: количество ремонтных органов и
приоритет обслуживания, т. е. порядок, в котором ремонтируются
отказавшие элементы.
Описание функционирования системы осуществляется с помощью построй
ния графа состояний и составления системы линейных алгебраических
дифференциальных уравнений.
Граф состояний системы строится в следующем порядке [5]:
П намечаются в виде горизонтальных линий уровни графа, которые ну^е"
ются сверху вниз, считая верхний уровень нулевым;
□ возможным состояниям системы ставятся в соответствие узлы графа» Р ^
полагаемые на определенных уровнях в виде точек (или кружков,^ ^
квадратов). На нулевом уровне помещается узел, соответствуют1* ^
стоянию, когда все элементы системы исправны (состояние (0)); на пер

Тематика курсового проектирования 391
уровне помещаются узлы, соответствующие состояниям, когда отказал
один любой элемент системы; на втором уровне помещаются узлы,
соответствующие состояниям, когда отказали любые два элемента системы и
т. д.; на последнем уровне располагаются узлы, соответствующие только
отказовым состояниям системы;
0 узлы графа соединяются ветвями, которые соответствуют переходам
системы из состояния в состояние. Ветви размечаются интенсивностями
отказов (восстановлений) элементов, из-за которых осуществляются переходы
из состояния в состояние;
О узлы графа, соответствующие отказовым состояниям системы,
помечаются, например, крестами.
Замечание
Узлы графа, соответствующие одинаковым по надежности элементам, входящим в
одну резервную группу, могут объединяться, и соответствующая интенсивность перехода
в укрупненный узел умножается на число элементов резервной группы. Общее число
узлов графа при этом существенно сокращается.
Разработаем математическую модель функционирования системы, для чего
получим, пользуясь графом состояний, выражения для показателей
надежности и риска системы.
Пусть Е — множество всех состояний системы; Е+ — множество
исправных; Е_ — множество отказовых состояний; pt{t) — вероятность
пребывания системы в момент времени / в состоянии /, / е Е; XitJ- — интенсивность
перехода из состояния / в состояние j. Если переход из состояния / в
состояние j отсутствует, то Xfj = 0.
tto графу состояний формально составляется система линейных дифференци-
зльных уравнений с постоянными коэффициентами, описывающая процесс
Функционирования нерезервированной и резервированной технической
системы [5]:
/>;(') = -£ Ч/ЛЮ+ I *7,//>>)> i*E. (1.13)
jeE jeE
предполагая, что в момент времени / = 0 система полностью исправна,
зачтем начальные условия функционирования:
/>0(0) = 1, Л(0) = 0, ieE\{0}. (1.14)
*^ениё системы (1.13) с заданными начальными условиями позволяет найти
Роятность безотказной работы технической системы за время / при усло-
**» что все состояния отказа являются поглощающими:
ТО=1а(0. (1Л5>

392
ЧАСТЬ ///. Курсовое проектирование. Глав
Для определения среднего времени безотказной работы по графу состояни4*
составляется система линейных алгебраических уравнений относительн
средних времен пребывания технической системы в исправных состояни
ЯХ Xjl
JeE jeE '
Тогда средняя наработка до отказа находится суммированием среднего
времени пребывания системы в исправных состояниях:
4=ZV (1.17)
Суммарный риск системы за время / находится по формуле:
*(')= £*мА(0, (1.18)
ieE_
где гкщ — риск системы из-за отказа /-го элемента.
2.3. Пример выполнения курсового проекта
Рассмотрим один вариант выполнения курсового проекта со следующими
исходными данными: и = 4, / = 1 год, m = 100, восстановление полностью
ограниченное, приоритет обслуживания назначенный: первым ремонтируется
элемент с большим риском. Остальные данные приведены в табл. 1.2.
Таблица 1.2. Исходные данные курсового проекта
Характеристики
элементов
Г, лет
ТЛ, час
г, усл. ед.
Номера элементов
I
3
1
10
2
15
240
10s
3
6
2
40
4
10
48
103
2.3.1. Определение показателей надежности
исходной системы и суммарного риска из-за ее отказа
Находим интенсивности отказов элементов:
А, =1 = 0,33333 лет"1, Х2 = — = 0,06667 лет-1,
1 3 2 15
Х2 =1 = 0,16667 лет"1, Х4 = — = 0,10000 лет-1.
3 6 10

Статика курсового проектирования 393
ааходим суммарную интенсивность отказов системы:
д = ^1+Х2+А.3+>-4=0'33333 + 0'06667 + 0.16667 + 0,10000 = 0,66667 лет""1.
flo формулам (1.1) находим вероятность и среднее время безотказной работы
системы за время / = 1 год:
Р(1) = е-°>666671 =0,51342,
7J = = 1,5 год.
1 0,66667
Суммарный риск системы определяется по формуле (1.2):
На основании этой формулы риск системы в момент времени t = 1 год будет
иметь значение:
Д(1) = (10-0,33333 + 105-0,06667 + 40-0,16667 + 103 -0,10000)-
.'-0'51342М946.
0,66667
2.3.2. Разработка структурной схемы системы,
риск которой в m раз меньше риска исходной
Второй элемент, отказ которого ведет к отказу системы, имеет наибольший
Риск. Зарезервируем его идентичным по надежности элементом. Тогда
вероятность безотказной работы каждой группы элементов равна:
/K0 = e-x>', P2(t) = \-(\-e-^)2, P3(t) = e~ht, />4(/) = g-V.
io формуле (1.12) находим риск за время / = 1 год:
ад=1 i№)*i mitmt)dt+r2 рк/шо/ко/к***+
о о
о о
Результате расчетов с помощью системы Derive получим
ед = 100,25036 + 1050,00283 + 400,12518 + 103 0,07511 = 366.

394 ЧАСТЬ III. Курсовое проектирование. Глада
Видим, что суммарный риск системы уменьшился более чем в 10 раз, одна^
он еще не достиг требуемого уровня. Резервируем повторно второй элемент
Вероятность безотказной работы каждой группы элементов будет равна:
/j(0 = e"v, P2(0 = l-(1-<?~X2')3, P3(t) = e-x>', P4(/) = ^4'.
Используя снова формулу (1.12) и систему Derive, получим следующий сум,
марный риск системы за время t = 1 год:
Я(1) = 10-0,25064 + 105-0,00017 + 40-0,12532 + 103 -0,07519 = 100.
Риск из-за отказа системы снова не достиг требуемого значения.
Зарезервируем теперь четвертый элемент, отказ которого вызывает наибольшую
опасность в отказе системы. Вероятность безотказной работы каждой группы
элементов равна:
fl (/) = *-*•', />2(/) = 1-(1-^2')3> 3(0 = е~Хз', AC) = l-(l-e"*4')2.
В третий раз используя формулу (1.12) и систему Derive, получим
следующий суммарный риск системы за время / = 1 год:
Л(1) = 100,26158 + 1050,00018 + 40-0,13079 + 103.0,00656 = 32,41.
Риск из-за отказа системы достиг требуемого значения, поскольку
4946
32,41 <-^ = 49,46.
100
Итак, структурная схема системы имеет вид, представленный на рис. 1.3.
Рис. 1.3. Оптимальная структурная схема системы
2.3.3. Расчет показателей надежности
усовершенствованной системы
Произведем расчет показателей надежности спроектированной системы-
роятность безотказной работы можно найти по формуле (1.11):
P(/) = e-V (l _(i -e-V)3 Je-V (i _(i _«f V)2 j}

foHiarma курсового проектирования
395
а
фи после упрощения получим:
1 P(t) = e~At(3-3e~^' +е-2^')(2-е-^1).
вычисляя значения функции P(t) от 0 до 1 с шагом 0,1, получим табл. 1.3.
График вероятности безотказной работы изображен на рис. 1.4.
Таблица 1.3. Значения функции P(t)
/, лет
0,000
0,100
0,200
0,300
0,400
0,500
0,600
0,700
0,800
0,900
1,000
Pit)
1,00000
0,95113
0,90448
0,85995
0,81746
0,77692
0,73826
0,70140
0,66626
0,63278
0,60088
Рис. 1.4. Вероятность безотказной работы усовершенствованной системы
Считаем наработку на отказ по формуле (1.11):
7] = \P(t)dt = ]<ГЛ' (3 - Зе'^' + <Г2*2' )(2 - е~х*' )dt,
о о

396
ЧАСТЬ III. Курсовое проектирование. Глайя
откуда получим:
„,6623 3 1 , ОЛ.Л<ч
т- + + = 1,89403 гоп
1 Л А + Х2 Л + 2Х2 А + Х4 А + \2+Х4 А + 2Х2+ХА д-
2.3.4. Расчет показателей надежности новой системы
для резерва замещением
В соответствии с (1.5) вероятности безотказной работы подсистем
вычисляются по формулам
( ,22 \
fl(/) = e"x'/, P2(t)= l + ^2/ + -~ e~X2'> Pi(t) = e~h', /i(0 = 0 + V^.
v 2 )
Вероятность и среднее время безотказной работы, а также риск системы
определяются по формулам (1.11) и (1.12).
Сравнительный анализ методов введения структурной избыточности следует
провести самостоятельно. Надо численно показать и объяснить повышение
надежности системы и уменьшение ее риска в случае использования резерва
замещением.
2.3.5. Вычисление показателей надежности
и риска системы при наличии восстановления
Предположим, что количество ремонтных органов достаточно для того,
чтобы подсистемы были независимы по восстановлению (неограниченное
восстановление). В этом случае можно воспользоваться формулами (1.11) и
(1.12). Поскольку восстановление элементов значительно повышает
надежность системы и снижает риск из-за отказа элементов, то в каждой резервной
группе можно оставить лишь по одному резервному элементу. Таким
образом, для ремонтируемой системы ее структурная схема имеет вид,
показанный на рис. 1.5.
Рис. 1.5. Структурная схема восстанавливаемой сисгемы
Постоянно включенный резерв
Поскольку первая и третья подсистемы являются нерезервированными, <*
рая и четвертая представляют собой дублированные подсистемы, то в с

тематика курсового проектирования
етствии с формулой (1.7) для постоянно включенного резерва получим
следующие формулы для вероятности безотказной работы подсистем:
/>(/) = e-Xl/, P2(t) = x2e^'+y2e^t) />3(0 = e"V, Р4(0 = х4еа*'+у4е^1,
где:
-»/+ЗЯ.,) + У01,+ЗЯ,,)2-8Я,? _-(>*/+ЗХ/)-У(ц<+ЗХ/)2-8Х?
а,- 2 . Р/- 2
у ,_сх/+Ц/+ЗХ/ _ ft + ц, + ЗА,,-
«/-ft Р/~а/
1-1
!^=— час — интенсивность восстановления элементов i-w подсистемы,
'в/
/-1,2,3,4.
Теперь для вычисления показателей надежности системы можно
воспользоваться соотношениями (1.11). В результате получим:
/>(/) = ^''(V2' +У2^)е~^(х4е^' +y4fA')9
г_ *2*4 , УгЧ , х2у4 [ у2у4
ос2 + а4 + Xj + Я.3 Рг + а4 + ^i + ^з а2 + Р4 + ^i + ^з Р2 + Р4 + ^-i + ^-3
Расчеты с помощью системы Derive показывают, что:
Р(1) = 0,60632, Г, =2,00142 год.
Аналогично, используя (1.2), найдем риск системы в момент / = 1 год:
ВД = 10-0,26227 + 105-0,00018 + 40-0,13114 + 103-0,00009 = 26,38.
Резерв замещением
° соответствии с формулой (1.9) для резерва замещением получим
следующие формулы для вероятности безотказной работы подсистем:
fl(0 = e~V, P2(t) = x2ea>'+y2e^, />з(') = ^з/, P4{t) = x4e^'+y4e^,
a ^-(Н<+2Я/) + >/(ц/.+2^)2-4^' о -(Ц/+2Х/)->/(>а/ + 2Я,/)2--4Я,?
'~ J ~~' Р'~ 2 '
_а/+ц/+2Л,/ _Р/+Ц,+2*./
*'- a,-ft ,Л ft-а, *

398
ЧАСТЬ III. Курсовое проектирование. Глава
Вычисление показателей надежности и риска системы производится, как и
ранее, на основе равенств (1.11) и (1.12).
2.3.6. Определение показателей надежности
и суммарного риска усовершенствованной системы
Рассмотрим структурную схему ремонтируемой системы с постоянно вклю.
ченным резервом, представленную на рис. 1.5. Ориентированный граф со.
стояний такой системы изображен на рис. 1.6. Он имеет 21 узел. Направление
стрелок сверху вниз соответствует отказовым переходам, а снизу вверх —
восстановлению элементов. На графе кружками отмечены исправные
состояния, а квадратами — отказовые.
Рис 1.6. Граф состояний восстанавливаемой системы
Интенсивности отказового перехода из каждого узла равны соответственно
Х1, Х2, А,3, Х4, умноженным на число исправных элементов данной
резервной группы. Интенсивности ремонта для второй и четвертой подсистем РаВ"
ны соответственно ц2 и Ш- Согласно заданной дисциплине обслуживани
первыми восстанавливаются элементы второй подсистемы, а затем —- эЛ
менты четвертой подсистемы.
Для удобства записи системы уравнений пронумеруем узлы графа в есте
венном порядке. Тогда узлы (0), (2), (4), (8), (10) соответствуют исправны^'
остальные узлы— отказовым состояниям. По графу составляется сисТ^
обыкновенных дифференциальных уравнений, которая в данном случае и
ет вид:

ратина курсового проектирования 399
рШ>
аЧО =
Р'2(0 =
Рз(0 =
/*(') =
Рз(0 =
р'б(0 =
р'ЛО =
pW) =
р'9(0 =
<рШ-
рШ-
рШ-
рШ-
№>
PisiO-
А'б(0 =
рШ-
рШ--
рШ-
А(0
: ~(Х] + 2Х2
*<iA)(0;
:ЩРо(*)~
hPoiO;
■2X4p0(t)-
: ^1^2(0;
:hP2(0',
■•hMOi
2X4p2(t)-
Xxp4{t)\
= 2X2p4(t)-
= hP^)>
= X4p4(t);
= hp*(0>
= hP*(ty,
= hP^0\
= X4p%(t);
= ^iPio(0;
= ^2Ao(0;
= ^зЛо(0;
= KP\o(0-
+x3
+ 2X
(A., + 2A,2
(X, + 2>.2
(Я.,ч
"(*•!
-A.24
+ V
4 )#>(') +
+ X3 + 21
+ X3 + X4
■ x3 +x4 -
•h X3 + X4
Ц2Л(0+ц4А(0;
ч+ц2)/?2(/);
+^4 W)+ъМО+1ЗДо(0;
ьц2)л(0;
+ Цг)Рю(0;
Сбитая, что при / = 0 все элементы системы исправны, получаем начальные
Условия: а>(0) = 1, /7,(0) = О, / = 1,2, ...,20.
Система уравнений может быть решена численно с использованием метода
*унге — Кутты. Для этого необходимо подготовить исходные данные,
содержащие матрицу коэффициентов системы дифференциальных уравнений,
бальные значения искомых функций, начальное и конечное значения аргу-
ента, шаг интегрирования и точность расчетов.
^етим, что при вводе данных надо обязательно привести значения интен-
Ивностей переходов к одной размерности. Для этого следует интенсивности
^становления элементов умножить на 8760, что соответствует переводу
часа в годы.

400 ЧАСТЬ III. Курсовое проектирование. Глав*
Поэтому
8760 „, 8760 .,
Lb = = 36,5 лет , 1Хл = =182,5 лет .
2 240 4 48
В результате вычислений надо получить два файла. В первом файле содер.
жатся значения всех 21 функций p,{t), / = 0,1, 2,..., 20 в зависимости от
значения аргумента t, изменяющегося от 0 до 1 года с шагом 0,1 года. Далее
представлены значения искомых функций только для конечного значения
/ = 1 год:
р0(\) = 0,60345, р,(1) = 0,26106, /?2(1) = 0,00219,
/?3(1) = 0,13054, /?4(1) = 0,00066, /?5(1) = 0,00092,
/?6(1) = 0,00018, /?7(1) = 0,00046, у>8(1) = 0,00001,
/?9(1) = 0,00029, /?10(1) = 0,00000, /?и(1) = 0,00014,
/?12(1) = 0,00009, /?,3(1) = 0,00001, />14(1) = 0,00000,
/>15(0 = 0,00000, /%,()) = 0,00000, />,7(1) = 0,00000,
р18(1) = 0,00000, /?19(1) = 0,00000, /?20(1) = 0,00000.
Приведенные значения используются дальше при нахождении риска
системы. Во втором файле содержатся значения вероятности безотказной работы
системы для значений / от 0 до 1 года с шагом 0,1 года. Эти значения
получены суммированием вероятностей />Д/) по всем исправным состояниям,
т. е.
/*(/) = Ро(0 + Л(0 + А(0+Л(0 + Ло(0.
Данные второго файла приведены в табл. 1.4.
Из таблицы следует, что Р(\) = 0,60632 для ремонтируемой системы
несколько больше, чем Р(\) = 0,60088 для неремонтируемой системы.
Для определения наработки на отказ составим следующую систему линейны*-
алгебраических уравнений:
-(Х{ + 2Х2 + Х3 + 2^4 )т0 + И2Т2 + М-4Т4 = "~U
2\2т0 - (X, + 2Х2 + Х3 + 2X4 + ц2 )t2 = 0;
< 2Х4х0 - (Х] + 2Х2 + Х3 + Х4 + U4)x4 = 0;
2л4х2 - (Х1 + Х2 + Х3 + Х4 + ц2 )Ц - 0;
2Х2т4 - (A.J + Х2 + Х3 + Х4 + ц2 )тш = 0.

Тематика курсового проектирования
401
Таблица 1.4. Вероятность безотказной работы системы
Л лет
0,000
0,100
0.200
0,300
0,400
0,500
0,600
0.700
0,800
0,900
1.000
АО
1,00000
0,95120
0.90478
0,86062
0.81862
0,77867
0,74067
0.70452
0.67014
0,63743
0.60632
Решение этой системы даст следующие результаты:
х0 =1,98926, т2 =0,00712, т4 =0,00218, х8 =0,00004, т,0 =0,00001.
Следовательно, среднее время безотказной работы системы будет равно:
Т{ = т0 + т2 + т4 + т8 + т,0 = 1,99860 год,
что также больше, чем 7J = 1,89403 лет для неремонтируемой системы.
Найдем суммарный риск системы в соответствии с формулой (1.18). Для
этого по графу необходимо найти все состояния отказа и для каждого из них
определить номер элемента, отказ которого привел к отказу системы.
Соответствие отказовых состояний и номеров отказавших элементов приведено в
табл. 1.5.
Таблица 1.5. Номера элементов и их состояний
Номер
состояния
1
3
5
6
7
9
Номер
элемента
1
3
1
2
3
1
Номер
состояния
11
12
13
14
15
16
11омер
элемента
3
4
1
2
3
4
Номер
состояния
17
18
19
20
11омер
элемента
1
2
3
4

402
ЧАСТЬ III. Курсовое проектирование. Глава i
По формуле (1.18) получим:
Л(/) = /1(л(0 + Л(0 + Л(0 + Аз(0 + А7(0) + ^(л(0 + Р14(0 + Л8(0) +
+'5(Л(0 + Л(0 + Ри(0 + А5(0 + Л9(0) + ',4(Л2(/) + Аб(0 + Ло(0).
Следовательно,
R(\) = 10(0,26106 + 0,00092 +0,00029 + 0,00001) + 105 -0,00018 +
+40(0,13054 +0,00046 + 0,00014) +103-0,00009 = 25,96.
Суммарный риск из-за отказа системы, равный R(\) = 25,96, стал меньше
риска, полученного для системы без восстановления и равного 32,41.
2.3.7. Определение показателей надежности
и суммарного риска усовершенствованной системы
(резерв замещением)
Граф состояний будет такой же, что и на рис. 1.6. Другими будут только
значения интенсивностей перехода вследствие отказов элементов. Этот раздел
выполняется аналогично разд. 2.3.6.
2.3.8. Выводы по работе
По результатам проведенных исследований составлена табл. 1.6, в которой
содержатся значения показателей надежности и риска системы для постоянно
включенного резерва.
Таблица 1.6. Значения показателей надежности и риска резервированной системы
Система
Неремонти руемая
Ремонтируемая
(неограниченное восстановление)
Ремонтируемая
(ограниченное восстановление)
Показатели надежности
Р(\)
0,60088
0,60632
0,60632
Т\, лет
1,89403
2,00142
1,99860
Риск системы
R{\)
32,41
26,38
25,96
На основании данной таблицы необходимо сделать выводы о целесообразн
сти мероприятий по восстановлению отказавших элементов. Следует отм
тить, что возможность ремонта элементов приводит к уменьшению кратное
резервирования и сокращению объема оборудования.

матка курсового проектирования
403
2.4. Варианты заданий на курсовой проект
курсовой проект выполняется по приведенной ранее методике. Варианты
заданий приведены в табл. 1.7.
Таблица 1.7. Варианты заданий на курсовой проект
Вар.
1
2
3 ■
4
5
6
7
8
9
п
4
4
4
5
4
4
5
4
4
m
ПО
90
ПО
ПО
100
120
120
80
80
/, лет
1,9
1,8
2
1,6
1,9
1,1
1,4
1,2
1,1
Характ.
Г, лет
Ть, час
г, у. е.
Т, лет
Та, час
г, у. е.
Г, лет
Тв, час
г, у. е.
Г, лет
Гв, час
г, у. е.
Г, лет
Гв, час
г, у. е.
Г, лет
Г„, час
г, у. е.
Г, лет
Г„ час
г, у. е.
Г, лет
7,, час
г, у. е.
Г, лет
Та, час
г, у. е.
Элем. 1
12
24
1000
10
120
10000
5
100
50
14
120
10000
14
100
1000
2
50
40
4
30
30
2
60
30
4
70
30
Элем. 2
2
24
30
16
240
1000000
3
100
30
4
96
10
20
200
100000
16
200
1000000
18
200
100000
14
180
100000
10
200
1000
Элем. 3
16
120
1000000
5
60
30
16
240
100000
5
20
40
3
50
10
14
120
10000
12
100
1000
10
96
1000
2
50
10
Элем. 4
2
50
20
3
90
30
14
100
1000
18
200
100000
4
50
20
5
90
40
5
50
50
2
40
30
14
180
100000
Элем.5
5
24
40
2
40
10

404
ЧАСТЬ III. Курсовое проектирование. Глава i
Таблица 1.7 (продолжение)
Вар.
10
11
12
13
14
15
16
17
18
19
п
4
4
5
5
4
4
5
5
4
4
m
120
90
120
90
80
90
90
90
120
80
/, лет
1,5
1,2
1,6
1,3
1,6
1,8
1,6
1,7
1,0
1,9
Характ.
Г, лет
Тв, час
г, у. е.
7', лет
Г8, час
г, у. е.
Г, лет
Тв, час
г, у. е.
Г, лет
Т„ час
г, у. е.
Т, лет
Та, час
г, у. е.
Г, лет
Гв, час
г, у. е.
Г, лет
Ть, час
г, у. е.
Т, лет
Тп, час
г, у. е.
Т, лет
Г„, час
г, у. е.
Г, лет
Тв, час
г, у. е.
Элем.1
3
40
50
10
200
1000
4
80
20
5
60
40
2
60
10
10
юб
1000
5
100
40
4
60
40
4
80
40
4
100
30
Элем. 2
12
150
100000
2
30
50
16
180
10000
3
100
30
20
150
100000
3
30
30
4
160
30
16
120
10000
16
100
100000
4
30
20
Элем. 3
12
120
10000
20
120
100000
4
50
20
2
50
50
4
100
50
14
200
1000000
5
50
50
4
60
50
4
100
40
14
200
1000
Элем. 4
4
90
40
5
30
40
5
40
10
12
180
100000
12
80
1000
2
40
50
18
200
100000
3
80
30
14
100
1000
20
40
1000000
Элем. 5
__
16
130
100000
14
100
1000
16
130
1000
18
150
юоооо
^^______
____—-—
__————
_______

Тематика курсового проектирования
405
Таблица 1.7 (продолжение)
Вар.
20
2L
22
23
24
25
26
27
28
29
л
4
5
5
4
4
4
4
5
4
4
/и
120
80
120
9
ПО
100
120
120
100
80
/, лет
1,0
1.6
1,6
1,8
1,7
1,6
1,0
1,4
1,7
1,39
Характ.
Т, лет
Тв, час
г, у. е.
Т, лет
Гв, час
г, У- е.
Г, лет
Гв, час
г, У- е.
Г, лет
Тв, час
г, у. е.
7', лет
Тн, час
г, у. е.
7", лет
Гв, час
г. у. е.
Г, лет
Гв, час
г, у. е.
Г, лет
Тш, час
г, У- е.
Г, лет
Г„, час
Л у. е.
Т, лет
7*,, час
г, у. е.
Элем. 1
4
100
50
16
100
1000
3
60
40
3
80
3
' 16
100
10000
14
100
1000000
20
160
100000
18
120
1000000
10
120
10000
12
100
1000
Элем.2
3
160
20
4
160
40
3
120
10
10
100
100000
3
30
20
12
160
10000
12
100
1000
3
120
30
5
100
20
16
200
100000
Элем.3
20
50
100000
4
50
30
4
60
20
10
100 .
10000
18
200
100000
3
50
20
3
50
30
4
60
20
16
120
100000
4
100
50
Элем. 4
18
200
1000
2
200
20
18
200
100000
4
100
20
2
40
20
3
70
10
2
50
10
10
100
1000
3
100
20
3
60
30
Элем. 5
18
130
100000
12
150
10000
5
150
20

406
ЧАСТЬ III. Курсовое проектирование. Глава j
Таблица 1.7 (окончание)
Вар.
30
п
4
m
ПО
/, лет
1,6
Характ.
Т, лет
Тв< час
г, у. е.
Элем. 1
2
100
30
Элем. 2
5
100
50
Элем.3
20
200
1000000
Элем. 4
18
200
10000
Элем. 5
Тема 3. Анализ надежности системы
по данным эксплуатации
3.1. Задание на курсовой проект
Статистические данные об отказах систем самолета в процессе его
эксплуатации приведены в табл. 1.8. Они получены из эксплуатации восьми
самолетов ТУ-154М в течение двух лет их функционирования. Отказы обобщались
поквартально.
1
2
3
4
5
6
7
8
9
10
11
Таблица 1.8. Статистические данные об отказах систем самолета ТУ-
Система
Управление самолетом
Рад иооборудован ие
Электроснабжение
Управление полетом
Топливная система
Гидравлическая
система
Приборное
оборудование
Шасси
Пилотажио-навигационная
система
Вспомогательная
силовая установка
Фюзеляж
1 кв.
17
31
2
11
9
6
0
14
23
5
7
154М
Число отказов по годам и кварталам
1997
2 кв.
24
55
6
15
12
9
1
35
30
5
6
3 кв.
31
39
9
13
10
6
2
30
23
15
12
4 кв.
13
38
1
11
11
3
1
27
27
7
7
1978
1 кв.
33
20
4
13
2
3
2
34
14
17
4
2кв.
25
38
4
10
6
3
3
28
26
6
5
3 кв.
27
42
9
13
12
10
1
30
35
16
10
4 кв.
29
29
3
8
18
7
5
29
34
9
7

Тематика курсового проектирования
407
Таблица 1.8 (окончание)
12
13
14
15
16
17
18
19
20
Система
Крыло
Газотурбинный двигатель
Топливная система
двигателя
Система управления
двигателем
Приборы контроля
двигателя
Система запуска
Радиоаппаратура
самолетовождения
Бортовые системы
контроля
Налет, час
Число отказов по годам и кварталам
1997
1 кв.
6
13
14
6
3
3
36
8
2351
2кв.
12
19
11
8
6
2
68
19
4066
3 кв.
4
15
10
8
6
3
70
16
4596
4 кв.
7
9
3
4
1
1
40
15
3381
1978
1 кв.
7
13
11
11
7
10
41
12
2630
2кв.
11
12
6
9
3
15
44
20
3665
3 кв.
14
14
18
18
7
24
59
21
4585
4 кв.
6
8
4
4
7
11
43
16
3158
Необходимо определить:
О P{i) — вероятность безотказной работы в течение времени /;
О \{t) — интенсивность отказов системы в течение времени /;
О /(/) — плотность распределения времени до отказа.
Решение получить в виде формул, таблиц и графиков.
3.2. Сведения из теории
Самолет является системой восстанавливаемой, а интересующие нас
показали надежности необходимо определить в течение времени полета, когда
самолет и его оборудование не ремонтируются. То есть необходимо по дан-
нЬ1м об отказах восстанавливаемой системы оценить ее надежность в течение
времени t, когда она не подлежит ремонту.
Зависимости между показателями надежности невосстанавливаемой и вос-
^навливаемой техники можно получить путем решения следующего инте-
гРального уравнения:

408 ЧАСТЬ III. Курсовое проектирование. Глава i
i
<о(0 = /(/) + Jco(x)/(/ -x)dx, (1.19)
о
где ю(0 — параметр потока отказов восстанавливаемой системы; /(/) __
плотность распределения времени до отказа невосстанавливаемой системы.
Согласно заданию на проектирование, решение необходимо получить в
аналитическом виде.
Методика определения показателей надежности систем самолета, основанная
на решении уравнения (1.19), состоит в следующем:
О по данным об отказах системы определяется параметр потока отказов со(^);
П со(0 представляется в виде формулы путем решения задачи
интерполяции;
О определяется преобразование Лапласа функции ш(0;
□ на основе формулы (1.19) находится преобразование Лапласа функции
fit):
Д*) = 7^т; (1-20)
1 + G)(s)
□ находится плотность распределения времени до отказа /(/) путем
обратного преобразования Лапласа функции (1.20);
□ по известной плотности /(/) определяются искомые показатели
надежности:
P(t) = \-)f{t)dt,
о
/>(/)
Приведенная методика может быть реализована с помощью универсальных
программных средств символьной математики. Наиболее эффективными из
них для решения задач настоящего проекта являются Mathematica и Мар»е-
Они позволяют получить решение в виде формул, таблиц и графиков. Пр0-
грамма решения задач приведена в [5, гл. //]. Анализ результатов расчетов
позволит сделать ряд важных выводов о надежности систем воздушноГ
судна.
Замечание сТ
Технических систем самолета ТУ-154М, приведенных в табл. 1.8, много, поэтому им
смысл оценить их надежность в нескольких курсовых проектах.

Тематика курсового проектирования
409
Тема 4. Разработка структурной схемы
системы длительного использования,
удовлетворяющей требованиям надежности
и ограничениям на техническую реализацию
Дано:
О структурная схема системы в виде основного соединения элементов;
CJ число элементов системы;
О допустимый вид структурного резервирования и его кратность;
О показатели надежности элементов;
О вид законов распределения отказов элементов;
Ь время работы системы;
О допустимое значение снижения нагрузки элементов (нагрузочное
резервирование).
Один из вариантов задания приводится в табл. 1.9.
Таблица 1.9. Исходные данные на проектирование оптимальной системы
Ти час
Закон
распределения
Структурное
резервирование
m
п
№ элемента
. 1
2180
Ехр
—
—
—
2
1200
G
Пос.
1
—
3
1250
R
—
—
1,4
4
980
Ехр
Зам.
1
5
920
N
—
—
2
6
2000
W
Др. кр.
1/2
—
7
1800
G
—
—
1,4
8
1600
Ехр
П,3.
1
—
9
1500
W
Пос.
1
—
10
1980
Е
—
—
—
Предполагается, что система длительного использования. Время ее
непрерывной работы — 840 часов.
Определить оптимальную структуру системы. Оптимальной считается такая
^уктура, которая имеет среднее время безотказной работы 7j > 500 час,
**Меет минимальное число элементов и минимальный объем резервирования.
" табл. 1.9 приняты следующие обозначения: 7] — среднее время
безотказной работы элемента, m — допустимая кратность резервирования, п — чис-

410 ЧАСТЬ III. Курсовое проектирование. Глава i
ло, показывающее, во сколько раз увеличивается среднее время безотказной
работы элемента, если применить нагрузочное резервирование.
Эта тема может иметь большое число вариантов, если в таблице исходных
данных изменять значения 7}, m, n, вид закона распределения отказов и вид
резервирования.
Пример выполнения проекта не приводится, т. к. методика его выполнения
ясна из предыдущих тем.

ГЛАВА 2
ТЕМАТИКА КУРСОВЫХ РАБОТ
В этой главе приводится семь тем курсовых работ, затрагивающих
следующие направления теории надежности:
О влияние дисциплины обслуживания на надежность технических систем
(Тема 1, 2);
О анализ переходных процессов при оценке надежности восстанавливаемых
систем (Тема 3, 4, 5);
О анализ надежности систем методом статистического.моделирования
(Тема б, 7).
Тема 1. Оценка влияния
дисциплины обслуживания на надежность
дублированной восстанавливаемой системы
Структурная схема дублированной восстанавливаемой системы с разнона-
Дежными элементами приведена на рис. 2.1.
Рис. 2.1. Дублированная система с разнонадежными элементами
необходимо оценить влияние дисциплины обслуживания на надежность сис-
Темы. За критерии надежности следует принять коэффициент готовности и
Заработку на отказ. Рассмотреть случаи прямого, обратного и назначенного
пРиоритетов при одной обслуживающей бригаде и при неограниченном об-
СлУживании. При назначенном приоритете рассмотреть два случая: приори-

412 ЧАСТЬ ///. Курсовое проектирование. Глава ♦>
тет более и менее надежному элементу. Коэффициент готовности и
наработку на отказ получить в аналитическом виде. Вычисления выполнить для
следующих случаев:
1. Приоритет наименее надежному элементу и с низкой
ремонтопригодностью (X велико, ц мало).
2. Приоритет наименее надежному элементу, но с высокой
ремонтопригодностью (X велико, р. велико).
3. Приоритет наиболее надежному элементу, но с низкой
ремонтопригодностью (X мало, ц мало).
4. Приоритет наиболее надежному элементу и с высокой
ремонтопригодностью (А. мало, ц велико).
Рассмотреть случаи при следующих исходных данных:
^,=2,3-1(Г3 час"1, Л,2 =1,2-10_3 час"1, р., = 0,05 час"1, \i2=0,\ час~'-
Тема 2. Оценка влияния
дисциплины обслуживания
на надежность энергетической системы
Энергетическая система состоит из трех генераторов разного типа, имеющих
интенсивности отказов Х{, Х2, Х3. При отказе одного из генераторов
интенсивность отказов исправных увеличивается, т. к. возрастает нагрузка на
каждый из генераторов, и становится равной А,п, Х12, А,13. Интенсивность
восстановления генераторов постоянна и равна ц. Отказ системы наступает при
отказе любых двух генераторов.
Необходимо исследовать влияние дисциплины обслуживания на надежность
системы. Критериями надежности являются: коэффициент готовности и
наработка на отказ. Рассмотреть случаи неограниченного восстановления, а
также полностью ограниченного при прямом, обратном и назначенном
приоритетах. Исследовать два варианта: приоритет более и менее надежном,
элементу.
Интенсивности отказов имеют следующие значения: ^ =1,2-10 чаС
А,2=2,4-1(Г5 час"1, Х3=3-10~5 час"1. Среднее время восстановления
отказавшего генератора Тъ - 23 час. По результатам расчетов установить зна
ния выифышей надежности по коэффициенту готовности GK и нарабо

Тематика курсовых работ 413
ла отказ Gr для каждого приоритета обслуживания по сравнению с
неограниченным восстановлением.
Тема 3. Анализ влияния законов
распределения отказов
на переходные процессы при оценке
показателей надежности и готовности
восстанавливаемой системы
Дана структурная схема системы, представляющая собой основное
соединение элементов. Данные о надежности элементов приведены в табл. 2.1.
Таблица 2.1. Данные о надежности системы
№ элем.
Г, час
Г„ час
1
1860
12
2
1000
9
3
980
2,4
4
2100
15,6
5
1320
12
6
1570
9,7
7
2200
15,5
8
1740
8,5
9
2300
16,5
10
1950
9
Определить показатели надежности системы Kr(t), Кг, Т при законах
распределения: экспоненциальном, нормальном, гамма-, Вейбулла. Оценить
влияние законов распределения на показатели надежности. Исследовать
длительность переходных процессов. Установить значение т, при котором
можно оценивать готовность системы лишь по коэффициенту готовности, не
анализируя функцию готовности Kr(t).
Тема 4. Влияние параметров
резервированной восстанавливаемой
системы на длительность переходных
процессов при оценке ее готовности
Дано:
^ резервированная восстанавливаемая система при общем постоянном
резервировании;
" кратность резервирования m = 1, 2, 3,4;
" Диапазон интенсивностей отказов системы:
^ = 0,21(Г3 час-1, А, = 0,6-10~3 час"1, А. = 1,2-Ю-3 час"1, Х = 2-10"3 час"1;

414
ЧАСТЬ III. Курсовое проектирование. Глапп
О среднее время восстановления Гв =8,24 час;
О приоритет обслуживания: одна бригада и т + \ бригад (независимое вое
становление).
Определить:
О коэффициент готовности, функцию готовности и среднее время
безотказной работы системы для всех вариантов задания;
О длительность т переходного процесса.
В результате исследований дайте ответы на следующие вопросы: какова дли-
тельность переходных процессов и как она зависит от кратности
резервирования, числа ремонтных бригад, интенсивности отказов системы; через какое
время от начала эксплуатации можно оценивать готовность системы
коэффициентом готовности, игнорируя функцию готовности АГГ(/).
Решение представить в виде следующей таблицы:
m
X
Кг
т
1
0,2
0,6
1,2
2
2
0,2
0,6
1,2
2
3
0,2
0,6
1,2
2
4
0,2
0,6
1,2
2
Решить для ограниченного и неограниченного восстановлений и представить
в виде графиков функции готовности Kr(t) для всех вариантов задания.
Указание: при исследовании переходных процессов необходимо
воспользоваться методом Рунге — Кутты и одним из программных средств символьной
математики (см. часть IV). Вычисления выполнить с точностью три
значащие цифры.
Тема 5. Влияние параметров
резервированной восстанавливаемой
системы на длительность переходных
процессов при оценке ее готовности
(случай резервирования замещением)
Исходные данные те же, что и в теме 4. Решение получить для случая обШ
резервирования замещением.

Тематика курсовых работ
415
Замечание
При выполнении курсовых работ необходимое их количество можно получить из
предложенных тем путем варьирования исходных данных.
Тема 6. Установление закона распределения
времени безотказной работы системы
по известным законам распределения
элементов
разработка математических моделей и методов, позволяющих определить
время безотказной работы системы аналитически, является сложной, а подчас
и неразрешимой задачей. С этой целью часто используется метод
статистического моделирования с последующей обработкой результатов эксперимента.
^Предметом статистического моделирования является изучение сложных
процессов и систем, подверженных, как правило, воздействию случайных
факторов, путем проведения экспериментов с их моделями.
Суть метода проста— имитируется "жизнь" системы при многократном
повторении испытаний. При этом моделируются и регистрируются случайно
Меняющиеся внешние воздействия на систему. Для каждой ситуации по
уравнениям модели просчитываются системные показатели. Существующие
современные методы математической статистики позволяют ответить на
вопрос: можно ли и с каким доверием использовать данные моделирования.
Если эти показатели доверия для нас достаточны, мы можем использовать
модель для изучения данной системы.
Можно говорить об универсальности статистического моделирования,
поскольку оно является одним из наиболее эффективных средств исследования
и проектирования сложных систем по критериям надежности и часто
единственным практически реализуемым методом исследования процесса их
функционирования.
Целью курсовой работы является изучение студентами методов
статистического моделирования применительно к задачам нахождения законов
распределения времени безотказной работы и показателей надежности технических
систем с использованием прикладных программных средств. Далее будут
Рассмотрены характерные этапы выполнения курсовой работы.
в.1. Задание на курсовую работу
Техническая система S состоит из трех элементов, схемы соединения
которых приведены в вариантах заданий на курсовую работу (см. разд. 6.5).
Времена безотказной работы Х], Х2, Х3 элементов системы являются непре-

416 ЧАСТЬ III. Курсовое проектирование. Глав* *
рывными случайными величинами с известными законами распределены
вероятностей. Внешняя среда Е оказывает воздействие на работу системы a
виде случайной величины V с известным дискретным распределением вер0.
ятностей.
Требуется оценить надежность системы S методом статистического модели,
рования на ЭВМ с последующей обработкой результатов эксперимента.
Последовательность выполнения работы следующая:
1. Разработать алгоритмы разыгрывания случайных величин Хх, Х2, Х2 и
V с использованием генераторов случайных чисел, содержащихся в
математических пакетах, например в Microsoft Excel или в StatGraphics.
2. Определить время безотказной работы системы Y в зависимости от
времен безотказной работы Хх, Х2, Х3 элементов на основе структурной
схемы расчета надежности.
3. Определить время безотказной работы системы с учетом влияния внешней
среды в соответствии с формулой Z = У/(1 + 0,1 V).
4. Построить моделирующий алгоритм, имитирующий работу системы S и
учитывающий возможность отказа элементов и случайные воздействия
внешней среды Е. Реализовать полученный алгоритм на ЭВМ и создать
файл со значениями случайных величин Х^ Х2, Х3, V, Y и Z. Число
опытов для машинного эксперимента принять равным 100.
5. Выполнить статистическую обработку полученных результатов. Для этого
необходимо:
• для каждой случайной величины рассчитать основные статистические
характеристики: выборочное среднее, выборочную дисперсию,
выборочное среднее квадратическое отклонение, наименьшее и наибольшее
значения, размах выборки, асимметрию, эксцесс;
• данные для случайной величины Z разбить на 10 групп и
сформировать статистический ряд, содержащий границы и середины частичных
интервалов, а также соответствующие частоты; вычислить
относительные, накопленные и накопленные относительные частоты;
• для величины Z построить полигон и кумуляту частот, построить
гистограмму по плотностям относительных частот;
• для величин Хх, Х2, Х3, V установить их соответствие заданным за
- 2
конам распределения, используя критерии % ;
• для случайной величины Z рассмотреть три непрерывных распреДеЛ
ния (равномерное, нормальное, гамма-), изобразить на гистограмме Д
Z плотности этих распределений;

<е^атика курсовых работ
417
• с помощью критерия % выполнить проверку справедливости гипотезы
о соответствии статистических данных выбранным распределениям,
уровень значимости при подборе подходящего распределения принять
равным 0,05.
6# Определить плотность распределения, математическое ожидание,
дисперсию и среднее квадрата чес кое отклонение времени безотказной работы Z
системы. Определить основные характеристики надежности системы:
среднее время безотказной работы 7] и вероятность безотказной работы
P(t) в течение времени /. Найти вероятность безотказности системы за
время 7].
6.2. Алгоритм статистического моделирования
Проведем имитацию работы системы, структурная схема которой изображена
на рис. 2.2. Согласно схеме, сначала работают элементы 1 и 3, а элемент 2
находится в резерве. При отказе элемента 3 наступает отказ системы. При
отказе элемента 1 в работу включается элемент 2, но это событие не является
отказом системы. Система откажет, если после этого произойдет отказ
элемента 3 или 2.
Рис. 2.2. Структурная схема системы
Законы распределения времени безотказной работы элементов и воздействия
8нешней среды сведены в табл. 2.2.
Таблица 2.2. Законы распределения времени безотказной работы элементов и V
Хх
LN(2; 1,4)
Хг
LN(2; 1,4)
х,
Е(2; 0,05)
V
G(0,7)
табл. 2.2 приняты следующие обозначения законов распределения:
LN — логнормальное;
Е •— Эрланга;
U о
^ ■— геометрическое.
скобках указаны параметры распределений.
14 Зак.553

418
ЧАСТЬ III. Курсовое проектирование. Глава *
На листе Excel (табл. 2.3) предусмотрим место для значений случайных вели
чин. Колонки А и В — вспомогательные, в них заносятся равномерно распре.,
деленные случайные числа (РРСЧ) из промежутка [0; 1]. В колонки С, D, {? и
F заносятся значения заданных случайных величин Хх, Х2, Хъ и V соот.
ветственно, полученные путем преобразования РРСЧ. Колонка G служит для
значений случайной величины Y, а колонка Н — для значений случайной
величины Z.
Таблица 2.3. Получение случайных чисел
1
2
3
• ••
101
А
РРСЧ
0,215
0,088
...
0,915
В
РРСЧ
0,493
0,731
...
0,305
С
Хх
10,608
18,973
...
54,505
D
Хг
10,608
18,973
...
54,505
Е
А'з
44,772
54,838
...
25,53
F
V
2
3
...
1
G
Y
21,216
37,946
...
25,53
Н
2
17,68
29,19
23,21
В ячейки первой строки А1, В1,..., HI помещаются заголовки таблицы.
В ячейки А2 и В2 помещаются РРСЧ в соответствии с формулами:
А2 = СЛЧИС(), В2 = СЛЧИС().
В ячейки С2, D2, Е2 помещаются значения случайных величин Хх, Х2, Х^,
первые две из которых имеют логарифмически нормальное распределение, а
третья — распределение Эрланга в соответствии с формулами разыгрывания,
приведенными в [5, табл. 5.6]:
С2 = ЕХР(2 + l,4*KOPEHb(-2*LN(B2))*COS(2*nH()+A2),
D2 = EXP(2 + l,4*KX>PEHb(-2*LN(B2))*COS(2*IH!()*A2),
Е2 = -(LN(A2) + LN(B2))/0,05.
В ячейку F2 помещается значение дискретной случайной величины V,
подчиненной геометрическому распределению вероятностей с параметром 0,7:
F2 = ЦЕЛОЕ(LN(A2)/LN(1 - 0,7)) + 1.
Рассмотрим структурную схему, изображенную на рис. 2.2. Отказ пары э
ментов 1 и 2 произойдет тогда, когда откажет первый, а затем второй э
мент, т. е. время до отказа этой пары равно сумме Хх + Х2- Считая пару э
ментов 1 и 2 одним элементом, имеем последовательное соединение с э
ментом 3. Время до отказа этой пары равно самому минимальному вРеМгГо,
до отказа составляющих ее частей. Это значит, что Y = min(Xj + Х2, %v'

Тематика курсовых работ
419
этому в ячейку G2 помещается формула, расчет по которой даст значение
<»лучайной величины Y:
G2 - МИН(С2 + D2; Е2).
р ячейку Н2 помещается формула для расчета значения случайной величины Z:
%2 = G2/{1 + 0,1*F2).
В результате этих действий будут заполнены ячейки второй строки А2,
В2,..., Н2. По заданию необходимо получить 100 значений данных
случайных величин. Поэтому содержимое ячеек А2, В2,..., Н2 копируется в
следующие строки, вплоть до 101 строки (табл. 2.3).
Также следует отметить, что при вводе какой-либо информации на лист Excel
содержимое ячеек А2 : HI 01 будет изменяться. Чтобы этого не происходило,
целесообразно выполнить следующие действия:
CJ выделить указанный блок ячеек и скопировать его в буфер (<Ctrl>+<C>);
О загрузить Microsoft Word и вставить содержимое буфера в документ Word
(<Ctrl>+<V>);
р выделить содержимое таблицы Word и скопировать его в буфер
(<Ctrl>+<C>);
О перейти на новый лист Microsoft Excel и вставить содержимое буфера в
документ Excel (<Ctrl>+<V>).
6.3. Статистическая обработка данных
6.3.1. Вычисление основных характеристик выборки
Основными числовыми характеристиками выборочной совокупности
являйся: выборочное среднее, выборочная дисперсия, выборочное среднее квад-
ратическое (или стандартное) отклонение, наименьшее и наибольшее
значения, размах выборки, асимметрия, эксцесс.
Для
расчета указанных характеристик в Excel необходимо поставить курсор в
ячейку, в которую будет записано значение характеристики, вызвать
соответствующую функцию и в качестве ее аргумента указать блок ячеек со
статистическими данными.
Для удобства следующих операций значения случайной величины Z
(статистические данные) перепишем на другой лист в прямоугольный блок ячеек,
Иапример в ячейки А1 : J10.
Значения вычисляемых характеристик будем располагать в ячейках с G12
0 G19, как показано в табл. 2.4.

420 ЧАСТЬ III. Курсовое проектирование. Глав.
Таблица 2.4. Расчет выборочных характеристик
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
А
17,68
38,68
2,87
28,55
4,86
12,84
33,74
13,24
42,10
11,04
В
29,19
9,52
6,58
14,08
28,76
17,23
16,93
14,71
17,22
20,31
С
17,75
16,03
4,86
4,53
2,61
84,86
8,92
4,64
29,16
23,33
D
34,38
9,53
8,98
16,62
26,79
15,76
58,53
5,90
15,64
10,48
Е
6,29
27,22
8,53
27,99
43,88
56,95
4,52
28,99
4,38
12,85
F
4,98
15,66
24,33
30,43
17,28
5,46
20,64
43.44
17,55
17,93
G
5,70
19,10
19,38
7,87
19,70
16,34
9,94
53,56
13,45
26,95
Н
3,44
13,64
39,52
18,60
20,41
25,38
27,92
23,23
6,95
15,20
I
21,96
25,46
41,72
9,58
15,08
35,96
12,78
24,53
17.31
11,86
J
17.51
5,91
27,54
2,58
20,05
9,76
35,14
15,20
20,73
23,21
Выборочное среднее
Выборочная дисперсия
Выборочное ср. квадр. отклонение
Наименьшее значение
Наибольшее значение
Размах выборки
Асимметрия
Эксцесс
19,79
190,76
13,81
2,58
84,86
82,28
1,69
4,62
Вычисление выборочных характеристик осуществляется по формулам:
□ выборочное среднее: G12 = срзнач (А1: Л0);
□ выборочная дисперсия: G13 = ДИСП(А1:Л0);
□ выборочное среднее квадратическое отклонение:
G14 = СТАНДОТКЛОН(А1:Л0) RT1HG14 = КОРЕНЬ (G13);
□ наименьшее значение: G15 = МИН(А1:Л0);
О наибольшее значение: G1 б = МАКС(А1: Л0);
□ размах выборки: G17 = G16 -G15;
□ асимметрия: G18 = СКОС(А1:Л0);
О эксцесс: G19 = ЭКСЦЕСС (А1:Л0).

Тематика курсовых работ
421
5.3.2. Формирование статистического ряда
А графическое представление данных
Для наглядного представления статистических данных используется
группировка. Числовая ось разбивается на интервалы, и для каждого интервала под-
считывается число элементов выборки, которые в него попали. Группировка
данных производится в следующей последовательности:
0 наименьшее значение округляется в меньшую сторону, а наибольшее —
в большую сторону до "хороших" чисел xmin и хтах; ,
О выбирается количество групп к, удовлетворяющее неравенству 6 < к < 20;
иногда оно определяется по формуле k = [5\gn]. Например, если объем
выборки п = 100, то к = 10;
О находится шаг по формуле И = —, где R = xmsx - jcmin — длина промежут-
к
ка, в котором содержатся статистические данные;
О определяются границы частичных интервалов:
Ло=*пип» ax=aQ+h, а2=щ+И, ... , ак = %_, + h = *тах; (2.1)
- - Щ-\ + ai
D в каждом интервале вычисляются средние значения jc; = —LJ ;
О для каждого интервала [#,_,, ц], /' = 1, 2,... Д находятся:
• частоты «,, т. е. число выборочных значений, попавших в интервал;
Щ
• относительные частоты —;
п
• накопленные частоты м>, = щ + п2 +... + л,;
• накопленные относительные частоты —-.
п
Для выборочной совокупности (табл. 2.4) результаты группировки в Excel
Представлены в табл. 2.5.
Сначала следует указать объем выборки, максимальное и минимальное
значения, размах выборки, количество групп и шаг:
^3 = юо, В23 = 100, С23 = 0, D23 = В23 - С23,
^3 = Ю, F23 = D23 / Е23.
8 ячейках А25 : Н25 указываются заголовки будущей таблицы. В этой табли-
^е колонки В и С можно заполнить в соответствии с формулами (2.1) или за-

422 ЧАСТЬ III. Курсовое проектирование. Гла^
полнить две строки и скопировать их в последующие так, чтобы всего полл
чилось k = 10 строк. Колонку D можно заполнить, используя формулу:
D26 = (В26 + С26) / 2
с последующим копированием в ячейки D27 : D35.
Таблица 2.5. Группировка статистических данных
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
А
п
100
Группа
1
2
3
4
5
6
7
8
9
10
В
•*тах
100
Левая
граница
0
10
20
30
40
50
60
70
80
90
С
•*min
0
Правая
граница
10
20
30
40
50
60
70
80
90
100
D
Я
100
Середина
5
15
25
35
45
55
65
75
85
95
Е
к
10
Частота
27
34
24
7
4
3
0
0
1
0
F
А
10
Относ,
частота
0,27
0,34
0,24
0,07
0,04
0,03
0
0
0,01
0
G
Накоп.
частота
27
61 '
85
92
96
99
99
99
100
100
Н
Накоп.
относ,
частота
0,27
0,61
0,85
0,92
0,96
0,99
0,99
0,99
1
1
Для заполнения колонки Е следует выделить ячейки Е26 : Е35 и обратиться к
функции ЧАСТОТА, указав массив статистических данных и массив правы*
границ интервалов:
{= ЧАСТОТА(A1-.J10; С2б:С35) }.
Одновременное нажатие клавиш <CtrI>+<Shift>+<Enter> приведет к заполн
нию выделенных ячеек.
Заполнение колонки F производится по формуле:
F26 = Е26 / $А$23
с последующим копированием в ячейки F27 : F35.

Тематика курсовых работ
Далее заполняются две ячейки колонки G по формулам:
G26 = Е26, G27 = G26 + Е27
с последующим копированием G27 в ячейки G28 : G35.
Колонка Н заполняется по формуле:
826 = G26 / $А$23
с последующим копированием в ячейки Н27 : Н35.
Рис. 2.4. Кумулята частот
Рис. 2.3. Полигон частот

424 ЧАСТЬ III. Курсовое проектирование. Глава о
Данные, собранные в табл. 2.5, нуждаются в наглядном представлении. ф0*
мами такого наглядного представления являются:
□ полигоны частот — графическая зависимость частот (относительных
частот) от середин интервалов (рис. 2.3);
О кумуляты частот — графическая зависимость накопленных частот
(накопленных относительных частот) от середин интервалов (рис. 2.4).
6.3.3. Подбор подходящего закона
распределения вероятностей
При достаточно большом объеме выборки статистические данные позволяют
подобрать подходящее распределение вероятностей. С этой целью можно
рассмотреть некоторые известные распределения, например равномерное,
нормальное и гамма-распределение.
Предположим, что случайная величина X имеет функцию распределения
F(x). Будем называть это предположение гипотезой о виде распределения
случайной величины X. Чтобы иметь полную информацию о распределении
случайной величины, надо знать параметры этого распределения или их
некоторые оценки. Как правило, параметры распределений берутся такими,
чтобы математическое ожидание случайной величины X было равно
выборочной средней, а среднее квадратическое отклонение случайной величины
X — выборочному среднему квадратическому отклонению. Указанные
выборочные характеристики находятся в ячейках G12 и G14 соответственно.
Откроем новый лист Excel и поместим эти значения в ячейки А2 и В2
соответственно (табл. 2.6). Определим параметры равномерного, нормального и
гамма-распределений в соответствии с формулами:
2 2
flr = /w-av3, & = /?/ + av3, a = ——, р = —
a m
и запишем их в ячейки:
85 = А2 - В2*КОРЕНЬ(3),
86 = А2 + В2*КОРЕНЬ(3),
88 = А2,
89 = В2,
811 = (А2/В2)л2,
812 = В2Л2/А2.
Далее построим таблицу, шапка которой располагается в ячейках А14 : Ь

Тематика курсовых работ
425
Таблица 2.6. Значения плотностей распределения
1
2
3
4
5
6
7
8
9
ю
11
12
13
14
15
16
17
18
19
20
21
22
23
24
А
Матем. ожидание
19,79
В
Сред. кв. отклон.
13,81
Параметры равномерного
распределения
a
b
-4,13
43,71
Параметры нормального
распределения
m
a
19,79
13,81
Параметры
гамма-распределения
а
Р
Середина
5
15
25
35
45
55
65
75
85
95
2,05
9,64
Плотность
относит.
частот
0,027
0,034
0,024
0,007
0,004
0,003
0,000
0,000
0,001
0,000
С
Плотность
равномер.
распред.
0,021
0,021
0,021
0,021
0,000
0,000
0,000
0,000
0.000
0,000
D
Плотность
нормал.
распред.
0,016
0,027
0,027
0,016
0,005
0,001
0.000
0,000
0,000
0,000
Е
Плотность
гамма-
распред.
0,030
0,034
0,021
0,010
0,005
0,002
0,001
0,000
0,000
0,000

426
ЧАСТЬ III. Курсовое проектирование. Глава ?
В ячейках А15 : А24 содержатся середины частичных интервалов, взятые ц3
ячеек D26 : D35 предыдущего листа. В ячейках В15 : В24 вычислены
плотности относительных частот как частное от деления относительных частот
предыдущего листа (ячейки F26 : F35) на шаг (ячейка $F$23).
Плотности равномерного, нормального и гамма-распределений
рассчитываются в соответствии с формулами:
С15 = ЕСЛИ(А15<$В$5; 0; ЕСЛИ(А15 <= $В$6; 1/($В$6-$В$5); 0)),
D15 = НОРМРАСП(А15; $В$8; $В$9; ЛОЖЬ),
Е15 = ГАММАРАСП(А15; $В$11; $В$12/ ЛОЖЬ),
затем они копируются в блок ячеек С16 : Е24.
Построим гистограмму частот, совмещенную с плотностью каждого из
указанных ранее распределений. Гистограмма частот— это графическое
изображение зависимости плотности относительных частот njnh от
соответствующего интервала группировки. В этом случае площадь гистограммы равна
единице, и гистограмма может служить аналогом плотности распределения
вероятностей случайной величины X. Графическое изображение
гистограммы и кривых различных распределений приведено на рис. 2.5—2.7. При этом
используется нестандартная диаграмма типа "График | гистограмма".
Рис. 2.5. Сглаживание гистограммы плотностью равномерного распределения
По внешнему виду этих графиков вполне можно судить о соответствии крй"
вой распределения данной гистограмме, т. е. о том, какая кривая ближе к п
лученной гистограмме.
Используя критерий %2, надо установить, верна ли принятая нами гипотез
распределении случайной величины X, т. е. о соответствии функции РасП"
деления F(x) экспериментальным данным, чтобы ошибка не превышала

Тематика курсовых работ
427
данного уровня значимости а (вероятность того, что будет отвергнута
правильная гипотеза).
0,040
0,035
0,030
0,025
0,020
0,015
0,010
0,005
0,000
Рис. 2.6. Сглаживание гистограммы плотностью нормального распределения
0,040
Рис. 2.7. Сглаживание гистограммы плотностью гамма-распределения
Для применения критерия у} необходимо, чтобы частоты nt,
соответствующие каждому интервалу, были не меньше 5. Если это не так, рядом стоящие
Интервалы объединяются, а их частоты суммируются. В результате общее
Количество интервалов может уменьшиться до значения к'. Далее
вычислялся следующая сумма:
^ = jpzmt, (2.2)

428 ЧАСТЬ III. Курсовое проектирование. Глава о
где Pj — теоретическая вероятность того, что случайная величина X прим^
значение из интервала [а^, а{]. Мы предположили, что случайная величина
X имеет функцию распределения F(x), поэтому pt =F(aj)-F(ai_l).
Образец расчетов по формуле (2.2) в Excel для трех распределений показан
табл. 2.7.
Таблица 2.7. Подбор распределения на основе критерия %2
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
А
Левая граница
0
10
20
30
40
В
Правая граница
10
20
30
40
100
С
Частота
27
34
24
7
8
D
Вероятности
Равномерное
распределение
0,209
0,209
0,209
0,209
0,078
Сумма
0
10
20
30
40
10
20
30
40
100
27
34
24
7
8
Нормальное
распределение
0,163
0,267
0,264
0,158
0,072
Сумма
0
10
20
30
40
10
20
30
40
100
27
34
24
7
8
Гамма-
распределение
0,263
0,335
0,208
0,106
0,086
Сумма
Критическое значение критерия
Е
->
X"
1,778
8,206
0,459
9,247
0,008
19,698
6,978
2,004
0,220
4,916
0,097
14,214
0,017
0,007
0,477
1,243
0,045
1.789
5,991

^Тематика курсовых работ 429
\
ft колонке А содержатся левые, а в колонке В — правые границы интервалов.
Р колонке С находятся соответствующие частоты. Заметим, что интервалы
с 5-го по 10-й объединены в один, чтобы все частоты были не менее пяти.
Количество интервалов вместо к = 10 стало равным к' = 5. В колонке D
рассчитываются теоретические вероятности в зависимости от вида
распределения. Как обычно, вычисляется одно значение, которое копируется в другие
ячейки:
О для равномерного распределения:
D45 = ЕСЛИ(В45 < $В$5; 0; ЕСЛИ(В45 <= $В$6;
(В45 - $В$5)/{$В$б - $В$5); 1)) - ЕСЛИ(А45 < $В$5; 0;
ЕСЛИ(А45 <= $В$б; (А45 - $В$5)/($В$6 - $В$5); 1));
О для нормального распределения:
D52 = НОРМРАСП(В52; $В$8; $В$9; ИСТИНА) - НОРМРАСП(А52;
$В$8; $В$9; ИСТИНА);
О для гамма-распределения:
D59 = ГАММАРАСП(В59; $В$11; $В$12; ИСТИНА) - ГАММАРАСП(А59;
$В$11; $В$12; ИСТИНА).
В колонке Е рассчитываются слагаемые соотношения (2.2) по формуле:
Е45 = (С45 - 100*D45)A2/(100*D45),
которая копируется в другие ячейки колонки Е.
Согласно (2.2) для каждого рассмотренного распределения определяются
итоговые суммы:
Е50 = СУММ(Е45:Е49),
Е57 = СУММ(Е52:Е5б),
Е64 = СУММ(Е59:Е63),
которые равны соответственно 19,698, 14,214 и 1,789.
Гипотеза о виде закона распределения должна быть принята, если
вычисление значение Хвыч достаточно мало, а именно не превосходит критического
значения %кр» которое определяется по распределению % в зависимости от
Жданного уровня значимости а и числа степеней свободы г = к' - s -1.
Здесь л- — число неизвестных параметров распределения, которые были
определены по выборке (для равномерного, нормального и гамма-
Распределений s = 2). В данном примере г = к'-5-1 = 5-3 = 2. Полагая

430 ЧАСТЬ III. Курсовое проектирование. Глава о
а = 0,05, критическое значение критерия %2 в Excel рассчитывается по фор,
муле:
Ебб = ХИ2ОБР(0,05;2)
и, как следует из табл. 2.6, равно 5,991.
Поскольку 1,789 < 5,991, то принимается гипотеза о том, что статистические
данные имеют гамма-распределение с параметрами а = 2,05 и (3 = 9,64
соответственно.
6.4. Определение характеристик
надежности системы
В разд. 6.3 было установлено, что случайная величина Z принадлежит
множеству Г(2,05; 9,64) с плотностью распределения вероятностей:
1,05 __£_
/(*) = ^ е9'64.
9,642>05Г(2,05)
Основными характеристиками надежности невосстанавливаемой системы
являются среднее время безотказной работы и вероятность безотказной
работы в течение времени /.
Среднее время безотказной работы системы 7j равно математическому
ожиданию m, т. е. 7} =19,79 час.
Вероятность безотказной работы вычисляется по формуле:
Pz(t) = \-)f(x)dx. (2-3)
-оо
Построим график функции Pz(tJ, используя Excel. В ячейках А71 : А91
запишем значения аргумента /, изменяющегося от 0 до 20 часов с шагом 1 час.
Так как случайная величина Z имеет гамма-распределение, то в ячейку В/1
записывается формула:
В71 = 1 - ГАММАРАСП(А71; $В$11; $В$12; ИСТИНА),
которая затем копируется в ячейки В72 : В91 (табл. 2.8). При этом
используется аргумент ИСТИНА, который, согласно равенству (2.3), соответствует
интегральной функции распределения (а не плотности распределения).
В результате будет получена таблица значений вероятности безотказной р
боты Pz(t), график которой представлен на рис. 2.8.

'ематика курсовых работ 431
Таблица 2.8. Значения вероятности безотказной работы системы
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
А
В
Вероятность безотказной работы
/, час
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/>(/)
1,000
0,996
0,984
0,965
0,941
0,912
0,880
0,846
0,811
0,774
0,737
0,699
0,662
0,626
0,590
0,556
0,522
0,490
0,459
0,430
0,401
tto табл. 2.8 и графику функции Pz(t) (рис. 2.8) можно определить
вероятность того, что система безотказно проработает в течение заданного времени,
^пример, вероятность безотказной работы в течение пяти часов
**г(5) = 0,912, а в течение средней наработки Pz (19,79) = 0,407 .

432
Рис. 2.8. График вероятности безотказной работы системы
6.5. Варианты заданий на курсовую работу
В табл. 2.9 содержатся исходные данные к курсовой работе: законы и
параметры распределений случайных величин Х], Х2, Х$, V и номера
структурных схем расчета надежности. Обозначения случайных величин
содержатся в [5, разд. 5.6]. На рис. 2.9 приведены соответствующие структурные
схемы. Эти схемы включают нерезервированные и резервированные участки
с постоянно включенным резервом и резервом замещением.
Время до отказа нерезервированной системы равно времени до отказа
наименее надежного элемента. Время до отказа резервированной системы с
постоянно включенным резервом равно времени до отказа наиболее надежного
элемента. Время до отказа системы с резервом замещением равно сумме
времен до отказа элементов.
Таблица 2.9. Варианты заданий на курсовую работу
Вариант
1
2
3
4
5
6
7
Х\
LN(I,5;2)
U(18;30)
W(l,5;20)
Ехр(0,1)
N(18; 2)
Е(3; 0,2)
W(2,l;24)
Хг
LN(1,5;2)
U(18;30)
W(l,5;20)
Ехр(0,1)
N(18; 2)
E(3; 0,2)
W(2,l;24)
Хг
E(2;0,l)
N(30; 5)
U(10;20)
W(2; 13)
Exp(0,05)
LN(2; 0,5)
E(3; 0,25)
V
B(5; 0,7)
G(0,6)
П(2)
B(4;0,6)
G(0,7)
П(0,8)
B(3;0,5)
Схема
рис. 2.9, в
рис. 2.9, д
рис. 2.9. а
рис. 2.9, б
рис. 2.9, г
рис. 2.9, и
рис. 2.9, е
ЧАСТЬ III. Курсовое проектирование, /лада Л

Тематика курсовых работ
433
Таблица 2.9 (окончание)
Вариант
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Хх
Ехр(0,03)
U(12; 14)
N(13; 3)
LN(2; l)
E(2;0,l)
W(l,4;20)
Ехр(0,08)
U(25; 30)
N(17; 4)
LN(3; 0,4)
Е(2;0,15)
W(2,3; 25)
Ехр(0,02)
U(15;22)
N(15; 1)
LN(2; 0,3)
E(3;0,5)
W(l,7; 19)
Exp(0,06)
U(15; 17)
N(29; 2)
LN(1,5; 1)
E(2;0,09)
X2
Exp(0,03)
U(12; 14)
N(13; 3)
LN(2; 1)
E(2;0,l)
W(l,4;20)
Exp(0,08)
U(25; 30)
N(17; 4)
LN(3; 0,4)
E(2;0,15)
W(2,3; 25)
Exp(0,02)
U(15;22)
N(15; 1)
LN(2; 0,3)
E(3; 0,5)
W(l,7; 19)
Exp(0,06)
U(15; 17)
N(29; 2)
LN(1,5; 1)
E(2;0,09)
*,
N(30; 0,4)
W(l,8;22)
W(2; 18)
Exp(0,04)
LN(1;2)
U(30; 50)
LN(2; 1,5)
N(30; 1,7)
E(2;0,04)
Exp(0,02)
W(2,3; 24)
U(34; 40)
LN(3,2; 1)
N(19; 2,2)
E(3; 0,08)
Exp(0,02)
W(3;2)
U(15;20)
LN(2; 1,6)
N(12; 4)
E(2; 0,07)
Exp(0,08)
W(2,4;25)
V
G(0,8)
Щ3,1)
B(4;0,4)
G(0,9)
П(4,8)
B(3;0,2)
G(0,3)
П(2,8)
B(2;0,3)
G(0,4)
П(1,6)
B(4;0,9)
G(0,7)
П(0,5)
B(4;0,6)
G(0,5)
П(3,6)
B(5;0,7)
G(0,2)
П(4,5)
B(2;0,7)
G(0,7)
П(2,9)
Схема
рис. 2.9, ж
рис. 2.9, з
рис. 2.9, д
рис. 2.9, а
рис. 2.9, б
рис. 2.9, в
рис. 2.9, г
рис. 2.9, и
рис. 2.9, ж
рис. 2.9, з
рис. 2.9, е
рис. 2.9, б
рис. 2.9, д
рис. 2.9, г
рис. 2.9, в
рис. 2.9, ж
рис. 2.9, и
рис. 2.9, а
рис. 2.9, е
рис. 2.9, з
рис. 2.9. а
рис. 2.9, д
рис. 2.9, г
о табл. 2.9 содержатся обозначения следующих дискретных распределений:
"В — биномиальное распределение;
^ П — распределение Пуассона.

434
ЧАСТЬ III. Курсовое проектирование. Глава о
Рис. 2.9. Структурные схемы расчета надежности

Тематика курсовых работ 435
"ема 7. Сравнение надежности систем
1ри различных видах
структурного резервирования
7.1. Задание на курсовую работу
Исходными данными к курсовой работе являются:
р две схемы резервирования последовательно-параллельной структуры
одинаковой размерности;
О число элементов нерезервированной системы п;
О число резервных систем m;
О закон распределения времени безотказной работы элементов системы (все
элементы системы имеют одинаковый закон распределения времени до
отказа).
Требуется рассчитать вероятность и среднее время безотказной работы
каждой системы и определить более надежную систему. Для расчетов
использовать метод статистического моделирования на ЭВМ с последующей
обработкой результатов эксперимента. Последовательность выполнения работы
следующая:
1. Разработать алгоритм разыгрывания случайных величин Ху в
зависимости от закона распределения и размерностей системы тип. При этом
используется генератор случайных чисел, равномерно распределенных на
промежутке [0; 1], приведенный в [5, разд. 5.6.2] или содержащийся в
математических пакетах, например в Microsoft Excel или StatGraphics. Объем
выборки принять равным 100, 500, 1000.
2. Определить время безотказной работы системы Хс1 в зависимости от
времени безотказной работы XtJ- элементов на основе первой схемы
расчета надежности.
•*• Определить время безотказной работы системы Хс2 в зависимости от
времени безотказной работы Ху элементов на основе второй схемы
расчета надежности.
4- Статистическая обработка полученных результатов. Для этого необходимо:
• для случайных величин Хс1 и Хс2 рассчитать основные
статистические характеристики: выборочное среднее, выборочную дисперсию,
выборочное среднее квадратическое отклонение, наименьшее и
наибольшее значения, размах выборки;

436 ЧАСТЬ III. Курсовое проектирование. Глава о
• данные для случайных величин Хс] и Хс2 разбить на 10 групп
сформировать статистический ряд, содержащий границы и середины
частичных интервалов, соответствующие частоты; вычислить
относительные, накопленные и накопленные относительные частоты;
• для величин Хс1 и Хс2 построить полигон и кумуляту частот, а также
гистограмму по плотностям относительных частот;
• определить вероятность безотказной работы каждой схемы (таблично и
графически);
• определить среднее время безотказной работы каждой схемы.
5. Выбрать из двух заданных систем более надежную. Определить, во
сколько раз одна схема надежнее другой по критериям вероятности и среднему
времени безотказной работы. Найти интервалы времени, где выигрыш в
надежности самый высокий (самый низкий).
Варианты заданий содержатся в разд. 7.4.
7.2. Методика сравнения надежности систем
последовательно-параллельной структуры
Основными видами структурного резервирования являются: общее и
раздельное при постоянно включенном резерве и по способу замещения.
Структурные схемы этих видов резервирования приведены на рис. 2.10—2.13. На
рисунках приняты следующие обозначения: п — число элементов
нерезервированной системы, m — число резервных систем. '
Пусть Ху — случайное время до отказа элемента, стоящего в /*-м ряду иу-и
колонке, т.е. элемента с номером (/.У), Хс — случайное время до отказа
системы. В [5, гл. 6] получены выражения, связывающие Хс с Xtj для раз*
личных схем расчета надежности.
Схема общего резервирования с постоянно включенным резервом приведен
на рис. 2.10. Время до отказа системы равна:
Хс = max min Xu. V'
/=0.!,2,...,ту=1,2,...,и J
Схема общего резервирования замещением приведена на рис. 2.11. Вре^я
отказа системы равна:
Хс = ± min Xv. <2'5)
/=0 У = 1»2.-'л

Тематика курсовых работ
437
Рис. 2.10. Схема 1. Общее резервирование с постоянно включенным резервом
Рис. 2.11. Схема 2. Общее резервирование замещением
Схема раздельного резервирования с постоянно включенным резервом
приведена на рис. 2.12. Время до отказа системы равна:
Хс = min max Xg. (2.6)
У=1,2,...,л /=0,1,2,-./и
Рис. 2.12. Схема 3. Раздельное резервирование с постоянно включенным резервом
Схема раздельного резервирования замещением приведена на рис. 2.13. Вре-
м* до отказа системы равна:
от
Jfc= min 14- (2-7)
7 = 1,2,...,я/=0

438
ЧАСТЬ III. Курсовое проектирование. Глава о
Рис. 2.13. Схема 4. Раздельное резервирование замещением
Каждая из рассмотренных схем резервирования имеет одинаковое количество
элементов, по-разному соединенных между собой. Важной задачей при
проектировании сложных технических систем является определение наиболее
надежной системы.
Целью курсовой работы является сравнение различных видов резервирования
по критерию вероятности безотказной работы P(t). Для этого необходимо
иметь способы вычисления P(J) систем на основе показателей надежности ее
элементов.
Расчет вероятности безотказной работы систем
последовательно-параллельной структуры с использованием аналитических методов требует
привлечения программных средств, особенно при больших значениях m и п.
Поэтому для проведения анализа надежности таких систем целесообразно
применить метод статистического моделирования.
Идея метода статистического моделирования в данном случае состоит в
следующем. Проводится серия из N независимых испытаний. Каждое
испытание состоит в разыгрывании (/я + 1)х/? случайных величин,
соответствующих времени безотказной работы системы с заданным законом
распределения. Согласно допущению все элементы системы имеют одинаковое
распределение времени до отказа, поэтому в результате испытания будет
получено (ю + 1)хи реализаций одной и той же случайной величины. Формулы
разыгрывания случайных величин с различными распределениями
вероятностей приведены в [5,разд. 5.6].
Рассчитываются значения времени работы до отказа заданных схем
резервирования в соответствии с формулами (2.4)—(2.7). В результате будет полу4
но два значения Хс1 и Хс2 .
Повторяя подобные испытания N раз, будут получены две выборки объе
N, из которых одна соответствует времени до отказа первой системы, а РРУ
гая — времени до отказа второй системы. Эти совокупности чисел являю

Тематика курсовых работ
439
первичным материалом для последующей статистической обработки.
Обозначим их \хР\ , Ы2Н соответственно.
Из этих совокупностей выберем максимальное значение Гкон . Промежуток
[0; Гкон ] разобьем на к равных частей: 0 = /0 <tx <...<tk_l <tk =ТК0И
Значение к можно принять равным 50.
Обозначим через \Jp количество элементов выборки Ы1*} , меньших /,,
а через w; ' — число элементов выборки Ы 1 , меньших /,,
/ = 1,2, ...Д.
Эмпирическая вероятность безотказной работы системы может быть
вычислена по формулам:
О для первой системы:
Р(,)(/,.) = 1-^-; (2.8)
Л'
Р для второй системы:
/>(2)(/,) = 1 i—. (2.9)
Результаты расчетов целесообразно свести в табл. 2.10.
Таблица 2.10. Значения вероятностей безотказной работы двух систем
г, час
0
/i
h
...
tk
Первая система
Р{,)(0)=1
/*,}(/,)
P{l\h)
...
P^\tk)
Вторая система
1*2\0) = 1
/*2)(/,)
P(2\h)
...
Р{2\'к)
Полученная таблица позволяет построить графики вероятностей безотказной
Работы систем, сравнить их по надежности и определить величину выигрыша
"Олее надежной системы по отношению к менее надежной. Если, например,
^рвая система оказалась более надежной, то выигрыш составит величину:
0(0=4^- (2Л0)
Р(2)(0

440 ЧАСТЬ III. Курсовое проектирование. Глав* ^
Среднее время безотказной работы каждой системы можно определить прц>
ближенно с помощью формулы Симпсона:
Tx = \P{t)dt= \P{t)dt = - P(0) + P(rKOH>]T(3^-l)V(/*/0 ,(2.11)
0 0 i\ 1 = 1 J
T
где h — K0H' — шаг интегрирования; k — число промежутков, определяю-
k
щее точность формулы.
Расчеты следует провести при различных объемах выборочной совокупности
и оценить сходимость полученных показателей надежности к истинным
значениям. Тогда будет получена количественная оценка метода
статистического моделирования в расчетах надежности резервированных систем.
7.3. Расчет вероятности безотказной работы
системы последовательно-параллельной
структуры
Рассмотрим схему общего резервирования по способу замещения (схема 2),
изображенную на рис. 2.11. Предположим, что нерезервированная система
содержит п - 2 элемента, а число резервных систем m = 1. Общее количество
элементов в системе равно (/и + 1)хи = 4. Все элементы системы имеют
время безотказной работы, подчиненное распределению Вейбулла с
параметрами а = 4 и (3 = 100 час. Требуется вычислить показатели надежности
системы методом статистического моделирования. Объем выборки N = 200 и
N = 400.
Структурная схема в нашем случае будет иметь вид, показанный на рис. 2.
Неслучайные величины X0i, Х02, Хп, Х12 характеризуют время безотказной
работы элементов системы.
Рис. 2.14. Схема расчета надежности
Время безотказной работы всей системы, согласно (2.5), равно:
Xc=m\n(X0l,XQ2) + m\n(Xu>Xl2). (2'l2)

Тематика курсовых работ
441
Получим значения случайных величин X0i, Х02, Хп, Хп и Хс в Microsoft
Excel.
g ячейки Al : El поместим наименования указанных величин, в ячейки
Д2 : D2 — одинаковые формулы для разыгрывания случайной величины
с распределением Вейбулла * = р(-1п£)а . Здесь cj — равномерно
распределенные случайные числа из интервала [0;1], которые генерирует функция
СЛЧИС():
А2 = 100*(-1п(СЛЧИС()))А(1/4),
В2 = 100*(-In(СЛЧИС()))л(1/4),
С2 = 100*(-In(СЛЧИС()))л(1/4),
D2 = 100*(-In(СЛЧИС()))л{1/4).
Согласно (2.12) в ячейку Е2 поместим формулу:
Е2 = МИН(А2; В2) + МИН(С2; D2).
Скопируем содержимое ячеек А2 : Е2 на блок ячеек A3 : Е201. В результате
получим табл. 2.11.
Таблица 2.11. Формирование выборочной совокупности
1
2
3
4
5
6
...
201
А
*01
96,1
131,3
43,6
59,5
67,6
...
57,2
В
ш
106,1
134,2
81,7
103,4
54,7
...
75,2
, С
ХМ
79,1
78,6
65,1
99,2
103,3
...
77,9
D
Л'12
63,7
74,2
72,6
71,2
69,8
...
31,4
Е
Хс
159,8
205,5
108,7
130,8
124,5
...
88,6
d колонке Е содержатся 200 значений выборочной совокупности,
характеризующих время безотказной работы системы Хс.
^Ыберем в этом столбце наибольшее значение и округлим его в большую
Сторону, в результате получим Гкон = 250 час.
Побьем промежуток [0; 250] на к = 50 равных частей. Полученные точки
_ деления поместим в колонку F, как показано в табл. 2.12. В ячейках колонки

442 ЧАСТЬ III. Курсовое проектирование. Глава
G содержатся частоты выборочных значений. Чтобы их получить, надо
выполнить следующее:
□ выделить блок ячеек G2 : G52;
□ вызвать функцию частота;
□ указать в качестве аргументов массив выборочных значений Е2 : Е20] и
массив точек деления F2 : F52;
О нажать одновременно клавиши <Ctrl>+<Shift>+<Enter>.
Тогда в строке формул появится выражение:
{= ЧАСТОТА(Е2:Е201; F2:F52)}}
а в ячейках колонки G — соответствующие частоты.
В колонке Н располагаются накопленные частоты w,, которые вычисляются
по формулам:
Н2 = G2,
НЗ = К2 + G3.
Последняя формула копируется на блок Н4 : Н52.
В колонке I рассчитываются значения вероятности безотказной работы по
формуле (2.8):
12 = 1 - Н2/200,
которая копируется на блок ячеек 13 :152.
В результате будут заполнены колонки F, G, Н, I табл. 2.12.
Таблица 2.12. Образование эмпирической вероятности безотказной работы
1
2
3
4
5
6
7
8
9
10
F
1. час
0
5
10
15
20
25
30
35
40
G
щ
0
0
0
0
0
0
0
0
0
н
Wi
0
0
0
0
0
0
0
0
0
I
P{t)
J
с,
1
4
2
4
2
4
2
4
2
К
с, • P(t)
1,000
4,000
2,000
4,000
2,000
4,000
2,000
4,000
2,000

Тематика курсовых работ 443
Таблица 2.12 (продолжение)
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
F
45
50
55
60
65
70
75
80
85
90
95
100
105
ПО
115
120
125
130
135
140
145
150
155
160
165
170
175
180
185
190
G
0
0
0
2
0
0
1
1
0
1
0
J
1
4
6
7
6
5
10
11
9
14
12
14
15
10
16
9
9
6
Н
0
0
0
2
2
2
3
4
4
5
5
8
9
13
19
26
32
37
47
58
67
81
93
107
122
132
148
157
166
172
I
1
1
1
0,99
0,99
0,99
0,985
0,98
0,98
0,975
0,975
0,96
0,955
0,935
0,905
0,87
0,84
0,815
0,765
0,73
0,665
0,595
0,535
0.465
0,39
0,34
0,26
0,215
0,17
0,14
J
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
4
2
К
4,000
2.000
4,000
1,980
3,960
1,980
3,940
1,960
3,920
1,950
3,900
1,920
3,820
1,870
3,620
1,740
3,360
1.630
3,060
1,420
2,660
1,190
2,140
0,930
1,560
0,680
1,040
0,430
0,680
0,280

444
ЧАСТЬ III. Курсовое проектирование. Глапя о
41
42
43
44
45
46
47
48
49
50
51
52
53
F
195
200
205
210
215
220
225
230
235
240
245
250
СумМа
G
6
5
2
4
4
2
3
2
0
0
0
0
200
Таблица 2.12 (окончание)
Н
178
183
185
189
193
195
198
200
200
200
200
200
I
0,11
0,085
0,075
0,055
0,035
0,025
0,01
0
0
0
0
0
J
4
2
4
2
4
2
4
2
4
2
4
1
К
0,440
0,170
0,300
0,110
0,140
0,050
0,040
0,000
0,000
0,000
0,000
0,000
93,870
По таблице (колонки F и I) строится график вероятности безотказной работы
системы, изображенный на рис. 2.15.
Рис. 2.15. Вероятность безотказной работы при N = 200
Табличные значения и график являются приближенными, зависящими
объема выборки N = 200. Для их уточнения увеличим N до 400 и повтор

Тематика курсовых работ
Рис. 2.16. Вероятность безотказной работы при N- 400
Сопоставляя эти графики, убеждаемся в том, что они практически совпадают.
Это значит, что метод статистического моделирования дает вполне
приемлемые оценки вероятности безотказной работы системы. Отметим, что даже
при пг = \ применение аналитических формул для вычисления вероятности
безотказной работы системы с резервом замещения— значительно более
сложная задача.
Определим среднее время безотказной работы системы, используя формулу
Симпсона (2.11). В колонку J табл. 2.12 запишем коэффициенты формулы
Симпсона, в колонку К — произведения коэффициентов на соответствующие
значения функции P(t):
К2 = 12 * J2,
которые скопируем на блок ячеек КЗ : К52. В ячейке К53 вычисляется сумма:
Н53 = СУММ(К2:К52),
Равная 93,870. Тогда время безотказной работы будет* равно:
Г,=--93,870 = --93,870 = 156,45 час.
3 3
0писанные действия. В результате получим график P(t), представленный на
рис. 2.16.

446
ЧАСТЬ III. Курсовое проектирование. Глад-
7.4. Варианты заданий на курсовую работу
Варианты заданий выбираются из табл. 2.13 в соответствии с номером сту.
дента в групповом журнале. Обозначения случайных величин содержатся &
[5, разд. 5.6].
Таблица 2.13. Задания к курсовой работе но вариантам
Вариант
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
11омер первой
схемы
2
1
2
3
1
1
2
1
2
3
1
1
2
1
2
3
1
1
2
1
2
3
1
1
2
Но4мер второй
схемы
3
2
4
4
3
4
3
2
4
4
3
4
3
2
4
4
3
4
3
2
4
4
3
4
3
m
5
7
9
3
2
4
5
6
8
6
7
9
3
2
4
5
6
8
4
7
9
3
2
4
5
п
10
8
3
5
6
4
7
Закон распределения времени
до отказа элемент
Е(2;0,1)
N(30; 5)
U(10;20)
W{2; 13)
Ехр(0,05)
LN(2; 0,5)
Е(3; 0,25)
2 j N(30; 0,4)
9
10
8
3
' 5
6
4
7
2
9
10
8
3
5
6
4
7
W(l,8;22)
W(2; 18)
Ехр(0,04)
LN(l;2)
U(30; 50)
LN(2; 1,5) .
N(30; 1,7) __
E(2: 0.04) __
Exp(0,02) ____,
W(2,3; 24) __________
U(34;40) _ .
LN(3,2; 1) ___ _-
N(19; 2,2) .^
E(3;0,08) ^
Rxp(0.02) ____^
W(3; 2) _..^-"-
U(15;20) ___^

Хематика курсовых работ
447
Таблица 2.13 (окончание)
Вариант
26
27
28
29
30
Номер первой
схемы
1
2
3
1
1
Номер второй
схемы
2
4
4
3
4
Di
6
8
6
4
8
п
2
9
6
9
6
Закон распределения времени
до отказа элемента
Щ2; 1,6)
N(12:4)
Е(2; 0,07)
1£хр(0,08)
W(2,4; 25)

• ЧАСТЬ IV
КОМПЬЮТЕРНЫЕ ТЕХНОЛОГИИ
РЕШЕНИЯ ЗАДАЧ НАДЕЖНОСТИ
Глава 1. УНИВЕРСАЛЬНЫЕ МАТЕМАТИЧЕСКИЕ СИСТЕМЫ
СИМВОЛЬНОЙ МАТЕМАТИКИ И РЕШЕНИЕ
ЗАДАЧ НАДЕЖНОСТИ
Глава 2. СПЕЦИАЛИЗИРОВАННЫЕ ПРОГРАММНЫЕ СРЕДСТВА
АНАЛИЗА НАДЕЖНОСТИ СЛОЖНЫХ СИСТЕМ
Глава 3. РЕШЕНИЕ ЗАДАЧ НАДЕЖНОСТИ С ПОМОЩЬЮ
УНИВЕРСАЛЬНЫХ И СПЕЦИАЛИЗИРОВАННЫХ
ПРОГРАММНЫХ СРЕДСТВ
!5 Зак 553

ГЛАВА 1
УНИВЕРСАЛЬНЫЕ
МАТЕМАТИЧЕСКИЕ СИСТЕМЫ
СИМВОЛЬНОЙ МАТЕМАТИКИ
И РЕШЕНИЕ ЗАДАЧ НАДЕЖНОСТИ
В информатике появилось новое научное направление — компьютерная ал
гебра. Технической основой компьютерной алгебры являются универсальны*
программные средства символьной математики. Среди них наибольшее рас
пространение получили системы Mathematica, Maple, Derive, Mathcad и Mat
lab. Интеллектуальность является одной из наиболее важных характеристи
этих систем. Она определяется возможностью системы получать решени
задачи в аналитическом виде. Из перечисленных систем наиболее интеллек
туальными являются первые три. Возможности символьных вычислени
Mathcad и Matlab достаточно скромные, хотя эти системы имеют ряд пре
имуществ перед другими. Мы выбрали систему Derive 5 по ряду причин, кс
торые указаны далее ъразд. 1.1. J описания этой системы.
В теории и практике надежности часто появляется необходимость иметь р«
шение в аналитическом виде. Это происходит в следующих случаях:
О когда необходимо получить показатели надежности при различных вар!
антах исходных данных;
О когда нужно выполнить математические операции над показателями н;
дежности при анализе эффективности, безопасности, риска и т. д.;
О когда требуется провести анализ эффективности различных методов п<
вышения надежности;
О когда необходимо получить математическую модель объекта в смысле ei
надежности.
Незаменимым помощником в таких случаях являются универсальные пр
граммные средства символьной математики. Убедимся в этом на примера
Которые приводятся после краткого описания системы Derive 5.

452 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 1
При расчетах показателей надежности сложных систем, когда приходится
выполнять громоздкие вычисления, весьма полезным может быть табличный
процессор Excel. Мы часто обращаемся к нему при решении примеров и
задач. Краткие сведения об Excel приводятся далее ъразд. 1.19.
1.1. Основы работы в системе Derive
1.1.1. Derive 5 как универсальная система
символьной математики
Система Derive 5 является наиболее интеллектуальной из всех известных
систем символьной математики. Ее интеллектуальность определяется
большим количеством символьных вычислений, множеством функций, простотой
и исключительной ясностью диалога с пользователем, наличием
превосходной системы помощи, большим числом примеров. К сожалению, все это
реализовано только на английском языке.
Derive 5 является самой производительной и безаварийной системой из всех
известных систем символьной математики, с высокой корректностью и
достоверностью решений.
Derive 5 под Windows реализует диалог пользователя с системой по
следующей схеме: ввод выражения — команда действий — ответ. Например, пусть
необходимо найти производную функции f(x). Пользователь вводит
выражение функции, обращается к команде дифференцирования путем щелчка
мыши на соответствующей кнопке и после нажатия клавиши <Enter>
получает ответ. Пользователь самостоятельно не вводит команды в память ЭВМ и
не пользуется клавиатурой, кроме ввода исходного математического
выражения, функции или уравнения.
Такая схема решения математических задач обеспечивает пользователю
максимум удобств и делает процесс решения задачи легким и даже приятным,
похожим на компьютерную игру. Иногда в сложных случаях приходится
набирать на клавиатуре и вводить в память команды. Но даже в этих случаях
все достаточно удобно благодаря автоматизации таких действий, как
подстановка данных в математические выражения, установка опций, ввод
начальных значений и начальных условий и многое другое.
til
Запуск Derive 5 осуществляется двойным щелчком мыши на пиктограмме
рабочем столе Windows. На экране монитора появляется красочная заставк >
а затем основное окно системы, содержащее вверху строку заголовка, стр° У
главного меню, панель инструментов, внизу — окно выражений, панели м
тематических символов, строку состояния системы.

Универсальные математические системы символьной математики 453
1.1.2. Основное окно системы
Главное меню содержит следующие пункты:
О File — работа с файлами и принтером;
О Edit — редактирование выражений;
О Insert — открытие графических окон, аннотация к графикам;
О Author — ввод математических выражений и текстов для их дальнейшего
использования;
О Solve — решение уравнений и систем уравнений;
О Calculus — вычисление производных, интегралов, пределов, сумм,
произведений, разложений в ряд Тейлора;
О Declare — задание функций и переменных;
О Options — задание необходимых установок системы Derive;
О Window — открытие окон и работа с ними;
О Help — открытие справочной системы.
Активизация команд главного меню осуществляется с помощью левой
кнопки мыши или с помощью "горячих" клавиш: сочетаний <Alt> и клавиши с
подчеркнутой буквой в названии команды. Эти способы управления
применяются и для других команд, для которых "горячие" клавиши указываются
после имени команды.
Главное меню изменяется в зависимости от состояния системы. Так,
например, если в Derive закрыты все окна, то главное меню будет иметь только
команды File, Window, Help. Графическое меню содержит свое меню. В ряде
случаев некоторые пункты главного меню недоступны пользователю
(надписи затененным шрифтом) или вовсе отсутствуют.
Панель инструментов расположена в третьей строке вверху основного окна.
Она содержит кнопки быстрого управления системой, дублирующие
команды главного меню. Каждая из кнопок вводит лишь одну команду из
множества команд главного меню. Набор кнопок зависит от вида окна, открытого в
Данный момент.
Наиболее часто приходится пользоваться кнопками быстрого управления при
работе с математическими выражениями. Далее приводятся их значения,
классифицированные по группам (слева направо). Их названия появляются
при подведении курсора к данной кнопке.
•J Команды работы с файлами:
• New — открытие нового окна;
• Open — вывод окна загрузки файла;

454 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава i
Save — сохранение в файле под текущим именем;
Print — печать содержимого окна.
Команды редактирования:
Cut — удаление выделенного выражения (множества выделенных
выражений);
Сору — создание копии;
Paste — восстановление последнего удаленного выражения;
Delete Object— удаление выделенного выражения без его
восстановления.
Команды ввода:
Insert Text — создание аннотаций;
Author Expression — ввод математических выражений;
Author Vector — задание вектора необходимой размерности;
Author Matrix — задание матрицы необходимой размерности.
Команды вычислений:
Simplify — символьные и точные вычисления в цифровой форме,
упрощение математических выражений;
Approximate — вычисления в цифровом виде с представлением чисел
в естественной форме;
Solve Expression — решение уравнений и систем уравнений;
Variable Substitution — подстановки для переменных.
Команды специальных вычислений:
Find limit — вычисление пределов функций;
Find Derivative — вычисление производных;
Find Integral — вычисление интегралов;
Find Sum — вычисление сумм рядов;
Find Product — вычисление произведений рядов.
Команды графических окон:
2D-plot window — вывод окна двумерной графики;
3D-plot window — вывод окна трехмерной графики;
Help About Derive — информация о системе Derive.

Универсальные математические системы символьной математики 455
Строка состояния системы расположена в нижней части основного окна.
Она предназначена для оперативного контроля за работой системы. В ней
выводятся текстовые комментарии о действиях, выполняемых над
выражениями, пояснения о выполняемых командах, сообщения о времени
выполнения расчетов, правильности их завершения, о параметрах графиков для
графических окон.
Диалоговое окно ввода выражении активизируется (мигающий курсор в окне)
с помощью пункта меню Author | Expression. Его также можно вызвать,
переместив курсор в область окна и щелкнув левой кнопкой мыши.
Диалоговое окно служит для ввода математических выражений и текстов.
Редактирование выражений, уже введенных и отображенных в основном
окне, осуществляется только путем вызова выражения в диалоговое окно с
последующим его вводом как нового выражения. Редактирование
осуществляется аналогично тому, как это делается в среде Windows.
Слева от диалогового окна ввода выражений расположены пять кнопок:
О Author Expression (Enter) — ввод выражения (кнопка, дублирующая <Еп-
ter>);
О Simplify — упрощение вводимого выражения или его вычисление;
П Author and Simplify— ввод выражения с одновременным его
упрощением или вычислением (на экране появляется выражение и упрощенное или
вычисленное его значение);
□ Approximate — вычисление выражения;
О Author and Approximate — ввод и вычисление выражения (на экране
появляется выражение и его вычисленное значение).
Например, если в диалоговом окне ввести выражение ехр(-1) + 1п{12), то
после нажатия кнопок на экране будут следующие выражения:
О Author Expression:
#1: exp(-l)+ln(12)
О Simplify:
#2: Ln(12)+e
Q Author and Simplify:
#3: exp(-l)+ln(12)
#4: Ln(12)+e
О Approximate:
#5: 2.852786

456 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава i
П Author Approximate:
#6: exp(-l)+ln(12)
#7: 2.852786
1.2. Ввод выражений
Ввод математических выражений осуществляется латинскими буквами.
Последовательность команд при вводе выражений выглядит так:
□ нажать кнопку Alitor Expression панели инструментов (или <Ctrl>+<A>);
□ записать выражение в диалоговом окне;
□ нажать клавишу <Enter> или кнопку с символом "V" слева от диалогового
окна.
На экране появится выражение с префиксом (#1:), что означает номер
строки, в которой оно находится. При вводе выражений можно пользоваться
панелями математических символов, находящихся в двух нижних строках
экрана. Это бывает полезным при вводе таких выражений, как ё или корень
квадратный, которые традиционно записываются в виде ехр(х) и sqrt(x),
или при вводе выражений с символами греческого алфавита.
УПРАЖНЕНИЕ. Введите следующие выражения:
х2+2х-1, sin(x), Л + 2Д = £, ё3+ях.
При вводе сложных выражений полезно вводить их по частям, а затем
собирать в общее выражение, оперируя номерами строк, в которых находятся
отдельные части выражения. При таком вводе исчезают сложности с
применением скобок и записью многоэтажных дробей.
ПРИМЕР. Необходимо ввести выражение:
f Ух + 2я!-1 Л 2a2+Qex-\)x
, sin(jc) + cos(x) I (Л sin(x) ^
\ \ cos(x)J )
Процедура ввода этого выражения:
#1: Vx+3*n!-l
#2: sin(x)+cos(x)

универсальные математические системы символьной математики
457
#3: 2*ал2 + (3*ел(х)-1)*х
#4: n*(l+sin(x)/cos(x) )
#5: #1/#2*#3/#4-5
После нажатия клавиши <Enter> на экране появится исходное выражение.
Часто при решении математических задач приходится вводить выражения,
в которых имеются переменные с индексами, например: ах, Р0, КаЬс и т. п.
Если не настроить систему на ввод переменных с индексами, то система
будет выводить выражения в виде: а*1, Р*0, К*а*Ь*с,т. е. как
произведения переменных и их индексов. Для настройки системы на ввод переменных
с индексами необходимо выбрать пункт меню Declare | Input, и в
появившемся окне щелкнуть мышью по кнопке Word. После нажатия клавиши <Еп-
ter> на экране появится соответствующее сообщение о настройке системы на
прием переменных с индексами. Теперь при вводе на экране будут
появляться выражения: а2, Р0, КаЬс.
1.3. Вычисление
математических выражений
Вычисление математических выражений, в которых константами и
аргументами функций являются числа, осуществляется с помощью кнопок Simplify
или Approximate панели инструментов, которые имеют вид (=) и (»)
соответственно. После щелчка мыши по одной из этих кнопок в середине экрана
появляется ответ в виде числа. Если точное решение отсутствует, то команда
Simplify обычно повторяет исходное выражение в преобразованном виде.
Такая ситуация возникает, например, при вычислении элементарных
функций с числовыми значениями аргументов. В табл. 1.1 приведены примеры
вычисления выражений по команде Approximate.
Таблица 1.1. Примеры вычислений математических выражений
Выражение в строке
ввода
Ехр{-0.25)
Pi
sin(0.6)A2 + cos{x)A2
Выражение на экране
после ввода
ЕХР(-0.25)
к
sin(0.6)2 + c.os(x)2
Ответ
0.2865047968
3.141592652
cos(x)2 + 0.3188211227
Если выражение содержит символьные переменные, то его вычисление
возможно при любых значениях переменных. Для этого необходимо присвоить

458 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Гла
переменным численные значения и выполнить вычисления, как было описа
ранее. °
Для присвоения переменным численного значения служит команда Substitut
for Variables. На панели инструментов этой команде соответствует кнопк
Sub.
Технология вычислений в системе Derive выглядит следующим образом:
□ ввести выражение с символьными переменными;
□ щелкнуть мышью по кнопке Sub панели инструментов, на экране
появится окно Substitute for Variables; в поле Variables находятся переменные
введенного выражения;
О поочередно присвоить символьным переменным численные значения в
поле New Values;
□ нажать кнопку ОК, на экране отобразится выражение с численными
значениями переменных;
О нажать кнопку Approximate или Simplify; в первом случае появится ответ
в виде числа, представленного в естественной форме, во втором — в виде
точного решения.
УПРАЖНЕНИЕ. Вычислить выражения:
при a = 0,5 , Ъ = -3,25, * = 7,5 ;
sin(x)
сш\
— при а = 2, и = 5; при я = 2, и = 10; при <я = 2, w = 20;
a-n\
хсТ™ + a при а = 0,1, х = 1,5; при я = 1, * = 1; при а = 5, х = 3.
Вычислить значения е икс точностью 10 и 100 знаков после запятой (число
знаков после запятой устанавливается в окне Digits, которое открываете
с помощью пункта меню Declare | Output Settings.
При вычислениях пользуйтесь командами Approximate и Simplify.
1.4. Преобразование выражений
Пункт Simplify главного меню содержит следующие команды символь
математики: Basic..., Expand..., Factor..., Approximate...
Команда Expand называется командой расширения. Она позволяет РасК^е-
вать скобки в алгебраических выражениях, осуществлять разложение на

Универсальные математические системы символьной математики
459
-ентарные дроби, выполнять сокращение дробей. Технология этих
преобразований проста и состоит в выполнении следующих процедур:
г\ ввести выражение;
rj вызвать пункт меню Simplify | Expand, на экране появится окно Expand
Expression;
CJ активизировать необходимые переменные в поле Expression Variables и с
помощью переключателя Amout задать один из четырех типов
выражения: Trivial (Тривиальное), Square Free (Свободное от радикалов),
Rational (Рациональное), Radical (Радикальное);
О щелкнуть мышью на кнопке Expand или ОК; в первом случае на экране
появится ответ, во втором — команда Expand; для ее выполнения
необходимо щелкнуть мышью кнопку Simplify панели инструментов.
Щ. табл. 1.2 приводятся примеры преобразования выражений с помощью
команды Expand.
Таблица 1.2. Примеры
Исходное выражение
(х + а)5
3 3
х -а
х -а
3
х -а
х-а
124
16
(х - 1)2(х3 - 2)
преобразования выражений командой Expand
Выражение после команды
х5 + 5ах" + 10а2х3 + 10а3х2 + 5а4х + а5
х2 + ах + а2
a(az-l) 2 2
+ х +ах + а
х-а
31
4
х5 - 2х4 + х3 - 2х2 + 4х - 2
"^манда Factor дает возможность выполнения операций разложения на
Сожители, выноса за скобки, приведения к общему знаменателю. Так же как
!* команда Expand, команда Factor имеет следующие опции: Trivial, Square
^е, Rational, Radical, Complex (Комплексная).
ори Установке опции Trivial выражения приводятся к общему знаменателю,
суидествляется вынос за скобки. При разложении, свободном от радикалов
уЧиаге Free), выполняются те же операции, что и при наличии опции
^ttvial. Отличие состоит лишь в различных формах представления результа-
°в- При разложении с опцией Rational в конечном выражении отсутствуют
аДикалы. При задании опции Radical осуществляется разложение с возмож-

460
ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 1
ностью представления чисел с дробными степенями. При установке опции
Complex в разложении используются комплексные числа.
Технология преобразований с помощью команды Factor такая же, как и при
реализации команды Expand.
В табл. 1.3 приведены примеры преобразования выражений с помощью
команды Factor.
Таблица 1.3. Преобразование выражений командой Factor
УПРАЖНЕНИЕ. С помощью команд Expand и Factor преобразуйте
следующие выражения:
2 3 1 5_9 (sin(jc)2 +cos(jc)2)cos(jc)
x + a x + a x2-a2' ' sin(2x)
(* + l,2X*-3,6X* + 7), ^ + b) ~° , x4-3x3j + 3xj + 9x2-\Q.
a + b + c
Проверьте правильность преобразования, используя те же команды Expand и
Factor, а также их опции.
1.5. Специальные вычисления
1.5.1. Табулирование функций
Получить значение функции у = /(х) при множестве ее аргументов м0>к
путем многократного ее вычисления методом, описанным в разд. 1.3. Под
Исходное выражение
а с
— +
b a + b
ах2 + bx
9х3 + 22.5х2 + 0.5х - 7
а2 + а - 1
Выражение после команды
а + ab + cb
b{a + b)
х(ах + Ь)
(2х-1) (Зх + 2) (Зх + 7)
2
или при опции Radical
9 х + — 1 х+-|(2х-1)
2
( -Гъ Л( 41 А
а + +_ а_ + _
. V 2 2)\ 2 2)

Универсальные математические системы символьной математики
461
ные вычисления требуют много времени. Система Derive позволяет
достаточно просто получить множество значений функции путем ее
табулирования. Функция табулирования имеет вид:
VECTOR([x;f(x)], х, xn, xk,h),
где f (x) — табулируемая функция, х — аргумент функции, xn — начальное
значение аргумента, хк — конечное значение аргумента, h — шаг таблицы.
Технология табулирования функции в системе Derive выполняется так:
О ввести функцию f(x), на экране функция отобразится в строке #1;
О набрать и ввести команду:
VECTOR([x,#l], х, xn, xk, h);
О выполнить команду Simplify или Approximate, на экране появится
таблица функции /(*).
ПРИМЕР. Необходимо протабулировать функцию sin(.v)/jc в диапазоне
изменения аргумента [0; 1] с шагом /7 = 0,1. В этом случае команда будет иметь
вид:
VECTOR([x,sin(х)/х], х, 0, 1, 0.1).
Если функция была введена предварительно:
#1: sin(x)/x
то команда будет выглядеть так:
VECTOR ( [х,#1], х', 0, 1, 0.1).
После выполнения команды Approximate получим ответ в виде следующей
таблицы:
"о ?
0.1 0.998334
0.2 0.993346 .
• * • • ■ •
1 0.841471_
Знак вопроса в таблице при х = 0 означает, что программа "не знает", чему
равно значение sin(jc)/jc при дг = 0 (деление на ноль).
Команда VECTOR позволяет табулировать одновременно несколько функций.
В этом случае она имеет вид:
VECTOR([x, fl(x), f2(x), ... , fn(x)], x, xn, xk, h),
где fi (x), i = 1, 2, ... , n — /-я функция.

462 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Главя у
ПРИМЕР. Пусть необходимо протабулировать функции ^ = ехр(дл
у = \п(х), у = sin(jc). В этом случае команда VECTOR будет иметь вид:
VECTOR([x,exp(x),ln(x),sin(x)], х, 0, 1, 0.1).
Если до ввода команды VECTOR функции у = ехр(х), у = \п(х), у = sin(;c)
были введены в строках #1, #2, #3, то команда будет иметь вид:
VECTOR([x,#l,#2,#3], х, 0, 1, 0.1).
Команда VECTOR позволяет табулировать функцию с переменным шагом.
В этом случае она представляется так:
VECTOR([x,f(x)], х, [xl, х2, ... , хп]),
где xl, х2, ... , хп — значения аргументов функции f (х).
ПРИМЕР. Необходимо протабулировать функцию п\ при л = 1, 4, 5, 7 .
В этом случае команда будет иметь вид:
VECTOR([n,nl], n, [1,4,5,7]).
После ее исполнения значения факториала будут представлены следующей
таблицей:
~1 1
4 24
5 120
J 5040_
Команда VECTOR позволяет табулировать функцию многих переменных. Для
этого ее необходимо повторить столько раз, сколько переменных содержит
табулируемая функция.
1.5.2. Команда Table
Команда Table — наиболее простой способ табулирования функции. Она
находится в меню Calculus, а соответствующая функция имеет вид:
TABLE(f(x), x, xn, xk, h),
где f (x), x — табулируемая функция и ее аргумент, хп, xk— начальное и
конечное значения аргумента, h — шаг табуляции.
Технология табулирования выполняется так:
□ ввести табулируемую функцию;
О вызвать пункт меню Calculus | Table, на экране появится окно CalcuWs
Table;

универсальные математические системы символьной математики
463
0 записать переменную табулируемой функции в поле редактирования
Variable; в полях Starting Value, Ending Value, Step Size записываются
соответственно начальное, конечное значения аргумента и шаг таблицы;
0 выполнить команду Simplify или Approximate; при нажатии кнопки
Simplify решение выдается в символьном виде (в виде точного решения), при
нажатии кнопки Approximate решение выдается в естественной форме
представления чисел.
функция table позволяет табулировать функции с переменным шагом.
В таком случае она имеет вид:
TABLE(f(x), x, [xl, x2, ... , xn]),
где xl, x2,..., xn — значения аргументов.
1.6. Разложение функций в ряд Тейлора
Разложение функций в степенной ряд реализуется в Derive с помощью
команды Taylor Series, которая находится в меню Calculus.
Соответствующая команда имеет вид:
Baylor(f(x), х, xo, п),
где f (х) — функция, разлагаемая в ряд, х — аргумент функции f (х), хО —
значение х, вокруг которого происходит разложение функции f (x), n —
число членов разложения.
Технология разложения функции в ряд Тейлора в системе Derive следующая:
О ввести функцию f(x), на экране она отобразиться в строке #1;
О вызвать пункт меню Calculus | Taylor Series, на экране появится окно
Calculus Taylor Series;
О в поле Variable активизируется аргумент х, а в полях Expansion Point и
Order вводятся соответственно хО и п;
О выполнить команду Simplify, на экране появится ответ: функция в виде
степенного ряда.
Упражнение. Разложить в ряд Тейлора следующие функции:
у = е~х при х0 = О и л-0 = 1, /7 = 4;
sin х л с.
у = при дг0 = 0 и п = 5;

464 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 1
х-\
у ПрИ х0 = 0 и п = 5;
х + I
у = Inх при jc0 = I и п-5.
1.7. Вычисление пределов
Пределы в Derive вычисляются с помощью команды Limit, находящейся в
меню Calculus.
Технология вычисления предела выглядит следующим образом:
□ ввести выражение;
О выполнить Calculus | Limit или нажать кнопку Lim панели инструментов,
на экране появится окно Calculus Limit;
П установить имя переменной в поле редактирования Variable, ее
предельное значение — в поле Limit Point; в поле Approach From
устанавливается область изменения переменной: Left— слева, Right— справа, Both —
слева и справа;
О выполнить команду Simplify или Approximate, на экране отобразится
ответ.
УПРАЖНЕНИЕ. Найти следующие пределы функций:
I
.. sin(.v) *-l , ,1 (ax+bx)x .. „ 4_L
lim , lim , limu + A'h-, lim , lim (1 -x\\-x.
1.8. Вычисление суммы ряда
Вычисление суммы ряда осуществляется в Derive командой Sum. Далее
приводится технология суммирования членов ряда:
□ ввести функцию суммирования;
□ вызвать пункт меню Calculus | Sum или щелкнуть мышью на кнопке Ь
панели инструментов, на экране откроется окно Calculus Sum;
П установить в поле Variable индексную переменную, переключатель Sum
устанавить в положение Definity, а в поле Defmity Sum задать пределы
суммирования;
□ выполнить команду Simplify или Approximate, на экране появится отве
соответственно в символьной или числовой форме.

универсальные математические системы символьной математики
465
Суммирование элементов вектора в Derive осуществляется с помощью
функции ELEMENT и команды Sum. В этом случае применяется следующая
технология решения задачи суммирования:
О образовать вектор элементов суммирования;
О ввести команду element (#1,п), где #1 — номер строки вектора (в
данном случае строка #1), г. — переменная суммирования;
П выполнить Calculus | Sum или щелкнуть мышью на кнопке £ панели
инструментов, на экране появится окно Calculus Sum;
О установить переменную в поле Variable (в нашем случае и),
переключатель Sum установить в положение Definite, а в поле Definite Sum задать
пределы суммирования: нижний (Lower Limit) и верхний (Upper Limit);
CI щелкнуть мышью на кнопке Simplify или Approximate, на экране
появится ответ: значение суммы чисел элементов вектора суммирования.
УПРАЖНЕНИЕ. Вычислить сумму следующих рядов:
144"4 + - + ^' 2 + 22+23-к.. + 2,°, £*, £*2, £*\ £*Д \q\<\,
2 3 10 j_j k=i k=i ,uo
CO 1 CO 1 CO 1 00 K. CO 1
«—» I ir-i 1 ^-4 1 <r-\ Л г-< J
h{2k-\)2' *=o*!' *=i*(4*2-l)' £i (* + !)!* *=!*?'
[2,2; 6,7; 12,3;-27,8; 14,6; 20].
1.9. Вычисление произведения ряда
Вычисление произведения ряда осуществляется командой Produkt.
Технология вычисления произведения отличается от технологии вычисления суммы
ряда лишь тем, что вместо кнопки £ панели инструментов используется
кнопка П.
Упражнение. Вычислить произведения следующих рядов:
ю ю ю ГГ оо / 1 \
П«* П(в + 0, ПЛ> П 1—Г ' [2; 5; 7; 9; П; 13; 15; 17; 19; 21],
1=1 /=o i=i V'! к=г\ кг)
« ( ^ Л
П i — •

466 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 1
1.10. Вычисление производных
Вычисление производной любого порядка в системе Derive осуществляется
с помощью команды Differentiate. Технология вычисления производной
в системе Derive выглядит так:
□ ввести функцию f(x);
О вызвать пункт меню Calculus | Differentiate или щелкнуть мышью на
кнопке д панели инструментов, на экране появится окно Calculus
Differentiate;
П установить переменную дифференцирования в поле редактирования
Variable, а порядок производной — в поле Order; после нажатия кнопки
Simplify на экране появится искомая производная.
УПРАЖНЕНИЕ. Найти первую, вторую и седьмую производные функции:
х-\
У(х) = г.
дс + 1
Найти первую производную следующих функций:
( 1 Y+1 1 ь
y(x) = eax + \n(bx)+ - , у(х) = - , у(х) = х\, у(х) = ахх .
\\ + х) sinjr + cos*
1.11. Вычисление интегралов
Вычисление интегралов в системе Derive осуществляется с помощью
команды Integrate.
Технология вычисления интеграла следующая:
О ввести подынтегральную функцию /(#);
О вызвать пункт меню Calculus | Integrate или щелкнуть мышью на кнопке J
панели инструментов, на экране отобразится окно Calculus Integrate #1»
где #1 — номер строки подынтегральной функции (в данном случае преД"
полагается, что подынтегральная функция находится в первой строке
экрана);
П установить в поле Variable переменную интегрирования, переключате
Integral установить в положение Indenfmite при вычислении неопреД ^
ленного интеграла или в положение Definite при вычислении определ6
ного интеграла с последующим заданием в полях Upper Limit и k°>v
Limit соответственно верхнего и нижнего пределов интегрирования; в
ле Indenfmite integral записывается постоянная интегрирования;

универсальные математические системы символьной математики 467
ХУ щелкнуть мышью на кнопке Simplify, на экране появится значение
интеграла.
УПРАЖНЕНИЕ. Вычислить интегралы от производных, полученных в
упражнении разд. 1.10. Убедиться, что первообразные совпадают с
исходными функциями.
Вычислить интегралы:
rslnx , /«sin* , rcosjc sin*. . i* cos* sin*. , rx-\ .
dx, I ax, ( —)dx> ( r-)<&> :<&>
J x Л x J x x~ * x x Jx + l
dx, f dx, f dx, [ — + ln(jc + l) + \dx.
x + \ 3x + \ Л x + \ *{x2+2x + \ x + \J
Вычисляя интегралы, следует иметь в виду, что если программа не может
найти первообразную, то вместо решения Derive повторяет выражение
интеграла без его вычисления.
При вычислении несобственных интегралов с бесконечными пределами
следует указывать тип параметров: положительный, отрицательный и т. п.
Пусть, например, необходимо вычислить интеграл
[e-axdx.
Если значение параметра а будет отрицательным, то интеграл будет
расходящимся и Derive после нажатия кнопки Simplify лишь повторит выражение
интеграла, возможно в преобразованном виде. Системе Derive необходимо
указать, что параметр а является положительным. Для этого необходимо
вызывать пункт меню Declare | Variable Domain. На экране появится окно
Declare Variable Domain. В поле Variable Name ввести переменную а .
Переключатель Interval установить в положение Positive(0, oo). После щелчка
мыши на кнопке ОК на экране появится сообщение:
AasReaMO,?).
Теперь вычислим интеграл указанным ранее способом. Ответом будет l/a.
1-12. Решение уравнений
с одним неизвестным
Мщение алгебраических и трансцендентных уравнений осуществляется с
п°Мощью функции SOLVE. Эта функция может иметь один из следующих
*Идов:
SOLVE(f(x), x),
S°LVE(f(x), x, Real),

468 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава /
NSOLVE(f(x}, х),
NSOLVE(f(x), x, Real),
APPROXSOLVE(f(x) , x),
APPROXSOLVE(f(x), x, Real),
NSOLVE(f(x), x, a, b).
В функциях приняты следующие обозначения: f (x) —левая часть
алгебраического или трансцендентного уравнения /(*) = 0, х— неизвестное,
[а, Ь] — область изоляции корня.
Технология определения корней с помощью приведенных функций
исключительно проста и состоит в следующем:
□ ввести команду;
О щелкнуть мышью на кнопке Simplify панели инструментов, на экране
появится'ответ: значение корней уравнения.
Такая технология очень проста, но пользователю неудобна. Например, если
уравнение сложно и приходится применять скобки. Кроме того, набор
команды занимает много времени, особенно у неопытного пользователя, когда
приходится многократно редактировать команду из-за орфографических или
синтаксических ошибок. Система Derive освобождает пользователя от набора
команд, а требует набора только уравнения.
Компьютерная технология определения корней уравнения состоит в
следующем:
О ввести уравнение f(x) = 0. Уравнение может быть представлено в любой
форме, например:
, .2
ах + Ьх -1 = 0, ах + Ьх -1, ах -1 = -Ьх, ах + Ьх = 1, х = —г >
Ъ
П вызвать меню Solve | Expression или щелкнуть мышью кнопку Solve
Expression панели инструментов, на экране появится окно Solve Expression c
четырьмя полями редактирования: Solution Variables, Solution Method*
Solution Domain, Solution Bounds.
В поле Solution Variables отражены все переменные уравнения. Пользовэ
тель должен выделить искомое неизвестное. Остальные поля предназн
чены для образования функций, перечисленных ранее, с помощью УсТ
новки переключателей в соответствующие положения. Каждой из пер
численных ранее функций соответствует определенная комбинат
положений переключателей (табл. 1.4).

Универсальные математические системы символьной математики 469
Таблица 1.4. Варианты функции SOLVE
Комбинация положений
переключателей
Algebraically + Complex
Algebraically + Real
Numerically + Complex
Numerically + Real
Numerically + Bounds +
Lower-a, Upper-b
Either + Complex
Either + Real
Функция
SOLVE(f(x), X)
SOLVE(f{x), x, Real)
NSOLVE{f(x), X)
NSOLVE(f(x), x, Real)
NSOLVE(f(x), x, a, b)
APPROXfSOLVE{f(X), x))
APPROX(SOLVE(f(x), x, Real))
Содержание функции
Решение уравнений в
аналитическом виде
Определение только
действительных корней
Определение корней в
численном виде
Определение
действительных корней в численном
виде
Определение численного
значения корня из области
изоляции [а, Ь]
Аналогично функции
NSQLVE(f (х)," х)
Аналогично функции
NSOLVE(f(x), х, Real)
Откликом функции NSOLVE (f (х), х, а, Ъ) будет лишь один корень из
области [а, ь], хотя в этой области может быть несколько корней. Если в
области [а, Ь] корней нет, то Derive повторно выведет функцию на экран;
О после выбора команды нажать одну из кнопок ОК или Solve,
расположенных в нижней части окна- Solve Expression. При нажатии кнопки J^olve на
экране появится ответ: значение искомого корня (корней). При нажатии
кнопки ОК на экране высветится команда, которую нужно выполнить
нажатием кнопки Simplify панели инструментов.
ПРИМЕР. Необходимо решить уравнение (*4 - \)(х2 - 2а +1) = 0.
Решение:
О ввести уравнение, на экране отобразится:
#1: (хЛ4 - 1)(хл2 - 2-а + 1);
О вызвать меню Solve | Expression, на экране появится окно Solve
Expression #1;
Q выделить переменную х в поле Solution Variables и установить
переключатели в положение Algebraically и Complex;
О нажать кнопку Solve.

470 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава ?
На экране отобразится ответ:
х = - i , x = i, x = - v (2 • а -1) , х = >/( 2 • а -1) , х = -1, х = 1.
Программа нашла все шесть корней уравнения. При выполнении функции:
SOLVE(f(x), x, Real)
при установлении опций Algebraically и Real в ответе будут только
действительные корни: х = -1 , х = 1, х = ->/(2 • а -1) , х = л/(2-а-1) .
Все остальные функции, приведенные в табл. 1.4, решения не дадут, т. к. они
не решают уравнения с символьными переменными.
УПРАЖНЕНИЕ. Решите следующие уравнения:
х3+5*2-17,84*-26,88 = О, sin* — = 0, х3-Зх + 1 = 0,
г5-3,2х2+27*-3,6 = 0, х5-1 = 0, x4-a = 0,
2*-4jc = 0, xsinjt-l = 0, x~ +21nx —3 = 0.
Перед решением определите область изоляции корня и функцию из табл. 1.4
для получения полного ответа. Проверьте правильность решения методом
подстановки результата в исходное уравнение.
1.13. Решение систем
линейных алгебраических уравнений
Системы линейных алгебраических уравнений в Derive решаются с помощью
функции SOLVE, имеющей вид:
Solve ( [fl (xl, x2, ... , xn) , f2(xl, x2, ... , xn) , ••• '
fn(xl, x2, ... , xn], [xl, x2, ... , xn]),
где f i (xl, x2, ... , xn) — z'-e уравнение системы, xi — Z-e неизвестное,
которое необходимо определить, i = 1, 2, ... , п.
Технология решения систем уравнений следующая:
П выполнить Solve | Sistem, на экране появится окно Solve Sistem Setup;
□ установить в поле Number размерность системы (число уравнений) и
нажать кнопку ОК, на экране отобразится новое окно Solve2 equations
пустыми строками вектора уравнений;
□ ввести последовательно все уравнения, пользуясь клавишей табуляции Д
перемещения курсора по строкам таблицы; в поле Solution Variables о
ределить, выделяя мышью переменные, все искомые неизвестные;

универсальные математические системы символьной математики 477
О нажать кнопку Solve или ОК, расположенные внизу окна Solution
Variables. В первом случае на экране появится команда и значения
неизвестных, во втором — только команда; для ее исполнения необходимо нажать
кнопку Simplify или Approximate.
УПРАЖНЕНИЕ. Описанную ранее технологию решения систем уравнений
изучите в процессе решения следующей системы уравнений:
щ + Ьх2 = 3;
<
2,Х\ — Ху = — 1.
Прежде чем решать эту систему уравнений, настройте Derive на прием
переменных с индексами (пункт меню Declare | Input | Word).
Решив приведенную систему уравнений, получите следующий ответ:
3-Ь _ а+6
*1~а + 2Ь' *2~a + 2b'
Решить следующие системы уравнений:
a\xi + #2*2 + азх3 = 1> ГЗ,2JC| - 7,3*2 + хз ~ -4;
< fy*i + byx2 + £3*3 = ^» 1 ~1 1*1 + 1 7*2 + $хз = 2;
Z*i — Ху •+■ СХ\ — —Z, *i + Ху — /Х-у —\2..
Правильность расчетов проверить методом подстановки решений в каждое
из уравнений. Вторую систему решить методом символьных вычислений
(Simplify) и методом приближенных вычислений (Approximate).
Эффективным методом решения систем линейных алгебраических уравнений
является матричный метод.
Пусть А — матрица коэффициентов системы уравнений, X — вектор
неизвестных, В — вектор правых частей системы уравнений. Тогда решение сис-
"^мы уравнений в матричной форме будет иметь вид: X = А_1В.
Пример. Система уравнений имеет вид:
[2дг, - 3*2 = 1;
[*1 + 5*2 = -4-
Тогда
А= 2 "3 , В = [1,-4], Х = А_,В.
L1 5_Г

472 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глав*
Технология решения системы уравнений в Derive следующая:
О выполнить Author | Matrix или нажать кнопку Author Matrix панели
инструментов, на экране отобразится окно Matrix Setup;
□ ввести размерность матрицы в поле Matrix dimension: Rows (Число
строк), Colums (Число столбцов), в нашем случае две строки и два столб-
ца; после нажатия кнопки ОК на экране появится окно Author 2x2 matrix
□ заполнить пустые поля элементами матрицы А, нажать кнопку ОК или
Simplify, на экране в строке #1 отобразится матрица А;
□ щелкнуть мышью кнопку Author Vector панели инструментов, на экране
появится окно Vector Setup;
□ набрать в поле Elements число элементов вектора В, в нашем случае два
элемента, и щелкнуть кнопку ОК, на экране появится окно Author 2
element Vector;
□ заполнить пустые поля элементами вектора В, в нашем случае это 1 и -4,
после нажатия кнопки ОК на экране выведется вектор:
#2: [1,-4]
□ набрать в строке пользователя выражение #1Л(-1)*#2 и нажать <Enter>,
на экране появится выражение:
~2 -ЗТ1
#3: [1 -4]
1 5 J
П щелкнуть мышью кнопку Simplify панели инструментов, на экране
появится ответ в виде вектора:
''-— -—'
13 13_
При нажатии кнопки Approximate панели инструментов на экране выве-
дется ответ в виде следующего вектора:
[-0.5384615, -0.6923076]
Матричный способ позволяет также решать системы линейных алгебраи
ских уравнений с символьными переменными.
УПРАЖНЕНИЕ. Приведенные ранее в упражнении данного раздела сИС
мы уравнений решить матричным методом и сравнить полученные резу-Л
ты с предыдущими.

универсальные математические системы символьной математики 473
1.14. Решение систем нелинейных уравнений
Системы нелинейных алгебраических уравнений в Derive решаются
методами Ньютона — Рафсона и итераций.
1.14.1. Метод Ньютона — Рафсона
функция, реализующая метод Ньютона, имеет вид:
NEWTONS([fl(xl, х2, ... , xn) , f2(xl, x2, ... , xn), ... ,
fn(xl, x2, ... , xn)], [xl, x2, ... , xn], [xlO, x20, ... ,
xnO], n),
rnefi(xl, x2, ... , xn), i = 1, 2, ... , n—i-e уравнение
системы; xi — /-e неизвестное; xiO — i-e начальное приближение для
неизвестного xi; n — число итераций, задаваемое пользователем.
Технологию решения нелинейных уравнений в среде Derive рассмотрим на
примере. Необходимо решить следующую систему нелинейных уравнений:
xy + xz + yz = -19;
<x2+y2+2z2=63;
_L JL-11
2y 2x 12
Начальными приближениями пусть будут следующие значения неизвестных:
*о=-2, ^0=-1,5, z0=3.
Решить систему можно путем набора и ввода функции:
NEWTONS([x*y + x*z + y*z = -19, хЛ2 + ул2 + 2*zA2 = 63,
х/(2*у) + у/(2*х) = 13/12], [х, у, z), [-2, -1.5, 3], 10).
После нажатия кнопки Approximate получим ответ в виде таблицы значений
неизвестных на каждой итерации.
чцнако на практике более рациональной может оказаться следующая
технология решения системы нелинейных уравнений:
™ ввести уравнения в любой последовательности, на экране появятся
следующие три уравнения:
#1: xy + xz + yz + 19
#2: x2+y2+2z2-63
n_ x у 13
#3: + —
2у 2х 12

474 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава i
П ввести функцию:
NEWTONS([#l,#2,#3],[x,y,z],[-2,-1.5,3],10)
на экране появится функция, в которой вместо номеров строк будут
вписаны уравнения;
□ нажать кнопку Approximate, на экране появится решение системы
уравнений в виде следующей таблицы:
-2 -1.5 3
-2.526 -1.68 6.008
-2.746 -1.83 5.175
-2.952 -1.968 5.025
-2.998 -1.998 5.001
-2.999 -1.999 5.000
-3-2 5
-3 -2 5
-3 -2 5
-3 -2 5
-3 -2 5
Из таблицы видно, что решением системы нелинейных уравнений является
* = -3, У = -2, Z = 5 и получено оно за шесть итераций.
1.14.2. Метод итераций
Функция решения систем нелинейных уравнений методом итераций имеет
вид:
FIXED_POINT([fl(xl, х2, ... , xn), f2(xl, х2, ... , хп) , ••• '
fn(xl, х2, ... , хп)], [xl, х2, ... , хп] , [х10, х20, ••• '
хпО], п).
Сравнивая эту команду с функцией NEWTONS, видим, что они отличаютс
лишь названием. Процедуры решения систем уравнений те же, что и в метод
Ньютона — Рафсона. В большинстве случаев метод Ньютона по сравнению
методом итераций позволяет получить решение за меньшее число итерации-
Метод итераций при его практической реализации требует преобразован
уравнений и проверки условий сходимости итераций. Уравнения доля*
быть представлены в виде: х = fl(x,y,z)t у = f2(x,y,z), z = f3(x,y,z).
При этом в функцию fixedpoint входят лишь правые части уравнений.

Универсальные математические системы символьной математики 475
Сходимость будет обеспечена, если выполнены условия сходимости
итераций. Если эти условия не выполнены, то необходимо преобразовать каждое
уравнение к виду, когда условия сходимости выполняются. Команды
NEWTONS и fixed_point можно также использовать для решения уравнений
с одним неизвестным.
1.15. Решение
дифференциальных уравнений
Система символьной математики Derive содержит несколько десятков
функций решения дифференциальных уравнений первого и второго порядков в
символьном и числовом виде. Эти функции позволяют решать уравнения
специального вида с представлением решений в аналитическом виде, в виде
чисел и числовых рядов. Наиболее важной является функция RK решения
дифференциальных уравнений и систем методом Рунге — Кутты.
Функция RK имеет вид:
RK(r, u, uO, h, n),
где:
Or — вектор правых частей уравнений, разрешенных относительно
производных, при этом система уравнений представляется в виде, когда каждое
из уравнений является уравнением первого порядка;
О и — вектор неизвестных;
О uO — вектор начальных условий;
Oh — шаг интегрирования;
On — число итераций.
Векторы представляются в виде квадратных скобок. Квадратные скобки
опускаются, если решается дифференциальное уравнение первого порядка.
Откликом при реализации функции RK является матрица неизвестных с
числом строк п и шагом h. Функция RK находится в файле ODEAPPR.mth, к
которому необходимо обратиться перед решением уравнений.
Технология решения дифференциальных уравнений следующая:
S выполнить обращение к файлу ODE_APPR.mth: File | Load | Utility File |
ODE_APPR.mth, на экране появится:
#1: LOAD(Ode_appr.mth);
^ ввести функцию RK (r, u, uO,h,n);
О Щелкнуть кнопку Approximate, на экране появится ответ в виде матрицы.

476 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава i
При решении дифференциальных уравнений высокого порядка
целесообразно перед вводом функции RK ввести поочередно правые части всех
уравнений. После ввода они будут расположены на экране в отдельных строках,
помеченных символами #к, где к = 1, 2,..., п — номера строк, в которых
находятся правые части всех п дифференциальных уравнений. Только после этого
ввести функцию RK, записав вектор г в виде: [# 1, #2, ... , #п].
ПРИМЕР. Необходимо решить следующее дифференциальное уравнение:
у" + ху' - 2у +1 = 0 с начальными условиями у(0) = 1, /(0) = 2.
Прежде чем обратиться к системе Derive, представим уравнение второго
порядка в виде системы двух дифференциальных уравнений, каждое из которых
первого порядка, разрешенное относительно производной. Такие
преобразования выполняются методом подстановок. Обозначим у' -z. Тогда система
дифференциальных уравнений будет иметь вид:
ГУ=г.
z' = -xz + 2y-\.
Теперь запишем функцию RK:
RK([z,-xz+2y-l], [x,y,z], [0,1/2], 0.2, 8).
После ввода этой функции и нажатия кнопки Approximate получим ответ в
виде следующей матрицы:
"О 1 2
0.2 1.4226 2.2398
0.4 1.9011 2.5578 .
_1.б 6.6975 5.7267_
1.16. Интерполяция
1.16.1. Интерполяция точная в узлах
Система Derive имеет две функции интерполяции точной в Узла'
POLY_INTERPOLATE И LAGRANGE.
Первая функция имеет вид:
POLY_INTERPOLATE(A, x),

универсальные математические системы символьной математики
477
где А— матрица функции y = f(x), представленной в виде таблицы, х —
аргумент функции y = f(x). Функция реализует полиномиальную
интерполяцию и выдает решение в виде многочлена степени п -1, где п — число
узлов интерполяции.
Технология интерполяции в среде Derive выглядит следующим образом:
О создать матрицу А размерности шх«, где m — число строк, равное числу
узлов интерполяции, п — число столбцов, равное в данном случае двум;
О ввести функцию POLY_lNTERPOLATE(#k, х), где #к— номер строки,
в которой находится матрица А, на экране отобразится функция с
матрицей А;
О выполнить команду Simplify, на экране появится ответ в виде полинома
степени п -1, в котором числа представлены в форме точных значений
(с числителем и знаменателем); при использовании команды Approximate
ответом будет многочлен степени п -1, коэффициентами которого
являются числа, представленные в естественной форме.
ПРИМЕР. Функция f(x) задана в виде следующей таблицы:
X
Л*)
1
12
2
9
3
7
4
2
5
1
Решая задачу интерполяции по описанной методике, получим на экране
монитора следующие выражения:
~1 12"
2 9
#1: 3 7
4 2
_5 1_
|Tl 12] ^
2 9
*'2: POLY_INTERPOLATE 3 7 ,х
4 2
I* lj ,

478 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава i
Их4 -126х3+493х2-834х + 744
#3:
24
#4: 0.041ббб(11х4-126х3+4 93х2-834х + 74 4)
Функция LAGRANGE имеет вид:
LAGRANGE(А, х),
где А — матрица, полученная по функции f(x), представленной в виде
таблицы, х— аргумент функции /(*)• Команда осуществляет интерполяцию
многочленами степени п -1 по методу Лагранжа.
Технология интерполяции в среде Derive выглядит так:
□ вызвать утилиту решения задачи интерполяции: File | Load | Utility File |
Hermite, на экране отобразится:
#1: LOAD{Hermite.mth);
О ввести матрицу исходных данных;
□ вызвать функцию LAGRANGE(#2, х), на экране отобразится функция
с матрицей исходных данных, расположенной в строке #2;
О выполнить команду Simplify или Approximate, на экране появится ответ:
в первом случае в виде точного решения, во втором — с представлением
чисел в естественной форме.
1.16.2. Сплайн-интерполяция
Сплайн-интерполяция реализуется в Derive функцией SPLINE. Эта функция
имеет вид:
SPLINE(А),
где А — матрица, полученная по функции f(x) и заданная в виде таблицы.
Технология решения задачи сплайн-интерполяции в среде Derive:
□ вызвать утилиту решения задачи сплайн-интерполяции: File | Load | Utility
File | Splines.mth, на экране появится:
#1: LOAD(Spline_s.mth);
О ввести матрицу А исходных данных, на экране появится матрица, напр
мер, в строке #2;
О вызвать функцию SPLINE (#2), на экране отобразится команда с матр
цей А;

Универсальные математические системы символьной математики
479
О выполнить команду Simplify или Approximate, на экране появится ответ:
в первом случае в виде точного решения, во втором — в виде
приближенного решения с представлением чисел в естественной форме.
1.16.3. Интерполяция
приближенная в узлах (аппроксимация)
Аппроксимация в Derive реализуется с помощью команды FIT, имеющей
вид:
FIT (А),
где А — матрица исходных данных. Первой строкой матрицы должна быть
строка вида [х, ср(х)], где (р(х) — функция аппроксимации, х— аргумент
функции <р(х). Функцией аппроксимации может быть полином,
показательная, степенная, логарифмическая и другие функции по выбору пользователя.
Вслед за строкой [х, ф (х) ] располагаются табличные данные исходной
функции у = f(x). Пусть, например, функция у = f(x) задана в виде следующей
таблицы:
дг
Лх)
I
3,2
3
7
7
9,65
12-
П.З
18
16,8
Пусть функцией интерполяции является полином третьей степени
у = я0 + ахх + а2х + а$х . Тогда матрица А будет иметь вид:
2 3~
х aQ+ajX + ajX +a3x
1 3.2
3 7
7 9.65
12 Ц.З
.18 16.8
Аппроксимация с помощью команды FIT в системе Derive осуществляется по
Методу наименьших квадратов.
Технология аппроксимации в среде Derive следующая:
СЭ ввести матрицу А, в строке #1 появляется матрица;
О ввести функцию fit (#1), на экране отобразится функция FIT с матрицей
данных;

X
Л*)
1
2
2
4
3
8
4
12
и пусть функцией интерполяции будет полином у = а + Ьх + сх2. Тогда поел
ввода матрицы А на экране будет матрица следующего вида:
х а + Ьх + сх
1 2
#1: 2 4
3 8
_4 12
После набора в строке пользователя функции у = fit(#1) и нажатия
клавиши <Enter> на экране появится строка #2:
х a + bx + cx
1 2
#2: y = FIT 2 4
3 8
После выполнения команды Approximate на экране отобразится ответ:
у=0.5х2+0.9х+0.5.
Сделаем несколько важных замечаний о команде FIT:
1. Если число неизвестных коэффициентов интерполяции равно числ>
исходной таблицы данных, то с помощью команды FIT решается з ^
интерполяции, точной в узлах. Если число неизвестных меньше н.
строк исходной таблицы, то решается задача интерполяции, при сЛа
ной в узлах (аппроксимация). Если же число неизвестных болыие
строк таблицы, то задача не решается. ^
2. Функция аппроксимации может быть практически любого вида, пр мер,
в аргументе функции не должно быть искомых переменных. На
480 ЧАСТЬ IV. Компьютерные технологии решения задач надежности г
-Lj^aea 1
П выполнить команду Approximate, на экране появится ответ в виде rb
мулы. ^Р*
ПРИМЕР. Пусть функция у = f(x) задана в виде следующей таблицы:

х/иивврсальные математические системы символьной математики 481
функция у = a + b • In x вполне может быть аппроксимирующей, а функция
yz=a + b-\ncx нет, т. к. произведение сх программой воспринимается, как
аргумент.
3. Команда FIT позволяет решать задачи аппроксимации функций многих
переменных. Пусть, например, функция задана в виде следующей
таблицы:
.Y
У
2
W
1
2.3
12,4
2,5
2
6.1
8
4,6
4
7,4
7,2
7,4
8
9
5,4
10,2
14
12
3,1
13,8
20
16,5
1,9
15,6
FIT
X
1
2
4
8
14
20
У
2.3
6.1
7.4
9
12
16.5
z
12.4
8
7.2
5.4
3.1
1.9
a + bx + cy+ dz
2.5
4.6
7.4
10.2
13.8
15.6
Если теперь функцию w(x,y,z) принять за квадратичную, то следует
изменить лишь первую строчку таблицы: вместо линейной функции
записать следующую квадратичную:
a+b1x+b2Xz+Ciy+Coy2+d1z+d2z2+e1xy+e2xz+e3y2/
Правда, в этом случае наша задача не будет решена, т. к. число
неизвестных функции аппроксимации больше числа узлов интерполяции (числа
строк таблицы). Для решения необходимо иметь не менее 10 строк
исходной таблицы (по числу коэффициентов квадратичной функции).
Ункция all_seven имеет вид:
AL4_SEVEN(.A),
в е А — матрица исходных данных. Данная функция позволяет интерполиро-
ь Функцию, заданную в виде таблицы, семью функциями вида: линейной
'б Зад. 553
И пусть функция w(x,y,z) является линейной, тогда команда FIT будет
иметь вид:

X
м
1
6,5
2
20
3
53,5
4
167
5
473
6
1470
После выполнения всех перечисленных действий на экране появится ответ в
следующем виде:
251.142t-514
г.г^бэе1-07812'
3.83192t2'94214
591.1561nt-283.227
974.732
763.015
t
4.07641.10"7
1.18175.10б-1. 94317.105t
1.28619.107t
1.27441.10б-2.06659.105t
В ответах аргумент функции обозначен символом t, вместо привычного х-
482 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава j
y = a + bx, показательной у-аеЬх, степенной у = ахь, логарифмической
i . <- b а ах
y = a\nx + b и дробно-линейными вида: у = а + —, у = , у = .
х b + cx b + cx
Технология решения задачи интерполяции в среде Derive выглядит следую,
щим образом:
□ обратиться к утилите решения задачи интерполяции: File | Load | Utility
File | Curv_fit, на экране отобразится:
#1: LOAD(Curv_fit.mth);
О ввести матрицу исходных данных, на экране отобразится матрица в
строке #2;
О выполнить функцию ALLSEVEN (#2), на экране появится функция с
матрицей исходных данных;
□ выполнить команду Approximate, на экране появится ответ в виде семи
формул.
ПРИМЕР. Функция задана в виде следующей таблицы:

Универсальные математические системы символьной математики 483
Следует иметь в виду, что некоторые из формул могут иметь большие
погрешности, хотя все они получены на основании одного и того же метода —
метода наименьших квадратов. Окончательный выбор формулы
аппроксимации остается за пользователем.
Команда ALLSEVEN полезна в тех случаях, когда пользователь не знает вида
функции, а поэтому не может воспользоваться командой FIT.
1.16.4. Паде-аппроксимация
Паде-аппроксимация служит для аппроксимации нелинейных функций
дробно-рациональными функциями вида:
, N Ьп+Ых + Ых2 + ... + bmxm
У(Х) = — ! *—= ~ .
aQ + щх + a2x +... + anx"
Метод является одним из наиболее точных. Его реализация в Derive
возможна лишь в том случае, если нелинейная функция задана в виде
аналитического выражения.
Функция Паде имеет вид:
PADE(y, х, хО, га, п),
где у, х — функция и ее аргумент; хО — значение аргумента, вблизи
которого обеспечивается высокая точность аппроксимации; m — степень
многочлена числителя; п — степень многочлена знаменателя.
ПРИМЕР. Нелинейная функция имеет вид: у(х) = 2е~х,2хcos(jc) . Необходимо
функцию аппроксимации представить в виде дробно-рациональной функции
вблизи значения аргумента хО = Оприш = 2, п = 3.
Последовательность решения задачи аппроксимации Паде в среде Derive
выглядит так:
О загрузить файл утилиты решения задачи аппроксимации Паде: File | Load |
Utility File | Approx.mth, на экране отобразится:
#1: LOAD(Approx.mth);
О вызвать функцию pade(2*exp(-1.2*x) *cos (х), х, 0, 2, 3);
О выполнить команду Simplify или Approximate.
Откликом будет следующая дробно-рациональная функция:
10(679..jc2-848..jc-115)
161...jc3 + 239...*2+493...x + 576...

484 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава i
1.17. Визуализация вычислений
Построение графиков всегда полезно, а иногда и необходимо. Графики почти
всегда строятся в следующих случаях:
О при визуализации функций, являющихся моделями физических и других
изучаемых явлений;
□ для наглядного представления о пространственных фигурах;
П для изучения особенностей математических функций: наличие экстрему,
мов, точек перегиба, разрывов непрерывностей и т. п.;
О при выборе вида функции интерполяции;
О при определении областей изоляции корней уравнения.
Derive является наиболее простой системой визуализации математических и
физических понятий. Ее освоение не требует детального описания способов
построения графиков. Для этого достаточно знать лишь назначение команд
меню и особенно кнопок панели инструментов графических окон двумерной
и трехмерной графики. Эти окна открываются соответственно кнопками
2D-plot window и 3D-plot window панели инструментов главного окна Derive 5.
Далее приводится назначение пунктов меню и кнопок панели инструментов.
Меню двумерной графики выглядит следующим образом:
О File — просмотр графиков, вывод их на принтер, выход из графического
окна, закрытие окна;
О Edit — создание и уничтожение аннотаций, удаление последнего графика,
копирование графика в буфер;
□ Insert — открытие графических окон, аннотация графика;
П Set — установка масштабов и размеров графика, выравнивание графика по
центру;
П Options — установка опций;
О Windows — управление окнами;
П Help — вывод справки о Derive.
В большинстве случаев при работе с графикой нет необходимости
обращаться к командам главного меню. Быстрый способ построения графиков осуше"
ствляется с помощью кнопок панели инструментов. Перечислим их и укаже
кратко их назначение.
□ Копирование и печать графика:
• New — открытие нового окна Derive;
• Open — открытие окон, демонстрация примеров решения задач;

Универсальные математические системы символьной математики 485
• Save — сохранение графика;
• Print — вывод графика на принтер;
• Copi Plot Window — копирование графика в буфер обмена.
О Управление построением графика:
• Plot expression — построение графика выделенного выражения;
• Delete last plot — удаление с экрана последнего построенного графика;
• Insert Annotation — создание аннотаций.
О Центрирование и масштабирование графика:
• Trace plots — режим перемещения графического курсора по кривой;
• Center on cross — центрирование графика относительно курсора;
• Center on origin — центрирование графика по самому себе;
• Set range with box — развертывание выделенного графика во все окно.
Р Расширение области графика:
• Zoom out (F10) — расширение графика по горизонтали и вертикали;
• Zoom vertical out (F8) — расширение графика по вертикали;
• Zoom horizontal out (F6) — расширение графика по горизонтали.
О Сжатие области графика:
• Zoom in (F9) — сжатие области графика в обе стороны;
• Zoom vertical in (F7) — сжатие области графика по вертикали;
• Zoom horizontal in (F5) — сжатие области графика по горизонтали.
• Algebra window (Ctrl + 1) — возврат в окно выражений.
Графическое изображение кнопок на экране столь очевидно, что нет
надобности их подробно описывать. Вполне достаточно приведенного списка.
Процедуры графического представления функции в Derive выглядят
следующим образом:
О ввести функцию f(x) и выделить ее на экране монитора;
О щелкнуть мышью на кнопке 2D-plot window панели инструментов, на
экране появится окно двумерной графики с сеткой координат 2D-plot 1.1;
О щелкнуть мышью на кнопке Plot Expression панели инструментов окна
двумерной графики, на экране появится график выделенной функции.
° ряде случаев Derive устанавливает масштабы графика автоматически.
Однако часто масштабы приходится устанавливать пользователю с помощью
кнопок расширения и сжатия графика.

486 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 1
Возврат в окно выражений осуществляется с помощью нажатия кнопки AlgC-
bra window панели инструментов. При этом предыдущий график
сохраняется, и, если необходимо, повторяя описанные действия, можно построить в
том же окне второй график. Удаление первого графика осуществляется
нажатием кнопки Delete Last Plot.
Система Derive 5 также строит графики параметрически заданных функций и
функций в полярных системах координат. Для построения графиков
параметрически заданных функций необходимо записать функции в виде вектора,
отделив их запятой. Векторное задание функций осуществляется их
представлением в квадратных скобках, например (sin(t) • (cos (t) i-i) ,
3sin (2t) 1. После ввода такого вектора и нажатия кнопок 2D-plot window и
Plot Expression панели инструментов появляется окно задания параметров
Parametric Plot Parameters. Задав необходимые параметры и щелкнув по
кнопке ОК, получим график функции.
При построении графика в полярной системе координат необходимо
выполнить следующие процедуры:
□ ввести функцию г{0);
□ открыть окно двумерной графики с помощью кнопки 2D-plor window;
П установить с помощью меню Set | Coordinate Sistem полярную систему
координат Polar;
П щелкнуть кнопку Plot Expression панели инструментов, появляется окно
Parametric Plot Parameter;
П уточнить (при необходимости) параметры построения графика и нажать
кнопку ОК, на экране появится график в полярной системе координат.
В процессе работы с графикой эффективным средством анализа является
графический курсор. Он позволяет: определить координаты точек графика
(режим Autoscale New Plots), посмотреть график за пределами видимого окна
путем перемещения курсора в нужную сторону (режим Follow Cross),
повысить точность определения координат графика (режим Trace Plots). В
последнем режиме курсор превращается из крестика в маленький квадратик,
устанавливается на необходимую кривую и перемещается мышью или
клавишами точно по кривой.
Все перечисленные режимы действия графического курсора устанавливаются
по команде Options графического меню.
Главное меню трехмерной графики не отличается от меню двумерной граф11
ки. Панели инструментов группы копирования и печати также идентичнь-
Остальные кнопки панели инструментов трехмерной графики имеют ель
дующие назначения:

Универсальные математические системы символьной математики
487
О Delete Plot — удаление графика;
О Plot — построение пространственного графика выделенного выражения;
CJ Insert Annotation — создание аннотаций;
О Trace Plots — трассирование графика;
О Set Plot Range — установка масштабов по осям координат;
О Set Eye Position — установка размеров области графика;
О Zoom out (F10) — расширение графика в обе стороны;
D Zoom in (F9) — сжатие графика в обе стороны;
□ Rotate Plots — вращение графика;
□ Rotate left — поворот графика влево на одну позицию;
О Rotate right — поворот графика вправо на одну позицию;
□ Rotate up — поворот графика в сторону от пользователя;
D Rotate down — поворот графика в сторону пользователя;
П Magnify plot — расширение области графика;
О Shrinkt plot — сжатие области графика;
□ Algebra window — возврат в окно выражений.
Процедуры построения пространственных графиков достаточно просты и
мало чем отличаются от процедур построения двумерных графиков. При
наведении курсора мыши на кнопки панели инструментов всплывают
подсказки с их названиями. Пиктограммы на кнопках являются хорошей подсказкой
для пользователя, поэтому нет необходимости детально описывать
процедуры построения трехмерных графиков. Пользователь легко в них разберется
уже при первом построении графика.
1.18. Функциональные возможности
табличного процессора Excel
Электронная таблица — самая распространенная технология для
профессиональной работы с данными. В ячейках (клетках) таблицы могут быть
записаны данные различных типов: текст, даты, числа, формулы, функции и др.
Главное достоинство электронной таблицы — возможность мгновенного
автоматического пересчета всех данных, связанных формульными
зависимостями, при изменении значения любого компонента таблицы.
В Microsoft Excel вычислительные возможности объединены с богатым
набором функций, присущих текстовому и графическому редакторам, а также

488 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 1
другим приложениям пакета Microsoft Office. В переводе с английского
Excellent означает "отличный", "превосходный".
Рассмотрим некоторые возможности табличного процессора Excel в связи
с решением задач анализа и синтеза надежности технических систем.
Программа Excel позволяет:
П выполнять табличные вычисления (в том числе как обычный
калькулятор);
П вычислять значения и исследовать функции, строить графики функций;
О решать уравнения, системы уравнений, работать с матрицами,
комплексными числами и т. п.;
□ осуществлять математическое моделирование, проводить численные
эксперименты;
О проводить статистический анализ данных и наглядно их представлять в
виде графиков и диаграмм;
О выполнять оптимизацию, осуществлять прогнозирование и поддержку
принятия решений;
П выполнять обмен данными с другими программами, вставлять текст,
рисунки, таблицы, подготовленные в других приложениях;
О использовать более 400 встроенных функций: математических,
статистических, финансовых, логических, инженерных, информационных,
функций даты и времени, функций управления базами данных и списками;
□ реализовать инструментальную поддержку технологий сети Интернет,
пользоваться средствами создания HTML-документов и выполнять их
публикации в локальных и глобальных сетях.
Расчеты показателей надежности без помощи ЭВМ, как правило, являются
сложными и требуют применения многочисленных таблиц функций и
справочников, содержащих значения квантилей стандартных распределений. Речь
идет не о замене математического мышления программой, а о новом виде
"справочника формул". В отличие от простого справочника по математике
налицо такие преимущества, как удобство и быстрота расчетов, наличие
большого количества дискретных и непрерывных распределений, изменение
исходных данных и автоматический пересчет результатов, большие
графические возможности.
Перечислим некоторые стандартные функции распределения вероятностей и
приведем их обозначения:
О FPACn — F-распределение (распределение Снедекора);
О бетарасп—г-бета-распределение;

Универсальные математические системы символьной математики 489
О биномрасп — биномиальное распределение;
О ВЕЙВУЛЛ — распределение Вейбулла;
О гаммарасп— гамма-распределение;
О логнормрасп — логарифмически-нормальное распределение;
□ нормрасп — нормальное распределение;
О пуассон — распределение Пуассона;
О стьюдрасп — распределение Стьюдента;
О ХИ2РАСП — хи-квадрат распределение;
П ЭКСПРАСП — экспоненциальное распределение.
Для статистического моделирования незаменимой является функция
СЛЧИСО, генерирующая псевдослучайные числа, равномерно
распределенные от 0 до I. На основе этой функции разыгрываются другие дискретные и
непрерывные случайные величины. Генерация случайных величин позволяет
проследить за изменениями в гистограммах и сглаживающих кривых
распределений.
При изменении исходных данных в задаче автоматически изменяются
результаты. Тем самым пользователь имеет возможность в определенной
степени управлять процессом вычислений, почувствовать элемент новизны в
изучаемом материале.
С помощью Excel можно решать уравнения и системы уравнений. Решение
систем алгебраических уравнений осуществляется с помощью пункта меню
Сервис | Поиск решения. Решение систем дифференциальных уравнений
можно выполнить с помощью реализации известного алгоритма, например
Эйлера или Рунге — Купы.
В Excel имеется возможность оперативной обработки статистических
экспериментальных данных. Для компактного представления данных очень
удобной оказывается функция ЧАСТОТА, позволяющая группировать большие
массивы данных и давать их наглядное представление.
Использование программы Excel целесообразно еще и потому, что она имеет
широкое распространение и, как правило, знакома студентам.
Оценка надежности систем при неэкспоненциальных законах распределения
часто требует использования табличных функций, таких как функция
Лапласа, гамма-функция и неполная гамма-функция. Значения этих функций легко
получить в Excel. Реализуются они по следующей технологии:
1 ' —
О Функция Лапласа Ф0(/) = —j= \e 2 dx.
v2ti о

490 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 1
В ячейку А1 помещается аргумент (значение t), а в ячейку А2—
функция:
А2 = НОРМРАСП(А1; 0; 1; 1) - 0,5.
Результатом является значение функции Лапласа.
00
О Гамма функция Г(а) = jxa~le~xdx:
о
В ячейку А1 помещается аргумент (значение а), а в ячейку А2—
функция:
А2 = ЕХР(ГАММАНЛОГ(А1)).
Результатом является значение гамма-функции.
О Неполная гамма-функция 7(а,0 = \xa~xe~xdx.
Г(а)^
В ячейку А1 помещается первый аргумент (значение а), в ячейку А2 —
второй аргумент (значение t), в ячейку A3 — функция:
A3 = ГАММАРАСП(А2; А1; 1; 1).
Результатом является значение неполной гамма-функции.
Большим достоинством Excel является возможность представления рядов и
столбцов данных в виде диаграмм и графиков, позволяющих наглядно
оценить имеющиеся величины. Excel поддерживает 34 типа различных двух- и
трехмерных диаграмм. Работа с диаграммами исключительно проста, описана
в многочисленной литературе и поэтому здесь не приводится.

ГЛАВА 2
СПЕЦИАЛИЗИРОВАННЫЕ
ПРОГРАММНЫЕ СРЕДСТВА
АНАЛИЗА НАДЕЖНОСТИ
СЛОЖНЫХ СИСТЕМ
2.1. Требования, предъявляемые
к интегрированной системе
Реализация новых методов анализа надежности сложных систем
предусматривает создание программных средств для их практического использования.
В целях повышения эффективности работы специалистов данные
программные средства должны удовлетворять следующим требованиям:
О их основу должны составлять научно-обоснованные методы расчета и
прогнозирования надежности систем;
О обеспечивать требуемую точность расчетов и работать в реальном
масштабе времени;
П иметь дружественный графический интерфейс, структура и способы
управления графическими объектами которого должны быть
унифицированы для всех программных средств;
О создавать базу исходных данных и результатов для оперативного их
просмотра и редактирования, для чего необходима реализация таких операций
с данными, как их создание, сохранение, копирование, удаление и т. п.;
О предоставлять возможность документирования результатов расчетов;
О создавать графическое представление результатов расчетов;
О быть удобными в приобретении и бесплатными.
Далее приведены алгоритмы и программные средства расчета надежности
Технических систем и их краткая характеристика. Алгоритмы и программные
средства разработаны авторами на основе методов, представленных в кни-

492 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
ге [5]. Программные средства выполнены в операционной системе Windows
ХР и используют язык программирования C++ Builder 6.
Интегрированная система 1SANT находится на сайте по адресу: http://
www.gurov.spb.ru/isant/isant.html.
Следует иметь в виду, что постоянное совершенствование интегрированной
системы может приводить к изменению перечня программных средств на
сайте и их содержимого.
2.2. Структура интегрированной системы
Общая структура интегрированной системы представлена на рис. 2.1.
На схеме приведены наиболее важные программные средства для оценки
надежности систем с большим числом состояний, переменной структурой и
произвольными законами распределения параметров, отказов и
восстановлений элементов. В последующих разделах данной главы приводятся
назначение и описание работы некоторых программных средств, содержащихся на
рис. 2.1.
Рис. 2.1. Структура интегрированной системы
Пользовательский интерфейс представлен в виде диалога с компьютеров
когда на экране сосредоточены исходные данные и результаты решения зада

Специализированные программные средства анализа надежности сложных систем 493
чи надежности. Пользователи могут создавать и модифицировать описание
функционирования системы и исходные данные об отказах и
восстановлениях элементов. Имеются также контекстные справки, предупреждения и
сообщения об ошибках.
2.3. Методика и алгоритм
программы Relass
Инструментальная система Relass предназначена для анализа и
прогнозирования надежности технических систем в процессе их проектирования.
Система позволяет рассчитать надежность невосстанавливаемых и
восстанавливаемых, нерезервированных и резервированных изделий при общем,
раздельном резервировании и при резервировании с дробной кратностью.
Рассчитываются стандартные показатели надежности. Уникальность системы
определяется возможностью анализировать широкий класс структур,
моделировать собственное время работы элементов системы, учитывать
последействие отказов, контроль состояния элементов и различных дисциплин
восстановления.
Исходными данными для расчета являются структурная схема и показатели
надежности элементов при различных способах их задания. Структурная
схема может представляться и редактироваться на экране. Результаты
расчетов отображаются в виде графиков, числовых значений и выходных
текстовых файлов.
Программная система .Relass позволяет также оценить надежность системы
по следующим показателям:
G функция оперативной готовности;
П среднее время безотказной работы Т{1) и среднее время восстановления
TR(t) на интервале [0, /];
О параметры потоков отказов. co(f) и восстановлений сов(7);
П интенсивности отказов X(t) и восстановлений \i(t);
О плотность распределения времени безотказной работы /(0 и времени
восстановления g(t);
О среднее число отказов и восстановлений на интервале [0, /].
На основе Relass разработано программное средство Dens, предназначенное
Для расчета первых двух моментов распределения времени пребывания
системы в подмножестве состояний, таких как среднее время безотказной
работы, наработка на отказ, среднее время восстановления системы. Функция

494 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава р
оперативной готовности сложной системы по программе Opgot также
рассчитывается с использованием файлов результатов программы Relass.
В следующих разделах приводится методика и алгоритм программной
системы Relass, использующей аналитическую оценку надежности. Разработанный
метод является универсальным для большого класса технических и
программных систем. Метод базируется на возможности описания
функционирования системы графом состояний. Однако в отличие от известных методов
он использует специальное интегрированное представление графа с целью
существенного сокращения времени расчетов и уменьшения памяти. Новизна
Relass состоит также в создании собственного языка описания и
формализации структурных схем, в методе создания и редактирования структурных
схем и исходных данных об элементах, в учете времени простоя отдельных
элементов системы.
Математические модели, предназначенные для оценки надежности сложных
невосстанавливаемых и восстанавливаемых систем, как правило, не
учитывают ряд важных специфических особенностей их функционирования, таких
как наличие интервалов простоя элементов, последействие отказов, контроль
состояний элементов, дисциплину обслуживания и т. д. Однако в реальных
системах игнорирование этих особенностей может привести к серьезным
ошибкам и иметь нежелательные последствия. Некоторые особенности
функционирования системы могут привести к улучшению, а некоторые к
ухудшению характеристик надежности системы. Рассмотрение этих особенностей
позволяет установить степень их влияния на надежность системы. А это
является важным инструментом для эффективного исследования систем.
2.3.1. Возможности и ограничения программы
Программа Relass предназначена для анализа и прогнозирования надежности
сложных технических систем с большим числом состояний
(Ю6 и более).
Исходными данными для расчетов являются: структурная схема системы,
данные о надежности и времени функционирования элементов системы, данные
о характеристиках и дисциплине обслуживания элементов и системы в
целом. Программа позволяет:
П представить и модифицировать структурную схему системы и исходные
данные;
О задавать исходные данные о надежности элементов в виде интенсивности
отказов, среднего времени безотказной работы, вероятности безотказной
работы за определенное время;
О отображать результаты работы в виде численных данных, таблиц и
графиков;

Специализированные программные средства анализа надежности сложных систем 495
О формировать выходные документы, содержащие исходные данные о
структуре и элементах, а также результаты расчета;
D вычислять надежность по всем стандартным показателям с учетом
неодновременности работы элементов, наличия последействия отказов,
различной дисциплины обслуживания, контроля состояния элементов
системы.
С помощью программы Relass вы имеется возможность:
О выбрать из множества вариантов структурных схем наилучшую;
D выбрать рациональную дисциплину обслуживания системы;
П выявить наиболее слабые места в системе и наметить пути повышения ее
надежности;
П оценить эффективность применения структурного резервирования.
Relass обладает одним очень важным ограничением — все элементы системы
имеют экспоненциальные распределения. Однако наличие интервалов
простоя элементов делает распределение времени их жизни не
экспоненциальным, что несколько ослабляет указанное ограничение.
2.3.2. Представление и формализация
структуры исследуемой системы
Одной из проблем анализа систем посредством инструментальных
программных средств является представление и формализация структурных
схем, точнее — выработка языка описания технических систем, который
учитывал бы сложные структурные схемы, наличие ремонта, различные
дисциплины восстановления, различные законы распределения отказов элементов
и т. д.
Программа Relass содержит способ трансформирования структур в удобный
вид для последующего применения численных алгоритмов оценки
надежности. Представление структурной схемы системы должно удовлетворять
следующим условиям:
П универсальность описания схем;
О гибкость в описании вложенных структур;
О возможность включения в описание узлов нового типа;
О удобство доступа к базе данных с информацией о схеме;
О малый объем памяти, занимаемый на диске.
Система представляется иерархической типовой структурой. Нижний
уровень состоит из элементов. Каждый следующий уровень содержит типовые

496 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
структуры, состоящие из типовых структур предыдущего уровня. В качестве
примера рассмотрим систему, представленную на рис. 2.2.
Рис. 2.2. Структурная схема расчета надежности
Эта система состоит из 10 элементов И представляется так, как показано в
табл. 2.1.
Номера
подсистем
11
12
13
14
15
16
Число Число основных Номера элементов
элементов элементов и подсистем
2
2
2
2
4
3
1
0
1
1
3
0
1;2
11; 3
5; 4
13; 12
6; 7; 8;9
14;15;10
Тип
связи
3
1
2
3
2
1
В таблице приняты следующие обозначения для типов связей: 1 — основное
соединение, 2 — основное соединение, когда при отказе элемента остальные
элементы подсистемы не выключаются, 3 — нагруженный резерв, 4 — нена-
груженный резерв. Использование данной формы представления структур
позволяет производить оценку надежности как всей системы, так и любой
п системы.
Таблица 2.1. Представление структуры системы

Специализированные программные средства анализа надежности сложных систем 497
Приведем исходные данные для расчета надежности восстанавливаемой и
невосстанавливаемой системы:
О период функционирования системы (для учета собственного времени
работы элементов);
□ время работы системы;
D число элементов в системе, число подсистем, число ремонтных бригад на
всю систему;
О данные по структурной схеме с учетом вложенности подсистем. Для
каждой подсистемы должны быть заданы следующие характеристики:
• номер подсистемы;
• тип связи (основное соединение; основное соединение, когда при
отказе элементы не выключаются; нагруженный резерв; ненагруженный
резерв);
• состояние (включена, выключена);
• общее количество элементов и подсистем;
• количество основных элементов и подсистем;
• номера элементов и подсистем в данной подсистеме;
П данные об элементах. Для каждого элемента должны быть заданы
следующие характеристики:
• номер элемента;
• интенсивность отказа;
• интенсивность отказа после отказа некоторого одного элемента;
• интенсивность отказа после отказа двух элементов;
• интенсивность восстановления;
• вероятность обнаружения отказа;
• количество интервалов простоя, границы интервалов простоя;
О данные о ремонтных бригадах. Для каждой ремонтной бригады должны
быть заданы следующие характеристики:
• номер бригады;
• количество ремонтных единиц в бригаде;
• приоритет обслуживания (прямой, обратный, назначенный);
• количество элементов, обслуживаемых бригадой;
• номера элементов, обслуживаемых бригадой.
'7 Зак. 553

498 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
Алгоритм расчета показателей надежности включает в себя:
О построение графа состояний;
О выявление типа состояния системы (исправное, отказовое, поглощающее
отражающее);
П вычисление суммарного времени пребывания в каждом состоянии
(суммарная наработка и суммарное время восстановления), а также
суммарного числа переходов (отказов и восстановлений) из состояния в состояние;
□ перестройку структуры системы вследствие отказа или восстановления
некоторого элемента;
П учет неодновременности работы элементов, наличие последействия
отказов, возможность появления необнаруженных отказов;
□ расчет нестационарных и стационарных характеристик надежности
системы.
Результатами расчетов являются:
□ наработка на отказ системы;
П среднее время восстановления системы;
□ коэффициент готовности системы;
□ среднее время безотказной работы системы;
О таблица значений функций готовности и простоя системы;
П таблица значений параметров потоков отказов и восстановления системы;
□ таблица значений среднего суммарного времени работы и среднего
суммарного времени восстановления системы;
П таблица значений среднего числа отказов и среднего числа
восстановлений системы;
О таблица значений наработки на отказ и среднего времени восстановления
системы в зависимости от времени;
П таблица значений вероятности безотказной работы и вероятности отказа
системы;
О таблица значений среднего времени безотказной работы системы в
зависимости от времени;
О графики всех табличных функций.
2.3.3. Описание системы графом состояний
Вычисление требуемых характеристик надежности основано на возможное
описания функционирования технической системы графом состояний. Око

Специализированные программные средства анализа надежности сложных систем 499
ветви графа указываются интенсивности переходов, которые вычисляются
следующим образом. Пусть i = (/l5 /2,..., ik) состояние системы, полученное
при последовательном отказе элементов с номерами /',, i2,... , ik ; a j —
состояние системы, полученное из состояния / при отказе еще одного элемента
ik+]. Тогда соответствующая интенсивность перехода равна Xtj = Xi , где
Я., — интенсивность отказа элемента с номером ik+x. При этом, если этот
элемент входит в резервированный узел, в котором ранее уже был отказ
некоторого одного элемента (или двух элементов), то, учитывая последействие
отказов, полагаем Ху=Х] i (или Ху=Х] ), где X) (X" ) —
интенсивность отказа элемента с номером ik+l после одного отказа (или двух отказов)
других элементов резервированного узла.
Интенсивность ц-перехода из состояния i определяется следующим образом.
Набор элементов (i{, /2, •••, **) разбивается на группы, соответствующие
одной ремонтной бригаде. Для каждой такой группы в зависимости от
количества ремонтных единиц и приоритета обслуживания определяются номера
ремонтируемых элементов. Для каждого найденного элемента определяется
состояние /, в которое переходит система при его восстановлении. Тогда р.
есть интенсивность перехода из состояния / в состояние /.
Без контроля состояния элементов ремонт невозможен, если не известен сам
факт отказа. При вычислении интенсивности перехода, связанного с
ремонтом некоторого элемента, необходимо учитывать вероятность обнаружения
отказа а < 1. Пусть X и ji — интенсивность отказа и интенсивность ремонта
элемента без учета контроля. Определим влияние скрытого отказа на
интенсивности X и ц. Пусть (0)— состояние исправной работы элемента, (1) —
состояние обнаруженного отказа, (2)— состояние скрытого отказа, (3) —
состояние обнаруженного отказа после состояния скрытого отказа
(рис. 2.3, а).
Рис. 2.3. Граф состояний с учетом скрытого отказа: исходный (а),
содержащий -эквивалентные интенсивности переходов (6)

500 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава ?
Интенсивности переходов равны соответственно Х0]=аХ, ц10 = ^
XQ2=(\-a)X, Р-зо=И-
Пусть р; — вероятность пребывания системы в /-м состоянии. Тогда
эквивалентные интенсивности переходов (рис. 2.3, б) с учетом контроля
определяются следующим образом:
-^аХр0+(]-а)Хр0 =х M^i+M-Рз = а^1
pQ ' P\+P2+Pi сО, + (1-сф"
Таким образом, наличие контроля не влияет на интенсивность отказа
элемента, но влияет на интенсивность его ремонта. Если ц; — интенсивность
ремонта /'-го элемента без учета контроля, то интенсивность ремонта с учетом
возможности обнаружения отказа вычисляется как:
а^+(1-а,-)Ц; '■
и контроль уменьшает интенсивность ремонта, поскольку р/. <\ir
Формирование самого графа состояний осуществляется с помощью рекурсии,
позволяющей не запоминать состояния системы в массивах или в файле на
диске, а использовать для хранения информации стековую память
компьютера. Одновременно рекурсия делает расчетный алгоритм более гибким и
компактным.
2.3.4. Алгоритм уменьшения
размерности графа состояний системы
Важной особенностью сложных систем является сильное увеличение числа
состояний системы при незначительном увеличении количества элементов.
Например, для системы с нагруженным резервированием кратности m, со-
стоящей из элементов разной надежности и обслуживаемой одной бригадой,
число состояний равно N - £ А'т+] . Зависимость N от т приведена в
i = 0
табл. 2.2.
Таблица 2.2. Зависимость числа состояний системы
от кратности резервирования
т
N
0
2
1
5
2
16
3
65
4
326
5
1957
6
13700
7
109601
8
986410
9
9864101

Специализированные программные средства анализа надежности сложных систем 501
Программа Relass позволяет установить, что для системы, изображенной на
рис. 2.2, количество состояний равно 52630.
Следовательно, невозможно использовать точные методы, которые
рассматривали бы все состояния системы и были бы пригодны для оценки ее
надежности. В связи с большим числом состояний невозможно сформировать
матрицу переходов для последующего решения систем алгебраических или
дифференциальных уравнений. Поэтому для проведения дальнейших расчетов по
графу состояний необходимо преобразовать его к более простому виду таким
образом, чтобы можно было провести расчеты в разумные временные сроки.
Наиболее простым графом со сравнительно небольшим количеством узлов
является такой, на каждом уровне которого содержатся не более двух узлов,
соответствующих работоспособному и отказовому состояниям (такой граф
назовем простейшим или свернутым). Указанное преобразование
выполняется так, чтобы были сохранены параметры потоков отказов и
восстановлений, рассчитанные для стационарного режима функционирования. Это
объясняется тем, что все характеристики надежности системы выражаются
именно через эти параметры. Согласно принятому допущению
интенсивности переходов для укрупненного графа рассчитываются по их определению,
приведенному в [5, гл. 2]. Например, интенсивность перехода из
работоспособного состояния k-го уровня в другое работоспособное состояние (к + 1)-го
уровня равна:
п -id
ak ~ sr
i
где суммирование производится по всем /-м исправным состояниям к-го
уровня и всему-м исправным состояниям {к+ ])-го уровня. Веса pt
вычисляются в соответствии со следующей формулой:
—/?/_!, если ц*0;
А НИ
[l, если ц = 0, или /-0,
где А. и ц. — суммарные интенсивности переходов в i-e и из /-го состояния
соответственно. Процесс накопления сумм для параметров и вероятностей
происходит одновременно с построением полного графа состояний.
Определение стационарных Т, Тв, К{. и нестационарных Р(/), Кг(1)
характеристик системы производится путем составления и решения систем
алгебраических и дифференциальных уравнений. Вычисление переходных
характеристик надежности является результатом решения системы
дифференциальных уравнений методом Рунге — Кутты с автоматическим выбором шага.

502 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
2.3.5. Анализ систем при наличии интервалов
простоя элементов
Согласно сделанному ранее предположению элементы системы могут
работать лишь некоторое время и простаивать в течение остальной его части.
Интервалы простоя могут быть как детерминированные, так и случайные. Мы
ограничиваемся здесь рассмотрением только детерминированных интервалов
простоя. Моменты времени изменения интенсивностей отказов для части
элементов являются моментами реконфигурации всей системы. Между
моментами реконфигурации системы все элементы имеют постоянные
интенсивности отказов и восстановлений. Предполагается, что функционирование
системы повторяется через определенный период. Однако это не означает,
что система в начале каждого периода становится новой. Надежность
системы зависит от ее предыдущего функционирования, и в начале каждого
периода система имеет другой ресурс по сравнению с началом предыдущего
периода. В каждый момент времени, соответствующий началу и концу
простоя, приходится перестраивать граф состояний и получать новые значения
для интенсивностей переходов. Однако на каждом таком интервале процесс
функционирования системы может рассматриваться как марковский.
Начальные условия в начале каждого интервала образуются из расчетов для
предыдущего интервала, что обеспечивает непрерывность перехода через момент
реконфигурации системы.
Для вычисления стационарных характеристик можно воспользоваться
следующим приемом. Предположим, что на периоде функционирования /0
произошло п перестроек системы в моменты времени /j,f2».» »f„, отвечающих
изменению интенсивностей переходов в графе состояний. Длительность /-го
этапа равна (/,- -*,_i), / = 1, 2,..., п, f0 = 0. Далее будут использоваться
обозначения, принятые в [5, гл. 2].
Средняя наработка между отказами для системы есть отношение суммы
средних суммарных наработок на всех этапах в течение времени tQ к сумме
среднего числа отказов на всех этапах в течение того же времени, т. е.
к " _ _
S 2>/(ty>+'/-i>fob+'/)
г ,. к=0 /=1
К-»оо * " _ _
*=0 /=1
Так как средняя суммарная наработка выражается через интеграл от функии
готовности, а среднее число отказов выражается через интеграл от параметр
потока отказов:

Специализированные программные средства анализа надежности сложных систем 503
h h
да,(/„/2) = J*r(')A. ^(/,,/2)= /<о(/)Л,
то по теореме о среднем существуют точки £, и rj, из промежутка (tltt2)
такие, что:
поэтому средняя наработка между отказами для системы равна:
К п
rj, ,. 4 = 0 /=1
Г= hm -j— ,
I 1<»(Пи)('м-',)
4=0 /' = 1
ИЛИ
T- \ш .
К-*<х> Д 1 А,
/=1Л+1Л=0
Поскольку ^, А ->.оо и х\ц -> со, то по свойству Чезара — Фейера средние
арифметические имеют те же пределы, что и сами слагаемые:
1 к 1 к
1Ш -^-7 I кг ft/,* ) = * г/. J'"1 -^-7 I ®(П/д) = ®/.
следовательно:
ixc-i-',) £-^(/,_,->,)
Аналогично можно показать, что среднее время восстановления,
коэффициент готовности и наработка до первого отказа вычисляются по формулам:
£^5и'н-'/) ix,cw-<<) 7
г _ /=!*/ +/в< „ _i=l __ т 'О
i» — , Лг — — , 1\ — „
"1 'г ^ 1 я , _j
Z т . т ^'-! ~ ''^ Z ^

504 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глав*
Приведенными здесь соотношениями удобно пользоваться для расчетов,
поскольку в них содержится зависимость только от предельных значений
показателей надежности и не учитывается нестационарный режим
функционирования.
2.4. Методика программы Kasm
Современные сложные системы (АСУ ТП, вычислительные системы и пр.)
отличаются большим числом элементов, наличием различных видов
резервирования, многофункциональностью, возможным последействием отказов,
зависимостью по восстановлению, распределением ремонтных бригад по
группам элементов, различными приоритетами обслуживания. Оценка
надежности таких систем с необходимой точностью невозможна без
применения вычислительной техники. Метод декомпозиции структурной схемы
расчета надежности, рассмотренный в гл. 5 части /, является одним из
машинных методов анализа надежности систем с большим числом элементов.
Однако он используется, как правило, в случае основного соединения групп
элементов функциональной схемы.
Аналитико-статистический метод основан на объединении узлов полного
графа состояний исследуемой системы с большим числом элементов. Метод
позволяет рассчитать наработку на отказ, среднее время безотказной работы,
среднее время восстановления, вероятность безотказной работы и
коэффициент готовности при следующих допущениях:
□ интенсивности отказов и восстановления элементов постоянные;
□ непрерывность контроля функционирования системы;
О полное восстановление надежности системы в процессе ремонта
элементов;
□ начало восстановления отказавшего элемента сразу же после его отказа
при наличии свободной ремонтной бригады или по очереди согласно
приоритету обслуживания.
Метод позволяет оценить надежность системы при любом виде структурного
резервирования и произвольной дисциплине восстановления.
Рассмотрим произвольную систему, удовлетворяющую приведенным ра«е
ограничениям. Полный граф состояний системы с большим числом элеме^
тов имеет сложную конфигурацию и огромное количество узлов и вегве, '
поэтому представление, хранение и обработку информации о таком грач
невозможно осуществить с помощью современных (и возможно, перспект
ных) ЭВМ. Сформируем граф состояний системы, имеющий на кажД '
уровне не больше двух узлов, соответствующих исправным и отказовым
стояниям (рис. 2.4).

Специализированные программные средства анализа надежности сложных систем 505
Рис. 2.4. Свернутый граф состояний
Такой граф образуется путем объединения соответствующих узлов полного
графа. Узлы 1, 2,..., п соответствуют исправным, а узлы 1, 2,..., п — отка-
зовым состояниям системы. Узлы графа соединяются ветвями переходов
согласно процессу функционирования системы. Ветвям приписываются, в
общем случае, приближенно вычисляемые интенсивности переходов Ajt /?,-,
С,, D,, Ej из одного укрупненного состояния в другое, являющиеся
функциями времени. Интенсивности переходов свернутого графа рассчитываются
по формуле:
/ее
где1 е, f — состояния свернутого графа; /?,(/) — вероятность пребывания
системы в момент времени t в состоянии /ее; au — интенсивность перехо-

506 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
да из состояния / в состояние j исходного (полного) графа состояний.
Таким образом, интенсивность Леу(/) равна среднему взвешенному сумм ин-
тенсивностей выходов из каждого состояния множества е во все состояния
множества / . При этом весами служат значения вероятностей /?,(/)
состояний /ее.
Показано [5,разд. 2.6], что система дифференциальных уравнений,
описывающая функционирование исследуемой системы по полному графу
состояний, справедлива и для свернутого графа, ветвям которого приписаны
интенсивности переходов, вычисляемые по приведенной формуле.
Ограничиваясь стационарными значениями интенсивностей переходов Ае ,,
получим систему линейных алгебраических уравнений, описывающих
стационарный режим функционирования. При этом вероятность /?,,
подставляемая в формулу, рассчитывается приближенно как произведение передач
ветвей, взятых вдоль монотонного пути, ведущего из начального состояния в
/-е состояние, где под передачей понимается отношение интенсивности
отказа ветви, входящей в какой-либо узел и лежащей на пути, к сумме
интенсивностей восстановлений для ветвей, выходящих из этого узла.
При вычислении значений этих интенсивностей до некоторого назначенного
уровня к > 1 учитываются все пути полного графа, а для следующих
уровней — только случайно выбираемые по равномерному закону пути, ведущие
в исправные и отказовые состояния.
Свернутый граф состояний системы позволяет описать ее функционирование
с помощью систем линейных алгебраических или дифференциальных
уравнений относительно невысокой размерности. Простые циклические
алгоритмы позволяют определить по уравнениям требуемые показатели надежности.
Описанный метод реализован в виде программы Kasm. Оценки показателей
надежности по этой программе для больших резервированных систем,
состоящих из сотен элементов, отличаются высокой точностью, вполне
достаточной для инженерных расчетов. Например, для резервированной системы,
состоящей из последовательного соединения 100 дублированных пар
элементов с различными интенсивностями отказов и восстановления,
обслуживаемой пятью ремонтными бригадами (по 20 пар элементов на каждую бригаду)
с различными приоритетами обслуживания, получены следующие
относительные погрешности:
8^<0,5%, 5><5%, 6Гв<3%, 87;<4%.
Точность оценок повышается с ростом надежности элементов системы и
с увеличением числа уровней свернутого графа, учитываемых при расчетах.

Специализированные программные средства анализа надежности сложных систем 507
2.5. Возможности программы Redopt
Программа Redopt предназначена для определения структуры и
характеристик обслуживания системы по критерию минимальной стоимости,
надежность которой не ниже заданной. Исследуется восстанавливаемая система,
состоящая из п подсистем, образующих основное соединение. Каждая
подсистема состоит из одинаковых элементов и представляется как система с
дробной кратностью резервирования (типа m/n) с нагруженным или нена-
груженным резервом. Кроме того, каждая подсистема может обслуживаться
некоторым количеством ремонтников. Все законы распределения времени до
отказа и времени восстановления элементов произвольные.
Программа позволяет определить количество резервных элементов в каждой
подсистеме и число ремонтных единиц, обслуживающих каждую
подсистему, обеспечивающих требуемую готовность системы Kg в заданный момент
времени / . Критерием оптимальности является минимальная стоимость
проектируемой системы.
Основными допущениями являются следующие:
□ время безотказной работы и время восстановления элементов имеют
произвольный закон распределения;
П переключающее устройство является абсолютно надежным;
□ восстановление отказавших элементов осуществляется по прямому
приоритету;
П отказавшие элементы из разных подсистем могут ремонтироваться
одновременно.
Математическая модель Redopt и примеры описаны в [5, гл. 10].
Программа Redopt позволяет определить:
П оптимальное количество резервных элементов при заданном числе
ремонтных бригад;
О оптимальное количество ремонтных бригад при заданном количестве
резервных элементов;
□ оптимальное количество резервных элементов и ремонтных бригад,
необходимых для обеспечения требуемой надежности и минимальной
стоимости системы вместе с оплатой обслуживающего персонала.

508 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
2.6. Программные средства анализа
надежности сложных систем
с произвольными распределениями отказов
и восстановлений элементов
Приведем краткую характеристику программных средств, позволяющих
оценить надежность неизбыточных и избыточных систем с большим числом
состояний и произвольными распределениями отказов и восстановлений
элементов (см. рис. 2.1).
П Программа Consexp позволяет рассчитать надежность системы с основным
соединением элементов и экспоненциальными законами распределения
времени безотказной работы при произвольных законах распределения
времени восстановления. Количество элементов, а значит, и число
состояний может достигать нескольких тысяч. Показатели надежности
элементов случайные из некоторого интервала. Программа позволяет рассчитать
следующие показатели надежности системы: Т, Тв, КГУ P(t), Kv{t).
Описание метода содержится в [5,разд. 6.1].
П Программа Conspz предназначена для анализа надежности
нерезервированной восстанавливаемой системы, состоящей из групп разнонадежных
элементов. Имя исполняемого файла — Conspz.exe.
Исходными данными являются:
• время работы системы;
• количество точек (для построения таблиц и графиков);
• количество групп.
Для каждой группы вводятся:
• количество элементов;
• вид закона распределения времени до отказа элемента
(экспоненциальный, гамма-, нормальный, равномерный, Вейбулла, Рэлея);
• математическое ожидание времени до отказа (нижняя граница);
• математическое ожидание времени до отказа (верхняя граница);
• среднее квадратическое отклонение врсмеЕШ до отказа (нижняя
граница);
• среднее квадратическое отклонение времени до отказа (верхняя гра
ница);
• вид закона распределения времени восстановления элемента (эксп
ненциальный, гамма-, нормальный, равномерный, Вейбулла, Рэлея);

Специализированные программные средства анализа надежности сложных систем 509
• математическое ожидание времени восстановления (нижняя граница);
• математическое ожидание времени восстановления (верхняя граница);
• среднее квадратическое отклонение времени восстановления (нижняя
граница);
• среднее квадратическое отклонение времени восстановления (верхняя
граница);
• математические ожидания и средние квадратические отклонения
времени до отказа и времени восстановления элементов генерируются
случайным образом в заданных промежутках по равномерному закону.
Результатами расчетов являются следующие показатели надежности
системы:
• средняя наработка на отказ;
• среднее время восстановления;
• коэффициент готовности;
• таблица значений функции готовности (нижняя граница, верхняя
граница, среднее значение);
• графики функции готовности и ее граничных значений.
Описание метода содержится в [5, разд. б. 1].
О Программа Magor позволяет рассчитать надежность системы с дробной
кратностью резервирования (типа т/п). Законы распределения времени
безотказной работы и восстановления элементов произвольные,
восстановление неограниченное. Исследование надежности системы возможно
при больших значениях т и п. Программа позволяет рассчитать
следующие показатели надежности системы: 7*(0» ^i(0» ^V» ДО» ^г(0»
X(t), ц.(/). Описание метода содержится в [5,разд. 7.4].
О Программа Magorc позволяет рассчитать показатели надежности системы
с дробной кратностью резервирования (типа т/п). Отказ системы
наступает при отказе (т + 1)-го элемента с последовательными номерами.
Законы распределения времени безотказной работы и восстановления
элементов произвольные, восстановление элементов неограниченное.
Исследование надежности системы возможно при больших значениях т и п.
Программа позволяет рассчитать Г, Тв, Кг и двусторонние оценки
Кг((). Описание метода содержится в [5, разд. 7.5].
О Программа Mizn позволяет рассчитать надежность систем с дробной
кратностью резервирования (типа т/п). Восстановление ограниченное и неог-

510 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
раниченное. Резерв нагруженный и ненагруженный. Количество
элементов определяется только ресурсами ЭВМ. Законы распределения времени
безотказной работы и восстановления элементов произвольные.
Программа позволяет рассчитать двусторонние оценки Kr(t). Описание метода
содержится в [5, разд. 7.6].
2.7. Программные средства расчета
и прогнозирования надежности систем
с переменной структурой
Приведем краткую характеристику программных средств, позволяющих
оценить надежность систем с переменной структурой (см. рис. 2.1).
□ Программа Reconf позволяет оптимизировать моменты реконфигурации
невосстанавливаемой системы и определять максимальное значение
вероятности безотказной работы в течение периода эксплуатации системы.
Законы распределения времени безотказной работы произвольные.
Описание метода содержится в [14].
О Программа Vreconf выполняет анализ восстанавливаемой системы с
динамической реконфигурацией при произвольных распределениях времени
безотказной работы и времени восстановления. Допускается любое число
этапов реконфигурации системы со случайными длительностями,
имеющими также произвольные распределения. Программа дает возможность
рассчитать стационарные характеристики надежности: Т, Тв, Кг.
Описание метода содержится в [13].
О Программа Recstr предназначена для оценки надежности сложных
восстанавливаемых систем с дробной кратностью резервирования (типа mjn),
общее число элементов в которой постоянно, но происходит динамичное
изменение числа резервных, а значит, и основных элементов. Тем самым
структура системы в некоторые моменты времени дискретно изменяется.
При этом длительности интервалов реконфигурации структуры могут
быть постоянными или случайными величинами. Число структур
ограничено только ресурсами ЭВМ. Порядок изменения структур может быть
определен заранее или носить случайный характер. Программа позволяе
определить показатели надежности системы с переменной структурой, т
кие как: коэффициент готовности, наработка на отказ, среднее время во
становления, вероятность безотказной работы, функция готовности, ере
нее время безотказной работы. Она выполняет графическое отображен
функционирования системы во времени и динамического изменения

Специализированные программные средства анализа надежности сложных систем 511
быточности, что дает возможность пользователю визуально следить за
поведением системы и управлять ее поведением по мере необходимости.
Описание метода содержится в [13, 15].
О Программа Multifim позволяет вычислять коэффициент готовности
восстанавливаемой двухфункциональной системы с "памятью". Законы
распределения времени безотказной работы и времени восстановления
произвольные. Время выполнения каждой функции также имеет произвольное
распределение. Анализ надежности выполняется по критерию Кг.
Описание метода содержится в [5,разд. 12.9].
2.8. Другие программные средства
В настоящем разделе приводится описание некоторых вспомогательных
программных средств системы ISANT, не отображенных на рис. 2.1.
2.8.1. Анализ показателей надежности системы
при различных законах распределения времени
до отказа
Имя исполняемого файла программы — P_t.exe.
Возможны два варианта работы программы в зависимости от исходных
данных: '
1. Задаются вид закона распределения времени безотказной работы системы
(экспоненциальный, равномерный, гамма-, усеченный нормальный, Рэлея,
Вейбулла, нормальный), первые два момента (математическое ожидание и
среднее квадратическое отклонение).
2. Задаются вид закона распределения времени безотказной работы системы
(экспоненциальный, равномерный, гамма-, усеченный нормальный, Рэлея,
Вейбулла, нормальный) и его параметры.
В первом варианте рассчитываются параметры всех имеющихся
распределений, а во втором — математические ожидания и средние квадратические
отклонения выбранных распределений.
Общими результатами расчетов для выбранных законов распределения
являются:
О таблицы и графики вероятности безотказной работы;
О таблицы и графики интенсивностей отказов;
П таблицы и графики плотностей распределения времени безотказной рабо
ты системы;

512 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
П среднее время безотказной работы нерезервированной системы,
состоящей из элементов с выбранными распределениями;
□ три файла результатов probab.txt, intcns.txt и plotn.txt, содержащие
показатели надежности системы в зависимости от времени ее
функционирования.
2.8.2. Анализ надежности резервированной системы
при наличии подключающего устройства
Имя исполняемого файла — Switching.exe.
Исходные данные:
□ количество резервных элементов;
□ вид закона распределения (экспоненциальный, гамма-, нормальный);
О параметры распределения (математическое ожидание и среднее квадрати-
ческое отклонение);
□ длительность времени переключения на резерв;
О время работы системы;
□ количество точек (для построения графиков).
Результаты расчетов;
□ таблица значений функции готовности системы;
□ график функции готовности системы;
□ файл результатов svvitching.txt.
2.8.3. Оценка последействия отказов
и его влияния на надежность
невосстанавливаемой дублированной системы
Имя исполняемого файла — Aftereffect.exe.
Исходные данные:
П математическое ожидание времени до отказа элемента;
□ среднее квадратическое отклонение времени до отказа элемента;
□ математическое ожидание времени до отказа элемента после отказа
другого элемента;
□ среднее квадратическое отклонение времени до отказа элемента после
отказа другого элемента;
П вид закона распределения (экспоненциальный, равномерный, гамма-,
усеченный нормальный, Рэлея, Вейбулла, нормальный).

Специализированные программные средства анализа надежности сложных систем 513
Результаты расчетов:
О среднее время безотказной работы системы при наличии последействия
отказов;
О среднее время безотказной работы системы при отсутствии последействия
отказов;
О графики вероятности безотказной работы системы при наличии и
отсутствии последействия отказов элементов;
□ файл результатов aftereffect.txt.
2.8.4. Анализ надежности
невосстанавливаемой системы
при неодновременной работе ее элементов
Имя исполняемого файла — Timeout.exe.
Исходные данные:
G математическое ожидание времени до отказа;
G среднее квадратическое отклонение времени до отказа;
□ период работы и простоя системы;
G время работы системы;
G вид закона распределения (экспоненциальный, равномерный, гамма-,
усеченный нормальный, Рэлея, Вейбулла, нормальный).
Результаты расчетов:
О среднее время безотказной работы системы при наличии интервалов
простоя;
П среднее время безотказной работы системы при отсутствии интервалов
простоя;
О графики вероятности безотказной работы системы при наличии и
отсутствии интервалов простоя;
CJ файл результатов timeouUxt
2.8.5. Анализ надежности системы
с временным резервированием
Имя исполняемого файла — Timerezerv.exe.
Исходные данные:
СЗ распределение времени до отказа (экспоненциальное, равномерное, гамма-,
усеченно нормальное, Рэлея, Вейбулла, нормальное);

514 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
П математическое ожидание времени до отказа;
П среднее квадратическое отклонение времени до отказа;
О распределение времени восстановления (экспоненциальное, равномерное,
усеченно нормальное, гамма-, Рэлея, Вейбулла, нормальное);
О математическое ожидание времени восстановления;
□ среднее квадратическое отклонение времени восстановления;
□ величина временного резерва.
Результаты расчетов;
О показатели надежности системы с резервом времени:
• наработка на отказ;
• среднее время восстановления;
• коэффициент готовности;
П показатели надежности системы без резерва времени:
• наработка на отказ;
• среднее время восстановления;
• коэффициент готовности;
О таблица и графики вероятности безотказной работы системы с резервом
времени и без резерва времени;
П файл результатов timerezerv.txt.
2.8.6. Оценка влияния профилактики
на надежность системы
Имя исполняемого файла — Prevention.exe.
Исходные данные:
□ показатели надежности системы:
• вид закона распределения времени безотказной работы (равномерный,
гамма-, усеченный нормальный, Рэлея, Вейбулла, нормальный);
• математическое ожидание времени безотказной работы;
• среднее квадратическое отклонение времени безотказной работы;
• вид закона распределения времени восстановления (равномерный, raN
ма-, усеченный нормальный, Рэлея, Вейбулла, нормальный);
• математическое ожидание времени восстановления;
• среднее квадратическое отклонение времени восстановления;

Специализированные программные средства анализа надежности сложных систем 515
G показатели профилактики:
• время между очередными профилактиками (частота профилактики);
• время проведения профилактики (глубина профилактики).
Результаты расчетов:
О при наличии профилактики:
• наработка на отказ;
• среднее время восстановления;
• коэффициент готовности;
О без профилактики:
• наработка на отказ;
• среднее время восстановления;
• коэффициент готовности;
• зависимость коэффициента готовности, наработки на отказ и среднего
времени восстановления системы от частоты и глубины профилактики
(таблицы, графики);
□ файл результатов prevention.txt.
2.8.7. Оценка вероятности безотказной работы
последовательно-параллельных схем
Имя исполняемого файла — Posl_par.exe.
Программа предназначена для вычисления вероятности и среднего времени
безотказной работы резервированных систем при общем и раздельном
резервировании. Резерв может быть как постоянно включенным, так и
замещением. Количество элементов нерезервированной системы п и количество
резервных систем m ограничены только быстродействием компьютера.
Элементы системы предполагаются равнонадежными. Расчет надежности
осуществляется методом статистического моделирования. Точность расчетов
гарантируется надлежащим значением объема выборочной совокупности.
Исходные данные:
О математическое ожидание времени до отказа элементов;
О среднее квадратическое отклонение времени до отказа элементов;
О вид закона распределения (экспоненциальный, равномерный, гамма-,
усеченный нормальный, Рэлея, Вейбулла, нормальный), один и тот же для
всех элементов;
О число элементов нерезервированной системы п;

516 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
П число резервных систем m ;
□ объем выборки.
Результаты расчетов:
О вероятность безотказной работы систем:
• при общем резервировании с постоянно включенным резервом
(система 1);
• при общем резервировании замещением (система 2);
• при раздельном резервировании с постоянно включенным резервом
(система 3);
• при раздельном резервировании замещением (система 4);
О графики вероятности безотказной работы систем;
П среднее время безотказной работы систем 1—4:
П файл результатов posl_par.txt.
2.8.8. Анализ надежности
структурно резервированных восстанавливаемых
систем с постоянными интенсивностями отказов
и восстановлений элементов
Имя исполняемого файла — Rezerve.exe.
Программа рассчитывает стационарные показатели надежности
восстанавливаемых систем с постоянно включенным резервом целой и дробной
кратности, с резервом замещением, со скользящим резервом. Элементы системы
равнонадежны и имеют постоянные интенсивности отказов и
восстановлений.
Исходные данные:
П интенсивность отказов элементов;
D интенсивность восстановления элементов;
О общее число элементов в системе;
□ количество резервных элементов;
□ количество ремонтных бригад;
П вид резерва (постоянно включенный, замещением).
Результаты расчетов:
□ коэффициент готовности;
П наработка на отказ;

Специализированные программные средства анализа надежности сложных систем 517
О среднее время восстановления;
П среднее время безотказной работы.
0 файл результатов rezerve.txt.
2.8.9. Решение систем
линейных дифференциальных уравнений
методом Рунге — Кутты с автоматическим
выбором шага
Имя исполняемого файла — Rungekutt.exe.
Расчет надежности системы в течение времени t > как правило, требует
решения системы обыкновенных дифференциальных уравнений. Программа
позволяет оперативно выполнять эту задачу. Шаг интегрирования выбирается
автоматически.
Исходные данные:
1 время работы системы;
Э количество точек (для построения графиков);
3 число уравнений в системе;
П матрица коэффициентов.
Результаты решения системы дифференциальных уравнений выводятся на
экран и записываются в файл rungekutt.txt.
2.9. Выводы
1. В настоящей главе представлен общий подход к созданию программного
продукта по расчету и анализу надежности сложных технических систем.
Составные программы базируются на научных методах, обеспечивают
требуемую инженерную точность и работу в реальном масштабе времени.
Они имеют унифицированную структуру и интерфейс, независимый от
решаемой задачи и области ее применения, что делает программы
универсальными с точки зрения анализа большого класса технических систем.
2. Программа Relass предназначена для анализа и прогнозирования
надежности технических систем в процессе их проектирования. Она позволяет
рассчитать надежность невосстанавливаемых и восстанавливаемых,
нерезервированных и резервированных систем при любом виде
резервирования по всем стандартным показателям надежности. Уникальность системы
определяется возможностью анализа широкого класса структур,
моделирования собственного времени работы элементов системы, учета после-

518 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 2
действия отказов, учета контроля состояния элементов и различных
дисциплин восстановления. Программа производит анализ и хранение
структурных схем произвольной сложности в формате, удобном как для
автоматического программного построения графа состояний исследуемой
системы, так и для компактного хранения информации. Процедура,
реализующая эти действия, является новой и универсальной для дальнейшего
использования при анализе надежности в перспективных системах.
3. Программа Redopt предназначена для определения структуры и
характеристик обслуживания системы по критерию минимальной стоимости,
надежность которой не ниже заданной. Программа позволяет определить
оптимальное число избыточных элементов и ремонтников, необходимых для
обеспечения требуемой надежности, при произвольных распределениях
отказов и восстановления элементов.
4. Программа Recstr предназначена для оценки надежности сложных
восстанавливаемых систем с дробной кратностью резервирования (типа m/n),
общее число элементов в которой постоянно, а число резервных и
основных элементов динамично изменяется. Длительности интервалов
реконфигурации структуры могут быть как детерминированными, так и
случайными величинами. Программа Recstr позволяет рассчитать надежность
системы с переменной структурой и провести ее исследование по
стационарным и нестационарным показателям надежности.
5. Созданные программные средства используют методику анализа систем с
интервальным заданием исходных данных по надежности элементов,
позволяющую существенно ускорить расчеты характеристик надежности.
Рассмотренные программные средства позволяют эффективно вычислять
нестационарные характеристики надежности восстанавливаемых систем с
произвольными распределениями случайных параметров, отказов и
восстановлений.

ГЛАВА 3
РЕШЕНИЕ ЗАДАЧ НАДЕЖНОСТИ
С ПОМОЩЬЮ УНИВЕРСАЛЬНЫХ
И СПЕЦИАЛИЗИРОВАННЫХ
ПРОГРАММНЫХ СРЕДСТВ
3.1. Решение задач надежности
на основе Derive 5
3.1.1. Определение среднего времени
безотказной работы
Система Derive 5 позволяет вычислить среднее время безотказной работы
сложной системы в аналитическом виде. При этом структурная схема (схема
расчета надежности) может быть любого вида и любой кратности резервиро-
.00
вания. Решение определяется по формуле 7]с = jPc(t)dt с помощью кнопки
о
Integrate панели инструментов.
Компьютерная технология определения 7jc выглядит так:
О ввести подынтегральное выражение для вероятности безотказной работы
системы;
□ установить диапазон изменения параметров функции Pc(t);
со
О образовать выражение ^Pc(t)dt с помощью кнопки Integrate панели ин-
о
струментов;
П вычислить интеграл с помощью кнопки Simplify.
ПРИМЕР 3.1. Определить среднее время безотказной работы системы при
общем резервировании с постоянно включенным резервом кратности т.
Предполагается, что справедлив экспоненциальный закон распределения
времени до отказа.

520 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
Решение. Процедуры решения задачи на экране имеют вид:
#1: 1-(1-е-А'иГ + 1
#2: Л :е Real(0,oo)
#3: m :e Real (0,со )
#4: ](1-(1-е'х"Ъ"Н)^
о
#5: VECTOR m, |(1-(1-ё~Х'*)т + 1} dt , m, 0, 10
М_ о • J )
1
0 -
к
3
1
2-Х
11
2
6-Л
25
#6: 3
12«А
137
4
60-Х
49
5
20-Л
363
140-Л.
Строка #1 содержит выражение для вероятности безотказной работы системы.
имеющей интенсивность отказа А, и кратность резервирования m. В строках
#2 и #3 указаны диапазоны изменения переменных Хит (положительные
числа). В строке #4 находится результат выполнения команды Integrate. Для
получения среднего времени безотказной работы системы с кратностью
резервирования т- 1-ИО используется функция табуляции vector
(строка #5), Результаты решения задачи приведены в строке #6 в диапазоне
1 ™±}\
т = О -s- 6. Они соответствуют известной из теории формуле Т1с = — 2^ т •
ПРИМЕР 3.2. Определить среднее время безотказной работы системы при
общем резервировании замещением кратности ///. Предполагается, что crip*1'
ведлив экспоненциальный закон распределения времени до отказа.

Решение задач надежности с помощью программных средств 521
Решение. Далее приведены процедуры и результаты решения задачи. Они
аналогичны примеру 3.1.
П: А :е Real(0,oo )
&2: m :e Real (0,°o )
(A-t)1
ft .5 '. ~^~~~~
i!
ji4: 2,
i-o i!
,5: r-.fi^:
i =c i !
_ ."f.-.4.t f(A-.t)1
*6: e • > dt
— i'
00' m (A • t )*
#7: VECTOR m, je~'Vr - £—; dt , m, 0, 6
\L о ;=o i! J J
l"
0 -
A
2
1 -
A
3
2 -
A
з 1
A
5
4 -
A
б
5 -
A
7
6 -
A.
По результатам решения видно, что 7JC = . Так элементарно просто с
Л,
помощью компьютерной алгебры получена формула среднего времени
безотказной работы системы, резервированной по методу замещения.

522 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
ПРИМЕР 3.3. Структурная схема невосстанавливаемой системы приведена
на рис. 3.1. Интенсивности отказов элементов имеют значения: a = 0,0008 час-1,
6 = 0,003 час"1, с = 0,002 час-1, </ = 0,001 час-1, е = 0,0015 час"1. Определить
среднее время безотказной работы в аналитическом и численном виде.
г ■
Рис. 3.1. Структурная схема резерви^энной системы
Решение. Далее приведены процедуры решения задачи:
#1: e"a,t
#2: e"bt'(l + b-t)
#3: 1-{1-е"с'сГ
#4: l-(l-rat)-(l-e"e,t)
#5: а :е Real{0,*> )
#6: b :£ Reai(0,oo )
#7: с :б Real (0,ос )
#8: d :e Real (0,00 )
#9: е :е Real(0,oo )
#10: e"a,t-(i"b't-(l + b-t))-(l-(l-e-c"t)2)-(l-(il-e-d-t)-(l-e"e't))
ОС
#11: Je"at-(i"b't-(l + b-t)}-(l-(l-e"ct)2)-(l-(l-e"d't)-{l-e"et))dt
о
#12: ь г+ 1 . ь ^
(a + b + 2-c + d + e)" a + b + 2-c + d + e (a + b + 2-c + dT
1 b 1 2-b
a + b + 2'C + d (a + b + 2-c + ef a + b + 2-c + e (a + b + c + d + e)2
2 2-b 2 2-b
+. + + _ +
a + b + c + d + e (a + b + c + d)2 a+b+c+d (a + b + c + e)
2
a+b+c+d

Решение задач надежности с помощью программных средств 523
X 1 Л
#13: г +
(Л + Л + 2-Л4Л + ХГ Х + А + 2-Х + Х + Х (Л + Л + 2-Л + ЛГ
1 X 1 2-Х
Х + Х + 2-Х + Х (Х + Х + 2-Х + Х)2 Х + Х + 2-Х + Х (Х+Х+Х+Х+ХГ
2 2-Х 2 2-Х
( + + _ +
Х+Х+Х+Х+Л (Х + Х + Х + Х)2 Х + Х + Х + Х (Х + Х + Х + Х)2
2
Х + Х + Х + Х
109
-14:
225 X
«о
», г Г--0.0008-t ,--0.003-t ,-. ,л ««-, ... ,т ,-, »-C.002-t,2. ,, ,,
#15: Je -(е •(- + 0. 003-t) )-(1-(1-е ))-(1-(1-
о
е )-{1-е ) ) dt
si 6: 313Л5654131
В первых четырех строках находятся результаты ввода вероятностей
безотказной работы нерезервированного элемента (#1), дублированного элемента с
замещением (#2), дублированного элемента с постоянно включенным
резервом (#3), дублированной пары разнонадежных элементов с постоянно
включенным резервом (#4).
В строках #5—#9 приведены результаты выполнения пункта меню Declare |
Variable Domain (интенсивности отказов элементов положительны).
В строке #10 находится выражение вероятности безотказной работы системы,
полученное при вводе выражения #1*#2*#3*#4.
В строке #11 приведен результат нажатия кнопки Find Integral панели
инструментов.
Среднее время безотказной работы системы в аналитическом виде находится
в строке #12 и является результатом интегрирования выражения,
находящегося в строке #11, с помощью кнопки Simplify панели инструментов и
команды меню Simplify | Expand.
В строках #13—#14 находятся выражения среднего времени безотказной
работы системы при условии равенства интенсивностей отказов элементов
системы: a-Ь-с =d = e = X. Подстановка осуществлена с помощью кнопки
Sub панели инструментов.
В строке #15 приведено выражение интеграла при численных значениях
интенсивностей отказов элементов. Численное значение интеграла находится в
строке # 16.

524 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
ПРИМЕР 3.4. Пусть невосстанавливаемая система состоит из трех
элементов, соединенных последовательно в смысле надежности. Первый элемент
имеет закон Рэлея распределения времени до отказа с параметром a = 0,0001,
закон распределения времени до отказа второго элемента —
экспоненциальный с параметром Л, = 0,01, закон распределения времени до отказа третьего
элемента — Вейбулла с параметрами h = 50 , с = 2.
Определить среднее время безотказной работы системы в аналитическом и
численном видах.
Решение. Процедуры решения задачи на экране монитора имеют вид:
#1: e~a,t'
#2: e"x-t
#3: ё-(с/Ь)С
#4: e-*<e-vt-r(t/b!C
#5: а :е Real (0,oo )
#6: b :е Real(0,oc )
#7: с :е Real (0,ос )
#8: А :е Real(0,oo)
#9: Je-^.e^-^e-'^dt
о
#10: ]e-<t/b)C-a't2-Atdt
о
#11: Je-^of-o.oooi.t'-o.oi.tdt
о
#12: lO-^-^-i^-lO-Vs-V^.e^-ERFl^
#13: 31.32521802
#14: ]i-at2.e"xt.e"(t/b,Cdt
о

Решение задач надежности с помощью программных средств 525
( ( W
Vn • b■ERF ,
.,, .ьЧ2/('.-(а-ьг+П) Уп-b 42->/(a-b- +1)J
а5' е ' / ,. 1 -.
2-^/(a-b- + l) 2-y{a-b"+l)
v У
Не будем объяснять содержание строк, т. к. оно практически не отличается от
предыдущего примера.
Из приведенных примеров видно, что системы компьютерной алгебры, в
частности система Derive 5, позволяют достаточно просто вычислить среднее
время безотказной работы системы при любых видах резервирования и
произвольных законах распределения времени до отказа. При этом во многих
практически важных случаях решение удается получить в аналитическом
виде. Ограничение здесь единственное: интеграл от вероятности безотказной
работы "не берущийся", и P(t) не выражается в элементарных функциях.
3.1.2. Определение вероятности
безотказной работы системы
Вероятность безотказной работы сложной системы вычисляется достаточно
просто: находится произведение вероятностей безотказной работы элементов
системы с учетом резервирования и неодновременности их работы. Однако
эта простота только кажущаяся. Конструктору приходится при расчете
надежности учитывать возможность физической реализуемости структурной
схемы, представлять решение в виде таблиц и графиков. Задача существенно
усложняется. В таких случаях целесообразно использовать математические
системы компьютерной алгебры.
Приведем примеры решения подобных задач.
ПРИМЕР 3.5. Структурная схема системы приведена на рис. 3.2. Физически
она представляет собой энергетическую систему, состоящую из двух
генераторов Г( и Г2, регулятора R и потребителей Н. Необходимо определить
вероятность и среднее время безотказной работы энергетической системы.
Решение представить в аналитическом виде, а также в виде таблиц и графиков.
Система работает следующим образом: при отказе одного из генераторов
нагрузка на исправный генератор возрастает, от чего увеличивается
интенсивность его отказа; при этом также возрастает интенсивность отказа
регулятора. Предполагается, что интенсивность отказа потребителей электроэнергии
при этом не меняется.

526 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
Рис. 3.2. Структурная схема энергетической системы
Введем следующие обозначения:
Е Р(0 — вероятность безотказной работы генератора в течение времени /
в нормальном режиме функционирования, когда все устройства системы
исправны;
Е Р\(0 — вероятность безотказной работы регулятора в течение времени /
в нормальном режиме функционирования;
ОХ — интенсивность отказа генератора в нормальном режиме
функционирования;
□ /Ц — интенсивность отказа регулятора в нормальном режиме
функционирования;
О {j'(T) — производная от вероятности отказа генератора в момент т.;
□ р(х) — вероятность безотказной работы генератора в течение времени т:
□ р{(х) — вероятность безотказной работы регулятора в течение
времени т:
П pa{t -т) — вероятность безотказной работы генератора в течение
времени / - х после отказа резервного генератора;
□ pb{t-x) — вероятность безотказной работы регулятора в течение
времени / - х после отказа резервного генератора;
Па — интенсивность отказа генератора после отказа резервного;
□ Ъ — интенсивность отказа регулятора после отказа резервного
генератора.
Исходные данные о надежности элементов: X = 10 час , А., =2-10 час >
я = 2-10"3 час-1, 6 = 3-КГ4 час-1. Предполагается, что интенсивности отказа
потребителей не меняются при отказе генератора, а поэтому они в
дальнейших расчетах не учитываются.

Решение задач надежности с помощью программных средств 527
Решение. Результаты расчетов на экране монитора имеют вид;
#1: InputMode:= Word
#2: pt -pit
#3: pt = e~'vt
H: plt = e~*1-t
n5: 2-q'x-pT'pa'plx-pib
ire: ]2-q'i-pi-pa -plt-plb di
о
=?7: q i = Л-е
--Л-Т
-о: pi = e
-••a-It-i)
: у : pa = e
:r10: p 1 т = e '
:r li: plb = e
-+12: plt-pt =e
t
#13: J2-(A-e )-e -e -e -e ат
о
t
(U4: e + J2-(A-e )-e -e -e -e di
с
е-2Л'^л:с-(а + Ь-Л1) 2-h-e~at-bt
#15: :
a + b-2-A-Al a + b-2-A-Al
*16: A :e Real(0,x )
#17: Al :e Real(0,<x>)
#18: a :e Real(0foc ) ■
#19: b :e Real (0,oo)
<r>{ д-2-Л -L-Xl-t , , , s,, ^ v -v-a-t-b-t \
#20: Г* -(a + b-Al)_ 2-A-e )
0y a + b-2-A-Al a + b-2-Л-М,

528 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
а + b + 2 • Л
#21:
(а + Ь)-(2-Л + Л1)
#22: (l-{l-i"A't)2)-e"'41t
#23: J(l-(l-e_xt)2)-e"Xltdt
о
3-Л + Л1
#24:
(Л + Л1)-(2-Л + Л1)
#25: 21.е-°-0022(:-20-ё-0-0023-с
215000
#26:
253
#27: 849.8023715
. #28: (l-(l-e-10"3t}2).i-(2-10"4K
40000
#29:
33
#30: 1212.121212
В строке #1 находится информация о настройке программы на прием
переменных с индексами.
Энергетическая система исправна в следующих случаях:
а) все элементы системы исправны;
б) в момент времени т отказал один из генераторов, второй генератор и
регулятор продолжают работать в течение всего оставшегося времени / - т
работы системы с новыми значениями интенсивностей отказов л > л,
Вероятность гипотезы (а) представлена на экране в строках #2. #3. #4.
В строке #2 находится произведение вероятностей безотказной работы
генераторов и регулятора. В строках #3, #4 вероятности представлены через
интенсивности отказов элементов.
В строках #5 и #6 реализована гипотеза (б), которая представлена в строке
#13, в которой вероятности состояний выражены через интенсивности
отказов элементов. В строках #7—#12 находятся выражения строки #6.
Сумма вероятностей гипотез (а) и (б), т. е. вероятность безотказной работы
системы, представлена в строке #14.

Решение задач надежности с помощью программных средств 529
В строке #15 находится выражение для вероятности безотказной работы
системы в аналитическом виде, полученное с помощью кнопки Simplify панели
инструментов.
В строке #21 находится выражение для среднего времени безотказной работы
системы, как интеграл от вероятности безотказной работы в пределах от О
до оо (выражение #20). Строки #16—#19 определяют допустимый диапазон
изменения значений интенсивностей отказов элементов системы
(интенсивности положительны).
Вероятность и среднее время безотказной работы системы без учета
последействия отказов находятся в строках #22—#24.
В строках #25—#27 отображены значения вероятности и среднего времени
безотказной работы системы при наличии последействия отказов и исходных
данных, сформулированных в задаче. Те же данные, но в случае отсутствия
последействия приведены в строках #28—#30.
Из сравнения результатов расчетов видно, что учет последействия отказов
необходим: значение среднего времени безотказной работы существенно
отличается от идеального случая, когда последействие отсутствует. Система
Derive 5 существенно облегчила процесс решения задачи и позволила
получить решение в виде формул.
Рис. 3.3. Вероятность безотказной работы системы без учета (кривая 1)
и с учетом последействия отказов (кривая 2)
На рис. 3.3 приведены графики вероятности безотказной работы системы без
Учета (кривая 1) и с учетом (кривая 2) последействия отказов. Построение
графиков в системе Derive 5 осуществляется с помощью нажатия двух кно-
IX Чаи «;<;з

530 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
пок: на панели инструментов основного окна (2D-plot window) и на панели
инструментов графического окна (Plot Expression)
Далее приведены результаты табулирования функций вероятности
безотказной работы с учетом и без учета последействия отказов (выражения #1 и #2).
Результаты табулирования с помощью функции VECTOR приведены в
строке #4.
#1: 21.ё-с-ОС2^-20-с-°-пС23-и
#2: (l-(l-e-°'C01t)2}-e-C-00C-
„_ /r 01 A-o.0022-t • on --0.0023-t ,, ,- A-G.001-t.2i д-О-0002-t,
#3: VECTOR![t, 21■е -20-е ,(1-(^-е ) )-е ],
t, 0, 500,50)
"О 1 1
50 0.9851939630 0.9876949318
100 0.9622227072 0.9713220754
150 0.9329913326 0.9516166893
200 0.8990919326 0.9292193010
#4: 250 0.8618486417 0.9046866309
300 0.8223566430 0.8785013176
350 0.7815159033 0.8510805713
400 0.7400603235 0.8227838719
450 0.6985828929 0.7939198137
_500 0.6575573700 0.7647521884_
3.1.3. Определение показателей надежности
восстанавливаемых систем
Критериями надежности восстанавливаемых систем являются: функция
готовности Kr(t), коэффициент готовности Кг, наработка на отказ Т . Во
многих случаях приходится также вычислять вероятность P(t) и среднее время
7J безотказной работы восстанавливаемой системы.
Вычисление этих показателей требует решения алгебраических и дифферен"
циальных уравнений. Система Derive 5 имеет богатые возможности решения
уравнений. Она позволяет решать:
О алгебраические линейные и нелинейные уравнения в аналитическом
численном видах;

Решение задач надежности с помощью программных средств ' S31
О дифференциальные уравнения первого и второго порядков в
аналитическом виде;
□ системы дифференциальных уравнений высокого порядка в
преобразовании Лапласа;
□ системы дифференциальных уравнений в численном виде.
Рассмотрим эти возможности на примерах.
ПРИМЕР 3.6. Структурная схема системы приведена на рис. 3.2. Условия ее
функционирования те же, что в примере 3.5. Необходимо определить:
□ P(t) — вероятность безотказной работы системы;
□ Т] — среднее время безотказной работы;
П /Сг(/) — функцию готовности;
□ Кг — коэффициент готовности;
П Т — наработку на отказ.
Интенсивности восстановления элементов имеют значения:
О ц = 0,02 час"1 — интенсивность восстановления генератора;
О Ц] =0,1 час"1 — интенсивность восстановления регулятора.
Решения представить в аналитическом и численном видах. Граф
функционирования системы приведен на рис. 3.4.
Рис. 3.4. Граф состояний системы
Решение
Определение вероятности и среднего времени безотказной работы системы
Узлы (0) и (1) соответствуют исправным, а узлы (2), (3), (4) — отказовым
состояниям системы. Тогда вероятность безотказной работы P(t) будет равна

532 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
сумме вероятностей состояний (1) и (2), т. е. P(t) = P^t) + P2(t) при наличии
экранов из состояний (2), (3), (4).
Система дифференциальных уравнений, соответствующая исправным
состояниям, имеет вид:
^^ = -(2^+^)^(0 + ^(0;
at
<
. at
Представим эту систему уравнений в преобразовании Лапласа при начальных
условиях Р0(0)=:1, Р,(0) = 0:
Г(л- + 2Х + X, )Р0 (s) - ц^ (л) = 1;
[2XP0(s) + (5 + а + b + u)/j (л*) = 0.
Далее приведены процедуры решения системы уравнений с помощью
Derive 5 и результаты определения вероятности и среднего времени безотказной
работы системы:
#1: InputMode: = Word
#2: (s + 2-A + Al)-pO-p'pl = l
#3: -2-A-pO + (s + a + b + y)'pl = Q
(s + 2-A + Al)-pO-u-pl = l
[-2 ■ A • pO -H s + a + b + p) • pi = 0_
(\ (s + 2-A + Al)'pO-ypl = l 1 ^
#5: SOLVE ,[pO, pi], Real
\J_-2-A-p0 + {s + a + b + p)-pl = 0j j
„,- ^ s+a+b+u
#6: p0 = — лр1 =
s2+s-(a + b + 2-A + Al + n) + a-(2-A + Al) + b-(2-A + Al) + Al-M
2j_A
s2+s-(a + b + 2-A + Al + y) + a-(2-A+Al) + b-(2-A + Al) + Al-u_
#7: p = p0 + pl =
s + a-J-b + 2-А + ц
s:!-t-s-(a + b + 2-A + Al + )j) + a-{2'A + Al)+-b-(2-A + Al) + Al-ii
#8: t- а + Ь + 2-Л + р
a-(2-A + Al) + b-(2-A + Al)+Al-ii

Решение задач надежности с помощью программных средств 533
5000-(10000-s + 243)
#9: pO + pl =
50000000-s2+1225000-s+4 53
405000
#10: t =
151
#11: t = 2682.119205
В строке #1 находится результат настройки программы на прием переменных
с индексами.
Система уравнений представлена в строке #4 как матрица 2x1, составленная
из уравнений, находящихся в строках #2 и #3. Решение найдено с помощью
функции SOLVE (строка #5) и представлено в строках #6 (значения P0(s) и
Рх (s)) и #7 (значение PQ(s)+P} (s)).
Среднее время безотказной работы, полученное в результате подстановки
s = 0 в изображение вероятности безотказной работы системы, приведено
в строке #8 (обозначено t).
В строках #9 и #10 получены выражения вероятности безотказной работы
в преобразовании Лапласа и среднего времени безотказной работы при
исходных данных задачи.
Далее приведено выражение вероятности безотказной работы системы как
функции времени, являющееся оригиналом функции Pq(s) + P{(s) (строка #9):
5000 00000^243)
50000000 • л-2 +1225000 • s + 453
Обратное преобразование Лапласа получено с помощью системы Math cad:
( -W ) J 1 /777777 1 241 f -49 ^ г^гтг:
ехр / -cosh V56401/ + ехр 1 -V56401-
И000 )ff U0000 J 56401 44000 J
•sinhf—! V56401-r .
Uoooo J
В результате преобразования последнего выражения и обращения к Derive 5
получим:
#1: 1. 007392034 ■e-°-00C3755526444-t-0.007392034305.e-0-02412444735,t
00
#2: J( 1. 007392034•ef0,0003"'55526444''1-0.007392034305-
о
~-0.0241244473S-L. ,.
е ) at
#3: 2682.119204

534 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
В строке #1 находится выражение вероятности безотказной работы системы,
полученное в результате преобразования точного решения, расположенного в
предыдущей строке, с помощью команды Approximate.
В строках #2 и #3 вычисляется среднее время безотказной работы системы с
целью проверки предыдущего решения. Из ответов видно, что решения
совпадают.
Восстановление позволило существенно повысить надежность системы.
Среднее время безотказной работы системы возросло с 850 до 2682 часов.
Определение показателей готовности восстанавливаемой системы
В данном случае функционирование системы описывается графом рис. 3.4
при условии отсутствия экранов. Система дифференциальных уравнений
имеет вид:
^^ —(2Я, + X, )/>0 (/) + цР, (/) + ц, />2 (/);
at
^Р = 2ХР0 (0 - (а + Ь + ц)/>, (0 + цР3 (0 + МЛС);
.^Р = Х1/Ь(/)-ц,Л(/);
at
4Ш = ыК/)-М>4(0.
at
В преобразовании Лапласа эта система уравнений имеет вид:
2\P0(s) + (S + a + b + ix)Pl(s)-VLP3(s)~vA(*) = b
aP](s) + (s + ]i)P3(x) = 0y
-bPl(s) + (s + [il)P4(s) = 0.
Система получена при начальных условиях Р0(0) = 1,
/j(0) = />2(0) = ?3(0) = A(0) = 0.

Решение задач надежности с помощью программных средств 535
Определение функции и коэффициента готовности системы в
аналитическом виде
Далее приведено решение системы уравнений в преобразовании Лапласа
аналитическим методом. Получено выражение функции и коэффициента
готовности системы.
#1: InputMode: = Word
#2: (з + 2-А + А1)-рО-ур1-у1-р2 = 1
#3: -2-A-pO+(s + a + b + vO-pl-p-p3-pl-p4=0
#4: -Al'p0 + (s + pl)-p2 = 0
#5: -a-pl + (s + p)-p3 = 0
#6: -b-pl + (s + yl)-p4 = 0
(s + 2-A + Al)-pO-p-pl-yl-p2 = l
-2-A-pO + (s + a + b + p)-pl-p-p3-|il-p4 = 0
#7: -Al-p0 + (s + pl)-p2 = 0
-a-pl + (s + p)'p3 = 0
-b-pl + (s + pl)-p4 = 0
T (s + 2-A + Al)-pO-y-pl-yl-p2 = l 1 N
-2-A«pO + (s + a+b + y)-pl-ii-p3-iil-p4=0
#8: SOLVE -Al-p0 + (s + pl)-p2 = 0 , [pO, pi, p2,p3, p4]
-a-pl-r{s + p)-p3 = 0
\_ -b-pi + (s + pl)-p4 = 0 J j
un л п (pl+s)-(a-s-(vil + s)+
#9: pO + pl= -
s-(a-(yl + s)-(2-A-(yl + s) + s-(Al + )jl+s) ) + (y + s)-(b-(2-A-
(yt + s)-(b-s + (yil + s)-
(yl + s) + s-(Al + pl + s)) + (ul + s)-(2-A-(pl + s) +
(2-A + p + s)))
(Al + pl + s)-(li + s) ) ) )
500'(10'S + l)-(500000-s3+72150-s2+2423-s +
#10: pO + pl = - — r—
s-(2500000000-s4 + 611250000 -s + 4 8272650-sz +
гг±
1325983-S+11123)

536 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
500 ■( 1 0-s +1 )•( 500000-s3+72150-s2+2423-s +
#11: p04-pl= L1
2500000000-s4+611250000-s3+48272650-s- +
22)
1325983-S+11123
11000
#12: pO+pl=
• 11123
#13: p0 + pl = 0.9889418322
В строке #7 находится система уравнений в виде матрицы, образованной из
уравнений, находящихся в строках #2—#6. Решение системы уравнений
получено с помощью функции SOLVE (строка #8).
Функция готовности системы в аналитическом виде, как сумма вероятностей
Pq + Р[, находится в строке #9. Вероятности остальных состояний системы с
экрана удалены. В строке #10 находится выражение функции готовности в
преобразовании Лапласа, полученное в результате подстановки в #9 значений
исходных данных задачи.
Коэффициент готовности легко вычислить, если воспользоваться формулой
Кх - lim Kr(t) = lim sKr(s).
Значение Кг получено путем сокращения символа s в знаменателе
выражений #9 и #10 и подстановки s = 0 в сокращенные выражения (#11).
Аналитическое выражение коэффициента готовности (на экране отсутствует) имеет
вид:
v ЦЦ[(2Я, + ц)
лг ~ 2 '
2bXyi + 2л,Ц[(д. + а) + ц. (Xt +]i\)
Из ответа видно, что восстановление обеспечило достаточно высокий
коэффициент готовности системы.
Определение функции готовности в численном виде
Определение функции готовности в данном случае требует решения системы
дифференциальных уравнений численными методами. В системе Derive 5
таким методом является метод Рунге — Кутты, реализованный функцией RK.
Технология решения системы уравнений исключительно проста. Далее
приведены процедуры решения нашей задачи и конечные результаты:
#1: InputMode : = Word
#2: LOAD(C:\DfW5Trial\DfW\MATH\ODE_APPR.MTH)

Решение задач надежности с помощью программных средств 537
#3: -(2-Л + Л1)-рО + и-р1 + р1-р2
#4: 2-А-рО-(а + Ь + р)-р1+р-рЗ + р1-р4
#5: Л1-р0-ц1-р2
#6: a-pl-p-рЗ
#7: Ь-р1-уЬр4
#8: RK( [-(2-Л + Л1)-рО+р-р1+у1-р2, 2-Л-рО-(а + Ь + ц)-р1 + у-рЗ +
ц1-р4, Л1-р0-р1-р2, a-pl-y-p3, b-pl-pl-p4] , [t, pO, pi,
Р2,рЗ,р4],[0,1,0,0,0,0],1,300)
#9: RK ([-(2-0.001+ 0.0002 )-р0+ 0.02-pl +0.1-р2, 2-0. 001-рО-
(0.002 + 0.0003 + 0.02)-р1+0.02-рЗ + 0.1-р4, 0.0002-рО-
0.1-р2,0.002-pl-0.02-p3,0.0003-pl-0.1-p4], [t,p0,pl,
р2,рЗ,р4], [0,1,0/0,0,0], 1,300)
"О 1 О
1 0.9978319022 0.001975725073
2 0.9957256123 0.003903785279
3 0.9936782975 0.005785474318
4 0.9916873249 0.007622042697
Й1 Г) ■
296 0.8996668554 0.08946810381
297 0.8996569864 0.08947500455
298 0.8996472735 0.08948179440
299 0.8996377141 0.08948847519
300 0.8996283059 0.08949504871_
В строке #2 находится результат обращения к утилите ODE_APPR.MTH
решения дифференциальных уравнений методом Рунге — Кутты. В системе
дифференциальных уравнений, представленной в строках #3—#7, вводятся
лишь правые части уравнений без указания аргумента /. В строках #8 и #9
находится обращение к функции RK решения системы дифференциальных
уравнений с исходными данными задачи. В строке #10 приведена таблица
результатов в виде матрицы, элементами которой являются вероятности Р0 и
I]. Их сумма и является функцией готовности системы. Решение выполнено
с шагом h = 1 и числом строк равном 300, что соответствует времени работы
системы в часах.

538 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
Определение наработки системы на отказ
Наработку на отказ вычислим по формуле:
где Р(), Р|, Р2, ^з» Л — финальные вероятности состояний системы. Для их
определения на основании графа состояний системы рис. 3.4 составим и
решим следующую систему алгебраических уравнений:
'-(2X + A.])PQ+iiPl+^P2=Q-
2Щ -(а + Ь + р)Р{ + цР3 + М]?4 = 0;
a,/b-jnIP2=0;
^-u^=0;
Эта однородная система имеет бесконечное множество решений. Заменим
одно из уравнений следующим нормировочным: Р{] + fj + Р2 + Ръ + Р4 -1.
Решение получим с помощью функции SOLVE, а затем воспользуемся
приведенной ранее формулой определения наработки на отказ.
Технология решения очевидна. Вычислительные процедуры имеют
следующий вид:
#1: InputMode : = Word
#2: -(2-Л + Л1)-рО + р-р1 + р1-р2 = 0
#3: p0 + pl + p2 + p3 + p4 = l
#4: Л1-р0-ц1-р2 = 0
#5: а-р!-р-р3=0
#6: b-pl-pl-p4 = 0'
"- (2 • Л + Л1) • рО + у • pi + р 1 • р2 = О"
p0 + pl + p2 + p3 + p4=l
#7: Л1-рО-ц1-р2 = 0
a-pl-y-р3 = 0
b-pl-pl-p4 = 0

Решение задач надежности с помощью программных средств 539
T-(2-A + Al}-pO + p-pl + pl-p2 = o] N
рО + рИ-р2 + рЗ + р4 = 1
#8: SOLVE Л1 -pO-pl-р2 = 0 , [рО, pi, р2, рЗ, р4 ]
a-pl -р 'р3 = 0
ч|_ b-pl-pl-p4 = 0 J y
ц" -pi
#9: —
2-a-A-pl + p-(2-b-A + 2-A-pl + p-(Al + pl))
#10: —
2-a-A-pl + p-{2-b-A + 2-A-pl + p-(Al + pl))
М-р2
#11:
2-a-A-pl + p-{2-b-A + 2-A-pl + p-(M + pl))
2-а-А-р1
#12:
2-a-A-pl + p-{2-b-A + 2-A-pl + p-(Al + pl))
2-Ь-А-р
§12 • -
2-a-A-pl + p-{2-b'A + 2'A-pl + p-(Al+pl) }
2 • А + р
#14 :
2-а-А + 2-Ь-А + А1-р
#15: 2558.139534
„_ 2-а-А<р1 + р-(2-Ь-А + А1-р)
#16:
p-pl-(2-a-A + 2-b-A + Al-p)
#17: 28.60465116
В строке #7 находится система уравнений, образованная из уравнений
состояний (строки #2—#6). Решение системы выполнено с помощью функции
SOLVE (строка #8). На экране для удобства дальнейших вычислений
оставлены выражения финальных вероятностей без их обозначений. Вероятность Р0
находится в строке #9, Р} — в #10, Р2 — в #11, Р3 — в #12, Р4 — в #13.
Решение, полученное по формуле коэффициента готовности, находится в
строках #14 и #15. В строке #16 получено выражение для среднего времени
восстановления, вычисленное по формуле:
т Р2 + Р3 + Г4
В Р2\1Х + Р3\1+Р4Щ'
Эти вычисления очевидны, поэтому они не приводятся.

540 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
Система Derive 5, как и другие системы компьютерной алгебры, позволяет
решать множество других задач, встречающихся при расчетах надежности.
Однако и этих примеров достаточно, чтобы убедиться в полезности
применения этой системы в научных и инженерных расчетах.
3.2. Использование
специализированных программ
для решения задач надежности
Далее будут рассмотрены лишь некоторые из программных средств,
описание работы которых было приведено в гл. 2 части IV. Их практическое
применение требует от пользователя минимального количества операций. В то
же время предполагается знание теоретических основ надежности по
изучаемой проблеме.
3.2.1. Программное средство Relass
Программа Relass позволяет рассчитывать показатели надежности сложных
систем по всем основным критериям. Система может состоять из большого
количества элементов и иметь миллионы возможных состояний.
Интенсивности отказов и восстановлений элементов предполагаются постоянными.
Учитываются следующие особенности функционирования системы: наличие
последействия отказов, неполнота контроля, возможные интервалы простоя
элементов.
На рис. 3.5 представлено окно для ввода исходной информации и
отображения результатов в программе Relass.
Назначение и возможности Relass описаны в разд. 2.3 части IV. Там же
приведены способы представления структурной схемы системы и необходимые
данные об отказах и восстановлениях ее элементов. Особенностями
функционирования системы являются: большое число состояний, наличие
последействия отказов, интервалов простоя, неполнота контроля.
ПРИМЕР 3.7. Требуется рассчитать показатели надежности сложной
резервированной системы из 12 элементов, структурная схема которой
представлена рис. 3.6. Подсистема 15, состоящая из элементов 4, 5, 6, имеет кратность
резервирования 1/2. Подсистема 16, состоящая из элементов 7, 8, 9,
представляет собой резервное устройство (резерв замещением) кратности 2.
Интенсивности отказов и восстановлений постоянные и приведены в
табл. 3.1. Интенсивность отказа элемента 3 равна 0,0001 час" . Однако при

Решение задач надежности с помощью программных средств
541
отказе любого из элементов I или 2 интенсивность отказа третьего элемента
становится равной 0,0003 час4. Аналогично при отказе элемента 10
возрастает интенсивность отказа элемента 11 с 0,005 до 0,008 час"'.
Вероятности обнаружения отказа для элементов 3, 7, 8, 9 равны
соответственно 0,8, 0,5, 0,7, 0,8. Для остальных элементов эти вероятности равны 1.
Время работы системы составляет 20 000 часов.
Рис. 3.5. Диалоговое окно системы Relass
Рис. 3.6. Структурная схема расчета надежности сложной системы с разбиением
на подсистемы

542 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
Таблица 3.1. Данные о надежности и ремонтопригодности элементов
Номер элемента /
1
2
3
4
5
6
7
8
9
10
11
12
Интенсивность отказа
X/, час-1
0,0001
0,0002
0,0001
0,0001
0,0001
0,0005
0,002
0,002
0,002
0,004
0,005
0,0001
Интенсивность восстановления
М/, час"1
2
1
10
5
5
0,5
0,1
0,3
0,5
7
5
2
Элементы с номерами 4, 5 и 6 имеют интервалы простоя. На каждом периоде
длительности 1000 часов элемент 4 простаивает в течение времени от 100
до 500 часов, элемент 5 — в течение времени от 500 до 1000 часов, элемент
5 — в течение времени от 200 до 700 часов. Остальные элементы
структурной схемы работают непрерывно.
Систему обслуживают 4 бригады с различной дисциплиной обслуживания.
Бригады распределены по подсистемам 14, 15, 16, 19. Первая, третья и
четвертая бригады имеют по одной ремонтной единице, а вторая бригада имеет
две ремонтные единицы. Приоритет обслуживания для бригад 1 и 4 прямой,
для бригады 2 — обратный, для бригады 3 — назначенный. В случае
образования очереди в подсистеме 16 первым обслуживается элемент 7, а затем
элемент 8 и 9.
Решение. Решение задачи с помощью Relass следует начинать с
декомпозиции структурной схемы, показанной на рис. 3.6. Подсистема с номером 13
состоит из двух элементов 1 и 2. Подсистема 14 представляет собой
дублирование подсистемы 13 и элемента 3. Подсистема 15 имеет дробную кратность
резервирования и состоит из элементов 4, 5, 6. Подсистема 16 с кратностью
резервирования, равной 2, состоит из элементов 7, 8, 9. Подсистема 17
представляет собой основное соединение подсистем 14, 15 и 16. Подсистема 18
есть дублированная система из разнонадежных элементов 10 и 11 с последей-

Решение задач надежности с помощью программных средств
543
ствием отказов. Подсистема 19, составленная из подсистемы 18 и
элемента 12, является нерезервированной. Анализируемая система 20
представляется как дублированная система, составленная из двух подсистем с номерами
17 и 19.
Перечислим теперь исходные данные о системе, которые вводятся в
диалоговом окне программы.
Общими данными являются:
О период работы системы — 1000 часов;
О время работы системы — 20 000 часов;
П число элементов — 12;
О число подсистем — 8;
О число бригад — 4.
Данные о подсистемах, вводимые в окне программы, приведены в табл. 3.2.
Таблица 3.2. Данные о подсистемах
Номер
подсистемы
13
14
15
16
17
18
19
20
Тип связи
Основное соединение
Нагруженный резерв
Нагруженный резерв
Ненагруженный
резерв
Основное соединение
Нагруженный резерв
Основное соединение
Нагруженный резерв
Номера элементов
и подсистем
1,2
13,3
4,5,6
7,8,9
14, 15, 16
10,11
18,12
17,19
Общее число
элементов
2
2
3
3
3
2
2
2
Число основных
элементов
1
1
2
1
1
1
1
1
Данные об элементах приведены в табл. 3.3.
Таблица 3.3. Данные об элементах
Номер
элемента
1
2
3
Интенсивность
отказа
0,0001
0,0002
0,0001
Интенсивность
отказа 1
0,0001
0,0002
0,0003
Интенсивность
отказа 2
' 0,0001
0,0002
0,0003
Интенсивность
восстановления
2
г
10

544 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
Таблица 3.3 (окончание)
Номер
элемента
4
5
6
7
8
9
10
11
12
Интенсивность
отказа
0,0001
0,0001
0,0005
0,002
0,002
0,002
0,004
0,005
0,0001
Интенсивность
отказа 1
0,0001
0,0001
0,0005
0,002
0,002
0,002
0,004
0,008
0,0001
Интенсивность
отказа 2
0,0001
0,0001
0,0005
0,002
0,002
0,002
0,004
0,008
0,0001
Интенсивность
восстановления
5
5
0,5
0,1
0,3
0,5
7
5
2
Номер
элемента
1
2
3
4
5
6
7
8
9
10
11
12
Вероятность
обнаружения
отказа
1
1
0,8
1
1
1
0,5
0,7
0,8
1
1 .
1
Число
интервалов
простоя
0
0
0
1
1
1
0
0
0
0
0
0
Левая
граница
100
500
200
Правая
граница
500
1000
700
Левая
граница
Правая
граница
В столбце "Интенсивность отказа 1" записывается интенсивность отказа
элемента после первого отказа любого элемента данной подсистемы. В столбце
"Интенсивность отказа 2" записывается интенсивность отказа элемента после
второго отказа некоторого элемента данной подсистемы. Таким образом,
учитывается последействие отказов элементов.

Решение задач надежности с Помощью программных средств
545
Столбец "Число интервалов простоя" служит для указания количества
интервалов простоя элемента на периоде. Левая и правая границы являются
моментами времени начала и окончания простоя элемента.
В соответствии с условиями задачи в табл. 3.4 приведены данные о
ремонтных бригадах, которые вводятся в соответствующую таблицу окна
программы.
Таблица 3.4. Данные о бригадах
Номер
бригады
1
2
3
4
Число
ремонтных
единиц
1
2
1
1
Приоритет
обслуживания
Прямой
Обратный
Назначенный
Прямой
Номера
обслуживаемых
элементов
1,2,3
4,5,6
7,8,9
10, 11, 12
Количество
обслуживаемых
элементов
3
3
3
3
После ввода данных на диске создается текстовый файл inputs, где N—
порядковый номер файла, с исходными данными:
1000 2000
12 8 4
13 1 1 2 1 1 2
14 3 1 2 1 3 13
15 3 1 3 2 4 5 б
16 4131789
17 1 1 3 1 14 15 16
18 3 1 2 1 10 11
19 1 1 2 1 12 18
20 3 1 2 1 17 19
1 0.0001 0.0001 0.0001 2 10
2 0.0002 0.0002 0.0002 110
3 0.0001 0.0003 0.0003 10 0.8 0
4 0.0001 0.0001 0.0001 5 1 1 100 500
5 0.0001 0.0001 0.0001 5 1 1 500 1000
6 0.0005 0.0005 0.0005 0.5 1 1 200 700
7 0.002 0.002 0.002 0.1 0.5 0

546 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
8 0.002 0.002 0.002 0.3 0.7 0
9 0.002 0.002 0.00.2 0.5 0.8 0
10 0.004 0.004 0.004 7 10
11 0.005 0.008 0.008 5 10
12 0.0001 0.0001 0.0001 2 10
1113 12 3
2 2 2 3 4 5 6
3 13 3 7 8 9
4 1 1 3 10 11 12
Результаты решения содержатся в текстовом файле outputN:
Т = 32177 час, Тъ =0,47 час, Кг =0,999985, 7] =32582 час.
Этот файл содержит также таблицу значений показателей надежности
системы в зависимости от времени. График вероятности безотказной работы для
значений / от 0 до 20 000 часов изображен на рис. 3.7.
Рис. 3.7. Вероятность безотказной работы системы
Результаты расчетов показывают, что система является высоконадежной, она
входит в стационарный режим при / = 700 час. Поэтому график функции
готовности изображен на рис. 3.8 для диапазона значений / от 0 до 800 часов.
При сделанных ранее допущениях программа Relass позволяет рассчитывать
надежность систем с большим числом состояний. Для системы,
изображенной на рис. 3.6, количество узлов графа равно 83384.

Решение задач надежности с помощью программных средств
547
Рис. 3.8. Функция готовности системы
3.2.2. Программа Conspz
На рис. 3.9 представлено окно для ввода исходной информации и
отображения результатов программы Conspz. Назначение и возможности этой
программы описаны ъразд. 2.6 частиIV.
Рассмотрим 2 примера работы с этой программой.
Рис. 3.9. Диалоговое окно программы Conspz

548 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
ПРИМЕР 3.8. Рассмотрим неизбыточную восстанавливаемую систему,
состоящую из 4-х групп элементов. Время работы системы — 15 000 часов,
число точек для табличного и графического отображения результатов равно
1000. Число элементов в каждой группе, а также данные по надежности и
ремонтопригодности элементов каждой группы приведены в табл. 3.5.
Требуется определить показатели надежности системы в условиях неполной
информации об отказах и восстановлении элементов. Неполнота информации
связана с тем, что математическое ожидание (МО) и среднее квадратическое
отклонение (СКО) времени безотказной работы элементов случайно,
равномерно распределено на промежутках, указанных в табл. 3.5.
Таблица 3.5. Данные о надежности и ремонтопригодности элементов
Номер
группы
1
2
3
4

Количество
элементов
12
18
20
15
Закон распределения
времени до отказа
Рэлея
Вейбулла
Усеченный
нормальный
Экспоненциальный
МО
(нижнее)
5000
5600
5200
5000
МО
(верхнее)
5500
6000
5800
5200
СКО
(нижнее)
Не задается
2000
1400
Не задается
СКО
(верхнее)
Не задается
2000
1800
Не задается
Номер
группы
1
2
3
4
Закон распределения
времени восстановления
Гамма
Экспоненциальный
Равномерный
Вейбулла
МО
(нижнее)
15
10
5
10
МО
(верхнее)
15
10
18
14
СКО
(нижнее)
10
Не задается
2
5
СКО
(верхнее)
10
Не задается
4
8
Табличные данные показывают, что первая группа содержит 12 элементов,
имеющих распределение Рэлея времени до отказа, причем математические
ожидания времени до отказа этих элементов равномерно распределены на
интервале от 5000 до 5500 часов. То же относится и к элементам других
групп.
После ввода данных создается текстовый файл inputiV с исходными данными:
4 15000 1000
1 12 4 5000 5500 0 0 2 15 15 10 10
2 18 5 5600 6000 2000 2000 0 10 10 0 0

Решение задач надежности с помощью программных средств
549
3 20 3 5200 5800 1400 1800 1 5 18 2 4
4 15 0 5000 5200 О О 5 10 14 5 8
Результаты решения сохраняются в файле outputs, который содержит
значения стационарных показателей надежности системы:
Г = 83,565208 час, Тъ = 11,902401 час, Кг =0,875325.
На основе табличных значений функции готовности системы, содержащихся
в файле, строится график (кривая 1), изображенный на рис. 3.10.
О 1500 3000 4500 6000 7500 9000 10500 12000 13500 15000
Рис. 3.10. Функция готовности нерезервированной системы
Обратим внимание, что при / = 0 Kr(t)*\. Объяснение этому факту дает
следующий пример.
ПРИМЕР 3.9. Рассматривается система, аналогичная предыдущей, но с
одним отличием. Элементы 4-й группы имеют гамма-распределение с
математическим ожиданием в пределах от 5000 до 5200 часов и средним квадрати-
ческим отклонением от 1000 до 2000 часов.
Решение. Результаты расчетов показывают, что стационарные показатели не
изменились, поскольку они не зависят от законов распределения, а зависят
только от их математических ожиданий.
Функция готовности существенно изменилась. На рис. 3.10 ей соответствует
кривая 2. В примере 3.8 элементы 4-й группы имели экспоненциальные рас-

550 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
пределения времени до отказа, для которых наблюдается быстрое вхождение
в стационарный режим. Поэтому на начальном этапе функционирования
происходит резкое снижение готовности системы (кривая 1) по сравнению
с примером 3.9, когда все элементы имеют гамма-распределение.
3.2.3. Программа Posl_par
На рис. 3.11 представлено окно для ввода исходной информации и
отображения результатов программы Posl_par. С помощью этой программы можно
определить вероятность безотказной работы невосстанавливаемых систем
последовательно-параллельной структуры. Это могут быть системы с
постоянно включенным резервом и по методу замещения при общем и раздельном
резервировании. Элементы системы предполагаются равнонадежными. Закон
распределения времени до отказа произвольный.
Рис. 3.11. Диалоговое окно программы Posl_par
ПРИМЕР ЗЛО. Время до отказа каждого элемента системы имеет гамма-
распределение с математическим ожиданием 200 часов и средним квадрати-
ческим отклонением а = 200 час. Число элементов нерезервированной сие-

Решение задач надежности с помощью программных средств 551
темы w = 20, число резервных систем m-Ъ . Требуется определить
вероятность и среднее время безотказной работы системы для четырех схем
соединения элементов:
П общее резервирование с постоянным резервом (схема I);
□ общее резервирование замещением (схема 2);
П раздельное резервирование с постоянным резервом (схема 3);
П раздельное резервирование замещением (схема 4).
Решение. Используя программное средство Posl_par, получим графики
вероятности безотказной работы для указанных схем резервирования (рис. 3.12).
Номер схемы
7"ic, час
I
21,0
2
39,9
3
И 5,0
4
246,8
Заметим, что в данном примере элементы системы имеют экспоненциальное
распределение времени до отказа, поскольку математическое ожидание
совпадает с а.
Для сравнения рассмотрим второй пример.
Рис. 3.12. Вероятность безотказной работы для четырех схем резервирования (а = 200 час)
Как видно из графиков, надежность систем возрастает с увеличением номера
схемы резервирования. Среднее время безотказной работы берется из
диалогового окна (табл. 3.6).
Таблица 3.6. Среднее время безотказной работы систем (о = 200 час)

552 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
ПРИМЕР 3.11. Для систем последовательно-параллельной структуры из
примера 3.10 определить вероятность и среднее время безотказной работы при
условии, что среднее квадратическое отклонение времени до отказа
элементов составляет а = 100 час.
Решение. Результаты расчета с помощью программы Poslpar показывают,
что графики вероятности безотказной работы для четырех схем
резервирования имеют вид, представленный на рис. 3.13.
Рис. 3.13. Вероятность безотказной работы для четырех схем резервирования (а = 100 час)
Из графика следует, что надежность всех четырех схем резервирования
заметно повысилась, причем схема общего резервирования замещением
(схема 2) стала более надежной., чем схема раздельного резервирования с
постоянно включенным резервом (схема 3). Этот факт вновь подтверждает
важность анализа надежности систем при произвольных законах распределения
времени до отказа элементов. Среднее время безотказной работы для
заданных схем резервирования содержится в табл. 3.7.
Таблица 3.7. Среднее время безотказной работы систем (о = 100 час)
Номер схемы
Г), час
;_t;(0 = ioo)
7^ (а = 200)
1
84,3
4,0
2
245,2
6,1
3
166,4
1,4
4
474,0
1,9

Решение задач надежности с помощью программных средств
553
Из рис. 3.13 видно, что самой высокой надежностью обладает схема
раздельного резервирования замещением, у которой вероятность безотказной работы
превышает P(t) остальных схем,
В табл. 3.7 приведен показатель роста надежности систем к по среднему
времени безотказной работы при уменьшении а в 2 раза. Наибольшее
увеличение надежности имеют схемы общего резервирования, в особенности схема
общего резервирования замещением.
3.2.4. Программное средство Redopt
Назначение программы Redopt состоит в решении трех задач:
1. Выбор оптимальной структуры системы при заданном количестве
ремонтных органов.
2. Определение количества ремонтных бригад при известном числе
резервных элементов.
3. Выбор оптимальной структуры системы и определение оптимальной
стратегии ее обслуживания.
В полном объеме методика, алгоритм и примеры оптимизации для всех трех
задач изложены в [5, гл. 10] и частично в разд. 2.5 части IV данной книги.
Здесь будет рассмотрена только третья задача, как наиболее общая.
Исходными данными для расчетов являются:
□ время работы системы;
О количество точек дискретизации (для таблиц и графиков функций);
О момент времени оптимизации /д;
□ требуемое значение функции готовности системы КЛ\
□ количество нерезервированных подсистем.
Для каждой подсистемы известно:
П вид резервирования (постоянно включенный или замещением);
П число основных элементов kt;
П максимально возможное число резервных элементов mi;
П вид и параметры распределения времени безотказной работы элементов;
□ вид и параметры распределения времени восстановления элементов;
О максимально возможное число ремонтных единиц rt;
П стоимость каждого резервного элемента си ;
G стоимость одной ремонтной единицы с2/.

554 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
Результатами расчетов является оптимальное число резервных элементов xi
и число ремонтных единиц у, в каждой подсистеме, так, чтобы выполнялось
неравенство К,.(/д) > Кл, и система имела минимальную стоимость.
Диалоговое окно для ввода исходной информации и отображения результатов
по программе Redopt представлено на рис. 3.14.
Рис. 3.14. Диалоговое окно программы Redopt
ПРИМЕР 3.12. Структурная схема системы приведена на рис. 3.15. Она
состоит из трех подсистем (обведены пунктирными линиями).
Данные по всем трем подсистемам содержатся в табл. 3.8.
Рис. 3.15. Структурная схема с неизвестным числом резервных элементов

Решение задач надежности с помощью программных средств 555
Таблица 3.8. Исходные данные для оптимизации системы
Подсистема
Вид резерва
*,
т,
0
Время до отказа
N40
СКО
Время восстановления
МО
СКО
C\i
Сц
2 ! з -
Постоянный
2
5
4
Усеченный нормальный
1000
350
Равномерный
100
45
20
8
Замещением
1
10
10
Гамма
700
150
Усеченный нормальный
120
70
12
15
Замещением
3
4
5
Рэлея
2500
1250
Рэлея
80
40
40
22
Из таблицы следует, что первая подсистема имеет 2 основных и х] резервных
элементов, Х] < 5. Она может обслуживаться ^ < 4 ремонтниками. Элементы
первой подсистемы имеют время до отказа, подчиненное усеченному
нормальному закону с математическим ожиданием 1000 часов и средним квадра-
тическим отклонением 350 часов. Время восстановления имеет равномерное
распределение с математическим ожиданием 100 часов и средним квадрати-
ческим отклонением 45 часов. Стоимость одного элемента первой
подсистемы — 20 ден. ед„ стоимость одной ремонтной единицы оценивается в
8 ден. ед. Аналогичные данные имеют вторая и третья подсистемы.
На функцию готовности системы задано ограничение: Кл=0,99 в момент
времени /д = 1000 час.
Результаты оптимизации по программе Redopt представлены в табл. 3.9.
Таблица 3.9. Результаты оптимизации системы
11одсистема
Число резервных элементов .t/
Число ремонтных единицу
1
2
3
2
3
1
3
1
1

556 ЧАСТЬ IV. Компьютерные технологии решения задач надежности. Глава 3
Фактическая готовность системы в момент /д = 1000 час составляет
АГГ(1000) = 0,990397, что превышает заданное значение. Общая стоимость
системы является минимальной и составляет с-Ml ден.ед. Абсолютная
погрешность расчетов равна 0,0057.
Программа выдает файл output^ со значениями функции готовности, которые
здесь не приводятся. График Kr(f) системы, полученный после оптимизации,
изображен на рис. 3.16.
Рис. 3.16. Функция готовности системы после оптимизации: Кг(\000) = 0,99
Рис. 3.17. Функция готовности трех подсистем

Решение задач надежности с помощью программных средств 55/
Из графика видно, что в момент времени t = 1000 часов значение функции
готовности превышает требуемое значение К}1 - 0,99.
Дополнительно программа рассчитывает и выдает в виде файла goW
функцию готовности для каждой подсистемы. Соответствующие графики
представлены на рис. 3.17.
Графики показывают, что самой надежной является подсистема 3 со
скользящим резервированием.

СПИСОК ЛИТЕРАТУРЫ
1. Аладьев В. 3., Шишаков М. Л. Автоматизированное рабочее место
математика. — М: Лаборатория базовых знаний, 2000.
2. Аладьев В. 3., Шишаков М. Л. Введение в среду пакета Mathemati-
са2.2. — М.: Филин, 1997.
3. Говорухин В. Н., Цибулин В. Г. Введение в Maple. — М.: Мир, 1997.
4. Гуров С. В., Герасин М. Л. Моделирование систем. Учебное пособие. —
Сыктывкар: Лесной институт, 2001.
5. Гуров С. В., Половко А. М. Основы теории надежности. — СПб.: БХВ-
Петербург, 2005.
6. Дьяконов В. П. Системы символьной математики. Mathematica 2 и Mathe-
matica 3. — М: СК Пресс, 1998.
7. Дьяконов В. П. Mathcad 8/2000. Специальный справочник. — СПб.:
Питер, 2000.
8. Курицкий В. Я. Поиск оптимальных решений средствами Excel 7.O. —
СПб.: BHV — Санкт-Петербург, 1997.
9. Манзон Б. М. Maple 5 Power Edition. — М.: Филин, 1998.
10. Половко А. М. Derive 5 для студента. — СПб.: БХВ-Петербург, 2005.
11. Соболь И. М. Метод Монте-Карло. — М.: Наука, 1968.
12. Тюрин Ю. Н., Макаров А. А. Анализ данных на компьютере.— М.:
ИНФРА-М, Финансы и статистика, 1995.
13. Gurov S. V., Utkin L. V. Reliability of repairable systems with periodic
modifications, Microelectron. Reliab. Vol. 36, No. 1, pp. 27—35, 1996.
14. Gurov S. V., Utkin L. V. Fuzzy reliability of gracefully degrading systems
with the composite software, Reliability, Quality and Safety Engineering,
Vol. 3, No. 2, pp. 153—165, 1996.
15. Gurov S. V., Utkin L. V. Reliability and optimization of systems with periodic
modifications in the probability and possibility contexts, Microelectron.
Reliab., Vol. 37, No. 5, pp. 801—808, 1997.