Текст
опорный вуз ~--_---~—^—--------------_--_-
А. Г. ПИНУС
основы
УНИВЕРСАЛЬНОЙ
АЛГЕБРЫ
———__^^^_ СЕРИЯ -
* УЧЕ НИКИ
Η Τ
•
РЕДАКЦИОННАЯ КОЛЛЕГИЯ
СЕРИИ «УЧЕБНИКИ НГТУ»
д-р техн. наук, проф. (председатель) А.А. Батаев
д-р техн. наук, проф. (зам. председателя) Г. И. Расторгуев
д-р техн. наук, проф. СВ. Брованов
д-р техн. наук, проф. А.Г. Вострецов
д-р техн. наук, проф. А.А. Воевода
д-р техн. наук, проф. В.А. Гридчин
д-р техн. наук, проф. В.И. Денисов
д-р физ.-мат. наук, проф. В.Г. Дубровский
д-р филос. наук, проф. В.И. Игнатьев
д-р техн. наук, проф. Н.В. Пустовой
д-р техн. наук, проф. Х.М. Рахимянов
д-р филос. наук, проф. М.В. Ромм
д-р техн. наук, проф. ЮТ. Соловейчик
д-р физ.-мат. наук, проф. В.А. Селезнев
д-р техн. наук, проф. А.А. Спектор
д-р техн. наук, проф. А.Г. Фишов
д-р экон. наук, проф. М.В. Хайруллина
д-р техн. наук, проф. А.Ф. Шевченко
д-р техн. наук, проф. Н.И. Щуров
А. Г. ПИНУС
ОСНОВЫ
УНИВЕРСАЛЬНОЙ
АЛГЕБРЫ
4-е издание, переработанное и дополненное
НОВОСИБИРСК
2019
УДК 512(075.8)
Π 326
Рецензенты:
д-р физ.-мат. наук В.А. Артамонов,
д-р физ.-мат. наук Б.М. Берников,
д-р физ.-мат. наук В.М. Волков,
академик РАН С.С. Гончаров
Пинус А.Г.
Π 326 Основы универсальной алгебры: учебное пособие /
А.Г. Пинус. - 4-е изд., перераб. и доп. - Новосибирск: Изд-во
НГТУ, 2019. - 184 с. (Серия «Учебники НГТУ»)
ISBN 978-5-7782-3794-0
Учебное пособие посвящено универсальной алгебре, молодой
развивающейся науке, нашедшей свои приложения как внутри
математики, так и в информатике и ряде других наук. Адресовано
студентам и аспирантам-математикам, информатикам, а также
научным работникам в этих областях.
УДК 512(075.8)
ISBN 978-5-7782-3794-0 © Пинус А.Г., 1998, 2000. 2005, 2019
© Новосибирский государственный технический
университет, 1998, 2000, 2005. 2019
Оглавление
Предисловие к первому изданию. 7
Предисловие ко второму изданию 8
Предисловие к третьему изданию 9
Предисловие к четвертому изданию 9
Глава 1. Основные понятия универсальной алгебры 11
§1. Универсальные алгебры, модели и алгебраические
системы. Эквивалентность на множестве 11
§ 2. Подалгебры и теоремы представлений для групп,
булевых алгебр, дистрибутивных решеток 31
§ 3. Алгебраические решетки 47
§ 4. Гомоморфизмы, конгруэнции и фактор-алгебры ... 53
§ 5. Прямые и подпрямые произведения,
ультрапроизведения. Операторы на классах алгебр 67
Глава 2. Многообразия и свободные алгебры 83
§ 6. Абсолютно свободные алгебры. Свободные алгебры
многообразий 83
§ 7. Тождества и эквациональные классы 91
§ 8. Исчисление тождеств 94
§ 9. Конгруэнц-перестановочные, конгруэнц-модулярные,
конгруэнц-дистрибутивные многообразия.
Дискриминаторные многообразия 97
§ 10. Рациональная эквивалентность многообразий .... 109
Глава 3. Условные термы и условные многообразия 115
§ 11. Условные термы и условно термальные функции . .115
§ 12. Условные тождества и условные многообразия . . . 124
§ 13. Условно рациональная эквивалентность условных
многообразий и алгебр 129
5
Оглавление
Глава 4. Некоторые приложения универсальной
алгебры 135
§ 14. Клоны и соответствие Галуа 135
§ 15. Шкалы потенциалов вычислимости конечных алгебр 148
§ 16. Конечные автоматы, языки
и грамматики 154
§ 17. Алгебры Халмоша и базы данных 162
§ 18. Некоторые приложения группоидов и полугрупп . . 167
Заключение 173
Указатель терминов 175
Библиографический список 180
б
Моим сыновьям Константину
и Филиппу посвящается
Предисловие к первому изданию
Универсальная алгебра — сравнительно молодая наука,
изучающая поведение функций на произвольных множествах. Ее
основы были заложены работами Г. Биркгофа 1930-х годов.
Впоследствии значительный вклад в нее внесли работы А. Тарского,
А.И. Мальцева, Б. Йонсона, Р. МакКензи и многих других.
Возникшая на стыке математической логики и классической алгебры
универсальная алгебра, в свою очередь, оказала влияние как на
эти разделы математики, так и на более далекие области этой
науки. Развитие универсальной алгебры связано не только с
решением внутренних математических проблем, но и с большим
числом приложений ее методов и результатов в различных областях
знаний от социологии до информатики. В частности,
непосредственное применение универсальная алгебра нашла в
программировании, в теории баз данных и ряде других областей,
получивших развитие в нынешнюю эпоху широкого применения
вычислительных машин. Тем не менее круг людей, знакомых с
универсальной алгеброй и владеющих ее методами, довольно узок.
Сам курс универсальной алгебры читается в виде спецкурсов в
довольно ограниченном числе университетов. В связи с этим
смелым и новаторским шагом было решение руководства факультета
прикладной математики и информатики Новосибирского
государственного технического университета и, в частности, его бывшего
декана, профессора В.И. Хабарова, о введении этого курса в
обязательную программу обучения прикладных математиков НГТУ.
Чтение этого курса было предложено мне, за что я благодарен
руководству факультета. Одна из проблем, с которой я
столкнулся при подготовке и чтении этого курса, — отсутствие
подходящей учебной литературы на русском языке. Классический
учебник А.И.Мальцева "Алгебраические системы" является в
настоящее время библиографической редкостью, да и материал этой
книги, написанный в 1960-е годы, далеко не полностью отражает
современные достижения универсальной алгебры. То же можно
Предисловие ко второму изданию
сказать и о имеющейся на русском языке книге П. Кона
"Универсальная алгебра". Учебники А.Г. Куроша "Лекции по общей
алгебре" и Л.А. Скорнякова "Общая алгебра" вопросов
универсальной алгебры касаются лишь косвенно. Книга Д.М. Смирнова
"Многообразия алгебр" носит скорее монографический, а не
учебный характер, да и изданная малым тиражом, она малодоступна
студентам. На английском языке можно указать книги Г. Грет-
цера "Универсальная алгебра" и С. Барриса, Х.П. Санкапанавара
"Курс универсальной алгебры", но они велики по объему
материала и недоступны для российского студенчества. Прекрасным
учебником по универсальной алгебре является книга Т. Ирингера
"Общая алгебра", соответствующая по объему университетскому
курсу, но, написанная на немецком языке и практически
отсутствующая в России, она также является вещью в себе для
студентов НГТУ.
Эти обстоятельства и подтолкнули меня на написание
учебника под тот курс универсальной алгебры, который в течение
нескольких лет читается мной студентам,НГТУ,
специализирующимся по прикладной математике. Результат перед вами.
Безусловно, на содержании курса сказались и личные пристрастия
автора в широкой области универсальной алгебры, в том числе в
виде включения в книгу главы 3, в которой представлены
результаты его исследований. Автор искренне надеется, что этот
учебник послужит более широкому знакомству молодых математиков
с методами и результатами близкой ему науки.
А. Г. Пинус
Мэдисон. Висконсин.
Февраль, 1998 г.
Предисловие ко второму изданию
В настоящем издании исправлен ряд опечаток, замеченных в
первом.
А. Г. Пинус,
Новосибирск, Россия.
Июнь 2000 г.
8
Предисловие к третьему изданию
Предисловие к третьему изданию
В настоящем издании исправлен ряд опечаток, замеченных в
предыдущих изданиях, расширен круг задач и добавлена глава 4,
посвященная приложениям универсальной алгебры.
А. Г. Пинус
Новосибирск, Россия.
Июнь, 2004 г.
Предисловие к четвертому изданию
В настоящем, четвертом издании помимо исправления
огрехов третьего, добавлены § 14 "Клоны и соответствие Галуа" и
§ 18 "Некоторые приложения группоидов и полугрупп".
В очередной раз хочу отметить, что настоящий учебник
посвящен лишь основам универсальной алгебры и не касается многих
современных областей универсальной алгебры, таких, к примеру,
как теория квазимиогообразий алгебр, алгоритмические
проблемы универсальной алгебры, теория коммутаторов, теория ручных
конгруэнции, строение конечных алгебр и других. Далеко не все
области возможных приложений универсальной алгебры
затронуты и в главе 4. К примеру, там не рассматриваются вопросы
приложения языка квазитождеств (фрагмента языка условных
тождеств) в логическом програмировании, не рассматриваются
вопросы о роли универсальной алгебры в целом ряде иных
областей дискретной математики: в теории кодирования, в теории
функциональных схем и в других.
Среди вышедших в последнее время учебников по
универсальной алгебре необходимо отметить электронный учебник Я. Ежека
[36] и единственный в настоящее время задачник [18] специально
посвященный задачам по универсальной алгебре.
Материалы настоящего учебника могут быть использованы
как основа для стандартного годового курса по универсальной
алгебре, как основа для ряда спецкурсов по избранным областям
универсальной алгебры, а так же для самостоятельного
знакомства с этой областью математики.
9
Предисловие к четвертому изданию
Наконец я хочу поблагодарить Евгения Николаевича Поро-
шенко и Ирину Львовну Кескевич за неоценимую помощь при
подготовке данного издания этого учебника.
А.Г.Пинус.
Новосибирск, Россия.
Октябрь, 2018 г.
10
Глава 1
Основные понятия
универсальной алгебры
§ 1. Универсальные алгебры, модели
и алгебраические системы.
Эквивалентность на множестве
Как уже сказано выше, основным предметом изучения
универсальной алгебры являются множества с наборами функций,
определенных на этих множествах. Однако на протяжении всего курса
важную роль будут играть не только функции на множествах, но
и различные отношения, определенные на этих множествах.
Мы будем предполагать известными читателю в пределах
"наивного курса" понятия множества, его элемента,
подмножества, декартова и прямого произведения множеств,
отображения одного множества в другое, η-местной функции и
η-местного отношения на множестве, мощности множества.
На протяжении всего курса мы будем отождествлять п-мест-
ное отношение, определенное на множестве А, с соответствующим
подмножеством n-й декартовой степени множества А. Более
точно, η-местное отношение R(xi,..., хп) на множестве А ставит в
соответствие каждому набору элементов αχ,..., αη множества А
элементы двухэлементного множества {И;Л}: истину либо ложь.
Если R(ai,..., ап) = И, то будем говорить, что отношение R
истинно на элементах αχ, ...,αη, если R(ai,..., αη) = Л, то
соответственно R ложно на αχ,... ,αη. В первом случае будем часто
ограничиваться записью Л (αχ,..., αη), во втором — ->/ί(αχ,..., ап).
Каждому η-местному отношению R на множестве А мы можем
поставить в соответствие некоторое подмножество n-й степени Ап
Глава 1. Основные понятия универсальной алгебры
множества А (как правило, обозначаемое той же буквой R),
определяемое следующим образом:
(ai,...,an) e R <=> R(ai,...,an) = И Ф=> Л(аь ... ,ап).
Очевидно, что это сопоставление является взаимно
однозначным отображением совокупности всех η-местных отношений на
множестве А на совокупность всех подмножеств n-й декартовой
степени Ап множества А. Как сказано выше, в дальнейшем мы,
пользуясь этим сопоставлением, будем отождествлять п-местные
отношения на Л и подмножества множества Ап.
Аналогичным образом мы будем отождествлять понятие п-
местной функции / на множестве А / : Ап —> А с некоторым
подмножеством grf (η + 1)-й степени множеств А — графиком
этой функции: для любых а1;..., αη, Ъ из А
f(al,...,an) = b 4=^ (αι,...,α„,6)€5τ/ςΛη+1.
В силу этих двух замечаний возможно сопоставление
каждой η-местной функции / : Ап —> А на множестве А некоторого
(п + 1)-местного отношения Rf такого, что для любых элементов
а1;... ,an,b из А
/(αχ,..., an) = b 4=» R/(alf..., α„, b) (т.е. Rf(ai, ...,an,b) = И).
Очевидно, что для различных η-местных функций / и д на
множестве А отношения Rf и Rg также будут различны. Однако
далеко не любое (п + 1)-местное отношение на множестве А будет
иметь вид отношения Rf для некоторой функции / : Ап —>· А.
Необходимым и достаточным условием для этого является
функциональность отношения.
(п + 1)-местное отношение R на множестве А назовем
функциональным, если имеет место условие
Vai,... ,an е А 3! Ъ £ А Д(аь... ,an,6).
В дальнейшем мы довольно часто будем пользоваться
стандартными сокращениями в математических текстах вида V (для
12
§1. Универсальные алгебры, модели и алгебраические системы
всех...), 3 (существует...) и 3! (существует единственный...).
Таким образом, приведенное выше условие функциональности
отношения R читается так: для любых элементов αι,...,αη
множества А существует и единственный элемент b E А такой, что
R(ai,..., αη, b). Нетрудно заметить, что если R — (п + 1)-местное
функциональное отношение на А, то существует η-местная
функция / на множестве А такая, что R = Rf. Таким образом,
сопоставление η-местной функции / на А (п + 1)-местного
функционального отношения Rf является взаимно однозначным
отображением совокупности всех η-местных функций на множестве А
на совокупность всех (п + 1)-местных функциональных
отношений на А.
Одно- и двухместные функции и отношения, определенные на
конечных (и небольших) множествах А, удобно задавать с
помощью их так называемых таблиц Кэли. Проиллюстрируем это
на примерах, избегая многословного и нудного описания. Пусть
А = {1,2,3} и функции / и <? являются соответственно одно- и
двухместной функциями на множестве А со следующими
таблицами Кэли:
для /: для д:
х\у
1
2
3
1
1
1
1
2
1
2
3
3
2
1
3
X
1
2
3
/(*)
2
3
2
Это будет означать, что имеют место следующие равенства:
/(1) = 2, /(2) = 3, /(3) = 2 и
9(1,1) = 1, 9(2,1) = 1, 9(3,1) = 1, д(1, 2) = 1, д(2, 2) - 2,
5(3, 2) = 3, 9(1, 3) = 2, 9(2,3) = 1, 5(3, 3) = 3.
Если R и Q — соответственно одно- и двухместное отношения
на А с таблицами Кэли
для R: для Q:
х\у
1
2
3
1
И
И
Л
2
Л
И
и
3
и
и
л
X
1
2
3
R(x)
И
л
и
13
Глава 1. Основные понятия универсальной алгебры
то это, в свою очередь, означает, что имеют место R(l), -R(3) и
Q(l,l), Q(2,l), Q(2,2), Q(3,2), Q(l,3), Q(2,3), а для остальных
ситуаций отношения Rh Q ложны.
Перейдем теперь к определению понятий "универсальная
алгебра", "модель", "алгебраическая система". Важную роль при
этом будет играть понятие сигнатуры — списка обозначений
для основных рассматриваемых (на фиксированном множестве)
функций, отношений, констант. В дальнейшем мы будем для
простоты рассматривать, как правило, лишь конечные сигнатуры,
хотя это ограничение часто не является принципиальным. Под
сигнатурой σ мы понимаем конечный кортеж
(последовательность) элементов трех типов fa (i < г), Pj (j < m), ci (I < k),
где г, m, к — некоторые натуральные числа, при этом каждому
из элементов /*, Pj будут поставлены в соответствие некоторые
положительные натуральные числа Sj и qj называемые их
местностью или арностью. Итак,
σ=(№,...,№,Ρ2\...,Ρ«Γ,θο,...,α*}.
Элементы /j будем называть функциональными
символами сигнатуры σ, элементы Pj — предикатными символами
(или символами отношений), a q — константными
символами сигнатуры σ. Фиксация сигнатуры означает, что в дальнейшем
мы будем иметь дело с Sj-местными фиксированными
функциями на некотором множестве А, обозначаемыми как fi (г < г), с
^-местными отношениями (предикатами) па том же множестве
А, обозначаемыми как Pj (j < m), и с константами
(некоторыми фиксированными элементами) из А, обозначаемыми как q
(I < к). Сигнатуру σ будем называть функциональной, если
предикатные символы Pj3 в ней отсутствуют, и предикатной —
если в σ отсутствуют символы //*. Под алгебраической
системой 21 = (Л; σ) сигнатуры σ мы будем понимать некоторое
фиксированное множество А (базовое или основное множество
алгебраической системы 21) с фиксированным на нем набором
Si-местных функций /; (г < г), ^-местных отношений Pj (j < m)
и константами qj,..., Ск (элементами множества А).
Алгебраическую систему 21 = (Α; σ) будем называть универсальной
алгеброй, если ее сигнатура σ функциональна, или моделью, ес-
14
§1. Универсальные алгебры, модели и алгебраические системы
ли ее сигнатура σ предикатна. Заметим также, что константы q
в сигнатуре σ могут отсутствовать. Функции /j : ASi —> А
будем называть базовыми или основными, или сигнатурными
функциями (операциями) алгебраической системы 21,
отношения Pj С Aqj — базовыми или основными, или сигнатурными
отношениями (предикатами) алгебраической системы 21.
Приведем ряд примеров, иллюстрирующих введенные
понятия.
Пусть σ = (/ο,/χ,/2,^*0,с<ъCi). Первый пример
алгебраической системы 91 = {Ν; σ) этой сигнатуры имеет в качестве
основного множества совокупность N = {0,1,2,..., η, η + 1,...} всех
натуральных чисел и сигнатурные символы интерпретируются в
системе 9ΐ следующим образом:
для любых п,т € N
/o(n, m) = n + m, /i(n, m,) = n- τη, /2(η) = η + 1,
Ро(п, т) — И 4=» η < т, со = 0, ci = 1.
Мы можем на том же основном множестве N строить
абсолютно иные алгебраические системы, иным образом интерпретируя
сигнатурные символы. К примеру, пусть ЙЯ = (Ν; σ) и для любых
п,т £ N
/o(n,m) = 0, /i(n,m) = пт, /2(п) = 2п,
Ро(п, т) — И <==> пит взаимно просты, Со = О, с\ — 0.
Другие примеры алгебраических систем этой сигнатуры
получим, рассматривая для любого множества А алгебраическую
систему 21 = (Р(А); σ). Здесь и далее Р(А) будет обозначать
совокупность всех подмножеств множества А. В качестве
интерпретации сигнатурных символов в системе 21 выберем следующие: для
любых В, С С А
fQ(B,C) = BnC,f1{B,C) = BuC1
/2(В) = ~<В (т.е. дополнение подмножества В в множестве А),
Р0(В, С) = И 4=Ф В С С, со - 0, С! = А.
Наконец, в качестве последнего рассмотрим следующий
пример алгебраической системы сигнатуры σ: *8 = (Β;σ), где В —
совокупность всех геометрических векторов трехмерного
пространства. При этом для любых a,b € В
/о(а, Ь) = α + δ, Λ_(α, 6) = α х 6, /2(α) = -α,
Ρ0(α, Ь) =И φ>· α||ί>, Cq = cx = 0.
15
Глава 1. Основные понятия универсальной алгебры
Еще раз подчеркнем, что единственным ограничением при
построении алгебраической системы сигнатуры σ на любом
основном множестве А является то, что функциональные символы
сигнатуры σ должны интерпретироваться на А функциями
соответствующей арности, предикатные символы — отношениями
соответствующей арности на Л, а константные символы —
фиксированными элементами из А.
Мы введем сейчас в наш обиход ряд алгебраических систем
различных сигнатур, которые будут в дальнейшем играть
принципиально важную роль при работе с произвольными
универсальными алгебрами.
1. Частично упорядоченное множество — это любая
модель 21 = (Α;σ) сигнатуры σ = (Ρ2), удовлетворяющая
следующим условиям для любых элементов а, Ь, с из А:
1) Р(а, а) — рефлексивность Р,
2) из Р(а, Ь) и Р(Ь, а) следует, что а = b — антисимметричность
Λ
3) из Р(а, Ь) и Р(Ь, с) следует Р(а, с) — транзитивность Р.
Поскольку отношение Ρ на частично упорядоченном
множестве призвано интуитивно отображать сравнение элементов по
принципу "больше - меньше", в дальнейшем предикат Р{х,у)
будем обозначать как отношение χ < у.
Примеры частично упорядоченных множеств:
I. 91 = (Ν;<), здесь отношение χ < у является стандартным
отношением порядка: χ не превышает у.
И. 9Ί = (R; <), здесь R — совокупность всех действительных
чисел и χ < у — стандартное отношение порядка на R.
III. 21 = {Р(А); <}, здесь В < С (для В, С С А) имеет место и
тогда, когда В С С.
IV. С = (Ν1; <), здесь Ν' — N \ {0} и η < m тогда и только
тогда, когда η нацело делит т.
Далее через а < b будем обозначать ситуацию, когда а < b и
а ф Ъ.
Нам будет удобно в дальнейшем конечные (небольшие)
частично упорядоченные множества (С; <) задавать с помощью
диаграмм Хассе, в которых элементы множества С изображаются
точками плоскости и отрезок, соединяющий точку α с точкой Ь,
идущий сверху вниз, соответствует отношению покрываемо-
16
§1. Универсальные алгебры, модели и алгебраические системы
сти элемента Ь элементом а, т. е. ситуации: Ъ < α и для любого
с Ε С из b < с < α вытекает, что с = b или с = а.
В этом случае для c,d £ С отношение с < d соответствует
наличию ломаной, идущей из точки d в точку с сверху вниз.
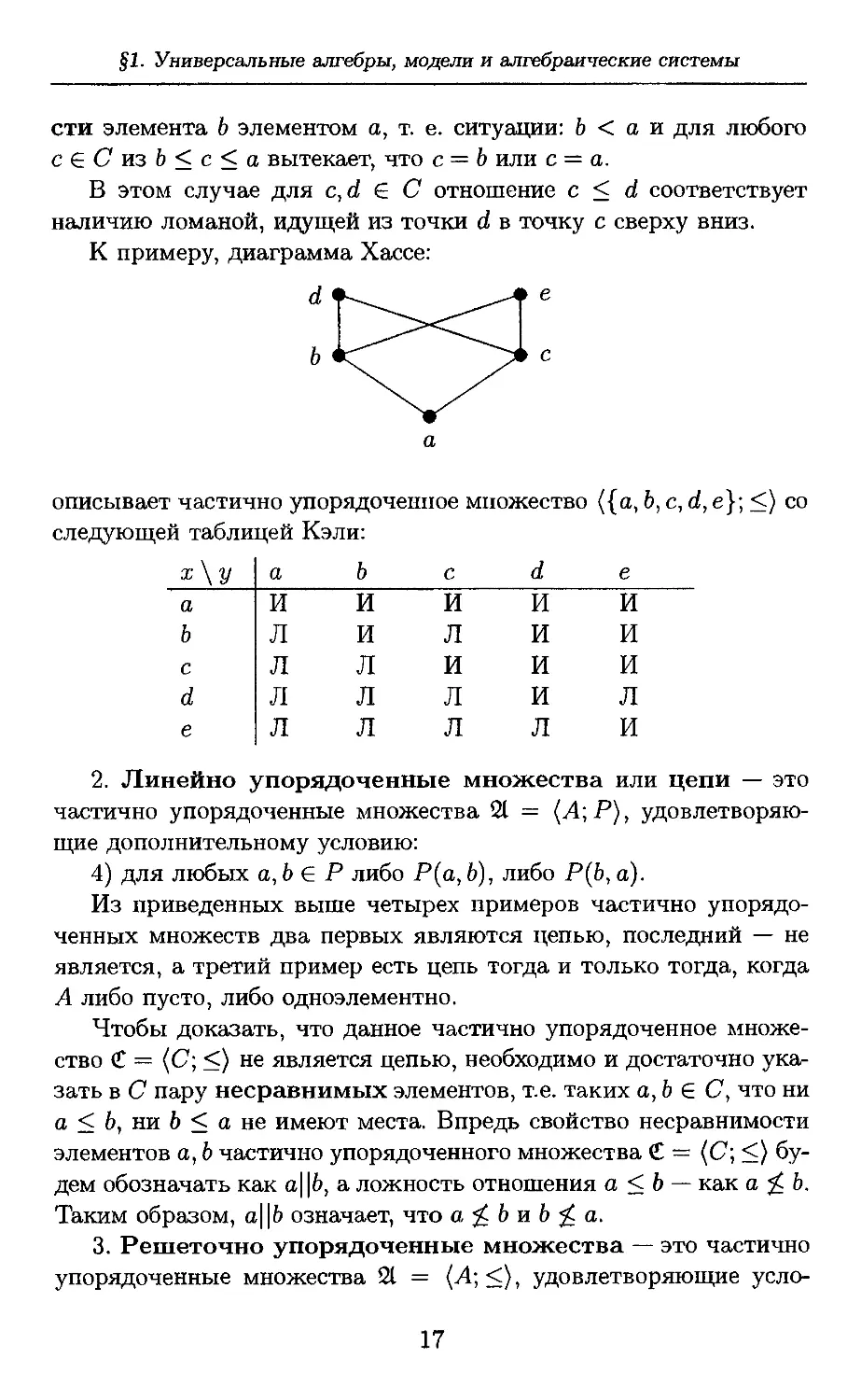
К примеру, диаграмма Хассе:
d f-~^^ ^^* e
а
описывает частично упорядоченное множество ({а, Ь, с, d, e}; <) со
следующей таблицей Кэли:
х\у
а
Ь
с
d
е
а
И
Л
Л
Л
л
ь
и
и
л
л
л
с
и
л
и
л
л
d
И
И
и
и
л
е
И
и
и
л
и
2. Линейно упорядоченные множества или цепи — это
частично упорядоченные множества 21 — (А;Р),
удовлетворяющие дополнительному условию:
4) для любых а,Ь € Ρ либо Р(а, Ь), либо Р(Ь, а).
Из приведенных выше четырех примеров частично
упорядоченных множеств два первых являются цепью, последний — не
является, а третий пример есть цепь тогда и только тогда, когда
А либо пусто, либо одноэлементно.
Чтобы доказать, что данное частично упорядоченное
множество € = (С; <) не является цепью, необходимо и достаточно
указать в С пару несравнимых элементов, т.е. таких a, b 6 С, что ни
а < Ь, ни Ь < а не имеют места. Впредь свойство несравнимости
элементов а, Ъ частично упорядоченного множества € = (С; <)
будем обозначать как а||6, а ложность отношения а < Ь — как а ■£ Ь.
Таким образом, а\\Ь означает, что а ■£ b a b ■£ а.
3. Решеточно упорядоченные множества — это частично
упорядоченные множества 21 = (А; <), удовлетворяющие усло-
17
Глава 1. Основные понятия универсальной алгебры
вию: для любых элементов a, b € А в 21 существуют их
наименьшая верхняя (обозначаемая как sup<a(a, Ъ) или просто sup(a, b)) и
наибольшая нижняя (infa(a, b) или inf (a, 6)) грани. Напомним, что
элемент с £ Л называется верхней гранью элементов α и Ь, если
имеют место отношения a < с и b < с. Элемент с называется
наименьшей верхней гранью или супремумом элементов α и Ь,
если с — верхняя грань элементов α и Ь и для любой верхней
грани d элементов α и b имеет место неравенство с < d. Аналогично
определяются понятия нижней грани и наибольшей нижней
грани или инфинума пары элементов из 21. Частично
упорядоченное множество с приведенной на предыдущей странице
диаграммой Хассе не является решеточно упорядоченным: элементы
d и е вообще не имеют верхней грани, нижними гранями для них
будут элементы a, b, с, но среди этих нижних граней нет
наибольшей.
Очевидным образом любая цепь является решеточно
упорядоченным множеством. Пример III частично упорядоченных
множеств также является решеточно упорядоченным множеством
(причем не являющимся цепью в случае, когда А содержит более
одного элемента). При этом для любых В,С £ Р{А) sup(f?, С) =
ВиСиЩВ,С) = ВПС.
4. Решеткой будем называть универсальную алгебру 21 =
(Α;σ) сигнатуры σ = (/ο,Λ2), удовлетворяющую условиям 1) -
4). В написании этих условий будем использовать традиционные
знаки V, Λ вместо /о, /ι, т.е. далее вместо /o(a, b) будем писать a\/b,
а вместо /χ(a, b) — α Λ b. Итак, в решетке для любых a,b,c Ε Α
должны выполняться условия:
1) α\/ α = α, а А а = а — идемпотентность операций V и Λ;
2) a V b = b\/ α, а ЛЬ = b Λα — коммутативность операций V и
Λ;
3) a\/(bVc) = (aVb)\/c, аЛ(ЬЛс) = (аЛЬ)Лс — ассоциативность
операций V и Λ;
4) α Λ (α V b) = a, a V (α Λ b) = a — поглощаемость операций V
и Λ.
Для любого множества А алгебра 21 = (Р(А); σ), где σ = (V, Λ)
и для произвольных В,С е Р(А) ВлС = ВГ\С,ВчС = ВиС
является решеткой.
(*) Если 21 = (Л; <) — решеточно упорядоченное множе-
18
§1. Универсальные алгебры, модели и алгебраические системы
ство, то определим двухэлементные операции V и Л на Л
следующим образом: для любых а, Ь из А пусть а V b = sup(a, b) и
a /\b — inf(a, b). Универсальная алгебра 21' = (A;V,A) является
решеткой. Обратно, если <8 = (В; V, Λ) — произвольная решетка,
то на В определим двухместное отношение <: α <Ь ■<=>· aAb = a
(что эквивалентно равенству a V b = b). Частично упорядоченное
множество (Bord = (В;<) является решеточно упорядоченным,
причем для любых a, b из В sup!BOrd(a, b) — a\/b, ini<&ord(a, b) — aAb.
Кроме того, для любой решетки € и любого решеточно
упорядоченного множества 21 имеют место равенства (Cord)' = £ и
(2l')ord = 21.
В дальнейшем, работая с решетками, будем постоянно
использовать отношение порядка < на элементах решетки, определенное
выше.
5. Модулярной решеткой будем называть решетку 21 =
(А; V, Л), удовлетворяющую условию: для любых а, Ь, с из А
(а Л 6) V (6 Л с) = Ъ Л ((а ЛЬ) V с).
Проверьте, что решетка (Р(А); V, Л) является модулярной для
любого множества А.
6. Дистрибутивная решетка — это любая решетка 21 =
{А;У,Л), удовлетворяющая условию: для любых элементов a, b
и с из А
aA(bVc)=(aAb)v(aAc).
Проверьте, что решетка (Р(А); V, Л) является дистрибутивной
для любого множества А.
Любая дистрибутивная решетка 21 = (А; V, Λ) является
модулярной.
Действительно, пусть а, Ь, с из Л, тогда &A((a/\6)Vc)= (в силу
дистрибутивности 21) (bA(aAb))V(bAc). В силу коммутативности,
ассоциативности и идемпотентности операции Λ имеет место
цепочка равенств:
bA(aAb)=bA(bAa)=(bAb)Aa=bAa=aAb.
Тем самым bA((aAb)\/c = (aAb)v(bAc) и модулярность
дистрибутивной решетки 21 доказана.
7. Булевой алгеброй называется универсальная алгебра
21 =< Α\σ > сигнатуры σ=(ν,Λ,/3,0,1) (одноместная операция fl
обозначается далее как ->: ,β(α)=->α и 0, 1 - константные символы
сигнатуры σ), удовлетворяющая условиям:
19
Глава 1. Основные понятия универсальной алгебры
1) (A;V,A) — дистрибутивная решетка и
для любого α из Л:
2) 0Vct=a, αΛΐ=α,
3) aV(->a)=l, αΛ-Ό=0.
Для любого множества Л универсальная алгебра (Р(Л);\/,Л,
-ι,0,1} является булевой алгеброй. Здесь под -\В для В из Р(Л)
понимаем теоретико-множественное дополнение множества В в
множестве А и 0 отождествляем с множеством 0, а 1 — с
множеством Л.
8. Полугруппой называется универсальная алгебра 21 =
(Л;ст) сигнатуры σ = (/о), если она удовлетворяет условию
ассоциативности операции /0. Далее традиционным образом операцию
/о для полугруппы будем обозначать как умножение · (/ο(α,6)=α·6).
Таким образом, универсальная алгебра 21=(А; ■) является
полугруппой, если для любых элементов а, Ь, с из А имеет место
равенство a-(b-c)=(a-b) -с.
Через АА обозначим совокупность произвольных отображений
множества А в себя. На А определим операцию · как обычную
суперпозицию отображений. Таким образом, для /, д из А и любого
а; из АА имеет место равенство {f-g)(x)~f(g(x})-
Универсальная алгебра 21 = (АА; ·) является полугруппой.
9. Группой называется универсальная алгебра 21 = (Л; σ)
сигнатуры σ = (·, /*, е) (Д1 — одноместная операция на Л,
обозначаемая далее как _1, т.е. /ι(α) = а-1 и е — константный символ),
если она удовлетворяет следующим условиям:
1) (Л; ■} полугруппа и
для любого α из Л:
2) at = е-a — a,
3) a-or1 = α~ι·α = е.
Для произвольного множества А через Bi(A) обозначим
совокупность всех взаимно однозначных отображений множества Л
на себя. Таким образом, Bi(A)C AA. Операцию умножения · на
В1(Л) определим так же, как и на множестве АА. Через / _1
обозначим обратное отображение к отображению /из В1(Л). Таким
образом, ί~χ{χ) = у <$■ f{y) — х для , из Л. Через idA обозначим
тождественное отображение на Л: для любого а; из Л idA(x)—x.
Универсальная алгебра (Bi(A);-,~l,idA) является группой.
20
§1. Универсальные алгебры, модели и алгебраические системы
Группа 21 = (Л;-,-1,е) называется абелевой (или
коммутативной), если для любых а, 6 из А имеет место равенство a-b=b-a.
10. Кольцом называется универсальная алгебра 21 = (Л; σ)
сигнатуры (+,/ι,·,0) (Д1 — одноместная функция на Л,
обозначаемая далее как —, т.е. /ι(α)=—α, 0 — константный символ), если
она удовлетворяет условиям:
1) (Л; +, —, 0) абелева группа
2) {А; ·) полугруппа и
для любых а, Ь, с из Л:
3) а · (Ь + с) = (а · 6) + (а · с), (Ь + с) · а = (6 · а) + (с ■ а).
Пусть Ζ — множество всех целых чисел и операции +,·,—,
константа 0 определяются на Ζ как традиционное сложение,
умножение, взятие противоположного элемента и нуль. Тогда
универсальная алгебра (Ζ;+,—,·,0) является кольцом.
Как неоднократно говорилось выше, основным предметом
изучения универсальной алгебры являются действия различных
функций на произвольных множествах. В этом случае
конкретное представление элементов этих множеств не играет
принципиальной роли. Таким образом, копирование или клонирование
элементов универсальной алгебры создание алгебры-близнеца не
порождает при изучении этих алгебр существенно новой
ситуации. К примеру, рассмотрим алгебру 21 = ({1,2,3};σ) сигнатуры
σ =(/ο) со следующей таблицей Кэли для функции /0:
X
1
2
3
/о(х)
3
2
1
Мы переобозначим (закодируем) элемент 1 как новый элемент
а, элемент 2 - как Ь, элемент 3 — как с и рассмотрим функцию
/о, определенную на множестве {а, Ь, с} с помощью таблицы Кэли:
X
a
b
с
fo(x)
с
b
a
В этом случае новая алгебра *В = ({а, Ь, с};а), полученная из
алгебры 21 указанной кодировкой, сохранит очевидным образом
21
Глава 1. Основные понятия универсальной алгебры
все родовые черты алгебры 21, связанные с действием функции
fo на основном множестве алгебры. Таким образом, с точки
зрения универсальной алгебры 21 и 23 представляют собой одну и ту
же универсальную алгебру. Однако изучение алгебры 21 вместо
алгебры 23 или наоборот может быть предпочтительнее с точки
зрения наглядности, интуитивной прозрачности и так далее,
связанной с конкретной природой множества {1,2,3} или {a,b,c}.
Данный подход закреплен в понятии изоморфизма,
рассматриваемом нами в более общем контексте алгебраических систем,
а не только универсальных алгебр. Фиксируем некоторую
сигнатуру
σ — (/о°> ■■·) /rriPq ι ···> Ρmm> со> ■•■,Ск) ·
Пусть 21 = (Α\σ) и 23 = (Β;σ) — пара произвольных
алгебраических систем сигнатуры σ. Пусть φ — некоторая биекция
основного множества А алгебры 21 на основное множество В алгебры
23. Биекцию ψ назовем изоморфизмом системы 21 на систему
23, если выполняются следующие условия:
1) для любого 1<г, для любых элементов аь ...,aSl из А имеет
место равенство φ(/ι(αι, ...,α3ι))=/ι(φ(α1), ...,φ(α3ι)) (здесь символ /г
из левой части равенства означает функцию, интерпретирующую
сигнатурный символ fi в системе 21, а символ fi из правой части
равенства — аналогичную функцию в системе 23);
2) для любого I <тп, для любых элементов aj, ...,aqi из А,
Ρι(αι,...,α4ι)=Ή^Ρι(φ(αι) ,..., ψ{ ад|))=И (здесь, как и выше,
символ Pi слева от равенства означает отношение, интерпретирующее
сигнатурный символ Pi в системе 21, а справа — в системе 23);
3) для любого 1<к (p(ci)=ci (здесь также левое q означает
элемент, интерпретирующий константный символ q в системе 21, а
правое q — в системе 23).
Очевидно, что приведенное понятие изоморфизма
соответствует интуитивному понятию копирования алгебраических
систем.
Еще раз попытаемся проиллюстрировать понятие
изоморфизма алгебраических систем сигнатуры σ—($, Pq, с0) (см. рисунок).
Здесь P0(2l)-{aeA|P0(a)} и Р0(23)={ЬбВ|Р0(&)}.
Укажем несколько конкретных примеров изоморфизма
алгебраических систем.
22
§1. Универсальные алгебры, модели и алгебраические системы
В
Рис. 1.1
1) Пусть алгебраические системы 21 = (Ν;σ) и <8 = {{2п|п €
Ν}; σ) имеют сигнатуру σ=(β, Pq,Cq) и таковы, что для любых
αϊ,02 из 21, bi,b2 из <8 имеет место:
/ο(αι,α2) = αϊ +«2, /ο(διΛ) =Ъ\ · &2,
Ρο(αι,θ2) ^ «ι < «2, Д)(£>1,Ы <* *>ι < &2,
4 = о,с$ = ι.
Здесь +, · и < — традиционные сложение, умножение и
отношение порядка на натуральных числах. Нетрудно заметить, что
отображение φ : N —> {2η|η € iV}, определенное как ί^(η)=2η,
является изоморфизмом алгебраических систем 21 и *8.
2) Пусть алгебры 21 = ({0,1}, σ) и <8 = (P(b),a) имеют сигна-
ТУРУ σ = (/о» /ι> /г> ^ ci) и таковы, что σ-символы алгебры 23
определяются на Ро{{Ь}) условиями: для любых С, D С {Ь}
/о(С, £>) = С U Д /Х(С, £>) = С П Д /2(С) = - С,
с? = 0, с? = {Ь}.
Пусть σ-символы алгебры 21, определяются следующими
таблицами Кэли:
23
Глава 1. Основные понятия универсальной алгебры
для /о а:\у
0
1
0 1
0 1
1 1
для /i x\y
0
1
О 1
0 0
О 1
ДЛЯ /2 X
О
1
/2(χ)
1
О
Нетрудно проверить, что отображение </?:{0,1}—>Р{{Ь}) такое,
что φ(Ο)=0, у>(1)={Ь}, является изоморфизмом алгебр 21 и 23.
Непосредственно проверяется следующее утверждение:
(**) а) тождественное отображение любой алгебраической
системы 21 на себя является изоморфизмом 21 на 21;
б) если φ — изоморфизм алгебраической системы 21 на систему
23, то обратное отображение φ'1 является изоморфизмом
алгебраической системы 23 на 21;
в) если φ — изоморфизм алгебраической системы 21 на 23, а ф
— изоморфизм алгебраической системы 23 на С, то суперпозиция
отображений φ и ψ, т.е. отображение φφ является изоморфизмом
алгебраической системы 21 на €.
Алгебраические системы 21 и 23 назовем изоморфными, если
существует некоторый изоморфизм систем 21 на 23. Эту ситуацию
будем обозначать как 21 = 23.
Автоморфизмом алгебраической системы 21 будем называть
любой изоморфизм этой системы на себя.
К примеру, пусть 21 = (Ζ; σ), где Ζ — совокупность всех целых
чисел, сг=(+). Тогда тождественное отображение idz множества
Ζ на себя и отображение φ : Ζ—^Ζ такое, что φ(η)= —η, являются
автоморфизмами алгебры 21 и других автоморфизмов алгебры 21
не существует.
Для любой алгебраической системы 21 = (Α; σ) сигнатуры σ и
любой биекции φ множества А на множество В мы можем
определить систему 23 = (Β;σ) с основным множеством В так, что
24
§1. Универсальные алгебры, модели и алгебраические системы
ψ будет изоморфизмом системы 21 на систему 93, полагая: для
любых l<r, i<m, j<kvi любых элементов &ι,..., bSl, αχ,..., aqu из В
Мы закончим этот параграф более подробным рассмотрением
отношения эквивалентности на произвольном множестве и
конструкциями, связанными с отношениями эквивалентности.
Отношением эквивалентности на множестве А называется
двухместное отношение Θ, удовлетворяющее следующим
условиям: для любых а, 6, с из Л:
1) Q(a,a) — рефлексивность Q,
2) из Q(a,b) следует Q(b,a) — симметричность Q,
3) из <5(а,Ь) и <5(Ь,с) следует Q(a,c) — транзитивностьQ.
Очевидно, что отношение равенства (Q(a,b) <& a= b) является
отношением эквивалентности на любом множестве А. Далее
будем обозначать это отношение как Δ^ (т.е. Ад (α,Ь) ■& а = Ь).
Отношение коллапса (или универсальное отношение) на А также
является отношением эквивалентности на A (Q(a,b)=W для
любых элементов a, b множества А).
Обозначим в дальнейшем это отношение как Уд- Очевидно,
что для любого отношения эквивалентности Q на А имеют место
включения Δ/ΐί-ΞφζνΆ-
Пусть А = {0,1,2,3} и отношения Q\ и Q2 определяются на А
следующими таблицами Кэли:
для Qi
х\у
0
1
2
3
0
И
И
Л
л
1
и
и
л
л
2
Л
Л
И
л
3
л
л
л
и
для Q2
х\у
0
1
2
3
0
И
И
Л
л
1
и
и
л
л
2
Л
Л
И
и
3
л
л
и
и
25
Глава 1. Основные понятия универсальной алгебры
Убедитесь, что оба этих отношения являются отношениями
эквивалентности на Л.
Пусть Л — произвольное множество. Набор непустых
подмножеств <8 = {Bi\i Ε 1} назовем разбиением множества Л, если
выполнены следующие условия:
1) U Д = Л,
iei
2) для различных ц, ii Ε I Bix Π Bi2~0.
Мы покажем, что в каком-то смысле понятия отношения
эквивалентности на множестве А и разбиения множества А
равносильны.
Пусть Q — отношение эквивалентности на А. Для любого
элемента α из Л классом эквивалентности Q для элемента α назовем
подмножество {bE A\Q(a,b)} множества А. Будем в дальнейшем
обозначать это подмножество как [o\q или a/Q.
Покажем, что совокупность попарно различных классов
эквивалентности Q образует разбиение множества А. Прежде всего
заметим, что в силу рефлексивности отношения Q, для любого α
из А имеет место включение α€[α]<2. Пусть теперь [aj^n [b]g φ 0.
Покажем, что в этом случае [а]д=[^]<з· Достаточно показать, что
имеет место включение [o\qQ [Ь}<з, тогда в силу симметричности
ситуации будет иметь место и включение [Ь]дС [ci]q, а значит, и
равенство [α]ζ}= [&]q. Действительно, пусть de[a]Q. Так как [o\qC\
ЩоФ 0, то найдется элемент cGfaJg П [6]q, т.е. имеет место Q(a,c)
и Q(b,c). В силу симметричности отношения Q истинно отношение
θ(ο,α) и, значит, по транзитивности Q, имеет место Q(b,a). Опять
же в силу транзитивности Q из Q(b,a) и Q(a,d) следует Q(b,d), что
и доказывает включение <fc[6]Q. Как замечено выше, последнего
достаточно для доказательства равенства [α]ς>—[δ]ς>·
Совокупность всех (попарно различных) классов
эквивалентности по Q множества А назовем фактор-множеством
множества А по отношению эквивалентности Q. Обозначать этот
фактор-множество будем как /η· Таким образом, для любого
элемента χ включение χ Ε ™/η равносильно тому, что для
некоторого α из Л ζ=[α]ς). Заметим, что ^jn образует разбиение
множества Л. Действительно, так как для любого α из Л aGfaJg, то
26
§1. Универсальные алгебры, модели и алгебраические системы
U [а3<э= &· С ДРУг°й стороны, как доказано выше, если для
α, b из Л имеет место неравенство [а]^^ [&]<?) то[а]<эП [6]q = 0. Это
и доказывает, что Α/q является разбиением множества А
(разбиением, соответствуюищм эквивалентности Q).
Пусть теперь <8 = {Bi\i € /} —произвольное разбиение
множества А. На А определим отношение 9<в следующим образом: для
любых а, 6 из A: Q<^(a,b) «Φ существует i£/ такой, что α € Β(ά Ь
е Bi.
Предоставим читателю самому убедиться в том, что Qb
является отношением эквивалентности на А и, более того, имеет место:
(***) а) для любого отношения эквивалентности Q на А имеет
место равенство Q =Q л ;
IQ
б) для любого разбиения ^В множества А имеет место
равенство <&=A/q^
Таким образом, эквивалентность, построенная по
фактор-множеству относительно некоторой эквивалентности, совпадает с
исходной эквивалентностью, а фактор-множество, построенное по
отношению эквивалентности, порожденному некоторым
разбиением, совпадает с этим разбиением.
Заметим, что разбиение /д . состоит из одноэлементных
множеств, а /у, состоит из одного-единственного множества А.
На совокупности Eq(.«4) всех отношений эквивалентности на
множестве А введем отношение <, совпадающее с
теоретико-множественным включением: для Qi,Q2^ Eq(A) пусть Q\ < Q2 тогда
и только тогда, когда Q\ С Q2 (как подмножества множества
А х А). Непосредственно замечается, что (Eq(A);<) является
частично упорядоченным множеством. Более того:
(****) (Eq(A);<) — решеточно-упорядоченное множество, где
для любых Qi,Q2 £ Eq(A) отношение mi(Qi,Q2) определяется как
пересечение отношений Qi и Q2, рассматриваемых как
подмножества множества А х А, т.е. для любых а, 6 из Л
mi(Qi,Q2)(a, Ь) & Qt(a, Ь) и Q2(a, 6).
Наименьшая верхняя грань отношений <5ι и Q2(sup(<5i,<52))
в (Eq(A);<) определяется более сложным образом:
27
Глава 1. Основные понятия универсальной алгебры
для любых a, b из A sup (фьОг )(«,&) О существует конечная
последовательность α = ao,ai,a2r..,avn-i,a2n=b (необязательно
различных) элементов множества Л такая, что для любого % < п— 1
имеют место Qi((hi,a^i+i) и(52(121+1,121+2)·
Доказательство утверждения (****) предоставляем читателю.
Решетку (Eq(^);V,A ), соответствующую решеточно-упорядо-
ченному множеству (Eq(^);< ), будем называть решеткой эк-
вивалентностей на множестве А.
ЗАДАЧИ
1. Пусть 21 = (Л; <) — частично упорядоченное множество.
Определим новое двухместное отношение Ρ на Л следующим
образом: для любых а,бе А пусть P(a,b) истинно тогда и только
тогда, когда b<a. Покажите, что модель (А;Р) также
является частично упорядоченным множеством. Отношение порядка Ρ
на А называется двойственным к порядку < и обозначается как
< *(а< *Ь <& b<a). Будет ли частично упорядоченное множество
двойственное к цепи (к решеточно упорядоченному множеству)
само являться цепью (решеточно упорядоченным множеством)?
2. Покажите, что частично упорядоченное множество из
примера IV частично упорядоченных множеств является решеточно
упорядоченным. Какие числа играют роль sup(n,m) и inf(n,m) для
m.ne./V в этом частично упорядоченном множестве?
3. Докажите утверждение (*) из данного параграфа.
4. Пусть £ — произвольное линейное пространство (над любым
полем) и Sub£ — совокупность всех подпространств пространства
£. На Sub£ определим операции V и Λ : для любых £χ, £2 GSub£
пусть £χ Λ £г = £ι П £2 и £ι V £2 является подпространством,
порожденным множеством элементов £j и£г пространства £.
Докажите, что (Sub£; Λ, V) является модулярной решеткой.
5. Докажите, что для любого множества А решетка (Р(А); U,
П) дистрибутивна.
6. Пусть £ в условиях задачи 4, — двухмерное линейное
пространство геометрических векторов. Докажите, что модулярная
решетка (Sub £; Λ, V) не является дистрибутивной.
7. Докажите, что условие, определяющее модулярность
решетки 21 = (Л; Λ, V), эквивалентно следующему: для любых a,b,ce Л,
если a<b, то aV(bAc) = bA(aVc).
28
§1. Универсальные алгебры, модели и алгебраические системы
8. Докажите, что условие, определяющее дистрибутивность
решетки 21 = (Α;Λ,ν), эквивалентно следующему: для любых
a,b,c£ А имеет место aV(bAc) = (aVb) A(aVc).
9. Является ли решетка С, где С — решеточно упорядоченное
множество из примера IV частично упорядоченных множеств,
модулярной, дистрибутивной?
10. Пусть <8 = (В; Л, ν) — произвольная решетка, < —
отношение порядка, определенное на β с помощью решетки <8
стандартным образом. Покажите, что 25* ={В\ /ο,/ι) — решетка,
определяемая решеточно упорядоченным множеством (£?; <*), такова, что
для любых а,бе В fo(a,b) = a\/b, f\(a,b) — aAb.
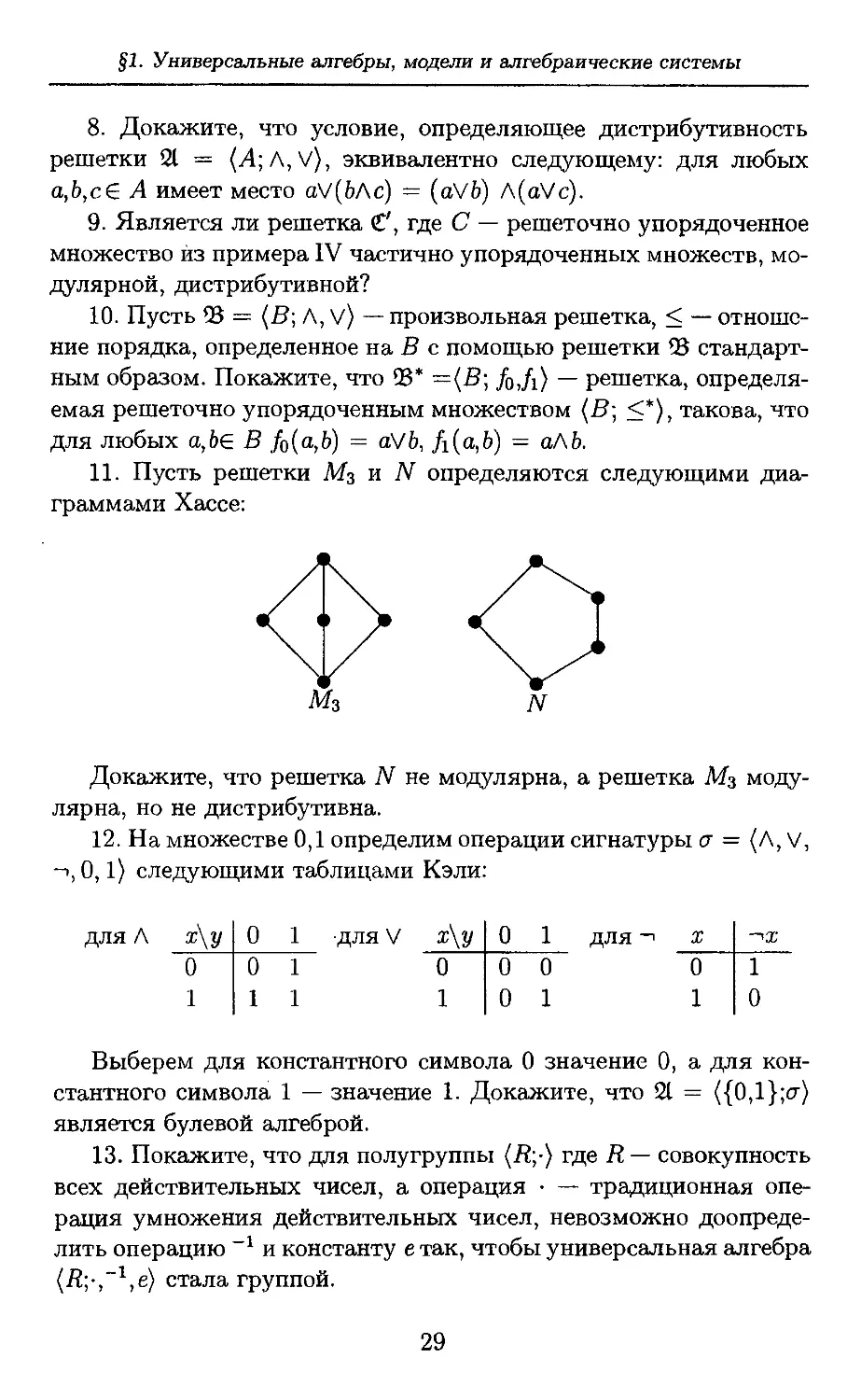
11. Пусть решетки М3 и N определяются следующими
диаграммами Хассе:
Докажите, что решетка N не модулярна, а решетка М3 моду-
лярна, но не дистрибутивна.
12. На множестве 0,1 определим операции сигнатуры σ = (Λ, V,
-ι,0,1) следующими таблицами Кэли:
для Λ
х\у
0
1
0
0
1
1
1
1
■для V
х\у
0
1
0 1
0 0
0 1
для
X
0
1
->х
1
0
Выберем для константного символа 0 значение 0, а для
константного символа 1 — значение 1. Докажите, что 21 = ({0,1};σ)
является булевой алгеброй.
13. Покажите, что для полугруппы (R;·) где R — совокупность
всех действительных чисел, а операция · — традиционная
операция умножения действительных чисел, невозможно
доопределить операцию -1 и константу е так, чтобы универсальная алгебра
(Я;-,_1,е) стала группой.
29
Глава 1. Основные понятия универсальной алгебры
14. Покажите, что для полугруппы (i?;+), где роль
полугрупповой операции умножения · играет традиционная операция
сложения действительных чисел, возможно (как?) доопределить
операцию _1 и константу е таким образом, чтобы универсальная
алгебра (Д;+,-1,е) стала группой.
15. Пусть 21 = (Л; ·,~ι,έ) — группа. Для произвольных
элементов a,b,cE А выразите элементы (а · Ь)-1, a ■ (Ь ■ с)-1, ((а · Ь)*1^ ■
(а-1)) · b))~l через произведения элементов а, Ь, с, сГ1, б-1, с-1.
16. Пусть 21 = (Л;-,_1,е) — группа. Докажите, что е —
единственный элемент хяз А такой, что для любого α 6 А имеют место
равенства αχ = χα = ακ для любого элемента b € А элемент
Ь-1 — это единственный в А элемент у такой, что b ■ у — у ■ b = е.
17. Покажите, что если множество А содержит, по крайней
мере, три элемента, то группа (В1(Л); ·,-1, гал) не является абелевой
18. Докажите утверждение (***) из данного параграфа.
19. Докажите утверждение (****) из данного параграфа.
20. Пусть *Bi = {Bi I zG/} и ©2 = {Cj; Ι ψ Ε J) — разбиения
множества А. Сформулируйте на языке подмножеств <8i и Cj
множества А отношение Q5i < 932, имеющее место тогда и только
тогда, когда имеет место отношение QeSl < <5<в2- Опишите
разбиения множества Л, отвечающие эквивалентностям Q<sl V Q<$2
и Q^j Λ Q<b2 на языке подмножеств В ι и Cj множества Л.
Через РагЦЛ) будем впредь обозначать совокупность всех разбиений
множества Л. Тем самым (РагЦЛ);<) — решеточно упорядоченное
множество. При этом sup(93i,932) = A/{Q<Si vQ<b2), inf(<8i,<82) =
Л/(<5«в1 Λ Q<82)· Обозначая, как обычно, sup(5S!,*B2) как Я^ЛЯЗг,
a inf(*Bi,232) как <8iV<82 получаем решетку (Part^);V,A)
разбиений множества Л.
21. Докажите утверждение (**) из данного параграфа.
22. Пусть К — некоторая совокупность алгебраических систем
сигнатуры σ. Докажите, что отношение изоморфности (21 = *8)
на совокупности К является отношением эквивалентности.
23. Докажите, что частично упорядоченные множества 91,91,
21, € из примеров I - IV частично упорядоченных множеств не
являются изоморфными.
30
§2. Подалгебры и теоремы представлений
24. Докажите, что для любой алгебраической системы 21 =
(Α; σ) совокупность Aut 21 всех автоморфизмов системы 21,
относительно операций суперпозиции, взятия обратного отображения
с константой id а, образует группу.
§ 2. Подалгебры
и теоремы представлений для групп,
булевых алгебр,
дистрибутивных решеток
К важнейшим понятиям универсальной алгебры относится
понятие подалгебры. Пусть 21 = (Α; σ) — некоторая универсальная
алгебра сигнатуры σ — (f^0,..., f*r,CQ,...,ck). Подмножества
множества А разбиваются на два принципиально различных класса:
первый — содержащие константы со,...,сд. алгебры 21 и замкнутые
относительно сигнатурных функций /о,...,/г и второй — не
удовлетворяющие какому-либо из этих условий. Мы говорим, что
подмножество В множества А замкнуто относительно
функции fi(xi,..., xSi), если для любых i>i,..., bSi из В значение fi(h,...,
bSi) также лежит в В. На подмножествах В первого типа не
составляет труда определить алгебру сигнатуры σ — наследницу
алгебры 21, используя для интерпретации сигнатурных функций
и констант сигнатурные функции и константы алгебры 21.
Подобную новую алгебру ^В = {Β;σ} и будем называть подалгеброй
алгебры 21. Итак, алгебра <8 = (Β;σ) является подалгеброй
алгебры 21 = (А\ σ), если выполнены следующие условия:
1) ВСА;
2) qf=Cq ,..., cf=c% и тем самым cf € В для любого г < к ;
3) для любого j < г и любых &i,..., bSj € В ff(bx,..., bSj) —
ff(b\,..., bSj) и тем самым ff(bi,..., bSi) e В. Здесь, как и во всех
подобных случаях, индекс С у констант и функций cf', /j8
означает, что рассматривается интерпретация константного,
функционального сигнатурного символа Cj, fj в алгебре С
К примеру, пусть σ—{+), 21 = (Ν;+) и В = {п — четное | η G
Ν}, тогда <8 = (В; +) (и в 21 и в <8 Η—- это стандартное сложение
натуральных чисел) будет подалгеброй алгебры 21. Легко видеть,
31
Глава 1. Основные понятия универсальной алгебры
что если С — произвольное конечное подмножество множества
N, отличное от {0}, или С — совокупность всех нечетных
натуральных чисел, то невозможно определить подалгебру алгебры 21
с основным множеством С.
Отношение теоретико-множественного включения С между
основными множествами подалгебр алгебры 21 очевидным
образом является частичным порядком на множестве Sub 21 —
множестве всех подалгебр алгебры 21. Обозначим это частично
упорядоченное множество как
Sub 21 =( Sub 21; С).
Заметим, что сама алгебра 21 является подалгеброй алгебры
21. С другой стороны, если сигнатура σ не содержит констант, то,
чисто формально, пустое подмножество 0 удовлетворяет
условиям 1)-3), и тем самым в случае бесконстантной сигнатуры σ мы
будем говорить о пустой подалгебре 0^ алгебры 21. Подалгебра 21
— наибольший элемент, а подалгебра 0и — наименьший элемент
частично упорядоченного множества Sub 21 (последнее — в случае
бесконстантной сигнатуры). Подалгебры алгебры 21, отличные от
Л и от 021, будем называть собственными подалгебрами
алгебры А.
Для любой совокупности {$ii=(Ai;a )| гЕ/} подалгебр алгебры
21 непосредственно проверяется, что множество Π Μ содержит
ier
все константы алгебры 21 и замкнуто относительно всех
сигнатурных функций. Таким образом, на множестве Π Μ существует
iei
подалгебра алгебры 21. Обозначим эту подалгебру как f) 2li. Для
ier
любого гЕ/ имеет место включение Π 2lj С 2lj. Кроме того, для
ier
любой подалгебры € алгебры 21, если для любого i e/ имеют
место включения € С 21ь справедливо и включение € С р| Ai. Ина-
ier
че говоря, подалгебра f) M является наибольшей нижней гранью
ier
совокупности подалгебр {21г|гб./} в частично упорядоченном
множестве Sub 21. В частности, для любых подалгебр 23, <£ алгебры
21
inf (Q3,C)=93 П €.
32
§2. Подалгебры и теоремы представлений
Пусть D — произвольное подмножество основного множества
А алгебры 21 и {2lj \ίξ.Ι) — совокупность всех подалгебр
алгебры 21, основные множества которых включают в себя
подмножество D. Таким образом, основное множество алгебры Π 2U также
iei
включает в себя множество D. С другой стороны, любая
подалгебра <8 алгебры 21, включающая в себя D (одна из 2lj), будет
включать в себя и подалгебру Π 2Ц. Тем самым f) 2t» — наимень-
шая из подалгебр алгебры 21 включающая в себя множество D.
Будем обозначать эту подалгебру как (D)a и назовем ее
подалгеброй алгебры 21, порожденной множеством D. Заметим, в
частности, что для любых подалгебр <8 = (Β;σ) и С=(С;а)
алгебры 21 в частично упорядоченном множестве Sub2l имеет место
равенство
<suc)a = suP(<B,e).
Таким образом частично упорядоченное множество Sub2l
подалгебр алгебры 21 является решеточно упорядоченным.
Соответствующую решетку { Sub2l; Λ,ν) мы будем обозначать тем же
символом Sub2l и называть решеткой подалгебр алгебры 21.
Итак, еще раз, для <8 = (В; σ) и €=(0;σ) € Sub2l:
<8 V € = (В U С)и,
<вле=®пс.
Остановимся теперь более подробно на конструкции
подалгебры, порожденной данным множеством. Итак, пусть 21 = (Α; σ) и
D С А. Рассмотрим подмножество ТУ множества А, определенное
следующим образом:
ТУ = £>U { /iK,..., d8i)\i<rn rflr.., dSie £>} U {<*,,...,<*},
т.е. £>' получается добавлением к D всех констант алгебры 21 и
всех значений сигнатурных функций на произвольных элементах
из D. Очевидно, что D С D'. Обозначим теперь множество D как
Do и для любого натурального числа η определим подмножество
Dn+i равным (Dn)'. Таким образом, мы имеем дело с
неубывающей бесконечной последовательностью
D = £>0С DiC Д>С ... С DnC ... С А.
33
Глава 1. Основные понятия универсальной алгебры
Пусть Д»= U Дг· Покажем, что £><*, замкнуто относитель-
ηζΝ
но сигнатурных функций алгебры 21. Действительно, пусть άχ,...,
d-si^ Д», тогда найдется η Ε Ν такое, что di,...,dSi € Dn. В
силу определения Dn+\ = (Dn)' имеет место включение /Дс^,...,
dSi)<E: Dn+iC Doo. Также в силу определения Dx , все константы
алгебры 21 содержатся в Д». Тем самым существует подалгебра
алгебры 21 с основным множеством Д». С другой стороны, если
€ = (С; σ) — некоторая подалгебра алгебры 21, включающая в
себя D, без труда, индукцией по натуральному п, доказываются
включения DnC С для любого ηξΝ. Таким образом, U DnC С.
neN
Последнее означает, что Дх,= U Дг является основным множе-
neN
ством наименьшей в Sub 21 подалгебры алгебры 21, содержащей
множество D, т.е.
(U £>„;σ> = <£>)α.
neN
Опишем теперь строение подалгебры, порожденной
множеством D в иных терминах. Для этого нам понадобится понятие
терма сигнатуры σ. Пусть X — некоторое фиксированное
счетное множество символов: X = {xq, х\, ..., хь, ■ ■ ·} — множество
переменных. Пусть с=(/о°, ·.·, /,?г,со,...,с*;} — фиксированная
сигнатура. Термами сигнатуры σ будут конечные последовательности
символов множества XUaU{(,)}. Здесь (,) — чисто технические
символы — скобки. Понятие терма сигнатуры σ будет
определяться следующей индукцией по длине терма (длина терма —
длина соответствующей последовательности символов):
1) переменные из X и константы сигнатуры σ являются
термами сигнатуры σ (базис индукции, определяющий самые короткие
термы);
2) если fjJ€cr и ii,..., tSi — термы сигнатуры σ, то /?' (ii,..., tSi)
также терм сигнатуры σ (индукционный шаг);
3) любой терм сигнатуры σ строится за конечное число шагов
согласно правилам 1), 2).
Для любого терма t сигнатуры σ определяется (опять же
индукцией по построению терма) совокупность переменных Var(f),
от которых зависит терм t:
1) Var(xj) = Xit Уаг(^) = 0;
34
§2. Подалгебры и теоремы представлений
2) VarCfi(ii,..., t$i)) = U Varfe).
1=1
Таким образом, терм t зависит от переменной ж$, если эта
переменная в явном виде входит в запись терма L В случае когда
Var(i) = {xii,-.-,Xik} мы будем употреблять запись i(xil5 ...,a;ifc)
или t(x) , обозначая через χ кортеж {xilt ...,xik).
К примеру, если σ— (+,·,0,1), то следующие
последовательности символов являются термами сигнатуры σ:
1) t1=(((x1+x2)-0)+(l-x3 ))·χι, здесь Var(i1)={o;1, Х2, хц}, т.е.
h=h(xi, Х2, хц);
2) ί2=(((χ1+α;1)·0)+(1·α;1 ))·%, здесь Var(i2)={a;1}, т.е. к=кЫ)\
3) ί3=(0·1)+(1·0), здесь Var(fe)=0.
Для удобства записи в написании этих термов, как и ранее,
запись +(х,у) и -(х,у)- заменяется на традиционную (χ+y) и (х-у).
Нетрудно убедиться, что приведенные ниже
последовательности символов не являются термами сигнатуры σ:
1) (Χι+Χ2)·Χι·Χζ\
2) (χι;
3) χ?;
4) 1+1+1+1.
Каждому терму t{x\,...Xn) сигнатуры σ на любой
универсальный алгебре 21 =< Α; σ > этой сигнатуры соответствует
термальная функция ^(хгг, ...,Xin), обозначаемая далее просто как
t(xilt ...,Xin) и определенная индукцией по построению терма:
1) если t=t(xi)—Xi , то для любого aG A t(a)=a; если i=Q, то
рассматриваем t как 0-местную функцию, принимающую одно и
то же значение cf (константу);
2) если t(xh,...,xin) =/i(ii(S1),...,iSi(xSl)) (здесь ^ - некоторые
подмножества переменных из множества {xix,..., χ%η}), то для
любых ab...,a„G A i(ai,...,a„) = b, если fi(di,...,dSi)=b и i1(a1)=di,...,
t$i(u$i) =d$i. Здесь tj(uj) — значение термальной (более простой
чем t и тем самым уже определенной по индуктивному
предположению) функции tj(xj) на переменных из Xj, принимающих
соответствующие значения из элементов ^,.,.,Οη.
К примеру, нетрудно подсчитать, что для термов h,t2,t3,
35
Глава 1. Основные понятия универсальной алгебры
из приведенных выше примеров термов на алгебре 21=(ЛГ;+,-,0,1)
имеют место равенства:
1) ί1(0,1,2)=0Λ(2,2,3)=6 ;
2) fc(0)=0, fe(l)=l, fe(2)=4 ;
3) fe=0.
Если вместо алгебры 21 рассмотрим алгебру
93 = (Р({1,2,3});и,П,0,{1,2,3}>,
т.е. алгебру с основным множеством Р({1,2,3}), на котором
двухместные сигнатурные функции +, · интерпретируются как U и Π
соответственно, а константные символы 0 и 1 как 0 и {1,2,3}, то
получаем следующие равенства:
1) h ({1},{2,3},{1,3})={1}, ί1({1,2,3},0,{1,2})={1,2,};
2) t2{A) = А для любого А С{1,2,3}.
Индукцией по длине терма t(xi,...,Xn) нетрудно доказать, что
(*) для любой подалгебры ^В = (£?; σ) алгебры 21 — (Α; σ) и
любых элементов bi,...,bn£ В имеет место включение t(bi,...,bn)E
В.
Таким образом, подалгебры замкнуты относительно
термальных функций.
Пусть теперь D — произвольное подмножество множества А.
Определим множество DT следующим образом:
DT—{t(air..,an)\t(xi,...,xn) — произвольный терм сигнатуры σ,
αχ,...,On — произвольные элементы из D}.
Множество DT содержит все константы алгебры 21 и замкнуто
относительно сигнатурных функций. Действительно, если fi(xi,
. ..,ж„) € σ и di,..., dSie DT,jro найдутся термы ii(xi),...,iSl.(zSi)
и кортежи элементов bx,...,bSi множества D такие, что d\ =
ίχ(6ι),..., dSi — tSi(bSi). При этом можно считать, что
совокупности переменных xi,...,xSi попарно дизъюнктны. В этом случае
fi(di,..., dSi) = t(bu...,bSi),
где t(xu ...,xSi) = fi(h(xi),...,tSi(xSi)) — терм сигнатуры σ. Тем
самым действительно fi(di,...,dSi)£ DT, т.е. DT замкнуто
относительно термальных функций. С другой стороны, рассматривая терм
χ убеждаемся в справедливости включения D С DT .
36
§2. Подалгебры и теоремы представлений
Доказанные свойства множества DT , наряду с утверждением
(*), демонстрируют справедливость равенства
(Ότ· σ) = (Ό)Λ
для любой алгебры 21 и любого ее подмножества D.
Перейдем теперь к доказательству некоторых теорем
представлений для "классических" алгебр введенных в § 1. Ряд
примеров этих алгебр представленных в том же параграфе, являются
достаточно естественными и наглядными: группы биекций
некоторого множества самого на себя, булевы алгебры подмножеств
некоторого множества и т.д. Основная цель доказываемых ниже
теорем представления и состоит в том, чтобы показать, что ряд
абстрактно определенных (через свойства этих алгебр, а не
через природу их элементов и сигнатурных функций) классических
алгебр с точностью до изоморфизма можно представлять как
подобные наглядно устроенные алгебры. Полезность такого
представления заключается в возможности использовать нашу
интуицию, основанную на наглядных представлениях, при изучении
произвольных абстрактно заданных алгебр.
Начнем с групп. В § 1 для любого множества А была
определена группа (B\(A);-~1,idA) — группа всех биекций множества А
самого на себя. Обозначим далее эту группу как Sym А и будем
называть ее симметрической группой множества А.
Подалгебры произвольной группы будем далее именовать ее
подгруппами. Имеет место следующая теорема представления для групп.
ТЕОРЕМА КЭЛИ. Для любой группы & = (С;-,-1^)
существует изоморфизм этой группы на некоторую подгруппу
симметрической группы множества G.
Доказательство. Для любого элемента а из G через φα
обозначим отображение множества G в себя, определенное
равенством
<ра(х)=а-х
для любого хе G. Так как χ = α·(α~ι·χ) — φα{<ί~ι·χ), то
отображение φα будет отображением G на G. Если φα(χ) = <ра(у),
то φα-ι(φα(χ)) = φα-ι(φα(ν)) и, значит, х = е-χ = (а ~1-а)-х =
37
Глава 1. Основные понятия универсальной алгебры
о 1·(α·χ)= φα-ι(φα(χ)) = ψα-ι{φα{ν)) = a l(a-y) = (a l-a)-y = e-y
= У-
Таким образом, любое отображение вида φα является биекцией
множества G самого на себя, т.е. cpa€zBi(G)
Так как для любого хЕ G (ре(х)=е-х=х, то φβ=ιάο-
Для любых ο,ί)€ G и любого χ из G
φα+{χ) = №)·χ=αφχ)=φα^{χ))=(φα·φύ(χ)·
Последнее произведение <ра-<Рь подразумевается как
произведение в группе Sym G. Таким образом, имеет место
ψα-Ь = ψα·ψ^
В силу того, что имеют место равенства
ιάα(χ)=χ=6-χ=(α'ι-α)-χ=α'ι-(α-χ)=φα-ι(φα(χ))=(φα-ι-φα)(χ)
ida(x)=x=e-x=(a-a ι)·χ=α·(α ι·χ)=φα{φα-ί{χ))τ={ψα·ψα-^){^),
ψα-ι является биекцией, обратной к биекции φα, т.е.
Кроме того, если для некоторых a, b € G и любого χ Ε G имеют
место равенства ψα{χ) — φь(x), то, в частности, φα(ε) — <{>ь{е) и,
значит,
a=a-e=(pa(e)=ipb(e)=b· e~b.
Тем самым, во-первых, совокупность {φα\αΕ G} является
подгруппой группы Sym G и, во-вторых, отображение φ : G —> Bi(G),
определенное как
φ(α) = φα
38
§2. Подалгебры и теоремы представлений
для любого а€ G, является изоморфизмом группы <5=(G;-,-1,e)
на подгруппу {{φα\αζ. G};·,~l,idc) симметрической группы Sym
G. Теорема доказана.
В § 1 для любого множества А рассмотрена полугруппа (АА;·)
всех отображений множества А в себя. Обозначим эту полугруппу
далее как F(A) и будем называть ее полугруппой отображений
множества А.
Аналогично доказательству теоремы Кэли с добавлением к
полугруппе единицы доказывается следующая теорема
представления для полугрупп.
ТЕОРЕМА 1. Для любой полугруппы &=(S;·) существует
изоморфизм этой полугруппы на некоторую подалгебру
(подполугруппу) полугруппы отображений некоторого множества.
Теорема Кэли и теорема 1 позволяют при работе с
произвольными группами и полугруппами интуитивно считать их
элементы некоторыми биекциями, соответственно отображениями в
себя, какого-либо множества.
Перейдем теперь к доказательству теоремы представления для
булевых алгебр.
Для доказательства этой теоремы нам потребуется аксиома
выбора, точнее, некоторое утверждение (лемма Цорна),
эквивалентное аксиоме выбора и играющее в алгебре важную роль.
Аксиома выбора представляет собой следующее теоретико-
множественное утверждение: для любой функции F,
определенной на произвольном множестве / и принимающей в качестве
значений F(i) (гб/) некоторые непустые множества, существует
функция /:/—>■ (J F(i) такая, что f{i)eF(i) для любого г € /, т.е.
iei
аксиомой выбора утверждается возможность одновременно (для
любого г Ε I) выбирать во множествах F(i) некоторые элементы
/(г). Возможность такого выбора для конечных множеств /не
вызывает сомнения. Проблематичным это становится в случае
бесконечного / и произвольных непустых множеств F(i). Проблема
принятия или непринятия аксиомы выбора относится к
основаниям математики и не будет здесь дискутироваться. Было доказано,
что аксиома выбора является независимой от стандартных,
общепризнанных аксиом теории множеств, известных под
аббревиатурой ZF-аксиом Цермело-Френкеля, т.е. как принятие утвержде-
39
Глава 1. Основные понятия универсальной алгебры
ния аксиомы выбора, так и принятие отрицания ее утверждения
не ведут к противоречиям с аксиомами ZF. В начале этого века
была широкая дискуссия вокруг возможности использования
аксиомы выбора в математике, поскольку ее принятие влекло в
качестве следствий некоторые парадоксальные, на первый взгляд,
утверждения. Однако непринятие аксиомы выбора существенно
обедняло интуитивно приемлемое содержание конкретной (не
связанной с вопросами философии математики и теории множеств)
математики, в том числе и алгебры. В результате аксиома
выбора стала широко использоваться в конкретных математических
исследованиях. Не будем чураться этого использования и мы.
Нам потребуется некоторое эквивалентное аксиоме выбора
(относительно ZF) утверждение известное под именем леммы Цор-
на. Доказательство эквивалентности утверждения леммы Цорна
и аксиомы выбора мы опускаем, желающие могут найти его, к
примеру, в книге [10].
Для формулировки леммы Цорна нам потребуются некоторые
определения. Подмножество С некоторого частично
упорядоченного множества (Л;< } называется цепью в (Л;< }, если для
любых a,b € С имеет место либо a<b, либо b<a. Иными словами,
подмножество С является цепью в (Л;< ), если частично
упорядоченное множество (С;< ), с порядком индуцированным на С
порядком из (А; <), является цепью. Как и ранее, элемент d из А
называется верхней гранью для С, если для любого Ь из С имеет
место неравенство Ь< d. Элемент α частично упорядоченного
множества (Л;< } называется наибольшим, если для любого Ье А
имеет место неравенство b<a. Элемент α множества (Л; <}
называется максимальным в (Л;< ), если в Л нет элементов строго
больше чем а, т.е. если для любого b из Л неравенство a<b влечет
равенство a=b. Очевидно, что наибольший элемент частично
упорядоченного множества, если он существует, единственен и
является максимальным в этом множестве. В отличие от наибольших
элементов множества (Л; <) число максимальных элементов в
частично упорядоченном множестве неограниченно. В то же время
максимальных элементов в частично упорядоченном множестве
может и не быть. Следующие примеры призваны прояснить
введенные понятия.
1) В частично упорядоченных множествах (N;<) и
40
§2. Подалгебры и теоремы представлений
(iV\{0};<!) (где < — обычное отношение порядка на
натуральных числах, а для m,n € Л?\{0} отношение η <\т означает, что η
нацело делит т) нет ни максимальных, ни наибольших элементов.
2) Пусть ({1,2,3,4};<ι} — частично упорядоченное множество с
отношением порядка <ι, определенным следующей таблицей Кэ-
ли:
х\у
1
2
3
4
1
И
Л
л
л
2
И
И
л
л
3
л
л
и
л
4
Л
л
и
и
Очевидно, что это множество не имеет наибольшего элемента,
а элементы 2,4 являются максимальными.
Будем говорить, что элемент о содержится в элементе b
частично упорядоченного множества (А;< ), если имеет место a<b.
ЛЕММА ЦОРНА. Если любая цепь β частично
упорядоченном множестве (А;< ) обладает верхней гранью, то любой
элемент этого множества содержится в некотором
максимальном элементе, т.е. для любого аЕ А существует в А
максимальный элемент Ь такой, что а<Ь.
Рассмотрим теперь произвольную булеву алгебру <8 = (В; V,
Λ,-·, 0,1). Непустое подмножество С множества В называется
фильтром булевой алгебры 23, если выполняются условия:
1) для любого с Ε С и любого Ь € В неравенство с < b влечет
включение b € С;
2) для любых cx,c<i € С имеет место включение c\f\oi e С.
Здесь и далее под отношением порядка < на булевой алгебре
*8 имеется в виду порядок, определенный на *8 как на решетке,
т.е.
а<Ь ^ аЛЬ = а <=$ aVb = Ъ.
В качестве примеров фильтров в булевой алгебре *В прежде
всего укажем на само множество В. Кроме того, для любого
элемента α из β через Fa обозначим подмножество {с Ε В | а < с}.
Очевидно, что для любого а Е В множество Fa является
фильтром булевой алгебры 2$ (главным фильтром порожденным
41
Глава 1. Основные понятия универсальной алгебры
элементом а). В данном контексте В = F0 (т.к. для любого
αξ. Β 0<α). Фильтры булевой алгебры 23, отличные от В = F0,
будем называть собственными фильтрами. Заметим также, что
из неравенства о<1 для любого элемента α να В следует, что
любой фильтр булевой алгебры содержит единицу 1 этой булевой
алгебры.
Нетрудно заметить справедливость следующего утверждения:
(**) Любой фильтр конечной булевой алгебры Ш является
главным.
С другой стороны на любой бесконечной булевой алгебре 23
существует неглавные фильтры. Не доказывая в полном объеме,
проиллюстрируем это на примере булевой алгебры 23 = (Р(А); U,
Π, -ι, 0, А) для бесконечного множества А. Пусть F$ = {С С
Л|-1С конечно}. Предоставляем читателю самому убедиться в
том, что F.J, — фильтр булевой алгебры 23 (именуемый в
дальнейшем фильтром Фреше). Очевидно также, что F$ — неглавный
фильтр этой алгебры.
Пусть F(23) — совокупность всех собственных фильтров
булевой алгебры 23. Теоретико-множественное отношение С является,
очевидно, частичным порядком на множестве F{B).
Максимальные элементы частично упорядоченного множества (F(23); С)
будем называть ультрафильтрами булевой алгебры 23.
Прежде всего докажем, что любой фильтр булевой алгебры 23
содержится в некотором ультрафильтре. Для этого, в силу леммы
Цорна, достаточно доказать, что любая цепь в частично
упорядоченном множестве (F(23); С) фильтров булевой алгебры 23 имеет
верхнюю грань. Действительно, пусть {F1 | г G /} — некоторая
цепь упорядоченного множества (F(23);C), т.е. F1 собственные
фильтры булевой алгебры 23 и для любых i,j € I либо F1 С F\
либо F·7 С F\ Положим F = \J F1. Нетрудно заметить, что F
ш
является фильтром на 23. Т.к. О £ F1 для любого i € /, имеем
О £ (J F1, т.е. фильтр F — собственный. Очевидно, что для лю-
бого г Ε I F1 С F. Итак, в частично упорядоченном множестве
(F(23); С) цепь {Fl | г 6 /} имеет верхнюю грань F, а значит,
каждый фильтр булевой алгебры 23 содержится в некотором
ультрафильтре.
42
§2. Подалгебры и теоремы представлений
Сформулируем и докажем теперь иную более конструктивную
характеризацию ультрафильтров.
ЛЕММА 1. Фильтр F булевой алгебры Ъявляется
ультрафильтром тогда и только тогда, когда для любого элемента а
из 23 выполнено ровно одно условие: либо а Ε F, либо ->а Ε F.
Доказательство. Пусть F — некоторый ультрафильтр
булевой алгебры 23. Прежде всего заметим, что ни для какого
элемента а условия а Ε F и ->а Ε F не могут быть выполнены
одновременно. Действительно, в противном случае О—аА^аЕ F, что
противоречит собственности фильтра F. Допустим теперь, что для
некоторого элемента аЕ 23 ни ->а, ни а не входят в F. Рассмотрим
множество D = {а А Ь\Ь Ε F}. Заметим, что для любых Οχ,ο^Ε D
элемент с\Ас2 также входит в D. Действительно, существуют &ι,
Ь2€ F такие, что С\= αΛ&ι, C2=aAb2- Но тогда
c\Ac2—(aAbi)A(aAb2)=aA((biAa)Ab2) — aA((aAbi)Ab2)=
=αΛ(αΛ(&ιΛ&2))=(αΛα)Λ(&1Λ&2) =aA(b1Ab2)
и так как btAb2E F, получаем CiAc2E D. Заметим также, что
0^ D. Иначе найдется bE F такой, что 0=аЛЬ. Но тогда ->о =
^aVO = -raV(aAb) = (^aVa)A(^aVb) = lA(--aVb) = -<aVb, т.е. b<->a
и, так как bEF, получаем ->aE F. Противоречие с условием, что
а<£ F, ->а£ F и доказывает требуемое: 0 ^ £>.
Пусть теперь F' = {d Ε 23 | для некоторого с из D имеет
место неравенство с < d}. Очевидно, что F С F' и α Ε F'.
Предоставляем читателю убедиться в том, что F является собственным
фильтром булевой алгебры 23. При этом F' строго больше F в
частично упорядоченном множестве (F(23); С), что противоречит
выбору F как ультрафильтра. Таким образом, действительно, для
любого ультрафильтра F булевой алгебры 23 и любого элемента
а из 23 выполняется ровно одно из условий: либо а Е F, либо
-пае F.
Докажем обратное. Пусть F — фильтр булевой алгебры 23 и
для любого а Е В имеет место либо а Е F , либо -ία Ε F.
Допустим, что F не ультрафильтр. Тогда найдется некоторый
собственный фильтр F* включающий F и отличный от него. Пусть
с Ε F* \ F, но тогда -\с Ε F и, значит, 0 = ->с А с Ε F, что
противоречит собственности фильтра F*. Лемма доказана.
43
Глава 1. Основные понятия универсальной алгебры
Мы можем, наконец, приступить к доказательству теоремы
представления для булевых алгебр. Через St 23 будем обозначать
совокупность всех ультрафильтров булевой алгебры 23.
ТЕОРЕМА СТОУНА. Для любой булевой алгебры 23
существует подалгебра булевой алгебры (Р (StQ3);U,n>-l»0»St*8) всех
подмножеств множества St23, изоморфная булевой алгебре 23.
Доказательство. Отображение φ : 23 —> P(St23) определим
следующим образом: для b£ 23 </?(6)={F €St23|&€l F}, т.е. tp(b) —
это совокупность всех ультрафильтров алгебры 23, содержащих
элемент 6.
В силу замеченного вслед за определением фильтров, φ(Ο)=0
и y>(l)=St<B.
Пусть bi,&2>£23. Покажем, что:
ipibxVb^ipibx) U ¥>(Ь2),
V?(f>iA&2) =y>(bi) П</?(Ь2)>
φ(^)= St23V(bx).
Действительно, если F € <p(bi), то Ьг € F, но &i <b{\/b2 и,
значит, 6jVb2 € -F\ т.е. <^(i>i)C (^(διΝ/ί^). Точно также имеет место
включение <p(b2)C ¥>(biVi>2). Включение φ(^)υ <p(b2) С </?(biV&2)
доказано. Пусть теперь F € <f(hVb2) и F ^ (^(Ь^и^Ьг), тогда
i»iVb2 € F, &χ ^ F,62 ^ F. В силу того, что F — ультрафильтр,
по лемме 1, ->i>i G F, -'Ьг е F и значит -i(&iV&2)=->biA-'&2 G F.
Включения 6iνέ>2 € F, ->(6iV&2)€ F противоречат лемме 1. Таким
образом, ip(biVb2) ί= ν(&ι)υί^(62) и первое равенство ip{b]\/b2) =
y>(bi)Uy>(&2) доказано.
Доказательство равенств </?(&ιΛ&2) = (^(-'bi) Π <p(b2), V?(M =
St23 \(^(6ι). предоставляем читателю.
Для доказательства теоремы теперь достаточно доказать, что
для Ь\фЬ2 из В имеет место (р(Ьг) Φ <p(b2).
Действительно, если bi^b2, то либо biA->b2 ^0, либо foA-'bi ф0.
Допустим первое (второе рассматривается аналогично). В этом
случае главный фильтр FinA-,b2 содержится в некотором
ультрафильтре F и, тем самым, biA-'foe F- В этом случае &ιΛ-ι&2 < Ъ\
и, значит, b\ G F, т.е. F е v^C&i)· В то же время F ^ ^(Ы» так
как в противном случае, &26 F и так как ί>ιΛ->62Ε F, имеет место
0 = Ъ\ Л 0 = Ъ\ Л (->&2 Л Ь2) = (&J. Л ->&2) Л Ъ2 £ F в противоречии с
собственностью фильтра F.
Итак, действительно, доказано, что отображение φ является
44
§2. Подалгебры я теоремы представлений
изоморфизмом булевой алгебры <8 на некоторую подалгебру
булевой алгебры (P(St<8); U, П, -\ 0, St<8). Теорема доказана.
Основной смысл утверждения теоремы Стоуна сводится к
тому, что работая с произвольной булевой алгеброй, мы можем
считать элементы булевой алгебры подмножествами некоторого
фиксированного множества, а операции сигнатуры σ = < ν,Λ,-',Ο,Ι^
— теоретико-множественными объединением, пересечением,
дополнением соответственно.
Без доказательства приведем также следующий результат
(теорему представления для дистрибутивных решеток).
ТЕОРЕМА 2. Для любой дистрибутивной решетки 23
существует множество А и некоторая подалгебра (подрешетка)
дистрибутивной решетки (Р(А); U, П), изоморфная решетке *8.
Полное доказательство этого результата см., к примеру, в [8].
В заключение параграфа сформулируем без доказательства на
языке подалгебр критерии модулярности и дистрибутивности
решеток.
Решетки М3 и N определены в задаче 12 § 1.
ТЕОРЕМА ДЕДЕКИНДА—БИРКГОФА. Решетка 93
является модулярной тогда и только тогда,когда она не
содержит подрешеток, изоморфных решетке N. Решетка 2$ является
дистрибутивной тогда и только тогда, когда она не содержит
подрешеток, изоморфных решеткам Μ^,Ν.
Полное доказательство этого результата можно найти в [8].
ЗАДАЧИ
1. Приведите примеры бесконечного числа различных
подалгебр алгебры 2l=(iV;+).
2. Сколько подалгебр имеет алгебра 21={Р({1,2,3}); U, П, -ι, 0,
{1,2,3}). Укажите все эти подалгебры.
3. Пусть 21 = ({0,1, ...,п — 1};/о), где функция /о определена
на {0,1,...,п-1} по правилу /0 (m)=m+l (mod η), т.е. fo(m) — т+1
для т < η — 1и /о (п— 1) = 0. Найдите все подалгебры алгебры
21.
4. Пусть 21 = ({0,1, ...,п — 1}; /^), где функция /о определена
на {0,1,...,п — 1} по правилу f0(m,k)=m+k(mod η). Найдите все
подалгебры алгебры 21.
45
Глава 1. Основные понятия универсальной алгебры
5. Докажите, что в решетке (Sub 21) подалгебр алгебры 21 =
(Z; +, —) наименьшая подалгебра ({0}; +, —) не имеет покрытий.
6. В алгебре 21= (ЛГ;·) укажите наиболее простой общий вид
элементов подалгебры порожденной множеством {2,3,4}.
7. Подалгебра 25 алгебры 21 называется конечно
порожденной, если существует конечное подмножество С основного
множества алгебры 21 такое, что <8 = (С)%. Докажите, что в решетке
Sub 21 для любых двух конечно порожденных подалгебр 2$, €
алгебры 21 подалгебра <8 V € также является конечно порожденной.
8. Пусть a,b — различные элементы, отличные от
элементов множества целых чисел Z. Сигнатура σ равна (/о).
Алгебру 21 = (Z U (α,ί>};σ) определим следующими условиями: для
любых m,n из Z: fQ(n,m) — η + 1, fQ(a,n) = fo(b,n) = —η,
/ο(η, α) = /ο(η,6) = 0, /ο(α,α) = /0(6,6) = /0(α,6) = /0(6,α) = 0.
Приведите примеры двух конечно порожденных подалгебр <8 и €
алгебры 21 таких, что алгебра <8 Л € не является конечно
порожденной.
9. Пусть сигнатура алгебры 21 содержит константы со,..., с&0.
Какая подалгебра алгебры 21 является наименьшим элементом
решетки Sub 21? Укажите общий вид элементов этой подалгебры.
10. Докажите утверждение (*) из данного параграфа.
11. Укажите все подгруппы групп Sym{l,2} и Sym{l,2,3}.
12. Пусть <τ=(+,·,0,1) и 21=(Ζ;+,·,0,1), где сигнатурные
символы сигнатуры σ имеют традиционную интерпретацию на
множестве Ζ всех целых чисел. Докажите, что любая термальная
функция /(ж) одного аргумента χ на алгебре 21 имеет вид многочлена с
натуральными коэффициентами от х.
13. Докажите теорему 1 из данного параграфа.
14. Докажите утверждение (**) из данного параграфа.
15. Элемент α булевой алгебры Ш=(£?; V, Л,-·, 0,1)
называется атомом, если а^Ои для любого элемента Ь £ В либо оЛб=о,
либо аЛЬ=0. Докажите, что элемент α является атомом булевой
алгебры *8 тогда и только тогда, когда a — минимальный
элемент в частично упорядоченном множестве ненулевых элементов
булевой алгебры <8. Докажите, что главный фильтр ¥ь булевой
46
§ 3. Алгебраические решетки
алгебры 23 является ультрафильтром тогда и только тогда, когда
Ь — атом булевой алгебры 23.
16. Для булевой алгебры 23 = (Р({0, ...,η — 1});ϋ,Π,-·, 0,
{О,..., η — 1}} докажите, что число ее подалгебр совпадает с
числом разбиений множества {0,..., η — 1}. Затем докажите
изоморфизм решеток (Sub 23) и (Part {0,..., η — 1}; V, Л).
§ 3. Алгебраические решетки
Предметом рассмотрения этого параграфа являются так
называемые алгебраические решетки, играющие важную роль в
универсальной алгебре.
Решетку 23 = (В; V, Л) назовем полной, если любое
подмножество С множества В обладает в 23 наименьшей верхней (sup
С) и наибольшей нижней (inf С) гранью, т.е. в В существуют
элементы a=sup С и b=inf С такие, что:
1) для любого с Ε С справедливы неравенства Кс<аи
2) для любых &ι, θχ€ В таких, что для произвольного с€ С
h<c<ai имеют место неравенства Ьг<Ь и α<αχ.
В качестве примера полной решетки укажем на решетку
(Р(А); и,П) для любого множества А. Действительно, если С =
{Bi\i е /} — некоторая совокупность подмножеств множества Д
то
sup С = U Bi и inf С = Π -Si· С другой стороны, решетка
iei iei
Ql—(Z;A,V), где для m,neZ mAn=mm(m,n) и mVn=max(m,n)
дает пример неполной решетки: само множество Ζ не имеет в 21 ни
наименьшей верхней, ни наибольшей нижней грани.
Из последнего примера вытекает следующее требование к
полной решетке: любая полная решетка обладает наибольшим и
наименьшим элементами. Действительно, если 23 = (В; Л, V) полная
решетка, то sup В (inf В) является наибольшим (наименьшим)
элементом этой решетки.
Далее наибольший элемент любой решетки 23 (если он
существует) будем называть единицей этой решетки и обозначать
как 1<8, а наименьший — нулем 0<в решетки 23. Решетка, облада-
47
Глава 1. Основные понятия универсальной алгебры
ющая единицей и нулем, называется ограниченной решеткой.
Таким образом, всякая полная решетка ограничена.
Следующий пример показывает, что требование
ограниченности решетки слабее требования ее полноты. Пусть <8={Ζ;Λ,ν) и
для любых n,m € Ν (Ζ \N) mAn=m.m(m,n) и mVn=max(m,n), a
для η G N и m € Z\N m\/n=m, mAn=n. Проверьте, что в этой
решетке *В множество N не имеет наименьшей верхней, а
множество Ζ \Ν — наибольшей нижней грани. В то же время —1 — 1<в
и 0 = О».
Большим и естественным классом полных решеток является
класс решеток подалгебр Sub2l произвольных алгебр 21.
Действительно, не представляет труда убедиться в том, что
(*) для любого множества D — {£; = (d\a)\i € /} подалгебр
алгебры 21 подалгебра Π С{ совпадает с inf D в решетке Sub 21, а
iei
подалгебра (Π Cj)a — с sup D.
Элемент α решетки <8 = (В] Л, V) назовем компактным, если
для любого подмножества С множества В неравенство α < sup
С влечет существование конечного подмножества С\ С С такого,
что a < sup Οχ.
Пусть *8=(P(i4);U,Π), тогда для любого С С. А имеет место
равенство С =sup{{ci} | dG С}. Тем самым, компактными
элементами в решетке <В являются конечные подмножества множества
А и только они.
Выясним теперь, каковы компактные элементы в решетке
Sub 21 для любой универсальной алгебры 21. Для любого
множества В через Ρω(Β) обозначим совокупность всех конечных
подмножеств множества В. Подалгебра <8 = (В; σ) алгебры 21
называется конечно порожденной, если существует конечное
подмножество D С В такое, что *8=(D)ai- Для любой подалгебры
€ — (С; σ) алгебры 21 имеет место равенство
€ = sup{(D)*\D 6 Ρω(0)}.
Таким образом, если С компактна, то должна существовать
конечная совокупность Di,...,Dn конечных подмножеств
множества С такая, что
€ = sup{(£>1)ia,..., (DM = (A U · · · U £>„>*,
48
§ 3. Алгебраические решетки
т.е. С должна быть конечно порожденной подалгеброй алгебры 21.
Нетрудно заметить справедливость и обратного утверждения:
(**) любая конечно порожденная подалгебра произвольной
алгебры 21 является компактным элементом решетки Sub 21.
Итак, компактные элементы решетки Sub 21 суть конечно
порожденные подалгебры алгебры 21.
Нетрудно заметить, что если a,b — компактные элементы
некоторой решетки 21, то и aVb является компактным элементом этой
решетки.
Решетка 23 = (В;\/,Л) называется алгебраической
решеткой, если она полна и любой ее элемент является наименьшей
верхней гранью какой-либо совокупности компактных элементов.
Решетка 21 = (Р(Л); и,П) является алгебраической для
любого множества А. Действительно, если С С Л, то справедливо
равенство
с= и в.
веРш(С)
Аналогично замечается алгебраичность решетки Sub 21 для
любой универсальной алгебры 21. Пусть 2$ = (В; σ) — подалгебра
алгебры 21, тогда очевидно равенство
® = U {D)%.
Ω£Ρω(Β)
На самом деле справедливо и обратное утверждение: любая
алгебраическая решетка изоморфна решетке подалгебр
некоторой универсальной алгебры. Правда, при этом нам придется
отказаться от ограничения на рассмотрение лишь конечных
сигнатур. То есть в утверждении следующей теоремы предполагается,
что сигнатура универсальной алгебры может быть произвольной
(не обязательно конечной) совокупностью символов.
ТЕОРЕМА БИРКГОФА — ФРИНКА. Для любой
алгебраической решетки 2$ = (В; V, Λ) существует универсальная
алгебра 21 = (Α;σ) такая,что 23 = Sub 21.
Доказательство. Пусть А — совокупность всех компактных
элементов решетки 23. Заметим, что А ф 0, так как элемент О®,
49
Глава 1. Основные понятия универсальной алгебры
являющийся, очевидно, компактным элементом решетки <8,
должен входить в А. На совокупности Р(А) всех подмножеств
множества А рассмотрим операцию ( ) : Р(А) —> Р(А): для любого
С С А пусть
{С) = {Ье А\Ь< sup С}.
Так как *8 — полная решетка, то sup С существует и операция
( ) на Р(А) определена корректно. При этом sup(C) = sup С.
Отметим следующие свойства операции ( ):
1) для любого С С А имеет место включение С С (С);
2) для любых С, D С А включение С С D влечет включение
(С) С (D);
3) для любого С С А имеет место равенство ((C)) = (С);
4) для любого С С. А имеет место равенство (С) = (J (£>).
DePu{C)
Справедливость свойств 1), 2) очевидна в силу определения
операции (). Покажем справедливость свойства 3). В силу свойств
1) и 2) имеем включения С С (С) и (С) С ((C)). Пусть теперь
d e ((C)), то есть d £ А и d < sup(C) = sup С. Тем самым, d e (С)
и равенство ((C)) = (С) доказано.
Пусть С С А, тогда для любого D Ε Ры{С) включение
(£>) С (С) имеет место в силу свойства 2) и, тем самым,
справедливо включение (J (£>)С(С). Пусть теперь d G (С), т.е. d ком-
DeP„(C)
пактный элемент решетки *В и d < sup С. В силу компактности d
найдется конечное подмножество D С С такое, что d < sup £>, то
есть d € (D) С (J (R). Последнее и завершает доказательство
RePu(C)
свойства 4) для операции ( ).
Для любого натурального η и любой последовательности а=
(αι,...,θη) элементов из Л, для элемента α€({αι,...,Οη}) определим
на А ^местную операцию /„,0 следующим образом:
t /l l \ ία, если αϊ = 6ь...,ап = 6П,
/α,αΙΟΐ,.-.,Οη) = < ,
Ι Οχ, в противном случае.
Пусть сигнатура σ состоит из всех попарно различных
функциональных символов вида /й)а и константного символа cq.
Алгебру 21= (Α; σ) определим, интерпретируя на 21 функциональные
50
§3. Алгебраические решетки
σ-символы соответствующими функциями, а константу cq —
нулем Οβ решетки <8. Покажем, что <8 = Sub 21.
Отображение *В в Р(А) определим следующим образом: для
любого Ъ € 55 пусть <р(Ь) - (Сь), где Сь = {a G Л|а < 6}.
Прежде всего заметим, что </?(&) Ε Sub 21, т.е. что <£>(Ь) содержит
константу со и замкнуто относительно функций вида /й<а.
Действительно, так как 0<в < Ъ и 0<в Ε Л для любого 6 £ <8, то
0<в € Сь и, значит, 0<в € V?(&)· Рассмотрим теперь любую
функцию вида /δ)0) где а= (αϊ,..., α„) и любые элементы 6χ,...,6η из у>
(6). Если αϊ фЪх, либо оаф h., ..., либо а^фЬ^ то /й)а (Ьь...,6„) =
6i G <^(&)· В противном случае, т.е. когда αχ=61; а^=Ь2, ·.., On = &п,
/α,α (&ι,···>Μ = α· Но по определению /й>а имеет место включение
ае ({αι,.,.,Οη}) = ({bu...,bn}) и, так как {6Ь...,6П}С у>(&) а, значит,
({&ь...,{>„}} С (у>(6)> = ((Сь)) = (Сь) = (р{Ь), то ае ср(Ь). Тем самым
действительно, φ (Ь) является подалгеброй алгебры 21 для любого
Покажем, что для различных элементов Ь\,Ь2 из <8 подалгебры
<р(Ъ\) и ν?(&2) также различны. Действительно, в противном случае
(Cbi)—<p{bi)=<p{b2)=( Сь2)· Покажем, что тогда Ь\< Ь^. Для этого
в силу равенства &i=sup С\Л достаточно показать, что для
любого d 6 Cbi, имеет место неравенство d < Ъч. Но если d Ε Сьх, то
d Ε {Сь^) = (Сь2) и, значит, d < supC^ = &2· Аналогично
замечается справедливость неравенства 62< &ь а тем самым и равенство
элементов 61=62 B противоречии с предположением. Итак,
действительно, ψ является разнозначным отображением решетки ^В
в Sub 21.
Покажем, что φ является отображением <8 на Sub 21, т.е. то,
что для любой подалгебры £ = (С; σ) алгебры 21 существует
элемент Ъ Ε В такой, что φ (6) = £. Так как ψ (Ь)=(Сь), то требуется
доказать равенство (Сь) = С для некоторого элемента 6.
Положим 6 = sup С. Имеем d < 6 и d Ε А для любого d Ε С. Тем
самым, de Сь С (Сь). Т.е. С С (Сь). Обратно, пусть d £ (Сь), т.е.
d < sup Сь = sup{e Ε Л|е < 6}. Но тогда, в силу компактности
d найдутся натуральное η и элементы еь ... ,еп из {е Ε Л|е < 6}
такие, что d < sup {ei,...,^}. Так как каждое из ti компактно и
ti<b — sup С, то найдутся конечные подмножества С* множества
С такие, что е*< sup С*. Пусть С = IJ ^={θι,...,«ν„}ζ С. Тогда
51
Глава 1. Основные понятия универсальной алгебры
d < sup С" и, значит, a=fed (ci,...,^), где с = (ci,...,^). Так как
С = (С; σ) подалгебра алгебры 21, то de С и включение (Сь) ζ С,
а вместе с тем и требуемое равенство С = (Сь) = у>(Ь) доказаны.
Заметим теперь, что φ является монотонным отображением
решетки *3 на решетку Sub 21, т.е. для любых 6i, &2 из 23
неравенство &ι< &2 влечет включение ψ {h)C φ (&2) (неравенство у> (6ι) <
<р (b2) в решетке Sub21). Действительно, если Ъ\ < 62, то С^ С Сб2
и, значит, у? (6i)=(Cb1) С (С&2) = φ (Ь2)· Так же замечается, что
монотонным является и φ~ι.
Утверждение теоремы о том, что ψ является изоморфизмом
решеток 25 и Sub 21, следует теперь из более общего факта:
(***) Любое взаимно однозначное монотонное отображение ψ
решетки *Βχ на решетку 3$2, для которого отображение ψ"1 также
монотонно является изоморфизмом решеток <8j и В2.
Доказательство этого последнего утверждения, завершающего
доказательство всей теоремы, предоставляется читателю.
Таким образом, алгебраические решетки с точностью до
изоморфизма суть решетки подалгебр универсальных алгебр.
ЗАДАЧИ
1. Докажите утверждение (*) из данного параграфа.
2. Докажите, что в решеточно упорядоченном множестве
(N; <) все элементы компактны, а в решеточно упорядоченном
множестве (Q; <) нет компактных элементов.
3. Докажите, что любая конечная решетка является
алгебраической.
4. Для любой булевой алгебры <8 пусть (F(<8);<) —
решеточно упорядоченное множество всех фильтров (включая
несобственные) этой булевой алгебры упорядоченное отношением теоретико-
множественного включения. Докажите, что компактные
элементы множества (F(<8);<) суть главные фильтры булевой алгебры
<8 и что решетка, соответствующая множеству (F(25);<) является
алгебраической.
5. Докажите утверждение (**) из данного параграфа.
6. Пусть <8 = (В; Λ, ν) — решетка удовлетворяющая условию:
для любого подмножества С множества В существует sup С. При
52
§4. Гомоморфизмы, конгруэнции и фактор-алгебры
этом будем считать, что sup0 = О®. Докажите, что <8 — полная
решетка.
7. Докажите утверждение (***) из данного параграфа.
8. Постройте примеры решеточно упорядоченных множеств 21
= (-4; <} и <8 = (В; <) не изоморфных, но для которых существует
монотонная биекция 21 на <8.
§4. Гомоморфизмы, конгруэнции
и фактор-алгебры
В § 1 было введено понятие изоморфизма, т.е. точного
копирования универсальных алгебр. Теперь нам понадобится более
общее понятие подобия алгебр: сохранение каких-то черт алгебры
без экстремистских требований абсолюта.
Для двух алгебр 21 = (А\ σ) и <8 = (В; σ) одной и той же
сигнатуры σ = (/q0, ..., /*r, c0)..., ck) отображение φ множества А
в множество В назовем гомоморфизмом алгебры 21 в алгебру ^В,
если отображение φ сохраняет константы и действия сигнатурных
функций, т.е. если:
1) для любого е< г, для любых элементов oi,...,oSe из А имеет
место равенство ip(fe(alr., aSc)) = ϊε{φ(αχ),...,φ( αββ));
2) для любого e<k φ(ο*) = cf.
а ж
53
Глава 1. Основные понятия универсальной алгебры
(*) Легко заметить, что для любых алгебр 21, 23 и любого
гомоморфизма φ алгебры 21 в алгебру 23 </?-образ алгебры 21 является
подалгеброй алгебры 23.
Если гомоморфизм φ является отображением алгебры 21 на
алгебру 23,то назовем его эпиморфизмом.
Гомоморфизм ψ алгебры 21 в алгебру 23 является
изоморфизмом тогда и только тогда, когда φ — эпиморфизм и он
разнозначен, т.е. для различных элементов a, b из 21 их (^-образы φ(α), cp(b)
также различны.
Остановимся на примерах гомоморфизмов:
1) 2l=(Z;+,—,0), где + и — традиционные сложение и
вычитание целых чисел. Пусть п€.М\{0} и 21η={Ζη={0,1,..., η—1};+,-,0),
где операция + интерпретируется как сложение по модулю η и
для любых т, к G Zn.
(т — к, если m — к > 0.
га- А; = <
Ι η — |га — к\, если т — к < 0.
Отображение </?: Ζ—> Zri, определенное как φ(τή)= остатку от
деления m на п, является гомоморфизмом алгебры 21 на алгебру
2) 21 = (Р(Л); U, П, -, 0, Л), Б С А и 23 = (Р(В); U, П, -., 0, В).
Отображение φ: Р(А) —> Р{В), определенное как φ{0) = С Π В
для любого С € Ρ (А), является гомоморфизмом алгебры 21 на
алгебру 23.
Легко заметить, что тождественное отображение алгебры 21 на
себя является гомоморфизмом и для любых гомоморфизмов φ :
21—» 23, ^> : 23 —^ £ их суперпозиция ^><£> является гомоморфизмом
алгебры 21 в алгебру €.
Индукцией по длине терма доказывается следующее
утверждение.
(**) Если φ — гомоморфизм алгебры 21 = (Α; σ) в алгебру 23,
то для любого терма ί(α;ι,...,ανι) сигнатуры <т, для любых αι,...,αη
из А имеет место равенство </?(£(αχ,..., αη))=ί(^(αι),...,ν?(οη)).
С каждым гомоморфизмом φ алгебры 21 = (Л; σ) в алгебру 23
свяжем некоторое двухместное отношение ker^, на множестве А
54
§4. Гомоморфизмы, конгруэнции и фактор-алгебры
именуемое далее ядром гомоморфизма φ и определенное
следующим образом:
для любых а, бе A kerv(a, 6) Φ>· p(a)=(p(b).
Очевидно, что отношение kerv является отношением
эквивалентности на множестве А. Более того, оно обладает важным
дополнительным свойством: для любой //* € σ, для любых е\, ...,
eSi, di, ..., dSie А отношения ker^ (e1; di), ..., ker^, (eSi, dSi) влекут
отношение ker^, (/j(eb..., e$i), fi(dh ..., ds,)). Действительно,
v(/i(ei, -, O) =/»(¥>(ei), -, ¥>(ee<)) = /i(</?K), ..., v>(dei)) =
¥>(/i(di, ·.., de.))
и, значит, kerv(/i(eb..., eSi), fi(du..., dSi)).
Отношение эквивалентности θ на основном множестве А
алгебры 21 = (Α, σ) назовем конгруэнцией алгебры 21, если оно
обладает свойством: для любой /?* € σ, для любых eiy..,eSi, c?i,...,ciSiG
Л отношения 9(ei,di),...,9(eSi,dSi) влекут отношение #(/i(elv.., eSi),
/t(4,..., deJ).
Таким образом ядро любого гомоморфизма алгебры 21
является конгруэнцией этой алгебры.
Верно и обратное: любая конгруэнция θ алгебры 21
является ядром некоторого гомоморфизма этой алгебры (естественного
гомоморфизма конгруэнции Θ). Пусть θ — конгруэнция алгебры
21 = (А; /о°, ...,/rSr,co, ...,с*;}. Определим фактор-алгебру
алгебры 21 по конгруэнции θ — алгебру *у # следующим образом. В § 1
было определено фактор-множество А/ q по отношению эквива-
лентности 0. Константы Cj' алгебры ™/# определим с помощью
равенств
"А
с/'= [#]·>
а действия функций $€ σ на множестве A q — с помощью ра-
Μ[αι]θ,-,[ αβ<]β)=[/(αι,...> a*)]*.
венств
55
Глава 1. Основные понятия универсальной алгебры
Заметьте, что в силу того, что 0 является конгруэнцией
алгебры 21, определение действий функций /ί€σ на множестве ^Jq
корректно, т.е. не зависит от выбора конкретных элементов (ц из
классов эквивалентности [(ц]е.
Теперь нетрудно проверить, что
(***) отображение φβ алгебры 21 на алгебру ™/#, определенное
как φ9() = [a]e, будет гомоморфизмом алгебры 21, ядро которого
совпадает с конгруэнцией 0.
Назовем подобное отображение φβ естественным
гомоморфизмом алгебры 21 по конгруэнции Θ. Непосредственно
замечается, что:
(****) а) гомоморфизм φ алгебры 21 в <8 является изоморфным
вложением алгебры 21 в алгебру <8 тогда и только тогда, когда
kerv=Aa;
б) для любого гомоморфизма ψ алгебры 21 в алгебру <8
гомоморфный образ φ{^) алгебры 23 (подалгебра алгебры <8,
состоящая из </?-образов элементов алгебры 21) изоморфна фактор-
алгебре ^/keV
Таким образом, гомоморфные образы универсальных алгебр
исчерпываются с точностью до изоморфизма их
фактор-алгебрами.
Заметим, что для любой алгебры 21 алгебра ™ /дЛ изоморфна
21, а алгебра ™ /у , — единственная, с точностью до изоморфизма,
одноэлементная алгебра сигнатуры σ.
Совокупность всех конгруэнции алгебры 21 обозначим как
Con 21. Так как каждая конгруэнция алгебры 21 = (Α;σ)
является, в частности, отношением эквивалентности на множестве А,
то Con 21 С Eq(A). Таким образом, отношение частичного
порядка < (являющееся отношением теоретико-множественного
включения на эквивалентностях множества А, рассматриваемых как
подмножества множества А х А) будет отношением частичного
порядка и на совокупности Con 21.
Непосредственно проверяется, что
(*****) для любых двух конгруэнции #ι,#2 на алгебре 21
отношение #ιΛ#2, определенное на А как
для Ь, с е А 01 Λ 02(Ь, с) <=ϊ 01 (Ь, с) и 02(Ь, с),
56
§4. Гомоморфизмы, конгруэнции и фактор-алгебры
является конгруэнцией на алгебре 21. Более того, 0iA02=inf(0i,02)
в частично упорядоченном множестве (Con21; <).
Точно так же замечается, что для любой совокупности ^ =
{θί\ί ζ. 1} конгруэнции на алгебре 21, отношение Πθ,
определенное как
для а, Ь 6 Α Π £>(а, Ь) Ф>· для любого г € /^(а, Ь),
также является конгруэнцией на 21 и П5= inf ίϊ в частично
упорядоченном множестве (Соп21;<).
В силу этого если для любых #ι,#2 £ Con21 отношение #iV#2
определим как
θχ\/θ2 = П$,
где δ = {Θ € Con21 | θχ < θ и 02 < θ}, то (так же как и в § 1 для
эквивалентностей на множестве А) нетрудно заметить что
0iV02= sup (θι,θ2)
в частично упорядоченном множестве конгруэнции на алгебре 21.
Тем самым (Con 21; Λ,ν) является решеткой — решеткой
конгруэнции алгебры 21, обозначаемой далее как Соп21.
Заметим, что операции V, Λ в решетках Con21 и (Eq(^); Λ,ν)
совпадают на конгруэнциях алгебры 21, являющихся
одновременно эквивалентностями на А (см., задачу 8 этого параграфа).
Как замечено выше, ПЗ является наибольшей нижней гранью
совокупности Э в частично упорядоченном множестве (Соп21;<)
для любой совокупности 9ί конгруэнции алгебры 21. Тем самым
(******) решетка Con 21 конгруэнции любой алгебры 21
является полной.
Более того, она является алгебраической. Но для
доказательства этого нам понадобится понятие конгруэнции порожденной
некоторой совокупностью пар элементов алгебры.
Пусть С — некоторая совокупность пар (неупорядоченных,
т.е. двухэлементных подмножеств) элементов основного
множества алгебры 21. Пусть $ = {Θ G Соп21| для любых {a,b} € С
имеет место 9(a,b)}. Очевидно, что конгруэнция Πθί является
наименьшей конгруэнцией алгебры 21 в решетке Con 21, относительно
которой любая пара элементов входящая в С эквивалентна.
Назовем эту конгруэнцию конгруэнцией, порожденной совокупностью
57
Глава 1. Основные понятия универсальной алгебры
С, и обозначим ее как 9с- Конгруэнцию алгебры 21 порожденную
некоторой конечной совокупностью С будем называть конечно
порожденной конгруэнцией алгебры 21. Для С = {{а, Ь}}
конгруэнцию 6с назовем главной конгруэнцией алгебры 21 и будем
обозначать как 9а<ь- Таким образом, 9а^ — наименьшая
конгруэнция алгебры 21, относительно которой элементы а и b
эквивалентны.
Имеет место следующее конструктивное описание
конгруэнции вида 9с-
ЛЕММА МАЛЬЦЕВА. Для любой алгебры 21 = (Α; σ),
любой совокупности С пар элементов множества А и
произвольных элементов a, b из А следующие условия эквивалентны:
1) 9с(а,Ь);
2) для некоторого натурального η и некоторых термов
Pi(x,y~i), ...,Pn(x,yn) сигнатуры σ существуют кортежи
элементов ei,..., ёп множества А и пары {с\, άχ},..., {сп, dn} из С
такие, что = pi(ci, e~i),b = pn(dn, ёп) и для 1 < г < η Pi(di,ei) =
Pi+i(ci+i,ei+i).
Доказательство. Пусть для некоторых термов р\(х, у~\),.~,
Рп(х, Уп), элементов Εχ,..., Еп из А и пар {θχ,άχ},...,{θη,άη} из С
выполнено условие 2). Тогда так как для любого 1<г<п имеет место
9с(<кА)> то 9с(Рг((к, ei), Рг(а\, Ει)) истинно для 1<г<п. С другой
стороны, равенства Ρί(α\, Ei) = pj+i(ci+i, &ί+ι) также влекут
отношения 9c(pi(di, ei), pi+i(ci+x, Ei+i)). Все это в силу транзитивности
отношения вс и равенств α=ρχ(θχ, Εχ), b=pn(dn,en) и влечет
истинность отношения 9с(а,Ь). Итак, из условия 2) следует истинность
условия 1).
С другой стороны, пусть 9* = {{и,ν) £ А х А | существует
натуральное п, термы ρχ{χ, Ух),--,рп(х, yn) сигнатуры σ,
кортежи элементов Εχ,...,Εη множества А и пары {cx,di},...,{cn,dn} из С
такие, что и = рх(с,ёх), р{(а\, ё{) = pi+1(ci+i, Ei+1) для 1<г<п и
v—pn{dn, en)}. Без труда проверяется, что
(*******) отношение 9* является конгруэнцией на алгебре 21,
для любой пары {с, d} из С имеет место 9* (с, d).
Тем самым истинность отношения 9с(а, Ь) влечет отношение
9*{а,Ъ), т.е из условия 1) вытекает условие 2). Лемма доказана.
Вернемся к рассмотрению решеток Con 21 для произвольных
алгебр 21. В силу определения конгруэнции 9а^ имеет место утвер-
58
§4. Гомоморфизмы, конгруэнции и фактор-алгебры
ждение: для любых элементов a, b из А и любой конгруэнции θ
на А отношение 9(a,b) влечет неравенство θα^ < θ.
В следствие этого для любой конгруэнции θ алгебры 21 имеет
место равенство θ =sup{0Oib|0 (a,b)}.
Докажем, что компактными элементами решетки Соп21
являются конечно порожденные конгруэнции алгебры 21 и только они.
Действительно, если θ = θαι^ V ... V θαη^ и для некоторой
совокупности конгруэнции ^={θι | i€l} имеет место неравенство θ
< sup 55, то для любого г<п θαί^ < θ < sup £> = 0м θ.. По лемме
Мальцева для каждого г < η найдется конечное подмножество С{
пар элементов из множества U θι такое, что 0Oi ^ < θ€■■ Тем
саге/
мым, найдется конечное подмножество U множества / такое, что
θατΑ <9Ci< V θ,. Но тогда, θ = θαιΜ V ... V 0Ori,6„ <( V 0,-)V...
V( V Gj) = sup {9j | φ €liU...Uln} и компактность конечно по-
jehn
рожденной конгруэнции θ доказана.
С другой стороны, если θ компактна, то равенство
e = sup{ea>b\9(a,b)}
влечет равенство
θ = 6>0lifel V ... V 0ап)Ьп
для некоторой конечной совокупности пар элементов {αϊ, bj},...,
{an, bn} из θ, т.е. конечную порожденность конгруэнции Θ. Итак,
действительно, компактные элементы решетки Con 21 суть
конечно порожденные конгруэнции алгебры 21.
Таким образом, отмеченная выше полнота решетки Con 21 и
равенство θ ~ sup { 0Oib|0(a,&)} доказывают алгебраичность
решетки Con 21 для любой алгебры 21.
Без доказательства сформулируем обратный результат.
ТЕОРЕМА ГРЕТЦЕРА — ШМИДТА. Для любой
алгебраической решетки € существует универсальная алгебра 21
такая, что € = Соп21.
Здесь, как и в теореме Биркгофа—Фринка, не предполагается
конечность сигнатуры алгебры 21. Полное доказательство этого
результата можно найти в [34].
59
Глава 1. Основные понятия универсальной алгебры
Алгебру 21 назовем простой, если 21 неодноэлементна и Con 21
= {Agt,V<2i}, т.е. любая конгруэнция алгебры 21, отличная от
нулевой (от равенства), является единичной (тотальной) на 21.
Очевидно, что простота алгебры 21 эквивалентна равенству 6а,ь — Va для
любых различных элементов а,Ь алгебры 21. В силу замеченного
выше о том, что гомоморфные образы алгебры 21 исчерпываются
с точностью до изоморфизма ее фактор-алгебрами, из простоты
алгебры 21 следует, что ее гомоморфные образы суть с точностью
до изоморфизма — сама алгебра 21 и одноэлементная алгебра
соответствующей сигнатуры. Обратное утверждение, вообще говоря,
неверно.
Докажем теперь несколько утверждений, играющих важную
роль в работе с конгруэнциями и гомоморфизмами. Прежде всего
отметим, что:
(********) а) если φ — некоторый гомоморфизм алгебры 21 в
алгебру 23, то для любой подалгебры € алгебры 21 ее φ-образ φ(€)
образует подалгебру алгебры 23;
б) если φ — некоторый гомоморфизм алгебры 21 в алгебру 23,
С — подалгебра алгебры 2$ такая, что £ С φ(%1), то φ~1(2) —
подалгебра алгебры 21.
Для любой конгруэнции θ на алгебре 21 и любой
подалгебры 23 этой алгебры через 23[Θ] обозначим U [Ь]е. Очевидно, что
бе<8
23[0] = φ~1(φ(^Β)), где φ — естественный гомоморфизм алгебры 21
на фактор-алгебру ®|y] Iq. В силу отмеченного выше 23[Θ]
является подалгеброй алгебры 21. В этой же ситуации через θ\<$
обозначим ограничение отношения θ на подалгебру 23, т.е. такое
отношение на элементах алгебры 23, что для a,b£ 23 9\<^(а,Ь) истинно
тогда и только тогда, когда истинно 6(а,Ь). Непосредственно
проверяется, что 0|<в является конгруэнцией алгебры 23.
ПЕРВАЯ ТЕОРЕМА ОБ ИЗОМОРФИЗМЕ. Пусть 21
— произвольная алгебра, 23 —подалгебра алгебры 21 и θ —
конгруэнция алгебры А, тогда имеет место изоморфизм ™[Щ /β =
Β/θ\*>
Доказательство. Определим отображение φ : 23 -τ^Ψΐ/β
следующим образом: (p(b) = [b]g для любого b € В .
По определению алгебры 23 [Θ] отображение φ является отоб-
60
§4. Гомоморфизмы, конгруэнции и фактор-алгебры
ражением на алгебру ®И/б· Равенство же элементов φ(α) = у>(&)
для a,be 25 равносильно равенству 0-классов [α]θ = [Ь]в, т.е.
тому, что истинно отношение в\ъ(а,Ь). Непосредственно
проверяется, что φ гомоморфизм алгебры 95 на алгебру ^И/б»· Тем самым
ядро φ суть θ\% и в силу доказанного ранее имеет место
изоморфизм алгебр ®/θ\χ и ®^/0· Теорема доказана.
Пусть теперь конгруэнции θχ и θ2 алгебры 21 таковы, что θχ <
θ2. На алгебре ^IQx определим отношение θ*/θχ так' что
VMH*» [ь]в1) ^ е2(а,ь),
где а,Ь — произвольные элементы алгебры 21.
Прежде всего отметим корректность определения отношения
Qz/q , т.е. независимость его определения от выбора элементов а,Ь
из классов [α]θι , [b}6i. Действительно, если [α]βι= [cJ^h [ί»]βι= [d]v
то отношения θχ(α,ό) и #ι(Μ) имеют место, а значит,
02(а,6) ^0i(a,c) & 02(а,6) & ^(М) =► в2(с,(£).
Непосредственно проверяется, что отношение 2/θχ
является отношением эквивалентности на множестве /#,· Более того,
2 θχ конгруэнция алгебры ™/0,, так как если /,Si € σ и для
некоторых ai,...,aSi, bi,...,bSi, из Л имеют место отношения
т.е. e2(a1,bi),...,e2(aSi,bSi), то имеет место и отношение
02(/i(ai,···, asi),fi(h,-, bs.)).
В этом случае
ν^^'-,αΟΚ, lfi(&i, ..., 6β4)]βι).
В силу же определения алгебры ^/#,
[/i(ab...,aei)]tfi =Λ([αι]βι,...,[αβ.]βι),
I/i(bb-.b4)U = /i([fri]ei,..., Κ}θι).
61
Глава 1. Основные понятия универсальной алгебры
Тем самым имеет место отношение
%(MMv ■·- Kh), ΜΝ*, -. [b.Jei)),
и проверка того, что "з/ρ является конгруэнцией алгебры ^yV,
закончена.
Рассмотрим теперь на фактор-алгебре ^у #, произвольную
конгруэнцию Ф. Определим отношение Φ θι на алгебре 21
следующим образом: для a,be A
Φβι(αί)^Φ([α)θιΜθι).
Заметим, что отношение Φ θι является конгруэнцией алгебры
21 и θχ < Φ θι. Непосредственно замечается, что отношение Φ θι
является отношением эквивалентности на А. Пусть теперь для
некоторых %,..., aSi, &i,..., bSi, из А имеют место отношения Φ θι (aj,bi),
..., Φ&1 (aSi,bSi). Тогда, по определению Φθι имеют место
отношения Φ([θι]βι[6ι]βι), ...,Φ (Κ]βι[6βί]βι) и, значит, Ф(Л([ах]в1,..., [αβί]βι),
fiilbiU'-AbsileJ)· Тем самым истинно Φ([/ί(αι,...,αβ.)]βι, [fi(bu
■■•■•bsi)]^) и по определению Φθι отношение Фб1(/г(аь ...,a.sJ,
/»(Ьь-, beJ) истинно.
Неравенство #ι<Φ&1 имеет место в силу следующих
импликаций:
вх{а,Ъ) =► [о]в1 = [Ь]в1=* Φ ([α]θιΜθι) =► φ·ι (β,6).
Заметим теперь, что для любой конгруэнции 02 алгебры 21
такой, что θι < θ2 имеет место равенство у2/о ) =θ2.
Действительно, для любых о,6 из А:
(Θ%Ϋ (α.6) * θ% {[о\вЛЬ\) * Ч*Я
Очевидно также, что для любой конгруэнции на алгебре ^/Q,
имеет место равенство Φ /q = Φ.
Для любого элемента α произвольной решетки £ через £[>а
обозначим множество {Ье£|Ь>а} с индуцированными на нем
операциями V, Л из решетки £. Очевидно, что £[>а является подре-
шеткой решетки £.
62
§4. Гомоморфизмы, конгруэнции и фактор-алгебры
Отмеченные свойства конгруэнции ^/q ηΦΘι резюмируем
следующим утверждением.
ТЕОРЕМА 1. Для любой алгебры 21 и любой конгруэнции
θ алгебры 21 отображение φ: Соп(^у #)->Соп21[> Θ, определенное
равенством φ(Φ) = Φθ (для любой Φ € Соп(™/#)), является
изоморфизмом решетки Соп(™/$) на решетку Соп21[> Θ. При этом
обратное отображение φ~ι определено на Соп21[> θ равенством
Доказательство. Выше было доказано, что ψ является биек-
цией решетки Соп(™/#) на решетку Соп21[> θ и что φ~χ является
обратным к отображению φ. Очевидна также монотонность
отображений ψ и ψ"1. Как уже замечалось, любая монотонная биекция
одной решетки на другую, для которой отображение ψ~χ также
монотонно является изоморфизмом этих решеток.
ВТОРАЯ ТЕОРЕМА ОБ ИЗОМОРФИЗМЕ. Пусть Θ,
Φ конгруэнции алгебры 21 такие, что θ < Ф. Тогда имеет место
изоморфизм
«У»/*/, = Я/Ф.
Доказательство. Определим отображение φ алгебры ™/# в
алгебру ™/ф следующим образом: для любого [а]д € ™/#
φ([α]θ) = [α]φ.
Непосредственно замечается, что φ является гомоморфизмом
алгебры ™/# на алгебру ™/#. При этом ядро ψ суть ®/q. Таким
образом, в силу изоморфизма гомоморфного образа алгебры и
ее фактор-алгебры по ядру гомоморфизма получа,ем требуемый
изоморфизм
*/в/*/в - я/Ф.
Теорема доказана.
63
Глава 1. Основные понятия универсальной алгебры
ЗАДАЧИ
1. Докажите утверждение (**) из данного параграфа.
2. Пусть φ — гомоморфизм алгебры 21 = (Л; σ) в алгебру
25 = (В; σ), t\(x) и ί2(ζ) — термы сигнатуры σ, α — элемент
множества Л, являющийся решением уравнения ij.(:r) = t2(x) (в алгебре
21). Тогда элемент φ(α) является также решением этого уравнения
(в алгебре <8).
3. Докажите, что существует лишь два гомоморфизма алгебры
21= (£;+;■) в себя: φ0 и φχ , где
φ0(η)=0 для любого η Ε Ζ и
Vi(n)=n для любого η Ε Ζ.
4. Докажите утверждение (*) из данного параграфа.
5. Докажите корректность определения фактор-алгебры 21 по
конгруэнции θ и утверждение (***) из данного параграфа.
6. Докажите, что все гомоморфные образы алгебры 21 из
примера 1 гомоморфизмов алгебр изоморфны либо 21, либо некоторой
алгебре вида <8n(nE./V\{0}) из того же примера. Для этого
опишите все возможные конгруэнции алгебры 21.
7. Докажите утверждение (****) а) и б) из данного параграфа.
8. Пусть θχ, Θ2Ε Con21 для некоторой алгебры 21. Докажите,
что отношения θ\ Veq θ2 и θχ Vcon #2, где VEq, Vcon операции
соответственно в решетках (Eq(A);V, Λ) и Con 21, совпадают. То есть
решетка Con 21 является подрешеткой решетки (БдЛ; V, Λ).
9. Докажите утверждение (*****) из данного параграфа.
10. Докажите утверждение (******) из данного параграфа.
11. Докажите утверждение (*******) из данного параграфа.
12. Докажите, что для алгебры 2l=(Z;4-,-), для любых τη,ηΕΖ
справедливо равенство
θο,η V #0,m = #0,НОД(п,т)> ^>.« Λ ^°>т ~ ^Ο,ΗΟΚ(η,τη)
где НОД(п, т) — наибольший общий делитель чисел η и m, a
НОК (п, т) — наименьшее общее кратное этих чисел.
13. Докажите простоту следующих алгебр:
1) решетка М$ (диамант) со следующей диаграммой Хассе:
64
§4. Гомоморфизмы, конгруэнции и фактор-алгебры
2) для любого простого числа peN алгебры 21р = (Zp = {0, 1,
..., р— 1}; +), где Η сложение по модулю р;
3) любое поле (коммутативное кольцо с единицей, в котором
каждый ненулевой элемент имеет обратный).
14. Докажите утверждение (********) а) и б) из данного
параграфа.
15. Для любой решетки <8 = (L;A,V), любых ее элементов
a,b,c и любой конгруэнции θ на В докажите следующие
импликации:
в(а,Ь) -> 6(aAb,aVb),
в(а,аЛЬ) -> 0(6, α V 6),
6(a,aVb) -> 9(b,aAb),
а < с < Ь и θ(α, Ь) ~+ θ(α, с) ->· 0(6, с).
16. Постройте диаграмму Хассе для решетки Con JV, где N
(пентагон) — решетка с диаграммой:
N
17. Пусть алгебра 21 = (N; f^) такова, что
f(n,m,k) =
О, если η > га, /с
к, в противном случае.
65
Глава 1. Основные понятия универсальной алгебры
Докажите, что для любой конгруэнции θ на 21, отличной от V
существует η Ε N такое, что [0]# = {0,... ,п — 1}, а для m > η
[m]e = {rn}. Верно и обратное: для любого η эквивалентность
θ определенная разбиением {{0,...,η — 1},{то}|т > п}
множества N является конгруэнцией алгебры 21. В силу этого любой
гомоморфный неодноэлементный образ алгебры 21 изоморфен ей
самой, но простой алгебра 21 не является.
18. Пусть <8 = (В; V, Л, ->, 0,1) — произвольная булева алгебра
и F некоторый фильтр этой алгебры. Отношение θρ на <8
определим следующим образом: для a,b Ε В пусть θρ·(α, b) тогда и только
тогда, когда ->((аЛ->Ь) V (bA->a)) Ε F. Докажите, что θ ρ является
конгруэнцией на булевой алгебре <8. Докажите, что для любой
конгруэнции θ на В множество [1]# является фильтром и θ = θ\^θ.
Докажите, что отображение ψ : F = (F(B);V,A) —> СопОЗ, где
F(<8) совокупность всех (включая несобственные) фильтров
алгебры 93 на решетку Соп<8, определенное равенством <p{F) = θρ·,
является изоморфизмом решетки $ на решетку Соп*8.
19. Пусть <5 = (G;-,_1,e) — произвольная группа.
Подгруппу (В;-,_1,е) группы <5 назовем нормальной, если для любого
b Ε В и любого элемента α из G элемент a"xba снова входит в
В. Докажите, что для любых двух нормальных подгрупп Шг, 2$2
группы <5 их пересечение ςΒχΓ\ς&2 также является нормальной
подгруппой группы <5. Докажите, что для любых двух нормальных
подгрупп *Βι, Я$2 группы (5 существует наименьшая
(относительно теоретико-множественного включения) нормальная подгруппа
группы (5, включающая в себя подгруппы 23χ и <8г· Тем самым
совокупность N((5) всех нормальных подгрупп группы (5 является
решеточно упорядоченным множеством относительно теоретико-
множественного включения. Для любой конгруэнции θ на
группе <5 докажите, что класс [е\е является нормальной подгруппой
группы <5. Для любой нормальной подгруппы <8 группы <5 на G
определим отношение θ<% следующим образом: для a,b Ε G пусть
6<s(a,b) тогда и только тогда, когда a~lb Ε В. Докажите, что
отношение 0<в является конгруэнцией на группе <5. Исходя из этого,
докажите, что отображение φ : N((5) —»■ Con (5, определенное как
φ{4$) = 0<в> является изоморфизмом решетки (N (<5);V,A) всех
нормальных подгрупп группы <5 на решетку ее конгруэнции.
66
§5. Прямые и подпрямые произведения, ультрапроизведения
§ 5. Прямые и подпрямые произведения,
ультрапроизведения. Операторы
на классах алгебр
В предыдущих параграфах мы уже рассматривали некоторые
способы построения новых алгебр исходя из имеющихся:
образование подалгебр и фактор-алгебр. В настоящем параграфе мы
рассмотрим еще ряд подобных конструкций.
Пусть {2lj = {Ai,a)\i El} — некоторая совокупность алгебр
одной и той же сигнатуры σ. Через Π Μ обозначим прямое про-
iei
изведение множеств Д (г G /), т.е. совокупность таких
функций /из /в U Ai, что /(г) 6 Аг для любого г € /. В силу ак-
сиомы выбора, непустота множеств Ai (г 6 /) влечет непустоту
множества Π Ai- На множестве Π А определим интерпретацию
iei iei
символов сигнатуры σ следующим образом:
для константных символов с, из σ положим Cj(i)— of* для
любого г€1;
для функциональных символов /? из σ и элементов gi,.-,gSj
из Π Ai положим fj(gi,..., gaj)(i)= ff{ (ffi(*),-, &,-(*)) для любого
iei
iei.
Определяя подобным образом σ-символы на множестве Π А>
iei
получаем алгебру ( Π Α;σ) сигнатуры σ, именуемую далее пря-
мым произведением алгебр 2lj(ie/) и обозначаемую как Π 2lj-
iei
В случае конечности множества /= {г1;..., in} алгебру Π 2li будем
iei
называть также декартовым произведением алгебр 21; (гб/) и
обозначать ее как 21^ х ... х Ql,n. Элементы д£ Π 21г в этом случае
iei
будем обозначать кортежами (g(h), ..-, д(гп)).
С прямым произведением Π 21» алгебр ШЛгеТ) связаны есте-
iei
ственные гомоморфизмы щ алгебры Π 2lj на алгебры Qlj
именуете/
мые в дальнейшем проекциями алгебры Π 21* на алгебры %, и
iei
определенные следующим образом:
т<(0) = 9{г)
67
Глава 1. Основные понятия универсальной алгебры
для любого д € Π 21г·. Самостоятельно убедитесь, что действи-
iei
тельно 7Tj является эпиморфизмом алгебры Π 21» на алгебру 21*.
iei
Через θi обозначим ядра проекций π^ίξί). В решетке Con Π 21»
iei
конгруэнции алгебры Π 21г справедливо следующее равенство
Ы (Щ iel})= Δ^.
iei
Действительно, если inf {9i\iel)= 0, то для любых g,h£ Π 21,, θ
iei
(g,h) влечет отношение 9i(g,h), т.е. равенство g(i)=h(i) для любого
гЕ/. Таким образом, действительно, θ (g,h) <& g—h.
С другой стороны, для любых различных г, j из /
Действительно, пусть gi,g2 € Π 21» и элемент /ι из Π 21г опре-
iei iei
делен условиями
·./ \ )9i(e), если е = г,
\д2{е), если е ψ г.
Тогда имеют место отношения 9i(gi,h) и 0Д/1, <?2) и, значит,
9i\/9j{gi,g2). Равенство 0iV0j=Vr[gi. тем самым доказано.
Пусть К — некоторый класс (совокупность) универсальных
алгебр фиксированной сигнатуры и алгебры 21Дгб7)
разложимы в прямые произведения /^-алгебр, т.е. существуют
множества 3i(iel) и алгебры 21^·(ie 3i) из К такие, что 21» — Π 2Ц··
Тогда прямое произведение алгебр 21г· само изоморфно
некоторому прямому произведению Я'-алгебр. Действительно, пусть S =
{(i,j)\i £ I,j G 3i} и φ — отображение алгебры П 21г в алгебру
iei
Π 21у такое, что для де Ц 2lj, г el, j е 3i имеет место равенство
4>{g)((iJ)) = 9Ш-
68
§5. Прямые и подпрямые произведения, ультрапроизведения
Нетрудно заметить, что φ является изоморфизмом алгебры
Π 2lj на алгебру Π 2Ц·.
ш (i,j)es
Остановимся теперь на условиях, когда алгебра 21
разложима в нетривиальное прямое произведение, т.е. когда алгебра
21 изоморфна прямому произведению неодноэлементных алгебр.
Пусть 21 = 21ι χ 2Ι2, где 2^ и 212 неодноэлементны. Более того,
будем считать, что 21 = 2lj χ 212. Пусть θχ и θ2 — ядра проекций
πχ и π2 алгебры 21 на алгебры 2^ и 212 соответственно. В силу
замеченного выше
Θϊ Л 0j = Δα, θί V 0j = V21,
а в силу неодноэлементности алгебр 21х и 212, θ\ и 02 отличны от
Δα и Va.
Введем понятие произведения R\ о Л2 двух двухместных
отношений Rx и R2 на множестве Л: для любых a,b £ A R\oR@(a, Ь)
тогда и только тогда, когда существует с € Л такой, что Ri(a,c)
и R2(c,b).
Отметим, что если θ — отношение эквивалентности, то для
любого отношения Л на Л имеют место равенства и включения
θοθ = θ, RC9oR, RCRo9.
В силу определения произведение отношений обладает
свойством ассоциативности, т.е. для любых двухместных отношений
Ri, R2, R3 на множестве Л справедливо равенство:
Λι о (Д2 о Дз) = (Rx о R2) о Д3.
В дальнейшем в силу ассоциативности операции о в
произведении недкольких отношений Ri}..., Rn на множестве Л мы будем
опускать скобки и записывать его просто как
Rx о R2 о ■ ■ ■ о Rn.
Нетрудно доказать, что
(*) если #1,02 GConSl, то имеет место равенство
0lV02= U (θιοθ2ο...οθη),
neN\{0}
69
Глава 1. Основные понятия универсальной алгебры
где для четных г £iV\{0} θ1 есть θχ, а для нечетных г — Θ'1 = θ2.
Конгруэнции θχ, θ2 алгебры 21 назовем перестановочными,
если имеет место равенство
θχθθ2 = θ2θθχ.
Заметим что в этом случае, — в случае перестановочности
конгруэнции θχ, θ2, — любое произведение отношений из (*)
Θ1 о Θ2 о · · · о θη равно отношению θχ ο θ2 = θ2 ο θχ. Таким
образом, если θχ и #2 перестановочны, то
θχνθ2 = θχθ θ2.
Вернемся к алгебре 21=21ι χ 212, разложимой в нетривиальное
прямое произведение. Покажем перестановочность ядер θχ ,θ2
проектирования алгебры 21 на алгебры 2li и 212. Действительно,
достаточно доказать, что 0xo02=Va (в силу симметрии будет иметь
место и равенство θ2οθχ=ν%). Пусть (01,02), (бь&г) — элементы
алгебры 21ι χ 212 (здесь ax,bx e 2li и 02,62 € 212). Пусть с = (01,62)
— элемент из Αχ х А2. Тогда очевидно, что #ι((οι,θ2), (θι,62)) и
02((αι,62), (61,62)), т.е. 6>ιο6>2((αι,α2), (6Ь62)). Равенство θχθθ2 = Va
доказано.
Имеет место
ТЕОРЕМА 1. Алгебра 21 разложима β нетривиальное
прямое произведение тогда и только тогда, когда на 21 существуют
перестановочные конгруэнции θχ,θ2, отличные от А<^и V^ и та-
кие,что Θχ4θ2=ν<&, θχ/\θ2—^.
Доказательство. Необходимость существования подобных
конгруэнции θχ и θ2 для разложимости алгебры 21 в
нетривиальное пря.мое произведение отмечена выше. Покажем
достаточность этих условий. Положим 2li=^/^1 и Q12=A/q2. В силу
того, что θχ, θ2 отличны от Va, алгебры 21х и А2 неодноэлементны.
Рассмотрим теперь отображение φ алгебры 21 в алгебру 21г х 212
определенное следующим образом:
ψ(α) = (Mex'Kj-
Докажем, что φ — изоморфизм алгебры 21 на алгебру 21ι χ %.
Разнозначность ψ следует из равенства θχΑθ2—Δ51. Так как
ψ{α) = (<Рх(а), φ2(α)}, где ψχ, ψ% — естественные гомоморфизмы
70
§5. Прямые и подпрямые произведения, ультрапроизведения
алгебры 21 на алгебры a/q и Λ/β2, то φ очевидным образом будет
гомоморфизмом. Таким образом, остается лишь заметить, что φ
есть отображение А на алгебру 21χ χ 212. Пусть 61=[αί1]θι е 21х и
Ь2=[с?2]в2 £ 21г, где ί»χ,62 € 21. Так как #io02=V2i, то найдется
элемент се 21 такой, что имеют место отношения θχ(άι,ό) и ^2(с,с^),
т.е. [c]e1=[cii]e1=6i и [c]02=[d2]i>2=b2· Тем самым <^(с)={ЬьЬ2), а
значит, φ — изоморфизм алгебры 21 на алгебру 21ι χ 212. Теорема
доказана.
В качестве следствия отметим, что любая алгебра, решетка
конгруэнции которой является линейно упорядоченной, в
частности любая простая алгебра, неразложима в нетривиальное прямое
произведение.
Пусть теперь 21 — подалгебра прямого произведения Π 21» ал-
iei
гебр 2li(zGi). Если для любого i€/^(2l)=2lj, то алгебра 21
называется подпрямым произведением алгебр 21г(г€/). Через θ[{ι €i)
обозначим конгруэнции 0j[2l алгебры 21, т.е. ядра гомоморфизмов
π* алгебры 21 на алгебры 21, (ге/).
Так же как и выше, нетрудно заметить справедливость
равенства
inf {{θ[\% el}) = Δα.
На самом деле это равенство является критерием
представимости (изоморфности) алгебры 21 подпрямым произведением алгебр
&■ (*е-0- Действительно, если конгруэнции θ{(ΐ(ΞΓ) алгебры 21
таковы, что
inf ({0t|t £/}) = Да,
то рассмотрим отображение φ алгебры 21 в алгебру Π ^/й , опре-
деленное следующим образом: для любого ае 21 и любого iEl
φ{α){ϊ) = [α]θ. .
Нетрудно заметить, что ψ является изоморфизмом алгебры 21
на некоторую подалгебру алгебры Π /θ·· Причем, так как для
любого a G 21 и любого i € (I) имеет место πι{φ(α)) = [α]θ., то
алгебра φ(%1) является подпрямым произведением алгебр ™/0..
71
Глава 1. Основные понятия универсальной алгебры
Алгебра 21 называется подпрямо неразложимой, если для
любого изоморфизма φ алгебры 21 с подпрямым произведением <8
каких-либо алгебр 21;(гЕ/) найдется го €/такое, что отображение
ιτίηφ является изоморфизмом. Изоморфизм алгебры 21 и
некоторого подпрямого произведения каких-либо алгебр будем называть
далее подпрямым представлением алгебры 21.
ТЕОРЕМА 2. Алгебра 21 подпрямо неразложима тогда и
только тогда, когда для любой совокупности конгруэнции #Дг £/)
алгебры 21 равенство inf {{9i\i €/}) = Δα влечет равенство θίο —
Ди для некоторого io El.
Доказательство. Предположим, что 21 — подпрямо
неразложимая алгебра и совокупность {9i\iEl} ее конгруэнции такова,
что
inf ({0£|» €/}) = Ал-
Определяя для любого а€ 21 элемент φ(α) алгебры Π /θ Ра~
iei ' г
венствами
φ{α){ΐ) = [α]β.,
получаем изоморфное вложение алгебры 21 в алгебру Π /#·> яв~
ляющееся подпрямым представлением алгебры 21. В силу подпря-
мой неразложимости алгебры 21, для некоторого г0 Ε /
гомоморфизм ΐΐί0φ является изоморфизмом, а это равносильно тому, что
θί0= Да-
Пусть теперь для алгебры 21 выполнено конгруэнц-условие из
формулировки теоремы и допустим, что ψ — подпрямое
представление алгебры 21, т.е. ψ — изоморфное вложение алгебры 21 в
алгебру Π 21ί такое, что для любого ге/7г^(21) = 2lj. Через 0* обозиа-
чим ядра гомоморфизмов Έίψ. В силу того, что у? — изоморфное
вложение, имеет место равенство
inf ({04|i €/}) = Δα.
Но тогда, в силу предположений о 21, имеет место равенство 0jo
= Δ21 для некоторого ^ из /. Гомоморфизм π^ψ алгебры 21 на
алгебру 2lj0 с нулевым ядром (равным Δ^) является изоморфизмом.
Теорема доказана.
72
§5. Прямые и подпрямые произведения, ультрапроизведения
Пусть теперь 21 — произвольная подпрямо неразложимая
алгебра. Пусть {9i\i£l} — совокупность всех конгруэнции алгебры
21, отличных от Да (ненулевых). В силу утверждения теоремы 2
inf ({0<|» €/})^ΔΑ.
Но тогда inf ({9{\i Ε Ι}) — это наименьшая ненулевая
конгруэнция алгебры 21. Наименьшую ненулевую конгруэнцию алгебры
(если таковая существует) назовем монолитом алгебры. Итак,
любая подпрямо неразложимая алгебра 21 обладает монолитом.
Опираясь на теорему 2, непосредственно проверяем и обратное:
алгебра, имеющая монолит, является подпрямо неразложимой.
Таким образом, наличие монолита — родовой признак подпрямой
неразложимости алгебр.
Важная роль подпрямо неразложимых алгебр в общей теории
универсальных алгебр определяется следующим утверждением.
ТЕОРЕМА БИРКГОФА О ПОДПРЯМЫХ
РАЗЛОЖЕНИЯХ. Любая алгебра 21 изоморфна подпрямому
произведению подпрямо неразложимых алгебр.
Доказательство. Для любых различных элементов а, 6 из
21, пусть $R0]b ~ {θ £ Соп21|а07^ be}. Совокупность Э£0)Ь непуста,
так как Δα € $Ra,&. Рассматривая традиционный порядок < на
совокупности $R0)b, замечаем, что любая цепь С из (Э£0,ь; <) имеет
в Э£0,г, верхнюю грань. Действительно, пусть θ = sup в решетке
Con 21. Тогда θ G Э£0,ь, так как иначе, в случае если в(а,Ь) истинно,
то найдется конечная совокупность конгруэнции θ^, ..., θίη из С и
элементы со = a, ci, ..., сп = Ъ алгебры 21 такие, что имеют место
отношения ^(со, сх), 6^{със2), ..., 6in(cn-i, cn). Так как С — цепь,
то найдется конгруэнция, скажем 0^, наибольшая среди
конгруэнции {А*!, ···, θίη}. Но тогда совокупность отношений 6ix(cQ, Ci),
···, #i„(cn-i, Сп) влечет отношение ^(со, £η)> т-е- ^{а,Ь).
Полученное противоречие и доказывает, что θ = sup С € 3£0>ь. Наличие
для каждой цепи в частично упорядоченном множестве (Э£0,ь",<)
верхней грани, по лемме Цорна, влечет наличие в (Эв0>ь;<)
максимального элемента. Пусть фа,ь — одна из таких конгруэнции
алгебры 21. Итак, в силу включения фа<ь € Э£0,ь, [а]у, φ [b]^a ь и
для любой конгруэнции Θ, большей чем фа,ь·, имеет место
равенство [α]θ = [Ь]в, т.е. ва<ь<9.
73
Глава 1. Основные понятия универсальной алгебры
Рассмотрим алгебру ^/ф ,· В силу утверждений теоремы 1
из §4, конгруэнция @а,ъ V фа<ь ι φ является монолитом алгебры
Ι φ bi а сама алгебра ™/»Л ■ подпрямо неразложима.
Докажем теперь равенство inf ({^>а,ь|а, Ъ € 21 и α ψ Ь})=А%.
Допустим противное, пусть сфЬ — элементы из 21 такие, что
inf ({tl>ajb\a, be 21 и α ^ 6})(c,d).
Но тогда имеет место и отношение t/}Ctd(c,d), что противоречит
определению конгруэнции ^>С|^.
Доказанное равенство
inf ({^„,ь|а,Ье 21 и α^6})=Δα,
как замечалось выше, влечет, что отображение φ алгебры 21 в
алгебру Π аЛл ь, где 5 = {(а, Ь)е21х21|а^6}и φ(ά)((α, 6»
~ И^о ь' будет подпрямым представлением алгебры 21. Подпрямая
неразложимость алгебр ^ /ф . влечет утверждение теоремы.
Следующий результат, приводимый без доказательства,
более конструктивно описывает строение подпрямых произведений
двух алгебр в некоторых ситуациях.
ТЕОРЕМА ФЛЕЙШЕРА. Пусть все конгруэнции
алгебры 21 перестановочны. Тогда, если ψ — изоморфизм алгебры 21 в
алгебру 21χ χ 212 и φ (01) — подпрямое произведение алгебр 2li и
21г, то существуют алгебра 21' и гомоморфизмы ф{ алгебр 21* на
алгебру 21' такие, что у>(21) = (αι,α2) € 21χ χ 212/ι/>ι(αι) = ^2(^2)·
Полное доказательство этого утверждения см., к примеру, в
[34].
В § 2 было определено понятие ультрафильтра булевой
алгебры. Пусть 21Дг €:/) — некоторая совокупность алгебр
фиксированной сигнатуры σ и F некоторый ультрафильтр булевой
алгебры (P(i); U, П, -ι, 0, I). Будем называть F ультрафильтром на
множестве /. Для любых элементов «ji, 52 прямого
произведения Π 2li алгебр 2lj под экволизатором элементов <?ь #2 будем
iei
понимать следующее подмножество [[<?i = g2]] множества /:
[[9i=92]] = {i€l\gi(i) = 92(i)}-
74
§5. Прямые и подпрямые произведения, ультрапроизведения
На прямом произведении Π 2li алгебр 2lj определим двухмест-
iei
ное отношение θρ следующим образом: для <?ь gi Ε Π 2li
0f{9i,92) ** [Iffi = &]]€ ^-
Покажем, что отношение 0p является конгруэнцией на
алгебре Π 21ί· Так как [[^ι = 91]] = / € F, то отношение 9F рефлек-
сивно. Если 9F(gi,g2), то [[91 = gi}] = [[g2 = gi]}, тем самым
#f(#2, #1) и отношение θρ симметрично. Если вр(д\,дч) и 9р{дъ, #з),
то [[91=92]], [b2=#jl]<EF. Но тогда [\дх = £2]]П[[#2 = Sb]]eF и, так как
[foi=Ss]P[[ffi = 92]]П[[92=9з]], то [[pi=psl]e F. Тем самым 9F(gug3)
и доказано, что отношение θρ транзитивно.
Пусть теперь /f<E σ, gu ...,&., hi, ...,hSi^U % и имеют место
отношения 6F(guhi), ..., 9F(gSi,hSi), т.е. [[^ = fti]],..., Н^ЛЛ^ F.
Следующее включение очевидно в силу определения экволизато-
ра:
[\gi=h1]]n..n[[ gaiKM\fi(9i,-, 9ч)= Ж V-, К)]].
Тем самым [[/г(<7ь···,^) = fi{hi,..., ^sJlJ^F и имеет место
отношение eF(fi(gi, ..., gSi), fi(hi, ..., hSi)). Доказательство того, что θρ
является конгруэнцией алгебры Π 2lj> завершено.
Алгебру П^/йр назовем ультрапроизведением алгебр
%i (г€Г) по ультрафильтру F и будем обозначать далее как
Пусть К — некоторый класс универсальных алгебр
фиксированной сигнатуры и алгебры 21* (гЕ/) являются
ультрапроизведениями /f-алгебр, т.е. существуют множества Ii(iGl),
ультрафильтры Fi на этих множествах и алгебры 21^ (j £ 3i) из К
такие, что 2lj = Π ^'/V·· Тогда для любого ультрафильтра F
на множестве I, алгебра Π ^/F изоморфна ультрапроизведе-
ш ' г
нию /Г-алгебр. Действительно, пусть S — {(i,j)\i € I,j € Λ},
£> - {В С 5|{г Ε /|{j € JiKi,i> € В} е F*} e F}. Пусть ^ -
75
Глава 1. Основные понятия универсальной алгебры
отображение алгебры Π VF в алгебру []^т определенное
iei ' *е/ '
следующим образом:
¥>(Ыв,) = \h\eD >
где для любого д € Π 21», если g(i) = [hi]eF , то h Ε Π 21„,
ie/ l (ij)6s
таков, что h((ij)) = /^(j), для любых i £ I,j e J{.
Тогда:
(**) а) отображение у> определено корректно, т.е. не зависит
от выбора элемента д в классе [д}0 ',
б) у> является изоморфизмом алгебры Π VF Ha алгебру
ie; '
Таким образом, ультрапроизведение ультрапроизведений К-
алгебр изоморфно некоторому ультрапроизведению /^-алгебр.
Заметим, что в случае выбора ультрафильтра F главным в
булевой алгебре (P(/);U, П,->, 0,7) операция ультрапроизведения не
дает новых алгебр. Действительно, как замечено в § 2, главный
ультрафильтр F на булевой алгебре (P(/);U,n,-', 0,7)
порождается некоторым ее атомом, т.е. найдется некоторый элемент i0 Е/
такой, что F= {3 С I\i0 E 0}· Но в этом случае непосредственно
проверяется, что
(***) отображение φ алгебры Π VF в алгебру 2lj0, опреде-
ie/ '
ленное равенством <p([g]eF) — g(io), определено корректно и
является изоморфизмом алгебры n^VF на алгебру 21» .
ie/ '
Таким образом, продуктивной в смысле получения новых
алгебр конструкция ультрапроизведения может быть только для
неглавных ультрафильтров на множествах.
Оператором X на классах (совокупностях) алгебр назовем
отображение, сопоставляющее любому классу К алгебр
фиксированной сигнатуры некоторый класс Х{К) алгебр той же
сигнатуры.
На операторах введем операцию умножения, определенную
как суперпозиция, т.е. для любых операторов Χ, Υ и любого
класса К алгебр некоторой фиксированной сигнатуры класс (ΧΥ)(Κ)
76
§5. Прямые и подпрямые произведения, ультрапроизведения
определяется равенством
(XY)(K) = X(Y(K)).
Заметную роль в дальнейшем будут играть следующие
операторы:
1(К) — {21|21 изоморфна некоторой /^-алгебре};
S(K) = {2l|2l является подалгеброй некоторой /^-алгебры};
Η (К) = {21|21 является гомоморфным образом некоторой К-
алгебры};
Р(К) — {21|21 является прямым произведением некоторых К-
алгебр};
Ps(K) = {2l|2l является подпрямым произведением некоторых
iC-алгебр};
Ри(К) — {21|21 является ультрапроизведением некоторых К-
алгебр}.
Отметим ряд тривиальных, а также вытекающих из
предыдущих рассмотрений, равенств и включений, имеющих место для
любых классов К универсальных алгебр фиксированной
сигнатуры:
(****) К С 1(К), К С S(K), К С Н{К), К С PS(K), К С Р(К),
К С Рц(К), П(К) = I(K), SS(K) = S(K), HH(K) = Н(К),
РР(К) = Р(К), PsPs(K) = PS(K), PuPu(K) = PV(K),
IS (К) = SI(K), I(K) С Η (Κ), ΙΡ {К) Э ΡΙ(Κ),
IPs(K) D PSI(K), IPu{K) D PuI(K).
Важную роль в дальнейшем будут играть следующие
включения так же легко вытекающие из предыдущих рассмотрений:
(*****) 1) SH(K) С HS(K);
2) РН(К) С НР(К);
3) PS(K) С SP(K);
4) PSH(K) С #Ps(tf);
5) Ру(К-) С #Р(#).
Заметим, что включения 1)-5) из (*****), вообще говоря, не
могут быть заменены на равенства.
Класс К алгебр фиксированной сигнатуры назовем
многообразием, если имеют место включения Н{К) С К, S(K) С К,
Ρ (К) С К. Очевидно, что совокупность всех алгебр данной
фиксированной сигнатуры σ является многообразием. Так как пересе-
77
Глава 1. Основные понятия универсальной алгебры
чение любой совокупности многообразий является, очевидно,
многообразием, то для любого класса К алгебр фиксированной
сигнатуры существует наименьшее многообразие, включающее в себя
этот класс — пересечение всех многообразий, включающих
рассматриваемый класс К универсальных алгебр. Назовем это
наименьшее многообразие, включающее класс К, многообразием
порожденным классом К, и будем обозначать его как Μ (К).
ТЕОРЕМА БИРКГОФА О МНОГООБРАЗИЯХ. Для
любого класса К универсальных алгебр фиксированной сигнатуры
имеет место равенство
М(К) = HSP(K).
Доказательство. Включение HPS(K) С М(К) очевидно в
силу определения многообразий. Таким образом, для
доказательства теоремы достаточно заметить, что класс HPS(K)
является многообразием, т.е. замкнут относительно образования
гомоморфных образов, подалгебр и прямых произведений. В самом
деле, из отмеченных выше утверждений (****) и (*****)
вытекают, в частности, следующие равенства и включения:
HHSP(K) = HSP(K)-
SHSP(K) С HSSP(K) = HSP(K);
PHSP(K) С HPSP(K) С HSPP(K) = HSP(K).
Теорема доказана.
Важную роль в изучении многообразий играет также
следующее утверждение приведенное здесь без доказательства.
ТЕОРЕМА КОГАЛОВСКОГО О
МНОГООБРАЗИЯХ. Для любого класса К универсальных алгебр фиксированной
сигнатуры имеет место равенство
Μ (К) = HPS{K).
Из определения многообразия очевидно, что совокупность, всех
(изоморфных друг другу) одноэлементных алгебр сигнатуры σ
образует многообразие. Назовем его тривиальным
многообразием. Заметим теперь, что если Μ — нетривиальное
многообразие алгебр, то Μ содержит алгебры любой бесконечной мощности.
Под мощностью алгебры 21 = (Α;σ) имеется в виду мощность
основного множества А. Действительно, пусть 21 € М, \А\ > 2 и
78
§5. Прямые и подпрямые произведения, ультрапроизведения
N — произвольная бесконечная мощность. Пусть {21* | г € /} —
совокупность алгебр совпадающих с алгеброй 21 и \1\ — N. Тогда
мощность М-алгебры Π %, не меньше мощности 2Ν > N. Пусть
С — подмножество основного множества алгебры Π 21; > имею-
iei
щее мощность N. В силу того, что каждый элемент подалгебры
<8 = {В; σ) М-алгебры Π 2li» порожденной множеством С, яв-
ie/
ляется значением некоторой термальной функции на элементах
множества С, а число различных термов конечной сигнатуры σ
счетно (его мощность равна Н0), то для мощности множества В
выполняются неравенства:
« = |С| < |5| < U «ο«η = Ν·
ηζΝ
Таким образом, действительно, М-алгебра ^В имеет мощность
N.
Для любого класса К универсальных алгебр, через Ksi
обозначим совокупность всех подпрямо неразложимых /^-алгебр. Так
как в представлении какой-либо алгебры 21 подпрямым
произведением алгебр 2lj(i€i) каждая алгебра 21; является гомоморфным
образом алгебры 21 (при проектировании щ), то в силу теоремы
Биркгофа о подпрямом представлении алгебр для любого
многообразия алгебр Μ включающего в себя алгебру 21 алгебры 21;
также входят в М; с другой стороны, если 2lj(iG7) являются М-
алгебрами, то любое подпрямое произведение алгебр 2lj (»€./)
также входит в многообразие М. Отсюда следует истинность
следующих формул для любых многообразий универсальных алгебр М1
иМ2:
М1 = М(М^), Мг = М2& Mlj = M2SI.
ЗАДАЧИ
1. Докажите, что прямое произведение решеток (полугрупп,
групп, колец) и само является решеткой (полугруппой, группой,
79
Глава 1. Основные понятия универсальной алгебры
кольцом). В то же время прямое произведение полей полем не
является.
2. Постройте диаграммы Хассе для решеток 21 χ <8 и 21 χ С,
если решетки 21, Ш, € заданы следующими диаграммами Хассе:
21 93 €
3. Докажите утверждение (*) изданного параграфа.
4. Пусть 21 = (Ζ;+,—}, докажите, что 21 неразложима в
нетривиальное прямое произведение.
5. Элемент α решетки <8 называется коатомом, если он
отличен от наибольшего элемента решетки 23 (от 1в) и для любого
с € В неравенство а<с влечет равенство с = 1#, т.е: если \в
покрывает элемент а. Докажите, что алгебра 21 представима подпря-
мым произведением простых алгебр тогда и только тогда, когда
пересечение коатомов решетки Con21 равно Да-
6. Докажите, что единственной подпрямо неразложимой неод-
ноэлементой булевой алгеброй является двухэлементная булева
алгебра из задачи 12 §1. На основе этого замечания и теоремы
Биркгофа о подпрямом представлении алгебр выведите
утверждение теоремы Стоуна (§ 2) о представлении булевых алгебр.
7. Постройте представление алгебры 21 = (Z\+) в виде
подпрямого произведения алгебр 2lfl(n e 7V\{0}) вида (21η =
{0,1,... ,η — 1}; +), где + на 21п определяется как сложение по
модулю п.
8. Пусть p,q — различные числа. Докажите, что алгебра 2lpg
из задачи 7 разложима в прямое произведение алгебр 2lp, 2lg.
9. Докажите утверждение (**) из данного параграфа.
10. Докажите утверждение (***) из данного параграфа.
11. Докажите, что для любых алгебр 2li и 212 решетка Con 21 j x
Соп21г изоморфно вложима в решетку Con(2li χ 212).
80
§5. Прямые и подпрямые произведения, ультрапроизведения
12. Докажите, что для любых алгебр 011 и 212, если
решетка Con (21χ χ 212) дистрибутивна, то решетки Con (Qlj. χ 212) и
Con 211 x Con2l2 изоморфны.
13. Приведите примеры алгебр 21χ и 212 таких, что ни 21х, ни
212 не являются изоморфно вложимыми в алгебру 21г х 212.
14. Приведите пример неизоморфных бесконечных алгебр 21х
и 212 таких, что 2lx x 2Ц = 2l2 x 2l2. Заметим, что, как доказал
Ловач, для конечных алгебр Щ и 212 это невозможно.
15. Приведите примеры произвольно больших подпрямо
неразложимых (простых) решеток.
16. Докажите, что любое многообразие, порожденное
некоторым конечным числом конечных алгебр, может быть порождено
одной конечной алгеброй.
17. Докажите, что ультрапроизведение решеток (полугрупп,
групп, колец, полей) и само является решеткой (полугруппой,
группой, кольцом, полем).
18. Пусть для любого ϊεΝ алгебры 21* суть одна и та же
алгебра (£;+), пусть F — неглавный ультрафильтр на множестве N.
Докажите, что алгебры Гр^/F и (^5+) неизоморфны.
19. Докажите, что любая алгебра изоморфно вложима в
некоторое ультрапроизведение своих конечно порожденных
подалгебр.
20. Докажите утверждение (****) из данного параграфа.
21. Докажите утверждение (*****) из данного параграфа.
22. Докажите, что совокупность всех решеток (полугрупп,
групп, колец) является многообразием. Совокупность всех полей
многообразием не является.
23. Докажите, что класс полных решеток не является
многообразием.
24. Докажите, что существует лишь два многообразия
булевых алгебр: тривиальное, состоящее из одноэлементных булевых
алгебр и многообразие всех булевых алгебр.
25. Докажите, что если 21 — конечная алгебра, то для любого
81
Глава 1. Основные понятия универсальной алгебры
множества /, любого ультрафильтра F на /, если алгебры Ql^ieT)
суть алгебра 21, то алгебры П^-ч ρ и ^ изоморфны.
26. Докажите, что совокупность всех дистрибутивных
решеток является многообразием и любое нетривиальное
многообразие решеток включает в себя многообразие всех дистрибутивных
решеток.
27. Докажите, что совокупность всех абелевых групп
является многообразием. Пусть ρ — простое натуральное число. Группа
65 = (G; ·,-1, е) называется группой экспоненты р, если для
любого элемента Ь € G справедливо равенство ЬР = е. Докажите, что
совокупность всех абелевых групп экспоненты ρ является
многообразием и любое нетривиальное многообразие групп включает в
себя некоторое многообразие абелевых групп экспоненты р.
82
Глава 2
Многообразия
и свободные алгебры
§ 6. Абсолютно свободные алгебры.
Свободные алгебры многообразий
Основным предметом изучения в этой главе будут
многообразия универсальных алгебр. Важным инструментом при этом будет
понятие свободной алгебры.
Фиксируем некоторую сигнатуру σ = (/ό°,. ■ ·, /rSr, Со, ■ ■., ск).
В §2 было определено понятие терма сигнатуры σ. Через Τ(σ)
обозначим совокупность всех термов этой сигнатуры над
множеством переменных X — {χ0,Χχ,...,χη,...}. На множестве Τ(σ)
мы можем определить действие сигнатурных функций /*,
полагая значение функции /j на элементах ίχ(5ι),..., tSi(xSi) равным
терму fi(ti(xx),..., tSi(xSi)). Интерпретируя при этом константные
символы Ci сигнатуры σ самими этими константами ci; входящими
в Т(сг), получаем алгебру сигнатуры σ с основным множеством
Τ{σ). Назовем эту алгебру абсолютно свободной алгеброй
сигнатуры σ и будем обозначать ее как F(a) = (Τ(σ); σ).
Очевидно, что алгебра F(a) порождена множеством X. При этом алгебра
F(a) обладает некоторым принципиальным свойством,
определяющим ее роль при изучении произвольных алгебр сигнатуры σ.
Пусть 21 = (Л; σ) — произвольная алгебра сигнатуры σ и гр —
некоторое отображение множества X в множество А. Это
отображение φ допускает продолжение до некоторого гомоморфизма
φ-Φ алгебры F(a) в алгебру 21, т.е. существует гомоморфизм ψψ
алгебры F(a) в алгебру 21, совпадающий с отображением φ на
множестве X С F(a). Отображение ψψ: Τ(σ) —> А определим
следующим естественным образом:
ψψ(ί(Χι, ...,Хп))= ίκ(φ(χι), . . . , ф(хп)),
Глава 2. Многообразия и свободные алгебры
где через t(xi,... ,хп) обозначается произвольный терм
сигнатуры σ, а через ί%(χχ,... ,хп) — термальная функция алгебры 21,
соответствующая терму t{xx, ...,xn). Непосредственно
проверяется, что:
(*) 1) отображение ψψ является гомоморфизмом алгебры F{a)
в алгебру 21, продолжающим отображение ф.
2) подобный гомоморфизм (алгебры F{a) в алгебру 21,
продолжающий отображение ф) единственен (доказательство —
индукцией по длине терма).
Отсюда, в частности, следует, что любая не более чем
счетная алгебра сигнатуры σ представима (изоморфна) некоторой
фактор-алгеброй абсолютно свободной алгебры F(a).
Действительно,
пусть 21 = (Α; σ) конечна или счетна (конечно или счетно
множество Л), пусть φ — произвольное отображение множества X на
множество Л. В этом случае, описанный выше гомоморфизм ψψ
алгебры F(a) в алгебру 21 будет эпиморфизмом. Тем самым если
θ — ядро гомоморфизма ψψ) то 21 =F\<?) Iд. Выбирая при этом
различные отображения множества X на А, получаем различные
представления алгебры 21 в виде фактор-алгебр алгебры F(a).
Редуцируем эти свойства абсолютно свободной алгебры F(a) с
произвольных σ-алгебр на алгебры некоторого многообразия М.
Алгебру 21 = {Α; σ), порожденную множеством 1С Ли лежащую
в М, назовем М-свободно порожденной множеством X М-
алгеброй, если для любой алгебры <8 = (В\ и) из Μ и любого
отображения φ : X —> В существует некоторый гомоморфизм ψψ
алгебры 21 в алгебру 23, продолжающий отображение ф.
Как и выше, индукцией по длине терма (любой элемент
алгебры 21 есть значение некоторой термальной функции на элементах
из X U {cq, ... ,с£}), доказывается, что подобный гомоморфизм
алгебры 21 в алгебру 2$, продолжающий отображение ф,
единственен.
Заметим теперь единственность, с точностью до изоморфизма,
М-свободно порожденной множеством фиксированной мощности
М-алгебры, т.е. то, что в случае равномощности множеств X и
Υ М-свободно порождающих М-алгебры 21 и <8 соответственно,
алгебры 21 и <8 изоморфны.
84
§6. Абсолютно свободные алгебры
Действительно, пусть φ — взаимно однозначное отображение
множества X на множество Υ. Рассмотрим гомоморфизмы ψφ
алгебры 21 в алгебру 25 и ψφ-ι — алгебры <8 в алгебру 21.
Отображение ψφ-ι ■ ψφ, совпадающее на. X с отображением ф~х ■ ф,
тождественно на X. Пусть ϊάχ — тождественное отображение на
множестве X. В силу того, что 21 — М-свободно порожденная
множеством X М-алгебра, отображение ιάχ продолжается до
единственного гомоморфизма ψ ίάχ алгебры 21 в себя. Таким образом,
в роли этого единственного гомоморфизма должны выступать и
гомоморфизм ψφ-ι ■ ψφ алгебры 21 в себя и тождественный
гомоморфизм id<a алгебры 21. Тем самым, ψφ-ι · ψφ — ida-
Последнее же равносильно тому, что ψφ-ι = (ψφ)*1, т.е. гомоморфизм
ψφ является разнозначным гомоморфизмом алгебры 21 на
алгебру *В. Но таковые суть изоморфизмы, и требуемая однозначность
(с точностью до изоморфизма) задания М-свободно порожденной
М-алгебры мощностью М-свободных порождающих доказана.
Докажем теперь само существование М-алгебр, М-свободно
порожденных множествами любой мощности для нетривиальных
многообразий М. Если Μ — тривиальное многообразие, т. е.
состоит только из одноэлементных алгебр фиксированной
сигнатуры, то очевидно, что любая из этих алгебр и есть М-свободная
однопорожденная алгебра, а других просто нет. Тем самым будем
считать, что Μ нетривиально. Фиксируем некоторую мощность Η
и какое-либо множество X этой мощности. Рассмотрим
совокупность R всех троек (21, Υ, φ), состоящих из М-алгебры 21,
некоторого множества Υ порождающих алгебры 21, имеющего мощность
не более чем К, и некоторого отображения φ множества X на
множество К. В § 5 отмечено существование М-алгебр мощности К.
Если 21 = (Α; σ) подобная алгебра, то тройка (21, А, ф), где φ —
любое отображение X на А, входит вйи, значит, R не пусто.
Тройки (ΟΙ,Ζ,φ) и (2$, К, h) назовем изоморфными, если существует
изоморфизм ψ алгебры 21 на алгебру <8 такой, что ψ(Ζ) = Υ и
ψ ■ φ = h. В каждом классе попарно изоморфных троек
выделим по одному представителю. Получим некоторую совокупность
{(2li,Xi,y,) | i Ε 1} попарно неизоморфных троек такую, что для
любой тройки из R в {(2lj,Xj,i/,) | i E 1} существует изоморфная
ей тройка.
85
Глава 2. Многообразия и свободные алгебры
Рассмотрим теперь прямое произведение Π 21, алгебр 21* и его
ш
подмножество Z, имеющее вид φ(Χ), где отображение φ
определено на X следующим образом: для любого χ е X и. любого i € /
φ(χ)(ί) = yi(x). Мощность Ζ очевидным образом равна К.
Пусть <8 — подалгебра алгебры Π 21*, порожденная множе-
iei
ством Z. Так как Μ — многообразие, то Π %, € Μ, а значит, и
iei
!В е Μ. Покажем, что <8 является М-алгеброй М-свободно
порожденной множеством Ζ (множеством мощности К).
Действительно, пусть 21 = (Α; σ) — произвольная М-алгебра и h —
некоторое отображение множества Ζ в А. Пусть <£ — подалгебра
алгебры 21, порожденная множеством h(Z). Для тройки (С, Η{Ζ),Ηψ)
найдется тройка (21*0)Χί0,^>ί0) (to — некоторый элемент из /) ей
изоморфная. Обозначим изоморфизм пары (ΌΙί0,Χί0,φί0) на
пару (£,h(Z),hip) как φίο. Тогда отображение ψίυπ'ίο (здесь π8·0 —
ограничение проектирования щ0: Π 21* —> Д0 до алгебры 93) бу-
дет гомоморфизмом алгебры 23 на алгебру €. При этом так как
KJ = Фго И ^г0Фг0 = V, Τ» ¥>вд<, Ψ = ψϊοΦτο = V· В СИЛу Же ВЗа-
имной однозначности отображения φ на множестве X получаем
совпадение отображений φί0π'ίο и h на множестве Ζ = <^(Х).
Таким образом, гомоморфизм φί0π[ο является продолжением
отображения h, и доказательство существования М-алгебр, М-свободно
порожденных множествами любой бесконечной мощности (<8 и
есть такая алгебра с М-свободными порождающими Ζ мощности
Н), завершено.
Нетрудно доказать, что
(**) если 21 — М-алгебра, М-свободно порожденная
бесконечным множеством X, и {хг,..., хп} — η-элементное подмножество
множества X, то подалгебра <8 алгебры 21, порожденная
множеством {χι,... ,хп}, будет М-алгеброй, М-свободно порожденной
множеством {χι,..., хп}.
Тем самым завершено доказательство существования
М-алгебр, М-свободно порожденных множеством любой мощности.
В дальнейшем, через -Fm(N) будем обозначать (единственную
с точностью до изоморфизма) М-алгебру, М-свободно
порожденную множеством порождающих мощности N. Таким образом, для
любой М-алгебры 21, мощности не превышающей Н, существует
86
§6. Абсолютно свободные алгебры
конгруэнция θ алгебры Fm(N) такая, что алгебры 21 и Fm{")/q
изоморфны. Отсюда, в частности, следует, что любое
многообразие Μ порождается совокупностью своих М-свободных алгебр
(Fm(N) | N — произвольная мощность}, т.е. Μ = M({FM(H) | Η —
произвольная мощность}).
В следующем параграфе мы докажем, что на самом деле в этой
формуле можно ограничиться лишь одной счетно-порожденной
М-свободной алгеброй .Fm(No) (^о — счетная мощность) или
счетной совокупностью М-свободных конечно порожденных алгебр
{FM(n) \neN}.
Так как совокупность всех алгебр сигнатуры σ является
многообразием (обозначим его далее как Μσ), то очевидно, что
абсолютно свободная алгебра сигнатуры σ будет изоморфна Μσ-
алгебре, М^-свободно порожденной счетным множеством X, т.е.
FH = FM,(Ko)·
При этом, для любого многообразия М-алгебр сигнатуры σ
существует конгруэнция θ алгебры F{cr) такая, что ^\σ) I q =
FmO&o)· Остановимся на характеризации конгруэнции θ
абсолютно свободной алгебры F(er), фактор-алгебры ^(σ) I q, по которым
изоморфны М-свободно порожденной М-алгебре для некоторого
многообразия М.
Любые гомоморфизмы алгебры 21 = (Α; σ) в себя называются
эндоморфизмами алгебры 21. Совокупность всех
эндоморфизмов алгебры 21 обозначим через End(2l). Конгруэнцию θ
алгебры 21 назовем вполне инвариантной конгруэнцией, если для
любого ψ € End(2l) и любых а, 6 € Л отношение θ(α, b) влечет
отношение θ(φ(α),φ(ο)). Имеет место
ТЕОРЕМА 1. Конгруэнция θ алгебры F(a) является вполне
инвариантной тогда и только тогда, когда алгебра ^ \σ) /q
является алгеброй некоторого многообразия М, М-свободно
порожденной множеством {[х]в | х € X}.
Доказательство. Пусть θ — вполне инвариантная
конгруэнция абсолютно свободной алгебры F(a). Через Xе обозначим
совокупность {[х]в | х £ X}. Таким образом, совокупность Xе
порождает алгебру F\a) /q. Покажем, что совокупность Xе
является М-свободно порождающей совокупностью М-алгебры ** \°>Q
многообразия Μ = Μ{^\σ) q) порожденного алгеброй ^\σ) /β.
87
Глава 2. Многообразия и свободные алгебры
Прежде всего, заметим, что любое отображение φ : Xя —>
^σ' Ι θ продолжается до гомоморфизма алгебры ** ^a'Q самой в
себя. Действительно, пусть для любого Χι Ε Χ ф([хг\е) = [&i\e, где
di Ε F(a). Рассмотрим отображение φ : Χ —> F(a), определенное
как ф(хi) = α,ί. Тогда существует эндоморфизм φψ алгебры F(o)
в себя продолжающий отображение ф. Отображение φψ алгебры
{σ' Ι θ в се^я определим следующим образом: для любого [α]θ Ε
В силу того, что θ вполне инвариантная конгруэнция
алгебры F(a), определение отображения φψ корректно (не зависит от
выбора элемента α в классе [α]θ). В силу того, что φ ψ —
эндоморфизм алгебры F(a), отображение φψ будет эндоморфизмом
алгебры F(a) Iq При этом, очевидно, ограничение φψ на множестве
Xе совпадает с ф.
Покажем теперь, что Xе является М-свободно порождающим
множеством М-алгебры F\a) q Пусть 21 = (Α; σ) Ε Μ. Тогда по
теореме Биркгофа о многообразиях, для некоторого множества
/, для некоторой подалгебры *8 алгебры { \σ> ι β) существует
гомоморфизм h алгебры <8 на алгебру 21. Здесь y\a)/Qj —
прямое произведение алгебр <8Дг Ε /), каждая из которых совпадает
с алгеброй ^\σ) q.
Пусть ф — некоторое отображение множества X9 в алгебру 21.
Для любого χ Ε Xе пусть дх Ε 23 и таков, что h(gx) = ф(х). Для
г Ε Ι определим отображение yi множества Xе в алгебру F(a) /^
полагая Уг(х) = дх(г). По доказанному выше существуют
эндоморфизмы φψ. алгебры ^(σ)/0, продолжающие отображения yi для
любого г Ε I. Отображение ψ' алгебры ?{<*)§ в алгебру F(a) q
определим равенствами: для любого г Ε Ι φ'(α)(г) = φψν(α).
Так как множество Xs порождает алгебру ^ψ) ιq и φ'^)(ϊ) —
Уг(Ь) Ε 55 для любого элемента Ь = \x]q из Χθ, то φ'^(σ) ^ q fg
Отображение φψ алгебры F(a) /q b алгебру 21 определим
равенством φυ = Υιφ'.
Непосредственно проверяется, что
88
§6. Абсолютно свободные алгебры
(***) отображение φψ является гомоморфизмом алгебры
(σ) Ι θ Β алгебру 21, продолжающим отображение ψ.
Таким образом, действительно, фактор-алгебра абсолютно
свободной алгебры, по вполне инвариантной конгруэнции,
является свободной алгеброй многообразия, порожденного этой фактор-
алгеброй.
Докажем обратное, что для любого многообразия М, если
^°'Q является М-свободной алгеброй М-свободно
порожденной множеством {[χ]θ \ х € X}, то θ — вполне инвариантная
конгруэнция алгебры F(a).
Пусть φ — эндоморфизм алгебры F(a). Требуется показать,
что для любых элементов a,b Ε F(a) отношение θ(α, b) влечет
отношение θ(φ(α),φφ)).
Прежде всего заметим, что если θ ф V<a, т.е. многообразие Μ
нетривиально, то для различных х,у из X классы [x]g, [y]e
также различны. В противном случае, пусть a,b Ε F(a), [α]β ф [b]e
и, рассмотрев какое-либо отображение ψ : χ —> F(a) такое, что
ψ(χ) = а,ф(у) = Ь, для эндоморфизма φψ алгебры F(a),
продолжающего ψ, получили бы противоречие с условием: 9(х,у) —>
θ(φψ(χ),φφ(υ)).
Определим отображение ф множества Xе в алгебру F\a) I q
с помощью равенств ф([х]е) = [ψ(χ)]θ- Замеченное выше о
различности классов [х]в, [у]в для различных х,у Ε Χ доказывает
корректность подобного определения ψ. Так как ^ (σ) /q — М-
свободная алгебра, М-свободно порожденная множеством Xе, то
существует гомоморфизм φψ алгебры F\a) q в алгебру F\o~) /^
продолжающий отображение ψ.
Пусть а,Ь Ε F(a) и имеет место отношение 9(а,Ь), т.е.
[а]е — [b]g. В силу определения алгебры F{cr) существуют
термы ti(xu...} хп) и t2(x'l,...,x'rn), где жь ... ,хГ1,х[,... ,х'т Ε Χ
такие, что а = ίι(χι, . ..,жп) и Ь = t2(x[, ■. ■ ,х'т)· Но тогда
[φ(α)]θ = [ip(ti(xi,... ,жп))]* = [h(ip(xi),..., φ(χη))]θ =
= hiMxjh, · · ·, MOW = tiMi&i]*). · ■ ■, Φ([Χη]β)) =
= к(<Рф([х1]о),...,(рф([хп]е)) =(fi,([h(xi1...,xn)\e) = ψφ([α]ο) =
= φψ([6\θ) = φψ{[ί2{χ'χ,..., x'm)]e) = ί2(φψ([χ[}θ), ■ ■ ·, Ρψ(Κ,Μ) =
= ЧПА\е), ■■-, Ф(Ыв)) = ta(M*i)b, ■ ■ ■, 1Ф'т)}е) =
89
Глава 2. Многообразия и свободные алгебры
Инвариантность конгруэнции θ алгебры F(a), а вместе с тем
и вся теорема полностью доказаны.
ЗАДАЧИ
1. Докажите утверждение (*) из данного параграфа.
2. Докажите, что алгебра 21 = (Ν \ {0}; +} является свободной
однопорожденной полугруппой в многообразии всех полугрупп.
Опишите все конгруэнции алгебры 21 и опишите с точностью до
изоморфизма строение всех однопорожденных полугрупп.
3. Докажите, что алгебра 21 = {Z; +, —ж, 0) является свободной
однопорожденной группой в многообразии всех групп.
Опишите с точностью до изоморфизма строение всех однопорожденных
групп.
4. Докажите, что алгебра 2lm = 21 χ · · · χ 21 (га раз), где 21 —
алгебра из задачи 3, является свободной М-порожденной
абелевой группой в многообразии всех абелевых групп.
5. Докажите, что алгебра 2lm = 21 χ · · · χ 21 (га раз), где
21 = ({0,1,...,р— 1};+,— х,0), ρ — простое число, а
операции +, —х рассматриваются по mod p, является свободной М-
порожденной алгеброй в многообразии Μ всех абелевых групп
экспоненты р.
6. Докажите, что решетка с диаграммой Хассе
<>
является свободной двупорожденной решеткой в многообразии
всех решеток.
7. Пусть X — некоторое множество (алфавит) и X* —
совокупность всех конечных последовательностей элементов из X (слов в
алфавите X). На X* введем операцию умножения (конкатенацию)
следующим образом: для a,b € X* под α · b понимаем слово из X*,
получающееся приписыванием слова b непосредственно вслед за
словом а. Докажите, что полугруппа (X*; ·) является свободной
90
§7. Тождества и эквациональные классы
|Х|-порожденной (здесь \Х\ — мощность множества X)
полугруппой в многообразии всех полугрупп.
8. Докажите, что алгебра 21 х 21, где 21 — двухэлементная
булева алгебра, является свободной однопорожденной булевой
алгеброй в многообразии всех булевых алгебр.
9. Докажите утверждение (**) из данного параграфа.
10. Докажите утверждение (***) из данного параграфа.
11. Докажите существование изоморфного вложения алгебры
FM(&) в алгебру Fm(W) для любых мощностей Н,Н' таких, что
К < К' и любого многообразия М.
§ 7. Тождества
и эквациональные классы
Под тождеством сигнатуры σ мы будем понимать
формальные равенства двух термов этой сигнатуры
tl(xl,...,xn) =t2{x'v...,x'm).
Здесь ΐι,ί2 € Τ(σ) и Var tx = {xly.. .,xn}, Var t2 = {x\,. .-,χ^}
(заметим, что термы ίχ(χχ,..., хп), t2(x[,..., х'т) могут иметь
общие переменные). Истинность тождества ίχ(χχ,..., хп) = t2(x'x,
..., х'т) на алгебре 21 сигнатуры σ означает совпадение значений
соответствующих термальных функций при любых подстановках
значений элементов алгебры 21 вместо переменных, входящих в
тождество (входящих во множество Var ίχ \J Var i2). Мы будем
говорить, что тождество истинно на классе алгебр К, если это
тождество истинно на каждой алгебре этого класса.
Соответствующие ситуации (истинность тождества ίχ(χ) = t2(x') на алгебре
21, на классе алгебр К) будем обозначать следующим образом :
211= ίχ(χ) = t2(x'), K\=tx(x) = t2(x').
Если Г — некоторая совокупность тождеств, то запись 21 И Г
(К Ν Γ) будет означать, что каждое из тождеств входящих в Г
истинно на 21 (истинно на К).
В дальнейшем через Ы(К), для класса К алгебр сигнатуры
σ будем обозначать совокупность всех тождеств сигнатуры σ,
истинных на классе К. Для любой совокупности Г тождеств сигна-
91
Глава 2. Многообразия и свободные алгебры
туры σ через Μοά(Γ) будем обозначать совокупность всех алгебр
сигнатуры σ, на которых истинны тождества из Г.
Класс К алгебр сигнатуры σ называется эквациональным
классом алгебр, если он имеет вид Μοά(Γ) для некоторой
совокупности тождеств Г.
Вспомнив определение решеток, модулярных решеток,
дистрибутивных решеток, полугрупп, групп, колец, определяемых
как классы алгебр соответствующей сигнатуры, обладающих
теми или иными свойствами (выражаемыми тождествами),
убеждаемся, что все эти классы алгебр являются эквациональными
классами.
Нетрудно непосредственно заметить, что для любого
тождества ti(x) = t2(x') и любых алгебр 2lj(i € /) соответствующей
сигнатуры имеют место следующие свойства:
(*) а) если 21; 1= ίχ(χ) = t2(x') и <8 — подалгебра алгебры 2lj, то
25 1= t\(x) = t2(x'), если (Г — гомоморфный образ алгебры 21^, то
С N h(x) = t2(x');
б) если для любого iElимеет место 2lj t= t\{x) — Ьг(х'), то Π 21ί
Ν φ) - h(x').
В силу этого замечания, к примеру, для любого
многообразия алгебр М, любого тождества ti(x) =t2(x') соответствующей
сигнатуры, утверждения Μ \= ti(x) = t2(x') и {Fm(N) | N —
произвольная мощность} t= ti(x) = t2(x') равносильны.
Заметим также, что если тождество ti(x) — fa{x') зависит от
η переменных, то для любой алгебры 21, 21 t= t\{x) — ^(ж') тогда
и только тогда, когда тождество ίχ(χ) = h{x') истинно на любой
^порожденной подалгебре алгебры 21.
Покажем теперь, что эквациональные классы алгебр — это в
точности многообразия.
ТЕОРЕМА БИРКГОФА ОБ ЭКВАЦИОНАЛЬНЫХ
КЛАССАХ. Класс К универсальных алгебр сигнатуры σ
является многообразием тогда и только тогда, когда он является
эквациональным классом.
Доказательство. В силу отмеченных выше свойств (*) любой
эквациональный класс является многообразием. Покажем
обратное.
Пусть Μ — некоторое многообразие алгебр. Докажем, что Μ яв-
92
§7. Тождества и эквациональные классы
ляется эквациональным классом. Достаточно показать, что Μ =
Mod(Id(M)). Включение Μ С Mod(Id(M)) очевидно. Пусть
теперь 21 = (Α;σ) eMod (Id(M)). Пусть мощность алгебры 21 не
превосходит некоторой бесконечной мощности N. Пусть Fm(N) —
М-алгебра, М-свободно порожденная некоторым множеством С
мощности Η и φ некоторое отображение множества С на
множество А. Продолжим отображение С на Л до отображения ψψ
алгебры Fm(^) на алгебру 21 следующим образом. Для
любого элемента α Ε -Fm(N) существует терм ί(χχ,...,χα) сигнатуры σ
и элементы άχ, ...,dnE С такие, что α = t(dx, ...,dn). Положим
ψφ{α) = ί%(φ(άι),... ,φ(άη)). Прежде всего отметим корректность
определения отображения ψψ. Пусть α = ίχ(άχ, ...,dn) — fa(d\,
...,d'n), где di,djE С. Так как совокупность С является М-свободно
порождающей М-алгебры Fm(ct), то для любых элементов еь
...,еп,е'1г..,е'т алгебры Fm(p) (выбранных с условием, что если
di=dj, то &1=е',) существует гомоморфизм η алгебры Fm(<?) в себя
такой, что η(άχ) = еь... ,η(άη) = en^(d[) = e'v ... ,v(d'm) = e'm
(любое отображение α\—>β{ и d'j—te'j продолжимо до
эндоморфизма алгебры Fm(N))· Таким образом, имеет место равенство ίχ(βχ,
■ ■•,^n)—h(e'i,-.-,e'm). Тем самым на алгебре Fm(&) истинно
тождество ίχ(χχ, ...,xn)^t2(x'l, ...,х'т), где xi=x'j если di—d!y
Как замечено выше, это означает истинность тождества t\{x)
— h{x') на многообразии М. Включение 2l€Mod(Id(M)) влечет, в
свою очередь, истинность этого тождества на алгебре 21. Тем
самым равенства а= ίχ(άχ, ...,dn) = h{d\, ■■■,d'm) — b влекут равенства
кл({ф(ах), ...,φ(άη)) = i2A((-0(d'i). -Ж<0)> те- определение φ+
корректно. Непосредственно проверяется, что φψ является
гомоморфизмом алгебры FM(H) на алгебру 21, т.е. 21 G H({FM(H)}) С
Н(М). Но поскольку Μ — многообразие, то Н(М) С М, и мы
имеем включение 21 Ε Μ. Таким образом, включение Mod(Id(M))C
Μ, а вместе с тем и теорема полностью доказаны.
Отметим ряд непосредственных следствий этой теоремы и ее
доказательства.
СЛЕДСТВИЕ 1. Если Μ — многообразие алгебр и е1; ...,&π,
β'χ, ...,ε^ некоторые элементы из М-свободно порождающей
совокупность элементов алгебры Fm(^), wo любое тождество ίχ(χχ,
...,Хп) = biix'x, ...,x'm), (здесь ίχ(χχ, ...,Хп), h{x'x, -,^) некоторые
термы такие, что Χι = χ1- тогда и только тогда, когда е^ = е'-
93
Глава, 2. Многообразия и свободные алгебры
истинно на многообразии Μ β том и только β том случае, когда
элементы ij_(ei, ...,e„)u ^(e^, ...,e^J, алгебры Fm(&) равны.
СЛЕДСТВИЕ 2. Для любого многообразия Μ любой
бесконечной мощности N имеют место равенства Μ = ({-Рм(^)}) и
Μ = M({FM(n) I neN}).
Отметим, что для любого ηζ,Ν существуют многообразия Μ
такие, что Μ φ М[\¥м{р)\) (см., к примеру, задачу 4).
СЛЕДСТВИЕ 3. Для любых алгебр Qli(iel)u любого
ультрафильтра F на множестве I, если тождество ti(x) — fa(x')
истинно на алгебрах ΟΙί(ίζΓ), то оно истинно и на
ультрапроизведении Π ι/F-
Утверждения следствия 3 непосредственно вытекают из
утверждения теоремы и отмеченного в §5 включения Ри(К) С М(К)
для любого класса алгебр К.
ЗАДАЧИ
1. Докажите утверждение (*) из данного параграфа.
2. Докажите утверждение следствия 2 из данного параграфа.
3. Докажите утверждение следствия 3 из данного параграфа
непосредственно (без использования утверждения теоремы) на
основе понятия истинности тождества на алгебре.
4. На основе результата задачи б предыдущего параграфа
докажите, что если Μ — многообразие всех решеток (всех
модулярных решеток), то Μ φ M(Fm{2)).
5. Докажите, что любое тождество tx{x) = ^(^') сигнатуры s
= (+, — ,·) истинно на алгебре 21 = (Z,+,—, ■) тогда и только тогда,
когда оно истинно на алгебре 25 = (R;+,—,·). Здесь Z(R) —
совокупность всех целых (всех действительных) чисел со стандартным
определением на них операций +, — ,-.
§ 8. Исчисление тождеств
Основным вопросом, рассматриваемым в данном параграфе,
является вопрос, когда истинность некоторых тождеств Τ на
произвольной алгебре влечет истинность на этой алгебре какого-либо
иного тождества t\{x) = <г(ж'). На основе введенных ранее обозна-
94
§8. Исчисление тождеств
чений, нас будет интересовать характеризация таких
совокупностей тождеств Τ и тождеств ίχ(χ) = ίο,{χ'), что имеет место
отношение
mod (Τ) Ν ti(x) = t2(x').
В этом случае мы будем говорить, что тождество ti(x) = h(x')
является следствием совокупности тождеств Т, и обозначать
этот факт следующим образом:
Tt=t1(x) = t2(x').
Мы построим в этом параграфе некоторое формальное
исчисление (аналогичное исчислению высказываний и исчислению
предикатов первого порядка), дающее более конструктивное
описание отношения следования 1= между тождествами.
Формулой исчисления тождеств сигнатуры σ будем
называть любое тождество этой сигнатуры. Совокупность всех
подобных формул обозначим как 1άσ.
Совокупностью аксиом исчисления тождеств назовем
совокупность тождеств Αχσ = {t(x) = t(x) \ t(x)E Τ(σ)}.
Правилами вывода исчисления тождеств назовем
следующие четыре правила вывода:
ti(xi)=t2(x2) .
' t2(.X2)=tl(xiV
9ч ti(xi)=t2{X2), ^2(^2)^3(^3) ■
' χ ^Щ=^(х3) '
^/(^(xi),...,^^))^/^^),:.,^))'
где / — любой η-местный символ сигнатуры σ;
4) _ fl(gl.-Mgn)=^2(gl,---»a?n)
}ti(qi{xi)y.yqn{Xn))=t2{qi{xi),...,qn{xn)))
где q\{xi),...,qn{%n) ~ произвольные термы сигнатуры σ.
Для любой совокупности тождеств Τ<Ζ\άσ последовательность
тождеств
h\xi) ~Ч\Х2)> ■•■■>h\xi) =^2\X2J
сигнатуры σ называется выводом тождества ΐ"(χ") =Щ(Х2) из
совокупности тождеств Т, если для любого г < η тождество
^ι(^ι) = ^2(^2) ЛН[бо входит в совокупность Τ[]Αχσ, либо
получается из тождеств {^(ж*) =£2(^2)» ·■·> *1-1(^1-1) =ί2_1(^2_1)} по °Д"
ному из правил вывода 1)-4). Если существует вывод тождества
95
Глава 2. Многообразия и свободные алгебры
*ι(^ι) =^2(^2) из совокупности тождеств Т, то назовем тожде-
ство ΐ1(^1) =Ь2{%2) выводимым из Τ и обозначим эту ситуацию
следующим образом
Τ Ь фх) =t2{x2).
Через h ίχ(χι) = ^2(^2) обозначим выводимость тождества
ti(x~i) = t2(x2) из пустой совокупности тождеств.
ТЕОРЕМА ПОЛНОТЫ ДЛЯ ИСЧИСЛЕНИЯ
ТОЖДЕСТВ. Для любой совокупности тождеств Τ и тождества
ίι(^ι) = ^2(ж2) отношения Τ h ^(ίχ) =^2(^2) и Τ \= ί1(^1) =t2(x2)
равносильны.
Доказательство. Индукцией по длине вывода тождества
*ι(^ι) = £2(^2) из совокупности тождеств Τ (используя то, что из
истинности посылки правил вывода 1) - 4) на некоторой алгебре
очевидным образом следует истинность заключения правила
вывода на этой же алгебре) непосредственно замечается импликация
Τ l· ^(xj) =£2(^2) ^ Τ \= tx(xx) =t2{x2). Покажем обратное. Пусть
Через Τ' обозначим совокупность всех тождеств, выводимых
из совокупности тождеств Т. Пусть θ = {(ί'(χ'), t"(x")) \ (t'(x') —
t"{x")) € Τ'}. В силу правил вывода 1) - 3) очевидно, что
отношение θ является конгруэнцией алгебры F(a). В силу правила
вывода 4) и того, что Τ С Т' на алгебре F\a) q истинны любые
тождества из совокупности Τ (правило вывода 4) по сути утверждает
вполне инвариантность конгруэнции θ на алгебре F(a)). Тем
самым в силу отношения Τ \= h(xi) — t2(x2) имеет место Ρ\σ) /q t=
k(xi) = Φ2), т.е. (^(жц), fe(i2)> € θ и (t^) = fc(z2)) € Г. По
определению совокупности Τ' имеет место Τ l· ti(x~i) = £2(^2) и
теорема доказана.
СЛЕДСТВИЕ 1 (теорема компактности для
исчисления тождеств). Для любой совокупности тождеств Τ и любого
тождества t\{x\) = £2(^2) отношение Τ t= ίι(χχ) = £2(2:2)
равносильно существованию конечного подмножества Т\
совокупности Т, для которого истинно отношение Τ t= ίχ(χι) = ^(жг)-
СЛЕДСТВИЕ 2. Отношение Τ h tx(x{) = ^{χ2) (и
равносильное ему отношение Τ \= ti(x\) = £2(^2)) эквивалентно
вхождению пары элементов {ti(xi),t2(x2)) алгебры F(a) во вполне ин-
96
§9. Конгруэнц-перестановочные многообразия
вариантную конгруэнцию, порожденную на алгебре F(a)
совокупностью пар {(t'(x'), t"(x")) I (t'(x') = t"(x")) e T}.
ЗАДАЧИ
1. Пусть σ = (/q), докажите, что для любого терма t(x) этой
сигнатуры от одной переменной χ имеет место отношение fo(x,x)
= χ \= t(x) = χ.
2. Докажите утверждение следствия 1 из данного параграфа.
3. Докажите утверждение следствия 2 из данного параграфа.
4. В исчислении тождеств постройте выводы тождеств уУ((хЛ
у) V ζ) = у Л (у V ζ) и χ Л (у Л ζ) — (χ Л у) V (х V ζ) из
совокупности тождеств, являющихся аксиомами класса дистрибутивных
решеток.
5. В исчислении тождеств постройте вывод тождества х~1у~1ху
= е из совокупности тождеств, являющихся аксиомами класса
абелевых групп.
6. Докажите утверждение теоремы компактности для
исчисления тождеств непосредственно (используя лемму Мальцева
из §4).
§9. Конгруэнц-перестановочные,
конгруэнц-модулярные,
конгруэнц-дистрибутивные
многообразия.
Дискриминаторные многообразия
Свойства совокупности конгруэнции универсальной алгебры
существенно влияют на многие другие свойства этой алгебры.
Особенно наглядно это проявляется при рассмотрении не
отдельно взятой алгебры, а при работе со всеми алгебрами, входящими в
некоторые многообразия (или при работе со свободной алгеброй
этого многообразия). В частности, целый ряд свойств
совокупностей конгруэнции алгебр многообразия оказался эквивалентен
требованиям о существовании некоторого терма,
удовлетворяющего на рассматриваемом многообразии тем или иным
тождествам. Условия подобного рода для многообразий (о
существовании терма, удовлетворяющего некоторым тождествам) называ-
97
Глава 2. Многообразия и свободные алгебры
ют условиями Мальцева. В данном параграфе мы рассмотрим
некоторые из этих условий.
Напомним, что алгебра 21 называется конгруэнц-перестано-
вочной, если для любых θ ι, Θ2& Con 21 имеет место равенство
0j.o02 = #2°#ι· Ранее замечалось, что в этом случае θ\\/02 =
подмногообразие алгебр называется конгруэнц-перестановоч-
ным, если все алгебры этого многообразия коыгруэнц-перестано-
вочны.
ТЕОРЕМА МАЛЬЦЕВА О КОНГРУЭНЦ-ПЕРЕСТА-
НОВОЧНЫХ МНОГООБРАЗИЯХ. Для любого
многообразия Μ следующие условия эквивалентны:
1) Μ — конгруэнц-перестановочно;
2) алгебра Fm(3) конгруэнц-перестановочна;
3) существует терм p(x,y,z) (сигнатуры многообразия М)
такой, что на Μ истинны тождества ρ(χ,ζ,ζ) = χ,ρ(χ,χ,ζ) = ζ.
Доказательство. Импликация 1)—>2) тривиальна. Пусть
теперь выполнено условие 2) и множество {а, 6, с} М-свободно
порождает М-алгебру Fm(3). Пусть θ = 0oi), Φ = Qbc. Так как 0оф
= Фо# и (а,с}<Е0оФу то найдется элемент d € FM(3) такой, что
(α,(ί)€Φ, (d,c)^9. Элемент d имеет вид р(а, 6, с) для некоторого
терма р(х, у, ζ) сигнатуры многообразия М. Таким образом,
(а,р(а,Ь,с)) еФ
и значит, так как {p(a,b,c),p(a,b,b)) € Φ, то (a,p(a,b,b)) ΕΦ.
Заметим теперь, что ограничение Φ на подалгебру ^В,
порожденную в Fm(3) элементами а, 6, равно Δβ. Действительно, пусть
и,υ € В и (и,у)€Ф = 0ь,с · По лемме Мальцева (§4) найдутся
натуральное η и термы pi(x,y~i),...,pn(x,yn), а также кортежи
элементов ёх, ...,ёп алгебры Fm(3) такие, что
и = Pi (<7i, ei), Pi {di, ei) = pi+1 (gi+1, ё4)
для 1<г<пиг» = pn{dn, ёп)· При этом {qi,di} — {b,c} для
любого г < п. Рассмотрим эндоморфизм φψ алгебры FM(Z) в
себя, продолжающий отображение ψ : {a,b,c} —> Fm(3) такое, что
ψ(α) -- а, ф(Ь) = Ь, ф(с) = Ъ. Тогда термы pi{x,yi), ■■■,рп{х,Уп) и
кортежи элементов φψ(&ι), • •·,φψ(εη) удовлетворяют заключению
леммы Мальцева и тем самым имеет место включение
98
§9. Конгруэнц-перестановочные многообразия
(и, V) = (φφ(η),φφ(ν)) Ε ^(6),^(с) = 0%ь = Ав.
Итак, действительно Ф\В = Δβ.
Но а, р(а, Ь, Ь)еШи выше замечено, что
(a,p(a,b,b)) e Ф.
Тем самым p(a,b,b) = α. Аналогично доказывается равенство
p(a,a,b) = b. А так как эти равенства имеют место для М-свободно
порождающих М-алгебры FM(3), то на Μ будут истинны
тождества
ρ(χ,ζ,ζ) = χ,ρ(χ,χ,ζ) = ζ.
Импликация 2) —> 3) доказана.
Пусть теперь выполнено условие 3), 21 £ Μ, Θ,Φ € Con 21,
α, Ь,с G 21 и (а, 6) G 0, (Ь, с) G Ф. Положим d=p(a,b,c). Так как
р(а,Ь,6)=аи (6,с)бФ, то (а,р(а,6,с)=й)еФ. Аналогично замечается,
что (d,c)G0. Тем самым имеет место включение
0оФ СФо0.
Симметричность ситуации для 0 и Φ влечет включение Φ ο θ С 0
о Φ а, значит, и равенство
0 о Φ = Φ о θ.
Импликация 3)—>1), а вместе с тем и теорема доказаны.
В качестве следствия этой теоремы отметим конгруэнц-пере-
становочность многообразий групп и колец. Действительно,
термы p(x,y,z) = χ ■ у'1 ■ ζ в первом и p(x,y,z) — x—y+z во втором
случае удовлетворяют тождествам
p(x,z,z) — х и ρ(χ,χ,ζ) = ζ на многообразиях групп и колец
соответственно.
Алгебра 21 называется конгруэнц-модулярной (конгру-
энц-дистрибутивной), если решетка Con 21 модулярна
(дистрибутивна). Многообразие Μ называется конгруэнц-модуляр-
ным (конгруэнц-дистрибутивным), если все алгебры этого
многообразия конгруэнц-модулярны (конгруэнц-дистрибутивны).
99
Глава 2. Многообразия и свободные алгебры
Без доказательств (которые аналогичны доказательству
теоремы Мальцева о конгруэнц-перестановочных многообразиях),
которые можно найти, к примеру, в [15], приведем характеризации
конгруэнц-модулярных и конгруэнц-дистрибутивных
многообразий с помощью условий Мальцева.
ТЕОРЕМА ДЕЯ О КОНГРУЭНЦ-МОДУЛЯРНЫХ
МНОГООБРАЗИЯХ. Для любого многообразия Μ следующие
условия эквивалентны:
1) Μ — конгруэнц-модулярно;
2) алгебра Fm(4) конгруэнц-модулярна;
3) для любой М-алгебры 21 и а, Ь, с, d (Ξ 21
(«,^<cV((uvio)AftvO);
4) для некоторого натурального η существуют термы
p0(x,y,z,u), pi(x,y,z,u),... ,pn(x,y,z,u) сигнатуры многообразия Μ
такие, что для г — 0, 1, ..., п— 1 на Μ истинны тождества:
pQ(x,y,z,u) = χ, pn(x,y,z,u) = и, pi(x,y,y,x) = ж,
Pi(x,y,y,u) — pi+i(x,y,y,u) для нечетных г,
Pi(x,x,u,u)=pi+i(x,x,u,u) для четных г.
ТЕОРЕМА ЙОНССОНА О
КОНГРУЭНЦ-ДИСТРИБУТИВНЫХ МНОГООБРАЗИЯХ. Для любого
многообразия Μ следующие условия эквивалентны:
1) Μ — конгруэнц-дистрибутивно;
2) алгебра Fm(3) конгруэнц-дистрибутивна;
3) для любой М-алгебры 21, любых а,Ь,с € 21 имеет место
включение
(«.^(CA^VlCAt);
4) для некоторого натурального η существуют термы
Po(x,y,z), pi(x,y,z), ...,pn(x,y,z) сигнатуры многообразия Μ такие,
что для г— 0, 1, ..., п— 1 на Μ истинны тождества:
Po(x,y,z) = χ, pn{x,y,z) = z, Pi(x,y,x) = χ,
Ρί(χ,χ,ζ) = pi+i(x,x,z) для четных i,
Pi(x,z,z)=pi+i(x,z,z) для нечетных г.
В качестве следствия теоремы Дея отметим следующий факт,
который может быть доказан и непосредственно.
СЛЕДСТВИЕ 1. Любое конгруэнц-перестановочное
многообразие является конгруэнц- модулярным.
100
§9. Конгруэнц-перестановочные многообразия
Доказательство. Пусть Μ — конгруэнц-перестановочное
многообразие и терм p(x,y,z) удовлетворяет условию Мальцева.
Тогда очевидно, что при η = 2 термы po(x,y,z,u) = χ, px(x,y,z,u)
= p(x,y,z), p2(x,y,z,u) — u удовлетворяют условию теоремы Дея и,
значит, Μ — конгруэнц-модулярно.
В качестве примера конгруэнц-дистрибутивных многообразий
укажем на любое многообразие решеток (любое подмногообразие
многообразия всех решеток). Действительно, если Μ —
некоторое многообразие решеток, то непосредственно проверяется, что
условию 4) теоремы Йонссона удовлетворяют термы p0(x,y,z) = ж,
Ριίχ,ν,ή = ((xAy)V(yAz)\/(zAx)), p2(x,y,z) = ζ.
Важную роль в исследовании многообразий, как это
замечено в конце § 6, играет класс Ms τ всех подпрямо неразложимых
алгебр входящих в многообразие М. Справедливость многих
результатов, доказанных для конгруэнц-дистрибутивных
многообразий, основана на следующем утверждении, приведенном здесь
без доказательства.
ЛЕММА ЙОНССОНА. Если многообразие Μ = М(К),
порожденное классом алгебр К, является конгруэнц-дистрибутив-
ным, то имеет место включение
Msj С HSPU{K).
Доказательство этой леммы см., к примеру, в [15].
Наличие для многообразия одновременно свойств конгруэнц-
перестановочности и конгруэнц-дистрибутивности позволяет
существенно упростить совокупность условий Мальцева для конгру-
энц-перестановочности и конгруэнц-дистрибутивности. Алгебру
21 будем называть арифметической, если она одновременно кон-
груэнц-перестановочна и конгруэнц-дистрибутивна.
Многообразие состоящее из арифметических алгебр, назовем
арифметическим многообразием. Для арифметических многообразий
имеет место следующая характеризация условием Мальцева.
ТЕОРЕМА ПИКСЛИ ОБ АРИФМЕТИЧЕСКИХ
МНОГООБРАЗИЯХ. Для любого арифметического
многообразия Μ следующие условия эквивалентны:
1) Μ — арифметично;
2) существует терм р(х,у,£) сигнатуры многообразия Μ
такой, что на Μ истинны тождества
101
Глава 2. Многообразия и свободные алгебры
р(х, у, х) = р(х, у, у) = р(у, у, х) - х.
Доказательство. Пусть Μ — арифметическое многообразие.
По теореме Мальцева о конгруэнц-перестановочных
многообразиях найдется терм m(x,y,z) такой, что на Μ истинны тождества
m(x,z,z) — χ и m(x,x,z) = ζ.
Пусть {α, b, с} — совокупность М-свободных порождающих ал-
гебры FM(3) и θ = <Г(3\ Φ = <Л Ψ = <Г(3)· Так как
(α, с) G Φ Λ (θ V ψ) = (Φ Λ θ) V (Φ Λ ψ) и, в силу конгруэнц-
перестановочности алгебры FM(3), (ΦΛ^)ν(^Λψ) = (ΦΛ0)ο(ΦΛψ),
то найдется элемент d £ А такой, что (α,φξΦΛθ и (й,с)сФЛф. Тем
самым для некоторого терма q(x,y,z) сигнатуры многообразия Μ
имеют место равенства и включения:
d= q(a,b,c), (α, q(a,b,c)) еФАв, (q(a,b,c),с) еФАл\>.
Так как (а,с)еФ, то включение (a,q(a,b,с)) €ΦΑθ влечет
включение
(а,9(а,Ь,а)) еФ.
Как показано в доказательстве теоремы Мальцева о
конгруэнц-перестановочных многообразиях, ограничение Ф[^В,
конгруэнции Φ на подалгебру <8 алгебры Fm(3) порожденную
элементами а, 6, равно Δβ. Тем самым имеем равенство
a = q(a,b,a).
Аналогично замечается, что a — q(a,a,c) и 6 = q(a,b,b).
Рассмотрим терм
p(x,y,z) = m(x,q(x,y,z),z).
Тогда:
p(a,a,c) = m(a,q(a,a,c),c) = с,
p(a,b,b) = m(a,q(a,b,b)yb) = α,
p(a,b,a) — m(a, g(a, 6, α),α) = a.
А так как эти равенства имеют место для М-свободно
порождающих М-алгебры F^(3), то на Μ будут истинны тождества
р(х, у, х) = р(х, у, у) = р(у, у, х) = х.
Покажем обратное. Пусть на многообразии Μ истинны
тождества
102
§9. Конгруэнц-перестановочные многообразия
р(х, у, х) = р(х, у, у) = р(у, у, х) = χ
для некоторого терма p(x,y,z). Непосредственно в силу теоремы
Мальцева о конгруэнц-перестановочных многообразиях замечаем,
что Μ конгруэнц-перестановочно.
Рассмотрим терм
q(x,y,z) =p{x,p{x,y,z),z).
Тогда
q(x,x,y) = x, q(x,y,x) = x, q(x,y,y)=y,
т.е. для η = 2 и для термов
pQ(x,y,z) = x, pi(x,y,z) = q(x,y,z), p2(x,y,z) = z
имеет место истинность условия 4) теоремы Йонссона о конг-
руэнц-дистрибутивных многообразиях. Тем самым Μ конгруэнц-
дистрибутивно. Арифметичность М, а вместе с тем и вся теорема
доказаны.
Важную роль в главе 3 будут играть так называемые дискри-
минаторные алгебры и связанные с ними многообразия.
Алгебру 21 назовем дискриминаторной, если существует терм d(x,y,z)
сигнатуры этой алгебры такой, что для любых a,b,c € А имеет
место
ία, если α φ 6,
d(a,6,c) = <
I с, если a = о.
Любую трехместную функцию на произвольном множестве Л,
обладающую этим свойством, будем называть
дискриминатором на Л. А любой терм с этим свойством — дискримина-
торным термом алгебры 21. Класс К алгебр фиксированной
сигнатуры назовем дискриминаторным, если существует терм
d(x,y,z), являющийся дискриминаторным для каждой из К-&я-
гебр. Многообразие Μ назовем дискриминаторным, если оно
порождается некоторым дискриминаторным классом К, т.е.
классом, для которого некоторый терм d(x,y,z) определяет дискрими-
наторные функции на каждой /^-алгебре.
103
Глава 2. Многообразия и свободные алгебры
Нормальной трансформацией на множестве А называется
четырехместная функция n(x,y,z,u) такая, что для любых a,b,c,e Ε A
. . . I с, если α = Ь,
n{a,b,c,e) = <
I е, если α ψ о.
Для любой алгебры 21 существование термов, определяющих на
А дискриминаторную функцию и нормальную трансформацию,
равносильно в силу следующих, непосредственно проверяемых
равенств:
п(х, у, z, u) = d(d(x, у, z),d(x, у, и), и),
d(x,y,z) = n(x,y,z,x).
Заметим, к примеру, что двухэлементная булева алгебра 2$ =
({0,1};Л, V, -ι, 0, 1) является дискримииаторной алгеброй.
Действительно, непосредственно проверяется, что терм
d(x, у, ζ) = (χ Л -.(я Θ у)) V (ζ Λ (χ Θ у))
является дискриминаторным на алгебре 25. Здесь х®у = (->xAy)V
(жЛ->у).
Точно так же непосредственно проверяется следующее: для
любого конечного поля F = (F; +, —, ·,0,1} состоящего из η
элементов, терм
d(x, y,z) = z + (x-z)(y- x)n~l
определяет дискриминаторную функцию на F.
Далее докажем ряд простых свойств дискриминаторных
алгебр и дискриминаторных многообразий.
ЛЕММА 1. Любая неодноэлементная дискриминаторная
алгебра является простой.
Доказательство. Пусть терм d(x,y,z) является
дискриминаторным термом алгебры 21 и θ Ε Con 21, θ φ Δ^. Тогда существуют
различные элементы a,b Ε А такие, что (а,Ь) Ε θ. В этом случае
для любого элемента с из А
(d(a, b, с) — a, d{a, а, с) = с) Ε θ,
104
§9. Конгруэнц-перестановочные многообразия
т.е. θ = Va· Простота алгебры 21 доказана.
Так как ограничение дискриминаторной функции на любое
подмножество остается дискриминаторной функцией, то любая
дискриминаторная алгебра наследственно проста (т.е.
простыми являются все подалгебры данной алгебры).
ЛЕММА 2. Любое дискримнаторное многообразие арифме-
тично.
Доказательство. Пусть Μ — М(К), К — дискриминаторный
класс и терм d(x,y,z) определяет дискриминаторные функции на
.ίΓ-алгебрах. Тогда на К, а в силу равенства Μ = М(К) и на М,
будут истинны тождества
d(x1y,y)=x, d(x,y,x) = x, d(y,y,x) = x.
В силу теоремы Пиксли об арифметических многообразиях Μ
арифметично.
Пусть Μ — дискриминаторное многообразие, К —
дискриминаторный класс, терм d(x,y,z) — дискриминаторный терм для К
и Μ — М(К). Через Мд обозначим класс всех М-алгебр на
которых терм d(x,y,z) определяет дискриминаторную функцию. Тем
самым, в частности, К С М^.
ЛЕММА 3. Для любого дискриминаторного многообразия Μ
имеет место равенство
MSi = Md.
Доказательство. В сиду леммы 2 многообразие Μ
арифметично и, в частности, конгруэнц-дистрибутивно. По лемме Йонс-
сона
Msi С HSPU(K).
На классе К истинна следующая формула исчисления
предикатов первого порядка:
Уж, у, z(d(x, χ, ζ) = zk,{x = у V d(x, у, ζ) = χ)),
утверждающая, что терм d(x,y,z) определяет дискриминаторную
функцию на основном множестве алгебры.
Хорошо известна ТЕОРЕМА ЛОСЯ (приводимая здесь без
доказательства, доказательство ее см., к примеру, в [13]): для
любых алгебр 2lj (i€l), любого ультрафильтра F на множестве I и
105
Глава 2. Многообразия и свободные алгебры
любой формулы φ исчисления предикатов первого порядка, если
%, 1= φ для всех iel, то Π^γ F 1= φ·
Таким образом, терм d(x,y,z) определяет дискриминаторные
функции на всех алгебрах из Ри(Ю- В силу замеченного
выше алгебры из SPU(K) также будут дискриминаторными. По
лемме 1 дискриминаторная алгебра является простой и, значит,
HSPU(K) = (SPu(K))e. Здесь Ке означает класс, получаемый
добавлением к классу К одноэлементной алгебры
соответствующей сигнатуры. Тем самым все М5/-алгебры являются
дискриминаторными (с дискриминаторным термом d(x,y,z)) и
включение Msi С Md доказано. Обратное включение Md С М^/следует
из леммы 1 и включения М3 С MSi, имеющего место для
любого многообразия М. Здесь Ms — совокупность всех простых
М-алгебр. Лемма доказана.
Многообразие Μ называется полупростым, если
MSI = Ms,
т.е. если каждая подпрямо неразложимая М-алгебра проста.
В силу леммы 1 М^-алгебры просты и, таким образом, имеет
место
СЛЕДСТВИЕ 1. Дискриминаторные многообразия
полупросты.
ЛЕММА 4. Для любой алгебры 21 из дискриминаторного
многообразия М, для любых элементов а,Ь,с,е из А включение
{с,е)€.в£ь (и эквивалентное ему включение в£е С в£ь)
равносильно равенству d(a,b,c) ■■= d(a,b,e).
Доказательство. Так как на Msi истинно тождество d(x,x,y)
— у, то это тождество истинно на всем многообразии М. Тогда,
если 211= d(a,b,c) — d(a,b,e), то
*/<ЬN d{aie^bh^chib)-chib &
т.е.
aAbN сАь=е/<ь
106
§9. Конгруэнц-перестановочные многообразия
Таким образом, равенство d(a,b,c) — d(a,b,e) действительно
влечет включение (с,е) е 9®ь.
Покажем обратное. Непосредственно проверяется
(отправляясь от его истинности на Л^-алгебрах), что на Μ для любого
η-местного символа / сигнатуры многообразия Μ истинно
тождество
d(xt у, f(zu ..., ζη)) = d(x, у, f(d(x, y,zi),..., d(x, у, zn))).
Рассмотрим совокупность
Ρ = {(с, е) е 2l2|d(a, b, с) = d(a, b, e)}.
В силу истинности на Μ указанного выше тождества Ρ
является конгруэнцией на 21. С другой стороны, на Μ истинны
тождества d(x,y,x) = χ и d(x,y,y) = χ, а, значит, d(a,b,a) = d(a,b,b). Таким
образом, (о,Ь)Е Р. Тем самым б£ь С Ρ т.е. для любых с, е (Ξ 21,
если (с,е)е^6, то d(a,b,c) = d(a,b,e). Лемма доказана.
Многообразие Μ обладает свойством продолжимости
конгруэнции, если для любой М-алгебры 21, любой ее подалгебры
93, любой конгруэнции θ на алгебре 93 имеет место равенство θ
(21) [93 = Θ, где θ (21) — наименьшая конгруэнция на алгебре 21
включающая в себя все пары ^-эквивалентных элементов
алгебры 93.
Из утверждения леммы 4, в силу того, что для любой алгебры
21 из дискриминаторного многообразия М, для любых элементов
a,b,c,e из А включение (с,е)£в*ь определяется равенствами термов
от элементов a,b,c,e имеет место
СЛЕДСТВИЕ 2. Любое дискриминаторное многообразие
обладает свойством продолжимости конгруэнции.
Без доказательств приведем еще ряд свойств дискриминатор-
ных многообразий. Доказательство этих свойств можно найти, к
примеру, в [17].
ЛЕММА 5. а) Если 21 — алгебра из дискриминаторного
многообразия М, то для любых ее элементов а,Ь,с,е равенство
в*ь=в*е равносильно равенству
d(d(a,b,c), d(a,b,d(a,c,b)), d(a,c,b)) = е.
б) Если 21 — алгебра из дискриминаторного многообразия М,
то для любых ее элементов а,Ь,с имеют место равенства
107
Глава 2. Многообразия и свободные алгебры
^а,Ь V ^а,с — ^о,п(а,6,с,6) > @а,Ь Л ^а,с ~ Vn(o,6,6,c) ·
Многообразие Μ называется конгруэнц-регулярным, если
для любой алгебры 21 из Μ, любых конгруэнции 0, ι/> на 21 и
любого ее элемента а из равенства [α]# = [α\ψ вытекает равенство θ
= φ, т.е. многообразие Μ конгруэнц-регулярно, если для любой
алгебры 21 из Μ и любых конгруэнции 0, ^ на 21 из совпадения
некоторых классов ^-эквивалентных и ^-эквивалентных
элементов алгебры 21 вытекает совпадение конгруэнции θ η ψ.
Многообразие Μ называется конгруэнц-униформным, если
для любой алгебры 21 из Μ и любой конгруэнции θ на 21 мощности
всех ^-классов на 21 равны, т.е. для любых a,b£ A
\Ш = |[ь]*|.
На основе утверждения леммы 5а) доказывается утверждение
следующей теоремы.
ТЕОРЕМА 1. Любое дискриминаторное многообразие
конгруэнц-регулярно и конгруэнц-униформно.
В силу леммы 5а) для любой алгебры 21 из дискриминаторного
многообразия М, для любых ее элементов а,Ь,с существует
элемент ее А такой, что 9®ь = 9®е. Отсюда и из утверждений леммы
56) вытекает следующее утверждение.
СЛЕДСТВИЕ 3. Для любой алгебры 21 из
дискриминаторного многообразия, любая конечно порожденная конгруэнция на
21 является главной и пересечение любых конечно порожденных
конгруэнции на 21 также является главной конгруэнцией.
Таким образом, совокупность главных конгруэнции алгебры 21
образует подрешетку решетки Con 21.
Конечные дискриминаторные алгебры называются квази-
примальными. Приведем без доказательства следующую харак-
теризацию квазипримальных алгебр.
ТЕОРЕМА 2. Конечная алгебра 21 квазипрималъна тогда и
только тогда, когда многообразие Μ(21) арифметично и алгебра
21 наследственно проста.
Алгебра 21 называется примальной, если любая функция на
основном множестве алгебры 21 является термальной и 21 конечна.
В заключение параграфа сформулируем характеризацию при-
мальных алгебр.
108
§10. Рациональная эквивалентность многообразий
ТЕОРЕМА 3. Алгебра 21 примальна тогда и только тогда,
когда она квазипримальна, не .содержит собственных [отличных
от нее самой) подалгебр и не имеет нетривиальных [отличных
от тождественных) автоморфизмов.
Доказательство теорем 2 и 3 можно найти, к примеру, в [17].
ЗАДАЧИ
1. Приведите непосредственное доказательство утверждения
следствия 1.
2. Докажите, что любое нетривиальное многообразие групп,
колец не является конгруэнц-дистрибутивным.
3.Будет ли декартово произведение двух дискриминаторных
алгебр 21 χ = (Αχ\σ) и 2l2 = (Α2;σ) дискриминаторной алгеброй?
4. Докажите, что единственной дискриминаторной булевой
алгеброй является двухэлементная булева алгебра.
5. Докажите, что никакая группа не является
дискриминаторной алгеброй.
6. Докажите, с использованием теоремы 3 и непосредственно,
что двухэлементная булева алгебра примальна.
7. Постройте пример трехэлементной примальной алгебры
конечной сигнатуры.
8. Постройте пример двухэлементной
конгруэнц-перестановочной (конгруэнц-дистрибутивной) алгебры 21 такой, что
порожденное ею многообразие Μ(21) не является конгруэнц-переетановоч-
ным (конгруэнц-дистрибутивным).
§10. Рациональная эквивалентность
многообразий
В качестве одной из прикладных трактовок понятия
универсальной алгебры 21 = (А; а) можно рассматривать следующее:
на множестве А (множестве объектов, с которыми производятся
вычисления, преобразования) задан некоторый первоначальный
набор вычислительных, преобразовательных процедур, команд —
сигнатурных функций. С'помощью суперпозиции мы можем,
исходя из этого первичного набора, строить программы более
сложных вычислений на А. Очевидно, что подобными программами
будут термы сигнатуры σ. Этим программам — термам на самой
109
Глава 2. Многообразия и свободные алгебры
алгебре 21 — соответствуют термальные функции — реальные
вычислительные процедуры на множестве А. При этом в учет не
берется программа вычисления, а рассматривается лишь его
результативная сторона: результат вычислений на таких-то
объектах (элементах множества А — значениях аргументов
термальной функции) равен такому-то объекту (элементу из А —
значению термальной функции). Набор термальных функций алгебры
21 = (Α; σ) — это набор вычислительных возможностей
обеспечиваемых на множестве А алгеброй 21, если в качестве
единственного принципа построения более сложных программ вычислений,
исходя из первичных программ, команд (сигнатурных функций),
используется принцип суперпозиции. В этом случае определенный
интерес представляют собой алгебры 21χ = {Α; σχ) и А2 = (Α;σ2)
с одним и тем же основным множеством, но различными
сигнатурами, обладающие однако равными вычислительными
возможностями — совокупностями термальных функций. Решение
задачи характеризации пар подобных алгебр открывает в
дальнейшем возможность наложения каких-либо дополнительных
условий на первичные программы, команды вычислений алгебр (на
совокупность сигнатурных функций этой алгебры) с сохранением
вычислительных возможностей алгебры (совокупности
термальных функций). К сожалению, удобная характеризация пар алгебр
с равными в указанном смысле вычислительными
возможностями невозможна. Однако возможна подобная характеризация пар
многообразий универсальных алгебр с равными
вычислительными возможностями. Этому соответствует понятие рациональной
эквивалентности многообразий.
Напомним, что через Τ(σ) мы условились обозначать
совокупность всех термов сигнатуры σ. Рассмотрим пару многообразий
Мх и М2 универсальных алгебр, имеющих сигнатуры σχ и σ2
соответственно. Многообразия Μχ и М2 назовем рационально
эквивалентными, если существуют отображения ^(i^), ставящие в
соответствие символам сигнатуры σχ термы сигнатуры σ2
(символам сигнатуры σ2 — термы сигнатуры σχ) с сохранением арности
(числа аргументов функции / Ε σ; и терма Fi(f) совпадают) и
такие, что:
а) для любой Μχ-алгебры 21 = (Α; σχ), алгебра F2(2l) = (Л; σ2)
ПО
§10. Рациональная эквивалентность многообразий
входит в Мг, здесь а2-операции алгебры F2(2l) определяются на
А соответствующими ^(ег2)-термами алгебры 21;
б) для любой М2-алгебры 21 = (А;а2), алгебра Fi(2l) = (Α;σχ)
входит в М\, здесь алгебра ·Ρ\(21) определяется аналогично
алгебре F2(2l) в пункте а);
в) для любой Mi-алгебры 21 имеет место равенство .Fi(F2(2l))
= 21;
г) для любой М2-алгебры 21 имеет место равенство F2(Fi(QV))
= 21.
Под категорией многообразия универсальных алгебр Μ
мы будем понимать совокупность всех М-алгебр — совокупность
объектов категории и совокупность отображений между этими
алгебрами, являющихся гомоморфизмами М-алгебр друг в друга
— морфизмов категории. Через Нот(Л, В) для М-алгебр 21 и
23 будем обозначать совокупность всех морфизмов из Λ в β (всех
гомоморфизмов алгебры 21 в алгебру *8). В категории
многообразия Μ определена частичная (т.е. не всюду определенная)
операция произведения морфизмов: для φ еНот(Л,£?), ψ €Hom(f?,C)
под произведением ф ■ φ понимаем элемент из Нот(Д С),
являющийся суперпозицией гомоморфизмов φ и ф. Категорию
многообразия Μ будем впредь обозначать как М~*\
Под натуральным изоморфизмом категорий М-* и Ν~*
многообразий универсальных алгебр Μ и N соответственно, мы
будем понимать совпадение совокупностей основных множеств
алгебр из М"4 и алгебр из Ν~* и совпадение совокупностей
отображений между этими множествами являющихся гомоморфизмами
М- и iV-алгебр друг в друга.
Имеет место следующая характеризация рационально
эквивалентных многообразий на языке натуральных изоморфизмов
категорий.
ТЕОРЕМА МАЛЬЦЕВА О РАЦИОНАЛЬНО
ЭКВИВАЛЕНТНЫХ МНОГООБРАЗИЯХ. Для любых двух
многообразий Μ и N универсальных алгебр следующие условия
эквивалентны:
а) многообразия Μ и N рационально эквивалентны;
б) категории М~* и Ν~* натурально изоморфны.
Доказательство. Пусть многообразия Μ и N рационально
111
Глава 2. Многообразия и свободные алгебры
эквивалентны и отображения Fi:a\—> Τ(σ2), F2:tf2—>■ Τ (σι)
удовлетворяют определению рациональной эквивалентности
многообразий Μ и N. Непосредственно замечается, что для любых М-
алгебр 21 = (Α; σχ), <8 = (Β;σχ), если отображение φ : А —> В
является гомоморфизмом алгебры 21 в алгебру *8, то φ является
также гомоморфизмом iV-алгебры F2(2l) в iV-алгебру F2(<8) (так
как гомоморфизмы сохраняют действия термальных функций).
Тем самым имеет место включение Hom(2l, *8) С Hom(F2(2l),
F2((B)). Аналогично, с использованием отображения Fi,
доказывается включение Hom(C, 3))С Hom(F1(£), ·Ρχ(ΐ£)) для любых N-
алгебр С, 2D. Наряду с равенствами Fx(F2(2l)) = 21 и F2(Fi(€)) = €
для любых М-алгебры 21 и iV-алгебры С, это и доказывает
равенства Hom(2l, <8)=Hom(F2(2l), F2(<8)) и Hom(C, ©) = Hom(Fi(€),
Fifo)) для любых пар М-алгебр 21, <8 и iV-алгебр С, 3). Все вместе
это доказывает натуральный изоморфизм категорий М~* и N~* в
случае рациональной эквивалентности многообразий Μ и N.
Покажем обратное. Пусть многообразия Μ и N таковы, что
категории М~* и Ν~* натурально изоморфны. Прежде всего
заметим, что существуют такие отображения Fi-. σχ—ϊ Τ(σ2), F2:
σ2—> Τ(σχ), что имеют место равенства F2(Fm(&q)) = F/v(Ko)>
Fi(Fn(&o)) = Fm(&q). Так как понятие М-свободной алгебры
Fm(^o), М-свободно порожденной множеством X = {ζχ,...,
хп,...}, определяется в терминах отображений и
гомоморфизмов (напомним: для любого отображения ψ множества X в
произвольную М-алгебру <8 существует гомоморфизм ψψ
алгебры Fm(&o) в алгебру 23 продолжающий отображение ψ), то
натуральный изоморфизм категорий Μ и N влечет, что Ν-
алгебра, соответствующая М-алгебре Fm(N0), будет iV-алгеброй,
TV-свободно порожденной тем же множеством X. В силу
результатов § 6 (все счетно порожденные iV-свободные алгебры
изоморфны между собой с изоморфизмами, переводящими iV-свободные
порождающие одной алгебры в iV-свободные порождающие
другой TV-свободной алгебры) можно считать, что основные
множества алгебр Fm(^o) и F^(H0) совпадают и совокупность X =
{χι,..., хп,... } является М-свободно и iV-свободно
порождающей для алгебр Fm(^o) и Fn(#q) соответственно. Для любого
функционального TV-местного символа / сигнатуры σχ элемент
[Дхх, ..., Хп)]м алгебры FM(No) совпадает с некоторым элемен-
112
§10. Рациональная эквивалентность многообразий
том [ί/(ϋ, ..., Xm)]N алгебры Fjv(No)» где tf(xu ..., д^) — терм
сигнатуры σ2. Здесь [Джь ..., ^)]м и [(/(а*, ..., χ„)]Ν -
элементы алгебр Fm(#o) и Fn(N0) содержащие термы /(жь ... ,а^) и tf{x\,
■ ■ · ,Xm) соответственно. Рассматривая подалгебру Fm(h) алгебры
FmO&o), М-свободно порожденную множеством Х^ = {χι,..., хп}
и содержащую элемент [Дж1; ..., Хп)]м, и используя
натуральный изоморфизм категорий М~* и N~*, получаем, что подалгебра
алгебры Fiv(H0), порожденная термами tXl = хх, ..., tXn — Хп,
является ЛГ-свободно порожденной этими элементами и так как
f(xi,...,Xn)]M^([xi]M, ■••,Nm)fm(Ho), то [tffa, ···> ^)]лг€ <[xi]jv,
■ · ■ > [3Vi]at)fn(n0) = ^v(i). Таким образом, m < п.
Симметричное рассмотрение, основанное на многообразии N
вместо М, доказывает равенство п= т.
Для любых элементов αχ, ..., α„€ F^ (No) рассмотрим
отображение h : Χ —γ Fm(&o) такое, что h(xi) = щ для i<n и h(xi) = Xi
для % > п. Пусть ψΗ — гомоморфизм алгебры Fm(No) в самою себя,
продолжающий отображение h. Через ψ'}ι обозначим гомоморфизм
алгебры F^(K0) в самою себя, продолжающий отображение h. В
силу однозначной определимости гомоморфизмов срн и ψ'Η
отображением h и натурального изоморфизма категорий М~* и N~*,
отображения ψκ и ψ'κ совпадают. При этом,
(*) /(αχ,..., On) = f(h(xi),..., h(xn)) = <ρ*,(/(χι, · ■ ·, xn)) =
= ^(*/(жъ · · ·,Χη)) = tf(h(xi),..., Цхп)) = «/(αχ,..., On).
Определим отображение Fx : αχ —» Τ(σ2), полагая Fx(f)=tf.
Аналогичным образом определяется отображение F2:tf2—> Τ(σ{).
На основе равенства (*) и аналогичного равенства для
отображения F2 получаем требуемые равенства:
(**) F2(FM(K0)) = Fw(«0) и F1(Fiv(Ho))=FM(Ho).
Отображения Fx и F2, удовлетворяющие условию (**), будут
удовлетворять аналогичному условию для прямых произведений,
т.е. F2 (Π 2li) = Π F2(2lj), где алгебры %{iel) совпадают с алгеб-
iei iei
рой Fm(^o)· Если 21 — подалгебра М-алгебры 93, то F2(2l) будет
подалгеброй алгебры F2(<8). Если φ — гомоморфизм М-алгебры
21 на алгебру <8, то φ будет гомоморфизмом алгебры F2(2l) на
алгебру F2(23). Аналогичные замечания имеют место для
отображения Fi и TV-алгебр.
По теореме Биркгофа о многообразиях, Μ = HSP(Fm(&o))
113
Глава 2. Многообразия и свободные алгебры
и Ν = HSP(Fn(&o)). Таким образом, отображения F\ и F2
осуществляют рациональную эквивалентность многообразий Μ и N.
Теорема доказана.
Заметим, что в доказательстве теоремы мы предполагали
наличие в сигнатурах рассматриваемых многообразий лишь
функциональных символов (отсутствие констант). Рассмотрение
случая присутствия в сигнатурах константных символов требует
несущественных корректировок рассуждений, и мы его опускаем.
В связи с приведенной теоремой Мальцева о рационально
эквивалентных многообразиях как о многообразиях с
натурально изоморфными категориями представляет интерес результат
Р. МакКинзи о Морита эквивалентных многообразиях, то есть о
многообразиях с изоморфными (как частичные полугруппы)
категориями. А именно, им доказано, что Морита эквивалентность
многообразий сводится к рациональной эквивалентности любого
из них некоторой идемпотентной и обратимой редукции
подходящих матричных степеней алгебр другого многообразия. Точные
определения, формулировки и доказательства см., к примеру, в
[16].
ЗАДАЧИ
1. Докажите рациональную эквивалентность многообразия
Μι — булевых алгебр и многообразия М2 алгебр вида 21 —
(А; V, ф, 0,1), где А — основное множество некоторой булевой
алгебры <8 = (A;V, Л, -ι, 0,1), операции V и константы 0, 1 на
алгебрах 21 и 25 идентичны и операция φ алгебры 21 суть операция
симметрической разности булевой алгебры *8, т. е. для a,b € A
α φ b = (-πα Λ b) V (->Ъ Л a).
2. Пусть многообразия алгебр Μχ и Μι рационально
эквивалентны. Следуют ли из конгруэнц-перестановочности (конгруэнц-
модулярности, конгруэнц-дистрибутивности, конгруэнц-арифме-
тичности, конгруэнц-дискриминаторности, конгруэнц-униформ-
ности, конгруэнц-регулярности) многообразия М1; аналогичные
свойства для многообразия М{1
114
Глава 3
Условные термы
и условные многообразия
§11. Условные термы
и условно термальные функции
В § 10 говорилось о возможности трактовки понятия терма
сигнатуры σ как программы вычислений, составленной из
простейших подпрограмм (соответствующих сигнатурным
функциям) с помощью принципа суперпозиции. В программировании для
построения более сложных программ помимо оператора
суперпозиции используется условный оператор, строящий новые
программы, которые, в зависимости от полученных на данном шаге
результатов, осуществляют дальнейшие вычисления по
различным подпрограммам. Понятие условного терма переносит
принцип действия условного оператора в контекст рассмотрений
универсальной алгебры.
Для удобства дальнейших обозначений через =х будем
обозначать обычное равенство, а через =° — его отрицание. Условием
сигнатуры σ будем называть конечную совокупность Т(х)
равенств и неравенств вида
t\(x\)=htl(xl),
Ш) =int2n(x2n),
где tlj{x1-) — термы сигнатуры σ, ^€{0,1} и χ — \Jx]· Пол-
г,3
ной системой условий сигнатуры σ будем называть набор
(Г^ж),..., Гк(х)} условий данной сигнатуры такой, что формула
Г(х) =
Глава 3. Условные термы и условные многообразия
к
\/х( V &Гг(ж)) является тождественно истинной и для различных
г=1
l,m <к формулы &Гг(х)& &Гт(ж) невыполнимы.
Понятие условного терма сигнатуры σ определяется
индукцией за конечное число шагов с помощью следующих правил:
а) любая переменная и константа сигнатуры σ являются
условным термом;
б) если ti(xi), ...,tSi(xn) — условные термы сигнатуры σ и /?'
ζ. σ, то fi(ti(xi),..., tSi(xn)) также условный терм сигнатуры σ;
в) если ti(x),..., tn(x) — условные термы сигнатуры σ, а (Г^х),
..., Тп(х)} — полная система условий этой сигнатуры, то
Тг{х) -> ίχ(χ),
t(x) = I
Хп{х) -> tn(χ)
также является условным термом сигнатуры σ;
г) любой условный терм сигнатуры σ строится за конечное
число шагов согласно правилам а) - в).
Пусть 21 = (Α;σ) — произвольная алгебра сигнатуры σ.
Каждому условному терму t(x) сигнатуры σ поставим в
соответствие на основном множестве А алгебры 21 некоторую функцию
(условно термальную функцию), которую будем обозначать
как ία(χ) или просто t(x). Для правил а), б) из определения
условного терма мы предполагаем стандартные интерпретации,
имеющие место при интерпретации термов сигнатуры σ термальными
функциями на алгебрах этой сигнатуры. Если же условный терм
t(x) построен по правилу в) определения условного терма, то для
любых элементов α из 21 (соответствующих переменным χ
условного терма t(x)) положим t(a) = b (b € А) тогда и только тогда,
когда для некоторого г < η на элементах α алгебры 21 истинно
условие Ι\(α) и ti(a) = Ь.
Очевидно, что значение условно термальной функции t(x)
определено и определено однозначно на любом наборе элементов
α алгебры 21. Функции, определимые на алгебре 21 с помощью
условных термов, будем называть условно термальными
функциями алгебры 21.
В качестве простейшего естественного, но принципиально
важного примера условно термальных функций укажем на дискри-
116
§11. Условные термы и условно термальные функции
минатор. Действительно, дискриминатор d(x, у, ζ) определим на
любой алгебре произвольной сигнатуры с помощью следующего
условного терма:
td(x,y,z) = < ^ у '
Обычные термы сигнатуры σ будем далее называть
стандартными. Любой стандартный терм, в частности, является и
условным. Как и ранее, через Τ(σ) обозначим совокупность всех термов
сигнатуры σ, а через СТ(а) будем обозначать совокупность всех
условных термов сигнатуры σ.
В приведенных определениях условий и условного терма в
качестве условий используются системы равенств и неравенств
стандартных термов. На самом деле можно проводить одновременную
индукцию при определении понятий условия и условного терма
(т.е. допускать в определении условия произвольные конечные
системы равенств и неравенств условных термов). Нетрудно
заметить, что при этом для любой алгебры сигнатуры σ мы получим
тот же класс условно термальных функций, что и при нашем
первоначальном определении условия. Будем говорить, что условный
терм t(x) имеет нормальную форму, если t(x) — либо
стандартный терм, либо
Г Γι(5)-^ίι(5),
t(x) = {
( Гп(х) -> tn(x),
где и(х) — стандартные термы рассматриваемой сигнатуры.
Таким образом, нестандартный условный терм t(x) имеет
нормальную форму тогда и только тогда, когда правило в) из определения
условного терма применялось лишь единожды на
заключительном шаге построения t{x).
ЛЕММА \.Для любого условного mepMat(x) сигнатуры σ
существует условный терм ί'{χ) этой сигнатуры, имеющий
нормальную форму и такой, что для любой алгебры 21 сигнатуры
σ условным термам t(x)u t'(x) соответствует на 21 одна и та
оке условно термальная функция.
Для доказательства утверждения леммы индукцией по
сложности условного терма достаточно заметить, что если
117
Глава 3. Условные термы и условные многообразия
Г}(х)-►*}(*), Г Γ?(χ)^ί?(χ),
Ш={ ,...,^(х)={
и а)
f(x) =
Γχ(χ) ^ Ь(х),
Γη(χ) ->ίι(χ)
или б)
<(я) =/(*i(iCi),-,in(ic„)),
где / (xi,—,3Cn)€ с, то терм ί(χ) на любой алгебре 21 сигнатуры σ
вычисляет ту же функцию, что и терм
tl{x) = <
( Tx{x)\JY\{x)-+t\{x),
Гп(х)иГ?(х)->*?(х),
( rn(x)uri(x)^ti(x)
в случае а) и терм
ί2(χ) =
' г}(х)иг?(х)и-··игу(х)->/(<}(5).*1(5).··■.'?(*)).
Γ^(χ)υΐ1(χ)υ-·-υΓ5(χ)->/(^(χ),ί1(χ),...,ί5(χ)),
в случае б).
Таким образом, работая далее с условно термальными
функциями, всегда можно предполагать, что они заданы условными
термами в нормальной форме.
В силу леммы 1 условно термальные функции на алгебре суть
кусочно термальные. Иначе говоря, если / (х1;...,£„) —
условно термальная функция на алгебре 21, то существует разбиение
118
§11. Условные термы л условно термальные функции
Τγ,.,.,Τίς (к € Ν) декартовой степени Ап алгебры 21, определяемое
полной системой условий Γι(χ),...,Γ^) сигнатуры алгебры 21, и
существуют термы (стандартные) ti(x),...,tk(x) этой сигнатуры
такие, что функция / на кортежах элементов алгебры 21,
входящих в Τι (г < к), совпадает с термальной функцией, определяемой
термом и(х) на алгебре 21. Здесь χ = (χχ,...,χη).
Очевидно, что любая условно термальная функция f{xxr..,xn)
на алгебре 21 определима на этой алгебре с помощью
бескванторной формулы исчисления предикатов первого порядка, т.е.
существует бескванторная формула Φf(x^,..., а^, у) сигнатуры алгебры
21 такая, что для любого кортежа элементов α алгебры 21 и
элемента Ь из 21 f(a)=b тогда и только тогда, когда 211= Ф(а, Ь). Нетрудно
показать что обратное неверно (см. задачу 3 этого параграфа).
Формулу Φ (χ, у) исчисления предикатов первого порядка
назовем у-функциональной на классе алгебр К, если имеет место
К \= \/жЭ!уФ(ж,у). Формулу Ф(х,у) назовем у-зависимой, если
любая атомная подформула формулы Φ (ж, у), содержащая
переменную у, имеет вид у = h(x), где h(x) — терм, не содержащий у,
и у не входит в отрицания атомных подформул, содержащихся в
Ф(х,у). Напомним, что атомные подформулы формулы
исчисления предикатов первого порядка функциональной сигнатуры суть
равенства термов этой сигнатуры, а сама формула исчисления
предикатов первого порядка строится из атомных подформул за
конечное число шагов с помощью образования дизъюнкций,
конъюнкций, отрицаний формул и навешивания кванторов 3, V (или
без такового навешивания, в случае бескванторности
рассматриваемой формулы).
Синтаксическое описание условно термальных функций
содержится в следующем утверждении.
ТЕОРЕМА 1. Формула Φ (χ, у) исчисления предикатов
первого порядка определяет условно термальные функции на
алгебрах некоторого класса К тогда и только тогда, когда на
классе К формула Ф(х,у) эквивалентна некоторой бескванторной у-
функциональной у-зависимой формуле.
Доказательство. Непосредственно из определения условных
термов замечается, что условно термальные функции определимы
бескванторными у-функциональными у-зависимыми формулами
исчисления предикатов первого порядка.
119
Глава 3. Условные термы и условные многообразия
Покажем обратное, пусть на некоторой алгебре 21 у-зависимая
бескванторная формула Φ (ж, у) является у-функциональной.
Будем считать, что Ф(ж, у) представлена в дизъюнктивной
нормальной форме. Пусть
Щх,у)= V ά Фу (ж, У),
г=1 j=l
где Фу (ж, у) — атомные формулы или их отрицания. Прежде
всего, если какая-то из формул & Фу (х, у) не содержит переменной
3=1
у, то в силу у-функциональности формулы Ф(ж, у) эта формула
& Ф^(ж, у) либо ложна, либо следует из формулы V &Ф«у(£>у)·
Тем самым с точностью до эквивалентности формул можно
считать, что переменная у содержится во всех формулах вида
& Фу(ж, у). В силу у-зависимости формулы Ф(ж,у) эти вхожде-
3=1
ния должны иметь вид у = h(x). С другой стороны, если формула
к,
& Фу (ж, у) содержит два подобных равенства у = /г(ж) и у = у (ж),
.7=1
ki _
то конъюнкция у = h(x)]ky = <?(ж), входящая в & Фу (ж, у), мо-
жет быть заменена в этой формуле (с сохранением
эквивалентности формул) на конъюнкцию у = h(x)&.h(x) = д(х). Таким
образом, можно считать, что переменная у в каждой из формул
& Фу (ж, у) встречается ровно один раз, т.е. для любого / < η
.7 = 1
fc( _ Τι _ _
формула & Фу (ж, у) имеет вид & Ру(ж)&Лг(ж) = у, где Ру(ж) —
3=1 3=1
атомные формулы и их отрицания, не содержащие переменную у.
Очевидным образом, используя у-функциональность формулы
!S\ Sn I
& Pij(x),..., & Рту (ж) f есть полная
3=1 3=1 J
система условий. Тем самым в конечном итоге функции,
определимые на ЛГ-алгебрах 21 формулой Ψ (ж, у), совпадают с
функциями, определимыми на алгебрах 21 условным термом
120
§11. Условные термы и условно термальные функпри
ί '^ΡιΛχ)-> ht(x),
& Pnj(^) -> hn(x),
что и требовалось доказать. Теорема доказана.
Из определения условно термальных функций (индукцией по
определению условных термов) без труда замечается, что:
(*) а) для любого условного терма t(x) любой алгебры 21 и
любой подалгебры 23 алгебры 21, если ае23, то i(a)e23;
б) для любого условного терма t(x), любого изоморфизма φ
алгебр 21 и 23, для любых α = (αϊ,..., αη) ζ. 21 имеет место
равенство
ip{t{ai,..., αη)) = t(<p(ai),..., v?(aTt)).
В отличие от термов вычисление условных термов не
коммутирует с гомоморфными отображениями и декартовыми степенями,
т.е.:
(**) а) существуют алгебры 21, 23 и гомоморфизм φ алгебры
21 в 23, существует условный терм t(x) и элементы αϊ, ..., α„ из 21
такие, что
V?(ia(ai,..., αη)) ^ ί»(ν(αι)> ■ · ·, <p(an));
б) существуют алгебры 21х, 212, элементы aj, ...,a*;af, ...,a^ из
алгебр 2li и 212 соответственно и условный терм t(x) такие, что
<aix«a((ai,ai), · · ·, Κ.αη)) ^ (%« · · ·, <£),ία2(αι> ■ · · >αη))·
Алгебра 21 называется локально конечной, если для любого
η € N и любых элементов αϊ, ..., оГ1 из 21, подалгебра алгебры 21,
порожденная этими элементами, конечна. Алгебра 21 называется
равномерно локально-конечной, если существует функция к
Ν—> N такая, что для любого η € Ν, любых αχ, ..., ortG 21
мощность подалгебры (аь ...,αη)α, порожденной элементами αχ,..., α„,
не превосходит /ι(η).
Без доказательства приведем следующую алгебраическую ха-
рактеризацию условно термальных функций на равномерно
локально конечных алгебрах.
ТЕОРЕМА 2. Для любой конечной алгебры или
равномерно локально-конечной алгебры 21 = (Α, σ) конечной сигнатуры,
121
Глава 3. Условные термы и условные многообразия
произвольная функция: д : Ап —»■ А будет условно термальной
функцией алгебры 21 тогда и только тогда, когда подалгебры
алгебры 21 замкнуты относительно g (т.е. для любой
подалгебры 05 алгебры 21, любых aj, ..., α„ Ε 25 имеют место включения
д(а\,... ,ап) Ε *Β) и функция g коммутирует с
изоморфизмами подалгебр алгебры 21 (т.е. для любых подалгебр €, 05 алгебры
21, любого изоморфизма φ подалгебры 95 на подалгебру €, любых
αι,...,ατι Ε Я5 имеет место равенство φ(ς(αχ, ..., On)) = g {φ(α\),
■■; φ(θη)))-
Для любой алгебры 21 через Т(21) обозначим совокупность всех
термальных функций алгебры 21, а через СТ(21) — всех условно
термальных функций алгебры 21. Через F(2l) обозначим
совокупность произвольных функций на основном множестве алгебры 21.
Таким образом, для любой алгебры 21 имеют место включения
Т(21) Ε СТ(Я) ε F(2l).
Напомним, что алгебра 21 называется примальной, если она
конечна и T(2l) = F(2l). Алгебру 21 назовем условно примальной,
если она конечна и CT(2l) = F(2l).
На основе теоремы 2 можно доказать следующее утверждение
СЛЕДСТВИЕ 1. Конечная алгебра 21 условно примальна
тогда и только тогда, когда она не имеет собственных
подалгебр и нетривиальных автоморфизмов.
Переформулируем последние результаты на языке программ
вычислений. Пусть А — некоторая конечная совокупность
объектов, на которой заданы простейшие программы вычислений,
команды (соответствующие сигнатурным функциям алгебры 21 =
(Α;σ)), тогда для произвольной функции g : Ап —> А
существует некоторая программа, составленная из простейших программ с
помощью суперпозиций и условного оператора и вычисляющая на
А функцию g в том и только в том случае, когда все подалгебры
алгебры 21 замкнуты относительно функции g n g коммутирует с
изоморфизмами подалгебр алгебры 21. При этом любая функция
g : Ап —> А будет вычислима некоторой подобной программой в
том и только в том случае, если 21 не имеет собственных подалгебр
и нетривиальных автоморфизмов.
Для любой алгебры 21 = (Α;σ) через 2ld = (A; a\J (d3))
обозначим обогащение алгебры 21 добавлением в сигнатуру алгебры 21
122
§11. Условные термы и условно термальные функции
нового трехместного функционального символа d,
интерпретируемого на алгебре 2ld дискриминатором множества А.
Имеет место следующее утверждение.
ЛЕММА 2. Для любой алгебры 21 выполняется равенство
СТ(21) = T(2ld).
СЛЕДСТВИЕ 2. Для любой алгебры 21 равенство СТ(21) =
Т(21) имеет место тогда и только тогда, когда 21 — дискрими-
наторная алгебра.
ЗАДАЧИ
1. Даны условные термы t(xi,X2) и q{xi,X2,Xz) сигнатуры (+,·):
^хг,х2) = <
XI ■ Х2 = Х2
χι·χιφχι^>-
q{x\,X2,x%) =
Ιζχ -Х2 фхъ -> <
( Xl φ Χ2 ->■ Χι · Χι + Χ2,
\ Xl = Χι -> Χ2,
Χ\ + %2 — Χχ -> Χχ + Χ2 · Χΐ,
Χι + Χι Φ Χχ -> Χι',
Xl ■ Χ2 = ^3 -> (Χχ + Χ2) ■ Χ3,
( X\—X2^t X'S,
\ XX Φ Χ2 —> ^1 · Χχ,
Xl +X2 Φ Χ3 -> Χ2-
XX + Χ2 — ^3
вычислите значения ί(1,2), ί(0,3) и g(0,1,2), g(l,2,3) на алгебре
α = (ζ;+,·>.
2. Для условного терма t{xi,X2)
t(xl,x2) = хг +
{
\
Х\ + Х2 — х\ · Х2 ->■ ^ι
\
^1 + Х2 Φ Χχ ■ Х2 ->■
Ж χ = Ж2 ->■ Ж2
\
^2
Si т^ ^2 -> жх + xj
/
постройте условный терм t'(x), имеющий нормальную форму и
определяющий на всех алгебрах сигнатуры (+,·) те же условно
термальные функции, что и условный терм t(xi,x2).
3. На алгебре 21 = (Z;f), где Дж) = х+1, укажите функцию,
определяемую бескванторной формулой исчисления предикатов
первого порядка не являющуюся условно термальной функцией
этой алгебры.
4. Докажите утверждения (*) а) и б) из данного параграфа.
5. Докажите утверждения (**) а) и б) из данного параграфа.
123
Глава 3. Условные термы и условные многообразия
6. Докажите, что любая булева алгебра является равномерно
локально-конечной.
7. Приведите пример алгебры сигнатуры (/о)
локально-конечной, но неравномерно локально-конечной.
8. Будут ли алгебры 21 = (Zn = {О, 1, ..., п-1},/о) и <8 =
(Zn; +, ·) примальными, условно примальными? Здесь j{k) = k+\
для к<п~ 1 и Дп—1) = 0, а операции + и · определены на Zn как
сложение и умножение по модулю п.
§12. Условные тождества
и условные многообразия
По аналогии с понятием тождества введем следующее
определение.
Условным тождеством сигнатуры σ будем называть
формальное равенство двух условных термов этой сигнатуры ίι(χι,
...,Χη) = h{%'i, ···> х'т)· Истинность условного тождества на
алгебре 21 сигнатуры σ означает совпадение значений
соответствующих условно термальных функций при любой подстановке
значений элементов алгебры 21 вместо переменных, входящих в
условное тождество. Мы будем говорить, что условное тождество
ίχ(χ) =t2(x') истинно на классе алгебр К, если это условное
тождество истинно на каждой алгебре этого класса. Подобно тому
как это делали раньше, соответствующие ситуации мы будем
обозначать как 21 t= ti(x) =£2(2') и Я' N tx{x) =ί2(χ'). Мы сохраним
и остальные обозначения и определения, касающиеся истинности
тождеств на классах алгебр, перенося их на случай условных
тождеств и их совокупностей. Под условным многообразием мы
будем понимать класс всех алгебр фиксированной сигнатуры, на
которых истинна некоторая совокупность условных тождеств.
Стандартным образом, поскольку пересечение любой
совокупности условных многообразий и самоочевидным образом является
условным многообразием, для любого класса алгебр К
фиксированной сигнатуры существует наименьшее условное
многообразие, включающее этот класс К. Обозначим его как М*(К).
124
§12. Условные тождества и условные многообразия
Заметим, что любое условное многообразие является
универсальным классом алгебр (аксиоматизируемо V-формулами
исчисления предикатов первого порядка). Действительно,
истинность условного тождества ti(x) =£2(2') на алгебре 21, где
условные термы ti(x) и t2(x') имеют нормальную форму (а именно
таковыми можно ограничиться в силу леммы 1 § 11) и определены
как
Г\(х) -+ t\(x),
ГЦх) -► tl(x),
ГЦх') -+ t\{x'),
Γΐ(χ') -+ φ'),
очевидным образом равносильна истинности на алгебре 21 V-φορ-
мулы
W (к к (kT\{x)kkT)(x')^t\{x)=t){x'))\
Здесь χ" = χ U х1.
Поскольку любое условное тождество истинно на
одноэлементной алгебре соответствующей сигнатуры, любое условное
многообразие содержит соответствующую одноэлементную алгебру.
Как оказывается, отмеченные свойства полностью
характеризуют условные многообразия.
ТЕОРЕМА 1. Для любого класса алгебр К
неодноэлементная алгебра 21 входит в условное многообразие М*(К) тогда и
только тогда, когда на 21 истинны все универсальные формулы,
истинные на классе К. Иначе говоря, М*(К) — это наименьший
универсальный класс алгебр, включающий в себя класс К и
одноэлементную алгебру соответствующей сигнатуры.
Доказательство. Пусть К — произвольный класс алгебр
фиксированной сигнатуры σ. Тогда одноэлементная алгебра этой
сигнатуры входит в М*(К). Пусть 21 — некоторая
неодноэлементная алгебра сигнатуры σ, входящая в М*(К) и φ = \/χψ(χ) —
некоторая универсальная формула сигнатуры σ, истинная на всех
/('-алгебрах (здесь ф{х) бескванторная формула). Для
доказательства теоремы достаточно показать, что 211= ψ. Выберем представ-
h(x) =
t2(x')
125
Глава 3. Условные термы и условные многообразия
ление формул ψ(χ) и ^{х) в дизъюнктивной нормальной фор-
к г
ме: ψ(χ) — V Гг(ж), ψ(χ) = V ГДя). Здесь Гг(х) — некоторые
i=l i=k+l
условия сигнатуры σ. Очевидным образом можно считать, что
(Г1(ж), ...,Гг(ж)} — полная система условий. Определим условный
терм t(x) следующим образом:
' Γι (ж) ->χι,
t(x) = \ lkW-?Xl*
v ' Гк+1(х) ^x2,
k Гг(х) ->· x2.
Очевидно, что формула φ на одноэлементных алгебрах
сигнатуры σ эквивалентна условному тождеству t(x) = х\ и тем самым
действительно, 211= у>. Как замечено выше, это и завершает
доказательство теоремы.
Хорошо известно (теорема Тарского), что наименьшим
универсальным классом, содержащим произвольный класс К,
является класс ISPU(K). Таким образом, аналог формулы Биркгофа
для М(К) в случае условных многообразий имеет вид М*(К) =
ISPu(Ke) = (ISPu(K))e. В частности, если 21 — конечная алгебра,
то IPu(Ql) = 7(2l)„ имеет место (см. Задачу 16 из § 5). Здесь Ке —
класс алгебр, получаемый добавлением к классу К
одноэлементной алгебры соответствующей сигнатуры.
СЛЕДСТВИЕ 1. Для любой конечной алгебры 21 имеет
место равенство М*(К) = /5"(21)е.
Отметим так же следующее утверждение.
СЛЕДСТВИЕ 2. Класс алгебр К сигнатуры σ является
условным многообразием тогда и только тогда, когда К —
универсальный класс, содержащий одноэлементную алгебру
соответствующей сигнатуры.
Пусть теперь Г — некоторая совокупность условных тождеств
сигнатуры σ и t\(x) =t2(x') — еще одно условное тождество этой
сигнатуры. Через Г t= h(x) =t2(x') обозначим тот факт, что для
любой алгебры 21, на которой истинны условные тождества из Г,
истинно и условное тождество ti(x) —t2{x').
126
§12. Условные тождества и условные многообразия
Через Αχσ (где σ — некоторая фиксированная сигнатура)
обозначим следующую совокупность условных тождеств:
(
.,, , X = Ζ —> Ζ
' ' χ ψ ζ —¥ χ
2)
3)
χ = у —> χ
χ φ у —> χ
χ — χ —> ζ
Χ φ Χ —> Χ
= χ\
Ζ]
4)
у;
х = у -> zfc
χ Φ У —* χ
5) для любой функции f{x\,...,Xk) из σ
ί χ = у->/(«ι,...,zfc)
\ хфу-+ χ
χ φ у -»■ χ;
Ζ\ = Ζ2 -> Ζ3
^1 7^ ^2 -»■ Ζ\ =
kхфу^х
x-y-^ζχ _{ х — у-ь zi
χ фу —ϊ χ \ χ φ у —* χ
X — y-^Ζχ ,\ Χ — у -^ Ζι
хфу -* χ \ χ φ у -> χ
^ хфу-+х\
7) ί(χ) = ί(χ), для любого условного терма ί(χ) сигнатуры σ.
Рассмотрим также следующие правила вывода:
б)
χ = у -*
Ж = J/-+
.г = г/ ->· ζ3
χ φ у —> χ
χ = г/ -> ζ\
χ Φ у -ϊ χ,
Ч
ti(x) =t2(x')
2)
t2(x)=tl(x'Y
h(x) =t2(x'), 4х') =<з(5")
3)
ίχ(5) =ί3(ζ")
127
Глава 3. Условные термы и условные многообразия
4ч h(xi,...,xn) =t2{xi,...,xn)
*ι(9ι(^ι). -Λη(Χη)) =h(qi(xi), ...,g„(x„))'
где tl{x)M{x')M{^^\{x\,---,ql{xn)^q\x'i)^ql{x'r,) -
произвольные условные термы сигнатуры σ, Дх1,...,жп)б^.
Аксиомами исчисления условных тождеств будем
называть совокупность условных тождеств Αχσ, а правилами
вывода этого исчисления — правила вывода 1) - 4), указанные выше.
Если Г — некоторая совокупность условных тождеств, то под
доказательством условного тождества ti{x) —t2{x') в
исчислении условных тождеств из совокупности Г будем понимать
последовательность Ρι(χχ) = р\{х\), ·■■■> Ρι(%ι) = £2(^2) условных
тождеств такую, что условное тождество р"(ж") = р2(Щ) и есть
условное тождество t\{x) —t2{x'), а для любого г<п условное
тождество р\(х\) = РгС^г) либо входит в совокупность Αχσ U Г, либо
получается из некоторых предшествующих условных тождеств по
одному из правил вывода 1)-4).
Существование доказательства условного тождества
ti(x) =t2{x') из совокупности Г в исчислении условных тождеств
обозначим как Г h ch{%) =t2(x')-
Без доказательства приведем следующий результат. Его
доказательство базируется на использовании свойств дискриминатор-
ных многообразий и приведено, к примеру, в [16].
ТЕОРЕМА ПОЛНОТЫ ДЛЯ ИСЧИСЛЕНИЯ
УСЛОВНЫХ ТОЖДЕСТВ. Для любой совокупности Г
условных тождеств сигнатуры σ и любого условного тождества
ti(x) —t2{x') той оке сигнатуры отношения Г t= t\(x) —t2(x') и
Г h cti(x) —t2(x') равносильны.
ЗАДАЧИ
1. Является ли любое многообразие алгебр условным
многообразием?
2. Является ли класс всех полей, рассматриваемых в
сигнатуре (+,-,0,1), условным многообразием?
3. В каком случае является условным многообразием класс,
состоящий из всех алгебр, изоморфных некоторой фиксированной
алгебре 21 = (Α;σ), алгебре из {21, €}, где <£ — одноэлементная
алгебра?
128
§13. Условно рациональная эквивалентность
4. Непосредственно проверьте, что все аксиомы исчисления
условных тождеств истинны на любой универсальной алгебре.
§13. Условно рациональная
эквивалентность
условных многообразий
и алгебр
Рассматривая совокупность условно термальных функций
алгебры 21 как программно вычислительные возможности этой
алгебры (условный терм — программа вычислений на алгебре,
составленная из простейших программ, команд — сигнатурных
функций с помощью суперпозиций и условных операторов, а
условно термальная функция на А — программируемая
условным термом процедура вычислений на алгебре 21), приходим к
проблеме изучения алгебр с одинаковыми вычислительными
программируемыми возможностями при варьировании простейших
программ вычислений — сигнатурных функций. Эта проблема
уже обсуждалась нами в § 10 для термов и термальных
функций на алгебрах, но решить ее в этом случае оказалось
возможным не для отдельно взятых алгебр, а лишь для многообразий
алгебр. Рассмотрение условных термов позволяет работать с
отдельно взятыми конечными и равномерно локально-конечными
алгебрами.
Классы алгебр Κι и К2 сигнатур соответственно σχ и σ2
назовем условно рационально эквивалентными, если существуют
отображения Fx(F2), ставящие в соответствие символам
сигнатуры σι условные термы сигнатуры σ2 (символам сигнатуры σ2 —
условные термы сигнатуры σι) с сохранением арности (числа
аргументов функции /6 σι и терма Fi(f) совпадают) и такие, что:
а) для любой /Сх-алгебры 21 = (Α; σι), алгебра F2(2l) = {Α;σ2)
входит в К2, здесь σ2 — операции алгебры F2(2l) — определяются
на А соответствующими F2(ct2) — термами алгебры 21 ;
б) для любой Яг-алгебры 21 = (Α; σ2Ζ, алгебра -£\(21) = (Α; σχ)
входит в Κι, здесь алгебра Fx(2l) определяется аналогично алгеб-
129
Глава 3. Условные термы и условные многообразия
ре -F2(2l) в пункте а);
в) для любой /^-алгебры 21 имеет место равенство Fi(F2(Ql)) =
21;
г) для любой /^-алгебры 21 имеет место равенство F2(Fi(2l)) =
21;
Под категорией вложимости класса алгебр К будем
понимать совокупность всех /f-алгебр — совокупность объектов
категории и совокупность отображений между этими алгебрами,
являющихся изоморфизмами произвольной iC-алгебры на подалгебру
какой-либо /^-алгебры (являющихся вложениями iC-алгебр друг
в друга), а так же отображения, являющиеся эпиморфизмами К-
алгебр на одноэлементную алгебру соответствующей сигнатуры,
если последняя входит в К, — морфизмов категории вложимо-
сти. Через Hom(2l, 23), для Я-алгебр 21 и 23 будем обозначать
совокупность всех морфизмов из 21 в 23 (всех изоморфных
вложений алгебры 21 в алгебру 23 или эпиморфизм 21 на 23, если
23 — одноэлементная алгебра). В категории вложимости класса
К определена частичная (т.е. не всюду определенная) операция
произведения морфизмов: для φ € Hom(2l, 23), ψ € Hom(23, С)
ι-)·
под произведением ψ · ψ понимаем элемент из Нот (21, €)
являющийся суперпозицией отображений φνιφ. Категорию вложимости
класса алгебр К будем впредь обозначать как К-
Под натуральным изоморфизмом категорий вложимости
Κι и Κι классов универсальных алгебр К\ и Кч соответственно,
мы будем понимать совпадение совокупностей основных множеств
алгебр из К\ и из Κι и совпадение совокупностей отображений
между этими множествами, являющихся морфизмами категорий
>—> >—*
Κι и Кг соответственно.
Имеет место следующая характеризация условно
рационально эквивалентных условных многообразий на языке натуральных
изоморфизмов категорий вложимости. Ограничиваясь лишь
формулировкой результата, заметим, что его доказательство основано
на теореме Мальцева о рационально эквивалентных
многообразиях и структурных теоремах о дискриминаторных многообразиях.
Полностью доказательство теоремы см. в [16].
130
§13. Условно рациональная эквивалентность
ТЕОРЕМА ОБ УСЛОВНО РАЦИОНАЛЬНО
ЭКВИВАЛЕНТНЫХ УСЛОВНЫХ МНОГООБРАЗИЯХ. Для
любых двух условных многообразий Κι и Κ-ι универсальных
алгебр следующие утверждения равносильны:
а) условные многообразия Κι и К% условно рационально
эквивалентны;
б) категории вложимости Κι и Кг натурально изоморфны.
Теорема 2 из § 11 (алгебраическая характеризация условно
термальных функций на конечных и равномерно локально-конечных
алгебрах) является следствием приведенного результата.
Отметим еще ряд следствий теоремы об условно рационально
эквивалентных условных многообразиях. Через Ьзо(Л) будем
обозначать совокупность всех внутренних изоморфизмов алгебры 21
(изоморфизмов между подалгебрами алгебры 21). Из теоремы об
условно рационально эквивалентных условных многообразиях и
отмеченного выше факта, что для конечной алгебры 21 условное
многообразие М*(А), порожденное этой алгеброй, состоит из
алгебр, изоморфных подалгебрам алгебры 21, плюс одноэлементная
алгебра, вытекает следующее утверждение.
СЛЕДСТВИЕ 1. Для любых двух конечных алгебр или
равномерно локально-конечных универсальных алгебр 21ι = (Α; σι) и
21г = (Л; σ-ι) конечной сигнатуры с одним и тем же основным
множеством А следующие условия эквивалентны:
1) CT(2li) = СТ(21г), совпадают совокупности условно
термальных функций алгебр 21χ и 212;
2) Iso(2li) = Iso(2l2), совпадают совокупности внутренних
изоморфизмов алгебр 2li и 212.
Таким образом, совпадение совокупностей внутренних
изоморфизмов алгебр %ι и 212 является критерием равных
вычислительных возможностей этих алгебр, где под вычислительными
возможностями алгебры мы понимаем совокупность функций на
основном множестве алгебры, вычислимых по программам
вычислений, составленных из простейших подпрограмм (сигнатурных
функций) с помощью операторов суперпозиции и условных
операторов.
Для любой биекции π множества А на множество В и любой
131
Глава 3. Условные термы и условные многообразия
функции / : Ап —> А, через /π обозначим η-местную функцию на
множестве В, определенную следующим образом:
/π(6ΐ,...,Μ=τ/(τ"1(Μ,···»τ"1(Μ)
для h,...,bn е в.
Функцию /π будем называть π-сопряженной к функции /.
Алгебры 21 = {Α; σι) и 23 = (В; σι) будем называть условно
рационально эквивалентными, если существует биекция π
множества А на множество В такая, что СТ(п(Ш)) — СТ(23), где
алгебра π(21) определена на множестве В и для jfl€cri
интерпретацией функционального символа fc в алгебре π (21) является
функция (/щ)*-. Фактически, условно рациональная эквивалентность
алгебр 21 и 23 означает условно рациональную эквивалентность
классов алгебр /({21}) и /({23}). Условно рациональная
эквивалентность алгебр 21 и 23 фактически равносильна тому, что (с
точностью до кодировки элементов алгебры 21 их π-образами в
алгебре 23) алгебры 21 и 2$ обладают одинаковыми
вычислительными возможностями (функции, вычислимые с помощью
программ — условных термов на алгебре 21, суть, с точностью до
π-сопряжения, те же, что и функции, вычислимые с помощью
программ — условных термов на алгебре 23).
СЛЕДСТВИЕ 2. Для любых двух конечных или
равномерно локально-конечных универсальных алгебр 21 — (А; аг) и 23 =
(Β;σ2) следующие условия эквивалентны:
а) алгебры 21 и 23 условно рационально эквивалентны;
б) существует биекция π множества 21 на множество 23
такая, что Iso23 = {/π Ι / G Iso2l}.
Ввиду утверждения этого следствия для любого
натурального числа η существует лишь конечное число S(n) попарно
условно рационально неэквивалентных η-элементных алгебр (алгебр с
различными вычислительными возможностями) таких, что любая
η-элементная алгебра условно рационально эквивалентна одной
из этих S(n) алгебр (имеет те же вычислительные возможности,
что и одна из этих S(n) алгебр).
Следующее утверждение дает значения и оценки чисел я-эле-
ментных алгебр с различными вычислительными возможностями.
132
§13. Условно рациональная эквивалентность
ТЕОРЕМА 1. S(2) = 5, 5(3) = 53, для любого η > 4
S(n) <2n+(V -еУ Ί).
Доказательство этой теоремы см. в [16].
В качестве иллюстрации приведем пример пяти
двухэлементных алгебр, имеющих различные вычислительные возможности
и таких, что любая двухэлементная алгебра имеет равные
вычислительные возможности с одной из этих пяти алгебр:
Я1 = <{0,1}
Яа = ({0,1}
Яз = ({0,1}
ац = <{о,1}
Кь = ({0,1}
ν);
;0>·
Здесь Η сложение по модулю 2, V и -ι — стандартные
операции дизъюнкции и отрицания на множестве {0,1}, а сигнатура
алгебры 215 не содержит никаких функциональных и константных
символов т.е. пуста.
Описание 53 попарно условно рационально не эквивалентных
трехэлементных алгебр также можно найти в [16].
В [16] можно найти, в частности, необходимые и достаточные
условия на полугруппы внутренних изоморфизмов конечных
алгебр при которых эти алгебры условно рационально
эквивалентны полурешеткам, решеткам (дистрибутивным, модулярным
решеткам), булевым алгебрам, унарам, полям. Кроме того там же
приведены необходимые и достаточные условия на полугруппы
частичных биекций множества в себя с тем что бы эта
полугруппа являлась полугруппой внутренних изоморфизмов некоторой
универсальной алгебры с данным основным множеством.
В этой же монографии изложены теории некоторых
обобщений условных термов: позитивно условных термов и
элементарно условных термов для которых аналогами инвариантов
рациональной эквивалентности конечных алгебр являются полугруппы
внутренних гомоморфизмов и пары — группы автоморфизмов и
решетки подалгебр этих алгебр.
ЗАДАЧИ
1. Будут ли условно рационально эквивалентными решетки М3
и N из задачи 11 § 1?
133
Глава 3. Условные термы и условные многообразия
2. Будут ли условно рационально эквивалентными
двухэлементная группа (5 — ({0,1};+,—, 0), где Η сложение по mod 2
и—0 = 0, —1 = 1,и двухэлементная булева алгебра?
3. Будут ли условно рационально эквивалентными полугруппа
(5 = ({0, 1, ..., п— 1};+} (Н сложение по mod (η — 1)) и решетка
L = ({0,...,п— 1}; V, Л), где решеточный порядок на L
определен неравенствами 0 < 1 < 2 < · · · < η — 1?
4. Найдите некоторые необходимые условия, которым должна
удовлетворять любая алгебра, условно рационально
эквивалентная некоторой конечной решетке (группе, булевой алгебре).
5. Докажите, что приведенные выше алгебры 2li-2ls попарно
условно рационально неэквивалентны друг другу и любая
двухэлементная алгебра условно рационально эквивалентна одной из
алгебр 2li,... ,215.
6. Докажите, что любая алгебра условно рационально
эквивалентна некоторой дискриминаторной алгебре.
7. Докажите, что дискриминаторные алгебры условно
рационально эквивалентны тогда и только тогда когда они рационально
эквивалентны.
134
Глава 4
Некоторые приложения
универсальной алгебры
В этой главе будут конспективно рассмотрены некоторые
приложения универсальной алгебры: к функциональным системам на
множествах (§14), к оценке вычислительных возможностей
вычислительных машин (§15), к теории автоматов и языков (§16),
к теории баз данных (§17), а также приложения группоидов в
биологии и других далеких от математики областях (§ 18).
Безусловно, эти рассмотрения носят лишь демонстрационный
характер и далеко не исчерпывают приложения универсальной алгебры
в теории вычислительных машин, программировании,
информатике и других областях науки.
§14. Клоны и соответствие Галуа
Из стандартных курсов дискретной математики и
математической логики известны основы теории булевых функций (функций
на двухэлементном множестве {0, 1}) и ее приложения к теории
переключательных схем. Аналогичные вопросы могут быть
рассмотрены в более общем плане — для функций, определенных на
произвольном конечном множестве {0,1,..., η — 1}, по сути — для
конечных универсальных алгебр. В настоящем параграфе будут
рассмотрены некоторые аспекты этой теории.
Для любой совокупности функций F, определенных на
некотором фиксированном множестве А, через (F) обозначим
наименьшую совокупность функций на множестве А, включающую в себя
F и замкнутую относительно суперпозиций. Совокупность F
назовем замкнутой в случае когда F = (F). Если при этом замкну-
Глава 4. Некоторые приложения универсальной алгебры
тая система функций F включает в себя все функции-селекторы
efc \.*С1 > · · · > хп) = хк
для любых натуральных η и к < п, то F называется клоном
функций на множестве А. Через (F) обозначим наименьший
клон, содержащий совокупность F.
Для любого множества А и любого натурального η через Од
обозначим совокупность всех η-местных функций на множестве
А а через Яд — всех η-местных отношений на А. Положим
оА = и о?\ ra = у я?>.
Для f(xu...,xn) e Од и R(xi,..., xm) e R}™ будем говорить,
что / сохраняет отношение R или R стабильно
относительно /, если для любой матрицы
/ ац · · · ain \
\ Q-ml ' ' ' ®mn )
элементов множества А такой, что все ее столбцы связаны
отношением R (т.е. R(an,... ,ami) для 1 < г < п), имеет место и
отношение R(f (а1Ь ..., а1п), ..., / (атЬ ..., amn)). Для любых
совокупностей F С О а и Q С RA введем следующие обозначения:
РоГ<5 = {/ Ε О а | / сохраняет каждое из отношений,
входящих в Q};
Pol F = {/ € О а | / сохраняет отношения grg для каждого g
H3F};
Inv F = {R e Да | R стабильно относительно каждой / из F}.
Таким образом, к примеру, для любой универсальной алгебры
А = (Α; σ) имеют место равенства:
SvX>A = R\{\lnv{T(A)); Con Л = ЩА1~}\т{Т{А))-
Aut A = Sym Лр|Ро1(Т(Л)).
Введенные операторы Pol и Inv определяют Галуа-соответ-
ствие между подмножествами множества Qa и
подмножествами множества RA, а именно имеют место следующие очевидные
136
§14. Клоны и соответствие Галуа
свойства этих операторов для любых F, F', F, (г G /) С QA и
Q,Q\Qi{ieI)QRA:
F С Pol Inv F, QCInfPoig,
Pol Inv Pol Q = Pol Q, Inv Pol Inv F = Inv F,
F CF' => InvF' С Inv,F, QCQ4 PolQ' С PolQ,
Poi (u Qi) = П Po1 «*. Inv fU F) = ΠΙην Fi-
\iei J iei Vie/ / iei
Для любых Q Ε Ra> F Q О а через Rf(Q) обозначим наименьшее
отношение на множестве А, включающее в себя Q и стабильное
относительно функций из F.
Пусть F С Оа и Q Ε Л^ · Тогда очевидным образом имеет
место равенство RF(Q) = {{д(ап,..., а1п),..., д(аг,а,..., атп))\д е
ί а-п · · · ciin \
(F) Π Од ,п Ε ω и I — произвольная матрица эле-
\ С1т\ · · · йтп /
ментов из А такая, что для 1 < г < η Q(au,..., amj)}.
Пусть X = {xi\i e /} - произвольное множество
переменных и Q — совокупность некоторых отношений на множестве А.
Под схемой отношений над Q от X будем понимать произвольную
тройку
где Σ — некоторая совокупность формул вида Р(х^, ■ ■ ■, Xjs), где
Xjl,...,Xjs Ε Χ, Ρ Ε Qf]0A' и (xiu... ,Xin) —
фиксированный кортеж переменных из X. Будем говорить, что совокупность
(сц|г € /) элементов из А удовлетворяет совокупности формул Σ,
если (а^,..., a,js) Ε Ρ для любой формулы Р(х^,... ,Xjs),
входящей в Σ. Через R^ обозначим η-местное отношение на А такое,
что R^ = {(ctij,. ■ -, ain) I существует совокупность (а{\г Ε /),
удовлетворяющая Σ}.
При этом отношение R^ будем называть обобщенным
произведением отношений из Q, соответствующим схеме ψ.
Под клоном отношений на множестве А будем понимать
любое подмножество Q С RA такое, что:
137
Глава 4. Некоторые приложения универсальной алгебры
а) Q содержит все диагональные отношения
Δ^ = {(αχ,...,am) e Am\(i,j) (Ee^ai = aj},
где е € Eq {1,..., га} , m е ω;
б) Q замкнуто относительно любых обобщенных
произведений.
Для любого Q С RA через [Q] будем обозначать наименьший
клон отношений на множестве А, включающий в себя
совокупность Q.
Заметим, что такие операции над отношениями, как
бесконечные конъюнкции, перестановки аргументов, отождествление
аргументов, введение фиктивных аргументов, произведение
отношений и другие, очевидным образом являются частными случаями
обобщенного произведения.
Пусть F С О a n R С RA. Для любого натурального η введем
следующие обозначения;
п — LocF = {/ G О™' | для любого В С А™ такого, что \В\ <
п, существует £ е F такая, что f\B = g\B,m € α;}, LocF =
Πηεω η - Loc F,
η—Loci? — {Q e RA I для любого В С Am такого, что \В\ <
п, существует Ρ € R такое, что Q\B = P\B,m € ω}, LocR —
Πηεω n ~ Loc R-
Здесь f\B и Q\B — ограничения / и Q на В соответственно.
Имеет место (доказательство см., к примеру, в [17]) следующее
описание Галуа-замыканий функций на множестве А.
ТЕОРЕМА РОМОВА. Для любого F С 0А:
1) для любого η (Ξ ω η — Loc(F) = Po\(lnvF()RAn));
2) Loc(F)=PolInvF.
Галуа-замыкания Inv Pol для совокупностей отношений
описывает следующая
ТЕОРЕМА САБО. Для любого Q С RA:
1) для любого η € ω η — Loc[Q] = Inv(PolQnoSl));
2)Loc[Q]=InvPoig.
Доказательство этой теоремы можно найти, к примеру, в [17].
Из этих теорем вытекают следующие описания Галуа-замкнутых
функциональных клонов и клонов отношений.
138
§14. Клоны и соответствие Галуа
СЛЕДСТВИЕ 1. Для F С О а следующие условия
равносильны:
1) F = (F) (т.е. F есть функциональный клон) и Loc F = F;
2) F = PolInvF;
3) существует Q С Я,д такое, что F = Pol Q.
СЛЕДСТВИЕ 2. Для любого Q С RA следующие условия
равносильны:
1) Q = [Q] (т.е. Q есть клон отношений) и LocQ = Q;
2) Q = InvPolQ;
3) существует F С 0^ такое, что Q = Inv F.
В случае конечности множества А обобщенные произведения
отношений при порождении клонов отношений [Q] могут быть
заменены на конечное число более привычных операций над
отношениями.
На множестве Яд определим операции ξ,τ,π и о следующим
образом. Для Pi G Яд и Р2 G Яд положим:
C(-Pi) = {(α2,α3,···,αη,αι}Και,α2,...,αη) G р^
r(^i) = {(а2,а1,а3,...,ап)|(аьа2,...,ап) б Pi},
π(ρι) = {(αι,α2, ...,αη_ι)|(αι,α2, ...,an) G Px},
Pi oP2 = {(ai,o2,...,afH.m_2) | За; G Л{аьа2,... ,αη_χ, χ) G Ρχ и
(χ, a„,..., an+m_2) G P2}.
Через Rel(^) обозначим алгебру (Яд;£, τ, π, ο, Δ^ \ т Ε ω n
ε G Eq{l,..., m}) сигнатуры, состоящей из одноместных функций
ξ, τ, π, двухместной функции о и констант Δ^. Алгебра Rel(^)
называется полной алгеброй отношений на множестве А.
Имеет место (доказательство см., к примеру, в [41])
ТЕОРЕМА ПЕШЕЛЯ-КАЛУЖНИНА. Для любого
конечного множества А, любых F С Од, Q С RA, Ρ G Лд имеет
место:
1) InvF является подалгеброй алгебры Rel(^);
2) подалгебра алгебры Rel(^), порожденная совокупностью Q
совпадает с Inv Pol Q;
1. Следующие условия эквивалентны:
а) Р = Inv Pol Q ;
139
Глава 4. Некоторые приложения универсальной алгебры
б) существует 3-примитивная формула ф(хг,... ,хп)
сигнатуры, соответствующей предикатам, входящим в совокупность Q,
такая что для любых αϊ,..., αη Ε Α
Ρ{αχ,...,αη) & (A;Q)\ = ф(аъ... ,an).
Напомним, что формула φ логики первого порядка
сигнатуры σ называется 3-примитивной, если получается из предикатов
сигнатуры σ с помощью конъюнкции и навешивания кванторов
3.
Очевидным образом совокупность всех функциональных
клонов на множестве А образует некоторую решетку (обозначаемую
далее как LA = (LA; Л, V)) относительно теоретико-множественного
включения С. При этом для Fb F2 € LA F\ Л F2 = F\ Π F2. В
случае когда А = {0,1,... ,η — 1} для некоторого натурального п,
решетки ВА будем обозначать как Вп. В силу приведенных
выше результатов решетки Вп коалгебраичны (двойственны
алгебраическим решеткам подалгебр алгебр Rel{0,1,... ,η — 1}
соответственно). Приводимая ниже теорема Розенберга дает описание
коатомов решеток Вп и, в частности, утверждает их конечность.
Предварительно введем ряд новых понятий.
Частичный порядок (А; <) называется ограниченным,
если существуют наибольший и наименьший элементы в (А;<).
Двухместное отношение на конечном множестве А назовем
простым перестановочным, если оно является графиком
некоторой перестановки на А, все циклы которой имеют
фиксированную простую длину. Эквивалентность на А нетривиальна, если
она отлична от отношений Δ и V. Четырехместное отношение
Ρ С Л4 на множестве А называется аффинным, если на А
определима операция + такая, что (А; +) — абелева группа и
для любых a, b,c,d £ АР(а, b,c,d) <=ϊ а + b = c + d. Аффинное
отношение Ρ на Л примитивно, если соответствующая
группа (А;+) является элементарной абелевой р-группой для
некоторого простого р. η-местное отношение Ρ С Ап на множестве
А называется тотально симметричным, если для любой
перестановки π на {1, 2,..., п} и любых а1;..., ап 6 А включения
(аь...,ап) е Ρ и (απ
(1)) · · ■ > ^тг(я)
) 6 Ρ равносильны. Для любого
натурального η на множестве А определим η-местное отношение
Ап = {(αχ,..., an)|aj = о, для некоторых г -ф j}.
140
§24. Клоны и соответствие Галуа,
η-местное отношение Ρ на Л называется тотально
рефлексивным, если Ап С Р. Центром η-местного отношения Ρ на Л
назовем множество {а € А\ для любых а2,..., ап € Л имеет место
(а,аг,... ,ап) G Р}. η-местное отношение Ρ на Л назовем
центральным, если оно тотально симметрично, тотально
рефлексивно и имеет непустой центр, отличный от самого множества Л.
Заметим, что одноместное отношение, выделяющее
подалгебру алгебры 21 = (Α\σ), является, по определению, центральным.
Наличие же нетривиального автоморфизма алгебры 21 влечет
наличие либо собственных подалгебр алгебры 21 (совокупности
неподвижных точек степеней этого автоморфизма), либо
автоморфизма Л некоторого простого порядка и без неподвижных точек, т.е.
автоморфизма, график которого соответствует простому
перестановочному отношению на Л.
Пусть η — некоторое натуральное число, η = {0,1,..., η — 1}.
Для 1 < г < т, где m — натурально, пусть π™ : nm —> η
является проектированием множества пт на η по r-й координате.
На множестве пт определим η-местное отношение ωτη следующим
образом: (αϊ,..., ап) € шт <& для любого 1 < г < т имеет место
(π™(αι),... ,7Γ™(α„)) € пп. Отношение Ρ С Ап (при η > 2)
называется η-регулярно порожденным, если для некоторого т > 1
существует отображение φ множества Л на множество пт такое,
что Ρ = φ-1(ωηι), т.е. (аь ... ,α„) G Ρ ^ (φ(α>ι),... ,φ(αη)) G um.
Очевидно, что если Р — η-регулярно порожденное отношение на
п, то Ρ тотально рефлексивно и тотально симметрично.
Следующее утверждение описывает коатомы решетки Вп.
ТЕОРЕМА РОЗЕНБЕРГА. Для любого натурального η >
2 и любого клона F из Ln следующие условия эквивалентны:
1) F — коатом решетки Вп;
2) F состоит из функций на множестве {0,1,... , η — 1},
сохраняющих некоторое фиксированное отношение Ρ на η одного
из следующих видов:
а) ограниченный порядок на п, либо
б) простое перестановочное отношение на п, либо
в) нетривиальная эквивалентность на п, либо
г) простое аффинное отношение на п, либо
д) центральное отношение на п, либо
е) к-регулярно порожденное отношение на п.
141
Глава 4. Некоторые приложения универсальной алгебры
В случае η = 2 теорема Розенберга превращается в хорошо
известный критерий полноты систем булевых функций
(доказательство см., к примеру, в [25]).
СЛЕДСТВИЕ (ТЕОРЕМА ПОСТА). Клон функций F на
множестве 2 = {0,1} совпадает с клоном Ο-ι (не содержится ни
в одном из коатомов решетки Вг) тогда и только тогда, когда
для каждого из следующих пяти классов функций То, Ti, S, Μ, L
в F существует функция, не входящая в этот класс.
Здесь Т0 — функции на 2, сохраняющие значение 0
(сохраняющие центральное отношение с центром {0}); Тх — функции на 2,
сохраняющие значение 1 (сохраняющие центральное отношение с
центром {1}); S — совокупность самодвойственных функций
(сохраняющие простое перестановочное отношение на 2); Μ —
совокупность монотонных функций (сохраняющих ограниченный
порядок на 2); L — совокупность линейных функций (сохраняющих
простое аффинное отношение на 2).
На самом деле Постом доказано (доказательство см., к
примеру, в [25]) более сильное утверждение.
ТЕОРЕМА ПОСТА. Решетка В2 счетна и имеет
следующую диаграмму Хассе (см. Рис. 4..1.)
Постом же получено (см., к примеру, [25]) полное описание
клонов из этой решетки. Мы приведем здесь лишь характери-
зации этих клонов и примеры их конечных базисов. Напомним,
что совокупность функций G называется базисом клона F, если
(G)' = F и для любого собственного подмножества G\ С G
имеет место неравенство (Gi)' Φ F. Иначе говоря, если множество
Д на котором определены функции из F, то F = Т(21) для
алгебры 21 = (A;G), но совокупность термальных функций любого
обеднения алгебры 21 меньше совокупности F.
Для формулировки результатов Поста нам понадобятся еще
следующие определения и обозначения. Функция f(x\,..., хп) на
множестве 2 = {0,1} называется α-функцией (/3-,7-,^-функцией),
если она удовлетворяет тождеству
/=(ж,...,а;) =
=ж(/(х, · · ·, х) = 1, /(я, · · ·, х) = 0, /(я,..., я) = -«я).
Функция /(ях,..., хп) на множестве 2 — {0,1}
удовлетворяет условию Ak(ak) при к > 2, если любые к наборов аргументов,
142
на которых функция обращается в единицу (в ноль), имеют
общую единичную (нулевую) компоненту. Функция f(x\, ■ ■ ■, хп) на
множестве 2 = {0,1} удовлетворяет условию Асо(асо) , если все
наборы аргументов, на которых функция равна 1 (0) имеют
обитую единичную (нулевую) компоненту. Через h(xi,... ,χη,χη+ι)
n+l
■•Ετι+1)
обозначим далее функцию равную V х\ · χι ·... -Xi-χ ■ ж,+1 ■
а через h * (χχ,..., χη+ι) — двойственную к к(хг,..., χη+ι)
функцию, через х\у — функцию "штрих Шеффера".
№
1
2
Ох
о4
Перечень входящих функций
Все функции, равные функции ж,
и все функции получающиеся из
них путем переименования
переменных без отождествления
Все функции, равные функциям
χ или -ιχ, и все функции,
получающиеся из них путем
переименования переменных без
отождествления
Пример базиса
{х}
Ьх}
143
Глава 4. Некоторые приложения универсальной алгебры
№
3
4
5
6
7
8
9
10
11
о5
о6
о8
о9
Si
s3
S5
s6
Ρχ
Перечень входящих функций
Все функции, равные функциям
1 или х, и все функции,
получающиеся из них путем
переименования переменных без
отождествления
Все функции, равные функциям
0 или х, и все функции,
получающиеся из них путем
переименования переменных без
отождествления
Все функции, равные функциям
0, 1 или х, и все функции,
получающиеся из них путем
переименования переменных без
отождествления
Все функции, равные функциям
0,1,а; или -1Я) и все функции,
получающиеся из них путем
переименования переменных без
отождествления
Все логические суммы (т.е.
функции вида V"=i Xi, n = 1,2,... и все
функции, получающиеся из них
путем переименования
переменных без отождествления)
Все логические суммы и все
функции, равные 1
Все логические суммы и все
функции, равные 0
Все логические суммы и все
функции, равные 0 или 1
Все логические произведения (т.е.
функции вида &"=1, η = 1,2,...
и все функции, получающиеся из
них путем переименования
переменных без отождествления)
Пример базиса
{х,1}
{х,0}
{х.0,1}
Ьх,0}
{xVy}
{хУуЛ}
{xVy,0}
{χ ν у, ο,ι}
{xky}
144
§14. Клоны и соответствие Галуа
№
12
13
14
15
16
17
18
19
20
21
Рз
Рь
Ре
Lx
L2
Ьз
U
Lb
Dx
D2
Перечень входящих функций
Все логические произведения и
все функции, равные 0
Все логические произведения и
все функции, равные 1
Все логические произведения и
все функции, равные 0 или 1
Все линейные функции
Все линейные а- и ^-функции
(т.е. функции вида Eeiari + 1»
EfiV х» г = 0,1, 2... и все
функции, получающиеся из них путем
переименования переменных без
отождествления)
Все линейные а- и η-
функции (т.е. функции вида
Σ1=ι Χί, s = 0,1,2 ..., и все
функции, получающиеся из них путем
переименования переменных без
отождествления)
Все линейные а-функции
(т.е. функции вида
ElLi1*» s = 0,1,2..., и все
функции, получающиеся из них
путем переименования
переменных без отождествления)
Все линейные
самодвойственные функции (т.е.
функции вида Е^ТХ^ + 1,
Σ*£14, С = 0,1,2... и все
функции, получающиеся из них
путем переименования
переменных без отождествления)
Все самодвойственные а-
функции
Все самодвойственные
монотонные функции
Пример базиса
{х&У,0}
{хку,1}
{zfe/,0,1}
{х + У,1}
{х + у + 1}
{х + у}
{x + y + z}
{х + у + z 4-1}
{xkyVxk-izVyk")
{хку Vifi^v
-ι?/&:-ΐζ} ________ '
145
Глава 4. Некоторые приложения универсальной алгебры
№
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
D3
Мх
м2
м3
м4
Сг
с2
С3
с4
ρμ
F£
F£
F4"
П
К
F?
η
Foo
poo
r2
Poo
r3
Перечень входящих функций
Все самодвойственные функции
Все монотонные функции
Все монотонные а- и /^-функции
Все монотонные а- и 7-функции
Все монотонные а-функции
Все функции на {0,1}
Все а- и /^-функции
Все а- и /^-функции
Все α-функции
Все α-функции,
удовлетворяющие условию (αμ)
Все монотонные α-функции,
удовлетворяющие условию (αμ)
Все монотонные функции,
удовлетворяющие условию (αμ)
Все функции, удовлетворяющие
условию (αμ)
Все α-функции,
удовлетворяющие условию (Αμ)
Все монотонные α-функции,
удовлетворяющие условию (Αμ)
Все монотонные функции,
удовлетворяющие условию (Αμ)
Все функции, удовлетворяющие
условию (Αμ)
Все α-функции,
удовлетворяющие условию {а°°)
Все монотонные α-функции,
удовлетворяющие условию(а°°)
Все монотонные функции,
удовлетворяющие условию (а°°)
Пример базиса
{хк->у V xk ->z V
yk-^x)
{^,ιν^,Ο,Ι}
{xky,xVy,l}
{xky,xVy,0}
{xky,xVy}
{xVy}
{xVy, x + y+1}
{xVy, x + y}
{xVy, xk(y + z + l)}
{xyykz,h;(x)}
{x V ykz, hl(x)},npa
μ = 2; {/г;(х)},при
/x>3
{1, h,;(x)}
{xVy^h^x)}
{xV->y,h;(x)}
{xk(yVz), h2(x)},
при μ = 2\{Ημ{χ)},
при μ > 3
{0, Λμ(ϊ)}
(χ&-ηί/,/ιμ(χ)}
{or V ί/&-·ζ}
{χ V y&z}
{1,ж V ykz}
146
§14. Клоны и соответствие Талу в,
№
42
43
44
45
46
F4°°
Foo
17*00
^6
F7TO
^8
Перечень входящих функций
Все функции, удовлетворяющие
условию (а°°)
Все α-функции,
удовлетворяющие условию (А°°)
Все монотонные α-функции,
удовлетворяющие условию (А00)
Все монотонные функции,
удовлетворяющие условию(Л°°)
Все функции, удовлетворяющие
условию (А°°)
Пример базиса
{χ ν ~<у}
{хк{у V -.ζ)}
{xk(yVz)}
{0,xk(yVz)}
{xk-iy}
Данная таблица при отождествлении описанных в ней
клонов сопряженных перестановкой (0,1) на множестве 2 = {0,1},
дает классификацию с точностью до рациональной
эквивалентности всех двухэлементных алгебр. Иначе говоря, попарно не
сопряженные таким образом клоны из этой таблицы описывают при
определении на 2 = {0,1} сигнатуры как базовых функций клона,
попарно не рационально эквивалентные алгебры, и любая
двухэлементная алгебра рационально эквивалентна некоторой
подобной алгебре, соответствующей клону из этой таблицы.
Существенно иная ситуация для функциональных клонов на
более мощных, чем двухэлементные, множествах. Имеют место
следующие утверждения (доказательства см., к примеру, в [26]).
ТЕОРЕМА ЯНОВА. Для любого натурального η > 3 на
множестве η = {0,1,... ,п — 1} существует функциональный
клон, не имеющий базиса.
ТЕОРЕМА МУЧНИКА. Для любого натурального η > 3
на множестве η — {0,1,. ..,η — 1} существует функциональный
клон со счетным базисом.
СЛЕДСТВИЕ 3. Для любого натурального η > 3 решетки
Вп континуальны.
ЗАДАЧИ
1. Докажите, что для любой совокупности Q отношений на
множестве А совокупность функций PolA является клоном.
2. Докажите, что следующие операции над отношениями:
конъюнкции, ξ, г, π, о (определение их см. перед формулировкой
147
Глава 4. Некоторые приложения универсальной алгебры
теоремы Пешеля — Калужнина) являются частными случаями
операции обобщенного произведения.
3. Докажите, что если функция f(xi,. ■. , хп) на множестве
{0,1} не самодвойственна (/ £ S), то из нее путем
подстановки функций χ и ->х можно получить константную функцию.
4. Докажите, что если функция /(χι,...,χη) на множестве
{0,1} не монотонна (/ £ М), то из нее путем подстановки
констант 0 и 1 и функции χ можно получить функцию -ιχ.
5. Докажите, что если функция f(xi,· · · ,хп) на множестве
{0,1} не линейна (/ ^ L), то из нее путем подстановки констант 0
и 1 и функций χ и -ιχ, а также, быть может, путем навешивания
отрицания над / можно получить функцию χχ&χ2.
6. Докажите, что из всякой совокупности функций F на
множестве {0,1} такой, что (F) = 0{од}, можно выделить
совокупность Fi С F такую, что |FX| < и (Fi)' = 0{од}·
§15. Шкалы потенциалов вычислимости
конечных алгебр
В настоящем параграфе на основе результатов § 13 будет
предложена некоторая классификация конечных универсальных
алгебр 21 на основе их программно-вычислительных возможностей,
т. е. на основе совокупностей СТ(21) их условно термальных
функций. Как было показано в § 13, следствия 1 и 2, пара п-элемснтных
алгебр 21 = (Α; σι) и <8 = (β;σ2) имеют одинаковые программно-
вычислительные возможности или, иначе, условно рационально
эквивалентны (т. е. для некоторой биекции π множества А на
множество В справедливо равенство СТ(<8) = {/π | / € СТ(21)})
тогда и только тогда, когда для этой же биекции π имеет
место равенство Iso 23 = {<?π|<? € Iso 21}. Иначе говоря, совокупность
Iso 21 внутренних изоморфизмов конечной алгебры 21 выступает с
точностью до сопряжения перестановками основного множества
алгебры инвариантом программно-вычислительных
возможностей этой алгебры.
Элементы совокупности Iso 21 суть частичные перестановки
(внутренние изоморфизмы алгебры 21) основного множества ал-
148
§15. Шкалы потенциалов вычислимости конечных алгебр
гебры 21, т.е. некоторая совокупность биекций между какими-то
подмножествами множества А. Причем сами подмножества А,
играющие роль областей определения и значения этих биекций,
— это основные множества подалгебр алгебры 21, т.е.
совокупность этих подмножеств является решеточно упорядоченным
множеством относительно отношения С теоретико-множественного
включения между ними.
Таким образом, чтобы была возможность построить
классификации конечных алгебр на основе их программно-вычислительных
потенциалов, прежде всего необходимо описание совокупностей /
биекций между некоторыми подмножествами произвольного
конечного множества А таких, что / = Iso 21 для некоторой
универсальной алгебры 21 = (Α; σ), определенной на этом множестве.
Говоря, что совокупность S £ Р(А) подмножеств
некоторого конечного множества А образует решетку, будем иметь
в виду, что S является решеточно упорядоченным множеством
относительно порядка, определенного как теоретико-множественное
отношение быть подмножеством, при этом решеточная операция
Л на элементах из S является теоретико-множественным
пересечением этих элементов как подмножеств множества А (в то
время как решеточная операция V не обязана быть теоретико-
множественной операцией объединения) и. А е S.
Пусть S — некоторая решетка подмножеств конечного
множества А, а / — некоторая совокупность биекций между
подмножествами из S.
Принципом обратимости для / назовем следующее ее
свойство: для любого gel отображение д~х также входит в /.
Принципом композиции для / назовем свойство /: для
любых g,h £ I если rang h = dom д, то gh £ /.
Принципом неподвижных точек для S и / назовем
следующее свойство: для любого д Ε I множество Fix(p) = {α £ А \
д(а) = а} входит в S.
Принципом ограничения для S Ά Ι назовем свойство: для
любых д е I и С € S, если С С domд, то д\С G /.
Принципом согласованности S и I назовем следующее
свойство: для любого С G S имеет место включение idcG /; для
любого д Ε I имеют место включения dom <?, rang g € S.
Принципом одноэлементных подалгебр назовем свой-
149
Глава 4. Некоторые приложения универсальной алгебры
ство: для любых a, b G А, если {а}, {b} G S", то существует h e I
такое, что domh = {α},rangh = {Ь}.
Имеет место следующее утверждение, полное доказательство
которого можно найти в [16] — описание инвариантов
программно-вычислительных возможностей конечных алгебр.
ТЕОРЕМА 1. Для любого конечного множества А и
некоторой совокупности I частичных биекций множества А
{совокупности некоторых биекций между некоторыми
подмножествами множества А) следующие условия эквивалентны:
1) / = Iso2l для некоторой универсальной алгебры 21 = {А; а)
с основным множеством А;
2) для некоторой решетки S подмножеств множества А
пара (S, I) удовлетворяет принципам обратимости, композиции,
неподвижных точек, ограничения, согласованности и
одноэлементных подалгебр; при этом S = Sub 21 для алгебры 21 из
условия 1).
Перейдем теперь непосредственно к определению шкалы
потенциалов вычислимости конечных универсальных алгебр — к
классификации η-элементных алгебр (или, если угодно,
вычислительных машин, работающих на η-элементном множестве
объектов) по их программно-вычислительным возможностям.
Как уже замечалось ранее, само основное множество
алгебры не играет никакой роли в оценке программно-вычислительных
возможностей этой алгебры (эти возможности оцениваются с
точностью до условно рациональной эквивалентности алгебр). В
силу этого будем далее считать, что рассматриваемые п-элементные
алгебры заданы на множестве η = {0,1,...,п— 1}. На
совокупности СТ(п) = {СТ(21) | 21 — η-элементная алгебра} введем
отношение эквивалентности ~:
CT(2ti) ~ СТ(212) тогда и только тогда, когда алгебры 21] и 212
условно рационально эквивалентны, т.е. существует перестановка
π на множестве {0,1,... ,п — 1}, которая сопрягает совокупности
функций CT(Sli) и СТ(012), т.е. такая, что СТ(212) = {Д | / €
СТ(01г)}.
В силу теоремы 2 из § 11 и следствий 1 и 2 из § 13 для любых
конечных алгебр 21 = (π; σγ) и 23 = (η; σ2) и для любой перестановки
π на множестве {0,1,..., п— 1} следующие условия эквивалентны:
а) имеет место равенство (включение)
150
§15. Шкалы потенциалов вычислимости конечных алгебр
СТ{Ъ) = {/π | / € СТ(Щ
. (СТ(«8) С {/„ | / € СГ(а)});
б) имеет место равенство (включение)
Ι8θ» = {0π |flf€lso(Sl)}
■(Ι80®2{5π|5€ΐ80(3)}).
Через СТП обозначим фактор-множество СТ(п)/~ ■ Таким
образом, в силу теоремы 1 множество СТП конечно, и мощность
множества СТ„, число S(n) из § 13, соответствует числу попарно
условно рационально неэквивалентных η-элементных алгебр, т. е.
n-элементных алгебр, имеющих различные
программно-вычислительные возможности — различные вычислительные потенциалы.
В силу сказанного выше под вычислительным потенциалом
алгебры 21 = (η;σ) естественно понимать класс [СТ(Щ]„.
Через < обозначим отношение частичного порядка на СТП,
индуцированное отношением теоретико-множественного включения
между элементами из СТ{п) при факторизации по отношению ~ :
т.е. [СТ(21)]^ < [СТ(£)]^ тогда и только тогда, когда для
некоторой алгебры £ имеют место СТ(21) С СТ(£) и СТ(£) ~ СТ(Ъ).
При этом, естественно, отношение СТ[(21)]~ < [СТ(*8)]^
фактически означает, что программно-вычислительные возможности
алгебры 21 меньше либо равны программно-вычислительным
возможностям алгебры Ш.
В силу сказанного частично упорядоченное множество
(СТ(п);<) называется шкалой потенциалов вычислимости
η-элементных алгебр и позволяет классифицировать
вычислительные машины, работающие на η-элементных совокупностях
объектов с точки зрения их вычислительных возможностей.
Далее вычислительный потенциал СТ[(21)]^ алгебры 21 будем
обозначать как 21.
Напомним, что мощности шкал потенциалов η-элементных
алгебр, числа S(n), при η = 2,3,4 и верхняя оценка этих мощностей
при η > 4 приведены в конце § 13.
Диаграмма Хассе для шкалы (СТ2\ <) представлена на Рис. 4.2.
Ключом к построению этой диаграммы и к изучению свойств
шкал (СТП; <) служит теорема 1.
Прежде всего заметим, что любая из шкал обладает
наименьшим 0 и наибольшим 1 элементами определяемыми соответствен-
151
Глава 4. Некоторые приложения универсальной алгебры
Л?1
<8
4
<в2«
V
<<?Т2; <}
Рис. 4.2
но алгебрами 21 = (η;σχ) и <8 = (η;σ2) такими, что Iso2l = Bin
— все возможные биекции между любыми подмножествами
множества η — {0,1,... ,τι — 1}, a Iso<8 = {idn}. Очевидным образом
замечается, что совокупности Bin и {idrt} удовлетворяют
условиям 2) теоремы 1.
При этом любая функция на множестве п = {0,1,...,п—1}
является программно вычислимой (условно термальной) функцией
на алгебре 23, а программно вычислимыми (условно
термальными) функциями на алгебре 21 являются лишь функции вида (так
называемые обобщенно селекторные функции):
f(xi,...,xm) = <
Ul\%\i ·■·) ■Km) ^ %ίι
D[(xi,...,xm) -> хц
где D\(x\, ...,xm), ...,Di(xi, ...,xm) — всевозможные
максимальные, попарно несовместные условия, состоящие из равенств и
неравенств между переменными Χι,...,χηι (при условии, что
%\ι · ■ · > %m t ΤΙ) И Χ{ί, . . . , Хц с: \Χ\, ■ ■ ■ , Χτη[·
Диаграмму Хассе для шкалы (СТ3; ^) можно найти в [16].
Имеют место также следующие утверждения (доказательство
их см. в [16]).
ТЕОРЕМА 2. Графы, соответствующие диаграммам Хассе
шкал (СТП; <), не являются планарными при η > 3.
ТЕОРЕМА 3. При η > 3 шкала (СТп; <) не является реше-
точно упорядоченным множеством.
О сложности строения шкал (СТп; <) говорит и следующее
утверждение.
152
§15. Шкалы потенциалов вычислимости конечных алгебр
ТЕОРЕМА 4. Для любой конечной решетки L существуют
натуральное число η и элементы 21 и 93 шкалы (СТП; <) такие,
что интервал Щ,Щ = {£ G СТПЩ < £ < Щ шкалы {СТП;<)
является решеткой и решетка £ изоморфно вложима в решетку
Представляет интерес нахождение различных параметров
конечного частично упорядоченного множества (СТП;<).
Атомами частично упорядоченного множества (А; <) с
наименьшим элементом 0 называются элементы, покрывающие этот
наименьший элемент, т.е. такие элементы а Е А, что для любого
элемента с Ε А такого, что 0 < с < а имеет место одно из равенств
с = 0 либо с = а. Коатомами частично упорядоченного
множества (А; <) с наибольшим элементом 1 называются элементы,
покрываемые элементом 1, т.е. такие элементы Ь, что для любого
элемента с 6 А такого, что b < с < 1 имеет место одно из равенств
с = 1 либо с = Ь.
Справедливо следующее утверждение (полное его
доказательство см. в [14]).
ТЕОРЕМА 5. Число атомов шкалы (СТП;<) равно § +
1 + R(n) где [т] — целая часть числа га, a R{n) — число
максимальных транзитивных на η подгрупп полной симметрической
группы на п, попарно не сопряженных в этой группе. Число
коатомов шкалы (СТп; <} равно (п — 1) + К(п), где К(п) — число
различных простых делителей числа п, отличных от единицы.
Длиной частично упорядоченного множества (А; <}
называется максимальное число элементов этого множества,
образующих цепь.
Следующее утверждение (доказательство см. в [16] описывает
длину шкалы (СТп;<).
ТЕОРЕМА 6. Длина шкалы (СТп; <) равна Е^=2С™1т +
2п+1 — 2п — 2, где С™ — число сочетаний из η по т, а 1т =
г, ιΊ [i°g24 г η
ψψ - Σ [Щ] mod 2.
г=0
В частности, длина (СТ2; <) равна 3, длина (СТз; <} равна 13,
длина (СТ4; <) равна 40.
Дальнейшее описание шкал (СТп; <}, а также ряд открытых
вопросов, связанных с их строением, можно найти в работе [16].
153
Глава 4. Некоторые приложения универсальной алгебры
Подводя итоги рассмотрений данной главы, мы можем
сформулировать, что программно-вычислительные возможности
(потенциал вычислимости) вычислительных машин (универсальных
алгебр) в конечном счете определяются двумя факторами:
1) совокупностью замкнутых относительно команд областей
объектов, с которыми имеет дело данная машина (решетки
подалгебр универсальной алгебры) и
2) совокупностью "симметрии" между этими областями
(совокупностью внутренних изоморфизмов универсальной алгебры).
ЗАДАЧИ
1. Докажите, что для любой универсальной алгебры 21 =
{Α; σ), конечной либо бесконечной, совокупность Iso2l
удовлетворяет условию 2) из формулировки теоремы 1.
2. Докажите, что шкала (СТ2; <) имеет диаграмму,
представленную на Рис. 4.2, стр. 152.
§ 16. Конечные автоматы, языки
и грамматики
Пусть А — некоторое конечное множество, А* — совокупность
всех конечных последовательностей элементов из А. Элементы
множества А будем называть буквами алфавита а элементы из
А* — словами алфавита А. Добавим к совокупности А* еще
один символ λ, который будем интерпретировать как пустое
слово. Пусть А^ — A* U {λ}. На элементах из А^ введем
двухместную операцию умножения (конкатенацию слов) следующим
образом: для ах...&„,, Ьх .. .bm G А* пусть αχ.,.Οη · Ь\ ... Ьт= αι...α„
b\ ...bm и λ ■ αχ.,.α,ι = αχ ... α„, α\...θη ■ λ = αχ ... α™, λ · Α — λ.
Очевидно, что операция · ассоциативна на совокупности А^*\ А
играет роль единицы в полугруппе (А^; ·), а (А*; ·) — свободная
полугруппа, порожденная множеством А в многообразии всех
полугрупп. Произвольное подмножество L С ЛМ будем называть
языком в алфавите А.
Пусть G = (V; Е) — некоторый конечный орграф без кратных
дуг. Пусть каждая его дуга помечена одной или несколькими
буквами алфавита Σ, т.е. задана функция ψ из Ε в Ρ(Σ) — функция
154
§16. Конечные автоматы, языки и грамматики
разметки дуг. Предположим, что в V выделены непустое
подмножество S — множество начальных вершин или входов и
подмножество Τ — множество заключительных вершин или
выходов.
Подобный набор (V; Е\ φ; S\ Г), состоящий из размеченного
орграфа без кратных дуг с выделенными начальными и конечными
вершинами, будем называть конечным автоматом.
К примеру, рассмотрим автомат, G\ = {{А, В, С, D,M, К};
{(A,M),(A,B),(M,K),(K,M),{B,K},(B,C),(C,D)};
φ((Α,Β)) = {α}, φ((Α,Μ)) = {b}^((M,K)) = {α},φ((Κ,Μ)) =
{α, 6}, φ((Β, Κ)) = {α}, φ((Β, C» = {a, b}, ψ{{0, D)) = {Ь}; {Α, Β},
{С, £>}). Графически автомат Gi можно представить следующим
образом:
Любому конечному маршруту в автомате мы будем
приписывать одно или несколько слов из Σ*, считывая буквы вдоль этого
маршрута. Все слова такого вида будем называть помечающими
словами данного маршрута. К примеру, для автомата G слова
a, b, ab, 6Ь, aa, aab, abb образуют полный список помечающих слов
всех маршрутов из начальных вершин в заключительные
вершины автомата G.
Языком L(G), порожденным конечным автоматом G,
назовем совокупность всех помечающих слов в алфавите для
маршрутов из начальных в заключительные вершины автомата
G. Таким образом, L{G\) = {a, b, ab, bb, aa, aab, abb}. Для
маршрута, не содержащего дуг, помечающим словом будем считать слово
λ. Тем самым для конечного автомата G имеет место включение
λ € L(G) тогда и только тогда, когда некоторая вершина автомата
G является одновременно и начальной и заключительной.
Язык L С Σ* называется представимым (над алфавитом),
если L = L(G) для некоторого конечного автомата G.
155
Глава 4. Некоторые приложения универсальной алгебры
Без труда замечается, что
(*) любой конечный язык представим.
Условие конечности языка здесь существенно.
Покажем, к примеру, что язык L = {а1Ьг \ г € N} не
представим, здесь сг — слово длины г, образованное одной буквой с.
Действительно, от противного, пусть L = L(G) для некоторого
конечного автомата G. Рассмотрим в G маршрут с помечающим
словом ааг Ьг, где г превышает число вершин в G:
a a abb Ъ
->--♦^—*)—· · · · ·-!—·->—m—· · · · ·-»—·-->
А0 Αι А2 Л-1 Ai Вг В2 Β*-ι В{
Так как число вершин на участке от Aq до Ai больше числа
вершин в G, то для некоторых 0 < к < I < г имеет место равенство
Ak — Αι. Выкинем из маршрута цикл А&, Ak+i, ■ ■ ■, Αι и получим
снова маршрут от Aq до Bi с помечающим словом вида а·7 Ьг, где
< j < i, т.е. aj Ь' G L(G) = L, в противоречии с выбором L.
Конечный автомат G назовем детерминированным, если он
имеет только одну начальную вершину и для любой вершины А и
любой метки а € Σ имеется в точности одна дуга (А, В) с меткой
а. На самом деле, ограничение детерминированностью не
сказывается на представимости языков. Иначе говоря:
(**) для любого конечного автомата G существует конечный
детерминированный автомат G' такой, что L(G) — L(G').
Можно показать, что подобный конечный детерминированный
автомат G', содержащий наименьшее число вершин (зависящее,
конечно, от автомата G), единственен с точностью до
изоморфизма.
Рассмотрим теперь другой подход к детерминированным
конечным автоматам G — (V;E;p; {υ},Τ). Элементы множества V
будем называть состояниями автомата G, элементы из Σ —
входными сигналами автомата, υ — начальным
состоянием автомата, а Т — конечными его состояниями. Автомат G
"работает" в дискретной временной шкале по следующему
правилу: если и € V — состояние автомата G в данный момент времени,
а α € Σ — входной сигнал, то в следующий момент времени
автомат G переходит в состояние υ £ V такое, что φ((η, υ)) = а.
В силу детерминированности автомата G функция φ может быть
156
§16. Конечные автоматы, языки и грамматики
заменена на другую функцию ф, отображающую декартово
произведение V χ Σ в V, такую, что φ((u, a)) = v. Очевидно, что
функции φ и ф взаимно определяют друг друга. Функция ф
называется функцией переходов автомата G.
Таким образом, детерминированный автомат G можно
представлять себе как некую машину с конечным числом внутренних
состояний, которые будут рассматриваться нами как вершины
орграфа. Метки алфавита Σ — это входные сигналы. Автомат
описывает поведение машины, показывая нам, в какое новое
состояние Υ она переходит из состояния X, получив входной сигнал
а, для этого служит дуга (Χ, Υ) такая, что φ((Χ,Υ)) — α, или
иначе такая, что ф((Х,а}) = Υ. Машина всегда начинает работу
в начальном состоянии. Слово w (Ξ L(G), если оно вызывает
переход машины, последовательно получающей его буквы как
входные сигналы, из начального состояния в одно из заключительных
состояний.
Подобный подход к детерминированным автоматам позволяет
изучать их с точки зрения универсальной алгебры. Правда, при
этом удобнее использовать не односортные универсальные
алгебры, рассматриваемые нами выше, а некоторое их обобщение —
многосортные универсальные алгебры.
Для этого мы фиксируем некоторое множество / —
множество сортов, под сигнатурой σ = {f£°,..., /£*, с0,..., Сщ) мы будем
по-прежнему понимать совокупность функциональных символов
Ζ/4 и символов констант с,·, но при этом для каждого
функционального символа //* фиксируется еще некоторое отображение ft
множества щ + 1 = {0,1,..., щ} во множество /, а также
отображение h множества {cq, ..., cm} во множество /. Тогда, говоря об
/-сортной универсальной алгебре 21, мы будем иметь в виду
набор (Ai\i € /) непустых множеств — основных множеств алгебры
21 и набор отображений ff. ЛЛ(°) х ... х Ακ(η4-ΐ) -> Ак(ш)
(сигнатурных функций алгебры 21), а также фиксированных элементов
Cj G Ah(j) (констант алгебры 21).
Таким образом, в случае, когда / = {г} одноэлементно,
многосортная алгебра 21 представляется универсальной алгеброй,
изучаемой ранее.
Тем самым конечный детерминированный автомат G = (V\ E;
ф; {ν}, Τ) — это двусортная универсальная алгебра 21 при / =
157
Глава 4. Некоторые приложения универсальной алгебры
{0,1} сигнатуры σ = (/^,Со,сь... ,ссп), где η = \Т\ и д(0) =
0,д(1) — 1,д(2) — 0,h(0) = 0,...,h(n) = 0 и основные
множества А0 и Αι алгебры 21 таковы, что Aq = V, Αι = Σ, при этом для
и е А0, a G Σ f0(u,a) = ψ((υ,,α)), Cq = υ, ci = ti,... ,Cm = tn,
если Τ — {ίχ,..., tn}. В контексте перехода от односортных
универсальных алгебр к многосортным естественным образом
обобщаются понятия изоморфизма, гомоморфизма, подалгебры, ядра
гомоморфизма, конгруэнции, фактор-алгебры, прямого и подпря-
мого произведения, многообразия алгебр, тождества и т.д. Таким
образом, возникают понятия подавтомата, изоморфизмов и
гомоморфизмов автоматов, фактор-автоматов по их конгруэнциям,
прямых и подпрямых произведений автоматов, их многообразий
(важнее — псевдомногообразий) и тождеств истинных на
автомате. Все эти понятия и утверждения, имеющие место для этих
понятий как обобщения соответствующих утверждений об
односортных алгебрах, оказываются весьма продуктивными в
контексте изучения автоматов и языков, ими представляемых.
Заметим также, что в ряде случаев удобно рассматривать
конечный детерминированный автомат G = (V;E;ip;{v},T) и как
обычную одноосновную универсальную алгебру 25 = (V;a), где
сигнатура σ состоит из одноместных функций /α(α G Σ), таких,
что fa(X) = У, если ψ((Χ,Υ)) = α для любых Χ, Υ €. V, и
констант с0 = ν, сх = ίχ,..., cn = ίη, если Τ — {ίχ,..., tn}.
Еще один подход к изучению представимых языков связан с
понятием системы продукций. Под последней имеют в виду
пару (Σ, Р), где Σ — по-прежнему конечное множество (алфавит),
а Р — конечное подмножество множества
£(*) χ £(*). Элемент
(ΐϋχ,κ^) € Ρ называется правилом подстановки или
продукцией. Далее продукцию (ΐϋι,ιι^) будем обозначать как ΐϋχ —¥ ги2.
Для заданной системы продукций (Σ,Ρ) определим отношение
=>■ продуцируемости на множестве Σ*·*) слов алфавита Σ
следующим образом: для слов и^щ € Σ^*' имеет место отношение
ωχ =Φ· щ (говорим, что слово щ продуцирует слово щ) тогда и
только тогда, когда существуют слова ι>χ,ι>2 € Σ^ такие, что
Щ = ViWiV2, Ul = ViW2V2 ДЛЯ НвКОТОрОЙ ПРОДУКЦИИ Ίϋχ —> W2
из Р. Рефлексивно-транзитивное замыкание отношения =Ф·
обозначим далее как =4>* (отношение выводимости для системы
продукций (Σ, Р) на множестве слов Σ^*^ алфавита Σ). Таким об-
158
§16. Конечные автоматы, языки и грамматики
разом, для слов и, ν Ε Σ,^ имеет место и =4>* υ тогда и только
тогда, когда и = υ, либо для некоторых слов щ, щ,... ,ит Ε Σ(*)
имеет место
U = Щ => Щ => U2 => ... =>■ Um = V.
К примеру, пусть Σ = {χ, у, z,a,b} α Ρ = {χ —ϊ ay, у —» ay, z —>■
αχ, ж —>■ Ьг;,у —»■ bx,z —» Ьу, χ —>■ λ}. Тогда, в частности, имеет
место
χ =>■ ay ==> aay => aaay => aaabx =Φ· aaabbz =Φ· aaabb, т.е. χ =>*
aaabb.
Грамматикой называется набор G = (Σ, Ρ, Σ^,Σ^, Στ), где
(Σ, Ρ) — система продукций, Σλτ С Σ, Στ = Τ\ΈΝ, 0 φ
Σ5 Q Σ#. Элементы из Σ^ называются нетерминалами, из Στ
—терминалами, а из Σ^ — начальными элементами. Языком,
порождаемым грамматикой G, называется множество
L(G) — {w Ε Σ^ I существует a £ Σ$ такое, что a =>* w}.
К примеру, для приведенной выше системы продукций (Σ,Ρ),
если грамматика G = (Σ, Р, {х}, {х, у, ζ}, {α, Ь}), то aaabb Ε b(G).
Грамматика G называется праволинейной, если каждая ее
продукция имеет один из следующих видов:
1) χ —¥ ay, для некоторых х, у € Σ^, α Ε Στ;
2) χ —» λ, для некоторого χ Ε Σ^.
Продукции вида 2) будем называть стирающими.
Нетрудно показать, что представимые языки — это в
точности языки, порожденные некоторой праволинейной грамматикой.
Таким образом, справедлива
ТЕОРЕМА 1. Для любого языка L С Σ^*) следующие условия
эквивалентны:
1) L представим конечным автоматом;
2) L представим конечным детерминированным автоматом;
3) L порождается праволинейной грамматикой.
Пусть, по-прежнему, Σ — некоторый конечный алфавит.
Рассмотрим булеву алгебру <8 = (Ρ(Σ^); Ц Π, ~·, Φ, Σ^*Λ всех
подмножеств множества ΣΜ всех слов в алфавите Σ. Алгебру <8
назовем булевой алгеброй языков над алфавитом Σ. Определим
на Ρ(Σ(*)) еще одну двухместную операцию · — катенацию
языков на основе операции конкатенации слов, определенной выше:
159
Глава 4. Некоторые приложения универсальной алгебры
для L\, Li С Σ^*) полагаем L\ · L2 = {w% ■ W2\w\ 6 Lj и №2 G L2).
Очевидно, что алгебра {Ρ (т№\ ; ·} является полугруппой. На
множестве Ρ(Έ^) определим новую одноместную операцию *:
L —* L* катенативного замыкания, полагая
оо
L* = U U\
п=0
считая, что L0 = {λ} и Ln+l = Ln · L. Очевидно, что слово w
входит в L* тогда и только тогда, когда w = λ, либо w является
конкатенацией некоторой конечной совокупности слов из L.
Алгебру Js = (Ρ(Σ(·>); U, Π, -, ·, *, </>, Σ<*>) будем
называть алгеброй языков над алфавитом Σ. Операции Ц ·, * над
языками алфавита Σ называются регулярными операциями.
Простейшими языками над алфавитом Σ будем называть
пустой язык 0 и любой язык вида {а}, где а е Σ.
Язык L над алфавитом Σ называется регулярным, если он
может быть получен из простейших языков с помощью конечного
числа применений регулярных операций, т.е. если он
принадлежит подалгебре, порожденной простейшими языками в алгебре
(Ρ(Σ(*>); U, ·, *)·
Без особого труда можно показать, что
(***) совокупность представимых языков над алфавитом Σ
замкнута относительно операций Ц ·, *·
Опять же без труда замечается, что любой простейший язык
представим. В силу этого и утверждения (***) получаем
представимость любого регулярного языка. На самом деле можно
доказать и обратное. Таким образом, имеет место
ТЕОРЕМА КЛИНИ. Язык представим тогда и только
тогда, когда он регулярен.
Полное доказательство теоремы Клини см., к примеру, в [2].
Заметим также, что совокупность представимых языков на
самом деле замкнута не только относительно регулярных операций
U, ·, *, но и относительно операций П> ~1· Тем самым
совокупность R(E^) представимых (регулярных) языков над алфавитом
Σ образует подалгебру в алгебре языков Σ — алгебру
представимых языков
ΛΣ = (Λ(Σ*); U, П, -., ., *, φ, Σ*}.
160
§16. Конечные автоматы, языки и грамматики
ЗАДАЧИ
1. Докажите утверждение (*) данного параграфа.
2. Докажите утверждение (**) данного параграфа, выбирая
в качестве вершин автомата G' = ty'\E'\iff\S';T') совокупность
V = P(V), где G = .(V,Ε,φ,S,T),b качестве S' = {S},Τ' = {В е
V = P(V)|P ПГ^}. Алфавиты для G и G' совпадают, и для
любой буквы α € Σ пусть Ва = {С € V| существует дуга (Л, £>) €
Ε такая, что ¥>((С,£>» = α>· ТогДа (#,#«.) € J? и φ((Β,Βα)) = а.
Докажите, что L(G) = L(G').
3. Пусть G = (У, #, у>, 5", Т) — некоторый конечный автомат
над алфавитом Σ. Рассмотрим следующую право линейную
грамматику G" = (Σ" = VUΣ, Ρ, Σ3 = S,ΣΝ = К, ΣΓ = Σ). При этом
Ρ = {А -+ аВ\{А,В) е Ε и у>((Л,Я» = a}U{A -+ Х\А е Т}.
Докажите, что Z/(G) = L(G'). Тем самым любой язык, предста-
вимый некоторым конечным автоматом, порождается некоторой
праволинейной грамматикой.
4. Докажите, что для любой праволинейной грамматики G
существует конечный автомат G' такой, что L{G) = L(G'). Тем
самым решение задач 1-4 содержит полное доказательство
теоремы 1.
5. Пусть U = L(Gi) и L2 = L(G2), где Gx = (Σι,Λ,Σ^,Συν,
Σ it) и G2 = (Σ2, Ρ2,Σ25,Σ2λτ,Σ2τ} — праволинейные
грамматики такие, что Ец" = Σ2τ = Σ. Предположим, что Συν Π Σ2λτ =
ф. Грамматику (?з = (Е3,Рз^з5,Езлг^3т) определим, полагая
Σ3/ν = ΣΧΝ U Σ2τν,Σ3τ = Σ, Ρ3 = Pi U P2, грамматику G\ =
(Σ4,Ρ4, Σ45, Σ4Λτ, Σ4Τ) — полагая Σ45 = Σ15, Σ4Τ = Σ,Σ4Λτ =
Συν U Σ2λτ, Ρ4 = {все продукции из Рг, за исключением стирающих
продукций}иРги {А —> w\ где А—> λ G Рь Р» —» ги е Рг и Ρ —
начальный символ из G2}. Грамматику G5 = (Σ5,Ρ5,Σ5£,Σ5λτ,Σ5γ)
определим, полагая Σ5λτ = EuvU{-Ao}, где А0 — некоторый
новый символ, не входящий в Σχχ, Σ^ = Σΐ£υ{Αο}, Σ5τ = Σ, Ρ =
Ρ! U {Α0 -> λ} U {Α -> ω| где Α -> λ e Pi, Ρ -»■ ω 6 Ρ2 и Ρ -
начальный символ из G\}. Докажите, что L(Gz) = L\ \]L%, L(Gi) =
Lx · Ζ/2, L(Gb) = L\. Тем самым утверждение этой задачи
доказывает утверждение (***) настоящего параграфа.
161
Глава 4. Некоторые приложения универсальной алгебры
§17. Алгебры Халмоша и базы данных
Основная цель данного параграфа — продемонстрировать
возможности алгебраического подхода к изучению баз данных. При
этом изложение носит лишь эскизный, демонстрационный
характер. Систематическое изложение этого вопроса можно найти в
монографии [20].
База данных — это информационная автоматизированная
система, хранящая и перерабатывающая информацию и способная
выдавать ответы на запросы. Можно запрашивать то, что
непосредственно хранится в базе, но можно запросить и производную
информацию — информацию, как-то выражаемую через
базисную. Мы рассмотрим далее лишь одну из возможных моделей баз
данных — реляционную, когда информация хранится в виде
отношений между данными.
Для большей ясности начнем с простейшего примера.
Рассмотрим информацию о некотором производственном
коллективе. Пусть Д — это множество членов этого коллектива, Д —
совокупность должностей, исполняемых членами этого
коллектива, Д — совокупность конкретных обязанностей членов
рассматриваемого коллектива. Пусть Φ — набор некоторых отношений
между элементами множеств Д. К примеру,
Ф = {φ,ψ,η,α,β,Ύ,δ,ξ,μ,...}.
При этом для a,b G Д, с, е £ Д, d € Д; вхождение
(а, Ь) € φ означает, что α занимает в настоящее время должность
Ь; (а, Ь) е ψ — означает, что α потенциально способен справиться
с обязанностями, предполагаемыми при исполнении должности Ь;
(а, Ь) € η — что а стремится занять должность b; (a,d) 6 α —
что α способен успешно справиться с поручением d; (a,d) € β —
что при дополнительном обучении α справится с поручением d\
(α, d) Ε 7 — что α исполнять поручение d будет без всякого
желания; (6, d) € δ — что поручение d входит в круг функциональных
обязанностей должности Ь; (а, Ь) € ξ — что отношение а к Ь
неприязненное; (с, е) €. μ — что должность с находится в подчинении
должности е и т.д.
Указанный набор Φ определяет базисную информацию о
данном производственном коллективе на данный момент. Эта инфор-
162
§17. Алгебры Халмоша и базы данных
мация хранится в виде подмножеств соответствующих
декартовых произведений множеств Di,D2,D3 : φ,ψ,η Q Dx χ £>2) α,/?,
7 C£>x x £>3, <* € £>2 X Аь ξ С £>! χ £>!, /χ С D2 x Α>·
Обработка информации предполагает определенные действия
с базисными подмножествами, входящими в Ф, и для реализации
этих действий необходимо всю базисную информацию «уравнять»
в одном и том же большом декартовом произведении. Для этого
рассмотрим декартово произведение D = D[ x D[ x D2 x D2 x £>3,
где D[ = D'2 = £>ь £>3 = D'4 = D2 и £>£ = Di и с
подмножествами, входящими в Ф, отождествим подмножества £>, отвечающие
им при фиксированных проектированиях D на некоторые
фиксированные произведения сомножителей, образующих множество
D. К примеру, φ отождествим с φ' С D следующим образом:
(а, Ь, с, о?, е) € V3' тогда и только тогда, когда (а, с) € у?.
Поскольку объекты имеющейся у нас базисной информации
имеют разную природу: члены коллектива (элементы множеств
D[ и £>з), наименования должностей (элементы множеств £>3 и
ЕУ4), конкретные поручения (элементы множества D'b), — мы
будем далее рассматривать так называемое многосортное
исчисление предикатов для формирования наших запросов к базе
данных. Для этого переменные в нашем исчислении предикатов
x,y,z,... будут снабжаться индексами 1,2,3,4,5 и переменная х1
(ж2, χ3, а;4, ж5) будет пробегать множество значений (домен) D\
(D'2, D'3, D'4, D'5) соответственно.
К примеру, нас интересует список лиц, способных после
дополнительного обучения занимать все вышестоящие над ними
должности и не имеющих неприязненного отношения ни к кому из
членов рассматриваемого коллектива. Очевидно, что требуемый
список - это те элементы множества ϋχ которые удовлетворяют
формуле
p{xl) = VyX*\ у2) -+ V*fy(ya, ζ2) -+
\/u3(S{z2,u3) ^ β(χ\υ?))))&\/νι->ξ(χ\νι).
При этом при обработке в нашей базе данных вместо
отношений φ, μ, δ, β, ξ будут использоваться φ', μ', δ', β', £' С D. Тогда
логическим связкам —>,-■,& в формуле запроса соответствуют
операции (D\X)\JY, D\X, X Г\У наД подмножествами множества
163
Глава 4. Некоторые приложения универсальной алгебры
D. Действиям же кванторов 3 и V при желании по-прежнему
работать с подмножествами множества D соответствуют
следующие конструкции. Пусть Φ (χ) — это некоторые свойства пятерки
{a;1,y1,z2,u2,i>3) из множества D и этому свойству соответствует
подмножество А множества D, тогда формула Зж1Ф(ж) выделяет
совокупность тех элементов (а1, 6х,с2, d2,e3) из D, что для
некоторого г1 G D[ имеет место включение {г^Ь^с2,^2, е3) € А. При
этом квантор Va;1 трактуется с помощью известной
эквивалентности
\/χ1Φ(χ) ~ -ι3χ1-ιΦ(χ).
Поясним определение квантора 3 при изложенной его
трактовке как преобразований подмножеств множества D на более
простом «двухмерном», а не «пятимерном» примере.
Если φ — бинарное отношение между элементами множества
А и множества В, т.е. φ С А х В и χ (у) — переменная,
соответствующая домену А(В), то формула
р(у) = 3χφ(χ, у)
при стандартной трактовке интерпретируется одноместным
отношением ρ на множестве В — фактически проекцией множества φ
по второй координате
В В
φ Α Ρ А
В контексте работы с базами данных удобнее рассматривать,
как уже замечалось выше, отношение р(у) как двухместное
отношение (р С А х В), в котором χ участвует как фиктивная
переменная, т.е. ρ является цилиндром, натянутым на множестве φ
по направлению множества А. Иначе, точка (a,b) £ ρ С А х В
тогда и только тогда, когда существует точка (а', Ь) Ε φ С А х В.
Впрочем, обо все этом говорилось выше в рассмотренном
примере, когда мы от двухместных отношений φ,ψ,α,... переходили к
164
§17. Алгебры Халмоша и базы данных
пятиместным φ',φ',α',— Таким образом, возвращаясь к
нашему примеру и добавляя к указанным выше интерпретациям
логических связок —>,&,-! рассмотренную интерпретацию кванторов
Зх^Зх^Зх^Зх^За;5, мы ПОЛуЧаем новые одноместные операции
над подмножествами множества D. При этом отметим следующие
свойства этих операций:
(*) А С ЗхМ, Зх1А = Эж*'ЭжМ, Зх* (A U В) = ЗхМ U Зх*5,
За;* (Л П В) С ЗхгЛ П Зх*5, Зх'0 = <£, Зх* ЗхМ = Зх^'Зх'А
Теперь мы можем сформулировать понятие кванторной
алгебры. Пусть <8 = {В; V, Λ, -ι, 0,1) — некоторая булева алгебра и
фиксировано множество / — множество сортов переменных
(имена доменов), под соответствующей кванторной алгеброй <8/ мы
будем понимать обогащение алгебры <8 введением в ее сигнатуру
дополнительных одноместных операций Зхг (где i € I),
удовлетворяющих условиям (*).
Таким образом, рассмотренный выше пример базы данных
производственного коллектива может быть описан как некоторая
конкретная кванторная алгебра / = {1,2,3,4,5}. Однако при
работе с базами данных приходится учитывать самые разные
изменения, которые могут происходить с зафиксированными
данными. В нашем примере: у конкретного члена коллектива
изменилась должность, изменились функциональные поручения,
связанные с этой должностью, какие-то должности ликвидированы или
введены новые, изменился состав коллектива и т. д. Все это
приводит к необходимости рассматривать еще целый ряд
преобразований базы данных. Удобнее всего это представить следующим
образом: фиксируется некоторая абстрактная полугруппа (5 = (S; ·)
с единицей е и на кванторной алгебре 93/ вводится еще ряд
одноместных операций fs, где s € S, при этом выполняются
следующие требования:
(**) fsAfs2(A)) = /WA), fe(A) = Л, fs^fsA =
SxVsA
Полученная таким образом алгебра
BItG = (В; V, Λ, -., 0,1, Зх\ /5|t € /, s € S)
и носит название алгебры Халмоша.
165
Глава 4. Некоторые приложения универсальной алгебры
Тем самым различные базы данных могут рассматриваться
как алгебры Халмоша. Обратимся теперь к взаимодействию
запросов с конкретными базами данных. Как мы видели выше,
запросы в базу данных могут быть сформулированы в виде
формул исчисления предикатов с дополнительными операциями: s-
элементами полугруппы (5. Но вообще сами эти формулы могут
рассматриваться как элементы абсолютно свободной алгебры Fa
сигнатуры σ = (V,&, -ι, 0,1,3а;1, \/х\ fs \ί G I, s G S). Однако при
формулировании запроса один и тот же запрос мы можем
формулировать с помощью различных формул и от конкретной
формулировки запроса может зависеть время обработки запроса.
Например, мы можем не использовать кванторы W, так как для
любой формулы ψ имеет место эквивалентность
Ух1 φ ~ ->3χι->φ.
Приведенный выше запрос к базе данных производственного
коллектива мы можем, к примеру, на основе стандартных эквива-
лентностей математической логики привести к пренексной конъ-
юктивной нормальной форме:
VyWWVu^b^i1, у2) V -μ(2/2, ζ2) V -φ2, ν?) V β {χ1, u3)}k
и результаты данного и указанного ранее запроса будут
тождественны. В частности, при обработке запросов можно
использовать равенства (*) и (**), указанные выше. Кроме того, возможны
еще какие-то специфические эквивалентности между формулами,
связанные с конкретным типом рассматриваемых баз данных; к
примеру, можно потребовать, чтобы в коллективе любой
начальник относился к своим подчиненным благожелательно, т.е. ввести
в рассмотрение дополнительную эквивалентность
\/χ1\/ν'\/ζ2,\/η2(φ(χ\ζ2)&:φ{ν\η2)&:μ(υ,2,ζ2) -> ^{y\z2)) = 1·
Подробные логические и «конкретные» эквивалентности на
множестве формул рассматриваемого исчисления предикатов
определяют конгруэнцию θ относительно сигнатуры σ в абсолютно
свободной алгебре Fa — конгруэнцию эквивалентных запросов.
166
§18. Некоторые приложения группоидов и полугрупп
Тем самым запросы можно представлять как элементы фактор-
алгебры Халмоша ^σ Iq — свободной алгебры в многообразии
алгебр Халмоша, определяемом тождествами, соответствующими
конкретной специфике рассматриваемых баз данных.
При этом база данных конкретного коллектива для данных
фиксированных множеств Dl,..., D5 и данных фиксированных
отношений φ',..., ξ',... будет представлять собой некоторую
конкретную алгебру Халмоша 21 и можно рассмотреть отображение /
свободных образующих φ, ...,ξ,... свободной алгебры Халмоша *W#
в данную алгебру, определяемое равенствами
/И = ¥/,...,/(О = £',-■
Тогда ответом на запрос Φ €. **σ /β к нашей конкретной базе
данных очевидно будет значение д(Ф), где д — это единственное
продолжение отображения / до гомоморфизма свободной алгебры
?σ q в алгебру 21. Эти соображения и лежат в основе применения
универсальной алгебры в теории баз данных.
§18. Некоторые приложения
группоидов и полугрупп
В этом параграфе будут приведены несколько примеров
возможного применения понятий и конструкций универсальной
алгебры в контексте теории группоидов и полугрупп (как частного
случая универсальных алгебр) как в различных областях чистой
и прикладной математики, так и в биологии, химии и других,
далеких от математики, областях знаний. Напомним, что алгебра
21 — (А; ·) сигнатуры из одной бинарной операции (как
правило, обозначаемой как умножение) называется группоидом.
Если при этом операция ассоциативна, то группоид 21 называется
полугруппой. Если полугруппа 21 обладает единицей, то она
называется моноидом.
Первый рассматриваемый здесь пример будет посвящен
взаимосвязи теории группоидов с комбинаторикой.
Тройной системой Штейна на множестве А называется
любая система S трехэлементных подмножеств этого множества
такая, что любая пара различных элементов из А содержится ровно
167
Глава 4. Некоторые приложения универсальной алгебры
в одном подмножестве из S. Мощность |Л| называется порядком
тройной системы Штейна (A;S).
Если \А\ = 1,2 то S = 0, если \А\ = 3, то S = {А}, Без
труда замечается, что для конечного множества Л на Л
существует тройная система Штейна (A; S) тогда и только тогда, когда
\А\ = 1 или 3(mod6), при этом \S\ = |A|(lghl).
Следующий рисунок дает пример тройной системы Штейна
порядка 7 на множестве {1,2,3,4,5,6,7}. При этом три точки
входят в систему S тогда и только тогда, когда эти точки лежат на
одной прямой либо на одной окружности.
Вопрос о построении новых тройных систем Штейна с
помощью уже известных легко решается путем перехода от этих
систем к соответствующим им универсальным алгебрам
(группоидам). Пусть (A; S) — некоторая тройная система Штейна. На
множестве А определим операцию умножения ·: для a,b,c € A
a ■ b = с, если {а, 6, с} € S и a ■ a — a
Ha группоиде 21 = (A; ·) очевидным образом истинны тождества
х-у = у -х,
х(х -у) = у.
Любой группоид 21 = (А; ·}, на котором истинны эти
тождества, называется квазигруппой Штейна.
Покажем, что любая квазигруппа Штейна связана указанным
выше образом с некоторой тройной системой Штейна.
Действительно, пусть 21 = {А; ·) — квазигруппа Штейна. Для любых
различных элементов а, Ь из А и любого с Ε А положим
{a,b,c} e S <&a-b = с
Очевидно, что S — система трехэлементных подмножеств
множества А и любая пара различных элементов из А входит в
некоторое единственное подмножество из S.
168
§18. Некоторые приложения группоидов и полугрупп
Так как совокупность всех квазигрупп Штейна образует
многообразие, то, в частности, переходя от декартовых произведений
квазигрупп Штейна (соответствующих известным тройным
системам Штейна) к соответствующим им тройным системам Штейна,
получаем возможность построения новых подобных систем.
Рассмотренным примером далеко не ограничиваются
взаимосвязи универсальной алгебры и комбинаторики.
Рассмотрим теперь некоторые взаимосвязи теории полугрупп
и теории кодирования. Традиционным образом передаваемая
информация рассматривается в виде сообщений (слов) —
последовательностей сигналов (букв некоторого алфавита Σ). Таким
образом, мы будем иметь здесь дело с множеством Σ всех слов
рассматриваемого алфавита Σ, наделенным операцией конкатенации
• (см. § 16). Т.е. со свободной полугруппой F% = (Σ*; ·).
Пустое слово λ играет роль единицы в свободном моноиде
F'E = (£*U{A};·).
Пусть Μ — подмоноид моноида F'e и М+ = μ\ {λ}.
Традиционно определим совокупность (М+) = {uv\u,v € М+}. Без труда
замечается, что подмоноид Μ имеет единственное минимальное
множество порождающих С = М+/(М+). Подобное С
называется базисом моноида М.
Столь же непосредственно доказывается следующий
критерий Шютценберже — Шеврина — Кона: подмоноид Μ свободного
моноида F'a свободен (изоморфен свободному моноиду) тогда и
только тогда, когда для любого ω Ε Σ*; если ΜωΓ)Μ0 и ωΜΓ\Μ0,
то α; € Μ.
Подмножество С свободного моноида F'e называется кодом
над Σ, если С является базисом некоторого свободного подмоно-
ида Μ моноида F's. Обозначим эту ситуацию как Μ = С*.
Пусть С — произвольное подмножество из Σ* и у — биекция
некоторого множества В на С. Отображение у продолжимо до
гомоморфизма у моноида F'b на подмоноид Μ моноида F'y^,
порожденного С.
Таким образом, С — код тогда и только тогда, когда у —
изоморфизм. При этом биекция у называется кодированием
множества В в алфавите Σ.
169
Глава 4. Некоторые приложения универсальной алгебры
Изложенная система понятий и является основой для
применения теории полугрупп в теории кодирования. Более подробно
об этом см., к примеру, [12].
Допустим теперь, что в изучении некоторых процессов мы
имеем дело с набором реагентов {αχ,..., αη,...}, которые в изучаемых
процессах вступают в некоторое попарное (бинарное) отношение
(реакцию) друг с другом, результатом которого является один из
реагентов из данного набора. Реально это могут быть химические
реагенты, при химической реакции пары из них друг с другом
возникает опять один из этих реагентов. Либо реагенты — это
биологические особи (точнее, типы этих особей), в результате
скрещивания которых возникает (рождается) новая особь (одного из
рассматриваемых типов αχ,..., αη,...). Таким образом, на
множестве А = {αχ,..., α„,...} задана бинарная операция а;, а, —>■ а4 · а,
— результат реакции реагента а* с реагентом а,-, и мы имеем дело
с группоидом (Л; ·).
Приведем два примера, конкретизирующих эту схему и взятые
из книги [12].
При селекции породы крупного рогатого скота рассматривают
два цвета: черный и бурый и признаки одноцветности или
пятнистости. Известно, что черный цвет доминантен, а бурый
рецессивен и что одноцветность доминирует над пятнистостью. Таким
образом, мы имеем четыре типа скота: a — черный одноцветный, b
— черный пятнистый, с — бурый одноцветный, d — бурый
пятнистый. Результат (по цвету) скрещивания пары скота определяет
операцию · на множестве {a,b,c,d}. С учетом сказанного выше о
доминантности операция · на {а, Ь, с, d} задана следующей
таблицей Кэли:
•
α
6
с
d
a
a
a
a
a
b
a
b
a
b
с
a
a
с
с
d
a
b
с
d
Непосредственно замечается, что у нас полугруппа с
единицей d (и нулем — а). Различные свойства подобных полугрупп (в
более общей ситуации) могут быть проинтерпретированы как
соответствующие результаты биологических процессов. К примеру,
170
§18. Некоторые приложения группоидов и полугрупп
подмножество {с, d} является подалгеброй А = {{а, Ь, с, d}; ·)
полугруппы А, т.е. результаты скрещивания пятнистых особей не
могут дать одноцветную. Условие же вида: некоторый тип не
входит в п-ю степень подобной полугруппы означает исчезновение
(вырождение) этого типа в результате η-го этапа скрещиваний и
прочее и прочее.
Второй пример применения подобных группоидов (полугрупп)
в биологии будет связан с генетикой. Как и предыдущий, он
страдает рядом неточностей и преследует здесь в основном
демонстрационную цель. Генетическая информация организма содержится
в так называемой дезоксирибонуклеиновой кислоте (ДНК).
Молекула ДНК состоит из двух нитей, которые, соединяясь друг с
другом, образуют двойную спираль. Каждая нить, будучи
полимером, построена из нуклеотидов, структурных единиц четырех
различных видов. Рассмотрим одну нить. Отдельные ее отрезки —
суть гены — несут неделимые порции генетической информации.
Обозначим нуклеотиды символами 0,1,0,2,0,3,0,4, тогда гены
можно рассматривать как слова над алфавитом {αϊ, α2, α3,α4}. При
этом каждый ген «кодирует» синтез одного-единственного белка.
Сама молекула ДНК не может непосредственно реализовать
генетическую информацию. Эта информация копируется
(«транскрибируется») с каждого гена путем построения соответствующей
рибонуклеиновой кислоты, с помощью которой в процессе так
называемой трансляции на рибосомах синтезируются белковые
цепи. Каждая белковая цепь является полипептидом, состоящим из
аминокислот 20 различных видов, которые мы обозначим
символами &ι,... ^го-
Аналогично генам каждую белковую цепь можно
рассматривать как слово над алфавитом {Ьг,..., &го}·
Огрубляя ситуацию, мы допустим, что последовательность
нуклеотидов в каждом гене однозначно определяется
последовательностью аминокислот в соответствующей белковой цепи.
Таким образом, если считать, что любые полипептидные цепи
отвечают каким-либо «белкам», то должен существовать
мономорфизм (вложение, кодирование) свободной 20-порожденной
полугруппы F20 = {Ь\,..., Ьго}* в свободную 4-порожденную
полугруппу F4 — {αχ,... ,α4}*. В этом контексте становится важным
ответ на вопрос существуют ли, а если «да», то сколько, вложения
171
Глава 4. Некоторые приложения универсальной алгебры
«большой» полугруппы F20 в «малую» F4. Ответ выглядит
следующим образом.
ТЕОРЕМА. Существует бесконечно много различных
вложений (кодирований) полугруппы F2q в полугруппу F4.
Доказательство. Прежде всего определим вложение φ
множества {bi,..., 620} в F4 = {αχ,..., α4}* следующим образом:
¥>(&ι) = αιαιαι,<ρ(62) = αιαι^,ψ^) = а^^з, · ■ ■ ,¥>(£>2θ) =
o-20-xo-i (слова в правых частях равенств выписаны в
лексикографическом порядке). Так как {&ι,·..,ί>2ο} ~~ свободные
порождающие свободной полугруппы F20, то существует
однозначно определенный гомоморфизм φ полугруппы F2q в
полугруппу F4, продолжающий отображение φ. Заметим, что φ —
мономорфизм. Пусть Tp{bn,bi2,■ ·.,bir) = ip(bji,bj2,.. ■,bja), тем
самым, ψ(^ι)φ(^2)... Tp{bir) = Ψθ>α)ψφ3-2)... Tp(bj8), т.е. <p{biX)
<p(bi2)...<p(bir) = 4>(bji)ip(bj2). .-ipibjs). Из определения
равенства в свободной полугруппе, учитывая, что все слова ip(bk)
имеют одну и ту же длину 3, получаем равенства г — s и (р(Ьц) =
¥>(bji),...,^(bir) = ¥>(Μ·
Инъективность у> влечет равенства 6^ = Ьд,... , Ь$г = bjs, т.е.
и равенство bii,bi2,... ,bir = bji,bj2, ■ ■ .,6,-s. Таким образом,
гомоморфизм φ действительно является мономорфизмом.
Очевидно что, выбирая отображение φ различными
способами, например, используя слова длины 4 или 5 и т.д., можно
получить бесконечно много таких мономорфизмов.
Другие применения теории полугрупп в биологии, социологии
и других науках можно найти, к примеру, в книге [12].
Ограничиваясь приложениями универсальной алгебры,
изложенными в §§ 14-18, заметим лишь, что ими далеко не
исчерпывается круг приложений универсальной алгебры.
172
Заключение
Рассмотренные в данном тексте вопросы касаются лишь основ
универсальной алгебры и избранных тем, отвечающих
индивидуальным интересам автора. За этими рамками остался большой
массив вопросов, рассматриваемых на современном этапе
развития универсальной алгебры. Упомянем здесь традиционные
вопросы, связанные со строением решеток многообразий и
квазимногообразий универсальных алгебр (см., к примеру, [7, 13, 21,
30, 37]), с алгоритмическими проблемами — описание
многообразий с разрешимыми элементарными теориями (см. [27]), с
разрешимой проблемой тождества слов (см. [30]), вопросы конечной
и неконечной базируемости многообразий и квазимногообразий
(см. [27, 36, 39]), вопросы строения алгебр близких к примальным,
функционально полных и пр. (см. [32, 38, 42]), вопросы, связанные
с производными структурами (см. [б, 17]), с Галуа
соответствием (см. [41]). В последние десятилетия возникли новые подходы и
направления в универсальной алгебре, получившие значительные
и значимые результаты: теория коммутаторов на универсальных
алгебрах (см. [33]), классификация конечных алгебр (см. [23]),
минимальные алгебры и подмножества (см. [36]), категорные
эквивалентности классов универсальных алгебр (см. [37]),
вопросы интерпретируемости одних эквациональных теорий в других
(см. [31]), самые различные приложения универсальной алгебры
(см. [4, 12]) и другие.
Наконец отметим близкую связь универсальной алгебры и
теории моделей имеющих очень близкие между собой объекты
исследования: универсальные алгебры и модели, объединяемые общим
родовым понятием алгебраической системы. Тем не менее
каждая из этих областей математики имеет свои специфические цели
и методы исследований.
В последнее время появилось направление исследований
которое наиболее близко сводит между собой универсальную алгебру и
теорию моделей: универсальная алгебраическая геометрия.
Пионерами этих исследований стали Б.И.Плоткин и В.Н.Ремесленников
Глава 4. Некоторые приложения универсальной алгебры
с соавторами. При этом работы Б.И.Плоткина шли от идеологии
классической алгебраической геометрии, в то время как подход
В.Н.Ремесленникова базировался на традиционных теоретико-
модельных понятиях.
Все это показывает насколько живой, актуальной,
развивающейся остается область математики именуемая универсальной
алгеброй.
174
Указатель терминов
Автомат конечный, 155
конечный
детерминированный, 156
Автоморфизм, 24
Аксиома выбора, 39
исчисления тождеств, 95
Аксиомы исчисления
условных тождеств, 128
Алгебра абсолютно свободная,
83
арифметическая, 101
булева, см. Булева алгебра
дискриминаторная, 103
квазипримальная, 108
кванторная, 165
конгруэнц-дистрибутивная,
99
конгруэпц-модулярная, 99
конгруэнц-перестановочная,
98
локально-конечная, 121
наследственно простая, 105
подпрямо неразложимая, 72
представимых языков, 160
иримальная, 108
простая, 60
равномерно локально-конечная,
121
разложимая в
нетривиальное прямое
произведение, 69
свободно порожденная в
многообразии, 84
универсальная,14
многосортная, 157
условно примальная, 122
Халмоша, 165
языков, 160
Алгебраическая система, 14
Алгебры условно
рационально эквивалентные, 132
Арность предикатного
(функционального) символа,
14
Атом булевой алгебры, 46
частично упорядоченного
множества, 153
Буква алфавита, 154
Булева алгебра, 19
Вход автомата, 155
Вывод тождества, 95
Выход автомата, 155
Вычислительный потенциал
алгебры, 151
Гомоморфизм, 53
естественный по
конгруэнции, 56
Грамматика, 159
праволинейная, 159
Грань верхняя, 18
наибольшая нижняя, 18
наименьшая верхняя, 18
нижняя, 18
Группа, 20
абелева (коммутативная), 21
175
Указатель терминов
симметрическая множества,
37
Группоид, 167
Диаграмма Хассе, 16
Дискриминатор, 103
Длина частично
упорядоченного множества, 153
Доказательство в исчислении
условных тождеств, 128
Единица решетки, 47
Замыкание катенативное, 160
Изоморфизм, 22
категорий вложимости
натуральный, 130
натуральный, 111
Инвариант
программно-вычислительных
возможностей алгебры, 148
Истинность тождества на
алгебре, 91
на классе алгебр, 91
Истинность условного
тождества на классе алгебр,
124
Исчисление тождеств, 95
условных тождеств, 128
Категория вложимости
класса алгебр, 130
многообразия, 111
Катенация языков, 159
Квазигруппа Штейна, 168
Класс алгебр универсальный,
125
алгебр эквациональный, 92
Классы алгебр условно
рационально эквивалентные,
129
Клон отношений, 137
функций, 136
Коатом частично
упорядоченного множества, 153
Кольцо, 21
Конгруэнции перестановочные,
70
Конгруэнция, 55
вполне инвариантная, 87
главная, 58
конечно порожденная, 58
порожденная совокупностью
пар, 57
Константа, 14
Лемма Йонссона, 101
Мальцева, 58
Цорна, 40
Линейно упорядоченное
множество, 17
Многообразие, 77
арифметическое, 101
дискриминаторное, 103
конгруэнц-дистрибутивное,
99
конгруэнц-модулярное, 99
конгруэнц-перестановочное,
98
конгруэнц-регулярное, 108
конгруэнц-униформное, 108
полупростое, 106
порожденное классом
алгебр, 78
тривиальное, 78
176
Указатель терминов
условное, 124
Многообразия рационально
эквивалентные, ПО
Множество, 11
конечных вершин, 155
начальных вершин, 155
Модель, 14
Моноид, 167
Монолит алгебры, 73
Морфизм категории, 111
Мощность алгебры, 78
Нормальная форма
условного терма, 117
Нуль решетки, 47
Объект категории, 111
Оператор на классах алгебр,
76
Отношение п-местное, 11
п-регулярно порожденное,
141
аффинное, 140
примитивное, 140
базовое (основное,
сигнатурное), 15
выводимости для системы
продукций, 158
перестановочное простое, 140
покрываемости, 17
тотально рефлексивное, 141
симметричное, 140
функциональное, 12
центральное, 141
эквивалентности, 25
Отображение множеств, 11
Подалгебра, 31
конечно порожденная, 48
порожденная множеством,
33
собственная, 32
Подмножество, 31
замкнутое относительно
функций, 31
Полугруппа, 20
отображений множества, 39
Порядок частично
ограниченный, 140
Правила вывода
исчисления тождеств, 95
исчисления условных
тождеств, 128
Правило подстановки, 158
Предикат, 14
базовый (основной,
сигнатурный), 15
Представление алгебры под-
прямое, 72
Принцип композиции, 149
неподвижных точек, 149
обратимости, 149
ограничения, 149
одноэлементных подалгебр,
149
согласованности, 149
Продукции стирающие, 159
Проекция, 67
Произведение
алгебр
декартово, 67
подпрямое, 71
прямое, 67
множеств прямое, 11
отношений, 69
обобщенное, 137
177
Указатель терминов
Разбиение множества, 26
Решетка, 18
алгебраическая, 49
дистрибутивная,19
конгруэнции, 57
модулярная, 19
ограниченная, 48
подалгебр, 33
подмножеств, 149
полная, 47
эквивалентностей, 28
Решеточно упорядоченное
множество, 17
Свойство продолжимости
конгруэнции, 107
Сигнал автомата входной, 156
Сигнатура, 14
Символ сигнатуры
константный, 14
предикатный, 14
функциональный, 14
Система продукций, 158
условий полная, 115
Штейна тройная, 167
Слова алфавита, 154
помечающие данного
маршрута, 155
Соответствие Галуа, 136
Состояние автомата, 156
конечное, 156
начальное, 156
Таблица Кэли, 13
Теорема Биркгофа
о многообразиях, 78
о подпрямых
разложениях, 73
об эквациональных
классах, 92
Биркгофа-Фринка, 49
Гретцера-Шмидта, 59
Дедекинда-Биркгофа, 45
Дея о конгруэнц-модулярных
многообразиях, 100
Йонссона о
конгруэнц-дистрибутивных
многообразиях, 100
Клини, 160
Когаловского, 78
компактности для
исчисления тождеств, 96
Кэли, 37
Лося, 105
Мальцева о конгруэнц-пе-
рестановочных
многообразиях, 98
о рационально
эквивалентных
многообразиях, 111
Мучника, 147
об изоморфизме вторая, 63
первая, 60
об условно рационально
эквивалентных условных
многообразиях, 131
Пешеля-Калужнина, 139
Пиксли об арифметических
многообразиях, 101
полноты для исчисления
тождеств, 96
для исчисления
условных тождеств, 128
Поста, 142
Розенберга, 141
Ромова, 138
178
Указатель терминов
Сабо, 138
Стоуна, 44
Тарского, 126
Флейшера, 74
Терм дискриминаторный, 103
сигнатуры, 34
условный, 116
Тождество, 91
выводимое из других
тождеств, 96
условное, 124
Ультрапроизведение, 75
Ультрафильтр, 42
на множестве, 74
Условие Мальцева, 98
сигнатуры, 115
Фактор-алгебра, 55
Фактор-множество, 26
Фильтр, 41
главный, 41
собственный, 42
Формула у-зависимая, 119
у-функциональная, 119
Функция п-местная, 11
π-сопряженная, 132
базовая (основная,
сигнатурная), 15
кусочно-термальная, 118
переходов автомата, 157
разметки дуг, 155
термальная 35
условно термальная, 116
Цепь, 17
Частично упорядоченное
множество, 16
Шкала потенциалов
вычислимости η-элементных
алгебр, 151
Экволизатор, 74
Элемент компактный, 48
максимальный, 40
множества, 11
наибольший, 40
Эндоморфизм, 87
Эпиморфизм, 54
Ядро гомоморфизма, 55
Язык, 154
порожденный грамматикой,
159
порожденный конечным
автоматом, 155
представимый, 155
простейший, 160
179
Библиографический список
[l] Артамонов В.А. Универсальные алгебры / В. А. Артамонов
// Общая алгебра. - Москва: Наука, 1996. — Т.2.
[2] Баранский В.А. Введение в общую алгебру и ее приложения
/ В. А. Баранский. - Екатеринбург: Изд-во УрГУ, 1988.
[3] Баранский В.А. Сборник задач по общей алгебре и
дискретной математике / В. А. Баранский, Ю. М. Важенин,
М. В. Волков - Екатеринбург: Изд-во УрГУ, 2003.
[4] Биркгоф Г. Современная прикладная алгебра / Г. Биркгоф,
Т. И. Барти. - Москва: Мир, 1976.
[5] Богомолов A.M. Алгебраические основы теории дискретных
систем / А. М. Богомолов, В. Н. Салий. - Москва: Наука,
1997.
[6] Бунина Е.И. Элементарная и близкие к ней логические
эквивалентности классических и универсальных алгебр./
Е. И. Бунина, А. В. Михалев, А. Г. Пинус.-Москва: Изд-во
МЦМНО, 2015.
[7] Горбунов В.А. Алгебраическая теория квазимногообразий /
В. А. Горбунов. - Новосибирск: Изд-во НИИМИОО, 1998.
[8] Гретцер Г. Общая тоерия решеток / Г. Гретцер. - Москва:
Наука, 1982.
[9] Кон П. Универсальная алгебра / П. Кон. - Москва: Мир,
1968.
[10] Курош А.Г. Лекции по общей алгебре / А. Г. Курош. -
Москва: Наука, 1973.
[11] Лаллеман Ж. Полугруппы и комбинаторные приложения /
Ж. Лаллеман. - Москва: Мир, 1985.
180
Библиографический список
[12] Лидл Р. Прикладная абстрактная алгебра / Р. Лидл,
Р. Пильц. - Екатеринбург: Изд-во УрГУ, 1996.
[13] Мальцев А.И. Алгебраические системы / А. И. Мальцев. -
Москва: Наука, 1970.
[14] Мальцев А.И. Итеративные алгебры Поста./ А. И .Мальцев,
И. А. Мальцев.- Новосибирск: Изд-во Института математики
СО РАН, 2009.
[15] Пину с А. Г. Конгруэнц-модулярные многообразия алгебр /
А. Г. Пинус. - Иркутск: Из-во ИрГу, 1986.
[16] Пинус А.Г. Условные термы и их применение в алгебре и
теории вычислений / А. Г. Пинус. - Новосибирск: Изд-во НГТУ,
2002.
[17] Пинус А.Г. Производные структуры универсальных алгебр /
А. Г. Пинус. - Новосибирск: Изд-во НГТУ, 2007.
[18] Пинус А.Г. Задачи и упражнения по универсальной алгебре
/ А. Г. Пинус. - Новосибирск: Изд-во НГТУ, 2008.
[19] Пинус А.Г. Дискретные функции (дополнительные главы
дискретной математики)./ А. Г. Пинус- Новосибирск: Изд-
во НГТУ, 2016.
[20] Плоткин Б.И. Универсальная алгебра, алгебраическая
логика и базы данных / Б. И. Плоткин. - Москва: Наука, 1991.
[21] Скорняков Л.А. Элементы общей алгебры / Л. А. Скорняков.
- Москва: Наука, 1983.
[22] Смирнов Д.М. Многообразия алгебр / Д. М. Смирнов. -
Новосибирск: Наука, 1992.
[23] Хобби Д. Строение конечных алгебр./ Д. Хобби,
Р. МакКензи.- Москва: Мир, 1993.
[24] Цаленко М.Ш. Основы теории категорий / М. Ш. Цаленко,
Е. Г. Шульгейфер. - Москва: Наука, 1974.
181
Библиографический список
[25] Яблонский СВ. Функции алгебры логики и классы Поста. /
С. В. Яблонский, Г. П. Гаврилов, В. Б. Кудрявцев. - Москва:
Наука, 1966.
[26] Яблонский СВ. Введение в дискретную математику /
С. В. Яблонский. - Москва: Наука, 1979.
[27] Burns S. Decidability and Boolean representations./ S. Burris,
R. McKenzie.- Memoirs Amer. Math. Soc, v.32, 1981.
[28] Burris S. A course in universal algebra / S. Burris,
H. P. Sankappanavar. - New York: Heidelberg; Berlin: Springer-
Verlag, 1981.
[29] Chajda I. A basic course on general algebra / I. Chajda,
K. Glasek. - Zielona Gora: Technical University Press, 2000.
[30] The Concise Handbook of Algebra.- Dordrecht-Bjston-London:
Kluwer Academic Publishers, 2002.
[31] Garcia O.C The Lattice of interpretability types of varieties./
О. С Garcia, W. Taylor.- Memoirs Amer. Math. Soc, v.50,1984.
[32] Denecke K. Preprimal Algebras./ K. Denecke.- Berlin: Akademie-
Verlag, 1982.
[33] Freest R. Commutator Theory of congruence modular varieties./
R. Freese, R. McKenzie.- London: Cambridge Univ. Press, 1987.
[34] Gratzer G. Universal algebra / G. Gratzer. - 2nd ed. - New-York:
Heidelberg; Berlin: Springer-Verlag, 1979.
[35] Ihringer T. Algemeine Algebra / T. Ihringer. - Stuttgart:
Teubner-Verlag, 1988.
[36] Jesek J. Universal Algebra/ J. Jesek.- www.karlin. Mff.
Cuni.cz/ jezek/un.pdf.
[37] Jonsson B. Topics in universal algebra / B. Jonsson. - Berlin;
Heidelberg: Springer-Verlag, 1972.
182
Библиографический список
[38] Kaarli К. Polynomial Completeness in Algebraic Systems./
K. Kaarli, A. Pixley.- Boca Raton - London - New York -
Washington: Chapman and Hall/CRC, 2001/
[39] McKenzie R. Algebras. Lattices. Varieties./ R. McKenzie,
G. McNulty, W. Taylor.- Montrey Calif.: Wadworth and Book
Publ., 1987.
[40] Pinus A.G. Boolean constructions in universal algebra /
A. G. Pinus. - Dordrecht; Boston: Kluwer Academic Publ.,1993.
[41] Poschel R. Funktionen- and Relationen-algebras. / R. Poschel,
L. A. Kaluznin. - Berlin: Deutscher Verlag Wissensch, 1978.
[42] Werner H. Discriminator algebras / H. Werner. - Berlin:
Academic-Verlag, 1978.
183
УЧЕБНОЕ ИЗДАНИЕ
Пинус Александр Георгиевич
ОСНОВЫ УНИВЕРСАЛЬНОЙ АЛГЕБРЫ
Учебное пособие
4-е издание, переработанное и дополненное
Редактор И. Л. Кескевич
Выпускающий редактор И. П. Брованова
Художественный редактор А. В. Ладыжская
Компьютерная верстка Е. Н. Порошенко
Подписано в печать 29.01.2019
Формат 70 х 100 1/16. Бумага офсетная
Уч-изд. л. 14,83. Печ. л. 11,5
Тираж 3000 экз. (1-й з-д - 1 - 50 экз.)
Изд. №94/16. Заказ №222.
Налоговая льгота - Общероссийскмй классификатор продукции
Издание соответствует коду 95 3000 ОК 005-93 (ОКП)
Издательство Новосибирского государственного
технического университета
630073, г. Новосибирск, пр. К. Маркса, 20
Тел. (383) 346-31-87
E-mail: officeSpublish.nstu.ru
Отпечатано в типографии
Новосибирского государственного технического университета
630073, г. Новосибирск, пр. К. Маркса, 20
УЧЕБНИКИ
НГТУ
Серия основана в 2001 году
ί
ч
•
ПИНуС Александр Георгиевич - доктор физико-
математических наук, профессор, профессор
кафедры алгебры и математической логики
Новосибирского государственного технического университета.
Специалист в области универсальной алгебры
и теории моделей, автор шести монографий и более
двухсот научных статей в этой области.