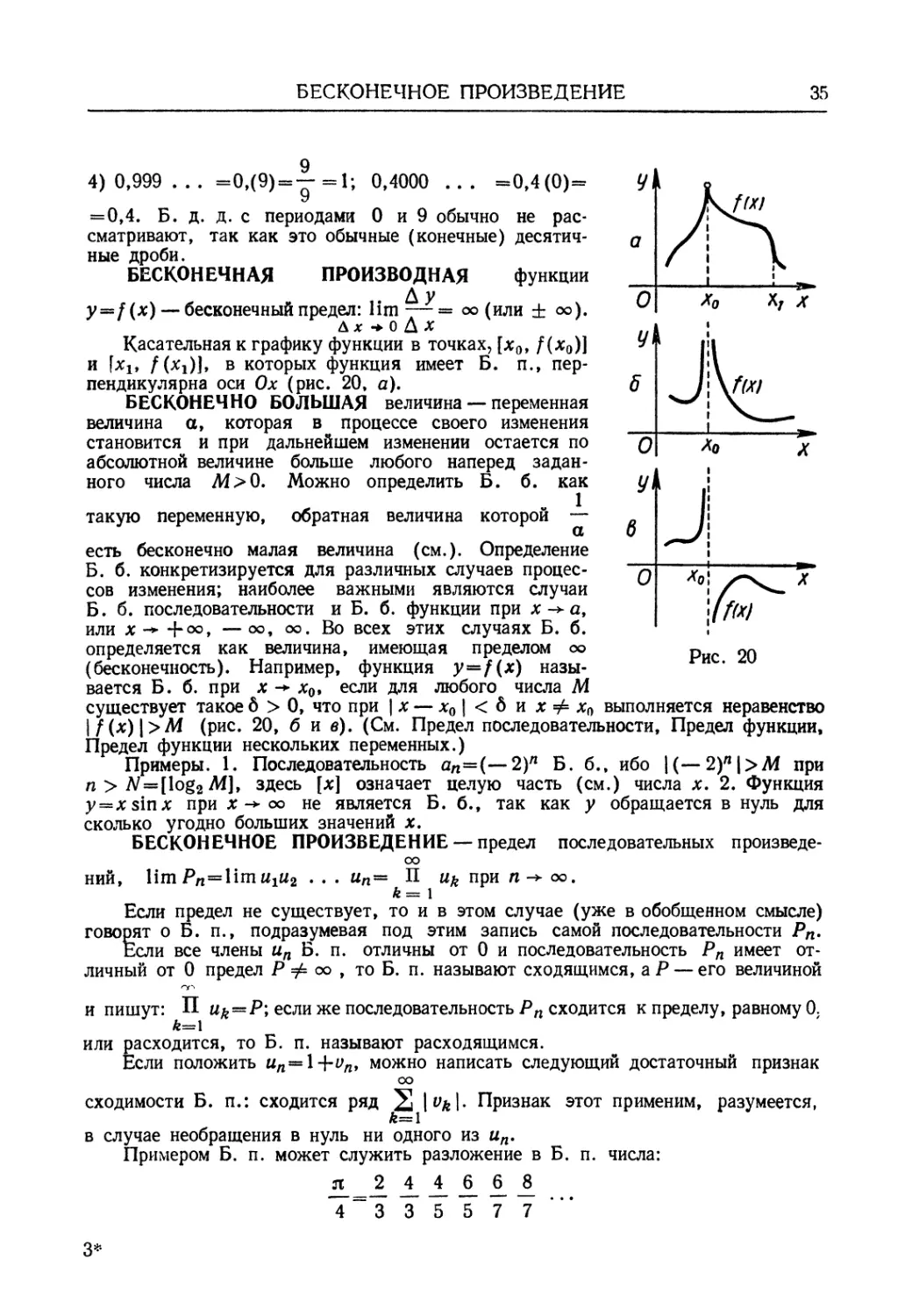
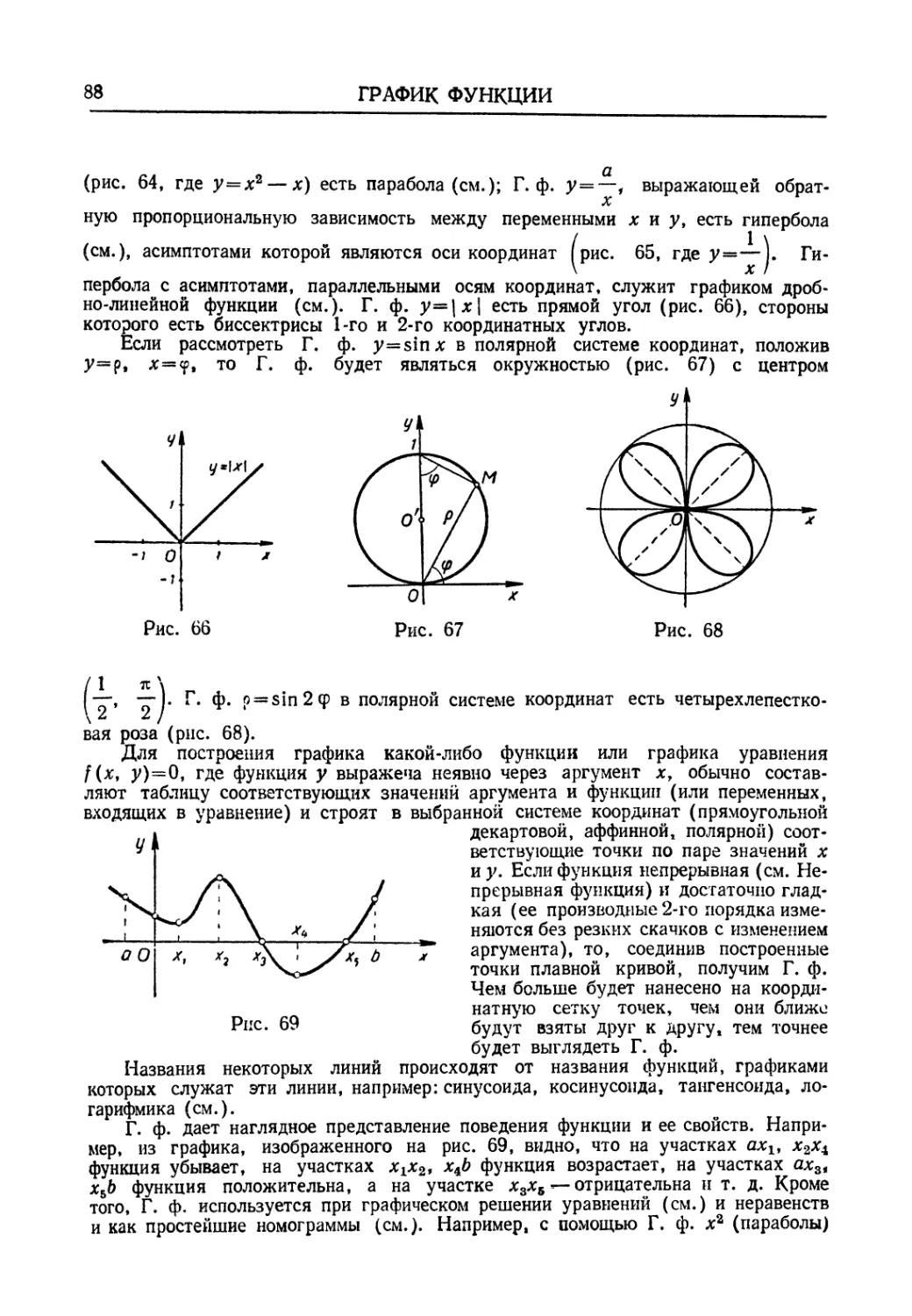
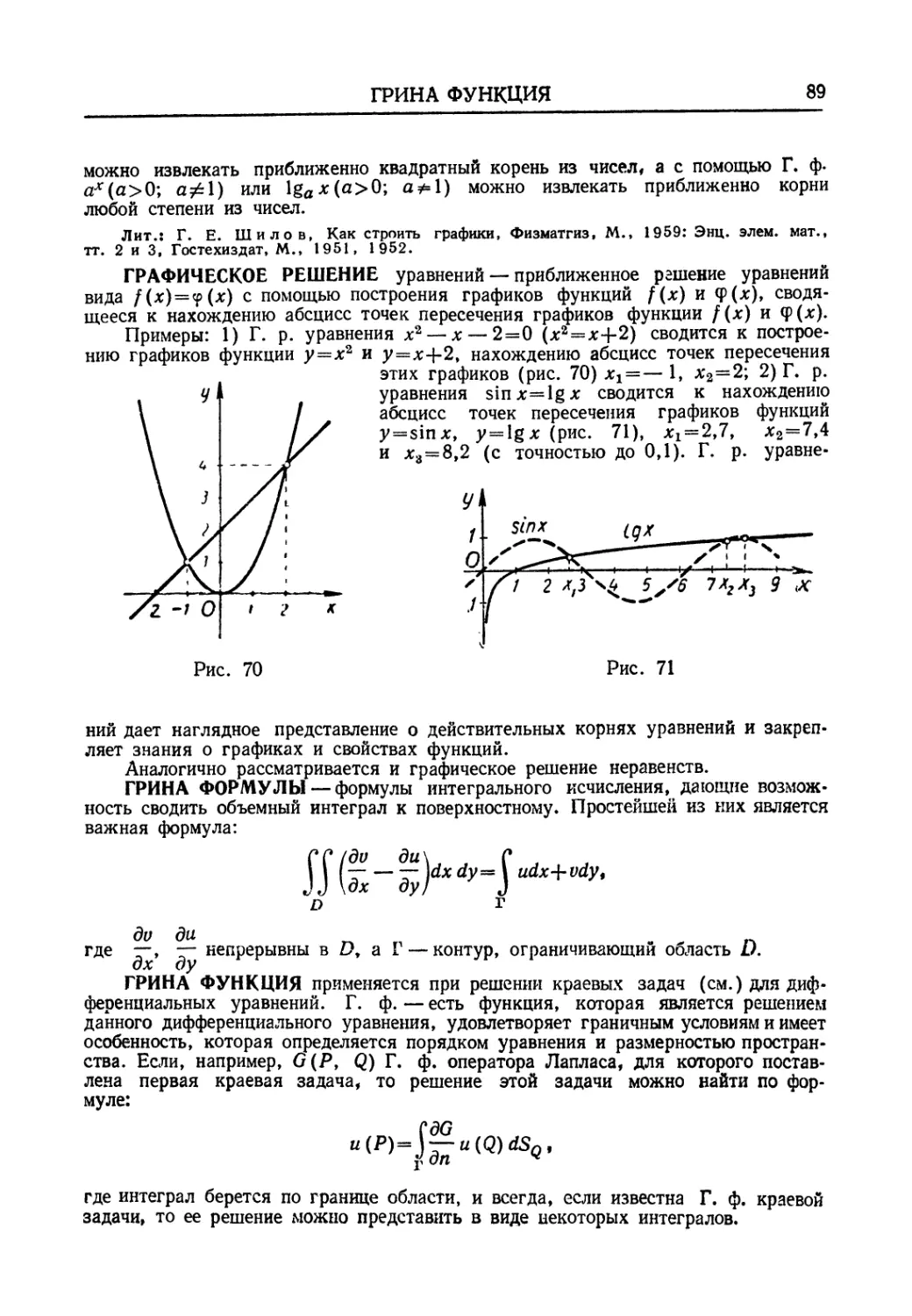
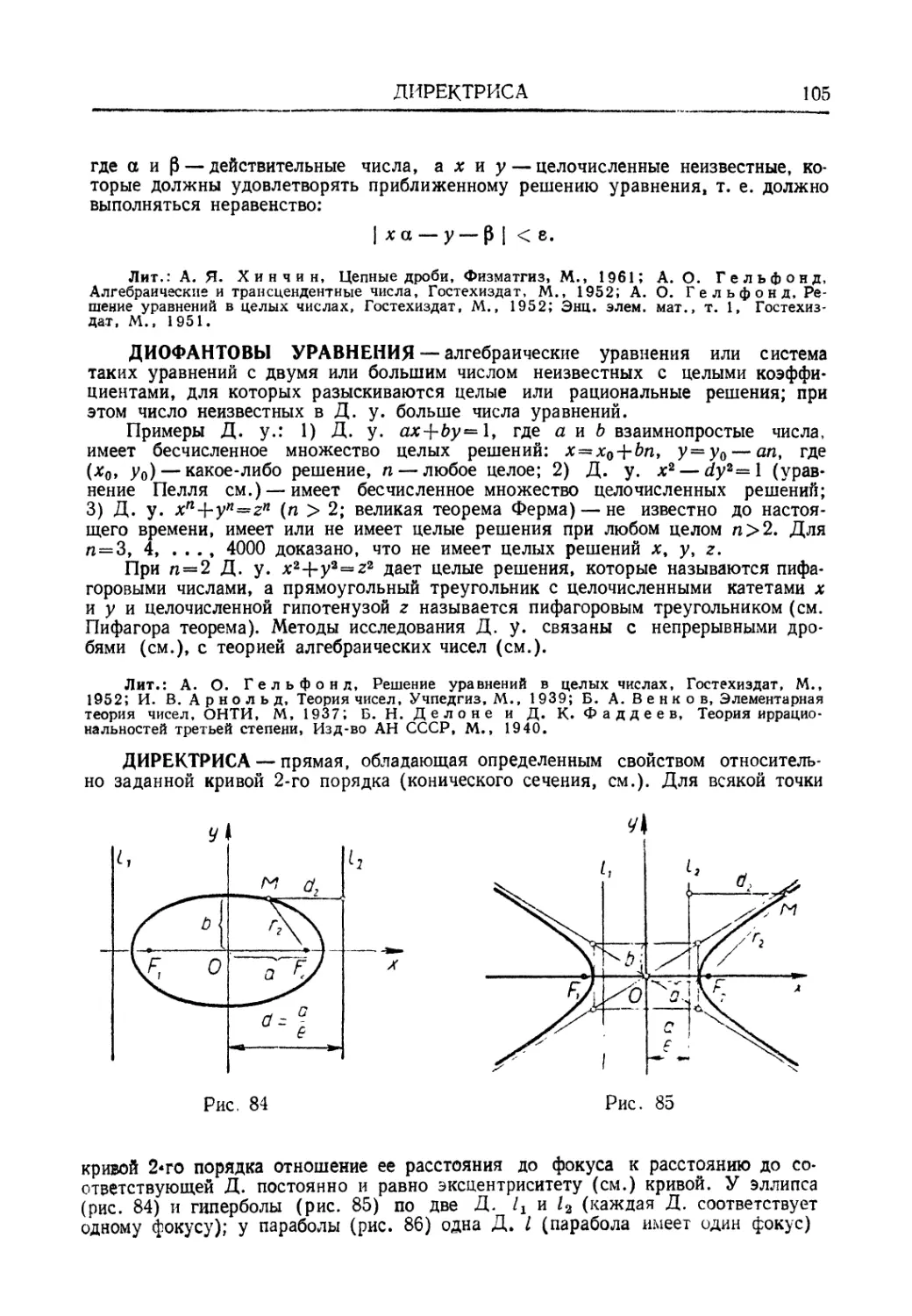
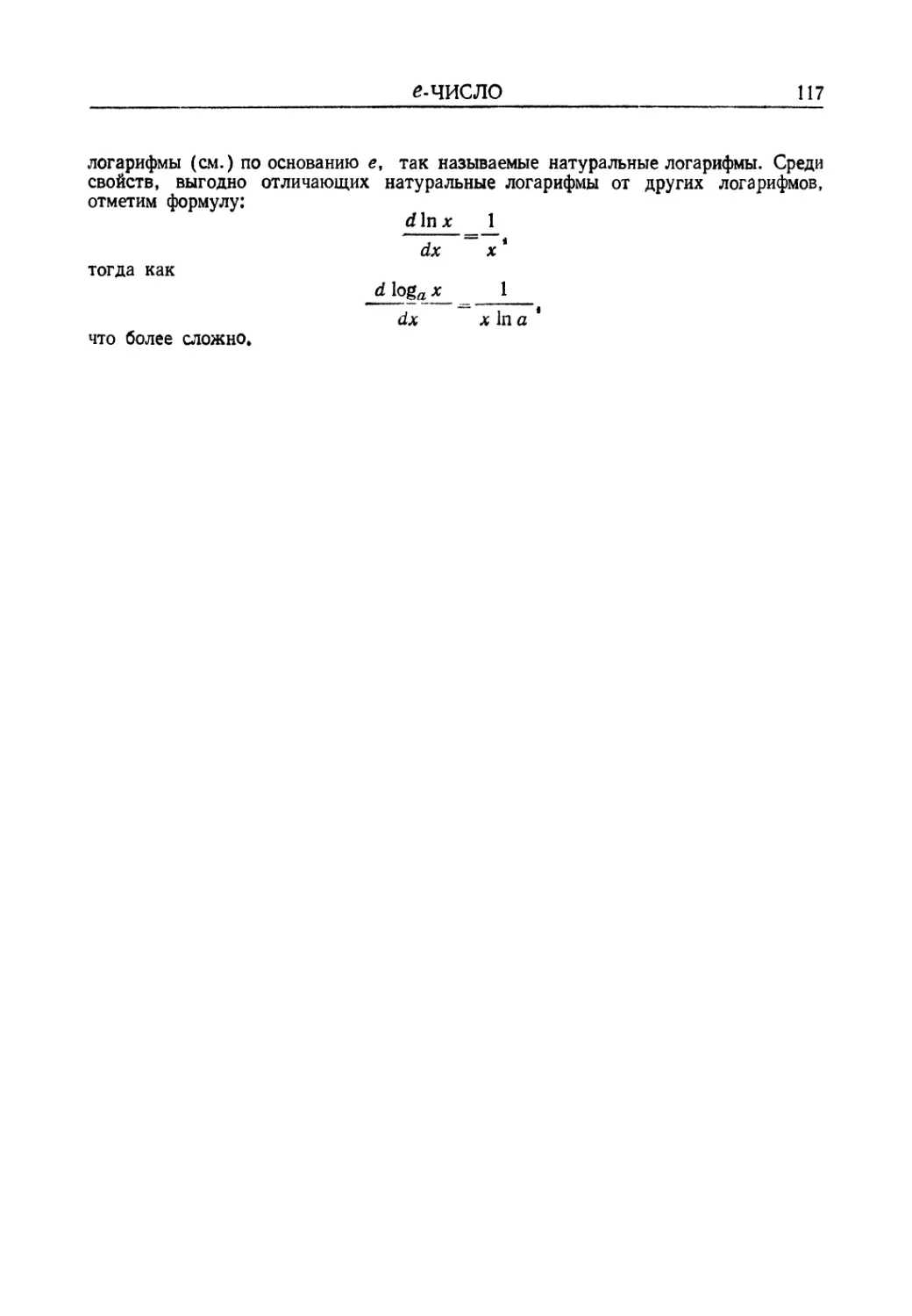
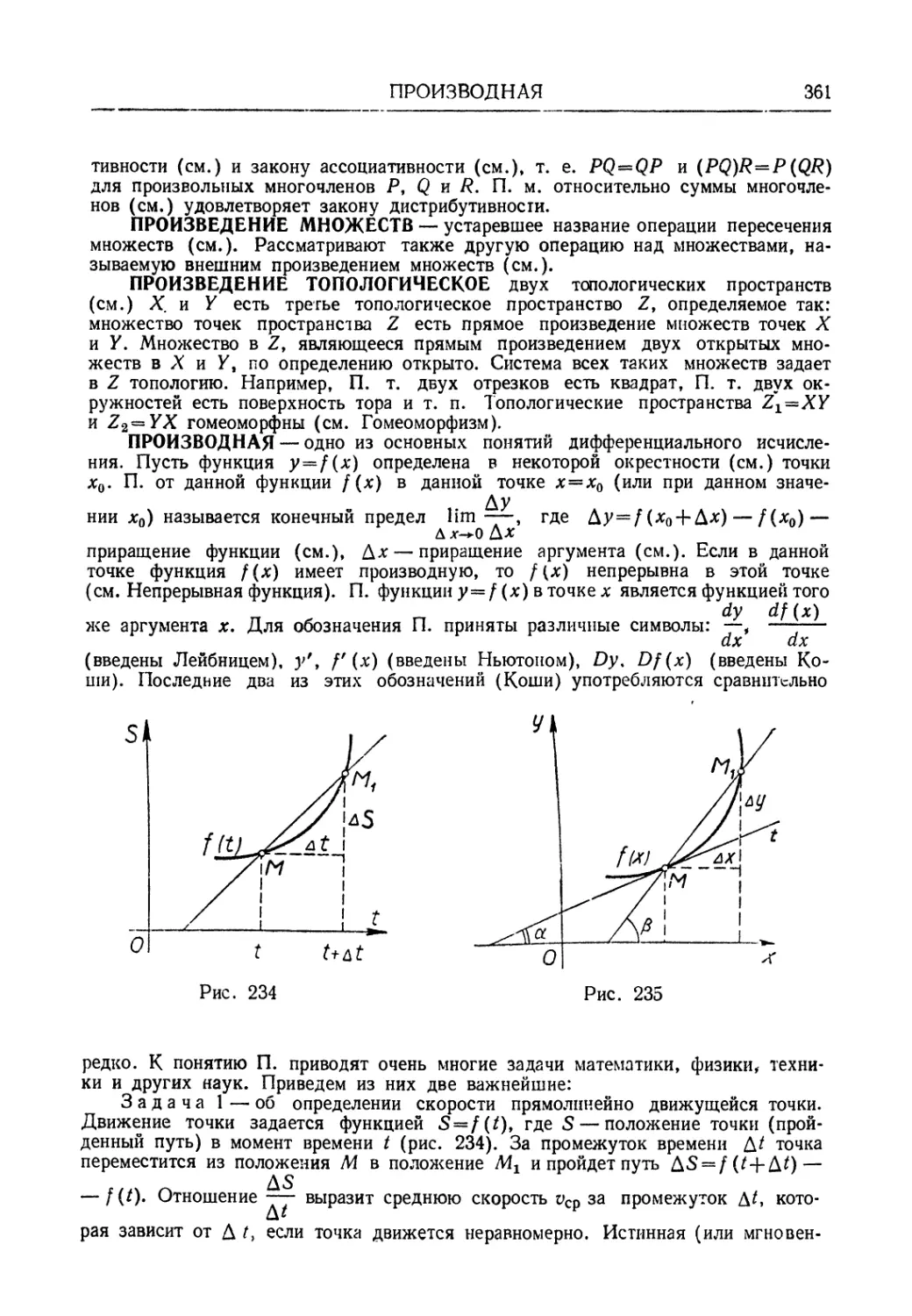
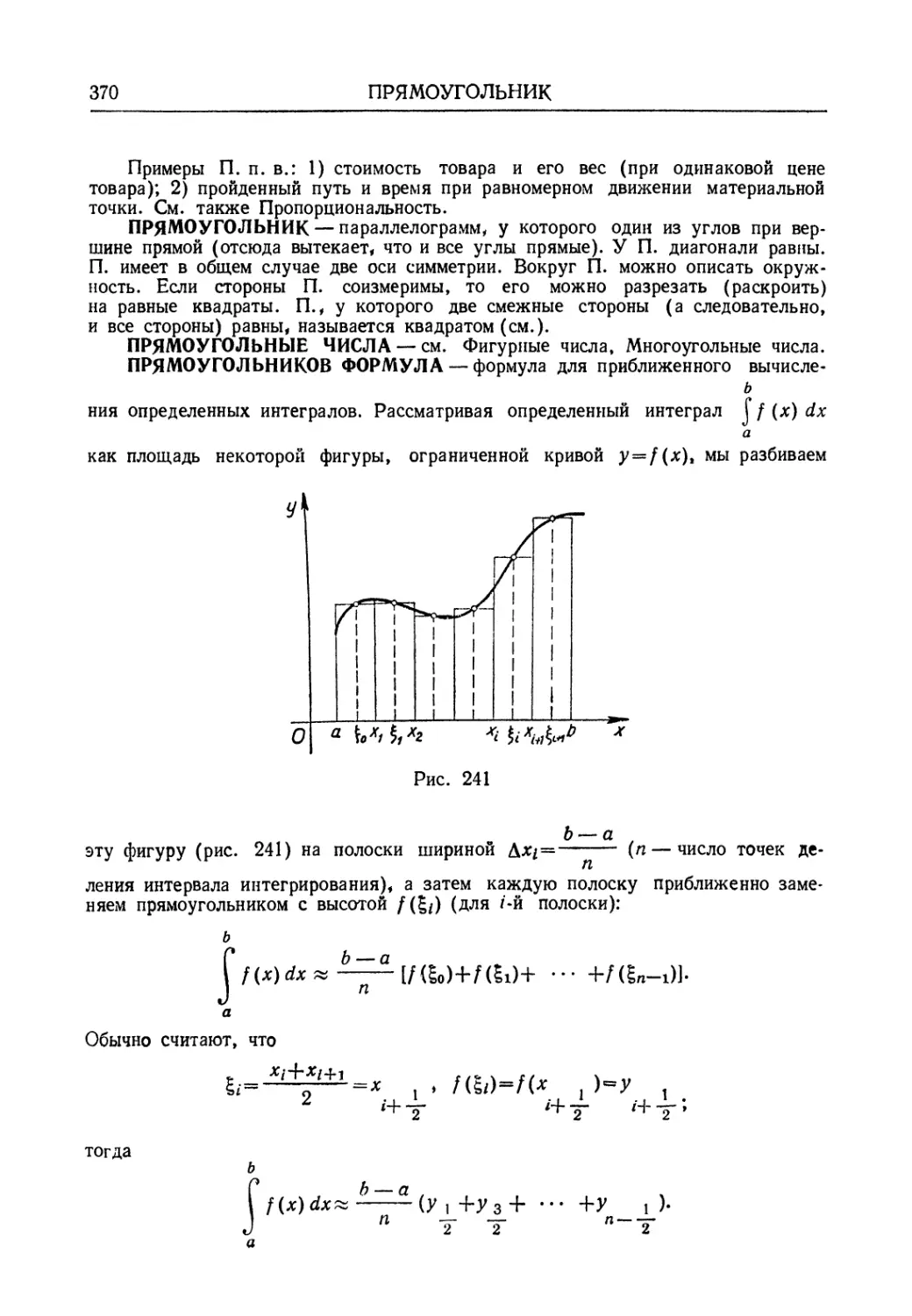
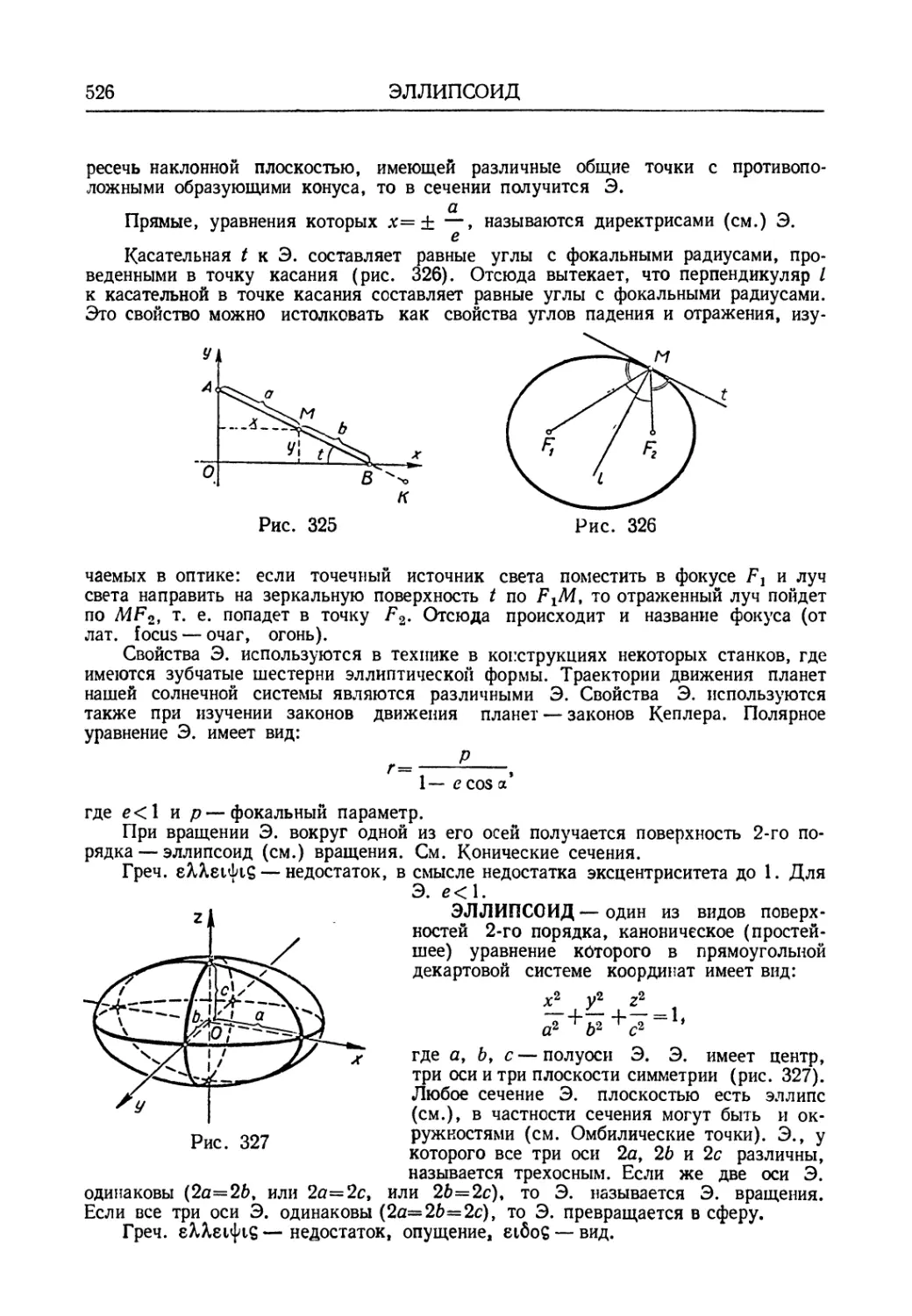
Толковый словарь математических терминов - Мантуров О.В., Солнцев Ю.К., Соркин Ю.И., Федин Н.Г.

Автор: Мантуров О.В. Солнцев Ю.К. Соркин Ю.И. Федин Н.Г.

Теги: словарь математические термины

Год: 1965

Похожие

Болгарско-русский словарь терминов изобразительного искусства

Русско-итальянский технический словарь. Около 40000 терминов. Издание 2-е

Шахматный словарь

Англо-русский словарь математических терминов

Текст

5жШ
ЮлиСоркт,1Ъ
АТЕМАТИЧЕСКИХ
ТЕРМИНОВ

О. В. МАИТУРОВ. Ю. К. СОЛНЦЕВ,
/О, И. СОРКИН, Н. Г. ФЕДИН
Толковый
СЛОВАРЬ
МАТЕМАТИЧЕСКИХ
ТЕРМИНОВ
ПОСОБИЕ
ДЛЯ УЧИТЕЛЕЙ
Под редакцией
проф. В. А. ДИТКИНА
ИЗДАТЕЛЬСТВО
«ПРОСВЕЩЕНИЕ»
Москва 1965

Рукопись данной книги обсуждалась на секции
математики Учебно-методического совета
Министерства просвещения РСФСР. Ее рецензировали: доктор
физ.-мат. наук С. П. Пулькин, кандидат физ.-мат.
наук В. А. Кондратьев, кандидат пед. наук В. И.
Мишин, учителя И. Б. Вейцман, Е. Г. Крейдлин и
А. М. Пышкало.

ПРЕДИСЛОВИЕ
Предлагаемая читателю (и прежде всего советскому учителю) книга имеет
целью собрать многочисленные и наиболее важные термины математики и дать их
современное толкование.
Ранее изданные терминологические словари устарели как по составу
терминов, так и по их толкованию и являются к тому же библиографической редкостью.
Нам кажется, что решение поставленной задачи очень важно, и в особенности
в настоящее время, когда математические методы проникают в самые
разнообразные разделы науки и широко применяются в народном хозяйстве. В связи
с этим в школьную программу вводятся элементы высшей математики.
Математика в школе претерпевает качественные изменения.
Новые программы требуют от учителя более широких знаний высшей
математики и умения ориентироваться в главных направлениях развития математики.
При написании книги мы старались обратить внимание на принципиально
новые моменты, возникающие при переходе от элементарной математики к высшей.
Термины математики изложены несколько шире, чем они затрагиваются
программой физико-математических факультетов пединститутов. Мы стремились оттенить
логическую сторону в толковании встречающихся понятий, теорем, методов-
Естественно, термины написаны по объему неравномерно.
Как часто бывает, удачно выбранный термин или знак (символ) в науке
ускоряет и облегчает процесс усвоения того или иного раздела соответствующей
дисциплины, а неудачно придуманный термин или знак затрудняет усвоение
теории. С развитием науки и общества часть терминов устаревает, видоизменяется
или совсем исчезает, выходя из употребления (например, относительные числа,
варианта, произведение множеств и др.); в то же время появляются другие,
новые термины.
Работа над терминологией по различным отраслям знаний ведется как в СССР,
так и за границей.
Словарь охватывает около 1800 терминов по математике. Отметим, что он
является терминологическим, а не этимологическим; в нем дано толкование,
раскрытие содержания термина, а не его этимология (происхождение).
Термины в Словаре расположены по алфавиту, в том числе и термины,
состоящие из нескольких слов. Однако для удобства пользования Словарем
в многословных терминах приняты следующие перестановки: в терминах,
содержащих слова «точка», «теорема», «метод», эти слова ставятся в конце термина.

4
ПРЕДИСЛОВИЕ
Перечень терминов настоящего Словаря, т. е. его словник, и его отдельные
статьи неоднократно обсуждались математической общественностью, редакцией
математики издательства «Просвещение», отдельными педагогическими институтами
и институтами усовершенствования учителей Российской Федерации, а также
многими учителями средних школ и методистами-математиками. Отзывы и
пожелания учителей средних школ и преподавателей пединститутов, детально
ознакомившихся со Словарем, были по возможности учтены коллективом авторов.
Термины по алгебре, теории чисел, теории групп написаны Ю. И. Сор к и-
ным, термины по тригонометрии, элементарной, аналитической, проективной
геометрии, основаниям геометрии и методики математики — Н. Г. Фединым,
термины по математическому анализу, теории множеств, дифференциальной
геометрии и др. — О. В. Мантуровым и Ю. К- Солнцевым.
Авторы благодарят СП. Π у л ь к и н а, Е. Г. Ш у л ь г е й φ е ρ а, В. А.
Кондратьева, В. И. Мишина, Б. А. Розенфельда, В. И. Левина,
И. Б. Вейцмана, Е. Г. Крейдлина, Э. Е. Евзерихину, Т. Н. Фи-
делли, Г. Г. Бунатяна, Н. С. Авраменкои других товарищей за
ценные замечания, способствовавшие улучшению книги.
Авторы

АБАК —счетная доска у древних греков и риМЛян, а впоследствии
перешедшая и в средневековую Западную Европу. А. использовался для арифметических
вычислений и имел различную конструкцию. Первоначально А. представлял
гладкую доску, посыпанную песком и разделенную на полосы, в которых
передвигались счетные марки (камешки, косточки, монеты). Затем счетные марки
стали нанизывать на проволоки, и А. стал представлять собой раму с
проволоками. А. встречается и до настоящего времени у некоторых народов Востока,
например в Китае. В России с давних пор для арифметических вычислений
использовались счеты. В номографии название А. применяется к специальным счетным
номограммам.
АБА ЦИСТЫ — название средневековых математиков, пользовавшихся в своих
вычислениях абаком (см.). А. вели борьбу с алгоритмиками — сторонниками
алгоритмизации арифметических вычислений, т. е. письменных вычислений,
выполняемых по определенному общему правилу (см. Алгоритм).
АБЕЛЕВА ГРУППА — группа (см.), удовлетворяющая закону
коммутативности (см.) ab=ba. Например, группа комплексных корней п-й степени из 1
относительно операции умножения абелева, а группа подстановок п-и степени· не
абелева (см. Симметрическая группа). А. г. названа по имени норвежского
математика Абеля.
АБЕЛЯ ТЕОРЕМЫ — важные теоремы теории рядов. Одна из них
утверждает, что если степенной ряд
00
p(z)=2Xzn
гс=0
сходится в некоторой точке z0, то он равномерно сходится в каждом замкнутом
круге \z\<R<zQ. Кроме того,
со
limp (z) существует и равен ^αηζ",
если z-*z0, и остается на полупрямой argz=argz0.
См. также Руффиии — Абеля теорема.
АБРИС — очертание, контур проекции фигуры. Так, например, А. шара
в ортогональной проекции есть окружность, А. же шара в произвольной
параллельной проекции есть эллипс (см.).
Нем. АЬгф — контур, очертание.
АБСОЛЮТ — кривая 2-го порядка, по отношению к которой устанавливается
проективная метрика (отрезков и углов) в проективной плоскости.
АБСОЛЮТНАЯ ВЕЛИЧИНА действительного числа χ (обозначается |дс|)
есть неотрицательное число, определяемое следующим образом: если число х>0,
то |я|=х, если число х<О, то \х\=—х.
Из определения А. в. вытекают следующие соотношения:
|α|Η —α|; | α|2=| я2 |=α2; I a | — \b \< | a+b | <
|-|6|<|α-6ΐ<|α|+|6|; |α·*Μα1-Ι*|; 7ГГ
a\+\b\;
a ,

б
АБСОЛЮТНАЯ ГЕОМЕТРИЯ
Например, А. в. чисел 1,6; — 5и 2 соответственно равны: |1,6|=1,6, |—5| =
= 5 и |2| = 2. А. в. противоположных по знаку чисел равны друг другу: Ц-5| =
= |—5|=5. Геометрически А. в. числа выражает расстояние от точки, являющейся
изображением этого числа, до начала отсчета числовой прямой (оси).
В случае комплексного числа z—a-\-bi обобщением понятия А. в. является
модуль этого числа, что записывают так: \z\ = y а2+Ь2, откуда \z\ > 0; термин
«модуль» применим также и к действительным числам. Геометрически модуль
числа ζ выражает расстояние точки г до начала координат комплексной
плоскости. Аналогично рассматривают понятия А. в. и модуля функции |/(х)|. А. в.
числа иногда называют абсолютным значением числа. Понятие А. в. часто
используется в математике при решении уравнений и неравенств, при построении
графиков, при рассмотрении сходимости и расходимости рядов (см. Ряд).
Используя определение А. в., легко получить, например, следующие
утверждения: 1) уравнение |х|«х имеет бесчисленное множество решений: χ > 0;
2) система уравнений: |*-fy|=l, х — у=3 имеет два решения (2; — 1) и
(1; —2); 3) графиком функции у^\х% — \\ является кривая ABODE (рис. 1),
У;
\
\/
V
-ί\ О
\
ч
* \х'-г\
μ
\/
Уо.
''/ <*
/
/
I It ч 1
naif
I'll" 1
f L
~2<\Z\<3
ы
Hill
/ 2'Ίΐ: !3
Рис. 1
Рис. 2
полученная из параболы у= х2 — 1 путем зеркального отражения ее дуги BMD
в оси 0х\ 4) геометрическое место точек ζ комплексной плоскости, для которых
выполняется условие: 2 < \ζ\ < 3, есть множество точек плоскости, заключенных
между двумя концентрическими окружностями (кольцо) с центром в начале
координат и радиусами, равными 2 и 3 (рис. 2).
Лит.: Н. Муравьев, Понятие абсолютной величины действительного числа в
средней школе, «Математика в школе», 1952, № 6; Н. Г. Федин, Абсолютное значение числа
в курсе математики средней школы, сб. статей сИз опыта работы учителей математики»,
Изд-во АПН РСФСР, М., 1957.
АБСОЛЮТНАЯ ГЕОМЕТРИЯ — геометрия, построенная на аксиомах
геометрии Евклида, за исключением аксиомы (постулата) о параллельных прямых
(см.). А. г. является общей частью как геометрии Евклида, так и геометрии
Лобачевского (см.). Известно, что система аксиом геометрии Евклида отличается
от системы аксиом геометрии Лобачевского только аксиомой о параллельных
прямых; поэтому те теоремы, в которых не используется аксиома о
параллельных прямых или ее эквиваленты (см. Аксиома о параллельных прямых), будут
принадлежать к А. г., например теоремы: а) во всяком треугольнике сумма двух
сторон больше третьей; б) во всяком треугольнике против большего угла
лежит большая сторона; в) теоремы-признаки равенства треугольников и др.
Термин А. г. введен венгерским математиком Яношем Бойаи.

АБСЦИССА
7
АБСОЛЮТНОЕ ДИФФЕРЕНЦИРОВАНИЕ тензорных полей (см.) (и вообще
геометрических объектов) — вычисление ковариантных производных и
абсолютного дифференциала. Ковариантная производная тензора ζ1χ1*··Λκ (xit хъ . . ..
хп) по направлению /-го базисного вектора касательного пространства
(обозначается ¥jzlli* ··· '*) есть предел отношения разности ζ'1'2 ··*'* (xlt x2t . . ., xj—ι*
Xj+bxj* xj+i, ·. ч χη) — *1ιί*'"ίκ(Χι* χ2> ···» χη) κ Δ*/ при Δ*/-»0;
г1г1*...1к означает координаты тензора 2 в системе координат, параллельно
перенесенной из точки М(х1¥ х2, . . ., хп) в точку M(xlt x2t . . .» xj—lt xj+
+Axj, Xj+i* · · ·♦ xn)·
А. д. вводится в произвольном пространстве аффинной связности (см.
Аффинной связности пространство). Обладает инвариантностью относительно
преобразований координат. С помощью символов Кристофеля (см.) ковариантная
производная векторного поля ξ£ записывается так:
VA* -
1ΞΪ
дх'
η
2 *}#
Абсолютный дифференциал связан с ковариантными производными
следующим образом:
η
Qzixi* ... //ς = 2 VjZ'1'1 '" ίκ dxs .
s=l
А. д. является важной главой тензорного исчисления (см.).
Лит.: П. К. Ρ а ше в с к и й, Риманова геометрия и тензорный анализ, ГИТТЛ, М., 1953.
оо
АБСОЛЮТНО СХОДЯЩИЙСЯ РЯД — числовой ряд 2 ап> Для которого
п=1
сх>
ряд i |ал|, составленный из абсолютных величин членов данного ряда, является
п=1
сходящимся (см.). Любой А. с. р. является сходящимся. В А. ср. можно
произвольно переставлять и объединять члены, не изменяя его суммы.
оо
Аналогично функциональный ряд ^ип(М) называется А. с. р. в обла-
п = 1
оо
сти D, если для любой точки Μζϋ соответствующий числовой ряд 2 ап (М)
/ι=1
сходится абсолютно. Например, ряд 1— — Η h ··· -f-(—l)n~^* + ··· аб
1 1 1
солютно сходящийся, так как сходится ряд 1-}-^~+"Т + *** +"ό7+ '" (гео*
метрическая прогрессия).
АБСОЛЮТНЫЙ ЭКСТРЕМУМ — экстремум (см.) функции нескольких
переменных; словом «абсолютный» подчеркивается отличие его от относительного
экстремума (см.).
АБСЦИССА — первая из координат (декартовых или аффинных) точки.
А. обычно обозначается буквой χ латинского алфавита.
Лат. abscissus — отрезанный.

8
АВТОМОРФИЗМ
АВТОМОРФИЗМ — изоморфное отображение множества с данной системой
операций на себя (см. Изоморфизм). Например, всякое невырожденное линейное
преобразование есть А. линейного пространства относительно операций сложения
векторов и умножения вектора на число.
АВТОМОРФНАЯ ФУНКЦИЯ —аналитическая функция комплексного
переменного, значение которой не изменяется при преобразовании комплексного
аргумента некоторыми дробно-линейными преобразованиями. Совокупность всех
таких преобразований образует группу (см.) — подгруппу группы всех
дробно-линейных преобразований.
АДАМСА МЕТОД численного интегрирования дифференциальных уравнений
у' = /(#, у) с начальным условием у0 = /(*о) основан на применении формулы:
1 5
АУЛ=%+—ΔηΛ-ι+~ Δ2%-2+ ···. (*)
гделЛ=у^/г=/(л;п, yn)h.
Если в формуле (*) ограничиться разностями второго порядка, то для
применения этого метода необходимо каким-либо образом найти сначала уг и у2,
соответствующие значениям x1—x0-\-h и JC2=JC0-f 2/г. Тогда, применяя формулу (*),
можно получить значение Δ Уг и найти yz=y (х0+3/г), а также определить η3
и конечные разности Δη2 и Δ2Τ]ι, затем Δ Уз и т· Д·
Решения уравнения по А. м. даются обычно в виде таблиц (см. для
сравнения Рунге метод, Эйлера — Коши метод). См. также Численное интегрирование.
Лит.: А. Н. Крылов, Лекции о приближенных вычислениях, Гостехиздат, М., 1954.
АДДИТИВНАЯ ГРУППА — то же, что абелева группа; групповая операция
в А. г. записывается символом + и называется сложением. Название
происходит от латинского слова additivus — прибавленный.
АДДИТИВНАЯ ТЕОРИЯ ЧИСЕЛ — раздел теории чисел, в котором
изучаются вопросы, связанные с разложением натуральных чисел 1, 2, 3, ... на
слагаемые определенного вида. Характерными задачами для А. т. ч. являются
Варинга проблема (см.), Гольдбаха проблема (см.) и др. Название А. т. ч.
происходит от латинского слова additivus — прибавленный.
АДДИТИВНЫЕ ВЕЛИЧИНЫ — числовые функции /(*), определенные на
множестве Е% для элементов которого определено сложение, и удовлетворяющие
условию:
/<*i+*i) = /(*i)+/(*a).
Примерами А. в. могут служить объем тела, площадь поверхности, длина
линии, масса, вес и т. д. Название А. в. происходит от латинского слова
additivus — прибавленный.
АДЪЮНКТА —то же, что и алгебраическое дополнение (см.). Название
А. происходит от латинского слова adjunctus — присоединенный.
АКСИАЛЬНЫЙ ВЕКТОР —то же, что и осевой вектор (см).
АКСИОМА — предложение, принимаемое без доказательства, рассматриваемое
как исходное при построении той или иной математической теории. Система Α.,
являющаяся логическим фундаментом обоснования математической теории, не
является раз навсегда законченной и совершенной и, как и сами А.» изменяется
и совершенствуется.
К системе А. предъявляются требования: непротиворечивости, независимости
и полноты (см. Независимость системы аксиом, Непротиворечивость системы
аксиом, Полнота системы аксиом).
Примеры: 1) А. параллельности Евклида (А. Плейфера): через точку А, не
лежащую на данной прямой а в плоскости, определяемой точкой А и прямой а%

АЛГЕБРА
9
можно провести не более одной прямой а\ параллельной прямой а; 2)
Архимеда А. (см.); 3) Лобачевского А. (см.); 4) Дедекинда А. (см.). Для каждой
геометрии (аффинной, евклидовой, проективной и др.) имеется своя система А.
С другой стороны, каждая геометрия может быть также определена своей
группой преобразований (см. Эрлангенская программа) или дифференциально-
геометрическими свойствами пространства этой геометрии.
Известны аксиоматические построения геометрии, арифметики, теории
вероятностей и других математических дисциплин.
А. называется также постулатом (см.).
См. также Основания геометрии.
Греч, αξίωμα — предложение, достойное уважения, бесспорное; почет,
уважение, авторитет.
АКСОНОМЕТРИЯ — параллельная проекция фигуры, когда на плоскости
чертежа изображается фигура вместе с пространственной прямоугольной
декартовой системой координат, к которой отнесена эта фигура, и вместе с
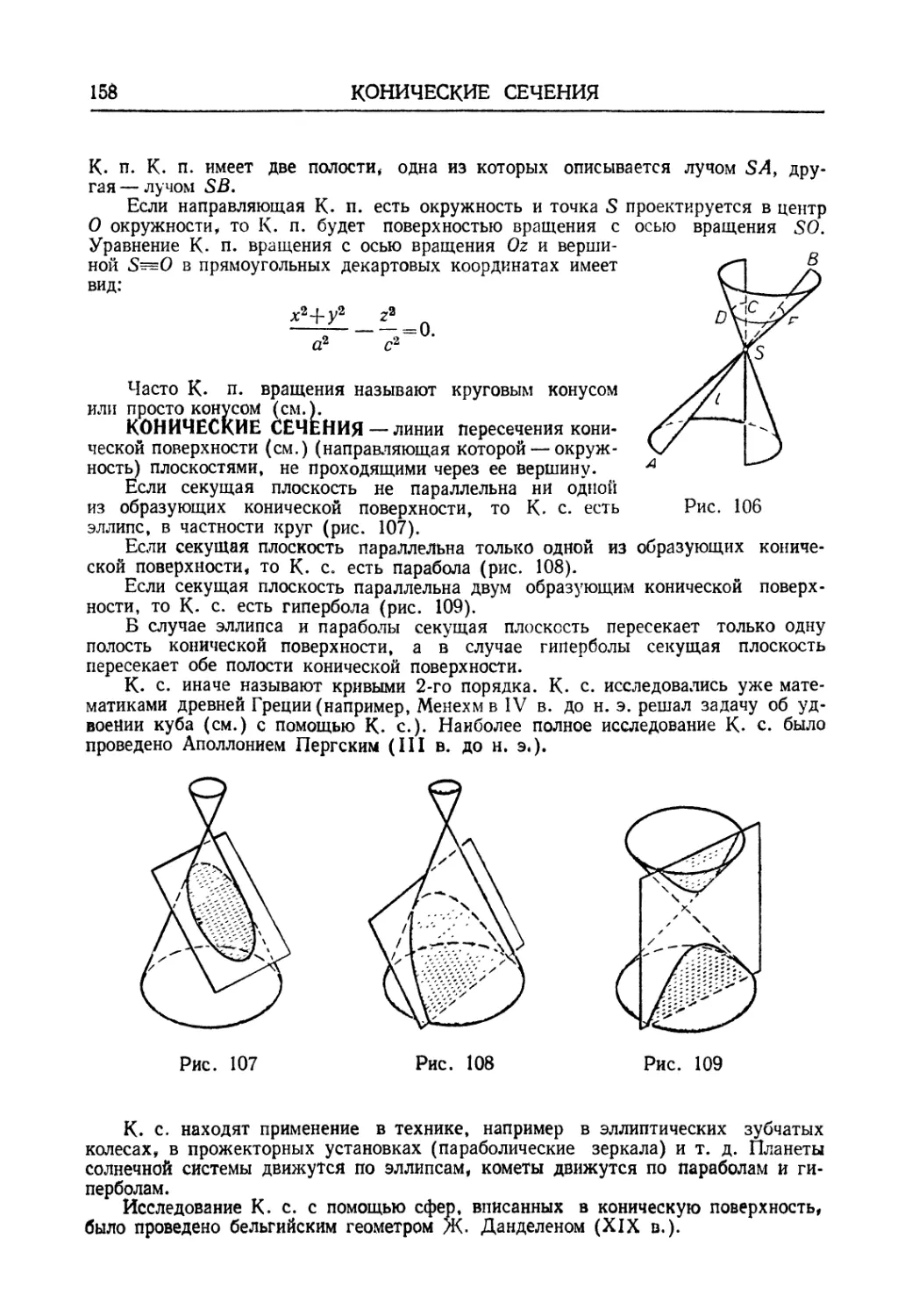
проекцией (вторичной) фигуры на одну из координатных плоскостей (на рис. 3 на
плоскости л: Ό'у'). А. позволяет восстановить форму и расположение фигуры
относительно системы координат.
А. имеет преимущество перед фронтальными
проекциями (см.) (на две или три плоскости)
в наглядности. Если в ортогональных проекциях
изображение пространственной фигуры расчле- . . . χ
няется на отдельные, разрозненные проекции \ I \ У С
(на две или три перпендикулярные плоскости),
то в А. изображение фигуры воспринимается
как целостное и наглядное.
В зависимости от углов наклона между осями
аксонометрических координат 0'х'9 О'у', О'г'
и длины единичных отрезков (аксонометрических
единиц) этих осей А. имеет частные случаи:
изометрия, диметрия, кабинетная проекция.
В А. всякая точка А изображается в виде >ч^я"
двух точек: первичной проекции А' и вторичной
проекции А" (на какую-нибудь координатную Рис. 3
плоскость).
А. иначе называется аксонометрической проекцией.
Греч, αξον (axon) — ось, μετρειν (metrein) — измеряю.
АЛГЕБРА: 1°. А. — математическая наука, объектом изучения которой
являются группы, кольца, поля, структуры и др. Отдельной ветвью А. является
элементарная алгебра (см.).
В первоначальном понимании А. мыслится как учение о решении уравнений.
В более широком смысле под А. мыслится наука, изучающая операции над
элементами множества произвольной природы, обобщающие обычные операции
сложения и умножения чисел. Существенным признаком А. является то
обстоятельство, что в А. отсутствует идея предела, идея бесконечной близости
элементов, как это имеет место в анализе или топологии (см.).
2°. А. над полем К — кольцо Л, в котором, кроме обычных для кольца
действий, определяется умножение на элементы из поля /С.
Требуется выполнение следующих свойств:
2'
о;
I
5'
4β\),
1 м4^ >
1) 0·α=0<
2) 1·α=α,
3) k(la) = (kl)ay
для любых at b£A н k,
4) (k+l)a=ka-hta,
5) k(a+b) = ka+kb
/£/C.

10
АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ
Кольцо многочленов с целыми коэффициентами не есть Α., а кольцо
многочленов с вещественными коэффициентами является А.
Лит.: Энц. элем, мат., т. 2, Гостехиздат, М., 1951; М. Я. Выгодский,
Справочник по элементарной математике, Физматгиз, М., 1951.
АЛГЕБРАИЧЕСКАЯ ГЕОМЕТРИЯ — дисциплина геометрического характера,
в которой изучаются алгебраические кривые и поверхности, вообще
алгебраические многообразия (см.).
АЛГЕБРАИЧЕСКАЯ КРИВАЯ — частный случай алгебраического
многообразия (см.) при η — s—1.
АЛГЕБРАИЧЕСКАЯ ПОВЕРХНОСТЬ — частный случай алгебраического
многообразия (см.) при я —s=2.
АЛГЕБРАИЧЕСКАЯ ФУНКЦИЯ — такая функция y=f(x)> для которой
существует многочлен F (у, х) такой, что F (у, *)ξ=0 при y=f(x).
Например, функция у, связанная с аргументом χ зависимостью
у=*— ι / __Σ—, есть А. ф. Функции, не являющиеся А. ф., называются
У 5-f-*2
трансцендентными функциями (см.).
АЛГЕБРАИЧЕСКИ ЗАМКНУТОЕ ПОЛЕ —такое поле Р, в котором
всякий многочлен степени п(п> 1) с коэффициентами из Ρ имеет в этом поле η
корней, если кратные корни засчитывать столько раз, какова их кратность.
Поле алгебраических чисел (см.) является А. з. п. Поле комплексных чисел
также является А. з. п. Последнее утверждение является одной из возможных
формулировок основной теоремы алгебры (см.).
АЛГЕБРАИЧЕСКОЕ ВЫРАЖЕНИЕ — выражение, составленное из букв
и чисел, соединенных между собой знаками алгебраических действий (сложения,
вычитания, умножения, деления, возвышения в целую степень и извлечения
корня с целым показателем) и, возможно, знаками последовательного
выполнения действий — скобками (см. Скобки).
Если А. в. не содержит знаков корней (радикалов) от чисел и букв, то оно
называется рациональным А. в.; если А. в. содержит радикалы, то оно
называется иррациональным А. в. (относительно буквы или числа, входящих под
знак корня). Рациональное А. в. называется целым, если оно не содержит
деления на выражение, содержащее буквы. Всякое А. в. есть алгебраическая
функция (см.) от букв, входящих в это выражение, если при этом буквы
считать переменными. Однако не всякая алгебраическая функция может быть
представлена в виде А. в.
3 аЬ — с
Примеры: 1) 2a+b2c— -~ab — целое А. в.; 2) · —дробное А. в.;
3) а у 2 — Ь\ Ъу а-\-Ь — иррациональные А. в.
Некоторые частные случаи А. в. называются одночленами (см.) и
многочленами (см.).
АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ какого-либо элемента (или к какому-
либо элементу) а^\ квадратной матрицы есть минор этого элемента М/у-, взятый
со знаком (—l)i+J, т. е. А. д. элемента а^ совпадает с его минором Мц, если
сумма его индексов четна, и является противоположным числом к минору, если
сумма его индексов i+j нечетна. А. д. используется для разложения
определителя (см.) по его строке или столбцу, что в свою очередь используется для
вычисления определителей.

АЛГОРИТМ
II
АЛГЕБРАИЧЕСКОЕ МНОГООБРАЗИЕ — совокупность всех точек, декартовы
координаты которых удовлетворяют системе уравнений вида:
Μ*ι. *а. · · ·. *л)=0,
F2(xltXt, ... , *я) = 0,
Μ*ι. Ч *я)в0,
где F/(/=l,2, . . ., s) — многочлены от неизвестных хи х2 хп.
АЛГЕБРАИЧЕСКОЕ ЧИСЛО — корень многочлена с целыми рациональными
коэффициентами. Как показал Г. Кантор, множество А. ч. образует счетное
множество.
Числа, не являющиеся А. ч., называются трансцендентными числами (см.).
А. ч. образуют поле, т. е. сумма, разность, произведение и частное А. ч. вновь
являются А. ч. Поле А. ч. является алгебраически замкнутым полем (см.).
т. е. всякий многочлен (степени η > 1), коэффициентами которого являются
А. ч., имеет своими корнями также А. ч.
Примеры. Всякое рациональное число p/qt где ρ и q — целые числа, будет
А. ч., так как оно является корнем многочлена qx — ρ с целыми коэффициента-
17
ми. Числа i и у 39 — А. ч., так как они являются корнями соответственно
многочленов x2-f-l и х17— 39 с целыми коэффициентами.
См. также Степень алгебраического числа.
Лит.: А. О. Гель фонд, Трансцендентные и алгебраические числа, Гостехиздат, М., 1952.
АЛГОЛ — универсальный (единый) язык и единая символика составления
программ для электронных вычислительных машин. Этот алгоритмический язык
(алгол-60) принят на Международной конференции, состоявшейся в Париже
в январе 1960 г.
Основными символами этого международного языка являются: латинские
буквы (26 прописных и 26 строчных), арабские цифры (от 0 до 9), два
логических значения («истина» и «ложь»), набор специальных символов — ограничителей
(знаки операций, разделителей и скобок) и, наконец, некоторый набор
служебных слов (около 20) на английском языке.
Таким образом, А. представляет собой своего рода систему или средство,
позволяющее выражать с помощью указанных символов точную
последовательность решения той или иной конкретной задачи.
При непосредственном применении А. для каждой конкретной электронной
вычислительной машины составляется программа, переводящая международный
язык (А.) на язык данной машины. При помощи такой программы —
«переводчика» машина уже сама «понимает» этот язык. По существу Α., являясь
принципиально универсальным языком для выражения (описания) вычислительных
алгоритмов, ликвидирует дорогостоящий параллелизм в научных исследованиях,
открывает перспективы в автоматизации программирования и широкого обмена
вычислительными программами и информацией.
АЛГОРИТМ (алгорифм) — точное предписание о выполнении в
определенном порядке некоторой системы операций, позволяющее решать совокупность
задач определенного класса.
А. приводит от исходных данных к искомому результату через конечное
число шагов (действий); при этом данные варьируются в известных
границах.
Много различных А. рассматривается в алгебре и теории чисел, а также
в других математических дисциплинах. Например, простейшие алгоритмы —
правила, по которым выполняются арифметические действия, А. Евклида (см.), А.
извлечения квадратного корня и А. для вычисления определителей я-го порядка,
правило Саррюса (см.)— А. для вычисления определителей 3-го порядка, А.

12
АЛГОРИТМИКИ
для вычисления ранга матриц (см.), А. для определения числа действительных
корней алгебраического уравнения — правило Штурма (см.) и т. д.
Слово А. возникло в-результате искажения имени великого узбекского
математика IX в. Хорезми (по-арабски —аль-Форезми, что означает: «из Хорезма»,
или латинизированное Algorithmi). Хорезми были написаны основополагающие
труды по арифметике и алгебре, которые переведены с арабского языка на
латинский в XII в.; по ним в Европе познакомились с индийской десятичной
позиционной системой счисления (часто ошибочно называемой арабской) и
основными правилами алгебры.
Долгое время понятие А. в математике не имело точного определения как
ввиду трудности уточнения объема этого понятия; так и ввиду того, что оно
понадобилось лишь тогда, когда пришли к открытию отсутствия А. для решения
некоторых задач. Точные определения А. были даны лишь в XX в. несколькими
математиками. Эти определения, различные по форме, впоследствии оказались
эквивалентными.
Было доказано отсутствие А. для решения ряда массовых задач. Наиболее
замечательный результат в этом направлении принадлежит советскому математику,
лауреату Ленинской премии, академику П. С. Новикову, доказавшему отсутствие
какого-либо алгоритма для решения проблемы тождества в теории групп.
Важность нахождения различных алгоритмов, доказательства их отсутствия
для ряда задач и создания общей теории алгоритмов исключительно повысилась
в связи с бурным развитием машинной математики (см.), дающей возможность
реализовать практически почти любой алгоритм в виде построения
соответствующей вычислительной машины.
Лит.: Б. А. Трахтенброт, Алгоритмы и машинное решение задач, Физматгиз
М., I960. *
АЛГОРИТМИКИ — средневековые математики, использовавшие в своих
арифметических вычислениях письменные вычисления, выполняемые по определенному
правилу (см. Алгоритм) и более совершенные, чем вычисления абацистов (см )
производившиеся на абаке (см.). ''*
АЛЕФ —первая буква финикийского алфавита, используется, следуя
F. Кантору, для обозначения мощностей бесконечных множеств. Например
мощность счетного множества (см.) обозначается #0 (читается А.-нуль).
АЛИДАДА —линейка, имеющая на концах перпендикулярные стойки
(пластинки) с щелями, называемые диоптрами. А. вращается вокруг центра лимба-—
круга или полукруга с делениями. А. является составной частью ряда
простейших измерительных (геодезических) приборов, предназначенных для измеоений
на местности.
Араб, ал-идада — линейка.
Лит.: см. термин Астролябия.
АНАГЛИФ — стереоскопический чертеж, отличающийся от обычного тем
что состоит из двух частей (чертежей), помещенных одна над другой и
выполненных в двух красках (бледно-красная и бледно-зеленая) А. рассматривается
через специальные очки — светофильтры (стереоочки), имеющие разные цвета
(чаще всего красный для левого глаза и сине-зеленый для правого)
По известным законам физики и физиологии каждый глаз воспринимает
только одно из двух изображений, так как каждый из саетофильтров очков
взаимно поглощает соседнее изображение, создавая таким образом при
совмещенном двойном (бинокулярном; рассмотрении анаглифа единое стереоскопичное
(объемное) впечатление.
А. используется для иллюстраций по стереометрии, кристаллографии и
объемной мультипликации (например, при рассмотрении сердца в медицине)
Греч, ana gluphen — рельефно.

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
13
Лит.: Г. А. Владимирский, Альбом стереоскопических чертежей-анаглифов к
задачнику Рыбкина, Учпедгиз, Стереофабрика, М., 1938; Г. Д. Михайлов, Набор
«Конструктор» и стенные анаглифы, Сб. «Изготовление наглядных пособий по геометрии», под
ред. А. Д. Семушина, Изд-во АПН РСФСР, М., 1953; И. Пал, Начертательная
геометрия с анаглифными иллюстрациями, Будапешт, 1961.
АНАЛИЗ — метод (способ) рассуждения или доказательства, при котором
мы отправляемся от неизвестного к известному, от искомого к данному.
А. используется в преподавании всех учебных предметов и дисциплин в
школе: арифметики, алгебры, геометрии, тригонометрии и высшей математики.
Так, например: а) при решении арифметической задачи методом А. мы
отправляемся в своих рассуждениях от неизвестного, от вопроса задачи и приходим к
данным величинам и зависимостям между ними; б) при решении задач на
составление уравнений с одним или несколькими неизвестными отправляемся в
рассуждении от неизвестного (одного или нескольких) и устанавливаем зависимости
между данными величинами и неизвестными; в) при решении задач на построение
начинаем рассуждать с рассмотрения искомой (неизвестной) фигуры, которую надо
построить, и устанавливаем ее связь с данными элементами. Аналогичную схему
рассуждения мы встречаем при доказательстве теорем, при решении задач на
доказательство в математике.
Пример. Доказать, что sin2a<2sina (1), если 2а — острый угол. Для
доказательства соотношения (1) запишем его в виде: 2 sin a cos a<2 sin a (2), или,
так как sin a>0, после упрощения имеем: cosa<l (3). Неравенство (3) при
указанных ограничениях угла α верно. Отсюда, рассуждая в обратном порядке
и используя свойства неравенств и формулу для синуса двойного угла, получим,
что верно и неравенство (2), а следовательно, и данное неравенство (1).
Обращение Α., τ. е. рассуждение в обратном порядке, есть синтез (см.). А.
ведет к более глубокому и сознательному усвоению учебного материала и
способствует активному и творческому развитию логического мышления учащихся,
нежели синтез. Но А. учащиеся усваивают труднее, чем синтез, в котором
рассуждения идут от данных известных величин.
При решении задач часто пользуются как Α., так и синтезом одновременно.
Всякий А. включает в себя элементы синтеза, и всякий синтез включает в себя
элементы А. А. и синтез взаимно связаны друг с другом, они представляют
собой две стороны одного и того же процесса рассуждения. Ф. Энгельс,
характеризуя А. как метод в научных исследованиях, говорит: «...мышление состоит
столько же в разложении предметов сознания на их элементы, сколько в
объединении связанных друг с другом элементов в единство. Без анализа нет синтеза»
(Ф. Энгельс, Анти-Дюринг, Госполитиздат, М., 1957* стр. 40).
Греч, analysis — разрешение, освобождение.
Лит.: В. В. Репьев, Общая методика преподавания математики, Учпедгиз, М.,
1958; любая другая книга по методике математики.
АНАЛИЗ МАТЕМАТИЧЕСКИЙ — общее название для ряда математических
дисциплин, основанных на понятиях функции и предельного перехода. К А. м.
обычно относят дифференциальное и интегральное исчисление, теорию рядов,
теорию дифференциальных уравнений, теорию аналитических функций,
вариационное исчисление, теорию интегральных уравнений, функциональный анализ.
В более узком смысле термин А. м. часто служит общим назначением первых
трех из указанных выше разделов математики.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ — часть математики, в которой
исследуются геометрические образы средствами алгебры на основе метода координат.
В А. г. на плоскости ставятся две основные задачи: 1) зная
геометрические свойства линии (как геометрического места точек), найти ее уравнение,
т. е. уравнение, связывающее координаты ее текущих (переменных) точек, и

14
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
2) зная уравнение линии, связывающее ее текущие координаты χ к у, найти
геометрические свойства этой линии. Например, уравнение окружности с центром
(а, Ь) и радиусом г в прямоугольной системе координат есть уравнение второй
степени, в котором отсутствует член с произведением координат и
коэффициенты при jc2 и у2 равны. И обратно, если имеется уравнение второго
порядка между текущими координатами χ и у, в котором отсутствует член с
произведением координат и коэффициенты при х2 и у* равны, то это уравнение
есть уравнение окружности (действительный или мнимый). Так, уравнение
х2-\-2х+у2=3 есть уравнение окружности в прямоугольных декартовых
координатах с центром (—1,0) и радиусом г=2.
Сущность метода координат на плоскости заключается в том, что положение
всякой точки определяется пересечением двух линий, принадлежащих к двум
различным системам координатных линий, которые, образуя координатную сетку,
должны удовлетворять требованию: через каждую точку плоскости должна
проходить одна и только одна линия каждой системы. Так устанавливается взаимно
однозначное соответствие между точками плоскости Евклида и парами чисел χ и
у — координатами точки, определяющими положение точки рассматриваемой
плоскости. Аналогично устанавливается взаимно однозначное соответствие между
точками трехмерного пространства и тройками чисел (х, у, г) — координатами
точки, определяющими положение точки в пространстве.
Исторически сложившееся название А. г. хотя и прочно удерживается, но
не вполне отвечает содержанию этой науки. Для А. г. характерным является не
только и не столько приложение алгебры к геометрии, а следовательно,
использование метода анализа (см.), сколько применение метода координат, почему и
следовало бы ее назвать скорее координатной геометрией.
Идея координатного метода не является достижением нового времени, а
уходит своими истоками в глубь античной истории: элементы идеи координат мы
находим у древних математиков. Древние египтяне пользовались при
выполнении строительных работ параллельными координатами (отрезками), греческие
астрономы Гиппарх (II в. до н. э.) и Птолемей (II в. н. э.) пользовались
сферическими координатами (широта и долгота) для определения положения
различных точек земной поверхности. Однако отсутствие буквенной символики
и общего представления о числе тормозило развитие координатного метода
у греков.
Наибольший вклад в создание А. г. внесли французские ученые Ферма и
Декарт. Пользуясь буквенной символикой, введенной французским ученым Виетом,
Декарт и Ферма одновременно и независимо друг от друга дали науке новый
метод— метод координат, лежащий в основе созданной ими в XVII в. А. г.
Великий мыслитель Декарт понимал, более чем его современник Ферма,
ограниченность и специфичность характера синтетической геометрии древних.
Большой заслугой Декарта по сравнению с Ферма было введение в математику
переменной величины, создание более удачной символики, установление тесной
связи пространства с числом, алгебры с геометрией. Поэтому Декарта считают
наиболее видным создателем А. г. Декартова переменная величина явилась,
по словам Ф. Энгельса, «поворотным пунктом в математике», в результате чего
стало возможным бурное развитие всей высшей математики и смежных с ней
разделов естествознания.
Творец А. г. Декарт не мог до конца провести «арифметизацию» геометрии;
он не распространил метод координат на пространство и ограничился изучением
только плоских кривых; система координат была у него несовершенной; была
только одна горизонтальная ось, а ординаты представлялись переменными
параллельными отрезками; не было четкого различия знаков координат.
Перенесение координатного метода на трехмерное пространство было
осуществлено лишь в конце XVII в. и продолжено в XVIII в. работами нескольких
ученых, прежде всего Клеро и Эйлера.

АНАЛИТИЧЕСКАЯ ФУНКЦИЯ
15
Во второй половине XIX в. в связи с бурным развитием физики и
совершенствованием техники наблюдается прогресс в математике. В геометрии
появляются новые понятия: вектор (см.)* тензор (см.) и др. Для характеристики
материальной системы требуется большее число параметров, чем три. Трехмерное
евклидово пространство становится тесным. В теории относительности
рассматривается четырехмерное пространство, в квантовой механике состояние системы
характеризуется бесконечномерными величинами. В математике стали прибегать
к пространствам четырех измерений, η измерений и бесконечного числа
измерений (функциональные пространства).
Лит.: СВ. Бахвалов и др., Аналитическая геометрия, Учпедгиз, М., 1958;
С. С. Бюшгенс, Аналитическая геометрия, ч. I, II, Гостехиздат, М., 1946; Б. Н. Де-
лонеиД. А. Райков, Аналитическая геометрия, ч. I и И, Гостехиздат, М.,
Н. И. Мусхелишвили, Курс аналитической геометрии, Гостехиздат, М., 1947.
АНАЛИТИЧЕСКАЯ ФУНКЦИЯ— основное понятие теории функций
комплексного переменного. Однозначная функция w—f(z) комплексного переменного
г=#-И'у называется А. ф. в точке г0, если в некотором круге \z — г0| <г с
центром г0 и радиусом г>0 она определена и представима степенным рядом:
/(2)=α0+α1 (г — ζ0)+α2 (ζ — z0)2-f · .. +ап (г — г0)"+ · · ·
(этот ряд обязательно является рядом Тейлора). Функция /(г) называется А. ф.
в области D плоскости комплексного переменного, если она аналитична в
каждой точке области D. А. ф. в точке z0 является А. ф. в некоторой окрестности
этой точки. Аналогично определяется понятие А. ф. действительного
переменного y=f(x), где требуется сходимость степенного ряда к f(x) не в круге, а в
интервале \х — *0| <г.
А. ф. в области D имеет в каждой точке z0 области D конечную
производную:
/'(*0)=lim — ,
Αζ+Ο ΔΖ
верно и обратное: если /' (ζ) существует и конечна в D, то f(z) является А. ф.
в области Di поэтому понятие однозначной А. ф. совпадает с понятием
голоморфной функции (см.).
А. ф. в связной области D однозначно определена, если заданы ее значения
для бесконечного множества точек, имеющего предельную точку внутри
области D\ в частности, А. ф. определяется своими значениями в произвольно
малой окрестности или на произвольно малой дуге, лежащими в D. Это свойство,
называемое теоремой единственности А. ф., показывает, насколько тесно
значения А. ф. связаны между собой. Например, А. ф. y=f(x) действительного
переменного может быть распространена в А. ф. комплексного переменного лишь
единственным образом (см. Аналитическое продолжение).
Интеграл от А. ф. в односвязной области D по любому замкнутому
контуру равен нулю (теорема Коши); обратное утверждение также справедливо, если
предполагать /(г) непрерывной в области D(теорема Морера). А. ф. имеет
производные всех порядков, которые также являются А. ф. в той же области.
Для того чтобы функция w=f(z) (которую всегда можно задать парой
функций и(ху у) и и(ху у) двух действительных переменных х, у) была А. ф. в
области £>, необходимо и достаточно, чтобы в области D функции и(х, у)
ди ди ди до
v(xt у) были дифференцируемы и Т"=Т'* Т~= —- Т" (условия Коши —Римана,
или, точнее, Даламбера— Эйлера). При выполнении этого условия и(х, у) и
ν (*, у) составляют пару сопряженных гармонических функций.

16
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
А. ф. w=f(z)t не принимающая одинаковых значений в связной области D
(однолистная), дает конформное отображение области D плоскости ζ на область
Dx плоскости w.
Многозначная (может быть бесконечнозначная) функция, полученная
аналитическим продолжением (см.) А. ф., также называется А. ф.; каждая однозначная
ветвь функции /(г) является однозначной А. ф.
Многозначная (быть может однозначная или бесконечнозначная) функция
/(г), полученная из А. ф. всевозможными аналитическими продолжениями»
называется полной А. ф. в смысле Вейерштрасса.
К классу А. ф. принадлежит большинство элементарных функций, напри-
П j
мер У ζ , ег , sin ζ, и многие неэлементарные, например гамма-функция,
эллиптические функции, бесселевы функции. Алгебраическая сумма и произведение
конечного числа А. ф. являются А. ф., частное А. ф. есть А. ф. (в области,
где знаменатель отличен от нуля). Сложная функция s=fx [/2(г)], составленная
из А. ф. s=f1(w) и w=f2(z), является А. ф.
Лит.: А. И. Маркушевич, Теория аналитических функций, Гостехиздат, Μ., 1950;
И. И. Привалов, Введение в теорию функций комплексного переменного, Гостехиздат,
М., 1954.
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ — распространение функции,
аналитической в некоторой области, на более широкую область. Если fx(z) — аналитическая
функция (см.) в области Dx и область D2 имеет общую часть S с областью Dx
(рис. 4.), то может существовать только одна аналитическая в области D2 функ-
Рис. 4 Рис. 5 Рис. 6
ция f2(z)y принимающая в области S те же значения, что и fx(z) (т. е.
fx(z)^f2(z) для всех точек ζ области 5); функция f2(z) называется А. п.
функции /х(г) в область D2 (наоборот, fx(z) есть А. п. f2(z)B область Dx). Можно
считать функции fx(z) и f2(z) частями одной аналитической в D1VD2 функции
f(z)i совпадающей с f1(z) в области Dx и с f2(z) в области D2\ эта функция
f(z) называется А. п. функции /1(2) на более широкую область Dx UD2 и
обозначается снова символом /χ(ζ). Если f2(z) — А. п. fx(z) в область D2i fz(z)—
А. п. /2 (ζ) в область D3, /4(z) —А. п. /3(z) в область D4, то эта цепь А. п.
функции fl(z) в совокупности даст А. п. fi(z) на более широкую область
D1.UD2UD3UD4; область £>4 (или даже £>3) может иметь общую часть К с
областью Dx (рис. 5), но значения f4 (z) B области К не обязаны совпадать со
значениями Mz), поэтому А. п. функции fx(z) приводит к понятию многозначной
аналитической функции, так как продолженная функция fx (z) может быть
двузначной в области К (а при дальнейших А. п. даже бесконечнозначной).
А. п. функции f(z) можно строить следующим образом. Пусть дан элемент
аналитической функции /(ζ), τ. е. дан степенной ряд a^a^z — Zy)-\-a2(z —
— 2х)г4-· · ·-И/ι (г — 2ι)"-1 » представляющий /(г) в круге ΛΥ, функция f(z)

АНАЛОГИЯ 17
в окрестности точки z2 внутри круга Кг представляется степенным рядом £>04·
-\-bl(z — z2)-\-b2 (ζ — z2)2H \-bn (ζ — z2)n-\ , который имеет круг
сходимости /С2 (не лежащий, быть может, целиком в круге Κι) и является А. п. f (z)
на /С2 (рис 6); этот степенной ряд называется А. п. заданного ряда.
Таким образом, исходный элемент функции / (ζ) определяет бесконечно
много новых элементов (с центрами внутри Κι), каждый из которых может
быть в свою очередь принят за исходный для дальнейшего продолжения /(г).
Если этот процесс продолжен неограниченно, то получается полная
аналитическая функция /(ζ) в смысле Вейерштрасса, вообще говоря многозначная,
определенная в некоторой области D, называемой областью существования полной
аналитической функции f(z).
Примеры: 1) при А. п. функции / (л:) = -Ь К х действительного переменного
получается двузначная функция f(z)=±y ζ , область существования которой
вся плоскость ζ, за исключением бесконечно удаленной точки и точки ζ=0;
2) при А. п. / (х) = 1п χ получается бесконечнозначная функция /(z) = Lnz.
АНАЛОГИЯ — умозаключение по сходству частных свойств (признаков),
имеющихся у двух математических понятий (фигур, отношений и т. д.).
А. широко используется в преподавании математики благодаря своей
наглядности и доступности; так, например, а) при изучении десятичных дробей
подчеркивается их аналогия с натуральными числами (сравнение, действия);
б) свойства алгебраических дробей аналогичны свойствам арифметических
(обыкновенных) дробей; в) методика решения задач на составление уравнений второй
степени аналогична методике решения задач на составление уравнений первой
степени; г) свойства членов геометрической прогрессии во многом аналогичны
свойствам членов арифметической прогрессии; д) свойства неравенств во многом
аналогичны свойствам равенств; е) свойства биссектральной плоскости
двугранного угла аналогичны свойствам биссектрисы плоского угла; ж) многие свойства
геометрических мест точек пространства аналогичны свойствам геометрических
мест точек плоскости (сфера — пространственный аналог окружности; плоскость,
перпендикулярная к отрезку АВ и проходящая через его середину, есть
пространственный аналог оси симметрии отрезка АВ).
Заключение по Л. схематически можно представить так: А имеет признаки
а, 6, с, d\ В имеет признаки а*, 6*, с*\ свойства а*, 6*, с* аналогичны
свойствам а, Ь. с. Тогда В имеет признак d*.
Следует признать, что заключение по А. не является строгим: если объекты
А и В имеют сходство в одном или нескольких свойствах а, 6, с, то мы не
можем еще заключить, что объект В имеет с Л и другое сходство в свойстве d.
Поэтому необходимо предостеречь учащихся от возможных ошибок при
пользовании А. Например, учащийся, производя сокращение дроби и записав в виде
2а 2 л
может по А. ошибочно записать:
ab b'
sin 2 α
—-—=sina (?).
Используя распределительный закон (см.) a (6-f c)=ab-\-ac, учащийся может
по А. ошибочно записать: lg(a-f-&) = lga-Hg& или sin (a-}-P) = sina-bsinP или
У a+b^Va+Vb.
Иногда действия над арифметическими корнями (см.) распространяют на
действия над корнями в поле (см.) комплексных чисел. Например, записав
2 Толковый словарь математических терминов

18
АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ
равенство У +3—у +3=0 по Α., учащийся ошибочно считает, что справедливо
и равенство
Индукция (см.) связана с аналогией по характеру знания, получаемого в
заключении. Как и индукция, А. может привести к ложным выводам.
Греч, analogia — пропорция.
Лит.: О. А. А рак ел ян. Аналогия в процессе повторения, «Ученые записки МОПИ»,
т. XIII, вып. 1, 1958: Д. Π ой а, Математика и правдоподобные рассуждения, ИЛ, М.,
1957; В. В. Репьев, Общая методика преподавания математики, Учпедгиз, М., 1958.
АНГАРМОНИЧЕСКОЕ ОТНОШЕНИЕ четырех точек (прямых, плоскостей) —
то же самое, что и сложное отношение (см.) точек (прямых, плоскостей).
См. также Гармоническая четверка точек.
АНТИЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ — преобразование А линейного
пространства (см.) над полем комплексных чисел, такое, что
А(х+у) = А{х)+А(у) и А(1х)=ТА(х)
при любых векторах χ и у пространства и при любом комплексном λ (~λ
означает число, комплексно сопряженное λ). Другое, не общеупотребительное
название А. п. — антигомография. Понятия А. п. используются в некоторых
главах теории непрерывных групп.
АНТИЛОГАРИФМ числа η (обозначается antlogyi) есть число N, логарифм
которого при данном основании а равен числу п: ant\ogan=;N=an или logflA/=/i.
Например, antlog102= 100.
Если η есть логарифм числа Ν, то N есть антилогарифм числа η при этом
же основании логарифмов.
А. называют также обращенным логарифмом.
АНТИНОМИИ теории множеств — логические противоречия в теории
множеств, возникающие при слишком «вольном» обращении с понятием множества.
В качестве примера А. отметим вопрос о множестве Μ всех кардинальных чисел
(см.). Кардинальное число μ этого множества должно было бы быть наибольшим
кардинальным числом, так как оно содержит все кардинальные числа, но,
образовав множество всех подмножеств этого множества, мы приходим к большему
кардинальному числу 2μ. А. теории множеств до сих пор не получили
удовлетворительного разъяснения. Одним из возможных путей устранения А. из
математики представляется аксиоматизация теории множеств, начатая К. Гёделем;
однако на этом пути возникают свои большие трудности.
Греч, αντινομία — противоречие.
АНТИПАРАЛЛЕЛОГРАММ — непростой четырехугольник ABCD (рис. 7) с
одной осью симметрии /. Боковые стороны и диагонали равнобедренной трапеции
образуют А. Подобно параллелограмму, его противоположные стороны АВ и
CD(AD и ВС) равны и антипараллельны (см. Антипараллельные прямые)
относительно двух других сторон AD и ВС (АВ и CD), поэтому его называют А. или
контрпараллелограммом.
АНТИПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ относительно сторон угла. Прямые а и b
называются антипараллельными относительно сторон угла KOL, если они
пересекают стороны этого угла так, что образуют равные углы, но с разными
сторонами угла KOL\ при этом равные углы входят в треугольники, содержащие
вершину О (рис. 8). А. п., вообще говоря, не являются параллельными, за
исключением того случая, когда они обе перпендикулярны биссектрисе угла KOL.
Понятие А. п. используется при изучении преобразования инверсии (см.).
Иногда аналогичное определение А. п. дают не относительно сторон угла,
а относительно двух других прямых, которые пересекаются первыми. Во всяком

АПОФЕМА
19
вписанном в окружность четырехугольнике (выпуклом или звездчатом)
противоположные стороны антипараллельны относительно двух других сторон.
Иногда также определяют А. п. относительно третьей прямой: прямые а и b
называются А. п. относительно прямой с9 если они образуют с ней равные
внутренние односторонние углы. Боковые стороны равнобедренного треугольника —
А. п. относительно основания.
Рис. 7
Рис. 8
АНТЬЕ от числа —то же, что и целая часть от числа (см.).
АПОРИЯ — парадокс (см.)* к которому прибегали в своих рассуждениях
древнегреческие ученые — противники школы Демокрита. А.—это ложный
вывод, к которому приходили древние всякий раз, когда стремились заменить
непрерывные процессы суммой дискретных величин, не пользуясь предельным
переходом, а опираясь только на атомистические соображения Демокрита.
Известны, например, апории Зенона (V—IV в. до н. э.), одна из которых
следующая: Ахиллес не может догнать черепаху, так как ему надо пройти
бесконечную последовательность тех пунктов, в которых находилась черепаха:
пройти одну половину пути, затем еще другую половину пути и т. д.
Математически апория Зенона сводится к отрицанию равенства:
/с=1
12*
= 1.
Лит.: К. А. Рыбников, История математики, изд. МГУ, 1 960.
АПОФЕМА: 1°. А. правильного многоугольника — длина перпендикуляра,
опущенного из центра правильного я-угольника на какую-либо его сторону. А.
правильного «-угольника равна радиусу гп вписанного в него круга и связана с
длиной его стороны ап и его площадью Sn соотношениями:
ал=2гл tg
180°
2х 180°
Последнее соотношение
вид:
при л, равных соответственно 3, 4, 5 и 6, принимает
2°. А. правильной пирамиды — высота треугольника, являющегося боковой
гранью правильной пирамиды, проведенная из вершины правильной пирамиды
2*

20
АППЛИКАТА
Площадь боковой поверхности S^0K правильной пирамиды связана с А. п. п. и с
периметром Ρ основания пирамиды соотношением: 5бок=-~- ^'^» гДе Λ есть
А. п. п.
3°. А. правильной усеченной пирамиды — высота трапеции, являющейся
боковой гранью правильной усеченной пирамиды. Площадь боковой поверхности
S00K связана с А. п. у. п. соотношением:
5б0к-у (Pi+PaM.
где Ρ χ и Р2 равны соответственно периметрам нижнего и верхнего оснований
правильной усеченной пирамиды, а Л есть А. п. у. п.
АППЛИКАТА — одна из декартовых координат точки в пространстве,
третья по счету после абсциссы (см.) и ординаты (см.) и обозначаемая обычно
буквой г.
АППРОКСИМАЦИЯ — приближенное выражение математических величин
(чисел, функций и пр.) через другие, более простые. Обычно стараются
построить А. с любой степенью точности (при каком-либо определенном способе
измерения величины отклонения А. от фактического значения аппроксимируемой
величины).
А. непрерывной на отрезке α*ζχ<δ функции y=f (x) алгебраическими или
тригонометрическими многочленами возможна с любой степенью точности
(теорема Вейерштрасса), где мерой отклонения р(Р, /) многочлена Р(х) от функции
f(x) служит максимум абсолютной величины разности между f(x) и Р(х):
ρ (Ρ, /)=тах |/ (х) — Ρ (χ)\ (так называемая равномерная А. функции).
а<х<Ь
Асимптотические выражения (см.) дают примеры А. с малой относительной
погрешностью. Частные суммы ряда Фурье функции f (х) с интегрируемым
квадратом (см.) аппроксимируют f(x) «в среднем». Другими словами, за меру
отклонения частной суммы Sn(x) ряда Фурье от f(x) принято:
λ(5*, /)-у _Ш (*)-S« (*)]2 dx .
22
А. числа π является его любое приближение, например ~.
Метод А. может служить для определения некоторых понятий. Например,
длина кривой определяется как предел длин ломаных, геометрически
аппроксимирующих данную кривую, когда длина наибольшего звена ломаной стремится к
нулю.
Лат. approximo — приближаюсь.
Лит.: В. Л. Гончаров, Теория интерполирования и приближения функций, Гостех-
издат, М., 1954.
АРАБСКИЕ ЦИФРЫ — название следующих десяти математических знаков:
0, 1, 2, 3, 4, 5, 6, 7, 8,9. По десятичной системе счисления с помощью А. ц.
можно записать любое сколько угодно малое или сколько угодно большое число.
А. ц. на самом деле пришли к арабам из Индии около XI в., а затем от
арабов в Европу. (См. также Цифры, Римские цифры, Счисление.)
Лит.: Я. И. Депман, История арифметики, Учпедгиз, М., 1959.
АРГУМЕНТ КОМПЛЕКСНОГО ЧИСЛА а-\-Ы — угол между положительным
направлением оси абсцисс и направлением от начала координат к числу а+Ы.

АРИФМЕТИЧЕСКИЙ РЯД
21
Α., к. ч. г~а-\-Ы часто обозначают символически: argz. А. к. ч. рассматри-
Ь а
вается с точностью до 2π. Ясно, что sin argz—— и cos argz=—, где г —
модуль комплексного числа (см.). Аргумент произведения комплексных чисел
равен сумме аргументов сомножителей, т. е. arg(21^2)=argz1-f-arg22.
Единственным комплексным числом, не имеющим аргумента, является число 0.
АРГУМЕНТ ФУНКЦИИ — независимая переменная (см. Функция).
АРИФМЕТИКА — наука о числах и операциях над ними. В А. изучаются в
первую очередь натуральные и дробные числа. А. является одной из
древнейших отраслей человеческого знания.
А. как учебный предмет в школьном преподавании изучается в I—VI
классах и строится на описательных определениях. На физико-математических
факультетах педагогических институтов А. изучается весьма углубленно в трех
теоретических курсах: в арифметике рациональных чисел, в теории чисел и в
основаниях арифметики.
Название А. происходит от греческого αριθμοζ— число.
АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ — последовательность чисел, каждое из
которых, начиная со второго, получается из предыдущего прибавлением к нему
постоянного (для всех членов) числа d, называемого разностью А. п. Если
первый член А. п. есть alt то А. п. имеет вид:
alt βχ-f-d, ax-\-2dt . . ., a^nd, . ..
Таким образом, А. п. вполне определяется первым ее членом и ее разностью
л-й член А. п. an=*aL+(n~- l)d. Сумма η первых членов А. п. равна:
• d(n-\)
«1 + "
А. п. является арифметическим рядом (см.) первого порядка. А. п. иногда
обозначается символом -*-.
Лат: progressio — продвижение вперед.
АРИФМЕТИЧЕСКАЯ ПРОПОРЦИЯ — равенство вида: а — Ь==с — d, где а,
Ьу с, d — суть арифметические числа (см.). А. п. иначе называется разностной
пропорцией.
АРИФМЕТИЧЕСКИЙ КОРЕНЬ — неотрицательное значение корня четной или
нечетйои степени из неотрицательного числа, например: А. к. г 16=2, А. к.
3/—- Ъг
У 27=3. А. к. у —27 не существует в силу определения А. к.
4/"~~
Если рассматриваются два значения корня: у 16= ±2, то говорят об ачгеб-
раическом значении корня (см.) в области действительных чисел; если же
рассматриваются все четыре значения корня у 16, то говорят об алгебраическом
значении корня в области комплексных чисел.
АРИФМЕТИЧЕСКИЙ РЯД порядка т — последовательность значений
некоторого многочлена р(х)=атхт+ат—1хт~~х ■] \-αχχ+α0 с целочисленными
коэффициентами и с атф0 при целых неотрицательных значениях аргумента
jt—0, 1, 2, ... Если blt 62, 63, ... есть А. р. порядка /я, то его разности:
с1=62 — b1% c2=bs — b2, . . . сл=6л+х — bnt ...образуют А. р. (т — 1)-го
порядка, вторые разности: dx = c2—- cly d2=c3 —= с2, .. ., dn^=cn^.1 — cni ...
образуют А. р. (т — 2)-го порядка и т. д.

22
АРИФМЕТИЧЕСКОЕ ДОПОЛНЕНИЕ
А. р. 1-го порядка является арифметической прогрессией (см.). А. р. 2-го
порядка образуют, например, треугольные числа (см.), фигурные числа (см.),
и в частности квадратные числа (см.).А. р. 3-го порядка образуют, например,
пентагональные числа.
АРИФМЕТИЧЕСКОЕ ДОПОЛНЕНИЕ числа А (0<Л<1) есть разность
между единицей и этим числом. Например, А. д. числа 0,3547 есть число 0,6453
(число 0,6453 дополняет число 0,3547 до единицы).
А. д. часто используется при логарифмических вычислениях, когда
требуется заменить логарифм с отрицательной мантиссой логарифмом с положительной
мантиссой, т. е. значение логарифма заменяется его записью в искусственной
форме — логарифмом с отрицательной характеристикой, но положительной
мантиссой, с целью замены вычитания сложением. Например, lgN± — lgN2=
=2,1326 —0,3547 = 2,1326+Т 6453= 1,7779. Число Т,6453 читается обычно так:
«единица с минусом (или: единица под минусом) шестьдесят четыре пятьдесят
три» («телефонным» способом). Иногда А. д. рассматривают не до единицы, а
до десяти. См. также Кологарифм, Дополнительный логарифм.
АРИФМЕТИЧЕСКОЕ СРЕДНЕЕ нескольких чисел аъ а2у . . ., ап есть число
П
А. с. чисел ^=1, α2 = 3, σ3=— 0,4 равно :— = 1,2. А. с. часто
о
встречается в практике измерений физических величин (температуры, длины
и др.) и вычислений.
Вместо А. с. (число) также говорят: арифметическая средняя (величина).
А. с. нескольких чисел, как и любая другая средняя этих чисел, заключена
между наименьшим и наибольшим числами из данных чисел. См. также
Средние.
АРИФМЕТИЧЕСКОЕ ЧИСЛО —в первоначальном понимании всякое
неотрицательное число. В более широком понимании (см. Теоретическая арифметика)
под А. ч. понимают любое число. Термин А. ч. иногда встречается в
преподавании арифметики в школе как противопоставление числу, изучаемому в алгебре,
где изучаются не только положительные числа и нуль, но и отрицательные числа.
А. ч., понимаемое в первоначальном смысле, изображается геометрически точкой
на числовом луче, всякое же действительное число в алгебре изображается
точкой на числовой прямой.
АРИФМОМАНТИЯ — лженаучное представление о магической роли чисел,
гадание с помощью чисел. От халдеев, египтян и евреев А. перешла к грекам;
особенно верили в силу А. члены школы Пифагора.
Греч, arithmos — число, manteia — прорицание (ср. хиромантия — гадание
по руке).
АРККОСЕКАНС — функция, обратная косекансу (см). А. обозначается так:
Arccosec χ. А—многозначная (бесконечнозначная) функция. Однозначная ветвь
ее называется главным значением А. и обозначается через arccosec x, где
— — <arccosec χ < —- и |дс| > 1. Функция arccosec χ — нечетная, ограниченная
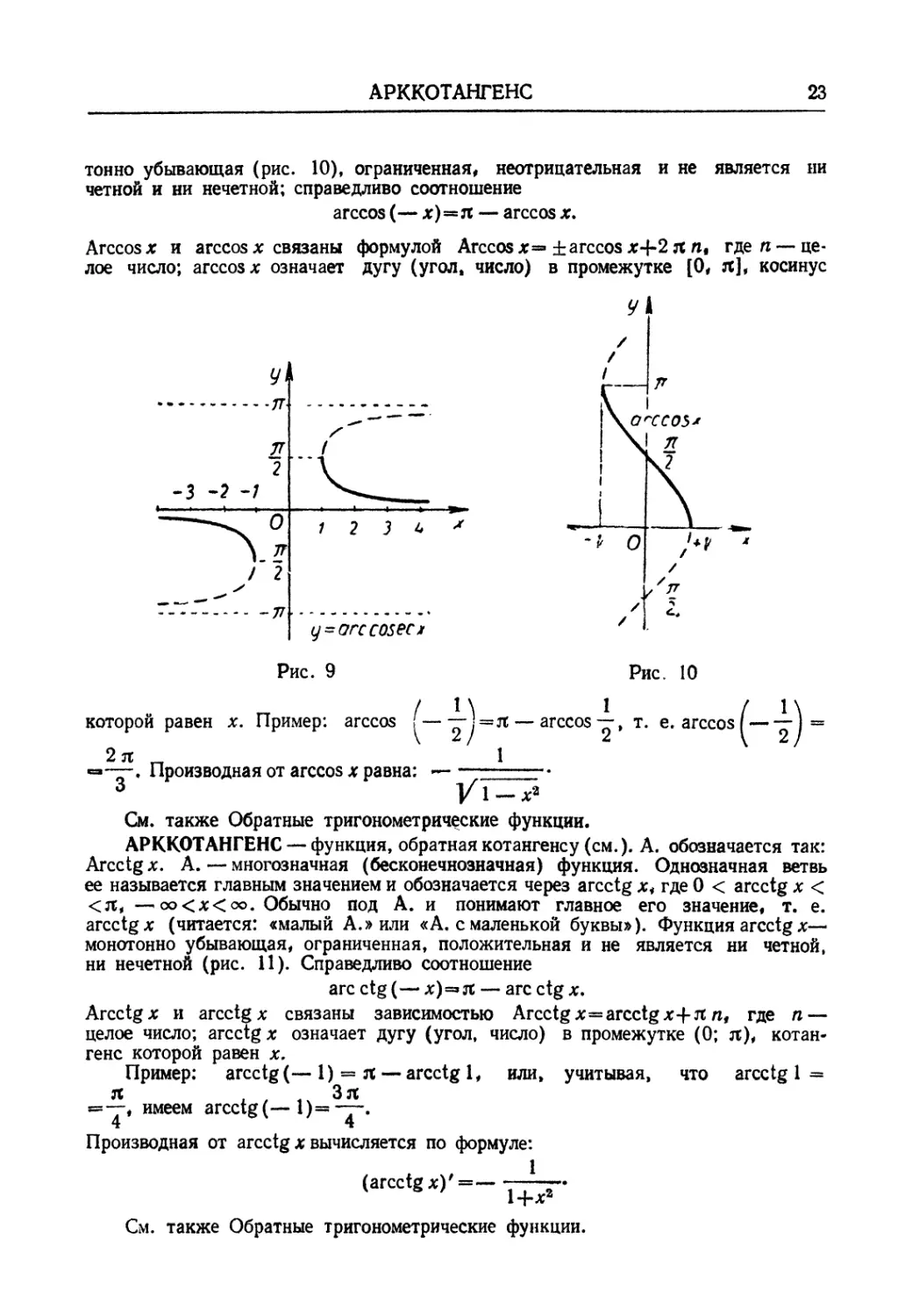
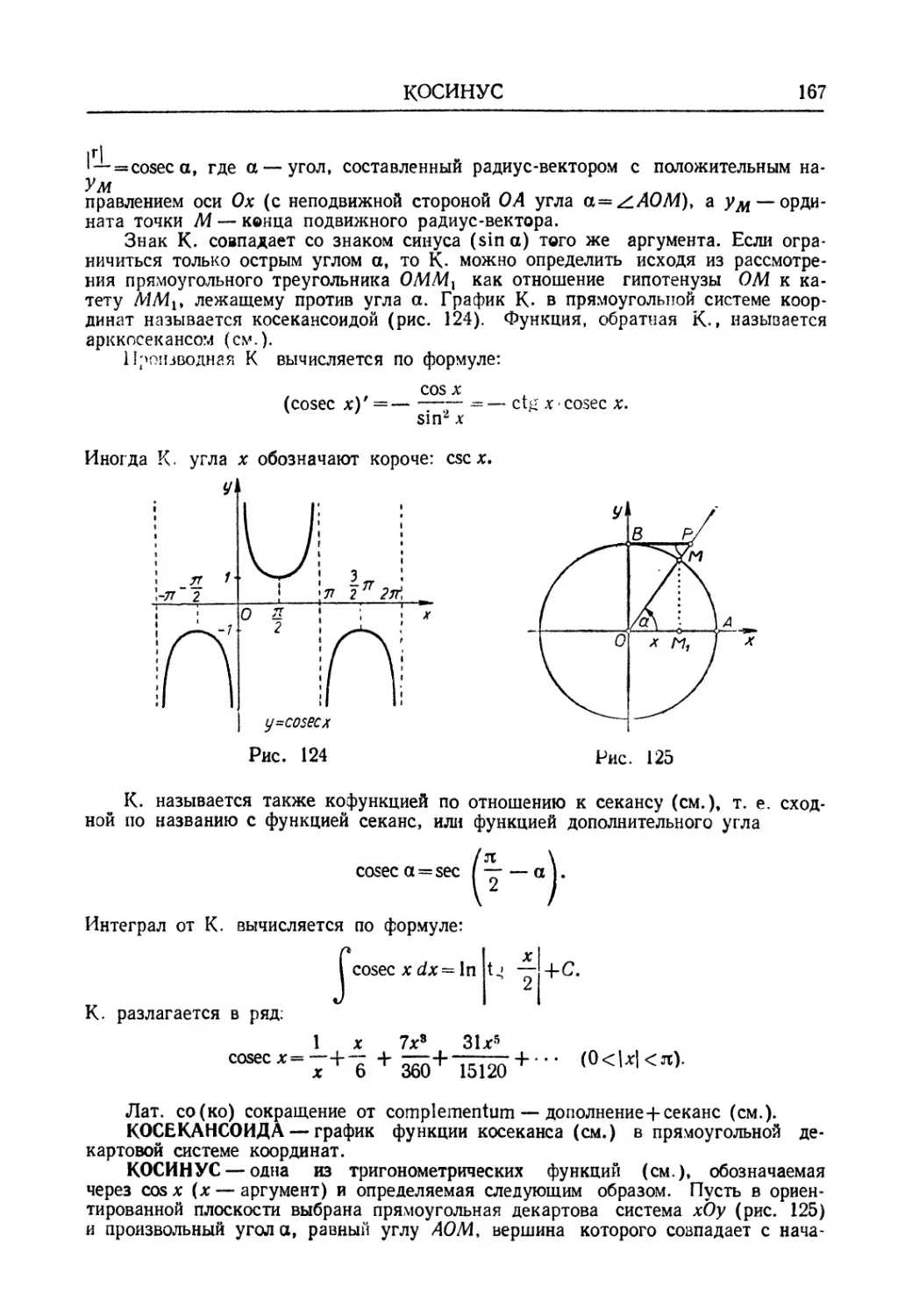
(рис. 9). График функции А. состоит из двух ветвей (дуг).
См. также Обратные тригонометрические функции.
АРККОСИНУС — функция, обратная косинусу (см.). А. обозначается так:
Arcsoc*. А.—многозначная (бесконечнозначная) функция. Однозначная ветвь
ее называется главным значением А. и обозначается через arccos χ, где 0 < arccos χ <
<π, —1<#<1. Обычно под А. понимают его главное значение, т. е. arccos*
(читается: «малый А.» или «А. с маленькой буквы»). Функция arccos χ | моно-

АРККОТАНГЕНС
23
тонно убывающая (рис. 10), ограниченная, неотрицательная и не является ни
четной и ни нечетной; справедливо соотношение
arccos (— *)=π — arccos x.
Arccos χ и arccos χ связаны формулой Arccos χ =- ± arccos х+2 я η, где η —
целое число; arccos χ означает дугу (угол, число) в промежутке [0, π], косинус
У1
7Т
2
-3 -2 -7
""Ν °
λ π
1
... ί
^
1 2 3 и
y^orecosec*
ж
/
/
/
\ О"
\
[
,. I
п
г cos*
η
\2
•ь о\ J+v
/
А.1-
Рис. 10
arccos -~, т. е. arccos
Ю-
Рис. 9
/ 1\
которой равен х. Пример: arccos —7Г/ rt—
„ Производная от arccos χ равна: -
3 Vl-x*
См. также Обратные тригонометрические функции.
АРККОТАНГЕНС — функция, обратная котангенсу (см.). А. обозначается так:
Arcctg*. А. — многозначная (бесконечнозначная) функция. Однозначная ветвь
ее называется главным значением и обозначается через arcctg xi где 0 < arcctg x <
<π„ -—οο<#<οο. Обычно под А. и понимают главное его значение, т. е.
arcctg χ (читается: «малый А.» или «А. с маленькой буквы»). Функция arcctg χ—
монотонно убывающая, ограниченная, положительная и не является ни четной,
ни нечетной (рис. 11). Справедливо соотношение
arc ctg (— χ) =» jt — arc ctg x.
Arcctg χ и arcctg л; связаны зависимостью Arcctg *=arcctg лг-f л п, где л —
целое число; arcctg χ означает дугу (угол, число) в промежутке (0; π),
котангенс которой равен х.
Пример: arcctg (— 1) = π — arcctg 1, или, учитывая, что arcctg 1 =
«=--, имеем arcctg(— 1)=—.
4 4
Производная от arcctg x вычисляется по формуле:
(arcctg *)'=— ——·
1-f x2
См. также Обратные тригонометрические функции.

24
АРКСЕКАНС
АРКСЕКАНС — функция, обратная секансу. А. обозначается так: Arcsec*.
А. — многозначная (бесконечнозначная) функция. Однозначная ветвь ее
называется его главным значением и обозначается через arcsec *, где 0<arcsec*< π.
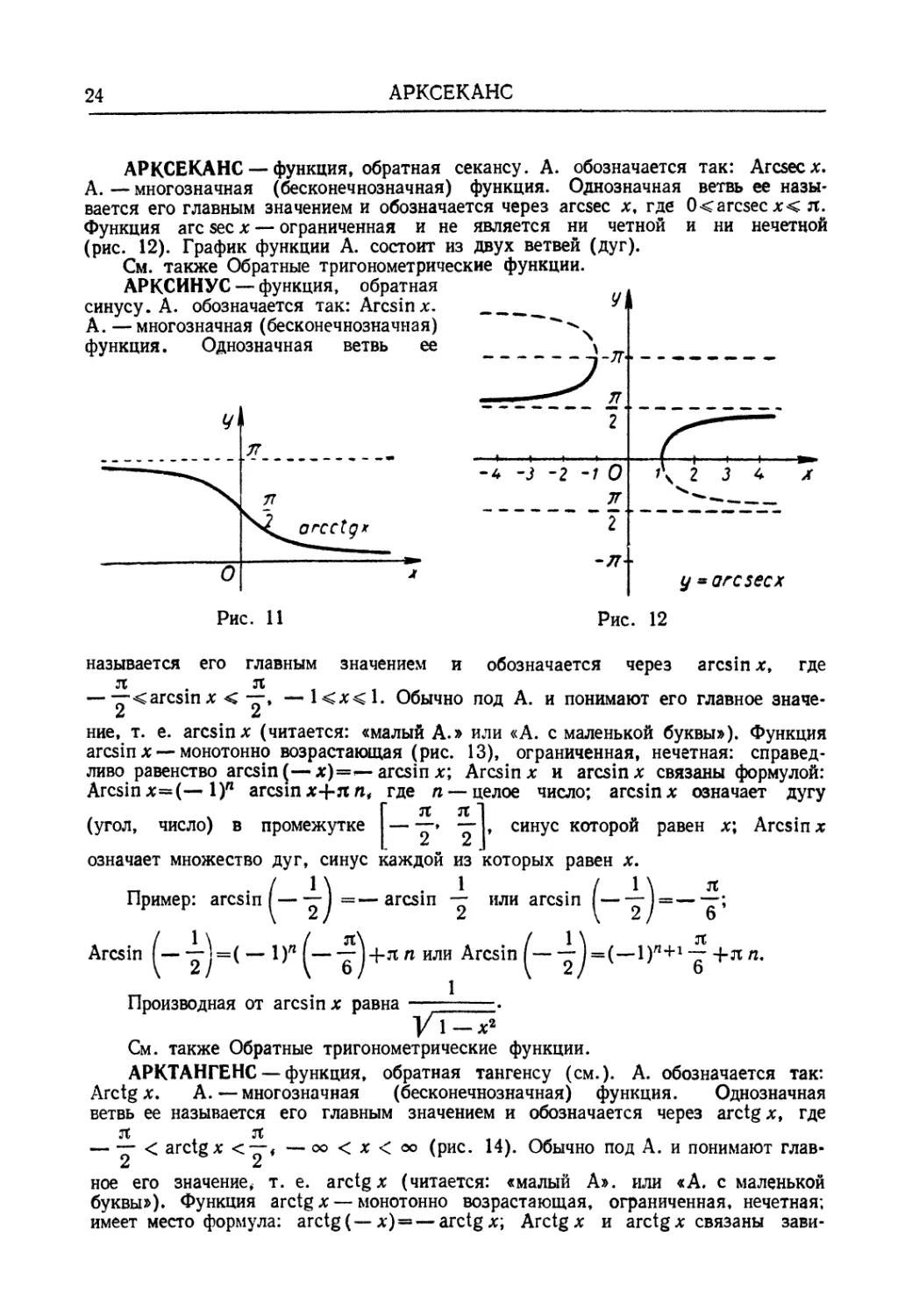
Функция arc sec л: — ограниченная и не является ни четной и ни нечетной
(рис. 12). График функции А. состоит из двух ветвей (дуг).
См. также Обратные тригонометрические функции.
АРКСИНУС — функция, обратная
синусу. А. обозначается так: Arcsin*. ^1
А. — многозначная (бесконечнозначная) "^
функция. Однозначная ветвь ее >
(/<
О
\
7Т
п
л
у = arc secx
Рис. 11
Рис. 12
называется его главным значением и обозначается через arcsin*, где
— -т-< arcsin* < -—, — 1 <х< 1. Обычно под А. и понимают его главное
значение, т. е. arcsin* (читается: «малый А.» или «А. с маленькой буквы»). Функция
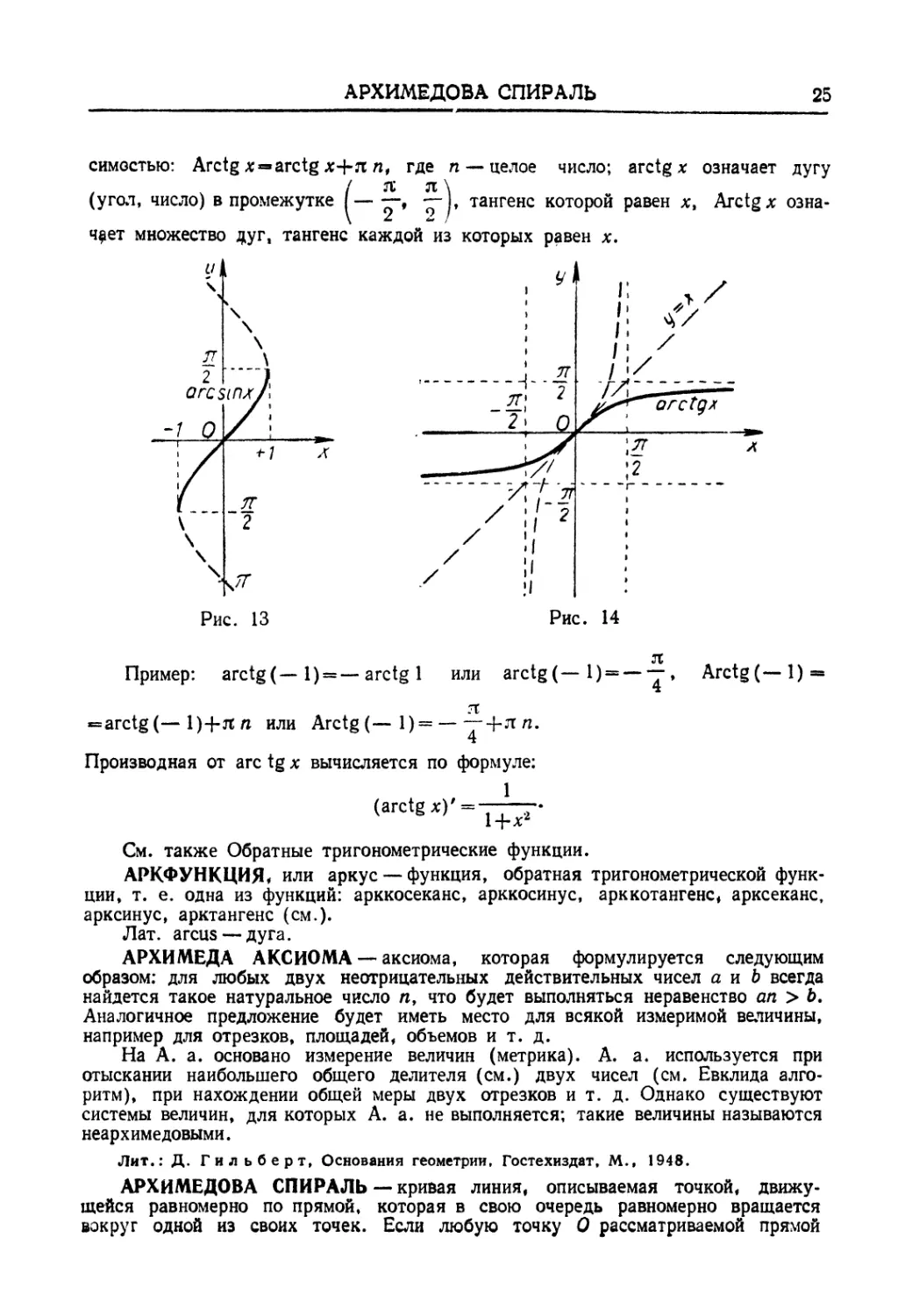
arcsin *~ монотонно возрастающая (рис. 13), ограниченная, нечетная:
справедливо равенство arcsin(—*)=—arcsin*; Arcsin* и arcsin* связаны формулой:
Arcsin *=(— 1)" arcsin х+л п, где η — целое число; arcsin* означает дугу
(угол, число) в промежутке
Г U 5-1
Г 2* 2>
синус которой равен х\ Arcsin x
означает множество дуг, синус каждой из которых равен *.
гт · / 1\ · Х ■ ( 1\ *
Пример: arcsin f— -—I =—arcsin -— или arcsin ——1=——;
1)-(-|)+«η
Производная от arcsin x равна
Arcsin (—-£■)=(
или Arcsin
1
К)-<-
1)η+1-+π«.
Ό
У 1 — jc2
См. также Обратные тригонометрические функции.
АРКТАНГЕНС — функция, обратная тангенсу (см.). А. обозначается так:
Arctg*. А. — многозначная (бесконечнозначная) функция. Однозначная
ветвь ее называется его главным значением и обозначается через arctg *, где
jt jt
— -г- < arctg* <~*— <χ> < * < оо (рис. 14). Обычно под А. и понимают
главное его значение, т. е. arctg л; (читается: «малый А», или «А. с маленькой
буквы»). Функция arctg* — монотонно возрастающая, ограниченная, нечетная;
имеет место формула: arctg (—*) = — arctg*; Arctg* и arctg* связаны зави-

АРХИМЕДОВА СПИРАЛЬ
25
симостью: Arctg * = arctg х+я η, где η — целое число; arctg χ означает дугу
/ л π \
(угол, число) в промежутке ι— --, —I, тангенс которой равен *, Arctg x
означает множество дуг, тангенс каждой из которых равен х.
Ц\
\
>
π
2
1
1
\
\
\
ι \
orcsinx/\
-г I °J
\
\
\
\
Ри
*7
π
2
Vr
с. 13
λ
У[
! я
<π> 2
7Т\ с
2> О
rf
y-t-j
/ \ г
/ '
/ ч
/ !
1 !; ,>'
: <'/
ν /
/:/
ТЛ^~*
js*^ arctg/
\Tt λ
;2
Рис. 14
Пример: arctg (— 1)==— arctg 1 или arctg (— 1) = — — , Arctg (— 1) =
π
«arctg (— l)-f-я п или Arctg (— 1)= — т"+я п.
Производная от arc tg x вычисляется по формуле:
(arctg х)> =Ί±7·
См. также Обратные тригонометрические функции.
АРКФУНКЦИЯ* или арку с — функция, обратная тригонометрической
функции, т. е. одна из функций: арккосеканс, арккосинус, арккотангенс, арксеканс,
арксинус, арктангенс (см.).
Лат. arcus — дуга.
АРХИМЕДА АКСИОМА —аксиома, которая формулируется следующим
образом: для любых двух неотрицательных действительных чисел а и Ь всегда
найдется такое натуральное число л, что будет выполняться неравенство an > b.
Аналогичное предложение будет иметь место для всякой измеримой величины,
например для отрезков, площадей, объемов и т. д.
На А. а. основано измерение величин (метрика). А. а. используется при
отыскании наибольшего общего делителя (см.) двух чисел (см. Евклида
алгоритм), при нахождении общей меры двух отрезков и т. д. Однако существуют
системы величин, для которых А. а. не выполняется; такие величины называются
неархимедовыми.
Лит.: Д. Гильберт, Основания геометрии, Гостехиздат, М., 1948.
АРХИМЕДОВА СПИРАЛЬ — кривая линия, описываемая точкой,
движущейся равномерно по прямой, которая в свою очередь равномерно вращается
вокруг одной из своих точек. Если любую точку О рассматриваемой прямой

26
АРЦЕЛА ТЕОРЕМА
принять за полюс, а данную прямую с выбранным на ней направлением — за
полярную ось, то уравнение А. с. в полярных координатах (см.) будет иметь
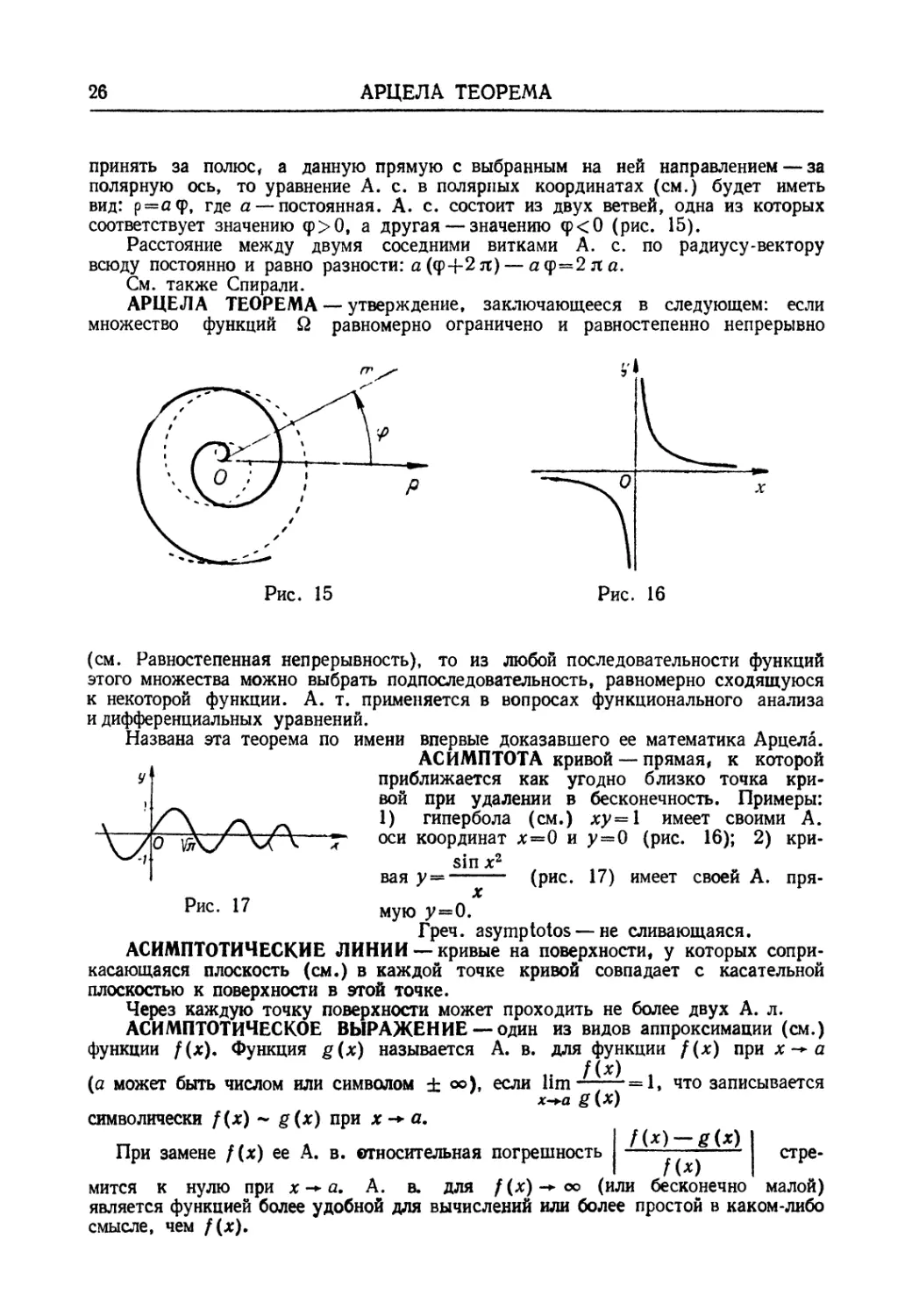
вид: ρ=αφ, где а —постоянная. А. с. состоит из двух ветвей, одна из которых
соответствует значению φ>0, а другая — значению <р<0 (рис. 15).
Расстояние между двумя соседними витками А. с. по радиусу-вектору
всюду постоянно и равно разности: α (φ-f 2 π) — α φ=2 π α.
См. также Спирали.
АРЦЕЛА ТЕОРЕМА — утверждение, заключающееся в следующем: если
множество функций Ω равномерно ограничено и равностепенно непрерывно
Рис. 15
Рис. 16
(см. Равностепенная непрерывность), то из любой последовательности функций
этого множества можно выбрать подпоследовательность, равномерно сходящуюся
к некоторой функции. А. т. применяется в вопросах функционального анализа
и дифференциальных уравнений.
Названа эта теорема по имени впервые доказавшего ее математика Арцела.
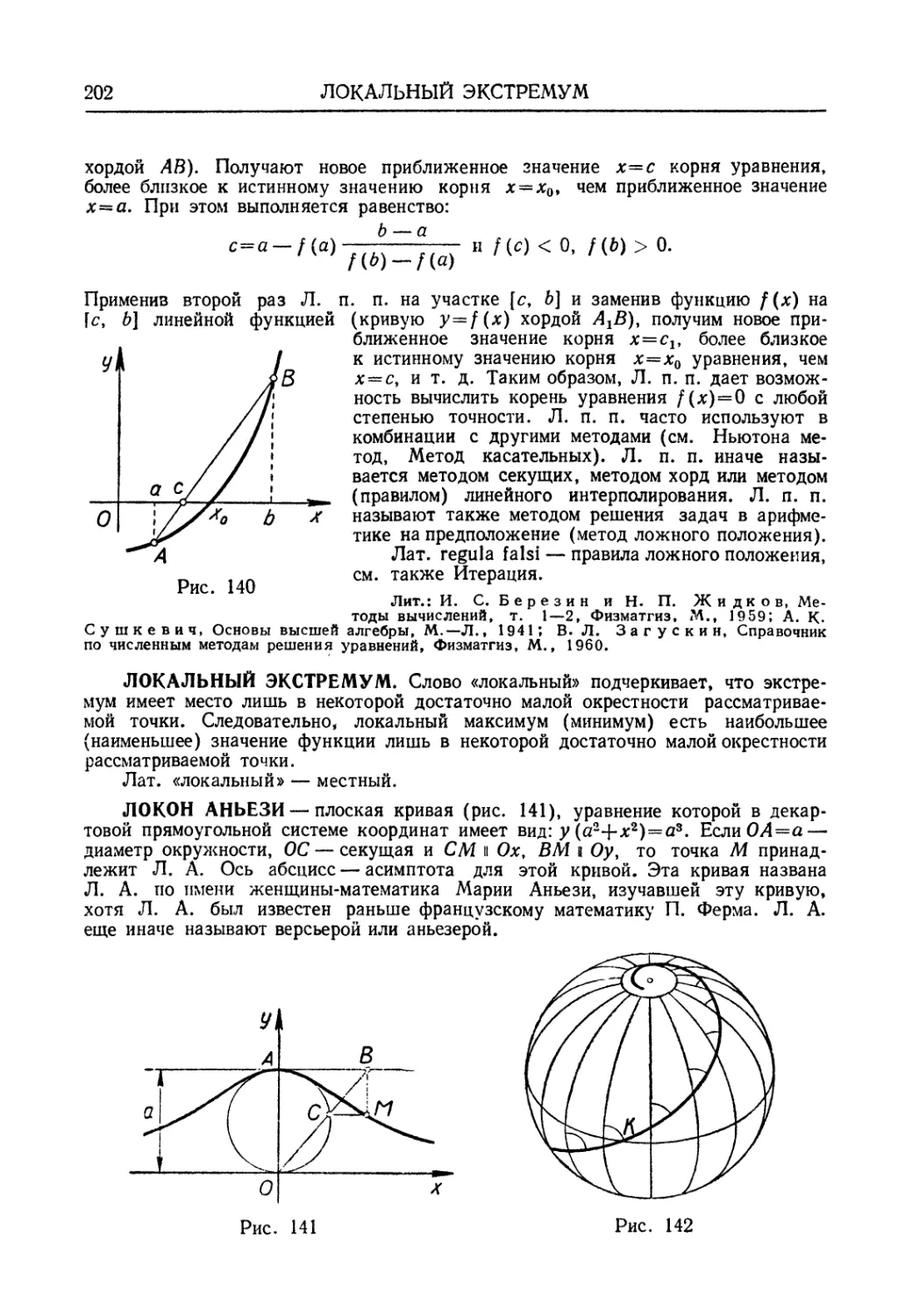
АСИМПТОТА кривой — прямая, к которой
приближается как угодно близко точка
кривой при удалении в бесконечность. Примеры:
1) гипербола (см.) ху=\ имеет своими А.
оси координат х=0 и у=0 (рис. 16); 2) кри-
(рис. 17) имеет своей А. пря-
м
вая у =
sin jt
Рис. 17
мую у=0.
Греч, asymptotos — не сливающаяся.
АСИМПТОТИЧЕСКИЕ ЛИНИИ —кривые на поверхности, у которых
соприкасающаяся плоскость (см.) в каждой точке кривой совпадает с касательной
плоскостью к поверхности в этой точке.
Через каждую точку поверхности может проходить не более двух А. л.
АСИМПТОТИЧЕСКОЕ ВЫРАЖЕНИЕ —один из видов аппроксимации (см.)
функции /(*). Функция g(x) называется А. в. для функции f(x) при χ -* а
(а может быть числом или символом ± оо), если am——* = 1, что записывается
x^ag(x)
символически f(x) ~ g(x) при χ -► α.
Ι /(*) — g(x) I
При замене f(x) ее А. в. относительная погрешность —
стремится к нулю при х-+а. А. в. для f(x)-+oo (или бесконечно малой)
является функцией более удобной для вычислений или более простой в каком-либо
смысле, чем /(*).

АСТРОИДА
27
Важными примерами А. в. являются Стирлинга формула (см.):
п\ ~<> у 2лηппе—п при /ι-*»οο, закон распределения простых чисел: π(#) —
при χ
\пх
Специальным видом А. в. является асимптотическое разложение (см.)
данной функции.
АСИМПТОТИЧЕСКОЕ РАЗЛОЖЕНИЕ — представление данной функции рас-
оо
ходящимся рядом. Более точно — ряд 2 Ф*(*) = Фо (*)+Φι (*)+ ···■+■
k - о
+ф* (*)+··· называется А. р. функции f (х) при χ -> а (или χ -> оо и т. п.),
если при χ -> а
f (х) **> Фо (*)» / (*) ~ Фо (*) ^ Φι (*)> / (*) - Фо (*) - Φι (*) ^ ф2 (*)>
. · ·> /(*) — Фо(*) — фл*) — ··· —q>k(x) - φ*+ι(*)> . ··,
α
где α *ν, β означает* что lim — =1 и частные суммы Sk(x)=q>0 (*)-τ·Ψι(*)4-
х -+а ρ
+ ··· -Ьф^(^) представляют асимптотические выражения для /(#), все более
* /(*) — S*+i(*)
точные в том смысле, что отношение ошибок - стремится к нулю
H*) — Sk(x)
при χ -*· а.
Нередко ограничиваются лишь несколькими первыми членами А. р., когда
трудно найти полное А. р.
Примером А. р. может служить формула:
Qn~lnn+C+— -—-+ ... .
2п 12л2
дающая А. р. суммы Qn—1+"Г"-т--г + ··· +~~ первых η членов гармониче-
2 о η
ского ряда (см.) при η -> оо (здесь дг=/г принимает лишь целочисленные
значения), где С — Эйлера постоянная (см.).
Иногда А. р. называют следующий частный вид А. р.:
/(*)~a0+-J-+-J-+ ··· +-£+ -(*--):
здесь
*-Ji»^W-*-f ^].
Понятие А. р. применимо к функциям комплексного переменного, в
особенности указанный выше частный тип. А. р.
АССОЦИАТИВНОСТЬ —см. Закон ассоциативности.
АСТРОИДА — кривая, описываемая точкой окружности С (г), катящейся
по неподвижной окружности радиуса R и внутри ее и имеющей радиус
D
г = — (рис. 18). А. представляет собой частный случай гипоциклоиды (см.).
Если радиус неподвижной окружности R=a, то уравнение А. в прямоугольных

28
АСТРОЛЯБИЯ
ч
о'' 1
<<~^ /
А\У
1 s\
\ X
\ \
х . ^ \
1
Г -^
\ " >
\ _ ^
/ Ν/'
/ /
1 „'
л
Рис. 18
декартовых координатах имеет вид: χ
2
+У
=а . Отрезок касательной к Α., заключенный
между осями координат, имеет постоянную длину
а. Длина А. равна 6 а.
Греч. αστρον — звезда , ε ι δ ο ζ — вид, форма;
астроида — звездообразная.
АСТРОЛЯБИЯ — угломерный прибор для
измерения углов, расположенных в горизонтальной
плоскости. Имеются различные конструкции А.
Лит.: М. А. Знаменский, Измерительные работы
на местности, Учпедгиз, М., 1959.
АФФИКС комплексного числа z=a+bi при геометрическом его
представлении— точка, соответствующая этому числу а+Ы9 т. е. точка с декартовыми
координатами (а; 6). Часто А. к. ч. не различают с самим комплексным числом ζ.
Лат. affiqo — приколачиваю, приковываю к чему-либо.
АФФИННАЯ ГЕОМЕТРИЯ — геометрия, изучающая аффинные свойства
фигур, т. е. такие свойства фигур, которые остаются инвариантными
относительно аффинных преобразований (см.).
В А. г. не сохраняется, вообще говоря, расстояние между двумя точками А
и β и им соответствующими точками А' и £', т. е. АВ φ Α'Β'. Вообще
понятие расстояния между двумя точками не принадлежит А. г.
Теоремы, например, о делении медиан треугольника точкой их пересечения
в определенном отношении, о свойстве сопряженных диаметров эллипса
являются теоремами А. г., в то время как понятия о высоте или биссектрисе
треугольника не являются аффинными.
А. г. можно также определить как геометрию, все предложения которой
вытекают из определенной системы аксиом, или как геометрию, определяемую
(характеризуемую) группой аффинных преобразований (см.).
Лат. affinus —- родственный, соответственный.
АФФИННЫЕ ПРЕОБРАЗОВАНИЯ плоскости α в плоскость а' (или
плоскости а в себя, или пространства в себя) есть произведение
перспективно-аффинных преобразований (параллельных проекций).
Если точки А% Bt С, . . . плоскости α проектируются в направлении /
в точки /40, В0, С0
плоскости а0 (рис. 19), а точки А0, В0, С0
.
проектируются параллельной проекцией в направлении /' в точки А'\ В\ С, ... на
плоскость а', то соответствие между
плоскостями а и а', в котором точкам
Ау Б, С, ... плоскости α сопоставляются
точки Л% В\ С, ... плоскости а',
будет аффинным.
При А. п. плоскости прямые
переходят в прямые, точки в точки,
параллельные прямые переходят в
параллельные, сохраняется инцидентность точек и
прямых и сохраняется простое отношение
(см.) трех точек (ochobhoi инвариант А.
п.) Поэтому при А. п. плоскости
трапеция перейдет в трапецию, квадрат в
параллелограмм.

АФФИНОР
29
А. п. дзух плоскостей или плоскости в себя задается тремя парами
соответственных "точек: (А, Л'), (В, В') и (С, С), из которых никакие три точки
одной плоскости не коллинеарны; другими словами, А. п. плоскости задается
двумя невырожденными треугольниками /\АВС и ДЛ'В'С
А. п. образуют группу.
А. п. плоскости α в плоскость а' можно определить аналитически,—как
такое, при котором координаты точки (х', у') плоскости а' и точки (х, у)
плоскости а связаны линейными формулами:
где ^ l·^ °·
у' =a2x+b2y+c2i \a2 b2\
Отношение площадей двух фигур при А. п. остается неизменным, т. е. является
инвариантом А. п.; А. п. плоскости в себя могут как изменять, так и не
изменять ориентацию фигуры.
Наиболее важные А. п. — это сжатие плоскости к прямой, сдвиг, гомотетия,
симметрия. Таким образом, все преобразования, изучаемые в элементарной
геометрии средней школы, являются частными случаями А. п.
При А. п. плоскости эллипс переходит в эллипс (в частности, в
окружность); поэтому эллипс и окружность — аффинно-родственные фигуры (или
аффинно-равные). Парабола при А. п. переходит в любую другую параболу,
гипербола — в гиперболу. Поэтому все эллипсы составляют один аффинный тип
(класс) кривых второго порядка, параболы — другой аффинный тип и
гиперболы— третий тип кривых. При А. п. кривая одного аффинного типа не может
перейти в кривую другого аффинного типа.
А. п. часто используется как метод решения геометрических задач; при
этом данную фигуру аффинно преобразуют в более простую, где находят
указанное свойство, а затем выполняют обратное А. п. и находят искомое свойство
данной фигуры.
Так, например, задачу: построить касательную из данной точки Μ
к эллипсу, если он задан парой сопряженных диаметров,—можно решить,
если один из диаметров принять за ось родства и диаметр окружности,
родственной данному эллипсу. Тогда сопряженные диаметры эллипса перейдут в
перпендикулярные диаметры окружности; точка Μ перейдет в выбранном родстве
в некоторую точку М'. Построив касательную к окружности из М', строив
ей аффинно-соответственную прямую,, которая и будет искомой касательной
к эллипсу.
Лат. affinus — родственный, соответственный.
Лит.: И. Ф. Чет веру хин, Проективная геометрия, Учпедгиз, М., 1953;Б. Н.
Делоне и Д. А. Райков, Аналитическая геометрия, т. I, Гостехиздат, М., 1948.
АФФИНОР — термин линейной алгебры и векторного исчисления. А. есть
оператор (см.), посредством которого выражается линейное (аффинное)
преобразование (линейная однородная вектор-функция). При заданной системе
координат А. задается п2 числами Aji компонентами А. (/=1, 2, . . ., п)\ η —
размерность линейного пространства. Именно: вектору а (а1, я2, . . ., ап) А.
ставит в соответствие вектор b(bx, b2t . . ., bn)t определяемый формулой:
Ь'- Σ ^yV(/«l, 2, ..., я),
где координаты векторов а и b взяты относительно некоторого базиса линейного
пространства. А. является тензором (см.) второй валентности (см.) один раз
ковариантным (см.) и один раз контра вариантным (см.). При преобразовании
координат линейного пространства числа Alj изменяются по закону,
характерному именно для таких тензоров.

Б
БАЗИС векторного пространства (см.)—линейно независимая система
векторов, такая, что любой вектор, принадлежащий этому пространству, может быть
выражен в виде линейной комбинации векторов этой системы. Так. в
пространстве полиномов степени не выше η базисом будет, например, система 1, xt
х\ . . . , хп.
Если в векторном пространстве введено скалярное произведение (см.),
то можно говорить об ортогональном Б. Б. называется ортогональным, если все
векторы Б. попарно ортогональны. Если, кроме того, норма каждого из
векторов равна единице, то Б. называется ортонормированным.
Существуют пространства как с конечным, так и с бесконечным Б.
Примером первого является л-мерное евклидово пространство, примером второго
может служить пространство со счетным ортонормированным Б.:
(1, 0, 0, . .., О, ... ), (0, 1, 0, .... О, ... ), ...
Лит.: А. Г. Курош, Курс высшей алгебры, Физматгиз, М., 1962; А. Н.
Колмогоров и С. В. Фомин, Элементы теории функций и функционального анализа, изд.
МГУ, 1954.
БАРИЦЕНТРИЧЕСКИЕ КООРДИНАТЫ. Пусть в трех точках Alt А2, АЛ9
не лежащих на одной прямой, сосредоточены соответственно массы т1ъ тъ т3;
тогда в плоскости этих точек найдется единственная точка А — центр тяжести
этих точек, имеющая массу т, и такая, что будет выполняться равенство:
Ш ι -f- ftl 2 -f* Ttlz = /72.
И обратно, каждой точке А> лежащей в плоскости трех фиксированных
точек Alt A2i Az и имеющей массу т(тФ 0), соответствуют три определенные
массы mlt т2, тг% которые, будучи сосредоточены соответственно в точках Alt
А2у Л3, имеют своим центром тяжести материальную точку А с массой m=m1-f
+m2-\-mz. При этом массы mlt т2% tnz могут принимать как положительные,
так и отрицательные значения.
Числа ти т2, т3 можно поэтому рассматривать как координаты точки Л,
имеющей массу т. Эти числа mlt m2, mz называют Б. к. материальной
точки А.
Если массу т точки А изменить в k раз, то ее координаты mlt tn2, m3
изменятся также в k раз. Поэтому одна и та же геометрическая точка А может
иметь различные Б. к. Геометрическое положение точки А определяется
отношением чисел mlt m2t m3 к одному из них. Геометрически точка А с массой т,
имеющая Б. к. ти т2, т9, может быть расположена как внутри треугольника
AxA2AZt так и вне этого треугольника или на его контуре. Аналогично
определяются Б. к. точки в трехмерном и вообще в «-мерном пространстве.
Б. к. являются простейшим типом однородных координат (см.).
Б. к. были введены Мёбиусом. В настоящее время Б. к. имеют ограниченное
применение, ио представляют исторический интерес при объяснении
возникновения однородных координат и векторного исчисления.
Лит.: A. F. Мб b i u s, Der baryzentriesche Calcul, Lp. z, 1827; С. С. Бюшгенс,
Аналитическая геометрия, ч. I, Гостехиздат, Μ., 1946; Μ. Б. Б а л к, Геометрические
приложения понятия о центре тяжести, Физматгиз, М., 1959.

БЕЗУ ТЕОРЕМЫ ОБОБЩЕНИЕ
31
БЕЗУ ТЕОРЕМА — теорема об остатке от деления произвольного многочлена
на линейный двучлен. Она формулируется следующим образом: остаток от
деления произвольного многочлена f(x) на двучлен χ— а равен f(a). Б. т. названа
по имени впервые сформулировавшего и доказавшего ее французского
математика XVIII в. Безу.
Из Б. т. вытекают следующие весьма важные следствия: 1) если многочлен
f(x) делится (без остатка) на χ — α, то число а является корнем f(x)\ 2) если
число а является корнем многочлена /(*), то f(x) делится (без остатка) на
двучлен χ — а; 3) если многочлен f(x) имеет по крайней мере один корень (ср.
Основная теорема высшей алгебры), то этот многочлен имеет ровно столько
корней, какова степень этого многочлена (при этом учитывается кратность корней).
БЕЗУ ТЕОРЕМЫ ОБОБЩЕНИЕ. М. В. Яковкиным указана также весьма
проедая закономерность образования остатка от деления произвольного
многочлена на двучлен не только первой, но и любой степени. Она выражается
следующим образом: остаток от деления произвольного многочлена
/(*)=αο+αι*-τ-α2*2+ '" +<*пхп (*)
на двучлен хт — Ь равен:
*W-/eo(«+/oiW*+/oi(b)*f+ ··· +/о («-!)(*) я"1-1'
где n=mq+r (О < г < т —· 1) и
я
/о*(*>- Σ **/+**'(*-°- *' 2' ···· т~1)·
/ = о
В качестве следствия из этой формулы вытекают условия, необходимые
и достаточные для делимости (без остатка) произвольного многочлена на
двучлен хт — Ь любой степени. Для этого, очевидно, все коэффициенты остатка
R(x) должны быть равны нулю.
Следовательно, для делимости любого многочлена (*) на двучлен хт — Ь
необходимо и достаточно, чтобы число Ь было корнем одновременно следующих
т подмногочленов (или, что то же самое, корнем их общего наибольшего
делителя):
/оо(*)=Яо+ат+о*+а2т+о*2-Ь ··'
/oi(*)=ai+am+i*+a2m+i*2+ ···
fo2(x)=a2+am+2x+a2m+2x2+ ···
fo(m- \)(x)=am-i+am+m-1x+a2m+m-lx2+ ....
Как видно, коэффициенты всех этих т подмногочленов не требуют никаких
вычислений, а непосредственно выписываются из основного многочлена f(x)
по очень простому правилу: в каждый &-й подмногочлен /0л(*) из основного
многочлена выписываются все те и только те коэффициенты, индексы которых
сравнимы с k по модулю т, т. е. следуя от младших к старшим
коэффициентам, начиная от А;-го, выписывается каждый m-й коэффициент.
В случае двучлена общего вида bmxm--<b0, т. е. когда старший
коэффициент двучлена отличен от единицы, условие делимости f(x) на этот двучлен
запишется в следующем виде:
(А \ 9
-4=0 или 2 ami+kbqm~'b^0 (*-0. 1, 2, .. ., /п-1).
"ml I - О

32
БЕЗУСЛОВНОЕ НЕРАВЕНСТВО
Примеры: 1. Делится ли на двучлен х2 — 5 следующий многочлен:
f(x)=2x4-x5 — 7*4 — 5х3 —Нх2 — 5?
В данном случае т=2, поэтому выписываем два подмногочлена с
коэффициентами, выбранными (через два) из основного многочлена:
/оо(*) = -5 - Их - 1х2+2х\
/οι(*) = 0 —5*+*а.
Легко видеть, что /00(5)=—5 — 14-5 — 752-f25з = 5(—1—14—13-f50)=-0
и /01(5)=—5-5-f-52=0. Значит, f(x) делится на xz — 5.
2. Делится ли многочлен
f(x)=—15jc84- 15а:7 — ΙΟχβ — 25х~°+9х*+6х* — 4х2 — 10jc+6
на двучлен 5x4-f-2? Найти остаток от деления этого многочлена на х3+2.
В двучлене 5х4-Ь2 степень т=4, поэтому составляем 4 многочлена,
выбирая для них коэффициенты (через четыре) из основного многочлена f(x):
/оо (*)=6+9х— 15а;2= — 3 (5х+2) (х — 1),
/οι (*) =—Ю — 25а: ==— 5 (5а:+2),
/о2 (*)=— 4 - 10*=- 2 (5*+2),
/o8U) = +6+15x=3(5a:+2).
Затем, вычисляя значения этих многочленов или только их общего наиболь-
2
шего делителя D04(a:)=5a:-{-2 при jc=——-, убеждаемся, что:
5
/о»(-|)-/01(-|) = /о2(-|)=/о,(-{)=0
или
«-(-|)-в(-т)+2-0·
Значит, данный многочлен f{x) делится на 5л:4+2.
Найдем коэффициенты остатка от деления этого же многочлена на х8+2.
Здесь т=3, поэтому составляем три подмногочлена, выбирая для них
коэффициенты (через три) из основного многочлена /(#), а затем вычисляем значения
этих подмногочленов при х=—2:
/ooW=6+6a:-10a:2, /00 (-2) = 6+ 6 (-2)- 10(-2)2 = -46,
foi(x)=-10+9x+\5x2, /01 (—2)=— 10-Ь9(— 2)-Ы5 (— 2)2==32,
/о2(*) = —4-25*—15**, /«а (—2) = —4 — 25 (— 2) —15 (— 2)2=—14.
Следовательно, искомый остаток равен:
Я <*)-/оо ( -2)+/οι (-2) *+/о2 (-2) х2- 46+32а: - Ux2.
В этой же работе М. В. Яковкиным доказана теорема о кратности
двучленных делителей: степень кратности делителя хт— Ь многочлена (*) равен степени
кратности делителя χ—Ъ ОНД JX0m(x) подмногочленов многочлена (*).
Лит.: М. В. Яковкин, Свойства чисел, аналогичные теореме Безу. «Математика в
школе», 1952. М. 1.
БЕЗУСЛОВНОЕ НЕРАВЕНСТВО — то же, что и тождественное неравенство,
т. е. неравенство, справедливое при всех допустимых значениях букв,
входящих в это неравенство, или верное числовое неравенство.
Например, (2+ва)а>3 есть Б. н.; 3-fa2>2 есть Б. н.

БЕРНУЛЛИ ЧИСЛА
33
Термин Б. н. устарел и выходит из употребления. Понятие Б. н. было
введено в противоположность условным неравенствам, т. е. тем неравенствам,
которые справедливы не при всех допустимых значениях букв, входящих в них,
а только при некоторых допустимых значениях этих букв. Например, 2-f-a>3 —
условное неравенство, справедливое лишь при а>1. Термин «условное
неравенство» также выходит из употребления.
БЕРНУЛЛИ ЗАКОН — частный случай важнейшего предложения теории
вероятностей — больших ·чисел закона (см.), открытый Я. Бернулли. Согласно
Б. з. можно с вероятностью, близкой к достоверности, утверждать, что при
большом количестве испытаний относительная частота появления события весьма
близка к вероятности его появления в отдельном испытании. Более точно: пусть
проводится η независимых испытаний, в каждом из которых вероятность Ρ (А)
наступления события Л равна р; пусть k — число наступления события Л в η
испытаниях. Тогда, каково бы ни было ε>0, lim P(J3)=1, где Р(В) означает
η -*-оо
k
~ —PI
вероятность выполнения неравенства
<ε. Б. з. вытекает из неравенства
Ρ (В) > 1 — , позволяющего оценить вероятность Ρ (В).
Пример. При увеличении числа бросаний монеты вероятность того, что
отношение числа появления решетки к общему числу бросаний близко к половине,
стремится к единице.
БЕРНУЛЛИ ЧИСЛА — особые числа, обозначаемые Вп> введенные в
математический анализ Я. Бернулли, который пришел к ним при изучении сумм
степеней последовательных натуральных чисел с натуральными же показателями.
Б. ч. играют важную роль во многих вопросах анализа: они могут быть
записаны в виде:
оо
2(2я)1 УЧ 1
" (2 π)2" £Л тш'
т — 1
откуда видно, что числа Вп положительны и бесконечно возрастают (хотя
и не монотонно) при возрастании номера п. Приведем значения некоторых Вп:
1 о __!_ д _1 я _1 174611
*1_6' 2~30* *3~42' *4~30' Bl0= 330 ·
Б. ч. встречаются, например, в разложениях:
оо
_!__ LBnX%n-i.
п= 1
оо
(2л)!
sin* ^1 2*п(2*п—1)Вп x*n
~~~ (2л)! ' 2п ;
22п(22П—\)Вп х2п
In
χ лшш
η = 1
In cos χ =
оо
Σ.
(2п)\ 2п
число таких разложений в анализе очень велико.
° Толковый словарь математических терминов

34
БЕРТРАНА ПОСТУЛАТ
С помощью Б. ч. получаются выражения для многих несобственных
интегралов (см.), например:
°Г х2х—\ Ви
I rfx =
о е 1
Б. ч. входят во многие важные формулы анализа, например в формулу
Стерлинга (см.), Эйлера — Маклорена. Для Б. ч. составлены таблицы.
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
т. II, Физматгиз, М., 19 63.
БЕРТРАНА ПОСТУЛАТ — предложение, высказанное, но не доказанное
французским математиком Бертраном в связи с одной его теоремой в теории
групп "подстановок. Б. п. утверждал, что при η > 3 между числами η и 2л —2
существует простое число. (Часто формулируя Б. п. в более слабом виде,
говорят, что между числами η и 2п найдется простое число.) Б. п. был
доказан великим русским математиком П. Л. Чебышевым в 1852 г.
БЕСКОНЕЧНАЯ ДЕСЯТИЧНАЯ ДРОБЬ — одна из форм записи
действительного числа. Б. д. д. имеет вид:
а0, ад^з · · · ап · · ·, (*)
где Оо — целое неотрицательное число, а19 а2, . . . , ап> ... —одно из чисел
О, 1, 2, . . . , 9; при этом если в выражении (*) начиная с некоторого номера все
щ равны нулю или все а/ равны 9, то выражение (*) обычно не называют
Б. д. д. Б. д. д. можно представить в виде суммы ряда:
со
У Б. д. д. за каждым знаком (цифрой) следует еще какой-либо знак, и поэтому
эта дробь не имеет последнего знака в своей записи.
Б. д. д. бывают периодические (см. Периодическая дробь), когда начиная
с некоторого знака группа цифр (период Б. д. д.) периодически повторяется,
и непериодические, когда такой группы цифр, повторяющейся неограниченное
число раз, нет. Периодические Б. д. д. в свою очередь подразделяются на
чистые Б. д. д., когда период начинается сразу после целой части, после запятой,
и смешанные Б. д. д., у которых период начинается не сразу после запятой;
при этом группа цифр, стоящая у смешанной Б. д. д. между целой частью
и периодом, называется предпериодом. Период периодической Б. д. д. может
быть сколько угодно большим. Всякое рациональное число (см.) может быть
представлено в виде конечной десятичной дроби или Б. д. д.—чистой
периодической или смешанной периодической. Всякое иррациональное число (см.) есть
непериодическая Б. д. д.
Примеры: 1) 0,333. . . =0,(3) (читается: «нуль целых и три в периоде») —
3 1
чистая периодическая Б. д. д.; 0,(3)=--=-— — рациональное число; 2)0,3(2) —
9 о
смешанная периодическая Б. д. д.; число 3 — предпериод, число 2—период
этой дроби; 0,3(2)=———=— —рациональное число; 3) у^2= 1,4142
90 90
lg2=0,3010 ... —непериодические Б. д. д., т. е. иррациональные числа;

БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ
35
4) 0,999 . . . =0,(9) = — =1; 0,4000
=0,4(0)=
У\ 8
rSt!1"
а
О
А \
Хо X/ X
у\ к
δ
0
-I'kL
*0
^
Л
о
и
*0
(т
Рис. 20
= 0,4. Б. д. д. с периодами 0 и 9 обычно не
рассматривают, так как это обычные (конечные)
десятичные дроби.
БЕСКОНЕЧНАЯ ПРОИЗВОДНАЯ функции
Ду
у=/(*) — бесконечный предел: lim—= оо (или ± оо).
Δ* ·*0 Δ*
Касательная к графику функции в точках, [x0t f(x0)]
и fxi, /(*i)J, в которых функция имеет Б. п.,
перпендикулярна оси Ох (рис. 20, а).
БЕСКОНЕЧНО БОЛЬШАЯ величина — переменная
величина а, которая в процессе своего изменения
становится и при дальнейшем изменении остается по
абсолютной величине больше любого наперед
заданного числа М>0. Можно определить Б. б. как
такую переменную, обратная величина которой —
α
есть бесконечно малая величина (см.). Определение
Б. б. конкретизируется для различных случаев
процессов изменения; наиболее важными являются случаи
Б. б. последовательности и Б. б. функции при χ-* а,
или # -» -f-oo, — оо, оо. Во всех этих случаях Б. б.
определяется как величина, имеющая пределом оо
(бесконечность). Например, функция У=/(*)
называется Б. б. при χ -+- х0, если для любого числа Μ
существует такое δ > 0, что при \х — х0\ < δ и χ φ х0 выполняется неравенство
|/(*)|>Λί (рис. 20, бив). (См. Предел последовательности, Предел функции,
Предел функции нескольких переменных.)
Примеры. 1. Последовательность αΛ=(— 2)п Б. б., ибо |(— 2)п\>М при
η > A/ = [log2 Μ], здесь [χ] означает целую часть (см.) числа х. 2. Функция
y=jtsinjt при χ -*· оо не является Б. б., так как у обращается в нуль для
сколько угодно больших значений х.
БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ — предел последовательных произведе-
оо
ний, limP/I=lim«1«2 . . . ип= Π щ при η-+ оо.
k = ι
Если предел не существует, то и в этом случае (уже в обобщенном смысле)
говорят о Б. п., подразумевая под этим запись самой последовательности Рп.
Если все члены ип Б. п. отличны от 0 и последовательность Рп имеет
отличный от 0 предел Ρ Φ оо , то Б. п. называют сходящимся, а Р — его величиной
и пишут: Π Uk=Ρ; если же последовательность Рп сходится к пределу, равному 0.
k=\
или расходится, то Б. п. называют расходящимся.
Если положить un=\+vnt можно написать следующий достаточный признак
оо
сходимости Б. п.: сходится ряд 2 \vk\- Признак этот применим, разумеется,
k=\
в случае необращения в нуль ни одного из ип.
Примером Б. п. может служить разложение в Б. п. числа:
JL jL .1.1 JL UL Л.
4 = 3 3 5 5 7 7 '"
3*

36
БЕСКОНЕЧНО МАЛАЯ
Другое разложение для л вытекает из следующего Б. п.:
^ φ sin φ Л
*?ΛΥ*=Τ при φ=Τ·
Лит.: Г. М. Фих'тенгольц, Курс дифференциального и интегрального исчисления,
т. II, Физматгиз, М., 1963.
БЕСКОНЕЧНО МАЛАЯ величина — переменная величина а, которая в
процессе своего изменения становится и при дальнейшем изменении остается по
абсолютной величине меньше любого наперед заданного положительного числа ε > О,
т. е. для любого ε > 0 существует такое значение ае величины а, что для всех
значений а, следующих за ае выполняется неравенство | α | < ε. Можно
определить также Б. м. как переменную величину, имеющую предел, равный нулю.
Приведенное выше определение Б. м. конкретизируется и становится
математически точным для различных случаев задания процессов изменения основной
переменной, функцией которой является величина а. Наиболее важными являются
случаи: 1) Б. м. последовательности, 2) Б. м. функции a=/(jc) при х->а, или
при χ -* a-fO (справа), χ -> а — 0 (слева), или при χ -> -f- со, —со, со, 3) Б. м.
функция нескольких переменных а=/(Р) при Ρ -> Р0. Во всех этих случаях
определение Б. м. есть иное изложение определения понятия предела для
случая, когда предел равен нулю. Например, последовательность а19 а2, . .. , ап, ...
называется Б. м. последовательностью, если для любого ε > 0 существует
номер N такой, что при η > N выполняется неравенство | ап | < ε.
Используя понятие Б. м., можно определить понятие предела величины a
как такого постоянного числа Ь, от которого величина а отличается на Б. м.,
т. е. разность a — Ь является Б. м. Основные свойства Б. м.: 1) алгебраическая
сумма или произведение конечного числа Б. м. есть величина Б. м., 2)
произведение ограниченной величины на Б. м. есть Б. м., 3) величина, обратная Б. м.#
есть бесконечно большая величина (см.), 4) величина, обратная бесконечно
большой, есть Б. м.
^ sin χ
Примеры: 1) Функция у= при χ -»· + οο есть Б. м., так как
произведение ограниченной функции sin* на Б. м.— есть Б. м:, 2)
последовательность ап = —т- есть Б. м., так как \ап\ < ε при η > Ν=\ л/ ϊ-\ , [χ] озна-
η'
"VH
чает целую часть (см.) числа х\ в частности, |ал|=| — I <8Тол ПРИ
/2>Ν=14; 3) y=sin* — Б. м. функция при*-*0, ибо |sin*|<8 при |*—· 0|<δ,
где можно взять Ь—ε.
Для сравнения одних Б. м. с другими введено понятие порядка Б. м. Б. м. a
и β называются одного порядка, если существует конечный, не равный нулю
предел их отношения lim —. Это записывают: α = 0(β) или α=ββ, β=/4α, где
Ρ
α
А и В — ограниченные величины. В частности, когда lim=—-=1, тогда α и β
называются эквивалентными друг другу (это записывают: α « β).
Если lim -— = 0, то α называется Б. м. высшего порядка по отношению
к Б. м. β, а β называется Б. м. низшего порядка по отношению к Б. м. а.
Это записывают: α=ο(β) или α=βγ, где γ —Б. м.

БЕССЕЛЕВЫ ФУНКЦИИ
37
Если же lim — = ± оо, то, наоборот, α называется Б. м. низшего порядка
по отношению к Б. м. β, а β называется Б. м. высшего порядка по отношению
к Б. м. а. Это записывают: β=ο(α) или β=αγ, где γ —Б. м.
Если некоторая Б. м. α принята за основную, то Б. м. одного с ней
порядка называются Б. м. 1-го порядка. Б. м. одного порядка с а2 называются
Б. м. 2-го порядка; вообще, величина одного порядка с оРл где ρ постоянное,
называется Б. м. порядка р.
Примеры: 1) β=2δίη2α—1 есть Б. м. второго порядка по отношению к а,
osin2 а ι
так как lim = 1п2; 2) Б. м. ег-х дг-^-f-oo имеет высший порядок, чем
/1 \*г
I—I , где N — сколь угодно большое фиксированное число.
См. Предел последовательности, Предел функции, Порядок бесконечно малой.
БЕСКОНЕЧНО УДАЛЕННЫЕ элементы в геометрии — тоже, что и
несобственные элементы (см.).
БЕССЕЛЕВЫ ФУНКЦИИ — важный класс функций, являющихся решением
уравнения:
jc2/'+xy'+(*2--v2)y=(). (*)
Решение этого уравнения, имеющее вид:
ja*)-2^(-w_.i2:. ...» с·)
с=ъ k\T(k+v+\)
называется Б. ф. первого рода порядка v. Ряд в правой части формулы (* )
сходится при всех*. Если v=m-f — , где т целое, то Б. ф. сводится к
элементарной функции, например:
yi=l/-
2 γ ЛХ
SUl*.
Функции (**) и уравнение (*) называются бесселевыми. Б. ф. второго рода
называется функция:
J v(x)cosvn—J_v(x)
γ = . s
v sin πν
если ν — не целое число, и при η целом
y»W = Hmyv(x)-iy„(x)l„-!-
/i-l
-* —1)!
2 ,л-2* 1 7j ^2/ ГГ'(п+*+1) _
\Ί) ТЛЯ *!(»+*)! [ (n+k)
Г'(*+1)1

38
БЕТТИ ЧИСЛА
Если ν не целое число, то CXJ v 4-С2/^ есть общее решение уравнения (*).
В любом случае функции Z^(x)=C1J>) +C2Y^ исчерпывают все решения
уравнения (*).
Б. ф. детально изучены как в действительной, так и в комплексной области,
и существует большое число таблиц Б. ф. Термин Б. ф. эквивалентен термину
«цилиндрические функции».
Лит.: Г. Н. В а т с о н, Теория бесселевых функций, перев. с англ., ч. 1—2, ИЛ,
1949; Е. Янке и Ф. Эмде, Таблицы функций с формулами и кривыми, перев. с нем.,
Гостехиздат, М., 1948.
БЕТТИ ЧИСЛА — важные числовые характеристики топологических
пространств. Наиболее простое представление Ь. ч. дает κονбинаторная топология
(см.). Рассматривая топологическое пространство (см.) как комплекс (см.),
можно ввести группу цепей (конечной совокупности ориентировочных
симплексов) (см.), взятых с некоторыми (обычно целыми) коэффициентами.
В терминах этой группы и операции взятия границы (ориентированному
симплексу ставится в соответствие совокупность его определенным образом
ориентированных граней) строятся группы Бетти различных размерностей. Эти
группы коммутативны (см.). Количество бесконечных циклических групп, на
которые разлагается группа Бетти данной размерности, называется Б. ч. данной
размерности. Б. ч. — инвариант топологического пространства: два гомеоморф-
ных (см.) топологических пространства имеют одинаковые Б. ч.
БИВЕКТОР — кососимметрический тензор (см.) второй валентности, задает
двумерное направление в пространстве. В трехмерном евклидовом пространстве
всякий Б. эквивалентен вектору. Эквивалентность устанавливается векторным
произведением (см.).
БИКВАДРАТНОЕ УРАВНЕНИЕ — уравнение вида ax*+bx2+c=0, где α=£θ.
Б. у. является частным случаем трехчленного уравнения (см.) и решается
заменой х2 через у, а затем решением системы квадратных уравнений, ay2+by-j-
-f-c=0, х2=у, или же непосредственно по формуле решения Б. у.:
*Ь2»3
..-±j/-
Ъ±У Ъ2 — \ас
2а
максимум (минимум) лежит выше,
БИКВАДРАТНЫЙ ТРЕХЧЛЕН — многочлен вида ах*+Ьх2+с (при а Ф 0).
Б. т. имеет ось ординат осью симметрии, так как Б. т.— четная функция.
График Б. т. при а > 0 имеет вид, изображенный на рисунках 21 и 22.
Рис. 21 характеризуется тем, что Ь > 0; в зависимости от с>0, с=0, с<0
на или ниже оси абсцисс, а рис. 22
характеризуется условием того, что Ь<0\
положение экстремумов (максимума и двух
минимумов) графика относительно оси
абсцисс зависит от знаков чисел с и
4ас — Ь2 _
. Ьсли а<0, то графики Б. т.
4а
будут симметричны относительно оси
абсцисс с соответствующими графиками при
а> Q (рис. 21 и 22).
Подробное исследование Б. т. см.,
например, в книге С. И.
Новоселова «Специальный курс элементарной
алгебры» («Советская наука», М., 1958,
стр. 403—405).
Рис. 21
Рис. 22

БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ
39
БИКОМПАКТЫ ОСТЬ — термин топологии. Свойство Б. для широкого класса
топологических пространств (см.) тождественно компактности (см.)
топологического пространства. Б. топологического пространства означает, что из всякого
покрытия (см.) топологического пространства открытыми множествами можно
выбрать конечное покрытие. Термин Б. введен советским ученым академиком
П. С. Александровым.
БИКУБИЧЕСКОЕ УРАВНЕНИЕ— частный случай трехчленного уравнения
(см.) при п = 3.
БИЛИНЕЙНАЯ ФОРМА — фор*ма (см.) второй степени от двух групп пере-
п
менных хъ хъ . . . , хп и ylt у2 уп> имеющая вид: 2 aijXiyj· На-
/,/=1
пример:
а11Х1У1+а12х1у2+а1ъх1уъ+а21х2у1+а.22х2у2^а2^2Уъ+
+азЛУ1-Ьаз2*зУ2+азз*зУз.
Б. ф. является частным случаем квадратичной формы (см.). Так,
вышеприведенная Б. ф. является частным случаем квадратичной формы от шести
переменных xlt х2, х3> У ι* Уг» Уз с матрицей:
/° ° 0 α1ιαι2α13χ
I 0 0 0 а21 а22 а2з
JLJ ° ° ° α3ΐ α32 °зз
2 I аи а21 а31 О О О
I ^12 α22 α32 О О О
V Qi3 ^23 а3з 0 0 0 / *
БИЛЛИОН — число 109, т. е. миллиард — тысяча миллионов (у французов,
американцев и в прошлом у русских), или число 1012, т. е. тысяча
миллиардов— миллион миллионов (у немцев, англичан и других народов). В нашей
литературе термин Б. выходит из употребления.
Лит.: И. Я. Депман, История арифметики, Учпедгиз, М., 1959.
БИНОМ — то же, что двучлен (см.). Термин образовался от латинского
слова Ы ...—дву (х) и греческого слова nomos — область, часть, член (ср.
Ньютона бином).
БИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ — коэффициенты бинома Ньютона,
η
т. е. числа С* в формуле (a-\-b)n=^ Cknan-kbk при л=0, 1, 2, . . . Б. к.
Скп обозначаются часто символом I ? ). Одним из основных свойств Б. к.
являйся формула C*-f-C^l*=C*Jj, в силу которой Б. к. составляют треугольник
Паскаля (см.). Б. к. С* выражают число сочетаний (см.) из η элементов по k
в комбинаторике. Б. к. удовлетворяют ряду соотношений, например:
η
(п
-к
-1)
1
η
Σ
*=0
2 .
(я-
. k
2Λ,
-k+\)
η
*=0
η\
k\ (η —
1)*C* = 0
k)\
и
~~ >
т.
д

40
БИНОМИАЛЬНЫЙ РЯД
БИНОМИАЛЬНЫЙ РЯД — разложение степени (1 + х)* бинома в
степенной ряд при произвольном действительном показателе а. Если а является целым
неотрицательным числом, то Б. р. становится биномом Ньютона (см.). Впервые
возможность распространения формулы бинома Ньютона на случай Б. р. была
указана Ньютоном в 1676 г., хотя строго обоснована много позже Абелем,
в 1826 г.
Пример. Б. р. (1-Ьа:)-1 = 1 — JC-f-JC2-b ··· +(— \)пхп+ ··· сходится при
1*1 < 1·
БИНОРМАЛЬ пространственной кривой / в точке ее Μ — прямая,
перпендикулярная к соприкасающейся плоскости (см.) кривой в той же точке М.
Подвижной триэдр (см.) с вершиной в точке Μ (рис. 23), играющий
большую роль в изучении свойств пространственной кривой /, имеет один из трех
его единичных векторов 6, η и t, направленный по Б. (это вектор Ь); вектор η
направлен по главной нормали и вектор t — по касательной к кривой / в точке М.
Рис. 23 Рис, 24
БИПОЛЯРНАЯ СИСТЕМА координат на плоскости — система координат
(см.), в которой выбираются две фиксированные точки Ог и 02 (рис. 24) за
полюсы (начальные точки) и единица масштаба, а координатными линиями служат
два семейства концентрических окружностей 01(г1) н 02(г2). Пересечение этих
окружностей дает две точки Мг и Λί2; в случае касания в точке Μ окружностей
точка Μ будет лежать на линии полюсов Ох02. Положение точки МХ(М2)
определяется на плоскости расстояниями гх и г2 этой точки от полюсов Ох и 02.
Б. с. координат используется редко.
БИПОЛЯРНЫЕ КООРДИНАТЫ точки Μ на плоскости — два числа
(расстояния гх и Го от точки Μ до двух фиксированных точек Ог и 02), определяющие
положение точки Μ на плоскости в биполярной системе координат (см.). При
этом Б. к. точки гх и г2, вообще говоря, определяют две геометрические точки
на плоскости Мг и М2 (рис. 24). Если г1-{-г2 = 0102 или | τλ — г21 = Ох02, то
точки Мг и М2 совпадают в одну точку Λί, которая будет расположена на
прямой Ог02. Б. к. используются для вывода уравнений кривых» имеющих ось
симметрии Ог02. Уравнение эллипса (см.) в Б. к. имеет вид: rl-fr2 = 2a (a — большая
полуось эллипса); уравнение гиперболы в Б. к. имеет вид: \гг — г2|=2а, где
а— действительная ось ее. Б. к. — частный случай криволинейных координат (см.).
БИССЕКТОР — то же, что и биссектриса (см.) угла или биссектриса
треугольника. Б. называется также прибор (инструмент), делящий угол пополам.
Ср. с трисектором (см. Трисекция угла).
БИССЕКТРАЛЬНАЯ ПЛОСКОСТЬ двугранного угла — полуплоскость,
ограниченная ребром двугранного угла и делящая этот угол пополам. Б. п. есть
пространственный аналог биссектрисы (см.) плоского угла. Под Б. п. часто
понимают и плоскость, проходящую через ребро двугранного угла и делящую его
пополам.

БОЛЬШИХ ЧИСЕЛ ЗАКОН
41
БИССЕКТРИСА УГЛА — полупрямая (луч), исходящая из вершины угла
и делящая его пополам. Б. у. есть его ось симметрии. Б. у. есть геометрическое
место точек, расположенных внутри угла и равноудаленных от его сторон.
БИССЕКТРИСА ТРЕУГОЛЬНИКА— отрезок биссектрисы внутреннего угла
треугольника, одним из концов которого является вершина этого угла, а
другим— точка пересечения биссектрисы угла со стороной треугольника. Б. т.
пересекаются в одной точке — центре вписанной в треугольник окружности
(вписанного круга). Точка пересечения Б. т.—одна из четырех замечательных точек
треугольника (см.).
Во всяком разностороннем треугольнике Б. т. заключена между высотой и
медианой, выходящими из той же вершины. В равнобедренном треугольнике Б. т.,
заключенная между равными сторонами, является одновременно высотой,
медианой и осью симметрии треугольника.
Во всяком треугольнике биссектриса его внутреннего угла делит
противоположную сторону на части, пропорциональные прилежащим сторонам.
Справедливо и обратное предложение. Биссектриса внешнего угла разностороннего
треугольника пересекает продолжение противоположной стороны треугольника
в точке, отстоящей от концов этой стороны на расстояниях, пропорциональных
прилежащим сторонам треугольника. Справедливо и обратное предложение.
Четыре точки (Л, В, /С, L), две из которых Л, В—вершины треугольника,
а две другие К и L — основания биссектрис, проведенных из третьей вершины С
треугольника ABC, образуют гармоническую четверку точек (см.).
Биссектрисы внутреннего и внешнего углов треугольника, исходящие из одной
вершины, взаимно перпендикулярны.
Биссектрису иногда называют биссектором. Под биссектрисой < понимают
(например, в аналитической геометрии) и прямую, проходящую через вершину
угла и делящую его пополам.
Аналогично определяется биссектриса и сферического треугольника.
Биссектрисой сферического треугольника называют как большой круг, делящий
пополам угол сферического треугольника, так и дугу этого большого круга от
вершины до точки пересечения большого круга с противоположной стороной
треугольника.
БЛИЗНЕЦЫ-пары. Пара простых чисел ρ и q называется Б.-п., если
\р — σ|=2. До сих пор не решена так называемая проблема близнецов о том,
конечно ли множество Б.-п. или бесконечно. Наряду с небольшими Б.-п., такими,
как 3 и 5, 5 и 7, 11 и 13 и т. д.^ известны Б.-п. довольно большие,
например: 10 016 957 и 10 016 959.
См. Четверки-близнецы.
БОЛЬШАЯ ОСЬ ЭЛЛИПСА —ось симметрии эллипса, на которой лежат его
фокусы. Другими словами, Б. о. э. называется max (2α, 2b) в каноническом
уравнении эллипса в декартовой системе координат:
-4-^ = 1
а2 + 62 '
См. также Эллипс.
БОЛЬШИХ ЧИСЕЛ ЗАКОН—теорема, утверждающая, что при η -> со
Ει+Ει+··-+Εη
стремится к нулю вероятность того, что среднее арифметическое
случайных величин (см.) glf ξ2» · · · » ζη отличается от среднего арифметического
Α4ξι + Μξ2-}- ··· +Μξη
—Ξ их математических ожидании (см.) (М — знак
математического ожидания) более чем на ε (ε — любое положительное число).
Различные формы этой теоремы установлены Я. Бернулли, Пуассоном, П. Л. Чебыше-

42
БОЛЬШОЙ КРУГ
вым, А. А. Марковым и другими математиками. П. Л. Чебышев доказал Б. ч. з.
в следующих предположениях: случайные величины ξ1? ξ2 ζ,η попарно
независимы и их дисперсии (см.) D |1# £>ξ2» · · · » & ίη ограничены: D£/<c<oo,
где /=1, 2, . . ., п.
В наше время важные результаты об условиях справедливости Б. ч. з.
получены С. Н. Бернштейном. А. Н. Колмогорову принадлежит уточнение
формулировки Б. ч. з., носящее название усиленного закона больших чисел.
БОЛЬШОЙ КРУГ сферы (шара) — окружность, полученная от пересечения
сферы с плоскостью, проходящей через центр сферы. Радиус Б. к. с. равен
радиусу сферы, на которой он расположен.
Через две любые точки сферы, не являющиеся концами ее диаметра,
проходит только один Б. к. с. Два любых Б. к. с. пересекаются в двух
диаметрально противоположных точках сферы.
БОКОВАЯ ПОВЕРХНОСТЬ. 1°. Б. п. призмы — поверхность призмы (см.),
заключенная между двумя ее параллельными гранями, принятыми за основания,
или поверхность, состоящая из всех боковых граней призмы.
2°. Б. п. пирамиды — поверхность, состоящая из всех боковых граней этой
пирамиды (см.).
3°. Б. п. усеченной пирамиды — поверхность, состоящая из всех боковых
граней ее.
4°. Б. п. конуса — поверхность, заключенная между вершиной и
основанием конуса (см.).
5°. Б. п. усеченного конуса — поверхность, заключенная между его верхним
и нижним основаниями. Аналогично Б. п. усеченного конуса определяется и
Б. п. шарового слоя (см.), Б. п. цилиндра; аналогично Б. п. конуса
определяется Б. п. шарового сегмента (см.).
БРАХИСТОХРОНА — кривая наикратчайшего спуска. Если две точки Л и В,
не лежащие на одной вертикали и на одном уровне, соединить семейством
всевозможных кривых линий, то тяжелая материальная точка, двигаясь под действием
силы тяжести от вышележащей точки А к
нижележащей В (рис. 25), затратит наименьшее время, следуя
по брахистохроне.
Б. была открыта И. Бернулли в 1696 г., что
послужило толчком к развитию вариационного исчисления
(см.). По форме Б. полностью совпадает с циклоидой
(см.). — от греч. βραχιστσζ — кратчайший и Χρονοζ —
время.
БРИАНШОНА ТЕОРЕМА. Во всяком шестисторон-
нике, описанном около кривой второго порядка, пря-
Рис. 25 мые, соединяющие противоположные вершины,
пересекаются в одной точке — точке Брианшона. Б. т.
является одной из важнейших теорем проективной геометрии (см.). Б. т.
двойственна (см. Двойственности принцип) теореме Паскаля. Б. т. позволяет построить
какую-либо прямую пучка прямых второго порядка (касательных к кривой
второго порядка), если даны пять прямых этого пучка, и решить другие
конструктивные задачи проективной геометрии (с помощью односторонней линейки).
БРИГГОВЫ ЛОГАРИФМЫ — логарифмы (см.) по основанию 10. Названы
по имени Бригса.
БУНЯКОВСКОГО ГИПОТЕЗА. В прошлом веке выдающийся русский
математик В. Я. Буняковский выразил следующее предположение (гипотезу):
Для того чтобы значения целочисленного неприводимого многочлена
f(x) = a0xn-ba1xn^+ ··· +ап(а0>0)
равнялись простым числам при бесконечном множестве различных натуральных
значений аргумента х, достаточно, чтобы не существовало натуральное число,

БЭРА КЛАССЫ
43
отличное от единицы, которое было бы делителем чисел f(k) при каждом целом
значении k.
Недавно ученик В. Серпинского — польский математик А. Шинцель высказал
следующую более общую гипотезу: если //(*)(/=1, 2, . . . , s) — целочисленные
неприводимые многочлены с положительными старшими коэффициентами и если
не существует целое число, большее единицы, которое было бы делителем
произведения fx (k) /2 (k) ... fs (k) при всех целых значениях k, то существует
бесконечное множество натуральных чисел т, для которых каждое из чисел fi(m),
f2(tn) fs(m) является простым.
Гипотеза Шинцеля легко следует из Б. г., однако она имеет более
громоздкую формулировку, чем Б. г.
Утверждение Б. г. в сущности является обобщением утверждения известной
теоремы Дирихле о бесконечности простых чисел в арифметических прогрессиях:
теорема Дирихле, относящаяся к значениям неприводимых целочисленных
многочленов только первой степени, в Б. г. распространяется на целочисленные
неприводимые многочлены любой степени.
Из справедливости Б. г. сразу бы следовали решения многих, до сих пор
не решенных проблем. Например, существование бесконечного множества
простых чисел вида п2+\ или вида ла-Ь/*-Ь41 ПРИ натуральных значениях п.
Из более общей гипотезы Шинцеля также вытекали бы многие, до сих пор
не доказанные теоремы о простых числах. Например, существование
бесконечного множества простых чисел каждого из следующих видов:
х*п 4-1, Jt2*-f-3, д»я 4-7, х*п 4-9 (/г— натуральное).
Лит.: В. Серпинский, Что мы знаем и чего не знаем о простых числах, пер. с
польского, Физматгиз, М., 1963.
БУНЯКОВСКОГО НЕРАВЕНСТВО — одно из важнейших неравенств
математического анализа. Б. н. является интегральным аналогом Коши неравенства (см.)
для конечных сумм. Б. н. — частный случай найденного позже Гёльдера
неравенства (см.) — часто ошибочно связывают с именем Шварца, которым это
неравенство было использовано в работах лишь в 1884 г., тогда как В. Я. Буняков-
ским оно было опубликовано в 1859 г.
БЭРА КЛАССЫ — множество функций заданных на отрезке [а, Ь] и
определяемых индуктивно. Нулевой Б. к. состоит из непрерывных на [а, Ь] функций.
Пусть определены Б. к. с индексами 0, 1, 2, . . . , т— I: #0, Нг Hm—i·
Тогда Нт — множество функций /(*), не входящих ни в один из классов Ни
/=0, 1, 2, . . . , т — 1 и представимых в виде:
f(x)=\\mfn(x)t
п-*оо
где все fn(x) принадлежат Ят__1.
Рассматривают Б. к. #Xf где λ — трансфинитное число (см.) второго класса.
Последние определяются с помощью трансфинитной индукции (см.): если же все Н,
при β < α (α, β — трансфинитные числа) определены, то Яа состоит из всех
функций, не входящих ни в один из //β и представимых в виде:
/(*)-Ит/„(*).
п-»оо
где fn (χ) принадлежит #^ , βΛ < α.
Все функции, входящие в Б. к., измеримы, их множество имеет мощность
континуума; Б. к. не пусты.
Б. к. впервые рассматривались Р. Бэром.
Лит.: М. П. Натансон, Теория функций вещественного переменного, Гостехиэдат,
М., 1957.

4
ВАЛЛИСА ФОРМУЛА выражает число -- в виде бесконечного
произведи
дения (см.):
я *=2 H*f2) '
В. φ. была им получена в связи с задачей о квадратуре круга и явилась одним
из первых примеров рассмотрения бесконечных произведений. В. ф. может
служить для приближенного вычисления л. В. ф. в современных курсах
математического анализа находит ряд применений, например при выводе Стерлинга
формулы (см.).
ВАНДЕРМОНДА ОПРЕДЕЛИТЕЛЬ — определитель вида:
1
я2
1
1
-1 пп — \
tide, а.
т. е.
определитель, в котором элементы ι-й строки являются (ι — 1)-ми степе-
нями элементов 2-й строки. В
(cii — aj), где 1 < / < ι < η, τ
о. равен произведению всевозможных разностей
\ е. равен Π (α,- — aj). Например:
1 ^J<l^n
1 1
1
2 5 7
4 25 49
= (7 — 5) (7 — 2) (5 — 2)=2·5·3=30.
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ — раздел математики, изучающий
экстремумы функционалов (см.). Простейшей задачей В. и. является задача на-
ь
хождения экстремума функционала L (y) = ^F (χ, у, у') dx, где у (х) — неиз-
а
вестная функция. Аналогично тому, как при нахождении экстремума функции fix)
находятся корни уравнения /' (*)=0f при решении задач В. и. приравнивается
нулю вариация функционала 6L. Уравнение 6L=0 называется уравнением
Эйлера (см.). К задачам о нахождении экстремума функционала приводят многие
задачи практики: изопериметрическая задача, задача о геодезической линии и др.
Толчком к развитию В. и. послужила задача о брахистохроне (см.): по какой
кривой должно двигаться тело под действием силы тяжести и реакции опоры,
чтобы в минимальный срок из точки А попасть в точку В? Эта задача была
решена И. Бернулли. Общие методы В. и. были разработаны Л. Эйлером и

ВЕКТОР
45
Ж. Лагранжем. Большой вклад в теорию В. и. внесли советские математики
Н. Н. Боголюбов, Н. М. Крылов, М. А. Лаврентьев, Л. А. Люстерник и др.
Лит.: М. А. Лаврентьев и Л. А. Люстерник, Курс вариационного
исчисления, Гостехиздат, М., 1950; Г. А. Б лис с, Лекции по вариационному исчислению, ИЛ,
М., 1950.
ВАРИНГА ПРОБЛЕМА — задача в теории чисел, состоящая в
доказательстве того, что для любого натурального числа η > 2 существует такое число г,
зависящее от п, что всякое натуральное число N может быть представлено в
виде суммы г чисел, каждое из которых есть я-я степень некоторого целого числа,
г
т. е. Ν= 2 α?· β- π. была поставлена Варингом в 1770 г. Однако первое полное
г=1
решение В. п. было найдено лишь в 1909 г. Гильбертом (ранее были получены
частные решения В. п., например, для η = 2 Лагранж доказал, что г=4). В
дальнейшем развитии теории чисел были получены новые доказательства В. п.
В частности, в 1942 г. Ю. В. Линник нашел элементарное решение В. п. в том
смысле, что его доказательство не требует привлечения методов высшей
математики.
Лит.: А. Я. Хинчин, Три жемчужины теории чисел, Гостехиздат, Μ., 1948;
А. О. Гельфонд и Ю. В. Линник, Элементарные методы в аналитической теории
чисел, Физматгиз, М., 1962.
ВВЕДЕНИЕ МНОЖИТЕЛЯ под знак корня — преобразование в области
действительных чисел иррационального выражения вида Αν В (А > 0) к виду
V АпВ, т. е. всякий положительный множитель перед корнем (радикалом) можно
ввести под корень, возводя этот множитель в степень с показателем, равным
показателю корня:
aVW=V~A*B (A>0).
Если Л<0, то операция В. м. п. з. к. в случае, когда показатель корня η —
четное число, выполняется так: А у В=— / АпВ\ например: —2 /з =—/ 64-3.
В. м. п. з. к. используется иногда при вычислениях.
ВЕКОВОЕ УРАВНЕНИЕ —см. Характеристическое уравнение.
ВЕКТОР — направленный отрезок прямой, или отрезок, один из концов
которого называется началом В., а другой — его концом.
К понятию В. приводят различные задачи физики, механики и математики,
где изучаются величины, характеризуемые не только числом, но и направлением;
например, сила, скорость — это векторные величины.
В. обозначается буквами жирного шрифта или светлого шрифта со стрелкой
сверху; например В., начало которого в точке А, а конец — в точке В, обозначается
так: АВ. Длиной или модулем вектора АВ называется длина отрезка А В.
Над В. можно производить действие сложения, действие умножения В. на
число (см. Векторное исчисление).
В., начало и конец которого совпадают, называется нуль-вектором. Модуль
нуль-вектора равен нулю. Нуль-вектору не приписывается никакое направление.
В., модуль которого равен единице, называется единичным В. (своего
направления) или ортом. Два В. считаются тождественными, если один из них может
быть получен из другого параллельным переносом. Такое определение
тождественности двух В. характеризует так называемый свободный В. В физике и механике
применяются еще скользящий В. (см.) и связанный В. (см.).
Всякий В. на плоскости или в пространстве может быть изображен
направленным отрезком, отложенным от начала координат. Каждый же В. с началом

46
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
в точке О (О, 0) на плоскости определяется положением его конца, т. е.
определяется парой действительных чисел — координат его конца. Следовательно, под В.
плоскости можно понимать упорядоченную пару действительных чисел (х, у).
Аналогично можно определить В. и в «-мерном пространстве: В. я-мерного
пространства есть упорядоченная совокупность η действительных чисел (х19 х2, . . ., хп).
Слово «вектор» происходит от латинского vector — переноситель.
См. также Векторное пространство.
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ —математическая дисциплина, изучающая
различные операции над векторами (см. Вектор). Иногда В. и. подразделяют на
векторную алгебру и векторный анализ. В векторной алгебре рассматриваются
такие операции над векторами, как сложение и вычитание векторов, произведение
вектора на число (на скаляр) (см. Коллинеарные векторы, Компланарные векторы)
и произведение вектора на вектор (см. Скалярное произведение, Векторное
произведение и Смешанное произведение).
В векторном анализе изучаются вектор-функции (см. Вектор-функция), или
векторные функции точки. Основными понятиями векторного анализа являются
градиент (см.), дивергенция (см.), ротор (см.) и др. (см. также Поле векторное).
Суммой a-f-b-f-c-f- ··· 4-1 векторов а, Ь, с, . . ., 1 называется такой
вектор х, который строится следующим образом: из произвольной точки О
пространства откладывают вектор а, из конца а откла-
^ r дывают вектор Ь, из конца b откладывают
rv J?] вектор с и т. д. и, наконец, из конца предпослед-
Ъ^/ него вектора откладывают последний вектор —
__Wj слагаемое I. Тогда вектор с началом в точке О
а и концом в конце вектора 1 будет суммой дан-
β ных векторов, или их вектор-суммой (правило
замыкающей стороны многоугольника). В случае
Рис. 26 двух векторов сумма a-f-b (рис. 26, а) — вектор
ОВ — строится или как замыкающая сторона
треугольника ОЛВ или как диагональ ОС параллелограмма, построенного
на векторах а и b (ОА и АВ), исходящих из общего начала О. Разность
а — ь двух векторов определяется другой диагональю ВА (рис. 26, б)
параллелограмма: ВА=а — Ь, т. е. разность а — b двух векторов определяется как
вектор, идущий от конца вычитаемого вектора b к концу уменьшаемого
вектора а. Сложение векторов подчиняется ассоциативному и коммутативному
законам.
Произведением λ а числа λ на вектор а называется вектор, коллинеарный
вектору а, длина которого равна |λ| |а| и который одинаково направлен с
вектором а, если λ>0, и противоположно направлен с ним, если λ<0.
Лит.: Η. Ε. К о ч и н, Векторное исчисление и начало тензорного исчисления, Изд.- во АН
СССР, Μ., 196Γ, И. А. Гольдфайн, Элементы векторного исчисления, Гостехиздат,
М., 1948; Я. С. Дубнов, Основы векторного исчисления, Гостехиздат, М., 1950,
П. С. Моденов, Сборник задач по векторному анализу, изд. МГУ, 1963; М. Л а г а л л к.
Векторное исчисление, ОНТИ, М.. 1936.
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ двух векторов а и b трехмерного евклидова
пространства есть третий вектор с, удовлетворяющий следующим условиям:
1) длина вектора с равна произведению длин перемножаемых векторов на синус
угла α между ними: |с| = |а| |b| sin α; другими словами, длина вектора с
численно равна площади параллелограмма, построенного на векторах а и Ь; 2) вектор с
перпендикулярен плоскости, в которой лежат векторы а, Ь; 3) вектор с
выбирается так, что три вектора а, Ь, с составляют правую тройку (правую
ориентацию, правый репер), т. е. если три вектора а, Ь, с, приведенные к общему
началу, располагаются соответственно как большой, указательный и средний
пальцы правой руки, то большой и указательный пальцы находятся в плоскости
ладони, а средний отклонен в сторону ладони и перпендикулярен к ней.
Следует отметить, что В. п. определяется лишь для трехмерного пространства.
Α * β
0^ О

ВЕКТОРНОЕ ПРОСТРАНСТВО
47
В. п. обозначается так: [а, Ь], или axb.
Свойства В. п.: 1) В. п. равно нулю, если векторыколлинеарны; 2) fa, b]==
=—[b, а], т. е. В. п. антикоммутативно; 3) [λ a, b]=X[a, b] и [a, Xb]=X[a, bj,
т. е. числовой множитель, стоящий при одном из сомножителей В. п., можно
выносить за знак В. п.; 4) В. п. обладает распределительным свойством:
[а, b-f-c] = [a, ЬЖа, с].
Если векторы а и b заданы своими декартовыми прямоугольными
координатами: a{xlt ylt zL)t Ь{лг2, у2, z2\> то их В. п. записывается в виде определителя:
[а, Ь] =
i j k
Χι Уг Ч
Η Уч *г
где ι, j, к — единичные векторы (орты) правой прямоугольной декартовой
системы координат (т. е. орты составляют правую тройку).
В. п. широко используется в аналитической геометрии (при вычислении
площади треугольника, при выводе уравнения плоскости, проходящей через три
точки, и т. д.). В. п. иначе называется внешним произведением двух векторов.
ВЕКТОРНОЕ ПРОСТРАНСТВО — понятие, обобщающее обычное (трехмерное)
пространство.
В. п. определяется так. Рассматривается множество R элементов любой
природы, называемых векторами, в котором установлены правила: 1) любым двум
элементам х, у из R соответствует определенный 3-й элемент х-Ьу из R,
называемый суммой элементов х, у; 2) каждому элементу χ из R и каждому
действительному числу λ отвечает определенный элемент из R, называемый произведением
λ на χ и обозначаемый λχ.
Назовем это множество В. п., если: 1) х-Ьу=у-|-х, 2) (x-fy)-hz=x-Hy4-z),
3) каковы бы ни были χ и у, существует вектор ζ такой, что x-f z=y, 4) λ(μχ)=(λ μ)χ.
5) (λ+μ)χ=λχ+μχ, 6) X(x-f-y) = Xx-^y, 7) 1·χ=χ.
Если существует система элементов из R еь е2, ..., еЛ такая, что любой
вектор χ из R представляется, и притом единственным образом, в виде х^Х^-Ь
+^ае3т- ··· 4-λ„βη, где λ1% λ2, . . . , λη —- действительные числа, то множество
элементов, удовлетворяющее этим свойствам, называется /2-мерным В. п., а
система elt е3, . . . , еЛ —его базисом (см.). При этом векторО-ех-ЬО-едН Ь0-еЛ
называется нулевым. Простым примером В. п. является множество всех
направленных отрезков или векторов в обычном трехмерном пространстве, с
определенными обычным образом операциями сложения, вычитания и умножения на число
(см. Векторное исчисление).
Другим примером В. п. может служить множество всех многочленов степени
не выше п. Не меняя сути аксиом (1—7), можно считать λ, μ, Xlt λ2, . . . , ϊη
элементами произвольного поля (см.), например поля комплексных чисел. В этом
случае говорят о комплексном /2-мерном В. п.
Нетрудно заметить, что указанные свойства В. п. являются обобщением
свойств обычного трехмерного В. п., но не всех таких свойств. Дальнейшим
обобщением таких понятий, как длина вектора, скалярное произведение двух
векторов (см. Векторное исчисление), можно прийти к понятию евклидова
/2-мерного пространства (см.). Все эти понятия и операции могут быть обобщены
и на бесконечномерный случай.
См. также Гильбертово пространство, Метрическое пространство.
Лит.: А. Г. Курош, Курс высшей алгебры, Физматгиз, М., 1962; А. И.
Мальцев, Основы линейной алгебры, Гостехнздат, М., 1956.

48
ВЕКТОР-ФУНКЦИЯ
ВЕКТОР-ФУНКЦИЯ скалярного аргумента — функция (см.), у которой
зависимая переменная г является вектором, а аргумент / принимает значения из
области действительных (иногда комплексных) чисел: r=i(/). Задание В.-ф. f(/)
равносильно заданию трех функций x=f1(t)1 у=/2(0» г=/з(0» выражающих
координаты вектора г=х\-\-yj-f-zk (i, j, k — орты системы координат). Если г —
радиус-вектор, то В.-ф. изображает кривую, описываемую его концом.
Дифференцирование (аналогично интегрирование) В.-ф. сводится к обычному диффе-
dx , ,
ренцированию: "7=/1(0>-}-/2(03+/з(0к· В.-ф. нескольких переменных
определяется аналогично.
См. также Векторное поле.
Пример. В.-ф. r=acos/i-f-a sin tj+btk задает винтовую линию (см.).
ВЕРНЬЕР — приспособление с прямолинейной или круговой шкалой,
предназначенное для измерения соответственно шкалам длин отрезков или величин углов.
В. встречаются в ряде измерительных приборов: в планиметре, астролябии и др.
В., служащий для измерения длин отрезков, называется нониусом (см.).
ВЕРОЯТНОЕ ОТКЛОНЕНИЕ — мера рассеяния случайных величин (см.).
Если Л есть математическое ожидание случайной величины ξ, то В. о. £» — число
такое, что вероятность отклонений ξ от Л, больших по абсолютной величине, чем
£^ равна вероятности отклонений, по абсолютной величине (см.) меньшей,
чем£^ . Если, в частности, ζ имеет нормальное распределение, то £ξ =0,67456 σ,
где σ — дисперсия распределения ξ.
ВЕРОЯТНОСТЬ — числовая характеристика возможности появления некоторого
определенного события в цепи событий, могущих повторяться неограниченное
число раз. В некоторых случаях численное значение В. получается как отношение
числа возможных случаев, благоприятствующих данному событию, к числу всех
равновозможных случаев вообще. Нельзя смешивать В. с частотой появления
данного события, которая, как правило, лишь мало отличается от В. появления
этого события. Строгое определение В. было дано в 30-х годах нашего столетия
A. Н. Колмогоровым и связано с теорией меры.
Лит.: А. Н. Колмогоров, Основные понятия теории вероятностей, ОНТИ, Μ., 1936.
ВЕРТИКАЛЬ — прямая, параллельная вертикальной плоскости проекции, но
не перпендикулярная горизонтальной плоскости проекций при рассмотрении
проекций этой прямой на две взаимно перпендикулярные плоскости (плоскости
проекций). В. — устаревший термин, употреблявшийся в начертательной геометрии.
B. теперь называется фронталью (см.).
ВЕРТИКАЛЬНЫЕ УГЛЫ — то же, что и противоположные углы (см.).
ВЕРХНИЙ ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ чисел alt a2, .... ая, ... —
самая правая из предельных точек (см.) этой последовательности, если
последовательность ограничена сверху; обозначается В. п. символом lim an. Если после-
п -»- оо
довательность не ограничена сверху, то полагают lim ап= + ос, если последо-
П -VOO
вательность ограничена сверху и не имеет предельных точек (это возможно лишь
в случае lim ап=—°о), то полагают lim ап =—оо. В случае существования
η -*■ оо η -> оо
конечного или бесконечного предела последовательности В. п. совпадает с этим
пределом. Если В. п. конечен, то его можно характеризовать следующим образом:
число / будет В. п. последовательности, если в любой окрестности / найдется
бесконечное множество членов последовательности и если при любом ε > 0 имеется
лишь конечное число членов последовательности, больших, чем /-fe.

ВЕТВЛЕНИЯ ТОЧКА
49
Примеры: 1) для последовательности
1 1
1.-.2, -,3, .... „
3 4
2) 2, -1, -. -2, -, -3
3) ιΤπϊ -
η -> оо
ВЕРХНИЙ ПРЕДЕЛ ФУНКЦИИ y=f(x) в точке а —наибольший (конечный
или бесконечный) из частичных пределов функции в точке а\ обозначается
символом lim /(#). Это определение сохраняет силу и в тех случаях, когда точка а
χ -*> а
заменяется на символы + оо, —оо, а также когда χ стремится к а справа или
слева (односторонний В. п. ф.).
Примеры: 1) fim 2 sin —=2; 2) Пт
г,^й-
• · · »
/г2
•
η
—оо.
, Пт ап =
η -~ оо
— /2, . .
= + <»;
. lim
η ->ос
:-1 (JC — 1 )2
3) lim xcos Jt = + оо; 4) lim — = -f-oo, но lim —= — со.
χ -+ + оо *-ю+о х х -* ° ~ ° х
ВЕРХНЯЯ ГРАНЬ МНОЖЕСТВА Ε действительных чисел — наименьшее из
чисел, ограничивающих данное множество сверху, т. е. число М,
удовлетворяющее следующим условиям: 1) любое χ из множества Ε удовлетворяет неравенству
х<М\ 2) для любого ε>0 существует в множестве Ε такой элемент χ', что
χ' >Μ — ε. В. г. м. обозначается символом sup£'=Ai. У всякого ограниченного
сверху множества существует В. г. м. Если В. г. м. не принадлежит этому
множеству, то она обязательно является предельной точкой этого множества (см.).
Примеры: 1)£{1, —, — —, . . .}, sup£=l; 2) Ε (a, b) — конечный
Δ Ο ΤΙ
интервал, sup E=b\ 3) Ε — последовательность a„=sinrt, sup£=l.
ВЕРХНЯЯ ГРАНЬ ФУНКЦИИ y=f(x) [или U=f(xlt x2, .. ., хп)\ на
данном множестве Ε — верхняя грань множества (см.) значений функции, которое
она принимает, когда аргумент χ [или (х19 х2, . . . , хп)] пробегает множество Е.
В. г. ф. обозначается символом sup f(x) [или sup U(х1у хъ . . ., хп)\- Если
х€Е XG E
при некотором χ из Ε /(*)= sup f(x), то В. г. ф. на Ε является наибольшим
χ е Ε
значением функции на множестве Ε (говорят, что функция достигает своей
верхней грани).
Примеры: 1) sup (1—х2)=\—наибольшее значение функции; оно
— ОО < X < ОО
достигается при л;=0; 2) sup (1—*2) = 1, но функция не имеет наибольшего
о <х<\
значения на интервале (0,1); 3) sup 2х не существует, или, условно, равняется
0<x<oo
+ 00, так как функция не ограничена сверху на данном множестве.
ВЕТВЛЕНИЯ ТОЧКА многозначной аналитической функции есть точка,
обход которой в комплексной плоскости по окружностям сколько угодно малых
радиусов с центром в этой точке, сопровождаемый непрерывным изменением
значений данной функции, приводит к значениям, отличным от первоначально
выбранных. Количество различных значений в каждой точке может быть как
4 Толковый словарь математических терминов

50
ВЕТРЯНАЯ МЕЛЬНИЦА
конечным (например, у ζ в окрестности 0), так и бесконечным (например,
Ln z=Ln ρ е* φ = In ρ+ί φ в окрестности 0, ос, arc tg ζ — в окрестности ± ι).
См. также Аналитические функции.
ВЕТРЯНАЯ МЕЛЬНИЦА — плоская кривая, являющаяся одной из кривых
некоторого семейства, называемого узлами (см.). Полярное уравнение узлов имеет
вид: p=actg£q>. При k—2 узел (одна из кривых семейства) называется В. м.
Форма В, м. напоминает в какой-то степени лопасти
ветряной мельницы (рис. 27). В. м. имеет асимптоты,
уравнения которых:
х=±ау у=±6.
- синоним термина
ВЕЩЕСТВЕННЫЕ ЧИСЛА
«действительные числа» (см.).
ВЗАИМНООБРАТНЫЕ ЧИСЛА—два числа а^О
и —. Произведение В. о. ч. равно 1. Понятие В. о.
а
ч. используется иногда при устном решении
уравнений; например, уравнение χ J =2,5 можно пред-
Рис. 27
1
1
откуда легко усматриваются корни хх = 2,
ставить в виде х-\- — = 2-1--
х
*а=—. В. о. ч. используются при делении дробей (обыкновенных) и при
возведении чисел в степень с отрицательным показателем. Отметим свойство В. о. ч.:
а+—>2, если а>0.
а
ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ — такое соответствие между
элементами двух множеств, при котором каждому элементу первого множества
соответствует только один элемент второго множества, и обратно — каждому
элементу второго множества соответствует только один элемент первого. В. о. с. —
частный вид функции, или отображения (см.).
Пример: между точками отрезка (0, 1) и отрезка (0, 2) можно установить
В. о. с.—достаточно отнести числу λ отрезка (0, 1) число 2 λ отрезка (0, 2).
ВЗАИМНО ПРОСТЫЕ МНОГОЧЛЕНЫ. Многочлены /1# /2, . . ., fh, (k>2)
называются В. п. м., если их наибольший общий делитель (см.) является
многочленом нулевой степени. Одно из важных свойств В. п. м. состоит в том, что
если многочлен g взаимно прост с каждым из многочленов /lf f2, .. ., /д, то
многочлен g взаимно простой и с произведением /ν/2· ... ·/*.
ВЗАИМНО ПРОСТЫЕ ЧИСЛА —целые числа αΐ9 α%% . . ., ak, k>2, не
имеющие общих делителей, кроме 1 и —1. Например, числа 18, 35 и 121 (здесь
/? = 3) суть В. п. ч., но числа 14, 35 и 49 не суть В. п. ч., так как они имеют
общие делители 7 и —7, наряду с 1 и —1. Основные свойства В. п. ч.: 1) если
каждое из чисел alt аг% .... ak является В. п. ч. с Ьу то произведение
aL-a2- ... «flfe и Ь — В. п. ч.; 2) если аъ a2t . . ., а^ — В. п. ч., то сущест-
k
вуют целые числа xlt x2t ,.., Xk такие, что 2 α**<~1· 3) наименьшее об-
щее кратное (см.) В. п. ч. совпадает с их произведением. Понятие В. п. ч. не
следует путать с понятием попарно взаимно простых чисел (см.).

ВИНТОВАЯ ЛИНИЯ
51
ВЗВЕШЕННОЕ СТЕПЕННОЕ СРЕДНЕЕ η положительных чисел alt
а2, .... ап — обобщение степенного среднего (см.). В. с. с. выражается
формулой:
/ Pi я* +Ρ2α" + ··· +Pnfll
β __ [ 1 1
" \ Ρι+Ρ2+ ··· +Ρη
В. с. с. является средним (см.) и обращается в степенное среднее (см.) при
р1==р2= ... =/7п. Так же как из степенного среднего при некоторых
конкретных значениях α получаются специальные виды средних, так и из В. с. с.
получаются взвешенное арифметическое среднее, взвешенное гармоническое среднее
и т. д. В. с. с. применяется в различных
вопросах математики и математической статистики,
например при математической обработке
результатов наблюдений, когда измеряемые величины
flit 02» · · ·» ап получаются с различной
точностью — с разным весом (см. Веса результатов
измерений).
ВИВИАНИ КРИВАЯ — линия пересечения
сферы 0(R) и кругового цилиндра, радиус
которого вдвое меньше радиуса R сферы, а
образующая проходит через центр сферы (рис. 28).
Параметрические уравнения В. к. имеют вид:
x=R cos2 ut y=R cos и sin и, z—±Rs\nu,
где параметр и есть угол АОМ' или долгота
точки М.
ВИЕТА ФОРМУЛЫ (Вьета формулы) —фор- рис. 28
мулы* устанавливающие связь между
коэффициентами многочлена я-й степени (с коэффициентом при старшем члене, равным
единице) хп+а1хп"1+ · · · +ап и его корнями αΐ9 α2, .. ., ал. В. ф. имеют вид:
αι = — (ах-Юз-Ь ··· -f-an),
a^-l· (aiaa-f-ajcta-f ··· +αη—гап),
«β^—(а1а2«8-Ьа1«2«4+ ··* -fCtn—2 «Л—1 ««)»
««=(—1)яа1а2 . . . ап.
В частном случае при η=2 получаем В. ф. для многочлена второй степени
хг-\>рх-\-ц, а именно: с^-Ьаз™—р, а1а2=з=^. Эти формулы впервые были
получены французским математиком Франсуа Виетом (Вьетом).
ВИЛЬСОНА КРИТЕРИЙ (теорема) — число т является простым в том
и только в том случае, если (т—1)!-{-1= O(modm), т. е. когда (т—1 )l-f-1
делится на т.
ВИНОГРАДОВА ТЕОРЕМА —одно из крупнейших достижений в теории
чисел первой половины текущего столетия. В. т. утверждает, что всякое
достаточно большое нечетное число является суммой трех простых чисел. Другими
словами, существует такое число С (константа Виноградова), что всякое нечетное
число riy большее, чем С, представляется суммой трех простых чисел. Число С
было оценено в 1939 г. Бороздкиным, который показал, что оно не больше, чем
41,96
ее . В. т. явилась решением проблемы Гольдбаха-Эйлера (см.) для
нечетного случая. В. т. была доказана акад. И. М. Виноградовым в 1937 г.
ВИНТОВАЯ ЛИНИЯ — линия, описываемая точкой Αί, движущейся равномерно
по образующей кругового цилиндра, если сама образующая равномерно вращается
4*

52
ВИНТОВАЯ ПОВЕРХНОСТЬ
вокруг оси цилиндра. Кривая ΑΜΕ (рис. 29, а) есть В. л. Различают правую
В. л. (рис. 29, б) и левую В. л. (рис. 29, в) в зависимости от того, как
движется образующая: против часовой стрелки или по часовой стрелке, если
смотреть со стороны положительного направления оси ζ цилиндра. Расстояние MB=hy
которое проходит точка Μ за время
полного оборота вокруг оси цилиндра,
называется шагом В. л.
Параметрические уравнения В. л.
имеют вид:
jc=rcos/, y=rsin/, z=—/,
2π
где г — радиус цилиндра, h — шаг,
t — угол поворота радиуса ОМ' (М' —
проекция точки Μ на плоскость
основания цилиндра, т. е. t^^OAM', где
А — начальное положение точки Λί).
Если цилиндрическую поверхность
развернуть на плоскость, то В. л.
превратится в прямую.
Проекция В. л. на любую плоскость, проходящую через ось цилиндра или
ей параллельную, есть синусоида.
ВИНТОВАЯ ПОВЕРХНОСТЬ — поверхность, описываемая плоской кривой
линией при своем винтовом движении вокруг неподвижной оси, т. е.
вращающейся вокруг оси с постоянной угловой скоростью ω и одновременно
перемещающейся поступательно с постоянной линейной скоростью υ в направлении оси
вращения.
Если прямая линия совершает винтовое движение, то В. п. называется
геликоидом (см.). Если прямая линия пересекает ось вращения под прямым
углом, то геликоид называется прямым или обыкновенной В. п.
ВИХРЬ ВЕКТОРНОГО ПОЛЯ (или, короче, вихрь вектора) — векторное поле:
tdR dg\ /дР j)R\. (dQ дР\
[ду дг)1+[дг- дх)*+[дх- дуГ
определяемое данным векторным полем:
F=P(x, у, z)\+Q(x, у, z)i+R(xt у, г) к.
В. в. п. обозначается символом rot F (читается: «вихрь F» или: «ротор F») и
может быть записан в виде символического определителя:
rotF =
!
д
дх
Ρ
i
д
к
д
ду dz
Q
R
при раскрытии которого «произведение» оператора — и функции Q означает
частая
dQ
ную производную —· и т. п.
Символ rot происходит от сокращения латинского слова rotatio — вращение.

ВНУТРЕННЯЯ ТОЧКА
53
ВНЕВПИСАННАЯ ОКРУЖНОСТЬ треугольника—окружность,
расположенная вне треугольника и касающаяся одной из его сторон и продолжений двух
других. Для каждого треугольника ABC f можно построить три В. о. Центрами
#i» О2, 03 этих окружностей (рис. 30) являются
точки пересечения биссектрис внешних углов
треугольника.
Понятие В. о. используется при решении
задач на построение.
ВНЕШНЕЕ ПРОИЗВЕДЕНИЕ множеств А
и В — множество Ах В всевозможных
упорядоченных пар вида (а, Ь), где α ζ А и b ζ Β.
Аналогично определяется В. п. м. для трех,
четырех и вообще произвольного множества множеств.
В. п. м. называют также прямым
произведением, декартовым произведением (по имени
Р. Декарта) или картезианским произведением
(от слова «картезиус»— латинизированного имени
Декарта).
Пример. Пусть А — множество целых чисел,
тогда В. п. м. Ах А—множество всех
двумерных целочисленных векторов.
ВНЕШНИЙ УГОЛ треугольника — угол, смежный (см.) с одним из его
внутренних углов. В. у. треугольника больше каждого внутреннего угла, не
смежного с ним (теорема доказывается без аксиомы параллельности, т. е. это
теорема абсолютной геометрии).
ВНЕШНЯЯ ТОЧКА: 1°. В. т. множества действительных чисел —точка,
для которой существует открытый промежуток (см.), содержащий эту точку
и целиком состоящий из точек, не принадлежащих данному множеству. Другими
словами, В. т. —точка, не принадлежащая множеству вместе с некоторым
содержащим ее интервалом.
2°. В. т. множества я-мерного евклидова, или метрического, пространства —
точка, для которой существует открытый шар (см.) соответствующего
пространства, содержащий эту точку и состоящий целиком из точек, не принадлежащих
данному множеству. Другими словами, В. т. — точка, не принадлежащая
множеству вместе с некоторым содержащим ее открытым шаром.
ВНУТРЕННЯЯ ГЕОМЕТРИЯ — раздел геометрии, в котором изучаются
свойства поверхности, инвариантные при ее изгибании (внутренние свойства
поверхности). Так, длина дуги кривой на поверхности не изменяется при изгибании
этой поверхности, в то время как кривизна кривой при том же изгибании
поверхности изменяется.
Понятие длины дуги кривой, угла между кривыми в точке их пересечения,
площади фигуры являются основными понятиями В. г. Аналогами прямых на
поверхности во В. г. являются геодезические линии (см.), которые называются
просто геодезическими. В основе изучения внутренних свойств поверхности лежит
первая квадратичная форма (см.), введенная Гауссом. В. г. составляет
специальный раздел теории поверхностей. В. г. кратко определяют как геометрию на
поверхности; так, В. г. плоскости есть планиметрия. Можно также
рассматривать В. г. на сфере, на плоскости Лобачевского.
Лит.: П. К. Ρ а ш е в с к и й, Курс дифференциальной геометрии, Гостехиздат, Μ., 1950;
А. Д. Александров, Внутренняя геометрия выпуклых поверхностей, Гостехиздат,
М., 1948.
ВНУТРЕННЯЯ ТОЧКА: 1°. В. т. множества действительных чисел —точка
данного множества на числовой оси, для которой существует содержащий эту
точку открытый промежуток (см.)» целиком состоящий из точек множества.
Рис. 30

54
ВОГНУТОСТЬ
Другими словами, В. т.—точка, принадлежащая множеству вместе с некоторым
содержащим ее интервалом.
2°. В. т. множества «-мерного евклидова, или метрического, пространства —
точка данного множества, для которой существует открытый шар (см.)
соответствующего пространства, содержащий эту точку и целиком состоящий из точек
данного множества. Другими словами, В. т. —точка, принадлежащая множеству
вместе с некоторым содержащим ее открытым шаром.
ВОГНУТОСТЬ —свойство графика у=/(х) (кривой). Кривая f(x) называется
вогнутой в точке х=х0, если существует окрестность точки х0 такая* что в этой
окрестности каждая дуга кривой лежит ниже своей хорды. Вместо слова
«вогнута» говорят также, что кривая обращена вогнутостью кверху (или
выпуклостью книзу). Если существует Г(х), то вогнутость в точке х=х0
характеризуется условием: f"(xo)>®·
ВОЗВЕДЕНИЕ В СТЕПЕНЬ — операция, состоящая в нахождении
произведения:
а-а а—ап.
η раз
Здесь η — целое положительное число, называемое показателем степени, а —
основание степени и ап — степень. В алгебре и математическом анализе понятие
степени обобщается на случай, когда показатель η является произвольным
действительным и произвольным комплексным числом (см. Показательная функция).
Термин В. в с. употребляется также в абстрактной алгебре (в теориях
групп, колец и т. д.), вообще для произвольной мультипликативной операции
(см. Мультипликативная группа).
ВОЗВРАТА ТОЧКА —одна из особых точек (см.) кривой, в которой
направление кривой меняется на противоположное. Различают В. т. первого рода
(рис. 31, а) и второго рода (рис. 31, б) в
зависимости от расположения ветвей кривой относительно
касательной к кривой в В. т.: в некоторой
окрестности В. т. Λίχ первого рода ветви кривой
расположены по разные стороны от касательной, в
окрестности же В. т. Μ2 второго рода ветви кривой
расположены по одну сторону относительно
касательной t.
В. т. иначе называется точкой заострения.
ВОЗВРАТНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — последовательность чисел а0,
аъ а2, . . ., ап, . . . , удовлетворяющих соотношению:
Qn+p+Cxdn+p—!+ ··· +срап=0,
где cv c2i ...» с ρ — постоянные величины для данной В. п. Это соотношение
позволяет* зная первые ρ членов В. п., последовательно (рекуррентно) вычислять
ее последующие члены. Примером В. п. может служить Фибоначчи ряд (см.),
в котором α0=α! = 1 и выполняется соотношение αη+2==αη+ι-τ-#я Для остальных
членов. Термин В. п. предложен А. Муавром, рассмотревшим степенные ряды
(см.), коэффициенты которых образуют В. п.
Лит.: А. И. Маркушевич, Возвратные последовательности, Гостехиздат, М., 1947.
ВОЗВРАТНОЕ УРАВНЕНИЕ л-й степени — алгебраическое уравнение:
α0χη+αχχη-ι + ··· +αη-ιΧ+αη=0, (*)
в котором ak = an-k' гДе * = °. U 2, . . ., п. Часто В. у. определяют как
уравнение вида (*), в котором коэффициенты членов, равноотстоящих от начала и
κέ-·^-,,
α δ
Рис. 31

ВОЗРАСТАЮЩАЯ ПРОГРЕССИЯ
55
конца, одинаковы. Последнее определение менее удачно, так как может привести
к недоразумению (например, уравнение л;5-ЬЗл:34-Зл;2-Ьл;=0 не является В. у.,
так как в нем α0 = 1, αι=0, α2=3, α3=3, α4=1 и аъ=0, т. е. α0 Φ αδ1
ахФ а4, хотя α2=#3)·
Термин В. у. был введен Л. Эйлером в 1733 г.
Корни В. у. отличны от нуля. Если α — корень В. у., то~ также
является корнем этого В. у. (В. у. нечетной степени имеет корень Χχ =—1; делением
его левой части на χ-И сводится к В. у. четной степени).
Решение В. у. четной степени 2 т подстановкой у=х+-~ сводится к
решению уравнения m-й степени и 2т квадратных уравнений. К В. у. сводится
уравнение деления круга. Близкими к В. у. являются косовозвратное уравнение
н возвратное уравнение второго рода.
Пример. Решим В. у. χδ+3χ* — 6x8 — 6x2-f-3x-H=0.
*! =—1. Поэтому исходное уравнение сводится к В. у. четвертой степени:
jc4+2jc8 — 8jca-b2jc-f l=0.
Разделив обе части уравнения на х2(хф0) и сделав замену y=*-f-—, откуда
у2 — 2=*2+— , получаем ya-f-2y — 10=0. Отсюда уь 2= — 1 ± VW . Далее
имеем:
- 1 ~УУ\ ± V 8+2]/И -1 +У\\±У 8—2Т/ТГ
ВОЗРАСТАНИЕ ФУНКЦИИ в точке. Функция У=Д*), определенная в
окрестности точки а, называется возрастающей в этой точке, если существует
такая окрестность точки а, что для любых значений хг и х2 из этой окрестности
хг<а<х2 выполняются неравенства / (хх) <f(a)< /(jc2).
Другими словами, знак приращения функции в точке а совпадает со знаком
приращения аргумента. В случае выполнения нестрогих неравенств /(*ι)</(α)<
<> / (*г) функция называется неубывающей в точке а. Дифференцируемая в точке
а функция является неубывающей в этой точке тогда и только тогда,
когда /' (а)>0.
Пример. Функция
*+2*2sin—· при χ Φ 0
0 при л:=0
возрастает в точке #=0, но не является возрастающей в любой окрестности этой
точки, так как в любой окрестности производная меняет знак бесчисленное
число раз.
ВОЗРАСТАЮЩАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ-последовательность^, а2
аПУ . . ., для которой следующий член больше предыдущего: α„+ι>αη{η=\, 2,
3, . . .). В случае выполнения нестрогого неравенства ап+1>ап
последовательность называется неубывающей. Неубывающая ограниченная сверху (см.)
последовательность имеет конечный предел.
ВОЗРАСТАЮЩАЯ ПРОГРЕССИЯ: 1°. В. п. арифметическая — такая
прогрессия (см.), разность которой больше нуля (d>0).
/(*) =

56
ВОЗРАСТАЮЩАЯ ФУНКЦИЯ
2°. В. п. геометрическая — такая прогрессия, знаменатель которой больше
единицы (?> 1) и первый член положителен.
ВОЗРАСТАЮЩАЯ ФУНКЦИЯ на отрезке а<х<Ь (или интервале, или
множестве)— функция у=/(х), для которой при любых х1<х2 из отрезка
(интервала, множества) выполняется неравенство f(X\)<f(Xi)\ в случае выполнения
нестрогого неравенства f {X\)<f (хг) функция называется неубывающей на
отрезке. Дифференцируемая на отрезке [а, Ь] или соответственно на интервале (а, Ь)
функция является неубывающей на нем в том и только в том случае, когда
/' (х)>0 для а<х<Ь или соответственно для а<х<Ь. Возрастание функции на
отрезке и интервале не следует смешивать с возрастанием функции в точке.
ВПИСАННЫЙ МНОГОУГОЛЬНИК (в кривую или в другой многоугольник) —
многоугольник, все вершины которого лежат на кривой или на сторонах другого
многоугольника. Так говорят о многоугольнике, вписанном в кривую второго
порядка, о квадрате, вписанном в круговой сегмент, о треугольнике, вписанном
в квадрат, о прямоугольнике, вписанном в треугольник, и т. д.
ВПИСАННЫЙ УГОЛ —угол, вершина которого лежит на окружности, а
стороны пересекают окружность. На рис. 32 угол ABC есть В. у. Дуга АКС>
не содержащая вершины В. у., называется дугой, на
которую опирается В. у. В. у. измеряется половиной дуги, на
которую он опирается. В. у., опирающийся на диаметр
окружности (или дугу в 180°) —прямой.
ВПОЛНЕ УПОРЯДОЧЕННОЕ МНОЖЕСТВО —
множество, в котором введено отношение порядка (обозначается
а{ Ь, а читается: «Ь следует за а»), обладающее свойствами:
1) каждый элемент не следует за самим собой; 2) из любых
двух элементов а и Ь один следует за другим; 3) если а\ Ь
и Μ с, то а{ с, и такое, что в любом его подмножестве
существует первый элемент. Например, натуральный ряд рис 32
чисел с порядком, определенным отношением >, есть В. у. м.
Лит.: П. С. Александров, Введение в общую теорию множеств и функций,
Гостехиздат, М.—Л., 1948.
ВРАЩЕНИЕ с центром О и углом вращения φ есть такое преобразование
точек плоскости, при котором всякой точке Μ плоскости ставится в
соответствие точка М' той же плоскости так, что при
этом выполняются два условия:
1) ОМ'=ОМ; 2) LMOM'^y.
При В. все точки (Μ, Ρ, ...) плоскости
описывают дуги концентрических окружностей с
центром в точке О — центре В. (рис. 33). При
В. прямые преобразуются в прямые,
окружности — в равные им окружности. В. есть
частный случай движения (см.), при котором по
крайней мере одна из точек плоскости остается
неподвижной.
Аналогично определяется В. относительно прямой в пространстве. В. на
плоскости аналитически задается формулами:
х* ==х cos φ — у sin φ, у' = χ sin φ-f-y cos φ,
где φ —угол В., точка О(0, 0) —центр В.
Преобразование В. используется при решении некоторых задач на геометрические
построения (см.), особенно в том случае, когда искомая фигура должна
занимать определенное положение по отношению к данным фигурам. Например,
задача: построить квадрат, три вершины которого по одной лежали бы на трех
данных параллельных прямых, — решается проще всего методом В.

ВЫПРЯМЛЕННЫЙ УГОЛ
57
ВРОНСКИАН—определитель, составленный из η функций /х(х), /2 (jc),
., fn(x) и их производных до (п— 1)-го порядка:
\f\ Ц · · · /я
/ι /г · · · ίη
W(x) =
/iJ
(л-1)
/2
/(1-1)
Такое название дано по имени польского математика Ю. Вронского.
Тождественное обращение В. в нуль является необходимым и достаточным
условием линейной зависимости функций. Если /lt /2, . . ., fn являются
решениями линейного дифференциального уравнения вида у(п)-\-р1(х)у{п—\)^г ..._[-
Л-р^У=®* то обращение В. в нуль в точке х0 — необходимое и достаточное
условие линейной зависимости flt /2» · · ·» fn- В теории систем линейных
дифференциальных уравнений В. системы η вектор-функций yi(i=\, 2, . . ., η)
называют определитель;
' (ι) (2) (п)
Ух У\ · · · У\
(υ
(2)
У2
(Л)
Уъ
(1) (2)
Уп Уп
Уп
где у\л — /-ая компонента вектора jf/. Обращение его в нуль также
необходимое и достаточное условие линейной зависимости решений yt.
ВТОРАЯ КРИВИЗНА пространственной кривой — синоним термина Кручение
(см.) кривой.
ВУРФ — упорядоченная совокупность точек л-мерного проективного
пространства, состоящая из 4 точек при /2=1 (случай прямой), и из («4-2) точек
при n>U при этом в случае п>\ любые п+\ точек не принадлежат никакому
(п—1)-мерному пространству. Например, при л=3 никакие 4 точки из 5 не
должны лежать в одной плоскости.
Понятие В. было введено Штаудтом.
Четверка точек Л, В, С, D прямой, взятая в определенном порядке,
называется В. на прямой и обозначается так: {ABCD}. Два В. {ABCD} и
[A'B'C'D'} равны, если образующие их четверки точек проективны: {ABCD}=
= {A,B,CtD,}y если ABCDaA'B'C'D'. Аналогично рассматриваются плоские
и пространственные В. Над В. можно производить операции сложения и
умножения, как и над числами в арифметике.
Лит.: Н. А. Глаголев, Проективная геометрия, ОНТИ, М., 1936; X. С. М.
Ко к стер, Действительная проективная плоскость, Физматгиз, М., 1959.
ВЫБОРОЧНЫЙ МЕТОД — метод статистического наблюдения, при котором для
определения сводных характеристик какой-либо совокупности изучаются не все
единицы совокупности, а лишь часть их, случайно взятая на выборку. Например,
для определения среднего срока службы большой партии электрических
лампочек отбирается сравнительно небольшая часть их и испытывается; средний срок
службы испытанных лампочек принимается за приближенное значение среднего
срока службы во всей партии. Широкое применение В. м. начал получать в
конце XIX в. В. м. широко применяется в практике советской статистики.
Основной задачей классической теории В. м. является определение дисперсий
случайных величин.
Лит.: см. термины Статистика и Математическая статистика.
ВЫПРЯМЛЕННЫЙ УГОЛ — другое название развернутого угла (см.).

58
ВЫПУКЛАЯ КРИВАЯ
ВЫПУКЛАЯ КРИВАЯ относительно декартовой системы координат — кривая,
обладающая тем свойством, что каждая дуга ее лежит не ниже своей хорды.
Если уравнение ее y = f(x) и f (х) имеет две непрерывные производные, то
выпуклая кривая характеризуется неравенством /"(л;)<0. Кривая называется В. к.
в точке М, если она выпукла в некоторой окрестности точки М.
ВЫПУКЛАЯ ОБЛАСТЬ — область, обладающая тем свойством, что если
две точки принадлежат к ней, то к ней принадлежит и отрезок прямой,
соединяющий эти точки.
ВЫПУКЛАЯ ПОВЕРХНОСТЬ — поверхность г = /(л:, у) называется выпуклой,
если обладает следующим свойством, касательная плоскость лежит не выше
данной поверхности. Достаточное условие выпуклости такое:
/ ay fay*/ 0.
[дхду) дх2 ду* '
если f(x, у) имеет вторые непрерывные частные производные.
ВЫПУКЛАЯ ФИГУРА: Г. В. ф.— выпуклое тело (см.) и 2°. В. ф
—выпуклая область (см.).
ВЫПУКЛАЯ ФУНКЦИЯ—функция, обладающая тем свойством, что для
любой тройки чисел χΎ^ #2<*з> принадлежащей интервалу, на котором
определена φ(я), выполняется неравенство:
(*з — *г) Φ (*ι) + (*ι — *з) Φ (*2) +(*2 — *ι) Φ (*s) < °·
Примерами выпуклой функции являются: у=—ekx, у=ха при х>0 и 0<а<1.
Сумма двух В. ф. выпукла. Предел последовательности В. ф. — выпуклая
функция. Всякая В· ф. непрерывна. Если φ(*) дважды дифференцируема, то
условие выпуклости: φ/"(χ)<0.
ВЫПУКЛОЕ ТЕЛО — тело, обладающее тем свойством, что
прямолинейный отрезок, соединяющий две любые точки тела, сам целиком содержится в
этом теле. Примерами В. т. могут служить шар, куб, шаровой сегмент.
Лит.: Л. А. Люстерник, Выпуклые тела, Гостехиздат, М., 1941.
ВЫПУКЛОСТЬ — свойство графика функции У=/(*)» заключающееся
в том, что в некоторой окрестности точки х=х0 каждая дуга кривой лежит
выше своей хорды. В этом случае говорят, что график функции f (х) в точке
х—х0 обращен выпуклостью кверху (вогнутостью книзу), и сама функция в этой
точке называется выпуклой.
Если существует /"(#)> то В. в точке х=х0 характеризуется условием
Г(*о)>0.
ВЫРОЖДЕННАЯ МАТРИЦА (вырождающаяся, особенная матрица)
—квадратная матрица, определитель которой равен нулю.
ВЫСОТА. 1°. В. плоской фигуры относительно отрезка (основания),
входящего в контур этой фигуры, есть наибольший из перпендикуляров,
опущенных из точек контура фигуры на отрезок (основание) или его продолжение.
О А В D L D К
Рис. 34 Рис. 35 Рис. 36
Примеры: высота (стрелка) CD кругового сегмента АС В (рис. 34); CD —
пысота треугольника ABC относительно стороны (основания) АВ или высота
треугольника ABCt соответствующая основанию АВ (рис. 35); С К (ML) — высота

ВЫЧИСЛЕНИЯ ПРИБЛИЖЕННЫЕ
59
параллелограмма ABCD (основание AD или ВС) — расстояние между
параллельными прямыми AD и ВС (рис. 36).
2°. В. пространственной фигуры относительно плоского основания (плоской
области), входящего в границу этой фигуры, есть наибольший из
перпендикуляров, опущенных из граничных точек этой фигуры на плоскость основания.
Примеры: CD —высота (стрелка) сферического сегмента ABC (рис. 37);
KL — высота наклонного цилиндра (рис. 38); SO — высота пирамиды
относительно основания ABC (рис. 39).
Рмс. 37
Рис. 39
ВЫСШАЯ ГЕОМЕТРИЯ — цикл геометрических дисциплин: основания
геометрии (аксиоматическое обоснование элементарной геометрии), проективная
геометрия (см.), изучаемых на физико-математических факультетах университетов и
педагогических институтов. Термин В. г. чисто условный. К В. г. иногда
относят и аналитическую и дифференциальную геометрии.
Лит.: Н. Ф. Ефимов, Высшая геометрия, Физматгиз, М., 1961.
ВЫСШАЯ МАТЕМАТИКА—цикл математических дисциплин (аналитическая
геометрия, дифференциальное и интегральное исчисления, дифференциальные
уравнения, дифференциальная геометрия и др.). изучаемых в высших учебных
заведениях. Однако этот термин является весьма условным.
В. м. противопоставляется элементарной математике* где изучаются в
основном постоянные величины и применяются частные методы исследования
математических вопросов, в отличие от В. м., где изучаются переменные величины,
где используются общие методы исследования. Резкого различия между ними
нет, и их выделение объясняется лишь структурой образования в стране и
методикой преподавания математики в школе. Ф. Энгельс указывал: «Элементарная
математика, математика постоянных величин, движется, по крайней мере в общем
и целом, внутри границ формальной логики; математика переменных величин, самый
значительный отдел которой составляет исчисление бесконечно малых, есть по
своей сущности не что иное, как применение диалектики к математическим
отношениям» (Ф. Энгельс, Анти-Дюринг, 1957, стр. 127).
См. также Элементарная математика.
ВЫЧЕТ: 1°. В. аналитической функции /(г) относительно изолированной
особой точки 20 называется коэффициент при (г — г0)—1 в разложении этой
функции в ряд Лорана (см.) в окрестности этой точки. Знание вычетов в
некоторых случаях позволяет вычислить интегралы функции /(г) по замкнутому в
комплексной плоскости контуру (в частности, по действительной оси от —оодо-Ьоо).
2°. В. в теории чисел В. числа а по модулю т называется остаток
отделения а на т.
ВЫЧИСЛЕНИЯ ПРИБЛИЖЕННЫЕ — вычисления, в которых данные и
результат (или только результат) являются числами, приближенно представляющими

60
ВЫЧИСЛЕНИЯ ПРИБЛИЖЕННЫЕ
истинные значения соответствующих величин. Числовые данные, полученные
измерением реальных объектов, редко бывают точными значениями
соответствующей величины, а обычно имеют некоторую погрешность (см.). Наконец,
имея дело даже с точными значениями, мы не всегда имеем возможность
пользоваться ими, например, используя их при счете на вычислительных машинах,
допускающих ввод в них чисел лишь с ограниченным (хотя, может быть, и
большим) числом знаков. Источником приближенных чисел могут быть и те
приближенные формулы (см.), по которым ведется иногда вычисление.
О приближенных числах следует всегда говорить с указанием на
погрешность. На практике обычно применяют такой принцип: приближенное число
пишется так, чтобы в нем все цифры, кроме последней, были верными, а последняя
сомнительна не более чем на единицу.
Используются также следующие способы для указания погрешности: 1)
точное неравенство а<х<Ь, где а и b соответственно нижняя и верхняя границы х\
2) указание абсолютной погрешности Δα, т. е. такого положительного числа,
что а—Δα<*-^α+Δ#. где а—приближенное значение х\ 3) указание относи-
Δα
тельной погрешности —, иногда выражаемого в процентах.
Если приходится считаться не только с величиной погрешностей данных, но
и с вероятностью различных возможных значений этих погрешностей (см.
Ошибок теория, Математическая статистика), то вычисляют по определенным
правилам средние квадратические погрешности результатов действий.
В своей основе элементарная теория В. п. состоит в оценке точности
результатов вычисления по формулам: z=f(xlt х2, . . ., хп). Например, в сумме или
разности приближенных чисел следует сохранять столько цифр после запятой,
сколько их в приближенном числе с наименьшим количеством цифр после
запятой.
Если даже значения х1% х2, ...» Хп известны точно, то значение ζ может
получиться лишь приближенным в силу погрешностей вычисления, полученных
при пользовании таблицами, приближенными формулами, округлением
результатов действий. Для учета влияния погрешностей используют формулу:
ΙΔ*|<
дхх
\дх2\ \дхп
\Ьхп\
З^есь | Дг | — абсолютная погрешность результата, а | Δ χχ |, | Δχ21,
| Ахп | — абсолютные погрешности аргументов. Эта формула дает линейную часть
ошибок.
Если Δ*ι, Δ#2, . . .? Δ*η — такие погрешности, что их можно считать
независимыми случайными величинами, то Δι — случайная величина, и
приближенно:
—-ШЧ+©Ч+- +(ЭЧ·
Здесь (Χχ,,<Χχ8, . . ., αχ„ — средние квадратические ошибки соответствующих
величин.
Например, пусть известно, что у числа #=2,154123 Есе знаки Еерные, а у
числа jc2=2,215 верен только один знак после запятой. Тогда x1-j-x2==4»3, так
как остальные знаки не будут верными в сумме.
Произведение двух приближенных чисел, имеющих k точных значащих,
имеет погрешность, не превышающую 5,5 единицы разряда k-й значащей цифры.
Это правило иллюстрируем на следующем примере. Пусть в числе л?!» 1,112 все
знаки верны, а в числе х2~1,21 верна только одна цифра после запятой. Тогда
ххх2 имеет погрешность, не превышающую 0,1 · 5,5=^0,55.

ВЫЧИСЛЕНИЯ ПРИБЛИЖЕННЫЕ
61
Следующие практические правила просты и общеупотребительны: 1) при
умножении и делении следует сохранять в результате столько значащих цифр,
сколько их имеет приближенное данное с наименьшим числом значащих цифр;
2) при возведении в квадрат и куб в результате следует сохранять столько
значащих цифр, сколько их имеет возводимое в степень приближенное число; 3) при
извлечении квадратного и кубического корней в результате следует брать
столько значащих цифр, сколько их имеет подкоренное число.
Лит.: Энц. элем, мат., т. I, Гостехиздат, М., 1954.

г
ГАЛЕРКИНА МЕТОД — прямой метод (см.) решения вариационных и
краевых задач (см. Вариационное исчисление, Краевые задачи), представляющий
собой весьма широкое обобщение Ритца метода (см.). Приближенное решение
уравнения L[u] = 0(L — некоторый дифференциальный оператор) в области D с
однородным краевым условием и = 0 ищут в виде:
η
где ifo(x, у), (/=1, 2, .. ., л)— линейно независимые функции,
удовлетворяющие краевым условиям и являющиеся первыми η функциями некоторой системы
функций 1|>! (х, у), ψ2(*, У). · · ·> Ψη(*. У), .... полной bD; коэффициенты аг
определяются из условия ортогональности функций L [ип] η первым функциям
семейства ψ/ (χ, у). Метод Галеркина может быть обобщен для решения задач
функционального анализа (см.). Широкое распространение метод Галеркина
получил при решении различных задач математики, а также теории упругости, после
работ Галеркина (1915).
Полное теоретическое обоснование метода Галеркина было дано в 1942 г.
советским математиком М. В. Келдышем.
Лит.: Л. В. Канторович и В. И. Крылов, Приближенные методы высшего
анализа. Физматгиз, М., 1962.
ГАЛУА ГРУППА алгебраического уравнения:
χη -{-а^п— l-f- ... +ап-\х+ап=0. (*)
Рациональным соотношением между корнями ξχ, ξ2. · · ·ϊ ξ л уравнения (*)
называется многочлен F (хъ х2* ...» Хп) от η независимых переменных,
обращающийся в нуль при *ι = ξι, #2 = ξ2» · · · » χη=ζ>η, причем коэффициенты
многочлена F выражаются с помощью операций сложения, вычитания, умножения и
деления через коэффициенты alt a2, .... ап-
Множество всех перестановок переменных xlt хг% . . ., хп, переводящих
рациональное соотношение снова в рациональное соотношение, образуют Г. г.
относительно операций умножения подстановок.
Г. г. впервые рассматривал Э. Галуа в связи с исследованием
алгебраических уравнений л-й степени.
Лит.: М. М. Постников, Теория Галуа, Физматгиз, М., 1960; Н. Г. Чебота*
рев, Теория Галуа, ОНТИ, М., 1936.
ГАЛУА ТЕОРИЯ — созданная Э. Галуа теория алгебраических уравнений с
одним неизвестным, т. е. уравнений вида:
χη +α1χη-ι+α2χη-2+ ··· + αη_χχ+αη=*0. (*)
Задача ставится так: выразить корни уравнения (*) через его коэффициенты аи
аъ . . ., ап с помощью четырех арифметических операций и операции извлечения
корней. Поэтому задача часто именуется задачей о разрешимости уравнения (*) в
радикалах. При л=1 и 2 решение этой задачи было известно еще в античной

ГАРМОНИКА
63
древности. При /2 = 3 и 4 задача была решена в эпоху Возрождения (XVI в.)
итальянскими математиками Бомбелли, Ферро, Кардано, Тарталья, Феррари.
В течение трех следующих веков все попытки решить в радикалах уравнение
(*) для /2 = 5 были безуспешными. В 1824 г. Абель доказал, что общее
уравнение (*) при /2=5 (следовательно, и при любом /2>5) не имеет решения в
радикалах. Возник вопрос о том, каковы необходимые и достаточные условия
разрешимости в радикалах того или иного конкретного уравнения вида (*)» и другие
сходные вопросы.
Г. т. решает эти вопросы, следуя такой схеме: каждому уравнению
сопоставляется некоторая конечная группа (см.) подстановок ее корней. Эта группа
называется группой Галуа (см.) уравнения (*). Далее надо проверить,
выполнено ли в этой группе некоторое свойство (разрешимости группы) или нет. В
соответствии с ответом на этот вопрос аналогичным будет ответ и на вопрос о
разрешимости в радикалах уравнения (*).
Таким образом, в Г. т. был решен основной вопрос (того времени) теории
алгебраических уравнений с одним неизвестным. Г. т. имеет ряд приложений к
другим вопросам математики; в частности, с ее помощью удалось установить
необходимые и достаточные условия (критерии) разрешимости задач на
построение с помощью циркуля и линейки.
Г. т. продолжала бурно развиваться вплоть до наших дней. Крупный вклад
в ее развитие был сделан И. Р. Шафаревичем, которым была решена так
называемая обратная задача Г. т., состоящая в том, что по заданной группе С
требуется построить уравнение (*), для которого группа С была бы группой
Галуа. Эта работа (наряду с другими работами И. Р. Шафаревича) в 1957 г.
была удостоена Ленинской премии.
Лит.: М. М. Постников, Теория Галуа, Физматгиз, М., 1964.
ГАММА-ФУНКЦИЯ — функция, определяемая формулой:
оо
Г(*)= \sx-ie-sds.
о
Если η — целое положительное число, то Г (п) = (/2 — 1)! Г. ф. может быть
аналитически продолжена в комплексную область. Основные соотношения дляГ.-ф.:
Г(*+1)-гГ(г), Г(г).Г(1-г) =
sin π 2
Через Г.-φ. выражается большое число определенных интегралов. В
комплексной области Г.-ф.—мероморфная функция с полюсами: г=0, —1, —2,
Г.-ф. введена Эйлером.
ГАРМОНИКА — функция вида Л sin (ω х-Ьф). Г. есть периодическая функ-
2π
ция с периодом Т=—. Колебательное движение, совершаемое по формуле:
ω
у=А sin (ω χ-\-φ) (переменная χ — время), называется простым гармоническим
колебанием; при этом число А называется амплитудой колебания, ω — круговой
частотой (круговой скоростью), φ — начальной фазой колебания. Функции
Λ sin (2 ω *-fq>2), Λ sin (3 ω χ+φ3), ... называются соответственно второй,
третьей и т. д. высшими Г. относительно основной Г. A sin (ω Jt-f-φ).
Число ν=—-=-— называется частотой колебания. Если Vi =——ча-
Т 2π Γ
стота первой, или основной, Г., то частоты высших Г. равны ν=2νχ (вторая
Г.). v3 = 3v! (третья Г.) и т. д.

64
ГАРМОНИЧЕСКАЯ ПРОПОРЦИЯ
Часто периодическую функцию y=f(x) можно аналитически представить в
виде бесконечного числа Г. (см. Гармонический анализ):
у=а0-\-аг cos (2πν1/+φ1)+α2α)5(2πν2/+φ2)+ . . .,
где а0 — постоянная средняя величина функции у, около которой происходит
колебание, alt φχ — амплитуда и фаза первой (основной) Г., а2, φ2 — амплитуда и
фаза второй Г. и т. д.
Общий вид простой Г. с частотой ω можно записать и в виде: acoscox+
4-6 sin ω χ, где а и Ь — любые действительные числа, что следует из
представления точки (Ь, а) в полярных координатах (Л; φ):
α cos cox-f-6 sinti) x=A sin φ cos ω x+A cos φ sin ω x=A sin (ω λ:-f φ).
График Г. получается из графика у=si η χ путем последовательного построения
и преобразования графиков функций:
sin x; A sin χ; Л sin cox; A sin
: + —j = Л sin (ωχ+φ);
график sin λ: растягивают в направлении оси Оу в А раз, затем полученный
график сжимают по оси Ох в ω раз и, наконец, полученный график переносят
φ
(сдвигают) в направлении оси Ох на — — единицы длины.
ω
См. также Синусоида.
ГАРМОНИЧЕСКАЯ ПРОПОРЦИЯ — пропорция вида:
a: c=(a — b): (b — с),
в которой первое число (или отрезок) так относится к третьему, как разность
между первым и вторым относится к разности между вторым и третьим. Число
b в Г. п. есть среднее гармоническое чисел α и с, Ь=Н(а, с), т. е.:
2ас
Ъ— .
а+с
ГАРМОНИЧЕСКАЯ ФУНКЦИЯ — непрерывная функция, являющаяся
решением уравнения Лапласа:
д2и д2и д2и Λ
дхх дх2 дхп
Г. ф. двух переменных тесно связаны с аналитическими функциями (см.).
Вещественная и мнимая части аналитической функции есть Г. ф. Всякая Г. ф.
является аналитической функцией всех своих аргументов. Важным свойством Г. ф.
является то, что среднее значение ее по поверхности любого шара равно
значению ее в центре этого шара. Многие свойства Г. ф. вытекают из формулы
Грина, связывающей интеграл по объему f с интегралом по поверхности |:
t s
С С I ди ди \ _, Λ
\ (и Αν — υ Δ и) <*<·>■+· I \и— "~УТ") ^σ==°·

ГАРМОНИЧЕСКАЯ ЧЕТВЕРКА
65
Из этой формулы можно получить, что
дп
^ 1 Г dG л
S
где G —функция Грина (см.).
Таким образом, зная и на какой-либо замкнутой поверхности, можно узнать
значение и в любой внутренней точке области, или, как говорят, решить задачу
Дирихле. Большое значение для приложения теории Г. ф. имеют численные
методы.
ГАРМОНИЧЕСКАЯ ЧЕТВЕРКА точек —четыре точки А, В, С, D прямой,
для которых сложное отношение (см.) равно (—1), т. е. (ABCD) =—1.
Аналогично определяется Г. ч. прямых пучка (см.) первого порядка: четыре прямые
а, b, ct d образуют Г. ч., если их сложное отношение равно —1, т. е. (abcd)=
=— 1. Г. ч. точек при проектировании переходит в Г. ч. точек; это свойство
Г. ч. точек используется при доказательстве ряда теорем проективной
геометрии (см.).
При различных перестановках букв внутри Г. ч. точек получается всего
три различных сложных отношения, а не шесть, как в случае сложного
отношения четырех точек общего расположения на прямой.
Если точка С — середина отрезка АВ, то гармонически сопряженная с ней
точка D относительно точек А к В будет несобственной. Это свойство Г. ч.
точек используется для построения с
помощью только линейки (математической,
односторонней) прямой, параллельной
данному отрезку, если известна его середина.
Если А и В — две вершины
треугольника, а точки К и Μ — основания
биссектрис (внутренней и внешней),
проведенных из третьей вершины треугольника, то
точки Л, В, К, Μ составят Г. ч. точек.
Г. ч. точек иначе называется
гармонической группой или гармонически
расположенными точками.
Доказывается, что на каждой сто- Рис. 40
роне и каждой диагонали полного четы-
рехвершинника (см.) ABCD имеется Г. ч. точек В, С, Я, Lh/C, L, Μ, N (рис. 40).
Поэтому в проективной геометрии дается и другое определение Г. ч.,
свободное от метрики и основанное на понятии полного четырехвершинника: пара
точек S и Τ произвольной прямой / называется гармонически сопряженной с
парой точек Ρ и Q той же прямой, если Ρ и Q — диагональные точки некоторого
четырехвершинника ABCD, а 5 и Τ — точки пересечения прямой / с двумя
противоположными сторонами, проходящими через третью диагональную точку R.
Таким образом, PQRT — Г. ч. точек. В проективной геометрии доказывается,
что к данным трем точкам Р, Q, S четвертая гармоническая точка Τ
однозначно определяется, так как построение точки Τ — четвертой гармонической к
точкам Р, Q, 5 — не зависит от того, каким полным четырехвершинником мы
пользуемся для ее построения.
Понятие Г. ч. является основным в проективной геометрии (см.); при
проектировании Г. ч. точек из какого-либо центра на другую прямую, как мы
отметили выше, она снова переходит в Г. ч. точек.
Г. ч. прямых пучка аналогично определяется с помощью полного
четырехсторонника (см.). Г. ч. прямых является двойственной ф°Рм°й Г. ч. точек
(см. Двойственности принцип). При проективных преобразованиях (см.) Г. ч.
точек (прямых) снова переходит в Г. ч. соответствующих элементов.
5 Толковый словарь математических терминов

66
ГАРМОНИЧЕСКИЙ АНАЛИЗ
ГАРМОНИЧЕСКИЙ АНАЛИЗ — отдел математики, посвященный разложению
функций в тригонометрические ряды и интегралы. Произвольную гладкую
периодическую функцию / (х) периода 2 π можно представить в виде
тригонометрического ряда
а0 %-у
/(*) = — + / ,Qn cos nx+bn sin nxt
коэффициенты которого определяются формулами:
f(x)dx,
an= — I f(x)cos nx dx,
я J
—π
-τΐ
f (x) sin nx dx.
При определенных условиях роста на (—оо, -f °°) произвольная гладкая
функция f(x) представляется в виде интеграла Фурье. Так, если обозначить
+00 4-00
F($)=—— \ f(t)e~ist dt, то окажется, что /(х)=—— Г F(s)ei8Xds\
V2nJM Ϋ2π)
—оо
функция F (s) называется преобразованием Фурье функции /(*). В основных
случаях вычисление коэффициентов Фурье проводится при помощи численных
методов, которые, особенно при вычислении высших гармоник, требуют
проведения большого числа операций. Тригонометрические ряды и интегралы имеют
важную роль в ряде разделов науки и техники, особенно в математической
физике, где методом Фурье можно решить известные задачи о колебаниях струны,
мембраны, упругого стержня, уравнение теплопроводности. Вопросы о
представлении различных функций тригонометрическими рядами и интегралами
изучались еще Риманом, Лебегом. В этот раздел большой вклад внесен советскими
математиками Н. Н. Лузиным, Д. Е. Меньшовым, А. Н. Колмогоровым,
Н. К. Бари и др.
Лит.: И. И. П рива л о в, Ряды Фурье, ГТТИ, М., 1959; А. 3 и г м у н д,
Тригонометрические ряды, ОНТИ, М., 1939.
ГАРМОНИЧЕСКИЙ РЯД —числовой ряд (см.)
, ι ι ι
1+ϊ+7+ - + ^+ -■
члены которого являются числами, обратными числам натурального ряда.
Г. р. — расходящийся ряд; расходимость его была доказана Г. Лейбницем
в 1673 г.

ГАУССОВА КРИВИЗНА
67
Название Г. р. связано с тем, что каждый член этого ряда, начиная со
второго, есть среднее гармоническое (см. Гармоническое среднее) двух соседних
членов — предыдущего и последующего.
ГАРМОНИЧЕСКОЕ СРЕДНЕЕ η положительных чисел аи а2, . . ., ап (л>2) —
число, равное
1 1 1
—+—+ ■·· 4—
at a2 ап
Г. с. является средним (см.) чисел aXi а2, ... , ап. Г. с. чисел α,, ав,...
..., ап является обратной величиной к среднему арифметическому величин,
обратных к аи а2 ап.
ГАУССА ЛЕММА о приводимости многочленов формулируется так: если
целочисленный многочлен приводим в поле рациональных чисел, то он приводим
в кольце целых чисел. Иными словами, если многочлен с целыми рациональными
коэффициентами разлагается на множители с рациональными коэффициентами,
то он разлагается также и на множители с целыми коэффициентами. Иногда
эту лемму называют теоремой Гаусса.
В учебниках высшей алгебры приводится еще и следующее предложение,
именуемое Г. л.: произведение примитивных функций равно примитивной функции.
ГАУССА ФОРМУЛА — формула для приближенного вычисления
определенных интегралов:
]f{x)dx = ib-a)[Alf{x1)+AJ{x2)+ ··· +Anf(xn)],
а
где коэффициенты Αι и абсциссы χ ι даются в специальных таблицах. Г. ф.
является гораздо более точной, чем формулы математических квадратур (см.
Численное интегрирование).
Г. ф. дает совершенно точный результат, если подынтегральная функция —
многочлен степени не выше, чем 2п — 1.
Лит.: А. Н. Крылов, Лекции о приближенных вычислениях, Гостехиздат, М.,
1954.
ГАУССОВА КРИВИЗНА поверхности в точке Μ определяется формулой
k= , где #! и /?2 —* радиусы главных кривизн в точке, т. е. радиусы мак-
R1R2
симальной и минимальной кривизны плоских кривых (нормальных сечений),
которые получаются от пересечения данной поверхности с плоскостями,
проходящими через нормаль к поверхности в рассматриваемой точке Λί.
Г. к. иначе называется полной кривизной. Г. к. играет важную роль при
рассмотрении вопроса об изгибании (см.) поверхности. Всякая поверхность,
имеющая Г. к. (полную кривизну), равную нулю, допускает развертывание на
плоскость.
Полусумма (иногда сумма) главных кривизн в точке называется средней
кривизной (см.) Я, т. е. #="- ίϊΓ+Ίό/» в то вРемя как Г* к' пРеДставляет
собой произведение главных кривизн.
При изгибании поверхности средняя кривизна, вообще говоря, изменяется,
а гауссова остается инвариантной в каждой точке поверхности.
5*

68
ГАУССА РАСПРЕДЕЛЕНИЕ
ГАУССА РАСПРЕДЕЛЕНИЕ — распределение вероятностей, выражаемое
формулой:
Κ2πσ J
Ф(*)=
2σ2
Λ.
Это распределение встречается во многих приложениях. Его можно обобщить на
случай многих случайных величин. См. также Нормальное распределение.
Лит.: Б. В. Гнеденко, Курс теории вероятностей, Физматгиз, Μ., 1961.
ГЕЙНЕ — БОРЕЛЯ ЛЕММА — лемма о конечном покрытии. Г. — Б. л.
заключается в следующем: если бесконечная система отрезков Μ покрывает
отрезок [а, Ь], т. е. каждая точка отрезка [а, Ь) лежит внутри по крайней мере
одного из отрезков системы М, то из нее можно выделить конечную систему
отрезков М*у также покрывающую отрезок [а, Ь].
Эта лемма используется в математическом анализе и названа по имени двух
математиков — Э. Гейне и Э. Бореля.
Лит.: Г. М. Фихтенгольц, Курс дифференциального интегрального исчисления,
т. 2, М., Физматгиз, 1963; А. Я. X и н ч и н, Краткий курс математического анализа,
Физматгиз, М., 1961.
ГЕКСАЭДР — шестигранник. Примеры: пятиугольная пирамида,
параллелепипед, усеченная четырехугольная пирамида суть Г. Правильный Г.—куб (см.
Куб, Правильные многогранники).
Греч.: hex — шесть-f hedra — грань.
ГЕЛИКОИД — одна из форм винтовой поверхности (см.), когда образующая
линия есть прямая / (рис. 41). Г. получается, если прямая / вращается
равномерно вокруг оси ζ, расположенной в одной плоскости с /,
и вместе с тем движется равномерно и поступательно в
направлении оси ζ. Если образующая прямая перпендикулярна
оси /, то Г. называется прямым, если же не
перпендикулярна, то Г. называется косым.
ГЁЛЬДЕРА НЕРАВЕНСТВО для конечных сумм имеет
вид:
. χ 1 , ,1
Σ αφλ
<= ι
<
(Jj^j^.jjw)"
или, в интегральной форме:
i\f(xWdx
)p(W
)\9dx
W(x)g(x)dx\
где ρ > 1 и ~--f-—=l. Г. н. часто применяется в математиче-
Р Я
ском анализе. Г. н. является обобщением неравенства Коши
(см.) в алгебраической форме и неравенства Буняковского
(см.) в интегральной форме, в которые Г. н. обращается
при ρ=2.
ГЕЛЬФОНДА ТЕОРЕМА относится к вопросу об алгебраичности и
трансцендентности чисел. Г. т. утверждает, что всякое число вида α^ , где а —
алгебраическое число, отличное от 0 и 1, и β — иррациональное алгебраическое
число, будет трансцендентным числом. Пример: З^3 трансцендентно. Г. т. была
Рис. 41

ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ
69
доказана в 1934 г. советским математиком Гельфондом, чем была решена
седьмая из двадцати трех проблем Гильберта.
ГЕНЕРАТРИСА последовательности функций <р0 (jc), <px (*), ... — это
функция
/(*> 0=φο(*)+φι(*)/+φ2(*)/2+ ···
Например, если уп(х)— полиномы Лежандра (см.), то
/(* п= , 1 —·
у \ — 2xt + t2
ГЕОДЕЗИЧЕСКАЯ КРИВИЗНА кривой, расположенной на поверхности, —
кривизна проекции рассматриваемой кривой на плоскость, касающуюся
поверхности в данной точке. Подобно тому как обычная кривизна (см.) плоской
кривой служит мерой искривления кривой на ее плоскости, так и Г. к. служит
мерой искривления кривой на ее поверхности. Как обычная кривизна кривой
характеризуется уклонением кривой от прямой — касательной к кривой в данной точке,
так Г. к. кривой характеризуется уклонением кривой от геодезической линии,
касающейся кривой в данной точке.
Г. к. кривой на поверхности не изменяется при ее изгибании, т. е.
принадлежит внутренней геометрии (см.) поверхности.
ГЕОДЕЗИЧЕСКАЯ ЛИНИЯ — линия на поверхности, геодезическая
кривизна (см.) которой в каждой точке равна нулю. Достаточно малые дуги Г. л.
являются кратчайшими путями между их концами на поверхности. Поэтому
Г. л. играют на поверхности ту же роль, что и прямые на плоскости.
Г. л. на шаре — это большие круги, на цилиндре — винтовые линии (см.).
Лит.: Л. А. Л ю стер ник, Геодезические линии. Кратчайшие линии поверхности,
Гостехиздат, М., 194 0; П. К. Рашевский, Курс дифференциальной геометрии,
Гостехиздат, М., 1950.
ГЕОДЕЗИЧЕСКИЕ КООРДИНАТЫ — криволинейные координаты точки,
лежащей на поверхности, когда роль координатных линий и и ν играют
геодезические линии, проходящие через эту точку.
ГЕОДЕЗИЧЕСКОЕ КРУЧЕНИЕ кривой на поверхности — величина, равная:
J. ^?
ρ ds '
где ρ — радиус кручения кривой, φ — угол между направлением нормали к
поверхности и направлением главной нормали кривой, ds — элемент длины дуги.
На линиях кривизны Г. к. обращается в нуль.
ГЕОДЕЗИЧЕСКОЕ СООТВЕТСТВИЕ между точками двух поверхностей —
такое соответствие, при котором всякой геодезической линии (см.) одной
поверхности соответствует геодезическая линия другой. Например, если спроектировать
сферу из ее центра на плоскость, то большие круги сферы преобразуются в
прямые на плоскости, т. е. это соответствие (отображение одной поверхности на
другую) будет геодезическим.
Г. с. находит применение при составлении морских карт.
ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ — последовательность чисел, каждое из
которых, начиная со 2-го, равно предыдущему, умноженному на некоторое
постоянное для данной прогрессии число q (знаменатель прогрессии). Общее
выражение геометрической прогрессии можно записать так:
a, aq, aq2, . . ., aqn
где а — первый член, q — знаменатель Г. п.

70
ГЕОМЕТРИЧЕСКАЯ СУММА
Г. п. (при аг > 0) называют возрастающей, если значение знаменателя этой
прогрессии больше единицы (д > 1), и убывающей, если q < 1. Например,
возрастающие Г. п.: 3, 6, 12, 24, ... (</ = 2); 8, 16, 32, 64, ... (? = 2); убы-
11 / 1 \ 1 / 1 \
вающие: 3, 1, —, —, ... \Я=-£\\ 8, 4, 2, 1, γ , . . . \q= — I.
Сумма η первых членов Г. п. выражается 4°РмУлои:
а — aqn
Если \q\ < I, то при неограниченном числе членов (п-*ос) сумма Sn стремится
а
к определенному пределу S = , что записывают так: a+aq+aq*+ ··· -f·
\—q
а
-Ьа<7л-г* ··· = . Левую часть последнего равенства называют геометриче-
1 —<7
оо
ским рядом, который можно записать и так: Σ ciqn—1.
Свойства убывающей Г. п. иногда используют в тождественных
преобразованиях, при решении уравнений, при исследовании сходимости рядов методом
сравнения.
Пример: решить уравнение
1 -Ь х+х2+ *3-Ь ··· =2.
Так как левая часть уравнения есть геометрический ряд, то уравнение можно
записать так:
1 л 1
=2, откуда Х-. + —-.
Свойства Г. п. во многом аналогичны свойствам арифметической прогрессии
(см.). Иногда встречается в литературе знак Г. п. -Н-.
Термин Г. п. связан со свойством любого члена этой прогрессии
ал=Уап-1Ал+1 , т. е. любой член Г. п. с положительными членами есть
геометрическое среднее (см.) между предыдущим и последующим ее членами.
ГЕОМЕТРИЧЕСКАЯ СУММА — устаревшее название суммы векторов (см.
Векторное исчисление).
ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ (или теория геометрических
построений) — учение о построении геометрических фигур (см.) с помощью тех или иных
инструментов или средств построения. Г. п. в основном затрагивают вопросы
построения фигур (прямых, «-угольников, окружностей и др.), удовлетворяющих
определенным условиям: при этом средства построения заранее предписаны —
это или классические инструменты: циркуль и линейка (математическая
односторонняя), или ограниченные средства построений: угольник (модель прямого угла),
линейка с параллельными краями, или только одна линейка при условии, если
на плоскости начерчена окружность и ее центр (построения Штейнера), или
только один циркуль (построения Мора — Маскерони), или другие средства. Г. п.
как на плоскости, так и в пространстве опираются на постулаты
(конструктивные аксиомы) построения, т. е. на простейшие, элементарные задачи. Задача
считается решенной, если она сведена к конечному числу простейших задач-по

ГЕОМЕТРИЧЕСКОЕ МЕСТО
71
стулатов построения. При этом каждому инструменту будет отвечать
определенный набор постулатов.
Основными из методов решения задач на Г. п. в средней школе являются:
метод геометрического места точек, метод геометрического преобразования,
в частности гомотетии (см.) и подобия, и алгебраический метод.
Приведем пример решения задач на построение, считая, что постулаты
построения известны. Разделить данный отрезок на три равные части циркулем
и линейкой.
1-й способ — на основе теоремы Фалеса (рис. 42). Проведя произвольный
луч AM и отложив на нем равные произвольные отрезки АМ1^М1М2 = М2М3,
проведем ВМ^ а затем через Мг и Λί2 — прямые, параллельные ВМ3, которые
пересекут АВ в искомых точках деления: Ак^КгК^КъВ.
К кг
^1 /
wNy ι
<iSs/
",
Рис. 42
_J Д
/
/
^М
Рис. 44
2-й способ. Проведем произвольную прямую / || АВ (рис. 43) и отложим
на ней три равных произвольных отрезка А'К''«/('L'=L'B''. Проведя АА'
и ВВ', получим точку пересечения 5 (считая, что А'В'ФАВ).
Спроектировав К' и U из 5 на АВ, получим искомые точки К и L.
3-й способ. Примем отрезок АВ за медиану некоторого треугольника
(рис. 44) и воспользуемся свойством медиан треугольника. Проведем через В
произвольную прямую/и отложим на ней произвольные равные отрезки BC=BD.
Соединив Л и С, А и D, получим треугольник ACD, в котором данный отрезок
АВ — медиана. Проведя в нем вторую медиану СМ, получим точку L
пересечения АВ и СМ, так что BL^-rAB. Затем строим LK=LB, тогда AK = KL=LB.
о
Лит.: Η. Φ. Четверухнн, Методы геометрических построений, Учпедгиз, Л.,
194 0; Б. И. А р г у н о в и М. В. Бал к, Геометрические построения на плоскости,
Учпедгиз, 1958; А. Адлер, Теория геометрических построений, перев. с нем., Учпедгиз, Л.,
1940; А. И. Фетисов, Геометрия в школе, «Детская энциклопедия», Изд-во АПН
РСФСР, М.
со
ГЕОМЕТРИЧЕСКИЙ РЯД — ряд Σ ап, где последовательность {ап},
η = I
и=1, 2, , , . — геометрическая прогрессия (см.).
ГЕОМЕТРИЧЕСКОЕ МЕСТО каких-либо фигур (точек, прямых и др.) на
плоскости или в пространстве есть множество всех таких фигур на плоскости
или в пространстве, которые обладают определенным (данным) свойством.
Обычно рассматривают Г. м. точек, Г. м. прямых, Г. м, плоскостей и т. д.
Примеры: 1) Г. м. точек, расположенных внутри данного угла и одинаково
отстоящих от сторон угла α (α<180°), есть биссектриса этого угла; 2) Г. м.
точек, находящихся на расстоянии, равном единице, от данного отрезка АВ

72
ГЕОМЕТРИЧЕСКОЕ СРЕДНЕЕ
(рис. 45), есть замкнутая кривая KLMNPQ, состоящая из двух равных
параллельных отрезков KL и PN и двух полуокружностей А(1) и В(\); 3) Г. м.
прямых, проходящих через данную точку А и параллельных данной плоскости
а, есть пучок прямых с центром в точке А, плоскость которого параллельна
(или совпадает) с данной плоскостью а; 4) Г. м. прямых, параллельных данной
плоскости и отстоящих от нее на данном
расстоянии, есть пара параллельных плоскостей;
5) Г. м. плоскостей, проходящих через данную
прямую / и касающихся данной сферы О (г),
есть две, одна или ни одной плоскости в
зависимости от расположения прямой / и сферы О (г)
и др.
Часто один и тот же геометрический образ
Рис. 45 (или множество точек) можно рассматривать как
Г. м. одних или других фигур. Например, пару
параллельных плоскостей аг и <х2 можно
рассматривать и как Г. м. точек, находящихся на данном расстоянии от данной
плоскости а, и как Г. м. прямых, параллельных данной плоскости α и отстоящих
от нее на данном расстоянии.
ГЕОМЕТРИЧЕСКОЕ СРЕДНЕЕ η положительных чисел ах, а2, ...» ап есть
арифметический корень (см.) степени η из произведения этих чисел:
G—y afi^· ... ·αη или
Г. с. двух чисел аг и а2 называется также средним пропорциональным между
ах и α2·
Г. с. нескольких положительных чисел, как и всякое среднее (см.) этих
чисел, есть число, заключенное между наименьшим и наибольшим из данных
чисел (см. также Средние).
ГЕОМЕТРИЯ. Г. в первоначальном своем значении понималась как наука
о фигурах, о взаимном расположении и размерах их частей, а также о
преобразованиях фигур.
История Г. теряется в глубокой древности, но колыбелью ее, несомненно,
является Восток. Развитие Г. можно характеризовать четырьмя периодами,
границы которых нельзя отделить какими-то определенными годами. Первый
период— период зарождения Г. — относится ко времени примерно до V в. до н. э.
и связан с развитием культуры землемерия (откуда и происходит само название
Г.) в древнем Египте, Вавилонии и Греции.
Религиозные обряды связывались с построением жертвенников (см. Делос-
ская задача), практические потребности людей приводили к необходимости
измерения площадей земельных участков, объемов (емкости) сосудов, корзин и
зернохранилищ.
Геометрические сведения и факты в основном сводились к правилам о
вычислении площадей и объемов, и надо полагать, что эти правила носили больше
эмпирический, чем логический характер. В VII в. до н. э. геометрические
сведения были, по мнению греческих историков, перенесены из Египта и Вавилонии
в Грецию. Греческие философы стали знакомиться с египетской и вавилонской
мудростью. С этого времеьи начинается второй период развития Г. — период
систематического изложения Г. как науки, где все предложения доказывались.
К этому периоду были уже известны в Греции теоремы Фа леса (VI в. до н. э.).
Фалес путешествовал в Египет и заимствовал сведения по геометрии и
астрономии у жрецов о сумме углов в треугольнике, о вписанном угле и др. Анаксагор
(VI в. до н. э.) занимался квадратурой круга и перспективой. Пифагор
открывает несоизмеримые отрезки (иррациональные числа), доказывает теорему, нося-

ГЕОМЕТРИЯ
73
щую его имя. Гиппократ Хиосский (V в. до н. э.) — последователь
Пифагора — изложил систематически Г. («Элементы» геометрии) и определил площадь
луночки.
Платон и его ученик Аристотель (IV в. до н. э.) хотя и не оставили
никаких трудов по Г., но придавали большое значение системе и обоснованию Г.;
они положили начало определениям и аксиомам. Таким образом, Г. достигла
такого развития в Греции, что необходимо было ее систематизировать.
Таким систематизатором был Евклид (III в. до н. э.), изложивший Г.
(элементарную) на базе основных предложений — аксиом в своих знаменитых
книгах «Начала» (элементы), содержащих 13 томов. После Евклида появляется
в Греции ряд выдающихся математиков — Архимед, Аполлоний, Эратосфен (III в.
до н. э.) и др., которые обогатили Г. новыми открытиями.
Падение античного рабовладельческого строя привело к застою в развитии
Г. в Греции, однако Г. развивалась в странах арабского Востока, в Средней
Азии и Индии.
Зарождение капитализма в Европе привело к новому, третьему периоду
развития Г.—созданию в первой половине XVII в. аналитической Г. (см.),
творцами которой были Декарт и Ферма. Аналитическая Г. изучает свойства
геометрических фигур по их алгебраическим уравнениям, опираясь на метод
координат. В связи с развитием дифференциального исчисления и исследованием
геометрических свойств фигур локального характера (в окрестности данной
точки) возникла в XVIII в. дифференциальная Г. (см.) в работах Эйлера, Мон-
жа. В работах Ж. Дезарга и Б. Паскаля зародилась в первой половине XVII в.
проективная Г. (см.), которая возникла сначала при изучении изображения
перспективы, а затем при изучении тех свойств фигур, которые не изменяются при
проектировании с одной плоскости на другую из какой-либо точки пространства
(центральное проектирование), и впоследствии была завершена в трудах
Ж- Понселе.
Четвертый период развития Г. знаменуется созданием неевклидовых Г.,
первой из которых является Г. Лобачевского, созданная им при исследовании
обоснования Г., и в частности аксиомы о параллельных прямых (см.).
Содержание своей Г. Н. И. Лобачевский впервые доложил на заседании
физико-математического факультета Казанского университета в 1826 г. Работа была
опубликована в 1829 г. Венгерский математик Янош Бойаи опубликовал работу по тому
же вопросу в 1832 г. и в менее развитой форме. С момента создания Г.
Лобачевского роль аксиоматического метода (см.) в математике вообще ивГв
частности стала весьма важной. Евклидова Г. (обычная элементарная Г.,
изучаемая в школе) получила впоследствии свое аксиоматическое обоснование.
Аксиоматическое обоснование получили и другие Г.: Лобачевского, проективная,
аффинная, многомерная евклидова (л-измерений) и др.
В настоящее время Г. содержит многочисленные Г. и теории, между
которыми нет точных границ. При этом отдельные геометрические теории тесно
переплетаются с анализом (дифференциальная Г.), с теорией множеств (теория
точечных множеств, топология). Каждая Г. отличается от другой тем, какое
пространство она изучает (Евклида, Лобачевского), какими методами
(например аналитическая теория кривых 2-го порядка в аналитической Г. или чисто
геометрическая, синтетическая теория кривых 2-го порядка в синтетической Г.
(см.), какие объекты (фигуры) или свойства их она исследует (например, можно
рассматривать многогранники и их свойства, кривые и поверхности и т. д.).
Вопросы метрики (измерение длины отрезков, углов и площадей) приводят к
понятию метрической Г. Вопросы же инциденции (принадлежности,
расположения) приводят к понятию Г. положения, т. е. проективной.
Вопросы обоснования Г. приводят к разделу элементарной Г., изучающей
ее логическое обоснование, ее аксиоматику и построение, — эта научная
дисциплина называется основаниями Г.

74
ГЕОМЕТРИЯ ПОЛОЖЕНИЯ
Каждую из Г. можно также охарактеризовать (определить) по предложению
Клейна (см. Эрлангенская программа) соответствующей группой (см.) тех
преобразований, которые она изучает. Так, элементарная Г. определяется группой
евклидовых движений, аффинная — группой аффинных преобразований,
проективная— группой всех коллинеаций (проективных преобразований).
Греч.: γεω — земля и μετρεω — мерю — дословно означает землемерие.
JlHf.: Ж. Адамар, Элементарная геометрия, ч. 1 и 2. Учпедгиз, М., 1958;
Д. И. Перепелки н, Курс элементарной геометрии, ч. 1, 2. Гостехиздат, М., 1948;
Ф. Клейн, Элементарная математика с точки зрения высшей, т. И, ОНТИ» М., 1935;
Евклид, Начала, Гостехиздат, М., 1950; Б. Л. В а н д е ρ В а р д е н,
Пробуждающаяся наука, Физматгиз, М., 1959.
ГЕОМЕТРИЯ ПОЛОЖЕНИЯ — то же самое, что и проективная
геометрия (см.).
ГЕРОИ А ФОРМУЛА — формула, выражающая площадь треугольника через
три его стороны:
S~V р{р-а)(р-Ь)(р-с)<
где S — площадь треугольника, а, Ъу с — его стороны й ρ — полупериметр, т. е.
а -\-Ь+с
р=—^-.
Формула названа по имени древнегреческого инженера и ученого Герона,
работавшего в Александрии примерно в I в. н. э. Герон рассматривал треугольник со
сторонами: а= 13, Ь—14, с=> 15 и а=5, Ь= 12, с~ 13, у которых стороны и площади
(84 и 30) выражались целыми числами. Впоследствии такие треугольники с
целочисленными сторонами и целочисленной площадью стали называть героновыми.
Прямоугольные же треугольники с целочисленными сторонами (катетами и
гипотенузой) называются пифагоровыми треугольниками (они Же будут и героновыми
треугольниками).
ГЕССИАН — функциональный определитель, элементы которого — вторые
частные производные функции f от η переменных. Для функции трех
переменных, например, Г. имеет вид:
I &[_ д^ дЧ_ I
дх2 дхду дхдг
d2f д*1 _а*/_
дудх ду2 дудг
ay ay ау
дгдх дгду дг2
Если в особой точке М(х, у, г) Г. не равен нулю, то Μ — невырожденная
особая точка поверхности f(xy у, z)=0.
ГИЛЬБЕРТА ПРОБЛЕМЫ — двадцать три проблемы в математике,
выдвинутые Д. Гильбертом в 1900 г. на Международном конгрессе математиков
в Париже и относящиеся к различным областям математики (теории чисел,
теории множеств, теории функций, теории групп, топологии и др,).
Йот некоторые из Г. п.:
I. Проблема, касающаяся мощности континуума. Существует ли
множество, мощность которого больше мощности счетного множества, но меньше
мощности континуума?

ГИПЕРБОЛА
75
II. Проблема, касающаяся непротиворечивости аксиом арифметики. Можно
ли доказать непротиворечивость системы аксиом арифметики путем конечного
числа дедуктивных рассуждений?
III. Проблема о равносоставленности двух равновеликих тетраэдров. Будут
ли два равновеликих тетраэдра равносоставленными?
VII. Проблема об алгебраических и трансцендентных числах. Будут ли
числа вида а^ трансцендентными, где α — алгебраическое (α Φ 0); 1 и β —
алгебраическое иррациональное?
Не все Г. п. уже решены. Так, из приведенных проблем первая (проблема
континуума) еще не решена.
ГИЛЬБЕРТОВО ПРОСТРАНСТВО — обобщение «-мерного евклидова
пространства на бесконечномерный случай. Элементом (вектором) Г. п. является по-
со
следовательность чисел х19 х2, . . ., хп> · · · такая, что ряд Σ х\ сходится.
г= 1
Обычным образом определяется сложение векторов и умножение вектора на
число. Скалярное произведение (см.) двух векторов χ (хъ х2, . . ., хп, . . .)
оо
й у (ylt у2, · · ·♦ Ут · · ·) равно по определению (*) (х, у)= Σ */У/* причем
этот ряд всегда сходится, если сходятся ряды 2*f» 2^* **· п*
можнотолковать как пространство интегрируемых в квадрате функций (см. функция,
интегрируемая в квадрате). Именно, если каждой такой функции, заданной, скажем,
на отрезке [—Jt, л], поставить в соответствие последовательность ее
коэффициентов Фурье, то скалярное произведение функций fug
-f-rt
(Λ g)= J/(*) Six) dx
— π
в терминах этих коэффициентов запишется в виде (*). В этой интерпретации
две различные функции с одинаковыми коэффициентами Фурье задают один
элемент. Существуют также и другие модели Г. п. Из свойств Г. п. весьма
важным является полнота (см. Полное пространство) в смысле нормы (см.),
определяемой скалярным произведением:
и/п-У(Г7).
Г. п. рассматривалось впервые в работах немецкого математика Гильберта.
Понятие Г. п. встречается во многих отделах математики: в функциональном
анализе, теории вероятностей, интегральных уравнениях и др.
ГИПЕРБОЛА — кривая, получаемая сечением кругового конуса плоскостью,
параллельной двум образующим конуса (рис. 46). Г. можно определить и
многими другими способами. Г. есть геометрическое место точек Μ плоскости,
разность расстояний которых (по абсолютному значению) до двух данных точек
постоянна. Если Fx и F2 — данные точки —фокусы Г., 2а — данный отрезок
и Μ — текущая ее точка, то свойство Г. можно записать в виде:
\MFX — MF2\ = 2a
или
а2 «* '
где а и Ь — полуоси Г., а х,У — текущие координаты точки М. Из
уравнения вытекает, что Г. есть кривая второго порядка, имеющая

76
ГИПЕРБОЛИЧЕСКАЯ ГЕОМЕТРИЯ
V
Ϊ
ύ
J?
У\
\У0
\α
Ν* **
X
Рис. 46
центр и две оси симметрии. Ось χ называется действительной осью Г., ось у —
мнимой осью (отрезки 2а и 26 также называются соответственно действительной
с
и мнимой осями Г.). Если положить F1F2e=:2ci то число е= — называется экс-
а
центриситетом Г. (для Г. е > 1).
Ъ
Г. состоит из двух ветвей. Уравнение асимптот Г. имеет вид: у=±—-*,
а
а
уравнение директрис (см.): *=±— (на рисунке άχ и d2 — директрисы).
Г. есть геометрическое место точек плоскости, отношение расстояний
которых до ближайшего фокуса к расстоянию до
ближайшей директрисы постоянно (равное
эксцентриситету).
Если асимптоты Г. принять за оси
координат, то уравнение ее запишется в виде
у=—, т. е. Г. будет являться графиком
обратной пропорциональной зависимости.
Если а—Ь, то Г. называется равнобочной;
в этом случае биссектрисы координатных
углов будут асимптотами Г. Г. как график
зависимости у=— может быть использована
X
как простейшая номограмма (см.) для графического решения некоторых систем
уравнений 2-й степени и неравенств 2-й степени.
Ряд физических процессов (приближенно) протекает по закону, выраженно-
k
му уравнением Г.: у= — , отнесенной к своим асимптотам. См. также
Конические сечения.
Греч, hyperbole — избыток, преувеличение (площадь 2рх больше площади
у2; эксцентриситет Г. превышает 1).
ГИПЕРБОЛИЧЕСКАЯ ГЕОМЕТРИЯ —то же, что и геометрия
Лобачевского (см. Лобачевского геометрия). Название Г. г. связано с тем, что в
основных соотношениях этой геометрии гиперболические функции sh χ и ch x
играют такую же роль, какую в обычной, евклидовой геометрии играют роль
тригонометрические функции sin χ и cos x.
ГИПЕРБОЛИЧЕСКАЯ СПИРАЛЬ — плоская кривая, описываемая точкой Μ
при движении ее по вращающемуся лучу ОЛ так, что ее расстояние от центра
вращения О обратно пропорционально углу
а
поворота ρ = —, где а — расстояние
полюса О до некоторой прямой / — асимптоты
Г. с. (рис. 47); асимптота Г. с.
параллельна полярной оси х.
Если записать зависимость между ρ
и φ в декартовых координатах (в виде
у=а: х)% то графиком этой обратной
пропорциональной зависимости будет
гипербола. Отсюда и происходит название Г. с.
См. также Спирали.
Рис. 47

ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
77
ГИПЕРБОЛИЧЕСКАЯ ТОЧКА поверхности —точка, в которой гауссова
кривизна (см.) поверхности отрицательна. Вблизи Г. т. поверхность имеет
седлообразное строение.
ГИПЕРБОЛИЧЕСКИЕ ЛОГАРИФМЫ —то же, что и натуральные
логарифмы (см.).
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ. Гиперболические синус (shjc) и косинус
(chjc) определяются следующими равенствами:
sh* =
е?— β—χ
ch jc=
е* -\~е~
Гиперболические тангенс и котангенс определяются по аналогии с
тригонометрическими тангенсом и котангенсом:
,« shx chx
thχ = -—, cth jt=-—■.
ch x sh x
Аналогично определяются гиперболические секанс и косеканс:
sech jt=
1
chjc'
cosech jc=
1
shjc
Имеют место формулы:
Sh^^fr+lr+
ch*-l+2i+ir+
f
χ2Π+ΐ
(2/1 + 1)!
x2n
+ (2/г)!
+
+
Свойства Г. ф. во многом аналогичны свойствам тригонометрических
функций (см.). Уравнения jc=cos/, y=sin£ определяют окружность jc2-fy2=l;
уравнения jt=ch/, y=sht определяют гиперболу х2 — у2=1. Как
тригонометрические функции определяются из окружности единичного радиуса, так и Г. ф.
определяются из равнобочной гиперболы х2— у2=1. Аргумент t есть двойная
площадь заштрихованного криволинейного треугольника ОМЕ (рис. 48),
аналогично тому как для круговых (тригонометрических) функций аргумент /
численно равен удвоенной площади криволинейного треугольника ОКЕ (рис. 49):
пл. OKE=--(^KE.R) = --(^KE).l=-ti т. е. *=2 пл. ОКЕ;
Рис. 48
Рис. 49

78
ГИПЕРБОЛИЧЕСКИЙ КОСИНУС
ί^κ^Κ Ε для круга и t—\jME для гиперболы. Теоремы сложения для Г. ф.
аналогичны теоремам сложения для тригонометрических функций:
sh (jt-f-y) = sh χ ch у-Ь ch χ sh yt
ch (x+y) = ch χ ch y-f-sh χ sh y.
Эти аналогии легко усматриваются, если за аргумент χ принять комплексное
переменное г. Г. ф. связаны с тригонометрическими функциями следующими
формулами:
sh*=—ι sin ix9 ch*=cos/x,
где / — одно из значений корня У— 1. Г. ф. sh х, а также и chx могут
принимать сколько угодно большие значения (отсюда, естественно, и большие
единицы) в отличие от тригонометрических функций sin xy cos xf которые для
действительных значений не могут быть по модулю больше единицы.
Г. ф. играют роль в геометрии Лобачевского (см. Лобачевского геометрия),
используются при изучении сопротивления материалов, в электротехнике и
других отраслях знаний.
Встречаются в литературе также обозначения Г. ф. такие sinh jc; cosh x\
tgh*.
Лит.: В. Г. Шерватов, Гиперболические функции, Гостехиздат, М., 1958;
И. Я. Штаерман, Гиперболические функции, ОНТИ, М., 1935; А. Р. Ян польский,
Гиперболические функции, Физматгиз, М., I960.
ГИПЕРБОЛИЧЕСКИЙ КОСИНУС — функция
2~~
. Обозначается Г. к.
ch(jc). Производная от
символом ch χ. Г. к. есть четная функция: ch (
Г. к. вычисляется по формуле (ch *)'=sh jt.
См. также Гиперболические функции.
ГИПЕРБОЛИЧЕСКИЙ ПАРАБОЛОЙ Д — поверхность, каноническое уравне
ние которой в декартовых координатах имеет вид:
2р 2? Zy
Р> q> 0.
Это поверхность 2-го порядка, нецентральная, имеющая форму седла (рис. 50).
В сечении Г. п. плоскостями, параллельными координатным плоскостям,
получаются параболы и гиперболы* откуда
происходит и название Г. п. Поверхность Г. п.
можно получить перемещением параболы КОМ
в пространстве так, чтобы ее плоскость
оставалась параллельной самой себе, а вершина
О скользила бы по параболе ЛОВ. Через
каждую точку Г. п. проходят две прямые,
целиком лежащие на его поверхности, — это
так называемые прямолинейные образующие
Г. п. Г. п. можно получить также путем
перемещения некоторой прямой, пересекающей
три попарно скрещивающиеся между собой
прямые. Поэтому Г. п. относится к
линейчатым поверхностям (см.), как однополост-
ный гиперболоид, конусы, цилиндры,
плоскость и др.
Рис

ГИПЕРБОЛОИДЫ
79
ГИПЕРБОЛИЧЕСКИЙ СИНУС — функция
е* — е—х
Обозначается Г. с.
символом sh#. Г. с.—функция нечетная; sh(—х)=*—shx. Производная от
Г. с. вычисляется по формуле (sh jt)'«ch#. См. также Гиперболические
функции.
ГИПЕРБОЛИЧЕСКИЙ ТАНГЕНС — функция **J7 *~* . Обозначается Г. т.
sh#
ех+е-
символом th χ. Следовательно, th χ=~τ--ί где sh x — гиперболический синус
ch*
(см.), a chx — гиперболический косинус (см.). См. также Гиперболические
функции.
ГИПЕРБОЛИЧЕСКИЙ ЦИЛИНДР —цилиндрическая поверхность, у которой
направляющей линией является гипербола. Каноническое (простейшее) уравнение
Г. в декартовых координатах имеет вид:
х^ у*
а2~~Ь*~1'
Таким образом, Г. ц. — поверхность 2-го порядка. Г. ц. имеет целую
прямую (ось ζ) центров симметрии.
ГИПЕРБОЛОИДЫ — центральные поверхности 2-го порядка. Различают два
вида Г.: однополостные(рис. 51) и двуполостные (рис. 52). Однополостный
гиперболоид относится к числу линейчатых
поверхностей (см.); через любую точку
его проходят две прямые, целиком
лежащие на его поверхности. Эти прямые
называются прямолинейными образующими.
Рис. 51
Рис. 52
В сечении его различными плоскостями получаются различные кривые 2-го по
рядка: эллипс* гипербола и пересекающиеся прямые. В сечении двуполостного Г.
различными плоскостями получаются также эллипс, параболы и гиперболы. Оба
гиперболоида имеют асимптотический конус, к которому они приближаются,
однополостный Г. имеет внутренний, а двуполостныи Г. — внешний
асимптотический конус.
Канонические уравнения Г. имеют вид:
ν2 ,,2 -2
Л
&
- = 1 (однополостный),
?!
~ь*
1 (двуполостныи).

80
ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ
ГИПЕРГЕОМЕТРИЧЕСКИЕ ФУНКЦИИ — аналитические функции, опреде-
ляемые при \х\ < 1 с помощью гипергеометрического ряда (см.). Г. ф.
являются интегралами гипергеометрического уравнения
х(1—х)У"+[У — 1*+9+1)*]У' — *&У=Ь
Важнейшие специальные функции математического анализа являются
решениями гипергеометрического уравнения. Имеется большое число соотношений
между различными Г. ф., например:
у (а, 1, γ. χ)=γ^-χν\Χ-α, 1, Υ, ^Ζΐ)'
Лит.: В. В. Голубев, Лекции по аналитической теории дифференциальных
уравнений, 1950.
ГИПЕРГЕОМЕТРИЧЕСКИЙ РЯД — ряд вида
ч , α·β α(α-Η)β(β-Μ) 0
у(а. β, ν, х)^1 + т±х+ \ , ,* х +
1·γ b2.v(Y-H)
α(α+1)(α+2) β(β+1)(β+2) ,
Ь2.3 Y(Y + l)(Y+2) *~*~ '"
Г. р. был впервые изучен Л. Эйлером (1778).
Ряды Тейлора (см. Тейлора ряд) многих функций представляют собой
частные случаи Г. р., например:
(1+х)а=у(-а, β, β, χ),
ln(l + jc) = jcy(l, 1, 2, —χ).
ГИПЕРПЛОСКОСТЬ — плоскость размерности η — 1 в /г-мерном евклидовом
пространстве Rn. Уравнение Г. в однородных координатах имеет вид:
п+\
аЛ+аг^2+ ··· +ая*л+вл+1*л+1=0 или Σ 0№ = 0. (*)
Если /г=3, то Г. есть обычная плоскость, если /*=2, то Г. есть прямая
обычной евклидовой плоскости (или одномерная плоскость). Всякая /я-мерная
плоскость пространства Rn может быть рассматриваема как пересечение (п — т) Г.,
т. е. как множество точек, координаты которых удовлетворяют (п — т)
линейно независимым уравнениям типа (*).
См. также Гиперповерхность.
ГИПЕРПОВЕРХНОСТЬ — поверхность размерности η ·— 1 (см.) в /г-мерном
евклидовом пространстве.
См. Гиперсфера, Гиперплоскость.
Греч, υιερ (hyper) — сверх, над, по ту сторону.
ГИПЕРСФЕРА — сфера размерности п — \ (см.) в «-мерном евклидовом
пространстве Rni т. е. это геометрическое место точек пространства Rn,
находящихся на данном расстоянии (радиус Г.) от данной точки (центр Г.). При
/*=3 Г. является сферой, при /г=2 — окружностью.
См. также Гиперповерхность.
ГИПЕРЦИКЛ — то же, что эквидистанта (см.).
ГИПОТЕНУЗА — сторона прямоугольного треугольника (плоского или
сферического), лежащая против прямого угла. Две другие стороны прямоугольного
треугольника называются катетами (см.); при этом предполагается» что в сфери-

ГЛАВНАЯ ДИАГОНАЛЬ
81
ческом треугольнике имеется только один прямой угол. Г. и катеты
прямоугольного треугольника евклидовой плоскости связаны согласно теореме Пифагора
(см.) зависимостью: с2=а2+Ь2, где с — длина Г., a, b — длины катетов.
Греч, hypoteinusa — тянущаяся под чем-либо (под прямым углом).
ГИПОТРОХОИДА — плоская кривая, описываемая точкой Mt связанной
неподвижно с окружностью ω, катящейся внутри и без скольжения по другой
неподвижной окружности L (рис. 53). На чертеже кривая / — гипотрохоида точки,
жестко связанной с окружностью ω. Если
точка Μ лежит на окружности, то Г.
называется гипоциклоидой (см.).
Греч, ιπυ — под, τροχοειδης —
колосообразный,, круглый.
ГИПОЦИКЛОИДА — кривая,
описываемая произвольной точкой окружности,
катящейся без скольжения по другой
неподвижной окружности и имеющей с ней
внутреннее касание. В зависимости от
соотношения радиусов неподвижной и подвижной
окружностей получаются различные виды Г.:
астроида (см.), циклоида (см.) и др. Если
радиус подвижной окружности равен половине
И)·
Рис. 53
радиуса неподвижной окружности
то Г. вырождается в отрезок прямой—,
диаметр неподвижной окружности. Этим свойством
конструировании зубчатых передач для превращения
прямолинейное (в печатных машинах), в некоторых часовых механизмах. Г. и
эпициклоиды (см.) принадлежат к кривым более общего вида — рулеттам (см.).
Параметрические уравнения Г. имеют вид:
иногда пользуются при
кругового движения в
*=(#-— /-)cos0-f-rcos
y=(R — /■) sin 0 — г sin
[,*-„i].
[<*-„ f ].
окружности,
где R — радиус неподвижной окружности, г — радиус катящейся
О — угол, стягиваемый дугой между точками касания окружности.
Греч, ιπυ — под, κοχλο — окружность, круг.
ГИППОКРАТОВЫ ЛУНОЧКИ — фигуры, ограниченные дугами двух
окружностей, для которых с помощью циркуля и линейки можно построить
равновеликий прямоугольник. Гиппократом найдены три такие фигуры. В 1840 г. Клау-
зен (Германия) нашел еще две луночки, для которых можно построить
равновеликий прямоугольник.
ГЛАВНАЯ ДИАГОНАЛЬ матрицы —(упорядоченная) совокупность
элементов ап, а22» · · ·> апп квадратной матрицы || atj || :
ап1 апг ... ап
6 Толковый словарь математических терминов

82
ГЛАВНАЯ НОРМАЛЬ
ГЛАВНАЯ НОРМАЛЬ — та из нормалей пространственной кривой, которая
лежит в соприкасающейся плоскости (см.).
ГЛАВНЫЕ КРИВИЗНЫ поверхности в точке — это наибольшая и
наименьшая кривизны нормального сечения (см.) поверхности в этой точке. Обратные
величины Rx и R2 главных кривизн поверхности в точке называются
радиусами Г. к.
ГЛАВНЫЕ НОРМАЛЬНЫЕ СЕЧЕНИЯ —те из нормальных сечений (см.)
поверхности, для которых кривизна (см.) достигает наибольшего или наименьшего
значения.
ГЛАВНЫЕ ОСИ центральной кривой (центральной поверхности) 2-го
порядка— оси симметрии этой кривой (поверхности).
ГОЛОМОРФНАЯ ФУНКЦИЯ—однозначная аналитическая функция (см.).
ГОЛЬДБАХА ПРОБЛЕМА часто называется также проблемой Гольдбаха—
Эйлера. Г. п. заключается в гипотезе, что всякое нечетное число, начиная с 5,
может быть представлено суммой трех простых чисел, а всякое четное число,
начиная с 4, может быть представлено суммой двух простых чисел. Г. п. для
нечетных чисел была высказана петербургским академиком Христианом
Гольдбахом в письме к Леонарду Эйлеру в 1742 г. и в ответном письме Эйлера была
высказана Г. п. для четного случая. Решению Г. п. посвящена Виноградова
теорема (см.).
ГОМЕОМОРФИЗМ (или топологический изоморфизм) — взаимно однозначное и
взаимно непрерывное отображение двух топологических пространств. Взаимно
однозначное и непрерывное отображение компактного пространства на некоторое
топологическое пространство является Г. Г. — основное понятие топологии» которая
изучает топологические пространства с точностью до Г.
Пример. Многоугольник (контур), не имеющий самопересечений, гомеоморфен
окружности. Г. устанавливается так. Пусть Μ и ΛΓ—две точки многоугольника
и окружности, / и /'—периметры многоугольника и окружности. Точке N
многоугольника, отстоящей на расстоянии χ от Μ по периметру многоугольника,
ставим в соответствие точку Ν' окружности, находящуюся на расстоянии
X
*' =—/' от М' по длине окружности. Все расстояния вычисляются в одном
направлении обхода. Отображение полуоткрытого интервала 0 < / < 2π на
окружность единичного радиуса #=cos/, y=sin/ по формуле /-»(cos/, sin/) не есть Г.,
так как обратное отображение разрывно в точке (cos 2π, sin 2л).
ГОМОЛОГИЯ в проективной геометрии — взаимно однозначное преобразование
точек проективной плоскости в себя, при котором сохраняется коллинеарность
(прямолинейность) точек и неподвижность точек
некоторой прямой (оси Г.). В Г., не являющейся
тождественным преобразованием, все прямые, соединяющие
соответственные точки (А и Л', В и В'), пересекаются
в одной точке — центре Г., а соответственные прямые
(АВ и А'В') пересекаются на оси гомологии.
Если центр 5 не лежит на оси Г., то Г.
называется неособенной (или гиперболической, рис. 54); если
центр S лежит на оси Г., то Г. называется особенной
(или параболической). Обычно Г. задается центром
S, осью и парой соответственных точек Л,Л'. Г. с
собственным (конечным) центром и несобственной
(бесконечно удаленной) осью (рис. 55) есть гомотетия (см.); Г. с несобственным
центром Soo и собственной осью χ есть растяжение и сжатие к оси (рис. 56).
Г. с несобственным центром Soo и несобственной осью (центр лежит,
следовательно, на оси) есть параллельный перенос. Особая Г. с несобственным центром Soo*

ГОМОМОРФИЗМ
83
но с собственной осью χ (цнтр лежит на оси) есть сдвиг (рис. 57). Всякое
проективное преобразование плоскости есть произведение двух преобразований:
Г. и перемещения.
От греч. γομολογια — соответствие, согласие.
Рис. 55 Рис. 56 Рис. 57
ГОМОМОРФИЗМ (групп G, Gf , колец /С, К', алгебр А, А') ■— отображение φ:
G-+G' (соответственно К-+К'9 А-+А'), обладающее свойствами: Φ(£ι#2) =
=Φ(£ι)φ(£2) при любых g1? g2£G для групп, φ(£ι — £2)=Φ(£ι) — Φ(£2),
φ(^2)=Φ(^ι)Φ(^2) при любых klf k2£K для колец, φ(αια2)=Φ(αι)φ(α2)»
φ(λαι)=λφ(α1) при любых αι# α2ξΑ и любого числа λ из поля, под которым
заданы А и А' (см. Алгебра) для алгебр.
Г. называется тривиальным, если φ (£)=£, где е — единица G' для всех g£G
(в случае групп), φ(&) = 0, φ(α)=0 для всех &ζ/(, а£Л в случае колец и
алгебр.
Множество всех элементов g£G (соответственно К, А) таких, что ф(£)=е
(соответственно φ(&)=0, φ(α)=0), называется ядром Г.
Если Г. есть отображение на всю G' (соответственно К', А')у то Г.
называют эпиморфизмом, если ядро Г. состоит только из единицы группы G
(соответственно нуля, К или А), то Г. называют мономорфизмом. Г. группы G
(соответственно кольца К или алгебры А) в себя называют эндоморфизмом.
Г., являющийся эпиморфизмом и мономорфизмом, есть взаимно однозначное
отображение G (соответственно К, А) на G' (соответственно на К', Л'),
называемое изоморфизмом (см.). Изоморфизм G (соответственно К, А) на самое себя
называется автоморфизмом.
Примеры: 1. Пусть G — группа всех невырожденных матриц порядка п, а
Q' —группа чисел, не равных нулю относительно операции умножения.
Положим,
φ(£)-<ϊβϊ£,
где def g означает определитель матрицы g. Из свойств умножения матриц следует,
что φ—-Г.
2. Рассмотрим кольцо многочленов К одного переменного с целыми
коэффициентами. Пусть К'—кольцо целых чисел. Поставим в соответствие каждому
многочлену его старший коэффициент. Полученное отображение К-+К' есть Г.
3. Пусть А — алгебра всех матриц порядка η над полем комплексных чисел,
пусть Л==Л'. Определим отображение φ формулой:
φ(α)=(α'ΓΛ
где (а')"*"1 означает транспонированную обратную к а матрицу. Отображение φ
есть автоморфизм.
б*

84
ГОМОТЕТИЯ
Рассматривают также Г. квазигрупп, полугрупп, структур и др., понимая
под этим отображение, сохраняющее заданные в указанных алгебраических
системах операции.
Лит.: Б. Л. Ван дерВарден, Современная алгебра, ч. 1 и 2, Гостехиздат, М-,
1947; А. Г. Курош, Курс высшей алгебры, Физматгнз, М., 1962.
ГОМОТЕТИЯ — преобразование, в котором каждой точке Μ плоскости или
пространства ставится в соответствие точка М' такая, что выполняется
равенство:
SM'=SM-k,
где S —данная точка, называемая центром Г., a k — постоянное число, не
равное нулю, называемое коэффициентом Г.
При k>0 соответственные точки Ми М' лежат на одном луче с началом
в точке S (рис. 58, а), при k<0 точки Μ к М' лежат на разных лучах прямой,
имеющих своим началом точку S (рис. 58, б).
Простейшие свойства Г.: 1) Г. есть взаимно однозначное преобразование точек
плоскости в себя; 2) Если &=1, то Г. есть тождественное преобразование точек
S ММ'
ι ιθ О' О ι ι ι ι. ■
а
Mf S Μ
——Qi. Ο μι 'О—
δ
Рис. 58 Рис. 59
плоскости; при любом k=£0 точка S — центр Г.— двойная, т. е. она
преобразуется в себя; 3) Всякая прямая, проходящая через центр Г., преобразуется
в себя; 4) Всякая прямая АВУ не проходящая через центр S, преобразуется
при Г. в параллельную ей прямую А* В'\ отсюда углы между прямыми при Г.
сохраняются (рис. 59); 5) Отрезки при Г. переходят в параллельные им отрезки
и уменьшенные или увеличенные в \k\ раз. Поэтому Г. есть сжатие (растяжение)
плоскости к точке S; 6) Всякая окружность при Г. преобразуется в окружность,
при этом центр одной из них переходит в центр другой.
Г. задается обычно центром S и парой соответственных точек и обозначается
при этом так: #(S, Л, А'). Г. есть частный случай аффинного преобразования
(см.), при котором имеется только одна двойная точка.
Преобразование Г. используется при подобном копировании с помощью
пантографа (см.) при съемках плана местности (мензульная съемка), при решении
задач на построение.
Г. есть частный случай более общего преобразования — подобия (см.), при
котором всякий отрезок АВ переходит в Л'Б', так что выполняется равенство
A'B'=ABk, k^O. Но АВ и А'В' могут быть и не параллельны.
Греч, ομοζ — одинаковый, равный, θετοζ — расположенный.
ГОМОТОПИЯ — важное понятие топологии. Два непрерывных отображения
/(х) и g(x) топологического пространства (см.) А в топологическое
пространство В называются гомотопными, если существует непрерывная по совокупности
(х, t) функция /(*, t) (χ — точка пространства Л, / — число, 0</<1) такая,
что/(.*, 0)=/(я) и/(*, !)=£(*). В топологии рассматриваются задачи клас-

ГРАДИЕНТ
85
сификации отображений с точностью до Г. Особое значение имеет случай
отображения сферы в топологическое пространство.
ГОНИОМЕТРИЯ — учение о тригонометрических функциях и соотношениях
между ними. Г. есть вводная часть тригонометрии (см.). Термин Г. выходит из
употребления.
Греч, γωνία — угол, μετρεω — измеряю.
ГОРИЗОНТАЛЬ — прямая, параллельная горизонтальной плоскости проекций
и не перпендикулярная вертикальной плоскости проекций. На эпюре (см.)
вертикальная проекция а2 Г. (прямой а) будет
параллельна оси проекций хх, а горизонтальная ее
проекция aL может занимать любое положение
относительно оси проекций хх, но не может
быть перпендикулярна ей (рис. 60). На рисунке
прямая α (αχ, α2) есть Г.
Термин Г. употребляется в начертательной
геометрии (см.). См. также Фронталь.
ГОРНЕРА СХЕМА —способ деления
многочлена л-й степени а0хп-}-а1хп—1+ \-ап на линейный двучлен χ — α,
основанный на том, что коэффициенты неполного частного Ь0хп—1+Ь1хп—2+ · · · •\-ЬПг-1
и остаток г связаны с коэффициентами делимого многочлена и с α формулами:
60=00, bk^abfr-x+ah, £=1, 2, . . ., л — 1 и г=аЬп—х+ап. Вычисления по Г. с.
располагают в таблицу:
Рис.
а
<*0
Ь0
αϊ
&ι = αδ0+αι
<*2
Ьг=аЬх+аг
αη-ι
t>n-i= abn-2+an-i
Qn ι
r = abn-x+ani
Г. с. позволяет быстро вычислить коэффициенты неполного частного и остаток.
Пример. Разделить f(x)=x*+2x* — 4jc-f-3 на x-f3.
Ι ι
I
—3
1
2
—1
i °
3
—4
— 13
3
42
Неполное частное равно χ3—x2-f-3x—- 13 и остаток равен 42=/ (—3).
Г. с. позволяет быстро вычислять значения многочлена при х—ау т. е. /(а).
Г. с. является частным случаем Яковкина схемы (см.) деления многочленов.
Лит.: С. И. Новоселов, Специальный курс элементарной алгебры, «Высшая школа*,
М., 1956; М. В. Яковкин, Вычислительные действия под многочленами, Учпедгиз,
М., 1961.
ГРАД — сотая часть прямого угла, обозначается \ό. Один Г. делится на 100
частей, называемых метрическими минутами (1'), сотая часть которых
называется метрическими секундами (1"). Г. как единица измерения угла был введен
вместе с метрической системой мер (конец XVIII в.). Широкого практического
применения Г. не получил.
ГРАДИЕНТ функции u = f(xt у, г),
странства х, у, г,—вектор (см.) с
заданной в некоторой области про-
ди да ди
проекциями —-, —, —, обозначаемый сим-
дх ду дг

86
ГРАДУС
ди ди ди
волами: gradH=*--i-f---j-f-T-' к или grad f (χ, у, ζ). Г. является функцией
ох ду дг
точки (х, у, г), т. е. образует векторное поле (см.). Производная в
направлении Г. в данной точке достигает наибольшего значения и равна
■-■"-/(течи·.
т. е. направление Г. является направлением наибыстрейшего возрастания
функции. Г. в данной точке перпендикулярен поверхности уровня (см.), проходящей
через эту точку. Производная по направлению, перпендикулярному Г., т. е. по
направлению, лежащему в касательной плоскости к поверхности уровня,
равна нулю. Г. является потенциальным векторным полем, потенциалом
которого является данная функция / (х, у, г).
ГРАДУС — единица измерения плоских углов, т. е. это плоский угол,
равный -— части прямого угла. Угол в один Г. обозначается так: 1°.
90
Лат. gradus — шаг, ступень.
ГРАММА ОПРЕДЕЛИТЕЛЬ —определитель матрицы || α/y ||, составленной
по формуле
Q//=J Φ/ (x)<Pj(x)dxt
где <Ρχ, φ2, . . ., φη*-данная система функций. Г. о. всегда неотрицателен.
Функции <plt φ2, . . ., Ф/2 линейно независимы тогда и только тогда, когда Г. о.
положителен. Г. о. введен датским математиком И. Граммом.
ГРАНИЦА МНОЖЕСТВА — совокупность граничных точек (см.) этого
множества.
ГРАНИЧНАЯ ТОЧКА: 1°. Г. т. множества действительных чисел — такая
точка, что в любом содержащем ее открытом промежутке найдутся как
точки, принадлежащие множеству, так и точки, не принадлежащие множеству.
Г. т. множества сама может как принадлежать множеству, так и не
принадлежать ему.
Примеры: 1) для множества рациональных чисел χ на отрезке [0,1],
0<дг<1 граничными точками являются все (как рациональные, так и
иррациональные) точки отрезка [0,1]; 2) для множества точек *=—(я=1, 2, . . .)
η
1
граничными точками являются точки множества х=— и, кроме того, нуль;
η
3) граничными точками открытого промежутка (а, Ь) служат точки а и Ь.
2°. Г. т. множества /г-мерного, или метрического, пространства — такая
точка, что в любом, содержащем ее открытом шаре (см.) имеются как точки,
принадлежащие множеству, так и точки, не принадлежащие множеству. Г. т.
множества может как принадлежать множеству, так и не принадлежать ему.
Примеры: 1. Для множества точек Μ (jc, у) плоскости, удовлетворяющих
условиям г0<У х2+у2 <гх (г0<гг), граничными точками являются точки двух
концентрических окружностей с центром в начале координат О(0, 0) и
радиусами г0 и гj (в случае г=0 одна из окружностей заменится одной точкой —
началом координат, рис. 61).

ГРАФИК ФУНКЦИИ
87
Рис. 61
Рис. 62
2. Граничными точками множества точек Μ (χ, у, ζ) в пространстве,
определяемого условиями x2-\-y2<z<ht служат точки параболоида вращения с
уравнением х24-У2=г, лежащие ниже плоскости г=/г, и точки круга, лежащего
в этой плоскости и ограниченного окружностью, являющейся пересечением
параболоида с плоскостью г=h (рис. 62).
ГРАНЬ: 1°. Г. многогранника — плоский многоугольник, являющийся
частью поверхности многогранника (см.) и ограниченный его ребрами.
2°. Г. многогранного (телесного) угла — плоский угол его при вершине.
3°. Г. в арифметике — группа цифр' числа. Для облегчения чтения числа,
записанного более чем тремя цифрами, его разбивают справа налево на Г.
(классы), по три цифры в каждой. При извлечении квадратного корня из числа его
также разбивают на Г. по направлению справа налево, по две цифры в каждой,
а при извлечении кубичного (кубического) корня —по три цифры в каждой.
4°. Г. в смысле границы действительных чисел или точек числовой прямой —
см. Верхняя грань.
ГРАФИК ФУНКЦИИ у=/(лг) (действительного переменного) —
геометрическое место точек плоскости, декартовы прямоугольные координаты которых
удовлетворяют соотношению (равенству) у=/(*). Геометрически Г. ф. обычно
представляет некоторую плоскую линию, координаты точек которой есть
соответствующие значения аргумента и функции. Например, график линейной функции
у=ах+Ь (рис. 63, где у=2х+\) есть прямая линия; Г. ф. у=*ах2+Ьх+с
ч\
Рис. 63
Рис. 64
Рис. 65

88
ГРАФИК ФУНКЦИИ
(рис. 64, где у=х2— х) есть парабола (см.); Г. ф. у= — , выражающей
обратную пропорциональную зависимость между переменными χ и у, есть гипербола
(см.), асимптотами которой являются оси координат (рис. 65, где у=—I.
Гипербола с асимптотами, параллельными осям координат, служит графиком
дробно-линейной функции (см.). Г. ф. у=|*| есть прямой угол (рис. 66), стороны
которого есть биссектрисы 1-го и 2-го координатных углов.
Если рассмотреть Г. ф. y=sinjt в полярной системе координат, положив
y=pt jt=<p, то Г. ф. будет являться окружностью (рис. 67) с центром
Рис. 66
у\
/I ^ \
/ V >■ \
/ \ >■ А
/ V N
I ^ч'*—^
s^"\
\ / / {
\ ι ' 1
\\ ' J
\Л / /
/ / тч
1 / )\
ι / У \
\ / У '
\/ ^*^
Г^~*>>4
Is X )
V ^ λ /
\ \ 1/
V \У
X
Рис. 68
(т- т)·
Г. ф. o = sin 2 φ в полярной системе координат есть четырехлепестко-
вая роза (рис. 68).
Для построения графика какой-либо функции или графика уравнения
f(x, y)=0, где функция у выражеча неявно через аргумент х, обычно
составляют таблицу соответствующих значений аргумента и функции (или переменных,
входящих в уравнение) и строят в выбранной системе координат (прямоугольной
декартовой, аффинной, полярной)
соответствующие точки по паре значений χ
и у. Если функция непрерывная (см.
Непрерывная функция) и достаточно
гладкая (ее производные 2-го порядка
изменяются без резких скачков с изменением
аргумента), то, соединив построенные
точки плавной кривой, получим Г. ф.
Чем больше будет нанесено на
координатную сетку точек, чем они ближе
будут взяты друг к другу, тем точнее
будет выглядеть Г. ф.
Названия некоторых линий происходят от названия функций, графиками
которых служат эти линии, например: синусоида, косинусоида, тангенсоида, ло-
гарифмика (см.). «и
Г. ф. Дает наглядное представление поведения функции и ее свойств.
Например, из графика, изображенного на рис. 69, видно, что на участках ахъ χ2χ4ι
функция убывает, на участках χλχ2ι x*b функция возрастает, на участках axst
χώ функция положительна, а на участке хъхъ — отрицательна и т. д. Кроме
того, Г. ф. используется при графическом решении уравнений (см.) и неравенств
и как простейшие номограммы (см.). Например, с помощью Г. ф. хг (параболы)
Рис. 69

ГРИНА ФУНКЦИЯ
89
можно извлекать приближенно квадратный корень из чисел, а с помощью Г. ф.
ах(а>0\ аф\) или \gax(a>0; α*=1) можно извлекать приближенно корни
любой степени из чисел.
Лит.: Г. Е. Шилов, Как строить графики, Физматгиз, М., 1959: Энц. элем, мат.,
тт. 2 и 3, Гостехиздат, М., 1951, 1952.
ГРАФИЧЕСКОЕ РЕШЕНИЕ уравнений — приближенное решение уравнений
вида /(*) = ?(*) с помощью построения графиков функций f(x) и ф(х),
сводящееся к нахождению абсцисс точек пересечения графиков функции f(x) и φ(χ).
Примеры: 1) Г. р. уравнения л:2 — л: — 2=0 (х2=х-\-2) сводится к
построению графиков функции у=х2 и y=*-f-2, нахождению абсцисс точек пересечения
этих графиков (рис. 70) хг = — 1, λ'2=2; 2) Г. р.
уравнения s\ux=\gx сводится к нахождению
абсцисс точек пересечения графиков функций
y=sinл:, y = \gx (рис. 71), ^ = 2,7, х2=7А
и л;3=8,2 (с точностью до 0,1). Г. р. уравне-
2 /Г,3 \£ 5/5 7Л2л3 9 {χ
Рис. 70
Рис. 71
ний дает наглядное представление о действительных корнях уравнений и
закрепляет знания о графиках и свойствах функций.
Аналогично рассматривается и графическое решение неравенств.
ГРИНА ФОРМУЛЫ — формулы интегрального исчисления, дающие
возможность сводить объемный интеграл к поверхностному. Простейшей из них является
важная формула:
ίίίΐ-^^ί"^1^
до да
где —-, г" непрерывны в D, а Г —контур, ограничивающий область D.
ГРИНА ФУНКЦИЯ применяется при решении краевых задач (см.) для
дифференциальных уравнений. Г. ф. — есть функция, которая является решением
данного дифференциального уравнения, удовлетворяет граничным условиям и имеет
особенность, которая определяется порядком уравнения и размерностью
пространства. Если, например, G(P, Q) Г. ф. оператора Лапласа, для которого
поставлена первая краевая задача, то решение этой задачи можно найти по
формуле:
CdG
u(P)=) — u(Q)dSQ9
где интеграл берется по границе области, и всегда, если известна Г. ф. краевой
задачи, то ее решение можно представить в виде некоторых интегралов.

90
ГРУППА
В краевых задачах математической физики с нулевыми граничными
условиями:
Lu(xlt x2t . . ., xn) = f(xlt x2t . . ., xn)
Γ. φ. G(x, x0) определяется следующим образом: пусть us (χ, χ0) —- решение
уравнения:
L\u]=% (χ, χ0),
где
( 0 при |^·—λ'Ρ|>ε, /=1, 2 η
Фе (*· Χθ) = ) 1 I 0| . , п
— при Ι χι — xjf Ι < е, / = 1, 2, . . ., /2.
Тогда
G(x, je0) = limi/e (χ, χ0).
4-*0
В этом случае
и(х)-$СЦх,х0)Пх0)ах0.
С этим определением связаны другие названия Г. ф.—функция источника,
функция влияния.
Лит.: С. Л. Соболев, Уравнение математической физики, Гостехиздат, М.—Л.,
1950.
ГРУППА — множество G элементов я, Ь, с, . . ., для которых определена
операция умножения (композиция) такая, что любым двум элементам a, b из G,
взятым в определенном порядке, однозначно поставлен в соответствие некоторый
элемент с из того же множества, который называется произведением элементов
а и b и обозначается ab\ при этом для всех элементов множества G
относительно указанной операции выполняются следующие требования (аксиомы, постулаты):
1) произведение любых двух элементов или квадрат какого-либо элемента мно*
жества принадлежит тому же множеству; 2) для любых трех элементов
множества выполняется ассоциативный (сочетательный) закон: a(bc)=(ab)c; 3) в
множестве существует элемент е такой, что ае=еа~а. Элемент е называется
единичным, или единицей группы, или нейтральным элементом; 4) для любого
элемента а существует элемент а—1, принадлежащий тому же множеству, что
αα—1=β—1α=β. Элемент а—1 называется элементом, обратным а.
Примечание. В аксиомах 3 и 4 достаточно положить ае=а и аагт1=е
(или еа—а и α~1α=β), откуда следуют соотношения: еа—а и а—га^е.
По своей природе элементы Г. могут быть самыми различными (числа,
матрицы, функции, геометрические объекты и т. д.).
Если операция, определенная в Г., коммутативна (для любых двух
элементов ab=ba), то группа называется коммутативной или абелевой. Если
групповая операция называется не умножением, а сложением, то вместо произведения
употребляют сумму и в аксиомах Г. вместо знака умножения пишут знак
сложения. При этом вместо единицы группы говорят о нуле группы и обозначают его
символом 0; в этом случае вместо обратного элемента употребителен термин
«противоположный элемент».
Если число элементов Г. конечно, то она называется конечной Г., а число
ее элементов называется порядком Г. Если Г. состоит из элемента а и его
последовательных степеней а2, а3, ... аР*=е% то она называется циклической Г.
порядка р, где ρ — наименьшее натуральное число, для которого аР*=*е. Порядок
циклической группы ρ называют также порядком элемента а.

ГУРВИЦА КРИТЕРИЙ
91
Следует заметить, что множество элементов, образуя Г. при одной
композиции (групповой операции), может не составлять Г. при другой композиции.
Например, множество всех целых чисел (положительных, отрицательных и нуля)
образует Г. при операции сложения и не образует Г. при операции обычного
умножения.
Примеры: 1) Множество всех целых чисел относительно операции сложения
есть группа (аддитивная Г. всех целых чисел). 2) Множество всех рациональных
чисел, отличных от нуля относительно операции умножения, есть группа
(мультипликативная Г. отличных от нуля рациональных чисел). 3) Множество всех
векторов на плоскости относительно сложения векторов есть Г. 4) Четыре числа
1, —1, /, —ι образуют Г. относительно операции умножения. Эта Г.
циклическая четвертого порядка, порождаемая степенями элемента / или —Л
Можно дать второе определение Г., равносильное предыдущему: множе*
ство О, в котором определена операция над любыми двумя ее элементами,
называется группой, если: 1) эта операция ассоциативна, 2) для любых двух
элементов а, Ь из Q существует единственный элемент χ из G такой, что ax=bt и
единственный элемент у из G такой, что уа=Ь.
См. также Ли группа, Абелева группа, Галуа группа, Преобразование,
Федоровские группы, Фактор-группа, Непрерывная группа.
Лит.: А. Г. Курош, Теория групп, Гостехиздат, М., 1953.
ГРУППОИД — множество, в котором для любой пары его элементов
определена одна бинарная операция и результат ее однозначен. Другими словами, Г.—
это множество элементов {а, Ь% , . .} произвольной природы» в котором каждой
упорядоченной паре его элементов а, Ь однозначно сопоставлен некоторый третий
элемент с, обычно называемый произведением а на b (обозначение ab=*c).
Произведение является условным названием. Оно в общем случае не совпадает с
понятием произведения чисел, так как даже сами элементы Г. не обязаны быть
числами.
Понятие Г. является очень общим. В различных разделах математики
находят применение более узкие классы Г., получаемых из общего понятия
наложением на бинарную операцию тех или иных дополнительных ограничений,
например: группа (см.), полугруппа (см.), квазигруппа (см.) и др.
Лит.: А. Г. Курош, Лекции по общей алгебре, Физматгиз, М., 1962.
ГУРВИЦА КРИТЕРИЙ — условие, необходимое и достаточное для того,
чтобы все корни многочлена P(x)=aQxn+alxn—1-Ь ··· -\-ап имели
отрицательные действительные части. В частности, если а0>0 и все коэффициенты
многочлена вещественны, то все корни многочлена Ρ (χ) имеют отрицательные
действительные части тогда и только тогда, когда выполняются неравенства:
«1
а0
0
0
0
Дз
^2
ч
«0
0
аь ..
а4 . .
а3 .·
а2 ..
0 ..
. a2ft—ι
• агЬ-2
• Q2ft-3
• fl2fe-4
• ал I
при Λ»1, 2, . . ., п. Г. к. имеет важное значение в теории дифференциальных
уравнений. При помощи Г. к. определяется устойчивость (см.) решении системы
дифференциальных уравнений. Объектом применения Г. к. в этрм случае
является характеристический многочлен (см.) матрицы линеаризированной системы.
Г. к. впервые был дан немецким математиком А. Гурвицем.

ДАЛАМБЕРА ЛЕММА — лемма к одному из наиболее распространенных
доказательств основной теоремы алгебры (см.). Д. л. утверждает, что для
всякого многочлена f(x) с комплексными коэффициентами степени л>1, не
обращающегося в нуль при х=х0, т. е. если f(x0)?=0, найдется комплексное число h
(по модулю сколько угодно малое) такое, что | f(x0+h) |<| /(jc0) |.
Геометрический смысл Д. л. состоит в том, что функция I/(jc)| не может достигать
ненулевого минимума.
ДАЛАМБЕРА УРАВНЕНИЕ (Лагранжа уравнение) — дифференциальное
уравнение вида:
У=*Ф(У')+/(У').
где φ и / — некоторые дифференцируемые функции. Изучалось впервые Ш. Да-
ламбером в 1748 г.
ДВИЖЕНИЕ — преобразование пространства в себя, при котором выполняются
два условия: 1) сохранение расстояния между точками АВ=А'В'\ 2)
сохранение ориентации пространственных фигур. Всякое Д. в пространстве есть или
вращение вокруг некоторой оси, или параллельный перенос, или винтовое Д.,
т. е. вращение вокруг некоторой оси с последующим параллельным переносом
вдоль этой оси.
Если в преобразовании пространства в себя выполняется только одно
условие 1), то это преобразование называется ортогональным. Примером может
служить преобразование симметрии относительно плоскости, при котором меняется
ориентация фигуры (правая рука при зеркальном отражении представляется нам
левой рукой).
В прямоугольной декартовой системе координат Д. в пространстве
определяется формулами:
*' eau*+ei2y+(iis*+a,
У' =а21х+а22у+a2zZ+bt
ζ' =аьХх+аъ2у+амг+с,
где коэффициенты а& удовлетворяют условию:
, ( 1, если /=&,
аиа1к+а21а2к+а^азк=^0^ ^^ {фк^
и определитель, составленный из коэффициентов, равен 1:
П1
Qi
12
"18
α2ΐ α22 α23
α«
<*32
-*38
- + 1.
В ортогональных преобразованиях возможно равенство Δ = — 1. что отличает
их от Д.
Аналогично определяется Д. на плоскости, но, в отличие от Д. в
пространстве, Д. на плоскости определяют как преобразование, сохраняющее только
расстояние между точками. Отсюда на плоскости различают два рода Д.: Д. первого

ДВОЙНАЯ ТОЧКА
93
рода, не выводящее из плоскости и не меняющее ориентации фигур (рис. 72),
и Д. второго рода, выводящее из плоскости (переворачивание плоскости в
пространстве) и меняющее ориентацию фигуры (рис. 73).
Всякое Д. первого рода на плоскости есть или параллельный перенос, или
вращение (см.) вокруг некоторой точки. Всякое Д. второго рода есть симметрия
относительно некоторой прямой с последующим переносом или вращением.
Д. первого рода на плоскости в прямоугольной системе координат
выражается формулами:
х' = х cos φ — у sin φ-fa,
у' =х sin φ-f-y cos φ+6,
где α, b — координаты нового начала, (χ', у1
соответствующей координатам (х, у) точки
положительным направлением оси Ох и ее
образом— осью О'х'.
Д. второго рода в прямоугольной
системе координат выражается формулами:
х' =х cos φ-Ьу sin φ-f α,
у* =х sin φ — у cos ψ+b.
При надлежащем выборе осей координат
формулы преобразований Д. могут быть упрощены.
) — координаты точки М' (образа),
Μ (прообраза), φ —угол между
Рис. 72
Рис. 73
Множество Д. как в пространстве, так и на плоскости составляет группу
Д. может быть введено в элементарной геометрии аксиоматически, т. е. как
основное понятие, и может быть производным понятием, т. е. определяется через
другие понятия, например через понятие равенства (конгруэнтности). В средней
школе Д. принимается как основное и выражается в терминах «наложение»,
«поворот» и др.
ДВОИЧНАЯ СИСТЕМА счисления — позиционная система счисления (см.)
с основанием g=2. В Д. с. с. всего две цифры 0 я 1, что весьма удобно
поддается физическому моделированию — двумя физическими состояниями. Так, в
электронных вычислительных машинах электронная лампа (например, триггер) может
находиться в одном из двух состояниях: пропускать ток (в фиксированном
направлении) или не пропускать, что соответственно моделирует 0 или 1 (или
наоборот). Поэтому во многих вычислительных машинах пользуются Д. с. с. На
практике в устных и письменных немашинных вычислениях пользоваться Д. с. с.
неудобно, так как сравнительно небольшие числа в Д. с. с. записываются как
весьма многозначные. Например, число 900 в Д. с. с. записывается как 11-знач-
ное число: 11 110101000.
ДВОЙНАЯ ТОЧКА кривой — простейший тип особой точки (см.) кривой
f(xt y)=0t характеризующейся тем, что в этой точке имеют место равенства:

94
ДВОЙНОЕ ОТНОШЕНИЕ
—■=—=0 (признак особой точки вообще) и по крайней мере одна из частных
дх ду
d*F d2F
производных второго порядка -—■ или —-, отличная от нуля.
дх* дуг
Д. т. к. может быть узловая или точка самопересечения (рис. 74),
изолированная (рис. 75), точка возврата (рис. 76).
Υ
Μ
Рис. 74 Рис. 75 Рис. 76
ДВОЙНОЕ ОТНОШЕНИЕ четырех точек прямой (четырех прямых пучка,
четырех плоскостей пучка) — то же самое, что и сложное отношение (см.) или
ангармоническое отношение (см.).
ДВОЙНОЙ РЯД — выражение вида:
βιι+βΐ2 + ··· +а1п+ ··.
... +a21-f-a22-f- ··· +а2п+ ···
··· +ат1+ат2+ ... +атп+ -·.
Д. р. удобно записывать таблицей с бесконечным числом строк и столбцов.
Если dij — числа, Д. р. называется числовым, если а^ — функции, Д. р.
называется функциональным.
Как и в случае обыкновенных рядов (см.), важным понятием является
т η
частичная сумма Д. р. 2 2ααβ ^тп% Говорят, что числовой Д. р. сходится
α=:1 В=1
к числу S (сумме ряда), если для всякого ε>0 существует N такое, что при
m>N и n>N выполняется неравенство
\Smn-S\<e.
оо
С Д. р. связан повторный ряд — ряд с элементами Ьт= ^атп (конечно,
оо \ оо
если 2а^Л СХ°ДИТСЯ )· Сумма 2j bm> если она существует, называется суммой
л=»1 / т—1
Д. р. по строкам. Аналогично определяется сумма по столбцам. У сходящегося
Д. р. суммы по столбцам и по строкам существуют, совпадают между собой
и равны сумме Д. р. Обратное неверно. Имеются такие Д. р., у которых
существуют суммы по строкам Sx и по столбцам S2, но Sij£S2·
ДВОЙНОЙ ЭЛЕМЕНТ геометрического преобразования — точка (прямая или
плоскость), которая переходит (преобразуется) сама в себя, т. е. точка, для ко-

ДВОЙСТВЕННОСТИ ПРИНЦИП
95
торой образ М' и прообраз Μ совпадают: М'=М. Так, например, центр
гомотетии (см.) является двойной точкой; точки оси симметрии и сама ось
симметрии являются двойными элементами в преобразовании симметрии. Д. э.
преобразования также называют неподвижным элементом геометрического
преобразования.
ДВОЙСТВЕННОСТИ ПРИНЦИП—одна из основных теорем проективной
геометрии (см.): 1°. Д. п. в проективной плоскости (малый Д. п.) заключается
в следующем. Если какое-нибудь предложение, выраженное в терминах
инцидентности «точек» и «прямых», верно, то будет также верно и другое предложение
(двойственное первому), в котором все слова «точка» заменены словами «прямая»
и, наоборот, все слова «прямая» заменены словами «точка».
2°. Д. п. в проективном пространстве (большой Д. п.) состоит в том, что
если какое-нибудь проективное предложение, выраженное в терминах
инцидентности «точек», «прямых» и «плоскостей», верно в проективном пространстве,
Рис. 77
то будет верно также и другое предложение (двойственное первому), в котором
все слова «точка» заменены словами «плоскость» и, наоборот, все слова
«плоскость» заменены словами «точка».
На проективной плоскости двойственными предложениями (которые обычно
записываются в 2 столбца) будут:
1. Теорема Паскаля: Во
всяком шестивершиннике,
вписанном в кривую 2-го порядка, точки
пересечения противоположных сторон
лежат на одной прямой хх — прямой
Паскаля. На рисунке 77 в
шестивершиннике 123456 противоположными
сторонами являются: 12 и 45; 23 и 56; 34 и 61.
Точки пересечения /С, L, Μ
противоположных сторон лежат на одной
прямой— прямой Паскаля.
2. Две различные точки
определяют только одну прямую.
1. Теорема Брианшона: Во
всяком шестистороннике, описанном
около кривой 2-го порядка, прямые,
соединяющие противоположные
вершины, пересекаются в одной точке —
точке Брианшона. На рисунке 78 в шести -
стороннике 123456 вершины 1 и 4; 2 и
5; 3 и 6 являются противоположными.
Прямые, проходящие через
противоположные вершины 14, 25 и 36,
пересекаются в одной точке S — точке
Брианшона.
2. Две различные прямые
пересекаются только в одной точке.
Если одна теорема проективной геометрии доказана, то двойственная
ее теорема будет верна по Д. и. Впервые Д. п. был высказан французским

96
двоякой кривизны кривая
ученым Понселе. Многие понятия проективной геометрии носят двойственный
характер; так, ряд 1-го порядка двойствен пучку 1-го порядка, ряд 2-го порядка
(кривая 2-го порядка) двойствен пучку 2-го порядка (кривой 2-го класса).
Д. п. иногда называют принципом взаимности или дуальным принципом.
Имеется также Д. п. в абстрактной теории множеств, в математической логике
(в исчислении высказываний и в исчислении предикатов) и в топологии.
Лит.: Н. Ф. Чет вер у хин, Проективная геометрия, Учпедгиз, М., 1953;
Н. В. Ефимов, Высшая геометрия, Фнзматгиз, М., 1961; Д ж. Юнг, Проективная
геометрия, пер. с англ., ИЛ. М., 1949; П. С. Александров, Введение в общую
теорию множеств и функций, Гостехнздат, М., 1948; Д. Г и л.ь бе ρ τ и В. Аккерман,
Основы теоретической логики, пер. с нем., ИЛ, М., 1947.
ДВОЯКОЙ КРИВИЗНЫ КРИВАЯ — синоним пространственной кривой (см.),
д. к. к. характеризуется в каждой своей точке двумя числами — первой и
второй кривизной (кручением пространственной кривой). См. Кривизна, Кручение.
ДВУГРАННЫЙ УГОЛ — совокупность двух полуплоскостей, исходящих
из общей прямой (рис. 79). Общая прямая называется ребром Д. у., а
полуплоскости— гранями Д. у. Д. у. с ребром / и гранями α
и β обозначается так: α / β, или Ζ (α, β), или ζ. (Ι).
Д. у. называется развернутым, если обе его грани вместе
с ребром составляют одну плоскость. Д. у., отличный от
развернутого, делит пространство на две области, из
которых одна выпуклая, другая невыпуклая, аналогично
делению плоскости углом на две области. Обычно выпуклую
область пространства называют внутренней областью Д. у.,
а невыпуклую — внешней областью Д. у. Если за
внутреннюю область принимается выпуклая, то говорят, что Д. у.
меньше развернутого. Если же за внутреннюю область
принимается невыпуклая, то говорят, что Д. у. больше
развернутого, или входящий двугранный угол. Плоскость,
перпендикулярная к ребру Д. у., пересекает его по углу,
который называется линейным углом Д. у. Д. у., У которого
линейный угол прямой, называется прямым.
ДВУПОЛОСТНЫЙ ГИПЕРБОЛОИД — одна из поверхностей 2-го порядка,
каноническое уравнение которой в прямоугольных декартовых координатах имеет
вид:
Рис. 79
г2 У1
а2_Ь62
~—-h
где а, 6, с — отрезки (числа), называемые полуосями
Д. г. Пересекая Д. г. (рис. 80) координатными
плоскостями z=0, у=0, лг=0# получим в сечении
соответственно мнимый эллипс и
ζ χ
гиперболы — — — = 1
с2 а2
(в плоскости χΟζ) и — — — = 1 (в плоскости yOz). Д. г.
с1 ой
состоит из двух частей (полостей). При а=Ь Д. г.
называется Д. г. вращения, он получается вращением гиперболы
ζ2 х2
— —— = 1 вокруг оси Oz. Уравнение Д. г. вращения
имеет вид:
jc2+ys
= 1.
Рис. 80

ДЕДУКЦИЯ
S7
Д. г. имеет центр симметрии — точку О(0, 0, 0); координатные плоскости
являются его плоскостями симметрии.
См. также Гиперболоиды.
ДВУЧЛЕН (бином) — многочлен, содержащий в точности два члена
многочлена (см.).
ДВУЧЛЕННОЕ УРАВНЕНИЕ — уравнение вида хп — а=0, где а — любое
комплексное число, η — натуральное. В поле комплексных чисел Д. у. имеет
η решений (корней), которые в комплексной плоскости располагаются на
окружности с центром в начале координат и радиусом, равным арифметическому
корню /2-й степени из модуля числа а.
Д. у. вида хп — 1=0 называется уравнением деления круга (окружности),
так как деление круга (окружности) на η равных частей эквивалентно решению
этого уравнения.
Корни уравнения хп—1=0 есть корни я-й степени из 1; все они
располагаются на окружности радиуса, равного 1* имеющей центр в начале координат.
Корни уравнения хп — 1=0 имеют вид:
2nk . . 2π£ , Λ „ rt
Sb = cos -Η sin (где £ = 0, 1,2, . . . , я—- 1).
η η
Зная хотя бы один корень уравнения хп+— а=0, можно путем умножения его
на корни той же степени из 1 получить все остальные корни этого уравнения.
Произведение ek >гк и частное ek :ek двух любых корней л-й степени
из единицы есть корень той же степени из единицы.
Существуют такие корни n-й степени гк из 1, что все остальные корни той
же степени из 1 есть степени корня ε#. Такие корни ε# называются
первообразными (см.). Если левую часть уравнения деления круга представить в виде
произведения неприводимых многочленов (л; — 1) fx (χ) /2 (χ) ... fi(x) с целыми
(действительными) коэффициентами, то один из этих многочленов fj(x) будет
иметь все корни первообразные. Для того чтобы корень ek был первообразным,
необходимо и достаточно, чтобы кип были взаимно простыми числами.
Например, εχ — всегда первообразный: гк=г^-
Д. у. также называется уравнение вида ахт+bxn = 0 (m, η —
натуральные), решение которого сводится к решению рассмотренного выше уравнения.
ДЕДЕКИНДОВО СЕЧЕНИЕ — аксиоматический метод введения
иррациональных чисел. Впервые дан Дедекиндом в 1872 г. Согласно этому методу
иррациональное число определяется как разбиение множества рациональных чисел
на два класса, «верхний» и «нижний», такое, что: 1) любое число «верхнего»
класса больше любого числа «нижнего» класса и 2) в «верхнем» классе нет
наименьшего числа, в «нижнем» классе нет наибольшего.
В множестве таких чисел-разбиений естественным образом вводятся понятия
сложения, вычитания и других арифметических действий.
Рациональное число а можно также истолковать как разбиение множества
рациональных чисел на два класса (числа меньшие или равные а относятся
к одному классу, а числа большие а — к другому).
Пример: У 3 — иррациональное число, разбивает рациональные числа на два
класса: один класс — отрицательные числа, нуль и положительные числа а такие,
что а8<3, а другой класс — положительные числа Ъ такие, что 63>3.
ДЕДУКТИВНЫЙ МЕТОД в методике преподавания математики — то же, что
и дедукция (см.).
ДЕДУКЦИЯ —метод рассуждения (доказательства), при котором
отправляются от общего предложения (суждения) к частному. Старинный пример Д.:
«Все люди — смертны (большая посылка). Сократ — человек (малая посылка).
» Толковый словарь математических терминов

98
ДЕЗАРГА ТЕОРЕМА
Следовательно, Сократ — смертен (вывод-заключение)». Если известно, что
предложение: «Всякое натуральное число, сумма цифр которого делится на три, само
делится на три», — верно, а мы хотим узнать, делится ли данное конкретное
число, например 456, на 3, то достаточно убедиться в том, что сумма его цифр
4+5-г6=15 делится на 3.
Аналогично теорему, доказанную для любой фигуры (любого треугольника,
любого параллелограмма и т. д.), применяем для частной, какой-то данной
фигуры. В настоящее время Д., или дедуктивным методом доказательства,
называется доказательство, основанное на системе определенных аксиом. И поэтому
дедуктивный метод, или Д., называется аксиоматическим методом. Д. является
строгим, логически обоснованным методом доказательства в математике. Д.
является обращением индукции (см.). Всякая Д. включает в себя элемент
индукции. Математическая индукция (см.) является примером Д., так как она
основана на аксиоме (принципе) математической индукции.
Дедуктивные рассуждения и доказательства в школе проводятся после
индуктивных, на более поздней ступени обучения учащихся. В начальной
же школе учитель больше использует индукцию, конкретные, наглядные
доказательства, которые не столько доказывают, сколько убеждают.
Д., наряду с синтезом (см.), анализом (см.), индукцией (см.) и аналогией
(см.), является одним из научных методов исследования.
Лат. deductio — выведение.
ДЕЗАРГА ТЕОРЕМА. Если соответственные стороны трехвершинников ABC
и А'В'С пересекаются в трех точках х, у, ζ, принадлежащих одной прямой,
то прямые, соединяющие соответственные вершины, проходят через одну точку
S — первая теорема Дезарга (рис. 81).
Справедливо и обратное предложение: если
прямые, соединяющие соответственные
вершины трехвершинников ABC и А'В'С,
проходят через одну точку, то соответственные
стороны этих трехвершинников пересекаются
в трех точках, принадлежащих одной прямой
(вторая теорема Дезарга). Справедливость
второй теоремы Дезарга следует из первой
по принципу двойственности (см.
Двойственности принцип). Д. т. справедлива как для
трехвершинников, лежащих в одной
плоскости, так и для трехвершинников, лежащих
в разных плоскостях.
Рис. 81 Д. Гильберт доказал, что если трех-
вершинники ABC и А 'В'С9 лежат в одной
плоскости, то доказать Д. т. (первую, считая, что вторая Д. т. еще не
доказана) без обращения к трехмерному пространству нельзя, т. е. ее нельзя
логически вывести из принятых аксиом проективной плоскости. Следовательно,
Д. т. можно рассматривать как независимую аксиому (см.) плоской проективной
геометрии (см.).
Д. т. — одна из важных теорем проективной геометрии. Д. т. можно
использовать и в элементарной геометрии при решении конструктивных задач.
Например, задача: провести через точки А и В прямую с помощью линейки,
длина которой меньше длины ABf — решается на основании Д. т.
Трехвершинники, упоминаемые в Д. т., называются гомологичными, поэтому
Д. т. часто называют Д. т. о гомологичных треугольниках.
ДЕЗАРГОВА ГЕОМЕТРИЯ — геометрия, основанная на системе аксиом,
состоящей из аксиом проективной плоскости и аксиомы (предложения) Дезарга
о гомологичных треугольниках (см. Дезарга теорема, а также Недезаргова
геометрия).

ДЕКАРТОВ ОВАЛ
99
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА — это все рациональные и иррациональные
числа (см.). Д. ч. образуют поле (см.). Термин Д. ч. противопоставляется
числам мнимым (комплексным мнимым) (см.). Д. ч. иначе называются
вещественными числами.
ДЕКАРТОВА СИСТЕМА КООРДИНАТ — прямолинейная система координат
(см.) на плоскости или в пространстве, в которой масштабы по осям одинаковы
(длины векторов, направленных по осям, равны), Д. с. к. — частный случай
аффинной системы координат, когда векторы-реперы имеют равную длину.
Д. с. к. названа по имени французского ученого Р. Декарта, однако система
координат у самого Декарта сводилась лишь к одной координатной четверти,
была, вообще говоря, косоугольной. Если оси координат взаимно
перпендикулярны, Д. с. к. называют прямоугольной.
ДЕКАРТОВ ЛИСТ — плоская кривая, уравнение которой в прямоугольной
декартовой системе координат (см.) имеет вид:
*3-f-ys — 3а*у=0. (*)
Д. л. — кривая 3-го порядка. Прямая дс-Ьу-}-я=0 есть асимптота (см.)
Д. л. (рис. 82). Если положить y^xt (**), то из (*) и (**) получим
параметрическое уравнение Д. л.:
Sat
Х~ 1-W3 '
За/2
У 1-М3
Полярное уравнение Д. л. имеет вид:
a cos φ sin φ
pass .
cos3 φ+sin3 φ
Так как координаты χ я у входят в уравнение (*) симметрично, то
Д. л. расположен симметрично относительно биссектрисы 1-го и 3-го
координатных углов. Начало координат есть узловая точка
(см.) Д. л. Оси координат *=0 и у=0 являются
касательными к Д. л. в узловой точке. Кривая
пересекает сама себя в начале координат под
прямым углом.
Д. л. впервые был упомянут как кривая,
обладающая определенным свойством, в письме Декарта
к Ферма в 1638 г. Форма Д. л. была установлена
Робервалем. Окончательная форма кривой вместе
с ее асимптотой была определена в конце XVII в.
Гюйгенсом и И. Бернулли. Название Д. л. прочно
вошло в математику лишь с начала XVIII в.
Лит.: А. А. С а ве л ов
М.. 1960.
Плоские кривые, Физматгиз,
ДЕКАРТОВ ОВАЛ — плоская кривая, обладающая тем свойством, что
расстояния гх и г2 любой ее точки Μ от двух данных точек Fx и F2 (фокусов)
связаны неоднородным линейным уравнением г1+тгй=а (т и а — постоянные
числа). Это уравнение Д. о. в биполярных координатах (см.).
Д. о. кривая 4-го порядка. При т=\ Д. о. превращается в эллипс (см.)
при т = — 1 Д. о. превращается в гиперболу (см.).
7*

100
ДЕКРЕМЕНТ ПОДСТАНОВКИ
Частным случаем Д. о. является также улитка Паскаля (см.). Впервые
Д. о. исследован Декартом в его «Геометрии» (1637) в связи с задачами
по оптике: требовалось найти такую кривую, которая преломляла бы лучи,
Еыходящие из одной точки так, чтобы преломленные лучи проходили через
другую заданную точку.
И. Ньютон дал другое определение Д. о.: как геометрическое место точек
плоскости, отношение расстояний которых от двух заданных окружностей,
лежащих в той же плоскости, постоянно; центры этих окружностей есть фокусы
овала.
Существует также стереометрический способ определения (построения) Д. о.:
Д. о. есть проекция линий пересечения двух круговых конусов с
параллельными осями на плоскость, перпендикулярную к этим осям.
Лит.: А. А. Савелов, Плоские кривые, Физматгиз, М., 1960.
ДЕКРЕМЕНТ ПОДСТАНОВКИ. Пусть подстановка (см.) п-и степени разложена
в произведение циклических подстановок (см.) без общих действительно
перемещаемых символов. Пусть s — число циклических подстановок-сомножителей
плюс число символов, оставляемых рассматриваемой подстановкой на месте.
Тогда Д. п. равен разности η — s. Д. п. четен для четной подстановки (см.)
и нечетен для нечетной подстановки (см.).
Пример.
Мз 8 ? ί 4 2 ? б) =<' 3 5 4> (286Н7>·
Д. п. равен 8 — 3=5, так как здесь участвуют две циклические подстановки
и один символ 7 остается на месте. Подстановка 5 нечетна.
ДЕЛЕНИЕ — операция (действие), обратная умножению, т. е. действие,
позволяющее находить по данному произведению и одному из сомножителей
другой сомножитель. Таким образом, разделить а на Ъ значит найти такое jc,
что Ьх=а или xb=a. Заданное произведение а называется делимым, заданный
сомножитель Ъ называется делителем и неизвестный (искомый) другой
сомножитель χ называется частным от Д. а на Ь или отношением а к Ь. Операция
Д. а на Ь обозначается с помощью двух точек (а: Ь) или горизонтальной
или косой черты (ajb). В кольце целых чисел Д. не всегда выполнимо.
Например, 12 делится на 6, но не делится на 5. Если при Д. целого числа а на
целое Ь в частном получается целое число, то говорят, что первое число делится
нацело (без остатка) на второе или, кратко, а делится на Ьл что часто
записывают так а \ Ь. В поле рациональных чисел Д. всегда выполнимо и однозначно,
кроме деления на нуль, так как если 6=£0, то при афО афЬ*0. При Д. а=0
на 6=0 частное χ может быть любым числом. Однако, чтобы не нарушать
однозначности операции, Д. на нуль считают невозможным.
Д. с остатком двух целых неотрицательных чисел а на Ь — это нахождение
двух неотрицательных чисел χ и у, удовлетворяющих требованиям: 1) а~Ьх-\-у,
2) у < Ь. Число а называется делимым, b — делителем, χ — неполным частным
(при уфО) или частным (при у«=0), у — остатком.
Аналогично определяется Д. и Д. с остатком для многочленов.
См. также Деление комплексных чисел, Деление отрезка в крайнем и
среднем отношении (Золотое деление), Гармоническая четверка, Евклида алгоритм.
Лит.: И. В. Арнольд, Теория чисел, Учпедгиз, М., 1939: А. Г. К у ρ о ш,
Курс высшей алгебры, Физматгиз, М., 1962.
ДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ производится по формуле:
а+Ы ac+bd be—ad
~c+di " с2-Ы2 с2-М8

ДЕЛИТЕЛЬ ЦЕЛОГО ЧИСЛА
101
При Д. к. ч. в тригонометрической форме модуль частного равен частному от
деления модуля делимого на модуль делителя, а аргумент частного равен
разности аргумента делимого и аргумента делителя:
/^(costPi-f-Zsintpt) гг
r2(cos φ2Ή δΐηφ2) r2
ДЕЛЕНИЕ КРУГА (окружности) на η равных частей с помощью циркуля
и линейки — это одна из древнейших задач. Древнегреческие математики могли
делить круг циркулем и линейкой на 3, 4, 5, 15 частей, а также неограниченно
удваивать число делений. Гаусс доказал, что можно осуществить Д. к. на 17
равных частей, а следовательно, и построить циркулем и линейкой правильный
17-угольник, изображение которого имеется на могиле Гаусса. Он также
доказал, что Д. к. на η равных частей можно выполнить циркулем и линейкой
тогда и только тогда, когда число η имеет вид:
п=2тр1р2 ... pst
где рг-=22* + 1 — различные простые числа Ферма, /= 1, 2, . . . , s, а к —
натуральное число.
Задача о Д. к. сводится к решению двучленного уравнения (см.) вида
хп— 1 = 0; если корни этого уравнения, называемого уравнением деления круга
(окружности), выражаются через квадратные радикалы, то их можно построить
циркулем и линейкой рогласно критерию разрешимости задач на построение
этими же инструментами (см. Критерий); отсюда вытекает, что можно построить
правильный л-угольник при тех же условиях. Например, правильный 7-, 9-,
11-угольники циркулем и линейкой построить нельзя.
См. также Трисекция, Правильные многоугольники.
Лит.: Б. И. Аргунов и М. Б. Балк, Геометрические построения на плоскости.
Учпедгиз, Μ., 1957.
ДЕЛЕНИЕ ОТРЕЗКА в крайнем и среднем отношении — см. Золотое
деление.
ДЕЛИЙСКАЯ ЗАДАЧА — неправильное название делосской задачи (см.
Удвоение куба).
ДЕЛИТЕЛИ НУЛЯ в кольце —два элемента α и Ь в кольце такие, что
α=£θ, ЪФЬ, но ab=*0. В числовых кольцах Д. н. нет, но в произвольном
кольце [например, в кольце матриц (см.)] Д. н. могут быть. В поле (см.) Д. н.
нет.
ДЕЛИТЕЛЬ ЕДИНИЦЫ в кольце — такой элемент α в кольце, для
которого существует обратный элемент or-1, т. е. такой элемент, что αα—г = е% где
е—единица кольца (см.). Например, в кольце целых чисел Д. е. будут числа
±1, в кольце многочленов над произвольным полем Д. е. являются
произвольные многочлены нулевой степени.
ДЕЛИТЕЛЬ МНОГОЧЛЕНА. Многочлен d называется Д. м. /, а многочлен
/ называется делящимся на многочлен d в том и только в том случае, если
существует многочлен атакой, что f — dg. Другими словами, многочлен d(x) из
кольца Р(х) является Д. м. f(x) из того же кольца, если при делении с
остатком f(x) на d(x) получается остаток, равный нулю.
ДЕЛИТЕЛЬНЫЙ ЦИРКУЛЬ —то же самое, что и пропорциональный
циркуль (см.).
ДЕЛИТЕЛЬ ЦЕЛОГО ЧИСЛА a — целое число, на которое делится
(нацело без остатка) число а. См. также Деление, Наибольший общий делитель.

102
ДЕЛОССКАЯ ЗАДАЧА
ДЕЛОССКАЯ ЗАДАЧА — то же самое, что и задача об удвоении куба (см.
Удвоение куба).
ДЕЛЬТОИД — выпуклый четырехугольник ABCD, имеющий одну ось
симметрии, совпадающую с его диагональю BD (рис. 83). Д. иначе называют
ромбоидом. Название Д. происходит от названия греческой буквы Δ (дельта),
имеющей форму треугольника.
ДЕСКРИПТИВНАЯ ТЕОРИЯ множеств — отдел теории
множеств (см.), изучающий строение точечных множеств
в евклидовом пространстве. Д. т. м. имеет своей
задачей описать множества, полученные из данной системы
некоторых простых множеств при помощи операций
суммы, пересечения, проекции и т. д.
ДЕСЯТИЧНАЯ ДРОБЬ — дробь — , знаменатель ко-
Я
торой q есть целая (положительная) степень числа 10.
Неправильную Д. д. записывают без знаменателя,
отделив запятой справа налево в числителе столько
знаков, сколько нулей в знаменателе. Правильную
десятичную дробь можно также записать без знаменателя,
поставив перед числителем ρ минимальное число нулей,
сколько их надо приписать после него, чтобы дробь была неправильной; при этом
первый нуль (целых единиц) отделяется десятичной запятой. См. Бесконечная
десятичная дробь. Периодическая дробь.
2341 38 3
Примеры: 1) ^-2.341; 2) -=0,38; 3) -=0,03.
Д. д.—одна из систематических дробей (см. Систематическая дробь).
Действия над Д. д. во многом сходны с действиями над натуральными числами.
Д. д. находят большое применение в практике вычислений.
ДЕСЯТИЧНАЯ СИСТЕМА счисления — позиционная система счисления (см.)
с основанием q, равным 10. В Д. с. с. всего имеется 10 цифр (знаков): 0, 1,
2, 3, 4, 5, 6, 7, 8, 9.
Десять единиц 1-го разряда (место, занимаемое в числе) образуют единицу
следующего разряда — число 10, десять единиц 2-го разряда образуют единицу
3-го разряда — число 100, и т. д. Д. с. с. весьма широко распространена во
многих странах мира в связи с использованием десятичной системы мер. Наряду
с Д. с. с. в науке и технике (машинной математике) большое значение имеет
двоичная система счисления (см.). У нас имеются остатки шестидесятеричной
системы счисления (градусы, минуты, секунды), остатки двенадцатеричной
системы счисления (счет дюжинами).
ДЕСЯТИЧНЫЙ ЛОГАРИФМ числа N-— логарифм (см.) этого числа, взятый
по основанию (при основании) 10, т. е. число Ь такое, что 10^=N. Д. л. ч. N
обозначается знаком \gN, что означает lgN=log10N.
Д. л. иначе называется бригговым логарифмом (см.).
ДЕТЕРМИНАНТ — синоним термина определитель (см.).
Лат. determino — определяю.
ДЕФЕКТ ТРЕУГОЛЬНИКА в геометрии Лобачевского — разность между
числом π и суммой углов треугольника (угловых мер треугольника).
Обозначается Д. т. буквой Dabc или Ьавс; следовательно, Оавс^п — (Л+B-fC).
Д. т. в некотором масштабе пропорционален площади треугольника. Для Д. т.
справедливо неравенство 0<Одвс<л-
Д. т. иначе называется недостатком этого треугольника.
Лат. defectus — недостаток (изъян, недочет).
ДЗЕТА-ФУНКЦИЯ Римана £(s) для s«a-{-tf. Res>l определяется как

ДИАМЕТРАЛЬНАЯ ПЛОСКОСТЬ 103
00
значение абсолютно сходящегося ряда £(s) = ^j~~7 · Для произвольных комп-
n=s
лексных значений s Д. ф. определяется как аналитическое продолжение (см.)
Д.ф. Д.ф. играет важную роль в аналитической теории чисел, и в частности
в вопросе о распределении простых чисел в натуральном ряду.
Лит.: Э. Ч. Титчмарш, Теория дзета-функции Римана, ИЛ, М., 1953; А.
Ингам, Распределение простых чисел, ОНТИ, М.—Л., 1936.
ДИАГОНАЛЬ: 1°. Д. многоугольника — отрезок прямой, соединяющей две
вершины многоугольника, не принадлежащие одной его стороне. Для всякого
/2-угольника число его диагоналей равно числу сочетаний С% без числа сто-
п(п — 1) /г(/г —3)
рон л, т. е. равно — л= .
2°. Д. многогранника — отрезок прямой, соединяющей две его вершины,
не принадлежащие одной грани. В проективной геометрии Д.—прямая линия,
проходящая через несмежные вершины.
3°. Д. определителя (или квадратной матрицы) есть совокупность элементов
а//(*> /β1> 2> ···» я) или элементов αιη, β2(η—ι). fls (л—з)» ···» ат- Диагональ,
на которой лежат элементы au(i=\, 2, . . . , /г), называется первой или
главной, диагональ, на которой лежат элементы αιη, α2(η—ι), · · · , ащ, называется
второй или побочной диагональю.
См. Определитель.
Греч, δίαγωηίοξ— идущий от угла к углу.
ДИАГОНАЛЬНАЯ ПЛОСКОСТЬ многогранника — плоскость, проходящая
через две диагонали многогранника (или диагональ и ребро его). Д. п. может
у многогранника и не существовать, если его диагонали не пересекаются или их
совсем нет (как, например, у тетраэдра).
Д. п. часто используется при решении задач по геометрии, когда
рассматриваются так называемые диагональные сечения многогранника, т. е. сечения
многогранника Д. п.
ДИАГРАММА — один из способов изображения зависимости между
величинами. Наибольшее распространение получили столбчатые (прямоугольные) и
секторные (круговые) Д. На прямоугольных Д. высота каждого столбика берется
пропорционально изображаемой величине. На секторных Д. круговые секторы
берутся пропорционально изучаемым величинам (явлениям).
Д. наглядно показывают зависимость между изучаемыми величинами.
Прямоугольные Д. содержат в себе элементы прямоугольной системы координат,
круговые Д. — элементы полярной системы координат.
Греч, διάγραμμα — рисунок, фигура.
ДИАМЕТР: 1°. Д. замкнутой фигуры — наибольшая из хорд.
2°. Д. кривой 2-го порядка — геометрическое место середин параллельных
хорд (пересекающих кривую в действительных или мнимых точках). Д. эллипса
(см.) и гиперболы (см.) будут прямые, проходящие через центр, Д. параболы —
ось ее и прямые, параллельные оси.
Примеры: 1) Д. прямоугольника будут его диагонали; 2) Д.
равностороннего треугольника — его стороны; 3) Д. круга (окружности) — любая хорда,
проходящая через центр; 4) Д. куба есть его диагональ; 5) Д. замкнутого
точечного множества есть верхняя грань всех расстояний между двумя
произвольными его точками.
Греч, δίαμβτροξ — поперечник.
ДИАМЕТРАЛЬНАЯ ПЛОСКОСТЬ поверхности 2-го порядка —
геометрическое место середин всех параллельных хорд неасимптотического направления г.

104
ДИВЕРГЕНЦИЯ
Эта Д. п. называется сопряженной направлению г. Если уравнение поверхности
2-го порядка имеет вид:
a11x2+a22y2i-a3Sz2^2a12xyi-2a13xz-\-2a2Syz-h2auxi--2a24y+2a^z+au^0i
а вектор г {α, β, γ}, то уравнение Д. п., сопряженной вектору г
неасимптотического направления, имеет вид:
(aux+a12y+a13z+au)a+(a21x+a22y+a23z+au)$^
ДИВЕРГЕНЦИЯ (или расходимость) векторного поля (Χ, Υ, Ζ) в точке
с координатами (х, у, ζ) есть скаляр, равный
ЭХ dY dZ
дх ду oz
Д. не зависит от системы координат, в которой заданы компоненты (Χ, Υ, Ζ)
поля. Геометрический смысл Д. таков: Д. есть предел отношения потока (см.)
векторного поля через замкнутую поверхность, окружающую данную точку,
к объему, ограничиваемому ею, когда эта поверхность стягивается к точке. См.
Остроградского формула.
ДИНАМИЧЕСКАЯ СИСТЕМА — однопараметрическая непрерывная группа
(см.) преобразований метрического пространства (см.) в себя. В большинстве
случаев Д. с. определяется системой дифференциальных уравнений вида:
dxi
— = fi(xlf *a. · .., Хп) (*)
в л-мерном евклидовом пространстве (хи х2, .... хп) следующим образом.
Каждая точка ( jt(j0), х^°К · · ·. ^0)) переводится в точку [xl (t), x2(t), . .. ,
Xn(t)\, где [Xi(t), *2(0. ···» xn(t)] есть решение системы (*), проходящее
при /=0 через точку ( χ\°Κ х^ *я°*)· Параметром здесь является t.
Можно проверить, что совокупность таких преобразований образует группу.
Лит.: В. В. Немыцкий и В. В. Степанов, Качественная теория
дифференциальных уравнений, Гостехиздат, М.—Л., 1949; Д. Д. Биркгоф, Динамические системы,
перев. с англ., Гостехиздат, М.—Л., 1941.
ДИОФАНТОВ АНАЛИЗ — раздел теории чисел, изучающий решение
алгебраических уравнений или систем таких уравнений с целыми коэффициентами
в целых или рациональных числах. Так, уравнение ах — my=*b fajt==6(mod m)],
где α, bt m — целые и а и т взаимно простые, имеет решения, записываемые
в виде формул: x=x0-\-mk, y^yo+mk, где (x0i y0) — одно любое решение
уравнения, k — любое целое. Д. а. называли еще неопределенным анализом.
Д. а. назван по имени греческого математика Диофанта (из Александрии).
См. Диофантовы уравнения.
ДИОФАНТОВЫ ПРИБЛИЖЕНИЯ — раздел теории чисел, изучающий решение
в целых числах линейных или нелинейных неравенств или систем неравенств
с действительными коэффициентами. В теории Д. п. большое значение имеют
непрерывные дроби (см.) и принцип Дирихле (см.Дирихле принцип).
Глубокие исследования по Д. п. принадлежат русским математикам
А. А. Маркову, П. Л. Чебышеву, а также немецким математикам Кронекеру
и Минковскому. Минковский использовал для решения задач Д. п.
геометрические методы.
Простейшим примером неоднородных линейных уравнений указанного типа
является следующее:
ха-у — β-о.

ДИРЕКТРИСА
105
где α и β — действительные числа, ахи у— целочисленные неизвестные,
которые должны удовлетворять приближенному решению уравнения, т. е. должно
выполняться неравенство:
| *а — у — β | < ε.
Лит.: А. Я. X и н ч и н, Цепные дроби, Физматгиз, М., 1961; А. О. Гельфонд,
Алгебраические и трансцендентные числа, Гостехиздат, М., 1952; А. О. Гельфонд,
Решение уравнений в целых числах, Гостехиздат, М., 1952; Знц. элем, мат., т. 1,
Гостехиздат, М., 1951.
ДИОФАНТОВЫ УРАВНЕНИЯ — алгебраические уравнения или система
таких уравнений с двумя или большим числом неизвестных с целыми
коэффициентами, для которых разыскиваются целые или рациональные решения; при
этом число неизвестных в Д. у. больше числа уравнений.
Примеры Д. у.: 1) Д. у. ах-\-Ьу=\, где а и Ь взаимнопростые числа,
имеет бесчисленное множество целых решений: х=х0+Ьп, у=у0— cm, где
(χο> Уо) — какое-либо решение, η — любое целое; 2) Д. у. х2 — dy2=l
(уравнение Пелля см.) — имеет бесчисленное множество целочисленных решений;
3) Д. у. хп-\-уп=гп (п > 2; великая теорема Ферма) — не известно до
настоящего времени, имеет или не имеет целые решения при любом целом /г>2. Для
/2=3, 4, . . . , 4000 доказано, что не имеет целых решений х% у, г.
При /г = 2 Д. у. *2-bya=z2 дает целые решения, которые называются
пифагоровыми числами, а прямоугольный треугольник с целочисленными катетами χ
и у и целочисленной гипотенузой ζ называется пифагоровым треугольником (см.
Пифагора теорема). Методы исследования Д. у. связаны с непрерывными
дробями (см.), с теорией алгебраических чисел (см.).
Лит.: А. О. Гельфонд, Решение уравнений в целых числах, Гостехиздат, М.,
1952; И. В.Арнольд, Теория чисел, Учпедгиз, М., 1939; Б. А. В е н к о в, Элементарная
теория чисел, ОНТИ, М, 1937; Б. Н. Делоне и Д. К. Фаддеев, Теория иррацио-
нальностей третьей степени, Изд-во АН СССР, М., 1940.
ДИРЕКТРИСА — прямая, обладающая определенным свойством
относительно заданной кривой 2-го порядка (конического сечения, см.). Для всякой точки
Рис. 84 Рис. 85
кривой 2*го порядка отношение ее расстояния до фокуса к расстоянию до
соответствующей Д. постоянно и равно эксцентриситету (см.) кривой. У эллипса
(рис. 84) и гиперболы (рис. 85) по две Д. 1г и /2 (каждая Д. соответствует
одному фокусу); У параболы (рис. 86) одна Д. / (парабола имеет один фокус)

106
ДИРИХЛЕ ЗАДАЧА
Рис. 86
Уравнения Д. эллипса и гиперболы,
заданных простейшими уравнениями, имеют вид
jc= ± — , где а — большая ось эллипса, или
е
действительная ось гиперболы, е —
эксцентриситет кривой.
Так как для эллипса е < 1, то обе Д.
эллипса отстоят от его центра на расстоянии
большем а. Для гиперболы е > 1, поэтому обе Д.
отстоят от центра на расстоянии меньшем а,
т. е. Д. гиперболы расположена ближе к
центру, чем ее вершины.
Для параболы у2=2рх (е=1) уравнение Д.
Ρ
такое: *=— -— .
Лат. directrix — направляющая.
ДИРИХЛЕ ЗАДАЧА — задача нахождения функции f(xlt хъ ..., хп),
удовлетворяющей уравнению Лапласа (см. Лапласа уравнение), т. е.
гармонической функции (см.):
d*f ду d*f
дх\ dxf дх2п
внутри некоторой области G и удовлетворяющей граничному условию:
f(P) = g(P),
где Ρ-—точка границы области, g (Ρ) — заданная (обычно непрерывная)
функция.
ДИРИХЛЕ ПРИНЦИП — утверждение о том, что при разбиении множества
из я-f 1 элемента на η классов в одном из классов будет по крайней мере два
элемента. Д. п. иллюстрируется такой задачей. В лесу 10 000 елок, на каждой
из них не менее 50 000 иголок. Доказать, что найдутся две елки с одинаковым
количеством иголок. Д. п. находит применение в теории чисел, в теории
гармонических функций и др.
ДИРИХЛЕ РЯДЫ —ряды вида
us
Д. р. используются в аналити-
ческой теории чисел, в частности в вопросе о распределении простых чисел
в арифметических прогрессиях и других последовательностях натуральных
чисел.
ДИРИХЛЕ ТЕОРЕМА в теории чисел. В 1788 г. высказал французский
математик Лежандр и лишь в 1837 г. доказал немецкий математик П. Г. Лежен
Дирихле следующую теорему, называемую Д. т.: если разность и первый член
арифметической прогрессии являются натуральными взаимно простыми числами,
то в этой прогрессии содержится бесконечное множество простых чисел.
Доказательство Д. т. весьма сложно и опирается на аналитический аппарат
так называемых рядов Дирихле (см. Дирихле ряды). В последнее время (Ван
дер Варден,. 1928) было найдено элементарное доказательство Д. т., не
опирающееся на теорию функций комплексного переменного.
ДИСКРЕТНОЕ ПРОСТРАНСТВО — один из видов топологических
пространств (см.). Окрестностью любой точки такого пространства служит, в
частности, сама точка. Таким образом, точка в Д. п.—открытое множество (см.).

ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
107
ДИСКРЕТНОСТЬ — прерывность. Множество точек обладает свойством Д.,
если оно не имеет предельных точек.
ДИСКРИМИНАНТ трехчлена ах2+Ьх+с, где аФО и а, 6, с — действитель
ные числа; число Δ = 62 — 4ас. Если Д. т. Δ > 0, то два корня трехчлена дей
ствительны и различны. Если Д. т. Δ=Ό, то трехчлен имеет двукратный
действительный корень. Если Д. т. Δ < 0, то трехчлен имеет два различных
комплексно сопряженных корня.
ДИСПЕРСИЯ случайной величины (см.) — важная характеристика случайной
величины. Д. отражает степень кучности случайной величины около своего
математического ожидания (см.). Д. есть по определению математическое
ожидание квадрата разности между величиной и ее математическим ожиданием. Д
случайной величины в случае непрерывного распределения (см.) выражается:
Dr^\\-Mi\*p%d\,
где Р. — плотность вероятности (см.), Λίξ — математическое ожидание.
Основные свойства Д: 1) D достоверной случайной величины равна нулю:
2) D (λξ) «=■ λ2 D ξ, здесь λ — скаляр, ξ — случайная вели чина.
Например, Д. равномерно распределенной (см. Распределение) на отрезке
[0, 1] величины равна:
ι / 1\2
Χύ
3
χ2 χ
1
1 1
!'з 2 + 4Г
12'
ДИСТРИБУТИВНОСТЬ —см. Закон дистрибутивности.
ДИФФЕРЕНЦИАЛ функции — главная линейная часть приращения функции
Д. функции f(x) обозначается символом df(x) или df. Если функция f(x)
одного переменного имеет производную (см.), то приращение Δ/ = / (χ+Δχ) — f(x)
можно представить в виде Δ/=/' (x)&x+R* где R— величина бесконечно малая
более высокого порядка по сравнению с Δ*. Выражение df = f'(x)\x линейно
относительно Δ* и при Δ^-^Q составляет основную часть величины Д/. Идея
разложения приращения функции одной переменной на главную линейную часть
и бесконечно малую высшего порядка находит применение и в теории функций
многих переменных.
Пусть Δ/=/(*ι-γ·Δλ;ι, *2+Δ*2. · · · » *η+ΔΧη) — Λ*ι, *2 *л), прира-
df
щение функции f(xx, χ2 χη)> Непрерывность частных производных —
όχι
является условием, достаточным для существования дифференциала; в этом случае
Δ/
-Σ
dxi
Δχί+Ri,
где R бесконечно мало по сравнению с у Δ*ι+Δ*2+ ··* + Δ*ϋ· Выражение
η
df= у .—Δχΐ является Д. функции многих переменных. В литературе
JmAdxi
i=\
встречается также термин Д. отображения одного многообразия (см.) в другое.
Д. отображения — главная линейная часть отображения, задаваемая некоторой
матрицей (см.).
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — ветвь геометрии, изучающая
геометрические образы (кривые, поверхности и их семейства) средствами матема-

108
ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА
тического анализа (см.), и в первую очередь средствами дифференциального
исчисления (см.).
Основными понятиями Д. г. являются кривизна (см.) и кручение (см.)
кривой, изгибание (см.) поверхности, первая и вторая основные квадратичные формы
поверхности и др.
Лит.: П. К. Рашевский, Курс дифференциальной геометрии, Гостехиздат, М.,
1950; А. П. Норден, Дифференциальная геометрия, Физматгиз, М., 1952; А. В. По·
горело в, Лекции по дифференциальной геометрии, изд. Харьковского ун-та, 1955;
М. Я. Выгодский, Дифференциальная геометрия, Гостехиздат, М., 1949.
ДИФФЕРЕНЦИАЛЬНАЯ ФОРМА — выражение целое однородное
относительно дифференциалов ряда переменных. Степень однородности называется
степенью Д. ф. Например, форма Пфаффа (см. Пфаффа уравнение) — форма
первой степени; f=a(x)dxdy— b(x, у) dy2—форма второй степени. Во многих
вопросах дифференциальной геометрии и топологии особое значение имеют кососим-
метрические Д. ф. (см. Кососимметричность). Примером такой Д. ф. может
служить элемент площади поверхности (см. Элемент поверхности). См. также
Формы.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — отдел математики, который
занимается исследованием функций при помощи производных и дифференциалов.
Центральными понятиями Д. и. являются понятия производной (см.) и
дифференциала (см.), которые в свою очередь связаны с понятием предела (см.)
последовательности или функции и бесконечно малой величины (см.).
Знание производной у функции дает возможность сказать, где функция
убывает или возрастает, где она имеет точки максимума, минимума и перегиба.
Эти же понятия применяются и при изучении функций многих переменных.
Первые попытки создания Д. и. были сделаны Декартом, Ферма и другими
математиками XVII в. при решении задач о проведении касательных к кривым.
Окончательное создание Д. и. связано с работами И. Ньютона и Г. Лейбница.
Границы понятия Д. и. весьма неопределенные. Сюда включаются обычно и ряды,
и теория пределов. Более глубокий анализ исходных понятий Д. и. связан
с развитием теории множеств и теории функций действительного переменного.
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального
исчисления, т. 1, 3, Физматгиз, М., 1963; А. Я. X и н ч и н, Восемь лекций по математическому
анализу, Гостехиздат, Μ., 1953; А. Я. Хинчин, Курс математического анализа,
Гостехиздат, М., 1953.
ДИФФЕРЕНЦИАЛЬНО-РАЗНОСТНЫЕ УРАВНЕНИЯ — уравнения,
связывающие аргумент, искомую функцию, ее производную при разных значениях
аргумента. Например: у' (х)=Ау (х+Ь).
В связи с приложениями изучались уравнения, в которых отклонение
аргумента у искомой функции и ее производных постоянно. Важнейший класс
Д.-р. у. образуют уравнения с запаздывающим аргументом. Эти уравнения во
многом напоминают обыкновенные дифференциальные уравнения, но в ряде
отношений отличаются от них.
Лит.: А. Д. Μ ы ш к и с, Линейные дифференциальные уравнения с запаздывающим
аргументом, Гостехиздат, М., 1951.
ДИФФЕРЕНЦИАЛЬНЫЕ ИНВАРИАНТЫ относительно некоторой системы
преобразований переменных — выражения, составленные из функций, их
производных и дифференциалов различных порядков, обладающие тем свойством, что
они не меняют структуры при рассматриваемом преобразовании переменных.
Одним из простейших Д. и. является двойное отношение четырех направлений:
#3 "-1 &4 "Ч
Ла — ""3 ^2 — *^4

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
109
где £/= —" (/=1, 2, 3, 4) есть отношение дифференциалов координат, со-
\dvli
ответствующих бесконечно малому смещению точки по одному из четырех
данных направлений (система координат и, ν — произвольная). Этот Д. и. есть
инвариант любых преобразовании плоскости.
Лит.: Г. Be иль, Классические группы, их инварианты и представления, пер.
с англ., ИЛ, М., 1947.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ — уравнения, содержащие искомые
функции, их производные любых порядков и независимые переменные. Д. у.
возникли в XVII в. ввиду потребностей механики и других отделов
естествознания.
Приведем простейшую задачу, решение которой сводится к Д. у. Если
тело имеет температуру Τ и находится в среде, температура которой нуль, то
падение этой температуры тела за время Д^ с достаточной точностью дается
формулой: ДУ=—kT&t, где к— некоторый постоянный коэффициент. Если
в этом соотношении устремить Δ^ к нулю, получим: Г'=—кТ. Для полученного
уравнения можно указать все частные решения—они даются формулой T=Cer-kt>
где С — постоянно.
Д. у. делятся на обыкновенные (см.), в которые входят как неизвестные
функции только одного переменного, и уравнения с частными производными
(см.), содержащие частные производные функций нескольких аргументов.
1°. Д. у. обыкновенные. Среди этих уравнений простейшим является
уравнение 1-го порядка, т. е. уравнение вида:
РЛ*. у> у')=о.
Иногда его можно записать в виде:
У'=/<*,У). Г)
Последнее уравнение является частным случаем более общего уравнения:
Р(х, y)dx+Q(x, y)dy=0.
Решить это уравнение — значит найти все кривые на плоскости, вдоль которых
оно выполняется.
Уравнение (*) допускает геометрическую интерпретацию.· В каждой точке
плоскости (х, у) можно провести вектор с направлением &=/(*, у). Таким
образом, получается поле направлений. Кривая у (х) будет решением (*), если
она в каждой своей точке касается некоторого вектора поля направлений.
Каждое Д. у. обыкновенное имеет, вообще говоря, бесчисленное множество решений.
Поэтому для нахождения частного решения надо указать начальные данные,
т. е. должно быть задано, через какую точку проходит решение. Таким образом,
семейство решений есть однопараметрическое семейство кривых:
y(x) = F(x, с). (**)
Если из (**) соответствующим выбором с можно получить любое решение,
то оно называется общим решением Д. у. обыкновенных.
В теории Д. у. обыкновенных изучаются также уравнения высших порядков,
а именно уравнения вида:
F(Jt, у, у', у\ .... у*»-1), у<*))=0
и системы уравнений. Как правило, решить Д. у. обыкновенные в конечном
виде невозможно, поэтому для их решения широко применяются приближенные
методы: метод конечных разностей, графическое разложение в ряды. Большое
значение имеют качественные методы (см.).

110
ДИФФЕРЕНЦИАЛЬНЫЙ БИНОМ
2°. Д. у. с частными производными. Их главным отличием от обыкновенных
является то, что общее решение зависит не от произвольных постоянных, а от
д2и д*и
произвольных функций. Например, общим решением Д. у. ~г"=Т~ является
at2 ох2
выражение и(х, t)=f(x-\-t)-\-g(x — t)t где / и g — произвольные функции.
Типичной задачей для Д. у. с частными производными является задача
Коши: найти решение u(t, x)t которое при / = 0 обращается в заданную
функцию Φι(#), а производные до (п—1)-го порядка ыг· (где η — порядок уравнения
по г) —в некоторые заданные функции (ft (x). Для уравнении порядка выше
1-го рассматриваются также краевые задачи (см.). Д. у. с частным
производным являются основным математическим аппаратом в гидромеханике,
аэромеханике, теории упругости и т. п.
Лит.: В. В. Степанов, Курс дифференциальных уравнений, Физматгиз, М, 1959;
И. F. Петровский, Лекции об уравнениях с частными производными, Физматгиз, М.,
1961.
ДИФФЕРЕНЦИАЛЬНЫЙ БИНОМ — выражение вида хт(а+Ъхп)Р dx, где
а и Ь постоянные, отличные от нуля, а т, /г, ρ— рациональные числа. Основная
задача для Д. б — указать все случаи его интегрируемости в элементарных
функциях. Л. Эйлер указал три случая его интегрируемости: 1) ρ— целое число,
2) целое число, 3) -f-p — целое число. П. Л. Чебышев доказал,
η η
что других случаев интегрируемости Д. б. нет.
ДИФФЕРЕНЦИАЛЬНЫЙ ОПЕРАТОР— оператор, который переводит
функцию /(*ь *2. · · ·» *п) из некоторого классам функцию
Ф=^ U /V /χ,. ...,/,,..., . дЧ .) ·
V п &С . . . dxrn)
4 1 η '
Наибольшее развитие имеет теория линейных Д. о. Если рассматривать
функции / одного независимого переменного, то линейный Д. о. имеет вид:
*=0
Часто на область определения линейных Д. о. накладывают ограничения,
имеющие следующую форму:
гс-1
V а{у№(х)+?>1у(х)(х) = 0* /-1. 2, .... т.
В теории линейных Д. о. наибольшее число исследований посвящено случаю
самосопряженного оператора.
Линейный Д. о. с частными производными определяется формулой:
(ь ъ dku
L(u)= 2 а " л> ~ΤΊ Γ~·
*i+Vb· · · + *„<« ι * · · · oxnn
Возможностей задания области определения здесь гораздо больше, чем в случае
обыкновенных линейных Д. о. Например, для оператора L(u)^=uxx4-Uyy
ди
область определения может быть задана соотношением α—4-β«=0 на границе
дп

ДЛИНА КРИВОЙ
111
некоторого открытого множества. По существу теория линейных Д. о. является
главой функционального анализа. Основными вопросами в ней являются:
исследование спектра Д. о., разложение по собственным функциям. Д. о. применяются
в квантовой механике.
Лит.: Б. М. Левитан, Разложение по собственным функциям, Гостехиздат, М.,
1950; М. А. На ймарк, Линейные дифференциальные операторы, Гостехиздат, М., 1954.
ДИФФЕРЕНЦИРОВАНИЕ — вычисление дифференциалов (см.) или
производных (см.), частных производных, полных дифференциалов. Д. является основной
операцией в дифференциальном исчислении, где выводятся правила дифферент*
рования (см.) и формулы дифференцирования (см.).
ДИФФЕРЕНЦИРУЕМАЯ ФУНКЦИЯ. Функция называется
дифференцируемой в точке, если существует дифференциал в этой точке. Функция называется
дифференцируемой в области, если она дифференцируема во всех точках области.
Для функций одного переменного дифференцируемость эквивалентна
существованию производной. Непрерывная функция может ни в одной точке отрезка не
иметь производной.
ДЛИНА ОТРЕЗКА АВ прямой в евклидовом пространстве — неотрицательное
число р (АВ), удовлетворяющее следующим условиям (требованиям, свойствам):
1) р (Л£)=0 тогда и только тогда* если АВ=0л т. е. если точки А и В
совпадают; 2) р (АВ)-\-р (ВС)>ρ (АС) — «неравенство треугольника»; 3) если AB=CD%
то p(AB)=?(CD), т. е. конгруэнтные (равные) отрезки должны иметь равные
длины; 4) если АВ и ВС — два отрезка прямой, не имеющие общих внутренних
точек, то р(ЛС) = р (АВ)+р (ВС)* т. е. длина суммы двух отрезков без общих
точек равна сумме длин этих отрезков (свойство аддитивности Д. о.); 5)
существует такой отрезок АхВи что ρ (А1В1)=\; отрезок АгВг называется единицей
измерения длин, или единичным отрезком.
Если можно сопоставить каждому отрезку KL число p(/CL)>0,
удовлетворяющее условиям 1—5, то говорят, что установлена система измерения отрезков,
или система длин отрезков.
В элементарной геометрии и основаниях геометрии доказывается, что
каждому отрезку АВ при выбранном единичном отрезке АХВХ отвечает
единственное действительное число ?(АВ)>0, удовлетворяющее условиям i—5. При
решении этой задачи используется аксиома Архимеда (см.). Справедливо и обратное
предложение. Для каждого действительного числа а>0 существует отрезок,
длина которого в данной системе измерения равна а. Обратная задача измерения
отрезков доказывается с привлечением аксиомы Дедекинда (см.).
ДЛИНА ЛОМАНОЙ есть сумма длины отрезков — ее звеньев.
ДЛИНА КРИВОЙ (дуги кривой) — предел, к которому стремится длина
вписанных в эту кривую (дугу кривой) ломаных при неограниченном увеличении
числа их звеньев, когда длина наибольшего звена стремится к нулю. Длина
окружности может быть рассмотрена как предел периметров вписанных или описанных
выпуклых /г-угольников, когда число сторон их неограниченно возрастает и длина
наибольшей стороны стремится к нулю. Длина окружности О (г) вычисляется по
формуле 1 = 2 π г. Для непрерывных кривых упомянутый предел всегда
существует конечный или бесконечный. Если этот предел конечный, то кривая (дуга
ее) называется спрямляемой. Условие спрямляемости кривой было установлено
Жор даном (см. Жордана кривая).
Если плоская кривая задана в прямоугольных декартовых координатах
уравнением у=/(х), где а<х<Ь и функция / (х) имеет непрерывную производную
/' (х), то длина ее вычисляется по формуле:
а

112
ДЛИНА ПОДСТАНОВКИ
если кривая задана параметрическими уравнениями x=x(t), У=У(0» гДе
α <ζ t ^ bx то длина ее
/^ТЛя'СОР-НУ'СО]2 dt.
а
Аналогично определяется длина пространственной кривой.
Лит.: Р. Н. Бончковский, Площади и объемы, Изд-во АН СССР, М., 1937;
A. Лебег, Об измерении величин, перев. с франц., Физматгиз, М.„ I960.
ДЛИНА ПОДСТАНОВКИ циклической (или длина цикла)—число символов,
действительно перемещаемых данной циклической подстановкой (см.). Пример:
5= (3 i 5 4 ΐ) = (135)· Д' ц* п* S равна 3*
ДОДЕКАЭДР — двенадцатигранник. Правильный Д. — правильный
двенадцатигранник — один из пяти типов правильных многогранников (см.). Грани
правильного Д. — правильные пятиугольники. Правильный Д. имеет 20 вершин,
12 граней и 30 ребер. К каждой вершине правильного Д. сходится по 3 ребра.
Правильный Д. двойствен (дуален) правильному икосаэдру (см.); центры
граней правильного икосаэдра являются вершинами правильного Д., и обратно
(см. Двойственности принцип).
Греч, dodeka — двенадцать, hedra — грань, основание.
ДОКАЗАТЕЛЬСТВО есть рассуждение, в ходе которого устанавливается
истинность или ложность какого-либо утверждения (суждения, высказывания,
теоремы). При Д. теоремы мы опираемся либо на аксиомы, либо на ранее
доказанные теоремы, привлекая при этом определения понятий. В зависимости от
способа Д. они подразделяются на: аналитическое (см. Анализ), синтетическое
(см. Синтез), индуктивное (см. Индукция, Математическая индукция),
дедуктивное (аксиоматическое; см. Дедукция), Д. от противного (см.) или Д.
приведением к нелепости (к абсурду, к противоречию).
Лит.: И. С. Град штейн, Прямая и обратная теорема, Физматгиз, М., I960;
B. В. Репьев, Общая методика преподавания математики, Учпедгиз, М., 1958.
ДОКАЗАТЕЛЬСТВО ОТ ПРОТИВНОГО — метод доказательства теоремы
(предложения), состоящий в том, что доказывают не саму теорему, а ей
равносильную (эквивалентную), противоположную обратной (обратную
противоположной) теорему. Д. от п. используют всякий раз, когда прямую теорему
доказать трудно, а противоположную обратной легче. При Д. от п. заключение
теоремы заменяется ее отрицанием, и путем рассуждения приходят к отрицанию
условия, т. е. к противоречию, к противному (противоположному) тому, что
дано; это приведение к абсурду и доказывает теорему.
Д. от п. очень часто применяется в математике. Д. от и. основано на
законе исключенного третьего, заключающегося в том, что из двух
высказываний (утверждений) А и Ά (отрицание А) одно из них истинно, а другое ложно.
См. также Доказательство, Теорема.
Лат. ad absurdum — к нелепости.
ДОЛЯ ЕДИНИЦЫ —часть единицы, или дробь вида */я (п > 2)> например:
пятая доля числа 1 есть 1/5. Доля также называется единичной дробью. См.
также Дробь.
ДОПОЛНИТЕЛЬНОЕ МНОЖЕСТВО. Если множество А является
подмножеством в множестве В, т. е. если ЛСВ, то Д. м. множества А в множестве
В называется разность множеств (см.) В — А. Д. м. обозначается символом
~А, С А или С в А, если хотят подчеркнуть, в каком множестве рассматривается
Д. м.

ДРОБЬ
ИЗ
Пример: Д. м. к замкнутому множеству (см.) является открытым
множеством, и обратно.
ДОПОЛНИТЕЛЬНЫЙ ЛОГАРИФМ —то же, что кологарифм (см.); ср.:
функция и кофункция.
ДОПОЛНИТЕЛЬНЫЙ УГОЛ к углу β — угол а, который в сумме с углом
β составляет прямой угол. Каждый из углов α и β является Д. у. для другого
угла.
ДОСТАТОЧНОЕ УСЛОВИЕ для выполнения какого-либо верного
утверждения (предложения, суждения) — всякое условие, из которого следует это утвер
ждение. Например, для делимости целого многозначного числа на 4 Д. у.
является окончание этого числа по крайней мере двумя нулями. Но это условие —
равенство двух последних цифр целого числа нулю — не является необходимым
условием (см.) для делимости целого числа на 4. Однако можно указать такое
условие делимости целого многозначного числа на 4, которое будет и
необходимым и достаточным; это условие состоит в том, что двузначное число, на
которое оканчивается многозначное число, должно делиться на 4. Действительно,
если двузначное число, на которое оканчивается многозначное число, делится на
4, то и все многозначное число делится на 4, и обратно — верно, если
многозначное число делится на 4, то и двузначное число, на которое оно оканчивается,
делится на 4.
Д. у. является одним из важнейших понятий математики и часто
встречается в формулировках теорем наряду с необходимым условием. Д. у. называется
также достаточным признаком для выполнения какого-либо верного
утверждения. Для выполнения какого-либо утверждения можно указать не один, а
несколько Д. у. Например, для того чтобы выпуклый четырехугольник был
параллелограммом, достаточно одного из условий: 1) чтобы любые две его
противоположные стороны были равны и параллельны друг другу; 2) чтобы в точке
пересечения его диагонали делились пополам; 3) чтобы этот четырехугольник
имел центр симметрии. См. также Необходимое условие, Критерий, Теорема.
Лит.: В. В. Репьев, Общая методика преподавания математики, Учпедгиз, М..
1958; П. С. Моденов, Сборник задач по специальному курсу элементарной математики,
гл. XIV, «Советская наука», М., 1957; Н. С. Г рад штейн, Прямая и обратная теорема,
Фнзматгиз, М., 1960; Д. Π о й а, Математика и правдоподобные рассуждения; ИЛ, М.,
1957.
ДРОБНАЯ ЧАСТЬ действительного числа χ — разность χ -
целая часть (см.) х. Д. ч. числа χ обозначается символом (л:},
Д. ч. и целая часть числа связаны
соотношением: х=\хЦ-{х}. Пример: у\
[3,87} =0,87; J—5 i-Ι = 3 3
-[*], где [*] —
Таким образом,
4J 4'
π={3,14... }=0,14...
График функции у={х] изображен на
y-w
рис. 87.
ДРОБЬ: 1°. Д. в арифметике — число,
состоящее из целого числа равных долей единицы.
В общем случае Д. можно записать в виде —»
Я
где целое число ρ называется числителем Д., а
q— знаменателем Д. Числитель ρ показывает число взятых долей единицы,
разделенной на столько долей, сколько показывает (знаменует) знаменатель q.
о Толковый словарь математических терминов

114
ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ
Числитель и знаменатель называются членами Д. Если ρ не делится нацело
(точно) на qt то Д. -Е- называется дробным числом. Если ρ делится на q (без
Q
остатка, точно, нацело), то Д. есть целое число /i_=3|.
И /
Если p>q, то Д. называется неправильной, если p<q, то Д. называется
правильной. Неправильная Д. может быть записана в виде суммы целого числа
и правильной дроби, т. е. в виде смешанного числа (см.); например, —=2-f-
3
-Ь_==2— есть смешанное число. Отношение двух Д. называется сложной дро-
3 3
бью (см.). Если знаменатель Д. есть степень 10, то Д. называется десятичной,
она может быть записана без знаменателя, например 423/100«4,23. Д. вида
11п (n>2, n — целое) называются единичными или долями. Арифметическая дробь
иначе называется обыкновенной дробью или простои дробью.
2°. В алгебре под Д. понимают выражения вида ajbt где а и b —
алгебраические выражения.
См. также Цепная дробь, Непрерывная дробь, Бесконечная дробь,
Систематическая дробь.
Лит.: Энц. элем, мат., т. 1, Гостехиздат, М., 1951; И. В. Арнольд,
Теоретическая арифметика, Учпедгиз, М., 1939; И. Я. Д е π м а н, История арифметики, Учпедгиз,
М., 1959; М. Я. Выгодский, Арифметика и алгебра в древнем мире, Гостехиздат, М.,
1941; И. Н. Шевченко, Арифметика, Учпедгиз, М., 1961.
ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ —функция вида
ах+b
У== cx+d9
т. е. функция, представляющая отношение (дробь) двух линейных функций
(см.). Если определитель Δ — L· j —0, то Д.-л. ф. есть постоянная величина;
если Д=£0> но с=0, то Д.-л. ф. есть целая линейная функция y=kx-\-l. При
Δ^Ο и сфо график Д.-л. ф.—равнобочная гипербола с асимптотами,
параллельными осям координат. Если а, 6, с, d — комплексные числа, χ —
комплексный аргумент, то Д.-л. ф. осуществляет конформное и взаимно однозначное
отображение (см.) комплексной плоскости на себя. Прямые и окружности
комплексной плоскости переводятся Д.-л. ф. снова в прямые и окружности.
Д.-л. ф. есть частный случай дробно-рациональной функции.
Лит.: И. И. Привалов, Введение в теорию функций комплексного переменного,
Гостехиздат, М., 1948; А. И. Маркушевич, Теория аналитических функций,
Гостехиздат, М., 1950.
ДРУЖЕСТВЕННЫЕ ЧИСЛА — менее распространенное наименование
содружественных чисел (см.).
ДУГА —часть кривой, заключенная между двумя любыми ее точками.
См. также Простая дуга.

Ε
ЕВКЛИДА АЛГОРИТМ — метод для нахождения наибольшего общего
делителя для целых чисел, а также двух многочленов от одного переменного.
Первоначально был изложен в «Началах» Евклида (см.) в геометрической форме как
способ нахождения общей меры двух отрезков. Е. а. для нахождения
наибольшего общего делителя как в кольце целых чисел, так и в кольце многочленов
от одного переменного является частным случаем некоего общего алгоритма в
евклидовых кольцах (см.)'
Е. а. для целых чисел состоит в следующем. Пусть а и b целые числа,
причем а>Ь. Тогда разделим с остатком а на Ъ — получим неполное частное ηΎ и
остаток гх такой, что 0<гх<Ь. Затем разделим с остатком b на гх — получим
неполное частное q2 и остаток г2(0<га<г1). Затем разделим с остатком гх на
г2 и т. д. Получим цепочку равенств
a^bq1-\-rl (0<г1<6),
Ь=ггд2+г^ (0</,2</'i)<
Гп-2-Гп-1Яп+Гп (0<гл<г„-.1),
в которой через конечное число шагов получается очередной остаток, равный
нулю (/-,.+! =,()), так как последовательность остатков является убывающей
последовательностью неотрицательных целых чисел:
b>rx>r2>r3> ... >гп>гп+1
и, значит, должна через конечное число шагов закончиться нулем. Тогда
наибольший общий делитель чисел а и 6 равен последнему отличному от нуля
остатку гп в схеме последовательного деления (*).
Пример. Найти наибольший общий делитель чисел 1981 и 378. Выполняем
последовательное деление:
1981-378.5+91,
378= 91-4+14
91= 14*6+ 7,
14* 7*2+ 0.
Последний отличный от 0 остаток 7 и есть наибольший общий делитель чисел
1981 и 378.
Е. а. для нахождения наибольшего общего делителя двух многочленов / (х)
и g(x) также состоит в последовательном делении с остатком f(x) на g(x),
затем g{x) на первый остаток гх{х), затем гх(х) на второй остаток г2{х) и т. д.:
f(x)=g{x)q1(x)+ri{x)t
g(x)-r1(x)q2(x)^rr2(x)t
Гх(х) = г2(х) q3(x)-\-r3{x),
rn-2(x)=rn-i M Qn (x)+rn (*)ι
rn-i (x) = 'n (*) Qn+i (*)+0·
8*

116
ЕВКЛИДОВА ГЕОМЕТРИЯ
Так как степени остатков, являющихся натуральными числами, убывают, то
через конечное число шагов приходим к остатку, равному нулю. Последний
отличный от нуля остаток гп(х) и является наибольшим общим делителем многочленов
/(*) и g(x).
Аналогично определяется Е. а. для отрезков (см. Отрезки соизмеримые и
Отрезки несоизмеримые).
ЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, построенная на базе аксиом
абсолютной геометрии (см.) и аксиомы Евклида о параллельных (через точку Л, не
принадлежащую прямой а, в плоскости, определяемой точкой А и прямой с,
можно провести только одну прямую, не пересекающую а).
Часто Е. г. называют элементарной геометрией (см.). Геометрию, изучаемую
в средней школе, лакже часто называют Е. г. Название Е. г. связано с тем, что
первое систематическое ее построение было изложено древнегреческим геометром
Евклидом (III в. до н. э.) в его книге «Начала» (см. «Начала» Евклида).
Первой геометрией, отличной от Е. г., была геометрия Лобачевского,
созданная великим русским математиком Н. И. Лобачевским.
См. также Эрлангенская программа.
Лит.: Евклид, Начала, Гостехиздат, М., 1950.
ЕВКЛИДОВО ПРОСТРАНСТВО — пространство, свойство которого
описывается аксиомами абсолютной геометрии (см.) и постулатом (аксиомой) Евклида о
параллельных прямых.
Более общо, —Е. п. называют /2-мерное метрическое пространство, в
котором возможно ввести декартовы координаты так, что метрика будет определена
следующим образом: расстояние между точками Μ с координатами (xl9 x2t . . .,
хп) и М' с координатами (хг, х2 хп) вычисляется по формуле:
р-ЛШ'- У (*1 — *i)* + (*a — *2)2 + ···+ [x'n — χη)2·
См. также Пространство, Геометрия.
ЕДИНИЦА ГРУППЫ —такой элемент е в группе, что ае^а для всякого
элемента а из этой группы. Тогда еа^а. Е. г. есть в каждой группе, и
притом двух различных Е. г. в одной группе быть не может.
ЕДИНИЦА КОЛЬЦА —такой элемент е в кольце, что ае=а для всякого
элемента а из этого кольца. Е. к. имеется в кольце не всегда. Например, в
кольце многочленов над полем Ρ единица есть, а в кольце четных чисел
единицы нет. В поле единица есть всегда.
ЕДИНИЦА МНИМАЯ — комплексное число (см.) вида (0; 1). Е. м.
обозначается знаком / и представляет собой одно из двух значений корня квадратного
из (— 1), т. е. V~l=±i.
ЕДИНИЧНАЯ МАТРИЦА — квадратная матрица, в которой по главной
диагонали стоят единицы, а на всех остальных местах нули. Е. м. в кольце
матрип играет роль единицы кольца (см.).
ЕДИНИЧНЫЙ ВЕКТОР — вектор, длина которого равна единице. Е. в.
иначе называется ортом (см.). См. также Вектор.
6-ЧИСЛО — одна из важнейших постоянных математического анализа.
.. / 1 \п .. sin л;
e=lim 1 + —ι . Этот предел и urn =1 часто называют замечатель-
ГС-»эо\ П/ X-+Q X
ными пределами (см.) £-ч. — трансцендентное и приближенно равно
2,7182818284590452353... В математике и ее приложениях удобно рассматривать

2-ЧИСЛО
117
логарифмы (см.) по основанию е, так называемые натуральные логарифмы. Среди
свойств, выгодно отличающих натуральные логарифмы от других логарифмов,
отметим формулу:
d\r\x 1
dx x *
тогда как
d \oga x 1
dx Λ' In α
что более сложно.

ж
ЖЕНЕРАТРИСА —- устаревшее название термина генератриса (см.).
ЖЕРГОНА ТОЧКА — точка пересечения прямых, соединяющих вершины
треугольника с точками касания его сторон, противолежащих вершинам, со
вписанной окружностью. Названа по имени французского математика Жергона,
изучавшего эту точку.
ЖОРДАНА КРИВАЯ — геометрическое место точек плоскости, задаваемое
уравнениями: x=f(t)% y=g(t), где функции f(t) и g(t) непрерывны. Ж. к.
может иметь вид, совершенно не похожий на кривую в обычном представлении.
Так, Пеано построил Ж. к., проходящую через каждую точку квадрата (см.
Пеано кривая). Более короткое определение Ж. к. —- непрерывный образ отрезка.
Задание кривой по Жордану есть один из возможных способов определения
кривой.
ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА — см. Нормальная жорданова форма.

3
ЗАВИСИМАЯ ПЕРЕМЕННАЯ величина — синоним термина «функция» (см.).
ЗАДАЧА АПОЛЛОНИЯ — одна из геометрических задач на построение на
плоскости, которая состоит в следующем: построить окружность, касающуюся
трех данных окружностей. Решение этой задачи обычно проводится методом
инверсии. 3. А. важна не только сама по себе, но и по своим частным
(предельным) случаям, когда отдельные окружности вырождаются в точку
(окружность нулевого радиуса) или прямую («окружность» бесконечно большого
радиуса). Например, задача: построить окружность, касающуюся двух данных
(пересекающихся или параллельных) прямых и проходящую через данную точку —
частный случай 3. А.
Задача названа по имени греческого математика Аполлония Пергского (III в.
до н. э.), впервые изучавшего ее.
ЗАДАЧА ПОТЕ НОТА (Потенота —Снеллиуса задача) — задача, состоящая
в нахождении точки χ на плоскости (на местности), из которой данный отрезок
АВ виден под углом а, а другой данный отрезок ВС виден под углом β.
Задача названа по имени французского математика Л. Потенота, давшего
одно из геометрических решений этой задачи. Еще в начале XVII в. решение
3. П. было дано голландским ученым В. Снеллиусом. Отдельные решения 3. П.
даны еще в XVI в. Известно более 100 решений этой задачи.
Лит.: А. С. Чеботарев, Геодезия, ч. 1, Геодезиздат, М., 1962; Г. П. С е н н и ко в,
Решение задач на построение в VI — VIII классе, Учпедгиз, М., 1955, стр. 143; М. А.
Знаменский, Измерительные работы на местности, Учпедгиз, М., 1960, стр. 135.
ЗАКОН АССОЦИАТИВНОСТИ — закон, которому может удовлетворять
бинарная операция (см.). Если бинарную операцию мыслить как умножение, то
3. а. имеет вид: a(bc)=(ab)c. 3. а. часто называют сочетательным законом.
Название происходит от латинского associatio — соединение. Примерами
операций, удовлетворяющих 3. а., могут служить сложение и умножение чисел,
сложение и умножение матриц (см.), умножение подстановок (см.). Примером
операции, не удовлетворяющей 3. а., может служить векторное умножение (см.).
Операции вычитания и деления чисел также не удовлетворяют 3. а, так как,
вообще говоря, (а: Ь): с Φ a:(b : с). 3. а. является одной из аксиом группы.
ЗАКОН БОЛЬШИХ ЧИСЕЛ — см. Больших чисел закон.
ЗАКОН ДИСТРИБУТИВНОСТИ — закон, которым могут быть связаны две
бинарные операции (см.), определенные в одном и том же множестве. Если одну
операцию мыслить как умножение, а другую как сложение, то 3. д. имеет вид:
a(b+c)=^ab-\-ac.
Ввиду того что операции (умножения и сложения) входят в 3. д.
несимметричным образом, часто 3. д. называют 3. д. умножения относительно сложения. Так
как далее операция умножения может оказаться некоммутативной, то наряду с
вышеприведенным 3. д., называемым левым 3. д., рассматривается правый 3. д.:
(b-\-c)a=ba-\-ca.
3. д. часто называют распределительным законом. Название происходит от
латинского distributus — распределенный. Операции объединения множеств (см.) и

120
ЗАКОН КВАДРАТИЧНОЙ ВЗАИМНОСТИ
пересечения множеств (см.) взаимно дистрибутивные, т. е. имеют место
следующие 3. д.:
ЛП (В0С)=(АПВ) U МПС); (Би С) ПА=(В[)А) U (СП Л);
Ли (ВГ)С)=(А()В) П ΜUС); (В(]С) 1М=(Я1М) П (СЦА).
Умножение чисел дистрибутивно относительно сложения, но сложение чисел не
дистрибутивно относительно умножения чисел, т. е., вообще говоря, ab~\-c Φ
&(а+с)(Ь+с).
ЗАКОН КВАДРАТИЧНОЙ ВЗАИМНОСТИ — одно из наиболее глубоких
свойств теории квадратичных вычетов (см.). открытое К. Ф. Гауссом. Если ρ
и q — различные простые нечетные числа, то 3. к. в. утверждает, что
Й)-«-"
Я)
где ( —) и (-")— символы Лежандра (см. Лежандра символ).
ЗАКОН КОММУТАТИВНОСТИ — закон, которому может удовлетворять
бинарная операция (см.). Если бинарную операцию мыслить как умножение,
то 3. к. имеет вид: аЬ—Ьа.
3. к. часто называют переместительным законом. Примерами операций,
удовлетворяющих 3. к., могут служить сложение и умножение чисел, пересечение
множеств (см.) и объединение множеств (см.). Примерами операций, не
удовлетворяющих 3. к., могут служить деление и вычитание чисел (так как, вообще
говоря, а: Ь φ b: а и а — Ь Φ Ъ — а), умножение подстановок (см.), умножение
матриц (см.), векторное умножение.
Лат. commutare — перемещать.
ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ. В курсе математического анализа
выводятся следующие два 3. п.:
Кщ—=1 и Hm (l + —)* = в=2,718281 828 459...
Эти пределы замечательны тем, что, пользуясь ими, можно очень просто и
легко находить численные значения бесконечного множества других пределов,
которые другими путями выводятся гораздо сложнее.
Из первого 3. п., например, сразу вытекает эквивалентность друг другу
следующих бесконечно малых: ах, sin ax, tg ax, arc sin ax, arc tg ax, т. е.
пределы отношений любых двух из этих функций при х-+0 будут равны единице.
Из второго 3. п. также непосредственно получаются, например, следующие
пределы:
- ( χ Υ ± 1
lim(l+*)*=*, Mm —) -β-1, lim (\+ax)bx =eb и т. д.
х->о х-юо \1-Ь */ v-*o
Следует отметить, что в первом 3. п. переменная χ рассматривается не в
градусной, а в радианной мере угла.
См. Предел функции, Предел последовательности чисел, £-число.
ЗАМЕЧАТЕЛЬНЫЕ ТОЧКИ в треугольнике. Во всяком треугольнике
имеются следующие четыре 3. т.:
Три перпендикуляра к сторонам треугольника, проведенные через их
середины, пересекаются в одной точке. Эта 3. т. является центром описанного круга.
Три биссектрисы внутренних углов треугольника пересекаются в одной
точке. Эта 3. т. является центром вписанного круга.
Три высоты треугольника пересекаются в одной точке. Эта 3. т.
называется ортоцентром треугольника.

ЗВЕНО НЕПРЕРЫВНОЙ ДРОБИ
121
к которой присоединены все
Μ n-мерного или метриче-
Три медианы треугольника пересекаются в одной точке. Эта 3. т. является
центром тяжести треугольника (сплошного, двумерного). См. Треугольник.
Точка пересечения медиан и точка пересечения биссектрис всегда лежат
внутри треугольника, а две другие 3. т. могут лежать как внутри и вне
треугольника, так и на самих сторонах треугольника.
Точка пересечения медиан (центр тяжести) треугольника делит каждую
медиану в отношении 2:1, считая отрезки медианы от вершины треугольника до
основания медианы.
Кроме перечисленных выше четырех 3. т., известно еще довольно много
других не менее замечательных точек, связанных с треугольниками, но они
значительно реже встречаются на практике. Эти более «специальные» 3. т.
треугольника обычно называются именами тех математиков, которые впервые их
обнаружили, например: Торричелли точка (см.), Нагеля точка (см.), Жергона точка
(см.), Лемуана точка (см.) и др.
ЗАМКНУТАЯ СФЕРА — открытая сфера (см.),
ее граничные точки (см.). 3. с — множество точек
ского пространства, удовлетворяющих
условию ρ(Λί0, Μ)<δ, где δ>0,
Аффиксированная точка, а ρ(Λίη, Αί) —
расстояние (см.) между точками Μ и М0
(в соответствующем пространстве).
ЗАМКНУТОЕ МНОЖЕСТВО —
множество, которое содержит все свои
предельные точки (см.).
Примеры 3. м.: 1) Отрезок [а, Ь]\ 2)
множество, состоящее из конечного числа
точек (на числовой оси, в л-мерном или
метрическом пространстве); 3) множество
точек прямой или отрезка на плоскости
или в пространстве; 4) множество на
плоскости, состоящее из точек кривой у=sin —
X
(0<jc<1) и точек отрезка — 1 <у < 1, Рис. 88
дг=0, лежащего на оси Оу (рис. 88).
ЗАМКНУТЫЙ ПАРАЛЛЕЛЕПИПЕД в л-мерном пространстве — иначе
просто параллелепипед в л-мерном пространстве (см.).
ЗАОСТРЕНИЯ ТОЧКА —то же, что возврата точка (см.).
ЗВЕНО НЕПРЕРЫВНОЙ ДРОБИ
*k
41U Di
Ί7
— дробь . в разложении
непрерывной дроби. Дробь -~ (k — натуральное) — называется звеном k-го по-
рядка непрерывной дроби, которую можно написать так:
а0+-
«1
*1 +
Q2
Ьп+
или кратко:
См. Непрерывная (цепная) дробь.
Г αν 1°°
L h Jv-l

122
ЗЕРКАЛЬНОЕ ОТРАЖЕНИЕ
ЗЕРКАЛЬНОЕ ОТРАЖЕНИЕ от прямой на плоскости (от плоскости в
пространстве)— то же, что и симметрия (см.) относительно этой прямой на
плоскости (или относительно плоскости в пространстве).
ЗНАКИ МАТЕМАТИЧЕСКИЕ — условные обозначения (символы), служащие
для записи математических понятий, предложений и вычислений. Так, отношение
длины окружности к длине ее диаметра записывают в виде знака π. Сумму
k оо
конечного или бесконечного числа слагаемых обозначают в виде 2 ап, 2 ап·
О роли 3. м. великий русский математик Н. И. Лобачевский писал:
«Подобно тому, как дар слова обогащает нас мнениями других, так язык
математических знаков служит средством еще более совершенным, более точным и
ясным, чтобы один передавал другому понятия, которые он приобрел, истину,
которую он постигнул, и зависимость между всеми частями, которую он
открыл. ..» (Н. И. Лобачевский, Наставления учителям математики в гимназиях).
Многие математические теории (например* тензорное исчисление) в XIX в.
успешно были развиты благодаря удачно созданной символике. 3. м. прошли
длительную и сложную историю своего развития, прежде чем стали иметь
окончательный, современный вид.
3. м. в основном подразделяются на три группы:
1) знаки математических объектов,
2) знаки операций, 3) знаки отношений.
Примеры: 1) Точки, прямые, плоскости обычно обозначаются соответственно
буквами: Л, Б, С, . . .; af bf с, . . .; α, β, γ, . . .
2) 3. м. операций: -f и — (сложение и вычитание) ввели немецкие
математики в конце XV в.; 3. м. · и : (умножение и деление) ввел Г. Лейбниц
(1698); 3. м. а2, а3, . . . — (степени) — Декарт (1637); 3. м. Vч V, . . .
(корни) — X. Рудольф (1525) и А. Жирар (1629); 3. м. Log —И. Кеплер (1624),
log — Б. Кавальери (1632); 3. м. sin, cos, tg (тригонометрические функции) —
Эйлер (1753); 3. м. ! (факториал) — X. Крамп (1808); 3. м. dxy ddx, . . .,
J'yd* (дифференциалы и интеграл) — Г. Лейбниц (1675) (в печати — 1684 г.);
3. м. |л;| (модуль)— К. Вейерштрасс (1841) и др.
3) 3. м. отношений: = (равенство) — Ф. Рекорд (1557); >, < (больше и
меньше) — Т. Гарриот (1631); || (параллельность) — У. Оутред (1677); J_
(перпендикулярность) — П. Эригон.
ЗНАКОПЕРЕМЕННЫЙ РЯД — ряд, члены которого имеют как
положительные, так и отрицательные знаки. 3. р. противопоставляется понятию
знакопостоянного ряда — ряда, у которого все члены имеют одинаковые знаки. Частным
случаем 3. р. является знакочередующийся ряд (см.).
ЗНАКОЧЕРЕДУЮЩИЙСЯ РЯД — знакопеременный ряд (см.), члены
которого попеременно (поочередно) положительны и отрицательны, т. е. это ряд
"ι — «2-Нз -Ь (— 1)л""1 ип+
где числа ui — положительны.
3. р. сходится (признак Лейбница), если ип-+0 и члены его монотонно
убывают по абсолютному значению (\ип+г\<\ип\). Например:
3. р. 1 ■——+-—-_ —-| сходится к In 2; (1)
3. р. 1 —--f — — —· · сходится к —-. кч
о о 7 4

ЗОЛОТОЕ ДЕЛЕНИЕ
123
Остаток сходящего 3. р. гп=(— 1)лип+Н меньше своего первого члена
"м+1 (первого из отброшенных членов) и имеет знак этого члена. Это свойство
используется при приближенном вычислении суммы 3. р.
Например, сумма трех первых членов в первом из приведенных примеров
I S3=l — ТГ+Т^т) бУдет отличаться от суммы этого ряда (S = ln2) меньше,
чем на первый из отброшенных членов, т. е. меньше чем на —-.Следовательно,
5
— — приближенное значение этого ряда, взятое с избытком (гп<0).
6
ρ
ЗНАМЕНАТЕЛЬ арифметической (обыкновенной) дроби — (см. Дробь) —
Я
число ?, показывающее (знаменующее), на сколько равных долей разделена еди-
Р
ница. 3. алгебраической дроби —, гдеРиС? — алгебраические выражения (см.),
Ц
есть алгебраическое выражение Q.
ЗНАЧАЩИЕ ЦИФРЫ приближенного числа (в десятичной записи) — все
верные цифры его, кроме нулей, стоящих слева от первой отличной от нуля
цифры.
Например, если в результате измерений или вычислений мы получили
окончательный ответ с точностью до 0,001 в виде приближенных чисел: 3,240; 0,0372,
то 3. ц. первого числа будут 3, 2, 4 и 0; 3. ц. второго числа будут 3 и 7.
Или, например, числа 137; 13,7; 1,37; 0,137; 0,0137 имеют одни и те же три
3. ц.: 1, 3 и 7.
Число 3. ц. приближенного числа называется значностью этого числа.
Понятие 3. ц. используется при вычислении на логарифмической линейке и на
электронных вычислительных машинах (при действиях над числами со скользящей
запятой).
ЗНАЧНОСТЬ ЧИСЛА — число значащих цифр (см.) этого числа.
ЗОЛОТОЕ ДЕЛЕНИЕ — деление отрезка на две части так, что большая из
них есть средняя пропорциональная между меньшей частью и всем отрезком,
т. е. при 3. д. отрезка справедливо
соотношение:
а: х=х : (а — х), (*)
где а — весь отрезок, χ — большая из двух
его частей (рис. 89).
Решая уравнение (1) х2+ах — а2 = 0,
получим *==—-ί |/5—1)«0,62 а (с
точностью до 0,01 а). Отрезок х, длина
которого удовлетворяет уравнению (1), строят Рис. 89
так: в конце В отрезка АВ=а восставляют
а
перпендикуляр ВС= -—. Затем строят отрезок АС и откладывают на нем CD=
а
==СБ= —. Тогда отрезок AE=AD будет искомым отрезком х, т. е. будет
выполняться равенство (*). 3. д. было известно еще в древности; так, в книге II
«Начал» Евклида встречается построение, равносильное решению уравнения (*).
В книгах IV и XIV «Начал» Евклид применяет 3. д. для построения правиль-

124
ЗОЛОТОЕ СЕЧЕНИЕ
ных пяти- и десятиугольников. В стереометрии Евклид использует 3. д. для
построения правильных двенадцатигранников и двадцатигранников.
3. д. часто встречается наряду с другими пропорциями в архитектуре и
искусстве. Некоторые авторы называли эту пропорцию «божественной». 3. д.
называют также золотым сечением, гармоническим делением, а также делением
в крайнем и среднем отношении.
Лит.: Г. Ε. Тимердинг, Золотое сечение, Петроград, Научные кн. изд-ва, 1924;
Е. И. Игнатьев, В царстве смекалки, ч. 2, ГИЗ, Петроград, 1924 — 1925.
ЗОЛОТОЕ СЕЧЕНИЕ — синоним термина «золотое деление» (см.).
ЗОНА —то же* что и шаровой пояс (см.).

и
ИДЕАЛ кольца R (см.) — подкольцо Ρ такое, что при любых x£R и γζΡ
произведение ху принадлежит Р. Например, в кольце целых чисел подкольцо
четных чисел является идеалом; в кольце непрерывных на отрезке [0; 1]
функций подкольцо функций / таких, что /(0)=0 есть идеал.
Лит.: Б. Л. Ван дер В а р д е н, Современная алгебра, ч. 1, 2, Гостехиздат, М.,
1947.
ИДЕМПОТЕНТНОСТИ ЗАКОН —закон, которому может удовлетворять
бинарная операция (см.). Если бинарную операцию мыслить как произведение, то
И. з. имеет вид: аа—а.
Примерами операций, удовлетворяющих И. з., могут служить пересечение
множеств (см.) и объединение множеств (см.), а также конъюнкция (см.) и
дизъюнкция (см.). Примерами операций, не удовлетворяющих И. з., могут
служить сложение и умножение чисел.
ИЗВЛЕЧЕНИЕ КОРНЯ — алгебраическое действие, обратное возведению в
степень (см.), состоящее в том, что по данной степени и по данному ее
показателю ищется основание степени. Извлечь корень /2-й степени из числа а значит
найти такое число х, /2-я степень которого равна а. И. к. /2-й степени из числа
а записывается так: уа=х, где α называется подкоренным числом (выражением),
η — показателем корня, а число (выражение) χ называется корнем (или
радикалом) /2-й степени из числа а.
Если л—2, то корень 2-й степени у а называют квадратным; при /2—3 ко-
3/—
рень 3-й степени у а называется кубичным или кубическим.
Если И. к. л-й степени из числа а рассматривают в поле комплексных
чисел, то этот корень будет иметь ровно η значений.
Если а > 0, то под корнем /2-й степени из а часто подразумевают
положительное значение корня, т. е. арифметический корень (см.).
Корень /2-й степени (п — натуральное число, л>1) из натурального числа
Ν>\% не являющегося л-й степенью другого натурального числа, есть число
всегда иррациональное (см.).
При нахождении арифметических корней часто пользуются их
рациональными приближениями, в частности таблицами корней, счетной (логарифмической)
линейкой, приближенными формулами, биноминальными рядами и т. д.
Лат. radix — корень.
ИЗГИБАНИЕ — преобразование поверхности, при котором сохраняется длина
ее линий. При И. сохраняется величина углов и площадь фигур, расположенных
на поверхности. Наглядный пример И. — свертывание листа бумаги в цилиндр
или конус. Поэтому И. связано с наглядным представлением о поверхности как
о гибкой, нерастяжимой и несжимаемой пленке.
Преобразование гомотетии с коэффициентом кф ±1 не является И. При
И. полная (главная гауссова или эйлерова) кривизна/г, равная произведению
главных кривизн, в любой точке поверхности не изменяется. Всякая поверхность,
изгибаемая на плоскость, есть развертывающаяся поверхность (см.).
См. также Внутренняя геометрия.

126
ИЗМЕНЕНИЕ ФУНКЦИИ
ИЗМЕНЕНИЕ ФУНКЦИИ f(x) — важная характеристика функции действи-
/ ь
тельного переменного. И. ф. f(x) на отрезке [а, Ь] обозначается Уд/или| \df\
а
и означает верхнюю грань сумм:
η
где а=х0<х1<. . .<хп—ι<хп = δ при всевозможных разбиениях отрезка на
конечное число частей. Геометрический смысл \ьа /, если / непрерывна, состоит в
том, что Vbaf равняется длине проекции графика у=/(*) на ось ординат, считая
кратность покрытия. Существуют непрерывные функции, И. ф. которых
бесконечно. Так, функция y=X'sin—обладает указанным свойством на [0,1]. Класс
функций, обладающих конечным изменением, обладает многими интересными
свойствами и часто рассматривается в теории тригонометрических рядов, геометрии
и функциональном анализе.
ИЗМЕРЕНИЕ ОДНОРОДНОЙ ФУНКЦИИ /(*, у$ гш .. ., t), удовлетворяю-
щей равенству:
f(\x, λ у, \г, . .., lt) = lnf(x, у. г, .. .» t),
где λ — любое действительное число (λ Φ 0), есть число п. И. о. ф. называется
также степенью однородности этой функции. Например, И. о. ф. f(xt у)=х2^-
χ у
— Ъху+у2 равно 2; И. о. ф. /(*, у)= равно 0.
ИЗМЕРЕНИЕ ОДНОЧЛЕНА относительно некоторых букв —сумма всех
показателей этих букв, входящих в одночлен; при этом если буква, относительно
которой устанавливается И. о.# не входит в одночлен, то ее измерение
принимается равным 0.
Примеры: И. о. 2ах2уъ относительно букв χ и у равно 7 (7=2+5); И. о.
Зх2у относительно буквы ζ равно 0.
И. о. называется также степенью одночлена.
ИЗМЕРЕНИЕ МНОГОЧЛЕНА относительно некоторых букв, входящих в
него,—измерение его старшего члена, т. е. члена, имеющего наивысшее
(наибольшее) измерение. Например, И. м. 7x4-f 6дг2у3г равно 6 относительно букв х,
у и г, но равно 4 относительно буквы х.
ИЗМЕРИМАЯ ФУНКЦИЯ — функция f(xlt x2f . . ., хп) такая, что
множество точек с координатами хи x2f . . ., хп, удовлетворяющих неравенству
f(xv x2i ...» *η)<Λ, измеримо при любом А (см. Измеримое множество).
Функции, с которыми имеет дело математический анализ, измеримы. Пример
неизмеримой функции дается относительно сложным построением.
Лит.: П. С. Александров и А. Н. Колмогоров, Введение в теорию функции
действительного переменного, М.—Л., 1938; И. П. Натансон, Теория функций
вещественной переменной, Гостехиздат, М-, 1957; Η. Η. Лузин. Теория функций
действительной переменной, Учпедгиз, М., 1948.
ИЗМЕРИМОЕ МНОЖЕСТВО — множество, для которого существует мера в
смысле Лебега (см. Мера множества). Всякое замкнутое или открытое
ограниченное множество измеримо. И. м. £ в смысле Лебега иногда обозначают так: £ (L.)

ИЗОМОРФИЗМ
127
ИЗОГОНАЛЬНАЯ ТРАЕКТОРИЯ данного семейства линий —линия,
пересекающая все линии данного семейства под одним и тем же углом а. Если а=90°,
то И. т. называется ортогональной. Ортогональной траекторией пучка прямых
y=kx будет любая окружность x2+y2 = rz в декартовой прямоугольной системе
координат (рис. 90), И. т. пучка прямых y=kx будут логарифмические спирали
р = аек? в полярной системе координат (рис. 91). См. также Локсодромия,
Конфокальные кривые.
Греч.: ισοξ — равный, одинаковый и γωνία — угол.
Рис. 90 Рис. 91
ИЗОКЛИНА — линия, во всех точках которой правая часть дифференциаль-
dy
ного уравнения ~- = /(*. у) постоянна.
ах
ИЗОЛИРОВАННАЯ ТОЧКА множества — такая точка, у которой существует
окрестность (см.)* не содержащая других точек этого множества. В
геометрии рассматриваются И. т. кривой или поверхности. Например, точка (0, 0)
является И. т. кривой у2—х*— 4jc2.
ИЗОМЕТРИЯ: 1°. И. есть отображение одной поверхности (вообще рима-
нова пространства) на другую поверхность (другое риманово пространство), при
котором сохраняется длина всех кривых. Например4 изгибание (см.) цилиндра
на плоскость есть И.
2°. И. есть частный случай аксонометрии (см.), когда показатели
(коэффициенты) искажения по всем трем осям координат равны.
ИЗОМОРФИЗМ — важное понятие современной математики. Пусть Ρ и Q —
два множества, а {φ/} и {^-} (ι — Ι, 2, , . ., η)·— системы преобразований
множеств {Рх. . .хР} и (Qx. . .xQ) в Ρ и Q соответственно. (Через χ обозна-
щ раз πι раз
чена операция прямого произведения.) Тогда И. —взаимно однозначное
отображение Л множества Ρ на Q такое, что Α q>/ (ух. . .ху) = % (ЛухАух.. .хАу) для
η ι раз щ раз
любого у ζ Р. Понятие И. очень широко. В алгебре рассматривается И. полей
(см.), колец (см.), алгебр (см.), групп (см.). Например, группа подстановок
(см.) из двух элементов 1 и 2 изоморфна группе по умножению чисел -И и —1:
И. в этом случае задается отображением (12) —> 4-1* (21)—*—1. Любые два

128
ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА
л-мерных линейных пространства изоморфны между собой, Ρ и Q — два гоме-
оморфных (см.) топологических пространства, аф и ψ — семейства непрерывных
отображений Ρ и Q в себя. Тогда гомеоморфизм (см.) А пространств Ρ и Q
есть изоморфизм двух множеств Ρ и Q относительно систем φ и ψ. Определения
И. групп, колец, алгебр см. в термине Гомоморфизм.
Два изоморфных множества неразличимы по своим свойствам, определяемым
в терминах φ и ψ. Два различных изоморфных множества являются различными
конкретными моделями некоторого абстрактного математического понятия.
Лит.: А. Г. Курош, Курс высшей алгебры, Физматгиз, М.—Л., 1962; Энц. элем,
мат., т. 2, Гостехиздат, М., 1951.
ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА — одна из основных задач
вариационного исчисления, заключающаяся в следующем: среди всех кривых данной
длины найти ту, для которой некоторая величина, зависящая от кривой, имеет
максимальное или минимальное значение.
Например, среди всех замкнутых плоских кривых данной длины
(одинакового периметра) наибольшую площадь ограничивает окружность.
Лит.: Д. А. Кр ы ж а но в с к и й, Изопериметры, Физматгиз, М., 1959; М. А.
Лаврентьев и Л. А. Люстерник, Курс вариационного исчисления, Гостехиздат, М., 1950;
И. М. ЯгломиВ. Г. Болтянский, Выпуклые фигуры, Гостехиздат, М., 1951.
ИЗОТРОПНЫЕ ПРЯМЫЕ — прямые в комплексной плоскости, уравнение
которых в прямоугольных декартовых координатах имеет вид: x±iy+c=0, где
/ — мнимая единица, а координаты точки (х, у) принимают комплексные
значения. «Расстояние» между двумя точками Мг (х19 уг) и М2 (*2, у2) одной и той
же И. п., вычисленное по формуле Μλ M2 = V(х2 — Х\УЛ-{Уъ—)Ί)2, равно
нулю. Через каждую точку (х0, у0) комплексной плоскости проходят две И. п.,
уравнения которых: (х — х0) ± i(y — Уо)=0. Если комплексную плоскость
дополнить несобственными элементами, то среди несобственных точек будут две
круговые точки (см.). И. п. можно определить как прямую, проходящую через
одну из круговых точек.
Греч, izos — равный, одинаковый, tropos — поворот, направление.
ИКОСАЭДР — двадцатигранник. Правильный И. — правильный
двадцатигранник— один из пяти типов правильных многогранников (см.), имеющий 20
треугольных граней, 12 вершин и 30 ребер, сходящихся по 5 к каждой вершине.
Правильный И. двойствен (дуален) (см. Двойственности принцип) правильному
додекаэдру (см.) и получается из него, если центры граней правильного
додекаэдра принять за вершины правильного И.
Греч, eikosi — двадцать, hedra — грань, основание.
ИМЕНОВАННОЕ ЧИСЛО — число, записанное вместе с наименованием
единиц измерения рассматриваемой величины, например: 5 м (пять метров), 2° (два
градуса), 3 га (три гектара), 40 кв. см или 40 см2 (сорок квадратных
сантиметров).
ИНВАРИАНТ — функция от координат преобразуемой величины, не
изменяющая своего значения при данной совокупности преобразований этой величины.
Например, функция f (xt у, г)«х2+у2-т-г2 — И. относительно всевозможных
вращений евклидова пространства около начала координат. И. квадратичной
формы с матрицей
I Дц я12 fli31
А— \агг а22 «2з |
I «81 fl3 2 «з:
являются: Яп-г-агг-Изз» def Α· Совокупностью преобразований здесь является
совокупность всех вращений евклидова трехмерного пространства.
ИНВЕРСИЯ: 1° И. в геометрии относительно данной окружности О (г)—

ИНВЕРСОР
129
преобразование точек плоскости этой окружности, при котором каждой точке М,
отличной от точки О, ставится в соответствие точка М' той же плоскости такая,
что при этом выполняются требования: 1) М' лежит на луче ОМ, 2) ОМ-ОМ' =
=г2. Окружность О (г) при этом называется окружностью И., точка О—
центром (полюсом) И., г2 — коэффициентом (степенью) И.
Если положить г=1, то ОМ= 7Г777(р = т)» 0ТКУДа происходит другое
название И.: преобразование обратными радиус-векторами. Упомянутая выше И.
называется гиперболической. Если же точка М' лежит на противоположном луче
по отношению к лучу ОМ, то такую И. называют эллиптической.
Свойства И.: 1) И. есть взаимно однозначное преобразование точек
плоскости (за исключением точки О); 2) И. есть инволюционное преобразование точек
плоскости; 3) всякая внутренняя точка окружности О (г), кроме точки О,
преобразуется во внешнюю точку, при этом чем дальше отстоит от центра точка М,
тем ближе к центру находится ее образ М'; 4) прямая, проходящая через центр
И., преобразуется в себя; 5) окружность И. преобразуется в себя, т. е.
окружность О (г) И. есть геометрическое место двойных точек И. (см. Двойной
элемент); 6) всякая прямая, не проходящая через центр, преобразуется в
окружность, проходящую через центр И. (при этом точка О исключается из
окружности), и обратно; 7) окружность, не проходящая через центр, преобразуется
в окружность, не проходящую через центр; при этом центры взаимно инверсных
окружностей не являются соответственными точками; 8) И. есть конформное
преобразование (см.) 2-го рода, т. е. в И. сохраняются углы между линиями,
но ориентация фигур при И. изменяется на противоположную; 9) окружности,
ортогональные к окружности И., преобразуются в И. сами в себя, хотя точки
этих окружностей не являются двойными, за исключением только двух точек
пересечения этой окружности с окружностью И.
Преобразование И. используется при решении задач на построение, в
особенности в тех задачах, где рассматривается вопрос о построении окружности,
касающейся других окружностей (прямые и точки могут считаться как
предельные (частные) случаи окружностей (см. Задача Аполлония). И. используется
также в теории функций комплексного переменного, в основаниях геометрии
(модель Пуанкаре плоскости Лобачевского).
Если вместо окружности О (г) взять сферу О (г), то аналогично можно
определить И. и для пространства. Две фигуры Φ и Ф', соответственные в И.,
называются взаимно инверсными. Преобразование фигуры Φ в фигуру Ф' в И.
называется также инвертированием фигуры Φ в фигуру Ф'.
2°. И. в комбинаторике — всякое нарушение нормального (обычного,
алфавитного) порядка двух элементов независимо от того, стоят ли они рядом или
нет. Например, в перестановке Ьса
элементы Ъ и а, с и а образуют И., если за
нормальное расположение элементов
считать такое: аЬс.
Лат. inversio — перестановка,
превращение.
ИНВЕРСОР —прибор, с помощью
которого строятся фигуры, соответствующие
данным в данной инверсии (см.).
Существует несколько конструкций И.
Например, инверсор Поселье состоит из 6
стержней, соединенных шарнирно (рис. 92), при этом ОЛ = ОВ и АМВМ' — ромб,
О — фиксированная (неподвижная) точка. Если Μ описывает какую-либо фигуру
Ф, то точка М' опишет фигуру Ф', соответственную в инверсии с центром в
точке О и коэффициентом инверсии, равным О А2 —ОМ2.
9 Толковый словарь математических терминов

130
ИНВОЛЮТА
И. используется в технике для превращения кругового движения в
прямолинейное. См. также Инверсия.
Лит.: А. Адлер, Методы геометрических построений, Учпедгиз, М., 1940.
ИНВОЛЮТА — то же самое, что эвольвента (см.).
ИНВОЛЮЦИОННОЕ ПРЕОБРАЗОВАНИЕ — преобразование точек плоскости
(пространства), повторное применение которого дает тождественное
преобразование, т. е. И. п. есть преобразование, квадрат которого есть тождественное
преобразование. Примеры И. п.: симметрия (центральная или осевая), инверсия,
полярное преобразование. И. п. иначе называется инволюцией.
Лат. involutio — свертывание, скрученное состояние листьев.
ИНДЕКС — Числовой, буквенный или иной значок, при помощи которого
отличаются выражения, обозначаемые одинаковыми символами. Например:
ν, *г. У1; У}\ *ι; ν. *т\ βτ\
Лат. index — указатель.
ИНВОЛЮЦИЯ —то же, что и инволюционное преобразование (см.).
ИНДИКАТРИСА Дюпена — плоская кривая, которая наглядно дает
представление об искривлении поверхности в данной на ней точке.
Если от произвольной точки Ρ(ы, ν) поверхности в каждом направлении
(duidu) отложить отрезок, равный |1 : £|°»&, где k — Кривизна нормального
сечения (см.) поверхности в том же направлений, то геометрическое место концов
этих отрезков называется И. Д. поверхности в точке Р.
В зависимости от типа точки, лежащей на поверхности, И. Д. в этой точке
может иметь различный вид: в эллиптической точке И. Д. — пара эллипсов, один
из которых мнимый; в гиперболической точке И. Д. — пара сопряженных
гипербол; в параболической точке И. Д. —■ пара параллельных прямых.
И. Д. называется также индикатрисой кривизны поверхности в точке Р.
И. Д. названа по имени французского инженера и математика Шарля Дюпена
(ученика Монжа), впервые применявшего ее к изучению поверхности.
ИНДУКЦИЯ (индуктивный метод) ■— заключение (вывод) от частного к
общему, т. е. общий вывод, основанный на изучении свойств отдельных, частных
фактов (частных экспериментов или наблюдений).
Пример И.: построив графики конечного числа линейных уравнений с двумя
неизвестными (леременными), например, уравнений 2х—у+3=*»0 и x-f-2)>+4~Q,
и убедившись в том, что графики этих уравнений в прямоугольной декартовой
системе координат представляют прямые линии, мы заключаем, что графиком
всякого уравнения вида ax-{-by-\-c=0 в той же системе координат будет
прямая.
Если общий вывод делается на основании изучения (рассмотрения) всех
частных фактов (объектов, фигур, чисел и т. д.), то И. называется полной, или
совершенной. Если же общий вывод делается на основании изучения только
части множества всех фактов (объектов), то И. называется неполной, или
несовершенной. Приведенный выше пример рассуждения есть пример неполной
индукции.
Если доказать теорему ό вписанном в окружность угле, рассматривая при
этом все частные случаи расположения центра окружности по отношению к
сторонам угла (центр лежит на одной из сторон, центр лежит внутри угла и центр
лежит вне угла), то полученный вывод (доказательство) будет представлять
собой полную И.
И. иначе называют индуктивным выводом (рассуждением) или индуктивным
методом. И. может привести как к верным, так и к неверным выводам.
Например, рассмотрим числа вида (2а -|-1) (числа Ферма). Давая η
значения 1, 2, 3, получим соответственно простые числа 5, 17, 257.

ИНЕРЦИИ ЗАКОН
131
Вывод: все числа вида (22 -Ь1) — простые. Этот вывод оказался неверным; уже
при /г = 5, как доказал Эйлер, число (22 +1) делится на 641.
И. широко используется в школе при выводе правил (признаков) делимости
чисел, при изучении действий над рациональными числами и т. д.
Всякая И. включает в себя элементы дедукции (см.) и с ней неразрывно
связана. «Общее существует лишь в отдельном, через отдельное» (В. И.
Ленин, Философские тетради, 1947, стр. 329). «Чтобы понять, нужно
эмпирически начать понимание, изучение* от эмпирии подниматься к общему» (В. И. Ле-
н и н. Там же, стр. 178).
Лат. inductio — наведение.
Лит.: В. В. Реп ь е в, Общая методика преподавания математики, Учпедгиз, М/,
1958; И. С. Соминский, Метод математической индукции, Гостехиздат, М., 1950;
И. Я. Депман, Метод математической индукции, Учпедгиз, М., 1957; Д. Пойа,
Математика и правдоподобные рассуждения, ИЛ, М., 1957; Л. И. Головина-Копей-
кина и И. М. Яг лом, Математическая индукция в геометрии, Физматгиз, М., 1961.
ИНДУКЦИЯ МАТЕМАТИЧЕСКАЯ —один из важнейших методов
доказательства в математике, основанный на аксиоме (принципе) И. м. Аксиома И. м.
состоит в следующем. Пусть: 1) свойство Л справедливо при п=\\ 2) из
предположения о том, что свойством А обладает какое-либо натуральное число п,
вытекает, что этим свойством А обладает и число η 4-1. Тогда свойством Л
обладает любое натуральное число.
Пример. Доказать, что справедлива формула:
1+2+3+ ... +»-!^. о
Для п=\ формула, как показывает проверка, верна. Пусть формула (*) верна
для некоторого n=k. Докажем, что она будет верна и для следующего числа
n=k+\. Рассмотрим формулу (*) при /г=£+1:
(\-\-k) k
1+2+3-г ... +k+(k+l)= +(1+Ь),
или после упрощения правой части равенства имеем:
1+2+8+...+*+(*+„.i*±a*±ii.
т. е. мы получили формулу (*), в которой вместо η стоит (&4-1).
Следовательно, на оснований аксиомы И. м. заключаем, что формула (*) верна для любого
натурального числа п.
И. м. широко используется и в школе при выводе формул арифметической и
геометрической прогрессии, формул, встречающихся при изучении логарифмов,
формул бинома Ньютона и комбинаторики и др.
И. м. является строгим, дедуктивным методом доказательства, но, как
всякая дедукция, включает в себя элемент индукции* элемент непосредственной
проверки рассматриваемого предложения (свойства) для числа nt равного
единице.
См. также Индукция.
ИНЕРЦИИ ЗАКОН действительных квадратичных форм — утверждение о том,
что число положительных и число отрицательных квадратов в нормальном виде
квадратичной формы с действительными коэффициентами, к которому она
приводится невырожденным линейным преобразованием, не зависит от выбора этого
преобразования. Сформулированное предложение является одной из основных
теорем теории действительных квадратическйх форм.
9*

132
ИНТЕГРАЛ
ИНТЕГРАЛ — важнейшее понятие математического анализа. Неопределенным
И. функции f(x) [обозначается: \f(x)dx] называется совокупность функций
F(x), у которых производная в каждой точке равна / (х). Эти функции
называются первообразными, или примитивными, для /(*)· Функции из этой
совокупности отличаются на постоянную величину, так что можно записать: \f(x)dx—
Ь
=F(x)i-C. Определенным И. функции f(x) от а до Ь [обозначается: J f(x)dx]
а
называется разность F (Ь) — F(a)t где F(х)—любая из первообразных. Если
Ь
функция f(x) непрерывна, то [f(x)dx равен площади фигуры, ограниченной
а
кривой у=/(х), осью абсцисс и прямыми х=а, х=Ь.
Такому определению понятия определенного И. [если f(x) — непрерывная
функция] эквивалентно следующее. Разобьем отрезок [а, Ь] на отрезки [xit
xi+i*h z===l» 2, .... л — 1, Xn—bi xQ—a. Взяв на каждом отрезке произвольную
точку ti, составим сумму:
S-fltiHXi--Xo)+nt%)lx%—Xi)+ ··· +/(*л)(*л-*п-1). (*)
ь
Предел этой суммы при max | χ ι — χ;—г |, стремящемся к нулю, равен Г / (х) dx.
а
Понятие И. обобщается и на разрывные функции. Если в (*) вместо /(//),
брать верхнюю (нижнюю) грань f(x) на [*;, #/+χ], то получим верхнюю
(нижнюю) сумму Дарбу. Если нижняя грань верхних сумм совпадает с верхней
b
гранью нижних сумм, то их общее значение J / (χ) dx называется интегралом
а
Римана.
Дальнейшее развитие понятия интеграла Римана привело к важнейшему в
математике понятию интеграла Лебега и интеграла Стильтьеса. Понятие
интеграла Лебега включает случай, когда интегрирование ведется не на отрезке [а, Ь]ч
а на любом измеримом множестве (см.) рассматриваемого пространства. Понятие
И.— еще более общее —дали А. Данжуа и А. Я. Хинчин.
Лит.: Г. М. Фихтенгольц, Курс дифференциального исчисления, т. 2, Физ-
матгиз, М., 1963; П. С. А л екса н д ρ о в и А. Н. Колмогоров, Введение в
теорию функций действительного переменного, Гостехиздат, М., 1948; И. П. Натансон,
Теория функций вещественной переменной, Гостехиздат, М. 1950; С. Сакс, Теория
интеграла, перев. с англ., ИЛ, М., 1949.
ИНТЕГРАЛ ВЕРОЯТНОСТИ — интеграл вида
X
о
И. в. не выражается через элементарные функции. Этот интеграл используется
в теории вероятностей, когда рассматривается вероятность попадания случайной
величины, подчиненной нормальному закону распределения (закону Гаусса), в
заданный интервал.
И. в. иначе называется функцией Лапласа.

ИНТЕГРИРОВАНИЕ
133
ИНТЕГРАЛЬНАЯ ГЕОМЕТРИЯ — математическая дисциплина, изучающая
определенные числовые характеристики — меры (см.) геометрических образов
с помощью интегрирования.
Лит.: В. Бляшке, Лекции по интегральной геометрии, «Успехи математических
наук», вып. 5, 1938; «Математика в СССР за тридцать лет, 1917—194 7» (обзорная статья
П. К. Рашевского); А. А. Сан та л о, Введение в интегральную геометрию, ИЛ, М.,
1956.
ИНТЕГРАЛЬНАЯ КРИВАЯ—кривая, изображающая решение
дифференциального уравнения или системы дифференциальных уравнений.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ — отдел математики, в котором изучаются
свойства и способы вычисления интегралов. Сюда входят и способы
приближенного вычисления интегралов. Зачатки И. и. возникли в античную эпоху из задач
на определение площадей и объемов и окончательно И. и. было завершено
в трудах И. Ньютона и Г. Лейбница в XVII и XVIII вв.
ИНТЕГРАЛЬНЫЙ ИНВАРИАНТ динамической системы (см.)— интеграл
вида jj ... §M(xlt х2, . . ., xn)dx1dx2 .. . dxn> взятый по некоторой обла-
D
сти D и сохраняющий свое значение при замене D областью G, в которую она
переходит в любой момент времени t.
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ — уравнения, содержащие неизвестные
функции под знаком интеграла. Наиболее разработана теория линейных И. у.,
которые имеют вид
<Р(Р)+\К(Р, Q)<V(Q)dF=f(P), (*)
G
где φ (Я) — неизвестная функция. При этом функция К(Р, Q) называется ядром.
И. у. такого вида, если область G конечна, а ядро К(Р, Q) ограничено,
называют уравнением Фредгольма. Частным случаем их является уравнение Воль-
терра:
X
φ (x)-t-J*/С (дс, s)<f(s)ds=f(x).
а
В приложениях часто встречаются уравнения вида (*), где К(Р, Q)=
=/C(Q, P)i т. е. уравнения с симметрическим ядром. К И. у. может быть
сведено решение краевых задач для эллиптических "уравнений. Теория И. у.
включается в теорию линейных операторов. Ряд результатов имеется также для
нелинейных И. у. вида
и(х)=Х$К(х< y)f и(у), y]dy.
Лит.: И. Г. Петровский, Лекции по теории интегральных уравнений, Гостехиз-
дат, М., 1951.
со
^ С COS t dt.
ИНТЕГРАЛЬНЫЙ КОСИНУС — функция ci (*)=— I —— И. к. не вы-
X
ражается в конечном виде через элементарные функции.
χ
ИНТЕГРАЛЬНЫЙ ЛОГАРИФМ — функция /(*)= I—. И. л. не выра-
Jlni
О
жается в конечном виде через элементарные функции.
ИНТЕГРИРОВАНИЕ — отыскание неопределенного интеграла.

134
ИНТЕГРИРУЕМОСТЬ
ИНТЕГРИРУЕМОСТЬ дифференциального уравнения в квадратурах —
выражение общего решений этого уравнения через элементарные функции и
неопределенные интегралы от них.
Важнейшие типы интегрируемых в квадратурах уравнений: а) с
разделяющимися переменными:}/' =*F (χ) Φ (у); б) однородные 1-го порядка: y' = f I ■·—1;
в) линейные 1-го порядка: у'-\-р(х)y = q(х)\ г) уравнение Бернулли: у'-\-р(х)у=
= q(x)yn.
Класс уравнений, интегрируемых в квадратурах, мал. При решении
практических задач часто встречаются дифференциальные уравнения, решение Которых
не выражается в квадратурах. Для решения таких уравнений разработаны
Мощные приближенные численные методы.
ИНТЕГРИРУЮЩИЙ МНОЖИТЕЛЬ —множитель, после умножения на
который левая часть дифференциального уравнения:
Р(х, y)dx+Q(xt y)dy=0
обращается в полный дифференциал некоторой функции ы(л;, у). И. м., вообще
говоря, есть функция двух переменных л: и у, но в частных случаях ой может
зависеть от одной переменной. Так, например, для дифференциального уравнения
ydx — xdy—Ο И. м. является функция — *—. И. м. μ(#, у) должен удовлетво-
X1
рять уравнению в частных производных
ду дх
это уравнение есть условие того, что выражение μ (Pdx+Qdy) является полным
дифференциалом.
Всякое дифференциальное уравнение 1-го порядка Pdx+Qdy= 0 имеет беско-
нечное множество И. м. Для целей интегрирования уравнения достаточно знать
какой-нибудь один И. м. Для многих видов дифференциальных уравнений 1-го
порядка И. м. заранее известен. Так, для линейного дифференциального
уравнения:
Ldy+(My+N)dx^0
выражение е* L есть И. м.
ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ — уравнения, содержащие
неизвестную функцию как под знаком интеграла, так и под знаком производной.
оо
ИНТЕРВАЛ СХОДИМОСТИ степенного ряда ^j α*χη ~~ интервал, в каж-
rt=0
дой точке которого ряд абсолютно сходится, а в точке, не принадлежащей
этому интервалу, ряд расходится. На концах И. с. ряд может сходиться или
расходиться. Интервал сходимости может быть пустым, а может и совпадать
со всей прямой.
ИНТЕРВАЛ ЧИСЛОВОЙ ОСИ (или промежуток) — множество
действительных чисел, удовлетворяющих неравенствам а<:х<Ь (знаки равенств исключа-
а+Ь
ются!), где а и Ъ — действительные числа, называемые концами И. Число——
называется центром И., Ъ — а*—длиной И. И. может быть определен
неравенством \х — х0\<Ь\ здесь х0 — центр И., а 25—длина И. Такой И. называется
также δ-окрестностью точки х0.
См. Отрезок.

ИНТУИЦИОНИЗМ
135
ИНТЕРПОЛЯЦИЯ — построение приближенного или точного аналитического
выражения функциональной зависимости» если о ней известны только
соотношения между значениями независимой переменной и соответствующими значениями
функции в дискретном ряде точек.
Так, основной задачей И. является нахождение значений функции f(x) во
всех точках интервала (х0, хп) числовой оси, если известные значения ?/=/(#/)
этой функции в конечном числе точек (x0i xlt x2t . . *, Хп) данного интервала.
Наиболее прост метод линейной И. При линейной И. значение функции f(x)
в точке χ(χί<χ<χί_^{) принимается равным значению
χ^\—χι
линейной функции, совпадающей с f(x) в точках xt и xt^v
Ошибка И. остается неопределенной, если на функцию/(ж) или на ее
производные не наложены некоторые количественные ограничения, т. е. сама
функция или ее производные не подчинены некоторым неравенствам. Так, если для
нахождения значения функции f(x) в точке χ(χι<χ<Χί^_{) применяется метод
линейной И., то оценка ошибки станет вполне определенной при ограничении,
наложенном, например, на вторую производную f(х) приXi<x<x^l9 \f"(x)\<M.
Ошибка при линейной И. может быть оценена неравенством:
[/(*)- Х~~Х'\ [/(*/+!) ~/(*i)]| M'
gi* —*ί)(*ί+ι —
сосуществуют более сложные интерполяционные методы, но ими обычно
пользуются при условии, что функция обладает достаточным числом не слишком
быстро возрастающих производных.
Такова Лагранжа интерполяционная формула (см.).
В случае, когда сегмент [*<>, Хп] разбит точками *t· на разные интервалы,
полином Рп(х) можно записать с помощью Ньютона интерполяционной формулы
(см.).
Если число точек χ ι очень велико, то лучше разбить интервал (х0, хп) на
части и интерполировать на каждой части в отдельности. При обработке данных
наблюдений, когда имеют место ошибки наблюдений, применяется обычно в
качестве интерполяционного многочлен не очень высокой степени, мало
уклоняющийся в точках χι от заданных значений, по способу наименьших квадратов
(см.). См. также Экстраполяция.
Лит.: А. Н. Крылов, Лекции о приближенных вычислениях, Гостехиздат, М.,
1954.
ИНТЕРПРЕТАЦИЯ системы аксиом — система объектов, выражающих
основные понятия и сохраняющих отношения между ними, как указано в системе
аксиом.
Построение И. с. а.—один из способов доказательства непротиворечивости
данной системы аксиом. Одна и та же система аксиом может допускать
множество интерпретаций.
И. с. а. иначе называют моделью или реализацией системы аксиом.
Лат. interpretatio — истолкование, раскрытие смысла чего-либо, разъяснение
чего-либо.
ИНТУИЦИОНИЗМ — одно из философских направлений в математике.
Содержание И. заключается в отрицании математики как науки, отражающей
некоторые стороны явлений природы. Интуиционисты считают математику
«деятельностью» отдельного человека, опирающегося на интуицию. Основателем И. является
голландский математик Л. Брауэр. Его идеи» предназначавшиеся, по мысли

136
ИНФОРМАЦИЯ
автора, для объяснения не вполне установившихся в математике некоторых
понятий теории множеств, приводят к громоздким и запутанным построениям.
Интуиционисты отрицают, в частности, закон исключенного третьего для
бесконечных множеств (см. Антиномии). Понять идеи И. можно, только приняв
ложную философскую концепцию Брауэра. И. был поддержан некоторыми
крупными математиками (Г. Вейль и др.). И. приводит к отрицанию многих
достижений математического анализа. Им отрицается также элементарная геометрия.
Брауэром получены некоторые результаты конструктивной логики (см.
Математическая логика), поэтому на Западе эту науку часто неправомерно называют
интуиционистской.
ИНФОРМАЦИЯ — одно из основных понятий теории информации (см.).
ИНЦИДЕНТНОСТЬ — термин, употребляемый в геометрии для выражения
таких понятий, как «лежать на ...» или «проходить через . . .»; например,
предложения: «точка лежит на прямой» или, что то же, «прямая проходит
через точку», можно заменить одним предложением «прямая и точка
инцидентны». Для обозначения И. применяются знаки: 5~6» или £ » И*'1И С · Если
точка А и прямая α И., то пишут: А^)—ζ α.
ИРРАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебраическое выражение (см.), со-
держащее радикалы (корни), например,
Υ а2 и др.
Следует отметить, что И. в. может не быть иррациональным числом (см.).
Например, И. в. Υ а при а=4 — рациональное число.
ИРРАЦИОНАЛЬНОСТЬ л-й степени — корень многочлена л-й степени с
целым коэффициентом, неприводимого в поле рациональных чисел. При п=2 мы
приходим к понятию квадратичной иррациональности (см.). Понятие И. л-й с.
совпадает с понятием «алгебраическое число (см.) степени л». Большой вклад в
изучение И. л-й с. был сделан украинским математиком Г. Ф. Вороным и
другими учеными из Петербургской школы теории чисел. Подробнее об этом см.
в книге Б. Н. Делоне «Петербургская школа теории чисел» (Изд-во АН СССР,
М., 1950).
ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ — уравнения, содержащие
неизвестные под знаком радикала. Например, уравнения!/* — 2=5 и Υ χ — 2 -f-
-b*=Vχ2— 4— иррациональные. Понятие степени И. у. не устанавливают.
К методам решения иррациональных уравнений относятся: 1) метод введения
вспомогательной неизвестной, в результате чего решение И. у. сводится к
решению системы рациональных уравнений; например, решение уравнения 2) заменой
переменных y-\-x=s, Ух — 2 =у, Υ χ2 — 4=s сводится к решению системы:
χ — 2=у2; y-}-x=s, χ2 — 4=--s2; б) изолирование (уединение) радикала и
возвышение в квадрат обеих частей уравнения, в результате чего приходят к
уравнению с меньшим числом (или не содержащим) радикалов; 3) умножение обеих
частей уравнений на выражение, сопряженное одной из его частей.
И. у. могут иметь и бесчисленное множество решений: например, уравнение
У дгЧ-8 — 6l/"x— 1 +V х+Ъ — ±Ух~^Т=\
имеет бесчисленное множество (континуум) корней 5 < jc < 10.
Решения И. у. обычно рассматривают в области (в поле) действительных
чисел, а корни, входящие в уравнение, — только арифметические.
При решении И. у. необходимо обращать внимание на законность
преобразований уравнений, на возможность нарушения равносильности уравнений (см.),
появления новых (посторонних) корней и потери корней уравнения.

ИТЕРАЦИЯ
137
ИРРАЦИОНАЛЬНЫЕ ЧИСЛА — числа* записываемые в виде бесконечной
десятичной непериодической дроби, например числа: ±0,1010010001 . . .;
±V 2; ±lg5; ±sin 31°; ±(Уъ-У 2) и др. И. ч. не могут быть
представке?
лены в виде —, где р, q — взаимно простые числа (<7¥=0). Строгая теория И. ч.
была разработана во второй половине XIX в. немецким математиком Дедекиндом.
Всякое И. ч. можно с любой степенью точности выразить приближенно
рациональным числом. И. ч. может быть алгебраическим (см.) или трансцендентным
(см.). На практике при действиях над И. ч. их обычно заменяют
рациональными приближениями. И. ч. возникают сначала при извлечении корня в алгебре
и при измерении отрезков в геометрии.
См. Дедекиндово сечение, Число, Иррациональность п-й степени, Галуа
теория.
Лит.: А. И. Маркушевич, Действительные числа и пределы, Изд-во АПН РСФСР,
М., 1948.
ИСКЛЮЧЕНИЕ НЕИЗВЕСТНЫХ — переход от системы уравнений,
содержащей несколько неизвестных* к системе уравнений (или к одному уравнению),
содержащей меньшее число неизвестных.
См. также Результант.
ИСКОМАЯ ВЕЛИЧИНА (фигура) — величина (фигура), подлежащая
определению. И. в. часто называют искомым; так, говорят об искомом геометрическом
месте точек, об искомой сумме нескольких слагаемых и т. д.
ИСТИННОЕ ПОДМНОЖЕСТВО множества А — подмножество множества Л,
отличное от самого множества А.
ИСЧИСЛЕНИЕ БЕСКОНЕЧНО МАЛЫХ— раздел математики, охватывающий
дифференциальное исчисление (см.) и интегральное исчисление (см.). Название
происходит от того, что основные понятия И. б. м. — производная и интеграл —
образованы с помощью рассмотрения бесконечно малых величин.
ИСЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ — см. Теория вероятностей.
ИСЧИСЛЕНИЕ КОНЕЧНЫХ РАЗНОСТЕЙ —см. Конечных разностей
исчисление.
ИТЕРАЦИЯ — результат многократного применения какой-либо
математической операции. Пусть у=/(*), тогда последовательность f(x), f [f (x)]t /{/[/(*)]}»
.. . есть последовательность итераций функции f(x). В частности, если /(*) =
=ах, то эта последовательность записывается в виде а*, а2х, а3х, . . ., апх, . . .
Число, показывающее, сколько раз применена операция, называется показателем
И. Процесс составления И. — итерирование — находит многочисленные
приложения в математике (см., например, Последовательный приближенный метод).

к
КАВАЛЬЕРИ ПРИНЦИП —предложение, состоящее в следующем: если
при пересечении двух плоских фигур любой прямой, параллельной некоторой
другой прямой, получаются в сечении равные хорды, то площади этих фигур
равны. Аналогичное предложение имеет место и для пространственных фигур.
К. п. является теоремой, доказательство которой принадлежит итальянскому
математику Кавальери.
Это предложение было известно еще древнегреческим математикам, которые
принимали его без доказательства.
КАНОНИЧЕСКОЕ УРАВНЕНИЕ кривой 2-го порядка или поверхности 2-го
порядка — простейшее уравнение этой кривой или поверхности в прямоугольных
х2 у2
декартовых координатах. Например, К. у. эллипса (см.) имеет вид: —(:4—г= 1,
а2 Ь2
где а и Ъ — его полуоси. К. у. однополостного гиперболоида (см.) имеет вид:
Всякое общее уравнение кривой 2-го порядка или поверхности 2-го порядка
может быть приведено путем преобразования координат к одному из своих К. у.;
свойства кривых и поверхностей 2-го порядка проще исследовать по их К. у.
См. также соответственно термины о кривых и поверхностях 2-го порядка.
Греч, χάνων — правило, канон, норма.
КАНОНИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ многочлена. Если в некотором
многочлене выполнить приведение подобных членов (см.) во всех случаях, когда это
возможно, и выбросить все получившиеся члены с нулевыми коэффициентами,
то в результате получим К. п. м. Если при этом окажется, что выбрасываются
все члены, то К. п. м. считаем 0, а исходный многочлен в этом случае
называется нуль-многочленом. Можно легко показать, что для всякого многочлена
К. п. м. единственно с точностью до порядка следования членов многочлена
(см.). Все члены многочлена в его К. п. м. попарно неподобны (см. Подобные
члены).
Греч, χάνων — правило, норма, канон.
КАНТОРА —БЕРНШТЕЙНА ТЕОРЕМА в теории множеств утверждает,
что если множества А и В таковы, что множество А эквивалентно
подмножеству В' множества В и множество В эквивалентно подмножеству А'
множества Л, то множества А и В эквивалентны (равномощны).
КАНТОРА МНОЖЕСТВО — простейшее совершенное множество на прямой,
не содержащее ни одного отрезка. Состоит из точек отрезка [0,1], которые
записываются с помощью троичной дроби, не содержащей цифру 2. К- м. имеет
меру (см.) нуль. Мощность К- м., как и всякого совершенного множества,—
континуум. К. м. играет важную роль во многих отделах математики.
КАППА — геометрическое место точек касания касательных прямых,
проведенных из начала координат к окружности радиуса а, центр которой
перемещается по оси абсцисс. Полярное уравнение К. имеет вид:
p = arctg<p.

КАРДИОИДА
139
В декартовой прямоугольной системе
координат К. имеет уравнение: (х2-\-у2)у2 =
=а2х2, которое является уравнением 4-го
порядка (рис. 93). Начало координат —
узловая точка (см.) К. Прямые у=*±а
являются асимптотами для К. Кривая
является частным случаем кривой
семейства кривых — узлов (см. узлы). Кривая К.
имеет форму греческой буквы χ (каппа).
КАРДАНО ФОРМУЛА — формула,
выражающая корни кубического
уравнения вида:
x*+px+q=0 (*)
через его коэффициенты. К виду (*) приводится всякое кубическое уравнение.
К. ф. записывается так:
Рис. 93
■У -ι+/м+/ -* У?
+
27
Выбирая произвольно значение первого кубического радикала, следует выбрать
то значение второго радикала (из трех возможных), которое в произведении
с выбранным значением первого корня радикала дает
ю-
Таким
образом, получают все три корня уравнения (*). До сих пор не ясно, кому
принадлежит К. ф.: Дж. Кардано, Н. Тарталье или С. Ферро. К. ф. относится к XVI в.
КАРДИНАЛЬНОЕ ЧИСЛО — важное понятие абстрактной теории множеств
(см.). К. ч. характеризует множество с точки зрения запаса его элементов —
мощности (см.) множества. К. ч. является обобщением понятия количественного
числа на бесконечные множества. Интересным при таком обобщении является то
обстоятельство, что одно и то же бесконечное множество можно по-разному
упорядочить (см. Вполне упорядоченные множества) и в связи с этим К. ч.
резко отличается от трансфинитных чисел (см.) — обобщения порядковых чисел.
Для конечных множеств К. ч. совпадает с трансфинитным числом и равно
количеству элементов множества.
Лит.: П. С. Александров и А.Н.Колмогоров, Введение в общую теорию
множеств и функций, Гостехиздат, Μ., 1948.
КАРДИОИДА — плоская кривая, описываемая какой-либо точкой Μ
окружности радиуса ΟλΜ, равного а, катящейся без скольжения по неподвижной
окружности того же радиуса и имеющей с
первой окружностью внешнее касание (рис. 94).
К. является частным случаем эпициклоиды
(см.). К. можно рассматривать как подэру
(см.) окружности относительно какой-либо из
ее точек. К. является также одной нз
конхоид (см.) и улиток Паскаля (см.).
Если над параболой выполнить
преобразование инверсии (см.) с центром в фокусе
параболы, то парабола перейдет в К.
Уравнение К. в полярных координатах
имеет вид:
P = 2a(l+cos(p),
а в декартовых —
(х2-ЬУа — 2α*)2 = 4α2(χ2-Β>2).

140
КАРНО ТЕОРЕМА
Из последнего уравнения вытекает, что К. является алгебраической кривой 4-го
порядка.
Греч, χαρδια — сердце, είδος — вид; сердцевидная.
КАРНО ТЕОРЕМА. Пусть ABC — треугольник с указанной на нем
ориентацией и f(x) — плоская алгебраическая кривая порядка т, пересекающая
каждую из сторон треугольника или ее продолжение в т точках. Если
обозначить точки пересечения кривой f(x) с прямой АВ через С19 С2 Ст, с
прямой ВС —через А19 А2 Ат, с прямой С А— через В1% В2 Вт и
составить 3 т отношений:
CjA_ Αβ Bfin-y о Ч
Cfi9 Afi9 БИ(
m).
CiA
то произведение этих отношений будет равно +1. Отношение —г > 0, если
С (В
точка Ci лежит между А и В или, что то же, направления отрезков АС ι и С,£
С-А
совпадают, в противном случае отношение -7гт;<0· ^Ри т=1 получаем теоре-
му Менелая, при т=2 получаем теорему о пересечении конического сечения со
сторонами треугольника.
Теорема названа по имени французского математика Л. Карно,
установившего ее.
КАСАНИЕ — свойство двух кривых или кривой и поверхности иметь в
некоторой точке общую касательную прямую (см.) или свойство двух
поверхностей иметь в некоторой точке общую касательную плоскость (см.). Точка, в
которой две кривые (кривая и поверхность или две поверхности) имеют К·*
называется точкой касания или точкой соприкосновения.
КАСАТЕЛЬНАЯ к кривой линии / в точке Μ— прямая t, являющаяся
предельным положением секущей ММ', когда вторая точка М' кривой
неограниченно приближается к точке Μ (рис. 95).
Далеко не всякая непрерывная кривая t2 |
имеет К. Так, на рис. 96 кривая в точке
Μ не имеет определенной касательной, в
точке Μ кривая имеет две предельные
прямые tx и t2. Непрерывная кривая
может не иметь касательной ни в одной
своей точке.
Μ
L
t,
Рис. 95
Рис. 96
Если уравнение плоской кривой в прямоугольных координатах имеет вид
У=/(*)> то уравнение К. в точке М, имеющей абсциссу х0, запишется так:
У —/(*о) = /'(*о)(* — *о),
где производная /' {х0) есть угловой коэффициент К.
К. к поверхности 5 в точке Μ называют любую прямую, проходящую
через Μ и лежащую в касательной плоскости (см,) к S в точке М.

КАТЕТ
141
КАСАТЕЛЬНАЯ ПЛОСКОСТЬ к поверхности S в точке Μ — плоскость,
проходящая через точку Μ и характеризующаяся тем свойством, что расстояние
от переменной точки М' поверхности при стремлении Μ' κ Μ до этой плоскости
есть бесконечно малая по сравнению с расстоянием ММ'.
Если поверхность задана уравнением/(л:, у, ζ)=0, то уравнение К. п. к
этой поверхности в точке M(x0i y0i zQ) имеет вид:
д1
дх
df df
(х - xo)+J (У - Уо)-Ь - (г - zQ) =
•0>
где
■значение частных производных в точке (дг0, у0, г0).
д[ df df
дх* ду дг
К. п. к сфере О (г) в точке М, лежащей на сфере, перпендикулярна
радиусу сферы, проведенному в точку касания. К. п. к конусу и цилиндру
(конической и цилиндрической поверхности, см.) в точке Μ проходит через одну только
образующую этих поверхностей, принадлежащую точке М.
КАССИНИ ОВАЛ — плоская кривая, представляющая собой геометрическое
место точек, произведение расстояний которых от двух данных точек постоянно.
Простейшее уравнение К. о. в декартовой системе координат имеет вид:
(х2+у2)2 — 2с2 (х2 — у2)=а* — с*,
где с — половина расстояния между двумя данными точками Fx и F2, α2 —
Данная константа, равная произведению MF1*MF2 (рис. 97). _^
Если а>су 2, то К. о. — выпуклая кривая вида /, если с<а<с\ 2, то
о. имеет вид кривой 2% если а=су то К. о. вырождается в лемнискату
К
Рис. 97
Рис. 98
Бернулли Я- (см.) вида 3, если с>а, то К- о. —- двухсвязная кривая вида 4,
состоящая из двух овалов.
К. о. назван по имени французского ученого Джона Кассини, впервые
рассмотревшего эту кривую.
КАТЕНОИД — поверхность, образуемая вращением цепной линии (см.)
вокруг ее директрисы (рис. 98). К.—единственная минимальная поверхность (см.)
среди поверхностей вращения. Модель К. можно сделать так: расположить два
проволочных круга так, чтобы их плоскости были перпендикулярны к линии
центров. Тогда мыльная пленка, заключенная между плоскостями этих кругов,
образует под действием сил поверхностного натяжения поверхность, имеющую
форму К.
КАТЕТ — каждая из двух сторон прямоугольного треугольника (плоского
или сферического), заключающих прямой угол. При этом прямоугольным сфери-

142
КАЧЕСТВЕННАЯ ТЕОРИЯ
ческим треугольником называется треугольник, имеющий только один прямой
угол.
См. также Пифагора теорема.
Греч, κάθετος (катетос) — отвес.
КАЧЕСТВЕННАЯ ТЕОРИЯ дифференциальных уравнений — изучение свойств
решений дифференциальных уравнений без нахождения самих решений. Так как
в большинстве случаев решение в явном виде найти невозможно, ясно, что
К. т. д. у. имеет большое значение. Основателями К. т. д. у. являются
русский математик А. М. Ляпунов и французский математик А. Пуанкаре. В
дальнейшем большой вклад в развитие К. т. д. у. внесли советские математики
А. А. Андронов, Н. Н. Боголюбов, Н. М. Крылов, В. В. Немыцкий, И. Г.
Петровский, В. В. Степанов и др.
Основные разделы К. т. д. у.: линейные проблемы, нелинейные проблемы
и зависимость решений от параметров.
Линейные проблемы. Рассматривается система линейных
дифференциальных уравнений:
dx- n
~77= Σ PikV)XkV) 0=1. 2, ..., η)
или одно уравнение:
2 Р/(ОУ(/) = 0 (/=1, 2, ..., я).
г=0
В К· т. д. у. изучается вопрос об асимптотическом поведении решений
таких уравнений при /—*-f-°°· В зависимости от коэффициентов получаются
оценки роста решений. Выводятся критерии устойчивости решений. Первым их
изучал А. М. Ляпунов. К. т. д. у. занимается также исследованием нулей
решений линейных дифференциальных уравнений (число их, чередование нулей
линейно-независимых решений).
Нелинейные проблемы. Рассматривается система уравнений:
dx:
—=/i(*i, *2> .--ι хп, t)(i=\t 2, ..., η),
at
Наиболее важными являются вопросы об устойчивости решений по
Ляпунову и о существовании периодических решений. При решении этих вопросов
в основном применяются методы, разработанные Ляпуновым. Подробно изучено
поведение решений около особой точки. Важной задачей является исследование
интегральных кривых в целом, а не в окрестности особой точки.
Зависимость решений от параметров. Исследуется вопрос
о сохранении периодических решений при изменении параметров, от которых
зависят правые части. Большое число работ посвящено исследованию уравнений с
малыми параметрами при старших производных.
Лит.: А. М. Ляпунов, Общая задача об устойчивости движений, Гостехиздат,
М. — Л., 1950; А. Пуанкаре, О кривых, определяемых дифференциальными
уравнениями, М. — Л., 1949.
КАЧЕСТВЕННЫЕ МЕТОДЫ — методы, дающие возможность указать те или
иные свойства решения задачи без нахождения его. Примерами задач, решаемых
К. м., могут служить следующие: 1) выяснить, устойчивы ли решения
дифференциального уравнения, колеблются ли они, какого типа особые точки
встречаются; 2) указать особенности расположения корней уравнения /(г) = 0,
например выяснить, вещественны ли они, в какой полуплоскости расположены.

КВАДРАТИЧЕСКАЯ ОШИБКА
143
С отдельными вопросами качественного характера математика сталкивалась
давно, но широкое распространение К- м. получили лишь в XX в. Так, основы
качественной теории дифференциальных уравнений заложены трудами русского
математика А. М. Ляпунова. Наиболее значительные результаты в области К. м.
в вариационных задачах получены советскими математиками Л. А. Люстерником
и Л. Г. Шнирельманом.
Лит.: А. М. Ляпунов, Общая задача об устойчивости движения, Гостехиздат, М.,
1950; Л. А. Люстерник и Л. Г. Шнирельман, Топологические методы в
вариационных задачах, ОНТИ. М., 1930; В. В. Немыцкий, Метод неподвижных точек
в анализе, «Успехи математических наук», вып. 1, 1936.
КВАДРАНТ — один из четырех прямых углов, образованных двумя
перпендикулярными осями координат.
Нумерацию К- производят в направлении против движения часовой стрелки.
Первым К. считают тот, который заключен между положительными
направлениями полуосей Ох и Оу.
Четвертый К. иногда называют первым отрицательным К., третий — вторым
отрицательным и т. д. Если вершина угла МОК совпадает с началом координат
О, неподвижная сторона ОК угла совпадает
с полуосью Ох, а подвижная сторона ОМ
расположена внутри какого-либо К.* то
говорят < что угол МОК лежит (расположен) в
этом К.# например угол МОК (рис. 99) лежит
во втором К- (четверти).
К. называют также координатным углом
или четвертью.
КВАДРАТ — прямоугольник, две смежные
стороны которого равны (отсюда вытекает,
что и все стороны равны). К. можно
определить и так: К. есть ромб, у которого один из
углов при вершине прямой (отсюда следует,
что и все углы прямые). Можно дать и такое
определение К·: К. есть параллелограмм, все
стороны и все углы которого равны.
К. имеет четыре оси симметрии: две
диагонали и две средние линии (отрезки,
соединяющие противоположные стороны). Вокруг
К. можно описать и в него можно вписать окружность. К. является одним из
правильных многоугольников (или /2-угольников, см.). Диагональ К.
несоизмерима с его стороной (см. соизмеримые и несоизмеримые величины).
КВАДРАТИЧЕСКАЯ ОШИБКА — выражение
Ч у1
\м
ι»4
V,
I
Рис. 99
V'-
ΔΤ + Δ2
-ΎΨ·
где Δ — ошибка измерения, т. е. разность между действительным, истинным
значением величины и ее измеренным значением, η — число измерений, [Δ2] —
обозначение суммы по Гауссу.
К. о. является хорошим мерилом точности произведенных измерений и
достоинства данного ряда измерений по следующим причинам: во-первых, на
величину К. о. сравнительно мало влияют большие по абсолютной величине случайные
ошибки, во-вторых, К- о. устойчива, так что практически достаточно
сравнительно небольшого числа измерений, чтобы определить значение этой ошибки
с удовлетворительной степенью точности.

144
КВАДРАТИЧНАЯ ИРРАЦИОНАЛЬНОСТЬ
Чем меньше К. о. оценки, тем более эффективной считается сама оценка.
К- о. иногда называют квадратичной ошибкой.
См. также Ошибка округления, Погрешность, Округление.
Лит.: В. И. Романовский, Элементарный курс математической статистики, изд.
АН Узбекской ССР, Ташкент, 1963.
КВАДРАТИЧНАЯ ИРРАЦИОНАЛЬНОСТЬ —иррациональный корень
квадратного уравнения с целыми (рациональными) коэффициентами. Другими словами,
К. и. — корень квадратного уравнения, не приводимого в поле рациональных
a+bVc
чисел. К. и. всегда может быть представлена в виде — , где Л, Б, С,
D — целые числа, D^O и С не является квадратом другого целого числа.
Основной теоремой о К- и. является Лагранжа теорема (см.) и теорема,
обратная ей.
См. также Квадратное уравнение и Иррациональность л-й степени.
КВАДРАТИЧНАЯ ФОРМА — однородный полином второй степени
η η
F(xlt x2i .... xn) = 22v/·
г=1 у=1
К. ф. характеризуется квадратной матрицей Λ = ||α/;·||. При помощи линейного
преобразования переменных χ с комплексными коэффициентами К. ф. может
быть приведена к виду:
У21+У22+ '" +У1 *<"·
Если αϊ/—вещественны, а линейные преобразования переменных χ
рассматриваются над полем действительных чисел, то К. ф. F приводится к виду:
у!+у1+ ··· +y2s-ys2+i >&*<*,
причем независимо от способа приведения F к этому виду количество
положительных квадратов s остается неизменным (см. Инерции закон К. ф. и
Сигнатура К. Ф·)· При линейном преобразовании переменных xlt х2, . . ., хп с
матрицей С матрица К. ф. А переходит в матрицу САС (С — транспонированная
(см.) матрица).
Ортогональными преобразованиями (см.) над переменными xlf х2, . . ., χη
можно привести F к виду:
^У2+Х2у2-Ь ... -ЬХлу2, (*)
где λ1? λ2, . . ч λΛ — вещественные числа, инварианты К- ф.
Вышеописанные теоремы находят важные и многочисленные применения
во многих отделах математики. Так, в определении типа (вида) кривой
(поверхности) 2-го порядка в аналитической геометрии по существу решается задача
о приведении К. ф. к виду (*), а вычисление, например, полуосей эллипса,
гиперболы и т. п. сводится к вычислению чисел λ в формуле (*).
В дифференциальной геометрии рассматриваются К. ф. с переменными
коэффициентами: aij=aij(xlt x2i . . ., хп), в связи с чем теория К. ф. наполняется
новым содержанием. Большое значение среди К. ф. имеют положительно
определенные К. ф. (см.), у которых λ|>0, ι = 1, 2, . . ., п. Рассматриваются также
отрицательно определенные К. φ. (λ/<0, ι = 1, 2 η).
Лит.: И. Μ. Гельфонд, Основы линейной алгебры, Гостехиздат, М., 1951;
Г. Е. Ш и л о в, Введение в теорию линейных пространств, Гостехиздат, М., 1952.

КВАДРАТИЧЕСКИЙ ВЫЧЕТ
145
КВАДРАТИЧНОЕ ОТКЛОНЕНИЕ — отклонение величин xlt x2t . . . , хп
от некоторой величины с, равное
Наименьшее значение К. о. имеет при с=х, где л;— среднее
арифметическое величин:
- *ι-τ·*2+ ·'· Л-Хп
х— ·
η
В этом случае К. о. может служить мерой рассеяния системы величин xlt
х2, .... хп. Взвешенное К- о. определяется как квадратный корень из
выражения
Ρι(Χι — с?+Р2 (*2 — с)2+ ··· +Рп(Хп — с)2
Pi-bP2-b ··· +Рп
где числа рь р2» · · · » Рп — веса, соответствующие величинам xlt x2t .... хп.
Наименьшее значение взвешенное К- о. принимает при с, равном взвешенному
среднему:
Pi*i-f-P2*2-b ··· +РпХп
Pi+Pz-l· ··· +Рп
В теории вероятностей К. о. σ случайной величины ξ от ее математического
ожидания (см.) называют квадратным корнем из дисперсии:
К. о. употребляется как мера качества статистических оценок и называется
в этом случае квадратической ошибкой (см.) соответствующей оценки.
КВАДРАТИЧНОЕ СРЕДНЕЕ η чисел аи а2, . . . , ап(п > 2) — число, равное
fa\W2+ ··· +а\
К. с. является средним (см.) чисел al9 a2i . . ., ап. К. с. чисел аи а*. . . . $ ап
является корнем квадратным из среднего арифметического квадратов данных
чисел.
КВАДРАТИЧНЫЕ ЧИСЛА —* натуральные числа вида л2, где л = 1,
2, . . . , п. К. ч. образуют арифметический ряд (см.) второго порядка, первые
разности которого составляют натуральный ряд, а вторые разности равны
единице. К. ч. являются частным случаем фигурных чисел (см.).
КВАДРАТИЧЕСКИЙ ВЫЧЕТ по модулю р. Число а, взаимно простое с р,
называется К. в. по модулю ρ в том и только в том случае, если сравнение χ2 ξξ a(mod p)
имеет решения, и называется квадратическим невычетом в том и только в том
случае, если указанное сравнение не имеет решений. Если ρ — простое число,
то половина из чисел приведенной системы вычетов (см.) по модулю ρ будет
К- в., а половина будет квадратическими невычетами, т. е. и тех и других будет
по —-—. Для распознавания К. в. и квадратических невычетов служит
Эйлера критерий (см.). Этот же вопрос легко решается с помощью символов
Лежандра и Якоби (см. Лежандра символ, Якоби символ).
10 Толковый словарь математических терминов

146
КВАДРАТИЧЕСКИЙ НЕВЫЧЕТ
Пример. По модулю 13 числа 1, 3. 4, 9, 10 и 12 будут К. в., а числа 2,
5, б, 7, 8, 11 будут квадратическими невычетами.
КВАДРАТИЧЕСКИЙ НЕВЫЧЕТ по модулю ρ — см. Квадратический вычет.
КВАДРАТНО^ УРАВНЕНИЕ — уравнение вида ax%+bx+c=0t где афО.
Коэффициенты а, Ь, с могут быть как действительными, так и комплексными
числами. Обычно К. у. рассматривают с действительными коэффициентами. К. у.
над полем комплексных чисел имеет всегда два корня.
Если а=1, то К. у. называется приведенным, которое обычно пишут в виде:
x2+px+q— 0. Если 6=0, или с=0, или 6=с;=0, то К. у. называется неполным.
Если К- у. с целыми коэффициентами имеет один иррациональный корень
x1=r1-jra1 то оно имеет и другой иррациональный корень х2=г1 — а, где гг —
рациональное число, α — иррациональное число.
Если а, 6, с — вещественные и u+vi (νφΟ) — корень К. у.» то
сопряженное ему число и — vi также корень К. у. Иррациональные корни К. у. с
целыми (или рациональными) коэффициентами называются квадратическими ирра-
циональностями (см. Иррациональность п-й степени).
» „ ь ъ
Сумма корней К- у. равна ——, т. е. ^+^2= — —, а произведение его
а , а
с с
корней равно —, т. е. хх-хг=— (см. Виета теорема).
К- у. называется также уравнением второй степени с одним неизвестным.
КВАДРАТНАЯ МАТРИЦА — матрица, которая имеет одинаковое число строк
и столбцов.
КВАДРАТРИСА — плоская кривая, уравнение которой в прямоугольных де-
л χ Λ .
картовых координатах имеет вид: y=*-ctg — , где/- — радиус О А окружности
с центром в начале координат (рис. 100).
К. может быть определена как
геометрическое место точек Ρ пересечения прямых ОМ,
равномерно вращающихся вокруг точки О (по
часовой стрелке), и прямых А'В', параллельных
оси Оу и равномерно перемещающихся в
направлении оси Ох\ при этом, когда прямая ОМ
повернется на прямой угол, прямая А'В'
переместится по оси Ох на отрезок ОА=г.
К. была известна древнегреческим
математикам: Гиппию Элитскому (V в. до н. э. )*
использовавшему ее для решения задачи о
трисекции угла (см.), и Динострату (IV в. до н. э.), использовавшему К. для
решения задачи о квадратуре круга (см.).
Рис. 100
Если я-* 0, то из уравнения К. получим:
у0 = \\т xctg—= hm-
х *о 2г х-+о
2г
tg"
π χ
~2r
откуда* зная отрезок у0, можно построить квадрат, равновеликий кругу
радиуса г.
Лит.: Г. ф. де Л'Опиталь, Анализ бесконечно малых, Гостехиздат, М., 1936;
Г. Г. Цейтен, История математики в древности и в средние века, ОНТИ, М., 1938.
КВАДРАТУРА: 1°. К.—величина площади, выраженная в квадратных
единицах. 2°.К. — построение квадрата, равновеликого данной фигуре. 3°. К. —*
вычисление интеграла. Ср. Кубатура.

КВАЗИГРУППА
147
КВАДРАТУРА КРУГА — задача о построении квадрата, равновеликого
данному кругу. Эта задача неразрешима с помощью циркуля и линейки, как и
трисекция угла (см.) и удвоение куба (см.). К. к. сводится к решению уравнения jr=jtr2
(где χ — сторона искомого квадрата, а г — радиус данного круга) или к
построению отрезка х=у яг · г. Но отрезок χ построить циркулем и линейкой нельзя
согласно критерию (см.) построения отрезка с помощью циркуля и линейки, так
как число π (отсюда и Υπ ) трансцендентное, т. е. оно не может быть
корнем никакого алгебраического уравнения с целыми коэффициентами.
Существуют, однако, другие средства построения отрезка х^У η г-г, т.е.
решения задачи К. к., например с помощью квадратрисы (см.), приближенные
способы решения и механические способы решения задачи о К- к. (например,
с помощью цилиндра Леонардо да Винчи).
Лит.: Φ. Ρ у д и о, О квадратуре круга, ОНТИ, М., 1936; А. Адлер, Теория
геометрических построений, Учпедгиз, М., 194 0.
КВАДРАТУРНЫЕ ФОРМУЛЫ — формулы, служащие для вычисления
определенных интегралов по значениям подинтегральной функции в некоторых
точках. Примерами К. ф. могут служить формулы Симпсона (см. Симпсона
формула), Котеса и др. Одна из наиболее простых К. ф. — формула трапеций:
ь
Г Ъ — а (b — af m
f (х) dx= —j- [/ (a)+f (b)} - —^- Г tt).
a
где a < I < b.
Лит.: С. М. Никольский, Квадратурные формулы, Гостехиздат, Μ , Ι ΌΖ8,
КВАДРИЛЛИОН — число, изображаемое единицей с 15 нулями (во Франции
и США), т. е. число 1015. В некоторых странах (Англии, Германии) К.
называют число 1024.
В советской математической литературе термин К. почти вышел из
употребления.
КВАДРИРУЕМАЯ ОБЛАСТЬ — область, имеющая определенную площадь
(см.), или, что то же самое, определенную плоскую меру в смысле Жордана
(см. Мера множества).
Для того чтобы область была квадрируемой, необходимо и достаточно,
чтобы ее граница имела площадь, равную нулю. Существуют области, не
удовлетворяющие этому условию и, следовательно * неквадрируемые.
Лит.: В. В. Немыцкийи др., Курс математического анализа, тт. 1,2, Гостехиздат,
М., 1944; Г. Μ. Φ и χ τ е н г о л ь ц, Курс дифференциального и интегрального исчисления,
тт. 2, 3, Физматгиз, М., 1963; Э. Лебег, Об измерении величин, Учпедгиз, М., 1960.
КВАЗИГРУППА — группоид (см.), в котором каждое из уравнений
ax=by ya — b (*)
имеет решение, и притом единственное. Таким образом, К. — это множество
G={a, by ... }, в котором определена одна бинарная операция, называемая
умножением и обозначающаяся ab=c, которая удовлетворяет условию
однозначной разрешимости уравнений (*). Если на операцию квазигруппы наложить
какие-либо дополнительные ограничения, то будет выделен тот или иной
специальный класс К. Наиболее важным классом К. .являются группы (см.),
получающиеся из К-, если потребовать, чтобы операция удовлетворяла закону
ассоциативности (см.): (ab)c=a(bc).
10*

148
КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ
Другим интересным классом К. являются дистрибутивные К-, получающиеся
при условии, что операция в К. удовлетворяет законам дистрибутивности:
(ab)c=(ac)(bc) и c(ab) = (ca)(cb).
Примером дистрибутивной К- может служить множество всех
действительных чисел относительно операции взятия среднего арифметического (см.) чисел.
Если потребовать, чтобы при любых элементах a, b уравнения (*) имели
одно и то же решение е, то такие К. называются лупами.
Лит.: А. Г. Курош, Лекции по общей алгебре, Физматгиз, М., 1962.
КВАЗИЛИНЕЙНЫЕ УРАВНЕНИЯ — уравнения вида:
η
γ jQj (*ь *2> · · · > *m u) J^+ b(xi* χ2> · · · . *л. «0-0. (*)
К. у. (*) линейно относительно производных от и, но не относительно самогон,
т. е. если дифференциальное уравнение содержит производные порядка выше
первого, то оно называется квазилинейным, в случае если оно линейно
относительно старшей производной от ы, но нелинейно относительно производных от и
более низкого порядка.
КВАЗИПЕРИОДИЧЕСКИЕ ФУНКЦИИ — функции, определяемые тем
свойством, что они могут быть равномерно приближены на всей действительной оси
посредством обобщенных тригонометрических полиномов вида:
>^ /(rtjaj+rtjaj -f · · · +nk *k) x
^antn9 · · · nke
где nlt n2 tifc—любые числа, alf a2, . . · , a^ — заданные
действительные числа. Этот класс функций был впервые рассмотрен и подробно исследован
латвийским математиком П. Болем в 1893 г. Боль указал ряд необходимых и
достаточных условий квазипериодичности функции. В частности, всякая
функция вида:
/<*)=/ι <*)+Ы*)+М*)+ ··· +/*<*).
где каждая из функций /х (х), /2 (х), . . . , /^ (х) непрерывна и периодична
(периоды их могут быть различными), является К. ф. Теория К. ф. послужила
основой для создания позднейшей теории почти-периодических функций (см.).
КВАТЕРНИОНЫ — выражение a-\-bi-\-cj-\-dk, где а, 6, с, d — вещественные
числа, а /, /, k — некоторые символы, связанные между собой и с числом 1
следующей таблицей умножения:
1
I
/
k
1
1
i
i
k
i
i
—1
—k
i
i
f
k
—1
—/
k
k
—/
i
—1
В таблицу выписаны произведения символов, стоящих в столбце, на символы,
стоящие в строке. При этом необходимо сохранять (не переставлять) порядок
сомножителей. Чтобы перемножить два К-, надо поступить согласно правилам умножения
многочлена на многочлен и учесть приведенную выше таблицу умножения.
Произведение двух К. зависит от порядка сомножителей. Число j/a2 -f b2 -j- с2 -j- d2

КЛАССИФИКАЦИЯ БЭРА
149
называется нормой К-, а произведение (a-\-bi-\-cj-\-dk)(a— Ы — с] — dk)
равняется квадрату нормы. К. а — Ы — с\ — dk называют К. сопряженным
a+bi+cj+dk. Ненулевые К- образуют группу по умножению. Норма
произведения равна произведению норм.
К. введены в 1843 г. англичанином Гамильтоном в связи с задачей об
обобщении комплексных чисел. Фробениусу принадлежит следующая теорема: все
ассоциативные алгебры с делением конечного ранга над полем вещественных чисел
исчерпываются тремя: алгеброй вещественных чисел, алгеброй комплексных чисел
и алгеброй кватернионов. Значение К· в современной математике невелико.
Лит.: Л. Я. О к у н е в, Высшая алгебра, Учпедгиз, М., 1958; Ф. Клейн,
Элементарная математика с точки зрения высшей, перев. с немец., т. 1, ОНТИ, М., 1935.
КВИНТИЛЛИОН — число 1018 (во Франции и США) или число 1030
(в Англии и Германии).
КЕПЛЕРА УРАВНЕНИЕ —уравнение вида у — asmy=x. Это уравнение
впервые рассматривалось И. Кеплером в связи с задачами небесной механики.
КИБЕРНЕТИКА — наука об общих закономерностях процессов управления и
связи в организованных системах — машинах, живых организмах и их
объединениях. К. также определяют как науку о способах восприятия, передачи,
хранения, переработки и использования информации (см. Теория информации) в
машинах, живых организмах и их объединениях.
Большую роль в создании К. сыграли работы И. Винера, К. Шеннона,
Дж. Неймана, А. Н. Колмогорова, А. М. Ляпунова, И. В. Вышнеградского
и работы по физиологии И. П. Павлова.
См. также Программирование, Алгоритм.
Лит.: Н. Винер, Кибернетика, или управление и связь в животном и машине, ИЛ.,
М., 1958; А. Н. Колмогоров, Кибернетика, БСЭ, изд. 2, т. 51, 1958; Б. А. Трах·
тенброт, Алгоритмы и машинное решение задач, Физматгиз, Μ., 1960.
КЛАСС — термин, имеющий различные значения. Например, при разбиении
некоторого множества на непересекающиеся подмножества, родственные по какому-
либо признаку элементов, говорят о разбиении множества на К. Часто разбиение
множества на К. определяется некоторым отношением эквивалентности
(обозначается ~), удовлетворяющим требованиям: 1) х~х (рефлексивность); 2) если
х~У> У~г, то *~г (транзитивность); 3) если х~у, то у^х (симметричность).
В этом случае К. является совокупностью эквивалентных между собой
элементов.
Примеры: 1. Пусть дана группа (см.) G и ее подгруппа Н. Введем в G
отношение эквивалентности: x~yt если xy—ΐζΗ. К., возникающие при этом,
называются классами смежности группы G по подгруппе Н.
2. Пусть дано число апапг^.1 ··· α3α2αλί где а/=0, 1, 2, . . . , 9. Тогда
всякую группу цифр ai+2ai+iai> *"=1 (mod 3) называют К.* читая справа
налево. Группа цифр ага2аг — первый К. (К. единиц), α6α5α4 — второй К. (К. тысяч)
и т. д. К. цифр пишутся друг от друга с некоторым промежутком.
КЛАССИФИКАЦИЯ БЭРА — разбиение множества функций на классы,
определяемое рекуррентно. К первому классу Бэра относятся разрывные функции,
которые являются пределами последовательностей непрерывных функций,
сходящихся всюду. К нему, например, относятся функции, имеющие конечное число
разрывов. Каждая функция, которая не входит в первый класс, но является
пределом сходящейся всюду последовательности функций первого класса, относится
ко второму классу. Аналогично определяются дальнейшие классы, причем
нумерация не ограничивается числами, а может быть продолжена при помощи
трансфинитных чисел (см.).
Лит.: И. П. Натансон, Теория функций вещественной переменной, Гостехиздат,
М., 1950.

150
КЛЕЙНА ПОВЕРХНОСТЬ
КЛЕЙНА ПОВЕРХНОСТЬ —одна из односторонних поверхностей. В
трехмерном пространстве К. п. может быть получена из трубы, открытой с обоих
концов (рис. 101), если ее изогнуть так, чтобы более узкий ее конец прошел
через стенку внутрь трубы, и оба круговых конца трубы склеить (рис. 102).
К- п. была впервые рассмотрена немецким математиком Ф. Клейном. К· п.
иначе называют «бутылкой» Клейна.
Рис. 101 Рис. 102
КЛЕРО УРАВНЕНИЕ —уравнение вида:
у=рх+Ч>(р). (*)
dy
Здесь /?=--, φ — дифференцируемая функция.
ах
Общее решение К. у. получается заменой в уравнении (*) ρ на
произвольное постоянное число С.
КЛОТОИДА—то же самое, что и спираль Корню (см. Корню спираль).
КОВАРИАНТНОСТЬ — понятие линейной алгебры и тензорного анализа. Пусть
в я-мерном линейном пространстве заданы своими координатами две величины (см.
Тензор и Спинор); х(хх, х%, · · · . *а). У(Уъ Уг. · · · > Ук)· Если при изменении
базиса линейного пространства обе они преобразуются при помощи одинаковой
матрицы, то χ и у называют ковариантными. Если же матрица Л преобразования
величины χ связана с матрицей В преобразования величины у соотношением
i4=«(fl')—1[(fi')""1—транспонированная, обратная В матрица], то лги у
называются контравариантными(контрагредиентными). Например, вектор и линейная форма
(ем.) контрагредиентны (координаты вектора и коэффициенты линейной формы
преобразуются так, как указано выше).
Лат. со (cum) — совместно, сообща, contra — напротив, наоборот, vario —
изменяюсь.
КОГРЕДИЕНТНОСТЬ — понятие линейной алгебры и тензорного исчисления,
то же, что ковариантность (см.).
КОЛЕБАНИЕ ФУНКЦИИ на множестве Я —разность между верхней гранью
и нижней гранью значений функции на множестве Е.
КОЛИЧЕСТВЕННОЕ ЧИСЛО — то же, что кардинальное число (см.) или
мощность множества (см.). Для бесконечных множеств К- ч. отличаются от
трансфинитных чисел (см.) — обобщения порядковых чисел, так как в одном и
том же бесконечном множестве можно по-разному ввести типы упорядочения.
КОЛЛИНЕАРНЫЕ ВЕКТОРЫ — векторы, лежащие на одной прямой или
на параллельных прямых. Для того чтобы два вектора a {xlf уг) и b {x2, у2}, от*
личные от нулевого вектора, были коллинеарны, необходимо и достаточно, чтобы
их одноименные координаты были пропорциональны:
Ч Уг '
Условие коллинеарности двух векторов иногда записывается так: α+λδ*=0, где
λ*0.
Лат. со (cum) — вместе, сообща, linea — линия.

КОМБИНАТОРИКА
151
КОЛЛИНЕАЦИЯ — преобразование точек плоскости (пространства) в точки
той же или другой плоскости, при котором точки, лежащие на одной прямой,
переходят в точки, также лежащие на одной прямой. Так в евклидовом
трехмерном пространстве всякое движение (см.) есть К., гомотетия (см.) есть также
К. Однако инверсия (см.) не является К. Всякое аффинное преобразование есть
также К· В проективном пространстве К. является проективным
преобразованием (см.).
КОЛОГАРИФМ числа N при основании а(а>0, αψ\)—логарифм числа
—. Обозначается К. так: cologfl N. К. встречается иногда при
логарифмических вычислениях, чтобы избежать действий с отрицательными мантиссами, за-
2
меняя вычитание сложением. Например: lg-r- = lg2—lg3=lg2-f-colg 3; colg3=
о
« _lg3= —0,4771 = Т,5229; lg—=0,3010+ Τ,5229-1,8239.
о
В настоящее время термин К. в советской литературе выходит из
употребления.
КОЛЬЦО — совокупность элементов произвольной природы, для которых
определены две операции — сложение (обозначается +) и умножение
(обозначается ·)· Каждая из этих операций ставит в соответствие всякой
упорядоченной паре элементов некоторый элемент К.» причем должны выполняться
следующие условия: 1) α-f Ь=Ь+а — коммутативность сложения; 2) {a+b)+c=ai-(b+
-i-c) — ассоциативность сложения; 3) для любых а и Ъ уравнение а+х=Ь имеет
единственное решение; 4) дистрибутивность умножения по отношению к
сложению:
a(b+c)=ab+ac, (b+c)a = ba-\-ca.
В К. может отсутствовать ассоциативность умножения (неассоциативные К.)
и коммутативность умножения (некоммутативные К·)» необязательным для К.
является также наличие единицы. Не следует путать операции сложения и
умножения в К., определенные на элементах произвольной природы, с обычным
сложением и умножением чисел. Общим для первого и второго являются только
законы 1—4.
Примеры К.: 1) вещественные числа, взятые с обычными операциями
сложения и умножения; 2) совокупность многочленов от одной переменной
относительно операций сложения и умножения многочленов; 3) совокупность всех ко-
сосимметрических матриц п-го порядка с естественной операцией сложения
матриц и с операцией умножения, определяемой формулой a-b^ab — ba, где ab и
Ьа означают обычное произведение двух матриц. Это К. без единицы, а также
без ассоциативного и коммутативного законов умножения.
КОМБИНАТОРИКА — раздел элементарной математики, в которой для
конечных множеств рассматриваются различные соединения (см.) элементов, такие,
как сочетания, размещения, перестановки (см.), а также все эти виды
соединений с повторениями и сходные понятия. Задачи К. впервые рассматривались
в XVI— XVIII вв. в связи с возникновением теории вероятностей, где к
задачам К- приводит подсчет вероятностей на основе гипотезы «равновозможных»
элементарных событий. К. используется также в алгебре многочленов,
например в формуле бинома Ньютона (см,) и в ее обобщении — полиномиальной
теореме (см.), В школьном преподавании элементы К. изучаются в связи с
формулой бинома Ньютона. В пединституте К- изучается в виде раздела в курсе
«Специальный курс элементарной алгебры».
Лит.: С. И. Новоселов, Специальный курс элементарной алгебры, «Советская
наука», М., 1958.

152
КОМБИНАТОРНАЯ ТОПОЛОГИЯ
КОМБИНАТОРНАЯ ТОПОЛОГИЯ — часть топологии (см.), которая изучает
топологические пространства (см.), разбивая их на более простые [симплексы
(см.), полиэдры (см.) и т. д.]. В терминах К. т. определяются группы Бетти
(см. Бетти числа) и другие важнейшие характеристики топологических
пространств.
Лит.: Л. С. П о н τ ρ я г и н, Основы комбинаторной топологии, Гостехиздат, М., 194 7.
КОММУТАНТ — термин теории групп. Элементами коммутанта являются
всевозможные коммутаторы (см.). Коммутант есть нормальный делитель (см.)
группы. Факторгруппа группы по коммутанту — абелева (см. Абелевы группы).
КОММУТАТИВНАЯ ГРУППА —то же, что абелева группа (см.).
КОММУТАТИВНОСТЬ — см. Закон коммутативности.
КОММУТАТОР — термин алгебры, применяемый в изучении
некоммутативных групп (см.), алгебр (см.), колец (см.) и т. д. К. элементов а и b равен
аЪ — Ьа (в кольцах), a—1b—1ab (в группе). К. называется также основная
операция алгебры Ли (см. Ли группа).
КОМПАКТ — компактное метрическое пространство, в частности любое
ограниченное замкнутое множество евклидова пространства.
КОМПАКТНОСТЬ — важное понятие топологии, широко используемое во
многих отделах математики. Множество Μ топологического пространства (см.)
называется компактным, если любая бесконечная последовательность точек этого
множества имеет предельную точку (см.), принадлежащую множеству М. Если
Μ лежит в конечномерном евклидовом пространстве, то Μ компактно тогда и только
тогда, когда оно ограничено и замкнуто. Сфера гильбертова пространства, хотя и
является ограниченной и замкнутой, компактной не является. Непрерывные
функции на компактном множестве обладают рядом замечательных свойств:
ограниченностью, достижением максимума и минимума и др.
Лит.: П. С. Александров и А. Н.Колмогоров, Введение в общую теорию
множеств и функций, Гостехиздат, М., 1938.
КОМПЛАНАРНЫЕ ВЕКТОРЫ — векторы, лежащие водной или в
параллельных плоскостях. Для того чтобы три вектора а(л:ь ylt гг), Ъ(х2, у2, z2),
с(*3. Уз» гз) были компланарны, необходимо и достаточно, чтобы их смешанное
произведение (см.) равнялось нулю:
Χι Ух ζι
х-2 Уч Ч
хз Уз гз
Если же это условие не выполняется, то векторы называются некомпланарными.
Условие компланарности трех векторов записывают и так: аа+рЬт-ус=0, где
по крайней мере одно из чисел α, β или γ не
равно нулю.
Аналогично прямые, лежащие в одной
плоскости, называются компланарными, а не лежащие
в одной плоскости — некомпланарными. В
частности, две скрещивающиеся прямые —
некомпланарные.
КОМПЛЕКС — одно из основных понятий
комбинаторной топологии (см.). Изучение
широкого класса топологических пространств сводится к изучению топологических
свойств комплекса. К. есть совокупность симплексов (см.) различных
размерностей, расположенных правильно, т. е. любые два симплекса, принадлежащие
К-, или не пересекаются, или пересекаются по общей грани, и т. д. Наряду со
всяким симплексом К. принадлежат также все грани симплекса. Размер-
Рис. 103

КОМПЛЕКСНЫЕ ЧИСЛА
153
ностью К. называется наибольшая размерность симплекса, входящего в К.
Например, К., показанный на рис. 103 и состоящий из двух заштрихованных
треугольников и отрезков ЛВ, ВС и ED, имеет размерность 2.
Лит.: Л. С. Понтрягин, Основы комбинаторной топологии, Гостехиздат, Μ.,
1947; П. С. Александров, Комбинаторная топология, Гостехиздат, М., 1947.
КОМПЛЕКСНО-СОПРЯЖЕННЫЕ ФУНКЦИИ —две функции комплексного
переменного, у которых действительные части равны, а мнимые части
противоположны по знаку.
КОМПЛЕКСНО-СОПРЯЖЕННЫЕ ЧИСЛА — комплексные числа (см.) вида
z=a-\-bi и ζ=α — Ы. Такие два числа_называют также взаимно сопряженными,
или, что то же, каждое из чисел гиг называют сопряженным с другим (или
другому), — это соответствует более общему термину сопряженных чисел (см.).
Если обозначать переход от комплексного числа ζ к сопряженному с ним ζ
(с черточкой над числом z)t то имеют место следующие равенства:
2l4~Z2 = ^1 + ^2» Ζ1Ζ2— Z1Z2* 2 = 2,
которые могут быть прочитаны словами так: число, комплексно-сопряженное
сумме (произведению), равно сумме (произведению) комплексно-сопряженных
слагаемых (сомножителей) и число, комплексно-сопряженное с
комплексно-сопряженным г, равно исходному комплексному числу.
Сумма К.-с.ч.—действительное число, равное удвоенной (их общей)
действительной части (см.), т. е. ζ -f- г= (а+ bi)-\-(a — bi)=2a. Произведение
К.-с.ч. — также действительное число, равное квадрату (их общего) модуля (см.),
т. е. z.l=(a+bi)(a— bi)=a2+b2=r2.
Число совпадает со своим сопряженным тогда и только тогда, когда оно
действительно. Отображение множества всех комплексных чисел в комплексно-
сопряженные с ними является автоморфизмом (см.) поля комплексных чисел.
При геометрической интерпретации комплексных чисел такое отображение
означает симметрию относительно действительной оси.
КОМПЛЕКСНЫЕ ЧИСЛА — в первоначальном представлении — выражения
вида a-\-bii где а и b — вещественные числа, / — некоторый символ. Сложение,
умножение и деление К. ч. задается формулами:
(а+Ы)1-(х+у1) = (а+х)+(Ь+У)1,
(a+bi) (x+yi)=(ax — by)+(ay + bx) /,
a+bi ax-\-by bx — ay .
x-t-yi "V-fr х2+У2
В К. ч. z=a+bi число а называется действительной его частью
(обозначается a=Rez), а число b называется мнимой частью (обозначается b=lmz).
Чисто мнимым называется комплексное число г такое, что Rez=0.
Вещественные числа являются частным случаем комплексных чисел (когда
коэффициент при ι равен нулю). Хотя К. ч. не выражает количества, как это
имеет место у действительных чисел, применение их бывает полезно в решении
задач, составленных в терминах действительных чисел, например задач о
прохождении тока через проводник, о профиле крыла самолета (с использованием
функции Жуковского) и др.
Не менее важным является применение К. ч. для чисто математических
задач. Так, нахождение действительных корней кубического уравнения требует
действий с К. ч. Исторически К. ч. были введены в связи с решениями
уравнений второй степени. Тот факт, что К. и. не выражают количества, дал пищу
для идеалистического толкования К. ч. (Г. Лейбниц). Большая заслуга в смысле

154
КОМПЛЕКС ПРЯМЫХ
материалистического истолкования понятия К. ч. принадлежит Л. Эйлеру. К. ч.
аксиоматически определяются как упорядоченная пара действительных чисел
(а, Ь). Формулы сложения, умножения, деления постулируются так:
(я, Ь)+(х, У) = (а+х, 64-у),
(а, Ь)-(х, y)*=(ax-~byy ay-\-bx)t
(α, b) idx+by bx — ay
(х* У)
Чу2
*2-Ьу2
(*)
Пара (0; 1) называется мнимой единицей и обозначается символом i. Из
формулы (*) вытекает, что /2 = — 1. Действия над К. ч. удовлетворяют обычным
законам коммутативности, дистрибутивности и ассоциативности (как и в случае
действительных чисел). Однако действия с К. ч. под радикалами Несколько
отличаются от аналогичныхдействий с вещественными числами. Так,- —1 = /2=
^/—χγ—1>/(-1) (-1) = 1.
Одним из важнейших свойств К. ч. является то, что любой многочлен
степени η с комплексными коэффициентами имеет ровно η комплексных корней,
считая их кратность. Это следует из основной теоремы алгебры (см.) и Безу
теоремы (см.).
Иногда удобно записывать К. ч. в тригонометрической форме:
а-\-Ы=$ (coscp-H* sin φ),
Ρ
-V*
И
φ —arcig— для α>0 и φ = π-
arcig— для α" 0;
а
при а=0, φ=-
если by 0, и φ= — —- , если Ь<0. Число ρ называется мо-
Z=a+bi
дулем К. ч., а φ —его аргументом. В такой форме очень удобно
производить умножение К. ч.: при умножении К. ч.
их модули перемножаются, а аргументы
складываются. Из этого правила вытекает формула
Муавра:
(cos φ-И sin <р)л= cos η φ -f- /sin n φ.
К. ч. часто изображают векторами на
комплексной плоскости (рис. 104). Геометрический
смысл чисел а, Ь, ρ и φ виден из чертежа. При
Рис. 104 сложении К. ч. их векторы складываются по
правилу параллелограмма. К. ч. в
тригонометрической форме тесно связаны с показательной функцией мнимого аргумента; имеет
место формула Эйлера:
е1 φ = ΰο$φ+/sirup;
с ее помощью определяются возведение в степень К. ч., логарифм К. ч. и др.
К- ч. образуют алгебраически замкнутое поле (см. Поле и Алгебраическое
замкнутое поле). Поле К. ч. является расширением поля действительных чисел
путем приобщения (расширения) к последнему элемента i такого, что ζ'2**-—ι.
Лит.: А. Г. Курош, Курс высшей алгебры, Физматгиз, М., 1962; Энц. элем, мат.,
кн. 1, Гостехиздат, М., 1951; И. И. Привалов, Введение в теорию функций
комплексного переменного, Гостехиздат, М., 1954.
КОМПЛЕКС ПРЯМЫХ — совокупность прямых, зависящих от трех
параметров. К. п. заполняет все пространство или его часть так, что через каждую
точку проходит бесконечное множество прямых этой совокупности. Прямые К. п.,

КОНЕЧНЫХ ПРИРАЩЕНИЙ ФОРМУЛА
155
проходящие через некоторую точку, образуют конус с вершиной в этой точке.
Если конус вырождается в плоские пучки прямых, то К. п. называется
линейным. См. также Линейчатая геометрия.
Лит.: Ф. Клейн, Высшая геометрия, М., ОНТИ, 1939.
КОМПОЗИЦИЯ — общее название для операции, ставящей в соответствие
двум упорядоченным элементам а и b некоторого множества третий с.
Обозначается а * Ь = с. Например, К. является составление сложной функции h (*) =
= /1# (*)] (h — f * g); другим примером К. является свертка функций (см.) и т.д.
Лат. compositio — составление.
КОМПОНЕНТА — составная часть. Так, координаты вектора (см.) можно
назвать его К. Каждое из слагаемых суммы или каждый из сомножителей
произведения называется К. действий соответственно сложения и умножения. К.
иногда называется компонентом.
Лат. componens — составляющий.
КОНВЕНЦИОНАЛИЗМ — лженаучное идеалистическое философское
направление в математике. К. отрицает отражение во многих отделах математики
явлений окружающего мира и толкует математику как науку, развивающуюся
на основе произвольных соглашений (конвенций), касающихся признания аксиом.
Выбор же этих аксиом производится из соображений удобства мышления
(принцип «экономии мышления» Маха). Принцип «экономии мышления» был
разгромлен В. И. Лениным в книге «Материализм и эмпириокритицизм».
Основатель К·* крупный французский математик А. Пуанкаре, создавая это течение,
неправомерно абсолютизировал аксиоматический метод построения математики.
Для конвенцион а листов вопрос об истинности различных геометрий (см.
Неевклидовы геометрии) не существует. Они отрицают тот факт, что разные геометрии
(например, Евклида и Лобачевского) отражают реальные свойства нашего
пространства, приближая их с разных точек зрения.
КОНГРУЭНТНОСТЬ — одно из основных отношений между основными
понятиями при аксиоматическом обосновании элементарной геометрии по схеме
Д. Гильберта. Если же за основное отношение между «вещами» (точками,
прямыми и плоскостями) принято движение, то К. становится уже производным
понятием.
К. иногда называют равенством.
КОНГРУЭНЦИЯ: 1°. К. прямолинейная — совокупность прямых (лучей К·)*
зависящих от двух параметров. К. заполняет все пространство или часть его
так, что через каждую точку проходит одна или несколько прямых К.,
например: совокупность нормалей к данной поверхности (нормальная К·)» совокупность
общих касательных к двум данным поверхностям.
2°. К. криволинейная — двупараметрическое семейство кривых.
Понятие К. впервые встречается в работах Г. Монжа (1781) и относится
к дифференциальной геометрии.
Лит.: П. С. Фиников, Теория конгруэнции,
Гостехиздат, Μ., 1950.
КОНЕЧНАЯ ГРУППА — группа (см.),
состоящая из конечного числа элементов. Число
элементов К- г. называется порядком группы.
КОНЕЧНЫХ ПРИРАЩЕНИЙ ФОРМУЛА
(Лагранжа формула) — формула, выражающая
связь между приращением дифференцируемой
функции f(x) и значением ее производной; эта
формула имеет вид: / (b)—f(a) = f (с) (6 — а), где
с—некоторое число, удовлетворяющее
неравенству а<с<Ь. К. п. ф. имеет место для любой
Рис. 105

156
КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ
функции f(x), если она определена и непрерывна в замкнутом промежутке [а, Ь\у
а ее производная /'(*) существует по крайней мере в открытом промежутке
[а, Ь]. Геометрически (рис. 105) К. п. ф. выражает тот факт, что на дуге АВ
всегда найдется по крайней мере одна точка сг в которой касательная
параллельна хорде АВ.
К- п. ф. часто записывают в виде:
/ (*о +Δ х) - f (*ο) = /'(*ο + θΔ χ) Δ χ,
где θ — неизвестное число, зависящее, вообще говоря, от х0 и от Δ χ и
удовлетворяющее неравенству 0 < θ < 1.
Для случая функций от многих переменных К. п. ф. записывается в виде:
F(Xo-rbx, Уо + АУ, · · · , z0 + &z) — F(x0, у0, . . . , г0) =
= bxF'x(x0+ebx, уо+еду, ..., *0+βΔ*)+
-hAyfyiXo + Q/ix, Уо + ^ЬУ. ^> + θΔζ)+ ...
··· + bzF'2(x0 + Bbxiy0 + 9byt . ... г0+вд г).
К. п. ф. была открыта французским математиком Лагранжем (1797).
КОНЕЧНЫХ РАЗНОСТЕЙ ИСЧИСЛЕНИЕ — раздел математики, в котором
изучаются функции при дискретных значениях аргумента, в отличие от
дифференциального и интегрального исчисления, где аргумент предполагается
непрерывно изменяющимся.
Задачи интерполирования (см.), численного дифференцирования и
интегрирования (см.), приближенного решения дифференциальных уравнений являются
основными задачами К. р· и.
Пусть функция y^=f(x) определена для всех значений вида xn=a-\-nh
(a, h — фиксированные числа, η — любое целое число). Можно образовать
некоторый аналог производной f(x):
Уп+ι - У η β f(xn+i) — f(Xn) = f[a+(n + l)b] — f(a+nh)
χη+ι— хп χη+ι — хп h
Выражение /[а+(/г + 1)й]— f(a+nh) обозначается Ahf(x) и называется
конечной разностью 1-го порядка функции f (х) в точке хп. Конечные разности 1-го
порядка могут служить для образования конечных разностей 2-го порядка,
ΔΛ/(*) = /(*+Λ)-/(*).
Δ)[/(*)=Δλ/(*+Λ)-Δλ/(*),
Akhf{x)=Akh-Xf{xi-h)-Akh-X f(xY
Разности Δ^ f (x) (в отличие от соответствующих дифференциалов dKf(x)
называют конечными разностями.
По аналогии с дифференциальным исчислением отыскиваются конечные
разности от элементарных функций. Так, в предположении, что разность двух
последовательных значений аргумента равна единице и k > п, получено:
A"jc(jc—1) ... [jc — (Λ— 1)]=Λ(Λ— 1) ... (fc — Λ+Ι) χ(χ—1)... [χ-
-(6-/2-1)],
дла*=(а—1)/1я*,
Δ" sin α x= I 2 sin —■ \ sin
[a*+"(f+f)]·

КОНИЧЕСКАЯ ПОВЕРХНОСТЬ
157
Эти формулы соответствуют формулам дифференциального исчисления
(положено dx=\):
dnxk=k(k—\) ... (k — n + \)xk-n%
dnax= (In a)nax,
dn sin dx = dn sin (ax-f/i· —
Аналогом формулы Тейлора в дифференциальном исчислении является
формула Ньютона в К. р. и. Так, если известно значение функции f(x) и ее
последовательных разностей при некотором х=а, то формула Ньютона
позволяет вычислить значение функции при другом значении аргумента:
,/ * ίΜ, χ-α \f{a) Ax-a){x-a-h) Δ2/(л)
/(*)-/(«)+-1Γ·-Τ-+ 5 JT+-..
. (x —aX-y —g —/t) - ·- lx-a-(n-\)h] Anf(a) , n
... + - · -j^r+Rn,
где остаточный член
(χ — α)(* — α — Α) ... (* — α — яЛр Δ"*1/^)
Λ*-1
α< ξ <a+nh.
Β Κ· р. и. важное значение имеет задача суммирования разностей. Если
F{x) — функция, для которой φ(χ) — разность первого порядка, то
q>(a)=F(a+h)~- F (а),
φ (a+h)=F (a+2h) — F (a+h),
φ [a+(k — 1) h]=F (a+kh) — F [a+(k — \)h].
Складывая все эти равенства, получим:
k- ι
2 9(a+mfc)=F(a+fcfc)--F(a)
m—О
— равенство, являющееся аналогом формулы интегрального исчисления,
выражающей определенный интеграл через первообразную функцию.
Для приближенного решения дифференциального уравнения часто заменяют
входящие в него производные соответствующими разностями, деленными на
разные степени аргументов, и решают полученное таким образом уравнение в
конечных разностях.
Лит.: А. О. Гельфонд, Исчисление конечных разностей, Физматгиз, М., 1959.
КОНИЧЕСКАЯ ПОВЕРХНОСТЬ есть поверхность, образуемая движением
прямой / так, что она все время проходит через неподвижную (данную) точку S
и пересекает неподвижную (данную) линию CDE (рис. 106). Прямая /
называется образующей К. п., точка S — ее вершиной, линия CDE — направляющей

156
КОНИЧЕСКИЕ СЕЧЕНИЯ
К. п. К. п. имеет две полости, одна из которых описывается лучом SA,
другая — лучом SB.
Если направляющая К. п. есть окружность и точка S проектируется в центр
О окружности, то К. п. будет поверхностью вращения с осью вращения SO.
Уравнение К. п. вращения с осью вращения Ог и
вершиной fe=0 в прямоугольных декартовых координатах имеет ^ι β
вид;
х2+у2
= 0.
Часто К. п. вращения называют круговым конусом
или просто конусом (см.).
КОНИЧЕСКИЕ СЕЧЕНИЯ — линии пересечения
конической поверхности (см.) (направляющая которой —
окружность) плоскостями, не проходящими через ее вершину.
Если секущая плоскость не параллельна ни одной
из образующих конической поверхности, то К. с. есть Рис. 106
эллипс, в частности круг (рис. 107).
Если секущая плоскость параллельна только одной из образующих
конической поверхности» то К. с. есть парабола (рис. 108).
Если секущая плоскость параллельна двум образующим конической
поверхности, то К- с. есть гипербола (рис. 109).
В случае эллипса и параболы секущая плоскость пересекает только одну
полость конической поверхности, а в случае гиперболы секущая плоскость
пересекает обе полости конической поверхности.
К. с. иначе называют кривыми 2-го порядка. К. с. исследовались уже
математиками древней Греции (например, Менехм в IV в. до н. э. решал задачу об
удвоении куба (см.) с помощью К. с). Наиболее полное исследование К. с. было
проведено Аполлонием Пергским (III в. до н. э.).
Рис. 107
Рис. 108
Рис. 109
К. с. находят применение в технике, например в эллиптических зубчатых
колесах» в прожекторных установках (параболические зеркала) и т. д. Планеты
солнечной системы движутся по эллипсам, кометы движутся по параболам и
гиперболам.
Исследование К. с. с помощью сфер, вписанных в коническую поверхность,
было проведено бельгийским геометром Ж. Данделеном (XIX в.).

КОНИЧЕСКИЕ СЕЧЕНИЯ
159
Уравнение К. с. в полярных координатах имеет вид:
Ρ
г— ,
1 — е cos cp
где г —фокальный радиус-вектор (рис. ПО, F — правый фокус К- е.);
ρ — фокальный параметр;
е — эксцентриситет;
φ — полярный угол.
Если е<1, то это уравнение определяет эллипс (см.); при этом угол φ
изменяется от 0 до 2π. Если e—\t то это уравнение определяет параболу (см.); при
этом угол φ изменяется от 0 до 2 π. Если е>\, то это уравнение определяет
гиперболу (см.); при этом для угла φ, изменяющегося от φ0 до 2π — φ0 (где
Ь\
2фо — угол между асимптотами tgcp0=—I, получим правую ветвь гиперболы,
а для углов φ, изменяющихся от — φ0 до φ0, получим левую ветвь гиперболы.
О _
](_
~" ' \у 2а-*
Рис. ПО
Рис. 111
Название конических сечений (эллипс, парабола и гипербола) объясняется у
древних геометров их методом решения задач, сводящихся к решению линейных
или квадратных уравнений, — методом приложения площадей, или
параболическим методом, который также называют методом геометрической алгебры.
Пусть АВ=2а —-диаметр эллипса (рис. Ill), AE**2pt CF — перпендикуляр
к АВ\ тогда квадрат, построенный на CD, будет равен площади
прямоугольника (AF):
CD*=ACCF, т. е. CF--Z-CB /—== —
а Ι 2ρ 2α
Положив АС = х, CB=2a — xt CD=yt получим:
Ρ
у2=л (2а— χ) χ,
а
*=2рх — - х2
а
Аналогично для гиперболы будем иметь:
у2=— (2а+х)х, или y2*=2p*+— χ2.
а а
В случае эллипса в формуле стоит знак минус, т. е. площадь
прямоугольника (СЕ) используется с недостатком (греч. ελλει/ψιζ — недостаток). В случае
гиперболы в формуле стоит знак плюс, т. е. площадь прямоугольника (СЕ)
используется с избытком (греч. υπερβολή — превышение, избыток).

160
коноид
Если имеет место простое равенство плсщади квадрата и площади прямоугольника
(СЕ) (в формуле нет ни минуса, ни плюса — ни избытка, ни недостатка), т. е.
γ2=2ΰχ, то кривая (коническое сечение) называется параболой (παραβολή —
приложение площадей, приравнивание).
КОНОИД — поверхность, образованная движением прямой, параллельной
данной плоскости (направляющей плоскости), пересекающей данную прямую
(направляющую прямую) и данную линию (направляющую линию); при этом
если направляющая линия плоская, то она не должна лежать в направляющей
плоскости. К- является линейчатой поверхностью. Примером К. может служить
геликоид (см.), у которого направляющая плоскость перпендикулярна оси,
направляющая линия— винтовая линия (см.), а направляющая прямая — ось
вращения.
Греч, κωνοεόηζ от κωνοξ — конус и ειδοξ — вид.
КОНСТАНТА — постоянная величина. Если χ есть К., то это символически
обозначают так: х=const.
Лат. constans — постоянный, неизменный.
КОНСТРУКТИВНАЯ ГЕОМЕТРИЯ — раздел геометрии, где изучаются
методы и теория геометрических построений. К. г. иначе называется
геометрическими построениями (см.).
Лат. constructio — построение.
КОНСТРУКТИВНАЯ ТЕОРИЯ функций изучает свойства функций, исходя
из их приближенных представлений. К. т. ф. окончательно оформилась в
работах С. Н. Бернштейна, который исходил из трудов П. Л. Чебышева. К. т. ф.
интенсивно развивается в настоящее время.
КОНТАКТНЫЕ ПРЕОБРАЗОВАНИЯ — преобразования кривых на плоскости
(или поверхности в пространстве), при которых касающиеся кривые (поверхности)
преобразуются тоже в касающиеся.
Лат. contactus — прикосновение.
КОНТИНУУМ — название мощности множества (см.) L чисел отрезка
0<*<1. Известно, что L нельзя взаимно однозначно отобразить на множество
целых положительных чисел (счетное множество). Термин «математика континуума»
употребляется тогда, когда говорят о теориях, связанных с понятием непрерывности,
противопоставляя их «математике дискретной». В то время как последняя
обычно имеет дело лишь со счетными множествами, математика К. оперирует более
мощными множествами, в частности множеством L, мощность которого К.
Лат. continuum — непрерывный.
КОНТИНУУМА ПРОБЛЕМА — вопрос о том, существует ли множество,
мощность (см.) которого больше мощности счетного множества и меньше
мощности континуума (см. Континуум). К. п. не решена, хотя поставлена
несколько десятков лет назад. См. Гильберта проблемы.
КОНТРАВАРИАНТНОСТЬ — понятие линейной алгебры и тензорного
исчисления (см.). См. также Ковариантность и Контравариантность.
КОНТРАГРЕДИЕНТНОСТЬ — то же, что и контравариантность (см.). В
теории представлений групп (см.) отношение контрагредиентности распространяется
на представление. Представление называется К. данному, если оно задается
матрицами транспонированными (см.) и обратными к матрицам данного
представления.
КОНТРПАРАЛЛЕЛОГРАММ — то же, что антипараллелограмм (см.). См.
также Параллелограмм и Антипараллельные прямые.
КОНУС — геометрическое тело, ограниченное одной из двух полостей
замкнутой конической поверхности (см.) и пересекающей плоскостью, не проходящей
через вершину 5 (рис. 112). Часть этой плоскости (ABCDE), лежащая внутри
конической поверхности, называется основанием К· Расстояние от вершины 5 до
секущей плоскости называется высотой К. Часть конической поверхности,
заключенная между вершиной и основанием, называется боковой поверхностью К.

КОНФИГУРАЦИЯ
161
Если основание К. есть круг, то К. называется круговым; при этом если
вершина S его проектируется в центр этого круга, то К. называется прямым
круговым (иногда также круглым К.)· Отрезок SM, где Μ — точка окружности
основания К-, называется образующей К. Прямой круговой К- может быть
получен вращением прямоугольного треугольника вокруг одного из катетов (рис. 113).
В элементарной геометрии чаще всего рассматривают прямой круговой К.»
называя его К. (без слова «круговой»).
Рис. 112
Боковая поверхность К. (прямого кругового) вычисляется по формуле:
где / — образующая, а г — радиус основания К.
Объем К. (прямого кругового) вычисляется по формуле:
где h — высота К.
Пирамида (см.) есть частный случай К., когда его основание —
направляющая конической поверхности (см.) — есть многоугольник.
В аналитической геометрии часто К. называют также коническую
поверхность (см.). См. Усеченный конус, Симпсона формула.
Греч, κωνοζ — сосновая шишка * остроконечная верхушка шлема.
КОНФИГУРАЦИЯ: 1°. К. на плоскости — система η точек и т прямых,
расположенных таким образом, что через каждую точку проходит одинаковое
число (k) прямых и на каждой прямой лежит одинаковое число (е) точек.
Например, К. Дезарга (см. Дезарга теорема) состоит из 10 прямых и 10
точек (л = т), при этом через каждую точку проходит по три прямых, и на
каждой прямой лежат три точки (k—e). К. Дезарга обозначается так: щ
или 108.
2°. К. в пространстве типа ( nba, mdci г*} состоит из η точек, т прямых и г
плоскостей, при этом через каждую точку проходит а плоскостей и Ь прямых,
каждая прямая проходит через d точек и лежит на с плоскостях, а каждая
плоскость содержит / точек и е прямых.
Примером пространственной К. может служить К. Рейе, состоящая из 12
точек и 12 плоскостей, которую можно иллюстрировать на модели куба. За
точки этой К. берутся 8 вершин куба, центр куба и три бесконечно удаленные
точки, принадлежащие параллельным ребрам куба. За плоскости К. берутся
Рис. 113
И Толковый словарь математических терминов

162
КОНФОКАЛЬНЫЕ КРИВЫЕ
6 граней куба и 6 диагональных плоскостей, каждая из которых проходит через
противоположные ребра куба. В каждой точке в этом случае будут пересекаться
6 плоскостей, а в каждой плоскости будут находиться 6 точек (как
собственных, так и несобственных). Эту К. символически обозначают так: 126.
Лит.: Д. Гильберт и С. Кон-Фоссен, Наглядная геометрия, Гостехиздат, М.,
1951; Б. И. А р г у н о в и Л. А. С к о ρ н я к о в, Конфигурационные теоремы,
Гостехиздат, М., 1959, Н. Ф. Четверухин, Проективная геометрия, Учпедгиз, М., 1953.
КОНФОКАЛЬНЫЕ КРИВЫЕ — кривые 2-го порядка (конические сечения),
имеющие общие фокусы. К. к. иначе называются софокусными кривыми (см.).
Лат. con (cum) — вместе, сообща, focus — фокус, буквально — очаг.
КОНФОРМНАЯ ГЕОМЕТРИЯ — ветвь геометрии, в которой изучаются
конформные свойства фигур, т. е. свойства, инвариантные при всех конформных
преобразованиях пространства.
Лит.; Ф. Клейн, Высшая геометрия, ОНТИ, М., 1939.
КОНФОРМНО-ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — ветвь
дифференциальной геометрии (см.), в которой изучаются свойства фигур, инвариантные при всех
конформных преобразованиях (см.) пространства.
Лит.; А. П. Норде н, Пространства аффинной связности, Гостехиздат, М., 1950
КОНФОРМНОЕ ОТОБРАЖЕНИЕ — взаимно однозначное непрерывное
соответствие между точками двух областей на поверхностях, при котором сохраняются
углы между линиями; угол между касательными к двум линиям (в их общей
точке) на первой поверхности равен углу между касательными к их образам на
другой поверхности. Так, стереографическая проекция является К- о. сферы на
плоскость. При К. о. областей плоскости бесконечно малым фигурам соответствуют
подобные бесконечно малые фигуры. С этим свойством связано само название
К. о., происходящее от латинского слова conformis — сходный, подобный.
Аналитическая функция w~f(z), однолистная в области D плоскости
комплексного переменного, дает К. о. области D на область D' плоскости W.
Обратно, любые две односвязные области D и D', отличные от полной плоскости
или плоскости с выключенной точкой, могут быть конформно отображены друг
на друга с помощью аналитической функции, которая определится однозначно,
если потребовать, чтобы данной точке из D и данному направлению в ней
соответствовала определенная точка из D' с заданным в ней направлением. Эта
важнейшая теорема теории К. о. была доказана Риманом.
Выше имелись ввиду К. о. первого рода, т. е. есть такие К. о., при которых
сохраняется направление обхода (по замкнутой кривой и ее образу). К. о., при
котором направление обхода меняется на противоположное, называется К. о.
второго рода. К. о. второго рода задается функцией w=f (z)=u — iu,
сопряженной с аналитической функцией f (z) = u-{-iv.
Рис. 114
Рис. 115

КОНХОИДА
163
Примеры: 1) функция w=zn дает К. о. угла 0<φ<— (рис. 114)
плоскости ζ (φ — аргумент ζ) на верхнюю полуплоскость плоскости w (рис. 115);
2) функция w=ez дает К. о. полосы —ос < л; <-f-oo, Q<y<2n(z=*x-\-iy)
плоскости ζ (рис. 116) на плоскость w, из которой исключена положительная часть
вещественной оси (рис. 117).
Лит.: А. И. Марку ш евич. Комплексные числа и конформные отображения, Гос-
техиздат, М., 1954 («Популярные лекции по математике», вып. 13).
Рис. 116
Рис. 117
КОНФОРМНОЕ ПРЕОБРАЗОВАНИЕ — переход от данной фигуры к ее
образу при конформном отображении (см.).
КОНФОРМНОЙ СВЯЗНОСТИ ГЕОМЕТРИЯ — раздел дифференциальной
геометрии, изучающий пространства конформной связности. С каждой точкой
такого пространства связано некоторое «касательное» конформное пространство и
задан закон, по которому «касательное» пространство одной точки конформно
отображается на «касательное» пространство соседней точки.
Лит.: А. П. Норде н, Пространства аффинной связности, Гостехиздат, М., 1950.
КОНХОИДА некоторой кривой — плоская кривая, получающаяся уменьшением
или увеличением радиуса вектора каждой
чину d. Если полярное уравнение кривой
имеет вид: г=/(ср), то уравнение ее К.
будет иметь вид: r=*f((p)±d. На
рисунке 118 сплошной линией изображена К.
эллипса, начерченного пунктиром. Обычно
под К- понимают К. прямой, так
называемую конхоиду Никомеда — по имени
древнегреческого геометра Никомеда (ок.
250—150 гг. до н. э.), который
использовал ее для решения задачи о трисекции
угла (см.) и удвоении куба (см.).
Если расстояние от полюса О
полярной системы до данной прямой равно а,
то уравнение конхоиды Никомеда имеет вид:
точки кривой на одну и ту же
Белила ±d,
cos φ
или в декартовых координатах с началом в полюсе:
(* —а)*(*а+У2) — Л2=0.
Рис. 118
11*

164
КОНЦЕНТРИЧЕСКИЕ ОКРУЖНОСТИ
Конхоида Никомеда — это алгебраическая кривая 4-го порядка^ состоящая из
двух ветвей. В зависимости от соотношения and одна из ветвей конхоиды
Никомеда будет иметь разную форму; при этом полюс О может быть узловой
точкой (d>a, рис. 119, а), точкой заострения (d=>at рис. 119, б) и изолированной
точкой (d<at рис. 119, в). Обе ветви конхоиды Никомеда асимптотически
приближаются в обоих направлениях к прямой. К. окружности относительно полюса,
лежащего на окружности, называют улитками Паскаля (см.).
Греч, κονκοειόηξ — ракообразная.
КОНЦЕНТРИЧЕСКИЕ ОКРУЖНОСТИ — см. Окружности концентрические.
КООРДИНАТЫ — числа, взятые в определенном порядке и
характеризующие положение точки на линии, на плоскости, на поверхности или в
пространстве. В зависимости от целей и характера исследования того или иного объекта
Уз "
Уг
и — -—
У/
Уо
У'1
У-г
У-з'
/ - 1
' - 1
У1
о
t I
\
J
м\
Г 1
м
f
"
Рис. 120
/К.Э Х-2 X-t χ *1 *2 λ3
Рис. 121
выбирают различные системы К., с помощью которых каждой точке
пространства относят определенную совокупность чисел —К. точки. Так, например, в
некоторой области плоскости или во всей плоскости рассматривают два
семейства несамопересекающихся линий U (M)=const, и V(M)=const. таких, что
каждая линия одного семейства пересекается с каждой линией другого семейства
только в одной точке М. Тогда, выбрав за начальные линии U = 0 и V' = 0,
получим точку Μ пересечения линий i/=const, и V=const. (рис. 120). Числа

КОРЕНЬ ИЗ ЧИСЛА
165
U(М) и V (М) и будут К. точки Μ на плоскости. Аналогично определяются К.
точки на любой поверхности и в пространстве. Линии U=const, и V= const,
называют координатными линиями.
Если линии £/=const. и V = const.—прямые, то К. называют
прямолинейными, если одна из линий семейств £/=const. и V=const. или обе линии —
кривые, то К. называются криволинейными, или гауссовыми.
Так, простейшие прямолинейные К. на плоскости — прямоугольные декартовы,
простейшие криволинейные К. на плоскости — полярные К. В случае
прямоугольных декартовых К. координатные линии χ и
у— взаимно перпендикулярны, и единица
измерения длины по осям (нулевым
координатным линиям) одна и та же (рис. 121).
Если оси К., вообще говоря, не взаимно
перпендикулярны и единица измерения длины
по осям χ и у разная, то К. любой точки
в этой системе К. называются аффинными
или общими декартовыми К.
В случае полярной системы К. (рис. 122)
линии U есть концентрические окружности
с центром в некоторой начальной точке О —
полюсе, а линии V — лучи, выходящие из
точки О; при этом каждой точке плоскости
Μ отвечает единственная пара чисел (р, ф)—
К. точки М, где 0<р<ос, 0<φ<2π.
См. также Барицентрические координаты
(координаты Мёбиуса), Биполярные
координаты, Тангенциальные координаты.
Однородные координаты, Трилинейные (треугольные) координаты, Проективные
координаты.
Лит.: См. в конце термина Аналитическая геометрия.
КОРЕНЬ ИЗ ЧИСЛА. Корень л-й степени из числа а (^обозначается 1
число х> п-я степень которого равна а, т. е. запись V а =х равносильна
записи хп — а=0. Корень второй степени (п=2) иначе называется квадратным.
Корень третьей степени (п=3) называется кубичным; при этом показатель
корня η у квадратного корня не пишется, аналогично тому как не пишется
основание 10 у десятичного логарифма (см. Логарифм). Нахождение числа χ
называется извлечением корня. Для извлечения квадратного и кубичного корня
существуют определенные общие правила — алгоритмы (см.), при которых
используются формулы (а+Ь)2 и (a+by, хотя эти алгоритмы на практике применяют
редко, а пользуются для извлечения корня (п=2; 3) счетной линейкой, таблицами
и приближенными формулами (выведенными из формулы бинома Ньютона для
дробного показателя); пользуются также графическими способами извлечения
корней и номограммами. Корень я-й степени из числа а в поле комплексных
чисел имеет ровно η значений, которые находятся по формуле:
Рис. 122
№)-
Va
-У\а\
cos -\-i sin
где |α| — модуль числа а, φ^-его аргумент, £ = 0, 1, 2, .. .s (л—1).
Корень л-й степени из натурального числа N^n* (где пг — натуральное
число) есть иррациональное число α — иррациональность я-й степени: /№*а.

166
КОРЕНЬ УРАВНЕНИЯ
КОРЕНЬ УРАВНЕНИЯ. Корень алгебраического уравнения вида
ц,хл+а1дсл-Ч-...+ая=0
есть численное значение аргумента х, обращающее данное уравнение в
тождество. Всякое алгебраическое уравнение /2-й степени над полем комплексных
чисел имеет ровно η корней [это следует из основной теоремы алгебры (см.)
и Безу теоремы (см.)]. Если при этом среди η корней т равны между собой
{\<т<п)% то каждый из т равных корней называется корнем кратности т,
или m-кратным корнем (см. Кратный корень).
К. у. /(*)=0*называется также его решением. К. у. /(а:) —0, где
1(х)=а0хп+ахх*-1 + --.+ап,
называется также корнем или нулем многочлена (функции) f(x).
КОРНЮ СПИРАЛЬ — спиралевидная кривая, параметрическое уравнение
которой имеет вид:
t t
cos—— du, y=a l sin —-
du.
К. с. состоит из двух ветвей,
(а а\
— -— 1 и В
симметрично расположенных относительно
а а\
-—f — — являются
2 2/
асимптотическими (см. Особые точки). Кривая названа по имени французского
физика Корню, использовавшего ее при изучении
дифракции света. К. с. иначе называют клотоидой,
а также спиралью Эйлера.
КОРРЕЛЯЦИЯ (коррелятивное преобразование):
1°. К-—взаимнооднозначное соответствие между
точками и прямыми проективного пространства,
сохраняющее отношение инцидентности (см.)
прямых и точек. Важным частным случаем К. является
полярное преобразование (см.).
2°. К. в математической статистике —
вероятностная зависимость, не имеющая, вообще говоря,
строго функционального характера.
Лит.: Н. А. Глаголев, Проективная геометрия,
«Высшая школа», М., 1963; Г. Крамер,
Математические методы статистики, перев. с англ., ИЛ, М., 1948.
КОСЕКАНС — одна из тригонометрических функций, обозначаемая cosec x
(χ — аргумент) и определяемая формулой:
1
cosec *= ,
sin χ
где sin λ; — синус (см.) того же аргумента (угла) х. Областью определения К.
является вся числовая ось (радианная мера изменяется от —оо до + оо), за
исключением точек, абсциссы которых:
х=лп (/2=0, ±1, ±2, . . .).
К. является функцией неограниченной (1< |cosec а:|< оо), нечетной (рис. 124),
периодической (с периодом 2 π).
Если рассматривать произвольный радиус-вектор (подвижный вектор) ОМ=
=г, начало которого совпадает с началом координат (рис. 125), то отношение

КОСИНУС
167
' —=coseca, где α —угол, составленный радиус-вектором с положительным на-
Ум
правлением оси Ох (с неподвижной стороной О А угла α=ζ:ΛΟΛί), а у ^ —
ордината точки Μ — конца подвижного радиус-вектора.
Знак К. совпадает со знаком синуса (sin a) т©го же аргумента. Если
ограничиться только острым углом а, то К· можно определить исходя из
рассмотрения прямоугольного треугольника ОММх как отношение гипотенузы ОМ к
катету MMlt лежащему против угла а. График К. в прямоугольной системе
координат называется косекансоидой (рис. 124). Функция, обратная К-, называется
арккосекансом (см.).
Производная К вычисляется по формуле:
/ W C0SX ,
(cosec χ) =— ~г~г~ =— ct£ χ · cosec x.
sin2 x
Иногда К. угла χ обозначают короче: esc*.
Μ
-π 2 \ !
y=cosecx
Рис. 124
Рис. 125
К. называется также кофункцией по отношению к секансу (см.), т. е.
сходной по названию с функцией секанс, или функцией дополнительного угла
cosec a=sec
Интеграл от К. вычисляется по формуле:
К. разлагается в ряд:
π \
τ-·
и f +с.
1 χ 7х» 31х»
cosec,= _+_ + _+__ + ... (0<ΐΛΓ,<π).
Лат. со (ко) сокращение от complementum — дополнение+секанс (см.).
КОСЕКАНСОИДА — график функции косеканса (см.) в прямоугольной
декартовой системе координат.
КОСИНУС — одна из тригонометрических функций (см.), обозначаемая
через cos а: (л: — аргумент) и определяемая следующим образом. Пусть в
ориентированной плоскости выбрана прямоугольная декартова система хОу (рис. 125)
и произвольный угол а, равный углу АОМ, вершина которого совпадает с нача-

168
КОСИНУС
лом координат, неподвижная (фиксированная) сторона его совпадает с осью O.v,
а подвижная (переменная) сторона ОМ при вращении вокруг вершины О
составит различные углы α с осью Ох. К. угла α (или угла х) называется отношение
—-, или — , где хм — абсцисса произвольной точки М, принадлежащей
подвижной стороне ОМ угла а, а |ОМ[ — длина радиус-вектора точки М. Отрезок
ОМ часто называют подвижным радиус-вектором, а координаты точки Μ —
координатами конца его. К. угла α есть функция этого угла; график К. показан
на рисунке 126. Наименьший положительный
период К. равен 2 π, т.е. cos x=cos (x-f 2 π /г),
где /2 = 0, ±1, ±2, ...
Областью определения К. является вся
числовая ось (радианная мера угла
изменяется Xj./ c/| zl\j^ &( * ся от —оо до 4-°°)» областью значений —
сегмент [—1; 1]. К.—функция
ограниченная, четная и периодическая.
С возрастанием угла от 0° до 90° K.f
как и все тригонометрические кофункции (см.)«
убывает; К. убывает от 1 до 0.
К. и синус (см.) связаны формулой: sin2*-fcos2A;=l; левая часть формулы
называется тригонометрической единицей. К. и секанс связаны формулой:
cosx=l:secA;.
Производная К. вычисляется по формуле: (cosx)' = —sin*. Интеграл от К.
находится по формуле: J cos* dx = sm x -J- С. К. разлагается в степенной ряд:
COSX=l — — + -у (—оо<*<оо).
Функция, обратная К-, называется арккосинусом (см.).
Если рассматривать только острый угол а, то К. угла α можно определить
как отношение катета, прилежащего к углу а, к гипотенузе (из прямоугольного
треугольника OMMlt рис. 125).
К. и синус (см.) комплексного аргумента г связаны с показательной функцией
формулой Эйлера:
из которой получаются выражения для sin χ и cos χ (χ — действительное число),
зависящие от показательной функции чисто мнимого аргумента:
cosx= г , sinx= ——.
2 2/
Эти формулы могут быть использованы для вычисления cos г (и sine). Если z=
— ιχ (чисто мнимое число), то
е*+ er-x
cos ix= = ch xt
где chχ — гиперболический косинус (см.).
Справедливо также равенство cos Jt=ch ix. К. комплексного аргумента —
cos? (как и sin г) может принимать любые значения, большие 1. Имеет место
формула;
cos 2=^cos lx+iy) — cos л ch у — / sin л sh y%

КОСОСИММЕТРИЧЕСКИЙ ОПРЕДЕЛИТЕЛЬ
169
Если 2=rt-f-'\ то согласно этой формуле получим:
£_!>£—1
cos (π-f- /)=cosnch 1 — /sin rtsh 1 = — ch 1= ——-—«— 1,5,
т. e. |cos 2[> 1.
К. также является одной из тригонометрических кофункций (см.).
Лат. со (сокращение слова complementum) — дополнение+синус (см.),
т. е. функция дополнительного угла или функция, сходная по названию с
синусом.
КОСИНУС-ВЕРЗУС угла α-^отношение (*) (рис. 125), где М2 —
проекция конца подвижного радиус-вектора на ось Оу, а г=ОВ. К.-в. угла α
обозначается так: cosversa. Если положить в (*) ВМ2=г — ОМ2, то К.-в. будет
равен 1—sin a. Понятие К. в., как и понятие синус-верзуса (см.), было введено
в математику в XVII в., а в настоящее время почти не употребляется.
К.-в. так же, как и тригонометрические функции (см.), является функцией
угла.
См. также Синус-верзус.
Лат. со (сокращение слова complementum) — дополнение, sinus —
выпуклость, вздутие, versus — обращенный; косинус-верзус — обращенный косинус.
КОСИНУС ГИПЕРБОЛИЧЕСКИЙ —см. Гиперболический косинус.
КОСИНУСОВ ТЕОРЕМА: 1°. К. т. плоской тригонометрии — утверждение
о том, что во всяком треугольнике квадрат любой его стороны равен сумме
квадратов двух других его сторон без удвоенного произведения этих сторон на
косинус угла между ними:
c2 = a2+b2 — 2abcosC,
где а, Ьу с — длины сторон треугольника, а С — угол, заключенный между
сторонами а и Ъ. К. т. часто используется при решении задач элементарной
геометрии и тригонометрии.
2°. К. т. для стороны сферического треугольника: косинус одной стороны
сферического треугольника равняется произведению косинусов двух других его
сторон плюс произведение синусов тех же сторон на косинус угла между ними:
cos a=cos Ь cos с4- sin b> sin с cos A.
3°. К. т. для угла сферического треугольника: косинус угла сферического
треугольника равен произведению косинусов двух других углов, взятому с
противоположным знаком, плюс произведение синусов двух других углов на
косинус стороны, противолежащей первому углу:
cos А = — cos В cos C-f-sin В sin С cos a.
КОСИНУСОИДА — график функции y=cos* в декартовой прямоугольной
системе координат (см. рис. 126). К. есть та же синусоида (см.), только сдви-
π
нутая по оси Ох влево на —, так как
л"
cos jc=sin { χ Α—
1 2
КОСОСИММЕТРИЧЕСКИЙ ОПРЕДЕЛИТЕЛЬ—определитель, в котором
элементы, симметричные относительно главной диагонали, противоположны по знаку,

170
КОСОСИММЕТРИЧНОСТЬ
т. е. в котором α^=—α μ. Для К. о. л-го порядка d справедливо соотношение
d=(—\)ndf откуда следует, что К. о. нечетного порядка η всегда равен 0.
КОСОСИММЕТРИЧНОСТЬ: 1°. К. функции— свойство функции f(xlt х2,
хп) нескольких переменных, заключающееся в том, что знак функции меняется
на противоположный при любой нечетной перестановке (см.) аргументов и не
меняется при любой четной перестановке. Например, функция трех переменных
/О, у, z)*=(x — y)(y — ζ)(ζ — χ) — кососимметрична.
2°. К. тензора (коварнантного или контравариантного) — свойство тензора
(см.), заключающееся в том, что координаты, отличающиеся только порядком
индексов, равны между собой, либо отличаются знаком. Первое имеет место в
случае четной перестановки индексов, второе — в случае нечетной. К. тензора
не изменяется при замене одной ортонормированной (см.) системы координат
пространства другой ортонормированной.
КОСОУГОЛЬНЫЕ КООРДИНАТЫ — частный случай аффинных координат
(общих декартовых) на плоскости или в пространстве, когда оси координат не
перпендикулярны друг другу, но единичные (базисные) отрезки по осям равны
между собой. См. также Координаты.
КОТАНГЕНС — одна из тригонометрических функций, обозначаемая ctg x
(χ — аргумент) и определяемая формулой:
COSJC
ctg jc=——,
sin χ
где cos λ: — косинус (см.), sin л; — синус (см.). Областью определения К. является
вся числовая ось, за исключением точек, абсциссы которых:
лг=ял(л = 0, ±1, ±2, . . .).
График К. состоит из отдельных ветвей (рис. 127). К. является функцией
неограниченной, принимающей значение, равное любому действительному числу;
К. также является функцией нечетной и периодической, с наименьшим
положительным периодом, равным π.
К. можно определить и иначе. Если рассмотреть произвольный
радиус-вектор (подвижный радиус ОМ=г), начало которого совпадает с началом координат
(рис. 128), то отношение — =ctg α, где α — угол, составленный радиус-вектором
УМ
с положительным направлением оси Ох (с неподвижной стороной О А угла а =

КОХЛЕОИДА
171
« < АОМ), а хм и Ум — координаты точки Μ — конца подвижного
радиус-вектора. К. и тангенс (см.) связаны соотношением:
ctga=-—,
tga
где a — допустимое значение аргумента для К. и тангенса. Знак К. совпадает
со знаком тангенса.
Если ограничиться только острым углом а, то К. можно определить из
рассмотрения прямоугольного треугольника ОММг или подобного ему
треугольника (рис. 128) как отношение катета OMlt прилежащего к углу а, к
катету MMlt противолежащему этому углу.
График К. в прямоугольной декартовой системе координат называется котан-
генсоидой. Функция, обратная К-, называется арккотангенсом (см.).
Производная К. вычисляется по формуле:
(ctg*)' — 4i .
sin2*
Интеграл от К. определяется по формуле:
Jctg χ dx*= In |sin x\+C*
К. разлагается в ряд:
1 χ χ3
(0< |x| <oo); это разложение справедливо и в комплексной плоскости. Для
комплексного аргумента ζ К. является мероморфной функцией, нули которой
находятся в точках г=лл, где л=0, ±1, ±2, . . .
К. также называется тригонометрической кофункцией (см.), т. е. функцией
дополнительного угла.
Лат. со (сокращение слова complementum) — дополнение-f-тангенс (см.).
КОТАНГЕНСОИДА — график функции котангенса (см.) y=ctgjc в
прямоугольной декартовой системе координат. К. состоит от отдельных ветвей
(рис. 127).
КОТЕСА ФОРМУЛА — формула для приближенного вычисления
определенных интегралов, имеет вид:
Ь
f/<*) **—^f5- [*&9+Η*ηγι+Η&%+ . . . +Нппуп\%
a
где η — число точек деления промежутка [a, b]f а коэффициенты Н1п
приводятся в специальных таблицах. К. ф. является наиболее общей формулой
механических квадратур (см. Численное интегрирование). Формула трапеций (см.)
получается при применении к каждому из отрезков (*/, xt+i) К. ф. для л=1,
формула парабол (см.) соответствует случаю /2 = 2.
Лит.: С. М. Никольский, Квадратурные формулы, Гостехиздат, М., 1958.
КОХЛЕОИДА —кривая, полярное уравнение которой имеет вид:
sin φ
Ρβα φ

172
КОШИ ЗАДАЧА
(рис. 129). К. относится к числу квадратрис (см.). Название кривой ввиду ее
сходства с проекцией раковины было предложено Юнгом (1883).
Греч, κοκλοη — улитка.
КОШИ ЗАДАЧА—-одна из основных задач теории дифференциальных
уравнений (см.), впервые систематически изучавшаяся французским математиком Коши.
К задаче Коши приводят процессы, характеризуемые некоторым
дифференциальным законом и определенным начальным состоянием. К. з. и заключается в
отыскании такого решения дифференциального
уравнения, которое удовлетворяет данному начальному
условию. Так? для обыкновенного дифференциального
уравнения
yn = f(x, у', у\ ..., у**-1))
К. з. состоит в отыскании решения при заданных
значениях:
У, У', . . ., У(л—*> для х=х0.
В случае линейного дифференциального уравнения с
двумя независимыми переменными
ди ди
а(х, у, и)---\-Ь(х, у, и) — =С{х, у, и).
дх ду
Рис. 129
К. з. состоит в нахождении решения этого уравнения при условии и(х0у)=(р(у),
где q>(y) — заданная функция.
Вообще, в случае дифференциального уравнения η-ro порядка с частными
производными К. з. заключается в нахождении решения дифференциального
уравнения:
дпи (
*т> ">
а*о +*ι+
+ *„
tf°oxf* ... dxl
(*)
(£ο+*ι+ ··· +km<ny k0<n),
ди дп - *и
если заданы ui —, . . . , ———-— для некоторого фиксированного значения
dt otn —l
аргумента t. На языке геометрии, этому соответствует случай (m-f 2)-мерного
пространства с координатами (t^, x2t ... хт, и), К. з. в случае линейного
уравнения вида:
ди ди
(h{xlt х«9 ..., хп, и) — + ··· +αη(Χι, х2, ■·· *л* и) τ— =
дхг дхп
= C(xlt хш и)
состоит в определении интегральной поверхности и=и(хъ хъ . . . , хп) этого
уравнения, проходящей через заданную (п—1)-мерную кривую.
Коши в 1842 г. и независимо от него С. Ковалевская в 1874 г. доказали
существование и единственность решения К. з. при условии аналитичности
функции F [см. (*) J и функций, входящих в начальные условия.
К. з. и теорема Коши — Ковалевской имеют место также для систем
дифференциальных уравнений.

КОШИ НЕРАВЕНСТВО
173
Адамар в 1923 г. показал, что постановка К. з. для эллиптических
уравнений не корректна, т. е. решение К. з. не является непрерывным зависящим
от начальных условий.
КОШИ ИНТЕГРАЛ — интеграл вида:
1 С V(z)dz
2 π/ J z —a '
(с)
где /— мнимая единица, {с) — спрямляемая замкнутая кривая и φ (г)— функция
комплексного переменного г, аналитическая как на границе (с), так и внутри
области. Если замкнутая кривая охватывает некоторую точку области а,
то К. и. равен ф(а), т. е. любая аналитическая функция может быть выражена
посредством К. и. через ее значения на границе.
Как обобщение К. и. известны интегралы типа Коши; они имеют тот же вид,
но кривая с не обязательно замкнута и функция φ (ζ) не обязательно
аналитическая.
Лит.: А. И. Марк у ш ев и ч, Теория аналитических функций, Гостехиздат, М.—Л.,
1950.
КОЭФФИЦИЕНТ при алгебраическом выражении — множитель при этом
выражении. Например, К. при х2 в выражении 2ух2 есть множитель 2у; К. при
(а-\-Ь) в выражении с(а+Ь) есть число с\ К. при с в том же выражении есть
множитель (а-\-Ь).
Иногда понятие К. относят к множителям в различных формулах
специального содержания: угловой К. — число k в уравнении прямой y=kx+b на
плоскости, выражающий тангенс угла наклона этой прямой с положительным
направлением оси абсцисс; К. гомотетии (см. Гомотетия), К. расширения и К. трения
(в физике) и др.
Лат. cum — с, вместе в соединении со словами, начинающимися с
согласной буквы, переходит в со (сравните с кофункцией, кологарифмом); efficiens
(родительный падеж — efficientis) — производящий, вызывающий причину чего-
либо; буквально: коэффициент — содействующий.
КОШИ КРИТЕРИИ: 1°. К. к. сходимости последовательности — см.
Фундаментальная последовательность.
2°. К. к. существования предела функции. Для существования конечного
предела функции lim f(x) необходимо и достаточно, чтобы для любого е>0
χ -*■ а
существовало 6>0 такое, что при
0<|*' — αΚδ и 0 :\х" — а\<Ь
справедливо неравенство:
|/(д:/)-/Ю|<е.
3°. К. к. сходимости ряда. Для сходимости числового ряда иг-\-
4-^2+ ·*· -Ь"л+ ··· необходимо и достаточно, чтобы для любого ε>0
существовал номер N такой, что при всех η>Ν и р>0 справедливо неравенство:
l«n+i+W/I+2+ ··· +"л+р|<е.
КОШИ НЕРАВЕНСТВО — неравенство
/ П \2 П П
Σ *ьЛ< Σ 4 Σ b\t
\k=i j /г = 1 Λ= 1

174
КОШИ — РИМАНА УРАВНЕНИЯ
имеющее место для конечных сумм; очень важное и наиболее употребительное
в различных областях математики и математической физики неравенство.
Впервые было установлено Коши в 1821 г. Интегральный аналог К. п.:
/ Ъ \2 ь Ь
I J a(x)-b(x)dx < j a2(x)dx J b2{x)dx,
\a } a a
установлен русским математиком В. Я. Буняковским.
КОШИ — РИМАНА УРАВНЕНИЯ (более правильное название — уравнения
Эйлера — Даламбера) — система уравнений с частными производными:
ди _ ди ди ди
дх ду' ду дх*
Решения К. —Р. уравнений суть сопряженные гармонические функции (см.).
Пару функций и и ν этого решения можно рассматривать соответственно как
действительную и мнимую части некоторой аналитической функции (см.)
комплексного переменного. Наоборот, действительная и мнимая части аналитической
функции комплексного переменного x+iy удовлетворяют уравнениям К.—Р.
КРАЕВАЯ ЗАДАЧА — задача, состоящая в том, чтобы найти функцию,
которая является решением дифференциального уравнения и удовлетворяет
краевым условиям, т. е. некоторым условиям на границе области. Например,
найти решение уравнения Лапласа, которое на границе области обращается
в заданную функцию. Такая задача называется первой К- з. Если потребовать,
чтобы производная по нормали у гармонической функции обращалась в
заданную непрерывную функцию, то это будет вторая К. з. В решении К. з.
большую роль играет функция Грина (см.). Среди многих методов для решения
К. з. большую роль играет сведение их к интегральным уравнениям. В ряде
случаев, когда К. з. не имеет обычного решения, в рассмотрение вводят
обобщенные решения.
Лит.: С. Л. Соболев, Некоторые применения функционального анализа в
математической физике, Гостехиздат, М.—Л., 1950.
КРАЙНИЕ ЧЛЕНЫ ПРОПОРЦИИ a:b=c:d — члены а и d этой пропорции.
а с
Происхождение термина К. ч. п. -г=—; особенно понятно, если записать про-
Ь d
порцию в виде: a:b=c:d. Члены бис называются средними членами
пропорции. Если пропорцию a:b—c:d записать в виде: b:a=d:ct то К. ч. п. будут
средними членами, и наоборот.
КРАТНАЯ ПРОПОРЦИЯ—-то же, что и пропорция (см.). К. п. называют
также геометрической пропорцией, в отличие от арифметической пропорции (см.).
КРАМЕРА ПРАВИЛО — правило решения систем линейных уравнений.
Система η уравнений с η неизвестными, определитель (см.) которой отличен
от нуля, всегда имеет решение. Это решение единственно и определяется таким
К. п.: значение каждого из неизвестных ^(/=1, 2, 3 п) равно дроби,
где знаменателем является определитель D φ 0 системы (см.), а числитель D/
получается из определителя системы путем замены столбца коэффициентов при
искомом неизвестном X/ столбцом свободных членов.
Пример. Решить систему:
хх — *2-Ь*з=1*
ΖΧγ-\~οΧ2 — 2Хз==2<
*ι + *2 + 3*3~—·4.

КРАТНЫЙ КОРЕНЬ
175
По правилу Крамера выписываем определитель D, стоящий в знаменателях,
и определители Dlf £>2 и D3, стоящие в соответствующих числителях:
[1—1 1
2 3—2
1 1 3
. Si-
1—1 1
2 3—2
-4 1 3
, #2 =
1 1 1
2 2—2
1—4 3
. 0з =
1-1 1
2 3 2
1 1—4
Вычислив эти определители и убедившись, что D Φ О, можем написать:
_^ι_23 __02__?2 _ϋ_ ??
*1_D ""18' *2~ D 18' *3~ D 18-
КРАТНОЕ натурального числа η — натуральное число Ν, которое делится
(без остатка, нацело) на число п. Например, число 65 есть К. числа 13.
Общее К. двух натуральных чисел пг и п2 есть натуральное число Ν,
делящееся как на nlt так и на л2· Наименьшее из всех К. чисел пх и п2
называется наименьшим общим К. (см.) этих чисел (обозначается НОК(Лц пг)-
Натуральные числа, К. двум, называются четными, а не К. двум, —
нечетными.
Слово «кратное» употребляется как существительное и как прилагательное:
десять — число, К. двум; десять — К. (существительное!) двух.
КРАТНЫЙ ИНТЕГРАЛ — интеграл от функций, заданных в определенной
области на плоскости, в трехмерном или /2-мерном пространстве. К. и.
называют двойными, тройными и т. д. п-кратными интегралами.
Пусть функция f(x, у) задана в некоторой области D на плоскости.
Разобьем всю область D на η частичных областей dh площади которых 5/;
выберем в каждой области dL точку (ξ/, η/) и составим интегральную сумму:
i - ι
Устремим к нулю максимальный диаметр частичных областей di# Предел HmS,
если он существует и не зависит от способа разбиения области на части S/,
называется двойным интегралом от функции f{xt у) по области D; его
обозначают j J\ f{x, y)dS.
D
Аналогично определяется тройной интеграл и вообще «-кратный интеграл.
Для существования двойного интеграла необходимо, чтобы область D была квад-
рируемой (см.).
Существуют формулы Грина и Остроградского, сводящие К. и. к интегралам
меньшей размерности. К. и. находят многочисленные применения в механике
и физике.
КРАТНЫЙ КОРЕНЬ многочлена
f(x)=a0xn+a1xn-*+ ... +ап
*— число х0 такое, что f(x) делится (нацело» без остатка) на степень бинома
(х — jc0)*, где 1<&</г, к — натуральное, но не делится на (х— x0)k+1· При
этом корень х0 называется корнем кратности k. Если х0 — корень кратности k
многочлена f{x), то х0—корень кратности (k — /) /-й производной / = 1,
2, . . . , k—1. К. к. многочлена f(x) называется также К. к. уравнения
/(x)=0. Корень х0 многочлена / (х) первой кратности (однократный) называется
также простым корнем этого многочлена (или простым корнем уравнения
/(х)=0). См. также Корень.

176
КРАТЧАЙШЕЕ РАССТОЯНИЕ
КРАТЧАЙШЕЕ РАССТОЯНИЕ между двумя множествами метрического
пространства (см.) — нижняя грань расстояний между точками первого множества
и точками второго множества. Так как все такие расстояния неотрицательны,
то вышеуказанная нижняя грань существует и неотрицательна. Однако может
оказаться, что К. р. двух непересекающихся множеств равно нулю. Например,
два множества точек на прямой [0,1) (полуоткрытый интервал) и (1,2] обладают
этим свойством.
К. р. между скрещивающимися прямыми а и Ъ является длина их общего
перпендикуляра АВ. К. р. между двумя непересекающимися окружностями
является длина отрезка МгМ2 линий центров, как показано на рисунках 130
и 131.
К. р. двух пересекающихся множеств равно нулю.
Рис. 130 Рис. 131
КРИВАЯ — геометрическое понятие, абстракция обычного представления
К. линии. В разных разделах математики термин К. определяется по-разному,
в зависимости от целей и методов исследования. К. есть геометрическое место
точек пространства, координаты которых являются функциями одной
переменной. Различные определения К. требуют различной гладкости этих функций.
Например, К. в смысле Жордана (см. Жордана кривая) задается непрерывными
функциями и может сильно отличаться от обычного представления К. линии.
Если координаты точек К. есть непрерывно дифференцируемые функции
параметра, то К. называется спрямляемой. У такой К. можно ввести понятие длины
дуги (см. Длина). Важным классом К. являются алгебраические К. (см.). Они
задаются уравнениями:
F^x, у, г) = 0, F2(*, у, г)=0,
где Ft и F2 — многочлены от трех переменных. В частности, прямая линия
есть алгебраическая К.
Лит.: Л. С. Пархоменко, Что такое линия, Гостехиздат, М., 1954; П. К. Ра-
шевский, Курс дифференциальной геометрии, Гостехиздат, М. — Л., 1956.
КРИВАЯ ОШИБОК — линия на плоскости, являющаяся графиком закона
нормального распределения (см.).
КРИВАЯ РАСПРЕДЕЛЕНИЯ — графическое изображение функции
распределения вероятностей.
КРИВИЗНА плоской кривой — величина, характеризующая степень
отклонения ее от прямой в окрестности некоторой точки М. Направление кривой
в точке Μ можно охарактеризовать углом Θ, составленным касательно к
кривой в точке Μ с осью Ох (рис. 132). Скорость изменения угла θ при
равномерном движении точки Μ по кривой называется К. кривой в точке М.

КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ
177
Угол θ можно рассматривать как функцию от длины дуги М0М, где Λί0
фиксированная (начальная) точка, откуда К. кривой в точке Μ запишется
в виде формулы:
К =
dS
= lim
Λ5*0
'Δ β Ι
|ASl·
где Δ Θ — угол между касательными к кривой в точках Μ и М0, Δ S — длина
дуги ЛШ0.
К. окружности k=—, т. е. обратна радиусу окружности.
R
В случае произвольной плоской кривой (при определенных условиях диффе-
ренцируемости) в любой точке Μ можно построить так называемую
соприкасающуюся окружность (круг К.)· которая
наиболее тесно примыкает к кривой в точке
Mt по сравнению с другими окружностями,
касающимися кривой в той же точке М.
Центр соприкасающейся окружности и ее
радиус называются центром К. и радиусом К.
К. и радиус К. ρ связаны соотношением
k=—. Если кривая задана в прямоугольных
Ρ
декартовых координатах, то ее К.
вычисляется по формуле:
з
\dx2
1 +
d2V
dx)
9l
О
ι
-*""
■^f
Mo/
/ψ+Δθ
/
Рис. 132
Если зна:< абсолютного значения не пишут, то получают К. со знаком 4-
или —, в зависимости от выпуклости (см.) или вогнутости кривой в точке М.
Если рассматривается пространственная кривая, то вместо соприкасающихся
окружностей (кругов К.) рассматривают соприкасающиеся плоскости (см.)
в точке Μ и в соседней с ней точке М', т. е. плоскости соприкасающихся
окружностей в точках Μ и ДГ. Пусть β — двугранный угол между этими
плоскостями, Δ 5 — длина дуги ЛШ'; тогда выражение
lim --=о
Δ s -* о Δ5
определит абсолютное значение кручения (второй К.) пространственной кривой
в точке М. Кручению σ приписывают знак по «правилу буравчика» (правовин-
тового или левовинтового).
Лит.: К. П. Рашевский, Курс дифференциальной геометрии, Гостехиздат, М.—Л.,
1956; В. Бляшке, Дифференциальная геометрия, перев. с нем., ОНТИ, М.—Л., 1935.
КРИВОЛИНЕЙНЫЕ КООРДИНАТЫ точки на поверхности — координаты
(см.), устанавливаемые с помощью двух систем кривых координатных линий и
и ν таких, что через каждую точку поверхности проходит только одна линия
каждого семейства. Одно из семейств координатных линий может состоять
из прямых. Например, в случае полярной системы координат одно из семейств
координатных линий есть пучок прямых, другое семейство —
концентрические окружности, каждая из которых ортогональна любой прямой пучка.
Другим примером К. к. точки на поверхности являются географические
координаты — долгота и широта точки на поверхности сферы.
12
Толковый словарь математических, терминов

178
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ
Аналогично определяются К. к. точки в пространстве, где рассматриваются
уже не два, а три семейства координатных поверхностей.
К. к. называются также гауссовыми координатами. К. к. широко
используются в теории поверхностей (см. Поверхностей теория).
КРИВОЛИНЕЙНЫЙ ИНТЕГРАЛ— интеграл, взятый вдоль некоторой
кривой на плоскости или в пространстве. Различают К. и. 1-го и 2-го типов.
К. и. 1-го типа встречается, например, при рассмотрении задачи о
вычислении массы кривой переменной плотности. Он имеет вид:
[f(p)ds,
С
где С — заданная кривая, ds — дифференциал ее дуги, a f (ρ) — функция точки
на кривой, и представляет предел соответствующих интегральных сумм. Для
плоской кривой С (у=/ (х)) К. и. 1-го типа сводится к обычному:
ь
J7 (p)ds=J/[*, y(x)\V\+{y')2dx.
С а
К. и. 2-го типа встречается, например, при вычислении работы силового
поля в случае плоской кривой С. Он имеет вид:
§Р(х, y)dx+Q(x, y)dy
с
и является пределом соответствующих интегральных сумм. Если уравнение
кривой задано в параметрической форме:
x=x(t), y=y(0, (a<t< β),
то К. и. 2-го типа можно свести к обыкновенному интегралу по формуле:
\Р(х, y)dx+Q(x, y)dy=l {P[x(t)t y{t)\x'(t)+
C α
+Q[x(t), y(t)]y'(t)}dt,
η к К. и. 1-го типа по формуле:
JP(jc, y)dx+Q(x. y)dy«J|Pcos3-f-Qsina] ds,
с
где a — угол между осью Ох и касательной к кривой, направленной в сторону
возрастания дуги. Аналогичные формулы существуют для пространственной
кривой. Применительно к К. и. известны Грина и Стокса формулы (см.).
КРИВОЛИНЕЙНЫЙ УГОЛ—совокупность двух
простых дуг /х и /2 кривых, дифференцируемых в
точке Λί, исходящих из общей точки М. Общая
точка Μ называется вершиной К. у., дуги /х и
12 — его сторонами. К. у. измеряется
прямолинейным углом (см. Угол), заключенным между
касательными t1 и £2» проведенными к сторонам К. у.
в его вершине (рис. 133).
Аналогично определяется угол между кривыми
/г и /2 в точке их пересечения. Понятие К. у.
используется в сферической тригонометрии (см.) и
дифференциальной геометрии (см.). Рис. 133

КРИТЕРИИ НЕПРИВОДИМОСТИ
179
КРИСТОФФЕЛЯ СИМВОЛ дифференциальной квадратичной формы
Г, S=l
риманова пространства (поверхности при я=2) есть выражение вида:
2\dxj~b dxi + дхк I
К. с. обозначается так: К7]. Символ VA называют К. с. 1-го рода, в
отличие от К. с. 2-го рода: {'/]* определяемого соотношением:
{V}-i;«*[Vl·
f= 1
где
К. с. обозначают и так:
± «^-ί;·если ;г
к~{ 10, если t=£s.
или
К. с, называют также скобками Кристоффеля. В литературе встречается другое-
название К. с. — Христоффеля символ.
Для К. с. справедливы равенства Γ^=Γ^. К. с. не является тензором: при
изменении системы координат его компоненты изменяются по более сложному,
чем тензорный, закону. При помощи К. с. в римановом пространстве вводится
понятие параллельного переноса (см.), и, таким образом, всякое риманово
пространство является в то же время пространством аффинной связности (см.).
К. с. евклидова пространства тождественно равен нулю. К. с. введен немецким
математиком Э. Кристоффелем.
КРИТЕРИИ НЕПРИВОДИМОСТИ многочленов. Ввиду того что применение
на практике общих методов разложения на неприводимые множители встречает
большие трудности (ср. Кронекера метод), в разное время различными авторами
было найдено довольно большое количество частных критериев, позволяющих
по тем или иным признакам сразу устанавливать неприводимость многочленов.
Наиболее ранним (1850) из таких критериев следует считать, по-видимому,
критерий Эйзенштейна (см.), который, правда, содержится в еще более ранне!
работе (1846) Шёнемана.
Все найденные к настоящему времени К. н. можно разбить по близости
их содержания на своего рода классы (типы).
В#т, например, один из таких типов К. н. В 1919 г. Пвйа двказал, что
если значения целочисленного многочлена степени η > 17 при η различных
целых значениях аргумента по абсолютной величине равны одному и то.м>
же простому числу р, то этот многочлен неприводим над полем рациональных
чисел или разлагается на произведение многочленов одинаковой степени.
Позднее А. Брауер (1934) доказал, что эта теорема верна для η > 6 и уже
неверна для 'п=6. Почти одновременно с Брауером в совместной работе Дор-
12*

180
КРИТЕРИЙ
варт и Оре дали полное исследование этого вопроса и распространили свои
результаты на неприводимость в мнимых квадратических полях.
В дальнейшем все К. н. указанного типа были значительно улучшены
М. В. Яковкиным. Он доказал, что для неприводимости целочисленного
многочлена любой степени достаточно равенства этого многочлена простому числу
хотя бы при одном значении аргумента, лежащем вне некоторого конечного
(практически не очень большого) отрезка.
Продолжая исследования этого рода, М. В. Яковкин пришел к новому
классу К. н. В ряде работ (опубликованных в «Докладах АН СССР» и
«Известиях АН СССР») им доказаны теоремы, позволяющие утверждать о
неприводимости многочлена тогда, когда его значение равно не только простому «
но и составному числу. Точнее, теоремы Яковкина по природе делителей
значения многочлена позволяют судить о природе делителей самого многочлена.
Так, например, если все существующие К. н. других авторов содержали
условия лишь достаточные для неприводимости и распространялись лишь
на некоторые частные виды многочленов, то М. В. Яковкиным доказаны довольно
простые теоремы, содержащие условия необходимые и достаточные, для
приводимости или неприводимости любых многочленов над полем рациональных
чисел.
Лит.: Г. М. Шапиро, Высшая алгебра, Учпедгиз, М., 1938; А. Г. Курош,
Курс высшей алгебры, Физматгиз, М., 1962; Н. Г. Чеботарев, Основы теории Галуа,
ч. I и И, ОНТИ, М., 1934; М. М. Постников, Теория Галуа, Физматгиз, М., 196 3;
М. В. Яковкин, Численная теория приводимости многочленов,. Изд-во АН СССР,
ΜΙ 959.
КРИТЕРИЙ — признак необходимый и достаточный.
Примеры: 1) К. разрешимости задач на построение циркулем и линейкой
на плоскости состоит в том, чтобы длина некоторого отрезка (к построению
которого сводится задача) выражалась как положительная функция от длин
данных отрезков через конечное число основных операций (сложение,
вычитание, умножение, деление и извлечение квадратного корня); 2) К· Больцано —
со
Коши для сходимости ряда состоит в следующем: ряд 2 ип сходится тогда
п= 1
и только тогда, если для любого сколько угодно малого числа ε>0 существует
такое число Ν, зависящее от ε, что
\Un+l+Un+2+ ··· +υη+ρ\<ε
для всякого η>Ν и всякого р>\.
Следует иметь в виду, что К. часто называют лишь достаточные признаки,
например критерий неприводимости многочленов (см.), Эйзенштейна критерий
(см.) и др.
Греч, κρ/τηρ/ον — средство для решения.
КРИТИЧЕСКАЯ ТОЧКА функции — точка, в которой градиент функции
(см.) равен нулю.
См. также Особая точка.
КРОНЕКЕРА—КАПЕЛЛИ ТЕОРЕМА — одна из основных теорем линейной
алгебры, выражающая необходимое и достаточное условие решения системы
η линейных уравнений с т неизвестными. К.—К. т. формулируется так: для
tofo чтобы система уравнений:
^11*1+^12*2+ ··· +£im*m=&i*
α21*1+α22*2+ ·'· +α2/7Ι*/7Ι = 62*
СЛ1*1 + ДЛ2*2 + '·· "\~аПтхт" Ьп·

КРОНЕКЕРА МЕТОД
181
имела хотя бы одно решение, необходимо и достаточно, чтобы ранг матрицы
(см.) системы (основной матрицы) был равен рангу расширенной матрицы.
* При этом матрицей системы называется матрица \\ щь \\ (/=1, 2, .... л),
(£=1, 2, . .., т), составленная из коэффициентов a-ik при неизвестных
данной системы, а расширенной матрицей называется матрица, составленная
из коэффициентов aik и свободных членов £>/(/= 1, 2, . . . , п).
Теорема названа по имени немецкого математика Кронекера и
итальянского математика Капелли, доказавших эту теорему.
КРОНЕКЕРА МЕТОД разложения многочленов на множители. Пусть
требуется решить вопрос, приводим или неприводим многочлен
f(x)=a0i-a1xi-a2x2-\' ... +апхп
над полем рациональных чисел, а в случае приводимости найти по крайней
мере два его сомножителя.
С точностью до постоянного множителя можно f(x) считать целочисленной,
а по лемме Гаусса (см.) можно полагать целочисленными также и искомые
множители этого многочлена.
Итак, если f(x) приводим, то должно иметь место тождество / (х)—
= Φ(*)Ψ(*) Для целочисленных многочленов f(x), φ (χ) и ψ (χ). Не нарушая
общности рассуждений, степень т функции ф(х) можно полагать не выше
л/2, т. е. т < [п/2\ — целой части л/2. Вычислим теперь значения f(x\ при
m-f-1 различных целых значениях x=x0i xlt x2, . . . , xmi тогда
соответствующие значения искомых множителей φ (jc) и ψ (χ) также должны быть целыми.
Но, с другой стороны, значениями φ(χ^) и ψ(^) могут быть только
делители числа /(*fc)(& = 0, 1, 2, . . . , т). Но так как каждое целое число
f(Xk) может иметь лишь конечное множество целых делителей, то значением
Ф(х0)может быть только один из целых делителей числа f(x0)> значением
φ (^i) может быть только один из целых делителей числа /(*i) и т. д.
Наконец, значением φ (хт) может быть только один из целых делителей числа /(*m).
Следовательно, система истинных значений φ{χ0), Φ(#ι), ф(*2), . . . f 4>(xm)
искомого множителя φ (χ) находится среди всевозможных комбинаций
делителей (как положительных, так и отрицательных) чисел /(*0)« /(*ι)« /(*2)» · · · *
f(xm). Для каждой комбинации m-f-1 делителей этих значений находим многочлен,
например, по интерполяционной формуле Лагранжа (см.), а затем на
полученный многочлен делим заданный многочлен /(*).
Таким путем продолжаем испытывать всевозможные комбинации делителей
значений f(x) до тех пор, пока не получим многочлен ф(#), на который
делится (без остатка) заданный многочлен f(x). Тогда частное от деления f(x)
на ψ(χ) даст второй сомножитель ψ(*) эгого многочлена f(x). После этого
можно применить К. м. к каждому из двух найденных многочленов φ(χ)
и ψ (л:) и тем самым решить вопрос о разложении f(x) уже не на два,
а на большее число сомножителей (если они имеются).
Этот метод был найден и разработан (1845) немецким математиком
Леопольдом Кронекером.
Несмотря на то, что после Кронекера некоторые математики (Мандль,
Рунге и др.) внесли в этот метод существенные усовершенствования, тем
не менее в большинстве случаев он все-таки приводит к практически очень
большому числу комбинаций делителей значений заданного многочлена, и
применение этого метода остается чрезмерно громоздким и трудно выполнимым.
Следует отметить, что во всех отношениях намного проще и практически
доступнее новые методы, найденные и детально разработанные М. В. Яковки-
ным.
Лит.: Л. Я. О к у нев, Высшая алгебра, ОНТИ, М.. 1937; Н, Г. Чеботарев,
Основные теории Галуа, ОНТИ, М., 1934; М. В. Яков кии, Численная теория
приводимости многочленов, Изд-во АН СССР, М., 1959.

182
КРОНЕКЕРА СИМВОЛ
КРОНЕКЕРА СИМВОЛ — тензор (см.) второй валентности, один раз
ковариантный (см.) и один раз контравариаитный (см.). Обозначается К. с.
через 5у. К. с, по определению, равен нулю, если / ψ /, и единице, если /="/.
К. с. удобен в выкладках тензорной алгебры и тензорного анализа (см.
Тензорное исчисление). В других областях математики часто отвлекаются от
тензорного характера К. с. и определяют его как функцию двух целочисленных
аргументов, равную нулю, когда аргументы неравны, и равную единице, когда
аргументы совпадают. К. с. введен Л. Кронекером в 1866 г.
КРУГ с центром О и радиусом г — геометрическое место точек плоскости,
отстоящих от точки О на расстоянии, не превосходящем г, т. е. это множество
точек Μ плоскости, в которой расположена точка О, таких, что ОМ < г.
К. есть замкнутое множество точек плоскости.
См. также Большой круг, Окружность, Круг кривизны.
КРУГ КРИВИЗНЫ — то же самое, что соприкасающийся круг (см.). См.
также Кривизна, Радиус кривизны.
КРУГ СХОДИМОСТИ степенного ряда:
αο+М2 — c)+a2(z— cf+ ··. +ап(г — с)п+ ·.·
— круг радиуса R с центром в точке z=c комплексной плоскости, для всех
внутренних точек ζ которого ( \z — a\<R) степенной ряд абсолютно сходится.
Радиус R К. с. называется радиусом сходимости степенного ряда. На границе
К. с. степенной ряд имеет особую точку (см.). Радиус сходимости степенного
ряда может быть равен 0 или оо; в последнем случае степенной ряд сходится
в любой точке комплексной плоскости. Для всякого степенного ряда областью
сходимости является всегда круг, за исключением, быть может, некоторого
множества точек, лежащих на его границе.
См. также Интервал сходимости. Абеля теорема.
КРУГЛЫЕ ТЕЛА (в элементарной геометрии) — шар, прямой круговой
конус и прямой круговой цилиндр.
Название К. т. весьма условное.
КРУГЛЫЙ КОНУС (в элементарной геометрии) — конус, направляющая
которого есть окружность. К. к., вершина S которого проектируется в центр
основания, называется прямым; если вершина S проектируется не в центр
основания, то К. к. называется наклонным или косым. Прямой К. к. получается
вращением прямоугольного треугольника вокруг катета. В сечении
наклонного К. к. плоскостью, не параллельной основанию, можно получить круг.
К. к. называют также круговым конусом. Обычно имеют в виду прямой К. к.,
который просто называется конусом.
См. также Круглые тела, Конус.
Лит.: О. Те π л и ц и Г. Радемахер, Числа и фигуры, Физматгиз, М., 1962;
Ж. Адама р, Элементарная геометрия, ч. II, Учпедгиз, М., 1952.
КРУГЛЫЙ ЦИЛИНДР (в элементарной геометрии) — цилиндр,
направляющая которого есть окружность. Если образующая К. ц. перпендикулярна
основанию его* то К. ц. называется прямым; если же образующая — наклонная
к основанию цилиндра, то К. ц. называется наклонным, или косым.
К. Ц. называется также круговым. Обычно под цилиндром понимают
прямой К. ц. Прямой К. Ц. можно представить как фигуру, образованную
вращением прямоугольника вокруг его стороны.
См. также Круглые тела. Цилиндр.
КРУГОВОЕ ПРЕОБРАЗОВАНИЕ плоскости — преобразование, при котором
каждая окружность или прямая переходит в окружность или в прямую. К. п.
представляет собой произведение двух преобразований: инверсии и подобия.

КУБ
183
Примеры К. п.: движение (см.)» подобие (см.), инверсия (см.). К. п.
представляют собой конформные преобразования (см.).
КРУГОВАЯ ТОЧКА: 1°. К. т. на плоскости, дополненной мнимыми и
бесконечно удаленными точками, — каждая из двух мнимых бесконечно удаленных
точек, однородные координаты которых удовлетворяют уравнению любой
окружности. Однородные координаты этих точек (1; /; 0) и (1; —/; 0). Прямые,
проходящие через К. т., называются изотропными прямыми (см.). К. т.
называется также циклической точкой.
2°. К. т. на поверхности — точка, в которой все нормальные сечения
(см.) имеют одну и ту же кривизну, например, точка пересечения поверхности
вращения с осью вращения есть К. т., на сфере любая точка есть К. т.
К. т. на поверхности иначе называется точкой округления, или омбилической
точкой.
КРУГОВЫЕ ФУНКЦИИ — иное название тригонометрических функций (см.).
Иногда К. ф. называются также аркфункции, т. е. функции, обратные
тригонометрическим (см.), хотя это название К. ф. менее оправдано.
КРУЧЕНИЕ кривой — скорость вращения соприкасающейся плоскости
(см.) кривой в точке А при равномерном движении точки с единичной
скоростью. Строго К. кривой определяется аналитически из формул Френе
(см. Френе формулы) коэффициентом κ:
— =κν,
as
пяти типов правильных
и 8 вершин. Гранями
где β — единичный вектор бинормали (см.), у — единичный вектор нормали
(см.), s—длина дуги. К. характеризует степень отклонения кривой от
соприкасающейся плоскости в данной точке. К. наряду с кривизной являются
основными характеристиками кривой: имея две произвольные гладкие функции
k(s) и x(s) (кривизну и кручение от длины дуги), можно восстановить всю
кривую с точностью до положения в пространстве. Например, кривой
постоянного К. является винтовая линия; прямая линия имеет неопределенное
К.; всякая плоская кривая имеет К., равное нулю.
Лит.: П. К. Ρ а ш е в с к и й, Курс дифференциальной геометрии, Гостехиздат, М.—Л.,
1956.
КУБ — правильный шестигранник. К. —один из
многогранников (см.), имеющий 6 граней, 12 ребер
К. являются квадраты, к каждой вершине К.
сходится по 3 ребра (грани). Поверхность К. с ребром
а равна 6а2, объем того же К. равен а3.
К. имеет центр симметрии, 9 осей симметрии
и 9 плоскостей симметрии. К. обозначается: ABCDA'B'
CD' (восемью своими вершинами) или АС (какой-
либо своей диагональю) (рис. 134).
К. (правильный гексаэдр) двойствен (дуален)
правильному октаэдру: вершины К. являются центрами
граней правильного икосаэдра (см. Двойственности
принцип), /г-мерным К. называется совокупность п-ок
(«энок», — в частности, двоек, троек, четверок и т. д.)
чисел (*,, х2, . . . , хп), где каждое 0 ^ *,· < 1 (ребро равно единице),
n-мерный куб имеет вершины, ребра, двумерные, трехмерные, четырехмерные и т. д.
грани. Каждая такая грань есть куб меньшего измерения. У /2-мерного куба
2п вершин. Координаты вершин состоят только из единиц и нулей. В
Московском университете имеется фильм, иллюстрирующий вращение
четырехмерного куба в четырехмерном пространстве вокруг неподвижной плоскости.

184
КУБАТУРА
КУБАТУРА: 1°. К. — число кубических единиц
в объеме данного тела. 2°. К- —построение куба,
равновеликого данному телу. 3°. К. — вычисление
объема тела.
КУБИЧЕСКАЯ ПАРАБОЛА — плоская кривая,
уравнение которой в декартовой системе координат
имеет вид y=kx*9 где кфО (рис. 135). Если £>0,
то К. п. проходит в первом и третьем
координатных углах. К. п. (при k = \) может быть
использована как номограмма (см.) для приближенного
вычисления кубических корней из чисел.
КУБИЧЕСКОЕ УРАВНЕНИЕ —уравнение вида:
αο*3+αι*2-Η2*+α3 = 0,
где а0» аи а2* as — произвольные комплексные чис-
ла, причем <20=£0. Подстановкой лг=у — — К. у.
общего вида приводят к
У3+РУ-Н=0,
где
Рис. 135
2а\ ага2 аг
21а%
Ы
а0
Последнее уравнение решается по формуле Кардано (см. Кардано формула).
Таким образом, корни К. у. в принципе могут быть выражены через
коэффициенты уравнения в явной форме. Однако случай, когда все три корня К. у.
вещественны, требует извлечения кубичного корня из комплексных чисел, что
нельзя свести к вычислению кубичных корней из действительных чисел. На
практике формула Кардано употребляется редко. Она связана с громоздкими
вычислениями. Поэтому чаще применяются приближенные методы решения К. у.:
Штурма метод (см.), Ньютона метод (см.), Лобачевского метод (см.) (метод
Греффе). К. У· иногда называют также и кубичным.

л
ЛАГРАНЖА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — формула для нахождения
многочлена L(x) степени mt принимающего в т-\-\ точках промежутка [а, Ь]
задания функции f(x) данные значения /(*/)/=1, 2„ ..., /я. Л. и. ф. имеет
вид:
L . у (х — *о) (x — Xi)...(x — *fe-i) (X *-Xk+i)---(x — Xm)
k=o ^ (Xk — Xo){xk — Xi)--^Xk—Xh--i)(Xk--Xk + i)---(Xk--Xm)'
Погрешность, совершаемая при замене функции f (x) выражением L(x), не
превышает
м (х — Хо) (х — *ι)· ·· (х — Хт)
(т+1)!
где Αί — наибольшее значение абсолютной величины (т-Н)-й производной
f(m+1)(x) функции f(x) на отрезке [x0t xm]. Л. и. ф. найдена (1793)
французским математиком Лагранжем.
ЛАГРАНЖА ИНТЕРПОЛЯЦИОННЫЕ КОЭФФИЦИЕНТЫ— выражения
L(n)( (х — Хо)· · ·(* — */-ι)(* — Xj+i)■ .(x — Xn)
J (Xj — X0)...(Xj — Xj-x)(Xj — X/+1)...(Xj — Xn) '
содержащиеся в интерполяционной формуле Лагранжа (см.). Ввиду сложности
вычислений Ljn)(jc) по указанной формуле в разное время различными авторами
составлялись таблицы Л. и. к. Например, в изданиях 1956 г. такие таблицы,
содержащие Л. и. к., опубликованы в изданиях Академии наук СССР. См. Лагранжа
интерполяционная формула.
Лит.: Л. Н. Кармазина, Л. В. Курочкина, Таблицы интерполяционных
коэффициентов, Изд-во АН СССР, М., 1956.
ЛАГРАНЖА МЕТОД неопределенных множителей для отыскания
относительных экстремумов (см.) функции и—[(хг, jc2s ·.., Xn) при условиях:
Фх(*1. Хъ .··* *л)=0* * = 1« 2 т<п%
называемых уравнениями связи, состоит в том, что вводят вспомогательную
функцию:
F(xu х2, .... Хп> ^ι» ^2» ···> ^ж)=/(■*!, хъ ···> χη)-\-
+λιΦι(*ϋ χ2 Α:η)-Γ*λ2φ2(χ1> х21 ..., χη)+... Xmq>m (д^, *2, ..., *„),
где Xlf λ2, ... * Xm называются неопределенными множителями. При помощи
функции F необходимые условия относительного экстремума (см.) могут быть
записаны в виде:
dF dF
аналогичном необходимым условиям экстремума функции F.

186
ЛАГРАНЖА РЯД
ЛАГРАНЖА РЯД — ряд, дающий разложение аналитической функции от
корня уравнения ζ=α+λφ(ζ) по степеням «малого параметра» λ;
ЧП λ" d«-i
Полагая /(z) = z, получают Л. р. для самого корня г:
2)ndn-i
Л. р. представляет собой весьма важные предложения Теории функций
комплексного переменного.
ЛАГРАНЖА ТЕОРЕМА о квадратических иррациональностях утверждает,
что всякая квадратическая иррациональность (см.) разлагается в периодическую
(бесконечную) цепную дробь (см.). Например,
лг— „ 10251—2/69477
У 11 =(3,(3,6)); — =(2, 4, (7, 5, 9, 1)).
44оо
Справедлива и теорема, обратная Л. т.: всякая периодическая цепная дробь
является квадратической иррациональностью.
Таким образом, Л. т. и обратная ей теорема дают арифметическую
характеристику для периодических цепных дробей.
ЛАГРАНЖА УРАВНЕНИЕ (Даламбера уравнение) — обыкновенное
дифференциальное уравнение 1-го порядка, линейное относительно зависимой и
независимой переменных, имеющее вид:
y=xy(y')+f(y')>
ay
где у' = -, афи / — заданные дифференцируемые функции своего аргумента.
Общий интеграл Л. у. может быть найден в параметрической форме
дифференцированием уравнения по х\ он выражается через квадратуры. Частным случаем
Л. у. является уравнение Клеро (см.). Название Л. у. не является исторически
оправданным, так как это уравнение ранее Лагранжа исследовано французским
математиком Даламбером.
ЛАГРАНЖА ФОРМУЛА — см. Конечных приращений формула.
ЛАПЛАСА ОПЕРАТОР — линейный дифференциальный оператор 2-го поряд-
:<а. Определен на пространстве дважды дифференцируемых функций.
Обозначается символом Д. Л. о. переводит данную функцию φ в функцию:
д2Ф с2 φ д2Ф
Δφ=—+—+ ■·+—-.
дх\ dx\ дх\
Важность Л. о. во многих вопросах математики обусловлена следующим его
основным свойством: Л. о. является единственным из всех дифференциальных
операторов 2-го порядка, инвариантным при любом ортогональном
преобразовании (см.) переменных хг, х2, ...« Хп* т. е. при замене х19 х2, ...» хп
координатами ylt у2 У η ортогональным преобразованием имеет место равенство:
д2Ф д2Ф d2W д2Ф д2Ф д2Ф
—-Ч—Ч-. .. + —£- + + ·.. -I- ,
дх\ дх\ дх* ду\ ду\ ду\
где
Ф(Уь Уч Уп) = Ф(*1> х* ..., ХпУ

ЛАПЛАСА ТЕОРЕМА
187
С помощью Л. о. уравнение (см. Лапласа уравнение) записывается так: Ды = 0.
См. также Гармоническая функция.
ЛАПЛАСА ПРЕОБРАЗОВАНИЕ — преобразование, переводящее функцию
действительного переменного f (t) (оригинал) в функцию комплексного
переменного g(p) (изображение) по формуле:
со
Lf(t) = g(p) = $e~ptf(t)dL
о
Изображение g(p) обладает некоторыми замечательными свойствами, например:
i)4/(«0J-7*(f); 3)L
J/(0 л
JAR)
ρ
2) М/'(0]=те(Р)-/(0);
Свойство 3) означает, что если оригинал проинтегрировать, то изображение
разделится на аргумент р. Эти и некоторые другие свойства Л. п. используются
в операционном исчислении. Л. п. часто применяется при решении задач,
связанных с автоматическим регулированием. Л. п. введено французским математиком
П. Лапласом в 1812 г.
Лит.: В. А. Диткин и П. И. Кузнецов, Справочник по операционному
исчислению, Гостехиздат, М. — Л., 1951.
ЛАПЛАСА ТЕОРЕМА об определителях. Выделим (зафиксируем) в
определителе л-го порядка совершенно произвольные k (k < η) строк или столбцов; тогда
Л. т. можно сформулировать следующим образом: определитель п-го порядка
равен сумме произведений всех миноров £-го порядка, составленных из элементов
любых зафиксированных k строк (столбцов), на их алгебраические дополнения.
Пример. В определителе D выделим, например,
первые две строки и составим всевозможные
миноры 2-го порядка, содержащиеся в этих двух строках:
D=
2 0
—3 4
0 —6
5 —8
Ai,-|
Λί4=|
—7 9
—4 —2
1 —1
3 7
2 0
—3 4
0 -7
4 —4
|. Η-3:ϊΙ· м>=\4Л\>
Λί-Ι ° 9
M*\ 4 —2
лл ι — 7 9
Λ*·-| -4 -2
Соответствующими алгебраическими дополнениями для этих миноров будут:
^1 = (—1)(1+2; + (1+2) 11-11 Л2 = ( —1)(1 + 2) + (1 + 3) | __б U
| 3 7 I * J —8 7| ·
Л3 = (—l)(i+2)+(i+4) | —6 1 I Л4-(—1)(1+|)+(|+8) 1 0 —1 I
—8 3 * 5 7 *
А=( — 1У1+2) + (2+4) I 0 1
I 5 3
Лв = ( — 1)(М-2)+<3 + 4) | 0 —6
5 -8
Тогда по Л. т. определитель D удовлетворяет следующему равенству:
£>=ΛΜι + МгА2+М9Аа -f MtAt+MbA5 + М6АЪ.
Для вычисления определителя D достаточно в это равенство подставить
численные значения соответствующих миноров и их алгебраических дополнений.

188
ЛАПЛАСА ФОРМУЛА
Л. т. является обобщением правила разложения определителей по элементам
строки или столбца. Это простейшее правило раскрытия и вычисления
определителей получается из Л. т. как частный случай, при k=\ или при k=n—1.
С помощью Л. т. доказывается правило умножения определителей, впервые
установленное французскими математиками Бине и Коши.
ЛАПЛАСА ФОРМУЛА для приближенного вычисления определенных интег-
ь
ралов — формула, дающая выражение для интеграла \f(x)dx через значения
а
функции f(x) з некоторых точках и конечные разности (см.) этих значений:
lf(x)dx=h\-
а V·
~ f(a)+f(a+h)+ · ·. +/[«+(« - 1) AJ+ \ f(b)\
--[Лул-1-ДУо1-Ь-[Д2ул-2-А2Уо]-^[Л3уя~з~Д3Уо]-
3/ι 863
- Wo ΙΔ-У*- - Δ* У·! - ^ fΔ^η-6 - Д«У1 - · · ·
ДУл=ул+1 — у* Ъ}ук=ь}-хУк+\ - а'-Ъъ.
Эта формула получается из формулы Эйлера для вычисления определенных
интегралов, если в последней записать приближенно производные с помощью
конечных разностей. Л. ф. находит широкое применение в современной
вычислительной математике, в частности при численном решении интегральных уравнений
с помощью быстродействующих электронных цифровых машин.
Лит.: А. Н. Крылов, Лекции о приближенных вычислениях, Гостехиздат, М., 1954.
ЛАПЛАСА ФУНКЦИЯ — синоним термина Интеграл вероятностей (см.).
ЛЕБЕГА ИНТЕГРАЛ — интеграл, определяемый при помощи специальной
конструкции и понятия меры множества. Разделим точками
• · -У-г < У-1 <Уо < Ух < · " < Ук < · · ·
область возможных значений функции /(*), определенной на некотором
измеримом множестве М. Пусть через Μ ι обозначено множество значений х<
удовлетворяющих соотношению yi—\ < f(x) < yi. Составим сумму 5 = Ση/μ(Λί/), где
t]i — произвольное число такое, что ^/_1<η < yit а μ(Λί/) есть мера множества
М(. Если предел S существует при стремлении к нулю максимума у ι — у/_ и
то он и называется Л. и. от f(x) по множеству М. Для интегрируемости
ограниченной функции но Лебегу необходимо и достаточно, чтобы она была
измеримой. Понятие Л. и. есть обобщение понятия интеграла Римана.
Лит,.: А. Лебег, Интегрирование и отыскание примитивных функций, Учпедгиз, М.,
1960.
ЛЕВАЯ КАСАТЕЛЬНАЯ —см. Односторонняя касательная.
ЛЕВАЯ ПРОИЗВОДНАЯ — см. Односторонняя производная.
ЛЕЖАНДРА СИМВОЛ. Если ρ— простое нечетное число и α не делится
на Pi то под Л. с, обозначаемым { —1, понимают +1, если а — квадратический
вычет (см.) по модулю р, и понимают —1, если а — квад
модулю р. Л. с. читается: «символ а по отношению к р»
Л. с. обладает следующими свойствами:
1) если α sa ах (mod pj, то (—«(—]; 2) ,'— 1 = 1;
\Pj \Ρ J \PJ

ЛЕМНИСКАТА
189
,,,_i)=(_;r;1)^.Hi)(f)...(,..);
ρ2 -ι
5) (— ]=(— 1) 2 ; б) закон квадратичной взаимности (см.).
Л. с. используется для практического выяснения вопроса о том, является
ли число а квадратическим вычетом по модулю ρ или нет.
ЛЕЙБНИЦА ФОРМУЛА — формула для нахождения я-й производной
произведения двух функций:
(м«У/,) = С°и(я)у+С;Ул-%' +C2nii(n-*)v" -f
+ .. · +С%~киШ^к)+.. .+С%~1 и'tt"-1)+€№">.
ЛЕЙБНИЦА — НЬЮТОНА ТЕОРЕМА — теорема о представлении функции
через интеграл ее производной. Если / (х) — непрерывно дифференцируемая
функция, то
а
Л. н. т. называется также формулой Лейбница-^-Ньютона.
ЛЕКСИКОГРАФИЧЕСКИЙ МЕТОД разложения многочленов на множители
предложен Л. Кронекером для нахождения множителей многочлена f(xf уч г,
5, ..., t) от многих переменных над полем рациональных чисел. Он состоит
в замене многих переменных (аргументов) xt у, г, s, ..., t одной переменной и:
г Г2 Г* a rk—1
x=u, y=urt z*=ur , s=w , ..., t=ur
где k — число переменных (аргументов) заданного многочлена /(*, у, z, s,
..., t)
Полученный в результате таких подстановок многочлен от одной
переменной и разлагается на множители обычными методами. После этого в найденных
сомножителях многочлена от одной переменной степени аргумента и обратно
заменяются через первоначально заданные переменные (аргументы) дс, у, z, st
..., t. Очевидно, что обратная замена переменных всегда однозначна. Слишком
большим недостатком этого метода является очень высокая степень многочлена
от одной переменной, получаемого после замены многих переменных
(аргументов).
Для отыскания разложения многочленов от многих переменных на
множители над полем рациональных чисел несравненно проще и во всех отношениях
удобнее, чем Л. м.» новые методы* найденные и детально разработанные
М. В. Яковкиным.
Лит.: Н. Г. Чеботарев, Теория Галуа, ОНТИ, М., 1936; М. В. Яковкин,
Численная теория приводимости многочленов. Изд-во АН СССР, М., 1959.
ЛЕММА — вспомогательное предложение, используемое для доказательства
одной или нескольких теорем.
Греч, λήμμα — взятка, прибыль, доход, корысть.
ЛЕМНИСКАТА — плоская кривая, произведение расстояний каждой точки
которой до двух данных точек (фокусов) F1(—at 0) и F2(fl* 0) равно аК Эта
кривая впервые изучалась Я. Бернулли и называется лемнискатой Бернулли. Л.
имеет форму восьмерки (рис. 136). В прямоугольных декартовых координатах
уравнение Л. имеет вид:
(*2-by2)2 — 2α2 (jc2 — α2)=0.

190
ЛЕМУАНА ТОЧКА
Рис. 136
В полярных координатах уравнение Л. может быть записано в виде:
p2=2a2cos2q>.
Л. — уникурсальная алгебраическая кривая 4-го порядка. Если равнобочную
гиперболу подвергнуть преобразованию инверсии с центром, совпадающим с
центром гиперболы, то гипербола преобразуется в Л. Л. есть частный случай овалов
Кассини (см.), фигур Лиссажу (см.) и
синус-спиралей (см.). Под Л. л-го
порядка понимают плоскую кривую,
произведение расстояния каждвй точки
которой до заданных точек (фокусов)
Fu ^2. · · · ι Ρ η равно заданному числу.
В этом смысле окружность есть Л. с
одним фокусом, а овалы Кассини — Л.
с двумя фокусами. Греч, λημνισχοξ —
бант, лента; лат. lemniscatus —
украшенный лентами.
ЛЕМУАНА ТОЧКА— точка
пересечения симедиан треугольника, т. е.
прямых, проходящих через вершины
треугольника и делящих (внутренним образом) противолежащие стороны его на
части, пропорциональные квадратам прилежащих сторон.
Л. т. названа по имени французского математика Э. Лемуана (1873).
3 XIX в. метрическим исследованиям треугольника уделялось большое внимание.
3 это время стали изучаться и другие точки треугольника, связанные с
вписанной, вневписанной, описанной окружностями, например Жергонна точка (см.),
Нагеля точка (см.) и др.
Лит.: СИ. Зетель, Новая геометрия треугольника, Учпедгиз, М. I960.
ЛИ ГРУППА — группа, множество элементов которой есть многообразие
;см.) аналитической структуры (см.) и групповые операции аналитичны в этой
структуре. Например, с каждой точкой окружности (прямой или тора) можно
связать единственное преобразование всей окружности (прямой, тора) в себя,
переводящее некоторую фиксированную точку — единицу группы в данную. При
этом указанное отображение аналитично (записывается аналитическими
функциями в локальных координатах (см. Многообразие). Л. г. впервые изучалась в тру-
цах норвежского математика Софуса Ли в связи с некоторыми задачами
дифференциальных уравнений. В изучении Л. г. весьма важным и плодотворным
оказался метод локального рассмотрения группы и введение алгебр Ли (см.) — более
простого, чем Л. г., математического объекта. Свойства алгебр Ли дают много
:ведений о Л. г. Теория Л. г. имеет многочисленные и разнообразные
приложения к математике и физике. Особое значение имеет теория Л. г. для геометрии
вообще и геометрии однородных пространств в частности. Эрлангенская
программа Клейна трактует геометрию как науку об изучении тех свойств фигур,
которые не изменяются при заданной группе (обычно Л. г.) преобразований.
На этом пути получены важные результаты. В теории относительности
Эйнштейна огромную роль играет группа Лоренца (см.), являющаяся Л. г. Аппарат
теории Л. г. и ее главы — теории представлений (см.). Л. г. является мощным
методом теории относительности. Теория Л. г. — бурно развивающаяся
математическая дисциплина. Фундаментальные результаты этой теории получены Кил-
лингом, С. Ли, Э. Картаном, Г. Вейлем и др. Труды советских математиков
в области теории Л. г. получили всемирную известность. Крупные результаты
получены А. И. Мальцевым и Л. С. Понтрягиным.
"См. также Непрерывные группы.

ЛИНЕЙНАЯ ЗАВИСИМОСТЬ
191
ЛИНЕЙКА — инструмент для проведения (черчения) прямых линий. Прямая,
начерченная с помощью Л., —овеществленный образ прямой линии в математике,
т. е. физически начерченная мелом на доске (карандашом или чернилами на
бумаге) прямая является наглядной моделью абстрактной математической прямой.
Л., имеющая параллельные края, с помощью которой можно проводить
параллельные прямые, называется двусторонней; Л., имеющая только один
прямолинейный край, называется односторонней. Л. (односторонняя) является основным
инструментом в геометрических построениях Штейнера (см.) и в построениях
проективной геометрии. С помощью только одной Л. (которая обычно мыслится
как односторонняя) нельзя разделить отрезок пополам, но можно, например,
провести касательную к начерченной окружности (см. Паскаля теорема, Полюс
и Поляра). В элементарной геометрии Л.— один из основных инструментов в
геометрических построениях на плоскости наряду с циркулем.
См. также Логарифмическая (счетная) линейка.
ЛИНЕЙНАЯ АЛГЕБРА — раздел алгебры, изучающий линейные
преобразования в конечномерных линейных пространствах. Возникновение Л. а. связано
с решением систем линейных уравнений, т. е. уравнений первой степени
относительно переменных (неизвестных). Развитыми отделами Л. а. являются теория
матриц, теория форм (в частности, квадратичных), теория инвариантов.
Некоторые идеи Л. а. используются в доказательстве фундаментальных теорем анализа
и дифференциальных уравнений: теорема о неявных функциях, теорема об
устойчивости решений автономной системы дифференциальных уравнений и др.
Л. а. имеет важные приложения во многих разделах науки и практики
(симплекс— метод в линейном программировании и др.).
Объекты изучения Л. а. обобщаются в различных направлениях в таких
разделах математики, как тензорное исчисление, функциональный анализ (см.)
и др.
Лит.: И. М. Гельфанд, Лекции по линейной алгебре, Гостехиздат, М.—Л., 1951;
А. И. Мальцев, Основы линейной алгебры, Гостехиздат, М., 1953; Ф. Р. Гант-
м а х е р, Теория матриц, Гостехиздат, М., 1953.
ЛИНЕЙНАЯ ВЕКТОР-ФУНКЦИЯ —функция, определенная на векторах
линейного пространства, принимающая векторные значения (быть может, из
другого пространства) и линейная, т. е.
А(х+у)=А (x) + A (у),
Α(λχ)=λ Α (χ),
где χ и у — любые векторы исходного пространства, λ — произвольное число.
Л. в.-ф. задает линейное отображение пространства в себя или в другое
пространство.
ЛИНЕЙНАЯ ЗАВИСИМОСТЬ — свойство конечной совокупности векторов
линейного пространства. Говорят, что векторы alt а2, ..., а.п линейно-зависимы
над полем (см.) &, если при некотором подборе чисел \lt λ2, ..., λη из
данного поля справедливо равенство:
Xi aj-f λ2 a2-j hXnan=0 (0 — нуль-вектор),
причем хотя бы одно λ/^O. Система векторов может обладать Л. з. над одним
полем, но быть линейно-независимой над другими. Так, два вектора (1, 0) и
(/, 0) линейно-зависимы над полем комплексных чисел, но линейно-независимы
над полем вещественных чисел. В η -мерном линейном пространстве всякая
линейно-независимая система векторов содержит не более η векторов. Система
векторов, содержащая нулевой вектор, всегда линейно-зависима.

192
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ
Лит.: И. М. Гельфанд, Лекции по линейной алгебре, Гостехиздат, М.—Л., 1951;
А. И. Мальцев, Основы линейной алгебры, Гостехиздат, М., 1953; Ф. Р. Гант-
махер, Теория матриц, Гостехиздат, М., 1953; Л. Я. О к у н е в, Высшая алгебра,
Учпедгиз, М.—Л., 1958; Е. С. Ляпин, Высшая алгебра, Учпедгиз, М.—Л., 1955.
ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ. Если известно значение непрерывной
функции f(x) в точках а и 6, то на отрезке [а, Ь] ее можно приближенно заменить
прямой:
,/ ч ,/ *,/ . f(b)-f(a)
о — а
или, как говорят, интерполировать линейно. Если f(x) имеет ограниченную
вторую производную, то ошибка при этом будет меньше, чем max | f(x) \ (Ь —а)2,
т. е. чем меньше отрезок, тем более точный результат дает Л. и.
ЛИНЕЙНАЯ ФОРМА — функция первой степени, не содержащая свободного
члена: γ=α1χι+α2χ2-) hdnXnt где коэффициенты α ι от xj не зависят. Л. ф.
есть линейный функционал (см.) в /2-мерном линейном пространстве переменных
Хц X<i> ...» Хп»
ЛИНЕЙНАЯ ФУНКЦИЯ — функция первой степени относительно всех ее
переменных (аргументов). В частности, Л. ф. является функция вида y=kx-\-b.
Если /гиб — числа вещественные, то график ее есть прямая, наклоненная к оси χ
под углом, тангенс которого равен k9 и пересекающая ось у в точке (О, Ь).
При этом число k называется угловым коэффициентом прямой, а Ь — начальной
ординатой.
ЛИНЕЙНОЕ ПРЕОБРАЗОВАНИЕ — преобразование А линейного
пространства X (см.) в линейное пространство У, и в частности в себя, удовлетворяющее
свойствам: Л(х+у)= А(х)-М(у), Α(λχ) = ΙΑχ, где χ и у — произвольные
векторы линейного пространства, а λ — произвольное число. Например,
преобразование В пространства аналитических функций (см.) по формуле βφ=φ'
является линейным. В конечномерном пространстве при выбранном базисе Л. п.
задается матрицей.
Лит.: И. М. Гельфанд, Лекции по линейной алгебре, Гостехиздат, М.—Л., 1953.
ЛИНЕЙНОЕ ПРОСТРАНСТВО — то же, что векторное пространство (см.).
ЛИНЕЙНОЕ УРАВНЕНИЕ — уравнение, содержащее неизвестные
(переменные) только в первой степени. Например, уравнение
аххх+а&2-\ +апХп=Ъ (*)
есть Л. у. с η неизвестными (а/т^О, /=1, 2, ..., п). Если в уравнении (*) все
коэффициенты а/=0, / = 2, 3, ...» п, но αι=£θ, это уравнение принимает вид
агх=*Ь или ах=Ь (αχ=α)ι которое называется Л. у. с одним неизвестным.
Совокупность нескольких Л. у. вида (*) относительно одних и тех же неизвестных
называется системой Л. у., которую можно записать в виде:
а11х1+а12х2+ · · ·Л-О-лпХп^Ъ^
0mi*i+flm2*2H hamnXn = bm.
Под решением система (**) понимают всякую совокупность (набор) чисел а19
^2* · · ·» ап> которые при подстановке вместо соответственно xlt x2, ..., хп
обращают все уравнения этой системы в тождества. Вопрос о разрешимости
системы Л. у. (**) сводится к сравнению рангов (см.) двух матриц.— основной А
и расширенной В:
(аи а12 ... а1П\ / аи а12 ... ат Ьг
а21 а22 · ·· а2П 1 β^Ι #21 β22 ··· а2П ^2
ат\ атъ · · · атп) л \ ат\ °тг · · · атп ЬП1

ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 193
Если ранги матриц А и В совпадают, то система Л. у. (**) совместна, если
ранг матрицы В больше ранга матрицы А, то система Л. у. (**) несовместна
(теорема Кронекера — Капелли).
Если все bi системы (**) равны нулю, то система Л. у. называется
однородной. Если т=*пу т. е. число уравнений системы равно числу неизвестных,
то для нахождения решения системы уравнения (**) применяют правило
Крамера (если определитель системы D=/=0) или приближенные методы решения
уравнений или решение системы уравнения находят на специальных машинах.
При исследовании системы Л. у. часто используют геометрические понятия
(см. Вектор, Прямая, Плоскость, Линейный оператор). См. также
Неопределенное уравнение.
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ — уравнения вида:
Po(x))*n)+Pi(x))tn-»+---+Pn(x)y=f(x) . (*)
Предполагается, что Ро(*)^0. Если /(*)==0, то уравнение называется
однородным, если же f(x)¥=0, то — неоднородным. Линейное однородное
дифференциальное уравнение имеет η линейно-независимых решений. Если их обозначить
Уг* Учу ···» Ум, то общее решение будет иметь вид: y=C1y1-f-C2y2H \-СпУп*
где Clt С2, ..., Сп — произвольные постоянные. Линейно-независимые решения
обладают тем свойством, что их вронскиан (см.) не обращается в нуль ни
в одной точке. Общее решение линейного неоднородного уравнения есть сумма
общего решения соответствующего однородного уравнения и произвольного
частного решения неоднородного уравнения.
Уравнение вида (*) можно легко решить, если коэффициенты постоянные.
Рассмотрим сначала однородное уравнение:
У<л)+р1у(л-1)+...+р|1у=0.
Составим характеристическое уравнение:
Пусть Х1э λ2, ..., λΛ — различные корни характеристического уравнения. Тогда
общее решение записывается так:
y = QleXl*+Q2*Xl*+ ··· + Qr*Xf* *
где Qi(x) — произвольный многочлен степени на единицу меньшей кратности
корня λ;. Если λ/— число комплексное (λ = α-}-β/), то вместо решения е^а±^х
можно взять е*х cos β χ и ee* sin β χ. Линейные неоднородные уравнения с правой
частью вида Fm (x) e*x sin β χ, где Fm(x) — многочлен степени т, имеют
частные решения вида:
Xs iQm (х) е*х ^п β x+Rm (x) e*x cos β*],
где s — кратность корня α+β/ в характеристическом уравнении, a Qm (x) и
Rm (x) — многочлены степени т с неопределенными коэффициентами. В случае
же произвольной правой части применяется другой метод — метод вариации
произвольных постоянных, который состоит в том, что решение неоднородного
уравнения ищут в виде Ciy^C^y^ У^пУт гДе У\> >'г» ···» У η — линейно-
независимые решения однородного уравнения, a Cl9 C2t ..., Сп считаются
функциями X.
В теории Л. д. у. наиболее полно изучено уравнение 2-го порядка. Большое
число исследований посвящено также системам линейных уравнений. В теории
13 Толковый словарь математических терминов

194
ЛИНЕЙНЫЙ ОПЕРАТОР
уравнений с частными производными линейные уравнения занимают большое
место. Это суть уравнения вида:
Σ Σ Α (*ιΛ, · · · . хп) —; ~ =
*=о Λι+**-γ-·· + *λ=* dxf*dx%*.. .дх п
=/(*i, *2. .... х„).
Лит.: В. В.Степанов, Обыкновенные дифференциальные уравнения, Физматгиз,
М., 1959.
ЛИНЕЙНЫЙ ОПЕРАТОР — преобразование А линейного пространства в себя
или в другое линейное пространство такое, что
А(х+у)=А(х)+А(у), Α(\χ)=λΑ(χ),
где а: и у— произвольные векторы линейного пространства, λ — произвольное
число. В конечномерных линейных пространствах Л. о. при определенном
выбранном базисе может записываться матрицей. Коэффициентами этой матрицы
являются коэффициенты разложения Ле;(/=1, 2 h) по векторам базиса.
В бесконечномерных пространствах Л. о. часто записывается в виде интеграла.
χ
Например, в пространстве непрерывных функций оператор A(y)=\y(x)dx
о
является линейным. Теория Л. о. составляет большой и весьма важный раздел
функционального анализа (см.).
Лит.: Г. Е. Шилов, Введение в теорию линейных пространств, Гостехиздат, М.—Л.,
1952.
ЛИНЕЙЧАТАЯ ГЕОМЕТРИЯ — ветвь геометрии, в которой в качестве
основного элемента пространства рассматриваются прямые линии. Как известно,
прямые в пространстве, не параллельные оси г, определяются четырьмя постоянными
коэффициентами a, b, р, q в уравнениях x=az+p9 y = bz+q. Поэтому числа а,
Ь, р, q можно рассматривать как координаты прямой. Если эти координаты есть
функции от одного, двух и трех параметров, то соответствующие совокупности
прямых образуют линейчатые поверхности (см.), конгруэнции (см.) и комплексы
прямых (см.), которые и изучаются в Л. г.
Лит.: Д. Н. 3 е й л и г е р, Комплексная линейчатая геометрия поверхности и
конгруэнции, 1934; СП. Фиников» Теория поверхностей, ОНТИ, М., 1934; С. П.
Фиников, Теория конгруэнции, Гостехиздат, Μ., 1950..
ЛИНЕЙЧАТАЯ ПОВЕРХНОСТЬ —поверхность, образуемая движением
прямой (образующей) по некоторой линии (направляющей). Л. п. можно
рассматривать как совокупность прямых, зависящую от одного параметра. Л. п. бывают
двух видов: развертывающиеся и косые. Развертывающиеся Л. п. можно
посредством изгибания (см.) наложить на плоскость (например, цилиндр и конус).
Касательная плоскость к развертывающимся Л. п. в различных точках одной
и той же образующей будет одна и та же. Косые Л. п. обладают тем
свойством, что касательные плоскости в различных точках одной и той же
образующей будут различные, т. е. при перемещении вдоль образующей косой Л. п.
касательная плоскость вращается вокруг этой образующей. Примером косой
Л. п. может являться коноид (см.).
Изгибаемые друг на друга Л. п. можно катить одну по другой, что
используется в теории механизмов, например при зубчатых передачах.
Лит.: СП. Фиников, Теория поверхностей, М.—Л., 1934.
ЛИНИИ КРИВИЗНЫ поверхности—линии, имеющие в каждой своей точке
главное направление. Главное направление поверхности в данной точке есть
такое направление, что кривизна (см.) нормального сечения поверхности дости-

ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ
195
гает экстремума. В общем случае из каждой точки исходят две Л. к.,
образующие между собой прямой угол. Характеристическим является такое свойство:
нормали вдоль Л. к. образуют развертывающуюся поверхность (см.), первая
и вторая квадратичные формы (см.) поверхности пропорциональны вдоль Л. к.^
См. также Родрига формулы.
Лит.: А. П. Η орден, Дифференциальная геометрия, Физматгиз, М., 1952.
ЛИНИЯ — то же, что и кривая (см.).
ЛИНИЯ ЦЕПНАЯ — плоская кривая, являющаяся графиком функции
у=а chx (см. косинус гиперболический) в прямоугольной системе координат.
Название этой линии происходит оттого, что гибкая нерастяжимая тяжелая
однородная нить (цепь) с концами, закрепленными в двух точках, провисает по
Л. ц. При небольшом провисании цепи, концы которой закреплены на одном
уровне, ее форма близка к параболе (см.), что используется для приближенных
расчетов в практике. Поверхность, возникающая при вращении Л. ц. вокруг
оси абсцисс, называется катеноидом (см.).
ЛИПШИЦА УСЛОВИЕ. Функция f{x) удовлетворяет Л. у. на отрезке
[а, Ь]9 если существует k > О такое, что
\f(x)-f{x')\<k\x-x'\
для всех д; и х' из [а, Ь].
Л. у. входит в формулировку теоремы о существовании и единственности
решения дифференциального уравнения
У'-/(*. У)·
Всякая непрерывно дифференцируемая функция удовлетворяет Л. у.
ЛИУВИЛЛЯ ТЕОРЕМА — теорема о приближениях иррациональных чисел
рациональными: если α — вещественное иррациональное число л-й степени, то
существуют постоянные с такие, что соотношение
Ρ
а — —
Я
с
< -- не будет вы-
Я
полняться ни при каких целых числах ρ и q. Иными словами, всякое рациональ-
р
ное число — будет отличаться от иррационального числа α по меньшей мере
Я
с
на —, т. е. неравенство
гебраического числа α степени η > 2 неравенство
а—£|
Р\ с *
а — — > — будет справедливо при любых целых ρ
и q. Этот результат был получен французским математиком Лиувиллем.
Л. т. позволяет строить сколько угодно конкретных непрерывных дробей,
выражающих трансцендентные (т. е. неалгебраические) числа.
Л. т. в 1908 г. была уточнена Туэ, который доказал, что для всякого ал-
с
< -~ при любом с>0
Яп
допускает лишь конечное число решений в целых числах ρ и q. См. также Туэ
теорема.
ЛОБАЧЕВСКОГО ГЕОМЕТРИЯ — геометрическая теория, основанная на тех
же аксиомах, что и обычная евклидова геометрия, за вычетом аксиомы о
параллельных, которая заменяется на противоположную.
Аксиома о параллельных прямых евклидовой геометрии формулируется так:
через точку, не лежащую на данной прямой, проходит не более одной прямой,
лежащей с данной в одной плоскости и не пересекающей ее.
В Л. г. принимается вместо приведенной евклидовой аксиомы следующая
(аксиома Лобачевского): «Через точку, не лежащую на данной прямой,
проходят по крайней мере две прямые, лежащие с данной прямой в одной плоскости
и не пересекающие ее».
13*

196
ЛОБАЧЕВСКОГО МЕТОД
Л. г. так же непротиворечива, как геометрия Евклида, хотя следствия
(теоремы), вытекающие из аксиом Л. г., на первый взгляд, носят парадоксальный
характер и кажутся противоречащими нашим обычным представлениям. Так,
в Л. г. сумма углов в треугольнике непостоянна и всегда меньше 2d\ не
вокруг всякого треугольника можно описать окружность. Не существует подобных
и неконгруэнтных (неравных) треугольников и т. д. Л. г. применяется как
в математике, так и в физике.
Л. г. иначе называется гиперболической неевклидовой геометрией (в
противоположность эллиптической геометрии Римана, см. Неевклидовы геометрии,
Римана геометрия).
Л. г. названа по имени ее творца, великого русского математика Н. И.
Лобачевского.
ЛОБАЧЕВСКОГО МЕТОД — метод приближенного нахождения корней
алгебраических уравнений. Л. м. состоит в следующем.
Пусть требуется найти корни х1у хъ . . ., хп уравнения:
a0xn+alXn-i+ ... +α„«0. (*)
С помощью указанных Лобачевским формул:
а{{)-а2
ап1-1=ап-\ — 2ап-^ги
строится многочлен:
корни которого являются квадратами корней уравнения (*).
Продолжая этот процесс — квадрирование, строят многочлены /2 (*), /3 (χ)
и т. д., где многочлен
Ы*)«а&*)*я+а1*)*л-1+ ·■· +а(пк)'.
k к k
его корнями будут числа х\ , х\ , . . ., х\ ; при этом коэффициенты а}*+1)
многочлена fu+i(x) получаются возведением в квадрат коэффициентов а№
многочлена /&(#), τ· е. имеет место приближенное равенство: а\к+Х) ж f б|·^]*
в пределах устанавливаемой точности, следовательно, и корни многочлена f(x)
могут быть найдены приближенно по тем же формулам:
2*/ «!*>
Знак корня определяется подстановкой в исходное уравнение. При этом
предполагается, что корни действительны и различны и такие, что удовлетворяют
условию:
Ы > Ν>·- ->|*л|.
где знак > означает «значительно больше». При выводе формулы (**)
используется зависимость (обобщенная теорема Виета) между корнями и коэффициента-

ЛОГАРИФМ
197
ми уравнения. Нарушение отмеченной закономерности между корнями (когда
корни по значению близки или комплексные) влечет за собой нарушение
указанной аналогичной закономерности между коэффициентами.
Л. м. может быть использован и для приближенного вычисления
комплексных корней, хотя при этом вычисления усложняются, а действительные корни
находятся по приближенной формуле (**).
Л. м. был описан Лобачевским в его книге «Алгебра или исчисление
конечных» (1834).
Л. м. в литературе встречается как Греффе метод — по имени швейцарского
математика К. Греффе, или Данделена метод — по имени бельгийского
математика Ж. Данделена, открывших этот метод независимо от Лобачевского.
Лит.: Н. И. Лобачевский, Алгебра или исчисление разностей, Полное собрание
сочинений, т. 4, Гостехиздат, М.—Л., 1948; Энц. злем. мат., т. 2, Гостехиздат, М.—Л.,
1951; А. Н. Крылов, Лекции о приближенных вычислениях, Гостехиздат, М.—Л.,
1954; И. С. Б е ρ е з и н и Н. П. Ж и д к о в, Методы вычислений, Физматгиз, Μ. , 1959;
В. Л. Загускин, Справочник по численным методам решения уравнений, Физматгиз,
М., 1960.
См. Ложного положения правило, Ньютона метод, Итерация.
ЛОГАРИФМ числа N при данном основании а (а > 0, аф\) есть
показатель /2-й степени, в которую надо возвысить число а, чтобы получить число N.
Л. числа N при основании а обозначают так: loga N. Итак, согласно
определению, \ogaN = n равносильно равенству an = N. Отсюда следует, что только
положительные числа имеют Л., так как а > 0.
Л. числа N при основании а можно определить как решение показательного
уравнения вида ax=N.
Всякое положительное число имеет единственный Л. при данном основании.
Л. принимает любые действительные значения.
Если основание Л., т. е. число а, равно 10, то такие Л. называются
десятичными и обозначаются \gN. Десятичный Л. числа N, отличного
от 10q , где ρ и д — целые числа, есть трансцендентное число, поэтому
в таблицах такие Л. даны лишь приближенно конечной десятичной дробью.
Целая часть десятичного Л. называется его характеристикой, а дробная —
мантиссой. Например, lg 200=2,3010, где характеристика Л. равна 2 и мантисса
0,3010. Основные свойства Л. такие (Μ, Ν — положительные):
\oga(MN) = loga M+\oga N%
Μ
loga JJ = logaM— logfl Ν,
\ogaNk~k\ogaN,
br— 1
\0gaV N =— loga N,
k
\ogan Nn=\ogaN
/например, Tog5 7 = log25 49=log _V 7 ). Между Л. двух различных систем
\ /s J
существует зависимость:
ι<*»λτ-τΗγ или log^= ϊΖΤΐ0**Ν·
loga Ь 10ga 0

198
ЛОГАРИФМИКА
Постоянный множитель Λί«=
1
при переходе (пересчете) от системы Л.
logfl6
с основанием а (при основании а) к системе Л. с основанием Ь называется
модулем перехода от одной системы Л. к другой.
В высшей математике и в теоретических вопросах большое значение имеют
Л. с основанием, равным трансцендентному числу е=2,71828 . . ., которые
называются натуральными Л. и обозначаются In N. Натуральные Л. иначе
называются гиперболическими, так как они связаны с площадью фигуры,
ограниченной дугой равносторонней гиперболы у=—, осью абсцисс и ординатами,
соответствующими абсциссам 1 и *.
В теории функции комплексного переменного рассматриваются Л.
(натуральные) комплексных чисел. По определению Л. комплексного числа ζ
(обозначается Lnz) равен:
Lnz=In|z|-f-i hxgz.
Л. появились как ответ на вычислительные потребности человеческого общества,
во время бурного развития астрономии и мореплавания в XV—XVI вв.
Первые таблицы Л. появились почти одновременно и были составлены
независимо друг от друга шотландским математиком Дж. Непером (1614),
английским математиком Бриггом (по другим написаниям Бригсом)— в 1617 г.,
швейцарским математиком И. Бюрги (1620). Термин «натуральный логарифм» и
понятие о модуле перехода принадлежит Меркатору, термин «характеристика» — Бриг-
гу, «мантисса», в нашем понимании, — Эйлеру, «основание логарифма» ввел также
Эйлер. Десятичные Л. иначе называются бригговыми. См. также
Логарифмическая функция.
Греч, λογοζ — (в смысле) отношение, αριθμό— число.
Лит.: А. И. Маркушевич, Площади и логарифмы, М,—Л., 1952; Л. Я. Гриш·
вальд, История открытия логарифмов, Харьков, 1952; И. Б. А бе ль сон, Рождение
логарифмов, М.—Л., 1948; Г. Г. Цейтен, История математики в XVI и XVII вв., 1959.
ЛОГАРИФМИКА — график логарифмической функции (см.).
ЛОГАРИФМИРОВАНИЕ — действие, заключающееся в нахождении
логарифма (см.) числа. Л. есть одно из двух действий, обратных возведению
(возвышению) в степень; если аь=с, то а=у с, b = \ogac. Л. используется при
сведении действий второй (умножение и деление)
и третьей (возведение в степень и
извлечение корня) ступеней к действиям
соответственно первой (сложение и вычитание) и
второй ступеней (умножение и деление).
ЛОГАРИФМИЧЕСКАЯ БУМАГА —
бумага, на которой нанесена функциональная
(логарифмическая) сетка (рис. 137, см.
Номография). Л. б. вычерчивается так: на осях
прямоугольной системы координат
откладываются логарифмы чисел x=\ogu и у = log v
и через точки деления (имеющие пометки и
и ν) проводятся прямые, параллельные осям
Ох и Оу. В более общем виде координатные
линии прямоугольной Л. б. имеют уравнения
x=m\gtt и y=n\gv, где т и л—
масштабы по осям.
9
7
ε
5
3
с.
i 3 Ь
Рис. 137
5 6 78910

ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
199
Если уравнения линий прямоугольной сетки на бумаге имеют вид х—ти%
y=n\gv, то такая бумага называется полулогарифмической.
Л. б. используется для построения некоторых графиков функций, которые
на Л. б. имеют более простую форму (выпрямляются). Так, например, графиком
функции v=aub на Л. б. будет прямая линия, так как после логарифмирования
это уравнение принимает вид:
1 Ь
Η v=b\gu-\-\ga, или — у= — x+lga,
η т
где а и Ъ — постоянные числа.
ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА — инструмент, предназначенный для
выполнения различных вычислений: умножения, деления, возведения в степень,
извлечения корня, тригонометрических вычислений, решения уравнений и пр.
Л. л. имеет различные формы и размеры. Точность вычислений на
25-сантиметровой Л. л. составляет три знака. Л. л. иначе называется счетной
линейкой.
При объяснении выполнения действий на Л. л. в аудиторных (классных)
занятиях используются так называемые демонстрационные Л. л. длиной в
1—2 м.
Лит.: Д. Ю. Панов, Счетная линейка, Физматгиз, М., 1953; Энц. элем. мат. ,■ т. 1,
Гостехиздат, М., 1951.
ЛОГАРИФМИЧЕСКАЯ ПРОИЗВОДНАЯ — производная от логарифма данной
функции. Нахождение Л. п. функции называется логарифмическим
дифференцированием, которое используется в том случае, если легче найти производную
от логарифма данной функции, чем производную самой функции. Производная
у' функции y=f(x) выражается через Л. п. по формуле:
у'=у(1пу)\
Пример: если у=хх, то
lny=Jt In xt
откуда
y'=r*(lnx-fl).
ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ — кривая (рис. 138), уравнение которой
в полярных координатах имеет вид:
Л. с. является интегральной кривой дифференциального уравнения
*р ?'
Подера (см.) и эволюта Л. с. есть снова Л. с. Л. с. была известна многим
математикам XVII в. (например, Декарту и Торричелли). Л. с. пересекает все
свои радиус-векторы под одним и тем же углом а. Форма некоторых раковин
напоминает Л. с.
ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ — функция, обратная показательной
функции (см.). Л. ф. обозначают так: y = logax, где а (а > 0, аф\)-—
произвольное основание Л. ф. Значение функции у, соответствующее определенному
значению аргумента *, называется логарифмом при основании а числа х.
В теоретических вопросах и в высшей математике особую роль играет Л. ф.
/ / 1 \п \
при д=е (число е= lim (1-f — I =2,71828. . . , которая обозначается так:
V п-+оо\ η J J
#v=ln*.

200
ЛОГАРИФМИЧЕСКИЕ ТАБЛИЦЫ
Область определения Л. ф. y—\ogax есть множество чисел χ > 0. График
Л. ф. называется логарифмикой (рис. 139). Л. ф. можно определить и как
непрерывную при х>0 функцию, удовлетворяющую функциональному уравнению:
fixy)4(x)+f(y)
при х> О, у > 0.
Л. ф. впервые наиболее подробно была изучена шотландским математиком
Дж. Непером (1614). Л. ф. комплексного значения аргумента ζ является мно-
Рис. 138
Рис. 139
гозначной (бесконечнозначной) функцией, определенной для всех значений гфО
и обозначаемой In ζ. Справедливо соотношение:
In г = In Ι ζ Ι + /arg 2+2£π,
6 = 0, ±1, ±2 .. .
При этом In z= In \z\+i arg2 — однозначная ветвь (— n<arg2<ji). Л. ф.
называется ее главным значением.
ЛОГАРИФМИЧЕСКИЕ ТАБЛИЦЫ. Первые Л. т. опубликованы (1614)
Д. Непером. Его таблицы в связи со специальными целями содержали
логарифмы тригонометрических величин, отличные от десятичных и так называемых
натуральных (с основанием, равным е) логарифмов: в неперовских таблицах
логарифм числа а равен ΙΟ7· 1η (107:α). Л. т., близкие к неперовым, издал (1620)
швейцарский математик И. Бюрги.
В 1617 Бригг опубликовал таблицы десятичных логарифмов для первой
тысячи с 14 знаками, а затем (1624) также с 14 знаками для чисел от 1 до 20 000
и от 90 000 до 100 000.
Голландский математик А. Влакк выпустил (1628) вторым изданием
таблицы Бригга, восполнив пробел чисел от 20 000 до 90 000, но уже не с 14, а
только с 10 знаками. На основе таблиц Влакка стали выпускаться Л. т. во многих
странах. На русском языке первые Л. т. появились в 1703, а затем в 1716
для чисел от 1 до 10 000 (Андрей Фархварсон, Стефан Гвьтна и Леонтий
Магницкий).
Из всего исключительно большого множества Л. т., издававшихся
различными авторами в различных странах, наибольшее распространение имели,
по-видимому, семизначные таблицы Г. Вега. Они выдержали только за первые сто
лет после их появления более 100 изданий и до сих пор продолжают издаваться
во многих странах.
В настоящее время (до 1950) наиболее обширными являются, по-видимому,
следующие Л. т.: 1) Астрономические таблицы, составленные Паркурстом (США,
1889) со 102 знаками для всех чисел от 1 до 109; 2) Бригговы логарифмы, со-

ЛОЖНОГО ПОЛОЖЕНИЯ ПРАВИЛО
201
ставленные Мольтепером (Германия, 1937) с 52 знаками для всех чисел от 1 до
1 100; 3) недавно в нашей стране переизданы фотоспособом таблицы Томсона
в двух томах, содержащие десятичные логарифмы с 20 знаками для
пятизначного аргумента (т. е. для всех чисел от 10 001 до 99999).
Лит.: А. В.Лебедев и Р. М. Федорова, Справочник по математическим
таблицам, Изд-во АН СССР, М., 1956; Η. Μ. Бурунова, Справочник по математическим
таблицам. Дополнение № 1, Изд-во АН СССР, Μ., 1959.
ЛОГАРИФМИЧЕСКОЕ УРАВНЕНИЕ — уравнение, содержащее неизвестное
под знаком логарифма. Способы решения Л. у.: потенцирование (см.); введение
новых неизвестных (переменных); приведение уравнения к виду IgA^lgB;
использование логарифмических формул
lgn'V = (lfoA0:(lg*a), ^a^^Ua^n (·);
графические и другие приближенные способы решения уравнений.
Примеры: 1) \g(x — 5)-flg * = lg(l — χ).
Это уравнение не имеет решений, так как правая часть определена для χ < 1,
а левая для χ > 5.
2) lgjc=2. Из уравнения непосредственно получаем *=102=100.
3) lgjc2 = 2, 2 lg |*| = 2, lgjx| = l. Из уравнения имеем
N = 10, х=±10; 4) Ig^ + lg* 4 = 2,5;
используя первую из формул (*), получим
lg**+i = 2,5;
или, положив lg4x = y, придем к уравнению
Я—=2,5,
У
откуда
у2 — 2,5у+1=0;
или
у1==2 и У2=у. или lgi*!«2 и lg4x, = —·
Отсюда л;1 = 1б и х2^=2.
См. Уравнение, Показательные уравнения.
ЛОГИКА МАТЕМАТИЧЕСКАЯ — см. Математическая логика.
ЛОЖНОГО ПОЛОЖЕНИЯ ПРАВИЛО — один из классических способов
приближенного вычисления корней уравнения /(*)=0 — алгебраического или
трансцендентного. Сущность Л. п. п. сводится к следующему. Рассматривают два
значения а и b аргумента функции действительного переменного f (х) (х —
действительное), близких к простому корню χ этой функции (два ложных
положения), таких, что функция в этих точках х=а и χ=b принимает разные по
знаку значения (рис. 140); /(a) < 0, f (b) > 0. При этом предполагается, что
в окрестности точки x=xQ функция f (х) вместе с /' (х) и f" (х) непрерывна,
и /'(*) и Г'(*) в окрестности точки х{) не меняют знака. На отрезке [а, Ь]
функцию f{x) заменяют линейной функцией (график кривой у = [{х) заменяют

202
ЛОКАЛЬНЫЙ ЭКСТРЕМУМ
Примениз второй
\с, Ь] линейной
хордой АВ). Получают новое приближенное значение х=с корня уравнения,
более близкое к истинному значению корня х = х0» чем приближенное значение
х=а. При этом выполняется равенство:
«-«-/О д6)1да) ■/(«)<<>. /W>0.
раз Л. п. п. на участке [с, Ь] и заменив функцию f (х) на
функцией (кривую y=f(x) хордой АгВ), получим новое
приближенное значение корня x=clt более близкое
к истинному значению корня х=х0 уравнения, чем
х=с, и т. д. Таким образом, Л. п. п. дает
возможность вычислить корень уравнения /(х)=0 с любой
степенью точности. Л. п. п. часто используют в
комбинации с другими методами (см. Ньютона
метод, Метод касательных). Л. п. п. иначе
называется методом секущих, методом хорд или методом
(правилом) линейного интерполирования. Л. п. п.
называют также методом решения задач в
арифметике на предположение (метод ложного положения).
Лат. regula falsi — правила ложного положения,
см. также Итерация.
Лит.: И. С. Березин и Н. П. Жидков,
Методы вычислений, т. 1—2, Физматгиз, М., 1959; А. К.
Сушкевич, Основы высшей алгебры, М.—Л., 1941; В. Л. Загускин, Справочник
по численным методам решения уравнений, Физматгиз, М., I960.
Рис. 140
ЛОКАЛЬНЫЙ ЭКСТРЕМУМ. Слово «локальный» подчеркивает, что
экстремум имеет место лишь в некоторой достаточно малой окрестности
рассматриваемой точки. Следовательно, локальный максимум (минимум) есть наибольшее
(наименьшее) значение функции лишь в некоторой достаточно малой окрестности
рассматриваемой точки.
Лат. «локальный» — местный.
ЛОКОН АНЬЕЗИ — плоская кривая (рис. 141), уравнение которой в
декартовой прямоугольной системе координат имеет вид: у (а2~{-х2)=а3. ЕслиОЛ=а —
диаметр окружности, ОС — секущая и СМ и Ох, ВМ в Оу, то точка Μ
принадлежит Л. А. Ось абсцисс — асимптота для этой кривой. Эта кривая названа
Л. А. по имени женщины-математика Марии Аньези, изучавшей эту кривую,
хотя Л. А. был известен раньше французскому математику П. Ферма. Л. А.
еще иначе называют версьерой или аньезерой.
'\у
\
У|
А
V
о
I
β
/j "
λ
Рис. 141
Рис. 142

ЛОПИТАЛЯ ПРАВИЛО
203
ЛОКСОДРОМА — линия двоякой кривизны, лежащая на сфере, сфероиде
или какой-либо другой поверхности вращения и пересекающая все меридианы
этой поверхности под постоянным углом К (рис. 142). Форму Л. имеет путь
корабля в океане или самолета над земной поверхностью при постоянном
истинном курсе (направлении) К. Термин Л. был введен в 1624 г. голландским
ученым В. Снеллиусом. Л. называют также локсодромией, локсодромной спиралью
или локсодромной кривой.
При k=0 или 180° Л. совпадает с меридианом поверхности вращения, при
£=90°—с параллелью. Если k — острый или тупой угол, то Л. образует
бесконечное число витков вокруг полюса, все приближаясь к нему.
Греч, λοξοζ — косой, σρομοξ — бег; локсодрома — кособежная (линия).
ЛОПИТАЛЯ ПРАВИЛО — правило вычисления предела:
/4= lim * v '
χ^α g(x)
когда lim/(#)=0 и limg(jt)=0 [или lim/(*) = lim g(#) = oo].
x-+a x-+a x-+a x-+a
Л. п. может быть применено при следующих условиях: а) функции f(x)
и g(x) дифференцируемы в некоторой окрестности точки jc=c, быть может, за
исключением самой точки х = а\ б) существует предел
η ,im fix)
D=lim —-—.
x-+a g' (Χ)
При наличии этих условий имеет место равенство:
a_ilmii£l_Iim£W,_B. («,
х-+а g(x) х-»а gf (X)
К вычислению пределов вида (*) раскрытию неопределенностей (см.) типа -~
оэ
сводятся вычисления других пределов; неопределенностей типа —, оо — оо,
оо
Охоо, 0°, 1°°, оо°. В случае, когда функции /' (х) и g' (х) правой части
равенства (**) удовлетворяют условиям:
Нт/'(*)=0 и limg'(*) = 0
х-*а х-*а
и условиям а) и б), упомянутым выше, возможно повторное применение Л. п.:
lim ——= hm ——- = lim —-— и т. д.
x-+ag(x) x+ag (х) χ-+α g" (x)
Л. п. является мощным инструментом для вычисления пределов (см.
Раскрытие неопределенностей). Например,
cos л:— 1-Ь-— .
2 , —smx+x —cos^-M
lim = lim =lim
x+o xl x-~o 4x3 x^q \2xl
sin* , cos л: 1
= lim = lim—-—=- — .
x-*0 24л *^o 24 24

204
ЛОРАНА РЯД
χ2 sin —
S* 1 Х
Здесь Л. п. применено многократно. С другой стороны, хотя lim ; су-
х-+о sin χ
шествует, однако этот предел не может быть вычислен по Л. п., так как не
выполняется условие б).
Л. п. названо по имени Лопиталя — французского математика, впервые
опубликовавшего его, хотя этим правилом пользовались и до Лопиталя.
ЛОРАНА РЯД — важное понятие теории функций комплексного
переменного. Известно, что всякую аналитическую в точке z0 функцию (см.) f(z) можно
представить в виде степенного ряда:
f(z)=c0+c1(z — г0)-К2(г — ζ0)24- ···♦
который сходится в некотором круге (см. Абеля теоремы), т. е. надлежащий
степенной ряд в некотором круге может задавать произвольную аналитическую
в точке ζ0 функцию. Л. р. решает аналогичную задачу (представить
аналитическую функцию) в более сложной, чем круг, области, именно в кольце. Под
кольцом подразумевают множество точек ζ комплексной плоскости,
удовлетворяющих неравенству:
г < |ζ — а| < #, (*)
где г и R — действительные числа 0 < г < R < оо, а — фиксированная точка
комплексной плоскости. Имеет место теорема Лорана; всякая аналитическая
в кольце (*) функция /(г) может быть единственным образом представлена
в виде:
ϊ(ζ)=α0+αι(ζ-α)+αζ(ζ-α)*+ ... +jj^+ *fl)8 + ··· (**)
Выражение, стоящее в правой части этой формулы, и называется Л. р.
функции /(ζ) в кольце (*). Коэффициенты ak, bt, k, /=0, 1, 2 . . . вычисляются
по формулам:
1 г fll)d(t) 1 Г
Υ Υ
Здесь интегрирование ведется по произвольной окружности γ, лежащей внутри
оо
кольца и имеющей центром точку а. Часть Л. р. 2 α^(ζ — а)к называется
оо
Х^ bl
правильной частью Л. р., а ряд > f — главной частью Л. р.
/ = ι
Областью сходимости Л. р. (**) является кольцо, быть может, более
широкое, чем кольцо (*). Если область сходимости правильной части Л. р. (*)
есть круг с центром в α и радиусом рь а область сходимости главной части
Л. р. есть множество точек, лежащих вне круга с центром а и радиусом р2»
то область сходимости Л. р. (*) есть кольцо 0<ρ2<|ζ — a|<pi< оо,
причем R < Ρχ, р2 < г·
Важен частный случай Л. р. — разложение аналитической функции /(г)
в Л. р. в окрестности ее изолированной особой точки (см.). Если главная часть
такого разложения состоит из конечного числа слагаемых, то особая точка
является полюсом (см.). Порядок полюса равен индексу последнего слагаемого
в главной части Л. р. Если же главная часть состоит из бесконечного числа

ЛОРЕНЦА ПРЕОБРАЗОВАНИЯ
205
слагаемых, то особая точка есть существенная особая точка. Коэффициент 6,
в разложении в Л. р. функции f(z) в окрестности особой точки z0 называется
вычетом (см.) функции f (z) в точке z0. Значение вычета аналитической
функции видно из следующей фундаментальной теоремы.
Если f(z) имеет конечное число особых точек в области, ограниченной
замкнутым контуром γ, то интеграл \f(z)dz равен 2ш\ умноженному на сумму
τ
вычетов функции f(z) во всех особых точках, лежащих внутри замкнутой
кривой γ. В частности, если внутри γ нет особых точек функции /(ζ), то
U(z)dz—0 (теорема Коши).
ι
Примеры: 1) разложение функции /(г) = — в кольце 1 < |z|<2
(ζ 1) (ζ 2)
в Л. р. таково:
1
(Ζ_1)(ζ_2)
k= 0 k= 1
а в кольце 2 < \z\ < -f-oo записывается так:
oo
1 V 2*-i — 1
(Z_l)(z_2)
2) разложением функции е z в окрестности особой точки (здесь в кольце
0 < ζ < оо) в Л. р. будет:
ι
7 1 1
_L
Вычет ez в точке 2=0 равняется 1.
Лит.: И. И. Привалов, Введение в теорию функций комплексного переменного,
Гостехиздат, М,—Л-, 1948; А. И. Маркушевич, Элементы теории аналитических
функций, Учпедгиз, М., 1944; В. И. Смирнов, Курс высшей математики, т. 3, Μ.,
Физматгнз, 1958.
ЛОРЕНЦА ПРЕОБРАЗОВАНИЯ — линейные преобразования четырехмерного
пространства
2
л о 9 Х4
такие, что квадратичная форма (см.) f^x^+x^x^ — — не изменяет своего
вида от замены *-ов у-ми по формулам (*), т. е. при такой замене квадратич-
ная форма / переходит в у\\-у\-тУ\ — ~- Л. п. играют большую роль в тео
рии относительности Эйнштейна. Они являются преобразованиями
пространственно-временного многообразия (хъ х2, х3 — координаты пространства, л:4=/—
время, с — скорость света), находящимися в соответствии с физическими
постулатами Эйнштейна. Л. п. интересны и с чисто математической точки зрения.

206
ЛУДОЛЬФОВО ЧИСЛО
Их рассматривают* например, при элементарном введении геометрии
Лобачевского. Л. п. образуют группу.
Лит.: П. К. Рашевский, Риманова геометрия и тензорный анализ, Гостехиздат,
М.—Л., 1954.
ЛУДОЛЬФОВО ЧИСЛО — приближенное значение с 32 верными
десятичными знаками иррационального числа π (см. Пи-число). Названо по имени Лу-
дольфа ван Цейлена. Л. ч. опубликовано в 1615 г. Иногда необоснованно
называют Л. ч. само число π. См. также Мециево число.
ЛУЧ — см. Полупрямая.
ЛЮИЛЬЕ ЗАДАЧИ — две задачи элементарной геометрии следующего
содержания: а) Если г — радиус вписанной в треугольник окружности, a rlf г2,
г3 — радиусы вневписанных в него окружностей, то
г гх г2 г3
б) Если г — радиус вписанной в треугольник окружности, а гь г2, г3 —
радиусы вневписанных в него окружностей и Q — площадь треугольника, то
ф=ггхгггъ.
Л. з. названы по имени математика С. А. Люилье.
Лит.: Г. Н. Попов, Исторические задачи по элементарной математике, ГТТИ,
М.-Л., 1932.

Μ
2
7
6
9
5
1
4 J
3
8
МАГИЧЕСКИЕ КВАДРАТЫ — квадратные (т.е. с одинаковым количеством
столбцов и строк), таблицы натуральных чисел, имеющие одинаковые суммы чисел
по всем строкам, столбцам и двум диагоналям.
Возникновение М. к. относится к глубокой древности. Наиболее ранние
сведения о них содержатся, по-видимому, в китайских книгах, написанных в IV—
V вв. до н. э. Из дошедших до нас древних М. к. самым «старым» является
таблица Ло-шу (2200 до н. э.).
Таблица Ло-шу состоит из 9 клеток: 3 строк и 3
столбцов, заполненных натуральными числами от 1 до 9.
В этом М. к. суммы чисел по всем строкам, столбцам и
двум диагоналям равны одному и тому же числу 15.
Следующие по времени сведения о М. к. дошли до нас из
Индии и Византии. В Европе изображение М. к. впервые
встречается на гравюре «Меланхолия» немецкого художника
Альбрехта Дюрера (1514). Этот М. к. состоит из 16
клеток: 4 строк и 4 столбцов, заполненных натуральными
числами от 1 до 16. В нем сумма чисел по каждой строке,
каждому столбцу и двум диагоналям равна 34. Средние числа в нижней строке
(15 и 14) означают дату 1514 — год издания этой гравюры А. Дюрера.
Этот М. к. замечателен еще и другими
интересными свойствами: в нем одному и тому же чи-1
слу (34) равна сумма не только чисел, стоящих в
строках, столбцах и двух диагоналях, но и суммы
чисел, стоящих в квадратах из четырех клеток, I
расположенных по углам и в середине, а также!
сумма чисел, стоящих в вершинах этого М. к. [
Такие квадраты, в отличие от обычных М. к.,
следовало бы называть как-нибудь иначе, например |
волшебными, сверхмагическими и т. п.
Способами составления М. к. занимались
многие математики: в XVI в. А. Ризе и М. Штифель, I
в XVII в. А. Кирхер и Баше де Мезериак. Тео-1
рией М. к. занимался французский математик Де-
лаир. Для составления М. к. с нечетным числом клеток имеется очень простой
общий способ. Для составления же М. к. с четным числом клеток все
имеющиеся способы значительно сложнее.
В настоящее время понятия М. к. обобщены (расширены) в различных
направлениях. В частности, под М. к. понимают квадратные таблицы,
заполненные не обязательно первыми натуральными и последовательными числами.
Легко видеть, что из любого М. к. можно получить бесконечное множество
других М. к. путем умножения всех его чисел на одинаковый множитель или
прибавления к ним одного и того же слагаемого.
16
5
9
4
1,
3
10
6
15
2
11
7
14
13
8 1
12
ι |

2)8
МАЖОРАНТА
Приведем еще два М. к., состоящие из 16 и 9 клеток и заполненные
натуральными (не подряд) числами. Суммы одного из них по строкам, столбцам
и диагоналям равны 77, а другого—105.
Эти два М. к. представляют особенный интерес как в смысле трудности их
составления, так и в смысле законов распределения простых чисел, а именно:
если все числа этих М. к. умножить на 10, а затем ко всем числам большего
из них прибавить 7, а ко всем числам меньшего прибавить 9, то получатся сно-
26
65
14
23
35
47
56
5
44
36
3
4
1 34
13
25
27
12
22
10
15
30
6
39
31
1 1
ва М. к., заполненные только одними простыми числами, и притом различными
(не повторяющимися).
М. к. свое название магических или волшебных получили от арабов,
которые усматривали в подобных сочетаниях чисел нечто чудесное, мистическое и
смотрели на них как на талисманы.
Лит.: М. М. Постников, Магические квадраты, «Наука», 1963; А. П. До
моря д, Математические развлечения и игры, Физматгиз, М., 1958; В. Серпинский,
Что мы знаем и чего не знаем о простых числах, перев. с польского, Физматгиз, М., 1963.
МАЖОРАНТА — функция F(x)t значения которой в рассматриваемой
области превосходят значения данной функции f(x) или значения системы функций
Ф, т. е. — более точно — функция F (х) удовлетворяет неравенствам F(x)>f(x)
или F(x) > φ(χ), где φ (χ) любая функция системы Ф. При этом F (х)
называется мажорирующей, а / (х) и любая функция φ (χ) f (χ) из Φ — мажорируемой.
Например, в области действительных значений χ функция x2-f-l является Μ.
функции sinjc; она же является М. системы функций y=s\n\x, где λ — любое
вещественное. Во многих вопросах анализа дифференциальных уравнений понятие
М. бывает полезным. Например, справедлива теорема: неубывающая
последовательность функций сходится, если существует М. семейства всех функций, составляю-
со
щих эту последовательность. М. аналитической функции (см.) /(*)= 2 ak*k
6 = 0
00
часто называют F (х)= 2 \ak\xk-
k = о
Франц. majorante от majorer — объявлять большим.
МАКЛОРЕНА РЯД — функции / (х) — частный случай ряда Тейлора (см.)
при #=0. М. р. функции f(x) записывается так:
i/mL/'(0) ^Г(О) /(/1)(0)

МАНТИССА
209
Например, Μ. р. функции ех таков:
1 + х +
2! ' 3!
х'1
Если М. р. функций f{x) сходится к самой /(*), то говорят о разложе
нии f(x) в М. р. Впервые М. р. дан Тейлором в 1715 г. Название М. р.
исторически неправильно.
МАКСИМУМ ФУНКЦИИ: Г. М. ф. одной переменной у=/ (*) — значение
f(x0) функции, не меньшее значений, принимаемых этой функцией при всех
достаточно близких к х0 значениях аргумента (рис. 143). Формальное
определение М. ф.: функция f(x) имеет максимум в точке x0i если существует
принадлежащая области определения функции окрестность (д:0 -—δ, λ*0+δ) такая,
что для всех ее точек χ выполняется неравенство:
/(*)</(*о). О
2°. М. ф. нескольких переменных u = f(xlt x2, x3i . . ., xn) = f (ρ) —-
значение /(дг10, *2си ·· ·* Xno)-f(Po)» не меньшее значений, принимаемых функ-
У%
1 !
Рис. 143
Рис. 144
цией во всех точках, достаточно близких к точке р0 (рис. 144, где п—2,
x1^=xi Хч=У)· Формальное определение М. ф. u=f(xlt х2, . . ., лгл)=/(р);
функция u=f(xlt х2, . . ., хп) имеет максимум в точке р0(*ю**2о» . · .» хПо)
(другими словами, f(p0) = f(xio, *го» · . ·, хПо) есть Μ· Ф-Ь если существует
окрестность (см.) точки p0i лежащая внутри области определения функции,
TaKafls что для всех точек ρ этой окрестности выполняется неравенство:
/<Р)</(Ро).
/**\
В случае выполнения в соотношениях (*) и (**) строгого неравенства гозо
рят, что имеет место строгий (в узком смысле) М. ф., в противном случае —
в широком смысле М. ф. Иногда М. ф. называют абсолютным максимумом,
в отличие от относительного максимума (см.).
См. также Необходимые условия экстремума и Достаточные условия
экстремума.
Лат. maximum — наибольшее.
МАЛЫХ ЧИСЕЛ ЗАКОН — устаревшее название Пуассона теоремы (см.).
МАНТИССА — дробная часть десятичного логарифма (см.). М. десятичных
логарифмов, приведенные з логарифмических таблицах (см.), вычислены
приближенно с точностью до определенного десятичного знака. М. логарифма
числа N не изменится, если число умножить или разделить на 10", где η — це·
14 Толковый словарь математических терминов

210
МАРКОВА НЕРАВЕНСТВО
лое. Например, если lg 200= 2,3010, то число 0,3010 есть М., а число 2
—характеристика логарифма.
Лат. mantissa — прибавка, добавка.
МАРКОВА НЕРАВЕНСТВО — неравенство, дающее оценку производной от
многочлена, если известна оценка для самого многочлена на некотором отрезке.
Например, если на отрезке [—■ 1, +1] многочлен л-ой степени рп(х) не
превосходит по модулю единицу, то | р'п (дг)| < п2. Это неравенство установлено
А. А. Марковым в 1889 г. В 1892 г. оно было обобщено В. А. Марковым,
братом А. А. Маркова.
МАРКОВА ЦЕПИ часто называются также марковскими цепями. М. ц.
называется последовательность случайных испытаний, обладающая тем
свойством, что вероятности результатов последующего
<? Ρ испытания зависят лишь от результата
непосредственно предшествующего испытания. Одним из
простых примеров М. ц. является случайное
блуждание по целочисленным точкам прямой,
/л-/ т т + 1 рассматриваемое в целые моменты времени. Это
ρ 145 блуждание определяется так: если в момент t=n
с* частица находится в некоторой точке прямой
(рис. 145) с абсциссой т, то в момент t = n-{-1
частица будет в точке т-{-\ с вероятностью ρ и в точке т — 1с вероятностью
q, причем p-\-q=\. Μ. ц. Бпервые изучены А. А. Марковым, доказавшим
ряд их важных свойств.
Лит.: Б. В. Гнеденко, Курс теории вероятностей, Физматгиз, М., 1961.
МАРКОВСКИЕ ПРОЦЕССЫ — вероятностные процессы (см.), обладающие
тем свойством, что при известном значении процесса в момент t поведение
процесса в более поздние моменты времени ке зависит от его поведения до
момента t. Типичным примером М. п. является процесс броуновского движеьия
(идеализация реального броуновского движения). Если известно положение
броуновской частицы в момент времени /, то ее положение в любой более
поздний момент не зависит от того, как двигалась частица до момента t. Строгая
математическая теория М. п. впервые дана А. Н. Колмогоровым в 1930 г. Эта
теория основана на рассмотрении так называемой переходной вероятности —
г,ероятности того, что движущаяся случайным образом частица попадет
в момент s в некоторое множество, если известно ее положение в момент ί,
где t < s.
МАСКЕРОНИ ПОСТРОЕНИЯ — исторически неправильное название
геометрических построений, выполняемых с помощью только одного циркуля. М. и.
названы по имени итальянского математика Лоренцо Маскерони, изучавшего
геометрические построения, осуществляемые с помощью одного только циркуля.
Однако более чем за 100 лет до Маскерони такие построения были изучены
датским математиком Г. Мором. Поэтому М. п. правильнее было бы называть
построениями Мора—Маскерони (см. Мора—Маскерони построения).
Теоретическое обоснование М. п. дал австрийский математик А. Адлер,
который в 1890 г. доказал, что всякая задача на построение, разрешимая
циркулем и линейкой, может быть разрешима с помощью одного только циркуля.
См. также Геометрические построения.
Лит.: А. Адлер, Методы геометрических построений, Учпедгиз, М., 1940;
Б. Б. Кутузов, Геометрия, Учпедгиз, М., 1955; Б. И· Аргунов и М. Б. Балк,
Геометрические построения на плоскости, Учпедгиз, М.» 1957*
МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ —см. Индукция математическая.
МАТЕМАТИЧЕСКАЯ ЛОГИКА — наука, изучающая математические
доказательства. Объектами исследования М. л. являются высказывания (суждения), над
г^гл

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
211
которыми производятся операции, аналогичные операциям над числами в алгебре.
М. л. иногда называют метаматематикой. М. л. применяется в теории
электронно-вычислительных машин.
См. также Алгебра и Алгебры.
Лит.: П. С. Новиков, Элементы математической логики, Физматгиз, М., 1959;
И. С. Град штейн, Прямая и обратная теорема, Физматгиз, М., 1959; А. И.
Фетисов, О доказательстве в геометрии, Гостехиздат, М., 1954.
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА — наука об общих способах обработки
результатов экспериментов. Эксперименты в различных науках — физике, химии,
биологии, медицине и др. — обладают тем общим свойством, что на их результат
влияют не только факторы, регулируемые экспериментатором, но еще и огромное
множество случайных факторов. Результат эксперимента, следовательно, обычно
является случайной величиной. Задача ученого — увидеть за случайными
колебаниями действие причинного закона. Применяемые при этом приемы могут быть
общими для различных наук. Эти приемы и изучаются М. с.
Пусть, например, результат эксперимента А есть случайная величина ξ,
результат эксперимента В есть случайная величина η (скажем, ξ есть урожай
при применении агротехнического комплекса Л, η — урожай при применении
комплекса В). Мы хотим выяснить, можно ли считать, что Μξ = Μη, где Μ —
знак математического ожидания (см.), т. е. что комплексы А и В в среднем
обеспечивают одинаковую урожайность. Для этого нужно проверить гипотезу
Μ(ξ--η)=0.
Другим важным примером вопросов, рассматриваемых в М. с, является
вопрос о распределении (см.) случайной величины, являющейся результатом
опыта. Часто бывает известно, что результат опыта имеет нормальное
распределение (см.), и ставится вопрос об оценке его математического ожидания (см.) а
и дисперсии (см.) σ2. Для этой цели повторяют некоторое число (п) раз опыт,
получая в первый раз результат хх< во второй — х2 и т. д., в последний раз —
хп. За оценку математического ожидания принимают величину
- *Н -г-*к
χ — *
η
за оценку дисперсии — величину
По значениям χ и s2 можно построить интервалы, в которых неизвестные
параметры а и σ содержатся с некоторой заданной вероятностью, например 0,99
(доверительные интервалы).
В последние годы развивается общая теория статистических решений, тесно
связанная с теорией игр (см.). Эта теория рассматривает следующую общую
задачу. Предположим, что результат опыта зависит от неизвестного для
статистика состояния изучаемой системы ω. Статистик наблюдает результаты опытов
xlf *2* · · ·» χη и принимает по ним решение а. Если система находится в
состоянии ω, а статистик принял решение а, то он несет потери L(o>, а)
(выраженные, скажем, в деньгах). Например, пусть мы изучаем работу какого-нибудь
автомата, производящего детали заданного размера. Система имеет два
состояния: (Oi — автомат налажен правильно и ω2 — произошла разладка, которая
может вызвать отклонения от заданного размера деталей. Решений можно
принять тоже два: аг—продолжать производство, а2 — остановить автомат для
наладки. Функция потерь дается равенствами: L((ult αχ)=0 и £(ω2ι 02)=O»
14*

212
МАТЕМАТИЧЕСКИЕ ЗНАКИ
a L((u2, cti) — стоимость брака, L((ult α2) — стоимость лишней наладки.
Ставится задача, как должен действовать статистик, чтобы математическое
ожидание потерь было минимальным.
Дальнейшее обобщение этой теории — теория последовательных
статистических решений, в которой учитывается стоимость повторения эксперимента.
Лит.: Б. Л. Вандер Варден, Математическая статистика, ИЛ, М., I960;
А. В а л ь д, Последовательный анализ, Физматгиз, М., 1960; В. Романовский,
Математическая статистика, Изд-во АН Узбекской ССР, Ташкент, 1963.
МАТЕМАТИЧЕСКИЕ ЗНАКИ — см. Знаки математические.
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ — термин теории вероятностей. М. о.
случайной величины (см.), имеющей дискретное распределение (см.), есть^^'Р*
(pi — вероятность того, что случайная величина ξ принимает значение gt-, /
пробегает некоторое множество индексов Ω). Μ. о. случайной величины, имеющей
непрерывное распределение (см.), есть [ χ ρ (χ) d x, где ρ (χ) — плотность
вероятен
ности (см.) случайной величины; Ω — область значений случайной величины.
Свойства М. о. (основные): 1) линейность:
М(а1+Ьг1)=аМ(1)+ЬМ(г))
при любых коэффициентах а и Ь\ 2) М. о. постоянного равно этому постоянному
М(с)=с\ 3) М. о. произведения двух независимых случайных величин (см.)
равняется произведению их математических ожиданий.
МАТЕМАТИЧЕСКОЙ ФИЗИКИ УРАВНЕНИЯ — см. Уравнения
математической физики.
МАТРИЦА — прямоугольная таблица, составленная из элементов
произвольной природы. Элементы М. располагаются в строки и столбцы (иногда их
называют колонками). Строки и столбцы часто называют собирательным термином
«ряды матрицы». Элементы М. часто обозначают двойными индексами — а^\
первый индекс / означает номер строки М., в которой стоит элемент а.ц, а
второй индекс / означает номер столбца М., в котором стоит элемент α,·;·. В
символическом обозначении матрица обычно заключается в круглые скобки или (реже)
в двойные вертикальные черточки:
^11^12
umium2
• · · а„
апа12
α,λα22
amiam2
Пользуются также краткими обозначениями Μ.: (αφ или ||ах-у||. Если
элементами М. являются элементы некоторого кольца R, то для таких матриц
определяются различные операции (см. Кольцо матриц).
МАТРИЦА КВАДРАТИЧНОЙ ФОРМЫ — квадратная матрица, составленная
η η
из коэффициентов квадратичной формы 2 2 aijxixj- Μ. κ. φ. является всегда
г=1 у=1
симметрической (см. Симметрическая матрица).
МАТРИЦА СИСТЕМЫ — матрица, составленная из коэффициентов при
неизвестных из системы т линейных уравнений с η неизвестными:
βιΛ+αΐ2*2-τ- ··· +а\пХп=*Ьи
021*1 + ^22*2+ "· +а2Л*Л=в*2.
a/nixi~ram2xil· "· +с/;гм*/г=^/71·

МЕНЕЛАЯ ТЕОРЕМА
213
Этой системе уравнений соответствует М. с:
ι апа12... flin
α21β22 · · · а2П
amiam2 · · · атп/
МЁБИУСА ЛИСТ — поверхность (рис. 146, а), получающаяся при
склеивании противоположных сторон АВ и А'В' прямоугольника ABB'А' (рис. 146, б)
так, что точка А совпадает с Б', точка А' совпадает с Б и сторона АВ
совпадает с А'В' всеми своими точками.
М. л. —односторонняя (см.)
поверхность. Если рассмотреть какую-либо
«окружность» с указанным на ней направле- _ ____
нием обхода и двигать ее по М. л., не β Ь β'
пересекая его границы, то можно при- | ——j
вести «окружность» в первоначальное по- L J
ложение, но при этом направление обхода А /{'
ее изменится на противоположное. рис# J46
Если М. л. разрезать по «средней»
линии, то он не распадется на две части,
а получится двусторонняя поверхность с двумя граничными линиями,
которая может быть получена из прямоугольной ленты уже путем двукратного
перекручивания. М. л. впервые был изучен независимо друг от друга немецкими
математиками А. Мёбиусом и И. Листингом, как пример односторонней
поверхности. ..
МЕБИУСА ФУНКЦИЯ —функция μ (л), определенная для целых
положительных значений аргумента п\ М. ф· Равна !. если η==1» Равна °» если п
делится на квадрат какого-либо простого числа р, и, наконец, равна (—1)*,
если ««Pipa. · -Pft. где plf p2, . . ., pft —различные простые числа. М. ф.
является мультипликативной функцией. Используется в различных
теоретико-числовых вопросах. М. ф. получила название по имени немецкого математика Мёбиуса
(Mobius), введшего ее в математику.
МЕДИАНА: Г. М. треугольника — отрезок прямой, соединяющий вершину
треугольника с серединой противоположной стороны. Три М. треугольника
пересекаются в одной точке —центре тяжести треугольника (двумерного, или
треугольной пластинки). Точка пересечения М. треугольника делит каждую
медиану на две части, отношение между которыми равно 2:1, считая первый
отрезок от вершины.
2°. М. тетраэдра (треугольной пирамиды) — отрезок прямой, соединяющий
вершину тетраэдра с центром тяжести противоположной его грани. Четыре М.
тетраэдра пересекаются в одной точке.
См. также Замечательные точки треугольника.
Лат. medianus — средний.
МЕДИАТРИСА отрезка АВ — прямая, перпендикулярная к этому отрезку и
проходящая через его середину. М. отрезка АВ может быть рассмотрена как
геометрическое место точек (см.) плоскости, равноудаленных от концов
отрезка АВ. М. отрезка АВ называют также М. точек А и В> а также серединным
перпендикуляром к отрезку АВ или симметралью отрезка АВ (или симметралью
точек А и В).
МЕНЕЛАЯ ТЕОРЕМА. Если прямая пересекает стороны треугольника ABC
или их продолжения в точках С, /Г и В' (рис. 147), то справедливо
соотношение:
С В ' А'С В'А

214
МЕНЬЕ ТЕОРЕМА
ь^
Отношение отрезков берется положительным, если прямая пересекает сторону
треугольника, и отрицательным, если прямая пересекает продолжение стороны.
Справедливо и обратное предложение: если выполняется равенство (*), где
д^В£—-вершины треугольника, а Л'Б'С'—точки, принадлежащие сторонам
треугольника или их продолжениям, то точки Л',Б',С лежат на одной прямой.
М. т. можно сформулировать в виде критерия рас-
g положения трех точек Л', В' и С на одной пря-
л мой: для того чтобы три точки Л', В\ С лежали на
Ху\ одной прямой, необходимо и достаточно, чтобы
выполнялось соотношение (*), где Л, В, С — три вершины
треугольника, а точки Л', В' к С принадлежат
соответственно прямым ВС, АС и АВ.
, М. т. была доказана древнегреческим ученым Ме-
с ° нелаем (I в.) для сферического треугольника и, по-
Рис. 147 видимому, была известна Евклиду (III в. до н. э.).
М. т. является частным случаем более общей теоремы
Карно (см. Карно теорема).
МЕНЬЕ ТЕОРЕМА — теорема дифференциальной геометрии,
устанавливающая зависимость между кривизной — плоского сечения к поверхности в точке Μ
. ι р
и кривизной -— нормального сечения поверхности в той же точке М. Именно —
имеет место формула:
-С05в=^, (*)
Ρ R
где θ — угол между плоскостью сечения π поверхности и нормалью ΜΝ к
поверхности. Формула (*) и есть аналитическая запись М. т., которая была
установлена французским математиком Ж. Менье в 1776 г., а опубликована
в 1785 г.
Лит.: любой курс дифференциальной геометрии.
МЕРА МНОЖЕСТВА — неотрицательная аддитивная функция μ (Ε)
множества Ε евклидова пространства: μ(£)>0 и μ(Ε1)·{·μ(Ε2)=μ(Ε1 (J E2), если
£ι Π ^2 = 0· Единственной Μ., обладающей свойством счетной
аддитивности, т. е.
(оо \ оо
U Η/) = 2>ί£ί> при Et П ErQ ιφΐ
/=ι / /=ι
и такой, что мера отрезка на прямой равна его длине, является мера
множества Лебега. Те множества, у которых можно определить меру Лебега,
называются измеримыми. Пример неизмеримого множества строится" довольно
сложно с использованием аксиомы Цермело (см. Цермело аксиома). М.
множества — важное понятие дескриптивной теории множеств, теории функций,
теории вероятностей.
Лит.: И. П. Натансон, Теория функций вещественной переменной, ГостехиздаГ,
М.—Л., 1950.
МЕРАНСКАЯ ПРОГРАММА—проект программы по математике для германской
общеобразовательной средней школы, составленный комиссией общества
естествоиспытателей и врачей и обсуждавшийся на съезде общества в Меране (1905).
М. п. выражала идеи «реформистского» движения в преподавании математики,
инициатором которого был немецкий математик Ф. Клейн. М. п. отводила
центральное место при изучении математики понятию функции, которая имеет

МЕТОДИКА ПРЕПОДАВАНИЯ МАТЕМАТИКИ
215
большое приложение в естествознании и технике. При этом в М. п. требовалось,
чтобы на первых ступенях обучения не давать строгого логического обоснования
понятий и выводов в математике, а больше прибегать к наглядным пособиям,
графикам и примерам из жизни. М. п. включала в себя элементы высшей
математики (производная, дифференциал, интеграл) и их приложения. М. п. повлияла
на преподавание в ряде стран: во Франции, России (в кадетских корпусах
элементы математического анализа были введены еще в середине XIX в. по
инициативе М. В. Остроградского, а требования о введении в среднюю школу идеи
функциональной зависимости были сформулированы В. П. Шереметьевским еще
задолго до М. п.).
МЕРОМОРФНАЯ ФУНКЦИЯ — однозначная аналитическая в плоскости ζ
функция w(z), у которой особые точки, отличные от z=oo, могут быть только
полюсами (см.). М. ф. представляется в виде w(z) = f(z): g(z)< где f(z) и g(z) —
целые функции (см.). К М. ф. относятся многие важные классы функций (см.
Аналитические функции).
Греч, μεροξ — часть (здесь — дробь) и μορφοξ — форма, вид.
МЕРСЕННА ЧИСЛА —числа вида МЛ«2Л—·1, где η — натуральное число.
М. ч. иначе можно определить как натуральные числа, которые в двоичной
системе счисления записываются только одними единицами (без нулей).
Действительно, М. ч. Мп = 2п—1 в двоичной системе запишется в следующем виде:
Λ4η=2" — 1 = 2л-1+2л-2-{- ·.· +2+1 = 1 1 1 ... 1 (п раз 1).
Можно определить М. ч. и как сумму η первых членов геометрической
прогрессии с первым членом 1 и со знаменателем 2.
С помощью М. ч. в разное время находили самые большие из известных
простых чисел, а также большинство из известных совершенных чисел (см.).
Легко видеть, что при любом составном η Μ. ч. является также составным.
Отсюда следует, что М. ч. могут быть простыми только тогда, когда η —
простое число. До настоящего времени (1963) найдены пока 20 простых М. ч.,
которые получены при следующих простых индексах п = р=2, 3, 5, 7, 13, 17,
19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253 и 4423. Восемь
наибольших из этих М. ч. найдены совсем недавно (в последнее десятилетие)
с использованием электронных вычислительных машин (ЭВМ).
Так, например, чтобы установить, что число 23217— 1 (состоящее из 969
цифр) является простым, понадобилось произвести несколько тысяч возведений
чисел в квадрат, а затем делений на 23217— 1 таких чисел, которые состояли из
более чем 696 знаков (цифр). Все такие вычисления в 1957 г. заняли 5,5 часов
работы шведской ЭВМ. Или, например, чтобы установить, что число 28191— 1
(состоящее из 2466 цифр) является составным, понадобилось 100 часов работы
ЭВМ, однако до сих пор ни один из его делителей не найден.
Не найдено ни одного делителя и для других гораздо меньших М. ч., хотя
сравнительно давно известно, что они являются составными и даже известны
сами числа. Таковы, например, числа 2101— 1, состоящее из 31 цифры, и2257— 1,
состоящее из 77 цифр.
Известно, что все четные совершенные числа (см.) имеют вид 2Р—г(2Р—1),
где ρ и 2^—1—простые числа (Эйлер, XVIII в.). Отсюда следует, что каждое
новое простое М. ч. одновременно открывает и новое четное совершенное число.
Лит.: В. Серп и некий, Что мы знаем и что не знаем о простых числах, перев.
с польск., Физматгиз, М., 1963.
МЕТОДИКА ПРЕПОДАВАНИЯ МАТЕМАТИКИ — наука о методах и
приемах преподавания математики в средней школе. Другими словами, М. п. м.-—

216
МЕТРИКА
наука о том, как преподавать математику учащимся средней школы с тем,
чтобы достигнуть при этом наибольшего успеха.
Великий русский математик Н. И. Лобачевский придавал огромную роль
М. п. м., он писал: «Самое важное в математике — способ преподавания» (его
статья «Наставление учителям математики в гимназиях»; см. собрание сочинений
Лобачевского).
Центральным местом в содержании М. п. м. является изучение наиболее
трудных и принципиально важных тем и разделов курса математики в средней
школе, например: 1) функция (см. Меранская программа), 2) геометрическое
преобразование (см. Эрлангенская программа), 3) уравнение и неравенство,
4) тождественное преобразование (в алгебре, тригонометрии, в математическом
анализе), 5) идея развития понятия о числе, 6) понятие предела (на его основе
строится понятие производной, интеграла, измерение геометрических величин—
длина, площадь, объем), 7) развитие пространственного представления и
воображения учащихся, 8) вопросы политехнической подготовки (культура вычислений,
графические навыки у учащихся, вопросы прикладной математики и др.), 9)
развитие логического мышления у учащихся и ряд других.
М. п. м. тесно связана с педагогикой, историей математики, математической
логикой и самой математикой. Развитие математики и требования жизни
оказывают влияние и на развитие М. п. м. См. также: Индукция, Дедукция, Синтез,
Анализ, Аналогия, Теорема.
Лит.: В. М. Брадис, Методика преподавания математики в средней школе,
Учпедгиз, М.—Л., 1954; СЕ. Ляпин (ред.), Методика преподавания математики, тт. 1 и 2,
Учпедгиз, М.—Л., 1952 и 1956.
МЕТРИКА — способ определения (задания) расстояния между двумя
точками (элементами) или определение меры угла в той или иной геометрической
системе.
В дифференциальной геометрии (см.) М. определяется заданием элемента
длины дуги при помощи дифференциальной квадратичной формы (см. Римановы
геометрии).
В топологии М. вводится заданием расстояния ρ (х, у) между элементами
χ и у, превращающего данное множество в метрическое пространство (см.).
В линейных векторных и функциональных пространствах М. задается
скалярным произведением, позволяющим определить понятия расстояния и угла.
МЕТРИЧЕСКАЯ ГЕОМЕТРИЯ — геометрия, изучающая свойства того или
иного пространства, в котором установлена метрика. Обычная евклидова
геометрия является М. г.; в проективной, например, геометрии тоже устанавливается
своя проективная метрика, поэтому ее тоже можно отнести к М. г.
МЕТРИЧЕСКОЕ ПРОСТРАНСТВО — множество, в котором каждой паре
элементов Μ и М1ч называемых точками пространства, отнесено число
ρ(Λί, Μχ)>0, называемое расстоянием от М до М19 удовлетворяющее
следующим условиям (аксиомам М. п.): 1) (аксиома тождества) о (Λί, МХ)=Ъ в том и
только в том случае, когда Μ = Μι\ 2) (аксиома симметрии) р(М, Atf^pfMiM);
3) (аксиома треугольника) р(М, М1)^(М19 М2)>р (ММ2).
Примеры: 1) числовая ось (см.) р(^, #2)Н *2— xi I'» 2) /2-мерное
пространство? (Aflf Mt)=Y(x\2)-x[l))2+ ··· +(42)-4°)2; 3) пР0СТРанстй0
Гильберта (см.) р(М1э М2) = Т/ 2 ( *£2)—*£υ)2 ; 4) ΠΡ°^Ρ3Η0ΤΒ0 "епрерыв-
ных на отрезке функций (см.) ρ (/, q)= max | f(x) — q(x) i, 5) пространство

МИНИМУМ ФУНКЦИИ
217
. 7)-]/ J[/(
функций с интегрируемым квадратом (см.) р(/, <7)= I/ \[f(x) — q(x)]*dx.
В этих примерах расстояние удовлетворяет аксиомам М. п.
МЕЦИЕВО ЧИСЛО—-приближенное значение числа π (см. Пи число) с
точностью до 10—7, которое было вычислено из приближенного представления
355
числа пи: π ^ —-. Приближенное значение числа π до 7-го знака было известно
1 \о
еще в Китае в V в. М. ч. названо по имени голландского математика
А. Меция (1543—1620), вычислившего число π с точностью до 10—7; правильная
фамилия Меция — Антониец (Андриан Антониец), но он был уроженец г. Меца,
поэтому его и назвали Мецием. (Сравните происхождение названия Региомотана
355
формулы (см.). Дробь-— есть одна из подходящих дробей разложения числа л
11о
в непрерывную дробь (см.). Иногда необоснованно число π называют М. ч.
[.сравните Лудольфово число (см.)].
МИНИМАЛЬНЫЕ ПОВЕРХНОСТИ —поверхности, у которых средняя
кривизна в любой ее точке равна нулю (см. Кривизна). М. п. возникли при
решении следующей вариационной задачи: среди всех поверхностей, проходящих
через данную замкнутую пространственную кривую, найти ту, которая имеет
минимальную площадь поверхности (отсюда происходит и название),
ограниченной данной кривой. В случае плоской кривой решением будет часть плоскости,
ограниченная данной замкнутой кривой. В случае же пространственной кривой
необходимым условием того, чтобы поверхность была М. п., является равенство
нулю ее средней кривизны во всех ее точках; хотя это условие не является
достаточным, однако поверхности, удовлетворяющие этому условию, стали
называть М. п.
М. п. имеют во всех своих точках неположительную полную кривизну, т. е.
являются седлообразными поверхностями. Бельгийский физик Плато предложил
простой экспериментальный способ получения М. п. с помощью использования
мыльных пленок, натянутых на проволочный каркас.
Лит.: Р. Курант и Г. Роббинс, Что такое математика, Гостехиздат, М.—Л.,
1947.
МИНИМУМ ФУНКЦИИ: 1°. М. ф. одной переменной у= /(*) — значение
f(x0) функции, не превосходящее значений, принимаемых этой функцией при
всех достаточно близких к х0 значениях аргумента (рис. 148). Формальное
определение М. ф.: значение f(x0) является М. ф. f{x)> если существует
принадлежащая области определения функции окрестность (х0— δ, *04-δ) такая, что для
всех ее точек выполняется неравенство
f(x)2zf(Xo). (*)
(Говорят, что функция f(x) имеет минимум в точке х0.)
2°. М. ф. нескольких переменных u=*f(xlt х2, . . ., хл)«/(Р) —значение
/(*ю> *2о> · · ·» *ло)=/(Л>)> не превосходящее значений, принимаемых функцией
во всех точках, достаточно близких к точке Р0 (см. рис. 149, где η=2, х^х,
х2=У).
Формальное определение М. ф. u = f(xly x2t . . ., xn)=f(P); функция
" = /(*ι, *2* · · ·. Xn) = f(P) имеет минимум в точке ρ0(Χι0, χ20, · · ·, Хпо),
Другими словами, f(P0)=f(XiQ, *2o» · · ·» *по) есть М. ф., если существует
окрестность (см.) точки Р0, лежащая внутри области определения функции, такая,
что для всех точек Ρ этой окрестности выполняется неравенство
f(P)>f(Pth <··)

218
МИНКОВСКОГО НЕРАВЕНСТВО
В случае выполнения в соотношениях (*) и (**) строгого неравенства
говорят, что имеет место М. ф. в узком смысле, в противном случае — в широком
смысле. М. ф. называют иногда абсолютным в отличие от относительного
минимума (см.). См. также Необходимые условия экстремума и Достаточные условия
экстремума.
Лат.: minimum—наименьшее.
У*
О
y*fM
Рис. 148
Λ
ο\-
/
y*™
u*f(x,
Ik
/\
\/
\Aw
У)
У "у
Рис. 149
МИНКОВСКОГО НЕРАВЕНСТВО — неравенство для р-х степеней чисел,
имеющее вид:
( 21 **+ Ьк ψ\7<\ 21 ак \р)т+\ 21 Ьк |Йг,
U=i J U=i J U=i J
где целое р>1, а ак и Ьк—неотрицательные числа. Μ. н. является обобщением
известного «неравенства треугольника», утверждающего, что длина одной
стороны треугольника не больше суммы длин двух других его сторон; для
«-мерного пространства расстояние между точками x=(xlt x2t . . ., хп) и >>=()Ί«
У21 · · ·* Уп) определяется числом
М. н. было установлено немецким математиком Г. Минковским в 1896 г. См.
также Гельдера неравенство.
МИНОР £-го порядка определителя D (или матрицы А) — определитель £-го
порядка, составленный из элементов, стоящих на пересечении любых k строк и
k столбцов определителя D (или матрицы А).
М. определителя /2-го порядка (или квадратной матрицы л-го порядка),
составленный из элементов, стоящих на пересечении k(k<n) столбцов и k строк,
и М., составленный из элементов, стоящих на пересечении остальных η—k
столбцов и η—k строк, называются взаимно дополнительными М.
Из определения М. следует, что алгебраическое дополнение (см.) минора
совпадает с его дополнительным минором Μ или отличается от него только
знаком.
См. также Алгебраическое дополнение, Ранг матрицы, Кронекера — Капел-
ли теорема, Крамера правило.

МНОГОГРАННЫЙ УГОЛ
219
МИНУС — математический знак, имеющий вид горизонтальной черты и
используемый для обозначения действия вычитания и при обозначении
отрицательных чисел.
Лат. minus — менее.
МИНУТА — единица измерения плоских углов, равная 1/в0 части градуса.
М. обозначается косым штрихом ': так, угол а, содержащий пять минут, можно
записать так: α=5'. 1/β0 часть М. называется секундой (см.).
МНИМАЯ ЕДИНИЦА — комплексное число (см.) вида (0,1). М. е.
обозначается буквой /. Квадрат М. е. равен —1, /2=—1, /3 = —ι, ζ"4=1 и вообще
/4/г=-=1 (п — целое). М. е. связана с корнем квадратным из —1 равенством
V-l-±i.
МНИМАЯ ЧАСТЬ комплексного числа а+Ы — действительное число Ь.
Иногда М. ч. комплексного числа z=a+bi называется также чисто мнимым
числом Ы, а число b тогда называется коэффициентом при М. ч. См.
Комплексное число.
МНИМОЕ ЧИСЛО — комплексное число (см.): а+Ы% где Ь?=0; а, Ь —
действительные числа, т. е. М. ч.— это комплексное число z=a+bi при 6^0.
М. ч. а+Ы, где а=0, 6?=0, называется чисто мнимым. М. ч. г на комплексной
плоскости изображаются точками, не лежащими на действительной оси х.
МНОГОГРАННИК трехмерного евклидова пространства — в первоначальном
представлении — геометрическое тело, ограниченное плоскими многоугольниками.
Эти плоские многоугольники называются гранями М., стороны многоугольников
называются ребрами М., а вершины многоугольников — вершинами М. Более
строгое определение: М.— совокупность конечного числа плоских
многоугольников таких, что: 1) каждая сторона многоугольника является стороной еще
другого многоугольника (смежного с первым по общей стороне — ребру М.), 2} от
каждого многоугольника можно перейти к любому другому многоугольнику,
проходя последовательно через смежные многоугольники.
Если М. гомеоморфен сфере и имеет при этом своими гранями простые
многоугольники, то он называется простым. Простые М. иначе называются М.
нулевого рода (см. Род поверхности). Для М. нулевого рода справедлива
теорема Декарта-Эйлера (см.). Простой М. называется выпуклым, если он весь лежит
по одну сторону от плоскости его любой грани, или простой М. называется
выпуклым, если любой отрезок АВ, с концами, принадлежащими М., весь
принадлежит этому М. Из этого определения следует, что выпуклый М. есть
частный случай выпуклой фигуры (см.). Выпуклый М. называется правильным,
если у него все грани — правильные одноименные многоугольники и все
многогранные углы равны (правильны). Правильных М. всего пять типов (тела
Платона), что было доказано еще в «Началах» Евклида (см. рисунки к термину
Правильный многогранник).
Выпуклые М., у которых все грани — правильные разноименные
многоугольники, а все многогранные углы или равны или симметричны, называются полу-
правильными (архимедовыми). См. Правильные многогранники, Многогранный
угол, Призма, Пирамида, Параллелепипед, Куб, Многоугольник.
Лит.: А. Д. Александров, Выпуклые многогранники, М.—Л., 1950; П. С.
Федоров, Начала учения о фигурах, Спб., 1885; Д. И. Перепелки н, Курс
элементарной геометрии, ч. 2, Гостехиздат, М.—Л., 1949; В. Г. Ашкинузе, «Математическое
просвещение», 1957, № 1.
МНОГОГРАННЫЙ УГОЛ — геометрическая фигура, образованная одной из
двух полостей (частей) конической поверхности, направляющей которой является
простой многоугольник. Вершина S конической поверхности называется
вершиной М. у. (рис. 150); лучи с началом в точке S и проходящие через вершины
направляющей (многоугольника) называются ребрами М. у. Углы, образованные

220
МНОГОЗНАЧНАЯ ФУНКЦИЯ
Рис.
соседними ребрами, называются плоскими углами М. у. Части плоскостей,
ограниченные соседними ребрами, называются гранями М. у. В зависимости от числа
граней М. у. бывают трехгранные, четырехгранные и т. д. На рисунке
изображен четырехгранный угол SABCD. Если направляющий многоугольник
выпуклый, то М. у. называется выпуклым. Если все плоские и двугранные углыМ. у.
соответственно равны, то такой М. у. называется
правильным.
В трехгранном угле любой плоский угол меньше
суммы двух других плоских углов и больше их разности.
Сумма плоских углов выпуклого М. у. меньше 360°.
МНОГОЗНАЧНАЯ ФУНКЦИЯ —расширение понятия
функции (см.), когда предполагается, что каждому
значению аргумента χ (из области определения) соответствует
одно или несколько (может быть, бесконечно много)
значений переменной у. М. ф. часто выражают при
помощи нескольких однозначных функций. Например,
двузначная функция у, определенная соотношением у2=х,
может быть задана с помощью двух функций: у= + ух,
у=— ух. Пример М. ф. y=Arcsinx (см. Арксинус).
См. также Аналитическая функция, Аналитическое
продолжение.
МНОГОМЕРНОЕ ПРОСТРАНСТВО (л-мерное пространство, линейное
пространство (см.) η измерений) — обобщение понятия трехмерного пространства,
которое в свою очередь есть некоторая абстракция реального физического
пространства. К подобному обобщению часто естественным образом приводят
некоторые практические задачи алгебры. Например, совокупность решений т
линейных однородных уравнений с k неизвестными есть М. п.
Изучение геометрии М. п. часто помогает давать ответы на многие
практические и чисто математические задачи. Реальное физическое пространство
трехмерно, т. к. при выбранной системе отсчета положение тела (в данный
момент) определяется тремя числами (координатами).
МНОГОМЕРНЫЙ ИНТЕРВАЛ —то же, что и полиинтервал (см.).
МНОГООБРАЗИЕ — математическое понятие, обобщающее на
случай понятие поверхности без самопересечений и краев. Неудобство
даже такой простой поверхности, как сфера,
заключается в невозможности задать на ней единую систему
координат без особенностей. Но, однако, можно
разбить сферу на куски, частично налегающие друг на
друга, гомеоморфные (см.) кругу евклидовой плоскости
(рис. 151), и в каждом из кусков ввести систему
координат при помощи упомянутого гомеоморфизма S/.
Именно — если точка Ргго куска при гомеоморфизме Si
переходит в точку (х, у) круга, то числа * и у мы
считаем координатами точки Ρ сферы. Если точка Ρ
принадлежит сразу двум кускам и,- и Oj, то она имеет
координаты xlt у19 связанные с «Slt и координаты х2,у2,
связанные с S2. Таким образом, х2 и у2 являются
функциями хг и Ух (и наоборот).
Абстрактное определение М. во многом следует изложенной конструкции для
сферы М.: во-первых, есть топологическое пространство X, покрытое конечным,
или счетным, числом множеств {у,·}, гомеоморфных η -мерному евклидову открытому
л-мерный
изучения
шару
V
*?+*!+
+ д^<1 (я называют размерностью М.). Гомеоморфизмы

МНОГОУГОЛЬНЫЕ ЧИСЛА
221
St: Vi-+S задают в топологическом пространстве системы координат (S/ задает
систему координат в ι>/). Если точка Р$У/ПУ/. она имеет два набора координат
(xlt х2* ...» Хп) и (χ'ι, х'г, . . ., *„'), в силу чего лсД/»1, 2, .... л) являются
функциями jclt jc2, . . ., хп. Пространство X будет М. класса С^, если^(/=1,
2, .... /г) являются k раз дифференцируемыми функциями дсу (/=1, 2, . . ., л).
Если эти функции аналитические, то М.— аналитическое. Множества {υ{\ с
гомеоморфизмами S/ называются системой локальных координат М.
Примеры: сфера* тор, плоскость — двумерные М. Множество прямых на
плоскости является также двумерным М. (прямая мыслится как точка М.).
Лит.: П. С. Александров и В. А. Ефремович, Очерк основных понятий
топологии, ОНТИ, М.—Л., 1936.
МНОГОСВЯЗНАЯ ОБЛАСТЬ — область (см.), не являющаяся односвяз-
ной (см.). Другими словами, в М. о. существует замкнутая кривая, которая не
может быть стянута в точку, оставаясь в пределах области. Простейшим
примером М. о. является кольцо — множество точек, координаты которых
удовлетворяют неравенствам:
r<x2+y2<R,
где 0<r<R.
МНОГОУГОЛЬНИК — замкнутая ломаная линия. При этом если все
вершины М. лежат в одной плоскости, то он называется плоским, если не все
вершины лежат в плоскости, то М. называется пространственным. Обычно
рассматривают плоские М., которые просто называются М. Отрезки (звенья) ломаной
называются сторонами М., а вершины ломаной (концы отрезков) —
вершинами М. Если М. гомеоморфен (см.) окружности, то он называется простым.
Другими словами, простой М. —это М. без самопересечений, т. е. когда: 1) из
каждой вершины его исходят только две стороны, 2) стороны не имеют общих точек
(вершины не принадлежат сторонам), 3) вершины не лежат на сторонах.
Непростой М. иначе называется звездчатым. В элементарной геометрии чаще всего
рассматривают простые М. Иногда М. называют часть плоскости, ограниченную
замкнутой ломаной линией. М. называется выпуклым, если он весь лежит
по одну сторону от прямой, на которой лежит какая-либо его сторона, или М.
называется выпуклым, если отрезок, соединяющий две его любые точки Л и В,
целиком (всеми своими точками) принадлежит этому М. Сумма углов при
вершинах всякого простого М. равна 180°-(п — 2), где η — число сторон.
Многоугольник удобно бывает называть и
«-угольником, где η — число сторон (вершин, п>3).
См. также Деление круга, Правильные
многоугольники.
МНОГОУГОЛЬНЫЕ ЧИСЛА — числа,
связанные определенным образом с плоским
многоугольником. Простейшими из М. ч. яв- Рис. 152
ляются треугольные числа. Это числа
последовательности
1,3,6, 10, 15,21 n-i2±ii
которые, начиная со второго, геометрически получаются из треугольника,
вершины которого дают три точки (рис. 152) — треугольник с наименьшим
числом точек, затем треугольник больший, стороны которого увеличены в 2 раза
(6 точек), затем в 3 раза (10 точек) и т. д.
Квадратными числами будут числа последовательности 1, 4, 9, 16, 25,

222
МНОГОЧЛЕН
36, . . ., η2 (рис. 153). Пятиугольными числами будут числа последовательности
1, 5, 12, 22, 35, 51, . . ., /|(3/|"~1>> . . . (рис. 154), и т. д.
Таким образом, получают М. ч. различных порядков. Обозначается я-ое
^-угольное число символом р^, оно определяется по формуле:
*-+<«-2, iiufu.
Эту формулу можно истолковать еще и так:
Pqn = n+Sn,
где η — порядковый номер ^-угольного числа, Sn—сумма первых членов
арифметической прогрессии, первый член которой равен нулю (<з1 = 0), а разность равна
q — 2. Μ. ч. называются также полигональными числами.
Рис. 153 Рис. 154
Есть основание предполагать, что М. ч. возникли у вавилонян при расчетах
мощения пола кирпичом. Из Вавилона М. ч. перешли к грекам (начиная с
пифагорейцев), Диофант написал целую книгу о М. ч. (III—IV вв. до н. э.).
Историки-математики утверждают, например, что треугольные числа были известны
в Индии (во II в. до н. э.), в Китае (в 1309 г.).
М. ч. занимались многие математики: Ферма, Эйлер, Лагранж, Лежандр,
Гаусс и др. См. также Фигурные числа, Арифметический ряд.
Лит.: И. Я. Депман, История арифметики, Учпедгиз, М., 1959.
МНОГОЧЛЕН (полином) от η неизвестных (переменных) над полем Ρ —
сумма произвольного числа одночленов (см.) от η неизвестных над полем Р.
Порядок суммирования членов М. можно произвольно менять. Можно добавлять
произвольные одночлены М. с нулевыми коэффициентами и выбрасывать такие
члены. Множество всех М. от η неизвестных над полем Ρ образует
кольцо Μ (см.) относительно операций суммы М. и произведения их (см.).
В М. можно выполнять приведение подобных членов (см.). Для М. возможно
каноническое представление М. (см.).
Иногда в элементарной математике М. называют алгебраическое выражение,
в котором последним действием является сложение (вычитание), например
5а:3 — 31ga-f-Jt)4-4y.
МНОГОЧЛЕН ДЕЛЕНИЯ КРУГА — многочлен (хР— 1):(х—1)=/(*)=
—χΡ—γ-\-χΡ—2+ ··· +лс+1. М. д. к. имеет своими корнями корни р-й
степени из 1, отличные от 1. М. д. к. неприводим над полем рациональных
чисел. С М. д. к. тесно связана геометрическая задача о построении циркулем
и линейкой правильных р-угольников. См. также Уравнение деления круга,
Деление круга.
МНОГОЧЛЕН НУЛЕВОЙ СТЕПЕНИ. При рассмотрении многочленов над
полем Ρ Μ. н. с. называют элементы поля Рй отличные от нуля, т. е. кон-

МНОЖЕСТВО ЗНАЧЕНИЙ ФУНКЦИИ
223
станты. В теории делимости многочленов большинство вопросов рассматривается
с точностью до делимости на М. н. с.
МНОЖЕСТВО — одно из важнейших понятий математики. Вводится
аксиоматически и не может быть определено через какие-либо элементарные понятия.
Описательное объяснение термина М.: совокупность, объединение некоторых
объектов произвольной природы — элементов М. Хотя М. могут состоять из
элементов произвольной природы, однако каждое конкретное М. представляет собой
объединение элементов по каким-либо общим для них свойствам (признакам).
Эти общие свойства элементов М. содержатся в самом названии (задании)
каждого М. Так, например, в М. целых чисел все элементы суть целые числа,
и это свойство является общим для всех элементов. Все объекты, обладающие
этим свойством, в данном случае представляют собой объединение М.
Аналогично можно рассматривать М. звезд во вселенной, М. точек на плоскости,
М., элементами которого являются все конечные М. (т. е. М., состоящие из
конечного числа элементов), и т. д.
МНОЖЕСТВ ТЕОРИЯ — отдел математики, изучающий множества (см.),
отвлекаясь от конкретной природы элементов множества. М. т. рассматривает
множества с точки зрения таких отношений, как взаимно однозначное
соответствие (см.), упорядочение (см. Вполне упорядоченное множество), отображение
множеств. Понятие взаимно однозначного соответствия естественным образом
приводит к понятию мощности (см.) множества, кардинальных чисел (см.);
отношение порядка вводит трансфинитные числа (см.), а затем трансфинитную
индукцию (см.). Простейшими операциями над множествами являются: 1)
объединение (сумма) множеств в любом «количестве» (обозначается (J А , где α—
α tt
символ, определяющий множество) — означает совокупность всех элементов,
принадлежащих хотя бы одному множеству А ; 2) пересечение произвольной
совокупности множеств (обозначается ()Аа) — означает множество всех эле-
α
ментов, принадлежащих каждому множеству А . Являясь весьма абстрактной
теорией, М. т. не свободна от противоречий (см. Парадоксы математические),
которых стараются избежать, отказываясь от некоторых «очевидных»
положений— аксиом (см. Цермело аксиома). Существуют два больших течения в М. т.:
одно признает аксиому Цермело, а другое отрицает.
М. т. занимает видное место в математике. В конце прошлого века М. т.
произвела революцию в анализе, дав его строгое обоснование (учение о числе
Дедекинда и т. п.). В XX в. идеи М. т. все более пронизывают математику.
Теоретико-множественная аксиоматика теории вероятностей оказалась наиболее
прочным фундаментом этой математической дисциплины. М. т. широко
применяется в качественной теории дифференциальных уравнений (см.), топологии (см.),
вариационном исчислении, теории функций вещественной переменной. Отдельная
глава М. т. занимается вопросами строения точечных множеств в л-мерном
евклидовом пространстве (см. Дескриптивная теория множеств). Основателями
М. т. являются чешский математик Б. Больцано, немецкие математики Г.
Кантор и Р. Дедекинд, получившие фундаментальные результаты теории (XIX в.).
Лит.: П. С. Александров, Введение з общую теорию множеств и функций, Гос-
техиздат, М.—Л., 1948; Η. Η. Лузин, Теория функций действительного переменного,
Учпедгиз, М., 1948.
МНОЖЕСТВО ЗНАЧЕНИЙ ФУНКЦИИ — множество значений, принимаемых
зависимой переменной (см. Функция). М. з. ф. называют также областью
изменения функции. Часто рассматривают М. з. ф. на данном множестве Ε
значений аргумента, т. е. множество значений, принимаемых функцией, когда
аргумент пробегает множество £; например, М. з. ф. y=;e2-f-3 на отрезке
— 1 ^jc<4 является отрезком 4<у<Л9.

224
МНОЖИТЕЛЬ
МНОЖИТЕЛЬ — число или выражение, на которое умножается другое число
или выражение, называемое множимым. В произведении α-b число α —
множимое, число Ъ — М. Как множимое, так и М. в совокупности называются
сомножителями. Иногда М. имеет при себе специальное прилагательное:
нормирующий множитель (см.), интегрирующий множитель (см.).
π ас
При сложении дробей с разными знаменателями, например — 4-—- по ос-
b ab2
новному свойству дроби их приводят к наименьшему общему знаменателю (см.
Наименьшее общее кратное), умножая числитель каждой дроби на определенное
число, разное для каждой дроби. Каждый из М. для этих дробей называется
дополнительным М. Дополнительный М. (для первой дроби ab, для второй 1)
обычно ставят слева вверху над числителем дроби и подчеркивают его косой
чертой или дугой:
Ь + ab'1 ab2
МОДУЛЬ КОМПЛЕКСНОГО ЧИСЛА z=a+bi — действительное
неотрицательное число У a2f б2 . При геометрическом представлении комплексных чисел
М. к. ч. равен расстоянию от начала координат до аффикса (см.) комплексного
числа ζ. Модуль произведения комплексных
чисел равен произведению модулей сомножителей.
М. к. ч. г обозначается так: \г\ (рис. 155),
следовательно, |г|=|/а2+62, или \z\ = r. См.
также Абсолютная величина числа.
МОДУЛЬ ПЕРЕХОДА от системы
логарифмов (см.) при основании а к системе
логарифмов при основании b — число М=- . Если
Рис l«W A l°ga
^ис· 10° известны логарифмы при основании а, то,
умножая их на М, получим логарифмы при
основании 6, т. е. \ogbX=M\ogax. Например, М. п. от десятичных логарифмов
(см.) к натуральным логарифмам (см.) равен М=2,30258 .. . М. п. от
натуральных логарифмов к десятичным равен Αί=0,43429. См. также Логарифм.
МОДУЛЬ СРАВНЕНИЯ — всякая совокупность чисел с тем свойством, что
вместе со всякими двумя числами она содержит их разность и сумму. В теории
чисел рассматривают модули, состоящие из целых чисел. Всякий такой М. с.
состоит из всех чисел, кратных некоторому числу т. В теории чисел говорят,
что а сравнимо с b по модулю т [(символически: a=b (modm)], если разность
а — b делится на т, т. е. принадлежит к М. с. чисел, кратных т.
МОДУЛЯРНАЯ ФУНКЦИЯ — аналитическая функция (см.), значения которой
не меняются при некотором целочисленном дробно-линейном преобразовании аргу-
ах+Ь
мента с определителем, равным 1, т. е. при замене χ на j, где а, о, с
и d — некоторые целые числа и определитель J = l. Μ. φ. является
частным случаем автоморфной функции (см.). Периодические функции (см.) являются
частным случаем М. ф. (например, cos π л- не меняется при замене χ на x-f-я,
где η — любое целое число; здесь a=d=l, b=ng с=0).
yj
b
0
ι
<^
a
2
ι
ι
1 -m
Χ

МОНТЕ-КАРЛО МЕТОД
225
МОЛЬВЕЙДЕ ФОРМУЛЫ — формулы плоской тригонометрии, выражающие
следующую зависимость между сторонами (их длинами) и углами треугольника:
а+Ь
с
А —В
cos—-—
2
С '
sin—
2
а — b
с
А —В
sin
2
С
cos-
где at b, с — стороны, а А, В, С — углы треугольника. М. ф. названы по
имени немецкого математика К. Мольвейде, использовавшего их, хотя эти формулы
были известны и другим математикам.
МОМЕНТ степени k случайной величины (см.) ξ — математическое
ожидание (см.) величины (ξ — M)k, где Μ — математическое ожидание ξ. Дисперсия
(см.) величины ξ является М. 2-го порядка.
МОНОГЕННАЯ ФУНКЦИЯ —обобщение понятия аналитической функции
комплексного переменного. Если функция комплексного переменного /(г)
определена на произвольном множестве Ε комплексных чисел и имеет производную
в некоторой предельной точке этого множества г0, то /(г) называется М. ф.
в точке г0. Если /(г) есть М. ф. в каждой точке множества £, то говорят,
что f(z) есть М. ф. на множестве Е. Понятие М. ф. совпадает с понятием
аналитической функции, когда Ε — область. Не будучи, вообще говоря,
аналитическими, М. ф. имеют с ними много общих свойств (например, правила
дифференцирования, свойство единственности).
Лит.: А. И. Маркушевич, Теория аналитических функций, Гостехиздат,
М. -Л., I960.
МОНОТОННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ (или функция) —не
возрастающая или не убывающая последовательность (или функция) (см.).
МОНОТОННО ВОЗРАСТАЮЩАЯ (убывающая) последовательность или
функция — возрастающая (убывающая) функция или последовательность (см.).
МОНТЕ-КАРЛО МЕТОД —метод, широко применяемый в настоящее время
для приближенного решения различных задач вычислительной математики:
вычисление кратных интегралов, решение дифференциальных уравнений и т. п.
Сущность М.-к. м. заключается в следующем: величине х9 которую нужно
приближенно вычислить, ставится в соответствие некоторая случайная величина
ξ, математическое ожидание (см.) которой Μ ξ равняется χ. Затем каким-нибудь
способом эта случайная величина многократно реализуется, из получаемых
значений образуется некоторое среднее, которое и принимается за приближенное
значение величины х. Случайные числа берутся либо из таблицы случайных
чисел, либо от некоего физического датчика, либо вычисляются методами
теории чисел (так называемые псевдослучайные числа).
\
Например, чтобы найти j f(x)dXi где f(x) — ограниченная интегрируемая
о
функция, берется последовательность случайных чисел |lf .. . f ξ#, равномерно
распределенных на отрезке [О, 1], и образуется величина — ■- ,
t
которая и принимается за приближенное значение f / (χ) dx. Ошибка при этом будет
о
с вероятностью, практически равной единице, не больше чем —, где С— неко-
У N
15 Толковый словарь математических терминов

226
ΜΟΡΑ - МАСКЕРОНИ ПОСТРОЕНИЯ
торая константа, зависящая от f(x). Название М.-к. м. связано с названием
города, знаменитого своими игорными домами.
МОРА — МАСКЕРОНИ ПОСТРОЕНИЯ — геометрические построения на
плоскости, выполняемые с помощью только одного циркуля. М. — М. п. названы
по имени датского математика Г. Мора и итальянского математика Л. Маскеро-
ни, изучавших эти построения. См. также Геометрические построения, Маске-
рони построения.
МОЩНОСТЬ МНОЖЕСТВА — обобщение на произвольные множества (как
конечные, так и бесконечные) понятия «число элементов». М. м. определяется
как то общее, что присуще всем множествам, эквивалентным данному
множеству, т. е. всем множествам, элементы которых могут быть поставлены во
взаимно однозначное соответствие с элементами данного множества.
Понятие М. м. введено в математику Г. Кантором, основоположником
теории множеств (1879), которым было показано существование различных
мощностей для бесконечных множеств. См. Счетное множество,
Континуум-проблема. М. м. Л часто называют кардинальным числом этого множества и
обозначают, по Кантору, через £[(алеф, см.)].
МУАВРА ФОРМУЛА — формула, позволяющая возводить в степень
комплексное число, представленное в тригонометрической форме. М. ф. имеет вид:
гл*= [р (cos φ+ι sin φ)]Λ=ρΛ (cos η φ-f/ sin η φ),
где ρ — модуль (см.), а φ — аргумент комплексного числа. М. ф. используется
для выражения cos я φ и sin л φ через степени cos φ и sin φ. Μ. ф. названа по
имени английского математика И. Муавра, друга И. Ньютона. Современный
вид ей придал Л. Эйлер. М. ф. иногда называют Моавра формулой.
МУЛЬТИПЛИКАТИВНАЯ ГРУППА — группа (см.), в которой основная
групповая операция записывается символом · и называется умножением.
Лат. multiplicatio — умножение.
МУЛЬТИПЛИКАТИВНАЯ ФУНКЦИЯ. Функция Q(n), определенная для
всех натуральных значений аргумента п, называется М. ф.; если: 1) Q(k)^0
хотя бы для одного kt т. е. Q(n) не равна тождественно нулю, и 2) если
(klt k2) = l, то Q(^i^2)=0(^i),Q(^2)· Если условие 2) выполнено для
произвольных двух чисел кх и k2 (не обязательно взаимно простых), то функция
называется вполне М. ф.
Примеры М. ф.: Эйлера функция (см.); Мёбиуса функция (см.); функция
τ (л), равная числу (натуральных) делителей натурального числа п\ функция
а(л), равная сумме (натуральных) делителей натурального числа п\ степенная
функция f(n) — ns будет не только М. ф., но и вполне М. ф.

Η АБ Л А ОПЕРАТОР (V-оператор или оператор Гамильтона) —
дифференциальный оператор вида:
д_. _д_ _д_
дх ду dz
где I, j, к — единичные ортогональные векторы. Если / (х, у, ζ)— скалярная
функция, то
df df df
VZ—I + 'j-J + T-k-grad/.
дх dy dz
Если F (χ, у, ζ) — векторная функция F (χ, у, z)=u (xt у, ζ) i-\-v(x, y$ z)j-J-
-\-w(x, у, ζ) kf то
„ du ди dw ,. „
VF= —- + —--{-—- -div Fu
дх ду dz
понимая под произведением векторов V и F скалярное их произведение (см.).
Для векторного произведения
r „, [dw dv\. /du dw\ido du\t
Операции 2-го порядка: A/=divgrad, где Δ — Лапласа оператор (см.),
[VVfl = rotgrad/=0,
WF = graddiv/\
[VfvFjj-rotrotF,
v[vF] = divrotF=0.
См. также Оператор.
НАГЕЛЯ ТОЧКА — точка пересечения прямых, соединяющих вершины
треугольника с точками прикосновения (касания) противоположных сторон с вне-
вписанными окружностями. Названа по имени немецкого математика Нагеля,
изучавшего эту точку.
НАИБОЛЬШИЙ "ОБЩИЙ ДЕЛИТЕЛЬ: 1°. Н. о. д. нескольких натураль
ных чисел alf a2i . . . , αη есть наибольшее из положительных чисел, на которое
делится каждое из данных чисел. Например, Н. о. д. чисел 16 и 24 есть 8,
что часто записывают так: (16; 24) =8 или: Н. о. д. (16; 24) = 8.
Понятие Н. о. д. используется при сокращении дробей. Для отыскания
Н. о. д. нескольких чисел надо разложить их на простые множители и соста
вить произведение из общих множителей в наименьшей степени. Так, 16= 24,
24=23·3, следовательно, Н. о. д. данных чисел будет равен 23=8.
При отыскании Н. о. д. двух чисел в общем случае пользуются алгоритмом
Евклида (см.). Если Н. о. д. двух чисел равен 1, то эти числа называются
взаимно простыми (см.). Произведение Н. о. д. (a; b) и наименьшего общего
кратного (см.) этих чисел равно произведению ab.
15*

228
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ
2°. Η. о. д. многочленов /lt /2, ···♦/* — такой общий делитель
многочленов (см.) flt f2l . . . , fk, который делится на всякий другой их общий
делитель. Н. о. д. многочленов определяется однозначно с точностью до
множителя нулевой степени. Н. о. д. многочленов /1# /2, . . . f fk часто записывают
символом: (/,, /2, ... ,· fk)· Практическое отыскание Н. о. д. многочленов /lf
/2» · · · » fk B кольце многочленов от одного неизвестного р(х) производится
с помощью последовательного применения алгоритма Евклида (см.). Одно из
важных свойств Н. о. д. многочленов, имеющее приложения к другим вопросам,
состоит в том, что если d = (flt /2, . . . , fk)t то существуют многочлены glf
g2> · · ·* gk такие, что
figi + f*g2+ ··· +fkgk = d-
НАИЛУЧШЕЕ ПРИБЛИЖЕНИЕ. Пусть /(х) — произвольная непрерывная
функция, а Φι (а:), <p2(*), ..., φ« (х) — фиксированная система непрерывных
функций на отрезке [а, Ь\. Максимум выражения | / (х) — аг q>i(x) — а2 ф2 (х) —
— ··· —апуп(х)\ на отрезке [а, Ь] называют уклонением функции f{x) от
рп{х)=а1у1(х)-\-а2у2(х)+ ··· -ЬалФл(-*). Минимум уклонения при
всевозможном выборе коэффициентов а19 а29 ..., ап называется наилучшим
приближением функции f(x) посредством системы <pt (χ), φ2(χ), .. . , φΛ (χ).
Понятие Η. п. впервые введено П. Л. Чебышевым.
НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ. Н. о. к. нескольких натуральных
чисел аг, а2, ... * ап есть наименьшее натуральное число* делящееся на
каждое из данных чисел. Например, Н. о. к. чисел 6; 28; 15 есть число 420, что
записывают так: Н. о. к. (6; 28; 15) = 420. Понятие Н. о. к. используется при
сложении и вычитании обыкновенных дробей.
Для отыскания Н. о. к. данных чисел следует разложить каждое из чисел
на простые множители и составить произведение, взяв каждый из множителей
в наибольшей степени. Так, 6=2-3, 28=2-2-7, 15=3·5, следовательно,
Н. о. к. этих чисел есть число: 2·2-7·3-5 = 420.
Н. о. к. нескольких многочленов над каким-либо полем есть многочлен
наинизшей степени, делящийся на каждый из данных. Например, Н. о. к. (х — 3;
х2~{-3х+9) = х3 — 27 над полем рациональных чисел.
НАИМЕНЬШИХ КВАДРАТОВ СПОСОБ — применяется в теории ошибок для
нахождения одной или нескольких величин по результатам измерений,
содержащим случайные ошибки. Н. к. с. используется также для приближенного
представления заданной функции другими (более простыми функциями). Пусть для
разыскания значения неизвестной величины χ произведено η независимых
измерений, давших значения у19 y2t ...» Уп* т. е. У/^χ+δ/ (/«1, 2, . . . , η),
где случайные ошибки δ/ являются независимыми случайными величинами (см.)
с математическим ожиданием (см.) /Ηδ/=0 и дисперсией (см.) D δι=σ2έ.
Согласно Н. к. с, в качестве величины χ берут такое Xt для которого будет
наименьшей сумма квадратов:
S(X)=j^Pi{yi-X?.
IS
Здесь pi =—. Коэффициент /С>0 можно выбрать произвольно. Для того
<**
чтобы сумма S была наименьшей, необходимо в качестве λ выбрать
η
Σ Ptyt
1=1
так в простейшем случае применяется Н. к. с.

НАТУРАЛЬНОЕ ЧИСЛО
229
Этот способ применяется и для приближения функций. Пусть, например,
функция y**f(x) задана таблицей значений xit у ι (/**1. 2, .. . , п) и пусть
задано некоторое семейство функций φ0 (х)я фх (х), .... <рт (х). Требуется так
приблизить функцию / (х) функцией вида
т
η
чтобы сумма квадратов S = 2 Pi 1У1 — S (*/)J2 была наименьшей. Задача прибли-
жения функций по Н. к. с. была изучена П. Л. Чебышевым.
НАКЛОННАЯ: 1°. Н. к прямой / — всякая прямая тч пересекающая
прямую I под углом, отличным от прямого. Точка пересечения 5 прямой т с
прямой / называется основанием наклонной (рис. 156).
Длина отрезка Н. от какой-либо фиксированной ее
точки Л, отличной от основания S, до S
называется длиной Н. (сравните с определениехМ длины
касательной). Иногда Н. к прямой называют всякий
отрезок AS, не перпендикулярный к /, один из
концов которого принадлежит прямой /.
2°. Н. к плоскости — всякая прямая,
пересекающая плоскость под углом, отличным от прямоге.
Основание и длина Н. к плоскости определяется
аналогично основанию и длине Н. к прямой. рис 156
НАПРАВЛЯЮЩАЯ ЛИНИЯ линейчатой
поверхности — линия* по которой движется точка
прямой, описывающей эту поверхность. Если Н. л. является многоугольник, а
образующая при перемещении остается параллельна самой себе, то линейчатая
поверхность будет призматической поверхностью. См. также Цилиндр, Конус.
НАПРАВЛЯЮЩИЕ КОСИНУСЫ прямой / — косинусы углов α, β, γ,
образуемых направляющим вектором г прямой (г || /) с положительными
направлениями осей координат Ох, Оу, Ог прямоугольной декартовой системы
координат. Н. к. связаны соотношением:
cos2 a-f-cos2 β-i-cos2 γ=1.
Η. κ. вектора определяют направление этого вектора: они равны координатам
единичного вектора данного направления.
НАТУРАЛЬНАЯ ГЕОМЕТРИЯ — геометрия, построенная на основе
представлений, получаемых нами от материальных «точек», материальных «прямых»,
материальных «плоскостей» и других материальных «геометрических» образов.
Н. р. называют также наглядной геометрией, реже — опытной геометрией.
Н. р. широко используется на первых ступенях обучения геометрии в школе.
Лит.: Α. Μ. Α ο τ ρ я б. Методика преподавания наглядной геометрии (в кн.: Η. Μ. Бе-
скина, Методика геометрии, М. — Л., 1947).
НАТУРАЛЬНОЕ УРАВНЕНИЕ*— уравнение, выражающее кривизну k и
кручение о кривой как функции ее дуги s:
k=k(s), a = a(s).
Название Η. у. связано с тем, что функции k (s) и σ (s) не зависят от
расположения кривой в пространстве (от выбора системы координат), а зависят
только от формы кривой.
НАТУРАЛЬНОЕ ЧИСЛО — всякое целое положительное число, т. е. любое
число натурального ряда (см.).

230 НАТУРАЛЬНЫЙ ЛОГАРИФМ
НАТУРАЛЬНЫЙ ЛОГАРИФМ — логарифм, основанием которого является
/ 1 \п
трансцендентное число e=lim( 1-Ь—I «2,71828 . . . (обозначается \ηΝ). Η. л.
п-*оо\ П /
связывают с именем Непера, однако таблицы логарифмов почти одновременно
были составлены независимо друг от друга несколькими математиками (Непер,
Бригг, Бюрги и др.). Термин Н. л. принадлежит немецкому ученому Меркатору.
Н. л. иначе называются гиперболическими логарифмами или неправильно их
называют неперовыми логарифмами. Н. л. имеют большое применение в высшей
математике. См. также Логарифм.
НАТУРАЛЬНЫЙ РЯД — в первоначальном понимании это
последовательность целых положительных чисел, расположенных в порядке их возрастания:
1, 2, 3, 4, 5, 6, . . . f л, . . . Всякое множество, эквивалентное множеству
чисел Н. р., называется счетным. Например, множество квадратов чисел является
счетным, так как оно эквивалентно всему множеству чисел Н. р. (пример
Галилея). При более строгом подходе к понятию Н. р. дается аксиоматическое его
определение, выраженное в аксиомах (см. Пеано аксиомы).
Лит.: И. В.Арнольд, Теоретическая арифметика, Учпедгиз, М., 1939; Эиц.
элем, мат., т. 1, Гостехиздат, М., 1951.
«НАЧАЛА» ЕВКЛИДА. «Начала» — сочинение по элементарной математике
древнегреческого ученого Евклида (III в. до н. э.). «Η.» Ε. состоят из
13 книг и представляют собой систематическое изложение греческой математики
того периода по разделам: элементарной геометрии, теории чисел, алгебры,
теории измерения геометрических величин, элементов теории пределов.
«Н.» Е.—прекрасный образец построения геометрии дедуктивным методом
(см.). Элементарная геометрия, изучаемая в средней школе во многих странах
мира, мало чем отличается от геометрии, изложенной в «Η.» Ε. Однако ряд
определений (точки, прямой и др.) в «Η.» Ε. являются теперь устаревшими.
Ряд аксиом из «Η.» Ε. теперь уже не являются аксиомами. Например, Евклид
считал за аксиому предложение: «Все прямые углы равны». Теперь это
предложение, при строгом (дедуктивном) построении курса элементарной геометрии,
доказывается.
Существует мнение, что ряд книг, входящих в «Η.» Ε., были написаны не
Евклидом, а другими математиками; например, книги X и XIII, по мнению
голландского математика Ван дер Вардена, написаны древнегреческим математиком
Теэтетом. Ряд теорем и геометрических фактов, изложенных в «Η.» Ε., были
известны задолго до Евклида.
Греч. SfoOCeta — азбука, элементы; в переносном смысле — основы, начала.
Лит.: Евклид, «Начала», перев. с греч. и комм. Д. Д. Мордухай-Болтовского,
т. 1—6. Гостехиздат, М.—Л., 1940, т. 7—10; Ван дер Варден, Пробуждающаяся
наука, Физматгиз, М., 1959.
НАЧАЛО КООРДИНАТ — точка пересечения осей координат (см.).
НАЧАЛЬНЫЕ УСЛОВИЯ—состояние изучаемого процесса в какой-либо
момент времени* принимаемый за начальный. Если процесс описывается системой
дифференциальных уравнений:
а%г / **% \
=Fi\ t, хг хп, — »
/=1, 2, .... л; /=1, 2, .... я,
50 = 0, 1 л8 — 1,
5<>4-$1-г- ··· -г-5л=£/у,

НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
231
то Н. у. определяется значениями функции:
[др*иА
-Ч 1=1, 2, .... я; pfe=0, 1, т-1.
a*p*J/-/.
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ — геометрическая дисциплина, изучающая
способы изображения пространственных форм на плоскости и решение
пространственных задач на плоскости при помощи этих изображений. Особое значение
в Н. г. имеют чертежи, получаемые при помощи проектирования данной
фигуры на плоскость, т. е. проекционные чертежи. В Н. г. рассматриваются в
основном два вида проекции: центральная (перспектива) и параллельная. В
технике часто используют ортогональные проекции фигуры на две и три плоскости
(комплексный чертеж), однако такие чертежи не обладают наглядностью.
Поэтому для построения наглядного чертежа в Н. г. используется другой способ
построения изображений, называемый аксонометрией (см.), при котором фигура
проектируется на плоскость вместе с пространственной системой координат, к
которой она отнесена.
На практике пользуются различными частными случаями аксонометрии,
когда берутся различные коэффициенты (показатели) искажения по осям и
различные углы между осями: изометрия (см.), диметрия и триметрия.
Лит.: Η. Α. Ρ ы н и н, Материалы к истории начертательной геометрии, Ленинградский
автодорожный ин-т им. В. В. Куйбышева, 1938; Н. А. Глаголев, Начертательная
геометрия, Гостехиздат, М., 1963; Н. Ф. Ч етверухин (ред.), Вопросы современной
начертательной геометрии (сб. статей), Гостехиздат, М. —Л., 1947; Е. А. Глазунов
иН. Ф. Четверухин, Аксонометрия, Гостехиздат, М., 1953.
НЕВЫРОЖДЕННАЯ КВАДРАТИЧНАЯ ФОРМА — квадратичная форма (см.),
матрица которой является невырожденной матрицей (см.).
НЕДЕЗАРГОВА ГЕОМЕТРИЯ — геометрия, в которой не имеет места
предложение Дезарга (о гомологических треугольниках). Н. г.—одна из
неевклидовых геометрий.
МодельН. г. имеется в книге Н. А. Глаголева «Проективная геометрия»,
«Высшая школа», М., 1963.
«НЕДЕЛИМЫХ» МЕТОД — различные способы определения отношений
площадей или объемов фигур. Сущность «Н.» м. состоит в том, что
сравниваются «неделимые» элементы (или их совокупности), образующие
рассматриваемые фигуры, отношение площадей или объемов которых требуется найти.
Идея этого метода уходит своими корнями в глубокую древность. Так,
древнегреческий ученый Демокрит считал, что тело состоит из «суммы» очень
малых «неделимых» частиц — атомов. Архимед, используя механические
принципы рычагов, вычислил площади и объемы многих фигур, рассматривая плоскую
фигуру как состоящую из бесчисленного множества параллельных отрезков
прямых, а пространственную фигуру как состоящую из бесчисленного множества
параллельных плоских сечений. Архимед считал, что результаты, полученные
«Н.» м., следует проверять еще методом исчерпывания (см.). Идеи «Н.» м.
были возрождены в математике на рубеже XVI—XVII вв. немецким астрономом
И. Кеплером и особенно итальянским математиком Б. Кавальери, с именем
которого чаще всего и связывают «Н.» м. (см. Принцип Кавальери). В
дальнейшем «Н.» м. был использован также математиками Торричелли, Дж. Валлисом,
Б. Паскалем и др. и послужил началом в создании интегрального исчисления.
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ — в широком смысле все геометрические
системы (геометрии), отличные от геометрии Евклида. Однако чаще всего под Н. г.
(в узком смысле) понимают геометрию Лобачевского (см.) и геометрию Рима-
на (см.).
Геометрия Лобачевского по своей аксиоматике отличается от геометрии
Евклида лишь аксиомой о параллельных, утверждающей, что через точку,

232
НЕЕВКЛИДОВЫ ГЕОМЕТРИИ
не лежащую на прямой, проходит только одна прямая, лежащая с данной прямой
в одной плоскости и не пересекающая ее. В геометрии Лобачевского
допускается существование по крайней мере двух таких прямых, а затем доказывается,
что таких прямых бесконечно много. В геометрии'Римана утверждается
аксиоматически, что две прямые, лежащие в одной плоскости, пересекаются.
Имеются также другие аксиомы (аксиомы порядка, разделенности точек на прямой),
отличающие Н. г. друг от друга. Расположение точек на прямой в геометриях
Евклида и Лобачевского линейное, т. е. соответствует расположению множества
действительных чисел, в геометрии же Римана порядок точек на прямой
циклический, т. е. соответствует расположению точек на окружности (топологической
моделью плоскости Римана является проективная плоскость). В геометрии
Лобачевского сумма внутренних углов треугольника меньше двух прямых; в
геометрии Римана сумма внутренних углов треугольника больше двух прямых, а в
геометрии Евклида эта сумма равна двум прямым. Площадь треугольника в
геометрии Лобачевского выражается формулой:
S=R2(n — α — β — γ),
где α, β, у — углы треугольника, R— некоторая постоянная, зависящая от
выбора единицы измерения площадей. В геометрии Римана площадь
треугольника имеет вид:
5=/Ρ(α+β+γ-π).
где буквенной символике придается аналогичный смысл. В геометрии Евклида
между площадью треугольника и суммой его углов никакой зависимости не
существует.
Существуют другие сходства и различия в Н. г. при синтетическом их
построении.
Н. г. рассматриваются также в плане дифференциальной геометрии, где
дифференциальные свойства их плоскостей аналогичны дифференциальным
свойствам поверхности евклидова пространства. Вводя внутренние координаты и ии
неевклидовой плоскости, дифференциал дуги ds, соответствующий
дифференциалам du и dv координат и и и, определяется формулой:
ds2= Edu2+2Fdu dv+G dv2. (1)
При соответствующих координатах и и υ формула (1) в плоскости Лобачевского
примет вид:
ds2~du2+ch2(-~]dv2, (2)
где сп — косинус гиперболический, R — постоянная (радиус кривизны), а в
плоскости Римана
ds2=du2+co$* [~-j dv\ (3)
При R**oo формулы (2) и (3) принимают вид:
ds2=du2+dv2,
т. е. метрическую форму евклидовой плоскости. Трехмерное пространство
Лобачевского имеет постоянную риманову кривизну k= — — (как, например,
псевдосфера) и относится, как и трехмерное пространство Римана, к числу ри-
мановых пространств (см.) в широком смысле. Пространство Римана имеет по-

НЕЙЛЯ ПАРАБОЛА
233
стоянную положительную кривизну £ = — (как, например, сфера).
Пространство Евклида занимает промежуточное положение между ними и имеет нулевую
кривизну.
Движения в Н. г. можно также рассматривать в теоретико-групповом
плане— как группу автоморфизмов (см.) относительно некоторого абсолюта
(некоторой кривой). При этом абсолют на проективной плоскости модели геометрии
Лобачевского задается уравнением в однородных проективных координатах:
абсолют геометрии Римана имеет уравнение:
В соответствии с уравнениями абсолютов на моделях Н. г. эти геометрии
называются гиперболической (геометрия Лобачевского) и эллиптической (геометрия
Римана).
Модель двумерной евклидовой геометрии задается вырожденным абсолютом:
т. е. группа автоморфизмов рассматривается относительно мнимых точек (1, /, 0),
(1, —/, 0), которые называются круговыми точками (см.).
Лит.: П. С. Александров, Что такое неевклидова геометрия, Изд-во АПН
РСФСР, М., 1950; Ф. Клейн, Неевклидова геометрия, ОНТИ, М. — Л., 1936;
Н. В. Ефимо в. Высшая геометрия, Физматгиз, М., 1953.
НЕЗАВИСИМОСТЬ системы аксиом — одно из основных требований (условий,
свойств) непротиворечивой системы аксиом. Непротиворечивая система аксиом
{Л/} /=1, 2 η называется независимой, если никакая из аксиом At этой
системы не является следствием других аксиом этой же системы. Другими
словами, Н. системы аксиом сводится к минимальности числа аксиом этой системы.
Доказательство Н. системы аксиом сводится к доказательству независимости
каждой аксиомы Л/ от всех остальных аксиом данной системы. Доказательство
же независимости аксиомы Л, от всех остальных сводится к доказательству
непротиворечивости всей системы аксиом, в которой Л,- заменена аксиомой Л/,
противоположной аксиоме Лг·. Например, доказательство независимости аксиомы
параллельности прямых от всех остальных аксиом геометрии Евклида сводится
к доказательству непротиворечивости геометрии Лобачевского.
Вопрос о Н. непротиворечивой системы аксиом рассматривается в
основаниях геометрии, в математической логике. См. также Аксиома,
Непротиворечивость, Полнота.
Лит : Н. В. Ефимов, Высшая геометрия, Физматгиз, М., 1953; П. С.
Новиков, Элементы математической логики, Физматгиз, М., 1959.
НЕЗАВИСИМОСТЬ СЛУЧАЙНЫХ СОБЫТИЙ — важное понятие теории
вероятностей. Применительно к двум случайным событиям А и В независимость
означает следующее: вероятность наступления одновременно двух событий А и В
равна произведению вероятностей наступления каждого из них в отдельности.
В предположении Н. с. с. доказываются многие теоремы теории вероятностей.
Лит.: Б. В. Гнеденко. Курс теории вероятностей, Физматгиз, М., 1961.
НЕЙЛЯ ПАРАБОЛА — иначе полукубическая парабола (см.). Н. п. названа
по имени английского математика У. Нейля, нашедшего длину ^е дуги.

234
НЕЙМАНА ЗАДАЧА
НЕЙМАНА ЗАДАЧА — состоит в отыскании решения уравнения Лапласа
\и=0 в некоторой области, имеющего на границе области заданную нормаль-
ди I
ную производную: — =/(s). Необходимое и достаточное условие
разрешись |г
мости: f/(s)ds=0. Решение определяется с точностью до аддитивной
произвольной постоянной. Граница области в условии задачи должна в каждой точке
иметь касательную плоскость.
НЕОБХОДИМОЕ УСЛОВИЕ для выполнения какого-либо верного
утверждения (предложения, суждения) — всякое условие, без осуществления которого
данное утверждение заведомо неверно.
Например, Н. у. делимости целого числа на 4 является делимость его
последней цифры на 2, т. е. деление последней цифры на 2 должно быть
обязательным (минимальным) условием того, чтобы данное целое число делилось на 4.
Но это Н. у. еще не является достаточным (см. Достаточное условие), т. е.
число может оканчиваться на четную цифру, однако оно может и не делиться
на 4. Достаточным условием делимости целого многозначного числа на 4
является, например, то, что оно оканчивается на 28. Однако это достаточное
условие не является необходимым, т. е. число может делиться на 4 и без того,
чтобы оканчиваться на 28. Необходимым и достаточным условием делимости
целого числа Ν(Ν>\0) на 4 является следующее: двузначное число, на которое
оканчивается данное число, должно делиться на 4.
Необходимое и достаточное условие называют также необходимым и
достаточным признаком. Если прямая и обратная теоремы Еерны, то эти две
взаимно обратные теоремы можно сформулировать в виде одной теоремы в терминах
«необходимо и достаточно». Таким образом, Н. у. и достаточное тесно связаны
с прямой и обратной теоремами. Выражение «необходимо и достаточно» в
формулировках теорем часто заменяется выражением «тогда и только тогда», «в том
и только втом случае», «те и только те». Понятие о необходимом и достаточном
условии является одним из важнейших в математике.
См. также Теорема, Взаимно обратные теоремы, Геометрическое место
точек.
Лит.: В. В. Репьев, Общая методика преподавания математики, Учпедгиз, М.,
1958; П. С. Моденов, Сборник задач по специальному курсу элементарной
математики, «Советская наука», М., 1957; И. С. Г ρ адштейн. Прямая и обратная теорема,
Физматгиз, М., 1959.
НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА: 1°. Н. у. э. функции одной
переменной y=f(x) в точке х0 состоит в том, чтобы производная /'(*) в этой
точке была равна нулю [/' (х0)=>0] или не существовала.
2°. Н. у. э. функции нескольких переменных в точке (х°{, х°2, ...» х„)
состоит в том, чтобы все частные производные u~f(xlt х2, . . . , Хп ) обращались
в этой точке в нуль:
= 0, / = 1, 2, . . . , η
dxi
или хотя бы одна из частных производных не существовала.
η η
НЕОПРЕДЕЛЕННАЯ ФОРМА — квадратичная форма ^ $3 aUxix/ с дей-
/=1 /=!
ствительными коэффициентами, которая при действительных значениях
переменных может принимать как положительные, так и отрицательные значения;
например, х\ — х\.

НЕОПРЕДЕЛЕННЫЕ ВЫРАЖЕНИЯ
235
НЕОПРЕДЕЛЕННОЕ УРАВНЕНИЕ — уравнение, содержащее более одного
неизвестного. Н. у. имеет, как правило, бесконечное число решений. Обычно
ищут решения Н. у. в целых или рациональных числах. См. также Диофанто-
вы уравнения.
НЕОПРЕДЕЛЕННЫЕ ВЫРАЖЕНИЯ. Иногда при формальной подстановке
числа а под знак функции F(x) и дальнейшем вычислении значения функции
приходят к выражениям вида:
О оо
а) "Г. б) —". в) оо — оо, г) 0°, д) 1», е) оо°.
0 оо
Э^и выражения с точки зрения алгебры являются бессмыслицей, но исходя из
понятий математического анализа удобно придавать им в некоторых случаях
определенный смысл. Именно, если F(х) непрерывна (см.) в некоторой
окрестности точки х=а, исключая саму точку а, под F(a) понимают
\imF(x).
х-*а
Вычисление этого предела есть раскрытие неопределенности (см.) (см. также
Лопиталя правило). Функцию F (х), имеющую в точке х=а неопределенность
одного из указанных выше типов, можно изменить так, чтобы неопределенность
0
новой функции имела вид а) —, а именно:
б) limq>(;:)=oo, lim\|)(x) = oo, Р(л) = -Ф(х) °°
х-*а х~»а ψ (χ)
1
lim—^—= 0, Πηι—[—=-0; ρΜ = Λίύ-=1.
χ->α Ψ (χ) χ-*α <Κ*) 1 0
φ(χ)
β) lim φ(χ)=οο, 1ίπιψ(χ)=οο§ F(x)=y(x) — Ψ(λ;)=οο—>οο§
χ-*α χ->α
1ίΓηβ-Ψ^ = 0, lim*-*<*> = 0; ^(*>β«=*^β-£;
χ-^α χ-*α e—φ(*) 0
г) <P(Jt)>0 (*=£0), Нтф(л:)=0, Пт\|)(л:)=0<
х->а х-*а
F(*H φ (*)*<*> = О0.
1 ψ (а:) 0
1ίπιψ(χ)=0, lim— — -0, \nF(x)= , =-;
к-*а x-+a In φ (χ) Ι 0
In φ (α:)
д) <p(*)>0 (хфа), lim ψ (*)=«>. lim<p(x)=l, F (χ) = ψ(χ)'Ηχ)= Ι00,
χ->α χ-+α
Ππι1ηφ(χ) = 0,
X-+CL
1 , Ιπφ(λ') 0
lim =0, lnF(*)= -л—- = 7Γ*.

236 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
е) <р(х)>0 (хфа), lim φ (*)-<», Нтг|?(*)=0, F(x) = y(x)]* <*) = оо°.
1 ф(х) О
Нт*(*)-0, Нт- 7~Г=0, lnF(*) = -—.
х^а х-»а In φ (л:) / 1 \ О
\ Ιηφ(χ) /
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ — совокупность всех примитивных, или
первообразных, функций (см.) для данной функции /(*), обозначается j f(x) dx.
Разность любых двух таких функций равна константе. Н. и. связан с
определенным интегралом (см.) формулой Ньютона — Лейбница (см.):
ь
§f(x)dx=F(b)-F(a),
а
где F (х) — одна из первообразных, если f{x) — непрерывная функция.
Н. и. обладает следующими свойствами: 1) f α f(x)dx*=a \f(x)dxt где α —
произвольное число; 2) Г [/ (x)-\-g (x))dx= f / (χ) dx-\- fg (χ) dx (свойства
линейности Η. и.); 3) $f(x)dg{x)-fix)gix) — jg(x)dfix).
Достаточным (но не необходимым) условием существования Н. и. является
непрерывность данной функции f(x) на рассматриваемом интервале.
НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ МЕТОД — метод, применяемый
для нахождения коэффициентов выражения в случае, когда вид этого выражения
заранее известен. Например, всякая рациональная функция (см.) может быть
разложена на сумму простых дробей. Пусть требуется найти такое разложение,
например, для функции
Зд:2 — 1
x(x2—1)'
Записываем ее в виде:
Зх2 — 1 _Л В С
х(х2— 1)" х+ х — 1 + л + 1 '
где коэффициенты А, Вч С подлежат определению. После освобождения от
знаменателя и группировки подобных членов получаем:
(А+В+С) х2+(В- С)х— ,4=3*2 _ h
Так как последнее равенство должно выполняться при всех х, то коэффициенты
при одинаковых степенях χ в левой и правой частях должны быть равны, откуда
Л+£-гС = 3, Б—С=0, Л=1. Следовательно, Л=£=С=1 и
За:2—1 _ 1 1 1
λ:(λ:- — Ι)"" χ + х— 1 + х+1 *
Этот метод широко применяется в математике.
НЕОСОБЕННАЯ МАТРИЦА-—квадратная матрица ,4 = (а,у) порядка л (число
строк равно числу столбцов), определитель которой D(A) отличен от нуля.
Ранг Н. м. А порядка η равен /г.

НЕПЕРА ПАЛОЧКИ
237
Если ранг квадратной матрицы меньше п, т. е. £>(Л)=0, то матрица
называется особенной. Всякая Н. м. А имеет единственную обратную матрицу Л—1,
т. е. такую, что АА—1=A-~1A=Et где Ε — единичная матрица, определяющая
в я-мерном пространстве тождественное линейное преобразование (см.). Всякая
Н. м. А в n-мерном пространстве задает невырожденное линейное
преобразование в любом базисе. Формулы преобразования координат также определяются
Ы. м. Н. м. называется также невырожденной матрицей или регулярной. См.
Матрица, Единичная матрица.
НЕПЕРА ПАЛОЧКИ — простейшее приспособление для выполнения
операции умножения многозначных чисел. Н. п. состоят из набора нескольких
полосок (картонных, деревянных или каких-либо других), на которых изображены
цифры, как указано на рисунке 157, а% т. е. сверху каждой полоски стоит
Рис. 157
цифра от 0 до 9, а ниже в клеточках, разделенных диагональю, записаны все
произведения этих цифр на все однозначные числа. При этом цифра десятков
двузначного произведения стоит в клетке слева, выше цифры единиц
произведения, т. е. цифра десятков стоит над диагональю клетки, а цифра единиц
произведения — под диагональю той же клетки. Для выполнения действия
умножения может потребоваться несколько одинаковых полосок.
Пусть требуется умножить число 6723 на однозначное число. Берем Н. п.
с цифрами сверху 6, 7, 2 и 3 (рис. 157, б), т. е. 6-ю, 7-ю, 2-ю и 3-ю палочки,
и кладем их рядом. Тогда произведение, например, числа 6723 на 4 читается
справа налево по горизонтальной линии (полосе), стоящей под номером 4, при
этом произведение состоит из таких цифр (указанных стрелкой в направлении
диагонали): из 2 единиц, 8-f 1 = 9 десятков, 8-f-0=8 тысяч, 4+2=6 десятков
тысяч, 2 сотен тысяч. Итак, 6723-4=26 892.
Н. п. удобнее применять вместе с другими средствами вычислений (счеты,
арифмометр и др.).
Н. п. редко употребляются, однако умножение на них производится
быстрее, чем письменно, но, конечно, гораздо больше потребует времени, чем
умножение на арифмометре, на счетной линейке (приближенное вычисление) или
умножение с помощью специальных таблиц (О'Рурка или М. В. Яковкинаи др.).
Лит.: В. М. Бр а д и с, Устный и письменный счет. Вспомогательные средства
вычислений с*нц элем матем., т. 1, Гостехиздат, М., 1951.

238
НЕПЕРОВЫ АНАЛОГИИ
НЕПЕРОВЫ АНАЛОГИИ. Н. а. называются следующие формулы
сферической тригонометрии (см.):
a— b a — b
_ sin cos
А —В 2 С A+B 2 С (*\
*«-2—^TctgT; tg—=~^jTctgT:
sin cos
A-B A-B
sin—-— t cos —
g 2 Λ+β tg 2' g 2 Л+β g 2* ( }
sin—-— cos—-—
Эти формулы удобны для логарифмирования при «решении» сферических
треугольников по данным двум сторонам а и b и углу С между ними (*) или по
данной стороне с и прилежащим к ней углам А и В (**). Формулы (*) и (**) в
некоторой степени аналогичны и были получены английским математиком Г. Бриг-
гом (*) и шотландским математиком Д. Непером (**) в виде пропорции.
Греч, αυαλογια — пропорция.
НЕПЕРОВЫ ЛОГАРИФМЫ— то же самое, что и натуральные логарифмы
(см.). Название Н. л. исторически неоправданно. См. также Логарифм.
НЕПЕРОВО ЧИСЛО —число e=\im(n+—Υ* = 2,718281828459 ... Η. ч.—
трансцендентное число (доказано впервые французским математиком Ш. Эрмитом
з 1873 г.). Играет большую роль в высшей математике и ее приложениях.
Название числа по имени шотландского математика Непера мало обоснованно.
См. также Натуральные логарифмы.
НЕПОДВИЖНАЯ ТОЧКА преобразования — точка, которая в
рассматриваемом преобразовании соответствует сама себе (переходит сама в себя).
Например, в преобразовании симметрии с данной осью симметрии / каждая точка
оси симметрии является Н. т., т. е. остается на месте в этом преобразовании; в
преобразовании гомотетии H(S, k) с центром s и коэффициентом кфО точка
S есть Н. т.
Кроме Н. т., рассматривают также неподвижные прямые, неподвижные
плоскости, неподвижные окружности например, в инверсии (см.) и т. д.
Неподвижные прямые могут быть как точечно-инвариантные, когда каждая точка
прямой преобразуется в себя, так и не являющиеся точечно-инвариантными,
когда прямая остается неподвижной в целом, но каждая ее точка (или
некоторое множество ее точек) преобразуется в другие точки, лежащие на той же
прямой. Так, ось симметрии есть точечно-инвариантная прямая, в то время как
прямые, перпендикулярные оси симметрии, не являются точечно-инвариантными.
Н. т., неподвижная прямая, неподвижная плоскость и т. д. называются
неподвижными или двойными элементами преобразования.
В терминах Н. т. может быть сформулирован ряд глубоких теорем
анализа и дифференциальных уравнений. Так, теорема существования и
единственности решения уравнения y' = f(x, у), у(0)=0 при выполнении обычных условий
эквивалентна утверждению, что у преобразования
X
z=lf(x, y(x))dx
О

НЕПРЕРЫВНАЯ ГРУППА
239
в пространстве функций есть единственная Н. т. — искомая функция у (х).
Имеет место знаменитая теорема о Н. т. в топологии (см.). Сформулируем ее
частный случай. При любом непрерывном отображении круга x2-f-y2^l в себя
существует по крайней мере одна Н. т.
Лит.: Д. М. Гильберт и Кон Фоссен, Наглядная геометрия, Гостехиздат,
М. — Л., 1951; Л. С. Понтрягин, Основы комбинаторной топологии, Гостехиздат,
М. — Л., 1947.
НЕПОЛНОЕ КВАДРАТНОЕ УРАВНЕНИЕ— квадратное уравнение, в кото
ром равен нулю коэффициент при неизвестном в первой или нулевой степени,
или оба эти коэффициента вместе (одновременно). Следовательно, Н. к. у. имеет
одно из следующих видов:
ах*-f-fo=0 (α=£0), или ах2+с=0 (афО), или ах2=0 (афО).
НЕПОЛНОЕ ЧАСТНОЕ: 1°. Н. ч. в арифметике — целая часть отношения
двух целых чисел а и Ь, из которых а>Ь и а не делится на Ь. Например,
7
Н. ч. отношения -— равно 2, число 7 — делимое, число 3 — делитель, остаток
о
от деления 7 на 3 равен 1. Делимое равно Н. ч., умноженному на делитель,
сложенному с остатком.
2°. Н. ч. в алгебре — многочлен q(x), который получается при делении
многочлена f(x) на ц(х)фО из кольца Р[х] и удовлетворяет соотношению:
f(x) = g(x)q(x)+r(x),
где степень г(х)^0 меньше степени g(x). Многочлен г (х) называется остатком
от деления f(x) на g(x). Иногда Н. ч. q(x) от деления f(x) на g(x) при
г(х)фО называется также частным, а деление f(x) на g(x) называется
делением с остатком г (х)Ф0. Для любых двух многочленов f(x), g(x) из кольца
Ρ [χ] многочлены q (χ) и г (χ) однозначно определяются.
Лит.: С. И. Новоселов, Специальный курс элементарной алгебры, «Советская
наука», М., 1956; А. И. Маркушевич, Деление с остатком в арифметике и алгебре,
Изд-во АПН РСФСР, 1949; Энц. элем, матем., т. 2, Гостехиздат, М. —Л., 1951.
НЕПРАВИЛЬНАЯ ДРОБЬ: 1°. Н. д. в арифметике — обыкновенная дробь,
3 8
у которой числитель больше или равен знаменателю, например: —, —.
2 8
Н. д. первого вида можно записать в виде смешанного числа, состоящего из
целой и дробной части:
3 1 1
—«1-f-—=1—. Всякое смешанное число можно записать в виде Н. д., на·
3 2.7+3 17
пример: 2у=——=у.
/(■*)
2°. Н. д. в алгебре — отношение двух многочленов , где степень
g(x)
f(x) не ниже степени g(x). См. также Дробь.
НЕПРЕРЫВНАЯ ГРУППА (или топологическая группа) — группа (см.),
множество элементов которой образует топологическое пространство (см.);
операции группового умножения и перехода к обратному элементу непрерывны в
топологии пространства. Например, множество рациональных чисел на прямой,
взятых в их естественной метрике (см.), образуют Н. г. Одним из самых
глубоких результатов теории Н. г. является теорема: Н. г., являющаяся в то же
время многообразием (см.), есть группа Ли (см.).
Лит.: Л. С. Понтрягин, Непрерывные группы, Гостехиздат, М., 195*

240
НЕПРЕРЫВНАЯ ДРОБЬ
НЕПРЕРЫВНАЯ ДРОБЬ — выражение вида
1
I
αι+
t
где Яо — любое целое число (не обязательно положительное), аь а2» · · ·» αη —
натуральные числа, называемые неполными частными, или элементами данной
Н. д. Н. д. кратко обозначается так: [а0, alt α2» · · · » яп]или[а0, #ι» #2 · · · »
αηί ...,], в зависимости от того, конечная ли Н. д. или бесконечная.
Всякое рациональное число может быть представлено в виде конечной
Н. д., иррациональное же число Н. д. представляется в виде бесконечной Η. д.;
эти разложения единственны, при этом квадратические иррациональности
разлагаются в периодические Н. д. (см. Лагранжа теорема), например: у^=[1; 2,
2, . . .J. Н. д. [Oq, alf α2* · · · · ci/il (k<n)f записанная в виде несократимой
Ph
дроби —, называется подходящей дробью порядка k. Числитель и знамена-
Qh
те ль подходящей дроби связаны рекуррентной формулой:
^Λ+ιβα*+ι^+^Α—ь Qk+i=ak+iQh+Qh-i-
Для каждой бесконечной Н. д. существует единственный предел
hm— = α,
который называется значением этой Н. д. Н. д. используются для
приближенного выражения иррациональных чисел рациональными — подходящими дробями.
22
Например, приближенные значения числа π есть подходящие дроби — и
335
—. Французский математик Лиувилль доказал, что если α — алгебраическое
11«3
число степени η > 1, то можно подобрать такую постоянную с, что для любой
χ Ι χ
рациональной дроби — будет выполняться неравенство α — —
гими словами, нельзя заменить алгебраическое иррациональное число α рацио-
х
нальной дробью—(с любым фиксированным знаменателем) так, чтобы разность
У
между ними по абсолютному значению была сколько угодно малой. Действия
над Н. д. весьма громоздки, что затрудняет их использование на практике.
Н. д. иначе называются цепными дробями.
Н. д. также называют и выражение вида:
а0+ !
г/.,
ь + ^ .
'и
>-^. Дру-

НЕПРЕРЫВНАЯ ФУНКЦИЯ
241
Г а> 1°°
которое обозначают кратко так: α0; —~- , или, если ах и Ьг следуют
другому закону, чем все остальные ап и bn, H. д. обозначают так:
ап
Дробь— называется я-ным звеном Н. д., ап и Ьп — членами я-го звена Η. д.;
°п
числа аъ а2* · · · называются частными числителями Н. д., а числа 6Х,
Ьъ ... — частными знаменателями Н. д.
Термин Н. д. (лат. fractio) был впервые введен Л. Эйлером (1737).
Лит.: А. Я. Хин чин, Цепные дроби. Г©стехиздат, М.—Л., 1949; Л. Эйлер,
Введение в анализ бесконечно малых, т. 1, перев. с лат., М.—Л.. 1931; Т. И. Стильтьес,
Исследования о непрерывных дробях, перев. с франц., Харьков — Киев, 1936; А. Н.
Хованский, Приложение цепных дробей и их обобщений к вопросам приближенного
анализа, Гостехиздат, М., 1956; Энц. элем, мат., т. 1, Гостехиздат, М.—Л., 1951; Н. Г.
Чеботарев, Теория непрерывных дробей, Казань, 1938.
НЕПРЕРЫВНАЯ ПРОПОРЦИЯ— геометрическая пропорция (см.), у которой
средние члены равны. Например, пропорция 9:6=6: 4 есть Н. п.; каждые три
последовательных члена геометрической прогрессии, следовательно, образуют
Н. п. Н. п. также называется и арифметическая пропорция вида а — b=b—с,
однако термин «непрерывная арифметическая пропорция» мало употребителен.
НЕПРЕРЫВНАЯ ФУНКЦИЯ в точке Р0(х°{, xjj, . . . , х°) — функция
/(P)—f(хц *2* ·· -f Xn)> удовлетворяющая условию: для любого ε>0
найдется такое б, что для всех точек Р(хг, х2 хп)> подчиняющихся
условиям \Xi — Xi\ <δ, /=1, 2 л, выполняется неравенство | f(P) —f(P0) [<ε.
Другими словами, f(P) непрерывна в точке Р0, если при стремлении Р—>Р0
f(P) стремится к f(P0)· Функция, непрерывная в каждой точке множества М,
называется Н. ф. на множестве Λί.
График Н. ф. одного переменного на связном множестве есть непрерывная
линия* которая, однако, может сильно отличаться от наивного представления о
непрерывной кривой. Так, существуют Н. ф., нигде не имеющие производной.
Их графики представляют собой непрерывные кривые, нигде не имеющие
касательной. Пример такой функции впервые был построен немецким математиком
Вейерштрассом.
Н. ф. обладают многими важными свойствами: Н. ф. на компактном
множестве (см.) достигает своего наименьшего и наибольшего значения;
сумма, разность, произведение Н. ф. являются Н. ф.; суперпозиция
(см.) двух Н. ф. есть также Н. ф. (см. также Ролля теорема). Всякую Н. ф.
}(х) на отрезке \а, Ь\ с любой степенью точности можно приблизить многочле
ном (теорема Вейерштрасса). Н. ф. на компактном множестве является равно
мерно непрерывной. Все эти свойства придают особую важность Н. ф. для
многих разделов математики.
По классификации Бэра Н. ф. относятся к нулевому классу. В более
абстрактной форме Н. ф. рассматриваются не только на множествах в
пространстве переменных хи x2t . . ., хп* но и на произвольном множестве
топологического пространства (см.). Примеры: все многочлены, а также функции е*,
sin*, cos x являются Н. ф. на всей числовой прямой; y=tgx непрерывна всю·
я:
ду, кроме точек *= — (2£-fl), А = 0, 1, 2, —, п, где она не определена;
y*=\gx непрерывна во всей области определения 0<х<оо; у=χ sin — [у (0)«
χ
~0] непрерывна на всей прямой, однако в точке *=0 не имеет производной.
16 Толковый словарь математических терминоз

242
НЕПРЕРЫВНОСТИ АКСИОМЫ
НЕПРЕРЫВНОСТИ АКСИОМЫ — аксиомы, выражающие в той или иной
форме непрерывность прямой линии. Одной из Н. а. является аксиома Деде-
кинда: если все точки отрезка прямой разбить на два класса, каждый из
которых не пуст, так, что: 1) каждая точка отрезка АВ принадлежит только
одному классу, — точка Л ζ первому классу, точка В ^второму классу; 2) каждая
точка χ первого класса, отличная от А, лежит между точкой А и произвольной
точкой у второго класса; 3) каждая точка у второго класса, отличная
от Б, лежит между произвольной точкой χ первого класса и точкой β, — то
существует такая точка С, что она принадлежит любому отрезку [х> у], где
χ и у — произвольные точки первого и второго классов соответственно. Сама
точка С может принадлежать или первому или второму классу точек. Можно
доказать, что точка С (граничная точка или точка дедекиндова сечения)
единственная. Аналогично аксиома Дедекинда формулируется для прямой и луча. Иногда
вместо неопределимого термина «между» используют также неопределимые
термины «предшествует»,' «лежит левее», «лежит правее».
Вместо одной Н. а. — аксиомы Дедекинда — иногда используют
равносильные ей две аксиомы: аксиому Кантора (любая последовательность вложенных
друг в друга сегментов, стремящихся к нулю, имеет одну общую точку), и
Архимеда аксиому (см.), или другие равносильные аксиомы.
Н. а. позволяют установить взаимно однозначное соответствие между
множеством всех точек прямой и множеством всех действительных чисел. Н. а. дают
возможность доказать ряд теорем элементарной геометрии: пересечение прямой,
проходящей через внутреннюю точку круга, с его окружностью только в двух
точках, пересечение двух окружностей, расположенных определенным образом
на плоскости; позволяют установить существование длины отрезка и решить
обратную задачу при измерении отрезков: доказать теорему о том, что для
всякого действительного числа α существует отрезок, длина которого равна
этому числу а. См. Длина.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ—свойство функции быть непрерывной. См.
Непрерывная функция.
НЕПРЕРЫВНОСТЬ ФУНКЦИИ СПРАВА (соответственно слева) — функция
y=f(x) называется непрерывной справа (слева) в точке х=а, если бесконечно
малому приращению Δ*>0 (соответственно Δ*<0) независимой, переменной
соответствует бесконечно малое приращение функции
Ay=f(x+bx) — f(a),
или, что равносильно, если lim /(#)=/(α), (соответственно lim /(*) = /(α), т.е.
х-+а-\-0 *-*α—0
предел функции справа (см.) (соответственно слева) равен значению функции
НЕПРИВОДИМОЕ УРАВНЕНИЕ над полем Р—алгебраическое уравнение (см.),
/(*)=0,
где f(x) — неприводимый многочлен (см.) над тем же полем Ρ (см.). Например:
х2-|-1=0 — Н. у. в поле вещественных чисел, но приводимое над полем
комплексных чисел. Если / (х) — приводимый многочлен, то разложение его на
множители
f{x) = p(x)-q(x)
позволяет свести уравнение f(x)=0 к эквивалентной совокупности уравнений:
Р(*) = 0,
д(х)=0
меньшей степени и, следовательно, более простых.
НЕПРИВОДИМЫЙ МНОГОЧЛЕН над заданным полем (см.) Ρ— многочлен,
не разлагающийся на множители — многочлены степени выше нуля с коэффи-

НЕРАВЕНСТВО
243
циентами из поля Р. Во всяком алгебраически замкнутом поле (см.)
единственными Н. м. являются многочлены степени не выше первой.
Примеры: над полем вещественных чисел всякий Н. м. с вещественными
коэффициентами есть либо константа, либо многочлен первой степени, либо
квадратный трехчлен с дискриминантом (см.), меньшим нуля; в поле
рациональных чисел существуют Н. м. любой (сколько угодно высокой) степени.
Роль Н. м. в кольце (см.) многочленов Ρ [χ] аналогична роли простых
чисел в кольце целых чисел. Справедлива основная теорема теории делимости
многочленов, аналогичная основной теореме арифметики в кольце целых чисел.
Как видно из примеров, многочлены, неприводимые над одним полем, могут
быть приводимыми над другим полем.
Ввиду громоздкости общих методов практического решения вопроса о
приводимости или неприводимости многочленов в разное время различными
математиками было найдено и доказано довольно большое число частных критериев
неприводимости многочленов. Однако все эти критерии содержали лишь условия
достаточные (а не необходимые) для неприводимости многочленов, т. е.
позволяли устанавливать неприводимость многочленов только того или иного весьма
частного типа.
В 1938 г. М. В. Яковкиным были найдены, а в 1940 г. опубликованы
весьма простые критерии, содержащие условия необходимые и достаточные для
приводимости или неприводимости любых многочленов в поле рациональных чисел,
т. е., в отличие от других критериев, позволяющие решать вопрос о
неприводимости многочленов в общем виде.
Лит.: А. Г. Курош, Курс высшей алгебры, Гостехиздат, М., 1952; Г. М.
Шапиро, Высшая алгебра, Учпедгиз, М., 1938; Б. Л. Ван дер Варден, Современная
алгебра, перев. с. нем., ч. 1 и 2, Гостехиздат, М., 1947; М. В. Яковкин, Численная
теория приводимости многочленов, Изд-во АН СССР, М., 1959.
НЕПРОТИВОРЕЧИВАЯ СИСТЕМА уравнений — то же, что и совместная
система уравнений (см.).
НЕПРОТИВОРЕЧИВОСТЬ системы аксиом — одно из важнейших требований
(условий, свойств) системы аксиом. Система аксиом называется
непротиворечивой, если из нее нельзя логически вывести два взаимно исключающих друг
друга предложения. Если система аксиом не обладает этим свойством, то она
называется противоречивой. Противоречивая система аксиом не может быть
пригодной для обоснования научной дисциплины.
Доказательство Н. системы аксиом сводится к построению модели
(реализации, интерпретации), т. е. такому набору элементов, играющих роль основных
объектов (но уже другой природы), для которых устанавливаются основные
отношения между ними, в точности отображающие основные отношения между
основными объектами первоначальной системы аксиом. Н. системы аксиом
называется также совместностью системы аксиом.
См. также Аксиома, Независимость, Полнота.
НЕРАВЕНСТВО — два алгебраических выражения, соединенные знаком
неравенства (>, <—знаки Н.). Решением Н., содержащего неизвестные
(переменные), называется множество всех действительных значений этих неизвестных,
удовлетворяющих Н. Например, решение Н. х>2 есть множество всех
действительных чисел, расположенных на числовой оси правее точки с абсциссой х=2.
Решением Η. χζ<χ является множество чисел промежутка (0; 1), т. е.
0<*<1 (рис. 158). Решением Н. \х — 21<5 является множество значений χ
(рис. 159), удовлетворяющих двойному неравенству —3<jc<7 (т. е. трем алгес*-
раическим выражениям, соединенным двумя знаками Н. вида А<В<С или
А>В>С и т. д.).
При решении Н. широко используют геометрические (графические)
интерпретации.
16·

244
НЕСОБСТВЕННОЕ ПОДМНОЖЕСТВО
Алгебраическое Н., справедливое при любых допустимых значениях букв
(известных и неизвестных), входящих в Н., а также верное числовое
неравенство, называются тождественными Н. Например, a2-f*a-J-l>0; а2>а2—1; 5>3 —
тождественные Н.
Два Н., содержащие одни и те же неизвестные, называются равносильными
(эквивалентными), если они имеют одно и то же решение. Например,
неравенства: | дс | < 2 и дг2 — 4<0 — равносильны. Решение Н. рассматривается
относительно только действительных чисел или какого-либо их подмножества
(например, относительно целых чисел, относительно положительных чисел).
с>
а.
/ 2
■*/
У//////////<(//(//{///////////<
J -J-2-* 0 1 2 3 4 5 6 7
Рис. 158 Рис. 159
Аналогично определяется равносильность двух систем Н.; система же
неравенств определяется аналогично системе уравнений. Два алгебраических
выражения, соединенные знаком > (большее или равно, т. е. не меньше), или
< (меньшее или равно, т. е. не больше), или знаком > (значительно больше),
или < (значительно меньше), также называют Н.
Свойства Н., классификация их во многом аналогичны свойствам и
классификации уравнений.
Примеры:
ах + Ь9 а Ф 0— уравнение пер- ах+Ь>0, α Φ О, — Н. первой
вой степени (линейное уравнение); степени (линейное Н.);
ax2+bx+c=0 — уравнение второй ах2+Ьх-\-с>0 или ax2+bx+c<0 —
степени (квадратное уравнение); Н. второй степени (квадратное Н.);
а^+а^х"—*+ ··· +ал=0 — ал- α^χη+α\Χη~χ+ ··· +ап>0 (или
гебраическое уравнение л-й степени <0) — алгебраическое Н. я-й степени;
с одним неизвестным; \gx>2 (lg χ < 2) —- логарифмиче-
lg χ=2 — логарифмическое (транс- ское (трансцендентное) Н.
цендентное) уравнение.
Понятие Н. используется в оценочных (приближенных) формулах во многих
разделах математики. См. также Гёльдера неравенство, Коши неравенство, Лаг-
ранжа неравенство, Минковского неравенство, Средние.
Лит.: П. И. Коровкин, Неравенства, Гостехиздат, М.—Л., 1951; Г. Л. Η е в я
некий, Неравенства, Учпедгиз, М., 1947; X а р д и Г. Г. и др., Неравенство, ИЛ, М.,
1948.
НЕСОБСТВЕННОЕ ПОДМНОЖЕСТВО множества Л —пустое множество (см.),
а также само множество А, рассматриваемое как свое подмножество.
НЕСОБСТВЕННЫЙ ИНТЕГРАЛ — обобщение понятия интеграла Римана,
для существования которого необходимо, чтобы подынтегральная функция была
ограниченной, а отрезок интегрирования имел конечную длину. Если функция
f{x) интегрируема на любом конечном отрезке [ал М] с фиксированной
начальной точкой и для достаточно больших М% то
м
lim [f(x)dx,
Μ-χχ>ί

НЕСОБСТВЕННЫЙ ИНТЕГРАЛ
245
если он существует, называется Н. и. функции f(x) на [at oo] и обозначается
lf{x)dx.
а
В этом случае говорят также, что Н. и. сходится. Аналогично
Ъ ь
f / (*)</*=lim \f(x)dx
со Μ
lim 11
Μ -*οο Λ'
ί f(x)dx= lim \f(x)dx.
*> \Л -*.rv> λ/
N
Если функция f(x) интегрируема на отрезке [α+ε> Ь] при любом достаточно
малом ε и неограничена в окрестности точки я, то по определению
ь ъ
\f(x)dx=\\m f f(x)dx>
если он существует, называется Н. и. функции f(x) на отрезке \а, 6].
Аналогично— для случая, когда f(x) не ограничена в точке Ь. Общий случай Н. и.
сводится к рассмотренным с помощью разбиения участка интегрирования на
подходящие части. Так, например,
оо —Ι —ε
l — dx^ lim i ■ dx -f lim I
J V x(x*+\) A— J V x(x* + \) ~°J
/ x{x4+\)
—1
1 Μ
+ lim l -dx+ lim I - dx = 0.
ε 1
b\ oo
Если Η. и. ( I /( χ) I dx сходится, то сходится и соответствующий Н. и. для
—oo; a
f(x) (абсолютная сходимость). Возможны случаи, когда обратное неверно
(условная сходимость). Н. и. находят в математике большое применение. Так,
преобразование Фурье f(t)-+g(u)4 имеющее многочисленные применения при
решении задач математической физики, определяется с помощью Н. и:
оо
e(u)=——\f{t)e dt.
(")="—~ Г/
Гамма-функция, широко используемая в аналитической теории чисел и
теории специальных функций, определяется формулой:
оо
T(z)=\ xz-4~xdx.
О

246 НЕСОБСТВЕННЫЙ ОТНОСИТЕЛЬНЫЙ ЭКСТРЕМУМ
Преобразование Лапласа выражается через Н. и.:
F(p)-L[/(0J-T/(0«-p,«tt.
о
Лит.: Л. В. Канторович, Определенные интегралы м ρ "да Фурье, изд.
Ленинградского ун-та, 1940; Г. М. Фихтенгольц, Курс диффере»н/«адьного и интегрального
исчисления, т. 2, Гостехиздат, М.—Л., 1951; П. П. Коровкин, Определенный интеграл
и ряды, Учпедгиз, М., 1959.
НЕСОБСТВЕННЫЙ ОТНОСИТЕЛЬНЫЙ ЭКСТРЕМУМ объединяет понятия
несобственного относительного максимума и несобственного относительного
минимума; о них см. термины Относительный максимум и Относительный минимум.
НЕСОБСТВЕННЫЙ ЭКСТРЕМУМ объединяет понятия несобственного
максимума и несобственного минимума, о которых см. термины Максимум и
Минимум.
НЕСОБСТВЕННЫЕ ЭЛЕМЕНТЫ в геометрии — элементы (точки, прямые,
плоскости), которыми пополняются соответственно евклидова прямая, плоскость
и пространство при изучении проективной геометрии (см.). Если в евклидовой
плоскости из центра S (рис. 160) проектировать
точки прямой 1Х на прямую /2, то М1-+М2 (Мх
проектируется в Λί2), но М0 (SM0 || /2) ни в
какую точку евклидовой прямой не спроекти-
руется. Чтобы устранить этот недостаток —
отсутствие взаимно однозначного соответствия
между точками прямой 1г и /2, прямые
дополняют несобственными (бесконечно
удаленными) точками. При этом пополнении
прямых Н. э. точке М0 ζ Ιχ будет соответствовать
точка Μ £°£ /2; аналогично точке у2 прямой
h(Sy2 II ^ι) будет соответствовать точка у™
прямой 1г. Все параллельные прямые
евклидовой плоскости в расширенной (проективной) плоскости,
пополненной несобственными точками (несобственной прямой), будут иметь общую
несобственную точку пересечения. Но введя Н. э. на плоскости, мы уже их не
отличаем от обычных (конечных), собственных элементов, они равноправны
с собственными элементами. Аналогично вводится несобственная прямая и
несобственная плоскость в пространстве.
Заметил!, что при пополнении пространства Евклида Н. э. мы получаем
новые неевклидовы геометрии (см.).
НЕСОВМЕСТНАЯ СИСТЕМА уравнений — система, не имеющая решений.
Например:
sin х+ sin у=1,
х-г-У^О.
Это Н. с. у., так как у=— х, sin χ+·sin (— jt)=sin x — sin x=0, что
противоречит первому уравнению системы. В линейной алгебре рассматриваются
Н. с. у. линейных (см. по этому поводу Кронекера—Капелли теорему). Н. с. у.
иначе называется противоречивой системой.
НЕСОИЗМЕРИМЫЕ ВЕЛИЧИНЫ— однородные величины, не имеющие
общей меры (см.). Отношение Н. в. есть число иррациональное. Например: 1)
диагональ квадрата и сторона его — Н. в.; 2) площадь круга радиуса г=\ и
квадрата со стороной, равной единице, —Н. в. Н. в.были известны еще в древности.
См. также Соизмеримые величины.
Рис, 160

НЕЧЕТНАЯ ПОДСТАНОВКА
247
НЕСОКРАТИМАЯ ДРОБЬ — дробь (арифметическая или обыкновенная),
числитель и знаменатель которой взаимно простые числа, т. е. числитель и зна-
3
менатель дроби не имеют общих делителей, отличных от ±1. Например, —.
4 8
--Н.д.
Всякую дробь, члены которой имеют наибольший общий делитель (см.),
отличный от 1, можно привести к Н.д., разделив члены дроби на общий
наибольший делитель (основное свойство дроби). По аналогии с обыкновенной Н. д.
Δ
рассматривают также в алгебре Н. д., т. е. алгебраическую дробь —-, где А
В
и β — алгебраические выражения, не имеющие общих делителей, отличных
2а За2
от ±1 (как буквенных, так и числовых). Например, -—, — алгебра-
Ь о — а
ическиеН. д.
НЕСЧЕТНОЕ МНОЖЕСТВО — бесконечное множество, мощность которого
больше, чем мощность счетного множества (см.). Множество всех
действительных чисел, например, является Н. м. (Кантор). Множество всех подмножеств
натурального ряда также является Н. м. (Кантор).
НЕЧЕТНАЯ ПЕРЕСТАНОВКА — перестановка (см.), содержащая нечетное
число инверсий (беспорядков; см. Инверсия). Например, перестановка, элементами
(предметами) которой являются натуральные числа (3, 5, 4, 1, 2),— есть Н. п., так
как общее число инверсий, образуемых парами элементов, входящих в
перестановку, равно 7— нечетному числу: число 3 образует инверсию с числами 1, 2, т. е.
всего две инверсии; число 5 образует инверсию с числами 4, 1, 2, т. е. всего
три инверсии; число 4 образует инверсию с числами 1, 2, т. е. две инверсии.
Таким образом, общее число инверсий в перестановке равно 7. Пары же
элементов (3, 5), (3,4), (1,2) образуют нормальное (естественное) расположение
(порядок).
Если перестановка содержит четное число инверсий, то она называется
четной. Например, перестановка (3, 2, 5, 4) — четная, так как общее число
инверсий всевозможных пар элементов в ней равно 2 — четному числу. Четность
и нечетность перестановки используется при определении знака членов
определителя, при определении четности и нечетности подстановок.
НЕЧЕТНАЯ ПОДСТАНОВКА — подстановка
/ ал а2 а3 . . . ап \ / I 2 3 ... η \
[ *ix aia ais . . . ain ) или [ ^ φ^ φ^ ... φ (/г) j
п-й степени, если она разлагается в произведение нечетного числа транспозиций
(см.)или если вторая строка (перестановка первой строки, записанной в
нормальном порядке) содержит нечетное число инверсий (беспорядков), когда за большим
числом рассматриваемой пары элементов следует меньшее (см. Инверсия).
Например:
/ 12345 \ _
1) подстановка из пяти элементов: I 19- I = (35) —- Н. п. (одна
транспозиция);
/ 12345 \
2) подстановка из тех же элементов? 0 _Q =(12) (34) (45) — Η. п. (три
транспозиции).
См. Подстановка.

248
НЕЧЕТНАЯ ФУНКЦИЯ
НЕЧЕТНАЯ ФУНКЦИЯ — функция f(x)> имеющая область определения,
симметричную относительно нуля, для которой справедливо равенство /(— х)=*
=—/(*)> т· е· функция, которая при изменении знака у аргумента изменяет
и свой знак. Например, функции: у=ах, y==sin a:, y=tgx, у=х3,
y=arcsin.x; суть Н. ф. График (см.) Н. ф. симметрично расположен
относительно начала координат, т. е. имеет центр симметрии — начало координат.
Сумма (разность) Н. ф. f(x) и φ(#) есть снова Н. ф.; произведение двух
Н. ф. есть четная функция (см.). Множество всех функций не сводится только
к четным и нечетным; есть функции, которые не являются ни четными, ни
нечетными, например функции: у=ах-\-Ь (аЬфЬ)у y=arccosjc.
Существуют функции, не являющиеся ни четными, ни нечетными, также
и потому, что для х>0 они могут быть определены, а для х<0 они не
определены, т. е. область их определения не всегда симметрична относительно
начала отсчета (нуля), например функции: y=lg#, у=л! («эн факториал» —
функция, определенная для /2=0, 1, 2, ... , п).
НЕЧЕТНОЕ ЧИСЛО — целое число (положительное или отрицательное), не
делящееся (нацело, без остатка) на 2. Н. ч. может быть записано в различных
формах, например: 2л-|-1, 2л—1, \п ± 3, где η — любое целое число.
Квадрат Н. ч. есть снова Н. ч., произведение двух любых Н. ч. есть
также Н. ч.
См. также Четное число.
НЕЯВНАЯ ФУНКЦИЯ. Соотношение F(xt у)=0 определяет у функцией χ
следующим образом: у(х) есть такое значение переменной у, которое вместе
с данным значением χ удовлетворяет условию F (х, у (#))=0. Иначе — у (х) есть
решение уравнения F(x% у) = 0 при фиксированном х. Такой способ задания
функции у(х) называется неявным заданием функции, а сама функция — Н. ф.
Особое значение во многих вопросах математики имеет случай, когда функция
у(х) однозначна (см.), т. е. когда решение уравнения F (х% у)=0 при
произвольном фиксированном χ единственно. На этот вопрос дает ответ теорема
о Н. ф., имеющая много различных вариантов. Самый простой из них такой.
Пусть
dF dF
Fix.. Уо)=0; -(*,у>, -(*,у)
непрерывны в точке (х0, у0); пусть, далее, — (х0, у0) φ 0. Тогда в
достаточно малой окрестности точки х0 существует одна и только одна непрерывная
функция у(х)> такая, что
У(х0) = Уо-
Более того,
dF(x4 v)
У <*)--■ дх
dF (л, у)
ду
Аналогичная теорема справедлива для системы Н. ф. Если:
Fy (*ι, Хъ · · . . *л. Уь · · · f Ук)=0<
РЛ*ъ *2» · · · . χη, Ун · · · * Ук)=0' (*>
Fk{xl9 х2ч . . ., хп, у19 ... ,ук )=0,

НИЖНИЙ ПРЕДЕЛ ФУНКЦИИ
249
6Fa
OF,
где -χ-^-, —^- — непрерывны в окрестности точки Р% /=1, 2,
dyj
, kt точка Ρ {χ®, х\,
όχι
-1, 2, .
стеме (*) и
л, s, /=
D(Fl9 F2, ..., Fk)
£>(Уи у*, .... Ук)
У\>
у1
, у%) удовлетворяетси-
Ф О в точке Ρ (см. Якобиан), то
существует единственная система непрерывных в некоторой окрестности (х\, х\, . . . ,
.... х°п) функций ух(хи х2 хп\ y2(Xl1 x2i .. ., χη), . .., yk(Xl%
χ2, . . . , χη), удовлетворяющих системе (*)итаких, что У/(*р х\> .... *„) =
«yyt /=1, 2, . .. , k. При этом ylf у2» · · · * Vk обладают непрерывными
частными производными. др $р
Примеры: 1. F (х, у)=у2+л;=0, — = 2у, — =^ О,
ду ду
Ρ (Ч> Уо) удовлетворяет уравнению F(x, y)=0, то
при у0 Φ 0 (следовательно, χ φ 0) в некоторой
окрестности х0 найдется единственная непрерывная
функция у(х) = ±У~-х с условием: у0=± v—xQ.
Знак квадратного корня определяется знаком у0.
dF\
2. F(x, у)=х* — у2=0, — -0. Однозначное
ду |о
определение у в виде функции от χ в окрестности
точки #=0 невозможно, как показывает график
Н. ф. (рис. 161).
Лит.: Г. М. Фихтенгольц, Курс
дифференциального и интегрального исчисления, т. 1, Физматгиз, Μ.,
1953.
НИЖНИЙ ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ чисел аи а2, . . . , ant ...—
самая левая из предельных точек (см.) этой последовательности, если
последовательность ограничена снизу; Н. п. обозначается символом limo^. Если после-
n-»-f-oo
довательность не ограничена снизу, то полагают lim ап=—со; если последо-
вательность ограничена снизу и не имеет предельных точек (т.е. liman—-f-oo),
/ι-*►+«>
то полагают ΠτηαΛ==-}-οο. Β случае существования конечного или бесконечного
предела последовательности Н. п. совпадает с этим пределом. В случае, когда
Н. п. конечен, его можно характеризовать следующим образом: число / будет
Н. п. последовательности, если: 1) в любой окрестности / найдется бесконечно
много членов последовательности, и 2) при любом ε>0 имеется лишь конечное
число членов последовательности, меньших чем / — е.
Примеры: 1) для последовательности:
1, — —, 2» — Τ * · · · · п> — —~ > · · · Нтап=0;
Рис. 161
2) 1, —1, 2, —2,
оч ,. п2+1
3) lim Γ~ = -τ-<*>·
η + 1 ,^+οο
rt-»-J-00
Я^5 Ή-2
НИЖНИЙ ПРЕДЕЛ ФУНКЦИИ y=f(x) в точке а — наименьший (конеч
ный или бесконечный) из частичных пределов функции б точке а (см.); обозна-

250
НИЖНЯЯ ГРАНЬ МНОЖЕСТВА
чается символом lim/(jc). Это определение сохраняет силу и в тех случаях,
х-*а
когда точка а заменяется на символы +°°» —°°ι а также когда χ стремится
к а справа или слева (односторонний Н. п.).
Примеры: 1) ИтЗ sin — = — 3;
x-*Q X
2)Й1^=+оо;
3) limA:cosA: =—оо;
Х-+ЭО
4) lim — = —оо, но Пт —= -f *>.
НИЖНЯЯ ГРАНЬ МНОЖЕСТВА £, являющегося подмножеством
множества действительных чисел, — наибольшее из чисел, ограничивающих данное
множество снизу, т. е. число т, удовлетворяющее следующим условиям: 1)
любое χ из множества Ε удовлетворяет неравенству χ > m, 2) для любого ε>0
существует в множестве Ε такой элемент х't что х'<т-\-г. Н. г. обозначается
символом inf£=m. У всякого ограниченного снизу множества существует Н. г.
Если Н. г. не принадлежит множеству, то она обязательно является предельной
точкой этого множества (см.).
( 1 2 η ) 1
Примеры: 1) Е~(- , - — , . . . j , infE--;
2) £ — отрезок a<x<b, inf£=a;
3) Ε — множество периметров правильных многоугольников, описанных
около круга радиуса R, inf £ = 2π#. Если Ε не ограничено снизу, то полагают
inf Е= — оо.
НИЖНЯЯ ГРАНЬ ФУНКЦИИ y=f(x) (или M = flxlf x2t . . . , хп) на дан-
ном множестве Ε — нижняя грань множества (см.) значений функции, которые
она принимает, когда аргумент χ [или (xlt х2, . . . , хп)] пробегает множество
Е\ Н. г. обозначается символом inf f(x) (или inf/(л^, х2, . . . , хп). Если при
некотором х1 из Ε /(*')= inf f\x), то Η. г. функции на Ε является
χζΕ
наименьшим значением функции на множестве Ε (говорят, что функция
достигает своей Н. г.).
Примеры: 1) inf / (л:2 — 2)=—2 — наименьшее значение, принимаемое
функцией при *=0; -2<*<2
2) inf 2—х=0, но функция не имеет наименьшего значения на
0<*<оо
0<*<оо;
3) inf (——) не существует или условно равен —оо, так как функция
0<*<1
не ограничена снизу на данном множестве.
НИКОМЕДА КОНХОИДА —это конхоида (см.) прямой /. В зависимости
от выбора полюса О и отрезка d> Η. к. может иметь различный вид. Н. к. состоит
из двух ветвей. Если расстояние полюса О до данной прямой / равно а и
данный отрезок равен dx то уравнение Н. к. в полярных координатах имеет вид:
о
р- ±<*.
cos φ

НОМОГРАММА
251
а в прямоугольных декартозых координатах с полюсом в начале координат:
(х — а)2(х2+у2) — d2x2^=0.
d=a и d<aH. к. со-
а), точку заострения
У τ
d>o
О!
Рис. 162
Н. к.—алгебраическая кривая 4-го порядка. При d>a
ответственно будет иметь в полюсе О узел (рис. 162
(рис. 162, б) или изолированную точку (рис.
162, в).
Н. к. названа по имени древнегреческого
геометра Никомеда, который использовал ее для
решения геометрических задач о трисекции угла
(см.) и удвоения куба (см.).
Лит.: ВандерВарден, Пробуждающаяся
наука, Физматгиз, М., 1959; А. А. С а в е л ов, Плоские
кривые, Физматгиз, М., 1960.
НИЛЬПОТЕНТНЫЙ ЭЛЕМЕНТ в группе —
такой элемент g, что его некоторая степень
(т. е. произведение g»g g) равна единице
η раз
группы. Так, в группе невырожденных матриц
2-го порядка матрица
Π
есть Н. э. Очевидно, единица группы всегда
является Н. э.
НОМОГРАММА — специальный чертеж,
предназначенный для решения определенного типа
задач вычислительного характера. Так, бывают Н. для решения приведенных
квадратных уравнений, для определения фокусного расстояния линзы (если
известно расстояние до предмета и его изображения) для вычисления площади
трапеции, для определения температуры смеси двух жидкостей с одинаковой
теплоемкостью и др.
В зависимости от способа изображения Н. и способа задания
функциональной зависимости между данными величинами, Н. разделяются на три основных
типа: Н. из выравненных точек, Н. сетчатые и Ы. транспарантные.
Н. из выравненных точек уравнения F (и% ι/, ш)=0 состоит из трех шкал
переменных и, v, w9 область изменения которых задается этими шкалами.
Шкалы построены так, что пометки (числа) из них, удовлетворяющие уравнению
F(u% у, шНО, лежат на одной прямой, откуда происходит и название. На
рис. 163 изображена Н. из выравненных точек для вычисления среднего
арифметического двух чисел.
Сетчатая Н. уравнения F(u% ι/, ш) = 0 состоит из трех семейств помеченных
линий (шкал), изображающих область изменения переменных и, у, w. Шкалы
построены таким образом, что каждые три из них, пометки которых
удовлетворяют уравнению F(u, v, w)=0, пересекаются в одной точке.
Транспарантная Н. в простейшем случае состоит из двух плоских полей
(плоскостей): основного (рис. 164 горизонтального) поля и транспаранта (часто
изготовленного из прозрачного материала), с изображением на них помеченных
линий хх и уу (хх±уу) бинарных полей (множество точек, каждая из которых
помечена парой чисел — значениями соответствующих переменных и немых линий
и точек). На рис. 164 изображена номограмма для вычисления среднего гео-
/ /То—
метрического двух чисел ΙθΛί=Ι/ —·6 «4,5 j

252
НОМОГРАФИЯ
Примером трансларантной Н. также является логарифмическая линейка, где
транспарант совершает лишь поступательное движение. См. также Номография.
Греч, νομός — закон, γράμμα — письменный знак, изображение.
НОМОГРАФИЯ — раздел математики,
в котором изучается теория и практика
построения номограмм (см.) — специальных
чертежей, предназначенных для решения
задач определенного типа.
Большая заслуга в развитии
отечественной Н. и организации номографиро-
τ9
t-8
~
с*
-'
,
-7
-6
ϊ5 ι
-4 _^^"^"
\-^^^
-3
\- 2
\л
L
Рис. 163
х/
|1||πρ .И
*' 3
ΙιιιΛιιι
2
\У
т
X/
~f )90*
J N,
'τ 2
„,,],, ,.||m,L.i....I....i....I...
;
'"'"Ί Ί"
0 7 2
lli'tl.n
3
4
Χνί/
5 Γ4
Рис. 164
вания инженерных расчетов принадлежит профессорам Н. А. Глаголеву и
А. А. Глаголеву, возглавлявшим советскую номографическую школу.
Лит.: Н. А. Глаголев, Курс номографии, «Высшая школа», М., 1961; М. В. Π β н т-
ковский, Считающие чертежи (номограммы), Физматгиз, М., 1959; А. П. Д о м о ρ я д,
Численные и графические методы решения уравнений, Энц. элем, мат., т. 2, Гостехиздат.
М., 1951.
1±Л\ ' ? з <·
ιΊΊ' ι1 .'
5 6 ? 8 9 ·0|
π—ι—г
12 13 )н
НОНИУС — приспособление, предназначенное для измерения длин
прямолинейных отрезков с точностью до 10—к долей единицы измерения (k — целое
положительное, обычно k — \\ 2). Η. представляет собой линейку, у которой 9
делений масштаба разделены на 10
равных частей или 99 делений на 100
равных частей.
Если конец измеряемого отрезка
АВ (рис. 165) не совпадает с делением
масштаба, то к концу его приставляют
Н. и смотрят, какое целение Н.
совпадает с делением масштаба. На рисунке
длина отрезка ,4/2=5,6 ед. масштаба.
НОРМА — понятие* обобщающее абсолютную величину числа, а.также
длину вектора. Н. есть функция вектора χ линейного пространства L (см.)*
удовлетворяющая следующим трем условиям (Н. обозначается || χ || ):
1) ||х||>0 при х^О, || χ ||=0 при х=0;
2) Ι1αχ||==|α| ||χ|| для любого *£L и действительного а;
3) II х+У II < II х H+-II УII Для любых χ и у из Ц,
Рис. 165

НОРМАЛЬ
253
Во всяком евклидовом пространстве (см.) Н. может быть определена при
помощи скалярного произведения (см.): || χ ||=* ν (χ·χ). В пространстве
непрерывных функций на отрезке \ач Ь] рассматривается Н.:
ll<F(0ll-max|q>(01.
a<t<b
Существует много других Н. Линейное пространство, в котором
определена Н., называется нормированным. Функциональный анализ (см.) оперирует
понятиями Н. линейного оператора А (см.) и Н. линейного функционала Ρ (см.).
Первое означает: || ^ Ц = sup
x6L
Ах\
\\Р*\\
а второе: ||P|| = sup .
x€L II х i|
Норма кватерниона а+Ь\+с)+dk — действительное неотрицательное число
у аа+624-£2-М2. Н. кватерниона α равна корню из произведения кватерниона α
на сопряженный с ним кватернион α (см.). В частности, при c=d=0 норма
у а2+Ь2 кватерниона paerfa модулю комплексно-сопряженных чисел a+bi
на — Ы.
Лит.: Г. Е. Шилов, Введение в теорию линейных пространств, Гостехиздат, М., 1952.
НОРМАЛЬ — к кривой (к поверхности) в данной ее точке — прямая,
проходящая через эту точку и перпендикулярная к касательной (см.) прямой
(касательной плоскости) в этой же точке кривой (поверхности). Если кривая плоская,
то в каждой своей точке она имеет единственную нормаль. Если χ=/(ί),
y=g(t) — параметрические уравнения плоской кривой в декартовой
прямоугольной системе координат, то уравнение Н. в точке (*0, у0), соответствующей
значению параметра t = t0t имеет вид:
df
dg
1^0
= 0.
Если плоская кривая задана уравнением F (х, у)=0, то уравнение Н. в точке
(*о. У0) имеет ВИД·'
Пространственная кривая в каждой своей точке имеет бесчисленное
множество Н.# лежащих в нормальной плоскости (см.). Из множества Н. к
пространственной кривой в данной ее точке выделяется главная Н., расположенная
в соприкасающейся плоскости (см.), и бинормаль (см.)—Н., перпендикулярная
к этой плоскости. Касательная, главная Н. и бинормаль образуют так называемый
подвижный триэдр (см.) кривой. Уравнение Н. для поверхности F(х, у, г)»0
имеет вид:
х — Хо _ У — Уо _ г^гь
oF dF $ρ
дх (χ°' У°* г°) ду ^х°* У°* г°) ТТ"^*6· ^°* г°)
Понятие Н. играет большую роль в дифференциальной геометрии, в
геометрической оптике (законы преломления и отражения света), в механике (материаль-

254
НОРМАЛЬНАЯ ЖОРДАНОВА ФОРМА
ная точка при движении по гладким линиям или поверхностям испытывает
реакцию, направленную по Н.). Если вместо кривой рассматривается прямая I, то
в этом случае Н. к прямой называется перпендикуляром или перпендикулярной
прямой к прямой /.
Лат. normal is — прямой.
НОРМАЛЬНАЯ ЖОРДАНОВА ФОРМА матрицы Л — матрица вида:
Άχ О ... О
О О
где Аи /=1, 2,
ρ есть квадратная матрица:
'λ, 1 0 ... О
1 ·
λ/1
О О
h.
некоторого порядка. Числа λ; и порядок матрицы At могут быть определены
непосредственно по матрице Л. Если порядок матрицы Αι равен единице, то она
есть число λ/. Надо иметь в виду, что λ/ с различными индексами могут быть
равными друг другу.
Имеет место теорема: для всякой матрицы А найдется невырожденная
матрица С такая, что САС—1 имеет вид Н. ж. φ. Η. ж. ф. матрицы А единственна с
точностью до произвольной нумерации жордановых «клеток» Л/. Алгебраический
смысл Н. ж. ф. матрицы А таков. Пусть линейное преобразование Ρ в данном
базисе комплексного линейного пространства записывается с помощью
матрицы Л. Спрашивается, нельзя ли изменить базис линейного пространства так,
чтобы матрица линейного преобразования стала возможно более простой.
Н. ж. ф. матрицы А является тем наиболее простым видом, в котором может
быть записана матрица линейного преобразования Р.
Числа λ/, упомянутые выше, есть собственные значения или
характеристические числа матрицы (см.) (они являются корнями векового уравнения). Жор-
дановы «клетки» Л/ имеют порядок больше единицы только в случае, когда
корень Xj является кратным. Однако кратность корня λ/, вообще говоря, не
равна порядку Л/. Частным случаем Н. ж. ф. являются диагональные матрицы.
Н. ж. ф. таких важных видов матриц, как ортогональные (см.), унитарные (см.),
симметрические, кососимметрические, является диагональной матрицей. Н. ж. ф.
матриц часто используется в теории дифференциальных уравнений, теории групп
Ли (см.), а также в линейной алгебре, чьим понятием она является. Вот как
решается, например, матричное уравнение:
Х*=
'—\ О ..
О —1 .·
0>
О 0 ... —Г
Предположим, что Х0 — решение этого уравнения. Приведем ее к И. ж. ф.
Y=CXQC-\ тогда
У2=СХ0С-*СХ0С-ь=СХ0Х0С-*=:С(-~ £)С~1 = — £,

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
255
т. е. матрица Н. ж. φ. Υ удовлетворяет уравнению
У2= — Е.
Непосредственно убеждаемся, что У с таким условием диагональна.
Следовательно,
/λ, 0 ... О
/о λ. ... о
где λΛ=± /, &=1, 2, . . . ? п.
Х0 легко выражается через У: X=C~~lYC% С — произвольная
невырожденная матрица.
Лит.: И. М. Гельфанд, Лекции по линейной алгебре, М.—Л. ,1954.
НОРМАЛЬНАЯ ПЛОСКОСТЬ пространственной кривой в данной ее
точке Μ — плоскость, проходящая через точку /И и перпендикулярная к касательной
(см.) прямой в той же точке. Н. п. содержит все нормали (см.) к кривой,
проходящие через данную точку. Если кривая в прямоугольной декартовой системе
координат задана уравнениями в параметрической форме: *=/(/), y=g(t),
z=h(t), то уравнение Η. п. в точке М(х0, у0, ζ0), соответствующей
параметру *-Ио» будет иметь вид:
df
Ну—у*)
+(* —*b)
dh
dt ,
= 0.
Η. π. прямой / в какой-либо ее точке Μ называется также плоскостью,
перпендикулярной к прямой /.
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ —один из наиболее важных типов
распределений (см.) случайной величины (см.). Плотность вероятности (см.)
случайной величины ξ, имеющей Н. р., есть функция:
1
(х — ту
2σ*
Р(х) = г=ге
ау 2л
где т — математическое ожидание, а σ2 — дисперсия (см.) величины ξ.
Очень давно было замечено, что распределение погрешностей наблюдения
довольно близко к Н. р. Например, если по оси χ откладывать разницу
между средним ростом мужчины и ростом
данного индивидуума, а по оси у —
количество людей данного роста, получается
кривая, весьма близкая к кривой у=р(х).
Эмпирические данные вскоре нашли строгое
математическое обоснование. Если считать, что
отклонение является результатом совместного
действия бесконечно большого числа незначительных
факторов, вызывающих каждый незначительное
изменение, то случайная величина (отклонение)
оказывается распределенной нормально. График
у=р(х) при σ=«1 и /я«3 показан на рис. 166.

256
НОРМАЛЬНОЕ СЕЧЕНИЕ
Вероятность того, что случайная величина ξ (чаще всего — ошибка наблю-
ь
дения) будет заключена в пределах α<ξ<6, равна \ p{x)dx,
а
Важность Н. р. так велика, что для функции:
у= Г —L- е * dXi
J ]/Г2л
о г
весьма тесно связанной с р(х), составлены таблицы. Н. р. широко
используется в статистике, артиллерии, инженерном деле и др. См. Интеграл вероятности,
Лапласа функция.
Лит.: Б. В. Гнеденко, Курс теории вероятностей, Физматгиз, М., 1961; Г. К ρ а-
мер, Математические методы статистики, перев. с англ., ИЛ, М., 1948.
НОРМАЛЬНОЕ СЕЧЕНИЕ поверхности — всякая плоская кривая,
получаемая от пересечения рассматриваемой поверхности плоскостью, проходящей через
нормаль к поверхности.
НОРМАЛЬНЫЙ ВИД квадратичной формы. Всякая квадратичная форма (см.)
η η
с действительными коэффициентами ^ ^ai/Xixj может быть приведена
невырожденными вещественными линейными преобразованиями к виду:
где ε/ равно -f-Ι или —1, г — ранг квадратичной формы (см.), г/ — линейные
формы от xj, /, /=1, 2, . . . , п. Выражение (*) называется Н. в. квадратичной
формы ^aijXjXj.
НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ группы G—подгруппа Η такая, что при лю-
^ом g£G gHg^1dHt где под gHg—1 понимается множество элементов вида
ghg—1, g£G, h ζ Я. Классы смежности G по // образуют группу, называемую
фактор-группой G/H.
Примеры: если G абелева (см.), то любая подгруппа ее является Н. д.
В группе унитарных (см.) матриц подгруппа унимодулярных (см.) унитарных
матриц есть Н. д.
Лит.: А. Г. Курош, Теория групп, Гостехиздат, М., 1953.
НОРМИРУЮЩИЙ МНОЖИТЕЛЬ уравнения прямой /4x-f-fiy-f-C=0 — число
± —ZZZZZ" » знак которого противоположен знаку С. После умножения урав-
Va2+b2
нения прямой на Н. м. оно принимает нормальный вид:
χ cos α-f-y sin α — р=0, ρ > 0.
Аналогично определяется Η. м. уравнения плоскости Ах+By+Cz+D=*Q.\
±(l:V A*+B*+C*).
НУЛЕВАЯ МАТРИЦА—матрица, состоящая сплошь из нулей. Н. м.
играет в кольце матриц (см.) роль нуля кольца (см.).
НУЛЬ-ВЕКТОР — вектор, длина которого равна нулю, или Н.-в.—вектор,
начало и конец которого совпадают. Н.-в. обозначается так: 0, или жирной
цифрой нуль (О). Определенного направления Н.-в. не имеет. Н.-в. введен для

НЬЮТОНА БИНОМ
257
общности рассуждений при действиях над векторами: при сложении двух
противоположных векторов или при умножении вектора на число (скаляр) λ=0; в
результате мы получаем Н.-в., а не скаляр. Н.-в. называется еще и нулевым
вектором. См. также Вектор.
НУЛЕВОЕ РЕШЕНИЕ: 1°. Н. р. линейной однородной системы уравнений:
βιι*ι+αΐ2*2+ ··· 4-αιη*η=0*
am*i+em2*2+ ··· +атпхп=0
есть решение х^О, х^—0, . . . * хп=0.
2°. Н. р. линейного однородного дифференциального уравнения я-го
порядка:
апУ{п)+ап-1У{п~1)+ ··· +а1У'+а0у=0
есть решение у(х) = 0. Н. р. в подавляющем большинстве случаев относится
к тривиальным.
НУЛЕВОЙ ПОКАЗАТЕЛЬ — показатель степени, равный нулю. По
определению а°=\ при любом афО, выражение 0° лишено смысла. См.
Неопределенность, Степень, Показатель степени.
НУЛЬ поля (кольца, алгебры) — такой элемент 0, что для любого-ν из поля
(кольца, алгебры) выполняется
х+0=х,
где равенства понимаются в смысле сложения в поле (кольце, алгебре). В поле
(кольце, алгебре) существует один и только один Η. Η. обладает также
свойством 0·λ;=0, для любого χ. Η. является особым элементом поля: деление
на Н. не определено. Обычное число 0 есть Н. в полях рациональных<
алгебраических, вещественных, комплексных чисел, а также в кольцах целых чисел,
четных чисел и т. д.
В школе при изучении арифметики Н. определяется как число, от
прибавления которого любое число не изменяется, или как число, от умножения
на которое любое число равно Н.
Лит.: Б. Л. Ван дер Варден, Современная алгебра, ч. 1, Гостехиздат, Μ., 1947.
НУЛЬ-МНОГОЧЛЕН — многочлен (см.), каноническое представление
которого есть нуль (см. Каноническое представление многочлена). Справедлива
теорема о Н.-м.: Если многочлен при любых значениях аргументов равен нулю, т. е.
тождественно равен нулю, то он является Н.-м.
НУЛЬ ФУНКЦИИ f{x) — точка xQ такая, что /(л:0)=0. Иначе Н. ф. суть
решения уравнения /(х)=0.
НУМЕРАЦИЯ — совокупность приемов наименования и обозначения чисел.
В истории математики различных народов были известны различные Н.: римская,
которой мы пользуемся для обозначения съездов, сессий, глав книг и т. д.,
арабская (перешла из Индии) и т. д. Н. иначе называется счислением (см.).
Лит.: И. Я. Депман, История арифметики, Учпедгиз, М., 1959.
НЬЮТОНА БИНОМ — название формулы, выражающей целую
неотрицательную степень двучлена а+b в виде суммы степеней его слагаемых. Н. б. имеет
вид:
к=0
17 Толковый словарь математических терминов

258
НЬЮТОНА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА
где & — биномиальные коэффициенты, равные числу сочетаний (см.) из η
элементов по k, т. е.
ck п(п—\)(п — 2) ··· (Λ2 — ^-Ь1)
П~ Ь2.3 k
Если биномиальные коэффициенты для различных я=0, 1, 2, .... записать
в последовательно идущие строки, то придем к треугольнику Паскаля (см.).
В случае произвольного действительного числа (а не только целого
неотрицательного) Н. б. обобщается в биномиальный ряд (см.), а в случае увеличения
числа слагаемых с двух на большее число — в полиномиальную теорему (см.).
НЬЮТОНА ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА — формула, дающая явное
выражение для многочлена я-й степени, принимающего заданные значение в/г-f-l
точках, расположенных на равных расстояниях друг от друга, т. е., если
заданы точки χ0<Χχ<χ2< ··· <хп и числа У/ = /(*/), *=0, 1, 2, . .. , nf то
Η. и. φ. дает выражение для многочлена Рп(х) такого* что Рп(х1)=У1 B
следующем виде:
Рп1*)=Уо+-ц- АУо+ 2| Д*Уо+- £| LA3y0-f ··· +
я!
где *=-
АУо = У1 — Уо. А2Уо=У2 —2у!+Уо. · · · ,Δ* Уо=У* — Clk yk-i +
Эта формула используется при интерполяции (см.). Ошибка, совершаемая при
замене функции f(x) выражением Рп(х), т. е. \f(x) — Pn(x)\> не превышает
/(/-1) ... (t-n)
hn+*M
(я+1)!
где Μ — наибольшее значение абсолютной величины (я-f· 1)-й производной
fln+l)(x) функции f(x) на отрезке [х0, хп].
Н. и. ф. названа по имени И. Ньютона, хотя она, по-видимому, была
известна ранее шотландскому математику Дж. Грегори. См. также Лагранжа
интерполяционная формула, Итерация.
НЬЮТОНА МЕТОД решения уравнений метод приближенного нахождения
корня х0 уравнения f(x) — Q. Метод заключается
в следующем. Берется какое-то число а1# по
возможности ближе к корню х0 (рис. 167). ах
принимается за первое приближение корня xQ. Затем
через точку А1(а1, /(αχ)) проводится
касательная к графику у=/(х) до пересечения с осью Ох.
Точка пересечения а2 принимается за второе
приближение корня х0. Повторяя этот процесс,
получают все более и более точные значения а1%
До, Д8» · · · корня λ*0.
На практике Н. м. комбинируется часто с
методом хорд (см. Ложного положения метод).
Н. м. называется также методом касательных.
НЬЮТОНА-ЛЕЙБНИЦА теорема (формула)
— см. Лейбница-Ньютона теорема (формула).

о
ОБЕЛИСК — выпуклый многогранник, основаниями которого являются
одноименные многоугольники, лежащие в параллельных плоскостях, а боковые грани
есть трапеции. О. есть частный случай призматоида (см.). Если основание О.—
подобные многоугольники, то О. есть усеченная пирамида. Термин О. редко
встречается в литературе.
См. Симпсона формулы.
ОБЛАСТЬ ЗАМКНУТАЯ (или закрытая область) в л-мерном пространстве —
открытая область (см.), дополненная всеми ее граничными точками (см.). О. з.
является замкнутым множеством (см.).
Примеры О. з. можно получить из примеров термина Область открытая
(рис. 168 и 169), если добавить к этим областям (фигурам) ограничивающие их
контуры или поверхности.
ОБЛАСТЬ ИЗМЕНЕНИЯ функции — множество значений функции, которые
она принимает для всех значений аргумента из области определения ее (см.).
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ функции действительного переменного —
множество значений, принимаемых независимой переменной (см. Функция). О. о. ф. не
обязана являться областью. Для функции, заданной некоторой формулой, под
О. о. ф. часто понимают (если О. о. ф. прямо не указана) множество
допустимых значений аргумента, т. е. всех тех его значений, для которых формула
дает действительное значение для функции; например, О. о. ф. г=1п!Л — *2—у2
считают внутренность круга с центром в начале координат радиуса единицы:
#2+у2<1.
ОБЛАСТЬ ОТКРЫТАЯ (или просто ОБЛАСТЬ): Г. О. в /г-мерном
пространстве — связное множество точек этого пространства, целиком состоящее из
т Ιβ! ^ ISt
Рис. 168
внутренних точек (см.). Любые две точки О. можно соединить ломаной (см.),
целиком состоящей из точек О.
Примеры О. на плоскости и в пространстве: 1) Внутренность (а также
внешность) круга прямоугольника, многоугольника, угла (контуры этих фигур не
включаются в рассматриваемое множество) представляют собой О. на плоскости
(рис. 168).
17*

260
ОБЛАСТЬ СХОДИМОСТИ
2) Внутренность (а также внешность) шара, параллелепипеда,
многогранного угла (поверхности, ограничивающие эти тела, не включаются в множество)
представляют собой О. в пространстве (рис. 169).
В л-мерном пространстве при /г>3 такое наглядное изображение О.
невозможно (примеры таких О. даны в термине Окрестность точки).
Рис. 169
2°. О. в метрическом пространстве — связное открытое множество этого
метрического пространства, т. е. связное множество (см.), состоящее только из
внутренних точек (см.). Пример О. см. в термине Окрестность точки.
ОБЛАСТЬ СХОДИМОСТИ функционального ряда (см. Ряд функций) —-
множество точек, при которых ряд сходится. О. с. не всегда будет областью (см.)
в смысле открытого связного множества. О. с. степенного ряда есть интервал
| χ — а\<г (интервал сходимости (см.)), причем граничные точки этого
интервала могут как принадлежать О. с, так и не принадлежать ей.
00 Г*
•ν 1 *^
Примеры: 1) Ряд jj sin" χ имеет О. с. множество χ Φ ~--\-п k, т. е. все
ч=\ 2
π
точки числовой оси, кроме точек с координатами ~-\-nk> & = 0, ±1, ±2, ...
2)0. с. ряда 2 (α^4-"~) включает в себя множество r<\x\<Rt
г>0, 0 < R < со и некоторые точки, абсциссы которых равны по модулю г
или R (см. также Лорана ряд).
оо .
3) О. с. ряда 2 \У *2+У2—U есть множество точек плоскости, коор-
п= ι
динаты которых хну удовлетворяют условию 0<ух2-\-у2 <2.
Существует несколько способов нахождения О. с. данного ряда (признаки
Даламбера, Коши, Раабе и др.).
ОБОБЩЕННАЯ ФУНКЦИЯ — линейный непрерывный функционал (см.),
определенный в пространстве бесконечно дифференцируемых функций, обращающихся
в нуль вне некоторого отрезка. Каждая обычная ограниченная функция f(x)
оо
является обобщенной, ибо она определяет такой функционал: J f(x) φ (x)dx.
— оо
К О. ф. относится, например, дельта-функция ό (*). Это есть функционал, который
функции φ(*) ставит в соответствие число ф(0). Это формально можно записать
оо
так: J δ (*) φ (χ)άχ=φ (0).
— 00
О. ф. обладают рядом свойств, которых нет у обычных функций. Например,
всякая О. ф. имеет производную в обобщенном смысле. О. ф. можно
рассматривать как функционалы и в других пространствах. Понятие О. ф. широко

ОБРАТНАЯ ФУНКЦИЯ
261
применяется в дифференциальных уравнениях. Впервые понятие О. ф., по существу,
появилось в работах советского математика С. Л. Соболева. Систематически
изучал их Л. Шварц, а затем многие советские математики.
Лит.: И. М. Г е л ь φ а н д и Г. Е. Шилов, Обобщенные функции и действия над
ними, Физматгиз, М., 1960.
ОБРАЗ элемента α ζ А при отображении (см.) φ множества Л на
множество В— тот элемент 6ζ£, в который отображается элемент а, т. е. 6=ср(а).
Если рассматривается отображение множества точек, функций, векторов и т. д.,
то говорят об О. точки, функции, вектора и т. д. О. подмножества А'
множества А при отображении φ множества А на множество В— множество всех
элементов φ (α'), где а' пробегает подмножество Л'. О. подмножества Л'
обозначается ф (Л'). Ясно, что φ (Л') с: Б.
ОБРАЗУЮЩАЯ ЛИНИЯ — прямая, пересекающая при своем движении
данную линию (направляющую; см.) и образующая линейчатую поверхность (см.).
Если О. л., перемещаясь по направляющей, остается все время параллельной
самой себе, то при этом образуется цилиндрическая поверхность (см.); если
О. л., перемещаясь по направляющей, все время проходит через одну и ту же
точку S, то О. л. опишет коническую поверхность (см.).
ОБРАТНАЯ МАТРИЦА к квадратной матрице Л—такая матрица Л—1, что
произведение А-А—1 равно единичной матрице (см.). Не всякая квадратная
матрица имеет обратную. Необходимым и достаточным условием существования
О. м. А—1 для квадратной матрицы Л является невырожденность матрицы Л,
т. е. отличие от нуля определителя матрицы Л. О. м. Л-"1 к невырожденной
матрице Л имеет вид:
Агг
D
А12
D
Ащ
D
Л21
D
Л22
D
А2п
D
Апг
D
АП2
D
Ann
D
где Aij — алгебраическое дополнение (см.) к элементу а/у в матрице Л и D —
определитель матрицы Л.
Для О. м. справедливо Л—1 = —п-А*, где Л* — присоединенная матрица
(см.).
ОБРАТНАЯ ТЕОРЕМА для данной теоремы (или к данной теореме) —
теорема, в которой условием является заключение, а заключением — условие данной
теоремы. Данная теорема по отношению к О. т. называется прямой (исходной).
В то же время О. т. к О. т. будет данной теоремой; поэтому прямая и обратная
теоремы называются взаимно обратными (см.). Если прямая (данная) теорема
верна, то О. т. не всегда верна. Например, если четырехугольник — ромб, то его
диагонали взаимно перпендикулярны (прямая теорема). Если в четырехугольнике
диагонали взаимно перпендикулярны, то четырехугольник есть ромб — это
неверно, т. е. О. т. неверна. Взаимно обратные теоремы тесно связаны с
необходимым и достаточным условиями (признаками) (см.).
Лит.: И. С. Градшт штейн, Прямая и обратная теоремы, Физматгиз, М., I960.
ОБРАТНАЯ ФУНКЦИЯ для данной функции у = Дх) — функция (быть может,
многозначная) *=<р(у), задающаяся тем же законом соответствия между
переменными χ и у, как и данная функция/ (х), но в обратном направлении: у-+х = у(у),

262
ОБРАТНОЕ ЧИСЛО
когда χ считается функцией, а у — независимой переменной; другими словами,
каждому значению у ставятся в соответствие все такие значения х=(р(у), для которых
/(,v)=y. Например, для функции y=f(x)=x2 О. ф. будет двузначная функция
x=<p(y)=±Vy, ибо f(+Vy) = ( + Vy)* = y и f(-Vy)=(-Vy)2 = y-
Областью определения О. ф. является множество значений F данной (прямой)
функции, а множеством значений О. ф. является область определения Ε прямой
функции. Для О. ф. л:=Ф(у) справедливо соотношение /[ф(у)]=У для всех у
из F и при любом выборе (если φ (у) многозначна) значения φ (у). Если О. ф.
однозначна, то Φ [/(#)]=# Для всех χ из Ε и данная функция y = f(x) является
О. ф. для своей О. ф. *=ф(у) — в этом случае функции / и φ называются
взаимно обратными. Если О. ф. многозначна, то часто ее представляют как
совокупность однозначных функций, также называемых часто О. ф. (точнее,
ветвями О. ф.)· Например, полная О. ф. для y=sinxt обозначаемая x=Arcsinyt
— 1<у«1, может быть представлена как
совокупность функций а;=(—l)rtxarcsiny-t-Jtrt (л=0, ±1,
±2, . . .), где функция jc = arcsiny есть
однозначная ветвь О. ф., определяемая дополнительным усло-
π л
вием — "т<х<7Г и называемая главным значением
2 2
арксинуса; функция #=arcsiny и функция y=sin*
с областью определения — ·— < χ < — — взаимно об-
ратны. График О. ф. *=Ф(у) совпадает с графиком
прямой функции y=f(x). Если же в О. ф.
обозначения функции χ и аргумента у изменены на у и *,
т. е. рассматривается функция* у=φ (χ), то ее график симметричен графику
y=f(x) относительно биссектрисы первого и третьего квадрантов системы
координат. Например, на рис. 170 показан график функции y=-f-V 4х—- х2 — 3 и
двузначной О. ф. (с изменением обозначений) у=2±у I—х2.
Справедлива теорема об О. ф.: для всякой непрерывной монотонной
функции У=/(х), заданной на [а, Ь] и с областью значений [/(а), /(&)], существует
однозначная монотонная и непрерывная О. ф., отображающая [/(а), /(6)] на
[at b].
ОБРАТНОЕ ЧИСЛО для числа а Φ 0 — число, равное — . Произведение
а
числа а и О. ч. — всегда равно 1. Если число — есть обратное для числа
а а
а Φ 0, то и число а есть обратное для числа —; поэтому числа а Φ 0 и —
а а
называются взаимно обратными (см.). Взаимно обратные числа связаны
неравенством:
а+—>2(а>0).
а
ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ВЕЛИЧИНЫ — такие две величины * и у,
что увеличение (уменьшение) одной из них в несколько раз влечет за собой
уменьшение (увеличение) другой величины во столько же раз. Иначе: две
величины χ и у называются О. п. в., если их произведение ху в процессе изменения
остается постоянным, т. е. xy—k. Обратно пропорциональная зависимость
величин — одна из простейших функциональных зависимостей между величинами χ и v.

ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 263
Графиком (см.) обратно пропорциональной зависимости ух=£(или y=*kjxt x=k/y)
является равносторонняя гипербола.
Пример: S=u·/; если путь S — постоянный, то чем больше скорость и, тем
меньше (во столько же раз) потребуется времени t для прохождения этого пути.
Следовательно, скорость υ и время / являются О. п. в.
См. также Пропорциональность, Прямо пропорциональные величины.
ОБРАТНЫЕ ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ— функции, обратные
гиперболическим функциям (см.) shx, ch.v, thx; они выражаются формулами:
Arsh*=ln(*-fl/ х2+1), — οο<λ-<οο, ]
Archx=ln(x+]/ χ2—1), 1 < χ < οο, Ι /*\
11+* Ι
Arthjt=-— In- , — 1<λ;<1.
2 Ι — χ )
Читается: «apea — синус гиперболический, ареа — косинус гиперболический,
ареа — тангенс гиперболический».
Производные О. г. ф. имеют вид:
(Arsh χ)' = * ,
У *2+ι
(Arch λ·)'-— ,
j/*2-l
(Arth*)'=-j-Ц.
x£ — 1
О. г. ф. часто появляются при интегрировании рациональных дробей и квадра-
тических иррациональностей.
В комплексной плоскости О. г. ф. многозначны. Если в формулах (*) брать
главные значения логарифмов, то получим однозначные ветви О. г. ф. (главные
их значения), обозначаемые arshz, arch z, artgz.. О. г. ф. связаны с главными
значениями обратных тригонометрических функций (см.) формулами:
arshz=-rarcsin/z,
ι
arch z=i arc cos z,
arthe=-T arc tg/г.
Лат. area — площадь.
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ— функции, обратные
тригонометрическим функциям (см.) sinx, cos*, tgx, ctgx, sec χ, cosecjc.
О. т. ф. соответственно тригонометрическим функциям обозначаются так:
Arcsinx (арксинус), Arccosx (арккосинус), Arctgx (арктангенс), Arcctgx
(арккотангенс), Arcsecx (арксеканс), Arccosecx (арккосеканс).
Обычно рассматривают только первые четыре О. т. ф. О. т. ф. являются
многозначными. Однозначные ветви О. т. ф., взятые в определенных интервалах
монотонного изменения значений функции, называются главными значениями
О. т. ф. и обозначаются так: arcsinx (см.), arccosx (см.), arctg,v (см.),
arcctgx (см.), arcsecv (см.), arccosec x (см.). О. т. ф. часто появляются при
интегрировании рациональных дробей и квадратических иррациональностей. О. т. ф.

264
ОБРАТНЫЕ ФИГУРЫ
иначе называются аркфункциями, а иногда аркусами. О. т. ф, не являются
тригонометрическими функциями, поэтому правильно было бы их называть
функциями, обратными тригонометрическим, или аркфункциями.
Лат. arcus — дуга (угол).
Лит.: СИ. Новоселов, Обратные тригонометрические функции, Учпедгиз, М., 1956.
ОБРАТНЫЕ ФИГУРЫ — две фигуры Φ и Ф', каждая из которых является
соответственной для другой в заданном преобразовании инверсии (см.). О. ф.
называются также взаимно инверсными или взаимно обратными.
ОБРАЩЕННОЕ ЧИСЛО по отношению к данному, многозначному числу,
значность которого не меньше двух, есть число, записанное теми же цифрами,
но в обратном порядке. Например, О. ч. для чисел 20; 24; 58 есть
соответственно числа 02, т. е. 2; 42; 85.
Если трехзначное число имеет цифру единиц х% цифру десятков у, цифру
сотен г, то его можно записать в виде: ζ- lOO-f-У* Ю+jt или кратко — гух, где
знак черты указывает, что цифры г, у, χ не перемножаются, а записаны одна
за другой,—то О. ч. по отношению к нему можно кратко записать так: хуг.
Понятие О. ч. и краткая его форма записи иногда используются при решении
задач на составление уравнений.
ОБЩАЯ МЕРА данных величин (отрезков, углов и др.) есть величина того
же рода (отрезок, угол и др.), содержащая целое число раз в данных
величинах.
Если, например, данные отрезки имеют О. м., то они называются
соизмеримыми (см.), если не имеют, то — несоизмеримыми.
ОБЩЕЕ НАИМЕНЬШЕЕ КРАТНОЕ — см. Наименьшее общее кратное.
ОБЩЕЕ РЕШЕНИЕ: 1υ. Ο. ρ. обыкновенного дифференциального
уравнения y(n) = f(xt у, у', . . . , у(л—ι)) представляет собой семейство функций
У = ф(** Сг, . . . , Сл), непрерывно зависящих от η произвольных постоянных
Сь С2, . . . , Сп. Выбирая соответствующим образом значения этих постоянных,
можно получить любое частное решение, за исключением, быть может, особых
решений (см.) уравнения. Выбор определенных значений постоянных
эквивалентен заданию начальных (граничных) условий. Начальные условия однозначно
выделяют частное решение из общего. Если соотношение, связывающее *, у и η
произвольных постоянных, дано в виде, не разрешенном относительно у:
Ф(*. у, Си С2, . .. , С„) = 0,
то такое соотношение называется общим интегралом обыкновенного дифференци-
dy у | х\
ального уравнения. Пример: —=—-\-у\ In — -f- x -f C=0 — общий интеграл,
dx χ J у I
a y = Cxex есть О. р.
Аналогично определяется О. р. системы обыкновенных дифференциальных
уравнений.
2°. О. р. дифференциального уравнения в частных производных
/ dz_ dz__ d*z д2г dkz \
Fl Хц #2» · · · » Xtl% -. -л » о * г» γι * · · · * ib\ \ ~
у дхх дхп дх* dXldx2 дхт J
представляет собой функционал, зависящий от одной или нескольких
произвольных, непрерывных и дифференцируемых функций. Частные решения получаются
из общего заданием начальных условий (начальных данных Коши). См. Коши
задача, Коши теорема.
3°. О. р. неоднородного линейного дифференциального уравнения является
суммой О. р. соответствующего однородного уравнения и частного решения
данного неоднородного уравнения.

ОБЪЕДИНЕНИЕ МНОЖЕСТВ
265
d2y
Пример: неоднородное уравнение —- -\- Зу = х имеет частное решение
1 _. d2y
У\—1ГХ' О. р. однородного уравнения —:+Зу=0 является:
3 dx2
у2=Сг sin V3jc+C2cos1/3x.
Тогда О. р. данного неоднородного уравнения является:
У°~У1+Уъ=*Сг$\п\ 3*-f-C2cosy 3*+—.
о
4°. О. р. линейного однородного дифференциального уравнения 2-го
порядка y"+Piy'+р-2У=0 получается из одного из частных решений этого уравнения уг
квадратурами
где Clf C2 — произвольные постоянные.
5°. О. р. неопределенного уравнения. В теории чисел рассматриваются
неопределенные (диофантовы) уравнения, т. е. уравнения с несколькими
переменными, для которых ищутся целые (или же рациональные решения). Такие
уравнения имеют О. р., зависящее от целочисленных параметров. Например,
уравнение x2-\-y2=z2 имеет общее решение x2=m2 — л2, y=2m/zt z2=m2+/22,
где m, n — целые числа.
6°. О. р. тригонометрического уравнения есть множество всех его решений.
Например: sinjt=a,
*—Arcsina ( | а\ <* 1)
или
jc=(—1)л arcsin α-bJt м, гс = 0; ±1; ±2; ...
О. р., как видим, может быть представлено в разной форме.
ОБЩИЙ ДЕЛИТЕЛЬ МНОГОЧЛЕНОВ. Многочлен d называется О. д. м.
/ъ /2. · · · * fk* если Для каждого /£-(/=1, 2, . . . , k) многочлен d является
делителем многочлена (см.).
ОБЩИЙ ИНТЕГРАЛ — см. Общее решение.
ОБЩИЙ НАИБОЛЬШИЙ ДЕЛИТЕЛЬ —см. Наибольший общий делитель.
ОБЪЕДИНЕНИЕ МНОЖЕСТВ А и В есть множество, состоящее из тех
и только тех элементов, каждый из которых есть элемент хотя бы одного из
множеств А или В. О. м. А и В обозначается символом А{]В (или А-\-В) и
называется иногда суммой множеств Л и Б. О. м. Л и В на рис. 171
схематически изображено заштрихованной областью.
Аналогично, если даны множества Аа , где α
пробегает конечное или бесконечное множество индексов АиВ
щ, то О. м. Ла(а£пт) называется множество,
состоящее из тех и только тех элементов, которые
принадлежат хотя бы одному множеству Аа при
некотором α=α0ζιη. (Если некоторый элемент а входит
в несколько множеств Аа f то в О. м. Аа он входит
лишь один раз.) О. м. Ла(а£т) обозначается Рис.171
СИМВОЛОМ [}Аа (ИЛИ Σ ^х )· 3 В СЛУчае» КОГДЭ Щ,
a 6ju « em

266
ОБЪЕМ
конечно, и состоит из η чисел 1, 2, . . . , п, О. м. Alt А2, .... Ап обознача-
ется символом ^lU-^U ... [}Ап (или Л1-т-Л2+ ··· + Ап или (J А{).
ί'= 1
Если щ — счетное множество и состоит из чисел натурального ряда 1,
оо оо
2, .... то О. м. Alt А2, . . . обозначается символом U Л/ (или 2 ^/· или
* - ! * = ι
^iU^2U , ...» или i41-hi4a-h ···)·
О. м. является одной из основных операций над множествами. О. м.
удовлетворяет законам коммутативности, ассоциативности и идемпотентности (см.);
О. м. связано с пересечением множеств (см.) двумя законами дистрибутивности
(СМ°' А Г) ( U в* )- U (А П В* ) и А и ( η βα ) - П {A U θ. ).
α em «em α ещ «б nt
Эти два закона дистрибутивности двойственны (см. Двойственность).
Примеры: 1) пусть А — множество четных чисел и В — множество нечетных
чисел; тогда A U В — множество всех целых чисел; 2) пусть Αι — множество
всех действительных чисел х, удовлетворяющих неравенствам /—l<x<i-t-i*
оо
где i — пробегает множество натуральных чисел: 1, 2, 3, ...; тогда \j Αι
является множеством всех неотрицательных действительных чисел. ""
ОБЪЕМ — неотрицательная аддитивная функция (см. Аддитивная величина)
множества точек трехмерного пространства (в обобщениях — n-мерного
пространства), не меняющаяся при любых движениях пространства. Это значит, что
множеству точек трехмерного пространства ставится в соответствие
неотрицательное число, называемое О., причем два множества точек, которые можно
совместить движением в пространстве, имеют одинаковый объем. О.
объединения конечного или даже, может быть, счетного (см.) множества
непересекающихся множеств равен сумме О. этих множеств.
О. есть мера количества пространства, занимаемого точками множества
(тела, в частности). К описанному определению понятия О. приводят
интуитивные представления об измерении количества пространства. Единицей измерения
О. служит О. куба, ребро которого равняется единице длины. Если тело, О.
которого мы измеряем, не может быть составлено из конечного числа кубов,
поступаем так: заполняем данное тело кубиками со стороной h так, чтобы два
соседние куба имели общую грань, до тех пор пока нельзя будет добавить ни
одного куба со стороной h без того, чтобы не выйти за пределы тела. С другой
стороны, рассматриваем множество кубиков, примыкающих друг к другу, как
описано выше, покрывающих все точки тела и таких, что ни один кубик не лежит
вне тела. Их О. обозначим vn\ О., занимаемый внутренними кубиками,
обозначим ν^. Тогда О. тела равен Игл ^=Пшуй, при всевозможных способах
h -> о
заполнения тела кубиками. Конечно, не для всех тел существует lim v^ и не
всегда lim ν·ι= lim щ. Поэтому О. определяется не для всех точечных мно-
h -+ о h -* О
жестз трехмерного пространства. О. обобщается в понятии меры множеств (см.).
Те множества, которые не имеют меры (объема), называются неизмеримыми.
Примеры: 1) О. пирамиды равняется -— Sh, где S — площадь основания,
о
h — высота; 2) О. многогранника, в который можно вписать сферу, равен ~ T-R,
где Т —полная поверхность многогранника, а /? —радиус вписанной сферы;

ОВАЛЫ
267
3) О. тела, полученного вращением кривой y=f(x), a<x<bt f(x)>0 вокруг
ь
оси Ох, равен π \f2(x)dx.
а
Лит.: Э. Лебег, Об измерении величин, Физматгиз, М., 1960.
ОБЪЕМЛЕМАЯ есть выпуклая дуга или выпуклая ломаная /, имеющая
с другой выпуклой дугой L или выпуклой ломаной (объемлющей первую) общие
концы А и В (рис. 172) и не содержащая внешних точек фигуры, ограниченной
кривой / (или выпуклой ломаной) и хордой А В (рис. 173). Всякая О. короче
всякой объемлющей. Иногда О. может являться вписанной кривой (ломаной)
в другую (объемлющую) кривую (ломаную).
А ВА ЗА ВА В
В А
Рис. 172
Рис. 175
ОБЪЕМЛЮЩАЯ есть выпуклая дуга кривой или выпуклая ломаная,
имеющая с другой выпуклой дугой / или выпуклой ломаной (объемлемой первой)
общие концы Л и Б и не имеющая внутренних точек фигуры,
ограниченной кривой / (или выпуклой ломаной) и хордой АВ (см. рис. 172 и 173).
Всякая О. длиннее всякой объемлемой.
ОБЫКНОВЕННАЯ ТОЧКА: 1°. О. т. кривой, заданной уравнением
F(jc, у) = 0, есть точка М0(х0, у0), в которой частные производные от F не
обращаются одновременно в нуль.
2°. О. т. дифференциального уравнения у'=/(*, у) — точка М0 (х0, у0),
в окрестности которой существует единственное решение, удовлетворяющее
условию у(х0)=Уо-
3°. О. т. однозначной аналитической функции — точка, в которой не
нарушается аналитичность функции.
ОВАЛЫ — замкнутые выпуклые плоские кривые. О. обладают рядом
интересных свойств, например: 1) при некоторых условиях на всяком О. имеется не
менее четырех точек, в которых кривизна его достигает максимума или минимума
(теорема о четырех вершинах; у эллипса, который, как и окружность, является О.,
таких вершин ровно четыре — концы его большой и малой осей); 2) если
расстояние между любыми двумя параллельными, касательными к О., постоянно для
всех направлении (О. постоянной ширины), то длина О. равна произведению
этого расстояния на число π.
Простейшим примером О. постоянной ширины
является окружность. Другим примером такого О. может
служить О., который получается следующим образом
(рис. 174): из вершин равностороннего треугольника
со стороной а описывают дуги шести окружностей —
три произвольным радиусом с, три другие радиусом,
равным а+с.
В алгебраической геометрии (см.) О. называют
также всякие замкнутые (не обязательно выпуклые)
ветви плоских алгебраических кривых, не имеющие
точек самопересечения.
Франц. ovale — от лат. ovum — яйцо.
Рис. 174

268
ОГИБАЮЩАЯ
ОГИБАЮЩАЯ семейства линий на плоскости (поверхностей в пространстве) —
линия (поверхность), которая в каждой своей точке касается по меньшей мере
одной линии (поверхности) семейства.
Если уравнение семейства линий на плоскости имеет вид f(x, у, с) = 0, то,
исключив параметр с из системы уравнений:
/(*, у, с)=0, f'c(xt у, с) = 0
(предполагая при этом существование непрерывных частных производных 1-го
порядка по всем трем аргументам), получим уравнение О. с, куда могут войти
и особые точки семейства, т. е. точки, для которых одновременно
/;=о, /;=о.
Примеры: 1) О. с. окружностей (х — c)2+y2 = R2 будет состоять из двух
параллельных прямых y=R и y=—R (рис. 175); 2) всякая кривая является
О. с. своих касательных и О. с. своих
кругов кривизны; 3) если в каждой точке
кривой построить к ней нормаль, то О. с.
этих нормалей будет эволюта (см.)
данной кривой; 4) О. с. сфер радиуса R с
центрами, лежащими на одной прямой,
будет круговой цилиндр того же радиуса
R с осью, совпадающей с линией центров
сфер: цилиндр касается каждой сферы по
окружности; 5) О. с. сфер радиуса R,
центры которых лежат в одной
плоскости, есть пара плоскостей, параллельных
плоскости центров и отстоящих от нее в ту
и другую сторону на расстояние R.
Лит.: Г. П. Толстов, К отысканию огибающей семейства плоских кривых, «Успехи
математических наук», 1952, т. 7, вып. 4; Г. И. В а л л е-П у с с е н, Курс анализа
бесконечно малых, т. 2, Гостехиздат, М., 1933; П. К. Рашевский, Курс дифференциальной
геометрии, Гостехиздат, М., 1956.
ОГРАНИЧЕННАЯ ВЕЛИЧИНА — переменная, которая в процессе своего
изменения остается всегда по абсолютной величине меньше некоторого
постоянного числа. См. Ограниченная последовательность, Ограниченная функция.
ОГРАНИЧЕННАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — последовательность (чисел,
точек и т. д.), члены которой составляют ограниченное множество (см.).
Аналогично последовательность называется ограниченной сверху (снизу), если ее члены
составляют ограниченное сверху (снизу) множество (см.).
ОГРАНИЧЕННАЯ ФУНКЦИЯ V=f(x) илим = /(л:1, *2, . . . , хп) на данном
множестве Ε — функция, для которой множество значений, принимаемых ею,
когда аргумент пробегает Е> есть ограниченное множество (см.).
Примеры: 1) функция у=— — О. ф. на интервале 1<д:<оо и не является
О. ф. на интервале 0 < а: < 1; 2) и = х2+у2 на любом ограниченном множестве
плоскости является О. ф.
Аналогично функция называется ограниченной сверху (снизу), если
множество ее значений есть ограниченное сверху (снизу) множество (см.).
ОГРАНИЧЕННОЕ МНОЖЕСТВО: 1°. О. м. действительных чисел
—множество {х} на числовой оси, для которого существует число В такое, что для
любого элемента χ из множества |χ|<£.
2°. О. м. в я-мерном или метрическом пространстве — множество, для
которого существует замкнутая сфера (см.), целиком его содержащая.

ОДНОПОЛОСТНЫЙ ГИПЕРБОЛОИД
269
Аналогично п. 1° определяется ограниченное сверху (снизу) множество
действительных чисел как такое множество Е, для которого существует число 5,
не меньшее (не большее) любых элементов из Ef т. е. любое число χ из Ε
удовлетворяет неравенству х<В (х>В).
ОДНОЛИСТНАЯ ФУНКЦИЯ — аналитическая функция (см.) ш=/(г) в
области D, не принимающая одинаковых значений, т. е. /(г1)=^/(г2) при гх Φ г2.
Производная О. ф. не обращается в нуль внутри области. О. ф. осуществляет
конформное отображение (см.) области D на область Dx плоскости w. Обратная
функция z=F(w) есть однозначная аналитическая функция в области Dv
2тг
Примеры: 1) функция w=zn является О. ф. в области г>0, 0<φ< —
(рис. 176), где г= | ζ \ — у х2+у2— модуль и (p=arg2 — аргумент
комплексного переменного г=*+/)/=г (cos ψ+/ sin φ); 2) функция w=sinz является О. ф.
в области — ~<х<~г,
• °° <У<+оо.
ОДНОЛИСТНОСТИ ОБЛАСТЬ — область плоскости комплексного переменного.
г—χ-}-/>', в которой аналитическая функция w=f(z) является однолистной
функцией (см.). Например, для функции
w=s\nz= — sin л;-Η ~ cos λ:
О, о. служит любая полоса а<х<а+я, —oo<y<-f-oo ширины π (рис. 177),
в которой присоединена любая пара множеств точек (а, уг), (α+Jt, у2), где
Рис. 176
Рис. 177
3Ί€£ι* Угё^г. ^ι Π ^2=0» ^i (J Е2 есть вся ось Оу. Для /(г), рассматриваемой
в О. о., обратная функция z=F(w) однозначна и называется ветвью полной
обратной функции. Так, обратная для w = sinz функция z^Arcsinoy имеет
бесконечно много ветвей, соответствующих О. о.
(2*-1)-|<*<(2Λ+1)γ, /г=0; ±1; ±2; ...
ОДНОПОЛОСТНЫЙ ГИПЕРБОЛОИД-^дцна из поверхностей 2-го порядка,
каноническое уравнение которой в декартовой прямоугольной системе координат
имеет вид:

270
ОДНОРОДНАЯ ФУНКЦИЯ
Если д=6, то О. г. называется О. г. вращения. О. г. является центральной
поверхностью, имеющей прямолинейные образующие (см.). О. г. относится
к числу линейчатых поверхностей (см.). См. также Гиперболоиды.
ОДНОРОДНАЯ ФУНКЦИЯ — функция одного или нескольких переменных,
для которой выполняется тождество
/(λ Χυ λχ2 λ Xn)--=bk Д*1* **2» · · · * *п)
при всевозможных λ,- где k — некоторая постоянная (степень однородности
функции). О. ф. имеет ряд интересных свойств. См. по этому поводу, например,
Эйлера теорему.
Примеры: 1) / (х, yf z)=(x — у) (у — г) (г — 2*), £=3; 2) /(*, у)=
- , * *--!-; 3) /(*. У)=У*Т~У< *=4; 4>
есть О. ф. длин его сторон:
площадь треугольника
о ι /~/а+Ь+с\ (а+Ь+с \ ( а+Ь+с \ / α-И+с \
S=V (—2—)(—2—а)[——ή[——ή
(формула Герона); 5) /(*, у)=1п—, £=0.
ОДНОРОДНОЕ ПРОСТРАНСТВО — многообразие (см.), допускающее
совокупность взаимно однозначных гладких преобразований в себя, причем для
любых двух точек найдется преобразование из указанной совокупности,
переводящее одну точку в другую. О. п. определяется непрерывной группой (см.)
таких преобразований и подгруппой (см.) тех преобразований, которые оставляют
некоторую точку неподвижной (стационарная подгруппа). В такой
интерпретации точкой пространства является класс смежности (см.) группы по подгруппе.
Значительное место в теории О. п. занимают римановы О. п., группа
преобразований которых сохраняет заданную на О. п. риманову метрику (группа
движений). Примером риманова О. п. служит обычная сфера трехмерного евклидова
пространства. Группа движений сферы есть всевозможные вращения вокруг
центра, стационарная подгруппа — вращения вокруг фиксированной оси.
ОДНОРОДНОЕ УРАВНЕНИЕ —уравнение вида f(xlt x2t ..., хп) = 0, где
/ — однородная функция (см.). Уравнение g(xi, х2, . · . . хи* Уи Уй> · · · » χι)=®
называется О. у. по переменным xl9 x2 *ь если функция g однородна по
этим переменным.
Дифференциальное уравнение п-го порядка:
F(x, У, У\ ..., У<Л>) = 0
называется однородным, если F однородна по переменным у, у, . . . , у(п).
Система линейных О. у. (конечных или дифференциальных) зсегда имеет
тривиальное (нулевое) решение.
ОДНОРОДНЫЕ КООРДИНАТЫ точки (прямой) на плоскости — это тройки
пропорциональных чисел (xlt x2, *3), не равные нулю одновременно, которые
связаны с декартовыми координатами точки χ и у формулами:
Х\ *2
— = Х, -=У.
Хз Хз
Если точка имеет О. к. (хи х2* х3), то та же точка имеет О. к. (р хи
Ρ #2* Р*з)* гДе ?—любое действительное число =£ 0. Аналогично определяются
О. к. точки и в пространстве трех и большего числа измерений.

ОДНОСТОРОННЯЯ КАСАТЕЛЬНАЯ
271
Уравнения кривых линий и поверхностей, записанные в однородных
координатах, имеют часто простой и симметричный относительно текущих координат
вид. Введение О. к. было вызвано необходимостью дополнить евклидову
плоскость бесконечно удаленными (несобственными) точками (xlt х2, 0), третья
координата которых равна нулю, что приводит к понятию проективной плоскости
в проектирной геометрии.
В системе О. к. бесконечно удаленные точка и прямая (уравнение
последней х8=0) не играют никакой особой роли по сравнению с любыми другими
точками и прямыми плоскости. В этом состоит все значение О. к. Мы можем
исследовать поведение кривой в бесконечно удаленных точках, так же как и
поведение этой кривой в любой другой (собственной) точке; мы можем говорить
о касательных в несобственных точках, о двойных (кратных) несобственных
точках кривой и т. д.
Например, уравнение параболы у2=2рх в О. к. имеет вид: %\ = 2рхгх3 (*),
откуда заключаем, что парабола имеет с несобственной прямой xz**0 точку
касания, так как из уравнения (*) вытекает, что точка (xlt 0, 0), где хх Φ 0—
любое действительное число, л^О, лг3=0,—двойная точка пересечения
параболы и несобственной прямой. Следовательно, несобственная прямая есть
касательная к параболе.
Аналогично показывается, что гипербола имеет с несобственной прямой две
точки пересечения, а эллипс — ни одной общей точки.
ОДНОРОДНЫЙ МНОГОЧЛЕН —то же, что форма (см.).
ОДНОСВЯЗНАЯ ОБЛАСТЬ — область (не обязательно открытая) (см.),
обладающая следующим свойством: любой замкнутый контур, лежащий в области,
можно непрерывным образом стянуть в точку, не покидая пределов области.
Например, интервал, круг, шар (безразлично, открытые или замкнутые и т. п.)
суть О. о. Кольцо (множество точек с координатами xi у, удовлетворяющими
неравенствам а<х2+у2<Ь) не является О. о. Зато шар без ядра (множество
точек пространства, координаты которых удовлетворяют неравенствам а<х2+
-f-y2-f-22<6) есть О. о. О. о. имеют ряд свойств, выделяющих их среди других
областей. Например, справедлива теорема: если функция f(xt у) гармонична
в О. о. С на плоскости, то интеграл по любой окружности, целиком лежащей
в G, деленный на длину окружности, равняется значению функции в центре
окружности. Теорема перестает быть верной, если отказаться от односвязности
области G.
ОДНОСТОРОННИЕ ПОВЕРХНОСТИ — поверхности, не имеющие двух сторон, в
отличие, например,от сферы, поверхности куба или квадрата. Примеры О. п. — лист
Мёбиуса, бутылка Клейна. Класс О. п. в
трехмерном пространстве совпадает с
классом неориелтируемых поверхностей. См.
Ориентируемая поверхность.
ОДНОСТОРОННИЕ УГЛЫ—см. Угол.
ОДНОСТОРОННИЙ ПРЕДЕЛ
функции — общее название для предела
функции справа (см.) или предела функции
слева (см.).
ОД НОСТОРОН НЯЯ КАСАТЕЛЬНАЯ
к графику функции y=f(x) в точке
М0 — правая (или левая) касательная, т. е.
предельное положение секущего луча М0М,
когда точка Μ стремится к М0, оставаясь
справа (соответственно слева) отточки М0.
На рис. 178 MQN — правая и М0Р — левая
касательные.
Рис. 178

272
ОДНОСТОРОННЯЯ ПРОИЗВОДНАЯ
ОДНОСТОРОННЯЯ ПРОИЗВОДНАЯ функции у=/(*) — конечный
односторонний предел (см.):
f. Ay .. ί(χο+Δχ) — ί(χο)
urn -—β iim .
δ*-*-ο Δχ Δ*-* ο Δχ
При Δ х —> +0 О. п. называется правой производной, а при Δ л:—* —0 — левой
производной (предполагается, что функция f(x) определена в правой и
соответственно левой полуокрестности данной точки х0). В случае равенства правой
и левой производных функция имеет производную (см.); если же эти производные
не равны, то точка \х0, f(x0)] графика
функции является угловой,
односторонние касательные (см.) к графику
функции образуют угол, отличный от
нуля, и функция в точке х0 не имеет
производной (рис. 179).
У\
fM/
Рис. 180
Если правая (левая) производная в данной точке существует, то функция
непрерывна справа (слева) в этой точке (см. Непрерывная справа (слева)
функция). Пример несуществования односторонних производных: функция
!xsin—, если χ Φ 0,
*
0, если *=0
не имеет правой и левой производной в точке *=0 (рис. 180).
ОДНОЧЛЕН — целое алгебраическое выражение, представляющее собой
произведение двух или большего числа сомножителей, каждый из которых есть либо
число, либо буква, взятая в некоторой положительной степени.
Одно число или одну букву в некоторой положительной степени также
5
можно рассматривать как О. Примеры: 2а3Ь; -—х6у2 — одночлены. О., которые
или ничем не отличаются, или отличаются только коэффициентами при одинаковых
буквенных множителях, называются подобными. Например, —а и а; 2аЬ и ЪаЬ —
подобные О.
ОКРЕСТНОСТЬ ТОЧКИ: 1°. О. т. на числовой оси —любой интервал
[открытый промежуток (см.)], содержащий данную точку а. В частности,
открытый промежуток (а — δ, a-f-δ). с центром в точке а, называется б-окрестностью
точки а (число о>0 — радиус δ-окрестности).
2°. О. т. в «-мерном пространстве — любая область (см.) n-мерного
пространства, содержащая данную точку. В частности, совокупность точек
М(хх, х-2, . . . , хп), удовлетворяющих неравенству:
V
(*1
фЧ
+(*«-
-*у
<».

окружность
273
является шаровой окрестностью точки М0 (х\, х®, . . . % х„) с центром в
этой точке и радиуса 6>0. Совокупность точек, удовлетворяющих системе
неравенств:
|*ι-*?|<δΐ' |*2-*2|<б2, ···. \хп-х°п\<Ъп,
является параллелепипеидальной окрестностью точки М0 (все δ/ положительны),
называемой также полиинтервалом.
3°. О. т. в метрическом пространстве — любая область (см.) метрического
пространства, содержащая данную точку. В частности, совокупность точек М,
расстояние каждой из которых до данной точки М0 меньше некоторого
числа 6>0, является сферической окрестностью с центром в данной точке М0
радиуса δ.
ОКРУГЛЕНИЕ действительного положительного числа — замена этого числа
приближенным значением его с определенной точностью. Обычно О. заключается
в отбрасывании конечного или бесконечного числа всех последних знаков (цифр)
данного числа а, начиная с некоторого разряда (О. по недостатку или О. с
недостатком); при отбрасывании цифры, начиная с некоторой, предшествующая
последняя цифра оставшегося («укороченного») числа может быть увеличена на
единицу (О. с избытком) или же оставлена без изменения (О. с недостатком).
Например, до разряда десятков О. числа α = 21,46 с недостатком дает число
20, стоящее ближе к числу α = 21,46, чем О. с избытком (которое дает
число 30).
О. числа связано с ошибкой О., т. е. разностью |а — а0|, где а — данное
число, а0 — «укороченное» округленное число, т. е. его приближенное значение.
См. Приближенные методы, Численные методы, Ошибка округления.
Лит.: И. Н. Шевченко, Начальные сведения о приближенных вычислениях, Изд-во
АПН РСФСР, М., 1958; В. М. Б ρ а д и с, Как надо вычислять, Учпедгиз, М., 1960.
ОКРУГЛЕНИЯ ТОЧКА —см. Круговая точка.
ОКРУЖНОСТИ КОНЦЕНТРИЧЕСКИЕ — окружности, имеющие общий центр
и лежащие в одной плоскости. Неконцентрические же окружности иначе
называют эксцентрическими или эксцентричными. О. к. иногда называют
концентричными. Ср. Конфокальные кривые.
Лат. соп — вместе, centrum — центр.
ОКРУЖНОСТЬ — замкнутая плоская кривая, все точки которой находятся
на одинаковом расстоянии от некоторой точки О, лежащей в плоскости этой
кривой и называемой ее центром. Расстояние от любой точки О. до ее центра
измеряется отрезком, называемым радиусом О., который обычно обозначается
буквой г (или R). О. с центром О и радиусом г иногда обозначается О (г).
О. с центром О и радиусом г можно определить как геометрическое место
точек (см.) плоскости, находящихся на данном расстоянии г от данной точки О,
расположенной в той же плоскости.
Уравнение О. в прямоугольных декартовых координатах имеет вид:
{x-af+(y-bf=r\ (*)
где (а, Ъ) — координаты центра, а г —радиус О. Из уравнения (*) следует,
что О. — кривая 2-го порядка. Касательная к О. перпендикулярна радиусу в
конце его.
О. используется при решении задач на построение, при графическом
решении уравнений и неравенств. О. имеет постоянную кривизну (см.) в любой
точке, равную —. Длина окружности О (г) равна 2 π г, площадь круга радиуса
г равна π/-2.
18 Толковый словарь математических терминов

274
ОКРУЖНОСТЬ АПОЛЛОНИЯ
ОКРУЖНОСТЬ АПОЛЛОНИЯ — геометрическое место точек Μ (см.)
плоскости, отношение расстояний которых до двух данных точек А и В, лежащих в
этой плоскости, есть постоянная величина λ(λ^=0, λ?=1): ΑΜ:ΒΜ=λ. Ο. Α.
используется при решении задач на геометрические построения (см.) методом
геометрических мест точек (см.), например при построении треугольника по
a, hat b:c или по а, Л, Ь:с (или по отношению высот hc\hb) и др. Окружность
названа по имени изучавшего ее древнегреческого ученого Аполлония Пергского
(III в. до н. э.).
ОКРУЖНОСТЬ ДЕВЯТИ ТОЧЕК — окружность, на которой расположены
середины сторон треугольника, основания его высот и середины отрезков высот,
заключенных между вершиной и ортоцентром. Центр О. д. т. совпадает с
серединой отрезка, соединяющего ортоцентр данного треугольника с центром
описанной окружности; радиус О. д. т. равен половине радиуса описанной окружности.
О. д. т. иначе называется окружностью Эйлера.
Лит.: П. С. Моденов, Сборник задач по специальному курсу элементарной
математики," «Советская наука», М., 1960; Д. И. Перепелки н. Курс элементарной геометрии,
Гостехиздат, М., 1948.
ОКРУЖНОСТЬ КРИВИЗНЫ пространственной кривой в точке Μ —
окружность, лежащая в соприкасающейся плоскости кривой в точке М, радиус
которой равен —-, где k — кривизна (см.) кривой в точке М, а центр О лежит
k
на нормали (см.) к кривой в точке Λί, на расстоянии МО=—. О. к. не
k
существует в точке* где кривизна кривой равна нулю. О. к. имеет с кривой
касание в точке Μ не ниже 2-го порядка. О. к. иначе называется соприкасающейся
окружностью (см.).
ОКТАЭДР — восьмигранник. Правильный О.—один из пяти типов
правильных многогранников (см.), имеет 6 вершин, 8 граней и 12 ребер, т. е. является
фигурой двойственной (см. Двойственности принцип) правильному гексаэдру (см.)—
кубу. Правильный О. имеет центр симметрии и 9 плоскостей симметрии, как и
куб. Правильный О. легко получить из куба, если центры граней куба принять
за вершины правильного О. О, иногда называют четырехугольной бипирамидой.
Греч. оутсэ— восемь, δερα — грань, основание.
ОМБИЛИЧЕСКАЯ ТОЧКА —то же, что и круговая точка на
поверхности (см.).
ОПЕРАТОР — математическое понятие, означающее, в самом общем смысле,
соответствие между элементами двух множеств X и У, относящее каждому
элементу χζΧ некоторый элемент у ζ У. Эквивалентный смысл имеют термины:
«отображение, преобразование», функция. Элемент у называют образом элемента
х, а χ называют прообразом элемента у.
Если X и У — числовые множества, то чаще всего пользуются термином
«функция». Оператор, отображающий (бесконечномерное) пространство функций
в числовое множество, называется функционалом.
Примеры: 1) оператор дифференцирования каждой дифференцируемой
функции f(x) ставит в соответствие функцию /' (х)\ 2) пусть (ξ^ ξ2» Is) — вектор
трехмерного пространства /?3 при линейном преобразовании пространства в себя
переходит в вектор ( ξ'ρξό* £з)« так что Ιί^^Σι а*&г α/—фиксированные чис-
7=1
ла; мы имеем, таким образом, оператор линейного преобразования векторного
пространства #3> заданный квадратной матрицей || α/JJ порядка 3; 3)
примером нелинейного оператора А является A[f(x)]=f2(x).

ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
275
Наиболее важный класс операторов — линейные операторы (см.) в
гильбертовом пространстве (см.). Большое значение в математической физике и в теории
дифференциальных и интегральных уравнений имеют дифференциальные
операторы (см.) и интегральные операторы (см.).
ОПЕРАТОРНОЕ ИСЧИСЛЕНИЕ — часть функционального анализа,
посвященная изучению свойств операторов и применению их к решению различных
задач.
О. и. возникло в результате развития теории интегральных уравнений,
решения задач на нахождение собственных значений операторов, связанных с
теорией колебаний и другими проблемами математической физики. В связи с
большой общностью понятия оператора О. и. установило связи между
различными областями математики.
Наиболее широкий и разработанный класс операторов — линейные операторы
в линейных нормированных пространствах (в частности, в функциональных
пространствах).
Примеры линейных операторов: 1) оператор дифференцирования функций;
2) оператор определенного интегрирования на данном отрезке суммируемых
функций; 3) оператор линейного преобразования в конечномерном пространстве
(задаваемый квадратной матрицей порядка п).
В последнее время развивается также теория нелинейных операторов,
связанная с нелинейными интегральными уравнениями в физике и механике. Этой
теме посвящены работы Н. Н. Назарова, В. В. Немыцкого и др.
Лит.: Л. А. Люстерники С. Л. Соболев, Элементы функционального анализа,
Гостехиздат, М., 1951; Н. И. Ахиезер и И. М. Глазман, Теория линейных
операторов в гильбертовом пространстве, Гостехиздат, М., 1950.
ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ — совокупность методов прикладного
математического анализа, позволяющих экономными и непосредственно ведущими к
цели средствами получать решения линейных дифференциальных уравнений, а
также разностных и некоторых типов интегральных уравнений.
В связи с этим методы операционного исчисления находят самое широкое
применение в механике, электротехнике, автоматике и в других самых
разнообразных отраслях науки и техники. В основе операционного исчисления лежит
идея функционального преобразования: некоторой функции вещественного
переменного t* определенной при положительных значениях аргумента, называемой
начальной функцией или оригиналом, с помощью линейного интегрального
преобразования ставится в соответствие функция другого переменного р,
называемая изображением.
Подобное преобразование «оригинал — изображение» можно осуществить так,
чтобы операциям дифференцирования и интегрирования начальных функций
соответствовали алгебраические операции в области изображений. Это дает
возможность находить с помощью простейших алгебраических действий
изображения решений» исходных дифференциальных уравнений, затем разыскивать
соответствующую начальную функцию, т. е. решение осуществляется с помощью
некоторых простых правил и «каталога» наиболее часто встречающихся
изображений. В более сложных задачах приходится прибегать к обратному
функциональному преобразованию: изображение — оригинал.
Первые сочинения, посвященные операционному исчислению, появились в
середине прошлого века. Русским математиком Μ. Ε. Ващенко-Захарченко в
монографии «Символическое исчисление и приложение его к интегрированию
линейных дифференциальных уравнений», вышедшей в Киеве в 1862 г., были
поставлены и частично разрешены основные задачи того метода, который в
дальнейшем получил название операционного.
18*

276 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ
Систематическое применение операционного исчисления к решению
физических и технических задач началось с появления в 1892 г. работ английского
ученого О. Хевисайда. Сущность О. и. можно проиллюстрировать на примере с
наиболее часто встречающимся в прикладных задачах классом начальных
кусочно-непрерывных функций f (t) вещественной переменной /, определенных при
*>0 и принимаемых равным нулю при /<0. Из класса кусочно-непрерывны χ
начальных функций выделяется и в дальнейшем рассматривается подкласс
функций, характеризуемых определенным порядком роста при весьма больших
значениях аргумента t, а именно: \f(t)\<MeSot, гДе Μ и so — независимые от t
числа.
Если p=s+/a —некоторое комплексное число, то при указанных
ограничениях, накладываемых на функцию / (t), интеграл
оо
M/(0}=f*-"/(0<ft С)
о
существует и представляет регулярную в полуплоскости Re ρ >s0 функцию от
/?, называемую лапласовым интегралом функции / (t).
Функцию F{p), введенную по закону:
f(t)dt, (··)
называют изображением начальной функции или оригинала /(/).
Ряд свойств изображения (**), например изображения производной /' (t):
М/#(0}-р^{/(0}-/(0)
и изображения интеграла
*(0-f/(0*:
ΜΨ
(Οίο
L{f(t))
делают очевидным тот факт, что преобразование (*) переводит операции
дифференцирования и интегрирования в операции умножения и деления на
комплексное переменное р.
Пользуясь основными свойствами изображения, составляются изображения
некоторых простейших функций — «каталог» изображений. «Каталог»
изображений простейших функций и теоремы разложения Хевисайда, дающие возможность
отыскать начальную функцию, когда изображение F (р) является полиномом или
отношением двух полиномов, позволяют простейшим способом найти решение
большой группы обыкновенных линейных дифференциальных и разностных
уравнений с постоянными коэффициентами.
Но многочисленные задачи приводят к изображениям, не сводящимся к
имеющимся в «каталоге». Существует общее средство построения начальной функции
по ее изображению — так называемая формула обращения Римана—Мсллина:
о-{-юо
/(О =-—-(' e«F(p)dp
Ρ

ОПОРНАЯ ПЛОСКОСТЬ
277
где интегрирование производится по любой прямой в плоскости p=o+iw,
параллельной мнимой оси и расположенной в полуплоскости Rep>s1>s0.
В математической физике при интегрировании дифференциальных уравнений
с частными производными применяется многомерное О. и.
В последнее время обоснованием О. и. занимались польский ученый Ян
Минусинский и советский математик В. А. Диткин.
Лит.: Л. Н. Лурье, Операционное исчисление и его приложения к задачам механики,
Гостехиздат, М., 1950; Б. ВандерПольи X. Бреммер, Операционное исчисление
на основе двустороннего преобразования Лапласа, ИЛ, М., 1952; В. А. Диткини
П. И. К у зн ец о в, Справочник пооперационному исчислению, Гостехиздат, М., 1950;
В. А. Диткин и А. П. Прудников, Интегральные преобразования и операционное
исчисление, Физматгиз, М., 1961.
ОПИСАННЫЕ ФИГУРЫ (в элементарной геометрии). Рассматриваются
фигуры, описанные вокруг выпуклых многоугольников и вокруг выпуклых фигур.
О. ф. вокруг выпуклого многоугольника называются выпуклыми фигурами
(замкнутые ломаные и кривые линии), на которых расположены вершины много-
й < м
Рис. 181 Рис. 182 Рис. 183 Рис. 184
угольника; этот многоугольник по отношению к О. ф. называется вписанным
(см.). О. ф. вокруг выпуклой фигуры Φ называются выпуклыми фигурами
(ломаные и кривые линии), если они касаются фигуры Φ (называемой вписанной)
по крайней мере в двух точках и так, что при обходе по контуру фигуры Φ по
часовой стрелке (или против ее) мы не встретим внешних точек (см.) О. ф.
О. ф. могут быть как конечные (например, окружность, описанная около
треугольника, рис. 181), так и бесконечные (неограниченные) (например, угол,
описанный около окружности, рис. 182). На рис. 183
многоугольник Alt Л2, . . ., Ап описан около треугольника
ABCt на рис. 184 кривая ω описана (является О. ф.)
вокруг фигуры Ф.
Аналогично определяются О. ф. и в пространстве,
где вместо многоугольника рассматривается многогран- ч ^ ,—^~
ник, а вместо плоской фигуры поверхность (чаще 'а »ч )
всего сфера, конус, цилиндр).
Иногда в математике также говорят об О. ф., кото- Рис. 185
рые могут быть и невыпуклыми; например, на рис. 185
изображена невыпуклая (вогнутая) фигура ω, описанная вокруг квадрата ABCD.
В проективной геометрии также говорят о вписанном в кривую 2-го
порядка (ряд точек 2-го порядка, коническое сечение) шестиугольнике (см. Паскаля
теорема) и описанном около кривой 2-го порядка шестиугольнике (шестисторон-
нике, стороны которого принадлежат пучку прямых 2-го порядка; см. Брианшона
теорема). См. также Вписанные фигуры.
Лит.: Д. И. Перепелки н, Курс элементарной геометрии, ч. 1—2, Гостехиздат, М.,
1948 — 1949.
ОПОРНАЯ ПЛОСКОСТЬ — плоскость, имеющая общие точки с границей
Bbinv^ofi пространственной фигуры и не содержащая внутренних точек этой
фигуры. Например, всякая касательная плоскость к шару будет его опорной

278
ОПОРНАЯ ПРЯМАЯ
плоскостью, или всякая плоскость, в которой лежит какая-либо грань
тетраэдра, будет его опорной плоскостью.
Можно доказать, что если α — опорная плоскость к выпуклой фигуре Φ
(выпуклому телу), то вся фигура Φ лежит по одну сторону от плоскости а.
О. п. есть пространственный аналог понятия опорной прямой (см.) для выпуклых
плоских фигур.
Лит.: Л. А. Люстерник, Выпуклые фигуры и многогранники, Гостехиздат, М.,
ОПОРНАЯ ПРЯМАЯ выпуклой фигуры Φ на плоскости есть прямая,
содержащая только граничные точки фигуры Φ и не имеющая общих
внутренних точек с той же фигурой. Фигура Φ по отношению к своей О. п. вся
лежит по одну сторону от нее. Например, касательная к окружности круга О (г)
есть О. п. к этому кругу. Или, например, прямая, на которой расположена
сторона треугольника, будет О. п. к этому треугольнику. Понятие О. п.
используется в теории выпуклых фигур, например, при рассмотрении изоперимет-
рической задачи (см.).
Лит.: Л. А. Люстерник, Выпуклые фигуры и многогранники, Гостехиздат, М.,
1956; И. М. Яг лом и В. Г. Болтянский, Выпуклые фигуры, Гостехиздат, М.,
1951.
ОПРЕДЕЛЕНИЕ математического понятия — раскрытие смысла, содержания
этого понятия. При этом раскрытие смысла (сущности) понятия может быть
дано различными способами: 1) генетически — когда указывается способ
образования данного понятия; 2) сведением данного понятия к понятиям ранее
известным — чаще всего через понятия рода и вида, т. е. через родовой признак и
видовое отличие; 3) аксиоматически — когда определение понятия дается неявно,
в аксиомах (см., например, Точка, Прямая, Плоскость).
Примеры О. : 1. Сферой (трехмерного евклидова пространства) называется
поверхность, полученная от вращения окружности вокруг ее диаметра. Это
генетическое О. понятия сферы. Однако сферу можно определить через понятие
геометрического места точек пространства или аналитически (см. Сфера).
2. Логарифм числа Л/>0 при основании а>0, аФ\ можно определить как
решение показательного уравнения αχ—Ν% что записывается так: *=lgaAf, а
можно определить как некоторое непрерывное решение функционального уравнения
f(xy)=f(x)+fM (см. Логарифм).
Выяснение сущности того или иного математического понятия в школе
проще всего устанавливается при рассмотрении конкретных примеров.
Лит.: В. В. Репье в, Общая методика преподавания математики, Учпедгиз, М.,
1958; Д. Пой а, Математика и правдоподобные рассуждения, ИЛ, М., 1957.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ (см. Интегральное исчисление) — важное
понятие математического анализа. К вычислению О. и. сводятся многие задачи
геометрии, механики, физики. Обозначается
О. и.:
ь
\f(x)dx
а
и по определению равен:
Ь > а
Рис. 186 /(П-*°
где Τ — разбиение отрезка \а, Ь\ на отрезки Дь»
%к — произвольная внутренняя ючка отрезка Ak (рис. 186),
1(Т) — длина наибольшего отрезка Δ/ι при разбиении Т.

ОПРЕДЕЛИТЕЛЬ
279
О. и. существует для функций, лебеговская мера (см. Лебега интеграл)
множества точек разрыва (см.) которых равна нулю. Геометрический смысл
О. и.—площадь криволинейной трапеции, ограниченной прямыми х=а< х=Ь,
у==0, и кривой y=f(x) (с учетом знака площади).
ОПРЕДЕЛИТЕЛЬ (детерминант) л-го порядка — алгебраическая сумма п\
слагаемых» составленных из элементов квадратной матрицы (таблицы):
Ч
/а11«12
α2ΐα22
аМ<*П2 · · · а
по следующему закону: каждое слагаемое есть произведение η элементов,
взятых по одному и только по одному из каждой строки и каждого столбца
матрицы. Каждый член со знаком (—1)', где t — число инверсий (см.) во
вторых индексах члена, когда первые индексы члена расположены в натуральном
порядке.
Для обозначения О. используется символ:
det Л =
а1Ха12 . . . а1п\
α21α22 · · · а2п\
аШап2 · · · аПП
т. е. элементы матрицы заключаются в прямые вертикальные черточки. Этот
символ был введен в XIX в. английским математиком Кэли. Следовательно,
det А=2(—1)^1^2/ · · · ank* гДе сумма берется по всем перестановкам (см.)
из чисел 1, 2, . . .* л, a t — число инверсий в подстановках ( . . * * * ?).
Таким образом, совокупность всех определителей образует числовую
функцию на множество всех квадратных матриц.
О. обладает рядом свойств, которые лежат в основе практических способов
их вычислений. Основные свойства О. следующие: 1) О. не изменяется при
транспонировании (см.) строк и столбцов; 2) если один из столбцов (строк)
состоит из нулей, то О. равен нулю; 3) если один О. получен из другого О.
перестановкой двух столбцов (строк), то О. отличаются друг от друга знаком;
4) О., содержащий два пропорциональных, в частности два равных столбца
(строки), равен нулю; 5) О. не меняется, если к какому-либо столбцу (строке)
прибавить линейную комбинацию других столбцов (строк); 6) если все элементы
какого-либо столбца (строки) О. умножить на некоторое число £, то весь О.
умножится на k, т. е. общий множитель любой строки или любого столбца
можно выносить за знак О.; 7) если элементы какого-либо ί-го столбца (строки)
О. являются суммами двух слагаемых, то такой О. равен сумме двух О., в
первой из которых в качестве /-го столбца (строки) взяты первые слагаемые, а во
втором — вторые слагаемые; при этом элементы всех остальных строк (столбцов)
у каждого из трех определителей одинаковы.
Свойство 2 и более общее свойство 4 дают лишь достаточные условия для
равенства нулю О. Необходимое и достаточное условие равенства нулю О.
состоит в том, чтобы какой-либо столбец (строка) был линейной комбинацией
других столбцов (строк).
О. имеют многочисленные приложения к различным вопросам математики и
физики. См., например, Крамера правило и опирающуюся на него Кронекера—
Капелли теорему, Остроградского определитель, Вронского определитель, Грама
определитель и т. д.
Начало зарождения О. относится, по-видимому, к концу XVII в. Лейбниц
(1693) в одном из писем Лопиталю сообщает, что он сделал открытие, пользу-

280 ОРДИНАЛЬНОЕ ЧИСЛО
ясь системой двойных индексов коэффициентов уравнений. Однако результаты
Лейбница не были опубликованы, поэтому они остались неизвестными.
В 1750 г. Крамер указывает общий закон составления О. и общие
формулы для решений систем η линейных уравнений с η неизвестными. Общая теория
О. была начата Вандермондом (1771) и дальнейшее существенное развитие
получила (1812) в работах Бине и Коши.
В настоящее время О. применяются почти во всех разделах математики, а
также в очень многих ее приложениях.
Лит.: А. Г. Курош, Курс высшей алгебры, Физматгиз, М., 1955; Л. Я. О к у н е в,
Высшая алгебра, Учпедгиз, М., 1957.
ОРДИНАЛЬНОЕ ЧИСЛО — то же самое, что и порядковое число. О. ч.
названо в противоположность понятию кардинального числа (cm.J, или
количественного числа. См. Трансфинитные числа.
Лат. ordinal is — порядковый.
ОРДИНАТА — вторая по порядку из координат (прямоугольных декартовых
или аффинных) точки на плоскости или в пространстве. О. точки обычно
обозначается буквой у.
Лат. ordinatus — упорядоченный.
ОРИЕНТАЦИЯ: 1°. О. базисов. Говорят, что два базиса [два репера (см.)]
«-мерного пространства (еи е2, . . ., еп) и (/lf /2, . . ., fn) одинаково
ориентированы, если линейное преобразование Λβ,· = //(/=1, 2 п) задается
матрицей с положительным определителем (см.). Если же матрица преобразования А
имеет отрицательный определитель, то базисы (elt e2, ...» еп) и(/1э /2» · · ·» fn)
ориентированы различно.
2°. О. поверхности. Разобьем поверхность на частично налегающие друг на
друга куски ш/ такие, что уравнение каждого куска может быть дано в виде:
х=х{и, υ), у*=у(и, ν), ζ=ζ(ιι, ν), 0<ы<1, 0<у<1
(для поверхности в целом такие уравнения, вообще говоря, написать
невозможно).
На каждом таком куске задается два векторных поля (два упорядоченных
линейно независимых касательных вектора в каждой точке поверхности,
непрерывно зависящих от точки). Каждая пара указанных векторных полей задает О.
куска. Две пары векторных полей задают одну и ту же О. куска, если в
любой точке куска векторы ξ, и η, первой пары векторных полей одинаково
ориентированы с (ξ2, η·2> — векторами второй пары векторных полей. В
противоположном случае две пары векторных полей задают различные ориентации.
Если куски Wi, покрывающие поверхность, можно ориентировать так, чтобы
на пересечениях wi f) wj совпадали ориентации кусков до,- и wj, то поверхность
называется ориентируемой, а ее О. определяется О. каждого из кусков.
Для наглядности вместо пары векторных полей рассматривают в каждой
точке поверхности векторное произведение векторов из векторных полей. Тогда
в каждом куске задается поле векторов, ортогональных поверхности и
направленных в «одну сторону» от поверхности. Если на каждом куске (рис. 187)
рассмотреть такое поле и если на пересечении до/П^/ поля wi и wj совпадают по
направлению, говорят, что поверхность ориентируема и задана ее О. Отсюда
непрерывное семейство нормальных к поверхности векторов задает О.
поверхности. Та сторона поверхности, куда направлены нормальные векторы, называется
положительной стороной относительно данной О.
Примеры: 1. Семейство векторов (рис. 188), ортогональных сфере и
направленных от центра, задает О. сферы, объявляя положительной внешнюю
сторону поверхности сферы. Возможна другая О. Ее задают нормальные векторы

ОРТОГОНАЛЬНАЯ МАТРИЦА
281
сферы, направленные внутрь сферы. 2. На листе Мёбиуса невозможны
непрерывные семейства ненулевых нормальных векторов. Лист Мёбиуса неориентируем.
3°. О несамопересекающейся кривой — один из двух возможных способов
движения вдоль кривой.
Рис. 187 Рис. 188
ОРИЕНТИРУЕМЫЕ ПОВЕРХНОСТИ — поверхности, допускающие
ориентацию (см.). О. п. имеют две стороны. Лист Мёбиуса (см.) неориентируем, у
него одна сторона: вектор нормали, обнесенный по листу, возвращается в
первоначальную точку, имея направление, противоположное первоначальному.
ОРИСФЕРА — поверхность в пространстве Лобачевского, полученная от
вращения орицикла (см.) вокруг одной из его осей: О., таким образом, есть
пространственный аналог орицикла. О. можно определить и как геометрическое
место концов секущих равного наклона, проведенных из некоторой точки Μ
прямой а ко всем прямым пространства, параллельным этой прямой в
определенном направлении. Точка Μ считается точкой О. Прямая а называется осью
О. О. задается осью а и точкой М, принадлежащей этой оси.
О. иначе называется предельной поверхностью.
ОРИЦИКЛ—кривая в плоскости Лобачевского, являющаяся геометрическим
местом концов секущих равного наклона, проведенных из некоторой точки А
прямой а к прямым, параллельным ей в определенном направлении и лежащим
с ней в одной плоскости. Точка А считается точкой О. Прямая а,
определяющая систему параллельных прямых в определенном направлении, называется
осью О.
Всякая прямая, параллельная оси орицикла, также может быть принята за
ось. О., как и эквидистанта (см.), есть кривая линия. Любая прямая
пересекает О. не более чем в двух точках. О. иначе называют предельной линией.
О. инвариантен относительно вращений вокруг бесконечно удаленной точки Ооо,
в которую направлена его ось а.
ОРТ — единичный вектор евклидова пространства, т. е. вектор е (см.),
длина которого равна единице. Если дан вектор а, то его О. (обозначим его через
а
е) можно выразить так: е=р, где |а| — длина вектора а. Всякий вектор а на
1а1
плоскости можно разложить по двум неколлинеарным векторам ех и е2: a=jtej-f
Н-уе2, где х, у— координаты вектора а, а е, и е2 — единичные векторы (базис)
соответственно осей координат χ и у.
Обычно О. в прямоугольной декартовой системе координат обозначают
буквами i, j, k, направленными соответственно по осям хч у, г.
Термин О. есть сокращение слова лат. orientation — ориентация, т. е.
направление данного вектора или данной оси.
'.ОРТОГОНАЛЬНАЯ МАТРИЦА — невырожденная матрица, обратная к
которой совпадает с ее транспонированной матрицей.

282
ОРТОГОНАЛЬНАЯ ПРОЕКЦИЯ
Существует много других» эквивалентных приведенному определений О. м.
Важность понятия О. м. предопределена тем, что О. м. соответствуют
ортогональные линейные преобразования неизвестных (см.).
ОРТОГОНАЛЬНАЯ ПРОЕКЦИЯ — частный случай параллельной проекции,
когда проектирующие лучи перпендикулярны оси проекций или плоскости
проекций (см. Проекции). О. п. иначе называют прямоугольной проекцией. Абрис
(см.) шара в О. п. есть окружность.
ОРТОГОНАЛЬНОЕ ПРЕОБРАЗОВАНИЕ я-мерного евклидова пространства —
линейное преобразование (см.), сохраняющее длину каждого вектора. О. п.
есть обобщение вращений трехмерного евклидова пространства вокруг начала
координат [быть может, с отражениями (см.)] на многомерный случай. В ортонор-
мальном базисе (см.) матрица ||я/у|| О. п. (см.)обладает следующими свойствами:
1) сумма квадратов элементов одной строки (одного столбца) равняется
единице:
η а
2) SflWtyk-O (/>/), ^akiakr0 (i+j).
Матрица ||ау||, обладающая свойствами 1) и 2), называется ортогональной.
Матрица Л—1, обратная (см.) ортогональной матрице А, совпадает с
транспонированной А'. Все собственные значения ортогональной матрицы или О. п. по
модулю равны единице. Совокупность всех О. п. образует группу, которая
называется ортогональной группой.
Справедлива теорема: всякую квадратичную форму О. п. переменных можно
привести к сумме квадратов с некоторыми коэффициентами. Эти коэффициенты
вещественны, если коэффициенты квадратичной формы вещественны.
Примеры: 1) вращение трехмерного евклидова пространства вокруг начала
координат есть О. п.; 2) преобразование переменных у,-=—Х[ (/=1, 2, .... п)
ортогонально относительно скалярного произведения (см.); 3) матрица
(cos φ — sin φ 0
sin φ cos φ 0
О 0—1
ортогональна;
4) если {е^ е2, е3} и {flf f2# f3} — системы ортонормальных векторов, то
линейное преобразование А, задаваемое формулами: Л(е/)=1,, /=1, 2, 3, есть О. п.
Пусть ау означает косинус угла между е; и!/, ί,/=1, 2, 3. Тогда матрица,
составленная из этих коэффициентов, есть ортогональная матрица. В базисе
{βχ, е2, е3} она задает О. п. А О. п. рассматривается во многих отделах
математики. В частности, в аналитической геометрии задача о приведении
уравнения кривой (поверхности) 2-го порядка к каноническому виду эквивалентна задаче
о приведении квадратной формы О. п. к сумме квадратов с некоторыми
коэффициентами.
Различают собственные и несобственные О. п. Определитель (см.) матрицы
собственных О. п. равен 4-1, а несобственных —1. Несобственные О. п. есть
вращение евклидова пространства вокруг начала координат с отражением.
Лит.: И. М. Гельфанд, Лекции по линейной алгебре, Гостехиздат, М., 1951.
ОРТОГОНАЛЬНЫЕ ТРАЕКТОРИИ — кривые, пересекающие под прямым
углом каждую из линий или каждую из поверхностей заданного семейства.
Например, гипербола -~ — т-2-^-у-14 λ>ο0 является О. т. семейства

ОРТОЦЕНТР
283
эллипсов —— -j - = 1, 0<μ<<: (см. Софокусные кривые), где λ и μ
—параметр семейства. Прямые пучка есть О. т. семейства концентрических
окружностей с центром, совпадающим с центром пучка.
ОРТОГОНАЛЬНЫЕ ФУНКЦИИ. Пусть в некотором линейном пространстве
функций определено скалярное произведение (см.). Две функции этого
пространства / и g ортогональные, если их скалярное произведение равно нулю.
Например, четная функция /(см.) и нечетная (см.) g ортогональны
относительно скалярного произведения:
(A g)~$flx)g(x)dx.
—\
ОРТОНОРМИРОВАННАЯ СИСТЕМА функций относительно некоторого
скалярного произведения — система функций <plt φ2* . . ., φη, . . . такая, что
скалярный квадрат (см.) каждой функции семейства равен единице, а скалярные
произведения (см.) любых двух различных функций системы равны нулю.
Например, система функций
1 sin пх cos пх # Λ
—=, —, ζζ (л=1. 2, ...)
1//2π Vk Υπ
ортонормирована относительно скалярного произведения:
η
(/. g)=$fWg(x)dx.
—π
Одной из главных задач теории О. с. ф. является задача о разложении
функции в ряд по функциям О. с. ф.:
оо
/(*)-2ся<м*). (*)
п==1
Предполагая возможность почленного интегрирования, получаем формулу для
коэффициентов Сп (скалярное произведение в данном случае записывается:
Ь
(A *)-Jp (*)/(*) *(*)<**■
а
где р(х) — некоторая функция):
Ь
Сц-J p(x)f(x)<Pn(x)dx.
а
Если α=—π, Ь*=л< р{х)=\, то разложение (*) — обычное разложение
функции / в ряд Фурье.
Теория О. с. ф. находит свое основное применение в решении краевых
задач уравнений математической физики.
ОРТОЦЕНТР — точка пересечения трех высот треугольника. Существует
ряд теорем относительно О., например: 1. Центр тяжести треугольника (точка
пересечения медиан), центр описанного круга и О. лежат на одной прямой.
2. О. треугольника ABC (рис. 189) является центром окружности, вписанной
в треугольник KLMt вершины которого есть основания высот данного
треугольника ABC. 3. О. остроугольного треугольника лежит внутри его, тупоугольного
треугольника — вне его и прямоугольного треугольника — совпадает с вершиной
прямого угла.

284
ОСЕВОЙ ВЕКТОР
Понятие О. иногда используется при решении задач на геометрические
построения (см.). Например, дан (начерчен) круг с диаметром АВ (рис. 190);
построить из данной точки М, лежащей вне круга, перпендикуляр на АВ
с помощью только одной линейки; при этом центр окружности не дан.
Построение выполняем таким образом: проводим AM и BMt получаем точки К и L,
затем проводим AL и ВК — высоты треугольника АВМ. Точка 5
пересечения AL и ВК есть О. треугольника АВМ, следовательно, третья высота
пройдет через ортоцентр S; отсюда прямая MS — искомая. Если Μ проектируется
Рис. 189 Рис. 190
на продолжение диаметра АВ, то построение перпендикуляра выполняется
несколько иначе; если В Μ (или AM) имеет с окружностью только одну общую
точку В (или Л), то ВМ (или AM) и будет искомым перпендикуляром.
Греч, ορθοξ — прямой, правильный; лат. centrum — центр.
ОСЕВОЙ ВЕКТОР — вектор а (обычный, полярный) в ориентированном
пространстве, который при изменении ориентации пространства на противоположную
преобразуется в противоположный вектор (—а).
Примеры: 1. Векторное произведение (см.) двух векторов является О. в.,
так как оно изменяется на противоположный вектор при переходе от левой
системы координат к правой или обратно. 2. Угловая скорость вращения
твердого тела вокруг некоторой оси может быть О. в., так как ее можно
изобразить вектором, направленным в ту или другую сторону оси вращения, в
зависимости от выбора положительного направления этой оси.
О. в. также называют псевдовектором или аксиальным вектором.
ОСНОВАНИЕ ПИРАМИДЫ — грань (см.) пирамиды (см.), лежащая в
плоскости, пересекающей все грани многогранного угла, из которого получается
пирамида.
ОСНОВАНИЕ СИСТЕМЫ СЧИСЛЕНИЯ— любое натуральное число g>2.
Всякое целое число в системе счисления с основанием g может быть записано
с помощью не более g различных знаков, называемых цифрами: 0, 1, 2, . . .,
(g — 1). Например, число gig2g3 · · · gm гАе g/ —одно из чисел 0, 1, 2, . . .,
(g—· 1), может быть записано в виде
*1вл-1+*1Яя-л+ - · · +gnr-ig+8n-
Если основание g мало (например, g=2), то сравнительно небольшие
числа будут иметь громоздкие, длинные представления (записи), если же g велико
(например, g=60), то в этой системе счисления придется записать 60 цифр
(от 0 до 59), что создает излишние трудности при записях чисел и тем более
при действиях над ними. Система счисления с О. с. с. g= 10 общеупотребительна.
См. Счисление, Двоичная система счисления. Десятичная система счисления.
ОСНОВАНИЕ СТЕПЕНИ а* — число а. См. также Степень, Возведение
в степень.

ОСОБАЯ ТОЧКА
285
ОСНОВАНИЕ ТРЕУГОЛЬНИКА — любая из его сторон, которая выделяется
по каким-либо соображениям из сторон треугольника. Например, если на
сторону АВ проводится высота из противоположной вершины С треугольника, то
сторона АВ — О. т. Основанием равнобедренного треугольника ABC (AC^BC)
называется сторона АВ этого треугольника.
ОСНОВАНИЯ ГЕОМЕТРИИ — математическая дисциплина, изучающая
дедуктивное (аксиоматическое) построение различных геометрий: элементарной
геометрии (евклидовой), геометрии Лобачевского и др.
В О. г. входит также вопрос об истории попыток доказательства пятого
постулата Евклида, общие вопросы исследования системы аксиом:
непротиворечивость, независимость и полнота. При изучении О. г. студенты педагогических
институтов и университетов знакомятся с ролью аксиоматического метода
в математике.
Лит.: Н. В. Ефимов, Высшая геометрия. М., 1953; А. В. Π о г о ρ е л о в, Лекции
по основаниям геометрии, Харьков, 1958; В. И. Костин, Основания геометрии, М.,
1948.
ОСНОВНАЯ ТЕОРЕМА АЛГЕБРЫ комплексных чисел — теорема,
заключающаяся в том, что всякий многочлен степени η (п>0):
/(2)-αυε"+α^-ι+ ... +ап,
где а0 φ О, над полем комплексных чисел имеет по крайней мере один корень ги
так что /(г1)=0. Из О. т. а. и из теоремы Безу вытекает, что многочлен
f(z) имеет в поле комплексных чисел ровно η корней (с учетом их кратностей).
Действительно, согласно теореме Безу /(г) делится на ζ— ζ1 (без остатка),
т. е. f(z)^fx(z) (г — гг), аотсюда многочлен fx(ζ) (я-— 1)-й степени по О. т. а.
также имеет корень ζ2 и т. д. В конечном счете мы придем к заключению, что
/(г) имеет ровно η корней:
/ (ζ) =α0 (г — ζγ) (ζ — ζ2)...(ζ — ζη).
О. т. а. называется так потому, что основное содержание алгебры в
XVII—XVIII вв. сводилось к решению уравнений. О. т. а. была доказана
впервые в XVII в. французским математиком Жираром, строгое же доказательство
было дано в 1799 г. немецким математиком Гауссом.
В настоящее время известно несколько доказательств О. т. а.
ОСОБЕННАЯ МАТРИЦА —см. Вырожденная матрица.
ОСОБАЯ ТОЧКА: 1°. О. т. кривой, заданной уравнением F (х, у)=0, —
dF \ dF \
точка Р0(х0, у0) такая, что — =0 и — =0. Из уравнения F(x, y) = 0
ох \х0 оу \Уо
ни одно из переменных х, у, вообще говоря, не может быть выражено как
функция другого даже в как угодно малой окрестности точки Р0. Если вторые
частные производные F не все одновременно обращаются в нуль в точке Р0, то
поведение кривой в окрестности Р0 во многом определяется знаком:
d2F
d*F
Ро ду~
_ I d2F У
Я0 [дхду;
Ро
Если Δ >0, то О. т. изолированная (например, начало координат для кривой
у2 —х3-г-л;2=0); если Δ <0, то в этой О. т. кривая самопересекается
(например, кривая л:2 — у2 = 0 имеет начало координат точкой самопересечения); если
Δ=0, то необходимо более глубокое исследование вопроса о характере особой
точки.

286
ОСОБОЕ РЕШЕНИЕ
2°. О. т. в теории дифференциальных уравнений — точка Р0, в которой
одновременно обращаются в нуль числитель и знаменатель правой части
уравнения
dy_A(x, у)
dx В (х, у)*
где А(х, у) и В (х, у) непрерывны вместе со своими первыми производными
в Р0.
Для исследования интегральных кривых (см.) в окрестности особой точки
составляют характеристическое уравнение матрицы:
*о. Уо
'Её. I dJL
дх U. у0 ду
дА\ £d.|
дх\х9. уо дУ U Уо„
, т. е.
дВ \ дВ
дх U, у0 ду
£11 дА.
дх U. уо ^У
Х0* Уо
—λ
*о. Уо
=0.
Рис. 191
Если корни этого уравнения 1г и λ2 вещественны и λ1λ2>0, то О. т.
называется узлом (см.). Качественно-интегральные кривые в узле имеют вид,
изображенный на рисунке 191.
Если Xj Φ λ2 и λ1λ2<0, то О. т. есть седло (см.). При комплексных, но
не чисто мнимых λχ и λ2 О. т. есть фокус кривой. Всякая интегральная кривая
бесконечное число раз закручивается вокруг фокуса.
Чисто мнимые корни \ и λ2 не определяют
полностью характер О. т. Этот случай и случай \г12=0
представляют предмет более глубокого исследования.
3°. О. т. однозначной аналитической функции
(см. Аналитическая функция) — точка, в которой
нарушается аналитичность функции. Если существует
окрестность О. т., не содержащая других О. т., то
точка называется изолированной. Изолированная О. т.
называется устранимой, если существует lim/(z)(*).
Z-»20
Если Нт/(г) = оо, то О. т. г0 называется полю-
ζ-*·ζ0
сом, а если предел (*) не существует в расширенной плоскости комплексного
переменного (см.), то г0 называется существенно О. т. Ряд Лорана (см. Лорана
ряд) не содержит отрицательных степеней ζ — г0, если г0 является устранимой,
не содержит г — г0 в степени меньшей, чем — ρ (ρ — целое положительное
число), если г0 является полюсом (наибольшее такое ρ называется порядком
полюса). В существенно О. т. ζ — г0 встречается в отрицательной степени
бесконечно много раз.
Справедлива теорема: на границе круга сходимости степенного ряда функции
существует по крайней мере одна О. т. функции, представляемой этим рядом.
ОСОБОЕ РЕШЕНИЕ (или особый интеграл) дифференциального уравнения —
решение, в каждой точке которого нарушается единственность. Если уравнение
1-го порядка, то в каждой точке О. р. по направлению касательной к О. р.
проходит еще одна интегральная кривая. В точках О. р. уравнения у'=/(л;, у)
не выполняется условие Липшица (см. Липшица условие).
О. р. есть огибающая семейства интегральных кривых F (х, у, С),
образующих общий интеграл (см.) дифференциального уравнения. Например, общий
интеграл дифференциального уравнения у'=Уу есть у=^— (семейство
парабол). О. р. у = 0 — огибающая этого семейства.

ОСТРОГРАДСКОГО МЕТОД
287
ОСТАТОЧНЫЙ ЧЛЕН приближенной формулы — разность между точным и
приближенным значениями представляемого данной формулой выражения.
Задача исследования О. ч. состоит в том, чтобы получить для него оценки.
Например, приближенной формуле
1^2"» 1,41
соответствует точное равенство
1/2"=1,41+Я,
где R является О. ч. для приближения 1,41 к числу У 2, и известно, что
0,004 < R < 0,005.
О. ч. встречается также в асимптотических формулах. Например, для числа
π (χ) простых чисел, не превосходящих jc, имеем асимптотическую формулу:
π(^=^+0[*β-<1η*>μ],
4
где μ. —любое положительное число, меньшее —-; здесь О. ч., являющийся
разностью между функцией π (χ) и · для х>2, записан в виде 0[хе L
In л;
где буква О обозначает, что О. ч. не превосходит по абсолютной величине
выражения Схе ипх> , а С — некоторая положительная постоянная.
Существует О. ч. в формулах, дающих приближенное представление
функции. Так, в формуле Тейлора (см. Тейлора формула) О. ч. Rn(x) в форме
Лагранжа имеет вид:
f(«+i)(jc+ θ h)
где h—x—α, θ — некоторое число, причем 0<θ<1. В этом случае оценка
О. ч. зависит от поведения (п-И)-й производной. Можно говорить об О. ч.
квадратурной формулы, формулы суммирования, интерполяционных формул.
ОСТРОГРАДСКОГО МЕТОД —метод выделения рациональной части
неопределенного интеграла
ί;
Q(x)
где Q — многочлен степени η, имеющий кратные корни, а Р (χ) — многочлен
степени ηι*ζη.
Если Ρ (χ): Q(x) представляет собой правильную несократимую дробь и
знаменатель Q(x) разлагается на простые множители, т. е. (?(*) =
=(jc — a)k ... (х2+рх +q)m , то интеграл от этой дроби представится в виде
суммы интегралов от дробей следующих двух видов:
Аг А2 Ak Mlx+N1 Mmx+Nm
χ —а (х — а)°~' ' ' + (x—a)ki χ*+ρΧ+9^· ' (x*+px+q)m'
где Alf A2% ..., Aki Mlt M2i . . .? Mmi Nlf N2, . . ., Wm ■—некоторые
постоянные коэффициенты. Если k (или т) больше единицы, то интегралы всех
дробей первого вида (кроме интеграла от первой дроби) находятся по формуле:
ί
А , А !
;<**= — τ—г· -; ^-т-4-С,
(x — a)k £ — I (jc — α)*~Α

288
ОСТРОГРАДСКОГО МЕТОД
а интегралы всех дробей второго вида представляются в следующей форме:
Г Mx+N J R(x) Л f dx
J (x*+px+q)m (x2+px+q)m-i ^ J x2 + px+q
После объединения (суммирования) всех этих результатов получим равенство
вида:
ГР(х)._ Ρι(χ),ΓΡ*(χ).
JQW QiW+J Q.W '
где рациональная часть интеграла Рх (х): Qx (x) получается путем сложения
выведенных выше рациональных частей и представляет собой правильную дробь
со знаменателем
QiixXx-a)*-1 ... {x*+px+q)m~\
Дробь Ρ2 (χ): Q2 (x)у оставшаяся под знаком интеграла, получается от сложения
дробей вида
A Mx+N
х — а x2+px+q
и поэтому также является правильной со знаменателем
Q2 (*) = (* —я) .-. (x*+px+q),
не имеющим кратных множителей (корней), т. е. этот знаменатель Q2(x)
содержит все те же множители (корни), что и знаменатель Q(x) первоначальной
дроби, но уже только в первой степени.
Очевидно,
QM-Qi<*)-Q2<*).
Остроградский нашел метод выделения рациональной части Рх (х): Qt (x)
интегралов от правильных рациональных дробей чисто алгебраическим путем, не
пользуясь методами интегрального исчисления.
Прежде всего находим Qi(x) как общий наибольший делитель функции
Q(x) и ее производной Q' (х) (например, с помощью алгоритма Евклида);
определив Qx(χ), найдем Q2(jc) = Q(jc) : Qx(jc). После этого в равенстве
(формуле) Остроградского остается определить два многочлена Рг (х) и Р2 (х)- Так
как степени искомых многочленов Рг (х) и Р2 (х) соответственно ниже степеней
найденных уже многочленов Qt (x) и Q2 (x)f то мы их в равенство
Остроградского запишем с неопределенными коэффициентами, а затем,
продифференцировав обе части этого равенства, получим следующее тождество:
Р{х) _/Рг(х)У РЛх)
<?(*)' [QAx) ) Qi(x)'
После приведения к общему знаменателю, приравняв друг к другу
коэффициенты при одинаковых степенях χ в числителях левой и правой частей этого
тождества, получим систему уравнений относительно неопределенных
коэффициентов искомых многочленов Рх (х) и Р2 (#). Решая эту систему, найдем
неизвестные коэффициенты (а значит, и сами многочлены).
Теперь для получения интеграла от первоначально заданной дроби P(x):Q(x)
остается проинтегрировать дробь Р2 (х): Q2 (*)» которая выражается уже только
через трансцендентные функции (логарифмы и арктангенсы).
Итак, в равенстве (формуле) Остроградского имеем: P(x):Q(x), Pi(x)'Qi(x)
и P2(x):Q2(x) — правильные рациональные дроби, Ql (χ) — общий наибольший
делитель Q(x) и Q' (х)< а Q2(x)=Q(x):Qi (*)· Pi(x) и Р2(х) — многочлены,
находимые методом неопределенных коэффициентов.

ОТКРЫТАЯ СФЕРА
289
ОСТРОГРАДСКОГО ФОРМУЛА —формула, дающая преобразование
интеграла, взятого по некоторому объему у, ограниченному поверхностью 2, в интеграл
по этой поверхности:
f f f ifl·1"F4"IF) dx dy dZ= [ [Xdydz+Ydzdx+Zdxdy>
σ a
где Χ, Υ, Ζ — функции точки (я, у, ζ) объема V.
В представлениях векторного анализа О. ф. означает, что поток вектора
через замкнутую поверхность равен объемному интегралу от расхождения вихря,
а сама О. ф. имеет вид:
[jjdiv ρ dv=JJpn d σ,
где ρ — вектор поля, заданного в области у, dv— элемент объема,
do—элемент поверхности, η — единичный вектор внешней нормали к поверхности. Если
/(*!, *2> · · ·» *л) = 0 есть уравнение поверхности Σ, ограничивающей область
у, то:
Я
дХг дХшдХ. Мп\. . .
—- + -—+-— + . . .+ -— dxx dx2 . . . dxn
дхх дхо οχ.ό дхп
df df df
X\ л +^2 -, +· · · + Χ Π Ζ
охг οχ2 ο χ η
ds,
Σ
где в правой части интеграл взят по поверхности Σ с элементом площади ds.
В гидродинамике О. ф. устанавливает равносильность двух способов
подсчета жидкости, вытекающей из оболочки Σ в единицу времени: 1) исходя из
производительности точечных источников, заполняющих область υ (левая часть
равенства): 2) исходя из скорости частиц жидкости в момент их прохождения
через оболочку Σ (правая часть равенства).
О. ф. была установлена М. В. Остроградским в 1828 г., а опубликована
в 1831 г.
ОСТРЫЙ УГОЛ — угол, меньший прямого угла, или, иначе — О. у. есть
угол, меньший своего смежного. См. Угол, Смежные углы.
ОСЬ СИММЕТРИИ фигуры — прямая или часть прямой (отрезок, луч),
относительно которой любая точка Л фигуры имеет симметричную точку Л',
принадлежащую той же фигуре.
Примеры: 1) высота равностороннего треугольника является его О. с,
2) биссектриса угла является его О. с; 3) любой диаметр сферы —ее О. с;
4) куб имеет девять О. с. О. с. также называют осью отражения или просто
осью. См. Симметрия.
ОТВЛЕЧЕННОЕ ЧИСЛО —то же самое, что и число (см.). О. ч. иногда
также называют абстрактным числом. Термин О. ч. используется при изучении
арифметики в школе как противопоставление термину «Именованное число» (см.).
ОТКРЫТАЯ ОБЛАСТЬ — связное открытое множество. Подробнее см.
Область открытая.
ОТКРЫТАЯ СФЕРА.: 1°. О. с. в я-мерном пространстве — множество
точек М(хъ х2, . . ., хп) этого пространства, удовлетворяющих неравенству:
ρ(Λι, М0) = У(хг- *?)2+(*2- д$)*+. · .+(*«- х°п)2 <*.
19 Толковый словарь математических терминов

290
ОТКРЫТОЕ МНОЖЕСТВО
где число δ>0 называется радиусом О. с, а фиксированная точка Мй(х°х%х°2,
.... хп) называется центром О. с. Символом р (М, М0) обозначено расстояние
между точками Μ и М0 «-мерного пространства. На плоскости (л=2) О. с.
есть внутренность круга. В пространстве (гс = 3) О. с. есть внутренность шара.
2°. О. с. в метрическом пространстве — множество точек метрического
пространства, отстоящих от некоторой фиксированной точки М0 (центра О. с.) на
расстоянии, меньшем числа δ>0 (δ называется радиусом О. с), т. е.
множество точек М, удовлетворяющих условию:
ρ(Λί, Μ0)<δ.
ОТКРЫТОЕ МНОЖЕСТВО в n-мерном пространстве — множество точек,
содержащее вместе с каждой своей точкой некоторую окрестность этой точки.
Справедливы такие утверждения об О. м.: объединение произвольной
совокупности О. м. есть О. м.# пересечение конечного числа О. м. есть О. м.
Примеры: 1) множество точек трехмерного пространства, координаты х, у,
г которых удовлетворяют неравенству х2+у2+г2< 1, есть О. м.; 2) множество
точек четырехмерного пространства, координаты х1% х2, х3» χι которых
удовлетворяют неравенству Aq-f-jeii-f-*!^"*^ 1» есть О. м.; 3) интервал а < χ < Ъ
есть О. м. на прямой, однако не является О. м. на плоскости; 4) пустое
множество считается О. м. (и замкнутым тоже).
См. также Замкнутое множество.
Лит.: И. П. Натансон, Теория функций вещественной переменной, Гостехиздат,
М.-Л., 1950.
ОТКРЫТЫЙ ПАРАЛЛЕЛЕПИПЕД я-мерного пространства — полиинтервал
см.). См. также Параллелепипед в n-мерном пространстве.
ОТНОСИТЕЛЬНЫЕ ЧИСЛА — устаревший и вышедший из употребления
термин для противопоставления отрицательных чисел положительным.
ОТНОСИТЕЛЬНЫЙ МАКСИМУМ — максимум функции f(хъ х2, ..., хп)
нескольких переменных, когда эти переменные связаны дополнительными
условиями— уравнениями связи <Р/(хь х2, · · ·, хп)х® (*=1. 2, . . ., т), т<п.
Формальное определение О. м.: функция w=/(a:1, x2i . . ., хп) имеет О. м. в
точке Ρ0(χ°ιι *2* · · ·» *л)» удовлетворяющей уравнениям связи, т. е. ф/(*р
jtij. · · ·* *°)=0 (/=1, 2, . . ., ш), если существует окрестность Р0,
содержащаяся в области определения функций / и φ,·, такая, что для всех точек
Р(х\, *2» · · ·» хп) этои окрестности, удовлетворяющих уравнениям связи,
выполняется неравенство f(xl4 х2 xn)^f(x°\* х2* · · ·* х<п)· В случае
выполнения строгого неравенства f(xx% . . ., xn)<f(x°\* · · ·» х°п) (для ? 5* ?о) О· м·
называется собственным О. м., в противном случае — несобственным О. м.
См. также Необходимые условия относительного экстремума, Достаточные
условия относительного экстремума, Лагранжа метод неопределенных множителей.
ОТНОСИТЕЛЬНЫЙ МИНИМУМ функции f(xlt x2t . . ., хп) нескольких
переменных определяется аналогично относительному максимуму (см.), с
изменением знаков неравенств на противоположные.
ОТНОСИТЕЛЬНЫЙ ЭКСТРЕМУМ. Два термина — «относительный максимум»
(см.) и «относительный минимум» (см.) вместе называются О. э.
ОТНОШЕНИЕ двух чисел есть частное от деления первого числа на второе.
3 2 9
О. дробных чисел можно заменить О. целых чисел, например,--: "Г=7Г =9:8.
4 о о
О. двух однородных величин (отрезков, углов и др.) называется О. их числен-
ных мер (для отрезков —длин).
См. также Сложное отношение, Простое отношение.

ОШИБКА ОКРУГЛЕНИЯ
291
ОТОБРАЖЕНИЕ — одно из основных понятий математики. О. есть
какое-либо правило или закон соответствия множеств. Говорят, что задано О.
множества Μ в множество Ν, если каждому элементу множества Μ поставлен в
соответствие некоторый элемент множества N. Если каждый элемент множества N
соответствует при О. некоторому элементу множества М, то говорят, что
задано О. Μ на N. Важным частным случаем О. является взаимнооднозначное
соответствие (см.).
Примеры: 1) всякая функция есть О. области определения функции (см.) на
множество значений функции (см.); 2) если каждому слову русского языка
поставим в соответствие его первую букву, то получим О. множества слов в
множество букв русского алфавита.
ОТРЕЗОК: 1°. О. прямой — часть прямой, заключенная между двумя ее
точками. В этом случае О. с концами А п В обозначается АВ.
При аксиоматическом обосновании элементарной геометрии (аксиоматика
Гильберта, см. Аксиома) отрезок прямой определяется как система двух точек
А и В и доказывается, что между точками Ли В существует бесконечное число
точек.
2°. О. числовой оси — множество точек числовой прямой, заключенных
между двумя ее точками А (а) и В (Ь), т. е. множество точек, координаты χ
которых удовлетворяют условиям а ^ χ «ζ b. В этом случае О. называется
также сегментом (см.), обозначается [а, Ь].
ОТРИЦАТЕЛЬНО-ОПРЕДЕЛЕННАЯ КВАДРАТИЧНАЯ ФОРМА —
невырожденная квадратичная форма (см.) с действительными коэффициентами,
нормальный вид которой состоит лишь из отрицательных квадратов. Квадратичная форма
(см.) является О. о. к. ф. тогда и только тогда, когда ее ранг (см.) и
отрицательный индекс инерции равны числу входящих в нее неизвестных.
ОТРИЦАТЕЛЬНЫЕ ЧИСЛА. По определению разность 0 — а, где а>0,
называется О. ч. и обозначается —а. При пополнении множества
положительных чисел О. ч. сохраняются все законы сложения и умножения, а также
многие свойства неравенств, при этом становится всегда выполнимой операция
вычитания. На числовой оси О. ч. изображаются слева от числа нуль.
ОШИБКА ОКРУГЛЕНИЯ «-— абсолютная величина разности между величиной
а и величиной а* — округлением величины а. О. о. иначе называется
погрешностью округления. См. Погрешность.
19*

π
ПАЛОЧКИ НЕПЕРА — см. Непера палочки.
ПАНТОГРАФ — прибор для вычерчивания гомотетичных фигур (планов,
карт, рисунков и т. д.). С помощью П. производят подобное копирование.
Прибор имеет различные конструкции, в которых по-разному учитываются
соображения устойчивости и простоты устройства прибора. П. (рис. 192) состоит:
а) из четырех равных планок АВ, ВС, CD и DA, соединенных шарнирно бол-
тиками и составляющих модель ромба;
В б) из подвижной планки KL, которая
устанавливается так, чтобы она была
параллельна ВС (AD) и чтобы при
заданном коэффициенте гомотетии k
выполнялось соотношение: DC:LC=AC:C'C
(где вершина А принимается за центр
гомотетии, k—DC.LC — за коэффициент
гомотетии); в) из четырех штифтов и
карандаша; три штифта
устанавливаются в вершинах А, В и £>, а
четвертый штифт с острием для обвода
фигуры устанавливается в отверстие С'
(при увеличении фигуры), а в
отверстие С устанавливается карандаш; при
уменьшении фигуры карандаш и штифт (С и С) меняются местами.
Пусть дана фигура Р' и требуется построить фигуру, ей подобную, с
отношением соответственных элементов, равным k. Для определенности полагаем
k—2. Подвижную планку KL устанавливаем с учетом значения &, а именно —
чтобы отношение £>C:LC=2, т. е. L устанавливаем в середине DC. Штифт с
острием для обвода фигуры устанавливаем на планке KL в точке С так,
чтобы выполнялось соотношение
KL:C'L=DC:LC=2.
ПАПИРУСЫ — дошедшие до нас математические памятники древнего Египта
(конца Среднего Царства), которые датируются приблизительно XVI —XVIII вв.
до п. э. К ним относится папирус Райнда (по имени английского египтолога,
занимавшегося изучением этого папируса), хранящийся в Британском музее, и
Московский П. (из коллекции Голенищева), хранящийся в Государственном
музее изобразительных искусств им. А. С. Пушкина. Расшифровкой его
занимался русский египтолог профессор Тураев.
К той же эпохе (XXII династия) относятся Кахунские П., затем
Берлинский «6619» с задачами на квадратные уравнения, и, наконец, из
Византийской эпохи (VI — IX вв.) до нас дошел П. из Акима на греческом языке,
хранящийся в Гизехе. Особенно ценен по богатству материала папирус Райнда,
расшифрованный профессором А. Эйзенлором в 1877 г. Папирус Райнда называют
также часто по имени его составителя — писца Ахмеса. В папирусе содержатся
решения задач с практическим содержанием. В папирусе Райнда их 84, в
Московском — 25.
Из этих П. видно, что в древнем Египте знали действия с дробями,
площади простейших геометрических фигур (прямоугольника, треугольника, трапе-

ПАРАБОЛА
293
ции), а также умели приближенно определять площадь круга, причем роль числа
л играло число (16:9)2==3,16...f а иногда просто 3. В некоторых задачах
вычисляются объемы прямоугольного параллелепипеда и цилиндра, используются
пропорции. Часто, по существу, решаются уравнения с одним неизвестным.
Наибольший интерес представляют: вычисление суммы геометрической
прогрессии (задача 79 папируса Раинда), точная формула объема усеченной
пирамиды с квадратным основанием (задача 14 Московского П.), вычисление боковой
поверхности цилиндра (задача 14Московского П.). Однако никаких рассуждений
общего характера не проводится. Система счисления, применявшаяся в древнем
Египте, была десятичной, но не имела нуля и по существу не была позиционной.
Сложение и вычитание производилось обычным способом; при умножении
один из сомножителей представляли в виде суммы чисел 1, 2, 4, 8, 16, . . .,
умножение на которые производилось с помощью таблиц, после чего оставалось
произвести сложение. Техника обращения с дробями, основанная на
представлении всякой дроби в виде суммы дробей с единицей в числителе, также облег-
. 2 1 1 г.
чалась применением таблиц. Так, дробь — представлялась в виде -τ"+~· π· яв"
5 3 15
ляются основным материалом, который позволяет судить о математической
культуре древнего Египта.
Лит.: В. В. Бобынин, Математика древних египтян, М., 1882; М. Я. Выгодский,
Арифметика и алгебра в древнем мире, Гостехиздат, М., 194 1; И. Н. Веселовский,
Египетская наука и Греция, «Труды института истории естествознания АН СССР», т. 2, Изд-
во АН СССР, М., 1948; Г. Н. Попов, Исторические задачи по элементарной математике,
ГТТИ, М.—Л., 1932.
ПАРАБОЛА — геометрическое место точек (см.) плоскости, равноудаленных
от данной точки F (фокуса) и данной прямой / (директрисы, см.), лежащих
в той же плоскости. На рисунке 193 MK=MF.
Простейшее уравнение П. в прямоугольных декартовых координатах имеет
вид: у2 = 2рх, где p=2FO — расстояние от данной точки F — фокуса до данной
У\
.^г
О
ι
V--
VF x
У
κί
Τ
ί
0
η
i
ν
14
!>
<
*··
λ
Рис. 193 Рис. 194
прямой / — директрисы П. Уравнение П. показывает, что П. — кривая 2-го по-
р
рядка. Уравнение директрисы П. имеет вид: *= — —·. Эксцентриситет (см.)
параболы равен единице (е—\). П. может быть получена как сечение конуса
плоскостью, когда эта плоскость параллельна одной из образующих конуса (см.
Конические сечения).
Ряд траекторий движения тел представляет собой П. Так, тело, брошенное
под углом к горизонту (если пренебречь сопротивлением воздуха), движется по
П. Вращая параболу вокруг ее оси Ох, получим поверхность 2-го порядка:
параболоид (см.) вращения.

294
ПАРАБОЛИЧЕСКАЯ СПИРАЛЬ
Касательная к П. образует равные углы с осью П. и фокальным радиусом
точки касания (рис. 194). Отсюда вытекает, что луч света, параллельный оси
параболоида, отразившись от его поверхности, пройдет через фокус, и,
обратно, луч, выходящий из фокуса, после отражения будет параллелен оси П. Это
свойство используется в прожекторных установках или в фарах автомобиля.
ПАРАБОЛИЧЕСКАЯ СПИРАЛЬ — кривая, уравнение которой в полярных
координатах имеет вид г=ау φ, где а — константа, а (г, φ) — полярные
координаты. На рис. 195 ветви П. с. проведены сплошной линией при а>0 и
пунктирной линией при а<0. П. с. иначе называются спиралью Ферма.
ПАРАБОЛИЧЕСКАЯ ТОЧКА —точка на поверхности, в которой гауссова
(или полная) кривизна (см.) равна нулю: k=k1-k2 = 09 где k — полная кривизна
поверхности, a kx и k2 — главные кривизны в той же точке поверхности.
2
Рис. 195
Рис. 196
ПАРАБОЛИЧЕСКИЙ ЦИЛИНДР —одна из поверхностей 2-го порядка,
простейшее уравнение которой в прямоугольных декартовых координатах имеет
вид: у2=2р:с. Направляющей П. ц. является парабола y2 = 2pxt где ρ—
расстояние от фокуса до директрисы (см.) параболы, а образующей — прямая,
параллельная оси Ог (рис. 196).
ПАРАБОЛОИДЫ — поверхности 2-го порядка, простейшие уравнения кото-
jc2 у2
рых в прямоугольных декартовых координатах имеют вид: 1) — -f-—=2z (pt q>
р q
χ2 у2
>0) — эллиптический параболоид (см.), 2)— — —-=2г— гиперболический па-
Р Я
раболоид (см.).
ПАРАБОЛ ФОРМУЛА (Симпсона) — формула для приближенного
вычисления определенных интегралов:
ь h
J>^= J(Уо+4у1+2уа+4у8 + . · •+2У«-2+4уя-1+уя). (*)
Промежуток интегрирования разбивается на четное число n = 2k равных
частей и для точек деления вычисляются значения подынтегральной функции
б — о
Уп* h-
~. Для оценки ошибки, получаемой при вычислении интеграла по
П. ф., вычисляют вспомогательную сумму:
^()OT4y2+2y4+. . .+4у„_г+Уя),
(··)

ПАРАЛЛЕЛЕПИПЕД
295
представляющую собой ту же П. ф. для h1^2hi получающуюся при
отбрасывании ординат с нечетными индексами. Символически можно записать
приближенное равенство:
]ydx-n=
15
Рис. 197
Лит.: Г. М. Фихтенгольц. Курс дифференциального и интегрального исчисления,
т. 2, Гостехиздат, М., 1951.
ПАРАДОКС (математический) — верное утверждение (вывод), но кажущееся
неверным в силу наших житейских и психологических причин.
Примеры: 1) сумма условно сходящегося ряда изменяется от перестановки
его членов (см. Ряд); 2) если лист (ленту) Мёбиуса (см. Мёбиуса лист)
разрезать ножницами по средней его линии, то он не
распадется на две части; 3) при вращении прямоугольника
ABCD (рис. 197) вокруг оси /, лежащей в его
плоскости и параллельной одной из его сторон (/1| AD),
объем тела, полученного от вращения треугольника
BCD, больше объема тела, полученного от вращения
треугольника ABD (см. Гюльдена теорема).
П. также называют и софизмы (см.), а также
неверные выводы, полученные на основании
использования таких понятий и рассуждений, границы
применимости которых неизвестны: например, при
перенесении свойств конечных множеств на бесконечные
можно получить неверные выводы.
ПАРАЛЛЕЛЕПИПЕДАЛЬНАЯ ОКРЕСТНОСТЬ
точки— открытый я-мерный параллелепипед, или
полиинтервал (см.), с центром в данной точке.
ПАРАЛЛЕЛЕПИПЕД в «-мерном пространстве — множество точек Р(хг*
*2» · · ·» хп) «-мерного пространства, удовлетворяющих неравенствам: βι<#ι<
—9—*
. . . , —-— Ι называется центром П. В случае выполнения строгих неравенств
a^Xi^bi множество точек называется открытым параллелепипедом или
полиинтервалом (см.). П. называют также замкнутым П., чтобы подчеркнуть его
отличие от открытого П. Точки П., не являющиеся точками соответствующего
открытого П., образуют совокупность граней П. Отдельная грань П.
определяется неравенствами вида:
<*ι < *ι < &ъ . . ., а,-! < х^-х < Ь|—1э а|+1 < х1+1 < bi+lf . . ., ап < хп < ЬП9
и равенством **=а/ (или */=&/) П. имеет 2/г граней, так как индекс / может
меняться от 1 до п. В пространстве (л=3) П. совпадает с обычным
прямоугольным параллелепипедом. На плоскости (я=2). П. превращается в прямоугольник;
грани в этом случае превращаются в стороны прямоугольника.
ПАРАЛЛЕЛЕПИПЕД (в элементарной геометрии) — призма (см.),
основанием которой является параллелограмм. Если боковые ребра или грани П.
перпендикулярны к плоскости основания, то П. называется прямым. Если боковые
ребра П. наклонны к плоскости основания, то П. называется наклонным. Прямой
П., основанием которого является прямоугольник, называется прямоугольным;
например, куб — прямоугольный П. Боковая поверхность П. вычисляется по
формуле:
s=p-ht
где р — периметр перпендикулярного сечения, а h>— длина бокового ребра П.
<ЬХ

296
ПАРАЛЛЕЛОГРАММ
Объем П. равен:
где Q — площадь основания, а Я — высота П. (расстояние между основаниями).
Все диагонали П. пересекаются в одной точке — центре симметрии П.
Наклонный П., у которого все грани — равные ромбы, называется
ромбоэдром (см.).
ПАРАЛЛЕЛОГРАММ — четырехугольник, противоположные стороны
которого параллельны. Противоположные стороны П. равны и противоположные
углы его равны. Углы, прилежащие к любой стороне П., в сумме составляют
2d. Диагональ П. делит его на два равных треугольника. Диагонали
параллелограмма в точке их пересечения делятся пополам. Точка пересечения
диагоналей П. есть центр его симметрии.
Эти свойства (признаки) являются не только необходимыми, но и
достаточными для того, чтобы простой четырехугольник был П. Расстояние между
параллельными сторонами называется высотой П. У П. имеются две высоты, вообще
говоря, различные. П., у которого один из углов прямой (отсюда следует, что
и все углы прямые), называется прямоугольником (см.). П., у которого две
смежные стороны равны (отсюда следует, что и все стороны равны),
называется ромбом (см.).
ПАРАЛЛЕЛОЭДРЫ — выпуклые многоугольники, которыми можно заполнить
трехмерное пространство с помощью их параллельных переносов так, чтобы не
было пустот и пересечений, — например, куб или правильная шестиугольная
призма.
См. также Многогранники.
Греч, παραλληλοζ — параллельный и έδρα — основание.
ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ в геометрии Евклида — прямые, лежащие в
одной плоскости и не имеющие общих точек. Если прямая а параллельна
прямой Ьу то это записывается так: а || Ъ> где две вертикальные черточки означают
знак параллельности прямых а и Ь.
В геометрии Лобачевского (см.) термин П. п. имеет другой смысл.
Греч, παραλληλοζ — дословно «рядом идущий».
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС: 1°. П. п. в аффинной геометрии —
преобразование пространства на себя, при котором все точки смещаются на один и
тот же вектор.
2°. П. п. в пространстве аффинной связности — линейное преобразование
касательного пространства к одной точке в касательное пространство к другой
точке, зависящее от кривой, соединяющей эти две точки. Уравнения П. п. есть
обыкновенные дифференциальные уравнения 2-го порядка, определяемые
символами Кристоффеля (см.).
Лит.: П. К. Рашевский, Риманова геометрия и тензорный анализ, Гостехиздат,
М., 1953; А. П. Η орден, Пространство аффинной связности, Гостехиздат, М.—Л.,
1950.
ПАРАМЕТР — величина, входящая в формулы и выражения, значение
которой является постоянным в пределах рассматриваемой задачи, но в другой
задаче меняет свои значения. Например, в декартовых координатах уравнение
(х — а)2+(у— 6)2 = 1 определяет множество всех окружностей единичного
радиуса на плоскости хОу. Для определенных а и Ь, например а»1, 6=2, мы
получаем вполне определенную окружность с центром в точке (1, 2); а и Ь —
параметры окружности в рассматриваемом множестве.
См. также Параметрическое представление функций.
Греч, παραμετρον — отмеривающий.
ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ функций — выражение
функциональной зависимости между несколькими переменными с помощью
вспомогательных переменных — параметров. Например, Ρ (а*, у)«О —уравнение некоторой

ПАСКАЛЯ ТЕОРЕМА
297
плоской кривой. Если величина t определяет положение точки (#, у) на этой
кривой (например, длина дуги, отсчитываемая со знаком ·+■ или — от
некоторой точки кривой, принятой за начало отсчета), то эту величину t можно
принять за параметр, а х и у будут функциями этого параметра: х=φ (t), y=^(0-
Эти функции и дадут П. п. функциональной зависимости между χ и у.
П. п. аналитических функций (см.) посредством однозначных аналитических
функций составляет предмет теории униформизации.
В случае трех переменных х, у и ζ уравнение F (х, у, г)=0 представляет
собой поверхность. Для определения точки на поверхности нужны два
параметра s и t. Например, для зависимости x2+y2=z* имеем П. п.: x=u2cosv,
y=*u2s'mvt г—u. П. п. дает возможность: 1) изучать неявные функции, 2)
выражать многозначные функции через однозначные.
ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ. Уравнения вида: χ«φ(0» У=*(0
называют П. у. соответствующей плоской кривой. Так, например, для случая
х2 у2
зависимости "Г+^Г^ имеет параметрическое представление (см.) *=2cos/,
y=3sini, (0 < t < 2 π). Это — П. у. эллипса. Если параметр t можно выбрать
таким, что функции φ(£) и ψ(/) будут рациональными, то кривую называют
уникурсальной (см.). П. у. прямой в пространстве имеют вид: x=xQ-{-att y=
=)>04-β/, z=z{)+it.
ПАРСЕВАЛЯ РАВЕНСТВО — равенство вида:
я2
L η= ι
где α0, ап, bn — коэффициенты функции Фурье f(x). П. р. справедливо для
любых функций с интегрируемым квадратом.
ПАСКАЛЯ ТЕОРЕМА. Во всяком шестивершиннике, вписанном в ряд
точек 2-го порядка (кривую 2-го порядка, коническое сечение), три точки
пересечения противоположных сторон лежат на
одной прямой — прямой Паскаля.
П. т. является одной из основных
теорем проективной геометрии (см.).
Так, если 6 вершин, взятых на кривой
2-го порядка, занумеровать цифрами 1, 2,
3, 4, 5, 6 в указанном порядке, то пары
сторон 12 и 45; 23 и 56; 34 и 61 будут
противоположными и три точки пересечения К,
L, Μ будут лежать на одной прямой χ —
прямой Паскаля (рис. 198).
Из 6 точек — вершин шестивершинника,
лежащих на кривой 2-го порядка, можно
получить 60 различных шестивершинников,
если соединять данные точки в различном порядке, откуда следует, что для
данных 6 точек кривой 2-го порядка можно получить соответственно 60
различных прямых Паскаля.
П. т. названа по имени французского ученого Б. Паскаля, доказавшего ее
в 1639 г.
Частный случай П. т. для кривой 2-го порядка, распадающейся на пару
пересекающихся прямых, был известен еще в древности (теорема Паппа, IV в. н. э.).
П. т. используется: 1) для построения точек кривой второго порядка,
когда задано только 5 точек или 4 точки кривой и касательная к кривой в одной

298
ПАСКАЛЯ ТРЕУГОЛЬНИК
из них; 2) для построения касательной (с помощью только линейки) к кривой
в данной ее точке, если кривая дана (начерчена) или даны ее 5 точек, и для
других задач. П. т. двойственна Брианшона теореме (см.).
ПАСКАЛЯ ТРЕУГОЛЬНИК—-треугольная таблица чисел, являющихся
биномиальными коэффициентами (см.):
С°о
С°С\
го г1 г2
2 2 2
СО г>\ /~»2 /^3
3 и3 и3 и3*
В числовом виде П. т. выглядит так:
1
1 1
1 2 1
13 3 1
14 6 4 1
В силу сзойства биномиальных коэффициентов:
каждое число П. т. равно сумме двух чисел, над ним стоящих (при этом
считается, что на периферии П. т. стоят нули). П. т. приведен в сочинении
Паскаля «Трактат об арифметическом треугольнике» — отсюда П. т. называют
также иногда арифметическим треугольником. П. т. был известен в Китае в 1303 г. #
у Штифеля в 1544 г., у Паскаля в 1665 г. Поэтому в разных странах его
называют по-разному: в Германии его чаще называют треугольником Штифеля,
в Италии — треугольником Тартальи, у нас следовало бы его называть
треугольником Омара Хайяма, в честь таджикского поэта, философа и математика, у
которого встречается этот треугольник. В Индии поэт Пинтала (II в. до н. э.)
пользовался Т. п. при решении вопросов поэзии.
Лит.: И. Я. Депман, История арифметики, Учпедгиз, М., 1959.
ПАША АКСИОМА. П. а. формулируется так: если прямая а, лежащая
в плоскости треугольника ABC и не проходящая ни через одну из вершин,
проходит через точку отрезка (стороны) АВ, то эта прямая
Q а либо проходит через точку отрезка АС, либо через
Δ точку отрезка ВС, Другими словами, если прямая
пересекает одну из сторон треугольника, то она должна
пересечь и другую сторону его (рис. 199).
П. а. является одной из основных аксиом при акси-
£ оматическом (дедуктивном, строго логическом) построении
курса элементарной геометрии (см. Основания
геометрии). П. а. названа в честь немецкого математика
β Паша, одного из первых математиков, положивших
начало исследованию аксиоматического обоснования гео-
Рис. 199 метрии.

ПЕРВУШИНА ЧИСЛО
299
ПЕАНО АКСИОМЫ натуральных чисел предложены в 1891 г. итальянским
математиком и логиком Пеано. Они служат для определения понятия
натурального числа. Натуральными числами называются элементы всякого непустого
множества N, в котором существует отношение «следует за» (число, следующее
за а, будем обозначать через а*), удовлетворяющее следующим аксиомам:
1. Существует число 1, не следующее ни за каким числом. 2. Для любого
числа а существует следующее за ним число а* и притом только одно, т. е. из
а—Ь следует а* = 6*. 3. Любое число следует не более чем за одним числом,
т. е. из а* — Ь* следует а=Ь. 4. (Аксиома индукции.) Пусть любое множеством
натуральных чисел обладает свойствами: 1) единица принадлежит М\ 2) если
число а принадлежит М, то а*=а-\-\ также принадлежит М. Тогда Μ содержит
все натуральные числа, т. е. множество всех натуральных чисел совпадает сМ.
Лит.: Энц. элем, мат., т. 1, Гостехиздат, М., 1951.
ПЕАНО КРИВАЯ — непрерывная кривая в смысле Жордана (см. Жордана
кривая), проходящая через все точки некоторого квадрата. Рассмотрена
впервые итальянцем Пеано в 1890 г.
Лит.: Η. Η. Лузин, Теория функций действительного переменного. Общая часть,
изд. 2, М., 1948.
ПЕЛЛЯ УРАВНЕНИЕ —уравнение вида *2 — Dy2=l, где D —- натуральное
число, не являющееся квадратом другого натурального числа. П. у. легко
решается в целых числах. Это уравнение названо П. у. Л. Эйлером, который по
ошибке принял переводчика одной книги по теории чисел за автора этой книги.
См. также Диофантовы уравнения.
ПЕНТАГОНАЛЬНЫЕ ЧИСЛА (пятиугольные числа) — натуральные числа
вида(3л2— я): 2, т. е. числа: 1, 5, 12, 22, .... П. ч. являются частным случаем
фигурных чисел (см.) и составляют арифметический ряд (см.) 2-го порядка.
Название П. ч. происходит от того, что ими выражается число шаров,
выложенных на плоскости в виде последовательно наращенных пятиугольников.
ПЕРВООБРАЗНАЯ ФУНКЦИЯ —то же, что и примитивная функция (см.).
ПЕРВООБРАЗНЫЙ КОРЕНЬ по модулю т — такое число gy что наименьшее
положительное число k, для которого разность gk — 1 — делится на т (gk
сравнимо с 1 по модулю т), совпадает с ср(т), где у(т) — функция Эйлера
(см.), равная числу натуральных чисел, меньших т и взаимно простых с т.
Например, П. к. * по модулю 7 является число б, так как φ (7)=6, а числа
31— 1=2, З2 — 1 = 8, З3— 1 = 26, 3* —1 = 80, З5 — 1=242 не делятся на 7 и
лишь число З3 — 1=728 делится на 7. П. к. существует, когда m=2, т=4,
т=р* f m=2pa , где ρ— простое нечетное число, a — целое > 1. Число П. к.
в этих случаях равно φ [φ (яг)] (числа, разность которых кратна тч не
считаются различными); для других модулей их нет. Советский математик
академик И. М. Виноградов установил в 1926 г., что в интервале
(l, 22/с у ρ In ρ) найдется П. к. по модулю р, где ρ — простое нечетное
число, к — число различных простых делителей числа ρ—1.
Лит.: И. М. Виноградов, Избранные труды, Изд-во АН СССР, М., 1952, стр.
54-57.
ПЕРВУШИНА ЧИСЛО. В 1883 г. талантливый уральский
математик-самоучка прислал в Петербургскую Академию наук заметку «Число 2й1—1 =
= 2 305 843 009 213 693 951 есть простое». В науке это число принято называть
первушинским.
Со времени Эйлера, который доказал, что число 231—1 — простое,, П. ч.
было первым самым большим из известных простых чисел. К сожалению,
имеется очень мало сведений о той работе, которую Первушин выполнял в связи
с доказательством простоты числа 2lJ1 — 1 в глухой сельской провинции, вдали
от культурных центров.

300
ПЕРВЫЙ ИНТЕГРАЛ
Академия наук отказалась опубликовать П. ч., так как академик В. Я. Бу-
няковский не решался принять на себя ответственность за непогрешимость
представленного П. ч. и так как «для проверки потребовалось бы очень много
времени даже от вычислителя, вполне привыкшего к этого рода труду».
И только в 1887 г. после того как Зеельхоф тоже доказал, что 261 — 1
есть простое число, было решено опубликовать работу Первушина для
обеспечения за ним права приоритета.
Лит.: А. Е. Раик, Уральский математик Иван Михеевич Первушин, сб. «Историко-
математические исследования», вып. 6, Физматгиз, М., 1953; И. В. Арнольд, Теория
чисел, Учпедгиз, М., 1939.
ПЕРВЫЙ ИНТЕГРАЛ системы обыкновенных дифференциальных уравнений:
~Г = //(*.У1. Уь · · ·» Ул)/==1' 2 п
ах
— соотношение вида:
*Ч*. Уь У* .· ·, Ул) = С
обращающееся в тождество при подстановке любого решения системы
У1 = У1(х)> У*=У*(х), ···, Уп = Уп(х)*
причем функция F не тождественно равна константе. П. и. есть уравнение
гиперповерхностей (см.) в пространстве переменных х, у19 у2, · · ., Уп таких,
что каждая гиперповерхность содержит некоторое подсемейство интегральных
кривых. Например, система:
dy
j-=a(x)y+b(x)z,
~ = b{x)y+a(x)z
имеет П. и.:
In 13 τ·г] — J [а (х) + Ь(х)] dx=C.
ПЕРЕГИБА ТОЧКА плоской кривой — точка Μ такая, что кривая в
некоторой окрестности этой точки лежит по разные стороны от касательной в
точке М. Для кривых y=f(x), где f(x) — достаточное число раз
дифференцируема, первая отличная от нуля производная в П. т. имеет нечетный порядок.
Кривизна кривой (см.) в П. т. равна нулю. Например, для кривых у=х2п+1ш
я=1, 2, . . ., начало координат есть П. т.
ПЕРЕМЕННАЯ ВЕЛИЧИНА — величина, которая принимает различные
значения. Например, при сжимании идеального газа давление и объем газа
изменяются. Введение П. в. в математику в XVII в. является революционным
скачком в развитии науки вообще. Оно означало новую ступень познания
явлений природы в их взаимной связи и движении. Мощные математические
методы и удобный аппарат дифференциального и интегрального исчислений,
основанные трудами Декарта, Ньютона, Лейбница, подверглись значительному
изменению, а главное — строго научному обоснованию в XIX в. В это время была
создана теория пределов, а вслед за ней теория непрерывных функций. Для
современной математики прежнее определение П. в. не является
удовлетворительным. Основания современной математики проникнуты идеями теории
множеств (см.) и топологии (см.). В частности, под величинами понимают не только
число, но и элементы произвольной природы некоторого множества. Старое
понятие П. в. остается удобным для многих инженерных задач, а также в
преподавании общего курса математики.

ПЕРЕСТАНОВКА ДИФФЕРЕНЦИРОВАНИЙ
301
ПЕРЕМЕСТИТЕЛЬНЫЙ ЗАКОН —см. Закон коммутативности.
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ. П. м. А и В называется множество,
состоящее из тех и только тех элементов, которые принадлежат как множеству Л,
так и множеству В, т. е. оно состоит из всех общих для множеств А и В
элементов. П. м. А и В обозначается символом Af\B (или АВ) и называется
произведением множеств А и В (этот термин устарел). П. м. А и В схематически
изображено на рисунке 200 заштрихованной областью.
Аналогично, если даны множества Аа , где α
пробегает конечное или бесконечное множество индексов /, то
П. м. Аа (αζ/) называется множество, состоящее из тех
и только тех элементов, которые принадлежат всем Ла ,
т. е. каждому Ал при любом α ζ/. П. м. Αα(αζί)
обозначается символом η Λ* ( или Π А„ ) , а в случае, Рис 200
<хе/ v ae/ /
когда множество / конечно и состоит из η чисел: 1#
2, .. ., п, П. м. А19 . . ., Ап обозначается символом А1[\А2П ... {\Ап
Ι η η \
(или А* А* . ш . Ап, или Π Л/, или П Ап]. Если / — счетное множество н
V /=1 /=ι /
состоит из чисел натурального ряда 1, 2, . . ., то П. м. AtA2. .. обозначается
оо / оо
символом Π Ai (или Π Ait или Аг П^гП · · ·» или АХА2...).
ι: == 1 \ i = 1
П. м. является одной из важнейших операций над множествами. Для
сравнения ее с другими операциями см. Теоретико-множественные операции.
П. м. может быть пустым множеством (см.). Такие множества, для
которых П. м. — пустое, называются непересекающимися. П. м. удовлетворяет
законам коммутативности, ассоциативности и идемпотентности (см.): А[\В~ВГ\А\
(АГ\В)Г\С=А(](ВГ\С)\ Af)A=A. П. м. связано с объединением множеств (см.)
двумя законами дистрибутивности (см.):
Ап№в-)-&(Апв-)· "(.РЛ)"-?' {ΑυΒή·
Эти два закона дистрибутивности двойственны (см. Двойственности принцип).
Примеры: 1) пусть А — множество всех четных чисел и В — множество
всех чисел, кратных 3. Тогда А(]В — множество чисел, кратных 6.
2) А — множество всех окружностей и В — множество всех эллипсов с
длиной большой полуоси, равной 1. Тогда Af]B — множество всех окружностей
единичного радиуса.
ПЕРЕСТАНОВКА СИМВОЛОВ — всякое размещение (см.) из η символов по
л. Число различных П. из η символов равно п\. П. является одним из
основных понятий в разделе алгебры — комбинаторике (см.).
ПЕРЕСТАНОВКА ДИФФЕРЕНЦИРОВАНИЙ — изменение порядка
дифференцирований. При П. д. результат дифференцирования не изменится, если
смешанные производные непрерывны. Точнее, справедлива теорема о П. д.: Пусть
частные производные ———» τ—τ функции u=u(x, у) непрерывны в точке
дхду дудх
д2и д2и ди ди
xQr у* и, следовательно, -——, -—г-, г*; Т" существуют в некоторой окрест-
дх dy ду дх дх ду
д2и д2и
ности точки (дг0, у0); тогда в этой точке ■——==—--. Немецкий математик
дх ду ду дх
Шварц показал, что в этой теореме достаточно предположить, кроме сущест·

302
ПЕРЕСТАНОВКА С ПОВТОРЕНИЯМИ
ди ди
вования — и г~ в окрестности точки, непрерывность в точке (л;0, у0) лишь
д2у д2у
одной из смешанных производных -——■„ -——-. См. Частные производные выс-
дх ду ду дх
шего порядка.
Ихмеет место более общая теорема о П. д.: Пусть в точке (х0, у0) частные
производные до (k—1)-го порядка включительно и смешанные производные k-το
порядка функции и—и(х1Щ х2, . . ., хп) непрерывны; тогда значение любой k-\\
смешанной произюдной в точке (х0$ у0) не зависит от порядка
последовательности дифференцирований. В этом случае число различных частных производных
&-го порядка равно числу сочетаний с повторениями (см.) из η элементов по k>
(л+£—1)!
Т' 6· раВН° AI0.-1)! *
х2 — у2
Пример изменения результата от П. д.: для функции и=ху—-—j- при
д2и д2у
^2-ЬУ > 0 и и—0 в точке *=0, у=0, =—1, = 1. В этом случае
дх ду ду дх
при перемене П. д. меняется результат, так как смешанные производные в
точке лг=0, у=0 разрывны.
ПЕРЕСТАНОВКА С ПОВТОРЕНИЯМИ из η элементов множества Μ {alt а2,
. . .9 ап}—частный случай размещения с повторениями (см.) из η элементов
множества Μ по к. Если в некотором размещении с повторениями из η
элементов по k элемент аг повторяется wx раз, а2 повторяется w2 раз и т. д. (а^-Ь
+а>2+ ··· -т-а>л=А!), то такое размещение называют П. с п. Число различных
П. сп., в которых элементы alt a2i .. ,t an повторяются соответственно wu
Щ% · · ·» и>п Раз* равно:
(Σ^/)! (wx+w2+ ··· +wn)\
П(^!) w^.Wnl ··· wn\
ПЕРИМЕТР замкнутой линии — длина этой линии. П. многоугольника
определяют так же, как сумму длин его сторон. П. окружности есть длина этой
окружности.
Греч, perimetron — окружность, от perimetreo — измеряю вокруг.
ПЕРИОДИЧЕСКАЯ ДРОБЬ — бесконечная десятичная дробь (см.), у
которой, начиная с некоторого места, бесконечно повторяется одна и та же группа
цифр. Например, 2,7136136136... сокращенно можно записать так: 2,7(136),
т. е. поместить бесконечно повторяющуюся группу цифр (называемую периодом)
в скобки (в этом примере говорят: «136 в периоде»), П, д. называется чистой,
если период начинается сразу после запятой (например, 8,333. . .), и
смешанной, если после запятой имеются цифры, стоящие перед периодом (например,
3,512626...).
При представлении рациональных чисел, т. е. обыкновенных дробей,
десятичными дробями конечные десятичные дроби получаются, если знаменатель
несократимой простой дроби не содержит других простых множителей, кроме 2
и 5; в других случаях получается П. д., которая является чистой, если
знаменатель данной несократимой простой дроби не содержит множителей 2 и 5,
и смешанной, если хотя бы один из этих множителей содержится в знаменателе.
Всякую П. д. можно обратить в простую дробь (т. е. она равна некоторому
рациональному числу). Чистая П. д. равна простой дроби, числителем которой
служит период, а знаменатель изображается цифрой 9, повторенной столько

ПЕРИЦИКЛОИДА
303
раз, сколько цифр в периоде. При обращении в простую дробь смешанной П. д.
надо числителем сделать разность между числом, изображаемым цифрами,
предшествующими второму периоду, и числом, изображаемым цифрами,
предшествующими первому периоду, а знаменатель изобразить цифрой 9, повторенной
столько раз* сколько цифр в периоде, приписав справа столько нулей, сколько
цифр до периода. Эти правила применяются для преобразования правильных
(т. е. не содержащих целых единиц) дробей, так как целая часть при этом
записывается без изменения.
ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — функция у = /(*), для которой
существует такое число τ > 0, что для всех χ и х+ τ из области определения /(jc-|-t) =
= /(jt). Наименьшее число Τ из всех таких чисел τ называется периодом
функции f(x). Если П. ф. y=f(x) непрерывна для —oo<*<-f-<x и не является
постоянной величиной у Φ const, то среди всех ее периодов τ найдется
наименьший Τ > 0, который, собственно, и называется в этом случае периодом; все
периоды τ являются целочисленными кратными Г, х=пТ, п=\, 2, .... Полный
график П. ф. получается последовательными сдвигами (в положительном и
отрицательном направлениях) на период части ее графика, построенной для
отрезка а < χ < а+Т, длины Т.
Примеры: 1) функция Дирихле:
J 1, при χ рациональном,
\ 0, при χ иррациональном
имеет периодом любое рациональное число; наименьшего периода нет; 2) у = sin x
2π г
имеет период Γ=2π; 3) y = tgjt, Γ=π; 4) y=cosa*, T=—; 5) у=У cosjc,
a
jt jt
область определения ——-\-2k π < χ < — 4-2&jt, k = 0t ±1, ±2, . . .s ±n<
. . ., Γ=2π.
ПЕРИОД ФУНКЦИИ — см. в термине Периодическая функция.
ПЕРИОДИЧЕСКОЕ РЕШЕНИЕ — системы дифференциальных уравнений:
-~-=ЫУ1> Уъ · · ·. Уп, t) /-1, 2, ... «,
решения У/ = фг(0. ГДе ф/— периодические функции одного и того же периода#
т. е: существует τ > 0 такое, что φ/(ί+τ)=φ/(/) для всех / и для всех
1 = 1, 2, . . ., п. П. р. описывают правильно повторяющиеся физические
процессы. П. р. есть некоторая переходная ступень от неограниченных решений к
затухающим.
Методы нахождения П. р. разработаны русским математиком А. !Л.
Ляпуновым и французским А. Пуанкаре. П. р. представляют интерес для небесной
механики, теории колебаний и т. п.
ПЕРИЦИКЛОИДА — плоская кривая, относящаяся к циклоидальным
кривым. Существует кинематический способ образования П. Пусть окружность
радиуса t, называемая производящей, катится по неподвижной окружности
радиуса R, причем производящая располагается с внутренней стороны неподвижной
окружности; тогда точка, находящаяся на окружности производящего круга*
описывает циклоидальную кривую, которая будет П., если г > R (П. является
частным видом эпициклоиды). П. описывается параметрическими уравнениями
x=(R+mR) cos mt — m R cos (t+mt),
y=(Ri-mR) sin mt — mR sin(t-\-mt)t

304
ПЕРПЕНДИКУЛЯР
где т=-~^> причем т
0 и \т\ > 1, a t — угол между радиусами, проведенны-
производящей окружности и в точку его касания
См. Циклоидальные кривые, Гипоциклоида, Эпи-
М
Рис. 201
ми в вычерчивающую точку
с неподвижной окружностью,
циклоида.
Греч, περί — возле, около и κυιλοειδηζ — круглый.
Лит.: А. А. С а ве л о в, Плоские кривые, Физматгиз, М., 1960.
ПЕРПЕНДИКУЛЯР к данной прямой а есть прямая, пересекающая данную
прямую под прямым углом. Если П. проходит через данную точку Л, не
лежащую на прямой а, и точка Μ есть точка
пересечения П. с прямой а, то в этом случае длину отрезка
AM (рис. 201) называют длиной П. Длина П.
определяется по аналогии с длиной касательной (см.)
к окружности.
0 Аналогично определяется П. к данной плос-
кости: П. к данной плоскости α есть прямая,
образующая прямой угол с любой прямой, лежащей в
плоскости а.
Лат. perpendicularis и греч. perpendiculum —
отвес.
ПЕРСПЕКТИВА — способ изображения геометрических фигур на плоскости,
заключающийся в следующем. Пусть дана некоторая плоскость а', фигура Φ
(фи) и некоторая точка S, не принадлежащая ни плоскости а', ни фигуре Φ
(рис. 202). Проведя прямую SM, где Μ — любая точка фигуры Ф, мы получим
точку пересечения М' этой прямой с плоскостью а'. Точка ΛΓ и будет П. или
центральной проекцией точки М. Построив,
таким образом, проекцию каждой точки фигуры
Ф, получим П. Ф' этой фигуры на плоскости а'.
Метод П. положен в основу проективной
геометрии. Точка S называется центром
проекций, плоскость а' называется картинной
плоскостью или плоскостью проекции, прямые SM —
проектирующими лучами или лучами зрения.
При П. сохраняется сложное отношение
(см.) четырех точек. Изображение фигуры,
построенное по методу П., близко к тому, которое
получается на сетчатке человеческого глаза,
помещенного в центр проекции. Изображение
предметов в П. применяется в живописи, а
также в черчении, когда требуется создать представление о протяженности и
глубине оригинала (предмета). В педагогической практике этот метод изображения
фигур не применяется в силу его сложности и неудобств.
Две плоские фигуры Φ иФ' называются перспективными, если их
соответственные точки Μ и М' лежат на одной прямой, проходящей через центр
перспективы проекций. П. иначе называется центральной (конической) проекцией.
Лат. perspicere — видеть, сквозь.
ПЕРСПЕКТИВНЫЕ ПУЧКИ 1-го порядка (1-й ступени) —это пучки 1-го
порядка, проектирующие один и тот же ряд 1-го порядка. Перспективность двух
пучков есть частный случай их проективности, когда общий элемент этих
пучков сам себе соответствует. Перспективность обозначается знаком л. Так, на
рис. 203 изображены два перспективных пучка Sx и 52, что записывается так:
Si(ai» ^i» "-) Л Sz(ait b2t . . .). Пучок прямых и прямолинейный ряд то-
S^--
м
Рис. 202

ПЕТЕРБУРГСКАЯ ИГРА
305
чек называются также перспективными, если каждая прямая пучка проходит
через соответствующую точку этого ряда. Так, ряд точек 1(А, В, С, .. .)
перспективен пучку прямых Si (alt blt . . .) и пучку S2 («2» Ьъ · · ·)·
П. п. являются двойственной формой (см. Двойственности принцип)
перспективных рядов 1-го порядка (1-й ступени) (см. Перспективные ряды). Для
того чтобы два проективных ряда (пучка) 1-го порядка были перспективны
(см.), необходимо и достаточно, чтобы их общий элемент сам себе соответ-
ствовал.
Важным случаем П. п. с общим носителем является инволюция (см.). См.
Формы геометрические.
ПЕРСПЕКТИВНЫЕ РЯДЫ 1-го порядка (первой ступени) —это ряды,
являющиеся сечениями одного и того же пучка 1-го порядка. Перспективность
обозначается знаком "л. Так, ряд 5(Л, В, С, D, . . .) л ряду 5'(Л', В', С,
Рис. 203 Рис. 204
D', . . .). Перспективное расположение двух рядов является частным случаем
их проективного расположения, когда их общий элемент (точка) сам себе
соответствует. Точка 5 — центр перспективы (рис. 204).
Пучок прямых и прямолинейный ряд точек называются также
перспективными, если каждая прямая пучка проходит через соответствующую точку этого
ряда. Так, ряд точек s(A, В, С, D, . . .) л пучку прямых 5 (а, 6, с, d, ...J.
См. Формы геометрические. Перспективные пучки.
ПЕТЕРБУРГСКАЯ ИГРА состоит в следующем. Первый игрок бросает
монету до тех пор, пока не выпадет герб, после чего игра считается законченной.
Если герб выпадет при первом бросании, то второй игрок уплачивает первому
1 рубль, если при втором — 2 рубля, если при третьем — 4 рубля, и т. д.
Вообще, если герб выпадет впервые при л-м бросании, то второй игрок
уплачивает первому 2п—г рублей. Спрашивается, какую сумму должен уплатить первый
игрок второму за право участия в игре, чтобы игра была безобидной, т. е.
математическое ожидание (см.) выигрыша равнялось стоимости участия в игре?
Трудность решения здесь в том, что математическое ожидание выигрыша в такой
игре равно:
ОО 00 00
η = 1 η = 1 /2=1
где Ап — вероятность того, что герб выпадет при л-м бросании. Эта
трудность возникла потому, что в игре допускаются сколько угодно большие
выплаты второго игрока первому, что невозможно из-за ограниченности капитала
второго игрока.
20 Толковый словарь математических терминов

306
ПИРАМИДА
//
//
/ι
11
/ ι
/fc'
/'/ti
//
//
W
\ \\
\ \\
Λ-Ά
-i cn
£
Рис. 205
Правильная постановка задачи такова: второй игрок уплачивает первому
2·4—ι рублей, если 2п-~1 не превосходит всего его капитала, и весь свой капитал —
в противном случае.
ПИРАМИДА — многогранник, полученный от пересечения многогранного
угла S плоскостью, пересекающей все его грани. Грань, лежащая в секущей
плоскости, называется основанием П., остальные грани
называются боковыми гранями, которые всегда являются
треугольниками. Отрезки ребер многогранного угла от
вершины его до секущей плоскости называются
сторонами основания или ребрами основания. Вершина
S многогранного угла называется вершиной П.
Перпендикуляр, опущенный из вершины пирамиды на
плоскость основания, называется высотой. Если основанием
-. П. является некоторый /г-угольник, то П. называется
k U я-угольной. Таким образом, /2-угольная пирамида
имеет я-f-l граней. П. определяется заданием
основания и вершины. Для построения «-угольной П.
требуется 3 (я-Ь 1) — 6 условий. Например, для
построения треугольной П. требуется 6( = 3·4 — 6) данных
(например, три плоских угла и три ребра).
П. называется правильной, если основание ее — правильный я-угольник и
вершина S проектируется в центр основания. Высота боковой грани правильной
П. называется апофемой П. (см.). Треугольная пирамида называется также
тетраэдром (см.).
Объем П. вычисляется по формуле
где Q — площадь основания, Η — высота П.
Если 5 — вершина П., a ABCDE — основание, то П. обозначается так:
SABCDE (рис. 205).
ПИФАГОРОВА ТЕОРЕМА. Если стороны прямоугольного треугольника
измерены одной и той же единицей длины, то квадрат длины гипотенузы равен
сумме квадратов длин катетов (кратко: квадрат гипотенузы равен сумме
квадратов катетов).
Доказательство П. т. приписывается древнегреческому ученому Пифагору
(VI в. до н. э.)» хотя, очевидно, она была известна и до него. Первоначально
П. т. устанавливала зависимость между площадями квадратов, построенных на
гипотенузе и катетах прямоугольного треугольника: площадь квадрата,
построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах.
Имеет место обобщение П. т.: если на гипотенузе, катетах а и b
прямоугольного треугольника построены произвольные, но подобные фигуры Фс, Фл,
Ф^, например, полукруги, то их площади связаны соотношением: пл. Фс=
«пл. Фд-Нпл. Ф&- В настоящее время известно свыше ста доказательств П. т.
Она является одной из важнейших теорем евклидовой геометрии.
Лит.: Г. Г. Цейтен, История математики в древности и в средние века, М. — Л.,
1938; В. Лит'цман, Теорема Пифагора, Физматгиз, М., 1960; А. А. Колосов,
Книга для внеклассного чтения по математике для учащихся VIII класса, Учпедгиз, М., 1958;
Ван дер Варден, Пробуждающаяся наука, Физматгиз, М., 1959.
ПИФАГОРОВЫ ЧИСЛА — тройки целых положительных чисел х, у, г,
удовлетворяющих уравнению x2-\-y2=z2. Все решение этого уравнения, а,
следовательно, и все П. ч. выражаются формулами x=a2 — b2t y=>2ab, z=a2-\-b2*
где a, b — произвольные целые положительные числа (а > Ь). П. ч. могут быть
истолкованы как длины сторон прямоугольного треугольника. Первыми
(наименьшими) П. ч. являются 3, 4, 5 и 5, 12, 13. См. Герона формула.

пи-число
307
ПИ-ЧИСЛО —число, равное отношению длины окружности к ее диаметру.
П.-ч. представляется бесконечной десятичной дробью 3,14159265 .. .
Обозначением этого числа греческой буквой π впервые пользовался английский
математик У. Джонсон (1706), и оно стало общепринятым после одной из работ
петербургского математика Л. Эйлера (1736).
В конце XVIII в. немецким математиком И. Ламбертом и французским
математиком А. Лежандром было доказано, что П.-ч. является
иррациональным, а в 1882 г. немецкий математик Ф. Линдеман доказал, что П.-ч. не
может удовлетворять никакому алгебраическому уравнению с целыми
коэффициентами, т. е. является трансцендентным. Из теоремы Линдемана следует
невозможность построения с помощью циркуля и линейки отрезка прямой длиной,
равной л; эта теорема окончательно устанавливает невозможность решения
задачи о квадратуре круга.
Уже в глубокой древности делались попытки найти приближенное
выражение для числа П.-ч. с помощью рациональных чисел. В древнем Египте при
/16\2
вычислении площади круга для П.-ч. использовали значение π « I —J =
= 3,16049... Древнегреческий ученый Архимед (III в. до н. э.),
рассматривая окружность как предел последовательностей правильных описанных и
вписанных многоугольников, когда число их вершин бесконечно растет, нашел,
10 1
что П.-ч. заключено между 3 —=3,14084 . . . и 3—=3,14285 ... Приближе-
355
ние π « — = 3,1415929. . . найдено было сначала китайским математиком Цзу
11 о
Чуи-чжи во второй половине V в., а затем, значительно позднее, в Европе
(в XVI в.); это приближение содержит ошибку лишь в седьмом знаке. В
дальнейшем делались многочисленные попытки найти более точное выражение для
П.-ч. Например, самаркандский ученый Джемшид ибн-Мауд-аль-Каши (первая
половина XV в.) вычислил 17 десятичных знаков П.-ч., голландский математик
Лудольф ван Цейлен (начало XVII в.) —32 десятичных знака. В настоящее
время благодаря применению вычислительных машин π найдено с огромной
точностью — известно более тысячи десятичных знаков. Для практических целей
в справочниках обычно даются значения π, —, π2„ IgJi и т. д. К П.-ч. при-
π
водит также разыскание пределов некоторых арифметических
последовательностей и рядов. Впервые это обнаружил французский математик Ф. Виет.
В 1674 г. Лейбниц получил медленно сходящийся ряд, представляющий число:
4 ~ 3*5 7 + 9 11 +
Удобнее для вычислений ряд, получаемый разложением arctgjc при
1 / . 1 π
6 ~yj\ 9 + 5*3a 7 'зз_Ь '")'
Наилучшую формулу для вычисления П.-ч. получил Дж. Мэчин, пользуясь
также разложением arctg* в ряды. Он вычислил П.-ч. с точностью до 100
десятичных знаков.
Число π встречается и в некоторых формулах неевклидовой геометрии, где
оно, конечно, не является отношением длины окружности к ее диаметру* а оп-
20*

308
ПЛАНИМЕТР
ределяется чисто аналитически. Число π участвует и в известной формуле
Эйлера е = I, из которой еще глубже выясняется природа числа л. Название и
обозначение П.-ч. происходит от начальной буквы греческого слова περιφέρεια —
периферия, окружность. См. также Мециево число, Лудольфово число.
ПЛАНИМЕТР — механический прибор, позволяющий приближенно
вычислять площади плоских фигур. Существуют различные виды конструкций П.
(рис. 206), П. используется в конструкторских бюро (при раскройке материала,
Рис. 206 Рис. 207
при работе с топографической картой и т. д.). На рис. 207 показан пример
отсчета на П.: 3254 (отсчет на циферблате, барабане и верньере). Если первый
отсчет равен 3254, а второй — 7868, то разность 7868 — 3254=4614 выражает
площадь обведенной фигуры в делениях П. Если цена деления, например, равна
30 (м2) для указанного масштаба плана участка 1 : 1000, то площадь
измеренного участка равна 30x4614—138 420 (ж2).
Лит.: Α.ιΜ. Лопшиц, Вычисление площадей в ориентированной плоскости, Гостехиздат,
М., 1956; Б. Н. Делоне, Краткий курс математических машин. Гостехиздат, М., 1952;
М.~Л., 1952; А. Н. Крылов, Лекции о приближенных вычислениях, Гостехиздат, М.,
1954.
ПЛАНИМЕТРИЯ — часть элементарной геометрии, в которой изучаются
свойства фигур, расположенных в одной плоскости.
После изучения П. в средней школе обычно приступают к изучению другой
части элементарной геометрии — стереометрии (см.), изучающей свойства фигур,
как угодно расположенных в трехмерном евклидовом пространстве.
Иногда обе части элементарной геометрии изучают совместно (см. Фузио-
низм).
Наиболее полное и систематизированное изложение П. впервые было
приведено в книге «Начала» древнегреческого ученого Евклида.
Лат. planum — плоскость, греч. μ ε τ ρ ε ω — измеряю.
ПЛОСКАЯ ЗАДАЧА математической физики — частный случай задачи
в пространстве, когда изучаемое явление одинаково во всех" плоскостях,
параллельных данной, что позволяет решать задачу только в этой плоскости, —
например, движение заряженной частицы в электрическом поле равномерно
заряженной нити. П. з. встречаются в теории упругости, гидродинамике и т. п.
В некоторых П. з. применяются методы конформного отображения (см.).
ПЛОСКАЯ КРИВАЯ — кривая, все точки которой принадлежат одной
плоскости. Кручение (см.) П. к. равно нулю.
ПЛОСКОСТЬ — одно из основных понятий геометрии. При первоначальном
ознакомлении с понятием П. представление о П. сравнивается с
представлением о гладкой поверхности воды, отполированного стола и т. д. При дальней-

ПЛОЩАДЬ
309
шем изучении систематического курса геометрии П. принимается за исходный
объект, косвенное определение которого дается в аксиомах геометрии. Важные
свойства плоскости выражены в таких, например, аксиомах: 1. Если две точки
прямой принадлежат плоскости, то и все точки прямой принадлежат плоскости.
2. Три точки, не лежащие на одной прямой, принадлежат только одной
плоскости, и др.
Великий русский математик Н. И. Лобачевский принимал за определение
П. следующее: П. есть геометрическое место точек пространства,
равноудаленных от'двух данных точек. При этом Лобачевский исходил при построении
геометрии из понятия движения, а следовательно, и из понятия расстояния
между двумя точками. Великий немецкий математик Г. Лейбниц определял
понятие П. как поверхность, разделяющую пространство на две конгруэнтные
(т. е. совмещаемые при движении) части. Однако этим свойством обладает,
например, цилиндрическая поверхность, образующая которой есть синусоида
или правильная пилообразная бесконечная ломаная.
Лит.: Н. В. Ефимов, Высшая геометрия, Физматгиз, М., 1961; У. А м а л ь д и.
О понятиях прямой и плоскости, сб. «Вопросы элементарной геометрии», перев. с нем., Спб..
1913; Д. Гильберт, Основания геометрии, Гостехиздат, М., 1948.
ПЛОТНОЕ МНОЖЕСТВО. Множество Μ плотно в топологическом
пространстве PzdM, если в любой окрестности любой точки множества Ρ найдется
точка множества М. Например, множество рациональных чисел плотно во
множестве всех действительных чисел. Когда P=Mt говорят, что Μ плотно в себе.
ПЛОТНОСТИ ТОЧКА данного множества, в котором определена мера
(см.),—такая точка, что отношение меры (см.) этого множества, лежащего
в окрестности этой точки, к мере окрестности стремится к единице, когда
окрестность стягивается к точке. Например, во множестве трансцендентных
чисел (см.) каждая точка есть П. т.
ПЛОТНОСТЬ ВЕРОЯТНОСТИ случайной величины ξ —функция р(х) такая,
ь
что при любых а и Ь вероятность неравенства α<ξ<6 равна J p(x)dx. Напри-
а
мер, случайная величина, распределенная по закону треугольника в интервале
(—1, 1), имеет плотность вероятности
{1 -f χ при — 1 < χ < 0,
0 при |х|>1,
1 — χ при 1 > χ > 0.
Если ρ непрерывна, то вероятность неравенства Jt<£<je-f-d* приближенно равна
ρ (χ) dx. Для П. в. удовлетворяются соотношения:
-j-oo
р(х)>0, j p(x)dx=\.
— со
См. Вероятность.
ПЛОЩАДЬ — одна из основных математических величин, характеризующих
геометрические фигуры на плоскости или на поверхности. В простейших случаях
П. измеряется числом заполняющих плоскую фигуру единичных квадратов, т. е.
квадратов со стороной, равной единице длины. Измерение П. плоских
многоугольников основано на возможности «перекроить» любой многоугольник в
прямоугольник^ для которого величина П. равна произведению его сторон. Для
произвольной плоской фигуры (Р), представляющей собой ограниченную и
замкнутую область, границей которой (Д) является замкнутая кривая, понятие П.
определяется следующим образом.

310
ПЛОЩАДЬ
Пусть (А) — всевозможные многоугольники, целиком содержащиеся в (Р),
а (В) — многоугольники, целиком содержащие (Р) (рис. 208); А и В
соответственно их П., тогда А < В. Множество чисел {А} имеет точную верхнюю
границу p*=sup {А}, а множество {В}—точную нижнюю границу p„e=inf {b}
( {А} ограничено сверху любым В* а {В} ограничено снизу любым А). Если
обе границы д. и р* совпадают, то общее их значение р*=р#=р* называется
П. плоской фигуры (Р); фигуру (Р) называют квадрируемой. Если фигура (Р)
разложена на две фигуры (Рг) и (Р2). то квадрируемость двух из этих фигур
.οί влечет за собой квадрируемость третьей, причем
(β) у) всегда Р=Р1+Р2, т. е. понятие П. аддитивно.
^ ^ Для того чтобы фигура (Р) была квадрируема,
необходимо и достаточно, чтобы ее контур (К)
имел П., равную нулю, т. е. мог быть покрыт
многоугольной областью с произвольно малой
П. П., равную нулю, имеет любая
непрерывная кривая, выражаемая с явным уравнением вида:
y=f(x) или *=£(у),
α < χ < b, с < у < d.
Рис. 20S Если фигура (Р) ограничена одной или
несколькими гладкими кривыми, то она заведомо
квадрируема. П. различных плоских фигур
вычисляются при помощи обычных определенных интегралов. Так, П.
криволинейной трапеции, ограниченной кривыми fx{x) и /2(*) (рис. 209), дается
формулой:
в в
J"·
П. ρ сектора АОВ, ограниченного кривой ABf заданной полярным
уравнением р=£(Ф) и двумя радиус-векторами О А и ОВ (рис. 210), дается
формулой:
1 β 1 Ρ
р j Γνφ=- j [g(<p)J2tfq>.
a a
П. плоских фигур могут вычисляться и с помощью криволинейных интегралов*
а именно: П. фигуры (D), ограниченной кусочно-гладким контуром а, дается
формулами:
■ ydx.
D=— ^ydx, D= J xdy, P=— \ xdy — ι
<*> <*> /!Λ
(«)
(Указанные формулы для вычисления площадей могут рассматриваться как
частные случаи формулы Грина; см. Грина формула.) П. плоской фигуры может
быть вычислена и с помощью двойного интеграла D—$$ dxdy, взятого
по П. фигуры.
В случае криволинейных координат ξ, η вместо элемента П. в декартовых
координатах имеем элемент П. в криволинейных координатах:
1 ηη'ίΐ 1^η = /(ξ,η)^η,
ι υα* η) ι
где /—якобиан (см.) преобразования от декартовой системы координат
х% у к криволинейной системе координат ξ, η.

ПОВЕРХНОСТЕЙ ТЕОРИЯ
311
В общем случае П. поверхности дается формулой:
S=UV EG-F*dudv,
(Δ)
где E,G% F — гауссовы коэффициенты поверхности (см. Гауссовы коэффициенты),
Δ — область изменения и и υ, соответствующая поверхности S. В частном случае,
когда поверхность задана явным уравнением z=f(x% у), где (*, у) изменяются
в области (D) на плоскости хОу, П. поверхности дается формулой:
S=jJVl+P2+q2dxdyt
дх ду
П. поверхности, образованной вращением кривой y^f(x) вокруг оси
х[а < χ ^ b, f(x) > 0] (поверхности вращения), дается формулой:
Ь
5=2π( fix)V\+lf (x)\2dx.
а
Вычисление П. с древнейших времен было одним из важнейших
приложений геометрии (отсюда само название геометрии — землеизмерение). За несколько
столетий до нашей эры греческие ученые располагали правилами вычисления
некоторых П. У Евклида в его «Началах» (III в. до н. э.) эти правила даны
в форме теорем. До сих пор в школьном преподавании сохранилось
вычисление П. многоугольников приемами разложения и дополнения, изложенными
в «Началах».
Лит.: Г. Μ. Φ и χ τ е н г о л ь ц, Курс дифференциального и интегрального исчисления,
тт. 1—3; В. Ф. Каган, Основания геометрии, т. I.
П.ЛЮККЕРОВЫ КООРДИНАТЫ прямой / — шесть чисел ρέ (/=1, 2f 3, 4.
5, 6), из которых первые три выражают координаты направляющего вектора
прямой/, а остальные три — координаты момента этого вектора относительно
начала координат. П. к. широко применяются в линейчатой геометрии
(см.) и были введены в 1846 г. немецким математиком Плюккером.
ПЛЮС — знак -Ь для обозначения действия сложения (см. Сложение)
и положительных величин. См. также Математические знаки.
Лат. plus — больше.
ПОВЕРХНОСТЕЙ ТЕОРИЯ — см. Теория поверхностей.

312
ПОВЕРХНОСТИ ВРАЩЕНИЯ
ПОВЕРХНОСТИ ВРАЩЕНИЯ — поверхности, образуемые вращением плоской
линии вокруг прямой — оси П. в., расположенной в плоскости этой линии.
Например, сфера — поверхность, полученная вращением полуокружности вокруг
ее диаметра; прямой круговой конус (см.) — поверхность, полученная
вращением прямой вокруг другой прямой, пересекающей первую, и др.
Линии пересечения П. в. с плоскостями,
проходящими через ось П. в;, называются меридианами
(на рисунке 211—MQR)', линии пересечения П. в. с
плоскостями, перпендикулярными оси, называются
параллелями (на рисунке 211—KLM). Меридианы и
параллели образуют на П. в. две системы линий
кривизны (см.).
ПОВЕРХНОСТНО-ОДНОСВЯЗНАЯ ОБЛАСТЬ —
область трехмерного пространства, в которой каждая
замкнутая поверхность, гомеоморфная сфере, может
быть стянута в точку (не выходя за пределы области).
Примерами П.-о. о. могут служить все пространство,
пространство с удаленной из него прямой, внутренность
тора; не являются П.-о. о. пространство с выколотой
точкой, область между двумя концентрическими
сферами и т. п.
ПОВЕРХНОСТНЫЙ ИНТЕГРАЛ — интеграл от функции /(*), заданной
на некоторой поверхности «S. П. и. равен по определению:
Hf(x)dS = Urn 2 nh)dSl9
где S^ —кусок поверхности с неограниченно убывающим диаметром (см.
Диаметр множества), ^/ — площадь «S,·, ξ{· — точка внутри St·. Если поверхность
Рис. 211
задана параметрически:
χ =
70
χ (и, υ), у = у{иу ν), ζ = ζ(ιι, ν),
(*)
\\fdS = ^fYEG-F4udv.
(S)
τζζ Ε, G, F — коэффициенты первой квадратичной формы поверхности,
Для поверхности z = f(x, у)
dS
-/■Ч
.*)+У dxdy-
В некоторых задачах вместо площадей dSi рассматриваются площади
их проекции на три координатные плоскости. При этом площади проекции
получают определенный знак в зависимости от заданного на поверхности
направления нормали (см. Ориентация поверхностей). Пределы таких сумм называют,
в отличие от (*), П. и. второго рода и обозначают:
J* J Pdydz+Qdzdx+Rdxdy. (**)
П. и. второго рода зависит от ориентации поверхности. На неориентируемых
поверхностях (см.) рассматриваются только П. и. первого рода.
В теории П. и. второго рода имеет место важная формула Остроградского,
связывающая П. и. с объемным (см. Остроградского формула).
ПОВЕРХНОСТЬ — двупараметрическое множество точек пространства,
т. е. множество точек пространства, координаты которых являются функциями
от двух параметров и и ν (например, от криволинейных координат точки на П.).

ПОВТОРНОГО ЛОГАРИФМА ЗАКОН
313
При этом предполагается, что эти функции дифференцируемы достаточно
большое число раз. Если и и ν — криволинейные координаты точки на П., то П.
можно задать уравнениями:
х=х(и, и), у==у(и, v), z^z(u% ι>),
которые называются параметрическими уравнениями П.
Например, сферу O(R) можно задать параметрическими уравнениями:
*=R cosh cos υ% y=R cosusmv, z—Rsmu, где и — широта, υ — долгота точки
на сфере. Исключая из этих уравнений и и ν, получим известное уравнение
сферы: jc2-f-y2-f 22=^2. Уравнение П. может быть задано и в других формах,
например в виде f (x, yt z)=0 или z=f(x, у) и др.
ПОВЕРХНОСТЬ 2-ГО ПОРЯДКА — геометрическое место точек,
пространства, прямоугольные декартовы координаты которых х, у, ζ удовлетворяют
уравнению вида:
aux2^a22y2+a33z2+2al2xy^2auxz+2a2uyz+2aux+2a2^y+2auz+au===0t
где не все коэффициенты α^(ί, Λ=1, 2, 3) равны нулю. Это определение
П. 2-го п. справедливо для любой системы (декартовых или аффинных)
координат (xf, у', ζ'), так как координаты (л/, у', ζ') выражаются линейно через
координаты (х, у, ζ) в преобразованиях координат.
Всего различных видов П. 2-го п.—17: цилиндры (см.) (эллиптический —
действительный и мнимый, параболический и гиперболический), конусы (см.)
(действительный и мнимый), эллипсоид (см.) (действительный и мнимый), гиперболоид
(см.) (однополостный и двуполостный), параболоид (см.) (эллиптический и
гиперболический), пара плоскостей действительных пересекающихся, пара параллельных
плоскостей (действительных и мнимых), пара мнимых плоскостей
(пересекающихся по действительной прямой), пара совпавших плоскостей.
П. 2-го п., имеющие центр (см. Центр), называются центральными.
П. 2-го п., содержащие прямолинейные образующие (см.), называются
линейчатыми П. 2-го п. (см. Конус, Цилиндр, Однополостный гиперболоид,
Гиперболический параболоид). Иногда говорят и о мнимых прямолинейных образующих
х2 у2 ζ2
П. 2-го п. Например, на эллипсоиде ---f —; 4* ~; = 1 расположены два семей*
аг Ъ% с2·
ства мнимых прямых:
, х · z , I. У\ х . z 1 Λ У\
1) —μ—«λ ΐ_-£. ; __,-»— i + 2L;
а с \ Ь] а с λ \ Ь}
2) - + '--λ 1 + ϋ- . __f:_ [Ι-η-1
а с \ οία с λ \ ο)
Линия пересечения П. 2-го п. плоскостью есть кривая 2-го порядка (см.).
ПОВЕРХНОСТЬ УРОВНЯ функции « = /(*, у, ζ) или П. у. скалярного
поля —поверхность, задаваемая уравнением f (х, у, z) = C, где С — постоянная.
В точках П. у. функция принимает заданное постоянное значение и —С.
Примеры: 1) и=^х--\-у2— ζ, П. у. х2-\-у2 — ζ —С являются параболоидами
вращения с осью Ог и вершинами на оси Οζ (рис. 212); 2) « =
==У 1~^2 — у2 —г2 П. у. являются сферами с центрами в начале координат
и радиусами, изменяющимися от 0 до 1 (рис. 213).
ПОВТОРНОГО ЛОГАРИФМА ЗАКОН—теорема теории вероятностей,
уточняющая закон больших чисел (см. Больших чисел закон). В случае, когда

314
ПОГРЕШНОСТЬ
Рис. 212
Рис. 213
ξι» ?2» »··ί ξπ» ···—независимые случайные величины (см.), принимающие
значения -f 1 и — 1 с вероятностью ■—-. П. л. з. формулируется так: пусть
S/l=g1-b|2-f- ··· -τ-ξη. тогда для каждого 6>0 при п-+оо с вероятностью
1 выполняется неравенство;
5Л < (1+δ) |/ 2я1п1шх,
и найдется бесконечно много значений η таких, что
S/i>(l—й)У"2я1п1пя.
Впервые П. л. з. установлен советским математиком А. Я. Хинчиным (1924).
ПОГРЕШНОСТЬ: 1°. П. абсолютная данного числа F (выражения, формулы
и т. д.), которое рассматривается как приближенное значение другого числа /
(формулы, выражения /), есть разность^— /|. Точность приближенного
равенства характеризуют границей абсолютной П. Δ F > \ f — F\. Чем меньше Δ F,
тем лучшим приближением является F для /. Если абсолютная граница П. равна
Δ F, то говорят, что / равно F с точностью до Δ F> и записывают: f=F ±Δ Fs
что равносильно двойному неравенству F — &F<f<F + &F.
2°. П. относительная определяется как отношение абсолютной П. к самой
Δ F
величине F. Относительная П. представляет собой отношение —- и обычно
выражается в %:
Δ/7
100% = Р. При этом говорят, что / известно с
точностью до Р% (или f=F±P%). О П. при вычислении интегралов по
приближенным формулам см. Парабол формула, Прямоугольников формула, Трапеций
формула. О П. при замене функций рядами см. Приближенные формулы,
Приближенные функции.
ПОДГРУППА группы G — подмножество Η элементов группы, замкнутое
относительно операций группы, т. е. если ^(Я и /г2 ζ Н* то hxh2 ζ //,
и если h £ Я, то h—x ζ Η.
Примеры. Группа ортогональных матриц (см.) есть П. группы неособых
матриц (см.), мультипликативная группа рациональных чисел (исключая нуль)
есть П. мультипликативной группы всех вещественных чисел, исключая нуль.

ПОДОБИЯ ПРЕОБРАЗОВАНИЕ
315
ПОДЕРА данной плоской кривой ω относительно точки О — геометрическое
место оснований перпендикуляров, опущенных из точки О на касательные
к кривой ω. Кривая ω по отношению к своей П. называется антиподерой.
П. окружности относительно ее центра есть сама окружность.
Франц. podaire; греч. ποδηρηξ — подошва, основание (перпендикуляров на
касательные).
ПОДКАСАТЕЛЬНАЯ к плоской кривой ω в точке М(х, у) — направленный
отрезок QT (рис. 214), заключенный между точкой пересечения касательной
t к кривой ω в точке Μ с осью χ и проекцией точки
Μ на ось х. Отрезок QN — поднормаль (см.) к
кривой ω в точке M(MN J_t). Если кривая ω
имеет в прямоугольных декартовых координатах
уравнение у=/(*), то имеет место равенство:
QT= __ ISA (из &MQT).
/' (*>
Лит.: П. К. Рашевский, Курс дифференциальной
геометрии, Гостехиздат, М., 1956. Рис. 214
ПОДМНОЖЕСТВО. Если каждый элемент
множества А является элементом множества В, то
множество А называется П. множества В (символически это обозначается знаком
включения: АаВ* или Ad В, или Bid А, или Bzz_A). Например, множество
всех положительных четных чисел является П. множества всех натуральных
чисел, которое в свою очередь является П. множества всех целых чисел, и. т. д.
Пустое множество (см.) является П. всякого множества. Множество всех П.
произвольного множества Μ имеет мощность большую, чем мощность множества
Μ (Г. Кантор). Среди П. данного множества различают собственные
(истинные) и несобственные.
ПОДНОРМАЛЬ к плоской кривой ω в точке М(х> у) — направленный
отрезок QN (см. рис. 214), заключенный между точкой пересечения нормали
η к кривой ω в точке Μ с осью χ и проекцией точки Μ на ось х. На рис. 214
прямая * — касательная к кривой ω в точке M(n±t). Если кривая ω имеет
в прямоугольных декартовых координатах уравнение y=f(x)t то имеет место
равенство:
QN=f(x)-f'(x)(u3 Д MQN).
Лит.: П. К. Рашевский, Курс дифференциальной геометрии, Гостехиздат, М.,
1950.
ПОДОБИЯ ПРЕОБРАЗОВАНИЕ точек плоскости (или пространства) — такое
преобразование, при котором всякий отрезок АВ переходит в отрезок А'В',
равный AB-ky где число k Φ 0 называется коэффициентом П. п. П. п. есть
частный случай аффинного преобразования (см.). Всякое П. п. можно
рассматривать как произведение (результат последовательного выполнения) гомотетии
(см.) и движения (первого или второго рода), при этом коэффициент
П. п. и коэффициент гомотетии совпадают.
Две фигуры, соответственные в П. п., называются подобными (см.).
В П. п. углы между двумя любыми линиями и им соответственными равны.
П. п. составляют группу. Частным случаем П. п. является гомотетия.
П. п. тесно связано с постулатом (аксиомой) о параллельности прямых,
который эквивалентен существованию хотя бы одной пары подобных и неравных
треугольников. В геометрии же Лобачевского (см.) не существует подобных
и неравных треугольников.
П. п. широко используется при решении конструктивных задач, при
изготовлении моделей и чертежей (подобное копирование). П. п. двух фигур часто
называют их подобием.

316
ПОДОБНЫЕ МАТРИЦЫ
ПОДОБНЫЕ МАТРИЦЫ. Две квадратные матрицы А и В одинакового
порядка называются подобными, если существует невырожденная матрица
С такая, что В^САС-1.
Если линейное преобразование Ρ линейного пространства L в базисе
{elt е2< . . . i ед} записывается матрицей Л, то в базисе {Celt Се2, . . . , Сеп]
его матрицей будет САС—1. Иными словами, ГЛ. м. задают одно и то же
линейное преобразование в различных базисах.
Отношение подобия матриц транзитивно, рефлексивно, симметрично
(см. Транзитивность, Рефлексивность, Симметричность), так что множество всех
матриц разбивается на классы попарно П. м. В каждом классе существует так
называемая каноническая матрица.
Классификация матриц по отношению подобия и определение канонической
матрицы даются в теореме Жордана (см. Жорданова нормальная форма).
П. м. имеют одинаковые определители (см.), собственные значения (см.),
ранги (см.), характеристические уравнения (см.).
Для подобия ортогональных (см.), унитарных (см.), симметрических (см.),
кососимметрических (см.) матриц необходимо и достаточно совпадения
собственных значений.
Вопросы, связанные с подобием матриц, рассматриваются, кроме алгебры,
в теории линейных дифференциальных уравнений, во многих вопросах
геометрии и др.
Лит.: Ф. Р. Гантмахер, Теория матриц, Гостехиздат, М., 1953; И. М. Гель·
φ а н д, Лекции по линейной алгебре, Гостехиздат, М., 1951.
ПОДОБНЫЕ ФИГУРЫ — две фигуры, соответственные в преобразовании
подобия (см. Подобия преобразование).
У П. ф. соответственные линейные элементы пропорциональны, а углы
между ними равны. С наглядной точки зрения П. ф. имеет одинаковую форму,
но различные размеры. Учение о П. ф. опирается на понятие пропорциональности
отрезков. В «Началах» Евклида П. ф. и преобразованию подобия посвящена
книга VI.
Наряду с общим определением П. ф. обычно дают иное определение
подобных многоугольников в такой форме: два многоугольника называются
подобными, если их соответственные стороны пропорциональны, а углы, заключенные
между пропорциональными сторонами, равны. Для подобия треугольников
необходимым и достаточным признаком является каждый из следующих: 1) стороны
одного пропорциональны соответственным сторонам другого; 2) два угла одного
равны двум углам другого; 3) две стороны одного пропорциональны двум
сторонам другого, а углы между этими сторонами равны. В подобных
треугольниках любые сходственные (соответственные) линейные элементы (высоты,
медианы, биссектрисы, радиусы вписанных и описанных кругов и т. д.)
пропорциональны сходственным (соответственным) сторонам.
Отношение расстояния между точками А и В одной фигуры к расстоянию
между соответственными точками А' и В' другой равно постоянному числу
кфОу называемому коэффициентом подобия (или подобного преобразования).
Площади замкнутых подобных фигур относятся как квадраты, а объемы —
как кубы их коэффициентов подобия. Если фигура Φ подобна фигуре Ф',
то это записывается так: Фс/эФ', где знак подобия с/>—повернутая латинская
буква S. П. ф. вычерчиваются с помощью пантографа (см.).
Лат. similis — подобный.
ПОДОБНЫЕ ЧЛЕНЫ многочлена. Если даны два члена многочлена:
л «ι «о an г> Pt ν Ρ» $п
Αχγχζ? . . . χ™ и Βχ\ х 2 .. . Χη ·

ПОЗИЦИОННАЯ СИСТЕМА
317
то они называются П. ч. в том и только в том случае, если аг«*=р^(/=1,
2, . . . , л), т. е. если степени обоих членов относительно каждого из
неизвестных (аргументов) xlt x2 хп равны. Если коэффициент А при некотором
члене равен нулю, то такой член считается подобным любому другому члену.
ПОДПОСЛЕДОВАТЕЛЬНОСТЬ — бесконечное подмножество (см.)
множества элементов последовательности, упорядоченное согласно порядку
последовательности. Справедливо утверждение: если последовательность имеет предел,
то каждая подпоследовательность имеет тот же предел.
ПОДПРОСТРАНСТВО — множество Р' элементов пространства Р, которое
само является пространством в том же смысле, что и пространство Р. Так,
например, всякое множество элементов метрического пространства само является
пространством метрическим. В трехмерном векторном пространстве R3 любая
прямая или плоскость являются П. одного и двух измерений пространства Rz.
П. R называется инвариантным относительно оператора Л, если А переводит
векторы П. R в векторы этого же П. Если линейный оператор, действуя
на базисные векторы П., переводит первый вектор во второй, второй в третий
и т. д., последний же базисный вектор переводится оператором А в линейную
комбинацию базисных векторов, то такое П. называется циклическим
относительно оператора А. Под ^-мерным координатным П. в n-мерном векторном
пространстве R с базисом е^ . . . , ел понимают любое П. в R с базисом
е k » tk , . . . , efe (у < η). См. Векторное пространство, Гильбертово
пространство, Линейное пространство, Метрическое пространство.
Лит.: А. Г. Курош, Курс высшей алгебры, Физматгиз, М., 1962; Ф. Р. Гант-
м а х е р, Теория матриц, Гостехиздат, М;, 1953; В. И. Смирнов, Курс высшей
математики, т. 3, Физматгиз. М., 1961.
ПОДСТАНОВКА л-й степени — взаимно однозначное отображение
множества из η символов (как правило, берутся первые η натуральных чисел 1, 2,
3, ... , л) на себя. Число всех различных П. л-й степени равно п\.
Относительно операции умножения П. множество всех П. образует симметричную
группу (см).
Пример. Подстановка 5-й степени:
1 2 3 4 5\
2 5 4 3 1/'
ПОДХОДЯЩАЯ ДРОБЬ — см. Непрерывная дробь.
ПОЗИЦИОННАЯ СИСТЕМА (или поместная система) счисления — система
счисления, основанная на принципе позиционного, или поместного, значения
цифр, т. е. на том, что одна и та же цифра получает различные числовые
значения в зависимости от ее места в записи числа (см. Счисление). К П. с.
принадлежит общепринятая ныне десятичная система * а также используемые
в машинной математике двоичная, восьмеричная и шестидесятеричная системы
счисления.
Исторически первой П. с. была шестидесятеричная система древних вавилонян,
возникшая за 2000 лет до н. э. В этой системе основанием было число 60,
позиционный принцип еще не был в ней проведен вполне последовательно —
отсутствовал символ для нуля, из-за чего позиционная запись не нашла
абсолютного характера. Следы этой системы сохранились до наших дней: час
делится на 60 минут, минута — на 60 секунд; окружность делится на 360
частей — градусов.
Независимо друг от друга П. с. возникли у племени майя в начале новой
эры и в Индии в VIII—IX вв. Родоначальницей современной десятичной нуме-

318
ПОКАЗАТЕЛЬ СТЕПЕНИ
рации была индусская система; она имела основанием 10, и в ней был символ
для обозначения нуля. Принцип поместного значения распространился из Индии
в другие страны. К народам Европы начертание цифр и позиционный способ
обозначения перешли из Испании, куда они дошли из Индии через
мавританские государства Передней Азии.
В книге, изданной в русской типографии, индусская нумерация впервые
встречается в 1638 г. В 1647 г. в Москве была издана книга «Учение и хитрость
ратного строения пехотных людей», в которой все цифры были уже индусскими.
В знаменитой «Арифметике» Магницкого все вычисления в тексте делаются
на индусских числах.
Лит.: Энц. элем, мат., т. 1, Гостехиздат, М., 1951.
ПОКАЗАТЕЛЬ СТЕПЕНИ — см. в термине Степень.
ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ — функция вида у=ах (рис. 215) при
— оо <х< оо,0<у< оо (а — положительное
число, отличное от единицы). При а>1 П. ф.
монотонно возрастает, при а<\ — монотонно
убывает. П. ф. непрерывна и имеет непрерывные
производные любого порядка:
у'=ах\па\ у"=ах(\па)2я . . .; у(п) = ах(\па)п.
Частным важным случаем П. ф. является у=е*,
где е — основание натуральных логарифмов. Если
f(x)=ax, то для любых вещественных чисел
χ и у всегда имеет место равенство:
f(x+y)=fW-fM (*)
(функциональное свойство). Оказывается, что
этим свойством и непрерывностью П. ф.
определена вполне однозначно. Иными словами,
единственной функцией, определенной и непрерывной
+ оо) и удовлетворяющей в нем условию (*), яв-
•-ах дает решение функционального уравнения (*)
ф, у~ех представляется равномерно и абсолютно
во всем промежутке (— оо,
ляется П. ф. Формула f(x) =
в непрерывных функциях. П.
ходящимся рядом:
X Xй X* .
■1+ΪΪ+2Ϊ+8Ϊ +
хп
+ -Т+
оо
η- Ι
Если заменить в этом ряде вещественную переменную χ комплексной перемен-
ной z=x+iy, то получится сходящийся ряд 1|>"]' Его СУММУ прини-
ίτϊι
мают по определению за значение П. ф. ег при любом комплексном г.
Функция ez также непрерывна вместе со всеми своими производными и
удовлетворяет условию (*). При чисто мнимом показателе имеем соотношение:
•♦"-(■♦S^'S
л = 0
(2л+1)1
cos у-И sin у,

ПОЛЕ
319
впервые полученное Эйлером. Например:
-п'/ . ί π 2 π ί ζ + 2 π / „ 21: /
e2 =tt e =—1, e = 1, e =ez-e = e%
т. е. П. ф. оказывается периодической с чисто мнимым периодом 2 π/(2 π/·ft,
k=±l, 2, 3, ..., /г); других периодов нет у нее. П. ф. связана также
с гиперболическими функциями:
sh *=
ch* =
е*+<?~
решаются
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
тт. I, II, Физматгиз, М., 1963.
ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ — уравнения, в которых неизвестное
содержится в показателе степени. Например, 2*=4, 2х=х2. В школе
П. у. рассматривается только в области действительных чисел. П. у.
логарифмированием обеих частей уравнения,
заменой переменных (введением новых
переменных или подстановкой), уравниванием степеней
с равными основаниями, графически и другими
приближенными способами.
Примеры: 1) 2*=3*. Jtlg2-jtlg3, *(lg3 —
— Ig2) = 0, откуда * = 0. Можно решить и так:
2х (2\х
~ = 1 г-) =1, откуда х=0. Решение этого
уравнения легко усматривается и графически: графики
функций у= 2Х и у—3х (рис. 216) пересекаются
в точке Λ1 (0,1); отсюда корень уравнения равен
*=0. 2) 9*4-1 ох=25х. Это уравнение решается
путем деления обеих частей на любую степень,
входящую в уравнение, после чего данное
уравнение сводится к квадратному. 3) 2х =—3 —
уравнение решений не имеет, так как левая часть -
а правая — отрицательная.
П. у. являются частными случаями трансцендентных уравнений (см.).
ПОКРЫТИЕ МНОЖЕСТВА — совокупность точечных множеств таких, что
каждая точка данного множества принадлежит по крайней мере одному
подмножеству покрытия. Если множества покрытия открытые (см. Открытое
множество), то само П. м. также называется открытым. Важным утверждением
дифференциального исчисления является лемма Гейне —Бореля (см.).
П. м. участвует в некоторых определениях размерности множества.
ПОЛЕ — коммутативное, ассоциативное кольцо (см.) Р, обладающее
единицей, если оно состоит не только из одного 0 и если в нем деление выполнимо,
притом однозначным образом, во всех случаях, кроме случая деления на 0.
Иными словами, для любых элементов а и b из ρ (ЬфО) существует в ρ такой
элемент q, притом единственный, который удовлетворяет равенству bq—a.
Элемент q называется частным элементов а и b и обозначается символом
а
Числовое кольцо называется числовым П., если оно содержит частное
любых двух чисел. Существуют П. рациональных чисел, действительных чисел,
комплексных чисел, но кольцо целых чисел уже не П., так как частное двух
целых чисел может быть и не целым. П. рациональных чисел целиком содер-
- функция положительная,

320
ПОЛЕ АЛГЕБРАИЧЕСКИХ ЧИСЕЛ
жится во всяком числовом П. Примером числового П. может служить также
система чисел вида а+Ьу 2 с любыми рациональными а и Ь. Действительно,
частное
a+bV2 (a+bVi) {с -~ dVJP) ас -- 2bd be — ad у-
c+dy2~{c+dV2){c-dV2)~ c*~-2d* + *-**
является числом вида α-{-б]/2 . При этом предполагалось, конечно, что
c+dy 2, а следовательно, и с — dV 2 отличны от 0. П. является и
множество всех рациональных функций с действительными переменными. Кольцо
же многочленов с коэффициентами из некоторого числового П. не является П.,
так как многочлены могут не делиться без остатка. Во всяком П. всякое
равенство можно сокращать на общий, отличный от нуля множитель. Если все
целые, кратные единицы поля Ρ являются различными элементами поля Ρ
(т. е. /ι·1φΙ·19 если ίιφΐ), то говорят, что П. имеет характеристику 0.
Таковы все числовые П. Если при ί Φ к все же имеем / · 1=£· 1, то (/ — £)· 1 =0,
т. с. в поле Ρ существует такое положительное кратное единицы, которое
равно нулю. Тогда Ρ называют П. конечной характеристики. Для всякого П.
имеет место один из двух случаев: 1) для всякого элемента афО и любого
целого числа η Φ 0 кратное па также входит в Ρ и отлично от нуля,
2) существует единственное простое число, такое, что ра — 0 для любого
элемента. Характеристикой П. называют число 0, если па Φ 0 для любого
элемента а^Ои любого целого числа η Φ 0, и простое число р, такое, что ра = 0
для любого элемента а в противном случае.
Множество Μ поля Ρ называется подполем поля Р, если оно само является
П. при тех же определениях операций сложения и умножения, которые даны
в поле Р. Тогда Ρ называется надполем или расширением поля М. Например,
П. рациональных чисел является подполем П. действительных чисел, а П.
комплексных чисел — надполем П. действительных чисел.
Поле Ρ изоморфно полю Р', если существует взаимно однозначное
отображение Ρ на Р', при котором сумме и произведению любых элементов R
соответствуют сумма и произведение соответствующих элементов R'.
Лит.: А. Г. Курош, Курс высшей алгебры, Физматгиз, М., 1962; Л. Я. Окунев,
Курс высшей алгебры, Учпедгиз, М., 1958; Энц. злем. мат., тт. I и II, Гостехиздат, М.,
1951.
ПОЛЕ АЛГЕБРАИЧЕСКИХ ЧИСЕЛ — множество всех алгебраических
чисел (см.). П. а. ч. является алгебраически замкнутым полем (см.). Эти свой-
стса доказываются проще всего использованием основной теоремы о
симметрических функциях (см.).
ПОЛЕ ВЕКТОРНОЕ—область пространства, в каждой точке которой
приложен вектор. П. в. часто приходится рассматривать в связи с задачами
физики: поле гравитации, электрической напряженности и др. В математике
П. в. задается обычно системой дифференциальных уравнений. Интегральные
кривые системы образуют линии поля — линии, касающиеся в каждой точке
вектора, связанного* с этой точкой.
Важными характеристиками векторного поля являются дивергенция (см.)
и вихрь векторного поля. П. в. называется потенциальным, если существует
функция точки пространства / (Р) такая, что вектор поля в произвольной точке
Ρ равняется grad / (см. Поля теория).
П. в. соленоидально, если его дивергенция равна нулю. Поле называется
лапласовым, если оно соленоидально и потенциально.

полином
321
П. в. на поверхности определяется аналогично П. в. в пространстве, при
этом оговаривается лишь то обстоятельство, что векторы берутся в точке
поверхности.
ПОЛЕ НАПРАВЛЕНИЙ (или поле псевдовекторов) — область пространства
или поверхности, с каждой точкой которой связано направление. Всякое век*
торное поле можно рассматривать как П. н.
ПОЛЕ СКАЛЯРНОЕ — функция V (Р) в области пространства или на
поверхности (например, температура в каждой точке пространства, высота над
уровнем моря и др.). П. с. изображается с помощью поверхностей уровня,
т. е. поверхностей с уравнением U(P)=C. С каждым П. с. связано векторное
поле его градиента (см.), каждый вектор которого перпендикулярен
поверхности уровня в их общей точке (см. Поля теории). Если поверхности уровня —
концентрические сферы или концентрические цилиндры, то поле называют
соответственно сферическим и цилиндрическим.
ПОЛИВЕКТОР — ковариантный или контравариантный тензор (см. Кососим-
метрический тензор) по всем индексам. При количестве индексов 2, 3, ... П.
называется соответственно бивектор, тривектор и т. д. П. валентности к
(см. Тензор) в /z-мерном пространстве при k > η есть тождественный нуль.
Примером бивектора может служить угловая скорость вращения тела в
пространстве. Теория П. применяется во многих главах дифференциальной геометрии.
ПОЛИГАРМОНИЧЕСКАЯ ФУНКЦИЯ— функция f (xu x2f ..., хп) такая,
что т раз примененный к ней оператор Лапласа (см. Лапласа оператор)
переводит ее в нуль. Необходимым и достаточным условием того, чтобы / была
П. ф., является представление функции f в виде:
/=Фо-Ь'·2 Φι-f г* Ф24- · · · 4-r2m-2 φ*-!,
где г = у х\-\-х\-5г ··· -\-х„ , а φ0, ср1§ ..., ψ}η—1— гармонические
функции.
Задача нахождения П. ф. является важной задачей теории упругости.
Лит.: С. Л. Соболев, Некоторые применения функционального анализа в
математической физике, изд. Сибирского отд. АН СССР, Новосибирск, 1962.
ПОЛИЛИНЕЙНАЯ ФОРМА — функция η векторных аргументов, линейная
по каждому из этих аргументов, например объем параллелоэдра, натянутого на и
векторов (объем со знаком!). Важным объектом изучения во многих вопросах
дифференциальной геометрии, теории групп Ли и топологии являются кососим-
метрические полилинейные формы.
ПОЛИИНТЕРВАЛ в /г-мерном пространстве — совокупность точек M(xlt
*о, ..., хп)у координаты которых удовлетворяют неравенствам | хх—х® \ <Ьи
..'., | хп — Хп\ < δ/ι, ГДе все δ/>°· Точка М0(х*{, х%, ..., х%) называется
центром П. П. является одним из видов окрестности (см.) точки М0 в /г-мерном
пространстве. П. на плоскости (/2=2) является внутренность прямоугольника со
сторонами 2δ1§ 2δ2, параллельными осям координат, и центром M0(x0t y0).
П. в пространстве (/2 = 3) является внутренность прямоугольного параллелепипеда.
П. является обобщением понятия интервала (см.) на случай п>\. П. называют
также открытым параллелепипедом /г-мерного пространства.
ПОЛИНОМ — тоже, что и многочлен (см.). Термин употребляется в
настоящее время значительно реже, чем термин многочлен.
См. Целая рациональная функция, Бином.
Греч, πολύ — много и νομός — область, часть, член.
21 Толковый словарь математических терминов

322
ПОЛИНОМИАЛЬНАЯ ТЕОРЕМА
ПОЛИНОМИАЛЬНАЯ ТЕОРЕМА — обобщение формулы бинома Ньютона
(см.) на случай возведения в целую неотрицательную степень η суммы k
слагаемых (k>2):
... ХП - L· Aaitat α.χ\
/ = 1 / α,+ ι,+ ...+c^n *
где суммирование в правой части распространено на всевозможные наборы целых
неотрицательных чисел al9 a2f ..., α#, дающих в сумме п. Коэффициенты
А^ α α носят название полиномиальных и выражаются следующим
образом:
А(п)
ах ! а2 ! ... ап !
Πία,Ι)
При &=2 полиномиальные коэффициенты становятся биномиальными
коэффициентами (см.).
ПОЛИНОМИАЛЬНЫЕ КОЭФФИЦИЕНТЫ — см. в термине Полиномиальная
теорема.
ПОЛИЭДР — то же, что и многогранник (см.) в /2-мерном пространстве.
Греч, πολύ — много, έδρα — грань, основание.
ПОЛНАЯ АНАЛИТИЧЕСКАЯ ФУНКЦИЯ (в смысле Вейерштрасса)—
функция /(г) (возможно, многозначная), полученная всевозможными аналитическими
продолжениями одного какого-либо элемента функции f (ζ). См. Аналитическое
продолжение.
ПОЛНАЯ ВЕРОЯТНОСТЬ. Пусть А19 Л2, ..., Ап — события, обладающие
следующими двумя свойствами: 1) никакие два события не могут наступить
одновременно (несовместимые события); 2) при любом исходе случайного
эксперимента наступает одно из событий Л1? Л2, -.. ♦ Ап. В таком случае
вероятность Ρ (В) любого события В, называемая здесь П. в., дается формулой:
P(B)=fiP(B/Ai)P(Al),
где Ρ (Β/Αι) — условная вероятность (см.) события В при условии Л/, Ρ (Αι) —
вероятность события Л,·. Например, пусть событие В означает появление брака
в производстве, я=2 и событие Лх означает, что нарушения технологии не
произошло (брак в этом случае может быть вызван случайными причинами), а
событие Ас, означает, что произошло нарушение технологии. Если Р(Б/Л1)=0,01,
Р(Б/Л2)=0,99, P(;4i)=0,9f />(Л2)=0,1, то П. в.
/>(В) = 0,01.0,9+0,99-0,1=0,108.
ПОЛНАЯ КРИВИЗНА поверхности в окрестности какой-либо ее точки —
число, равное произведению главных кривизн (см.). Для плоскости и для
развертывающейся линейчатой поверхности П. к. равна 0, для сферы радиуса R
она равна —-. П. к. остается неизменной при изгибании поверхности, т. е.
при таком ее преобразовании, при котором длина линий не изменяется. П. к.
иначе называется гауссовой кривизной. См. также Теория поверхностей.

ПОЛНОЕ ИЗОБРАЖЕНИЕ
323
ПОЛНАЯ ПРОИЗВОДНАЯ — производная от функции у= /(*, xu х2* ..., хп)>
зависящей от переменной t как непосредственно, так и через посредство
аргументов *ι = *ι(Οι ·.., *λ = */ι(0 п° переменной t. П. п. выражается
формулой:
^^ ^bdf_dxk
dt dt \Zjdxk dt '
df df
где — , -— — частные производные (см. Частная производная, Производная).
dt dxfc
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
т. I, Физматгиз, М., 1963.
ПОЛНАЯ СИСТЕМА АКСИОМ — такая система непротиворечивых аксиом,
любые две интерпретации которой изоморфны. П. с. а. достаточна для
построения той или иной теории. Так, системы аксиом евклидовой геометрии,
геометрии Лобачевского, проективной геометрии являются П. с. а. Однако система
аксиом теории групп (см. Группа) не является полной, так как существуют
неизоморфные группы.
ПОЛНАЯ СИСТЕМА ВЫЧЕТОВ по модулю т — любая совокупность целых
чисел, содержащая по одному числу из каждого класса чисел по модулю т
(два целых числа а и Ь принадлежат одному классу по модулю т, если а — Ь
делится на т). Любые т чисел, принадлежащих различным классам по
модулю /и, образуют П. с. в. В качестве П. с. в. может применяться система
наименьших неотрицательных вычетов 0, 1, 2, ..., т—1 (см. Вычеты).
ПОЛНАЯ СИСТЕМА ФУНКЦИЙ в некотором линейном пространстве
функций L — система функций {Ф(*)} такая, что в L не существует функции,
ортогональной всем функциям семейства (см. Ортогональные функции) в смысле
определенного в L скалярного произведения. Если в L существует полная ортонор-
мированная (см.) система функций, то любую функцию из I можно разложить
в ряд по функциям этой системы.
Пример: система {1, sin nxt cos я*}, л=1, 2, ортонормированная
П. с. ф. относительно скалярного произведения
в пространстве непрерывно-дифференцируемых функций на [—π, π]. Система
функций, полная в одном пространстве, может оказаться неполной в другом.
ПОЛНОЕ ИЗМЕНЕНИЕ (полная вариация) функции одного переменного —
η
верхняя грань сумм: 2 I /(*/) — /(**'—ι) I Для всевозможных разбиений ас
ί=ι
<#o<*i< * * * <*л<& отрезка [а, Ь]. Функции, имеющие ограниченное Π и.,
называются функциями с ограниченной вариацией. Последние обладают рядом
интересных свойств. Например, каждая функция ограниченной вариации
является разностью двух ограниченных положительных неубывающих функций.
П. и. функции нескольких переменных так же рассматривается, но
определяется сложнее.
ПОЛНОЕ ИЗОБРАЖЕНИЕ фигуры — такое изображение, при котором
определяются позиционные свойства ее оригинала.
При П. и. всякая инциденция на оригинале определена также и на
изображении, т. е. любая инциденция двух элементов из множества точек, прямых
и плоскостей на П. и. определяется однозначно. Но П. и. не определяют
метрических свойств оригинала. Для того чтобы чертеж обладал и метрической полно -
21*

324
ПОЛНОЕ ПРИРАЩЕНИЕ
той (метрической определенностью), следует добавить к нему условия,
определяющие оригинал. Например, из условия задачи может быть известно, что тот или
иной параллелограмм является квадратом или ромбом, что пирамида,
изображенная на чертеже, является в оригинале правильным тетраэдром, и т. д.
Лит.: Η. Φ. Чет вер у хин, Чертежи пространственных фигур в курсе геометрии,
Учпедгиз, М., 1946.
ПОЛНОЕ ПРИРАЩЕНИЕ функции f(xlt χ,, ..., χη) — разность между
#2> · · · > хп)· Если / (х1, хъ ...,
,,.,хп) имеет непрерывные частные производные, то П. п. есть сумма полного
дифференциала (см.) и величины бесконечно малой по отношению к
1Ла*,)Ч-(А*2)2+---+(А*я)2.
ПОЛНОЕ ПРОСТРАНСТВО — метрическое пространство, в котором всякая
фундаментальная последовательность (см.) имеет предельную точку,
принадлежащую этому пространству. Например, евклидово пространство — полно, круг
с выколотым центром — не является П. п.
ПОЛНОТА СИСТЕМЫ АКСИОМ — одно из основных требований (условий,
свойств) непротиворечивой системы аксиом (см. Полная система аксиом). П. с. а.
аксиоматической системы определяется так: всякая система аксиом называется
полной, если все ее интерпретации (реализации, модели) изоморфны друг другу.
В математике все большую роль приобретают теории, основанные на
неполной системе аксиом; например, система аксиом, определяющая группу, является
неполной, так как существуют неизоморфные группы.
ПОЛНЫЙ ДИФФЕРЕНЦИАЛ функции f{xlt x2, ..., хп) — выражение
^ a/ df df
<*f =—Δ*ι+— Δ*2+··· + ~-Δ** (Axi = dxh i=\, 2, ..., η)
ΟΧ χ ΟΧ 2 0Χη
в случае, когда оно отличается от полного приращения (см.) на величину
бесконечно малую по сравнению с у (Δ*ι)4 \-(кхп)2 · Иначе, П. д. есть
главная линейная часть приращения функции.
ПОЛНЫЙ КВАДРАТ трехчлена — выражение ах*-\-Ьх+с, которое можно
представить в виде (kx+l)2. П. к. встречается при изучении формулы корней
квадратного уравнения (квадратного трехчлена), при интегрировании некоторых
функций, при изучении кривых второго порядка и т. д. П. к. называют также
натуральное число, равное квадрату другого натурального числа. П. к. иначе
называется точным квадратом.
ПОЛНЫЙ ЧЕТЫРЕХВЕРШИНКИК — это совокупность четырех точек
(вершин П. ч.), из которых никакие три не лежат на одной прямой, и шести
прямых (сторон П. ч.), определяемых каждой парой точек.
Если ABCD—-П. ч., то его сторонами будут шесть прямых АВ, ВС, CD,
DA, АС к BD. Стороны АВ и CD, ВС и AD, АС и BD называются
противоположными. Точки пересечения противоположных сторон называются
диагональными точками П. ч. Прямые, соединяющие диагональные точки, называются
диагоналями П. ч. На каждой стороне и диагонали П. ч. имеется гармоническая
четверка точек (см.; там же см. и рисунок).
Двойственной формой П. ч. является полный четырехсторонник, т. е.
четыре прямые (стороны П. ч.), из которых никакие три не проходят через одну
точку, и шесть их точек пересечения (вершин П. ч.).
Полный четырехвершинник называют также полным четырехугольником.
ПОЛОЖИТЕЛЬНО ОПРЕДЕЛЕННАЯ КВАДРАТИЧНАЯ ФОРМА — выраже-
η
ние вида /= ^ aikxi*ki гДе αίΛ==αΑ£» принимающее положительные значе-
ния, при всех вещественных χ ι, кроме Χχ=· · ·=χη=0.

ПОЛУИНТЕРВАЛ
325
Ортогональным преобразованием переменных П. о. к. ф. приводится к виду
/= 2λ>:*/ >где все λ*>0·
г = 1
Линейными произвольными невырожденными преобразованиями (с
вещественными коэффициентами) П. о. к. ф. приводится к сумме квадратов:
/- Σ χ< ·
/ = 1
Существует признак положительной определенности формы (см. Сильвестра
критерий).
Форма вида
(где aik=akh чертой сверху обозначено комплексно-сопряженное число) такая,
что g>0 при х, отличных от нуля, называется П. о. к. ф. Эрмита. Для нее
справедливы теоремы, во многом похожие на вышеприведенные.
ПОЛОЖИТЕЛЬНЫЕ ЧИСЛА — действительные числа, расположенные на
числовой оси справа от начала отсчета — нулевой точки. Например: 2, 3,
у 10 и т. д. Знак 4- перед П. ч. обычно не пишется. См. также
Отрицательные числа.
ПОЛОЖИТЕЛЬНЫЙ ИНДЕКС инерции действительной квадратичной
формы — число положительных квадратов в нормальном виде квадратичной формы.
П. и. и. является инвариантом действительной квадратичной формы относительно
ее невырожденных линейных преобразований.
ПОЛОСА: 1°. П. — множество точек плоскости, лежащих между двумя
параллельными прямыми этой плоскости. Задается аналитически неравенствами:
а<Ах+Ву<Ь,
где а, 6, Л, В — постоянны, Л и β не равны нулю одновременно.
2°. П. в дифференциальной геометрии — кривая в трехмерном евклидовом
пространстве, в каждой точке которой заданы три линейно независимых вектора,
один из которых направлен по касательной.
Лит.: В. Бляшке, Введение в дифференциальную геометрию, ОНТИ, М., 1935.
ПОЛУГРУППА — непустое множество Р, в котором любой паре взятых
в определенном порядке элементов Χ, Υ ζ Ρ поставлен в соответствие элемент
того же множества, называемый их произведением:
ί/=Χ7ζΡ,
причем для любых X, Υ, ΖζΡ всегда выполнено равенство
(ΧΥ)Ζ=Χ(ΥΖ).
При дополнительном условии существования решений уравнений ХА=В
и ΑΥ=Β при любых А и В П. является группой (см.).
Лит.: Е. С. Л я пин, Полугруппы, Физматгиз, М., I960.
ПОЛУИНТЕРВАЛ, иначе полуоткрытый интервал — множество точек
числовой прямой, удовлетворяющих условию
а < х<5 или а<х < Ь.
П. не является ни открытым (см.), ни замкнутым множеством на прямой.
П. иначе называется полусегментом.

326
ПОЛУКУБИЧЕСКАЯ ПАРАБОЛА
■it
ПОЛУКУБИЧЕСКАЯ ПАРАБОЛА — плоская кривая, уравнение которой
в некоторой декартовой системе координат имеет вид y2=kx'3.
П. п. имеет точку заострения («клюв») в начале координат (рис. 217). Ось
Оу является касательной к П. п. в начале координат. П. п. не является
параболой. П. п. иначе называется параболой Нейля (см.).
ПОЛУЛОГАРИФМИЧЕСКАЯ БУМАГА — бумага с
нанесенной на ней прямоугольной сеткой так, что по
одной из координатных осей отложена равномерная шкала,
а по другой функциональная — логарифмическая. П. б.
используется для построения графиков таких функций,
которые изображаются на ней довольно просто. См. также
Логарифмическая бумага.
ПОЛУНЕПРЕРЫВНАЯ ФУНКЦИЯ: 1°. П. ф. сверху
в точке х0— функция /(*), удовлетворяющая условию:
для всякого ε>0 найдется δ>0 такое, что как только
| χ — х0 | < δ, разность f(x) — / (х0) < ε. Непрерывная
Рис 217 функция является П. ф. сверху, но не наоборот.
2°. П. ф. снизу в точке х0 — функция f(x),
удовлетворяющая условию: для всякого ε > 0 найдется 6 > О
такое, что как только | а: — лг0 1 <: 6, разность f(x0)—f(x)<s. Например,
функция
х> О,
-jc, χ < О
полунепрерывна снизу в точке х0=0. Относительно П. ф. справедлив ряд теорем,
аналогичных теоремам о непрерывных функциях. Отметим, например, такую из
них: П. ф. снизу на данном отрезке достигает минимума.
Лит.: И. П. Натансон, Т. ф. в. п., Гостехиздат, М.—Л., 1950.
ПОЛУПЛОСКОСТЬ — одна из двух частей евклидовой плоскости, на
которые разбивается эта плоскость всякой лежащей в ней прямой /; прямая /
может быть отнесена к одной из двух П. Если уравнение прямой / имеет вид:
Ах+Ву+С=0 (А и В одновременно не равны нулю) и прямая / не
принадлежит ни к одной из П., то для точек одной П., определяемой этой прямой,
справедливо неравенство Ах+Ву+С > 0, для точек другой П.— Ах+Ву+С<0.
Для комплексной плоскости z—x+iy рассматриваются верхняя П. у—
= Imz >0 и нижняя П. y=lmz<0, левая П. x=Rez < 0 и правая П.
jt=Rez>0. Верхняя П. комплексной плоскости конформно отображается на
круг | w | < 1 с помощью дробно-линейной функции (см.):
ζ- β
где β — произвольное действительное число, a Im β > 0.
ПОЛ У ПОЛОСА — множество точек плоскости, координаты которых
удовлетворяют в прямоугольной декартовой системе координат трем неравенствам:
у < αχ+b, у > ах+с, у > — — x+d
(или у < — — x+d) , где с < Ъ
(открытая П.). Если знаки строгого неравенства заменить знаками >, <, то
получим замкнутую П.

ПОЛЯРА
327
ПОЛУПРОСТРАНСТВО — одна из частей евклидова пространства, на
которые разбивает его всякая плоскость Ax+By+Cz+D=0 (Л, В% С одновременно
не равны нулю). Сама полуплоскость может быть отнесена к одной из П.
Координаты точек одного П. удовлетворяют.неравенству:
Ax+By+Cz+D> О,
координаты точек другого П.—неравенству:
Ax+By+Cz+D < 0.
ПОЛУПРЯМАЯ — одна из частей евклидовой прямой, на которые
разбивается эта прямая любой ее точкой А. Точка А может быть отнесена к одной
из П. Если точка А отнесена к П., то П. называется замкнутой П. (или лучом),
а точка А — ее началом.
ПОЛЬКЕ ТЕОРЕМА. П. т. формулируется так: три отрезка произвольной
длины, лежащие в одной плоскости и исходящие из общей точки под
произвольными углами друг к другу, могут быть приняты за параллельную проекцию
пространственного ортогонального репера i, j, k( | i | «= | j| = | k | ).
Теорема была сформулирована немецким геометром К. Польке (1860) без
доказательства, а затем была обобщена немецким математиком Г. Шварцем,
который дал ее элементарное доказательство. Теорему Польке—Шварца можно
формулировать так: любой невырожденный четырехугольник с его диагоналями
можно рассматривать как параллельную проекцию тетраэдра, подобного любому
данному. П. т. имеет большое практическое значение (любой четырехугольник
с его диагоналями можно принять, например, за изображение правильного
тетраэдра) и является одной из основных теорем аксонометрии (см.).
Лит.: Е. А. Глазунов, Η. Φ. Четверухин, Аксонометрия, Гостехиздат, Μ.,
1953; Η. Μ. Беек и н, Основное предложение аксонометрии, сб. «Вопросы современной
начертательной геометрии», под ред. Н. Ф. Четверухина, Гостехиздат, М., 1947; Н. А.
Глаголев, Начертательная геометрия, Гостехиздат, М., 1953,
ПОЛЮС: 1°. П. координат — начало координат в полярной системе.
2°. П. шара— концы диаметра, перпендикулярного данному большому
кругу.
3°. П. прямой ρ относительно кривой 2-го порядка k — точка Р, для
которой прямая ρ является полярой (см.) точки Ρ относительно кривой k.
4°, П. функции — изолированная особая точка (см.) функции. В П.
функция / не определена, но выполняется условие:
lim/(z)=oo.
г·* г0
Следовательно, Ит (1:/(ζ)) = 0, τ. е. функция g(x)= ■;- при г~г0 обра-
щается в нуль. Если Нт[/(г)-(г — г0)*1 при некотором вещественном α коне-
чен и не равен нулю, то α называется порядком полюса.
Теория П. функций особенно развита для аналитических функций
комплексного переменного. Ряд Лорана в П. функции имеет конечное число
отрицательных степеней (г— г0). Существуют простые методы вычисления вычета (см.)
аналитической функции в ее полюсе. Например, w=—т*т-~""1 Г имеет два
г2 г г — 1
полюса: 2=0, порядок его равен 2 и 2=1 1-го порядка. См. Аналитические
функции, Лорана ряд.
ПОЛЯРА точки Ρ относительно кривой 2-го порядка k — геометрическое
место точек Q, гармонически сопряженных с Ρ относительно точек пересечения

328
ПОЛЯРНЫЙ ВЕКТОР
Οι
А'
I ■ ■(
/ / \К
J0k
Рт^,
Мх и М2 прямой PQ с кривой k (рис. 218). П. точки Ρ относительно кривой
2-го порядка k есть прямая линия р.
Точка Ρ относительно своей П. называется полюсом.
Если точка Ρ принадлежит кривой 2-го порядка /г, то П. точки Ρ совпадает
с касательной к кривой в этой точке. Если П. пересекает кривую в точках Q^
и Q2, то касательные к кривой в точках Qx и Q2 пересекаются в точке Ρ —
полюсе П. Полюс и П. удовлетворяют принципу взаимности, т. е. если поляра
точки Ρ проходит через точку Q, то поляра точки Q проходит через точку Р.
м П. точки Ρ относительно кривой 2-го
>[*1 порядка k можно определить и как
диагональ полного четырехвершинника.
Понятия П. и полюса играют
большую роль в конструктивных
задачах проективной геометрии.
Каждой П. относительно
невырожденной кривой соответствует
единственный полюс, и любому полюсу отвечает
определенная П. Таким образом, с
помощью невырожденной кривой 2-го
r r порядка между точками и прямыми
О проективной плоскости можно
установить взаимно однозначное соответст-
Рис. 218 вие> которое называется полярным (см.
Полярные преобразования) и является
частным случаем коррелятивного преобразования (см.).
Аналогично П. определяется понятие полярной плоскости точки Ρ (полюса)
относительно поверхности 2-го порядка. Связь между П. и полюсом отчасти
была известна древним, наиболее развита Дезаргом (1639) и особенно Понселе
и Жергоном. Эта связь послужила толчком к открытию принципа
двойственности (см.).
Лит.: Н. Ф. Четверухин, Проективная геометрия, Учпедгиз, М., 1953.
ПОЛЯРНЫЙ ВЕКТОР — термин, употребляемый по отношению к
обыкновенному (свободному) вектору, когда хотят подчеркнуть отличие этого вектора от
осевого вектора (см.).
ПОЛЯРНЫЕ КООРДИНАТЫ точки на плоскости — два числа, определяющие
положение этой точки относительно некоторой фиксированной точки О,
называемой полюсом, и некоторого фиксированного
луча Ох, называемого полярной осью (рис. 219).
Первая координата ρ точки Μ(ρ,φ)— полярный
радиус означает расстояние ее от полюса: ОМ — р;
вторая координата φ — полярный угол — есть
угол, на который надо повернуть ось Ох в
положительном или отрицательном направлении до
совпадения с лучом ОМ. Координату φ также
называют амплитудой или фазой точки М.
Обычно рассматривают для риф
промежутки изменения такие: 0<р < оо и 0<φ< 2π,
при этом устанавливается взаимно однозначное соответствие между точками
плоскости и П. к. (за исключением полюса, который определенного полярного угла
не имеет).
П. к. являются одним из видов криволинейных координат (см.), где одним из
семейств координатных линий являются лучи, исходящие из полюса, другим
семейством координатных линий являются концентрические окружности с центром
в полюсе.

ПОЛЯ ТЕОРИЯ
329
П. к. часто используются при изучении различных спиралей, кривых 2-го
порядка (полюс помещается в фокусе, полярная ось — ось симметрии кривой)
в математике, физике и астрономии.
ПОЛЯРНЫЙ УГОЛ —одна из полярных координат (см.) точки на
плоскости.
ПОЛЯ ТЕОРИЯ — отдел математики, изучающий гладкие скалярные,
векторные, тензорные поля, а также поля геометрических объектов (см. Поле
скалярное, Поле векторное, Тензорное исчисление). П. т. возникла и, в особенности,
развилась под влиянием новых идей физики, связанных, в частности, с теорией
относительности Эйнштейна. При рассмотрении скалярных полей удобно вводить
поверхности уровня (см. Уровня поверхности). Частные производные от функции
скалярного поля по пространственным переменным (если они существуют) задают
вектор-градиент скалярного поля:
(ди ди ди)
gradu=te· *· *j·
Этот вектор перпендикулярен к поверхностям уровня, направлен в сторону
наибольшего возрастания функции и и его длина равна производной от и в
направлении градиента.
С каждым векторным полем связаны векторные линии — линии, касающиеся
в каждой своей точке некоторого вектора поля. Например, силовые линии поля
электрической напряженности суть векторные линии. Векторные линии задаются
обычно системой дифференциальных уравнений вида:
dx dy dz
Ρ х Py Ρ ζ *
где p = {pr, pyt ρζ] —вектор поля.
Специальные виды векторных полей имеют названия:
1) плоскопараллельное — поле, в котором имеется направление такое, что
производные от всех координат вектора по этому направлению равны нулю;
задачи, связанные с таким полем, сводятся к плоским задачам (см.); векторные
линии такого поля — плоские кривые; 2) центральное поле, у которого все
векторы лежат на прямых, пересекающихся в одной точке; 3) цилиндрическое поле,
векторы которого лежат на прямых, ортогонально пересекающих некоторую
фиксированную прямую (см.), причем длина вектора поля зависит от расстояния
точки до оси.
Много сведений о строении векторного поля в данной точке дают
дивергенция (расхождение) и вихрь (ротация) поля. Интерпретируя векторное поле как
поле скоростей не зависящего от времени (стационарного) движения газа, можно
увидеть физический смысл дивергенции и вихря. Некоторый объем газа через
время Δ* в первом приближении повернется на некоторый угол φ и претерпит сжатие
(либо растяжение) по трем осям. Удвоенная угловая скорость вращения w есть
вихрь, а относительная скорость изменения величины объема ν — дивергенция.
В координатах они выражаются так:
(ду dz dz дх дх ду) %
дх ду dz
Используя формальный вектор (см. Набла оператор)
д_ ^Ц
ду ' dz\
=ί-.
(дх

330
ПОПАРНО ПРОСТЫЕ ЧИСЛА
эти формулы можно записать
rotp—Vxp (векторное произведение),
divps=(Vp) (скалярное произведение).
Потоком векторного поля через поверхность называется интеграл по поверхности
от скалярного произведения вектора поля и единичного вектора нормали к
поверхности. Формула Остроградского (см. Остроградского формула) очень просто
читается в терминах П. т.: поток векторного поля через поверхность равен
интегралу дивергенции вектора по объему, ограниченному этой поверхностью:
(j) pn° d$ = jdivpdv.
Σ Ό
Циркуляцией векторного поля по замкнутому контуру называется интеграл по
контуру скалярного произведения векторного поля на единичный касательный
вектор к контуру.
Формула Стокса (см. Стокса формула) в таких терминах выражается
следующим образом: циркуляция вектора по замкнутому контуру равна интегралу
вихря поля по любой поверхности, ограниченной данным контуром, т. е.
a dr«= f n° rot a ds.
По вихрю и дивергенции векторные поля подразделяются на потенциальные
(rotp=0), соленоидальные (divp=0) и лапласовы (divp==0). Последние связаны
с уравнением Лапласа (см. Лапласа уравнение)t именно — их потенциал (см.
Потенциальное поле) φ удовлетворяет уравнению:
да φ д2 φ д2 φ
дх* т dy2 T дг*
Лит.: А. Я. Хин чин, Краткий курс математического анализа, Гостехиздат, М.,
1955.
ПОПАРНО ПРОСТЫЕ ЧИСЛА— целые числа аъ ait ..., ak (k> 2) такие,
что каждая пара иь них а/ и a.j является взаимно простыми числами (см.). Если
числа alt a2i ..., α& сУть П. п. ч., то они являются и взаимно простыми все
вместе. Обратное неверно — числа alf α2, .♦., ад. могут быть взаимно простыми
числами, но не быть П. п. ч. Например, числа 6, 10 и 15 — взаимно простые
числа, но они не являются П. п. ч.
ПОПОЛНИТЕЛЬНЫЕ УГЛЫ—·два угла, сумма которых равна двум
прямым (Или 180°, или π радианов). П. у", таким образом, составляют в сумме
развернутый угол (см.). Термин П. у. малоупотребителен.
ПОРИЗМА — верное предложение, высказанное в такой общей форме,
которую можно всегда конкретизировать.
Примеры П. и соответствующих им теорем: 1. П.: произведение отрезков,
образуемых касательной к гиперболе на ее асимптотах (считая от начала
координат), есть величина постоянная. Теорема: произведение отрезков, образуемых
касательной к гиперболе на ее асимптотах, равно сумме квадратов полуосей
гиперболы.
2. П.: произведение двух отрезков — всей секущей (проведенной к окружности
из внешней точки) на ее внешнюю часть — есть величина постоянная. Теорема:
произведение двух отрезков — всей секущей (проведенной к окружности из
внешней точки) на ее внешнюю часть — равно квадрату касательной, проведенной
к окружности из той же точки.

ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ МЕТОД 331
П. встречаются у древних греков: у Евклида, Паппа, Прокла, а также
у европейских математиков, наиболее часто у французского геометра Шаля.
Греч, ποριζω — открываю путь, нахожу.
ПОРЯДОК — числовая характеристика многих математических объектов:
1°. П. алгебраической кривой /(#, у)=0 [где /(*, у) многочлен
относительно х> у]— степень многочлена f(x, у). Например, парабола у=ах2-f-bx-Ье-
кривая 2-го порядка.
2°. П. нуля (корня) х0 функции f(x) — такое число п, что существует
конечный предел lim [f(x): (χ — Χο)η], отличный от нуля.
х-*х0
3°. П. полюса функции f(x) — такое число, что существует отличный от
нуля предел lim (я — х0)п f(x).
х-+х0
4°. П. производной — число дифференцирований, произведенных над
функцией.
5°. П. дифференциального уравнения — наивысший П. входящих в него
производных (так, y'"-f-*2y'-bsin х^0— уравнение 3-го порядка).
6°. П. квадратной матрицы (и определителя) — число ее строк или столбцов.
7°. П. конечной группы — число ее элементов. П. элемента α — наименьшее
число п, для которого ап—Е (Е — единичный элемент группы).
8°. П. целой функции /(г)-—нижняя грань значений Л, для которых
отношение f(z)\eAZ ограничено.
9°. П. действий — последовательность, в которой производятся те или иные
действия.
10°. П. числа (величины). При оценках чисел (величин) говорят, что они
П. я, имея в виду, что они заключены между 5· 10л—α и 5· 10".
ПОРЯДОК БЕСКОНЕЧНО МАЛОЙ —см. Бесконечно малая.
ПОСЛЕДОВАТЕЛЬНОЕ ДИФФЕРЕНЦИРОВАНИЕ — вычисление производных
одна за другой. См. Производные высших порядков.
ПОСЛЕДОВАТЕЛЬНОСТЬ —функция, заданная на множестве натуральных
чисел; обозначается обычно:
аи аъ ..., ап или {α„}, п—\, 2, ...
ПОСЛЕДОВАТЕЛЬНОСТЬ РАСХОДЯЩАЯСЯ — последовательность чисел ап,
у которой нет конечного предела, т. е. либо ее предел бесконечность, либо не
существует вовсе (см. Предел последовательности). Функциональная
последовательность fn(x) называется расходящейся при данном значении х0, если
числовая последовательность fn(xo) расходится.
ПОСЛЕДОВАТЕЛЬНОСТЬ СХОДЯЩАЯСЯ — последовательность чисел аш
имеющая конечный предел lim ап=а (см. Предел последовательности). Последо-
п-*оо
вательность функций fn(x) называется сходящейся на отрезке а<х<6
(интервале, множестве), если при каждом фиксированном х0 из отрезка (интервала,
множества) получается сходящаяся числовая последовательность.
ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ МЕТОД —метод численного
решения математических задач. Состоит в способе находить по известному
приближению решение следующего, более точного приближения. Применяется только
в том случае, если последовательность указанных приближений сходится.
Например, для решения уравнения вида:
/(*>-о (s)
рассматривают равносильное ему уравнение:
x=F(x), где F(*)«/(*)+* (**)

332
ПОСТОРОННИЙ КОРЕНЬ
и составляют последовательность: х0 — произвольное, xx = F (jc0), x« = F (л^),
..., xn=F (*η—ι)» ··· Если последовательность \хп] имеет предел, то этот
предел есть корень уравнения <**), а следовательно, и (*). Процесс составления
последовательных приближений наглядно показан на , графике (рис. 220), где
кривая — график функции F (х)% прямая — биссектриса координатного угла.
Последовательность таких приближений обязательно сходится, если,
например, F (jc) > χ и 0 < F' (х) < 1—ε. Π. п. м. применяется также для
численного решения систем линейных
уравнений с большим количеством переменных. Этим
методом находят приближенные решения
дифференциальных и интегро-дифференциальных
уравнений. П. п. м. применяется также в вопросах
теории. При его помощи доказывается теорема
существования и единственности
дифференциального уравнения у'=/(*, у).
Возможность применимости П. п. м.
устанавливается принципом сжатых отображений
(см. Отображения).
ПОСТОРОННИЙ КОРЕНЬ уравнения /(*) =
=0 — корень уравнения f1(x) = 0,
неравносильного данному, но полученного при решении
данного уравнения. П. к. обычно появляются
при решении иррациональных, логарифмических,
тригонометрических и других уравнений.
Примеры: 1. При решении уравнения ух—1=*—7 возведением обеих
частей уравнения в квадрат получим #χ=5, х2= 10. Если корень V χ—1
рассматривать как арифметический (см.)(а такие корни только обычно и
рассматривают при решении иррациональных уравнений), то корень х=Ъ— П. к. для
данного уравнения.
2. Уравнение lgx-j-lg(jt— 3) = lg4 имеет только один корень *=4, в то
время как, потенцируя данное уравнение, получим уравнение χ (χ — 3) = 4, корни
которого хг=—1, jc2=4; при этом корень х=—1 есть П. к. для исходного
(первоначального) уравнения'.
3. Решая уравнение sin х+cos x=l возведением обеих частей уравнения
в квадрат, получим после упрощений уравнение sin 2x = 0, откуда 2х=лп или
однако при л=—I или при л=3, т. е. при
Рис. 220
2
/2=4λχ
л, /2=0, ±l, ±2,
Ι (^=0, ±l, ±2, ...), корни χ=
*— η будут посторонними для
данного уравнения. Поэтому из множества решений *=— η уравнения sin 2 χ=0
π
мы должны исключить корни jc= — (An—I), являющиеся корнями уравнения
sin χ ■
π
cosx= — I. Корнями данного уравнения будут хл=2лп и х2
=—+2 я л. Это ясно и геометрически, так как sinx-f-cos* может равняться
единице только при этих значениях, а в других случаях больше единицы (сумма
катетов треугольника больше гипотенузы) или меньше единицы. Другими
словами, для хф— η имеем ] sin χ { + | cos x J > Ι.

ПОТЕНЦИАЛА ТЕОРИЯ
333
Во избежание появления П. к. данное уравнение следует решить по схеме:
χ
sin χ = ι — cos л:, sinx = 2sin2—- и т. д., или sin jc-bsin(90° — х)= 1, а дальше
левую часть разложить на произведение множителей (по формуле суммы
синусов).
П. к. уравнения иногда называют лишними, непригодными или
паразитическими (так реже) корнями. См. также Потерянные корни.
ПОСТОЯННАЯ ВЕЛИЧИНА (константа) — величина, которая в данном
процессе сохраняет свое значение. П. в. χ часто обозначается *=const. Например,
при сжимании идеального газа, по закону Бойля — Мариотта, произведение
объема газа на давление остается П. в. См. Переменная величина, Параметр.
ПОСТРОЕНИЯ ГЕОМЕТРИЧЕСКИЕ — решение геометрических задач на
построение с помощью различных инструментов (линейки односторонней или
двусторонней, циркуля, угольника и др.)· П. г. называются также конструктивными
задачами или конструктивной геометрией. См. Геометрические построения.
ПОСТУЛАТ — то же самое, что и аксиома (см.). В «Началах» Евклида
аксиомы и П. различаются, однако логического различия Евклид не указывает,
и поэтому неясно, по какому признаку он относил одни предложения к П.,
а другие - к аксиомам.
Лит. postulatum — требование, от postulo — требую.
ПОТЕНОТА ЗАДАЧА—см. Задача Потенота.
ПОТЕНЦИАЛА ТЕОРИЯ — раздел математической физики, изучающий
потенциалы силовых полей. Таким образом, П. т. изучает потенциальные силовые
поля, т. е. такие силовые поля, в которых работа сил поля по любому
замкнутому пути равна нулю. Примерами таких полей могут служить поля тяготения,
электростатические поля. Именно в таких полях можно ввести понятие
потенциала V(P)=V(a;, у, ζ), где Р(х, у, ζ)— произвольная точка пространства
с координатами х, у* ζ. Потенциал V (Р) показывает работу, необходимую для
перемещения пробного тела из некоторой фиксированной точки (чаще всего
бесконечно удаленной) в точку Р. Само поле а(Р) оказывается связанным с
потенциалом V (Р) формулой a(P)=grad V(P). Для поля тяготения, образованного
точкой A (a, bt с) массы ту потенциал
V(P)~V(x, у. z)=X Y
Г V(x - α)2 + (У — bf+(z - cf
Где γ — постоянная тяготения при условии, что точка Ρ имеет единичную массу.
Потенциал поля тяготения, образованного конечной системой материальных точек
Λ/(α«» bit Ci) массы ть
V(P)=V(x, y, z) = y2" Щ
l Y^-aiY+iy-btf+iz-Cif
ибо при наложении двух силовых полей их потенциалы складываются. Потенциал
поля тяготения, образованного непрерывно распределенной по некоторому
объему Τ с плотностью ρ (α, 6, с) массой, выражается интегралом:
V(P) = V(xt у, ζ) = γ fff, P(Q' ' С) da.db-dc=
(Т)
(Г)

334
ПОТЕНЦИАЛЬНОЕ ВЕКТОРНОЕ ПОЛЕ
Этот потенциал (ньютонов потенциал) непрерывен вместе со своими частными
производными 1-го порядка на всем пространстве, кроме точек (Т). При удалении
точки Р(х, у, г) в бесконечность потенциал У(х, у, ζ) стремится к нулю и
эквивалентен бесконечно малой величине γ-m: у х2+у2+г2, где m — масса всего
объема:
/я=Г^р(а, Ь, c)da-db-dc.
(Τ)
Вне области Τ потенциал V (х, у, ζ) удовлетворяет уравнению Лапласа:
d2v d2v d2v
П. т. продолжает развиваться, в частности решаются обратные задачи П. т.,
по определению притягивающихся масс по значениям их ньютонова потенциала.
П. т. возникла в XIX в. в связи с изучением гравитационного и
электростатического полей. Большую роль в развитии П. т. сыграли работы русского
математика А. М. Ляпунова.
Лит.: Η. Μ. Гюнтер, Теория потенциала и ее применение к основным задачам
математической физики, Гостехиздат, М., 1953; Л. Н. Сретенский, Теория
ньютоновского потенциала, Гостехиздат, М.—Л., 1946.
ПОТЕНЦИАЛЬНОЕ ВЕКТОРНОЕ ПОЛЕ — векторное поле:
F=P(*, yt z)i+Q(x, у, z)j-ftf(*, у, г) к,
для которого существует потенциал, т. е. существует скалярное поле U (х, у, ζ),
градиент которого есть вектор F:
Μ г,
-τ-βΛ
дх
Μ Λ
—=Q,
ду
W «
—=#.
дг
Непрерывно дифференцируемое поле F, заданное в пространственно-односвязной
области V (см.) (т. е. частные производные от функций Р, Q, R непрерывны
в этой области), является П. в. п. тогда и только тогда, когда выполнено одно
из четырех равносильных условий: 1) Pdx+Qdy+Rdz есть полный дифференциал
некоторой функции U(х, у, г); 2) вихрь (см.) векторного поля F равен нулю
в области v\ 3) циркуляция вектора F по любому замкнутому контуру,
лежащему в области V, равна нулю; 4) линейный интеграл \ Pdx+Qdy+Rdz (или
работа вектора F) не зависит от путей, соединяющих данные точки Мх (х1% ylt zx)
и М2(хъ, Уч> z2), лежа1Дие в области у, а зависит лишь от точек Мх и М2 [он
равен разности значений потенциала U (#2. Уг» *ι) — U (*1> У\* Z\) в этих точках].
— k
Пример. Поле F= г силы тяготения, вызываемое материальной точкой,
помещенной в начале координат, является П. в. п. во всем пространстве (х, у* ζ)
с исключенной точкой 0(0, 0, 0). Здесь k — постоянная, r=x i -f-vj-fz k —
радиус-вектор произвольной точки, | г |=V *2-fy2-fz2 —ее расстояние до начала
координат. Потенциалом поля служит:

ПОЧТИ-ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ
335
ПОТЕРЯННЫЕ КОРНИ уравнения f(x)=Q — корни этого уравнения,
которые в результате решения уравнения и сведения его к неравносильному
уравнению /i(jc)=0 не являются корнями последнего. Потеря корней уравнения может
быть, если мы логарифмируем обе части уравнения, или извлекаем из обеих
частей корень четной степени, или делим обе части уравнения на выражение,
содержащее неизвестное, или в других случаях.
Примеры: 1. Уравнение х2—4=χ — 2 имеет корни хх^—1# λγ2—2, но если
мы разделим обе части на χ — 2, то получим уравнение *4-2=1, не
равносильное данному, имеющее только один корень *=— 1. Корень #=2 для данного
уравнения есть П. к. Чтобы не потерять корни, надо данное уравнение
представить в виде: (х — 2) (*+1) = 0[или *2—χ — 2=0], а затем его решить.
2. Логарифмируя уравнение х(х — 3) —4, имеющее корни хх**—1, x^—^t
мы придем к уравнению, не равносильному данному: \gx-\-\g(x— 3)=lg4,
имеющему только один корень х~4, следовательно, логарифмируя данное
уравнение, мы сузили область определения входящих в него функций и потеряли
корень *—— 1. См. также Посторонние корни.
Лит.: С. И. Новоселов, Специальный курс элементарной алгебры, «Высшая
школа», М., 1958; С. И. Новоселов, Специальный курс тригонометрии, Гостехиздат,
М.—Л., 1958.
ПОТЕНЦИРОВАНИЕ —действие, обратное логарифмированию. П. есть
нахождение числа по данному его логарифму (см.). Понятие П. используется при
решении логарифмических уравнений.
Нем. potenzieren от Potenz — степень.
ПОТОК векторного поля — понятие теории поля (см.). Если
п0—единичный вектор нормали к поверхности 5 (изменение его по поверхности S
предполагается непрерывным), а — {ах, αν, α2}, то П. в. п. а через поверхность S с
точностью до знака выражается поверхностным интегралом:
a n0 ds = J J" (axdydz+aydzdx -f· a2dxdy).
S
Для поля скоростей частиц жидкости П. в. п. равен количеству жидкости,
протекающей за единицу времени через поверхность.
ПОЧТИ-ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ — функция, значения которой
приближенно повторяются при добавлении к аргументам надлежащим образом
выбранных постоянных чисел. Точнее, каково бы ни было ε>0, можно указать
L(e)>0 такое, что в каждом интервале длины L найдется по крайней мере
одно τ, удовлетворяющее условию:
|/(x+t)-/(x)|<e.
Простейший пример П.-п. ф.— сумма конечного числа периодических функций
с несоизмеримыми периодами:
cos x-f-cos V 2 χ, 2 ake~~l X** »
где λ& — вещественные числа. Это понятие обобщается также на многообразие
(см.) с группой, т. е. на случай, когда функция f(x) определена на некотором
многообразии?}?, χ ζ Ш, a G есть группа преобразований этого многообразия в
себя, так что х-а£Ш, где αζΰ. Первое построение П.-п. ф. дал Бор (1923).
Частный случай П.-п. ф.—квазипериодические функции — построил латвийский
математик П. Боль. Новыми построениями и обобщениями понятия П.-п. ф.
занимались Н. Н. Боголюбов (1930), В. В. Степанов (1925), С. Бохнер,
Г. Вейль, Б. М. Левитан и др.
Лит.: Г. Бор, Почти-периодические функции, перев. с нем., М.—Л., 19С4; Б. М.
Левитан, Почти-периодические функции, Гостехиздат, М., 1963.
ff

336
ПОЯС ШАРОВОЙ
ПОЯС ШАРОВОЙ —см. Шаровой пояс.
ПРАВАЯ КАСАТЕЛЬНАЯ — см. Односторонняя касательная.
ПРАВАЯ ПРОИЗВОДНАЯ —см. Односторонняя производная.
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ — правила для вычисления производных
или дифференциалов, вместе с формулами дифференцирования дают
возможность вычислять производные и дифференциалы от сколько угодно сложных
элементарных функций (см.).
П. д., выраженные в производных (или частных производных), если С —
постоянная, uyv,w — функции, имеющие производные: \)(Си)'=Си'\ 2)(ιι·\-υ-\- · · · -Ь
-f-до)' =i/'-f ν' -\- · · · +W'\ 3) (UV . . . W)' =U'V · · · W+UV' . . . W-\- · · · +UV . . . W' \
• uv'
5) Если y=f(u)y u=y(x), т. e. y=f[4>(x)] (где / и φ —
4) (τ) -—
дифференцируемые функции), то yx=fu(u) φ^ (x)9 или короче: Ух—Уиих-
П. д., выраженные в дифференциалах, записываются аналогичными
формулами. Если z=f(ux, и2, . . ., ип)у ui=q>i(x, у, . . ., t)t т. е. z=f[y1(x, . . .,
..., О» · · ·» Ф/и (■*» · · ·» 01» то полный дифференциал ζ выражается формулой:
dz=-— dux-\-
дип
■Σ
dui
ПРАВИЛЬНАЯ ДРОБЬ — дробь (см.), у которой числитель меньше знамена-
112 6
теля, например: -—, -—, —, — и т. д. Число, обратное П. д., есть неправиль-
2, и и 11
ная дробь.
ПРАВИЛЬНАЯ ЧАСТЬ множества А — то же, что и собственное
подмножество (см.) множества А.
ПРАВИЛЬНЫЙ МНОГОГРАННИК — выпуклый многогранник, у которого все
грани — равные правильные многоугольники и все многогранные углы равны.
Число ребер, выходящих из вершины П. м., одно и то же для каждой его
вершины.
Евклид доказал, что существует только пять типов П. м.: правильный
тетраэдр (см. Тетраэдр) (рис. 221), правильный гексаэдр, или куб (см. Гексаэдр)
Рис. 221
Рис. 222
Рис. 223
(рис. 222), правильный октаэдр (см. Октаэдр) (рис. 223), правильный додекаэдр
(см. Додекаэдр) (рис. 224), правильный икосаэдр (см. Икосаэдр) (рис. 225).
Каждый из П. м. можно получить путем сечения куба плоскостями. Все П. м.,
за исключением правильного тетраэдра, имеют центр симметрии. Вокруг
всякого П. м. можно описать сферу и во всякий П. м. можно вписать сферу.
Правильный тетраэдр двойствен (дуален) сам себе (см. Двойственности принцип),

ПРЕДЕЛОВ ТЕОРИЯ
337
куб двойствен правильному октаэдру, правильный додекаэдр двойствен
правильному икосаэдру. У двойственных П. м. число вершин одного из них равно числу
граней другого и наоборот, а число ребер у двойственных многогранников одно
и то же. Центры граней П. м. являются вершинами двойственного ему П. м.
Для П. м., как для многогранников нулевого рода (простых), справедлива
формула (теорема) Декарта —Эйлера (см.): В-\-Г — Р=2, где В — число вершин,
Г— число граней, Ρ — число ребер многогранника.
Рис. 224 Рис. 225
ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК —плоский выпуклый многоугольник,
у которого равны все стороны и все углы при вершинах. Другими словами,
П. м.— равносторонний и равноугольный выпуклый многоугольник. В отличие
от существования конечного числа правильных многогранников г (см.) существует
бесконечное множество П. м., однако не всякий из них можно построить с
помощью циркуля и линейки. Например, правильные трех-, четырех-, пяти-, шести-,
десяти-, пятнадцатиугольники построить можно, а правильные семи-, девяти-,
одиннадцатиугольники построить нельзя циркулем и линейкой.
Гаусс доказал, что с помощью циркуля и линейки можно построить
правильный /2-угольник в том и только в том случае, если число η имеет вид:
п=2& Ριρ2· · -Рту гДе Pi—различные простые числа вида pi=22k-\- 1 (числа
Ферма).
Построение П. м. связано с делением окружности (круга) на η равных частей
или с решением уравнения ζη—1=0, которое поэтому называется уравнением
деления окружности (круга).
Вокруг всякого П. м. можно описать и во всякий П. м. можно вписать
единственную окружность. Всякий П. м. имеет центр симметрии. П. м. с четным
числом сторон 2п имеет (2я-Н) осей симметрии, из которых 2п осей лежат
в плоскости П. м. и одна ось проходит через центр П. м. перпендикулярно его
плоскости. П. м. с нечетным числом сторон (2я+1) имеет (2я-{-1) осей
симметрии, лежащих в плоскости П. м.
Иногда также рассматривают невыпуклые П. м. (звездчатые). Примером
таких звездчатых П. м. может служить правильная пятиугольная звезда, у
которой все стороны равны и все углы при вершинах равны.
ПРЕДЕЛОВ ТЕОРИЯ — теория, которая является основанием современного
математического анализа. Она изучает свойства пределов и устанавливает
условия их существования (см. Предел) и правила, по которым можно, зная пределы
нескольких простых переменных величин, найти предел простейших функций
этих величин.
Основой П. т. является понятие бесконечно малой величины (см. Бесконечно
малые), т. е. величины, имеющей своим пределом нуль. Чтобы переменная
величина хп имела своим пределом постоянное число а, необходимо и достаточно,
чтобы разность ап=хп — а была бесконечно малой. Если переменная величина хп
стремится к пределу а и а>р (a<q), то и все ее значения, начиная с некото-
22 Толковый словарь математических терминов

338
ПРЕДЕЛОВ ТЕОРИЯ
рого, тоже будут> ρ (<</). Переменная величина хп не может одновременно
стремиться к двум различным пределам.
П. т. устанавливает целый ряд теорем, облегчающих нахождение пределов.
Если для хп и уп при всех η справедливо хп>Уп и хп и уп имеют конечные
пределы lim*rt=a, \imyn=bt то α>6. Если хп<Уп^2п и существуют пределы
П-Р-ОО П-*00
\\mxn=\\mzn=a, то уп имеет тот же предел, т. е. Нтул=а.
Над переменными хп можно совершать арифметические операции. Если
существуют конечные пределы lim an=а и \imbn=b (причем Ь^О), то существуют
п+оо п->оо
также конечные пределы tim(an±bn)=a±b, limanbn=ab, lim —=— (ЬфО).
rt-*0O /2-*·0Ο П**СО Ьп Ь
Если же bn-+ оо или bn-*0, то соответственно отношение ~->0(ап->а^0) и -^ -> оо.
Если обе последовательности одновременно стремятся к 0 или оо, то в этих случаях
ап
говорят, что lim — представляет собой неопределенность соответственно вида
гс-*оо Ьп
0 оо
— или —. Для раскрытия таких неопределенностей, т. е. для отыскания пре-
0 оо
дела —, существуют различные способы. Наиболее общим и удобным из них
является правило Лопиталя (см. Лопиталя правило).
Если Нтал—О, а \\тЬп~ооч то говорят, что \\тапЬп представляет собой
п-юо п-*оо пчюо
неопределенность вида 0·οο. Если Нтал=оо, Нт6„=оо, то предел их разности
я-*>оо п+оо
Мт(ап—Ьп) называют неопределенностью вида (оо — оо) (см.
Неопределенности).
П. т. устанавливает критерии существования пределов (признаки
сходимости). Если ап монотонно не убывает (ап<ап+1) и ограничена сверху (ап<М), то
существует \iman (если ап не ограничено сверху, то ап-+оо при л->оо). Ана-
п-*со
логичное утверждение справедливо и для монотонно невозрастающей
последовательности. В общем случае, для того чтобы последовательность хп имела
конечный предел, необходимо и достаточно, чтобы для каждого числа 8>0
существовал такой номер /V, чтобы неравенство \хп— *л, |<ε выполнялось, как только
п> N и п' > /V (теорема Коши — Больцано); иными словами, значения переменной хп
должны безгранично сближаться между собой по мере возрастания их номеров.
В П. т. рассматривается также последовательность xn%t xnt, . . ., xtlh , . . .,
извлеченная из данной хП1 где пь— некоторая последовательность возрастающих
натуральных чисел: n1<n2<ns< ... <nk<nk+i<. . . Роль номера,
принимающего последовательно все натуральные значения, играет уже не п, a k\ п^—
варианта, принимающая натуральные значения; очевидно, nk-*oo при &->оо. Эта
последовательность χηχ , хП2 , . . .# хПк>> - - называется частной
подпоследовательностью. Если последовательность имеет предел, то тот же предел имеет и
частная подпоследовательность. Из любой ограниченной последовательности всегда
можно извлечь такую частную подпоследовательность, которая имеет конечный предел
(лемма Больцано — Вейерштрасса). Этот предел называют частным пределом
исходной последовательности. Существует всегда наибольший частный предел
(Шп хп = lim sup хп) и наименьший частный предел (Игл хпξ lim inf xn). Если

ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
339
lim xn=tim xni то хп имеет предел (в обычном смысле). Их общее значение
и является тогда этим пределом.
Все основные понятия, изложенные для случая переменной величины хп
(числовой последовательности), переносятся и на случай функций. Для того чтобы
f(x)-+b при х^-а, необходимо и достаточно, чтобы для всякой последовательно-
сти чисел Х\, х2, .... *rt, . . ., имеющей пределом число а, последовательность
соответствующих значений функции f (х), т. е. последовательность чисел /(яД
/(#2), · · ·» f (*п)> · · -* имела своим пределом число Ъ.
Еще древнегреческие ученые, вычисляя площади различных фигур, применяли
операцию предельного перехода, хотя термина «предел» у них не было. Общая
П. т. начинает создаваться в XVII в. Обозначение lim ввел И. Ньютон (1686),
развивавший П. т. для метода флюксий. Понятие предела монотонной
последовательности сформулировано французским математиком Ж. Даламбером (1765) и
русским математиком Гурьевым (1798). Современная теория пределов базируется
на внутреннем критерии сходимости Больцано — Коши (1817). Вполне современное
определение предела «на языке ε, δ» было дано немецким математиком К. Вей-
ерштрассом (1880). См. Предел, Дедекиндово сечение.
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
т. I, Физматгиз , М., 1963.
ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ: 1°. П. п. функций /J*), f2(x), . . .,
fn(x), . . ., заданных на отрезке а<х<& (интервале, множестве), есть функция
/(*) = lim/n(A;), значение которой /(л:0) для произвольного х0 есть предел
числовой последовательности {fn(Xo)}* этот предел должен существовать и быть
конечным для всех х0 из отрезка
(интервала, множества). G
2°. П. п. чисел. Число С назы- О С С С, С ι^~ι
вается П. п. чисел С1% С2, . . ., ' 2
Сп, . . м если для всякого 8>0
существует такой номер N> что при
n>N выполняется неравенство.
\Сп— С|<е. Номер N зависит от
ε, т. е. Ν—Ν (г). Изображая члены
Сп последовательности точками на (q q mtQ J
числовой оси (в случае последова- * * s n
тельности действительных чисел) Рис. 226
или на комплексной плоскости (в
случае последовательности комплексных чисел), можно определение П. п. чисел
сформулировать так: точка С является П. п. чисел Clf С2, . . ., Сп,
если в любой 8-окрестности точки С лежат почти все (т. е. все, кроме конечного
числа) члены последовательности (рисунки 226, а и 226, б).
Члены последовательности с различными номерами могут быть одинаковы и
изображаться, следовательно, одной геометрической точкой. Поэтому в
определении речь идет о числе членов последовательности, а не точек, их
изображающих. Точка может и не быть предельной для множества точек, изображающих
члены последовательности (это будет тогда и только тогда, когда все члены Сп
совпадают между собой, начиная с некоторого номера п0). Например,
последовательность С, = 1, С2 = 10, Cg-π, С4-1, ..., Сп=У~2 (п>Б) имеет предел
V 2, а множество изображающих точек конечно (состоит из точек 10 η
V*.
1) и не имеет предельной точки. Для П. п. чисел принят символ ИтСп
(иногда \\тСп). П. п. чисел могут служить также символы -+-«>„ — £Г°°оо
Последовательность действительных чисел Clt С2, . . ., Сп, ... имеет пределом
22*

340
ПРЕДЕЛ ФУНКЦИИ
4-оо, НтСд=4-0° (—°°> соответственно оо), если для всякого А существует
п-+оо
такой номер N, что при n>N выполняется неравенство Сп>А(Сп<А,
соответственно \Сп\>А). Если окрестностью -f-oo считать любой интервал числовой оси
вида (Л, 4·°°)» окрестностью— оо считать любой интервал вида (—оо, В), а
окрестностью оо — совокупность двух любых интервалов (— со, В), (Л, +оо), то
определения бесконечных П. п. чисел формулируются теми же словами, что и
в случае конечного П. п. чисел (только слова «точка С» надо заменить
соответствующими символами +оо, —оо или со). Последовательность, имеющая
конечный предел, называется сходящейся (к этому пределу).
Для последовательности комплексных чисел понятие П. п. чисел сводится
к П. п. чисел в действительной области, так как имеет место следующее
утверждение: число A+Bi является П. п. чисел Cn=an+bn i (п= 1, 2, . . .) тогда и только
тогда, когда число А есть П. п. чисел ап и число В есть П. п. чисел Ьп.
Считают HmCn=oo, если lirn | Сп\ = + оо.
Примеры: 1) последовательность а, у а , У а , \f а , . . ., у а , . . ., где
п/— 1 1 1
а>0, имеет lim у а =1; 2) последовательность 1, —-, 1, -—, 1, —, . . ., 1,
п+оо 2 3 4
—, 1. :, . . ., т. е. С2&—1=—"» С*2£=1 (&=1, 2, . . .), не имеет предела;
две подпоследовательности (см.), составленные одна из нечетных и другая из
четных членов, имеют пределы:
limCo^—!=0, HmC2fe=l;
2k— 1 -*οο 2&·>οο
3) последовательность Сп=- : сходится к пределу 11тС,г=—-; 4) последова-
2п — ι n-+Qo 2
1 / \\п -
тельность Cn=n2-\-i— имеет бесконечный предел HrnCn=oo; 5) lim [1-f-— =е
П Л—оо V tl I
(е — основание натуральных логарифмов).
ПРЕДЕЛ ФУНКЦИИ: 1°. П. ф. от одной переменной y=f(x) при х-+а
(или в точке х=а). Число Ъ называется П. ф. y=f(x) при х->а, если для
всякого е>0 существует такое 6>0, что при хфа и \х — а\<Ь выполняется
неравенство \f(x) — Ь\<г (определение П. ф. по Коши). Это определение
равносильно следующему: число Ь называется П. ф. y=f(x) при х-+а, если для
любой последовательности хп, сходящейся к а, причем хпфа, л=1, 2, . . .,
последовательность yn~f(Xn) сходится к Ь (определение П. ф. по Гейне, в котором
понятие П. ф. выражается через понятие предела последовательности чисел).
В приведенных определениях П. ф. предполагается, что функция y=f(x)
определена в некоторой окрестности точки х0, кроме, быть может, самой точки х0.
П. ф. обозначается символом lim f(x) = 6.
х-*х0
Геометрическая иллюстрация П. ф.: число Ь есть \\т?(х), если для всякого
Х-*Хо
β>0 можно указать такой прямоугольник с основанием 26>0, высотой 2ε и
центром в точке C(x0i b), что все точки графика функции y=f(x) на интервале
х0—6<х<х0+Ь1 за исключением, быть может, точки М0[х0, /(*0)], лежат
в этом прямоугольнике (рис. 227). Сформулированное выше понятие
конечного П. ф. распространяется на случай бесконечных пределов. Функция y=f(x)
имеет пределом -f-oo при х-+а% lim/(χ)=-f-oo (—оо, соответственно со), если
х-*а
для всякого Л существует такое δ>0, что при xjba и \х — а\<Ь выполняется

ПРЕДЕЛ ФУНКЦИИ СПРАВА
341
ь
b-ε
о
ftojtto)) φ
неравенство f(x)>A (f(x)<A, соответственно |/(л;)|>Л). Понятие П. ф.
y=f(x) при х-*а распространяется также на случай,, когда а является не
числом, а одним из символов -f-oo, — оо, оо. Если воспользоваться понятием
окрестности точки (см.) и понятием окрестности 4-оо, —оо или оо (см. Предел
последовательности чисел), то все случаи
П. ф. f (х) охватываются следующим
определением: число Ь называется пределом
функции f (х) при х-+а, если для
произвольной окрестности V (Ь) (числа или символа) b
существует такая окрестность U (а) (числа
или символа а), что для всех х,
принадлежащих U (а), кроме, быть может, самого а,
значения f(x) принадлежат V (Ь).
Предполагается, что / (х) определена в некоторой
окрестности а. Здесь а и b могут быт^ь
числами или символами 4-оо, —оо, оо.
В это определение укладывается также
случай П. ф. нескольких переменных (см.),
когда хна являются точками /2-мерного
W^
пространства.
Примеры:
4) lim(l+jc)T =
lim У χ =— оо.
1)
Итх = а\
х-+а
2)
.. sin*
lim = 1;
*-*о χ
3)
lim sin -
λγ-*0
χ0-δ
Рис.
1
λ0 Χ,
227
не существует;
3/—
(£ —основание натуральных логарифмов); 5) limy x=-f-c
2°. П. φ. от многих переменных. Число Ъ называется пределом функции
tf=/l*i. χ2<- · ·> Xn) = f(P) при.Р-Р0, т. е. при х^х0^ ха-
(функция определена в окрестности точки Ρ0=(χ°{
ко>
х^), кроме, быть
может, самой точки Р0), если для любого ε>0 существует такое δ>0, что при
|*ι—*?|<о» j а:2—лг§ j <са, ..., |хя—*£|<δ и Р^=Р0 выполняется
неравенство |/(*ι, Хъ ···> хп) — Ь\<г.
Равносильным будет требование, чтобы для любого ε < 0 существовало такое
δ<0, что при р(Р, Ρ0)<δ, где ρ — расстояние (см.) между точками Ρ и Р0
в л-мерном пространстве, т. е. для точек, лежащих в δ-окрестности точки Р0,
выполнялось неравенство I / (Р) — b \ < г.
Понятие П. ф. от многих переменных обобщается на случай бесконечных
пределов. Функция U=f(P) имеет пределом -Ь°° при Р-+Р0 (пишут:
lim/(P) = -{-oo), если для любого М>0 существует δ>0, что приО<р (Ρ, Ρ0)<δ
Ρ "*■* о
выполняется неравенство f(P)>M. Аналогично определяются П. ф. от многих
переменных для случаев — оо и оо.
Примеры: 1) lim *.sin — =0; 2) lim
*-*о χ
f(x,X2) =
λγ-*0 Х4+У*
2
не существует, ибо при y=*2
-—, а при у=2х2 имеем /(*, 2*2)=—-
2 5
ПРЕДЕЛ ФУНКЦИИ СПРАВА (соответственно слева). Число Ъ
называется П. ф. с. (соответственно слева) в точке а, если для любого ε >0 существует
δ>0 такое, что при α<χ<α-\-δ (соответственно а—-6<х<а) выполняется нера-

342
ПРЕДЕЛЬНАЯ СФЕРА
венство |/(л:) — 6J<ε; этот П. ф. с. обозначается lim/(x) = 6 или /(а+0)
[соответственно hm f{x) = b или /(α — 0)]. В отличие от предела функции (см.)
в точке а, аргумент χ изменяется не в полной окрестности точки а, а лишь
в правой (соответственно левой) полуокрестности. Понятие П. ф. с.
определяется и для случая бесконечных П. ф. с. аналогично понятию бесконечных
пределов функции. ν
Условие f(a — 0)=/(a-fO) является необходимым и достаточным для
существования предела функции Нт/(*)» который иногда называют двусторонним
пределом функции в отличие от односторонних пределов f(a — 0) и /(α-f-O)
Если а=0, то пишут: *-*+0 [х->— 0, /(4-0), /(—0)].
Примеры:
1) /(*) = —, Hm — =+<х>, Hm —= —оо;
X К-++0Х х-*—0Х
2) /(*) = г-, lim /(*)-0. Hm /W-1;
L χ·*+ο х-»—о
\ + ех
__ 1_
3) f(x)=2 \ lim /(x) = 0, lim /(*)=+«>.
ПРЕДЕЛЬНАЯ СФЕРА — то же, что и орисфера (см.) в геометрии Лоба*-
чевского.
ПРЕДЕЛЬНАЯ ТОЧКА: Р. П. т. множества — такая точка Af, что в любой
ее окрестности (см.) содержится по крайней мере одна точка данного
множества, отличная от Λί. Отсюда следует, что в любой окрестности П. т.
содержится бесконечное число точек данного множества. П. т. множества может как
принадлежать, так и не принадлежать самому множеству.
Примеры: 1) множество натуральных чисел η не имеет П. т.; 2) множество
чисел вида у η — —, где η и т пробегают независимо друг от друга все нату-
т
ральные числа: я=1, 2, . . .; т=1, 2, . . ., имеет бесконечно много П. т., а
именно 1, у 2, КЗ, . . .; 3) П. т. множества внутренних точек круга на
плоскости являются все внутренние точки круга и все точки окружности,
ограничивающей круг; 4) для множества точек М(х, у, 2) пространства, у которых все
координаты х% у, ζ — всевозможные рациональные числа, П. т. является любая
точка пространства; 5) в метрическом пространстве непрерывных на отрезке
Функций (см.), в котором расстояние ρ (/(*). £(*) 1=шах J f(x) —-g(x) |, для
множества, состоящего из всевозможных многочленов, любая точка пространства
(т. е. любая непрерывная на [а, Ь] функция) является П. т. Это утверждение
равносильно теореме Вейерштрасса о равномерном приближении непрерывной
функции многочленами.
2°. П. т. последовательности — частичный предел последовательности (см.).
ПРЕДЕЛЬНАЯ ФУНКЦИЯ —предел последовательности функций (см.).
ПРЕДЕЛЬНОЕ ЗНАЧЕНИЕ функции — предел функции (см.).
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ теории вероятностей — общее название теорем,
описывающих те или иные свойства случайной величины, зависящей от большого
числа случайных факторов. Так, например, Я. Бернулли впервые дал строгое
доказательство закона больших чисел (см.), А. Я. Хинчин уточнил закон
больших чисел —закон повторного логарифма (см.), П. Л. Чебышев получил силь-

ПРЕДСТАВЛЕНИЕ ГРУППЫ
343
ные результаты в этой области (см. Чебышева неравенство). Необходимые и
достаточные условия применимости закона больших чисел установил советский
академик А. Н. Колмогоров (1928).
Важное место в теории вероятностей занимает центральная П. т.,
доказанная А. М. Ляпуновым (1901).
Лит.: Б. В. Гн еден к о, Курс теории вероятностей, Физматгиз, 1963; Б. В. Г н е-
денко и А. Н. Колмогоров, Предельные распределения для суммы случайных
величин, Гостехиздат. М., 1949.
ПРЕДЕЛЬНЫЙ ЦИКЛ системы дифференциальных уравнений:
dx n \
7ГР(Х, у)\
— это замкнутая траектория фазового пространства хОу, т. е. частное решение
x—x(t)t y=y'(t) этой системы дифференциальных уравнений, дающее на
плоскости хОу замкнутую кривую, обладающую свойством: траектории, начинающиеся
в достаточно узкой кольцеобразной окрестности П. ц., приближаются к нему
либо при /-» + со (устойчивый П. ц.), либо при t-+—со (неустойчивый П. ц.),
либо частью при t->-\-oo и остальной частью при ί->—со
(полуустойчивый П. ц.).
С механической точки зрения устойчивый П. ц. соответствует
периодическому режиму системы, автоматически восстанавливающемуся при достаточно
малых нарушениях его.
Пример: dr \ Решение этой системы:
<#=г1"~ГЧ г-1— (1— г0)е~^
dt "* Ι
Если л и φ—-полярные координаты плоскости, то при г=1 в плоскости хОу
имеем П. ц.
Лит.: А. А. Андронов и С. Э. Хайкин, Теория колебаний, ч. 1, Гостехиздат,
М,— Л., 1937; В. В. Немыцкий и В. В. Степанов, Качественная теория
дифференциальных уравнений, Гостехиздат, М., 1949.
ПРЕДСТАВЛЕНИЕ ГРУППЫ — отображение Ρ группы G на некоторое
множество неособенных квадратных матриц порядка /г. удовлетворяющее условиям:
Pig-^-Pig)-1
для любых glt g2t g—1 из G> Элементы gx»g2 и g—1 означают умножение
и обратный элемент в группе, a P{gi)-P(g2) и Ρ(g)-1— умножение матриц
и обратную матрицу. Говоря более абстрактно, П. г. есть гомоморфизм (см.)
группы в группу всех невырожденных матриц порядка п. Число η называется
размерностью П. г. При выборе определенного базиса в /г-мерном линейном
пространстве (см.) L матрицы Ρ(g), g£G задают линейные преобразования этого
пространства. Если существует собственное ненулевое подпространство (см.) N<z.L
такое, что P(g)x£N для любого g£G и χζΝ, то говорят, что П. г.
приводимо, в противном случае П. г. называют неприводимым. К настоящему времени
теория П. г. является развитой теорией, лежащей на стыке алгебры, функцио-

344
ПРЕКРАЩЕНИЯ ТОЧКА
нального анализа и дифференциальной /z-мерной геометрии. Крупные результаты
получены здесь Дж. Юнгом, Э. Картаном, Г. Вейлем, И. Шуром, И. М. Гель-
фандом.
Примеры: 1) Группа подстановок (см.) из 3 элементов (123), (132), (213),
(231), (312), (321) получает П. г., если положить:
/100\ /100\ /010\
Р(123)= 010 |, Р(132)= 001 , />(213) = 100 ,
\001/ \010/ \001/
/001 \ /010\ /001
Я(231)= 100 , Ρ(312)= 001 L Р(321)= 010
\010/ \100/ \100
2) любая группа G имеет П. г., определяемое равенством:
P(g) = E для всех g£G.
Здесь £ — единичная матрица порядка п. Такое П. г. называется
тривиальным.
Лит.: Ф. Д. Мурнаган, Теория представлений групп, перев. с англ., ИЛ,
М.—Л., 1950.
ПРЕКРАЩЕНИЯ ТОЧКА— особая точка кривой,
в которой кривая обрывается (не существует).
Например, для кривой y=x\gx начало координат является
П. т. (рис. 228).
ПРЕОБРАЗОВАНИЕ — соответствие между
элементами двух множеств какой угодно природы, такое,
что каждому элементу χ некоторого множества X
сопоставляется вполне определенный элемент у некоторого
(вообще говоря, другого) множества У. Чаще всего
под П. понимают взаимно однозначное соответствие
между элементами χ и y=f(x) одного и того же мно-
Рис. 226 жества. В геометрии часто рассматривают точечные
П., в которых каждой точке некоторого многообразия
(см.) (линии, поверхности, пространства) ставится в соответствие, вообще говоря,
другая точка того же многообразия, т. е. точечные П.— это отображения
точечного множества (многообразия) на себя.
Если рассматривать точечные П. плоскости, то их можно задать
формулами:
*'=/(*, У). У'=Ф(*< У)»
где точка (х, у) — прообраз (оригинал), а точка (*', у') —образ (копия).
Многие точечные П. плоскости образуют группу (см.); так, известны группа
вращений плоскости вокруг фиксированной точки, например вокруг начала
координат, группа параллельных переносов, группа движений (первого и второго
рода), группа подобия, группа аффинных П. (центроаффинных и эквиаффинных),
группа проективных П., состоящая из всех взаимнооднозначных точечных П.
расширенной (проективной) плоскости, при которых прямая переходит в прямую:
ax+by+c * \аг Ьг сг I
ах+Ьу+с

ПРЕОБРАЗОВАНИЕ КООРДИНАТ
345
Из этих формул П. видно, что прямая ах-\-Ьу-\-с=0 переходит в бесконечно
удаленную (несобственную) прямую.
Известна также группа круговых П., состоящая из П. движения,
зеркального отражения, подобия и инверсии (см.) и переводящая окружности и прямые
в окружности или в прямые. В отличие от предыдущих групп П. (линейных
групп. П. переводящих прямые линии в прямые) упомянутые П. называются бира-
циональными преобразованиями (см.)* т. е. такими П., при которых
координаты χ и у точки плоскости выражаются рационально через координаты χ и у
соответствующей точки.
В геометрии рассматриваются также П., переводящие точки плоскости в
прямые и обратно, например полярное преобразование (см.) относительно кривой
2-го порядка. Каждая группа П. сохраняет некоторые свойства фигур
неизменными (инвариантными) относительно этой группы П. Поэтому каждая группа П.
определяет свои свойства геометрических фигур, свою геометрию. Так, изучают
метрические, аффинные, проективные и другие свойства фигур (см. Эрланген-
ская программа). Чем уже группа П., тем больше инвариантных свойств фигур
она изучает, тем богаче она содержанием. И чем шире группа, тем меньше
инвариантных свойств фигур она изучает, тем глубже эти свойства связаны
с самой фигурой. Наиболее общими свойствами фигур являются топологические
свойства, остающиеся инвариантными при всяких топологических
преобразованиях (взаимно однозначных и непрерывных). К топологическим свойствам фигур
относятся размерность, связность, ориентируемость.
Лит.: Н. В. Ефимов, Высшая геометрия, М.—Л., 1953; Ф. Клейн, Высшая
геометрия, М.—Л., 1939; Ф. Клейн, Элементарная математика с точки зрения высшей,
М.—Л., 1934; Ж. Адамар, Элементарная геометрия, ч. I, M., Учпедгиз, 1948.
ПРЕОБРАЗОВАНИЕ КООРДИНАТ — переход от одной системы координат
к другой. Задача П. к. состоит в том, что, зная координаты текущей точки Μ
в одной системе координат, надо найти координаты этой же точки в другой
системе координат. Формулы, которые связывают координаты точки Μ в одной
и другой (старой и новой) системах координат, называются формулами П. к.
Например, формулы П. к. при переходе от одной прямоугольной декартовой
системы координат хОу к другой прямоугольной декартовой системе координат х'Оу*
имеют вид:
х' =(х — х0) cos α-f (у — у0) sin a,
у ' = _ (χ — χ0) sin a -f (у — y0) cos a,
а формулы обратного перехода:
х=х' cos a — у' sin a-f-x0,
y=x' sin a-fy' cos a-f-Уо*
где x0, y0—координаты нового начала О' в старой системе координат, а a — угол
между осями Ох и О'х'.
Формулы П. к. при переходе от прямоугольной системы координат к
полярной (ось абсцисс совпадает с полярной осью):
p=V*2-f-y2, sinq>=— . cosq>=— .-
Vx2+y2 VWy2
а обратный переход осуществляется по формулам:
*=р cos φ, у — p. sin φ.
См. также Координаты.

346
ПРИБЛИЖЕНИЕ ФУНКЦИЙ
ПРИБЛИЖЕНИЕ ФУНКЦИЙ состоит в нахождении по данной функции
другой функции, достаточно мало отличающейся от нее и принадлежащей к
определенному семейству — семейству приближающих функций, В частном случае,
когда приближающая функция совпадает с данной в заданных точках, говорят
об интерполировании и интерполирующей функции (см. Интерполирование).
Задача замены одних функций другими, близкими к ним в определенном
смысле, постоянно встречается в математике и ее приложениях. Сложные
функции заменяют простыми для облегчения вычислений или функциями,
принадлежащими семейству, определяемому условиями задачи. Из обработки результатов
экспериментов получают эмпирические формулы (см.), являющиеся некоторым
приближением. П. ф. есть средство исследования самих функций.
Чаще всего для П. ф. используются алгебраические многочлены Ра(х)=
=а0хп-\-а1хп--1-{- ··· +ап фиксированной степени η, рациональные дроби /?(*) =
η
= Рп(х):Км (*)» тригонометрические полиномы вида: Тп (я)=~+ 2 (а# cos kx-\-
η
-\-$ksmkx) или вообще многочлены вида: ФОО^^СлФлМ. где <ρ&(χ) заданы.
Практические методы нахождения наилучших равномерных приближений
разработаны бельгийским математиком Балле Пуссеном, советскими математиками
Е. Я. Ремезом, С. М. Никольским, А. Н. Колмогоровым. Немецкий математик
Вейерштрасс доказал, что если семейством приближающих функций является
семейство алгебраических многочленов на любом отрезке fa, Ъ\, то, выбрав число
параметров, от которых зависит это семейство, достаточно большим, можно
сделать погрешность приближения сколько угодно малой для л;обой непрерывной
функции /(*). Это свойство именуется полнотой системы функций; им обладает
по отношению ко всем непрерывным и периодическим функциям также система
тригонометрических функций. Этим определяется наиболее частое использование
тригонометрических систем приближающих функций.
В настоящее время благодаря практическим потребностям, связанным с
широким развитием машинной техники вычислений, теория П. ф. представляет собой
обширную и очень быстро развивающуюся область математики. Основы этой
теории были заложены П. Л. Чебышевым, ряд фундаментальных результатов
получен в начале XX в. С. Н. Бернштейном. Существенный вклад в теорию
П. ф. внесли советские математики М. В. Келдыш, А. Н, Колмогоров, М. А.
Лаврентьев, С. М. Никольский, С, Н. Мергелян.
Лит.: П. Л. Чебышев, Полное собрание сочинений, тт. 2—3, Изд-во АН СССР,
М.—Л., 1947—1948; Н. И. А-хиезер, Лекции по теории аппроксимации, Гостехиздат,
М., 1947; С. Н. Мергелян, Равномерное приближение функций комплексной
переменной, УМН,7:2, 19525 С- М. Никольский, Приближенное представление
функций, 1963.
ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ — раздел вычислительной математики,
занимающийся приближенным решением дифференциальных уравнений. Первой
задачей П. и. является приближенное вычисление интегралов (которое
соответствует решению простейшего дифференциального уравнения yf = f(x)). В тех
случаях, когда точное интегрирование невозможно, так как интеграл не может быть
выражен в известных функциях, применяются аналитические методы П. и.,
которые заключаются в том, что подынтегральная функция приближенно заменяется
другой, интеграл от которой легко вычисляется. В качестве такой функции
обычно берут интерполяционный многочлен, т. е. многочлен, совпадающий
с подынтегральной функцией в некоторых точках хь (узлах интерполяции). Полу-

ПРИБЛИЖЕННОЕ ИНТЕГРИРОВАНИЕ
347
чающиеся в результате формулы (так называемые квадратурные формулы, см.)
имеют вид:
ь η
\f(x)dx^Ai(xli . ... χη, a, b)f(xi)+R,
α ί=1
где R=R(ri)— погрешность данной формулы П. и. Если число узлов
интерполяции равно п, то, очевидно, интегралы многочленов степени не выше η—1 будут
вычислены точно.
Однако за счет удачного выбора узлов интерполяции степень многочлена,
интеграл которого вычисляется точно с помощью квадратурной формулы, может
быть повышена. Формула П. и. считается тем точнее, чем выше эта степень
(при фиксированном /г). Часто для уменьшения погрешности и получения
возможно более простых коэффициентов Αι отрезок интегрирования [а, Ь] разбивают
на части и к каждой применяют выбранную формулу П. и. Разбивая отрезок
[а, Ь] на т равных отрезков и заменяя подынтегральную функцию на каждом
отрезке линейной (т. е. многочленом первой степени), совпадающей на его концах
с подынтегральной, получим формулу трапеций:
^(*)^-^[i^+y1+y.+ ··· +ym-i]+R.
(b — а)3
где jc0 = a, xm = b, У/=/(#;), ff< ln » M2, M2=max I/" (x)\. Если же на каж-
дом из т отрезков разбиения подынтегральную функцию f(x) заменить
многочленом второй степени, совпадающим с / (х) ка концах и середине отрезка,
то получится формула парабол (формула Симпсона):
Ϊ Ь — а
J/Wdx=-^-[yo+4yi+2ya-f4y8-f2y4+ ... +4уат_1+уш]+Д,
где х0~а, х2, х4, . . ., х2т«b — точки разбиения отрезка [а, 6] на т равных
частей, xlt х3 *2т—ι — середины этих частей, yj=f(xj) (/=0,1, . . ., 2m),
R<
(*-ϊΤ·& ^s'"v,<*
Отказавшись от требования, чтобы узлы интерполяции разбивали отрезок [а, Ь]
на равные части, можно повысить точность формулы. Такова, например, формула
Гаусса:
)f(x)dx=A\n)f(Xl) + A{2n>f(x2)-l· ··· +Л£Я>/(*Л)+Я(я).
Здесь χι — корни многочлена Лежандра л-й степени [который имеет вид:
1 dn
РпМа . 2п Γη (*2 — 0я и все корни которого действительны и лежат в
интервале (—1, 1)]:
1 "d-x^^M1 vn+mvnw f Hc)
для некоторого —1 <с< 1. Эта формула дает точное значение интеграла для
многочленов степени не выше 2/? — 1. Составлены таблицы величины xt η Α'·1
для многих п.

348
ПРИБЛИЖЕННЫЕ МЕТОДЫ
Существует также много других формул, выражающих приближенное
значение интеграла с помощью значений производных / (х) в узлах интерполяции,
конечных разностей в узлах интерполяции и т. д.
Неопределенный интеграл вычисляют как определенный с переменным
верхним пределом интегрирования, получая ответ в виде таблицы значений
первообразной функции. Формулы П. и. обобщаются и на кратные интегралы.
На практике П. и. пользуются также в тех случаях, когда интегрируемая
функция задана таблицей (или графиком) или если она быстрее приводит к цели
в рамках требуемой точности. В этих случаях, кроме аналитических методов,
используются графические методы П. и., которые заключаются в построении
графика первообразной по графику подынтегральной функции, а также
используются математические машины и приборы (вычислительные машины, интеграторы,
планиметры и т. п.). Основной задачей П. и. является приближенное решение
дифференциальных уравнений весьма общего вида. Здесь также существуют
аналитические методы, дающие результат П. и. в виде формулы. Основная идея
этих методов заключается в построении последовательности функций, равномерно
сходящейся к решению (метод рядов, метод Ритца, метод последовательных
приближений, метод Галеркина и т. д.). Беря член такой последовательности
с достаточно большим номером, получим результат с любой степенью точности.
Примером может служить метод, заключающийся в разложении искомой функции
в ряд Тейлора в окрестности подходящей точки, после чего может быть вычислено
любое число коэффициентов этого ряда.
Наряду с аналитическими применяются численные методы П. и.,
определяющие приближенные значения искомого решения в отдельных точках, т. е. в виде
таблицы (метод Рунге, метод Эйлера и др.).
Для решения дифференциальных уравнений применяются также графические
методы П. и. В основе их лежит использование поля направлений, определяемое
дифференциальным уравнением. Многие численные методы могут использоваться
в графической форме.
Методы П. и. приобретают все возрастающее значение для практики,
которая реализует их на быстродействующих вычислительных машинах дискретного
действия и на различных моделирующих устройствах.
Лит.: А. Н. Крылов, Лекции о приближенных вычислениях, Гостехиздат, М.,
1954; В. Э. Милн, Численный анализ, перев. с англ., ИЛ, М., 1951; Л. В.
Канторович и В. И. Крылов, Приближенные методы высшего анализа, Физматгиз, М.,
1962; Д. Ю. Панов, Справочник по численному решению дифференциальных уравнений
в частных производных, Физматгиз, М., 1962.
ПРИБЛИЖЕННЫЕ МЕТОДЫ — раздел вычислительной математики,
связанный с разработкой и применением различных методов доведения до числового
результата основных задач математической физики, математического анализа,
алгебры, геометрии и др. П. м. заменяют решение заданной задачи решением
некоторой другой.
П. м. можно разбить на следующие группы: 1) П. м. вычисления частных
значений функции, заданной некоторым аналитическим выражением, по данным
значениям ее аргументов; 2) П. м. решений алгебраических и трансцендентных
уоавнений с численными коэффициентами и систем таких уравнений; 3) П. м.
дифференцирования и интегрирования функций; 4) П. м. интегрирования
дифференциальных уравнений (обыкновенных и в частных производных).
Средствами П. м. являются: 1) таблицы формул; 2) таблицы значений
функций; 3) настольные вычислительные машины; 4) электронные вычислительные
машины.
При применении П. м. к решению каждой задачи приходится: 1) давать
математические характеристики точности приближенных величин; 2) оценивать
точность результата, когда известна точность исходных данных; 3) находить
точность исходных, обеспечивающую заданную точность результата; 4) согласо-

ПРИБЛИЖЕННЫЕ МЕТОДЫ
349
вывать ючность различных исходных данных с тем, чтобы не затрачивать
лишней работы при отыскании или вычислении одних данных, если другие даны
слишком грубо; 5) следить в процессе вычислений за точностью промежуточных
результатов, с тем чтобы, с одной стороны, обеспечить необходимую точность
окончательного результата и, с другой стороны, по возможности упростить
вычисления.
При использовании П. м. получаемые результаты неизбежно обладают
погрешностями (см.)· Различают погрешности округлений и погрешности метода.
Погрешность округления возникает, во-первых, из-за того, что всякая
система счисления (в том числе и десятичная) не позволяет конечным числом
разрядов выражать очень многие числа (например, число 1:6 нельзя записать в виде
конечной дроби), и, во-вторых, в результате отбрасывания лишних цифр,
получающихся при вычислениях.
Так как при пользовании П. м. исходная задача заменяется
приближенной другой, то в результате применения П. м. возникают ошибки метода.
Исходные данные в любой задаче, как правило, неизвестны точно, и приходится
при вычислениях пользоваться приближенными исходными величинами. Поэтому
и результат вычислений получается не точный, а приближенный, даже если
все вычисления производились точно, без округлений.
Погрешность полученного решения задачи П. м. определяется суммарным
действием погрешностей. Разность между истинным и приближенным значением
какой-либо величины называется абсолютной погрешностью. Точное значение
величины обычно неизвестно, поэтому неизвестна точно и абсолютная погрешность.
В практике пользуются указанием границ абсолютной погрешности. Отношение
абсолютной погрешности к абсолютному значению приближенной величины
называют относительной погрешностью. Относительная погрешность, как правило,
выражается в процентах и принимается за меру точности результата.
Погрешности результатов арифметических действий характеризуются
следующими правилами: 1. При сложении приближенных величин их абсолютные
погрешности складываются, а относительная погрешность суммы будет заключена
между наибольшей и наименьшей относительными погрешностями слагаемых.
2. Абсолютная погрешность разности двух приближенных величин равняется
сумме абсолютных значений абсолютных погрешностей уменьшаемого и
вычитаемого, а относительная погрешность разности двух приближенных чисел, близких
по величине, может оказаться большой величиной, даже если относительные
погрешности каждого из этих чисел в отдельности являются малыми. 3.
Относительная ошибка частного равняется сумме абсолютных значений относительных
погрешностей делимого и делителя. 4. При умножении приближенных величин
относительные погрешности складываются.
Пример. Умножим два числа Nx и N2. Пусть их относительные
погрешности равны соответственно εχ и ε2, следовательно, истинные величины этих
сомножителей:
^1=^(1+8,), Л^=Л/2(14-е2), ^1Λ^2=Λ/1Λ/2(1 + ε1)(1-τ-ε2) =
=^ι^2[ΐ4-(ε1+ε2)+ε1ε21;
так как гх и ε2 малы, то гхг2 можно пренебречь, и тогда
#2 ' ^2=ад [1 + (ε1+ε2)]=Λ/1Λ^2+^1^2(ε1+ε2).
При использовании формул П. м. следует учитывать, что одну и ту же
формулу можно использовать различным способом с раз личной результирующей
точностью. Например, можно вычислить
*3 хь
smx^x — — 4- —
6 120

350
ПРИБЛИЖЕННЫЕ ФОРМУЛЫ
двумя различными способами. Можно отдельно вычислить каждый член и потом
сложить. В этом случае ошибка округления может быть равна 1,5 единицы
последнего разряда. С Другой стороны, в выражении
[{u-oxt-i)x2+l\x
ошибка не может превзойти 0,5 единицы последнего разряда. В первом случае
было два деления, четыре умножения, два сложения и вычитание. В последнем
случае умножения сведены к трем.
П. м. в последнее время быстро развиваются в связи с широким
использованием быстродействующих вычислительных машин для научных и инженерных
расчетов.
Лит.: А. Н. Крылов, Лекции о приближенных вычислениях, Гостехиздат, М., 1954;
И. С. Березин и Н. П. Жидков, Методы вычислений, Физматгиз, М., т. I, 1 959,
т. II. 1960.
ПРИБЛИЖЕННЫЕ ФОРМУЛЫ для вычисления различных функций.
Основным методом получения приближенных формул является разложение функций в
ряд, чаще всего в ряд Тейлора. Для оценки разности между точным и
приближенным значением функций, полученным с помощью ряда, рассматривают
дополнительный член ряда Тейлора в какой-либо форме.
Ряд Тейлора с дополнительным членом в форме Пеано имеет вид:
/<*) = /(*о)+Яг (*-*о)+^(*-*о)Ч- ...+^ψΒ{χ^γ.
(α зависит от χ и стремится к 0 вместе с х — х0).
Дополнительный член в форме Шлемильха и Роша имеет вид:
г^ /<"+'> [*о-И (*-*,)] {1_Ь)П+1-р{х_Х())п+1 (0<9<1, р>0),
п\р
при р=я+1 получаем дополнительный член в форме Лагранжа:
(в+1)! ( 0) " ()
а при р=\ —в форме Коши:
п\
Из формулы Тейлора при х0=0 и из (*) получаем формулу Маклорена
с остаточным членом:
Г(0) Г(0) /(/1)(0) /<Л-Ы) (Θ jc)
Если (я-И)-я производная /(л+1)(дг) ограничена по абсолютной величине числом
М4 то погрешность гп приближенной формулы
/'(0) /"(0) 0 /(/1>(0)

ПРИБЛИЖЕННЫЕ ФОРМУЛЫ
351
полученной из точной отбрасыванием дополнительного члена, может быть
оценена следующим образом:
Мхп+*
Например (при малых х), приближенная формула
х xl Jt3 хп
имеет погрешность
*"+* 3
1'л (*)!<** , , п, ПРИ х~1> \гп\<-
(л+1)! (я+1)!
Для sinx«x—-+ ··· + (—Ι)"1-1- 777' I'aiiiMK—J
3! (2m-1)! ' лту "^ (2m+l)!
В частности, чтобы погрешность формулы sin*»* была меньше 10—3(#>0),
надо, чтобы —<0,001, т. е. л:<0,1817. Для формулы sin*^*— -г та же
6 о
точность достигается при χ< 0,6544.
χ2 χ* х2т Ы2/п+2
Для cosj^I—— +-7 — ··· -Ь(-1)т-г—Г,|r2w+1(xK-'
2Г 41 τι ж/ (2т)!"'2^1^л^(2т-Ь2)Г
для cosjt=l — ~- К(^)К~<Ю-4 при *<0,2213 («13°).
Существуют и приближенные формулы иного типа; так, для приближенного
спрямления дуги s окружности, малой по сравнению с радиусом г, имеем при
ближенную формулу:
ft4 2o —d
s«2o+——,
где d — хорда дуги s, а Ь — хорда, соответствующая половине s; ее
погрешность оценивается так:
|Δ5ΐ<'ΪΓο
(х — центральный угол, соответствующий s).
Для той же цели существует правило Чебышева: дуга приближенно равна
сумме равных сторон равнобедренного треугольника, построенного на хорде
лП
и имеющего высотой γ -~ стрелки. Для оценки погрешности этой формулы
о
справедливо соотношение: |As|<0#l ™δ.
Приближенные формулы для вычисления определенных интегралов см.
в терминах: Парабол формула, Трапеций формула, Прямоугольников формула.
Лит.: А. Н. Крылов Лекции о приближенных вычислениях, Гостехиздат, Мм 1ь54;
Л. С. Б е з и к о в и ч, Приближенные вычисления, Гостехиздат, М., 1949.

352
ПРИВЕДЕНИЕ ПОДОБНЫХ ЧЛЕНОВ
ПРИВЕДЕНИЕ ПОДОБНЫХ ЧЛЕНОВ многочлена. Если в некотором
многочлене (см.) дан некоторый член многочлена (см.) и совокупность всех ему
подобных членов (см.):
Atf х\* · · · *„"" » ЬА1 42 · · · х'пя<< ■ ■ ·. Ak*'14* · · · *>> (*)
то П. п. ч. многочлена называется замена в данном многочлене всей
совокупности подобных членов (*) одним членом:
(^1 + ^2-Ь ... +Ak)xVx*S . . . х°\
П. п. ч. есть один из видов тождественных преобразований (см.).
ПРИВЕДЕННАЯ СИСТЕМА ВЫЧЕТОВ — часть полной системы вычетов
(см.), состоящая из чисел, взаимно простых с модулем т. Любые Ц>(т) чисел,
не сравнимые по модулю т и взаимно простые с ним, образуют П. с. в. по
этому модулю. Здесь φ (т) —функция Эйлера.
ПРИВОДИМЫЙ МНОГОЧЛЕН над полем Р. Многочлен называется П. м.
над полем Ρ тогда и только тогда, когда он разлагается в произведение по
крайней мере двух многочленов ненулевой степени с коэффициентами из того же
поля. Если же такое разложение многочлена в произведение многочленов из
того же поля невозможно, то этот многочлен называется неприводимым.
Один и тот же многочлен может быть приводимым в одном поле или
кольце и неприводимым в другом. Так, например, многочлен f(x)=x2 — 5
неприводим в поле рациональных чисел, но приводим в поле вещественных чисел, так
как
*2 _ 5=(*+уТ)(*—VO·
Или, например, многочлен f[x)=x2-j-b неприводим в поле рациональных чисел
и в поле вещественных чисел, но приводим в поле комплексных чисел, так как
*2 + 5 = (*+ζ'1/ΊΓ)(χ— iV*)·
Вопрос о приводимости того или иного многочлена даже в поле
рациональных чисел до последнего времени имел весьма громоздкие общие методы
решения. Наиболее известными методами решения вопроса о приводимости
многочленов, а также нахождения множителей этого многочлена в поле рациональных
чисел были методы, разработанные в прошлом столетии немецким математиком
Л. Кронекером. Однако его методы настолько громоздки, что даже для
решения вопроса о приводимости многочленов пятой степени приходится испытывать
миллионы различных гипотез, причем испытание каждой гипотезы в свою
очередь требует также довольно много выкладок и вычислений.
В 1938—1940 гг. М. В. Яковкиным найдены и детально разработаны новые
методы решения вопроса о приводимости многочленов, гораздо проще и
совершеннее методов Л. Кронекера. Впервые эти методы опубликованы Яковкиным
в 1941 г. в «Ученых записках МГПИ им. В. И. Ленина», а затем в нескольких
номерах журнала «Доклады АН СССР». Наиболее полное и подробное
изложение этих методов содержится в книге М. В. Яковкина «Численная теория
приводимости многочленов» (Изд-во АН СССР, 1959).
ПРИЗМА — многогранник, полученный от пересечения призматической
поверхности (см.) двумя параллельными плоскостями. Равные многоугольники
(грани), полученные в сечении призматической поверхности с параллельными
плоскостями, называются ее основаниями, а другие грани (параллелограммы) —
боковыми гранями (рис. 229).

ПРИЗНАКИ ДЕЛИМОСТИ
353
П. называется прямой, если ее боковые ребра перпендикулярны основаниям.
П. называется правильной, если она прямая и основание ее — правильный
многоугольник. П. называется наклонной, если ее боковые ребра (грани) не
перпендикулярны основаниям. П. называется треугольной, если ее основание —
треугольник, четырехугольной, если ее основание — четырехугольник, и вообще
л-угольной, если основание ее — /г-угольник.
Чаще всего рассматривают выпуклую П.,
которую обычно и называют П. Определение П.
иногда в литературе дается неверно: призмой
называется многогранник, у которого две
грани — равные многоугольники с соответственно
параллельными сторонами, а все остальные
грани— параллелограммы (см., например, БСЭ,
изд. 2, слово «Призма»; Киселев, Геометрия,
ч.П, стр. 33, 1950). Такому определению
удовлетворяет, например, многогранник, изображенный
на рисунке 230, но не являющийся призмой.
Греч, πρίσμα — отпиленный (кусок), опилки
(πριω — пилю).
ПРИЗМАТИЧЕСКАЯ ПОВЕРХНОСТЬ —
поверхность, образованная движением прямой в
пространстве так, что эта прямая остается параллельной самой себе и
пересекает данную ломаную линию.
Подвижная прямая называется образующей П. п., а данная ломаная
линия—ее направляющей.
ПРИЗМАТОИД — выпуклый многогранник, две грани которого, называемые
основаниями, параллельны. В основаниях могут быть разноименные
многоугольники, например треугольник и четырехугольник (ЛВС и A'B'C'D',
см. рис. 231), а остальные грани (боковые)
могут быть треугольниками и трапециями.
Частными случаями П. являются обелиск (см.) и
призма (см.).
ПРИЗНАКИ ДЕЛИМОСТИ чисел —
простейшие критерии (правила), позволяющие судить
о делимости (без остатка) одних натуральных
чисел на другие. Решение вопроса о делимости
чисел П. д. сводят к действиям над
небольшими числами, обычно выполняемым в уме.
Так как основанием общепринятой системы
счисления является 10, то наиболее простыми и распространенными являются
П. д. на делители чисел трех видов: 10А, 10А — 1, 10^-f-1.
Первый вид — П. д. на делители числа 10fe: для делимости любого
целого числа N на любой целый делитель q числа 10* необходимо и достаточно,
чтобы последняя &-циферная грань (k—циферное окончание) числа N делилась
на q. В частности (при &=1, 2 и 3), получаем следующие П. д. на делители
чисел 101 = 10(1^, 102= 100 (12) и 103 = 1000 (18):
I,. На 2, 5 и 10 — одноциферное окончание (последняя цифра) числа должно
делиться соответственно на 2, 5 и 10. Например, число 80 110 делится на 2, 5
и 10, так как последняя цифра 0 этого числа делится на 2,5 и 10; число
37 835 делится на 5, но не делится на 2 и 10, так как последняя цифра 5
этого числа делится на 5, но не делится на 2 и 10.
12. На 2, 4, 5, 10, 20, 25, 50 и 100 — двуциферное окончание числа
должно делиться соответственно на 2, 4, 5, 10, 20, 25, 50 и 100. Например, число
7 840 700 делится на 2, 4, 5, 10, 20, 25, 50 и 100, так как двуциферное
окончание 00 этого числа делится на 2, 4, 5, 10, 20, 25, 50 и 100; число 10 831750
z>C
Рис. 231
*·& Толковый словарь математических терминов

354
ПРИЗНАКИ ДЕЛИМОСТИ
делится на 2, 5, 10, 25 и 50, но не делится на 4, 20 и 100, так как двуци-
ферное окончание 50 этого числа делится на 2, 5, 10, 25 и 50, но не делится
на 4, 20 и 100.
13. На 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 125, 200, 250, 500 и 1000 —
трехциферное окончание числа должно делиться соответственно на 2, 4, 5, 8,
10, 20, 25, 40, 50, 100, 125, 200, 250, 500 и 1000. Например, число 675 081000
делится на все перечисленные в этом признаке числа, так как на каждое
из них делится трехциферное окончание 000 заданного числа; число 51 184 032
делится на 2, 4 и 8 и не делится на остальные, так как трехциферное
окончание 032 заданного числа делится только на 2, 4 и 8 и не делится
на остальные.
Второй вид — П. д. на делители числа 10ft—1: для делимости любого
целого числа N на любой целый делитель q числа 10^—1 необходимо и
достаточно, чтобы сумма £-циферных граней числа N делилась на д. В частности
(при £=1, 2 и 3), получаем следующие П. д. на делители чисел 101—1 = 9
(IIJ, 103—1=99 (Н2) и 103 — 1 = 999 (Н3):
Hj. На 3 и 9 —сумма цифр (одноциферных граней) числа должна делиться
соответственно на 3 и 9. Например, число 510 887 250 делится на 3 и 9, так
как сумма цифр 5+1+0+8+8+7+24-54-0=36 (и 3+6 = 9) этого числа
делится на 3 и 9; число 4 712 586 делится на 3, но не делится на 9, так как
сумма цифр 4+7+1+24-5+8+6=33 (и 3+3 = 6) этого числа делится на 3,
но не делится на 9.
Н2. На 3, 9, 11, 33 и 99 — сумма двуциферных граней числа должна
делиться соответственно на 3, 9, 11, 33 и 99. Например, число 396 198 297
делится на 3, 9, 11, 33 и 99, так как сумма двуциферных граней 3+96+19+
+82+97=297 (и 2+97=99) делится на 3, 9, 11, 33 и 99; число 7 265 286 303
делится на 3, 11 и 33, но не делится на 9 и 99, так как сумма двуциферных
граней 72+65+28+63+03=231 (и 2+31 = 33) этого числа делится на 3, 11
и 33 и не делится на 9 и 99.
Н3. На 3, 9, 27, 37, 111, 333 и 999 —сумма трехциферных граней числа
должна делиться соответственно на 3, 9, 27, 37, 111, 333 и 999. Например,
число 354 645 871 128 делится на Есе перечисленные в этом признаке числа,
так как на каждое из них делится сумма трехциферных граней 354+645+
+871 + 128=1998 (и 1+998-999) этого числа.
Третий вид —П. д. на делители числа 10*+1: для делимости любого
целого числа N на любой целый делитель q числа 10й + 1 необходимо
и достаточно, чтобы разность между суммой £-циферных граней, стоящих
в #на четных местах, и суммой £-циферных граней, стоящих в Λί на
нечетных местах, делилась на q. В частности (при 6=1 2 и 3)
получаем следующие П. д. на делители чисел 10+1 = 11 (HIi), 10' +1 = 101 (П12)
и 103+1 = 1001 (III,). т
IIι На 11 —разность между суммой цифр (одноциферных граней), стоящих
на четных местах, и суммой цифр (одноциферных граней), стоящих на нечетных
местах должна делиться на 11. Например, число 876 583 598 делится на 11,
так как разность 8 — 7+6—5+8-3+5 — 9+8=11 (и 1-1=0) между
суммой цифр, стоящих на четных местах, и суммой цифр, стоящих на нечетных
местах, делится на 11.
Ш2. На 101 —разность между суммой двуциферных граней, стоящих в
числе на четных местах, и суммой двуциферных граней, стоящих на нечетных
местах должна делиться на 101. Например, число 8 130 197 делится на 101, так
как разность 8—13+01—97=101 (и 1—01=0) между суммой двуциферных
граней, стоящих в этом числе на четных местах, и суммой двуциферных граней,
стоящих на нечетных местах, делится на 101.
III . На 7, 11, 13, 77, 91, 143 и 1001 — разность между суммой
трехциферных граней, стоящих в числе на четных местах, и суммой трехциферных граней,

ПРИСОЕДИНЕННАЯ МАТРИЦА
355
стоящих на нечетных местах, должна делиться соответственно на 7, 11, 13,
77, 91, 143 и 1001. Например, число 539 693 385 делится на 7, 11 и 77, но не
делится на 13, 91, 143 и 1001, так как 539 — 693+385=231 делится на 7, 11
и 77 и не делится на 13, 91, 143 и 1001.
Лит.: М. В. Яковкин, Свойства чисел, аналогичные теореме Безу, «Математика
в школе», 1951, № 1.
ПРИКЛАДНАЯ МАТЕМАТИКА — этим термином пользуются, когда
говорят о применении математики в других областях науки и в технике (в физике,
химии, астрономии, экономике, геодезии, в военном и инженерном деле и т. д.).
Четкой границы между прикладной и неприкладной математикой провести
нельзя.
Любая математическая дисциплина имеет большее или меньшее, прямое или
косвенное прикладное значение. Так, теория чисел, решая некоторые задачи
теории функций комплексного переменного, может иметь тем самым значение для
механики. Употребляя термин П. м., обычно имеют в виду разделы математики,
имеющие непосредственное применение в других областях. Для таких разделов
математики характерно наличие важных нематематических интерпретаций (теория
вероятностей, теория информации, теория поля, теория операторов, теория
потенциала). Некоторые прикладные математические дисциплины возникают в рамках
старых теорий в связи с новыми практическими задачами (численные методы
решения дифференциальных уравнений и т. п.).
ПРИМИТИВНАЯ ФУНКЦИЯ (или первообразная функция) данной функции
f(x)— функция Φ (χ) такая, что Φ'(*)=/(*) на данном интервале. Отыскание
П. ф. является действием, обратным дифференцированию, оно не однозначно: для
f (x) существует бесконечно много П. ф.; однако любые две из них отличаются
друг от друга на постоянное слагаемое. Совокупность всех П. ф. называется
неопределенным интегралом (см.) от /(*). Эта совокупность выражается
формулой Φ (χ) = Φχ (χ) -f- С, где Φг(х) — какая-либо П. ф., а С — произвольная
постоянная. Например, х3 является П. ф. для Зх2 и все П. ф. для За:2 имеют
вид jc3-j-C (в этом примере интервал произволен). Основной факт о П. ф.: для
любой непрерывной на интервале функции / (х) существует П. ф.
ПРИРАЩЕНИЕ: 1°. П. аргумента — разность между двумя значениями
(новым и старым) аргумента: Дх=х1-д:0.
2°. П. функции y = f(x) определяется П. аргумента Δ * и равно Ду=
= ί(χ+Δχ) — f(x)· П. функции y — f(x) в данной точке χ — разность Ду=
= /(λ:4-Δλ:) — /(^), где Δ*— П. аргумента (см.).
ПРИСОЕДИНЕННАЯ МАТРИЦА (взаимная матрица) к квадратной матрице
А— матрица, в которой вместо каждого элемента ац поставлено его
алгебраическое дополнение (см.) Лг/·. Для матрицы /z-го порядка
П. м. будет матрица
/а1га12 . . . а1п\
1 = / а21а22 . . . а2п \
\ап1ап2 . . . annJ
IАХ1А21
А = I АХ2А22
АлпАпп
23*

356
ПРОВЕРКА С ПОМОЩЬЮ ДЕВЯТКИ
Произведение матрицы Л на П. м. Л* равно скалярной матрице (см.), в кото-
рои на главной диагонали стоит определитель £> = |Л| матрицы Л, т. е.
/D00 . .. 0\
АА* = А*А = О DO . . . О \
\000 . .. D /.
Поэтому обратная матрица (см.) Л—1 к невырожденной матрице (см.) А
выражается так:
Л-1-— Л*.
ПРОВЕРКА С ПОМОЩЬЮ ДЕВЯТКИ — прием, с помощью которого
выполняется контроль правильности вычислений. Чаще всего этот прием используется
при проверке результата умножения и заключается в следующем: сравниваются
остатки от деления суммы цифр произведения на 9 и от деления произведения
остатков сумм цифр каждого из двух множителей на 9. Если эти остатки не
равны, то умножение выполнено неверно, если же остатки равны, то
умножение выполнено или верно или допущена ошибка на число, кратное девяти.
Следовательно, П. с п. д. является необходимым, но недостаточным условием для
оценки правильности результата вычислений.
Пример: 827*563=465 601. Остатки от деления суммы цифр сомножителей
на 9 равны соответственно 8 и 5, произведение этих остатков (40) при делении
на 9 дает остаток 4. При делении суммы цифр произведения (465 601) на 9 мы
получаем остаток, равный тоже 4. Следовательно, умножение выполнено верно
(или допущена при вычислениях ошибка на число, кратное 9).
ПРОВЕШИВАНИЕ ПРЯМОЙ (линии) — нанесение на местности точек,
расположенных на одной прямой. П. п. осуществляется . различными способами
(с помощью вех, теодолита) при измерительных работах на местности, при
геодезических работах.
ПРОГРАММИРОВАНИЕ — составление программы решения математической
или логической задачи на электронных вычислительных машинах. Для
управления машиной существует определенная система команд. Каждая команда (или
операция) математическая или логическая имеет определенную форму записи
(код), обычно в восьмеричной (или двоичной) системе счисления, кодами
записываются и числа.
Например, машина «Стрела-3» оперирует с кодами, содержащими 43
двоичных разряда, операция сложения изображается для нее в восьмеричной системе
кодом 01, операция умножения —05, операция сравнения чисел (кодов)—16.
Команды и числа размещаются в определенных ячейках внутренней памяти
машины, имеющих определенные номера.
Программа (т. е. числа и команды) записывается на стандартных бланках.
Приведем небольшой отрывок программы для «Стрелы-3».
I
а+З
<2-Н
<2-f5
II
0
1
III
535
541
α-ЬЗ
IV
4
α+4
V
α+13
VI
0
0
VII
00
02
01
VIII
IX Ι
4
5
6

ПРОЕКТИВНАЯ МЕТРИКА
357
В первом столбце указывают номер в восьмеричной системе той ячейки,
куда засылается данная команда или число; во втором столбце пишут 0, если
засылаемое число положительно, или I — если отрицательно. В третьем,
четвертом и пятом столбцах следуют 1, 2, 3-й адреса: при записи числа в
виде Л-10в (0 < А < 1) они используются для записи А по три цифры в
каждом адресе, а при записи команды в 1-м и 2-м адресах указываются номера
ячеек, откуда берутся числа или команды, над которыми выполняется
указанная операция; в 3-м адресе стоит номер ячейки, куда посылается
результат. В шестом столбце пишут 0, если В > О, и 1, если В < 0. В седьмом столбце
указывается код данной операции или число В (для его изображения
используются два разряда в восьмеричной системе). Например, в ячейке о-{-3
записано число 0,535, в ячейке а+4 — число 54,14, в ячейке a-j-5 — команда:
«взягь число из ячейки а-\-3, взять число из ячейки а+4, сложить их и
результат направить в ячейку a-f-13». После выполнения данной команды маши»а
переходит непосредственно к выполнению следующей и т. д.
Написанная на бланках программа пробивается затем на перфокартах или
перфолентах, с которых и производится ввод в машину исходного числового
материала и команд программы. После ввода машина автоматически начинает
выполнять заданную программу, т. е. команды, пробитые на картах.
При решении различных задач стараются выбирать такие численные методы,
которые при достаточной математической корректности могут быть легко
запрограммированы и для которых выполнение программы займет минимальное
время. По выбранному числовому методу составляется общая схема программы,
т. е. решение всей задачи разбивается на решение некоторого числа простых
задач и указывается, в какой последовательности друг за другом они будут
решаться (однократно или с многократным повторением); затем для каждой из
простых задач, для каждого участка схемы составляется программа решения
этой задачи. Весь материал распределяется в памяти машины, и все участки
программы объединяются в одну программу.
При составлении программы предусматривают необходимость контролировать
правильность решения задачи (выполнения программы) машиной; для этого
существуют специальные методы. Для решения некоторых простейших задач
(например, вычисления элементарных функций) машине раз и навсегда заданы
стандартные подпрограммы, хранящиеся в ее памяти.
В настоящее время разрабатываются методы автоматического
программирования, т. е. составления программ для составления программы
(программирующие программы). Это оказывается необходимым при решении чрезвычайно
сложных задач за возможно более короткое время.
ПРОГРЕССИЯ — см. Арифметическая прогрессия и Геометрическая
прогрессия.
ПРОЕКТИВНАЯ ГЕОМЕТРИЯ — математическая дисциплина, изучающая
проективные свойства фигур, т. е. такие свойства фигур, которые остаются
инвариантными при всех проективных преобразованиях плоскости (пространства) в
себя; другими словами, П. г. есть геометрия, определяемая группой
проективных преобразований (см.). Основным понятием П. г. является сложное
отношение четырех точек (прямых) (см.).
Лит.: Н. Ф. Чет вер ухи н, Проективная геометрия, Учпедгиз, Л\., 1953;
Н. А. Глаголев, Проективная геометрия, ОНТИ, М., 1936; Н. В. Ефимов, Высшая
геометрия, Физматгиз, М., 1961; Дж. Юнг, Проективная геометрия, перев. с англ., ИЛ,
М., 1949.
ПРОЕКТИВНАЯ МЕТРИКА — метрика (измерение отрезков и углов,
площадей и т. п.), инвариантная относительно некоторого класса проективных
преобразований. Обычно таким классом преобразований [подгруппа (см.)
проективной группы] являются преобразования, сохраняющие некоторую кривую 2-го

358
ПРОЕКТИВНАЯ ПЛОСКОСТЬ
порядка (абсолют, см.). Свойства, инвариантные относительно такого рода
преобразований, составляют предмет изучения различных метрических геометрий
(в частности, геометрии Лобачевского, эллиптической геометрии и др.).
Лит.: Н. Ф. Четверухин, Проективная геометрия, Учпедгиз, М., 1953;
Н. В. Ефимов, Высшая геометрия, Физматгиз, М., 1961; Ф. Клейн, Неевклидова
геометрия, ОНТИ, М.—Л., 1936; Г. Буземан и П. Келли, Проективная геометрия
и проективные метрики, ИЛ, М., 19 57.
ПРОЕКТИВНАЯ ПЛОСКОСТЬ: Г. П. п. в проективной геометрии —
евклидова плоскость, пополненная бесконечно удаленными элементами (см.). Каждая
прямая дополняется бесконечно удаленной точкой и становится замкнутой.
Семейству параллельных прямых соответствует общая бесконечно удаленная
точка, двум непараллельным прямым соответствуют различные бесконечно
удаленные точки. С аналитической точки зрения П. п. определяется как множество
пропорциональных троек чисел (х1:х2'-*а) — однородных координат текущей
точки Λί# не равных одновременно нулю. В П. п. верна теорема: две
произвольные прямые пересекаются в одной точке или совпадают.
2. П. п. в топологии — топологическое пространство (см.), гомеоморфное
П. п. пункта 1°. Топологической моделью П. п. служит сфера в трехмерном
евклидовом пространстве с отождествленными диаметрально противоположными
точками.
ПРОЕКТИВНО-ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ — раздел
дифференциальной геометрии, изучающий дифференциально-геометрические объекты,
инвариантные относительно проективных преобразований пространства. Для
поверхностей примерами таких объектов могут служить сопряженные сети,
асимптотические направления. Важной главой П.-д. г. является теория конгруэнции (см.)—
двупараметрических семейств линий. В этой теории изучаются фокальные и
развертывающиеся поверхности, фокусы и т. п. Школа П.-д. г. в СССР
создана С. П. Финиковым.
ПРОЕКТИВНОЕ ПРЕОБРАЗОВАНИЕ плоскости (пространства) —такое
точечное взаимно однозначное отображение проективной плоскости (пространства)
в себя, при котором точки, лежащие на одной прямой, переходят в точки,
лежащие на другой прямой.
П. п. проективной прямой называется такое взаимно однозначное
отображение ее в себя, при котором гармоническая четверка точек (см.) этой прямой
переходит в гармоническую четверку точек. Основным инвариантом П. п.
прямой (плоскости или пространства) является сложное отношение (см.) четырех
точек. П. п. (прямой, плоскости, пространства) образуют группу (см.). П. п.
точек М' (х[:х2'.х'з) и Μ (х^-х^:xs) проективной плоскости задается формулами:
*1 = Ρ(αιι*ι+αΐ2*2+αΐ3*3).
*2 =Ρ(α2ΐ*1 + α22*2·Τ-α23*3)»
*з=Р (а31*1+Яз2^2+азз*з)*
Φ О, а р — любое действительное число, отличное от нуля.
где Δ-
а\1 ^12 °13
а21 а22 ^23
аЫ °32 °33
Рассматривают также П. п. евклидовой плоскости (евклидова
пространства), где декартовы координаты (*, у) точки Μ (прообраз) и координаты(χ', у')
точки М' (образ) связаны формулами:
ап*+Д12У+Д1з
У' =
Q2i^+Q22y-fQ23
аз1*-г-аз2у+а3з'

ПРОЕКТИВНЫЕ КООРДИНАТЫ
359
Точки прямой а31*-Ьаз2>'+азз ¥= 0 не имеют себе соответственных (образов), и
поэтому взаимно однозначное соответствие для точек этой прямой нарушается.
Наиболее важным и вместе с тем простейшим примером П. п. является
гомология (см.), оставляющая неподвижными точки некоторой прямой (оси
гомологии), а также некоторую точку вне этой прямой или принадлежащую
этой прямой (особая гомология).
ПРОЕКТИВНОЕ ПРОСТРАНСТВО — евклидово пространство, дополненное
бесконечно удаленными (несобственными) точками, бесконечно удаленными
прямыми, бесконечно удаленной плоскостью. Каждая прямая дополняется только
одной бесконечно удаленной точкой, каждая плоскость — одной бесконечно
удаленной прямой и все пространство — одной бесконечно удаленной плоскостью.
В П. п. нет параллельных прямых и плоскостей: любые две прямые
проективной плоскости пересекаются; любая плоскость пересекается со всякой прямой,
не принадлежащей плоскости; любые две плоскости пересекаются по прямой.
П. п. может быть определено и аксиоматически как совокупность объектов
трех родов: точек, прямых и плоскостей, для которых определены отношения
принадлежности и порядка так, что выполняются определенные требования
системы аксиом проективной геометрии (см.).
П. п. может быть определено и как совокупность точек (хх\ х2: xz: хА)
четверок пропорциональных чисел, из которых хотя бы одно не равно нулю,
являющихся однородными координатами (см.) текущей точки М. Две четверки
чисел (х1:х2:Хъ'-х*) и (λχ1:ίχ2:λχ3:λ xA)i где λ Φ 0, определяют одну и ту
же точку П. п. В П. п/ собственные и несобственные элементы (точки,
прямые, плоскости) совершенно равноправны по своим свойствам.
ПРОЕКТИВНОЙ СВЯЗНОСТИ ГЕОМЕТРИЯ — раздел дифференциальной
геометрии, изучающий пространства проективной связности: каждой точке такого
пространства отнесено «касательное» проективное пространство, а также задан
«проективный перенос» элемента этого касательного пространства по
произвольному пути в «касательное» пространство
произвольной точки. П. с. г. приложима ко многим
вопросам римановой (см.) геометрии.
ПРОЕКТИВНЫЕ КООРДИНАТЫ. П. к. точки
на проективной плоскости — три числа χν х2, хг<
одновременно не равные нулю, определяющие
однозначно положение точки на этой плоскости.
Проективная система координат на плоскости
задается треугольником А1А2А3 и единичной
точкой Е, не лежащей ни на одной из прямых —
сторон треугольника (рис. 232).
Пусть Μ — произвольная точка проективной
плоскости, не лежащая на прямой АгА2л Мх —
проекция ее из точки Аг на прямую А2А3,
Μ2 *— проекция ее из точки А2 на прямую АхАг. Положение точки Мх на прямой
А2АЬ однозначно определяется неоднородной координатой хм относительно
базисных точек /42, Л8, Elt а М2 на прямой АХАЪ определяется неоднородной
координатой Хм относительно базисных точек АгАгЕ2\ тогда точка Μ
однозначно определится как пересечение прямых А1М1 и А2М2.
Однородные П. к. xlt хъ хг точки Μ плоскости относительно базисных
точек Ati А2, А3 и Ε определяются равенствами:
Х2 Х3
Однородные П. к. (хь х2, х3) точки Μ и (I xlt λχ2, λ*3), где λ j= 0,
принимаются за координаты одной и той же точки.
Рис. 232

360
ПРОЕКТИВНЫЕ ФОРМЫ
Прямая на проективной плоскости задается линейным однородным
уравнением:
где числа uit u2t щ называются координатами прямой. Аналогично
определяются П. к. и в пространстве.
П. к. точки на плоскости называются также трилинейными или
треугольными координатами.
ПРОЕКТИВНЫЕ ФОРМЫ 1-й ступени (см. Формы геометрические) — всякие
две формы 1-й ступени, у которых сложные отношения (см.) любых четырех пар
соответственных элементов равны.
ПРОЕКЦИОННЫЙ ОПЕРАТОР —оператор в /2-мерном евклидовом (см.) или
бесконечномерном гильбертовом пространстве (см.), ставящий в соответствие
каждому вектору χ его проекцию на некоторое фиксированное подпространство.
Всякий П. о. является самосопряженным и удовлетворяет условию Р2 = Р.
Обратно, если оператор Ρ самосопряженный и Р2 = Р, то Ρ есть П. о.
Например, пусть Η — пространство интегрируемых на отрезке [—π, π] функций.
Отображение φ(*)->α0» где ао~"~ нулевой коэффициент Фурье функции φ (а:),
переводит все множество Η на подпространство всех функций-констант, заданных на
отрезке [—π, π].
ПРОЕКЦИЯ (центральная) точки Μ на плоскость α — точка М' пересечения
прямой, проходящей через точку Μ и некоторую другую фиксированную точку
S (Ξφα, S ψ Μ), с плоскостью α (рис. 233). При
этом точка S называется центром проектирования,
плоскость α — плоскостью П. или картинной
плоскостью, прямая MS— проектирующей прямой (или
проектирующим лучом). Иногда ради наглядности
точку S называют «глазом», а прямую MS — «лучом
зрения». Точку Μ также называют прообразом
(оригиналом), а точку М' — образом (копией). П. фигуры
Φ на плоскость α называют множество П. всех ее
точек. Центральная П. иначе называется
конической или перспективной. Если точка S удалена в
бесконечность* то в этом случае все проектирующие
прямые параллельны между собой и П.
(центральная) вырождается в параллельную П. или цилиндрическую. Если проектирующие
лучи параллельной П. перпендикулярны плоскости П., то П. называется
ортогональной или прямоугольной.
Параллельная и " ортогональная П. широко используются в начертательной
геометрии (см.). Существуют частные случаи параллельной и ортогональной П.
Аналогично определяется П. точки (прямой) на прямую.
Лат. projectio — отбрасываю вперед, по смыслу означает: изображение,
тень.
Лит.: Е. А. Глазунов и Η. Φ. Четверухин, Аксонометрия, Гостехиздат,
М., 1953.
ПРОИЗВЕДЕНИЕ МНОГОЧЛЕНОВ Ρ и Q определяется как сумма
одночленов, равных произведениям каждого члена многочлена Ρ на каждый член
многочлена Q, т. е. если Ах*1 /'. . . х*п — произвольный член многочлена Ρ и
Вх? х^г .. . хпп — произвольный член многочлена Q» то PQ будет суммой
членов вида АВх*1+$* х**+$* . . . χ*η*^η. Π. м. удовлетворяет закону коммута-
/
/а
Рис
lS
\м
V/
\ /
\
. 233

ПРОИЗВОДНАЯ
361
тивности (см.) и закону ассоциативности (см.), т. е. PQ—QP и (PQ)R=P(QR)
для произвольных многочленов Р, Q и R. П. м. относительно суммы
многочленов (см.) удовлетворяет закону дистрибутивности.
ПРОИЗВЕДЕНИЕ МНОЖЕСТВ — устаревшее название операции пересечения
множеств (см.). Рассматривают также другую операцию над множествами,
называемую внешним произведением множеств (см.).
ПРОИЗВЕДЕНИЕ ТОПОЛОГИЧЕСКОЕ двух топологических пространств
(см.) X. и У есть третье топологическое пространство Z, определяемое так:
множество точек пространства Ζ есть прямое произведение множеств точек X
и У. Множество в Ζ, являющееся прямым произведением двух открытых
множеств в Λ и У, по определению открыто. Система всех таких множеств задает
в Ζ топологию. Например, П. т. двух отрезков есть квадрат, П. т. двух
окружностей есть поверхность тора и т. п. Топологические пространства Ζ^ΧΥ
и Ζ2 = ΥΧ гомеоморфны (см. Гомеоморфизм).
ПРОИЗВОДНАЯ — одно из основных понятий дифференциального
исчисления. Пусть функция y=f(x) определена в некоторой окрестности (см.) точки
х0. П. от данной функции / (х) в данной точке х=х0 (или при данном значе-
АУ
нии х0) называется конечный предел lirn-—, где Δ)>=/(*ο + Δ*)— f(xo) —
δ χ-+ο Δ*
приращение функции (см.), Δ*— приращение аргумента (см.). Если в данной
точке функция f(x) имеет производную, то / {х) непрерывна в этой точке
(см. Непрерывная функция). П. функции у=/ (х) в точке χ является функцией того
™ г-, аУ df(*)
же аргумента х. Для обозначения П. приняты различные символы: —, —-—
(введены Лейбницем), у\ f (χ) (введены Ньютоном), Dy% Df(x) (введены Ко-
ши). Последние два из этих обозначений (Коши) употребляются сравнительно
SJ
О
1 /
/л1
/ \ \ г
t t+nt
Рис. 234
Рис. 235
редко. К понятию П. приводят очень многие задачи математики, физики,
техники и других наук. Приведем из них две важнейшие:
Задача 1 — об определении скорости прямолинейно движущейся точки.
Движение точки задается функцией S=f(t), где S — положение точки
(пройденный путь) в момент времени / (рис. 234). За промежуток времени Д^ точка
переместится из положения Μ в положение Мх и пройдет путь AS = /(i+AO —
— /(/). Отношение — выразит среднюю скорость vCp за промежуток At, кото·
[χι
рая зависит от Δ t> если точка движется неравномерно. Истинная (или мгновен-

362 ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
ная) скорость точки в момент / получится переходом к пределу: и= lim yco==
AS
= lim —. Таким образом, истинная, или мгновенная, скорость υ есть П. от
функции S==/(0» τ· е· П. от пути по времени.
Поэтому в общем случае говорят, что П. есть скорость изменения функции
(по отношению к аргументу).
Задача 2 —«о нахождении касательной к кривой. Пусть кривая задана
Ду
уравнением у=/(*) (рис. 235). Секущая ММг имеет угловой коэффициент fg β=—.
Δ*
Поэтому если функция y=f(x) имеет П. в точке х0, то существует касательная
Ду
к графику функции в х=х0 и tga = lim, tg β = lim —=у'=£ (где k — угловой
Δα'-*0 Δλγ-*·ΟΔΧ
коэффициент касательной). Примеры несуществования П. см. в термине
Односторонняя производная.
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ, заданному единичным вектором
e{cosa, cos β, cosy} or функции u=f{xt у, z) в точке M0(xot y0, z0),
называется конечный предел
,. /(*, у, z) — f(x0, y0, 2?o) du
lim e
Δί-»ο As de
где Д5 > 0, *=*0+As-cosa, y=y0-f-As-cos β, z=20-f-As cos γ. П. п. н.
характеризует скорость изменения функции и в точке М0 по направлению е; cos a,
cos β, cos γ — направляющие косинусы (см.) направления е. Если f(x, у, ζ) —
дифференцируемая функция (см.) в точке Λϊ0, то П. п. н. в точке Μ
существует и равна:
ди ди ди ди
т- = г- cos a + г- cos β+— cos у
dl дх ду dz
ди
или -r = /-grad и [gradи — градиент (см.) функции и], т. е. равна проекции гра-
dl
диента на направление е.
ПРОИЗВОДНАЯ ПРОПОРЦИЯ — пропорция, являющаяся следствием данной
а с a±b c±d а с a+b c+d
пропорции t^T- Примеры П. п.: = Т"» Г— ,* Г = : и АР·
b d с d a±b c±d a-—b c-—d
П. п. используются в тождественных преобразованиях и при решении
дробно-рациональных уравнений.
ПРОИЗВОДНОЕ МНОЖЕСТВО —есть совокупность всех предельных точек
(см.) данного множества. Таким образом, П. м. состоит из всех тех точек
прикосновения (см.) множества М, которые не являются изолированными точками
(см.) М. П. м. всегда замкнуто. См. также Множеств теория.
ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ. Производная порядка η > 2 (ля
производная) от функции y = f(x) в точке х0 есть производная (см.) в точке х0
от производной порядка η—1 (наличие л-й производной в точке х0
предполагает, следовательно, существование (л—1)-й производной в окрестности точки
jc0). Производная л-го порядка обозначается символами:
-^, у("). Dnyt d"/(*oL, /<">(*), Dn(x).
dxn dxn

ПРОМЕЖУТОЧНЫЙ ИНТЕГРАЛ
363
Таким образом, —= » y^=(y(n — *))' и т. д. Обычную производ-
dxr ах
ную называют производной 1-го порядка (первой производной). Производной
нулевого порядка называют самое функцию /(*). Ускорение в прямолинейном
движении s=*f(t) точки есть производная от скорости и, следовательно,
представляет вторую производную —■ от пути по времени (см. задачу 1 в
термине Производная).
ПРОМЕЖУТОК (открытый промежуток или интервал) — множество всех
действительных чисел х, удовлетворяющих неравенствам а < χ < Ъ (знаки
равенств исключаются!), где а и Ъ — некоторые действительные числа, называемые
концами П. Обозначается П. символом (а, Ь). См. Сегмент.
ПРОМЕЖУТОЧНЫЙ ИНТЕГРАЛ дифференциального уравнения F(x9 у,
у', . . ., у(л)) = 0 (*) есть соотношение ψ (jc, у, у', . . ., у(*\ C^+i, . . .«
Сл)=0 (**), в которое входят производные до &-го порядка включительно
(у^ входит непременно) ил — k произвольных постоянных при условии, что
в результате исключения из уравнения (**) и η — k уравнений:
2+2" - +'>+"=°·
dxn-k y -rdyk У
η — k постоянных Ci(i=k+\, . . ., я), мы получим уравнение (*).
В частности, если (**) содержит лишь одну произвольную постоянную, т.е.
Ψ (*» У» У'» У** - · ·» У*1""1· С)=09 то оно называется первым интегралом. П. и.
сам является дифференциальным уравнением порядка k (k < η) относительно у.
Общее решение этого уравнения (см. Общее решение) содержит, кроме η — k
постоянных, входящих в (**), еще k постоянных С19 С2, . . ., С^, т. е.
всего η постоянных и является общим решением уравнения (*). Следовательно,
значение П. и. вида (*) позволяет свести задачу решения уравнения п-го
порядка к решению уравнения порядка k < п.
В частном случае, когда уравнение (*) не содержит у и всех производных
у^т) до £-го порядка (1 < k < η— 1), т. е. имеет вид:
F(x, y{k\ y(k+lK ..., У(п)) = 0* (***)
можно подстановкой y^=z свести его к уравнению порядка η — k < η
F(Xy г, г', . . ., z(n-k))=Q. Общий интеграл уравнения
Ф(х, у<*>, Съ С„ .... С„_*)=0
есть П. и. уравнения (***), содержащий η — k постоянных.
Например, заменяя в уравнении у" — ху'"+У'"=0 у"' = z, имеем: ζ — χζ'+
-f2'=0, откуда находим П. и. исходного уравнения: сх — ζ—с=0, или сх —
сх^ сх^
— у* — с=0. Его общий интеграл у— —Η—— — схх — с2=0 является и об-
о 2
щим интегралом исходного уравнения.

364
ПРОМИЛЛЬ
В другом частном случае, когда уравнение (*) не содержит х, т. е. имеет
вид: F(yt у', у", . . ., у(п)) = 0, оно сводится заменой т~=Р (У — независимое
ах
переменное) к уравнению порядка η—1 относительно р:
общий интеграл которого
Φ (у, ρ, Съ С29 . . ., Сп-1)=0 или Φ (у, -£, Clt С2, . . ., Сп-1)=0
является П. и. и представляет собой уравнение 1-го порядка.
Например, уравнение (d-\-y)y"=yf заменой у'=р, у"=р — приводится к
dy
dp
уравнению (а-ЬУ)-р* τ=Ρ· ^г0 общий интеграл ρ — In [С(а-\-у)] = Ъ является
dy
П. и. для исходного уравнения.
Лит.: В. В. Степанов, Курс дифференциальных уравнений, Физматгиз, М., 1963.
ПРОМИЛЛЬ какого-либо числа — тысячная доля этого числа. Один П.
обозначается 1°/0о· Понятие П.—весьма близкое к понятию процента (см.).
Понятие П. используется в сплавах (проба золота 900, 800 и т. д., где на
1000 частей сплава приходится 900, 800 и т. д. частей чистого золота), в
аптекарских взвешиваниях и т. д.
Лат. promille — на тысячу, за тысячу.
ПРООБРАЗ: 1°. П. элемента b ζ В при отображении φ множества А в
множество В— это всякий элемент α ζ А такой, что элемент b является образом
(см.) элемента а, т. е. φ (а)=Ь.
В геометрии чаще всего под П. элемента понимают точку Μ (прямую,
плоскость и др.), которая преобразуется (отображается) в точку АГ (прямую,
плоскость и др.).
2°. П. подмножества В'аВ — всякое подмножество Л'с Л такое, что В'
является образом множества А\ т. е. φ(/Γ) = £\ Если Аг < Л, множество всех
элементов аг£А таких, что φ (α!) ζ Б', то А' является полным П. множества
В'. Полный П. множества В' (в частности, элемента Ь) обозначается символом
φ-1 (β').
ПРОПОРЦИОНАЛЬНОЕ ДЕЛЕНИЕ — деление какого-нибудь числа (или
отрезка) на части, прямо или обратно пропорциональные данным числам
(или отрезкам). Чтобы разделить данное число на части, пропорциональные данным
числам, надо это число разделить на сумму данных чисел и полученное частное
последовательно умножить на каждое из данных чисел; например, чтобы число
60 разделить на части пропорционально числам 1, 2 и 3, следует выполнить
действия:
(60:6). 1 = 10; (60:6)·2=20; (60:6)·3=30.
Таким образом, 10:20:30=1:2:3.
Для деления числа 60 на две части, обратно пропорциональные числам 1 и
1/3, достаточно разделить число 60 на части, пропорциональные числам,
обратным данным, т. е. на части, пропорциональные числам 1 и 3. Следовательно,
(60:4)· 1 = 15; (60:4).3 = 45. Таким образом, 15:45=1:3.
ПРОПОРЦИОНАЛЬНОСТЬ — один из наиболее простых видов
функциональной зависимости мгжду двумя величинами. Существуют два вида П. между
переменными величинами χ и у — прямая и обратная П. Две переменные величи-

ПРОСТАЯ ДУГА 365
ны χ η у называются прямо пропорциональными (или просто —
пропорциональными), если их отношение в процессе изменения остается постоянным:
bji= ... =const,
хх х2
т. е. при умножении одной из них на любое число вторая умножается на то
же число. Прямая П. между двумя переменными величинами аналитически
выражается формулой: y=kx, где число к называется коэффициентом П. Прямая
П. между двумя величинами графически выражается прямой линией^
проходящей через начало координат и имеющей угловой коэффициент, равный
коэффициенту П.
Две переменные величины χ и у называются обратно пропорциональными,
если их произведение в процессе изменения остается постоянным:
х1у1=х2У2= ··· =const,
т. е. при умножении одной из них на любое число вторая величина делится на
то же число. Обратная П. между двумя переменными величинами аналитически
выражается формулой: y=k:x, где £—-коэффициент П. Графически обратная
П. представляется равнобочной гиперболой (см.).
ПРОПОРЦИОНАЛЬНЫЙ ЦИРКУЛЬ — инструмент для уменьшения (или
увеличения) отрезков в некотором (ограниченном в своих пределах) отношении,
а также для деления отрезков на равные части. П. ц.
состоит из двух стержней, шарнирно скрепленных
между собой и несущих на себе шкалы (рис. 236)
наиболее распространенных отношений. На основании
свойства подобия фигур имеем отношения расстояний:
ab:AB=Oa:OA, т. е. отметка (х) — черточка будет
соответствовать числу (отношению), стоящему против
деления шкалы.
ПРОПОРЦИЯ — равенство двух отношений а:Ь=
= c:d. Числа а, 6, с, d называются членами П.,
причем а и d — крайними, Ъ и с — средними. Основное
свойство П.: произведение крайних членов П. равно
произведению средних (ad = bc). Прибавляя (или
вычитая) к обеим, частям (от обеих частей) П. по
единице и производя другие тождественные
преобразования, получим новые П., называемые производными
пропорциями (см.). См. также Арифметическая
пропорция.
ПРОСТАЯ ДРОБЬ (то же самое, что и обыкновенная дробь, или
арифметическая дробь, или дробное число) — число, составленное из одной или
нескольких равных долей (частей) единицы. Иными словами, арифметическая или П. д.
есть отношение двух натуральных чисел. Подробнее см. Дробь, Смешанное
число.
ПРОСТАЯ ДУГА — непрерывный и взаимно однозначный образ отрезка.
1°. П. д. на плоскости может быть задана уравнениями: Λ·=φ(ί), y=ty(t)y
где φ и ψ-—непрерывные функции параметра t, /0 < t < /α (t0 < tx), причем
различным значениям / соответствуют различные точки Λϊ(φ(/), ψ(/)). График
непрерывной на отрезке функции y=f(x) является П. д. *=/, y=f(t).
2°. П. д. в /г-мерном пространстве может быть задана уравнениями:
*ι = Φι(0. *2 = <Р2(0. ···> *я=Фл(0.
где ФЛО» Фг(0« · · ·* Ф« (0 — непрерывные функции параметра t\

366
ПРОСТОЕ ЧИСЛО
причем различным значениям t соответствуют различные точки П. д.:
Λ* (Φι (О. ..·. Фл<0)·
Примеры: 1. П. д. ОЛВ — часть синусоиды (рис. 237) можно задать
уравнениями:
η
x=tt y^sintt 0</<—;
П. д. COD (рис. 237) можно задать уравнениями: x=2t—1, y = \2t—1|,
0«ζ/< 1. 2. Более сложным примером П. д. может служить график функции
(рис. 238):
( χ sin χ при 0 < χ < 1,
\ 0 при *=0.
3. Уравнения x=acost, y=asin t, z=—t, 0 ^ t < 2jt задают П. д. в
пространстве — один виток винтовой линии AEF с шагом h = AF (рис. 239). П. д. может
быть также ломаная, как COD (рис. 237).
Рис. 237 Рис. 238 Рис. 239
ПРОСТОЕ ЧИСЛО — всякое натуральное число ρ > 1, натуральные
делители которого исчерпываются лишь двумя числами 1 и р. По определению 1 не
является простым числом, так как имеет лишь единственный натуральный
делитель (самого себя). Натуральные числа, отличные от 1 и не являющиеся
простыми, называются составными. П. ч. существует бесконечно много — это
содержание Евклида теоремы. Вопрос о распределении П. ч. в натуральном ряду
очень труден. Фундаментальные результаты в этом направлении получены
П. Л. Чебышевым.
Самое большое число, о котором было известно к 1958 г., что оно П. ч.,
является 23217— 1. В десятичной записи оно содержит 969 цифр.
Лит.: Р. Τ ρ о с т, Простые числа, ИЛ, М., 1959; Г. Н. Б е рма н, Число и наука о
нем, Гостехиздат, М., 1954.
ПРОСТРАНСТВЕННАЯ КРИВАЯ —■ кривая, не являющаяся плоской кривой
(см.). П. к. может быть задана в декартовых координатах как пересечение двух
поверхностей:
FAx, У, z)=0 и FAx, У, z)=0.
В параметрической форме П. к. может быть задана уравнениями:
*=Φι(0. У=Ф2(0. г=<Р3(0·

ПРОСТЫХ ЧИСЕЛ ТАБЛИЦЫ
367
П. к. иначе называется кривой двоякой кривизны. П. к. может быть
определена как кривая, кручение (см.) которой не тождественно равно нулю. Примерами
П. к. могут служить кривая Вивиани (см.) и винтовая линия (см.).
ПРОСТРАНСТВЕННО-ОДНОСВЯЗНАЯ ОБЛАСТЬ — область трехмерного
пространства, в которой каждый замкнутый контур можно стянуть в точку
(не выходя за пределы области). П.-о. о. часто просто называют односвязной
областью; полное название употребляется в отличие от поверхностно-односвязной
области (см.).
Примерами П.-о. о. могут служить все пространство, пространство с
выколотой точкой, область между двумя концентрическими сферами и т. д. Не
являются П.-о. о. пространство с удаленной из него прямой* внутренность тора
(см.) и др.
ПРОСТРАНСТВО — см. Линейное пространство, Топологическое
пространство, Метрическое пространство, Проективное пространство, Пространство функций.
ПРОСТРАНСТВО ФУНКЦИЙ, непрерывных на отрезке, — множество всех
непрерывных на отрезке [а, Ь] функций, рассматриваемое как метрическое
пространство (см.), в котором расстояние между точками пространства, функциями
f(x) и g(x) принимается максимум |/(х)— g(x)\ на отрезке [а, Ь]9 т. е.
Ρ (/(*)* g(x))= max \f(x) — £(*)!· ή· Φ· обозначается часто символом
С (а, Ь).
ПРОСТЫХ ЧИСЕЛ ТАБЛИЦЫ. Неограниченность числа простых чисел
среди всех натуральных чисел была известна еще в древности (во времена
Евклида). Самые ранние сведения о составлении П. ч. т. относятся к XVII в.: Ка-
тальди (1603) в Болонье составил П. ч. т. до 750, Шутен (1657) — до 10000.
Первыми, более значительными явились П. ч. т., составленные В. Лебегом
(1864). В это же время в глухом Уральском селе составлял П. ч. т.
талантливый математик-самоучка И. М. Первушин. Он посвятил этому труду более
сорока лет (1854—1897) своей жизни и составил П. ч. т. до 10 000 000. Это были
первые обширные (мощные) П. ч. т. в России. Петербургская Академия наук
нашла невозможным опубликовать таблицы Первушина из-за их большого
объема (на 750 листах, заполненных мелким бисерным почерком), и рукопись была
передана на хранение в архив Академии наук. К сожалению, этот огромный
труд Первушина остался забытым некоторыми позднейшими математиками, даже
занимавшимися теорией чисел (например, академиком Д. А. Граве).
В те же годы в Венскую Академию наук были представлены, казалось,
совершенно невероятные П. ч. т.—до 100 330 201 и притом содержащие не
только все простые числа, но и наименьшие делители всех чисел, взаимно простых
с 2, 3, 5 и 7. Автором этих таблиц явился выдающийся феноменальный
вычислитель, профессор Пражского университета Я. Ф. Кулик. Эти таблицы —
результат поистине титанического двадцатилетнего труда автора — не были
опубликованы из-за их очень большого объема и переданы на хранение в архив
Академии наук (см. Таблицы Кулика).
В 1914 г. в Вашингтоне Д. Н. Лемер опубликовал П. ч. т. от 1 до
10 006 721.
Таблицы Я. Ф. Кулика после проверки были использованы при составлении
П. ч. т. 11-го миллиона (от 10 006 741 до 10 999 997), изданных в 1951 г. в
Амстердаме (соавторы Я. Ф. Кулик, Л. Полетти и Р. Портер).
Недавно (1959) К. Л. Бейкер и Ф. Ю. Грунбергер составили П. ч. т.
(микрофильм) всех первых 6 миллионов простых чисел. Оказалось, что 6 000 000-е
простое число равно 104 395 301, т. е. π (104 395 302)=6 000 000.
К настоящему времени разными авторами составлены П. ч. т. для
отдельных интервалов натурального ряда, выходящих за пределы первых 10
миллионов, например для 16-го миллиона (Дарфи), для промежутка от 14 984 970 до
19 225 210 и для небольших промежутков 33-го, 35-го, 44-го, 53-го, 59-го и

368
ПРОТИВОПОЛОЖНЫЕ ТЕОРЕМЫ
77-го миллионов, а также других промежутков (Полетти). Самым большим из
таких списков простых чисел, составленных Полетти, является список 116 683
простых чисел, расположенных между 10 000 813 и 5 101 683 361.
Таким образом, в настоящее время наиболее полными и самыми мощными
П. ч. т. являются таблицы Кулика (в рукописи) — до 100 330 201 и таблицы
Бейкера и Грунбергера (в микрофильме) — до 104 395 301.
Лит.: И. Я. Д еп ма н, Замечательные славянские вычислители Г. Вега и Я. Ф. Кулик,
«Историко-математические исследования», вып. 6, Гостехиздат, М., 1953; Α. Ε. Ρ а и к,
Уральский математик Ива;! Михеевич Первушин, «Историко-математические исследования»,
вып. 6, Гостехиздат, М., 1953; В. Се ρ π и и с к и й, Что мы знаем и чего не знаем о
простых числах, перев. с польск., Физматгиз, М., 1963.
ПРОТИВОПОЛОЖНЫЕ ТЕОРЕМЫ — две теоремы, условие и заключение
любой одной из которых являются отрицанием условия и заключения другой.
П. т. называются также взаимно противоположными теоремами. См. также
Теорема, Обратная теорема, Необходимое условие, Достаточное условие,
Критерий.
Лит.: И. С. Град штейн, Прямая и обратная теоремы, Физматгиз, М., I960;
В. В. Репьев, Общая методика преподавания математики, Учпедгиз, М., 1958.
ПРОТИВОПОЛОЖНЫЕ УГЛЫ —
углы с общей вершиной, образуемые при
пересечении двух прямых, такие, что
стороны одного угла являются
продолжением сторон другого угла. На рис. 240
П. у. являются 1 и 2, 3 и 4. П. у. также
называются двугранные углы с общим
ребром, образуемые при пересечении двух
плоскостей, такие, что грани одного угла
являются продолжением граней другого
Рис. 240 угла (рис. 240). П. у., рассматриваемые как
в планиметрии, так и в стереометрии, равны
между собой. П. у. иначе называют вертикальными углами, хотя этот термин
является менее оправданным.
ПРОТИВОПОЛОЖНЫЕ ЧИСЛА — два действительных числа, равные по
модулю, но противоположные по знаку. Например, 2 и —2, у 3 и — V Ъ, а и
— а являются парами П. ч. На числовой оси П. ч. изображаются точками,
расположенными по разные стороны от начала отсчета (нулевой точки) и на равном
расстоянии от этого начала.
ПРОЦЕНТ какого-либо числа — сотая часть этого числа. П. обозначается
знаком %. Понятие П. часто используется в хозяйственных, финансовых,
статистических расчетах для характеристики и сравнения изучаемых величин или
явлений.
Если сумма а рублей положена в банк (сберкассу) при условии р% годовых
(р простых П.), то по истечении / лет сумма а превратится в сумму х, опре-
ра
деляемую формулой *—а+7^Г*· При этом предполагается, что по истечении
каждого года ρ % от первоначального вклада изымаются так, что П.
начисляются с первоначального взноса, а не с наращенного.
Если % годовых прибавляется к первоначальному взносу и через t лет
взнос а (руб.) принимает значение χ (руб.), то определяется формулой
а 1 +
100/

ПРЯМО ПРОПОРЦИОНАЛЬНЫЕ ВЕЛИЧИНЫ
369
В этом случае при каждом вычислении П. в новом году расчет ведется с
наращенного взноса, т. е. с денег, когда к первоначальному взносу
прибавляются ρ % годовых. Такие П., в отличие от обычных (простых) П., называются
сложными (проценты начисляются с учетом процентов), и сама формула
называется формулой сложных П.
Лат. pro cent — за сто, на сто.
ПРЯМАЯ ЛИНИЯ — одно из основных понятий геометрии, косвенное
определение которому дается при аксиоматическом построении курса геометрии.
П. л. евклидовой плоскости может быть определена как геометрическое место
точек (см.), декартовы (или аффинные) координаты которых удовлетворяют
уравнению:
Ах+Ву+С=0,
где числа А и В не равны нулю одновременно.
Немецкий ученый Г. Лейбниц определял П. л. как линию, делящую
плоскость на две конгруэнтные части, но под это определение подходят и другие
линии, например синусоида, и все правильные ломаные линии, каждые два
звена которых, взятые через одно, параллельны.
ПРЯМАЯ ПРИЗМА — призма (см.), ребра (или же грани) которой
перпендикулярны ее основанию.
ПРЯМОЕ ПРОИЗВЕДЕНИЕ двух множеств X и У — третье множество Z,
элементами которого являются всевозможные пары (х, у), где χζΧ, y^Y»
Понятие П. п. часто используется во многих отделах математики. См., например,
Произведение топологическое.
ПРЯМОЙ КРУГОВОЙ КОНУС (в элементарной геометрии) — конус (см.),
основанием которого является круг и вершина которого проектируется в центр
основания. Часто под конусом и понимают П. к. к. См. также Коническая
поверхность, Линейчатая поверхность.
ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД — параллелепипед, боковые ребра (или грани)
которого перпендикулярны его основанию. П. п. называется прямоугольным,
если основанием его служит прямоугольник. См. Параллелепипед, Призма.
ПРЯМОЙ УГОЛ — угол, равный (конгруэнтный) своему смежному (см.).
П. у. содержит 90°, или 0,5π радианов (см.). Часто П. у. обозначается буквой
d. П. у. можно разделить циркулем и линейкой на три равные части (см.
Трисекция угла). В основаниях геометрии доказывается, что П. у. существует и
что все П. у. равны друг другу.
ПРЯМОЙ ЦИЛИНДР — цилиндр (см.), образующие которого
перпендикулярны плоскости направляющей. П. ц., направляющая которого есть окружность,
называется прямым круговым цилиндром. См. также Цилиндрическая поверхность,
Линейчатая поверхность.
ПРЯМОЛИНЕЙНЫЕ ОБРАЗУЮЩИЕ поверхности — прямые, от движения
которых образуется поверхность. Так, на однополостном гиперболоиде и
гиперболическом параболоиде расположены два семейства П. о. На конусе,
цилиндре, плоскости, геликоиде также имеется П. о.
П. о. поверхности целиком принадлежит этой поверхности. См. Линейчатая
поверхность.
ПРЯМО ПРОПОРЦИОНАЛЬНЫЕ ВЕЛИЧИНЫ — две переменные величины χ
и у, отношение между которыми в процессе их изменения все время остается
постоянным, т. е. у : χ=const, или у: x=k, где число k называется
коэффициентом пропорциональности.
П. п. в. называют чаще пропорциональными величинами. П. п. в. можно
определить и как две переменные величины, увеличение (уменьшение) одной из
которых в несколько раз влечет за собой соответственно увеличение
(уменьшение) другой величины во столько же раз.
-4 Толковый словарь математических терминов

370
прямоугольник
Примеры П. п. в.: 1) стоимость товара и его вес (при одинаковой цене
товара); 2) пройденный путь и время при равномерном движении материальной
точки. См. также Пропорциональность.
ПРЯМОУГОЛЬНИК — параллелограмм, у которого один из углов при
вершине прямой (отсюда вытекает, что и все углы прямые). У П. диагонали равны.
П. имеет в общем случае две оси симметрии. Вокруг П. можно описать
окружность. Если стороны П. соизмеримы, то его можно разрезать (раскроить)
на равные квадраты. П., у которого две смежные стороны (а следовательно,
и все стороны) равны, называется квадратом (см.).
ПРЯМОУГОЛЬНЫЕ ЧИСЛА — см. Фигурные числа, Многоугольные числа.
ПРЯМОУГОЛЬНИКОВ ФОРМУЛА —формула для приближенного вычисле-
Ь
ния определенных интегралов. Рассматривая определенный интеграл { f (x) dx
а
как площадь некоторой фигуры, ограниченной кривой y=f(x)» мы разбиваем
Рис. 241
Ъ — а
эту фигуру (рис. 241) на полоски шириной Δ*/= (п — число точек
деления интервала интегрирования), а затем каждую полоску приближенно
заменяем прямоугольником с высотой /(ξ/) (для /-й полоски):
ί
/(*)^«-^·[/(ξο) + /(ξι)+ ··· +/<bi-i)l·
Обычно считают, что
Xi+Xi+г
= х ! . /(E/W(* , )-У , β
'+Т
'"+ у Н- -у '»
тогда
f(x)dxK (у , +у3+ ··· +У ι )·
п Ύ Τ ""Τ

ПСЕВДОСФЕРА
371
Дополнительный член Rn П. φ., характеризующий погрешность этой
приближенной формулы, имеет вид:
«и-
(Ь-
24/z2
-Г (ξ), гдеа<£<6.
Лит.: Г. Μ. Φ и χ τ е н г о л ь ц, Курс дифференциального и интегрального исчисления,
т. II, Физматгиз, М., 1963.
ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ — частный случай аффинных (общих
декартовых) координат, когда оси координат взаимно перпендикулярны. При
этом если длины единичных векторов по осям (масштабные единицы измерения)
равны, то П. к. называются прямоугольными декартовыми координатами. См.
также Координаты.
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК (в геометрии Евклида или геометрии
Лобачевского) — треугольник, имеющий прямой угол. Сторона с, лежащая против
прямого угла, называется гипотенузой П. т., стороны а и Ь, заключающие
прямой угол, называются катетами П. т. Для П. т. в геометрии Евклида
справедливо равенство c2=a2-f-&2. См. Пифагорова теорема.
ПСЕВДОГРУППА — совокупность элементов произвольной природы с
операцией, определенной, в отличие от группы (см.), не для всех упорядоченных пар
элементов. Элементы П. и операция должны удовлетворять следующим
требованиям: 1) если а* (6*с), (а*Ь)*с определены, то а*(Ь*с) = (а*Ь)*с\ 2)
существует элемент е такой, что еа—ае определены и равны а при любом a£G;
3) для любого а существует а—1 такой, что αα~~ι определено и равно е. Любая
группа есть в то же время П.
Пример. Совокупность преобразований вида:
Х' = , V :
b0i-b1x+b2y
Ср+СгХ+СгУ Р(х\ У')
' ά0+άχχ+ά&1 D(x, у)
фО
[где D(x/ y'):D(x, у) означает якобиан (см.) преобразования] образует П.
относительно суперпозиций (см.) этих преобразований. Эта П. не является
группой.
ПСЕВДОВЕКТОР— вектор, определенный с точностью до постоянного
множителя λ Φ 0 (вектор-направление). П.—то же, что и осевой вектор (см.)
или аксиальный вектор.
ПСЕВДОСКАЛЯР — число, отнесенное к некоторой системе координат и
меняющее знак на противоположный при переходе к другой системе координат,
если якобиан (см.) перехода отрицателен. Примером П. может служить
смешанное произведение базисных векторов евклидова пространства,
элемент площади поверхности (см.) и др.
ПСЕВДОСФЕРА — поверхность вращения трактрисы (см.)
вокруг ее базы (асимптоты) (рис. 242). Название П.
связано с тем, что ее полная (гауссова) кривизна (см.)
постоянна и отрицательна: k= — I : α2, где а — отрезок
касательной, заключенный между точкой касания к трактрисе и ее
базой, в то время как полная кривизна сферы 0(R)
постоянна и положительна: k—\ : R2 (П.—ложная сфера).
Важность П. состоит в том, что на ней частично
реализуется плоская неевклидова геометрия Лобачевского, что
было установлено уже после смерти Лобачевского
итальянским геометром Бельтрами в 1868 г. Этот факт положил
конец спорам о реальности геометрии Лобачевского.
24*

372
ПТОЛЕМЕЯ ТЕОРЕМА
В более общем понимании П. называется поверхность постоянной
отрицательной кривизны, на которой установлено движение в достаточно малой
окрестности (куске) ее. При этом роль прямых линий на П. играют геодезические
линии (см.) так, что через каждую точку поверхности проходит только одна
геодезическая линия.
ПТОЛЕМЕЯ ТЕОРЕМА — теорема элементарной
геометрии, устанавливающая зависимость между
сторонами и диагоналями четырехугольника, вписанного
в окружность: во всяком выпуклом четырехугольнике,
вписанном в окружность, произведение диагоналей
равно сумме произведений его противоположных сторон,
т. е. имеет место равенство (рис. 243):
AC-BD=AB.CD+BC-AD.
Рис. 243 П. т. названа по имени древнегреческого ученого
Птолемея Клавдия, доказавшего эту теорему. П. т.
используется при решении задач по элементарной геометрии, при доказательстве
частного случая теоремы (формулы) сложения синусов.
ПУАССОНА ИНТЕГРАЛ: 1°. П. и. в гармоническом анализе интеграл вида:
1 ρ Я2__ г2
— 1 /(Θ) ав=и(г, φ),
2jiJ П ' ^2_2^rcos(0-<p)-b/·2
о
где г, φ — полярные координаты. П. и. выражает значение гармонической
функции (см.) внутри круга радиуса R через значения этой функции на
окружности /(Θ). Впервые был дан Пуассоном в 1823 г.
оо β
2°. П. и, в теории вероятностей — интеграл f e~~x~dx= у π , похожий на
—оо
интеграл, который участвует в выражении нормального закона распределения;
впервые вычислен Эйлером.
ПУАССОНА РАСПРЕДЕЛЕНИЕ —важный частный случай распределения
случайной величины ξ, принимающей значения 0, 1, 2, . . . , k. Значение k
принимается с вероятностью Ρ^(λ) = (λ!°: k\) ё~~х\ здесь λ — параметр.
Математическое ожидание и дисперсия ξ равны λ.
П. р. возникло из следующей задачи: имеется η равновозможных событий
(вероятности —); какова вероятность того, что наступит ровно k из
рассматриваемых событий. Оказывается, что при больших η эта вероятность
приближенно равна Ρβ(λ).
ПУАССОНА ТЕОРЕМА — теорема, утверждающая, что если имеется η
независимых испытаний, в каждом из которых вероятность появления события А
равна р, где ρ мало, а п велико, то вероятность того, что событие А произошло
ровно т раз, приближенно равна (A,'f : т\) е~'\ где λ=ηρ (см. также
Пуассона распределение).
ПУСТОЕ МНОЖЕСТВО — множество, не содержащее ни одного элемента.
Введение П. м. в математику весьма удобно. П. м. является подмножеством
(см.) любого множества. Если два множества не имеют общих элементов, то
говорят, что их пересечение (см.) является П. м.
Пример. Множество действительных корней квадратного уравнения x2-f-3=0
является П. м.

ПУЧОК СФЕР
373
ПУЧОК — семейство линий на плоскости или поверхностей в пространстве,
линейно зависящее от одного параметра. Часто рассматривают следующую
конструкцию. Пусть Fx(x, у)=0 и F2 (х, у)—0 — уравнения плоских линий. Тогда
X1/71-f-X2F2=0 (где параметры λχ и λ2 не равны нулю одновременно) будет
уравнением П.; это уравнение фактически зависит от одного параметра (Xj: λ2).
Аналогично записывается П. поверхностей в пространстве. Линии Fx(x, у) =0,
F2(xt y)=0 называются образующими П. Множество точек пересечения каждых
двух линий П. называется носителем П. (для П. прямых называется также
центром пучка). Носитель П. плоских линий может состоять как из
действительных, так и из мнимых точек П. См. также Пучок окружностей, Пучок
плоскостей, Пучок сфер.
ПУЧОК ОКРУЖНОСТЕЙ — пучок (см.) плоских линий, образующими
которого являются окружности. Или иначе: П. о. есть семейство окружностей,
лежащих в одной плоскости и проходящих через две точки, которые могут быть
действительными (различными и совпадающими) или мнимыми. Соответственно
с этим и П. о. называется эллиптическим, параболическим или гиперболическим.
Существует бесконечное множество окружностей, ортогональных ко всем
окружностям П. о. Это множество окружностей само образует П. о., который
называется П. о., сопряженным данному. Эллиптический П. о. сопряжен с
гиперболическим, параболический — с параболическим. Понятие П. о. используется при
изучении радикальной оси (см.) и при решении задач на геометрические
построения. П. о. можно также определить как множество окружностей, общих
двум связкам окружностей, лежащим в одной плоскости.
Лит.: Д. И. Перепелкин, Курс элементарной геометрии, ч. 1—2, Гостехиздат,
М., 1948—1949; Ж. А д а м а р, Элементарная геометрия, Учпедгиз, М., ч. 1, 1948, ч. 3,
1938; Ф. Клейн, Высшая геометрия, М.—Л., 1939.
ПУЧОК ПЛОСКОСТЕЙ — множество плоскостей, проходящих через одну и
ту же прямую — ось П. п. или параллельных некоторой плоскости (П. п. с
несобственной осью). Если ось П. п. задана в виде пересечения двух плоскостей:
i41^+J31y+C1z-hD1«0 (^i^O),
A2x+B2y+C2z+D2=Q (F2=0),
то П. п. (любая его плоскость) может быть определен уравнением: λ1Ρ1+λ2Ρ2=0ί
где \γ и λ2 одновременно не равны нулю. Плоскости F^O и F2=0 называются
образующими П. п.; П. п. линейно зависит от одного параметра (отношения 1г: λ2).
Понятие П. п. довольно часто используется при решении задач в аналитической
геометрии (см.). См. также Пучок.
ПУЧОК ПРЯМЫХ — множество прямых, лежащих водной плоскости и
проходящих через одну и ту же точку S или параллельных одной и той же
прямой. Точка S называется центром или носителем П. п. Если (л:0, у0) — центр
П. п., то уравнения прямых пучка будут иметь вид: А (х — х0)=В(у— у0).
Если П. п. задан парой прямых:
AiX+Bj+C^O,
А2х+В2у+С2=0,
то уравнения прямых пучка будут иметь вид:
λχ (Ахх+Вху+d)+X2 (А2х+В2У+С2)=0.
П. п. представляет собой однопараметрическое семейство прямых, линейно
зависящих от параметра (Хг : λ2) (см. Пучок).
ПУЧОК СФЕР — семейство сфер, линейно зависящих от одного параметра.
Всякая пара сфер П. с. пересекается по некоторой окружности действительного,

374
ПФАФФА УРАВНЕНИЕ
нулевого или мнимого радиуса. В соответствии с этим П. с. называется
эллиптическим, параболическим или гиперболическим. П. с. есть пространственный
аналог пучка окружностей. См. Пучок, Пучок окружностей.
ПФАФФА УРАВНЕНИЕ —уравнение вида:
X1dx1-jrX2dx2+ ··· +Xndxn=:Qi
где Xlf X2t ... ι Χ η — функции переменных хг, х2, . . . , хп. Это уравнение
названо по имени немецкого математика Пфаффа, учителя Гаусса. П. у.
равносильно некоторой системе уравнений в частных производных. В отличие от
обыкновенных дифференциальных уравнений, произвол общего решения П. у., вообще
говоря, не определяется несколькими произвольными постоянными. Этот
произвол характеризуется несколькими функциями определенного числа переменных;
количество таких функций и количество их переменных определяются
характерами П. у. В самом простом случае решение П. у. имеет вид:
Ф(хг, *а, .. . , хп) = С-
Такое уравнение называется вполне интегрируемым. Критерием полной
интегрируемости являются равенства:
dXt dXf . . f o
я =я С' ' = 1' 2, .... я).
οχ; όχι
Теория П. у., а также теория систем П. у. играют большую роль в
механике неголономных систем и термодинамике. Системы П. у. систематически
использовались в трудах французского геометра Э. Картана, создавшего
мощный метод в многомерной дифференциальной геометрии (см. Метод внешних
форм).
Лит.: П. К. Ρ а ш е в с к и й, Геометрическая теория уравнений в частных производных,
Гостехиздат, М., 1953; СП. Фиников, Метод внешних форм Картана, Гостехиздат,
М., 1951.

Ρ
РАВЕНСТВО — два выражения, соединенные знаком =. Р. могут быть как
верные, так и неверные, как числовые, так и буквенные. Верное Р. обладает
свойствами: 1) рефлексивности (Л=Л); 2) симметричности, или взаимности,
Л = £, В=А\ 3) транзитивности А=В, В=С, тогда и Л = С. Частными случаями
верного Р. Р. являются уравнения и тождества.
По другому определению Р. к этому понятию относят только верные Р.,
а неверные Р. совсем не включаются в это определение.
РАВЕНСТВО МНОГОЧЛЕНОВ. Два многочлена над полем К по
определению считаются равными, если их канонические представления (см. Каноническое
представление многочлена) таковы, что для всякого члена в представлении
одного из них найдется подобный член с равным коэффициентом в представлении
другого многочлена. Разность равных многочленов является нуль-многочленом
(см.).
РАВЕНСТВО МНОЖЕСТВ. Два множества Ли В равны (символически А=В),
если множество А является подмножеством в множестве В и, обратно,
множество В является подмножеством в множестве Л, т. е. если АаВ и ВаА.
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК —треугольник, две"~стороны которого
равны. Две равные стороны Р. т. называют боковыми сторонами, а третью
сторону — основанием. Р. т. имеет по крайней мере одну ось симметрии. Углы
при основании Р. т. равны. Высота Р. т., проведенная из вершины на
основание, одновременно является его медианой и биссектрисой. Р. т. иначе
называется равнобочным. Если боковая сторона равна основанию, то Р. т. называется
равносторонним (см.).
РАВНОБОЧНАЯ ГИПЕРБОЛА —то же, что и равносторонняя гипербола
(см.).
РАВНОБОЧНАЯ ТРАПЕЦИЯ — трапеция, у которой углы при основании
равны. Боковые стороны Р. т. равны. Диагонали Р. т. равны. Сумма углов при
боковой стороне Р. т. равна двум прямым. Вокруг всякой Р. т. можно описать
окружность. Р. т. имеет ось симметрии. Р. т. иначе называется равнобедренной
трапецией. См. также Трапеция.
РАВНОВЕЛИКИЕ ФИГУРЫ — плоские фигуры, имеющие равные площади,
или пространственные фигуры (тела), имеющие равные объемы. Всякие два
простых равновеликих многоугольника будут и равносоставлены (Бойаи — Герви-
на теорема). Два равновеликих многогранника, вообще говоря, не будут равно-
составленными (Дена — Кагана теорема). См. Гильберта проблемы.
Лит.: В. Г. Болтянский, Равновеликие и равносоставленные фигуры, Гостехиздат,
М., 1960.
РАВНОМЕРНАЯ СХОДИМОСТЬ: 1©. Р. с. ряда функций flt f2t . . . , fni ...
на данном множестве k функции Φ означает, что для всякого ε>0
существует Ν (ε) такое, что при всех η>Ν выполняется неравенство \fn—Ф| < ε
при любых χ из данного множества. Так, например, ряд функций уп=хп на
любом отрезке [0; 1—ε] е>0 сходится равномерно к нулю (нуль-функция).
Ряд может сходиться равномерно на одном множестве и сходиться неравномерно
на другом. Рассмотренный ряд функций на отрезке [0, 1] сходится, но
неравномерно. Во многих задачах анализа применяется теорема, использующая понятие
равномерной непрерывности: если ряд /х, Д, . . ., fn, .. . равномерно сходится

376
РАВНОМЕРНОЕ ПРИБЛИЖЕНИЕ
к Φ (обозначается /£-*Ф), то ряд 2 {f/л (*)</*} равномерно сходится к
§Φ(χ)άχ.
2°. Р. с. несобственного интеграла, зависящего от параметра. Говорят, что
00
Г /(х, \)dx сходится равномерно к Φ (λ), если для всякого ε>0 существует
о
Ν (ε) такое, что при всех a>N(e) выполняется неравенство
j f(Xt λ)<**-Φ(λ)
<ε
при любых значениях λ. Ρ. с. интеграла дает возможность менять порядок
интегрирования у несобственных двойных интегралов.
РАВНОМЕРНОЕ ПРИБЛИЖЕНИЕ—-приближение функции Φ функциями
f\* fi* · · · 1 /η· · · · > когда за меру уклонения // от Φ взята верхняя грань
модуля разности:
р(Л, Ф) = вир|Ф —Л|,
χ 6 2
где Ω — множество чисел, на котором производится приближение.
Если Φ и /j(i = l, 2 η, . . .) непрерывны, а Ω компактно (см.), то
знак верхней грани можно заменить знаком максимума.
РАВНОМЕРНО НЕПРЕРЫВНАЯ ФУНКЦИЯ: 1°. Р. н. ф. от одной
переменной называется Р. н. ф. на отрезке а <; χ < Ь (интервале, множестве), если
для любого ε>0 существует такое 6>0, что для любых значений хх и х2
из отрезка (интервала, множества), отстоящих друг от друга меньше чем на
б>0 (|*1 — х3| < &)» выполняется неравенство: |/(х2) — /(*i)| <β·
Р. н. ф. на отрезке (интервале, множестве) непрерывна на этом отрезке
(интервале, множестве). Функция, непрерывная на отрезке, является Р. н. ф.
на этом отрезке; для интервала а<х<Ь это утверждение может быть неверным:
например, y=tgx непрерывна на интервале 0<*<0,5π, но не является Р. н. ф.
на этом интервале.
2°. Р. н. ф. от нескольких переменных u=f(xx xn) = f(P) называется
Р. н. ф. на множестве D, если для любого е>0 существует 6>0 такое, что
для всех точек Рх и Р2. Ρ(^ι. ^г)<^ выполняется неравенство \f(Px)—
ь—/(^2)1<8» гДе Ρ(^ι» Λί) обозначает расстояние (см.) между точками Рг иР2
в η -мерном пространстве.
Если функция u = f(P) непрерывна в замкнутой ограниченной области Di
то она является Р. н. ф. в этой области. Справедлива теорема: функция,
непрерывная в каждой точке компактного множества, является Р. н. ф. на этом
множестве. Для некомпактных множеств 1акая теорема неверна. См. Компактные
множества.
РАВНОМОЩНЫЕ МНОЖЕСТВА —то же, что и эквивалентные
множества (см.).
РАВНОСИЛЬНЫЕ УРАВНЕНИЯ — уравнения, имеющие одни и те же
корни с учетом их кратностей. Например, уравнения: а) х2—4=0, |л| = 2
равносильные, так как они имеют одни и те же корни: хх=--—2, х^—2\ б) χ — у=0,
х — y-f-1 = 1 также равносильны; в) х2—1=0 и χ—1=0 не будут
равносильными, так как первое из них имеет два корня ± 1, а второе только один
корень: дг=1; г) (х—1)2=0 и χ — 1 = 0 неравносильные, так как множества
корней этих уравнений не совпадают; д) }/ (x—>6)(x-\-\)='\f8 и }ί χ— 6 χ

РАДИАН
377
Х\/х-Н=У^ неравносильные, так как первое из них имеет в области
действительных чисел два корня: хг =—2, л:2 = 7, а второе только один корень: х=7\
е) χ=χ+\ и ех=— е равносильные, так как множество решений каждого из
них пустое.
Вопрос о Р. у. возникает уже при решении уравнений первой степени
с одним неизвестным, наиболее же полное освещение он получает при решении
иррациональных уравнений (см.) и простейших трансцендентных уравнений:
тригонометрических, показательных и логарифмических. Р. у. иначе называются
эквивалентными. Аналогично определяется и равносильность систем уравнений:
системы уравнений называются равносильными, если они имеют одинаковое
множество решений. Например, системы уравнений χ — у = 5, х+у = 7 и χ — 2у=4,
л:=б являются равносильными, так как они имеют одно и то же решение:
я = б, у=1.
Р. у. можно определить и так: уравнения (или системы) называются
равносильными, если каждое решение первого уравнения (или системы) является
решением второго уравнения (или системы), и наоборот.
РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ семейства функций — важное
свойство некоторых семейств функций. СемейстЕО функций {/ } равностепенно
непрерывно, если для любого ε > 0 существует такое δ> 0, что при любых хх и х2 \ xt — χ2\ <δ
неравенства | /а (хх) — /а (х2) \ < ε выполняются для всех функций / . В
теореме Арцела (см.) критерий компактности (см.) множества функций в равномерной
сходимости] используется термин Р. н.
РАВНОСТОРОННИЙ КОНУС —прямой круговой конус (см.), образующая
которого равна диаметру основания конуса. Плоскость, проходящая через ось
вращения (высоту) Р. к., пересекает его по равностороннему треугольнику.
РАВНОСТОРОННИЙ ТРЕУГОЛЬНИК —треугольник, у которого все
стороны равны между собой. Р. т.— один из видов правильных многоугольников (см.).
Р. т. имеет три оси симметрии, пересекающиеся в точке, которая одновременно
является центром его тяжести, ортоцентром (см.), центром вписанной и описанной
окружностей. Р. т. называется также равноугольным или правильным треугольником.
РАВНОСТОРОННИЙ ЦИЛИНДР—прямой круговой цилиндр, высота
которого равна диаметру его основания. Плоскость, проходящая через ось вращения
Р. ц., пересекает его по квадрату.
РАВНОСТОРОННЯЯ ГИПЕРБОЛА — гипербола (см.), у которой
действительная и мнимая оси равны. Простейшее уравнение Р. г. в прямоугольных
координатах имеет вид: х2— y2=a2i где а — действительная и мнимая полуось.
Асимптоты Р. г. взаимно перпендикулярны. Если за оси координат принять
асимптоты Р. г., то ее уравнение будет иметь вид: y=k : χ. График обратной
пропорциональной зависимости, изучаемой в курсе элементарной алгебры, есть
Р. г. Р. г. иначе называют равнобочной гиперболой.
РАВНОЧИСЛЕННЫЕ МНОЖЕСТВА — см. Эквивалентные множества.
РАДИАН — центральный угол, опирающийся на дугу (окружности), длина
которой равна радиусу (рис. 244). Если полный угол (360°) соответствует длине
360°
всей окружности 2π#4 то один Р. содержит ——=57° 17'44" с точностью до
1". или с точностью до 0,1 градуса; 1 радиан = 57,3°. Таким образомв имеем:
π
90е — -— радианам, 180° = π радианам, 360° = 2π радианам и т. д. При переводе
градусной меры угла в радианную и обратно используется зависимость:
180° л^
π α
где α — радианная, arc — градусная мера одного и того же угла (дуги).

378
РАДИАННАЯ МЕРА УГЛА
Если / — длина дуги, α ·— радианная мера угла, соответствующего этой дуге,
a R — радиус окружности, то имеет место формула / = #·α.
РАДИАННАЯ МЕРА УГЛА. Пусль ЛОБ —данный угол и окружность
с центром в точке О и радиусом R (рис. 245) пересекает стороны угла в точках
А и В. Тогда число, равное отношению длины дуги ЛВ окружности О (R) к ее
радиусу, называется Р. м. у. При этом если угол больше 360°, т. е.
R/ \^ = ^~- [радиан)
а \
Рис. 244 Рис. 245
^=360ο·Α2+α0ί где 0°<а0<360, то Р. м. у. а равна 2jt/z-fP. м. у. а0. За
единицу измерения Р. м. у. принят один радиан (см.). Р. м. у. играет большую
роль в вопросах высшей математики, так как, используя понятие Р. м. у.? ряд
формул в математике (нахождение производной тригонометрической функции,
разложение тригонометрической функции в степенной ряд и др.) упрощается.
Р. м. у. называется также радианной мерой дуги (окружности).
РАДИКАЛ — математический знак у , обозначающий действие извлечения
корня л-й степени из какого-либо числа а\ это записывается так: у а.
Лат. radix — корень.
РАДИКАЛЬНАЯ ОСЬ двух окружностей — геометрическое место точек
плоскости, имеющих одну и ту же степень (см. Степень точки) относительно этих
окружностей. Р. о. есть прямая, перпендикулярная к линии центров данных
окружностей. Концентрические окружности Р. о. не имеют. Из каждой точки
Р. о., внешней по отношению к данным двум окружностям, можно провести
к ним равные касательные.
РАДИКАЛЬНАЯ ПЛОСКОСТЬ двух сфер — геометрическое место точек
пространства, имеющих одну и ту же степень (см. Степень точки) относительно
этих сфер. Р. п. есть пространственный аналог радикальной оси (см.) двух
окружностей, поэтому свойства Р. п. аналогичны свойствам радикальной оси.
РАДИКАЛЬНЫЙ ЦЕНТР трех окружностей (сфер) — точка, имеющая одну
и ту же степень (см. Степень точки) относительно этих окружностей (сфер).
В Р. ц. пересекаются три радикальные оси (радикальные плоскости) этих
окружностей (сфер), взятых попарно. Если центры трех окружностей (сфер)
лежат на одной прямой, то Р. ц. или не существует, или их бесчисленное
множество.
РАДИУС окружности (сферы) — отрезок* соединяющий любую ее точку
с центром. Р. также называют и длину этого отрезка. Р. окружности (сферы)
также называют Р. круга (шара), граница которого есть данная окружность
(сфера).
Лат. radius — спица колеса, луч.
РАДИУС КРИВИЗНЫ — радиус круга кривизны (см.) в данной точке
кривой.
РАДИУС СХОДИМОСТИ— см. Круг сходимости.
РАДИУС-ВЕКТОР ТОЧКИ Μ плоскости (пространства) — вектор, или отрезок,
начало которого совпадает с некоторой фиксированной точкой О плоскости (про-

РАЗДЕЛЕННЫЕ РАЗНОСТИ
379
странства), а конец — с точкой М. Точка О может совпасть с полюсом полярной
системы координат или с началом декартовой прямоугольной системы координат.
РАДИУС СХОДИМОСТИ — радиус круга сходимости степенного ряда (см.) —
оо
такое число /*, что степенной ряд 2 anzn сходится при |z|<r и расходится
/г=0
при \z\>r. Для определения радиуса сходимости существует несколько формул,
например формула Даламбера
1
I I
или формула Коши
1
lim η/г ,
пчюоГ \ап\
РАЗВЕРНУТЫЙ УГОЛ — угол, стороны которого составляют одну прямую.
Р. у. равен 180°, или π радианам. Р. у. иначе называется выпрямленным углом.
РАЗВЕРТКА: 1°. Р. кривой — отрезок прямой, длина которого равна длине
этой кривой. Разыскание такого отрезка называется спрямлением или
ректификацией кривой. Иногда под Р. кривой понимают ее эвольвенту (см.).
2°. Р. многогранника — множество многоугольников — граней этого
многогранника, для которых указан порядок их склеивания по сторонам и вершинам
с тем, чтобы получить данный многогранник.
3°. Р. поверхности, допускающей изгибание (см.),— совокупность плоских
фигур, изометричных кускам данной поверхности, из которых можно склеить
эту поверхность. Например, Р. прямого кругового конуса есть круговой сектор
вместе с кругом — основанием конуса.
Понятие Р. используется в элементарной геометрии, в черчении, топологии
и в геометрии выпуклых поверхностей.
Лит.: Б. Кутузов, Геометрия, Учпедгиз, М., 1957; А. Д. Александров,
Внутренняя геометрия выпуклых поверхностей, Гостехиздат, М., 1948; П. С.
Александров, Комбинаторная топология, Гостехиздат, М., 194 7 (гл. 3).
РАЗВЕРТЫВАЮЩАЯСЯ ПОВЕРХНОСТЬ — поверхность (см.), которая при
помощи изгибания (см.) может быть наложена (развернута) на плоскость. Всякая
Р. п. линейчата, полная кривизна (см.) Р. п. равна нулю. См. также Ребро
возврата.
РАЗВЕТВЛЕНИЯ ТОЧКА многозначной аналитической функции f(z) —
точка, обход вокруг которой в комплексной области по окружности любого сколь
угодно малого радиуса с центром в этой точке, так что данная функция
изменяется непрерывно, приводит к значениям, не совпадающим с первоначально
выбранными. Например, для функций -/г—1 и Ln(z—1) точка 2=1
является Р. т. При однократном обходе вокруг нее значение первой функции меняет
знак, а значение второй приобретает слагаемое 2ш. Р. т. называется также
точкой ветвления.
См. также Аналитические функции, Аналитическое продолжение.
РАЗДЕЛЕННЫЕ РАЗНОСТИ— отношения разностей значений некоторой
функции к разностям соответствующих значений аргумента. Р. р. используются при
интерполировании и приближенных вычислениях, когда значения функций
рассматриваются при неравноотстоящих друг от друга значениях аргумента. Иногда
говорят «разностные отношения». См. Исчисление конечных разностей.

380 РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ
РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ на множители — тождественное
преобразование многочлена в произведение нескольких множителей. В средней школе Р. м.
выполняется (в основном) следующими способами:
1) вынесение за скобки общего множителя:
a2b*+ca2b* — а*Ь* = Ь*а2 (b+вс — а2)\
2) использование формул сокращенного умножения и деления:
аз _ £з=(а _ b) (a2+ab+b2yf
3) группировка слагаемых:
а2Ь ±аЧ — bc2+dc2+2acd=b(a2 — c2)+d (а2+2ас+с2) =
=6 (а+с) (а — c)+d (а+с)2 = (а+с) [Ь (а — c)+d {а+с)\;
4) разбиение слагаемых:
c2 + 12c-f-32 = c2-f-8c-f 16+4с-Ь
+ 16=(с+4)2+4(Н-4) = (с+4) (с+8).
Всякий многочлен от действительного переменного α0χη+α1χη—ι-\-...+αη
с действительными или комплексными коэффициентами представляется в виде
α0χη-\·αιχη-1+. . .+ап=а0(х — хг)(х — х2) · . .(* — *„),
где х1% х2, . . ., хп—корни многочлена. Многочлен с действительными
коэффициентами разлагается на множители первой и второй степени с действительными
коэффициентами. Существуют многочлены с рациональными коэффициентами, не
разлагающиеся на рациональные множители (см. Неприводимые многочлены).
Если многочлен с целыми коэффициентами разлагается на множители с
рациональными коэффициентами, то он разлагается на множители и с целыми
коэффициентами (см. Лемма Гаусса). Можно рассматривать также разложение
целых функций в бесконечные произведения:
оо
л=1
См. Бесконечные произведения.
РАЗМЕРНОСТЬ геометрической фигуры — число, равное единице, если фигура
есть линия, равное двум, если фигура есть поверхность, равное трем, если
фигура есть тело. Общее определение Р. любого замкнутого множества,
лежащего в w-мерном евклидовом пространстве, было дано советским математиком
П. С. Урысоном, который построил теорию Р.—одну из глубоких теорий
современной топологии (см.). Р. иначе называется числом измерений.
Лит.: П. С. Александров, Комбинаторная топология, Гостехиздат, М., 194 7
(гл. 5иб); Л. С. Понтрягин, Основы комбинаторной топологии, Гостехиздат, М.,
1947 (§3); В. Г у ре вич и Г. Волмэн, Теория размерности, 1948; П. С. Урысоп,
Труды по топологии и другим областям математики, тт. 1—2, 1951.
РАЗМЕЩЕНИЕ — одно из понятий комбинаторики (см.)· Р· из η элементов
по k называется всякое упорядоченное подмножество, состоящее из k элементов
множества из η элементов. Два Р. считаются различными, если они различаются
либо составом элементов, либо порядком элементов. Число различных Р. из η

РАЗРЫВА ТОЧКА
381
элементов по k обозначается символом А„ (А— начальная буква французского
. п\ ь
слова «размещение»). Число Р. Ап = связано с числом сочетания С„
(п — k)\
соотношением:
<-к\ С*.
Пример. Сколько существует трехзначных чисел, записываемых нечетными
цифрами: 1, 3, 5, 7, 9, и в записи каждого из которых участвуют различные
неповторяющиеся цифры?
Франц. arrangement — размещение.
РАЗМЕЩЕНИЕ С ПОВТОРЕНИЯМИ из η элементов множества М=
= {а19 аъ .... ап] по k — всякая конечная последовательность, состоящая из
k членов, причем члены ее являются элементами рассматриваемого множества М.
Два Р. с п, йг· a-t 9 . . ., aik и а, а, , . . ·, я*Л считаются различными,
если хотя бы на одном месте они имеют различные элементы множества Λί»
т. е. если хотя бы для одного r(l^r^k) справедливо неравенство air £a.]r .
Число различных Р. с п. из η элементов по k равно nk . Если в некотором Р. с п.
элемент af встречается на ρ местах и только на ρ местах, то говорят, что a-t
повторяется в рассматриваемом Р. с п. ρ раз.
РАЗНОСТНАЯ ПРОГРЕССИЯ — то же, что и арифметическая прогрессия (см.).
РАЗНОСТНАЯ ПРОПОРЦИЯ — то же, что и арифметическая пропорция (см.).
РАЗНОСТЬ — результат вычитания: 1°. Р. двух чисел а и b (уменьшаемого
а и вычитаемого Ь) — такое третье число с—а — Ь, что его сумма с b равна о,
т. е. с-\-Ь=а.
2°. Р. двух векторов А и В — такой вектор С,- что его сумма с В равна А»
т. е. С+В = А. Графически А, В, С образуют треугольник. См. Разность
арифметической прогрессии, Разность множеств, Векторное исчисление.
РАЗНОСТЬ АРИФМЕТИЧЕСКОЙ ПРОГРЕССИИ — число d, прибавлением
которого к любому члену арифметической прогрессии (см.) получается
следующий член прогрессии. Иными словами, Р. а. п. есть результат вычитания любого
предыдущего члена из следующего за ним.
РАЗНОСТЬ МНОЖЕСТВ А и В — множество всех тех элементов множества
Л, которые не входят в множество В. Р. м. А и В обозначается символом А\В
(или символом А — Б, или А-т-В). Иногда термин Р. м. применяют лишь к
случаю, когда В является подмножеством множества А. Р. м. является пустым
множеством (см.) тогда и только тогда, когда А является подмножеством Б,
т. е. Α<ζ3.
Р. м. является одной из основных операций над множествами. Для
сравнения Р. м. с другими операциями над множествами см. Теоретико-множественные
операции.
Пример. Пусть А — множество всех треугольников и В — множество
прямоугольных треугольников, тогда А\В — множество косоугольных
треугольников, т. е. треугольников, у которых ни один угол не является прямым.
РАЗРЫВА ТОЧКА — значение аргумента, при котором данная функция
разрывна (см. Разрывные функции). Р. т. разделяются на два рода. Р. т. первого
рода называется точка а, в которой существуют левый и правый пределы, т. е.
Игл/(а-) и lim/ (x).
χ-*α-~ 0 х-+а+0
(*)

382
РАЗРЫВНАЯ ФУНКЦИЯ
Когда эти пределы равны между собой, тогда функция / (х) может быть сделана
непрерывной при x~at если положить
f(a) = \\mf(x) = l\mf(x)
х-р-а—0 х-+а+0
(устранимый разрыв). Р. т. второго рода характеризуется тем, что по крайней
мере один из пределов (*) не существует (т. е. равен ±оо).
Еще более сложным видом Р. т. (относящимся также ко вюрому роду)
являются точки такие, что один из пределов (*) не существует и не равен
бесконечности, как, например, у функции y=sin (1 : χ) в ючке *=0.
РАЗРЫВНАЯ ФУНКЦИЯ — функция, которая хотя бы при одном значении
аргумента не является непрерывной (см. Непрерывная функция). Р. ф. относятся
к классам Бэра начиная с первого. Примеры: y=cos(l : χ) разрывна в точке *=0,
функция Дирихле (см.) разрывна в каждой точке.
РАЗРЯД (в арифметике) — место, занимаемое цифрой при написании числа
в позиционной системе (см.). В десятичной системе цифры 1-го разряда — единицы,
2-го — десятки и т. д.
РАНГ КВАДРАТИЧНОЙ ФОРМЫ —ранг матрицы этой квадратичной формы
(см. Матрица квадратичной формы).
РАНГ МАТРИЦЫ — наивысший порядок минора этой матрицы (таблицы),
отличного от нуля, т. е. если ранг матрицы равен /г, то среди миноров порядка к
этой матрицы есть по крайней мере один, отличный от нуля, но все миноры
матрицы порядка k-\-\ и более высокого равны нулю. Рассмотрим, например,
матрицу:
/1 3 6 3\
3 0 0 9
V2 2 4 6/,
содержащую 3 строки и 4 столбца. Вычеркивая строки и столбцы так, чтобы
число остающихся строк и столбцов было одинаково, составляем из оставшихся
строк и столбцов определители разных порядков этой матрицы. Все определители
3-го порядка, полученные таким путем:
113 6
3 0 0
2 2 4
>
1 3 3
3 0 9
2 2 4
»
1 6 3
3 0 9
2 4 6
»
3 6 31
0 0 9
2 4 6|
как легко видеть, равны нулю,
личные от нуля, например:
Среди же определителей 2-го порядка есть от-
6 3
О 9
3 О
2 2
Следовательно, ранг рассматриваемой матрицы равен 2. Справедлива теорема:
Р. м. равен максимальному числу линейно независимых строк матрицы, а также
максимальному числу линейно независимых столбцов. Понятие Р. м. часто
используется в линейной алгебре (см., например, Кронекера — Капелли теорему).
Лит.: И. М. Гельфанд, Основы линейной алгебры, Гостехиздат, М., 1951;
Ф. Р. Гантмахер, Теория матриц, Гостехиздат, М., 1953.
РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ. При формальной подстановке х0
вместо аргумента в функции, стоящей под знаком предела, и при дальнейших
вычислениях часто приходят к числовым выражениям типа:
— , -, О.оо, 0°, оо°, оо — оо, I00,
О оо

РАСПРЕДЕЛЕНИЕ
383
которые, взятые отдельно, лишены математического смысла. Однако при
значениях аргумента, близких к рассматриваемому, функция может иметь вполне
определенные значения. Поэтому естественно считать, что при х=х0 функция
принимает такое значение, которое мало отличается от соседних. Строго говоря,
мы полагаем, что
/(*0) = lim/(x),
(*)
если, конечно, такой предел существует.
Р. н. заключается в вычислении истинного значения предела (*). Все
неопределенности путем несложного преобразования приводят к неопределенности типа
О
-—. При Р. н. этого типа используется правило Лопиталя (см. Лопиталя
правило). См. также Неопределенные выражения.
РАСПАДАЮЩАЯСЯ КВАДРАТИЧНАЯ ФОРМА — квадратичная форма (см.),
представимая в виде произведения двух линейных форм. Квадратичная форма
над полем комплексных чисел является Р. к. ф. тогда и только тогда, когда ее
ранг меньше или равен 2.
Квадратичная форма над полем действительных чисел является распадающейся
тогда и только тогда, когда ее ранг меньше или равен 1 или же когда ее ранг
равен 2, а сигнатура (см.) равна нулю.
РАСПРЕДЕЛЕНИЕ — одно из основных понятий теории вероятностей. Р.
вероятностей случайной величины ξ, принимающей конечное число значений,
задается указанием, с какой вероятностью величина ξ принимает данное свое
значение. Р. таких величин удобно задавать таблицей. Аналогично задается Р.
величины ξ, принимающей значения^, х%, . . .»
...,xni... (дискретное Р,). Однако многие
случайные величины множеством своих
значений имеют множества чисел отрезка.
Обычно в подобных случаях
бессодержательно говорить о вероятности того,
что ξ принимает значение, равное данному
(такая вероятность равна нулю).
Вероятность Р(х, dx) неравенства χ<ξ<χ+άχ
есть бесконечно малая величина, в общем
случае того же порядка, что dx, т. е.
Р(х, dx) = q(x)dx+0(dx).
Функция q(x) называется плотностью
вероятности (см.). Ее графиком может
быть задано распределение
(дифференциальный закон распределения).
Рассматривается также F (х) — вероятность
неравенства ζ<χ. Функция F и ее график
называются интегральным законом
распределения. Легко видеть, что
Рис. 246
F(x)= ]q(t)dt.
Вероятность неравенства a<i<b в терминах F и q выражается так:
F(b) — F(a) и ]q(t)dt.

384
РАСПРЕДЕЛИТЕЛЬНЫЙ ЗАКОН
Примером дискретного Р. является Пуассона распределение (см.). Примерами
непрерывных Р. являются: 1) нормальное, или гауссово, распределение:
F{x)= I , e 2σ2 dt (рис. 246, α),
J 1/2 πσ
—oo
ι ΐχ~α)2
g(x)=—z=—e 2σ' (рис. 246,6),
ΐ/2πσ
где α, σ — параметры;
2) распределение по закону треугольника:
У=
О при | я — α |>с,
c+JC — а
при —c<x — a<0 (рис. 246, в,г),
с — х+а
при с>х — а>0,
где а, с — параметры. Важнейшими характеристиками Р. являются
математическое ожидание (см.) и дисперсия (см.) См. также Моменты.
РАСПРЕДЕЛИТЕЛЬНЫЙ ЗАКОН — см. Закон дистрибутивности
РАССТОЯНИЕ — неотрицательное число р (Mlt M), сопоставляемое всякой
упорядоченной паре точек какого-либо пространства (в частности, паре точек
прямой, плоскости, обычного трехмерного пространства). Это число называют
также Р. между точками Μ и Мх. Обычно требуют, чтобы Р. удовлетворяло
следующим аксиомам метрического пространства (см.): 1) аксиома тождества:
ρ (Αΐι, Μ)—0 в том и только том случае, когда Μ совпадает с М19 т. е. М^Мг;
2) аксиома симметрии: р (ML,M)=p{M, Mv)\ 3) аксиомы треугольника: ρ (Μ, Μχ) ■]-
+ ?(Mlt Λί2)>ρ(Λί, Μ2).
Примеры: 1. См. в термине Метрическое пространство. 2. За Р. между
точками на поверхности обычно принимается длина отрезка геодезической линии
(см.), соединяющей эти точки. В частности, на сфере расстояние между точками
измеряется длиной дуги окружности большого круга, проходящего через эти
точки (из двух дуг выбирается меньшая). 3. Для путешественника в гористой
местности естественно считать Р. между двумя пунктами наименьшее время,
необходимое для перехода из первого пункта во второй. В этом примере Р. не
удовлетворяет аксиоме симметрии.
Лит.: Ю. А. Шрейдер, Что такое расстояние? Физматгиз, Μ., Ι963.
со
РАСХОДЯЩИЙСЯ ИНТЕГРАЛ—интеграл вида § f (x) dx такой, что
а
А
lim [f(x)dx равен ±с© или же отсутствует вовсе, где f (х) определена в про-
межутке [а, со] и интегрируема в любой его части [α, Λ]. Такой Р. и. называют
также несобственным, в отличие от интеграла в собственном смысле. Например,
со
f cos x dx и I — являются Р. и., так как первый вообще не имеет значения на
верхнем пределе (sin x при jc->oo не стремится ни к какому пределу), а второй
равен бесконечности.

РАСХОДЯЩИЙСЯ РЯД
385
Если подынтегральная функция / (х) внутри промежутка интегрирования
Ь
[α, b] обращается в бесконечность в точке с, то интеграл | / (jc) dx понимают
а
в смысле предела:
Если этот предел конечен, то интеграл сходится, если бесконечен (т. е. равен
±оо) или его нет совсем, то имеем Р. и.
Существуют методы, позволяющие в некоторых случаях и расходящимся
интегралам приписывать обобщенные значения. Если f(x) определена для х>0 и
интегрируема в обычном смысле в любом конечном промежутке [0, χ], но не
интегрируема в промежутке [0, оо], и если существует конечный предел
X . X X
lim—\ F (u)du=ll среднего значения —\ F (и) du функции F (x)= \ f(t) dt\t
Х~*°° о \ о о /
то это число / и считают обобщенным значением интеграла, a f(x) — интегри-
X
руемой в обобщенном смысле. Например: {cosxdx = — sin x; его среднее значе-
о
1 Г · α ι· I 1 I · а Ι ι· — cosx+l
ние —\$,mudu имеет предел lim I — — \ sin χ dx\= lim , равный
χ J χ -#- л Ι χ ) Ι *->οο χ
ο ο
нулю; следовательно, Р. и. в обобщенном смысле равен нулю.
оо
Если для f(x) интеграл \ f(x)dx не существует, но сходится интеграл,
\f(x)e—kxdx (k>0) и существует конечный предел / = lim f e~kx f(x)dxt ίο
о *-*° о
этот предел можно также рассматривать как обобщенное значение интеграла,
расходящегося в обычном смысле. Например:
оо
lim I e—kx cos χ dx=\im-——г = 0.
fe-*oJ Λ-^ο^-τ-Ι
о
оо
Снова получили для обобщенного значения интеграла J cosa:c?x = 0 (см. Инте-
о
грал).
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального
исчисления, т. II, Физматгиз, М., 1963.
РАСХОДЯЩИЙСЯ РЯД —ряд, имеющий бесконечную сумму (т. е. сумма
00
его равна ±оо) или же вообще не имеющий суммы. О двух Р. р. ^ Сп и
25 Толковый словарь математических терминов

386
РАЦИОНАЛЬНАЯ ФУНКЦИЯ
У\ Сп говорят, что из них второй расходится медленнее, чем первый, если его
частичная сумма Sn является бесконечно большой низшего порядка по срав-
S'n оо
нению с частичной суммой Sn первого: lim—=0. Для каждого Р. р. 2 Сп
n->ooSn 71_j
можно построить ряд, медленнее расходящийся. С этой целью можно, например,,
взять ряд:
оо оо
Поэтому никакой Р. р. не может служить универсальным средством для
установления путем сравнения с ним расходимости других рядов. Для исследования Р. р.
вводится понятие обобщенного суммирования и обобщенной суммы (см. Ряды).
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
тт. II, III, Физматгнз, М., 1963.
РАЦИОНАЛЬНАЯ ФУНКЦИЯ — функция вида:
*/ ч PW _αοΧη+<*ιΧη-1+···+<'η
ПХ) Q(x) bQxm + b1x'n-^'^bmi
где α/, bi — постоянные числа (а0Ф0, b0^~Q)f a n и т — целые
неотрицательные числа. Р. ф. представляет собой отношение двух целых Р. ф.
(многочленов) (см.). Р. ф. определена для всех значений *, кроме тех, которые обращают
в нуль знаменатель Q {х). Если х0 — корень кратности k знаменателя Q (х)
и кратности r(r>k) числителя Р(х), то Р. ф. имеет в точке х0 устранимый
разрыв; при r<k P. ф. имеет в точке х0 бесконечный разрыв (полюс) (см.).
При т=0 Р. ф. называется целой Р. ф. или многочленом. При п=т = 1
Р. ф. называется дробно-линейной Р. ф. (см.), имеющей вид:
ах-\-Ь
у=
сх-\-а
РАЦИОНАЛЬНЫЕ ЧИСЛА—все целые и дробные числа, как
положительные, так и отрицательные, и число нуль. Всякое рациональное число можно
Ρ
представи!ь в виде отношения двух целых чисел: —, где ρ и q — взаимно
простые целые числа и q Φ 0.
2
Примеры: числа 1;—5;—; 0; 0,(3) — рациональные; множество Р. ч. всюду
о
плотное (см.), т. е. в множестве действительных чисел между любыми двумя
Р. ч. гх и г2 всегда найдется хотя бы одно (отсюда вытекает и бесчисленное
Г1 + Г2
множество) рациональное число, например число г3=—г—; множество Р. ч.—
счетное и представляет собой группу (см.) относительно операции сложения
(вычитания и умножения).
Лат. ratio—отношение; здесь понимается как отношение целых чисел.

РЕГУЛЯРНАЯ ТОЧКА
387
РАСШИРЕННАЯ МАТРИЦА системы уравнений-
щая системе т линейных уравнений с η неизвестными:
матрица, соответствую-
aii*i-bai2*2-b· *
'-\-а\пхп—Ьц
•-\-а2пхп = Ь2,
#mi*i+£tfz2*2+· '' Л-О-тп^п^Ьт.
Р. м. с. у. получается добавлением к матрице системы столбца из свободных
членов.
||а„ avl . .
; α2ι α22 .
Шт\ #/И2 ·
• ат bi\
. а2п b2\
• · атп ®γη\
Равенство рангов матрицы системы и Р. м. с. у. является необходимым и
достаточным условием для, совместности системы линейных уравнений. Это
утверждение является содержанием теоремы Кронекера-Капелли (см. Кронекера-Ка-
пелли теорема).
РЕБРО ВОЗВРАТА развертывающейся поверхности — линияf совокупность
точек касательных к которой составляет эту поверхность. Доказывается, что у
всякой развертывающейся поверхности,, кроме конуса, цилиндра и плоскости,
существует Р. в. Р. в. является кривой, состоящей из особых точек
поверхности. Каждая плоская кривая, принадлежащая развертывающейся поверхности и
пересекающая Р. в., имеет в точке пересечения точку возврата.
Другим определением Р. в. является следующее: если задана
развертывающаяся поверхность как однопараметрическое семейство прямых I (t)t тогда
основания общих перпендикуляров прямых I (t) и /(*+Δθ при Д^ —+ 0
образуют Р. в.
РЕГИОМОНТАНА ФОРМУЛА — формула плоской тригонометрии,
устанавливающая зависимость между длинами двух сторон треугольника и тангенсами
полусуммы и полуразности противолежащих им углов. Р. ф. имеет вид:
а-Ъ tg~^~
a+b
tg
А + В
где α, b — стороны треугольника, Л, В — соответственно противолежащие этим
сторонам углы.
Р. ф. также называется формулой (теоремой) тангенсов. Р. ф. названа по
имени немецкого астронома и математика Иоганна Мюллера (по-латински
Regiornontanus), установившего эту формулу. И. Мюллера называли «Кенигсбер-
жец», т. е. житель Кенигсберга: по-немецки Konig — король, царь, Berg —
гора, а по-латински «король» и «гора» в родительном падеже — regis и montis.
Отсюда «Региомонтан» — латинизированная фамилия И. Мюллера.
РЕГУЛЯРНАЯ ТОЧКА: 1°. Р. т. аналитической функции — такая точка,
что в некоторой ее окрестности функция может быть разложена в степенной
ряд.
2°. Р. т. дифференциального уравнения:
а2у dy
■^•2-bPi (x) — +Ръ (х) У = 0,
— точка, являющаяся полюсом функции рд порядка не выше k(k = lt 2).
25*

388
РЕЗОЛЬВЕНТА
3°. Р. т. разрыва функции / (х) — точка *0 такая, что выполняется равенство:
/(*) = у{/(*+0)+/(*-0)).
4°. Р. т. системы линейных уравнений с переменными коэффициентами —
значения параметров, при которых ранг матрицы системы не ниже, чем во всех
точках достаточно малой окрестности Р. т.
РЕЗОЛЬВЕНТА: 1°. Р. линейного оператора (см.) А — оператор Γχ ♦
обратный оператору Л—λ Ε и обозначаемый (А — λ £)—*. Здесь λ — произвольное
комплексное число, Ε— тождественный оператор. Р. оператора Л,
определяемого равенством:
ъ
Af(x)=$k(x,t)f(t)dt,
а
где k(x, t) непрерывна, есть мероморфная функция (см.) по λ, полюсы которой
совпадают с собственными значениями оператора Л. Зная Р. оператора Л,
можно сразу написать решение интегрального уравнения Фредгольма:
ъ
J*(x, t)y(t)dt-ly(x) = g(x)t
а
именно:
У=ГХ£(д:).
2°. Р. уравнения п-й степени:
/ (χ)=α0χη+α1χη-ι+ ·. · +ал=0,
неприводимого над данным полем ω, — уравнение g(x) =0 (g(x)— многочлен)
такое, что присоединение одного из корней уравнения g(x)—0 к полю ω дает
поле, содержащее все корни уравнения f(x)=Q.
Р. уравнения четвертой степени является уравнением не выше третьей
степени. Для уравнений степени л>4 степень Р., вообще говоря, больше п.
Знание корней Р. позволяет найти корни уравнения /(x)=0 при помощи решения
более простых уравнений.
Понятие Р. возникло в связи с задачей решения произвольного уравнения
п-й степени. Р. играет важную роль в классическом труде Э. Галуа. Важную
проблему теории, носящую ныне имя автора, решил советский математик
Н. Г. Чеботарев (1931).
См. также Поле, Неприводимый многочлен, Неприводимое уравнение.
Лат. resolvo — решаю, развязываю.
РЕЗУЛЬТАНТ двух многочленов:
ГМ-а^+а^-^+.-.+ап и g(x)^b9xm+blx^-^+. · .+Ьт (ап^0> Ьт^0)
есть определитель:
I а0 аг а2 . . . ап 0 0 ... О I
О а0 ах . . . α„_χ ап 0 ... О
О 0 Oq ... ап-2 ап-х ап . . . О
Ь\ Ь2 Ь3 . . . а0 аг а2 . . . ап
Ь0 Ьг Ь2 . . . Ът а0 аг . . . ап—1
О Ь0 Ьг . . . Ът—ι Ьт а0 . . . ап—2
6 0 0* .'. '. Ь0 ' b[ ' Ь2 . l.'b'm '

РЕКУРРЕНТНАЯ ФОРМУЛА
389
Если Р. равен нулю, то многочлены / (х) и g (x) имеют общий делитель степени
больше нуля, и наоборот. Р. /(х) и g (х) выражается через корни xlt x2, . . .,
хп функции f(x) и корни ylt y2» · · ч Ут функции g(x) по формуле:
η т
R(f, έΤ)=«Π Π (Xi-yk).
i=l k=\
Лит.: Б. Л. Ван дер В а р д ν н, Современная алгебра, пере в. с нем., Гостехиздат,
М., 1947.
РЕКУРРЕНТНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — последовательность,
удовлетворяющая рекуррентной формуле (см.). В частности, под Р. п. понимают
последовательность ип, л = 1, 2, . . . , удовлетворяющую равенству:
"/i+fc=ai"rt+fc-i+a2"n+*-2+ · · ·-¥akun(n>\). (*)
Такую Р. п. также называют возвратной последовательностью, а число k — ее
порядком. Равенство (*), называемое возвратным уравнением порядка k%
является по существу уравнением в конечных разностях, а теория Р. п. является
одним из разделов исчисления конечных разностей (см. Конечных разностей
исчисление). Частными случаями Р. п. являются арифметическая (k=2) и
геометрическая (£=1) прогрессии, а также последовательность л-х степеней
натуральных чисел (k=n-{-\). Последовательность коэффициентов в выражении
D0+Dlx+D2x*+ · · · +Dnxn+
полученном делением многочлена /-й степени на многочлен £-й степени,
расположенный по возрастающим степеням:
B0+B1x+B2x^---+Bkxk (В0Ф0),
также является, начиная с некоторого номера, Р. п. порядка k, а именно:
Dn+k=—-rDn+k-1 "TDn при п>1-п+\.
Последний пример носит весьма общий характер: оказывается, что произвольная
Р. п. ип(п=\, 2, . . .) порядка £, удовлетворяющая уравнению (*), есть
последовательность коэффициентов частного, полученного от деления некоторого
многочлена на многочлен
1 — ахх а^хк.
Теория Р. п. является аналогом теории линейных дифференциальных
уравнений с постоянными коэффициентами. Так, например, все Р. п.,
удовлетворяющие уравнению (*), образуют векторное пространство (см.) размерности к.
Если λ0 — корень характеристического уравнения \k=ax λΛ—1-f-a2 λΛ—2-f· \-a^t
то геометрическая прогрессия со знаменателем λ0 есть Р. п., удовлетворяющая
уравнению (*). Если все корни \lt λ2 . . ., λ# этого характеристического
уравнения различны, то геометрические прогрессии со знаменателями λΐ9 λ2, . . .,λ#
образуют базис векторного пространства решений уравнения (*).
Впервые Р. п. встречаются в работах А. Муавра и Д. Бернулли, однако
стройную теорию Р. п. мы имеем благодаря работам Эйлера.
Лит.: А. А. Марков, Исчисление конечных разностей, Одесса, 1910; А. О. Гель-
фонд, Исчисление конечных разностей, Физматгиз, М., 1959.
РЕКУРРЕНТНАЯ ФОРМУЛА — формула, выражающая каждый член
последовательности ап{п — \, 2, . . .) через ρ предыдущих членов вида:
ап=Г(п> ап-ъ ап-2> .... αΛ-ρ)ι п>р+\.

390
РЕКУРСИВНЫЕ ФУНКЦИИ
При помощи этой формулы, зная ρ первых членов последовательности, можно
определить всю последовательность, т. е. вычислить любой наперед заданный
член последовательности. Этот прием оказывается полезным при решении
многих задач. Примером Р. ф. является формула удвоения числа сторон
правильного вписанного многоугольника (р=1):
j/^7
ип—\
Если сторона аг исходного правильного вписанного многоугольника задана, то
ап есть сторона многоугольника, полученного из исходного (п—1)-кратным
удвоением числа сторон.
Р. ф. используется,- например, при вычислении /u=fsinnxdx.
cos χ · si nn—1x η—\τ
/n- —+—/»-,
Решение уравнения Бесселя:
^+ту'+(1-?)у-°
может быть записано в виде ряда:
оо
Чтобы определить коэффициенты ап, достаточно установить, что
4r2(n-{-v)an-bart-l=0, /г>1,
после чего сразу получается известный результат:
а„=(-1)« ~
v ' 22/Ι/ι!(1+ν)(2+ν) . . . (л + v)
Очень часто Р. ф. рассматривают в теории конечных разностей (см.
Конечных разностей исчисление).
РЕКУРСИВНЫЕ ФУНКЦИИ — функции y=f(xu . . ., хп), значения и
аргументы которых суть целые неотрицательные числа и для которых могут быть указаны
определенные правила, позволяющие фактически вычислить у по заданному
набору хи х2, . . ., хп, входящему в область определения /. Может быть введено
также понятие о частично-рекурсивных функциях, отождествляемых в настоящее
время с функциями, вычисляемыми с помощью произвольного алгоритма (см.).
Теория Р. ф. используется в математической логике (см.) и основаниях
математики, а также в теории современных быстродействующих электронных
вычислительных машин.
Первые работы по рекурсивным функциям были опубликованы немецким
математиком Г. Грассманом (XIX в.). Р. ф. интенсивно изучаются после работ
немецкого математика Гильберта (20-е годы XX в.). В 1931 г. австрийский
математик К. Гёдель доказал с их помощью теорему о невозможности полной
аксиоматизации арифметики. Окончательно теория Р. ф. становится особой отраслью
математики в 40-х годах.

РИМАНА ГЕОМЕТРИЯ
391
Лат. recursio — возвращение.
Лит.: Р. Петер, Рекурсивные функции, Гостехиздат, М., 1054.
РЕПЕР /ί-мерного евклндового пространства — упорядоченная совокупность
η линейно-независимых (базисных векторов е^ е2, . . ., е/г, исходящих из общего
начала отсчета—начала системы координат). Так, двумерным Р. будет
являться пара неколлинеарных векторов ег и е2, исходящих из общего начала
отсчета (из начала координат); трехмерным Р. (пли Р. трехмерного
пространства) является тройка некомпланарных векторов elt e2, е3,- исходящих из общего
начала отсчета. Если векторы е,, е2, . . ., еп Р. направлены по осям координат
гс-мерного пространства, то векторы, определяющие Р., называют также
координатными (базисными) векторами, а Р.—базисом «-мерного пространства.
Каждый вектор /г-мерного пространства г?=0 можно разложить по базисным
векторам е1# е2, . . ., е/г Р., т. е. представить его как линейную комбинацию
координатных векторов:
г=а! ег+а2 е2Н +ап еП9
где числа а/ называются координатами вектора г. Если на векторы трехмерного
Р. наложены определенные условия, то он часто носит особое название
(например, см. Триэдр).
Франц. гереге— метка, ориентир.
РЕФЛЕКСИВНОСТЬ — свойство бинарных отношений (см.), состоящее в том,
что если в множестве Μ определено бинарное отношение р, то всякий элемент
/ηζΜ находится в этом отношении к самому себе. Например, отношение
равенства чисел рефлексивно; отношение эквивалентности уравнений (или систем
их) рефлексивно. Отношение порядка < в множестве действительных чисел не
удовлетворяет условию Р.
РИККАТИ УРАВНЕНИЕ — дифференциальное уравнение вида:
dy
dx
где α, b, α — постоянные. Как показал Д. Бернулли, Р. у. интегрируется в
элементарных функциях при α = —2 или а = — 4к : (2k — 1) (k — целое). Р. у.
общего вида — дифференциальное уравнение:
du
—=P{x)y*+Q{x)y+R(x)> Ρ(χ)φθ.
dx
При R(x) = 0 это Р. у. называется уравнением Бернулли; последнее
интегрируется в конечном виде.
Лит.: В. В. Степанов, Курс дифференциальных уравнений, Физматгиз, М., 1959;
Э. Камке, Справочник по обыкновенным дифференциальным уравнениям, перев. с нем.,
Гостехиздат, М., 19 50.
РИМАНА ГЕОМЕТРИЯ (эллиптическая геометрия)—двумерная геометрия
сферы в трехмерном евклидовом пространстве с отождествленными диаметрально
противоположными точками (такая поверхность топологически эквивалентна
проективной плоскости). Р. г. моделируется на сфере в (п-И)-мерном евклидовом
пространстве (диаметрально противоположные точки отождествляются).
«Прямыми» Р. г. являются большие круги сфер (с указанным отождествлением).
Метрика (измерение длин, углов и т. п.) индуцируется метрикой сферы.
В Р. г. существуют движения, сохраняющие метрику и переводящие любую точку
пространства в любую другую (однородность Р. г.). Пространство, в котором

392
РИМАНА ИНТЕГРАЛ
действует Р. г. (эллиптическое пространство), имеет положительную постоянную
риманову кривизну (см.).
Р. г. может быть задана аксиоматически, подобно евклидовой геометрии.
Однако система аксиом Р. г. существенно отличается от системы аксиом
Евклида. Например, любые две прямые в Р. г. пересекаются, плоскость не разделяет
пространства и т. п. Р. г. одна из немногих неевклидовых геометрий, хорошо
изученных к настоящему времени.
РИМАНА ИНТЕГРАЛ — обычный определенный интеграл (см.).
Необходимые и достаточные условия его существования: 1) интервал интегрирования
конечен; 2) интегрируемая функция ограничена; 3) мера Лебега (см.) множества
точек разрыва функции на этом интервале равна нулю. Существуют обобщения
Р. и.—интеграл Лебега (см.), Стильтьеса (см.) и др. С их помощью можно
интегрировать более широкий класс функций.
РИМАНА СФЕРА — пополнение плоскости комплексного переменного одной
бесконечно удаленной точкой (расширенная плоскость комплексного
переменного). Расширенная плоскость взаимно однозначно отображается на обычную
сферу трехмерного евклидова пространства при помощи стереографической
проекции (см.). Таким образом, каждую точку сферы можно считать комплексным
числом (или оо). Р. с. используется в теории минимальных поверхностей и
гармонических функций.
РИМАНОВА ПОВЕРХНОСТЬ аналитической функции комплексного
переменного f(z) — одно из основных понятий теории функций комплексного
переменного. Аналитическая функция, рассматриваемая на своей Р. п., становится
однолистной (см.). Р. п., как правило, самопересекающаяся поверхность. Например,
^ Р. п. функции у=22 состоит из
комплексных чисел до=р (cos9-f /sinφ), причем
два комплексных числа νοχ и до2
соответствуют различным точкам Р. п., если
аргумент первого отличается от аргумента
второго менее чем на 4 π. Схематически
Р. п. может быть представлена так:
берутся две плоскости комплексного пере-
р 2д7 менного, разрезаются по вещественной
с* полуоси от 0 до оо. Затем склеиваются
(рис. 247) /х с т1% 12 с т2.
РИМАНОВО ПРОСТРАНСТВО — гладкое многообразие, каждой точке
которого задан тензор, дважды ковариантный gy (gy — непрерывно-дифференцируемые
функции точки). При помощи этого тензора определяется длина любой кривой
Р. п. χι=χι(ί), t=\, 2, . . ., η (η — размерность Р. п.), а также углы,
площади и т. п. Именно, эта длина равна:
W
Σ 8ij*xlV)dxHt)dt.
Примеры: 1) поверхность в трехмерном евклидовом пространстве, тензор gij ■—
первая квадратичная форма поверхности (см.); 2) поверхностьk измерений в
/2-мерном евклидовом пространстве М=*М (ult u2f . . . , un)t
(dM dM\
(скобки означают скалярное произведение векторов евклидова пространства).
Если дискриминант gij больше нуля, Р. п. называется собственно римановым.

РИМСКИЕ ЦИФРЫ
393
Абстрактное Р. п. определяется и весьма часто изучается вне связи с
объемлющим его евклидовым пространством (как это имеет место в примерах 1 и 2).
См. Римановы геометрии.
РИМАНОВЫ ГЕОМЕТРИИ — геометрии римановых пространств (см.)
—раздел дифференциальной геометрии, изучающий свойства римановых пространств,
которые могут быть выражены в терминах тензора gy. Геометрии римановых
пространств в окрестности некоторой точки совпадают с геометрией Евклида до
величин 1-го порядка малости включительно. Так, для измерений небольших
участков на земной поверхности с большой точностью применяется евклидова
геометрия. Риману же принадлежит идея вычисления длины кривой бесконечно
малыми шагами. При каждом таком шаге длина кусочка кривой вычисляется в
евклидовой метрике (см.):
но коэффициенты этой метрики меняются от точки к точке (см. Риманово
пространство). В Р. г. определяется некоторый аналог прямых линий евклидовой
геометрии — геодезические линии. Эти линии реализуют минимум расстояния
в достаточно малой области риманова пространства. Важнейшими понятиями
Р. г. являются кривизна риманова пространства в двумерном направлении (см.
Кривизна), аффинная связность (см.), порожденная метрическим тензором gy,
ковариантное дифференцирование в этой связности (см. Ковариантное
дифференцирование) и тесно с ним связанный параллельный перенос.
Развитие Р. г. шло одновременно с развитием аппарата тензорного
исчисления, созданного в основном математиками итальянской школы (Риччи, Леви-Че-
вита и др.)· Крупный вклад был сделан семинаром по Р. г. и тензорному
анализу при Московском университете (семинар основан в 1928 г. В. Ф. Каганом).
Много новых идей и методов было предложено французским математиком
Э. Картаном.
Проблемами геометрии римановых пространств являются вопросы
погружения в целом риманова пространства в евклидово, изучение специальных видов
римановых пространств, в частности однородных римановых пространств, и др.
Р. г. с момента своего возникновения имели большую область приложения
к различным задачам физики. В трудах Римана, Герца теория Р. г.
применялась к задаче распространения тепла в анизотропном теле, к механике и т. д.
Очень важным приложением Р. г. является теория относительности Эйнштейна,
который показал, что пространственно-временное многообразие можно
рассматривать как псевдориманово пространство четырех измерений. В свою очередь
развитие теории Р. г. во многом стимулировалось запросами теории
относительности.
РИМСКИЕ ЦИФРЫ — знаки, обозначающие числа:
Μ D С L X V I (*)
1000 500 100 50 10 5 1.
С их помощью можно записывать целые положительные числа. Если совокупность
Р. ц., означающих некоторое число, слева направо имеет порядок
последовательности (*), то эта совокупность означает число, равное сумме значений,
входящих в него Р. ц. Например, MCXXVIII означает число 10004-Ю04-104-104-
4-54-14-1 + 1 = 1128. Однако если в записи числа Р. ц. имеется инверсия (см.)
относительно порядка (*), значение числа вычисляется по другому правилу. Из
двух рядом стоящих Р. ц., образующих инверсию, первое берется со знаком
минус. Например, MCDLIX означает 1000—1004-5004-50—14-10=1459. Р. ц.
введены в древнем Риме. Правил, описанных выше, не всегда придерживались
сами римляне. Система записи чисел Р. ц. не является позиционной и потому

394
РИТЦА МЕТОД
весьма неудобна в вычислениях. В настоящее время Р. ц. употребляются для
нумерации съездов, часто глав книг и т. п.
РИТЦА МЕТОД —широко применяемый прямой метод (см.) решения
вариационных и краевых задач математического анализа (см. Вариационное исчисление,
Краевые задачи). Функцию у (х), доставляющую экстремум функционалу ν [у (х)]
и удовлетворяющую условиям: у(х0)=а, )>(*ι)=β, ищут не среди всех, вообще
говоря, возможных функций, а лишь среди функций, представляющих собой
линейные комбинации вида:
η
Ул(*)=]£а;Ф;(*)
/=1
с постоянными коэффициентами а/, составленные из η первых функции
некоторой выбранной системы Ц>г{х), ф2 (*)» · · · » Ф/* (*)» · · · и удовлетворяющие
условию уп{х0) = а, yn(xi) = $· При таком подходе к вариационным задачам
функционал v[y(x)] превращается в функцию Ф(аь а3. · · · » ап) от
коэффициентов ait и задача сводится к отысканию экстремума Φ (alt a2, .... ап).
Значения αί% доставляющие экстремум <b(alt a2, ..., cin)> а следовательно, и у/7,
доставляющие экстремум функционалу v[y(x)]t определяются из соотношений
άΦ
—=0 (/=1, 2, . . . , η). Найденное таким способом приближенное решение за-
dai
дачи уп стремится при некоторых условиях, касающихся полноты системы q>/
(см.), к точному решению у(х) при η —* <χ>.
Лит.: Л. В. Канторович и В. И. Крылов, Приближенные методы высшего
анализа, Физматгиз, Μ., 1962.
РОД ПОВЕРХНОСТИ — целое неотрицательное число, характеризующее
связность (см.) поверхности. Каждую замкнутую ориентируемую поверхность
можно топологически (непрерывной деформацией без разрывов и
склеиваний) отобразить на сферу с ρ ручками. Число ρ называется родом этой
поверхности. Так, сфера (рис. 248, а) —
поверхность рода О, тор (рис. 248, б) —
рода 1, крендель (рис. 248, в) — рода
2 и т. д.; грубо говоря, Р. п. равен
числу дыр в ней. Р. п. можно определить
β как наибольшее число взаимно
непересекающихся простых замкнутых кривых,
которые можно провести на
поверхности, не разбивая ее на части (рис. 248).
Если поверхность представляет собой многогранник, то его род связан с
числом вершин (β), граней (Г) и ребер (Р) формулой:
В+Г — Р=2(1 — р),
где р—г род многогранника. Для простого многогранника (см.) (р=0)
получается известная формула Декарта — Эйлера (см.):
В+Г — Р-2
(см. Эйлерора характеристика поверхности). Неориентируемая замкнутая
поверхность может быть представлена как сфера с h круговыми отверстиями, каждое
из которых заклеено листом Мёбиуса [граница отверстия склеена с границей
листа (ленты) Мёбиуса (см.)]. Число h называется родом этой поверхности.
Если две поверхности имеют один и тот же Р. п., то их можно
топологически преобразовать друг в друга. Поэтому Р. п. есть ее топологический инва-

РОМБ
395
риант (см.); например, крендель, изображенный на рисунке 248, в, и сфера с двумя
ручками имеют род 2, поэтому каждую из них можно деформировать в другую.
РОДРИГА ФОРМУЛЫ: 1°. Р. ф. в дифференциальной геометрии выражают
пропорциональноегь производных единичного вектора нормали к поверхности и
радиуса вектора к поверхности, взятых в одном из главных направлений
поверхности (см. Главное направление). Если 6i и δ2 — символы дифференцирования
в главных направлениях, η — единичный вектор нормали, Rt и R2 — главные
радиусы кривизны (см.), то:
δΤί= — -- бхг, δ3 п= — — о2г,
Αχ /<2
где г — текущий радиус-вектор поверхности.
2°. Р. ф. в специальных функциях иногда называют выражения многочленов
Лежандра (см. Лежандра многочлены) в виде:
Fn{X>~2"nl' dx" '
РОЗЫ — семейство плоских кривых, полярное уравнение которых имеет вид
p = asinkq> или p=acosky, где а и k — постоянные числа. Если k —
рациональное число, то Р. — алгебраические кривые четного порядка. Если k —-
иррациональное число, то Р. состоят из
бесчисленного множества лепестков, Пересе- к = ? **j
кающихся друг с другом, и уравнение Р.
в декартовых координатах в этом случае
не может быть алгебраическим.
Число различных Р. одного и того
же порядка η при /г, кратном 4, равно
значению функции π (η) (см.), т. е. числу
простых чисел, меньших п. Если η не
кратно 4, то число Р. одного и того же
, ч , (п\ Рис. 249
порядка равно π (п)-\-л ί -— I.
При k—2 Р. называются четырехлепестковыми (рис. 249), при £=3 трех-
лепестковыми (рис. 249). Полярные уравнения их соответственно будут иметь
вид p=asin2<p и p = asin3q>. В прямоугольной декартовой системе координат
четырехлепестковая Р. имеет уравнение:
(А:2+у2)зр_4а2л:2у2=0.
а трехлепестковая — уравнение:
(х*+у2)2 — а (3*2у — у3)=0.
Р. иначе называются кривыми Гвидо Гранди, по имени итальянского геометра,
впервые изучавшего их (172S).
РОЛЛЯ ТЕОРЕМА — одна из основных теорем анализа, Формулируется так:
если функция f(x) непрерывна на [а, 6], дифференцируема на интервале (a, b)
и Да)=/(6), то найдется по крайней мере одна точка х=с такая, что а<с<Ь
и /' (с)=0.
РОМБ — параллелограмм, у которого две смежные (отсюда и все) стороны
равны. Диагонали Р. взаимно перпендикулярны и делят углы его пополам.
Справедливы и обратные предложения: если диагонали параллелограмма взаимно
перпендикулярны или делят углы пополам, то этот параллелограмм есть Р.
Диагонали Р. являются осями его симметрии. Высоты Р. равна между собой.
В Р. можно вписать окружность. Площадь Р. равна половине произведения его

396
РОМБОИД
диагоналей или, как и для всякого параллелограмма, равна произведению его
основания на высоту.
РОМБОИД —см. Дельтоид.
РОМБОЭДР — параллелепипед (см.), все грани которого — равные ромбы.
Форму Р. имеют некоторые кристаллы, например кристаллы исландского шпата.
РОТОР векторного поля (иначе ротация) — то же, что и вихрь векторного
поля (см.).
РУЛЕТТЫ — траектории точек, жестко связанных с кривой, которая катится
без скольжения по другой неподвижной кривой (базисной), при этом обе кривые
и фиксированная точка лежат в одной плоскости. Если круг катится по прямой,
то Р. какой-либо точки М, неподвижно связанной с этим кругом, будет
циклоида (см.). Если же круг катится по окружности, то Р. какой-либо его точки
будут гипоциклоиды (см.) и эпициклоиды (см.). Каждая кривая многими способами
может быть рассмотрена как Р., например (см.) всякая кривая может быть
образована качением прямой по эволюте.
Франц. roulette, от router — катать.
РУНГЕ МЕТОД приближенного интегрирования дифференциальных
уравнений относится к числу методов приближенного интегрирования, в которых
dy
решение дифференциального уравнения —«=/(*, у) с начальным условием
Уо=У(*о) строят, находя по заданным х0, у0, Δ)Ό» т· е· приращение у при
некотором приращении х, равном h9 и определяя затем У1=У0~ЬАУо»
соответствующее значению x=x1=xQ-\-h. После этого находят по хг и ух Δ Ух и определяют
Уг^УхЛ-кУх* соответствующее x2=x1-\-h и т. д.
Метод Рунге основан на применении для Δ Уп формулы:
&yn = j{k[n)+Uin)+Uin)+kin)), где h = xJ-xJ-1=const,
k[n)=hf(xmyn) kM=hf(xn+ \, Уп+~<)>
£(") = /*/U„-by, Уя+-у-).Л1п)=Л/(д:„+Л, Уп+~у).
Полагая л=0, получаем Δ У0 и находим ух и т. д.
См. также Численное интегрирование.
Лит.: А. Н. Крылов, Лекция о приближенных вычислениях, Гостехиздат, М., 1954.
РУФФИНИ — АБЕЛЯ ТЕОРЕМА — теорема о неразрешимости в радикалах
общего алгебраического уравнения пятой и более высокой степени. Первым
доказательство (с пробелами) дал итальянский математик Руффини. Вполне
строгое доказательство было дано норвежским математиком Абелем (1824).
См. также Уравнение.
РЯД — последовательность символов, соединенных знаком +:
*х+а2+ · · . +ап+ · . . (*)
Символы а19 а2, . . ., ап> . . ., называемые членами Р., могут обозначать числа,
или функции, или векторы, или матрицы и т. п. Соответственно этому
различают Р. числовые, функциональные, векторов, матриц (см.). Вместо развернутой
оо
записи Р. (*) очень часто употребляется сокращенное обозначение 2 ап (или,
гс=1

РЯД АБСОЛЮТНО СХОДЯЩИЙСЯ
397
реже, 2ая)· Ρ· называется сходящимся, если существует конечный lim Sn=S,
где
Sn^Qi+^-l· · · · Λ-αηι
S — называется суммой Р. В противном случае Р. называется расходящимся.
Р. может иметь более общий вид:
,+ оо
2 ап= · · · -И-л-Ь · . · +α-ι4-α04-αι4- ■ · · ап+ · · ·
п=—оо
(см. Лорана ряд), а также вид:
00
2 а«*=
/, /г=1
, αιι-Μΐ2+ · . · +αΐη+ · . ·
^a2i-b«22-b . . . -Нгл-Ь · · ·
+Ял1+ал2+ · · · Λ-αηη+ · . .
См. Ряд двойной.
оо
РЯД АБСОЛЮТНО СХОДЯЩИЙСЯ — числовой ряд 2 ат Для которого
i=\
оо
ряд 2ΐα"Ι» составленный из абсолютных величин членов данного ряда, являет-
п=\
ся сходящимся (см.). Любой Р. а. с.—сходящийся. В Р. а. с. можно
произвольно переставлять и объединять члены, не изменяя его суммы.
Пример: ряд 1 — -—+—— · · . +(—l)n+1 __ + ... — абсолютно схо-
1 1
дящийся, так как сходится ряд 1-1-—+ ... +~^г:+ . · . = 2 (геометрическая
прогрессия).

САМОПЕРЕСЕЧЕНИЯ ТОЧКА —особая точка (см.) кривой, в которой
кривая пересекает себя. Например, для лемнискаты:
(х2-Ьу2)2 — 2а2 (л:2 — у2)=0
точка (0, 0) является точкой самопересечения (рис. 250). С. т. называется
также узловой или кратной.
САМОПРИКОСНОВЕНИЯ ТОЧКА —особая точка (см.) кривой, в которой
кривая касается самой себя. Например, для кривой у2 — лг4+л:6 = 0 точка (0, 0)
является С. т. (рис. 251).
Рис. 250
Рис. 251
САРРЮСА ПРАВИЛО — правило вычисления определителя 3-го порядка:
#11 #12 #13
U2\ #22 #23
= аи Я22 #33 + #12 #23 #31 + #13 #2 1 #32 — #13 #22 #31
#11 #23 #32
■ #12 #21 #33 —
Закон составления выражения для определителя 3-го порядка весьма прост.
Из членов, входящих со знаком -Ь, один будет произведением элементов
главной диагонали, каждый из двух других — произведением элементов, лежащих на
параллели к этой диагонали, с добавлением третьего множителя из
противоположного угла матрицы (рис. 252, а).
Члены, входящие со знаком —, строятся
таким же образом относительно другой
диагонали (рис. 252, б). С. п. называют также
правилом Саррюса или правилом
диагоналей и треугольников.
СВЕРТКА ФУНКЦИЙ Д и /2 —
функция φ (л:), определенная равенством:
/"Л
Рис. 252
Ф(*)= J М*-У)/2(У)#>.
С. ф. часто обозначается φ = / */2 и обладает свойствами: /ι*/2 = /2*/Ί;
/1*(/oHc/3)=(/1*/2)*f3· Операции С. ф. обладают рядом интересных свойств
относительно преобразований Фурье и Лапласа (см. Фурье преобразования и
Лапласа преобразования). Понятие С. ф. используется в теории вероятностей ,
в теории нормированных колец, функциональном анализе.

СВЯЗКА ОКРУЖНОСТЕЙ
399
СВЕРТЫВАНИЕ ТЕНЗОРА — операция тензорной алгебры, ставящая в
соответствии смешанному тензору (см.) Ζ тензор V меньшей валентности (см.) по
правилу:
.Л /2. . . if{ _viJi... ik, ρ
vJi У· ... У/ ~ ZiΔ J, . . .//, ρ ·
p==l
Операция С. т. линейна; С. т. перестановочна с операциями тензорного анализа
(см.), абсолютным дифференцированием (см.) и т. п.
Рассматривается также свертывание тензоров, определенное формулой:
1*1 . . . ί.Ζι ... 2 JL /ι . . . /. Ζλ . . . Ζ О
V k " =V7 k I) n
/Ί . . · У, sx . . . s ^-Ι^/Ί . . . y. p^sx . . . s
1 s p=l »
(см. Тензорное исчисление).
СВОБОДНЫЙ ВЕКТОР — вектор, начало которого может быть совмещено
с любой точкой пространства, в котором рассматривается данный вектор. С. в.
можно переносить параллельно самому себе в любую точку пространства. Таким
образом, С. в. задается своей длиной и направлением. Примерами С. в. могут
служить скорость и ускорение твердого тела, движущегося поступательно.
С. в. часто называют в математике просто вектором (см.). См. также
Связанный вектор, Скользящий вектор.
СВОБОДНЫЙ ЧЛЕН — член уравнения, приведенного к каноническому виду
/(#ι. х-2* ·♦·* *л) = 0> не содержащий неизвестных (переменных). Например,
С. ч. уравнения х2— 5*4-4 = 0 есть ЧИсло 4, С. ч. уравнения х2— у2=0 равен
0. С. ч. уравнения можно определить как член уравнения* содержащий
неизвестные (переменные) в нулевой степени, т. е. С. ч. уравнения f(xl9 х2 . · ., хп)=
=0— это член нулевого измерения.
СВЯЗАННЫЙ ВЕКТОР — вектор, начало которого совпадает с определенной
(фиксированной) точкой. Так, сила, приложенная к некоторой точке частицы
жидкости, является примером С. в. Понятие С. в. часто используется в физике.
См. также Вектор, Свободный вектор, Скользящий вектор.
СВЯЗКА — семейство линий на плоскости или поверхностей в пространстве,
линейно зависящее от двух параметров. Семейство линий на плоскости*
определяемое уравнением:
Xi/?1+X2f,a+X8f,8 = 0t (*)
где одновременно λχ, λ2, λ3 не равны нулю, a Flt F2t F3—функции от двух
переменных, есть С. Уравнение (*) фактически зависит от двух параметров
(двойного отношения λ1:λ2:λ3; ср.: Двойное неравенство, Двойное равенство).
Три линии Fx=0, F2=0, F3=0 определяют всю С, поэтому их можно назвать
образующими. Аналогично определяется уравнение С. поверхностей в
пространстве.
В геометрии рассматривают также С. прямых в пространстве, где
образующими С. являются не поверхности, а линии. В проективной геометрии
рассматривается одновременно С. прямых и плоскостей в пространстве — множество
прямых и плоскостей, проходящих через фиксированную точку (конечную или
бесконечно удаленную).
Обычно под образующими (элементами) С. понимают геометрические объекты:
прямые, окружности, плоскости, сферы. См. Связка окружностей, Связка
плоскостей, Связка прямых, Пучок.
СВЯЗКА ОКРУЖНОСТЕЙ — семейство окружностей линейно-зависящее от
двух параметров (см. Связка). Для каждой С. о. существует точка, имеющая
одну и ту же степень (см. Степень точки) относительно всех окружностей

400
СВЯЗКА ПЛОСКОСТЕЙ
связки; эта точка называется центром С. о. (см. также Радикальный центр).
Со. называется эллиптической, гиперболической или параболической в зависимости
от того, лежит ли центр С. о. внутри, вне или на окружностях связки.
Уравнение С. о.:
где \19 λ2, λ3 одновременно не равны нулю, a F,=0, F2 = 0, F^^O — уравнения
окружностей, образующих С. о. Совокупность общих элементов (окружностей)
двух различных С. о. образует пучок окружностей (см.).
СВЯЗКА Π ЛОСКОСТЕЙ — семейство плоскостей, линейно зависящее от двух
параметров (см. Связка). С. п. представляет собой совокупность
плоскостей, проходящих через одну и ту же фиксированную точку.Ср. Пучок плоскостей.
СВЯЗКА ПРЯМЫХ — множество прямых, каждая пара из которых лежит
в одной плоскости (см. Связка). С. п. в евклидовой геометрии представляет
собой множество прямых пространства, проходящих через фиксированную точку —
конечную.или бесконечно удаленную (соответственно эллиптическую или
параболическую С. п.).
СВЯЗКА СФЕР — семейство сфер, линейно-зависящее от двух параметров
(см. Связка). Геометрическое место точек (см.), имеющих одну и туже степень
(см. Степень точки) относительно каждой сферы из С. с, представляет собой
прямую — ось С. с. В зависимости от того, пересекает ли ось С. с. каждую из
сфер связки в двух действительных, двух комплексно-сопряженных или двух
слившихся точках, С. с. соответственно называется эллиптической,
гиперболической или параболической. С. с. есть пространственный аналог пучка
окружностей (см.). Сечение С. с. любой плоскостью, проходящей через ось С. с,
есть пучок окружностей.
СВЯЗНАЯ ОБЛАСТЬ—открытое множество евклидова пространства,
которое не может быть разбито на два непересекающихся непустых открытых
множества. Другое определение С. о. — область, любые* две точки которой могут
быть соединены непрерывной кривой. Например, множество комплексных чисел
w таких, что а< \w\ <b, есть С. о.
СВЯЗНОЕ МНОЖЕСТВО топологического пространства — множество,
которое нельзя разбить на два неперерекающихся непустых открытых в пространстве
множества (см. Топологическое пространство, Открытое множество).
СВЯЗНОСТЬ (в геометрии в целом
fy=j /7=j h^5 ив топологии) —натуральное число /г,
которое сопоставляется с каждым
классом многогранников (поверхностей).
Многогранник называется /ι-связным,
если на нем можно провести h — 1
ломаных, составленных из его ребер,
не разбивающих многогранник, но
всякие h ломаных разбивают его на две
части; при этом первая из этих ломаных
должна быть замкнутой, а
последующие соединяют две точки предыдущих.
Для /t-связного многогранника имеет место обобщенная теорема Декарта —
Эйлера (см.), которая выразится в этом случае формулой:
B+F — P = 3 — h,
где В — число вершин, Г — число граней, Ρ — число ребер, h — С.
многогранника. Простой многогранник (многогранник нулевого рода) разбивается на две
части каждой замкнутой ломаной линией, следовательно, его С. /г-= 1 (например,
куб, тетраэдр, призма).
о

СЕГМЕНТ
401
Аналогично определяется и С. поверхностей. Например, С. шара h=\
(рис. 253, а), С. тора /г=3 (рис. 253, б), С. кренделя h=5 (рис. 253, в); С.
кренделя с ρ дырами равна Л=2р-f-1.
Число дыр характеризует род (см.) поверхности. С. есть топологический
инвариант (см.) поверхности.
СВЯЗНОСТЬ АФФИННАЯ в дифференциальной геометрии — способ
перенесения вектора касательного пространства одной точки поверхности (вообще
некоторого пространства аффинной связности) по некоторому пути в касательное
пространство другой точки поверхности. С. а. задается обычно коэффициентами
объекта связности Г^. Эти коэффициенты в случае риманова пространства (см.)
называются символами Кристофеля (см.).
Введение связности в пространство позволяет определить операцию кова-
риантного (абсолютного) дифференцирования (см. Ковариантное
дифференцирование) — важный метод изучения геометрических свойств пространства аффинной
связности.
СГУЩЕНИЯ ТОЧКА (накопления точка) данного множества — точка, в
любой окрестности которой находится бесконечное число точек данного множества.
Устаревшее название предельной точки (см.).
СДВИГ — один из видов аффинного преобразования (см.) плоскости (или
пространства) в себя. С. плоскости относительно прямой /, лежащей в этой
плоскости, — такое преобразование точек плоскости
в себя, при котором прямая / остается
неподвижной (точечно-инвариантной), а все точки, лежащие
вне прямой /, сдвигаются по прямым, параллельным
/; при этом всякая точка Λί, отстоящая на
расстоянии 1 от прямой /, сдвигается на вектор &, а всякая
точка Λί0, отстоящая от / на расстоянии ρ той
же полуплоскости у сдвигается на вектор ρ -k (рис. 254)
(точки в другой полуплоскости сдвигаются в
обратном направлении).
Аналогично определяется С. пространства
относительно данной плоскости. С. плоскости в
аффинных координатах выражается формулами: Рис. 254
Ί
Ρ
1
MQ
[ м1
/
<έ-1—i
ρκ
^. . к „ Τ
V ' '°
К
>
ι
х'=х+ру, у'=у
(С. в направлении оси Од:).
Понятие С. используется при решении конструктивных задач.
Лит.: Б. Н. Делоне и Д. А. Райков, Аналитическая геометрия, т. I, Гостехиз-
дат, М., 1948; X. С. М. Кокстер, Действительная проективная плоскость, Физматгиз,
М., 1959.
СЕГМЕНТ: 1°. С. числовой или отрезок — множество точек числовой
прямой, координаты которых удовлетворяют условиям а < χ < 6, т. е. множество
точек прямой, расположенных между двумя данными
точками этой прямой, включающее данные две точки.
2°. С. плоской фигуры — часть фигуры, заключенная
между какой-либо дугой и стягивающей ее хордой; так, на
рис. 255 изображен С. круговой АтВу площадь которого
равна разности площадей сектора ОАтВ и площади
треугольника АО В.
3°. С. пространственной фигуры (или тела) — часть этой
фигуры (тела), заключенная между плоскостью и частью
поверхности фигуры, отсекаемой от фигуры этой плоскостью.
Так, шаровой или сферический С. есть часть шара, заклю-
26 Толковый словарь математических терминов

402
СЕДЛО
ченная между секущей плоскостью и одной из двух частей его сферической
поверхности. Шаровой С. можно получить вращением кругового С. вокруг
диаметра, перпендикулярного к хорде (основанию) С.
Объем шарового С. вычисляется аналогично площади кругового С. и равен
ν=π Нг lR — ■—1, где Η — высота С, R — радиус шара.
Лат. segmentum — отрезок, полоса, от seco — резать, рассекать.
СЕДЛО (седловина) — особая точка дифференциального уравнения. Между
интегральными кривыми, входящими в особую точку, находятся интегральные
кривые типа гиперболы, расположенные примерно так же, как линии уровня
гиперболического параболоида, имеющего форму С. Отсюда и происходит
название этого типа особых точек дифференциального уравнения (см. также Особые
точки дифференциального уравнения).
Пусть в окрестности (xot у0) функция f(x, у) не ограничена и не имеет
единственного предела. Простейшим примером
является /(х, y)=(ax+by):(cx+dy), для
которой точка (0, 0) является изолированной особой
точкой. В уравнении
*У_ аХ+Ь (*ч
ах cx+d
сделаем замену g=aAr-f-py, η=γ.ν-|-δ у —
однородное аффинное преобразование, подбирая α, β,
γ, о так, чтобы уравнение (*) имело вид:
dy λη
d% μΓ ( )
при этом λ и μ будут корнями уравнения:
х2 — (b+c) x+bc—da=0. (***)
Решение уравнения (**) имеет вид: η=£ Ι ξ Ι'Λ · Если корни (***) действительные
и разных знаков, то λ:μ=—k<0 и интегральные кривые даются решением
d η η
η=^|ξ|—k уравнения ■—=—k —. Два решения ξ = 0 и η=0 проходят через
особую точку (0, 0), а все другие — нет. Особая точка такого типа называется
d η η
С. Например, при —L= — -L общий интеграл (см.) £л = С, т. е. имеем семей-
β?ξ ξ
ство гипербол, отнесенных к осям» и две асимптоты, — они-то и проходят через
особую точку (рис. 256).
СЕКАНС — одна из тригонометрических функций, обозначаемая символом
sec χ (χ — аргумент) и определяемая формулой sec λ*= 1 :cos χ, где cos x — косинус
(см.) того же аргумента (угла) х.
Областью определения С. является вся числовая ось, за исключением точек,
π
абсциссы которых х= -—(2гс± 1), где я=0, ±1, ±2, ...С. является функцией
неограниченной (1 < | sec χ \ < оо), четной (рис. 257), периодической (с
периодом 2π).
Если рассматривается произвольный радиус-вектор (подвижной вектор ОМ=г),
начало которого совпадает с началом координат (рис. 258), то отношение
| г |:л:л/=$еса, где а — угол, составленный радиус-вектором с положительным
направлением оси Ох (с неподвижной стороной О А угла а = ЛОМ), а%-
абсцисса точки Μ — конца подвижного радиус-вектора.
Рис. 256

СЕКТОР
403
Знак С. совпадает со знаком косинуса (cos α) того же аргумента а. Если
ограничиться только рассмотрением острого угла а, то С. можно определить,
исходя из рассмотрения прямоугольного треугольника OMMlt как отношение
гипотенузы ОМ к катету ОМ1у прилежащему к углу а.
Рис. 258
График С. в прямоугольной декартовой системе координат называется секан-
соидой (рис. 258).
Производная С. вычисляется по формуле:
(sec*)' =
sin л:
cos2 χ
Интеграл С. находится по формуле:
:fg*-sec*.
Jsec*£i*-ln^tg^+-|j
+С
Разложение С. в ряд имеет вид:
л; 3π
sec*=
5π
Ш-' (τ)- (τ)*-
где χ — любое допустимое значение аргумента.
Функция, обратная С, называется арксекансом (см.). См.
Тригонометрические функции.
Лат. secans — секущая, от seco — режу, рассекаю.
СЕКАНСОИДА — график секанса (см.) (y=secx) в прямоугольной системе
координат.
СЕКСТИЛЛИОН — число 1021; в Англии и Германии — число 10м.
СЕКТОР: 1°. С. круговой — часть круга, ограниченная двумя радиусами и
дугой круга.
2°. С. плоской фигуры, граница которой есть кривая без самопересечений,—
часть этой фигуры, ограниченная двумя лучами, исходящими из внутренней
точки, и дугой контура. Так, рассматривают площадь С, описываемого фокаль-
26*

404
СЕКУНДА
ным радиус-вектором эллипса (при изучении законов Кеплера), площадь
параболического сектора и т. д.
3°. С. пространственной фигуры есть часть этой фигуры, ограниченная
конической поверхностью с вершиной внутри фигуры и поверхностью этой фигуры,
вырезаемой конической поверхностью. См. Шаровой (сферический) сектор.
СЕКУНДА: 1°. С. угла — единица измерения, равная 60—2 градуса (см.)
или 60—* минуты (см.). Одна С. обозначается 1" (единица с двумя косыми
штрихами вверху).
2°. С. времени — единица измерения времени, равная 60—2 часа.
Лат. secunda divisio — второе деление части градуса.
СЕКУЩАЯ — всякая прямая, имеющая с кривой по меньшей мере две общие
точки. См. также Касательная.
СЕМЕЙСТВО ЛИНИЙ — множество линий, непрерывно зависящих от одного
или нескольких параметров. С. л. на плоскости задается обычно уравнением вида
F(x, у, Съ . . ., Сп)=0 (*), где х, у —координаты точек на плоскости (см.),
aCj, . . ., Сп—параметры. При определенных значениях параметров уравнение
определяет одну линию. С. л. может быть определено и на поверхности; в этом
случае вместо хну следует рассматривать внутренние координаты ы, υ на
поверхности. С. л. в пространстве задается чаще всего в виде уравнений:
*=<p(f, Clf . . ., Сл), у=ф(*, Съ . . ., Сп), ζ=χ(/, Съ . . ., Сп)
(в параметрическом виде).
Зафиксировав значения параметров CJt . . ., Сп и меняя t, получаем одну
из линий семейства, которую можно рассматривать как траекторию точки
(,*, у, ζ). По числу параметров различают С. л. однопараметрические, двупара-
метрические и т. д. В исследовании свойств однопараметрических С. л. на
плоскости или произвольной поверхности (удовлетворяющей лишь условию гладкости)
важную роль играет понятие огибающей С. л. (см. также Дифференциальная
геометрия). Обычно предполагается, что функции Ζ7, φ, ψ, χ непрерывны и
непрерывно-дифференцируемы по своим аргументам. Если продифференцировать
уравнение (*) η раз [считая у=у(х)] и из полученных таким путем уравнений
исключить все η (Clf C2, .... Сп) параметров, то получится дифференциальное
уравнение С. л. Как видим, примером С. л. может служить семейство
интегральных кривых некоторого дифференциального уравнения (см. Общее решение).
Примерами С. л. являются: 1) однопараметрическое семейство концентрических
окружностей *2-f-y2=C, 2) четырех параметрическое семейство эллипсов и
гипербол:
3) двупараметрическое семейство винтовых линий:
x=C1cost1 y=Cis'mt, z=Cnt.
СЕМЕЙСТВО ПОВЕРХНОСТЕЙ — множество поверхностей, непрерывно
зависящих от одного или нескольких параметров. Аналитически С. п. определяется
либо одним уравнением вида:
F(x, у, z, Clf .... Сп)=0(*),
либо в параметрической форме тремя уравнениями:
*=<р(и, vt Съ . ... Сп), }'=·!>(«, у, С19 . . ., Сп),
г=у.(и, ν, С, Сп). (**)
Придавая параметрам Clf С2, . . ., Сп определенные значения, получают из
уравнений (*) или (**) определенную поверхность семейства. Обычно функции
F> Φ» ψ> 7. непрерывны и непрерывно-дифференцируемы по всем своим
аргументам. В исследовании одно- и двупараметрических С. п. играет важную роль

СЖАТЫЕ ОТОБРАЖЕНИЯ
405
понятие огибающей семейства (см.). Огибающая однопараметрического С. п.
называется развертывающей поверхностью (см.).
СЕРРЕ—ФРЕНЕ ФОРМУЛЫ — формулы, выражающие разложение
производных по длине дуги от единичных векторов касательной, нормали и бинормали
кривой по самим этим векторам. Если t, n, b — единичные векторы соответственно
касательной (см.), нормали (см.) и бинормали (см.), то С —Ф. ф. имеют вид:
dt d n db
— = k(s)nt —=—k{s)t+%{s)b, - = -y,(s)n, (*)
as as as
где k(s) и 7.(5) являются соответственно кривизной и кручением кривой (см.).
По С—Ф. ф., зная k(s) и *(s), отыскание конечных уравнений кривой сводится
к интегрированию системы дифференциальных уравнений (*) и уравнения
ds
где M(s) — текущий радиус — вектор кривой.
Справедлива теорема, что указанная система имеет единственное (с
точностью до положения в пространстве) решение при любых k(s) и x(s). Иногда
С.— Ф. ф. называют формулами Френе.
СЕТЬ ЛИНИЙ на поверхности — любая пара однопараметрических семейств
линий (см.) на поверхности, гладко-зависящая от параметра. В
дифференциальной геометрии С. л. изучается в малом, т. е. в некоторой окрестности
точки такой, чтобы линии каждого из семейств не пересекались между собой,
а пары линий, принадлежащие различным семействам, пересекались в
единственной точке.
Теория сетей является важной главой дифференциальной геометрии.
Примеры: С. л. кривизны, сеть асимптотических линий и др.
СЕЧЕНИЕ в области рациональных чисел — разбиение множества
рациональных чисел на два класса А и В, удовлетворяющих следующим условиям:
1) в каждом классе есть хотя бы одно число, 2) каждое рациональное число
отнесено в один и только один из классов, 3) любое число из класса А
(нижний или левый класс) меньше любого числа из класса В (верхний или правый
класс). С. могут быть трех видов: 1) в первом классе А есть наибольшее
число г, 2) во втором классе В есть наименьшее число г, 3) в первом классе А
нет наибольшего, а во втором классе В нет наименьшего числа. В случаях 1
и 2 С. определяет рациональное число г. В случае 3 С. определяет
иррациональное число — этот способ построения всех действительных чисел был
предложен Дедекиндом. Если аналогично определить С. в области действительных
чисел, то теорема Дедекинда (свойство непрерывности множества
действительных чисел) состоит в том, что случай 3 невозможен и С. могут быть только 1-го
и 2-го видов (см. Дедекиндово сечение).
СЕЧЕНИЕ ДЕДЕКИНДА — то же самое, что и дедекиндово сечение (см.).
СЕЧЕНИЕ ЗОЛОТОЕ— см. Золотое деление.
СЖАТЫЕ ОТОБРАЖЕНИЯ — отображения подмножества метрического
пространства самого в себя, при которых расстояния между точками уменьшаются
(сжимаются). Точнее: отображение А называется С. о., если существует число
0<Θ<1 такое, что р(Ах, Ау):р(х, у) С θ, где х, у— произвольные точки
подмножества, р(х, у) — расстояние между χ и у.
В современной математике существует теорема, устанавливающая
существование н единственность неподвижной точки множества при сжимающем
отображении (подробно см. Принцип сжатых отображений).
Лит.: И. Г. Петровский. Лекции по теории обыкновенных дифференциальных
уравнений, Гостехиздат, М.—Л., 1952.

406
СИГНАТУРА
СИГНАТУРА квадратичной формы 2 2 a4XiXJ — Разность между положи-
тельным индексом инерции (см.) этой формы и отрицательным индексом инерции
(см.) этой формы.
СИГНУМ от χ — функция от действительного числа х, равная 1, если χ
положительно, равная нулю, если χ равно нулю, и равная —1, если χ
отрицательно. Обозначается эта функция сим-
у к волом signx или sgnx. Таким образом,
/
-2
{-И, если х>0,
О, если л;=0,
— 1, если *<0.
-/
; ι λ Функция y=sgnx используется в различных
вопросах математики. График функции у=sgn x
изображен на рис. 259. В качестве примера
употребления функции у=sgn χ заметим, что
Рис 259 формула для извлечения корня из
комплексного числа (см.) при показателе корня 2 может
быть записана так:
-,/· г. ΐ/α+Ί/α2-^2 , Л/ —a+Va2+b*
Уа+Ы=±у +i(sgn&)|/ 2 .
Лат. signum — знак.
СИЛЬВЕСТРА КРИТЕРИЙ — критерий положительной определенности
квадратичной формы: квадратичная форма является положительно определенной
тогда и только тогда, когда все главные миноры матрицы квадратичной формы
положительны. Главный минор матрицы — минор, образованный первыми k
строками и столбцами матрицы.
СИММЕТРАЛЬ точек А и θ —прямая, перпендикулярная к отрезку АВ и
проходящая через его середину. С. точек А и В называется также С. отрезка АВ.
С. отрезка АВ (точек А и В) есть ось его симметрии. С. отрезка АВ называется
также срединным перпендикуляром его или его медиатрисой.
СИММЕТРИЧЕСКАЯ ГРУППА г—группа подстановок из η элементов
относительно операции умножения подстановок (см.). Содержит п\ элементов.
СИММЕТРИЧЕСКАЯ МАТРИЦА г-, квадратная матрица, в которой элементы,
симметричные относительно главной диагонали, равны, т. е. в которой
''^СИММЕТРИЧЕСКАЯ РАЗНОСТЬ МНОЖЕСТВ А и В — множество, получаю-
щееся из множеств А и В с помощью операций вычитания множеств (αι.
Разность множеств) и объединения множеств (см.). Если С. р. м. А и В обозначать
символом Л®£, то по определению:
A®B~(A/B)\J(B/A). Для С. р. м. справедливы законы:
А®В~В®А, (A®B)SC=A®(B8C)f
Ли(В®С)=(ЛЛЯ)®(ЛПС), A®B=(A\JB)\(Af)B).
Таким образом, С. р. м. Ли В<—это множество тех элементов, которые
входят хотя бы в одно из множеств А или В, но не входят в их пересечение,
т. е входят в одно π только одно из множеств А и В. Для сравнения С. р. м'.
с другими операциями над множествами см. Теоретико-множественные
операции.

СИММЕТРИЯ
407
Пример: если А — множество четных чисел и В — множество чисел,
кратных 3, то А®В — множество чисел, которые делятся на 2 или на 3, но не
делятся на 6.
СИММЕТРИЧЕСКАЯ ФУНКЦИЯ—-функция многих переменных, не
изменяющаяся при любых перестановках переменных, т. е. функция f (xit x*t ...., хп)
от нескольких переменных, удовлетворяющая равенству:
f(xi> *2 Xn)=f(xii, xi2> · · ·> *in)t
где (. . ' * ' f ] — произвольная подстановка (см.).
\*1*2 · · · hi/
/ η \k η η
Среди С. φ. I 2 χι) * 2 xi * Π *ϊ важными и наиболее изученными
являются симметрические многочлены. Основная теорема С. ф.: Любая целая
рациональная С. ф. представляется единственным образом в виде целой
рациональной функции от основных элементарных С. ф.:
η η
η
<Jk==2jxi\ xiz ··· xifc » · · ·» σΛβ*ΐ» λ'2» · · · χη
,1·'« Ά = 1
(суммирование распространяется на комбинации неравных между собой чисел
'ι. '*2· · · ·» *k)· Функция называется кососимметрической, если меняет знак при
перестановке любой пары аргументов. Кососимметрическая функция рационально
выражается через ои σ.2, . . ., ση и σ= П(#4 —Лу).
i<j
Лит.: А. Г. Курош, Курс высшей алгебры, Физматгиз, М., 1962; Л. Я.
Окуней, Высшая алгебра, Учпедгиз, М., 1958.
СИММЕТРИЧЕСКИЕ МНОГОЧЛЕНЫ— см. Симметрическая функция.
СИММЕТРИЧНЫЕ ТОЧКИ: 1°. С. т. относительно некоторой прямой / ·—
две точки Μ и М\ лежащие на прямой, перпендикулярной к /, по разные
стороны от / и на равном расстоянии от нее. Прямая / при этом называется осью
симметрии.
2°, С. т. относительно некоторой точки О —две точки Μ и Μ', лежащие
на прямой, проходящей через О, по разные стороны от точки 0 и на одинаковом
расстоянии от нее, т. е. ОМ=ОМ'.
СИММЕТРИЯ* 1°. С. относительно прямой /, лежащей в некоторой
плоскости Q, есть такое преобразование точек этой плоскости в себя, при котором
каждая точка А переходит в точку Л', симметричную с первой относительно
прямой / (рис. 260). Прямая / иначе называется осью С, а С. относительно
прямой — осевой С, или отражением от прямой, или зеркальным отражением от
прямой. Осевая С. есть взаимно однозначное, а также инволюционное
соответствие точек плоскости (см. Инволюция). При осевой С. длина отрезка
сохраняется, а ориентация фигуры меняется на противоположную, следовательно, осевая
С. есть движение (см.) второго рода. Прямые при С. преобразуются в прямые,
при этом прямые, перпендикулярные оси С, преобразуются в себя, а ось С,
оставаясь неподвижной, остается и точечно-неподвижной (точечно-инвариантной):
каждая точка ее двойная (см.).

408
СИМПЛЕКС
Понятие осевой С. часто используется при решении задач на геометрические
построения (см.)» при построении графиков четной функции (см.), в архитектуре,
в кристаллографии, в разрисовке тканей. Произведение двух осевых С. с
параллельными осями есть параллельный перенос (см.), произведение двух осевых С.
с пересекающимися осями не является С. ни относительно первой, ни
относительно второй осей С, т. е. множество всех С. на плоскости относительно заданных
осей не обладает свойством замкнутости. Другими словами, множество всех
осевых С. на плоскости не является группой (см.).
2°. С. относительно точки О, лежащей в некоторой плоскости Q, есть такое
преобразование точек этой плоскости, при котором каждая точка А переходит
в точку Л', симметричную с первой относительно точ-
А ϊ х- -^^^ ки О. Точка О при этом называется центром С, а С.
( ^ч относительно точки — центральной С.
ι \ Центральная С. является: а) взаимно однозначным
Χ^^ί^44^ преобразованием точек плоскости, б) инволюционным
ι преобразованием точек плоскости, в) преобразованием
\ 1 поворота плоскости на угол φ=180° и г) преобразо-
] ванием движения. Центральная С. имеет те же приме-
^—sa^^ « нения, что и осевая С.
г ^ ^ Произведение двух центральных С. на плоскости
У с различными центрами С. есть параллельный перенос
Ч^ У^ (см.) точек плоскости. Аналогично определяется С.
м ° относительно плоскости и относительно точки в про-
Рис 260 странстве.
С. называют также свойство фигуры,
симметричной относительно прямой (оси), или точки (центра)у
или плоскости; другими словами, С. есть также свойство фигуры, имеющей
ось С, или центр С, или плоскость С.
СИМПЛЕКС. Одномерным С. называется отрезок. Двумерный С. по
определению— треугольник, трехмерный С.— тетраэдр. Здесь треугольник и тетраэдр
рассматриваются соответственно как двумерная и трехмерная замкнутая область
(см.). В л-мерном евклидовом пространстве С. называется фигура η измерений,
обобщающая понятие треугольника (тетраэдра). Более точно — /г-мерный С. есть
множество точек я-мерного евклидова пространства, описываемое следующим
образом. Пусть ξ0, glt . . ., ξη означают я-f-l векторов в /z-мерном евклидовом
пространстве такие, что любые η векторов этой совокупности дают базис всего
пространства. С. состоит из точек, задаваемых векторами
при любых неотрицательных С/, /=0, 1, 2, . . ., я, сумма которых C0+C,-f-
-Ь ··· Л-С η равна единице. Те точки С, у которых ρ фиксированных
коэффициентов С/ равны нулю, образуют (п — р)-мерную грань С, которая, очевидно,
является (п — р)-мерным С. Таким образом, С. обладает С^ , 1 (п — р)-мерными
гранями, в частности, лг-f-1 (лг—1)-мерной гранью. Среди всех многогранников
«-мерного евклидова пространства С. имеет наименьшее количество (п— 1)-мерных
граней. В этом смысле С. является наиболее простым многогранником.
С. является важным понятием комбинаторной топологии (см.), свойства С.
используются в математических методах экономики (симплекс-метод).
Лат. simplex — простой.
Лит.: Л. С. Понтрягии, Основы комбинаторной топологии, Гостехиздат, Д\.—Л.,
1947.
СИМПСОНА ФОРМУЛА: 1°. С. ф. для интеграла — формула для
приближенного вычисления интегралов. То же самое, что парабол формула (см.).

СИНТЕТИЧЕСКАЯ ГЕОМЕТРИЯ
409
2°. С. ф. для объемов тел — формула для вычисления объемов тел с двумя
параллельными основаниями:
V = -£(Q«+Qe+4QC).
о
где QH— площадь нижнего основания, Qe— площадь верхнего основания, Qc—
площадь среднего сечения тела. Под средним сечением тела здесь понимается
фигура, полученная от пересечения тела плоскостью, параллельной плоскостям
оснований и находящейся на равном расстоянии от этих плоскостей. Через h
обозначена высота тела.
Из С. ф., как частный случай, получаются многие известные формулы
объемов тел, изучаемых в школе (усеченной пирамиды, цилиндра, шара и др.).
СИМСОНА ПРЯМАЯ — прямая, на которой расположены основания трех
перпендикуляров, опущенных из любой точки Μ окружности на стороны
треугольника, вписанного в эту окружность. С. п. названа ошибочно по имени
Симеона; эта прямая установлена ранее Валлисом.
СИНГУЛЯРНАЯ МАТРИЦА — то же, что особая матрица (см.),
вырожденная матрица (см.).
СИНТЕЗ — метод (способ) рассуждения или доказательства, при котором
следуют от неизвестного к известному, от искомого к данному. С. применяется
во всех разделах математики как элементарной, так и высшей. Большинство
теорем геометрии обычно доказывается синтетически, хотя для доказательства
теоремы приходится часто прибегать к анализу (см.) — обращению С, т. е.
рассуждению, проведенному в обратном порядке, а также к индукции, аналогии и
другим приемам.
Пример С. Доказать, что а-\-—>2, если а>0. Возьмем неравенство
а
(а—I)2 (*), которое является верным. Запишем неравенство (*) в виде:
α2+1>2α (**). Разделив обе части (**) на а (а>0), получим искомое
неравенство а-\-—>2. Знак равенства имеет место только при а—\.
а
С. более доступен для понимания учащихся, хотя он менее развивает
логическое мышление, чем анализ. Применяя С, учащиеся рассуждают вслепую,
пассивно; трудно догадаться, с чего начать доказательство, в то время как
рассуждая аналитическим путем, мы мыслим ясно и творчески, активно ищем путь
доказательства того или иного предложения.
С. в чистом виде никогда не встречается, а всегда включает в себя
элементы анализа, который при этом может быть использован устно (умозрительно)
целиком или частично. С. и анализ взаимно связаны и неотделимы друг
от друга.
В преподавании математики используется как С, так и анализ.
СИНТЕТИЧЕСКАЯ ГЕОМЕТРИЯ — геометрия, изучающая свойства фигур
на основе синтетического метода (см. Синтез), т. е. чисто геометрического в
элементарном значении этого слова, а не на основе алгебры и метода координат,
как это имеет место в аналитической геометрии (см.).
До создания аналитической геометрии Декартом и Ферма геометрия была
чисто С. г., как, например, в трудах древних геометров (Пифагор, Аполлоний,
Евклид и др.).
Один и тот же вопрос в геометрии можно изложить как синтетическими, так
и аналитическими методами; например, конические сечения (эллипс, парабола,
гипербола, см.) можно изучать с помощью сфер Данделена* методом С. г.
и методом аналитической геометрии (методом алгебры на основе идеи
координат).

410
СИНУС
К С. г. относится элементарная геометрия, изучаемая в средней школе,
а также конструктивная геометрия (теория геометрических построений) и
проективная геометрия, если последняя излагается в стиле Попселе, Шаля и Штейне-
ра, без привлечения аналитического аппарата.
Лит.: Извольский, Синтетическая геометрия, Учпедгиз, М., 1040; Адлер,
Теория геометрических построений, Учпедгиз, М.— Л., 1940; Η. Φ. Четверухин,
Проективная геометрия, Учпедгиз, М.—Л., 1953; Ж. А д а м а р, Элементарная геометрия,
Учпедгиз, М.—Л., 1958.
СИНУС —одна нз тригонометрических функций (см.), обозначаемая sin,v
(χ— аргумент) и определяемая следующим образом. Пусть в'ориентированной
плоскости выбрана прямоугольная декартова система координат хОу (рис. 261)
и произвольный угол α (или х), равный углу ЛОМ, вершина которого совпадает
с началом координат, неподвижная (фиксированная) сторона его совпадает
с осью Ох, а подвижная (переменная) сторона ОМ
при вращении вокруг вершины О составит различные
углы α с осью Ох. С. угла α (или угла х) назы-
У У
вается отношением т~г~777 или - , где у — орди-
| ОМ | | г|
ната произвольной точки Mf принадлежащей
подвижной стороне ОМ угла a, a J ОМ | — длина
радиус-вектора точки М. Отрезок ОМ часто
называют подвижным радиус-вектором, а координаты
точки Μ — координатами конца его. С. угла α
есть функция этого угла. Наименьший
положительный период С. равен 2я, т. е. sin x=sm{x-\-2zin)i
Рис. 261 ГДе ™°' ±Ь ±2, ... г
Областью определения С. является вся
числовая ось, областью значений — сегмент [—1; 1].
С.— функция ограниченная, нечетная и периодическая.
С возрастанием угла α от 0° до 90°, как и тригонометрические функции
тангенс (см.) и секанс (см.), С. возрастает.
С. и косинус (см.) связаны соотношением: sin2a-f-cos2 a=l (a — любое).
Левая часть этой формулы называется тригонометрической единицей. С. и
косеканс (см. ) связаны зависимостью: sin х= 1: cosec x.
Производная С. вычисляется по формуле: (sin jc)'=cos х\ для л:=0 имеем
(sin x)Ar==0=cosO=l> т. е. угловой коэффициент касательной, проведенной к
синусоиде y=s\nx в точке #=0 (у = 0), равный тангенсу угла наклона этой
касательной с положительным направлением оси Охч равен 1. Этот факт используется
при построении графика синуса (см. Синусоида); для лг>0 синусоида лежит ниже
прямой у=х (биссектриса первого координатного угла), а для х<0 — выше этой
прямей. Интеграл от С. находится по формуле: \ s'mxdx=— cos*-f-C.
С. разлагается в степенной ряд: sin*=jt— —-f-— — · · · (— со < χ <οο);
3! 5!
этот ряд используется для вычисления приближенных значений С.
Функция,^ обратная С, называется арксинусом (см.). Если рассматривать
только острый угол а, то С. угла α можно определить как отношение катета,
противолежащего углу а, к гипотенузе (из прямоугольного
треугольника ОММг).
С. и косинус комплексного аргумента г связаны с показательной функцией
формулой Эйлера:
^«cos г+ί sinz,

СИНУСОИДА
411
из которой получаются формулы, выражающие sin* и cos л; (л; — действительное
число) через показательную функцию чисто мнимого аргумента:
o/.V 0—IX
Если τ=ix t то s i η ι χ=/
βΙΛ
cx-
■he-
2
- e—
IX
χ
sin .* = -
2/
= / sh.\r,- где sh* = -
гиперболи-
2 2
ческий синус (см.).
В комплексной плоскости функция sin z может принимать любые
значения.
См. также Синусоида.
Лат. sinus — выпуклость, вздутие.
СИНУС-ВЕРЗУС угла α — отношение ' (*) (рис. 262), где
М1—проекция конца подвижного радиус-вектора на ось Ох, а г=\ОМ\. С.-в. угла α
обозначается так: sinversa. Если положить в (*) АМх = г — ΟΜλ, то С.-в. угла a
будет равен I—cos а. Понятие С.-в. было введено в XVII в. и в настоящее
у\
2
^
о
т\ 1*
2 ^-^
Рис. 263
'2π
j
V
время почти не употребительно. Следует отметить, что русский математик
П. Л. Чебышев считал, что понятие С.-в. будет играть в математике
важную роль.
Лат. sinus — выпуклость, вздутие, versus — обращенный; sinvers a —
обращенный синус.
СИНУС ГИПЕРБОЛИЧЕСКИЙ —см. Гиперболический синус.
СИНУСОВ ТЕОРЕМА — теорема плоской тригонометрии, устанавливающая
зависимость между сторонами a, b, с произвольного треугольника и синусами
противолежащих этим сторонам углов:
sin Л sin β sin С
где R — радиус описанной около треугольника окружности.
Для сферической тригонометрии С. т. аналитически выражается так:
sin a sin b sine
sin Л sin В sin С *
СИНУСОИДА — график тригонометрической функции y = sin* в
прямоугольной декартовой системе координат (рис. 263). Биссектриса 1-го и 3-го
координатных углов является касательной к синусоиде в начале координат; поэтому
для *>0 синусоида расположена под биссектрисой первого координатного угла.
Графики функций вида у=»Л sin(a>#-{-(p) называют также синусоидами, которые
получаются из С. у=*ъ\пх путем ее одного сдвига на (— φ) и растяжения (ежа-

412
СИСТЕМА СЧИСЛЕНИЯ
тия) в ω раз по оси χ и растяжения (сжатия) в А раз по оси у. При этом
число А называется амплитудой (размахом), ω — круговой частотой, φ —
начальной фазой колебания.
График функции y=cos,v (косинусоида) есть также синусоида, параллельно
π . / π \
сдвинутая по оси Ох на — —, так как cosje = sin \х+—1.
С. часто встречается в электротехнике, в механике и других разделах
физики при изучении колебательных движений. Так, колебания математического
маятника, колебания тока и напряжения в электрическом колебательном
контуре являются примерами синусоидаль-
Линия разреза
>-
у
Рис. 264
пых колебаний, если пренебречь
затуханиями.
Проекция винтовой линии (см.) на
плоскость осевого сечения кругового
цилиндра есть С, амплитуда которой
равна радиусу цилиндра, а период равен
шагу винтовой линии.
Для практического получения
модели синусоиды можно поступить так:
взять стеариновую свечу и обернуть ее
несколько раз тонкой бумагой, а затем
разрезать (рис. 264, а) под углом, не
равным 90°, к ее оси; тогда развертка
бумаги (рис. 264, б) даст модель С.
СИСТЕМА СЧИСЛЕНИЯ
(нумерация)— способ для наименования и обозначения чисел. В настоящее время
общепринята десятичная позиционная С. с.
Позиционные системы могут иметь основанием не обязательно число 10,
по и другие числа; употребляются восьмеричная, двоичная, шестнадцатеричная
позиционные С. с. Хотя десятичная позиционная С. с. и является широко
распространенной, однако возникла она сравнительно недавно и явилась
результатом длительного исторического развития. У первобытных народов
никакой С. с. вообще не было. Даже в середине XIX в. в Австралии и на
островах Полинезии обитали дикие племена, знавшие всего два числительных:
один и два.
Наиболее древней С. с. является египетская иероглифическая нумерация,
возникшая за 3000 лет до н. э. В этой десятичной непозиционной С. с. для
выражения чисел применялся только принцип сложения. Аналогичными были
греческая нродианова, римская, сирийская С. с. (нумерации). Более совершенными
являются алфавитные С. с. счисления, из которых наиболее древней была
возникшая в греческих колониях в Малой Азии в V в. до н. э. ионическая система;
алфавитными были и славянская (см.), еврейская, арабская, армянская,
грузинская С. с. Первой позиционной С. с. была вавилонская шестидесятеричная
система (2000 лет до н. э.). Современная С. с. возникла на основе существовавшей
в Индии в V в. до н. э. позиционной С. с.
После введения десятичных дробей десятичная позиционная С. с. стала
универсальным средством записи чисел.
Лит.: Энц. элем, мат., т. 1, Гостехиздат, М., 1951; И. Я. Депман, История
арифметики, Учпедгиз, М., 1959.
СИСТЕМАТИЧЕСКИЕ ДРОБИ—дроби, отнесенные к определенной
позиционной системе исчисления. Пусть в качестве основания позиционной системы взято
число k (см. Позиционная система); тогда говорят о представлении чисел
&-ичной С. д. Наиболее употребительны десятичные дроби, т. е. С. д., отнесен-

СИСТЕМА УРАВНЕНИЙ
413
ные к позиционной системе счисления с основанием 10. Числа 0, 1, 2, ...,
k — 1 именуют цифрами. Пусть дана бесконечная последовательность цифр alt a2t
а3, . . ., я/, . . ., ant . . ., 0<;#/<£. Тогда бесконечный ряд
ал а2 а* ап
— +—+—4· ··· 4·— (*)
называют &-ной С. д. Исключаются из рассмотрения такие последовательности,
в которых все а„, начиная с некоторого места, равны k—1. Обычно эту дробь
записывают в известной форме 0. alt a2 ... ап. С. д. вида (*) называют
конечной, если начиная с некоторого места все ее цифры равны нулю, и
бесконечной— в противном случае. Если \ -4=<х, то говорят, что С. д. представляет
1=1
число α или что она равна а. В этом случае для любого я>0 0<<х —
η
— \ ,-^<Т^· Любое действительное число а отрезка 0<ζα<1 представляется
ί=ι
одной и только одной £-ичной С. д. Всякая периодическая &-ичная дробь
представляет некоторое рациональное число а.
СИСТЕМА КООРДИНАТ — совокупность условий, определяющих положение
точки на прямой, на плоскости, в пространстве. Впервые понятие о С. к. было
введено в геодезии и астрономии для определения положения точки на земной
поверхности или на небесной сфере. В XIV в. французский математик Н. Орезм
пользовался С. к. на плоскости для построения графиков, он употреблял понятия
долготы и широты, соответствующие нашим понятиям абсциссы и ординаты.
В XVII в. благодаря трудам французского ученого Декарта было выяснено все
значение метода координат, позволяющего переводить задачи геометрии на язык
математического анализа и, обратно, давать различным результатам
математического анализа геометрическую интерпретацию. О различных С. к. см.
Координаты, Аффинные координаты, Декартовы координаты, Криволинейные координаты,
Сферические координаты.
Лат. со (cum) — приставка, означающая — совместно, и ordinatus —
упорядоченный, определенный.
Лит.: С. С. Бюшгенс, Аналитическая геометрия, ч. 1, Гостехиздат, М.—Л.,
194G.
СИСТЕМА УРАВНЕНИЙ — множество уравнений с η неизвестными xlt
х2 хп, для которых требуется найти значения неизвестных,
удовлетворяющие одновременно всем уравнениям системы. Совокупности x1=x\i jc2=jc?, . . .,
хп=х^ искомых значений неизвестных, удовлетворяющие всем уравнениям
системы, называются решениями системы. Две С. у. называются равносильными, если
каждое решение одной С. у. является решением другой Су., и наоборот»
причем обе С. у. рассматриваются в одной и той же области.
Всякая С. у. равносильна С. у. вида fk(X\, #2» . . ., #,г) = 0, где /г=1, 2, . . ., п.
С. у., у которых функции fk являются многочленами от xlt х2, . . ., хп,
называются алгебраическими. Простейшим случаем С. у. являются системы
линейных алгебраических уравнений (см. Линейное_уравнение).
Система дифференциальных уравнений—"конечное и бесконечное множество
дифференциальных уравнений (см.), для которых требуется найти все функции,
удовлетворяющие каждому из этих уравнений.

414
СКАЛЯР
СКАЛЯР — величина, значение которой характеризуется одним
действительным числом, без учета направления или другой какой-либо опенки, например
длина, площадь, объем, температура и др. В векторной алгебре С. называется,
в отличие от вектора, любое действительное число. С. также называется
скалярной величиной.
СКАЛЯРНАЯ МАТРИЦА — квадратная матрица вида
(с 0 ... 0\
О с . .. 0\
0 0 '. .'. с),
т. е. матрица, в которой а,-у= Щ?" /Ξ/ · Множество всех С. м. над полем Ρ
образует поле, изоморфное полю Р.
СКАЛЯРНОЕ ПОЛЕ —см. Поле скалярное.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ двух векторов а и Ь — число, равное
| а | · I b |-cos α, где | а |, | b | — модули векторов а и Ь, а а — угол между
этими векторами. С. п. векторов а и b обозначается так: ab; таким образом,
ab=[ а 11 b | cos α. С. п. двух векторов может быть выражено и так: ab =
=| а | ПР· ba =| b | пр. аь , где пр. Ьа или пр. аь — соответственно проекция
вектора b на вектор а и проекция вектора а на вектор Ь.
Если векторы а и b имеют в прямоугольной декартовой системе на плоскости
координаты a {xXi >ί}, b {x2, УгЬ то С. п. этих векторов может быть выражено
так: аЬ=*х1х2+У1У2· Аналогичная формула имеет место и для пространства трех
и большего числа измерений. С. п. обладает свойствами: 1) ab=ba (свойство
коммутативности), 2) (<xa)b=a(ab) (свойство ассоциативности относительно
скалярного множителя), 3) a(b-f-c)=ab-f-ac (свойство дистрибутивности); 4) ab=0
тогда и только тогда, когда или а=0, или Ь=0, или а±Ь. Если сила F на пути s
прямолинейного перемещения тела совершила работу Л, то работа, совершенная
телом, может быть выражена С. п.: /4 = F-s. С. п. аа=а2 = а2 называется
скалярным квадратом. Понятие С. п. находит большое применение в аналитической
геометрии (см.), физике и т. д.
В гильбертовых и η -мерных евклидовых пространствах С. п. определяется
как билинейная форма (см.), удовлетворяющая условию 4.
См. также Векторное произведение.
СКОБКИ — математические знаки (см.) ( ), [ ]*{},< >, употребляемые
для обозначения порядка действий. Первые из написанных С. называются
круглыми С, вторые — квадратными или прямоугольными, третьи — фигурными,
четвертые — угловыми или угольными.
СКОЛЬЗЯЩИЙ ВЕКТОР — вектор, начало которого можно произвольно
выбирать на прямой, на которой расположен вектор. С. в., таким образом, может
свободно скользить по прямой, на которой он расположен, не изменяя своего
направления. С. в., в отличие от свободного вектора (см.), нельзя, вообще говоря,
переносить с одной прямой на другую. Так, сила, приложенная к твердому телу,
является примером С. в. Понятие С. в. часто используется в физике.
См. также Вектор, Связанный вектор, Свободный вектор.
СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ — прямые, не лежащие в одной плоскости.
Через любые две С. п. а и Ь можно провести единственную пару параллельных
плоскостей аир (ааа, 6<ζβ) и бесчисленное множество пар взаимно
перпендикулярных плоскостей. Расстояние между параллельными плоскостями α и β
(аса, Ьа$) называется расстоянием между С. п.
Если три прямые а, 6, с являются попарно С. п., то можно построить
единственный параллелепипед, три ребра которого лежали бы на трех данных пря-

СЛОЖНАЯ ДРОБЬ
415
мых. Если четыре прямые а, Ьу с, d попарно скрещиваются, то можно построить
прямую, пересекающую все четыре данные прямые.
С. п. называют также некомпланарными прямыми.
СЛАВЯНСКИЕ ЦИФРЫ — цифры (см.), применявшиеся древними славянами
для обозначения чисел в алфавитной системе (см.) нумерации, возникшей в X в.
Считают,· что алфавитное обозначение чисел было введено одним из составителей
славянского алфавита — Кириллом (умер в 869 г.). Система обозначения чисел
была построена по типу ионинской, которой пользовались византийцы; числовые
значения получили лишь буквы, соответствовавшие буквам греческого алфавита.
Эта славянская система именовалась кириллицей. Во втором славянском способе
обозначения чисел — глаголице — сходства с ионической системой нет. Там
числовые значения букв строго соответствуют их алфавитному порядку. В обеих
системах для выделения в тексте чисел над каждой буквой или надо всем числом
ставился особый знак (титло).
В славянском языке для наименования высших десятичных разрядов
употреблялись названия «малое число», в котором названия не шли далее 106, и
«великое число», в которое входили числа до 1050. При этом одни и те же названия
обозначали в обеих системах различные числа. Так, тьма обозначала 10 000 в
малом числе и 1 000 000 в великом числе. Легион обозначал в малом числе 10 тем,
а в великом числе — тьму тем и т. д. 1050 называли колодой. Буквы алфавита,
соответствующие числам 1—9, обведенные кружком, обозначали тьмы,
обведенные кружком из точек — легионы, а кружком из лучей — леодры (леодр — в
малом числе равнялся 10 легионам, т. е. 1000, а в великом—1024=легион
легионов). Леодр леодров (1048) назывался вороном.
Лит.: Энц. элем, мат., т. 1, М.—Л., 1951; И. Я. Депман, История арифметики,
Учпедгиз, М., 1959.
СЛЕД МАТРИЦЫ
/я„ av2 ... я1л \
\ат ап2 · · · апп/
равен сумме элементов главной диагонали, т. е. С. м. А равен ац+а22+ · · · -r-flWz·
См. А является коэффициентом (с противоположным знаком) при хп—*
характеристическом уравнении (см.) для матрицы Л. См. является инвариантом матрицы
относительно преобразования А-+САС—1, где С — невырожденная матрица.
СЛЕД ПЛОСКОСТИ α — линия пересечения этой плоскости с одной из
плоскостей проекций: горизонтальной #, вертикальной V или фронтальной W.
Термин С. п., как и след прямой (см.)* употребляется в начертательной
геометрии (см.).
СЛЕД ПРЯМОЙ / — точка пересечения этой прямой с одной из плоскостей
проекций: горизонтальной Я, вертикальной V или фронтальной W. Термин С. п.,
как и след плоскости (см.), употребляется в начертательной геометрии (см.).
СЛОЖЕНИЕ в арифметике — одно из арифметических действий. Результатом
сложения чисел а и Ь является число а+Ь, называемое суммой слагаемых аи Ь.
При сложении справедлив переместительный (коммутативный) закон a-\-b=b-\-a
и сочетательный (ассоциативный) закон (a-f-6)-f-c==a-H6-f с). Помимо сложения
чисел, в математике рассматривают сложение, выполняемое над другими
объектами: многочленами, множествами, векторами, матрицами (см.). См. Сумма.
СЛОЖНАЯ ДРОБЬ («многоэтажная» дробь) — число, равное отношению
5 7
двух простых (обыкновенных) дробей (см.). Например, —, — — С. д. С. д. есть
1 4
б 3

416
СЛОЖНАЯ ФУНКЦИЯ
обобщение понятия дроби (см.), когда ее числителем и знаменателем могут быть
не только целые, но и дробные числа. С. д. иначе называется составной
дробью.
Ср. Сложное отношение (см.).
СЛОЖНАЯ ФУНКЦИЯ- Если ζ есть функция от у, а у в свою очередь есть
функция от х, то функция f(x)=z[y (χ)] называется С. ф. (иначе — композицией
функций от х). Переменная χ называется независимой переменной С. ф. /, а у—
промежуточной переменной. Если
z=/i(yi). У1 = ЫУ3)> У2 = /з(УзЬ
то
dz df-i df2 dfn-
dx
У/1-1 = /п(*).
dyx dy2
dyn-i
dfn
dx'
Это правило дифференцирования С. ф. выражает инвариантность дифференциала
функции относительно замены независимого переменного.
СЛОЖНОЕ ОТНОШЕНИЕ четырех точек (обозначается (ABCD)),
расположенных на одной прямой, — число, равное частному от деления простых
отношений (см.) трех точек:
(ABC) л „п ACDB
(ABCD) = 7Т^' или (ABCD) = -
(ABD)
CB-AD
Аналогично записывается С. о. четырех прямых (лучей) пучка:
(abed) =
(abc)
(abd)'
или (abcd) =
sin (ac)· sin (db)
sin (cb)·sin (ad) *
где (ас) —угол между а и с. С. о. —одно из основных понятий проективной
геометрии (см.) и важнейший инвариант проективных преобразований (см.), в то
время как в аффинной геометрии одним из
основных инвариантов является простое отношение
трех точек (прямых). В проективной геометрии
доказывается, что 4 различные точки,
расположенные на одной прямой, вообще говоря,
образуют 6 различных значений С. о.: \)(ABCD) = v\
2) (ABDC)= 1: ν; 3) (ACBD)= 1 — ν; 4) (ACDB) =
= 1: (1 —ν); 5) (ADBC) = 1 _(1 : ν) =^-=:^;
6) (ADCB)=v:(v — 1).
Если ряд / точек 1-го порядка (см.) проек-
тивен или перспективен пучку прямых (ряду /')
[см. Проективные ряды (пучки), или
Перспективные ряды (пучки)], то С. о. их соответственных
элементов равны:
(ABCD)=(abcd)=(A'BfC,D') (рис. 265).
С. о. четырех точек используется при доказательстве ряда теорем
проективной геометрии, в частности теоремы Чевы (см.) и теоремы Менелая (см.). С. о.
четырех элементов может равняться любому действительному числу. Если С. о.
равно (—1), то оно называется гармоническим (см.). С. о. иначе называют
двойным и реже — ангармоническим отношением.
СЛОЖНЫЕ ПРОЦЕНТЫ — проценты, насчитываемые в определенные сроки
как на основной взнос (вклад), так и на наращенные из этого взноса проценты
за предыдущий срок. Взнос а при р% годовых обратится за t лет в величину

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
417
100/ ·
а 1-Ь~ . если произведено исчисление по правилу простых (обычных) процен-
а{1+ш)'·
тов, и в величину a(l-b77pJ · если Расчет произведен по правилу С. п. Таким
образом, при С. п. вклад (взнос) а возрастает в геометрической прогрессии со
знаменателем <7= 1 + (р: 100).
См. также Процент.
СЛОЙ ШАРОВОЙ — см. Шаровой слой.
СЛУЧАЙНАЯ ВЕЛИЧИНА — величина, которая может принимать от случая
к случаю то или иное свое значение. Задается законом распределения (см.
Распределения закон). С. в. делятся на величины, распределенные дискретно и
непрерывно. Дискретные, случайные величины принимают каждая свое значение
с определенной вероятностью, в то время как непрерывные случайные величины
характеризуются плотностью вероятности (см.).
Многие свойства С. в. описываются математическим ожиданием (см.) и
дисперсией (см.).
Лит.: Б. В. Г я е д е н к о, Курс теории вероятностей, Гостехиздат, М., 1954.
СЛУЧАЙНОЕ СОБЫТИЕ (в теории вероятностей) — событие, которое может
произойти, а может и не произойти. Наступление С. с. характеризуется
вероятностью (см.) или плотностью вероятности (см.). Вероятность С. с.
характеризует частоту наступления С. с, если указанные события повторяются большое
количество раз. Последнее утверждение составляет содержание закона больших
чисел (см. Больших чисел закон), а также теоремы Лапласа (см. Лапласа
теорема).
СЛУЧАЙНЫЙ -ПРОЦЕСС (в теории вероятностей) — случайная величина,
зависящая от времени. Закон распределения (см. Распределения закон) такой
величины есть функция пространственных переменных и времени. Теория С. п. имеет
многочисленные и важные приложения к физике, технике (броуновское движение,
распространение радиосигналов при наличии помех и т. п.). Главные результаты
теории С. п. получены русским ученым А. А. Марковым (старшим), А. Н.
Колмогоровым, А. Я. Хинчиным, а также американскими математиками В. Феллером,
Н. Винером, Дж. Дубом и др. В настоящее
время теория С. п. быстро развивается.
СМЕЖНЫЕ УГЛЫ —два угла '(/*, k)
и Z(k, /), у которых k — общая сторона,
а две другие стороны h и / составляют одну
прямую. Так углы / и 2 — С. у. (рис. 266).
Сумма С. у. равна двум прямым: Ζ14-^2=
=2d, где d — прямой угол.
СМЕЖНЫЙ ИНТЕРВАЛ замкнутого мно- 9fi
жества (см.) Λ4, лежащего на прямой, — интер- ^ис* bb
вал (быть может, бесконечный), не имеющий
с Μ общих точек, концы которого принадлежат М. Термин С. и.
употребляется в формулировке теоремы о строении произвольного открытого множества
на прямой: всякое открытое множество на прямой есть конечное число или
счетное множество С. и., дополнительного к нему замкнутого множества.
СМЕШАННАЯ ДРОБЬ — то же, что и смешанное число (см.).
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ трех векторов а, Ь, с — число, равное
скалярному произведению двух векторов, один из которых равен векторному
произведению [а, Ь] первых двух векторов, а второй равен вектору с. Следовательно,
С. п. трех векторов а, Ь, с равно [а, Ь] с. С. п. трех векторов геометрически
равно обьему параллелепипеда, построенного на этих векторах а, Ь, с (рис. 267),
взятому со знаком плюс, если тройка векторов а, Ь, с и тройка координатных
векторов (реперов) i, j, k одинаково ориентированы, и взятому со знаком минус,
Толковый словарь математических терминов

418
СМЕШАННАЯ ПРОИЗВОДНАЯ
если эга тройка векторов имеет противоположную ориентацию. С. п.
векторов а, Ь, с не изменяется при круговой (циклической) перестановке векторов и
изменяет свой знак на противоположный при нарушении круговой перестановки
векторов (сомножителей).
Если координаты векторов а, Ь, с соответственно равны:
{*ι. У и ζι\, !*2> У2> гг}9 !*8. Уа» гъ)>
то С. п. векторов а, Ь, с выразится через координаты в виде определителя:
[а Ь]с=±
'*!
Хо
χ*
Ух 2Ί
У-2 *2
Уз Ч\
Рис. 267
С. п. трех векторов называется также векторно-
скалярным произведением этих векторов. С. п.
трех векторов а, Ь, с обозначается еще и так: abc.
Если три вектора компланарны (см.), то их
С. п. равно нулю. Справедливо и обратное
предложение: если С. п. трех векторов равно нулю,
то такие векторы компланарны. Понятие С. и.
трех векторов используется при вычислении
объема тетраэдра, построенного на этих векторах.
ПРОИЗВОДНАЯ — частная производная высшего порядка
СМЕШАННАЯ
(см.), взятая по различным переменным, например:
д2и д*и д*и
дхду' ду*дг2' дхЧудг "
О равенстве смешанных производных см. Перестановка дифференцирований.
СМЕШАННОЕ ЧИСЛО — число, состоящее из целой и дробной части, напри-
2 1
мер: 3—; —1—. С. ч. называют иногда смешанной дробью.
5 7
СОБСТВЕННАЯ ФУНКЦИЯ линейного дифференциального или интегрального
оператора А — функция /, обладающая свойством:
Л/=Х/, /^0,
где λ — постоянная. Число λ называется собственным значением (см.) Л.
Например, у оператора L(y)=—у9 в пространстве дважды дифференцируемых функций,
равных нулю на концах отрезка [0, π], собственными значениями являются числа
а собственными функциями — функции yn^sinnxt так как — уп-
■ п*уп.
СОБСТВЕННОЕ ЗНАЧЕНИЕ — см. Собственная функция и Собственный вектор.
СОБСТВЕННОЕ ПОДМНОЖЕСТВО множества А — всякое подмножество (см.)
множества Л, отличное от пустого множества (см.) и от самого множества А.
С. п. множества А называют также правильной частью множества А или
истинным подмножеством множества Л.
СОБСТВЕННЫЙ ВЕКТОР — понятие линейной алгебры. Пусть в линейном
пространстве Ρ задано линейное преобразование Н. Если преобразованием /7
вектор Ь, отличный от нуля, переводится в вектор, пропорциональный самому Ь,
//Ь = лЬ, где λ —некоторое действительное число, то вектор b называется С. в.
преобразований Н. Число λ называют собственным значением или корнем
преобразования Η и говорят, что С. в. b принадлежит собственному значению λ.
Другими словами, С. в. линейного преобразования — это такие векторы, которые
при данном преобразовании остаются параллельными (коллинеарными), т. е.
только умножаются на скаляр.

СОВМЕСТНЫЕ УРАВНЕНИЯ
419
Собственные значения λ линейного оператора А в /ι-мерном пространстве
удовлетворяют характеристическому уравнению (см.):
detl|a/y —A^yl^O,
где aij — матрица оператора А в произвольном базисе
Л __[1 при /=/,
Ч/~\0 при ίφΐ.
После вычисления соответствующего собственного значения С. в. (xlt х2, . . .,хп)
могут быть определены из системы уравнений:
η
^aijXj=lxi (/-1, 2 η).
С. в. и собственные значения являются важнейшими характеристиками
линейного оператора. Если все Св. образуют базис в пространстве, то матрица
оператора Η в этом базисе, составленном из С. в., имеет вид:
/λχ0 ··· О
/ 0λ2 ... О
\оо ... к
где λ/ (/=1, 2 η) —собственные значения А.
СОБСТВЕННЫЙ ОТНОСИТЕЛЬНЫЙ ЭКСТРЕМУМ —термин, объединяющий
понятия собственного максимума и собственного минимума, о которых см. термины
Относительный максимум и Относительный минимум.
СОБСТВЕННЫЙ ЭКСТРЕМУМ—термин, объединяющий понятия
собственного максимума и собственного минимума, о которых см. термины Максимум
и Минимум.
СОВЕРШЕННОЕ МНОЖЕСТВО — замкнутое множество, не имеющее
изолированных точек (см. Замкнутое множество). Примером является канторово С. м.
(см. Кантора множества). Всякое непустое См. в евклидовом пространстве
имеет мощность континуума (см.). Мера С. м. может равняться нулю.
СОВЕРШЕННОЕ ЧИСЛО — натуральное число /г, сумма натуральных
делителей которого, за исключением самого числа /г, равна п. Например, числа 6, 28,
496 и др. С ч. были введены Евклидом в «Началах» (см.). Евклиду было
известно четыре С. ч. В настоящее время известно двадцать четных С ч. Однако
не решен вопрос о том, конечно или бесконечно множество С ч. Неизвестно
также, существуют ли нечетные С ч. С древности известно, что всякое четное
число являе'1ся С. ч. тогда и только тогда, когда оно имеет вид:
2^-1(2^—1),
где ρ и 2Р — 1 — простые числа. Одно из самых больших совершенных чисел,
известных до 1957 г., было 23216 (23217—1). Совершенность этого числа была
установлена с помощью быстродействующих электронных вычислительных машин.
Самым большим из известных до настоящего времени (1962) является С. ч.
2*422 (24423 1).
Нечетных С. ч. не известно ни одного. Если они и существуют, то, вероятно,
очень большие.
СОВМЕСТНЫЕ УРАВНЕНИЯ — система уравнений, для которой существуют
значения неизвестных, удовлетворяющие всем данным уравнениям. Геометрически
совместность системы уравнении означает существование общих точек у
многообразий, изображаемых этими уравнениями (см. также Система уравнений).
27*

420
СОДРУЖЕСТВЕННЫЕ ЧИСЛА
СОДРУЖЕСТВЕННЫЕ ЧИСЛА —два числа, каждое из которых равно сумме
делителей другого, например числа 220 и 284. Делителями числа 220 являются
1, 2, 4, 5, 10, 20, И, 22, 44, 55, НО; их сумма равна 284. Делителями числа
284 являются 1, 2, 4, 71, 142; сумма их равна 220. С. ч. были введены в
школе Пифагора, где им придавали мистический смысл. Тогда было известно 4^
пары С. ч. До сих пор неизвестно, конечно или бесконечно множество С. ч. С. ч.
также называются дружественными числами.
Лит.: Б. Л. Ван дер Варден, Пробуждающаяся наука, Физматгиз, М., 1959-
СОЕДИНЕНИЕ — собирательный термин комбинаторики (см.). Под С.
понимают сочетания, размещения, перестановки (см.) без повторений. С. с
повторениями суть соответственно сочетание с повторениями (см.), размещение с
повторениями (см.) и перестановка с повторениями (см.).
СОИЗМЕРИМЫЕ ВЕЛИЧИНЫ —величины, имеющие общую меру (см.).
Величины, не имеющие общей меры, называются несоизмеримыми, например
диагональ квадрата несоизмерима с его стороной. Отношение несоизмеримых величин
есть число иррациональное (см.).
СОКРАЩЕНИЕ ДРОБИ — тождественное преобразование дроби, выполняемое
с использованием основного свойства дроби, т. е. путем деления числителя и
знаменателя дроби на их общий делитель.
, 25 5 а(Ь+с) Ь+с
Примеры: 1) -=-, 2) -д^—^. <β+0>.
СОЛЕНОИДАЛЬНОЕ ПОЛЕ — векторное поле и, не имеющее ни
источников, ни стоков, иными словами, векторное поле, для которого расходимость равна
нулю в любой его точке:
divu(p) = (V u(/?)) = 0.
Поток векторного дифференцируемого С. п. через любую замкнутую
поверхность, которую можно стянуть в поле в одну точку, равен нулю. Поэтому в С. п.
потоки вектора через различные сечения векторной трубки равны между собой.
Поле вихря любого дважды дифференцируемого векторного поля соленоидально,
так как
div-rotu = (V'[VXVl)=0.
Поэтому потоки через все сечения каждой вихревой трубки равны между собой,
их общее значение называют напряжением вихревой трубки. Всякое С. п. можно
представить в виде вихря некоторого другого, дважды дифференцируемого
векторного поля:
u = rot v=[VXv].
Примерами С. п. могут служить поле скоростей несжимаемой жидкости,
магнитное поле внутри бесконечного соленоида. См. Векторное поле, Поле.
Лит.: Η. Ε. Кочин, Еекторное исчисление и начала тензорного исчисления, Изд-во
АН СССР, М., 1951.
СООТВЕТСТВЕННЫЕ УГЛЫ — пары углов, образованные при пересечении
двух прямых а и b третьей прямой с (см. Угол). Если С. у. равны, то прямые
а и b параллельны в плоскости Евклида. Справедливо и обратное предложение:
если прямые а и b параллельны (в плоскости Евклида), то С. у., образованные
при пересечении этих прямых третьей прямой с, будут равны. Если же С. у.
рассматриваются в абсолютной геометрии (см.), то при равенстве их прямые а и b
не пересекаются (параллельны в плоскости Евклида и сверхпараллельны в
плоскости Лобачевского).
СООТВЕТСТВИЕ (отображение) — неопределимое, но интуитивно ясное
понятие. Являясь аксиоматическим, С. играет важнейшую роль во всей математике.

СОПРИКАСАЮЩАЯСЯ СФЕРА
421
Идеей отображения (в частности, функции) проникнута вся современная
математическая наука. Отображение есть С. элементов данных множеств, вообще говоря,
не однозначное и не взаимно однозначное.
Примеры: 1) функция одного переменного отображает множество чисел своей
области определения на множество своих значений; 2) функционал (см.)
отображает некоторое множество функций в некоторое множество чисел; 3)
стереографическая проекция (см.) отображает точки сферы на расширенную область
комплексного переменного.
СОПРИКАСАЮЩАЯСЯ ОКРУЖНОСТЬ в точке кривой Μ — окружность,
имеющая с кривой / в той же точке Μ касание порядка п>2 (см.
Соприкосновение). Радиус С. о. является радиусом кривизны (см.) кривой / в точке Mt a
центр С. о. — центром кривизны.
Если кривая плоская и задана уравнением у = /(*),
то се радиус кривизны р определяется по формуле:
з
Р^
|1 + (У)2]
У*
где у'* и у" — соответственно первая и вторая
производные функции в точке χ (рис. 268). С. о. в точке
Μ кривой / наиболее тесно подходит к этой кривой
в окрестности точки по сравнению с любой другой
окружностью, проходящей через точку М. С. о.
кривой лежит в соприкасающейся плоскости (см.). С. о. называется также
соприкасающимся кругом.
Лит.: П. К. Рашевский, Курс дифференциальной геометрии, Гостехиздат, М.,
1956.
СОПРИКАСАЮЩАЯСЯ ПЛОСКОСТЬ в точке Μ кривой / — плоскость,
имеющая с кривой / в той же точке Μ касание порядка п>2 (см. Соприкосновение).
С. п. кривой / в точке Μ наиболее тесно примыкает к кривой / в окрестности
точки Μ из всех касательных плоскостей кривой в той же точке М. С. п. может
быть определена как предельное положение
переменной плоскости, проходящей через три
точки кривой, когда эти точки стремятся
к точке М. На рис. 269 изображена кривая /
и С. п. а, когда кривая, соприкасаясь в точке
М, переходит из одного полупространства,
определяемого С. п. а, в другое.
Если кривая задана уравнениями: x=x{t)i
У=У (0» z=z{t), то уравнение С. п. имеет вид:
Рис. 269
х — х0 у —у0 г—г0
хх
х»
Уг
Уч.
= 0,
где х, у, г — текущие координаты, x0i у0, ?о —координаты точки М\ a xl9 ylt
2ι. *2» Уг. z2 — координаты точек Мг и М2, стремящихся к Λί.
Лит.: П. К. Рашевский, Курс дифференциальной геометрии, Гостехиздат, М.,
1960,
СОПРИКАСАЮЩАЯСЯ СФЕРА в точке Μ кривой / — сфера, имеющая с
кривой в точке Μ касание порядка п>Ъ (см. Соприкосновение). С. с. может быть
определена как предельное положение переменной сферы, проходящей через

422
СОПРИКАСАЮЩИЙСЯ КРУГ
четыре точки кривой /, когда они стремятся к точке Λί. Радиус С. с. кривой
вычисляется по формуле:
где р — радиус кривизны (см.) кривой в точке Λί, σ — кручение кривой в той же
точке, ds — дифференциал дуги кривой.
Лит.: П. К. Рашевский, Курс дифференциальной геометрии, Гостехиздат, M.t
1950.
СОПРИКАСАЮЩИЙСЯ КРУГ (в дифференциальной геометрии) — то же, что
и соприкасающаяся окружность (см.).
СОПРЯЖЕННЫЕ ГАРМОНИЧЕСКИЕ ФУНКЦИИ — две дифференцируемые
в некоторой области D плоскости (xt у) функции и (х, у) и υ (χ, у),
удовлетворяющие в этой области уравнениям:
ди ди ди dv
дх ду% ду
дх
С. г. ф. определяют в области D аналитическую функцию (см.) f(z) = u(x, )>) +
-\-iv(x, у). Каждая из С. г. ф. является гармонической (см.) в области D.
Функция v(x, у) называется сопряженной с гармонической функцией и(х, у)
и определяется ею с точностью до постоянной. Сопряженной с υ (χ, у) является
функция — и (xf у), т. е. ν (χ, у) и—и (х, у) также составляют пару С. г. ф. (Однако
ν (х, у) и ы=(л;, у) не составляют пару С.г. ф.)
Отношение сопряженности гармонических
функций не удовлетворяет условию симметричности.
СОПРЯЖЕННЫЕ ГИПЕРБОЛЫ — две
гиперболы, действительная ось одной из
которых является мнимой осью другой
гиперболы и, наоборот, мнимая ось одной из
гипербол является действительной осью другой.
С. г. в прямоугольной декартовой системе
координат имеют уравнения:
Рис. 270
г-*"1
Xй У3
:1.
С, г. имеют один и тот же центр и одни и те же асимптоты и оси (рис. 270).
СОПРЯЖЕННЫЕ ДИАМЕТРЫ кривой 2-го порядка — два диаметра, каждый
из которых делит пополам хорды этой кривой, параллельные другому диаметру.
С. д. окружности всегда взаимно перпендикулярны. Свойство сопряженности
диаметров кривой 2-го порядка сохраняется при параллельном проектировании этой
кривой, т. е. является инвариантом аффинного преобразования.
СОПРЯЖЕННЫЕ ЧИСЛА над полем Ρ — корни некоторого неприводимого
УТ 1/7
многочлена (см.) над полем Р. Например, четыре числа: (1 ±i) —— и (—1 ±i) ——.
являющиеся корнями неприводимого над полем рациональных чисел многочлена
дс4+1, будут С. ч. над полем рациональных чисел.
Числа, сопряженные над полем комплексных чисел, называются комплексно-
сопряженными. Взаимно сопряженными комплексными числами является пара
чисел вида а+Ы и а—Ыч где а и Ь — вещественные числа.
СОПРЯЖЕННЫЙ КВАТЕРНИОН с кватернионом L**a + bi+cj+dk есть ква.
терн ион L=a — Ы — cj — dk.

СОФИЗМ
423
СОСТАВНОЕ ЧИСЛО — натуральное число, имеющее более двух натуральных
делителей. Всякое С. ч. единственным образом, с точностью до "порядка
следования множителей, представляется в виде произведения простых чисел. Последнее
утверждение часто называют основной теоремой арифметики (см.).
СОФИЗМ—преднамеренно неверный вывод, неверное доказательство какого-либо
предложения. При этом ошибка в доказательстве бывает довольно искусно
замаскирована в одной из цепей доказательства. Приведем примеры различных
математических С:
1. Два произвольных действительных числа а и Ь равны. Рассмотрим
равенство:
(а — б)2=(6 — а)2.
Извлекая из обеих частей его квадратный корень, получим:
а — Ъ=Ь — а\ 2а = 26; а=Ь.
Ошибка в «доказательстве» состоит в том, что при извлечении арифметического
корня мы допускали записи ух2=х и у (— х)2=— х, в то время как следует
писать: Vx2=\xl У"(— х)2=| х\.
. / 1 \2 1
2. Докажем, что 2<1. Так как —I <—, то, логарифмируя обе части
неравенства, получим: 21g—-< lg-—, откуда, деля обе части неравенства на число
lg-—, будем иметь: 2<1.
Ошибка в «доказательстве» заключается в том, что при делении обеих частей
неравенства на отрицательное число мы не изменили знак неравенства.
3. Известно, что по формуле Эйлера e-v/=cosA;-b/sin.Y. Пользуясь этой
формулой, докажем, что /=0. Полагая х=2 π, получим: e27W=cos2jt-Wδίπ2π=1;
с другой стороны, е°=1; следовательно, e2:t'=e0,
откуда 2π/=0. Но так как 2π=£θ, то /=--0.
Ошибка в «доказательстве» состоит в том, что мы
на можем в комплексной области приравнивать
показатели равных степеней e2nt и е°, так как функция ez
в комплексной области периодическая с периодом 2 π /,
т. е. ez=ez'*m 2 г. тя
4. Сумма углов треугольника равна 2d.
Доказательство, не опирающееся на аксиому о параллельных
прямых.
Пусть сумма углов треугольника равна х.
Докажем, что x=2d. Проведем в данном треугольнике
ABC (рис. 271) любую секущую, тогда получим два треугольника ABC и BDC.
Запишем сумму образовавшихся при этом углов:
Ζ 14-/24- ^4-bX5-f-Z3+Z6=2*.
Так как Z44-./5=2d, то предыдущее равенство запишем так: Z14-^24-2с?4-
4-Z34-Z6=2jt, или Zl4-./24-Z34-Z6=2jt —2d; так как левая часть есть х,
то после преобразований получим jc=2d.
Ошибка в «доказательстве» состоит в том, что мы неявно пользуемся
предложением, равносильным аксиоме параллельности, состоящей в том, что сумма углов
треугольника неизменна. Известно, что такое утверждение не имеет места ни в
геометрии Лобачевского, ни в геометрии Римана.

424
СОФОКУСНЫЕ КРИВЫЕ
О роли С. В. И. Ленин писал: «. . . рассуждения, которые математики
называют математическими софизмами и в которых, — строго логичным, на первый
взгляд, путем, — доказывается, что дважды два пять, что часть больше целого
и т. д. Существуют сборники таких математических софизмов и учащимся детям
они приносят пользу» (В. И. Ленин, Соч., т. 7, стр. 78, изд. 4).
С. имеют педагогическую ценность, так как их анализ предупреждает
возможность повторения ошибок со стороны учащихся, воспитывает у них критическое
отношение к рассуждениям.
Лит.: Я. С. Дубнов, Ошибки в геометрических доказательствах, Гостехиздат, М.,
1956; В. М. Брадис и А. К. Харчева, Ошибки в математических рассуждениях,
Учпедгиз, М., 1938; В. Л. Минковский, Математические софизмы и их
педагогическая роль, сМатематика в школе», 1946, № 5—6.
СОФОКУСНЫЕ КРИВЫЕ—то же самое, что и конфокальные кривые (см.).
СОХОЦКОГО ТЕОРЕМА в теории функций комплексного переменного
утверждает, что аналитическая функция в окрестности особой точки принимает значения
сколько угодно близкие к любому наперед заданному. Усилением С. т. является
теорема Пикара.
Иногда С. т. неправильно называют теоремой Зейерштрасса. С. т. открыта
русским ученым Ю. В. Сохоцким и одновременно итальянским математиком
Ф. Казорати.
СОЧЕТАНИЕ — одно из понятий комбинаторики (см.). С. из η элементов
по k называется всякое подмножество, состоящее из k элементов множества из η
элементов. Два С. считаются различными, если некоторый элемент, входя в одно
из них, не входит в другое. Число различных С. из η элементов (некоторого
л-элементного множества) по k (элементов) обозначается символом Скп и
выражается формулой:
С*- 51_ИЛИС*-Д
п k\(n—k)l n Pk
где Л* — число размещений из η элементов по kt Pk — число перестановок из к
элементов. Числа Ckn являются биномиальными коэффициентами.
Пример. Сколько существует в выпуклом n-угольнике точек пересечения
диагоналей, считая, что никакие три из них не пересекаются в одной точке?
Решение. Каждая искомая точка вполне определяется двумя диагоналями.
Всякие две (пересекающиеся) диагонали вполне определяются четырьмя вершинами
π-угольника — теми, которые они соединяют. Обратно, всякие четыре вершины
гс-угольника определяют одну из искомых точек. Поэтому ответом на задачу будет
число С из η (вершин) по 4, т. е.:
,г(/2— 1) (Λ7 — 2)(Г2 —3)
п 43-2.1
Франц. combinaison — сочетание.
СОЧЕТАНИЕ С ПОВТОРЕНИЯМИ —понятие комбинаторики (см.). Пусть
— теоретико-множественное объединение k одинаковых конечных множеств М,
состоящих из η элементов аг, a2i . . . , ап, т. е. в множестве V каждый
элемент α ι содержится k раз. С. с п. из /г элементов множества Μ по k элементов
называется сочетание в обычном смысле (т. е. без повторений) из k+n — 1
элементов множества У^ по k. Два С. с п. считаются различными, если хотя бы
для одного номера г (1<г</г) в одном из этих С. с п. элементы ат имеются
большее число раз, чем в другом. Число различных С. с п. из η элементов
Σ

СПИРАЛЬ
425
по k равно — -—. Это число равно Ckn , k__x, где C^,k __. — число сочс-
k\ (η — 1)! "*" "*"
таний (без повторений из n+k— 1 элементов по k).
СОЧЕТАТЕЛЬНЫЙ ЗАКОН —то же, что и закон ассоциативности (см.).
СПЕКТР ОПЕРАТОРА — совокупность комплексных чисел, каждое из
которых таково, что оператор А — λ £, где Ε — оператор, переводящий каждый
элемент пространства в себя, не имеет ограниченного обратного, определенного на всем
рассматриваемом пространстве. С. о. принадлежат все его собственные значения,
т. е. такие числа λ, при которых существует нулевой элемент χ такой, что Αχ=λχ.
Однако С. о. не исчерпывается собственными значениями. Например, оператор
умножения на t в пространстве функций, интегрируемых в квадрате на отрезке
0^/<1, не имеет собственных значений, однако его спектр есть отрезок 0^λ<1.
СПЕЦИАЛЬНЫЕ ФУНКЦИИ — класс функций, часто встречающийся при
интегрировании уравнений математической физики. Основные С. ф. определяются
обычно как решения линейных дифференциальных уравнений 2-го порядка с
переменными коэффициентами. Важнейшие С. ф.: гипергеометрические,
цилиндрические, сферические, шаровые и др. Часто к С. ф. относят трансцендентные как
не выражающиеся через элементарные функции.
СПИНОР — математическая величина, принимающая в данной системе
координат значения, определенные с точностью до знака. При переходе от одной
системы координат к другой эти значения изменяются по особому закону. В
теории представлений групп рассматриваются представления в координатах
пространства С. (спинорные представления). С. применяются во многих вопросах
квантовой механики (см. Спинорное исчисление).
СПИНОРНОЕ ИСЧИСЛЕНИЕ — один из математических аппаратов квантовой
механики. Физическая величина изучается обычно в некоторой системе координат
и задается в ней набором чисел-компонент физической величины. При изменении
системы координат эти компоненты преобразовываются по определенным законам.
Физическими величинами с различными законами преобразования являются векторы,
тензоры, псевдотензоры, спиноры и т. п. С. и. изучает спиноры (см.). К понятию
спиноров наука подошла в начале XX в. с лвух различных сторон: при изучении
физического явления спина электрона и при разработке математической теории
представлений групп (французский ученый Э. Картан, 1913); подобно тензорному
исчислению, в С. и. различаются ковариантные и контравариантные спиноры,
вводится операция свертывания спинора.
Лит.: П. К. Рашевский, Риманова геометрия и тензорный анализ, Гостехиздаг,
М., 1953; П. К. Рашевский, Теория спиноров, «Успехи математических наук»,
вып. 2, 1955.
СПИРАЛЬ — плоская кривая, многократно обходящая некоторую
фиксированную точку О, приближаясь к ней с каждым обходом или удаляясь от нее. Если
точку О выбрать за полюс (см.) полярной системы координат, то уравнение С.
в этой системе можно записать в виде Р=/(ф) и будет справедливо неравенство
/(φ-1-2π)>/(φ) или /(φ+2π)</(φ) для всякого φ. Наиболее известные С:
архимедова С. (см.), логарифмическая С. (см.), Корню С, или клотоида (см.),
параболическая С. (см.), гиперболическая С. (см.), С. интегрального синуса
и интегрального косинуса (см.), жезл (см.), кохлеоида (см.).
Свойства многих С. находят применение при решении практических задач.
Так, свойство логарифмической С. пересекать под одним и тем же углом все
радиус-векторы используется при проектировании вращающихся ножей, фрез
и т. д. для получения постоянного угла резания; С. Корню (клотоида)
используется при графическом решении некоторых задач дифракции; название
некоторых С. связано с тем, что их полярные уравнения напоминают уравнения соответ-

426
СПРЯМЛЕНИЕ КРИВОЙ
ствующих кривых в декартовой системе координат: ρ2 = αφ —параболическая С,
а
р=— — гиперболическая С.
φ
Иногда С. называют также пространственные кривые, многократно обходящие
вокруг некоторой оси; например, винтовая линия (см.) называется также С.
Лит.: сГрафический справочник по математике. Атлас кривых», под ред. А. Ф. Берманта,
ч. 1, Μ — Л., 1937; С. Ρ о у, Геометрические упражнения с куском бумаги, Одесса, 1910;
А. А. Саве лов, Плоские кривые, Физматгиз, М., 1960.
СПРЯМЛЕНИЕ КРИВОЙ — нахождение длины этой кривой. Если кривая
имеет конечную длину (см.), то ее называют спрямляемой. Под длиной кривой
понимают предел последовательности длин ломаных, вписанных в кривую при
условии, что длина наибольшего звена ломаной стремится к нулю.
СПРЯМЛЯЮЩАЯ ПЛОСКОСТЬ — плоскость, проходящая через касательную
и бинормаль (см.) в данной точке Μ пространственной кривой. Огибающая (см.)
семейства С. п. данной кривой / называется спрямляющей поверхностью (см.)
этой кривой.
СПРЯМЛЯЮЩАЯ ПОВЕРХНОСТЬ пространственной кривой / — огибающая
(см.) семейство спрямляющих плоскостей (см.) этой кривой. На С. п. кривая /
является геодезической (см. Геодезическая линия). С. п. является
развертывающейся поверхностью (см.). При развертывании С. п. на плоскость кривая /
преобразуется в прямую, т. е. спрямляется, чем и объясняется термин С. п.
СРАВНЕНИЕ. Целые числа а и Ь, дающие одинаковые остатки при делении
па т, принято называть сравнимыми по модулю т и обозначать так: а =~ b (mod m).
Например, 2ξ — 26 (mod 7).
Сравнимые числа а и Ь по модулю т называются иначе равноостаточнымн.
Такие пары чисел в вопросах делимости обладают по отношению к числу т
некоторыми общими свойствами. Если а и Ь при делении на т дают остаток г, то
a=km+rt b=lm+r,
тогда a — b=(k--l)m делится на т, отсюда
a=qm+b% b=a — qm.
Отношение сравнимости — некоторое сходство подобия двух чисел. Установление
важнейших свойств этого отношения двух чисел и составляет содержание теории
сравнений, разработанной Гауссом. Вообще говоря, два числа, сравнимые по
модулю т% не имеют друг с другом ничего общего по другому модулю п.
Основные теоремы теории сравнений показывают, что с С., за исключением
некоторых случаев, можно оперировать как с обыкновенными равенствами. Очень
важная теорема теории сравнений устанавливает, что из
х~у (mod/и)
следует:
Ρ (х)^Р (у) (mod m),
где Р —многочлен с целыми коэффициентами.
Лит.: Энц. элем, матсм., т. 1, Гостехиздат, М., 1951; А. А. Бухштвб. Теория
чисел, Учпедгиз, М., 19GO.
СРЕДНЕЕ ЧИСЕЛ al9 α2» · · · » °п — числовая характеристика 5 этих чисел,
удовлетворяющая условию:
min {alt Go, ... , αη} <S < max {аъ а2, . . . , ап}.
Примерами С. могут служить: арифметическое С. ч. (см.), геометрическое
С. ч. (см.), гармоническое С. ч. (см.), квадратическое С. ч. (см.), степенное
С. ч. (см.), взвешенное С. ч. (см.), арифметико-геометрическое С. ч. (см.).
СРЕДНЕЕ ПРОПОРЦИОНАЛЬНОЕ положительных чисел_ а н Ь — число х,
равное корню квадратному из их произведения, т. е. х=у ab. Название С. п.

СТАТИСТИЧЕСКАЯ ПРОВЕРКА
427
как на диаметре, строится
Рис. 272
оправдывается тем, что число χ является средним членом пропорции а:х=х:Ь.
С. п. двух данных отрезков а и b легко строится с помощью циркуля и линейки
следующим образом (рис. 272). На отрезке а+Ь,
полуокружность. Из точки С, делящей отрезок
а-\-Ь в отношении а:Ь, восставляем перпендикуляр
χ до пересечения с полуокружностью. Величина
этого перпендикуляра χ равна С. п. отрезков а и Ь.
С. п. называется также средним геометрическим.
См. Среднее чисел.
СРЕДНЯЯ КРИВИЗНА поверхности в данной ее
точке Μ — полусумма главных кривизн этой
поверхности в точке М.
Если С. к. в каждой точке поверхности равна
нулю, то поверхность будет минимальной (см.
Минимальная поверхность, Главная кривизна, Кривизна).
СРЕДНЯЯ ЛИНИЯ· 1°. С. л. трапеции — отрезок, соединяющий середины
боковых сторон трапеции. С. л. трапеции параллельна ее основаниям и равна
их полусумме. С. л. трапеции не разбивает трапецию на подобные трапеции.
При аффинных преобразованиях трапеции ее С. л. переходит в С. л.
преобразованной трапеции.
2°. С. л. треугольника — отрезок, соединяющий середины двух сторон
этого треугольника: третья сторона при этом называется основанием
треугольника. С. л. треугольника параллельна основанию и равна его половине. Во
всяком треугольнике С. л. отсекает от него треугольник, ему подобный. Три С. л.
разбивают треугольник на четыре равных треугольника. При аффинных
преобразованиях треугольника С. л. остается С. л. преобразованного треугольника.
СТАТИСТИЧЕСКАЯ ПРОВЕРКА гипотез состоит в том, чтобы решить по
данным эксперимента, согласуется ли некоторая гипотеза о распределении
случайной величины с данными опыта. Например, пусть гипотеза, подлежащая
проверке, состоит в том, что математическое ожидание (см.) случайной
величины, получаемой в результате эксперимента, равно нулю. Тогда, в соответствии
с законом больших чисел (см.), среднее арифметическое результатов η экспериментов
(где η достаточно велико) должно быть близко к нулю. Если это среднее
оказывается далеким от нуля, то гипотеза отвергается. Точное правило, когда
следует принимать и когда отвергать гипотезу, получается применением
предельных теорем (см.). Это правило заключается в следующем. Пусть известна
дисперсия (см.) случайной величины, равная σ2, и в η независимых опытах были
получены результаты xlt x2i . . ., Xk (Xk есть результат &-го опыта). Если
гипотеза справедлива, то случайная величина имеет приблизительно нормальное
/ σ \
распределение (см.) с параметрами [ 0, —— · Условимся отвергать гипотезу,
. VnJ
если )*Π>β· Правило принимать или отвергать гипотезу определяется, таким
образом, числом β. Число β выбирается так, чтобы вероятность Ρ(|]Γ|>β}
отвергнуть гипотезу в том случае, когда она верна, была мала, например 0,01.
Таким образом, β является корнем уравнения:
р/7
0.01-/>{|*|>β) -Ρ
Ύη
aVn
2π J
~4x.

428 СТАЦИОНАРНЫЙ ВЕРОЯТНОСТНЫЙ ПРОЦЕСС
Приближенное решение этого уравнения легко находится с помощью таблиц
нормального распределения (см.).
Лит.: Б. Л. Ван дерВарден, Математическая статистика, ИЛ, М., 1960;
Б. В. Г н е д е н к о, Курс теории вероятностей, Физматгиз, М., 1961.
СТАЦИОНАРНЫЙ ВЕРОЯТНОСТНЫЙ ПРОЦЕСС — случайная величина,
зависящая от времени (т. е. вероятностный процесс), если ее вероятностные
характеристики [распределение (см.), математическое ожидание (см.) и др.] не
меняются с течением времени. С. в. п. играет большую роль в приложениях
теории вероятностей к радиоэлектронике, теории связи, прогнозу погоды и др.
Большое значение для практики имеет так называемая задача экстраполяции
(прогнозирования) С. в. п., т. е. задача возможно более точного определения
значения процесса в момент Т-\-х (τ>0) по известным значениям его за время
от to до Т. Эта задача рассмотрена впервые А. Н. Колмогоровым, затем Н.
Винером и рядом других математиков. Известно, например, что атмосферное
давление может считаться С. в. п., если только время, в течение которого оно
наблюдается, не слишком велико. Задача экстраполяции атмосферного давления есть
в сущности задача о возможно более точном прогнозе его значения в момент
7+τ по наблюденным значениям за время от tQ до Г. Эта задача
непосредственно связана с задачей прогноза погоды.
СТЕПЕННАЯ ФУНКЦИЯ--функция вида #=** , где а — постоянное. С. ф.
в вещественной области определена для всех x>0f а также если α рационально,
несократимо и с нечетным знаменателем для х<0. При <х<0. С. ф. определена
в нуле. С. ф. в своей области определения однозначна, кроме случаев рациональ·
у*
Рис. 273
Рис. 274
Рис. 275
У\
Рис. 276
ного несократимого α с четным знаменателем, когда С. ф. двузначна. В таких
случаях часто из двух значений С. ф. выбирается неотрицательное
(арифметическое значение). (При таком соглашении у Ь2= \Ь\ равенство У b2=b —
несправедливо.) При х>0 С. ф. — возрастающая, если а>0, и убывающая, если а<0.
С. ф. имеет производные любого порядка во всей области своего
определения, кроме точки *=0 при 0<а<1, когда ее первая производная обращается
x*+l Cdx
-+С, если аф— 1 и \ — = ln|jtl-fC.
α + l J x
Интегрирование ведется по интервалу, целиком принадлежащему области
определения С. ф.
Графики С. ф. для различных значений показателя степени α представлены
на рисунках 260—263. Для а=1 (рис. 273) графиком С. ф. является прямая.
Лля а = 2 (рис. 274) графиком С. ф. является парабола. Для « = 3/2 (рис. 275)
графиком С. ф. является полукубическая парабола. Для <х=— 1 (рис. 276)
графиком С. ф. является гипербола. В комплексной области С. ф. становится,
в бесконечность ί/' = α*α *, [x*dx=·

СТЕПЕННЫЕ РЯДЫ
429
вообще говоря, многозначной (принимает бесконечное число значений). В этом
случае С. ф. определяется формулой:
г» ^«Ln ζββ* (In |z|+/ urgz+2k*i)^ ^j
где k пробегает целые действительные числа (при α целом действительном С. ф.
однозначна). Из всех возможных значений С. ф. в комплексной области часто
рассматривают только главное ее значение, определяемое равенством (*) при
£=0 и — Jt<argz<:i.
СТЕПЕННОЕ СРЕДНЕЕ положительных чисел аи а2, ..., αΛ — числовая
η \ ι
характеристика S* этих чисел. С. с, равная S* =\ 1—-— I , где α — любое
η
действительное число, отличное от нуля. Выражение для С. с. при а = 0 дает
неопределенность, раскрыв которую, например, по правилу Лопиталя (см. Ло-
питаля правило), приходим к геометрическому среднему (см.). Поэтому можно
считать, что S0 является средним геометрическим и С. с. Значение Sa
определено для всех действительных чисел а. При а=— 1, 1 и 2 из С. с. получаем
соответственно гармоническое среднее (см.) S_lt арифметическое среднее (см.) Si.
и квадратичное среднее (см.) S2.
Основное свойство С. с. состоит в том, что оно относительно α является
монотонно возрастающей функцией (см.), т. е. если α<β, то Sa <S$ . Поэтому
среднее гармоническое, геометрическое, арифметическое и квадратичное: S—lf
50ι Si, S2 — удовлетворяют неравенствам S— i<S0<Si<S2. С. с. находят
различные применения во многих разделах математики и математической статистики.
См. также Взвешенное степенное среднее.
СТЕПЕННЫЕ РЯДЫ — важный частный случай функциональных рядов — ряды
вида ao-fQjX-f а2АГ2-г- . . . +αη*η+ .... где <з0, alf . . ., ant . . . — некоторые
постоянные. С. р. рассматриваются как в вещественной, так и в комплексной
области. В своей области сходимости С. р. представляет аналитическую
функцию.
С. р. сходится на множестве чисел х, удовлетворяющих неравенству \х\<г
и при некоторых или всех х, удовлетворяющих равенству |х|=г, где г — радиус
сходимости (см.). В вещественном случае областью сходимости является
интервал (—г, г), симметричный относительно х=0, а в комплексном случае
областью сходимости является круг радиуса г. Граничные точки круга и
интервала могут как принадлежать, так и не принадлежать области сходимости в
зависимости от конкретных С. р. Интервал и круг сходимости могут вырождаться в точку
(г = 0), во всю прямую или плоскость комплексного переменного (г—со).
00 ОО
Примеры: ряд 2 *п сходится при — 1 <: д; < 1, ряд ^ %п1хп сходится лишь
2хп
-~ = ех сходится во всей плоскости.
Существует несколько признаков сходимости (см.) С. р., например признак
Даламбера (см.), Коши (см. Кошн критерий) и др., а также способы
определения радиусов сходимости. С. р. сходится равномерно (см. Равномерная
сходимость) на всяком множестве |x[<rl<r# где в силу теорем анализа возможно
его почленное интегрирование.
Аналитические функции, являющиеся суммой С. р. в комплексной области,
обладают некоторыми замечательными свойствами (см. Аналитические функции).

430
СТЕПЕНЬ ЧИСЛА
СТЕПЕНЬ ЧИСЛА (или выражения) — произведение нескольких
сомножителей, равных этому числу (выражению), л-я С. ч. а кратко записывается так:
а", где а называется основанием степени, а натуральное число η называется
показателем степени. Показатель С. ч. показывает, сколько раз число а берется
сомножителем.
При дальнейшем обобщении понятия С. ч. рассматривается степень с целым
отрицательным показателем а—п (отрицательная С. ч.), которая по определению
принимается равной \:ап, т. е. а—п = \:ап. С. ч. с нулевым показателем
(нулевая С. ч.) определяется равенством α°=1 (α=£θ). С. ч. с дробным показателем
q Q/
(дробная С. ч.) определяется равенством а —уаР(а>0, ρ n q —
натуральные). Основные свойства С. ч.:
1) an-ak=an+k;
2) an:ak=an-k\ 3) (an)k = ank\
4) (ab)n = anbn\ 5) (a:b)n = an:bn = an'b-n.
Затем, при дальнейшем обобщении понятия С
с иррациональным показателем (иррациональная С.
2 означает предел последовательности чисел
ч., рассматривается степень
ч.) αα (α>0). Например,
И.4
■>1 .41
,414
где {гп} — любая последовательность рациональных
делом число у 2 . Степень
2^2 =Пт2г" ,
чисел, имеющая своим пре-
комплексного числа связана с формулой Муавра
(см. Муавра формула). В теории функций комплексной переменной
рассматриваются выражения г", где г и и — комплексные числа. По определению zu=euznz
(см. Логарифм, Степенная функция).
СТЕПЕНЬ ЧИСЛА АЛГЕБРАИЧЕСКОГО — наименьший из степеней
многочленов с целыми коэффициентами, для которых это число является корнем.
Иначе можно сказать, что С. ч. а. α — степень многочлена f(x), неприводимого
в поле рациональных чисел такого, что /(а) = 0. Если С. ч. а. а равна п, то
число α называют также иррациональностью л-й степени (см.).
СТЕПЕНЬ МНОГОЧЛЕНА от η неизвестных xlt x2, .... хп относительно
неизвестного */— максимальная из степеней членов (см.) относительно*/ в
каноническом представлении этого многочлена. Аналогично понятие С. м. по
совокупности неизвестных определяется как максимальная из степеней членов в его
каноническом представлении. С. м. по
определению отсутствует лишь у нуль-многочленов (см).
СТЕПЕНЬ ТОЧКИ Μ относительно данной
окружности — число, равное произведению длин
отрезков Μ A· MB всякой секущей, проходящей
через точку Μ (рис. 277), где А и В — точки
пересечения секущей с данной окружностью;
число ΜА>MB берется со знаком -К если ΛΊ —
внешняя точка окружности, и со знаком —,
если Μ — внутренняя ее точка. Если точка Μ
лежит на окружности, то ее степень равна нулю.
Степень внешней точки Μ равна квадрату
длины касательной МТ2 (рис. 277), проведенной из
точки Μ к окружности. Для любого располо-

СТИРЛИНГЛ ФОРМУЛА
431
жения точки Μ справедлива $м=*ОМ2 — г2, где s^ —степень точки Μ
относительно окружности О (г), О — центр и г — радиус данной окружности.^
Понятие С. т. играет большую роль в элементарной геометрии. См. также
Радикальная ось и Радикальный центр.
СТЕРАДИАН—единица измерения телесного угла (см.). Один С. есть
телесный угол с вершиной в центре сферы O(R), вырезающий на ее поверхности
фигуру, площадь которой равна R2. Вся сфера содержит 4 π С.
Греч, στερεοζ— пространственный, радиан — от лат. radius — луч, спина.
СТЕРЕОГРАФИЧЕСКАЯ ПРОЕКЦИЯ — проекция, которая ставит" в
соответствие каждой точке сферы Zc точку плоскости ΖΠ. Это соответствие
устанавливается следующим образом. Из точки С сферы Zc, называемой центром С. п.,
каждая другая ючка сферы проектируется на плоскость Ζπ, перпендикулярную
радиусу сферы, проведенному в точку С, и не проходящую через С. Чаще
всего плоскость проходит через центр сферы или через конец диаметра,
проведенного через точку С. С. п. устанавливает (после исключения из сферы самого
центра проекции) взаимно однозначное соответствие между точками сферы и
точками плоскости. Если плоскость Ζπ — плоскость комплексная и сфера
касается ее своим южным полюсом, а северный — центр проекции, то точки сферы
будут изображениями комплексных чисел, а сфера именуется числовой. Чтобы
распространить соответствие между точками сферы и плоскости на всю сферу,
на плоскости вводят бесконечно-удаленную точку (комплексное число г=со) и
считают ее соответствующей северному полюсу сферы). Окружностям на сфере
соответствуют окружности на плоскости, причем окружностям, проходящим
через С, соответствуют на плоскости прямые. С. п. сохраняет углы, т. е.
является конформным отображением.
С. п. широко применяется в астрономии, картографии, в теории
аналитических функций. См. Римана сфера.
Греч, στερεοζ — пространственный, γράφω — пишу.
СТЕРЕОМЕТРИЯ — часть элементарной геометрии, изучающая свойства
фигур, расположенных в пространстве. В противоположность С,
рассматривается планиметрия (см.), где изучаются свойства фигур, расположенных на
плоскости.
Греч, στερεοζ — пространственный, μετρ ε ω — измеряю.
СТИЛЬТЬЕСА ИНТЕГРАЛ — обобщение понятия интеграла. Определяется
как предел
00
Нт2/«*)[Ф(*к)-Ф(**-1)].
/С7>*0Л=1
Здесь Г — разбиение отрезка интегрирования, xk — точки деления, ξ^ —-
произвольная точка отрезка \Xk-\-Xk\* ф—-интегрирующая функция; она является
функцией с ограниченной вариацией. С. и. обозначается:
Ь
(S)$f(x)dy(x).
а
Если φ —дифференцируема, то С. и. совпадает с римановым, если последний
существует. С. и. широко применяется в теории вероятностей. Автором С. и.
является голландский математик Т. Стильтьес (см. Интеграл).
СТИРЛИНГА ФОРМУЛА — формула
л' / п\п — (1)
/i!«V 2лп1— \ ξ\2η (0<Θ<1);

432
СТИРЛИНГА ФОРМУЛА
эта формула служит для оценки величины факториала п\ при больших
значениях л. Имеет место асимптотическое разложение:
В. 1
In п\ ~С+ (п+ — \\п η — п + ~- —
I 2 j 1-2 л
3-4 л3""*"'"4"
+(-1)*-1^ί^-^Γ+·- (2)
где C= — In 2π, a β£· — числа Бернулли (см.). Из асимптотического разложения
для In (nl) можно получить и разложение для самого факториала:
ι/ ( п\п\ l l 139 571 )
п1~У2ЛП[7){1 + Ы1 + ^^-~Ш^~ 2488320** + '"]' (3)
Если оборвать ряд (2), называемый рядом Стирлинга, на &-том члене, то
получится формула Стирлинга:
1π(/ι)!-ΙΙπ2π+^+-| !„„-„+ _.---. -+
4- ... 4- ί — Π*—ι . 4-
Τ ^ V ' (2£—1)·26 /г2*-* τ
+ θ(_1) (2Λ+1)(2Λ + 2) ' 22*+ι' (4)
пригодная для практических вычислений; формула (1) получается из (4) при
оо
Для эйлерова интеграла второго рода (см.) Г(а)=( xa—1e—xdx (так назы-
"о
ваемая функция гамма) существует формула Стирлинга:
. / 1 \ Д 1 Д 1
1пГ(*)-1п /2π +[ α—J J 1ηα-α+ ^.---1+-+ ... +
K (2m — \)2m a*m-i y
χ ^L+J · — (0<θ<1); (5)
(2/ji+1Х2Ш+2) fl^-i l '
в простейшем случае при /л=0 формула примет вид:
/ ι \ й
1п Г (α) = 1η У 2π -f ( α — — | Ιηα —α+
Ι 2i 12
Отбрасывая дополнительный член и продолжая ряд членов в формуле (5)
до бесконечности, получим ряд Стирлинга, который расходится

СТРОФОИДА
433
ilim—-—ΓΓ'ή -=оо при п^оо) и является асимптотическим представле-
\ у лЛЪ 1) /ill ~~~ 1
нием функции Г (а). Так как V (п) = (п—1)! (п — натуральное), то из
формулы (5) можно получить все предыдущие, если положить а=п.
СТОКИ (источники) — точки векторного поля, в которых отличен от нуля
предел
lands
lim = q,
Σ-Ρ υ
равный по значению div а, где а — некоторый вектор, η — единичный вектор
нормали к поверхности 2, стягиваемой в точку Р, V — объем пространства,
замкнутого поверхностью JJ.
СТОКСА ФОРМУЛА — формула, связывающая криволинейный интеграл по
замкнутому контуру L с интегралом по поверхности, ограниченной этим
контуром. Поверхность и контур предлагаются ориентированными и их ориентации
согласованными (см. Ориентация поверхности). С. ф. записывается так:
.I"*+«*'+s<ft-j'j(S-f;) "*"+ |(f ~τ) ·>**+
Здесь Ρ, Q, R — непрерывные дифференцируемые функции χ, у, ζ. С. φ. в
векторной форме принимает вид:
[pdz=Jjnrot pds, (*)
1 D
где p=Pi-\-Qj+Rk> dz — элемент контура, ds — элемент площади поверхности,
π — единичный вектор нормали к поверхности. Равенство (*) словесно
выражается так: циркуляция векторного поля по замкнутому контуру L равна потоку
вихря поля через поверхность D.
С. ф. обобщается на я-мерные многообразия.
СТОХАСТИЧЕСКИЕ ПРОЦЕССЫ — то же, что и вероятностные и случайные
процессы (см.).
СТРЕЛКА СЕГМЕНТА — то же, что и высота сегмента (см. Высота).
СТРИКЦИОННАЯ ЛИНИЯ линейчатой поверхности — геометрическое место
центров прямолинейных образующих поверхности / (/) (/ — параметр семейства
образующих). Центром образующей называется основание предельного
положения общего перпендикуляра прямых /(/) и l(t-\-M), когда Δ* стремится
к нулю
Лит.: С. П. Фиников, Теория поверхностей, ОНТИ. М., 1У34.
СТРОФОИДА — плоская кривая 3-го порядка, каноническое уравнение которой
в прямоугольных декартовых координатах:
2 о а+х
а — х
а в полярных:
cos 2 φ
ρβα—^г*
cos φ
28 Толковый словарь математических терминов

434
СТРУКТУРА
где а — расстояние от О (полюса) до PQ — асимптоты С, т. е. OR = OS=a. С.
можно получить следующим образом. Пусть дана прямая Оу (рис. 278) и
фиксированная вне ее точка S, через которую проходят все возможные лучи SK,
пересекающие прямую Оу. Если отложить на луче по обе стороны от точки К
отрезки КМ = КМ' =ОК, то геометрическое место
точек Μ и М' при вращении луча SK вокруг
точки S и есть С.
См. также Углы.
Греч, στροφοξ — кручение.
СТРУКТУРА — частично упорядоченное
множество (см.) Р, любые два элемента которого
имеют наибольшую нижнюю грань или
пересечение хГ\У и наименьшую верхнюю грань или
объединение x\Jy. Теория структур — один из
важных разделов современной алгебры.
Лит.: Биркгоф, Теория структур, М,—Л., 1 952.
СТРУНЫ УРАВНЕНИЕ —
дифференциальное уравнение с частными производными,
описывающее малые поперечные колебания
однородной натянутой струны:
д2у д2у
У ~> \+F (χ, Ζ),
Рис. 278
dt2
дх2
где а — постоянная, характеризующая струну, χ — координата вдоль струны,
t — время, F (x, t) — некоторая известная функция, выражающая действие
внешних сил; у(х> t) — искомая функция — отклонение струны в точке χ в момент
времени / от положения равновесия. С. у. описывает также много других
физических процессов (колебания однородной среды и т. п.). С. у.—исторически
первый пример уравнения математической физики, а также гиперболического
уравнения. Свойства решений С. у. во многом характерны для гиперболических
уравнений (см.). С. у. решается обычно при некоторых граничных и начальных
условиях. Наиболее общий и мощный метод решения С. у. и некоторых
гиперболических уравнений предложен Д. Бернулли (1755). По этому методу U (x, t)
ищется в виде бесконечного ряда функций вида Х(х) Τ (t) (метод разделения
переменных, см.).
СТЮАРТА ТЕОРЕМА — предложение, заключающееся в следующем: если
Л, В, С — три вершины треугольника, a D — любая точка на стороне ВС, то
имеет место соотношение:
AD2-BC=AB2.CD+AC2-BD — BC.BD.CD.
С. т. названа по имени доказавшего ее английского математика М. Стюарта
и опубликовавшего ее в труде «Некоторые общие теоремы» (1746, Эдинбург).
Теорему сообщил Стюарту его учитель Р. Симеон, который опубликовал эту
теорему лишь в 1749 г. С. т. применяется для нахождения медиан и биссектрис
треугольников.
СУБГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функция f(xlt x2t . . ., хп),
удовлетворяющая условию:
д2/ ^/ д2/
дх\ дх\ дх2п
С. ф. обладает некоторыми свойствами гармонических функций (см.). Она
используется при доказательстве некоторых теорем о гармонических функциях
и часто рассматривается в теории уравнений с частными производными.

СУММИРОВАНИЕ
435
СУММА — результат сложения величин [чисел, векторов, тензоров,
определителей, матриц, множеств (см.) и т. д.]. Сумма обладает свойствами
перестановочности: a-\-b=b-\-a, сочетательности: a-\-(b-\-c)=(a-\-b)+c% а также
распределительности по отношению к умножению, если для рассматриваемых величин
умножение определено: (a-\-b)c=ac-\-bc.
СУММА МНОГОЧЛЕНОВ допускает две основные концепции определения.
Во-первых, так как многочлены являются частным случаем функций, то С. м.
может быть определена как сумма функций (см.). Во-вторых, С. м. можно
определить следующим образом. Если многочлены Ρ и Q имеют следующие
канонические представления (см. Каноническое представление многочлена):
Ахх*х ха* . . . я*п +Вгх$* jcPz ... *£/! + . ..
12 * 1 2 II
И
Αοχΐ* χ4* ... jtjn -f-βο ХЬх Χ*2 ... χ\η + . . .,
то каноническое представление многочлена:
Atf
χΊηη +Βλ χ^ χ$* . . . χ\η 4- . . . + Α2χ]
*2" +
+Β*χ°ι jc°2
Χ°η +
называется С. м. Р и Q.
Множество всех многочленов от η неизвестных над полем Ρ относительно
операции сложения многочленов образует абелеву группу (см.).
Если рассматриваются многочлены от одного неизвестного xt то С. м.
можно определить как многочлен, в котором коэффициент при х1 равен сумме
коэффициентов при х1 в многочленах-слагаемых; при этом предполагается, что если
в некотором слагаемом многочлена член с х1 отсутствовал, то в качестве его
коэффициента брался нуль.
СУММА МНОЖЕСТВ —см. Объединение множеств.
СУММАТОР — простейшее устройство для определения суммы двух
величин. Является основным арифметическим элементом математических машин (см.).
С. бывают дискретного и непрерывного
действия. С, складывающий величины,
задаваемые дискретной последовательностью
числовых значений, называется С. дискретного
действия. Он образует сумму путем сложения
цифр из соответствующих разрядов слагаемых
чисел и осуществляет необходимые
межразрядные переносы. С. непрерывного действия
оперирует не с цифрами, а со значениями
переменных, которые могут меняться
непрерывно. Простейшим С. является, например,
устройство (рис. 279), состоящее из трех
параллельных стержней, прикрепленных шар-
нирно в точках А, В, С к прямому стержню
/, так что АВ = ВС. Когда крайние стержни
средний смещается на (х+у):2.
СУММИРОВАНИЕ расходящихся рядов — способ построения обобщающей
суммы ряда, не имеющего суммы в обычном смысле. По определению
обобщенная сумма сохраняет многие свойства обыкновенной суммы Так, например, тре-
оо оо
буется, чтобы из того, что ряд ^ ап суммируется к Л и ряд 2 Ьп суммируется
л=0 п=0
Рис. 279
смещаются на величины χ и у,
29 Толковый словарь математических терминов

436
СУММИРУЕМАЯ ФУНКЦИЯ
к Б, следовало, что ряд 2 λ ап'Ы1 Ьп суммируется к λ Α-\-μ В и ряд
/ζ=0
оо
2 ^п суммируется к А — а0. Требуется также, чтобы суммирование сходящегося
л=1
ряда приводило к его обычной сумме. При С. расходящегося ряда
00
Σ°η
(*>
л=0
поступают следующим образом: рассматривают ряд
где ln(t) — функции такие, что ряд (*) сходится при t^t^ и lim )-„(/)= 1.
Обобщенной суммой ряда (*) называют lima(/), где σ(/) сумма ряда (**)
t-+t0
(если этот предел существует). С. расходящихся рядов применяется во многих
практических задачах теории электромагнитного поля и др.
СУММИРУЕМАЯ ФУНКЦИЯ — функция, для которой существует интеграл
Лебега, взятый по данному множеству. Будучи интегрируемыми по Лебегу, эти
функции должны быть одновременно измеримыми (по Лебегу). Функция с
суммируемым квадратом — измеримая функция, квадрат которой есть С. ф.
СУММИРУЮЩИЕ МАШИНЫ — вычислительные машины для нахождения
алгебраической суммы чисел (т. е. для выполнения действий сложения и
вычитания). Они представляют собой соединение счетчика с дополнительными
механизмами. Путем нажатия на определенные цифровые клавиши осуществляется
последовательное внесение каждого слагаемого в счетчик машины. При
этом происходят независимые добавления (с необходимыми меж разрядными
переносами) к цифрам, уже накопленным в одноразрядных решетках
счетчика, в то время как в обычном счетчике суммирование осуществляется путем
последовательного добавления единиц, составляющих вводимое число к числу
ранее накопленному.
Показания счетчика либо печатаются, либо считаются оператором.
Лит.: Б. Н. Делоне, Краткий курс математических машин, Гостехиздат, М., 1949.
СУПЕРГАРМОНИЧЕСКАЯ ФУНКЦИЯ — функция f(xu x2, .... х„),
обладающая свойством:
дх\ дхгп
С. ф. обладает рядом свойств гармонической функции (см.), применяется при
доказательстве некоторых теорем о гармонических функциях, часто
рассматривается в теории уравнений с частными производными.
СУПЕРПОЗИЦИЯ ФУНКЦИИ —составление из двух функций y=f(u)
и и=(р(х) сложной функции (см.) у=/(ф(л:)). Например, функция y=sinln;t
получена суперпозицией функций: натурального логарифма (см.) и синуса (см.).
_з_
4
Функция y=(sin In x) получена последовательным применением двух
суперпозиций: сначала получена функция u = sin\nx, а затем взята суперпозиция
полученной функции и степенной функции (см.). Понятие С. ф. относится и к функ-

СФЕРА
437
циям нескольких переменных. С. ф. *i=<Pi (xit jc2, . . ., хп), . . ., tm=*
=*Ут(х1> χ2 *п) и u = f(tlt . . ., tm) будет сложная функция (см.):
" = /[Φι(*ι, *2 *п) <Pm(*i» *2 *п)1
Суперпозиция происходит от латинского слова «наложение».
СУЩЕСТВЕННО ОСОБАЯ ТОЧКА аналитической функции /(г) —такая
точка а, что lim/(z) конечный или бесконечный не существует. Точка а тогда и
z-*a
только тогда является С. о. т. для функции /(ζ), когда главная часть лоранов-
ского разложения функции f{z) (см.) в окрестности точки а содержит
бесконечно много членов. Поведение функции в окрестности С. о. т. выясняет теорема,
установленная русским математиком Ю. В. Сохоцким (1862): если α есть С. о. т.
функции /(ζ), то для любого комплексного числа А существует
последовательность точек Ζ£->α такая, что Y\mf(zk) = A. Иными словами, в окрестности
С. о. т. а функция f(z) стремится по различным последовательностям к
любому наперед заданному пределу (конечному или бесконечному). Например, для
функций е , sin —, cos — начало координат является С. о. т. В самом
πει 2
7 ζ 111
ле, разложение е в ряд Лорана е =1+ —+—■ —+ . .. содержит в
окрестности z=0 бесконечно много членов с отрицательными степенями. Для А=
= оо последовательностью Zk служит ζ^ = ~γ (k=\, 2, . . .), так как очевидно,
k
что lim^ = oo. Для А =0 можно принять г& = —·-- (&=i, 2, 3, . . .), действи-
тельно, lim^~"/?=0. Для конечного АфО берем
£-*оо
тогда
zk = -——- (£=0, 1, 2, 3. . . .),
* \nA+2kw
hmf{zk) = hme =A.
Лит.: И. И. Привалов, Введение в теорию Функций комплексного переменного.
М.—Л., 1954.
СУЩЕСТВОВАНИЯ ТЕОРЕМЫ— теоремы теории дифференциальных и
интегральных уравнений, указывающие условия, при выполнении которых существует
решение, удовлетворяющее определенным краевым условиям (см.) или начальным
условиям. Например, если /(*, у)— непрерывная функция, то существует
решение уравнения y'=f(xt у), удовлетворяющее условию у(х0)=Уо·
СФЕРА есть геометрическое место точек пространства, расстояние которых
от данной точки О равно данному отрезку г. Данная точка О называется
центром С, а данный отрезок г — радиусом С. Уравнение С. в прямоугольных
декартовых координатах имеет вид:
(х - а)2-Ну - bf+{z - cf=r2.
29*

438
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ
где я, Ь, с — координаты центра, а г — радиус С. С. можно рассматривать как
поверхность, полученную от вращения окружности вокруг своего диаметра.
Площадь поверхности С. радиуса г определяется формулой:
S = 4:tr2.
Касательная плоскость к С. перпендикулярна радиусу, проведенному в точку
касания.
Абрис С. в ортогональной проекции есть окружность, в произвольной же
параллельной проекции абрис С. есть эллипс.
Всякое сечение С. плоскостью есть окружность. Сечение С. О (г)
плоскостью, проходящей через центр С, есть окружность радиуса г — большой круг;
всякое же другое сечение С. плоскостью есть окружность, радиус которой
меньше радиуса г С. — малый круг.
См. также Шар.
СФЕРИЧЕСКАЯ ГЕОМЕТРИЯ — геометрическая дисциплина, изучающая
свойства фигур, расположенных на сфере, аналогично тому как планиметрия
изучает свойства фигур, расположенных на плоскости.
Большие круги на сфере, являясь геодезическими линиями (см.), играют
роль прямых на плоскости: через две точки сферы, не являющиеся концами ее
диаметра, проходит только один большой круг, аналогично тому как на
плоскости две точки определяют только одну прямую. Однако на сфере нельзя
провести параллельных «прямых», в то время как на плоскости Евклида и
плоскости Лобачевского существуют параллельные прямые.
Основными фигурами С. г. являются сферические двуугольники,
сферические треугольники (см.), сферические многоугольники, т. е.
многоугольники на сфере, сторонами которых являются дуги больших кругов, меньших
полуокружности.
Лит.: Н. Н. Степанов. Сферическая тригонометрия, Гостехиздат, М.— Л., 1948;
Д. И. Перепелки н. Курс элементарной геометрии, ч. 2, Гостехиздат, М.—Л., 1949.
СФЕРИЧЕСКАЯ ИНДИКАТРИСА нормалей поверхности М = М (и, и) — часть
поверхности сферы или вся сфера с параметризацией, индуцируемой уравнением
поверхности. Более точно: в каждой точке поверхности М = М(м, υ)
рассматривается единичный вектор нормали (см.); таким образом, получается
вектор-функция п = п(ы, у), [п — единичный нормальный вектор в точке (м, υ)). Если
начала векторов находятся в фиксированной точке, то концы этих векторов
описывают часть сферы или всю сферу. Эта часть сферы или вся сфера вместе с
параметризацией называется С. и. Отображение М(ы, у)->п(ы, υ) называется
сферическим отображением поверхности. Это отображение часто и с большой пользой
рассматривается в дифференциальной геометрии. Имеет место теорема: полная
кривизна поверхности в точке равняется пределу отношения:
lim — =k,
As—О AS
где As — площадь некоторого кусочка поверхности, содержащего данную точку,
As'—площадь сферического изображения этого кусочка поверхности. Примеры:
С. и. плоскости есть точка, С. и. цилиндра есть большой круг сферы; С. и.
конуса (без вершины) есть малый круг сферы. Рассматриваются также С. и.
касательных к кривым и т. д.
СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ — тригонометрия сферического
треугольника (см.), т. е. учение о зависимости между сторонами и углами сферического
треугольника. В отличие от плоской (обычной) тригонометрии, в С. т. три угла
треугольника однозначно определяют его вид и размеры.

СФЕРИЧЕСКИЕ ФУНКЦИИ
439
См. также Косинусов теорема, Синусов теорема.
Лит.: Н. Н. Степанов, Сферическая тригонометрия, Гостехиздат, М.—Л., 1948:
М. К. Вентцель, Сферическая тригонометрия, Гостехиздат, М., 1948.
СФЕРИЧЕСКИЕ КООРДИНАТЫ точки М — три числа г, θ, φ,
определяющие положение этой точки в пространстве. С. к. можно определить так. Пусть
Ох> Оу, Ог — три взаимно перпендикулярные оси
декартовых координат (рис. 280), начало О которых
совпадет с центром сферы О (г). Тогда ОМ=г есть
расстояние точки Μ от точки О, угол θ = -^ΛίΟΖ,
т. е. угол, составленный радиус-вектором ОМ с
положительным направлением оси Οζ% угол φ=^χΟΝ,
где N — проекция Μ на плоскость хОу.
С. к. связаны с декартовыми прямоугольными
координатами следующими формулами:
x=r sin θ cos φ, y=r sin θ sin φ, z=r cos Θ.
СФЕРИЧЕСКИЕ ФУНКЦИИ: 1°. С. ф. Лежанд-
ра Рп(х) и Qn(x) служат решениями
дифференциального уравнения Лежандра: [(1 — х2) у' ]' -f-
+/2(/2-f-1) У=0 и могут быть представлены с помощью
рядов:
Рис. 280
4=0
где Cfc+2 =
(ft — n)(k+n+l)
(Λ+1)(Λ+2)
у=л Λ £(^^ + πίπ-2χπ+ΐχπ+1)^Μ>^Η
+в{х-
(/*-!)(/г+2) ч § (η—1)(/ι —3Χ/1+2Χ/1+4)
3'
дг3 +
X5_
с произвольными А и Ь.
Для любого целого числа /г>0 один из рядов обрывается, и
соответствующая С. ф. превращается в полином Лежандра Рп(х) (см.); второй ряд при
этом есть функция Лежандра второго рода.
Полиномы Рп(х) имеют производящую функцию (см.):
г оо
UV 1—2*;-И2 =2 PnWtn Для |ί|<1
п=0
1:1/1 — 2* *+*2 =2 Ρη(*)*~(η+Ι) Для W>1.
n=0
Если положить x=cosu, to Pn (cos υ) будет представлять функцию,
определенную на поверхности сферы,—«зональную С. ф.». Функция y=Prt(cos0)
удовлетворяет дифференциальному уравнению:
Л2У dy
TT+ctg£;—+/n/i+l)y=0.
άυ* άυ

440
СФЕРИЧЕСКИЙ ДВУУГОЛЬНИК
Функции rn Pn (cos υ) и г—(«Η-ΐ)Ρη называются шаровыми функциями Лапласа;
они удовлетворяют уравнению Лапласа Δ U—0.
2°. С. ф. присоединенные Р™(х) являются решениями дифференциального
уравнения:
т*
η (/г-И)—·
[О-^УЧЧ-
1—л:2
Они связаны с полиномом Лежандра формулой:
у-0.
т
2 <*"*
PjW-d-*·) —/>я(4
Если положить x=cosy, то функция Я™(cos у) представляет решение уравнения:
d2y 4 dy
TT+ctgy— +
dir dy
sin2 "
Щ
3°. С. φ. общие yn(v, φ) служат решениями дифференциального уравнения
с частными производными:
д'2у ду 1 д2у
■Jl-bctgyT-b-—- —f;4-/2 (/2+1) у=0; (*)
ду2 ди sin2 у д φ2
здесь υ и φ — сферические координаты (см.).
С ф. Уп(и> Ф) степени η называется тригонометрический многочлен:
η
Уп(*>* Ч)=а0Р n(cosv)+ 2 (Qmc°s^9-b^sin/7i9)P/(lm)(cosy).
m - I
Уравнение (*) получается при разделении переменных в уравнении Лапласа
в сферических координатах.
СФЕРИЧЕСКИЙ ДВУУГОЛЬНИК — фигура, образованная двумя
полуокружностями больших кругов сферы, исходящими из диаметрально
противоположных точек этой сферы.
СФЕРИЧЕСКИЙ ИЗБЫТОК — разность между суммой углов сферического
треугольника и суммой углов треугольника евклидовой геометрии, т. е.
разность (А+В+С)— π, где Л, β, С — углы сферического треугольника.
С. и. также называют эксцессом. Разность же между суммой углов
треугольника в плоскости Евклида и суммой углов треугольника в плоскости
Лобачевского называется дефектом или недостатком треугольника, т. е. дефект
треугольника есть разность π — (А-\-В-\-С)% где Α, β, С — углы треугольника
в плоскости Лобачевского.
СФЕРИЧЕСКИЙ СЕКТОР —то же, что шаровой сектор (см.).
СФЕРИЧЕСКИЙ ТРЕУГОЛЬНИК — совокупность трех точек сферы и трех
дуг больших кругов, каждая из которых меньше полуокружности и имеет
концы в этих точках. Сумма углов С. т. больше двух прямых и заключается
между π и 3π, т. е.:
л<Л+В+С<Зя,
где Л, Bf С — углы С. т.
Многие признаки равенства С. т. аналогичны признакам равенства обычных
плоских треугольников. Однако есть и иные: например, два С. т. (одной
и той же сферы) равны, если три угла одного треугольника равны трем углам

СЧЕТНО-АНАЛИТИЧЕСКИЕ МАШИНЫ
441
другого. См. также Сферическая тригонометрия, Косинусов теорема, Синусов
теорема.
СФЕРОИД — поверхность, полученная вращением сферы вокруг ее оси
с учетом сжатия поверхности сферы вдоль этой оси, возникающего за счет
влияния ускорения силы тяжести на экваторе и полюсе и за счет угловой
скорости вращения. С. имеет вид, близкий к сфере.
Греч, σφαίρα — шар, сфера, мяч. εζδος — вид.
СХОДИМОСТИ ТОЧКА функционального ряда (функциональной последова-
оо оо
тельности) 2 ип(х) такая точка х0, что числовой ряд 2 ип(хо)>
составлю п=1
ленный из значений функций ип(х) в данной точке x0i является сходящимся
(см. Ряды).
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
т. II, III, Физматгиз, М., 1959.
СХОДСТВЕННЫЕ СТОРОНЫ — каждая пара соответственных сторон двух
многоугольников, один из которых является соответственным другому в некотором
геометрическом преобразовании. Термин С. с. обычно употребляется при
рассмотрении двух подобных треугольников (многоугольников) и означает стороны
этих треугольников (многоугольников), лежащие против равных углов (сторон,
к которым прилежат равные углы).
См. Преобразование, Отображение, Соответствие.
со
СХОДЯЩИЙСЯ РЯД — ряд 2 ап, имеющий конечную сумму. Сходимость
η - ι
СО оо
комплексного ряда 2 ^п = 2 (an+ibn) к сумме C=A+iB равносильна
п=) п=1
сю со
сходимости двух вещественных рядов 2 ап и 2 ^псоответственнок Ли В.
η - ι η = ι
См. также Ряд.
СЧЕТ — математическое понятие, имеющее два значения. Во-первых, С.
понимается как операция, имеющая целью установить, сколько элементов
содержит данное конечное множество; во-вторых, С. совокупность первых четырех
арифметических действий, производимых над рациональными числами целыми
и дробными, т. е. С. — вычисление.
Лит.: Энц. элем, мат., Гостехиздат. ,\\., 1951: И. Я. Депман. История арифметики,
Учпедгиз, М., 1959.
СЧЕТНАЯ ЛИНЕЙКА — линейка, служащая для выполнения различных
вычислений. На обычной логарифмической линейке (см.) можно умножать,
делить, возводить в степень, извлекать корень, выполнять тригонометрические
вычисления.
Существуют также линейки со шкалами для решения специальных задач.
Например, на 17 шкалах навигационной счетной линейки, применяемой в
авиации, можно производить расчеты пути, времени и скорости полета по показанию
барометра, перевод мер длины и скоростей и другие вычисления.
СЧЕТНО-АНАЛИТИЧЕСКИЕ МАШИНЫ (или счетно-перфорационные
машины) — ряд машин, работающих с перфорационными картами (см.), на которых
путем пробивки отверстий нанесены коды различных чисел и команд или слов.
К числу счетно-аналитических машин относятся прежде всего перфораторы,
наносящие на перфокарты коды чисел, команд, слов. Сортировка группирует
карты по каким-либо признакам. Репродуктор применяется для размножения

442
СЧЕТНОЕ МНОЖЕСТВО
перфокарт с перфокарт-шаблонов. Расшифровочная машина расшифровывает
коды чисел, команд, слов, нанесенные на перфокарты. На базе
счетно-аналитических машин строятся входные устройства и выходные устройства
современных быстродействующих электронных счетных машин.
СЧЕТНОЕ МНОЖЕСТВО — множество, эквивалентное натуральному ряду,
т. е. множество, все элементы которого можно занумеровать натуральными
числами. Мощность С. м. является наименьшей мощностью бесконечных
множеств и обозначается Ъ0 (алеф-нуль). Примерами С. м. могут служить
множества всех четных чисел, рациональных чисел, алгебраических чисел. Всякое
бесконечное множество содержит своими множествами С. м. Бесконечное
множество, не являющееся С. м., называется несчетным множеством (см.).
СЧЕТНО-РЕШАЮЩИЕ УСТРОЙСТВА входят в различные математические
машины (см.) и предназначены для выполнения определенной математической
операции или группы операций. Они бывают непрерывного и дискретного
действия, в зависимости от того, пробегают ли переменные, входящие в решаемую
задачу, всю область своего изменения непрерывно или же принимают лишь
дискретные значения. С.-р. у. бывают суммирующие, множащие,
интегрирующие и дифференцирующие, а также функциональные, служащие для
автоматической резлизации заданной функциональной зависимости.
СЧЕТНЫЕ МАШИНЫ — математические машины (см.), предназначенные
для механизации математических операций над отдельными числами. Наиболее
распространены суммирующие машины, выполняющие сложение и вычитание,
и полуавтоматические и автоматические арифмометры (см.), производящие все
четыре арифметических действия. Они называются малыми счетными машинами
и состоят из установочного (для установки задаваемых чисел), переносного
и счетного устройств, которые весьма сходны: у всех у них числа, над
которыми должны выполняться действия, обычно задаются машине путем нажатия
клавиш специального устройства; таким же способом управляют машиной.
Результат получается на определенной шкале.
Лит.: И. С. Евдокимов, Г. П. Евстигнеев, В. Н. Крушин, Счетно-цифро
вые машины, Машгиз, М., 1953
СЧЕТЧИК — цифровой математический прибор для выполнения простейшей
арифметической операции — счета, т. е. для последовательного увеличения
числа, уже накопленного в счетчике, на единицу. В зависимости от
используемой системы счисления (см.) С. бывают десятичными, двоичными,
восьмеричными и вообще р-ичными, состоящими из одноразрядных /?-ичных регистров,
соединенных межразрядными переносами; накопление в данном разряде р единиц
вызывает увеличение показаний ближайшего старшего разряда на единицу
и переход данного регистра в нулевую позицию. Технически С. бывают
различные: механические, релейные, электрические, электронные. С. в том или ином
виде является необходимым элементом всякой математической вычислительной
машины, в том числе и электронных быстродействующих вычислительных
машин.
СЧЕТЫ — простейший прибор для арифметических вычислений (сложения
и вычитания), широко применяемый в простейшей практической счетной работе
и в качестве наглядного пособия в школе. В России в XVI в. появился так
называемый досчаный счет, явившийся прообразом современных счетов. Свой
современный вид счеты приобрели в начале XVIII в. Кроме СССР, счеты
русские используются в Иране. В западной Европе используются только созданные
на их основе школьные наглядные пособия. Существуют еще китайские счеты
(суан-пан), распространенные в Китае, Индокитае, Японии. Они значительно
старше русских и поныне сохраняют свое древнее устройство со счетом единиц до 5.
Лит.: И. Г. Спасский, Происхождение и история русских счетов. хИсторико-ма-
гематические исследования», вып. 5, Гостехиздат, м., 1952; И. Я. Депман, История
арифметики, Учпедгиз, М., 1959.

τ
ТАБЛИЦЫ КУЛИКА. В первой половине XIX века математики разных
стран при слабо развитой вычислительной технике с огромными усилиями
составляли таблицы простых чисел и наименьших делителей составных чисел
только для отдельных миллионов натуральных чисел, стремясь создать такие
таблицы хотя бы для первых десяти миллионов, например: Чернак(1811) — для
первого миллиона, Буркгардт (1814) — для второго миллиона, он же (1816) —
для третьего миллиона, Крелле, Дазе, Розенберг, Глейшер, В. Лебег и др.
(к 1865 г.) довели таблицы до девятого миллиона.
В те же годы в Венскую Академию наук были представлены, казалось,
совершенно невероятные таблицы наименьших делителей (отличных от 2, 3, 5,
7) для натуральных чисел до 100 миллионов (!). Эти таблицы являлись
результатом огромного титанического труда феноменального выдающегося вычислителя
профессора Пражского университета Я. Ф. Кулика. Из-за очень большого объема
Т. К. Венская Академия наук не нашла возможным опубликовать их, и
рукописные таблицы были переданы на хранение в архив Академии.
«Великий канон делителей . . . » Я. Ф. Кулика представлен был Академии
наук в восьми томах общим объемом в 4212 страниц. Начинались Т. К. от
3 033 001—с того числа, которым кончались самые полные в то время таблицы
Буркгардта. Кончались Т. К- числом 100 330 201. В 1911 г. было установлено,
что второй том Т. К. от 12 642 601 до 22 853 800 исчез и до сих пор не
обнаружен. В Т. К. на каждой странице (размером 14,5x11,5 дюйма) размещены
80 строк и 77 столбцов. Сокращение объема таблиц автором достигнуто за счет
введения дополнительных (более коротких) буквенных обозначений чисел.
Например, каждое двузначное число обозначено одной латинской буквой; сочетания
двух двузначных чисел также обозначены соответствующим сочетанием двух
латинских букв и т. д. Такими обозначениями достигнуто существенное (по тому
времени) сокращение объема таблиц — примерно в два раза, но зато усложнена
техника пользования таблицами и проверка верности их буквенно-чнслового
содержания.
См. Простых чисел таблицы.
Лит.: И. Я. Депман, Замечательные славянские вычислители Г. Вега и Я. Ф.
Кулик, «Историко-математическне исследования», вып. 6, Гостехнздат, М., 1953.
ТАБЛИЦЫ МАТЕМАТИЧЕСКИЕ — численные значения какой-либо
функции, вычисленные для соответствующих значений ее аргументов. Простейшим
примером является всем известная с детства таблица умножения.
Математические таблицы являются важным вспомогательным средством при разных расчетах
в математике, физике, химии, астрономии, технике и т. д. Число верных
значащих цифр, приводимых в табличных ответах для значений функции, называется
степенью точности таблицы. Таблицы характеризуются шагом (т. е. разностью
соседних значений аргумента) и диапазоном изменения аргумента. Составляя
таблицы, необходимо выбрать значения аргументов, для которых будут
приводиться значения функции, наилучшим образом расположить материал в таблице,
дать простые правила пользования таблицей. Так как в таблицу включаются
значения функций лишь для дискретных значений аргументов, то для значений
функций аргументов, не попавших в таблицу, необходимо производить
интерполяцию (см.). Диапазон и шаг таблицы определяются из практических потребно-

444
ТАБУЛИРОВАНИЕ
стей так, чтобы можно было производить интерполяцию с необходимой точностью
и чтобы интерполяция была наиболее простой — чаще всего линейной.
Уже в древнем Вавилоне, за 2000 лет до н. э., употреблялись таблицы
произведений натуральных чисел, таблицы чисел вида —, п2, я3, п2-\-пъ и т. п.
η
(η — натуральное). В связи с необходимостью обработки обширного материала
по астрономии в древней Греции были составлены первые таблицы
трансцендентных функций. Первые тригонометрические таблицы, дошедшие до нас,
приведены в сочинении Птолемея (II в.) «Алмагест». Математические таблицы
составлялись индийскими математиками, математиками Средней Азии и Ближнего
Востока. В X в. иранский ученый Абу-ль-Вефа составил таблицу тангенсов
и синусов с шагом 10 и с точностью 1 : 604. В Европе большое количество
таблиц создается в XV—XVII вв.
В XV в. немецкий ученый И. Региомонтан впервые использовал в таблицах
значений синусоз (шаг 1°, точность — семь знаков) десятичную систему
счисления (см.). Н. Коперник (1543) и его ученик Рэтик составили таблицы
тригонометрических функций, которые были расширены и дополнены (1613) немецким
ученым Питиском и послужили основой современных тригонометрических таблиц.
Таблицы логарифмов чисел впервые опубликованы (1614) шотландским
математиком Непером. С развитием науки число таблиц возрастает чрезвычайно
быстро. В XIX в. появляются таблицы различных специальных (см.) функций.
В составлении таблиц принимают участие знаменитые математики Л. Эйлер,
А. Лежандр, К- Гаусс. Большие работы по составлению таблиц ведутся
и в настоящее время. В СССР наряду с отдельными изданиями выпускаются
серии таблиц различными институтами АН СССР.
Лит.: А. В. Лебедев, Р. М. Федорова, Справочник по математическим таблицам,
11зд-в> АН СССР, М., 1956; Η. Μ. Бурунов а, Справочник по математическим
таблицам, дополнение № 1, 11зд-во АН СССР, М., 1959.
ТАБУЛИРОВАНИЕ — конструирование и вычисление различных
математических таблиц (см. Таблицы математические).
ТАБУЛЯТОР — счетно-аналитическая машина, автоматически выполняющая
нанесенные на перфокарты команды; табуляторы вычисляют алгебраическую сумму
чисел, коды которых также наносятся на перфокарты, и печатают результат вычисления.
ТАНГЕНС — одна из тригонометрических функций (см.), которая
определяется так. Пусть в ориентированной плоскости выбрана прямоугольная
декартова система координат (рис. 281) и произвольный угол a=Z.AOMy вершина
которого совпадает с началом координат, неподвижная (фиксированная)
сторона его совпадает с осью Ох, а подвижная (переменная) сторона его ОМ
при вращении вокруг вершины О составит различные углы α с осью Ох.
Т. угла α называется отношение ум : хм, где (хм\
Ум) — координаты любой точки Λί,
принадлежащей подвижной стороне ОМ угла а. Отрезок ОМ
часто называют подвижным радиус-вектором, а
координаты гочки Λί — координатами конца его. Т. угла
α есть функция этого угла. Т. угла α обозначается
tg α. Наименьший положительный период Т. равен π
или 180°, т. е. tg (a-f-jtAz)=tga, где л=0,
+ 1, +2, ... Т. является функцией неограниченной,
нечетной (tg (—a) = —tga) и определенной для
всех значений χ числовой оси, для которых спра-
π
ведливо неравенство χ φ ~к (2п 4-1), где η — любсе
Рис. 281
целое число.

ТАНГЕНЦИАЛЬНЫЕ КООРДИНАТЫ
445
С возрастанием угла α от 0 до —· (радианов) Т. возрастает от 0 до оо.
Т. связан с синусом и косинусом, а также с котангенсом формулами:
sin α
tga= , tga=l:ctga.
cos a
Функция, обратная Т., называется арктангенсом (см.). Производная Т.
вычисляется по формуле: (tgje)' = l : cos2 *. Интеграл от Т. находится по
формуле: J tgxdx =— In I cos χ \ ■+- С Т. разлагается в ряд:
χ* 2λ-5 / , π\
Если рассматривать угол α как острый угол прямоугольного треугольника,
то Т. можно определить как отношение катета, противолежащего углу а,
к катету, прилежащему к этому углу (из треугольника ОММх), т. е. tga==
=УМ: хм. Иногда Т. определяют как функцию, выражаемую формулой
sin a: cos а, а функции синус (см.) и косинус (см.) уже определяют особо. Так
как длина отрезка касательной АР (от конца неподвижного радиуса ОЛ = 1
до точки пересечения продолжения подвижного радиуса ОМ с касательной
к окружности в точке А) численно равна Т. угла а, т. е. tga = AP, то
отсюда — слово Т.
Лат. tangens — касательная (tango — касаюсь).
ТАНГЕНСОВ ТЕОРЕМА —см. Теорема
сложения и Региомонтана формула.
ТАНГЕНСОИДА — график
тригонометрической функции у=tg χ в прямоугольной
декартовой системе координат (рис. 282).
ТАНГЕНЦИАЛЬНЫЕ КООРДИНАТЫ.
Уравнение прямой на плоскости в
прямоугольных декартовых координатах, не проходящей
через начало координат, имеет вид: их+иу+
+ 1=0. Коэффициенты и и υ входят в это
уравнение на равных правах с координатами
точек (х, у), лежащих на прямой. Задание
/ 1 1
коэффициентов и и υ \и = — —, и=——,
\ а о
где а и Ь — отрезки, отсекаемые прямой на
осях координат) однозначно определяет
прямую на плоскости. Поэтому коэффициенты
(числа) и и υ могут быть приняты за особые
координаты прямой. Эти координаты и и υ
называются Т. к. прямой (неоднородными
Т. к. прямой). Если рассмотреть однородное уравнение прямой: u1Xi+U2*2+
+"s^s=r0# т0 числа их% u2i u3 называются однородными Т. к. прямой.
Аналогично определяются неоднородные и однородные Т. к. плоскости. Т. к.
плоскости, соответственно заданные уравнениями: ux-\-vy-\-wz+\=0 и u1x1+u2X2ml·
-Ьи3#3-Ь"4*4=0» устанавливают связь между и и и, то из оо2 прямых на плоскости
уравнением f(u, f)=0 мы выделяем оо1 прямых, которые образуют множество
(семейство) касательных (огибающих) (см.) к некоторой кривой F(x, у)=0,
Поэтому уравнение /(ы, у)=0 называется уравнением кривой F(jc, у)=0.
30 Толковый словарь математических терминов

446
ТЕЙЛОРА РЯД
но не в точечных, а в Т. к. Уравнение F(x, у) = 0 кривой можно получить,
исключая и и ν из уравнений:
/(и, »)=0,
d/ df Λ
at; aw
Обратная задача— переход от уравнения кривой F(x, y) = 0 в точечных
координатах к уравнению кривой f(u, υ) —0 в Т. к. — решается исключением
χ и у из уравнений:
ылг-Иу-Ь 1=0,
/Ч*. У)=0
dF dF
и — — υ— =0.
ay d#
Тангенциальное уравнение алгебраической кривой является алгебраическим
уравнением. Тангенциальное уравнение плоской кривой двойственно точечному
уравнению этой кривой (см. Двойственности принцип). Порядок (степень)
тангенциального уравнения кривой называется классом (см.) кривой. Класс кривой
2-го порядка совпадает с порядком этой кривой. Для кривых более высокого
порядка класс и порядок вообще различны.
Лат. tangens — род. пад. от tangentis — касающийся.
ТЕЙЛОРА РЯД функции f (х) в точке а есть ряд:
f (а) Г (а) Г" (а)
Здесь f(x) определена и обладает производной любого порядка в точке а.
Формально выписанный ряд Тейлора (1) может быть как сходящимся, так
и расходящимся, причем даже, будучи сходящимся, он может сходиться
к функции, отличной от f(x). Например, для функции f(x)—y χ" нельзя
выписать ряд Тейлора в точке а=0, так как в этой точке функция не имеет
производных.
Т. р. для ех\
„ „ X X2 X*
«*в1+П+™ + * + ···
1! 2! 3!
сходится везде к функции ех.
Т. р. для
/<*) =
является сходящимся, но не сходится к f(x), а тождественно обращается
в нуль.
Можно также привести примеры функций, Т. р. которых расходится или
сходится к другой функции. Если Sn(x) — сумма первых (л-f-l) членов

ТЕЛЕСНЫЙ УГОЛ
447
Т. р. (1), то разность Rn(x) = f(x) — Sn(x) называется остаточным членом
Т. р. Формула:
Λ = О
справедлива, если lim Rn(x)=Q.
η -»- со
При <з = 0 Т. р. обращается в ряд Маклорена (см. Маклорена ряд).
Наиболее распространенными разложениями в Т. р. являются разложения
функций:
*« , m(m—1) . . . (m —я+1)
(1 + *)*=1+/ιι*+ · · · +— —^ —V + . . .; (2)
Χ3 χ2η+1
sinjc-jc — — + ... +(— 1)" + . . .; (3)
ЗГ v ' (2/i+l)I
«,,-Ι--+... +<-!)· —+...; (4)
1п(1+ж)-дс-£+ ... +(-l)«->-+ .... (5)
Ряд (2) сходится: при— 1<#<1, если т<—1; при —-1<#<1, если
—1<т<0; при —1 <#< 1, если т>0. Ряды (3) и (4) сходятся для любых х.
Ряд (5) сходится при —1<#*ζ 1.
Необходимо знать две важные теоремы, касающиеся Т. р.:
1. Если функция f(x) разлагается в степенной ряд, то это обязательно
ее Т. р.
2. Если существует такое С > 0, что \f^n)(x)\<C (— r^jc<r,
п= 0, 1, 2, . . . ), то функция f (х) разлагается в степенной ряд на отрезке
—г < χ < г.
ТЕЙЛОРА ФОРМУЛА — формула, позволяющая приближенно находить
значения функции для заданного значения аргумента. Если а — любое
действительное число, то Т. ф. с остаточным членом выглядит так:
/' (a) fin) (a) f{n + 1) (х)
/(*W(e)+-I^*-«>+ - - ■+L7J(^fl)4 (n+l)\ (х-аГ+\
причем неизвестная точка х лежит между а и х. Ошибка Rn (x) оценивается
формулой (остаточный член):
fin + О (Т\
Для многочлена формула Тейлора выглядит так:
/' (а) , Г (а) о f(n) (а)
f(x) = f(a)+-L^\x-a)+J-^(x--a)*+ ... +'—^(*-α)«;
здесь η — степень многочлена.
ТЕЛЕСНЫЙ УГОЛ —часть пространства, ограниченная одной из двух
полостей конической поверхности (конуса), направляющая которой гомеоморфна
30*

448 ТЕЛО
окружности. Частным случаем Т. у. являются трехгранные углы (см.) и
многогранные углы (см.). За меру' Т. у. принимается площадь фигуры,
которую вырезает коническая поверхность на сфере радиуса R с центром в
вершине конической поверхности (рис. 283).
За единицу измерения Т. у. принимается
стерадиан (см.), т. е. Т. у., вырезающий на
сфере фигуру площади R2.
ТЕЛО: 1°. Т. алгебраическое есть кольцо,
у которого все элементы, отличные от нуля,
относительно операций умножения образуют группу.
Всякое поле (см.) есть Т., однако операция
умножения в Т., вообще говоря,
некоммутативна (см. Коммутативность). Примером Т., не
являющегося полем, служит кольцо
кватернионов (см.).
2°. Т. геометрическое иногда описательно
определяют как фигуру, ограниченную со всех
сторон частями поверхностей. Примеры
геометрических Т.: куб (см.), круглые тела (см.) и др.
ТЕЛО ВРАЩЕНИЯ — геометрическое тело,
полученное от вращения некоторой плоской
линии вокруг фиксированной прямой или вокруг частей прямой (отрезка, луча).
Пример: Т. в., полученное от вращения эллипса (см.) вокруг одной из его
осей, есть эллипсоид (см.) вращения.
См. также Круглые тела.
ТЕНЗОР. При исследовании некоторых математических или физических
объектов средствами алгебры и анализа часто приходится прибегать к помощи
системы координат, например, в задачах, связанных с кривыми 2-го, 3-го
и т. п. порядка, с угловой скоростью вращения, с напряжением упругих
пластин и т. д. Сама изучаемая величина имеет определенный (физический,
геометрический и т. д.) смысл, является единым целым и, конечно, обладает
свойствами, не зависящими от случайного выбора системы координат. Однако в
каждой системе координат величина характеризуется набором чисел-координат:
коэффициенты уравнения кривой 2-го порядка, коэффициенты полилинейной
формы, линейного преобразования и т. д. Большой класс величин объединяется
в понятие по связи между координатами величины в одной системе координат
и в другой системе. Точнее: если в каждой системе координат «-мерного
пространства задан набор чисел:
zi\i* ... ίρ /Λ=1, 2, . . ., η: 6=1, 2, . . ., ρ
J\h...jq //β1§ 2, ..., я: /=1, 2, . ... ?,
причем при замене данной системы координат другой системой с помощью
матрицы а) числа (*) изменяются по формуле:
„ixi% . . . /„ χΐ 'ι '» in J* и1* k^7-*l*8 · · · *o
zhl. ... fq - Ζ β*. a"> · ■ ■ % bh bu · · · ЬГЯ zhi, ■ ■. i/>
<t.l lq
где blj — матрица, обратная к aj, — говорят, что задан Т., ρ раз контрава-
риантный и q раз ковариантный.
Примеры Т. см. в терминах Полилинейная форма, Квадратичная форма,
Линейное преобразование, Аффинор, Поливектор.
Лит.: П. К. Рашевский, Риманова геометрия и тензорный анализ, Гостехиздат, М.—Л.»
1953.

ТЕОРИЯ ВЕРОЯТНОСТЕЙ
449
ТЕНЗОРНОЕ ИСЧИСЛЕНИЕ —отдел математики, изучающий тензоры (см.)
и тензорные поля средствами линейной алгебры и математического анализа. Над
тензорами в я-мерном линейном пространстве производятся алгебраические
действия сложения, свертывания (см. Свертывание тензора), симметризации,
альтернирования и т. д. Каждая такая операция имеет смысл геометрический или
физический, смотря по роду задачи, поставленной практикой. Однако указанные
действия и свойства тензоров можно и полезно изучать даже без связи с этими
задачами. Четыре упомянутых выше действия над тензорами и их свойства
составляют основное содержание важной составной части Т. и.— тензорной
алгебры.
Более глубоким отделом Т. и. является тензорный анализ — дисциплина,
в основу которой положено понятие предела, дифференцируемости. Объектом
исследования тензорного анализа являются тензорные поля. Понятие
дифференцируемости тензорных полей является более сложным, чем, например, диффе-
ренцируемость обычной функции многих переменных — скалярного поля.
Инвариантное (неизменное при различных выборах криволинейных координат)
дифференцирование тензорных полей может быть введено при помощи так называемого
абсолютного или ковариантного дифференцирования (см.). Частным случаем
Т. и., составляющим, пожалуй, самостоятельную дисциплину, является
векторное исчисление. Т. и. — мощное орудие исследования теории относительности
и дифференциальной геометрии.
Первоначальные идеи Т. и. появляются в XIX в. в связи с задачами диф
ференциальной геометрии у К- Гаусса и Б. Римана. Оформление Т. и. как науки
произошло в трудах итальянских математиков Г. Риччи-Курбастро и Т. Леви-
Чивита. Особенно широко и интенсивно развивается Т. и. в связи с идеями
теории относительности. В этом направлении больших успехов достигли советские
математики В. Ф. Каган, П. А. Широков, П. К. Рашевский.
Лит.: П. К. Рашевский, Риманова геометрия и тензорный анализ, Гостехиздат,
М., 1953; Н. Е. К о ч и н, Векторное исчисление и начала тензорного исчисления, Изд-во
АН СССР, М., 1951.
ТЕОРЕМА — математическое предложение, истинность которого устанавли
вается или опровергается при помощи доказательства.
Греч, τβορεμα — представление, зрелище.
См. также Взаимно обратные теоремы, Противоположные теоремы,
Необходимый признак, Достаточный признак, Критерий.
Лит.: И. С. Г ρ а д ш т е й н, Прямая и обратная теорема, Физматгиз, М., 1960
ТЕОРЕМЫ СЛОЖЕНИЯ в тригонометрии — формулы для синуса, косинуса и
тангенса суммы или разности двух углов.
ТЕОРИЯ ВЕРОЯТНОСТЕЙ — математическая наука, изучающая
закономерности случайных явлений. Математическое понятие вероятности есть отражение
объективной закономерности статистической устойчивости частоты, сущность
которой состоит в следующем.
Пусть имеется некоторый комплекс условий /С, с которым связано
событие Л, причем событие А при выполнении условий комплекса /( может как
произойти, так и не произойти. Например, А' может обозначать бросание
игральной кости, а событие А — выпадение единицы. Пусть комплекс К
воспроизводится некоторое число η раз, из которых т раз наступает событие А (в резуль
тате η бросаний кости единица выпала т раз). Тогда частотой событий А назы
вается отношение т: п. Явление статистической устойчивости частот состоит в том,
что при больших η частота события А почти не зависит от η и близка к
некоторому числу. Это число и называется вероятностью события А. В приведенном

450
ТЕОРИЯ ГРУПП
примере бросания игральной кости частота выпадения единицы при большом числе
бросаний близка к 1/6, следовательно, вероятность выпадения единицы равна 1/6.
Основываясь на том, что при большом числе наблюдений частота близка
к вероятности, Р. Мизес предлагал определить вероятность как предел частоты.
Однако проверка того, что частота стремится к вероятности как к пределу,
требует производства бесконечного числа опытов и потому неосуществима.
Поэтому принять определение Р. Мизеса — значит вообще отказаться от каких
бы то ни было применений теории вероятности.
Возникновение Т. в. связано с вопросами азартных игр (см. Петербургская
игра). Важный вклад в Т. в. внес Я. Бернулли: он дал доказательство закона
больших чисел в простейшем случае независимых испытаний. В первой половине
XIX в. теория вероятностей получает применение к анализу ошибок наблюдений.
Лаплас и Пуассон доказывали первые предельные теоремы. Развитие Т. в. во
второй половине XIX в. связано исключительно с именами русских ученых
П. Л. Чебышева, А. А. Маркова и А. М. Ляпунова. В это время были
доказаны закон больших чисел и центральная предельная теорема (см. Предельные
теоремы), а также разработана теория цепей Маркова (см.). В XX в. теория
вероятностей получает весьма серьезные применения в самых различных областях
науки и техники. Возникает теория случайных процессов (см.). Важнейшее
значение для этой теории имеют работы А. Н. Колмогорова и А. Я. Хинчина.
В частности, А. Н. Колмогоровым изучены в рамках введенной им аксиоматики
так называемые марковские процессы (см.).
Предельные теоремы обобщены на суммы зависимых случайных величин
С. Н. Бернштейном и рядом других математиков.
В конце XIX и начале XX в. создается математическая статистика (см.). См.
также Статистическая проверка гипотез. В 40-х годах нашего века в Т. в.
возникают теория информации (см.) и теория игр.
Таким образом, современная Т. в. является весьма разветвленной наукой.
В числе приложений можно указать приложения к теоретической физике
(статистическая физика, квантовая теория), радиоэлектронике, теории случайных помех
в линиях связи, теории автоматического регулирования при наличии случайных
помех. В биологии и медицине Т. в. применялась главным образом для
обработки результатов экспериментов. Однако в последние годы, по-видимому,
наметилась возможность применения теории информации в вопросах, связанных с
нервной деятельностью, а также в вопросах наследственности. Теория игр может быть
применена при решении многих военных задач, а также задач, связанных с
анализом экономики.
Лит.: Б. В. Гнеденко, Курс теории вероятностей, Физматгиз, М., 1961;
А. М. Я г лом, И. М. Яглом, Вероятность и информация. Физматгиз, М., 1960.
ТЕОРИЯ ГРУПП — раздел алгебры, изучающий свойства групп (см.).
Т. г. возникла первоначально в качестве вспомогательной дисциплины теории
алгебраических уравнений (см. Галуа теория). В дальнейшем она развивалась
в тесной связи с задачами разрешимости дифференциальных уравнений в
квадратурах. На этом пути С. Ли дал основы теории непрерывных групп (см.).
Весьма глубокие и разнообразные применения этой теории в алгебре, геометрии,
дифференциальных уравнениях, топологии дали основания для оформления
Т. г. в самостоятельную дисциплину. Т. г. рассматривает различные классы
групп, как-то: абелевы, нильпотентные разрешимые, полупростые, с конечным
числом образующих, свободные и т. п. Изучаются конструкции построения
по заданным группам новых групп (см. по этому поводу термины Фактор-группа,
Отображение, Гомеоморфизм). Т. .г. к настоящему времени достигла крупных
успехов: классифицированы абелевы группы, с конечным числом образующих,
полупростые группы Ли. Большими авторитетами Т. г. являются математики
Г. Вейль, Э. Картан, Н. Г. Чеботарев, О. Ю. Шмидт, Л. С. Поитрягин,
А. И. Мальцев и др.

ТЕОРИЯ ИГР
451
Лит.: О. 10. Шмидт, Абстрактная теория групп, ГТТИ, М.-—Л., 1933; А. Г. К у-
рош, Теория групп, Гостехиздат, М.—Л., 1953.; Л. С. Понтрягип, Непрерывные
группы, Гостехиздат, М., 1954.
ТЕОРИЯ ИГР — теория выбора наиболее выгодного поведения при
столкновении противоречивых интересов. Математическое понятие игры возникло
из рассмотрения различных игр (шахмат, шашек, карточных игр и т. д.).
Однако область его применения значительно шире и охватывает весьма
различные ситуации, в которых сталкиваются противоречивые интересы (конкурентная
борьба, военные действия и т. д.).
Типичная постановка задачи в Т. и. такова. Имеются два противника (первый и
второй игроки), каждый из которых выбирает независимо от другого
определенный способ действий — стратегию. Например, выбрать стратегию белых в
шахматах — значит указать первый ход и для каждого возможного первого, второго,
третьего и т. д. хода черных указать ответ белых; выбрать стратегию черных —
значит указать ответ черных на каждый возможный ход белых. Игра имеет
некоторое множество исходов, зависящих только от выбранных стратегий (и,
возможно, еще от случайного эксперимента, результат которого не зависит от
игроков). Если игра получила исход а, второй игрок уплачивает первому f (а)
рублей (если f(a) отрицательно, то второй получает от первого f(a) рублей).
Математическое ожидание М(х, у) выигрыша первого игрока зависит только от
стратегий л; и у, выбранных соответственно первым и вторым игроками. Т. и.
рассматривает следующие задачи: а) какую стратегию х0 должен выбрать
первый игрок, чтобы гарантировать себе возможно больший выигрыш независимо от
действий второго, т. е. чтобы
ггипЛ4(л;0, y) = max {rninM (x, у)};
у χ у
б) какую стратегию у0 должен выбрать второй игрок, чтобы независимо от
действий первого проигрывать как можно меньше, т. е. чтобы
тахМ(л;, y0)=min {max Μ (χ, у)}.
χ ух
Эти задачи получили принципиальное решение в случае, когда число
стратегий каждого игрока конечно. При этом оказалось, что обычно каждому
игроку бывает выгодно выбирать не какую-нибудь фиксированную стратегию, а при
каждом повторении игры выбирать одну из возможных стратегий xlt x2i . . ., хп
для первого игрока и ylt у2» · · ·* Ут для второго с некоторыми вероятностями,
соответственно р1# р2, . . ., рп и qu q2, . . ., qm- Наборы (plt p2l . . ., рп) и
(<7ь <72. · · ·« Qm) называются смешанными стратегиями игроков. Нахождение
этих наборов, а также математического ожидания выигрыша первого игрока
называется решением игры.
Рассмотрим в качестве примера следующую игру. Первый игрок прячет
либо монету в 10 коп., либо монету в 20 коп.; второй игрок должен угадать,
какая монета спрятана. Если он угадывает, то получает стоимость спрятанной
монеты, если не угадывает, то платит первому игроку 15 коп.
Применением методов Т. и. в этом случае можно получить, что наилучшая
7
стратегия первого игрока: прятать 10 коп. с вероятностью —-, а 20 коп.—с
5 „
вероятностью —. При этом математическое ожидание его выигрыша равно
5
- коп. при условии, что второй игрок применяет свою наилучшую стратегию:
7 5
называть с вероятностью — монету в 20 коп. и 10 коп. — с вероятностью — ·

452
ТЕОРИЯ ИНФОРМАЦИИ
Если второй игрок будет применять другую стратегию, то он не сможет умень-
/5
шить свой проигрыш!—- коп. в среднем при каждом повторении игры).
Необходимо иметь в виду, что Т. и. применима в том случае, когда игра повторяется
достаточно много раз [тогда выигрыш каждого игрока будет в силу закона
больших чисел (см.) мало отличаться от его математического ожидания].
ТЕОРИЯ ИНФОРМАЦИИ — один из разделов кибернетики, рассматривающий
общие закономерности передачи сообщений. Часто называется также теорией
передачи информации.
Основным понятием Т. и. является информация. Если имеются случайные
величины ξ и η, принимающие значения соответственно #,·, /=1, 2, . . ., η и
Уу, /=1, 2, . . ., т, то информацией /(ξ, η) о случайной величине ξ,
содержащейся в η, называется сумма:
η т
где ρ(ζ—Χί, fl^Vj) — вероятность того, что случайные величины ξ и η примут
соответственно значения *г· и уу·.
Энтропией Я (ξ) случайной величины ξ называется / (ξ, ξ). Т. и.
рассматривает передачу сообщений по каналам связи с помехами. Канал связи имеет вход,
на который подаются символы ylt у2, .. ., уп, и выход, с которого снимаются
символы ylt у2, · · ·» Уп- Например, в телеграфном аппарате Морзе символами
на входе являются точки, тире и пустые промежутки (паузы). Они же являются
символами на выходе. При этом в результате помех точка на входе может
перейти в тире или паузу на выходе. Поэтому в Т. и. рассматриваются
вероятности Ρ {yj/yi} перехода символа у ι на входе в символ у;- на выходе. Только эти
вероятности являются существенными для Т. и.; природа канала (состоит ли он
из электрических, или механических, или радиоприборов, или даже из живых
существ) не играет никакой роли. Именно эта общность Т. и. делает возможным
ее применение в самых различных областях, например в вопросе о путях
передачи информации о наследственных признаках при развитии зародыша.
В зависимости от вероятностей, с какими подаются на вход символы у/,
информация о случайной величине на входе, содержащаяся в случайной величине
на выходе, может принимать различные значения. Пропускной способностью
канала называется наибольшее значение этой информации. Для того чтобы
передавать по каналу сообщение (например, телеграмму по телеграфу Морзе), надо
сначала перевести сообщение в символы на входе (буквы — в точки и тире).
Эта операция называется кодированием. Затем символы на входе передаются по
каналу. Получившиеся символы на выходе надо декодировать (перевести точки
и тире обратно в буквы). Возникает вопрос: для каких сообщений можно
выбрать кодирование и декодирование так, чтобы вероятность ошибки, возникающей
из-за помех, была как угодно мала? Теорема К. Шеннона, являющаяся
центральным результатом Т. и., утверждает, что при широких предложениях для
того, чтобы такой выбор был возможен, необходимо и достаточно, чтобы
энтропия сообщения была меньше пропускной способности канала.
Теорема К. Шеннона была доказана самим К. Шенноном при сравнительно
узких предположениях. Эти предположения были затем расширены А. Райнстей-
ном (США) и советскими математиками А. Я. Хинчиным и А. Н. Колмогоровым.

ТЕТРАЭДРИЧЕСКИЕ ЧИСЛА
453
Идеи теории информации применены А. Н. Колмогоровым в некоторых других
областях математики.
Лит.: А. И. Яг лом, И. М. Яг лом, Вероятность и информация, Физматгиз, М.,
1960; А. Н. Колмогоров, Теория передачи информации, Изд-во АН СССР, М., 1956.
ТЕОРИЯ ПОВЕРХНОСТЕЙ — раздел геометрии, изучающий с локальной
точки зрения поверхности в трехмерном евклидовом пространстве средствами
дифференциального исчисления.
Основы Т. п. заложены в трудах Л. Эйлера. Классические результаты этой
науки получены французским математиком Г. Монжем, затем К. Ф. Гауссом.
Значительный вклад в Т. п. внесли русские математики П. Л. Чебышев, Петер-
сон (уравнения Петерсона — Кодацци). В Советском Союзе вопросами Т. п.
успешно занимались В. Ф. Каган, Я. С. Дубнов, С. П. Фиников, Г. Ф. Лаптев,
Вагнер, П. К. Рашевский, А. П. Норден.
Лит.: П. К. Рашевский, Курс дифференциальной геометрии, Гостехиздат, М.,
1956; А. П. Норден, Теория поверхностей, Гостехиздат, М., 1956; А. Д.
Александров, Внутренняя геометрия выпуклых поверхностей, Гостехиздат, М.—Л., 1949.
ТЕТА-функции — особый класс целых функций (см.). Основные четыре
Т.-ф. определяются рядами:
J. JL Η
6г (г) = 2<7 4 sin ζ — 2q 4 sin Зг+2<7 4 sin 5г— · · ·,
J- JL Hi
θ2(2) = 2<74 cos2-b2<74 cos3z-f-2<74 cos 5гН ,
03 (2)= 1 +2<7 cos 2г+2q* cos 4z+2q9 cos 62-{ ,
04 (г) = 1 — 2? cos 22-f2^4 cos 4z — 2q9 cos 62-\ ,
где |<7|<1. Т.-ф. имеют следующее характеристическое свойство: отношение
двух Т.-ф. есть эллиптическая функция (см.).
ТЕТРАЭДР — четырехгранник или треугольная пирамида. Правильный
Т. — правильный четырехгранник — один из пяти типов правильных
многогранников (см.), имеющий 4 треугольные грани, 4 вершины, 6 ребер. Правильный
Т., в отличие от остальных четырех правильных многогранников, не имеет
центра симметрии. Правильный Т. имеет 6 плоскостей симметрии, каждая из
которых проходит через его ребро и середину другого ребра, скрещивающегося
с первым. Правильный Т. легко получить из куба, если из любой его
вершины А провести три диагонали ABt AC, AD граней куба и соединить точки
Ву Ct D между собой. Правильный Т., как и вообще Т., согласно теореме
Польке— Шварца можно изображать в виде произвольного четырехугольника с его
диагоналями. Т. двойствен (дуален) сам себе.
Греч, τετοα—четыре, έδρα — грань,
основание.
ТЕТРАЭДРИЧЕСКИЕ ЧИСЛА
—натуральные числа вида п(п-\-\) (п-\-2): 6, /]
т. е. числа 1, 4, 10,20, ... Т. ч. являют- # ^ Jv
ся частным случаем фигурных чисел (см.) ^^l'
и составляют арифметический ряд (см.)
3-го порядка. Название Т. ч. происходит ц «
от того, что ими выражается число шаров,
выложенных в пространстве в форме
правильных тетраэдров (рис. 284, а, б, в). Рис. 284
\

454
ТОЖДЕСТВЕННАЯ ПОДСТАНОВКА
ТОЖДЕСТВЕННАЯ ПОДСТАНОВКА (или единичная подстановка) —
подстановка, отображающая символ в себя. Т. п. играет роль единицы в
симметрической группе и имеет вид:
(I 2 .... п\
[\ 2 ... п).
ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ: 1°. Т. п. в алгебре — замена
одного алгебраического (аналитического) выражения другим, тождественно равным
ему, т. е. принимающим те же значения при всех допустимых значениях букв,
входящих в это выражение. Т. п. алгебраического выражения /(а, 6, с, ... , /)
есть переход от этого выражения к выражению φ (α, 6, с> . . ., /), по внешнему
виду, вообще говоря, отличному от первого, но такому, что равенство /=φ есть
тождество (см.). Т. п. выражения / можно выполнять множеством способов.
Т. п. играет большую роль в алгебре при решении уравнений, при
доказательстве теорем и тождеств.
Примерами Т. п. служат: сокращение дробей, раскрытие скобок, вынесение
множителя за скобки, приведение подобных членов, приведение выражения
к логарифмическому виду, формулы сложений в тригонометрии и др.
2°. Т. п. в геометрии — преобразование я-мерного пространства в себя, при
котором все точки этого пространства остаются неподвижными (двойными).
ТОЖДЕСТВО — равенство (числовое, алгебраическое, аналитическое),
справедливое при всех допустимых значениях букв, входящих в это равенство.
]gN
Например: 1)(a — b)2=(b — α)2; 2)(α+6)3 = α3Η-3α26+3α64&3; 3)Ν = α α(α>0,
αφ\, Ν>0); 4) 1= si η2*-b cos2 χ\ lg(*-)>) = lg χ + lgy (*>0, У>0).
ТОПОЛОГИЧЕСКИЕ ИНВАРИАНТЫ — числовые или другие характеристики
топологического пространства (см.), которые не изменяются при гомеоморфизме
(см.). Изучение Т. и. есть предмет топологии. Примерами Т. и. служат:
эйлерова характеристика (см.), связность (см.), числа Бетти (см.), группы Бетти и др.
ТОПОЛОГИЧЕСКОЕ ПРОИЗВЕДЕНИЕ — см. Произведение топологическое.
ТОПОЛОГИЧЕСКОЕ ПРОСТРАНСТВО — понятие, обобщающее в
определенном смысле понятие метрического пространства. Т. п. есть множество
произвольных элементов, называемых точками Т. п., характеризуемых отношением
«бесконечной близости». Более точно: в множестве точек Т. п. выделяется класс
множеств, называемых открытыми множествами или окрестностями,—аналог
открытых множеств евклидова пространства. Окрестностью точки называется любое
открытое множество, содержащее данную точку.
Требуется, чтобы объединение любой совокупности и пересечение конечного
числа открытых множеств было открытым множеством. Этим определено
отношение «бесконечной близости»: точка χ предельная для множества Λ4, если любая
окрестность точки χ содержит точку множества М. Тем самым на
топологическом пространстве возможно рассмотрение непрерывных функций и непрерывных
отображений.
Т. п. может быть определено и другими способами, например с помощью
операции замыкания. Однако такое определение понятия Т. п. слишком общее
и поэтому имеет мало применений вне собственно топологии. Дальнейшим
сужением понятия Т. п. являются хаусдорфовы пространства (см.), нормальные
пространства и т. п.
Примеры: 1. Любое метрическое пространство есть Т. п. В самом деле,
назовем множество Μ открытым, если оно вместе с каждой точкой χ содержит
все точки у пространства, удовлетворяющие условию ρ (л:, у) <б, где о>0
произвольно. Эти множества удовлетворяют указанным выше требованиям.
2. Множество целых чисел превращается в Т. п., если определить окрестность
числа η как арифметическую прогрессию с разностью d, взаимно простой с п.
Лит.: П. С. Александров, Введение в общую теорию множеств и функций.
Гостехиздат, М., 1948.

ТОРРИЧЕЛЛИ ТОЧКА
455
ТОПОЛОГИЯ — наука, изучающая свойства топологических пространств (см.),
не изменяющиеся при гомеоморфизме (см. также Топологические инварианты). Так
как поверхности в геометрии и траектории в теории дифференциальных
уравнений можно рассматривать как топологические пространства, то топология
включает в себя исследования весьма общих свойств этих объектов.
Одним из первых занимался исследованиями топологических проблем
французский ученый А. Пуанкаре. Он впервые понял, что изучать общие свойства
сложных поверхностей, задавая уравнения различных их частей, неудобно. Ему
принадлежат идея триангуляции (см.) поверхности, идея комплекса и т. п.
В настоящее время Т. бурно развивается, особенно это касается
алгебраической Т. Советская топологическая школа продолжает занимать одно из
ведущих мест в мире. Весьма важные результаты в Т. получены советскими
математиками П. С. Александровым, П. С. Урысоном, Л. С. Понтрягиным.
Лит.: Л. С. Понтрягин, Непрерывные группы, М. — Л., 1938; П. С.
Александров, Введение в общую теорию множеств и функций, Гостехиздат, М. —Л., 1948.
ТОР — геометрическое тело, получаемое от вращения круга около оси /
(рис. 285), лежащей в плоскости этого круга и не пересекающей его. Иногда
Т. называют и поверхность, образованную вращением окружности вокруг оси /,
лежащей в плоскости этой окружности и не пересекающей ее, т. е. поверхность,
ограничивающую Т. Внешний вид Т.
напоминает баранку, бублик или спаса-
Рис. 286
Поверхность и объем Т. согласно теоремам Гюльдена (см.) вычисляются по
формулам:
S~2 7ttf.2jtr=4 7t2tfr#
1/«πΓ2.2π#«2π2/?Γ2<
где г — радиус данного круга, a R — расстояние центра круга до оси
вращения /.
Лат. torus — вздутие, выпуклость, узел.
ТОРРИЧЕЛЛИ ТОЧКА. Пусть на сторонах треугольника ABC (рис. 286)
построены правильные треугольники АВСХ% ВАХС% САВХ так, что вершины Ль
Вц С ι лежат по разные стороны с вершинами Л, В, С относительно прямых ВС,
АС, АВ. Тогда окружности, описанные около построенных правильных
треугольников (окружности Торричелли), пересекаются в одной точке Μ — точке Тор-
ричелли. Т. т. относительно треугольника ABC обладает тем свойством, что
сумма ее расстояний от вершин треугольника наименьшая (AM-\-ВМ~{-СM=min)
тельный круг (рис. 285).
I
I
Рис. 285

456
ТОЧКА
по сравнению с любой другой точкой, лежащей внутри того же
треугольника.
Т. т. названа по имени итальянского ученого Е. Торричелли, изучавшего
задачу об этой точке.
Лит.: С. И. Зетель, Новая геометрия треугольника, Учпедгиз, М., 1962.
ТОЧКА — одно из основных понятий геометрии, косвенное определение
которому дается в аксиомах при дедуктивном (аксиоматическом) построении самой
геометрии. Природа Т. может быть самой различной. Так, под Т. л-мерного
евклидова пространства понимают упорядоченную совокупность η чисел. Под Т.
проективной плоскости (см.) можно понимать упорядоченную тройку
пропорциональных чисел (хи х2, x3)t из которых хотя бы одно не равно нулю
(арифметическая модель Т.). Под Т. проективной плоскости в трехмерном евклидовом
пространстве можно понимать евклидову прямую в связке прямых и плоскостей
(евклидова модель проективной плоскости).
В дифференциальной геометрии рассматривают также Т.: особая Т.,
возврата Т., изолированная Т., перегиба Т., прекращения Т., самопересечения Т.,
прикосновения Т., угловая Т.
В теории функций и теории множеств рассматриваются Т., характеризующие
свойства изучаемых функций и множеств: предельная Т., граничная Т.,
плотности Т., особые Т. решений дифференциальных уравнений и др.
ТОЧКА НАКОПЛЕНИЯ множества — предельная точка множества (см.).
ТОЧКА СГУЩЕНИЯ числового множества или множества /2-мерного
пространства (или множества метрического пространства) — точка, в любой
окрестности которой находится несчетное множество (см.) точек Данного множества.
ТОЧКА ЭКСТРЕМУМА функции — точка, в которой функция имеет
экстремум (см.), т. е. максимум (см.) или минимум (см.).
ТРАЕКТОРИЯ — непрерывная кривая, которую описывает при движении
материальная точка. Движение может определяться системой дифференциальных
уравнений. В этом случае говорят о траектории системы дифференциальных
уравнений.
Лат. trajecio — перемещаю.
ТРАКТРИСА — плоская кривая, уравнение которой в прямоугольных
декартовых координатах имеет вид:
Т. является трансцендентной кривой. Т. есть эвольвента (развертка) (см.)
цепной линии (см.). Характеристическое свойство Т. состоит в том, что длина ее
касательной (от точки Μ до оси Ох) есть постоянная величина а (рис. 287),
MR—а. Ось Ох — асимптота Т. или база Т.
Точка А (О, а) — точка возврата Т. (см. Возврата
У* точка) — называется ее вершиной. Т. расположена
симметрично относительно оси Оу. Поверхность
вращения Т. вокруг ее асимптоты (базы) есть
псевдосфера (см.).
Если мыслить точку Μ как материальную,
к которой натянута нерастяжимая нить MR
длиной я, то при движении конца нити R по
некоторой прямой Ох точка Μ опишет траекто-
-•J- рию, называемую Т. Отсюда происходит и
название ее.
Лат. iracto —тащу, влеку; трактриса — ли-
Рис. 287 ния влечения.
Г\\ I/ ON

ТРАНСФИНИТНЫЕ ЧИСЛА
457
ТРАНЗИТИВНОСТЬ. Под Т. понимают одно из свойств системы
преобразований ψ данного множества, заключающееся в том, что для любых двух
элементов а и Ь множества ω найдется преобразование из совокупности ψ, переводящее
а в Ь. Если система ψ есть группа (см.), а ω — многообразие (см.), то пара
(ψ, ω) задает однородное пространство.
Кроме того, под Т. понимают одно из свойств логического отношения
элементов множества. Если элементы а и Ь находятся в отношении* (обозначается
а*Ь) и b*cf то из Т. следует отношение а*с.
Отношения равенства, эквивалентности, сравнимости чисел по некоторому
модулю обладает свойством Т. Примером отношения, не удовлетворяющего
свойству Т., служит отношение в множестве чисел, определяемое так: а* 6, если
|а — Ь\<1.
ТРАНСВЕРСАЛЬ — любая прямая, пересекающая стороны треугольника.
Имеется ряд теорем о Т. См., например, Менелая теорема, Чевы теорема.
Франц. transversal — поперечный, от лат. transversus — поперечный.
ТРАНСПОЗИЦИЯ — подстановка (см.), перемещающая лишь два символа,
а остальные символы оставляющая на месте. Т. является циклической
подстановкой, и длина циклической подстановки (см.), являющейся Т., равна двум.
Т. является нечетной перестановкой (см.). Применение одной Т. к перестановке
(см.) меняет ее четность на противоположную.
Лат. transponere — перемещать.
ТРАНСПОНИРОВАННАЯ МАТРИЦА к матрице А — матрица Л\
получающаяся из матрицы А переменой ролями ее строк и столбцов. Например, если
Λ —L ~"j 5J, то Т. м. к ней будет А1 = / __3 Λ. Если матрица Л квадратная,
\ 0 5/
то ее определитель равен определителю Т. м. к ней. Это одно из основных
свойств определителей. Матрица, транспонированная к произведению матриц,
равна произведению матриц, транспонированных с сомножителями, притом взятых
в обратном порядке, т. е.
\Αγ· Л2 . . . Ап) =ΑηΑη^χ .. . A2At.
ТРАНСФИНИТНАЯ ИНДУКЦИЯ — математический принцип, утверждающий
следующее: если из того, что какое-либо предложение справедливо для всех
трансфинитных чисел (см.) а, предшествующих данному трансфинитному числу β,
следует, что это предложение справедливо также для β, то предложение
справедливо для любого трансфинитного числа. Т. и. является обобщением метода
полной математической индукции и применяется при решении ряда задач теории
множеств.
Лит.: П. С. Александров, Введение в общую теорию множеств и функций, Гос-
техиздат, М. — Л., 1948.
ТРАНСФИНИТНЫЕ ЧИСЛА — обобщение понятия порядковых чисел для
бесконечных множеств. Если конечные множества допускают лишь один тип
упорядочения, который характеризуется порядковым числом, то бесконечное
множество, пусть даже самое простейшее, можно сделать вполне упорядоченным
(см.) многими различными способами. Например, множество из двух элементов
a, b допускает единственный порядок а, Ь или, что безразлично, Ь% а. Самое
простое бесконечное множество целых положительных чисел допускает, например,
такие упорядочения: 1) 1, 2, 3, . . . ; 2) 2, 3, 4, . . . , 1. Эти два
упорядочения различны хотя бы потому, что первое из них не имеет последнего элемента,
а второе имеет. Для каждого возможного порядкового типа вводится его обо-

458
ТРАНСЦЕНДЕНТНОЕ УРАВНЕНИЕ
значение — Т. ч. Над Т. ч. производится действие сложения, весьма сильно
отличающееся от сложения обычных чисел. В приведенном выше примере
порядковый тип 1 обозначается ω, порядковый тип 2 есть ω+l. Можно показать, что
1+ω = ω, хотя ω-Μ=£ω=1-}--ω.
По теореме Цермело (см. Цермело теорема) каждое множество, т. е.
множество любой мощности, может быть сделано вполне упорядоченным и, как
правило, не единственным способом. Итак, одинаковые кардинальные числа (см.)
(мощность множеств, обобщение понятия количественного числа) могут быть
заданы различными Т. ч., хотя в случае конечных множеств эти понятия
совпадают.
Трансфинитная индукция (см.) ведется по Т. ч.
Лит.: П. С. Александров, Введение в общую теорию множеств и функций,
Гостехиздат, М. — Л., 1948.
ТРАНСЦЕНДЕНТНОЕ УРАВНЕНИЕ — уравнение, содержащее
трансцендентные функции (показательные, логарифмические, тригонометрические и обратные
тригонометрическим) от неизвестного (переменного), например, уравнения:
sin x-\-\gx=*x, 2х — \gx=arccos χ.
Обычно рассматривают только простейшие из Т. у. — показательные,
логарифмические и тригонометрические, так как приемов решения, кроме
приближенных, общих Т. у., не существует.
ТРАНСЦЕНДЕНТНОЕ ЧИСЛО — число, которое не может быть корнем
никакого многочлена с целыми коэффициентами. Иначе, Т. ч. есть число, не
являющееся алгебраическим (см.). Примерами Т. ч. являются числа π и е.
Доказательства этих фактов довольно χ ложны.
Однако то, что Т. ч. существуют, можно показать простым рассуждением.
Множество всех многочленов с целыми коэффициентами счетно (см. Счетность
множества), у каждого многочлена конечное число корней. Следовательно,
множество алгебраических чисел счетно, а так как множество чисел имеет мощность
(см.) континуума (см.), то существуют не алгебраические, т. е. Т. ч. Мощность
Т. ч. — континуум.
Всякое Т. ч. иррационально, однако существуют иррациональные числа, не

заявляющиеся Т. ч. Например, число у 3-М есть корень уравнения (х—1)3 = 3,
следовательно, это число является иррациональным, но не трансцендентным.
Существование Т. ч. впервые установил Ж- Лиувилль (1844). Советский
математик А. О. Гельфонд доказал, что числа tf — трансцендентные, если α —
алгебраическое (а>0, аф 1) и β — иррациональное число. См. Гильберта проблемы.
Лит.: А. О. Гельфонд, Трансцендентные и алгебраические числа, Гостехиздат,
М., 1952.
ТРАНСЦЕНДЕНТНЫЕ КРИВЫЕ —линии на плоскости [или, в общем случае,
в произвольном векторном пространстве (см.)], не являющиеся алгебраическим
многообразием (см.). Примеры Т. к. — графики функций: у=sin xt у=cosx,
y=lg*, у=2*.
ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ — аналитические функции, которые не
являются алгебраическими (см.). Такими функциями, например* являются
логарифмические, показательные и тригонометрические функции (см.). Если Т. ф.
рассматривать как функции комплексного переменного, то у Т. ф. обязательно
будет особенность, отличная от полюсов и точек разветвления конечного порядка.
Например, ez и sin 2 имеют существенно особую точку г=оо.
Специальные Т. ф. изучаются в соответствующих курсах (например, теория
бессолевых, эллиптических функций и др.; см, Аналитические -функции).

ТРАПЕЦИЯ
459
ТРАПЕЦИЙ ФОРМУЛА — формула приближенного вычисления определенных
интегралов:
ь
/-J/Wrfr*-^£(^+/1+-+/„-1)-s.
а
Ъ — а
где fk = f(a+kh), Λ= .
Общая площадь криволинейной трапеции заменяется суммой площадей
прямолинейных трапеций, у которых основания — ординаты fmt /m + i (/w=0, 1, . . .,
лг—1).
Погрешность при применении Т. ф. равна:
(Ь — а)*
где а < ξ < Ь.
См. Приближенные методы интегрирования.
ТРАПЕЦИЯ — выпуклый четырехугольник, у которого две
противоположные стороны параллельны, а две другие не параллельны. Параллельные
стороны Т. называются ее основаниями, а непараллельные — боковыми сторонами.
Т., у которой боковые стороны равны, называется равнобедренной или равнобоч-
5
А
// V
/
/ \
о/и К \/
Рис. 288
ной. Т., у которой одна из боковых сторон перпендикулярна основанию,
называется прямоугольной.
Расстояние между параллельными сторонами называется высотой Т. Отрезок,
соединяющий середины боковых сторон Т., называется ее средней линией.
Средняя линия параллельна основаниям и равна их полусумме. Средняя линия KL
(рис. 288) не делит Т. на подобные Т.
В равнобедренной Т. углы при основании равны. Обратно, если углы при
основании равны, то Т. будет равнобедренной. У равнобедренной Т. диагонали
равны и сумма противолежащих углов равна 2d. Равнобедренная Т. имеет ось
симметрии; вокруг равнобедренной Т. можно описать окружность, и, обратно,
если вокруг Т. можно описать окружность, то она равнобедренная.
Для построения Т. необходимо задать (знать, иметь) четыре ее основных
элемента, среди которых должен быть хотя бы один линейный.
Площадь Т. вычисляется по формуле:
S=0,b(a+b)-h,
где а, Ь — основания, a h — высота Т.
Прямая, соединяющая точку пересечения О диагоналей и точку S
пересечения продолженных боковых сторон AD и ВС (рис. 289), делит основания Т.

460
ТРЕУГОЛЬНИК
пополам: AL=LB, DK=CK. Этим свойством трапеции пользуются для деления
отрезка пополам, если дана прямая, параллельная ему с помощью только
линейки, или для построения прямой, параллельной данному отрезку с помощью
только линейки, если известна середина отрезка.
У Евклида Т. означает четырехугольник общего вида.
Греч, τραπεζιον (трапедзион) — столик, обеденный стол (сравните: трапеза,
трапезная); буквально — четырехножник.
ТРЕУГОЛЬНИК: 1°. Т. прямолинейный (одномерный) — три точки, не
лежащие на одной прямой, и три отрезка с концами в этих точках. Т. есть
многоугольник (см.) с наименьшим числом сторон.
Отрезки, соединяющие каждые две из трех данных неколлинеарных точек
А< В и С, называются сторонами Т., а три точки — его вершинами. Углами Т.
(точнее, внутренними углами Т.) называются три угла, каждый из которых есть
совокупность двух лучей, исходящих из вершины Т. и проходящих через две
другие вершины.
В зависимости от углов Т. бывает остроугольный (все углы острые),
прямоугольный (один угол прямой) и тупоугольный (один угол тупой). В зависимости
от сторон Т. подразделяются на разносторонние (все стороны различные),
равносторонние, или правильные (все стороны равны, откуда следует, что и все углы
равны), и равнобедренные (две стороны равны).
Т. с вершинами Л, Б, С обозначают символически так: £±АВС или &ВСА
и т. д. (всего шесть обозначений одного Т.).
Стороны и углы Т. называются основными элементами Т. Одномерный Т.
иногда называют контурным или каркасным. Т. делит плоскость на две области,
из которых одна выпуклая, а другая — невыпуклая. Точки выпуклой области
называются внутренними точками Т., точки невыпуклой области — внешними.
Часто под Т. (двумерным) понимают Т. (одномерный) вместе с внутренними
точками Т. Двумерный Т. иногда называют сплошным или пластиночным.
Модели одномерного (контурного) и двумерного (сплошного) Т. имеют различные
центры тяжести: у первого Т. центр тяжести есть точка пересечения биссектрис,
у второго — точка пересечения медиан; если же Т. равносторонний, то цеьтры
тяжести одномерного и двумерного Т. совпадают. Из контекста обычно ясно,
какой треугольник рассматривают: например, говоря о площади Т., обычно
понимают двумерный Т. («треугольную пластинку»).
Сумма углов Т. равна 2d в геометрии Евклида, меньше 2d и непостоянна
в геометрии Лобачевского, больше 2d и непостоянна (л;<Л-Ь£-|-С<Зя) в
геометрии Римана.
Известные теоремы о зависимости сторон и углов в Т. (против равных
сторон лежат равные углы и др.) верны в абсолютной геометрии (см.), однако ряд
свойств Т. плоскости Лобачевского отличается от свойств Т. плоскости Евклида.
Например, в плоскости Лобачевского существуют треугольники, вокруг которых
нельзя описать окружность; если три угла одного Т. равны трем углам другого
Т., то Т. равны, т. е. в геометрии Лобачевского не существует подобных и
неравных треугольников.
2°. Т. криволинейный — совокупность трех точек А, В, С, не лежащих на
одной прямой, соединенных между собой дугами кривых или дугами кривых и
отрезками прямых, лежащими в плоскости, определяемой тремя точками Л,β,С.
Например, круговой сектор (см.) есть Т. криволинейный.
В проективной геометрии (см.) обычно под Т. понимают трехвершинник
(см.).
См. также Сферический треугольник.
ТРЕУГОЛЬНИК ПАСКАЛЯ--см. Паскаля треугольник.
ТРЕУГОЛЬНЫЕ ЧИСЛА — натуральные числа вида —^-—-. т. е. 1, 3,6,

ТРЕХГРАННЫЙ УГОЛ
461
10, ... Т. ч. являются частным случаем фигурных чисел (см.) и составляют
арифметический ряд (см.) 2-го порядка. Название Т. ч. происходит от того, что
ими выражаются числа шаров, выложенных на плоскости в форме правильных
треугольников (рис. 290, а — г). См.
также Многоугольные числа. ·
ТРЕХВЕРШИННИК в проективной
геометрии — три точки, не лежащие на одной щ %*# *· ···
прямой, и три прямые, проходящие через * * ··· · · . .
каждые две из трех точек. Три точки назы- О О д ι
ваются вершинами, а три прямые — сто-
ронами Т. Легко видеть, что Т. двойствен ™ис· 200
самому себе (см. Двойственности принцип),
т. е. Т. по принципу двойственности соответствует трехстороннику (три прямые,
не проходящие через одну точку, и три точки попарного их пересечения).
Т. также называют треугольником, но треугольник понимают в проективном
смысле (стороны треугольника, в отличие от метрической геометрии, понимаются
не как отрезки прямых, а как прямые целиком).
ТРЕХГРАННИК СОПРОВОЖДАЮЩИЙ кривой M«M(s) (где s — длина
дуги кривой) — три вектора единичной длины: касательный вектор t =—, нор-
ds
1 d2fA
мальный вектор π=-- — (здесь k — кривизна кривой) и вектор бинормали
k ds1
b = txn (здесь txn означает векторное произведение векторов t и п).
Если кривая М = М(/) отнесена к произвольному параметру / (а не к длине
дуги 5), то векторы t, n, b вычисляются по формулам:
dm dt
dt ds
1
d2M / dt \2 Md4_
dt2 \ds) + dt ds2
b = txn,
где ds=y dx2-\-dy2-\-dz2dt, a x(t)t y(t), ζ (/) — компоненты вектора М(/).
Итак, в каждой точке кривой (там, где &=£0) рассматриваются три вектора
t, n, b. При движении точки вдоль кривой эти векторы определенным образом
поворачиваются, так сказать, сопровождают точку.
Движение этих векторов при равномерном движении точки по
кривой описывается формулами Серре-Фреие (см.).
Расположение векторов t, n, b (или τ, ν, β)
относительно кривой можно обрисовать так (рис. 291): вектор t
направлен по касательной к кривой в направлении возрастания
параметра tt вектор η лежит в плоскости, «наиболее близкой» ρ oqi
к кривой в данной точке, — соприкасающейся плоскости,
перпендикулярен вектору t и направлен в сторону
вогнутости кривой в данной точке. Вектор b ортогонален t и π и направлен в
соответствии с правилом векторного произведения.
Т. с. является важнейшим средством исследования кривой.
Лит.: любой курс дифференциальной геометрии.
ТРЕХГРАННЫЙ УГОЛ--три луча SA, SB, SC, исходящие из одной точки
5 пространства и не лежащие в одной плоскости. Плоские углы AS В, BSC,
CSA называются гранями Т. у., точка S — его вершиной (рис. 292, а). Т. у.
31 Толковый словарь математических терминов

462
ТРЕХЧЛЕН
Рис. 292
обозначается так: SABC или LS (одной вершиной). Т. у. делит все пространство
на области (части), одна из которых выпуклая, а вторая невыпуклая (вогнутая).
Выпуклая часть пространства называется внутренней областью Т. у.,
невыпуклая — внешней его областью.
Если все плоские углы Т. у. равны, то Т. у. называется правильным.
Сумма всех плоских углов выпуклого Т. у. меньше четырех прямых (4d).
Каждый плоский угол Т. у. меньше суммы двух
других его плоских углов. Т. у. есть
многогранный угол (см.) с наименьшим числом его
граней. Два Т. у. SABC и S'A'B'C называются
симметричными, если у них плоские углы (грани)
равны, но расположены в обратном порядке,
как показано на рис. 292,6 (S~Sf). ZSABC и
^SA'B'C симметричны. Симметричные Т. у.
не равны, т. е. при наложении они не совпадут.
ТРЕХЧЛЕН — многочлен, содержащий в
точности три члена многочлена (см.). См.
Квадратный т., Биквадратный т.
ТРЕХЧЛЕННОЕ УРАВНЕНИЕ — уравнение,
сводящееся к квадратному уравнению вида:
ах2П+Ьхп+с=0,
где аЪс Φ 0. Т. у. разрешимо в радикалах. Решение Т. у. посредством подстановки
у^=хп сводится к решению квадратного уравнения ау2+&y-f-c=0, найдя корни
которого ул и у2> Далее, нужно будет решить два двучленных уравнения: хп=уг
и хп^у2. Т. у. в частных случаях п=2 и л=3 называют соответственно
биквадратным и бикубическим уравнениями.
ТРИАНГУЛЯЦИЯ — разбиение поверхности на треугольники, вообще говоря,
криволинейные. Разбиение должно проводиться так, чтобы треугольники
примыкали один к другому (т. е. если два треугольника
имеют общие точки, то это или их сторона, или
вершина). Например, Т. квадрата показана на рис. 293.
В трехмерном пространстве легко получить Т. сферы,
вписав в шар, например, тетраэдр и спроектировав его
поверхность из центра на поверхность шара.
Многомерная Т. (я-мерная Т. я-мерного полиэдра) — см. в
термине Комплекс. Топологическое пространство (см.)
считается триангулируемым в том случае, если оно
гомеоморфно (см.) некоторому полиэдру (см.).
Триангулируемые множества называются также криволиней-
D 0QQ ными полиэдрами. См. также Комбинаторная топо-
нис. Ло Д0ГИЯв
ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ — функциональные ряды вида:
~гН-2(яА cos kx+bk sin kx)~ -—- -j-ax cos ,ν-j-^i sin x-f
2 i& 2
-f-a2 cos2x-t-62 sin 2x+ ··· +an cos nx+bn sin nx+
Б комплексной форме Т. р. записывается так:
in x
'rfi
2 Crfi

ТРИГОНОМЕТРИЯ
463
где числа ап, ЬПУ сп называют коэффициентами Т. р. В математике и ее
приложениях Т. р. имеют большое значение. С Т. р. связаны решения некоторых
задач математической физики, например задачи о распространении тепла и задача
о колебании струны. Теория Т. р. способствовала развитию теории множеств,
теории функций действительного переменного, функционального анализа, теории
интегралов Фурье, положила начало общему гармоническому анализу. См. также
Фурье ряд.
Лит.: И. И. Привалов, Ряды Фурье, Гостехиздат, М., 1954; Г. П. Толстое,
Ряды Фурье, Физматгиз, М., I960; А. Зигмунд, Тригонометрические ряды, перев
с англ., ОНТИ, М., 1939; Н. К. Бари, Тригонометрические ряды, Физматгиз, Μ., 196Ι.
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ — уравнения, алгебраические
относительно тригонометрических функций от неизвестного аргумента λ*. Пользуясь
тождественными преобразованиями, Т. у. можно свести к алгебраическому виду:
адЯ+МГЧ ··· +fln=0, (*)
где yk (&=1, 2, 3, 4, 5, 6) есть одна из шести тригонометрических функций
sin λ jc, cos λ χ, tg λ χ и т. д.
Всякое трансцендентное уравнение, левая и правая части которого есть
алгебраические выражения, содержащие только тригонометрические функции от
аргумента (\x-\-k), на основании формул (теорема сложения и других тождественных
преобразований) сводится к Т. у.
Решение Т. у. обычно сводится к решению простейших (основных) Т. у.:
sin*=a, cos*=a, \gx—a. К способам решения Т. у. относят: сведение его к
виду (*), а затем к простейшим Т. у.; сведение Т. у. к виду fx (\г х)
/2(λ2*) = 0, где /i и /2 — тригонометрические функции от неизвестного аргумента,
а затем к простейшим Т. у.; использование формулы двойного и половинного
аргумента (понижение степени тригонометрической функции), формулы сложения;
применение рациональных подстановок (выражений sin x, cos x и других
тригонометрических функций рационально через tg-— J; замена суммы (разности)
тригонометрических функций через их произведение; введение функций неопределенного
угла tgq> или ctg9 и др. Важным при решении Т. у. является вопрос о
равносильности уравнений (случаи потери и появления корней).
Пример: Т. у. — — = tg8x проще решить исходя из формулы тангенса
ι · tg χ
суммы двух углов, т. е. заменить данное Т. у. таким: tg (45°+*) = tg8je, откуда
7λ'=45°4-180°·/2> или *=— (4я-М).
Лит.: И. К- Андронов и А. К. Окунев, Основной курс тригонометрии.
Учпедгиз. М., 1958; П. Я. Коже у ров. Курс тригонометрии для техникумов, Гостехиздат,
М., 1958; С. И. Новоселов, Специальный курс тригонометрии, «Высшая школа», м..
1958.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ — функции угла. См. термины Синус
Косинус, Тангенс, Котангенс, Секанс, Косеканс.
ТРИГОНОМЕТРИЯ — раздел математики, изучающий зависимость между
сторонами и углами треугольника (тригонометрия), а также свойства
тригонометрических функций и связь между ними (гониометрия). Если треугольник (или угол)
плоский, то Т. называется плоской.
Лит.: С. И. Новоселов, Специальный курс тригонометрии, /Высшая школа», М.,
1959.
31*

464
ТРИЛИНЕЙНАЯ ФОРМА
ТРИЛИНЕЙНАЯ ФОРМА — частный случай полилинейной формы (см.),
зависящий от трех систем переменных: xlt х2» . . ., хп\ уъ у2» · · ·» Уп*
zlf z2, ... , ζη. Таким образом, Т. ф. имеет вид:
η
Σ aijeXiy^e'=ci111x1ylz1i-all2x1y1z2+ ... +
it/. e«l
+αΛ—ι» л—ь nxn—хУп— 1гл+Дл—1|П» п^л—1Уп2/1+Яп» л» пхпУп*п»
ТРИЛЛИОН—тысяча миллиардов, или миллион миллионов, т. е. число
Ю12= 1 000 000 000 000. Кое-где (например, в Германии и Ажлии) Т. называют
число 1018.
ТРИСЕКЦИЯ УГЛА — задача о делении произвольного угла на три равные
части. Т. у.— одна из трех знаменитых задач на построение в древней Греции:
Т. у., квадратура круга (см.) и удвоение куба (см.), ни одна из которых
неразрешима с помощью циркуля и линейки.
Т. у. сводится к построению корня кубического уравнения вида х*-\-рх-\-
+(7=0, которое разрешимо в квадратных радикалах тогда и только тогда, когда
это уравнение имеет рациональный корень. Для произвольного данного угла
полученное уравнение не имеет рационального корня, отсюда, согласно критерию
построения отрезка с помощью циркуля и линейки, Т. у. не может быть
разрешена этими средствами построений. Например, деление угла в 60° на три
равные части не может быть выполнено циркулем и линейкой, отсюда вытекает, что
нельзя построить циркулем и линейкой угол в 20°, а следовательно, нельзя
циркулем и линейкой построить правильный 18-угольник (20°=—--360°), отсюда — и
18
правильный 9-угольник. Деление же угла пополам можно выполнить с помощью
циркуля и линейки. Существуют, однако, другие средства построений, которые
позволяют разделить произвольный угол на три равные части: 1) циркулем и
линейкой с эталоном длины на ней (с двумя отметками) — «вставкой»; этот
механический способ деления угла на три равные части был предложен Архимедом
в III в. до н. э.; 2) с помощью конхоиды Никомеда (см.) и 3) с помощью двух
прямых углов.
Лат. tri — три, sectio — разрезание, рассечение.
Лит.: А. Адлер, Теория геометрических построений, Л., 1940; Р. Курант и Г.
Робине, Что такое математика, М.—Л., 1947; Б. В. Кутузов, Геометрия, Учпедгиз,
М.. 1955.
ТРИЭДР — совокупность трех взаимно перпендикулярных единичных
векторов, исходящих из одной точки. Т. играет большую роль в дифференциальной
геометрии (см.) при изучении свойств пространственной кривой (см.), когда
рассматривается подвижный Т., вершина которого совпадает с текущей точкой
кривой, так что один вектор t его направлен по касательной к кривой, другой η —
по главной нормали, а третий b — по бинормали.
Т. также называется трехгранником сопровождающим (см.) или
трехгранником Серре-Френе.
Греч, τρι — в сложных словах — три, έδρα — основание, грань.
ТРОЙНОЕ ПРАВИЛО — устаревшее название правил (приемов) решения
арифметических задач, содержащих прямо или обратно пропорциональные
величины.
Лит.: В. Г. Ч и ч и г и н, Методика преподавания арифметики, Учпедгиз, М., 1949;
Е. С. Березанская, Методика преподавания арифметики, Учпедгиз, М., 1934.
ТРОХОИДА — циклоидальная кривая, которую описывает точка,
находящаяся на расстоянии h от центра круга, катящегося без скольжения по другому

ТРУБКА ВЕКТОРНАЯ
465
кругу. Если /t=r — радиусу катящегося (производящего) круга, то Т. переходит
в эпициклоиду (см.) или гипоциклоиду (см.). Если производящий круг катится
по внешней стороне неподвижного круга, то Т. называется эпитрохоидой, если
же по внутренней — то гипотрохоидой. При h>r (рис. 294) Т. называют
удлиненной, при h<r (рис. 295) — укороченной.
Рис. 294 Рис. 295
Параметрические уравнения эпитрохоиды:
x=(R+mR) cos mt — h cos (t+mt),
y=(R-\-mR) sin mt — h sin (t+mt),
а гипотрохоиды:
x=z(R — mR) cos mt+h cos (t+mt),
y=(R — mR) sin mt+h sin (t — mt)%
_ r
где R — радиус неподвижного круга, a m=— .
R
Особый интерес представляют собой трохоидальные розы. Для таких Т.
h=R-{-r=R+mR. Их уравнение в полярных координатах можно записать в виде:
?=2(R+mR)sin—— φ.
2/72+1
При R~r и любом h Т. представляет собой так называемую улитку
Паскаля, ее уравнение в полярных координатах:
ρ = 2 (г — h cos φ).
При R=2r гипотрохоида становится эллипсом.
Лит.: М. Б. С а в е л о в, Плоские кривые, Физматгиз, М., 1960.
ТРУБКА ВЕКТОРНАЯ — частный случай векторной поверхности в каком-
либо векторном поле. (Векторная поверхность характеризуется тем, что в
каждой ее точке /И соответствующий вектор Л (М) лежит в плоскости, касательной
к поверхности в этой точке. Если взять в векторном поле какую-либо
замкнутую линию, отличную от векторных линий поля, и через каждую ее точку
провести векторную линию, то геометрическое место этих линий и дает трубкообразную
векторную поверхность, называемую Т. в. Поток вектора (см.) через поперечное
сечение Т. в. называют интенсивностью векторной трубки; в соленоидальном поле
интенсивность есть величина постоянная.
Лит.: Н. Е. Ко чин, Векторное исчисление и начала тензорного исчисления, М., 1950.

466
ТУПОЙ УГОЛ
ТУПОЙ УГОЛ — угол, больший своего смежного (см.). Т. у. всегда
больше прямого угла, но меньше развернутого (см.).
См. также Угол.
ТУЭ ТЕОРЕМА — теорема, относящаяся к решениям неопределенных
уравнений и приближениям иррациональных чисел рациональными. Она доказана
в 1908 г. Туэ в следующей формулировке: неопределенное уравнение:
fix, y) = anxn+an-lxn-iy+ ... +а1хуп-1+а0уп=а(*)
совсем не имеет или имеет лишь конечное число целых решений χ и у, если
/(ζ) = απζ"+αη-.1ζ«-ι+ ... +αιζ+α0{αηΦθ)
есть целочисленный неприводимый многочлен степени выше второй.
Т. т. позднее была усилена и обобщена Зигелем, Морделем, Вейлем и
другими авторами. В частности, оказалось, что утверждение Т. т. справедливо, когда
в правой части (*) вместо а будет произвольный целочисленный многочлен с
некоторыми ограничениями для измерений его членов.
Лит.: И. В. Арнольд, Теория чисел, Учпедгиз,М., 1939.

УБЫВАНИЕ ФУНКЦИИ: Г. У. ф. в точке. Функция y=/(.v), определен
ная в окрестности точки а, называется убывающей в точке а, если существует
такая окрестность точки а, что для любых значений xlt x2 из этой окрестности
(хг<а<х2) выполняются неравенства /(Χχ)>f (a)>/(*2), т. е. знак приращения
функции в точке а противоположен знаку приращения аргумента. В случае
выполнения нестрогих неравенств: / (хг) > f (о) > f (х2) функция называется невозра-
стающей в точке а. Дифференцируемая в точке а функция является невозра-
стающей в этой точке тогда и только тогда, когда /' (а)^а. См. также пример
в термине Возрастание функции в точке.
У. ф. на отрезке — см. Убывающая функция.
УБЫВАЮЩАЯ АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ — арифметическая про
грессия (см.), разность которой отрицательна: d<0.
УБЫВАЮЩАЯ ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ — геометрическая
прогрессия (см.), знаменатель которой по модулю меньше единицы: |^|<1.
УБЫВАЮЩАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ — последовательность аъ а2, ...,
ап . . . , для которой следующий член меньше предыдущего: αη+ι<«η(Λ=1, 2,
3, . . . ). В случае выполнения нестрогого неравенства ап+г^ап
последовательность называется невозрастающей. Невозрастающая ограниченная снизу
последовательность имеет конечный предел.
УБЫВАЮЩАЯ ФУНКЦИЯ — на отрезке а<х<Ь (или интервале, или
множестве) — функция y=f(x), для которой при любых х2>хг из отрезка
(интервала, множества) выполняется неравенство: / (а:2)</(а'1). В случае выполнения
нестрогого неравенства / (л*2) < f (х\) функция называется невозрастающей на
отрезке. Дифференцируемая на отрезке [а, Ь] или интервале (а, Ь) функция
является невозрастающей на нем в том и только в том случае, когда f'(x) < 0 для
а < χ < Ъ. Убывание функции на отрезке не
следует смешивать с понятием убывания функции в
точке (см.).
УГЛОВАЯ ТОЧКА кривой у=/ (x) — такая
особая точка функции f(x), для которой сущест-
ДУ
вуют лишь односторонние пределы отношения —
Ах
при Δ* -> 0 или Δ х -> — 0; их называют
односторонними производными. На графике функции (для
кривой у=/(*)) в соответствующей У. т. существуют
лишь односторонние касательные, составляющие
угол. Например, для Рис. 296
АУ
y = \x\ = f(x)\ Игл — = 1 при Ах^ -fO
и Δ*
АУ
lim —=— 1 при Δ х -> — 0.
Δ*
Значит, для нее начало координат — У. т., а односторонние касательные
представляют собой биссектрисы первого и второго координатных углов (рис. 296).
У. т. называется также точкой излома.

468
УГЛОВОЙ КОЭФФИЦИЕНТ
Лит.: Г. М. Фихтенгольц,
Физматгпз, М., 1963.
Курс дифференциального и интегрального исчисления,
Рис. 297
УГЛОВОЙ КОЭФФИЦИЕНТ прямой на плоскости относительно декартовой
прямоугольной системы координат — тангенс угла между этой прямой и
положительным направлением оси χ данной системы координат. Если прямая задана
уравнением y=kx+b, то k является ее У. к. К такому виду может быть
приведено уравнение прямой общего вида ах+Ьу -f с=0, если Ь^О. При 6 = 0 У. к.
условно считается равным ос. В этом случае прямая перпендикулярна оси х.
По У. к. двух прямых kx и k2 можно определить тангенсы углов между этими
двумя прямыми:
&2 ky
1 +kxk2
УГОЛ — два луча (полупрямые), исходящие из одной точки. Лучи,
образующие У., называются сторонами У., точка, из которой они исходят, —вершиной У.
Под точками У. понимают его вершину и все точки его сторон. Если стороны У
образуют одну прямую, то У. называется
развернутым. У., отличный от развернутого, делит плоскость
на две области, из которых одна — выпуклая, а
другая — нет; одну из этих областей называют
внутренней областью У. (обычно это — выпуклая область),
а другую — внешней. Точки, принадлежащие
внутренней области У., называются внутренними, а
принадлежащие внешней области — внешними. Если
внутренняя область У. — выпуклая, то говорят, что
У. меньше развернутого. Если внутренняя область
У. — невыпуклая, то говорят, что У, больше
развернутого. Угол, равный (конгруэнтный) своему
смежному, называется прямым. При пересечении двух прямых третьей прямой
(рис. 297) углы называются: 1 и 5, 2 и 6, 4 и 8, 3 и 7 — соответственными,
2 н 5, 3 и 8 — внутренними односторонними, 1 и 6, 4 и 7 — внешними
односторонними, 3 и 5, 2 и 8 — внутренними накрест лежащими, 1 и 7, 4 и 6 — внешними
накрест лежащими.
УГОЛ ПАРАЛЛЕЛЬНОСТИ при точке А по отношению к прямой / (Аф1) —
острый угол α в плоскости Лобачевского, образованный перпендикуляром,
проведенным из точки А на прямую /, и одной из двух прямых {1г и /2),
проходящих через точку А и параллельных
прямой / в одном из двух направлений этой
прямой / (рис. 298). Длина перпендикуляра
АА0 называется стрелкой У. п.; она
зависит от У. п.; с возрастанием
(убыванием) стрелки У. п. убывает (возрастает).
См. Лобачевского геометрия.
УДВОЕНИЕ КУБА —задача о
построении куба, объем которого вдвое
больше, чем объем данного куба. Задача
У. к. сводится к решению уравнения
х3— 2=0, если положить ребро данного
куба а=1. Отсюда корень полученного
уравнения нельзя построить циркулем и линейкой согласно критерию построения
отрезков циркулем и линейкой. Задача об У. к. не может быть решена
циркулем и линейкой, так же как квадратура круга (см.) и трисекция угла (см.).
Неразрешимость У. к. с помощью циркуля и линейки строго доказал (1837)
французский математик П. Ванцель. У. к. называют также делосской задачей (непра-

УЛИТКА ПАСКАЛЯ
469
вильно — делийской) по названию острова Делоса (Эгейское море), на котором
разразилась, по преданию, эпидемия, и оракул посоветовал увеличить объем
кубического жертвенника вдвое, не нарушая его формы.
Однако, как показал еще Менехм (IV в. до н. э.), У. к. разрешимо
с помощью конических сечений (см.): отрезок χ (корень уравнения хг—2=0)
может быть построен как абсцисса одной из точек пересечений двух парабол:
х2 = оу и у2 = 2ах или параболы х2=ау и гиперболы ху — 2а- и другими способами.
Лит.: А. Адлер, Теория геометрических построений, перев. с нем., Л., 194 0;
Р. Куранти Г. Роббинс, Что такое математика? М.—Л., 1947; Б. В. К у ту з о в.
Геометрия, М-, 1955.
УЗЕЛ — всякая кривая из семейства узлов (см. Узлы). В частности, узлом
является каппа (см.), строфоида (см.). Инверсия У. с центром инверсии в начале
координат есть также У., конгруэнтный данному, но повернутый вокруг начала
на 90°. См. У. также в термине Особая точка.
УЗЛОВАЯ ТОЧКА — особая точка кривой, иначе называется самопересечения
точкой (см.).
УЗЛЫ — семейство плоских кривых, уравнение которых в полярных
координатах имеет вид: s=actg£(p. Все эти кривые имеют в начале координат (в
полюсе) узловую точку (см.) и асимптоты, параллельные осям координат (полярная
ось совпадает с осью ОХ).
При k=l У. есть каппа (см.); при £ = "Т* У· есть строфоида (см.); при
k=2 У. называется ветряной мельницей (см.).
УЛИТКА ПАСКАЛЯ — плоская кривая, определяемая как геометрическое
место точек Λ1 и М\ расположенных на прямых пучка с центром в точке О,
Рис. 299
Рис. 300
лежащей на данной окружности, и находящихся на равном расстоянии а по обе
стороны от точки пересечения Ρ прямых пучка с окружностью. На рис. 299
У. П. изображена сплошной линией. Полярное уравнение У. П. имеет вид:
p = 2/?cosq>+a,
где R — радиус данной окружности, φ — полярный угол радиуса вектора
текущей точки У. П. Если a=2Rt то петля У. П. (сплошная линия внутри данной
окружности) стягивается в точку, и У. П. вырождается в этом случае в
кардиоиду (см.). Если a>2R (рис. 300), то У. П. не имеет общих точек
пересечения с данной окружностью.
В прямоугольных координатах уравнение У. П. имеет вид:
(х2+у2— 2&t)a— а2 (х2+у2)=0.

470
УМНОЖЕНИЕ
Таким образом, У. П.— алгебраическая кривая 4-го порядка. У. П. названа
по имени французского ученого Б. Паскаля, впервые изучавшего ее.
УМНОЖЕНИЕ — операция образования по двум объектам а и Ъ
(сомножителям) третьего объекта с (произведения). Английский математик У. Оутред ввел
(1631) для обозначения У. знак х, а немецкий ученый Лейбниц (1698) — знак·;
при буквенном обозначении эти знаки часто опускают (вместо а хЪ или а-Ь
пишут ab). В зависимости от конкретной природы сомножителей в понятие
операции У. вкладывается различный смысл. Для целых а и Ь произведение с есть
сумма Ь слагаемых, каждое из которых равно а:
ab=a+a-{-. . .-f-α.
' Ъ ''
^ · т ρ тр
а — множимое, b—множитель. У. дробей определяют равенством —·—=—.
η q nq
При У. рациональных чисел получается число, равное произведению абсолютных
величин сомножителей со знаком +* если оба сомножителя имеют одинаковые
знаки, и со знаком — , если они имеют разные знаки. У. иррациональных чисел
понимают как У. их рациональных приближений. У. комплексных чисел
определяется равенствами:
(a+ib) (c+id) = ac — bd+i (ad+bc);
r(cos91+/sin91)-r2(cos92+isin92)=r1r2[cos(91+92)-b/sin(91-t-92)].
У. чисел однозначно и обладает свойствами коммутативности (ab=ba),
ассоциативности [a(bc) = (ab)c], дистрибутивности [a(6-f c)=ab+ac] и α·0 = 0, α·\=α.
См. также Векторное произведение, Умножение подстановок.
УМНОЖЕНИЕ ПОДСТАНОВОК — операция, ставящая в ссответствие
упорядоченной паре подстановок «-степени третью подстановку той же степени. Если
,/1, 2 ... л \ вПг /2 . . . i„\,
Λ-1/ΐ,/2. ...W "Μ/ι /2... Μ
то по определению
Множество всех подстановок л-й степени образует относительно операции У. п.
симметрическую группу (см.) л-й степени. Например, пусть
А~\Ъ 34 21J и ΰ-[\ 3 5 24,)'
тогда
AR(\ 2345\ и RA (I 2345\
AB~U 5 231J и ВА = \Ь 4 1 32>
У. п. некоммутативно, так как закон коммутативности для произвольных
подстановок не выполняется.
УНИКУРСАЛЬНАЯ КРИВАЯ — плоская кривая, которую можно обойти,
побывав дважды только в точках самопересечения. Будем называть точку кривой
четным узлом, если из нее еыходит четное число путей, и нечетным узлом, если
через точку проходит нечетное число путей. Так, все внутренние точки отрезка
есть четные узлы, а концы его — нечетные. Тогда верна теорема: для того чтобы
кривая была уникурсальной, необходимо и достаточно, чтобы у нее было не
более двух нечетных узлов. Легко видеть, что не существует кривой с одним
нечетным узлом. Таким образом, если кривая уникурсальна, то число нечетных
узлов равно либо 0 либо 2, и наоборот.

УНИТАРНЫЙ ОПЕРАТОР
471
В анализе важен особый случай У. к., а именно такие алгебраические
кривые, которые имеют максимальное число двойных точек, включая несобственные
и мнимые двойные точки. Максимальное число δ двойных точек для
алгебраической кривой п-го порядка вычисляется по формуле:
^- (η—1)(/ι —2)
2
причем точки кратности k рассматриваются как C"k двойных точек.
Алгебраические У. к. играют важную роль в теории интегралов
алгебраических функций. Всякий интеграл ^R(x,y) dx, где у— функция от х,
определяемая уравнением F (х* у) = 0, задающим алгебраическую У. к., a R (х% у) —
рациональная функция своих аргументов, приводит к интегралу от рациональных
функций и выражается в элементарных функциях.
УНИМОДУЛЯРНАЯ ГРУППА —- группа всех матриц с η строками и η
столбцами, определитель которых равен единице относительно операции матричного
умножения. В общем случае У. г. называют группу, изоморфную группе таких
матриц, элементами которых могут быть даже не матрицы. У. г. является
группой Ли (см.). Рассматриваются также унимодулярные подгруппы различных групп
матриц, т. е. подгруппы данной группы, состоящие из матриц данной группы
и имеющие определитель, равный единице.
УНИМОДУЛЯРНАЯ МАТРИЦА — квадратная матрица, определитель которой
равен единице. Линейные преобразования, задаваемые У. м., отнесенной к любому
базису, обладают одним замечательным свойством: они сохраняют объем любой
фигуры. Совокупность всех У. м. образует унимодулярную группу (см.). См.
также Матрица.
УНИМОДУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ — линейное преобразование
линейного пространства, при котором сохраняется объем. Матрица (см.) У. п. в любом
базисе имеет определитель, равный единице. Всевозможные У. п. образуют
унимодулярную группу (см.).
УНИТАРНАЯ МАТРИЦА — квадратная невырожденная (см.) матрица А,
удовлетворяющая условию Л~1 = Л', где А*"1 означает обратную матрицу, А —
транспонированную и комплексно-сопряженную матрицу. У. м. есть матрица
линейного преобразования комплексного линейного пространства, сохраняющего
эрмитову форму (см.):
где хи х2 Хп—координаты вектора пространства, и отнесенного к ортонор-
мированному относительно этой формы базису. Определитель У. м. по модулю
равен единице. Все корни У. м. по модулю равны единице. Эрмитову форму У. м.
можно привести к диагональному виду. Всякая ортогональная матрица (см.) есть
в то же время У. м.
УНИТАРНОЕ ПРЕОБРАЗОВАНИЕ конечномерного комплексного линейного
пространства — линейное преобразование, сохраняющее некоторую положительно
определенную эрмитову форму. В ортонормированном базисе относительно эрмитова
произведения, задаваемого этой формой, У. п. записывается унитарной матрицей
(см.). У. п. есть обобщение понятия вращения на случай комплексного линейного
пространства.
УНИТАРНЫЙ ОПЕРАТОР — обобщение понятия вращения евклидова
пространства на бесконечномерный случай. У. о. гильбертова пространства (см.) есть
линейное преобразование гильбертова просгранства, сохраняющее определенное там
скалярное произведение. У. о. обладает обратным оператором, который тоже
является унитарным. У. о. и обратный ему оператор являются сопряженными опера-

472
УНИЧТОЖЕНИЕ ИРРАЦИОНАЛЬНОСТИ
торами; примером У. о. служит преобразование Фурье (см. Фурье
преобразование). У. о.— важное понятие функционального анализа (см.) и операторного
исчисления (см.).
УНИЧТОЖЕНИЕ ИРРАЦИОНАЛЬНОСТИ в знаменателе дроби —
тождественное преобразование алгебраической дроби, в знаменателе которой есть
иррациональные выражения, к дроби, знаменатель которой не содержит иррациональных
выражений (радикалов).
Обычно У. и. в знаменателе дроби выполняется путем умножения обоих
членов дроби на выражение, сопряженное знаменателю (относительно некоторого
радикала).
а
Например, У. и. в знаменателе дроби — выполняется умножением
Ъ -У 2
членов дроби на Ь+ у 2, что приводит ее к виду:
а(ь + У2)
№— 2
не содержащему радикалов в знаменателе. У. и. в знаменателе часто упрощает
вычисление дроби; например, запись дроби —17 D виде десятичного ее прибли-
жения легче выполнить, если предварительно произвести У. и. в ее знаменателе,
приведя ее к виду:
У J 1,4
—— = — = 0,7 (с точностью до 0,1).
Аналогично определяется У. и. в числителе дроби.
УПОРЯДОЧЕННОЕ МНОЖЕСТВО. Множество Ω называется упорядоченным,
если в нем введено отношение порядка < , т. е. для любых двух элементов
α^Ω и ϋζΩ выполняется альтернатива: или а предшествует b (обозначается:
а < Ь), или b предшествует а (обозначается: b < a)t и выполняется свойство
транзитивности: если а < b и b < с, то а < с.
Например, любое подмножество (см.) множества действительных чисел есть
У. м.» если отношение порядка совпадает с отношением «больше». Множество
называется частично упорядоченным, если же не для всех, а только для
некоторых пар элементов а и b множества выполняется альтернатива: а < b или b < a
относительно заданной операции порядка (обозначаемой знаком < , причем, если
а < b и b < с, то а < с), то такое множество называется частично упорядоченным.
Пример. Дано множество Q. Рассмотрим множество А всех его
подмножеств. В множество А можно ввести отношение частичного порядка так, чтобы
А стало частично упорядоченным множеством. Именно: а < bt если а как
подмножество Ω содержится в подмножестве Ь. Следует отметить, что если одно
множество из двух данных целиком не содержится в другом, то отношение
порядка < для них не определяется. Понятие У. м. применяется в алгебре
и функциональном анализе. См. также Структура.
УРАВНЕНИЕ — в первоначальном понимании — есть равенство, в котором одна
или несколько букв считаются (называются) неизвестными.
При дальнейшем изучении математики неизвестные рассматриваются как
переменные и определяются с функциональной точки зрения: У. с одним
неизвестным есть равенство двух функций f^ (jc) = /2 (-^). рассматриваемых в общей
области их определения. Аналогично определяется У. с несколькими
неизвестными:
fi(xi> *2> · · ·» xn) — fi (*ι» #2» · · ·» *η)>

УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 473
Решениями У. называются те значения неизвестных (аргументов), при
которых значения рассматриваемых функций равны. Если функции, входящие в У.,—
многочлены от переменных (неизвестных) х19 х2, .... хп* то У. называется
алгебраическим. Алгебраическое У. с одним неизвестным можно записать в виде:
а^хп-\-агхп—Ч \-ап^Ъ (α0=^0), at — комплексные числа(/=0, 1, ...,/г), где
натуральное число η называется степенью алгебраического У. Всякое
алгебраическое У. имеет по крайней мере один корень — комплексный, мнимый или
действительный (см. Основная теорема алгебры). Алгебраическое У. степени
выше четвертой (я>4) в радикалах в общем виде неразрешимо (см. Руффини—·
Абеля теорема).
Примеры: 1) χ — 2=0 есть У. с одним неизвестным, его решением (корнем)
является, число χ=2; 2) х~\-2у=7 есть У. с двумя неизвестными, одним из его
бесконечного множества решений является пара чисел: х=\, у=3.
В зависимости от того, в какой области допустимых значений
рассматриваются неизвестные, данное У. может иметь (конечное или бесконечное число),
а может и не иметь решений. Так, У. х2 — 2 = 0 не имеет решений
(неразрешимо) в области рациональных чисел, но имеет два решения (разрешимо):
*! = ]' 2, х2 = —к 2 —в области действительных чисел. У. *2-f-l —0 не имеет
решений в области действительных чисел, но имеет два решения: xx~i и
jc2=—i — в области комплексных чисел.
Если в У. входят трансцендентные функции от неизвестных (переменных),
то такие У. называются трансцендентными. Например:
лг2 =3; sin*=l; \gx-\-x-s\nx\
2*=4; arcsin Jt=0,5; sinx=2 и т. д.
Последнее из этих трансцендентных У. совсем не имеет решений в области
действительных чисел. Практически трансцендентные У. решаются приближенными
методами: разложением функций в ряд, графическим путем, методом итераций
и т. д.
Два У. называются равносильными (эквивалентными), если каждое решение
первого У. является решением второго и, наоборот, каждое решение второго У.
является решением первого, или оба У. совсем не имеют решений. У. /ι (*)=/2(х)
называется дробно-рациональным, если функции fx (χ) и /2 (л;) — рациональные и
по крайней мере одна из них не является многочленом. Другими словами, в
дробно-рациональном У. неизвестное входит в знаменатель алгебраической дроби,
содержащейся в У.; решение таких У. сводится к решению алгебраических У.
См. Диофантовы уравнения, Галуа теория, Иррациональное уравнение*
Логарифмическое уравнение, Тригонометрическое уравнение, Трансцендентное урав
нение.
Лит : Энц. элем, матем., т. 2, Гостехиздат, М., 1951; С. И. Новоселов, Специ
альный курс элементарной алгебры, «Высшая школа», М., 1956.
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ— дифференциальные уравне
ния с частными производными, а также некоторые интегральные (см.) и инте-
гро-дифференциальные уравнения. Теория У. м. ф. является частью теории
дифференциальных уравнений в частных производных и тесно связана с различными
другими отделами математики (см. Краевые задачи, Аналитическая теория
дифференциальных уравнений). В основном У. м. ф. являются уравнения вида:
η η η
i'asl /=1 (si

474
УРОВНЯ ЛИНИИ
где aij—ciji, b[, с, f—заданные функции xlt х21 . . .* xn (n>2). Свойства
решения этих уравнений существенно зависят от знаков корней характеристического
уравнения | а^—λ|=0. Если все корни имеют одинаковый знак, то уравнение
(*) называют уравнением эллиптического типа, если знак одного корня
противоположен знаку всех остальных η — 1 корней, то — гиперболического типа, если
же один корень равен нулю, а все остальные одного знака, — то параболического
типа; другие комбинации знаков корней мало изучены.
К уравнениям эллиптического типа приводит изучение различных
стационарных процессов (электростатика, магнитостатика, потенциальное движение
несжимаемой жидкости и т. п.). Простейшими из них являются уравнения Δ ы=0
(Лапласа) и Ди=с (Пуассона), а также уравнение, рассматривавшееся Эйлером:
Au+ku=0, и полигармоиические уравнения (см.).
Уравнения параболического типа получаются при исследовании таких
физических явлений, как теплопроводность, диффузия, распространение
электромагнитных волн в проводящих средах, движение вязкой жидкости. Простейшим из
них является уравнение теплопроводности (см.).
К уравнениям гиперболического типа приводят задачи о колебаниях
сплошных сред и задачи об электромагнитных колебаниях. Простейшим из них является
ди
волновое уравнение — = α2Δ" (Эйлер, 1759).
д2и д2и
Для уравнения Ут^+Т^^^ (Трикоми, 1923) полуплоскость у>0 (—оо<
<*<оо) служит зоной эллиптичности, полуплоскость у<0 — гиперболичности,
прямая у=0 — параболичности; это уравнение смешанного типа. Решению У. м. ф.
посвящены работы известнейших математиков: Эйлера, Даламбера, Лапласа,
Римана, Фурье.
Лит.: А. Н. Тихонови А. А. Самарский, Уравнения математической физики,
Гостехиздат, М., 1956; Р. Курант и Д. Гильберт, Методы математической физики,
гт. I—II, Гостехиздат, М. — Л., 1951.
УРОВНЯ ЛИНИИ — линии в двумерном скалярном поле и (х% у), для
которых x(xt y)=C; при этом требуется, естественно, чтобы и(х, у) имела
непрерывные частные производные и чтобы эти производные не обращались все одно-
нременно в нуль. Каждому значению постоянной С соответствует определенная
У. л. У. л. не пересекаются между собой. Градиент скалярного поля (см.) в
каждой точке поля направлен по нормали к У. л.
Лит.: Н. Е. Кочин, Векторное исчисление и начала тензорного исчисления, Изд-во
АН СССР, М., 1951.
УРОВНЯ ПОВЕРХНОСТИ — поверхности в скалярном поле и (х, у, г),
определяемые уравнением и (х, у, г)=С [и (х, у, ζ) имеет непрерывные частные
производные, которые не обращаются все одновременно в нуль]. Каждой У. п.
соответствует свое значение константы С. Вся рассматриваемая область заполнена
этими поверхностями так, что через каждую точку ее проходит одна и только
одна У. п. Ясно, что У. п. между собой не пересекаются. Градиент скалярного
поля (см.) направлен в каждой точке по нормали У. п., проходящей через эту
ι очку.
Лит.: Η. Ε. Кочин, Векторное исчисление и начала тензорного исчисления, Изд-во
АН СССР, М., 1951.
УСЕЧЕННАЯ ПИРАМИДА — часть пирамиды (см.), заключенная между
основанием и плоскостью, пересекающей боковые ребра и параллельной
основанию. У. п. называется правильной, если она получена из правильной
пирамиды. По числу вершин η в основании У. п. называется л-угольной.
Расстояние между секущей плоскостью и плоскостью основания У. п. называется ее

УСЛОВНАЯ ВЕРОЯТНОСТЬ
475
высотой. На рис. 301 изображена треугольная У. п. ABC А'В'С \ треугольники
ABC и А'В'С называются основаниями У. п. Если У. п. правильная, то
отрезок KL апофемы (см.) SL полной пирамиды называется апофемой У. п.
Объем У. п. с площадями оснований q и Q и высотой h вычисляется по
формуле:
(ср. Усеченный конус).
УСЕЧЕННЫЙ КОНУС — часть конуса (см.), заключенная между основанием
и плоскостью, пересекающей его образующую и параллельной основанию. У. к.,
образованный из прямого кругового конуса, называется прямым круговым У. к.
Рис. 302
(или просто У. к.). Расстояние между секущей плоскостью и плоскостью
основания У. к. называется его высотой. Плоская фигура, полученная от
пересечения конуса и секущей плоскости α (рис. 302), параллельной основанию конуса S,
называется верхним основанием У. к.; основание же Q конуса S называется
нижним основанием У. к. Если площади верхнего и нижнего оснований У. к.
соответственно равны q и Q, а высота /г, то его объем вычисляется по формуле:
'ус.кон
. = \h(g+Q+ViQ).
(г) и O(R), то объем У. к.
Если q и Q — площади кругов соответственно О
выразится формулой:
У-—-Kh(r2+R'2+rR).
о
У. к. можно получить путем вращения равнобедренной трапеции вокруг ее
оси симметрии или вращением прямоугольной трапеции вокруг боковой стороны,
перпендикулярной основаниям (ср. Усеченная пирамида).
УСЛОВНАЯ ВЕРОЯТНОСТЬ события В при условии А обозначается Ρ (В/А)
и имеет смысл, если вероятность Ρ (А) события А отлична от нуля. У. в.
Ρ (В/А) определяется формулой:
где Ρ (АВ) — вероягноаь одновременного наступления событий А и В.

476
УСЛОВНАЯ СХОДИМОСТЬ
Понятие У. в. значительно обобщено А. Н. Колмогоровым в 1930 г. После
этого оно превратилось в центральное понятие современной теории марковских
процессов (см.).
00
УСЛОВНАЯ СХОДИМОСТЬ бесконечного ряда. Если ряд 2 at сходится,
/-1
а ряд, составленный нз модулей | αι |, расходится, то говорят об условной, или
неабсолютной, сходимости первоначального ряда.
Примерами могут служить ряды лейбницевского типа (см.):
Σ^-Σ
со
2;г—1.
Эти ряды сходятся, но ряды, составленные из абсолютных величин их
членов, расходятся. К числу неабсолютно сходящихся рядов относятся также ряды:
со со
У] ι ; (0<s<l): V / ,/ . „(0<s<l).
£—1 η \ns η £J η In /2 (In In ny
n= 2 /1=3
В противоположность абсолютно сходящимся рядам, условно сходящиеся ряды
не обладают переместительным свойством; в каждом таком ряду надлежащей
перестановкой членов можно изменить его сумму или даже вовсе нарушить
сходимость. Согласно теореме Римана, если ряд сходится неабсолютно, то какое бы
ни было наперед заданное число В (конечное или равное ±оо), можно так
переставить члены в этом ряду, что преобразованный ряд будет иметь своей суммой
именно число В. Так, например, если в ряде:
Σ
(_ л_1 111
* =1 — —+—— — -\ =1п2,
2п — 1 2Т3 4Т
переставить члены так, чтобы после одного положительного следовали два отри-
11111 1 1 1
цательных: ^--^-^^ + ...+^—^--—^—+...,10
получившийся ряд имеет сумму 0,5 In 2, т. е. вдвое меньшую.
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
Физматгиз, М., 1963.
УСЛОВНЫЕ УРАВНЕНИЯ — уравнения, в которых сделана замена части
неизвестных их измеренными каким-либо способом значениями; эти измерения
содержат случайные ошибки. Оценку оставшихся неизвестных обычно производят,
применяя к системе условных уравнений метод наименьших квадратов (см.).
УСЛОВНЫЙ ЭКСТРЕМУМ (относительный экстремум). Функция п+т
переменных f(xlt ..., хп+т) имеет в точке M0(x°lt . . ., *°+m), удовлетворяющей
уравнениям связи:
ФД*!, . . ., хп, хп+и . . . , x/z+w)=0, /=1, 2, ... /я,
У. э., если неравенство f(xlt . . . , xn+m)^f (х°{, . . ., *„+m) выполняется в
некоторой окрестности точки /И0 для всех ее точек (xlt . . ., xn+m)t
удовлетворяющих уравнениям связи.

УСТОЙЧИВОСТЬ
477
Для фактического отыскания У. э. функций применяется метод
неопределенных множителей Лагранжа (см.).
См. также Относительный экстремум.
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального
исчисления, т. I, Физматгиз. М., 1963.
УСТОЙЧИВОСТЬ решений дифференциальных уравнений — важнее понятие
качественной теории дифференциальных уравнений и имеет большое значение для
приложений в механике и технике.
Пусть имеется система дифференциальных уравнений:
и хг (/), . . ., xn(t) есть решение этой системы, принимающее при t=t0
начальные значения х®, х®> . . ., xQn. Оно называется устойчивым, если всякое другое
решение, начальные данные которого мало отличаются от х°{, х\, . . ., xjj,
будет тоже мало отличаться от него при всех значениях t.
Виднейшее место в теории У. занимают работы А. М. Ляпунова. Наиболее
часто приходится рассматривать случай, когда правые части системы от t не
зависят и на устойчивость надо исследовать нулевое решение, т. е. хг—0,
λ'2=0, . . ., хп=0 (предполагается, что оно существует). Обычно поступают так.
Разлагают функции Д· в ряд Тейлора (см.) в окрестности точки (0, 0, ... , 0)
и отбрасывают члены порядка малости выше первого. Тогда система запишется
так:
dxi_ "
dt ~ khPik4'
Если вещественные части характеристических корней матрицы pik отрицательны,
то нулевое решение системы устойчиво; если же хотя бы у одного
характеристического корня вещественная часть положительна, то нулевое решение системы
неустойчиво. Эту теорему доказал А. М. Ляпунов. Но из нее ничего не следует,
если есть характеристические корни матрицы р/£ чисто мнимые.
Однако А. М. Ляпунов создал другой метод исследования устойчивости,
основанный на понятии так называемой функции Ляпунова. В случае, когда
правые части системы (*) зависят от t, чаще всего изучаются уравнения с правыми
частями, периодическими по /. Здесь очень интересные критерии устойчивости
d2x
решений уравнения —=p(t)x получены А. М. Ляпуновым. За последние годы
at-
в связи с развитием техники теория У. приобрела очень большое значение.
Выходит очень большое число работ, посвященных этой теории. Большинство
этих исследований опирается на идеи А. М. Ляпунова.
Лит.: А. М. Ляпунов. Общая задача об устойчивости движения. Гостехиздат.
М. —Л., 1950; Н. Г. Четаев, Устойчивость движения, Изд-ао АН СССР, М. —Л.,
1962.
32 Толковый словарь математических терминов

φ
ФАКТОР-ГРУППА группы (см.) G по ее нормальному делителю (см.) Я —
группа Ζ, элементами которой являются классы смежности (см. Класс) группы G
по подгруппе И.
Групповые операции в Ζ вводятся так: для того чтобы перемножить два
класса смежности (два элемента группы G), нужно взять из каждого класса по
представителю, их перемножить в смысле групповой операции группы G и
рассмотреть класс смежности, к которому относится это произведение. Используя
свойства нормального делителя, какозым является группа //, легко доказывается,
что так определенное умножение в группе Ζ не зависит от случайного выбора
представителей классов смежности. Аналогично определяется операция перехода
к обратному элементу в группе Ζ. Ф.-г. обозначается G/H.
Пример Ф.-г. группы невырожденных матриц по подгруппе скалярных
матриц есть группа матриц с определителем, равным единице.
Лит.: А. Г. Курош, Теория групп, Гостехиздат, М. —Л., 1953.
ФАКТОРИАЛ — произведение всех натуральных чисел от 1 до данного
натуга
рального числа п. Ф. обозначается /г! = 1 -2·3- ··· п= Π /. Название Ф. проис-
г=1
ходит от английского слова factor — множитель. Обобщением Ф. является гамма-
функция (см.). Для приближенного вычисления Ф. при больших η пользуются
формулой Стирлинга (см. Стирлинга формула).
В математике Ф. пользуются в самых различных формулах, например, в
ряде Тейлора (см.), в полиномиальных коэффициентах (см.) и т. д.
По определению 0! принято считать равным единице.
ФАЛЕСА ТЕОРЕМА — одна из теорем элементарной геометрии о
пропорциональных отрезках. Ф. т. утверждает, что если на одной из сторон угла от его
вершины последовательно отложить равные между собой отрезки и через концы
этнх отрезков провести параллельные прямые, пересекающие вторую сторону
угла, то на второй стороне угла отложатся также равные между собой отрезки.
Частный случай Ф. т. выражает некоторые свойства средней линии треугольника
(см.).
Лит.: Н. А. Глаголев, Элементарная геометрия (Планиметрия), Учпедгиз, М.,
1944.
ФЕДОРОВСКИЕ ГРУППЫ — понятие геометрии, используемое в
кристаллографии. Совокупность ортогональных преобразований евклидова пространства
называется Ф. г., если: 1) она образует группу (см.); 2) хотя бы для одной
точки Μ пространства существует число г такое, что внутри шара радиуса г
с центром в точке Μ нет гомологических точек (см.) (условие дискретности);
3) существует такое R>0, что где бы ни вырезать из пространства шар радиуса
R, в этом шаре есть точки, гомологичные М. Имеется 230 различных
трехмерных федоровских групп (Федоров, 1890).
Лит.: С. А. Богомолов, Вывод правильных систем по способу Федорова,
Изд.-во «Кубуч», 1932—1934; И. И. Федоров, Симметрия и структура кристаллов.
Основные работы, Изд-во АН СССР, М., 1949.
ФЕЙЕРБАХА ТЕОРЕМА — предложение, утверждающее, что окружность
девяти точек (см.) касается вписанной окружности и трех вневписанных окруж-

ФИБОНАЧЧИ ЧИСЛА
479
ностей. Точки касания окружности девяти точек и окружностей, вписанной и вне-
вписанных, называются точками Фейербаха. Ф. т. названа по имени немецкого
математика Фейербаха, доказавшего эту теорему.
Лит.: С. И. Зетель, Новая геометрия треугольника, Учпедгиз, М., 1962.
ФЕРМА БОЛЬШАЯ ТЕОРЕМА, или Ферма великая теорема — утверждение
П. Ферма о том, что уравнение хп+уп = гп (где η — целое число большее двух)
не имеет решений в целых положительных числах. Несмотря на утверждение
П. Ферма о том, что ему удалось найти удивительное доказательство Ф. б. т.,
которое он не приводит из-за недостатка места (это замечание написано было
П. Ферма на полях книги Диофанта), до сих пор Ф. б. т. в общем виде не
доказана (и не опровергнута). Ф. б. т. удалось доказать для отдельных
показателей и групп показателей, например для всех η ^ 4002. Широкая известность
Ф. б. т. и нездоровый ажиотаж к поискам ее доказательства возникли в 1907 г.
в связи с объявлением премии в 100 тысяч немецких марок за ее решение. Эта
премия из-за ряда инфляции в Германии давно аннулирована. Однако Ф. б. т.
и в настоящее время представляет значительный интерес, так как ее решение
потребует создания новых глубоких методов в теории алгебраических чисел.
Лит.: А. Я. X ии чин, Великая теорема Ферма, Гостехиздат, М., 1932; В. Сер-
пинский, Решение уравнений в целых числах, перев. с польского, Физматгиз, М.,
1961.
ФЕРМА ВЕЛИКАЯ ТЕОРЕМА — см. Ферма большая теорема.
ФЕРМА МАЛАЯ ТЕОРЕМА — частный случай Эйлера теоремы (см.), когда
модуль т=р—простое число. Ф. м. т. формулируется так: если ρ простое
число, то aP = a(mod р). В том случае, когда а не делится на р, из^ Ф. м. т.
следует: аР—*ξ l(mod ρ). Φ. м. т. была открыта французским ученым Пьером Ферма.
Получила название малой, в отличие от другого высказанного Ферма
утверждения, называемого большой теоремой Ферма.
ФИБОНАЧЧИ ПОСЛЕДОВАТЕЛЬНОСТЬ (РЯД) —последовательность чисел
1, 1, 2,3, 5, 8, 13, . . . , составляемая по рекуррентному закону αΛ+ι—ап-\-ап—lf
т. е. каждый последующий член последовательности равен сумме двух
предыдущих. Ф. п. была введена итальянским математиком Фибоначчи (1202) в связи
с задачей о размножении кроликов. Ф. п. является частным случаем возвратных
последовательностей (см.). Существует формула, явно выражающая /2-й член
Ф. п. через число п:
/-2—1 η , 1—гх п \+Vs \-Vb
Лит.: Н. Н. Воробьев, Числа Фибоначчи, Гостехиздат, М., 1951.
ФИБОНАЧЧИ ЧИСЛА. На одном из турниров (1225) в г. Пизе, в
присутствии римского императора, знаменитому тогда искусному вычислителю Фибоначчи
была предложена следующая задача: найти полный квадрат, остающийся
полным квадратом как после увеличения, так и после уменьшения его на 5.
После некоторого размышления Фибоначчи нашел решение задачи:
/41 \2 /31\2 /41\2 /49\2
Записывая эту задачу в общем виде, получим три числа, содержащиеся в ее
условии:
' N2 / χ \2
(х 2 /х\2 (х
32*

480
ФИГУРА ГЕОМЕТРИЧЕСКАЯ
Эти три числа являются точными квадратами и последовательными членами
арифметической прогрессии с разностью, равной г, и называются Ф. ч.
В литературе название Ф. ч. иногда относят также и к членам
последовательности (ряда) Фибоначчи.
Лит.: Б. А. Кордемский, Математическая смекалка, Физматгиз, М., 1963.
ФИГУРА ГЕОМЕТРИЧЕСКАЯ — множество точек на плоскости или в
пространстве. Ф. г. может содержать как конечное, так и бесконечное множество
точек. Примеры: точка, три точки, отрезок, луч, прямая, треугольник, тетраэдр,
окружность, пространство — представляют собой Ф. г.
ФИГУРНЫЕ ЧИСЛА или ^-угольные числа — целые числа вида:
n+(k — 2)n*n~ ) при л=1, 2, . ..
Ф. ч. образуют арифметический ряд (см.) 2-го порядка. При &=3, 4 и 5 Ф. ч.
дают соответственно треугольные числа, квадратные числа и пентагональные
числа (см.). О Ф. ч. справедлива следующая основная теорема: всякое натуральное
число может быть представлено суммой не более чем k ^-угольных чисел,
например суммой не более чем четырех квадратов. Эта теорема была высказана Ферма
и доказана Коши. Исторически первое систематическое изучение Ф. ч.
содержится в сочинении Никомаха «Введение в арифметику». Пространственные аналоги
треугольных чисел в трехмерном пространстве называются пирамидальными (те-
траэдрическими) числами. Пирамидальные числа выражают число одинаковых
шаров, составляющих правильную пирамиду.
Ф. ч. встречаются в комбинаторике, а также в теории чисел при
вычислении суммы одинаковых степеней чисел натурального ряда. Ф. ч. известны были
в древней Индии, в Китае, Вавилоне, Греции. У европейских математиков Ф. ч.
назывались коэффициентами в разложении бинома {а-\-Ь)п при /2=1, 2, 3, . . .
См. также Паскаля треугольник, Многоугольные числа.
ФЛЮЕНТА — устаревший термин, введенный И. Ньютоном для выражения
переменной величины, зависящей от времени.
См. также Флюксия, Флюксий исчисление.
Лат. flure — течь, флюента — текущая.
Лит.: К. А. Рыбников, История математики, МГУ, I960.
ФЛЮКСИЙ ИСЧИСЛЕНИЕ (теория флюксий) — наиболее ранняя форма
анализа бесконечно малых величин и дифференциального и интегрального
исчисления. Ф. и. было создано И. Ньютоном и развивалось в работах английских
математиков. Символика Ньютона в Ф. и. была неудобна и была вытеснена
символикой дифференциального исчисления, введенной Лейбницем и сохранившейся до
настоящего времени. Переменные величины х, у, ζ, . . ., зависящие от времени,
Ньютон называл флюентами (см.), скорости изменения (течения) их он называл
флюксиями и обозначал х, у, г, . . . (первые флюксии), х, у, г, . . .
(вторые флюксии) и т. д. Следовательно, флюксии — это производные флюент по
времени. Бесконечно малые изменения флюент Ньютон называл моментами и
обозначал символом О (что соответствует дифференциалу флюенты). Момент времени
Ньютон обозначал через О, момент флюенты у —через оу. Иногда вводились
специальные символы флюент 'у или О У (символ квадратуры).
В теории флюксий ставились две основные задачи: 1) определить скорость
движения в данный момент времени по заданному пути (задача дифференцирования
неявной функции); 2) по заданной скорости движения определить пройденный за
данное время путь (задача интегрального исчисления).

ФОРМУЛА
481
Лит.: К· А. Рыбников, История математики, МГУ, 1960; И. Ньютон.
Математические работы, М. — Л., 1937; И. Ньютон, Математические начала натуральной
философии, вкн. «Собрание сочинений Д. Н. Крылова», т. 7, М. —Л., 1936; А. Н.
Колмогоров, Ньютон и современное математическое мышление, вкн.: «Московский
университет— памяти Исаака Ньютона», М., 194 6.
dy
ФЛЮКСИЯ — устаревшее название производной функции —-, введенное
at
Ньютоном н обозначаемое символом у (первая флюксия), у (вторая флюксия)
и т. д.-Символ Ф. сохранился, например, в механике и в векторном анализе.
См. также Флюента и Флюксий исчисление.
ФОКУС: 1°. Ф. кривой 2-го порядка — точка, лежащая в плоскости этой
кривой и обладающая тем свойством, что отношение расстояний любой точки
кривой до фокуса и до соответствующей директрисы (см.) есть постоянная
величина, равная эксцентриситету (см.) этой кривой. См. Гипербола, Парабола,
Эллипс. См. также Овалы, Декартов овал.
Термин Ф. был введен Кеплером в 1609 г.
2°. Ф. в теории дифференциальных уравнений — один из типов особых
точек дифференциальных уравнений: все интегральные кривые, проходящие через
эту точку, представляют собой спирали с бесконечным числом витков. См.
Особая точка.
Лат. focus — очаг, огонь.
Лит.: А. Г. Дорфман, Оптика конических сечений, Физматгиз, М., 1958.
ФОРМА степени т — многочлен от нескольких неизвестных, каждый член
которого имеет степень т относительно совокупности всех неизвестных.
Лат. forma — вид, наружность.
ФОРМАЛИЗМ в преподавании математики понимается двояко: во-первых,
отрыв содержания этой дисциплины от формы ее изучения, т. е. преподавание,
при котором математика изучается поверхностно, неглубоко; во-вторых,
преподавание математики, при котором обращается внимание на развитие только
логического, абстрактного мышления учащихся, без должного внимания на связь
математики с жизнью, без указания на прикладной характер математики.
Ф. в философии математики — одно из буржуазных течений, сводящееся к
аксиоматическому обоснованию математики и доказательству ее
непротиворечивости. Крупным представителем Ф. в философии математики является известный
немецкий математик Д. Гильберт и его школа.
Ф. возник в начале XX в. как ответ на критику интуиционистов (см.
Интуиционизм).
. Лит.*. А. Я. X и н ч и н, Об оснэвных понятиях математики в средней школе
(Педагогические статьи). Изд-во АПН РСФСР, М., 1963.
ФОРМУЛА — всякая символическая запись (алгебраическое выражение, а
также равенство), содержащая какое-либо утверждение (предложение, суждение).
Примеры: 1) 2п есть Ф. любого четного числа (где η — целое);
2) у=— qh — Φ. объема пирамиды (где q — площадь основания, h — высота пира-
о
миды); 3) (α-f6)2=>a2-f2ab+b2— Φ. квадрата суммы двух чисел а и Ъ\
4) 2лг=с\ 5) УТ+УТ-π; 6) е= lim (1+—Υ*; 7) 2χ2=3; 8) \χ\ < 5;·
9) /±ABC=&A'B'C.
См. также Стирлинга Φ., Эйлера Φ., Грина Φ., Тейлора Φ. Φ. могут
выражать как истинные, так и ложные утверждения. Например, Ф. 5 и 7 —
ложные, Ф. 9 Еыражает равенство двух треугольников. Ф. помогают заменить

482
ФОРМЫ
сложные рассуждения, громоздкие предложения в математике краткой
записью.
Лат. formula — уменьшительное от forma — образ, вид.
ФОРМЫ геометрические (в проективной геометрии). 1°. Ф. 1-й ступени
(основные):
а) прямолинейный ряд точек — множество точек Л, В, С, D, . . .,
принадлежащих данной прямой s; прямая s называется носителем ряда точек;
б) пучок прямых — множество прямых а, Ъ> с, d, . . . на плоскости,
принадлежащих данной точке S\ точка S называется носителем или центром пучка;
в) пучок плоскостей — множество плоскостей α, β, γ, δ, . . .,
принадлежащих данной прямой s\ прямая s называется носителем пучка плоскостей (или
осью пучка плоскостей).
Каждая из Ф. 1-й ступени с помощью проектирования или сечения может быть
приведена во взаимнооднозначное соответствие с любой другой Φ.Ι-й ступени.
2°. Ф. 2-й ступени (основные):
а) плоское поле точек — множество точек, принадлежащих данной
плоскости а; плоскость а при этом называется
носителем поля;
б) плоское поле прямых — множество
прямых, принадлежащих данной плоскости а;
плоскость а при этом называется носителем поля;
в) связка прямых — множество прямых про-
-X странства, принадлежащих данной точке S; точка
S называется носителем или центром связки;
г) связка плоскостей — множество плоскостей,
принадлежащих данной точке S; точка S
называется носителем или центром связки.
ρ οπό Иногда также рассматривают Ф. 3-й ступени:
с* пространство точек — множество точек
проективного пространства, которое называется носителем
точек; пространство плоскостей — множество плоскостей проективного
пространства, которое называется носителем плоскостей.
В проективной геометрии изучают еще и такие Ф. 2-й ступени: плоское
поле точек и прямых, которое двойственно связке прямых и плоскостей.
Ф. 1-й (2-й, 3-й) ступени также называют образами 1-й (2-й, 3-й) ступени.
В проективной геометрии устанавливают проективное соответствие в Ф. (в
образах) 1-й и 2-й ступени.
См. Проективные формы.
ФРОНТАЛЬ — прямая а, параллельная вертикальней плоскости проекций ν,
но не перпендикулярная горизонтальной плоскости проекций Н. На эпюре (см.)
горизонтальная проекция αγ Φ. (прямой а(ах, а2))будет параллельна оси
проекций хх, а вертикальная ее проекция а2 может занимать любое положение
относительно оси проекций хх, но не может быть перпендикулярна ей (рис. 303).
На рисунке прямая а(аг, а2) есть Ф.
Термин Ф. употребляется в начертательной геометрии (см.).
См. также Горизонталь.
ФУЗИОНИЗМ в преподавании математики — метод преподавания математики,
при котором различные ее разделы изучаются не постепенно и не раздельно, а
сразу, в одном, например, учебном году и в тесном переплетении различных
разделов между собой. Например, Ф. в преподавании геометрии выражается в
изучении планиметрии (см.) и стереометрии сразу, одновременно, а не раздельно.
За совместное изучение планиметрии и стереометрии высказывался наш великий
математик Н. И. Лобачевский. Советская методика математики не признает Ф.,
так как это направление в преподавании не учитывает возрастных особенностей
учащихся и развития их логического мышления и не ведет к положительным

ФУНКЦИОНАЛ
483
результатам в усвоении математики. Например, книга В. А. Богомолова
«Геометрия» (систематический курс) (Учпедгиз, М.—Л., 1949) построена на фузионист-
ской основе. Элементы Ф. встречаются и у нас в восьмилетней школе.
Лат. fusio — литье, сплавление, слияние,
ФУНДАМЕНТАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ действительных чисел
(точек я-мерпого или метрического пространства) — последовательность χλ, χ2,
. . ., хп, . . ., удовлетворяющая критерию Коши, т. е. любого ε > 0
существует номер N такой, что для любого η > N и любого ρ > О выполняется
неравенство: \хп+р —хп\ < ε (соответственно неравенство: ρ (χη+Ρι χη) < ε, где
символом ρ обозначено расстояние в η -мерном или метрическом пространстве). Для
того чтобы последовательность имела конечный предел (соответственно
единственную предельную точку), необходимо и достаточно, чтобы она являлась Ф. п.
(критерии Коши сходимости последовательности).
Метрическое пространство называется полным, если любая Ф. п. его точек
сходится к некоторой точке этого пространства.
ФУНКЦИЙ ТЕОРИЯ — раздел математического анализа, изучающий общие
свойства функций. Обычно под Ф. т. понимают теорию функций действительного
переменного. Относительно теории функций комплексного переменного см. термин
Аналитическая функция. Теория функций действительного переменного
подразделяется на три основных направления: 1) дескриптивная теория функций (см.);
2) конструктивная теория функций (см.); 3) метрическая теория функций.
Метрическая теория функций оперирует понятиями меры множества (см.),
измеримой функции, различными обобщениями понятия интеграла (см. Лебега
интеграл), сходимости и т. п. В основе этой теории лежат методы и идеи теории
множеств.
Развитие теории функции действительной переменной во многом было
обусловлено вопросами практики. Так, часто замечалось, что решения
дифференциальных уравнений оказывались функциями разрывными или с разрывными
производными (здесь решения — в некотором обобщенном смысле). φ
Крупные результаты Ф. т. получены Э. Борелем, Р. Бэром, А. Лебегом,
а также советскими математиками Д. Ф. Егоровым, Η. Η. Лузиным, А. Я. Хин-
чиным, Д. Е. Меньшовым, А. Н. Колмогоровым.
Лит.: П. С. Александров, Введение в общую теорию множеств и функций, Гос-
техиздат. М.— Л., 1948; И. П. Натансон, Теория функций вещественной переменной,
Гостехиздат, М.—Л., 1950; Н. А. Фролов, Теория функций действительного
переменного, Учпедгиз, М., 1961.
ФУНКЦИОНАЛ. Если каждой функции φ из некоторой совокупности
функций s ставится в соответствие некоторое число F (φ), то говорят, что задан Ф.
Говоря нестрого, Ф. есть функция от функции, при этом совокупность функций
называется областью определения Ф. Например, F (ф)=ф2 (0), F (Ф)= [ф2 (х) dx и т. п.
о
являются Ф.
Наибольшее значение в математике имеют так называемые линейные Ф. Если
F (ay-l-\-by2) = aF (q>i)+bF (φ2) для любых чисел а и Ь произвольных функций
Φι и φ2 из совокупности s, то Ф. F называется линейным. Область определения
линейного Ф. есть обязательно линейное пространство.
Примеры: 1) /7(Ф) = Ф(0); 2) F(q>)=—χ ; 3) F (φ)= f Ρ (χ) Φ (x) dx,
dx \χ = α 0
где Ρ (χ) — заданная функция.
Линейные Ф. называются иначе обобщенными функциями. Существует
обширная и глубокая теория, касающаяся обобщенных функций.
Лит.: Г. Е. Шилов, Введение в теорию линейных пространств, Гостехиздат, М.—
Л., 1952; И. М. Гельфанд и Г. Е. Шилов, Обобщенные функции и действия над
ними, Физматгиз, М., 1959.

484 ФУНКЦИОНАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
ФУНКЦИОНАЛЬНАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ - последовательность (см.),
члены которой являются функциями: /т (дг), /г (х), . . ., fn(x)
ФУНКЦИОНАЛЬНОЕ ПРОСТРАНСТВО —топологическое пространство,
элементами (точками) которого являются функции, в частности, Ф. п. являются
метрические Ф. п. Наибольшее значение в математике имеют линейные Ф. п.,
метрика которых определяется с помощью нормы (см.).
Например: С (а, Ь) — пространство непрерывных на отрезке [а, Ь] функций
с метрикой ρ (/, g) = max |/(/) — g(t)\\ пространство непрерывных финитных
а < t < ь
функций (т. е. функций, обращающихся в нуль вне некоторого интервала) с
метрикой о(/, £)=1/ J (f — g)2dx и т. д.
* -—со
Ф. п. часто рассматривается в функциональном анализе, операторном
исчислении и т. д.
ФУНКЦИОНАЛЬНОЕ УРАВНЕНИЕ — уравнение, в котором неизвестным
является функция и в котором искомая функция связана с известными (данными)
функциями при помощи операции образования сложной функции (помимо, быть
может, алгебраических операций).
Примеры: 1. / (x+y) = f(x)-\-f(y), где / — неизвестно. Это уравнение
имеет общее решение: f(x)=ax, если ищется непрерывное решение. Однако то же
уравнение допускает и другие решения [разрывные и, более того, неизмеримые
(см. Измеримая функция)]. 2. Некоторые элементарные функции (например,
Inx, ех) являются непрерывным решением простых Ф. у. [соответственно:
/(** у)ЧМ+Пу) и f(x+y)4(*)-f(y)h
Определение четной (см.), нечетной (см.), а также периодической функции
(см.) производится с помощью Ф. у.
ζ$ Лит.: Я. Ацель, Некоторые общие методы в истории функциональных уравнений,
«Успехи математических наук», т. 11, вып. 3, 1956, стр. 3—68.
ФУНКЦИОНАЛЬНОЕ УСТРОЙСТВО — механизм, при помощи которого
можно определить значение функции, зная значение ее аргумента. Примером Ф. у.
могут служить фигурные потенциометры, соединения электрических элементов,
приближающие функцию кусочно-линейной зависимостью, и другие
электрические устройства. См. Счетно-решающие устройства.
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ —важный раздел современной математики.
Как самостоятельная наука Ф. а. оформился на рубеже XIX и XX вв., когда
обнаружилась глубокая аналогия между некоторыми понятиями алгебры, анализа
и геометрии. Ф. а. объединяет и обобщает идеи различных отделов
классического анализа (например, вариационное исчисление, интегральное и
дифференциальное исчисление, интегральные и дифференциальные уравнения), теории
множеств, линейной алгебры и многомерной геометрии.
Наиболее важным понятием Ф. а. является общее понятие пространства
(см.). Для Ф. а. характерно рассмотрение бесконечномерных пространств,
состоящих из функций, последовательностей или каких-либо других общих
объектов, а также операций над элементами таких пространств. Понятие /2-мерного
пространства необходимо было ввести уже при геометризации теории функций
многих переменных. Пространства, точками которых являются функции или
числовые последовательности, называются функциональными пространствами (см.).
С развитием понятия пространства шло и обобщение понятия функции.
Переменные величины, зависящие не от числового аргумента, а от некоторой
функции, получили название функционалов (см.). Функционал — числовая функция,
определенная на некотором функциональном пространстве.
Было установлено, что многие свойства уравнений связаны с чисто
алгебраическими соотношениями между операторами (см.) дифференцирования, интег-

ФУНКЦИЯ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО 485
рнрования, умножения на функцию и т. д. Рассмотрение алгебраических свойств
этих операторов лежит в основе операционного исчисления (см.) — одного из
отделов Ф. а. Одной из важнейших идей Ф. а. является идея спектрального
разложения линейного оператора.
Методы Ф. а. широко применяются как в математике, так и в современной
физике и химии (например, квантовой физике и квантовой химии). Более того,
сам Ф. а. и пути дальнейшего его развития в значительной мере зависят от
идей и задач современной квантовой физики.
Лит.: Л. А. Люстерники С. Л. Соболев, Элементы функционального анализа,
Гостехиздат, М—Л., 1950; Ф. Рисе и Б. Сек ефальвн-Надь, Лекции по
функциональному анализу, перев. с франц., ИЛ, М., 1954.
ФУНКЦИОНАЛЬНЫЙ ОПРЕДЕЛИТЕЛЬ —определитель (см.), элементами
которого являются функции. Большую роль в математике играют следующие
частные случаи Ф. о.: вронскиан (см.), гессиан (см.), якобиан (см.),
определитель Грама (см.) и т. д.
ФУНКЦИЯ — одно из основных понятий математики. Элемент множества
Еу произвольной природы называется функцией элемента х, определенной на
множестве Ех произвольной природы, если каждому элементу χ из множества
Ех соответствует единственный элемент у ζ Εν. Элемент χ называется
независимой переменной или аргументом. Множество 'Ех называется областью
определения, или областью существования Ф. Множество Ау с Еу, состоящее из всех
у, которые соответствуют хотя бы одному χ ζ Ех, называется множеством
значений Ф. или областью изменения Ф. Таким образом, у есть Ф. от х, когда
установлено соответствие: каждому χ из множества Ех соответствует
определенное у из множества Еу. Обозначения дтя Ф.: у= f(x)t y=<p(x) и т. д.
В зависимости от природы множеств Ех и Еу получаются различные типы Ф.
Если Ех и Еу — некоторые множества действительных чисел, т. е. χ и у
принимают действительные числовые значения, то имеем Ф. действительного
(вещественного) переменного (см.), или просто Ф. Если Ех — некоторое множество
действительных чисел, а Еу — некоторое множество комплексных чисел, то
имеем комплексно-значную Ф. действительного переменного. Если Ех и Еу —
некоторые множества комплексных чисел, то имеем Ф. комплексного переменного
(см.). Если Ех — некоторое множество комплексов (совокупностей из η
элементов) (л;,, jc2, . .., хп)* где хХ1 х2, . . ., хп принимают числовые значения, а
Еу — некоторое множество действительных чисел, то имеем Ф. многих
переменных (см.): y=f(x) = f(xl9 χ2, . . ., хп).
Чаще всего рассматривают Ф., множество значений Ау которых есть
числовое множество. Иногда тот факт, что Ау не есть числовое множество,
указывается в названии Ф., например: вектор-функция, Ф., принимающая матричные
значения. Когда Ау является множеством более абстрактным, чем числовое,
более употребительны термины «оператор», «отображение».
Ф. может задаваться одним или несколькими аналитическими выражениями,
словесным определением, таблицей и т. д., — лишь бы был задан закон
соответствия:
x-+y=f(x).
Определение Ф. как переменной величины несовершенно, так как при этом
используется нестрогое понятие переменной величины.
Примеры Ф. см. в отдельных терминах, посвященных Ф. (Аналитическая
функция, График функции, Непрерывные функции» Тригонометрические
функции и др.).
ФУНКЦИЯ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО — функция, у которой
независимая переменная χ и сама функция у принимают значения из области
действительных чисел. Ф. д. п. часто называют просто функцией. Ф. д. п.
наглядно изображают при помощи графика (см. График функции). Если Ф. д. п.

486
ФУНКЦИЯ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
задана некоторым аналитическим выражением, ю ее областью определения Ех
обычно считают множество ее допустимых значений — всех тех действительных
значений ху для которых аналитическое выражение дает для у действительное
значение.
Примеры: 1. у=1—х2\ область определения Ех этой функции есть все
множество действительных чисел — оо < χ < -f-°°, множество ее значений Еу =
= {— оо <у^1), ее график — парабола (рис. 304). 2. Пусть у есть целая часть
2
1
-2
-/!
-/
т -2
Рис. 304
Рис. 305
3 λ
χ, т. е. у=[л*] есть наибольшее целое число, не превосходящее числа х. В этом
случае Ех—{—ос < χ < 4-со}, Еу есть множество всех целых чисел, а график
показан на рис. 305. Иногда эту функцию обозначают у=Е(х), где Ε·—
начальная буква французского слова Entier — целый.
3. Функция Дирихле y=D(x) определяется так: если χ — рациональное
число, то у=1, если χ—иррациональное число, то у=0. В этом случае об-
Ут
ΖΧ
-2л ~я О
ГЛ""ТЛ" .
4,
ласть определения Ех, как и в первых
двух примерах, есть вся числовая ось,
множество значении Еу состоит из двух
чисел 0 и 1.
4. Функция у=у sin χ. В этом
примере Ех состоит из отрезков: 0<ζχ^π,
2π < χ < 3π, — 2 π < χ < — π, . . .;
^У={0<У<1} (рис. 306).
5. Факториал у=х\ Здесь Ех есть множество натуральных чисел: 1, 2, 3,
. ., и, . . ., Еу — множество чисел: 1, 2, 6, 24, . . ./г!, . . .
я 2π зя λ
Рис. 306
Лит.: Г. Μ. Φ и χ те н г о л ь ц, Курс дифференциального и интегрального исчисления,
Физматгиз. М., 1963; Λ. Я. X и и ч н н, Кратким курс математического анализа, Гостехиз-
дат, М., 1956.
ФУНКЦИЯ КОМПЛЕКСНОГО ПЕРЕМЕННОГО — функция (см.), у которой
независимая переменная ζ и сама функция w=f(z) принимают значения из
области комплексных чисел.
Задание Ф. к. п. w=f(z) равносильно заданию двух функций: и=и(х, у)
и ν=υ(χ, у) от двух действительных переменных, где w=u-\-iv% z=x+iy.
Наиболее важный класс Ф. к. п. составляют аналитические функции (см.), которые
изучаются в теории функций комплексного переменного.

ФУРЬЕ ИНТЕГРАЛ
487
ФУНКЦИЯ МНОГИХ ПЕРЕМЕННЫХ — функция (см.), У которой аргумент
χ является комплексом (xlt х2, . . ., хп) из η переменных xlt x2t . . ., хп,
называемых независимыми переменными. Говоря о Ф. м. п. u = f(x)=f (xlt х2, . . .,
хп)у обычно считают, что независимые переменные xlt x2t . . ., хп и функция и
принимают значения из области действительных чисел (в других случаях термин
уточняют, например: функция многих комплексных переменных).
Функция z=f(x, у) двух переменных χ и у может быть наглядно
представлена в пространстве геометрическим местом точек, прямоугольные координаты
которых связаны соотношением z=f(x, у), ф. м. п. называют также функцией
точки .*=(*!, λ* 2, . . ., Хп) «-мерного пространства. Областью определения Ф.
м. п., заданной аналитическим
выражением, считают обычно множество всех
тех точек (xlt х2, . . ., хп) я-мерного
пространства, для которых функция \
принимает действительные значения. \у
Рис. 307
Рис. 308
Примеры: 1) областью определения функции z=yl —4*2— у2 служит
эллипс 4*2-Ьу2=1 и его внутренность, функция изображается верхней половиной
поверхности эллипсоида 4*2-|-y2-bz2 = l (рис. 307); 2) областью определения
функции трех переменных u = \x\(x2-\-y1-\-z1— 1) служит часть пространства,
лежащая вне сферы радиуса единицы с центром в начале координат (рис. 308).
ФУНКЦИЯ ОТ ФУНКЦИИ (или сложная функция) — функция y=F(x),
состоящая из функций y=f(u) и ы=Ф(л;), причем множество значений (см.)
функции и=ц>(х) должно являться частью области определения (см.) функции
у={ (и). Ф. о. ф. y=F(x) записывается в виде: y=f[q>(x)] и определяется
так: заданному χ ставится в соответствие значение функции y=f(u),
соответствующее тому значению аргумента х, которое является значением функции ί/=φ(χ)
для заданного х. Область определения f(u) есть часть области определения
функции φ (а:). Характеристика функции — как сложной — связана лишь со способом
задания функции, а не с природой функциональной зависимости. Например, пусть
u=cosx, 0<χ<π, у=У\—иг,
будет являться простои функцией у-
ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
величины.
ФУРЬЕ ИНТЕГРАЛ абсолютно интегрируемой функции / (х) —
несобственный интеграл вида:
оо оо оо оо
/(*)=— \dz f (и) cos (и —x)zdu = — \ dz j f (и) cos ζ (и — χ) du (*)
0 — оо — со — со
— 1 < и < 1. Тогда Ф. о
=sin jc, 0 < χ < π.
■ см. в термине Распределение
ф. у=у 1 — cos2jc
случайной

488
ФУРЬЕ КОЭФФИЦИЕНТЫ
или
оо оо
•ИМ
. . . iz (и — χ) ,
f(u)e du. (**)
Интегралы с бесконечными пределами понимаются в смысле главного
значения. Пусть f (х) в точке х0 в одном случае (*) непрерывна, а в другом случае
(**) имеет в этой точке разрыв первого рода. Положим в первом случае (*)
*о=/(*о)>
а в другом
/(*.»+0)+/(*о-0)
«о- δ ·
Тогда Ф. и. функции / (х) в точке х0 сходится и имеет значение s0, если
ПФ(01
при некотором h > 0 сходится интеграл 1—-—dt, где φ (0=/ (*ο + 04-/(*ο—
о
— t)—2s0 (признак Дини). Ф. и. функции f (х) в точке х0 сходится и имеет
значение s0, если в некотором промежутке [х0 — /г, x0-\-h] с центром в этой
точке функция f(x) имеет ограниченное значение (признак Дирихле-Жордана).
Ф. и. широко используются при решении различных задач математической
физики и в функциональном анализе.
Ф. и. является аналогом ряда Фурье (см.), поскольку Ф. и. представляет
функцию в виде непрерывной суммы гармоник (см.) с бесконечно малыми
амплитудами (ср. Фурье преобразование).
Лит.: И. С н е д д о н, Преобразование Фурье, ИЛ, М., 1955; Г. М. Фихтенгольц,
Курс дифференциального и интегрального исчисления, т. III, Физматгиз, М.,1963.
ФУРЬЕ КОЭФФИЦИЕНТЫ. Функции / (х) относительно ориентированной
системы (см.) функций <рь φ2 фл заданных на отрезке [а, Ь] числа
Ь
Ck={f(x) φ^(χ) dx. Важен частный случай Φ. к. периодической (периода 2Г)
а
1 тхпх 1 . πηχ 1
функции f (х) по орто нормирован ной системе: "ψ cos ~^Г~» "7Г sin ——, —;
т т
1 Г лпх 1 Г г . лпх
αη = γ f(x)cos — dx, Ъп = — \ f (x) sin — dx,
-г -г
а^1
f(x)dx\ /z=l, 2, . . .
—~г
См. также Парсеваля равенство, Фурье метод, Фурье ряды.
ФУРЬЕ МЕТОД — метод решения различных задач, использующий
разложение функций в ряды и интегралы Фурье. Такое разложение приводит к очень
удобному аналитическому представлению функции, которое оказывается зачастую
совершеннц незаменимым при решении различных задач математики, астрономии,
математической физики, теоретической физики, теоретической механики и т. д.

ФУРЬЕ ПРЕОБРАЗОВАНИЕ
489
Так, например, рассматривая распространение тепла в точном однородном
стержне длины /, решают уравнение теплопроводности (см.):
ди д2и
с граничными и (О, t)=u(l, t)=0 и начальными условиями и(х, ())»/(*), пред-
оо
An(t)sin— χ, где An(t) определяются из на-
/г = 1
чальных и граничных условий.
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
т. III, Физматгпз, М., 1963; И. Снеддон, Преобразования Фурье, ИЛ, М.. 1955;
А. Н. Тихонов и А. А. Самарский, Уравнения математической физики, Гостехиз-
дат, М., 1956.
ФУРЬЕ ПРЕОБРАЗОВАНИЕ функции / (х) — функция F (ζ), связанная с / (*·)
формулой:
+со
F(z) ^ Г f(u)e~l™du. П
— оо
При этом предполагается, что формула Фурье:
+оо -Ьоо
/(л:) = — I dz \ f(u)cosz(u — x)t
-СО — СО
имеет место для всех значений χ в промежутке (— оо, -f-oo), за исключением,
быть"может, лишь конечного числа точек.
Обратное Ф. п. выражается формулой:
-f-со
/(*) = —— Г F(z) eixzdz.
/2л J
Функции
^(Ζ) = Ί/ "—-\ f (и) cos zu du, /\9(ζ)=Ί/ —■ 1 f(u) sin zudu
CO CO
:(z) = l/ — \f(u)coszu du, Fs(z)=y ^-j/(a)sin;
^ о ' о
называются соответственно синус- и косинус-преобразованием Фурье.
Если f(x) — четная, то F (z)=Fc(z), если же f (х)—нечетная, то F(z) —
—iFs(z). В общем случае f(x) можно представить в виде суммы четной g и
нечетной h функций:
2=γ [/(*)+/(— х)Ъ h= , f=g+h.
Тогда F (z)=^Gc(z)i-iHs (ζ), поэтому можно ограничиться косинус- и синус-пре-
ΓΎ а
образованиями Фурье. Например, для /(*) = £—ах, ^(г)=1/ -—-
I/ «Т C*~~j~Z

490
ФУРЬЕ РЯД
Ι/ π a2-f-z2 10, χ > a
ρ π ζ y π
1 — cos αζ
Если /(jc) абсолютно интегрируема в промежутке (—со, 4-оо), то функция
+оо
1 (*
F(z)— zzz \ f (и) e—l2Udu непрерывна во всем этом промежутке и стремится
V2n J
— ОО
к нулю при z-*±oo. Если же абсолютно интегрируема в промежутке (—оо,
-j-oo) f (χ) хп (η — натуральное число), то F (ζ) имеет η производных: F' (ζ),
F"(z), . . ., Fn (z), которые при z-»-±co все стремятся к нулю.
Понятие Ф. п. можно обобщить на случай функции многих переменных.
В частности, если f(xit х2) абсолютно интегрируема по обеим переменным хх, х2
в промежутке (—оо, +<хэ), то ее Ф. п. имеет вид:
-j-OO +0°
п/ ч 1 Г j Γ г/ ч £(ζιαι+ζ*"ι).
F{*i, z2)=— dux f(ult u2)e du2;
— OO — OO
+ CO -j-OO
— OO —OO
Ф. п. применяется в функциональном анализе, гармоническом анализе,
операционном исчислении, в теории линейных систем и др.
Лит.: И. Снеддон, Преобразования Фурье, ИЛ, М., 1955; Г. М. Фихтен-
г о л ь ц, Курс дифференциального и интегрального исчисления, Физматгиз, М., 1963.
ФУРЬЕ РЯД функции f(x) относительно ортонормированной системы функ-
оо
ций (см.) φχ (χ), φ2 (χ), . . ., φΑ (χ), ... — ряд 2 скЧк (*). где Ch — коэф-
k == l
фициенты Фурье (см. Фурье коэффициенты). Часто рассматривается важный
частный случай Ф. р. периодической функции f (х) (периода 2Г) относительно орто-
1 1 π пх 1 π ηχ
нормированной системы —, —cos , —sin—-, /2=1, 2, 3 . . .:
оо
Х"1 zt пх . ~ пх ^
а0-Ь у ancos—;-+bnsin-—- (см. Фурье коэффициенты),
/:= 1
Если f(k) обладает непрерывной производной, то этот Ф. р. сходится к
функции /(*).
Ф. р. является мощным средством уравнений математической физики и
гармонического анализа. Введен Ж. Фурье в связи с задачами о распространении
тепла.
Лит.: Г. М. Фихте и голь ц( Курс дифференциального и интегрального
исчисления, т. III, М., 1955; А. Н. Тихонов и А. А. Самарский, Уравнения
математической физики, М., 1956.

χ
ХАРАКТЕРИСТИКА: 1°. Χ. логарифма — целая часть логарифма числа.
2°. X. в теории дифференциальных уравнений (см.) в частных производных.
Для дифференциальных уравнений 1-го порядка:
дг дг
дх ду
где /?, д, г — данные функции х< у, ζ. Χ. называют кривые, определяемые
системой дифференциальных уравнений:
ах dy dz
р~д~г "
Интегрируя, получаем семейство X.:
φ (л:, у, z) = Clt ψ (χ, у, г) = С2, (С^ C2 = const).
Это — совокупность кривых, касающихся в каждой своей точке вектора {р,
Я» '}·
Интегральная поверхность уравнения (*) является геометрическим местом X.,
пересекающих некоторую кривую. Уравнение поверхности — F [φ (χ, у, ζ), ψ (χ,
у, ζ)] = 0, где F — функция двух переменных.
Условие — кривая не является X. — необходимое и достаточное (см.) для
того, чтобы задача Коши (см.) с условиями, заданными на этой кривой, имела
единственное решение.
Понятие X. обобщается для случая трех и более независимых переменных.
Для дифференциального уравнения 2-го порядка:
д2у д2х д2у / ди ди\
«(*. Л-£Г+*<*. Л^+с(х. Л"^-/(*. У. «. Ъ a-j Г)
X. определяются как линии, вдоль которых удовлетворяется обыкновенное
дифференциальное уравнение:
ady2—bdxdy+cdx2 = 0. (***)
Понятие X. для этого случая было введено французским ученым Г. Монжем.
В случае, когда уравнение (***) гиперболического типа, получаются два
семейства X. с уравнениями:
К*. У) = Сг и μ (л:, у) = С2\
Сг и С2 — произвольные константы. Если взять ξ и η за новые аргументы,
то уравнение (***) приводится к виду:
д2и ί ди ди \
д£дц \ д$ дц!
Для уравнения параболического типа эти семейства совпадают, и если
выбрать правильно η, то уравнение (**) приводится к виду:
dhi [ ди ди\
Если уравнение (**) эллиптического типа, то вещественных X. нет.

492
ХАРАКТЕРИСТИКА ПОЛЯ
Записывая
ние (**):
решение уравнения (***) в виде ξ-Ηη=^, преобразуем
уравнены д2и
-+-
/ ди ди\
ag2 3η2
Зная значения решения вдоль X. и значения
ди
ди
дх
вдоль всей линии (см. Краевые
линий. Однако если значения
г~ в некоторой точке X.
можно определить значение этих производных
задачи). Такой зависимости нет для других
ди ди
и, —, —-, заданные на линии, не являющейся X., определяют значения реше-
дх ду
ния вблизи этой линии, то для X. это не так. Если два решении совпадают
по одну сторону линии и различны по другую, то эта линия является X.
Определения X. имеются также для уравнения и систем уравнений с
частными производными любого порядка.
3°. X. в дифференциальной геометрии — кривая, вдоль которой огибающая
касается данной поверхности семейства. X. плоскостей можно получить как
предельное положение прямой пересечения плоскости семейства с бесконечно
близкой плоскостью семейства.
4°. X. Эйлера-Пуанкаре — см. Эйлера теорема.
5°. X. в теории вероятностей. Числовые X. — числовые параметры,
до некоторой степени характеризующие существенные черты распределения
случайной величины. Назначение таких X. — в сжатой форме выразить наиболее
существенные особенности распределения. Например, какое-то среднее значение
около которого группируются возможные значения случайной величины; какое-
либо число, характеризующее степень разбросанности этих значений относительно
среднего, и т. д.
Литературу см. в терминах Уравнения математической физики,
Дифференциальная геометрия, Вероятностей теория.
ХАРАКТЕРИСТИКА ПОЛЯ. Если в поле Ρ равенство пе = 0 (где е—
единица поля Ρ и 0 — нуль поля Р, а п — целое неотрицательное число,
указывающее, чтое взято слагаемым η раз) возможно лишь при л=0, то поле Ρ
называется полем характеристики нуль. Например, все числовые поля имеют
характеристику 0. Иногда поля характеристики 0 называют полями без характеристики.
Если же равенство пе=0 выполняется и при некоторых положительных
л, то наименьшее из этих чисел называется X. п. X. п. могут быть лишь
простые числа Ρ и число 0. Поля не нулевой характеристики называются полями
конечной характеристики.
ХАРАКТЕРИСТИЧЕСКАЯ МАТРИЦА квадратной матрицы Л—матрица Л-Х£,
где Ε — единичная матрица, а λ — некоторое неизвестное. Таким образом, если
αηαί2 . . . αιη
α21α22 · · · а2п
аП1ап2
ее X. м. равна: Α — λ£ =
ап — λ α12
«in
0П2
.-λ .
ХАРАКТЕРИСТИЧЕСКАЯ ТОЧКА кривой семейства — предельное положение
точки пересечения данной кривой семейства с бесконечно близкой кривой семейства.
ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ: 1°. X. ф. множества точек —
функция* равная единице в точках множества и нулю в точках, не принадлежащих
рассматриваемому множеству. Например, функция Дирихле (см.) есть
X. ф. множества рациональных чисел.

ХОРДА
493
2°. Χ. φ. случайной величины ξ определяется равенством:
f(t) = Me£ix9
где Μ —знак математического ожидания (см.). Если q>(jt)—плотность
распределения (см.) случайной величины ξ, то
+ оо
/(*)= J eitx q>(x)dx.
— 00
Χ. φ. случайной величины применяются при доказательстве предельных теорем
(см.). Их применение основано на том факте, что X. ф. суммы независимых
случайных величин равна произведению X. ф. слагаемых.
Другие свойства X. ф.: 1) X. ф. однозначно определяют распределение
(см.) случайной величины; 2) /'(0/ = о=/'М£. Г (0/= о= "~" D S lD—знак
дисперсии (см.) ].
Пример X. ф. случайной величины, имеющей нормальное распределение
с параметрами 0 и 1, если плотность распределения (см.) равна
_£?
1 2
дастся формулой: j^ — e 2
Лит.: Б. В. Гнеденко, Курс теории вероятностей, Физматгнз, М., 1964.
ХАРАКТЕРИСТИЧЕСКИЕ ЧИСЛА — то же, что и собственные
значения (см.).
ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН квадратной матрицы А —
определитель характеристической матрицы (см.) для матрицы Л, т. е. \Л—λ£|.
Он, очевидно, является многочленом /2-й степени относительно λ.
ХАРАКТЕРИСТИЧЕСКИЕ КОРНИ квадратной матрицы А — корни ее
характеристического многочлена (см.) или ее характеристического уравнения (см.).
ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИЕ квадратной матрицы А — ее
характеристический многочлен (см.), приравненный нулю, т. е. \ Α — λ Е\=0. Если
в X. у. матрицы А подставить вместо λ матрицу А и выполнить (матричные)
операции, то получим нулевую матрицу (см.), т. е. матрица А является
матричным корнем своего X. у. Всякий многочлен £(λ), для которого матрица А
является матричным корнем, делится на характеристический многочлен
матрицы А. X. у. иначе называется вековым уравнением.
ХАРАКТЕРЫ ПРЕДСТАВЛЕНИЯ A(g) (см.) группы G являются следами
матриц A(g), т. е. функциями элементов группы, определенных равенством
η
λ(£)= Σ A(g)u· У всех эквивалентных представлений X. п. одинаковые.
/= ι
Необходимым и достаточным условием эквивалентности двух представлений
является совпадение всех их X. п. (см. Группа, Теория групп).
ХАУСДОРФОВО ПРОСТРАНСТВО — топологическое пространство (см.),
удовлетворяющее второй аксиоме отделимости . Хаусдорфа: для любых различных
точек χ и у пространства существуют окрестности U и V точек χ и у
соответственно такие, что uf\u=0. Другое название X. и. — Г2-пространство.
ХОРДА — отрезок прямой, соединяющей две какие-либо ι очки кривой (или
поверхности) и не пересекающей кривую (поверхность).
Греч, χορδή — струна.
33 Толковый словарь математических терминов

ц
ЦЕЛАЯ РАЦИОНАЛЬНАЯ ФУНКЦИЯ — функция вида:
у=а0хп+а1хп-1+ ··· +ая-1дг+ая,
где χ — независимая переменная, <з0, я,, α2 ап — постоянные. В частности,
квадратный трехчлен (см.) у=ахг-\-Ьх-\-с является Ц. р. ф. Если Ц. р. ф. имеет
степень я, то она содержит не более п— 1 экстремумов (см.) и не более (/2 — 2)
точек перегиба (см.).
ЦЕЛАЯ ФУНКЦИЯ — функция /(г), являющаяся аналитической (см.) во всей
плоскости комплексного переменного. Такими, например, являются функции:
f(z)=a0+a1z+ ... an+zn,
/(2)=sinef /(г)~в*.
Для того чтобы / (ζ) была Ц. ф., необходимо и достаточно, чтобы хотя
бы для одной точки 20 имело место
limj/l f(n)(Zo)
n-co у \ п1
-0.
В этом случае ряд Тейлора (см.) для /(г):
П')ЧМ+-^-(г-
•20)+-^—(г-г0)г-
будет сходиться во всей плоскости комплексного переменного.
Ц. ф. /(г) называется трансцендентной (см.), если точка г=оо является
существенно особой точкой. Например,
/(2)^=cos2, f(z) = ez.
Лит.: А. И. Map куше внч, Теория аналитических функций, Гостехнздат. Μ ,
1947.
ЦЕЛАЯ ЧАСТЬ действительного числа χ — наибольшее целое число, не
превосходящее х. Ц. ч. числа χ обозначается символом \х] или (реже)
символом Е(х). Читается так: «целая часть х» [или: «целая часть от я», или:
«антье х» (или: «антье от jc»)]. Последнее название происходит от французского
слова entiere—целый. Ц. ч. числа χ может быть определена как целое число
[λ'], являющееся решением двойного неравенства системы двух неравенств;
[*]<*<[*]+! .
Примеры: [}/з0] = 5,
3π
= 0, [-4,71=-5, fcos —
L 4

ЦЕНТР СИММЕТРИИ
495
Функция у=[х\ используется в
различных вопросах теории чисел,
математического анализа, теории рекурсивных
функций и в других вопросах математики.
График функции у=[л'] изображен на
рис. 309.
Ц. ч. числа [х] связана с дробной
частью (см.) {х} числа χ соотношением:
2\
-л
О
J-
;
3 λ
ЦЕЛОЕ АЛГЕБРАИЧЕСКОЕ ЧИС- \
ЛО — корень многочлена с целочисленными * >\-1
коэффициентами и с коэффициентом при
старшем члене, равным единице. Напри- рис 309.
5 .
мер, у 9 —Ц. а. ч., так как оно является
корнем многочлена хъ — 9 с целыми коэффициентами. Множество всех Ц. а. ч.
составляет кольцо. Это кольцо является подкольцом в поле алгебраических чисел.
ЦЕЛОЕ КОМПЛЕКСНОЕ ЧИСЛО — комплексное число а+Ы с целыми а и Ъ.
ЦЕЛОСТНОСТИ ОБЛАСТЬ — термин алгебры. Ц. о. есть коммутативное кольцо
(см.) без делителей нуля, т. е. такое кольцо, в котором из равенства ab=0
следует, что один из сомножителей равен нулю. Всякое поле (см.), тело (см.) есть
Ц. о. Кольцо многочленов — тоже Ц. о.
С другой стороны, кольцо матриц 2-го порядка относительно естественных
операций сложения и умножения не есть Ц. о. В самом деле, пусть
О 1
О О
Ь =
1 О
О О
а-Ь =
О О
О О
тогда а-6=0, хотя а Ф О, b Φ 0.
ЦЕЛОЧИСЛЕННАЯ ФУНКЦИЯ—функция, область определения которой
есть совокупность натуральных чисел. О значениях Ц. ф. говорят, что они
образуют последовательность. Например, f(x)=x\ — Ц. ф. Ее значения /(1)=1,
/(2) = 2, /(3)=6, . . . образуют последовательность.
/(*) = —_-Ц. ф., jc=1, 2, 3,... Значения /(!)=—> /(2)=т
2х
/(3) =
1
образуют последовательность (геометрическая прогрессия).
ЦЕЛЫЕ ЧИСЛА — числа вида ±пу где η ~~ натуральное число (см.) или
нуль. Понятие натурального числа введено в результате счета предметов.
Положительное Ц. ч. характеризует как количество предметов, так и
порядок предметов, расположенных в ряд.
Введение отрицательных Ц. ч. было вызвано развитием алгебры. Ц. ч.
образуют кольцо (см.). См. Пеапо аксиомы.
ЦЕНТР СИММЕТРИИ геометрической фигуры — такая точка О, что для
всякой точки Μ этой фигуры найдется такая ее точка М', что точка О будет
серединой отрезка ММ'. Другими словами, для любой точки Μ фигуры,
имеющей точку О своим Ц. с, найдется точка ее М', лежащая по другую сторону
от точки О прямой ОМ на расстоянии ОМ' = ОМ. Например, середина отрезка
есть его Ц. с.
Кривые и поверхности и вообще фигуры, имеющие Ц. с, называют
центральными (см. Эллипс, Гипербола, Эллипсоид, Однополостный гиперболоид
и Двуполостный гиперболоид, Параллелограмм и др.).
33*

496
ЦЕНТРАЛЬНО-ПОДОБНОЕ ПРЕОБРАЗОВАНИЕ
Два или любое конечное число η (η > 2) Ц. с. фигура иметь не может,
однако она может иметь бесконечное число Ц. с. — целую прямую или целую
плоскость Ц. с. Например, круговой цилиндр имеет целую линию Ц. с. — ось
цилиндра; две параллельные плоскости имеют целую плоскость Ц. с,
параллельную данным плоскостям и проходящую через точку, равноудаленную от
данных плоскостей.
См. также Симметрия.
ЦЕНТРАЛЬНО-ПОДОБНОЕ ПРЕОБРАЗОВАНИЕ - Синоним гомотетии (см.).
ЦЕНТРАЛЬНЫЙ УГОЛ — угол, вершина которого совпадает с центром
данной окружности (рис. 310). Ц. у. COD измеряется дугой окружности АВ,
где А и В — точки пересечения сторон Ц. у. с
окружностью, т. е. он содержит столько угловых градусов,
сколько дуга АВ — дуговых. Дуга АВ называется
дугой, на которую опирается Ц. у. См. также Угол.
Ц. у., длина дуги которого (на которую он
опирается) равна радиусу О А, называется радианом.
ЦЕНТР ГОМОЛОГИИ в проективной геометрии —
см. Гомология.
ЦЕНТР ГОМОТЕТИИ в элементарной геометрии —
см. Гомотетия.
ЦЕНТР ГРУППЫ — множество элементов Ζ группы
G таких, что zg=g-z для любых ζ ζ Ζ и g ζ ό.
Ц. г. является абелевой группой (см.), а также нормальным делителем
(см.) группы О. Например, в группе всех невырожденных матриц скалярные
матрицы (т. е. матрицы вида λ £, λ — произвольное число, Ε — единичная
матрица) образуют Ц. г.
ЦЕНТР КРИВИЗНЫ — центр круга кривизны (см.) в данной точке кривой.
ЦЕНТРО-АФФИННОЕ ПРЕОБРАЗОВАНИЕ — аффинное преобразование (см.),
имеющее по крайней мере одну двойную точку (см. Двойной элемент). Частным
случаем Ц.-а. п. является гомотетия (см.).
ЦЕНТРОИД треугольника двумерного — точка пересечения его медиан. Ц. т.
является также центром тяжести этого треугольника. См. Треугольник.
ЦЕНТР (ОСОБАЯ ТОЧКА) в теории дифференциальных уравнений — такая
особая точка (см.), в окрестности которой все интегральные кривые являются
замкнутыми и содержат эту точку внутри себя.
ЦЕНТР ТЯЖЕСТИ треугольника (двумерного, треугольной пластинки) —
точка пересечения его медиан. Ц. т. треугольника называется иначе центроидом
треугольника. Ц. т. двумерного треугольника не совпадает с Ц. т. одномерного
(каркасного) треугольника. См. Треугольник.
ЦЕПНАЯ ДРОБЬ — синоним непрерывной дроби (см.).
ЦЕПНАЯ ЛИНИЯ — плоская кривая, определяемая уравнением:
χ а [ Τ "Τ)
а £
Форму этой кривой принимает цепь или какая-нибудь другая однородная гибкая
и нерастяжимая тяжелая нить, у которой концы закреплены в двух точках и
расстояние между этими точками меньше длины нити. При небольшом провисании
Ц. л. для ее приближенного расчета можно пользоваться уравнением параболы:
Рис. 310

ЦИКЛОИДА
497
Радиус кривизны Ц. л.:
Длина дуги Ц. л., отсчитываемая от точки х=0:
у1 χ
а а
/= ash — = —· \е а — е
а 2
Если дугу Ц. л. вращать вокруг оси Ох, то получаемая поверхность
называется катеноидом.
ЦЕПНОЕ ПРАВИЛО — устаревшее правило арифметики, применявшееся при
переводе мер одной системы измерений в меры другой системы с помощью
третьей системы измерений.
ЦЕРМЕЛО АКСИОМА, или принцип произвольного выбора, утверждает,
что для любой системы непустых и непересекающихся множеств существует
функция, сопоставляющая каждому множеству один его элемент. Иначе говоря,
Ц. а. утверждает, что из каждого множества произвольной системы непустых
и не имеющих общих элементов множеств можно сразу выбрать по одному
элементу. Ц. а. была высказана Цермело (1904). На нее опирался Цермело в
доказательстве теоремы о возможности всякое множество сделать вполне
упорядоченным множеством (см.). Ц. а. вызвала много споров среди математиков, и ряд
математиков не признал ее, а следовательно, не считает установленной и теорему
о возможности вполне упорядочивать произвольные множества. Но оказалось,
что на Ц. а. опирается доказательство многих теорем классического
математического анализа.
ЦИКЛИЧЕСКАЯ ГРУППА — группа (см.), содержащая элемент а такой,
что всякий ее элемент g=aK при некотором целом показателе k, например:
группа комплексных корней я-й степени из единицы, аддитивная группа (см.)
целых чисел и др.
ЦИКЛИЧЕСКАЯ ПОДСТАНОВКА (или цикл) — подстановка такая, что любой
действительно перемещаемый ею символ может быть переведен в любой другой
из этих символов некоторой степенью этой подстановки, т. е. некоторым ее
повторным применением.
Пример:
/1 2 3 4 5^
S=\3 2 5 4 \j
Действительно перемещаемые символы здесь 1, 3 и 5. Подстановками
S, S2, S3 любой из этих трех символов может быгь переведен в любой другой
из них. Для Ц. п. используется запись,
при которой выписывают в круглых
скобках действительно перемещаемые
символы в том порядке, в каком они
переводятся друг в друга Ц. п.
Вышеприведенная Ц. п. записывается:
£=(1, 3, 5).
ЦИКЛОИДА — плоская кривая,
которую описывает фиксированная точка
Му неподвижно связанная с
окружностью, катящейся без скольжения по
неподвижной прямой. Если точка Μ
расположена на окружности, получим
т—обычную Ц., если внутри (на рис.311
Рис. 311

498
ЦИЛИНДР
точка Μ') — укороченную т', если вне окружности (на рис. 311 точка М") —
удлиненную Ц.
Ц. находит себе применение в технике (в зубчатом зацеплении, при котором
профили зубьев имеют очертания циклоидальных кривых) и теории механизмов.
Параметрические уравнения Ц. такие:
x=r\t
7 Η'
■)·
y=r 1 — — cost
где г — радиус подвижного круга, а — расстояние точки Μ до центра круга,
/ — параметр, угол, на который повернулся круг (или его радиус) при своем
качении по прямой.
Греч, κοκλοείδος — кругообразный, от κοκλος — круг, είδος —вид.
Лит.: Г. Н. Берма н. Циклоида, Гостехиздат, М., 1954.
ЦИЛИНДР: 1°. Ц. в аналитической геометрии — то же самое, что
и цилиндрическая поверхность (см.).
2°. Ц. в элементарной геометрии — тело (фигура), образованное
пересечением цилиндрической поверхности, имеющей замкнутую, несамопересекающуюся
плоскую направляющую ω, двумя параллельными плоскостями (рис. 312) α и β.
Рис. 312
Рис. 313
Плоские фигуры ω и ω' называются основаниями Ц: ω — нижним, ω' —верхним.
Если при этом сечение Ц. есть окружность, то Ц. называется круговым, если
же образующая / перпендикулярна плоскости сечения ω, то Ц. называется
прямым круговым. Обычно только прямой круговой Ц. и называют Ц.
Плоское сечение прямого кругового Ц. наклонной плоскостью есть эллипс
(ср. Конус).
ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ — поверхность, образованная
движением прямой /, перемещающейся параллельно самой себе и пересекающей
некоторую заданную плоскую кривую ω (направляющую Ц. п.). Прямая / при этом
называется образующей Ц. п. Если образующая Ц. п. есть эллипс, парабола
или гипербола (см.), то Ц. п. соответственно называется эллиптической,
параболической или гиперболической. В аналитической геометрии Ц. п. называется
также цилиндром.

ЦИЛИНДРОИД
499
ЦИЛИНДРИЧЕСКИЕ КООРДИНАТЫ г, θ, ζ точки Ρ — такие координаты,
для которых координатная поверхность (см. Координаты) г=const является
цилиндром с образующими, параллельными оси Oz (рис. 313). Ц. к. связаны
с декартовыми х, у, ζ соотношениями:
jt=rcos6, y=rsin0, z=z.
Якобиан преобразования (см.) от декартовых координат к цилиндрическим
имеет вид:
cos 0 sin θ Ο
—rsin 0 г cos θ 0
О 0 1
Р(х, у, ζ)
D(r, θ, ζ)
ЦИЛИНДРИЧЕСКИЕ ФУНКЦИИ — решения линейного дифференциального
уравнения 2-го порядка:
/Ч^у'+(1--^)у=о, (*)
где ν — произвольный параметр. Термин Ц. ф. обязан своим происхождением
тому обстоятельству, что уравнение (*) встречается при рассмотрении краевых
задач потенциала для цилиндрической области. Некоторые* классы Ц. ф.
известны под названием функций Бесселя, и иногда это наименование присваивается
всему классу Ц. ф.
Одно из решений уравнения (*) имеет вид:
л w=2(~1)'
k.
(τ/
αΞΓο Λ!Γ(Λ+ν+1)
Это решение называют Ц. ф. первого рода порядка v. Общее решение
уравнения (*) при нецелом запишется в виде:
y=cj„(jo+c8J_,(*).
где Сь С2 — постоянные. В случае целого ν yv (χ) и J_Ί(χ)
линейно-зависимы (см.), и в качестве второго частного решения берется Ц. ф. второго рода
(функция Неймана):
ΥΊ {х)= lim : ·
μ.-^. ν sin μ Jt
В практических задачах часто употребляются еще Ц. ф. третьего рода (функции
Ганкеля):
Н?> (χ) Λ (x)+iY4 (χ), Я<2> (·ν)=Λ (*) -Ι Υ., (χ).
Детально изучены также Ц. ф. для мнимых и комплексных значений аргумента.
Существует большое количество таблиц Ц. ф.
ЦИЛИНДРОИД — тело, ограниченное цилиндрической поверхностью
перпендикулярной к ней плоскостью (называемой основанием Ц.) и поверхностью,
которую каждый перпендикуляр к основанию Ц. пересекает в одной точке

500
циркуль
(рис. 314). В цилиндрической системе координат с осью Οζ, параллельной
образующей цилиндрической поверхности Ц., его объем выражается интегралом
ff/(*» y)dxdy, где Ρ—плоское основание Ц.,а/(х, у) — уравнение поверх-
(Я)
ности, ограничивающей его сверху. Ц. называется также линейчатая поверхность
(см.) 3-го порядка: (x2+y2)z=kxy, применяемая при изучении винтовых
движений твердого тела. Ц. иначе называется цилиндрическим брусом.
Греч, ν.νλίνδρος — цилиндр, ε/δος — вид.
ЦИРКУЛЬ: 1°. Ц. круговой—инструмент, служащий для вычерчивания
окружностей и дуг, а также для линейных измерений. Ц. состоит из двух
ffM)
Рис. 314
Рис. 315
металлических ножек, соединенных шарниром. Одна ножка оканчивается острием,
другая — карандашом или пером. Ц. в первой русской книге по геометрии Ели-
зарьева (см. «Историко-математические исследования», вып. XII) называема
кружальником.
2°. Ц. эллиптический служит для вычерчивания эллипсов (рис. 315). Если
а и Ь— полуоси эллипса, то муфту Μ и шарнир В следует закрепить так,
чтобы ЛМ=а и βΛί=6.
Лат. circulus — круг, окружность.
ЦИРКУЛЯТУРА КВАДРАТА — задача о построении циркулем и линейкой
круга, равновеликого данному квадрату Ц. к. в плоскости Евклида, как и задача
о квадратуре круга (см.), неразрешима.
ЦИРКУЛЯЦИЯ векторного поля а (г) вдоль замкнутой кривой L — интеграл
<j> adr. В координатной форме Ц. записывается в виде:
\axdx-\-aydy+azdz, a=a^i -J- ayj+azk, dx=dx\+dy\-\-dz\i.
'l
Ц. поля вдоль L равна работе, совершаемой силами силового поля а (г) при.
перемещении тела единичной массы, заряда и т. д.
В теории поля (см.) широко применяется теорема Стокса, по которой
Ц. дифференцируемого поля равна потоку вихря (см.) через какую-либо
поверхность S, ограниченную кривой L:
(j) adr = f rot an ds.
В поле кулоновского или ньютоновского притяжения, как и во многих
других потенциальных полях (см.), Ц. поля по любому замкнутому контуру равна
нулю: § aiir=0.

ЦИФРОВЫЕ МАШИНЫ
501
ЦИССОИДА ДИОКЛЕСА — плоская кривая 3-го порядка, уравнение которой
в прямоугольной декартовой системе координат имеет вид;
v3
Полярное уравнение Ц. Д. такое:
?с
2α — χ
2q sin2 φ
cos φ
У'
0
ι
4 \ '
г
Τ ^
λ
Рис. 316
где 2а—-диаметр окружности. Ц. Д. можно рассматривать как геометрическое
место точек Μ пучка прямых с центром О, лежащим на окружности (рис. 316).
для которых справедливо равенство OM = KL, где К и L — точки пересечения
прямой ОМ пучка соответственно с окружностью
и касательной t к окружности в точке Г,
диаметрально противоположной точке О. Вместо
окружности (производящей) можно брать другие кривые
2-го порядка.
Ц. Д. названа по имени древнегреческого
математика Диоклеса (III в. до н. э.), использовавшего
ее для решения делосской задачи (см.), т. е. задачи
об удвоении куба. Древние рассматривали только
часть циссоиды, заключенной внутри окружности;
эта часть ее вместе с дугой окружности
напоминает лист плюща.
Греч, χισσοιδεζ от χισσος — плющ, είδος —
вид, форма.
ЦИФРЫ — знаки для обозначения чисел (см.
Число). У разных народов были различные Ц.,
которые с течением времени, с развитием материальной
и общественной жизни этих народов, изменились и
все время совершенствовались. Наиболее примитивная запись Ц. была словесная,
которая сохранилась у математиков Средней Азии и Ближнего Востока вплоть
до X в. и даже встречалась позже.
Наиболее древними являются вавилонские и древнеегипетские Ц.
См. также Славянские цифры, Римские цифры, Индийские цифры (см.
другое название — Арабские цифры, так как в Европу они были занесены арабами
в X—XIII в.).
Лит.: Энц. элем, матем., т. 1, Гостехиздат, М., 1951; И. Я. Депман, История
арифметики, Учпедгиз, М., 1959.
ЦИФРОВЫЕ МАШИНЫ — математические машины дискретного действия.
В Ц. м. числа представляются в виде последовательности цифр, переменные
величины — в виде последовательности их значений. Для изображения каждой
цифры применяется какой-либо прибор; каждому состоянию этого прибора
(элемента) поставлена в соответствие определенная цифра. Число изображается с
помощью набора таких элементов. Ц. м. обеспечивают высокую точность расчетов
и являются универсальными математическими машинами. Вычисления на
простейших Ц. м., арифмометре (см.) и различных ручных счетно-клавишных машинах
требовали очень много времени. В настоящее время благодаря появлению
быстродействующих электронных Ц. м. с программным управлением этот недостаток
устранен. См. Электронные быстродействующие машины.
Лит.: А. И. Китов, Η. Α. Κ ρ и н и ц к и й. Электронные цифровые машины и
программирование» М., 1959; А. И. Китов, Электронные цифровые машины, М., 1956.

ч
ЧАПЛЫГИНА МЕТОД — метод приближенного решения дифференциального
уравнения, предложенный (1919) советским математиком С. А. Чаплыгиным. Этот
метод позволяет решать дифференциальные уравнения с заранее заданной степенью
точности, для чего строятся последовательности функций {ип} и [vn], все более
точно аппроксимирующие искомое решение у(х) заданного уравнения, для которых
справедливо ип>ип+1>у>ип+1>ип.
Способ построения ип и vni основанный на теореме Чаплыгина о
дифференциальных неравенствах (см.), представляет собой обобщение на случай
дифференциальных уравнений известного метода Ньютона (см. Ньютона метод), причем
так же, как и в последнем, начиная с некоторого η погрешность имеет порядок
(см.) ρ2" , р<1.
Лит.: С. А. Чаплыгин, Новый метод приближенного интегрирования
дифференциальных уравнений, М.—Л., 1950.
ЧАПЛЫГИНА НЕРАВЕНСТВА — дифференциальные неравенства, играющие
важную роль в численном интегрировании дифференциальных уравнений. Если
у'=/(л:, у) и и(х), и(х) удовлетворяют неравенствам: и'(х) — f(x, u)>0,
v'(x) — f(x, v)<0, *o<*<*i* u(x0) = v(x0)=y0i то решение у(х) уравнения
y'=/(jt, у), проходящее через точку (х0у0)> заключено между функциями
и(х) и υ(χ), т. е. и(х)>у (x)>v(x) (jc0<*<*i) (С. А. Чаплыгин, 1919, см.
Чаплыгина метод).
ЧАСТИЧНО-УПОРЯДОЧЕННОЕ МНОЖЕСТВО. См. в термине Упорядоченное
множество.
ЧАСТИЧНЫЙ ПРЕДЕЛ: 1°. Ч. п. последовательности чисел Сх, С2, . . .,
Сп, ... —число Ь (или один из символов 4-оо, —-оо) такое, что существует
подпоследовательность (см.) Сд, , Ck , . . ., C^m, . . . данной последовательности,
для которой HmCftm=6.
т-+оо
2°. Ч. п. функции y = f(x) в точке а (другими словами, при х-*а) — такое
число Ь (или один из символов -Ь°°» —°°)> что Для некоторой
последовательности xlt х2, .... хП1 · · ·, имеющей пределом а (причем хпФа)л
соответствующая последовательность значений функции f{xi), /(*г)> · · ·> /(λ'π)> · · · имеет
предел b (или соответственно + оо, —оо). Если все Ч. п. совпадают, то
функция f(x) имеет предел в точке я, совпадающий с общим значением Ч. п. Если
f(x) имеет в точке а два Ч. п. -f00 и — оо, то f(x) имеет предел оо в точке α
(при х-*а). Ч. п. справа (соответственно слева) функции y=f(x) в точке α, т. е.
Ч. п. при х-*а-\-0 (соответственно при х->а—0), определяется таким же
образом, но с дополнительным условием, что члены последовательности хп>а
(соответственно хп<а). Аналогично определяется понятие Ч. п. функции при *->-f-oo
или х->— оо.
Примеры: 1) Ч. п. функции y=sin — при х-+0 является любое число а, где
χ
— 1<а<1; напротив, *,,-= имеет lim*n—0 и lirnsin— =a\
arcsin tf-f-2<: η л-*· о л-^оо хп

ЧАСТНАЯ ПРОИЗВОДНАЯ
503
2) для функции y=*sin2A; частичными пределами при ^-►-Ь00 являются все
неотрицательные числа 0<а< +оо, а также символ -f-°°·
ЧАСТНАЯ ПРОИЗВОДНАЯ: 1°. Ч. п. функции u=f(xu χ,, . . ., хп)
нескольких переменных по переменному Х( в точке M0(xit χ , . . ., хп^ — ко-
I · Δ/ Μ / О О 0 ° ° , ж
нечныи предел lim , где Δ/" = /(*. х> .... */_ι> *,·» */+Δ.ϊ/,
Δλγ; - 0 Δ */ V ι г
*/j_i> ...» Ό— f(x°> x° > · · ·> *n)— частное приращение (см.) функции м в
точке Λί0; при этом предполагается, что функция и определена в некоторой
окрестности (см.) точки М0.
Ч. п. по χι является производной (см.) функции u=f(x0, . . ., *°_р Xi,
xi+ι, . . ., хп) одного переменного χ ι в точке xi (остальные переменные
зафиксированы на значениях χ , χ , . . ., *,·__ρ */_i_p · · ·» -Ο-
Ч. п. есть функция координат точки М0, τ. е. является функцией тех же
переменных xlt х2, . . . , хп, что и функция ы. Для обозначения Ч. п. приняты
ди df (jcj, дсо, . . ., *п)
символы: —, (исполь-
σχι όχι
зовать для Ч. п. круглое д вместо прямого
d в обозначении обычной производной
предложил Якоби), их\ , (х.{х\, хъ · · ·» хп\
Dx. и, Dx. f(xlt x2i · · ., Хп)· В случае функ-
ди
цииы=/(л;, у) двух переменных Ч. п. —-
в точке (х0, у0) имеет такой геометрический
смысл: плоскость у=у0 пересекает
поверхность u=f(x, у) по некоторой кривой L; если
ди
— существует, то существует касательная
дх
в точке Μ [х0, yQ, f{x0, y0)] к кривой L,
причем если α есть угол, образуемый этой касательной с плоскостью хОу,
ди
то —-=tga (рис. 317).
дх
2°. Ч. п. высшего порядка. Частная производная 2-го порядка от функции
u=f(x, у, ζ) по переменным χ и у определяется как Ч. п. по у от Ч. п. дан-
Рис. 317
нон функции по а: и обозначается
д2и d2f(x, у)
ди\
дхду дхду
или и = f (*, у). Таким
д2
и \дх1
образом, т~7~ =—7—· Аналогично определяется Ч. п. 2-го порядка по другим
парам переменных (взятых в определенном порядке):
2и *(*
д2и\ д2и
значается —: I
!дИ\
дхдх
ди
дх.
дх
(короче обо-
0Z!
дх2] дгди ду
и т. д. —всего 9=32 производных 2-го порядка от

504
ЧАСТОТА
функции u=>f(x< у, г). Ч. п. 3-го порядка определяется как Ч. п. от Ч. п.
2·γο порядка и обозначается аналогично предыдущему, например:
д3и \dxdyj д3и \dzdxl д3и д3и \дхду)
дхдудх дх дгдхду ду дхду2 дхдуду ду
и т. д.— всего 27=33 производных 3-го порядка.
Аналогично определяется и обозначается Ч. п. 4-го, 5-го и т. д. порядков
для функции u—f(xu . . ., хп) от η переменных. Ч. п. &-го порядка от
функции η переменных будет пк. Однако при широких условиях число
различных Ч. п. &-го порядка значительно уменьшается (см. Перестановка
дифференцировании). Приведем формальное индуктивное определение (см.) Ч. п. высшего
порядка. Ч. п. 1-го порядка по переменному */ в точке M0(x°{i . . ., jtjj) от
функции u = f(xli х2, . . ., хп) называется Ч. п. (см.) по переменному */ в
точке М0 от функции u = f(xlf x2i . . ., хп). Ч. п. £-го порядка по переменным
х-, , */„ , . . ., л'/ , х: [индексы (ί\, /2, . . ., /^) образуют некоторое
размещение с повторениями (см.) из цифр 1, 2, . . ., п] в точке М0 от функции
u=f(xlt χ2ι . . ., хп) называется Ч. п. по переменному jt/. в точке М0 от
функции, являющейся Ч. п. (k—l)-ro порядка по переменным хи х2, . . ., x-t
от функции u=f(xl9 х2, . . ., хп), предполагая, что эта Ч. п. (k — l)-ro порядка
существует во всех точках некоторой окрестности точки М0. Эта Ч. п. &-го
порядка обозначается символом:
д^и
ϋχίχ dxi2 . . . dxifc "
. Как следует из определения, для существования £-й Ч. п. в точке М0
необходимо существование предыдущей Ч. п. в некоторой окрестности точки М0.
ЧАСТОТА: 1°. Ч. периодической функции ω (см.) — величина, обратная
периоду,, т. е. такому изменению Τ аргумента / периодической функции /(i), что
/(Ο — Ζ^+Ό* ω=—. Так, например, периодическая функция sin 3/ имеет пе-
^ 2π 3
риод Т=-. а ω=- .
2°. Ч. случайного события, которое может произойти или не произойти
в результате эксперимента, есть отношение т:п числа т экспериментов, в
которых эло событие произошло, к числу η всех экспериментов. При больших η Ч.
события обычно близка к его вероятности (см. Теория вероятностей).
ЧАСТНОЕ ОТ ДЕЛЕНИЯ числа а на число Ь=£0— результат деления а на Ь.
Ч. о. д. числа а на число b есть такое число я, что выполняется равенство
bx—α или xb=a. Ч. о. д. а на Ь называется также отношением этих чисел
(отношением числа а к числу b или отношением чисел а и Ь).
Аналогично определяется Ч. о. д. многочлена / (х) на многочлен g (x).
См. также Деление.
ЧАСТНОЕ ДИФФЕРЕНЦИРОВАНИЕ — нахождение частных
производных (см.).
ЧАСТНОЕ ПРИРАЩЕНИЕ функции нескольких переменных ы=/ (jc, yf ...,/) —
приращение, получаемое величиной и, когда придано приращение одной из
независимых переменных. Например, Ч. п. по переменной х будет:
А*и«/ (*+Δ х, У, . . ., О — / (*. У. · · ·. О-

ЧЕБЫШЕВА МНОГОЧЛЕНЫ
505
ЧАСТНОЕ РЕШЕНИЕ какого-либо уравнения получается из его общего
решения (см. Общее решение) при определенных значениях χ произвольных
постоянных, входящих в общее решение. Эти конкретные значения произвольных
постоянных обычно определяются какими-либо дополнительными условиями,
задаваемыми вместе с уравнениями. Так, если требуется найти решение уравнения
y"=k-x при 0<д:<оо, обращающееся в 0 на бесконечности и равное 1 при х=0,
то в общем решении y = c1e~kx-{-Coekxt с> = 0, сх = \ и имеем Ч. p. у=е~kx
(*>0).
ЧАСТНЫЙ ИНТЕГРАЛ дифференциального уравнения F (х, у, у', . . .,
у(п)) =0 — интеграл этого уравнения, получающийся из общего интеграла (см.)
Φ (χ, у, Сц . . ., Сп)=0 при некотором конкретном наборе постоянных
Cl»' ^2» · · ·» (*П·
Лит.: В. В. Степанов, Курс дифференциальных уравнений, Гостехиздат, Μ.,
1959.
ЧЕБЫШЕВА ЗАКОН — одна из форм закона больших чисел (см. Больших
чисел закон).
ЧЕБЫШЕВА МНОГОЧЛЕНЫ — системы ортогональных многочленов. Названы
по имени русского математика П. Л. Чебышева, впервые определившего их и
занимавшегося их изучением. Ч. м. называются многочлены Гл(а:)=
=cos (n arccosx) (л=1,2, . . .), или
Тп {х)=2п~Чп— — 2п~*хп-*+?-^—^ 2"-V-4 —
1! 2!
я („-4) (/ι-5)
3! l X +
Ч. м. ортогональны на [—1, -4-1] относительно веса l:y I—х2. Для Ч. м.
справедливо рекуррентное соотношение Тп+1(х)=*2х»Тп(х) — Τη^.Ύ (χ), 4. м.
играют важную роль при разложении функции f(x), непрерывной на [—1, -f-1],
в ряд по многочленам. Важным свойством Ч. м. является то, что многочлен
Τ (χ)
п__ наименее уклоняется от 0 на отрезке [ + 1, —1].
Ч. м.— частный случай многочлена Якоби (см. Якоби многочлены). Кроме
Ч. м., известны еще многочлены Чебышева — Лагерра и многочлены Чебышева-^
Эрмита. Многочлены Чебышева — Лагерра определяются по формуле:
М^=(-1)л**£^ (*"*-*), " = 0, 1,2, ....
Они ортогональны на полупрямой х>0 относительно веса е—х.
Рекуррентное соотношение для многочленов Чебышева — Лагерра:
Wi (*)-(* — 2/z — 1) Ln (x) —rPLn-г (*).
Многочлены Чебышева — Эрмита определяются формулой:
Нп(х)=е*2£;е-*2(п=1, 2, . . .).
Они ортогональны на всей прямой относительно веса б"*"*2 . Рекуррентное
соотношение для многочленов Чебышева — Эрмита:
#/Η-ι(*) — 2хНп(х)+2пНп-1(х)=0 и Н'п(х) — 2пНп_1(х) = 0.
Лит.: П. Л Чебышев, Полное собрание сочинений, тт. 2—3, Изд-во АН СССР
М.— Л., 1947—1948.

506
ЧЕБЫШЕВА НЕРАВЕНСТВО
ЧЕБЫШЕВА НЕРАВЕНСТВО: 1°. Ч. н. в теории вероятностей — неравен-
ство Ρ { | ξ |>ε} < —, где ξ — случайная величина, Р { | ξ | >ε} — вероятность
ε-
того, что случайная величина ξ примет значение, по модулю большее ε, Ώξ,—
дисперсия (см.) случайной величины. Неравенство Чебышева и его обобщения
применяются при доказательстве закона больших чисел.
2°. Ч. н. в теории чисел. Если через π (χ) обозначить число простых чисел,
не превосходящих х, то существуют постоянные числа а и b (a<b) такие, что
выполняется неравенство
при х>2, называемое Ч. н. Далее П. Л. Чебышев показал, что в качестве а
и b в Ч. н. можно взять а=0,92129 и 6=1,10555. Ч. н. явилось крупнейшим
вкладом в развитие теории простых чисел. В частности, из него легко было
получено П. Л. Чебышевым доказательство Бертрана постулата (см.).
ЧЕВИАНА (Чевы прямая) — см. Чевы теорема.
ЧЕВЫ ТЕОРЕМА — предложение: Если прямые, соединяющие вершины
Δ ЛВС с точкой О, лежащей в плоскости треугольника, пересекают
противоположные стороны (или их продолжения) соответственно
в точках А*В'С (рис. 318), то справедливо равенство:
о
/\ АС В А' СВ'
CA^V\Af с'в ' А'с ' В'А~~ '
А £-^**~ °\^^^ При этом отношение отрезков рассматривается как
β' положительное, если эти отрезки (например, АС и
С'В) имеют одинаковое направление, и отрицательное —
Рис. 318 в противном случае.
Ч. т. можно записав и в такой форме:
(АВС').(ВСА'ПСАВ')=\9
где (ABC) — простое отношение (см.) трех точек Л, β и С. Справедлива и
обратная теорема: если точки С, А', В' расположены соответственно на сторонах
АВУ ВС и С А треугольника или их продолжениях так, что выполняется
равенство:
(АВС')-(ВСА'У(САВ')=\9
то прямые АА', ВВ' и СС пересекаются в одной точке или параллельны
(пересекаются в несобственной точке).
Прямые А А'', ВВ' и СС', пересекающиеся в одной точке и проходящие
через вершины треугольника, называются прямыми Чевы или чевианами. Ч. т. носит
проективный характер. Ч. т. метрически двойственна Менелая теореме (см.).
Ч. т. названа по имени итальянского геометра Джованни Чева, доказавшего
ее (1678).
Лит.: С. И. 3 е τ е л ь, Задачи на максимум или минимум, Гостехиздат, М.—Л.,
1948; Н. А. Глаголев, Проективная геометрия, М.—Л., 1936.
ЧЕТВЕРКИ-БЛИЗНЕЦЫ. До последнего времени в математической
литературе наименование «близнецы» σι носили только к парам самых ближайших друг
к другу в натуральной последовательности простых чисел (кроме 2 и 3), т. е.
к парам простых чисел вида рх=/г—1 и /?2=л+1.

ЧИСЕЛ ТЕОРИЯ
507
В последнее время занимаются также исследованиями самых ближайших друг
к Другу в натуральной последовательности уже не пар, а четверок простых чисел,
т. е. четверок простых чисел вида: pi=n — 4, р2=л — 2, р3—/г+2, р4=л-|-4.
Чтобы отличать близнецы, состоящие из двух простых чисел, от близнецов,
состоящих из четырех простых чисел, по-видимому, удобнее первые назвать
близнецами-парами, а вторые — близнецами-четверками.
Двумя наиболее редкими (т. е. с наибольшей разностью) арифметическими
прогрессиями, содержащими все близнецы-пары (кроме 3 и 5), являются
прогрессии 6п + 5 и 6л4-7 с разностью, равной 6. Аналогично четырьмя наиболее
редкими (т. е. с наибольшей разностью) арифметическими прогрессиями, содержащими
все близнецы-четверки (кроме 5, 7, 11, 13), являются прогрессии с разностью,
равной 30:
30/1 + 11, 30/2 + 13, 30л+ 17, 30/г+19.
Из последних выражений все первые Ч.-б. до 10 000 (кроме 5, 7, 11, 13)
получаются при /2=0, 3, 6, 27, 49, 108, 187, 314. Из этих же выражений видно,
что простые числа (соответственно в порядке их возрастания) в любой Ч.-б.
всегда оканчиваются цифрами 1, 3, 7 и 9.
Предполагают, что Ч.-б., так же как и пар-близнецов, имеется в
натуральной последовательности бесконечное множество. Однако как первое, так и
второе из этих предположений до сих пор никем не доказано и не опровергнуто.
В. А. Голубевым подсчитано (1959), что от I до 10 000 000 в натуральном
ряду имеется 899 Ч.-б., а от 1 до 15 миллионов—1209 Ч.-б. Самая большая
из известных в настоящее время Ч.-б. указана А. Ферье. Она состоит из
следующих четырех простых чисел:
2 863 308 731, 2 863 308 733,
2 863 308 737, 2 863 308 739.
Лит.: В. Серпинский, Что мы знаем и чего не знаем о простых числах, перев.
с польского, Физматгиз, М., 1963.
ЧИСЕЛ ТЕОРИЯ — отдел математики, посвященный изучению свойств целых
чисел, рациональных и алгебраических. Ч. т. изучает также и свойства
произвольных чисел, вытекающие из возможности приближения этих чисел числами
рациональными.
Ч. т. стала развиваться очень давно. Уже в VI в. до н. э. в
пифагорейской школе в Греции изучались различные свойства целых чисел (их делимость,
деление на подклассы: простые, составные, квадратные), структура совершенных
чисел (см.), было дано решение уравнения х2-\-у2=г2 в целых числах (см.
Пифагоровы числа).
Ч. т. были посвящены труды греческих математиков Евклида, Эратосфена,
Диофанта. В Китае в связи с составлением календарей Ч. т. занимались ученые
Сунь-цзы (II—VI вв.), Цинь Цзю-шао (XIII в.). В Индии исследовались
решения уравнений в целых числах (Барамагута, VII в., Бхаскара, XII в.).
В Европе интенсивное развитие Ч. т. начинается с работы Ферма (XVII в.)
(см. Ферма великая теорема). Огромный вклад в развитие Ч. т. внес
петербургский математик Л. Эйлер, заложивший основы аналитической Ч. т. Из
приведенных ниже трех знаменитых проблем Эйлера (см.), поставленных им в переписке
с Гольдбахом, две остались до сих пор нерешенными (а первая из них решена
в 1937 г. советским математиком акад. И. М. Виноградовым): 1) всякое нечетное
число N есть сумма трех простых чисел; 2) четное число N есть сумма двух
простых чисел; 3) нечетное число есть сумма вида N=p-\-2k2 (где k — целое
число, ар — простое).
В формировании Ч. т. в смысле строгой ее систематизации оказали
существенное влияние работы выдающегося немецкого математика К. Ф. Гаусса: им

508
ЧИСЛЕННОЕ ЗНАЧЕНИЕ
была построена теория сравнений (см.), заложены основы современной теории
форм, введены в рассмотрение тригонометрические суммы.
Выдающийся вклад в Ч. т. внес великий русский математик П. Л. Чебы-
шев, который получил ряд первоклассных результатов о простых числах (см. Че-
бышева неравенство в теории чисел, Бертрана постулат).
В настоящее время в Ч. т. используются элементарные и аналитические
методы для решения проблем распределения простых чисел в различных
числовых последовательностях; изучаются также алгебраические числа, являющиеся
обобщением понятия целых чисел (см. Алгебраические числа). Специальный
раздел Ч. т. составляет решение диофантовых уравнений (см.) и нахождение дио-
фантовых приближений (см.).
Лит.: И. М. Виноградов, Осиоеы теории чисел, Гостехиздат, М.—Л., 1952;
А. О. Гельфонд, Трансцендентные и алгебраические числа, Гостехиздат, М., 1952;
Энц. элем, матем., т. 1, Гостехиздат, М., 1951; А. А. Бухштаб, Теория чисел,
Учпедгиз, М., 1960.
ЧИСЛЕННОЕ ЗНАЧЕНИЕ (числовое значение) алгебраического выражения
(функции) f(a, bt . . ., ζ)— всякое число, полученное в результате подстановки
в выражение / вместо букв а, 6, . . ., ζ каких-либо конкретных действительных
чисел (из области допустимых значений букв) и выполнения над этими числами
тех же действий, которые должны производиться над буквами. Например, Ч. з.
2 2
/(a, b)=ab:(a2— b2) при α=2, b=\ равно—, т. е. /(2, 1)=—.
о о
Нахождение Ч. з. служит одним из видов упражнений на развитие
функциональной пропедевтики в шкале.
Лит.: В. Л. Гончаров, Вычислительные и графические упражнения с
функциональным содержанием, Изд-во АПН РСФСР, М., 1948; В. Л. Гончаров,
Арифметические упражнения и функциональная пропедевтика, Изд-во АПН РСФСР, М., 1947;
Η. Η. Полозова, Сборник упражнений и задач по алгебре для VI и VII классов,
Учпедгиз, Л., 1949.
ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ — раздел математики, посвященный
приближенному вычислению определенных интегралов (в тех случаях, когда точное
аналитическое вычисление невозможно или крайне сложно) и решению
дифференциальных уравнений. При аналитических методах приближенного вычисления
интегралов подынтегральную функцию заменяют каким-либо более простым
выражением, чаще всего интерполяционным многочленом, принимающим в некоторых
точках (узлах интерполяции) х^ значения f (Xk)· Тогда формулы Ч. п.
имеют вид:
Ь η
^f(x)dx=^lAkf(xk)i
а &=1
где Ak зависят от промежутка интегрирования, вида функции, узлов
интерполяции, их числа. Эти формулы именуются квадратурными или формулами
механических квадратур. Простейшими из них являются формулы Котеса (в них
точки xk делят отрезок [а, Ь] на равные части), к числу которых относятся
общеупотребительные формулы прямоугольников, трапеций, Симпсона (или
парабол). (См. Прямоугольников формулы, Парабол формулы, Трапеций формулы.)
В случае, когда узлы интерполяции не делят промежуток [а, Ь] на равные части,
были получены формулы для вычисления интеграла от многочлена степени не
выше 2п—1 (п — число узлов интерполяции) Гауссом, (2/2 — 3) — Марковым,
{п — 1) — Чебышевым. Ряд формул Ч. п. получил акад. В. А. Стеклов. Часто
употребляется формула Эйлера, дающая выражение интеграла через значения
подынтегральной функции и ее производных в некоторых точках и через числа
Берчулли (см. Эйлера формула, Бернулли числа), и формула Лапласа, которая

ЧИСЛИТЕЛЬ
509
даст выражение интеграла через значения функции и конечные разности эгих
значений (см. Лапласа формула).
Приближенное решение дифференциального уравнения получается, если искать
решение в Риде бесконечного ряда и ограничиться конечным числом его членов
(см. Неопределенных коэффициентов метод). При решении различных краевых
задач (см.) часто пользуются тригонометрическими рядами (см.) и более общими
рядами ортогональных функций. Если уравнение содержит члены с малыми
постоянными множителями, так что этими членами приближенно можно пренебречь
по сравнению с остальными, то решение этого уравнения ищут в виде ряда,
первым членом которого является решение без малых членов, а остальные члены
ряда расположены по возрастающим степеням малой величины, входящей в
уравнение (малого параметра). Для решения дифференциальных уравнений существуют
многочисленные аналитические методы. См. Последовательных приближений
метод, Чаплыгина метод, Ритца метод, Галеркнка метод.
Численные методы позволяют находить приближенное решение при некоторых
значениях аргумента, пользуясь известными значениями решения в одной или
нескольких точках.
Наиболее часто используются Рунге и Эйлера методы (см.), а также
различные разностные формулы, где решение ищется в виде линейной комбинации:
y(Xi), rn^hf(Xiyi), Δη;=η;+ι—η/, Д%— A''-^/+i— Δ''-1*)/.
Примером может служить Адамса формула (см.) и ее обобщение, полученное
Штёрмером.
Существуют графические методы решения дифференциальных уравнений,
многие из которых строятся на основании численных методов. В последнее время
для решения дифференциальных уравнений широко используются электронные
вычислительные машины.
Лит.: А. Н. Крылов, Лекции о приближенных вычислениях, изд. 6, Гостехиздат,
М., 1954; В. Э. Милн. Численный анализ, М., 1951; Я. С. Безикович,
Приближенные вычисления, Гостехиздат, Л.—ДА., 1949.
ЧЕТНАЯ ПЕРЕСТАНОВКА —- пепестановка, имеющая четное число инверсий
(см.).
ЧЕТНАЯ ПОДСТАНОВКА — подстановка (/2-й степени), в которой сумма
числа инверсий (см.) в обеих ее строках четна. Подстановка четна тогда и только
тогда, когда ее декремент (см.) четен. Число всех Ч. п. /г-й степени равно
—. Совокупность всех Ч. п. относительно операции умножения подстановок (см.)
образует знакопеременную группу (см.).
ЧЕТНАЯ ФУНКЦИЯ — функция y=/(jc), область определения когорой
симметрична относительно нуля и которая обладает свойством: /(—x) = f(x).
График Ч. ф. симметричен относительно оси у.
Примеры: 1) у=У 1— х'\ —1<а:<1; 2) y=cosx, — оо<#<оо; 3) у=
= 1 — 3jC2-f-15jC18f — οο<χ<οο.
ЧЕТНЫЕ ЧИСЛА —целые числа, кратные 2, например: 0, 2, 4, 6, 8
и т. д. Число является четным тогда и только тогда, когда в десятичной записи
оно оканчивается четной цифрой (0, 2, 4, 6 или 8).
ρ
ЧИСЛИТЕЛЬ. Г. Ч. арифметической дроби ·——число р, равное числу
q
д-х долей единицы. Число η называется при этом знаменателем дроби
(делителем). Ч. называется также делимым.
Па, Ь ζ) р , ч
2°. Ч. алгебраической дроби есть многочлен / (делимое).
φ (α, b ζ)
Многочлен φ называется при этом знаменателем дроби (делителем).
34 Толковый словарь математических терминов

510
ЧИСЛО
Ч. и знаменатель дроби (обыкновенной арифметической или алгебраической)
называются членами дроби (см. Дробь).
ЧИСЛО — одно из основных понятий математики, возникшее впервые в связи
с потребностями счета предметов и совершенствовавшееся затем по мере развития
математических знаний. Уже в трудах античных ученых было установлено, что
ряд натуральных чисел бесконечен (III в. до н. э.). Проблемы бесконечности
натурального ряда, ряда простых чисел и построение названий для сколь
угодно больших чисел обсуждаются в знаменитом произведении Евклида «Начала»
и в книге Архимеда «Об исчислении песка» («Псаммит»),
С введением понятий сложения (см.), вычитания (см.), умножения (см.)
и деления (см.) начинает развиваться наука о числах и действиях над ними —
арифметика (см.). Изучение глубоких закономерностей в натуральном ряду чисел
продолжается до настоящего времени и составляет теорию чисел (см.). Понятие
натурального числа кажется таким простым и естественным, что в науке долгое
время не ставился вопрос об определении его в терминах каких-либо простых
понятий.
Обоснование понятия натурального числа стало необходимым лишь в
середине XIX в. в связи с развитием аксиоматического метода в математике (см.) и
разработкой основ математического анализа. Это было сделано в 70-х годах
XIX в. в работах немецкого метематика Кантора (см.) на основании понятия
множеств (см.), их равномощности (см.), т. е. сопоставимости элементов одного
множества элементам другого. Число предметов в совокупности, число элементов
во множестве определяется как то общее, что имеет данная совокупность и
всякая другая ей равномощная. Другое понятие натурального числа было дано
итальянским математиком Пеано на основании сформулированных им аксиом (см.
Пеано аксиомы).
Первым обобщением натуральных чисел были дробные числа, возникшие
в связи с потребностью производить измерения какой-либо величины, что
заключается в сравнении ее с какой-либо другой величиной — эталоном (см. Дроби).
Все дальнейшие расширения понятия числа уже не были более вызваны
потребностями счета и измерения, а явились следствием развития науки. Первым из них было
введение отрицательных чисел, обусловленное развитием алгебры. В Европе
отрицательные числа ввел в употребление в XVII в. французский ученый Декарт.
Далее были введены иррациональные числа (см.). Изучение понятия
непрерывности в работах немецких математиков Дедекинда (см.), Кантора (см.), Вейерштрас-
са (см.) привело к дальнейшему уточнению понятия числа и его свойств.
Развитие теории алгебраических уравнений привело (XVIII в.) к понятию
комплексного числа (см.).
Комплексные числа образуют поле, и, как установил Вейерштрасс,
совокупность всех комплексных чисел не может быть далее расширена за счет
присоединения новых чисел так, чтобы в расширенной совокупности сохранились все
законы действий, имеющие место в совокупности комплексных чисел.
См. также: Натуральное число, Рациональное число, Иррациональное число,
Действительное число, Комплексное число, Алгебраическое число,
Трансцендентное число, Кардинальное число, Трансфинитное число, б-число, Пи-число.
Лит.: Энц. элем, матем., т. I, М,—Л., 1951; И. Я· Депман, История арифметики,
Учпедгиз, М., 1959.
ЧИСЛОВАЯ ОСЬ —прямая, служащая для изображения действительных
чисел, на которой заданы: 1) положительное направление (от О к А), 2) точка О—
начало отсчега и 3) единичный отрезок (масштаб) О А. Всякое действительное
число изображается точкой Ч. о. по следующим правилам: число нуль
изображается точкой О. Положительное действительное число χ изображается точкой В
(обозначаемой также х) такой, что отрезок ОБ направлен в ту же сторону, как

ЧЛЕН ОПРЕДЕЛИТЕЛЯ
511
и отрезок ОА (положительное направление на оси), и отношение длины отрезка
ОВ к длине отрезка ОА равно х.
Отрицательное действительное число х' изображается точкой С
(обозначаемой также х') такой, что отрезок ОС имеет направление, противоположное
направлению отрезка О А (т. е. отрицательное направление), и отношение длины ОС
к длине О А равно абсолютной величине числа х' (рис. 319).
Это соответствие между числами и точками Ч. о. взаимно однозначно.
Поэтому часто не делают различия между числом χ и соответствующей ему точкой
X1 О 7 X
1 1 \ , *_
С О Α β *
Рис. 319
на Ч. о., которая также может обозначаться точкой х. Расстояние между
точками Ч. о. хх и хо равно \х2 — хг\ — абсолютной величине разности
соответствующих чисел хг и х2.
ЧИСЛОВАЯ ПОСЛΕДОВАТЕЛ ЬНОСТЬ — последовательность (см.), члены
которой являются числами.
ЧИСЛОВАЯ ПРЯМАЯ —то же, что и числовая ось (см.).
ЧЛЕН МНОГОЧЛЕНА от η неизвестных (или переменных): хи х2, . . ., хп
в некотором поле Ρ-—выражение (функция) вида
Ax\*fj ... хп*п, (*)
где аъ σ2, .. ., ап — целые неотрицательные числа — показатели степеней
соответствующих неизвестных, а коэффициент А — элемент из того же поля Р.
Порядок следования множителей в Ч. м. можно произвольно менять.
Сумма нескольких Ч. м. называется многочленом (см.) в поле Р.
Если Ч. м. имеет вид (*), то при Л^О число а/ называется степенью члена
(*) относительно неизвестного xt·; степенью члена (*) по совокупности всех неиз-
п
вестных (переменных) называется число, равное 2 al·
ЧЛЕН ОПРЕДЕЛИТЕЛЯ я-го порядка:
1^11^12 · · · а1п\
К*21а22 · · · а2П\
\аП1ап2 · · · апп\
— всякое произведение η элементов этого определителя, взятых по одному из
каждой строки и каждого столбца.
Всего у определителя (*) существует п\ членов. Например, при η=4 у
этого определителя будет членом произведение α12, α2ι, α34. ^4з. н0 не будет Ч. о.
произведение α1ζαζ2α22α^ так как в последнем произведении участвуют два
элемента а2а и оз2, не лежащие в разных столбцах, а принадлежащие к одному и
тому же (второму) столбцу.
34*

ШАР — геометрическое тело, ограниченное сферой (см.). Ш. можно
рассматривать как тело, полученное от вращения круга около своего диаметра. Всякое
сечение Ш. плоскостью есть круг.
Площадь поверхности Ш. радиуса R определяется формулой S = 4- R",
4
объем Ш. — V=— r.R3. Ш. с центром О (а, Ь, с) и радиусом R есть геометри-
ό
ческое место точек (см.) (х, у, ζ) пространства, координаты которых
удовлетворяют условию:
0< V (х — а)2-Ь(У — bf+(z — df~<R.
ШАРОВОЙ ПОЯС — часть шаровой (сферической) поверхности, заключенная
между двумя секущими параллельными плоскостями. Ш. п. иначе называют зоной.
Ш. п. представляет собой боковую поверхность шарового слоя (см.).
ШАРОВОЙ СЕГМЕНТ — часть шара, заключенная между секущей плоскостью
и одной из двух частей его сферической поверхности. См. также Сегмент.
ШАРОВОЙ СЕКТОР — геометрическое тело, полученное от вращения круго-
зого сектора вокруг диаметра, не имеющего внутренних ючек с дугой кругового
сектора.
Различают Ш. с. первого и второго рода. Если радиус кругового сектора
расположен на оси вращения, т. е. на диаметре ЛК (рис. 320), то полученный
Рис. 320 Рис. 321
при этом Ш. с. (ВОВ') называется Ш. с. первого рода. Если же диаметр PL
не пересекает дуги АВ кругового сектора ЛОВ, то полученный при этом Ш. с.
АВОВ'А' называется Ш. с. второго рода (рис. 321).
Поверхность основания у Ш. с. первого рода — сегментная, у Ш. с.
второго рода — шаровой пояс. Ш. с. первого рода — выпуклая фигура (см.), Ш. с.
второго рода — невыпуклая (вогнутая) фигура.
ШАРОВОЙ СЛОЙ — часть шара, заключенная между секущими
параллельными плоскостями.

ШТУРМА ПРАВИЛО
513
ШАРОВЫЕ ФУНКЦИИ — однородные гармонические полиномы п-й степени:
ип= Σ ap,q%rxVyW.
Общее число линейно-независимых однородных гармонических полиномов л-й
степени, являющихся Ш. ф., равно 2/2-|-1. В случае сферических координат
(г, ν, φ) Ш. ф. выражаются через сферические функции (см.) Уп(и, Ф) по
формуле:
Un=rnyn(v,V).
Каждой Ш. ф. Un степени η соответствует Ш. ф. г^2п—г1)п (п—1)-й степени.
Ш. ф. являются решением уравнения Лапласа в задачах математической физики
для областей, ограниченных сферическими поверхностями.
ШЕННОНА ТЕОРЕМА — одна из основных теорем теории информации.
См. Теория информации.
ШТЕЙНЕРА ПОСТРОЕНИЯ — геометрические построения (см.) на плоскости,
выполняемые с помощью только одной линейки (односторонней, математической).
Ш. п. были в основном разработаны швейцарским геометром Я. Штейнером,
который доказал, что любую планиметрическую задачу на построение,
выполняемую с помощью циркуля и линейки, можно решить с помощью только одной
линейки, если на плоскости задан круг и известен его центр. Ш. п. носят
проективный характер и противопоставляются построениям Маскерони (см.),
выполняемым только одним циркулем.
ШТУРМА —ЛИУ ВИЛ Л Я ЗАДАЧА — граничная задача (см.) для
дифференциального уравнения:
[-p{x)y'Y+q(x)y-\yt
i4iy(fl)+Biy'(fl) = 0,
А2у(Ь)+В2у'(Ь) = 0.
Необходимо отыскать отличные от нуля решения (собственные функции, см.), а
также значения параметра λ (собственные значения, см.), при которых
существуют эти решения. Если на р(х) и q (χ) наложить некоторые условия, Ш. — Л. з.
сведется к аналогичной для уравнения:
— y"+q(x)y = ly. (*)
Показано, что если функция q (x) в уравнении (*) непрерывна и действительна
на [a, b], a AltBuA2yBz— действительные числа, то существует возражающая
последовательность действительных собственных значений λχ, λ2, . . ., λΛ, . . .,
стремящаяся к бесконечности, и каждому значению λη соответствует собственная
функция (с точностью до постоянного множителя) φ/2 (χ), которая имеет ровно η
нулей на участке а<х<Ь. Функции Фл(*) образуют полную, ортогональную
систему функций на [я, Ь].
Лит.: Б. М. Левитан, Разложение по собственным функциям дифференциальных
уравнений второго порядка, Гостехиздат, М.—Л., 1950.
ШТУРМА ПРАВИЛО — правило, позволяющее находить непересекающиеся
интервалы, содержащие каждый по одному корню данного многочлена. Ш. п.
состоит в следующем. Дан многочлен f(x) без кратных корней (метод отделения
кратных корней см. в термине Кратный корень). Рассмотрим систему
многочленов: /0 (x)t h (χ), . ... fs{x), где /„(*) = /(*), Λ (*)-/' (х), ...,/*+iW-
= //?(*) <7fc (*) — /*—ι (*) (A=1.2, 3, ..., 5—1), где qk (x) — многочлен такой,
что степень fk+1 (χ) меньше степени /д» (χ). Эта система обладает свойствами:
Π fk и /fc+i (£=0» 1» · · ·. 5 — О не имеют общих корней, 2) многочлен /s не
имеет действительных корней, 3) из /а(*о)=0 следует и ffi^.1 (*0)7a+i (*o)<

514
ШТУРМА ТЕОРЕМЫ
<0 (£=1, 2 s— 1), 4) из /(х0)=0 следует, что /х (x0)f (х0)>0 пп. 3
и 4. Обозначим fc>(*) число перемен знака в ряду чисел /0 (а), /(а), .... fs(a).
Тогда θ (b) — θ (α) равно числу действительных корней, заключенных между
а и 6.
Лит.: А. Г. Курош, Курс высшей алгебры, изд. 7, Физматгиз, М.—Л., 1962.
ШТУРМА ТЕОРЕМЫ — теоремы о нулях решений линейных
дифференциальных уравнений 2-го порядка. Пусть у1 (х) и у2 (х) — линейно-независимые
решения уравнения у"+д(х) у=0. Если хг, х2— последовательные нули ух (х), то
у2 (х) имеет в точности один нуль между хг и х2.
Очень важной является так называемая теорема сравнения, которая состоит
в следующем: даны два уравнения: /'-{-<7ι (х)=®, z"4-Q2(x)z=Q и q2(χ)>qx(x)
в интервале (я, b)\ тогда между двумя нулями любого решения ух (х) первого
уравнения содержится хотя бы один нуль каждого решения ζλ (χ) второго
уравнения.
Ш. т. применяются при исследовании собственных значений (см.) задачи
Штурма — Лиувилля (см.)— уравнения yff+Q(x)y—^y с однородными
граничными условиями.

э
ЭВОЛЮТА кривой / — геометрическое место центров кривизны (см.)
кривой /. Кривая / по отношению к своей Э. называется эвольвентой (см.) или
инволютой Э. Касательные к Э. являются нормалями к эвольвенте.
ЭВОЛЬВЕНТА кривой т — такая кривая /, для которой кривая т является
эволютой (см.). Э. может быть получена как траектория конца А или D нити,
которая наматывается на линию т или разматывается
с нее (рис. 322); отсюда и происходит название Э.—
«развертка».
Э. пространственной кривой можно определить
как ортогональную траекторию касательных к этой
кривой.
Лат. evolvo — развертываю, разворачиваю.
Лит.: П. К. Ρ а ш е в с к и й, Курс дифференциальной
геометрии, Гостехиздат, М., 1950.
ЭЙЗЕНШТЕЙНА КРИТЕРИЙ — достаточные
условия для того, чтобы многочлен с целыми
коэффициентами был неприводимым в поле
рациональных чисел. Если f(x)=a0xn-\-alxn—1-\- ··· +αη—i*+fl/i— многочлен с
целочисленными коэффициентами, то Э. к. утверждает, что для неприводимости много
члена f (х) в поле рациональных чисел достаточно существования простого числа
р, такого, что а0 не делится на р, аь делится на ρ при /=1, 2, . . ., /г, но ап
не делится на р2. Например, многочлены хп±2, хл±10, jc"±6 при любом
натуральном числе п>\ по Э. к. являются неприводимыми в поле рациональных
чисел.
ЭЙЛЕРА ИНТЕГРАЛЫ первого и второго рода — соответственно интегралы
вида:
1 оо
В (р, q)=*$xP~i (1 — Jt)?-1 dx и Г (z)=j e-4z-~4t.
о о
Первый Э. и. представляет собой функцию от двух параметров ρ и q — функцию
В (бета): он изучался И. Ньютоном, Дж. Валлисом, Эйлером, именем которого
и назван по предложению Лежандра. Функция В (р, q) симметрична, т. е.
В (р, q)=B(q, p); имеет место формула:
В(«, бИ^^а,*-!),
последовательное применение которой приводит (при Ь, равном натуральному
числу п) к
п— 1 п — 2 1
В (Яш Ό=— Г" ■- о · · · -Г7Г В (а> *) =
а+п-
1 a-f-rt-
Ь2.3·.
•2 α-f-l
.·(/»-1)
α(α+1)(α + 2) .. . (a-f-л— 1)'

516
ЭЙЛЕРА ИНТЕГРАЛЫ
если же и а равно натуральному числу т, то
(я — \)$т— 1)!
В (т, я) К I J (01 = 1).
(m-fn — 1)!
Имеют место также формулы:
оо
Г Ур~х π
] (1+У)р + / sin а г.*
i
0<«<1.в(± 1)-п.
Второй Э. и. Г (ζ) (гамма-функция) рассматривался Эйлером (1729—1730);
название дано Лежандром. Формула
оо
Г (г) =\е-Чг~Ч1
Ό
определяет справа от мнимой оси регулярную функцию, которая может быть
продолжена влево от мнимой оси. Оказывается, что Г (ζ)— мероморфная
функция (см.). имеющая простые полюсы 2=0, — 1, —2, . . ., —я, ... с вычетом
(—$п-п\ в полюсе ζ——я. Г (г) обладает рядом интересных свойств:
Г(г-Н)=гГ(г), Г (ζ) Г (1 — г)=я : sin π ζ, r( ~2 ] = Κπ.
Э. и. первого и второго рода связаны соотношением:
В(Р, ?)-Г(р) Г(д):Г(р+д).
При ζ=α>0 имеет место известная формула Эйлера — Гаусса:
ГМ-Нш , <"-'» -.
п-оо а(а+1) . . . (а+я —1)
При натуральном я Г(я+1)=я!, Г (я-f п) = (а+п — 1)(<з-Ья — 2) ... (a-f-
4-1)·α·Γ(α), при я — оо Г (а)-*со.
Для (Г (г))-1 может быть получено выражение в виде бесконечного
произведения (см.):
[Г(2)]-1 = е« ζ
k.
оо / ζ \ к
где С — постоянная Эйлера (см.), k — натуральное. Из этой формулы видно,
что есть целая функция (см.).
Г (2)
Имеет место также формула:
—(т—1) тг
Г (г) Г(г+-М г(' + |) ··· Г (г +2*Z^_(2 «) ' ^ Г<тг).

ЭЙЛЕРА ПОДСТАНОВКИ
517
Функция Г (ζ) может быть выражена также контурным
интегралом вида
У\
5©
Г(г)=(1 :е2гЛг — 1) f e-'^-i Λ,
(i> v\ ,(z)
где / — контур, представленный на рис. 323, <з, или « V—si ^ts
в виде:
1 :Г(г) = (1 :2πζ) f ez %-ζάτ
(ΪΊ
(контур /' дан на рис. 323, б). Через интеграл Эйлера Рис. 323
может быть выражена гипергеометрическая функция:
F(a, β, γ, 1) = Γ(γ).Γ(γ-α-β)·.Γ(γ~ά)Γ(α-β).
Лит.: В. И. Смирнов, Курс высшей математики, т. Ill, ч. 2, Гостехиздат, М., 1956;
Г. Μ. Φ и χ τ е н г о л ь ц, Курс дифференциального и интегрального исчисления, т. II;
Физматгиз, М., 1963.
ЭЙЛЕРА КРИТЕРИЙ в теории сравнений служит для распознавания
квадратичных вычетов (см.) и квадратичных невычетов (см.) по простому
модулю р. Э. к. формулируется так: если (at р)=1. где ρ — простое нечетное число, то
Р-1
2 /о/
а = 1 (modp),
где I — — Лежандра символ (см.).
ν Ρ I
ЭЙЛЕРА МЕТОД ломаных — один из простейших методов численного
решения дифференциальных уравнений: предложен Эйлером в 1768 г. Основная идея
этого метода состоит в применении рядов для вычисления приближенных
значений решения дифференциального уравнения у (х) в точках х1% х2> . . ., Хп
некоторого фиксированного отрезка [x0i b\t где х0 определяет начальное условие
Уо=УЫ-
Ь х
Для вычисления у(хх), где Xi^x0+h, Λ= ~, следует представить у (*,)
η
в виде ряда по степеням h=x1— хп, взяв затем конечное число членов этого
ряда. Если ограничиться лишь двумя первыми членами ряда, то получим:
y(*K)=*y(XK-i)+hf(xx-.u у*-,), xK=Xo+hb.
Это и есть метод ломаных: на каждом отрезке [хк, хка-\\ интегральная кривая
заменяется прямолинейным отрезком ломаной Эйлера. Доказывается при весьма
общих предположениях, что при /ί-*-0 ломаные Эйлера всегда стремятся к
интегральной кривой.
ЭЙЛЕРА ОКРУЖНОСТЬ — то же самое, что и окружность девяти точек (см.).
ЭЙЛЕРА ПОДСТАНОВКИ — три типа подстановок, приводящих интегралы
вида §R(xf y)dxy где у=у ax2+bx+c и R {χ, у) — рациональная функция
от * и у, к интегралам от рациональных функций.
Если а>0, то применяется первая Э. п.: у ах2-\-bx-\-c = t — χ να, если
О0, то — вторая Э. п.:]/ ах'1 -J- Ъх 4- с = xt -4- V с\ если корни трехчлена ax2i-
-f bx+c действительны и λ — один из корней, то применяется третья Э. п.:
V ax*+bx ±-c=t{x — λ).

518
ЭЙЛЕРА ПОСТОЯННАЯ
ЭЙЛЕРА ПОСТОЯННАЯ — предел
1 = с = 0,577215 . . .,
η 1
lim J Σ —- — In n
η-*·χ> Ι k— 1 k
рассмотренный Эйлером и давшим для С некоторые представления в форме рядов
и интегралов, например:
ι
-\[i-x+inx)dx' 1 с Jj»
О л=2
где ξ (s) — дзета-функция.
Э. п. встречается в различных классах специальных функций.
ЭЙЛЕРА ПРЯМАЯ — прямая, на которой расположен центр тяжести
треугольника Μ (точка пересечения медиан), центр О описанного круга и ортоцентр Я.
При этом справедливо равенство:
ОМ:МН=\ :2.
В разностороннем и равнобедренном треугольниках существует единственная
Э. п., при этом в равнобедренном треугольнике Э. п. — его ось симметрии.
В равностороннем треугольнике существует пучок Э. п.
Э. п. названа по имени великого математика Л. Эйлера, установившего
указанное свойс1во прямой.
Лит.: С. И. Зетель, Новая геометрия треугольника, Учпедгиз, М., 1940;
Д. И. Перепелки н, Курс элементарной геометрии, Гостехиздат, М.—Л., 1948.
ЭЙЛЕРА СПИРАЛЬ —то же самое, что и Корню спираль (см.), или
клотоида (см.).
ЭЙЛЕРА ТЕОРЕМА: 1°. Э. т. в теории сравнений утверждает, что если
(а, т)=1, то а?Ся)=:1 (modm), где φ (m) — Эйлера функция (см.).
2°. Э. т. о многогранниках утверждает, что для всякого многогранника
нулевого рода справедлива формула:
В+Г— Р=2,
где Б — число вершин, Г — число граней, Ρ — число ребер многогранника.
Однако впервые такую зависимость подметил еще Декарт. Поэтому Э. т. о
многогранниках исторически правильнее будет называть Декарта — Эйлера теоремой о
многогранниках. Число В-\-Г — Ρ называется эйлеровой характеристикой
многогранника.
См. также Род, Связность.
ЭЙЛЕРА ТОЖДЕСТВА: 1°. Э. т. о пятиугольных числах:
Zkz—к
n(i-*")= 2 (-1)**
л=1 /г=—оо
(см. Пентагональные числа).
2°. Э. т. о простых числах:
2М-*Г-
= 1
здесь произведение берется по всем простым числам р.

ЭЙЛЕРА ФОРМУЛА
619
3°. Э. т. о четырех квадратах:
(a2+b2+c2+d2)(p2+q2+r2+s2) =
= (ap+bq+cr+ds)2+(aq — bp+cs — dr)2+
+(ar — bs — cp — dq)2+(as+br — cq — dp)2.
См. также Эйлера формулы.
ЭЙЛЕРА УРАВНЕНИЕ дифференциальное: 1°. Э. у. д. обыкновенное —
дифференциальное уравнение вида:
„ dny n dn-^y dy
где alt а2, . · ·, а>п — постоянные. Заменой х=е* оно приводится к уравнению с
постоянными коэффициентами (см.). Например, для уравнения
xY+2xy' — я(л+1)у=0,
полагая х=е*, имеем:
d2y dy
- + __„(я+,)У-0.
2°. Э. у. д. уравнение вида
dx dy
Ух Уу
где
X=a0xi+o1xB+a2x2+a3x+alt a Υ=α(#*+α1γ*+α.#*+α3γ+αΑ,
рассматривалось Эйлером в ряде работ в 1753 г. Он показал, что общее решение
(см.) этого уравнения имеет вид: F(х, у) = 0, где F(x, у)—симметрический
многочлен (см.) четвертой степени от л; и у; этот результат Эйлера играет
важную роль в теории эллиптических интегралов (см.).
Лит.: В. В. Степанов, Курс дифференциальных уравнений, М., 1953.
ЭЙЛЕРА ФОРМУЛА для приближенного вычисления определенных интегра-
ь
лов — формула, дающая выражение интеграла J f(x)dx через значение функции
а
f(x) и ее производных в некоторых точках:
Ь
f(x)dx=h ]-£■ /(α)+/(α+Α)+/(α+2Α)+·
Г f(x)dx=h U-
+/[o+(n-l)lA]+j/(6) \-^[Г(Ь)-Г(а)]+
hA Bnfl2p
+720 U'"{b) ~ Г(а)] + ···+(- 1)" T^T l/(2P_1' (Ь) ~ ΡΡ~1) {a)]+RV

520
ЭЙЛЕРА ФОРМУЛЫ
где
ъ
Д2/7=(- ψϊΐΡ+ι Γ/2Ρ+1 (*) Q2p+l {χ) dx,
а
оо
Ж ^sin2rt η (χ — а)
Ч?2Р+1 = у l22p л2р + 1п2Р+1'
h= , Вр — числа Бернулли (см. Бернулли числа). Эта формула Эйлера
является весьма точной: если требуемая точность не очень велика, то можно
ограничиться лишь членами, содержащими производные нескольких первых порядков.
Э. ф. находит также применение при численном решении интегрального уравнения
Вольтерра второго рода (см. Интегральные уравнения).
Лит.: А. Н. Крылов, Лекции о приближенных вычислениях, изд. 6, М., 1954.
ЭЙЛЕРА ФОРМУЛЫ — некоторые наиболее важные формулы,
установленные Эйлером:
Э. ф., связывающие тригонометрические и показательные функции:
cos χ = , s ι π χ=
2 2/ '
e/A"=cos .ν г/sin x.
Э. φ., представляющие разложение функции sinjc в бесконечное
произведение:
sin., й / г
2 — °
Ы \ k*rJ
1
Э. ф. о кривизнах, дающая выражение кривизны — любого нормального
R
1 1
сечения поверхности через ее главные кривизны -— и —- и угол φ между
одним из главных направлений и данным направлением:
1 cos2 φ sin2 φ
Известны также формула суммирования Эйлера — Маклорена, формулы
Эйлера — Фурье, дающие коэффициенты разложения функций в тригонометрические
ряды.
См. также Эйлера тождества.
ЭЙЛЕРА ФУНКЦИЯ в теории чисел. Под Э. ф. φ (л), определенной для
целых положительных значений аргумента п, понимают число целых
положительных чисел, взаимно простых с я, не превосходящих п. Например, φ(10) = 4,
Φ(1)= 1, φ(17)= 16. Э. ф. является мультипликативной функцией (см.). Э. ф.
фигурирует в так называемой теореме Эйлера в теории сравнений (см. Эйлера
теорема). Если каноническое разложение в произведение простых чисел для числа
η имеет вид:
л=Р*1 Р%' · · · Pkki

ЭКВИВАЛЕНТНЫЕ МНОЖЕСТВА
521
то Э. φ. φ (η) выполняется по формуле:
т. е.
ЭЙЛЕРОВА ХАРАКТЕРИСТИКА — число В + Г — Р, характеризующее
количественное соотношение между числом вершин (Б), числом граней (Г), числом
ребер (Р) многогранника. Если многогранник выпуклый или гомеоморфен (см.)
выпуклому, то его Э. х, равна двум. См. Род поверхности, Связность.
ЭЙЛЕРОВЫ УГЛЫ — углы φ, ψ, θ, определяющие положение
прямоугольной декартовой системы координат Ох'у'ζ' (см.) относительно другой
прямоугольной декартовой системы координат Oxyz с той же ориентацией (см.); были
введены Эйлером (1748). Э. у. рассматриваются как углы последовательных
поворотов одной системы относительно осей другой, после которых обе системы
совпадут. Первый поворот делается вокруг оси Oz на угол φ, затем
промежуточная система Oxxyxzx поворачивается на угол θ вокруг оси Oxlt и, наконец,
полученная таким образом система поворачивается на угол ψ вокруг оси Oz'.
Э. у. ф, ψ, θ берутся с учетом направления поворота. Используя Э. у., можно
написать формулу перехода от координат х', у\ ζ' к х, у, ζ:
x=(cos<pcost|; — sin φ sin ψ cos θ) χ' —(cos φ sin ψ-bsin φ cos ψ cos 6)y'-f
-f-sin φ sin θ ζ';
y=(sin φ cos ψ+ΰ08φ5Ϊηψ cos θ) χ' +(—sin φ sin ([/-f-coscpcosa cos θ) у' —
— cos φ sin θ ζ';
z=sin φ sin θ χ1 -f-cos ψ sin θ-y'+cos Θ·2\
Этими формулами всегда пользуются в механике при изучении движения твердого
тела с неподвижной точкой.
ЭКВИВАЛЕНТНЫЕ ВЕЛИЧИНЫ: 1°. Э. в. бесконечно большие — бесконечно
а. (х\
большие α (χ) и β (χ) при х-+х0, для которых lim ΤΓΓΤ^Ι'» это пишут так:
х-*х0 Ρ Μ
% 1
α (λ')~β(#). Например, при х-> — —0 имеем tg χ , при л*-*-оо лг-fsin х~х~
-л;-И~л;-{-2.
2°. Э. в. бесконечно малые — бесконечно малые α (χ) и β(χ) при *-*·*<)* для
которых Нт-— = 1; это пишут так: α(χ)~β(χ). Например, при х^О sin*~A;.
ρ (χ)
При отыскании пределов любые бесконечно малые и бесконечно оольшие
можно заменять эквивалентными им величинами.
ЭКВИВАЛЕНТНЫЕ МНОЖЕСТВА — множества, между элементами которых,
можно установить взаимно однозначное соответствие. Э. м. называют также рав-
номощными (и, менее удачно, равночисленными) множествами. Таким образом,
всякие два множества либо эквивалентны, либо нет. Отношение эквивалентности
множеств рефлексивно, симметрично и транзитивно (см. Рефлексивность,
Симметричность, Транзитивность). Поэтому множество псех множеств распадается на
классы эквивалентных множеств. На этом пути мы приходим к понятию
мощности множества (см.) и кардинальных чисел (см.), являющихся обобщением
натуральных чисел (см.).

522
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ
ЭКВИВАЛЕНТНЫЕ УРАВНЕНИЯ —то же, что и равносильные уравнения
(см.).
Э KB И ДИСТ АНТ А — геометрическое место точек плоскости Лобачевского,
расположенных по одну сторону от прямой ы и на одинаковом от нее расстоянии.
Прямая и называется базой Э., а величина расстояния h — высотой Э. Каждую
прямую можно рассматривать как Э. с высотой /г=0. Всякая прямая имеет с Э.
не более двух общих точек. Если в плоскости Евклида геометрическое место
точек, расположенных по одну сторону от прямой на данном расстоянии /г, есть
прямая, то в плоскости Лобачевского это геометрическое место точек есть
кривая, называемая Э. В планиметрии Лобачевского Э. остаются инвариантными
относительно сдвигов в плоскости. Э. иначе называют гиперциклом. Э. можно
истолковать как кривую равных расстояний.
Лат. aequidistans — равноудаленный.
ЭКВИДИСТАНТНАЯ ПОВЕРХНОСТЬ — геометрическое место точек
пространства Лобачевского, расположенных по одну сторону от какой-нибудь плоскости
α и отстоящих от нее на одинаковом расстоянии. Плоскость α называется базой
Э. п., а перпендикуляр, опущенный из какой-либо точки Э. п. на базу,
называется высотой Э. п. Э. п. есть пространственный аналог эквидистанты (см.),
аналогично тому как в евклидовой геометрии, например, параллельные плоскости
являются пространственным аналогом параллельных прямых, а сфера является
пространственным аналогом окружности. Э. п. является поверхностью вращения
эквидистанты (гиперцикла) вокруг одной из ее осей.
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — функция е* или αχ(α>0), τ. е.
показательная функция. Э. ф. обозначают также ехр х.
ЭКСТРАПОЛЯЦИЯ — распространение результатов, полученных из
наблюдения над одной частью явления, на другую его часть. Так, если известны значения
функции y=f(x) на отрезке [х0, хп], то по ее значениям в точках х0, хХу . . . ,
χη(χο< · ·· <χη) можно определить значения функции в точках, лежащих вне
отрезка [x0f xn]. Аппаратом для этого служит, например, параболическая Э.,
при которой в качестве значения f (χ) в точке χ берется значение многочлена
Рп(х) степени nt принимающего в л-И точке χι заданные значения у*=/(#/).
Для параболической Э. используются обычные интерполяционные формулы,
например формула Ньютона для равноотстоящих точек Xi=x0+ih:
t t(t+l) β
Ρη (Хп + Щ=уп+ — Δ yn-i+ 2, Δ2 Уп-2+
,/(/+1)(/+2) Ш+1)...«тЯ-1)
-г «ι Δ Уп—3-г · · · ίγ j Δ у0.
где ΔΛyi=kk~~1 У1+1 — ЛЙ"~1У(. Например, если для функции y=f(x) составлен
ряд частных значений у0, ylf у2, · · · » Уп> соответствующих a, a-\-h, . . . > а+
-f nh, то
ЛУо=У1 — Уо. АУ1=У2 —Уь АУ2 = Уз —Уг ···
и Д2Уо = АУ1 — АУо, А2У1=Ау2 —АУх, А2У2 = АУ3.— Ау2 и т. д.;
наконец, A*y0= Δ*-^ι — ΔΛ~^0 Δ^=Δ*-^ί+ι — Ак-гУь
χ "~~" Χ η λ
t= ——->0 и х>хп.
h
Погрешность, совершаемая при вычислении по этой формуле значения / (х)
в точке x=xn+tht не превышает

ЭЛЕМЕНТАРНАЯ АЛГЕБРА
523
где Μ — максимум абсолютной величины л-{-1-й производной функции f(x) на
отрезке [х0* *]·
ЭКСТРЕМАЛЬ — интегральная кривая дифференциального уравнения Эйлера
(см.). встречающаяся в вариационном исчислении (см.).
ЭКСТРЕМАЛЬНАЯ ТОЧКА — точка, в которой функция имеет экстремум
(см.).
ЭКСТРЕМУМ — термин, объединяющий понятия максимума (см.) и минимума
(см.). В случае функции нескольких переменных иногда различают абсолютный
Э. (см.) от относительного экстремума (см.).
Лат. extremum — крайнее (значение).
ЭКСЦЕНТРИСИТЕТ кривой 2-го порядка (конического сечения) — число,
равное отношению расстояния от любой точки кривой 2-го порядка до фокуса к
расстоянию от этой точки до соответствующей директрисы (см.). Э. эллипса
меньше единицы, у гиперболы Э. больше единицы и у параболы равен единице.
Э. характеризует вид, форму кривой 2-го порядка: если у двух кривых 2-го
порядка Э. равны, то кривые подобны между собой (т. е. одинаково сжаты,
сплюснуты).
Для эллипса, если Э. приближается к нулю, то эллипс приближается по
своей форме к окружности, если же Э. эллипса будет приближаться к единице,
то эллипс будет более вытянутым (сжатым, сплюснутым) и будет стремиться
занять положение отрезка — большой оси эллипса 2а.
Для гиперболы, если Э. стремится к единице, то угловой коэффициент
асимптот по модулю стремится к нулю, а, следовательно, ветви гиперболы все
более приближаются (сжимаются) к действительной оси xf стремясь выродиться
в два луча; если же Э. гиперболы неограниченно возрастает (-*оо), то ветви
гиперболы все более распрямляются, стремясь занять положение двух прямых
х—а и jc=— а.
Лат. ех — вне, centrum — центр.
ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ МАШИНЫ — наиболее совершенные
вычислительные цифровые машины, позволяющие быстро и с большой точностью
решать различные математические и логические задачи. Технической
основой этих машин являются весьма сложные электронные схемы,
обеспечивающие быстрое и точное выполнение различных операций (команд). Э. ц. м.
состоит из: 1) арифметического устройства, предназначенного для выполнения
операций над числами; 2) запоминающего устройства, предназначенного для
приема, хранения и выдачи чисел и команд; 3) устройства управления,
предназначенного для управления автоматической работой машины.
Каждая операция выполняется машиной под воздействием специального
управляющего сигнала — команды. Последовательность команд образует программу
работы машины (см. Программирование). В современном виде основные идеи ίι
принципы работы таких машин были сформулированы американским математиком
Д. фон Нейманом (1946).
В СССР первая быстродействующая электронная счетная машина (БЭСМ)
была построена в 1953 г. под руководством акад. С. А. Лебедева. В настоящее
время наша промышленность выпускает весьма разнообразные Э. ц. м.,
выполняющие различные операции со скоростью, равной десяткам тысяч операций в
секунду, и имеющие большую внутреннюю память.
Лит.: А. И. Кнтое, Электронные цифровые машины, М., 1956; А. И. Китов и
Н. А. Криницкнй, Электронные цифровые машины и программирование, М., 1959.
ЭЛЕМЕНТАРНАЯ АЛГЕБРА — раздел элементарной математики (см.),
объектом изучения которой в основном являются и уравнения и неравенства первой и
второй степени, и частные случаи уравнений высших степеней, простейшие
(элементарные) функции, понятие числа и предела, тождественные преобразования

524
ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ
и вопросы комбинаторики. Границы содержания Э. а. четко не установлены
Э. а. составляет также часть алгебры (см.) в более широком понимании.
ЭЛЕМЕНТАРНАЯ ГЕОМЕТРИЯ — геометрия, определяемая в основном
группой движений (см. Движение) и группой подобия (см. Подобие).
Однако содержание Э, г. не исчерпывается указанными преобразованиями.
В Э. г. изучаются также преобразование инверсии (см. Инверсия), элементы
сферической геометрии, элементы геометрических построений (конструктивная гео
метрия), теория измерения геометрических величин и другие разделы математики
Четкого, как и точно очерченного, содержания Э. г. не имеет. Э. г., как и дру
гие геометрии, продолжает развиваться и по настоящее время.
Э. г., изучаемую в средней школе, называют евклидовой геометрией (см.)
ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА — несколько неопределенное понятие
охватывающее в основном разделы математики в объеме средней школы. Э. м
включает в себя разделы, задачи и методы математики, в которых не пользуются
общими понятиями переменной, функции, предела, общим понятием множества
т. е. включает такие предметы, как арифметику, элементарную теорию чисел
элементарную алгебру, элементарную геометрию и тригонометрию (см.). Э. м
характеризуют как «математику постоянных величин», однако это не совсем точно
В Э. м. рассматривают не только постоянные, но и переменные величины (на
пример, тригонометрические функции или геометрические фигуры), не обязательно
интересуясь их величиной, а, например, только расположением. Но в Э. м. речь
идет о некоторых конкретных функциях.
Точно так же, например, при определении длины окружности пользуются по
существу понятием предела, но не в общем виде, а для конкретной
последовательности (периметров вписанных и описанных многоугольников).
Вот характеристика, данная Ф. Энгельсом: «Элементарная математика,
математика постоянных величин, движется, по крайней мере в общем и целом, внутри
границ формальной логики;...» (Ф. Энгельс, Анти-Дюринг, Госполитиздат,
М., 1957, стр. 127). Общие понятия функции, предела, кривой, поверхности,
фигуры, не заданной каким-либо конкретным построением, выходят за пределы Э, м.
ЭЛЕМЕНТАРНЫЕ ДЕЛИТЕЛИ квадратной матрицы (см.)
ЛН|«Ы1?
-—степени двучленов (λ — λ χ)Ρι , (λ — λ2)Ρζ, . . ., (λ — ?.s )ps, получающихся из
характеристического уравнения (см.):
Δ(λ)=
λ — αη — α12 ... — aln
— CL21\ — α22 · · · — <*2П
αΠ\ #Л2 · · · λ аПП
= 0
следующим образом. Любой минор £-го порядка определителя Δ (λ) является
многочленом относительно λ. Пусть D^ (λ) — наибольший общий делитель всех
таких многочленов £>«(λ)=Δ(λ). Каждый последующий многочлен в
последовательности D0(X)==1, D1(k)i £>2(λ), . . ., Αι(λ)=Δ(λ) делится нацело на
предыдущий. Такие частные разложим на множители в поле комплексных чисел:
°"(λ) =(λ _λ')«. (λ -νΎ,,
Dn-ЛЦ
D0 (λ)
(λ —//)«. (λ — }"γ-.

эллипс
525
Степени (λ —λ')α\ (λ —λ")°2, . . ., (λ — λ')*1, (λ —λ")62 и образуют полную
систему Э. д. матрицы А (степени с нулевыми показателями исключаются).
Произведение Э. д. равно характеристическому многочлену. Э. д. определяют
жорданову форму матрицы (см.) А.
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ — класс функций, включающий в себя
многочлены, рациональные функции, показательные, степенные, логарифмические к
тригонометрические функции, обратные тригонометрические функции (см.), а
также функции, получающиеся из перечисленных с помощью четырех арифметических
действий и суперпозиций (образование сложной функции, см.), примененных
конечное число раз.
X* X -—X
* -8 , * + е
Например, у= —:— , у=спл;= и т. д.
sin 4х 2
Класс Э. ф. хорошо изучен и часто применяется в прикладной математике.
Производная от Э. ф. всегда является Э. ф., однако интеграл от Э. ф. может уже
не являться Э. ф.
ЭЛЛИПС — геометрическое место точек плоскости а, для каждой из которых
сумма расстояний до двух данных точек F, и F2" лежащих в а, есть величина
постоянная, большая, чем расстояние между FY и F2* и равная данному числу
2а (или отрезку 2а). Точки Fj и F2 называются фокусами Э. Расстояние между
фокусами, обозначаемое через 2с, называется фокальным. Данное число (отрезок)
2а называется большой осью.
Э. можно начертить так. Взяв нерастяжимую нить ^ ^м
длиной 2а, закрепим ее концы в точках Fx и F2 (рис. ^'^
324). Затем, натянув эту нить острием карандаша, будем /'
двигать острие карандаша по бумаге. Траектория дви- / / \ \
жения острия карандаша и опишет замкнутую кри- \ <г * )
вую — Э., для которой MFi -fMF2=2α, отрезки MFt \ F, Fz ι
и MF» называются фокальными радиусами. ч /
Каноническое (простейшее) уравнение Э. в прямо- ччч +*'
угольных декартовых координатах имеет вид: ^
ί! . ^!_ι Р»с. 324
а2+Ь*~1*
где 62 = а2— с2. Число (отрезок) 2Ь называется малой осью Э.
х2 у2
Из уравнения Э. вытекает, что — < 1 и -г- < 1. Отсюда следует, что
координаты точек эллипса удовлетворяют условиям | jc|'<a и \y\<bt т. е. Э.
расположен внутри прямоугольника со сторонами 2а и 2Ь. Из уравнения Э. также
следует, что Э. имеет центр и две оси симметрии.
с
Число е— — называется эксцентриситетом Э. Для Э. всегда е <1. Если
F^Fz (фокусы совпадают), то Э. вырождается в окружность, для которой
совпадающие фокусы являются центром, а эксцентриситет е—О (так как при этом с=0).
Параметрические уравнения Э. имеют вид x=acost и у=bsin/, которые
легко усматриваются из рис. 325: если отрезок постоянной длины скользит своими
концами по двум взаимно перпендикулярным прямым, то точка Μ этого отрезка
опишет Э. Если точку Μ взять на продолжении отрезка АВ (на рисунке точка /С),
то описываемая ею кривая будет также Э. На указанном свойстве построен
эллиптический циркуль (см.)— прибор, вычерчивающий Э. с различными осями.
Если спроектировать какую-либо окружность на плоскость, не
перпендикулярную и не параллельную плоскости окружности, то в проекции получится Э.
Если круговой цилиндр пересечь наклонной плоскостью или круговой конус пе-
Зо Толковый словарь математических терминов

526
ЭЛЛИПСОИД
ресечь наклонной плоскостью, имеющей различные общие точки с
противоположными образующими конуса, то в сечении получится Э.
а
Прямые, уравнения которых х=± —, называются директрисами (см.) Э.
е
Касательная t к Э. составляет равные углы с фокальными радиусами,
проведенными в точку касания (рис. 326). Отсюда вытекает, что перпендикуляр /
к касательной в точке касания составляет равные углы с фокальными радиусами.
Это свойство можно истолковать как свойства углов падения и отражения, изу-
Рис. 325
Рис. 326
чаемых в оптике: если точечный источник света поместить в фокусе Fj и луч
света направить на зеркальную поверхность t no FXM, то отраженный луч пойдет
по MF2, т. е. попадет в точку F2. Отсюда происходит и название фокуса (от
лат. focus — очаг, огонь).
Свойства Э. используются в технике в конструкциях некоторых станков, где
имеются зубчатые шестерни эллиптической формы. Траектории движения планет
нашей солнечной системы являются различными Э. Свойства Э. используются
также при изучении законов движения планет — законов Кеплера. Полярное
уравнение Э. имеет вид:
1 — е cos α
где е<\ и ρ — фокальный параметр.
При вращении Э. вокруг одной из его осей получается поверхность 2-го
порядка— эллипсоид (см.) вращения. См. Конические сечения.
Греч, ελλειψις — недостаток, в смысле недостатка эксцентриситета до 1. Для
Э. е<\.
ЭЛЛИПСОИД — один из видов
поверхностей 2-го порядка, каноническое
(простейшее) уравнение которого в прямоугольной
декартовой системе координат имеет вид:
а2+62+с2=1>
где at Ь, с — полуоси Э. Э. имеет центр,
три оси и три плоскости симметрии (рис. 327).
Любое сечение Э. плоскостью есть эллипс
(см.), в частности сечения могут быть и
окружностями (см. Омбилические точки). Э., у
которого все три оси 2а, 26 и 2с различны,
называется трехосным. Если же две оси Э.
одинаковы (2а=26, или 2я=2с, или 26=2с), то Э. называется Э. вращения.
Если все три оси Э. одинаковы (2а=26=2с), то Э. превращается в сферу.
Греч, ελλειψις — недостаток, опущение, είδος — вид.

ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
527
ЭЛЛИПСОИДАЛЬНЫЕ КООРДИНАТЫ — координаты, связанные с
семейством поверхностей 2-го порядка, которое задается уравнением:
ха у2 22
+ —-— 4- =1 (а>Ь>с>0); (*)
при этом каждой фиксированной точке Р(х, у, ζ) отвечают три различных
значения λ, μ, ν величины Θ, удовлетворяющие уравнению (*). Э. к. точки Ρ
называются числа α, β, γ, связанные с λ, μ, ν соотношениями:
λ=— (α сп α)2 — (6sna)2, μ= — (a en β)2 — (b sn β)2, ν= — (a en γ)2 — (b sn yf.
где sn α и en a — эллиптические функции (см.) Якоби. Э. к. находят применение
в различных задачах математической физики. Э. к. называются также
эллиптическими координатами в пространстве.
ЭЛЛИПТИЧЕСКАЯ ГЕОМЕТРИЯ — то же, что Римана геометрия (см.).
ЭЛЛИПТИЧЕСКАЯ ТОЧКА поверхности — точка, в которой главные
кривизны (см.) положительны. Индикатриса (см.) Дюпена в такой точке есть эллипс.
Если главные кривизны равны между собой, то индикатриса есть окружность,
а Э. т. называется омбилической точкой или точкой округления. Справедлива
теорема о том, что поверхность, каждая точка которой омбилическая, есть сфера.
В окрестности Э. т. поверхность расположена по одну сторону от касательной
плоскости в этой точке (в малом).
ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ — интегралы вида:
JV'a'. Vax*+bxu+cx+d) dx, Jtf (χ, V ax*+bx3+cx2+dx+c ) dx,
где R — рациональная функция своих аргументов. Эти интегралы, как правило,
не берутся в элементарных функциях; если же они могут быть вычислены в
элементарных функциях, то их называют псевдоэллиптическими. Все Э. и. с
помощью элементарных подстановок (с точностью до слагаемых, выражающихся
в конечном виде) приводятся к следующим трем стандартным интегралам:
гЧг
J |/(1-г2)(1-*222) ' J ■
V [\— г2)(1— £2г2) J V(\ — г2)(1 — £2z2)
dz
ί
(l+hz2)V (1 — ζ2)(1 — k2z2)
(0</Κ1).
Как показал Лиувилль, эти интегралы уже не берутся в конечном виде. Лежандр
назвал их Э. и. соответственно первого, второго и третьего рода. Первые два
зависят лишь от k, а третий еще от одного, вообще говоря, комплексного
параметра h. Они могут быть записаны также в форме Лежандра:
Если фиксировать произвольные постоянные параметра k, содержащиеся в двух
первых интегралах, потребовав, чтобы при φ=0 эти параметры обращались в нуль,
то получим вполне определенные функции F (k, φ) и E(k, φ). Эти функции
глубоко изучены и играют очень важную роль в анализе и его приложениях. При
тс
<р= — Э. и. Лежандра F (k) и E(k) называют полными.
Лит.: Г. М. Фихтенгольц, Курс дифференциального и интегрального исчисления,
II, III, Фнзматгиз, М., 19G3.
35*

528
ЭЛЛИПТИЧЕСКИЕ КООРДИНАТЫ
ЭЛЛИПТИЧЕСКИЕ КООРДИНАТЫ — координаты, связанные с семейством
софокусных эллипсов и гипербол. Э. к. и, υ точки Μ связаны с ее декартовыми
координатами хи у соотношениями: x=b chu cos υ, y—bshusinu. Э. к. можно
рассматривать как частный случай эллипсоидальных координат; они широко
используются в математике, физике, технике.
ЭЛЛИПТИЧЕСКИЕ ФУНКЦИИ представляют собой двоякопериодические
мероморфные функции, т. е. такие мероморфные функции /(г), для которых оба
основных периода τ и τ' отличны от нуля (см. Периодические функции), все их
периоды имеют вид: Т=п х-\-п' %' (п, п' = 0, ±1, ±2, . . .). Так как по теореме
τ
Абеля (см.) отношение — не может быть действительным, то начало координат О
и точки комплексной плоскости τ, τ' и τ-{-τ' являются вершинами
невырожденного параллелограмма; этот параллелограмм и каждый конгруэнтный (см.) ему
называют параллелограммом периодов.
Любая рациональная комбинация R(flt . . ., fn) Э. φ. с периодами τ и τ'
является тоже периодической функцией с периодами τ и τ'; это же верно и для
производной эллиптической функции.
ЭЛЛИПТИЧЕСКИЙ ПАРАБОЛОИД — поверхность 2-го порядка, простейшее
уравнение которой в прямоугольных декартовых координатах имеет вид:
х2 У2 Λ
—-{-—=22
Ρ Я
(постоянные величины р, q>0 называются параметрами Э. п.).
Э. п. имеет форму, изображенную на рис. 328.
Сечение Э. п. плоскостями z—ht параллельными
плоскости хОу> есть подобные эллипсы, проекция
которых на плоскость хОу имеет уравнение:
р q ar b2
где a=y 2ph, b=y2qh. Плоскости xOz и yOz
пересекают Э. п. по параболам я2=2рг и y2=2qz
(главные параболы), с параметрами ρ и q осью Oz.
Если p—qt то Э. п. называется параболоидом
вращения. Он получается вращением параболы вокруг
Рис. 328 ее оси. Параболическое зеркало, образованное
вращением дуги параболы вокруг оси, обладает тем
свойством, что если поместить источник света в фокусе, то отраженные от
зеркальной поверхности лучи будут параллельны, что используется в прожекторных
установках.
См. также Параболоиды.
ЭЛЛИПТИЧЕСКИЙ ЦИЛИНДР —одна из поверхностей 2-го порядка,
простейшее уравнение которой в прямоугольных декартовых координатах имеет вид:
х2 у2
02 + Ь2= *
Образующие этого Э. ц. параллельны оси г, а направляющей линией является
эллипс. См. Цилиндр.
ЭЛЛИПТИЧЕСКИЙ ЦИРКУЛЬ —см. Циркуль.
ЭМПИРИЧЕСКИЕ ФОРМУЛЫ — формулы, полученные hj опыта посредством
наблюдения и эксперимента. Имея серию исходных данных xlt x2, . . ., λ'Λ,

эпициклоида
529
в результате эксперимента получают соответствующие этим исходным данным
результаты:
Ух, Уч Уп·
Ставят задачу об отыскании такой функции из некоторого заранее заданного
класса функций, чтобы отклонение этой функции от реальной зависимости было
по возможности мало. Полученная зависимость называется Э. ф. Задача
нахождения Э. ф. неоднозначна. Мерой отклонения функции / (х) от реальной зависимости
η η
считают S1=2lyi—/ (*/) \ или 52=2(Уг—/(**) )2 и τ· Α· Считают Э. φ. более
точной ту, для которой рассматриваемая величина меньше, чем у других.
Противоположностью Э. ф. являются формулы теоретические, полученные
дедуктивным методом при тех или иных допущениях, относящихся к
рассматриваемым величинам.
ЭНДОМОРФИЗМ — отображение в себя множества, сохраняющее
алгебраические операции, заданные в этом множестве. Например, проекция линейного
пространства на некоторое полупространство есть Э. линейного пространства (этот Э.
сохраняет операцию сложения векторов и умножения на число). См. также
Автоморфизм, Изоморфизм, Гомоморфизм.
ЭНТРОПИЯ — одна из термодинамических функций, характеризующих
состояние и возможные изменения состояний материальных систем. Важность понятия Э.
заключается в том, что ее свойства отражают специфические черты теплового
состояния системы. Понятие Э. было введено в 1865 г. Дальнейшее обобщение
понятия Э. получило в статистической физике. В последнее время понятие Э. нашло
широкое применение в теории информации (см.).
Греч, εν — в, τροπή'—превращение.
ЭПИТРОХОИДА — циклоидальная кривая, представляющая собой частный
случай трохоиды (см.).
ЭПИЦИКЛОИДА — плоская кривая, описываемая произвольной точкой Μ
окружности, катящейся без скольжения по другой неподвижной окружности,
имеющей с первой внешнее касание. В зависимости
от соотношения радиусов подвижной и непо- у\
движной окружностей получаются различные
виды Э. Например, если радиусы указанных
окружностей равны, то получим кардиоиду
(см.).
Параметрические уравнения Э. имеют вид:
х = (r+R) cos Θ — /· cos (r+R) —
y=(r+tf)sin9
— rsinUr-f-/?)—1
Рис. 329
где г — радиус подвижной окружности, R —
радиус фиксированной окружности ив — угол,
опирающийся на дугу, концы которой есть
точки касания К и К\ окружностей.
Если /*=/?, то Э. имеет одну дугу (петлю) и называется кардиоидой; если
г=~, то Э. состоит из двух равных дуг; если /·=—, то Э. состоит из η равных

530
ЭПЮР
дуг. На рис. 329 рассмотрен случай, когда г=—. См. также Гипоциклоида.
4
Греч, επί — на, над, τ/υχ,λοξ — круг.
ЭПЮР — двукартинный (комплексный) чертеж пространственной фигуры,
который получается по методу Монжа — методу ортогональных проекций фигуры
на две взаимно ортогональные плоскости: Я (горизонтальную) и V (вертикальную)
с последующим совмещением этих плоскостей. При этом совмещение плоскостей
^ проекций Η и V происходит путем вращения V вокруг
Μ ty оси проекций χ — линии пересечения этих плоскостей.
!/\ На Э. точка, не лежащая на оси проекций и не ле-
уг ι жащая в одной из двух биссектральных плоскостей
yS \ двугранного угла (Я, 1/), изображается двумя точ-
r s ι л ками: горизонтальной ее проекцией Мг и верти-
\™i кальной проекцией М2, т. е. точка Μ проаранава
^ч! на Э. как бы раздваивается (Мг и М2 играют роль
Л^4^ координат точки М). Прямая / общего положения
^ на Э. также изобразится двумя прямыми: горизонталь-
Рис. 330 ной проекцией и вертикальной проекцией (рис. 330).
Э. является менее наглядным изображением
фигуры по сравнению с ее аксонометрической проекцией, или аксонометрией (см.).
См. также Начертательная геометрия.
ЭРАТОСФЕНА РЕШЕТО — один из наиболее древних методов выделения из всех
натуральных чисел («просеивания через решето») простых чисел. Принадлежит
древнегреческому ученому Эратосфену (III в. до н. э.). В Э. р. (как его
применяют теперь), чтобы выделить (просеять) все простые числа до л, выписывают все
натуральные числа от 2 до \ η. Затем, установив простоту числа 2, вычеркивают
каждое второе число, т. е. все числа, кратные двум; тогда первое оставшееся
не вычеркнутым число 3 — простое. После этого вычеркивают каждое третье число,
т. е. все числа, кратные трем; тогда первое оставшееся число 5 — простое, и т. д.
В настоящее время известен ряд «решёт», являющихся усовершенствованием
Э. р.
ЭРГОДИЧЕСКАЯ ТЕОРЕМА: 1°. Э. т. для стационарных вероятностных
процессов (см.) — теорема, устанавливающая условия, при которых средние по
времени от значений процесса χ (t) стремятся к его математическому ожиданию (Μχ(ί)
не зависит от / в силу стационарности процесса), т. е. условия, при которых
с вероятностью, равной единице, справедливо равенство:
Τ
limy j *(*)««-Μ* (/).
Γ-»-οο 0
Эта Э. т. имеет большое значение в статистической физике.
2°. Э. т. для цепей Маркова (см.) — теорема, утверждающая, что при
определенных условиях вероятность некоторого фиксированного исхода я-го испытания
стремится при л->оо к пределу, зависящему только от этого исхода. Эта теорема
впервые установлена русским ученым А. А. Марковым (старшим).
Лит.: Б. В. Г н еде и ко, Курс теории вероятностей, Гостехиздат, М., 1954.
ЭРЛАНГЕНСКАЯ ПРОГРАММА — единый подход к определению различных
геометрий с ючки зрения группы преобразований. Так, евклидова геометрия
определяется (характеризуется) группой движений (см. Группа, Движение), группа
аффинных преобразований определяет (характеризует) аффинную геометрию, группа
проективных преобразований определяет проективную геометрию, группа проектив-

ЭРМИТОВА ФОРМА
531
ных преобразований, переводящих в себя некоторый круг или произвольное
коническое сечение, определяет геометрию Лобачевского, и т. д.
Э. п. была сформулирована немецким математиком Ф. Клейном в лекции,
прочитанной в 1872 г. в университете города Эрлангена (Германия).
Различные геометрии можно также определять с аксиоматической точки зрения.
Лит.: Ф. Клейн, Сравнительное обозрение новейших геометрических исследований
(Эрлангенская программа), сб. «Обоснованиях геометрии», ГИТТЛ, М., 1956; Ф. Клейн,
Элементарная математика с точки зрения высшей, ОНТИ, М.—Л., 1934; Ф. Клейн,
Высшая геометрия, ОНТИ, М.—Л., 1939,
ЭРМИТОВА ФОРМА—выражение вида ^a/^x/x/t, где α/^=α^/(черта
означает комплексную сопряженность). При помощи Э. ф. задается квадрат длины
вектора в комплексном линейном пространстве (следовательно, и углы между
векторами). Теория Э. ф. во многом аналогична теории квадратичных форм. Так,
Э. ф. при помощи унитарных преобразований (см.) приводится к виду:
где λ — вещественные числа. Введена французским ученым Ш. Эрмитом,

я
ЯДРО: 1°. Я. интегрального оператора £(<P)=J&(a:, у) φ (у) dy — функция
*(*. У).
2°. Я. гомоморфизма (см.) — множество элементов кольца или алгебры,
переводящихся данным гомоморфизмом в нуль (в единицу в случае гомоморфизмов групп).
ЯКОБИАН — определитель вида:
дух
дхх
ду2
дхх
дуп
дхх
дух
дх2
ду2
дх2
дуп
дх2
дУг
дхп
ду2
дхп
дуп
дхп
п
где yi—fi(X\, Хо χη), l<i<n — функции, имеющие непрерывные
частные производные в некоторой области Д. Сокращенно Я. обозначается через
D (уь у* уп)
■— = . Название дано по имени немецкого математика Якоби.
D (*ъ *2» · · ·» хп)
Если заданы функции >Ί=/ι (хи х2), y2=f2 Ui, *г). а вместе с ними и
отображение области Δ плоскости хгх2 на область А плоскости уху2% то роль Я. в этом
отображении во многом аналогична роли производной для функции одной
переменной. Так, абсолютное значение Я. в некоторой точке равно коэффициенту
искажения площадей в этой точке. Я. применяется в формулах преобразования
кратных интегралов, например:
Я*(У1. УО^Уа-Я^ГМ*. *2). У2<*1. *.)]|-(У1' У2)]
Δ, Δ
dxxdx2.
D(xu x2)\
Я. находит многочисленные применения в теории неявных функции. Так,
например, для того чтобы явно выразить в окрестности точки Л4(*{\ x\t . . . , х^\
3^1 у^) функции уи уа, . . . , Ут> неявно заданные уравнениями:
Фк(Хг. · · - Хп, Уг Ут)=0 (1<*</я). (**)
требуется, чтобы координаты точки Μ удовлетворяли уравнениям (**) и Я.
— * —2L- в точке Μ был отличен от нуля.
£>()'!, .... Ут)
Для Я. имеет место следующая формула:
Р(г1ч ζ2 гп) Р(уг Уп) JD(zu г2, . . ., гп)
D{yu У2» · · ·> Уп) " ^1*1. · · ·. *л) DUi> -«2, · . ·. Хп) '

ЯКОВКИНА СХЕМЫ
533
ЯКОБИ МНОГОЧЛЕНЫ
Па· *4χ)=
2п-п\
■о-
многочлены, определяемые формулой:
dxn
λ')"α (1 + *)~β f- [(1-х) а+л (l+jc)
Я. м. ортогональны на отрезке (—1,1) относительно веса:
(1-*)»(1+*)β.
Я. м. были введены немецким математиком К. Якоби. Я. м. — частный случай
гипергеометрическои функции (см.). Справедлива следующая формула для Я. м.:
1- й г /» ш 12 2α+β+1 Γ(α+Λ+1)·Γ(β+«+1)
Я. м. используется в теории представлений групп (см.).
Лит.: И. П. Натансон, Конструктивная теория функций, М.—Л., 1949.
ЯКОБИ СИМВОЛ — обобщение Лежандра символа (см.). Я. с. обозначается
— (читается: «символ а по отношению к р» или «символ а над р»). Если а взаим-
Р
но просто с числом Р(р—р1р2 ... Pk)> где pltp2t .... Р/г — простые числа,
то Я. с. определяется как произведение символов Лежандра:
\Р) W W "" \Pk)'
Я. с. применяется как символ Лежандра к вопросу об установлении того, будет ли
число а квадратичным вычетом (см.) но модулю ρ или невычетом.
ЯКОВКИНА СХЕМЫ — схемы деления многочленов и извлечения квадратных
корней из многочленов, разработанные М. В. Яковкиным.
Операция деления с остатком заключается в переходе от делимого к первому
остатку, от первого остатка ко второму и т. д., вплоть до получения в остатке
многочлена степени меньшей, нежели степень делителя. Обычно эти единообразно
повторяемые операции выполняются при помощи так называемого деления углом,
при котором вычисления располагаются так, как это показано на следующем
примере:
__2x5-f-3*4— 2λ:3+7λ:2— 10α:+4
2л:5—4л:4 + 2х3—2л:2
л:3—2л:2-Ь л:—I
2л:2-г-7л:-И0
7x4— 4*3-b9x2— 10л:
~7л'4— 14х3-{-7л:2— 7л:
__1(к3+ 2л:2— Зх+ 4
Юл:3—20a:2-t- Юл:—10
22х2— 13*+14
Согласно Я. с. для нахождения членов неполного частного надо делить старшие
члены промежуточных остатков на старший член делителя, вследствие чего нет
надобности находить сами эти остатки, а достаточно знать лишь их старшие члены.
В применении к выше рассмотренному примеру Я. с. выглядит следующим
образом:
λ:3|2λγ5+3λγ*— 2л:3 4- 7л:2—10*+4
2х2
—χ
1
4л:*— 2л:3 + 2л:2
14л:3 — 7л:2 + 7 χ
20л:2—Юл:-МО
2л:24-7л:+10 Ц 22л:2—13л:-Ц4

534
ЯКОВКИНА СХЕМЫ
Здесь в верхнем левом углу записан старший член делителя, а затем в
столбец выписаны все остальные члены, взятые с противоположным знаком. Делимое
выписано в верхней строке. В нижней строке 2л:2 — старший член частного.
Произведение старшего члена делителя на старший член частного не выписано, так как
оно сократится при вычитании из делимого. Во второй строке выписано
произведение старшего члена частного на остальные члены делителя, взятые с обратным
знаком. Затем делится старший член первого остатка 3jc4+4jc4=7x4 на старший
член делителя, получается второй член частного 1ху и т. д. Остаток 22л:2 — 13л:+
-f-14 получается сложением записанных в столбце подобных членов.
В Я. с. степени χ можно опустить. В частном случае, когда делителем
является двучлен bmxm—b0t Я. с. обобщает известную схему Горкера (см.): из
этого частного случая Я. с. схема Горнера получается при т=\ и Ьт=\.
Схема, аналогичная делению многочленов, М. В. Яковкиным разработана
также и для извлечения квадратных корней из многочленов.
Лит.: М. В. Яковкин, О схеме деления многочленов, «Математика в школе», 1954,
№ 5; С. И. Новоселов, Специальный курс элементарной алгебры, Высшая школа,
М., 1956; М. В. Яковкин, Вычислительные действия над многочленами, Учпедгиз,
М., 1961.

ИМЕННОЙ УКАЗАТЕЛЬ
Абель Н. Г. 5, 8, 40, 63, 91, 151,
182, 204, 396, 450, 473, 529
Абу-ль-Вефа (Абу-ль-Уафа) 444
Адамар Ж. 173
Адаме Д. К. 8, 511
Адлер А. 210
Александров П. С. 39, 455
Анаксагор 72
Андронов А. А. 142
Аньези М. Г. 202
Аполлоний 73, 119, 158, 274, 409
Аристотель 73
Архимед 9, 25, 73, 231,242, 306,464,
510
Арцела 26
Ахмес (Ахмозе) 292
Барамагута 507
Бари Н. К. 66
Баше де Мезериак 207
Безу Э. 31, 32, 153, 166, 285
Бейкер К. Л. 367, 368
Бельтрами Э. 371
Бернулли Д. 389, 391, 434
Бернулли И. 42, 99
Бернулли Я. 33, 41, 44, 141, 189,342,
432, 450, 508, 520
Бернштейн Ф. 138
Бернштейн С. Н. 42,160, 346, 450
Бертран Ж. Л. Ф. 34, 506
Бессель Ф. В. 37, 499
Бетти 38, 454
Бинэ 188, 280
Боголюбов Η. Η. 45, 142, 335
Бойаи Я. (Больаи Я.) 7, 73, 375
Бойль Р. 333
Боль П. 148, 335
Больцано Б. 180, 223, 338, 339
Бомбе л л и Ф. 63
Бор Г. 335, 483
Борель Э. 68, 319, 483
Бороздкин К. Г. 51
Бохнер 335
Брауэр А. 179
Брауэр Л. Э. Я. 135
Брашман Н. Д. 42, 95
Брианшон Ш. 277
БриггГ. (Бриге Г.) 42, 198, 200, 230
Буняковский В. Я. 42, 68, 174, 300
Бурхардт 443
Бхаскара 507
Бэр Р. Л. 43, 149
Бюрги И. 198, 200, 230
Вагнер 453
Валле-Пуссен Ш. Ж. 346
Валлис Д. 231, 409, 516
Ван дер Варден Б. Л. 106, 230
Вандермонд 44, 280
Ванцель П. 468
Варинг Э. 8, 45
Ващенко-Захарченко Μ. Ε. 275
Вега Г. 200
Вейерштрасс К. Т. В. 16,20, 122, 322,
338, 339, 424, 510
Вейль Г. 136, 190, 335, 344, 450, 466
Вивиани 51
Виет Ф. 14, 51, 146, 196,306
Вильсон 51
Винер Н. 149, 417, 428
Виноградов И. М. 51, 81, 299, 507
да Винчи Л. 147
Влакк А. 200
Вольтерра В. 521
Вороной Г. Ф. 136
Вронский Ю. 57, 279
Вышнеградскин И. А. 149
Галёркин Б. Г. 62, 348, 509
Галилей Г. 230
Галуа Э. 62, 63, 91, 137, 388, 450
Гамильтон У. Р. 149, 227
Ганкель Г. 499, 505
Гарриот Т. 122
Гаусс К. Ф. 53, 57, 68, 101, 120, 125,
132, 222, 285, 311, 347, 371, 374,
380, 426, 444, 449, 453, 508, 516
Гвидо Г. 395
Гвына С. 200
Гедель 18, 390
Гейне Э. 68, 319, 340
Гёльдер 68, 218
Гельфанд И. М. 344
Гельфонд А. О. 68, 69, 344, 375, 453
Гервин 375
Герон-Александрийский 73
Герц 393
Гессе Л. О. 74

536
ИМЕННОЙ УКАЗАТЕЛЬ
Гильберт Д. 45, 69, 74, 75, 98, 155,
291, 375, 390, 414, 481
Гиппарх 14
Гиппий Элидский 146
Гиппократ Хиосский 73, 81
Глаголев А. А. 252
Глаголев Н. А. 252
Глейшер 443
Голенищев 292
Голубев В. А. 507
Гольдбах X. 8, 51, 81, 507
Горнер В. Г. 85, 534
Граве Д. А. 367
Грамм И. 86, 279
Грасман Г. 390
Грегори Д. 258
Греффе К. Н. 184, 197
Грин Д. 65, 89, 174, 175, 178, 310,
481
Грунбергер Ф. Ю. 367, 368
Гурвиц А. 91
Гурьев С. Е. 339
Гюльден П. 295, 455
Дазе 443
Даламбер Ж. Л. 15, 92, 174, 186,
260, 339, 379, 429, 477
Данделен 158, 197, 409
Данжуа 132
Дарбу 132
Дарфи 367
Дедекинде Ю. В. 9, 97, 137, 223, 242,
339 510
Дезарг Ж. 73, 98, 161, 231, 328
Декарт Р. 14, 53, 99, 108, 122, 300,
337, 394, 409, 413, 481, 510, 518
Делаир (Делагир) 207
Делоне Б. Н. 136
Демокрит 19, 231
Ден 375
Джонсон У. 306
Дини 488
Диоклес 501
Диофант 104, 146, 222, 479, 507
Дирихле П. Г. Л. 43, 65, 104, 106,
303, 488, 493
Диткин В. А. 277
Дорварт 180
Дуб Д. 417
Дубнов С. Я. 453
Дюпен П. Ш. 130, 527
Дюрер А. 207
Евклид 6, 8, 11, 14, 73, 100, 115, 116,
123, 124, 155, 196, 214, 228, 230,
231, 232, 233, 246, 285, 308, 311,
331, 333, 366, 367, 371, 392, 393,
409, 414, 419, 420, 438, 440, 460,
500, 507, 510
Егоров Д. Ф. 483
Жергон Ж. 118, 121, 190, 328
Жирар А. 122, 285
Жордан 111, 118, 176, 254, 299, 316,
488
Жуковский Η. Ε. 153
Зеельгоф 300
Зенон 19
Зигель 466
Кадацци 453
Казоратти Ф. 424
Кавальери Б. 122, 138, 231
Каган В. Ф. 375, 393, 449, 453
Кантор Г. 11, 138, 223, 226, 242, 247,
314, 510
Капелли 180, 181, 193, 218, 246, 382
Кардано Д. 63, 139, 184
Карно Л. Н. 140, 214
Картан Л. Ж. 190, 344, 374, 393,
425, 450
Кассини Д. Д. 141, 190
Катальди 367
аль-Каши 306
Келдыш М. В. 62, 346
Кеплер И. 122, 149, 231, 404, 527
Килинг 190
Кирилл 415
Кирхер А. 207
Клаузен 81
Клейн Ф. 150, 190, 214, 271, 532
Клеро А. К. 14, 86
Ковалевская С. Ф. 172
Колмогоров А. Н. 42, 66, 149, 343,
346, 417, 428, 450, 452, 453, 476,
483
Коперник 444
Корню 150, 166, 425
Котес 147, 171, 509
Коши О. Л. 8, 15, 43, 68, 172, 173,
174, 180, 188, 205, 238, 239, 260,
280, 340, 350, 429, 480, 483, 491
Крамер Г. 174, 188, 193, 218, 279,
280
Крамп X. 122
Крелле 443
Кристоффель Э. Б. 7, 179, 296
Кронекер Л. 104, 179, 180, 181, 182,
189,193, 218, 256, 279, 352, 382

ИМЕННОЙ УКАЗАТЕЛЬ
537
Крылов Η. Μ. 45, 142
Кулик Я. Ф. 367, 368, 443
Кэлли А. 279
Лаврентьев М. А. 45, 346
Лагерр (Лягерр) 505
Лагранж Ж. Л. 44, 45, 135, 155, 156,
185, 186, 222, 238, 258, 287, 291,
350, 477
Лаплас П. С. 89, 106, 132, 174, 186,
187, 188, 234, 246, 321, 330, 334,
398, 417, 440, 450, 474, 508, 510
Лаптев Г. Ф. 453
Лебег А. 66, 126, 132, 214, 392, 436,
483
Лебег В. 367, 443
Леви-Чивнта 393, 449
Лежандр А. М. 120, 145, 188, 222,
306, 347, 395, 444, 515, 516, 527,
533
Лейбниц Г. В. 67, 108, 122, 133, 153,
189, 236, 258, 279, 280, 300, 306,
309, 369, 476, 480
Левитан 335
Лемер 367
Лемуап Э. М. 121, 190
Ленин В. И. 131, 155, 424
Ли С. 91, 152, 190, 321, 450, 471
Линдеман Ф. 306
Линиик Ю. В. 45
Липшиц Р. 195, 286
Лиссажу 190
Листинг И. Б. 213
Лиувилль Ж. 195, 238, 458, 514, 515
Лобачевский Н. И. 6, 9, 53, 73, 78,
116, 122, 129, 155, 184, 195, 196,
197, 206, 216, 231, 232, 233, 281,
285, 309, 315, 323, 358, 371, 420,
423, 438, 440, 460, 468, 482, 522,
527 531
Лопиталь Г. Ф. 203, 204, 205, 279,
338, 383, 429
Лоран П. А. 59, 204, 260, 327, 397
Лоренц В. А. 190, 207
Ло-шу 207
Лузин Η. Η. 66, 483
Люилье С. 206
Люстерник Л. А. 45, 143
Ляпунов А. М. 142, 149, 303, 334,
343, 450, 477
Магницкий Л. Ф. 200, 318
Маклорен К. 34, 208, 209, 350, 447,
520
Мальцев А. И. 190, 450
Мандль М. 181
Мариотт 333
Марков А. А. 42, 104, 210, 417, 418,
450, 476, 508, 531
Марков В. А. 210
Маскерони Л. 70, 210, 226, 513
Мах Э. 155
Мёбиус А. Ф. 30, 213, 226, 271, 281,
295, 394
Меллинг 276
Менелай Александрийский 140, 213,
214, 216, 457, 506
Менехм 158, 469
Менье Ж. Б. М. Ш. 214
Меньшов Д. Е. 483
Мергелян С. Н. 346
Меркатор Н. 198, 230
Мерсенн М. 214
Меций А. 206, 217, 307
Мизес Р. 450
Микусинский Я. 277
Минковский Г. 104, 218
Мольвейде 225
Мольтепер 201
Монж Г. 73, 130, 155, 453, 530
Мор Г. 70, 210, 226
Морд ель 466
Морер 15
Морзе С. 452
Муавр А. 54, 153, 226, 389, 430
Мэчин Д. 307
Нагель 121, 190, 227
Назаров И. Н. 275
Нейль 234
Нейман Д. (Я.) 149, 234, 499
Немыцкий В. В. 142, 275
Непер Д. (Непир Д.) 198, 200, 230,
237, 292, 444
Никольский С. М. 346
Никомах 480
Никомед 163, 164, 250, 251, 464
Новиков П. С. 12
Норден 452
Ньютон И. 39, 40, 99, 108, 131,
133, 135, 151, 157, 165, 184, 189,
197, 202, 236, 257, 258, 300, 322,
339, 480, 502, 515
Оре 180
О'ру.рк 237
Остроградский М. В. 104, 175, 279,
287, 288, 289, 312, 330
Оутред У. 122

538
ИМЕННОЙ УКАЗАТЕЛЬ
Павлов И. П. 149
Папп 297, 331
Паркурст 200
Парсеваль 297, 488
Паскаль Б. 39, 42, 73, 95, 99, 139,
164, 231, 258, 277, 297, 298, 460,
465, 469, 470, 480
Паш 298
Пеано Д. 118, 230, 350, 511
Пелль 105, 299
Первушин И. М. 299, 300, 367
Петровский И. Г. 142
Петерсон А. М. 453
Пикар Э. 424
Пинтала 298
Питиск Б. 444
Пифагор 22, 72, 73, 105, 142, 307,
308, 409
Плато Ж. А. Ф. 217
Плейфер 8
Плюккер Ю. 311
Полетти Л. 367, 368
Псйа Д. (Г.) 179
Пойгенс 99
Польке 327
Понселе Ж. В. 73, 96, 328, 410
Понтрягин Л. С. 190, 450, 455
Портер Р. 367
Потенот 119, 333
Прокл 331
Птолемей К. 14, 372, 444
Пуанкаре А. 129, 142, 155, 303, 455,
492
Пуассон С. Д. 41, 209, 372, 450, 474
Пфафф И. Ф. 108, 374
Раабе 260
Райнд (Ринд) 292
Райнстейн 452
Рашевский П. К. 449, 453
Региомонтан И. 337, 444, 445
Рейе 161
Рекорд Ф. 122
Ремез Е. Я. 346
Ризе А. 207
Риккати 391
Риман Г. Ф. Б. 15, 66, 102, 132,
174, 188, 196, 231, 232, 233, 276,
391, 392, 393, 423, 431, 449, 460,
474, 476, 528
Ритц В. 62, 348, 394, 510
Риччи-Курбастро Г. 393, 449
Розенберг 443
Роберваль Ж. 99
Родрнг 395
Ролль М. 395
Рош 350
Рудольф X. 122
Рунге 8, 181, 348, 396 510
Руфини П. 396, 473
Рэтик Г. И. 444
Саррюс 11. 398
Серпинский В. 43
Серре 405
Сильвестр Д. Д. 325. 406
Симпсон Т. 147, 161, 219, 347 408
409, 509
Симеон Р. 434
Снелиус В. 119
Соболев С. Л. 261
Сократ 97, 98
Сохоцкий Ю. В. 424, 437
Степанов В. В. 142,'335
Стильтьес Т. И. 132, 392, 431
Стирлинг Д. 26, 34, 44, 431 478 481
Стоке Д. Г. 178, 330, 433, 500 '
Стюарт М. 434
Сунь-цзы 507
Тарталья Н. 63, 139 298
Тейлор Б. 80, 157, 208, 287, 348 350
446, 447, 481, 493
Теэтет Афинский 230
Тоисон У. 201
Торричелли Э. 121, 231, 455, 456
Трикоми 474
Туэ 195, 465
Урысон П. С. 380, 455
Фалес Милетский 71, 72, 478
Фарвархсон А. 200
Федоров Е. С. 91, 478
Фейербах 478
Феллер В. 417
Ферье А. 507
Ферма П. 14, 99, 105, 108, 130, 202
222, 294, 409, 479, 480, 507
Феррари Л. 63
Ферро Д. 63, 139
Фибоначчи Л. 479
Фиников С. Ф. 453
Фредгольм Э. И. 133, 388
Френе Ж. Ф. 183, 405
Фробениус Ф. Г. 149
Фурье Ж. Б. Ж. 20, 66, 75, 245, 283
297, 398, 472, 474, 487, 488, 489,'
490, 491, 521

ИМЕННОЙ УКАЗАТЕЛЬ
539
Хайям О. 298
Хаусдорф Ф. 454, 493
Хевисайд О. 276
Хинчин А. Я. 132, 314, 342, 417,
450, 452, 483
аль-Хорезми 12
ван Цейлен Л. 206, 217, 306, 307
Цермело 214, 223, 458, 497
Цзу Чун-чжи 306
Цинь Цзю-шао 507
Чаплыгин С. А. 503, 509
Чебышев П. Л. 34, 41, 42, 104, ПО,
160, 228, 351, 343, 346, 366, 411,
450, 453, 505, 506, 508
Чева Д. 457, 506
Чарнак 443
Шаль М. 331, 410
Шафаревич И. Р. 63
Шварц Г. А. 261, 301, 327
Шёнеман 179
Шеннон К. 149, 452, 513
Шинцель А. 43
Широков П. А. 449
Шлёмлих 350
Шмидт. О. Ю. 450
Шнирельман Л. Г. 143
Штейнер Я. 70, 191, 410, 513
Штермер К. Ф. 509
Штифель М. 207, 298
Штурм Ж. Ш. Ф. 184, 513, 514
Шур И. 344
Шутен 367
Эйзенлор 292
Эйзенштейн А. 179, 180, 515
Эйлер Л. 14, 15, 27, 34, 44, 51,55, 63,
73, 80, 81, 110, 122, 125, 131, 145,
153, 174, 188, 198, 215, 222, 226
274, 299, 306, 307, 319, 337, 348,
389, 394, 423, 432, 444, 453, 474,
479, 481, 492, 507, 508, 509, 515,
516, 517, 518, 519, 520
Эйнштейн А. 190, 205, 393
Энгельс Ф. 13, 14, 59, 525
Эратосфен 73, 507, 530
Эригон П. 122
Эрмит Ш. 238, 471, 505, 531
Юнг 172, 344
Якоби К. Г. Я. 145, 249, 499, 527,
532 533
Яковкин М. В. 85, 237, 533, 534

Олег Васильевич Манту роз
Юрий Константинович Солнцев
Юрий Исаакович Соркин
Николай Георгиевич Федин
ТОЛКОВЫЙ СЛОВАРЬ
МАТЕМАТИЧЕСКИХ ТЕРМИНОВ
Редактор М. В. Яковкин
Художник Е. П. Леонов
Художественный редактор А. В. Сафонов
Технический редактор В. В. Новоселова
Корректор Т. М. Графоеская
Сдано в набор 15/VIII 1964 г. Подписано к печати
12/IV 1965 г. 60X90V.6. Печ. л. 33.75.
Уч.-изд. л. 40.19. Тираж 102 тыс. экз.
(Пл. 1964 г. N9 159). А04420. Зак. 640.
Издательство «Просвещение» Государственного
комитета Совета Министров РСФСР по печати,
Москва, 3-й проезд Марьиной рощи, 41.
Типография изд-ва «Уральский рабочий»,
Свердловск, проспект Ленина. 49.
Цена без переплета 1 р. 09 к., переплет 15 к.