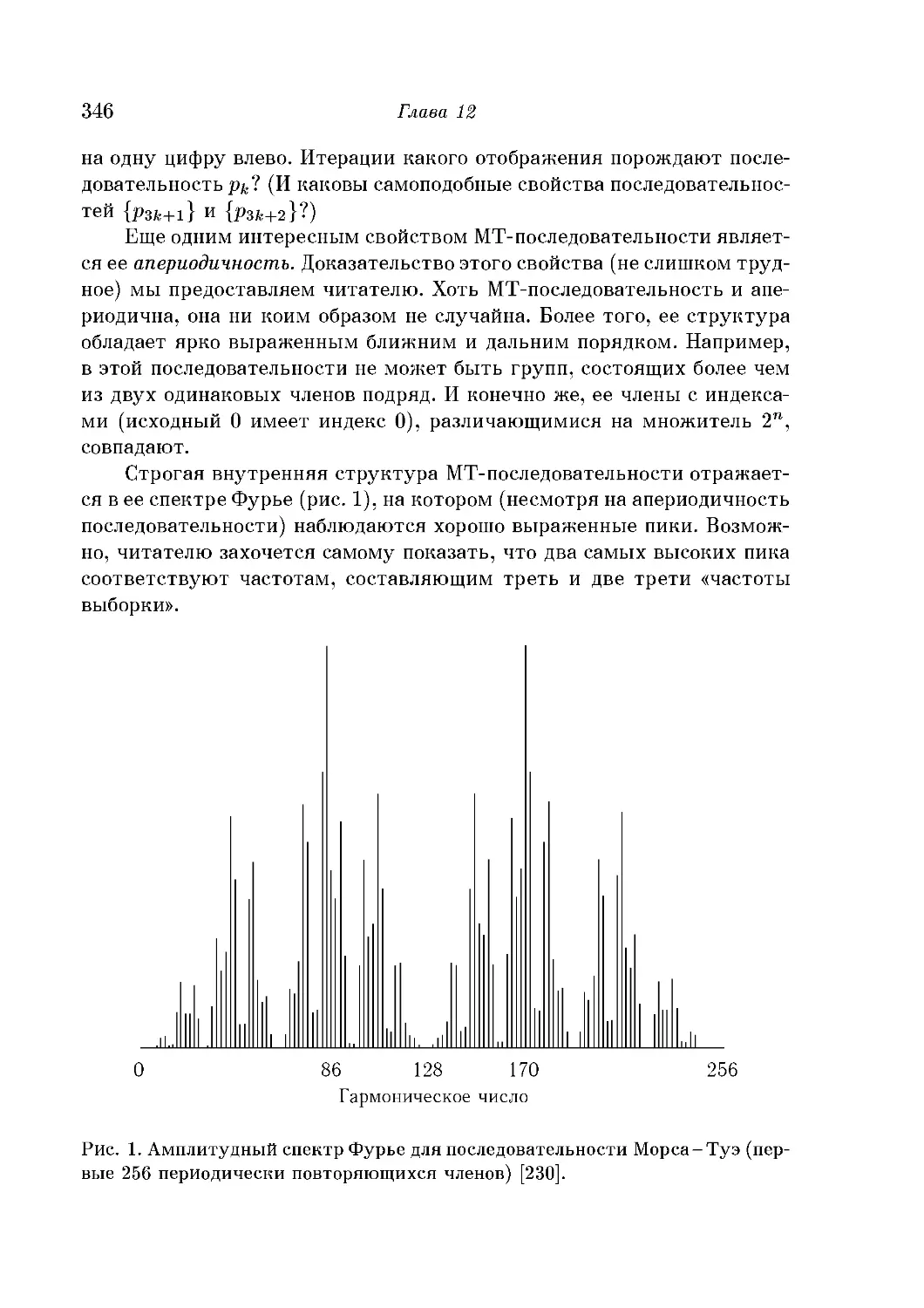
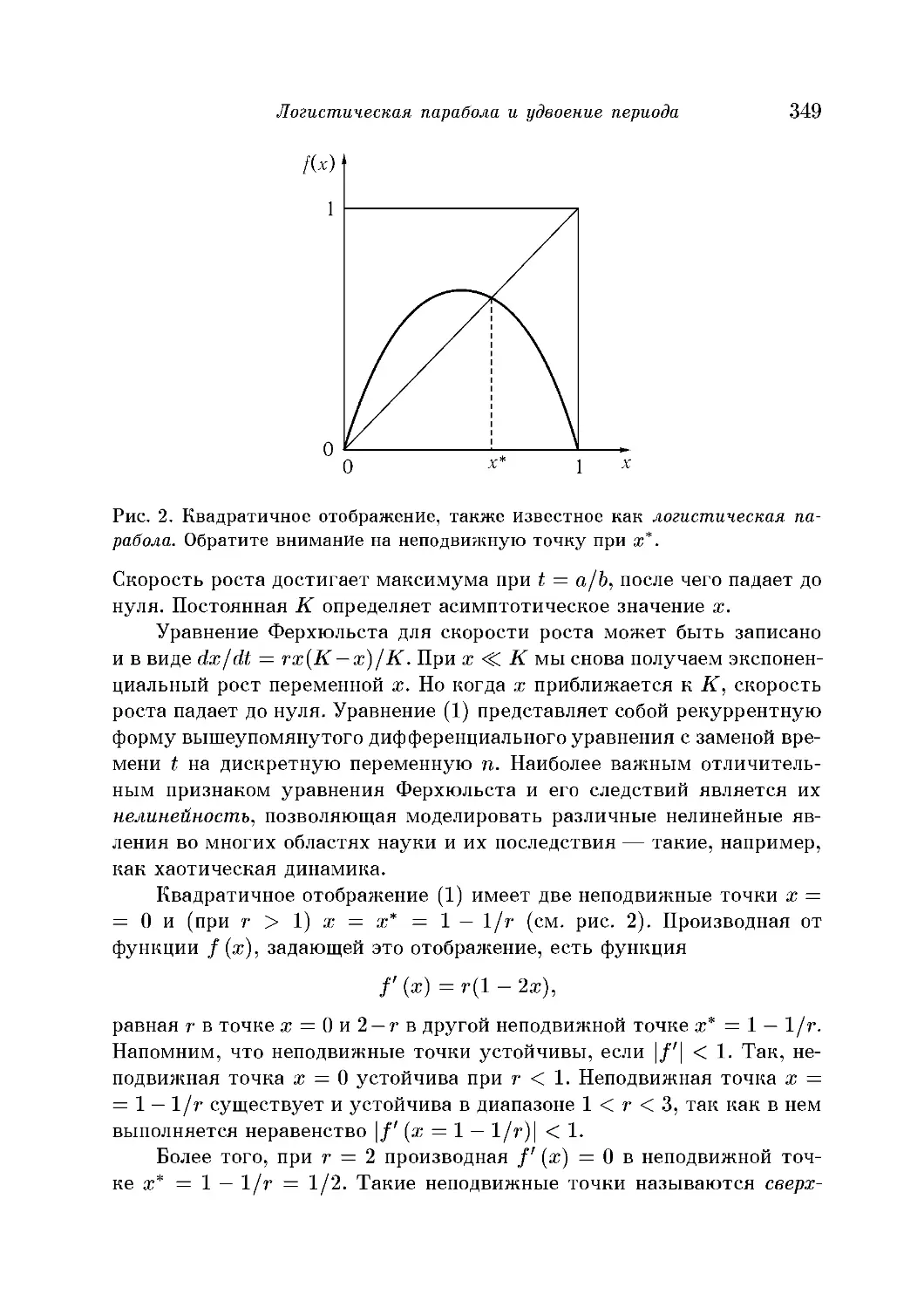
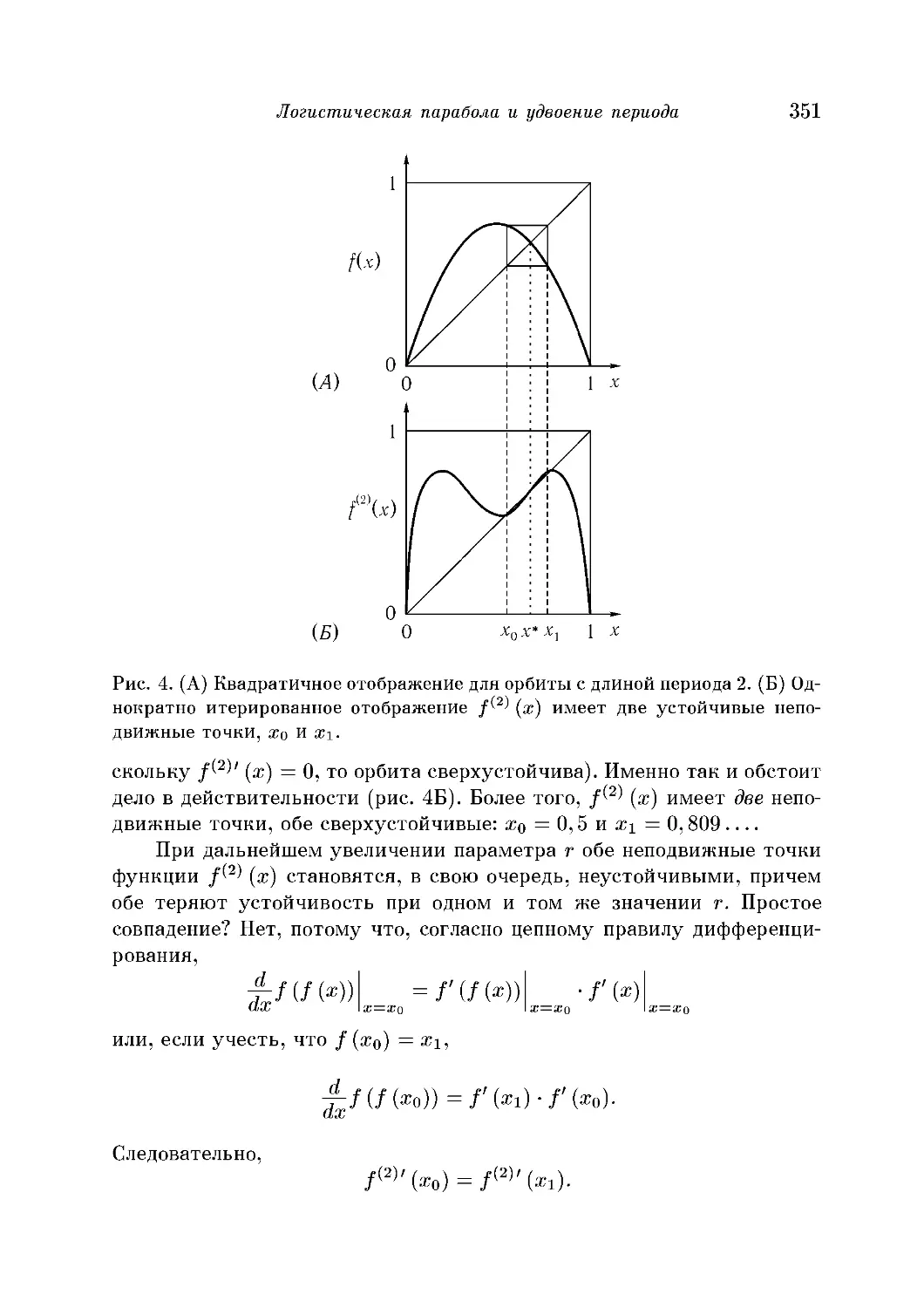
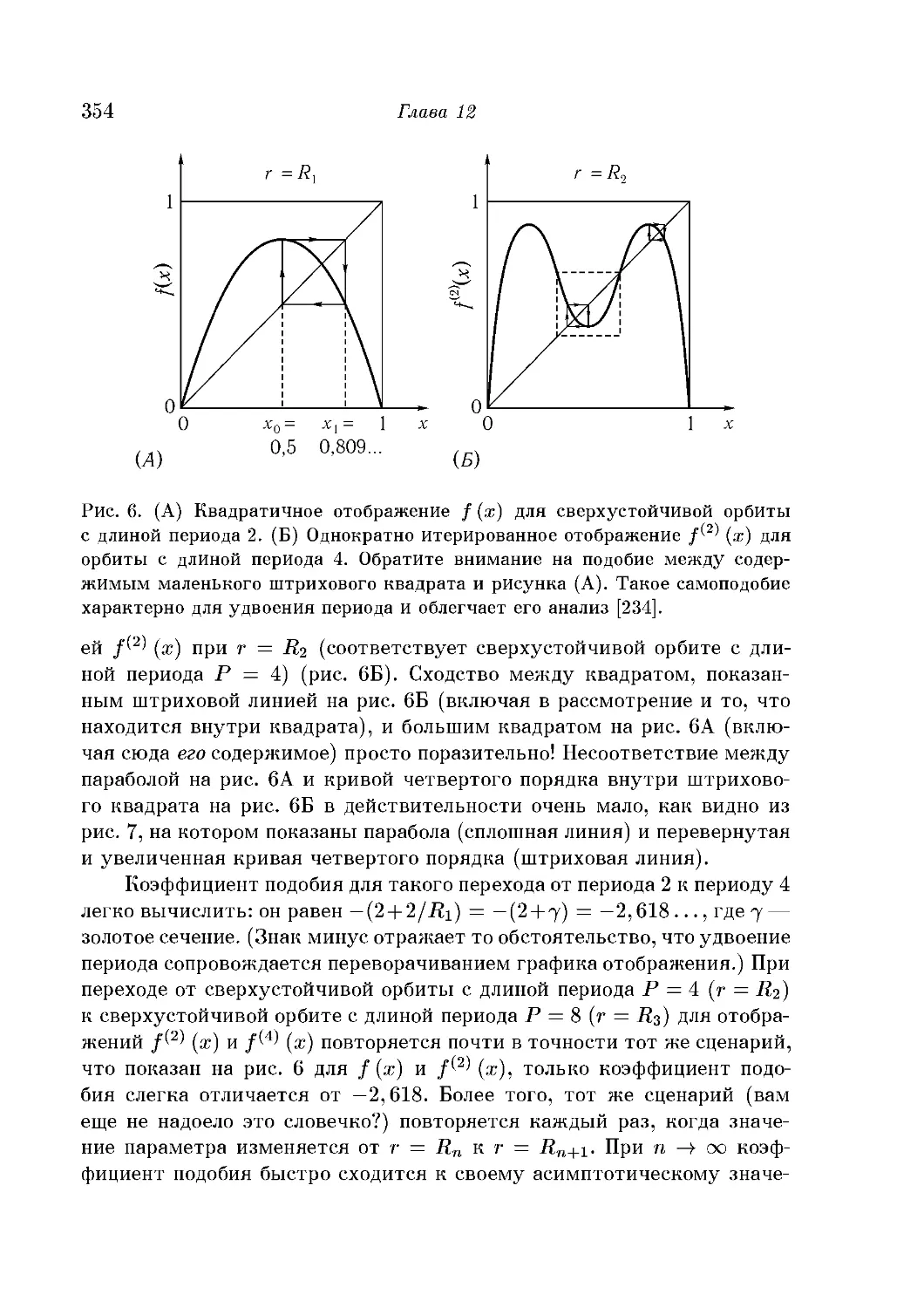
Текст
R&C
Fractals, Chaos,
Power Laws
Minutes from an Infinite Paradise
Manfred Schroeder
W. H. Freeman and Company
New York
М. Шредер
Фракталы, хаос, степенные
законы
Миниатюры из бесконечного рая
Научно-издательский центр
«Регулярная и хаотическая динамика»
2001
УДК 530
Интернет-магазин
http://rcd.ru/shop
Интересующие Вас книги, выпускаемые нашим издательством, дешев-
дешевле и быстрее всего приобрести через наш интернет-магазин. Регистрация в
магазине позволит вам
• приобретать книги по наиболее низким ценам;
• подписаться на регулярную рассылку сообщений о книгах;
• самое быстрое приобретение новых книг до поступления их в магазины.
Шредер М.
Фракталы, хаос, степенные законы. Миниатюры из бесконечного рая. —
Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001, 528 стр.
Основная цель книги — помочь читателю глубже понять, что такое
самоподобие — возможно, наиболее важную из встречающихся в природе
симметрии, а также продемонстрировать широчайший диапазон применений
масштабной инвариантности в физике, химии, биологии, музыке и, в особен-
особенности, в изобразительном искусстве. Материал изложен на доступном уровне
и снабжен множеством иллюстраций.
Книга будет полезна и интересна самому широкому кругу читателей.
ISBN 5-93972-041-2
© Перевод на русский язык
НИЦ «Регулярная и хаотическая динамика», 2001
http://rcd.ru
Георгу Кантору
\
i'v'- •?'•":•'¦-:,-
Никто и никогда не изгонит нас из его рая.
Давид Гильберт, в защиту канторовои теории множеств
Ich sage euch:
man muss noch Chaos in sich haben,
um einen tanzenden Stern gebaren zu konnen.
Ich sage euch:
ihr habt noch Chaos in euch.
Я говорю вам:
нужно носить в себе еще хаос,
чтобы быть в состоянии родить танцующую звезду.
Я говорю вам:
в вас есть еще хаос.
Фридрих Ницше
«Так говорил Заратустра»
(пер. с нем. Ю.М. Антоновского)
Оглавление
Предисловие 15
Глава 1. Введение 23
Эйнштейн, Пифагор и простое подобие 25
Самоподобная расстановка ферзей, не бьющих друг друга ... 28
Самоподобная снежинка 30
Новая размерность для фракталов 32
Самоподобное разбиение и «неевклидов» парадокс 36
У врат канторова рая 40
Ковер Серпинского 41
Игра сэра Пинского и детерминированный хаос 46
Хаос, вызываемый движением трех тел 52
Странные аттракторы, их области притяжения и игра в хаос . 54
Перколяционные случайные фракталы 59
Степенные законы: от Альвареса до Ципфа 63
Итерации Ньютона и упразднение межнациональных границ . 71
Мог ли Минковский услышать форму барабана? 73
Дискретное самоподобие: складки и центральные сгибы .... 80
Золотое и серебряное сечения и гиперболический хаос 85
Как выиграть в фибоначчиев ним 89
Самоподобные последовательности, порождаемые квадратны-
квадратными решетками 93
«Отчаянное пари» Джона Хортона Конуэя 96
Глава 2. Подобие и различие 99
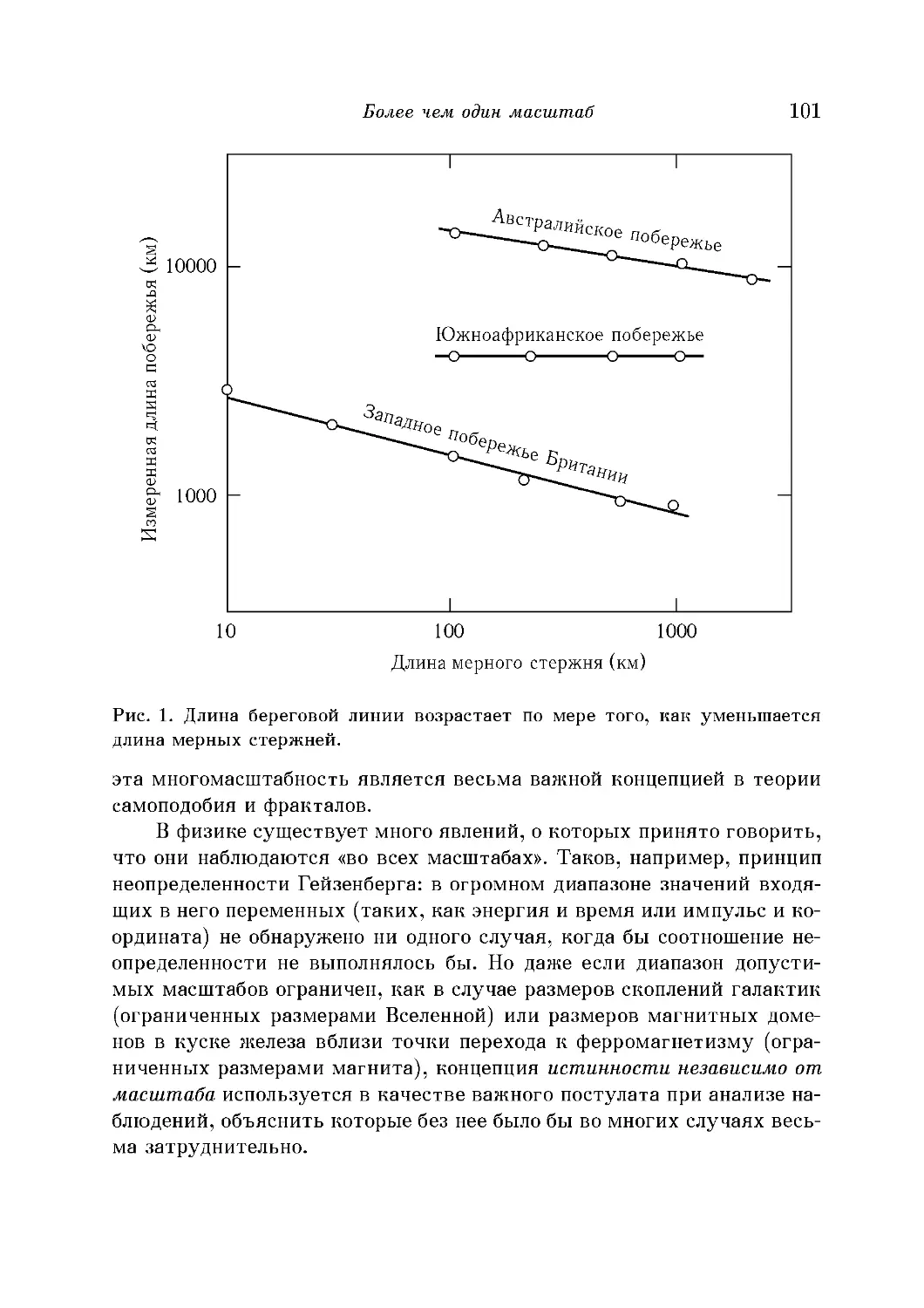
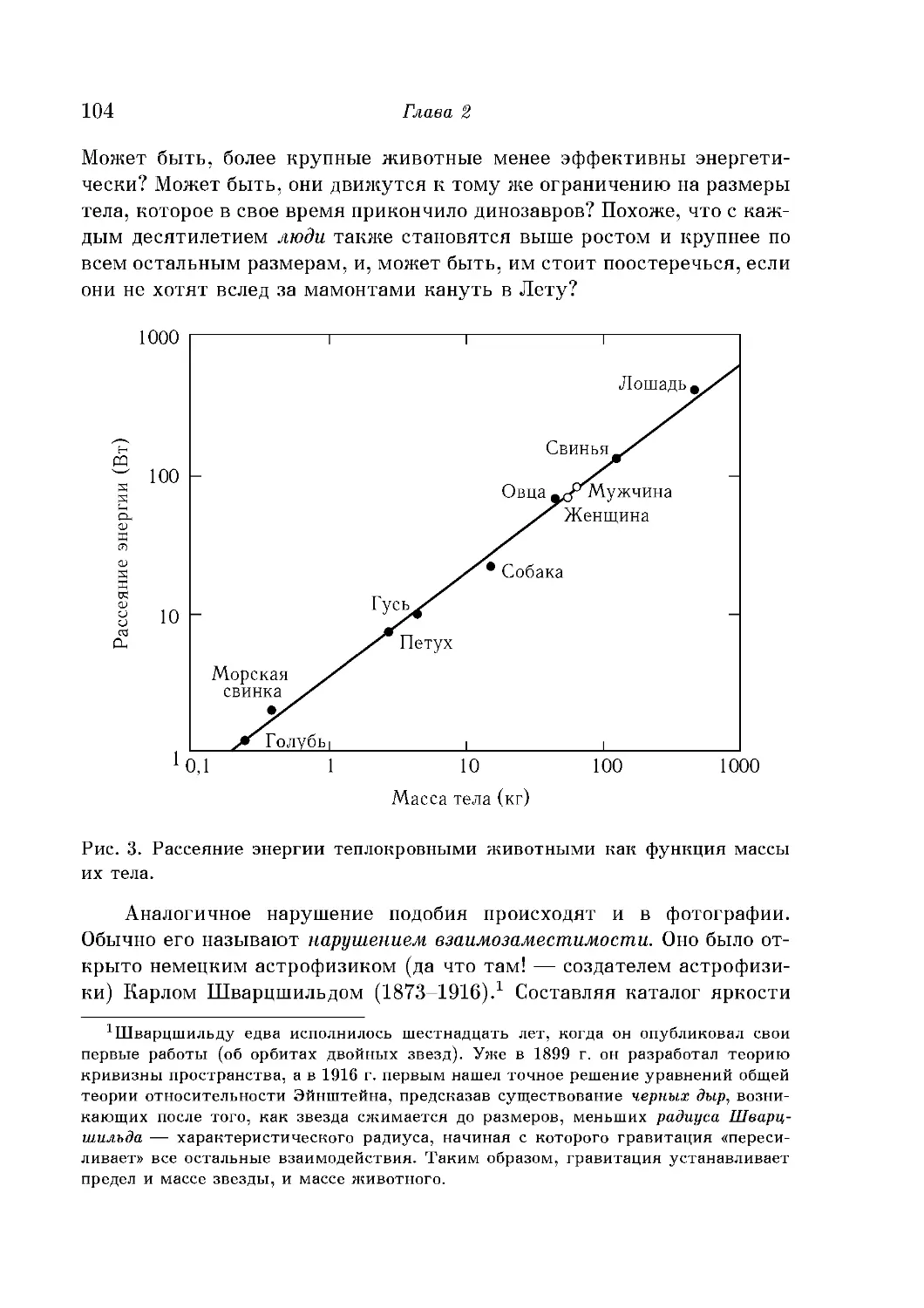
Более чем один масштаб 100
Быть или не быть масштабной инвариантности: немного из
биологии и астрофизики 102
Подобие в физике: некоторые поразительные следствия .... 105
Подобие в концертных залах, микроволнах и гидродинамике . 108
Масштабирование в психологии 111
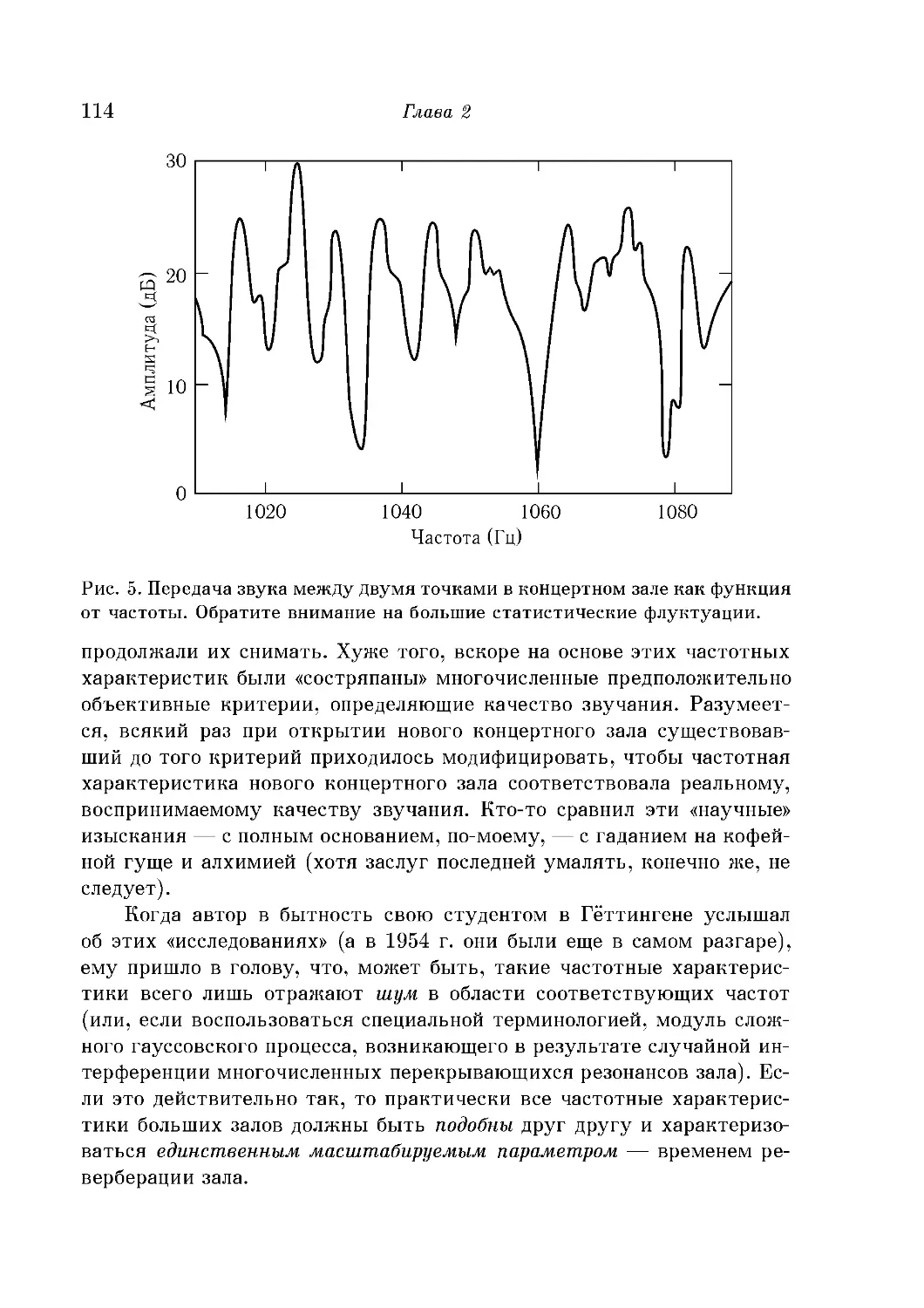
Специалисты по акустике, алхимия и концертные залы .... 113
Предпочтения и несходство: снова о концертных залах .... 115
8 Оглавление
Глава 3. Самоподобие — дискретное, непрерывное, строгое
и всякое другое 124
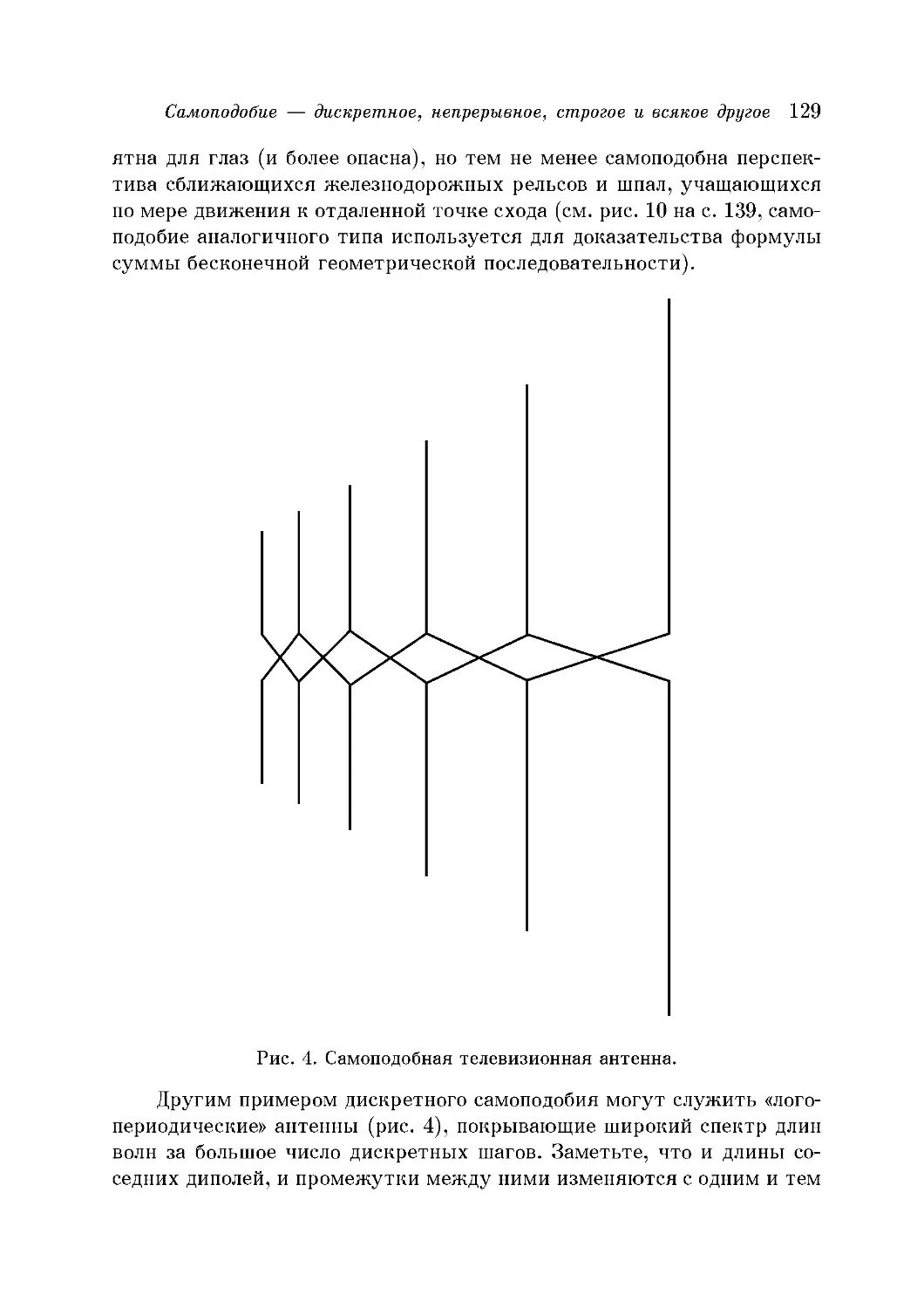
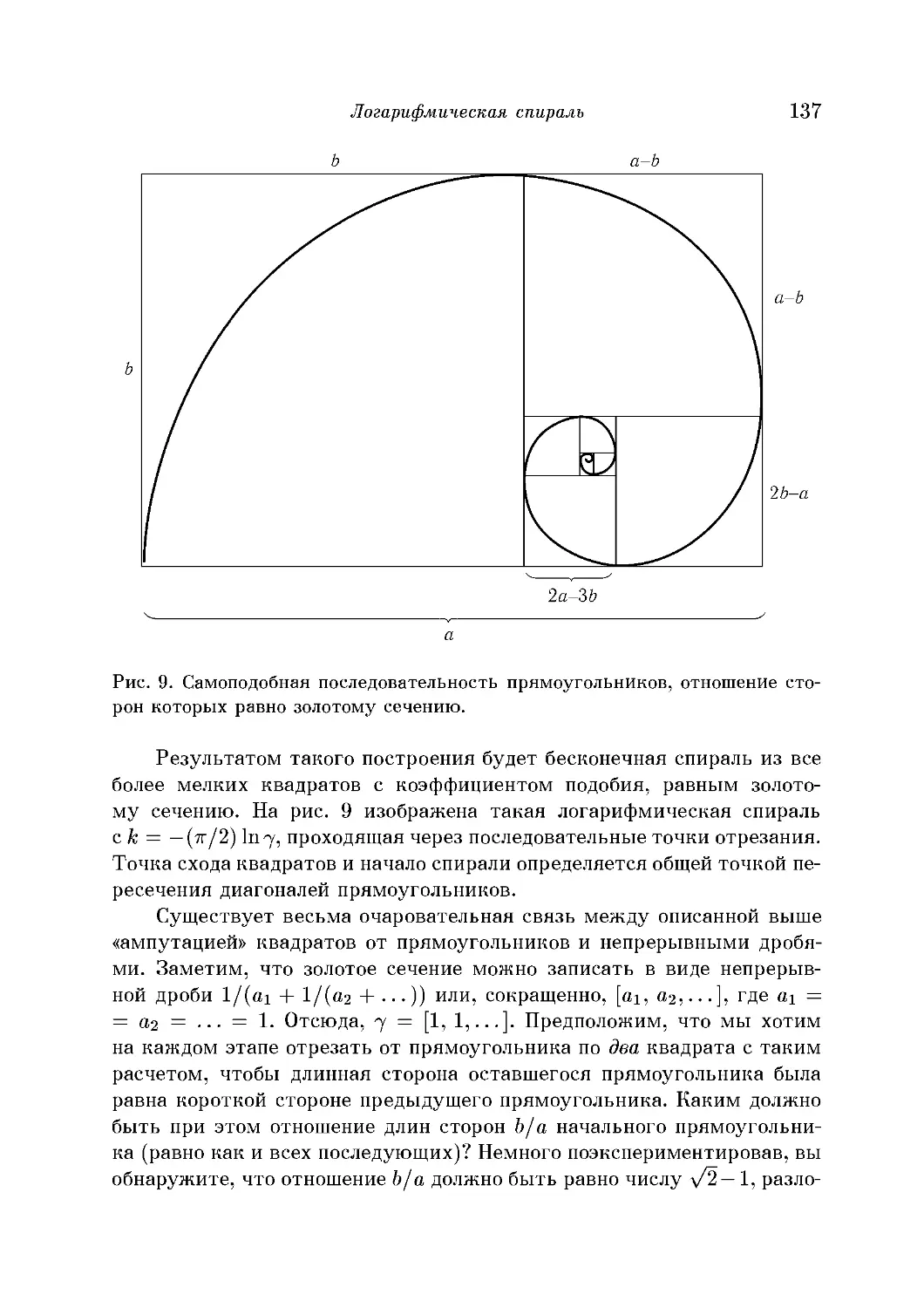
Логарифмическая спираль, режущие инструменты и широко-
широкополосные антенны 132
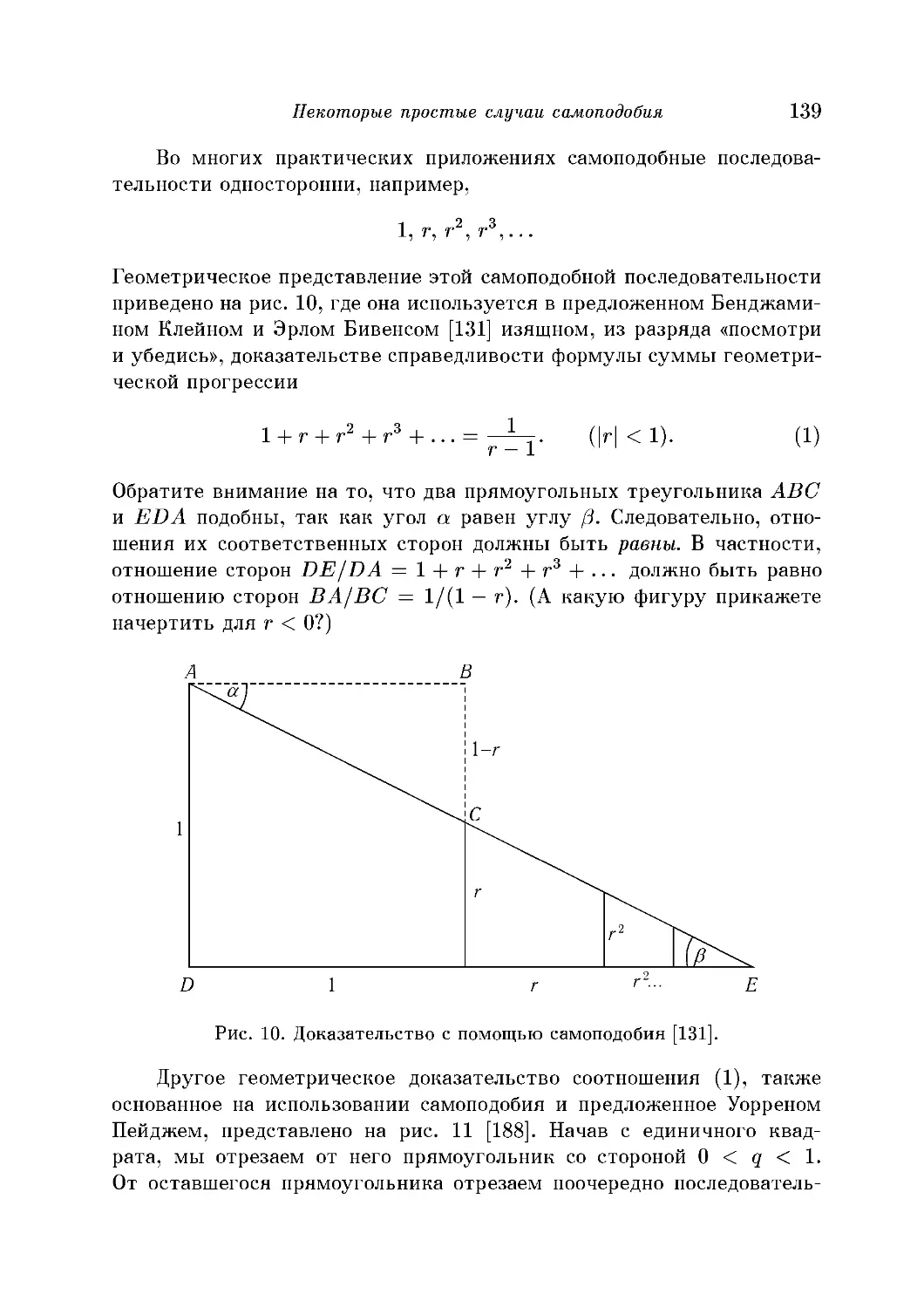
Некоторые простые случаи самоподобия 138
Функции Вейерштрасса и музыкальный парадокс 142
Еще о самоподобии в музыке: темперированный строй Баха . 146
Замечательные соотношения между простыми числами 3, 5 и 7 149
Глава 4. Степенные законы — неисчерпаемый источник
самоподобия 151
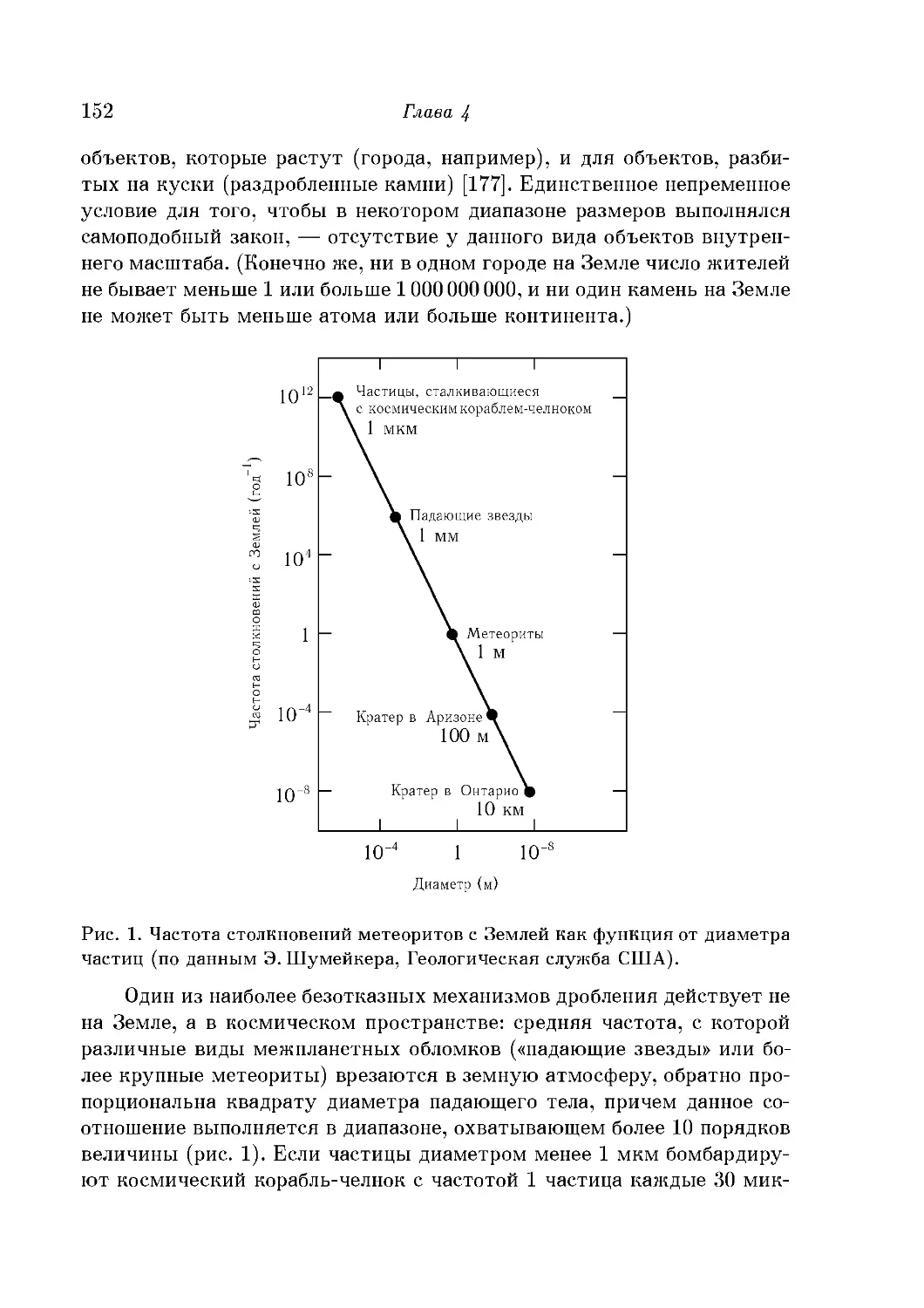
Размеры городов и метеоритов 151
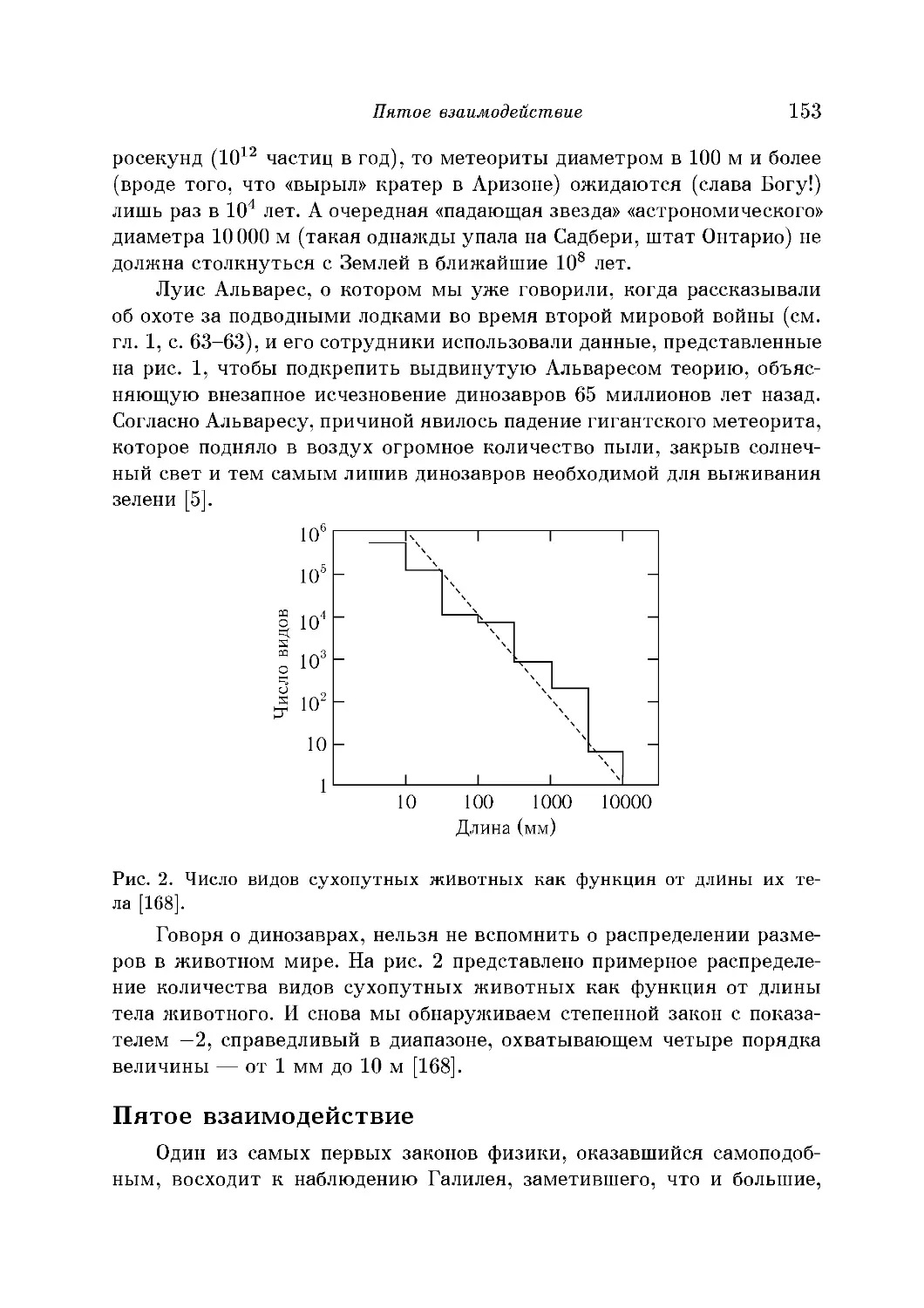
Пятое взаимодействие 153
Независимые от естественных масштабов 155
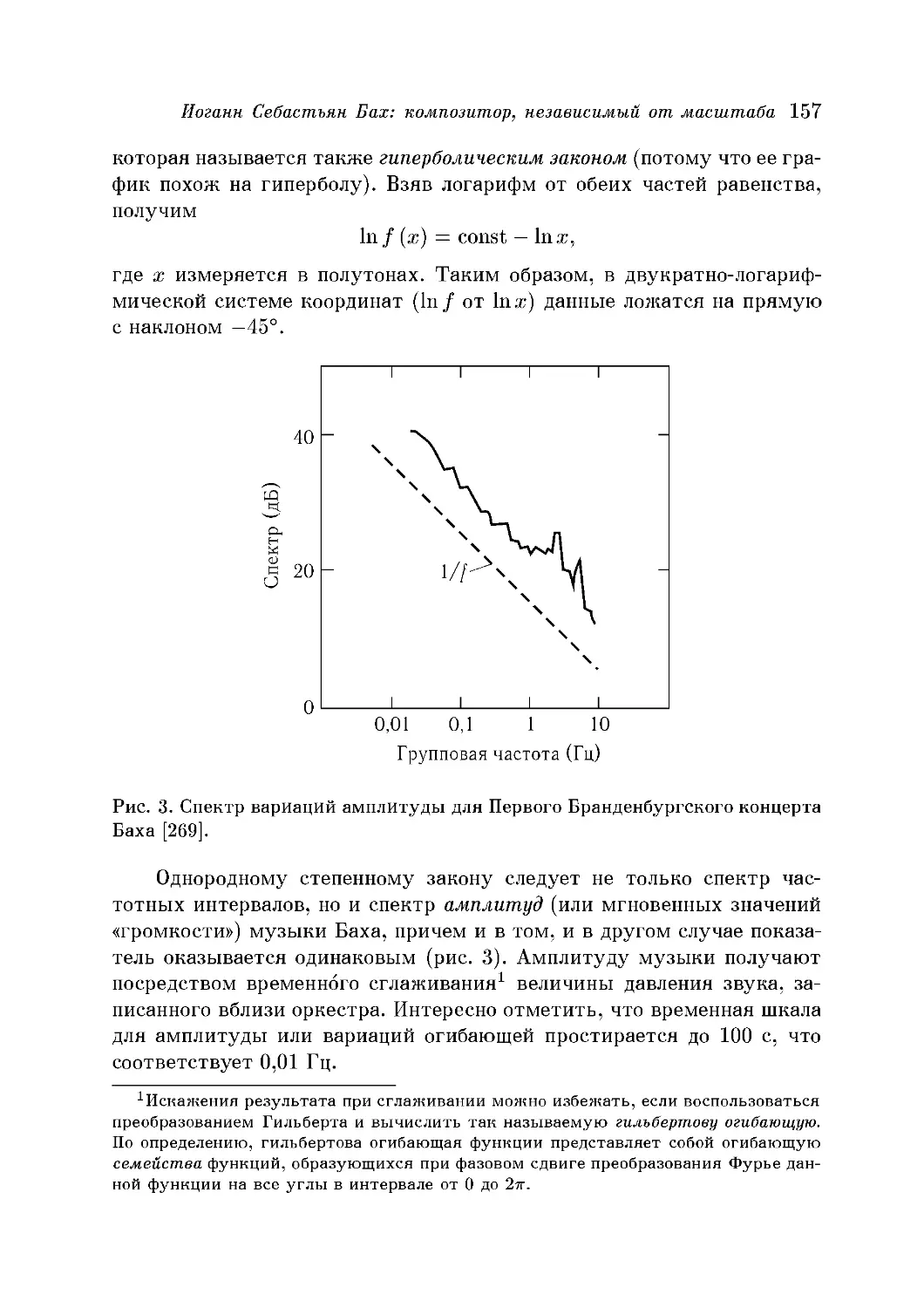
Иоганн Себастьян Бах: композитор, независимый от масштаба 156
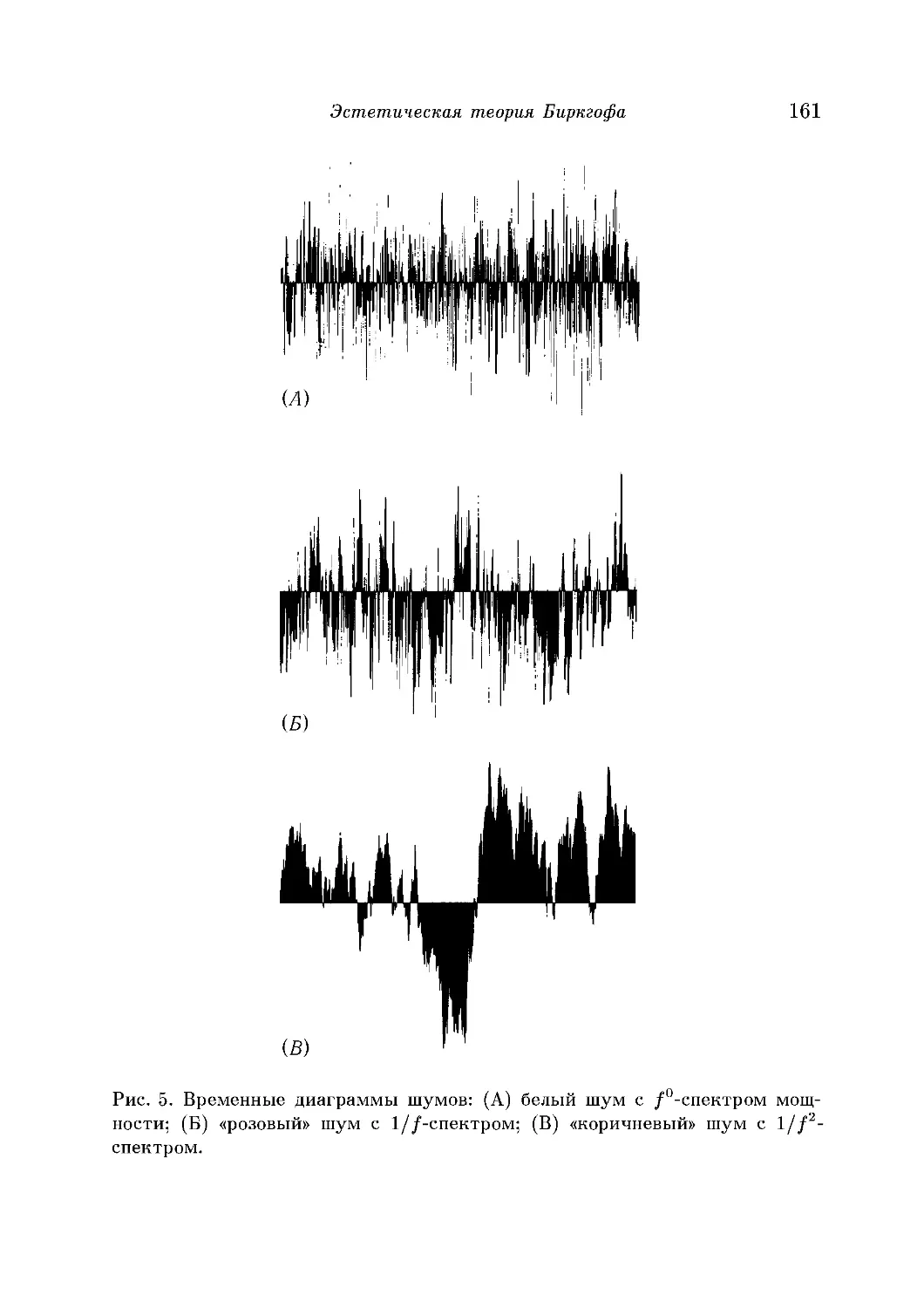
Эстетическая теория Биркгофа 158
Гиперболический принцип неопределенности Гейзенберга . . . 162
Дробные показатели 165
Необычное распределение первого знака 166
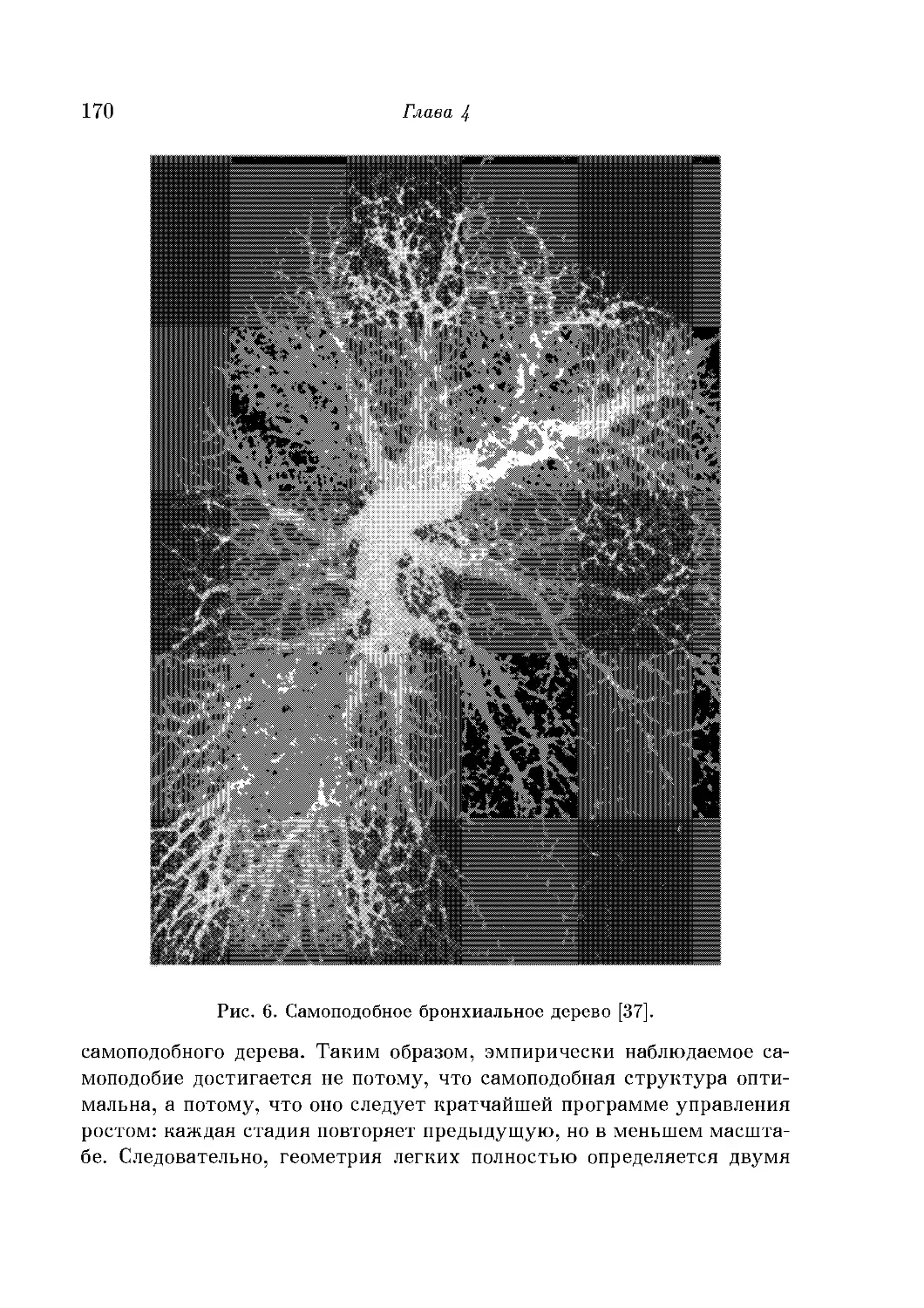
Показатели при поперечных сечениях: деревья, реки, артерии
и легкие 168
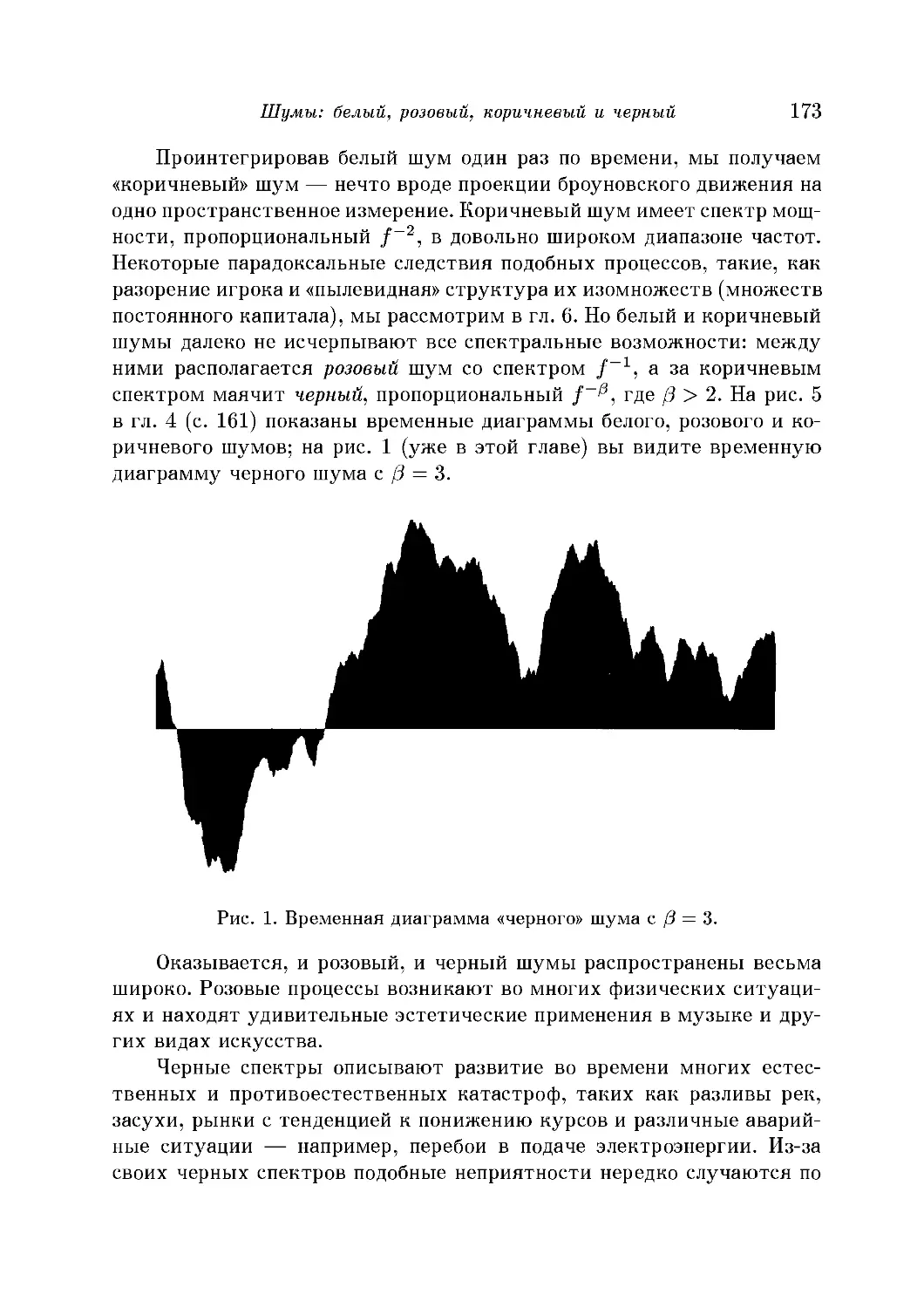
Глава 5. Шумы: белый, розовый, коричневый и черный 172
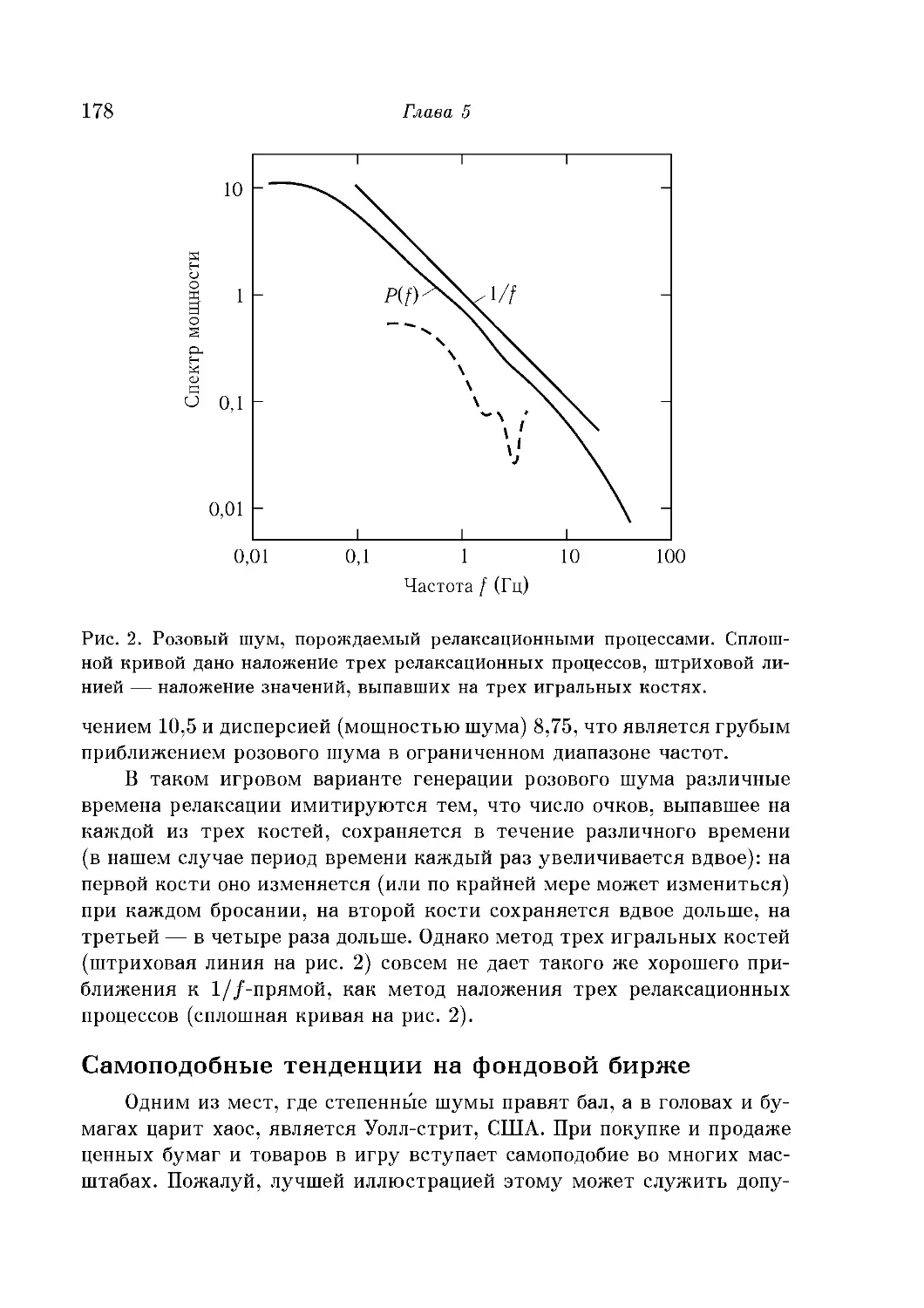
Розовый шум 174
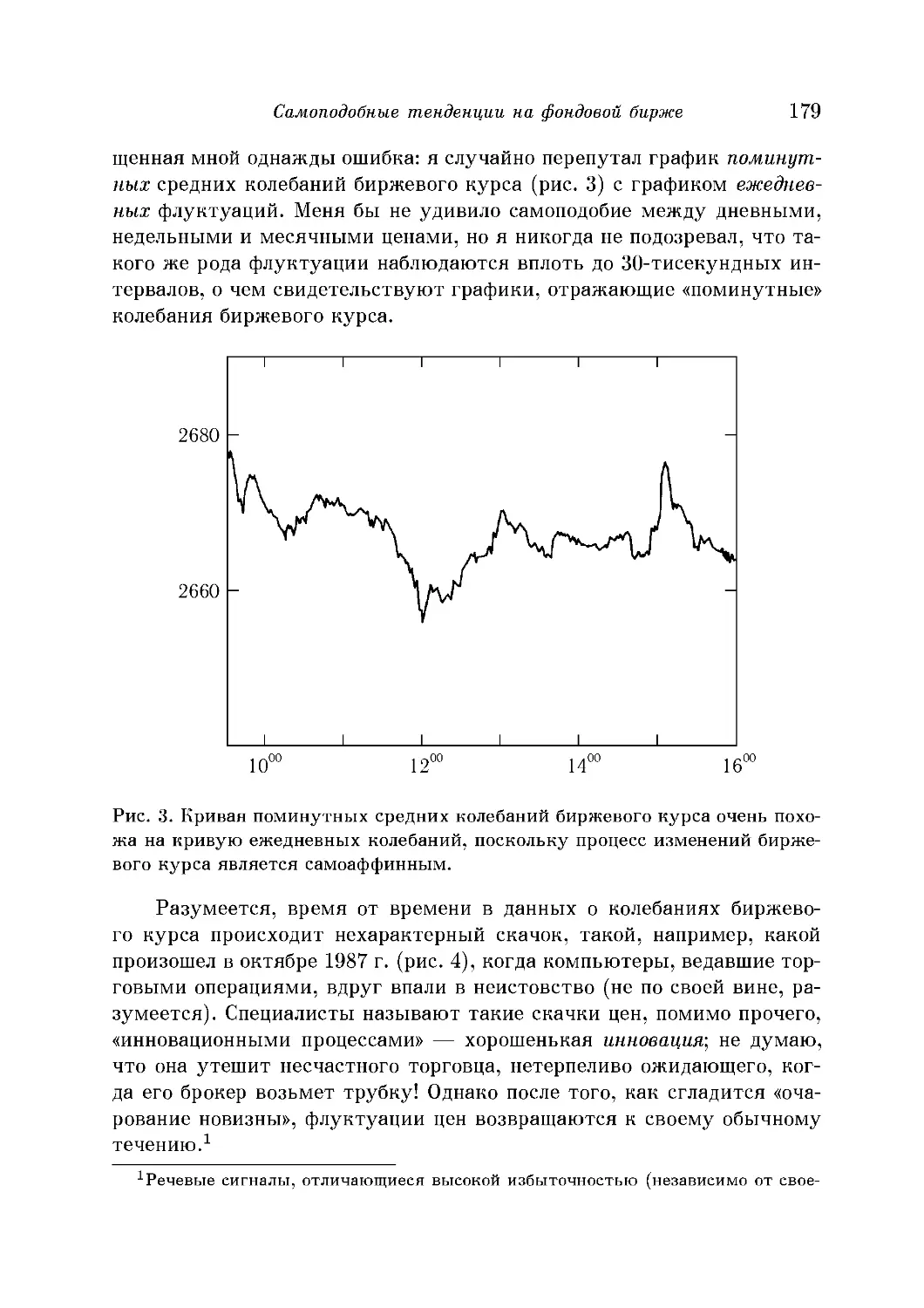
Самоподобные тенденции на фондовой бирже 178
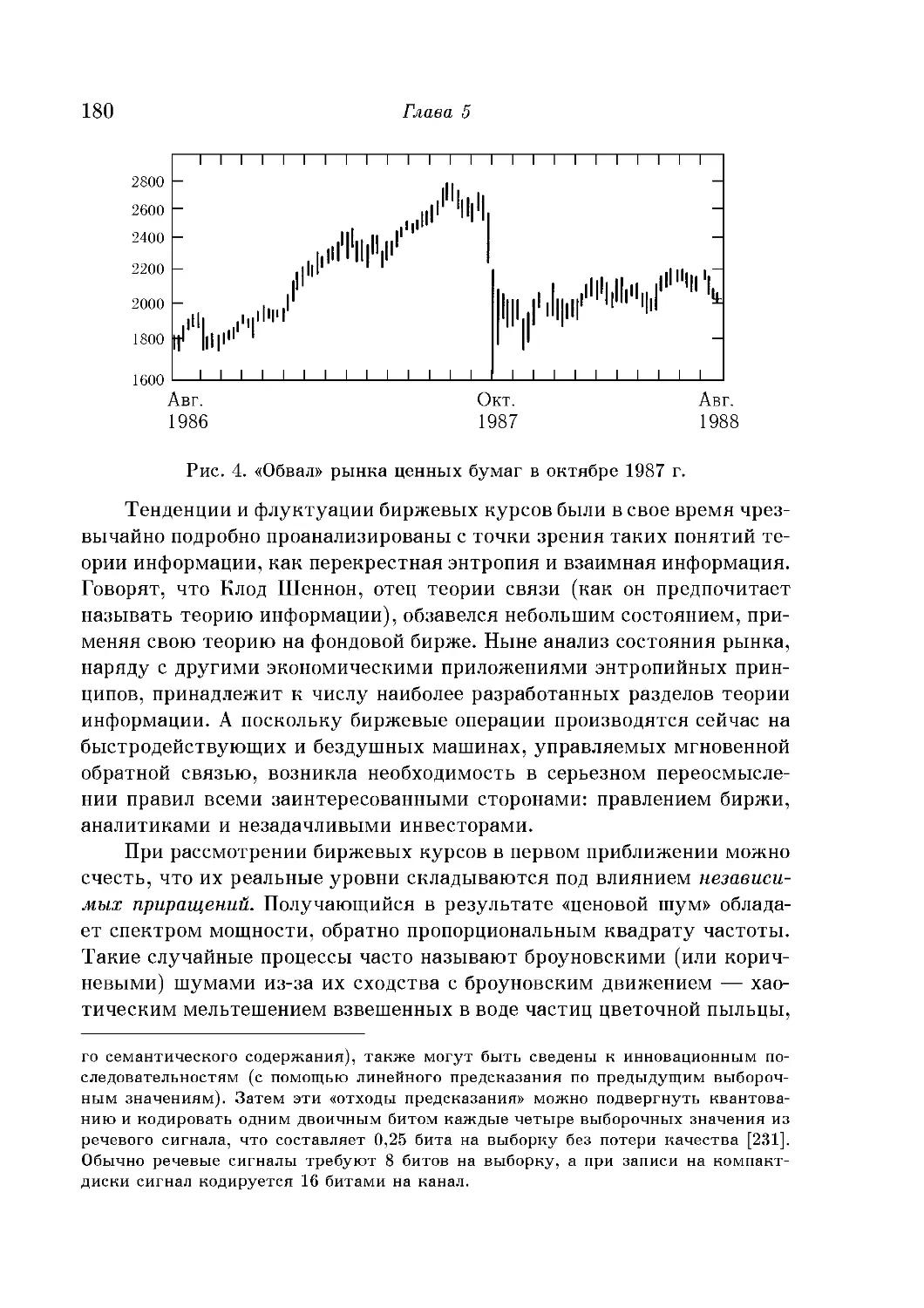
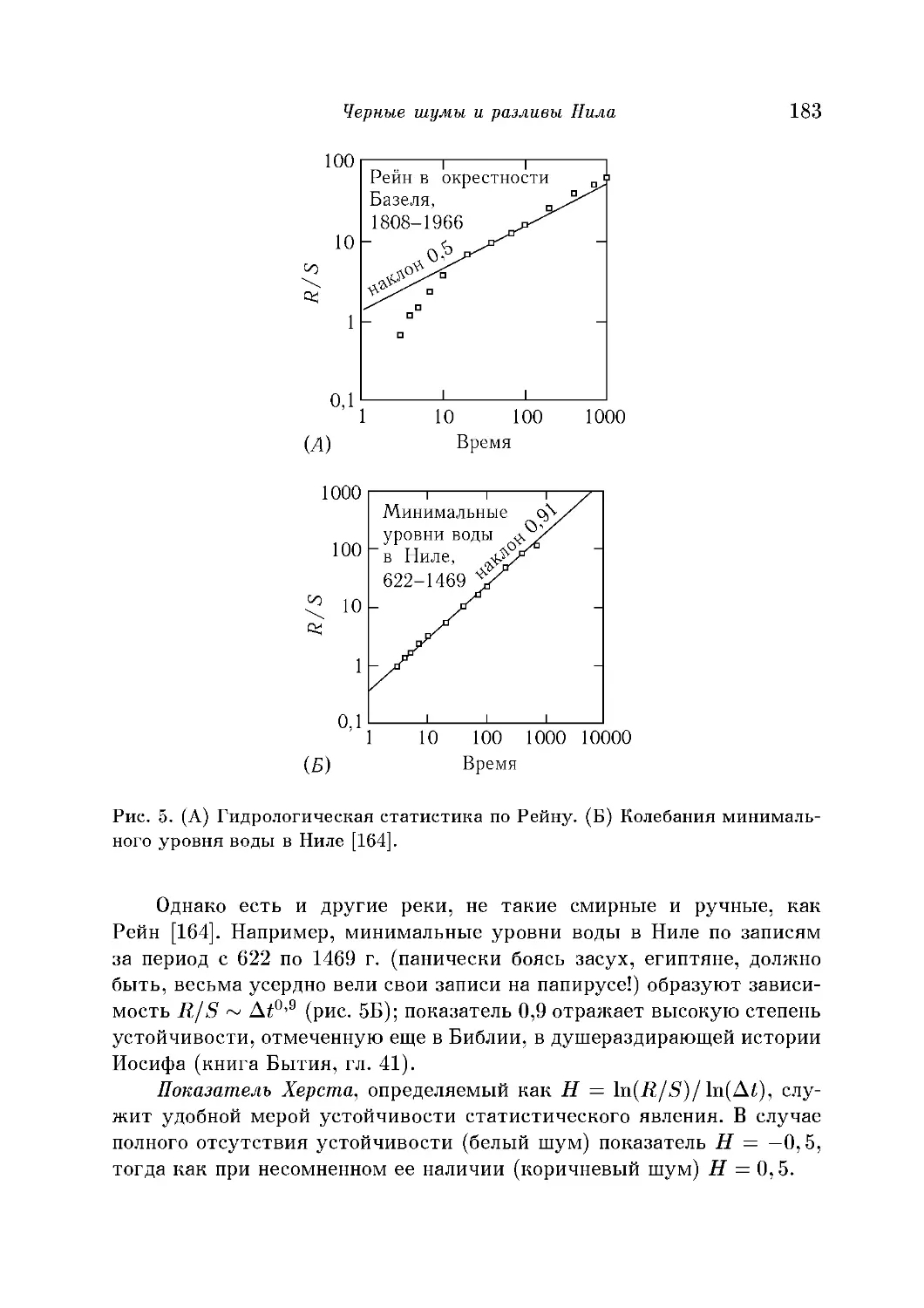
Черные шумы и разливы Нила 182
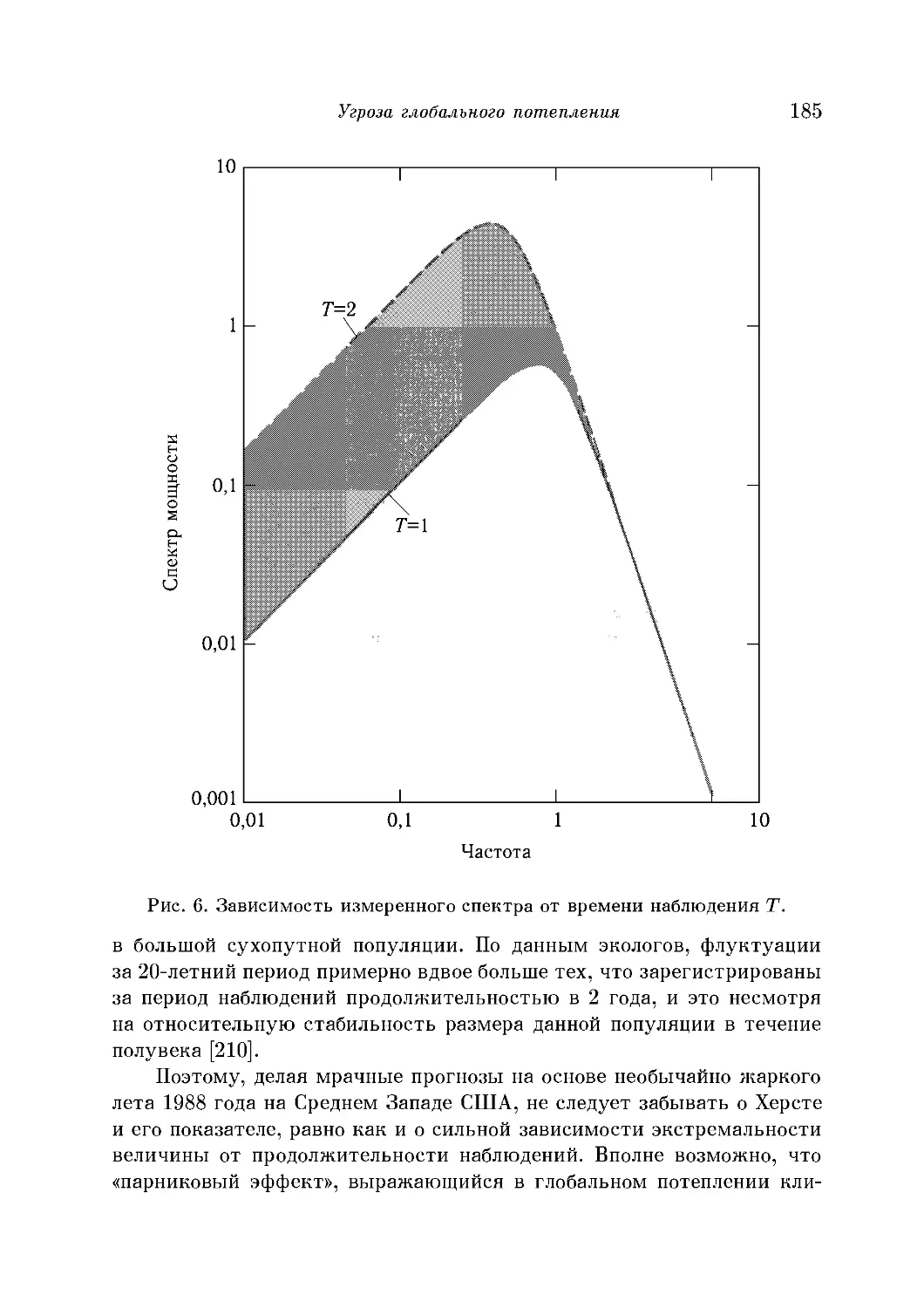
Угроза глобального потепления 184
Дробное интегрирование — современный инструмент матема-
математического анализа 186
Броуновские горы 187
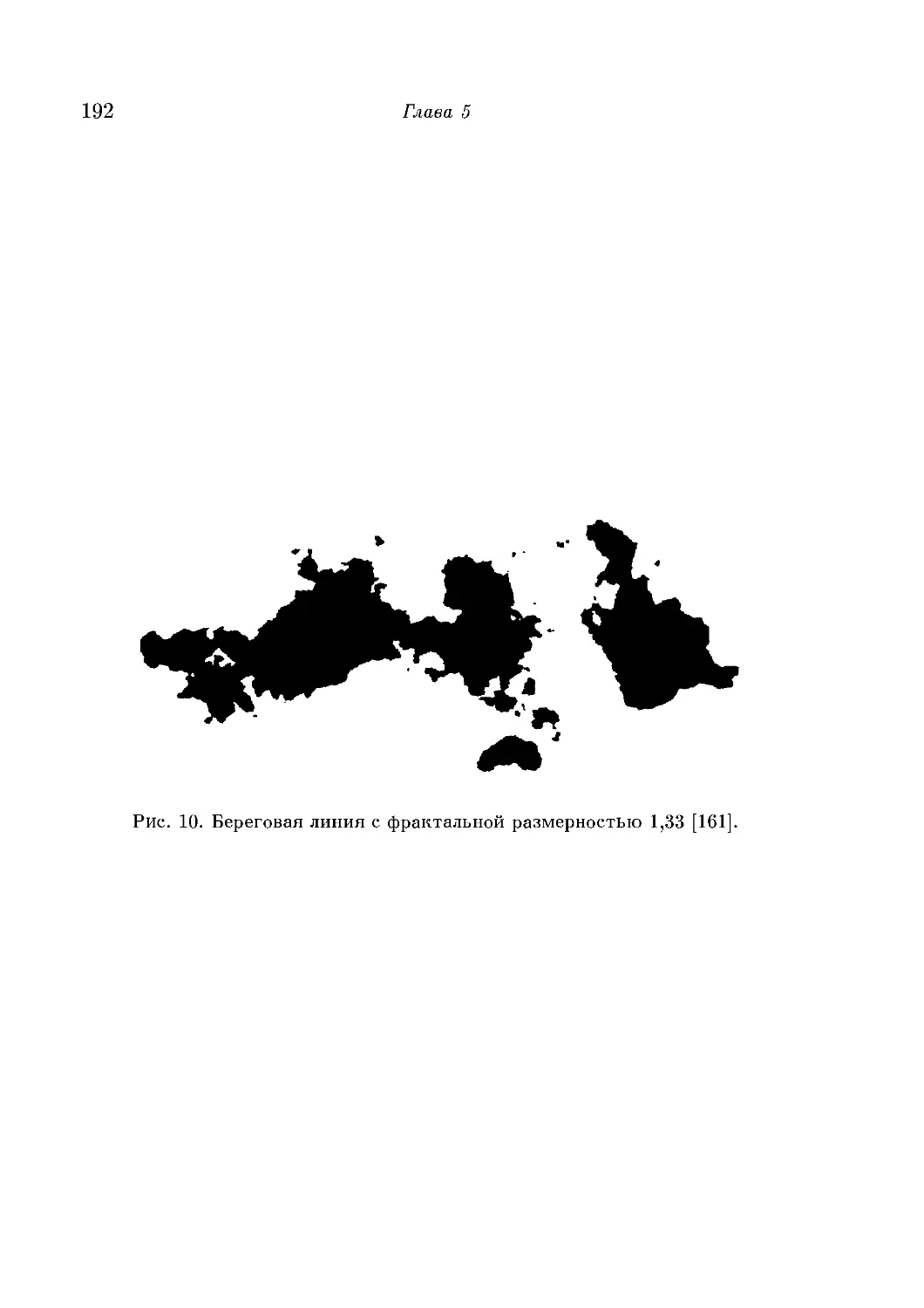
Преобразование Радона и компьютерная томография 188
Горы юные и старые 189
Глава 6. Броуновское движение, разорение игроков и меж-
межгалактическая пустота 193
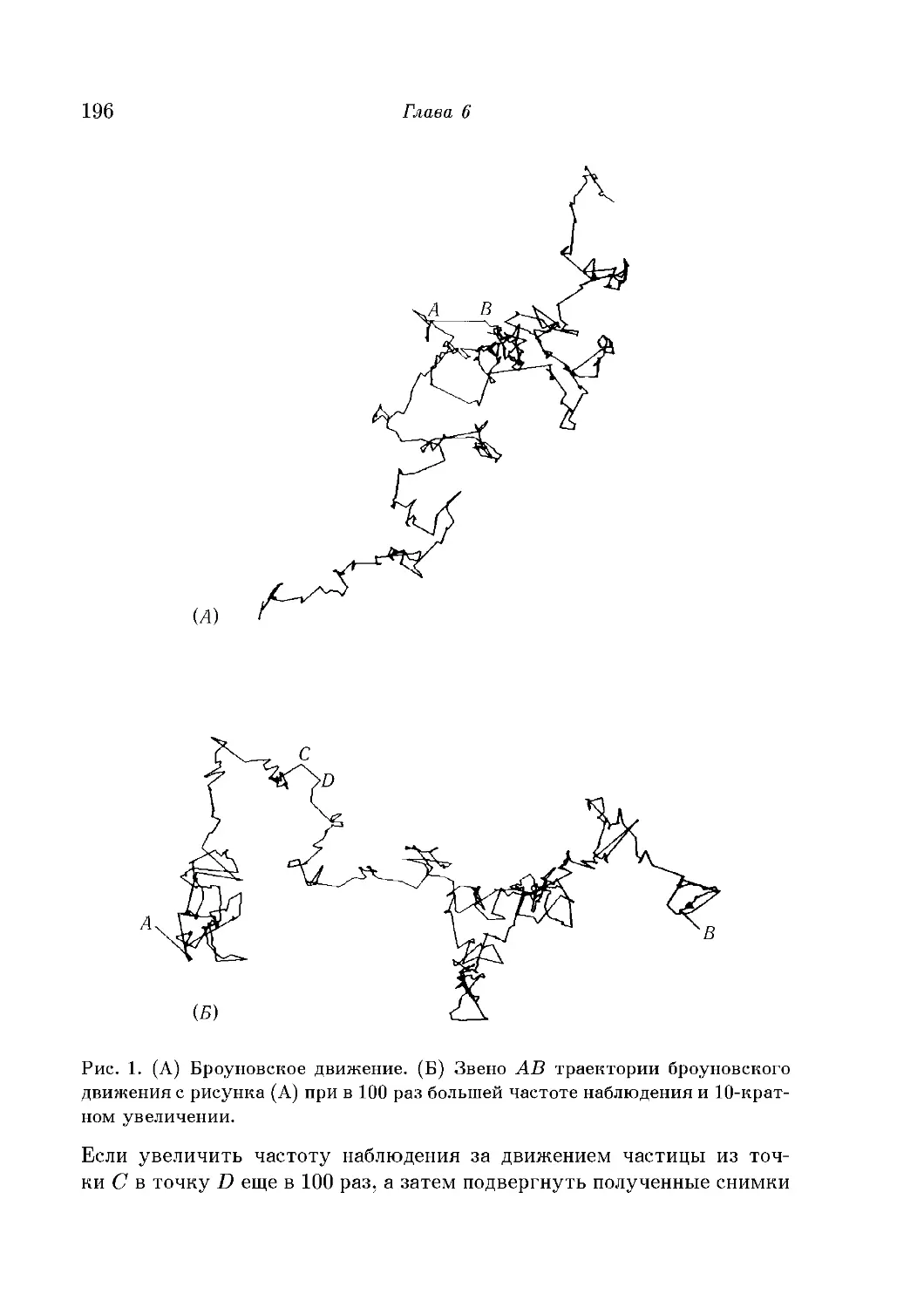
Укрощение броуновского зверя 194
Броуновское движение как фрактал 195
Много ли молекул в капле жидкости? 198
Спектр броуновского движения 199
Разорение игрока, случайные блуждания и теория информации 200
Оглавление 9
Крах здравого смысла в случайных испытаниях 201
Еще немного пищи для размышлений о справедливости .... 202
Петербургский парадокс 203
Угадывающая машина Шеннона 205
Классическая механика рулетки и пропускная способность ка-
канала по Шеннону 206
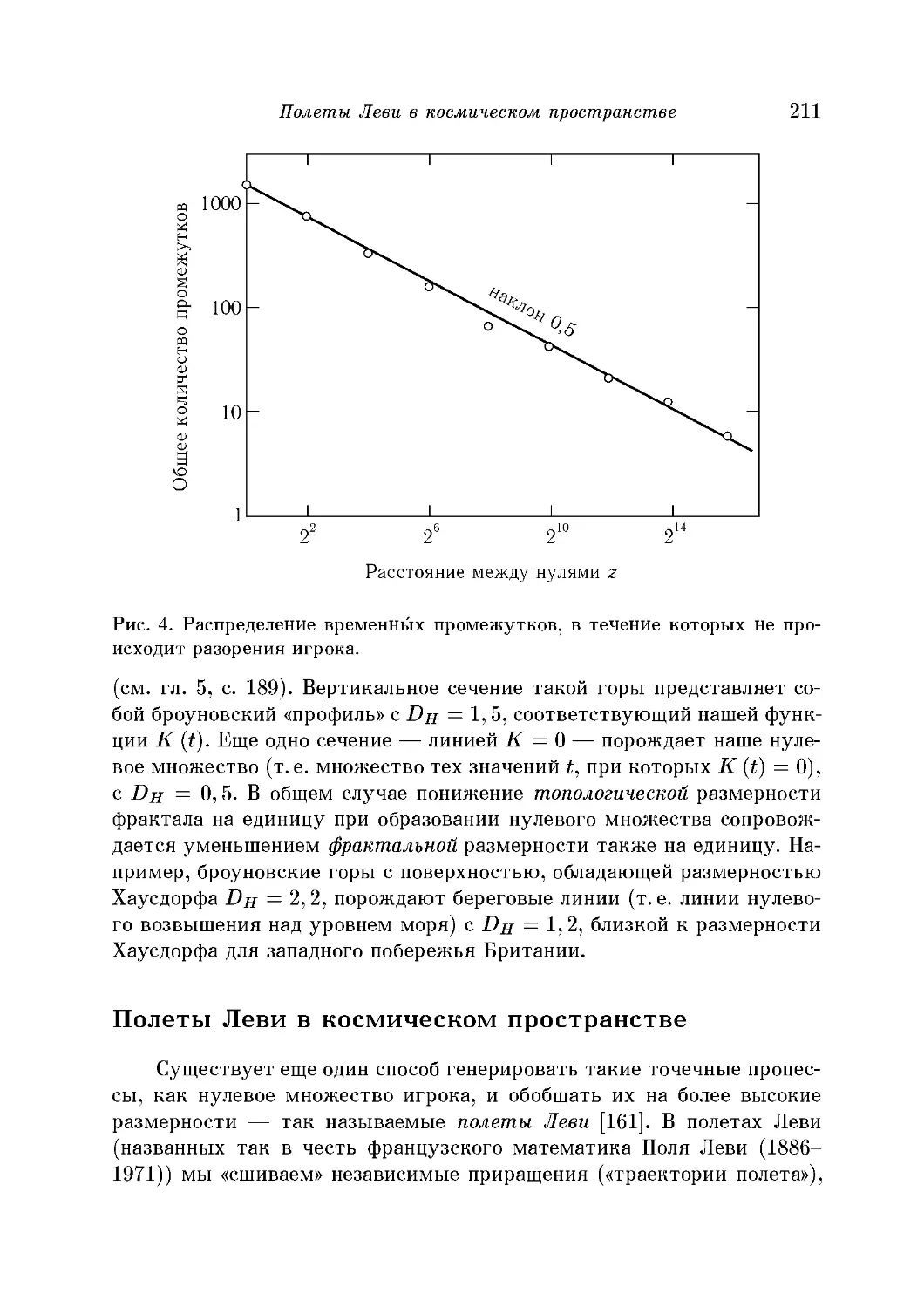
Скопления разорений и галактик 208
Полеты Леви в космическом пространстве 211
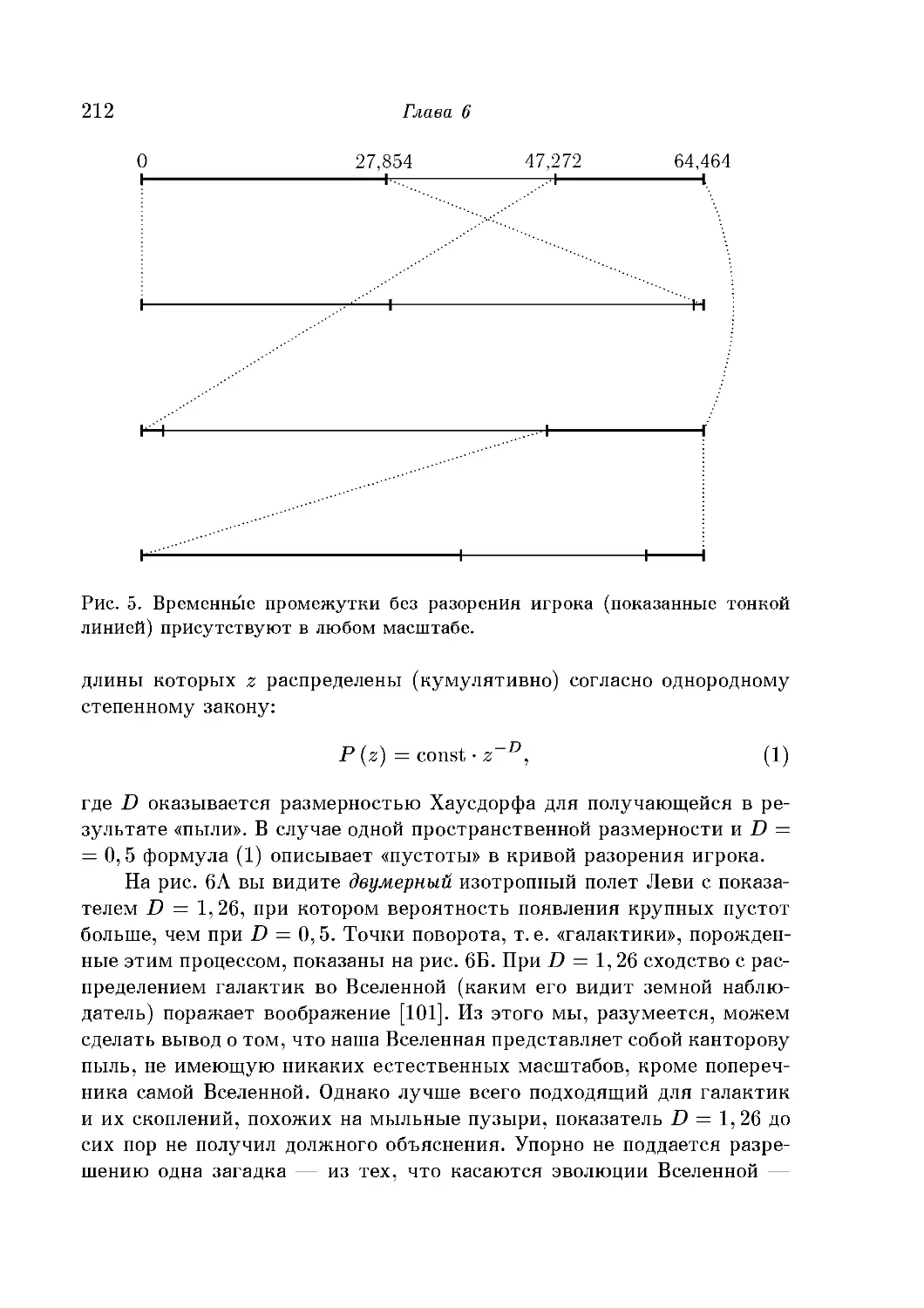
Парадоксы вероятностных степенных законов 214
Инвариантные распределения: Гаусс, Коши ... кто следующий?215
Глава 7. Канторовы множества: самоподобие и арифмети-
арифметическая пыль 220
Уголок канторова рая 220
Канторовы множества как множества инвариантные 225
Символическая динамика и детерминированный хаос 227
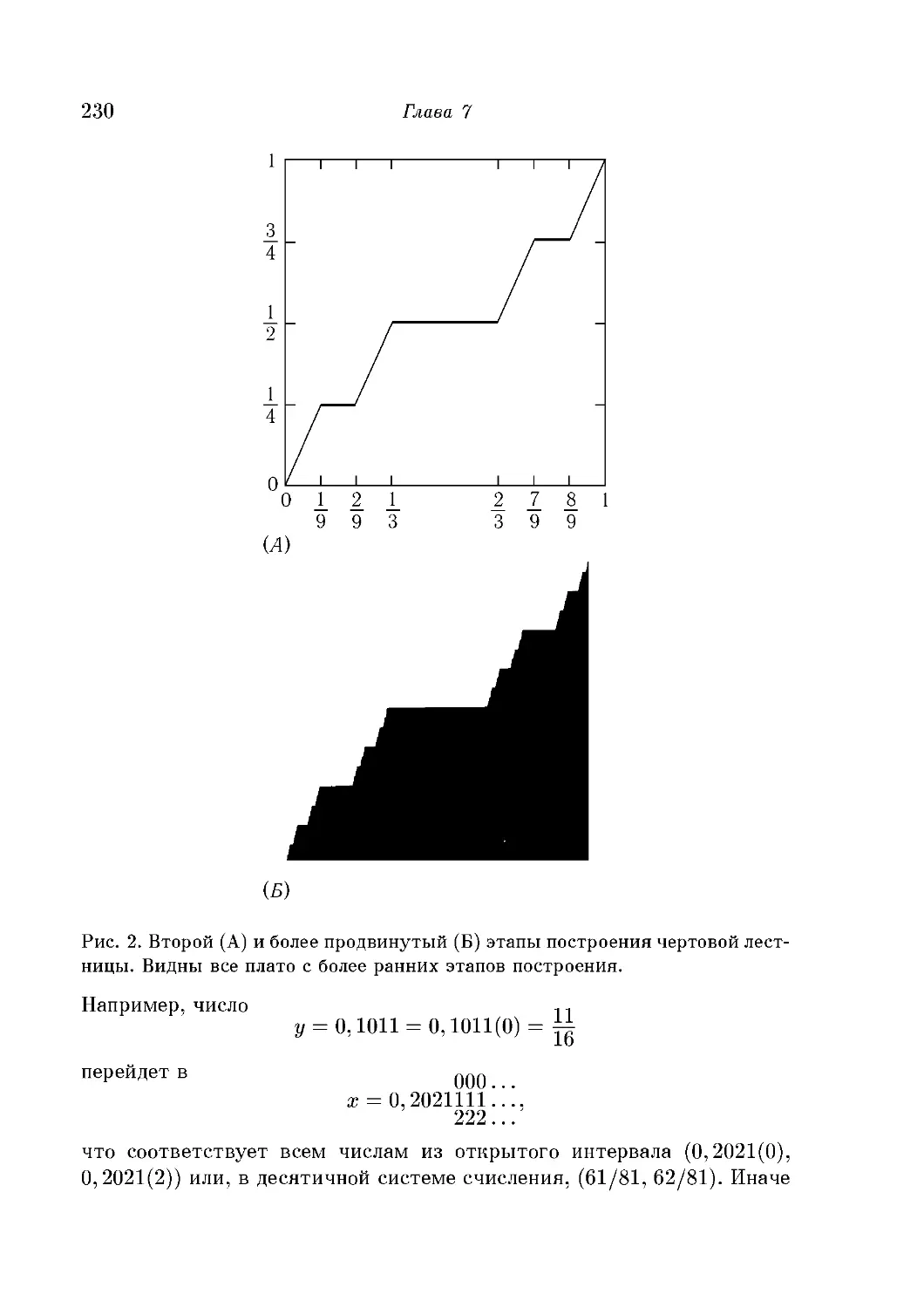
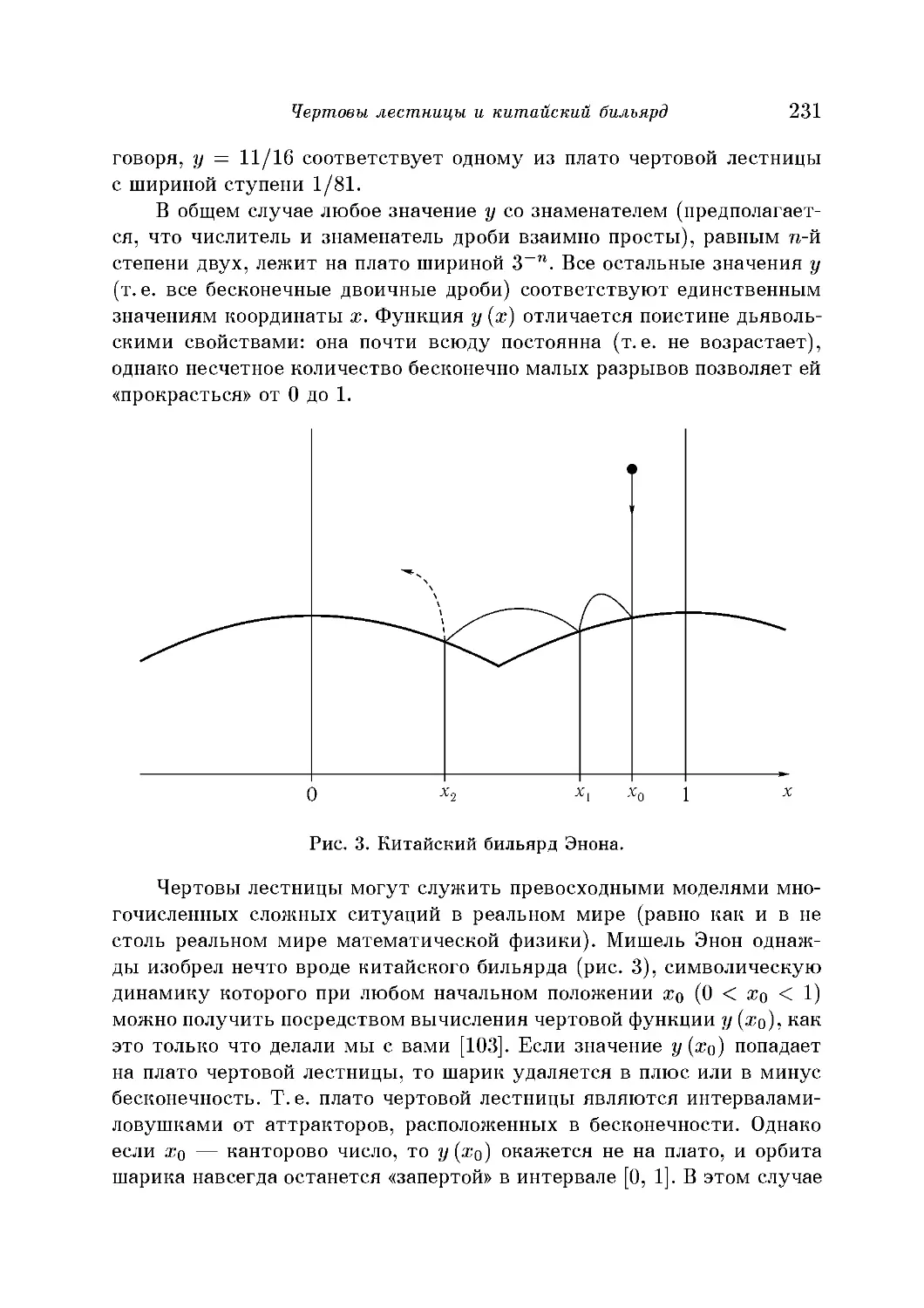
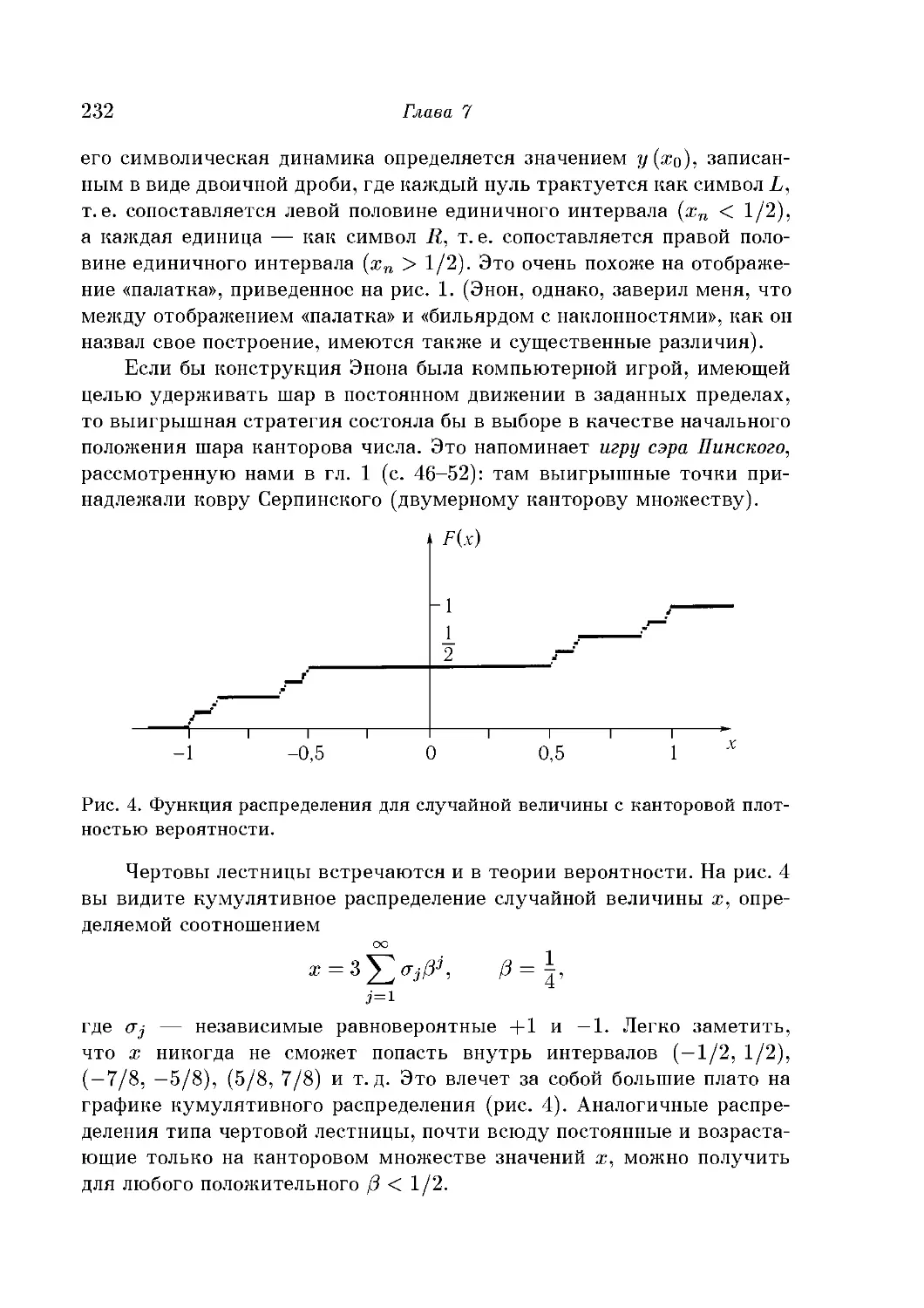
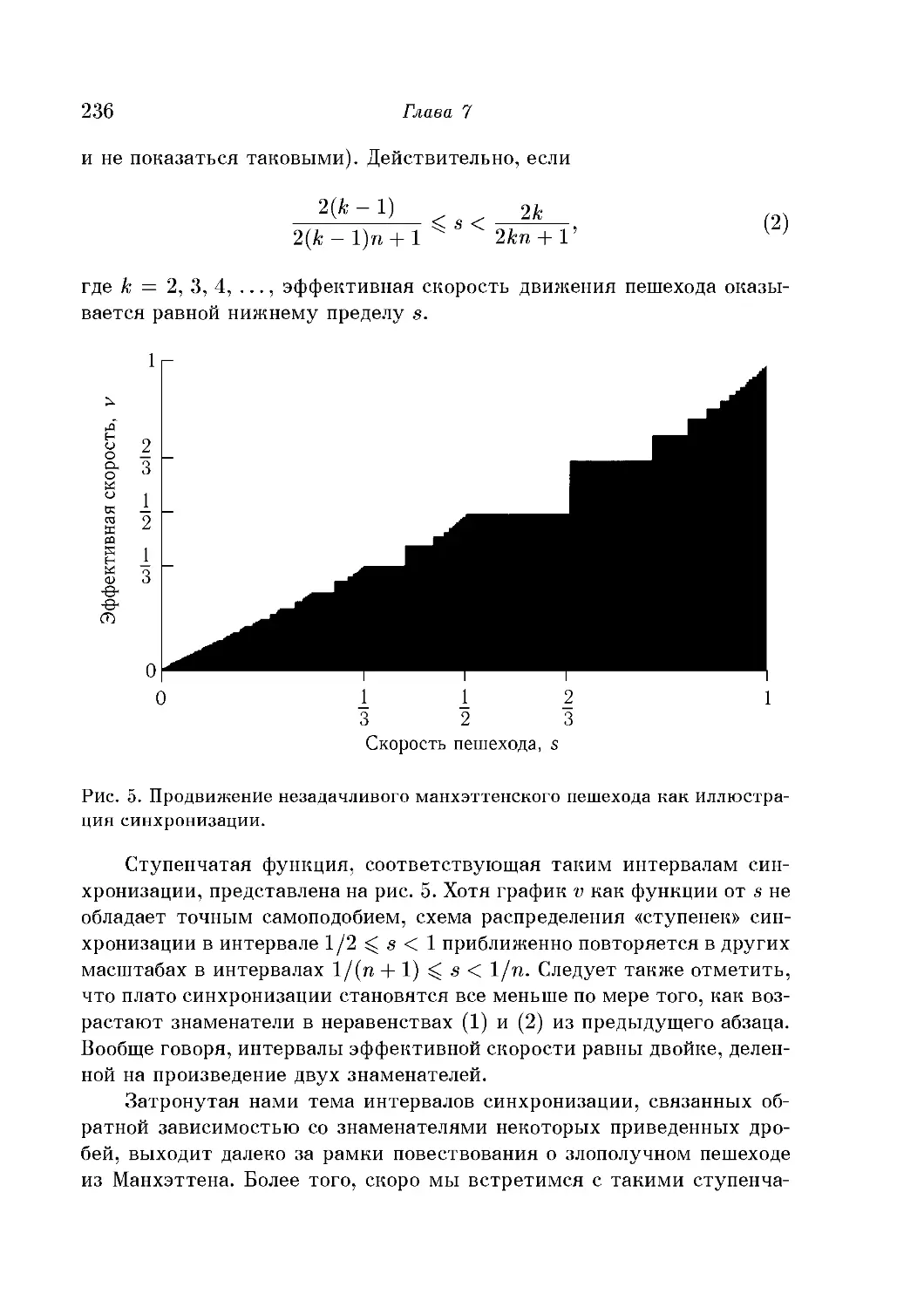
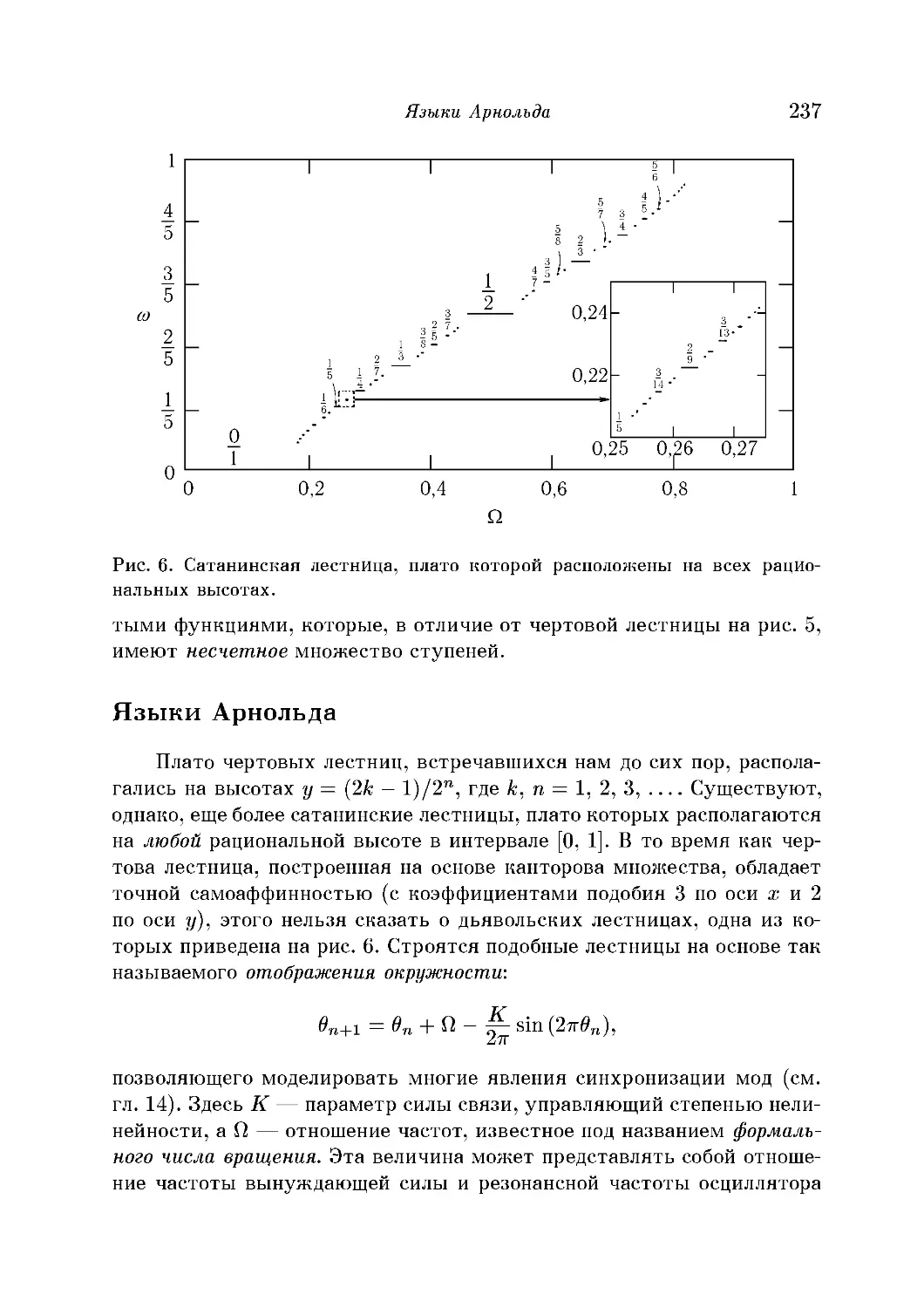
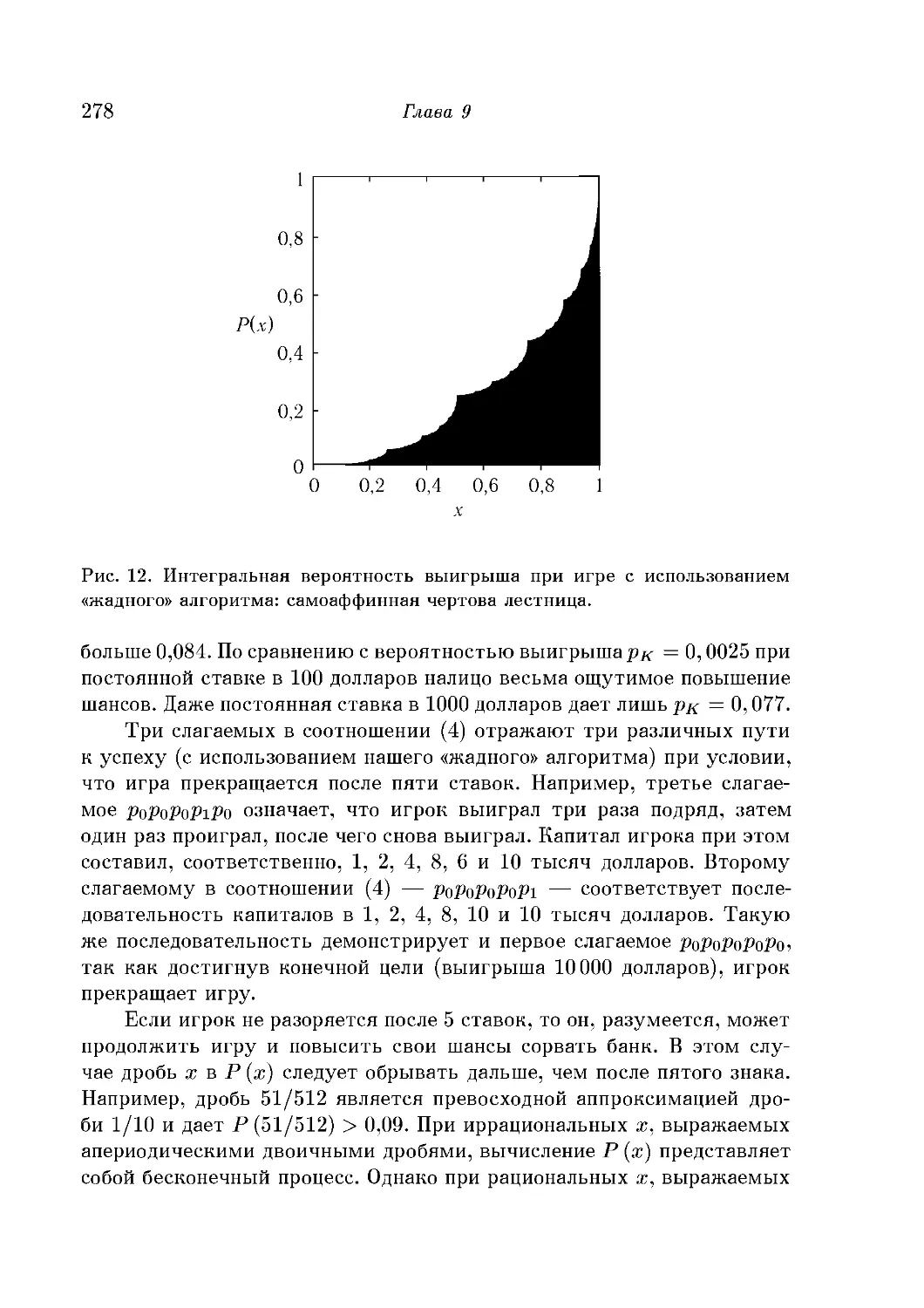
Чертовы лестницы и китайский бильярд 229
Синхронизация мод в качелях и часах 233
Незадачливый манхэттенский пешеход 235
Языки Арнольда 237
Глава 8. Многомерные фракталы и цифровые солнечные
часы 240
Декартовы произведения канторовых множеств 240
Дырявый ковер, мягкие губки и швейцарские сыры 241
Солнечные часы на основе канторова множества 244
Толстые фракталы 246
Глава 9. Мультифракталы, или фракталы, тесно перепле-
переплетенные между собой 251
Распределение: концентрация руды и плотность населения . . 252
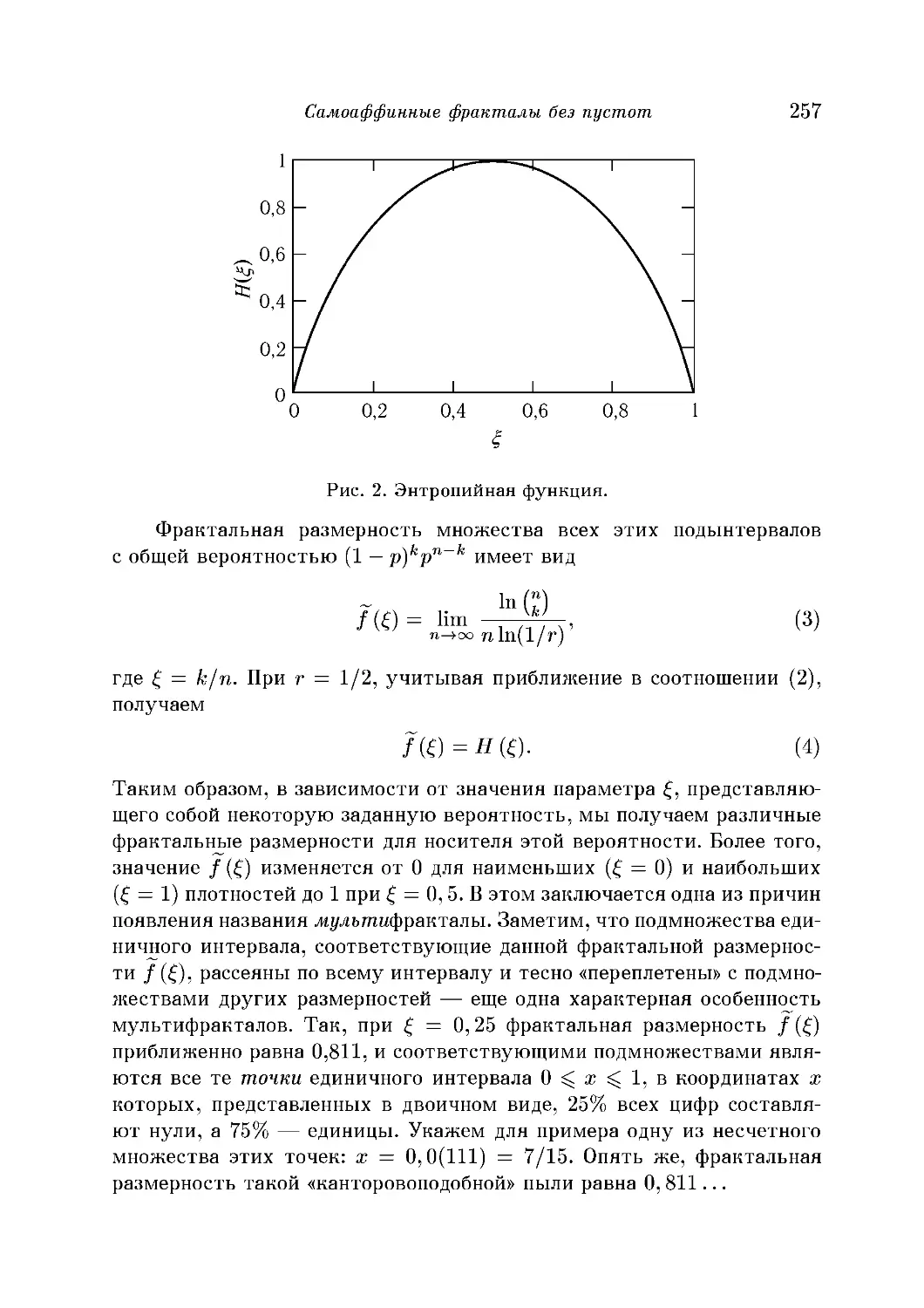
Самоаффинные фракталы без пустот 255
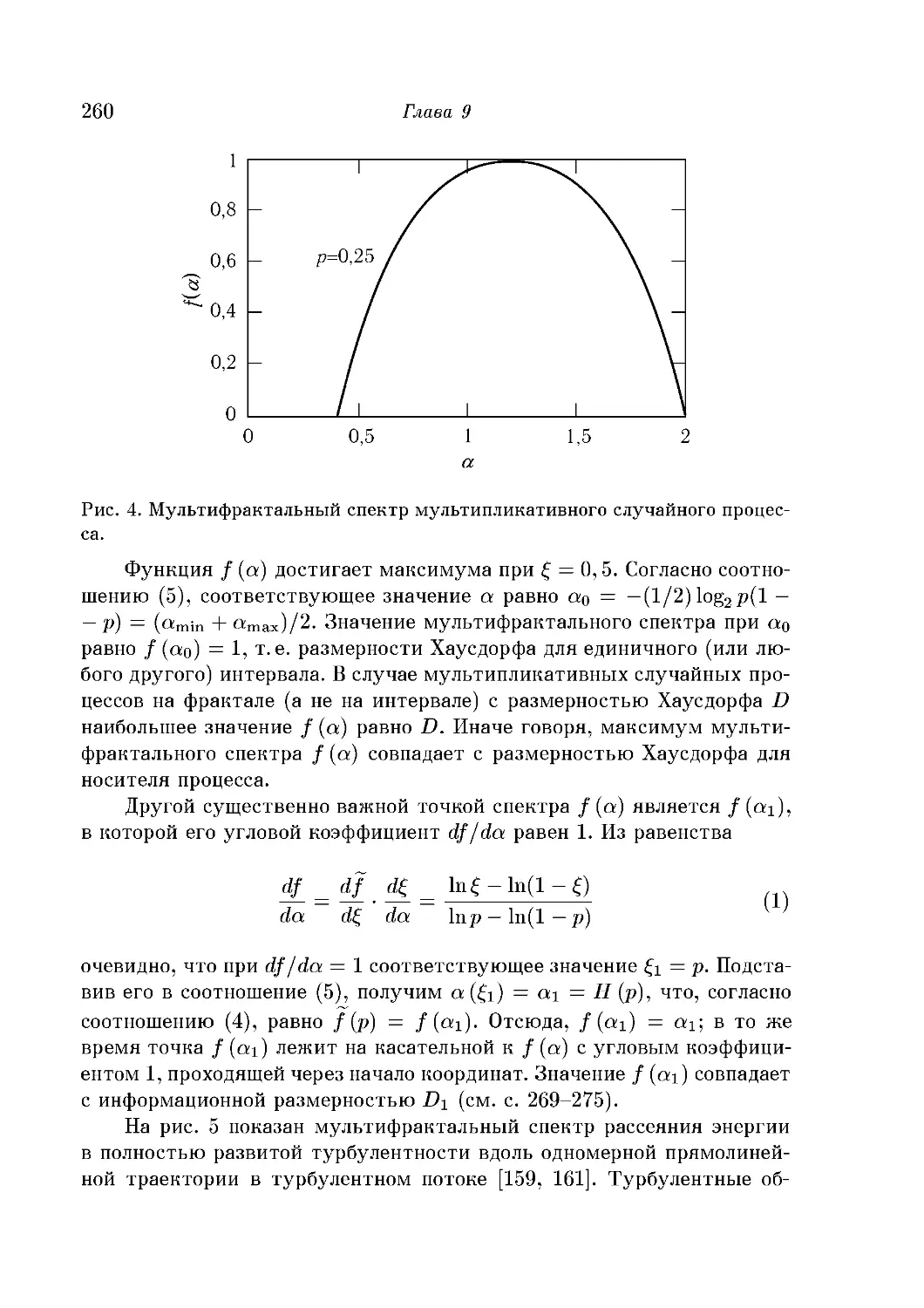
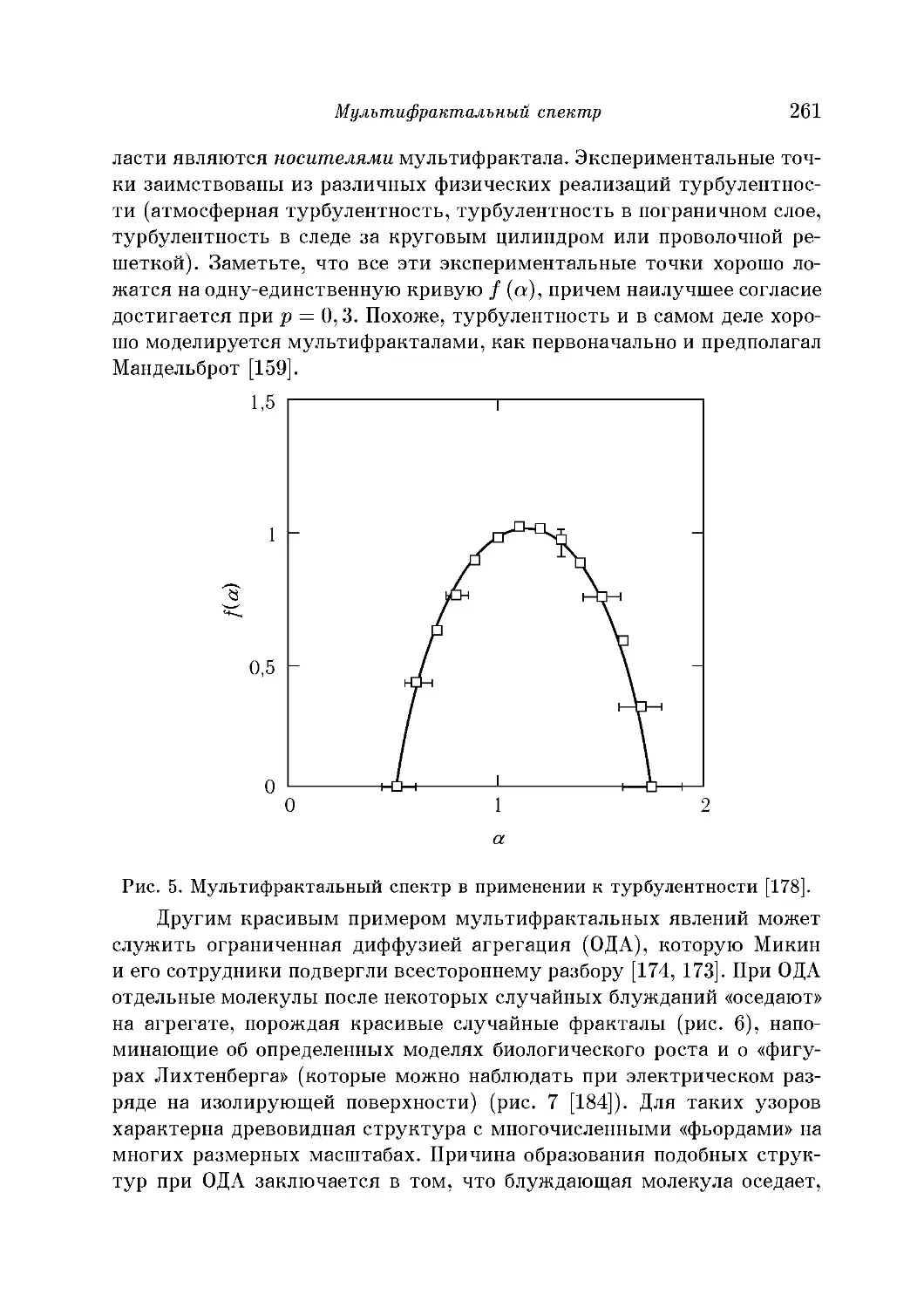
Мультифрактальный спектр: турбулентность и ограниченная
диффузией агрегация 259
Образование вязких языков 265
Мультифракталы на фракталах 267
Фрактальные размерности, получаемые из обобщенных энтро-
энтропии 269
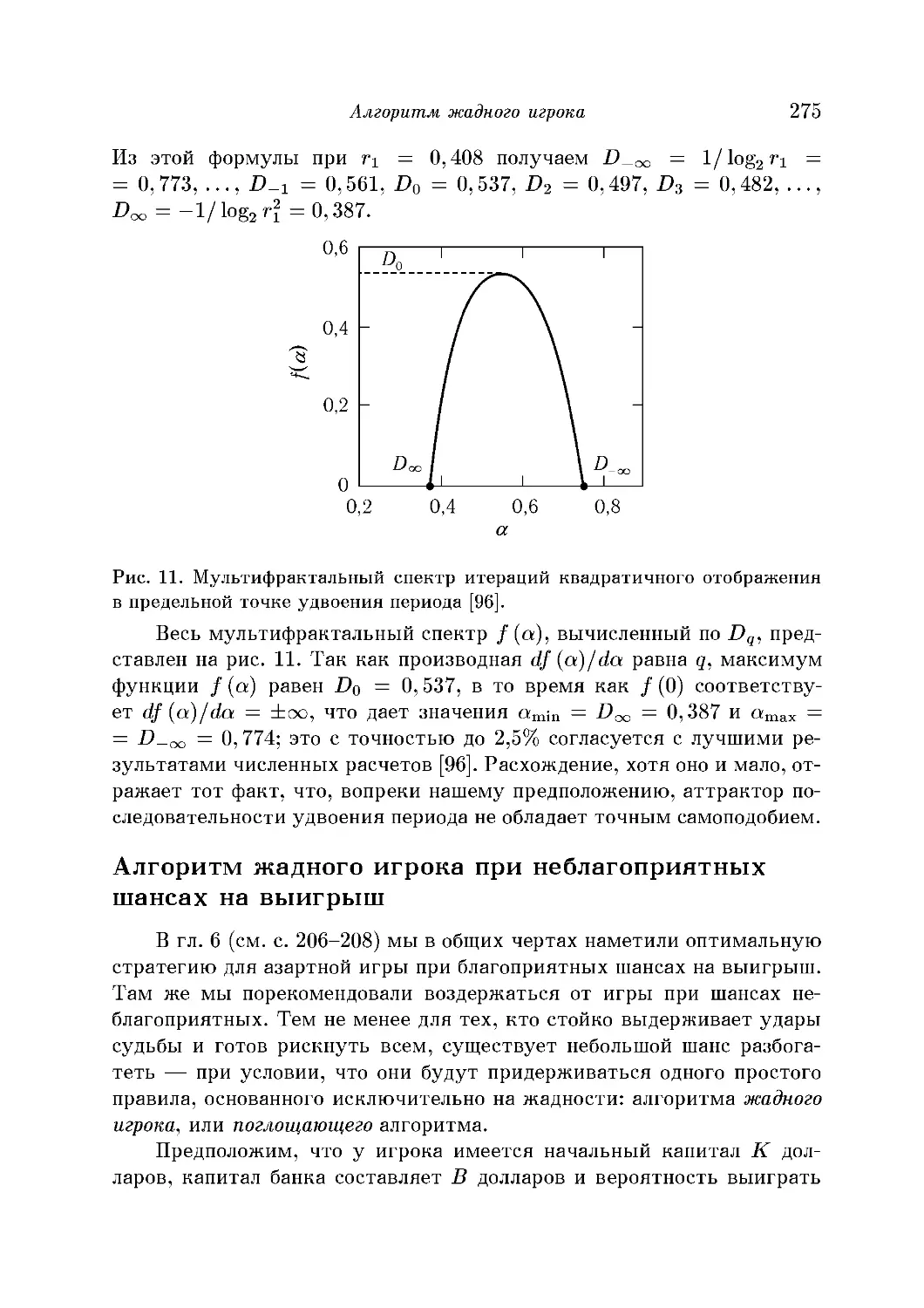
Соотношение между мультифрактальным спектром / (а) и по-
показателями массы т (q) 272
Странные аттракторы как мультифракталы 274
Алгоритм жадного игрока при неблагоприятных шансах на вы-
выигрыш 275
10 Оглавление
Глава 10. Некоторые реально существующие фракталы и
их измерение 280
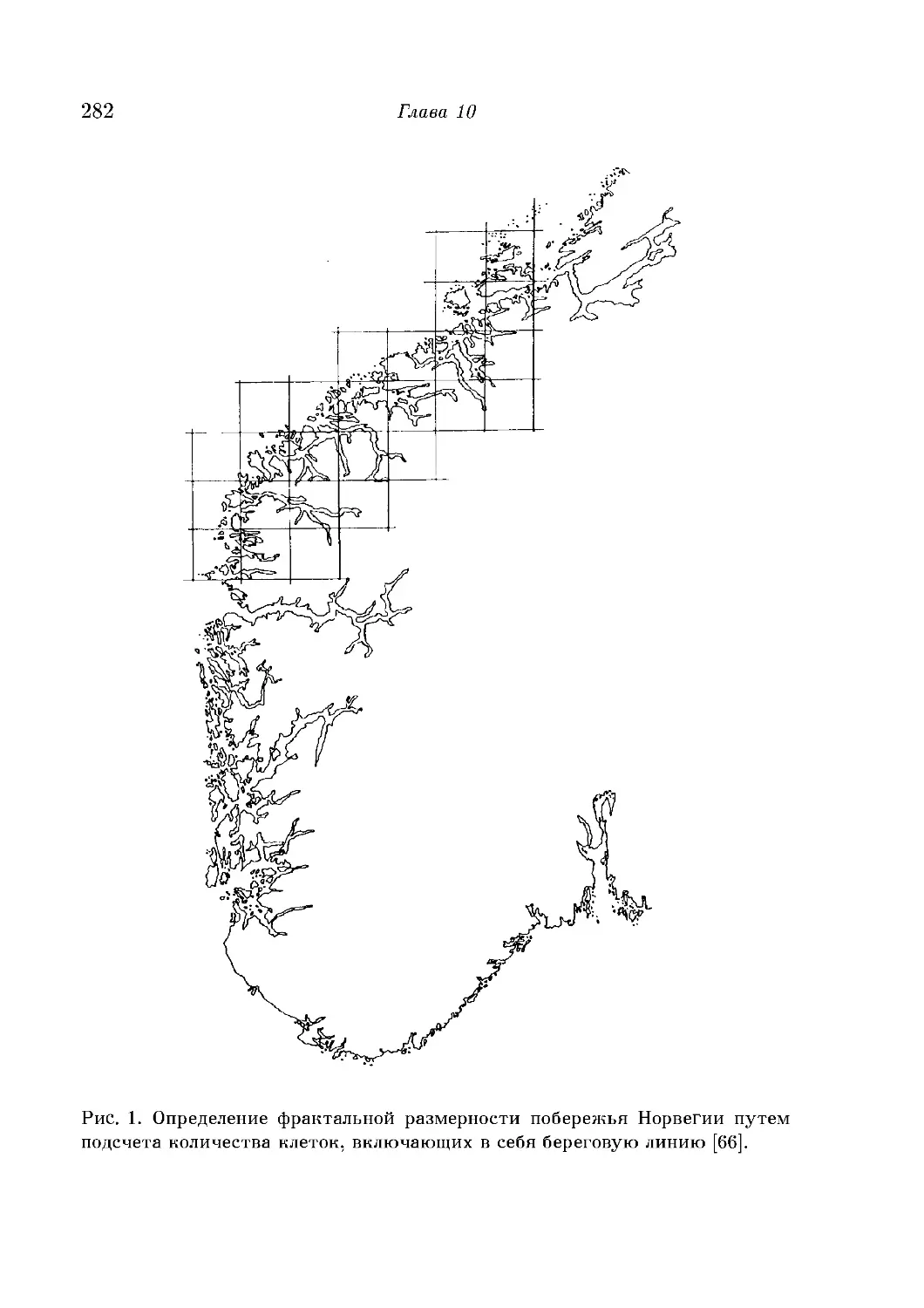
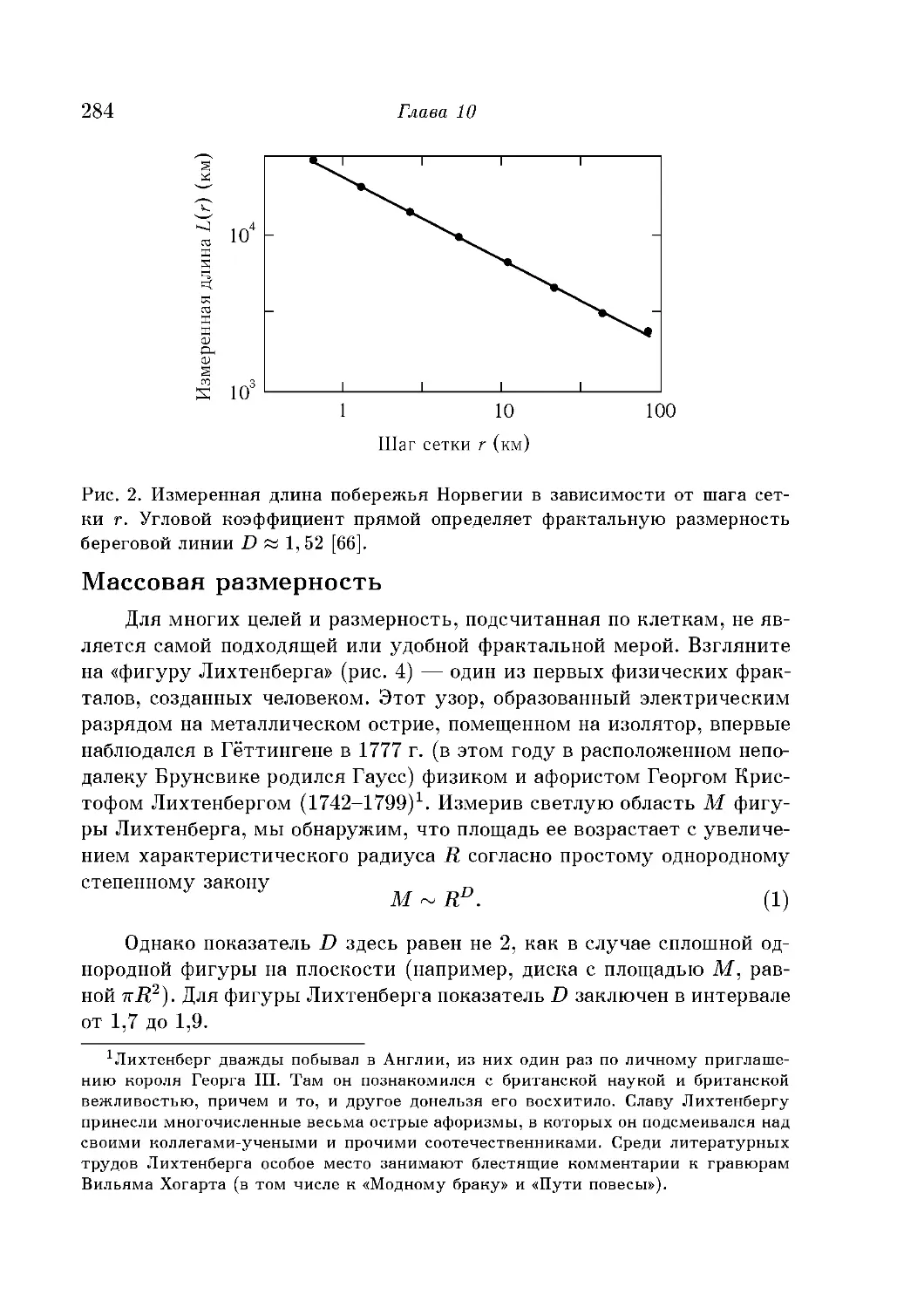
Размерности, определяемые путем подсчета клеток 283
Массовая размерность 284
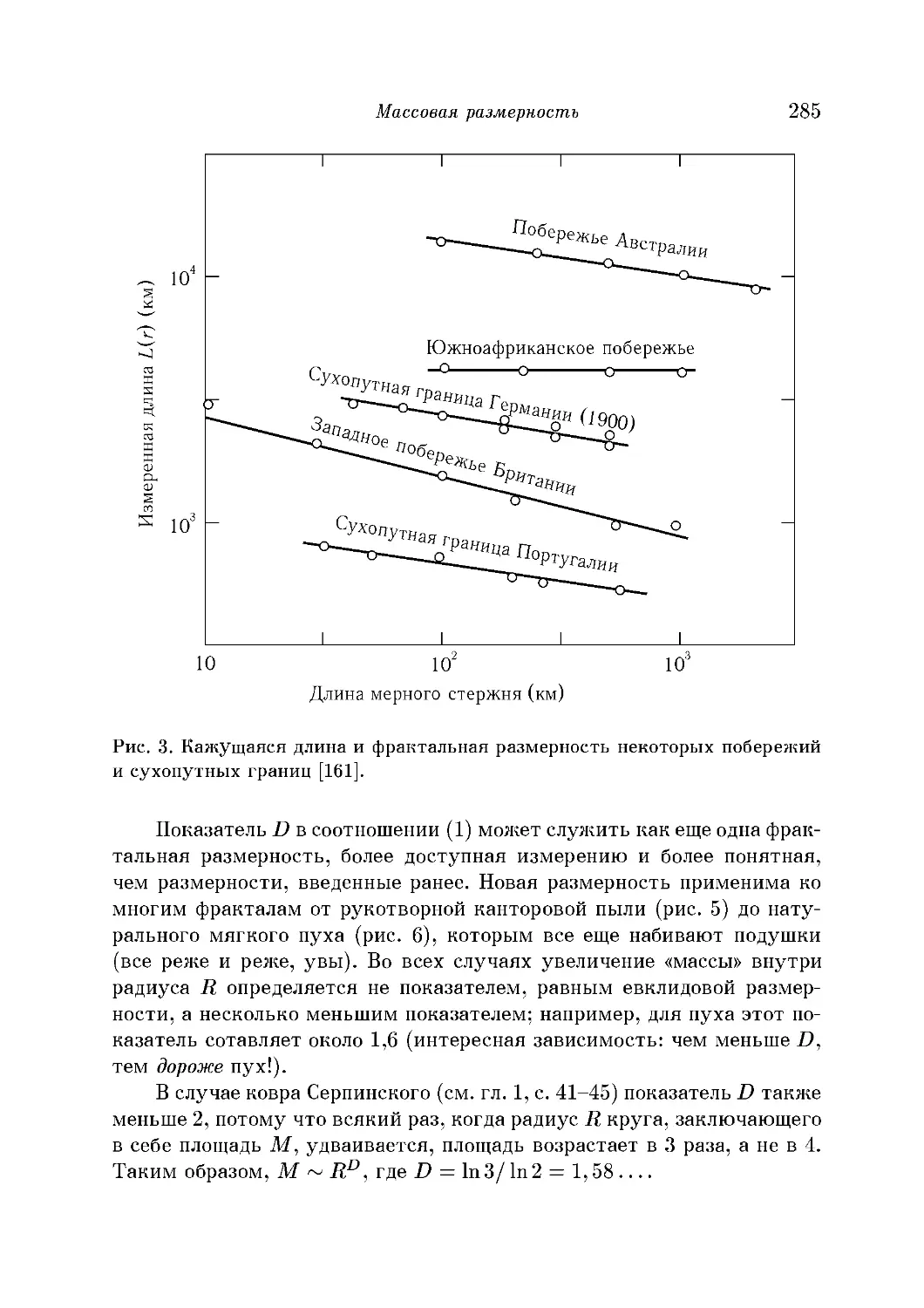
Корреляционная размерность 290
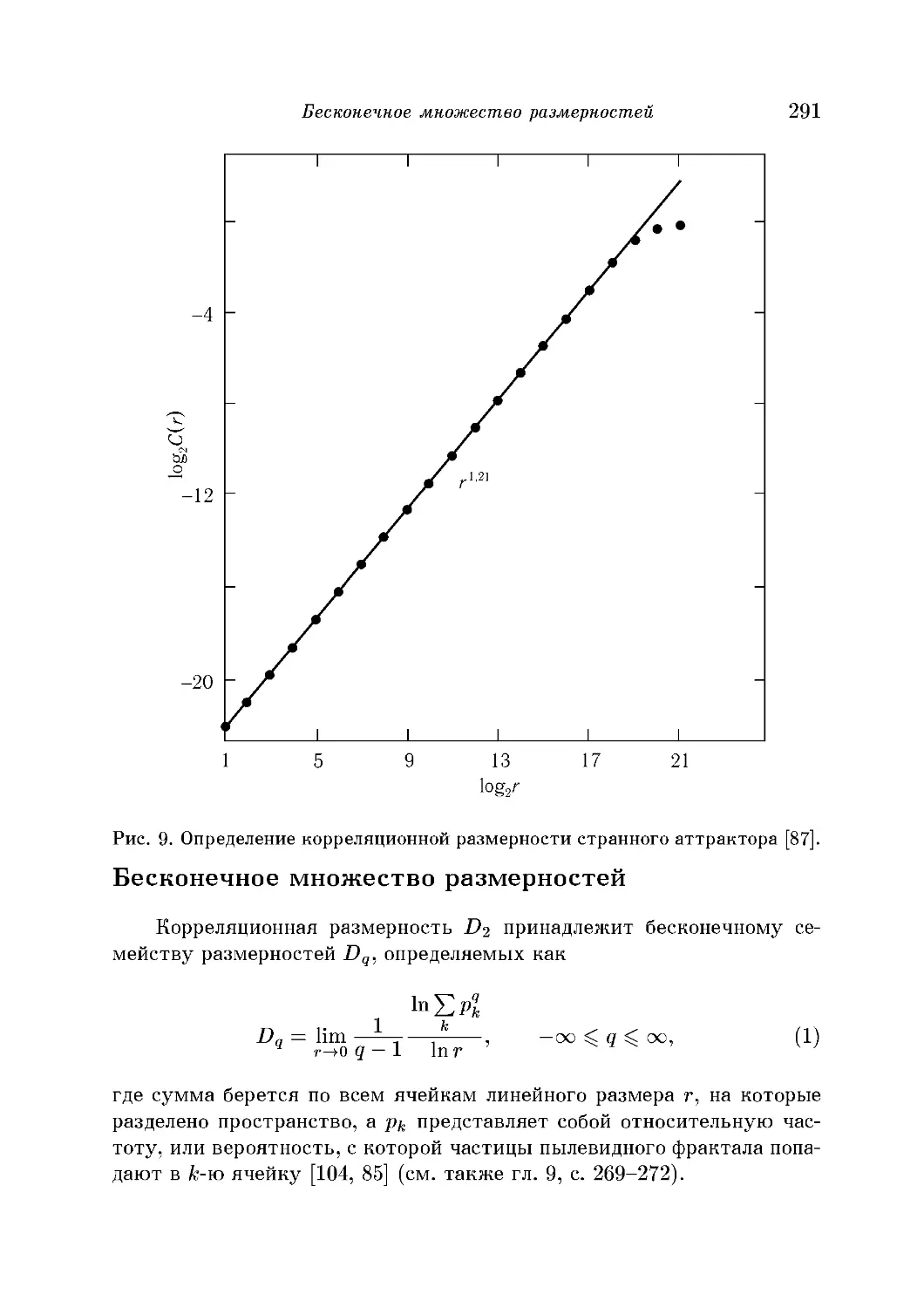
Бесконечное множество размерностей 291
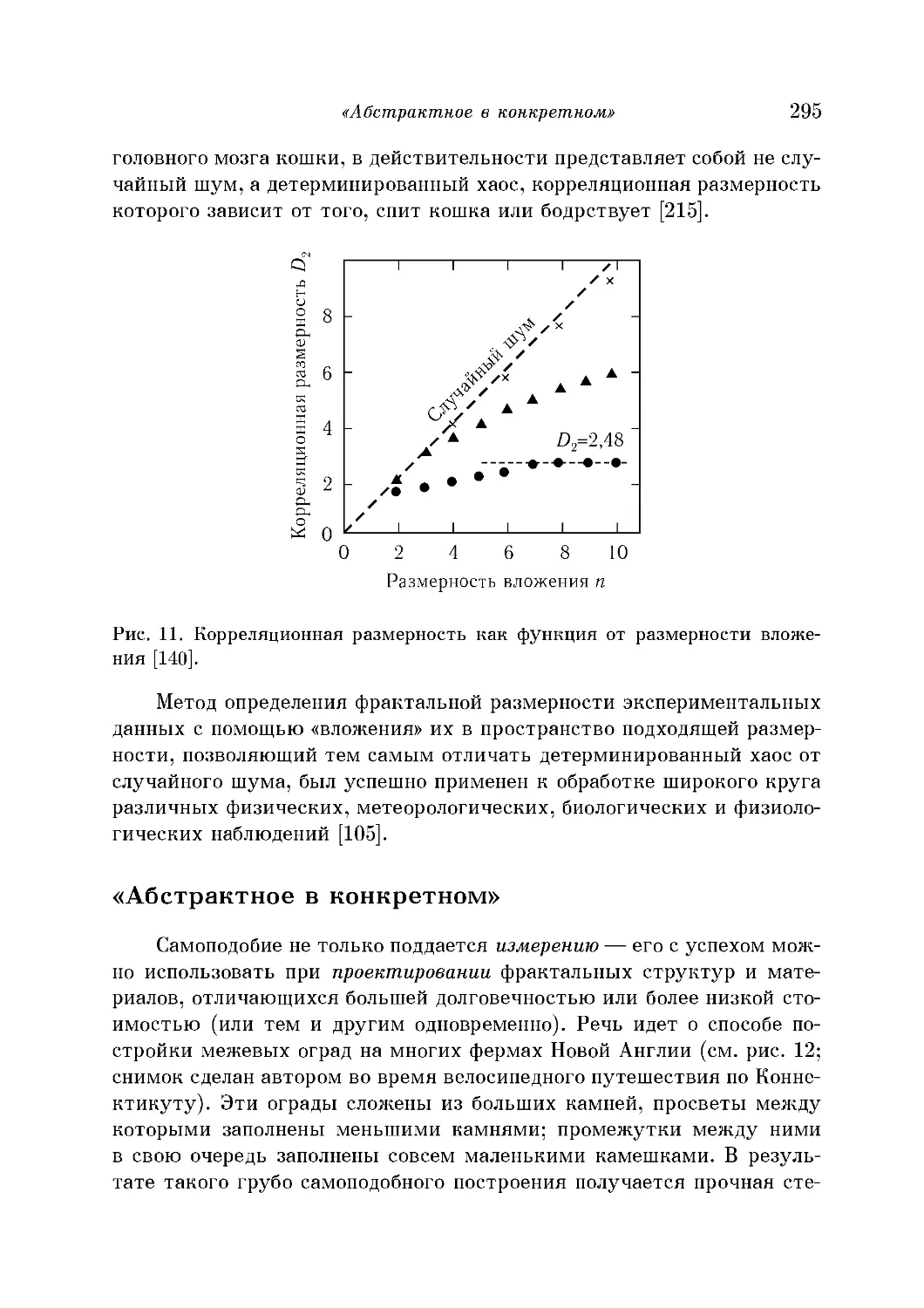
Определение фрактальных размерностей по временным рядам 294
«Абстрактное в конкретном» 295
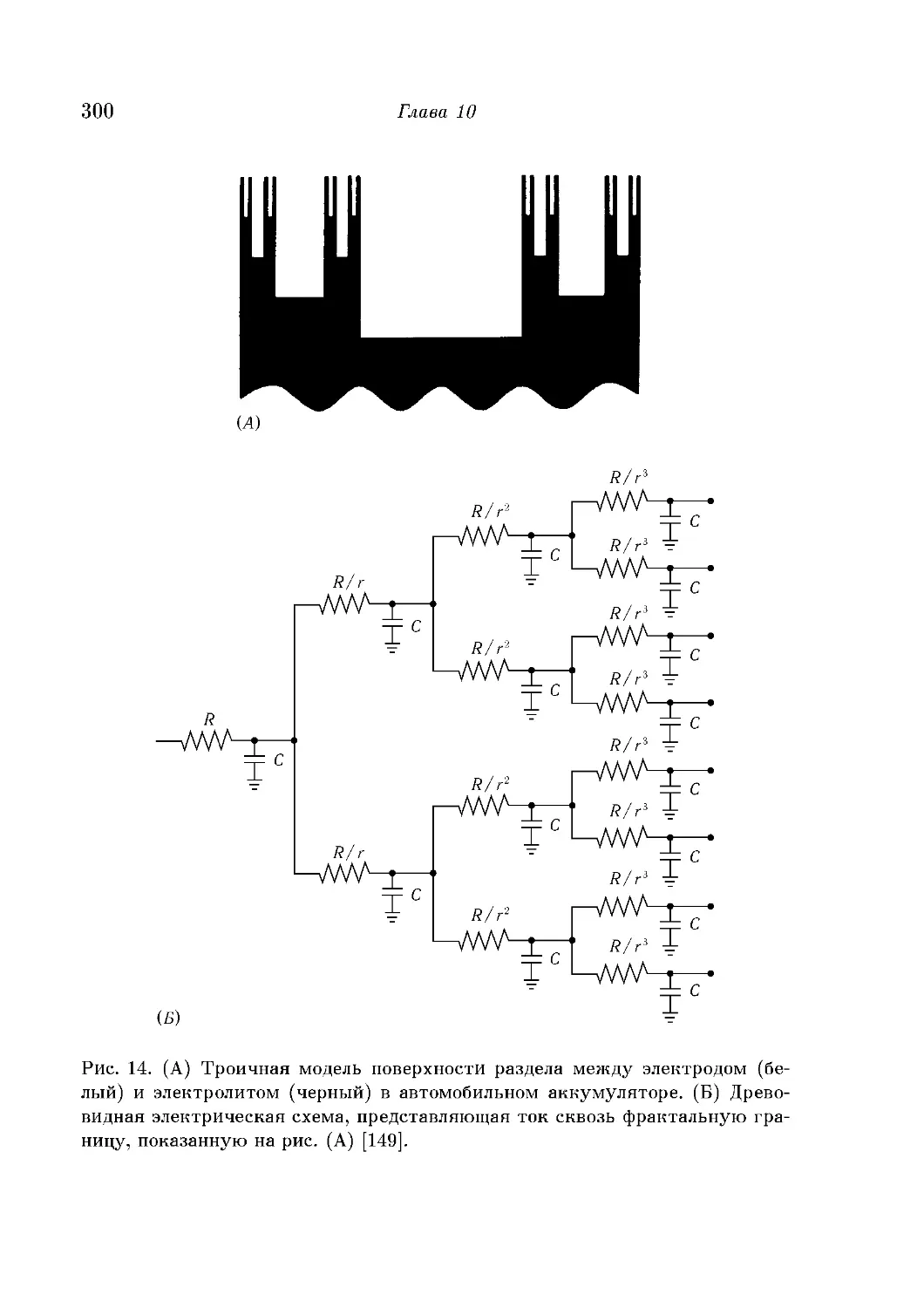
Фрактальные поверхности раздела как основа дробных пока-
показателей частоты 296
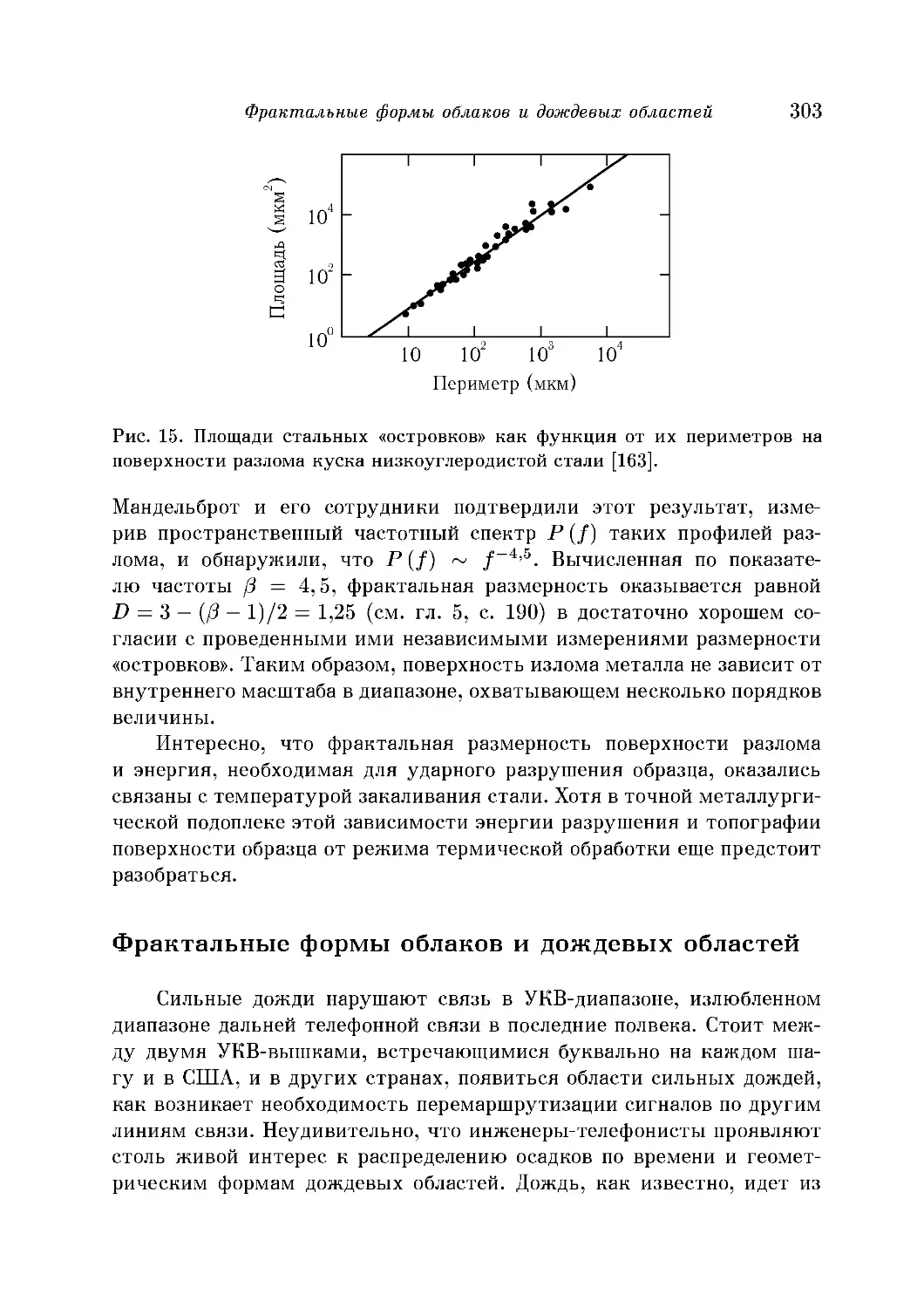
Фрактальные размерности поверхностей разлома 302
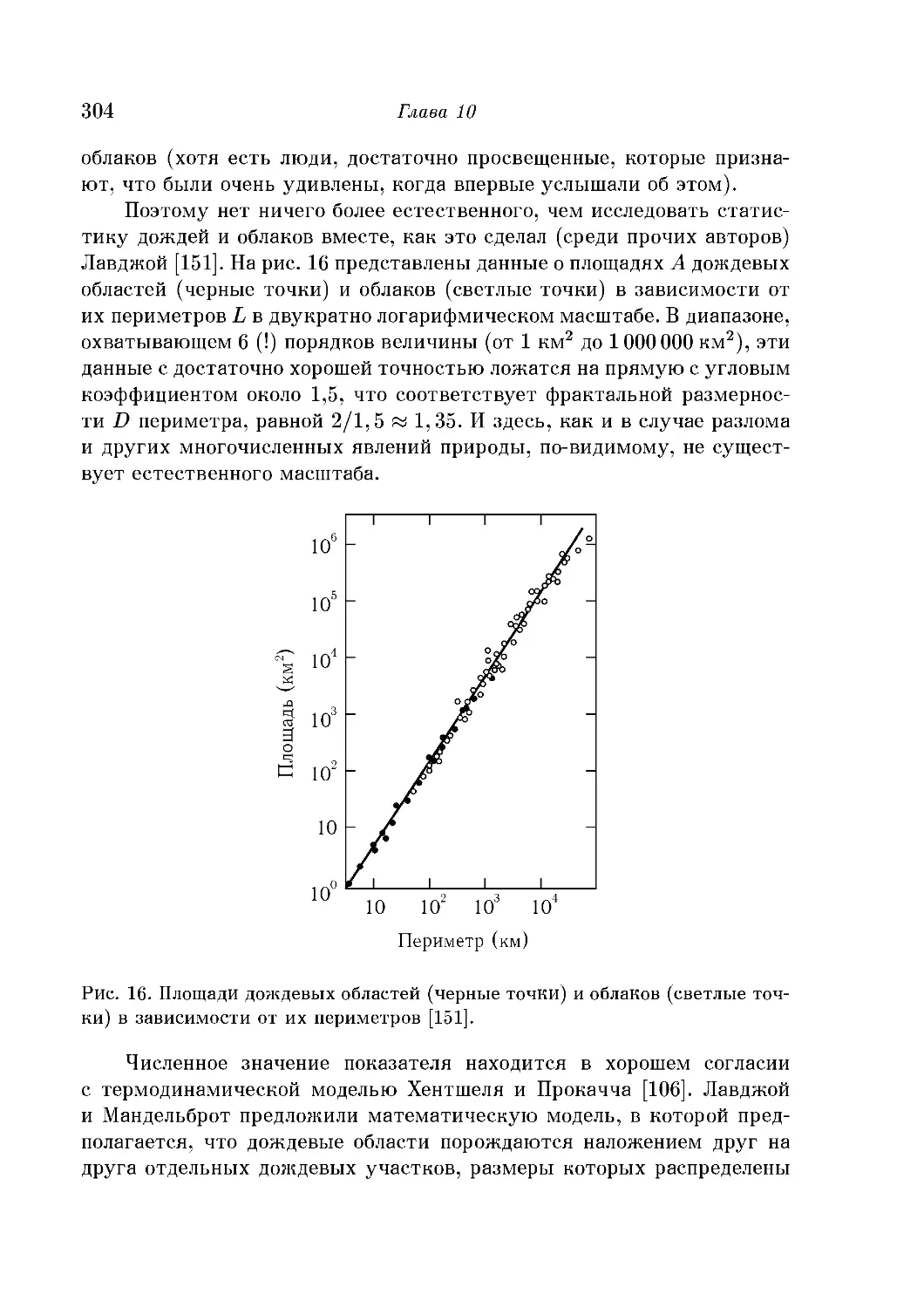
Фрактальные формы облаков и дождевых областей 303
Агломерация кластеров 305
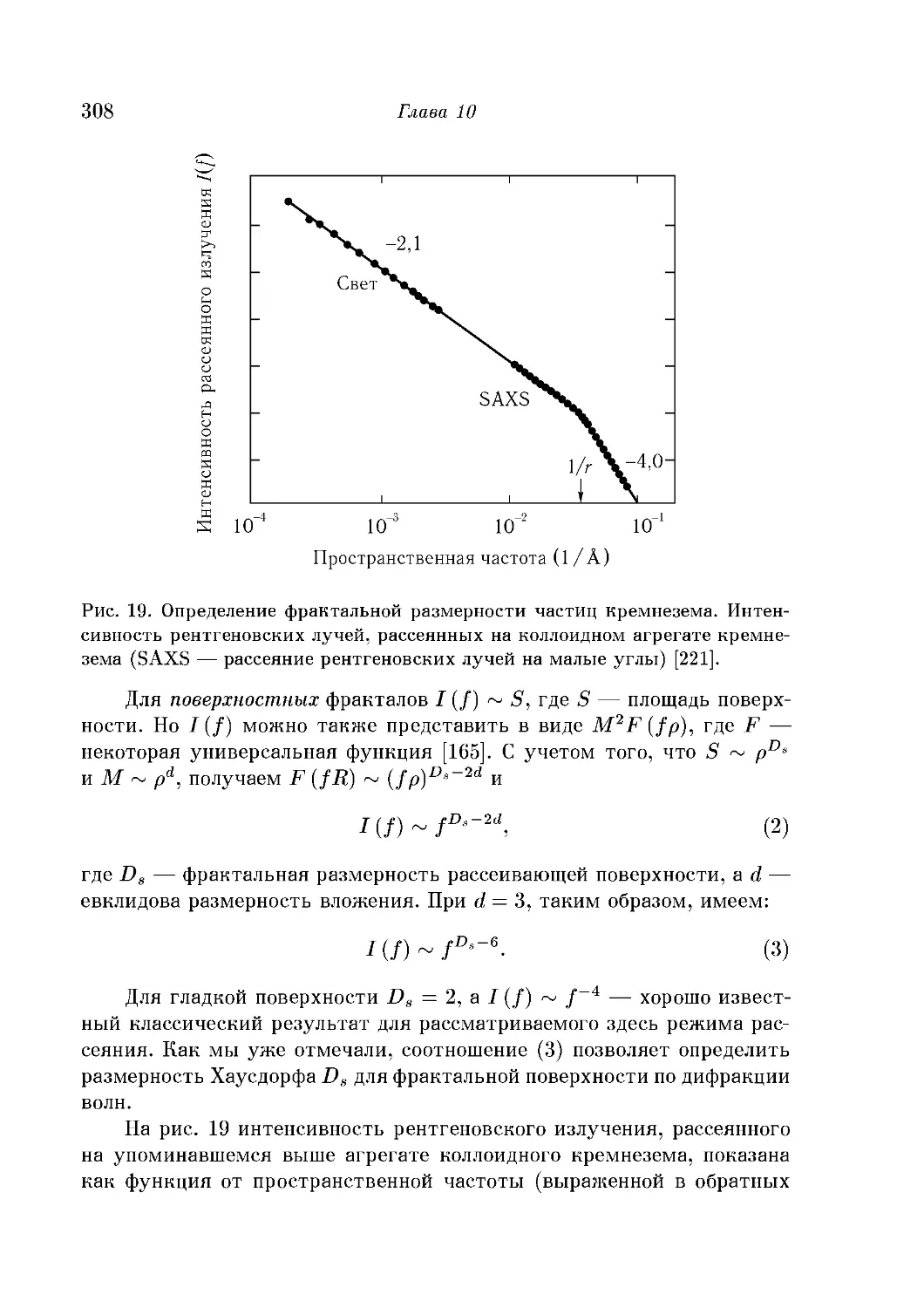
Дифракция на фракталах 307
Глава 11. Итерации, странные отображения и миллиард
знаков для 7г 311
Поиск нулей и встреча с хаосом 314
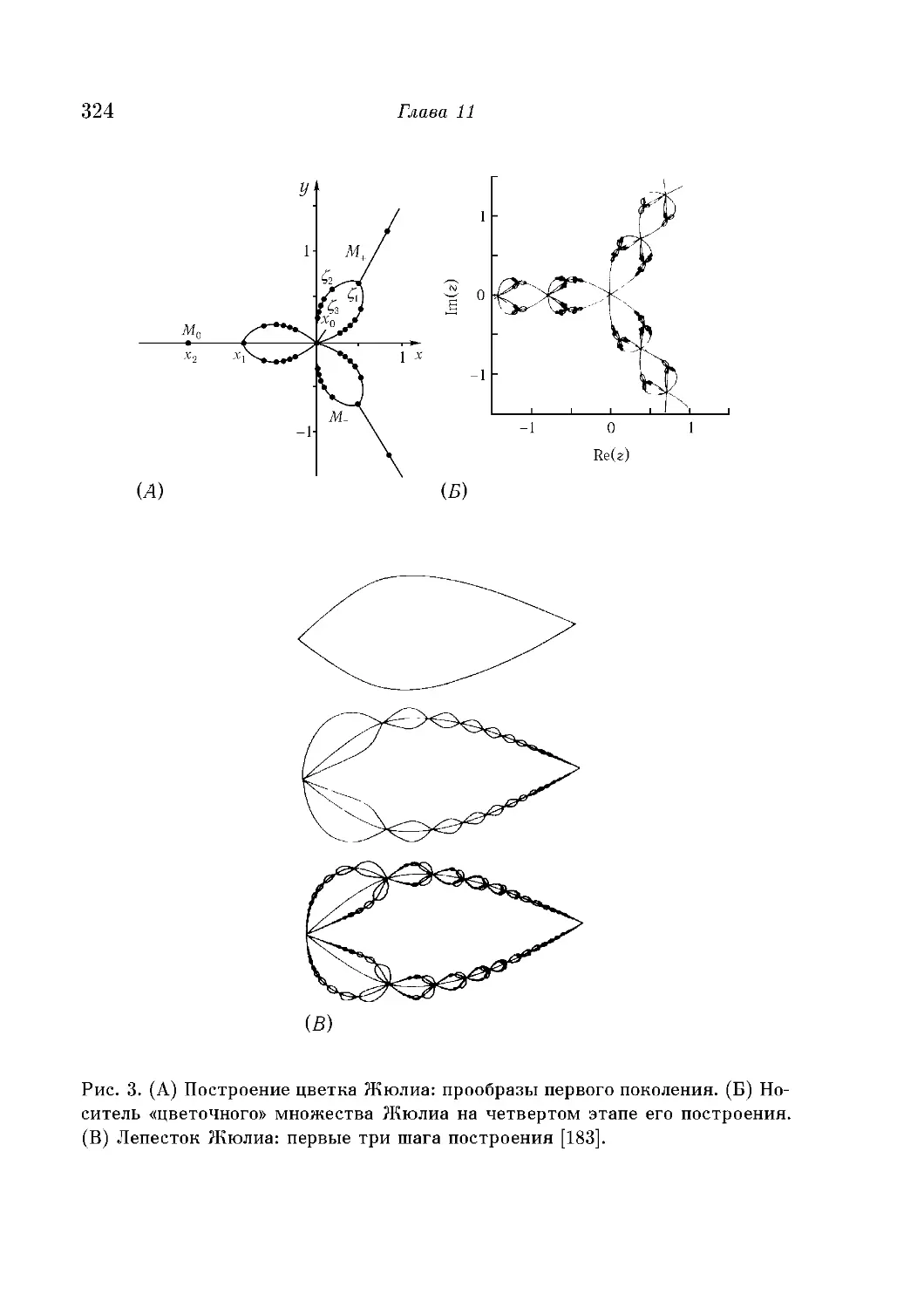
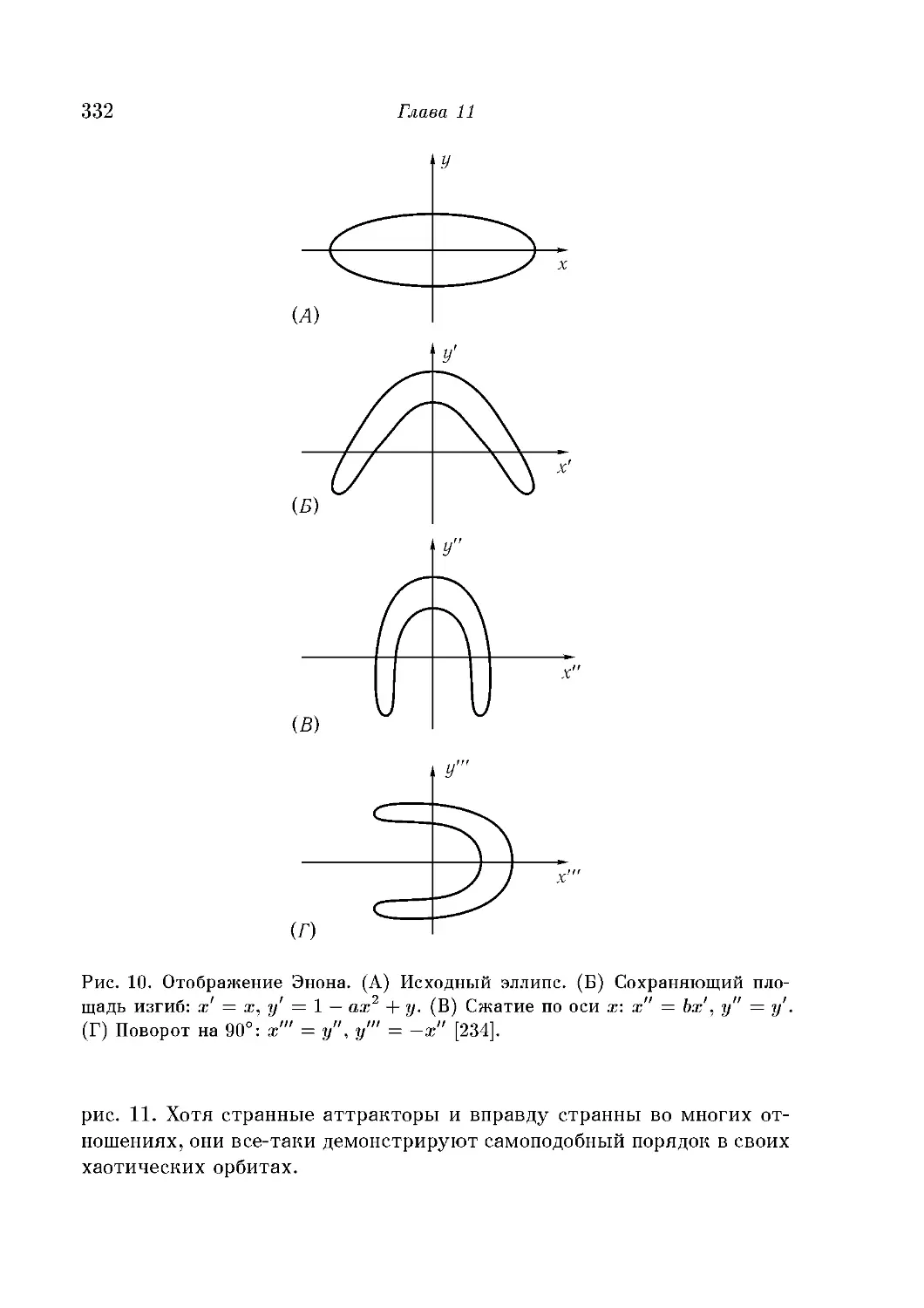
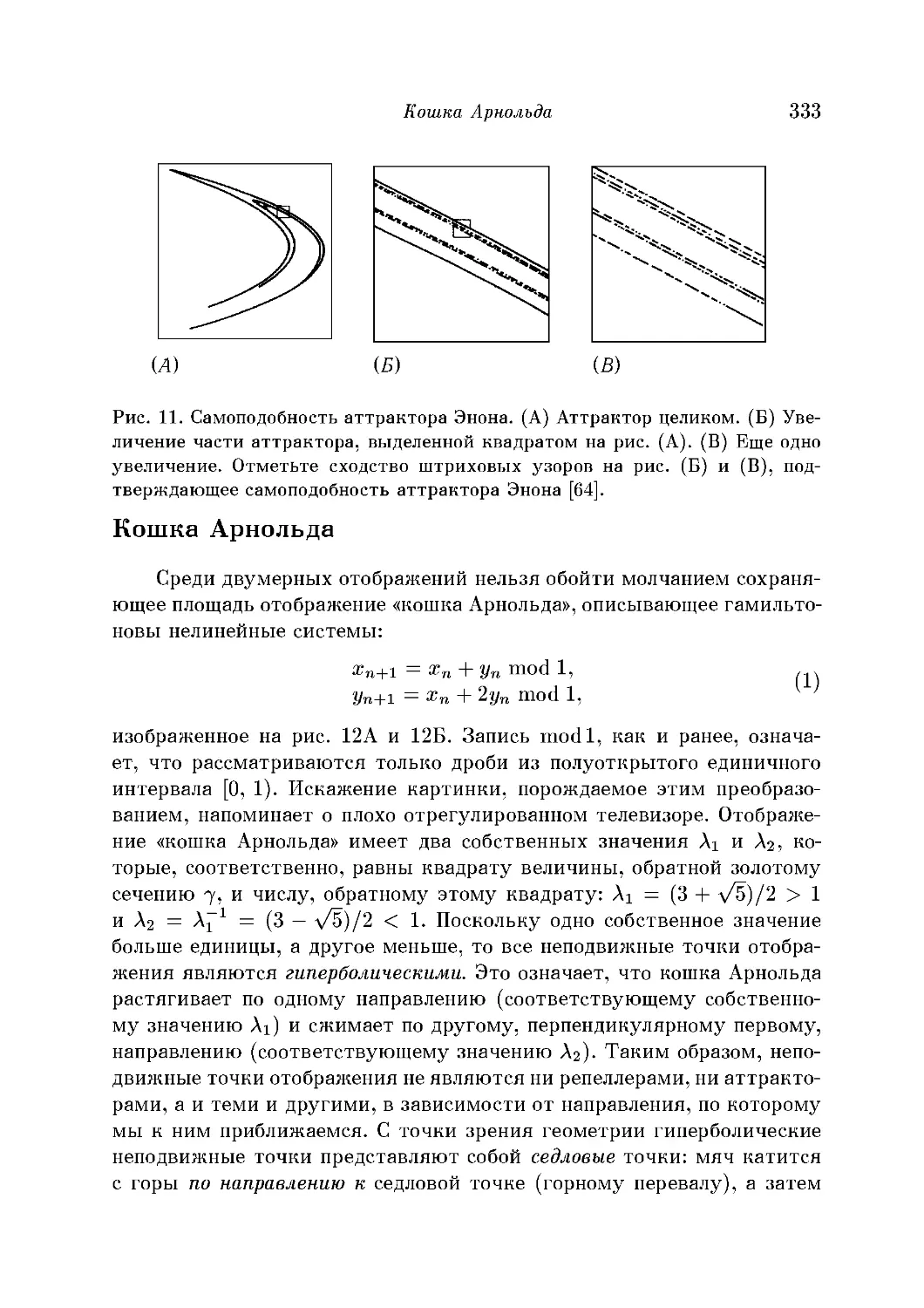
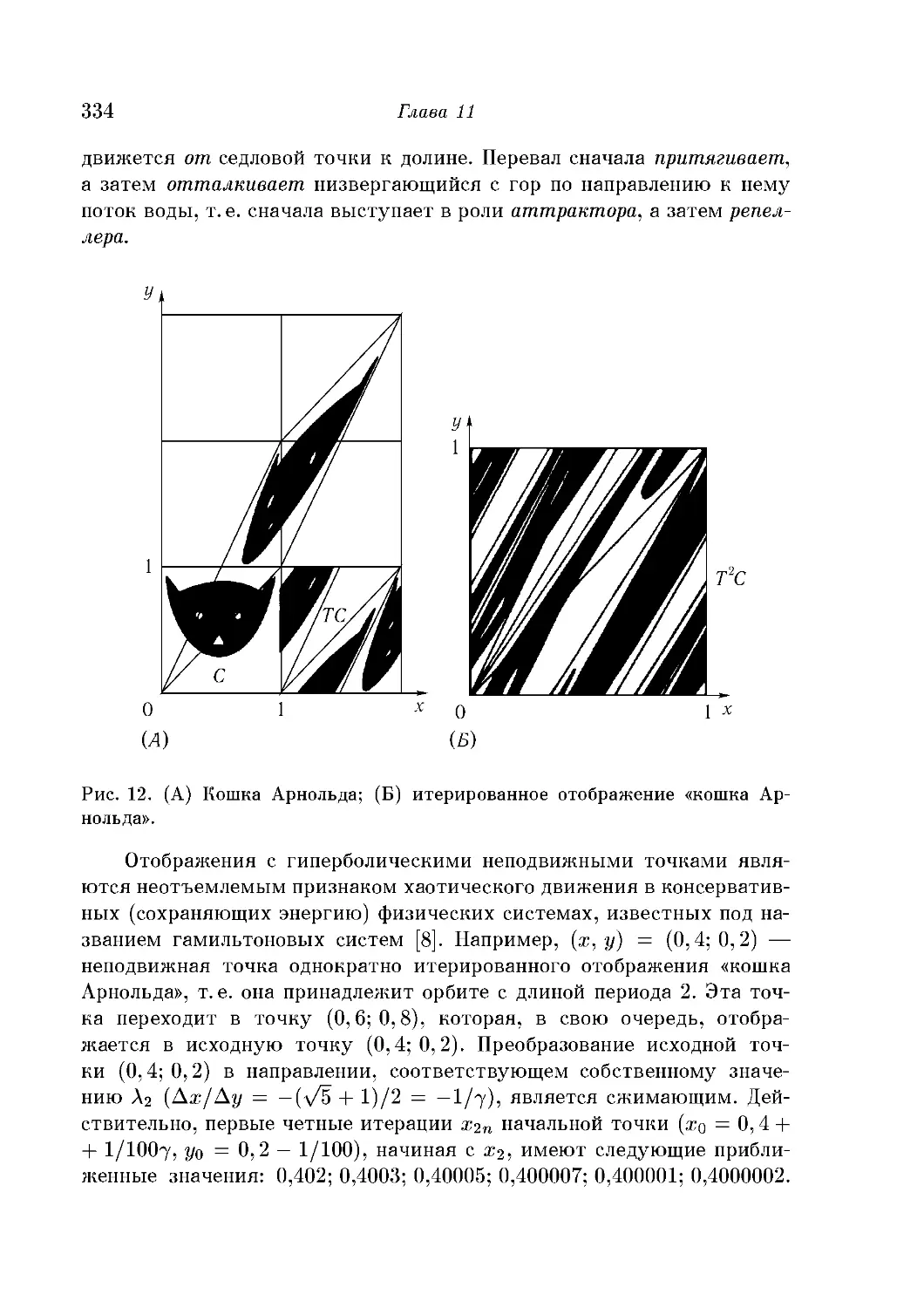
Странные множества Жюлиа 319
Мультифрактальное множество Жюлиа 322
Красота кусочно-линейных отображений 326
Преобразование пекаря и цифровой вариант игры в «стулья с
музыкой» 328
Кошка Арнольда 333
Миллиард знаков для тг 336
Кустарники и цветы от итераций 338
Глава 12. Самоподобная последовательность и логистичес-
логистическая парабола 342
Самоподобие от целых чисел 343
Логистическая парабола и удвоение периода 348
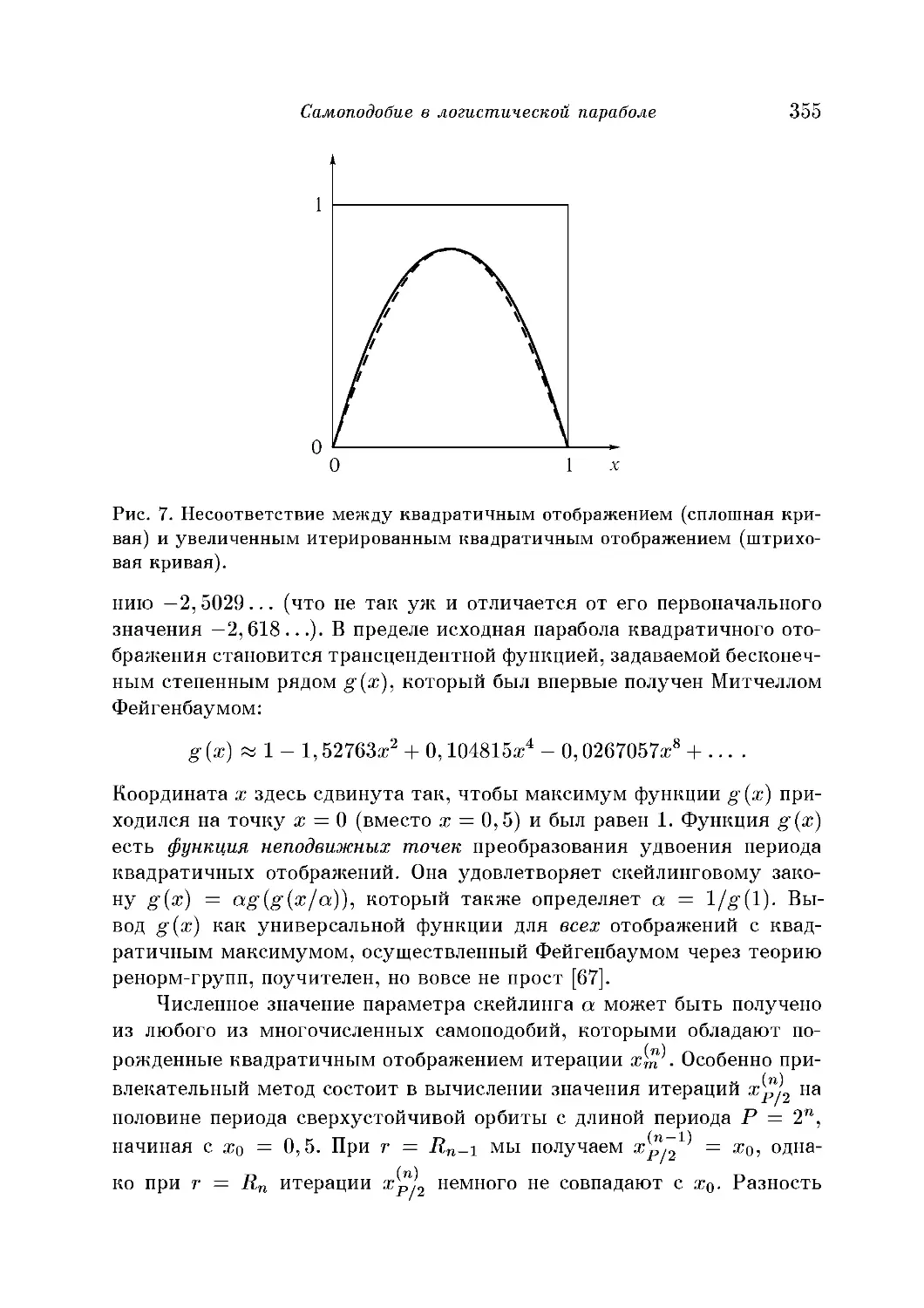
Самоподобие в логистической параболе 353
Скейлинг параметра роста 356
Самоподобная символическая динамика 359
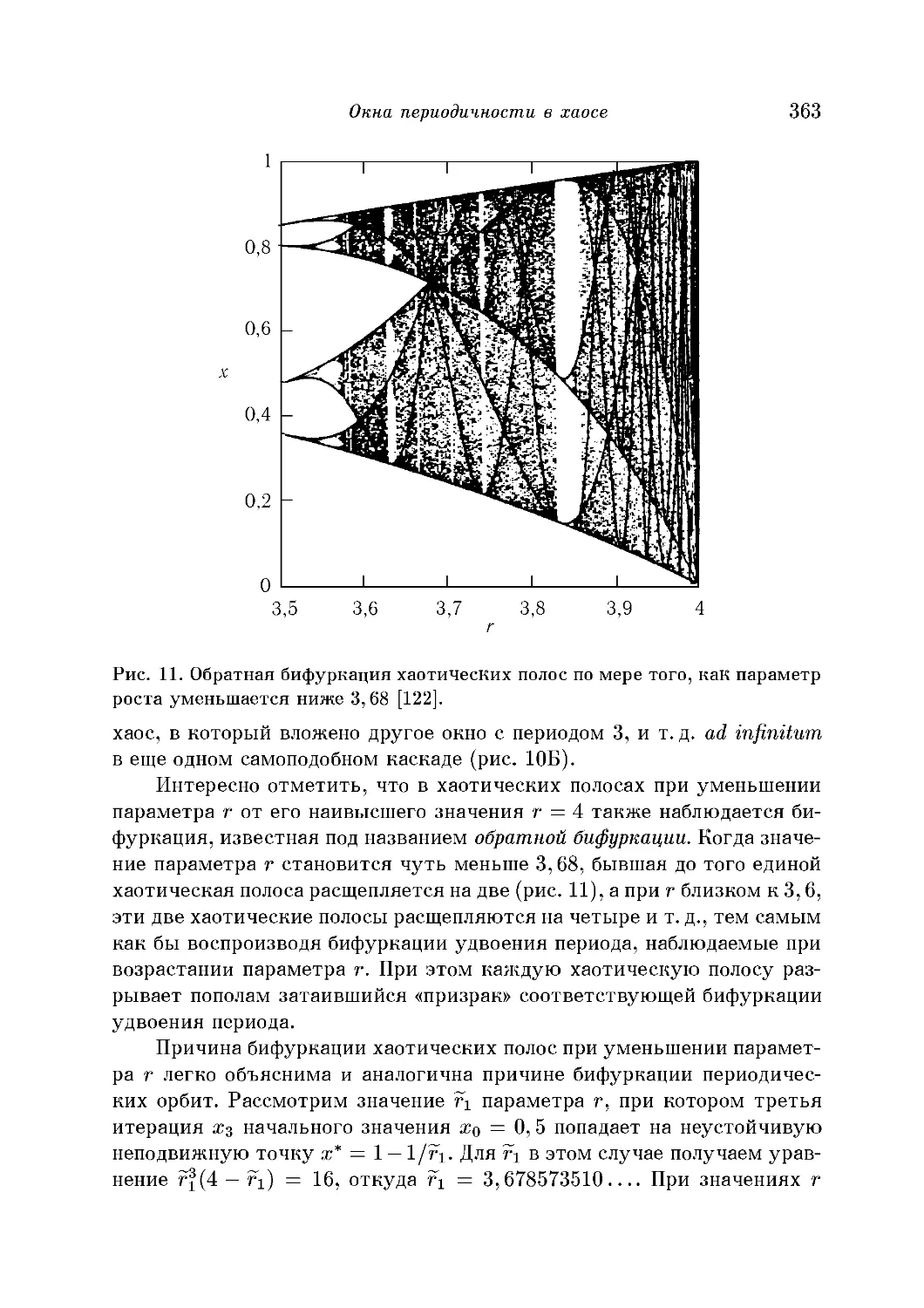
Окна периодичности в хаосе 361
Порождение новых орбит 365
Вычисление параметров роста для различных орбит 370
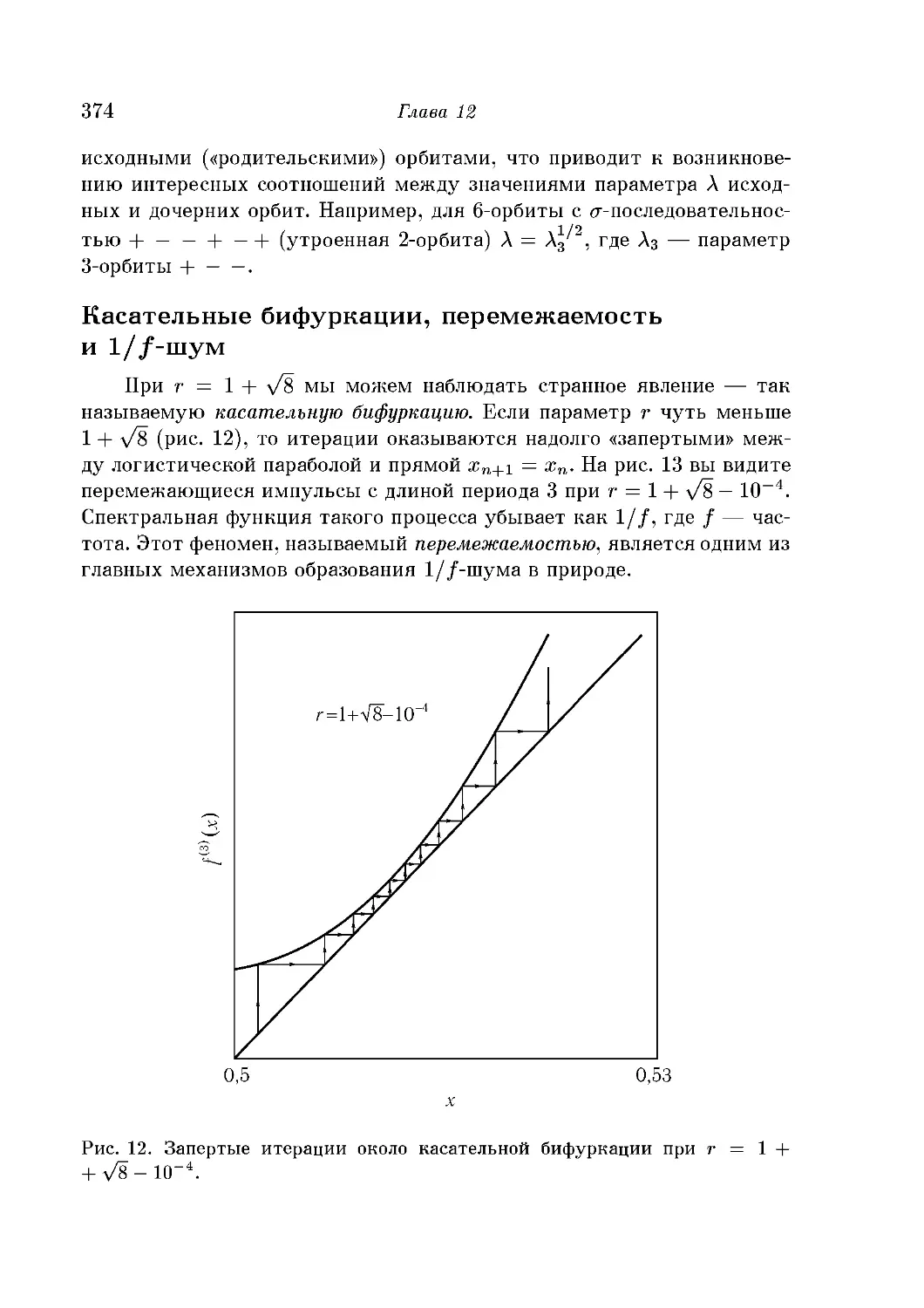
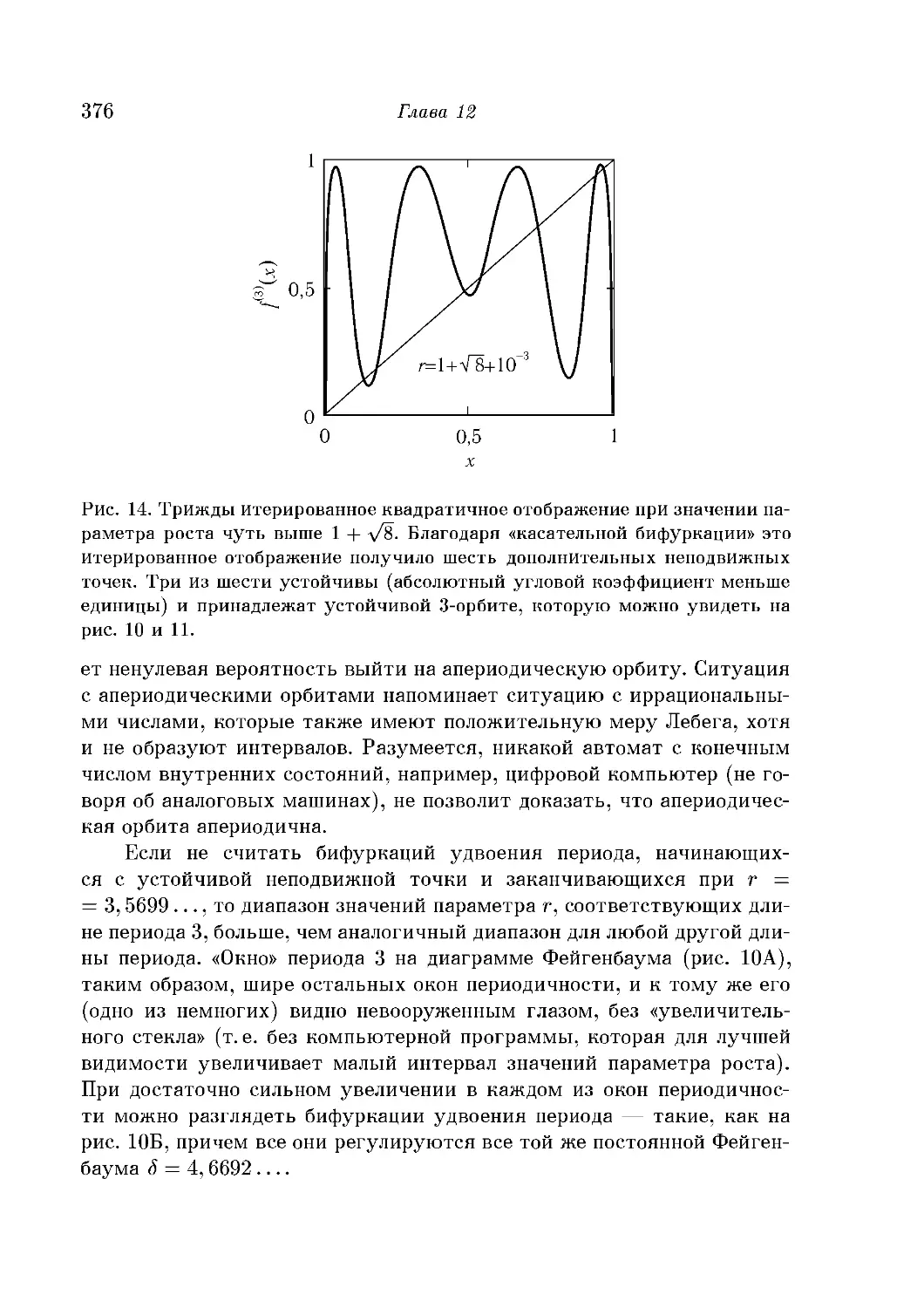
Касательные бифуркации, перемежаемость и 1//-шум 374
Полный хаос 377
Множество Мандельброта 381
Множества Жюлиа комплексного квадратичного отображения 383
Оглавление 11
Глава 13. Запрещенная симметрия, кролики Фибоначчи и
новое состояние вещества 387
Запрещенная симметрия пятого порядка 387
Дальний порядок, обусловленный взаимодействиями между
соседями 390
Построение кроличьей последовательности из последователь-
последовательности чисел Фибоначчи 396
Самоподобный спектр кроличьей последовательности 397
Самоподобие кроличьей последовательности 398
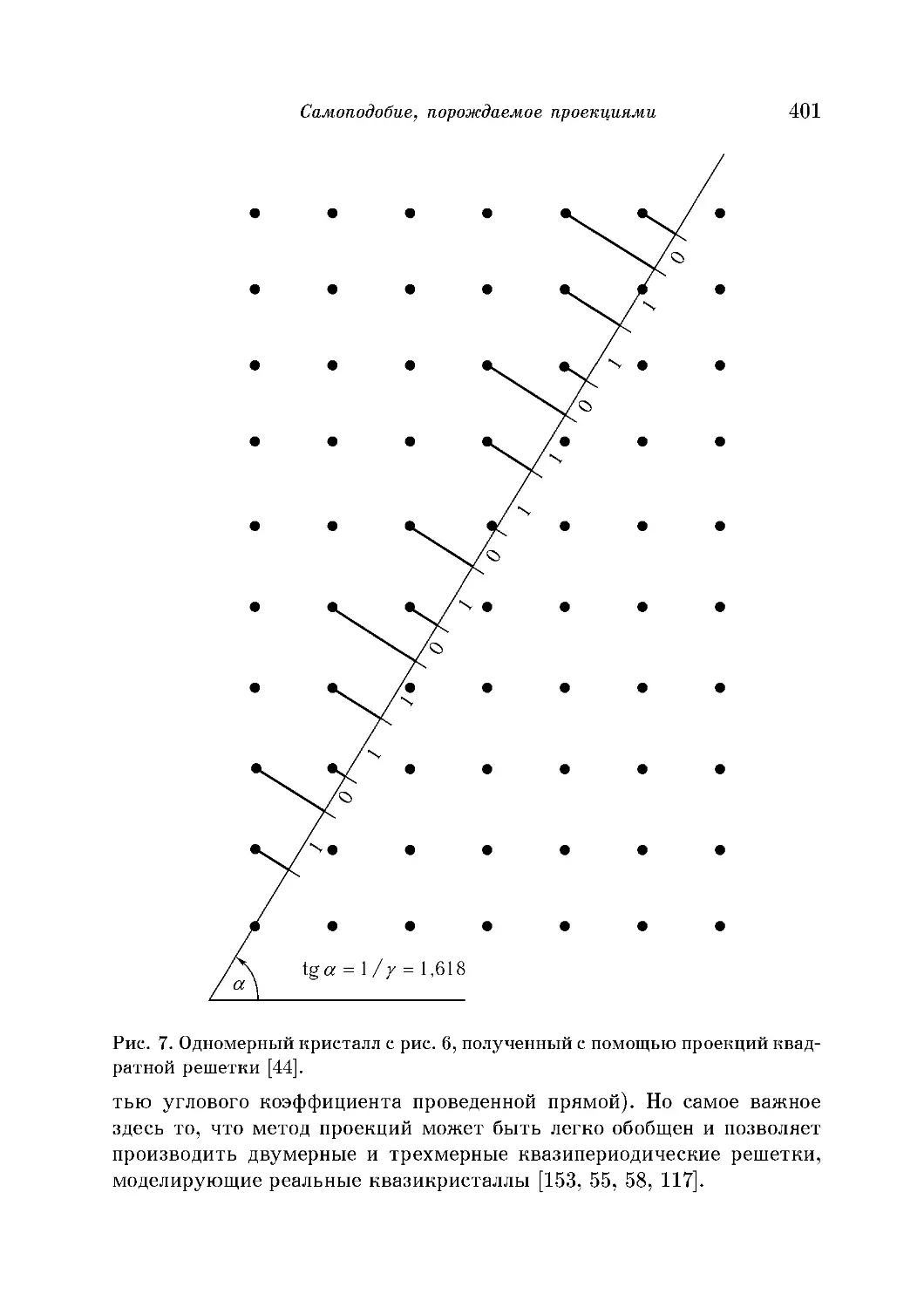
Одномерная квазипериодическая решетка 399
Самоподобие, порождаемое проекциями 400
Другие запрещенные симметрии 406
Глава 14. Периодические и квазипериодические структу-
структуры в пространстве 408
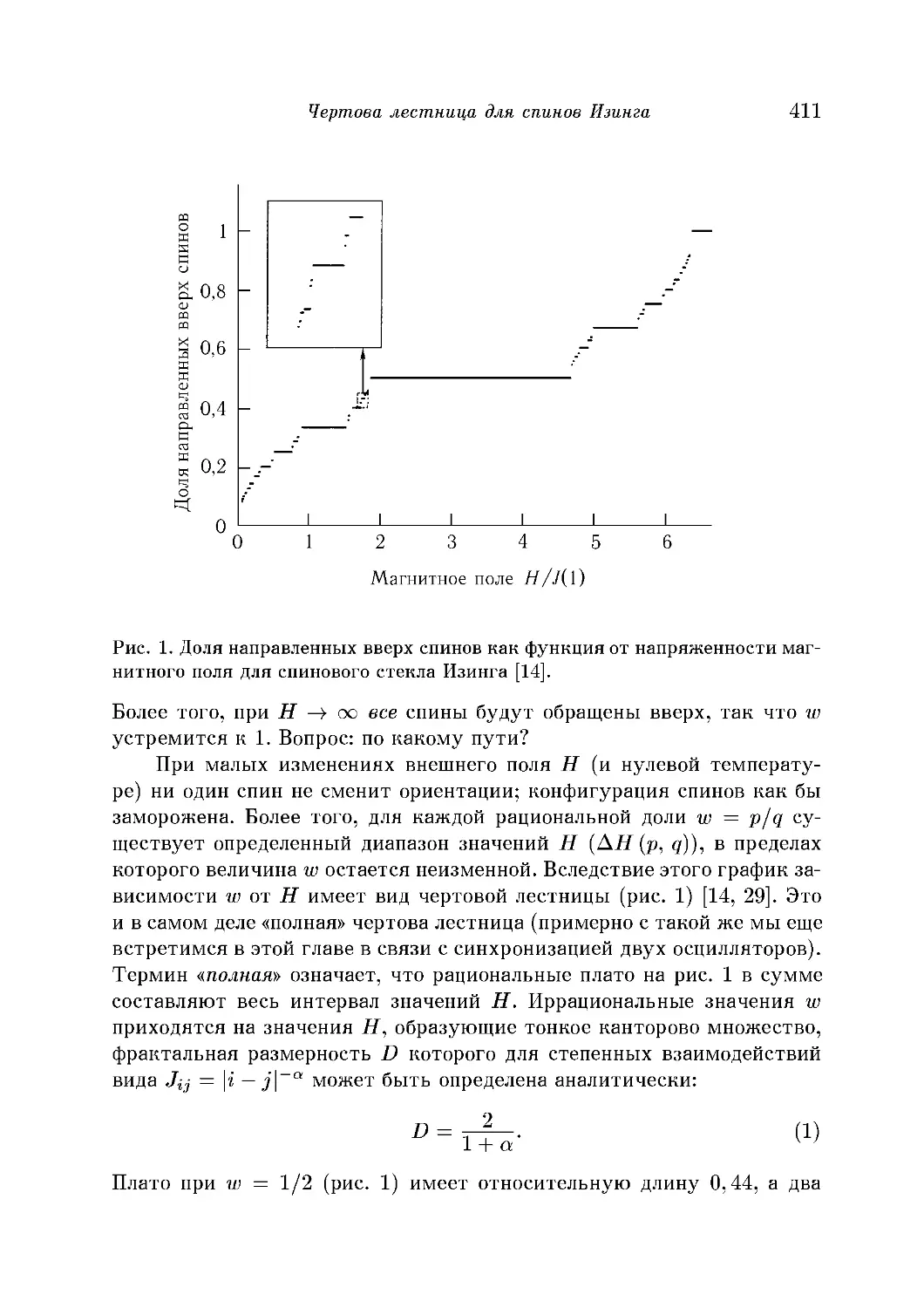
Периодичность и квазипериодичность в пространстве 410
Чертова лестница для спинов Изинга 410
Квазипериодические пространственные распределения .... 412
Спиновая последовательность Битти 415
Законы подобия для квазипериодических спинов 420
Самоподобные числа вращения 421
Отображения окружности и языки Арнольда 423
Медианты, последовательности Фарея и дерево Фарея 426
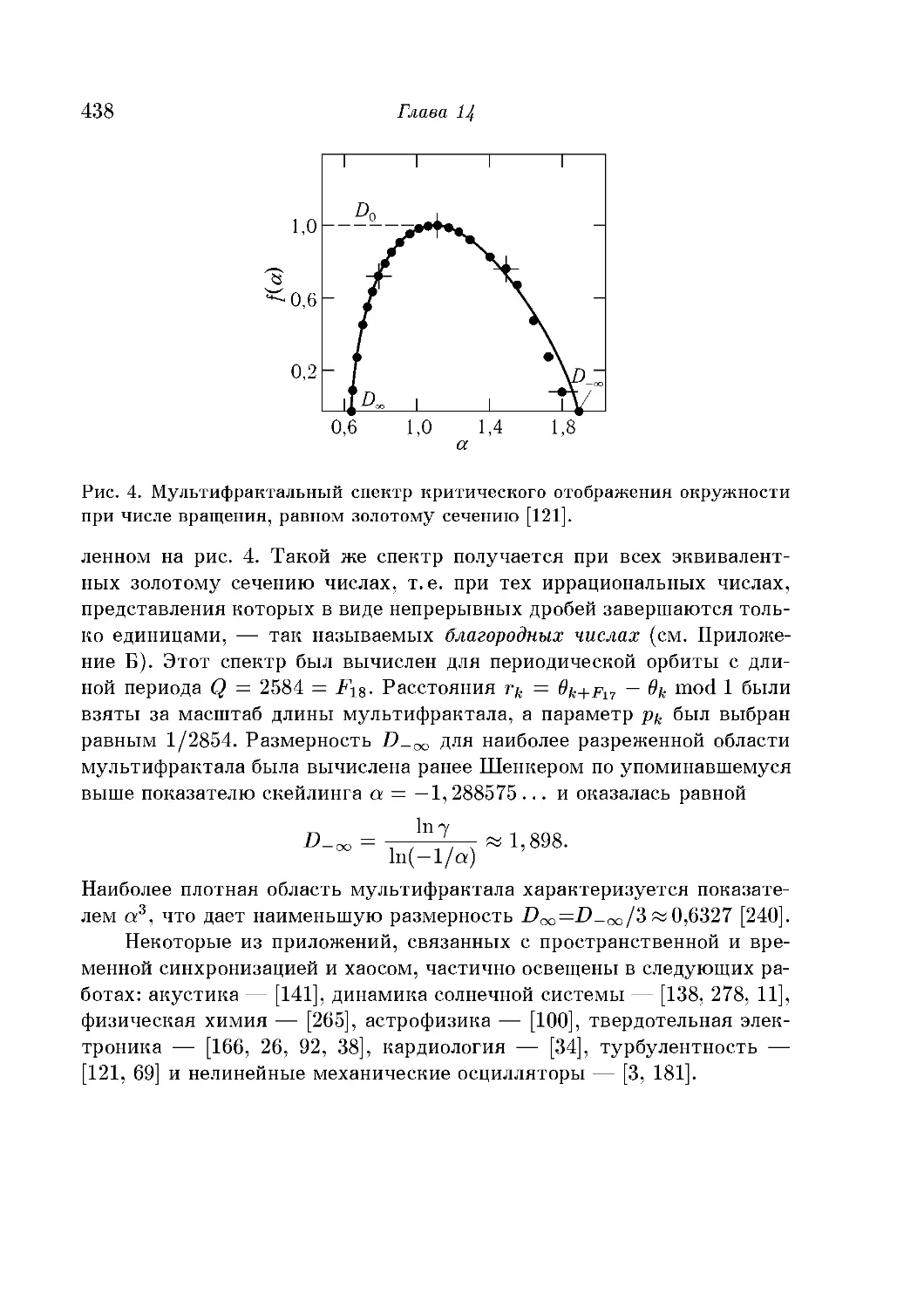
Путь к хаосу через золотое сечение 434
Глава 15. Перколяция: от лесных пожаров до эпидемий . 439
Критическое возгорание на квадратной решетке 440
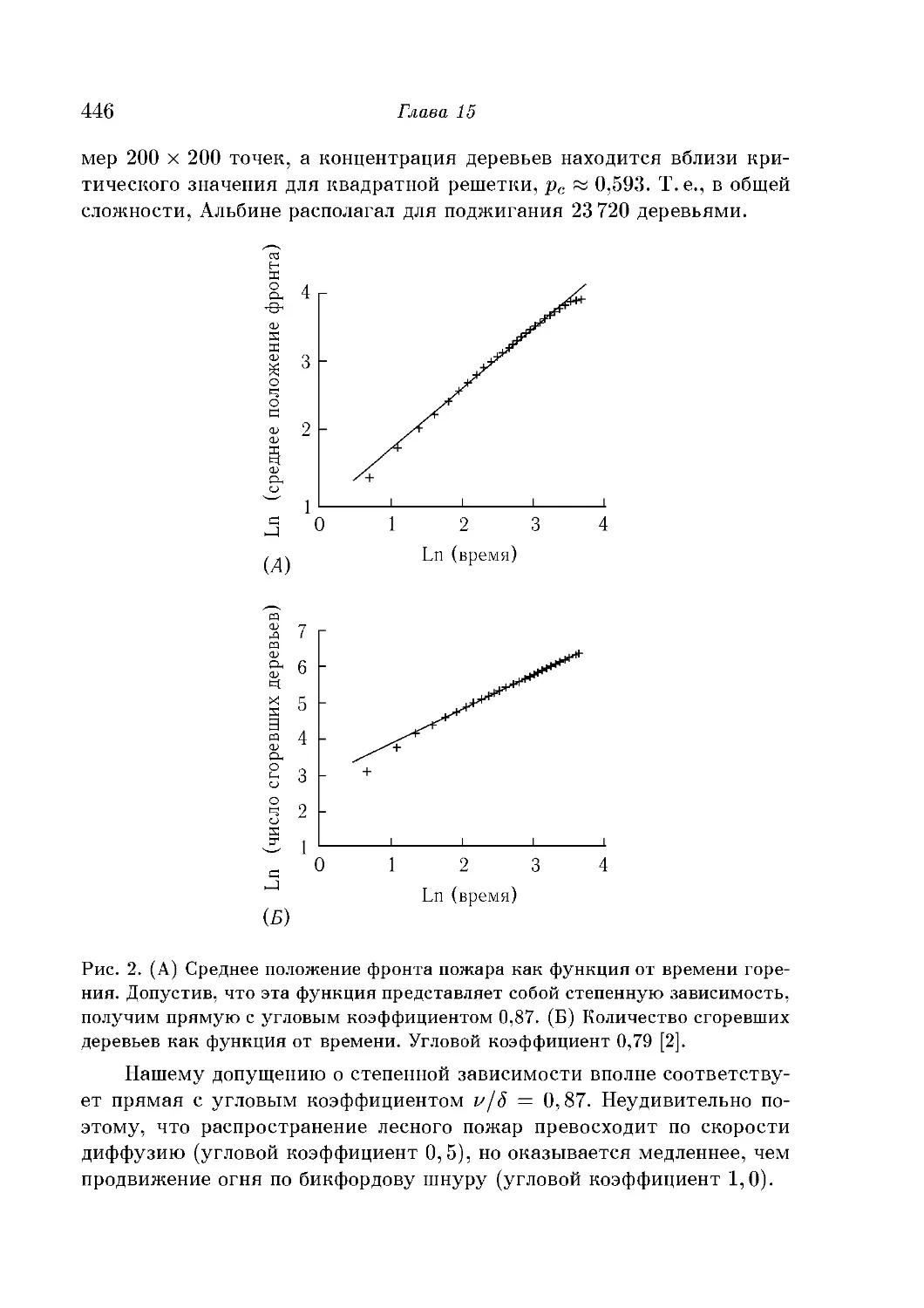
Универсальность 445
Критическая концентрация 448
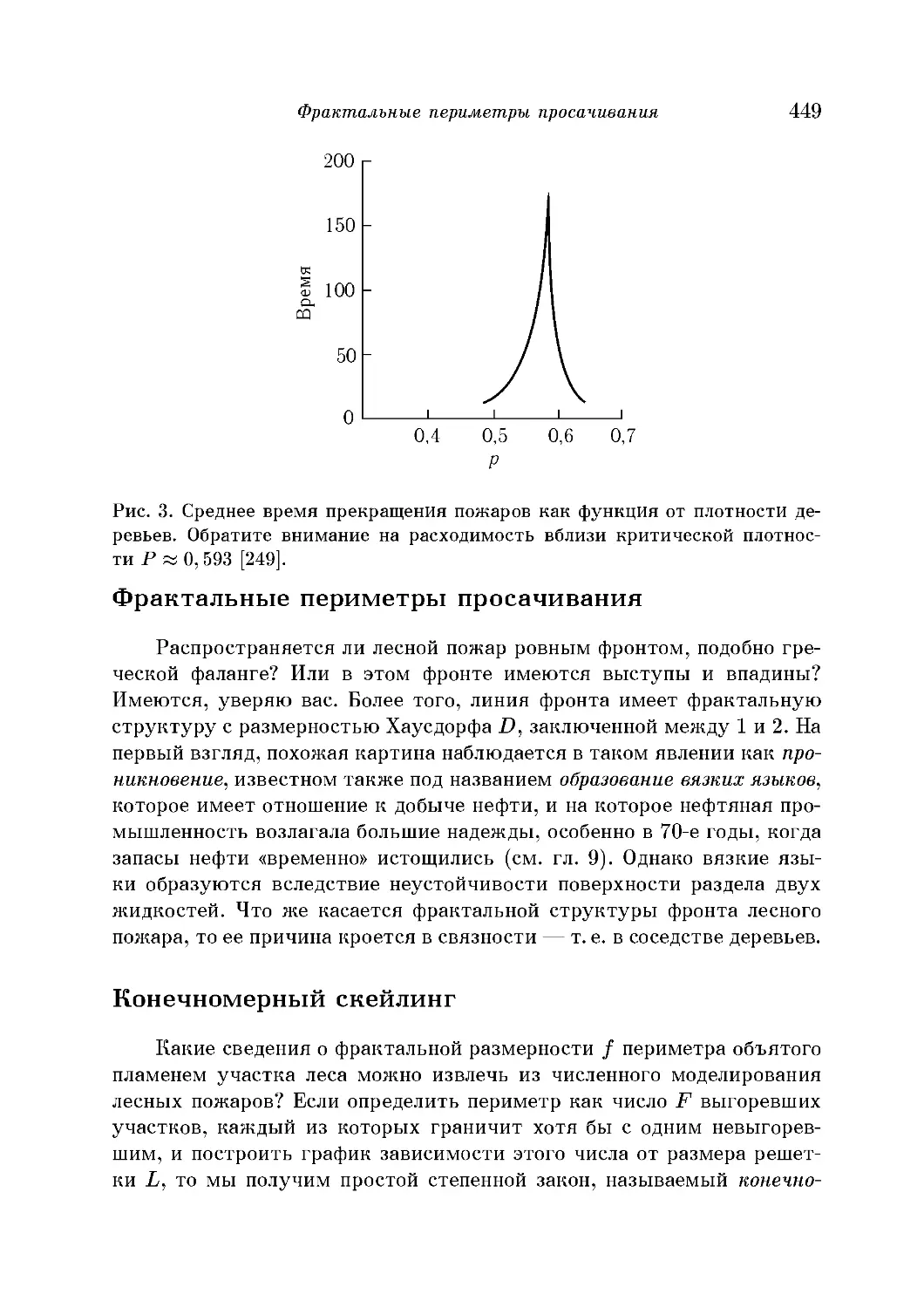
Фрактальные периметры просачивания 449
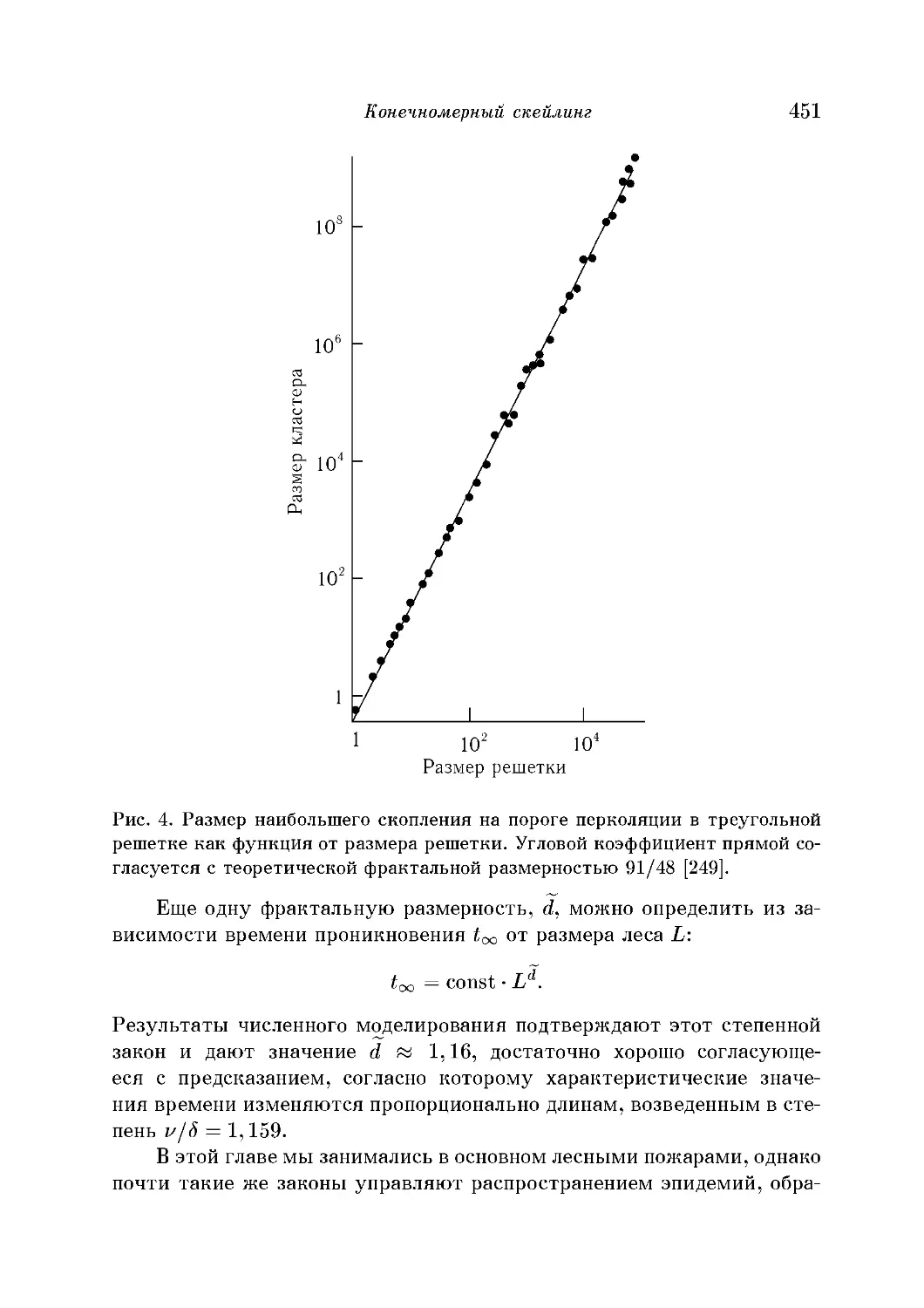
Конечномерный скейлинг 449
Глава 16. Фазовые переходы и перенормировка 453
Марковский процесс первого порядка 453
Самоподобные и несамоподобные марковские процессы .... 455
Скейлинг символов, порожденных марковским источником . . 456
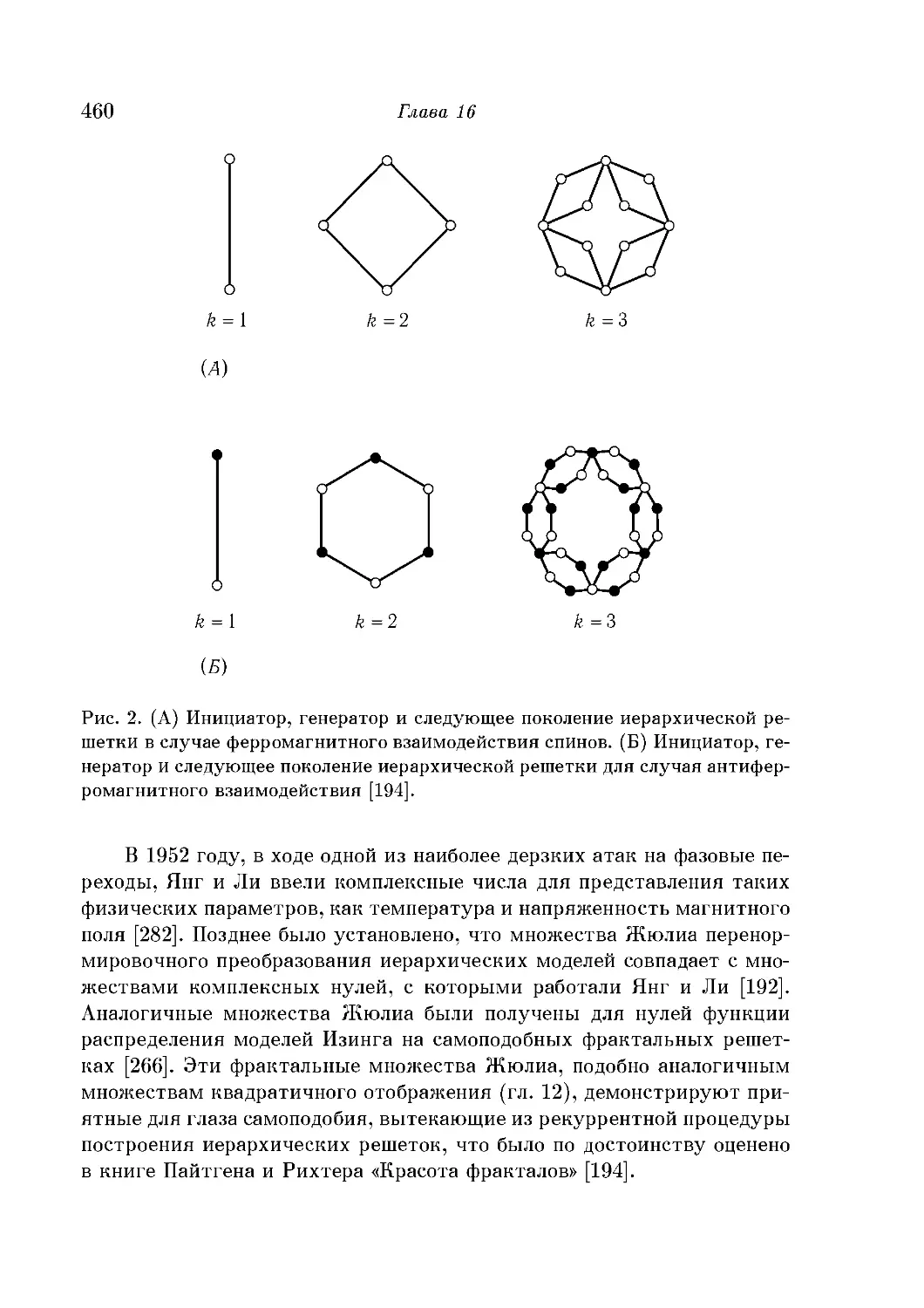
Перенормировка и иерархические решетки 459
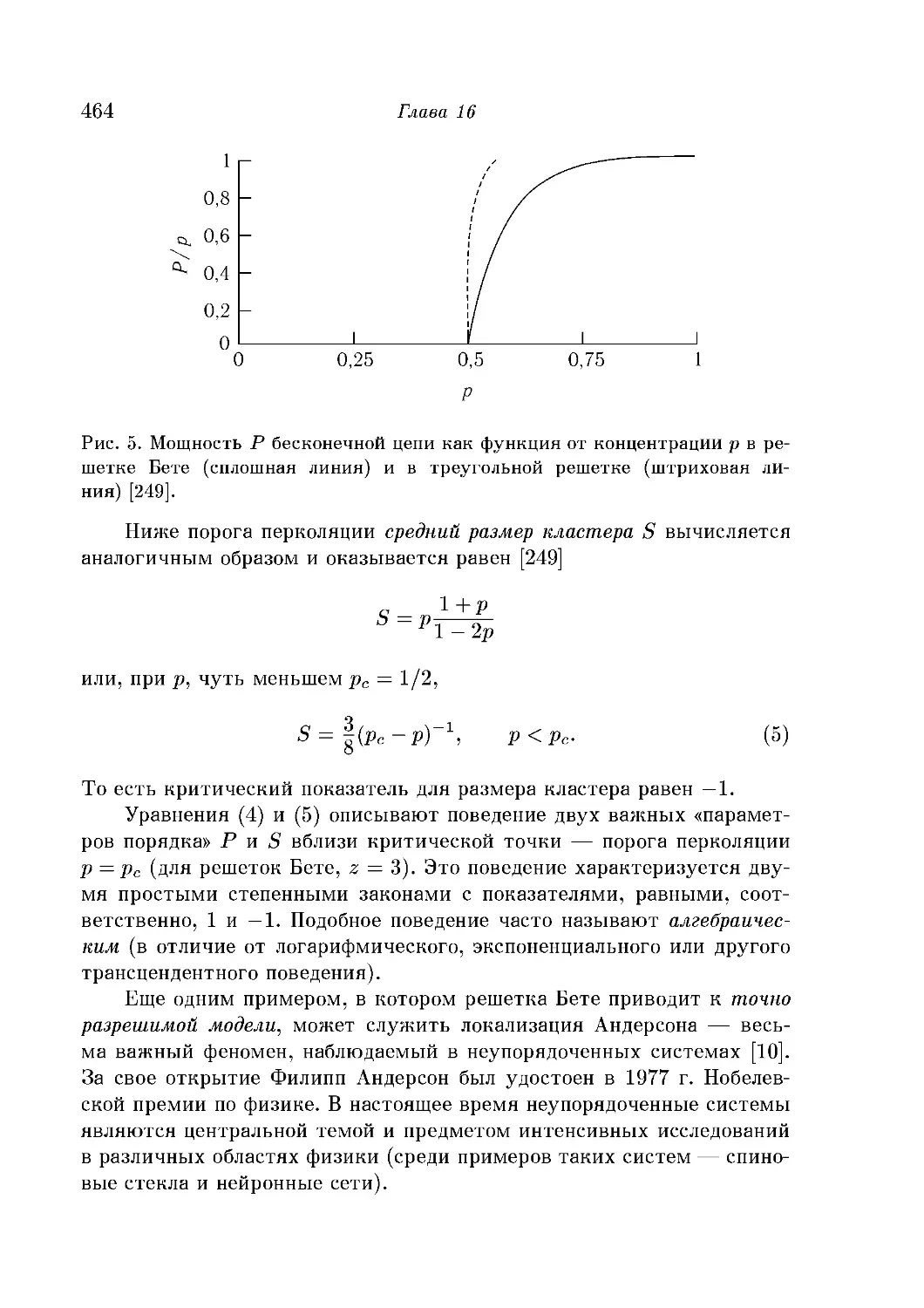
Порог перколяции решетки Бете 461
Простая перенормировка 465
12 Оглавление
Глава 17. Клеточные автоматы 469
Игра под названием «Жизнь» 471
Рост и гибель клеток 473
Формирование биологических конфигураций 481
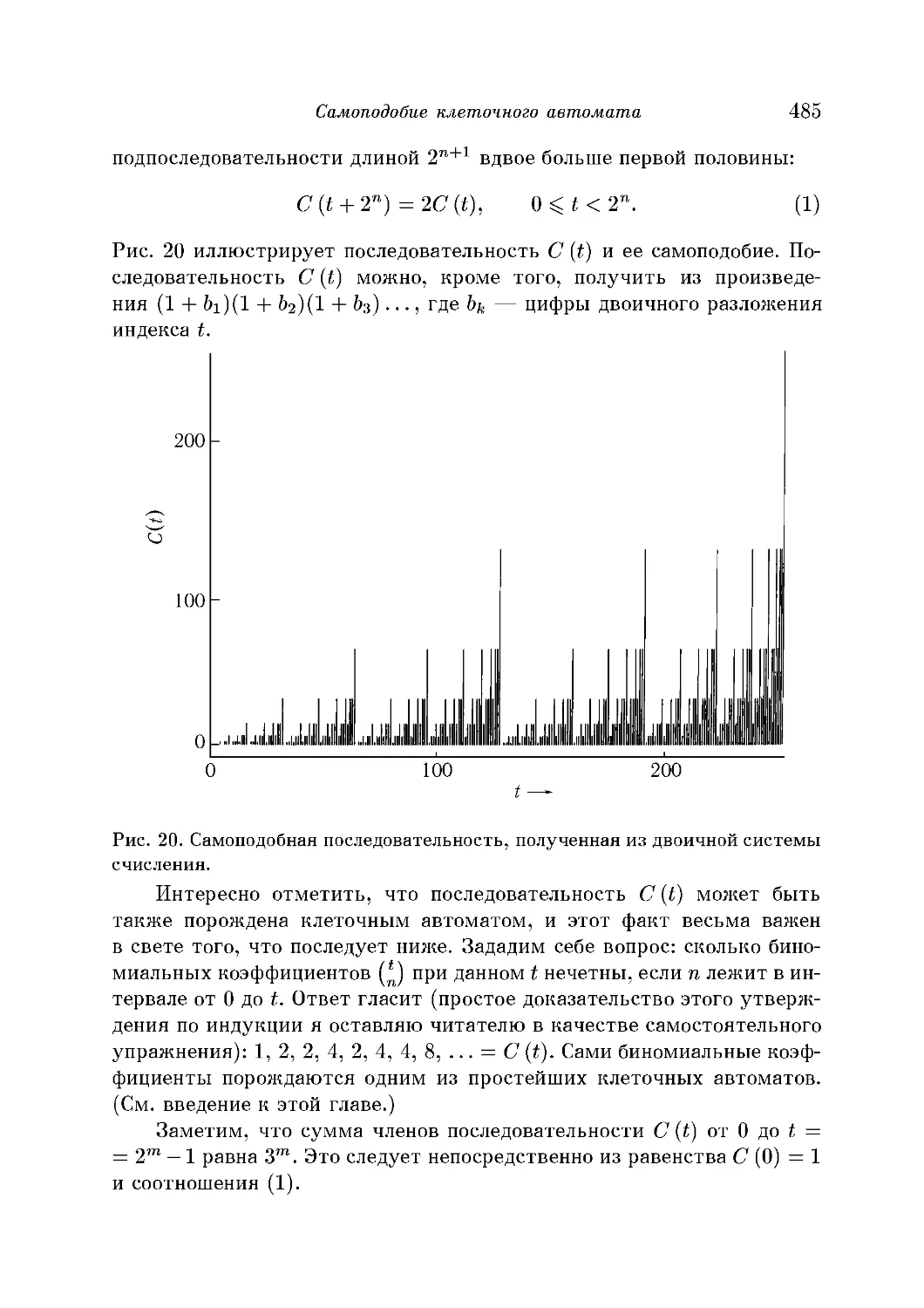
Самоподобие клеточного автомата 482
Каталитический конвертор как клеточный автомат 486
Треугольник Паскаля по модулю N 488
Самоорганизующиеся критические кучи песка по Баку .... 488
Приложение 491
Литература 495
Предметный указатель 512
Цветные вклейки
Вклейка 1. Встреча трех небесных тел. (А) При сближении двойной звез-
звезды (красная и желтая траектории, идет слева) и звезды-одиночки (синяя
траектория, идет справа) их орбиты становятся донельзя хаотическими. Че-
Через некоторое время они снова разлетаются в разные стороны: двойная звезда
уходит влево вверх, а одиночка — вправо вниз. (Б) При этой встрече трех тел
произошла смена партнеров. Желтый партнер оставил свою красную спутни-
спутницу и утанцевал с новой, синей, подругой влево вниз. Одинокая теперь красная
звезда удалилась вправо вверх. (Печатается с любезного разрешения Вольфа
Дитера Брандта.)
Вклейка 2. Этот причудливый самоподобный лист был получен итерациями
аффинных преобразований. (Печатается с любезного разрешения Хольгера
Беме.)
Вклейка 3. Три области притяжения итераций Ньютона («государства» по-
показаны красным, зеленым и синим цветом). Между этими государствами
проходит фрактальная граница, обладающая одним странным свойством: где
бы ни встречались территории двух государств, там же непременно присут-
присутствует и территория третьего. Парадоксальный факт: здесь нет государст-
государственных границ-линий, есть только трехгранные пограничные столбы-точки.
Интересно, может ли подобное устройство государственных границ помочь
делу мира во всем мире. (Печатается с любезного разрешения Хольгера Бе-
Беме.)
Вклейка 4. «Бесконечная радуга» — множество разноцветных логарифми-
логарифмических спиралей. (Печатается с любезного разрешения Хольгера Беме.)
Вклейка 5. «Облака над восточной Европой» — фотография, сделанная ав-
автором из окна своего дома рядом с осыпающейся «стеной».
Вклейка 6. Фракталы реального мира. (А) Облупившаяся краска на сте-
стене Плавательного клуба в Беркли, многосвязный фрактал. (Б) Фрактальный
рост микроорганизмов: красные водоросли на скале в Национальном парке
Пойнт-Рейес, штат Калифорния.
Вклейка 7. Цветы и прочие растения, полученные с помощью черепашьих
алгоритмов. (А) Лихнис, называемый также васильком (Lychnis Coronaria),
выращенный Пшемиславом Прусинкевичем и Джеймсом Хананом. (Б) Вер-
Вербена (Verbena). (В) Ветка сирени, выращенная Прусинкевичем и Хананом.
(Г) «Сад L», разбитый Прусинкевичем, Хананом, Дэвидом Фраккья и Деборой
14 Оглавление
Фаулер. (Д) Этапы цветения. (Е) Цветочный луг, удобренный стохастичес-
стохастическими L-системами. (©1988 P. Prusinkiewicz, University of Regina.)
Вклейка 8. (А) Множество Мандельброта (показано черным цветом) комп-
комплексных чисел с, для которых итерации zn+i = z^ + с (zo = 0) остаются
ограниченными. Цветные области символизируют значения с, при которых
итерации становятся неограниченными. Для значений с из основной «кардио-
идной» области М-множества длина периода итераций равна 1. Круг слева от
кардиоиды имеет период длиной 2 и т. д. Каждый круг («нарост») содержит
значения с для некоторой конечной длины периода. М-множество являет-
является связным множеством, однако неизвестно, можно ли назвать его локаль-
локально связным. (Б) Крупный план участка комплексной плоскости показывает
нарост и нити, связывающие его с уменьшенными копиями М-множества.
(В) При дальнейшем увеличении в комплексной плоскости обнаруживается
«водоворот» с одиннадцатью рукавами, в котором плавают еще меньшие ко-
копии М-множества. Сами рукава составлены из множества завитков, которые
несомненно сами состоят из меньших завитков. (Г) Самоподобное погруже-
погружение: увеличиваем одно из маленьких, «дочерних», М-множеств, резвящихся
в водовороте, и воочию наблюдаем фамильное сходство с «мамашей», изобра-
изображенной на рис. (А). (Печатается с любезного разрешения Хольгера Беме.)
Вклейка 9. Самоорганизующийся дрейф генов между шестнадцатью раз-
различными «видами» от п = 1 до п = 16 (показаны разными цветами). (А) На-
Начальная стадия — различные виды случайным образом перемешаны на квад-
квадратной решетке. По прошествии некоторой единицы времени на часах эво-
эволюции каждая клетка, занятая геном вида п, перекрасит по своему образу
и подобию любую клетку из четырех непосредственно соседствующих с ней
клеток, при условии, что эта соседняя клетка занята геном вида п — 1 (п = 0
соответствует п = 16). (Б) Более поздняя стадия — некоторые виды генов
занимают все большие и большие площади, однако не сдаются и многие мел-
мелкие генетические сообщества. (В) Эволюционный процесс продолжается —
возникает новый тип генетических конфигураций: спирали, в которых пери-
периодически повторяются различные виды. (Г) Хотя генетические взаимодей-
взаимодействия строго локальны, доминирующей конфигурацией становятся большие
спирали. Как и в квазикристаллах и многих других природных феноменах,
локальные правила порождают дальний порядок и влияют на процесс на гло-
глобальном уровне. (Печатается с любезного разрешения Хольгера Беме.)
Предисловие
Симметрия — как бы широко или узко
вы не определяли значение этого поня-
понятия — является той идеей, посредст-
посредством которой человек на протяжении ве-
веков пытается постичь и создать поря-
порядок, красоту и совершенство.
Герман Вейль
В основе фракталов, хаоса и степенных законов лежит объединя-
объединяющее понятие — самоподобие. Самоподобие, или инвариантность при
изменении масштабов или размеров, присуще многим законам природы
и бесчисленным явлениям в окружающем нас мире. Более того, самопо-
самоподобие — одна из важнейших симметрии, играющих формообразующую
роль в нашей Вселенной и лежащих в основе наших попыток постичь ее.
Симметрия сама по себе принадлежит к числу наиболее фун-
фундаментальных и плодотворных понятий, созданных человеческой
мыслью [275]. Под симметрией мы понимаем инвариантность при
каких-либо изменениях: нечто остается одним и тем же, несмотря на
потенциальную возможность изменения. По-видимому, сильнее других
бросается в глаза зеркальная симметрия, т.е. инвариантность при «пе-
«перемене местами» левой и правой сторон. Многие свои организмы при-
природа построила почти симметрично, и большинство фундаментальных
законов физики, таких, как закон всемирного тяготения Ньютона, об-
обладает точной зеркальной симметрией: в притяжении небесных тел
(равно как и большинства тел земного происхождения) нет различия
между левым и правым. Однако несохранение четности при радиоак-
радиоактивном распаде, т. е. нарушение точечной симметрии при «слабом» взаи-
взаимодействии, научило в конце концов даже физиков серьезно относиться
к различию между правым и левым.
Еще одна важная разновидность симметрии — инвариантность от-
относительно геометрических преобразований. Наша вера в инвариант-
инвариантность при смещениях в пространстве и времени столь безгранична, что
16 Предисловие
мы глубоко убеждены в одинаковости законов природы во всей Все-
Вселенной и в том, что законы природы всегда были такими и останутся
такими во все времена.
Столь же важна и другая разновидность симметрии — инвариант-
инвариантность относительно вращения. Окружность инвариантна при повороте
вокруг ее центра на любой угол. Квадрат можно совмещать с самим
собой, только поворачивая его на углы, кратные 360°/4 = 90°. Говорят,
что квадрат обладает осью симметрии четвертого порядка. Правиль-
Правильный шестиугольник обладает симметрией шестого порядка. Хотя пово-
поворотная симметрия цветка или морской звезды может быть не вполне
точной, точная изотропия, обнаруженная в фундаментальных законах
природы, является одним из наиболее мощных принципов, позволяю-
позволяющих понять и объяснить структуру отдельных атомов, сложных мо-
молекул и целых кристаллов. Трансляционная, поворотная и зеркальная
симметрии, действуя совместно, создают форму кристаллов от алмазов
до снежинок. И эти же три симметрии определяют многое из того, что
доставляет нам эстетическое наслаждение в орнаментальных узорах.
Еще более поразительна симметрия, проявляющаяся в точном тож-
тождестве однотипных элементарных частиц. Между электроном здесь
и электроном там — на далекой звезде, например, — просто не су-
существует никакой разницы. Абсолютное тождество фотонов — частиц
света — не позволило подойти к их подсчету как к подсчету иденти-
идентифицируемых отдельных частиц. Возникла новая разновидность статис-
статистики частиц, открытая Ш.Н. Бозе и облеченная в более удобоваримую
форму Эйнштейном — способ подсчета, ранее не виданный в мире, на-
наполненном осязаемыми объектами.
Впервые на связь между симметриями фундаментальных законов
физики относительно сдвигов в пространстве и времени и вращений,
с одной стороны, и законами сохранениями импульса, энергии и уг-
углового момента — с другой, обратила внимание Эмми Нётер, одна из
величайших математиков нашего века. (Благодаря Давиду Гильберту,
который вопреки глубоко укоренившимся предрассудкам коллег насто-
настоял на предоставлении ей должности в Гёттингенском университете,
Нётер получила возможность преподавать. После разгрома немецкой
науки в 1933 г. она была вынуждена покинуть Гёттинген. Умерла Эм-
Эмми Нётер в Брин-Море в 1935 г.)
Не менее глубокое воздействие на наше понимание мира оказы-
оказывают и другие симметрии. Инвариантность при равномерном прямо-
прямолинейном движении дала нам специальную теорию относительности,
слияние пространства и времени в единое пространство-время и соот-
Предисловие 17
ношение Е = тос2 как наиболее известное следствие теории относи-
относительности. Постулированная Эйнштейном эквивалентность ускорения
и гравитации (инертной и тяжелой масс) лишь усугубила переворот
в нашем восприятии пространства, времени и материи.
Среди всех симметрии, пышным цветом расцветаюших в Саду Ин-
Инвариантности, лишь один побег до недавнего времени не был взлеле-
взлелеян — буквально вездесущая инвариантность при изменении размеров,
называемая самоподобием, или, если речь идет более чем об одном
масштабном (скейлинговом) факторе, самоаффинностью. Чрезвычайно
плодотворные концепции самоподобия и самоаффиности пронизывают
всю природу — от распределения атомов в веществе до распределения
галактик во Вселенной. Самоподобие глубоко проникло и в математику.
Около трехсот лет назад немецкий философ и разносторонний матема-
математик Готфрид Вильгельм Лейбниц воспользовался масштабной инвари-
инвариантностью бесконечно длинной прямой для того, чтобы дать опреде-
определение прямой. Другими, столь же ранними, хотя и менее удобными
примерами самоподобных объектов в математике являются канторовы
множества и функции Вейерштрасса. Позднее к этим примерам доба-
добавились множества Жюлиа и другие чудеса теории множеств.
Есть нечто симптоматичное в том, что благодаря теории множеств
еще один абстрактный раздел математики глубоко проник в реальный
мир. «Непостижимая эффективность» (по выражению Юджина Вигне-
ра) математики, по-видимому, безгранична. Кто бы мог подумать, что
такие чисто математические конструкции, как канторовы множества,
изобретенные лишь для того, чтобы убедить скептиков в возможнос-
возможности существования несчетных множеств нулевой меры, найдут хотя бы
какое-нибудь практическое применение, не говоря уже о том, что ста-
станут одним из центральных понятий? Между тем, именно такими они
стали для многих природных явлений — от гелеобразования, полимери-
полимеризации и коагуляции в коллоидной физике и химии до нелинейных сис-
систем в бесчисленных разделах современного естествознания. Перколя-
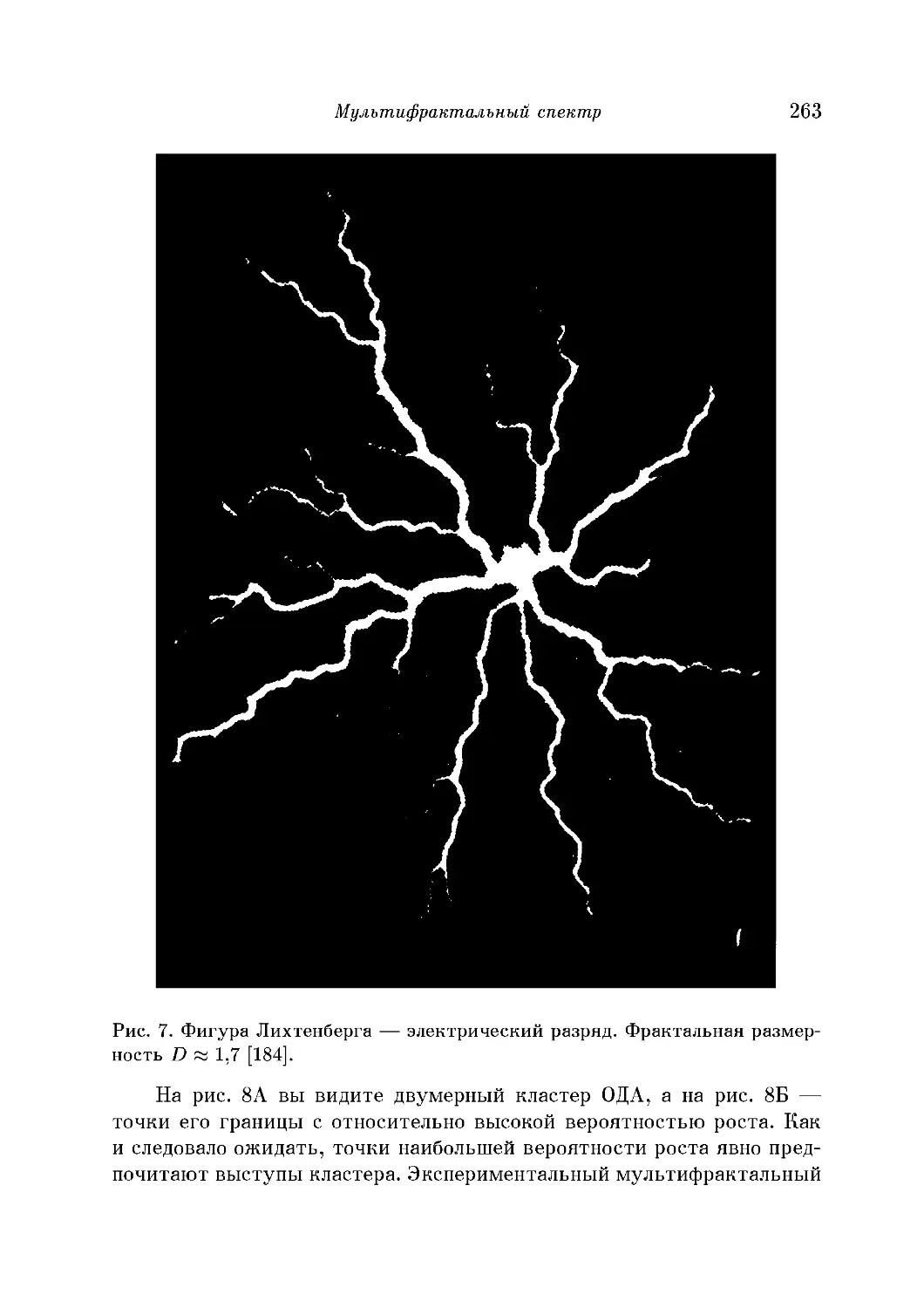
ция, древовидный рост, поверхности разрыва, электрические разряды
(молнии и фигуры Лихтенберга) и структура квазикристаллов лучше
всего описываются теоретико-множественными конструкциями.
Или взять хотя бы причудливую функцию, которую сто лет на-
назад Карл Вейерштрасс придумал только для того, чтобы показать, что
функция может быть всюду непрерывна и тем не менее нигде не диф-
дифференцируема. Поразительно уже то, что такая аналитическая патоло-
патология описывает нечто, существующее в реальном мире; еще более по-
поразительно, что она имеет фундаментальное значение для понимания
18 Предисловие
странных аттракторов нелинейных динамических систем (таких, как
двойной маятник или задача трех тел).
Слово симметричный — древнегреческого происхождения и озна-
означает «соразмерный», «упорядоченный», т. е. даже отдаленно не напоми-
напоминает ни о чем хаотическом. Тем не менее, как это ни парадоксаль-
парадоксально, самоподобие — основная тема нашей книги — это единственная
из всех симметрии, которая порождает саму антитезу симметрии —
хаос, состояние полного беспорядка и отсутствия какой бы то ни бы-
было соразмерности. Как мы постараемся показать, возникновение хаоса
тесно связано с самоподобием и внутренне присущим ему отсутствием
«гладкости».
Возможно, не следует удивляться тому, что самоподобие приво-
приводит к многочисленным парадоксам в измерениях времени, длины и
даже музыкальной тональности. Вспомним о медлительной черепахе
Зенона, за которой гонится (но которую так никогда и не догоняет)
быстроногий Ахилл. Почему длина некоторых отрезков неограничен-
неограниченно возрастает, когда мы измеряем их все укорачивающимися мерными
стержнями? Как Евклид объяснил бы плоские геометрические фигуры,
площадь которых пропорциональна не квадрату видимого периметра,
а некоторой меньшей, дробной его степени, например, 1,77? Что мы
должны подумать о музыкальных звуках, которые при повышении их
частоты звучат, каким бы невероятным это нам ни казалось, ниже то-
тоном? Как могут существовать подобные несообразности? И как можно
было бы дать непротиворечивое и осмысленное описание таких фено-
феноменов?
Здесь нам на помощь приходит одна необычайно счастливая идея
Феликса Хаусдорфа. Вместе с Абрамом Безиковичем Хаусдорф, по-
новому взглянув на размерность, низверг ее с целочисленного трона
в гущу вещественных чисел, дав нам тем самым острейшее орудие для
атаки на странные множества, порождаемые самоподобием, — размер-
размерность Хаусдорфа и ее многочисленные ответвления и обобщения.
Вспоминая славные имена прошлого, мы не должны забывать о
нашем великом современнике, несравненном Бенуа Б. Мандельбро-
те, который в одиночку спас наиболее хрупкие функции теории мно-
множеств и наиболее «пыльные» множества от почти полного забвения,
поместив их в самый центр нашего повседневного опыта и пред-
представлений. Как выяснилось, все эти годы мы жили с фрактальны-
фрактальными артериями неподалеку от фрактальных речных систем, собира-
собирающих влагу со склонов фрактальных гор под фрактальными обла-
облаками и катящих свои воды к фрактальным берегам морей и оке-
Предисловие 19
анов. Но, как и мольерову мещанину во дворянстве, нам не до-
доставало надлежащей прозы — существительного фрактал и при-
прилагательного фрактальный, которые мы обрели благодаря Бенуа
Мандельброту.
В истории, которую мы хотим рассказать вам, есть еще один ге-
герой, молчаливый и недвижимый: цифровой компьютер. Нет никаких
сомнений в том, что компьютеры действовали как мощные хирурги-
хирургические пинцеты, извлекая фракталы из темных закоулков абстрактной
математики и выставляя на яркий свет их тончайшие геометрические
особенности. Именно под влиянием фрактальных образов, нередко нево-
невообразимо красивых и привлекательных, компьютерная графика обрела
новое поразительное измерение.
Краткий обзор содержания книги
Мы открываем наш трактат рассказом о наиболее изящном из
когда-либо предложенных применений подобия: найденном юным Эйн-
Эйнштейном доказательстве теоремы Пифагора. Известная теорема дока-
доказывается сразу, легко и просто, стоит только провести в прямоугольном
треугольнике в нужном месте одну-единственную линию и воспользо-
воспользоваться подобием треугольников.
Затем мы вступаем на бескрайние просторы сажоподобия, столь
ярко проявляющегося в фракталах, мультифракталах и скейлинговых
законах физики, психофизики и бесчисленного множества других об-
областей человеческой деятельности.
В фазовых пространствах мы встречаем детерминированный ха-
хаос и странные аттракторы. Перколяция и другие фазовые переходы
приводят нас к критическим показателям и иерархии различных раз-
размерностей. Следуя Пуанкаре, мы погружаемся в самоподобие итери-
итерированных отображений — от преобразований пекаря и сдвигов Бер-
нулли до логистических парабол и отображений окружности. Ни торы,
ни кантор-торы, ни языки Арнольда не помешают нам взобраться по
чертовым лестницам и расположиться среди рациональных чисел вра-
вращения, гроздьями свисающих с ветвей деревьев Фарея.
Но коль скоро мы заговорили о нелинейной динамике, нельзя не
вспомнить некоторых из тех, кто внес в ее развитие наиболее зна-
значительный вклад совсем недавно: Зигеля, Мозера, Лоренца, Вильсона,
Фейгенбаума и, наконец (последнюю по счету, но не по значению), за-
замечательную русскую школу, представленную такими именами, как
А. М. Ляпунов, В. И. Арнольд, Я. Г. Синай, Б. В. Чириков, В. М. Алексеев,
20 Предисловие
Д.В.Аносов, Я. Б.Песин и недавно скончавшийся признанный мэтр
А. Н. Колмогоров.
Деревья Кэли, известные также под названием решеток Бете, по-
послужат нам удобной отправной точкой для понимания структур мно-
многих фракталов, встречающихся в реальной жизни — таких, как наша
бронхиальная и сосудистая системы. Нас также будут интересовать
клеточные автоматы как модели биологического роста и химических
реакций.
Мы испытаем странное влечение1 к символической динамике,
последуем за последовательностью Морса-Туэ и за «кроличьей» по-
последовательностью Фибоначчи, а также за их дискретными самопо-
самоподобиями, которые шепнут нам «по секрету» немало важных сведе-
сведений об удвоении периода, синхронизации мод, фрустрированных спи-
спинах Изинга и квазикристаллах с симметрией пятого порядка. Мно-
Многие из этих чудес были покрыты мраком таинственности и отяго-
отягощены парадоксами, до тех пор пока острые скальпели теорий мас-
масштабной инвариантности и ренорм-групп не рассекли покровы и не
сделали простым и ясным то, что ранее казалось столь загадоч-
загадочным. Не случайно все жизнеспособные фундаментальные полевые те-
теории в физике перенормируемы, иначе бы им не миновать мнимых
масштабов.
И, конечно же, мы без малейших колебаний бросимся в пучи-
пучину случайных фракталов от броуновского движения до диффузно-
ограниченной агрегации и «спазмов» на фондовой бирже (вспомним не-
некоторые из таких спазмов в недавнем прошлом). Разорение бедного иг-
игрока и петербургский парадокс дадут нам новую пищу для размышле-
размышлений на фрактальные темы.
Таковы некоторые из увлекательных и в высшей степени серьез-
серьезных тем, звучащих в нашей книге. Мы стремились помочь читателю
глубже понять самоподобие — возможно, наиболее чреватую важными
последствиями из всех существующих в природе симметрии, а так-
также продемонстрировать широчайший диапазон применений масштаб-
масштабной инвариантности в физике, химии, биологии, музыке и, в особен-
особенности, в изобразительном искусстве (убедительным подтверждением
тому является недавний ренессанс компьютерной графики, порожден-
порожденный фрактальными образами и их красотой, неизменной при любом
масштабировании).
1В оригинальном тексте игра слов: англ. attractor может быть передано и как
«аттрактор», и как «нечто влекущее, притягивающее к себе». — Прим. перев.
Предисловие 21
Благодарности
Эта книга обязана своим появлением многим источникам. Помимо
того, что я вкратце обсуждал в моей диссертации хаос в нормальных
модах концертных залов (вот, кстати, хороший пример «неинтегрируе-
мой» системы, если таковая вообще существует), моим главным стиму-
стимулом стали первые демонстрации фрактальных множеств Жюлиа, про-
произведенные Хайнцем-Отто Пайтгеном и Петером Рихтером. Чарующая
красота фрактальных образов и лежащая в их основе увлекательная
математика, описанная в книге этих авторов «Красота фракталов», про-
произвели на меня неизгладимое впечатление.
Моя первая встреча с работами Мандельброта произошла в связи
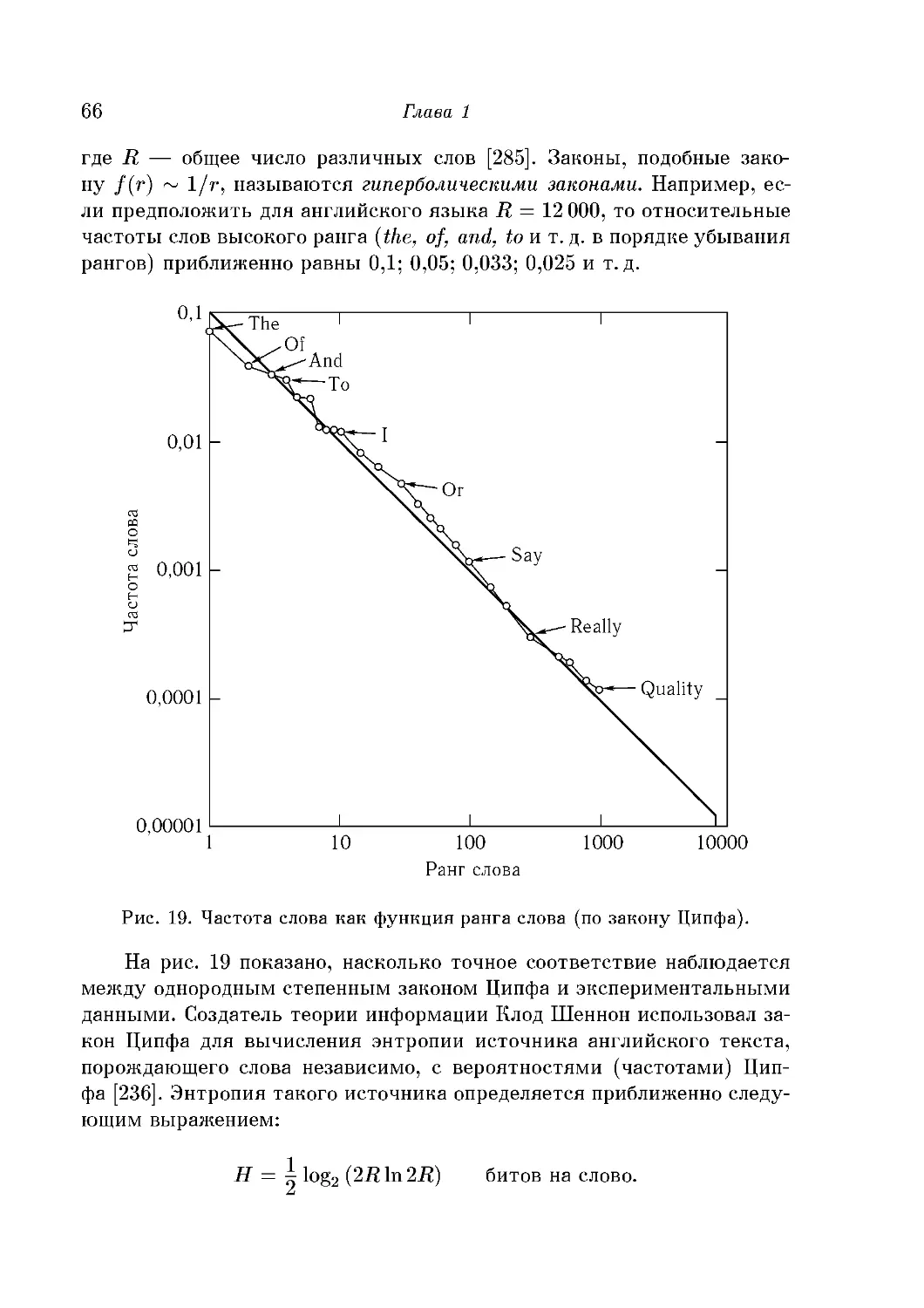
с произведенным им анализом частоты слов в естественных и искус-
искусственных языках, затронувшим мой собственный интерес к компью-
компьютерному синтезу и распознаванию речи. Монументальная монография
Мандельброта «Фрактальная геометрия природы» оказала на меня, как
и на многих других людей, ни с чем не сравнимое влияние.
Я также многое почерпнул для себя из книг Роберта Девани
и его лекций по хаосу, «Фракталов» Йенса Федера, «Фракталов повсюду»
Майкла Барнсли и очаровательного «Введения в теорию перколяции»
Дитриха Штауффера.
Много полезного о последних достижениях в этой области я узнал
на организованной Рихардом Фоссом и Полом Микином Гордоновской
конференции по фракталам, куда съехалось множество выдающихся
специалистов со всего мира.
В Гёттингенском университете (главным образом благодаря рабо-
работам Вернера Лаутерборна) я увидел хаос в действии — в нелинейных
динамических системах от кавитационных пузырьков до цепочек То-
ды. Мои собственные студенты в Третьем Физическом институте были
для меня и стимулом, и пробным камнем во время серии лекционных
курсов по самоподобию, фракталам и хаосу. Хайнрих Хенце и Карл Ла-
утшам умело дополнили демонстрации, сопровождавшие эти лекции.
Хольгер Беме, Вольф Дитер Брандт и Тино Грамс предоставили многие
из вошедших в книгу компьютерных изображений.
Ныне покойный Вальтер Кауфман-Бюлер из нью-йоркского отде-
отделения издательства Springer и мой давний коллега по работе в Bell La-
Laboratories Рональд Грэм оказали мне моральную поддержку на раннем
этапе работы над книгой.
Хильдегард Франке и Эсперанца Плата в Murray Hill (штат
Нью-Джерси) при поддержке Майи Зуттер и Ирены Шёнке из
22 Предисловие
Гёттингенского университета превратили мои почти не поддающиеся
прочтению каракули в удобочитаемую машинописную рукопись. Лиа-
Лиана Либе и Гизела Киршман-Шрёдер любовно позаботились об иллюст-
иллюстрациях. Как и во время наших предыдущих странствий, Анни Шредер
обеспечила мне столь необходимую логистическую поддержку.
Джерри Лайонс убедил меня отдать себя и рукопись в руки
W.H. Freeman and Company, и, последовав его совету, я ни разу не
пожалел об этом. Сотрудничество с Джерри Лайонсом, старшим редак-
редактором Джорджией Ли Хэдлер, дизайнером Нэнси Сингер и художес-
художественным редактором Биллом Пейджем доставило мне огромное удо-
удовольствие. Профессиональная компетентность моего редактора Ричар-
Ричарда Микки была вне всяческих сравнений.
Наконец (но отнюдь не в последнюю очередь), я хотел бы выра-
выразить свою признательность выдающимся специалистам Хансу-Вернеру
Штрубе, Аллану Херду, Виктору Клее и Полу Микину, взявшим на се-
себя труд по рецензированию рукописи, внесшим множество исправлений
и высказавшим важные замечания.
Мюррей Хилл и Гёттинген Манфред Шредер
Май 1990 г.
Глава 1
Введение
Я хочу узнать, как Бог создал этот мир.
Меня не интересует то или иное яв-
явление, спектр того или другого элемен-
элемента. Я хочу узнать, о чем Он думал, все
остальное — детали.
Альберт Эйнштейн
Природа изобилует периодическими явлениями — от движения ма-
маятника до колебаний атомов, от стрекотания кузнечиков до обращения
небесных тел вокруг Солнца. В этом вселенском менуэте участвуют
и наши земные тела — от сердцебиения и суточных ритмов до месяч-
месячных и более продолжительных циклов.
Разумеется, в природе нет строго периодических явлений. Всякое
движение имеет начало и конец, поэтому в математическом смысле
строгой периодичности в реальном мире не существует. И все же пери-
периодичность оказалась необычайно полезным понятием для объяснения
основополагающих законов и механизмов во многих областях.
Одна из причин универсальности простого гармонического движе-
движения — линейность (или почти линейность) многих физических систем
и инвариантность управляющих их поведением законов при сдвигах
в пространстве и времени.
Однако существуют многочисленные явления, в которых линей-
линейность нарушается, и вместо периодичности мы получаем апериодичес-
апериодическое и даже хаотическое движение: гладкие волны на поверхности спо-
спокойного озера сменяются сильной турбулентностью в горном ручье,
а ежедневный восход солнца — символ предсказуемости — скрывается
за завесой облаков, прибежищем хаоса, хотя и детерминированного.
Но сколь бы хаотичной ни становилась жизнь, на сколь бы мелкие
осколки ни разбивалась всякая регулярность, одна мощная крепость
остается незыблемой, гордо возвышаясь над турбулентным хаосом. Эта
крепость — самоподобие, инвариантность относительно изменения мас-
масштаба, или скейлинга; иначе говоря, не инвариантность при аддитив-
аддитивных сдвигах, а инвариантность при мультипликативных изменениях
24 Глава 1
масштаба. Кратко можно сказать, что самоподобный объект «выгля-
«выглядит» неизменным и после увеличения, и после уменьшения его разме-
размеров. Так, в турбулентных потоках крупные вихри порождают меньшие,
те, в свою очередь, — еще меньшие и так (почти) ad infinitum. В общем
случае одно из наиболее заметных следствий самоподобия — объекты
с необычайно тонкой структурой, которые ныне называются фракта-
фракталами по предложению Бенуа Мандельброта, ставшего их отцом [161]1.
Многие законы природы не зависят (или почти не зависят) от мас-
масштаба. То, что скейлинг обычно имеет предел (постоянную Планка —
когда объекты становятся слишком малыми, или скорость света — ког-
когда объекты движутся слишком быстро), не умаляет полезности «раз-
«размышлений в терминах самоподобия» — так отсутствие (за пределами
чистой математики) строгой периодичности не создает сколь-нибудь
серьезных препятствий для применения этого понятия в реальном ми-
мире. В некотором смысле самоподобие — это тоже периодичность, только
в логарифмической шкале.
Самоподобие — строгое или приближенное — царит во многих об-
областях под самыми различными обличьями, и в этой книге мы займем-
займемся изучением некоторых из многочисленных проявлений самоподобия
в окружающем нас мире. Среди прочих мы в той или иной степени
затронем следующие вопросы:
• Скейлинговые законы и их выражение в физике, психофизике
и физиологии.
• Случайные блуждания на фондовой бирже и под микроскопом; на-
наводнения, лесные пожары, распределение галактик и другие «сти-
«стихийные явления» со статистическим самоподобием.
• Масштабная (скейлинговая) инвариантность, самоподобие и не-
некоторые из их математических моделей — например, канторовы
множества и множества Жюлиа.
• Фракталы и их количественная характеристика по Хаусдорфу,
другие нецелые размерности; фрактальные парадоксы и их разре-
разрешение; функции Вейерштрасса и кривые Гильберта; снежинки Ко-
Коха, ковры Серпинского и другие неевклидовы конструкции в двух
и более измерениях; толстые фракталы и мультифракталы.
• Итерированные отображения и отбор следующих из них самопо-
самоподобий.
1 Ссылки в квадратных скобках указывают на список литературы, приведенный
в конце книги.
Эйнштейн, Пифагор и простое подобие 25
• Логистическая парабола и другие унимодальные отображения
с универсальными скейлинговыми законами; бифуркация удвое-
удвоения периода, ведущая к хаосу; постоянная Фейгенбаума, символи-
символическая динамика и последовательность Морса-Туэ; универсаль-
универсальное распределение орбит (порядок Шарковского).
• Комплексификация квадратичного отображения и множество
Мандельброта.
• Чертовы лестницы, деревья Фарея, языки Арнольда и синхрониза-
синхронизация мод; «кроличья» последовательность Фибоначчи и квазипери-
квазипериодический путь к временному и пространственному хаосу; спи-
спиновая решетка Изинга и квазикристаллы.
• Треугольник Паскаля и клеточные автоматы.
В настоящей главе мы приводим неформальное введение в некото-
некоторые из этих вопросов и представляем читателю основных действующих
лиц.
Эйнштейн, Пифагор и простое подобие
Я малость подумаю.
Альберт Эйнштейн, в Америке
Когда Якоб Эйнштейн стал обучать геометрии (евклидовой) сво-
своего одиннадцатилетнего племянника Альберта, юный Эйнштейн, уже
тогда стремившийся к предельной экономии мысли, почувствовал, что
некоторые из доказательств Евклида неоправданно сложны1. Напри-
Например, столь ли необходимо в типичном доказательстве теоремы Пифаго-
Пифагора а2 + Ь2 = с2 рассматривать помимо исходного прямоугольного тре-
треугольника с гипотенузой с и катетами а и b все эти дополнительные
линии, углы и квадраты?
«Малость подумав», острый разумом подросток придумал такое до-
доказательство, для которого требуется лишь одна дополнительная ли-
линия — высота, опущенная из вершины прямого угла на гипотенузу
(рис. 1). Эта высота делит большой треугольник на два меньших, по-
подобных друг другу и большому треугольнику. (Треугольники подобны,
если равны их соответствующие углы. С первого взгляда легко заме-
заметить, что именно так обстоит дело с треугольниками на рис. 1.)
1Эту историю мне рассказал Шнейор Лифсон (из Института Вейцмана в Тель-
Авиве), которому поведал ее ассистент Эйнштейна Эрнст Штраусе, слышавший ее
от самого старика Альберта.
26
Глава 1
Рис. 1. Теорема Пифагора: чертеж к доказательству на основе подобия тре-
треугольников, предложенному одиннадцатилетним Эйнштейном.
В евклидовой геометрии площади подобных (замкнутых) фигур от-
относятся как квадраты соответствующих линейных размеров. Следова-
Следовательно, площади Еа, Еь и Ес (Е — начальная буква немецкого слова
ЕЬепе — плоскость) трех треугольников на рис. 1 связаны с их гипо-
гипотенузами а, Ь и с соотношениями
Еа = та2,
Еь = mb2,
Ес = тс2,
A)
B)
C)
где т — некоторый безразмерный отличный от нуля множитель, один
и тот же во всех трех соотношениях.
Бросив на рис. 1 второй взгляд, мы обнаружим, что площадь боль-
большого треугольника равна сумме площадей двух меньших треугольни-
треугольников:
Еа + Еь = Ес.
Используя соотношения A)-C), получаем
та2 + mb2 = тс2.
Наконец, деля это равенство на общую меру т, мы приходим к знаме-
знаменитому выводу Пифагора:
а2 + Ъ2 = с2.
Теорема доказана одиннадцатилетним ребенком1 путем комбини-
комбинирования двух плодотворных научных принципов, которых впослед-
впоследствии неукоснительно придерживался взрослый Эйнштейн: простоты
xHa которого в его школьные годы в Мюнхене никто не обращал внимания [206].
Эйнштейн, Пифагор и простое подобие
27
и симметрии, частным случаем которой является самоподобие. Однако
истинная красота доказательства Эйнштейна не в том, что оно столь
просто, а в том, что оно вскрывает истинную суть теоремы Пифагора:
подобие и масштабируемость (скейлинг).
Рис. 2. Эйнштейн накануне открытия своей знаменитой формулы Е = тс2
(с точки зрения карикатуриста) [98] (©1991 Sidney Harris).
Разумеется, сходство соотношения C) с последующим открытием
Эйнштейна — его знаменитым соотношением Е = тс2 — чисто случай-
случайно. Эквивалентность массы т и энергии Е, лежащая в основе ядерной
энергетики во всех ее формах, следует из инвариантности при преобра-
преобразованиях Лоренца. Эта инвариантность, лежащая в основе специальной
28 Глава 1
теории относительности, была предсказана Эйнштейном в 1905 г., когда
он после нескольких фальстартов «еще малость подумал» (рис. 2).
Самоподобная расстановка ферзей, не бьющих друг
друга
Рассмотрим одну из многочисленных шахматных задач, состоя-
состоящую в расстановке на шахматной доске заданного размера как можно
большего количества не атакующих друг друга ферзей (ферзи не бьют
друг друга, если никакие два ферзя не стоят на одной горизонтали, од-
одной вертикали или одной диагонали доски). На доске к х к можно рас-
расставить самое большее к не бьющих друг друга ферзей. Но всегда ли
можно расставить ровно к мирно сосуществующих ферзей? А если чис-
число к очень велико? Не возрастает ли сложность расстановки ферзей экс-
экспоненциально с увеличением размера доски? Как мы сейчас убедимся,
расстановка ферзей осуществляется очень просто даже на произвольно
больших досках, если мы сосредоточим внимание на досках, размеры
или порядок которых к равен целой степени какого-нибудь целого чис-
числа (т.е. к = пт, где пит — целые числа) и разумно воспользуемся
принципом самоподобия при построении решения. (Как и прежде, мы
называем объект или структуру самоподобными, если при увеличении
их самих или надлежаще выбранной их части они выглядят так же, как
до увеличения.)
На рис. 3 вверху показана расстановка пяти не бьющих друг друга
ферзей на доске 5x5. (Чтобы расставить так ферзи, можно восполь-
воспользоваться поглощающим алгоритмом: начать с клетки, расположенной
в левом нижнем углу, и продолжать вертикаль за вертикалью, ставя
каждого следующего ферзя на самую нижнюю из «допустимых» кле-
клеток.)
Из решения для доски 5x5 мы можем немедленно построить реше-
решения для доски 25 х 25, которую можно считать состоящей из 5 х 5 = 25
досок размером 5x5. Мы просто оставим большинство из этих 25 досок
пустыми, за исключением пяти, соответствующих позициям, занятым
ферзями на доске 5x5. Эта расстановка изображена на рис. 3 и даль-
дальнейших пояснений не требует.
Чтобы расставить «мирные» (не бьющие друг друга) ферзи на дос-
доске 125 х 125, условимся рассматривать эту доску как составленную из
двадцати пяти досок размером 25 х 25. Пять из них, заполненных в со-
соответствии с решением для доски 25 х 25, расставлены по уже известной
Самоподобная расстановка ферзей, не бьющих друг друга
29
•
s
ш
ш
*
*
йг
•
•
•
\
\
•
•
*
*
•
*
*
*
•
*
*
•
•
*
Рис. 3. Пять не бьющих друг друга ферзей на доске 5x5 (вверху), и анало-
аналогичная расстановка 25 ферзей на доске 25 х 25, полученная из доски 5x5
с помощью подобия.
нам схеме, а остальные двадцать досок остаются пустыми. Продолжая
в том же духе, мы после п шагов получим доску размером 5п х 5п
с расставленными на ней 5п ферзями, не бьющими друг друга.
Этот процесс можно продолжать ad infinitum, получая каждый раз
безукоризненно самоподобную расстановку не бьющих друг друга фер-
ферзей. Действительно, выбирая одну из пяти непустых «поддосок» со сто-
стороной, составляющей одну пятую от стороны всей доски и увеличивая
ее в 5 раз, мы в точности получаем исходную доску. Множитель 5 на-
называется коэффициентом подобия доски.
30 Глава 1
Какие числа, кроме 5, можно использовать в качестве коэффициен-
коэффициента подобия в такого рода самоподобных схемах? Можно ли использовать
самоподобие для построения решений на досках со стороной, длина ко-
которой не представима в виде чистой степени целого числа (как 5га)?
Интересующийся читатель сможет найти дальнейшие указания в весь-
весьма содержательной статье Кларка и Шиши [35].
Самоподобная снежинка
Повторяя некую операцию снова и снова (во все меньшем и мень-
меньшем масштабе), мы почти неизбежно приходим к самоподобной струк-
структуре. Повторяющаяся операция может быть алгебраической, симво-
символической или геометрической, как в случае пяти спящих красавиц-
королев, которых мы на пути к совершенному самоподобию пробудили
от сна и позволили безгранично множиться.
Классическим примером такого повторяющегося построения мо-
может служить кривая фон Коха, предложенная в 1940 г. шведским мате-
математиком Хельге фон Кохом. Основной принцип и конечный результат
конструкций фон Коха в равной мере прекрасны. Возьмем отрезок пря-
прямой (инициатор, рис. 4А) и на его средней трети построим равносторон-
равносторонний треугольник, как показно на рис. 4Б. Результат этого построения
называется генератором. Заметим, что длина генератора составляет че-
четыре третьих от длины инициатора.
Повторяя еще раз построение равносторонних треугольников на
средних третях прямолинейных отрезков, мы получаем ломаную, изо-
изображенную на рис. 4В. Длина ломаной теперь составляет D/3J. По-
Повторяя процесс бесконечно много раз, мы приходим к «кривой» беско-
бесконечной длины, которая (хотя и всюду непрерывна) нигде не дифферен-
дифференцируема. Насколько позволяют перо и чернила, она воспроизведена на
рис. 4Г.
Такого рода ущербные «функции», которые непрерывны, хотя ни
в одной точке к ним невозможно провести касательную, были впер-
впервые построены в прошлом веке немецким математиком Карлом Вей-
ерштрассом лишь для того, чтобы показать своим скептически на-
настроенным коллегам (в том числе ужаснувшемуся Эрмиту), что такие
функции действительно существуют. Однако другие авторитеты (и сре-
среди них не в последнюю очередь великий австрийский физик Людвиг
Больцман) увидели забрезживший новый свет; в 1898 г. Больцман пи-
писал в письме к Феликсу Клейну, что недифференцируемые функции
могли бы быть изобретены физиками, поскольку в статистической ме-
Самоподобная снежинка
31
(А)
(Б)
Рис. 4. Инициатор (А) и генератор (Б) для кривой фон Коха. Следующая ста-
стадия построения кривой фон Коха (В) и аппроксимация высокого порядка
к кривой фон Коха (Г).
ханике имеются проблемы, для решения которых «недифференцируе-
«недифференцируемые функции абсолютно необходимы». Французский коллега Больцмана
Жан Перрен пошел еще дальше. В 1906 г. он, предвосхищая современное
отношение к такого рода математическим монстрам, заявил, что «кри-
«кривые, не имеющие касательных, являются общим правилом, а гладкие
кривые, такие, как окружность, — интересным, но весьма частным
случаем». Изысканно, не правда ли? Теперь, следуя Мандельброту, мы
называем такие недифференцируемые кривые просто фракталами.
32 Глава 1
Новая размерность для фракталов
Вселенная не только причудливее, чем
мы думаем, но даже причудливее, чем мы
можем предположить.
Дж. Б. С. Холдейн
Применив генератор фон Коха (рис. 4) к равностороннему тре-
треугольнику и закрасив внутренность построенной фигуры в черный
цвет, мы получим сплошную звезду Давида (рис. 5А). Бесконечная ите-
итерация такого построения приводит к снежинке фон Коха (промежуточ-
(промежуточные стадии построения показаны на рис. 5Б). Каков же периметр такой
снежинки? После п итераций периметр снежинки становится в D/3)га
раз больше периметра исходного треугольника. При п, стремящемся
к бесконечности, периметр снежинки становится бесконечно большим.
Следовательно, длина перестает быть удобной величиной для количест-
количественной характеристики периметра. Необходимо ввести какую-то новую
меру, которая позволила бы различать фракталы, порождаемые различ-
различными генераторами. Но, изобретая новые меры, мы хотим оставаться
как можно ближе к тому, что делали обычно при измерении длины.
W) (Б)
Рис. 5. Инициатор и генератор для снежинки фон Коха (А) и промежуточные
стадии построения снежинки фон Коха (Б).
Для гладкой кривой ее приближенная длина L (г) определяется как
произведение числа N прямолинейных отрезков, умещающихся на кри-
кривой, на длину такого отрезка г: L (г) = N ¦ г. Когда длина шага г стре-
стремится к нулю, величина L (г) стремится к конечному пределу — дли-
длине L рассматриваемой кривой.
Иначе обстоит дело в случае фракталов! Произведение N ¦ г об-
обращается в бесконечность, потому что когда г стремится к нулю, мы
учитываем все более мелкие извивы фрактала. Однако асимптотически
Новая размерность для фракталов 33
это стремление к бесконечности происходит по некоторому четко опре-
определенному однородному степенному закону от г. Иначе говоря, сущест-
существует некоторый критический показатель Dh > 1, такой, что произве-
произведение N ¦ гПн остается конечным. При показателях меньших, чем Dh,
произведение расходится, т.е. обращается в бесконечность, а при по-
показателях больших, чем Dh, — стремится к нулю. Этот критический
показатель Dh называют размерностью Хаусдорфа в честь немецкого
математика Феликса Хаусдорфа A868-1942). Справедливо следующее
соотношение:
Dh = Ип1
(это определение размерности Хаусдорфа эквивалентно приведенному
выше). Если при построении кривой или снежинки фон Коха и-го поко-
поколения (n-й итерации) шаг выбран равным г = Го/Зга, то число шагов N
пропорционально 4га. Таким образом,
1пЗ
То, что Dh лежит между 1 и 2, довольно понятно: бесконечно длин-
длинная кривая в некотором метрическом смысле представляет собой нечто
большее, чем просто одномерный объект, но в то же время «не дотягива-
дотягивает» до двумерной фигуры, так как такая кривая не покрывает никакой
области на плоскости. И действительно, как мы вскоре увидим, пред-
предложенное Хаусдорфом определение размерности, которая, как нам уже
известно, может принимать дробные значения, во многих отношениях
вполне разумно. Разумеется, для гладкой кривой Dh = 1, а для глад-
гладкой поверхности число N покрывающих дисков пропорционально 1/г2,
вследствие чего Dh = 2 (здесь г — диаметр N малых дисков, необхо-
необходимых для того, чтобы покрыть фигуру). Аналогично, для компактного
трехмерного тела размерность Хаусдорфа Dh равна 3.
Удивительно, однако, что при Dh = 2 мы отнюдь не обязатель-
обязательно получаем двумерную фигуру: вполне достаточно оказывается топо-
топологически одномерного объекта — линии. Хорошо известным приме-
примером может служить асимптотически самоподобная кривая Гильберта
(рис. 6А), проходящая сколь угодно близко от любой точки единич-
единичного квадрата. Последовательные этапы построения кривой Гильберта
изображены на рис. 6Б. Окончательный результат, разумеется, самопо-
добен: раздув любой надлежащим образом выбранный подквадрат в 2п
раз, мы получим кривую, в точности похожую на всю кривую.
34
Глава 1
я
н
а.
а>
>о
л
ч
&
JS
о
с
S
о.
и
ш
о
о.
н
о
о
с
с
а
35
н
о.
JS
о
а
S
о.
1
о
S
я
а>
о
О.
н
о
о
С
о
S
Он
Новая размерность для фракталов
35
Поскольку п-е поколение кривой Гильберта состоит из 22п — 1
звеньев длиной 1/2™, ее размерность Хаусдорфа равна 2, как и подоба-
подобает кривой, заполняющей плоскую фигуру. На рис. 7 вы видите вариант
кривой Гильберта, рожденный фантазией художника. Распознаете ли
вы в хитросплетениях и извивах кривой человеческое лицо?
Рис. 7. Деформированная кривая Гильберта; точка зрения художника.
Рекомендуется рассматривать издали. (Рисунок любезно предоставлен
В.-Й. Мёллером.)
Соседние точки на кривой Гильберта остаются соседними и в еди-
единичном квадрате. Однако обратное утверждение неверно! Это свойство
отличает кривую Гильберта от телевизионной развертки, претерпеваю-
претерпевающей разрывы на концах линии1, и от канторова полностью разрывного
¦'¦Интересно, что некоторые более сложные способы сканирования изображения
на телевизионном экране используют алгоритм Гильберта для построения кривой,
заполняющей все пространство. Дело в том, что точки, соседние во времени вдоль
36 Глава 1
отображения единичного квадрата на единичный интервал, переводя-
переводящего точку х = О, Ж1Ж2Ж3 ..., у = О,У1У2Уз ¦ • • единичного квадрата
в точку О, Х1У1Х2У2Х3У3 • • • единичного отрезка.
Когда Кантор впервые увидел, что плоская фигура может быть ука-
указанным выше способом обратимо отображена на линию, он написал:
«Я видел это, но я не могу в это поверить». Однако эволюция, кон-
конструируя наш мозг, обнаружила тысячелетия назад, что для заполне-
заполнения объема с сохранением двумерной близости серое вещество коры
больших полушарий должно быть сложено «по схеме», напоминающей
трехмерную кривую Гильберта.
Кривые Гильберта в пространствах более высокой размерности на-
нашли также интересные применения в теории информации — в кодах
Грея, названных так в честь изобретателя [80]. В двоичном коде Грея
для целых чисел при переходе от одного числа к следующему код из-
изменяется только на один бит. Например, четыре целых числа от 0 до 3
кодируются двумя двоичными битами следующим образом: 0 = 00,
1 = 01, 2 = 11, 3 = 10 (а не как в обычном двоичном коде, в ко-
котором 2 = 10 и 3 = 11, вследствие чего между кодами чисел 1 и 2
возникает скачок в два бита). На рис. 8 показаны последовательные
этапы построения кривой Гильберта в трехмерном пространстве, на-
наглядно демонстрируя обобщенные коды Грея [81].
Если канторово отображение квадрата на отрезок разрывно в обе
стороны, т. е. разрывны и прямое, и обратное отображения, то кривая
Гильберта разрывна только в одну сторону. Благодаря трудам Бернарда
Больцано A781-1848) и Джузеппе Пеано A858-1932), мы знаем и о дру-
других отображениях площади на линию, однако ни одно из них не является
непрерывным в обе стороны.
Самоподобное разбиение и «неевклидов» парадокс
Взгляните на семь фрактальных «плиток», изображенных на
рис. 9А. Они получены из семи правильных шестиугольников (рис. 9Б)
при замене каждой стороны трехзвенной ломаной, как показано на при-
примере одной из сторон. Если внутренние углы между звеньями рав-
равны 120°, то длины трех звеньев будут составлять \j\fl от первона-
первоначальной длины стороны правильного шестиугольника.
Бесконечно повторяя процесс взламывания прямолинейных отрез-
отрезков и замены их трехзвенными ломаными, мы приходим к разбиению
«гильбертовой развертки», оказываются соседними в пространстве и на сканируе-
сканируемом изображении, что упрощает его обработку.
Самоподобное разбиение и «неевклидов» парадокс
37
с
¦)
(А)
(Б)
Рис. 8. Построение трехмерного варианта кривой Гильберта (А); трехмерная
кривая Гильберта, иллюстрирующая коды Грея (Б).
плоскости на фрактальные плитки, которое приближенно представлено
на рис. 9А. В результате такого построения контур всей фигуры, со-
состоящей из семи фрактальных «шестиугольников» подобен каждому из
этих семи шестиугольников.
Таким образом мы приходим к самоподобному разбиению плоскос-
плоскости на «шестиугольники», в котором каждая плитка окружена шестью
такими же плитками. (Заметим, что хотя возможно разбить плоскость
на настоящие правильные — с прямолинейными сторонами — шести-
шестиугольники, это разбиение не самоподобно: правильный шестиугольник,
38
Глава 1
(А)
(Б)
Рис. 9. (А) Разбиение плоскости с помощью фрактальных плиток, плотно по-
подогнанных друг к другу. Совокупность семи плиток подобна одной плитке,
что порождает «неевклидов» парадокс. (Б) Разбиение плоскости на правиль-
правильные шестиугольники — инициатор фрактальных плиток, изображенных на
рис. А. Показан также один генератор, состоящий из трех прямолинейных
отрезков.
окруженный шестью такими же шестиугольниками, не образует пра-
правильный шестиугольник больших размеров.)
Взглянув на рис. 10А, нетрудно заметить, что периметры меньших
фрактальных шестиугольников укладываются в периметре большого
фрактального шестиугольника ровно три раза. Следовательно, по ев-
евклидову правилу соотношения площадей подобных геометрических фи-
фигур, площадь большого шестиугольника должна была бы быть в З2 = 9
раз больше площади любого из меньших фрактальных шестиугольни-
шестиугольников. Но это не так: площадь большого шестиугольника только в 7 раз
больше площади меньшего шестиугольника!
Самоподобное разбиение и «неевклидов» парадокс 39
Где же допущена ошибка? Где мы сбились с пути? Неужели нам
удалось застать врасплох Евклида? Нет, древние греки (за исключени-
исключением, быть может, Зенона Элейского) могут по-прежнему покоиться с ми-
миром. Фрактальные геометрические объекты, подобные изображенным
на рис. 9А, никогда не изучались в школе Евклида (и не использова-
использовались для мощения тамошних полов). Евклид, по-видимому, и не подо-
подозревал о существовании недифференцируемых функций или ограничен-
ограниченных кривых бесконечной длины. Но последующие поколения матема-
математиков занимались изучением таких объектов, и со времен Хаусдорфа
мы знаем, что размерности такого рода кривых не обязательно равны
единице, но могут превосходить ее. Например, размерность Хаусдор-
Хаусдорфа Dh периметра наших шестиугольных фракталов оказывается рав-
равной 1пЗ/1пл/7 = 1,12915 Поэтому, следуя идее Евклида о пропор-
пропорциональности отношения площадей подобных фигур, чтобы получить
соотношение площадей для нашего случая, мы должны были бы возвес-
возвести 3 («отношение» периметров) не в квадрат, а (поскольку периметр
имеет размерность 1,12915...) в степень 2/1,12915... = 1,77124
Если верить моему карманному калькулятору, то это дает отношение
площадей, равное 6,999999999 — что достаточно близко к истинному
отношению, равному 7, величина которого видна из рис. 9А. Таким об-
образом, мы имеем все основания для того, чтобы сформулировать заново
теорему Евклида об отношении площадей подобных фигур и получить
более общий результат, применимый и к фракталам, и к нефракталам:
Отношения соответствующих размеров подобных фигур рав-
равны, если их привести к одной и той же размерности на ос-
основе их размерностей Хаусдорфа.
Как раз из-за таких своих свойств размерность Хаусдорфа являет-
является столь полезной концепцией. Размерность Хаусдорфа — это необхо-
необходимое расширение понятия размерности на фрактальные объекты, мо-
моделирующее, хотя и приближенно, огромное количество явлений в ре-
реальном мире вокруг нас — и внутри нас. Вспомним хотя бы сосудис-
сосудистую систему человека или легкие с их иерархическим ветвлением на
бронхи, которое обеспечивает поразительно большую площадь полезной
поверхности. И сосудистая, и легочная системы великолепно описыва-
описываются фрактальными конфигурациями и размерностями Хаусдорфа.
Итак, понятие размерности Хаусдорфа разрешило чреватый ката-
катастрофическими последствиями парадокс, расширив наши представле-
представления о размерности на дробные и даже трансцендентные значения. Мы
еще не раз вернемся к этой теме в нашей книге и познакомимся с дру-
40 Глава 1
гими фрактальными парадоксами — например, с музыкальным аккор-
аккордом, который при воспроизведении с более высокой скоростью звучит
ниже] (См. с. 142-146 в гл. 3.)
У врат канторова рая
Я, некоторым образом, выступаю про-
против широко распространенных взглядов
на природу математической бесконеч-
бесконечности.
Георг Кантор
Размерность Хаусдорфа Dh полезна для описания не только фрак-
фрактальных кривых бесконечной длины, но и точечных множеств, или
«кривых» нулевой длины. Не удивительно, что для таких множеств
величина Dh, как правило, меньше единицы. Знаменитым примером
таких множеств служит построенное самим Георгом Кантором само-
самоподобное множество «стертой средней трети», которое он предъявил
изумленному и встретившему диковинку с недоверием математическо-
математическому сообществу своего времени в подтверждение того, что существуют
множества нулевой меры (нулевой «длины») с несчетно бесконечным
числом членов.
Свой в высшей степени неочевидный пример Кантор строил следу-
следующим образом. Он начал с замкнутого единичного интервала [0,1], т.е.
с прямолинейного отрезка длиной 1, содержащего обе конечные точки.
Затем Кантор «стер» открытую среднюю треть A/3, 2/3) и повторил
ту же операцию над каждым из двух оставшихся отрезков длиной 1/3
(рис. 10).
Повторяя снова и снова процесс стирания средней трети, мы не
оставляем ни одного связного прямолинейного отрезка. Общая длина,
или мера, оставшегося множества равна нулю. Тем не менее, как мы
увидим в дальнейшем, оставшаяся «пыль» все же содержит бесконечно
много, в действительности несчетно много, «точек». Оценить мощность
канторова множества можно уже по его арифметическому описанию:
элементами множества служат те дроби из замкнутого интервала [0,1],
в записи которых не встречается цифра 1, например, 0,2 или 0,2022.
Как охарактеризовать содержимое множества нулевой длины?
И снова нам на помощь приходит Хаусдорф. После и-кратного стирания
средних третей у нас останется N = 2™ прямолинейных отрезков, каж-
каждый из которых имеет длину г = A/3)га. Таким образом, размерность
Ковер Серпинского
41
II II
II II
II II
II II
1111 НИ
ни ни
Illl Illl
Illl Illl
Рис. 10. Построение канторова множества «стертой средней трети». Оно име-
имеет нулевую меру и тем не менее неисчислимо. Фрактальная размерность
In 2
такого множества равна
1пЗ
= 0,63....
Хаусдорфа Dh равна In 2/ In 3 = 0,63 ..., т. е. принимает значение меж-
между 0 и 1, как и следовало ожидать, поскольку канторова пыль больше
(гораздо больше!), чем точка (размерность 0), и много меньше, чем от-
отрезок прямой или кривой (размерность 1). Как и в случае фрактальной
кривой фон Коха значение Dh не является целым (в действительнос-
действительности Dh для канторова множества — трансцендентное число).
В нашей книге мы встретимся с «несчетным» множеством других
примеров пыльных множеств, подобных канторову, в самых разнооб-
разнообразных декорациях. Одно из таких множеств — знаменитый ковер Сер-
Серпинского — мы сейчас и рассмотрим.
Ковер Серпинского
Туман в тумане.
Герман Вейль, по поводу трансфи-
трансфинитных чисел Кантора.
Существуют ли двумерные множества, подобные канторовой пы-
пыли? Да, существуют. Начнем с равностороннего треугольника, изобра-
изображенного слева на рис. НА и удалим перевернутый центральный рав-
равносторонний треугольник со стороной, равной половине длины сторо-
стороны исходного треугольника. У нас останутся три равносторонних тре-
42 Глава 1
угольника со сторонами, вдвое меньшими стороны исходного треуголь-
треугольника. Повторяя эту операцию над оставшимися (не перевернутыми)
треугольниками, мы получаем после п итераций N = 3" треугольни-
треугольников со сторонами г = гоB~") (рис. 11Б). Множество, которое получает-
получается при бесконечном повторении данной процедуры, называется ковром
Серпинского в честь польского математика Вацлава Серпинского A882-
1969), автора многочисленных работ по теории чисел и топологии. Раз-
Размерность Хаусдорфа для такого множества равна In 3/In 2 = 1,58
Это иррациональное число меньше 2, несмотря на то, что ковер Сер-
Серпинского существует в двумерном пространстве.
Ш (Б)
Рис. 11. (А) Генератор для ковра Серпинского. (Б) К построению ковра Сер-
Серпинского — двумерного несчетного множества нулевой меры с фрактальной
размерностью -р— = 1, 58 ...
Ill 2i
Интересно отметить, что в ковре Серпинского самоподобие соче-
сочетается с другой важной, хотя и классической симметрией: симметрией
поворота. Действительно, форма ковра Серпинского не изменяется при
повороте вокруг его центра на угол 120° (или на любое целое кратное
угла 120°). Такие симметрии, сочетающие в себе бесконечный скейлинг
и поворот на конечный угол, наблюдаются во многих фрактальных по-
построениях и в работах Морица Эшера (рис. 12)
Заметим кстати, что «фрактальная» размерность фрактального
множества не обязательно должна быть нецелой. Например, размер-
размерность Хаусдорфа для самоподобной расстановки не бьющих друг друга
ферзей (см. с. 28-30) равна 1.
На рис. 13 вы видите трехмерное обобщение ковра Серпинского. По-
Построение его начинается с правильного тетраэдра (пирамиды, гранями
которой являются четыре равносторонних треугольника), из которо-
которого вырезается центральный перевернутый правильный тетраэдр вдвое
меньших размеров. Та же операция проделывается с каждым из че-
Ковер Серпинского
43
Рис. 12. Картина Эшера, в которой поворотная симметрия сочетается с бес-
бесконечным скейлингом.
тырех оставшихся тетраэдров и т. д. В результате мы получаем нечто
вроде ажурной башни.
Размерность Хаусдорфа для этой самоподобной конструкции сле-
следует непосредственно из первого этапа построения: имея N = 4 остав-
оставшихся тетраэдров размера г = 1/2, мы получаем Dh = In 4/In 2 = 2,
т. е. фрактальная размерность на этот раз оказывается целой, хотя и на
целую единицу меньше евклидовой размерности d = 3 несущего про-
пространства.
Двумерные и трехмерные аналогии ковра Серпинского моделиру-
моделируют многие природные явления и рукотворные сооружения. Взять хо-
хотя бы Эйфелеву башню в Париже, спроектированную Густавом Эйфе-
Эйфелем. Если бы вместо всемирно известной ажурной конструкции это
44
Глава 1
Рис. 13. Трехмерный вариант ковра Серпинского. Его фрактальная размер-
размерность 1п4/1п2 = 2 имеет целое значение, хотя она и меньше размерности
несущего пространства (равной 3).
сооружение было спроектировано в виде сплошной пирамиды, то на его
строительство было бы израсходовано дополнительно невероятное ко-
количество железа без сколько-нибудь заметного увеличения прочности.
Эйфель пошел по другому пути: он применил фермы, т. е. структурные
модули, элементы которых используют жесткость треугольника. (Тре-
(Треугольник в отличие от прямоугольника не может быть деформирован
без деформации по крайней мере одной из его сторон.) Однако отдель-
отдельные элементы больших ферм сами представляют собой фермы, которые
в свою очередь состоят из ферм еще меньшего размера. Такая самопо-
самоподобная конструкция гарантирует высокую прочность при низком весе.
Конструкция готических соборов также выдает глубокую веру их стро-
Ковер Серпинского 45
ителей в принцип достижения максимальной прочности при минималь-
минимальной массе. В то же время американский архитектор Бакминстер Фул-
лер A895-1983) и его ажурные купола наглядно продемонстрировали
всем, что прочность кроется не в массе, а в точках ветвления. Вопре-
Вопреки тому, что подсказывает нам наш здравый смысл, ковер Серпинского
и аналогичные ему конструкции состоят сплошь из одних лишь точек
ветвления. (В сколь угодно малой окрестности точки ветвления на кри-
кривой содержится более чем две точки.) Некоторые граничные множест-
множества (например, граничные множества странных аттракторов) разделяют
это свойство с ковром Серпинского (см. с. 71-73, где свойство состоять
из одних лишь точек ветвления используется для «решения» проблемы
международных границ).
Рассмотрим еще одно противоречащее здравому смыслу и вызы-
вызывающее удивление проявление ковра Серпинского. Для евклидовых тел
в d-мерном пространстве объем V пропорционален Rd, где R — неко-
некоторый характеристический линейный размер тела. Площадь поверхнос-
поверхности S изменяется пропорционально Rd~1. Таким образом, S ~ V^d~1^d.
Например, в трехмерном пространстве, т.е. при (d = 3), справедли-
справедлива зависимость S ~ У2/3 (вспомним, что для сферы S = 4тг_К2 =
= (ЗбтгI^ . у2'3).
Однако для фрактальных объектов это простое евклидово соотно-
соотношение часто нарушается. Как мы уже знаем, для ковра Серпинского
размерность Хаусдорфа равна In 3/In 2 к, 1,58. А чему равна размер-
размерность Хаусдорфа для краев ковра Серпинского? Легко заметить, что
всякий раз, когда мы уменьшаем мерный стержень в 2 раза, число от-
отрезков, образующих края, увеличивается в 3 раза. Следовательно, раз-
размерность Хаусдорфа для краев, или «поверхности», ковра Серпинского
равна 1пЗ/1п2, т.е. «объем» и «поверхность» имеют одинаковую раз-
размерность Хаусдорфа. В этом можно также убедиться, представив мас-
массу М (R) ковра, т. е. число точек внутри окружности радиуса R, как
функцию радиуса: мы обнаружим, что в среднем V (R) ~ _R1>58. Но для
полной протяженности краев ковра S (R) внутри окружности радиуса R
мы получаем ту же самую зависимость S (R) ~ _R1>58. Следовательно,
для ковра Серпинского площадь V и длина краев S пропорциональны
друг другу: V ~ S. Результат, что и говорить, парадоксальный!
Мы еще будем иметь удовольствие встретить ковер Серпинского
и в первоначальном его виде, и в дискретном варианте — в виде тре-
треугольника Паскаля по модулю 2 (в гл. 17). А пока развлечемся немного
одним из необычных следствий из фрактальных свойств ковра Серпин-
Серпинского — настольной игрой, изобретенной мифическим сэром Пинским.
46 Глава 1
Игра сэра Пинского и детерминированный хаос
Рассмотрим следующую «настольную игру», в которой могут учас-
участвовать два или более человека.
• Каждый игрок выбирает по своему усмотрению начальную точку
внутри равностороннего треугольника.
• Проведя через ближайшую вершину и выбранную точку прямую
и отложив на ней от этой вершины удвоенное расстояние до на-
начальной точки, игрок получает точку pi.
Выигрывает тот, кто сумеет повторить удвоение расстояния от
ближайшей вершины наибольшее число раз, не выходя при этом за
пределы треугольника. Как мы увидим, существует несчетно много
и в то же время очень мало точек, гарантирующих выигрыш или ни-
ничью. («Очень мало» надлежит понимать в том смысле, что случайно
выбранная точка имеет нулевую вероятность сколь угодно продолжи-
продолжительного «выживания» игрока при соблюдении правил игры.)
На рис. 14 изображен равносторонний треугольник. Начальная точ-
точка помечена цифрой 0, а три ее последующих положения, или образа, —
соответственно, цифрами 1, 2 и 3. Мы видим, что точка 3 лежит уже за
пределами треугольника. Значит, начальная точка выбрана неудачно.
Можно ли обезопасить себя от неудачных начальных точек? Мы отве-
ответим на этот вопрос сначала геометрически, а затем арифметически.
Заметим, что точка 2, лежащая внутри малого белого (перевер-
(перевернутого) треугольника, при следующем ходе отображается за пределы
исходного треугольника. Достаточно несложного размышления, чтобы
увидеть, что любая точка внутри малого белого треугольника отобра-
отобразится за пределы исходного треугольника. Следовательно, белый тре-
треугольник — неподходящее место для размещения удачной исходной
позиции. Более того, не годится и его прообраз, а также прообраз про-
прообраза, и так далее ad infinitum. Иначе говоря, любая точка, рано или
поздно отображаемая в белый треугольник, приводит к проигрышу.
Но каковы же прообразы белого треугольника? Как показывает
дальнейшее несложное размышление, эти прообразы состоят из трех
перевернутых треугольников вдвое меньшего размера, расположенных
по одному в каждом из трех оставшихся темных треугольников. В свою
очередь, прообразами этих трех прообразов являются девять перевер-
перевернутых треугольников со сторонами вдвое меньшего размера, вырезан-
вырезанных из середины девяти оставшихся темных треугольников, линейные
Игра сэра Пинского и детерминированный хаос
47
/
\
/
/'
/
/
•
•
1
1
\
\
\
\
/ \
у
Рис. 14. Игра в хаос сэра Пинского. Сколько раз вам удастся удвоить расстоя-
расстояние от ближайшей вершины, не выходя за пределы большого равностороннего
треугольника?
размеры каждого из которых в 4 раза меньше линейных размеров ис-
исходного треугольника.
Таким образом, выбирая неограниченное число раз выигрышные
начальные точки, мы в действительности строим самоподобную фигу-
фигуру, хорошо известную под названием ковра Серпинского (рис. 15), т.е.
канторова множества в двумерном пространстве с нулевой площадью
и размерностью Хаусдорфа, равной 1пЗ/1п2 и 1,58. Если же мы будем
выбирать начальную точку случайным образом, мы почти неизбежно
окажемся на белой территории — прелюдия к ужасной участи оказать-
оказаться в конце концов выброшенным за пределы большого треугольника.
48
Глава 1
Рис. 15. Ковер Серпинского как множество выигрышных начальных точек
для игры сэра Пинского.
Чтобы избежать возможных споров, вызванных неточным начер-
начертанием линий и точек, в вышеописанную игру сэра Пинского следует
играть арифметически, т.е. начальные точки и все последующие обра-
образы задавать их координатами в подходящей системе координат. Хотя
для задания точки на плоскости достаточно двух координат, в нашем
случае удобнее использовать систему координат, более приспособлен-
приспособленную к симметрии треугольника, т.е. систему трех координат х, у и z,
как показано на рис. 14. Вершины треугольника имеют единичные зна-
значения соответствующих координат, а противолежащие стороны — ну-
нулевые значения тех же координат. Например, середина горизонтальной
стороны треугольника имеет координаты х = 0, у = z = 1/2.
Разумеется, набор из трех координат на плоскости избыточен,
и мы не можем выбирать значения координат независимо друг от дру-
друга, поскольку они связаны соотношением x+y+z = 1. Кроме того, точки
Игра сэра Пинского и детерминированный хаос 49
внутри треугольника должны удовлетворять дополнительным услови-
условиям ж > О, у > 0 и z > 0.
Как действует наше отображение, определяемое как удвоение рас-
расстояния от ближайшей вершины, если его рассматривать арифметичес-
арифметически? Предположим, что для выбранной нами точки (жо, 2Лъ %о) ближай-
ближайшей является левая нижняя вершина (у). Тогда образ точки (жо, 2/о> zo)
имеет координаты Bжо, 2уо — 1, 2zo). Множители 2, встречающие-
встречающиеся в записи нашего отображения, наводят на мысль о записи ко-
координат в двоичной системе счисления. Тогда умножению на 2 со-
соответствует простой сдвиг на один знак влево. Следовательно, точ-
точку 0 на рис. 14 с приближенными координатами E/16, 39/64, 5/64) =
= @,0101; 0,100111; 0,000101) постигает следующая судьба:
ж0 = 0,0101; уо = 0,100111; z0 = 0,000101;
Ж1 =0,101; 2/1=0,00101; zi =0,00101;
ж2 = 0,01; J/2 = 0,0111; z2 = 0,0101;
ж3=0,1; 2/3 = -0,001; z3= 0,101.
Координата 2/з отрицательна, т.е. точка (жз, 2/з< z3) лежит вне треуголь-
треугольника, и игрок, выбравший начальную точку (жо, уо, zo), выходит из
игры.
Оказавшись за пределами треугольника, образы продолжают «убе-
«убегать» в бесконечность. Что же такое с точки зрения арифметики удачно
выбранные начальные условия, позволяющие оставаться внутри боль-
большого треугольника и никогда не выбывать из игры? Если нам удастся
найти полный ответ на вопрос, то мы вдобавок ко всему получим также
арифметическое описание ковра Серпинского!
Итак, что привело нас к нежелательному отрицательному значе-
значению 2/з при отображении? Ответ заключается в том, что 2/2 (наибольшая
из координат предыдущей точки) была меньше 1/2. Иначе говоря, на
первом месте после запятой в представлении координаты 2/2 в виде дво-
двоичной дроби стоял нуль, а не единица. Отсюда следует, что каждая из
позиций во всех трех координатах удачной начальной точки не долж-
должна быть занята только нулями. Это правило нарушается в выбранной
нами начальной точке (xo,j/o,zo), так как в двоичной записи ее коорди-
координат на третьем месте после запятой стоят одни лишь нули (и ни одной
единицы). В сочетании с условием ж + у + z = 1 это означает, что на
каждом месте двоичной записи координат ж, у и z удачных начальных
точек, т. е. точек, принадлежащих ковру Серпинского, должны стоять
одна единица и два нуля.
50 Глава 1
Здесь существует удивительно красивая аналогия с троичным
представлением канторова множества (стертой средней трети), кото-
которое содержит только нули и двойки, но не содержит единиц. Действи-
Действительно, существует весьма тесная взаимосвязь между арифметически-
арифметическими представлениями ковра Серпинского и конструкции Кантора: пер-
первая отсутствующая единица канторова числа (на первом месте после
«троичной запятой») соответствует стиранию средней трети A/3, 2/3)
единичного отрезка. Единица, отсутствующая на втором месте после
троичной запятой, соответствует последующему исключению двух ин-
интервалов A/9, 2/9) и G/9, 8/9) и т.д.
Что означает геометрически отсутствие трех нулей в одной и той
же позиции двоичного представления ковра Серпинского? Три нуля на
первом месте после двоичной запятой означали бы, что ни х, ни у, ни z
не превосходят 1/2. На геометрическом языке это означает, что со-
соответствующая точка принадлежит центральному перевернутому тре-
треугольнику, т. е. белому треугольнику на рис. 14, который, таким об-
образом, должен быть исключен. Так и происходит в действительности
на первом этапе построения ковра Серпинского. Можно было бы да-
даже утверждать, что единица на месте первого двоичного знака после
запятой в координатах х, у или z означала бы, что соответствующая ко-
координата больше (или равна) 1/2. Геометрически это значит, что точка
принадлежит одному из трех темных треугольников на рис. 14.
А чему соответствовали бы геометрически три нуля во втором дво-
двоичном знаке после запятой? Как показывает небольшое «треугольное»
рассуждение, эти три нуля соответствуют перевернутым треугольни-
треугольникам размером в одну четверть исходного треугольника, вырезанным
из середины трех темных треугольников половинного размера, остав-
оставшихся после первой операции вырезания центрального треугольника.
В общем случае три нуля на n-ом месте после двоичной запятой соот-
соответствуют вырезанию З" перевернутых треугольников со сторонами
длиной 2~п из З™ неперевернутых треугольников, оставшихся пос-
после к — 1 операций вырезания центральных перевернутых треугольни-
треугольников. Таким образом, двоичная запись ковра Серпинского знак за знаком
соответствует этапам геометрического построения ковра. Два описа-
описания — арифметическое и геометрическое — эквивалентны.
Верной точкой Серпинского является, например, точка A/3; 2/3; 0) =
= @,@1); 0,A0); 0), лежащая на левой боковой стороне треугольника
на расстоянии одной трети от левой нижней вершины. Под действием
нашего отображения удвоения расстояния эта точка переходит в точ-
точку B/3; 1/3; 0) и наоборот, образуя цикл с периодом 2, что ясно и из
Игра сэра Пинского и детерминированный хаос 51
геометрических построений и из того, что дроби 1/3 и 2/3 в двоич-
двоичной системе записываются в виде бесконечных периодических дробей
с периодом из двух знаков.
Существуют ли периодические точки с периодом 3? Если такие
точки существуют, то наше отображение должно оставаться эквива-
эквивалентным при повороте на 120°. Чтобы найти такие точки, нам необхо-
необходимо просто рассмотреть двоичные дроби с периодом из трех знаков.
Легко убедиться, что точкой с периодом 3 является, например, точ-
точка @,@10); 0,@01); 0,A00)) = B/7; 1/7; 4/7), отмеченная на рис. 14
звездочкой. Порождаемому этой точкой циклу принадлежат две другие
точки D/7; 2/7; 1/7) и A/7; 4/7; 2/7), в которые точка B/7; 1/7; 4/7)
переходит при одно- и двукратном повороте на 120° против часовой
стрелки. Кроме названного, существует лишь один цикл с периодом 3.
Он получается из первого, если поменять местами две координаты,
т.е. начать, например, с точки A/7; 2/7; 4/7), которая при поворотах
на 120° по часовой стрелке дает последовательно точки B/7; 4/7; 1/7)
и D/7; 1/7; 2/7).
Периодические точки существуют для периодов любой длины. На-
Например, точка A; 0; 0) — верхняя вершина треугольника — имеет пе-
период 1, т.е. является неподвижной точкой. То же самое можно сказать
и о двух других вершинах треугольника. В дальнейшем мы еще встре-
встретимся с этим сценарием и аналогичными отображениями, и выведем
формулу для различных циклов с периодом данной длины. (При выводе
этой формулы используется, в частности, функция Мёбиуса из теории
чисел — функция, о разнообразных применениях которой в высшей ма-
математике вы, вероятно, наслышаны. Функция Мёбиуса «перекручивает
все вокруг себя» подобно тому, как это делает гораздо лучше известный
лист Мёбиуса.)
По правилам игры, образ точки в игре Серпинского (называемый
точкой Серпинского) также является точкой Серпинского. Следователь-
Следовательно, точки Серпинского образуют то, что называется инвариантным
множеством отображения: раз назвавшись точкой Серпинского, оста-
останешься точкой Серпинского навсегда. Если в качестве начальной вы
выбираете точку Серпинского с иррациональными координатами, то
ее цикл может выглядеть совершенно хаотическим, однако последова-
последовательность точек-образов полностью определяется значениями коорди-
координат начальной точки. Именно поэтому такое поведение, весьма распро-
распространенное в природе, называется детерминированным хаосом: правила
«игры» однозначно определены, но ее исход в высшей степени непред-
непредсказуем, поскольку по иронии судьбы вещественный мир не признает
52 Глава 1
огромного большинства вещественных чисел, а именно чисел, задание
которых требует бесконечной точности.
Хаос, вызываемый движением трех тел
Поражаешься сложности этой фигуры,
которую я даже не пытаюсь изобразить.
Ничто не дает нам более ясного пред-
представления о сложности задачи трех тел
и вообще задач динамики, не имеющих
однозначного решения.
Анри Пуанкаре
Более привлекательное свойство точек Серпинского состоит в том,
что все они являются отталкивающими точками, или репеллерами, т. е.
точка, сколь угодно близкая к точке Серпинского, не перейдет под дей-
действием нашего отображения в точки, близкие к образам исходной точки
Серпинского, не говоря уже о том, чтобы притягиваться к ним. Напро-
Напротив, образы точки, сколь угодно близкой к точке Серпинского, будут
удаляться от соответствующих образов точки Серпинского. Более того,
расходимость расстояний будет экспоненциальной. Читатель, облада-
обладающий доступом к персональному (или неперсональному) компьютеру,
может убедиться в этом самостоятельно. Нетрудно понять, с чем связа-
связана экспоненциальная расходимость: она обусловлена тем, что наше ото-
отображение соответствует сдвигу влево двоичных знаков, «кодирующих»
координаты точек. Сдвиг влево приводит к тому, что первый «ошибоч-
«ошибочный» бит рано или поздно становится первым знаком после запятой.
Это означает, что начальное различие, сколь бы малым оно ни было, со
временем оказывается увеличенным до размера, равного половине вы-
высоты треугольника. После этого последующие биты становятся случай-
случайными ошибками: движение первоначально почти периодической точки
становится хаотическим. В действительности, этот простой пример со-
содержит то, что составляет самую суть хаоса, и полностью согласуется
с определением хаоса: малые начальные ошибки растут экспоненциаль-
экспоненциально и становятся с некоторого момента доминирующими в любом регу-
регулярном движении.
Хаотическое движение распространено в природе гораздо шире,
чем регулярное, хотя мы можем все еще не знать об этом [277]. Уче-
Ученые «присяжные» еще не вынесли своего вердикта относительно того, не
является ли планетное движение — воплощение регулярности — хаоти-
хаотическим на больших временных интервалах. Плутон и еще несколько не-
небесных тел уже находятся под подозрением как тела, вызывающие хаос
Хаос, вызываемый движением трех тел 53
Рис. 16. Ламинарное и турбулентное течение струйки сигаретного дыма.
54 Глава 1
(или страдающие от него). Струйка дыма, поднимающаяся в спокойном
воздухе от неподвижно лежащей сигареты, сначала образует регуляр-
регулярный (ламинарный) поток, а затем, всего лишь в нескольких дюймах над
пепельницей, ламинарное течение сменяется турбулентными клубами
(рис. 16). А что произойдет, если две звезды («двойная звезда»), обра-
обращающиеся вокруг друг друга по эллиптическим орбитам (послушные
детки!), столкнутся с третьей звездой? Их регулярное движение сме-
сменится совершенно хаотическим (см. цветную вклейку 1А). Однако, как
и в случае человеческого (любовного) треугольника, через некоторое
время какие-то две звезды могут снова образовать пару и выйти на ре-
регулярную орбиту (как это показано на вклейке 1А). Но в хаотической
неразберихе, возникающей при столкновении трех тел, один из членов
первоначальной пары может поменять партнера (см. вклейку 1Б).
Разумеется, закон всемирного тяготения Ньютона, которому под-
подчиняются движения наших трех небесных тел, является совершенно де-
детерминированным. Но отдаленная судьба трех партнеров может весьма
чувствительно зависеть от их начальных положений и скоростей. Здесь
перед нами еще один случай детерминированного хаоса. Устойчивость
(на бесконечном промежутке времени) движений планет нашей солнеч-
солнечной системы, в том числе и Земли, общего космического корабля всего
человечества, пока строго не доказана, даже без учета вмешательства
со стороны Немезиды, темной и далекой гипотетической сестры нашего
Солнца.
Нам еще предстоит неоднократно встретиться с другими приме-
примерами детерминированного хаоса, столь тесно связанного с самоподоби-
самоподобием, на страницах этой книги. А ненасытного читателя, который уже
пристрасился к идее детерминированного хаоса и захочет узнать о
нем побольше, мы отошлем к недавнему бестселлеру Джеймса Глейка
«Хаос» [82].
Странные аттракторы, их области притяжения
и игра в хаос
Детерминизм, подобно английской коро-
королеве, царствует — но не правит.
Майкл Берри
Обратимся теперь к обратному отображению игры сэра Пинского
(см. с. 46-52) и попытаемся выяснить, не таит ли оно в себе каких-
нибудь сюрпризов (а может, попробуем извлечь из него один-два по-
Странные аттракторы, их области притяжения и игра в хаос 55
лезных урока). Как правило, существует несколько причин для более
внимательного рассмотрения обратных отображений. Одна из них со-
состоит в том, что репеллеры превращаются в аттракторы (и наоборот).
Возникают и новые понятия, такие, как области притяжения и стран-
странные аттракторы.
В обратном отображении сэра Пинского, мы снова выбираем точку
внутри (или снаружи) равностороннего треугольника, не удваиваем,
а делим пополам расстояние от точки до самой далекой вершины. Мы
можем быть вполне уверены в том, что деление расстояния пополам
не приведет к взрывной расходимости. Однако в каких же точках мы
сойдемся при таких условиях?
Прежде всего напомним, что в игре сэра Пинского точка Серпин-
ского всегда остается точкой Серпинского, а поскольку отображение
удвоения расстояния имеет единственное обратное ему (за исключе-
исключением точек, находящихся на равном расстоянии от двух или всех трех
вершин треугольника), то же остается справедливым и относительно
обратного отображения.
А что произойдет со всеми остальными точками внутри треуголь-
треугольника? Арифметически обратное отображение выглядит следующим об-
образом. Если х — наименьшая координата (т. е. если вершина х — наи-
наиболее отдаленная из вершин), то образом точки (ж, у, z) при обратном
отображении является точка (A+ж)/2, у/2, z/2). В двоичной записи де-
деление на 2 означает сдвиг на один знак вправо, а при прибавлении 1/2
справа от двоичной запятой вставляется единица.
Начнем с точки, не являющейся точкой Серпинского, например,
с точки A/8; 1/4; 5/8) = @,001; 0,010; 0,101), и проследим за ее орби-
орбитой. По нашим правилам, она отобразится в точку @,1001; 0,001; 0,0101),
которая, в свою очередь, отобразится в точку @,01001; 0,1001; 0,00101)
и т. д. Заметьте, что каждый раз в результате отображения мы встав-
вставляем ровно одну единицу и два нуля на первое место после двоичной
запятой. С каждой новой итерацией отображения эта тройка передвига-
передвигается на один двоичный знак вправо. Следовательно, независимо от того,
с какого места начали, мы асимптотически приближаемся к числу Сер-
Серпинского, имеющему ровно одну единицу в каждой двоичной позиции
всех трех координат. (Если бы мы с самого начала выбрали точку Сер-
Серпинского, то, разумеется, и в дальнейшем не покинули бы множество
Серпинского.)
В действительности мы сходимся в одном из двух циклов с
периодом 3 (в цикле, состоящем из точки @,@01); 0,@10); 0,A00))
и двух ее последовательных образов, или в цикле, состоящем из точ-
56 Глава 1
ки @,@01); 0,A00); 0,@10)) и двух ее последовательных образов). К ка-
какому из двух циклов мы придем, зависит от координат начальной точки
(составляют ли упорядоченные значения координат четную или нечет-
нечетную перестановку координат х, у, z).
Помимо прочего, это обстоятельство также можно использовать
в игре, в которой требуется как можно точнее предсказать, где ока-
окажется, например, двенадцатая итерация, исходя из грубого начально-
начального приближения. Если для начальной точки выполняются неравенст-
неравенства Xq > уо > zq, то после Зп итераций ее образ приблизится к перио-
периодической точке с периодом 3, для которой будут выполняться неравен-
неравенства х > у > z, а именно, к точке @, A00); 0, @10); 0, @01)), с погреш-
погрешностью менее 2~3п (начальная точка находится внутри треугольника).
Эта периодическая точка является аттрактором для сектора с раство-
раствором в 60°, задаваемом неравенствами х > у > z (с вершиной в центре
фигуры, изображенной на рис. 14); а сектор представляет собой область
притяжения трехкратно итерированного обратного отображения сэра
Пинского. Пять остальных периодических точек с периодами 3 имеют
своими областями притяжения остальные пять секторов по 60°. Грани-
Границами между этими областями служат гладкие (более того — прямые)
линии — в отличие от фрактальных границ многих других областей,
с которыми нам еще предстоит познакомиться.
Обратная игра сэра Пинского сродни «игре», называемой игрой в ха-
хаос. Эту игру придумал Майкл Барнсли, а описание ее можно най-
найти в сравнительно недавно изданной книге «Фракталы повсюду» [19].
В игре Барнсли игроки по очереди бросают трехгранную кость, на гра-
гранях которой стоят буквы х, у, z, и в зависимости от результата броска
делят пополам расстояние от точки, заранее выбранной внутри данного
треугольника, до соответствующей вершины, т. е. вершины, помечен-
помеченной той буквой, что стоит на выпавшей грани. (Придумать конструк-
конструкцию трехгранной кости мы оставляем читателю в качестве упражне-
упражнения.) Вместо кости с тем же успехом можно использовать любой гене-
генератор случайных чисел с тремя возможными исходами.
Что же представляет собой область притяжения игры в хаос? Ока-
Оказывается, она имеет форму ковра Серпинского (аффинно преобразован-
преобразованного, если треугольник не равносторонний)! Доказательство следует не-
непосредственно из проведенного нами анализа игры сэра Пинского. Од-
Однако орбита любой начальной точки по мере приближения ее итераций
к аттрактору становится совершенно хаотической. Такой аттрактор,
состоящий из бесконечного, подобного канторову, множества точек, на-
называется странным аттрактором — странным потому, что известные
Странные аттракторы, их области притяжения и игра в хаос 57
нам аттракторы либо состояли из отдельных точек (неподвижные точ-
точки), либо из конечного набора точек (периодические орбиты), либо из
непрерывных многообразий, порождающих периодические или аперио-
апериодические орбиты.
Странные аттракторы встречаются во многих нелинейных фи-
физических, химических и биологических системах, «неинтегрируемых»
и поэтому демонстрирующих в высшей степени непредсказуемое хао-
хаотическое поведение. Славно интегрируемые примеры, обычно приво-
приводимые в учебниках, являются в действительности единичными исклю-
исключениями: реальный мир за страницами учебников, включающий «ат-
«аттракторы» романтического характера, остается во многом непредсказу-
непредсказуемым на своем пути по орбитам странных, иногда даже очень странных
аттракторов.
Впрочем, не все потеряно; в реальном мире еще не царит полный ха-
хаос. Странные аттракторы часто обладают упорядоченной структурой:
подобно ковру Серпинского, они самоподобны, точно или приближенно.
Они имеют фрактальные размерности и содержат важные путеводные
нити для наших попыток понимания таких хаотических систем, как,
например, погода.
Странные аттракторы в последнее время нашли еще одно порази-
поразительное применение. В своей книге «Фракталы повсюду» Барнсли пока-
показал, что многие обычные изображения, черно-белые или цветные, мож-
можно аппроксимировать с помощью наложения странных аттракторов,
подвергнутых ограниченному числу аффинных преобразований, каж-
каждое из которых случается с заданной вероятностью. Аффинное преоб-
преобразование на плоскости определяется поворотом, преобразованием по-
подобия (скейлингом) и сдвигом по каждой из двух координат. Посколь-
Поскольку аффинные преобразования на плоскости, таким образом, полнос-
полностью определяются шестью вещественными числами, то вся картинка
может быть задана некоторым целым числом, кратным семи, напри-
например, 7 • 13 = 91 числом1.
Чтобы лучше понять аппроксимацию изображений странными ат-
аттракторами, заметим прежде всего, что ковер Серпинского состоит из
трех треугольных областей, каждая из которых есть образ всего ковра
1В теории чисел число 91 пользуется некоторой юмористической известностью
как наименьшее составное число, которое выглядит как простое по той лишь при-
причине, что не существует простого правила (кроме деления) для распознавания двух
его простых множителей. Заметим, однако, что 91 • 11 = 1001, поэтому делимость
чисел, больших тысячи, на 7, 11 и 13 можно проверять, вычитая из них соответству-
соответствующее кратное числа 1001. Например, 9399 делится на 13 потому, что на 13 делится
число 390.
58 Глава 1
при сжимающем аффинном преобразовании. (Сжимающее преобразо-
преобразование уменьшает расстояние между любыми двумя точками.) Геомет-
Геометрически такие аффинные преобразования соответствуют перемещению
точки вдоль прямой с целью сократить вдвое расстояние от нее до од-
одной из трех вершин ковра Серпинского. Арифметически преобразова-
преобразования задаются вписыванием единицы после двоичной запятой в одной
из координат ж, у или z и нуля в каждой из двух оставшихся координат
при сдвиге всех двоичных цифр точки (ж, у, z) на один знак вправо.
Чтобы построить весь ковер, мы выбираем произвольную началь-
начальную точку (жо, 2/о> zo) где-то вблизи ковра и наугад одно из трех преоб-
преобразований — поворот, преобразование подобия или сдвиг — и получаем
точку (xi, ?/1, z\). При последующих отображениях эти три преобразо-
преобразования выбираются независимо с заданными вероятностями рг, Р2 w Рз-
Из правила вписывания единиц и нулей ясно, что образы точек
подступают все ближе и ближе к точкам Серпинского, т. е. к элемен-
элементам ковра. Из-за случайности выбора различных отображений точки
сгущаются не по «периодической колее», а беспорядочно «прыгают» и по-
постепенно «высвечивают» весь ковер.
В случае равных вероятностей, или при Pi = Р2 = Рз = 1/3, каждая
из трех частей ковра посещается с одинаковой вероятностью. Выбирая
другие значения ри, мы можем добиваться различных степеней осве-
освещенности или затененности для различных частей аттрактора.
Описанный выше процесс получения изображений допускает следу-
следующее обобщение. Вместо того чтобы выбирать три вершины равносто-
равностороннего треугольника, мы можем выбрать любые три точки на плос-
плоскости. Более того, мы можем задать любое число совершенно общих
аффинных преобразований — каждое со своей собственной вероятнос-
вероятностью быть выбранным. Но даже учитывая все эти обобщения, нельзя не
удивляться тому, что данный «странно притягательный»1 метод позво-
позволяет воспроизводить вполне реалистичные естественные изображения
при числе параметров меньше 100.
Высокоэффективный метод сжатия графических данных с помо-
помощью систем итерированных функций, как назвал этот метод Барнс-
Барнсли, представляется поразительно многообещающим, как только будет
обеспечена достаточная вычислительная поддержка, необходимая для
такого аттракторного разложения изображения. На вклейке 2 показано
изображение, полученное этим способом.
1В оригинальном тексте игра слов — ср. англ. attractive («притягательный»)
и attractor («аттрактор») (см. также прим. на с. 20). — Прим. перев.
Перколяционные случайные фракталы 59
Перколяционные случайные фракталы
Ковер Серпинского служит примером двумерного детерминирован-
детерминированного фрактала. Выбирая точку внутри треугольника, из которого выре-
вырезан ковер, мы сразу же знаем, принадлежит ли она фрактальному мно-
множеству или «проваливается в щели». Многие рукотворные фракталы,
наподобие ковра Серпинского, привлекательны с визуальной и интри-
гующи с алгебраической точки зрения. Однако большинство природных
фрактальных объектов лучше всего моделируются случайными фракта-
фракталами, порождаемыми стохастическими процессами. Среди многих яв-
явлений, рассмотренных с точки зрения случайных фракталов, упомянем
распространение эпидемий и лесных пожаров. Другими примерами та-
таких фракталов могут служить случайные резисторные цепи, полимер-
полимерные связи и, вероятно, льдины, дрейфующие в Беринговом море.
Рис. 17. Квадратная решетка со случайно занятыми узлами ниже порога пер-
коляции.
Чтобы изложить суть дела как можно проще и яснее, рассмотрим
большую квадратную решетку, узлы которой «заняты» независимо друг
60 Глава 1
от друга некоторыми объектами с вероятностью р < 1 (рис. 17). В роли
таких объектов может выступать что угодно — деревья, люди, атомы
или что-нибудь еще (не важно что). Доля не занятых («пустых») уз-
узлов решетки равна 1 — р. Важный вопрос заключается в следующем:
образуют ли занятые узлы непрерывный путь от нижнего края решет-
решетки до верхнего? Под непрерывным мы понимаем путь, соединяющий
один занятый узел решетки с соседним занятым узлом решетки. (Со-
(Соседями данного узла считаются узлы, расположенные в непосредствен-
непосредственном соседстве от него к северу, югу, востоку или западу.) Если такой
путь существует, то говорят, что решетка перколирует (от латинского
percolare — «протекать, течь сквозь»). Представьте себе кофейное си-
ситечко, в котором занятые ячейки заполнены воздухом, а «пустые» —
кофейной гущей; вода, налитая в такое ситечко, перколирует сквозь
кофе.
Наименьшая плотность р занятых узлов, при которой бесконеч-
бесконечная решетка перколирует, называется критической плотностью, или
порогом перколяции рс. Несмотря на столь простое определение, точ-
точный порог перколяции для узлов квадратной решетки все еще не
установлен. Как показали массированные расчеты по методу Монте-
Карло, рс к, 0,59275. По мере того, как для вычисления рс использу-
используются все более мощные компьютеры, количество десятичных знаков
увеличивается.
Помимо перколяции по узлам существует перколяция по связям: все
узлы решетки считаются занятыми, а между соседними узлами с ве-
вероятностью р < 1 возникают «связи». Вероятность отсутствия связи
равна 1 — р. Здесь перколяция означает непрерывный путь из связей
от одного края решетки до другого. Порог перколяции связей для бес-
бесконечной квадратной решетки установлен точно: рс = 0, 5. Однако для
доказательства этого, на первый взгляд «невинного», результата понадо-
понадобилось два десятилетия компьютерного моделирования и теоретичес-
теоретического анализа. Итак, в больших случайных сетях, состоящих из разме-
размещенных на квадратной решетке резисторов, между противоположными
сторонами решетки может течь электрический ток, если проводника-
проводниками являются по крайней мере половина возможных связей. Резисторы,
через которые течет ток, называются остовом кластера, а остальные —
болтающимися связями.
При достижении порога перколяции (р и 0,5927 для квадратной
решетки) занятые узлы бесконечной решетки образуют кластеры всех
размеров из связанных между собой узлов. Распределение кластеров
по размерам следует простому степенному закону: число n(s) клас-
Перколяционные случайные фракталы
61
теров, содержащих s занятых узлов, пропорционально s т, где т =
= 187/91 = 2,@54945) (для квадратной решетки) [249]. Степенной за-
закон n(s) ~ s~T означает, что отношение числа кластеров одного размера
к числу кластеров другого размера зависит не от их размеров s, а лишь
от отношения размеров.
Рис. 18. Квадратная решетка с вероятностью занятия узлов, равной порогу
перколяции. Встречаются кластеры различных размеров, образующие ста-
статистически самоподобную картину.
На рис. 18 показаны кластеры различных размеров — от пары уз-
узлов (s = 2) до «перекрывающего кластера», простирающегося от ниж-
нижнего края решетки до верхнего. На большой решетке — например, в 10
раз большей, чем изображенная на рис. 18, — распределение класте-
кластеров было бы таким же за исключением того, что кластеры стали бы
крупнее. Таким образом, перколяционные кластеры самоподобны, или
независимы от масштаба, на интервале от шага решетки до размера
всей решетки. Однако ниже порога перколяции верхняя граница раз-
62 Глава 1
мера, при котором сохраняется самоподобие, совпадает не с размером
решетки, а с корреляционной длиной ?, определяемой как расстояние,
при котором вероятность принадлежности двух узлов к одному и то-
тому же кластеру убывает до 1/е к, 0,368. На расстояниях, меньших
корреляционной длины ?, занятые узлы образуют фрактал; на рассто-
расстояниях, больших ?, превалирует евклидова геометрия, а число занятых
узлов равно М (R) ~ Rd, где d — евклидова размерность вложения.
При достижении порога перколяции корреляционная длина ? обращает-
обращается в бесконечность, и вероятность того, что два узла, даже при сколь
угодно большом расстоянии между ними, принадлежат одному и тому
же кластеру, ограничена снизу и не достигает нуля.
Будучи самоподобными фракталами, перколяционные кластеры
должны иметь фрактальные размерности. Первая размерность, кото-
которая приходит на ум в этой связи, — так называемый массовый пока-
показатель Dm, указывающий, сколько занятых узлов («масс») находится
в круге радиуса R: M (R) ~ RDrn. Разумеется, для евклидовых объ-
объектов показатель Dm равен евклидовой размерности; например, для
сплошного диска площадь М (R) = irR2, иначе говоря, Dm = 2. Но для
фракталов Dm обычно меньше, чем евклидова размерность пространст-
пространства (называемая также размерностью вложения), в котором существует
фрактал (в которое он вложен). Например, для троичного канторова
множества доля М (R) множества, попавшая внутрь круга радиуса R,
возрастает в среднем пропорционально Л0'63, т.е. показатель Dm равен
размерности Хаусдорфа Dh = In 2/In 3 и 0,63. Аналогично, для дву-
двумерного ковра Серпинского М (R) ~ Л1'58; т.е. показатель Dm снова
равен размерности Хаусдорфа Dh = In 3/In 2 « 1,58.
Чему равен массовый показатель для перколяционного кластера на
двумерной решетке? Теория дает значение Dm = 91/48 = 1,8958C), на-
находящееся в хорошем согласии с лучшими результатами, полученными
с помощью численного моделирования [249].
Целое число 91, входящее в численные значения т и Dm, наво-
наводит на мысль о том, что между т и Dm существует какая-то взаи-
взаимосвязь. Она действительно существует и имеет вид: т — 1 = 2/Dm.
Через некоторое время мы еще вернемся к интересным соотношениям
между характеристическими показателями (в гл. 15 — о перколяции и
в гл. 16 — о фазовых переходах). В гл. 10 мы увидим, что во многих
случаях массовый показатель равен корреляционной размерности ?>2 —
одной (весьма, кстати, важной) из размерностей в бесконечной иерар-
иерархии фрактальных размерностей.
Степенные законы: от Альвареса до Ципфа 63
Степенные законы: от Альвареса до Ципфа
Однородные степенные законы (например, открытый Ньютоном за-
закон всемирного тяготения F ~ г~2) в изобилии встречаются в приро-
природе — как в живой, так и в неживой. Поскольку однородные степенные
законы при изменении масштаба остаются однородными степенными
законами с тем же самым показателем (—2 в случае закона Ньютона),
такие законы по определению самоподобны. Иначе говоря, закон Нью-
Ньютона справедлив независимо от значения величины г — от длины волны
света до светового года, т. е. закон всемирного тяготения не имеет соб-
собственного, «встроенного», масштаба. Мы могли бы сжать или растянуть
гравитирующую вселенную Ньютона по своему усмотрению, если бы
у нас возникло такое желание1.
Тот же закон обратных квадратов, которому подчиняется тяготе-
тяготение, описывает и убывание мощности радарного сигнала с расстоянием.
Этим простым фактом часто пользовались во время второй мировой
войны немецкие подводные лодки. Измеряя скорость увеличения ин-
интенсивности сигнала, они оценивали быстроту приближения авиации
противника и успевали погрузиться прежде, чем вражеские самолеты
могли их атаковать.
Такая тактика великолепно работала на гросс-адмирала Карла
Дёница до тех пор, пока американский физик Луис Альварес A911
1988) не изобрел хитроумное устройство, получившее кодовое наиме-
наименование «Виксен»2. Альварес предложил уменьшить интенсивность ра-
радарного сигнала настолько, чтобы она была пропорциональна кубу рас-
расстояния до подводной лодки. В результате при приближении самолета
к ничего не подозревающей подводной лодке, интенсивность радиосиг-
радиосигнала падала, создавая у моряков ложное впечатление, будто самолет
удаляется. Идея была великолепна! (Для атакующего же самолета ин-
интенсивность принятого сигнала, отраженного от подводной лодки, воз-
возрастала по мере приближения к цели [4].K
¦"¦Впрочем, недавно на неограниченную применимость закона Ньютона все же
была брошена тень сомнения. Похоже, некая все еще таинственная «пятая сила»
потрясает самые основы ньютоновских построений и выводов, добавляя члены,
вносящие естественный масштаб длины порядка нескольких сотен метров [7]. При
очень малых величинах г действие закона Ньютона ограничивается планковской
длиной A0~35 м), что напоминает нам о том, что гравитацию необходимо, наконец,
должным образом квантовать и наделить неопределенностью.
2Vixen (англ.) — «лисица». — Прим. перев.
3Предложенная Альваресом хитрость наводит на мысли о «повелителе мира»
Чингиз-хане и о коварной тактике, применяемой воинами Золотой Орды. Броса-
64 Глава 1
Еще один широко известный пример однородного степенного зако-
закона — соотношение между площадью А подобных плоских фигур и их
диаметрами, периметрами или любыми другими характеристическими
линейными размерами /: площадь пропорциональна квадрату линейного
размера /, т. е. А ~ I2. Разумеется, для площадей на кривых поверхнос-
поверхностях это неверно: радиус кривизны привносит масштаб длины, который
разрушает истинность вышеприведенного соотношения «во всех подоби-
подобиях». Например, как всем известно, расстояния и площади на поверхнос-
поверхности сферы ограничены некоторой максимальной величиной, задаваемой
радиусом сферы.
В отличие от гравитации, межатомные силы принято моделировать
неоднородными степенными законами по крайней мере с двумя показа-
показателями. Такие (и экспоненциальные) законы зависят от масштаба; они
непременно вводят характеристический размер, связанный с размера-
размерами атомов.
Степенные законы описывают и спектры мощности всевозможных
шумов. Самый загадочный из них — вездесущий (хотя иногда и труд-
труднообъяснимый) фликер-шум 1// (где / — частота). Например, шум,
наблюдаемый во многих полупроводниковых приборах, не является ни
«белым» (т.е. независимым от частоты), ни «коричневым» (с зависи-
зависимостью I//2, как при броуновском движении1), а имеет некоторый
промежуточный показатель, вследствие чего его иногда называют ро-
розовым шумом. При акустических исследованиях предпочтение отдается
опять же розовому шуму, так как его мощность постоянна в интерва-
интервале октавы (а не герца) и поэтому хорошо соответствует шкале частот
внутреннего уха.
Как мы увидим на протяжении нашего экскурса в мир фракталов,
показатели степенных законов не обязательно должны быть целыми.
Они вполне могут быть (и часто бывают) дробными.
Неудивительно, что мы обнаруживаем однородные степенные за-
законы не только в неорганическом мире. Такие законы «присущи» и жи-
живой природе, и, в частности, человеческому восприятию. Так, в весьма
широком диапазоне амплитуд звуковых сигналов субъективная гром-
громкость L пропорциональна физической интенсивности звука / в степени
три десятых: L ~ /°'3. Это означает, что для увеличения громкости
ясь наутек от преследователей, всадники Чингиз-хана в действительности позволя-
позволяли тем приблизиться, после чего внезапно вставали на стременах, поворачивались
назад и обрушивали град стрел на онемевшего от изумления противника.
Английское слово brown («коричневый») совпадает по написанию с фамилией
Броун (Brown). — Прим. перев.
Степенные законы: от Альвареса до Ципфа 65
своей музыки вдвое рок-группа из пяти музыкантов должна увели-
увеличить свою численность в десять раз, т. е. довести ее до 50 участников
(при условии, что «выходная мощность» каждого музыканта останется
на прежнем уровне). (Эти несложные подсчеты объясняют просто кри-
кричащее пристрастие «производителей» поп-музыки к электронным уси-
усилителям.)
По той же причине, если мы хотим уменьшить вдвое громкость не-
непрерывного грохота от шоссе с напряженным движением, то интенсив-
интенсивность акустического шума необходимо уменьшить в десять раз! Сде-
Сделать это не так трудно, как может показаться, по крайней мере с чисто
физической точки зрения: шуршание шин (основной виновник дорож-
дорожного шума при постоянных скоростях движения) резко идет на убыль
при снижении скорости движения. Интенсивность шума приближенно
пропорциональна четвертой степени скорости.
С другой стороны, десятикратное повышение средней интенсивнос-
интенсивности дорожного шума, вызванное десятикратным увеличением плотнос-
плотности дорожного движения, может привести к стократному увеличению
потока жалоб со стороны раздраженных окрестных жителей: один гру-
грузовик, грохочущий каждые 5 минут, еще вполне терпим, но рев и гро-
грохот каждые 30 секунд превратили бы жизнь людей в кошмар и сделали
бы заведомо невозможным любой разговор на открытом воздухе. Ска-
Сказанное о грузовых автомобилях в полной мере относится и к низко
летящим самолетам.
Степенные законы широко распространены и в экономике. Почти
сто лет назад итальянский экономист Вильфредо Парето A848-1923),
работая в Швейцарии, обнаружил, что число людей с доходом, превы-
превышающим некоторую большую величину, следует простому степенно-
степенному закону [190, 156]. Другие примеры степенных законов в экономике
и логические ошибки, основанных на них экономических схем, были
проанализированы Мандельбротом [157, 158].
Одним из наиболее удивительных примеров степенных законов
в гуманитарных науках может служить закон Ципфа, определяющий
зависимость между рангом слова и частотой слова для многих нату-
натуральных языков. (Под словом ранга г понимается слово, стоящее на г-м
месте в списке слов данного языка, расположенных в порядке убыва-
убывания частоты их употребления.) Закон, сформулированный Джорджем
Кингсли Ципфом A902-1950), гласит, что относительная частота сло-
слова/в данном тексте в очень хорошем приближении обратно пропор-
пропорциональна рангу слова г:
f (r\ ~ 1
1 К ' ~ г1пA,78Д)'
66
Глава 1
где R — общее число различных слов [285]. Законы, подобные зако-
НУ J(r) ~ 1/г) называются гиперболическими законами. Например, ес-
если предположить для английского языка R = 12 000, то относительные
частоты слов высокого ранга (the, of, and, to и т. д. в порядке убывания
рангов) приближенно равны 0,1; 0,05; 0,033; 0,025 и т.д.
0,1
0,01 -
о
ч
о
Й 0,001 -
0,0001 -
0,00001
[V-The
\\.0f
-
i
^nd
-To
\
I
^-Say
\
1
I
- Really
\
1
_
- Quality
\
\
1
10
100
Ранг слова
1000
10000
Рис. 19. Частота слова как функция ранга слова (по закону Ципфа).
На рис. 19 показано, насколько точное соответствие наблюдается
между однородным степенным законом Ципфа и экспериментальными
данными. Создатель теории информации Клод Шеннон использовал за-
закон Ципфа для вычисления энтропии источника английского текста,
порождающего слова независимо, с вероятностями (частотами) Цип-
Ципфа [236]. Энтропия такого источника определяется приближенно следу-
следующим выражением:
Н = ±\og2BRln2R)
битов на слово.
Степенные законы: от Альвареса до Ципфа 67
При R = 12 000 мы получаем Яй9 битов на слово, в то время как R =
= 300 000 приводит к энтропии около 11,5 битов на слово. Разумеется,
приведенные значения указывают лишь верхнюю границу энтропии,
так как слова (пусть даже и независимые от действий) зависят друг от
друга (за исключением, разве что, слов в произведениях так называе-
называемой случайной поэзии). Взаимозависимость слов в осмысленном тексте
(их «избыточность») приводит к уменьшению энтропии.
Если учесть, что средняя длина английского слова составляет
4,5 буквы, или 5,5 «символов», в число которых входит и пробел между
словами, то легко заметить, что энтропия английского текста состав-
составляет приблизительно 2 бита на символ.
Из гиперболического закона Ципфа, применимого не только к язы-
языку как таковому, но и к языку отдельных писателей, вытекают не-
некоторые весьма любопытные следствия. Знаете ли вы, например, что
у хорошего писателя с активным словарем примерно в R = 100 000 слов
«верхние» 10 слов (т. е. слов наивысшего ранга) занимают 24 процен-
процента текста, тогда как в более примитивном английском (basic English),
на котором изъясняется большинство газет, со словарем в десять раз
меньшим (R = 10 000) доля наиболее часто употребляемых слов лишь
немногим больше (около 30 процентов)? Разумеется, любому писателю
трудно избежать таких слов, как the, of, and и to.
Ципф попытался вывести свой закон из анализа текста собствен-
собственного трактата «Человеческое поведение и принцип наименьшего уси-
усилия» A949). Однако Мандельброт в одной из своих ранних работ по-
показал, что обезьяна, случайным образом барабанящая по клавишам пи-
пишущей машинки, также создает «язык», подчиняющийся гиперболичес-
гиперболическому закону Ципфа [155]. Вот вам и наименьшее усилие в применении
к лексикографии!
Подробный анализ показывает, что если на клавиатуре пишущей
машинки, на которой «печатает» обезьяна, имеется N равновероятных
клавиш с буквами и одна клавиша для пробела (с вероятностью р0), то
порождаемые обезьяной слова (определяемые как последовательности
букв между пробелами) имеют относительные частоты
/ (г)
lnJV
При N = 26 и ро = 1/5 показатель величины г равен —1,068, что
лишь слегка меньше, чем —1. В общем случае обезьяньи слова мож-
можно моделировать как канторово множество с фрактальной размерное-
68 Глава 1
тью D, равной величине, обратной показателю дроби 1/г. В нашем при-
примере
D = - и 0,936.
l-ln(l-po)
lniV
Для алфавита из 9 букв и ро = 110 показатель равен —1,048, что
соответствует канторовой «пыли» с D « 0, 954. Арифметической мо-
моделью для слов (бесконечно большого количества слов) такого девяти-
буквенного «языка» служат все десятичные дроби между 0 и 1, в записи
которых после запятой не встречается ни одного нуля (не считая нулей
на концах конечных дробей).
Вот несколько «трехбуквенных» слов такого языка: 0,141; 0,241;
0,643; 0,442; 0,692; 0,121. А вот дроби 0,103; 0,702; 0,0C) словами не
являются, так как содержат нуль после десятичной запятой.
У такого рода языков не существует среднего ранга, но медиан-
медианный ранг слов нашего «образцово-показательного» языка имеет порази-
поразительное значение: 1895 761. Иначе говоря, лишь отсчитав от начала его
частотного словаря 1895 761 слов, мы достигнем слова, встречающего-
встречающегося с вероятностью 1/2. (Для сравнения: медианный ранг английского
текста находится между 100 для типичной газетной статьи и 500 для
произведения высокообразованного писателя.) Таким образом, обезья-
обезьяна, неукоснительно придерживаясь закона Ципфа, создает весьма мно-
многословный (и многосложный) язык.
Обезьяний язык обладает еще одной, не менее удивительной, «ре-
«речевой патологией»: построить для него словарь оказывается невозмож-
невозможным, поскольку его слова образуют несчетное канторово множество.
(Мы, возможно, не откажемся пользоваться даже бесконечно толстым
словарем, лишь бы статьи в нем располагались последовательно, но не
потерпим несчетного нагромождения слов.)
Но если обезьяний язык имеет фрактальную размерность, то обла-
обладает ли он какими-нибудь самоподобиями? Несомненно, обладает. Ум-
Умножим все слова этого «десятичного языка» на 10 и отбросим целую
часть (или просто отбросим самую левую «букву» каждого слова). У нас
получится еще один обезьяний язык (и скорее всего, на нем можно бу-
будет писать столь же бессмысленные предложения). Можно сказать, что
слова такого рода языков растут на самоподобных деревьях: выберите
любую ветвь, как бы высоко она ни росла и как бы мала ни была, и она
окажется тождественной всему дереву.
В этом особенно наглядно проявляется отличие обезьяньего языка
Степенные законы: от Альвареса до Ципфа 69
от языков естественных: языки, на которых говорят и пишут живые
люди, не растут на самоподобных деревьях, а если мы станем-таки
настаивать на том, чтобы и их туда повесить (Боже упаси!), то боль-
большинство ветвей окажутся мертвыми.
Действительно, в естественных языках многие комбинации букв
словами не являются. Вместе с тем многие английские слова омогра-
фичны словам других языков, т. е. имеют одинаковое с ними написа-
написание. Говоря о словах-омографах, мы отнюдь не имеем в виду такие
тривиальные случаи, когда одно и то же слово, например, GENERAL,
имеет одинаковое значение во многих языках. Нет, гораздо более ин-
интересны примеры одинакового написания слов, не родственных друг
другу, таких, как английское STRICKEN («пораженный» (параличом),
«охваченный» (ужасом)), означающее по-немецки «вязать», или англий-
английское FALTER («шататься, колебаться, запинаться»), означающее по-
немецки «бабочка», или английское LINKS («узы, связи»), означающее
по-немецки «слева, налево». А что говорить о таких триплетах, как анг-
английское слово ART («искусство, ремесло, умение»), которое по-немецки
значит «вид, порода, сорт, манера, способ», т. е. то же, что означает анг-
английское слово KIND, которое переводится с немецкого как «ребенок,
малыш», т.е. то же, что по-английски может означать слово MINOR
(«младший ребенок в семье»), которое встречается как термин в теории
определителей (и в немецком, и в английском языках). Или вот вам по-
последовательность из пяти слов: ROT — RED — TALK — STEATITE —
SOAPSTONE1. Может, придумаем цепочку из шести звеньев?
Существуют буквально сотни таких «англо-немецких» слов. Однаж-
Однажды я даже сочинил небольшой рассказ на немецком языке, в котором
использовал только английские слова. Когда я показал свое произведе-
произведение одному немецкоязычному венгру, жившему в Соединенных Шта-
Штатах, тот, зевнув, отозвался о моем опусе, как об «еще одном образчике
случайной поэзии», и не изменил своего вердикта даже после неодно-
неоднократных и настойчивых просьб непредвзято подойти к рассмотрению
текста, например, как к задаче о дискриминации изображения (разли-
(различения фигуры и фона), входившей в круг занимавших его исследова-
исследовательских проблем. Однако когда я через полгода показал тот же текст
¦'¦Английское ROT («гниение, гниль») — по-немецки «красный», что на английский
переводится как RED; в свою очередь, RED почти совпадает с немецким REDE —
«речь», что по-английски соответствует слову TALK; с немецкого это слово перево-
переводится как название минерала «тальк», одна из разновидностей которого называется,
в частности, «стеатит», по-немецки — STEATITE, что соответствует английскому
SOAPSTONE — «мыльный камень». — Прим. перев.
70 Глава 1
тому же венгерскому приятелю, к тому времени оказавшемуся в Гер-
Германии, он, прочтя, заметил: «Interessant! Interessant!»1 И не говорите
мне после этого, что контекст не влияет на человеческое восприятие!
(Я оставляю в качестве самостоятельного упражнения для читателя
с лингвистическими наклонностями сочинение рассказа, который имел
бы смысл и по-английски, и по-немецки или на любых двух других
языках — таких, в которых хотя бы частота использования букв сопо-
сопоставима.)
Некая француженка, впервые оказавшись в Соединенных Штатах
и увидев толпу под вывеской «Lingerie Sale»2, была несказанно удивлена
тем, что американцы охотно покупают грязное белье, да еще в таких
количествах.
Иногда слова с двойной смысловой нагрузкой порождают двоякое
понимание или точнее двоякое непонимание. Вскоре после моего приез-
приезда в Гёттинген комендант физического института, в обязанности кото-
которого входило доставлять из таможни поступившие в мой адрес зарубеж-
зарубежные посылки, доверительно сообщал сотрудникам: «Профессор Шредер
импортирует из Соединенных Штатов яд. На пакетах, которые он полу-
получает, так прямо и значится — ЯД!» Действительно, на моих бандеролях
крупными буквами было написано «GIFT»3, что по-немецки означает
«яд». Здесь необходимо признать, что слова эти все же происходят от
одного корня (в самом деле, и подарок, и яд, как правило, даются совер-
совершенно безвозмездно); кроме того, в немецком языке сохранилось слово
Mitgift — «приданое».
Когда я рассказал об этом случае химику Фрэнсису О. Шмитту
из Массачусетского технологического института, он тут же привел об-
обратный пример полного непонимания. По словам одного из студентов
Шмитта, побывавшего на стажировке в Германии, тамошняя химичес-
химическая промышленность отличается необычайной щедростью: на каждой
второй бутыли с реактивами в лаборатории красовалась наклейка с над-
надписью GIFT. Этот пример показывает, что в некоторых краях «подар-
«подарки» лучше не принимать внутрь!
Разумеется, не все омографы столь безобидны. Возьмите немецкое
слово NOT («нужда, необходимость; аварийная ситуация»). Один мой
приятель из Австралии (настоящий лингвист, никак не меньше) од-
однажды оказался в ловушке в каком-то здании в Австрии (уж не пожар
1«Интересно! Интересно!» (нем.). — Прим. перев.
Lingerie Sale — англ. «Распродажа дамского белья», франц. «грязное белье». —
Прим. перев.
3Gift — англ. «подарок, дар». — Прим. перев.
Итерации Ньютона и упразднение межнациональных границ 71
ли там был?): куда бы он ни пошел, на его пути неизменно возника-
возникала дверь со зловещей надписью NOTAUSGANG1 (очевидно, не-выход).
Тщетно мой друг, все больше впадая в панику, искал дверь с надписью
AUSGANG: в достаточной мере владея латынью и немецким (кроме
родного английского), он правильно расшифровал Aus-gang как ex-it2.
Но, подгоняемый настоятельной необходимостью срочно выбраться из
здания, он так и не сумел разрубить этот Гордиев узел. NOT не значит
«нет»!
Итерации Ньютона и упразднение
межнациональных границ
Как известно каждому школьнику, уравнение z2 = 1 имеет не одно,
а два решения: z = +1 и z = — 1. Предположим, однако, что мы этого
не знаем. Пытаясь решить это уравнение, мы могли бы начать с не-
некоторой начальной догадки Zq и воспользоваться методом касатель-
касательных Ньютона для отыскания более точного приближенного значения z\.
В нашем случае метод Ньютона дает z\ = (z2 + l)/2zo- При положитель-
положительном zq приближенное значение z\ будет лежать ближе к решению +1.
Например, при zq =0,5 мы получаем z\ = 1,25. Действительно, все Zq
с положительной вещественной частью при многократном применении
формулы Ньютона «мигрируют» к +1. Аналогично, все zq с отрица-
отрицательной вещественной частью сходятся к —1. Таким образом, линия на
комплексной плоскости, состоящая из точек zq с нулевой вещественной
частью (т. е. мнимая ось) является границей между областями притя-
притяжения двух решений: +1 и —1. Просто, как дважды два — четыре.
А что можно сказать об уравнении z3 = 1? Оно, разумеется, имеет
три решения: z = 1, z = и> и z = u>2, где u> — стандартное обозначение
для ехр(г'2тг/3). Если в качестве нулевого приближения мы выбрали
число zo, то для следующего приближенного значения метод Ньюто-
Ньютона дает Z\ = Bzq + l)/3z2. Вычисляя последующие итерации по этой
формуле, мы ожидаем, что приближенные значения будут сходиться
к одному из трех решений A, и> или и>2) в зависимости от сектора,
в котором расположено начальное приближение zq. Иначе говоря, мы
ожидаем, что существуют три области притяжения, которые разбивают
комплексную плоскость на три сектора по 120° каждый. Но, как обна-
обнаружил в 1879 г. к своему крайнему изумлению английский математик
1«3апасный выход» (нем.). — Прим. перев.
2Вы-ход (лат. и англ.). — Прим. перев.
72 Глава 1
Артур Кэли A821-1895), ничто не может быть дальше от истины. (Мы
еще встретимся с Кэли, когда дойдем до рассмотрения самоподобных
деревьев.)
В действительности безобидные, на первый взгляд, итерации zn+\ =
= R(zn) = Az\ + l)/3z^ ведут себя невероятно сложным образом. На-
Начать хотя бы с того, что области притяжения корней 1, и> и и>2 от-
отнюдь не напоминают круглый пирог, разрезанный на три равных сек-
сектора. В действительности на всей комплексной плоскости нет ни одного
сколь-нибудь связного фрагмента границы между любыми двумя облас-
областями притяжения. Предположим, что мы выбрали начальную точку zo,
итерации которой сходятся к +1; предположим далее, что итерации
другой точки, расположенной поблизости от первой, сходятся к ш. Ес-
Если это так, то всегда найдется третья точка, расположенная еще ближе
к zq, итерации которой сходятся к третьему решению и>2. Общая кар-
картина выглядит так, как если бы межгосударственные границы были
бы упразднены, дабы избежать межнационального соперничества (или
просто из предусмотрительности), и между любыми двумя странами
всегда вклинивалась бы третья.
Столь невероятно сложное поведение границ областей притяжения
решений простого, казалось бы, уравнения поразило не только профанов
в математике, но и высоких профессионалов. Впрочем, в 1918 г. Гас-
тон Жюлиа A893-1978) и Пьер Фату A878-1929) несколько рассеяли
всеобщее удивление, показав, что для итераций рациональных функ-
функций в общем случае граничные точки одной области притяжения явля-
являются граничными точками всех областей притяжения. Эти граничные
точки образуют множество, известное теперь под названием множес-
множества Жюлиа в честь Гастона Жюлиа (дополнительное множество точек
комплексной плоскости с полным основанием было названо множест-
множеством Фату). Таким образом, итерации, имеющие более двух областей
притяжения, не могут иметь границ между этими областями, пред-
представляющих собой связные отрезки линий. Такие границы неизбежно
должны быть фракталами, состоящими из множеств совершенно не свя-
связанных между собой точек — бесконечно тонким налетом несчетной
числовой «пыли».
На вклейке 3 красным, зеленым и синим цветом показаны области
притяжения трех решений 1, ш и w2 на комплексной гауссовой плос-
плоскости. В центре фигуры (z = 0) мы видим своего рода клеверный лист:
три области притяжения (каждая представлена дважды) встречаются
в одной точке. Центральный клеверный лист имеет три прообраза, так-
также в виде клеверных листьев, хотя и несколько искаженных. Эти три
Мог ли Минковский услышать форму барабана? 73
клеверных листа, в свою очередь, имеют прообразы в виде девяти еще
более мелких клеверных листьев и т. д. ad infinitum, причем все прооб-
прообразы вместе образуют изящный самоподобный орнамент. Именно так
любая граничная точка становится граничной точкой всех трех аттрак-
аттракторов — в точности так же, как точка z = 0. Последнее замечание не
случайно: множество Жюлиа есть не что иное, как множество прооб-
прообразов точки z = 0. Но истинную степень «пыльности» множества Жю-
Жюлиа невозможно оценить с помощью какого бы то ни было рукотворного
прибора, ибо разрешение любого прибора конечно. В действительности,
если множество Жюлиа не совпадает со всей комплексной плоскостью,
то оно не имеет ни одной внутренней точки. Вот так множества Жю-
Жюлиа «решили» проблему внутренних точек по принципу все или (почти)
ничего.
Мы также можем определить множество Жюлиа, взяв вместо ат-
аттракторов репеллеры. Действительно, множество Жюлиа Jr рациональ-
рациональной функции R содержит в себе все свои репеллеры (несчетно бесконеч-
бесконечное количество). На интуитивном уровне это понятно, поскольку мно-
множество Jr есть граница областей притяжения функции R, не принад-
принадлежащая самим областям притяжения. Однако несколько удивительно,
что при прямом отображении любой репеллер порождает орбиту, кото-
которая непременно должна «посетить» все остальные репеллеры.
Интересно отметить, что не только прямая, но и обратная (порож-
(порождаемая обратным отображением) орбита любого репеллера всюду плот-
плотна в Jr. Поскольку при обратном отображении репеллеры становятся
аттракторами, множества Жюлиа можно стабильно, хотя и неравно-
неравномерно, строить из одного-единственного репеллера, обратно отображая
его; при этом малые ошибки в ходе вычислений не возрастают экспо-
экспоненциально, как в случае прямого отображения. Все это великолепно из-
изложено в книге Пайтгена и Заупе «Наука о фрактальных образах» [196].
Мы еще вернемся к множествам Жюлиа на с. 319-326 в гл. 11, где
и углубим наши знания об этих удивительных и часто фрактальных
множествах.
Мог ли Минковский услышать форму барабана?
В конце 1910 г. великий голландский физик Хендрик А.Лоренц,
выступая с докладом на Вольфскелевских чтениях в Гёттингене1, вы-
1 Чтения проводились на проценты от Вольфскелевской премии, учрежденной
Гёттингенской Академией Наук и предназначенной тому, кто сможет доказать или
74 Глава 1
сказал некое предположение. Присутствовавший на докладе Гильберт
(принимавший Лоренца в качестве гостя) тотчас же заявил во всеуслы-
всеуслышание, что это предположение при его жизни не будет доказано. Суть
высказанного Лоренцем предположения, играющего важную роль в тер-
термодинамике (при вычислении удельной теплоемкости твердых тел),
теории излучения черного тела и акустике концертных залов, состо-
состоит в том, что число резонансов N3 (/), вплоть до некоторой большой
частоты /, зависит только от объема V резонатора и не зависит от его
формы.
Один из слушателей, молодой человек по имени Герман Вейль
(ставший впоследствии преемником Гильберта в Гёттингене), не раз-
разделил пессимизма великого математика. И вскоре Вейлю удалось до-
доказать, что при большой частоте / для резонаторов с достаточно глад-
гладкими, но в остальном произвольными границами асимптотически спра-
справедливо соотношение
где с — скорость звука (или света в случае излучения черного тела).
Соответствующая формула для двумерных резонаторов (например, ба-
барабанов или поверхностных волн на озере) имеет вид
где А — площадь поверхности резонатора. Этот результат асимптоти-
асимптотически верен с точностью до порядка /2 и, как и в трехмерном случае,
независим от формы границы (периметра).
Впоследствии эти поразительные формулы были усовершенствова-
усовершенствованы посредством введения в них дополнительных поправочных членов,
содержавших частоту / в меньших степенях [110]. Например, при неко-
некотором заданном граничном условии поправочный член для Л^г(/) имеет
вид
AN(f) = \pl,
где Р — длина периметра резонатора.
Что произойдет, если отбросить требование Вейля о гладкости
границы? Что если периметр резонатора представляет собой фрактал
опровергнуть последнюю теорему Ферма (эта премия, кстати, так и не была востре-
востребована). Первоначально размер премиального капитала составлял 100 000 золотых
марок, но инфляция, последовавшая за двумя мировыми войнами, уменьшила его
до 7 600 немецких марок.
Мог ли Минковский услышать форму барабана? 75
с фрактальной размерностью D > 1? М.В.Берри высказал предположе-
предположение [23], что
где L — постоянная длины, a D — размерность Хаусдорфа для пери-
периметра. Такое допущение вполне разумно, так как показатель степени
частоты / в любом из членов предыдущих формул, включая поправо-
поправочные члены, совпадает с евклидовой размерностью C, 2 или 1) меры
протяженности (объема, площади или длины) резонатора. Поэтому для
фрактального периметра, имеющего бесконечную длину и фракталь-
фрактальную размерность D, соответсвующей степенью частоты / вполне могла
бы стать fD.
Предположение Берри о том, что D в действительности представ-
представляет собой размерность Хаусдорфа, в некоторых случаях оказывается
неверным. Как показали Лапидус и Флекингер-Пелле [137], правильной
фрактальной размерностью в этом случае является размерность Мин-
Минковского— еще одна нетривиальная размерность, введенная для других
целей Германом Минковским A864-1909I и обобщенная на фракталы
Булиганом. Размерность Минковского не всегда совпадает с размернос-
размерностью Хаусдорфа.
Определение размерности Минковского Dm Для кривой (фракталь-
(фрактальной или гладкой) в общих чертах сводится к следующему. Пусть центр
небольшого круга радиуса г движется вдоль кривой, заметая площадь
Минковского, т.е. площадь F (г), возникающей в результате движе-
движения круга «сосиски Минковского» (рис. 20). Разделим площадь F (г)
на 2г и устремим г к нулю. В случае гладкой кривой мы получи-
получили бы в пределе длину кривой, но для фрактальной «кривой» резуль-
результат может превзойти любой мыслимый конечный предел. Действитель-
Действительно, отношение F(r)/2r пропорционально величине г1~?>м, которая —
при Dm > 1 — расходится для г —> 0. Значение величины Dm служит
мерой скорости расхождения и называется размерностью Минковского-
Вулигана. Эта размерность допускает и другое, эквивалентное, опреде-
определение: lnF(r)
DM = Hm )[ + 2
r-»0 ln(l/r)
хКак и Гильберт, Минковский родился в Кенигсберге, где и началась дружба
двух математиков, которую они пронесли через всю жизнь. Минковский соединил
геометрию с теорией чисел и снабдил специальную теорию относительности подо-
подобающими ей четырехмерными парусами (пространство-время) для плавания под
предводительством капитана Эйнштейна к берегам общей теории относительности
и современной космологии.
76
Глава 1
Рис. 20. Определение «протяженности» кривой с помощью «сосиски Минков-
ского».
при условии, что предел существует. (Для некоторых фракталов хо-
хороший вкус требует различать два конца сосиски.) В случае гладкой
кривой F (г) ~ги Dm = —1+2=1, как и следовало ожидать.
Предыдущая формула для Dm напоминает формулу для размернос-
размерности Хаусдорфа. Различие состоит в том, что вместо числа «покрывающих
элементарных областей» N (г) в размерность Минковского-Булигана
входит «площадь» F (г) — площадь сосиски Минковского. Кроме того,
к отношению логарифмов добавлено 2. (Впрочем, от члена +2 можно
избавиться, если заменить F (г) под логарифмом на F(r)/r2.)
Предполагается, что для всех строго самоподобных фракталов раз-
Мог ли Минковский услышать форму барабана? 77
мерность Минковского Dm равна размерности Хаусдорфа D. Если эти
размерности не совпадают, то Dm больше D.
Почему же числом резонансных мод, связанных с границей резо-
резонатора, управляет размерность Минковского, а не Хаусдорфа? На ин-
интуитивном уровне ответ прост: нормальным модам необходима некая
площадь (или объем), связанная с границей резонатора (а не некоторый
набор элементарных областей, как в случае размерности Хаусдорфа).
Что произойдет, если фрактальна сама область резонатора, а не
только ее граница, т. е. если резонатор представляет собой не спош-
ное твердое тело, а весь пронизан множеством дырок и дырочек все-
всевозможных размеров? Как будет вибрировать такая фрактальная «губ-
«губка»? Можно было бы предположить, что приведенную выше формулу
для N2(f) следовало бы в этом случае заменить на
N2(f)= (af-)\
где а — некоторая характеристическая длина, ad — подходящая фрак-
фрактальная размерность, называемая спектральной размерностью. В дан-
данном случае, однако, нам следует соблюдать осторожность, потому что
фрактал с D < 2, вложенный в двумерное пространство, часто является
не чем иным, как «пылью», а как может пыль быть носителем нормаль-
нормальных колебаний? Но, как мы узнаем в главе о перколяции (гл. 15), на
пороге перколяции и над ним существует бесконечно много «связанных»
кластеров «атомов», а такие кластеры имеют конечную массу и поддер-
поддерживают нормальные моды колебаний. При длинах волн, превосходящих
некоторый характеристический размер кластера, называемый корреля-
корреляционной длиной, плотность мод ничем не отличается от плотности для
сплошного однородного тела, т.е. пропорциональна fd~1, где d — ев-
евклидова размерность (целочисленная) пространства, в которое вложена
перколяционная сеть. Но при длинах волн ниже корреляционной длины
нормальные моды «видят» самоподобную фрактальную структуру клас-
кластеров, и показатель степени плотности мод падает с d — 1 до d — 1, где
спектральная размерность d обычно имеет дробное значение, которое
отличается от значений других фрактальных размерностей (например,
от размерностей Хаусдорфа и Минковского).
По аналогии с частицами света — вездесущими фотонами — нор-
нормальные моды колебаний, знакомые нам по звучанию музыкальных
инструментов, принято называть фононами (если моды квантованы).
Фононы имеют решающее значение для нашего понимания многих фи-
физических явлений, в том числе удельной теплоемкости твердых тел
78 Глава 1
и сверхпроводимости как при низких, так и при высоких температу-
температурах — возможно, даже при комнатной температуре (в комнате с широ-
широко раскрытыми окнами где-нибудь на Аляске, не иначе). Фононы жи-
живут в кристаллических решетках, но и в амфорных телах чувствуют
себя, как дома. В фрактальных средах фононы, если они существуют,
принято называть фрактонами (а как же еще?). Предполагается, что
фрактоны будут играть все возрастающую роль в нашем понимании
природы колебательных процессов.
С колебаниями тесно связана дифракция волн на фрактальных
структурах («дифракталах»). Так как дифракция на больших расстоя-
расстояниях от излучателя (или дифракция Фраунгофера) представляет собой,
по существу, преобразование Фурье, самоподобия (детерминированные
или статистические) фрактала рассеяния должны полностью отразить-
отразиться в дифракционной картине падающего излучения, будь то электро-
электромагнитное, звуковое или ультразвуковое излучение, или же электро-
электроны, нейтроны и нейтрино. (Интересно, можно ли наблюдать дифрак-
дифракцию нейтрино на фрактальной структуре Вселенной?) Очевидно, что
дифракция волн является весьма чувствительным инструментом не
только для классических тел, но и для фрактальной материи. Кроме
того, фрактальная дифракция служит (в каком, интересно, звании?)
для очень детальной имитации радиолокационных помех во всевозмож-
всевозможных масштабах (может быть, для того, чтобы затруднить обнаружение
противником цели?).
Что происходит с плотностью нормальных мод колеблющихся
фракталов, размерность которых превышает их евклидову размер-
размерность? Представьте себе скрипичную струну, локальная плотность мас-
массы которой изменяется на канторовский манер: средняя треть стру-
струны обладает плотностью, скажем, вдвое превышающей плотность двух
остальных третей, средние трети которых, в свою очередь, вдвое боль-
больше плотности их первых и третьих третей и т. д. ad infinitum. Для
«классической» струны длиной L с постоянной плотностью массы число
нормальных мод определяется выражением
По аналогии с формулами Вейля можно ожидать, что число мод такой
«животрепещущей» фрактальной струны будет изменяться по формуле
/ f\DM
Ni(f) = D) ,
где Dm > 1; здесь Ь — снова некоторая характеристическая длина.
Мог ли Минковский услышать форму барабана? 79
Эти размышления приводят нас к интересному и, как оказывается,
важному вопросу: можно ли вычислить толщину струны (переменную)
по ее резонансным частотам? Такого рода обратные задачи в том или
ином виде встречаются во многих областях человеческой деятельности.
(Например, можно ли локализовать опухоль в головном мозге по теням,
отбрасываемым ею на рентгеновских снимках, сделанных под разны-
разными углами? Ответ: можно — в определенных, разумеется, пределах —
с помощью компьютерной томографии.)
К сожалению, в случае скрипичной струны восстановить распреде-
распределение плотности по резонансным частотам не представляется возмож-
возможным. Но если известны резонансные частоты для двух независимых гра-
граничных условий, то в нашем распоряжении оказывается вся информа-
информация, необходимая для вычисления распределения масс в колеблющейся
(без потерь) струне.
Решение задачи о струне приобрело однажды весьма большую важ-
важность. Произошло это на одном из этапов проводившегося автором этой
книги исследования основных механизмов звукопроизводства в чело-
человеческой речи (в рамках проекта создания говорящих компьютеров,
чей «голос» был бы лишен того бесчувственного «электронного акцен-
акцента», который до сих отличает «речь» современных машин). Разумеется,
мы могли бы многое узнать о звукопроизводстве в человеческой речи,
если бы форму вокального тракта (например, положение языка) можно
было бы вывести из звуков записанной речи (отображающих резонансы
этого самого вокального тракта). Это также очень помогло бы глухим и
плохо слышащим людям как дополнение к чтению по губам, поскольку
они тогда могли бы «видеть» на своем видеомониторе положение языка
говорящего.
К сожалению, осуществление подобного замысла наталкивается на
большие трудности по только что изложенным причинам, а именно,
из-за необходимости иметь два набора резонансов. С другой стороны,
оказывается, что определение входного импеданса вокального тракта,
измеренного на губах, вместе с некоторыми другими предположения-
предположениями позволяет вычислить функцию площади вокального тракта и тем
самым восстановить последовательность движений языка при артику-
артикуляции субъектом различных звуков [224].
Таким образом, на вопрос о том, можно ли услышать форму во-
вокального тракта, следует отвечать с осторожностью. Да, мы можем ее
услышать (именно так, в конце концов, мы и воспринимаем речь), но
решение здесь не единственно: часто при различных положениях языка
звуки получаются весьма похожими. Эту артикуляционную неоднознач-
80 Глава 1
ность используют чревовещатели, которые умудряются разгваривать
с неподвижными губами, используя «в порядке компенсации» другие
артикуляторы.
Но довольно о Лоренце, Гильберте, Вейле, Минковском — и о чре-
чревовещателях!
Дискретное самоподобие: складки и центральные
сгибы
Повторение — почти безотказный источник самоподобия, даже ес-
если речь идет о таких простых вещах, как складывание бумаги. Возь-
Возьмем лист бумаги и сложим его один раз. В результате этой опера-
операции у нас получится V-обра.чная складка (рис. 21А, поколение 1). Сло-
Сложенный вдвое лист подвергнем еще одному складыванию (следя за
тем, чтобы новая линия сгиба была параллельна старой) и получим
три складки V V Л: слева от первоначальной складки V расположит-
расположится складка V, а справа — складка Л. Очередное складывание порож-
порождает последовательность сгибов V V Л V V Л Л (рис. 21А, поколе-
поколение 3). Дальнейшие складывания дают всё более длинные последова-
последовательности складок. Каждое новое поколение получается из предыду-
предыдущего путем вставления новых складок, таким образом, чтобы слева
от каждой складки предыдущего поколения, исключая самую первую,
центральную V-складку, оказывалась новая V-складка, а справа — но-
новая Л-складка. Так, последовательность складок четвертого поколения
имеет вид VVAVVAAVVVAAVAA. При альтернативном
способе построения поколение п + 1 получается из поколения п путем
копирования последовательности поколения п, добавления к ней справа
центральной складки V и приписывания далее «вывернутой» последо-
последовательности поколения п (прочитанной от конца к началу с заменой
букв V на буквы А и наоборот) [46]. Такая операция эквивалентна по-
повороту последовательности поколения п на 180° вокруг центральной
складки, что в действительности и происходит при очередном склады-
складывании.
Но где же, спросите вы, самоподобие в этой безумной последова-
последовательности складок? Развернем же скрытую истину! Извлечем каждую,
к примеру, вторую «букву» из последовательности V V А V V А А,
начиная со второй (с V). (Такая операция совершенно уместно назы-
называется развертыванием.) Мы получим «материнскую» последователь-
последовательность V V А, которая, при построении альтернативным способом, долж-
Дискретное самоподобие: складки и центральные сгибы 81
1 2
/
ч\
4
/
/
(А)
Рис. 21. (А) Основная кривая дракона, порождаемая правыми складками.
(Б) Самоподобие, возникающее в более поздних поколениях кривой дракона.
(В) Центральные сгибы (помеченные точками) точно ложатся на самоподоб-
самоподобную логарифмическую спираль.
82
Глава 1
1 1
IN
(В)
s.
\
ч
h-J
J
::
I
ь-
——-
/
/
Рис. 21. (продолжение)
на породить дочернюю последовательность V V Л V V Л Л. Таким обра-
образом, получающаяся в результате такого построения бесконечная после-
последовательность складок обладает точным самоподобием: изъяв каждую
вторую складку (вместо 2 здесь сгодится любое четное число), мы вос-
воспроизводим заново всю последовательность. Вряд ли найдется более
простой пример дискретного самоподобия!
Можете ли вы построить прямую нерекурсивную формулу для
определения n-й «буквы» в общем «складчатом слове»? Предположим,
что число п записано в двоичном виде и первой цифрой слева от первой
единицы является ...
Самоподобие, присущее последовательности складок, можно на-
наглядно продемонстрировать, представив все складки как сгибы под пря-
прямым углом (рис. 21А). Порождаемая такой конструкцией фрактальная
кривая называется кривой дракона, так как на более поздних этапах
построения она действительно напоминает дракона (рис. 21Б). Два та-
таких дракона образуют двойного дракона [43]. Кривая дракона самопо-
добна (рис. 21В). Последовательные центральные складки, помеченные
Дискретное самоподобие: складки и центральные сгибы
83
жирными точками, точно ложатся на логарифмическую спираль, ко-
которая и сама представляет собой один из основных (причем гладких!)
самоподобных объектов и имеет множество интересных практических
приложений (о последних см. с. 132-138 в гл. 3).
Двойной дракон (рис. 22А) оживает в одной весьма примечатель-
примечательной системе счисления с комплексным основанием. С появлением циф-
цифровых компьютеров наиболее широко применяемым способом записи
чисел стала двоичная система, использующая только две цифры — О
и I.1 Теперь же компьютерам приходится довольно часто иметь дело
с комплексными числами, т. е. с числами, состоящими из двух «компо-
«компонентов» — вещественной и мнимой частей. Для записи комплексного
числа необходимо, таким образом, два множества двоичных чисел. Ра-
Разумеется, было бы просто великолепно, если бы и комплексное число
можно было бы записать как одно двоичное число, но это, кажется, не-
невозможно (мы, разумеется, не принимаем в расчет такую грязную иг-
игру, как попеременную запись по одной цифре то из одной, то из другой
части комплексного числа).
Рис. 22. (А) Двойной дракон. (Б) Область, занимаемая на комплексной плос-
плоскости правильными дробями в комплексной двоичной системе счисления
с основанием 1 —г: зеркально-симметричный двойной дракон. Двойными дра-
драконами можно замостить плоскость [43].
1Правда, Клод Шеннон однажды построил компьютер под названием THROBAC,
основанный на использовании римских чисел A,11,III,IV и т.д.), однако это упраж-
упражнение в мазохизме почему-то не привлекло ничьего внимания и осталось без послед-
последствий (в отличие от его же теории информации, слава которой не померкла до сих
пор).
84 Глава 1
Тем не менее, система записи комплексных чисел, использующая
только цифры 0 и 1, но с основанием, отличным от 2, все же существует.
Ясно, что основание такой системы должно быть комплексным числом
и модуль этого числа не должен превышать л/2, иначе двум двоичным
цифрам пришлось бы обслуживать интервал, больший, чем 2. Если мы
теперь будем настаивать на равноправии вещественной и мнимой час-
частей, то наилучшим выбором будет основание A — г) = л/2ехр (—г'тт/4)
(или какой-нибудь другой из трех первообразных корней восьмой сте-
степени из 16).
Разумеется, при использовании этой хитроумной системы мы пла-
платим довольно высокую цену, когда дело доходит до «программирова-
«программирования». Например, число 2 в обычной, вещественной двоичной системе
записывается как 10, в системе же с основанием 1 — г то же число 2
выглядит несколько сложнее.
Действительно, назвать систему счисления с основанием 1—г комп-
комплексной означает не сказать ничего1. На рис. 22Б показаны все такие
числа на комплексной (гауссовой) плоскости, которые являются пра-
правильными дробями, т.е. числами, представимыми в виде набора толь-
только отрицательных степеней основания, например, 0,1 = A — г)
или 0, A) = A — г') + A — г')~2 Н = г. (Заметим, что периодическая
дробь 0,A) в периодической системе с основанием 1 — г не равна 1, как
в обычной, вещественной двоичной системе.)
Как ясно из приведенного примера, правильные дроби занимают
односвязную область с фрактальным периметром, т.е. образуют двой-
двойного дракона. Но в отличие от снежинки фон Коха и фрактальных «шес-
«шестиугольников», с которыми мы встречались в предыдущих разделах,
шкура двойного дракона порождена генератором, состоящим из прямо-
прямолинейных отрезков различной длины: одного отрезка длиной г\ = 1/\/2
и двух отрезков, расположенных под прямым углом к первому, дли-
длиной гг = г\ каждый (рис. 23). Размерность Хаусдорфа Dh для таких
фракталов можно рассматривать как прямое обобщение формулы для N
отрезков равной длины, которую можно записать в виде N ¦ г°н =
= 1. Заменяя единственную длину г генератора различными длина-
длинами п, гг,... , rjv (общим числом N), получаем
г\н +г?н +... + г°н =1.
Разумеется, при r\ = r-i = Гз = г± = 1/3 мы получаем известное
1В оригинальном тексте игра слов: англ. complex можно перевести и как «комп-
«комплексный», и как «сложный». — Прим. перев.
Золотое и серебряное сечения и гиперболический хаос 85
значение размерности Хаусдорфа для снежинки фон Коха: 4A/3)г>н =
= 1 или DH = In 4/ In 3.
Рис. 23. Генератор для шкуры двойного дракона: размерность Хаусдор-
Хаусдорфа 1,52 .. .
Чтобы найти Dh для генератора двойного дракона, необходимо ре-
решить кубическое уравнение относительно rfH, а именно, rfH +2r\DH =
= 1. Хотя для решения кубических уравнений существуют замкну-
замкнутые формулы с радикалами, я предпочитаю более консервативный под-
подход: мой микрокалькулятор говорит мне, что г\н = 0,5897545123...,
и при г = 1/л/2 я получаю DH = 1, 523627...
Двойного дракона можно разделить на четыре части, подобные ему
самому (рис. 24). Следовательно, согласно нашему обобщению теоре-
теоремы Евклида о соотношении площадей и периметров для фрактальных
фигур (см. с. 36-40), периметр шкуры дракона-мамаши должен содер-
содержать периметр шкуры одного из четырех драконов-отпрысков не 2 раза,
а 2°н = 2,875 ... раз. (Пожалуй, зря мы не стали решать то кубическое
уравнение «радикальными» методами, а то уже поняли бы, что может
значить это иррациональное соотношение.)
Золотое и серебряное сечения и гиперболический
хаос
Как уже отмечалось, итерация является одним из богатейших ис-
источников самоподобия. Если выбрана подходящая начальная точка, то
повторное применение некоторой одной и той же операции — геомет-
геометрической, арифметической или просто абстрактной, производимой над
символами — почти неизбежно приводит к самоподобию. Возьмем, на-
например, простое правило Fn+2 = Fn+i +Fn. При Fo = 0 и F\ = 1 эта ре-
рекуррентная формула порождает хорошо известную последовательность
чисел Фибоначчи 0, 1, 1, 2, 3, 5, 8, 13, 21, ... Что же в них самоподобно-
Глава 1
Рис. 24. Двойной дракон содержит четыре малых себе подобных дракона,
а его фрактальная шкура нарушает евклидово соотношение между площадями
и периметрами подобных фигур.
го? Умножим каждое из чисел на 1,6 и округлим до ближайшего целого
числа; в результате получаем 0, 2, 2, 3, 5, 8,13, 21, 34, т. е. за исключени-
исключением нескольких первых членов (и, возможно, нескольких более поздних)
ту же последовательность чисел Фибоначчи.
Вычислим отношение последовательных чисел и получим Fn/Fn+i =
= 0; 1; 0,5; 0, F); 0, 625; 0,615;... ; 0,619 ... Похоже, что эти числа схо-
сходятся к какому-то пределу. Действительно, как показывают неслож-
Золотое и серебряное сечения и гиперболический хаос 87
ные арифметические выкладки, отношения последовательных чисел
Фибоначчи стремятся к иррациональному числу j = (-у/5 — 1)/2 =
= 0,618 ... — знаменитому золотому сечению, т. е. такому разделению
прямолинейного отрезка на две части, что его короткая часть относит-
относится к длинной так же, как длинная — ко всему отрезку. Таким обра-
образом, п-е число Фибоначчи должно быть равно (приближенно) некото-
некоторой константе, умноженной на j~n. В действительности приближение
оказывается сверхъестественно точным: нужно просто разделить j~n
на аД, что дает 0,4... ; 0, 7 ... ; 1,1... ; 1, 8 ... ; 3,0 ... ; 4,9 ... ; 8,0 ...;
затем округлить до ближайшего целого, числа и — готово! — мы полу-
получим числа Фибоначчи даже для п = 0.
А что можно сказать о самом золотом сечении 7? Кроются ли в нем
какие-нибудь самоподобия? Может быть, эти самоподобия проявятся,
если записать число j подходящим образом, т.е. не в «детской» деся-
десятичной @,61803 ...), не в «двусмысленной» двоичной @,100111...) и не
в какой-нибудь другой из тех систем счисления, которые возносят чис-
число, выбранное за основание, выше того места, которое ему пристало
занимать. Попробуем вместо этого представить число j в более естес-
естественном виде, а именно в виде непрерывной дроби, т.е. j = [1, 1, 1, ...].
Напомним, что в теории непрерывных дробей запись [а®, а\, аг, ...]
означает
1 .
ао-{
a2
такое «многоэтажное» написание следовало бы запретить, даже в ка-
качестве наказания для наборщика.
На рис. 25 вы видите изображение периодической непрерывной
дроби для величины, обратной золотому сечению j, из которого видно,
что она геометрически самоподобна. А что можно утверждать относи-
относительно арифметического самоподобия 7?
Непрерывная дробь для данного положительного иррационально-
иррационального числа а < 1 вычисляется следующим образом: положим х0 = 1/а
и применим итерацию хп+\ = —-—, где угловые скобки с индексом 1
(xn)i
означают дробную часть числа, т. е. «взятие остатка по модулю 1» (на-
(например, (tt)i = 0,14...). Тогда непрерывная дробь для а запишется
как [[жо_|, |_Ж1_Ь 1_Ж2_Ь |_жз_Ь •••]; где скобки |_ J означают округление до
ближайшего целого числа, а [хо] — целую часть числа а. Так как все
члены непрерывной дроби для золотого сечения (за исключением пер-
Глава 1
1
1+
i+
i+
1+
\
Рис. 25. Геометрически самоподобная непрерывная дробь для величины, об-
обратной золотому сечению.
вого) равны 1, число j является неподвижной точкой итерации хп+\ =
= 1/{хп), называемой также гиперболическим отображением.
Особенно просто гиперболическое отображение выполняется в том
случае, если «отображаемое» число xq задано в виде непрерывной дроби:
нужно просто сдвинуть все члены дроби [а,о, ffli, аг, •••] на одно место
влево и отбросить первый член: [ai, аг, •••]• Таким образом, золотое
сечение j, равное [1, 1, 1, ...], и в самом деле является неподвижной
точкой гиперболического отображения.
Это отображение называется также гауссовым отображением, так
как именно Гаусс вывел многие его свойства, в том числе инвариантные
распределения для хна/. [230].
Существуют ли, кроме золотого сечения, другие драгоценные чис-
числа, представимые в виде периодических непрерывных дробей с длиной
периода 1? Заметим, что 1/j = j + 1. Заменив +1 на любое другое поло-
положительное целое число п, мы получим серебряные сечения тп, определя-
определяемые соотношением 1/т„ = т„ + пи представимые в виде непрерывных
дробей тп = [п. п, п, ...] = [(п)].
Как выиграть в фибоначчиев ним 89
Серебряные сечения [(п)] занимают весьма видное положение в од-
одной просто бескрайней стране чудес, в которой можно встретить такие
диковинки, как квазикристаллы, «изящные» спины Изинга, путь к хао-
хаосу через синхронизацию мод, размножение кроликов и некоторые дру-
другие еще более интересные забавы, например, фибоначчиева стрижка,
усовершенствованная с помощью золотого сечения.
Подобно многим другим самоподобным объектам, серебряные сече-
сечения несут в себе семена хаоса. Попробуем итерировать гиперболическое
отображение, начиная с какого-либо серебряного сечения, на компью-
компьютере, производящем вычисления с любой конечной точностью; резуль-
результатом будет полнейший хаос. В качестве примера выберем начальным
значением (\/ТЗ - 3)/2 = [3, 3, 3, ... ] = 0,3027756 ... — серебряное се-
сечение тз- Гиперболическое отображение, вычисленное с помощью мик-
микрокалькулятора, дает (запишем только первую цифру после запятой)
восемь раз подряд 0,3, а затем 0,2; 0,8; 0,2; 0,6; 0,4; 0,0; 0,2 и т. д. —
полностью непредсказуемая последовательность с совершенно хаоти-
хаотическим хвостом.
Аналогичная картина наблюдается и в том случае, если мы записы-
записываем результаты последовательных итераций гиперболического отобра-
отображения в виде непрерывных дробей: в конце концов непрерывная дробь,
получаемая гиперболическим отображением из тз, становится хаоти-
хаотической. Судите сами — сначала получаем девять раз подряд [3, ...]
(в записи оставлена только первая цифра дроби), затем [1, ...], [4, ...],
[1, ...], [2, ...], [10, ...], [4, ...], [11, ...], [90, ...], [1, ...] и т.д. От-
куда берется здесь этот хаос? Непрерывная дробь, выражающая лю-
любое иррациональное число, имеет бесконечно много членов. А компью-
компьютеры конечны, т.е. работают с конечной точностью, и, независимо
от того, сколь велика эта точность, менее значимые члены, начиная
с какого-то места, неизбежно останутся неопределенными. Так, в на-
нашем примере серебряное сечение тз представляет собой не непрерыв-
непрерывную дробь [C)], где C) означает бесконечно много троек, а последова-
последовательность [3, 3, 3, 3, 3, 3, 3, 3, 3, 1, 4, 1, 2, 10, 4, 11, 90, 1, ...]. После
девятикратного повторения гиперболического отображения случайные
числа «выходят на передний план» и доминируют в дальнейшем, порож-
порождая типичный случай хаоса.
Как выиграть в фибоначчиев ним
Попробуем теперь, не откладывая в долгий ящик, познакомиться
с золотым сечением j немного поближе. Рассмотрим две целочисленные
90 Глава 1
последовательности
k=[l\ =1'3'4'6'8'---
Перед нами пара так называемых последовательностей Битти.
Вместе они полностью охватывают все положительные целые числа.
Заметим, что Ъи = аи + к; и что аи — всегда наименьшее положитель-
положительное целое число, еще не встречавшееся ни как ап, ни как Ъп, где п < к.
Это свойство последовательностей Битти находит применение в од-
одной интересной игре, называемой фибоначчиевым нимом (а так же ни-
мом Витхофа). Два игрока поочередно берут фишки из двух кучек.
Каждый забирает не менее одной фишки. Если игрок берет фишки из
двух кучек, то он должен брать из каждой одинаковое количество фи-
фишек. Выигрывает тот из игроков, кто забирает последнюю фишку (или
фишки).
Предположим, что перед началом игры в одной кучке 7 фишек,
а в другой — 12, и что мне предстоит сделать первый ход. Чтобы вы-
выиграть, я должен оставить своему противнику две кучки, количество
фишек в которых составляет пару Битти (Ьи, аи), причем такой расклад
я могу получить из любой пары кучек, не составляющих пару Битти.
С меньшим1 из двух начальных чисел G = &з) пару Битти образует
число аз = 4, поэтому я забираю из большей кучки 12 — 4 = 8 фишек,
оставляя противнику пару Битти G, 4). Для него это означает верный
проигрыш, так как получить из пары Битти другую пару Битти у него
не получится.
Предположим теперь, что противник оставляет мне пару E, 4), ко-
которую я не могу превратить в G, 4). Заметим, однако, что разность
между 5 и 4 равна 1. Это означает, что, взяв из каждой кучки по 3
фишки, я получу пару Битти с разностью 1, т.е. пару B, 1). Предо-
Предоставляю читателям самостоятельно убедиться в том, что какой бы из
четырех возможных ходов ни сделал мой противник, я всегда могу за-
забрать последнюю фишку (или фишки) и тем самым выиграть. Раз уж
вы получили пару Битти, то вам от этого самостоятельно не оправиться
и приходится признать, что в этой игре вас побили.
Интересно, что существует простая игра на шахматной доске, на-
называемая «Королеву — в угол» [78], которая эквивалентна («гомоморф-
1Если фишек в обеих кучках поровну, то я забираю все и сразу же выигрываю.
Как выиграть в фибоначчиев ним
91
на») фибоначчиеву ниму. Возьмите шахматную доску и поставьте фер-
ферзя («королеву») на любое поле верхней горизонтали или правой верти-
вертикали (на рис. 26А эти поля затемнены). Оба игрока поочередно делают
ходы, двигая ферзя на «запад», «юго-запад» или «юг». На какие поля
мне следует ставить ферзя для того, чтобы, какой бы ход ни сделал
мой противник, я мог последним ходом попасть на поле, помеченное
звездочкой, и тем самым обеспечить себе выигрыш?
24
23
22
21
20
19
18
17
16
15
14
13
12
11
[II
q
8
7
6
ь
4
3
S
1
0
I
1
1
1
1
I
1
I
1
I
1
I
1
1
1
1
1
1
> 6 7 8 9 10111213141516171819
(A)
(Б)
Рис. 26. (А) Игра «Королеву — в угол», придуманная Руфусом П. Айзексом.
Начальная позиция ферзя выбирается либо на верхней горизонтали, либо на
правой вертикали (на рисунке затемнены). Цель игры состоит в том, чтобы
достичь поля в левом нижнем углу доски. (Б) «Верные» позиции для фер-
ферзя закрашены черным. Через две противоположные стороны «верных» полей
проходит либо прямая с угловым коэффициентом, равным золотому сечению,
либо прямая с угловым коэффициентом, равным величине, обратной золото-
золотому сечению.
Ходы ферзя на запад или юг соответствуют взятию фишек только
из одной из двух кучек игры в ним. Ход на юго-запад соответству-
соответствует взятию одинакового числа фишек из обеих кучек. Следовательно,
координаты «верных» полей образуют уже знакомые нам пары Бит-
ти, выведенные из золотого сечения: A, 2), C, 5), D, 7), F, 10), (8, 12)
и т. д. Эти «верные» поля показаны черным цветом на большой доске
(рис. 26Б).
Существует ли простой, чисто геометрический, способ нахождения
всех «верных» полей? Безусловно, существует. Проведем на доске пря-
92 Глава 1
мую, выходящую из левого нижнего угла, с угловым коэффициентом,
равным золотому сечению (рис. 26Б). Клетки доски, пронзенные про-
проведенной прямой справа и слева, образуют нижний ряд «верных» полей.
(Верхний ряд образован клетками, зеркально-симметричными клеткам
нижнего ряда относительно диагонали, проходящей через левый ниж-
нижний угол доски.)
Заметим между прочим, что «размножающимся» кроликам Фибо-
Фибоначчи такая выигрышная стратегия известна с давних пор (именно
поэтому ним-версия игры называется фибоначчиевым нимом).
В своем сочинении «Liber Abaci», изданном в 1202 г., итальянский
математик Леонардо Пизанский, более известный как Фибоначчи (сын
Боначчи), рассматривает задачу о числе пар кроликов после п периодов
размножения, если первоначально имеется лишь одна пара крольчат и
предполагается, что рост числа пар подчиняется следующим идеализи-
идеализированным правилам [71]:
• Крольчата достигают зрелости за один сезон с момента рождения.
• Каждая из пар взрослых кроликов производит по одной паре
крольчат за каждый сезон размножения.
• Кролики не умирают.
Нетрудно видеть, что при таких правилах число пар кроликов в каж-
каждом п-м поколении должно равняться сумме чисел пар в двух пре-
предыдущих поколениях: Fn = Fn-\ + -Fn-2- Полагая F\ = F% = 1,
мы приходим к знаменитой последовательности чисел Фибоначчи:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ... , фигурирующей в бесчисленном мно-
множестве ситуаций.
С кроликами связана еще одна числовая последовательность — по-
последовательность двоичных битов, которую я назвал кроличьей [230].
Рассмотрим два отображения 0 —>¦ 1 («крольчата взрослеют») и 1 —>¦ 10
(«взрослые кролики никуда не деваются и обзаводятся крольчатами»).
Начав с одного-единственного нуля, мы получаем в результате итера-
итераций 1, 10, 101, 10110, ... ив пределе бесконечную кроличью после-
последовательность 1011010110110 ... Самоподобна ли такая последователь-
последовательность? Вне всякого сомнения. Стоит лишь подчеркнуть все пары «10»
A0 110И) 110 1 И) ...) и прочитать их, как единицы, а все не подчерк-
подчеркнутые цифры — как нули, и бесконечная кроличья последовательность
воспроизведет сама себя: 10110101...!
Где расположены все единицы в кроличьей последовательности?
Они стоят на местах с номерами 1, 3, 4, 6, 8, 11, 12, ... , а это есть
Самоподобные последовательности 93
не что иное, как первая из вышеописанных последовательностей Битти
(ак). Нули расположены на местах с номерами 2, 5, 7, 10, 13, ... , об-
образующими вторую последовательность Битти (bk). Отсюда ясно, что
кроликам превосходно известны тайные пружины игры в фибоначчиев
ним, но им просто некогда — они заняты размножением.
Между кроличьей последовательностью и числами Фибоначчи су-
существует еще одна интересная связь, открытая Джоном Хортоном
Конуэем [78]: «кроличья постоянная», определяемая двоичной дро-
дробью 0,1011010110110 ..., которая, в свою очередь, образуется припи-
приписыванием 0 и запятой перед кроличьей последовательностью, равна не-
непрерывной дроби [2°, 21, 21, 22, 23, 25, 28, 213, 221, 234,... ], где показатели
степени у двоек — не что иное, как числа Фибоначчи.
Предоставляем читателю придумать аналогичные игры, основан-
основанные не на золотом, а на серебряном сечении. Какими окажутся соответ-
соответствующие правила размножения кроликов, например, при тг = [B)] =
/
Самоподобные последовательности, порождаемые
квадратными решетками
Возьмем квадратную решетку (рис. 27) и проведем через начало
координат прямую с угловым коэффициентом, равным золотому сече-
сечению 7 = [A)] = 0, 618... Условимся записывать единицу всякий раз,
когда наша прямая пересекает вертикальную линию решетки, и нуль
всякий раз, когда она пересекает горизонтальную линию. Полученная
последовательность единиц и нулей апериодична, так как золотое се-
сечение иррационально, но все же имеет дальний порядок с бесконечно
большим «радиусом действия», так как выведена из бесконечно протя-
протяженной жесткой квадратной решетки.
Какими еще свойствами обладает построенная нами последователь-
последовательность, которая начинается так: 1011010110110 ... ? Она самоподобна
в следующем смысле. Условимся считать каждую единицу началом но-
нового «предложения» и сокращать предложение 10 до 1, а предложение 1
заменять нулем. В результате мы снова получим оригинальный, бес-
бесконечно длинный «роман»: 10110101 ... В действительности наш роман
вовсе не так уж и оригинален, а списан со старой (и вечно юной) доброй
кроличьей последовательности, с которой мы только что встречались,
играя в фибоначчиев ним, только на этот раз кролики выскакивают
из квадратной решетки. (Просто невозможно побороть искушение —
какая же это решетка? Это же клетка!)
94
Глава 1
A
О*
Го
i
q
к
1
о;
ft
у
0
o,
1
0
0
<
1
1
Рис. 27. Квадратная решетка и прямая с угловым коэффициентом, равным зо-
золотому сечению 7, порождает «кроличью последовательность» 10110 ... Ниж-
Нижняя прямая имеет угловой коэффициент, равный серебряному сечению у/2 — 1,
и порождает еще одну самоподобную двоичную последовательность.
Если вместо того, чтобы сокращать «роман» золотого сечения, мы
захотим просто-напросто написать его с нуля, то (подобно большинст-
большинству авторов) мы с него и начнем, а затем будем итерировать кроличье
отображение 0 —>• 1, 1 —>• 10.
А что если угловой коэффициент секущей прямой равен одному из
серебряных сечений тп = [(п)]? При п = 2 получаем тг = 1/B + 1/B +
+ ...)) = у/2 — 1 (см. нижнюю секущую прямую на рис. 27). Она по-
порождает бесконечную последовательность 11011011101101110110110...
Эта последовательность также самоподобна — еще один всемасштаб-
ный роман. Но где начинаются или кончаются предложения, которые
воспроизводят роман? Условимся считать концом предложения каж-
каждый нуль и каждую первую единицу в тройке единиц. Предложение
первого типа A10) заменим единицей, предложение второго типа A) —
нулем. И что же получается? Все та же старая история: 1101101110 ...
И наоборот, секущая последовательность для т-i порождается ите-
итерацией отображения 0 —>¦ 1 и 1 —>¦ 110.
Для секущей прямой с угловым коэффициентом, равным следую-
следующему серебряному сечению тз = [C)] = (\/ТЗ—3)/2, секущая последова-
Самоподобные последовательности 95
тельность имеет вид 11101110111011110110 ... Где же «точки» между
предложениями? И как можно написать роман с помощью итераций,
начиная буквально с нуля?
Самоподобные последовательности, аналогичные тем, которые мы
только что продемонстрировали, недавно приобрели скандальную из-
известность как генераторы одномерных квазипериодических «решеток»,
которые — при обобщении их на трехмерный случай — служат хоро-
хорошими математическими моделями для недавно открытого нового со-
состояния материи, получившего название квазикристаллы (см. гл. 13).
Схожие последовательности играют заметную роль и в компьютер-
компьютерной графике — при оцифровке прямых линий. Независимо от значения
углового коэффициента (будь то золотое или серебряное сечение или
какое-либо другое значение) ступенчатая функция, наилучшим обра-
образом аппроксимирующая прямую, проведенную по целочисленной ре-
решетке, характеризуется последовательностью нулей и единиц, извест-
известной под названием цепного кода. Каждому горизонтальному участку
ступенчатой функции соответствует в цепном коде единица, каждо-
каждому вертикальному участку — нуль. Цепные коды обладают следую-
следующим свойством: один символ всегда изолирован, а другой встречается
сериями, причем серии имеют самое большее две различные длины.
Если длины серий различаются, то ровно на единицу. Действительно,
при то ^ 1 длины серий равны, соответственно, [то] и [то]. («Висели-
(«Виселицы» [ ] означают округление в большую сторону до ближайшего целого
числа.) При то < 1 длины серий равны [1/mJ и Г1/771!- Длины серий
различаются только при нецелых т и 1/то.
Один из методов перекодирования цепных кодов с различными дли-
длинами серий двумя символами состоит в том, что более коротким сери-
сериям ставится в соответствие один символ, а более длинным — другой.
В результате такого перекодирования мы получаем еще одну последо-
последовательность символов, один из которых встречается одиночно, а другой
сериями самое большее двух длин, отличающихся между собой на еди-
единицу. Эта инвариантность цепного кода была открыта Азриэлем Розен-
фельдом в 1973 г. [216], однако лежащая в ее основе теоретико-числовая
проблема (а именно, может ли данная последовательность целых чисел
быть получена в результате округления линейной функции?) была по-
поставлена еще одним из Бернулли [83].
Эти выводы нашли применение в эффективном кодировании изоб-
изображений и распознавании образов, в особенности для различения пря-
прямых линий и криволинейных контуров [274]. В настоящее время основ-
основные усилия исследователей в этой области сосредоточены на создании
96 Глава 1
эффективных вычислительных алгоритмов для обнаружения прямоли-
прямолинейных участков [135].
Существует другой метод перекодирования цепного кода, тес-
тесно связанный с первым. Он основан на подсчете числа знаков меж-
между двумя сериями символов различной длины. Например, цепной
код 1011010110110... при таком способе перекодирования переходит
в 10110101... Я предполагаю, что такое перекодирование цепных ко-
кодов соответствует сдвигу влево в непрерывной дроби, представляющей
угловой коэффициент т.
«Отчаянное пари» Джона Хортона Конуэя
Джон Х.Конуэй, английский математик, автор множества инте-
интересных работ, ныне основательно обосновавшийся в Принстоне (штат
Нью-Джерси), приобрел широкую известность (даже за пределами
математических кругов), придумав остроумную игру под названием
«Жизнь» (о ней см. гл. 17 «Клеточные автоматы»). В своей захватываю-
захватывающей лекции «О некоторых безумных последовательностях», прочитан-
прочитанной сотрудникам AT&T Bell Laboratories в Мюррей-Хилл (штат Нью-
Джерси) 15 июля 1988 г., Конуэй привел еще одно неопровержимое до-
доказательство того, что математика может быть не только заниматель-
занимательной, но и весьма забавной. После нескольких предварительных замеча-
замечаний о числах Фибоначчи и тому подобных материях, Конуэй представил
аудитории последовательность а(п), которая начиналась довольно без-
безобидно: 1, 1, 2, 2, 3, 4, 4, 4, 5, ... Простой итеративный закон для такой
последовательности имеет вид
а (п) = а(а(п — 1)) + а(п — а(п — 1))
с начальными членами аA) = а B) = 1. Как и в случае последова-
последовательности Фибоначчи, каждый новый член последовательности Конуэя
равен сумме двух ее предыдущих членов.
Данные числового анализа свидетельствуют, что а(п)/п при боль-
больших п стремится к 1/2, и Конуэй предложил аудитории найти такое
число щ, чтобы при всех п > щ абсолютная ошибка \а (п)/п — 1/2\ была
бы меньше, чем 0,05. Поскольку Конуэй и его жена (также математик
по специальности), сочли последовательность а(п) достаточно трудной
для исследования, Конуэй предложил премию в 100 долларов тому, кто
первым сообщит ему решение. Затем, как бы про себя, Конуэй негромко
(но отчетливо различимо на видеозаписи его лекции) предложил пре-
премию в 10 000 долларов тому, кто первым найдет наименьшее п0.
«Отчаянное пари» Джона Хортона Конуэя
97
Рис. 28. Джон Хортон Конуэй, увенчанный самоподобной рогатой сферой.
(Рисунок Саймона Фрейзера, любезно предоставленный Дж. X. Конуэем.)
Ровно через 34 дня — 18 августа 1988 г. — Колин Мэллоуз, спо-
способнейший математик из Bell Laboratories предложил решение деся-
титысячедолларовой задачи Конуэя (вместе со строгим доказательст-
доказательством): п0 = 317-337-3556. Я намеренно записал решение Мэллоуза так,
словно это телефонный номер (в Индиане, кстати): высказывалось пред-
предположение, что Конуэй просто вздумал пошутить, что он и сам знал ре-
решение, а если бы решивший задачу умник набрал номер C17) 337-5556,
то ему бы ответили, что номер, конечно, набран верный, но раздача
призов, к несчастью, уже закончена. (В действительности при наборе
номера по автоответчик просит набрать номер еще раз. Еще раз? И это
после всего, что мы вытерпели, разыскивая это номер?!)
98 Глава 1
Как вы уже, наверное, догадались, последовательность а(п), по-
порожденная простой рекурсией, просто переполнена весьма привлека-
привлекательными самоподобиями, которые и содержат ключ к решению задачи.
Эти самоподобия были быстро обнаружены Мэллоузом, специалистом по
математической статистике и анализу данных, который не использовал
при решении ничего более сложного, чем обычные численные расчеты
и пояснительные рисунки [154].
Предоставляем увлеченному читателю, имеющему в распоряжении
персональный компьютер, самостоятельно обнаружить упомянутые на-
нами самоподобия и другие симметрии последовательности Конуэя а (п)
или более простой последовательности Ь (п) = 2а (п) — п (чтобы почув-
почувствовать основную тенденцию). Что происходит с bin) при п = 2т
и почему? Какова размерность Хаусдорфа для фрактальной функции,
к которой сходится при стремящемся к бесконечности п надлежащим
образом нормированная между п и 2п последовательность Ь(п)? Су-
Существует ли простая прямая формула для Ъ (п)? В качестве размин-
разминки читатель может попытаться обнаружить закономерность изменения
длин серий одинаковых знаков для а (п).
Завоевавший «гран-при» Мэллоуз и Конуэй впоследствии согласи-
согласились, что Конуэй намеревался предложить приз размером не в десять,
а в одну тысячу долларов. Конуэй выслал победителю чек на меньшую
сумму, однако первоначальный призовой чек на десять тысяч долларов
Мэллоуз все же сохранил на память. (На рис. 28 вы видите Джона Хор-
тона Конуэя, увенчанного самоподобной короной, получившей весьма
меткое название рогатой сферы.)
Глава 2
Подобие и различие
Наш мир построен по плану, глубокая
симметрия которого каким-то образом
отражается во внутренней структуре
нашего интеллекта.
Поль Валери
Понятия подобия и различия издавна играют важную роль в де-
делах человеческих и в природе. Мы радостно приветствуем всякое про-
проявление подобия, но довольно часто нас гораздо сильнее привлекает
непохожее. Масса притягивает массу, но электроны тянутся к части-
частицам с противоположным зарядом — антиэлектронам, или позитронам.
Электроны и позитроны даже могут привести свое взаимное влечение
к достойному завершению — небольшому взрыву с выделением энергии
в миллион электрон-вольт. (Впрочем, различие очень часто вызывает
дискриминацию. Приведем лишь один далеко не самый яркий пример.
В русском языке за коренным жителем Германии закрепилось назва-
название немец, что означает «немой» или «не из наших». Читатель без труда
приведет и более красноречивые примеры.)
В естественных науках подобие напускало туману, и в то же время
проливало свет. Почему все электроны подобны, более того, тождест-
тождественны друг другу (судя по тому, что мы о них знаем)? Это лишь одна
из тех великих неразгаданных загадок, которыми Природа так любит
подразнить нас. Если бы мы знали ответ и понимали к тому же, по-
почему электроны и другие «элементарные» частицы обладают именно
такими массами, зарядами и спинами, то наши познания об окружа-
окружающем нас (и страдающем от нас) мире стали бы несравненно шире.
Прежде чем погрузиться в различные аспекты самоподобия, мы кос-
коснемся в этой главе некоторых практических применений идей подобия
и различия в физике, психофизике, биологии, геологии (альпинизме?)
и других областях человеческой деятельности, в которых масштабная
инвариантность, или скейлинг, является одним из ключевых понятий.
100 Глава 2
Более чем один масштаб
Измерение обычно считается пусть иногда и неточным, но без-
безусловно однозначным процессом. Футбольное поле имеет размеры при-
приблизительно 50 на 100 м. Следовательно, поле имеет площадь 5000 квад-
квадратных метров, по крайней мере, на взгляд футболиста или агента по
продаже земельных участков.
Однако площадь того же самого футбольного поля (как, впрочем,
и любой лужайки или поляны) может выражаться совсем другой ве-
величиной, если к ее оценке подходить с иной точки зрения — напри-
например, с точки зрения крохотной букашки, карабкающейся то вверх, то
вниз по травинкам. Площадь, соответствующая суммарной поверхнос-
поверхности всех травинок, гораздо (возможно, в 100 раз) больше обычной, «иг-
«игровой» площади футбольного поля. Новая, большая, площадь актуальна
и для фотонов солнечного света, поглощаемых хлорофиллом травы, что-
чтобы превратить содержащийся в воздухе углекислый газ в углеводороды
и кислород.
Таким образом, вопрос о площади применительно к футбольному
полю допускает по крайней мере два совершенно истинных ответа; фут-
футбольное поле характеризуется двумя масштабами площади, отличаю-
отличающимися друг от друга во много раз. В других случаях измерения могут
приводить к еще большему числу ответов. Например, протяженность
границы между какими-либо двумя европейскими странами, как пра-
правило, зависит от масштаба, в котором проводятся измерения. Так, изме-
измеренная по глобусу граница между Испанией и Андоррой (или Австрией
и Лихтенштейном, если это княжество вообще нанесено на глобус) ока-
окажется короче, чем та же граница, измеренная по карте Европы, а та,
в свою очередь, окажется короче границы, измеренной по карте Пире-
Пиренеев (или Альп).
Еще большую протяженность границ мы получим, измеряя их дли-
длину по более подробным картам, на которых нанесена только одна инте-
интересующая нас местность, или по туристическим картам-планам. А если
бы мы действительно прошли вдоль границы (кое-где нам, возможно,
пришлось бы плыть или взбираться на горы), то ее протяженность ста-
стала бы еще больше (рис. 1). Таким образом, не существует единственной
протяженности границы — таких протяженностей много. Как теперь
принято говорить, граница, как и фрактальная кривая фон Коха, о кото-
которой мы рассказывали в гл. 1 (с. 30- 31), имеет много масштабов длины;
Более чем один масштаб
101
10000 -
ХО
о
с
аз
X
К
ш
1000 -
Южноафриканское побережье
100 1000
Длина мерного стержня (км)
Рис. 1. Длина береговой линии возрастает по мере того, как уменьшается
длина мерных стержней.
эта многомасштабность является весьма важной концепцией в теории
самоподобия и фракталов.
В физике существует много явлений, о которых принято говорить,
что они наблюдаются «во всех масштабах». Таков, например, принцип
неопределенности Гейзенберга: в огромном диапазоне значений входя-
входящих в него переменных (таких, как энергия и время или импульс и ко-
координата) не обнаружено ни одного случая, когда бы соотношение не-
неопределенности не выполнялось бы. Но даже если диапазон допусти-
допустимых масштабов ограничен, как в случае размеров скоплений галактик
(ограниченных размерами Вселенной) или размеров магнитных доме-
доменов в куске железа вблизи точки перехода к ферромагнетизму (огра-
(ограниченных размерами магнита), концепция истинности независимо от
масштаба используется в качестве важного постулата при анализе на-
наблюдений, объяснить которые без нее было бы во многих случаях весь-
весьма затруднительно.
102 Глава 2
Быть или не быть масштабной инвариантности:
немного из биологии и астрофизики
Слоны и гиппопотамы настолько же не-
неуклюжи, насколько и огромны, а лось по-
поневоле менее грациозен, чем газель.
Д'Арси Томпсон
По иронии судьбы Галилей (рис. 2), открывший скейлинговый за-
закон для свободно падающих тел и тем самым положивший начало со-
современной экспериментальной физике, оказался также и тем, кто за-
заметил, что некоторые законы физики (и биологии) не остаются неиз-
неизменными при изменении масштабов. Размышляя над прочностью кос-
костей, Галилей рассуждал следующим образом. Животное вдвое боль-
большей длины, ширины и высоты, должно весить в 8 раз больше. Однако
его вдвое более широкие кости имеют лишь вчетверо большее попе-
поперечное сечение, а значит, способны выдерживать лишь вчетверо боль-
больший вес. Следовательно, чтобы выдерживать полный вес тела, попе-
поперечный размер костей должен был бы увеличиться более чем в 2 раза.
Такое отклонение от простого подобия вводит естественный масштаб
в строение тела животных, как сухопутных, так и водных: при некото-
некоторых предсказуемых в общих чертах размерах диаметр костей начинает
увеличиваться быстрее, чем остальные части тела животного, разру-
разрушая тем самым подобие, но сохраняя в живых животное (см. очерк
Дж. Б. С.Холдейна A892-1964) «Как важно быть нужного размера» [94].
Другим примером подобия в биологии может служить диссипация
энергии теплокровными животными как функция их веса или мас-
массы (рис. 3). Как можно было бы по наивности ожидать, диссипация
энергии Р, измеряемая по суточному потреблению калорий, должна
быть пропорциональна площади поверхности тела животного, которая
для «подобных» животных приближенно пропорциональна объему или
массе тела в степени две третьих: Р ~ т2/3. И в самом деле, угловой
коэффициент прямой на рис. 3 соблазнительно близок к ^, однако не-
О
большое, но систематическое отклонение от ожидаемого коэффициента
все же существует: более крупные животные рассеивают больше энер-
энергии, чем можно было бы предсказать, исходя из соотношения Р ~ то2/3.
Более того, данные для многочисленных видов, включая Homo sapiens,
гораздо лучше ложатся на прямую с угловым коэффициентом j. По-
Почему? Хороший вопрос, который заслуживает дальнейшего изучения.
Быть или не быть масштабной инвариантности
103
< Galileo Galilei Г
censured:
tomb fto«u: 1737
owmi.
' 19 SI
Рис. 2. Галилео Галилей полностью оправдан [98] (©1982 Sidney Harris). На
постаменте надпись: «Галилео Галилей. Родился в 1564 г. Осужден в 1616 г.
Умер в 1642 г. Надгробие сооружено в 1737 г. Памятник воздвигнут в 1842 г.
Реабилитирован в 1982 г.»
104
Глава 2
Может быть, более крупные животные менее эффективны энергети-
энергетически? Может быть, они движутся к тому же ограничению на размеры
тела, которое в свое время прикончило динозавров? Похоже, что с каж-
каждым десятилетием люди также становятся выше ростом и крупнее по
всем остальным размерам, и, может быть, им стоит поостеречься, если
они не хотят вслед за мамонтами кануть в Лету?
1000
100 -
10 -
1
у/
Морская у/
свинка yS
J* Голубь i
i
s Петух
i
i
Лошадь щ
Свинья^
Овца -(-/^Мужчина
yS Женщина
• Собака
i
0,1
10
Масса тела (кг)
100
1000
Рис. 3. Рассеяние энергии теплокровными животными как функция массы
их тела.
Аналогичное нарушение подобия происходят и в фотографии.
Обычно его называют нарушением взаимозаместимости. Оно было от-
открыто немецким астрофизиком (да что там! — создателем астрофизи-
астрофизики) Карлом Шварцшильдом A873-1916).1 Составляя каталог яркости
1Шварцшильду едва исполнилось шестнадцать лет, когда он опубликовал свои
первые работы (об орбитах двойных звезд). Уже в 1899 г. он разработал теорию
кривизны пространства, а в 1916 г. первым нашел точное решение уравнений общей
теории относительности Эйнштейна, предсказав существование черных дыр, возни-
возникающих после того, как звезда сжимается до размеров, меньших радиуса Шварц-
шилъда — характеристического радиуса, начиная с которого гравитация «переси-
«пересиливает» все остальные взаимодействия. Таким образом, гравитация устанавливает
предел и массе звезды, и массе животного.
Подобие в физике: некоторые поразительные следствия 105
звезд, Шварцшильд обнаружил, что звезда, обладающая вдвое мень-
меньшей яркостью, чем некоторая эталонная звезда, требует более чем вдвое
большей выдержки, чтобы зачернить фотографическую пластинку так
же, как эталонная звезда. Чтобы получить ту же степень почернения
при малой яркости Ь, требуемое время экспонирования t не должно
быть обратно пропорционально яркости (как это имеет место в случа-
случаях большей яркости и более короткого времени экспонирования), а, как
обнаружил Шварцшильд, должно выполняться равенство tp ~ Ь, где
показатель Шварцшилъда р меньше единицы.
Следовательно, когда темнеет (или вы слишком затемняете объ-
объектив вашего фотоаппарата диафрагмой), выдержку следует устана-
устанавливать длинней, чем может показаться на первый взгляд. Поскольку
у различных цветов наблюдается различное нарушение взаимозамести-
мости, в цветной фотографии при малой освещенности цветовой баланс
может измениться, если не воспользоваться специальными цветофильт-
рами.
И все же, несмотря на все эти нарушения, масштабная инвариант-
инвариантность (скейлинг) может принести очень много пользы в самых разных
областях человеческой деятельности, например, в физике.
Подобие в физике: некоторые поразительные
следствия
В физике дискуссии о подобии уже завели нас достаточно дале-
далеко. Но даже на элементарном уровне подобие существенно упрощает
решение различных задач. Взять хотя бы физическую систему с по-
потенциальной энергией U, представляющей собой однородную функцию
степени к от пространственных координат гт:
U{an,ar2,...) = akU(ri,r2,...). A)
Если мы изменим все пространственные координаты в а раз, а вре-
время — в /3 раз, то скорости изменятся в а//3 раз, а кинетическая энер-
энергия — в а21(З2 раз. Но если коэффициент а2//32 равен множителю ак
потенциальной энергии U, то лагранжиан физической системы умножа-
умножается на постоянный коэффициент ак, и уравнения движения остаются
неизменными. Траектории движения всех материальных точек («час-
(«частиц») сохраняют подобие исходным траекториям, изменяются только
масштабы [136].
106 Глава 2
Временные интервалы вдоль новой траектории изменяются в /3 =
= а1~к/2 раз, значения энергии — ва' раз, а угловые моменты, имею-
имеющие ту же размерность, что и квант действия Планка (энергия х вре-
время) — в а1+к/2 раз.
Какой вывод можно сделать из всего этого? Обратимся к линейно-
линейному осциллятору, потенциальная энергия которого представляет собой
однородную квадратичную функцию, т.е. функцию, для которой пока-
показатель к из соотношения A) равен 2. Простым примером линейного ос-
осциллятора может служить маятник, раскачивающийся с очень малой
амплитудой. Зависит ли период колебания от амплитуды колебаний?
Мы могли бы, конечно, решить уравнение движения и убедиться, что
не зависит, но для того, чтобы ответить на поставленный вопрос, со-
совсем не обязательно решать уравнение. Как мы заметили выше, время
при изменении масштабов изменяется в а1~к12 раз, т.е. при к = 2 —
в а0 раз. Непосредственно отсюда можно заключить, что все значения
времени, в том числе и период колебания, остаются неизменными: ес-
естественная частота линейного осциллятора, строго придерживающаяся
квадратичной функции потенциальной энергии, не зависит от амплиту-
амплитуды или энергии осциллятора. (В квантовой механике этот факт находит
отражение в эквидистантности уровней энергии: расстояние между лю-
любыми двумя соседними уровнями равно hv.)
А что можно сказать о нелинейном осцилляторе с восстанавливаю-
восстанавливающей силой, подчиняющейся кубическому закону, т. е. с однородным по-
потенциалом четвертой степени (к = 4)? В этом случае мы не можем най-
найти решение уравнения движения, используя простую тригонометричес-
тригонометрическую функцию. Однако подобие подсказывает нам, что время должно
изменяться как а1~к12 = а, т.е. что частоты пропорциональны а :
чем больше энергия осциллятора, тем больше его резонансная часто-
частота, чего и следовало ожидать от пружины с возрастающей жесткостью.
Точнее говоря, резонансная частота такого нелинейного осциллятора
изменяется как корень четвертой степени из его энергии. (В кванто-
квантовой механике Еп ~ и4/3.)
В однородном силовом поле потенциальная энергия является одно-
однородной линейной функцией пространственных координат, т.е. к = 1.
В результате значения времени изменяются как а1~к12 = а1/2, и это
действительно так, в чем имел возможность убедиться один из пер-
первых людей, практиковавших скейлинг, Галилей, который еще в давние
времена открыл, что для увеличения продолжительности свободного
падения в два раза, ему приходится взбираться по ступеням Пизанской
Подобие в физике: некоторые поразительные следствия 107
падающей башни на вчетверо большую высоту (красивая легенда, хоть
и апокриф).
В случае ньютоновского притяжения потенциальная энергия об-
обратно пропорциональна расстоянию. Следовательно, к = —1, и для кру-
круговых орбит вокруг массивного центра следует ожидать, что время бу-
будет изменяться в a1~kl2 = о?12 раз. Иначе говоря, квадрат периода
обращения планеты по орбите пропорционален кубу линейного разме-
размера орбиты. Так мы с вами только что заново открыли частный случай
одного из основных законов небесной механики — бессмертного треть-
третьего закона движения планет Кеплера — и не взяли при этом ни одного
интеграла!
Исаак Ньютон в своих «Началах» рассмотрел более общие законы
движения «планет». Он показал, что если выполняется скейлинговое со-
соотношение т ~ г", то для круговой орбиты радиуса г и с периодом
обращения т гравитационный потенциал подчиняется закономернос-
закономерности U ~ г2~2п. Тот же результат непосредственно следует из нашего
«подобного» принципа. При п = ^ мы возвращаемся к закону U ~ г
и реальному миру падающих яблок и лун, движущихся по орбитам.
В действительности только благодаря внезапному озарению1 Ньютон
увидел, что сила, с которой Земля притягивает яблоко, в 3600 = 602
раз больше, чем сила, с которой Земля притягивает Луну (расположен-
(расположенную в 60 раз дальше от центра Земли), и вывел, как следствие, закон
всемирного тяготения: сила гравитационного притяжения обратно про-
пропорциональна квадрату расстояния.
При U ~ г~2 одна из возможных орбит имеет форму логариф-
логарифмической спирали (в полярных координатах г (<р) = Г(,е1(р), т.е. само-
самоподобного объекта! Подробнее о логарифмической спирали рассказано
в главе 3 на с. 132-138, а с художественным взглядом на нее С.Кима
читатель может ознакомиться на рис. 4. Что может нам поведать скей-
линг о скоростях и времени для такого движения, когда «планета» па-
падает на свое солнце или удаляется от него по спирали?
При U ~ г~3 одна из возможных траекторий представляет собой
кардиоиду г = ro(l + sin<? (?)). Что же мы можем сказать об угле ip (?)?
Используя концепцию подобия, мы можем даже доказать теорему
вириала, которая устанавливает связь между средней потенциальной
энергией U и средней кинетической энергией Т для ограниченных дви-
движений. Так как кинетическая энергия Т — это однородная квадратич-
1Интересно отметить, что немецкое слово Einfall («озарение», «вдохновение») про-
произносится так же, как em Fall («падение»).
108
Глава 2
Рис. 4. Логарифмическая спираль, ведущая в бесконечность [129].
ная функция от скоростей, а потенциальная энергия U — однородная
функция степени к от пространственных координат, мы непосредст-
непосредственно (почти) получаем из соотношения A) формулу 2Г = kll.
А для линейного осциллятора (к = 2) мы, оказывается, имеем такое
хорошо известное соотношение между средней кинетической и средней
потенциальной энергией как Т = U.
Подобие в концертных залах, микроволнах
и гидродинамике
Особенно плодотворными преобразования подобия оказались в гид-
гидродинамике и других сложных областях физики. Еще в XIX веке Со-
фус Ли A842-1899), а впоследствии Джордж Дэвид Биркгоф A884-
1944) занялись поиском групп преобразований, которые оставляли бы
Подобие в концертных залах, микроволнах и гидродинамике 109
инвариантными данные дифференциальные уравнения, а следователь-
следовательно, и их решения. Такие решения получили название подобных (или
инвариантно-групповых) решений.
Предположим, что для решения ip (ж, у) существует следующий
предел:
lim ?<V (ebx, есу) = Ф (ж, у). A)
е—»0
Тогда подобное решение Ф (ж, у) подчиняется масштабному закону
Ф (ж, у) = ЛаФ (Льж, Лсг/),
который следует непосредственно из равенства A) и, более того, явля-
является обобщением соотношения A).
Но преобразование подобия не всегда так просто. Например, при
проектировании концертных залов и оперных театров применяется сле-
следующий разумный метод: сначала архитектор строит уменьшенные мо-
модели, подобные проектируемым сооружениям, и изучает передачу зву-
звука в них — вместо того, чтобы делать это в «полномасштабном» зда-
здании.1 Линейные размеры, длины волн и частоты масштабировать легко
и просто. Например, если модель сооружена в одну десятую натураль-
натуральной величины, то все ее линейные размеры в десять раз меньше соот-
соответствующих линейных размеров настоящего зала. Так как дифракция
звука на твердых поверхностях зависит только от отношения длины
волны к линейным размерам рассеивающих поверхностей, то длины
волны следует также уменьшить в 10 раз. При фиксированной скорос-
скорости звука (с = 343 м/с в сухом воздухе при комнатной температуре)
это означает, что частоты должны быть увеличены в 10 раз. Время рас-
распространения звука в нашей модели, разумеется, в 10 раз меньше, чем
в настоящем зале. Таким образом, время изменяется обратно пропор-
пропорционально частоте, и это хорошо, учитывая, что частоту принято из-
измерять в обратных секундах. Несколько труднее масштабировать по-
поглощение звука (самими слушателями, например). Тем не менее были
изобретены специальные материалы (известные под названием «публи-
«публики быстрого приготовления»), позволяющие имитировать поглощение
звука слушательской аудиторией при обычных, немасштабированных
частотах.
Альтернативный подход, т. е. постройка сначала полномасштабного концертного
зала и лишь затем его уменьшенных моделей, также был испробован проектиров-
проектировщиками и привел к катастрофическим последствиям, так как потребовал весьма
дорогостоящей «реконструкции» (вот так нужно употреблять эвфемизмы!).
110 Глава 2
Поглощение, трение и другие механизмы энергопотерь обычно
создают трудности при попытке их масштабировать. Например, при
уменьшении в 10 раз размеров микроволновой полости (полого металли-
металлического резонатора) ее резонансные частоты возрастают в те же 10 раз.
Однако минимальные значения ширины полос резонансных мод (опре-
(определяемые потерями на скин-эффект) увеличиваются в 103/2 и 32 раза,
так как малая глубина проникновения электромагнитных полей в про-
проводниках (конечная величина глубины проникновения и обуславливает
скин-эффект) пропорциональна не J, a J/2. (Относительная ши-
ширина резонансной полосы микроволновой полости приближенно опре-
определяется отношением двух объемов — площади внутренней поверхнос-
поверхности полости, умноженной на глубину проникновения электромагнитного
поля, — объема, в котором происходят потери энергии, — к полному
объему полости, или объему, в котором накапливается энергия.) Похо-
Похоже, все-таки есть хоть что-то простое и ясное во всей этой микровол-
микроволновой неразберихе.
Вот еще один пример проблем при масштабировании: на этот раз
источником их служит трение при испытании моделей судов в особых
испытательных бассейнах. Военный корабль, уменьшенный в 50 раз,
в гораздо большей мере подвержен действию влекущих сил потоков,
потому что эти силы создаются вязкими пограничными слоями, в ко-
которых, как и в случае скин-эффекта, действует другой масштаб.
О том, насколько ощутимым может быть влияние размера на мас-
масштабируемость, красноречиво свидетельствует следующее наблюдение
очевидца. Огромный океанский лайнер, входивший в нью-йоркскую га-
гавань во время забастовки портовых буксиров, был вынужден застопо-
застопорить свои двигатели за несколько миль до причала и затем дрейфовать
вместе с ослабевающим приливом по Гудзону с тем, чтобы добрать-
добраться до места своей стоянки точно в тот момент, когда прилив сменится
отливом. Маневр, надо сказать, не из легких: тормозной путь океанско-
океанского лайнера (при отсутствии посторонней помощи) значительно длиннее
тормозного пути многотонного грузовика на гладком льду.
И наоборот, в микроскопических масштабах тормозные пути в лю-
любой неидеальной (не-сверхтекучей) жидкости настолько малы, что
взвешенные в ней частицы кажутся неподвластными инерции. То же
наблюдает и современный исследователь, изучающий под микроско-
микроскопом гидродинамические течения в модели внутреннего уха: в момент
прекращения звука движение мгновенно замирает, как будто частицы
жидкости совершенно лишены массы. Такова «жизнь при малых числах
Рейнольдса», какой она описана в увлекательной статье Эдварда Пер-
Масштабирование в психологии 111
селла под тем же названием [204]. Числа Рейнольдса — лишь один из
представителей длинного списка безразмерных величин, отражающих
важность и сложность масштабирования в гидродинамике [170].
Масштабирование в психологии
Если в классической физике измерение можно считать вполне по-
понятным процессом, устанавливающим, как наблюдаемая величина свя-
связана с определенной единицей, то в психологии ситуация оставалась не
столь ясной до тех пор, пока физиолог Э.Г. Вебер A795-1878), брат фи-
физика Вильгельма Вебера A804-1891), сотрудника К.Ф.Гаусса, не про-
произвел тщательных исследований звуковых и тактильных ощущений,
заложив тем самым основы новой науки — науки об ощущениях. Со-
Согласно сформулированному Вебером закону, увеличение интенсивнос-
интенсивности раздражителя, необходимое для того, чтобы вызвать едва замет-
заметное усиление ощущения, не является раз и навсегда заданной величи-
величиной, а зависит от отношения приращения интенсивности раздражителя
к его первоначальной интенсивности. Впоследствии физик и философ
Г. Т.Фехнер A801-1887) несколько иначе сформулировал закон Вебера
(в новой редакции закон получил впоследствии название закона Вебе-
Вебера-Фехнера) и указал область его применимости1. Современным психо-
психологам (главным образом С. С. Стивенсу) удалось ввести в психологию
методы измерения почти столь же однозначные, как и объективные
измерения в физике [250]. Поэтому новая научная дисциплина вполне
обоснованно была названа психофизикой, а психоакустика и психовизу-
психовизуальные исследования стали ее разделами.
Одним из наиболее значительных вкладов Стивенса в науку стало
введение отношения масштабов для субъективных параметров (гром-
(громкость, яркость и т. п.), а также открытие простых степенных соотноше-
соотношений между этими субъективными параметрами и соответствующими
физическими величинами (поток энергии, интенсивность и т.п.).
Например, для того, чтобы громкость звука L возросла вдвое, его
интенсивность / должна увеличиться в 10 раз; это верно для большей
части диапазона интенсивности звука, воспринимаемого человеческим
ухом без болевых ощущений (диапазон охватывает более 12 порядков
величины при средних аудиочастотах). Поскольку lg 2 яз 0,3, мы полу-
1Фехнер также заложил основы экспериментальной эстетики, исследуя, какие
формы и размеры наиболее приятны глазу. Возможно, он был также первым чело-
человеком, проведшим опрос общественного мнения (для того, чтобы выяснить, какой
из двух картин Гольбейна отдает предпочтение большинство людей).
112 Глава 2
чаем следующий степенной закон для громкости как функции от ин-
интенсивности звука:
L-I0'3. A)
Кто-нибудь, никогда не принимавший участия в тестах психоакусти-
психоакустического масштабирования, возможно, возразит, что «удвоение громкос-
громкости» — понятие не вполне определенное. Однако, как это ни удивительно,
случайный разброс результатов тестирования оказывается на редкость
малым, даже при участии в нем различных слушателей.
Входящие в психофизические степенные законы показатели, такие,
как число 0,3 в соотношении A), не универсальны, но специфичны для
исследуемого ощущения (например, для субъективной яркости, кажу-
кажущегося веса груза или видимой длины) и подробнейшим образом про-
проанализированы психофизиками1. Один из важных вопросов, встающих
перед исследователями в этой области, связан с транзитивностью по-
показателей степеней при сравнении, скажем, громкости с весом или веса
с яркостью и с тем, что это может дать для понимания функциониро-
функционирования мозга.
Если интенсивность звука / в соотношении A) заменить звуковым
давлением р, то, поскольку интенсивность пропорциональна квадрату
давления, мы получим следующее соотношение:
Интересно отметить, что показатель 0,6 может быть выведен из пока-
показателя 0,5, который обнаруживается на более фундаментальном уровне
при разложении «критической» полосы частот звуков во внутреннем
ухе в некое подобие ряда Фурье. В свою очередь, показатель 0,5 об-
обращает наше внимание на статистический анализ и неопределенность,
из чего возникает следующая упрощенная модель восприятия громкос-
громкости. Если бы громкость воспринималась как средняя скорость нервных
импульсов, распространяющихся по слуховому нерву к высшим слу-
слуховым центрам в мозге и если бы эти импульсы представляли собой
модулированный пуассоновский процесс, средняя скорость распростра-
распространения которого пропорциональна звуковому давлению р, то неопреде-
неопределенность количества импульсов в данном временном интервале (напри-
(например, за 100 мс) была бы пропорциональна р0'5. Поскольку многие отно-
отношения масштабов в психофизике оказались непосредственно связанны-
связанными с неопределенностями восприятия («едва заметными различиями»),
1Таким образом, столь милая сердцу физиков универсальность не присуща пси-
психофизике.
Специалисты по акустике, алхимия и концертные залы 113
рассмотренный степенной закон, задающий субъективную громкость
как функцию от физической интенсивности звука, действительно мо-
может быть предсказан на основе такой статистической модели частот
возбуждения нейронов.
В действительности восприятие звука представляет собой более
сложный процесс, однако рассмотренные выше степенные законы и вхо-
входящие в них показатели снабжают исследователей важными путевод-
путеводными нитями и направляют их в нужную сторону.
Специалисты по акустике, алхимия и концертные
залы
Концертные залы строят для того, чтобы предавать приятные зву-
звуки от музыкантов-исполнителей к внимательным слушателям (а еще
для того, чтобы и те, и другие чувствовали себя при этом уютно и не
зависели от капризов погоды). Таким образом, вряд ли физик-акустик
может предпринять здесь что-либо более уместное, чем измерение «час-
«частотной характеристики» зала в пространстве между сценой и различ-
различными точками, в которых предполагается размещать слушателей. Час-
Частотная характеристика в данном случае означает эффективность,
с которой различные частоты (музыкальные тоны) передаются между
двумя разнесенными в пространстве точками зала. На рис. 5 показан
типичный образец такой частотной характеристики, т.е. зависимости
амплитуды сигнала от его частоты в логарифмическом масштабе.
Даже если рассматривать узкие интервалы частот, многочислен-
многочисленные пики и провалы такой частотной характеристики просто бросают-
бросаются в глаза. Обратил на это внимание и изобретатель конденсаторного
микрофона Эдвард Ч. Венте A889-1972), который первым опубликовал
такую частотную характеристику в 1935 г. Будучи экспертом по свя-
связи, Венте выразил в своей статье недоумение по поводу того, как люди
могут наслаждаться музыкой в концертных залах при столь больших
флуктуациях частотной характеристики — таких флуктуации не дают
даже самые дешевые громкоговорители. Ответ заключается в том, что,
воспринимая речь или музыку, ухо подсознательно «настраивается» на
высокочастотный спектральный анализ, при котором, в соответствии
с принципом неопределенности Гейзенберга, не заметны флуктуации
в столь мелком масштабе частот, какой показан на рис. 5.
Не обращая внимания на то, что воспринимающему звук уху глу-
глубоко безразличны частотные характеристики настолько высокого раз-
разрешения, специалисты-акустики всего мира, забыв о еде и сне, все
114
Глава 2
1020
1040 1060
Частота (Гц)
1080
Рис. 5. Передача звука между двумя точками в концертном зале как функция
от частоты. Обратите внимание на большие статистические флуктуации.
продолжали их снимать. Хуже того, вскоре на основе этих частотных
характеристик были «состряпаны» многочисленные предположительно
объективные критерии, определяющие качество звучания. Разумеет-
Разумеется, всякий раз при открытии нового концертного зала существовав-
существовавший до того критерий приходилось модифицировать, чтобы частотная
характеристика нового концертного зала соответствовала реальному,
воспринимаемому качеству звучания. Кто-то сравнил эти «научные»
изыскания — с полным основанием, по-моему, — с гаданием на кофей-
кофейной гуще и алхимией (хотя заслуг последней умалять, конечно же, не
следует).
Когда автор в бытность свою студентом в Гёттингене услышал
об этих «исследованиях» (а в 1954 г. они были еще в самом разгаре),
ему пришло в голову, что, может быть, такие частотные характерис-
характеристики всего лишь отражают шум в области соответствующих частот
(или, если воспользоваться специальной терминологией, модуль слож-
сложного гауссовского процесса, возникающего в результате случайной ин-
интерференции многочисленных перекрывающихся резонансов зала). Ес-
Если это действительно так, то практически все частотные характерис-
характеристики больших залов должны быть подобны друг другу и характеризо-
характеризоваться единственным масштабируемым параметром — временем ре-
реверберации зала.
Предпочтения и несходство: снова о концертных залах 115
Как показали дальнейшие измерения, так оно и есть. Например,
среднее расстояние по частоте (в герцах) между максимумами частот-
частотной характеристики оказалось равным 4, деленным на время ревербера-
реверберации (в секундах) — в совершенном согласии с теоретическим предска-
предсказанием [222] (или последний перевод на английский язык: [229]). Таким
образом, все эти годы вышеупомянутые специалисты измеряли не что
иное, как время реверберации, причем весьма сложным и окольным
путем. Ирония ситуации заключается в том, что «новые» критерии, из-
извлеченные из частотных характеристик, должны были по замыслу ис-
исследователей дополнить время реверберации, которое, согласно их же
вердикту, было признано не имеющим предсказательной силы в отно-
отношении качества звучания. Так немного интуиции и хороший аргумент,
основанный на соображениях подобия, избавили множество людей от
бесполезного занятия.
Частотные характеристики высокого разрешения пригодились впо-
впоследствии при решении проблемы стабильности звукоусилительных
систем, предназначенных для выступлений перед большими скоплени-
скоплениями людей; проблема заключалась в наличии нежелательной акусти-
акустической обратной связи («гула»). Как выяснилось, стабильность можно
существенно повысить посредством простого сдвига всех частотных
компонентов речевого сигнала на среднее расстояние между максиму-
максимумами и минимумами частотной характеристики помещения (согласно
статистической теории, о которой мы уже упоминали, эта величина
составляет всего лишь несколько герц). (Гулкие аплодисменты.) [223]
В более общем (и, возможно, более важном) плане теория случай-
случайно интерферирующих когерентных волн приобрела центральное зна-
значение при анализе многолучевого распространения электромагнитного
излучения и пятнистой структуры лазерных голограмм; вспомните о
портативных сотовых телефонах в машинах и беспроводных телефонах
в домах — великолепное изобретение, особенно учитывая, что такой те-
телефон позволяет достичь превосходного качества звучания, присущего
лучшим моделям телефонов «привязанных».
Предпочтения и несходство: снова о концертных
залах
В этом разделе мы кратко рассмотрим одну проблему психологи-
психологического масштабирования, с которой автор, не будучи психологом, все
же до некоторой степени знаком, — проблему оценки акустики кон-
концертных залов.
116 Глава 2
Для оценки акустических свойств концертного зала (или оперно-
оперного театра) издавна применяется глубоко укоренившаяся процедура —
сбор отзывов слушателей, музыкантов, дирижеров и музыкальных кри-
критиков. Затем эти субъективные оценки соотносятся с различными ар-
архитектурными и физическими характеристиками зала (ширина разме-
размещения слушателей, время реверберации и частотная характеристика).
Затем на основании этих соотношений строится математическая фор-
формула, способная предсказать качество звучания исходя из измеримых
объективных параметров зала (см., например, книгу Беранека «Музы-
«Музыка, акустика и архитектура» [21]).
Отзывы немецкоязычных любителей музыки об акустике концерт-
концертных залов содержат, как правило, такие замечательные словечки, как
glasklar, jammerlich, krankhaft, ruinos, unheimlich и — последнее, но толь-
только в этом алфавитном списке — wunderbar. Пытаться перевести эти
великолепно звучащие по-немецки слова на обычный английский было
бы пустой тратой времени, ибо на любом другом языке они не просто
смутно определены, а почти лишены смысла1.
Филармонический зал Линкольновского Центра Исполнительских
Искусств в Нью-Йорке (ныне Зал Эвери Фишера) был спроектирован
как раз на основе вышеупомянутого подхода. Неудивительно поэто-
поэтому, что для исправления положения потребовалась крупномасштабная
акустическая спасательная операция. Столкнувшись с подобным про-
проектированием, автор и его коллеги осознали, что наиважнейшая задача
отрасли состоит в данный момент в том, чтобы как можно скорее разра-
разработать более надежные методы субъективной (и объективной) оценки
акустических свойств концертных залов.
Новый объективный метод измерения [9] обнаружил, что подвес-
подвесные акустические панели («облака», см. рис. 6) не отражают с доста-
достаточной силой низкочастотных компонентов (особенно в звучании вио-
виолончели) в основное пространство размещения слушателей [232]. Отчас-
Отчасти это можно объяснить плохим масштабированием: для того, чтобы
музыкальные тоны с различными длинами волн хорошо отражались
от акустической панели, ее геометрические размеры должны быть по
крайней мере сравнимы с длиной самой длинной из присутствующих
в звуке волн. В действительности же размеры панелей оказались слиш-
1 Glasklar — от нем. Glas «стекло» и Шаг «ясный, прозрачный, светлый»;
jammerlich — нем. «жалобный» или «жалкий, ничтожный»; krankhaft — нем. «болез-
«болезненный»; ruinos — от нем. Ruin «разорение, упадок, гибель»; unheimlich — нем. «жут-
«жуткий, ужасный»; wunderbar — нем. «чудесный, удивительный, замечательный». —
Прим. перев.
Предпочтения и несходство: снова о концертных залах
117
№
Рис. 6. Акустические панели («облака») в филармоническом зале Линкольнов-
ского Центра Исполнительских Искусств, Нью-Йорк.
ком малы. Этот промах проектировщиков послужил поводом для мно-
многочисленных саркастических замечаний и шуток1.
Чтобы подвести под субъективную оценку акустических качеств
концертного зала твердое основание, автор этой книги предложил пол-
1Не слишком сдержанный в речах дирижер прославленного Кливлендского сим-
симфонического оркестра Джордж Селл был настолько раздражен всем этим без-
безобразием, что обозвал пресловутые панели «schwangere Prosche mit beleuchtetem
Bauchnabel» («беременными лягушками с подсвеченными пупками» — панели вы-
выполняли двоякую функцию, служа одновременно и для подвески ламп). На карика-
карикатуре из тогдашнего выпуска журнала «New Yorker» изображены две дамы, прогу-
прогуливающиеся в фойе под скульптурой Липшица (смутно напоминающей подвесные
акустические панели); одна из дам замечает, обращаясь к другой: «Неудивительно,
что акустика в зале так ужасна. Ведь все эти штуки развешаны здесь, а не там!»
118 Глава 2
ностью отказаться от всех смутных эпитетов, приведенных выше,
и ограничить оценки слушателей выражением предпочтения, отдава-
отдаваемого звучанию в одном из залов перед другим, или степени несход-
несходства воспринимаемого на слух звучания. Чтобы учесть индивидуаль-
индивидуальные различия в музыкальных предпочтениях, отзывы слушателей не
просто усреднялись, а анализировались с помощью современных алго-
алгоритмов многопараметрического скейлинга [233]. При достаточном числе
отзывов (даже если эти отзывы двоичны, как в случае двузначных вы-
выражений предпочтения) такие алгоритмы позволяют построить впол-
вполне определенное евклидово пространство, обычно дву- или трехмерное,
расстояния в котором пропорциональны воспринимаемому несходству
звучания или различию в предпочтениях.
На рис. 7 показан пример построенного таким образом пространст-
пространства предпочтений. Символы Ti,Qz и т. д. соответствуют различным кон-
концертным залам и расположению мест в этих залах (например, Qz озна-
означает, что речь идет о месте третьего слушателя в концертном зале Q).
Нумерованные стрелки — это единичные векторы, представляющие 10
слушателей, принимавших участие в данном тесте на предпочтение.
(То, что некоторые стрелки выглядят короче других, объясняется на-
наличием у них ненулевого компонента в третьем измерении, которое
также учитывалось при анализе, но не показано на рисунке.)
Для каждой пары из 10 тестовых условий, например для Тз и?г,
каждый из 10 слушателей указывал, какому из условий он отдает пред-
предпочтение. Собранные данные (общее число попарных сравнений соста-
составило 450) были подвергнуты многопараметрическому скейлингу с по-
помощью метрического линейно-факторного анализа [244].
Компьютерная программа, осуществлявшая этот факторный ана-
анализ, итеративно изменяла положение каждого из тестовых условий, на-
например, Т\, в пространстве предпочтений и направление вектора каж-
каждого слушателя в трехмерном евклидовом пространстве до тех пор, пока
нормальные проекции всех 10 тестовых условий на каждый из 10 слу-
слушательских векторов не дали как можно более полного согласия с дан-
данными о предпочтениях. Таким образом, из рис. 7 мы можем узнать
о том, что, скажем, слушателю 3 меньше всего нравится тестовое усло-
условие 7\, а больше всего — условие Qi-
Вообще говоря, для точного представления этих данных нам тре-
требуется десятимерное евклидово пространство. В действительности же
почти 90% всех колебаний значений можно наблюдать на двух первых
измерениях пространства предпочтений.
Поскольку стрелки почти всех слушателей на рис. 7 направле-
Предпочтения и несходство: снова о концертных залах
119
Индивидуальное различие
3
10
Общее предпочтение
Рис. 7. Пространство предпочтений для концертных залов.
ны в правую полуплоскость, абсциссу можно пометить как «направле-
«направление единодушного предпочтения». В самом деле, если бы в результате
некоторой архитектурной модификации зала положение точки в про-
пространстве предпочтений, соответствующей любому выбранному месту
в этом зале, сдвинулось вправо, то все слушатели, за исключением од-
одного (слушателя 4), сочли бы это место в зале более предпочтительным.
Что касается разницы в предпочтениях между верхней и нижней
полуплоскостями, то здесь мнения разделились почти пополам. Следо-
Следовательно, ордината явно отражает «индивидуальные различия» в музы-
музыкальных вкусах, олицетворяя собой некое личностное измерение, к ко-
которому надлежит относиться с должным почтением при проектирова-
проектировании помещений, где люди могли бы наслаждаться музыкой.
Субъективные тесты, основанные на суждениях слушателей о не-
несходстве звучания, дали весьма сходные результаты. Таким образом,
наша уверенность в том, что используя методы многопараметрическо-
многопараметрического скейлинга, можно строить пространства, достоверно описывающие
особенности нашего восприятия, получила новое подкрепление. Успеш-
120 Глава 2
ность применения этих методов не вызывает сомнений, а все благодаря
двум начальным условиям (точнее, запретам):
1) при описании качества звучания мы тщательно избегали пользо-
пользоваться смутными терминами или пустыми словами;
2) мы не пытались втиснуть музыкальные вкусы в одномерное про-
прокрустово ложе (несомненно, Прокрусту чрезвычайно понравилась
бы самая мысль об одномерном ложе).
В заключение нельзя не упомянуть об одной «технической детали»,
без которой вышеописанные результаты никогда бы не были получены.
Сопоставление акустических особенностей разных залов и обнаруже-
обнаружение различий в звучании (часто очень тонких различий) — дело весь-
весьма и весьма сложное. Суждения слушателей, разделенные днями или
даже неделями, основанные на различных музыкальных программах,
исполненных различными оркестрами, в высшей степени ненадежны.
Гораздо большего можно было бы достичь, если бы предоставилась воз-
возможность мгновенного переключения между различными залами. В вы-
вышеупомянутом исследовании эта возможность была реализована с по-
помощью остроумного метода, позволявшего точно воспроизводить му-
музыку, записанную в разное время в разных залах, используя магни-
магнитофонную запись симфонии Моцарта «Юпитер» (а также произведений,
представляющих другие музыкальные стили) в исполнении Английско-
Английского камерного оркестра, сделанную в безэховом помещении и любезно
предоставленную автору.
На рис. 8А вы видите трех главных участников этого проекта.
Метод воспроизведения звука [226] основан на том факте, что у боль-
большинства людей обычно имеется два уха. После надлежащей предвари-
предварительной обработки два аудиосигнала, исходящих от изображенной на
рис. 8А головы манекена, поступают на барабанные перепонки слушате-
слушателя, сидящего на некотором расстоянии перед громкоговорителями (см.
рис. 8Б). Предварительная обработка — своего рода обратная фильтра-
фильтрация — компенсирует перекрестные искажения, т.е. попадание сигнала
из громкоговорителя «не в то» ухо. Поскольку трансфер-матрица про-
прохождения звука между громкоговорителями и ушами при надлежащем
расположении громкоговорителей в безэховом помещении невырожде-
невырождена, то существует физически реализуемая обратная трансфер-матрица,
которая воплощена в соответствующих фильтрах, компенсирующих пе-
перекрестные искажения. Структура трансфер-матрицы и обратной ей
матрицы зависит от геометрии пространства вокруг головы слушате-
Предпочтения и несходство: снова о концертных залах
121
(Л)
Сигнал для левого Сигнал для правого
уха уха
Фильтр компенсации
перекрёстных искажений
Рис. 8. (А) Три основных участника проекта акустических измерений в кон-
концертном зале. (Б) Прослушивание звука через громкоговорители с компен-
компенсированными перекрестными искажениями.
122 Глава 2
ля и дифракции звука в нем; эти величины измеряются для некото-
некоторой «стандартной» формы головы. (В кои-то веки успех задуманного
предприятия зависит не столько от процессов, происходящих внутри
головы, сколько от ее внешней формы.)
Чтобы испытать предложенный метод воспроизведения звука, мы
имитировали звуковые волны, приходящие с двух сторон под уг-
углом 90°, с помощью двух громкоговорителей, расположенных под угла-
углами ±22,5°. Имитация оказалась настолько реалистичной, что многие
слушатели поворачивали головы на 90°, стремясь обнаружить третий
(не существующий) источник звука. (Разумеется, стоило им повернуть
голову, как эффект исчезал, поскольку изменялась геометрия простран-
пространства.)
Когда же этот метод воспроизведения звука был впервые приме-
применен к концертным залам, эффект был поистине ошеломляющим: одним
щелчком переключателя слушатель мог «переноситься» из, скажем, вен-
венского Musikvereinssaal в амстердамский Concertgebouw и назад. Такие
мгновенные сравнения сделали, наконец, возможными надежные оцен-
оценки качества звучания, столь долго ускользавшие от акустиков.
Координаты предпочтений, полученные в этих тестах, были по-
поставлены в соответствие различным физическим параметрам залов,
что позволило обнаружить отсутствие в менее предпочитаемых залах
сильных поперечно распространяющихся звуковых волн. Таким обра-
образом, хорошая акустика (при соответствующих времени реверберации,
балансе частот и отсутствии помех в виде эха) зависит от наличия силь-
сильных поперечных звуковых волн, обеспечивающих то самое «стереофо-
«стереофоническое» звучание, которому слушатели отдают предпочтение. В ста-
старинных узких и высоких концертных залах такие поперечные волны
естественным образом порождались архитектурными особенностями
помещения. Во многих же современных залах, имеющих в плане форму
веера и обладающих низкими потолками, доминирует «монофоничес-
«монофоническое» звучание, которое доходит до слушателя в плоскости симметрии,
проходящей через его голову, рождая у него нежелательное ощущение
обособленности от музыки.
Такова вкратце причина столь низкого качества звучания во мно-
многих современных залах. Стимулирующую роль, которую сыграли кон-
концепции сходства-несходства и многопараметрического скейлинга [241]
в выяснении тайны хорошего звука вряд ли можно переоценить.
Недавно, с целью увеличения числа поперечных звуковых волн
в современных концертных залах, были изобретены поверхности, эф-
эффективно рассеивающие звук [230]. Эти, как говорят физики, «фазо-
Предпочтения и несходство: снова о концертных залах 123
отражательные решетки» разработаны на основе теоретико-числовых
принципов (примитивные полиномы над конечными полями, квадра-
квадратичные вычеты и дискретные логарифмы) и обладают замечательным
свойством рассеивать звук (или электромагнитное излучение — в слу-
случае радаров) по всем направлениям с почти одинаковой интенсивнос-
интенсивностью. В настоящее время такие широко рассеивающие поверхности ис-
используются в студиях звукозаписи, церквях и даже в жилых помеще-
помещениях, — словом, где только ни используются!
Подобные звукорассеивающие структуры должны также найти ши-
широкое применение в решении проблемы снижения шума, так как рас-
рассеянный (и, следовательно, ослабленный) шум легче «замаскировать»
(т.е. сделать неслышимым) другими звуками.
Глава 3
Самоподобие — дискретное, непрерывное,
строгое и всякое другое
Блох больших кусают блошки,
Блошек тех — малютки-крошки,
Нет конца тем паразитам,
Как говорят, ad infinitum.
Дж. Свифт
Стихотворения, II, 651 A733)
Мы говорим, что некоторый объект, например, геометрическая фи-
фигура, инвариантен при преобразовании подобия, или, для краткости, са-
моподобен, если его можно воспроизвести путем увеличения какой-то
его части.
Самоподобие встречается во многих различных видах и формах.
Одни из разновидностей самоподобия непрерывны, другие — дискрет-
дискретны. Одни сохраняют точное подобие при увеличении в 10™ раз с очень
большим п, другие не выдерживают увеличение более чем в 10 раз. При-
Примеры самоподобия могут встречаться на каждом шагу, а могут быть
глубоко скрыты в поведении физических или биологических систем.
В одних случаях самоподобие полностью детерминистично, в других
носит лишь вероятностный характер. В некоторых случаях самоподо-
самоподобие математически точно, однако чаще всего оно встречается в реаль-
реальном мире асимптотически или почти асимптотически. Двумя хорошо
известными представителями от математики на нашем форуме высту-
выступают канторовы множества и функции Вейерштрасса (см. с. 142-146
и гл. 7). Броуновское движение представляет одновременно и естес-
естественные науки, и вероятностное самоподобие. А темперированный
двенадцатитоновый строй Баха свидетельствует о важности самоподо-
самоподобия в музыке.
Хорошо известны такие примеры дискретного, пусть и ограни-
ограниченного самоподобия, как китайские коробочки или русские деревян-
деревянные (как правило) матрешки: внутри большой матрешки благоразум-
Самоподобие — дискретное, непрерывное, строгое и всякое другое 125
но1 скрывается подобная ей матрешка меньших размеров, в той, в свою
очередь — матрешка еще меньших размеров и т.д. на протяжении еще
двух, трех или более «поколений». Если бы последовательность мат-
матрешек была двукратно бесконечной, т.е. бесконечной как в сторону
уменьшения, так и в сторону увеличения размера, причем отношение
размеров матрешек двух смежных «поколений» было бы постоянным,
то такой набор матрешек обладал бы точным дискретным самоподоби-
самоподобием. Разумеется, подобный набор может существовать только в нашем
воображении: реальные матрешки имеют конечные размеры: они, без-
безусловно, должны быть больше отдельных атомов и меньше всей Все-
Вселенной. (Если вы хотите увидеть зарождение самоподобия по Чарльзу
Аддамсу, взгляните на рисунок из посмертно изданного альбома его
работ, рис. 1).
Рис. 1. Самоподобие а 1а Аддамс. (Рисунок Чарльза Аддамса, ©1987 The New
Yorker Magazine, Inc.)
1B оригинале игра слов, основанная на одинаковом звучании английских слов
discrete «дискретный» и discreet «благоразумный, осторожный». — Прим. перев.
126 Глава 3
Рис. 2. Длинный ряд свечей. Самоподобие, порождаемое двумя параллельны-
параллельными зеркалами.
Самоподобие — дискретное, непрерывное, строгое и всякое другое 127
Другой пример дискретного, хотя и сильно ограниченного само-
самоподобия можно видеть на этикетках некоторых продуктов. Возьмите
бутылку пива, на этикетке которой изображена эта же бутылка пива
со своей собственной этикеткой, на которой изображена все та же бу-
бутылка пива.
Или взгляните на обложку «Наивной теории множеств» Пола Хал-
моша [95], на которой изображена обложка «Наивной теории множеств»,
на которой, в свою очередь, также изображена обложка «Наивной тео-
теории множеств» с изображением обложки «Наивной теории множеств»,
на которой уже нет очередного изображения обложки все той же книги.
Разумеется, расходы на печать (не говоря уже о других ограничениях)
очень быстро ставят предел такой последовательности уменьшающихся
изображений, обрывая ее на первых же членах. Существует более де-
дешевый способ получения длинной цепочки уменьшающихся изображе-
изображений — встаньте между двумя почти параллельными зеркалами, вроде
тех, что можно видеть в магазинах готового платья (рис. 2). Разумеет-
Разумеется, отображения высокого порядка искажаются и становятся нечетки-
нечеткими, так как ни одно реальное зеркало не является абсолютно плоским
(и не отражает 100% падающего на него света).
Результатом одной из ранних попыток воспроизвести самоподо-
самоподобие в архитектуре по праву можно считать замок Кастель-дель-Монте
(рис. 3), построенный по собственному проекту императором Священ-
Священной Римской империи, а также королем Сицилии, Германии и Иеруса-
Иерусалима Фридрихом II A194-1250), большим любителем соколиной охоты,
обладателем редких (по крайней мере, среди средневековых импера-
императоров) математических способностей и, наконец, безудержным стро-
строителем замков. Замок представляет собой в плане правильный вось-
восьмиугольник, в вершинах которого возведено восемь мощных башен,
каждая из которых также имеет в плане форму правильного восьми-
восьмиугольника. (Такие башни позволяли Фридриху II легко запускать и при-
приманивать охотничьих соколов.)
По иронии судьбы, сам Фридрих родился в палатке, наскоро соору-
сооруженной на рыночной площади небольшого городка Иези в Итальянской
Марке близ Анконы на побережье Адриатического моря.1 Фридрих, ко-
1То, что Фридрих родился в палатке на рыночной площади, было, скорее все-
всего, устроено преднамеренно, так как его мать, нормандская королева Констанция,
слишком долго не могла понести столь желанного для дома Гогенштауфенов будуще-
будущего монарха. И поэтому, дабы пресечь малейшее подозрение в подмене августейшего
младенца, роды должны были происходить в самом многолюдном месте и вокруг
ложа не должно было быть ни двойных стен, ни двойного пола, где могла бы спря-
128 Глава 3
tr
Рис. 3. Кастель-дель-Монте — ранняя попытка императора Фридриха II в соз-
создании самоподобия.
торый написал и собственноручно проиллюстрировал книгу о соколи-
соколиной охоте [73], обладал одним из наиболее колоссальных умов своего
времени (отсюда и его латинское прозвище stupor mundi1). Он вырос
в Палермо и Апулии и говорил, и читал главным образом по-арабски,
по-гречески и на латыни. Позднее он ввел в употребление (через поэ-
поэзию) разговорный итальянский, volgare, на котором говорили люди при
императорском дворе. Этим шагом Фридрих укрепил свои языковые
связи с Италией и придал народному языку официальный статус. Фрид-
Фридрих также был другом Фибоначчи (Леонардо Пизанского) и исправно
снабжал того алгебраическими задачами, решения которых стали не-
неотъемлемой частью истории математики.
Музыка также изобилует примерами самоподобия. Отношение час-
частот соседних нот хорошо темперированного строя постоянно (и рав-
равно 21/12 для октавы, разделенной на 12 полутонов). Отсюда же, благо-
благодаря обратной пропорциональности между резонансной частотой и дли-
длиной трубы, происходит самоподобие групп органных труб. Менее при-
таться «подменная» мать. В зрелые годы Фридрих вновь посетил Иези, который он
называл своим «Вифлеемом» (Фридрих родился во время рождественских праздни-
праздников).
1В вольном переводе с латинского — «повергающий мир в изумление». — Прим.
перев.
Самоподобие — дискретное, непрерывное, строгое и всякое другое 129
ятна для глаз (и более опасна), но тем не менее самоподобна перспек-
перспектива сближающихся железнодорожных рельсов и шпал, учащающихся
по мере движения к отдаленной точке схода (см. рис. 10 на с. 139, само-
самоподобие аналогичного типа используется для доказательства формулы
суммы бесконечной геометрической последовательности).
Рис. 4. Самоподобная телевизионная антенна.
Другим примером дискретного самоподобия могут служить «лого-
периодические» антенны (рис. 4), покрывающие широкий спектр длин
волн за большое число дискретных шагов. Заметьте, что и длины со-
соседних диполей, и промежутки между ними изменяются с одним и тем
130 Глава 3
же коэффициентом подобия. Таким образом, если не принимать во
внимание концевые эффекты, логопериодические антенны принимают
широкий диапазон длин волн почти с одинаковой чувствительностью
и пространственным разрешением. Телевизионные антенны, украшаю-
украшающие наши крыши, — всего лишь бедные родственницы антенны, изоб-
изображенной на рис. 4, но и они позволяют ловить множество различных
каналов с одинаковым коэффициентом усиления и четкостью1.
Еще один пример широкополосных «антенн», правда, на этот раз
для звуковых волн, — это основная перепонка, частотный анализатор,
расположенный в нашем внутреннем ухе. Различные частоты возбуж-
возбуждают различные участки основной перепонки. Тем самым эта резони-
резонирующая мембрана осуществляет отображение частоты в координату
точки. Чтобы охватить весь огромный диапазон частот, воспринима-
воспринимаемых человеческим слухом, — от 20 Гц до 20 000 Гц — и избежать
излишней тесноты на участках, «отведенных» под жизненно важные
низкие и средние частоты, ухо должно осуществлять отображение час-
частот в логарифмическом масштабе. И действительно, начиная примерно
с 600 Гц постоянным по величине сдвигам вдоль основной перепон-
перепонки соответствуют постоянные отношения частот. В диапазоне частот
от 600 Гц до 20000 Гц изменения отношения частот и сдвиги вдоль
перепонки (соответствующие местам расположения резонансов) проис-
происходят с сохранением почти идеального подобия; причем коэффициент
подобия составляет 5 мм сдвига на октаву.
Существует и другая, не менее основательная причина для такого
логарифмического отображения частот. Суть ее заключается в том, что
относительное изменение управляющих резонансом параметров (плот-
(плотность, масса, жесткость) при изменении выбора точки на основной пе-
перепонке постоянно вдоль всей перепонки. Следовательно, основная пе-
перепонка ведет себя, как экспоненциальный акустический рупор, такой
как, например, рупор низкочастотного громкоговорителя, минимизи-
минимизируя таким образом отражение акустической энергии при заданной пол-
полной длине и диапазоне частот. Должно быть, это было важным аргу-
аргументом при выборе надлежащей конструкции нашего уха в ходе его
эволюции и превращения в высокочувствительный акустический де-
детектор. (Здоровое ухо почти способно детектировать броуновское дви-
движение молекул воздуха.)
1К сожалению, вышеупомянутые концевые эффекты, ограничивающие точное
самоподобие, часто проявляются за счет общественных телевизионных каналов, ко-
которые занимают менее чувствительный край диапазона (таких, например, как аме-
американский канал 13 в УКВ-диапазоне).
Самоподобие — дискретное, непрерывное, строгое и всякое другое 131
Для физика относительно малая скорость изменения механических
параметров при движении вдоль основной перепонки (и в самом деле,
настолько малая, насколько это вообще возможно при данной полной
длине и диапазоне частот) означает, что он может анализировать вол-
волновое движение на основной перепонке в рамках известного приближе-
приближения Вентцеля-Крамерса-Бриллюэна [286]. Этот полезный метод был
создан Жозефом Лиувиллем A809-1882) и заново открыт тремя выше-
вышеназванными авторами, которые применили его в квантовой механике.
В диапазоне ниже 600 Гц отображение между местоположением на
основной перепонке и собственно частотой (а не отношением частот)
линейно. В противном случае пять октав диапазона ниже 600 Гц зани-
занимали бы на ней столько же места, сколько пять октав диапазона вы-
выше 600 Гц. Поскольку плотность слуховых нейронов вдоль основной пе-
перепонки приблизительно постоянна, нейронное представление высоких
частот было бы существенно более бедным, чем представление низких
частот.
Отклик основной перепонки обнаруживает еще одно интересное
подобие, выполняющееся для всего диапазона частот: локальная ско-
скорость волн пропорциональна локальной резонансной частоте. Постоян-
Постоянным коэффициентом пропорциональности служит характеристическая
длина, равная примерно 1 мм. Вследствие этого запаздывания акусти-
акустических сигналов вдоль основной перепонки обратно пропорциональны
координате точки детектирования. Благодаря такому подобию можно
построить простую интегрируемую математическую модель основной
перепонки [227].
Самоподобие часто присуще иерархическим структурам, таким
как филогенетические деревья. Примером могут служить математи-
математические деревья Кэли (называемые в физике решетками Бете). Дере-
Деревом Кэли называется граф без петель, имеющий в каждом узле одно
и то же число ветвей (на рис. 5 это число равно 2). Самоподобие таких
графов необязательно проявляется в их геометрическом представле-
представлении, но легко усматривается в их связности или топологии. Решетки
Бете, несмотря на то, что они в высшей степени нефизичны, нередко
представляют собой единственно возможные точно разрешимые модели
в таких сложных ситуациях, как локализация Андерсона и перколяция
(немаловажные концепции в современной физике; см. гл. 16).
Другой пример самоподобного дерева — дерево двоичного кода —
изображен на рис. 6. Интересно отметить, что если мы определим рас-
расстояние между двумя «листьями» (концевыми узлами) как число поко-
поколений, которое необходимо пройти вспять, чтобы вернуться к общему
132
Глава 3
Рис. 5. Художественное дерево Кэли с коэффициентом ветвления 1 : 2 [161].
предку, то порождаемое в результате пространство окажется ультра-
метрическим. Для филогенетических деревьев это означает, что из трех
расстояний между любыми тремя существующими узлами либо равны
все три расстояния, либо равны два расстояния, а третье — меньше.
Иначе говоря, все треугольники в построенном пространстве либо рав-
равносторонние, либо равнобедренные с коротким основанием, что при-
приводит к интересным следствиям для кодов Гензеля и безошибочных
вычислений [230].
Если для некоторой проблемы удается указать ультраметрическое
пространство, то за ним обычно маячит иерархическая структура, ко-
которая дает ключ к лучшему ее пониманию. Такие структуры встреча-
встречаются в самых различных задачах от таксономии до статистической фи-
физики и теории оптимизации. Превосходный обзор ультраметричности,
написанный для математиков-любителей, можно найти в работе [209].
Логарифмическая спираль, режущие инструменты
и широкополосные антенны
Замечательно простым примером самоподобного объекта, имею-
имеющего к тому же множество практических приложений, может слу-
Логарифмическая спираль 133
0
0
0
0
0
1
0
1
0
0
1
1
Рис. 6. Дерево двоичного кода: самоподобная иерархическая структура.
жить логарифмическая спираль, хорошо известная из школьного кур-
курса математики. В полярных координатах (г, <р) ее уравнение имеет
вид г (<р) = roexp(kip), где го > 0 и к — постоянные. Применяя к ра-
радиус-вектору г, т. е. к размеру спирали, преобразование подобия с ко-
коэффициентом s, получаем исходную спираль, повернутую на постоян-
постоянный угол (lns)/fc. Поскольку угол <р определен только по модулю 2тг,
при коэффициентах подобия, равных s = expB?rmfc), где т — целое
число, бесконечная спираль остается инвариантной, т.е. логарифми-
логарифмическая спираль самоподобна, причем коэффициент подобия равен s =
= ехрBтг|&|). Если пренебречь вращениями, то логарифмическая спи-
спираль оказывается самоподобной при любом вещественном коэффициен-
коэффициенте подобия.
Из самоподобия логарифмической спирали вытекают несколько ин-
интересных следствий и полезных приложений. Например, направление
касательной к спирали зависит только от угла <р и не зависит от того,
какую ветвь спирали мы рассматриваем (рис. 7). Это следует непосред-
непосредственно из масштабной инвариантности логарифмической спирали, но
может быть, конечно же, проверено и более окольными вычислениями.
Кроме того, поскольку повернутая логарифмическая спираль подобна
134
Глава 3
себе, угол /3 между радиусом-вектором и касательной в любой точке
должен быть одним и тем же для всей спирали. Небольшое размыш-
размышление (или столь же небольшой чертеж) показывает, что ctg/З должен
быть равен (dr/dip)/r = d(\nr)/dip = к. Вот в чем заключается геомет-
геометрический смысл величины к — это не что иное, как котангенс постоян-
постоянного угла между радиус-вектором и касательной в произвольной точке
логарифмической спирали. (При к = 0 угол /3 становится равным тг/2,
и спираль вырождается в окружность.)
г = гое"*
Рис. 7. Логарифмическая спираль: гладкая самоподобная кривая.
Это свойство логарифмической спирали находит одно интересное
применение. Представьте себе, что вам нужно спроектировать режу-
режущий инструмент с вращающимся ножом в виде диска. Какую форму
следует придать режущей кромке, чтобы угол резания был постоян-
постоянным, независимым от угла вращения ножа? Правильно, форму лога-
логарифмической спирали! Поскольку периметр режущей кромки неизбеж-
неизбежно должен быть однозначной функцией от угла вращения, при каком-то
значении этого угла должен, разумеется, происходить «скачок назад» на
величину roexpB7r|fc|).
Однако самое интересное только начинается! Как мы уже знаем,
логарифмическая спираль самоподобна, причем, если пренебречь вра-
вращением, коэффициент подобия может быть произвольным. Это значит,
что пока мы игнорируем вращение, логарифмическая спираль не име-
Логарифмическая спираль 135
em подобия по длине, вопреки впечатлению, создаваемому математи-
математической формулой спирали, г (<р) = Го exp(kip), множитель го которой, по
всей видимости, подразумевает наличие подобия по длине. Коэффици-
Коэффициент го, однако, может при вращении просто исчезнуть, в чем нетрудно
убедиться, если записать формулу в виде г (ф) = ещ>{к[уэ + (lnro)/fc]},
где (lnro)/fc — это просто некоторый постоянный угол.
Раз уж мы обнаружили нечто не зависящее от масштаба, ему долж-
должно найтись великое множество полезных применений. Людей всегда
сбивают с толку проблемы, возникающие в связи с изменением мас-
масштабов или размеров1. А вдруг нам удастся придумать обувь, незави-
независимую от масштаба — ботинки на любой размер. Какое благодеяние для
человечества! (Ну хорошо, не для всего.) С чулками, пожалуй, в опре-
определенных пределах, безразмерности мы достигли: эластичные чулки
подходят всем, независимо от размера ноги (или надо сказать, что не
подходят никому?).
Еще одна область, в которой весьма желательна независимость
от масштаба — это проектирование приемно-передающих антенн для
коммуникационных систем, которым приходится охватывать широкий
диапазон длин волн; примером такой антенны может служить изобра-
изображенная на рис. 4 логопериодическая антенна, самоподобная на некото-
некотором дискретном множестве длин волн. Если бы такие антенны были
столь же эффективны и в непрерывном диапазоне длин волн! Предпо-
Предположим теперь, что мы используем кругополяризованные волны. Тогда
поворот антенны на любой угол никак не отразится на коэффициен-
коэффициентах усиления и направленного действия антенны. А если мы придадим
антенне форму логарифмической спирали (в идеале из тонкой сверх-
сверхпроводящей проволоки), то она одинаково хорошо будет работать на
всех длинах волн в любом заданном диапазоне [39]. Антенны, осно-
основанные на использовании этого столь соблазнительного принципа, су-
существуют в действительности (и похожи на конусообразные диванные
пружины).
Природа также использует самоподобие логарифмической спирали.
У многокамерного моллюска наутилус (рис. 8) каждая камера представ-
представляет собой увеличенную копию предшествующей, причем для любых
двух смежных камер коэффициент подобия остается постоянным. Как
следствие, наутилус растет вдоль логарифмической спирали. Не толь-
только природа, но и художники вдохновляются спиралями. На цветной
1Говорят, что вечно погруженный в размышления сэр Исаак (Ньютон) прика-
приказал прорезать во входной двери два отверстия для двух своих любимцев — кошки
и собаки, имевших различные размеры.
136 Глава 3
вклейке 4 показано бесконечное множество бесконечно переплетенных
логарифмических спиралей всех цветов радуги.
Рис. 8. Самоподобная раковина многокамерного моллюска Nautilus име-
имеет форму логарифмической спирали. (Фото Эдварда Уэстона, ©Center for
Creative Photography, Arizona Board of Regents.)
Логарифмическая спираль с особенным коэффициентом подобия
встречается в следующей геометрической задаче. Возьмем прямоуголь-
прямоугольник со сторонами а > Ь и отрежем от него квадрат со стороной Ь (рис. 9).
От оставшегося прямоугольника отрежем квадрат со стороной а — Ь, как
показано на рис. 9. Для того чтобы построение «работало», разность а — Ь
должна быть меньше Ь, т.е. сторона а должна быть меньше 2Ь. На вто-
втором этапе построения неравенство выглядит как 2а > Э>Ъ, а на 2п-м эта-
этапе условие того, что при отрезании квадрата получится прямоугольник,
длинная сторона которого будет совпадать с короткой стороной преды-
предыдущего прямоугольника, принимает вид неравенства Fin-\a > F2nb,
где Fk — числа Фибоначчи. Аналогично должно выполняться неравен-
неравенство F2na < F2n+ib. Для того чтобы построение было осуществимо при
произвольно больших п, отношение сторон Ь/а исходного прямоуголь-
прямоугольника должно быть равно пределу отношения F2n-i/Fn при п —> сю, т.е.
золотому сечению 7 = (\/5 — 1)/2.
Логарифмическая спираль
137
а-Ь
2Ь-а
1а-ЪЪ
Рис. 9. Самоподобная последовательность прямоугольников, отношение сто-
сторон которых равно золотому сечению.
Результатом такого построения будет бесконечная спираль из все
более мелких квадратов с коэффициентом подобия, равным золото-
золотому сечению. На рис. 9 изображена такая логарифмическая спираль
с к = — (тг/2) In 7, проходящая через последовательные точки отрезания.
Точка схода квадратов и начало спирали определяется общей точкой пе-
пересечения диагоналей прямоугольников.
Существует весьма очаровательная связь между описанной выше
«ампутацией» квадратов от прямоугольников и непрерывными дробя-
дробями. Заметим, что золотое сечение можно записать в виде непрерыв-
непрерывной дроби l/(ai + 1/(«2 +•••)) или> сокращенно, [oi, «2, • • • ], где а± =
= а2 = • • • = 1- Отсюда, 7 = [1; !:•••]• Предположим, что мы хотим
на каждом этапе отрезать от прямоугольника по два квадрата с таким
расчетом, чтобы длинная сторона оставшегося прямоугольника была
равна короткой стороне предыдущего прямоугольника. Каким должно
быть при этом отношение длин сторон Ъ/а начального прямоугольни-
прямоугольника (равно как и всех последующих)? Немного поэкспериментировав, вы
обнаружите, что отношение Ь/а должно быть равно числу л/2— 1, разло-
138 Глава 3
жение которого в непрерывную дробь имеет вид [2, 2, 2,...]. В общем
случае п-й член ап в записи непрерывной дроби Ь/а говорит нам о том,
сколько квадратов необходимо отрезать на п-й стадии построения. Та-
Таким образом, самоподобные каскады и логарифмические спирали воз-
возникают в тех случаях, когда отношение сторон начального прямоуголь-
прямоугольника Ь/а равно периодической непрерывной дроби с длиной периода 1.
Получающиеся при этом иррациональные числа [п, п,...] (п > 1), ко-
которые я называю серебряными сечениями, играют также определенную
роль в построении квазипериодических решеток (см. гл. 14) и модели-
моделировании квазикристаллов (см. гл. 13).
Заметим кстати, что, подобно бесконечной прямой, логарифмичес-
логарифмическая спираль может служить образцом гладкого самоподобного объекта,
что резко отличает ее от обычно ассоциируемых с самоподобием фрак-
фрактальных объектов, таких, например, как очертания скалистых бере-
берегов, траектории броуновского движения и другие недифференцируемые
функции.
Некоторые простые случаи самоподобия
Одним из простейших самоподобных объектов можно считать бес-
бесконечную в обе стороны геометрическую прогрессию, например,
J. J. _1_ -| п а о
Умножив каждый член этой прогрессии на 2, получим последователь-
последовательность
2sn = ...,\, \, 1,2, 4, 8, 16,...,
которая, без сомнения, является той же самой прогрессией. Множи-
Множитель 2 называется коэффициентом подобия, или скейлинга. Очевидно,
что вместе с числом 2 все целые степени 2, в том числе \, 8 и -^, так-
же являются коэффициентами подобия вышеприведенной прогрессии.
Условимся называть наименьший из всех этих коэффициентов подобия,
превышающий 1, примитивным коэффициентом подобия. В нашем при-
примере 2 — это примитивный коэффициент, а 4 — нет. (Коэффициент ^,
хотя он также может порождать все остальные коэффициенты подо-
подобия, мы исключаем из числа примитивных по определению, так как он
меньше 1.)
Некоторые простые случаи самоподобия
139
Во многих практических приложениях самоподобные последова-
последовательности односторонни, например,
1, г, г2, г3,...
Геометрическое представление этой самоподобной последовательности
приведено на рис. 10, где она используется в предложенном Бенджами-
Бенджамином Клейном и Эрлом Бивенсом [131] изящном, из разряда «посмотри
и убедись», доказательстве справедливости формулы суммы геометри-
геометрической прогрессии
1 + г + г2
- Г
(И <
A)
Обратите внимание на то, что два прямоугольных треугольника ABC
и EDA подобны, так как угол а равен углу /3. Следовательно, отно-
отношения их соответственных сторон должны быть равны. В частности,
отношение сторон DE/DA = 1+г + г2+г3 + ... должно быть равно
отношению сторон В А/ВС = 1/A — г). (А какую фигуру прикажете
начертить для г < 0?)
А
Рис. 10. Доказательство с помощью самоподобия [131].
Другое геометрическое доказательство соотношения A), также
основанное на использовании самоподобия и предложенное Уорреном
Пейджем, представлено на рис. 11 [188]. Начав с единичного квад-
квадрата, мы отрезаем от него прямоугольник со стороной 0 < q < 1.
От оставшегося прямоугольника отрезаем поочередно последователь-
140
Глава 3
ность прямоугольников, площадь каждого из которых в 1 — q раз мень-
меньше площади предыдущего прямоугольника. Так как все эти прямо-
прямоугольники вместе покрывают исходный единичный квадрат, получаем:
q + q(l — q) + q(l — qJ + ... = 1. Полагая 1 — q = г, приходим к форму-
ле A).
q qil-qf
q{\-qf
q(\-qf
q(\-q)
q
qil-qf
•
•
•
qil-qf
qil-q)
Рис. 11. Другое доказательство с помощью самоподобия [188].
Уверен, большинство читателей уже успели познакомиться с лам-
лампами с тремя режимами накаливания и вовсю пользуются тремя удоб-
удобными уровнями освещения — слабым, средним и ярким. Не секрет,
что в большинстве коммерческих ламп три уровня освещения реа-
реализуются с помощью всего лишь двух спиралей, потребляющих, со-
соответственно, х Вт и у Вт в одиночных режимах и (х + у) Вт при
совместном включении. Обычно х = 50 Вт, а у = 100 Вт; к сожале-
сожалению, при ярком режиме A50 Вт) освещение оказывается не намного
ярче, чем при среднем A00 Вт). Более оптимальным был бы вари-
Некоторые простые случаи самоподобия 141
ант, при котором три мощности образовывали бы самоподобную гео-
геометрическую прогрессию, т.е. при у > х отношение (х + у)/у было
бы равно отношению у/х. Решение приводит нас к золотому сечению
7 = (^/5 — 1)/2 = 0,618. Действительно, если х/у = 7, то у/(х + у) так-
также равно 7-
Аналогично в лампе с тремя спиралями можно было бы реализовать
пять различных режимов, мощности которых образовали бы самоподоб-
самоподобную последовательность при условии, что третья спираль потребляла
бы мощность z = y/"f2- Например, при у = 100 Вт самоподобные зна-
значения мощностей (округленные до ближайшего целого числа Вт) соста-
составили бы последовательность х = 62 Вт, у = 100 Вт, х + у = 162 Вт,
z = 262 Вт и у + z = 424 Вт.
Разумеется, тому, кто читает при свете многоспиральной лампы,
вряд ли есть дело до того, что мощности режимов образуют самопо-
самоподобную последовательность; потребителя интересует субъективная яр-
яркость. К счастью, яркость В как функция от мощности W в довольно
широком диапазоне подчиняется простому степенному закону В ~ Wa.
Поскольку степенные законы сами самоподобны (см. гл. 4), наш выбор
спиралей остается-таки верным, даже если нам требуются равные от-
отношения яркостей.
Любопытный акустический парадокс, основанный на конечной са-
самоподобной последовательности музыкальных нот, был придуман Род-
Роджером Шепардом [242]. Парадоксальный звук возникает при суперпози-
суперпозиции 12 нот, каждая из которых на октаву выше, чем ее нижняя соседка.
Если за исходную принять ноту с частотой 10 Гц, то остальными 11
частотами в составном звуке будут 20, 40, 80, 160, 320, 640, 1280, 2560,
5120, 10 240 и 20 480 Гц. Увеличив все 12 частот на полтона (примерно
на 6%), мы получим звук с частотными компонентами 10,6; 21,2;...;
10 489 и 21698 Гц, чуть более высокий, поскольку все частоты увели-
увеличены на полтона (он и получился на полтона выше).
Снова увеличив частоты на полтона, получим еще более высокий
звук. Повторяя этот процесс, мы каждый раз будем получать все бо-
более высокий звук. Однако звук, полученный после двенадцатого уве-
увеличения частот оказывается неотличим от исходного! (Самая низкая
составляющая A0 Гц) исходного звука и самая высокая составляю-
составляющая D0 960 Гц) конечного звука неслышимы.)
Добавляя достаточное количество неслышимых низкочастотных
составляющих, Шепард смог создать последовательность звуков, высо-
высота которых возрастала неограниченно! Сейчас, имея персональный ком-
компьютер, подключенный к цифроаналоговому преобразователю, каждый
142
Глава 3
Рис. 12. Парадоксальный самоподобный сигнал. При удвоении частоты высо-
высота звука не изменяется.
может легко получить такую последовательность звуков, и я настоя-
настоятельно рекомендую тем, кого это заинтересовало, испытать на себе этот
таинственный парадокс нашего восприятия. На рис. 12 приведена вре-
временная диаграмма самоподобного сигнала, высота которого остается
неизменной при удвоении всех частот.
Функции Вейерштрасса и музыкальный парадокс
Вечно восходящие звуки Шепарда тесно связаны с недифференци-
руемыми функциями, продемонстрированными Карлом Вейерштрассом
A815-1897) в качестве примеров непрерывных, но нигде не дифферен-
дифференцируемых функций. На первый взгляд, такие функции противоречат
здравому смыслу, и в XIX веке они вызвали бурные споры. Функция
Вейерштрасса определяется рядом
w(t)= Y, akcos(j3kt), где
к=1
а — вещественно,
C — нечетно.
Вейерштрасс показал, что при аC > 1 + Зтг/2 функция w it) непрерыв-
непрерывна, но нигде не дифференцируема, как фрактальная снежинка фон Коха
или заполняющая все пространство кривая Гильберта, с которыми мы
уже встречались в гл. 1. Подобно канторовым множествам, недиффе-
ренцируемые функции служат неисчерпаемым источником парадоксов,
таких как последовательность вечно восходящих звуков Шепарда.
Функции Вейерштрасса и музыкальный парадокс 143
Приведем еще один пример музыкального аккорда, который по-
построен по образцу функции Вейерштрасса и обладает следующим
сверхъестественным свойством. Если записать такой аккорд на маг-
магнитофонную ленту и воспроизвести на скорости, вдвое превышающей
скорость записи, то высота звука не возрастет на октаву, как мож-
можно ожидать от всякой добропорядочной записи, а станет на полтона
ниже [213, 214, 228]. Как такое возможно? Построим конечную час-
частичную сумму, аппроксимирующую функцию Вейерштрасса (множи-
(множители ак, необходимые для сходимости бесконечного ряда, можно здесь
опустить):
к
fc=l
Применив к временному измерению t преобразование подобия с коэф-
коэффициентом /3, получим
К К+1
wk (f3t) = / j cos(/3 + i) = у cos(/3 i).
k=\ k=2
Иначе говоря, функция wk (Pt) с точностью до концевых эффектов сов-
совпадает с функцией wk (t), не подвергшейся преобразованию подобия.
Следовательно, функция wk (t) приближенно самоподобна (см. рис. 12,
где К = 7, а /3 = 2).1 Очевидно, что в пределе, при к —> ос, такая функ-
функция нигде не может иметь конечную ненулевую производную, посколь-
поскольку под действием преобразования подобия производные изменяются.
Выберем /3 = 213/12 и получим
функция wk (t), таким образом, станет слышимой как звук. Часто-
Частоты 2йA3/12)/2тг должны теперь охватывать только диапазон аудиочас-
тот (от 10 Гц до 20 000 Гц). Записав сигнал wk (t) на магнитную ленту
1Интересно отметить, что концепция самоподобия вошла в математику в двух
независимых точках — через канторовы множества и функции Вейерштрасса —
примерно в одно и то же время и по схожим причинам: дабы пролить свет на опор-
опорные столпы математики, числа и функции. Хотя еще раньше Лейбниц использовал
понятие самоподобия («миры внутри миров») в своем трактате «Монадология» [143]
и в определении прямой.
144 Глава 3
и воспроизведя ее с вдвое большей скоростью, получим
wK Bt) =Y,
где к' = к + 1. Поскольку эти суммы покрывают весь аудиодиапазон,
то для человеческого уха верно следующее равенство:
Следовательно, при удвоении скорости воспроизведения высота зву-
звука уменьшается в 21/12 раза. Пользуясь музыкальной терминологией,
можно сказать, что аккорд будет звучать не на октаву выше, а на пол-
полтона ниже. Вот такие парадоксы порождаются фракталами!
Нетрудно составить программу для персонального компьютера, ко-
которая будет генерировать сигнал wu (t) с 11 компонентами, охватываю-
охватывающими диапазон частот от 10,0 Гц до 18 245,6 Гц. При удвоении скорос-
скорости воспроизведения частота, скажем, шестой составляющей изменится
с 427,15 Гц на 854,3 Гц. Однако сравнивая два аккорда, слуховая систе-
система человека отождествляет удвоенную шестую компоненту (854,3 Гц)
с ближайшей к ней компонентой первоначального аккорда, т. е. с седь-
седьмой его компонентой (905,1 Гц). Поскольку частота 854,3 Гц как раз на
полтона ниже, чем частота 905,1 Гц, и поскольку эти рассуждения при-
применимы ко всем компонентам с удвоенной частотой, результирующий
аккорд будет звучать на полтона ниже.
Удвоение скорости прослушивания при отношении частот C =
= 214/12 приводит к понижению звука на целый тон, при отношении /3 =
= 215/12 — на три полутона и т. д. Однако при C = 224/12 = 4 восприятие
становится неоднозначным, потому что при удвоении чисел 1, 4, 16,
64,... результирующая последовательность B,8,32,...) может рас-
рассматриваться либо как звук на октаву выше, либо как звук на октаву
ниже.
Все физические «самоподобные» объекты в действительности обла-
обладают ограниченным самоподобием — просто потому, что в реальном
мире не существует идеальных, в математическом смысле, периоди-
периодических функций: большинство колебаний имеет начало и конец (ис-
(исключение, возможно, составляет наша Вселенная,1 при условии, что
1 Согласно некоторым из самых последних физических фантазий, Вселенная —
это нечто, случающееся время от времени.
Функции Вейерштрасса и музыкальный парадокс 145
она замкнута и начинает новый цикл жизни после каждого «Большо-
«Большого Взрыва»; см. замечательный — без единой формулы! — бестселлер
Стивена Хокинга «Краткая история времени» [101]). Тем не менее, са-
самоподобие — полезная абстракция, точно так же, как и периодичность,
которая представляет собой одно из наиболее полезных понятий в ес-
естественных науках, несмотря на всю свою ограниченность.
Одним из самоподобных, если не учитывать «концевых эффектов»,
математических объектов является функция
sine ж - жх ,
которая описывает картину дифракции на прямоугольной щели и игра-
играет важную роль в интерполяции выборочных функций, используемых
в цифровых системах с дискретным временем. (Под «щелью» в данном
случае понимается прямоугольное «окно», сквозь которое рассматрива-
рассматривается спектр функции.)
Применив к функции sine ж тригонометрическое тождество
sin 2ж = 2 sin ж cos ж,
получим
Следовательно, с точностью до множителя cos(ttx/2), функция sine ж
самоподобна с коэффициентом подобия 2.
Повторяя процесс факторизации, приходим к знаменитому беско-
бесконечному произведению Эйлера
Функция sine ж имеет нули при всех целых значениях ж, положитель-
положительных и отрицательных. Первый множитель в произведении Эйлера дает
нули функции sine ж при всех нечетных значениях ж. Второй множи-
множитель дает нули при значениях ж, равных удвоенным нечетным числам.
Третий множитель дает нули при значениях ж, равных учетверенным
нечетным числам, и т.д. Таким образом, мы получаем требуемые ну-
нули при всех целых значениях ж за исключением ж = 0. (Заметим, что
каждое ненулевое целое п может быть однозначно представлено в ви-
виде п = 2mfc, где к — нечетное целое число, a m ) 0.)
146 Глава 3
Во многих ситуациях мы можем наблюдать лишь приближенное са-
самоподобие: всегда возможны статистические или детерминированные
«возмущения». Например, основанная на еще одном хорошо известном
представлении 2/тг в виде бесконечного произведения последователь-
последовательность
к=1
где //. определяется через рекурсию
Л+1 = \^-^j , Л = о,
самоподобна только в пределе при п —> ос. При п = 1, 2, 3, 4,... полу-
получаем
sn = 0,070482; 0,01662; 0,004109; 0,0001024;...
Коэффициент подобия для членов этой последовательности стремится
к 4. Такие асимптотические самоподобия часто встречаются в рекур-
рекурсивных вычислениях.
В последующих главах мы встретимся с еще одним отклонением
от строгого самоподобия — со статистическим самоподобием, при ко-
котором масштабную инвариантность демонстрируют статистические
законы, управляющие поведением объекта. Сам объект может изме-
изменяться под действием преобразования подобия, но его вероятностные
аспекты остаются теми же.
Еще о самоподобии в музыке: темперированный
строй Баха
Древние греки, игравшие на множестве струнных инструментов,
обнаружили, что деление струны на две равные части дает приятный
для слуха музыкальный интервал, ныне называемый октавой. Соответ-
Соответствующее отношение физических частот равно 2:1.
«Отсечение» одной трети струны дает другой приятно звучащий
интервал, чистую квинту, с отношением частот 3 : 2.
Пифагорейцы задумались о том, можно ли получить целое число
октав из одной лишь квинты путем повторного применения простого
отношения частот 3/2. С математической точки зрения речь шла о ре-
решении уравнения
аг-
Еще о самоподобии в музыке: темперированный строй Баха 147
в целых положительных числах п и то. В то же время из фундаменталь-
фундаментальной теоремы теории чисел известно, что никакая целая положительная
степень числа 3 не может быть равна никакой целой положительной
степени числа 2, т.е. уравнение 3™ = 2к не имеет решений в целых
числах при п > 0.
Однако древних греков это не остановило, и они методом «проб и
ошибок» нашли превосходное приближенное решение
- I ~ 27
2/ '
основанное на почти точном равенстве чисел З1/19 и 21/12.
Систематический подход к получению таких почти точных ра-
равенств сводится к записи отношения логарифмов двух целых оснований
данного уравнения (в нашем случае, 2 и 3) в виде непрерывной дроби:
?§ = [1,1,1,2,2,...],
где последовательность в квадратных скобках представляет собой удоб-
удобную форму записи непрерывной дроби
1
1 +
1 +
1 +
2 + ...
Непрерывные дроби обычно дают хорошие рациональные аппроксима-
аппроксимации иррациональных чисел, например тг яз 355/113. Это превосходное
приближение к тг, использующее не очень большие целые числа, было
известно еще древним китайцам.
Обрывая вышеприведенную непрерывную дробь на пятом члене
(как показано в примере), мы получаем дробь, дающую очень хорошее
приближение для музыкальной квинты:
In2 _, 12
1пЗ 19'
откуда следует, что C/2I2 рй 27.
148 Глава 3
Здесь необходимо подчеркнуть еще одно важное обстоятельство:
показатели 12 и 7 представляют собой взаимно простые числа, поэто-
поэтому повторное применение чистой квинты по модулю октавы («квинто-
(«квинтовый круг») не даст в результате частоту, близкую к полученной ранее,
вплоть до двенадцатого шага. Что касается 12 различных частот в пре-
пределах одной октавы, то все они являются приближенными степенями
основного отношения частот 1 : 21/12, или полутона. Следовательно,
всегда существует некоторое значение к, при котором
й.\ ~ 2Г/12 г — 1 2 4
„I ~ ^ , Г — 1, Z, О . . .
Решение этого приближенного уравнения имеет вид k = r/7=7r mod 12.
Это означает, что треть октавы, например, или 21/3 (г = 4, отношение
частот я» 1,260), эквивалентна (по модулю октавы) к = 4 квинтам (от-
(отношение частот ра 1,266).
Треть октавы близка и к чистой большой терции (отношение час-
частот 5/4), что является счастливым следствием еще одного, независи-
независимого, теоретико-числового приближенного равенства 53 ра 27, которое
устанавливает связь между следующими за 3 простым числом (т. е. 5)
с наименьшим простым числом, 2.
Сама квинта аппроксимируется семью интервалами в полтона каж-
каждый с точностью до 0,1%: 27/12 ра 1,4983. Небольшое отличие от
точного значения 1,5 называется пифагорейской невязкой. Интерес-
Интересно отметить, что не только семь полутонов составляют одну квин-
квинту, но и семь квинт (по модулю октавы) составляют один полутон.
Это следует из еще одного теоретико-числового казуса: число 7 сов-
совпадает с обратным ему числом в арифметике вычетов по модулю 12
(т.е. 7-7 = 49 = 1 mod 12).
Чтобы на музыкальных инструментах с фиксированным набором
тонов, вроде фортепиано, можно было играть в различных тональнос-
тональностях, частоты этих тональностей должны выбираться из одного и то-
того же основного набора частот. Это подвигло И.С.Баха на разработ-
разработку темперированного строя, основанного на полутоне с отношением
частот 21/12. Музыкальный инструмент, настроенный в соответствии
с темперированной гаммой, имеет, таким образом, частоты, близкие
к следующим кратным самого низкого тона:
2 21/12 22/12 23/12 24/12 25/12
и т. д. до самой высокой ноты.
Замечательные соотношения между простыми числами 3, 5 и 7 149
Можно видеть, что частоты хорошо темперированного инструмен-
инструмента образуют самоподобную последовательность с коэффициентом по-
подобия 21/12. Если бы все эти ноты прозвучали одновременно, то такой
инструмент создал бы акустический выход (чтобы не сказать сильнее),
близкий к самоподобной функции Вейерштрасса. (В действительности
результат настройки фортепиано нельзя назвать в точности самоподоб-
самоподобным. Настраивая инструмент, настройщик несколько «перетягивает»
струны, чтобы минимизировать биение обертонов, которые не являют-
являются в точности гармоническими из-за конечного сопротивления струн
именно на изгиб.)
Превосходным введением в науку о музыкальном звуке может слу-
служить книга Джона Р. Пирса с тем же названием [199].
Замечательные соотношения между простыми
числами 3, 5 и 7
Несколько лет назад Джон Р. Пирс, известный своими работами по
спутниковой связи, заинтересовался вопросом о том, нельзя ли заме-
заменить отношение частот октавы 2 : 1 отношением частот 3 : 1 (соот-
(соответствующий интервал Пирс предложил назвать тритавой) и создать
самоподобный (равнотемперированный) строй с отношениями частот,
в которых участвуют следующие два простых числа — 5 и 7 [167]. Ина-
Иначе говоря, существует ли некоторый корень целой степени N из числа 3
такой, что его целыми степенями хорошо аппроксимируются
отношения | и \ (по аналогии с аппроксимациями ^ я» 27/12 и | и 29/12
о и 2 2
хорошо темперированного строя Баха)?
Систематически подходя к ответу на этот вопрос, необходимо раз-
разложить отношения In 3/In 5 и In 3/In 7 в непрерывные дроби. Для пер-
первого отношения получаем
?§ = [1,2,6,...].
Оборвав непрерывную дробь в правой части на числе 6, приходим к ра-
рациональной аппроксимации
1пЗ ^ 13
1п5 ~ 19'
т.е. З1/13 и 51/19. Это означает, что начальное отношение частот
1,088 ... представляет собой подходящий «полутон» для постро-
150 Глава 3
ения музыкального строя, который дает хорошее согласие, по модулю
тритавы, с нотами, порождаемыми отношением частот 5 : 3. В самом
деле, З6/13 совпадает с -| с точностью до 0,4%!
О
А что можно сказать об отношении частот 7 : 3? Разложе-
Разложение In 3/In 7 в непрерывную дробь дает превосходную аппроксима-
аппроксимацию З1/13 ss 71/23. И снова число З1/13 выступает как предпочтительный
начальный интервал для построения хорошо темперированного строя
Пирса — еще одно счастливое совпадение в теоретико-числовом духе!
Разница между ^ и одной из степеней основания З1/13, а именно, чис-
о
лом З4/13, невероятно мала и составляет всего лишь 0,16%. А отношения
частот снова образуют самоподобную последовательность
^ з1/13 з2/13 33//13
Несмотря на то, что теоретико-числовая основа этого нового му-
музыкального строя практически безупречна, оценить его эстетические
достоинства каждый должен для себя сам1.
1гГот терпеливый слушатель, который выступал в роли подопытного кролика
в музыкальных тестах строя Пирса, упорно отдавал предпочтение сочинениям, на-
написанным в традиционной манере.
Глава 4
Степенные законы — неисчерпаемый
источник самоподобия
Что меня действительно интересует, так
это вопрос, имел ли Господь Бог при сотво-
сотворении мира хоть какой-нибудь выбор?
Альберт Эйнштейн
Подобие не только господствует в планиметрии (о чем свидетель-
свидетельствует предложенное Эйнштейном доказательство теоремы Пифагора,
приведенное в гл. 1), но и лежит в основе значительной части алгебры.
Возьмите однородную степенную функцию
f(x) = cxa,
где с и а — постоянные. При а = 1, например, мы получаем част-
частный случай / (х) = сх, который при с < О описывает восстанавлива-
восстанавливающую силу линейной пружины. При а = — 2 (и по-прежнему отрица-
отрицательном с) наше уравнение становится законом всемирного тяготения
Ньютона f (х) = сх~2. Эти простые степенные законы, во множестве
встречающиеся в природе, являются, в действительности, самоподоб-
самоподобными: если подвергнуть х преобразованию подобия (умножив его на
некоторую константу), то функция f (х) по-прежнему будет пропор-
пропорциональна ха, хотя и с другим коэффициентом пропорциональности.
Как мы увидим в дальнейшем, степенные законы с целочисленными
или дробными показателями представляют собой один из наиболее пло-
плодоносных и изобильных источников самоподобия.
Размеры городов и метеоритов
Количественное распределение многих «разноразмерных» объектов
как функция от их размера подчиняется в широком диапазоне размеров
самоподобным степенным законам. Это утверждение справедливо и для
152
Глава 4
объектов, которые растут (города, например), и для объектов, разби-
разбитых на куски (раздробленные камни) [177]. Единственное непременное
условие для того, чтобы в некотором диапазоне размеров выполнялся
самоподобный закон, — отсутствие у данного вида объектов внутрен-
внутреннего масштаба. (Конечно же, ни в одном городе на Земле число жителей
не бывает меньше 1 или больше 1 000 000 000, и ни один камень на Земле
не может быть меньше атома или больше континента.)
1012
10s
10"
\ I I
Частицы, сталкивающиеся
с космическим кораблем-челноком
1 МКМ
Падающие звезды
1 ММ
етеориты
1 М
Кратер в Онтарио i
10 км
I |
1СГ4 1 Ю-8
Диаметр (м)
Рис. 1. Частота столкновений метеоритов с Землей как функция от диаметра
частиц (по данным Э. Шумейкера, Геологическая служба США).
Один из наиболее безотказных механизмов дробления действует не
на Земле, а в космическом пространстве: средняя частота, с которой
различные виды межпланетных обломков («падающие звезды» или бо-
более крупные метеориты) врезаются в земную атмосферу, обратно про-
пропорциональна квадрату диаметра падающего тела, причем данное со-
соотношение выполняется в диапазоне, охватывающем более 10 порядков
величины (рис. 1). Если частицы диаметром менее 1 мкм бомбардиру-
бомбардируют космический корабль-челнок с частотой 1 частица каждые 30 мик-
Пятое взаимодействие
153
росекунд A012 частиц в год), то метеориты диаметром в 100 м и более
(вроде того, что «вырыл» кратер в Аризоне) ожидаются (слава Богу!)
лишь раз в 104 лет. А очередная «падающая звезда» «астрономического»
диаметра 10 000 м (такая однажды упала на Садбери, штат Онтарио) не
должна столкнуться с Землей в ближайшие 108 лет.
Луис Альварес, о котором мы уже говорили, когда рассказывали
об охоте за подводными лодками во время второй мировой войны (см.
гл. 1, с. 63-63), и его сотрудники использовали данные, представленные
на рис. 1, чтобы подкрепить выдвинутую Альваресом теорию, объяс-
объясняющую внезапное исчезновение динозавров 65 миллионов лет назад.
Согласно Альваресу, причиной явилось падение гигантского метеорита,
которое подняло в воздух огромное количество пыли, закрыв солнеч-
солнечный свет и тем самым лишив динозавров необходимой для выживания
зелени [5].
106
10s -
?10'
104
io3h
ю
1
к
1
\
-
1
1
1
\|
1
\
-
10 100 1000
Длина(мм)
10000
Рис. 2. Число видов сухопутных животных как функция от длины их те-
тела [168].
Говоря о динозаврах, нельзя не вспомнить о распределении разме-
размеров в животном мире. На рис. 2 представлено примерное распределе-
распределение количества видов сухопутных животных как функция от длины
тела животного. И снова мы обнаруживаем степенной закон с показа-
показателем —2, справедливый в диапазоне, охватывающем четыре порядка
величины — от 1 мм до 10 м [168].
Пятое взаимодействие
Один из самых первых законов физики, оказавшийся самоподоб-
самоподобным, восходит к наблюдению Галилея, заметившего, что и большие,
154 Глава 4
и маленькие камни, брошенные с Пизанской башни, падают с одина-
одинаковой (почти) скоростью1. Если пренебречь аэродинамическим сопро-
сопротивлением, то время падения t прямо пропорционально квадратному
корню из высоты h, с которой падает камень, и не зависит от мас-
массы камня: t ~ /i1/2. На справедливость этого закона никак не влияет
масштаб входящих в него величин — почти никак, потому что если
подняться на астрономические высоты (или хотя бы взобраться на вы-
высокую гору), то притяжение Земли станет меньше. Таким образом, су-
существует естественный предел, ограничивающий масштабную инва-
инвариантность или самоподобие галилеевского закона t ~ /i1/2, а именно,
радиус Земли. Здесь можно говорить только о приближенном самоподо-
самоподобии. С аналогичной ситуацией мы столкнемся еще не раз: самоподобие
царит беспредельно, но лишь в ограниченных областях.
И даже только что упомянутый универсальный закон всемирного
тяготения Ньютона (который в полной записи выглядит как / (х) =
= GMx~2, где G — гравитационная постоянная, a f (х) — сила при-
притяжения, создаваемая массой М на расстоянии х от нее) в наши дни
поставлен под сомнение (не дожидаясь появления теории квантовой
гравитации, которая сплавит воедино постоянную Ньютона G с по-
постоянной Планка К). Критический анализ старых экспериментальных
данных по гравитации и тщательно проведенные новые измерения, по-
видимому, обнаружили некую неудовлетворяющую масштабной инва-
инвариантности поправку к закону Ньютона, которую некоторые наделен-
наделенные богатым воображением исследователи окрестили «пятым взаимо-
взаимодействием» (плюс к четырем уже известным взаимодействиям — гра-
гравитационному, электромагнитному и двум ядерным, сильному и слабо-
слабому). Пятое взаимодействие, какова бы ни была его природа (и реально
ли оно) зависит, очевидно, от расстояния х по закону ехр(—х/хс) ¦ х~2,
который не является однородным степенным законом и поэтому не
обладает самоподобием: в него входит характеристический размер —
длина обрезания хс, поскольку экспоненциальная функция требует без-
безразмерного аргумента.
Какой же смысл может иметь пороговая длина хс, порядок величи-
величины которой равен 100 м? В современной физике принято считать, что
силы действуют через посредство частиц-переносчиков с массой по-
покоя h/cxc, где h — постоянная Планка, ас — скорость света. В случае
сил с бесконечным радиусом действия (хс = ос), например, электро-
1В действительности Галилей скатывал шары по наклонным плоскостям, однако
легенда о падающей башне живет с некоторых пор своей собственной жизнью, и ей
нет дела до исторических фактов.
Независимые от естественных масштабов 155
магнитных полей, масса покоя соответствующей частицы равна нулю.
Считается, что именно такую массу имеет частица электромагнитно-
электромагнитного поля, обычно называемая фотоном. Скажем больше, все надежды
на определение верхнего предела массы покоя фотона связаны, в пер-
первую очередь, с отысканием радиуса действия электромагнитного поля.
То же относится и к массе покоя нейтрино — причем если эта масса
окажется отличной от нуля, то потенциальные последствия для общей
массы Вселенной (и ее окончательной судьбы) трудно даже вообразить.
Важность масштабной инвариантности при изменении расстояния
(или, точнее, неинвариантности) была с особой наглядностью про-
продемонстрирована, когда в 30-х годах японский физик Хидеки Юка-
ва A907-1981), размышляя о конечной пороговой длине ядерных
сил (хс ~ 1014 м), пришел к заключению о том, что в природе долж-
должна существовать частица с массой около 240 масс электрона, которую
он назвал мезоном. Немного позже такая частица действительно была
обнаружена (в ливнях частиц, «изливающихся» на Землю из космоса),
но она оказалась всего лишь тяжелой «сестрицей» обычного электро-
электрона; теперь ее называют мюоном (масса мюона в 207 раз больше мас-
массы электронаI. Поиски гипотетического мезона Юкавы продолжались,
и, наконец, он и впрямь был обнаружен, причем масса новой частицы,
получившей название пи-мезон или пион, оказалась равной 270 массам
электрона.
Какая же частица служит переносчиком пятого взаимодействия?
При хс и 100 м масса такой частицы должна быть меньше, чем 10~13
масс электрона, а масса электрона и сама чрезвычайно мала. Возможно,
что видимый радиус действия пятой силы является результатом сло-
сложения двух (или более) новых сил, почти полностью компенсирующих
друг друга. Не исключено также, если учесть подобие масс и послед-
последние экспериментальные данные, что пятого взаимодействия вообще не
существует [255, 25, 118].
Независимые от естественных масштабов
Как мы уже говорили, однородные функции обладают интересным
свойством масштабной инвариантности: при изменении масштаба они
воспроизводят сами себя. Такая инвариантность может пролить свет
на некоторые темные уголки физики, биологии и других наук и даже
помочь объяснить особенности нашего восприятия музыки.
1«А это-то кто заказывал?» — «крылатый» вопрос Исидора Раби A898-1987),
заданный им по поводу новой, абсолютно «никому не нужной» частицы.
156 Глава 4
Масштабная инвариантность обусловлена тем, что однородные сте-
степенные законы не имеют естественных масштабов; в них нет мес-
места характерной единичной мере (такой, как единичная длина, едини-
единица времени или единичная масса). Поэтому такие законы называют
масштабно-независимыми, или, что несколько парадоксально, «истин-
«истинными для всех масштабов». Разумеется, последнее утверждение спра-
справедливо в строгом смысле только для математических моделей. Реаль-
Реальная пружина не растягивается линейно вне зависимости от масштаба
длины: при некоторой характеристической длине растяжения наступа-
наступает разрыв. Даже закон всемирного тяготения Ньютона, если его надле-
надлежащим образом проквантовать, несомненно, породит какую-никакую
характеристическую длину1.
Концепция независимости от масштаба является одной из цен-
центральных тем настоящей книги. Говорят, что (причем первым, кто вы-
высказал это достаточно громко, был Мандельброт) горные ландшафты
интересны только тогда, когда их характерные особенности (скалы,
расщелины, пики и долины) повторяются во многих масштабах длины.
Это касается и музыки: неважно, в каком ключе написано то или иное
произведение — приятным для слуха оно будет только в том случае,
если в нем присутствуют изменения тональности во многих масшта-
масштабах частот и изменения ритма хотя бы в нескольких временных мас-
масштабах. Именно так сочиняли музыку представители семейства Бахов
(И. С. и другие), пусть даже они никому об этом ничего не говорили.
Иоганн Себастьян Бах: композитор, независимый от
масштаба
Когда Иоганн Себастьян Бах A685-1750) сочинял свои Бранден-
бургские концерты, он (несомненно, сам того не ведая) использовал
при выборе нот однородные степенные функции [269]. Спектр мощности
(квадрат амплитуды преобразования Фурье) / (ж) относительных час-
частотных интервалов х между последовательными нотами может быть
аппроксимирован в довольно широком диапазоне однородной степенной
функцией с показателем —1:
/ (х) к, сх
-1
1Гейзенберг провозгласил появление новой постоянной в фундаментальных зако-
законах физики — характеристической длины — более 50 лет назад, но дебют ее так
до сих пор и не состоялся. (Планковская длина (Gfo/c3I/2 fs 10~35 м, «управляв-
«управлявшая» Большим Взрывом, который, возможно, создал нашу Вселенную, — всего лишь
производная величина.)
Иоганн Себастьян Бах: композитор, независимый от масштаба 157
которая называется также гиперболическим законом (потому что ее гра-
график похож на гиперболу). Взяв логарифм от обеих частей равенства,
получим
In/ (ж) = const - In ж,
где х измеряется в полутонах. Таким образом, в двукратно-логариф-
двукратно-логарифмической системе координат (In/ от In ж) данные ложатся на прямую
с наклоном —45°.
0,01 ОД 1 10
Групповая частота (Гц)
Рис. 3. Спектр вариаций амплитуды для Первого Бранденбургского концерта
Баха [269].
Однородному степенному закону следует не только спектр час-
частотных интервалов, но и спектр амплитуд (или мгновенных значений
«громкости») музыки Баха, причем и в том, и в другом случае показа-
показатель оказывается одинаковым (рис. 3). Амплитуду музыки получают
посредством временного сглаживания1 величины давления звука, за-
записанного вблизи оркестра. Интересно отметить, что временная шкала
для амплитуды или вариаций огибающей простирается до 100 с, что
соответствует 0,01 Гц.
¦'¦Искажения результата при сглаживании можно избежать, если воспользоваться
преобразованием Гильберта и вычислить так называемую гильбертову огибающую.
По определению, гильбертова огибающая функции представляет собой огибающую
семейства функций, образующихся при фазовом сдвиге преобразования Фурье дан-
данной функции на все углы в интервале от 0 до 2тг.
158 Глава 4
Почему же Бах придерживался при сочинении музыки простого ги-
гиперболического степенного закона? Прежде всего надо сказать, что ни
Бах, ни бесчисленное множество других композиторов ничего такого
не делали. Создавая музыкальное произведение, композитор стремится
к тому, чтобы оно было интересным для слушателя. Так что, нам следо-
следовало бы спросить: «Почему спектры частотных интервалов и амплитуд
интересных музыкальных произведений (некоторых, по крайней мере)
являются гиперболическими?»
Эстетическая теория Биркгофа
Частичный ответ на вопрос, поставленный в конце предыдуще-
предыдущего раздела, может дать «теория эстетической ценности», предложен-
предложенная американским математиком Джорджем Дэвидом Биркгофом A884-
1944). Суть этой теории сводится вкратце к тому, что произведение
искусства приятно и интересно лишь при условии, что оно не слишком
правильно и предсказуемо и в то же время не таит в себе слишком мно-
много сюрпризов. Переведя сказанное на язык математических функций,
основную идею Биркгофа можно интерпретировать в следующем смыс-
смысле: спектр мощности «эстетической» функции не должен вести себя ни
как утомительно однообразный «коричневый» шум с зависимостью от
частоты /~2, ни как совершенно непредсказуемый белый шум с зави-
зависимостью /°.
В «белом» процессе любое значение переменной величины (напри-
(например, последовательные значения частоты мелодии) совершенно не зави-
зависит от своего прошлого — оно всегда неожиданно (рис. 4А). Напротив,
в «коричневой» музыке (броуновское движение — это тоже «коричне-
«коричневый» шум; см. также сноску на с. 64) только инкременты не зависят от
своего прошлого, в результате чего мелодия получается утомительно
однообразной (рис. 4Б). Очевидно, что большинству слушателей (и не
только во времена Баха) больше понравится такая музыка, в которой
последовательность нот не слишком предсказуема и не слишком неожи-
неожиданна, иначе говоря, спектр, изменяющийся по закону fa, где показа-
показатель а заключен в интервале между 0 и —2. Как обнаружил Рихард
Фосс, показатели, встречающиеся в большинстве музыкальных произ-
произведений, находятся как раз посредине этого интервала: а = — 1, что
дает гиперболический степенной закон J (рис. 4В) [269]. Как сказал
однажды Бальтазаар ван дер Поль о музыке Баха: «Это великая музыка,
потому что она неотвратима [подразумевая а < 0] и вместе с тем не-
Эстетическая теория Биркгофа
159
JJj^
4^
(?)
(fl)
Рис. 4. (А) «Белая» музыка, составленная из независимых нот; (Б) «коричне-
«коричневая» музыка, составленная из нот с независимыми инкрементами по частоте;
(В) «розовая» музыка — частоты и продолжительность звучания нот опреде-
определяются 1//-шумом (розовым шумом) [269].
160 Глава 4
ожиданна [а > —2]». (Я обнаружил это высказывание в захватывающе
интересной автобиографии Марка Каца «Загадки случая» [125].)
На рис. 5Б представлен образец шума с гиперболическим степен-
степенным спектром J. Такие функции известны также под названием розо-
розового шума, потому что они занимают промежуточное положение между
коричневым (броуновским) (/~2) и белым шумом (/°) (см., соответ-
соответственно, рис. 5В и 5А). Поскольку спектр мощности любого шума, под-
подчиняющегося однородному степенному закону (/"), самоподобен, соот-
соответствующая временная диаграмма также должна быть самоподобна.
Действительно, если масштаб вдоль оси частот изменить в г раз, то
по закону взаимности Фурье масштаб вдоль оси времени соответству-
соответствующей временной диаграммы изменится в 1/г раз. Разумеется, в слу-
случае шума (и других вероятностных явлений) самоподобие носит лишь
статистический характер: увеличенный фрагмент не является точной
детерминированной копией формы сигнала до изменения масштаба.
Кроме того, чтобы сохранить мощность при изменении масштаба
частот, амплитуды должны измениться в г~а12 раз. Поэтому, строго го-
говоря, такие стохастические процессы самоаффинны, т. е. имеют более
одного масштабирующего множителя: г для частот (или, что эквива-
эквивалентно, 1/г для значений времени) и г~а/2 для амплитуд.
Вообще говоря, розовый (а также белый и коричневый) шум яв-
является идеальным образчиком статистически самоподобного процесса.
Явления, спектры мощности которых представляют собой однородные
степенные функции1, не имеют собственных масштабов времени и час-
частоты: они масштабно-независимы. Здесь нет таких понятий как харак-
характеристическое время или характеристическая частота: то, что проис-
происходит в одном временном или частотном интервале, происходит при
любом масштабировании времени или частоты. Если такие шумы за-
записать на магнитную ленту и проиграть на различных скоростях, то
звучать они будут одинаково (в отличие от человеческого голоса, ко-
который при проигрывании с удвоенной скоростью становится похож на
голос Дональда Дака). Существуют даже такие самоподобные тоны, ко-
которые звучат ниже при воспроизведении их записи с удвоенной скорос-
скоростью (см. гл. 3, с. 142-144). Мы еще вернемся к разноцветным шумам
и продолжим их исследование в гл. 5.
ХВ оригинале автор дает здесь сноску о многозначности английского слова power
и возникающих в этой связи интересных совпадениях. Действительно, слово power
можно перевести и как «мощность» (power spectrum «спектр мощности»), и как «сте-
«степень» (power law «степенной закон»); среди других его значений «сила», «энергия»,
«власть» и т. д. — Прим. перев.
Эстетическая теория Биркгофа
161
(А)
Рис. 5. Временные диаграммы шумов: (А) белый шум с /°-спектром мощ-
мощности; (Б) «розовый» шум с 1//-спектром; (В) «коричневый» шум с I//2-
спектром.
162 Глава 4
Гиперболический принцип неопределенности
Гейзенберга
Гиперболические законы распространены настолько широко, что
нередко их даже трудно признать, особенно если они записаны в виде
произведения, равного некоторой постоянной. Именно так обстоит дело
со знаменитым соотношением неопределенности Гейзенберга в кванто-
квантовой механике:
Дд • Ар ^ h,
где q и р — две «канонически сопряженные» (в квантовомеханическом
смысле) переменные, например, координата и импульс (или энергия
и время), а Н — постоянная Планка, деленная на 27г.1 Принцип неопре-
неопределенности гласит, что чем меньше погрешность (в смысле статисти-
статистического среднеквадратичного отклонения) при определении одной пе-
переменной, тем больше погрешность при определении сопряженной пе-
переменной. Следовательно, если некто пожелает, в порядке Gedanken-
эксперимента (т.е. мысленного), измерить с очень высокой точностью
положение, скажем, электрона, то для этого ему придется воспользо-
воспользоваться фотонами (частицами света) с очень короткими длинами волн,
т. е. с очень большими импульсами. После того, как фотоны отразятся
от несчастного электрона, его состояние можно будет охарактеризовать
лишь весьма неопределенным импульсом. Последнее утверждение час-
часто формулируют в более качественном виде: «Любое наблюдение воз-
возмущает наблюдаемую систему».
Но как бы его ни формулировали, принцип неопределенности есть
не что иное, как следствие из хорошо известного обратного соотно-
соотношения для преобразования подобия, получаемого из теории Фурье-
преобразований для пары переменных Фурье. (Однако тот факт, что
преобразование Фурье и гильбертовы пространства являются естест-
1«Что это за штука такая, «аш перечеркнутое»?» — спросил недавно шепотом
один из участников физической конференции у соседа. По-видимому, планковско-
му «кванту действия» потребуется больше времени (или энергии), чтобы проник-
проникнуть в общественное сознание. Печально, но это относится и к сознанию некото-
некоторых вполне профессиональных физиков. Многотерпеливая кафедра Гёттингенского
Коллоквиума по общей физике однажды оказалась свидетелем следующего диалога:
некий докладчик заметил (как бы мимоходом), что затвор камеры, прерывая поток
мёссбауэровских гамма-квантов во времени, приводит (ну, разумеется) к расшире-
расширению их энергетического спектра. На что один из специалистов по мёссбауэровской
спектроскопии (!) возразил, что затвор, движущийся поперек пучка квантов, никак
не может изменить их энергию. Что ж, как заметил Ричард Фейнман в 1967 г.: «Ду-
«Думаю, можно смело сказать, что в квантовой механике никто ничего не понимает!»
Гиперболический принцип неопределенности Гейзенберга 163
венными математическими образами для квантовых систем, сам по
себе отнюдь не тривиален. Осознание его говорит о все более глубоком
проникновении человеческого разума в тайны природы.)
Наибольшая возможная точность пор и q достигается, если распре-
распределение обеих переменных соответствует гауссовскому нормальному
распределению вероятностей: в этом случае в предыдущем соотноше-
соотношении имеем знак равенства:
Хотя это соотношение минимальной неопределенности обычно не рас-
рассматривается как гиперболический закон, однако, раз уж оно записано
в таком виде, напрашивается вопрос: какова область его применимос-
применимости? Ответ на этот вопрос является, возможно, одним из самых устра-
устрашающих во всей физике: несмотря на многократные проверки и пере-
перепроверки соотношения Aq ^> Н/Ар в широчайших диапазонах энергии,
времени, координаты и импульса, так и не было обнаружено ни ма-
малейшего его нарушения. У физиков не осталось и тени сомнения в том,
что, подобно относительности, неопределенность имеет абсолютно фун-
фундаментальную природу, не допускающую никаких исключений. Теории
приходят и уходят, но «аш перечеркнутое» всегда остается с нами.
Сам размер атома представляет собой одно из фундаментальных
следствий принципа неопределенности (не будь неопределенности, атом
просто схлопнулся бы в бесконечно малую точку). Вообще говоря, мож-
можно вычислить радиус самого легкого атома, атома водорода, непосред-
непосредственно из соотношения неопределенности: потенциальная энергия ато-
атома U обратно пропорциональна его радиусу. Следовательно, при умень-
уменьшении радиуса величина потенциальной энергии увеличивается. По те-
теореме вириала (см. гл. 2, с. 105-108), это порождает пропорциональное
увеличение кинетической энергии атома Т, а это значит, что атом дол-
должен увеличиться в размерах. Минимальный размер атома (боровский
радиус) ГвоЬг определяется из соотношения неопределенности со знаком
равенства, Ах ¦ Ар = h; нам остается лишь отождествить гвоьг с Ах,
а импульс, соответствующий кинетической энергии, — с Ар. Точные
соотношения для потенциальной и кинетической энергии (U = е2/г4тгео
и Т = р2/2пге, где е и пге — заряд и масса электрона, а ?о — диэлектри-
диэлектрическая проницаемость вакуума) позволяют одним махом, без обычных
трудоемких вычислений, получить правильное значение для боровско-
го радиуса. Этот радиус, называемый также атомной единицей длины,
164 Глава 4
можно представить в виде комбинации четырех фундаментальных фи-
физических постоянных:
4тте0Н2
ГВоЬт =
тее
т.е. 5,3-10 п м. Отсюда, диаметр атома водорода, 2гв0Ьг, равен при-
примерно 1О~10 м, или 1 ангстрему (А).
Впечатляющей иллюстрацией необычайно широкого диапазона,
в котором истинно соотношение неопределенности, может служить
большая длина когерентности лазерного излучения, имеющая важное
значение в голографии и уточнении теории относительности. При от-
относительной неопределенности энергии АЕ/Е = 10~7 «неопределен-
«неопределенность длины» Ах (т. е. длина когерентности) для гелий-неонового лазе-
лазера с длиной волны Л = 630 нм достигает величины Ах = ХЕ/АЕ ¦ 2тг,
т. е. около 1м — макроскопическая длина, которая более чем в 1010 раз
превышает боровский радиус, выведенный из того же самого принципа.
В мёссбауэровской спектроскопии нам приходится иметь дело
с еще меньшими относительными неопределенностями энергии A0~14
и менее), однако принцип неопределенности Гейзенберга остается в си-
силе.
Хотя время когерентности (неопределенность времени) At для ла-
лазерного излучения, составляющее, скажем, около 10~9 с, не слишком
велико, нейтронная спектроскопия производит измерения энергии с не-
невероятно малой неопределенностью АЕ = 2 • 10~36 ватт-секунд (Вт-с),
возможной благодаря макроскопическому времени когерентности для
нейтронных волн E0 с!). И здесь гиперболическое соотношение неопре-
неопределенности выполняется незыблемо, охватывая более 10 порядков вели-
величины.
Вероятно, самым поразительным следствием неопределенности
стало исключение из нашей картины мира понятия «ничто», которое
мы невинно называли вакуумом. Вакуум в его классическом понима-
понимании не содержит ни материи, ни энергии. Но нулевая энергия значит
точно определенная энергия, а это запрещено принципом неопределен-
неопределенности. Поэтому в современном квантовомеханическом вакууме име-
имеются конечные флуктуации энергии, в соответствии с предписаниями
Гейзенберга, — и согласно тому же закону размеры наименьшего атома
в состоянии с наименьшей энергией конечны.
Реальность флуктуации энергии в вакууме стала ныне неотъем-
неотъемлемой частью квантовой физики и повлекла за собой многочисленные
следствия, которые подтверждаются экспериментально с величайшей
Дробные показатели 165
точностью (к числу таких следствий относится, например, сверхтон-
сверхтонкая структура атомных спектров). Существуют вполне респектабель-
респектабельные теории, которые объясняют происхождение Вселенной гигантской
«взбесившейся» вакуумной флуктуацией [101]. Как писал еще в 1550 г.
Томас Кранмер, архиепископ Кентерберийский, «природа не терпит
пустоты».1
Насколько нам известно, область применимости принципа неопре-
неопределенности неограничена. С другой стороны, любой однородный сте-
степенной закон, определяющий энергию как функцию от частоты (такая
функция называется спектром), должен, конечно же, иметь либо верх-
верхний, либо нижний предел (либо оба сразу), за которыми однородная
степенная зависимость перестает выполняться. Белый шум, например,
имеет плоский спектр мощности лишь до некоторой, возможно даже
весьма высокой, частоты. А розовый шум должен непременно иметь и
верхнюю («ультрафиолетовую»), и нижнюю («инфракрасную») частоты
перехода, пусть даже и отдаленные друг от друга, за пределами кото-
которых гиперболический закон нарушается, поскольку в противном случае
полная мощность сигнала (интеграл, взятый по всему спектру) стала бы
бесконечной. (Разумеется, физики все равно пользуются степенными
законами (ведь они так хорошо масштабируются), а потом жалуются
на ультрафиолетовые и инфракрасные «катастрофы».)
Дробные показатели
Степенные законы отнюдь не ограничены целочисленными показа-
показателями, как в случае белого, розового и коричневого шумов. В природе
в изобилии встречаются и дробные показатели. Самоподобию, в конце
концов, все равно, целочисленный у нас показатель или нет. Нередко
дробный показатель содержит важный ключ к решению запутанной
головоломки. Часто дробные показатели законов, описывающих совер-
совершенно разные явления (например, плавление и магнетизм), оказыва-
оказываются похожи, что служит указанием на существование аналогичных
«универсальных» механизмов, лежащих в основе этих явлений.
Простым примером проявления в природе самоподобного закона
с дробным показателем может служить соотношение между плотнос-
1«Naturall reason abhorreth vacuum» — точная цитата, приведенная в «Oxford
English Dictionary» [30]. Не следует путать ее с более современным высказыванием
Джона Робинсона Пирса по случаю рождения транзистора в 1948 г. (он же и крестил
младенца): «Природе отвратительны вакуумные лампы».
166 Глава 4
тью излучения рг и плотностью вещества рт в расширяющейся Все-
Вселенной, существовавшее вскоре после ее рождения:
Из этого простого соотношения Альфер и Герман сумели еще в 1948 г.
вывести нынешнюю плотность излучения во Вселенной [6]. Опираясь
на другие, хотя и неполные, данные, они предсказали существование
излучения черного тела (этого последствия Большого Взрыва, давшего
некогда жизнь Вселенной, а теперь «купающего» ее (точно младенца?)
в «теплом» фоновом излучении), соответствующего температуре око-
около 5 К (т.е. 5° выше абсолютного нуля). Впоследствии Арно Пензиас
и Роберт Вильсон, «настраивая» микроволновые антенны, обнаружили
космическое фоновое излучение (с температурой 2,7 К), и в 1978 г.
были удостоены Нобелевской премии за открытие этого реликтового
«следа» юной Вселенной.
В последующих главах мы поговорим и о других простых степен-
степенных законах с дробными показателями, демонстрирующих масштаб-
масштабную инвариантность с далеко идущими последствиями в самых раз-
разнообразных явлениях реального мира — от разливов Нила до разоре-
разорения игрока и распределения галактик во Вселенной. Вообще говоря, на
удивление часто сложные функции двух и более переменных ведут се-
себя вблизи «критических точек» как простые степенные законы. Напри-
Например, функцию двух переменных / (х, у) очень часто можно представить
в следующем общем виде:
f(x,y)=xag(y/x^,
где функция f(x, у) заменена функцией только одной переменной g.
Для любого интервала переменных, на котором функция g постоянна,
функция / (х, у) приближенно представима простым степенным зако-
законом от х.
Такого рода представление — через степенные законы и их показа-
показатели — оказывается необычайно плодотворным при анализе критичес-
критических явлений от перколяции (см. гл. 15) до ферромагнетизма и сверх-
сверхпроводимости.
Необычное распределение первого знака
В тех случаях, когда самоподобные данные приводятся в числовом
виде, степенные законы, или соотношения вида / (х) ~ ха, приводят
Необычное распределение первого знака 167
к асимметричным, неравномерным распределениям первого (самого ле-
левого) знака этих чисел. При показателе а = — 1 вероятность рт того,
что самая значащая цифра числа равна т > 0, определяется из форму-
формулы
Рт =log(,(l+ Ш
где b — основание используемой системы счисления [201, 207]. Для де-
десятичных данных эти вероятности имеют следующие приближенные
значения: pi = 0,301; рг = 0,176; рз = 0,125; ...; р9 = 0,046. Заметьте,
что р2 + Рз = P\i как и должно быть, потому что цифры 2 и 3 охваты-
охватывают тот же относительный диапазон данных, что и цифра 1.
Приведенные вероятности рт (свидетельствующие в пользу того,
что первая значащая цифра с наибольшей вероятностью равна 1) полу-
получаются при интегрировании функции ха, где а = — 1, от т до т + 1.
При других значениях а такое интегрирование дает
та+1 _ (т + !)а+1
где Ь — снова основание системы счисления, используемой для записи
самоподобных данных. Например, при Ь = 10 и а = — 2 вероятности
оказываются следующими: pi = 0, E); pi = 0, A85); рз = 0,0(925); ...;
р9 = 0, @12345679).
Разумеется, любые реальные данные никогда не бывают в точ-
точности масштабно-инвариантными, хотя бы из-за «концевых эффектов».
Ни в одной настоящей деревне не живет меньше 1 человека или боль-
больше, чем, скажем, 100 миллионов человек (за исключением пресловутой
«всемирной деревни»). Самые последние данные относительно первой
значащей цифры можно найти в работе П. Диакониса [49].
Кроме того, нельзя забывать и о том, что существует огромное
количество немасштабируемых «данных», таких, например, как теле-
телефонные номера или номера машин, к которым наши асимметричные
распределения знаков неприменимы.
Асимметричные распределения чисел (а не знаков) существуют
также в непрерывных дробях. Как показал Карл Фридрих Гаусс A777-
1855), для большинства иррациональных чисел асимптотическая веро-
вероятность того, что некоторый член ап в разложении непрерывной дроби
равен к, определяется выражением
(к + IJ
prob(an = k) = log2 fc , п ->• оо.
168 Глава 4
Исключительные иррациональные числа, такие как золотое сечение j =
= (-у/5 — 1)/2, для которых ап = 1 при любом п, имеют меру нуль.
И снова, как и в случае самоподобных степенных законов, число 1
имеет наибольшую вероятность: prob(an = 1) и 0,415.
В главах 5 и 6 мы рассмотрим взаимосвязь между степенными
законами и статистикой более подробно.
Показатели при поперечных сечениях: деревья,
реки, артерии и легкие
Рассмотрим ствол дерева диаметром d, который разделяется на
две главные ветви с диаметрами d\ и di- Существует ли некоторое
устойчивое соотношение между этими диаметрами по мере того, как
мы продвигаемся от ствола дерева ко все более тонким ветвям вплоть
до черенков листьев?
Леонардо да Винчи считал, что для беспрепятственного движения
соков вверх по дереву, поперечные сечения двух главных ветвей в сум-
сумме должны быть равны поперечному сечению ствола [217]. Иначе гово-
говоря, Леонардо полагал, что d2 = d\ + d\. Его гипотеза выдержала про-
проверку временем и ныне воплощена в «трубчатой модели» биологической
структуры дерева [284]. Трубчатая модель опирается на идеализирован-
идеализированное представление о том, как сок поступает от корней дерева к листьям
по многочисленным неветвящимся сосудам («трубкам»), занимающим
определенную долю сечения каждой ветви.
То же самое соотношение, а именно
dA = d?+d?, A)
где Д = 2, выполняется в месте слияния двух рек (d, d\ и di — ширина
рек). Установлено, что ширина d реки пропорциональна квадратному
корню из количества воды Q, переносимого рекой: d ~ Q0'5 [144]. Од-
Однако глубина реки t, как правило, изменяется в соответствии с зако-
законом t ~ Q0'4. Возникающая разница восполняется за счет увеличения
скорости течения v, которая пропорциональна Q0'1. Иначе говоря, река,
образовавшаяся от слияния двух притоков одинаковой величины и не-
несущая, таким образом, вдвое больший объем воды в секунду, обычно
в 1,4 раза шире каждого из своих притоков, но лишь в 1,3 раза глубже
их. Скорость же течения реки приблизительно в 1,1 раза больше, чем
скорость течения притоков. Разумеется, 1,1 х 1,3 х 1,4 и 2 (с достаточ-
достаточно высокой точностью), как и должно быть, учитывая, что вода при
слиянии никуда не теряется и ниоткуда не добавляется.
Показатели при поперечных сечениях 169
Как однажды заметил Мандельброт, невозможно оценить масштаб
карты, если ширины всех рек нанесены в соответствии с этим масшта-
масштабом. А если изгибы русла реки еще и самоподобны, то на всем своем
протяжении от истока до устья река не дает никаких «зацепок» для
оценки масштаба карты.
И наоборот, сливающиеся или разветвляющиеся дороги, не облада-
обладающие — в отличие от рек — глубиной, должны иметь ширину, удов-
удовлетворяющую соотношению A), где показатель Д = 1, при условии,
что транспортный поток, выраженный в количестве машин, пронося-
проносящихся по одной полосе за минуту, одинаков для всех дорог. Здесь по-
полосы движения играют ту же роль, что и сосуды с древесными соками
в трубчатой модели дерева.
Артерии и вены в сосудистой системе млекопитающих также удов-
удовлетворяют степенному закону A) в диапазоне, охватывающем пример-
примерно 20 бифуркаций от сердца до капиллярных сосудов. Оценки показате-
показателя Д дают значения около 2, 7 [253]. Эта величина выглядит вполне ра-
разумно для результата биологической эволюции, учитывая требование
о том, чтобы артерии и вены доходили до каждой точки тела, нужда-
нуждающейся в питании и избавлении от отходов. Идеальное для этих целей
значение Д = 3, конечно же, недостижимо, так как сосудистая систе-
система, заполняющая все пространство, оставляет слишком мало места для
других задач.
В отличие от сосудистой системы бронхи легкого достигают скей-
лингового показателя, очень близкого к Д = 3, — такое значение пока-
показателя имеет фрактал, заполняющий трехмерное пространство. И дей-
действительно, на протяжении 15 бифуркаций бронхиальное дерево оста-
остается почти самоподобным (рис. 6) [37].
Показатель Д = 3 можно вывести из предположения, что геомет-
геометрия бронхиального дерева определяется требованием минимального со-
сопротивления потоку воздуха во всей бронхиальной системе [256]. Это
требование подразумевает существование постоянного коэффициента
ветвления djd\ = d/d2 = 21/3. Учитывая соотношение A), показатель Д
должен быть равен 3 [276].
Однако Мандельброт привел гораздо более убедительный аргумент,
не требующий внесения коэффициента ветвления djd\ в генетический
код [161]. Он предположил наличие простого самоподобного процесса
роста на пренатальной стадии развития легких: «Рост начинается с поч-
почки. Из почки вырастает трубка, на которой образуются две новых поч-
почки, каждая из которых ведет себя вышеописанным образом».
Итерации по этим правилам образуют структуру легкого в виде
170
Глава 4
..¦» «.
.с.
"•Ч
•-.I,
Рис. 6. Самоподобное бронхиальное дерево [37].
самоподобного дерева. Таким образом, эмпирически наблюдаемое са-
самоподобие достигается не потому, что самоподобная структура опти-
оптимальна, а потому, что оно следует кратчайшей программе управления
ростом: каждая стадия повторяет предыдущую, но в меньшем масшта-
масштабе. Следовательно, геометрия легких полностью определяется двумя
Показатели при поперечных сечениях 171
параметрами: отношением ширина/длина ветвей бронхов и показате-
показателем при диаметре Д. В вышеописанной модели значение Д и 3 полу-
получается просто вследствие того, что большое число бифуркаций должно
заполнить почти все пространство, не вытесняя друг друга.
Глава 5
Шумы: белый, розовый, коричневый
и черный
И лился на землю дождь сорок дней и со-
сорок ночей.
Книга Бытия, гл. 7, стих 12.
Наблюдаемый рост доходов должен спо-
способствовать подъему рынка на новую вы-
высоту.
Э.Ф.ХАТТОН, брокерская фир-
фирма на Уолл-стрит. Из прогноза,
выпущенного 19 октября 1987 г.,
незадолго до катастрофического
падения курса ценных бумаг на
бирже.
Среди многих областей, в которых пышно расцветают самоподоб-
самоподобные степенные законы, весьма и весьма почетное место занимает ста-
статистика. Особую приверженность к простым однородным степенным
законам вида f~@ проявляют спектры мощности (квадраты амплитуд
преобразования Фурье), часто называемые шумами. Среди шумов ши-
широкой известностью пользуется белый шум со спектральным показа-
показателем /3 = 0. Иначе говоря, спектр мощности белого шума не зависит
от частоты. Однако белый шум, т.е. шум с постоянным, или плоским,
спектром мощности, представляет собой удобную абстракцию, так ска-
сказать, небольшую ложь во спасение. Подобно спектру белого света (от-
(отсюда и название — белый шум), спектр белого шума является плоским
только в некотором конечном диапазоне частот. Тем не менее, белые
спектры служат в высшей степени практической цели, позволяя моде-
моделировать бесчисленное множество процессов в широчайшем диапазоне
научных дисциплин. К числу таких процессов принадлежат, в частнос-
частности, инкременты броуновского движения и разные другие инновацион-
инновационные процессы (ученое название для любой последовательности неожи-
неожиданностей и сюрпризов). На членство в этой «бело-шумной компании»
претендуют электронный и фотонный дробовые шумы, тепловой шум
и всякого рода шипящие звуки, издаваемые человеком или животными.
Шумы: белый, розовый, коричневый и черный 173
Проинтегрировав белый шум один раз по времени, мы получаем
«коричневый» шум — нечто вроде проекции броуновского движения на
одно пространственное измерение. Коричневый шум имеет спектр мощ-
мощности, пропорциональный /~2, в довольно широком диапазоне частот.
Некоторые парадоксальные следствия подобных процессов, такие, как
разорение игрока и «пылевидная» структура их изомножеств (множеств
постоянного капитала), мы рассмотрим в гл. 6. Но белый и коричневый
шумы далеко не исчерпывают все спектральные возможности: между
ними располагается розовый шум со спектром J, а за коричневым
спектром маячит черный, пропорциональный f~@, где /3 > 2. На рис. 5
в гл. 4 (с. 161) показаны временные диаграммы белого, розового и ко-
коричневого шумов; на рис. 1 (уже в этой главе) вы видите временную
диаграмму черного шума с /3 = 3.
Рис. 1. Временная диаграмма «черного» шума с /3 = 3.
Оказывается, и розовый, и черный шумы распространены весьма
широко. Розовые процессы возникают во многих физических ситуаци-
ситуациях и находят удивительные эстетические применения в музыке и дру-
других видах искусства.
Черные спектры описывают развитие во времени многих естес-
естественных и противоестественных катастроф, таких как разливы рек,
засухи, рынки с тенденцией к понижению курсов и различные аварий-
аварийные ситуации — например, перебои в подаче электроэнергии. Из-за
своих черных спектров подобные неприятности нередко случаются по
174 Глава 5
нескольку штук кряду. Вот уж действительно, как сказано в «Кораб-
«Корабле дураков» Себастьяна Бранта, «И рек мудрец ... беда в одиночку не
ходит» [18].
Все вышеперечисленные явления имеют одну важную общую чер-
черту: в некотором достаточно широком диапазоне частот их спектры мощ-
мощности представляют собой однородные степенные функции вида f~@,
где C находится в интервале от 0 до 4.
Такие однородные спектры, а также пространственные и времен-
временные сигналы, из которых они получены, демонстрируют простую мас-
масштабную инвариантность: если такой процесс сжать с постоянным ко-
коэффициентом подобия s, то соответствующий спектр Фурье растянет-
растянется1 в 1/s раз. Однако изменение масштаба частот в любое (постоянное)
число раз не изменяет частотной зависимости для степенных спект-
спектров: форму свою они сохраняют. Это можно великолепно продемонст-
продемонстрировать на акустическом примере. Если такой процесс записать на
магнитофонную ленту (надлежащим образом изменив временной мас-
масштаб, чтобы исследуемый сигнал попал в область слышимых частот)
и прослушать с увеличенной или уменьшенной скоростью, то звук не
повысится и не понизится. Звук не изменится совсем, изменится только
громкость! Следовательно, черные спектры самоподобны, а описывае-
описываемые ими процессы статистически самоподобны или самоаффинны.
Розовый шум
Розовый шум, называемый также 1//-шумом, или фликкер-шумом,
обладает одинаковой мощностью в полосах частот шириной в октаву
или в любых постоянных интервалах в логарифмической частотной шка-
шкале. Благодаря этому свойству он находит множество применений. На-
Например, розовый шум является одним из излюбленных тестовых сиг-
сигналов в исследованиях слуха и акустических исследованиях в целом,
поскольку он близок к многим естественным шумам. Розовый шум
обладает также свойством возбуждать на приблизительно равных по
длине участках основной перепонки в нашем внутреннем ухе равные
по амплитуде колебания, тем самым стимулируя постоянное количест-
количество окончаний слуховых нервов, передающих звуковые сигналы в мозг
(см. гл. 3, с. 130- 131). Таким образом, розовый шум представляет собой
психоакустический эквивалент белого шума.
1 Фундаментальное свойство преобразования Фурье, лежащее в основе принципа
неопределенности (см. с. 162-165) и многих других реалий физики, не имеющих
столь красивого названия.
Розовый шум 175
Розовый шум встречается также в самых различных физических
системах, в том числе в полупроводниковых устройствах. Одной из при-
причин вездесущности 1//-шумов является то, что их порождают парал-
параллельные релаксационные процессы, в изобилии встречающиеся в приро-
природе [1]. В релаксационном процессе (представьте себе электроны, запер-
запертые между стенок потенциальной ямы в полупроводнике) запертая час-
частица переходит в возбужденное состояние, в котором и остается в те-
течение экспоненциально распределенного интервала времени с временем
релаксации т. Спектр мощности (т. е. квадрат амплитуды преобразова-
преобразования Фурье) такого процесса Рт (/) есть не что иное, как хорошо нам
знакомая лоренцева резонансная кривая, центрированная на частоте О
(инженер-электрик назвал бы такой спектр характеристикой первого
порядка фильтра низких частот):
|^. а)
Полная мощность Pq релаксационного процесса, т.е. интеграл
от Рт (/) по всему диапазону положительных частот, не зависит от т.
Многие физические, химические или биологические системы име-
имеют не одно релаксационное время т, а целый спектр таких времен,
зависящих от значений энергии потенциальных барьеров Е, которые
в течение некоторого времени удерживают запертую в потенциальной
яме систему в возбужденном состоянии. Отношение между временем
релаксации т и энергией барьера Е — знаменитый закон, названный
в честь Сванте Августа Аррениуса A859-1927) — имеет следующий
вид:
г = тое^г, B)
где Т — абсолютная температура, а к — постоянная Больцмана.
Предположим, что эти энергии равномерно распределены в интерва-
интервале [Ei, E2]. Тогда распределение времени релаксации р(т) может быть
получено из соотношения B) с помощью элементарных правил преоб-
преобразования вероятностей. Оно оказывается гиперболическим по т:
р(т)= кТ -\, Т1^т^т2, C)
где ti,2
Наложение большого числа независимых релаксационных процес-
процессов на спектры мощности типа A) и времена релаксации, распределен-
176 Глава 5
ные по формуле C), приводит к спектру
- arctgB7rM)],
где разность в квадратных скобках, несмотря на несколько громоздкий
вид, практически постоянна в интервале частот
* D)
Здесь необходимо подчеркнуть, что интервал частот D) может быть
очень широким и в многочисленных ситуациях действительно бывает
весьма широк. Допустим, к примеру, что значения энергии потенциаль-
потенциального барьера разделены интервалом шириной 7кТ; тогда T2Jt\ к, 103.
Соответствующие частоты, для которых 1//-закон Р (/) ~ J вы-
выполняется с точностью до 3 децибел (дБ), заполняют в 1200 раз более
широкий диапазон.
Распределения времени релаксации по широким диапазонам зна-
значений наблюдались во многих физических и биологических явлени-
явлениях [161]. Например, падение со временем электрического напряжения
на лейденской банке, одном из самых первых аккумуляторов, не под-
подчиняется экспоненциальному закону с одним-единственным временем
релаксации. Скорее, процесс разрядки лейденской банки имеет гипербо-
гиперболический характер, который подразумевает широкий диапазон времен
релаксации [133]. Утечка внутреннего заряда в вездесущем электрет-
ном микрофоне (современном аналоге лейденской банки) происходит
по сходному закону [235].
Приведем еще один пример. Как установил Джерри Леттвин, зна-
значения времени восстановления нейрона после возбуждения колеблются
в диапазоне от долей миллисекунд до часов и суток. А когда Вильгельм
Вебер по совету Карла Фридриха Гаусса измерил удлинение эластичных
шелковых нитей, используемых в сконструированном им приборе, он
обнаружил, что приложенная нагрузка вызывает не только мгновенное
растяжение, но и устойчивое последействие — непрерывное растяжение
нити, подчиняющееся гиперболическому закону от времени, истекшего
с момента нагружения [132].
Гиперболическое затухание наблюдается даже в концертных за-
залах с недостаточно сильным рассеянием звука. В результате затухание
звука в таких залах не может быть охарактеризовано одним временем
реверберации даже на одной частоте [226]. По-видимому, куда бы мы
Розовый шум 177
ни смотрели или что бы мы ни слушали, мы увидим или услышим,
что экспоненциальное поведение встречается гораздо реже, чем приня-
принято думать.
Позднее мы встретимся еще с одним механизмом гиперболическо-
гиперболического поведения, порождающего широкодиапазонные 1//-спектры. Я имею
в виду перемежаемость, возникающую при касательной бифуркации
в логистической параболе и других итерированных нелинейных отобра-
отображениях. Недавно Т. Гайзель [79] представил на суд публики генератор
типичного 1//-шума в хаотических гамильтоновых системах, этакого
заложника самоподобной иерархии «кантор-торов».
Если генерировать коричневый шум довольно легко (нужно лишь
суммировать независимые случайные числа), то получить розовый
шум несколько сложнее. Сравнительно простой метод генерирования
розового или 1//-шума на компьютере состоит в том, чтобы сложить
несколько релаксационных процессов со спектрами мощности типа A)
(характеристика фильтра низких частот первого порядка) и со значе-
значениями времени релаксации т, образующими самоподобную прогрессию
с коэффициентом подобия 10 (или меньше — для лучшей сходимости).
При таком подходе достаточно всего лишь трех значений времени ре-
релаксации для того, чтобы покрыть частотный диапазон шириной почти
в три десятичных порядка (рис. 2).
Релаксационный процесс с дискретными значениями времени хп
можно задавать с помощью имеющегося в компьютере генератора слу-
случайных чисел, который позволяет получать независимые случайные
числа г„ (нулевой меры), подставляемые затем в рекуррентное соот-
соотношение /- ;г
хп+1 = рхп + V1 - р^гп, х0 = 0.
Здесь р — требуемый коэффициент корреляции между соседними слу-
случайными значениями. С временем релаксации т этот коэффициент свя-
связан соотношением р = ехр( — 1/т). Таким образом, для набора значений
времени релаксации, каждое из которых в 10 раз превосходит пре-
предыдущее (т = 1,10,100,...), коэффициенты корреляции получают-
получаются вычислением последовательных корней десятой степени (т.е. р =
= 0,37; 0,90; 0,99...).
Если не требуется высокая точность, то генераторами случайных
чисел могут послужить три игральные кости: первую кость бросаем
для каждого нового значения розового шума, вторую кость бросаем
через раз, а третью — через три раза на четвертый. Этой остроумно
азартной идеей мы обязаны Рихарду Фоссу [76]. Сумма очков, выпав-
выпавших на всех трех костях, образует случайную величину со средним зна-
178
Глава 5
U
10
1
0,1
0,01
1
р({У
-
-
i
"V
1
1
-
\
1
0,01 0,1 1
Частота / (Гц)
10
100
Рис. 2. Розовый шум, порождаемый релаксационными процессами. Сплош-
Сплошной кривой дано наложение трех релаксационных процессов, штриховой ли-
линией — наложение значений, выпавших на трех игральных костях.
чением 10,5 и дисперсией (мощностью шума) 8,75, что является грубым
приближением розового шума в ограниченном диапазоне частот.
В таком игровом варианте генерации розового шума различные
времена релаксации имитируются тем, что число очков, выпавшее на
каждой из трех костей, сохраняется в течение различного времени
(в нашем случае период времени каждый раз увеличивается вдвое): на
первой кости оно изменяется (или по крайней мере может измениться)
при каждом бросании, на второй кости сохраняется вдвое дольше, на
третьей — в четыре раза дольше. Однако метод трех игральных костей
(штриховая линия на рис. 2) совсем не дает такого же хорошего при-
приближения к 1//-прямой, как метод наложения трех релаксационных
процессов (сплошная кривая на рис. 2).
Самоподобные тенденции на фондовой бирже
Одним из мест, где степенные шумы правят бал, а в головах и бу-
бумагах царит хаос, является Уолл-стрит, США. При покупке и продаже
ценных бумаг и товаров в игру вступает самоподобие во многих мас-
масштабах. Пожалуй, лучшей иллюстрацией этому может служить допу-
Самоподобные тенденции на фондовой бирже
179
щенная мной однажды ошибка: я случайно перепутал график поминут-
поминутных средних колебаний биржевого курса (рис. 3) с графиком ежеднев-
ежедневных флуктуации. Меня бы не удивило самоподобие между дневными,
недельными и месячными ценами, но я никогда не подозревал, что та-
такого же рода флуктуации наблюдаются вплоть до 30-тисекундных ин-
интервалов, о чем свидетельствуют графики, отражающие «поминутные»
колебания биржевого курса.
2680 -
2660 -
12
14и
16и'
Рис. 3. Кривая поминутных средних колебаний биржевого курса очень похо-
похожа на кривую ежедневных колебаний, поскольку процесс изменений бирже-
биржевого курса является самоаффинным.
Разумеется, время от времени в данных о колебаниях биржево-
биржевого курса происходит нехарактерный скачок, такой, например, какой
произошел в октябре 1987 г. (рис. 4), когда компьютеры, ведавшие тор-
торговыми операциями, вдруг впали в неистовство (не по своей вине, ра-
разумеется). Специалисты называют такие скачки цен, помимо прочего,
«инновационными процессами» — хорошенькая инновация; не думаю,
что она утешит несчастного торговца, нетерпеливо ожидающего, ког-
когда его брокер возьмет трубку! Однако после того, как сгладится «оча-
«очарование новизны», флуктуации цен возвращаются к своему обычному
течению.1
1Речевые сигналы, отличающиеся высокой избыточностью (независимо от свое-
180
Глава 5
2800
2600
2400
2200
2000
1800
Ifinn
1
-
-
-
-
_
Л
1
1 1
/I1
1 1
1 1 1
. Ill'
1 l"
,ir
I1
'I'l
1 1 1
1 1 1 1 1 1
1
1
llll 1
III1' "I
|"|l"
lll"|l'
1 1 1 1 1 1
Illll
1
'll||
"l|
1 1
1 1
¦ ¦I
1 1
1 1 1
II ill
И'''/
1 1 1
1 1
-
-
-
'ill l|~
11 'it
-
1 1
Авг.
1986
Окт.
1987
Авг.
1988
Рис. 4. «Обвал» рынка ценных бумаг в октябре 1987 г.
Тенденции и флуктуации биржевых курсов были в свое время чрез-
чрезвычайно подробно проанализированы с точки зрения таких понятий те-
теории информации, как перекрестная энтропия и взаимная информация.
Говорят, что Клод Шеннон, отец теории связи (как он предпочитает
называть теорию информации), обзавелся небольшим состоянием, при-
применяя свою теорию на фондовой бирже. Ныне анализ состояния рынка,
наряду с другими экономическими приложениями энтропийных прин-
принципов, принадлежит к числу наиболее разработанных разделов теории
информации. А поскольку биржевые операции производятся сейчас на
быстродействующих и бездушных машинах, управляемых мгновенной
обратной связью, возникла необходимость в серьезном переосмысле-
переосмыслении правил всеми заинтересованными сторонами: правлением биржи,
аналитиками и незадачливыми инвесторами.
При рассмотрении биржевых курсов в первом приближении можно
счесть, что их реальные уровни складываются под влиянием независи-
независимых приращений. Получающийся в результате «ценовой шум» облада-
обладает спектром мощности, обратно пропорциональным квадрату частоты.
Такие случайные процессы часто называют броуновскими (или корич-
коричневыми) шумами из-за их сходства с броуновским движением — хао-
хаотическим мельтешением взвешенных в воде частиц цветочной пыльцы,
го семантического содержания), также могут быть сведены к инновационным по-
последовательностям (с помощью линейного предсказания по предыдущим выбороч-
выборочным значениям). Затем эти «отходы предсказания» можно подвергнуть квантова-
квантованию и кодировать одним двоичным битом каждые четыре выборочных значения из
речевого сигнала, что составляет 0,25 бита на выборку без потери качества [231].
Обычно речевые сигналы требуют 8 битов на выборку, а при записи на компакт-
диски сигнал кодируется 16 битами на канал.
Самоподобные тенденции на фондовой бирже 181
открытым под микроскопом шотландским ботаником Броуном. (В бро-
броуновском движении инновационный процесс состоит из независимых
толчков, получаемых взвешенными частицами со стороны молекул той
жидкости, в которой они плавают.)
Другим, еще более чистым примером коричневого шума могут слу-
служить флуктуации капитала игрока, для которого роль инновационного
процесса выполняют независимые броски игральных костей. Предполо-
Предположим, что при каждом броске вероятность выиграть 1 доллар равна р
(а вероятность проиграть 1 доллар равна, соответственно, 1— р). Какой
же оптимальной стратегии рекомендует придерживаться теория ин-
информации? Ответ: если ваши шансы на выигрыш не превышают 50%,
то лучше не играть вообще! (Еще один пример того, как наука под-
подтверждает обычный здравый смысл.)
Но как быть и что делать, если р ^ 0, 5? Такая ситуация не столь
нереальна, как может показаться на первый взгляд. Игрок может по-
получить побочную информацию (легальную или нет) о механической
статистике рулеточного колеса. В этом случае теория информации дает
еще один полезный совет: делайте ставку, но не ставьте все свои деньги!
Чтобы максимизировать прирост вашего капитала, ставьте 2р— 1 от тех
денег, что имеются у вас в наличии [127]. В этом случае логарифмичес-
логарифмическая скорость прироста капитала достигнет наивысшего значения, зада-
задаваемого шенноновской информационной емкостью С (р) = 1—Н(р) дво-
двоичного симметричного канала с вероятностью ошибки р. Здесь Н (р) —
энтропия, или энтропийная функция Н (р) = — [р\пр+ A —р) 1пA —р)].
Например, в случае р = 0,6 игроку при каждом запуске рулетки сле-
следует делать ставку в размере 20% от своего текущего капитала. Взяв
логарифмы по основанию 2, мы получим энтропию Н (р) = 0,97 бита на
каждый запуск рулетки и 2е = 1,02. Таким образом, хорошо информи-
информированный игрок может ожидать, в среднем, двухпроцентной прибыли
на каждую ставку, что гораздо больше, чем те облагаемые налогом 2%
годовых, которые без зазрения совести предложил автору один крупный
европейский банк.
Более робкий игрок, ставящий только 5% своего капитала, выиг-
выигрывает в среднем менее 1% на ставку. После 200 ставок его прибыль
составит всего лишь одну десятую выигрыша «оптимального» игрока,
должным образом использующего теорию информации.
И наоборот, жадный игрок, который всегда ставит половину сво-
своего текущего капитала, проигрывает в среднем 3,5% своих денег при
каждом запуске рулетки и, в конце концов, после 200 ставок проиграет
практически все свои деньги (99,9%). Что касается беспечного игро-
182 Глава 5
ка, который каждый раз ставит все имеющиеся у него деньги, полнос-
полностью разорится после, в среднем, двух таких ставок. (См. также гл. 6,
с. 206- 208.)
Броуновское движение содержит несколько весьма тонких статис-
статистических самоподобий, и в последующих разделах и в гл. 6 мы еще
вернемся к броуновской теме, в том числе к азартным играм и к во-
вопросу о построении интересных топографических картин по шуму.
Черные шумы и разливы Нила
Если игрок сочтет, что броуновский шум для него недостаточно
хорош, он может обратиться к процессам со спектром мощности, про-
пропорциональным f~P, где /3 > 2, которые мы назвали черными шумами.
Диффузионный процесс с независимыми приращениями Ах расходит-
расходится, но только как квадратный корень из времени, прошедшего от его
начала:
Чтобы охарактеризовать черные процессы, нам потребуется новая ме-
мера расходимости. И такая мера была предложена Харольдом Эдвином
Херстом A900-1978) [111] и Бенуа Мандельбротом [161].
Величина, о которой идет речь, называется нормированным разма-
размахом R/S и по существу представляет собой размах R {At) данных на
временном интервале At (после вычитания любого линейного тренда),
деленный на стандартное отклонение выборки S(At). Для белого гаус-
гауссова шума отношение R/S при больших At стремится к постоянной.
В некотором смысле и R, и S служат мерой размаха данных, но R «рас-
«рассматривает» данные линейно, a S — после возведения в квадрат. Для
некоторых процессов нормированный размах R/S не дает новой ин-
информации и асимптотически стремится к постоянной, т.е. пропорци-
пропорционален At0. Однако в случае многочисленных геофизических записей,
относящихся к разливам рек, и множества других, столь же мрачных,
данных отношение R/S ведет себя иначе.
Для броуновской функции (спектр мощности которой пропорцио-
пропорционален /~2) величина R/S пропорциональна At0'5, что отражает крою-
кроющуюся за коричневыми процессами долговременную зависимость, на-
называемую устойчивостью. Статистика колебаний уровня воды в Рей-
Рейне (во всяком случае там, где сходятся границы Швейцарии, Фран-
Франции и Германии, недалеко от Базеля) вот уже на протяжении весьма
долгого срока демонстрирует тенденцию к аналогичному поведению
cR/S &At°>55 (рис. 5А).
Черные шумы и разливы Нила
183
100
10 -
1 -
Рейн в
Базеля,
1 1
окрестности п >
1808-1966 „^
.С
s^ и
п
и
<
1 1
10 100
Время
1000
0,1
(Б)
10 100 1000 10000
Время
Рис. 5. (А) Гидрологическая статистика по Рейну. (Б) Колебания минималь-
минимального уровня воды в Ниле [164].
Однако есть и другие реки, не такие смирные и ручные, как
Рейн [164]. Например, минимальные уровни воды в Ниле по записям
за период с 622 по 1469 г. (панически боясь засух, египтяне, должно
быть, весьма усердно вели свои записи на папирусе!) образуют зависи-
зависимость R/S ~ At0'9 (рис. 5Б); показатель 0,9 отражает высокую степень
устойчивости, отмеченную еще в Библии, в душераздирающей истории
Иосифа (книга Бытия, гл. 41).
Показатель Херста, определяемый как Н = ln(R/S)/ ln(At), слу-
служит удобной мерой устойчивости статистического явления. В случае
полного отсутствия устойчивости (белый шум) показатель Н = —0,5,
тогда как при несомненном ее наличии (коричневый шум) Н = 0,5.
184 Глава 5
Интересно, что между показателем Херста Н и спектральным по-
показателем /3 существует простое соотношение: /3 = 2Н+1. Следователь-
Следовательно, «нильский шум» имеет спектр мощности, пропорциональный f~@ =
= /~2'8, что, как и большой показатель Херста Н = 0,9, предполагает
долгосрочную устойчивость, при которой для сдерживания наводнений
и предотвращения разрушительных последствий необходимо сооружать
необычайно высокие преграды (такие, как Большая плотина в Асуане).
Угроза глобального потепления
Процессы с ярко выраженной статистической устойчивостью ста-
ставят перед нами головоломнейшие задачи, и предлагаемые интерпрета-
интерпретации таких процессов часто оказываются неверными. То и дело под-
поднимается крик о нависшей над нами страшной опасности, стоит толь-
только какому-нибудь паникеру столкнуться с данными, которые, на его
взгляд, свидетельствуют о какой-то угрозе, но беспристрастный ана-
анализ, как правило, не обнаруживает ничего более угрожающего, чем ста-
статистический артефакт.
Рассмотрим шум, напоминающий колебания уровня воды в Ниле,
со спектром мощности, затухающим при больших частотах / как /~3.
При малых частотах мы, разумеется, наблюдали бы расходимость
спектра, что означало бы бесконечную энергию процесса. Однако сколь
бы катастрофичными ни были реальные катастрофы, их энергия всегда
конечна. Даже при отсутствии других причин, конечные значения вре-
времени наблюдения Т поставили бы предел возможным эксцессам. Так,
реалистический спектр мощности Р (/) с асимптотической зависимос-
зависимостью /~3, построенный по данным за период Т, мог бы выглядеть сле-
следующим образом:
T4f
P(f) = J—- (f>0).
1 + Г4/4
График этого спектра для периода наблюдений Т = 1 (например, 1 год)
представлен на рис. 6.
А теперь предположим, что наблюдения продолжаются в течение
двух лет. «Новый» спектр мощности, построенный по расширенным на-
наблюдениям, изображен на рис. 6 штриховой линией. Таким образом,
весь этот «роковой» избыток мощности, изображенный на рис. 6 тем-
темным цветом, образуется с помощью простого продления периода наблю-
наблюдений с 1 года до 2 лет.
В качестве примера из реальной жизни можно взять наблюдае-
наблюдаемые на протяжении 50 лет годичные вариации количества животных
Угроза глобального потепления
185
о
о
ж
о
S
1 W
1
0,1
0,01
.001
7=:.'
-
I I
7 = 1
1 1
1
\
\
0,01
0,1
10
Частота
Рис. 6. Зависимость измеренного спектра от времени наблюдения Т.
в большой сухопутной популяции. По данным экологов, флуктуации
за 20-летний период примерно вдвое больше тех, что зарегистрированы
за период наблюдений продолжительностью в 2 года, и это несмотря
на относительную стабильность размера данной популяции в течение
полувека [210].
Поэтому, делая мрачные прогнозы на основе необычайно жаркого
лета 1988 года на Среднем Западе США, не следует забывать о Херсте
и его показателе, равно как и о сильной зависимости экстремальности
величины от продолжительности наблюдений. Вполне возможно, что
«парниковый эффект», выражающийся в глобальном потеплении кли-
186 Глава 5
мата, является суровой реальностью, но для подтверждения этого нам
необходимо набраться гораздо больше терпения (требуемое количество
углекислого газа мы, пожалуй, уже набрали [72, 272]).
С другой стороны, минимальные способные к выживанию популя-
популяции видов, которым грозит вымирание, должны быть значительно мно-
многочисленнее, чем это следует из существующих ныне оценок, основан-
основанных на наблюдениях, производившихся в течение ограниченного вре-
времени [142]. (Относительно других парадоксов, связанных со степенной
статистикой см. гл. 6.)
Дробное интегрирование — современный
инструмент математического анализа
Броуновское движение возникает и при суммировании независи-
независимых приращений. Суммирование (или интегрирование) приращений
преобразует спектр из /° (инновационные процессы) в /~2 (проинтег-
(проинтегрированный процесс). Возникает вопрос: нельзя ли получить с помо-
помощью интегрирования и процессы с /-1? Оказывается, можно, только
прежде мы должны заново изобрести дробное интегрирование, а для
этого нам придется его определить1.
Поскольку интегрирование приводит к умножению спектра мощ-
мощности на /~2, определим полуцелое интегрирование как операцию, кото-
которая умножает спектр мощности на /-1. Относительно сопряженной пе-
переменной Фурье (времени, скажем, или пространственной переменной)
такая операция представляет собой свертку, ядро которой равно обрат-
обратному Фурье-преобразованию функции I/I1/2 • ехр(г'(/> (/)), где </>(/) —
соответствующим образом выбранная фаза.
Вообще говоря, можно определить v-дробное интегрирование через
операцию умножения спектра мощности на f~2v. Соответствующее яд-
ядро свертки пропорционально tv~x [59].
Дробное интегрирование и дифференцирование уже довольно давно
с пользой применяются в квантовой механике и других областях науки.
Теперь они могут, кроме того, послужить удобными средствами для
автоматизированного построения фрактальных ландшафтов и других
самоподобных структур. Хотя вычисление свертки по временной или
1 Поразительно, но факт: как было уже отмечено, Лейбниц размышлял над дроб-
дробными производными и интегралами еще триста лет назад, едва успев заложить ос-
основы традиционного дифференциального и интегрального исчисления. Сдается мне,
что этот поразительный Лейбниц изобрел и канавки под шляпками гвоздей для луч-
лучшего их сцепления с материалом.
Броуновские горы 187
пространственной области может потребовать немалых затрат машин-
машинного времени и значительных объемов памяти, альтернативный подход
(синтез Фурье по заданному спектру) может привести к наложению па-
паразитных (не существующих в действительности) периодичностей на
образующийся в результате построения фрактал.
Броуновские горы
Можно ли обобщить броуновскую функцию В (?) и представить
ее в виде функции двух переменных В {t\,t2I Иначе говоря, мы хо-
хотим воздвигнуть над плоскостью (ii,^) броуновскую гору В (ii,^) так;
чтобы любое сечение такой горы плоскостью, перпендикулярной плос-
плоскости (fi, ?2), было типичной броуновской функцией B(t). Интересно
отметить, что решение этой задачи, как будет показано в следующем
разделе, связано с компьютерной томографией и, что столь же неправ-
неправдоподобно, с получением изображений с помощью вращающихся ци-
цилиндрических линз.
Прежде всего напомним, что функция В (?) имеет спектр мощ-
мощности, пропорциональный /~2. Следовательно, ее амплитудный спектр
пропорционален I/I. В двумерном случае нам необходим амплитуд-
амплитудный спектр, пропорциональный I/I, где / — вектор частот (/1,/г)
с компонентами /i (соответствует «временной» переменной t\) и /2 (со-
(соответствует t-ъ). Длина вектора частот равна |/| = (_ff + /II/2.
Таким образом, один из методов построения броуновской го-
горы В (t), где t — вектор «времени» (?i, ?2)? состоит в том, чтобы взять
достаточно много независимых (одинаково распределенных и случайно
выбранных) точек на квадратной решетке в плоскости частот, умно-
умножить их на |/|-1 и, проделав преобразование Фурье, перевести про-
произведение на временную плоскость. Разумеется, для настоящих гор
«временная» плоскость представляет собой «пространственную» равни-
равнину и измеряется в квадратных километрах.
Альтернативный метод построения B(t) заключается в том, чтобы
начать с выбора независимых точек на временной плоскости и выпол-
выполнить над ними операцию, эквивалентную умножению на I/I на плос-
плоскости частот. Эта эквивалентная операция представляет собой свертку
с обратным преобразованием Фурье функции |/|-1, которое в двух из-
измерениях совпадает с функцией l^l (с точностью до не представляю-
представляющего интереса постоянного множителя). Иначе говоря, функции I/I
и |4|-1 образуют пару Фурье для двумерного преобразования Фурье.
(Другим, более известным случаем, когда функция подобна своему пре-
188 Глава 5
образованию Фурье, является гауссово распределение. Причем для га-
гауссова распределения это подобие сохраняется при любом количестве
измерений.)
Итак, если обозначить через W (t) двумерный массив независи-
независимых, одинаково распределенных и случайно выбранных точек на вре-
временной плоскости, то броуновская гора определяется выражением
B(t)=W(t)*\t\-1, A)
где * означает операцию взятия интеграла свертки. На рис. 7 изоб-
изображен горный ландшафт, полученный таким способом. Другие методы
построения фрактальных ландшафтов и других самоаффинных фракта-
фракталов описаны Рихардом Фоссом [268] и Дитмаром Заупе в книге «Наука
о фрактальных изображениях» [196].
Преобразование Радона и компьютерная
томография
Как продемонстрировал Б. Юлес, получение изображения объекта
в ^-плоскости с помощью вращающейся цилиндрической линзы после
усреднения по времени эквивалентно свертке с функцией l^l [124]. То
же верно и для томографии (здесь для получения изображения исполь-
используется рентгеновское или какое-либо другое отбрасывающее тень из-
излучение) [220]. Преобразование в уравнении A), описывающее эти «рас-
«расплывчатые» методы получения изображений, называется также преоб-
преобразованием Радона. На рис. 8 приведено изображение буквы А, полу-
полученное с помощью вращающейся цилиндрической линзы и усреднения
по времени.
Для того чтобы восстановить резкое изображение W (t) из «раз-
«размытой картинки» B(t), необходимо подвергнуть функцию В (t) об-
обратному преобразованию Радона. Причем мы уже знаем, как это де-
делается. Применим преобразование Фурье к данным функции В (t) (вы-
(вычисления лучше производить на компьютере — ведь это компьютер-
компьютерная томография). Умножим полученный результат на |/|, чтобы со-
сократить множитель |/|-1, и, снова применив преобразование Фурье,
отобразим функцию обратно на плоскость t, в результате чего полу-
получаем резкое изображение W (t). He так уж и сложна эта компьютер-
компьютерная томография, если не вдаваться в ее унылые и смертельно скучные
подробности!
Горы юные и старые
189
Рис. 7. Броуновская гора, полученная с помощью компьютера [161].
Горы юные и старые
Поверхность броуновской горы со спектром мощности |/|~2 име-
имеет размерность Хаусдорфа D = 2,5 [267], поэтому такая гора выглядит
с геологической точки зрения очень молодой: время еще не успело сгла-
сгладить ее многочисленные расщелины и острые пики (рис. 9А).
Для того чтобы наши горы стали более гладкими — такими, напри-
например, как Скалистые горы в Северной Америке (за исключением Гранд-
Тетонс) — их спектр мощности должен спадать быстрее, чем |/|~2.
Хороший правдоподобный горный ландшафт получается при умноже-
умножении массива случайно выбранных точек на плоскости частот на |/|~т,
где 7 > 1- Последующее преобразование Фурье дает горы с фрактальной
размерностью поверхности D = 3,5 — 7- Спектральный показатель /3 =
= 27 в этом случае равен /3 = 7 — 2D.
На рис. 9Б изображен горный ландшафт с Dm = 2,1 и спектром
мощности, пропорциональным |/|~2'8.
Береговая линия многих горных озер (например, на рис. 9А) име-
имеет размерность Хаусдорфа Dc = D — 1. В броуновском случае (/3 = 2)
190 Глава 5
Г
1
Рис. 8. Образ буквы А, полученный с помощью вращающейся цилиндричес-
получаем'Дс = 1,5, а при /3 = 2,8 — Dc = 1,1 (рис. 9Б). Это не-
несколько меньше фрактальной размерности западного побережья Бри-
Британии (Dc ss 1,25).
На рис. 10 показана береговая линия с Dc к, 1,33, построенная
в сосВ'айщщиивлущмидам^рюнгала^ивпряинипайНв. ?-мерное евклидово
пространство, его фрактальная размерность D вычисляется по формуле
Существует также соотношение между D и введенным ранее показате-
показателем Херста Н (см. с. 182- 184). Так как /3 = 2Н+1, мы можем записать
D = Е + 1 - Я.
Поскольку многие образования в природе (например, горы и облака)
имеют фрактальную размерность D и Е + 0,2, то значение показа-
показателя Херста, близкое к 0,8, является превосходным и универсальным
выбором при генерации таких естественных форм. В настоящее время
фрактальные ландшафты, построенные с помощью компьютера, широ-
широко используются при создании художественных и мультипликацион-
мультипликационных фильмов.
Горы юные и старые 191
(А)
(Б)
Рис. 9. (А) Броуновская гора с фрактальной размерностью поверхности 2,5.
(Б) Гора с размерностью 2,1 [268].
192
Глава 5
Рис. 10. Береговая линия с фрактальной размерностью 1,33 [161].
Глава 6
Броуновское движение, разорение игроков
и межгалактическая пустота —
выдающиеся случайные фракталы
Пока законы математики соотносятся
с реальностью, они недостоверны; если
же они достоверны, они никак не соот-
соотносятся с реальностью.
Альберт Эйнштейн
Одна из наиболее плодоносных фрактальных нив — явления, так
или иначе связанные с флуктуациями. Природа просто изобилует са-
самоподобными структурами и процессами, статистическими по свое-
своему характеру; они изучаются самыми различными науками — от рас-
распределения галактик в астрономии до формирования облаков, климата
и погоды в метеорологии; от полимеризации и окисления в химии до
структуры легких и сосудистой системы человека и картин роста мно-
многих растений в биологии; от «языков», мешающих добыче нефти, от
структуры притоков и областей водосбора речных систем и частоты
наводнений в геофизике до собственно физики, где фракталы и статис-
статистическое самоподобие встречаются в броуновском движении, поверх-
поверхностях разлома, мыльных пузырях, коагуляции, перколяции, ограни-
ограниченной диффузией агрегации и диэлектрическом пробое (молния и фи-
фигуры Лихтенберга), не говоря уже о минимумах энергии («долинах»)
в спиновых стеклах и, наконец, в турбулентности.
Космические струны, эти тонкие нити, образовавшиеся, по-
видимому, при рождении Вселенной и потенциально ответственные за
кластеризацию галактик, также проявляют статистическое самоподо-
самоподобие по мере расширения Вселенной [264].
Ввиду столь всеобъемлющей вездесущности статистического само-
самоподобия, неудивительно, пожалуй, что фракталы вторглись даже в храм
искусства. Взяв на вооружение результаты первопроходческого труда
194 Глава 6
Мандельброта и следуя его вполне конкретным предположениям, ху-
художники все чаще стали генерировать горные ландшафты и прочие
«фоны» в видео- и кинофильмах, а также на обычных неподвижных
изображениях, пользуясь компьютерными программами, призванны-
призванными создавать образы самоподобных структур с приятной для глаз ста-
статистикой на любой вкус — говоря «на любой вкус», я нисколько не
преувеличиваю, потому что фракталы обладают прелюбопытнейшими
свойствами во многих масштабах.
В этой главе мы сначала рассмотрим наиболее выдающиеся случай-
случайные фракталы — броуновское движение и некоторые азартные игры.
Укрощение броуновского зверя
Броуновское движение, яркий пример случайного фрактала, впер-
впервые наблюдал в XIX веке шотландский ботаник Роберт Броун A773-
1858); он же в 1827 г. должным образом описал наблюдаемый эффект
как физическое1 явление.
Все было подготовлено для того, чтобы на сцене появилась матема-
математическая физика, и первый свет на сию покрытую мраком тайну про-
пролил не кто иной, как Альберт Эйнштейн в 1905 г. и, чуть позже, Мариан
Смолуховский A872-1917) [189]. Интересно, что когда Эйнштейн впер-
впервые задумался о случайном тепловом движении макроскопических объ-
объектов, он даже не знал наверняка о существовании броуновского дви-
движения.2 Однако он чувствовал, что молекулярное движение непременно
должно иметь какие-то макроскопические проявления и что, наблюдая
их, можно получить подтверждение молекулярной теории теплоты, до-
доказав тем самым существование атомов, имеющих конечные размеры.
Именно такую задачу поставил перед собой Жан Батист Перрен A870-
1942). В 1926 г. он был удостоен Нобелевской премии по физике за свою
1Вряд ли уместно пересказывать здесь те презабавные истории, которые породи-
породила причудливая пляска частиц цветочной пыльцы под микроскопом. Какие только
фантастические интерпретации ни предлагались — от живых молекул, наделенных
свободой воли, до прямого вмешательства сверхъестественных сил. Достаточно ска-
сказать, что когда Броун кипятил, замораживал и вновь нагревал жидкость, частицы
все так же продолжали свою безумную пляску, весьма напоминающую столпотво-
столпотворение на многих современных дискотеках.
2В своей первой статье по данной теме Эйнштейн писал: «Возможно, что рассмат-
рассматриваемое здесь движение идентично так называемому броуновскому движению мо-
молекул. Однако доступные мне источники содержат о последнем явлении настолько
неопределенные сведения, что я просто не смог сформировать о нем никакого мне-
мнения» [57].
Броуновское движение как фрактал 195
работу, посвященную броуновскому движению. Применив к наблюдае-
наблюдаемому под микроскопом движению частиц закон больших чисел, Перрен,
следуя идее Эйнштейна, сумел даже «подсчитать» число молекул в дан-
данном объеме.
Однако на этом перечень головоломных вопросов, связанных с бро-
броуновским движением, далеко не исчерпал себя. На сей раз, по причине
недифференцируемости броуновского движения, головы заболели уже
у математиков; спасение пришло в лице Норберта Винера A874-1964)
и его коллег, разрешивших и эту проблему. С тех пор броуновское
движение известно в математической физике как «процесс Винера» —
в нем в сущности не было ничего нового или неведомого, учитывая,
что к тому времени уже довольно давно были известны функции Вей-
ерштрасса — хорошая математическая модель нигде не дифференци-
дифференцируемых непрерывных функций. Более того, один из величайших умов
XIX века Людвиг Больцман A844-1906) уже тогда осознавал, что су-
существуют физические проблемы, которые лучше всего описываются
недифференцируемыми функциями, и что при должном рассмотрении
подобных проблем такие функции можно было бы уже изобрести1.
Броуновское движение как фрактал
На рис. 1А показано, как выглядит под микроскопом типичная тра-
траектория частицы пыльцы, совершающей броуновское движение. Однако
наблюдаемая картина способна ввести в заблуждение. В самом ли деле
частица между вершинами ломаной движется по прямой? Нет! Может
быть, она движется по кривым? Снова нет! Как же тогда в действи-
действительности движется частица из точки А в точку В на рис. 1?
Сфотографируем движение частицы, увеличив скорость затвора
камеры в 100 раз. Это позволит нам получить в 100 раз больше про-
промежуточных положений частицы между точками А и В. Результаты
такой съемки, увеличенные в 10 раз, представлены на рис. 1Б: прямая,
соединяющая точку А с точкой В, превратилась в 100 прямолиней-
прямолинейных отрезков, каждый из которых имеет (в среднем) такую же длину,
как прямолинейные звенья ломаной на рис. 1А (хотя в действитель-
действительности они в 10 раз короче, так как траектория на рис. 1Б показана
при 10-кратном увеличении).
Движется ли частица между точками С и D на рис. 1Б по пря-
прямой? И на этот вопрос мы снова вынуждены ответить отрицательно.
1В письме Феликсу Клейну A849-1925) от 15 января 1898 г.
196
Глава 6
(А)
(Б)
Рис. 1. (А) Броуновское движение. (Б) Звено АВ траектории броуновского
движения с рисунка (А) при в 100 раз большей частоте наблюдения и 10-крат-
10-кратном увеличении.
Если увеличить частоту наблюдения за движением частицы из точ-
точки С в точку D еще в 100 раз, а затем подвергнуть полученные снимки
Броуновское движение как фрактал 197
10-кратному увеличению, то полученная картина окажется статис-
статистически подобна той, которую мы видим на рис. 1Б. Именно поэтому
мы и называем броуновское движение статистически самоподобным1.
Всякий раз, когда мы увеличиваем пространственное разрешение в 10
раз, число звеньев ломаной увеличивается в 100 раз. В общем случае, ес-
если увеличить пространственное разрешение в 1/г раз, то для того, что-
чтобы построить траекторию, нам понадобится в 1/г2 раз больше звеньев.
Следовательно, размерность Хаусдорфа (см. гл. 1, с. 32-35) для броу-
броуновского движения определяется величиной
lnN(r)
DH = — = 2 A)
1пA/г)
которая по чистой случайности принимает целочисленное значение.
Имея Dh = 2, броуновское движение в двумерном случае могло бы
заполнить плоскость, однако в действительности этого не происходит
из-за множества самопересечений (см. рис. 1А и 1Б). Вообще, для бро-
броуновского движения в двумерном случае (представьте себе ферменты,
блуждающие по поверхности клетки) вероятность возвращения в лю-
любую, сколь угодно малую окрестность произвольно выбранной точки
равна 1. Что касается броуновского движения в трехмерном простран-
пространстве, то, поскольку размерность вложения C) превышает размерность
Хаусдорфа {Dh = 2), вероятность возвращения оказывается меньше I.2
Как мы уже отмечали, у каждого реального самоподобного процес-
процесса должен быть наибольший и наименьший масштаб: нельзя бесконечно
увеличивать или уменьшать масштаб. Однако в случае броуновского
движения диапазон масштабов, в пределах которого сохраняется само-
самоподобие, охватывает много порядков величины — от размеров сосуда
с жидкостью (допустим, 0,1 м) до длины свободного пробега молекул
между столкновениями, которая для малых пробных частиц может до-
достигать 10~9 м. Во многих случаях мы склонны называть объект са-
самоподобным, если его можно масштабировать с коэффициентом подо-
подобия 10 или даже меньше за, скажем, три дискретных шага. Броуновское
1Если говорить более точно, то геометрические фигуры, части которых могут
быть приведены в соответствие со всей фигурой с помощью преобразований подо-
подобия, проводимых по разным направлениям с различными коэффициентами подобия,
называются самоаффинными. Так, броуновское движение статистически самоаф-
финно с коэффициентом подобия, скажем, г по пространственным направлениям
и коэффициентом подобия г2 по временному направлению.
2По-видимому, именно по этой важной причине мать-природа предпочитает про-
проводить многие химические реакции, необходимые для поддержания жизни, не
в трехмерном пространстве, а на поверхностях.
198 Глава 6
же движение выдерживает преобразование подобия с коэффициентом
до 108, причем промежуточные шаги образуют континуум.
Броуновское движение очень близко подходит к недифференцируе-
мым функциям (насколько это вообще достижимо в физике). Как весь-
весьма здраво заметил Больцман в упоминавшемся письме к Клейну (тому
самому, знаменитому своей бутылкой), если бы Вейерштрасс не приду-
придумал недифференцируемые функции (в попытке показать миру, насколь-
насколько сильно может противоречить здравому смыслу нечто, столь невинно
называемое функцией), то физикам (или ботаникам) не осталось бы ни-
ничего другого, как самим изобрести столь необычного математического
зверя.
Много ли молекул в капле жидкости?
Физический закон, лежащий в основе подобия, приводящего к со-
соотношению A), называется уравнением диффузии
x? = 2Dt, A)
где х1 — среднеквадратическое смещение броуновской частицы за вре-
время t. Соотношение A) просто-напросто выражает тот математический
факт, что при сложении независимых случайных длин (с нулевым сред-
средним и распределением, имеющим второй момент) полное расстояние
можно вычислить сложением квадратов отдельных длин и извлечени-
извлечением из этой суммы квадратного корня. Коэффициент пропорциональнос-
пропорциональности в соотношении 1 мы обозначили через 2D, следуя первоначальному
обозначению Эйнштейна.
Так называемый коэффициент диффузии D необходимо соотне-
соотнести с «микроскопическими» переменными (которых, вообще говоря, ни
один ботаник под микроскопом не увидит), а именно со средней длиной
свободного пробега Л и средним временем между столкновениями т.
«Малость подумав», нетрудно сообразить, что соотношение между упо-
упомянутыми величинами имеет следующий вид:
2D = ^г, B)
или, если ввести скорость теплового движения v pa Л/т наблюдаемой
частицы,
2D = v*t, C)
Спектр броуновского движения 199
где v2 — среднеквадратичная скорость. Согласно термодинамическому
равнораспределению энергии,
^=3f, D)
где к — постоянная Больцмана, Т — абсолютная температура и то —
масса частицы.
Среднее время между столкновениями определяется по формуле
E)
vnF'
где п — число сталкивающихся с частицей молекул в единице объ-
объема, a F — поперечное сечение бомбардируемой частицы (которое, как
и масса частицы то, может быть измерено макроскопически).
Измеряя х1 и подставляя соотношения A)-D) в формулу E), мы
получаем возможность определить число молекул п в единичном объ-
объеме. Если результат оказывается конечным (а он и в самом деле коне-
конечен), то и число всех молекул в жидкости конечно. Поскольку известен
и общий вес жидкости, измерение броуновского движения под мик-
микроскопом позволило Перрену определить вес отдельной молекулы. То,
что Эйнштейн смог предвидеть возможность установления конечной
неисчезающей реальности атомов и молекул, является одним из вели-
величайших его вкладов в наше понимание окружающего нас физического
мира (стоя почти наравне с переопределением пространства и времени
в общей и специальной теориях относительности).
Спектр броуновского движения
Каков же спектр мощности броуновской функции В (?), кото-
которую мы определяем как проекцию броуновского движения на одно
пространственное направление в зависимости от времени? Броунов-
Броуновское движение порождается независимыми приращениями (отдельны-
(отдельными столкновениями молекул с частицей) и имеет плоский («белый»)
спектр мощности. Следовательно, сумма, или интеграл, приращений
имеет спектр мощности, пропорциональный /~2. Шумы с такими
спектрами теперь принято называть коричневыми шумами (см. гл. 5) —
что, помимо прочего, указывает еще и на то, что коричневый свет име-
имеет более сильную примесь красного (т.е. низших оптических частот),
чем белый свет.
200 Глава 6
Разорение игрока, случайные блуждания и теория
информации
Другими примерами коричневого шума могут служить колебания
биржевых курсов, выигрышей и проигрышей в других jeux d'hasard1,
а в более общем плане — всякого рода случайные блуждания, обуслов-
обусловленные независимым приращением. Рассмотрим печально знаменитый
пример, известный под названием «разорение игрока». Если при броске
монеты выпадает орел (с вероятностью р), игрок выигрывает 1 дол-
доллар, а если выпадает решка (с вероятностью 1 — р), игрок проигрывает
1 доллар. Капитал игрока как функция от времени (числа бросков) пред-
представляет собой броуновский процесс с фиксированными приращениями,
называемый также процессом Маркова-Винера в честь А.А.Маркова
A856-1922) и Норберта Винера.
Предположим, что первоначальный капитал игрока составляет К
долларов (К — Карл Маркс и «Капитал»). После первого опыта (весьма
удачное слово!) его капитал становится равным либо К + 1 (с вероят-
вероятностью р), либо К — 1 (с вероятностью q = 1 — р). Обозначив вероят-
вероятность окончательного разорения игрока через дк, получим следующее
разностное уравнение
Як = РЧк+i + qqK-i, 0 < К < В, A)
где В — капитал банка, до = 1 и дд = 0.
Такие разностные уравнения могут быть решены с помощью про-
производящей функции цк = zk (или ^-преобразования), которая позволя-
позволяет свести уравнение A) к квадратному уравнению по z (z = pz2 + q),
имеющему (при р ф q) два решения (г = 1 и г = я/р)- Таким образом,
при р ф q и частных решениях дк = 1 и g^r = (q/p)K общее решение
имеет вид
к
или, с «граничными условиями» до = 1 и 9о = 0;
д/р)в - ШК , 10,
qK= в——, рфч- B)
(q/p) - 1
В случае р = q применяем к пределу при р —> 0,5 правило Лопиталя
и получаем для вероятности окончательного разорения игрока следую-
1Jeux d'hasard (фр.) — азартные игры. — Прим. перев.
Крах здравого смысла в случайных испытаниях 201
щее простое выражение:
удовлетворяющее при р = 0,5 необходимой симметрии, т. е. цк +
+ Чв-к = 1- Разумеется, окончательное разорение небогатого игрока,
чей капитал К мал по сравнению с капиталом банка В почти неизбеж-
неизбежно1: qK ~ 1.
Крах здравого смысла в случайных испытаниях
Рассмотрим один из нескольких бросающих вызов здравому смыс-
смыслу фактов, связанных с бросанием нефальшивой монеты. Он заключа-
заключается в том, что в среднем 1 раз за игру игрок сможет увеличить свой
капитал на G долларов, прежде чем ему придется впервые изъять не-
некую сумму из первоначальной, причем величина G может быть сколь-
сколько угодно большои.1 Переведем сказанное на более понятный язык —
при ставке в 1 доллар игрок, бросая монету, сможет увеличить свой
капитал до 1000000 долларов в среднем один раз, прежде чем проиг-
проиграет какую-либо сумму (т. е. прежде чем его капитал станет меньше,
чем был до начала игры). Единственное утешение для банка состоит
в том, что ожидаемый выигрыш в конечном счете равен 0. (Как было
показано в предыдущем разделе, для неограниченной во времени игры
вероятность того, что игрок проиграет весь свой капитал, составляю-
составляющий К < В долларов, равна 1 — К/В, а вероятность разорения банка
равна К/В.)
Еше один, столь же фантастичный результат, связанный с продол-
продолжительностью честной игры Dk, можно получить при решении раз-
разностного уравнения, напоминающего по своей структуре уравнение A):
DK=K(B-K).
Иначе говоря, если у игрока имеется один-единственный доллар,
а в банке — миллион долларов, то ожидаемая продолжительность иг-
игры составит 999999 бросков монеты! Как станет ясно из дальнейшего,
столь поразительные заключения связаны с тем, что хотя обращения
к некоторому заданному капиталу в неограниченной (В = оо) игре,
хКак это ни удивительно, но один профессор-статистик, имени которого я назы-
называть не буду, оказался не в состоянии вывести формулу для вероятности разорения
игрока в конечной по продолжительности игре. Вывод этой формулы он предложил
в качестве упражнения своим студентам в начале летнего семестра 1948 г. На про-
протяжении всего семестра он повторял на каждом занятии: «А этим мы займемся на
следующей неделе». Так и не занялись.
202 Глава 6
происходят с вероятностью 1, они имеют структуру канторовых мно-
множеств с фрактальной размерностью 1/2.
Только что описанные удивительные результаты весьма характер-
характерны для несмещенных случайных блужданий, наиболее ярко выража-
выражаемых так называемым законом арксинуса. Сформулированный в тер-
терминах дискретного случайного блуждания диффундирующей частицы
в одном пространственном измерении, закон арксинуса гласит: веро-
вероятность р2П Bfc) того, что за временной интервал от 0 до 2п частица
проведет 2k единиц времени на положительной полуоси, определяется
по формуле [70]
H) \ n H J TT[k(n -
Это распределение вероятности сосредоточено в основном вблизи к — О
и к = п (подобно распределению амплитуды синусоиды, осциллирую-
осциллирующей между своими экстремальными значениями; на этом распределе-
распределении основана голография колеблющихся тел с усреднением по времени).
Закон арксинуса, получивший свое название потому, что интегра-
интегралом уравнения A) является арксинус, имеет много любопытных след-
следствий. Например, при честной игре вероятность того, что из 20 бросков
каждый игрок выиграет 10 раз (по-моему, достаточно честно) составля-
составляет лишь около 6%. Вероятность же того, что один из игроков выиграет
все 20 бросков (а вот это уже совсем нечестно!) превышает 35%! Ина-
Иначе говоря, более чем в одной трети всех игр выигрывает только один
игрок!
Еще немного пищи для размышлений
о справедливости
Еще один «нечестный» результат вполне честной игры с монетой
заключается в следующем. Рассмотрим 2п бросков, в половине из ко-
которых выпали орлы (а в половине — решки). А 2к пусть обозначает
количество раз, когда общее число всех выпавших орлов превышало об-
общее число всех выпавших решек. Тогда число возможностей 7V2n Bfc)
такого исхода определяется «числом Каталана»
которое не зависит от к.1
1Хотя числа Каталана, возможно, недостаточно широко известны, встречаются
они поистине на каждом шагу. Например, JV2n — это число способов, которыми 2п
Петербургский парадокс 203
Такого рода несоответствия со здравым смыслом неоднократно
приводили к ложным выводам в истории науки вообще и статисти-
статистики в частности. В 1876 г. сэр Фрэнсис Гальтон A822-1911), изобрета-
изобретатель доски Гальтона (своего рода факирского ложа для шариков), зани-
занимался исследованием некоторых данных о растениях, предоставленных
ему еще более знаменитым Чарльзом Дарвином A809-1982). Всего бы-
было выбрано 15 растений, подвергшихся обработке, и 15 необработанных
растений (контрольная группа). Упорядочивая данные, Гальтон обна-
обнаружил, что в 13 из 15 случаев подвергшиеся обработке растения опере-
опережают необработанные растения с тем же порядковым номером. Вполне
понятно, что Гальтон признал обработку эффективной, однако так ли
это? Предположим, что все измерения выбраны совершенно случайно
C0 измерений из одной и той же группы растений). Тогда вероятность
обнаружения Гальтоном положительных последствий обработки состав-
составляет 3/16. Иначе говоря, в 3 случаях из 16 абсолютно неэффективная
обработка выглядит чрезвычайно эффективной. Сколько неверных от-
ответов и ошибочных умозаключений было почерпнуто из одного только
этого источника «статистических преступлений»!
Петербургский парадокс
Азартные игры успели породить множество парадоксов, чаще все-
всего связанных с противными здравому смыслу аспектами случайных
блужданий и их внутренней фрактальной природой.
Около 1700 г. Николас Бернулли A687-1759), племянник Якова
A654-1705) и Иоганна Бернулли A677-1748), придумал любопытную
азартную игру с бесконечными средними выигрышами (пожалуй, не-
нетрудно предугадать точку зрения банкиров на подобные забавы). Игру
Николая Бернулли проанализировал другой Бернулли1, Даниил A700-
1782), на страницах «Комментариев» Санкт-Петербургской Академии,
печатного органа, в котором были опубликованы многие работы Эйле-
Эйлера.
Предположим, что монета выпадает вверх орлом с вероятнос-
вероятностью р > 1/2. Игрок бросает монету до тех пор, пока орел не выпадет
в первый раз. Если это происходит на п-м броске, то игрок выигры-
людей, сидящих за круглым столом, могут обменяться попарно рукопожатиями так,
что их руки при этом не пересекутся. Множество интереснейших сведений о числах
Каталана приведено в статье Эгглтона и Гая [56].
1На рис. 2 проведена параллель между многочисленными представителями слав-
славного рода Бернулли и вывеской типичной американской адвокатской фирмы.
204
Глава 6
T5O
5EE-
Рис. 2. Бернулли, Бернулли, Бернулли и К0 [98] (©1991 Sidney Harris). Под-
Подпись под рисунком гласит: «Какой Бернулли вам нужен — Бернулли по гид-
гидродинамике, Бернулли по дифференциальному исчислению, Бернулли по гео-
геодезическим, Бернулли по большим числам или Бернулли по теории вероят-
вероятности?»
вает 2™ долларов. Каков же будет его ожидаемый выигрыш W, ес-
если игра может продолжаться неограниченно долго? Ответ достаточно
Угадывающая машина Шеннона 205
прост: W = 2°p + 21(l-p)p + 22(l-pJp + ..., A)
ИЛИ Г)
W = Р
1-2A- р)
Например, при р = 0,55 ожидаемый выигрыш составит W = 5, 5 дол-
долларов, а при р = 0,51 — W = 25,5 долларов.
А что произойдет, если играть «честно»? При р = 1/2 геометри-
геометрическая прогрессия A) не сходится, а ожидаемый выигрыш становится
бесконечным! Стало быть, по справедливости, платой за игру должна
стать бесконечно большая первая ставка (так, по крайней мере, мог бы
рассудить раздраженный банкомет).
Однако благоразумный игрок, помимо того, что он «временно» не
располагает бесконечным капиталом, мог бы счесть бесконечный сред-
средний выигрыш, который сулит ему соотношение A), не совсем честным,
и предпочел бы основывать свою ставку на конечном медианном вы-
выигрыше, составляющем всего лишь один доллар. Банкомету и игроку
никогда не стать друзьями — слишком различны ставки!
Каким же образом среднее значение может так сильно отличаться
от медианного? Ответ состоит в том, что при р = 1/2 среднего значения
даже не существует, а то, что не существует, не может от чего бы то
ни было отличаться.
Расходящиеся средние выигрыши напоминают о бесконечной дли-
длине фрактальной кривой, и, действительно, как мы убедимся в последу-
последующих разделах, петербургский парадокс может быть укрощен с помо-
помощью введения фракталов и размерностей Хаусдорфа.
Угадывающая машина Шеннона
Не все азартные игры честны, и меньше всего, пожалуй, те, ко-
которые провозглашают свою честность громче других («Я не жулик!»).
Но некоторые игры и не претендуют на честность. Более того, самим
своим существованием они обязаны тому, что нечестны. Такова, на-
например, занимательная «угадывающая машина» Клода Шеннона [237].
Это хитроумное изобретение Шеннона в начале игры несколько
раз случайным образом выбирает сторону монеты, в то время как
соперник-человек делает ставки. Сразу после первого своего выигры-
выигрыша машина приступает к анализу «стратегии» оппонента на глубину до
двух бросков «монеты». Ставит ли человек на другую сторону моне-
монеты, если исход предыдущего броска оказывается для него неблагопри-
неблагоприятным? Продолжает ли игрок ставить на решку, если решка выпала
206 Глава 6
в двух предыдущих бросках? Или он из осторожности предпочтет сде-
сделать следующую ставку на орла? Большинство людей выбирает такие
стратегии подсознательно, но машина Шеннона исходит из допущения,
что человек действует, как марковский процесс второго порядка. Без-
Безошибочно вскрывая глубинные переходные вероятности и используя
их, машина Шеннона всегда выигрывает в длинной серии бросков за
исключением того случая, когда ей приходится играть против своего
создателя. Шеннон, постоянно отслеживая внутреннее состояние маши-
машины, может выиграть у нее 6 раз из 10. Разумеется, кто угодно может
выиграть у машины в среднем 5 раз из 10: нужно лишь делать ставки
случайным образом (например, в самом деле бросая монету). Но именно
этого и не делают люди (очевидно, по причине отсутствия необходимых
«шариков»), в чем нас снова и снова убеждает машина Шеннона, выиг-
выигрывая у множества самых различных людей-претендентов на победу.
По-видимому, есть нечто противное человеческому разуму в длинных
сериях однотипных исходов, которые выглядят вполне естественно в ис-
истинно случайных последовательностях.
Конечно же, у машины также бывают полосы неудач, в особеннос-
особенности на стадии начального угадывания. Однажды я хотел продемонстри-
продемонстрировать проницательность машины Шеннона одному своему иностран-
иностранному знакомому (математику Фрицу Хирцебруху), посетившему Bell
Laboratories. Так уж получилось, что Хирцебруху удалось выиграть
13 раз подряд, прежде чем он впервые проиграл. Однако затем машина
Шеннона отыгралась с лихвой: она обогнала знаменитого математика
на 31-м броске (т.е. машина выиграла в 16 из 18 последующих брос-
бросков)! и после этого уже не уступила ему, хотя Хирцебруху и объяснили
(в общих чертах) принцип работы машины.
Классическая механика рулетки и пропускная
способность канала по Шеннону
Если угадывающая машина Шеннона нечестна изначально (в пол-
полном соответствии с замыслом своего создателя), то многие на первый
взгляд честные азартные игры можно превратить в нечестные. Огром-
Огромные состояния (а иногда и жизни) были «спущены» за рулеточным
столом игроками, делавшими ставки в соответствии с причудливой
смесью «абсолютно надежных» стратегий. В конце концов банк всег-
всегда остается в выигрыше, так как даже при игре с «равными шансами»,
шансы банкомета относятся к шансам игрока как 19 к 18 (а на столах
с двумя «зеро», распространенных в американских казино, как 20 к 18).
Классическая механика рулетки 207
И все же автор этой книги, заядлый любитель понаблюдать за про-
происходящим в игорном зале, был склонен думать, что простая — класси-
классическая, а не квантовая — механика вкупе с быстрыми вычислениями
в реальном времени, могут несколько улучшить его шансы на выиг-
выигрыш. Облачившись в новенький с иголочки смокинг и вооружившись
несколькими спрятанными в карманах хронометрами, он отправился
в поход по самым известным казино мира — в Баден-Бадене в Шварц-
Шварцвальде («отце» Монте-Карло), Бадене близ Венского леса и Эвиан-Ле-Бен
на Женевском озере. Эти полевые исследования, предпринятые в нача-
начале 60-х годов, подкрепили выводы, сложившиеся у меня в результате
экспериментирования с настоящей рулеткой, устроенной по всем пра-
правилам в подвале моего дома: в момент, когда некий усредненный кру-
крупье объявляет: «Rien ne vas plus!» («Ставки больше не принимаются!»,
«Nichts geht mehr!»), окончательное положение шарика уже не является
совершенно непредсказуемым; распределение вероятностей здесь дале-
далеко не равномерно. Больше того, глубина модуляции амплитуды вероят-
вероятности по окружности рулеточного колеса обычно составляет около 10%.
Таким образом, вместо того, чтобы проигрывать в среднем 19 из 37
«равношансовых» ставок, можно выигрывать примерно 20 ставок из 37.
В некоторых казино шансы клиента на выигрыш еще выше. Например,
в Эвиане, где крупье за одним столом по небрежности запускал колесо
так медленно, что шарик, свалившись с верхнего круга, падал прямиком
в лунку, где и оставался, не подпрыгнув ни разу ни в ту, ни в другую
сторону.
Чтобы пожать обещанные плоды, необходимо прежде определить
коэффициенты трения для шарика и колеса (обычно очень малые)
и ввести эти параметры в небольшой портативный вычислитель.
(В свое время мы с приятелем построили для этой цели специализи-
специализированный аналоговый компьютер. Теперь, четверть века спустя, при
необходимости направить фишки на игорном столе в нужную для вас
сторону вы вполне можете положиться на цифровые компьютеры [20].)
Нажатием двух клавиш вы передаете компьютеру данные о времени
двух последовательных прохождений шарика и «зеро» вращающегося
колеса мимо некоторой заранее выбранной отметки на ободе рулетки.
Эти данные позволяют определить скорости и относительные положе-
положения колеса и шарика. (О трении мы уже позаботились заранее.) После
вычисления наиболее вероятный исход сообщается игроку через моди-
модифицированный слуховой аппарат.
Как же максимизировать ожидаемую скорость прироста капита-
капитала игрока, если известно, что вероятность выигрыша р больше, чем
208 Глава 6
один из двух (т.е. р > 0,5)? Какой долей капитала следует рисковать
при каждом запуске рулеточного колеса? Ответы дает теория инфор-
информации (вообще говоря, азартные игры — это одно из первых ее при-
приложений). В превосходной работе, о которой мы уже упоминали (гл. 5,
с. 181-182), Джон Л.Келли-младший [127] доказал следующее утвержде-
утверждение: чтобы максимизировать скорость увеличения капитала, необходи-
необходимо ставить Bр — 1) от текущего количества денег. При р ^ 0,5 следует,
разумеется, полностью воздержаться от игры в рулетку и найти себе
другое времяпрепровождение. При соблюдении упомянутого условия
ожидаемый (экспоненциальный) рост капитала определяется коэффи-
коэффициентом 2е (р\ где С (р) — пропускная способность по Шеннону двоич-
двоичного симметричного канала с вероятностью ошибки р:
Например, при р = 0,55 игроку следует при каждом запуске рулеточ-
рулеточного колеса рисковать долей своего капитала, равной 2р — 1, или 10%,
и ожидать скорости обогащения 2е (°>55) = 0,005, или 0,5%, за каждый
запуск. (Это означает, что за один уик-энд, сделав 138 ставок, игрок
может удвоить свое состояние — за вычетом чаевых и налогов).
Описанное выше применение теории информации было первым
(и, насколько мне известно, все еще остается единственным) приме-
примером того, какую пользу можно из нее извлечь, не прибегая к трудоем-
трудоемкому кодированию, необходимому для реализации обещанной теорией
Шеннона безошибочной передачи информации.
Много ли я выиграл, придерживаясь своей системы? По правде го-
говоря, когда я убедился, что классическая механика (так же, как и мой
аналоговый компьютер) работает, у меня пропал всякий интерес к про-
проекту. Кроме того, я знал, что в любом казино всякого, кто «слишком
много» выигрывает, могут без всяких объяснений выдворить из свя-
священных залов. И наконец, стоит лишь администрации казино ознако-
ознакомиться с научными основами нашего метода, как тотчас же последу-
последует распоряжение крупье запускать рулетку чуть быстрее и объявлять
«Rien ne vas plus!» чуть раньше. И все — волшебный сон развеется, рай
будет утерян.
Скопления разорений и галактик
Некоторые весьма простые статистические правила порождают
случайные последовательности точек, называемые точечными процес-
процессами, в которых наблюдаются неожиданно большие пустоты, облада-
Скопления разорений и галактик 209
ющие статистически самоподобной структурой. Хорошим тому при-
примером может служить распределение галактик во Вселенной: пустоты
между самыми большими скоплениями галактик лишь в несколько раз
меньше размера всей Вселенной. Пустоты между галактиками, в свою
очередь, сравнимы по размеру со скоплениями галактик и т. д. С ана-
аналогичной структурой мы встречаемся и в азартных играх (в «рассто-
«расстояниях» между последовательными разорениями) и в многочисленных
других явлениях, заполненных «дырами». Рассмотрим честную азарт-
азартную игру, в которой вероятность выиграть или проиграть иену рав-
равна р = 0, 5. Текущий капитал К (t) игрока в ходе игры может изме-
изменяться так, как показано на рис. ЗА: он обладает тенденцией к сдви-
сдвигу в сторону больших положительных или отрицательных значений,
но в конце концов возвращается к 0. (Разорившемуся игроку, растра-
растратившему весь свой капитал, разрешается продолжать игру в кредит).
Коль скоро капитал упал до 0, то вероятность того, что он в течение
короткого промежутка времени еще раз достигнет нулевой отметки, по
очевидным причинам очень высока. Иначе говоря, нули «капитальной»
функции К (t) образуют скопления.
500
04)
5000
Рис. 3. (А) Капитал игрока в честной азартной игре как функция от времени.
(Б) Флуктуации капитала игрока на протяжении длительного времени.
Что еще можно сказать о функции К (?)? Других масштабов, кроме
величины шага по оси времени (At = 1) и прироста капитала (АК = 1),
в интересующей нас задаче нет. Поэтому мы ожидаем, что разорение
игрока обладает самоподобием и самоаффинностью. Действительно, ес-
если построить график функции К (t) на большем интервале времени при
210 Глава 6
подходящем выборе масштабов по осям t и К, то новый график (рис. ЗБ)
будет сильно напоминать старый. Подходящим коэффициентом подо-
подобия для К является квадратный корень из коэффициента для t, как
и в броуновском движении.
Число ожидаемых нулей 7V0 во временном интервале t также про-
пропорционально квадратному корню из t [70]: Nq рй t1!2. При увеличении
временного интервала в 4 раза число разорений возрастет только в 2 ра-
раза (звучит неплохо!).
Какова вероятность р (z) того, что расстояние между последова-
последовательными нулями будет равно zl Поскольку в задаче при бесконечных
ресурсах капитала нет ограничения на масштаб, функция р (z) для про-
продолжительных игр должна стремиться к самоподобному степенному
закону:
р (z) ss const • za, I <C z ^ t.
Так как величина 7V0 пропорциональна i1/2, ему же пропорциональ-
пропорционально и среднее расстояние между последовательными нулями z = t/N0.
При Ж ?s const • ta+2 ~ t1!2 получаем а = —3/2 и, асимптотически,
p(z) и const-z~3/2, 1 « z ^ t.
Отсюда выводится кумулятивное распределение длин свободных от ну-
нулей отрезков, длина которых превышает z:
t
Р (z)=^p{k) к const-z-1'2. A)
k=z
Это распределение имеет очень длинный хвост, который, по мере воз-
возрастания расстояния между последовательными нулями, очень медлен-
медленно спадает к нулю. На рис. 4 представлены экспериментальные резуль-
результаты (полученные с помощью карманного калькулятора), подтвержда-
подтверждающие соотношение A) в диапазоне, охватывающем более пяти порядков
по величине.
На рис. 5 показана структура свободных от нулей областей —
«пустоты внутри пустот внутри пустот». Примерно половина каждо-
каждого «скопления нулей» не содержит на деле ни одного нуля! В пределе,
при непрерывной шкале времени, нули образуют весьма разреженное
облако пыли — канторово множество с размерностью Хаусдорфа, рав-
равной взятому с противоположным знаком показателю в уравнении ку-
кумулятивного распределения A): Dh = 0,5. Эту величину можно так-
также получить из значения Dh = 2, 5 для поверхности броуновских гор
Полеты Леей в космическом пространстве
211
Расстояние между нулями г
Рис. 4. Распределение временных промежутков, в течение которых не про-
происходит разорения игрока.
(см. гл. 5, с. 189). Вертикальное сечение такой горы представляет со-
собой броуновский «профиль» с Dh = 1, 5, соответствующий нашей функ-
функции К (t). Еще одно сечение — линией К = О — порождает наше нуле-
нулевое множество (т.е. множество тех значений t, при которых К (t) = 0),
с Dh = 0, 5. В общем случае понижение топологической размерности
фрактала на единицу при образовании нулевого множества сопровож-
сопровождается уменьшением фрактальной размерности также на единицу. На-
Например, броуновские горы с поверхностью, обладающей размерностью
Хаусдорфа Dh = 2, 2, порождают береговые линии (т. е. линии нулево-
нулевого возвышения над уровнем моря) с Dh = 1,2, близкой к размерности
Хаусдорфа для западного побережья Британии.
Полеты Леви в космическом пространстве
Существует еще один способ генерировать такие точечные процес-
процессы, как нулевое множество игрока, и обобщать их на более высокие
размерности — так называемые полеты Леви [161]. В полетах Леви
(названных так в честь французского математика Поля Леви A886-
1971)) мы «сшиваем» независимые приращения («траектории полета»),
212
Глава 6
27,854 47,272
64,464
1
Рис. 5. Временные промежутки без разорения игрока (показанные тонкой
линией) присутствуют в любом масштабе.
длины которых z распределены (кумулятивно) согласно однородному
степенному закону:
Р (z) = const •
A)
где D оказывается размерностью Хаусдорфа для получающейся в ре-
результате «пыли». В случае одной пространственной размерности и D =
= 0,5 формула A) описывает «пустоты» в кривой разорения игрока.
На рис. 6А вы видите двумерный изотропный полет Леви с показа-
показателем D = 1, 26, при котором вероятность появления крупных пустот
больше, чем при D = О,5. Точки поворота, т. е. «галактики», порожден-
порожденные этим процессом, показаны на рис. 6Б. При D = 1, 26 сходство с рас-
распределением галактик во Вселенной (каким его видит земной наблю-
наблюдатель) поражает воображение [101]. Из этого мы, разумеется, можем
сделать вывод о том, что наша Вселенная представляет собой канторову
пыль, не имеющую никаких естественных масштабов, кроме попереч-
поперечника самой Вселенной. Однако лучше всего подходящий для галактик
и их скоплений, похожих на мыльные пузыри, показатель D = 1,26 до
сих пор не получил должного объяснения. Упорно не поддается разре-
разрешению одна загадка — из тех, что касаются эволюции Вселенной —
Полеты Леви в космическом пространстве
213
(A)
(Б)
Рис. 6. (А) Двумерный полет Леви. (Б) Соответствующее скопление «галак-
«галактик».
214 Глава 6
таинственная роль темной материи, в том числе черных дыр и (на дру-
другом конце шкалы масс) вездесущих, но неуловимых нейтрино.1
Парадоксы вероятностных степенных законов
Распределения вероятности, описываемые самоподобными степен-
степенными законами, могут иногда приводить к весьма парадоксальным
следствиям. Рассмотрим случайную величину 1 ^ х < оо с вероят-
вероятностью того, что она превысит данное значение х на x~D. Условная
вероятность того, что при х > хо случайная величина превосходит
значение х, равна (xo/x)D.
При D > 1 среднее существует и равно D/(D — 1). Условное среднее
при х > Хо выглядит, на первый взгляд, достаточно невинно:
х - XqD A)
Как и следовало ожидать для случая самоподобного распределения,
условное математическое ожидание линейно зависит от хо-
Предположим теперь, что значения времени, необходимые для за-
завершения какой-то работы (например, для написания сложного до-
доклада), распределены согласно степенному закону с показателем, ска-
скажем, D = 1,5. Тогда ожидаемое время, необходимое для завершения
работы, составит D/(D — 1) = 3 часа, дня или любых других единиц
времени. Здраво рассуждая, если мы начали некую работу 5 дней на-
назад и не закончили ее, то время, необходимое нам сейчас для окончания
этой работы, окажется значительно меньше 3 дней — в конце концов,
мы же собирались сделать ее всю за 3 дня. Как бы то ни было, из фор-
формулы A) следует, что теперь, через 5 дней после начала работы, ожи-
ожидаемое время ее завершения составляет 15 дней. Если по истечении 60
дней после начала работа все еще не будет завершена, то ожидаемое
время ее окончания составит уже 180 дней! Иначе говоря, чем доль-
дольше ведется работа над каким-нибудь проектом, тем более отдаленной
становится дата ее окончания.
1Давно ожидающие решения вопросы, связанные с распределением квазизвезд-
квазизвездных объектов («квазаров») на дальних окраинах Вселенной, недавно были объяс-
объяснены эффектами гравитационной линзы, образованной темной материей, которая
окружает галактики, находящиеся на «переднем плане» [13]. Этот оптический эф-
эффект, предсказанный некогда Эйнштейном (Эйнштейн, впрочем, полагал, что он не-
ненаблюдаем), может еще оказаться наиболее четким «отпечатком» темной материи.
(Способность гравитационной линзы порождать множественные изображения мож-
можно сравнить с оптическими свойствами ножки бокала: если смотреть сквозь ножку,
изображение двоится.)
Инвариантные распределения: Гаусс, Коши ... кто следующий? 215
Так ли уж парадоксально последнее утверждение? Отнюдь: как по-
показывает человеческий опыт, наш старый добрый человеческий опыт,
многие проекты страдают именно из-за таких «убегающих» сроков их
завершения. Если говорить кратко, то подобная работа либо выполня-
выполняется быстро, либо не выполняется никогда. Хотя нельзя не удивиться
тому, что эту всеобщую загадку удается так просто смоделировать
с помощью самоподобного степенного закона. Пожалуй, было бы разум-
разумно разработать классификацию таких «затяжных» работ по их харак-
характеристическим показателям D и в соответствии с нею назначать нера-
нерадивым исполнителям зарплату. При D = 2 разность хХо — xq равна xq,
что характерно для пресловутых работ, завершение которых вечно от-
откладывается а тапапа1.
Инвариантные распределения: Гаусс, Коши ... кто
следующий?
Сумма двух гауссовых случайных величин является гауссовой слу-
случайной величиной. Поэтому принято говорить, что гауссово распределе-
распределение инвариантно относительно сложения. Дисперсия <т2 суммы гауссо-
гауссовых случайных величин равна сумме дисперсий этих величин (а2 и а2):
2.
A)
Инвариантность гауссова распределения тесно связана с централь-
центральной предельной теоремой теории вероятности. Теорема эта утверждает,
что надлежащим образом нормированная сумма большого числа неза-
независимых случайных величин с конечными дисперсиями сходится к га-
гауссову распределению.
Для правила суммирования A) гауссово распределение является
единственным распределением, инвариантным относительно сложения.
Однако, если ввести некоторый общий показатель D и заменить стан-
стандартные отклонения а (возможно, расходящиеся) какой-нибудь другой
мерой s ширины распределения, существование которой гарантировано
(например, интерквартильным размахом), то вместо соотношения A)
мы получим более общее правило
s^ = sf+sf. B)
Существуют ли распределения, инвариантные относительно сложе-
сложения с показателем D, отличным от 2? Существуют, причем они связаны
1А mafiana (исп.) — на завтра. — Прим. перев.
216 Глава 6
с самоподобными степенными распределениями, с которыми мы встре-
встречались в предыдущих разделах.
Для показателя D = 1 инвариантным распределением оказывается
колоколообразная плотность Коши
Р(х)= ..]_ 2,, C)
7ГA + X )
функциональная форма которой совпадает с формой резонанса интен-
интенсивности («резонансной линией») линейного осциллятора как функции
от частоты.
С распределением Коши, названным в честь французского матема-
математика Огюстена Луи Коши A789-1857), связано несколько заслужива-
заслуживающих внимания парадоксов. Оно не имеет первого момента и диспер-
дисперсии, поскольку соответствующие интегралы расходятся. Следователь-
Следовательно, нам не остается ничего другого, как характеризовать распределение
Коши с помощью его медианы и интерквартильного размаха. Напом-
Напомним, что медианой называется значение х, при котором распределение,
проинтегрированное от х до +оо, равно 1/2, т.е. применительно к рас-
распределению Коши,
откуда медиана равна 0. Интерквартильный размах есть разность
двух значений х, при которых величина Р (х) равна, соответственно,
3/4 и 1/4. Для распределения Коши C) интерквартильный размах ра-
равен 2.
Преобразование Фурье (так называемая характеристическая функ-
функция) распределения Коши C) имеет вид симметричной экспоненциаль-
экспоненциальной функции ехр(—1?|). (Раз уж мы признали, что распределение Коши
имеет форму резонансной линии, появления экспоненциальной функции
следовало ожидать, так как амплитуда колебаний линейного резонатора
убывает экспоненциально.)
Поскольку сложение двух случайных величин означает свертку их
распределений вероятностей или произведение их преобразований Фу-
Фурье, то очевидно, что преобразование Фурье суммы двух переменных,
распределенных по формуле C), запишется как функция ехр(—2|?|). Та-
Таким образом, соответствующая плотность вероятности будет такой же,
как и плотность, задаваемая формулой C), но с осью абсцисс, растя-
растянутой в 2 раза. Обобщая, можно сказать, что ширина s распределения
Инвариантные распределения: Гаусс, Коши ... кто следующий? 217
суммы двух случайных величин Коши равна сумме ширин распределе-
распределений слагаемых:
S = Si + 82-
Итак, для распределения Коши показатель D в соотношении B) дей-
действительно равен 1. Причина такого линейного поведения заключается
в том, что преобразование Фурье распределения Коши убывает экс-
экспоненциально, а при умножении двух экспоненциальных функций их
аргументы складываются линейно.
В результате такого линейного скейлинга распределение средне-
среднего значения N одинаково распределенных случайных величин Коши
совпадает с исходным распределением. Следовательно, усреднение слу-
случайных величин Коши не улучшает оценку, т.е. не дает никаких пре-
преимуществ. Этим распределение Коши резко отличается от остальных
распределений вероятности с конечной дисперсией <т2, для которых
усреднение по N случайным величинам уменьшает неопределенность
в 1/y/N раз. Такое нестандартное поведение распределения Коши явля-
является следствием медленно убывающих «хвостов», порождающих слиш-
слишком много «выбросов», которые отнюдь не способствуют получению
стабильного среднего.
Мы настоятельно рекомендуем читателю самостоятельно убедить-
убедиться в парадоксальном поведении распределения Коши, моделируя усред-
усреднение случайных величин Коши с помощью микрокалькулятора или
домашнего компьютера. В общем случае, случайную величину с про-
проинтегрированным распределением Р (х) можно получить из случайной
величины и, равномерно распределенной в интервале [0,1] (генераторы
таких величин имеются во многих калькуляторах), с помощью обраще-
обращения уравнения и = Р(х). Подставляя в его правую часть определение
величины Р (х) из соотношения D), получаем «рецепт»
х = tg[7r@, 5 - и)]
преобразования равномерно распределенной случайной величины и
в случайную величину Коши х.
Распределение Коши встречается в многочисленных практичес-
практических ситуациях. Например, отношение двух независимых одинаково
распределенных случайных величин с нулевым средним распределено
по Коши. Иначе говоря, для любого двумерного изотропного распре-
распределения р(х, у), центрированного в начале координат, отношение х/у
(или у/х) распределено по Коши. Из этого утверждения также следует,
218 Глава 6
что если какая-либо случайная величина распределена по Коши, то и об-
обратная ей величина распределена по Коши. Распределение логарифма z
случайной величины Коши также симметрично: l/(irchz). (Эта функ-
функция играет важную роль в некоторых разделах физики. Например, све-
световые лучи с профилем 1/ chz во времени или пространстве приводят
к солитонам в оптических волокнах. Профиль скорости звука в океане,
изменяющийся по закону 1/ chz в зависимости от глубины, приводит
к самофокусировке и тем самым к возможности передачи акустичес-
акустической энергии на межконтинентальные расстояния с малыми потерями.)
Как мы уже знаем, то, что показатель D в соотношении B) для рас-
распределения Коши равен единице, непосредственно следует из того фак-
факта, что преобразование Фурье распределения Коши представляет собой
экспоненциальную функцию (ехр(—\t\j) с линейной зависимостью аргу-
аргумента от переменной Фурье t. Аналогично: показатель D для гауссова
распределения равен двум, так как преобразование Фурье гауссова рас-
распределения есть экспоненциальная функция (ехр(—t2)) с квадратичной
зависимостью от переменной Фурье t. Следуя Коши, мы можем предпо-
предположить, что обратное преобразование Фурье функции ехр(—1^1"°) при-
приведет к случайной величине с инвариантным относительно сложения
распределением, имеющим некоторый показатель D. Так оно и есть
в диапазоне 0 < D ^ 2. (В случае D > 2 приведенный выше «рецепт»
Коши дает отрицательные значения вероятности, что есть verboten1.)
Милое нашему сердцу гауссово распределение с D = 2 предстает
здесь перед нами как крайний случай (пусть даже и весьма распро-
распространенный) из целого клана распределений. Это означает, что вместо
одной центральной предельной теоремы мы получаем много таких те-
теорем: в зависимости от показателя скейлинга D из соотношения B)
надлежащим образом нормированная сумма случайных величин будет
сходиться к тому или иному предельному распределению, инвариант-
инвариантному относительно сложения случайных величин.
Например, при D = 1/2 инвариантное распределение принимает
вид
Это есть не что иное, как плотность вероятности того, что
функция броуновского шума B(t) с нулевым начальным значением
(т.е. 5@) = 0) снова обратится в нуль в интервале х ^ t ^ х + dx.
1Verboten (нем.) — запрещено. — Прим. перев.
Инвариантные распределения: Гаусс, Коши ... кто следующий? 219
То, что показатель скейлинга D случайной величины, распределен-
распределенной по закону E), равен 1/2, очевидно непосредственно из распределе-
распределения, проинтегрированного от х до +оо, что дает Р (х) = ег1A/\/2ж).
Интерквартильный размах s = 9,12 этого распределения может быть
получен из таблиц интеграла ошибок [115]. Поскольку преобразование
Фурье функции р(х) E) имеет вид ехр(—l^1/2), добавление двух не-
независимых случайных величин изменяет переменную Фурье t на 4?,
а значит, и случайную величину х на ж/4. Интерквартильный размах
для суммы двух случайных величин при этом оказывается равен 4s =
= 36,5. Таким образом, среднее двух независимых случайных величин
такого рода имеет интерквартильный размах вдвое больший, чем раз-
размах каждой случайной величины в отдельности. В общем случае, сред-
среднее значение N независимых случайных величин, распределенных по
закону E), имеет ширину в N раз большую, а не в l/\/N раз мень-
меньшую, как в стандартных случаях. Неудивительно, что такую статис-
статистику иногда называют нестандартной — хотя в мире гораздо больше
нестандартной статистики, чем хотелось бы многим невинным мудре-
мудрецам.
При больших х распределение р (х) из соотношения E) пропор-
пропорционально ж~3/2, а проинтегрированное распределение пропорциональ-
пропорционально ж/2, т.е. x~D. Последнее утверждение допускает обобщение:
для всех инвариантных распределений, отличных от гауссова, проин-
проинтегрированное распределение асимптотически пропорционально x~D,
где D — показатель из соотношения B). И наоборот, поскольку нам
уже известно (см. с. 211), что полеты Леви с проинтегрированными
распределениями, удовлетворяющими степенному закону x~D, порож-
порождают фрактальные множества с размерностью Хаусдорфа D, мы уви-
увидим в показателе D из соотношения sD = sf + sf самую что ни на
есть «добропорядочную» фрактальную размерность для этой геометри-
геометрической реализации распределения. Заметим лишь, что показатели D не
всегда имеют смысл фрактальной размерности.
Глава 7
Канторовы множества: самоподобие и
арифметическая пыль
Eine Menge stelle ich mir vor wie einen Abgrund.
(Множество, по моему представлению, подобно бездне.)
Георг Кантор
(около 1888 г.,
цитир. по Эмми Нетер)
В этой главе мы продолжим наше знакомство с одним из наибо-
наиболее важных источников самоподобия — канторовыми множествами.
Первоначально построенные для чисто абстрактных целей, канторовы
множества впоследствии превратились в почти идеальные модели для
огромного числа явлений реального мира — от странных аттракторов
в нелинейных динамических системах до распределения галактик во
Вселенной.
Уголок канторова рая
Большинство чисел в континууме не мо-
может быть определено с помощью конеч-
конечного набора слов.
Марк Кац
Посреди жарких споров, происходивших в XIX столетии вокруг
основ математики (и затрагивавших самый смысл понятия числа), Ге-
Георг Кантор A845-1918) вознамерился продемонстрировать своим кол-
коллегам некое множество, состоящее из чисел, заключенных в интервале
от 0 до 1. Это множество имело нулевую меру (т.е. пущенная наугад
«стрела» вряд ли «поразила» бы какой-либо из его элементов), но в то
же время содержало так много чисел, что могло бы с полным правом
называться несчетным, как множество всех вещественных чисел меж-
между 0 и 1.
Многие математики, в том числе и сам Кантор (в течение некото-
некоторого времени), сомневались, что такое «безумное» множество вообще
Уголок канторова рая 221
может существовать1 — тем не менее, оно существует, причем про-
процесс его построения весьма прост. Представьте себе отрезок прямой
от 0 до 1 (начертите его мелом на доске, если уж вам так хочется)
и сотрите открытую среднюю треть, т.е. интервал от 1/3 до 2/3, ис-
исключая концы — точки 1/3 и 2/3. Затем сотрите открытую среднюю
треть в каждом из двух оставшихся отрезков, и так далее ad infinitum.
Результат первых семи стираний средней трети представлен на рис. 10
в гл. 1 (с. 41). Изобразить же окончательный результат, который Ман-
дельброт удачно назвал канторовой пылью [161], не представляется воз-
возможным. Действительно, пустоты в канторовой пыли присутствуют во
всех масштабах2: сколь бы сильное увеличение ни давал наш «мик-
«микроскоп» для рассматривания канторова множества, мы увидим только
пустоты (иначе говоря, во всем единичном интервале от 0 до 1 нет ни
одного сплошного подынтервала, сколь бы малым он ни был, а лишь от-
отдельные изолированные точки). Ни одно из канторовых чисел не может
похвастаться тем, что имеет в качестве непосредственного соседа дру-
другое канторово число. Канторова пыль совершенно разрывна, и в то же
время бесконечно делима, подобно континууму. Древних греков, оче-
очевидно, весьма позабавило бы то обстоятельство, что в данном случае
между разрывным (например, состоящим из атомов) и бесконечно де-
делимым не существует фундаментальной антиномии или философского
противоречия — канторова пыль представляет собой и то, и другое.
Формально канторово множество определяется как вполне разрыв-
разрывное, замкнутое и совершенное. Вполне разрывным называется множес-
множество, не содержащее ни одного интервала и, следовательно, не имеющее
внутренних точек. Замкнутым называется множество, которое содер-
содержит все свои граничные элементы. (Граничным называется элемент
множества, содержащий в любой своей сколь угодно малой окрестнос-
окрестности элементы как принадлежащие, так и не принадлежащие данному
множеству). Совершенным называется непустое множество, совпадаю-
1О нелегком жизненном пути Георга Кантора, возникновении и постепенном при-
признании его теории множеств можно прочесть в новой замечательной книге «Георг
Кантор» [205]
2Выражение во всех масштабах, как мы уже отмечали, отражает одну из главных
особенностей самоподобных структур. Например, кластеры при перколяции в кри-
критической точке (см. гл. 15) существуют во всех масштабах размера, а магнитные
домены в спиновых стеклах существуют во всех масштабах длины. Разумеется,
применительно к реальным физическим системам — в отличие от простых мате-
математических моделей — слово «всех» в выражении «во всех масштабах» надлежит
понимать с некоторыми оговорками. Например, в случае перколяции размеры клас-
кластеров лежат где-то между размером отдельного «атома» и размером всего образца.
222 Глава 1
щее с множеством его предельных точек. Множество, получающееся
в результате стирания средних третей — первоначальное канторово
множество — удовлетворяет всем трем условиям, т.е. оно вполне раз-
разрывно, замкнуто и совершенно.
Хоть канторово множество и противоречит здравому смыслу,
существует изящное теоретико-числовое описание канторовой пыли,
а именно, описание с помощью троичных дробей (т.е. дробей, в записи
которых используются только цифры 0, 1 и 2). Например, запись 0,5 =
= 1/3 +1/9 +1/27+... соответствует дроби 0,111... в троичной систе-
системе. Подобно представлению чисел в десятичной системе, запись числа
в троичном виде не является однозначной. Например, дробь 1/3 можно
записать либо как 0,1, либо как 0,0B), где двойка в скобках означа-
означает бесконечную последовательность двоек. Одним из способов придать
однозначность представлению чисел в троичной системе может стать
запрет конечных дробей. Т.е. записывать 1/3 в виде 0,1 «противоза-
«противозаконно» — вам придется воспользоваться записью 0,0B).
Для того чтобы сделать запись троичных дробей однозначной, при-
примем следующее соглашение: условимся не использовать представления
дробей, в которых вслед за единицей идут одни только нули или двойки.
Т. е., дробь 1/3 = 0,1 следует представлять в виде 0,0B), а дробь 2/3 —
в виде 0,2 (но не 0,1B)).
В рамках этого соглашения все числа в открытом интерва-
интервале A/3, 2/3) — это те числа, которые в троичной системе имеют пер-
первым знаком после запятой единицу. Стирая их на пути к построению
канторовой пыли, мы оставляем нетронутыми числа, троичная запись
которых начинается либо с 0,0, либо с 0,2.
Аналогично, вторым стиранием (третья «строка» на рис. 10 в гл. 1),
мы исключаем все числа, в которых единица стоит на втором месте
после запятой (в троичной записи). В конце концов, уже получив кан-
торову пыль, мы увидим, что все оставшиеся у нас троичные дроби
являются «правильными», т.е. единицы в них нет ни на каком месте,
например, 0,0B); 0,2; 0,2002 и 0,B002).
Элементы канторова множества образуют самоподобное множес-
множество в следующем смысле: возьмем любую строку на рис. 10 в гл. 1,
отбросим правую половину и увеличим оставшуюся часть в три раза.
У нас получится предшествующая строка (расположенная непосредст-
непосредственно над той, с которой мы производили все манипуляции). Выража-
Выражаясь более точно, канторово множество инвариантно по модулю 1 отно-
относительно преобразования подобия с коэффициентом 3. В троичной сис-
системе счисления такое преобразование представляет собой всего лишь
Уголок канторова рая 223
сдвиг запятой на один знак вправо и отбрасывание любой двойки, кото-
которая при этом выходит за запятую. Например, канторово число 0,202202
отображается в другое канторово число 0,02202.
Троичная система счисления позволяет легко понять, почему кан-
канторово множество имеет меру нуль: вероятность того, что случайно
выбранная дробь в интервале [0, 1] не содержит в своей троичной за-
записи ни одной единицы, разумеется, равна нулю. Более точно, вероят-
вероятность того, что п троичных знаков после запятой не содержат ни одной
единицы, равна B/3)™. При п —>¦ ос эта величина стремится к нулю.
Троичная система счисления помогает, кроме того, показать, что
никакие два канторовых числа не могут быть непосредственными со-
соседями. Например, к канторову числу 0,2 ближе всего канторово чис-
число 0,20...002. Удлиняя последовательность нулей в этом «соседнем»
числе, мы можем подойти сколь угодно близко к 0,2, однако между 0,2
и, скажем, 0,20002 всегда есть неканторовы числа, например, 0,200012.
Возникает вопрос: как же доказать, что элементы столь сильно
разреженного множества, как канторово, все же настолько многочис-
многочисленны, что даже не поддаются счету. (Заметим здесь, что целые, рацио-
рациональные и даже алгебраические иррациональные числа счетны.) При-
Причина несчетности заключается в том, что мы можем поставить эле-
элементы канторова множества, хоть оно и сплошь изрешечено дырами,
во взаимно однозначное соответствие со всеми вещественными числа-
числами, заключенными в интервале [0, 1]. Дабы совершить сей подвиг, мы
с каждым канторовым числом отождествим двоичное число, получаю-
получающееся заменой в данном канторовом числе всех двоек на единицы. На-
Например, канторову числу 0,020222 поставим в соответствие двоичную
дробь 0,010111 (= 23/64). Действуя таким образом, мы отобразим каж-
каждый элемент канторова множества в некоторое вещественное число и,
наоборот, каждое вещественное число, заключенное между 0 и 1, может
быть отображено в некоторое канторово число. Тем самым мы доказы-
доказываем, что мощность множества канторовых чисел совпадает с мощнос-
мощностью множества вещественных чисел.
Хорошо известный ныне факт, что вещественные числа образуют
несчетное множество, был доказан Кантором с помощью так называе-
называемого диагонального метода, известного еще Галилею. Кантор использо-
использовал диагональный метод в непрямом доказательстве, которое приведено
ниже.
Предположим, что все вещественные числа, заключенные между
0 и 1, образуют счетное множество. Тогда их можно выписать одно за
другим, так чтобы они составили перечисляющую последовательность.
224 Глава 7
Например, в десятичной системе счисления наш перечень мог бы вы-
выглядеть так:
0,91971...
0,29216...
0,36638...
0,55389...
Чтобы запись дробей в десятичной системе счисления была одно-
однозначной, условимся использовать только бесконечные дроби. Например,
десятичную дробь 0,5 будем записывать в виде 0,499999
Запишем теперь число, первая цифра которого после запятой отлич-
отлична от первой цифры первого числа в приведенном выше списке, вторая
цифра отлична от второй цифры второго числа и т. д. Во избежание
неоднозначности мы не будем при заменах использовать цифры 0 и 9.
Получившееся в результате замен число, скажем,
0,88578...,
не значится в списке, так как от каждого стоящего там числа оно от-
отличается по крайней мере в одном знаке. Следовательно, наш список не
полон, и допущение о том, что вещественные числа образуют счетное
множество, ложно.
Существует несколько способов доказать, что рациональные чис-
числа, напротив, счетны. Мне особенно нравится следующее доказательст-
доказательство [218]. Запишем рациональное число в виде т/п, где тип — взаимно
простые целые числа. Пусть т = р^р^2 ¦ ¦ -ре^ и п = q^q^2 ¦ ¦ ¦ q{' — раз-
разложения чисел то и и в произведения степеней простых чисел. Тогда
интересующая нас считающая функция для рациональных чисел при-
принимает вид / A) = 1 и
f(fTl\ _
J\~n) ~
_ 2ei 2e2 . 2е* 2^-1 2/2-1 „2/е-1
~ Pi Pz •¦• Рк (h (h •¦• Qe
Эта функция однозначно обратима. Например, рациональное число 2/3
стоит на двенадцатом месте в списке рациональных чисел, а восемна-
восемнадцатое место занимает рациональное число 3/2.
Еще одно, совершенно неинтуитивное следствие канторовой теории
множеств заключается в эквивалентности двумерных областей и одно-
одномерных линий. Два множества называются эквивалентными, если меж-
Канторовы множества как множества инвариантные 225
ду ними существует взаимно однозначное соответствие. Например, еди-
единичный квадрат (двумерная область) и единичный отрезок прямой (ли-
(линия) эквивалентны: каждой точке единичного квадрата соответству-
соответствует одна и только одна точка единичного отрезка и наоборот. Сообщая
об этом открытии своему другу Р. Дедекинду в Брунсвик B0 июня
1877 г.), Кантор писал: «Вижу, но не верю».
В действительности построенное Кантором отображение единично-
единичного квадрата на единичный отрезок почти тривиально. Например, точка
квадрата с прямоугольными координатами х = 0,123 и у = 0,456 ото-
отображается в точку 0,142536 на единичном отрезке. Видите ли вы, что
происходит, и верите ли своим глазам?
Пожалуй, не менее удивительно и то, что любое число из интерва-
интервала [0, 2] представимо в виде суммы двух канторовых чисел, невзирая на
чрезвычайную их разреженность в единичном интервале. Доказать это
противное здравому смыслу утверждение арифметическим либо гео-
геометрическим путем мы предоставляем читателю. Возможно, процесс
покажется ему поучительным (или, по крайней мере, позабавит его).
Канторовы множества как множества инвариантные
Одной из областей математики, в которой канторовы множества
чувствуют себя весьма привольно, являются так называемые инвари-
инвариантные множества итерированных отображений. (Элемент инвариант-
инвариантного множества под действием отображения переходит в некоторый
элемент того же множества. Все эти элементы вместе и образуют ин-
инвариантное множество.) Рассмотрим простое отображение, известное
под названием «палатки» (см. рис. 1):
п+1
= 1,5 - 3|ж„ - 0,
Поскольку угловые коэффициенты обоих скатов палатки по абсолютной
величине всюду больше единицы, это отображение не имеет аттракто-
аттракторов за исключением х = — ос. Две неподвижные точки х = 0 и х = 0, 75
являются репеллерами: оказавшись в их окрестностях, точки уходят
в бесконечность.
Существуют ли здесь точки, не уходящие в бесконечность, т.е. та-
такие точки, образы которых навсегда остаются в единичном интервале?
Чтобы ответить на этот вопрос, запишем хп в троичной системе счис-
счисления. Тогда из отображения на рис. 1 видно, что при хп ^ 0, 5 каждую
следующую итерацию хп+\ можно получить простым сдвигом вправо
226
Глава 7
ю,
V
I
ю
Рис. 1. Отображение «палатка». Инвариантное множество этого отображения
представляет собой канторово множество (см. также рис. 10 в гл. 1).
запятой в числе хп. Если х > 0,5, то, прежде чем произвести сдвиг
вправо, необходимо каждую цифру дополнить, т.е. заменить 0 на 2, 2
на 0, а все единицы оставить единицами.
Если где-то в первоначальном разложении числа Хо имеется еди-
единица, то в конце концов эта единица окажется на первом месте слева
от троичной запятой. Начиная с этой итерации, число хп и все его по-
последующие образы превосходят единицу и расходятся, т. е. удаляются
в бесконечность (за исключением тех случаев, когда дробь на единице
обрывается).
Но предположим, что в троичном разложении начального значе-
значения Хо нет ни одной единицы, т. е. Хо — канторово число. Тогда все его
образы также будут канторовыми числами @ —>¦ 0 или 2, 2 —>¦ 2 или 0,
не забыли?). Все образы такого числа навсегда останутся в единичном
интервале. Чтобы убедиться в этом, предположим, что хп = 0,2022 ...,
т. е. больше 0,5. Следуя нашему алгоритму, мы должны сначала допол-
Символическая динамика и детерминированный хаос 227
нить хп (и получить 0,0200...), а затем сдвинуть запятую на один
знак вправо — получим 0,2..., что меньше 1). Если же первой циф-
цифрой числа хп является 0, то xn+i также будет меньше единицы. Таким
образом, канторовы числа (и только они) всегда находятся в пределах
единичного интервала и неизменно остаются канторовыми числами.
Именно поэтому мы и говорим, что они образуют инвариантное мно-
множество отображения «палатка» xn+i = 1,5 — Э>\хп — 0,5|.
Отображение, аналогичное рассмотренному выше, но ограниченное
единичным интервалом, было описано Бо-Сен Ду [54].
Символическая динамика и детерминированный
хаос
Отображением, с которым мы познакомились в предыдущем разде-
разделе, можно проиллюстрировать еще один важный момент. Вместо под-
подробного описания последовательности образов (которая называется ор-
орбитой) путем указания точных величин хп, последние часто квантуют
лишь на два значения. Например, если хп меньше 0,5, т.е. лежит сле-
слева от 0, 5, то мы представляем такие значения хп одним символом L
(от англ. left — левый). Если же хп больше 0,5, то мы заменяем его
символом R (от англ. right — правый).
Любопытно отметить, что для любого данного начального значе-
значения хо, принадлежащего инвариантному множеству, мы можем сра-
сразу же предсказать последовательность символов L и R, которая на-
называется символической динамикой его образов. Например, началь-
начальное значение ж0 = 0,022020002... имеет символическую динами-
динамику LRLRRRLLR..., которую можно получить, записывая символ L
всякий раз, когда какая-либо цифра в числе Xq совпадает с ближайшей
слева цифрой, и символ R в противном случае. Символическая дина-
динамика описывает эволюцию во времени некоторой динамической систе-
системы — например, детских качелей или распределения голосов полити-
политически активного населения.
Еще любопытнее то, что по (дискретной!) символической дина-
динамике мы можем однозначно определить точное начальное значение xq
(если оно принадлежит инвариантному множеству). Например, орбита
с символической динамикой RLRLLLRRL... исходит из начальной
точки Хо = 0,220000200... Не может ли уважаемый читатель объяс-
объяснить, почему я так решил?
Ясно, что инвариантные множества (и их дополнения) играют ре-
решающую роль в динамических системах в целом, поскольку они спо-
228 Глава 1
собны сообщить нам о любом начальном состоянии то, что мы более
всего хотим узнать — какая судьба ожидает это состояние в конечном
итоге: будут ли образы его оставаться в определенных пределах или они
окажутся неустойчивыми и удалятся в бесконечность, а также какой
будет его орбита — периодической или апериодической?
Как видно из вышеприведенных примеров, инвариантные множес-
множества могут представлять собой (и часто так оно и бывает) самоподобные
канторовы множества, т. е. несчетные множества меры 0, обладающие
масштабной инвариантностью. Для канторова множества коэффициент
подобия равен 3, что соответствует сдвигу запятой в троичной записи
числа на один знак вправо.
Представление эволюции динамической системы во времени с по-
помощью сдвигов запятой вправо в соответствующей системе счисле-
счисления выявляет еще одно важное свойство систем, которые допуска-
допускают такое представление: независимо от того, с какой точностью из-
известно начальное состояние ж0 некоторой координаты, точность эта
всегда остается конечной, т. е. стоящие справа от последнего извест-
известного знака цифры числа хц, неизвестны. По мере того, как динами-
динамическая система эволюционирует во времени, эти неизвестные циф-
цифры сдвигаются влево, т. е. значимость их растет; рано или позд-
поздно они достигнут запятой и станут тем самым определять поведе-
поведение системы. А поскольку все эти цифры неизвестны, система ста-
становится полностью непредсказуемой. Возникающее в результате дви-
движение называется хаотическим. Чтобы подчеркнуть, что такого ро-
рода хаос порожден строго причинными, детерминированными прави-
правилами, его называют детерминированным хаосом. Как мы можем ви-
видеть, нет никакого противоречия между полным детерминизмом и
хаосом. Более того, детерминированный хаос весьма широко распро-
распространен в природе — от турбулентности до динамики численности
населения.
Проведенный выше анализ позволяет также понять, почему так
редко сбываются предсказания погоды. Причина заключается в том,
что описывающие погоду уравнения являются уравнениями хаотичес-
хаотической системы. Чтобы надежно предсказать погоду хотя бы на один лиш-
лишний день, необходимо знать начальные состояния температуры, давле-
давления воздуха, скорости ветра и других величин в огромном количестве
точек на Земле с точностью, намного превышающей современные воз-
возможности метеорологии, не говоря о трудностях сбора и обработки всей
этой огромной массы данных. Впрочем, появившиеся в последнее вре-
время на горизонте суперкомпьютеры, выполняющие крупномасштабную
Чертовы лестницы и китайский бильярд 229
параллельную обработку информации, обещают более надежное пред-
предсказание погоды на чуть больший период времени.
Чертовы лестницы и китайский бильярд
Одно из наиболее интересных построений на основе канторовых
множеств называется чертовой лестницей. Возьмем исходное канторо-
во множество, получающееся при стирании средних третей, и построим
график относительного веса у множества лежащих слева от х чисел, как
функции от х на единичном интервале. На первой стадии построения у
возрастает от 0 до 1/2 по мере того, как х проходит отрезок от 0 до 1/3.
Затем до точки х = 2/3 функция у остается постоянной. После этого
плато (у = 1/2) функция у снова возрастает от 1/2 до 1 по мере того,
как х проходит отрезок от 2/3 до 1. На второй стадии построения на
графике появляются еще два плато — у = 1/4 и у = 3/4 (рис. 2А).
В пределе ступенчатая функция у (х) имеет плато почти всюду, но
несмотря на это умудряется возрастать от 0 до 1 при несчетно многих
значениях х (на рис. 2Б можно видеть чертову лестницу на довольно
продвинутой стадии построения).
Чтобы узнать высоту лестницы для любого заданного значения х,
необходимо записать х в виде троичного числа и превратить его затем
в двоичную дробь, заменяя каждую цифру 2 вплоть до первой единицы
(при чтении слева направо) на единицу. Первую единицу (если таковая
имеется) оставляем в покое, а все стоящие справа от нее цифры заме-
заменяем нулями. Например, число
ж = 0,20210012...=
отображается в
у = 0,1011000...= Ц.
Таким образом, каждому значению х соответствует единственное зна-
значение у.
Чтобы вернуться от данного значения у к соответствующему зна-
значению (или значениям) х, необходимо записать у в виде двоичной дро-
дроби и заменить все единицы, кроме последней (если таковые имеются),
двойками, а каждый нуль, расположенный правее последней единицы,
заменить одной из трех цифр — нулем, единицей или двойкой. В ре-
результате проделанных манипуляций мы получим некоторый интервал.
230
Глава 7
0
04)
1
9
2
9
1
3
2
3
7
9
8
9
(Б)
Рис. 2. Второй (А) и более продвинутый (Б) этапы построения чертовой лест-
лестницы. Видны все плато с более ранних этапов построения.
Например, число
перейдет в
= 0,1011 = 0,1011@) = ^|
000...
ж = 0,2021111...,
222...
что соответствует всем числам из открытого интервала @,2021@),
0,2021B)) или, в десятичной системе счисления, F1/81, 62/81). Иначе
Чертовы лестницы и китайский бильярд
231
говоря, у = 11/16 соответствует одному из плато чертовой лестницы
с шириной ступени 1/81.
В общем случае любое значение у со знаменателем (предполагает-
(предполагается, что числитель и знаменатель дроби взаимно просты), равным п-й
степени двух, лежит на плато шириной 3~™. Все остальные значения у
(т. е. все бесконечные двоичные дроби) соответствуют единственным
значениям координаты х. Функция у (х) отличается поистине дьяволь-
дьявольскими свойствами: она почти всюду постоянна (т.е. не возрастает),
однако несчетное количество бесконечно малых разрывов позволяет ей
«прокрасться» от 0 до 1.
Рис. 3. Китайский бильярд Энона.
Чертовы лестницы могут служить превосходными моделями мно-
многочисленных сложных ситуаций в реальном мире (равно как и в не
столь реальном мире математической физики). Мишель Энон однаж-
однажды изобрел нечто вроде китайского бильярда (рис. 3), символическую
динамику которого при любом начальном положении xq @ < xq < 1)
можно получить посредством вычисления чертовой функции у (хо), как
это только что делали мы с вами [103]. Если значение у (хо) попадает
на плато чертовой лестницы, то шарик удаляется в плюс или в минус
бесконечность. Т.е. плато чертовой лестницы являются интервалами-
ловушками от аттракторов, расположенных в бесконечности. Однако
если Хо — канторово число, то у (xq) окажется не на плато, и орбита
шарика навсегда останется «запертой» в интервале [0, 1]. В этом случае
232 Глава 7
его символическая динамика определяется значением у(жо), записан-
записанным в виде двоичной дроби, где каждый нуль трактуется как символ L,
т.е. сопоставляется левой половине единичного интервала (хп < 1/2),
а каждая единица — как символ R, т. е. сопоставляется правой поло-
половине единичного интервала (хп > 1/2). Это очень похоже на отображе-
отображение «палатка», приведенное на рис. 1. (Энон, однако, заверил меня, что
между отображением «палатка» и «бильярдом с наклонностями», как он
назвал свое построение, имеются также и существенные различия).
Если бы конструкция Энона была компьютерной игрой, имеющей
целью удерживать шар в постоянном движении в заданных пределах,
то выигрышная стратегия состояла бы в выборе в качестве начального
положения шара канторова числа. Это напоминает игру сэра Пинского,
рассмотренную нами в гл. 1 (с. 46-52): там выигрышные точки при-
принадлежали ковру Серпинского (двумерному канторову множеству).
Fix)
-1
2
~г
и 1 г
-1 -0,5 0 0,5 1
Рис. 4. Функция распределения для случайной величины с канторовой плот-
плотностью вероятности.
Чертовы лестницы встречаются и в теории вероятности. На рис. 4
вы видите кумулятивное распределение случайной величины х, опре-
определяемой соотношением
где <jj — независимые равновероятные +1 и —1. Легко заметить,
что х никогда не сможет попасть внутрь интервалов (—1/2, 1/2),
(—7/8, —5/8), E/8, 7/8) и т.д. Это влечет за собой большие плато на
графике кумулятивного распределения (рис. 4). Аналогичные распре-
распределения типа чертовой лестницы, почти всюду постоянные и возраста-
возрастающие только на канторовом множестве значений х, можно получить
для любого положительного /3 < 1/2.
Синхронизация мод в качелях и часах 233
Синхронизация мод в качелях и часах
Одно из наиболее распространенных колебательных явлений в при-
природе известно под названием синхронизации мод, затягивания часто-
частоты, синхронизации фаз, или просто синхронизации двух осцилляторов.
И здесь чертовы лестницы играют весьма заметную роль. В примене-
применении к синхронизации высота чертовой лестницы соответствует отноше-
отношению частот двух осцилляторов, а плато представляют собой фиксиро-
фиксированные отношения частот, причем фиксированные на любом из рацио-
рациональных чисел (а не только на конечных двоичных дробях, как в случае
чертовой лестницы, построенной по первоначальному канторову мно-
множеству). Кроме того, самоподобие в случае синхронизации может быть
только асимптотическим, а не точным.
Рассмотрим в качестве примера детские качели. У них имеется
собственная частота, с которой они раскачиваются, когда ребенок, при-
приседая и распрямляясь, перемещает свой центр тяжести вверх и вниз
с частотой, равной удвоенной собственной частоте качелей — нужную
частоту ребенок быстро находит опытным путем задолго до того, как
впервые услышит о параметрических усилителях.
Но качели может раскачать и терпеливый родитель, подталкивая
их извне с некоторой частотой, не обязательно равной собственной час-
частоте качелей. Если внешняя сила достаточно «прочно» связана с каче-
качелями, то они начинают двигаться в такт с этой внешней силой, т.е.
синхронизируются с внешней частотой при некоторых значениях зада-
задающих частот.
Первым описал подобный феномен синхронизации голландский фи-
физик, математик и астроном Христиан Гюйгенс A629-1695) — тот са-
самый Гюйгенс, который сформулировал носящий ныне его имя прин-
принцип распространения волн. В письме из Парижа к отцу он описал, как
двое маятниковых часов, висевших по разные стороны одной стены,
разделявшей две комнаты, синхронизируют свой ход и начинают вско-
вскоре тикать совершенно согласованно (см. книгу Гюйгенса «Horologium
Oscillatorium» [112]). Как показывает этот пример, даже самая малая
связующая сила может «подчинить» один осциллятор другому, при
условии что отношение их собственных частот близко к рациональной
дроби с небольшими целыми числителем и знаменателем (такой, на-
например, как 1/1).
Еще одно давнее наблюдение синхронизации, на этот раз в косми-
космическом пространстве, относится к 1812 г., когда Гаусс открыл, что пе-
период обращения астероида Паллада связан с периодом обращения Юпи-
234 Глава 7
тера неизменным и точным отношением 7/18. Числа 7 и 18 представля-
представляют собой два числа Люка Ln, удовлетворяющие тому же рекуррентно-
рекуррентному соотношению, что и числа Фибоначчи, а именно Ln = Ln-i + Ln-2,
но с другими начальными условиями (L\ = 1 и 1г = 3). Гаусс так
и не опубликовал свое эпохальное открытие, если не считать краткой
заметки — и той в зашифрованном виде! — в Gelehrte Anzeigen, опера-
оперативном бюллетене Гёттингенской Академии. Впрочем, он все же пове-
поведал об этом поразительном наблюдении 5 мая 1812 г. своему близкому
другу астроному Фридриху Вильгельму Бесселю A784-1846), взяв с то-
того слово хранить сообщение в тайне «некоторое время». По-видимому,
Бессель полностью сдержал свое обещание, потому что Гаусс так и не
получил за свое открытие никаких почестей. Более того, впоследст-
впоследствии «принц математиков», явно позабыв о своем первоначальном на-
намерении хранить открытие в тайне, был немало раздосадован таким
поворотом событий. (Почему Гаусс так противился тому, чтобы мир
узнал о Палладе и Юпитере? Может быть, он опасался, что обнаружил
случайно некое божественное вмешательство в «часовой механизм» на-
нашей планетной системы? Нет, Гаусс отлично знал, что обнаруженная
им связь — это всего лишь простое следствие из законов нелиней-
нелинейной механики и ничего больше. Возможно, он опасался, что новость
слишком взбудоражит умы, как в случае с открытой им неевклидо-
неевклидовой геометрией, которую он держал «в столе» на протяжении десятиле-
десятилетий.)
Аналогичную синхронизацию можно наблюдать в некоторых ра-
радиоприемниках и телевизорах с автоматической подстройкой частот:
пользуясь регулятором (если таковой еще сохранился), можно вручную
сместить настройку приемника на некоторую величину, и, тем не ме-
менее, он будет принимать выбранный канал. Еще одним примером может
служить синхронизация с помощью внешнего сигнала горизонтальной
(или временной) развертки осциллографа или телевизора. Внутренний
генератор развертки синхронизируется с внешней частотой в пределах
некоторого частотного интервала, а затем скачкообразно перемещает-
перемещается к другому рациональному отношению частот, предпочитая отноше-
отношения с малыми числителем и знаменателем (такие, например, как 1/2
или 3/4). Частотные интервалы, перескакивая через которые две часто-
частоты синхронизируются в рациональное отношение, очень часто зависят
от величины целых чисел в числителе и знаменателе (особенно от зна-
знаменателя). Например, в данном случае частотный интервал, в пределах
которого происходит синхронизация, при отношении частот 1/1 шире,
чем при отношениях 1/2, 1/3 или 2/3.
Незадачливый манхэттенский пешеход 235
Интересно отметить, что такого рода интервалы синхронизации
обладают весьма высокой степенью универсальности и встречаются
в бесчисленных и, на первый взгляд, никак не связанных между со-
собой явлениях (например, осцилляции суперионных проводников [166]
и сердцебиение периодически раздражаемых куриных зародышей). Бо-
Более того, все эти явления могут быть смоделированы асимптотически
самоподобными фракталами, размерность Хаусдорфа для которых во
многих случаях оказывается одинаковой и равной D = 0,86 ... К раз-
разговору о периодических, апериодических и хаотических колебаниях мы
еще вернемся в гл. 14.
Незадачливый манхэттенский пешеход
Этот весьма настойчивый пешеход, совершая время от времени вы-
вылазки в Большое Яблоко (известное также под названием Нью-Йорк),
испытывает на себе последствия одной из самых «очаровательных» си-
ситуаций, связанных с синхронизацией. Проходя по одной из авеню Ман-
хэттена, он вынужден останавливаться на каждом перекрестке, потому
что, стоит лишь ему приблизиться, как зеленый сигнал светофора не-
неизменно сменяется красным.
Предположим, что скорость пешехода лишь немногим меньше двух
третей «скорости» светофора (т. е. расстояния между соседними пере-
перекрестками, деленного на продолжительность одного полного цикла сме-
смены сигналов — зеленый/желтый/красный). Тогда красные сигналы за-
заставят несчастного пешехода ожидать на каждом перекрестке и умень-
уменьшат его скорость наполовину.
Предположим для простоты, что зеленый сигнал (знак того, что пе-
пешеход может безопасно переходить улицу) горит на протяжении ровно
половины цикла, и что все сигналы идеально синхронизированы (что
заведомо неверно для улицы с односторонним движением). Тогда, при
условии, что скорость пешехода находится в интервале 1/2 ^ s ^ 2/3
сигналы светофора заставляют его двигаться с эффективной скорос-
скоростью v = 1/2. В общем случае, если скорость пешехода находится в ин-
интервале
< • < Л A)
где п = 1, 2, 3, ..., пешеход вынужден двигаться с эффективной ско-
скоростью v = 1/{п + 1). Однако можно заставить пешехода двигаться
и с другими, более рациональными, скоростями (хотя ему они могут
236 Глава 7
и не показаться таковыми). Действительно, если
2(к-1)п
s <
2к
B)
где к = 2, 3, 4, ..., эффективная скорость движения пешехода оказы-
оказывается равной нижнему пределу s.
112
3 2 3
Скорость пешехода, s
Рис. 5. Продвижение незадачливого манхэттенского пешехода как иллюстра-
иллюстрация синхронизации.
Ступенчатая функция, соответствующая таким интервалам син-
синхронизации, представлена на рис. 5. Хотя график v как функции от s не
обладает точным самоподобием, схема распределения «ступенек» син-
синхронизации в интервале 1/2 ^ s < 1 приближенно повторяется в других
масштабах в интервалах 1/(п + 1) ^ s < 1/п. Следует также отметить,
что плато синхронизации становятся все меньше по мере того, как воз-
возрастают знаменатели в неравенствах A) и B) из предыдущего абзаца.
Вообще говоря, интервалы эффективной скорости равны двойке, делен-
деленной на произведение двух знаменателей.
Затронутая нами тема интервалов синхронизации, связанных об-
обратной зависимостью со знаменателями некоторых приведенных дро-
дробей, выходит далеко за рамки повествования о злополучном пешеходе
из Манхэттена. Более того, скоро мы встретимся с такими ступенча-
Языки Арнольда
237
-
-
0
1
1
1
1
3
i it'-
2 3 •"
I 7.
1
1
2
1
5
8
7 -
1
5
7
5 • '
0,24
0,22
0,
3
4 ¦
_
25
-;.]¦-
i
2
9
3
14 •'
1
0,26
-
i
13-
1
0,27
-
—
0,2
0,4 0,6
Рис. 6. Сатанинская лестница, плато которой расположены на всех рацио-
рациональных высотах.
тыми функциями, которые, в отличие от чертовой лестницы на рис. 5,
имеют несчетное множество ступеней.
Языки Арнольда
Плато чертовых лестниц, встречавшихся нам до сих пор, распола-
располагались на высотах у = Bk — 1)/2™, где к, п = 1, 2, 3, Существуют,
однако, еще более сатанинские лестницы, плато которых располагаются
на любой рациональной высоте в интервале [0, 1]. В то время как чер-
чертова лестница, построенная на основе канторова множества, обладает
точной самоаффинностью (с коэффициентами подобия 3 по оси ж и 2
по оси у), этого нельзя сказать о дьявольских лестницах, одна из ко-
которых приведена на рис. 6. Строятся подобные лестницы на основе так
называемого отображения окружности:
позволяющего моделировать многие явления синхронизации мод (см.
гл. 14). Здесь К — параметр силы связи, управляющий степенью нели-
нелинейности, а О — отношение частот, известное под названием формаль-
формального числа вращения. Эта величина может представлять собой отноше-
отношение частоты вынуждающей силы и резонансной частоты осциллятора
238
Глава 7
(вспомним о различного рода ритмических колебаниях, в том числе
и исполняемых на танцевальной площадке, или об отношениях частот
обращения планет и спутников вокруг своих центральных тел и вокруг
собственных осей).
В отсутствие связи (К = 0) так называемое реальное число враще-
вращения w, определяемое как предел при п —>¦ ос отношения (9п — 9о)/п, сов-
совпадает с формальным числом вращения О. Однако при К > 0 реальное
число вращения w синхронизируется с рациональными отношениями
частот, предпочитая отношения с небольшими знаменателями.
На рис. 7 показаны некоторые области синхронизации частот на
плоскости (О — К). Темные области называются языками Арнольда
в честь открывшего их русского математика В.И.Арнольда. (Ни фрак-
фрактальные небеса, ни фрактальная преисподняя, по-видимому, не испы-
испытывают недостатка в значащих терминах).
со=\
Рис. 7. Языки Арнольда: интервалы синхронизации частот.
В применении к другим явлениям реальное число вращения w мо-
может представлять собой, скажем, относительное число направленных
вверх спинов в модели антиферромагнетика Изинга или относительным
содержанием данного элемента (или молекулярной структуры) в крис-
кристалле или квазикристалле (см. гл. 13).
При критическом значении параметра связи К = 1 бесконечно
большое количество частотных интервалов синхронизации, соответ-
Языки Арнольда 239
ствующих всем рациональным реальным числам вращения w от 0 до 1
в буквальном смысле слова покрывает весь диапазон формальных чи-
чисел вращения О. Иррациональные значения w соответствуют несчетно
бесконечному множеству нулевой меры, состоящему из значений п —
иначе говоря, канторовой пыли.
Глава 8
Многомерные фракталы и цифровые
солнечные часы
Jetzt Mengenlehre (А теперь — теория множеств).
Курт Гёдель, в 1937 г.,
когда, после завершения доказательства
неразрешимости в теории чисел, он решил обратить
острейший скальпель своего разума к теории множеств.
Многомерные самоподобные или самоаффинные множества явля-
являются моделями странных аттракторов и их областей притяжения,
а также пористых материалов, древовидного роста кристаллов и квази-
квазикристаллов, горных ландшафтов, броуновского движения и связанных
с ним стохастических процессов, которые описывают широкий ассорти-
ассортимент катастроф (плюс некоторое количество более счастливых проис-
происшествий). Некоторые из этих «практических фракталов» мы навестим
в гл. 10. А здесь обсудим некоторые из базовых понятий и разработаем
проект цифровых солнечных часов на основе канторова множества.
Декартовы произведения канторовых множеств
Исходное одномерное канторово множество может быть обобщено
для случая пылевидных множеств в двух и более измерениях несколь-
несколькими различными способами. Рассмотрим множество всех точек еди-
единичного квадрата, для которых как абцисса х, так и ордината у принад-
принадлежат канторову множеству С. Получившееся в результате декартово
произведение канторова множества на себя, которое обычно записывают
в виде С у. С, представляет собой канторову пыль, вложенную в дву-
двумерное пространство (рис. 1).
Какова размерность Хаусдорфа D для такой пыли? Множест-
Множество С х С может, очевидно, быть покрыто N (г) = 4™ квадратами с дли-
длиной стороны г = 1/3™. Следовательно,
D(CxC)= lim
>оо
Дырявый ковер, мягкие губки и швейцарские сыры
241
Рис. 1. К двумерной канторовой пыли: декартово произведение оригинально-
оригинального канторова множества на себя. Первый (А) и второй (Б) шаги в построении
канторовой пыли, фрактальная размерность которой составляет 1,26 ...
т. е. вдвое больше размерности исходного одномерного канторова мно-
множества. Нетрудно догадаться (и лишь немногим труднее доказать), что
для трехмерного декартова произведения С х С х С размерность Хаус-
Хаусдорфа равна
D(C,С,C) = ^I=3^
и т. д. При построении декартова произведения к канторовых множеств
мы умножаем размерность Хаусдорфа для одномерного канторова мно-
множества на к, т. е. поступаем так же, как с обычными евклидовыми раз-
размерностями. (Заметьте, что канторова пыль С х С х С, взвешенная
в трехмерном пространстве, настолько разрежена, что ее размерность
Хаусдорфа не достигает даже значения 2.)
Дырявый ковер, мягкие губки и швейцарские сыры
Рассмотрим другое декартово произведение — дополнения С" кан-
канторова множества С на себя: С'хС Дополнение к С'хС, т.е. (С'хС")',
может быть построено рекурсивно следующим образом. В качестве
инициатора возьмем единичный квадрат, а генератором будет единич-
единичный квадрат, из которого вынут центральный квадрат со стороной 1/3.
На следующей стадии построения из каждого из 8 оставшихся квадра-
квадратов со стороной 1/3 удаляются центральные квадраты со стороной 1/9
(рис. 2Б). После бесконечного числа итераций получаем канторов ковер,
приблизительное изображение которого вы можете видеть на рис. 2(Г).
242 Глава
Ш (Б) (В) (Г)
Рис. 2. Первые три шага в построении канторова ковра и приблизительный
окончательный результат (фрактальная размерность 1,89...).
Какова же размерность Хаусдорфа для такого ковра? Если судить
по рис. 2, размерность множества (С'хС)' должна быть больше размер-
размерности СхС. Так как канторов ковер строго самоподобен, нам необходи-
необходимо рассмотреть только генератор. Для того чтобы полностью покрыть
генератор, мы должны взять 8 квадратов со стороной 1/3. Тогда
такое же значение мы получили ранее для трехмерной канторовои пы-
пыли С х С х С.
А что вы скажете о множестве (С х С" х С")', прозванном канто-
ровым сыром? Его генератор можно заполнить 27 — 1 = 26 кубиками
с длиной ребра 1/3. Соответственно, получаем
п _ In 26 ^ 2 q7.
это значение близко к 3, потому что канторов сыр представляет собой
достаточно сплошную конструкцию с изолированными пустотами.
Обобщение канторова сыра на к евклидовых измерений — мно-
множество (С х С" х ... х С')' — имеет размерность Хаусдорфа D =
= lnCfc — 1)/ 1пЗ и к — l/Cfc 1пЗ). Это значение, как правило, чуть
меньше размерности вложения к.
В трехмерном пространстве существует еще одно симметричное
фрактальное множество, основанное на канторовом множестве С (на
месте С может быть любое другое одномерное фрактальное множест-
множество). Оно называется губкой Менгера в честь его создателя Карла Мен-
Менгера и изображено на рис. 3 [179]. Двумерных аналогов губка Менге-
Менгера не имеет. Пустоты в губке Менгера представляют собой откры-
открытые каналы, пронизывающие единичный куб насквозь. Применяя прин-
Дырявый ковер, мягкие губки и швейцарские сыры
243
цип включения-исключения, нетрудно понять, что в генераторе остает-
остается 27 — 9 + 3 — 1 = 20 кубов с длиной ребра 1/3. Следовательно, размер-
размерность Хаусдорфа для губки Менгера равна D = In 20/In 3 pa 2, 73 ...,
благодаря чему губка Менгера занимает промежуточное положение
между канторовой пылью и канторовым сыром — оказываясь, как и
следовало ожидать, ближе к последнему. Мандельброт, независимо от
других исследователей, предложил губку Менгера в качестве модели
турбулентной перемежаемости [159].
Рис. 3. Губка Менгера (фрактальная размерность 2,73...).
Можно построить хорошее теоретико-множественное описание,
позволяющее выявить симметрию губки Менгера по трем декартовым
координатам х, у и z. Обозначим канторово множество С по оси х сим-
символом X, а канторовы множества по двум другим осям — соответствен-
соответственно Y и Z. Тогда, если рассматривать только генераторы, запись Х'ПУ
соответствует центральной квадратной «дыре» в плоскости ху (рис. 2),
а выражение
(X' П У) U (У П Z') U (Z' П X')
244 Глава 8
опишет множество всех пустот генератора. Дополнение этого множес-
множества представляет собой генератор губки Менгера. Согласно правилу
Де Моргана [95], его можно записать в следующем виде:
(XUY) П (YUZ) П (ZUX). A)
Будет ли также фрактальным множество, генератор которого есть
дополнение генератора губки Менгера, и будет ли его размерность Хаус-
дорфа D заключена между 0 и 3? (Дополнение самой губки, разумеется,
имеет конечную меру Лебега и D = 3). Генератор-дополнение содер-
содержит 27 — 20 = 7 кубов с длиной ребра 1/3: центральный куб и 6 кубов
вокруг него. Следовательно, D = 1п7/1пЗ = 1,77 ... Весьма «тощее»
множество, надо сказать.
Итак, исходное канторово множество, обобщенное на более высо-
высокие размерности вложения, равно как и аналогичные ему множества,
порождают непрестанно разрастающийся «зоопарк» разнообразных пы-
пылевидных множеств.
Солнечные часы на основе канторова множества
Применяя канторово построение к двумерному случаю, мы полу-
получаем канторову «пыль», рассеянную на плоскости. Для этого достаточно
взять единичный квадрат и изъять центральные трети сторон по осям х
и у, а затем повторять эту операцию до бесконечности (рис. 1). Полу-
Получающееся при этом множество математики называют также прямым
произведением канторова множества С на себя и обозначают С х С. Как
мы уже знаем, его размерность Хаусдорфа D вычисляется непосредст-
непосредственно по генератору, который состоит из 4 оставшихся от 9 квадратов.
Так как множество СхС можно покрыть 4™ (но не меньше) квадратами
с длиной стороны 3~™, его размерность Хаусдорфа равна
D jn4 2]n2 -, 2,
D 2
U~ 1пЗ" 1пЗ -1'Д)--"
что вдвое больше размерности Хаусдорфа для канторова множест-
множества С. В общем случае размерность Хаусдорфа для декартова произ-
произведения множеств равна сумме размерностей отдельных множеств-
сомножителей. Так, например, канторова пыль С х С х С, взвешен-
взвешенная в трехмерном пространстве, имеет размерность Хаусдорфа D =
= 31п2/1пЗ = 1,89 ....
Солнечные часы на основе канторова множества 245
Арифметически такие n-мерные канторовы множества можно опи-
описать как совокупности наборов, состоящих из п канторовых чи-
чисел (xi, Х2, ... , хп), где каждое х/. есть канторово число, т.е. троичная
дробь, в записи которой содержатся только нули и двойки и нет ни од-
одной единицы (см. гл. 7, с. 221- 223).
Интересно отметить, что проецирование фрактальных множеств,
вложенных в многомерные евклидовы пространства, на евклидовы про-
пространства меньших размерностей дает фрактальные множества, чьи
размерности Хаусдорфа зависят от направления проецирования. Рас-
Рассмотрим, например, одномерное множество канторовского типа С4, ко-
которое получается при удалении из единичного интервала центральных
четвертей. Пыль в трехмерном пространстве, построенная из двукрат-
двукратного декартова произведения такого множества на себя, имеет размер-
размерность Хаусдорфа D = 31п2/1п(8/3) = 2,12 ..., что больше 2. Прое-
Проецирование этого множества (С4 x C4 x C4) вдоль одной из трех ко-
координатных осей дает множество С4 х С^ с размерностью Хаусдор-
Хаусдорфа 21п2/1п(8/3) = 1,41 ..., что меньше 2. Однако проекции этого же
множества в других направлениях могут представлять собой двумер-
двумерные множества, содержащие связные элементы. Иначе говоря, пыль кан-
канторовского типа С4 х С*4 х С± отбрасывает «бесплотные» тени в одних
направлениях и вполне зримые — в других.
Основываясь на этих соображениях, К. Дж. Фалконер [62] предло-
предложил наиболее парадоксальное, пожалуй, множество из всех, что когда-
либо были придуманы: цифровые солнечные часы (рис. 4). В зависи-
зависимости от положения солнца на небе это множество отбрасывает тень,
которая ежеминутно изменяет свои очертания в соответствии с мест-
местным временем. При желании множество можно «расширить», чтобы оно
заодно показывало правильную текущую дату между зимним и летним
солнцестояниями. Перед нами идеальный часовой механизм, работаю-
работающий на солнечной энергии.
Разумеется, такое отбрасывающее тень множество должно быть
весьма сложным, и изобретатель по понятным соображениям воздер-
воздерживается от публикации подробных инструкций по построению часов
(предположительно, на тот срок, пока рассматривается патент и про-
продолжаются попытки обойти дифракционнные ограничения). Однако ни-
никто не мешает нам намекнуть, каким образом можно было бы присту-
приступить к построению множеств, отбрасывающих тени различной величи-
величины и формы (см. рис. 5).
246
Глава 8
Рис. 4. Цифровые солнечные часы на канторовом множестве [62].
Толстые фракталы
«Часовой» фрактал, о котором шла речь в предыдущем разделе,
представляет собой пример фрактального множества, проекции которо-
которого по некоторым направлениям имеют ненулевую меру. Следует заме-
заметить, что существуют многочисленные «серьезные» области, в которых
фрактальные множества ненулевой меры находят достаточно широкое
применение. В особенности это верно для нелинейных динамических
систем и их областей притяжения. Например, такое фрактальное мно-
Толстые фракталы 247
\
%.
Рис. 5. Идея, лежащая в основе цифровых солнечных часов: набор стержней,
отбрасывающий весьма различные тени в зависимости от направления про-
проекции.
жество образуют значения параметра, при которых логистическая па-
парабола — прототип нелинейных динамических систем (см. гл. 12) —
демонстрирует апериодическое поведение [116].
Каждой периодической орбите соответствует некий конечный ин-
интервал значений параметра, который называется окном периодичности.
Объединение окон периодичности не исчерпывает всех значений пара-
параметра. Таким образом, значения параметра для апериодических орбит
имеют ненулевую меру Лебега. С другой стороны, распределение таких
значений параметра имеет фрактальную структуру: пустоты (окна пе-
периодичности) в нем существуют во всех масштабах. Такие фракталь-
фрактальные множества (ненулевой меры) получили название толстых фрак-
фракталов [61]. Приведем еще один пример толстого фрактала: множество
значений параметра, при которых подкритические отображения окруж-
окружности демонстрируют апериодическое поведение (т.е. множество зна-
значений параметра, не ведущих к синхронизации).
Очевидно, не имеет смысла характеризовать такие множества их
размерностью Хаусдорфа — она просто равна евклидовой размерности
пространства, в которую вложен толстый фрактал, и потому не несет
248
Глава 8
в себе никакой дополнительной информации. Толстые фракталы удоб-
удобнее описывать с помощью показателей скейлинга.
Простой пример толстого фрактала можно получить, взяв единич-
единичный интервал и удалив из него на первом этапе среднюю часть дли-
длиной 1/3; на втором этапе из каждой из двух оставшихся третей удаля-
удаляются средние части длиной 1/9; на третьем — из каждого из четырех
оставшихся отрезков удаляются средние части длиной 1/81 и т. д. На
каждом этапе мы удаляем центральные части, относительная длина
которых равна 1/C2 ) (рис. 6). После п итераций получаем 2™ отрез-
отрезков, общая длина которых равна
п-1
Mn =
A)
fc=0
При п —>• сю величина рьп стремится к ненулевому значению: рьж =
= 0,5851874....
1
Рис. 6. Построение толстого фрактала. В нем имеется бесконечное множество
пустот, однако остаток все же умудряется сохранять общую длину отличной
от нуля.
Несколько более тощий толстый фрактал мы получим, если будем
изымать при каждой итерации центральные части относительной дли-
длины 2>~к. В этом случае полная длина остающихся отрезков составит
= JJ(l-3"fc) = 0,560 ...
B)
k=i
Для характеристики толстых фракталов используется, как прави-
правило, один из нескольких показателей скейлинга. Самый полезный пока-
показатель скейлинга определяется следующим образом: заполним все пус-
пустоты, длина которых не превышает е, и аппроксимируем меру // (е)
Толстые фракталы 249
получившегося в результате множества степенным законом, е —> О,
сеР, C)
где с — постоянная, а /3 — показатель скейлинга; причем 0 ^ /3 ^ сю.
Положим в нашем примере (с удалением средних частей длиной 3~*)
е = 3~и; тогда
*=i ft (i-
k=n
ИЛИ
Отсюда, при п —> сю,
Таким образом, показатель скейлинга /3 для толстого фрактала, опре-
определяемого соотношением B), равен 1.
Обозначив меру пустот, меньших е, через F(e), мы можем запи-
записать показатель скейлинга также в следующем виде:
^. D)
е->оо 1п?
Показатель /3 определяется скоростью обращения в нуль меры малых
пустот.
Дж. Дойн Фармер определил численное значение рь @) для квадра-
квадратичного отображения: 0,89795 ±0,00005. Он же обнаружил, что как для
квадратичного, так и для тригонометрического отображения с квадра-
квадратичным максимумом (жп+1 = 7^'т(ттхп)) показатель скейлинга /3 со-
составляет 0,45 ± 0,04. Это указывает на то, что показатель /3 может
оказаться универсальным, т.е. одним и тем же для всех отображений
с квадратичным максимумом [65].
Чтобы получить другой показатель скейлинга а, следует умень-
уменьшить все пустоты на величину е. Это не только позволит заполнить
все малые пустоты, но и уменьшит размеры больших. Если обозначить
изменение меры через G (е), то показатель а определится соотношени-
соотношением
+G(e)\_
e-s-0 lne
250 Глава 8
Можно показать, что а ^ /3. Если а < /3, то величину а определяют
большие пустоты. Поскольку в большинстве практических ситуаций
мелкая структура фрактала имеет более важное значение, чем круп-
крупная, показатель /3 часто оказывается более полезным. Однако показа-
показатель а может все же содержать важную информацию в случае толстых
фракталов, описывающих, например, значения параметра, при которых
нелинейная система демонстрирует хаотическое движение. При а = /3
такие системы проявляют чувствительную зависимость от параметра,
иными словами, сколь угодно близко к некоторому значению парамет-
параметра, приводящему к хаотическому движению, существуют другие зна-
значения, при которых движение является периодическим. Когда а < /3,
подобной чувствительности не возникает. Таким образом, равенство
а = /3 указывает на важное свойство нелинейных динамических сис-
систем, которое получило название чувствительность к параметру.
Глава 9
Мультифракталы, или фракталы, тесно
переплетенные между собой
Канторизм — это болезнь, от которой
математике еще предстоит оправиться.
Анри Пуанкаре
Фракталы неизмеримо расширили наши возможности описания
природы. Абстрактные конструкции, связанные с именами Бернар-
Бернарда Больцано A781-1848), Георга Кантора и Джузеппе Пеано A858-
1932), снабдили нас моделями реальности гораздо более реалистичны-
реалистичными, чем вся евклидова империя целочисленных показателей и глад-
гладких форм. Однако в физике, химии, геологии и в особенности при
изучении роста кристаллов мы сталкиваемся со многими явления-
явлениями, требующими расширения понятия фрактала на сложные струк-
структуры с более чем одним показателем скейлинга. К тому же, мно-
многие из таких структур характеризуются целым спектром показате-
показателей, и размерность Хаусдорфа — лишь один из них. Расширенные
фракталы, созданные для таких случаев, принято называть мулъти-
фракталами. Они находят применение при изучении широкого кру-
круга явлений — от распределения плотности населения или концент-
концентрации минералов до рассеяния энергии в турбулентности или во
фрактальных резистивных цепях. Ограниченная диффузией агрега-
агрегация, образование вязких языков, распределение сбоев в компьютер-
компьютерных сетях или примесей в полупроводниках и тому подобные явле-
явления хорошо моделируются мультифракталами — равно как и неко-
некоторые азартные игры. Многие странные аттракторы нелинейных ди-
динамических систем также обладают ярко выраженной мультифрак-
тальной структурой. Именно с помощью мультифракталов «фрак-
«фрактальной геометрии природы» удалось одержать верх над классичес-
классической «гладкой» геометрией в битве за владычество в естественных
науках.
252 Глава 9
Распределение: концентрация руды и плотность
населения
Золото есть повсюду на Земле. В одних, весьма редких, местах
оно встречается в виде богатых жил; существуют тысячи других, бо-
более бедных месторождений, где можно добывать золото с некоторой
прибылью. Кроме того, известны миллионы мест, где золото есть, но
в таких малых количествах, что его добыча не окупит себя. Золото не
только повсюду вокруг нас, оно имеется и внутри нас. Запасы золо-
золота в мировом океане оцениваются в миллиарды тонн, но концентрация
его составляет менее 6 частей на 1 триллион частей морской воды. Та-
Таким образом, в распределении золота на Земле, похоже, нет абсолютно
пустых мест.
Такая же картина наблюдается и в отношении других минералов.
Как мудро заметил однажды голландский геолог X. Й. де Вис, ни один
минерал не бывает сосредоточен исключительно в рудных жилах: он
может находиться и между жил, хотя и в значительно меньших кон-
концентрациях. Впрочем, характеристические вариации концентрации на-
наблюдаются и в самих рудных жилах [45]. Вообще, всякий раз, когда
некоторый объем руды расщепляется вдоль жилы, относительные ко-
количества минерала в двух половинах объема составляют, соответствен-
соответственно, ри1 — р. Интересно отметить, что максимальное значение парамет-
параметра р, характеризующего изменчивость концентрации минерала, остает-
остается примерно постоянным от одного расщепления к другому. Но можно
ли считать, что подобная закономерность справедлива только для руд?
Как распределяется плотность населения на больших пространст-
пространствах суши (например, в Евразии или в обеих Америках)? Если некото-
некоторую обширную территорию разделить на две равные по площади час-
части, то может оказаться, что, скажем, 70% населения живет по одну
сторону нашей демаркационной линии, а остальные 30% — по другую.
В общем случае доля населения по одну сторону от линии может соста-
составить р (причем, р > 0,5), а доля живущих по другую сторону — всего
лишь 1 — р. В нашем примере р = 0, 7. Разумеется, размер избыточной
доли р зависит от того, как проведена линия. Предположим, что она
проведена так, чтобы максимизировать величину р.
Если теперь продолжить деление и разделить более густонаселен-
густонаселенную половину на четверти, следя за тем, чтобы раздел и на этот раз
обеспечил максимум численности населения в одной из четвертей, то
может оказаться, что доли населения составят р2 и рA — р). Аналогич-
Аналогично, проводя линию по менее населенной половине, мы получим две рав-
Распределение: концентрация руды и плотность населения 253
1-
1-
0,5-
0,25-
1
(Б)
(В)
(Г)
0 0,5 1
х
Рис. 1. Построение самоподобного распределения с помощью повторения опе-
операции деления пополам [200].
ные по площади территории с плотностями населения, соответственно,
A-р)риA-рJ.
Итерация такого разделяющего процесса приводит к асимптоти-
асимптотически самоаффинному распределению (рис. 1). Мы начинаем с одно-
однородного распределения вероятностей в пределах единичного интерва-
интервала (рис. 1А). После однократного деления интервала пополам находим
две вероятности 1 — р и р для двух половин единичного интервала.
При 1 — р < р получается одноступенчатое распределение, представлен-
представленное для р = 2/3 на рис. 1Б. Повторное деление приводит к четырем
интервалам и распределению вероятностей, приведенному на рис. 1В.
Результат третьего деления можно видеть на рис. 1Г. В пределе, пос-
после бесконечно многих делений, получаем самоаффинное распределение
вероятностей: левая половина распределения, растянутая с коэффици-
коэффициентом 2 в горизонтальном направлении и с коэффициентом 1/A — р)
в вертикальном, воспроизводит распределение в целом [200].
Если мы условимся считать, что вероятность р = 0, 7 характер-
характерна для населения всего земного шара, то после 18 делений всей су-
254 Глава 9
ши у нас останутся два отшельника, живущие на площади 576 км2 =
= 24 кмх24 км в самом малонаселенном районе планеты, где-нибудь,
скажем, посреди Сибири, в то время как на такой же территории
в каком-нибудь мегалополисе будут тесниться 8 миллионов человек. Со-
Согласно такой простейшей модели деления, большинство людей C,5 мил-
миллиарда человек) живут в 60 000 сообществ, каждое из которых насчи-
насчитывает от 20 000 до 300000 человек.
Сказанное о рудах и людях можно отнести и к фотонам. Возьми-
Возьмите пучок света, испускаемый старомодной лампой накаливания, и раз-
разделите его на две равные части. Число фотонов в половинных пуч-
пучках будет неодинаковым, как не будет одинаковым и число фотонов
в четвертных пучках, и т.д. Или рассмотрим электромагнитное излу-
излучение в полости, возникающее при нагреве ее стенок до определенной
температуры. (Проделайте в стенке такой полости крохотное отвер-
отверстие, и вы получите знаменитое излучение черного тела, описываемое
формулой Планка.) Число фотонов в одной фазовой ячейке или чис-
число колебательных мод резонатора находится в соответствии с геомет-
геометрическим распределением: добавьте один фотон, и соответствующая
вероятность уменьшится в постоянное число раз, равное т/(т + 1),
где т — среднее число фотонов (задаваемое распределением Бозе-Эйн-
Бозе-Эйнштейна). Дисперсия такого распределения а2 равна т2 + т, где пер-
первое слагаемое (т2) происходит от случайных флуктуации классичес-
классического электромагнитного поля, индуцированных нагретыми стенками.
Второе слагаемое (т) отражает «корпускулярность» энергии, обуслов-
обусловленную эйнштейновскими фотонами — частицами света, существова-
существование которых он вывел из добавочного т в выражении а2 = т2 + т.
(Эта корпускулярность первоначально была введена Планком, что-
чтобы согласовать теоретические выводы с экспериментальными данны-
данными.)
При больших т можно считать, что а2 и т2. Деление объема ре-
резонатора пополам приводит в этом случае к ожидаемой доле фотонов р
в одной его половине и 1 — р — в другой. Если деление произведено
так, чтобы максимизировать р, то р и 0,6, причем независимо от чис-
числа фотонов. При больших т геометрическое распределение масштабно-
инвариантно, или самоподобно, так как а ~ т. Таким образом, по-
повторные деления объема продолжают распределять имеющиеся фото-
фотоны с самоподобным коэффициентом ветвления р/{1 — р) ~ 1,5 до тех
пор, пока их число не уменьшится настолько, что отношение а/т не
будет более постоянным, а существование отдельных фотонов нарушит
строгое самоподобие.
Самоаффинные фракталы без пустот 255
В случае лазерного излучения фотоны подчиняются распределению
Пуассона с а2 = т. Следовательно, масштаб распределения а ~ л/т не
пропорционален его среднему (т), и самоподобия не возникает.
Самоаффинные фракталы без пустот
Многократное деление пополам и умножение приходящихся на
каждую половину долей на 1 — р для левой и на р для правой поло-
половины интервала, т. е. то, чем мы занимались в предыдущем разделе,
представляет собой частный случай мультипликативного случайного
процесса. Бесконечные итерации такого процесса приводят к самоаф-
самоаффинному распределению плотностей (см. рис. 1, на котором представ-
представлены первоначальная постоянная плотность на единичном интервале
и результаты первых трех итераций.)
После п итераций вероятность в открытом интервале
т ¦ 2~п < х < (т + 1) • 2~п определяется выражением ркA — р)п~к,
где к — число единиц в первых п двоичных знаках числа х. Напри-
Например, если п = 6 и х = 1/5 = 0,00110011..., то к = 2; вероятность
равна р2A — рL и остается таковой на всем интервале 0,001100 =
= 12/64 < х < 0,001101 = 13/64 длиной 2, содержащем х = 1/5.
После шестой итерации имеем (JJ) = (®) = 15 интервалов с таким зна-
значением плотности — те 15 интервалов, в которых числа х имеют ровно
по 2 единицы в первых шести знаках своей двоичной записи. Наибо-
Наиболее распространенная при п = 6 плотность соответствует к = 3: она
встречается (®) = 20 раз, причем самый левый из этих интервалов на-
начинается в точке х = 0,000111 = 7/64. Причина, по которой двоичное
представление числа х описывает распределение такого рода, состоит
в том, что каждый нуль в двоичной записи х соответствует левой по-
половине интервала, а каждая единица — его правой половине.
Отметьте зачатки самоаффинности, присущие этой рекурсивной
конструкции: правая половина каждого распределения (см. рис. 1) рав-
равна его левой половине, умноженной на р/A — р), а все распределение
целиком стремится остаться инвариантным при растягивании его ле-
левой половины в 2 раза по горизонтали и в 1/A — р) раз по вертикали.
В пределе при п —>• сю распределение Р (х) на всем единичном ин-
интервале равно распределению на левой половине интервала, растянуто-
растянутому по горизонтали в 2 раза и по вертикали в 1/A — р) раз:
256 Глава 9
С этим функциональным уравнением мы еще встретимся, рассматри-
рассматривая одну интригующую стратегию для азартной игры (см. с. 275-279).
Множители 2 и 1/р представляют собой два коэффициента подобия для
получающегося самоаффинного фрактала.
Как еще можно охарактеризовать эту фрактальную функцию? От
обычной размерности Хаусдорфа D, как предела при г —>• 0 величи-
величины lniV/ ln(l/r), в данном случае мало проку. После п итераций число
отрезков N составляет 2™, а длина г каждого из них равна 2~™. Поэ-
Поэтому D = 1, как и следовало ожидать, поскольку фрактал на рис. 1 не
содержит пустот.
С другой стороны, сосредоточив внимание на долях и их распре-
распределениях, мы обнаружим, что после п = 2т итераций вероятность на
большом количестве, а именно (^), отрезков равна A —р)трт. На еди-
единичном интервале им соответствуют как раз все те полуоткрытые ин-
интервалы длиной 2~™, абсцисса х которых содержит одинаковое число
нулей и единиц среди первых п знаков двоичного представления х.
Например, при п = 4 эти (t,) = 6 особых интервалов задаются зна-
значениями х = 0,0011... (интервал C/16,4/16)), х = 0,0101..., х =
= 0,0110..., х = 0,1001..., х = 0,1010... и х = 0,1100... (Мно-
(Многоточия здесь означают все возможные комбинации нулей и единиц,
указывая на то, что речь идет об интервале, а не об отдельном значе-
значении.)
В общем случае существует (™) отрезков длиной 2~™ с плотнос-
плотностью A — р)крп~к, что соответствует полной вероятности
Заметим, что
fc=O
Используя формулу Стирлинга для факториалов и опуская несу-
несущественный множитель (п/2тгк(п — к)I!2, можно записать
I.) ~ ( п) [1~ П) = 2" " ' B)
где Н — энтропийная функция, хорошо известная из термодинамики
и теории информации, т.е.
Н(О = -?log2? - A -Olog2(l -О
(график энтропийной функции Н представлен на рис. 2).
Самоаффинные фракталы без пустот
257
Рис. 2. Энтропийная функция.
Фрактальная размерность множества всех этих подынтервалов
с общей вероятностью A — p)kpn~k имеет вид
C)
где ? = кIп. При г = 1/2, учитывая приближение в соотношении B),
получаем
Таким образом, в зависимости от значения параметра ?, представляю-
представляющего собой некоторую заданную вероятность, мы получаем различные
фрактальные размерности для носителя этой вероятности. Более того,
значение f (?) изменяется от 0 для наименьших (? = 0) и наибольших
(? = 1) плотностей до 1 при ? = 0, 5. В этом заключается одна из причин
появления названия жг/льтыфракталы. Заметим, что подмножества еди-
единичного интервала, соответствующие данной фрактальной размернос-
размерности /(?), рассеяны по всему интервалу и тесно «переплетены» с подмно-
подмножествами других размерностей — еще одна характерная особенность
мультифракталов. Так, при ? = 0,25 фрактальная размерность / (?)
приближенно равна 0,811, и соответствующими подмножествами явля-
являются все те точки единичного интервала 0 ^ х ^ 1, в координатах х
которых, представленных в двоичном виде, 25% всех цифр составля-
составляют нули, а 75% — единицы. Укажем для примера одну из несчетного
множества этих точек: х = 0,0A11) = 7/15. Опять же, фрактальная
размерность такой «канторовоподобной» пыли равна 0,811...
258 Глава 9
Установив фрактальную размерность / (?) носителя мультифрак-
тала, уместно выяснить, как изменяются при п —>• сю вероятности
A — р)крп~кB~п) из соотношения A). С этой целью введем показатель
Липшица-Гёлъдера а (?), который определим с таким расчетом, чтобы
произведение pk(l — p}n~kr~na (Z) не обращалось бы в нуль и не удаля-
удалялось бы в бесконечность при п —>• сю. Таким образом, показатель Лип-
Липшица-Гель дера, характеризующий сингулярности вероятностей, зада-
задается соотношением
tt@ = > E)
где, как и прежде, ? = к/п, а величина г для интересующего нас про-
процесса равна 1/2.
Как показывает соотношение E), а (?) есть линейная функция от ?,
монотонно возрастающая при р < 0, 5. При ? = 0 имеем а = ат{п =
= -Iog2(l -р), а если ? = 1, то а = amax = -log2p. Так, при р = 0,3
показатель Липшица-Гёльдера а принимает значения от amin = 0,51
до атах = 1,74. Значение amin характеризует наименее вероятную
часть мультифрактала, а атах — его наиболее вероятную часть.
Хотя фрактальные подмножества мультифрактала абсолютно де-
терминистичны (в отличие от случайных фракталов), они обнару-
обнаруживают гораздо меньшую геометрическую правильность, чем ори-
оригинальное канторово множество. Например, на двенадцатой стадии
построения троичное канторово множество состоит из 212 отрез-
ков длиной S к, I , образующих правильный геометрический
узор. Напомним, что размерность Хаусдорфа для канторова множес-
множества D к, 0,631.
Мультифрактал без пустот, имеющий примерно такую же размер-
размерность Хаусдорфа (D к, 0,629), характеризуется двоичными дробями,
доля единиц в которых составляет 3/19. На девятнадцатой стадии его
построения имеем A39) = 969 отрезков длиной 2~19, как и в случае тро-
троичного канторова множества. Однако эти отрезки расположены весьма
нерегулярно, как того требуют девятнадцатизначные двоичные дроби
с тремя единицами; а вот не содержащие единиц троичные дроби, опи-
описывающие троичное канторово множество, дают вполне упорядоченное
расположение отрезков.
Еще одна нерегулярность нашего мультифрактала проявляется
в количестве его элементов. Если размерность Хаусдорфа для муль-
мультифрактала оценивать по числу элементов на девятнадцатой стадии
построения, то мы в результате получим D = In 969/ In 219 к, 0,522,
Мулътифракталъный спектр 259
что значительно меньше асимптотического значения D и 0,629. Даже
на 190-й стадии построения, когда число отрезков достигает 7, 74-Ю34,
расчетное значение D = 0,610 все еще на 3% не дотягивает до оконча-
окончательной размерности Хаусдорфа. На примере таких подмножеств муль-
мультифракталов мы можем убедиться, как медленно сходятся оценки фрак-
фрактальных размерностей, если фрактал не самоподобен, пусть даже поро-
породившая его структура идеально самоаффинна (рис. 1).
Рис. 3. Последовательные этапы построения подмножества с наивысшей ве-
вероятностью, принадлежащего мультифракталу, изображенному на рис. 1.
В качестве иллюстрации нерегулярности таких мультифракталов
на рис. 3 показаны последовательные этапы построения подмножест-
подмножества с к = [п/2\, принадлежащего мультифракталу, изображенному на
рис. 1.
Мультифрактальный спектр: турбулентность
и ограниченная диффузией агрегация
В большинстве случаев нельзя получить прямого доступа к пе-
переменной ? [66]. Более того, эта переменная зачастую несуществен-
несущественна, поскольку относится к весьма специфическому процессу. Важны-
Важными параметрами описания мультипликативных случайных процессов,
аналогичных рассмотренному в предыдущих разделах, являются фрак-
фрактальная размерность носителя /, показатель Липшица-Гель дера для
распределения плотностей а и связывающее их соотношение / (а) =
= /(?(«)), называемое «силой сингулярности» параметра а, т.е. раз-
размерностью Хаусдорфа для его носителя, или просто мультифракталь-
ным спектром. В нашем примере, где а есть линейная функция от пере-
переменной ?, спектр / (а) представляет собой просто-напросто растянутый
и смещенный вариант функции / (?) (рис. 4).
260
Глава 9
Рис. 4. Мультифрактальный спектр мультипликативного случайного процес-
процесса.
Функция / (а) достигает максимума при ? = 0, 5. Согласно соотно-
соотношению E), соответствующее значение а равно «о = —A/2) log2p(l —
— р) = (dmin +amax)/2. Значение мультифрактального спектра при ад
равно / (ао) = 1, т.е. размерности Хаусдорфа для единичного (или лю-
любого другого) интервала. В случае мультипликативных случайных про-
процессов на фрактале (а не на интервале) с размерностью Хаусдорфа D
наибольшее значение / (а) равно D. Иначе говоря, максимум мульти-
мультифрактального спектра / (а) совпадает с размерностью Хаусдорфа для
носителя процесса.
Другой существенно важной точкой спектра / (а) является / («i),
в которой его угловой коэффициент df/da равен 1. Из равенства
A)
df _df d? _ ln?
da d? da lnp — ln(l — p)
очевидно, что при df/da = 1 соответствующее значение ?i = р. Подста-
Подставив его в соотношение E), получим a(?i) = ot\ = Н (р), что, согласно
соотношению D), равно / (р) = f {а.\). Отсюда, /(ai) = «i; в то же
время точка / (а\) лежит на касательной к / (а) с угловым коэффици-
коэффициентом 1, проходящей через начало координат. Значение / (ai) совпадает
с информационной размерностью Di (см. с. 269-275).
На рис. 5 показан мультифрактальный спектр рассеяния энергии
в полностью развитой турбулентности вдоль одномерной прямолиней-
прямолинейной траектории в турбулентном потоке [159, 161]. Турбулентные об-
Мулътифракталъный спектр
261
ласти являются носителями мультифрактала. Экспериментальные точ-
точки заимствованы из различных физических реализаций турбулентнос-
турбулентности (атмосферная турбулентность, турбулентность в пограничном слое,
турбулентность в следе за круговым цилиндром или проволочной ре-
решеткой). Заметьте, что все эти экспериментальные точки хорошо ло-
ложатся на одну-единственную кривую / (а), причем наилучшее согласие
достигается при р = 0,3. Похоже, турбулентность и в самом деле хоро-
хорошо моделируется мультифракталами, как первоначально и предполагал
Мандельброт [159].
1,5
Рис. 5. Мультифрактальный спектр в применении к турбулентности [178].
Другим красивым примером мультифрактальных явлений может
служить ограниченная диффузией агрегация (ОДА), которую Микин
и его сотрудники подвергли всестороннему разбору [174, 173]. При ОДА
отдельные молекулы после некоторых случайных блужданий «оседают»
на агрегате, порождая красивые случайные фракталы (рис. 6), напо-
напоминающие об определенных моделях биологического роста и о «фигу-
«фигурах Лихтенберга» (которые можно наблюдать при электрическом раз-
разряде на изолирующей поверхности) (рис. 7 [184]). Для таких узоров
характерна древовидная структура с многочисленными «фьордами» на
многих размерных масштабах. Причина образования подобных струк-
структур при ОДА заключается в том, что блуждающая молекула оседает,
262
Глава 9
Рис. 6. Рост кристаллов посредством ограниченной диффузией агрегации
(ОДА) [107].
как правило, вблизи выступа фрактала, а не в глубине фьорда; веро-
вероятность проникновения в глубокий фьорд, не «застряв» где-нибудь по
пути, просто чрезвычайно мала. Таким образом, в различных точках
на границе фрактала вероятности роста различны: высокие у выступов,
они уменьшаются по мере углубления в фьорды. В точности по такому
рецепту и «пекутся» мультифракталы.
Мультифрактальный спектр
263
Рис. 7. Фигура Лихтенберга — электрический разряд. Фрактальная размер-
размерность D и 1,7 [184].
На рис. 8А вы видите двумерный кластер ОДА, а на рис. 8Б —
точки его границы с относительно высокой вероятностью роста. Как
и следовало ожидать, точки наибольшей вероятности роста явно пред-
предпочитают выступы кластера. Экспериментальный мультифрактальный
264
Глава 9
спектр / (а), охватывающий диапазон от ат[п ss 0,5 до атах > 5, доста-
достаточно хорошо воспроизводит спектр теоретический (см. обзор Стэнли
и Микина и приведенный там список литературы [247]).
04)
(Б)
Рис. 8. (А) Кластер ОДА. (Б) Места на нем с высокой вероятностью дальней-
дальнейшего роста [173].
На рис. 9 представлен результат одной из первых попыток ком-
компьютерного моделирования ОДА Уиттеном и Сандером. Как обнаружи-
обнаружилось, фрактальная размерность для двумерной ОДА лежит вблизи 1,7.
Это означает, что масса агрегата возрастает как L1'7, где L — линей-
линейный размер, а средняя плотность изменяется как L1'7/L2 = L~0'3, т.е.
убывает, в полном соответствии с внешним видом подобных форм рос-
роста. Для трехмерной ОДА фрактальная размерность обычно находится
вблизи 2,5 [279].
Внешнее сходство между фигурами Лихтенберга и формами ОДА
не случайно. Оба процесса описываются уравнением Лапласа из теории
потенциала, причем градиент потенциала соответствует полю диффу-
диффузии в ОДА, а поверхность кластера ОДА — эквипотенциальной поверх-
поверхности. При таком подходе к ОДА можно предположить, что частицы
будут с большей охотой прилипать к тем местам кластера, где высок
градиент потенциала, т.е. вблизи выступов.
Рассматривая молнии, фигуры Лихтенберга и тому подобные элек-
электрические пробои, мы, разумеется, должны будем воспользоваться
электрическим потенциалом. «Рост» молнии или разряда происходит
как правило в направлении наибольшего градиента потенциала. Глубо-
Глубокие же «фьорды» нашего узора хорошо заэкранированы и поэтому либо
Образование вязких языков
265
•¦=:":!"
.:•. :¦• .:
Г:: - ::.:.
: ::: ::**:
Рис. 9. Фрактальный кластер, выращенный с помощью компьютерного моде-
моделирования ограниченной диффузией агрегации [279].
растут весьма слабо, либо не растут вовсе. Такое соответствие между
теорией потенциала и фрактальным ростом было полностью подтверж-
подтверждено тщательными измерениями и численными решениями потенци-
потенциального уравнения [184].
Образование вязких языков
Аналогичную проблему представляет образование вязких языков,
которое удобнее всего наблюдать на границе раздела двух жидкостей,
заключенных между двумя стеклянными пластинами. В случае двух
266 Глава 9
смешивающихся жидкостей — например, воды и желатина — при втор-
вторжении одной жидкости в другую возникает структура, аналогичная
ОДА (рис. 10А). Этот процесс является результатом гидродинамичес-
гидродинамической неустойчивости между жидкостями. Как и в случае ОДА, любой
«бугорок» на поверхности раздела имеет тенденцию к росту, причем
рост происходит, как правило, у выступов, поскольку градиент дав-
давления, обусловливающий этот рост, достигает наибольшей величины
именно у выступов.
(А) (Б)
Рис. 10. Образование вязких языков на границе раздела двух жидкостей. Фор-
Форма «языков» зависит от степени взаимной смешиваемости жидкостей. (А)
В жидкий желатин впрыснуто через канюлю (черная полоса на рисунке) не-
некоторое количество подкрашенной воды (вода и желатин очень хорошо сме-
смешиваются). (Б) Вместо воды в желатин впрыснут концентрированный рас-
раствор сахара (смешиваемость хуже).
В случае несмешивающихся жидкостей, например, глицерина
и нефти, языки гораздо шире, потому что поверхностное натяжение
между этими двумя жидкостями препятствует образованию тонких
дендритов, т.е. выступов с большой кривизной (рис. 10Б). Когда в неф-
тесодержащий пласт под большим давлением закачивают воду, то из-
за этой особенности образования вязких языков много нефти остается
в земле. Повышая поверхностное натяжение воды с помощью специаль-
Мультифракталы на фракталах 267
ных добавок, вязкие языки можно сделать более округлыми, уменьшив
тем самым их фрактальную размерность и увеличив количество нефти,
которое можно извлечь до появления воды.
Мультифракталы на фракталах
Принимая во внимание благоговейный трепет, который мульти-
мультифракталы вызвали в определенных кругах, можно лишь удивлять-
удивляться, насколько простым оказывается обобщение, ведущее от фракталов
к мультифракталам. Рассмотрим мультифракталы с фрактальным но-
носителем. Возьмем единичный интервал, из которого удалено несколь-
несколько открытых интервалов, и от которого осталось несколько отдельных
отрезков длины г,-, разделенных пустотами. Поставим в соответствие
каждому отрезку гг- значение веса, или вероятности, pi. Итерируя этот
обобщенный процесс удаления открытых интервалов и приписывания
вероятностей оставшимся интервалам, мы приходим к обобщению кан-
торова множества, причем каждой «пылинке» поставлена в соответ-
соответствие некоторая вероятность. Это и есть тот самый прототипический
мультифрактал на фрактальном носителе, изучением которого мы зай-
займемся в настоящей главе.
Сопоставление каждому отрезку г, вероятности р, позволяет моде-
моделировать процессы фрактального роста, при котором различные отрез-
отрезки соответствуют различным точкам роста. Вероятности же pi пред-
представляют собой различные скорости роста в этих точках, как при огра-
ограниченной диффузией агрегации (см. с. 259-265). Применяя наше по-
построение к странным аттракторам, мы увидим, что отрезки г\ сходят-
сходятся к различным значениям, которые может принимать динамическая
переменная (множество таких значений называется носителем аттрак-
аттрактора), в то время как вероятности pi моделируют частоты, с которыми
«посещаются» эти отрезки.
Если самоподобное канторовское множество, порожденное сегмен-
сегментами одинаковой длины, характеризуется одним показателем скейлин-
га, а именно, размерностью Хаусдорфа D, то мультифракталы описыва-
описываются двумя показателями скейлинга — один для фрактального носителя
и другой для вероятностей.
Введем эти два показателя. Для этого нам понадобится вспом-
вспомнить определение размерности Хаусдорфа. Размерность Хаусдорфа D
для множества задается пределом выражения lniV/ln(l/r) при г —> О,
где N — наименьшее число элементов диаметра г, необходимое для
268 Глава 9
того, чтобы полностью покрыть множество:
D = Иш _ЬЛ^. A)
ю ln(l/r) V ;
Размерность Хаусдорфа D можно также задать в следующем неявном
виде:
\imNrD=c, 0<c<oo, B)
где с — некоторая постоянная. Соотношение B) демонстрирует одно
важное свойство размерности Хаусдорфа: это тот самый показатель,
при котором произведение NrD остается конечным и отличным от ну-
нуля при г —v 0. Стоит изменить D, пусть даже на ничтожно малую
величину, как произведение NrD либо обратится в 0, либо уйдет в оо.
При рекуррентном построении самоподобного множества число
частей N после п итераций равно Nq, где пс — число частей гене-
генератора. Аналогично, г равно Tq, где га — длина отрезка генератора.
(Предполагается, что на данном этапе эти отрезки имеют одинаковую
длину.) Тогда вместо соотношения B) мы можем записать
lim (NGrg)n = с, C)
п—юо
что, разумеется, верно лишь при
S = 1,
или
D = т^Ц. D)
ln(l/r)
Следовательно, в случае строго самоподобного множества нет необходи-
необходимости вычислять предел при г —> 0, как в соотношении A). Достаточно
воспользоваться параметрами генератора Nq и г<з-
Если отрезки генератора г, имеют различную длину, соотноше-
соотношение C) принимает вид
N
lim [2_jri ) = с> E)
i=i
что подразумевает
JV
y>f = i- F)
Фрактальные размерности, получаемые из обобщенных энтропии 269
Для обобщенного генератора с прямолинейными частями г\ и ве-
вероятностями pi введем два показателя: показатель т для интервалов
носителя г\ и показатель q для вероятностей р». Таким образом, вместо
предела в соотношении E) рассмотрим предел
G)
и найдем такие значения q и т, при которых выражение G) остается
конечным; иначе говоря, такие значения q и т, которые удовлетворяют
уравнению
N
Из уравнения (8) ясно, что пара значений q и т не единственна. Су-
Существует сплошной диапазон показателей т = т(д), соответствующий,
как мы увидим, континууму фрактальных размерностей.
В случае оригинального канторова множества (N = 2, г» = 1/3)
уравнение (8) принимает при pi = 1/2 следующий вид:
1Г = 1
и имеет решение т = A — <7Iп2/1пЗ. Учитывая, что размерность Ха-
усдорфа для оригинального канторова множества равна D = In 2/In3,
можно также записать это решение в виде т = A — q)D.
Полученное соотношение между т и D подтверждается также срав-
сравнением предела G) с соотношением E): при q = 0 показатель т соответ-
соответствует D в полном согласии с соотношением т = (l — q)D. Это сравнение
наводит на мысль, что величина т/A — q) может играть роль некоей
обобщенной размерности Dq, которая совпадает с размерностью Хаус-
дорфа при q = 0, но может отличаться от нее при других значениях q.
Другой метод образования новых размерностей мы рассмотрим
в следующем разделе.
Фрактальные размерности, получаемые из
обобщенных энтропии
Пытаясь обобщить понятие энтропии распределения вероятностей,
венгерский математик А.Реньи ввел следующее выражение, основан-
270 Глава 9
ное на моментах g-го порядка вероятностей р^:
N
где q не обязательно должно быть целым числом [211]. При q —> 1 опре-
определение A) приводит к хорошо известному выражению для энтропии
JV
B)
дискретного распределения вероятностей. Таким образом, величину,
определяемую соотношением A), можно считать (для чего Реньи все
это и затеял) обобщенной энтропией.
Взяв пример с Реньи, определим обобщенные размерности как
JV
9 r->i g-1 lnr '
где pi — вероятность того, что случайная величина попадет в «кор-
«корзинку» шириной г. Параметр q принимает значения от —оо до +оо.
Заметим, что для самоподобного фрактала с равными вероятностями
Pi = 1/N определение C) дает Dq = Do при всех значениях q. Для та-
таких фракталов необходимость в переходе к пределу при г —> 0 отпадает,
и мы получаем обобщенную размерность
! =
9 g-1 In r ln(l/r)'
не зависящую от q.
Очевидно, что при q = 0 определение C) совпадает с определением
размерности Хаусдорфа D. Именно поэтому мы называем величины Dq
обобщенными размерностями в надежде, что они станут еще одним по-
полезным инструментом для описания мультифракталов. И наши надеж-
надежды вполне оправдываются. Более того, обобщенные размерности Dq,
как оказалось, однозначно соотносятся с парой показателей q и т обще-
общего мультифрактала.
Соотношение между Dq и показателями q и т можно легко полу-
получить из предела G), если ввести N «корзинок» постоянного размера г\ =
= г, что при п —> оо никак не влияет на значения гид, при которых
Фрактальные размерности, получаемые из обобщенных энтропии 271
этот предел сходится:
N
in Ер?
и, учитывая определение C),
т (q) = A - gJ?g. D)
Для самоподобных фракталов размерности Dq можно получить не-
непосредственно из величину и г, генератора, используя соотношения (8)
и D):
«rf"^ = 1. E)
При q = 1 получаем т (д) = 0, и Dq определяется выражением
п — ^т
dq Л
4 4=1
которое с учетом соотношения (8) имеет вид
JV
Е Pi lnPi
Е Pi ln г*
г'=1
или, в случае N равных вероятностей pi = 1/N,
Dl = -?Ш-. G)
Е НУ г)
При <7 —у 1 из определения C) получаем
r->0 111 Г
где S\ — энтропия вероятностей pi, задаваемая соотношением B).
272 Глава 9
Энтропия Si и величина D\, называемая также информационной
размерностью, играют важную роль в анализе нелинейных динамичес-
динамических систем, особенно в описании потерь информации при эволюции
хаотической системы во времени. В этом контексте энтропия S\ назы-
называется энтропией Колмогорова.
При q = 2 формула C) дает так называемую корреляционную раз-
размерность
которая является еще одной важной фрактальной размерностью в до-
дополнение к Dq и D\. Ее главное практическое преимущество состоит
в том, что в случае «практических» фракталов ее можно сравнительно
легко определить (см. гл. 10). Теоретическая значимость размернос-
размерности ?>2 обусловлена ее тесной связью с таким фундаментальным поня-
понятием, как корреляция. Как мы увидим в гл. 10, размерность D<i опреде-
определяется непосредственно «корреляционной функцией» фрактального мно-
множества, т.е. вероятностью найти на расстоянии г от данного элемента
множества другой элемент того же множества. Таким образом, изме-
измерение корреляционной размерности D^ сводится к простому счету.
В принципе, обобщенные размерности Dq могут быть определены
для всех q в соответствии с C). Однако на практике при q > 0 иногда
встречаются трудности, так как положительные показатели q уменьша-
уменьшают члены с малыми р, (соответствующие «редко посещаемым» частям
фрактала). В результате предел при г —> 0 сходится очень медленно.
Этот недостаток можно преодолеть, если числитель в соотношении C)
вычислять сразу для г и г/2, требуя при этом, чтобы при г -> 0 их
отношение было равно 1 (см. [96]).
Соотношение между мультифрактальным
спектром / (а) и показателями массы т (q)
В предыдущих разделах мы ввели для описания мультифрактала
две различные функции:
• мультифрактальный спектр f (а), который задает фрактальную
размерность / подмножества с данным показателем массы Лип-
Липшица-Гёльдера а, и
• обобщенные фрактальные размерности Dq или, что эквивалентно,
показатели т (q) = A — q)Dq.
Соотношение между спектром и показателями массы 273
Так как обе эти функции (/ (а) и т (q)) описывают одни и те же
аспекты мультифрактала, они должны быть как-то связаны друг с дру-
другом. Такая взаимосвязь действительно существует и имеет вид
T{q) = f(a)-qa, A)
где а как функция от q определяется из решения уравнения
?(qa - f (а)) = 0. B)
И наоборот, если известна фрактальная размерность Dq (или по-
показатель т(д)), то мультифрактальный спектр может быть найден по
формуле
f(a{q))=r(q) + qa{q), C)
где
a(q) = -j-qr(q), D)
что подразумевает, учитывая соотношение C),
Соотношения C) и D) задают кривую / (а) параметрически (как функ-
функцию от параметра q). Эти два уравнения представляют собой преобра-
преобразование Лежандра от переменных q и т к переменным аи/. Такие
преобразования играют важную роль в термодинамике, позволяя пе-
переходить, например, от энергии как функции от объема и энтропии
к свободной энергии как функции от объема и температуры.
Вообще говоря, аналогии между мультифракталами и статистичес-
статистической механикой простираются гораздо дальше, чем замена переменных
с помощью преобразования Лежандра. Физики могут по достоинству
оценить тот факт, что равенство (8) выглядит в точности как функция
распределения, которую придумал знаменитый физик-теоретик и хи-
химик Дж. Уиллард Гиббс A839-1903). Следуя этой математической ана-
аналогии, некоторые из наших параметров можно считать формально эк-
эквивалентными таким термодинамическим понятиям, как энергия (а),
свободная энергия (т/q), энтропия (/) и температура A/q).
274 Глава 9
Странные аттракторы как мультифракталы
Странные аттракторы принадлежат к числу наиболее важных ре-
реализаций мультифракталов. Аттрактором отображения хп+\ = f (ж„)
является отдельная точка или неразложимое ограниченное множество
точек, к которым сходятся при п —у оо итерации начальных значе-
значений из «области притяжения» аттрактора. Странным называется ат-
аттрактор, итерации хп которого чувствительно зависят от начального
значения жо, т.е. сколь угодно близкие начальные значения при доста-
достаточно больших п расходятся на макроскопические расстояния. Стран-
Странный аттрактор — это фрактальная пыль с фрактальной размерностью
меньшей, чем евклидова размерность пространства вложения.
Прототипом странного аттрактора может служить логистичес-
логистическая парабола (см. гл. 12), определяемая квадратичным отображени-
отображением / (ж) = гхA — х). При г < Гоо = 3,5699456 ... итерации /(") (ж) ото-
отображения / (ж) имеют периодический характер на интервале 0 ^ х ^ 1
с длиной периода 2т. Но при г = Гоо итерации становятся апериодичес-
апериодическими и сходятся к странному аттрактору. Этот странный аттрактор
имеет структуру канторова множества, которое асимптотически хоро-
хорошо моделируется генератором с двумя интервалами длиной г\ = 0,408
и Г2 = г\ и двумя равными весами pi = Р2 = 0, 5.
Размерность Хаусдорфа D = Do для такого модельного аттрактора
определяется из уравнения E) при q = 0:
г? +г? = 1,
которое при гг = г\ имеет решение
Таким образом, D = Do к, In 0,618/In0,408 к, 0,537.
Информационная размерность определяется соотношением G).
При N = 2 и приведенных выше значениях г\ получаем Di = 0,575.
При всех остальных значениях q и pi = p<i = 0,5 соотношение E) при-
принимает следующий вид:
1 *^ 1 5
откуда
-g)lnri
Алгоритм жадного игрока
275
Из этой формулы при 7*1 = 0,408 получаем -D_oo = l/log2ri =
= 0,773, ..., ?>_i = 0,561, Do = 0,537, D2 = 0,497, D3 = 0,482, ...,
D00 = -l/log2ti= 0,387.
0,6
0,8
Рис. 11. Мультифрактальный спектр итераций квадратичного отображения
в предельной точке удвоения периода [96].
Весь мультифрактальный спектр f (а), вычисленный по Dq, пред-
представлен на рис. 11. Так как производная df(a)/da равна q, максимум
функции / (а) равен Do = 0,537, в то время как / @) соответству-
соответствует df (a)/da = ±оо, что дает значения am;n = D^ = 0,387 и amax =
= -D-oo = 0, 774; это с точностью до 2,5% согласуется с лучшими ре-
результатами численных расчетов [96]. Расхождение, хотя оно и мало, от-
отражает тот факт, что, вопреки нашему предположению, аттрактор по-
последовательности удвоения периода не обладает точным самоподобием.
Алгоритм жадного игрока при неблагоприятных
шансах на выигрыш
В гл. 6 (см. с. 206-208) мы в общих чертах наметили оптимальную
стратегию для азартной игры при благоприятных шансах на выигрыш.
Там же мы порекомендовали воздержаться от игры при шансах не-
неблагоприятных. Тем не менее для тех, кто стойко выдерживает удары
судьбы и готов рискнуть всем, существует небольшой шанс разбога-
разбогатеть — при условии, что они будут придерживаться одного простого
правила, основанного исключительно на жадности: алгоритма жадного
игрока, или поглощающего алгоритма.
Предположим, что у игрока имеется начальный капитал К дол-
долларов, капитал банка составляет В долларов и вероятность выиграть
276 Глава 9
одну игру равна р, где р < 0,5. Конечно же, разумный человек, реши-
решительно настроенный на положительную среднюю прибыль, вообще не
должен играть, если вероятность выигрыша меньше 0,5. Но допустим,
что наш игрок желает рискнуть всем своим капиталом в надежде на
малый шанс сорвать банк. Из формулы B) в гл. 6 мы знаем, что ве-
вероятность достичь желанной цели при постоянной ставке в 1 доллар
равна
гк -1
Рк = 1~дк = —ц -, A)
г — 1
где г = A — р)/р > 1. Если колесо рулетки идеально отрегулировано
и имеет 36 секторов с положительными числами и один нулевой сектор
(«зеро»), то для «равных» шансов р = 18/37, а г = 19/18. В более общем
смысле, К в соотношении A) есть первоначальный капитал игрока,
деленный на величину ставки, а В — капитал банка, также деленный
на величину ставки.
Предположим, что первоначальный капитал игрока составля-
составляет 1000 долларов (К = 1 000), а в банке находится 10 000 долларов (В =
= 10 000). Тогда из соотношения A) следует, что вероятность рк со-
сорвать банк равна примерно 10~211. Иначе говоря, шансы игрока проиг-
проиграть все свое состояние почти неотличимы от неизбежности.
Менее робкий игрок может отважиться сделать ставку в 10 долла-
долларов на игру. В этом случае К в соотношении A) становится равным 100,
а В = 1000. Это «повышает» шансы игрока на выигрыш 10 000 долла-
долларов до р ss 10~21. Еще более отчаянный игрок, который каждый раз
ставит 100 долларов (К = 10, В = 100), вознаграждается неслыханным
повышением вероятности до рк ~ 0,0025. Получается, что чем выше
ставка, тем больше у игрока шансов на выигрыш.
Почему же так получается? Очевидно, что игрок, делающий очень
небольшие ставки, например, в 1 или 10 долларов, должен сыграть очень
много партий, прежде чем сумма его выигрыша достигнет 10 000 долла-
долларов (если такое событие вообще произойдет), а всякий раз, делая став-
ставку, он тем самым испытывает судьбу. Это позволяет нам утверждать,
что при неблагоприятных шансах на выигрыш оптимальная стратегия
состоит в том, чтобы поставить все имеющиеся в наличии деньги. Вы-
Выражаясь более конкретно, пока х = К/В меньше 1/2, ставить нуж-
нужно весь капитал; в случае выигрыша вы его удвоите. Следовательно,
обозначив через Р (х) вероятность того, что используя наш «жадный»
алгоритм, игрок в конце концов все же выиграет, получим следующее
Алгоритм жадного игрока 277
функциональное рекуррентное соотношение:
Р(х)=рРBх) + A-р)-0, 0^ж^|. B)
Разумеется, если х > 1/2, то чтобы выиграть В долларов, необходимо
каждый раз ставить В — хВ долларов. Тогда даже в случае проигрыша
у игрока останется К — (В — К) = 2К — В долларов, чтобы продолжать
игру [24]. Отсюда,
Р(х)=р-1 + A-р)РBх-1), l^x^l. C)
Остается только один вопрос: как найти функцию Р (х) из уравне-
уравнений B) и C)? Конечно, при 0 < р < 1/2 из уравнения B) следует,
что Р @) = 0, а из уравнения C) — что Р A) = 1. Что касается осталь-
остальных значений х, то нетрудно заметить, что функция Р (х) должна быть
самоаффинной. Действительно, из уравнения B) видно, что, подверг-
подвергнув х сжатию в 2 раза и умножив Р на р, мы получим левую половину
функции Р (х).
По правде говоря, нам уже приходилось встречаться с функци-
функцией Р (х) (в этой же главе; правда, вместо р там было 1 — р — см. рис. 1
и соотношение A)). Но, подобно многим другим самоподобным или са-
самоаффинным функциям, Р (х) не отличается добронравным поведени-
поведением: ее производная обращается в нуль везде, кроме точек, абсциссы х
которых образуют канторово множество. Иначе говоря, функция Р (х)
представляет собой чертову лестницу (см. рис. 12, где изображен гра-
график Р (х) для случая р = 0, 25).
Чтобы вычислить Р(х), запишем х в виде двоичной дроби. Если
эта дробь бесконечна, оборвем ее после n-го знака. В нашем приме-
примере х = 1/10 в двоичной записи имеет вид бесконечной периодической
дроби х = 0,0@011), которую можно аппроксимировать конечной дро-
дробью х = 0,00011 = 3/32. Величина Р (х) задается следующим выраже-
выражением:
Р (ж) = роРоРоРоРо + PoPoPoPoPi + P0P0P0P1P0, D)
где ро = р и pi = A — р). Три последовательности индексов соответ-
соответствуют всем двоичным дробям с п = 5 знаками, меньшим х = 0,00011,
т.е. 0,00000; 0,00001 и 0,00010. Таким образом, если р0 = 18/37 и р± =
= 19/37, то Р(х) = р*(р0 + 2pi) и 0,084. Так как х < х, а Р (х) —
неубывающая функция, значение Р (х) в действительности несколько
278
Глава 9
О 0,2 0,4 0,6 0,8 1
Рис. 12. Интегральная вероятность выигрыша при игре с использованием
«жадного» алгоритма: самоаффинная чертова лестница.
больше 0,084. По сравнению с вероятностью выигрыша рк = 0,0025 при
постоянной ставке в 100 долларов налицо весьма ощутимое повышение
шансов. Даже постоянная ставка в 1000 долларов дает лишь рк = 0,077.
Три слагаемых в соотношении D) отражают три различных пути
к успеху (с использованием нашего «жадного» алгоритма) при условии,
что игра прекращается после пяти ставок. Например, третье слагае-
слагаемое PoPoPoPiPo означает, что игрок выиграл три раза подряд, затем
один раз проиграл, после чего снова выиграл. Капитал игрока при этом
составил, соответственно, 1, 2, 4, 8, 6 и 10 тысяч долларов. Второму
слагаемому в соотношении D) — PoPoPoPoPi — соответствует после-
последовательность капиталов в 1, 2, 4, 8, 10 и 10 тысяч долларов. Такую
же последовательность демонстрирует и первое слагаемое РоРоРоРоРо?
так как достигнув конечной цели (выигрыша 10 000 долларов), игрок
прекращает игру.
Если игрок не разоряется после 5 ставок, то он, разумеется, может
продолжить игру и повысить свои шансы сорвать банк. В этом слу-
случае дробь х в Р (х) следует обрывать дальше, чем после пятого знака.
Например, дробь 51/512 является превосходной аппроксимацией дро-
дроби 1/10 и дает Р E1/512) > 0,09. При иррациональных х, выражаемых
апериодическими двоичными дробями, вычисление Р (х) представляет
собой бесконечный процесс. Однако при рациональных х, выражаемых
Алгоритм жадного игрока 279
периодическими двоичными дробями, существует замкнутая формула,
открыть которую мы предоставляем читателю. Итак, чему же равно
значение Р A/10)?
И какова ожидаемая продолжительность игры до момента, когда
либо разорится игрок, либо лопнет банк (под тяжестью жадного ал-
алгоритма)? Как и Р(х), эта продолжительность должна представлять
собой самоаффинную функцию и быть меньше, чем ожидаемая продол-
продолжительность игры с любой постоянной ставкой [70]:
E)
При р = 18/37, г = 19/18 и ставке в 1 доллар К = 1 000 долларов, В =
= 10 000 долларов, а ожидаемая продолжительность игры Dk состав-
составляет 37000 раундов. При ставке в 100 долларов К = 10, В = 100, про-
продолжительность игры сокращается до 358 раундов. При ставке 1 000
долларов К = 1, В = 10, игра продлится только 25 раундов. Таким
образом, используя алгоритм жадного игрока, можно ожидать средней
продолжительности игры менее, чем 25 раундов.
Глава 10
Некоторые реально существующие
фракталы и их измерение
Равенство, которого мы требуем, явля-
является наиболее прочным воплощением не-
неравенства.
Георг Кристоф Лихтенберг
В этой главе мы нанесем запоздалый визит в мир реально сущест-
существующих фракталов. Как было метко замечено Мандельбротом и дру-
другими авторами, природа любит фракталы ничуть не меньше (если не
больше) регулярных форм. На каждую гладкую кривую или поверх-
поверхность в окружающем нас мире приходится много (чтобы не сказать
«очень много») весьма нерегулярных, а нередко даже фрактальных кри-
кривых и поверхностей, наделенных тончайшей структурой во многих мас-
масштабах.
Почему фракталы так распространены в природе? Решающей при-
причиной здесь является то, что гладкая искривленная поверхность содер-
содержит свой внутренний масштаб длины — радиус кривизны. И, конечно
же, такой внутренний масштаб тоже должен иметь какую-то причину.
Например, наша Земля выглядит со стороны как шар, и ее искривлен-
искривленная поверхность имеет свой радиус кривизны R. Чему равен этот ра-
радиус? Его можно выразить через полную массу Земли М и ее среднюю
плотность р:
з у/3
При М и 6 • 1024 кг и р й 6 ¦ 103 кг/м3 радиус Земли получается рав-
равным приблизительно 6 000 км. Таким образом, естественный масштаб
длины для земного шара в конечном счете определяется количеством
агрегированной пыли, из которой 4,7 миллиарда лет назад и образова-
образовалась допотопная Земля.
К счастью, многие объекты и законы природы лишены естествен-
естественного масштаба в том диапазоне, в котором мы их наблюдаем. Следова-
Следовательно, то, что верно при одном увеличении, должно быть верно и при
Некоторые реально существующие фракталы и их измерение 281
всех остальных увеличениях. Иначе говоря, объект должен обладать
самоподобием — статистическим, асимптотическим или даже строго
геометрическим. Если же объект обладает какой-либо структурой, то
аналогичная структура должна проявиться во многих масштабах. Дру-
Другими словами, отсутствие естественных масштабов порождает самопо-
самоподобие, а самоподобный объект, за исключением нескольких лишенных
характерных структурных особенностей построений (таких как беско-
бесконечная прямая), должен быть фрактальным.
Взглянем на матушку-Землю еще раз, но уже не из космического
пространства, а с более близкого расстояния, когда кривизна ее поверх-
поверхности становится несущественной. Многие береговые линии (равно как
и некоторые проведенные человеком границы) не имеют естественного
масштаба длины. Процессы, формирующие многие из границ раздела
между водой и сушей, подобны в широком диапазоне масштабов. На
рис. 1 показана часть побережья Норвегии — родины Йенса Федера,
из книги которого «Фракталы» [66] и позаимствован рисунок. Побере-
Побережье изрезано большими фьордами, маленькими фьордами и еще более
мелкими бухтами и бухточками. Если же мы рассмотрим еще более
подробные карты, а затем, наконец, сами отправимся (пешком или на
лодке) на прогулку вдоль побережья, то увидим, что берега бухт изре-
изрезаны заливами, заливчиками и т. д. вплоть до уровня воды, заполняю-
заполняющей узкие щели между отдельными камнями.
Как же измерить длину такого фрактального побережья? Ясно, что
чем подробнее наша карта, тем больше кажущаяся длина L. Более того,
если береговая линия самоподобна, то мы обнаружим самоподобный
степенной закон, устанавливающий связь между длиной побережья L
и масштабной единицей длины г, используемой при измерении:
L(r)~re, A)
где показатель е отрицателен, если L возрастает при уменьшении г.
В отличие от фрактальной кривой, длина гладкой кривой стремится
при г->0к некоторому асимптотическому значению, т. е. показатель е
равен нулю.
Как мы уже видели в предыдущих главах, для характеристики
фрактальных объектов используют фрактальную размерность — на-
например, размерность Хаусдорфа
lniV(r)
^^ B)
282
Глава 10
Рис. 1. Определение фрактальной размерности побережья Норвегии путем
подсчета количества клеток, включающих в себя береговую линию [66].
Размерности, определяемые путем подсчета клеток 283
где N (г) — минимальное число дисков диаметра г, необходимых для
покрытия фрактала. Если измерять таким образом длину L, то чис-
число N (г) окажется равным L (г)/г, а показатель е в соотношении A) —
1 — D. Размерность Хаусдорфа, таким образом, принимает вид
D = 1 - е C)
и при е < 0 превосходит единицу (размерность Хаусдорфа для гладкой
кривой).
Размерности, определяемые путем подсчета клеток
Предложенный Хаусдорфом рецепт — покрытие фрактала диска-
дисками — далеко не всегда представляет собой самый удобный способ из-
измерения фрактальной размерности (равно как и рецепт сосиски Мин-
ковского, тайна которого была раскрыта нами на с. 75-77 в гл. 1).
Для многих реальных фракталов метод определения размерности пу-
путем подсчета числа клеток, содержащих контур фрактала, оказывается
более предпочтительным. Для того чтобы определить таким способом
размерность фрактала, мы накладываем на него квадратную решетку
(рис. 1) и подсчитываем число клеток N(r), в которые попадает наш
фрактал. Когда расстояние г между параллельными линиями квадрат-
квадратной сетки становится достаточно малым, величина lniV (r)/ ln(l/r) схо-
сходится к конечному значению — размерности Хаусдорфа D.
На рис. 2 показан результат произведенного Федером подсчета дли-
длины береговой линии Норвегии с помощью квадратных сеток с шагом г
от 0,6 км до 80 км. При увеличении шага г длина L (г) уменьшилась в 12
раз — от примерно 30000 км до 2 500 км. В двукратно логарифмичес-
логарифмическом масштабе все результаты измерения достаточно хорошо ложатся
на прямую с угловым коэффициентом е = —0,52. Таким образом, со-
согласно соотношению C), размерность Хаусдорфа D = 1 — е = 1,52,
т.е. находится примерно посредине между евклидовыми размерностя-
размерностями гладкой кривой и гладкой поверхности.
На рис. 3 представлены опубликованные Мандельбротом [161] дан-
данные о кажущейся длине L (г) нескольких других берегов и сухопутных
границ, размерности Хаусдорфа для которых варьируются в диапазоне
от D ss 1 для гладкого побережья Южной Африки доВи1,3 для весь-
весьма изрезанного западного побережья Британии. Однако ни одна страна
и ни один берег не могут сравниться с Норвегией и ее D и 1, 52.
284
Глава 10
-А
X
X
CJ
CD
10* -
К 10°
1 10
Шаг сетки г (км)
Рис. 2. Измеренная длина побережья Норвегии в зависимости от шага сет-
сетки г. Угловой коэффициент прямой определяет фрактальную размерность
береговой линии D и 1, 52 [66].
Массовая размерность
Для многих целей и размерность, подсчитанная по клеткам, не яв-
является самой подходящей или удобной фрактальной мерой. Взгляните
на «фигуру Лихтенберга» (рис. 4) — один из первых физических фрак-
фракталов, созданных человеком. Этот узор, образованный электрическим
разрядом на металлическом острие, помещенном на изолятор, впервые
наблюдался в Гёттингене в 1777 г. (в этом году в расположенном непо-
неподалеку Брунсвике родился Гаусс) физиком и афористом Георгом Крис-
тофом Лихтенбергом A742-1799I. Измерив светлую область М фигу-
фигуры Лихтенберга, мы обнаружим, что площадь ее возрастает с увеличе-
увеличением характеристического радиуса R согласно простому однородному
степенному закону
Однако показатель D здесь равен не 2, как в случае сплошной од-
однородной фигуры на плоскости (например, диска с площадью М, рав-
равной tvR2). Для фигуры Лихтенберга показатель D заключен в интервале
от 1,7 до 1,9.
1Лихтенберг дважды побывал в Англии, из них один раз по личному приглаше-
приглашению короля Георга III. Там он познакомился с британской наукой и британской
вежливостью, причем и то, и другое донельзя его восхитило. Славу Лихтенбергу
принесли многочисленные весьма острые афоризмы, в которых он подсмеивался над
своими коллегами-учеными и прочими соотечественниками. Среди литературных
трудов Лихтенберга особое место занимают блестящие комментарии к гравюрам
Вильяма Хогарта (в том числе к «Модному браку» и «Пути повесы»).
Массовая размерность
285
Южноафриканское побережье
* ю3 -
10"
Длина мерного стержня (км)
Рис. 3. Кажущаяся длина и фрактальная размерность некоторых побережий
и сухопутных границ [161].
Показатель D в соотношении A) может служить как еще одна фрак-
фрактальная размерность, более доступная измерению и более понятная,
чем размерности, введенные ранее. Новая размерность применима ко
многим фракталам от рукотворной канторовои пыли (рис. 5) до нату-
натурального мягкого пуха (рис. 6), которым все еще набивают подушки
(все реже и реже, увы). Во всех случаях увеличение «массы» внутри
радиуса R определяется не показателем, равным евклидовой размер-
размерности, а несколько меньшим показателем; например, для пуха этот по-
показатель сотавляет около 1,6 (интересная зависимость: чем меньше D,
тем дороже пух!).
В случае ковра Серпинского (см. гл. 1, с. 41-45) показатель D также
меньше 2, потому что всякий раз, когда радиус R круга, заключающего
в себе площадь М, удваивается, площадь возрастает в 3 раза, а не в 4.
Таким образом, М ~ RD, где D = 1пЗ/1п2 = 1,58....
286 Глава 10
Рис. 4. Еще одна фигура Лихтенберга — электрический разряд на поверхнос-
поверхности стеклянной пластины. Массовая размерность D и 1,9 [185].
Для строго самоподобных математических фракталов (таких, как
ковер Серпинского и канторова пыль) массовая размерность совпада-
совпадает с размерностью Хаусдорфа (и любой другой из рассматриваемых
здесь фрактальных размерностей). Все эти размерности определяют-
определяются размерностью подобия скейлингового закона, которая задается по-
порождающими фрактал инициатором и генератором. Однако в случае
реальных («природных») фракталов между фрактальными размернос-
размерностями существуют значительные различия, в чем мы могли убедиться,
представляя размерность Минковского (см. гл. 1, с. 75-77) для учета
числа мод колебаний барабана с фрактальным параметром.
Массовая размерность особенно хорошо подходит для параметри-
параметризации упаковки порошков. Первичные частицы порошка обладают спо-
способностью образовывать кластеры с плотностью упаковки, скажем, р.
Предположим, что радиусы этих кластеров в г раз больше радиусов
первичных частиц. Кластеры, в свою очередь, очень часто образуют
новые, более крупные кластеры с теми же или близкими значениями р
и г, и т. д. в течение нескольких поколений (рис. 7) [186].
Массовая размерность
287
Рис. 5. Канторова пыль на выходе цифро-аналогового преобразователя. Мас-
Массовая размерность D и 1,26.
Через п поколений плотность порошка Р становится равной рп,
а радиус кластера R — г™. Разумеется, полная масса М пропорцио-
пропорциональна PRd, где d — евклидова размерность пространства, в которое
вложен порошок (для большинства порошков в трехмерном мире d = 3).
Таким образом,
М ~ PRd = RD,
где массовая размерность D = d + lnp/lnr меньше d, так как р < 1
и г > 1. На рис. 7 d = 2, г й 7 и р й 0, 7, что дает массовую раз-
размерность D к, 1, 82. Для сравнения скажем, что массовая размерность
ковра Серпинского (d = 2, г = 2 и р = 3/4) меньше и равна Вй2 +
+ 1пC/4)/1п2 и 1,58 (что совпадает с его размерностью Хаусдорфа).
Массовая размерность, как можно судить из названия, приме-
применима и к случаю более высоких евклидовых размерностей, особенно
к губчатым веществам, таким, как губка Менгера (рис. 3 в гл. 8)
с D = In 20/In 3 к, 2,73 и к кристаллам, выращенным посредст-
посредством ограниченной диффузией агрегации (ОДА) с характерным значени-
значением D к, 2,4 [172]. В случае ОДА (результат двумерного компьютерного
моделирования которой вы можете увидеть на рис. 9 в гл. 9) некоторый
288
Глава 10
*¦¦
I
Рис. 6. Натуральный пух. Его мягкость обусловлена низкой массовой раз-
размерностью D и 1,6.
Рис. 7. Три поколения самоподобной агломерации порошка [186].
источник, расположенный на большом расстоянии от растущего агре-
агрегата, испускает за цикл один «атом», который диффундирует до тех
Массовая размерность 289
пор, пока не попадает в сферу действия короткодействующих сил при-
притяжения ранее захваченных атомов и не присоединяется к растущему
агрегату. Простые вероятностные соображения показывают, что новые
атомы осаждаются на агрегате вблизи концов ветвей «дендритов», а не
в глубине кристаллических «фьордов».
Измерение массовой размерности дает значение D ра 2,4 для трех-
трехмерной и D ра 1,7 для двумерной ОДА. Однако точные значения D
зависят от физических и химических параметров процесса и содержат
важные указания относительно производства новых материалов, а так-
также относительно других практических приложений с преобладанием
фрактальных процессов.
Рассмотрим образование вязких языков (см. рис. 10 в гл. 9), воз-
возникающих вследствие неустойчивости поверхности раздела при втор-
вторжении жидкости или газа на «территорию» другой, более вязкой жид-
жидкости. (Читатель может попытаться собственноручно получить вязкие
языки с помощью воды и глицерина, стесненных в узком зазоре между
двумя стеклянными пластинами).
Выход
нефти
Введешк-
воды
Рис. 8. Вытеснение нефти из битуминозной породы.
Образование вязких языков наблюдается также при вытеснении
одной жидкостью (например, водой) другой жидкости (например, неф-
нефти) в пористой среде (скажем, сланце) — стандартный метод «выда-
«выдавливания» нефти из битуминозной породы (рис. 8). Фрактальная мае-
290 Глава 10
совая размерность водных языков чувствительно зависит от вязкости
жидкости, пористости породы и способности жидкости смачивать по-
поверхность породы [251]. Если бы граница воды была гладкой (D = 2),
то через удаленную скважину можно было бы извлечь большую часть
нефти, прежде чем вода достигнет откачивающего насоса. Но, к со-
сожалению всего мира, испытывающего острую нехватку нефти, D для
водной границы гораздо больше 2, и вода достигает насоса задолго до
того, как из нефтеносного пласта откачана вся нефть. Существует, од-
однако, возможность уменьшить фрактальную размерность воды путем
добавления к ней особых полимеров, увеличивающих вязкость. Нефте-
Нефтедобывающая промышленность надеется с помощью этих полимерных
добавок удвоить выход нефти при таком способе ее добычи. (Нефтеп-
(Нефтепромышленники надеются также, что стоимость полимерных добавок
будет меньше стоимости извлеченного с их помощью дополнительного
количества сырой нефти.)
Корреляционная размерность
Одной из наиболее широко используемых фрактальных размернос-
размерностей является так называемая корреляционная размерность. Измерить
ее проще всего экспериментально, особенно если фрактал представля-
представляет собой «пыль», т.е. изолированные точки, разбросанные по некоторой
области пространства.
Для определения корреляционной размерности необходимо прежде
всего подсчитать количество точек, попарные евклидовы расстояния
между которыми меньше заданного расстояния г. При изменении г
изменяется и относительная доля С (г) таких точек (С (г) определя-
определяется как отношение числа точек, попарные расстояния между кото-
которыми меньше г, к квадрату общего числа точек). Величина С (г) на-
называется также корреляционной суммой (или корреляционным интегра-
интегралом) [87, 84].
Корреляционная размерность, таким образом, определяется как
^. ,1)
г-И) In Г
На рис. 9 показано экспериментальное определение корреляционной раз-
размерности ?>2 Для странного аттрактора итерированного отображения
Энона: мы видим, что в диапазоне, охватывающем шесть порядков ве-
величины, зависимость log2 С (г) от log2 r имеет вид прямой с угловым
коэффициентом Di = 1,21 [87].
Бесконечное множество размерностей
291
-20 -
21
Рис. 9. Определение корреляционной размерности странного аттрактора [87].
Бесконечное множество размерностей
Корреляционная размерность Di принадлежит бесконечному се-
семейству размерностей Dq, определяемых как
Dq= lim—!—¦
4 r->o q - 1
111 Г
—сю
(X),
A)
где сумма берется по всем ячейкам линейного размера г, на которые
разделено пространство, a pf. представляет собой относительную час-
частоту, или вероятность, с которой частицы пылевидного фрактала попа-
попадают в к-ю ячейку [104, 85] (см. также гл. 9, с. 269-272).
292 Глава 10
При q = О мы снова приходим к нашему старому доброму дру-
другу — размерности подсчета клеток, или размерности Хаусдорфа Dh,
так как из суммы Y1 Р°к = ХI мы видим лишь, в скольких клетках,
к к
или ячейках, «присутствует» фрактал. Таким образом, Dh = -Do-
При q = 2 легко убедиться, что в пределе при г —> О сумма ^р].
к
совпадает с относительной долей С (г), с помощью которой мы в пре-
предыдущем разделе ввели корреляционную размерность [234].
При q —> 1 формула A) дает так называемую информационную раз-
размерность
x = lim \ , B)
r-Ю ln(l/r)
получившую свое название потому, что числитель в формуле B) пред-
представляет собой энтропию Шеннона в том виде, в каком он ввел ее в
своей теории информации (по аналогии с энтропией Больцмана в ста-
статистической механике). Размерность D\ и в самом деле измеряет по-
потерю информации в ходе динамической эволюции хаотических систем.
При q —> сю в сумме, стоящей в числителе формулы A), единст-
единственным значимым членом становится наибольшая вероятность ртах.
Отсюда
И наоборот, при q —> — ос значение суммы определяется наимень-
наименьшей вероятностью pmjn, и мы получаем
D-oo = lim
In г
Размерность D-oo, зависящую от наименьшей вероятности pm;n, весь-
весьма трудно измерить в случае реальных фракталов: места с низкой ве-
вероятностью посещаются свободно блуждающими частицами слишком
редко.
Заметим, что D_oo ^ -Doo- В общем случае для любых двух раз-
размерностей с различными q справедливо неравенство
Dq > Dq, при q < q'. C)
Таким образом, Dq — монотонно невозрастающая функция от q. Только
в исключительных случаях Dq не зависит от q и принимает одно и то
же значение во всем диапазоне —сю ^ q ^ сю.
Бесконечное множество размерностей 293
Одним из таких исключений является строго самоподобный фрак-
фрактал, порожденный «нестертыми» отрезками равной длины, такими как
отрезки, порождающие троичную канторову пыль. При вычислении Dq
по формуле A) мы считаем, что генератор фрактала состоит из N = 2
отрезков с равными вероятностями рг = Р2 = 1/2. Так как троичное
канторово множество является строго самоподобным фракталом, пре-
предел при г —> О становится излишним: мы можем вычислить Dq с г = 1/3
для генератора, что дает
1 Ц2A/2)] = in 2
" 1 1A/3) 1пЗ'
т. е. значение Dq и в самом деле не зависит от q.
Если генератор состоит из отрезков различной длины г и, то для
того, чтобы размерность Dq не зависела от q, вероятности pj. долж-
должны быть пропорциональны ri ". Для доказательства этого утверждения
воспользуемся уравнением (8) для самоподобных фракталов из главы 9:
&К = 1, D)
Ъ
где г = A - q)Dq.
При р^ ~ ri q в уравнении D) получаем
что, разумеется, означает независимость разности Dq от q.
Например, при п = 1/2 и ri = 1/4 получаем: D= In 7/ln(l/2) и 0, 694,
где 7 = (\/5 — 1)/2 — золотое сечение. Таким образом, pi = A/2I5 = j,
a p2 = A/4)?> = 72- Конечно же, вероятности pj = rf (за исключени-
исключением rj = г) носят весьма искусственный характер, и размерность ?>9
в общем случае зависит от q. Например, при Г2 = г\ и р\ = р-2, = 1/2 из
формулы D) получаем размерность
I Цл/l + 2«+2 - 1/2]
которая изменяется от D_oo = In2/ln(l/ri) до Doo = In2/ 1пA/г2).
294 Глава 10
Заметим, что при п > 1/2 размерность D_0О, характеризующая
самую плотную часть фрактала, больше единицы. В общем случае при
постоянных pk размерность ?*_оо определяется самым длинным отрез-
отрезком rmax, a Dqo — самым коротким отрезком гт\п (см. гл. 9).
Определение фрактальных размерностей по
временным рядам
Огромное количество данных, воспринимаемых человеком, посту-
поступает к нему в виде временных рядов, т. е. последовательностей неких
измеренных величин во времени. Таковы, например, электроэнцефа-
электроэнцефалограммы (ЭЭГ) — записи электроэнцефалографических потенциалов
(рис. 10). Что это — случайный шум или детерминированный хаос,
порожденный неким детерминированным, пусть и хаотическим, про-
процессом?
+ Слуховой отдел коры головного мозга
я
X Время —-
Рис. 10. Электроэнцефалограмма [215].
Чтобы ответить на эти вопросы, часто имеющие решающее зна-
значение, необходимо построить из d измерений, равноотстоящих друг от
друга по времени, d-мерные векторы данных и определить для получен-
полученного d-мерного точечного множества корреляционную размерность D^.
Если измеренные данные действительно были случайными, то при воз-
возрастании d вычисленная корреляционная размерность D<i также возрас-
возрастает. Но для детерминированной системы, сколь бы хаотичной ни ка-
казалась она «невооруженному глазу», вычисленная корреляционная раз-
размерность перестает возрастать, как только корреляционная размер-
размерность ?>2 данных оказывается меньше так называемой размерности
вложения d (рис. 11). Действуя таким образом, студент автора этой кни-
книги Й. Рёшке обнаружил, что казавшаяся на первый взгляд хаотической
энцефалограмма, снятая со слухового отдела коры больших полушарий
«Абстрактное в конкретном»
295
головного мозга кошки, в действительности представляет собой не слу-
случайный шум, а детерминированный хаос, корреляционная размерность
которого зависит от того, спит кошка или бодрствует [215].
5
8
6
4
2
п
1 1
-
сх
/ 1 1
I
4/
' ж
# • ^
1
1
х
Ж
L
1
/1
/ X
f
ж А -
J=2,48 "
-
i
О 2 4 6 8 10
Размерность вложения п
Рис. 11. Корреляционная размерность как функция от размерности вложе-
вложения [140].
Метод определения фрактальной размерности экспериментальных
данных с помощью «вложения» их в пространство подходящей размер-
размерности, позволяющий тем самым отличать детерминированный хаос от
случайного шума, был успешно применен к обработке широкого круга
различных физических, метеорологических, биологических и физиоло-
физиологических наблюдений [105].
«Абстрактное в конкретном»
Самоподобие не только поддается измерению — его с успехом мож-
можно использовать при проектировании фрактальных структур и мате-
материалов, отличающихся большей долговечностью или более низкой сто-
стоимостью (или тем и другим одновременно). Речь идет о способе по-
постройки межевых оград на многих фермах Новой Англии (см. рис. 12;
снимок сделан автором во время велосипедного путешествия по Конне-
Коннектикуту). Эти ограды сложены из больших камней, просветы между
которыми заполнены меньшими камнями; промежутки между ними
в свою очередь заполнены совсем маленькими камешками. В резуль-
результате такого грубо самоподобного построения получается прочная сте-
296 Глава 10
на, не требуя обычно применяемого в таких случаях дорогостоящего
цемента для заполнения просветов и укрепления конструкции. Если
представить количество требуемых для кладки камней как степенную
функцию от их размера, то каков же будет надлежащий показатель?
Рис. 12. Иерархическая структура межевой ограды в Новой Англии.
Дэвид Джонс в колонке «Абстрактное в конкретном» журнала
«Nature» высказывает соображения о том, что применяя все более мел-
мелкие частицы от самой крупной гальки до мельчайшей пыли, можно
сколь угодно уменьшить объем, который предстоит заполнить доро-
дорогостоящим связующим материалом, и тем самым снизить стоимость
конструкции либо получить возможность использовать более дорогие
и высокопрочные связующие материалы, такие как эпоксидная смо-
смола или даже полимид [123]. Аналогично, многие другие композитные
материалы, например, фибергласе, можно было бы усовершенствовать,
используя самоподобные структуры.
Фрактальные поверхности раздела как основа
дробных показателей частоты
Входные импедансы конечных электрических цепей, построенных
из пассивных «элементов с сосредоточенными параметрами», например,
сопротивлений и конденсаторов, являются рациональными функциями
Фрактальные поверхности раздела
297
от частоты. Так, конденсатор с емкостью С обладает импедансом Z =
= (iu>C)~1, где г = \/(—1), а и> —угловая частота (частота, умноженная
на 2тг). Таким образом, для конденсатора Z ~ ш, т.е. является рацио-
рациональной функцией от ш.
Инженеры-электрики давно обнаружили, что конечная электричес-
электрическая цепь, произвольным образом составленная из конечного числа эле-
элементов с сосредоточенными параметрами, всегда обладает импедансом,
который является рациональной функцией от частоты. Это обусловлено
тем, что рациональные функции образуют при сочетании группы, т. е.
если R (х) и S (х) — рациональные функции, то и S (R (х)) — также
рациональная функция.
Эта рациональность является в определенном смысле злом, по-
поскольку характеристический импеданс Zo линии связи (например, те-
телевизионного кабеля), необходимый для «согласованного» безэхового со-
соединения, не является рациональной функцией от частоты. Обычно Zo
зависит от частоты как uj~1I2. Таким образом, конечная цепь не может
в точности воспроизвести импеданс, который описывается квадратным
корнем из частоты; любая согласованная цепь всегда является лишь
приближением (и стандарты этого приближения, увы, варьируются от
страны к стране).
R
R
Рис. 13. Электрическая цепь лестничного типа, составленная из сопротивле-
сопротивлений R и проводимостей G.
Бесконечные же цепи способны порождать иррациональную зави-
зависимость от частоты. Например, бесконечная цепь «лестничного» типа,
представленная на рис. 13, имеет входной импеданс Zo, который лучше
всего представляется в виде непрерывной дроби
1
Z0=R
G +
1
R
G + ...
Конечную форму для значения Zq можно получить, если воспользовать-
298 Глава 10
ся периодичностью этой непрерывной дроби, которая позволяет запи-
записать ее в виде
Zo=R+ , . ,.
Перед нами квадратное уравнение относительно Zq. Физический смысл
имеет следующее его решение (с положительной вещественной частью):
() A)
При R = 1/G = 1 Ом (U) и конечном числе элементов импеданс Zo
равен рациональному числу, а именно, отношению двух последователь-
последовательных чисел Фибоначчи: 1/1, 2/1, 3/2, 5/3, Но если число элементов
бесконечно, то, как видно из формулы A), Zo перестает быть рацио-
рациональным. В этом случае Zq есть величина, обратная золотому сечению,
т.е. (л/5 + 1)/2 = 1,618
Чтобы получить иррациональную зависимость от частоты, можно
на место G поставить конденсаторы с обратным импедансом G = шС.
При малых частотах и> <С 1/RC величина Zo зависит от и> по простому
степенному закону и>~@ с дробным показателем /3 = 1/2:
B)
где и)с = 1/RC — верхняя «частота обрезания» используемого прибли-
приближения.
Однако реальный мир электропроводности, как правило, выходит
за рамки простых полуцелых показателей типа /3 = 1/2. Это следует
иметь в виду, поскольку однородные цепи описываются периодическими
непрерывными дробями, неизменно приводящими к квадратным кор-
корням и полуцелым показателям. Следовательно, если наблюдатель обна-
обнаруживает в физической системе нестандартную зависимость от часто-
частоты с дробным значением 2/3, то это свидетельствует о некоторой неод-
неоднородности структуры.
Более того, такие нестандартные частотные зависимости нередко
наблюдаются при прохождении электрического тока через шерохова-
шероховатые поверхности, например, через поверхности раздела между электро-
электродом и электролитом в автомобильном аккумуляторе. Простые модели,
представляющие токонесущие поверхности раздела в виде фракталов,
установили однозначное соотношение между фрактальной геометрией
и показателем частоты г].
Фрактальные поверхности раздела 299
На рис. 14А вы видите очень схематичную двумерную модель по-
поверхности раздела между электродом (белый) и электролитом (чер-
(черный) [149]. В основе этой модели лежит канторово множество с ге-
генератором, состоящим из двух отрезков равной длины г, которая на
рис. 14А равна 0,3. «Шероховатость» поверхности моделируется посто-
постоянно углубляющимися «канавками» в электроде; на каждом этапе по-
построения фрактала их глубина увеличивается на постоянную величину,
как показано на рис. 14А.
На рис. 14Б показана древовидная электрическая цепь, моделиру-
моделирующая проводимость такой поверхности раздела. Обратите внимание на
то, что сопротивления на каждом новом этапе построения увеличива-
увеличиваются в 1/г > 2 раз, отражая тот факт, что заполненные электролитом
канавки в поверхности электрода с каждым этапом все больше сужают-
сужаются. Построенная электрическая цепь в действительности представляет
собой самоподобное дерево Кэли, т. е. дерево с постоянным коэффициен-
коэффициентом ветвления (в рассматриваемом случае равным 2) и коэффициентом
подобия для сопротивлений, равным 1/г, что соответствует возраста-
возрастанию сопротивления постоянно сужающихся канавок.
Входной импеданс построенного дерева Кэли определяется непре-
непрерывной дробью
Z(u)=R+ 1— . C)
шС Н —
R/r
шС ¦
R/r2 +...
Двойки в числителях здесь — «отзвук» коэффициента ветвления нашего
дерева 2 : 1.
Непрерывная дробь C) также была бы периодической, если бы не
то обстоятельство, что коэффициент подобия г здесь отличен от 1/2.
Входной импеданс можно представить в следующем конечном виде:
Z(u)=R + 1— . D)
Заметим, что Z (ос) = R, как и следовало ожидать, глядя на схему,
изображенную на рис. 14Б. Для конечных частот справедливо неравен-
неравенство
Z{w)\ > R.
300
Глава 10
(Б)
Рис. 14. (А) Троичная модель поверхности раздела между электродом (бе-
(белый) и электролитом (черный) в автомобильном аккумуляторе. (Б) Древо-
Древовидная электрическая схема, представляющая ток сквозь фрактальную гра-
границу, показанную на рис. (А) [149].
Фрактальные поверхности раздела 301
Если
что подразумевает ш <С 1/RC, то соотношение D) упрощается к следу-
следующему масштабно-инвариантному виду:
*7 ( \ 7 (^ \ (К\
решением которого является степенной закон
Z(U>) ^LJ-13
с показателем
/3 = 1 " ТТ7ТТ = 1~D. F)
Здесь D — размерность Хаусдорфа для канторова множества, исполь-
использованного в модели (рис. 14А). Так как 0 ^ D $С 1, показатель /3 за-
заключен в том же интервале @ ^ /3 $С 1) и не обязательно ограничен
значением /3 = 1/2.
Размерность Хаусдорфа для одномерной поверхности раздела
электрод-электролит в двумерном пространстве равна D + 1 = 2 — /3.
Для двумерной поверхности раздела с изотропной шероховатостью со-
соотношения для /3 и ?) остаются неизменными. Соответствующая древо-
древовидная модель использует коэффициент ветвления, равный 4 (вместо
прежнего значения 2), а сопротивления изменяются с коэффициентом
подобия 1/г2 (вместо 1/г). Размерность же Хаусдорфа для такой по-
поверхности раздела становится равной 2?) + 1 = 3 — 2/3. Вот они, давно
ожидаемые соотношения между геометрией проводника и показателем
частоты. Заметим еще, что чем более шероховата поверхность раздела
(чем больше ?)), тем меньше показатель частоты /3.
На интуитивном уровне возрастание импеданса при уменьшении
частоты объясняется тем, что электрический ток все глубже прони-
проникает во все более узкие канавки на поверхности раздела, прежде чем
оказывается шунтированным емкостями. Для древовидной фракталь-
фрактальной поверхности глубина проникновения растет по степенному закону
с показателем /3, изменяющимся в некоторых пределах в зависимости
от шероховатости поверхности.
Если бы не экспоненциальный рост числа элементов, то древовид-
древовидные цепи, аналогичные изображенной на рис. 14Б, были бы полезны
302 Глава 10
для генерирования шумов или фильтрации сигналов, зависящих от час-
частоты по степенному закону с дробным показателем. Хотя 1//-шумы,
наблюдаемые во многих электронных материалах, могут в некоторых
случаях генерироваться фрактальными структурами, поддающимися
описанному выше моделированию.
Фрактальные размерности поверхностей разлома
Господь Бог создал объем; поверхности
же были изобретены дьяволом.
Вольфганг Паули
Разумеется, фрактальные поверхности отнюдь не исчерпываются
шероховатыми электродами. Разлом — вот еще один вездесущий источ-
источник двумерных фракталов. В своей классической работе Мандельброт,
Пассойя и Полле исследовали структуру поверхности разлома образцов
низкоуглеродистой стали, которая оказалась самоаффинной [163]. По-
Покрывая поверхность разлома толстым слоем никеля и последовательно
сошлифовывая слой за слоем, авторы получили островки стали, разме-
размеры которых увеличивались по мере того, как плоскость шлифования
приближалась к поверхности разлома. На рис. 15 представлена зави-
зависимость площадей А стальных островков от их периметров L в дву-
двукратно логарифмическом масштабе. В диапазоне, охватывающем более
четырех порядков величины, данные хорошо описываются степенным
законом А ~ X1'56, из чего следует, что периметры стальных островков
самоподобны. Значение показателя 1,56 заметно отличается от пока-
показателя в евклидовом законе А ~ L2. Показатель 1,56 означает так-
также, что размерность Хаусдорфа D для периметра равна 2/1,56 ~ 1,28.
Это значение близко к размерности Хаусдорфа для западного побере-
побережья Британии (D я» 1,3), но значительно превосходит размерность
«фрактального шестиугольника» (D = 1п9/1п7 и 1,13), с которым мы
уже встречались в гл. 1 (с. 36-40). Возможно, читатель вспомнит, что
для правильного предсказания площади фрактального шестиугольника
по его периметру, последний следует возводить в степень 2/D ра 1, 77
(а не 2).
Из значения D и 1,28 для стальных островков следует, что са-
самоаффинная поверхность разлома имеет фрактальную размерность
D + 1 = 2,28 — значение, характерное для несглаженных гор. Верти-
Вертикальный разрез, проведенный через такой изломанный горный ланд-
ландшафт, порождает профиль с фрактальной размерностью 2,28 — 1 = D.
Фрактальные формы облаков и дождевых областей
303
.мкм
Площадь
ю4
ю2
10°
1
-
10
1
1
ю2
Периметр
I
i
ю3
(мкм)
У
S
1
104
Рис. 15. Площади стальных «островков» как функция от их периметров на
поверхности разлома куска низкоуглеродистой стали [163].
Мандельброт и его сотрудники подтвердили этот результат, изме-
измерив пространственный частотный спектр Р (/) таких профилей раз-
разлома, и обнаружили, что Р (/) ~ /~4'5- Вычисленная по показате-
показателю частоты /3 = 4,5, фрактальная размерность оказывается равной
D = 3 — (/3 — 1)/2 = 1,25 (см. гл. 5, с. 190) в достаточно хорошем со-
согласии с проведенными ими независимыми измерениями размерности
«островков». Таким образом, поверхность излома металла не зависит от
внутреннего масштаба в диапазоне, охватывающем несколько порядков
величины.
Интересно, что фрактальная размерность поверхности разлома
и энергия, необходимая для ударного разрушения образца, оказались
связаны с температурой закаливания стали. Хотя в точной металлурги-
металлургической подоплеке этой зависимости энергии разрушения и топографии
поверхности образца от режима термической обработки еще предстоит
разобраться.
Фрактальные формы облаков и дождевых областей
Сильные дожди нарушают связь в УКВ-диапазоне, излюбленном
диапазоне дальней телефонной связи в последние полвека. Стоит меж-
между двумя УКВ-вышками, встречающимися буквально на каждом ша-
шагу и в США, и в других странах, появиться области сильных дождей,
как возникает необходимость перемаршрутизации сигналов по другим
линиям связи. Неудивительно, что инженеры-телефонисты проявляют
столь живой интерес к распределению осадков по времени и геомет-
геометрическим формам дождевых областей. Дождь, как известно, идет из
304
Глава 10
облаков (хотя есть люди, достаточно просвещенные, которые призна-
признают, что были очень удивлены, когда впервые услышали об этом).
Поэтому нет ничего более естественного, чем исследовать статис-
статистику дождей и облаков вместе, как это сделал (среди прочих авторов)
Лавджой [151]. На рис. 16 представлены данные о площадях А дождевых
областей (черные точки) и облаков (светлые точки) в зависимости от
их периметров L в двукратно логарифмическом масштабе. В диапазоне,
охватывающем 6 (!) порядков величины (от 1 км2 до 1 000 000 км2), эти
данные с достаточно хорошей точностью ложатся на прямую с угловым
коэффициентом около 1,5, что соответствует фрактальной размернос-
размерности D периметра, равной 2/1,5 к, 1,35. И здесь, как и в случае разлома
и других многочисленных явлений природы, по-видимому, не сущест-
существует естественного масштаба.
10° -
10 10 10 10
Периметр (км)
Рис. 16. Площади дождевых областей (черные точки) и облаков (светлые точ-
точки) в зависимости от их периметров [151].
Численное значение показателя находится в хорошем согласии
с термодинамической моделью Хентшеля и Прокачча [106]. Лавджой
и Мандельброт предложили математическую модель, в которой пред-
предполагается, что дождевые области порождаются наложением друг на
друга отдельных дождевых участков, размеры которых распределены
Агломерация кластеров 305
по гиперболическому закону [152]. Предложенная ими модель позволя-
позволяет получать в высшей степени реалистичные изображения облаков. На
цветной вклейке 5 на фотографии, снятой автором этой книги, видно,
что естественные облака соперничают в реализме с изображениями,
полученными с помощью компьютера. На вклейках 6А и 6Б показаны
еще два фрактала, наблюдаемых в природе. Один из них возникает при
распаде, другой — в процессе роста.
Агломерация кластеров
При ограниченной диффузией агрегации (ОДА) рост скоплений мо-
молекул происходит путем присоединения к агрегату по одной молекуле
за цикл. Еще одним важным процессом роста, который также приводит
к образованию фрактальных структур, является агломерация аэрозолей
и коллоидов. На рис. 17 вы видите сделанный с помощью электронно-
электронного микроскопа снимок частицы коллоидного золота, выращенной Вейт-
цем и Оливериа посредством кластерной агрегации [273]. Фрактальная
структура этого коллоида настолько разрежена, что даже на представ-
представленной на снимке двумерной проекции кластер прозрачен.
Процесс агломерации кластеров проиллюстрирован на рис. 18. Пер-
Первоначально отдельные частицы почти равномерно распределены в не-
некотором конечном объеме (рис. 18А). Затем частицы случайным об-
образом мигрируют, как при броуновском движении. При столкновении
две частицы слипаются и в дальнейшем движутся вместе как малень-
маленький «кластер». Эти маленькие кластеры, в свою очередь, также сли-
слипаются при столкновении, образуя более крупные кластеры; о таком
поведении частиц сообщает в своих наблюдениях Микин [171]. Подоб-
Подобные агломерационные процессы, как видно на рис. 18Б и 18В, приводят
к образованию все более крупных кластеров, которые обладают струк-
структурой статистически самоподобных фракталов. Двумерное компьютер-
компьютерное моделирование дает значение размерности Хаусдорфа D около 1,4.
В трехмерном случае Кольб, Боте и Жюльен получили D к 1,8 [134].
Экспериментально фрактальную размерность можно измерить по
рассеянию света, рентгеновского излучения или нейтронов на фракта-
фрактале. Для пространственных частот (обратных длин волн) / в диапазо-
диапазоне 1/R «С / <S 1/r, где R — размер всего фрактала, а г — величина
отдельной частицы, можно ожидать, что интенсивность рассеянного из-
излучения /(/) удовлетворяет простому степенному закону / (/) ~ f~D
(см. следующий раздел). Измеренная таким способом Шефером и его
306
Глава 10
Рис. 17. Частица коллоидного золота, выращенная посредством агрегации
кластеров [273].
сотрудниками фрактальная размерность частиц кремнезема оказалась
равной D к, 2,1 (см. рис. 19) [221]. Это значение, существенно большее,
чем найденные с помощью компьютерного моделирования, указывает
на то, что агломерация кремнезема происходит на основе иного меха-
механизма. Численные эксперименты, в которых кластеры образуются мед-
медленно, после многократных столкновений дают размерность D к, 2,0,
которая лучше согласуется с результатами измерений по рассеянию на
фракталах [63, 248].
Агломерация, кроме того, играет решающую роль в процессах элек-
электролитического осаждения и в каталитических реакциях. Кластериза-
Кластеризация во многом определяет также распространение эпидемий, слухов
и мнений. Грассбергер показал, что при опросах общественного мне-
мнения фрактальные структуры могут приводить к сильно смещенным и
поэтому ложным результатам [86].
Дифракция на фракталах
307
ьГ 1
s
4
1 ,_
.. t
J
-r
IT
J J
i
'1
J" '
¦*
T
p
4
В
/;
A-
>-
V - ,,
J-
-ь
1
>
h
(S)
Рис. 18. Агломерация кластеров: (А) однородное случайное распределение,
(Б) образование малых кластеров при случайном движении, (В) образование
больших кластеров [171].
Дифракция на фракталах
При некогерентной дифракции на фрактале, состоящем из неза-
независимых частиц, например, на коллоиде, интенсивность / (/) рассеян-
рассеянного излучения как функция от пространственной частоты / пропор-
пропорциональна всей «массе» М, содержащейся в объеме радиуса р = 1//.
Если М D
pD, то
Hf)~f
-D
A)
308
Глава 10
о
X
Свет^»-
-
-
i
i
SAXS
1
1
_
-
l/\-4,0-
\ \
X Wq 10" 10"
Пространственная частота A /A)
Рис. 19. Определение фрактальной размерности частиц кремнезема. Интен-
Интенсивность рентгеновских лучей, рассеянных на коллоидном агрегате кремне-
кремнезема (SAXS — рассеяние рентгеновских лучей на малые углы) [221].
Для поверхностных фракталов / (/) ~ S, где S — площадь поверх-
поверхности. Но I (/) можно также представить в виде M2F(fp), где F —
некоторая универсальная функция [165]. С учетом того, что S ~ р
и М ~ pd, получаем F (fR) ~ (fp)
D.,
D.-2d
tDa-2d
B)
где Ds — фрактальная размерность рассеивающей поверхности, ad —
евклидова размерность вложения. При d = 3, таким образом, имеем:
tDs-6
C)
Для гладкой поверхности Ds = 2, а / (/) ~ / 4 — хорошо извест-
известный классический результат для рассматриваемого здесь режима рас-
рассеяния. Как мы уже отмечали, соотношение C) позволяет определить
размерность Хаусдорфа Ds для фрактальной поверхности по дифракции
волн.
На рис. 19 интенсивность рентгеновского излучения, рассеянного
на упоминавшемся выше агрегате коллоидного кремнезема, показана
как функция от пространственной частоты (выраженной в обратных
Дифракция на фракталах 309
ангстремах A0~10 м)). Измерения были ограничены рассеянием на ма-
малые углы, так как при рассеянии на большие углы рентгеновское излу-
излучение разрешало бы молекулярную структуру, тогда как основной ин-
интерес в данном случае представляет структура кластеров. При / < 1/г,
где г = 27А — радиус нефрактальных мономеров, образующих фрак-
фрактальный коллоид, значения интенсивности рассеянного излучения ло-
ложатся на прямую с угловым коэффициентом —2,1 (в двукратно лога-
логарифмическом масштабе), который, таким образом, является размернос-
размерностью Хаусдорфа для данного фрактального коллоида.
При / > 1/г существует другой линейный режим изменения ин-
интенсивности рассеянного излучения с угловым коэффициентом, рав-
равным —4. Именно его предсказывает теория для нефрактальных моно-
мономеров, образующих фрактал. Таким образом, экспериментальный ре-
результат указывет на то, что мономеры в агрегате остаются неповреж-
неповрежденными.
Здесь мы подходим к самому важному применению волновой ди-
дифракции при анализе фрактальных структур — к анализу коллоидов.
Проблема понимания процессов, лежащих в основе агрегации коллои-
коллоидов, уже давно стоит на первом месте в определенных областях физи-
физики и химии, а также в многочисленных и разнообразных коммерчес-
коммерческих отраслях. Дифракция волн и без того всегда была превосходным
инструментом структурного анализа, теперь же область ее примени-
применимости успешно расширена от однородных тел к фрактальным струк-
структурам.
Еще одной фрактальной структурой, которую удалось расшифро-
расшифровать с помощью рассеяния рентгеновского излучения и нейтронов на
малый угол, стал лигнит, или «бурый уголь». Лигнит пронизан микро-
микроскопическими порами с фрактальной внутренней поверхностью. Имен-
Именно эти поры и их поверхности делают «активированный» уголь актив-
активным и многообещающим материалом для воздушных фильтров и дру-
других приспособлений, связанных с тонкой очисткой. Теория предсказы-
предсказывает, что интенсивность рассеянного излучения / (/) для гладких пор
должна быть пропорциональна /~4. Для крупных же пор с фрактальной
поверхностью величина / (/) должна быть, согласно соотношению C),
пропорциональна fD~6, где D — фрактальная размерность внутренней
поверхности пор. Этот закон должен выполняться для пространствен-
пространственных частот, соответствующих величине, обратной неровности поверх-
поверхности пор.
Экспериментальные результаты Бейла и Шмидта дают показа-
показатель —3,44 с ошибкой менее 1% в диапазоне интенсивностей, охваты-
310 Глава 10
вающем семь порядков величины [17]. Следовательно, поверхности пор
фрактальны, и их фрактальная размерность равна 6 — 3,44 = 2,56.
Интересно отметить, что тот же самый степенной закон / (/)~/D~6
получается и для гладких пор с самоподобным распределением размеров.
В частности, если число пор N (г) с радиусом, превышающим г, пропор-
пропорционально Г?>, то, как показывают результаты Пфайфера и Авнира, ин-
интенсивность рассеянного излучения следует закону /(/) ~ fD~6 [198].
Однако выполняется этот закон в другом диапазоне частот, который
определяется размерами пор, а не неровностями их поверхности. Это
еще один пример относительного упрощения ситуации при наличии са-
самоподобия и при должном его использовании.
Несколько лет назад автор этой книги предложил несколько
теоретико-числовых концепций (квадратичные вычеты, примитивные
многочлены и первообразные корни на конечных числовых полях, а так-
также логарифмы Цеха) в качестве основ проектирования отражательных
фазовых решеток с очень интенсивным рассеянием падающей энергии
по широким частотным диапазонам [230]. Диапазоны частот, эффектив-
эффективно рассеиваемые такими решетками, можно еще больше расширить, ес-
если использовать при их проектировании самоподобие, в результате чего
мы получим фрактальные дифракционные решетки [42].
Глава 11
Итерации, странные отображения
и миллиард знаков для тг
Что толку от Вашего изящного доказа-
доказательства [трансцендентности] тг ? К че-
чему заниматься исследованием таких за-
задач, если иррациональных чисел вообще
не существует?
Леопольд Кронекер,
из письма Фердинанду Линдеману
Одним из основных источников самоподобия, помимо степенных
законов, являются итерации. Под итерациями мы здесь понимаем мно-
многократное применение какого-нибудь правила либо операции, т.е. мно-
многократное выполнение одного и того же действия. (Как видно из рис. 1,
даже одно повторение может привести к самоподобию.) В этой главе
мы продолжим исследования некоторых странно притягательных по-
последствий итераций — одной из наших излюбленных тем.
С понятием итерации тесно связано другое понятие — рекурсия.
В наш век все возрастающей автоматизации и компьютеризации мно-
многие процессы и вычисления носят рекурсивный характер, а коль скоро
рекурсивный алгоритм в действительности периодичен, то где-то «за
сценой» ожидает своего часа самоподобие. Вспомним о рекурсивном вы-
вычислении золотого сечения (л/5 — 1)/2 = 0,618... по правилу: «прибавь
единицу и возьми обратную величину». Начав с 1, мы получим по-
последовательность 1, 1/2, 2/3, 3/5, 5/8, 8/13 и т.д., т.е. последователь-
последовательность дробей, сходящихся к золотому сечению. (Более того: погреш-
погрешность, с которой эти дроби стремятся к золотому сечению, убывает
в геометрической прогрессии, образуя асимптотически самоподобную
последовательность погрешностей с коэффициентом подобия, равным
квадрату золотого сечения.) Рекурсия является также одной из глав-
главных тем книги Хофштадтера «Гёдель, Эшер, Бах» [108].
312
Глава 11
Рис. 1. Итерации ведут к самоподобию (рисунок Sempe, ©1985 New Yorker
Magazine, Inc.).
Итерации, странные отображения и миллиард таков для тг 313
Одним из самых ранних примеров итеративного алгоритма может
служить алгоритм Евклида для нахождения наибольшего общего де-
делителя (НОД) двух натуральных чисел: разделить большее число на
меньшее, взять число, обратное остатку и итерировать до тех пор, по-
пока остаток не станет равным нулю. Знаменатель последнего ненулевого
остатка и есть НОД. Например, для чисел 182 и 78 имеем: 182/78 = 2 +
+ 26/78; 78/26 = 3 + 0. Следовательно, НОД чисел 182 и 78 равен 26.
(В основе метода Евклида лежит то простое обстоятельство, что целые
числа в числителе и знаменателе последнего остатка B6 и 78) имеют
такой же НОД, как и исходные целые числа A82 и 78).)
Еще одна древняя задача, решаемая с помощью рекурсивного алго-
алгоритма, реализована в знаменитой игре под названием ханойская башня:
стопку дисков различной величины нужно перенести с одного колыш-
колышка на другой по одному диску за один раз, следя за тем, чтобы диск
больших размеров не оказался поверх диска меньших размеров. Тре-
Третий колышек служит своего рода «запасным аэродромом», без которого
игра, конечно же, была бы невозможной. Если число дисков достаточно
велико, то игра вслепую, методом проб и ошибок, не приводит к жела-
желаемому результату, однако простой рекурсивный алгоритм дает опти-
оптимальное решение, не требуя никаких догадок.
Обратимся теперь к изобретенной Ньютоном простой итерацион-
итерационной схеме нахождения нулей функции. Алгоритм Ньютона позволяет
установить для этих нулей области притяжения, которые представля-
представляют собой хитроумно переплетенные мультифракталы. Применяя ите-
итерационный метод Ньютона к более земным задачам, можно с высокой
точностью вычислять обратные величины и корни с помощью одного
лишь умножения. Например, величина 1/z вычисляется из соотноше-
соотношения xn+i = 2хп — zx\, a z~xl2 — из соотношения xn+i = хпB> — zx^J/2.
(Чтобы итерации сходились к нужному результату, необходимо, разу-
разумеется, выбирать подходящие начальные значения жо.)
Эффективность итераций лежит в основе и таких замечатель-
замечательных алгоритмов, как быстрое преобразование Фурье (знаменитое БПФ)
и менее известное преобразование Адамара [99]. Важно здесь то, что
матрицы, описывающие эти преобразования, факторизуются в прямое
произведение меньших матриц [230]. В частности, матрица Фурье или
Адамара, состоящая из 2п строк и 2п столбцов, может быть итеративно
факторизована в п матриц 2x2; именно это итеративное разложение
позволяет существенно уменьшить объем вычислений (в 2п/2п раз).
Неудивительно, что порожденные с помощью итераций матрицы Ада-
314 Глава 11
мара, будучи представлены в виде графических образов или оптических
масок, обнаруживают самоподобие.
Итерации преобразования пекаря напоминают детскую игру
в «стулья с музыкой» с двоичными цифрами вместо детей, моделируя
в то же время нелинейные преобразования в двумерных пространст-
пространствах. Отображение «кошка Арнольда» дает еще одну порождающую ха-
хаос рекурсию для моделирования сохраняющих площадь преобразова-
преобразований. (Олицетворение нелинейного отображения — логистическую пара-
параболу— и ее двумерное обобщение {отображение Энона) мы рассмотрим
в гл. 12.)
Однако надлежащим образом направляемая рекурсия порождает
и красоту, будь то изящные узоры для вышивания, или цветы и де-
деревья самых изысканных форм. В самой математике рекурсия также
творит настоящие чудеса, позволяя, например, вычислить миллиард
знаков числа тг всего лишь за 15 итераций. Этот вычислительный ре-
рекорд опирается на труды великого индийского математика Шринивасы
Рамануджана A887-1920), поразительная интуиция которого выходит
за рамки человеческого разумения.
Поиск нулей и встреча с хаосом
Около 300 лет назад Исаак Ньютон A642-1727) предложил метод
нахождения нулей функции / (z) с помощью итераций, основанных на
проведении касательных. Если известно приближенное значение zn ре-
решения уравнения / (z) = 0, то следующее приближенное значение вы-
вычисляется по формуле
Zn+1=Zn-jwy A)
где /' (zn) — производная от функции / (z) в точке z = zn. Формула A)
имеет смысл, если угловой коэффициент касательной /' (zn) отличен от
нуля.
Для / (z) = z2 — 1 из формулы A) получаем
B)
Неудивительно, что при начальном значении z§ с положительной ве-
вещественной частью итерации zn сходятся к положительному корню
уравнения z2 — 1 = 0, а именно, к z = 1. Аналогично, при начальном
Поиск нулей и встреча с хаосом 315
значении Zq с отрицательной вещественной частью итерации сходятся
к отрицательному корню z = — 1.
Что же произойдет в случае чисто мнимого начального значе-
значения Zq = гго, где Го ф 0 — число вещественное? Оказывается, при таком
начальном значении итерации вообще не сходятся: они, фигурально вы-
выражаясь, никак не могут решить, куда же им двигаться, и скачут вдоль
мнимой оси в соответствии с отображением
гп+1 = 2
Например, золотое сечение 0,618 ... последовательно отображается
при итерациях в —0,5; 0,75; —0,291F); 1,566845... и т.д. Но некото-
некоторые го ведут себя совершенно иначе. Таково, например, начальное зна-
значение го = 1 + л/2, которое отображается в 1, 0 и сю (тоже своего рода
неподвижная точка, хотя и весьма удаленная).
Как можно привнести порядок в это хаотическое отображение?
Воспользуемся тригонометрической подстановкой
г = — ctg(Tra), D)
которая переводит отображение C) в необычайно простое соотношение
an+i = 2an mod 1, E)
где «modi» означает вычитание целой и сохранение только дроб-
дробной части, лежащей в полуоткрытом интервале [0, 1). Например,
2,618 mod 1 = 0,618.
При переходе на новую переменную а хаотическое отображение
переменной г становится вполне «прозрачным». Если записать ап в ви-
виде двоичной дроби, то знаки в an+i будут теми же, что и в ап, только
сдвинутыми на один знак влево. Единица, оказавшаяся левее двоич-
двоичной запятой, отбрасывается. Таким образом, периодическая двоичная
дробь «о порождает периодические орбиты (т. е. периодические после-
последовательности итераций). Например, «о = 1/3 = 0,@1) отображается
в число 0,A0) = 2/3, которое отображается обратно в а^ = 0,@1) = а$.
(Действительно, го = — ctg(?r/3) = —1/\/3 отображается по формуле C)
в число г\ = 1/\/3, которое отображается назад в гг = —1/\/3 = го-)
Аналогичным образом, предпериодические двоичные дроби, кото-
которые начинаются как непериодические и заканчиваются периодическим
316 Глава 11
«хвостом», такие, например, как, ско = 5/6 = 0,1A0), порождают пред-
периодические орбиты:
г0 = л/3, 7-1 = —, г2 = -—=, г3 = гх и т.д.
V3 /3
Конечные двоичные дроби представляют собой не что иное, как
частный случай предпериодических двоичных дробей — с периодичес-
периодическим хвостом @). Куда же приводят их итерации? Многократный сдвиг
влево и взятие дробных частей (остатков по modi) рано или поздно
приводит к а = 0, что соответствует г = сю. Например, ско = 7/8 =
= 0,111 отображается в дробь 0,11 = 3/4, а та — в 0,1 = 1/2, которая,
в свою очередь, отображается в 0. Более того, соответствующее значе-
значение го = — ctgG-7r/8) = 1 + л/2, как мы уже заметили, отображается
в 1, 0 и сю.
Приведенные выше соображения показывают, что любое иррацио-
иррациональное «о дает апериодическую орбиту вдоль мнимой оси на плоскос-
плоскости z. Таким образом, простое отображение, задаваемое ньютоновыми
итерациями для функции z2 — l = 0 приводит в случае начальных значе-
значений, расположенных на мнимой оси, к весьма странным последствиям.
По соответствующим значениям а все числа можно разделить на три
группы:
1) периодические двоичные рациональные числа;
2) предпериодические двоичные рациональные числа;
3) иррациональные числа.
Периодические и предпериодические двоичные рациональные числа «о
сходятся к неподвижной точке или порождают периодические орбиты.
В отличие от них несчетное множество иррациональных чисел ско по-
порождает апериодические орбиты: одно и то же значение никогда не
встречается дважды, и ни одна итерация ап не бывает рациональной.
Как ни удивительно, но простое отображение E) позволяет даже прово-
проводить некую тонкую границу между иррациональными числами различ-
различного типа — имеется в виду не обычное теоретико-числовое разделение
иррациональных чисел на алгебраические (например, л/2) и трансцен-
трансцендентные (например, тг), а разделение чисел на нормальные и ненормаль-
ненормальные, включая числа Лиувилля.
Нормальное число (в данной системе счисления) определяется как
число, в записи которого любая возможная группа цифр встречается
Поиск нулей и встреча с хаосом 317
с равной вероятностью. Например, судя по первым 100 миллионам зна-
знаков, число тг нормально в десятичной системе счисления [270]. Это озна-
означает, что где-то в десятичной записи числа тг встречается, скажем, во-
восемь семерок подряд. Более того, существует достаточно большая ве-
вероятность, что такая «великолепная восьмерка» встретится среди пер-
первых 108 знаков числа тг (или любого другого нормального десятичного
числа). Самые современные данные по этому вопросу можно почер-
почерпнуть в книге Клее и Вагона [130]. Итерации нормальных чисел по фор-
формуле E) порождают хаотические орбиты.
Некоторое представление о том, сколь необычными свойствами об-
обладает такой объект как нормальное число, можно составить, исходя из
следующих соображений. Все содержание «Британской энциклопедии»
можно закодировать одним-единственным десятичным числом (длиной
примерно в 1010 знаков), и в записи любого нормального числа непре-
непременно окажется блок цифр, совпадающий с «кодом» «Британской энцик-
энциклопедии». Более того, этот блок встретится там бесконечно много раз!
(Только не спрашивайте меня где!)
Существуют ли ненормальные иррациональные числа? Оказывает-
Оказывается, любая система счисления может похвастаться бесконечным множес-
множеством таких чисел! Например, канторовы числа (см. гл. 7) ненормальны
в троичной системе, потому что они не содержат единиц. В последую-
последующих главах мы познакомимся с постоянной Морса-Туэ 0,01101001...
и «кроличьей постоянной» 0,10110101...; в двоичной записи этих двух
постоянных вы не найдете трех единиц подряд, сколько бы ни иска-
искали. Значит, они никак не могут оказаться нормальными двоичными
числами.
Известны, однако, еще более необычные ненормальные числа, та-
такие, как двоичное число
оо
L = ^ 2"fc = 0,110001000000000000000001000...
k=l
и другие числа Лиувилля1, которые иррациональны, но очень близки
к рациональным числам.
¦'¦Названные так в честь Жозефа Лиувилля A809-1882), продемонстрировавше-
продемонстрировавшего первое трансцендентное число, прототипом которого является число L. Доказа-
Доказательства трансцендентности чисел е и тг были предложены позднее соответственно
Шарлем Эрмитом A822-1901) и Фердинандом Линдеманом A852-1939).
Другое доказательство существования трансцендентных чисел дал Георг Кантор,
показавший, что алгебраические числа (т.е. корни полиномов с рациональными ко-
коэффициентами) образуют счетное множество. Поскольку континуум представляет
318 Глава 11
В общем случае число Лиувилля /3 определяется как иррациональ-
иррациональное число, для которого существует такая пара рациональных чисел р
и q, что
"' :^ F)
при любом п. Чтобы число Лиувилля L удовлетворяло неравенству F),
положим q = 2n!. Тогда суммарная погрешность аппроксимации соста-
составит 2-(га+1)! + 2-(га+2)! + ..., что (при п > 1) меньше, чем 2"n!n = q~n.
(При п = 1 мы полагаем q = 4 и видим, что |Х — 3/4| < 1/4.) То, что
для алгебраических иррациональных чисел в степени п модуль разнос-
разности в неравенстве F) превосходит l/qn+1, доказывает существование
таких чисел, как L, которые «выходят за пределы» множества алгебра-
алгебраических чисел, т.е. трансцендентных чисел.
Итерации нормальных двоичных чисел «о по формуле E), как сле-
следует из их определения, плотно заполняют единичный интервал, при-
причем все подынтервалы одинаковой длины заполняются с равными ве-
вероятностями. Таким образом, стационарное распределение при итера-
итерациях, называемое инвариантным распределением, является в действи-
действительности плоским. Иначе обстоит дело с ненормальными числами. На-
Например, итерации числа L накапливаются в окрестности нуля и всех
отрицательных степеней числа 2 (т.е. чисел 1/2, 1/4, 1/8 и т.д.)
Итак, мы оказываемся перед лицом прелюбопытного факта: тон-
тончайшие различия (различия между рациональными и иррациональны-
иррациональными, а среди иррациональных — между нормальными и ненормальными
числами) приобретают решающее значение для конечной судьбы чис-
численных итераций. Принято думать, будто физика и, тем более, реальный
мир в целом, не зависят от чисто математических дихотомий между ра-
рациональными и иррациональными или нормальными и ненормальными
числами. В действительности же это не так. Хотя все в реальном мире
может в принципе быть адекватно описано с помощью рациональных
чисел, однако математическая модель, проводящая различие между те-
теми или иными классами чисел, может оказаться не только чрезвычайно
полезной, но и ухватить истинный, возможно, скрытый, дух проблемы.
Говоря конкретнее, два различных начальных состояния физичес-
физической системы, совершенно неразличимые посредством любого измере-
собой несчетное множество, должны существовать числа (более того, бесконечно
много чисел), «выходящие за пределы» множества алгебраических иррациональных
чисел, т.е. так называемые трансцендентные числа.
Странные множества Жюлиа 319
ния конечной точности, при эволюции системы во времени или в про-
пространстве рано или поздно значительно разойдутся. Для этого необхо-
необходимо лишь, чтобы соответствующее отображение, называемое отобра-
отображением Пуанкаре (см. гл. 14), было бы достаточно немонотонным (на-
(например, таким, как отображение E), которое обладает пилообразной
немонотонностью). Мерой скорости расхождения служит так называе-
называемый показатель Ляпунова А = ln(an+i/an) при п —>¦ сю. В нашем не-
незатейливом примере, построенном на отображении E), А = In2 и 0,693
(это если брать натуральный логарифм).
Хотя итерации, задаваемые отображением E), могут показаться
неестественно простыми, они верно передают сущность бесчисленных
нелинейных задач, связанных с бифуркациями удвоения периода и тем
самым следующих одной из двух наиболее протоптанных дорог к хаосу
(см. гл. 12). (Другая дорога вымощена квазипериодичностью, которая
моделируется так называемым отображением окружности, обсуждае-
обсуждаемым в гл. 14.)
Странные множества Жюлиа
Метод Ньютона A), примененный к кубическому уравнению
/ (z) = z3 — 1, дает отображение
с которым мы уже сталкивались в гл. 1 на с. 71-73.
Это отображение ведет себя еще более странно, чем предыдущее.
Во-первых, наивное предположение о том, что любое zo будет сходиться
к ближайшему из трех корней, следует сразу отбросить по причине его
несостоятельности. Например, начальное значение zq = —1 сходится
к 1, наиболее удаленному от него корню.
На цветной вклейке 3 показаны тесно переплетенные области при-
притяжения всех трех корней — совершенно безумное лоскутное одеяло
(может, следовало бы сказать «мнимо безумное»?). Более того, можно
доказать, что при отображении, задаваемом соотношением A), две об-
области притяжения (два цвета) не могут встретиться без того, чтобы
при этой встрече не присутствовал третий. Это может показаться не-
невозможным, да это и было бы невозможным — если бы не фрактальная
природа границ, изображенных на вклейке 3, которая демонстрирует,
помимо всего прочего, притягательное самоподобие, порождаемое нью-
ньютоновыми итерациями.
320 Глава И
Почему же эти три области притяжения не выглядят попросту как
три куска круглого пирога, т. е. как три сектора по 120° каждый? В кон-
конце концов, итерации Ньютона для z1 = 1 приводят к областям притя-
притяжения в виде двух полуплоскостей. То, что подобный исход недости-
недостижим для z3 = 1, становится понятным, если мы обратим внимание на
точку z = — 2/3, которая согласно уравнению A) отображается в точ-
точку z = 0. Окрестность точки z = 0 содержит точки, принадлежащими
всем трем областям притяжения (благодаря 120-градусной осевой сим-
симметрии задачи). Таким образом, исходя из того, что отображение, об-
обратное A), непрерывно, точка z = — 2/3 должна быть также окружена
точками, принадлежащими всем трем областям притяжения. Более то-
того, ее бесконечно малая окрестность должна содержать уменьшенную
копию «клеверного листа» в начале координат. Значит, ниже отрица-
отрицательной вещественной полуоси существуют точки, принадлежащие об-
области притяжения аттрактора z\ = ш = ехр(гтг/3), расположенного вы-
выше вещественной оси. Аналогично, выше отрицательной вещественной
полуоси существуют точки, сходящиеся к аттрактору zi = ш2, располо-
расположенному ниже вещественной оси. Таким образом, области притяжения
корней кубического уравнения никак не могут быть простыми сектора-
секторами с ровными границами: каждая из областей притяжения «откусывает
от пирога» другой области притяжения.
В общем случае для уравнения z11 = 1 метод касательных Нью-
Ньютона порождает в окрестности начала координат клеверный лист с п
лепестками. Поэтому прообраз начала координат, попадающий на гра-
границу между двумя аттракторами, перемешивает в этой точке все об-
области притяжения, а при п > 2 такое перемешивание не может не
порождать фрактальной границы, поскольку в двумерном простран-
пространстве только граница соприкосновения двух аттракторов может быть
гладкой. Кроме того, так как все граничные точки представляют собой
прообразы начала координат, они являются граничными точками для
всех п областей притяжения. Столь необычные множества граничных
точек принято называть множествами Жюлиа. По определению, мно-
множество Жюлиа J рациональной функции R (z) есть множество точек z,
в которых значения функции R(z) не нормальны. (Нормальными на-
называются значения в точках z, в окрестности которых функция R (z)
равностепенно непрерывна.)
Множество Жюлиа рациональной функции обладает следующим
удивительным свойством: если Zk — периодический аттрактор, aAj —
область его притяжения, то J = дАи при всех к. Здесь дАи — граница
области притяжения Аи, т.е. множество всех тех точек, в сколь угодно
Странные множества Жюлиа 321
малой окрестности которых найдутся точки, лежащие как внутри, так
и вне Ак. Следовательно, если точка z принадлежит границе, скажем,
области А\, то можно смело заявить, что эта же точка принадлежит
границам областей А2, Аз,
Еще одно важное свойство множества Жюлиа J заключается в том,
что периодические репеллеры рациональной функции R (z) плотны в J.
Более того, если zr — периодический репеллер, то J — замыкание мно-
множества всех прообразов точки zr. Следовательно, динамика на множес-
множестве Жюлиа является хаотической, т.е. чувствительной к начальным
условиям, в чем мы уже успели убедиться на стр. 314-316, когда рас-
рассматривали множество Жюлиа функции R (z) = (z + 1/'z) /2. Множест-
Множество Жюлиа всегда содержит несчетное множество точек, но оно не обя-
обязательно фрактально.
Множества Жюлиа, состоящие из репеллеров, чрезвычайно трудны
для изображения из-за их хаотической чувствительности, требующей
реально недостижимой числовой точности. Тому, кто все же решится
на такое, может прийти на помощь другое свойство этих множеств —
для любого числа z из множества J обратная орбита R~n (z) плотна
в J при п = 1, 2, 3, ... Для точек в J обратная орбита R~n (z) являет-
является аттрактором, поэтому никаких проблем с расходимостью чисел не
возникает. Но функция R~1 (z), вообще говоря, многозначна, поэтому
для равномерного покрытия всего множества Жюлиа требуются доста-
достаточно хитроумные алгоритмы. Они описаны в книге Пайтгена и Заупе
«Наука о фрактальных образах» [196]. На рис. 2 показано пылевидное
множество Жюлиа для отображения A), построенное с помощью тако-
такого алгоритма.
Даже такой простой пример рационального отображения с тремя
аттракторами и его множество Жюлиа, рассмотренные нами выше,
имеют свои физические приложения. Рассмотрим, например, маятник,
состоящий из подвешенного на конце нити железного шарика. Под маят-
маятником находятся три магнита, притягивающие шарик. После несколь-
нескольких колебаний маятник замрет, а шарик зависнет точно над одним из
трех магнитов. Но всегда ли шарик устремится к тому из аттракторов,
который окажется ближайшим к его начальному положению? Отнюдь!
Попробуйте, и вы убедитесь в этом сами. При различных начальных
условиях шарик описывает весьма замысловатую траекторию, а его
конечное положение представляется совершенно непредсказуемым. Бо-
Более того, оно нередко не только кажется непредсказуемым, но в дей-
действительности таковым и является, если только начальное положение
шарика не задано с какой-то сверхнеобыкновенной и совершенно нере-
322
Глава 11
Рис. 2. Пыль Жюлиа для итераций Ньютона [196].
альной точностью. Иначе говоря, области притяжения трех магнитов
определяются фрактальными множествами — так же, как множество
Жюлиа в итерациях Ньютона.
Мультифрактальное множество Жюлиа
В предыдущем разделе мы выяснили, что множества Жюлиа ра-
рациональных функций с более чем двумя аттракторами представляют
собой фракталы. В действительности такие множества мулыпифрак-
талъны. По традиции такие множества принято анализировать путем
построения их отдельных точек с помощью обратных численных итера-
итераций. Однако для анализа некоторых множеств Жюлиа можно воспользо-
воспользоваться аналитическими методами, несравненно более точными и сопря-
сопряженными с существенно меньшим объемом вычислений. Убедительным
тому примером может служить недавно произведенный Науэнбергом
и Шельнхубером анализ мультифрактальных свойств множества Жю-
Жюлиа, связанного с ньютоновым отображением A) для отыскания корней
кубического уравнения z3 — 1 = 0 [183].
Прежде всего необходимо построить носитель фрактального мно-
множества. Для исходного канторова множества носителем является еди-
единичный интервал: все его элементы «обитают» на единичном отрез-
Мулътифракталъное множество Жюлиа 323
ке прямой. Что же касается нашего ньютоновского множества Жю-
Жюлиа, то его носитель и сам обладает чрезвычайно сложной структу-
структурой — этакая бесконечное число раз вложенная в себя «паутина». По-
Построить это «убежище для пауков» Науэнбергу и Шельнхуберу по-
помогло одно немаловажное обстоятельство: один из трех прообразов
отрицательной вещественной полуоси есть полубесконечный интер-
интервал —оо < z ^ — 2/3, обозначенный на рис. ЗА через Mq. Два других
прообраза получаются из Мо поворотами на ±120°.
Два прообраза М+ и М_ множества Мо, не лежащие на отрица-
отрицательной вещественной полуоси, определяются выражением
Остальные четыре дугообразных прообраза второго порядка получают-
получаются при поворотах на углы ±120°. Эти шесть дуг и три прямолинейных
«шипа» на концах лепестков вместе образуют первое поколение носите-
носителя фрактала. Второе поколение состоит из 3 • 9 = 27 частей и т. д. На
рис. ЗБ показан носитель на четвертой стадии построения (т.е. состав-
составленный из первых четырех поколений, полученных с помощью обрат-
обратных итераций из центрального цветка). Уже на данном этапе отчетливо
видна иерархическая («вложенная») структура этого фрактала Жюлиа.
Прообразы хп более высокого порядка точки z = О, лежащие на
отрицательной вещественной полуоси, определяются соотношением
B)
где х\ = — 2/3. Асимптотический коэффициент подобия для хп
равен 3/2. Его можно вывести из производной прямой итерации:
dN/dz —>¦ 2/3 при больших z.
Прообразы С™ = С™ + Щп точек хп на М+ определяются соотноше-
соотношением
е„+1 = -хп sh2 [| sh ((-ж„)-3/2)], C)
и, как следует из формулы A), r]n+1 = ±{CJ+i ~ ?n+i)- Длины L Дуг
на М+ между ?„ и ?n+i асимптотически убывают как /„ ~ B/3)™/2.
Самая большая дуга имеет длину /i = 0,3834.
Чтобы вычислить фрактальные размерности Dq, сосредоточим
внимание на одном из трех лепестков центрального цветка (рис. ЗВ).
В первом поколении лепесток состоит всего лишь из двух больших дуг.
324
Глава 11
м„
У\
~ о
-1
м.
-1
о
Ке(г)
(А)
(Б)
Рис. 3. (А) Построение цветка Жюлиа: прообразы первого поколения. (Б) Но-
Носитель «цветочного» множества Жюлиа на четвертом этапе его построения.
(В) Лепесток Жюлиа: первые три шага построения [183].
Мулътифракталъное множество Жюлиа 325
В качестве следующего шага рассмотрим бесконечную последователь-
последовательность меньших дуг, концы которых, лежащие на двух больших дугах,
определяются прообразами первого порядка точек хп на отрицатель-
отрицательной вещественной полуоси. Заметим, что каждая дуга порождает по-
последовательность двойных дуг. На рис. ЗВ (внизу) показан результат
третьего шага построения: каждая меньшая дуга покрылась бесконеч-
бесконечной последовательностью еще меньших двойных дуг.
Интересующее нас множество Жюлиа, а именно, множество общих
граничных точек трех областей притяжения, состоит из точек вет-
ветвления носителя. (Аналогичным образом обстоит дело с исходным кан-
торовым множеством, которое состоит из концевых точек остающихся
интервалов.) Фрактальные размерности Dq нашего множества Жюлиа
определяются выражением
5Х = 1, T = (l-q)Dq D)
(см. гл. 9), где суммирование проводится по последовательным поколе-
поколениям построения носителя, а множитель 2 отражает то обстоятельст-
обстоятельство, что каждая материнская дуга порождает двух сестер-близнецов —
двойную дугу. Выбрав три прообраза с одинаковыми весами, полу-
получим рт = A/3)т. Длины дуг 1т вычисляются по формулам A)-C).
Из всех размерностей проще всего вычисляется D^,, потому что
при q —>¦ оо показатель т стремится к — ос, и вклад в сумму D) дает
лишь наибольшая длина 1т. Наибольшей из 1т является /i pa 0,3834.
Следовательно, при р\ = 1/3 мы получаем
А» =
При q = ±оо коэффициент 2 в соотношении D) становится несущест-
несущественным. Другая предельная размерность D_oo вычисляется столь же
легко. На этот раз главным слагаемым в сумме D) является наимень-
наименьшая длина /т, т.е. 1т при т —>¦ оо. Учитывая, что при больших т
и Рт = A/3)т длина изменяется по закону lm ~ B/3)m/2, получаем из
соотношения D)
-oo = lim -^2^-=5,419...
.1 1 3
2 2
Заметим, что в отличие от размерности Хаусдорфа Do предельная
размерность D_oo не имеет простого геометрического смысла. И поэ-
326 Глава И
тому то, что ее величина превосходит 2 (евклидову размерность про-
пространства вложения для фрактала Жюлиа), не составляет никакого про-
противоречия.
Интересно отметить, что при изложенном выше подходе числен-
численное значение размерности -D_oo определяется простым аналитическим
фактом, а именно тем, что lm ~ B/3O™/2. В отличие от аналитичес-
аналитического метода численные методы при q = — ос оказываются бессильны-
бессильными, так как в этом случае компьютеру пришлось бы работать целую
вечность, исследуя наиболее редко заселенные области множества Жю-
Жюлиа, которые и характеризуются размерностью D-oo- Учитывая это
обстоятельство, обычно возникает искушение оценить значение раз-
размерности -D-oo no Dq при больших q. Однако такой подход наталкива-
наталкивается на обескураживающе медленную сходимость. Другие размернос-
размерности, в том числе размерность Хаусдорфа Do, можно также определить
с помощью элементарных вычислений. Для получения хороших при-
приближений достаточно в сумме D) явно учесть лишь несколько длин 1т.
Что до остальных слагаемых, то для них вполне подойдет приближен-
приближенное значение 1т = 0,1986B/3)т/2. Такой подход дает для размерности
Хаусдорфа величину Do = 1,429..., намного более точную, чем те,
что получены «числодробительными» методами, на основании обработ-
обработки миллиона точек множества Жюлиа. Заметим, что Do < 2 — вполне
подобающее значение для двумерной пыли. Что же касается такой важ-
важной характеристики, как информационная размерность (см. гл. 9)
то для хорошей оценки D\ к. 1,2 достаточно учесть только две дли-
длины: h и 0,38 и 12 и 0,18.
Красота кусочно-линейных отображений
На рис. 4 вы видите результат применения кусочно-линейного «пи-
«пилообразного» отображения b = 8b mod 1 к локальной яркости 0 ^ Ь ^ 1
фотографии человеческого лица и последующем квантовании & в 0 (ес-
(если Ь > Ь) или в 1 (если Ь ^ Ь) [225]. На рис. 5 показан красивый узор,
образующийся при итерации другой простой кусочно-линейной функ-
функции [193].
Красота кусочно-линейных отображений
327
Рис. 4. Пилообразное отображение «Карен», из первых опытов автора в ком-
компьютерной графике [225].
Такие отображения представляют собой полезные математические
модели детерминированной диффузии [234]. В то время как традици-
традиционная (термодинамическая) диффузия является типичным случайным
процессом, кусочно-линейные отображения, аналогичные представлен-
представленному на рис. 6, обусловливают внешне случайное движение частицы —
при том, что ее дрейф является в действительности строго детермини-
детерминированным процессом. Этот дрейф может служить еще одним примером
хаотического движения, сильно зависящего от точного (хотя и не всег-
всегда точно определяемого) начального значения координаты. Как и при
обычной диффузии, пространственная корреляция между двумя перво-
первоначально близкими частицами со временем убывает до нуля [89]. В ре-
результате среднеквадратичное смещение х2 возрастает со временем ли-
линейно, как и при обычной диффузии:
а-2 = 2Dt при * » 1,
где D — коэффициент диффузии, пропорциональный ширине S, на кото-
которую итерированная функция «высовывается» из единичного квадрата.
328
Глава 11
Рис. 5. Вышитый узор в свете дробно-линейного преобразования [193].
Преобразование пекаря и цифровой вариант игры
в «стулья с музыкой»
Пекари месят тесто, раскатывая его, складывая и вновь раскаты-
раскатывая — бесконечная, на первый взгляд, последовательность итераций —
до тех пор, пока не добиваются достаточно однородной смеси ингреди-
ингредиентов.
На рис. 7 вы видите математически облагороженный вариант опе-
операций раскатывания и складывания теста, известный под названием
преобразование пекаря. Это полезная модель для всевозможных процес-
процессов перемешивания, в том числе хаотического перемешивания жидкос-
жидкостей. В арифметическом смысле точка (ж, у) в единичном квадрате пе-
переходит в точку Bж, у/2) при раскатывании и в точку (Bx)i, у/2 +
+ |_2ж_|/2) при последующем разрезании раскатанного теста пополам
и помещении правой половины над левой половиной. (Эта операция ма-
математически проще, чем складывание.) Здесь, как и ранее, угловые
Преобразование пекаря
329
Рис. 6. Дробно-линейное отображение для моделирования детерминирован-
детерминированной диффузии [89].
скобки означают взятие дробной части, а открытые сверху полуквад-
полуквадратные скобки — округление до ближайшего меньшего целого числа.
Рис. 7. Отображение пекаря: рецепт хаотического теста. Сначала «раскаты-
«раскатываем» единичный квадрат, затем отрезаем его правую половину и помещаем
ее над левой половиной.
330 Глава 11
Если х и у выразить в двоичной форме, то преобразование пекаря
значительно упрощается: цифры в записи координаты х сдвигаются
на один знак влево, цифры в записи координаты у сдвигаются на один
знак вправо, а самая левая цифра координаты х становится самой левой
цифрой координаты у. Двоичные цифры в х и у играют в своего рода
«стулья с музыкой»1. Например, пара координат
Ж1 = 0,10110001... ,
ух =0,01110100...
отображается в пару
х2 =0,0110001... ,
г/2 = о,1ошоюо...,
которая, в свою очередь, переходит в пару
х3 =0,110001... ,
г/з = о,о1ошоюо...
и т. д. Таким образом, любая конечная дробь х асимптотически стре-
стремится к началу координат @, 0), которое становится аттрактором для
таких значений х.
Периодические двоичные значения х сходятся к периодическим
орбитам. Например, координаты х = 1/3 = 0,@1), у = 2/3 = 0,A0)
сходятся к периодической орбите с периодом 2. Напротив, нормаль-
нормальные двоичные числа порождают хаотические орбиты, на которых даже
первоначально близкие точки вскоре разбегаются и следуют по своим
независимым орбитам (рис. 8). И хаотические, и нехаотические потоки
обсуждаются в статье Оттино «Перемешивание жидкостей» [187].
Иногда пекарь после каждой итерации отбрасывает какую-то часть
теста. В этом случае то, что остается, постепенно превращается в од-
одном направлении в канторову пыль. Такое обобщенное преобразование
пекаря представляет собой простую модель фазовых пространств не-
нелинейных динамических систем — пространств, которые сжимаются
по некоторым направлениям и потому обзаводятся странными аттрак-
аттракторами — такими, как множества Жюлиа, рассмотренные нами на
с. 319-326.
1Игра, в которой могут принимать участие любое число желающих. Играющие
ходят под музыку вокруг выстроенных в круг стульев, число которых на единицу
меньше числа участников. Музыка внезапно прекращается, и играющие бросаются
занимать свободные стулья. Проигрывает тот, кому не хватило стула. — Прим.
перев.
Преобразование пекаря
331
Рис. 8. Хаотическая орбита точки при преобразовании пекаря; начальная точ-
точка находилась вблизи периодической точки (жо = 2/3, j/o = 1/3) с периодом 2.
Среди родственных преобразований можно назвать отображение
«подкова Смейла» [246] (рис. 9) и отображение Энона (рис. 10), описы-
описывающих характерные особенности диссипативных физических систем
со странными аттракторами.
Рис. 9. Подкова Смейла. Пространство растягивается в одном направлении,
сжимается в другом, а затем складывается вдвое. Пара точек, оказавшихся
после нескольких итераций рядом, могли находиться очень далеко друг от
друга в начале процесса.
Где же в отображении Энона таится самоподобие? Взгляните на
рис. ЮГ и на аттрактор Энона после 104 итераций, представленный на
332
Глава 11
(А)
(Б)
G
Рис. 10. Отображение Энона. (А) Исходный эллипс. (Б) Сохраняющий пло-
площадь изгиб: х = ж, у = 1 — ах2 + у. (В) Сжатие по оси х: х" = Ьх', у" = у'.
(Г) Поворот на 90°: х'" = у", у'" = -х" [234].
рис. 11. Хотя странные аттракторы и вправду странны во многих от-
отношениях, они все-таки демонстрируют самоподобный порядок в своих
хаотических орбитах.
Кошка Арнольда
333
(Б)
Рис. 11. Самоподобность аттрактора Энона. (А) Аттрактор целиком. (Б) Уве-
Увеличение части аттрактора, выделенной квадратом на рис. (А). (В) Еще одно
увеличение. Отметьте сходство штриховых узоров на рис. (Б) и (В), под-
подтверждающее самоподобность аттрактора Энона [64].
Кошка Арнольда
Среди двумерных отображений нельзя обойти молчанием сохраня-
сохраняющее площадь отображение «кошка Арнольда», описывающее гамильто-
новы нелинейные системы:
хп+1 = хп + уп mod 1,
Уп+i = хп+ 2уп mod 1,
A)
изображенное на рис. 12А и 12Б. Запись modi, как и ранее, означа-
означает, что рассматриваются только дроби из полуоткрытого единичного
интервала [0, 1). Искажение картинки, порождаемое этим преобразо-
преобразованием, напоминает о плохо отрегулированном телевизоре. Отображе-
Отображение «кошка Арнольда» имеет два собственных значения Ai и Аг, ко-
которые, соответственно, равны квадрату величины, обратной золотому
сечению j, и числу, обратному этому квадрату: Ai = C + л/5)/2 > 1
и Х2 = Х^1 = C — л/5)/2 < 1. Поскольку одно собственное значение
больше единицы, а другое меньше, то все неподвижные точки отобра-
отображения являются гиперболическими. Это означает, что кошка Арнольда
растягивает по одному направлению (соответствующему собственно-
собственному значению Ai) и сжимает по другому, перпендикулярному первому,
направлению (соответствующему значению Аг). Таким образом, непо-
неподвижные точки отображения не являются ни репеллерами, ни аттракто-
аттракторами, а и теми и другими, в зависимости от направления, по которому
мы к ним приближаемся. С точки зрения геометрии гиперболические
неподвижные точки представляют собой седловые точки: мяч катится
с горы по направлению к седловой точке (горному перевалу), а затем
334
Глава 11
движется от седловой точки к долине. Перевал сначала притягивает,
а затем отталкивает низвергающийся с гор по направлению к нему
поток воды, т.е. сначала выступает в роли аттрактора, а затем репел-
репеллера.
Рис. 12. (А) Кошка Арнольда; (Б) итерированное отображение «кошка Ар-
Арнольда».
Отображения с гиперболическими неподвижными точками явля-
являются неотъемлемым признаком хаотического движения в консерватив-
консервативных (сохраняющих энергию) физических системах, известных под на-
названием гамильтоновых систем [8]. Например, (х, у) = @,4; 0,2) —
неподвижная точка однократно итерированного отображения «кошка
Арнольда», т.е. она принадлежит орбите с длиной периода 2. Эта точ-
точка переходит в точку @,6; 0,8), которая, в свою очередь, отобра-
отображается в исходную точку @,4; 0,2). Преобразование исходной точ-
точки @,4; 0,2) в направлении, соответствующем собственному значе-
значению Аг (Ах/Ay = — (л/5 + 1)/2 = —1/7), является сжимающим. Дей-
Действительно, первые четные итерации х^п начальной точки (xq = 0,4 +
+ 1/1007, 2/о = 0,2 — 1/100), начиная с х^, имеют следующие прибли-
приближенные значения: 0,402; 0,4003; 0,40005; 0,400007; 0,400001; 0,4000002.
Кошка Арнольда 335
Следовательно, точка @,4; 0,2), если приближаться к ней с направ-
направления, соответствующего собственному значению Лг, действует как
аттрактор. Но если мы продвинемся по этой сходящейся последова-
последовательности несколько дальше, воспользовавшись 12-разрядным каль-
калькулятором, который вносит небольшую погрешность в направле-
направлении Ai, то эти небольшие погрешности приведут нас в конце кон-
концов к расходимости, о чем свидетельствуют последующие итера-
итерации: 0,4000005; 0,400003; 0,40002; 0,4002; 0,401; 0,407; 0,45; 0,75 и т.д.
до полного хаоса. Дело в том, что в силу двойственной (аттракторно-
репеллерной) природы гиперболических неподвижных точек любое вы-
вычисление (равно как и любая физическая система, моделируемая кош-
кошкой Арнольда) рано или поздно демонстрирует хаотическое движение,
за исключением редких начальных условий нулевой меры. Такие на-
начальные условия, конечно же, не могут быть реализованы физически,
так как они соответствуют неустойчивым состояниям равновесия (на-
(например, поставленный на острие карандаш).
Одно из преимуществ кошки Арнольда состоит в том, что итерации
этого отображения легко анализировать. В матричной форме отображе-
отображение A) (кошка Арнольда) задается матрицей
1 2
которая переводит вектор-столбец (хп, уп) в вектор-столбец (xn+i,yn+i),
где все х и у берутся по модулю 1.
Зная рекуррентное соотношение для чисел Фибоначчи Fn = Fn-\ +
+ Fn-2, Fi = F2 = 1, нетрудно с помощью индукции доказать, что п-п
итерация отображения Арнольда имеет следующий вид:
F2n-1
Это преобразование наследует свойство Т сохранять площадь. (Дейст-
(Действительно, определитель матрицы Т™, т.е. i*2n-i-p2n+i ~~ F^, равен 1.)
Так как Тп — симметричная матрица, ее собственные значения (Aj™ =
= А™ > 1 и Aj = A2 < 1) всегда вещественны.
Неподвижные точки отображения Тп соответствуют орбитам
с длиной периода п (вместо п подойдет любое его кратное). Например,
при п = 2
^3 5;
336 Глава 11
Чтобы найти неподвижные точки с периодом 2, необходимо решить
уравнения
2х + Зу = х mod 1,
Зх + 5у = у mod 1.
Исключая у, мы, помимо решения х = у = О (длина периода равна 1),
получаем уравнение 5х = О mod 1, т.е. х = к/5, где к — целое число.
Так как 0 < х < 1, для к допустимы только значения 1, 2, 3, 4, каждое
из которых дает решение. Соответствующие значения у представимы
в виде у = к'/5, где к' = —2к mod 5. Эти четыре периодические точ-
точки с длиной периода 2 образуют две орбиты, а именно: B/5, 1/5) —>¦
—>¦ C/5, 4/5), с которой мы уже встречались, и A/5, 3/5) —>¦ D/5, 2/5).
Заинтересованному читателю мы рекомендуем произвести анализ
полной структуры орбит кошки Арнольда, что, на наш взгляд, весьма
поучительно.
Миллиард знаков для тг
Итерации принадлежат к числу наиболее мощных математичес-
математических инструментов. Для вычисления числа тг с помощью ряда Грегори-
Лейбница
4 3 + 5 7 + '"
с точностью лишь до трех десятичных знаков требуется учесть 500
членов ряда, между тем как рекурсия, использующая арифметико-
геометрическое среднее, позволяет с каждым шагом удваивать коли-
количество правильных знаков [27, 130]. А есть еще итеративные алгорит-
алгоритмы, основанные на работах Рамануджана, позволяющие с каждой ите-
итерацией увеличивать количество десятичных знаков в 4 и даже в 5
раз [28]. Тринадцать итераций такого алгоритма уже дали более 134
миллионов знаков числа тг, а вычислив еще две итерации, мы довели бы
точность тг до более чем двух миллиардов знаков. При этом относитель-
относительная погрешность составляет 10~10 (а не просто 10~9). Поразительная
точность!
Никому, разумеется, не нужно знать число тг с такой сверхъестес-
сверхъестественной точностью. Самые точные измерения в физике, использующие
эффект Мёссбауэра, производятся с точностью, скажем, до 14 десятич-
десятичных знаков. Такая точность соответствует погрешности в 1 секунду за
3 миллиона лет. Тридцать девять знаков в десятичной записи числа тг
достаточно для того, чтобы вычислить длину окружности известной
Миллиард знаков для -к 337
Вселенной с точностью до диаметра атома водорода. Однако вычисле-
вычисление знаков числа тг стало своего рода эталонным тестом для суперком-
суперкомпьютеров и сверхбыстрых алгоритмов. Излишне говорить, что такие
вычисления производятся не на карманных калькуляторах, поскольку
те не обладают ни необходимым объемом памяти, ни достаточно вмес-
вместительным дисплеем.
Одним из наиболее поразительных достижений Рамануджана по
праву считается следующая формула:
1 _ V8 у> Dn)![1103 + 26390n]
n=0
(n!L C964n)
v / v /
Даже при учете только самого первого члена суммы точность вычисле-
вычисления тг превосходит 3-10~8. Каждый последующий член дает еще восемь
десятичных знаков (т.е. увеличивает точность в 100 миллионов раз).
Очень быстро сходящиеся приближения тг основаны на одной из ос-
основополагающих работ Рамануджана, в которой он установил тесную
взаимосвязь между приближением A) и теорией преобразований эллип-
эллиптических интегралов [208]. Один из рекурсивных алгоритмов, происте-
проистекающих из этой связи, сводится к следующему. Пусть «о = 6 — 4\/2 и
Тогда
ап+1 = A + yn+i)Aan - 22п+3уп+1A + уп+1 + у2п+1)
приближается к ^ с погрешностью меньшей, чем 164n+1 ехр(—2тг-4и+1).
Уже первое приближение а\ дает 9 правильных знаков в тг, второе же а^
дает уже 40 правильных знаков. Число знаков n-го приближения ап
превышает 2 • 4й; оно асимптотически увеличивается в четыре раза
с каждой итерацией и после 15 шагов превышает 1 миллиард.
Существует даже пятикратный алгоритм, который увеличивает
число правильных знаков с каждым шагом в пять раз [28].
Насколько случаен первый миллиард знаков тг? Грегори и Дэвид
Чудновски из Колумбийского университета обнаружили, что цифры
числа тг более случайны, чем последовательности цифр, порождаемые
стандартными генераторами псевдослучайных чисел; поскольку такие
генераторы основаны на алгоритмах с конечным числом состояний, они
338 Глава 11
в конечном счете периодичны. В частности, при воспроизведении бро-
броуновского движения цифры числа тг порождают случайные блуждания,
которые, по-видимому, удовлетворяют закону повторного логарифма
(чего не скажешь об обычных генераторах псевдослучайных чисел).
Даже если это так, не существует строго математического доказа-
доказательства нормальности числа тг (напомним, что в записи нормального
числа любые группы цифр встречаются асимптотически равновероят-
равновероятно). Более того, сам факт, что тг можно определить такими компактны-
компактными и быстро сходящимися формулами, как A), внушает специалистам
подозрение в ненормальности числа тг при некотором подходящим об-
образом выбранном основании.
Кустарники и цветы от итераций
Итерирование простых правил принадлежит к числу наиболее
сильнодействующих рецептов для порождения не только математичес-
математических фракталов, но и интересных биологических форм [203]. Излюблен-
Излюбленным примером такого рода процессов является так называемый «чере-
«черепаший алгоритм» для рисования линиями.
Состояние «рисующей черепахи» определяется тройкой чисел
(х, у, а), где декартовы координаты (ж, у) указывают положение че-
черепахи, а угол а, называемый курсом черепахи, указывает, в какую
сторону черепаха «смотрит». Если заданы величина шага d и прираще-
приращение угла S, то черепаха откликается на команды, обозначаемые следу-
следующими символами:
F Ход вперед на один шаг длины d. Такое движение переводит исход-
исходное состояние черепахи в новое состояние (х1', у', а), где х' = х +
+ d cos а и у' = y + d sin а. Черепаха оставляет за собой след, вычер-
вычерчивая отрезок прямой, соединяющий точку (х, у) с точкой (х', у').
f Ход вперед на один шаг длины d без вычерчивания линии.
+ Поворот вправо (по часовой стрелке) на угол 5. В результате такого
хода черепаха переходит в состояние (ж, у, а + 5).
— Поворот влево на угол S. Состояние черепахи меняется на (ж, у, а—5).
Пусть и — упорядоченная последовательность команд, (хо,уо,ао) —
начальное состояние черепахи, d и S — фиксированные параметры. Кар-
Картина (совокупность линий), которую черепаха нарисует в ответ на по-
последовательность команд v называется черепашьей интерпретацией v.
Кустарники и цветы от итераций
339
На рис. 13 показан пример черепашьей графики — фрактальная картина
«Острова и озера», которую черепаха «нарисовала», начав с единично-
единичного квадрата, заданного последовательностью команд F — F — F — F.
В соответствии с вышеприведенными правилами, черепаха интерпре-
интерпретирует такую последовательность команд как последовательность пря-
прямолинейных отрезков, соединенных «голова к хвосту».
? О
о
о
о
%
°n
0
%
0
сэ
сэ
сэ
2,0°
сэ
сэ
0°
сэ
сэ
сэ
сэ
%
0
сэ
а
сэО
сэ
сэ
сэ
сэ
0а
сэ
сэ
0
°0
сэ
сэ
сэ
сэ
? 0
сэ
сэ
D
сэ
сэ
сэО
°о
0
°0
°0
?а
о
о
о
о
о
о
cd a a cd a
а а
F-F-F-F
f — ffffff
F — F-f+FF-F-FF-F-FF+f-FF+F+FF+Ff+FFF
? 0
? 0
Рис. 13. Вложенные друг в друга «Острова и озера», изображенные с помощью
черепашьего алгоритма [161].
При дальнейшей разработке черепашьего алгоритма Линденмайер
ввел специальные обозначения для представления теоретико-графовых
деревьев, используя последовательности со скобками [148]. Целью та-
такого нововведения было получение инструмента для формального опи-
описания ветвящихся структур, встречающихся во многих растениях —
от водорослей до деревьев. Это расширение черепашьей интерпретации
использует два дополнительных символа:
[ Запомнить текущее состояние черепахи (х, у, а) для последую-
последующего восстановления.
340
Глава 11
] Вернуться к состоянию до паркой открывающей скобки ([), и про-
продолжить выполнение команд, стоящих справа от закрывающей
скобки (]). Обратите внимание на возможность появления скобок
внутри скобок.
Примером последовательности команд со скобками и ее интер-
интерпретации черепахой может служить куст на ветру, изображенный на
рис. 14.
F -FF+[+F-F-F]-[-F+F+F]
Рис. 14. «Куст на ветру» (обратите внимание на его самоподобие) [203].
На цветных вклейках 7А-7Е показаны шесть напоминающих рас-
растения структур, которые создал указанным выше способом Прусинке-
вич [203]. Добавляя к своим конструкциям цвет, Прусинкевич получил
Кустарники и цветы от итераций 341
захватывающе красивые и вполне реалистичные цветы и кустарники,
в чем читатель может убедиться сам, взглянув на вклейку 7, воспро-
воспроизводимую с любезного разрешения автора.
Используя другой подход к кодированию образов, известный под
названием системы итерированных функций, Барнсли создал изображе-
изображения подсолнухов, папоротников и лесов с помощью поразительно малого
набора параметров (см. гл. 1, с. 56-58).
Глава 12
Самоподобная последовательность,
логистическая парабола и символическая
динамика
Я работаю в области статистической
механики, но отнюдь не мечтаю по-
попасть на Луну.
Марстон Морс
В этой главе мы глубже познакомимся с самоподобием, возникаю-
возникающим в результате итераций. Свое внимание мы сосредоточим на так
называемой логистической параболе — простом квадратном уравне-
уравнении, описывающем подъемы и спады численности хищников и жертв
и ограниченные процессы роста (ограниченные недостатком снабже-
снабжения1). Этот простой закон нашел широкое применение во многих об-
областях человеческой деятельности. Его итерации порождают многочис-
многочисленные универсальные характеристики и самоподобия. Мы попытаем-
попытаемся осветить такие знаменательные свойства логистической параболы,
как устойчивые и неустойчивые орбиты, детерминированный хаос, ка-
касательные бифуркации, перемежаемость, иерархия орбит, бифуркация
хаотических полос и инвариантные распределения. Мы коснемся также
некоторых математических методов, использующих присущее квадра-
квадратичному отображению самоподобие, и изучим несколько достоприме-
достопримечательных преобразований, проливающих свет на итерации логисти-
логистического и других отображений.
Среди предсказаний, данных логистической параболой и под-
подкрепленных наблюдениями многих явлений природы, можно назвать
появление периодических циклов, особенно циклов с длиной перио-
периода 2, 4, 8, 16, 32 и т.д. Речь идет о знаменитом сценарии удвоения пе-
периода, возникающего из самоподобия и приводящего в конце концов
10т англ. logistical — «тыловой», «снабженченский» (ср. logistic — «логистичес-
«логистический»). — Прим. перев.
Самоподобие от целых чисел 343
к полному хаосу, пусть и детерминированному. Мы попытаемся навес-
навести мост через, казалось бы, немыслимую пропасть, разделяющую са-
самоподобие двоичных целых чисел и удвоение периода в логистической
параболе, выковав прочную связь между этими двумя фундаменталь-
фундаментальными явлениями и дав ей имя символическая динамика. Однако, как
мы увидим из дальнейшего разговора, детерминированный хаос весь-
весьма тесно связан с одной простой операцией, производимой над цифрами
(двоичного) числа: многократным сдвигом влево до тех пор, пока перед
нашими глазами не предстанет его абсолютно непредсказуемый хвост.
Всласть налюбовавшись реальным миром логистической парабо-
параболы, мы последуем за Мандельбротом, совершив воображаемый прыжок
в мнимом направлении прямиком на комплексную плоскость, где ста-
станет явным многое из того, что представлялось тайным на вещественной
прямой. Иными словами, займемся комплексификацией ради симплифи-
кации. Между делом, в качестве дополнительного приза, мы откроем
для себя множество Мандельброта и познакомимся с его замысловатой
самоподобной структурой.
Наш экскурс в комплексную область мы начнем с простого рекур-
сировного упражнения в дискретном мире целых чисел.
Самоподобие от целых чисел
Числа Фибоначчи и треугольник Паскаля (см. гл. 17 «Клеточные
автоматы») далеко не исчерпывают самоподобных способностей це-
целых чисел. Рассмотрим последовательность неотрицательных целых
чисел 0, 1, 2, 3, 4, 5, 6, 7, ..., записанных в двоичной форме,
О, 1, 10, 11, 100, 101, 110, 111, ...
и извлечем из каждого двоичного числа «цифровой корень» (т. е. найдем
сумму его цифр по модулю 2). Мы получим последовательность
0, 1, 1, 0, 1,0, 0, 1, ... ,
которая называется последовательностью Морса-Туэ (МТ) в честь
норвежского математика Акселя Туэ A863-1922), который представил
ее миру в 1906 г. в качестве примера апериодической рекурсивно вы-
вычислимой последовательности символов, и Марстона Морса из Принс-
тона A892-1977), обнаружившего, что эта последовательность игра-
играет важную роль в символической динамике при описании поведения
344 Глава 12
некоторых нелинейных динамических систем в фазовом пространст-
пространстве [257, 182].
Интересно, что МТ-последовательность можно также получить,
итерируя отображение 0 —> 0 1 и 1 —>¦ 1 0, т. е. отображение, при ко-
котором вслед за каждой двоичной цифрой записывается ее дополнение.
Начав с единственного нуля, мы получим такие последовательные «по-
«поколения»:
О
01
ОНО
01101001
и т. д. Построенная таким образом последовательность называется са-
самопорождающей последовательностью [245].
Другой способ построения той же последовательности состоит
в том, что каждое поколение получается из предыдущего путем припи-
приписывания справа его дополнения:
0
01
ОНО
01101001
и т. д. Новый способ — это всего лишь следствие того, что отобра-
отображение 0 —> 01, 1 —> 10 непосредственно порождает отображение
01—^0110, 10—» 1 0 0 1 и т. д., где каждое отображение более высокого
порядка следует исходному правилу «повтори двоичное число и припи-
припиши к нему справа его дополнение». Иначе говоря, исходное правило,
порождающее отображение, наследуется всеми последующими поколе-
поколениями. Наследование такого рода является важным следствием итери-
итерированных отображений и часто приводит к самоподобным структурам.
Такие порождающие процессы известны также под названием инфляци-
инфляционных1 процессов — термин, который (в своем неэкономическом и не-
некосмологическом смысле) ассоциируется с мозаиками Пенроуза и их
замечательными скейлинговыми свойствами [91].
Бесконечная последовательность, получаемая итерированием ото-
отображения 0 —>• 0 1, 1 —>¦ 1 0, инвариантна относительно этого отобра-
отображения; инфляция никак ее не затрагивает. Более того, последователь-
1От лат. inflatio — вздутие. — Прим. перев.
Самоподобие от целых чисел 345
ность МТ самоподобна: сохраняя лишь нечетные члены этой бесконеч-
бесконечной последовательности (отмеченные чертой снизу), мы вновь получа-
получаем последовательность МТ:
01101001 ... .
Аналогично, сохраняя только нечетные пары двоичных чисел, мы также
воспроизводим МТ-последовательность:
011 11001 ... .
МТ-последовательность воспроизводится и после замены каждой па-
пары, четверки, октета и т. д. на их самую левую цифру. Такой про-
процесс «усечения» и отбрасывания «лишних» чисел эквивалентен тому,
что принято называть дефляцией в теории мозаик или переименова-
переименованием блоков в теории ренорм-групп. Все эти схемы просто следуют
из преобразования 0 1 —» 0, 1 0 —>• 1, обратного исходному преобразо-
преобразованию 0—^01, 1 —>• 1 0. Естественно, что если инфляция воспроизво-
воспроизводит некоторую заданную бесконечную последовательность, то же самое
делает и соответствующая дефляция. Тот факт, что собственное под-
подмножество может быть эквивалентно всему множеству, представляет
собой хорошо известное свойство бесконечных множеств.
Понять самоподобие МТ-последовательности очень легко. Сохране-
Сохранение только нечетных членов бесконечной последовательности эквива-
эквивалентно умножению исходных чисел на 2 (основание двоичной системы
счисления, в которой записаны члены последовательности). Так как
в двоичной системе умножение на 2 означает сдвиг цифр влево на один
знак, то цифровые корни чисел остаются неизменными, точнее, они
и образуют по определению МТ-последовательность. (Если мы сохра-
сохраним только четные члены, то МТ-последовательность по аналогичным
причинам перейдет в собственное дополнение.)
Разумеется, ни в числе 2, ни в двоичной системе нет ничего маги-
магического. Цифровые корни (т. е. суммы цифр по модулю 3) целых неот-
неотрицательных чисел, записанных в троичной системе счисления,
0, 1, 2, 10, 11, 12, 20, 21, ...
образуют самоподобную последовательность с коэффициентом подо-
подобия 3:
Рк = 0, 1, 2, 1, 2, 0, 2, 0, ... .
Действительно, рзк = Vk-, так как троичное представление числа ЗА; сов-
совпадает с троичным представлением числа к, если не учитывать сдвига
346
Глава 12
на одну цифру влево. Итерации какого отображения порождают после-
последовательность pj;? (И каковы самоподобные свойства последовательнос-
последовательностей {рзк+i} и {p3fc+2}?)
Еще одним интересным свойством МТ-последовательности являет-
является ее апериодичность. Доказательство этого свойства (не слишком труд-
трудное) мы предоставляем читателю. Хоть МТ-последовательность и апе-
риодична, она ни коим образом не случайна. Более того, ее структура
обладает ярко выраженным ближним и дальним порядком. Например,
в этой последовательности не может быть групп, состоящих более чем
из двух одинаковых членов подряд. И конечно же, ее члены с индекса-
индексами (исходный 0 имеет индекс 0), различающимися на множитель 2™,
совпадают.
Строгая внутренняя структура МТ-последовательности отражает-
отражается в ее спектре Фурье (рис. 1), на котором (несмотря на апериодичность
последовательности) наблюдаются хорошо выраженные пики. Возмож-
Возможно, читателю захочется самому показать, что два самых высоких пика
соответствуют частотам, составляющим треть и две трети «частоты
выборки».
86 128 170
Гармоническое число
256
Рис. 1. Амплитудный спектр Фурье для последовательности Морса-Туэ (пер-
(первые 256 периодически повторяющихся членов) [230].
Самоподобие от целых чисел 347
Особенно удобным исходным пунктом для вывода Фурье-преоб-
Фурье-преобразования МТ-последовательности в «алфавите» ±1 (т/. = 1, —1, —1,
1, 1, —1, ...) является ее производящая функция
k=0
Инвариантность МТ-последовательности ти при подстановке 1 —>• 1, —1
и — 1 —> — 1, 1 предполагает функциональное уравнение
H(z) = (l-z)H(z2),
которое, в свою очередь, дает производящую функцию
Н (z) = A - z)(l - z2)(l - z4)(l -z8)....
Если не учитывать замены z на z~x, эта производящая функция сов-
совпадает с так называемым «-преобразованием», широко используемым
инженерами-электриками для описания передаточных функций цифро-
цифровых фильтров.
Положим z = ехр(гш), где и) — угловая частота. Тогда из произво-
производящей функции следует Фурье-преобразование
оо
М(ш) = Д[1-ехр(ш2*)],
k=0
которое удовлетворяет масштабному закону М (ш) = [1—ехр(га>)] М Bш).
Этот закон, вкупе с симметриями М (—ш) = М* (ш) и М (ш + 2тт) =
= М (ш), и определяет самоподобную структуру спектра.
В физике МТ-последовательность была впервые обнаружена в сим-
символической динамике некоторых нелинейных динамических систем.
Марстон Морс доказал, что траектории динамических систем, фазовые
пространства которых имеют всюду отрицательную кривизну, полнос-
полностью характеризуются дискретной последовательностью нулей и еди-
единиц — поразительное открытие! Это означает, что какая-нибудь слож-
сложная кривая в М™, т.е. несчетно бесконечное множество в многомерном
пространстве, может быть отображено на дискретную двоичную по-
последовательность! Пользуясь МТ-последовательностью, Морсу удалось
также доказать возможность существования бесконечно долгих шах-
шахматных партий (при определенных ограничениях).
В следующем разделе мы исследуем один особенно простой и по-
поучительный случай символической динамики и его отношение к после-
последовательности Морса-Туэ.
348 Глава 12
Логистическая парабола и удвоение периода
Предположим, что в процессе экологического, экономического или
какого-нибудь другого роста некая величина xn+i для последующего
поколения (например, число животных) есть линейная функция от те-
текущего значения этой величины хп:
Хп+1 = ГХп,
где г > О — параметр роста. Неконтролируемый рост следует геомет-
геометрической прогрессии («экспоненциальному» закону):
хп = гпх0,
которая при г > 1 неограниченно возрастает.
Однако часто случается так, что ограниченное количество ресур-
ресурсов ограничивает рост. Иначе говоря, чем больше хп, тем меньше па-
параметр роста г. Проще всего уменьшение фактора роста моделируется
заменой г на гA — хп). Тогда при приближении хп к некоторому пре-
пределу (в нашем случае — к единице) параметр роста стремится к нулю.
В результате получаем закон роста
Хп+1 = f (ж„) = ГA - Хп)хп, A)
называемый квадратичным отображением, или — из-за его параболи-
параболической формы и отношения к снабжению1 — логистической параболой
(рис. 2).
Логистическое уравнение было представлено публике в 1845 г.
бельгийским социологом и математиком Пьером-Франсуа Ферхюльстом
A804-1849) в качестве модели роста популяций, ограниченного конеч-
конечностью ресурсов [261]. (Термин логистическое, однако, не получил ши-
широкого распространения до 1875 г. Происходит он от французского при-
прилагательного logistique, относящегося к тыловым службам, занимаю-
занимающимся расквартированием и снабжением войск.)
Первоначально логистическое уравнение выглядело как х (t) =
= К/[1 + ехр(а — Ы)], где х — число особей в исследуемой популяции как
функция от времени t. Постоянные а и Ъ задают начало отсчета и мас-
масштаб временной переменной. В зависимости от этих постоянных рост
переменной х происходит по приближенно экспоненциальному закону.
1См. прим. на стр. 342. — Прим. перев.
Логистическая парабола и удвоение периода
349
Рис. 2. Квадратичное отображение, также известное как логистическая па-
парабола. Обратите внимание на неподвижную точку при ж*.
Скорость роста достигает максимума при t = a/b, после чего падает до
нуля. Постоянная К определяет асимптотическое значение х.
Уравнение Ферхюльста для скорости роста может быть записано
и в виде dx/dt = rx(K — x)/K. При х <С К мы снова получаем экспонен-
экспоненциальный рост переменной х. Но когда х приближается к К, скорость
роста падает до нуля. Уравнение A) представляет собой рекуррентную
форму вышеупомянутого дифференциального уравнения с заменой вре-
времени t на дискретную переменную п. Наиболее важным отличитель-
отличительным признаком уравнения Ферхюльста и его следствий является их
нелинейность, позволяющая моделировать различные нелинейные яв-
явления во многих областях науки и их последствия — такие, например,
как хаотическая динамика.
Квадратичное отображение A) имеет две неподвижные точки х =
= О и (при г>1)ж = ж* = 1 — 1/г (см. рис. 2). Производная от
функции / (ж), задающей это отображение, есть функция
/' (х) = гA - 2х),
равная г в точке ж = 0 и 2 — г в другой неподвижной точке х* = 1 — 1/г.
Напомним, что неподвижные точки устойчивы, если |/'| < 1. Так, не-
неподвижная точка х = 0 устойчива при г < 1. Неподвижная точка х =
= 1 — 1/г существует и устойчива в диапазоне 1 < г < 3, так как в нем
выполняется неравенство |/' (х = 1 — 1/г)| < 1.
Более того, при г = 2 производная /' (х) = 0 в неподвижной точ-
точке ж* = 1 — 1/г = 1/2. Такие неподвижные точки называются сверх-
350
Глава 12
устойчивыми из-за очень быстрой к ним сходимости, в чем нетруд-
нетрудно убедиться с помощью любого карманного калькулятора. В общем
случае сверхустойчивая орбита возникает, когда точка х = 1/2, в ко-
которой /' (ж) = 0, принадлежит этой орбите. [Орбита — специальный
термин для обозначения последовательности итераций хп.) Значения
параметров сверхустойчивых орбит с длиной периода 2к обозначают
через R^; при г = Ro мы получаем сверхустойчивую неподвижную
точку (длина периода равна 1).
При г = 3 угловой коэффициент касательной к параболе в непо-
неподвижной точке х = 2/3 равен —1. Эта неподвижная точка «нейтраль-
«нейтральна», т. е. не притягивает и не отталкивает соседние точки. Что же
происходит при г > 3? Неподвижная точка становится неустойчивой
и расщепляется (претерпевает бифуркацию) в орбиту с длиной перио-
периода 2: жо, Ж1, а?2 = Xq (рис. 3). Например, при г = R\ = 3,2360679775
существует устойчивая (более того, сверхустойчивая) орбита с длиной
периода 2: 0, 5 ->• 0,8090169943 ...->0,5ит.д. (рис. 4).
Рис. 3. Неподвижная точка теряет устойчивость, порождая орбиту с длиной
периода 2.
Значение Ri мы получим, положив / (/ @, 5)) = 0,5 решением ку-
кубического уравнения R\ = AR\ — 8, которое как раз имеет квадра-
квадратичное иррациональное решение, связанное с золотым сечением j =
= 0,618 ...: Rx = 2/7 = \/5 + 1.
То, что длина периода орбиты равна 2, означает, что функ-
функция / (/ (ж)) (сокращенно /^ (ж)) имеет неподвижную точку (а по-
Логистическая парабола и удвоение периода
351
1 х
Рис. 4. (А) Квадратичное отображение для орбиты с длиной периода 2. (Б) Од-
Однократно итерированное отображение f^2' (ж) имеет две устойчивые непо-
неподвижные ТОЧКИ, Жо И Ж1.
скольку j'2'' (ж) = 0, то орбита сверхустойчива). Именно так и обстоит
дело в действительности (рис. 4Б). Более того, /^ (ж) имеет две непо-
неподвижные точки, обе сверхустойчивые: Жо = 0,5 и Xi = 0,809
При дальнейшем увеличении параметра г обе неподвижные точки
функции /B) (ж) становятся, в свою очередь, неустойчивыми, причем
обе теряют устойчивость при одном и том же значении г. Простое
совпадение? Нет, потому что, согласно цепному правилу дифференци-
дифференцирования,
d
dx
/(/И)
/'
или, если учесть, что / (жо) =
?f(f(xo))=f'(xi)-f'(x0).
Следовательно,
352 Глава 12
Из этого равенства можно заключить, что если точка Хо становит-
становится неустойчивой из-за того, что |/B)'(жо)| > 1> то теряет устойчи-
устойчивость и точка х\, причем при том же самом значении параметра г.
Это означает, что обе неподвижные точки отображения /B) (х) пре-
претерпевают бифуркацию при одном и том же значении г, порождая
в результате орбиту с длиной периода 4. Иначе говоря, теперь уже
отображение /{2)(/{2)(х)) = /D) (ж) = /(/(/(/ (ж)))) имеет непо-
неподвижную точку (точнее, четыре неподвижные точки). При г = В,2 =
= 3,498561699... этими четырьмя неподвижными точками являют-
являются: х0 = 0,500; хх = 0,874... ; х2 = 0,383...; и х3 =0,827.... Они
также образуют сверхустойчивую орбиту отображения / (ж) с длиной
периода 4: х0 -> х\ ->¦ х2 -> х3 -> х0 и т. д.
И снова в силу цепного правила дифференцирования четыре про-
производные во всех четырех точках орбиты равны. Следовательно, если
при некотором данном значении параметра г величина одной из произ-
производных превосходит единицу, то больше единицы окажутся все четыре
производные. Таким образом, все четыре итерации претерпевают би-
бифуркацию при одном и том же значении г, что приводит к возникно-
возникновению орбиты с длиной периода 8. Такой сценарий бифуркации повто-
повторяется снова и снова по мере увеличения параметра роста г, порождая
орбиты периода 16, 32, 64 и т. д. ad infinitum, когда каскад удвоений
периода завершается «хаотической» орбитой с бесконечной длиной пе-
периода при г = Гоо = 3, 5699
Рис. 5. Бифуркация-вилка: наружные «зубцы» соответствуют новым итераци-
итерациям после бифуркации, а средний отражает старые, теперь уже неустойчивые,
итерации.
Бифуркации удвоения периода известны также под названием би-
бифуркаций типа вилки, поскольку график зависимости значений итера-
итераций от параметра роста напоминает своей формой вилку (рис. 5). Два
зубца вилки, верхний и нижний, образованы новыми итерациями после
Самоподобие в логистической параболе 353
бифуркации, а центральный зубец (показанный на рис. 5 штриховой ли-
линией) соответствует старым (уже неустойчивым) итерациям, которые
превратились из аттрактора в репеллер.
Удвоение периода — весьма распространенное явление, встреча-
встречающееся во многих физических, экологических и экономических систе-
системах. Вспомните хотя бы о хищниках и их жертвах — например, о лисах
и зайцах. При умеренном уровне воспроизводства лис (г < 3) количест-
количество зайцев может оказаться вполне достаточным для того, чтобы насы-
насытить лисьи аппетиты, в результате чего установится устойчивое рав-
равновесие между численностью лис и численностью зайцев. Однако если
уровень воспроизводства лис превысит определенный предел (г > 3),
то лисы сожрут столько зайцев, что в следующем сезоне зайцев на всех
не хватит, и популяция лис пойдет на убыль. Уменьшение количест-
количества хищников даст зайцам шанс на восстановление своей популяции, но
как только зайцев станет больше, возрастет и поголовье лис. Таким
образом, возникает цикл с периодом в два сезона.
При каких значениях гп параметра роста г происходят бифур-
бифуркации, изменяющие длину периода с 2™ на 2й? И при каких зна-
значениях Rn мы получаем сверхустойчивые орбиты отображения A)
с длиной периода 2"? Что происходит с итерациями жо, х\, ... , жг»-1
при п —> оо? Чтобы ответить на эти вопросы, нам необходимо восполь-
воспользоваться самоподобиями, которые наверняка скрываются где-то в ите-
итерациях квадратичного отображения.
Самоподобие в логистической параболе
Рассмотрим сверхустойчивые орбиты отображения A) с длинами
периодов Р = 1, 2, 4, 8 и т. д. Значения параметра г = Rn, порождаю-
порождающие сверхустойчивые орбиты с длиной периода 2™, определены значи-
значительно лучше, чем точки бифуркаций г = гп (как экспериментально,
так и теоретически). Быстрая сходимость к окончательной орбите поз-
позволяет получать лучшие численные оценки, к тому же один элемент
орбиты всегда известен a priori: Хо = 0,5. Напротив, численное опреде-
определение бифуркационных значений гп сопряжено с несколько большими
трудностями.
Процесс удвоения периода характеризуется самоподобиями, облег-
облегчающими его анализ. Чтобы продемонстрировать одно из этих самопо-
самоподобий, сравним / (х) при значении параметра г = R\ (соответствует
сверхустойчивой орбите с длиной периода Р = 2) (рис. 6А) с функци-
354
Глава 12
г =Д,
Рис. 6. (А) Квадратичное отображение / (ж) для сверхустойчивой орбиты
с длиной периода 2. (Б) Однократно итерированное отображение /^ (ж) для
орбиты с длиной периода 4. Обратите внимание на подобие между содер-
содержимым маленького штрихового квадрата и рисунка (А). Такое самоподобие
характерно для удвоения периода и облегчает его анализ [234].
ей /B) (ж) при г = Ri (соответствует сверхустойчивой орбите с дли-
длиной периода Р = 4) (рис. 6Б). Сходство между квадратом, показан-
показанным штриховой линией на рис. 6Б (включая в рассмотрение и то, что
находится внутри квадрата), и большим квадратом на рис. 6А (вклю-
(включая сюда его содержимое) просто поразительно! Несоответствие между
параболой на рис. 6А и кривой четвертого порядка внутри штрихово-
штрихового квадрата на рис. 6Б в действительности очень мало, как видно из
рис. 7, на котором показаны парабола (сплошная линия) и перевернутая
и увеличенная кривая четвертого порядка (штриховая линия).
Коэффициент подобия для такого перехода от периода 2 к периоду 4
легко вычислить: он равен — B + 2/i?i) = —B + 7) = —2,618 ..., где j —
золотое сечение. (Знак минус отражает то обстоятельство, что удвоение
периода сопровождается переворачиванием графика отображения.) При
переходе от сверхустойчивой орбиты с длиной периода Р = 4 (г = Дг)
к сверхустойчивой орбите с длиной периода Р = 8 (г = Дз) для отобра-
отображений /B) (ж) и /D) (ж) повторяется почти в точности тот же сценарий,
что показан на рис. 6 для / (ж) и /B) (ж), только коэффициент подо-
подобия слегка отличается от —2,618. Более того, тот же сценарий (вам
еще не надоело это словечко?) повторяется каждый раз, когда значе-
значение параметра изменяется от г = Rn к г = Rn+i- При п —> ос коэф-
коэффициент подобия быстро сходится к своему асимптотическому значе-
Самоподобие в логистической параболе
355
Рис. 7. Несоответствие между квадратичным отображением (сплошная кри-
кривая) и увеличенным итерированным квадратичным отображением (штрихо-
(штриховая кривая).
нию —2, 5029... (что не так уж и отличается от его первоначального
значения —2,618...). В пределе исходная парабола квадратичного ото-
отображения становится трансцендентной функцией, задаваемой бесконеч-
бесконечным степенным рядом g(x), который был впервые получен Митчеллом
Фейгенбаумом:
g (ж) и 1 - 1,52763а;2 + 0,104815ж4 - 0,0267057а;8 + ... .
Координата ж здесь сдвинута так, чтобы максимум функции gix) при-
приходился на точку х = 0 (вместо х = 0,5) и был равен 1. Функция g(x)
есть функция неподвижных точек преобразования удвоения периода
квадратичных отображений. Она удовлетворяет скейлинговому зако-
закону g(x) = ag(g(x/a)), который также определяет а = 1/^A). Вы-
Вывод g(x) как универсальной функции для всех отображений с квад-
квадратичным максимумом, осуществленный Фейгенбаумом через теорию
ренорм-групп, поучителен, но вовсе не прост [67].
Численное значение параметра скейлинга а может быть получено
из любого из многочисленных самоподобий, которыми обладают по-
порожденные квадратичным отображением итерации ж„ . Особенно при-
привлекательный метод состоит в вычислении значения итераций XpL на
половине периода сверхустойчивой орбиты с длиной периода Р = 2™,
начиная с хо = 0,5. При г = Rn-\ мы получаем
р
Z =
одна-
однако при г = Rn итерации XpL немного не совпадают с xq. Разность
356 Глава 12
XpL— Xo\ изменяется асимптотически с коэффициентом подобия а
при увеличении п до п + 1. Точнее говоря,
(и) _
Хр i2 Xq
ап = > а при п -^ оо.
X р j2 *^0
С помощью программируемого калькулятора можно сначала опреде-
определить Rn и Д„+1 (подбирая параметр R до тех пор, пока не будет достиг-
достигнуто равенство хр = Хо = 0, 5 для Р = 2™ и Р = 2n+1), а затем найти
значение хр/2- Действуя так, мы быстро вычислим ач и —2,502905
с относительным отклонением от а около 10~6.
Скейлинг параметра роста
Только что мы узнали, что удвоение периода асимптотичес-
асимптотически самоподобно с коэффициентом подобия для переменной ж, рав-
равным —2,5029... А с каким коэффициентом подобия изменяются зна-
значения параметра г, соответствующие, скажем, сверхустойчивым орби-
орбитам Л„? На основании численных расчетов можно предположить, что
значения разности Rn+i —Rn становятся все меньше и меньше согласно
следующей геометрической прогрессии:
Rn — Rn-i
Rn+i -л„и ? при п -> оо,
д
где S — универсальная постоянная, знаменитая (и, возможно, транс-
трансцендентная) постоянная Фейгенбаума (впервые найденная С. Гроссма-
Гроссманом и С.Томе [90]). Это поистине магическое число заслуженно носит
эпитет «универсальное», потому что, как показал Фейгенбаум, оно при-
применимо ко многим различным нелинейным отображениям, независимо
от их характеристик, при условии, что абсолютный максимум отобра-
отображения квадратичен. Последовательность 8п = (Rn — Rn-i)/(Rn+i — Rn)
сходится к 6 очень быстро: Si « 4,7; <5г ~ 4,68, ... , Sq и 4,66918. Асимп-
Асимптотическое значение равно
S = 4,6692016091029...,
а точка сгущения параметра роста для удвоений периода определяется
величиной
Л» = 3,5699456....
Используя эти два значения и еще одну постоянную, можно запи-
записать Д„ и Дю - 1,542E"™.
Скейлинг параметра роста 357
Два параметра скейлинга а и S связаны между собой. Упрощенная
теория дает {йй2 + о + 1й 4,76 [67].
При критическом значении параметра роста г = Roo период ста-
становится бесконечным. Иначе говоря, орбита теперь апериодична и со-
состоит из бесконечного точечного множества никогда не повторяющих-
повторяющихся значений х. Однако это точечное множество, обладающее канто-
ровой структурой (рис. 8), служит аттрактором для других значе-
значений х. Отметим приближенное самоподобие точечного множества, о ко-
котором идет речь: левая половина нижней линии представляет собой
зеркальное отражение линии, расположенной непосредственно над ней
и сжатой в 2,5 раза; правая половина также повторяет верхнюю ли-
линию, только сжатую уже в 2,52 раза. Размерность Хаусдорфа D =
= 0, 538... для этого множества была выведена аналитически и чис-
численно П. Грассбергером [84]. Этот и другие аналогичные аттракторы
в многомерных пространствах получили название странных, хотя они
отнюдь не кажутся нам такими уж странными теперь — когда мы
знаем о канторовых множествах.
r=R0
0,0 0,25 0,5 , 0,75 1,0
r=R2 н-
r=R3
r=R4
Рис. 8. Самоподобное канторово множество итераций удвоения периода. Ите-
Итерации для г = В.5, обведенные рамкой, являются уменьшенной версией всех
итераций при г = Лз-
Предполагая, что предельное множество строго самоподобно, мы
можем воспользоваться хорошо известной формулой (см. Приложе-
Приложение А) размерности Хаусдорфа D для самоподобного канторова мно-
множества с двумя различными остатками «i и «2
358
Глава 12
и вычислить хорошее приближение размерности Хаусдорфа для стран-
странного аттрактора логистической параболы в точке сгущения удвоений
периода. При Si = 1/2,5 = 0,4 и S2 = s\, и полагая, кроме того, z = 0,4,
мы получаем из уравнения
z + z2 = 1
значения z = 7 ~ 0,618 и D = In-у/In 0,4 ~ 0,525 — удивительно хо-
хорошее согласие с более точным значением 0,538... Как часто бывает,
самоподобие может иметь исключительно приближенный характер, од-
однако если не обращать внимания на отсутствие точного подобия, можно
получить весьма хорошие результаты, которые могут быть улучшены
только большим количеством произведенных вычислений.
|о,5
(А)
Р = 16
ш
с
U
1
1
16
Частота k
т
(Б)
Рис. 9. (А) Итерации хт квадратичного отображения при длине периода 16.
(Б) Спектральная функция Фурье итераций хт [234].
Спектр Фурье периодической последовательности хт также обна-
обнаруживает ярко выраженное самоподобие (рис. 9). Пусть а% — коэффи-
коэффициенты Фурье членов последовательности хт, длина периода которой
равна Р = 2™. При переходе от орбиты с длиной периода Р = 2™ че-
через бифуркацию удвоения периода к орбите с длиной периода 2n+1 но-
новые коэффициенты Фурье с четными индексами приближенно равны
старым коэффициентам Фурье, т.е. a^jt1 ~ аи (так как %п+р ~ хп).
Коэффициенты же Фурье с нечетными индексами aj^, описываю-
описывающие субгармоники, которые появляются в спектре в результате удво-
удвоения периода, определяются разностью хп+р — хп. Как показывает
подробный анализ, квадраты абсолютных величин коэффициентов Фу-
Фурье
п+1
12к+1\
приближенно равны соседним компонентам предыдущей
орбиты, уменьшенным в 8а4/A + а2) и 40 раз, т.е. до 16 децибел (дБ)
Самоподобная символическая динамика 359
в логарифмических единицах [67]. (По определению, число децибел рав-
равно 20 log10 отношения модулей амплитуд или 10 log10 отношения квадра-
квадратов модулей амплитуд — такого, например, как отношение спектраль-
спектральных мощностей.)
Одно из первых подтверждений существования бифуркаций удво-
удвоения периода было получено в гидродинамическом (конвекция Рэлея-
Бенара) эксперименте Либхабера и Маурера, в котором роль парамет-
параметра г сыграло число Рейнольдса [147]. Исследуя вынужденные нели-
нелинейные колебания пузырьков в воде, Лаутерборн и Крамер обнаружи-
обнаружили аналогичное поведение: появление все новых и новых субгармоник
вплоть до наступления хаоса, называемого в данном контексте кави-
тационным шумом [139]. Эти эксперименты позволили, в частности,
разобраться в деструктивном механизме кавитации, основной причине
отказа судовых винтов.
Самоподобная символическая динамика
Вместо вычисления всей последовательности итераций хп часто
бывает достаточно лишь установить, куда попадает очередная точка —
в область слева от максимума (L), справа от него (R), либо в самый
максимум, или центр, отображения (С). Найденная таким образом по-
последовательность символов L, R, С называется символической дина-
динамикой для данной орбиты. Так, сверхустойчивая орбита с длиной пе-
периода 2 обладает символической динамикой, или «последовательностью
пекаря» СRCRCR. Ограничившись одним периодом, можно записать
только С R.
Нетрудно показать, что следующая сверхустойчивая орбита (с дли-
длиной периода 4) получается следующим образом. Прежде всего выпишем
два периода 2-орбиты (т.е. орбиты с длиной периода 2) — С RC R —
а затем заменим второе С на L, если число букв R слева от него нечет-
нечетно. Если же это число четно, то второе С следует заменить на R. Таким
образом, сверхустойчивые орбиты обладают следующей символической
динамикой:
Период 1 : С
Период 1 ->• Период 2: CC
Период 2 ->• Период 4: С RC Д -» CRLR
Период 4-» Период 8: СRLRCRLR ->• СRLRRRLR
и т. д. Орбиту с длиной периода 8 часто бывает удобнее записать в ви-
виде CRLR3LR. В той же манере сверхустойчивая орбита с длиной
периода 16 записывается как CRLR3LRLRLR3LR.
360 Глава 12
Алгоритм подсчета числа предшествующих второму С букв R
и установления его четности или нечетности непосредственно связан
с тем обстоятельством, что угловой коэффициент графика квадратич-
квадратичного отображения отрицателен для правой половины отображения.
Следовательно, всякий раз, когда точка хп попадает на правую полови-
половину единичного отрезка (хп > 0,5), происходит смена знака, сколь бы
мала ни была разность значений, причем нечетное число смен знака —
это тоже смена знака (тогда как четное — нет). Это одно из наибо-
наиболее важных свойств не только квадратичного отображения, но и всех
унимодальных («одногорбых») отображений. В результате изменение
порядка символов в символической динамике всех этих отображений
при изменении параметра роста имеет «универсальный» характер.
Говоря более конкретно, при г = Rn (т. е. при длине периода Р =
= 2") итерация Хр по определению совпадает с xq. При изменении
параметра роста г с Rn на Rn+i значение разности Хр — хо положи-
положительно (отрицательно), если разность Хт — Хо принимала положитель-
положительное значение четное (нечетное) число раз при т = 1, 2, ... , Р — 1.
Это и лежит в основе вышеупомянутого правила С —> R (или L) при
нечетном (четном) числе предшествующих букв R.
Последовательности символов самоподобны в следующем смысле.
Сохраняя каждый второй после С символ, мы воспроизведем последо-
последовательность для сверхустойчивой орбиты с половинной длиной пери-
периода, только L при этом меняется на Л и наоборот. «Прореживая» та-
таким образом символическую динамику, получим для орбиты с длиной
периода 16 последовательность CLRL3RL, что представляет собой
дополнение к последовательности CRLR3LR, описывающей орбиту
с длиной периода 8.
Как и в последовательности Морса-Туэ, сохранение каждого вто-
второго члена порождает аналогичную исходной, хотя и дополненную, по-
последовательность. Существует ли более тесная связь между последова-
последовательностью Морса-Туэ и символической динамикой сверхустойчивых
орбит? Вне всякого сомнения. Чтобы убедиться в этом, заменим сим-
символы Л на 1, а символы С и L — на 0. В этих обозначениях сверхустой-
сверхустойчивые орбиты с периодами 1, 2, 4, и 8 имеют следующий вид:
0
01
0101
01011101,
что, к сожалению, ничем не напоминает последовательность Морса-
Окна периодичности в хаосе 361
Туэ. Зато частичные суммы по модулю 2 членов этих орбит (начи-
(начиная с первого) и впрямь воспроизводят эту знаменитую последователь-
последовательность: Q
01
0110
01101001
и т.д. Вряд ли нужно говорить о том, что вычисление частичных сумм
по модулю 2 эквивалентно подсчету числа предшествующих симво-
символов R.
И наоборот, можно получить последовательности пекаря для уни-
унимодальных отображений в двоичной системе счисления @1011101...)
из последовательности Морса-Туэ путем вычисления сумм (или раз-
разностей) соседних элементов по модулю 2.
Такого рода связь позволяет нам непосредственно (без итераций)
записывать последовательность пекаря для орбиты с длиной периода 2т
при любом т. Правило же (я рекомендую читателю вывести его само-
самостоятельно) сводится к следующему: fc-й член в каждой такой последо-
последовательности символов выглядит как к = 29 ¦ j, где j — нечетное число.
Четность показателя q определяет выбор между L и R: нечетные q со-
соответствуют символу L, четные q — символу R (к = 0 по определению
подразумевает символ С). Таким образом, девяносто шестой, напри-
например, символ последовательности пекаря есть L, так как 96 = 3 • 25,
а 5 — число нечетное.
Одним из общих следствий нашего правила является то, что все
члены с нечетными к суть R (включая последний член каждой пе-
периодической орбиты с Р = 2п). А все члены с к, равными степеням
двойки (к = 2q), чередуют L и R.
Иррациональное число, построенное с помощью последова-
последовательности Морса-Туэ, интерпретируемой как двоичная дробь
0,0110100110010110... = 0,4124..., которую можно назвать постоян-
постоянной Морса-Туэ, имеет самое непосредственное отношение к сценарию
бифуркации удвоения периода и к множеству Мандельброта (см.
с. 381-386).
Окна периодичности в хаосе
Зрение должно учиться у разума.
Иоганн Кеплер
На рис. 10А показано «поведение» итерированной логистической
параболы, т.е. значения ее итераций хп при увеличении параметра г
362
Глава 12
3,83
Рис. 10. (А) Итерации квадратичного отображения как функция от парамет-
параметра роста. Каскад бифуркаций удвоения периода, начинаясь слева, переходит
в хаос справа, где итерации принимают хаотический характер. Полосы хаоса
перемежаются «окнами периодичности», в которых итерации снова стано-
становятся периодическими. Наиболее заметно окно с периодом 3, начинающееся
при г ~ 3, 83. (Б) На увеличенном центральном участке окна с периодом 3
виден еще один каскад удвоения периода, за которым следует второе окно
периода 3 (длина периода 9).
от 3 до 4. Каскад бифуркаций удвоения периода сменяется хаосом (плот-
(плотно заполненные полосы), который перемежается «окнами периодичнос-
периодичности». На самом деле значения параметра г, соответствующие окнам пе-
периодичности, всюду плотны, но на древообразном графике (рис. 10А),
иногда называемом деревом Фейгенбаума («фиговым деревом»1), видны
лишь немногие точки бифуркации. Наиболее заметно окно с периодом 3,
которое начинается при г = \/8 + 1 (рис. 10А). Из работы Ли и Йорка
нам известно, что коль скоро наблюдается период 3, то существуют
и все остальные периоды [146].
Заметим, что в окне периода 3 снова происходит удвоение, приво-
приводящее к орбитам с длинами периода 6, 12, 24 и т.д., и возникает новый
ига (нем.) — «фиговое дерево». — Прим. перев.
Окна периодичности в хаосе
363
0,8
0,6 -
0,4 -
0,2 -
3,5
1
-
i
щ
m
1
В
я
lif
1
1
ЯЯ
1
s
ft
1
a
1
?-'
i
is
1
jit
Ш
1
1
1
¦
3,6
3,7
3,8
3,9
Рис. 11. Обратная бифуркация хаотических полос по мере того, как параметр
роста уменьшается ниже 3,68 [122].
хаос, в который вложено другое окно с периодом 3, и т. д. ad infinitum
в еще одном самоподобном каскаде (рис. 10Б).
Интересно отметить, что в хаотических полосах при уменьшении
параметра г от его наивысшего значения г = 4 также наблюдается би-
бифуркация, известная под названием обратной бифуркации. Когда значе-
значение параметра г становится чуть меньше 3,68, бывшая до того единой
хаотическая полоса расщепляется на две (рис. 11), а при г близком к 3,6,
эти две хаотические полосы расщепляются на четыре и т. д., тем самым
как бы воспроизводя бифуркации удвоения периода, наблюдаемые при
возрастании параметра г. При этом каждую хаотическую полосу раз-
разрывает пополам затаившийся «призрак» соответствующей бифуркации
удвоения периода.
Причина бифуркации хаотических полос при уменьшении парамет-
параметра г легко объяснима и аналогична причине бифуркации периодичес-
периодических орбит. Рассмотрим значение г\ параметра г, при котором третья
итерация Жз начального значения Хо = 0, 5 попадает на неустойчивую
неподвижную точку х* = 1 — 1/г\. Для 7\ в этом случае получаем урав-
уравнение rfD — г{) = 16, откуда г\ = 3,678573510 При значениях г
364 Глава 12
несколько меньших, чем г\, третья итерация жз немного «недотягива-
«недотягивает» до ж*, а четвертая итерация ж 4 чуть превосходит ж*, что создает
в окрестности точки х* «окно», в которое не может попасть ни одна
итерация.
Аналогично при значениях г, чуть меньших, чем Г2=3,5925721841...,
при котором итерации начального значения х0 = 0, 5 попадают на не-
неустойчивую 2-орбиту, происходит бифуркация двух хаотических полос
в четыре. Более того, темные синусоидальные контуры, видимые на
диаграмме Фейгенбаума (рис. 11), включая верхний и нижний края
хаотических полос, являются образами стационарной точки х = 0,5.
В точках пересечения этих контуров происходит слияние хаотических
полос, а там, где контуры касаются верхнего и нижнего краев, откры-
открываются окна периодичности [150, 122].
Интересно, что значения параметра гт, при которых сливают-
сливаются 2m-1 и 2т хаотических полос, образуют убывающую асимптоти-
асимптотически геометрическую прогрессию с той же точкой сгущения (г =
= 3,5699...), что и при бифуркациях удвоения периода. Остается тем
же и коэффициент подобия — постоянная Фейгенбаума 6 = 4, 6692 ...
Значения гт соответствуют также значениям параметра для то-
точек сгущения последовательных строк порядка орбит, известного под
названием «порядка Шарковского» (см. с. 369), так как их символи-
символические динамики совпадают. Например, хаотические динамики двух
хаотических полос (начинающихся с жо = 0,5), т.е. CRLR2(RL)°°,
совпадают с символическими динамиками для точки сгущения орбит
с длинами периода 4 • 3, 4 • 5, 4 • 9, ... (см. с. 372).
Порядок, в котором итерации хп попадают в 2т различных хао-
хаотических полос, совпадает с порядком итераций в устойчивой орбите
с длиной периода Р = 2т. Например, как для 4-орбиты, так и для
четырех хаотических полос, итерации, начиная с наибольшей х\, рас-
располагаются в следующем порядке: х\ > Жз > ж 4 > жг- Этот порядок
получается из порядка х\ > жг при Р = 2 путем расщепления каждой
итерации ж« на две итерации ж« и Xi+p и обращения порядка в каж-
каждой второй паре итераций. Таким образом, мы легко получаем порядок
для Р = 8, т.е. Ж1 > Ж5 > Ж7 > Жз > Ж4 > Ж8 > Жб > жг, из поряд-
порядка Ж1 > Жз > Ж4 > Ж2 ДЛЯ Р = 4.
Упорядочение итераций хп в соответствии с их значениями можно
также получить из кода Грея (который, в свою очередь, связан с за-
заполняющей пространство кривой Гильберта; см. гл. 1, с. 34-36). На-
Например, чтобы вывести правильный порядок восьми итераций хп (п =
= 1, 2, ... , 8), представим трехзначные коды Грея (в которых при каж-
Порождение новых орбит 365
дом шаге меняется одна цифра, начиная с крайней левой) как обычные
двоичные числа и добавим единицу, чтобы получить индекс п итера-
итерации хп:
2 = 110 = ж7,
3 = 010 = ж3,
4 = 011 = ж4,
5 = 111 = ж8,
6 = 101 = ж6,
7 = 001 = ж2.
Тесное соответствие между бифуркациями удвоения периода и об-
обратными бифуркациями хаотических полос, с которыми мы бегло озна-
ознакомились — это лишь одна из многих увлекательнейших особенностей
квадратичного отображения.
Порождение новых орбит
На с. 359-360 мы привели описание алгоритма построения символи-
символической динамики сверхустойчивых орбит, возникающих при удвоении
периода. Этот алгоритм допускает существенное обобщение. Так, пра-
правило «записать последовательность символов CR ... дважды и заме-
заменить второй символ С на L (или R), если число символов R в исходной
последовательности нечетно (или четно)» применимо не только к фун-
фундаментальным периодам длиной Р = 2п, но к периодам любой дли-
длины. Действуя таким образом, можно видеть, что сверхустойчивая ор-
орбита, длина периода которой равна 3, а символическая динамика имеет
вид СRL, удваивается через СRLCRL в СRLLRL. Новая орбита,
в свою очередь, переходит после удвоения периода в орбиту с символи-
символической динамикой С RL2 RLR2 L2 RL и т.д. Возникает бесконечный
каскад орбит с периодами 3 • 2™.
В более общем виде: орбиты с периодами к • га11 могут быть полу-
получены из орбиты Р с длиной периода к и орбиты Q с длиной периода т.
Для получения периода к ¦ т мы копируем т раз символическую дина-
динамику орбиты Р и заменяем один за другим т — 1 символов С (кроме
первого) символами орбиты Q, заменяя L на R и R на L, если число
символов йвР нечетно. (Первый символ С в орбите Q во внимание не
принимается.) Например, 2-орбита С R утраивается с помощью 3-ор-
биты СRL следующим образом: прежде всего 2-орбита трижды копи-
366 Глава 12
руется (CRCRC R), затем второй и третий символы С заменяются
дополнениями второго и третьего символов орбиты С RL. В результате
мы получаем орбиту СRLRRR с длиной периода 6, отличающуюся
от ранее описанной орбиты С RL2 RL. (Алгоритм удвоения периода,
о котором шла речь в предыдущем разделе, представляет собой не что
иное, как частный случай рассматриваемого здесь закона композиции
cQ = CR).
Какая из только что описанных двух орбит с длиной периода 6 «до-
«доминирует» над другой? По определению, это зависит от первого сим-
символа, которым они отличаются. Если число символов R в начальных,
одинаковых, отрезках двух последовательностей нечетно (четно), то
доминирует та из орбит, у которой первый отличающийся от другой
последовательности символ есть символ L или С (R). Из сказанно-
сказанного следует, что орбита С RL2 RL доминирует над орбитой CRLR3.
Сверхустойчивое значение параметра г орбиты, доминирующей над
другой орбитой, есть наибольшее из двух сверхустойчивых значений.
Действительно, орбите CRL2 RL соответствует приближенное значе-
значение г ра 3,8445688, тогда как орбите CRLR3 соответствует значе-
значение г и 3,6275575.
Особенно привлекателен эквивалентный алгоритм «умножения»
двух орбит с длинами периодов pi и р2, порождающий орбиту пери-
периода piP2- Он заключается в следующем. Запишем символическую ди-
динамику орбиты как последовательность знаков плюс и минус (плюс
соответствует любому из символов L или С, минус — символу R).
Последнее соглашение отражает то обстоятельство, что угловой коэф-
коэффициент унимодальных отображений отрицателен справа от макси-
максимума. Так, сверхустойчивая орбита р\ = 3 с символической динами-
динамикой СRL записывается в виде + — +. Затем мы выписываем самый
левый знак, а каждый последующий знак заменяем его произведени-
произведением с предыдущим. В результате такого преобразования из последова-
последовательности знаков + — + получаем новую последовательность + — —,
которую условимся называть ^-последовательностью орбиты. Анало-
Аналогично ^-последовательность сверхустойчивой орбиты С R с длиной пе-
периода р2 = 2 имеет вид И—.
Введенные нами ^-последовательности позволяют свести умноже-
умножение периодов к простому приписыванию одной ^-последовательности
к другой. Например, удвоение периода любой орбиты мы получаем,
приписывая к ее ^-последовательности такую же последовательность,
но с измененными знаками — в соответствии с действием «операто-
«оператора» И—, т.е. ^-последовательности орбиты с длиной периода 2. Если
Порождение новых орбит 367
придерживаться такого правила, то каскад удвоений периода выглядит
следующим образом. Начнем с неподвижной точки С, которая имеет пе-
период р = 1 и поэтому соответствует ^-последовательности, состоящей
из одного-единственного знака (<то = +)• Тогда
Р=1 + С
р = 2 +- CR
р = 3 + + CRLR
р = 4 + + - + +- CRLR3LR
и т. д. Такое итеративное построение ^-последовательностей орбит
с длинами периода 2п («приписывание дополнения»), конечно же, при-
приводит к уже знакомой нам самоподобной последовательности Морса-
Туэ, порождаемой тем же правилом.
Чтобы восстановить символическую динамику, мы выписываем
символ С и приписываем к нему справа символы R и L в зависимос-
зависимости от того, отличается ли очередной знак в ^-последовательности от
предыдущего или совпадает с ним, как это было только что показано
для р = 2, 3, и 4.
Для того чтобы утроить длину периода орбиты, мы приписываем
к (Т-последовательности две ее «копии» со знаками, измененными в со-
соответствии с (Т-последовательностью + — — 3-орбиты. Таким образом,
каскад утроения периода состоит из следующих ^-последовательностей
(начиная е<то = +):
р = 1 + С
р = 3 + CRL
р = 9 + + + - + + CRL2RLR2L
и т. д. Получающуюся в результате такого построения бесконечную
самоподобную ^-последовательность a^k = <т* можно рассматривать
как обобщение последовательности Морса-Туэ.
Заметим, что fc-й символ Sk, к > 0, в символической динамике ут-
утроенного периода мы получим, представив индекс к в виде к = Зт • q,
где <7 = 1 или 2 mod 3: Sk = L, если оба числа т и (qK = q mod 3
являются четными или нечетными. Если же четности чисел т и (GK
различны, то Sk = R- Заменяя символ R числом —1, а символ L чис-
числом + 1, получаем Sk = (—1)т+<9Ь. Например, при к = 405 = З4 • 5
символ Sk равен (—1L+2 = 1 = L.
«Вторая гармоника» 3-орбиты CRL с ^-последовательностью -\
имеет ^-последовательность + — — — + +, соответствующую 6-ор-
бите с символической динамикой С RL2 RL. Она получается путем
368 Глава 12
приписывания ^-последовательности + — — к себе самой с противопо-
противоположным знаком. Аналогично ^-последовательность утроенной 2-орби-
ты CR (^-последовательность И—) получается в результате двукрат-
двукратного приписывания последовательности И— к себе самой с противо-
противоположными знаками, в соответствии с оператором утроения периода
+ — —. Это дает ^-последовательность + — — + —\-, соответствую-
соответствующую орбите СRLR3, которая была выведена нами ранее с помощью
менее изящного правила.
Мы еще встретимся с ^-последовательностями при вычислении па-
параметра роста линеаризованного логистического отображения (так на-
называемого отображения «палатка») в следующем разделе.
Другой алгоритм построения новой орбиты состоит в интерполя-
интерполяции между двумя известными орбитами Р и Q; для этого необходиимо
взять пересечение гармоники Н (Р) орбиты Р и антигармоники A (Q)
орбиты Q [180]. Гармоника орбиты Р строится, как и прежде, припи-
приписыванием символической динамики орбиты Р к самой себе и заменой
второго С на L (или R), если число символов R в орбите Р нечет-
нечетно (или, соответственно, четно). Антигармоника орбиты Q, которая,
вообще говоря, не является допустимой периодической орбитой, опре-
определяется также, как и гармоника, за исключением того, что при за-
замене второго символа С символы R и L меняются местами. Таким
образом, ^-последовательность антигармоники получается путем при-
приписывания исходной ^-последовательности к себе самой без изменения
знака. (Возможно, кто-нибудь из читателей захочет вывести правила,
позволяющие отличать допустимые орбиты от недопустимых.)
Например, гармоника орбиты Р = С R есть орбита Н (Р) =
= CRLR, а антигармоника орбиты Q = СRL°° есть последователь-
последовательность A(Q) = СRL°° RRL°°. Пересечением этих двух последователь-
последовательностей, т. е. последовательностью, в которой начальные символы по-
последовательностей Н (Р) и A (Q) совпадают, является «дочерняя» ор-
орбита СRL с длиной периода 3. Согласно этому правилу, значение па-
параметра г дочерней орбиты всегда лежит между значениями парамет-
параметров двух исходных орбит. Отсюда и название — интерполяция орбит.
Повторяя построение гармоник и интерполяцию, можно построить все
орбиты отображения от «первой» (С) до «последней» (С RL°°).
Различные длины периода Р устойчивых периодических орбит
унимодальных отображений следуют некоторому универсальному по-
порядку. Пусть гр — значение параметра роста г, при котором впер-
впервые при возрастании г появляется устойчивый период длиной р. Тог-
Тогда гр > rq, если р >- q (читается: р предшествует q) в следующем порядке
Порождение новых орбит 369
Шарковского:
Зу5у7у...
2-3 ^2-5^2-7^ ...
2П • 3 у 2п • 5 у 2п • 7 у ...
...у2ту...у4у2у1.
Так, минимальное значение г для орбиты с длиной периода р = 10 = 5-2
больше, чем минимальное значение г для орбиты с длиной периода р =
= 12 = 4 • 3, так как в этой колдовской алгебре 10 >- 12.
Перечислим некоторые следствия, проистекающие из порядка
Шарковского:
• Существование периода длиной р = 3 гарантирует существование
периода любой другой длины q для некоторого rq < гр.
• Если встречается только конечное число длин периодов, то
эти длины должны быть равны степеням двух, т.е. р =
= 2k, 2к~1, ... , 4, 2, 1 для некоторого к.
• Если существует период с длиной, отличной от степени двух, то
существует бесконечно много различных периодов.
Сверхустойчивые орбиты при наименьшем значении параметра гр
имеют символическую динамику СRLRP+3 при нечетных длинах пе-
периода р ^ 3. «Последняя» сверхустойчивая орбита с длиной периода р,
т.е. орбита с наибольшим значением гр, обладает символической ди-
динамикой СRLP~2 [36]. Например, последняя сверхустойчивая 6-орбита
имеет символическую динамику СRL4, г и 3,9975831.
Вышеприведенные рассуждения являются следствием из теоремы
Шарковского о существовании и упорядочении орбит в соответствии
с уже упомянутым определением предшествования по Шарковскому
при фиксированном значении г [238]. Однако большинство этих орбит
неустойчиво. (Они являются «призраками» тех орбит, которые были
устойчивы при меньших значениях г. Неподвижная точка х* = 1 — 1/г,
например, сохраняется даже при г > 3, где она становится неустойчи-
неустойчивой.) Более того, как показал Д. Сингер, унимодальные («одногорбые»)
отображения / (ж) с отрицательной производной Шварца
Г(х)
(
Г(х) 2\f'(x)
370 Глава 12
имеют самое большее одну устойчивую орбиту [243]. (Здесь предпола-
предполагается, что / (х) — трижды непрерывно дифференцируемая функция,
отображающая единичный интервал на себя.)
Например, при г = 3,83187405529 и ж0 = 0, 5 мы получаем сверх-
сверхустойчивую орбиту С RL с длиной периода 3, а выбрав xq = 1 — 1/г =
= 0, 73903108882 — неустойчивую орбиту с длиной периода 1. При Xq =
= 0,89208905218 получим неустойчивую орбиту с длиной периода 2.
Другие начальные значения приводят к неустойчивой 4-орбите, проис-
происходящей от орбиты СRLR. Однако 4-орбиту, происходящую от орби-
орбиты CRLL, невозможно реализовать при г = 3,83..., так как CRLL
доминирует над орбитой С RL. Предоставляем читателю самостоятель-
самостоятельно найти начальные значения для других длин периода (так как при г =
= 3,83 ... возможен период длины 3, то, согласно теореме Шарковского,
возможны и все остальные периоды).
Вычисление параметров роста для различных орбит
Предположим, что дана сверхустойчивая орбита с символической
динамикой Q = СRL Чему равно соответствующее ей значение
параметра роста г? Один из методов вычисления г состоит в итераци-
итерационной подгонке г в формуле / (х) = гхA — х) до тех пор, пока не будет
достигнуто равенство /^ @,5) = 0,5, где р — длина периода орби-
орбиты, а /(р) —р-я итерация отображения f (х). Однако для тех областей,
где скапливаются значения г для «подобных» орбит, этот метод, скорее
всего, неприменим. Под подобными мы понимаем в данном случае орби-
орбиты с одинаковой четностью (числом символов R) и длинами периодов,
на которые делится длина периода р. Кроме того, разумеется, важно
удачно выбрать начальное значение г.
Спутать нужную орбиту с какой-нибудь другой совершенно не-
невозможно, если при вычислениях значения г мы будем принимать во
внимание не только четность и период орбиты, но и ее символичес-
символическую динамику. Для того, чтобы воспользоваться предлагаемым нами
методом, удобно перейти к другой часто применяемой форме квадра-
квадратичного преобразования g(x) = 1 — fix2 с помощью линейной замены
независимой переменной х. Новый параметр роста fi связан с г соот-
соотношением fi = г (г — 2)/4, или г = 1 + -^/A + 4/х). При такой записи
квадратичного отображения максимум приходится на х = 0. Следова-
Следовательно, сверхустойчивая орбита содержит значение х = 0.
Рассмотрим в качестве примера 5-орбиту с наименьшим значени-
значением г, которая обладает символической динамикой CRLR2. Выбира-
Вычисление параметров роста для различных орбит 371
ем х0 = х5 = 0. Так как g@) = 1, gR (gR (gL (gR A)))) = 0. Индексы R
и L в последнем уравнении напоминают нам, какая ветвь параболы g(x)
вступает в игру при соответствующей итерации. Эти сведения необхо-
необходимы нам для того, чтобы обратить уравнение. Обращая его, получаем
где
м
Умножая уравнение A) на /л, получаем
Значение fi из этого соотношения можно определить с помощью ите-
итераций, как предложил Х.Каплан. Если начать с ц0 = 2, то правильное
значение параметра для орбиты CRLR2 получается быстро и без ка-
каких бы то ни было неоднозначностей: ji = 1,625413725 ..., что соответ-
соответствует г к, 3,738914913.
Для произвольной допустимой орбиты CRL... знаки плюс или
минус в соотношении B) определяются символической динамикой
(символ R соответствует знаку минус, а символ L — знаку плюс). Пер-
Первый знак под радикалом (плюс) соответствует первому символу L после
начальной группы СR в СRL
Соотношение B) особенно полезно для вычисления значений па-
параметра в точках сгущения некоторых орбит. Например, взглянув
на порядок Шарковского, мы, возможно, захотим узнать, при каком
значении fi сгущаются орбиты с нечетными длинами периода р =
= 3, 5, 7, 9, Как уже отмечалось, эти орбиты имеют символичес-
символическую динамику СRLRP~3, поэтому при р —>• сю соотношение B) при-
принимает вид
с бесконечной последовательностью знаков минус. Положим fi —
• • • = х- Тогда х = fi — у/х. Исключая х, приходим к ку-
372 Глава 12
бическому уравнению для fi, а именно, к уравнению fi3 — 2//2 + 2fi —
— 2 = 0 с корнем fi = 1,543689012..., который соответствует f\ =
= 3,67857351... (= fi3). Это также то самое значение параметра, при
котором сливаются две хаотические полосы, потому что они имеют
одинаковую символическую динамику (см. с. 361-364).
Поскольку орбиты с четными длинами периода вида р = 2 • 3, 2 • 5,
2-7, ... имеют ту же символическую динамику С R L Rp~3, что и ор-
орбиты с нечетными длинами периода, они сгущаются при одном и том
же значении параметра, но приближаются к нему снизу.
Аналогично определяется и значение параметра r<i точки сгущения
орбит с длинами периода р = 4-3, 4-5, 4-7, 4-9, ... и символической ди-
динамикой CRLR3 (LR)p/2~3. Параметр^ = 3,5925721841...; при этом
значении параметра, кроме того, происходит слияние четырех хаоти-
хаотических полос в две.
Орбиты CLn, п —>• сю, приводят в точке сгущения к соотноше-
соотношению // = i/a* + л/А* • • -5 т-е- А* = \Ла* + А*): с решением // = 2 (что соот-
соответствует г = 4).
Другое «одногорбое» отображение — кусочно-линейное отображе-
отображение «палатка» — имеет вид
/(ж) = АA-|ж-1|), 0^ж^2 C)
и гораздо лучше поддается анализу, чем квадратичное отображение [47].
Тем не менее, отображение C) имеет много общих с квадратичным ото-
отображением свойств, в частности, аналогичные порядок орбит и их сим-
символическую динамику при увеличении параметра Л от 1 до 2. (Правда,
некоторые орбиты, существующие при квадратичном отображении, от-
отсутствуют в отображении C) — например, те, что вытекают из удвое-
удвоения периода. Кроме того, поскольку |/' (ж)| > 1 при Л > 1, отображение
«палатка» не имеет устойчивых орбит.)
Особенно просто определить значение параметра Л для данной ор-
орбиты СRL ...; нужно лишь решить уравнение
У Ч = 0- D)
к=1 А
Для итераций с начальным значением, скажем, Л = 1,5, уравнение D)
удобнее представить в следующем виде (здесь также подразумевается,
что <г\ = 1 и 0-2 = -1):
к=з А
Вычисление параметров роста для различных орбит 373
Коэффициенты а^ равны +1 (или —1) в зависимости от того, четно
или нечетно число символов R слева от fc-ro символа орбиты СRL ...
(включая и fc-й символ). Например, для орбиты СRL с длиной пери-
периода Р = 3 уравнение E) имеет вид Л = 1 + 1/Л. Ему удовлетворя-
удовлетворяет решение Л = (л/5 + 1)/2 = 1,618 Для «низшей» из трех 5-ор-
бит (CRLRR) уравнение E) имеет решение Л = 1 + 1/Л — 1/Л2 +
+ 1/Л3 ра 1,5128763968. (Заметим, что коэффициент <тз всегда ра-
равен — 1, так как в противном случае уравнение E) не имело бы решений
при 1 < Л < 2.)
Коэффициенты а^ есть не что иное, как элементы сг-последователь-
ности, которую мы ввели на с. 366, чтобы упростить построение новых
орбит из уже известных. В определенном смысле ^-последовательности
являются наиболее полезной формой динамики квантованных орбит
унимодальных отображений.
С помощью уравнения E) можно очень просто найти общую точку
сгущения для орбит с нечетными длинами периода р и орбит с длинами
периода р вида 2 • 3, 2 • 5, 2 • 7, Как уже отмечалось, общая символи-
символическая динамика таких орбит имеет вид СRLRP~3. Ей соответствует
^-последовательность И 1 1 1— ..., т. е. аи = (—1)* при к ^ 3.
Следовательно, для р —>• сю получаем Л = 1 + 1/(Л + 1), откуда Л = л/2.
При конечном р решение определяется выражением
*2
или, асимптотически,
Таким образом, разности между значениями Л для последовательных
нечетных (или четных) орбит и их точкой сгущения Л = л/2 при уве-
увеличении периода в 2 раза образуют асимптотически геометрическую
прогрессию с знаменателем 1/2. Это значение сравнимо с знаменате-
знаменателем 1/4,669... для последовательности удвоения периода квадратич-
квадратичного отображения. Но если значения параметра орбит с удвоенными
периодами заключены в смежных интервалах, то между значениями
параметра, соответствующими 3 и 5 или другим последовательным не-
нечетным длинам периода, «вклиниваются» многие другие орбиты.
Еще одно полезное свойство ^-последовательности состоит в том,
что уравнение D) может быть факторизовано для орбит, порожденных
374
Глава 12
исходными («родительскими») орбитами, что приводит к возникнове-
возникновению интересных соотношений между значениями параметра Л исход-
исходных и дочерних орбит. Например, для 6-орбиты с сг-последовательнос-
тью + — — + —h (утроенная 2-орбита) А = А3 , где Аз — параметр
3-орбиты + — —.
Касательные бифуркации, перемежаемость
и 1//-шум
При г = 1 + \/8 мы можем наблюдать странное явление — так
называемую касательную бифуркацию. Если параметр г чуть меньше
1 + л/8 (рис. 12), то итерации оказываются надолго «запертыми» меж-
между логистической параболой и прямой xn+i = хп. На рис. 13 вы видите
перемежающиеся импульсы с длиной периода 3 при г = 1 + %/8 — 10~4.
Спектральная функция такого процесса убывает как 1//, где / — час-
частота. Этот феномен, называемый перемежаемостью, является одним из
главных механизмов образования 1//-шума в природе.
r=l+V8"-10
0,5
0,53
Рис. 12. Запертые итерации около касательной бифуркации при г = 1 +
+ V8-10.
Касательные бифуркации, перемежаемость и 1/ f-шум 375
Период 3 Хаос Период 3 Хаос
0,8
0,5
0,2-
Рис. 13. Перемежаемость при параметре роста чуть ниже параметра каса-
касательной бифуркации: импульсы с длиной периода 3 перемежаются со слу-
случайными импульсами.
Если г чуть больше 1 + %/8> то третья итерация квадратичного
отображения /^ (ж) (рис. 14) приобретает шесть дополнительных непо-
неподвижных точек: три с угловым коэффициентом, превышающим по абсо-
абсолютной величине единицу (принадлежат неустойчивой орбите с длиной
периода 3), и три с угловым коэффициентом, который по абсолютной
величине меньше единицы (принадлежат устойчивой орбите с длиной
периода 3). Это и есть та самая 3-орбита, гарантирующая существова-
существование орбит (пусть неустойчивых) с любыми другими длинами периода
при том же значении параметра. Это сосуществование бесконечного
множества неустойчивых орбит Ли и Йорк назвали хаотическим, а тот
факт, что «период 3 — предтеча хаоса», был обнародован ими в одно-
одноименной статье еще в 1975 г. [146].
При уменьшении параметра г ниже 1 + л/8 все эти орбиты ста-
становятся устойчивыми на малых, но конечных интервалах параметра
роста. Все периоды орбит, кроме р = 2 и р = 3, устойчивы на более
чем одном интервале значений г. Если р — нечетное простое число, то
число таких интервалов для различных орбит равно BР~1 — 1)/р. Ка-
Касательная бифуркация, вместе с бифуркацией удвоения периода (типа
«вилки»), является основным источником новых орбит.
Заметим, что интервалы значений г плотны, т.е. значения пара-
параметра, при которых не существует устойчивых орбит, не образуют ин-
интервалов. Тем не менее, они обладают положительной мерой Лебега.
Это означает, что при случайном выборе параметра роста существу-
376
Глава 12
З" 0,5
Рис. 14. Трижды итерированное квадратичное отображение при значении па-
параметра роста чуть выше 1 + \/8- Благодаря «касательной бифуркации» это
итерированное отображение получило шесть дополнительных неподвижных
точек. Три из шести устойчивы (абсолютный угловой коэффициент меньше
единицы) и принадлежат устойчивой 3-орбите, которую можно увидеть на
рис. 10 и 11.
ет ненулевая вероятность выйти на апериодическую орбиту. Ситуация
с апериодическими орбитами напоминает ситуацию с иррациональны-
иррациональными числами, которые также имеют положительную меру Лебега, хотя
и не образуют интервалов. Разумеется, никакой автомат с конечным
числом внутренних состояний, например, цифровой компьютер (не го-
говоря об аналоговых машинах), не позволит доказать, что апериодичес-
апериодическая орбита апериодична.
Если не считать бифуркаций удвоения периода, начинающих-
начинающихся с устойчивой неподвижной точки и заканчивающихся при г =
= 3,5699 ..., то диапазон значений параметра г, соответствующих дли-
длине периода 3, больше, чем аналогичный диапазон для любой другой дли-
длины периода. «Окно» периода 3 на диаграмме Фейгенбаума (рис. 10А),
таким образом, шире остальных окон периодичности, и к тому же его
(одно из немногих) видно невооруженным глазом, без «увеличитель-
«увеличительного стекла» (т. е. без компьютерной программы, которая для лучшей
видимости увеличивает малый интервал значений параметра роста).
При достаточно сильном увеличении в каждом из окон периодичнос-
периодичности можно разглядеть бифуркации удвоения периода — такие, как на
рис. 10Б, причем все они регулируются все той же постоянной Фейген-
Фейгенбаума ё = 4, 6692....
Полный хаос
377
Полный хаос
Для квадратичного отображения особенно интересно значение па-
параметра роста г = 4. Преобразование
У=\-\ arcsin(l - 2х), O^y^l A)
переводит квадратичное отображение в еще одно отображение «палатка»
уп+1 = 1 - \2уп - 1|,
состоящее из двух прямолинейных отрезков с угловыми коэффициен-
коэффициентами +2 и —2 и максимума при уп = 0,5 (рис. 15).
Рис. 15. Хаотическое отображение «палатка» yn+i = 1 — |2j/n ~ 1|-
Перевернув правую половину «палатки» (yn+i —>• 1 — yn+i Для
уп > 0,5), получим необычайно простое отображение двоичного сдвига
(сдвига Бернулли):
Уп+i =
mod 1.
B)
Если записать уп в виде двоичной дроби, то отображение B) представ-
представляет собой не что иное, как сдвиг цифр этой дроби влево на один знак
с отбрасыванием единицы, «выступающей» влево за двоичную запятую.
Под действием двоичного сдвига любое значение у, представимое в виде
378 Глава 12
конечной двоичной дроби, в конце концов отображается в нуль. В об-
общем случае рациональные значения у, представимые в виде периоди-
периодических двоичных дробей, порождают периодические орбиты. В отличие
от них иррациональные значения у, т.е. почти все значения у из ин-
интервала @, 1), порождают непериодические орбиты.
Хотя при г = 4 почти все начальные значения у из интервала @, 1)
приводят к апериодическим орбитам, такие апериодические значения у
не образуют интервалов. Более того, начальные значения, порождаю-
порождающие периодические орбиты, плотны в @, 1). Чтобы убедиться в этом,
оборвем некоторое данное значение у после сколь угодно большого чис-
числа двоичных знаков и периодически повторим оставшиеся знаки. На-
Например, ограничив у = 0,10110001... в пределах 2~5, получим началь-
начальное значение с длиной периода 5, т.е. уо = 0,A0110) (длина периода
может быть сколь угодно большой).
Если не выбирать в качестве начальных значений уо «ненормаль-
«ненормальные» двоичные числа (см. гл. 11, с. 316-319), то итерации иррацио-
иррациональных уо заполняют единичный интервал с равномерной плотнос-
плотностью. Такое распределение называется инвариантным распределением
отображения, так как если случайная величина первоначально имеет
такое распределение, то оно остается неизменным и после итераций.
Вследствие равномерного распределения значений у инвариантное рас-
распределение р(х), связанное с у соотношением A), представляет собой
[/-образное распределение, хорошо известное из закона арксинуса в те-
теории случайных блужданий:
Это распределение, представленное на рис. 16, после надлежащего мас-
масштабирования и сдвига, аппроксимирует также инвариантные распре-
распределения в хаотических полосах при других значениях параметра.
Отображение B) может также служить великолепной иллюстраци-
иллюстрацией того, что имеют в виду, когда говорят о детерминированном хаосе.
Предположим, что начальное условие физической динамической систе-
системы представлено значением уо с некоторой конечной точностью. Напри-
Например, ограничившись точностью в восемь двоичных знаков, получим
I/0 = 0,1011010lJJJ... ,
где двухъярусная запись после восьмого знака отражает то обстоятель-
обстоятельство, что мы не знаем, будет ли какой-либо знак, начиная с девятого,
Полный хаос
379
Рис. 16. Инвариантное распределение квадратичных итераций при г = 4.
Большинство итераций скапливаются около х = 0 и х = 1 [36].
нулем или единицей. Из-за такого неизбежного отсутствия абсолютной
точности, девятая и более высокие итерации начального значения у0
имеют вид
п 000
Ук = ' 111 ¦ ¦ ¦'
т.е. принимают любые возможные значения из единичного интервала
в абсолютно непредсказуемой последовательности. Именно так детер-
детерминированный закон, включающий в себя и соотношение B), дает хао-
хаотические результаты, которые весьма удачно называются детермини-
детерминированным хаосом. Даже при вполне детерминированных динамических
законах начальные условия, заданные с конечной точностью, при надле-
надлежащем увеличении в конце концов дают совершенно непредсказуемые
результаты.
Это, однако, произойдет только в случае, если определяющий ите-
итерации закон будет нелинейным и, более того, не обратимым однознач-
однозначно. К отображениям, удовлетворяющим этому требованию, относятся и
отображения с одним максимумом (квадратичные либо какие-нибудь
другие), и отображения, содержащие операции взятия вычета по не-
некоторому модулю, как в соотношении B). Кроме того, нелинейность
должна быть достаточно выраженной, чтобы начальная неопределен-
неопределенность возрастала экспоненциально. Например, в случае отображения
двоичного сдвига B) неопределенность возрастает вдвое с каждой ите-
итерацией.
380 Глава 12
Напротив, в случае логистической параболы любое начальное зна-
значение (отличное от 0 или 1), скажем, при г = 2 приводит к неподвиж-
неподвижной точке х" = 0, 5, и значения разности еп между последовательными
итерациями хп и точкой х* убывают с каждой итерацией в — 2е2п раз
(асимптотически). Именно это имеют в виду, когда говорят о квадра-
квадратичной сходимости. Например, если в качестве начального значения
выбрать х0 = 0,45 (е = —0,05), то последовательные разности оказы-
оказываются приближенно равными -0,0005; -0,00005; -0,000000005 и т.д.
Иначе говоря, «погрешность» быстро убывает: расстояние в 5 знаков
от десятичной запятой удваивается с каждой итерацией (в отличие от
смещения на один знак за итерацию при двоичном сдвиге B)).
Если значения параметра г не соответствует сверхустойчивым ор-
орбитам (как в случае г = 2, поскольку орбита включает в себя «плоскую
вершину» параболы при х = 0,5), то сходимость несколько замедляет-
замедляется. Например, при г = 2,5 неподвижная точка возникает при ж* =
= 1 — 1/2,5 = 0,6, отличном от 0,5, а значит, орбита не является
сверхустойчивой. Значение производной в неподвижной точке позво-
позволяет оценить сходимость итераций. При г = 2, 5 получаем
f(x*) = 2- г =-0,5.
Следовательно, значения разности между хп и х* убывают в геометри-
геометрической прогрессии с знаменателем —0,5 (асимптотически). Например,
начальное условие ж0 = 0,61 приводит к следующим последовательным
значениям разности: хп - х* = 0,01000; -0,00525; 0,00256; -0,00129;
0,00064 и т. д. Эта несверхустойчивая орбита сходится гораздо мед-
медленнее, и сходимость ее может быть описана как линейная. В нашем
примере она соответствует асимптотическому сдвигу влево цифр чис-
числа \хп — х*\ на log10 2 = 0,3 десятичных знаков (в среднем) при каждой
итерации — в отличие от удвоения сдвига в сверхустойчивых орбитах.
Резюмируя, можно сказать, что сверхустойчивые орбиты обладают
двумя основными преимуществами:
1) Они быстрее сходятся и более устойчивы при малых возмуще-
возмущениях (с чем, собственно, и связан эпитет — сверхустойчивые) и,
следовательно, легче поддаются экспериментальным измерениям.
2) Они допускают более простые теоретические описания, такие, на-
например, как символическая динамика, о которой мы говорили
выше.
Многие свойства квадратичного отображения являются образцом для
подражания не только среди унимодальных отображений, но также
Множество Мандельброта 381
и среди других нелинейных отображений. Последние отображения,
в свою очередь, моделируют широкий круг проблем, в которых су-
существенную роль играют различного рода нелинейности.
Множество Мандельброта
Кратчайший путь между двумя исти-
истинами в вещественной области проходит
через комплексную область.
Жак Адамар
Как было показано в предыдущем разделе, квадратичное отображе-
отображение при г = 4 может быть преобразовано в простое отображение «па-
«палатка», которое, в свою очередь, упрощается до отображения двоичного
сдвига Уп+i = %Уп mod 1. Последнее отображение позволяет непосред-
непосредственно получить орбиту любой начальной точки уо, записав уо в виде
двоичной дроби: периодические двоичные дроби порождают периоди-
периодические орбиты, а иррациональные уо с нормальными апериодическими
дробями приводят к хаотическим орбитам.
К сожалению, это простое отображение неприменимо при других
значениях параметра роста вещественного квадратичного отображе-
отображения, изучением которого мы до сих пор занимались. Однако стоит
нам «комплексифицировать» параметр роста и независимую перемен-
переменную, как квадратичное отображение становится гораздо «прозрачнее»
и намного легче поддается анализу. Как и во многих других областях
математики (например, в теории чисел), введение комплексных пере-
переменных позволяет существенно упростить многие доказательства и со-
соотношения (такие, например, как доказательство теоремы о простых
числах, лежащей в основе распределения простых чисел). Отсюда —
парадоксальный математический девиз «комплексифицируй, если хо-
хочешь упростить»1.
Комплексифицированный вариант квадратичного отображения час-
часто записывают в виде
Zn+l =Z2n+C, A)
где и переменная z, и параметр роста с могут принимать комп-
комплексные значения, графически представляемые точками на комплекс-
комплексной плоскости z и комплексной плоскости с. Вещественные с свя-
1Англ. complex «комплексный» имеет, среди прочих, значение «сложный». —
Прим. перев.
382 Глава 12
заны с уже встречавшимися нам параметрами /лиг соотношени-
соотношением с = —\i = —г(г — 2I А.
Один из первых вопросов, которые приходят на ум при взгляде
на соотношение A), можно сформулировать следующим образом: при
каких значениях параметра с итерации zn остаются ограниченными
при п —> ос? Очевидно, что при с = 0 и zq, находящемся внутри еди-
единичного круга \zq| ^ 1, итерации zn при п —у ос остаются в пределах
единичного круга. Однако даже при с = О начальное значение zq = 2,
например, дает z*i = 22 > 1038, т.е. седьмая итерация превышает диа-
диаметр Вселенной, измеренный в атомных единицах.
А если с ф О? Например, при с = — 2 и zq = 0 соотношение A)
дает z\ = —2, zi = 2, zz = 2 и т. д. Таким образом, с = —2 порождает
предпериодическую орбиту с длиной периода 1, иначе говоря, непо-
неподвижную точку z = 2.
В общем случае множество всех точек с, для которых итера-
итерации zn+i = z\ + с (zq = 0) остаются ограниченными при п —у оо,
называется множеством Мандельброта, или, для краткости, М-множе-
ством, в честь Бенуа Мандельброта, который открыл эти множества и
исследовал многие из их замысловатых свойств [160]. На вклейке 8А
черным цветом показано М-множество, состоящее из большой сердце-
сердцевидной области («кардиоиды»), к которой примыкают меньшие круглые
области, к тем, в свою очередь, прилепились еще более миниатюрные
круги и т. д. ad infinitum в приблизительно самоподобной прогрессии.
Ту же «кардиоиду», облепленную множеством меньших кругов, мож-
можно при надлежащем увеличении обнаружить во многих других облас-
областях плоскости комплексного параметра (см. цветные вклейки 8Б и 8В).
Компьютерный «микроскоп» обнаруживает также и другие характер-
характерные формы: дендриты, завитки и хвосты «морских коньков» (см. цвет-
цветные вклейки). На этих иллюстрациях черным цветом показаны области,
принадлежащие М-множеству, а другие цвета характеризуют различ-
различные скорости ухода итераций zn в бесконечность при значениях с, не
принадлежащих М-множеству. (Цвета были выбраны из компьютерной
палитры из соображений хорошей различимости и эстетической при-
привлекательности.)
Хотя М-множество в целом не самоподобно, оно обладает многочис-
многочисленными подструктурами, демонстрирующими приближенное самопо-
самоподобие, — кардиоидами, кругами, хвостами морских коньков и завитка-
завитками внутри завитков внутри завитков, образующими бесконечно тонкие
филигранные узоры. Удивительна сама мысль о том, что столь порази-
поразительная конструкция, как М-множество вместе со своим окружением,
Множества Жюлиа комплексного квадратичного отображения 383
порождена простым квадратичным отображением! Тончайшая мате-
математическая паутина М-множеств продолжает внушать благоговейный
трепет даже закаленным профессионалам. Сложность М-множества —
живое напоминание о том, что сложность, которую мы наблюдаем во
многих явлениях природы, включая и Саму жизнь (название известной
книги Ф. Крика), может быть следствием сравнительно простых зако-
законов [40]. Очевидно, что сложное поведение еще не означает сложности
основополагающих законов.
Хотя части М-множества выглядят как изолированные пятна (из-
(известны случаи, когда чрезмерно ревностные художественные редакто-
редакторы стирали такие «пятна»), в действительности, как показали Дуади
и Хаббард, М-множество является связным. Однако до сих пор неиз-
неизвестно, можно ли считать его всюду локально связным. (Круг, из кото-
которого выколота отдельная точка, по-прежнему остается связным, но его
уже нельзя считать всюду локально связным: точки, расположенные
по разные стороны от отверстия, пусть даже сколь угодно близко друг
от друга, могут быть соединены между собой только дугой, обходящей
отверстие.)
Большая кардиоидная область М-множества и каждый круг со-
соответствуют периодической орбите определенной длины: кардиоида —
периоду 1, самый большой круг — периоду 2, а остальные выстроивши-
выстроившиеся по горизонтали круги — периодам 2, 4, 8, ... , завершаясь точкой
сгущения последовательности бифуркаций удвоения периода Фейген-
баума. Самая большая из остальных кардиоид на вещественной оси
соответствует орбитам с длинами периода 3. Каждый из бесконечно
многих кругов, отпочковавшихся от кардиоид на комплексной плос-
плоскости, соответствует какой-то периодической орбите с определенной
длиной периода, связанной с длиной периода материнской кардиоиды,
причем каждый из этих кругов облеплен бесконечно большим количест-
количеством меньших кругов, похожих один на другой. Невооруженному глазу
заметно лишь одно отклонение от самоподобия в последовательности
кругов — зазор в «задней» части материнской кардиоиды.
Множества Жюлиа комплексного квадратичного
отображения
Разумеется, нам хотелось бы знать не только то, что некоторое
данное значение параметра принадлежит М-множеству. Мы были бы не
прочь узнать, как поведут себя итерации zn при различных начальных
условиях zq. При каких zq итерации zn ограничены? Множество началь-
384 Глава 12
ных значений zq, при которых итерации zn ограничены (при заданном
значении параметра с), образуют так называемое заполненное множес-
множество Жюлиа Jc. (Собственно множеством Жюлиа называется множество
граничных точек множества Jc.) Как показал компьютерный экспери-
эксперимент, различные значения параметра с могут порождать поразительно
разнообразные множества Жюлиа, причем малейшие изменения пара-
параметра с нередко приводят к весьма существенным метаморфозам мно-
множеств Jc (рис. 17А и 17Б).
Некоторые множества Жюлиа связны, другие представляют собой
«пылевидные» канторовы множества. Интересно, что абсолютно все зна-
значения параметра с, при которых Jc связны, принадлежат М-множеству,
поэтому последнее может быть определено и как множество всех зна-
значений параметра с, при которых Jc — связно. Эта эквивалентность
следует из теоремы, доказанной независимо друг от друга Гастоном
Жюлиа и Пьером Фату в 1918 г. и переоткрытой в совместной рабо-
работе Дуади и Хаббарда, которые существенно расширили наши все еще
отрывочные знания об обманчиво простом отображении z —> z2 + c [50].
Одно из наиболее важных открытий Дуади и Хаббарда состоит
в том, что граница множества Мандельброта может быть конформно
отображена на единичную окружность, и что итерации zn+i = z\ + с
соответствуют простому удвоению угла на единичной окружности. Та-
Таким образом, если измерять углы а в величинах кратных 2тг, то комп-
комплексное квадратичное отображение соответствует отображению ап+\ =
= 2ап mod 1. Если «внешний угол» а, как его принято называть, выра-
выразить в виде двоичной дроби, то такое отображение соответствует сдви-
сдвигу двоичных цифр влево по модулю 1. Например, значение параметра
с внешним углом а = 13/31 = 0, A1011) приводит к периодической
орбите с длиной периода 5. Конкретные цифры указывают, какая из
итераций zn попадет в верхнюю @), а какая — в нижнюю A) полу-
полуплоскость.
На рис. 18 изображено М-множество и указаны некоторые ра-
рациональные внешние углы. Точка сгущения бифуркаций удвоения пе-
периода с = —1,4011... (она отмечена буквой F в честь Фейгенба-
ума) имеет в качестве своего внешнего угла постоянную Морса-
Туэ 0,0110100110010110... = 0,412..., двоичные цифры которой об-
образуют последовательность Морса-Туэ.
Конформному отображению границы М-множества на единичную
окружность можно придать наглядный физический смысл, если его
интерпретировать как задачу электростатики. Рассмотрим бесконеч-
бесконечно длинный проводящий стержень, поперечное сечение которого совпа-
Множества Жюлиа комплексного квадратичного отображения 385
(?)
Рис. 17. (А) Заполненное множество Жюлиа, определяемое как множество
всех точек го, для которых итерации г„+1 = г^ + с ограничены. (Б) Еще одно
едва связное множество Жюлиа, иллюстрирующее огромное разнообразие
форм, получаемых при изменении параметра с [161].
дает с М-множеством, окружим его на большом удалении электродом
в форме кругового цилиндра и создадим между стержнем и цилинд-
цилиндром разность потенциалов. Тогда силовые линии электрического поля,
выходящие из точки на единичной окружности, проведенный через ко-
которую радиус образует с вещественной осью угол а, заканчиваются
в точке с с внешним углом а на границе М-множества. Так проис-
386
Глава 12
Рис. 18. Внешние углы для множества Мандельброта. Дробные значения опре-
определяют длины периода итераций zn при заданном параметре с. Точка «_F»
отмечает точку сгущения каскада удвоения периода [52].
ходит потому, что силовые линии электрического поля подчиняются
законам конформного отображения. А эквипотенциальные линии, орто-
ортогональные к силовым линиям, соответствуют значениям с с равными
скоростями расходимости итераций zn в бесконечность при zo = 0.
(Напомним, что лежащие вне М-множества значения параметра с при-
приводят к неограниченным итерациям zn.)
Еще более увлекательные подробности можно найти в книге Пайт-
гена и Рихтера «Красота фракталов», в которую, кроме того, входит
и доступно написанный очерк Дуади [194].
Глава 13
Запрещенная симметрия, кролики
Фибоначчи и новое состояние вещества
Приведенное выше предложение [1 + 1 = 2]
бывает иногда полезным.
А. Н. Уайтхед и Б.Рассел
«Principia Mathematica»
Современная теоретическая физика —
это роскошный, совершенно раблезианс-
раблезианский полнокровный мир идей, и матема-
математик может найти в нем все, что душе
угодно — кроме порядка, к которому он
привык.
Ю.И.Манин
В этой главе мы отведаем вкус некоторых запретных плодов из тех,
что произрастают на почве самоподобия, познакомимся с новым твер-
твердым состоянием вещества — с квазикристаллами, обладающими осью
вращательной симметрии пятого порядка (как у пятилучевой морской
звезды и многих цветов). Интересно отметить, что новое состояние ве-
вещества связано с простым итерированным отображением, описываю-
описывающим размножающихся кроликов, но не простых, а весьма редкой поро-
породы, из знаменитого семейства Фибоначчи. В свою очередь упомянутое
итерированное отображение тесно связано с непрерывной дробью для
золотого сечения, которая легко может быть «понижена» до так назы-
называемых серебряных сечений, что позволяет ожидать появления новых
запрещенных симметрии, причем некоторые из них уже были обнару-
обнаружены в реальных квазикристаллах.
Запрещенная симметрия пятого порядка
Люди всегда высоко ценили кристаллы — будь то снежинки или
драгоценные камни — т. е. такие образования, в которых отдельные
388 Глава 13
атомы расположены в узлах упорядоченных периодических решеток.
Однако нам известны также и неупорядоченные вещества (большинст-
(большинство жидкостей, например), в которых атомы распределены случайным
образом. Аналогично, большинство твердых веществ, встречающихся
в природе, неупорядочены, или аморфны, напоминая этим жидкости,
только затвердевшие. Прекрасным примером аморфных твердых тел
могут служить стекла. Более того, у физиков слово «стекло» стало с не-
некоторых пор собирательным названием для неупорядоченных систем
вообще. Так, под металлическим стеклом отнюдь не подразумевается
вставленный в оконную раму лист свинца, и с обычным стеклом это
вещество имеет мало общего: речь идет всего лишь о металле, атомы
которого расположены беспорядочно. Точно так же и спиновые стекла
не имеют никакого отношения ни к спинам, ни к спиннингу. Спино-
Спиновое стекло — это неупорядоченное расположение магнитных спинов
или, в общем смысле, значений любой другой физической переменной,
обладающей двумя1 предпочтительными состояниями, например, воз-
возбужденных и невозбужденных нейронов в нейронной сети.
Кроме названных существуют и весьма необычные состояния ве-
вещества. Вспомним хотя бы о жидких кристаллах, повсеместно исполь-
используемых ныне в буквенно-цифровых дисплеях наручных часов и микро-
микрокалькуляторов (т.н. ЖК-дисплеи). В жидком кристалле молекулы рас-
расположены случайным образом, но их ориентации упорядочены и управ-
1 Между спином (в том смысле, какой придают этому термину физики) и чис-
числом 2 (известным также как самое странное из простых чисел, поскольку 2 —
единственное четное простое число) существует прочная связь. Так как элемен-
элементарный спин — величина, способная принять одно из двух значений («верх» или
«низ»), два электрона могут находиться на одной и той же атомной орбите, что
(вместе с принципом запрета Паули) объясняет структуру периодической системы
химических элементов. Эйнштейн в единственном выполненном им собственноруч-
собственноручно (вместе с де Гаазом) эксперименте (по измерению гиромагнитного отношения
электрона) получил результат в 2 раза больший ожидаемого значения (погрешность
в 100%!). Однако это обстоятельство ничуть не обескуражило великого теоретика;
говорят, что он лишь невозмутимо заметил: «Достаточно близко». Впоследствии
оказалось, что экспериментальный результат Эйнштейна и де Гааза абсолютно то-
точен, а недостававший множитель 2 обусловлен спином электрона. Позднее и в физи-
физике, и в химии неоднократно возникали ситуации, когда результаты эксперимента
приходилось «умножать на 2 из-за спина». (Однако то, что цифру крепости на бу-
бутылке спиртного следует понимать как процентное содержание спирта, умноженное
на 2, по-видимому, не имеет отношения к спину, возникающему в головах любите-
любителей горячительных напитков, стоит им немного перебрать.) (Английское слово spin
переводится, среди прочего, и как «вращение»; ну а цифра крепости на россий-
российских бутылках соответствует (в идеале) действительному содержанию алкоголя,
т.е. спин, по-видимому, не учитывается вовсе, что, однако, не мешает «перебирать»
нашим отечественным любителям «спина в голове». — Прим. перев.)
Запрещенная симметрия пятого порядка
389
о
о
о
* •
о '
о
о
- t
•
* о
о
о
о '
' •
о
о
о
о "
°
о
*
' о
«
о
•
о
о
0
о
"
о
о
°
' о
о
в
•
0 '
о
¦:'»
о
о
° о
• * •
о
* о
о
. ¦ •
о
. ш .'
о
•
о
о
°
о
о
°
•
о
о
•
о
*
о
о
о
о
т
о
о
о
•
о
*
о
a
0
о
о
°
0
0
Рис. 1. Электронная дифракционная картина кристалла с запрещенной сим-
симметрией пятого порядка [239].
ляются приложенным извне напряжением, что позволяет изменять вы-
выводимую информацию.
Вплоть до недавнего времени вряд ли кто-нибудь подозревал, что
может существовать еще одно состояние вещества, которое обладало бы
существенными свойствами кристаллических и аморфных веществ од-
одновременно. Однако именно такое состояние и обнаружили Д. Шехтман
и его сотрудники при снятии электронограммы (рис. 1) быстро охлаж-
охлаждаемого образца алюминиево-марганцевого сплава (AleMn), отнесенно-
отнесенного ныне к особому разряду квазикристаллов [239]. На электронограмме,
или дифракционной картине (которая, в сущности, представляет собой
двумерное преобразование Фурье), квазикристаллов наблюдаются рез-
резкие пики, свидетельствующие о дальнем порядке, как в периодических
кристаллических решетках. Но на тех же электронограммах мы ви-
видим симметрию пятого порядка, запрещенную для периодических крис-
кристаллов. Простое доказательство этого приведено на рис. 2. Симметрия
пятого порядка означает, что решетку можно совместить с самой со-
собой, повернув на угол 360°/5 = 72°. Разрешенными же являются толь-
только оси симметрии второго, третьего, четвертого и шестого порядков;
все остальные вращательные симметрии противоречат трансляционной
симметрии периодического кристалла.
Что же происходит в квазикристаллах? После первого открытия
Шехтмана и его сотрудников было обнаружено еще несколько квази-
квазикристаллов с запрещенными симметриями других типов. Значит, ква-
390
Глава 13
Рис. 2. Простое доказательство невозможности симметрии пятого порядка в
периодическом кристалле. Существует такое понятие, как наименьшее рас-
расстояние между двумя атомами периодического кристалла. Предположим, что
отрезок АВ является одним из таких наименьших расстояний. Если кристалл
обладает симметрией пятого порядка, то точки С и D (полученные поворо-
поворотом на угол 360°/5 = 72е) также должны быть заняты атомами. Но рассто-
расстояние между точками С и D меньше (коэффициент подобия, между прочим,
равен 0, 382, т. е. золотому сечению в квадрате) длины отрезка АВ, что про-
противоречит начальному условию о минимальности длины отрезка АВ.
зикристаллы представляют собой не любопытный курьез, не редкую
диковину, а новое твердое состояние вещества — несмотря на не по-
покидающие Лайнуса Полинга сомнения в правильности подобных взгля-
взглядов [191]. Как мы вскоре увидим, объяснение существования квази-
квазикристаллов основывается на самоподобии.
Дальний порядок, обусловленный взаимодействиями
между соседями
Как мы уже знаем из теоретико-числовой последовательности Мор-
са-Туэ (см. гл. 12), острые пики в спектре и апериодичность отнюдь
не противоречат друг другу — до тех пор, пока господствует дальний
порядок. Простейшим примером апериодичности и дальнего порядка,
Дальний порядок 391
приводящих к резким пикам в спектре, может служить суперпозиция
двух синусоид с несоизмеримыми частотами:
s (t) = s'm((jJot) + s'm(aijJot),
где отношение частот а — иррациональное число. Не существует не-
ненулевого значения Т, при котором s (t) = s it + T) для всех t. Одна-
Однако Фурье-анализ функции s (t) (надлежащим образом преобразованной
для обеспечения сходимости преобразования Фурье), без сомнения, об-
обнаружит четко выраженные пики при несоизмеримых угловых часто-
частотах oj = и>о и и) = аи>о-
Периодичность в кристаллах легко объяснима. Например, в крис-
кристалле поваренной соли (хлорида натрия, химически выражаясь) атомы
натрия (Na) предпочитают в качестве соседей атомы хлора (С1), а те,
в свою очередь, предпочитают окружать себя атомами натрия. Таким
образом, взглянув вдоль любой из кристаллических осей, мы увидим,
что атомы натрия и хлора чередуются: Na—C1—Na—C1—Na—C1— и т.д.
Результат — идеальная периодичность и дальний порядок.
А как же объяснить дальний порядок в апериодическом квазикрис-
квазикристалле? Это не так просто. Если между атомами или молекулами раз-
различного рода нет взаимного притяжения (или если это притяжение раз-
разрушено высокой температурой), то дальнего порядка, как правило, нет
совсем: возникает случайная структура вроде той, что мы наблюдаем
в жидкостях (или в «замороженных» жидкостях — например, в оконном
стекле).
По-видимому, единственный способ построить дальний порядок из
короткодействующих сил, доминирующих в твердых телах, не порож-
порождая при этом периодической решетки (такой, как у поваренной соли),
состоит в том, чтобы воспользоваться итерированными отображени-
отображениями. Такие отображения можно считать моделями короткодействую-
короткодействующих сил. Например, нуль притягивает единицу, порождая отображе-
отображение 0 —у 01, а единица притягивает нуль, порождая отображение 1 —у 10.
Однако из анализа последовательности Морса-Туэ нам известно, что
итерированные отображения могут также порождать апериодический
дальний порядок. Поскольку итерированные отображения часто приво-
приводят к самоподобию, объяснить квазикристаллы с помощью такого под-
подхода можно только в том случае, если эти кристаллы (и их дифракци-
дифракционные «портреты») обладают масштабной инвариантностью. Более под-
подробное изучение дифракционной картины, представленной на рис. 1,
показывает, что так оно и есть, причем наиболее заметный коэффи-
коэффициент подобия равен золотому сечению -у = {\/Ъ — 1)/2 = 0,618...
392 Глава 13
(Примечание. Некоторые авторы — включая и вашего покорного слугу,
только в другой книге — называют золотым сечением обратную ему
величину 1/7 = (\/5 + 1)/2 = 1,618 ....)
Таким образом, квазикристаллы, скорее всего, можно моделиро-
моделировать с помощью некоторого итеративного отображения, связанного с зо-
золотым сечением. Чтобы найти такое отображение, нам придется загля-
заглянуть в прошлое.
Примерно в 1200 г. Леонардо Пизанский (около 1175-1250), более
известный как Фибоначчи, т. е. сын Боначчи, задумался над задачей
о размножении кроликов (по-видимому, уже в те далекие времена кро-
кролики были в этом деле весьма искусны) [71]. В наилучшем современ-
современном стиле Фибоначчи постулировал в высшей степени упрощенную мо-
модель процесса размножения: раз в сезон каждая взрослая пара кроликов
производит новую пару, которая достигает зрелости через поколение.
Предположим, что в самом начале имеется одна-единственная пара но-
новорожденных кроликов, и что кролики живут неограниченно долго. По-
Популяция кроликов при этом быстро растет (см. рис. 3).
С формальной точки зрения Фибоначчи занимался рассмотрением
итерированного отображения 0 —> 1 и 1 —> 10, где 0 означает незрелую
пару кроликов, а 1 — взрослую пару. Таким образом, первые шесть по-
поколений представлены следующими двоичными последовательностями
0
1
1 0
10 1 A)
10 110
10 110 10 1
которые, как и последовательность Морса -Туэ, являются самопорож-
самопорождающими. Количество пар кроликов в n-м поколении равно Fn (п-е чис-
число Фибоначчи, определяемое равенством F\ = F2 = 1 и рекуррентным
соотношением Fn+2 = Fn+i + Fn); числа Fn образуют известную после-
последовательность Фибоначчи 1, 1, 2, 3, 5, 8, 13,...). Существует простой
способ вычисления Fn при п > 0 — округление значения 7~™/v/5 до
ближайшего целого числа (здесь 7 = 0,618... — уже упоминавшее-
упоминавшееся золотое сечение). Таким образом, отношение двух последовательных
чисел Фибоначчи асимптотически стремится к золотому сечению, рав-
равно как и отношение количества нулей и единиц в каждой строке масси-
массива A). Более того, количество нулей и единиц в n-й строке в точности
Дальний порядок 393
11
Рис. 3. Размножение кроликов по Фибоначчи. Маленькие белые кролики —
молодняк, большие черные — взрослые особи.
равно Fn_2 и Fn-i, соответственно. (Заметим, что обратная рекурсия
дает Fo = 0 и F_i = 1.)
Другой способ построения бесконечной последовательности, нача-
начало которой представлено массивом A), и который я назвал кроличь-
кроличьей последовательностью, вполне очевиден: приписывая к каждой стро-
строке, начиная со второй, предыдущую строку, мы будем получать сле-
следующую строку. Это свойство является прямым следствием итера-
итераций отображения. Первая итерация отображения 0 —» 1, 1 —>• 10 да-
дает 0 —» 01, 1 —У 101. Следующая итерация приводит к отображе-
отображению 0 —У 10110, 1 —у 10110101 и т.д. Таким образом, пятую строку
A0110) массива A) можно считать порожденной третьей строкой A0)
посредством однократно итерированного отображения 1 —>¦ 101 и при-
приписывания справа результата отображения 0 —У 10. Но 101 — это не что
394 Глава 13
иное, как четвертая строка, а приписанная справа группа цифр 10 —
третья строка. Следовательно, можно утверждать, что каждая строка
массива A) может быть получена посредством приписывания к пре-
предыдущей строке лредпредыдущей строки — правило «инфляции», отра-
отражающее исходное отображение 0 —» 1, 1 —v 10. Такого рода структура
и обусловливает дальний порядок в кроличьей последовательности, хотя
последовательность эта была определена на основе лишь короткодейст-
короткодействующих «сил» 0 —» 1, 1 —у 10, затрагивающих только соседние символы.
Как было показано в гл. 11, итерированные отображения часто по-
порождают самоподобие, и кроличья последовательность в этом отноше-
отношении не является исключением: она просто изобилует самоподобиями.
Одно из самоподобий кроличьей последовательности можно продемон-
продемонстрировать, сохраняя первые два из каждой тройки символов для каж-
каждой единицы в последовательности и первый из каждой пары символов
для каждого нуля. Такое выборочное усечение воспроизводит исходную
бесконечную кроличью последовательность, в чем можно убедиться,
подчеркнув сохраняемые символы:
101101011011...
Это свойство кроличьей последовательности отражает тот факт, что
она воспроизводит сама себя при обратном отображении 10 —>¦ 1, 1—^0
(называемом также переименованием блоков или «дефляцией» в физи-
физической теории ренорм-групп). (Обратите внимание на то, что непод-
неподчеркнутые символы также воспроизводят единицы и нули кроличьей
последовательности — от этих пронырливых кроликов просто некуда
деться!)
Попытаемся теперь извлечь из наших кроликов хоть немного поль-
пользы. Рассмотрим следующую задачу о «синхронизации» (с потенциаль-
потенциальным применением в обеспечении согласованного функционирования ка-
каналов передачи цифровой информации — например, при передаче изоб-
изображений с отдаленных космических кораблей). На сколько шагов впра-
вправо необходимо сдвинуться в кроличьей последовательности
101101011011010110101...,
чтобы снова обнаружить некую заданную подпоследовательность сим-
символов (например, 10)? Для ответа на этот вопрос необходимо про-
произвести осмотр на месте. Сначала сдвигаемся на 3 знака, затем
на 2, затем снова на 3 и т. д. — в итоге получаем последователь-
последовательность 3, 2, 3, 3, 2, 3, 2, ... (числа Фибоначчи, кстати), которая похо-
похожа на кроличью последовательность. Да что там — похожа! которая
Дальний порядок 395
воспроизводит кроличью последовательность, если сделать подстанов-
подстановку 2 —>¦ О (F3 —> Fq) и 3 —> 1 (F± —> Fi). Чтобы справиться с большими
погрешностями синхронизации, необходимо использовать длинные по-
последовательности. В общем случае подпоследовательность длиной Fn — 1
встретится повторно не ранее, чем через Fn-\ шагов, но и не позднее,
чем через Fn+i шагов.
Существует простая формула (впервые мы ее встретили на с. 90),
позволяющая определять те индексы к, для которых элементы ги кро-
кроличьей последовательности равны единице:
к = \щ, п = 1, 2, 3, ...
Значения индексов к, для которых элементы г\. равны нулю, задаются
другой функцией:
— 1 О Q
— -L, Lt* О, ...
Г"
Здесь под значением функции \_х\ понимается наибольшее целое число,
не превосходящее х.
Эти два равенства можно интерпретировать как формулы, описы-
описывающие генерацию единиц и нулей двумя несоизмеримыми частота-
частотами 7 и 72- Заметим, что 7 + 72 = 1> единица в данном случае есть
частота появления либо единицы, либо нуля (инженеры называют ее
частотой дискретизации). Если число 7 заменить любым положитель-
положительным иррациональным числом w < 1, а т2 — числом 1 — го, то две
результирующие последовательности, вместе охватывающие все поло-
положительные целые числа, называются парой последовательностей Бит-
ти. Из-за своего свойства вкючать в себя все целые положительные
числа последовательности Битти оказываются полезными в качестве
последовательностей индексов [245].
Поскольку кроличья последовательность порождена частотами
7 ~ 0,618 и 72 ~ 0,382, неудивительно, что в спектре (т.е. наборе ам-
амплитуд преобразования Фурье) именно на этих частотах наблюдаются
два четко выраженных пика. На рис. 4 показан спектр, который получа-
получается после обрыва кроличьей последовательности на 144 члене и после-
последующего преобразования Фурье [230]. Два главных пика расположены
на 55-й и 89-й гармониках, что соответствует частотам 89/144 я» 7
и 55/144 ра 72- Построенный спектр отражает и самоподобие кроличь-
кроличьей последовательности. Более того, пики приходятся на частоты, от-
отношение которых равно золотому сечению 7 (ему же, кстати, равно
396
Глава 13
21 34 55 89 ПО 123 144
Гармоническое число
Рис. 4. Амплитудный спектр Фурье для двоичной кроличьей последователь-
последовательности (составленной из первых 144 ее членов, периодически повторяющих-
повторяющихся) [230].
и отношение двух последовательных чисел Фибоначчи в усеченной по-
последовательности), а отношение амплитуд приближенно равно j2.
Построение кроличьей последовательности из
последовательности чисел Фибоначчи
В большинстве случаев мы не испытываем особой потребности
в последовательностях индексов для единиц и нулей кроличьей после-
последовательности, но нам просто необходима сама кроличья последова-
последовательность и какая-нибудь формула, позволяющая непосредственно ее
строить. Попытаемся же получить такую формулу.
Рассмотрим выражение
ru = mr + I mod 2,
где тг — индекс наименьшего значащего члена в представлении к в фи-
боначчиевой числовой системе [230]. Число п в этой системе однозначно
представляется в виде суммы чисел Фибоначчи с убывающими индек-
индексами, начиная с числа с наибольшим индексом, не превосходящим п:
^ J7> _i_ Тр _|_ _|_ Тр
ltj — "m\ т Гтп2 ~Г • • • ~Г -^mr5
где mi > то2 > ... > mr. Например, 12 = 8 + 3 + 1 = F6 + F4 + F2.
Так как индекс 2 последнего члена разложения F% четный, r\i = 1.
(Обратите внимание на то, что в таком представлении чисел не может
Самоподобный спектр кроличьей последовательности
397
оказаться рядом двух последовательных индексов, т.е. rrij+i ^ 2 + то;.
Кроме того, по условию, 1 = i<2, поэтому т*1 = 1.) Хотя вышеописанный
подход и направлен на получение самих членов г/., однако вычисления,
производимые в фибоначчиевой системе, вряд ли можно назвать непо-
непосредственными.
Самоподобный спектр кроличьей
последовательности
Более прямым представлением кроличьей последовательности
является следующее:
1, если ((к + 1OI < 7)
О, в противном случае,
A)
где (x)i, как и прежде, означает дробную часть числа х. Эта формула
имеет красивое геометрическое представление (рис. 5).
Г
¦ 360°= 222,5
Рис. 5. Геометрическое представление кроличьей последовательности.
Член Гк равен 1, если угол {(к + 1OI • 360° попадает внутрь выделенной
дуги. В противном случае Гк = 0.
Запишем две прямые формулы, порождающие кроличью последо-
последовательность, из которых непосредственно видны и дальний порядок,
и апериодичность:
гк = [(к + 1OJ -
398 Глава 13
= \ + \ sgn[7 - ((к + lO>i] B)
(формула B) по существу представляет собой выражение A), только
иначе записанное), где sgn[a;] — функция, значением которой является
знак числа х (при ж /0 она равна +1 или —1; sgn[0] = 0 по определе-
определению).
Переведя соотношение B) на инженерный язык и рассматривая
при этом к как непрерывную переменную («время»), можно сказать,
что Г]. — это прямоугольная волна (совершающая скачки от 0 до 1)
с основной частотой -у (и «рабочим циклом» 7)- Однако в действитель-
действительности переменная к не непрерывна, а дискретна, и возрастает с ша-
шагом 1. Это означает, что наша прямоугольная волна дискретизирована
с частотой дискретизации 1. Так как частоты 7 и 1 несоизмеримы, воз-
возникающая в результате дискретизации последовательность апериодич-
на, хотя и сохраняет идеально жесткий дальний порядок. Например,
положив к = 144, мы обнаружим, что гщ = 1. Мы можем сразу же
убедиться в правильности полученного результата, заметив, что 144 =
= Fi2 и применив общее правило грп = A + (—1)™)/2. (Примечание.
При Fn = 1 следует брать п = 2.)
Так как период 7 — число иррациональное, значения г/., выбранные
с интервалом дискретизации, апериодичны. Вследствие этого в спект-
спектре Г}, наблюдаются ярко выраженные пики на определенных пред-
предпочтительных частотах, т.е. на частоте дискретизации, умноженной
на 72, 73; 745 75 и Т-Д-: и на соответствующих зеркальных частотах
A-72=7, 1-73,---)-
Математическое выражение для спектра ги можно получить, про-
произведя Фурье-преобразование функции г/., выраженной формулой B):
Rm = sincm7 на частотах fnm = п + ту,
где функция sine ж определяется как (sin7ra;)/7ra;.
Самоподобие кроличьей последовательности
Откуда же берутся все эти спектральные самоподобия? Судя по
всему, они должны быть заложены в самой последовательности. В са-
самом деле, если взглянуть на последовательность индексов [п/у\ для
единиц, то нетрудно заметить, что при уменьшении всех ее членов
Одномерная кваэипериодическая решетка 399
в 7 Раз, т-е- при подстановке п/у вместо п, она переходит в после-
последовательность индексов [п/у2\ для нулей. Следовательно, амплитуда
Фурье-преобразования функции г/, останется при таком уменьшении
неизменной (если пренебречь постоянным коэффициентом подобия).
Самоподобие наблюдается и в самой последовательности ги- Так
как коэффициент самоподобия равен I/7, то для того, чтобы добить-
добиться изменения масштаба в I/7 раз, нам необходимо пропускать в сред-
среднем 1,618... знаков. А поскольку асимптотическое отношение числа
единиц к числу нулей в точности равно у, мы могли бы пропускать
по два члена последовательности г\. всякий раз, когда встретим едини-
единицу, и по одному члену, когда встретим в исходной последовательности
нуль. Как нам уже, наверное, подсказывает нетерпеливый читатель,
в результате вновь получится последовательность г^:
1011010110110... = 10110...
Описанный выше процесс усечения последовательности является до-
дополнением упомянутого ранее процесса «дефляции», или переименова-
переименования блоков. В данном случае мы переименовали каждый блок 101 в 1,
а каждый блок 10 — в 0. Переименование блоков — операция, обрат-
обратная отображению 0 —» 1 0, 1 —у 1 01 (т. е. однократно итерированному
производящему отображению 0—^1, 1 —>• 1 0).
Одномерная квазипериодическая решетка
Можно ли те удивительные открытия, что мы сделали, наблюдая за
самоподобными последовательностями, порождающими апериодичес-
апериодический дальний порядок, перевести в более физическую форму? Например,
в одномерную решетку — этакий прообраз настоящего трехмерного
квазикристалла? Рис. 6 иллюстрирует один простой способ построения
одномерного квазикристалла. Расположим атомы на прямой по следую-
следующему правилу: для каждой единицы в кроличьей последовательности г/.
выберем межатомное расстояние в I/7 = 1,618... единиц (например,
ангстрем), а для каждого нуля — расстояние в одну единицу. В нижней
части рис. 6 изображена та же одномерная решетка, сжатая в 1,618 ...
раз. Легко заметить, что каждый атом в исходной решетке в точности
совпадает с некоторым атомом в сжатой решетке. (Разумеется, в сжа-
сжатой решетке, обладающей более высокой плотностью атомов, имеет-
имеется определенное количество «лишних» атомов, для которых не нашлось
партнеров в исходной решетке.) Следовательно, построенная вышеука-
400
Глава 13
занным способом одномерная решетка самоподобна. (Читатели могут
попытаться самостоятельно обобщить полученный результат на само-
самоподобные одномерные решетки, основанные на подходящих иррацио-
иррациональных числах, отличных от золотого сечения 7-)
1
о
1
1/7
1
1/7
I 1—1-
О
1
н—ь
Исходная решетка
7
0
7
0
Сжатая решетка
Рис. 6. Одномерный квазипериодический «кристалл», полученный из кро-
кроличьей последовательности. Коэффициент самоподобия — золотое сечение -у.
Если каждый атом в «кроличьей решетке» представить дельта-
функцией Дирака, мы получим следующее преобразование Фурье [283]:
sine I —— + то ) на частотах fnm =
V V 5 /
- то.
Самоподобие, порождаемое проекциями
На рис. 7 вы видите схему альтернативного метода построения од-
одномерной кроличьей решетки [44]. В квадратной двумерной целочис-
целочисленной решетке Z2 проводится прямая с угловым коэффициентом (тан-
(тангенсом угла между нею и положительным направлением оси абсцисс),
равным 1/7- На проведенную прямую нормально проецируется верх-
верхняя левая вершина каждого квадрата, ею пересекаемого. И — о чу-
чудо! — полученные проекции образуют одномерную кроличью решетку,
определение которой было дано выше. Обозначим большие интервалы
единицами, а меньшие — нулями, и перед нами вновь кроличья после-
последовательность. Сообразительный читатель, вероятно, уже понял, что
это геометрическое построение непосредственно следует из арифмети-
арифметического описания кроличьей последовательности A).
Метод проекций, основанных на идеально периодической квадрат-
квадратной решетке, вновь демонстрирует и дальний порядок одномерной кро-
кроличьей решетки, и ее апериодичность (обусловленную иррациональное-
Самоподобие, порождаемое проекциями
401
Рис. 7. Одномерный кристалл с рис. 6, полученный с помощью проекций квад-
квадратной решетки [44].
тью углового коэффициента проведенной прямой). Но самое важное
здесь то, что метод проекций может быть легко обобщен и позволяет
производить двумерные и трехмерные квазипериодические решетки,
моделирующие реальные квазикристаллы [153, 55, 58, 117].
402
Глава 13
Для построения двумерной квазипериодической решетки необхо-
необходимы четыре рационально независимых вектора [145]. Однако более
удобным представляется спроецировать область пятимерной «кубичес-
«кубической» решетки на плоскость с надлежащим образом выбранным накло-
наклоном. Результат такого проецирования представлен на рис. 8 (вряд ли
есть необходимость пояснять, что изображение было получено с по-
помощью компьютера, поскольку в реальном мире пятимерные решетки
пока недосягаемы). Интересно отметить, что точки на рис. 8 совпада-
совпадают с вершинами апериодической мозаики, получающейся при замоще-
замощении плоскости плитками двух различных форм — знаменитой мозаики
Пенроуза (рис. 9) (долгое время такое замощение считалось невозмож-
невозможным) [197, 153]. Апериодическая мозаика, образующаяся в результате
замощения плоскости плитками только одной формы, изображена на
рис. 10 [75].
Рис. 8. Двумерный квазикристалл, полученный с помощью проекций из пя-
пятимерной гиперкубической решетки.
Если слайд с рис. 8 поставить на пути лазерного луча, то возникнет
дифракционная картина, которую вы видите на рис. НА. Она демон-
демонстрирует непривычную и даже несколько ошеломляющую симметрию
Самоподобие, порождаемое проекциями
403
Рис. 9. Мозаика Пенроуза: замощение плоскости с помощью всего лишь двух
разновидностей плиток [153].
Рис. 10. Апериодическое замощение плоскости Хайнца Фодерберга с исполь-
использованием одной разновидности плиток [75].
пятого порядка (которая выглядит как симметрия десятого порядка
просто потому, что мы не можем различить знаков амплитуд рассеян-
404
Глава 13
(А)
Рис. 11. (А) Дифракционная картина рассеяния лазерного луча на квазикрис-
квазикристалле, изображенном на рис. 8. Ясно различима симметрия пятого порядка.
(Б) Та же картина при большей интенсивности лазерного луча. Количество
дифракционных точек увеличилось. (В) Практически плотная картина рассе-
рассеяния энергии лазерного луча, возникающая при дальнейшем увеличении его
интенсивности.
ного излучения в запечатленных на снимке интенсивно стях). Вообще
говоря, узор на рис. НА весьма напоминает дифракционную картину,
возникающую при рассеянии лазерного луча на реальном квазикрис-
квазикристалле. Особого внимания заслуживает самоподобие с коэффициентом j,
наблюдаемое на многих деталях картины, например, на многочислен-
многочисленных правильных пятиугольниках различных размеров.
Для достижения максимального эффекта только что описанный
эксперимент надлежит демонстрировать «живьем» перед достаточно
многочисленной аудиторией, используя большие телевизионные мони-
мониторы для показа изображения и безлинзовые телекамеры для съем-
съемки дифракционной картины1. При увеличении яркости дифракционной
1Я глубоко признателен Хансу Вернеру Штрубе за выращенный компьютером
«квазикристалл» и Хайнриху Хенце за великолепные дифракционные картины.
Самоподобие, порождаемое проекциями
405
406 Глава 13
картины (посредством усиления интенсивности лазерного луча) коли-
количество дифракционных точек будет увеличиваться, и в конце концов
экран монитора заполнится ими целиком. На рис. НА, Б и В пока-
показана одна и та же дифракционная картина при увеличении интенсив-
интенсивности лазерного излучения. Таким образом можно весьма убедительно
продемонстрировать одно из наиболее существенных различий между
дифракционными картинами при рассеянии на квазикристаллах и на
периодических кристаллах: хотя и в том, и в другом случае дифрак-
дифракционные картины состоят из дельта-функций, дифракционные карти-
картины квазикристаллов содержат бесконечный (счетно бесконечный) набор
таких функций, которые всюду плотны, в то время как дифракционные
картины периодических кристаллов состоят из конечного числа изоли-
изолированных дифракционных точек! Первые дифракционные картины ква-
квазикристаллов так напоминали дифракционные картины периодических
кристаллов лишь потому, что были получены при относительно низкой
интенсивности падающего излучения.
Чтобы получить трехмерную квазипериодическую решетку, необ-
необходимо спроецировать на трехмерное пространство шестимерную ку-
кубическую решетку [126].
Другие запрещенные симметрии
Вкусив от первого запретного плода симметрии пятого порядка,
вы вправе поинтересоваться, существуют ли квазикристаллы с дру-
другими незаконными осями симметрии, которые мы могли бы «выкрис-
«выкристаллизовать» из самоподобных итерированных отображений. Спешу вас
обрадовать — существуют.
Отображение 0 —>• 1, 1 —>• 1 0, порождающее кроличью последова-
последовательность, тесно связано с непрерывной дробью для золотого сечения 7,
7 =
которую можно записать как [1, 1, 1, ...] или, поскольку она периодич-
периодична, как [A)]. Заметим, что длина периода равна единице. Разложение
золотого сечения j в непрерывную дробь следует непосредственно из
определения числа j как положительного корня квадратного уравне-
уравнения х2 + х = 1, которое можно также записать в виде х = 1/A + х).
Другие запрещенные симметрии 407
Именно такая форма определяющего уравнения для j рекуррентно
приводит к непрерывной дроби [A)]. (Заметим еще, что, поскольку
|1 + 71 > 1? рекурсия сходится.)
А нельзя ли воспользоваться для построения самоподобных реше-
решеток менее благородными серебряными сечениями т^? Серебряные сече-
сечения определяются уравнением 1/т^ = N ± т^, т.е. все они являют-
являются квадратичными иррациональными числами, представимыми в виде
периодических непрерывных дробей с периодом 1 и числителем, рав-
равным il.1 Можно показать, что сечение т^~ = [2, 2, 2, ...] = л/2 — 1 по-
порождает квазикристалл с кристаллографически запрещенной симмет-
симметрией восьмого порядка, в то время как сечение т± = 2 — л/3 лежит
в основе также запрещенной оси симметрии двенадцатого порядка. Обе
эти симметрии (и восьмого, и двенадцатого порядка) недавно наблюда-
наблюдались экспериментально [113, 114, 33].
Наряду с золотым сечением j = т^, все сечения т^ (где N — п-е
число Люка, а знак в верхнем индексе равен (—1)™) также способны
порождать квазикристаллы с симметрией пятого порядка [230]. Чис-
Числа Люка Ln подчиняются тому же рекуррентному соотношению, что
и числа Фибоначчи, с тем лишь отличием, что L\ = 1 и Li = 3. Кроме
того, числа Люка 1, 3, 4, 7, 11, 18, ... также связаны с золотым сечени-
сечением 7- Более того, при п ^ 2 число Люка Ln определяется величиной f™,
округленной до ближайшего целого числа.
1 Благородные сечения — еще одно обобщение золотого сечения — определяются
как числа, разложения которых в непрерывные дроби заканчиваются бесконечной
последовательностью единиц. Благородные сечения играют важную роль и в струк-
структуре квазикристаллов, и в квазипериодическом пути к хаосу нелинейных динами-
динамических систем. Следуя этой терминологии, можно сказать, что золотое сечение —
это всего лишь благороднейшее из благородных сечений.
Щели Кассини в кольцах Сатурна могут служить примером того, что происходит,
когда вместо благородных сечений бал правят обычные рациональные числа: камни
и глыбы льда, из которых состоят кольца, обращаются вокруг планеты с перио-
периодами, находящимися в простых рациональных отношениях с периодами обращения
лун Сатурна, и возникающие при этом резонансные эффекты между соизмеримыми
периодами обращения просто сметают их с их орбит. Скажем больше: сама устой-
устойчивость солнечной системы зависит от благородства отношений между периодами
обращения планет вокруг Солнца.
Глава 14
Периодические и квазипериодические
структуры в пространстве: путь
к пространственному хаосу
Великой истиной может называться
лишь та истина, чья противополож-
противоположность — также великая истина.
Нильс Бор
Из предыдущей главы мы узнали, что помимо кристаллов с иде-
идеально периодическими решетками существуют квазикристаллы с ква-
квазипериодической пространственной структурой. В одномерных моделях
такую квазипериодичность можно описать с помощью двух несоизме-
несоизмеримых частот, связанных с золотым сечением или с другими квадратич-
квадратичными иррациональными числами, разложения которых в непрерывные
дроби имеют короткие периоды1. Что же касается аморфных веществ,
не обладающих сколько-нибудь различимой периодической структу-
структурой, то о них мы, безусловно, знали и раньше.
В 1984 г. (время их открытия) квазикристаллы были восприняты
как полная неожиданность: лишь очень немногие ученые предвидели
возможность существования пространственной структуры (отличной
от жидких кристаллов), которая занимала бы промежуточное положе-
положение между аморфными стеклами и правильными кристаллами. Но на
квазикристаллах неожиданности не закончились2. Между квазиперио-
квазипериодичностью и аморфным беспорядком проглядывает еще одна простран-
пространственная структура: пространственный хаос.
1 Периодические непрерывные дроби с длинными периодами и большими целыми
числами в качестве числителей порождали бы нереальные квазикристаллы с неправ-
неправдоподобно сложными молекулярными взаимодействиями.
2«Рано заканчивать, вон та толстуха еще не пела», как заметил Ф. У. Андерсон
в День св. Патрика в 1987 г. в Нью-Йорке на этаком «Вудстокском фестивале» Аме-
Американского физического общества по поводу новых высокотемпературных сверх-
сверхпроводников («комнатная температура на Аляске»).
Периодические и квазипериодические структуры в пространстве 409
Существование пространственного хаоса не должно вызывать
удивления ни у кого, кто знаком с временным хаосом, ведь пространст-
пространство и время — всего лишь составляющие единой физической сущности,
именуемой «пространство-время». Все, что может произойти во вре-
времени, может произойти и в пространстве (и наоборот). Во владениях
времени мы уже давно познакомились с периодическими, квазиперио-
квазипериодическими и случайными явлениями:
• Колебания маятника периодичны;
• Фазы Луны, например, каждое воскресенье в полночь, квазипери-
одичны, поскольку в основе их лежат две несоизмеримые (пока
несоизмеримые) частоты: частота обращения Луны вокруг Зем-
Земли и частота обращения Земли по эллиптической орбите вокруг
Солнца;
• Шипение воздуха, вырывающегося из проколотой велосипедной
шины, можно считать случайным шумом. Другим примером слу-
случайного процесса может служить тепловое движение1.
Сравнительно недавно физики созрели для того, чтобы по достоин-
достоинству оценить четвертый тип временного поведения — детерминирован-
детерминированный хаос, который апериодичен, как и случайный шум, но отличается
от него тем, что является следствием детерминированных уравнений.
В динамических системах детерминированный хаос часто характери-
характеризуется малыми фрактальными размерностями, поскольку хаотический
процесс в фазовом пространстве обычно заполняет лишь небольшую
часть всего энергетически доступного пространства.
По аналогии с временным хаосом следует ожидать, что хаос может
посягнуть и на пространственные владения. Более того, сейчас мы уже
рассматриваем турбулентность как разновидность пространственного
хаоса, хотя и весьма сложного. В этой главе мы сначала сосредото-
сосредоточим внимание на более простом случае пространственной квазипери-
квазипериодичности и хаоса, который имеет некоторые немаловажные аналогии
с хаосом во временных владениях — на одномерной спиновой модели
магнетизма Изинга.
1Если бы наш слух был чуть острее и если бы не было отвлекающих звуков, то
мы могли бы слышать тепловое движение молекул воздуха: постоянное шипение,
восприятие которого не дало бы ни лично нам, ни виду в целом никаких дополни-
дополнительных преимуществ в борьбе за выживание. Более того, такое «суперухо» стало бы
помехой на пути эволюции, учитывая дополнительные усилия, которые должен был
бы затратить биологический вид на его развитие, защиту и подержание в рабочем
состоянии.
410 Глава Ц
Периодичность и квазипериодичность
в пространстве
Рассмотрим одномерную систему электронных спинов s, = +1
или Si = — 1, расположенных через равные промежутки вдоль одного
пространственного измерения, как это сделано в статье [14]. При на-
наличии внешнего магнитного поля Н энергия Е системы определяется
выражением
E = -Y,Hsi+Y,JijSiSj, A)
i i-ф]
где Jij — антиферромагнитное взаимодействие («7^- > 0) между спи-
спинами Si и sj, убывающее с увеличением пространственного расстоя-
расстояния \г — j\ по степенному закону
Jij = \i-j\~a B)
с показателем, например, а = 2.
Тот факт, что величина J{j положительна, означает, что соседние
спины с большей вероятностью направлены в противоположные сторо-
стороны (минимизируя, тем самым, энергию Е). Именно поэтому взаимодей-
взаимодействие типа B) принято называть антиферромагнитным. (В «ферромаг-
«ферромагнетике» соседние спины предпочитают иметь одинаковое направление,
создавая сильное внешнее магнитное поле — как в случае подковооб-
подковообразных магнитов, например.)
Если соседние спины имеют противоположные направления, то
спины, расположенные через одного, направлены, конечно же, в одну
сторону, что дает положительный, хотя и небольшой, вклад в энергию Е
(при а > 0). Таким образом, в отсутствие внешнего поля Н минимум
энергии достигается, когда число спинов, направленных вверх, состав-
составляет w = 1/2 от общего числа спинов. Выбирая в качестве начального
условия so = +1; получаем
S2k = +1 И S2U+1 = -1, C)
т.е. идеально периодическое антиферромагнитное расположение спи-
спинов.
Чертова лестница для спинов Изинга
При ненулевых значениях внешнего магнитного поля Н доля
w = 1/2 направленных вверх спинов уже не дает минимума энергии Е.
Чертова лестница для спинов Иэинга
411
m
з 0,6
x
X
CJ
I 0,4
Z 0,2
§
2 3 4 5
Магнитное поле Н/]{\)
Рис. 1. Доля направленных вверх спинов как функция от напряженности маг-
магнитного поля для спинового стекла Изинга [14].
Более того, при Н —>• ос все спины будут обращены вверх, так что w
устремится к 1. Вопрос: по какому пути?
При малых изменениях внешнего поля Н (и нулевой температу-
температуре) ни один спин не сменит ориентации; конфигурация спинов как бы
заморожена. Более того, для каждой рациональной доли w = p/q су-
существует определенный диапазон значений Н (АН (р, </)), в пределах
которого величина w остается неизменной. Вследствие этого график за-
зависимости w от Н имеет вид чертовой лестницы (рис. 1) [14, 29]. Это
и в самом деле «полная» чертова лестница (примерно с такой же мы еще
встретимся в этой главе в связи с синхронизацией двух осцилляторов).
Термин «полная» означает, что рациональные плато на рис. 1 в сумме
составляют весь интервал значений Н. Иррациональные значения w
приходятся на значения Н, образующие тонкое канторово множество,
фрактальная размерность D которого для степенных взаимодействий
вида Jij =
i — j\ a может быть определена аналитически:
A)
Плато при w = 1/2 (рис. 1) имеет относительную длину 0,44, а два
412 Глава Ц
интервала при w ф 1/2 равны: г\ = т^ = О, 28. Если чертова лестни-
лестница для одномерного «антиферромагнетика» Изинга обладала бы точным
самоподобием, то ее размерность Хаусдорфа была бы равна
D = In ТУ = 1п2= Q 54
= = Q 54
1пA/0,28)
Поскольку соотношение A) дает D = О, F) при а = 2, чертова лест-
лестница не может быть в точности самоподобной. Но плато при w = 1/3
(и еще одно — при w = 2/3) с г\ = 0,47 и г^ = 0,23 предполагает фрак-
фрактальную размерность D = 0, 59, которую получаем из соотношения для
неравных остатков (ri ф гг)
Поэтому представляется вполне разумным ожидать, что чертова лест-
лестница на рис. 1 будет асимптотически самоподобной или самоаффинной.
Это заключение подтверждается и увеличенным в 10 раз фрагментом
лестницы, показанным на вставке на рис. 1. Наибольшее плато на встав-
вставке соответствует w = 3/7.
Квазипериодические пространственные
распределения
Не обладая точным самоподобием, чертова лестница для спинов
Изинга, в лучшем случае, асимптотически самоподобна. Как же прове-
проверить самоподобие такой лестницы? Из графика на рис. 1 можно пред-
предположить, что чем больше знаменатель q в отношении w = p/q, тем
короче «замороженное» плато.
Физическое осмысление задачи ведет к такому же заключению:
знаменатель q, в конце концов, есть не что иное, как длина периода
спиновой конфигурации, а интуиция подсказывает, что чем длиннее пе-
период, тем неустойчивее конфигурация и, следовательно, короче плато.
Как расположены спины при w ф 1/2? Ответ на этот вопрос дает са-
самая, наверное, простая из всех возможных формул, удовлетворяющих
основным симметриям. Пусть w = p/q, где р и q — взаимно простые
числа (т.е. их наибольший общий делитель равен II. Тогда р из каж-
каждых q спинов должны быть направлены вверх. Точнее, р из каждых q
1В теории чисел это довольно распространенное условие принято записывать
как (р, q) = 1. В общем случае равенство (р, q) = m означает, что m — наибольший
общий делитель чисел р и q.
Квазипериодические пространственные распределения 413
последовательных спинов должны быть направлены вверх. Таким обра-
образом, конфигурация спинов должна быть периодической, причем длина
периода равна q. В пределах каждого периода ровно р спинов направ-
направлены вверх, a q — р спинов — вниз, но какие спины направлены вверх
и какие вниз? Ясно, что, например, при w = 3/7, конфигурация, в кото-
которой три спина подряд направлены вверх, а следующие четыре — вниз,
не дает минимума энергии. Чтобы уменьшить энергию, спины, направ-
направленные вверх и вниз, должны быть лучше перемешаны. Но как имен-
именно? Как показывает подробный теоретический анализ, при начальном
условии so = +1 местоположения щ направленных вверх спинов опре-
определяются простой формулой
-\k\
* = ...,-2, -1, 0, 1, 2, 3, 4, 5, ..., A)
где |_aj означает наибольшее целое число, не превосходящее а.
При w = 1/2 из формулы A) видно, что k-й направленный вверх
спин, в полном соответствии с формулой C), находится на 2к-м месте.
Соответствующие местоположения d/. спинов, направленных вниз,
определяются множеством целых чисел, дополнительным к множест-
множеству ик:
где \а] — наименьшее целое число, большее а.
Например, при w = p/q = 3/7, согласно формуле A), направленные
вверх спины находятся в местах
ик = ... , -5, -3; 0, 2, 4; 7, 9, 11; ... , C)
в то время как спины, направленные вниз, могут быть обнаружены,
согласно формуле B), в местах
dk = ... , -4, -2; -1, 1, 3, 5; 6, 8, 10, 12; .... D)
Как нетрудно убедиться, оба множества uu и dk — периодичны (длина
периода q = 7) в том смысле, что если uu = n при некоторых к, то при
каких-то других к' (к' = к + 3) мы получаем Щ' = щ + 7. Аналогично
при к' = к + 4 справедлива формула d^ = d\. + 7. Узлы щ и d\. вмес-
вместе покрывают все целые числа, причем каждое число — ровно один
раз. (Простое доказательство для иррационального w приведено в моей
книге по теории чисел [230].)
414 Глава Ц
Формулы A) и B) распределяют спины, направленные вверх
и вниз, по возможности однородно при данных ограничениях — о чем-
то подобном мы уже догадались, когда рассматривали антиферромаг-
антиферромагнетик с минимальной энергией. Действительно, из последовательнос-
последовательности C) видно, что при w = 3/7 три промежутка на один период между
направленными вверх спинами равны 2, 2 и 3. Расстояния между че-
четырьмя направленными вниз спинами на один период при w = 3/7, как
видно из последовательности D), равны 2, 2, 2 и 1. В общем случае мож-
можно показать, что поскольку расстояния между спинами должны быть
целочисленными и сумма расстояний между спинами, направленными
вверх, и спинами, направленными вниз, должна быть равна периоду q,
то расстояния, порождаемые формулами A) и B), в действительности
обладают наименьшим разбросом.
Между описанными выше устойчивыми конфигурациями спинов
и движением в фазовом пространстве простых консервативных дина-
динамических систем с двумя степенями свободы (например, двух связан-
связанных осцилляторов) существует тесная связь. В зависимости от интен-
интенсивности (или просто силы) нелинейной связи движение может быть
периодическим, квазипериодическим или хаотическим. Если частоты
двух осцилляторов соизмеримы, т. е. если осцилляторы синхронизиру-
синхронизируются с некоторым рациональным отношением частот p/q, то фазовая
траектория такой системы на поверхности тора («бублика») будет пе-
периодической с периодом q. Совершив р оборотов по другому измерению
(по «меридиану») тора, траектория замкнется. Следовательно, плоское
сечение (называемое сечением Пуанкаре), нормальное к первому изме-
измерению («параллели») тора, окажется проколотым траекторией в q раз-
различных точках под углами в\, 02, • • • , 0q.
Чтобы еще больше упростить описание, углы в), можно заменить
их знаками: например, плюсом, если 0 ^ в{ < тг, и минусом, ес-
если 7г ^ 0k < 2тг. Полагая во = 0, мы получаем последовательные пять
углов (по модулю 2тг): ^/2тг = 0, 3/5, 1/5, 4/5, 2/5. Соответствующая
последовательность знаков, называемая также символической динами-
динамикой, имеет вид + — + — + и в точности совпадает с конфигурацией
спинов в нашей антиферромагнитной системе спинов Изинга для слу-
случая, когда доля направленных вверх спинов составляет w = 3/5. Дейст-
Действительно, обращаясь к формуле A), мы видим, что направленные вверх
спины находятся на местах с номерами к = 1, 2, 3, т.е. при и\. = 1, 2, 3.
Таким образом, конфигурация спинов имеет вид + — + — +•
Учитывая тесную аналогию между траекториями, наматыва-
наматывающимися на поверхность тора в фазовом пространстве, и (ква-
Спиновая последовательность Битти 415
зи)периодическими или хаотическими пространственными конфигу-
конфигурациями (например, спиновыми конфигурациями или квазикристалла-
квазикристаллами), специалисты часто называют отношение частот w = p/q числом
вращения.
При иррациональном числе вращения w конфигурация спинов не
периодична, а квазипериодична. Например, при w = (л/5 — 1)/2 (золо-
(золотое сечение) направленные вверх спины, как показывает формула A),
располагаются в узлах одномерной решетки
ик = 1, 3, 4, 6, 8, ... , к = 1,2,3,...,
а спины, направленные вниз, как показывает формула B), — в узлах
dk =2, 5, 7, 10, 13, ....
Заслуживает внимания следующее соотношение: dk — ик = к. Каждые
два числа (щ, dk) образуют так называемую пару Битти— выигрыш-
выигрышную комбинацию при игре в фибоначчиев ним (см. с. 89).
Спиновая последовательность Битти
Если энергетически предпочтительная доля направленных вверх
спинов равна w (в общем случае w ф 1/2), то местоположения щ от-
отдельных спинов определяются последовательностью Битти (форму-
(формулой A)). Что же касается местоположений спинов, направленных вниз,
то они задаются дополнительной последовательностью Битти (форму-
(формулой B)).
Вместо последовательностей Битти для местоположений спинов,
направленных вверх и вниз, мы можем указать простую формулу для
значений самого спина. При иррациональном w справедлива формула
sm = sgnw- ((m + l)w)i, A)
где sgn(x) — функция знака числа х, {х)\ — дробная часть числа х.
При w = (л/5 — 1)/2 (золотое сечение) последовательность зна-
знаков (направлений) спинов имеет вид +, —, +, +, —, +, —, +, +, —, +,
+,—,..., и может быть получена из итерированного «кроличьего» ото-
отображения (см. гл. 13):
" ~* + B)
416 Глава Ц
Если начать с одного знака минус, то получается следующая по-
последовательность поколений и их длин Lf.
L1 = l
+ L2 = l
+ - L3 = 2
+ - + L4 = 3
H h + - ^5 = 5
и т. д. Эквивалентное правило, позволяющее получать непосредст-
непосредственно п-е поколение, состоит в приписывании (п — 2)-го поколения
к (п — 1)-му поколению. Заметим, как следствие, что длина Ln п-го
поколения удовлетворяет рекуррентному соотношению Ln = Ln_\ +
+ Ln_2- При L\ = Li = 1 это приводит к числам Фибоначчи Ln =
= 1, 1,2,3, 5, 8, 13, ....
Доля спинов, направленных вверх, в п-м поколении равна Ln-\jLn.
Как и следовало ожидать, эта величина стремится к золотому сече-
сечению (л/5-1)/2 = 0,618....
Последовательность Битти при числе вращения w = (л/5 — 1)/2
приводит к одномерному аналогу квазикристалла с осью симметрии
пятого порядка (см. гл. 13). Такая симметрия запрещена для перио-
периодических кристаллов, однако наблюдалась экспериментально в 1984 г.,
когда были открыты квазикристаллы.
Отображение B) тесно связано с разложением золотого сечения
в непрерывную дробь: (л/5 — 1)/2 = [1, 1, 1, ...] = [A)]. Для другой
простой непрерывной дроби с периодом 1, а именно, w = л/2 — 1 = [B)],
соответствующее отображение, порождающее последовательность спи-
спинов по формуле A) (т.е. последовательность — + — + — — + — +
— — +...), имеет вид
~^~+ C)
Начиная с одного знака минус, отображение C) дает следующие после-
последовательные поколения:
L1 = l
-+ L2 = 2
- Н Ь - Ьз = 5
- + -Н + -Н + L4 = 12
и т. д. Альтернативное правило для получения n-го поколения заклю-
заключается в двукратном повторении (п — 1)-го поколения и приписыва-
Спиновая последовательность Битти 417
нии к полученной последовательности (п — 2)-го поколения. Начав с —
и —1-й воспользовавшись этим правилом, получим только что пока-
показанные поколения, длина Ln которых возрастает по рекуррентному за-
закону Ln+i = 2Ln + Ln_\. При L\ = 1 и Li = 2 получим последова-
последовательность длин 1,2,5,12,29,70,169. Заметим, что отношение Ln-i/Ln
стремится к величине w = л/2 — 1. Относительное число направленных
вверх спинов также приближается к w = л/2 — 1, как и должно быть.
Вообще, из Ln спинов п-го поколения ровно ?n_i спинов направлены
вверх и Ln - Ln-i = Ln-i + Ln-2 — вниз. Отношение Ln-i/Ln стре-
стремится к w так быстро, как только возможно (при данных ограничени-
ограничениях на знаменатели). Согласно полученным значениям длин отношение,
например, 70/B9 + 70) = 70/99 = 0,70707... должно быть хорошим
приближением к 1/л/2 = 0, 70710 ... (и так оно и есть).
Подстановка w = л/2 — 1 в формулу A) порождает ту же последо-
последовательность, что и отображение C). Формулы A) и B) при w = \/2 — 1
позволяют определить соответствующие места расположения направ-
направленных вверх и вниз спинов.
В квазикристаллическом контексте квадратичное иррациональное
число л/2 — 1 = [B)] лежит в основе одномерной модели квазикрис-
квазикристалла с «запрещенной» симметрией восьмого порядка, описанной в ста-
статье [271].
Аналогично последовательность спинов при w = [C)] = (\/ГЗ —3)/2
в формуле A)
1 1 Ь - ...
может быть также порождена итерированным отображением
> Ь
D)
+ ->¦ Ь - •
Эквивалентный подход: исходя из двух начальных поколений —
и — — +, можно получить поколение с номером п > 2 трехкратным
повторением (п — 1)-го поколения и приписыванием к полученной по-
последовательности (п — 2)-го поколения. Это непосредственно следует
из того, что длина Ln п-го поколения подчиняется рекуррентному со-
соотношению Ln = 3?n_i + -Ьп_2 = 1, 3, 10, 33, 109, 360..., а отноше-
отношение Ln-i/Ln стремится к w = [C)].
Следует ли из отображения D), что число направленных вверх спи-
спинов в поколении п (jn^), деленное на общее число спинов (Ln=m++m~),
стремится к желаемой величине w = [C)]? Вне всякого сомне-
сомнения. Прежде всего заметим, что при отображении D) каждый спин
418 Глава Ц
в (п — 1)-м поколении (независимо от того, направлен он вверх или
вниз) порождает ровно один направленный вверх спин в п-м поколе-
поколении. Следовательно, m+ = Ln-\. Значит, относительное число направ-
направленных вверх спинов равно величине Ln-i/Ln, которая, как мы уже
видели, стремится к
[C)]= ^~3 =0,3027756...
Причем стремится довольно быстро. Например,
^ = Ш =0,3027777...
Lq ЗоО
В общем случае конфигурация спинов при го, равном периодичес-
периодической непрерывной дроби с периодом 1 (ш = [(п)]), определяется отобра-
отображением
где (—)™~1 означает последовательность из п — 1 знаков минус.
Для w = [(п)] справедливо соотношение
Положительное решение этого квадратного уравнения
называется серебряным сечением, так как, подобно золотому сечению,
оно представимо в виде периодической непрерывной дроби с длиной
периода 1. В особом случае п = 1 серебро превращается в золото, и мы
получаем золотое сечение w = т^ = j = (л/5 — 1)/2.
Если не настаивать на условии, требующем, чтобы члены непре-
непрерывной дроби были положительными, то мы получим второе семейство
серебряных сечений
J-=n-T- n = 2, 3, ...
Спиновая последовательность Битти 419
с единственным корнем в интервале [0, 1]
п — у/п2 — 4
тп = г
и разложением в непрерывную дробь
тп = [п~, П-, П-, ...}.
Конфигурации спинов для этих серебряных сечений также порождают-
порождаются простыми итерированными отображениями. Например, при п = 4
получаем т± = 2 — \/3 = 0,268 Подставляя т± в формулу A),
находим, что направленные вверх спины расположены в узлах ии =
= 3, 7, 11, 14, 18, Таким образом, конфигурация спинов для т±
имеет вид
F)
Чтобы определить закон отображения спинов, необходимо вычис-
вычислить подходящие приближения непрерывной дроби: 1/4, 1/D — 1/4) =
= 4/15, 16/56 и т. д., где знаменателями D, 15, 56, ...) являются длины
периода. Длина n-го поколения Ln (n > 1) определяется рекуррентным
соотношением Ln = 4Xn_i — Ln-i при том, что Lq = 0 и L\ = 1.
Отделяя подпоследовательности с такими длинами периодов запятыми
(см. конфигурацию спинов F)), получаем отображение
которое, начиная с одного знака минус, порождает последовательные
поколения
L1 = l
- - + - L2 = 4
Н Н Н + - L3 = 15
и т. д. в поразительном согласии с конфигурацией спинов F).
Серебряное сечение т4~ = 2 — \/3 лежит в основе квазикрис-
квазикристаллов с запрещенной симметрией двенадцатого порядка, открытых
в 1988 г. [33].
Все серебряные сечения т^ (т^), где N — число Люка с чет-
четным (нечетным) индексом, принадлежат полю иррациональных чи-
чисел Q(\/5) и являются основой для квазикристаллов с осями симметрии
420 Глава Ц
пятого порядка. Числа Люка (Ln = 2, 1, 3, 4, 7, 11, 18, ...) определяют-
определяются тем же рекуррентным соотношением, что и числа Фибоначчи (Ln =
= Ln-i + Ln-2), но с другим начальным условием (Lq = 2, L\ = 1).
При п > 1 число Люка Ln может быть получено округлением j~n до
ближайшего целого числа.
Разумно предположить, что в общем случае отображение при т~
имеет вид
где (—)п 2 означает последовательность, состоящую из п — 2 минусов.
Возможно, читатель пожелает испробовать свои силы и самостоятельно
доказать следующий эквивалентный закон: при первых двух поколени-
поколениях—и (—)"~2 Н—, к-е поколение получается в результате (п — ^-крат-
^-кратного повторения предыдущего (к — 1) поколения и приписывания к по-
полученной последовательности (к — 1)-го поколения, из начала которого
исключено (к — 2)-е поколение.
Законы подобия для квазипериодических спинов
Формула A) позволяет вычислять знак любого спина непосред-
непосредственно, без обращения к рекурсии. Например, при w = (\/ГЗ —3)/2
1000-й спин имеет знак +. С другой стороны, самый факт того, что
при w, представимом в виде периодической непрерывной дроби [(п)],
антиферромагнитные спины Изинга могут быть вычислены рекурсив-
рекурсивно с помощью итераций некоторого отображения, свидетельствует о су-
существовании у таких спиновых конфигураций определенной масштаб-
масштабной инвариантности. Так и есть; более того, они демонстрируют мно-
многочисленные самоподобия.
Рассмотрим подробнее конфигурацию спинов при числе враще-
вращения w, равном золотому сечению. Выраженная в двоичных обозначе-
обозначениях {0, 1}, она представляет собой кроличью последовательность:
1011010110110.... A)
Бесконечная кроличья последовательность воспроизводит себя, если
каждый раз (начиная слева), встречая единицу, мы будем перепрыги-
перепрыгивать через два знака и вычеркивать третий, а встречая нуль, перепры-
перепрыгивать только через один знак и вычеркивать второй. Знаки, оставши-
оставшиеся от исходной последовательности после такой сумасшедшей скачки
Самоподобные числа вращения 421
и вычеркивания, в последовательности A) подчеркнуты, причем усе-
усеченная последовательность в самом деле воспроизводит исходную кро-
кроличью последовательность. Конфигурация, образуемая длинными и ко-
короткими линиями подчеркивания также дает кроличью последователь-
последовательность, хотя бы по построению. Поразительнее всего то, что и выбро-
выброшенные (неподчеркнутые) знаки тоже образуют исходную кроличью
последовательность. Можете ли Вы, читатель, объяснить почему?
Как видно из последовательности A), все эти «прыжки» через
двоичные знаки в действительности представляют собой отображе-
отображение 101—>10и10—>1. Такое «переименование блоков» (с которым мы,
кстати, уже встречались раньше) обратно отображению 1—^10—^101
(т.е. следующей итерации исходного отображения 0—^1—^10).
Переименование блоков 101—>10и10—>1 соответствует прос-
простому преобразованию подобия индекса к с коэффициентом w. Точнее,
индекс к в формуле для направленных вверх спинов A) заменяется
на к' = k/w, и спины сдвигаются в сторону на одну единицу:
Но, по формуле B), значения \_k/w2\ = [k/(l — w)\ = \k/(l-w)~\ -1
определяют места d*, в которых первоначально располагались спи-
спины, направленные вниз. Таким образом, в конфигурации спинов после
преобразования подобия, произведенного посредством переименования
блоков, оставшиеся направленные вверх спины расположены на одно
место левее исходных направленных вниз спинов. В самом деле, как
следует из формулы A), оставшиеся направленные вверх спины — это
как раз те, что имеют соседом справа нуль. Все остальные направлен-
направленные вверх спины «не пережили» процесса построения новой последова-
последовательности.
Предоставляем читателю самостоятельно доказать, что оставши-
оставшиеся направленные вниз спины располагаются на одно место левее ис-
исходных направленных вверх спиновых дублетов 11 (плотность кото-
которых w3 = \/5 — 2 = 0, 236 ..., как и плотность сохранившихся направ-
направленных вниз спинов).
Самоподобные числа вращения
Скейлинговый закон для антиферромагнитных спинов Изинга
можно также вывести из формулы A), которая описывает последова-
422 Глава Ц
тельность спинов в обозначениях ±1:
sm = sgn[w - ((то + l)w)i].
Ясно, что число sm никак не изменится от прибавления к стояще-
стоящему в угловых скобках ()i выражению любого целого числа, напри-
например, п(т + 1):
sm=sga[w-{(m + l)(w + n)I]. A)
Если число w равно золотому сечению, то w + 1 = 1/w. Следовательно,
при п = 1
sm = sgn[w- ((m + 1)-
откуда следует, что если подвергнуть индекс т+1 преобразованию
подобия с коэффициентом 1/w2, то конфигурация спинов останется не-
неизменной.
Какие еще числа вращения обнаруживают такого рода самоподо-
самоподобие? Соотношение A) показывает, что индекс т+1 можно преобразовы-
преобразовывать с коэффициентом подобия 1/w2 при любом w, для которого верно
равенство w+n = 1/w, где п — положительное или отрицательное целое
число. (Заметьте, что {а)\ = а— \а\ принадлежит интервалу [0,1), так
что если а, например, равно —4,7, то {а)\ = (—4,7)i = 0,3.) При поло-
положительных п эти числа вращения в точности совпадают с теми числа-
числами, которые представимы в виде периодических непрерывных дробей
с периодом 1:
w = т+ = [(п)], п > 0.
Это уравнение можно записать как
w=—^+-; B)
n + w v '
именно в таком виде оно необходимо нам для масштабной инвариант-
инвариантности соотношения A).
При положительных п, как уже было установлено, квадратное урав-
уравнение B) имеет следующее решение:
п >
При отрицательных п два корня уравнения лежат вне «законного»
интервала @, 1) для w. Но мы можем все-таки получить самоподобное
Отображения окружности и языки Арнольда 423
решение, а именно,
w = Тп = [(п-)], п < -1.
Решение, которое попадает в интервал @, 1), имеет вид
л/п2 - 4 + п
n < -2. C)
Числа т+ и т~ представляют собой серебряные сечения (еще одно
обобщение золотого сечения, с которым нам уже доводилось встречать-
встречаться прежде).
Как перевести скейлинговый закон для формулы, определяющей
расположение спинов A), в скейлинговый закон для спинов, направлен-
направленных вверх? Иначе говоря, как нужно изменить формулу A), чтобы она
позволяла определять, где находятся направленные вверх спины, уце-
уцелевшие после процесса усечения блоков при п > 1?
Отображения окружности и языки Арнольда
Наряду с квадратичным отображением, рассмотренным в гл. 12,
весьма важную роль при моделировании великого множества природ-
природных явлений играет другой нелинейный закон — знаменитое отобра-
отображение окружности:
"п+1 — "п "Г " " — q— olllt ATVUfi I. V /
Здесь К — константа связи, регулирующая степень нелинейности;
при К = О уравнение A) становится линейным. Переменная вп пред-
представляет собой угол (обычно в фазовом пространстве динамической
системы). Среднее приращение (инкремент) угла вп за одну итерацию
называется реальным числом вращения и определяется как
w = lim -^—-—-. B)
п—>оо
Параметр п в уравнении A) называется формальным числом вращения.
Столь необычная терминология связана с тем, что интересующее нас
фазовое пространство часто имеет вид тора, на который накручивается
траектория (совершая некоторое число оборотов, или вращений, вдоль
меридианов и параллелей тора). В типичном случае формальное число
424 Глава Ц
вращения представляет собой отношение частот (например, отношение
резонансной частоты осциллятора — скажем, маятника — и частоты
периодической силы, воздействующей на этот осциллятор). Реальное
число вращения w — это также отношение частот (как правило, рацио-
рациональное число, w = P/Q), при котором некое нелинейное взаимодейст-
взаимодействие «синхронизировало» систему. Разумеется, при К = О реальное чис-
число вращения w совпадает с формальным числом вращения О, и никакой
синхронизации мод при рациональном числе вращения w не происходит.
Однако при К = 1 (так называемое критическое отображение окруж-
окружности) области синхронизации покрывают весь интервал значений О
(см. рис. 7 в гл. 7), оставляя несинхронизированным только канторово
множество значений О. Эти области синхронизации получили назва-
название языков Арнольда в честь открывшего их российского математика
В.И.Арнольда.
Критическое отображение окружности имеет при вп = 0 кубичес-
кубическую точку перегиба и может быть аппроксимировано отображением
071+1 = "+ ~3~У7И (•>)
гДе \вп\ ^ 1- Большинство результатов, полученных для критическо-
критического отображения окружности, можно назвать универсальными, так как
они относятся ко всем отображениям, содержащим кубическую нели-
нелинейность с горизонтальной касательной. Похожую универсальность мы
наблюдали в случае унимодальных отображений с квадратичным мак-
максимумом. Взятые вместе, квадратичное и кубическое отображения мо-
моделируют многие нелинейные явления, характеризуемые либо симмет-
симметричной (четной), либо несимметричной (нечетной) нелинейностью.
При К > 1 отображение окружности немонотонно, и языки Ар-
Арнольда перекрывают друг друга, порождая хаотическое движение. По-
Подобно тому, как переход к хаосу в квадратичном отображении можно
проследить по бифуркациям удвоения периода, путь к хаосу в кри-
критическом отображении окружности может быть проанализирован по
орбитам с возрастающей длиной периода. Только в последнем случае
предпочтительные длины периода совпадают с числами Фибоначчи Fn,
а реальные числа вращения w (или 1 — w) — с отношениями соседних
чисел Фибоначчи. При п —>¦ оо эти числа вращения стремятся к золото-
золотому сечению.
Далее будет показано, что даже важнейшие символические дина-
динамики этих двух прототипических нелинейностей подобны.
Отображения окружности и языки Арнольда 425
На рис. 6 (гл. 7) показано реальное число вращения w = P/Q как
функция от формального числа вращения О для критического отобра-
отображения окружности. График имеет вид чертовой лестницы с горизон-
горизонтальными плато при всех рациональных значениях параметра w (в от-
отличие от чертовой лестницы на основе исходного канторова множества,
имеющей плато только при w = P/Q, где Q = 2т). Хотя строгой са-
самоаффинности, как в случае канторовой чертовой лестницы, здесь не
наблюдается, чертова лестница синхронизации, как видно на вставке,
обладает приближенной самоаффинностью.
Ширина плато имеет явную тенденцию к убыванию при увеличе-
увеличении значения Q — периода синхронизированного по частоте движения.
Это представляется интуитивно понятным, так как синхронизация мод
происходит преимущественно при отношениях частот, представимых
в виде отношения небольших целых чисел (например, отношение часто-
частоты обращения Меркурия вокруг Солнца к частоте его обращения вокруг
собственной оси равно 2/3).
На рис. 2 представлена зависимость ширины плато ДО от от-
отношения P/Q [120], в немалой степени самоподобная, судя по встав-
вставкам. Как обнаружили авторы статьи, ДО изменяется как Q в степе-
степени 1п(Д0)/1п<3 » -2,292.
Фрактал, образуемый теми значениями О, при которых не проис-
происходит синхронизации мод, является, в действительности, мулътифрак-
талом с размерностями Dq, лежащими в интервале от D-^ ss 0,924
до D^o =0,5. В гл. 9 мы уже упоминали о том, что размерность D-^
соответствует наиболее разреженной области фрактала, расположенной
в данном случае в окрестности формального числа вращения п, равного
золотому сечению — наиболее трудному для синхронизации отноше-
отношению частот. Как показал Шенкер, длины г а изменяются асимптотичес-
асимптотически по закону F~s ~ ¦у116, где 6 = 2,1644..., при О = Fn-\/Fn, n —>¦ ос
(путь к хаосу через золотое сечение) [240]. Если вероятности заданы
как рп ~ 72п иг„~ 7n<i1 то
D-x = lim -j^ = | и 0,924.
n-юо lnrn 6
Наиболее плотная область фрактала синхронизации расположена
сразу справа от интервала, синхронизированного при отношении час-
частот, равном нулю (вблизи от О = 1/2тг), т.е. там, где отношения час-
частот 1/Q приближаются к нулевому значению при <5 —>¦ сю. Это при-
приближающееся к нулю отношение представляет собой так называемый
426
Глава 14
0,3 -
0,2
а
<
0,1
0,5
P/Q
Рис. 2. Зависимость синхронизированных по частоте интервалов от отноше-
отношения частот. Обратите внимание на самоподобие, показанное с помощью по-
последовательного увеличения отдельных участков построения [120].
гармонический ряд, при котором синхронизация мод происходит срав-
сравнительно легко. Для гармонического ряда изменения реальных чисел
вращения асимптотически пропорциональны квадратному корню из из-
изменений формального числа вращения, т.е. рп ~ rj . Отсюда строгое
равенство D^ = 0,5.
Весь мультифрактальный спектр / (а) был вычислен по 1024 син-
синхронизированным интервалам в статье [41]. Максимум функции f (а)
приближенно равен 0,868 и соответствует размерности Хаусдорфа Do
для мультифрактала, лежащего в основе чертовой лестницы синхрони-
синхронизации.
Медианты, последовательности Фарея и дерево
Фарея
Для вычисления размерностей Dq фрактала синхронизации и его
мультифрактального спектра / (а) необходимо навести какой-никакой
порядок в рациональных числах P/Q, представляющих различные отно-
отношения частот. Одно из возможных упорядочений используется в стан-
Медианты, последовательности Фарея и дерево Фарея 427
дартном доказательстве того, что рациональные числа (в противопо-
противоположность иррациональным) образуют счетное множество. Однако сей-
сейчас нам необходимо другое упорядочение, которое бы лучше отражало
физику синхронизации мод.
Предположим, что параметр О в уравнении A) (формальное чис-
число вращения) таков, что реальное число вращения попадает в интервал
между 1/2 и 2/3, не синхронизируясь ни с одним из этих отношений.
Каково наиболее вероятное синхронизирующее отношение частот для
силы нелинейной связи чуть ниже той, которая вызвала бы синхрони-
синхронизацию при отношении частот 1/2 или 2/3? Разумно предположить, что
таким отношением должно быть отношение частот P/Q с наименьшим
возможным Q в интервале A/2, 2/3).
Именно это и происходит в динамических системах, моделируемых
отображением окружности. Выберем постоянную нелинейной связи К
и формальное число вращения п так, чтобы соответствующая им точка
располагалась чуть ниже пересечения двух языков Арнольда, символи-
символизирующих синхронизацию при отношениях частот 1/2 и 2/3. Реальное
число вращения w для данной точки на плоскости ?}-К должно быть
рациональным, так как К > 1. На самом же деле рациональное значе-
значение P/Q, принимаемое числом вращения w, удовлетворяет неравенст-
неравенству 1/2 < P/Q < 2/3 с наименьшим из всех возможных знаменателем Q.
В связи с этим возникает интересный математический вопрос,
ответ на который прост, но необычен: какое отношение из интерва-
интервала от 1/2 до 2/3 имеет наименьший знаменатель? Если вы попросите
дошкольника сложить 1/2 и 2/3, то он вполне может сложить отдельно
числители, отдельно — знаменатели и написать равенство
Самое удивительное, что, поступая таким образом, он действительно
найдет искомое отношение частот с наименьшим знаменателем1.
1Нечто подобное произошло, когда знаменитый индийский физик Ш.Н.Бозе
A894-1974) при выводе статистики фотонов «забыл» учесть различимость фото-
фотонов (в природе не существующую). Когда журнал «Nature» отверг его работу, Бозе
направил ее Эйнштейну, который узрел свет во тьме, признав в «ошибке» коллеги
долгожданное решение проблем статистической физики света. С тех пор имя Бозе
увековечено в таких понятиях, как статистика (или распределение) Бозе-Эйн-
Бозе-Эйнштейна, бозоны (частицы с целочисленным спином — фотоны, например) и конден-
конденсация Бозе, которой мы обязаны сверхпроводимостью и другими макроскопичес-
макроскопическими чудесами микроскопического квантового мира.
428 Глава Ц
Что бы мог означать столь странный способ образования проме-
промежуточных дробей? Физически отношение частот двух осцилляторов,
равное 1/2, можно представить комбинацией импульса A) и последу-
последующего «отсутствия импульса» @) более быстрого осциллятора в тече-
течение каждого периода более медленного осциллятора. То есть отношение
частот 1/2 может быть представлено последовательностью 101010...,
или просто A0). Аналогично отношение частот 2/3 представляется дву-
двумя единицами, повторяющимися с периодом 3, или A10).
Чтобы образовать промежуточное отношение частот, мы просто
чередуем отношения частот 1/2 (т.е. A0)) и 2/3 (т.е. A10)) и получа-
получаем последовательность A0110), представляющую отношение частот 3/5
(три импульса за каждые пять единиц времени). Таким образом, при
усреднении отношений частот взятие медиант (так называется эта опе-
операция) вовсе не выглядит таким уж странным делом.
В общем случае, если имеются две дроби P/Q и P'/Q' с взаим-
взаимно простыми числителями и знаменателями, то промежуточная дробь
определяется соотношением
Q" ~ Q + Q1'
Специалисты по теории чисел называют такую дробь медиантой. Ана-
Анализируя диофантовы уравнения, Джон Хортон Конуэй с присущей ему
проницательностью показал, что числители и знаменатели можно ин-
интерпретировать как компоненты двумерного вектора, а промежуточ-
промежуточную дробь с наименьшим знаменателем можно получить покомпонент-
покомпонентным сложением векторов [не опубликовано; из личной беседы A989)].
Так, например, медианта дробей 5/13 и 2/5 равен 7/18 (отношение час-
частот, которое Юпитер и Паллада выбрали для своих гравитационно свя-
связанных орбит вокруг Солнца). (Вообще говоря, между 5/13 и 2/5 просто
нет ни одной дроби со знаменателем, меньше 18.) Чтобы это правило
работало, две исходные дроби должны быть достаточно близки. Точнее,
они должны быть унимодулярными. Модулярность двух дробей с взаим-
взаимно простыми числителями и знаменателями P/Q и P'/Q', служащая
мерой их близости (для нашего случая), измеряется как абсолютная
величина разности \QP' — PQ'\. Унимодулярными называются дроби,
для которых \QP' - PQ'\ = 1.
Медианта двух дробей имеет такую же модулярность, какую ис-
исходные дроби имеют между собой: модулярность передается по наслед-
наследству. Вообще, наследование является одним из центральных свойств са-
Медианты, последовательности Фарея и дерево Фарея 429
моподобия, и самоподобия, которые обнаруживаются в синхронизации
мод, не являются исключением.
Медианты естественным образом возникают в последовательнос-
последовательностях Фарея. Последовательностью Фарея называется последователь-
последовательность дробей из интервала от 0 до 1 с заданным наибольшим знаме-
знаменателем (называемым порядком последовательности). Например, дроби
Фарея порядка 5 образуют следующую последовательность (в порядке
возрастания):
01112132341
1543525345 1"
Заметим, что каждая дробь является медиантой двух соседних дро-
дробей. Модулярность любых двух соседних дробей равна 1, но расположе-
расположены дроби неравномерно. Однако знаменитая гипотеза Римана о нулях
дзета-функции гарантирует, что расстояния между соседними дробями
относительно равномерны [230].
Хотя последовательности Фарея имеют множество полезных при-
приложений и занятных свойств (например, они позволяют классифициро-
классифицировать рациональные числа по величине их знаменателей. Да что там —
есть целые книги, не содержащие ничего, кроме дробей Фарея), они об-
обладают одним существенным недостатком: число дополнительных дро-
дробей при переходе от последовательности Фарея порядка п-1 к после-
последовательности порядка п задается сильно флуктуирующей функцией
Эйлера ф(п), определяемой как количество положительных целых чи-
чисел, меньших п и взаимно простых с п. Например, фE) = 4, ^>F) = 2,
а фG) = 6. Более регулярный характер рациональным числам прида-
придают деревья Фарея, в которых количество дробей, добавляемых каждым
поколением, равно соответствующей степени двух.
Начав с двух дробей, мы можем построить дерево Фарея, вычисляя
медианты всех численно близких («соседних») дробей. В интервале [0, 1]
можно начать с 0/1 и 1/1 в качестве начальных дробей, или «затравок».
Первые пять поколений дерева Фарея выглядят следующим образом:
0 I
1 1
1
2
1 2
3 3
12 3 3
4 5 5 4
12334554
57877875
430 Глава Ц
В бесконечном дереве Фарея каждое рациональное число, заключенное
между 0 и 1, встречается ровно один раз. Структура дерева в точнос-
точности соответствует интерполяции с помощью медиант, синхронизирован-
синхронизированных по частоте интервалов в отображении окружности. Таким образом,
дерево Фарея является своего рода математическим скелетом языков
Арнольда.
Положение каждой дроби на дереве Фарея может быть определено
двоичным адресом, в котором 0 соответствует сдвигу влево при пере-
переходе с п-го уровня на (п + 1)-й, а 1 — сдвигу вправо. Например, если
начать с 1/2, то рациональное число 3/7 имеет двоичный адрес 011.
Дополнение дроби 3/7 до единицы (т.е. дробь 4/7) имеет двоичный ад-
адрес 100 (дополнительный к адресу дроби 3/7). Такой двоичный код
рациональных чисел полезен при описании связанных осцилляторов.
Заметим, что любые две численно соседних дроби дерева Фарея
унимодулярны. Таковы, например, дроби 4/7 и 1/2, так как 2 • 4 —
-1-7 = 1.
Некоторые свойства дерева Фарея становятся более понятными,
если воспользоваться непрерывными дробями, которые для чисел w из
интервала [0, 1] имеют следующий вид:
w =
1
а2 Н
аз---
Непрерывные дроби удобнее записывать в строку w = [а\, п2, аз, ...],
где aj. — положительные целые числа. Непрерывные дроби, выражаю-
выражающие иррациональные числа w, бесконечны. В случае квадратичных ир-
иррациональных w числа aj. (начиная с какого-то места) повторяются пе-
периодически. Например, 1/л/З = [1, 1, 2, 1, 2, 1, ...] = [1, A, 2)] — пред-
периодическая непрерывная дробь с длиной периода 2; дробь l/vTf =
= [(8)] имеет период 1, а 1/\/бТ — период 11. (Очень действует на нервы
то, что до сих пор неизвестно никакого простого правила, которое поз-
позволяло бы предсказывать длину периода непрерывной дроби в общем
случае.)
Интересно, что для любой дроби на п-м уровне дерева Фарея сумма
всех чисел аи равна п:
\ аи = п, п = 2, 3, 4, ...
Медианты, последовательности Фарея и дерево Фарея 431
Предоставляем читателю самостоятельно доказать справедливость это-
этого равенства (например, с помощью простого комбинаторного рассуж-
рассуждения).
Для каждой дроби на (п — 1)-м уровне можно непосредственно вы-
вычислить две соседние дроби, или, иными словами, «прямых потомков»
на п-м уровне. Сначала нужно записать исходную дробь в виде непре-
непрерывной дроби двумя способами, что всегда возможно: для этого доста-
достаточно «отщепить» от последнего аи единицу. Например, 2/5 = [2, 2] =
= [2, 1, 1]. Затем необходимо прибавить к последнему члену каждой
из двух полученных непрерывных дробей единицу. Это дает две дро-
дроби [2, 3] = 3/7 и [2, 1, 2] = 3/8, которые действительно являются «пря-
«прямыми потомками» числа 2/5.
И наоборот, непосредственного предшественника любой дроби (то-
(того, что находится на предыдущем уровне) можно найти, вычитая еди-
единицу из последнего члена ее разложения в непрерывную дробь (в той
форме, в которой последний член больше единицы, так как аи в не-
непрерывной дроби не может быть равен 0). Другой (отдаленный) пред-
предшественник данной рациональной дроби может быть найден простым
выбрасыванием последнего члена. Например, у дроби 3/7 = [2, 3] име-
имеются два предшественника: прямой [2, 2] = 2/5 и отдаленный [2] = 1/2.
(Какой из предшественников, в общем случае, больше — ближайший
или отдаленный? И как вычислять медианты, используя только непре-
непрерывные дроби?)
Заметим, что если спускаться зигзагообразно по дереву Фарея из
правого верхнего «угла» A/1 —>¦ 1/2 —>¦ 2/3 —>¦ 3/5 —>¦ 5/8 и т.д.), то
мы будем каждый раз попадать на дроби, числители и знаменатели ко-
которых равны числам Фибоначчи Fn, определяемые соотношением Fn =
= Fn-i +Fn-2] Fq = 0, F\ = 1. Точнее говоря, начав с 1/1 и пройдя п-й
поворот зигзага, мы достигнем дроби Fn+i/Fn+2- При п —>¦ оо такая
дробь стремится к золотому сечению 7 = (л/5 — 1)/2 = 0,618... [230].
(Начав с 0/1, мы будем проходить через дроби Fn/Fn+2, которые стре-
стремятся к 72 = 1 — 7-) Золотое сечение 7 имеет на дереве Фарея двоичный
адрес 101010...
Разложение отношений Fn/Fn+i в непрерывные дроби выглядит
весьма просто. Например,
W = 1 = t1' !' Ч'
а в общем случае
w
= [1, 1, ... , 1], п единиц в квадратных скобках.
Fn
+1
432 Глава Ц
Очевидно, что при малых а\, непрерывные дроби сходятся относительно
медленно, причем медленнее всего сходятся те дроби, у которых все а\,
равны единицам. Так как
7= lim ^- = [1, 1, 1, •..] = [(!)],
где круглые скобки означают бесконечное повторение единицы, золотое
сечение 7 обладает самым медленно сходящимся из всех иррациональ-
иррациональных чисел разложением в непрерывную дробь. Поэтому физики и им
подобные люди иногда называют золотое сечение «самым иррациональ-
иррациональным из иррациональных чисел». Это свойство 7 имеет исключительно
важные последствия в самых разнообразных проблемах нелинейной фи-
физики — от двойного маятника до проблемы трех тел.
Ситуация приблизительно такова: если отношение частот двух свя-
связанных осцилляторов есть рациональное число P/Q, то связь между
вынуждающей силой и «порабощенным» осциллятором проявляется осо-
особенно эффективно из-за своего рода резонанса: через каждые Q циклов
внешнего воздействия возникает одна и та же физическая ситуация,
так что эффекты перекачки энергии нарастают резонансоподобным об-
образом. Этот резонансный эффект весьма силен, особенно если Q — ма-
малое целое число. Именно это произошло с Луной: резонансная переда-
передача энергии между Луной и Землей, осуществляемая посредством при-
приливных сил, замедлила вращение Луны вокруг собственной оси до та-
такой степени, что период ее вращения синхронизировался с 28-суточным
циклом обращения Луны вокруг Земли. В результате Луна всегда обра-
обращена к нам одной своей стороной, которая, кстати, слегка покачивается
из стороны в сторону (так называемая либрация).
Аналогично частота обращения Меркурия вокруг собственной оси
и частота его обращения вокруг Солнца синхронизировались при ра-
рациональном отношении 3/2. В результате день на Меркурии длится два
меркурианских года. (Когда-нибудь — надеюсь, не скоро — нечто по-
подобное может приключиться и с матушкой-Землей.)
Еще одно следствие этого резонансного механизма — кольца Сатур-
Сатурна, или, вернее, щели между ними. Периоды обращения вокруг Сатур-
Сатурна любых материальных тел (глыб льда или камня), попавших в щели
между кольцами, находятся в рациональном резонансе с некоторой пе-
периодической силой (например, с силой притяжения со стороны одной
из лун Сатурна — «пастухов» колец). В результате воздействие даже
слабых сил, постепенно накапливаясь на протяжении длительных вре-
временных промежутков, выметает весь мусор из этих самых щелей.
Медианты, последовательности Фарея и дерево Фарея 433
При рациональных отношениях частот с большими знаменателя-
знаменателями Q резонансный эффект относительно слаб, а при иррациональных
отношениях резонанс еще слабее или вообще отсутствует.
Если связь между осцилляторами достаточно сильна, то даже ир-
иррациональные отношения частот могут дать неплохой резонанс. Однако
одно иррациональное отношение частот всегда будет менее всех других
подвержено возмущениям — это золотое сечение. Дело в том, что ра-
рациональная аппроксимация золотого сечения с некоторой определенной
точностью требует наибольших знаменателей Q. Это свойство золото-
золотого сечения находит отражение и в дереве Фарея: на каждом уровне п
двумя дробями с наибольшими знаменателями являются Fn-i/Fn+i
и Fn/Fn+i, которые при п —>¦ оо стремятся, соответственно, к -у2 =
= 0,382... и 7 = 0,618... (И наоборот, дроби с наименьшими знаме-
знаменателями Q на некотором данном уровне дерева Фарея принадлежат
гармоническим рядам 1/Q и 1 — 1/Q.)
Еще один способ продемонстрировать уникальное положение зо-
золотого сечения среди иррациональных чисел основан на теории ра-
рациональной аппроксимации, составляющей важную часть теории чи-
чисел. Чтобы получить хорошую рациональную аппроксимацию, иррацио-
иррациональное число w необходимо разложить в непрерывную дробь и обо-
оборвать разложение на n-м члене, что приводит к рациональному чис-
числу [а\, п2, ... , ап] = Рп/Яп- Вообще говоря, такого рода рациональ-
рациональная аппроксимация иррационального числа w будет наилучшей при
данном максимальном знаменателе qn. Например, для w = 1/тг =
= [3, 7, 15, 1, 293, ...] и п = 2 мы получаем pn/qn = 7/22, и как бы
вы ни старались, вы не найдете лучшего приближения к 1/тг со знаме-
знаменателем, меньшим 22.
Даже при той оптимальной аппроксимации, которую дают непре-
непрерывные дроби, погрешности
_ ElL
для золотого сечения -у превышают cjq2n (где с — постоянная, мень-
меньшая 1/л/5, но бесконечно близкая к нему) при всех значениях п, боль-
больших некоторого щ. Сказанное верно только для золотого сечения -у
и «благородных чисел» (определяемых как иррациональные числа, раз-
разложения которых в непрерывные дроби заканчиваются только единица-
единицами). Таким образом, согласно этому точному определению, золотое се-
сечение (равно как и благородные числа) отстоит от рациональных чисел
дальше, чем любое другое иррациональное число. Поэтому не вызывает
434 Глава Ц
особого удивления тот факт, что золотое сечение играет исключительно
важную роль в проблемах синхронизации.
Рис. 3. Визуальная интерпретация золотого угла. (Печатается по [212] с лю-
любезного разрешения Т. Грамсса.)
Взглянув на рис. 3, мы сможем составить визуальное представле-
представление о золотом сечении. Перед вами построенное с помощью компьютера
изображение «подсолнечника», использующее в качестве углового при-
приращения при размещении (г„, фп) семян, где
(Гп, Фп) = (СГ„_1, фп-! + Аф),
шаг, равный золотому углу Аф = 360°7 ~ 225,5°. При таком постро-
построении получается довольно реалистичная картина расположения семян
подсолнечника (левая часть рис. 3) [212]. Но если выбрать в качест-
качестве приращения угол Аф = 222,4°, который всего лишь на 0,04% от-
отличается от золотого угла, то человеческий глаз отчетливо различит
отдельные спирали (правая часть рис. 3) — феномен психовизуальной
синхронизации!
Путь к хаосу через золотое сечение
Для критического отображения окружности
вп+1 = 9п + п-± нтBтгвп) A)
Путь к хаосу через золотое сечение 435
последовательность синхронизирующих отношений частот P/Q, сов-
совпадающая с последовательностью отношений соседних чисел Фибонач-
Фибоначчи Fn-i/Fn = [1, 1, ... , 1], представляет собой во многих смыслах наи-
наиболее интересный путь к апериодическому поведению переменной вп
и детерминированному хаосу. При переходе к хаотическому движе-
движению эти отношения частот (и эквивалентные им, например, Fn-2JFn =
= [2,1,1,..., 1]) обычно оказываются последними, не затронутыми
возрастающей степенью нелинейной связи. Под хаотическим здесь, как
и всегда, подразумевается то, что первоначально близкие значения в
в процессе эволюции системы во времени экспоненциально расходятся,
утрачивая какую бы то ни было предсказуемость.
Отношения Fn_i/Fn и Fn_2JFn лежат на зигзагообразной линии
в структуре дерева Фарея (см. предыдущий раздел), стремясь к золо-
золотому сечению 7 или его квадрату 1 —7 = 72> соответственно. Каждая из
дробей является медиантой двух предшествующих. Например, последо-
последовательность дробей Fn_2/Fn, начинающаяся с рациональных чисел 0/1
и 1/2, имеет вид 1/3, 2/5, 3/8, 5/13, 8/21, ... В записи соответству-
соответствующих непрерывных дробей, начиная с 1/2, с каждым новым членом
добавляется единица: [2], [2, 1], [2, 1, 1], [2, 1, 1, 1], [2, 1, 1, 1, 1] и т.д.,
вплоть до [2, A)] = 72-
Значение параметра О, который задает реальное число вращения,
равное отношению частот Fn-2/Fn, должно быть определено численно.
Простая программа для калькулятора, позволяющая подогнать п с та-
таким расчетом, чтобы при во = 0 выполнялось равенство Врп = Fn_2,
дает следующие приближенные значения параметра О:
П(|)=О,5
!) =0,3516697
|) =0,4074762
П (!) =0,3882635
A) =0,3951174
ii) =°>3927092
||) =0,3935608
и т.д., которые сходятся к Ооо и 0,3933377.
436 Глава Ц
Представленные выше значения приводят к сверхустойчивым ор-
орбитам, так как итерации вп включают в себя нулевое значение, при
котором производная критического отображения окружности обраща-
обращается в нуль. Следовательно, эти значения п соответствуют сверхустой-
сверхустойчивым значениям Rn квадратичного отображения, а 0^ соответству-
соответствует Roo.
Существует ли здесь универсальная постоянная, аналогичная по-
постоянной Фейгенбаума, которая характеризовала бы скорость сходи-
сходимости значения параметра Ога = ?}(Fn/Fn-i) к Ооо при п —>¦ ос? Ре-
Результаты расчетов позволяют надеяться, что существует, и что значе-
значения разности между последовательными значениями Ога уменьшаются
асимптотически с коэффициентом 8:
где S = —2,8336... (эта величина, таким образом, соответствует по-
постоянной Фейгенбаума 4,6692 ...). Отрицательное значение 6 означает,
что знаки последовательных разностей чередуются.
Итерации переменной вп демонстрируют и другие проявления са-
самоподобного скейлинга. Например, при О = ?}(Fn-2/Fn) значения раз-
разности Of,,-! — Fn-z сходятся к нулю в асимптотически геометрической
прогрессии:
0Fn-i ~ гп-z ~ а ,
где а = —1,288575..., что соответствует коэффициенту подобия
—2,5029... для итерируемой переменной квадратичного отображения.
Обе постоянные а и S универсальны для отображений, содержащих
кубическую точку перегиба с горизонтальной касательной. Это следует
из теории ренорм-групп для перехода таких отображений к хаосу че-
через золотое сечение. Функциональное уравнение функции неподвижных
точек для перенормированного кубического отображения имеет вид
f(x) = af(af(x/a2)).
(Соответствующее функциональное уравнение для перехода квадратич-
квадратичного отображения к хаосу через удвоение периода выглядит очень по-
похоже: g(x) = ag(g(x/a)), см. с. 355.)
Оба этих прототипических перехода к хаосу сходны еще в одном —
в их символической динамике. При О = ?l(Fn-2/Fn) и К = 0
Путь к хаосу через золотое сечение 437
Рассмотрим вп mod 1 в интервале (—0,5; 0,5] и будем записывать сим-
символ L при вп < 0, С при вп = 0 и R при вп > 0. Тогда, положив во = О,
мы получим при п —>¦ оо следующую символическую динамику:
CRLRRLRLRRLRRL...
Если не считать начального С, эта последовательность представляет
собой не что иное, как хорошо знакомую нам кроличью последова-
последовательность, в которой единица заменена символом R, а нуль — сим-
символом L. При К = 1 истинные значения итераций отличаются от зна-
значений при К = 0, но символические динамики задаются той же самой
последовательностью.
Как нам стало известно из обсуждения квазикристаллов в гл. 13,
эта последовательность может быть построена с помощью отображе-
отображения 0—^1, 1 —>¦ 1 0, или, в наших теперешних обозначениях, L —>¦ R,
R —>¦ RL. И снова мы можем наблюдать значительное сходство с пе-
переходом к хаосу через удвоение периода, символические динамики для
которого порождаются отображением L —>¦ RR, R —>¦ L R. Более того,
оба перехода к хаосу — и через золотое сечение, и через удвоение пе-
периода — рассматриваются в рамках единой теории ренорм-групп [202].
При конечных п символическая динамика может быть получена
из формулы для положений спинов Изинга (см. с. 412-414). Например,
для реального числа вращения P/Q = 3/8 положения символа L опре-
определяются формулой B) для направленных вниз спинов с 1 — w = 3/8,
а именно 2, 5, 7. Значит, символическая динамика сверхустойчивой ор-
орбиты с отношением частот 3/8 имеет вид СRLRRLRL — начальный
восьмичленный отрезок бесконечной последовательности.
При числе вращения P/Q = 2/5 символическая динамика, вычис-
вычисленная по вышеприведенному алгоритму, имеет вид СRLRL, причем
ее последний символ отличается от соответствующего символа беско-
бесконечной последовательности. Вообще, при Q = F2k+i на последнем месте
стоит L, а не R, как на соответствующем месте бесконечной последо-
последовательности. Однако эта небольшая неувязка вызвана не внешними,
а внутренними причинами. От нее нетрудно избавиться, если рассмат-
рассматривать вп mod 1 не в интервале (—0,5; 0, 5), а в интервале, слегка сдви-
сдвинутом, т.е. (—ж, 1-х), где х и 0,4461583 — решение трансцендентного
уравнения х = О^ + (sin27ra;)/27r.
Апериодические итерации вп критического отображения окруж-
окружности при реальном числе вращения, равном золотому сечению -у, об-
образуют мультифрактал со спектром сингулярностей f (а), представ-
438
Глава 14
4-0,6 -
0,2 -
Рис. 4. Мультифрактальный спектр критического отображения окружности
при числе вращения, равном золотому сечению [121].
ленном на рис. 4. Такой же спектр получается при всех эквивалент-
эквивалентных золотому сечению числах, т.е. при тех иррациональных числах,
представления которых в виде непрерывных дробей завершаются толь-
только единицами, — так называемых благородных числах (см. Приложе-
Приложение Б). Этот спектр был вычислен для периодической орбиты с дли-
длиной периода Q = 2584 = Fis- Расстояния r^ = 6k+F±7 — 6k mod 1 были
взяты за масштаб длины мультифрактала, а параметр pj. был выбран
равным 1/2854. Размерность D-^ для наиболее разреженной области
мультифрактала была вычислена ранее Шенкером по упоминавшемуся
выше показателю скейлинга а = — 1, 288575 ... и оказалась равной
B_tc = _J?1_ «i,898.
Наиболее плотная область мультифрактала характеризуется показате-
показателем а3, что дает наименьшую размерность ?>00=?>_00/3 и 0,6327 [240].
Некоторые из приложений, связанных с пространственной и вре-
временной синхронизацией и хаосом, частично освещены в следующих ра-
работах: акустика — [141], динамика солнечной системы — [138, 278, 11],
физическая химия — [265], астрофизика — [100], твердотельная элек-
электроника — [166, 26, 92, 38], кардиология — [34], турбулентность —
[121, 69] и нелинейные механические осцилляторы — [3, 181].
Глава 15
Перколяция: от лесных пожаров до
эпидемий
За наблюдением всегда стоит теория.
Эдвин Хаббл
Функция эксперта состоит не в том, что-
чтобы быть правым, когда остальные ошиба-
ошибаются, а в том, чтобы ошибаться по более
сложным причинам.
Дэвид Батлер
Перколяция (просачивание) буквально пронизывает всевозможны-
всевозможными способами как окружающий нас естественный мир, так и рукотвор-
рукотворные к нему дополнения. В кофеварке, например, вода перколирует, т. е.
просачивается сквозь размолотые зерна кофе, а мы на выходе получаем
восхитительный напиток.
Не вставайте пока из-за стола. Поговорим о вареных яйцах — чем
дольше они варятся, тем больше белковых связей сцепляется между
собой, и вскоре образуются мостики, пронизывающие все яйцо, от чего
оно твердеет, а вы получаете возможность спокойно есть его ложечкой,
не опасаясь пролить.
С другой стороны — и к счастью для нас — эпидемии не всегда
«просачиваются» сквозь все население целиком. Существует такое поня-
понятие, как порог перколяции, оказавшись ниже которого, эпидемия сходит
на нет прежде, чем сойдет на нет большинство людей. Яйцо всмятку —
еще один пример процесса, происходящего ниже порога перколяции.
В более грандиозном масштабе теория перколяции, красноречи-
красноречиво изложенная Дитрихом Штауффером [249], вносит весьма солидный
вклад в лучшее понимание процесса образования отдельных галактик
и скоплений галактик. На противоположном конце шкалы просачива-
просачивание проникло в микроскопический мир — до масштабов атомных ядер.
Например, деление ядер рассматривается теперь с точки зрения теории
перколяции [31].
440 Глава 15
Еще один знаменитый и излюбленный авторами пример просачи-
просачивания — лесной пожар. Что произойдет, если поджечь несколько де-
деревьев: сгорит весь лес, или к тому моменту, когда огонь затухнет,
большинство деревьев останутся стоять?
На пороге перколяции (который был явно превышен при самовозго-
самовозгорании леса в 1988 г. в Йеллоустонском национальном парке) существу-
существует множество статистических самоподобий, и именно эти самоподобия
позволяют построить математическую теорию перколяции и приводят
к простым законам подобия на пороге перколяции или вблизи него.
Теория перколяции может рассматриваться и как хорошая подго-
подготовка к исследованию более сложных физических явлений — таких,
например, как фазовые переходы в магнитных материалах и в термо-
термодинамике в целом. Например, корреляционная длина направлений спи-
спина в разреженном «ферромагнетике» становится бесконечной на пороге
перколяции, который в физике называется критической точкой, или
точкой Кюри. Это означает, что в образце появляются кластеры маг-
магнитных доменов, сравнимые с ним по размеру. Вообще говоря, возника-
возникают кластеры всех размеров, или масштабов длины, причем эти класте-
кластеры самоподобны. Во всем диапазоне размеров, от атомных расстояний
до размеров образца, кластеры выглядят похожими, а после приведения
к одному масштабу становятся стохастически неотличимыми.
Ниже порога перколяции {выше точки Кюри для магнетиков) су-
существуют только кластеры конечных размеров: жидкость не просачи-
просачивается сквозь кофейную гущу, а кусок железа обладает только «пара-
«парамагнитными» свойствами. Однако выше порога перколяции (ниже точ-
точки Кюри) бесконечные кластеры становятся обычным делом со всеми
вытекающими отсюда последствиями: лесной пожар накроет весь лес
от края до края, эпидемия перейдет в пандемию, а железо станет фер-
ферромагнетиком. Что касается ближайших окрестностей порога перколя-
перколяции, то здесь безраздельно властвует самоподобие!
Итак, познакомимся более подробно с одним из самых ярких при-
примеров из теории перколяции — лесными пожарами, с которыми люди
неустанно сражаются, а они по-прежнему полыхают.
Критическое возгорание на квадратной решетке
Предположим для простоты, что лес можно моделировать квад-
квадратной решеткой, в узлах которой располагаются деревья с вероятнос-
вероятностью р < 1 (рис. 1). Подожжем нижний ряд деревьев и посмотрим, как
распространяется огонь по мере того, как цифровые часы отсчитывают
дискретное время.
Критическое возгорание на квадратной решетке 441
Предположим также, что горящее дерево за единицу времени под-
поджигает всех своих ближайших соседей. За следующую единицу времени
дерево сгорает дотла.
Сложное компьютерное моделирование [249] подтверждает очевид-
очевидное: если концентрация деревьев рс находится ниже некоторой крити-
критической величины, пожар затухает прежде, чем огонь достигает про-
противоположного края леса (верхнего ряда деревьев на рис. 1). И наобо-
наоборот, при р > Рс огонь достигает противоположного края леса (а если
бы лес тянулся дальше, пожар угрожал бы уничтожить и остальные
деревья).
При р <€. Рс лес абсолютно пожаробезопасен, а при рси1 представ-
представляет собой естественную пороховую бочку, однако самое интересное
происходит на пороге перколяции, т.е. при р ~рс, или при
Оказывается, что при г -С 1 критические параметры подчиняются
простым законам подобия, отражающим самоподобие просачивания
вблизи порога, или критической точки (позаимствуем термин из фи-
физики фазовых переходов).
Обозначим через Z (n, t, e) отношение числа деревьев в n-м ряду
решетки, сгоревших дотла к моменту времени t, к среднему числу де-
деревьев в ряду. Предполагается, что параметры п и t много больше еди-
единицы. Данные численного анализа [249] показывают, что вблизи порога
(т. е. при е <$; 1) параметр порядка Z является однородной (обобщенной)
функцией от своих аргументов:
Z(Xn,X4,Xe)
Z(n,t,s) = , A)
п > 1, t » 1, s <€. 1.
Иначе говоря, Z есть некоторая универсальная функция, изменяющая-
изменяющаяся по закону A), с тремя показателями скейлинга: ап, at и ае [88]. Что
еще можно сказать об этой важной функции? Если подождать доста-
достаточно долго (т.е. при t —> сю) и уйти достаточно далеко (п —> сю), то
соотношение A) принимает следующий вид:
Z(oo, сю, ?)= V ' '-. B)
442
Глава 15
ффф ффф ф фф
ф ффффффффф ф
4 Н Ф ФФ Ф
ффф ф фф фффффф
ф фффффф ф ф фф ф
ффффф ф ффф ффф ф
ффф ф ф ф ффф
ф ф ф фф ффф фф
ф фф ФФФФ
(А)
ффф ффф ф
ф ффффффффф
ф фф Ф Фф
ффф ф фф ффф
ф фффффф ффф
ФФФ Ф
фф ф фффффф
ф фффффф
фф ф ффф
Ф Ф
Ф Ф „
ФФ __
фф
ф
ф
ффф
ф ф
ф
(Б)
Рис. 1. (А) Квадратная решетка, случайным образом засаженная деревьями;
плотность деревьев соответствует порогу перколяции. Нижний ряд деревьев
подожжен. (Б) Некоторое время спустя: занялись соседние деревья. (В) По-
Пожар достиг верхнего края леса. (Г) Пожар прекратился; большинство деревь-
деревьев сгорело. (Печатается с любезного разрешения X. Беме.)
Критическое возгорание на квадратной решетке 443
........
¦ ...
(В)
-i. —1_ ^,
Допустив, что функция Z(oo, сю, е) зависит от е по степенному закону,
т.е.
Z (сю, сю, е) = const • е'3, C)
444 Глава 15
получим из B) равенство е@ = (Aae?)^/A, или а? = 1//3. Показатель /3
называется критическим показателем, и нам только что удалось свя-
связать его с одним из показателей скейлинга ае.
Введем еще два параметра: характеристическую длину (например,
корреляционную) ? и характеристическое время в. Известно, что и ?,
и в расходятся при е —> О в соответствии с простыми степенными за-
законами:
D)
в = const -s~s. E)
Приведем зависимость Z (n, t, e) от е к этим характеристическим ве-
величинам и запишем (в порядке рабочей гипотезы)
F)
где функция g зависит только от двух переменных. Чтобы выполнялся
исходный закон подобия A), показатель х должен быть равен — /3/гл
Теперь мы связали все три показателя скейлинга в соотноше-
соотношении A) с тремя критическими показателями /3, v, S, характеризующи-
характеризующими, как Z, ? и в изменяются в зависимости от г вблизи критической
точки (г <?С 1).
Обозначим через
С = n-Plv
характеристическое число сгоревших деревьев. Тогда функциональное
уравнение F) можно записать в виде
Z (n, t, e)
С
=«(!•!)• <7»
Это наиболее симметричный и практичный способ записи степенной
зависимости Z от п и t, а с учетом формул C)-E) — йоте. Из этих
формул, в частности, видно, что при изменении параметра р (т.е. е)
мы можем получить новые значения функции Z (n, t, e) из той же са-
самой «универсальной» функции g, просто умножив ее на n~^/v', апи(,
соответственно, на г~" и e~s.
Универсальность 445
Универсальность
Уже довольно давно я установил для себя
такое правило: всякий раз, когда теоре-
теоретик заговаривает об «универсальности»,
я считаю это чистой чепухой.
Вольфганг Паули
Критические показатели v и S необходимо определять аналитичес-
аналитически или с помощью численного моделирования на компьютере, и мы
предоставляем критически настроенному читателю попытаться сде-
сделать это на своем компьютере. Самое удивительное состоит в том, что
для огромного множества задач в физике, химии, биологии и многих
других научных дисциплинах критические показатели не зависят от
конкретных деталей, а только от размерности пространства вложения
(равной двум в случае квадратной решетки) и от количества «степе-
«степеней свободы» рассматриваемой переменной (например, спин, который
может быть направлен вверх или вниз, имеет две степени свободы,
столько же степеней свободы у дерева, которое может сгореть или не
сгореть).
Такого рода универсальность является одной из наиболее горячо
обсуждаемых тем в современной физике и порождает немало жгучих
вопросов. Например, такой: как расходится данное случайное блужда-
блуждание на фрактальной решетке типа ковра Серпинского, скажем, вбли-
вблизи критической точки (порога перколяции)? Или такой: как проводят
электрический ток фрактальные цепи? И наконец: как зависит скорость
распространения пожара от концентрации р деревьев?
Из формул D), E) и G) следует, что величина Z/C, остается неиз-
неизменной, если п изменяется со временем t по закону
п = const • tv/s.
Следовательно, средняя скорость распространения пожара, которую
можно измерить, например, по продвижению фронта огня, изменяется
со временем как tv/s~1. Подсчитав количество только что загоревшихся
деревьев в компьютерной модели (сохраним леса и кислород!), можно
легко определить отношение двух критических показателей и/S [2].
На рис. 2А приведен один из результатов численного моделирова-
моделирования, выполненного Альбине и сотрудниками, в котором среднее поло-
положение фронта пожара дано как функция от времени в двукратно лога-
логарифмических координатах. В этом эксперименте решетка имеет раз-
446
Глава 15
мер 200 х 200 точек, а концентрация деревьев находится вблизи кри-
критического значения для квадратной решетки, рс и 0,593. Т.е., в общей
сложности, Альбине располагал для поджигания 23 720 деревьями.
X
о
•е-
ш
К
X
X
с
(А)
Ln (время)
х
X
са
ш
Оч
о
с
(Б)
Ln (время)
Рис. 2. (А) Среднее положение фронта пожара как функция от времени горе-
горения. Допустив, что эта функция представляет собой степенную зависимость,
получим прямую с угловым коэффициентом 0,87. (Б) Количество сгоревших
деревьев как функция от времени. Угловой коэффициент 0,79 [2].
Нашему допущению о степенной зависимости вполне соответству-
соответствует прямая с угловым коэффициентом и/8 = 0,87. Неудивительно по-
поэтому, что распространение лесного пожар превосходит по скорости
диффузию (угловой коэффициент 0,5), но оказывается медленнее, чем
продвижение огня по бикфордову шнуру (угловой коэффициент 1,0).
Универсальность 447
Отклонения от прямой при очень малых значениях времени объ-
объясняются остаточными эффектами расположения деревьев, подожжен-
подожженных первыми, а при больших — эффектами «насыщения» (т.е. полнос-
полностью выгоревшими участками леса).
Общее число сгоревших деревьев
Nb (t, e) = const • У^ Z (n, t, e)
изменяется со временем как t^v ^l6. Таким образом, простой, не огра-
ограниченный какими-либо условиями, подсчет приводит к отношению
(v — /3)/6, или /3/E, так как отношение и/8 уже определено. На рис. 2Б
показан результат другого компьютерного эксперимента. И в этом слу-
случае после того, как окончательно сойдут на нет начальные эффекты,
зависимость числа сгоревших деревьев от времени в двукратно лога-
логарифмических координатах имеет вид прямой с угловым коэффициен-
коэффициентом (i/ - /3)/5 = 0,79.
Третий критический показатель /3 определяется из формулы C),
т. е. путем подсчета мертвых деревьев после окончания пожара. Ре-
Результаты численного моделирования оказались весьма чувствитель-
чувствительны к ошибке выборки: /3 = 0,12 ± 0,03; теоретическое значение /3 =
= 5/36^0,139 [249].
Показатель /3 весьма мал — как и следовало ожидать, учитывая,
что доля сгоревших деревьев не так сильно зависит от е, как скорость
распространения пожара.
Еще один показатель, который можно вычислить аналитически, —
это показатель v, управляющий корреляционной длиной D); он ра-
равен 4/3 (точно). При v = 4/3 и и/8 = 0,87 критический показатель вре-
времени 8 равен 1,533, что близко к значению, найденному Петером Грас-
сбергером [86]. Следовательно, при е —> 0 характеристические времена
расходятся быстрее, чем корреляционные длины. Это имеет смысл, так
как при р, меньших рс, но близких к нему (т.е. при г <$; 1), может
случиться так, что огонь будет гореть в течение длительного периода
времени после остановки фронта пожара. Как хорошо известно лесным
пожарным, огонь распространяется не только вперед, но и назад.
Интересно отметить, что все критические показатели {у, 8 и /3),
как оказалось, не зависят от числа взаимодействующих соседних эле-
элементов. Значения этих показателей одинаковы в следующих трех слу-
случаях: во взаимодействии принимают участие только 4 ближайших со-
соседа на квадратной решетке, 8 соседей в квадрате 3x3 или 24 соседа
в квадрате 5x5.
448 Глава 15
Эта инвариантность иллюстрирует то, что мы назвали универсаль-
универсальностью: критические показатели зависят только от размерности вло-
вложения (d = 2) и количества степеней свободы (также 2) для всех трех
координационных чисел.
Что же касается критических концентраций рс, то они бывают раз-
различными. Например, для трех вышеупомянутых координационных чи-
чисел экспериментальные значения критических концентраций равны, со-
соответственно, рс = 0, 592745; 0,407355 и 0,168. Это неудивительно, так
как огонь может перебрасываться не только на ближайших соседей, но
и на деревья, стоящие за ними, или на те, что стоят еще дальше, и т. д.
Таким образом, даже сравнительно широкие просеки в лесу не могут
считаться непреодолимым препятствием на пути огня.
Критическая концентрация
На рис. 3 представлена зависимость среднего времени прекраще-
прекращения лесного пожара too от концентрации деревьев р для квадратной
решетки 300 х 300. Расходимость вблизи р = рс я» 0,593 выражена
вполне отчетливо и согласуется с теоретическим предсказанием too —
= const • |?|~т, где т и 1,5 [249].
Аналогичное поведение с тем же значением показателя т наблюда-
наблюдается и в треугольных решетках, за исключением того, что рси0,5 —
в точном соответствии с теоретическим предсказанием для критичес-
критической концентрации (рс = 0,5).
Треугольная решетка принадлежит к тем решеткам, для кото-
которых удается получить аналитическое решение. Другим примером ана-
аналитически разрешимой решетки может служить решетка Бете (см.
гл. 16), называемая в теории графов деревом Кэли: порог перколя-
ции рс в точности равен l/(z — 1), где z — число ближайших со-
соседних элементов. Как можно судить по рис. 3, компьютерное мо-
моделирование с изменением р является хорошим способом определе-
определения рс: в критической точке р = рс у многих параметров наблюдает-
наблюдается острый пик. В физике такие пики (в зависимостях удельной теп-
теплоемкости, например, или магнитной восприимчивости от темпера-
температуры) сигнализируют о фазовых переходах второго рода. Вообще го-
говоря, просачивание — это тоже фазовый переход, только гораздо бо-
более чистый и четко выраженный, чем «средний» термодинамический
фазовый переход, анализ которого может оказаться делом довольно
«пыльным».
Фрактальные периметры просачивания
200 г
150
449
к
S
ш
DQ
100
50
0,4
0,5
Р
0,6 0,7
Рис. 3. Среднее время прекращения пожаров как функция от плотности де-
деревьев. Обратите внимание на расходимость вблизи критической плотнос-
плотности Р и 0, 593 [249].
Фрактальные периметры просачивания
Распространяется ли лесной пожар ровным фронтом, подобно гре-
греческой фаланге? Или в этом фронте имеются выступы и впадины?
Имеются, уверяю вас. Более того, линия фронта имеет фрактальную
структуру с размерностью Хаусдорфа D, заключенной между 1 и 2. На
первый взгляд, похожая картина наблюдается в таком явлении как про-
проникновение, известном также под названием образование вязких языков,
которое имеет отношение к добыче нефти, и на которое нефтяная про-
промышленность возлагала большие надежды, особенно в 70-е годы, когда
запасы нефти «временно» истощились (см. гл. 9). Однако вязкие язы-
языки образуются вследствие неустойчивости поверхности раздела двух
жидкостей. Что же касается фрактальной структуры фронта лесного
пожара, то ее причина кроется в связности — т. е. в соседстве деревьев.
Конечномерный скейлинг
Какие сведения о фрактальной размерности / периметра объятого
пламенем участка леса можно извлечь из численного моделирования
лесных пожаров? Если определить периметр как число F выгоревших
участков, каждый из которых граничит хотя бы с одним невыгорев-
невыгоревшим, и построить график зависимости этого числа от размера решет-
решетки L, то мы получим простой степенной закон, называемый конечно-
450 Глава 15
мерным скейлингом [249]:
F = const • L*,
где / = 1, 75 для всех трех окрестностей; близость этого значения к 2
как-то тревожит, ведь топологически размерность периметра должна
быть равна единице. (Не следует, впрочем, забывать о том, что наше
определение периметра включает в себя и границы внутренних оази-
оазисов — невыгоревших участков леса.)
Другая фрактальная размерность, d, описывает число М сгорев-
сгоревших деревьев. Если сгорают все деревья (или какая-то определенная
доля от их общего количества), то М будет пропорционально общему
количеству деревьев или площади решетки: М = const • L2. Но вблизи
порога перколяции все иначе. Конечномерный скейлинг здесь описыва-
описывается другим степенным законом, а именно:
М = const • L1, A)
где d к, 1,9 — несколько меньше двух, так как на сцене все еще при-
присутствуют невыгоревшие участки леса. После прекращения пожара вы-
выгоревшие участки образуют нечто вроде двумерной губки (или швей-
швейцарского сыра) с множеством пустот в различных масштабах длины.
Штауффер [249] также приводит интересную взаимосвязь между
разностью фрактальной размерности d и размерности вложения d, с од-
одной стороны, и критическими показателями /3 и v — с другой:
d-d=%. B)
При d = 2, /3 = 5/36 и v = 4/3 соотношение B) дает d = 91/48 —
в превосходном согласии с экспериментальными данными (рис. 4).
Разумеется, вдали от критической точки зависимость числа сго-
сгоревших деревьев от г очень слаба. Значит, показатель /3 стремится
к нулю (см. формулу C)), a d —t d (согласно соотношению B)), чего
и следовало ожидать, так как лесные пожары фрактальны только вбли-
вблизи критической точки е <С 1.
Собственно говоря, вдали от критической точки корреляционная
длина во много раз меньше размеров леса (или магнита). Поэтому М
изменяется не как Ld с фрактальным показателем d (см. формулу A)),
а вполне «евклидовым» образом: М = const • Ld, где d — евклидова раз-
размерность пространства вложения. Короче говоря, просачивание фрак-
фрактально только вблизи критической точки; выше или ниже ее оно де-
демонстрирует классическое евклидово поведение.
Конечномерный скейлинг
451
КГ -
Рч
1 102 104
Размер решетки
Рис. 4. Размер наибольшего скопления на пороге перколяции в треугольной
решетке как функция от размера решетки. Угловой коэффициент прямой со-
согласуется с теоретической фрактальной размерностью 91/48 [249].
Еще одну фрактальную размерность, d, можно определить из за-
зависимости времени проникновения too от размера леса L:
too = const • Ld.
Результаты численного моделирования подтверждают этот степенной
закон и дают значение d к, 1,16, достаточно хорошо согласующе-
согласующееся с предсказанием, согласно которому характеристические значе-
значения времени изменяются пропорционально длинам, возведенным в сте-
степень и/5 = 1,159.
В этой главе мы занимались в основном лесными пожарами, однако
почти такие же законы управляют распространением эпидемий, обра-
452 Глава 15
зованием галактик, делением атомных ядер и бесчисленными другими
процессами [128].
Перколяция — весьма широкое понятие; как следствие, теория пер-
коляции способна объяснить множество ситуаций, которые кажутся, на
первый взгляд, совершенно различными. Поскольку просачивание по
сути своей геометрично, оно упрощает анализ сложнейших конфигура-
конфигураций и текстур, позволяя обойтись без излишних физических усложне-
усложнений. А самоподобие, господствующее в критических точках, способст-
способствует успешному раскрытию взаимосвязей между подобием и фракта-
фракталами.
Глава 16
Фазовые переходы и перенормировка
Является ли использование лишь пере-
перенормируемых взаимодействий попыткой
природы что-то нам сообщить?
Хайнц Пагельс
Понятия перенормировки и самоподобия тесно взаимосвязаны. Бо-
Более того, перенормировка по праву может считаться одним из наиболее
плодотворных применений самоподобия. В физике теории ренорм-групп
позволили пролить свет на нелинейную динамику и загадки фазовых
переходов в самых различных областях — от низкотемпературных про-
процессов до ферромагнетизма, спиновых стекол и самоорганизации [93].
Откуда берутся загадочные дробные показатели, описывающие по-
поведение процессов вблизи критических точек, и почему эти показатели
так часто совпадают в ситуациях, казалось бы, весьма далеких друг
от друга? И что же кроется за малыми целыми числами, в которых
они так нуждаются? На многие из подобных вопросов за последние
два десятилетия были найдены ответы благодаря работам Лео Кадано-
ва, Майкла Фишера и, в особенности, Кеннета Уилсона, удостоенного
за свои исследования Нобелевской премии по физике. Среди наиболее
впечатляющих фазовых переходов, получивших исчерпывающее объ-
объяснение, можно назвать критическую опалесценцию, при которой про-
прозрачная среда в критической точке становится оптически непрозрач-
непрозрачной из-за так называемой «мягкой моды», рассеивающей свет наподобие
густого дыма в накуренном помещении.
Мы лишь бегло коснемся упомянутой темы, не теряя, однако, на-
надежды на то, что разбросанные ниже редкие капли окажутся в состоя-
состоянии передать божественный букет.
Марковский процесс первого порядка
Марковским процессом называется стохастический процесс, в кото-
котором настоящее зависит от прошлого только на протяжении конечного
454 Глава 16
числа поколений. В марковском процессе первого порядка часть прошло-
прошлого, влияющая на настоящее, ограничена одним предыдущим поколени-
поколением: настоящее полностью определяется непосредственно предшествую-
предшествующим ему прошлым.
Такие процессы часто представляют с помощью диаграмм состо-
состояний (рис. 1) с различными вероятностями перехода. Рассмотрим, на-
например, простой марковский источник первого порядка, изображен-
изображенный на рис. 1. Если последним символом, порожденным источником,
был +1, то мы находимся в левом состоянии (помеченном знаком +),
а р есть вероятность порождения еще одного знака +. Этому событию
соответствует искривленная стрелка, начинающаяся и заканчивающа-
заканчивающаяся в левом состоянии.
р+_=1-р
Р++=Р
Рис. 1. Марковский процесс первого порядка с двумя состояниями (+ и —)
и четырьмя вероятностями перехода.
Источник может с вероятностью 1—р породить символ —1 и тем
самым скачкообразно перейти в правое состояние, помеченное зна-
знаком —. В этом состоянии источник с вероятностью q порождает еще
один знак —1 и, следовательно, остается в правом состоянии, или же
с вероятностью 1 — q порождает символ +1 и скачком возвращается
в левое состояние.
При р = q энтропия Нм такого марковского источника имеет вид
Нм = -plog2p - A - р) Iog2(l - p) (бит на выходной символ).
Как выясняется, она совпадает с энтропией Н (р) двоичного источника
без памяти с вероятностями р и 1 — р для двух возможных символов
на выходе. В этом совпадении легко убедиться, моделируя марковский
источник первого порядка с р = q в виде источника нулевого порядка
(т.е. источника без памяти), который изменяет полярность выходного
сигнала (т. е. заменяет + на — или — на +) с вероятностью 1 — р и не
Самоподобные и несамоподобные марковские процессы 455
изменяет полярность с вероятностью р. Выходные символы от обоих
источников могут быть обратимо преобразованы друг в друга (не счи-
считая общего изменения знака) и поэтому должны обладать одинаковой
энтропией.
Самоподобные и несамоподобные марковские
процессы
При р = q изображенный на рис. 1 марковский источник порожда-
порождает символы +1 или —1 с равной вероятностью. При р = 1/2 последо-
последовательные символы на выходе независимы: наш автомат превращается
в «беспамятного» бросателя «честной» монеты1. Выходная последова-
последовательность символов может служить примером статистически самопо-
самоподобного процесса: вычеркните каждый второй символ, и вы получите
усеченную последовательность, статистически неотличимую от исход-
исходной, потому что она снова состоит из независимых символов +1 и —1,
каждый из которых встречается с вероятностью 1/2.
Однако при р ф 1/2 самоподобие нарушается. Соседние выборки
коррелированы, и когда мы вычеркиваем часть символов, корреляция
между остальными символами ослабевает.
Более того, взглянув еще раз на рис. 1, мы обнаружим, что при р =
= q > 1/2 вероятность появления после любого данного символа та-
такого же символа выше, чем вероятность появления противоположного.
При р = q < 1/2 возникает обратная ситуация: символы предпочитают
чередоваться.
При р = q корреляция Ст между двумя символами sn и sn+m,
порождаемыми изображенным на рис. 1 источником, определяется вы-
выражением
JV
Ст = Jim — Vsnsn+m. A)
n=\
Так как наш марковский источник является стационарным и эр-
годическим при 0 ф р ф 1, усреднение по «времени» в соотношении A)
можно заменить средним ожиданием по ансамблю, которое мы обозна-
обозначим угловыми скобками:
Ст = \Snsn+m)-
1Не путать с забывчивым, но честным бросателем монеты (не обязательно
«честной»).
456 Глава 16
Для Ci, усредняя по четырем различным возможностям
—h, ), получаем:
При р = 1/2, как и следовало ожидать, С\ = 0. Заметим, что С\ < 0
при р < 1/2.
Запишем типичную «случайную» последовательность, порожден-
порожденную вашим покорным слугой, выступающим в роли закоренелого сто-
стохастического генератора (не используя никаких механических или
электронных устройств):
+ + - + h - + Н- + + + + -.
По случайному совпадению эта последовательность содержит равное
число знаков + и —. Выборочная корреляция равна —3/19, что позволя-
позволяет дать оценку параметра вероятности р = 8/19 и 0,42. Так как я на-
намеревался построить последовательность с р = 1/2, можно заключить,
что я «не дотянул» до намеченной цели около 16% — типичная чело-
человеческая ошибка. Пытаясь генерировать независимые двоичные собы-
события, большинство людей-генераторов случайных чисел ведут себя как
марковские источники с р < 1/2. Людям очень трудно быть истинно
случайными — они слишком часто изменяют знаки (еще один типич-
типичный недостаток; Клод Шеннон весьма остроумно использовал его в сво-
своей «угадывающей машине» [237], которая описана на с. 205-206 нашей
книги).
Скейлинг символов, порожденных марковским
источником
Поскольку в марковском процессе первого порядка настоящее пол-
полностью определяется непосредственно предшествующим прошлым, ко-
коэффициенты корреляции можно получить из соотношения
Ст = С? = Bр - 1)т
или, если ввести новый параметр /3, определяемый как
при р>1, A)
из соотношения
П —
Скейлинг символов, порожденных марковским источником 457
Вычеркнем каждый второй символ из последовательности, порож-
порожденной нашим марковским источником. Полученную в результате по-
последовательность можно интерпретировать как порожденную другим
марковским источником с другим параметром р (при р ф 1/2). Коэф-
фициент корреляции Ст усеченного процесса равен квадрату коэффи-
коэффициента корреляции исходного процесса:
М2) _ A _ р2 _ -20т
°т — °2т — L-m — 6
Мы видим, что наш параметр /3 удвоился. Это означает (см. A)), что ве-
вероятность нового перехода изменилась ср на р^2\ гдерB) определяется
из соотношения 2р^ — 1 = Bр — IJ, или
рB) = 2р2 - 2р + 1.
Упомянутое выше значение р = 8/19 ра 0,42 изменяется в этом слу-
случае на рB) ss 0,51. Если мы снова удалим каждый второй символ
(т.е. каждый четвертый символ исходной последовательности), то по-
получим С{т] = С4т = Ст и pW = 0,5003 (при р = 0,42). По мере того,
как мы будем вычеркивать все больше и больше промежуточных сим-
символов, рB") при п —> оо устремится к 1/2 сверху (значение 1/2, как
нам известно, описывает независимые символы).
Таким образом, несмотря на то, что порожденная нашим марков-
марковским источником последовательность не самоподобна (за исключением
случая с р = 0,5 или 1 при неотрицательном С\), умножение индекса
выходной последовательности Sk на г порождает усеченную последова-
последовательность sTk, что эквивалентно переходу к выходной последователь-
последовательности другого марковского источника с перенормированным парамет-
параметром ^г\ где /3(г) = г/3. Следовательно, параметр /3 изменяется по тому
же закону, что и индекс.
Параметр 1//3^ имеет физический смысл корреляционной длины,
которая стремится к нулю при г —^ сю. Это еще раз подтверждает тот
факт, что «вычеркивание» членов последовательности ослабляет корре-
корреляцию. В других ситуациях (как мы вскоре увидим) параметр /3 может
быть также идентифицирован с температурой.
Вместе с периодическими симметриями, проявляющимися в про-
пространственных вращениях и других периодических явлениях, симмет-
симметрия относительно преобразования подобия, с которой мы только что
познакомились, принадлежит в настоящее время к числу наиболее важ-
важных симметрии в физике и других областях человеческой деятельнос-
деятельности. Изобретательный голландский художник Мориц Эшер A898-1972)
458 Глава 16
в некоторых своих графических работах удачно соединил обе эти фун-
фундаментальные симметрии.
В физике перенормировка привела к ставшим ныне поистине везде-
вездесущими теориям ренорм-групп. В качестве типичного примера приме-
применения этих теорий можно привести такой: попытаемся вывести, исходя
из фундаментальных принципов, критический показатель а удельной
теплоемкости с (Г), скажем, вблизи критической температуры Тс. Как
показывают измерения, здесь выполняется простой степенной закон
типа
с(Т)-с(Тс)ъ\Т-Тс\-а.
Рассматривая подобные проблемы, мы всякий раз убеждаемся, что по-
показатель а не зависит от конкретной ситуации, а может быть одина-
одинаковым для самых различных физических систем: воды, гелия, ксенона
или любой другой жидкости вблизи критической точки жидкость-газ1.
В таких случаях принято говорить, что соответствующие системы по-
попадают в один и тот же класс универсальности, который, как правило,
зависит лишь от двух безразмерных величин: размерности пространст-
пространства, в котором происходит процесс, и числа степеней свободы параметра
порядка.
Разумеется, большинство физических систем настолько сложны,
что приходится полагаться лишь на достаточно простые модели реаль-
реальности — такие, например, как одна из простых моделей спиновых сис-
систем, названная в честь известного физика Изинга, родившегося в Гер-
Германии. В модели Изинга спины принимают лишь два возможных значе-
значения («вверх» и «вниз»), и обычно предполагается, что взаимодействуют
между собой только соседние спины («связь между ближайшими сосе-
соседями»).
Марковский источник первого порядка, рассматриваемый нами
в этой главе, соответствует одномерной модели Изинга. В этой модели
Изинга существуют две «критические температуры»: Тс = 0, при кото-
которой все спины направлены в одну сторону (что соответствует полнос-
полностью коррелированному случаю в марковской модели, /3 = 0), и Тс = сю,
при которой все спины ориентированы совершенно беспорядочно (что
соответствует случаю /3 = сю).
1При тщательно контролируемых условиях можно довести жидкость и до со-
состояний за критической точкой, получив в результате надкритическую жидкость.
Такие жидкости находят многочисленные полезные применения. Например, надкри-
надкритическая вода может быть использована для экстракции кофеина из зерен кофе, не
изменяя его вкуса (в отличие от химических растворителей).
Перенормировка и иерархические решетки 459
Компьютерное моделирование трехмерной модели Изинга дает сле-
следующее соотношение для среднего спонтанного намагничивания:
М ~ (Тс - Tf при Т < Тс,
где /3 = 0,325. Такой же показатель получается для всех трехмерных
систем с только одной степенью свободы параметра порядка (одно из
двух возможных направлений спина в модели Изинга).
Перенормировка и иерархические решетки
Для того, чтобы можно было применить перенормировку к атом-
атомной решетке, эта решетка должна быть подобна себе в том смысле,
в каком самоподобны снежинки фон Коха и другие фракталы. Чтобы
построить решетки, обладающие таким свойством, необходимо начать
с инициатора — например, с двух спиновых узлов (к = 1) — и генера-
генератора (к = 2) (рис. 2А). Следующая итерация порождает уже «решетку»
(к = 3 на рисунке). Такие самоподобные решетки в данном контексте
называются иерархическими [48, 194, 195].
В случае антиферромагнитной решетки спины на концах инициа-
инициатора должны быть различными (светлая и черная точки на рис. 2Б).
Генератор для антиферромагнитной иерархической решетки (шести-
(шестиугольник) неизбежно оказывается более сложным, чем генератор для
ферромагнитной решетки (ромб).
Отсутствие таких иерархических решеток в природе не мешает фи-
физикам играть в бесконечные компьютерные игры с ними — до того это
забавно! Причем, не прерывая игр, все с нетерпением ждут появления
еще более быстродействующих суперкомпьютеров и параллельных про-
процессоров, которые позволят исследовать более реалистичные модели.
(В свободное от работы время эти числодробители разлагают на мно-
множители гигантские числа — такие, например, как то 100-значное чудо-
чудовище, которое попало на первую страницу «New York Times» от 12 октяб-
октября 1988 года и которое удалось разложить в произведение двух простых
множителей, 41-значного и 60-значного.)
Так как иерархические решетки определены рекуррентно и об-
обладают самоподобием, неудивительно, что их можно охарактеризо-
охарактеризовать фрактальной размерностью. Однако надежды на универсальность
в данном случае не сбылись: оказалось, что можно построить иерар-
иерархические решетки с одинаковыми связностями и фрактальными раз-
размерностями, но с различными критическими показателями фазовых
переходов [109].
460
Глава 16
k=2
k=S
(А)
= 1
(Б)
k=2
Рис. 2. (А) Инициатор, генератор и следующее поколение иерархической ре-
решетки в случае ферромагнитного взаимодействия спинов. (Б) Инициатор, ге-
генератор и следующее поколение иерархической решетки для случая антифер-
антиферромагнитного взаимодействия [194].
В 1952 году, в ходе одной из наиболее дерзких атак на фазовые пе-
переходы, Янг и Ли ввели комплексные числа для представления таких
физических параметров, как температура и напряженность магнитного
поля [282]. Позднее было установлено, что множества Жюлиа перенор-
перенормировочного преобразования иерархических моделей совпадает с мно-
множествами комплексных нулей, с которыми работали Янг и Ли [192].
Аналогичные множества Жюлиа были получены для нулей функции
распределения моделей Изинга на самоподобных фрактальных решет-
решетках [266]. Эти фрактальные множества Жюлиа, подобно аналогичным
множествам квадратичного отображения (гл. 12), демонстрируют при-
приятные для глаза самоподобия, вытекающие из рекуррентной процедуры
построения иерархических решеток, что было по достоинству оценено
в книге Пайтгена и Рихтера «Красота фракталов» [194].
Порог перколяции решетки Бете
Порог перколяции решетки Бете
461
Еще один тип иерархической решетки представляет собой решетка
Бете (рис. 3), известная в теории графов как дерево Кэли. Каждый узел
дерева Кэли имеет одинаковое число z ветвей, или связей. Таким об-
образом, размер окрестности растет с увеличением «диаметра» экспонен-
экспоненциально — в отличие от степенного роста окрестности для физических
решеток, фрактальных или нет. Поэтому неудивительно, что решетка
Бете в некоторых отношениях ведет себя так, будто ее размерность бес-
бесконечна. Однако, будучи иерархической конструкцией, бесконечная ре-
решетка Бете позволяет вычислить и порог перколяции, и вероятность Р
того, что данный узел решетки связан с бесконечностью, причем сде-
сделать это путем замечательно простых рассуждений, основанных на со-
соображениях подобия.
Рис. 3. Дерево Кэли (решетка Бете для физиков); каждый узел здесь имеет
ровно три связи [249].
Выберем в качестве исходного произвольный узел решетки и пе-
перейдем из него в один из z соседних узлов. Там мы обнаружим z — 1
исходящих из него новых связей, или ветвей (ребер графа) (рис. 4).
Каждая из этих z — 1 ветвей ведет, в свою очередь, в какой-либо из
соседних узлов, который занят с вероятностью р. Значит, существует
в среднем (z — l)p новых занятых соседних узлов, к которым можно
проложить наш путь. Если это число меньше единицы, то вероятность
462
Глава 16
найти связный путь некоторой заданной длины убывает экспоненци-
экспоненциально по мере увеличения этой длины. С другой стороны, если величи-
величина [z — 1)р больше единицы, то существует положительная вероятность
того, что мы сможем двигаться по решетке бесконечно. Следовательно,
порог перколяции рс (для узлов или для связей) определяется соотно-
соотношением
Рс =
1
Z-1
A)
и при z = 3 равен 1/2, как в случае перколяции по узлам на треугольной
решетке или перколяции по связям на квадратной решетке [249].
Подветвь
Ветвь
Рис. 4. Иерархические окрестности: ветви и подветви в решетке Бете [249].
Однако вероятность Р того, что некоторый заданный узел решетки
связан с бесконечностью, не равна единице: существует, в конце кон-
концов, ненулевая вероятность A — p)z того, что z соседей данного узла не
заняты. А какова вероятность Р того, что данный узел решетки принад-
принадлежит бесконечному кластеру при р > рс1 (При р < рс вероятность Р,
очевидно, равна нулю.)
Пусть Q — вероятность того, что данный узел не связан с бес-
бесконечностью через какую-то одну исходящую из него фиксированную
связь. Вероятность того, что все z — 1 связей, исходящих из соседнего
узла, не связаны с бесконечностью, равна Qz~1. (Так как вероятности
занятости узлов статистически независимы, вероятности Q просто пе-
перемножаются.) Значит, pQz~x — вероятность того, что соседний узел
занят, но не связан с бесконечностью. С вероятностью 1 — р соседний
Порог перколяции решетки Бете 463
узел может быть вообще не занят; через такой узел с бесконечностью
не свяжешься, даже если все его ветви ведут туда. В результате при-
приходим к фундаментальному уравнению
Q = l-p+pQ*-1, B)
которое при z = 3 имеет два решения:
\-р
Q =
р
Вероятность р — Р того, что данный узел занят, но не связан с бес-
бесконечностью, равна pQz. Следовательно,
P = p(l-Qz) C)
или, при z = 3,
На пороге перколяции р = рс = 1/2 последнее соотношение дает Р = 0.
Это означает, что хотя бесконечный кластер и существует, он столь же
бесконечно разрежен.
На рис. 5 сплошной линией показана зависимость отношения Р/р
от р (штриховая линия — та же зависимость для треугольной решет-
решетки). Обратите внимание на резкое возрастание отношения Р/р для тре-
треугольной решетки. Например, при р = 0,6 вероятность Р того, что
данный узел решетки Бете принадлежит бесконечному кластеру, рав-
равна 0,422, тогда как для треугольной решетки вероятность Р того, что
занятый узел принадлежит бесконечному кластеру, практически равна
единице.
Решение Q = 1 уравнения B) (при Q = 1 соотношение C) да-
дает Р = 0), очевидно, соответствует р < рс. В самом деле, при z = 2
(т. е. при рс = 1, согласно уравнению A)) единственным решением урав-
уравнения B) для р < 1 является Q = 1, т. е. Р = 0.
При р, чуть большем рс = 1/2, зависимость величины Р от р вы-
выражается соотношением
Р = 6(р-Рс), Р>Рс- D)
Следовательно, критический показатель /3 вероятности Р равен еди-
единице.
464
Глава 16
1
0,8
о. 0,6
°^ 0,4
0,2
0
0,25
0,5
Р
0,75
Рис. 5. Мощность Р бесконечной цепи как функция от концентрации р в ре-
решетке Бете (сплошная линия) и в треугольной решетке (штриховая ли-
линия) [249].
Ниже порога перколяции средний размер кластера S вычисляется
аналогичным образом и оказывается равен [249]
S=p
1+р
1-2р
или, при р, чуть меньшем рс = 1/2,
Р<Рс-
E)
То есть критический показатель для размера кластера равен —1.
Уравнения D) и E) описывают поведение двух важных «парамет-
«параметров порядка» Р и S вблизи критической точки — порога перколяции
р = рс (для решеток Бете, z = 3). Это поведение характеризуется дву-
двумя простыми степенными законами с показателями, равными, соот-
соответственно, 1 и —1. Подобное поведение часто называют алгебраичес-
алгебраическим (в отличие от логарифмического, экспоненциального или другого
трансцендентного поведения).
Еще одним примером, в котором решетка Бете приводит к точно
разрешимой модели, может служить локализация Андерсона — весь-
весьма важный феномен, наблюдаемый в неупорядоченных системах [10].
За свое открытие Филипп Андерсон был удостоен в 1977 г. Нобелев-
Нобелевской премии по физике. В настоящее время неупорядоченные системы
являются центральной темой и предметом интенсивных исследований
в различных областях физики (среди примеров таких систем — спино-
спиновые стекла и нейронные сети).
Простая перенормировка
465
Существуют и другие решетки, для которых показатели могут
оказаться иными, однако поведение параметров порядка останется по-
прежнему алгебраическим. Например, вероятность Р для квадратной
решетки изменяется как (р — рс)^, где C — критический показатель,
равный 5/36. Само значение этого показателя указывает на то, что его
теоретический вывод отнюдь не тривиален.
Ш'//Ж'ШШЯ'ШШ
у.
v/,
у,
ff
/A
ft
M
/ft
\(
Yt
'/,
A
ft
'/{
44
4$
/A
'//
'/(
¦
У/
У,
У.
1
у,
У/
ш
У/
¦
У/,
¦
'А
V/
У/.
'У,
у,
У.
¦
Ye
У/
У/
1
у,
''л
У/
¦
'/'
У/
¦—1
Рис. 6. Случайная резистивная цепь с одной токопроводящей дорожкой (по-
(помечена стрелками) между двумя медными стержнями [249].
Важное приложение теория перколяции [249, 128, 88] нашла в реше-
решении задачи о проводимости Е случайных резистивных цепей (рис. 6).
Очевидно, что при р < рс проводимость равна нулю. Но и при р > рс
она растет с увеличением р весьма медленно по сравнению с ростом
вероятности Р (т. е. вероятности того, что данный узел принадлежит
бесконечному кластеру). Причина заключается в том, что большинство
узлов в бесконечном кластере вблизи порога перколяции принадлежат
не «магистральной линии», а болтающимся свободным концам, отнюдь
не способствующим увеличению проводимости.
Простая перенормировка
Для того чтобы перенормировка действовала, должно выполнять-
выполняться фундаментальное условие — самоподобие. Поскольку многие крити-
критические явления в физике обнаруживают самоподобное поведение вбли-
вблизи критической точки (например, порога перколяции или температу-
температуры Кюри), такие явления допускают анализ с точки зрения ренорм-
группового подхода, позволяющего определять критические показатели
для корреляционной длины ? и других важных параметров.
Следуя Штауфферу [249], мы продемонстрируем метод ренорм-
групп в действии, выбрав в качестве объекта треугольную решетку
466 Глава 16
(рис. 7) — структуру, критические показатели которой нам известны.
Для этой решетки порог перколяции по связям рс в точности равен 1/2,
а показатель корреляционной длины v предполагается равным 4/3. Те-
Теперь давайте посмотрим, удастся ли нам вывести значения рс и v с по-
помощью пространственной перенормировки решетки.
Рис. 7. Пространственная перенормировка треугольной решетки. Каждый
«сверхузел» (светлая крупная точка) заменяет собой три соседних узла ис-
исходной решетки, причем решетка, составленная из таких «сверхузлов», также
является треугольной [249].
Для этого заменим каждые три соседних узла в треугольной решет-
решетке одним «сверхузлом» (светлые «горошины» на рис. 7). Предположим,
что вероятность заполнения узлов исходной решетки равна р. Чему же
равна соответствующая вероятность (р') для сверхузлов? Условимся
считать сверхузел занятым, если входящие в него узлы исходной ре-
решетки образуют «несущий кластер», т. е. если по крайней мере два из
трех узлов заняты. Вероятность того, что заняты все три узла рав-
равна р3, а вероятность того, что заняты ровно два узла из трех, равна
C/2)р2A — р). Следовательно,
р'=р3+3р2A-р). A)
В критической точке р = рс должно выполняться равенство р' = р.
Таким образом, из уравнения A) находим три критические точки рс =
= 0, 1/2 и 1, из которых нетривиальна только точка рс = 1/2. Этот
результат, полученный с помощью перенормировки, в точности соот-
соответствует известному порогу перколяции по узлам рс для треугольной
Простая перенормировка 467
решетки. Похоже, перенормировка работает! Однако повезет ли нам так
же и с показателем корреляционной длины ul
Корреляционная длина ? вблизи критической точки определяется
выражением
? = с\р-РсГ", B)
где с — константа. В перенормированной решетке
где Ъ — коэффициент подобия между исходной решеткой и сверхре-
сверхрешеткой. Если положить ? = ?', то из соотношений B) и C) следует,
что
V = 4
Ц(р'-Рс)/(Р-Рс)] К)
Разлагая равенство A) в окрестности неподвижной точки р = рс = 1/2,
получаем
о
р' = Р + 2{Р-Рс) + •••
или
Р' -Рс = 3
р-рс 2'
При Ь = З1/2 (см. рис. 7) из соотношения D) находим, удерживая члены
первого порядка по (р — рс):
и 1пC/2)
что замечательно близко к точному значению ^ = 4/3.
Еще один, весьма мощный способ перенормировки известен под
названием конформное отображение [32]. Как и при самоподобном пре-
преобразовании, при конформном отображении сохраняются углы. Прак-
Практическая полезность конформного отображения проистекает из кон-
конформной инвариантности — реальной или предполагаемой — исследуе-
исследуемой системы. Хорошо известный пример конформного отображения —
зеркальное отражение данного пространства в неподвижной сфере. На
плоскости любая аналитическая функция определяет локальное кон-
конформное отображение в тех точках, где ее производная не обращается
468 Глава 16
в нуль. В качестве примера конформной инвариантности в физике мож-
можно упомянуть знаменитые уравнения Максвелла; их конформная инва-
инвариантность была установлена только в 1909 году — через несколько
десятилетий после того, как Максвелл их вывел.
Неохотно завершаем мы знакомство с теориями ренорм-групп и фа-
фазовыми переходами и переходим к самоподобиям, порождаемым кле-
клеточными автоматами.
Глава 17
Клеточные автоматы
Истина слишком сложна; нам же дано
постичь лишь приближения к ней.
Джон фон Нейман
Впервые идея клеточных автоматов была предложена Конрадом
Цузе и Станиславом Уламом и воплощена практически Джоном фон
Нейманом с целью воспроизвести поведение сложных пространственно
протяженных систем [258]. Еще в начале 40-х годов Цузе начал раз-
размышлять о «вычисляющих пространствах» (как он их многозначитель-
многозначительно окрестил) как о дискретных моделях физических систем. Улам вы-
выдвинул идею клеточных автоматов в конце 40-х годов, вскоре после
того, как он (совместно с Николасом Метрополисом) придумал метод
Монте-Карло. (О поразительно широких научных интересах Улама и
его достижениях можно узнать из сборника его избранных работ под
названием «Множества, числа и Вселенные» [259]. Также рекоменду-
рекомендуем обратить внимание на уникальную антологию, дающую обзор со-
современного состояния клеточных автоматов, под редакцией Стивена
Вольфрама [281]).
Одномерный клеточный автомат состоит из выстроенных в ряд
клеток, в каждой из которых хранятся некоторые начальные числа,
и набора правил, определяющих характер изменения этих чисел в каж-
каждый заданный момент времени. Предположим, что в начальном состо-
состоянии автомата все клетки заняты нулями, кроме одной, в которой хра-
нится единица: .01000000...
Предположим также существование правила, согласно которому число
в каждой клетке заменяется на сумму его самого и его соседа слева.
Тогда через единицу времени состояние автомата будет следующим:
...01100000...
Еще через один шаг состояние автомата будет таким:
...01210000... ,
470 Глава 17
затем
...01331000...
...01464100...
и т. д. Такие клеточные автоматы в действительности являются ком-
компьютерами, и надо сказать, что клеточные компьютеры находят все бо-
более широкое применение при вычислении сложнейших функций, пото-
потому что клеточные автоматы изначально приспособлены для параллель-
параллельной обработки данных. В приведенном только что примере клеточный
компьютер вычисляет биномиальные коэффициенты, встречающиеся
в разложениях по степеням биномов — таких, например, как (а + ЬL,
разложение которого равно а4 + 4a3b + %о?Ь2 + 4ab3 + Ь4.
Клеточные автоматы могут быть одно-, двух- или многомерными.
Чтобы рассчитать, например, поведение двумерного потока жидкости,
используют клеточные автоматы, представляющие собой двумерные
массивы клеток, в каждой из которых хранится некоторое число (пред-
(представляющее, скажем, плотность жидкости), которое изменяется с хо-
ходом времени по определенным правилам, действующим на некоторую
совокупность клеток. Правила эти, по существу, моделируют локаль-
локальные взаимодействия между соседними клетками, отражая динамику
исследуемой системы.
Клетки могут образовывать не только квадратные, но и, напри-
например, шестиугольные решетки, а «числа» в клетках могут и вовсе быть
векторами, представляющими скорость жидкости или газа в каждом
узле решетки (рис. 1). Такие клеточные автоматы физики называют
их моделями решеточного газа — оказались весьма удобными при ре-
решении казавшихся неприступными задач гидродинамики [219, 169].
На рис. 2 изображены потоки позади цилиндра, движущегося спра-
справа налево сквозь вязкий газ; отчетливо видно, как за цилиндром тя-
тянется знаменитый вихревой шлейф. Такие гидродинамические фено-
феномены и поныне исследуются на моделях в аэродинамических трубах
и опытных бассейнах. Но в настоящее время их все чаще изучают
с помощью компьютерного моделирования, основанного на клеточных
автоматах.
Поскольку типичные клеточные автоматы основаны на многократ-
многократном применении фиксированных правил, мы вполне можем рассчиты-
рассчитывать обнаружить здесь самоподобия — как мы обнаружили их во мно-
многих других итеративных процессах. Наши надежды не напрасны — мно-
многие клеточные автоматы и впрямь порождают самоподобные конфигу-
конфигурации, часто весьма привлекательные на вид.
Игра под названием «Жизнь»
471
Г Л Л Л Г '\ Л Л Г
Рис. 1. Гидродинамический поток, моделируемый клеточным автоматом
(«решеточный газ»). На рисунках показаны последовательные состояния газа.
Стрелки символизируют направление векторов скорости частиц.
Рис. 2. Поток за движущимся цилиндром, представленный с помощью модели
решеточного газа [219].
Игра под названием «Жизнь»
Наверное, самым известным из клеточных автоматов следует счи-
считать игру, придуманную Джоном Хортоном Конуэем и названную им
«Жизнь» [74]. «Жизнь» описывает рост и гибель популяций клеток в со-
соответствии с довольно простыми правилами, которые — при всей своей
простоте — породили целый зоопарк престранных существ, демонстри-
демонстрирующих поистине удивительное поведение [22].
472
Глава П
0 .
1 -
2 "
Ь
а
I
i
|
1
мерли
i
ь
4
-L
щ
г
4-
1 I
| |
1
н
1
Умерли
1
с
1
а
¦
_ Умерли
t-
d
1
-L
Hi
1
1
ж
i
¦
лок
Ml
йчи
>ина
вая -
ция
1
е
1
4
1
1
1
Мигалка
П
1
1
1
_
гриод 2
н
Рис. 3. «Жизнь» Конуэя: судьба пяти триплетов точек [77].
11
uL
t
J
H
Авианосец
1
1
1
•
1
1
__l Шляпа
t
и
1
Г
I
1
I
1
1
•
Д л и н н а я
змея
¦
¦
I
1
1
¦
¦
1
Тонущий
корабль
1
1
Л
и
>
1
•
_
Рь боловный
крючок
1
1
1
1
1
1
¦
1
•
Пчелш
соть
1
1
ь
1
е
I
\
1
и
•Г
1
И
+
1
1
•
_
Дубинка
1
I
i
¦
1
1
1
1
1
1
1
1
1
т
т
|±
_ г
- С
±
Озеро
Рис. 4. Натюрморт: неживые формы «Жизни» [77].
В игре «Жизнь», по замыслу Конуэя, каждая клетка либо мерт-
мертва @), либо жива A) и изменяет свое состояние в зависимости от со-
состояний соседних клеток и своего собственного следующим образом:
по прошествии единицы времени живая клетка остается живой, если
среди восьми соседних с ней клеток на квадратной решетке имеется
две или три живых клетки. Если число живых соседей больше трех, то
клетка чувствует себя стесненной и погибает «от удушья». Если число
живых соседей меньше двух, то клетка погибает от одиночества. С дру-
другой стороны, мертвая клетка оживает, если ее окружают ровно три
живых соседа (родители и повивальная бабка, так сказать). На рис. 3
вы можете проследить за судьбой пяти различных триплетов точек.
Рост и гибель клеток
473
н
п
1
н
од
I
1
1
1
1
н
3
1 1 1 1 1 1 1
и
LMJ
«W1
1П1
•П Ж ГР
ггГгп
ГП*Т1
1
J PTU1
i и Н
1_Ш ж
пч_рп
ГрП
1 П 1 1
- 1 1 1 1 1
¦
i
i
i
i
i
Период 4
1
1
1
I
Е
3
5_
Я
и
ГГ
±
4-
1
1
h
1
н
d
н
1
1
н
н
О
h
i
1
1
1
I
1
1
н—
м
ж
¦П
1
ш-
т Период 6 ~
Т1 '
1
1
I
г
1 и
Вт
щ
П
¦
I
1
м
г
и
т
А-
i
if
И
щ
_ГГ
444-
Рис. 5. Периодические формы «Жизни» [77].
-1
4 -
¦
»
i
Si
•
•
•
-i
*
•
-
¦ г
5 -s-
j *--
If ("
jl 1
i f
11
-88-j 6--
f
i i f
ill
i |
! i i|t T"
i n f "-+- 1
11 in i
t jiijiii •_
i i
1 1 1 1 1 1 1 1 1 -l-l-l-l-l-
'ii'
MM
j
! 1
Рис. 6. Чеширский кот @), оставляющий после себя лишь улыбку F), которая
затем превращается в неизменный след лапы G) [77].
Разнообразие конфигураций, порождаемых этими простыми правила-
правилами, поражает воображение — на рис. 4-8 представлена лишь весьма
скромная подборка стационарных, периодических, исчезающих и вы-
выживающих «организмов».
Предложенный Конуэем свод правил, или закон, — лишь один из
многих возможных. При данных начальных условиях (значение клетки
двоично, и каждая клетка окружена восемью воздействующими на нее
соседями) существуют 22 и 10154 различных «жизнеподобных» зако-
законов, из которых, похоже, только один, установленный Конуэем, оказал-
оказался жизнеспособен.
Рост и гибель клеток
Рассмотрим двумерный клеточный автомат, в котором клетка, как
и в игре «Жизнь», может находиться в двух возможных состояниях 0
и 1, но имеет только четырех соседей, воздействующих на нее — Вое-
Рис. 7. Семь цепочек по пять бит: начальное (темные точки) и конечное (свет-
(светлые точки) состояния [77].
ток, Запад, Юг и Север. Текущее состояние центральной клетки Ц и
ее соседей ВЗЮС определяется 5-значным двоичным словом, напри-
например, ВЗЮСЦ=11000. Следующее состояние клетки Ц, например, Ц = 1,
определяется доминирующим правилом 11000 —> 11001 (рис. 9). Пол-
Полный свод таких правил, называемый законом, задан в таблице из 32
475
Рис. 8. Убийство «Жизни»: единственный «вирус», помещенный в определен-
определенную клетку (светлая точка на рисунке), способен полностью разрушить кон-
конструкцию. Если поместить вирус в любую другую клетку, то конструкция
его уничтожает и восстанавливает свою исходную структуру [77].
возможных состояний соседей и последующих состояний центральной
клетки Ц (рис. 10). Для данных условий (значение клетки двоично, че-
четыре воздействующих соседа) существуют 232 я» 4 000 000 000 возмож-
возможных различных законов.
Рис. 9. «Включение» центральной клетки (переключение из положения 0 в по-
положение 1) в соответствии с правилом (Восток, Запад, Юг, Север, Центр) =
= 11000 ->• 11001.
Разнообразные конфигурации на рис. 11 получены с помощью по-
постоянного закона, заданного в таблице на рис. 10 и обозначаемого аб-
аббревиатурой HGLASS, при различных начальных условиях [258].
Согласно другому, чрезвычайно простому закону центральной
клетке Ц приписывается значение суммы по модулю 2, т. е. четность
содержимого пяти клеток окрестности (включающей и саму клетку Ц).
476
Глава П
EWSNC
00000
00001
00010
00011
00100
00101
00110
00111
^new
0
1
1
1
0
0
0
0
EWSNC
01000
01001
01010
01011
01100
01101
OHIO
они
t^new
0
0
0
1
0
0
0
0
EWSNC
10000
10001
10010
10011
10100
10101
10110
10111
^new
0
0
0
0
0
1
0
0
EWSNC
11000
11001
11010
11011
11100
11101
11110
11111
t^new
0
1
0
0
0
1
1
1
Рис. 10. Таблица правил HGLASS, один из четырех миллиардов возможных
сводов правил.
(А)
(Б)
Рис. 11. (А) Конфигурация, полученная в соответствии с законом HGLASS,
из случайного инициатора. (Б) То же, но из простого инициатора [258].
Начав с небольшого квадрата из единиц, плавающего в море нулей, мы
через 50 или 100 шагов приходим к конфигурациям, представленным на
рис. 12. Существуют ли здесь какие-нибудь самоподобия? Вне всякого
сомнения. Можно даже показать, что любая начальная конфигурация
на однородном фоне воспроизводится и через определенное число шагов
окружает себя четырьмя тождественными копиями. Еще через такое
же число шагов копий будет уже 25 и т. д. ad infinitum. Так как сумми-
суммирование по модулю 2 — линейная операция, различные конфигурации
могут проникать одна сквозь другую, причем это никак не влияет на
их будущий рост. В частности, любая конфигурация может быть полу-
Рост и гибель клеток
477
Рис. 12. Правило четности: (А) конфигурация, получаемая из квадрата 32x32
через 50 шагов; (Б) то же через 100 шагов [258].
Рис. 13. Самоподобный фрактал, построенный согласно правилу «одна-из-
восьми» [258].
чена путем суммирования по модулю 2 конфигураций, порожденных
одной изолированной точкой.
Еще один простой закон: клетка переходит в состояние A), если
жива ровно одна из восьми соседних с ней клеток, в противном слу-
случае клетка остается в прежнем состоянии. Возникающая в результа-
результате конфигурация представляет собой самоподобный фрактал (рис. 13),
478
Глава 17
размерность Хаусдорфа для которого читатель, возможно, пожелает вы-
вычислить самостоятельно.
А как вам понравится вот такой закон: состояние клетки зависит
от состояния большинства соседей: если из девяти клеток окрестнос-
окрестности (включая и центральную) четыре или меньше клеток мертвы, то
центральная клетка умирает (или остается мертвой), в противном слу-
случае центральная клетка оживает (или остается живой). Возникающие
в результате конфигурации напоминают спиновые системы Изинга при
низкой температуре и наводят на мысли о перколяции. На рис. 14А по-
показан узор, возникающий из исходной конфигурации случайно распре-
распределенных по половине решетки единиц.
(А)
(Б)
Рис. 14. (А) Конфигурация, образующаяся при эволюции клеточного автома-
автомата, половина клеток которого в исходном состоянии была случайным образом
занята единицами, согласно правилу «большинства». (Б) Эволюция по прави-
правилу «отжига» — небольшая модификация правила «большинства» [263].
О том, насколько конфигурации чувствительны к малейшим изме-
изменениям закона, можно судить по рис. 14Б. На нем изображен автомат,
эволюционирующий по следующему закону: центральная клетка мерт-
мертва, если мертвы либо все пять клеток окрестности, либо менее четырех.
Этот закон, предложенный Дж. Вишняком, моделирует процесс отжига
металла — как видно из рис. 14Б, домены и в самом деле консолидиру-
консолидируются [263]. Полученные конфигурации пространственно однородны, но
не самоподобны.
Рост и гибель клеток
479
Для того, чтобы возникли самоподобные спиновые домены, исход-
исходная случайная конфигурация должна обладать критической «энерги-
«энергией» [262]. В такой «энергетической» конфигурации происходит нару-
нарушение симметрии и наблюдаются магнитные домены всевозможных
масштабов (рис. 15).
Рис. 15. Магнитные домены всевозможных масштабов в равновесной конфи-
конфигурации спинов Изинга при критической температуре [262].
Все рассмотренные нами до сих пор законы носили «строго прину-
принудительный» характер, т.е. были детерминированными. Между тем мно-
многие клеточные автоматы действуют по случайным правилам, модели-
моделируя диффузию и другие стохастические процессы. В качестве примера
можно привести автомат, подчиняющийся «мягкому» закону, который
гласит: «Копируй случайного соседа». Если выбор любой из четырех
соседних клеток равновероятен, то исходный круг просто взрывается
(см. рис. 16, справа). Диффузию с дрейфом можно моделировать «час-
«частицами» (клетками-единицами), движущимися с вероятностью 3/8 на
восток или юг и с вероятностью 1/8 — на запад или север (рис. 17).
Из таких клеточных автоматов можно получить весьма правдо-
правдоподобные модели дрейфа генов. На цветной вклейке 9 показано про-
пространственное перемешивание шестнадцати конкурирующих видов ге-
генов [258].
480
Глава П
Рис. 16. Взрывающийся круг — результат эволюции по правилу «копируй-
ближайшего-соседа» [258].
Рис. 17. Диффузия с дрейфом и без: занятная ошибка программирова-
программирования [225].
Рассмотрим одну классическую задачу, которая в переводе на язык
клеточных автоматов может быть названа задачей о «единице в каж-
каждой клетке» [252]. Снабдим каждое поле (клетку) шахматной доски пхп
Формирование биологических конфигураций
481
лампой и кнопкой, нажатие которой включает лампы, входящие в не-
некоторую заданную окрестность этого поля (уже включенные лампы
тем же нажатием выключаются). Какие кнопки следует нажать, чтобы
загорелись все лампы на доске, если в начальный момент времени не
горит ни одна? Ясно, что число нажатых кнопок в окрестности каждого
поля должно быть нечетным. Такое расположение кнопок называется
нечетным покрытием. На рис. 18 представлены нечетные покрытия для
шахматных досок 4 х 4 и 5 х 5 (окрестность данного поля определяется
как само поле и четыре соседних поля, примыкающих к центральному
сторонами).
Рис. 18. Нечетные покрытия для шахматных досок 4 х 4 и 5 х 5 [252].
А как выглядит решение для доски 8x8? Под силу ли читателю
сформулировать правила, следуя которым клеточный автомат даст на
выходе требуемую конфигурацию нажатых кнопок, т. е. нечетное по-
покрытие для заданной окрестности? Разумеется, если искомое нечетное
покрытие окажется «райским садом», нам с вами его не найти. (По опре-
определению, конфигурация «райский сад» не имеет предшествующей кон-
конфигурации; единожды утратив райские кущи, мы никогда не сможем
обрести их вновь.)
Формирование биологических конфигураций
Клеточные автоматы доказали свои моделирующие способности
и в еще одной области — в формировании различного рода структур
у растений и животных. Мейнхардт, Гирер и другие, используя комби-
482 Глава 17
нации локальных и дальнодействующих автокаталитических и ингиби-
торных взаимодействий, смоделировали полосы на шкурах зебр и мно-
многочисленные другие структуры бесконечно разнообразных форм жиз-
жизни [175].
Простой клеточный автомат имитирует структуру раковины мол-
моллюска Olivia porphyria (рис. 19), для которой характерны диагональные
линии, исчезающие в точке встречи. Другой механизм обуславливает
бифуркацию одиночной линии для поддержания средней пигментации
на заданном уровне [176].
С помощью клеточных автоматов, использующих простые само-
самоподдерживающие и антагонистические реакции, были смоделированы
и многочисленные другие биологические процессы, включая формиро-
формирование рук и ног человека. Разнообразие возникающих при этом форм
поистине поразительно.
Самоподобие клеточного автомата
Самоподобие возникает в самых различных формах в самых раз-
различных областях. Пожалуй, наиболее известный пример дискрет-
дискретного, хотя и ограниченного, самоподобия — русские матрешки,
вложенные одна в другую. Самоподобие можно обнаружить даже
в такой дискретной и безыскусственной сущности, как целые чис-
числа 0, 1, 2, 3, 4, 5, 6, 7,... Запишем последовательные целые числа, на-
начиная с 0, в двоичной системе (которую Лейбниц, по всей видимости,
придумал во время ожидания аудиенции у Папы Римского в Ватикане,
куда он явился с планом воссоединения христианских церквей):1
О, 1, 10, 11, 100, 101, 110, 111,...
Значения суммы цифр для каждого числа образуют последовательность
В (t) = 0, 1, 1, 2, 1, 2, 2, 3, ... , t = 0, 1, 2, ... ,
которая может быть также получена итеративно следующим обра-
образом. Чтобы из подпоследовательности длиной 2п получить подпосле-
подпоследовательность длиной 2n+1, необходимо повторить первую, прибавляя
к каждому ее члену по единице. Так, начальная подпоследовательность
1 Компьютеры отдают особое предпочтение двоичной системе по той простой при-
причине, что она использует только две цифры @ и 1): любую двоичную цифру можно
однозначно и недвусмысленно представить одним из двух состояний переключате-
переключателя — «включено» и «выключено», и ничего больше.
Самоподобие клеточного автомата
483
(Б)
Рис. 19. (А) Поверхность раковины улитки Olivia porphyria. (В) Волнообраз-
Волнообразная структура, полученная клеточным автоматом с автокаталитическими
взаимодействиями, локальными и дальнего порядка [176].
484 Глава 17
длиной 2° = 1 (т. е. 0) порождает подпоследовательность длиной 21 = 2
(т.е. 01) путем добавления к исходному 0 числа 0 + 1 = 1. Придержива-
Придерживаясь этого алгоритма, получаем серию поколений подпоследовательнос-
подпоследовательностей длиной 2п:
0
01
0112
01121223
0112122312232334
По существу, это порождающее правило является прямым следствием
определения двоичного представления целых чисел: при к < 2п два
целых числа к и к + 2п отличаются ровно одной единицей в своих дво-
двоичных представлениях.
Интересно и важно отметить, что наше итеративное правило
порождения подпоследовательностей является быстрым алгоритмом:
каждая итерация удваивает длину подпоследовательностей, т.е. их
длина растет экспоненциально с числом итераций. (Линейные рекур-
рекуррентные соотношения — такие, например, как соотношение для после-
последовательности чисел Фибоначчи Fn+2 = Fn+i + Fn — с каждой итера-
итерацией добавляют только один новый член.)
Полученная описанным способом бесконечная последовательность
B(t) самоподобна в следующем смысле: она воспроизводится при уда-
удалении из нее всех членов с нечетными индексами. Члены же с четными
индексами (подчеркнутые) остаются, как показано ниже:
В (t) = 0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4, ...
Таким образом, В Bt) = B(t).
Это самоподобие является почти тривиальным следствием того,
что в двоичной системе умножение на 2 приводит всего лишь к сдвигу
цифр влево, что, разумеется, не изменяет сумму цифр.
Последовательность В (t) можно превратить в последовательность,
самоподобную и по величине ее членов. Более того, последовательность
C(t)=2B^=l, 2, 2, 4, 2, 4, 4, 8, ...
обладает одинаковым коэффициентом подобия (равным 2) не только
по индексу t ее членов, но и по их величине. Вторая половина каждой
Самоподобие клеточного автомата 485
подпоследовательности длиной 2п+1 вдвое больше первой половины:
2n)=2C(t),
A)
Рис. 20 иллюстрирует последовательность С (t) и ее самоподобие. По-
Последовательность С (t) можно, кроме того, получить из произведе-
произведения A + &i)(l + &2)A + Ьз) • • •, где bk — цифры двоичного разложения
индекса t.
200
100
100
200
Рис. 20. Самоподобная последовательность, полученная из двоичной системы
счисления.
Интересно отметить, что последовательность С (t) может быть
также порождена клеточным автоматом, и этот факт весьма важен
в свете того, что последует ниже. Зададим себе вопрос: сколько бино-
биномиальных коэффициентов (^) при данном t нечетны, если п лежит в ин-
интервале от 0 до t. Ответ гласит (простое доказательство этого утверж-
утверждения по индукции я оставляю читателю в качестве самостоятельного
упражнения): 1, 2, 2, 4, 2, 4, 4, 8, ... = С (t). Сами биномиальные коэф-
коэффициенты порождаются одним из простейших клеточных автоматов.
(См. введение к этой главе.)
Заметим, что сумма членов последовательности С (t) от 0 до t =
= 2т — 1 равна 2>т. Это следует непосредственно из равенства С @) = 1
и соотношения A).
486
Глава П
Каталитический конвертор как клеточный автомат
Последовательности, напоминающие С (t), где t интерпретирует-
интерпретируется как дискретное время, наблюдались в некоторых химических реак-
реакциях — например, в процессах каталитического окисления (рис. 21).
Какая, скажите на милость, может быть связь между химической ре-
реакцией и последовательностью C(t), т.е. последовательностью двоек,
возводимых в степени, равные суммам цифр двоичных представлений
последовательных целых чисел? Простой ответ на этот вопрос был най-
найден Андреасом Дрессом, занимавшимся моделированием таких катали-
каталитических процессов с помощью одномерных клеточных автоматов [53].
т
К
о
о
U
Время t~
Рис. 21. Скорость химической реакции как функция от времени в процессе
каталитического окисления [53].
В одномерном клеточном автомате каждый период времени харак-
характеризуется последовательностью символов или чисел. Как мы узнали
из введения к этой главе, последовательность gt (n) в момент време-
времени t строится из последовательности в момент времени t — 1 согласно
некоторому закону — такому, например, как закон
gt (п) = gt-i (п) + gt-i (п - 1)
с начальным поколением go @) = 1 и go (п) = 0 при других п, который
порождает биномиальные коэффициенты (^) в том порядке, как они
располагаются в треугольнике Паскаля. (Каждое число в треугольнике
Паскаля равно сумме двух чисел, расположенных непосредственно над
ним.) Построим треугольник Паскаля по модулю 2. Иначе говоря, если
биномиальный коэффициент (^) нечетный, заменим его единицей, если
же коэффициент четный, заменим его нулем. Возникающий в резуль-
Каталитический конвертор как клеточный автомат 487
Рис. 22. Треугольник Паскаля по модулю 2: дискретный вариант ковра Сер-
пинского.
тате треугольник Паскаля по модулю 2 представлен на рис. 22. Черные
клетки соответствуют единицам, белые — нулям.
Вернемся к химической реакции, моделируемой треугольником
Паскаля по модулю 2. Дресс предположил, что «молекула», представ-
представленная клеткой в позиции п, «инфицируется» (окисляется, например)
в момент времени t только в том случае, если один из ее соседей в по-
позициях п и га—1 был инфицирован (черный цвет) в момент времени t—1.
Но по построению, число черных квадратов (единиц) в момент вре-
времени t равно С (t). Значит, последовательность С (t) и в самом деле опи-
описывает скорость химической реакции в данном каталитическом кон-
488 Глава 17
верторе — как и предполагалось, исходя из приближенного самоподо-
самоподобия такой реакции, который отчетливо заметен на рис. 21.
Треугольник Паскаля по модулю N
Рекуррентное построение из одной единицы треугольника Паскаля
для биномиальных коэффициентов (^) — типичный образец клеточно-
клеточного автомата. По мере того, как сами числа (^) становятся все больше и
больше с увеличением t @ < п < t), их свойства делимости образуют
самоподобные конфигурации. Более того, четные коэффициенты распо-
располагаются в треугольниках, чрезвычайно похожих на пустоты в ковре
Серпинского (см. с. 41-45). Структура этих треугольников с легкостью
следует из того, что все биномиальные коэффициенты Q) при t = 2т
и 0 < п < t — четные. Две единицы (при п = 0 и п = t) постепенно по
мере увеличения t «поедают» четные коэффициенты до тех пор, пока
при t = 2m+1 — 1 все коэффициенты не становятся нечетными.
Аналогичные механизмы порождают самоподобные конфигурации
из треугольника Паскаля с биномиальными коэффициентами, взяты-
взятыми по модулю любого другого простого числа [280]. Имея под рукой
персональный компьютер, читатель может попытаться соорудить свой
клеточный автомат и получить с его помощью треугольник Паскаля по
модулю любого простого числа, степени простого числа и произволь-
произвольного составного числа, наблюдая возникающие самоподобия в черно-
белом или цветном исполнении. Чему равны размерности Хаусдорфа D
для предельных конфигураций? Размерность Хаусдорфа для треуголь-
треугольника Паскаля по модулю 2 (D = In 3/In 2) можно вывести исходя из
того, что общее число нечетных коэффициентов увеличивается втрое
каждый раз, когда число строк в треугольнике Паскаля удваивается
(начиная с самой первой строки, содержащей лишь одну единицу) —
так же, как увеличивается втрое площадь, покрываемая бесконечным
ковром Серпинского при каждом удвоении линейных размеров покры-
покрывающей области.
Самоорганизующиеся критические кучи песка
по Баку
В этой книге мы несколько раз встречались с тем, что многие
явления природы — от фликер-шума до разливов Нила — обладают
самоподобными спектрами мощности с зависимостью от частоты по
Самоорганизующиеся критические кучи песка по Баку 489
закону f~P. Такие процессы называются 1//-шумами (даже если спек-
спектральный показатель /3 не равен в точности единице), и их степенные
спектры свидетельствуют об отсутствии у процесса характеристичес-
характеристического масштаба времени, т.е. в описании процесса не фигурируют такие
типические значения времени, как, например, период полураспада в ра-
радиоактивном распаде.
Отсутствие характеристических масштабов наблюдается и в про-
пространственных аспектах многочисленных явлений природы; для них
не существует доминирующих характеристических длин, в отличие,
например, от ядерных сил или движения молекул в газе.
Чтобы как-то объяснить вездесущность таких самоподобных
структур, Пер Бак, Чао Тан и Курт Визенфельд не так давно ввели
понятие самоорганизующейся критичности [15]. В своей одноименной
статье и в последующих публикациях [254, 16] Бак и его сотрудники
убедительно доказывают, что пространственно протяженные динами-
динамические системы спонтанно эволюционируют в едва устойчивые струк-
структуры критических состояний, и что такая самоорганизующаяся кри-
критичность является общим механизмом, лежащим в основе многих са-
самоподобных и фрактальных феноменов.
Воплощая свои идеи в конкретную форму, Бак и его сотрудники
построили несколько моделей, в том числе простой двумерный клеточ-
клеточный автомат, имитирующий осыпание песчинок в куче песка. Если
крутизна склона в какой-то точке (ж, у) на поверхности кучи становит-
становится слишком большой, песчинка осыпается, уменьшая действующую на
нее силу тяжести z ценой увеличения силы тяжести, действующей на
четыре соседние точки (ж±1, у) и (ж, j/±l). Таким образом, если значе-
значение переменной z (целочисленное) превосходит некоторое критическое
значение zc, то оно обновляется (синхронно) по следующему закону:
z (ж, у) ->• z (ж, у) - 4
z (х ± 1, у) ->• z (х ± 1, у) + 1
z (ж, у ± 1) ->• z (ж, у ± 1) + 1.
Автомат начинает работать со случайно выбранных начальных
условий z 3> zc; граничные условия имеют вид z = 0. Как только все z
становятся меньше, чем zc, эволюция системы прекращается. Систе-
Система достигает минимального устойчивого состояния — минимального,
потому что добавление одной-единственной песчинки может спровоци-
спровоцировать лавину. Более того, вооруженный персональным компьютером
читатель, вознамерившись подтвердить выводы Бака, возможно, об-
490 Глава 17
наружит, что песчаные лавины во всех масштабах длины могут быть
вызваны малыми локальными возмущениями, т.е. добавлением одной
песчинки в случайно выбранной точке. Размеры кластеров точек, об-
образующихся с помощью этого физического «эффекта домино», распре-
распределены по степенному закону:
где т и 1 (для размера кластера s до 500 в массиве 50 х 50 точек)
или т и 1,35 (для трехмерного массива 20 х 20 х 20 точек) [15].
Время жизни таких лавин также следует степенным законам с по-
показателем а ра 0,43 в двумерном случае и а ра 0,9 в трехмерном; соот-
соответствующие показатели спектров мощности 2 — а равны 1,57 и 1,1.
Тан и Бак обнаружили также степенное поведение расхода пес-
песка, корреляционной длины, максимального размера кластера и других
параметров, наблюдаемое, когда среднее значение z удерживается по-
подальше от критического с помощью некоего «внешнего поля» [254]. Хотя
найденные ими критические показатели для перечисленных выше ве-
величин могут зависеть от конкретных особенностей рассматриваемой
системы, авторы полагают, что сама по себе масштабная инвариант-
инвариантность степенных законов более универсальна.
Если это действительно так, то самоорганизующаяся критичность
может стать «типовой» моделью для множества разнообразнейших
масштабно-инвариантных явлений: от всевозможных стекол, магнит-
магнитных доменов, гидродинамических потоков и турбулентности до транс-
транспортных пробок, экономических взаимодействий и землетрясений [12].
И еще: не являются ли минимально устойчивые состояния (че-
(чересчур долго поддерживавшиеся) причиной политических потрясе-
потрясений 1989 г. в Восточной Европе?
Приложение
Размерность Хаусдорфа при неравных остатках
Приводимое ниже доказательство было предложено X. В. Штрубе.
Пусть /д, С [0, 1] — интервалы генератора канторова множест-
множества F, a Sk — их длины. (В исходном «троичном» канторовом множестве
h = [0, 1/3], h = [2/3, 1] и si = s2 = 1/3.) Обозначим через Fk части
множества F, лежащие в 1^:
Fk=FnIk. A)
Пусть N (г) и Nk (г) — наименьшие числа интервалов радиуса г,
покрывающих, соответственно, F и Fj,- Кроме того, пусть L — длина
наименьшего зазора между /д,. При 2r < L имеем:
N(r) = Y,Nk(r) B)
к
ИЛИ
^^-i (з)
Так как Fj, — множество, подобное множеству F с коэффициентом
подобия Sk, справедливо соотношение Nk (s* r) = N (г), или
Следовательно, поскольку размерность Хаусдорфа D является в то же
время размерностью подобия (т.е. N (г) ~ r~D), при г —>• 0 выполняет-
выполняется соотношение
Подставляя его в соотношение C), получаем обобщенный результат
для размерности Хаусдорфа D канторова множества, генератор кото-
которого состоит из интервалов произвольной длины Sk-
492 Приложение
Благородные и почти благородные числа
Благородными по определению называются иррациональные чис-
числа v, разложения которых в непрерывные дроби завершаются только
единицами. При 0 < v < 1 имеем:
v= [au а2, ... , ап, A)], G)
где единица в скобках означает бесконечную последовательность еди-
единиц.
С помощью золотого сечения
7 = [A)] = 0,618... (8)
благородные числа могут быть представлены в виде «эквивалентных
чисел» [97]:
где Ak и Bk — соответственно, числитель и знаменатель дроби, пред-
представляющей собой к-е приближение («сходящееся») дроби [а\, п2, ¦ ¦ ¦, ап].
Например, простое благородное число, удовлетворяющее определе-
определению G), при и = 2са1 = 1иа2=2 есть число v = [1, 2, Т] = 0,7236 ...
Так как аппроксимирующие дроби его непериодического начала [1, 2]
равны Ai/Bi = 1/1 и А2/В2 = 2/3, число и, согласно формуле (9),
можно также представить в виде
В общем случае, поскольку j = (у/Ь —1)/2, благородные числа образуют
подмножество поля Q(\/5).
Почти благородные числа я определил как все вещественные
?@ < v < 1), разложение которых в непрерывную дробь периодично
с длиной периода Р, причем период состоит из (Р — 1) единиц, за кото-
которыми следует число п > 1:
v = [A, 1, ... , 1, п)], длина периода равна Р, A1)
где скобки означают периодическое повторение заключенных внутри
чисел. Примером простого почти благородного числа может служить
число [A,2)] = \/3-1.
Приложение 493
Чтобы узнать, какие числа v имеют разложения в непрерывную
дробь вида A1), запишем v следующим образом:
v= [l, I, ...,1, n, |], A2)
где последнее число \jv следует рассматривать как обычный член раз-
разложения в непрерывную дробь, хотя оно и не является целым. Напри-
Например,
[|] l g). A3)
Это квадратное уравнение относительно v имеет положительное реше-
решение v = \/3 — 1.
Вычисляя значение v по формуле A2), получаем
111...1 п \jv
10 11 2 ... Fp_2 FP_! nFp-x+Fp-2
01 123 ... Fp-xFp nFp+Fp-x (nFP + Fp^d'1 FP
где Fn — числа Фибоначчи [230]. Это позволяет нам записать следую-
следующее квадратное уравнение для v:
_ nFp-l + Fp-2 + vFp-X
v = , A4)
nFp+Fp^+uFp y '
допускающее решение
nFp-x+Fp-2
Для частного случая п = 2 находим:
Применив рекуррентные соотношения Fp + i*p_i = -Fp+i, Fp-i +
+ -Fp-2 = -Fp и _Fp +-Fp+i = -Fp+2, получим следующий окончательный
494 Приложение
результат:
A7)
Например, при Р = 3 из формулы A7) находим число v = \/5/2 — 1,
которое и в самом деле допускает разложение в непрерывную дробь
с длиной периода 3, причем период завершается числом 2: л/5/2 — 1 =
= [A, 1, 2)].
Асимптотически при Р —>• сю и любом фиксированном п на-
наши почти благородные числа стремятся к золотому сечению 7 =
= (\/5 — 1) и 0,61803. Например, при п = 2 и Р = 10 получаем почти
благородное число v к, 0,61808. Согласно формуле A6) или A7), после-
последовательные значения v при Р = 1, 2, 3, ... составляют по существу
приближение к золотому сечению через иррациональные (квадратич-
(квадратичные) числа.
Возможная последовательность для кубических иррациональных
чисел имеет вид
хп={у^У'\ A8)
где к = 3 (при к > 3 получим иррациональные числа четвертой и более
высоких степеней).
Литература
[1] AguM. A nonstationary time-series having 1/f-type power spectrum. //
J. Phys. Soc. Japan. 1976. V.40. P. 1510-1511.
[2] AlbinetG., SearbyG., StaufferD. Fire propagation in a 2-D random
medium. // J. Physique (Paris). 1986. V.47. P. 1-7.
[3] Alstr0mP., LevinsenM. T. Fractal structure of the complete devil's staircase
in dissipative systems described by a driven damped-pendulum equation with
a distorted potential. // Phys. Rev. 1985. V. B32. P. 1503-1511.
[4] Alvarez L. W. Adventures of a Physicist. N. Y.: Basic Books, 1987.
[5] AlvarezW., AsaroF., MichelH. V., Alvarez L. W. Iridium anomaly
approximately synchronous with terminal eocene extinctions, j j Science.
1982. V. 216. P. 886-888.
[6] AlpherR. A., HermanR. Evolution of universe. // Nature. 1948. V. 162.
P. 774-775.
[7] AnderM. E., ZumbergeM. A., LautzenhiserT., Parker RL, AikenC.L.V.,
GormanM.R., NietoM.M., Cooper A. P.R., FergusonJ. F., FisherE.,
McMechanG. A., SasagawaG., Stevenson J. M., Backus G., ChaveA. D.,
GreerJ., HammerP., HansenB.L., HilderbrandJ. A., KeltyJ.R., SidlesC,
Wirtz J. Test of Newton's inverse-square law in the Greenland ice cap. //
Phys. Rev. Lett. 1989. V.62. P. 985-988.
[8] Arnold V. I. Mathematical Methods of Classical Mechanics. Berlin: Springer,
1989. [Русский оригинал: Арнольд В. И. Математические методы клас-
классической механики. 3-е изд., перераб. и доп. М.: Наука, 1989.]
[9] AtalB. S., ShroederM. S., SesslerG. M., WestJ.E. Evaluation of
acoustic properties of enclosures by means of digital computers. //
J. Acoust. Soc. Amer. 1966. V.40. P.428-433.
[10] Anderson P. W. Absense of diffusion in a certain random lattices. //
Phys. Rev. 1958. V. 109. P. 1492-1505.
[11] AvronJ.E., SimonB. Almost periodic Hill's equation and the rings of
Saturn. I/ Phys. Rev. Lett. 1981. V.46. P. 1166-1168.
[12] BabcockK. L., Westerverlt R. M. Avalanche and self-organization in
cellular magnetic-domain patterns. // Phys. Rev. Lett. 1990. V. 64. P. 2168-
2171.
[13] BahcallJ., PiranT., WeinbergS. (eds.) Dark Matter in the Universe.
Singapore: World Scientific, 1987.
496 Литература
[14] ВакР., BruinsmaR. One-demensional Ising model and the complete
staircase, jj Phys. Rev. Lett. 1982. V. 49. P. 249-251.
[15] BakP., TangC, WiesenfeldK. Self-organized criticality: An explanation of
1/f-noise. I/ Phys. Rev. Lett. 1987. V. 59. P. 381-384.
[16] BakP., TangC, WiesenfeldK. Self-organized criticality. jj Phys.Rev.
1988. V. A38. P. 364-374.
[17] BaleH.D., SmithP.W. Small-angle x-ray scattering investigation of
submicroscopic porosity with fractal properties. j j Phys. Rev. Lett. 1984.
V.53. P. 596-599.
[18] Barclay A. The Ship of Fools. 1509. (Перевод сочинения Себастьяна Вран-
дта «Das Narrenschiff» A494 г.) — описание распрей внутри католичес-
католической церкви и предшественник протестантской Реформации.)
[19] BarnsleyM. Fractals Everywhere. San Diego: Academic Press, 1988.
[20] Bass T. A. The Newtonian Casino. N.Y.: Longman, 1990.
[21] BeranekL.L. Music, Acoustics and Architecture. N. Y.: Wiley, 1962.
[22] BerlekampE. R., ConwayJ.H., GuyR. K. Winning Ways for Your
Mathematical Plays, Vol.2. Ch. 25. N. Y.: Academic Press, 1982.
[23] Berry M.V. Diffractals. jj J.Phys. 1979. V.A12. P. 781-797.
[24] BillingsleyP. The singular function of bold play, jj Amer. Sci. 1983. V. 71.
P. 392-397.
[25] BizettiP. G., Bizetti-SonaA. M., FazziniT., TaccettiN. Search for a
composition-dependent fifth force, jj Phys. Rev. Lett. 1989. V. 62. P. 2901-
2904.
[26] BohrT., BakP., JensenM. H. Transition to chaos by interaction of
resonances in dissipative systems. II. Josephson junctions, charge-density,
and standard maps, jj Phys. Rev. 1984. V. A30. P. 1970-1981.
[27] BorweinJ. M., BorweinP. B. Pi and the AGM — A Study in Analytic
Number Theory and Computational Complexity. N. Y.: Wiley, 1987.
[28] BorweinJ. M., BorweinP. B. BailyD.H. Ramanujan, modular equations,
and approximations to pi, or how to compute one billion digits of pi. j j
Amer. Math. Monthly. 1989. V. 96. P. 201-219.
[29] BruinsmaR., BakP. Self-similarity and fractal dimension of the devils's
staircase in the one-dimentional Ising model, j j Phys. Rev. 1983. V. B27.
P.5824-5825.
[30] BurchfieldR.W. (ed.) Oxford English Dictionary. Oxford: Oxford
University Press, 1987.
[31] CampiX. Multifragmentation: Nuclei break up like percolation, jj J.Phys.
1986. V. A19. P. L917-921. (См. также Nucl. Phys. V.A459. P. 692.)
[32] Cardy J. L. Conformal invariance and the Yang-Lee edge singularity in two
dimensions, jj Phys. Rev. Lett. 1985. V. 54. P. 1354-1356.
Литература 497
[33] ChenH., LiD.X., KuoK.H. New type of two-dimensional quasicrystal with
twelvefold rotational symmetry. jj Phys. Rev. Lett. 1988. V. 60. P. 1645-
1648.
[34] ChiavaloD. R., JalifeJ. Nonlinear dynamics of cardiac excitation and
impulse propagation. jj Nature. 1987. V. 330. P. 749-752.
[35] ClarkD.S., ShishaO. Invulnerable queens on an infinite chessboard. jj
3rd Int. Conf. Combinatorial Math. Annals of the New York Academy of
Sciences. 1988.
[36] Collet P. C, EckmannJ.-P. Iterated Maps of the Interval as Dynamical
Systems. Boston, Cambridge, Mass.: Birkhauser. 1980.
[37] ComroeJ.H. The lung. jj Scientific American, February 1966, V. 214.
p. 56-68.
[38] CoonD.D., MaaS.N., Perera A. G. U. Farey fractions frequency modulation
in the neuron-like output of silicon p-i-n diodes at 4.2 K. j j Phys. Rev. Lett.
1987. V.58. P 1139-1142.
[39] CorzineR. G., MoskoJ. A. Four-arm Spiral Antennas. Norwood, Mass.:
Artech House, 1990.
[40] Crick F. Life Itself. N. Y.: Simon & Shuster, 1981.
[41] CvitanovicP., JensenM.H., Kadanoff L. P., Procaccial. Renormalization,
unstable manifolds, and the fractal structure of mode locking. j j
Phys. Rev. Lett. 1985. V. 55. P. 343-346.
[42] D'AntonioP. A new 1- or 2-dimensional fractal sound diffusor. jj
J. Acoust. Soc. Amer. 1990. Suppl. 1. V. 87. P.S10.
[43] DaviesC, KnuthD. Number representations and dragon curves, jj
J. Recreational Math. 1988. V. 3. P. 66-81, 133-149.
[44] de BruijnN. G. Sequences of zeroes and ones generated by special
production rules. jj Kon. Ned. Acad. Wetensch. Proc. Ser. 1981. V. A84.
(Indaginationes Mathematicae. V. 43) P. 27-37. См. также de BruijnN. G.
Algebraic theory of Penrose's nonperiodic tilings of the plane, jj
Kon. Ned. Acad. Wetensch. 1981. V.84. P. 39-66.
[45] de WijsH. J. Statistics of ore distribution, jj Geologie en Mijnbouw
(Amsterdam). 1951. V. 13. P. 365-375. (См. также Ibid, 1953. V. 15. P. 12-
24.)
[46] DekkingF. M., Mendes France M., van der PoortenA. Folds! jj
Math. Intelligencer. 1982. V.4. P. 130-138, 173-181, 190-195.
[47] DerridaB., GervoisA., PomeauY. Iteration of endomorphisms on the real
axis and representation of numbers, j j Ann. Inst. Henri Poincare. 1978.
V. XXIX. P. 305-356.
[48] DerridaB., De SezeL., ItzyksonC. Fractal structure of zeroes in hierarchical
models, jj J. Statist. Phys. 1983. V. 33. P. 559-569.
498 Литература
[49] DiaconisP. The distribution of leading digit and uniform distributions
modi. // Ann.Prob. 1977. V. 5. P. 72-81.
[50] DouadyA., HubbardJ.H. Iterations des polynomes quadratique complexes.
I/ Compt. Rend. Acad. Sci. Paris 1982. V. 294. P. 123-126.
[51] DouadyA., HubbardJ.H. On the dynamics of polynomial-like mappings.
I/ Ann. Sci Ecole Normale Sup. 4e Serie. 1985. T. 18. P. 287-343.
[52] DouadyA. Julia sets and the Mandelbrot set. В книге: PeitgenH.-O.,
RichterP.H. The Beauty of Fractals. Berlin: Springer. 1986. P. 161-173.
[53] Dress A. W. M., GerhardtM., JaederN.L, PlathP.J., Schuster H.
Some proposals concerning the mathematical modelling of oscillating
heterogeneous catalytic reactions on metal surfaces. В книге: RensingL.,
JaederN.L (eds). Temporal Order. Berlin: Springer. 1985. P. 67-74.
[54] DuB.-S. A chaotic function whose nonwandering set is the Cantor ternary
set. I/ Proc. Math. Soc. Amer. 1984. V. 92. P. 277-278.
[55] DuneauM., Katz A. Quasiperiodic patterns. // Phys. Rev. Lett. 1985. V. 54.
P. 2688-2691.
[56] EggletonR. В., GuyR. K. Catalan strikes again! // Mathematics Magazine.
1988. V.61. P. 211-219.
[57] Einstein A. Uber die von der molekularkinetischen Theorie der Wdrme
geforderte Bewegung von in ruhender Flussigkeiten suspendierten Teilchen.
Annalen der Physik. 1905. V. 17. P. 549-560. [Русский перевод: О дви-
движении взвешенных в покоящейся жидкости частиц, требуемом
молекулярно-кинетической теорией теплоты. В книге: Эйнштейн А.
Собрание научных трудов в четырех томах. Т. III. Работы по кине-
кинетической теории, теории излучения и основам квантовой механики.
1901-1955. М.: Наука, 1966. С. 108-117.]
[58] Eisner V. Indexing problems in quasi-crystal diffraction. // Phys. Rev. 1985.
V.B32. P. 4892-4898.
[59] ErdelyA. Tables of Integral Transforms. N.Y.: McGraw-Hill. 1954. [Русс-
[Русский пер.: ВейтменГ., ЭрдейиА. Таблицы интегральных преобразований.
В 2-х т. М.: Наука, 1969.]
[60] Escher М. С. The World of М. С. Escher. N. Y.: H. N. Abrams, 1971.
[61] Eykholt R., Umberger D. K. Characterization of fat fractals in nonlinear-
dynamical systems. // Phys. Rev. Lett. 1986. V. 57. P. 2333-2336.
[62] Falconer K. J. Digital sun dials, paradoxical sets, and Vitushkin's conjecture.
I/ Math. Intelligencer. 1987. V. 9. P. 24-27.
[63] Family F., Landau D. P. (eds.) Kinetics of Aggregation and Gelation.
Amsterdam: North Holland. 1984.
[64] Farmer J. D. Dimension, fractal measure and chaotic dynamics. В книге:
HakenH. (ed.). Evolution of Order and Chaos. Berlin. N. Y.: Springer. 1982.
Литература 499
[65] Farmer J.D. Sensitive dependence on parameters in nonlinear dynamics, j j
Phys. Rev. Lett. 1985. V. 55. P. 351-354.
[66] Feder J. Fractals. N. Y.: Plenum, 1988. [Русский пер.: ФедерЕ. Фракталы.
М.: Мир, 1991.]
[67] FeigenbaumM. J. The universal metric properties of nonlinear
transformations. // J. Statist. Phys. 1979. V. 21. P. 669-706.
[68] FeigenbaumM.J. Universal behavior in nonlinear systems. // Physica.
1983. V. 7D. P. 16-39. [Русский пер.: Фейгенбаум М. Универсальность в
поведении нелинейных систем. // УФН. 1983. Т. 141. В. 2. С. 343-374.]
[69] FeinA.P., HeutmakerM. S., GollubJ.P. Physical scaling at the transition
from quasiperiodicity to chaos in a hydrodynamic system, // Phys. Scr.
1985. V. T9. P. 79-84.
[70] Feller W. An Introduction to Probability Theory and Its Applications. N. Y.:
Wiley, 1968. [Русский пер.: Феллер В. Введение в теорию вероятностей
и ее приложения. В 2-х т. М.: Мир, 1984.]
[71] Fibonacci Leonardo. Liber Abaci. Pisa, 1202.
[72] Fisher D. E. Fire and Ice: The Greenhouse Effect, Ozone Depletion, and
Nuclear Winter. N. Y.: Harper & Row, 1990.
[73] Friedrich II. De Arte Venandi cum Avibus. (Латинский оригинал «Искус-
«Искусства охоты с птицами» с собственноручными иллюстрациями импера-
императора был похищен во время осады Пармы в 1248 г. и впоследствии утра-
утрачен. Копия, снятая сыном императора Манфредом, была опубликована
в 1789 г. Шнейдером в Лейпциге.)
[74] GardnerM. The fantastic combinations of John Conway's new solitaire
game of life, // Scientific American. (Mathematical Games. April 1970.)
V.223. P. 120-123.
[75] Gardner M. Extraordinary nonperiodic tiling that enriches the theory of
tiles. I/ Scientific American. (Mathematical Games. January 1977.) V. 236.
P. 110-121.
[76] Gardner M. White and brown music, fractal curves and one-over-f noise.
//Scientific American. (Mathematical Games. April 1978.) V. 238. P. 16-32.
[77] Gardner M. Wheels, Life and Other Mathematical Amusements. N. Y.:
W.H. Freeman, 1983.
[78] Gardner M. Penrose Tiles to Trapdoor Ciphers. N. Y.: W. H. Freeman, 1989.
[Русский пер.: Гарднер М. От мозаик Пенроуэа до надежных шифров. М.:
Мир, 1993.]
[79] GeiselT., ZacherlA., Radons G. Generic 1// noise in chaotic Hamiltonian
systems. // Phys. Rev. Lett. 1987. V. 59. P. 2503-2506.
[80] Gilbert E. N. Gray codes and paths on the n-cube. // Bell Syst. Tech. J.
1958. V.37. P. 815-826.
500 Литература
[81] Gilbert W. J. A cube-filling Hilbert curve. j j Math. Intelligencer. 1984. V. 6.
P. 78.
[82] GleickJ. Chaos: Making a New Science. N. Y.: Viking, 1987.
[83] Graham R. L., LinS., LinC.-S. Spectra of numbers. // Mathematics
Magazine. 1978. V.51. P. 174-176.
[84] Grassberger P. On the Hausdorff dimension of fractal attractors. //
J. Statist. Phys. 1981. V. 26. P. 173-179.
[85] Grassberger P. Generalized dimensions of strange attractors. // Phys. Lett.
1983. V.97A. P. 227-230.
[86] Grassberger P. On the spreading of two-dimensional percolation. // J. Phys.
1985. V.A18. P.L215-219.
[87] Grassberger P., Procaccial. Characterization of strange attractors. //
Phys. Rev. Lett. 1983. V. 50. P. 346-349.
[88] Grimmett G. Percolation. N. Y.: Springer, 1989.
[89] Grossmann S. Diversity and universality. Spectral structure of discrete time
evolution. В книге: HakenH. (ed.) Evolution of Order and Chaos. Berlin:
Springer, 1982.
[90] Grossmann S., Thomae S. Invariant distributions and stationary
correlations of one-dimensional discrete processes. // Zeitschrift fur
Naturforschung. 1977. V. 32a. P. 1353-1363.
[91] GranbaumB., ShephardG. C. Tilings and Patterns. N. Y.: W. H. Freeman,
1987.
[92] GwinnE. G., WesterveltR. M. Scaling structure of attractors at the
transition from quasiperiodicity to chaos in electronic transport in Ge. j j
Phys. Rev. Lett. 1987. V. 59. P. 157-160.
[93] HakenH. Synergetics. Berlin / N. Y.: Springer, 1978. [Русский пер.: Ха-
кен Г. Синергетика. М.: Мир, 1980.]
[94] Haldane J. В. S. On Being the Right Size. L: Oxford University Press, 1928.
[95] HalmosP.R. Naive Set Theory. N.Y.: Springer, 1974.
[96] HalseyT. C, JensenM. H., KadanoffL. P., Procaccial., ShraimanB.I.
Fractal measures and their singularities: The characterization of strange
sets. I/ Phys. Rev. 1986. V. A33. P. 1141-1151.
[97] Hardy G.H., WryghtE. M. An Introduction to the Theory of Numbers.
Oxford: Clarendon Press, 1984.
[98] HarrisS. What's So Funny about Science. Los Altos, Calif.: Kaufmann,
1977.
[99] HarwitM., SloaneN. J. A. Hadamard Transform Optics. N. Y.: Academic
Press, 1979.
[100] HasingerG., LangmeierA., SztajnoM., TrumperJ., LewienW. H. G.,
White N. E. Quasi-periodic oscillations in the X-ray flux of Cyg X-2. //
Nature, 1986. V.319. P. 469-471.
Литература 501
[101] Hawking S. A Brief History of Time. N. Y.: Bantam, 1988. [Русский пер.:
Хокинг С. От большого взрыва до черных дыр: Краткая история време-
времени. М.: Мир, 1990.]
[102] HenonM. A two-dimensional map with a strange attractor. //
Commun. Math. Phys. 1976. V. 50. P. 69-77.
[103] HenonM. Chaotic scattering modelled by an inclined billiard, jj Physica,
1988. V.D23. P. 132-156.
[104] HentschelH. G. E., Procaccial. The infinite number of generalized
dimensions of fractals and strange attractors. j j Physica, 1983. V. 8D.
P. 435-444.
[105] HentschelH. G. E., Procaccial. Fractal nature of turbulence as manifested
in turbulent diffusion. // Phys. Rev. 1983. V. A27. P. 1266-1269.
[106] HentschelH. G. E., Procaccial. Relative diffusion in turbulent media: The
fractal dimension of clouds. // Phys. Rev. 1984. V. A29. P. 1461-1470.
[107] HinrichsenE., Feder J., j0ssangT. DLA growth from a line. Report Series,
Cooperative Phenomena Project, Department of Physics, University of
Oslo, 1987. V. 87-11. P. 1-21.
[108] Hofstadter D. R. Godel, Escher, Bach: An Eternal Golden Braid. Vintage,
1980.
[109] HuB. Problem of universality in phase transitions on hierarchical lattices.
I/ Phys. Rev. Lett. 1985. V. 55. P. 2316-2319.
[110] HuntF.V. BeranekL. L., MaaD.Y. Analysis of sound decay in rectangular
rooms. I/ J. Acoust. Soc. Am. 1939. V. 11 P. 80-94.
[Ill] Hurst H.E., Black R. P., SimaikaY.M. Long Term Storage: An
Experimental Study. L.: Constable, 1965.
[112] HuygensC. Horologium Oscillatorium. Paris: Muguet, 1963. [Русский пер.:
Гюйгенс X. Три мемуара по механике. М.: Изд-во АН СССР, 1951. Маят-
Маятниковые часы.]
[113] IchimasaT., NissenH.-U., FukanoY. New ordered state between crystalline
and amorhous in Ni-Cr particles. // Phys. Rev. Lett. 1985. V. 55. P. 511-
513.
[114] IchimasaT., NissenH.-U., FukanoY. Electron microscopy of crystalloid
structure in Ni-Cr small particles. // Phil. Mag. 1988. V. A58. P. 835-863.
[115] JahnkeE., EmdeF. Tables of Higher Functions. Leipzig: Teubner, 1951.
[Русский пер.: ЯнкеЕ., ЭмдеФ., ЛешФ. Специальные функции: Формулы,
графики, таблицы. М.: Наука, 1977.]
[116] JakobsonM.V. Absolutely continuous invariant measures for one-
parameter families of one-dimensional maps. // Commun. Math. Phys.
1981. V.81. P. 39-88.
[117] JannerA. Symmetries in higher-dimensional crystallography. // Phase
Transitions. V. 16/17. P. 87-101.
502 Литература
[118] JekeliC, Eckhardt D. H., RomaidesA.J. Tower gravity experiment: No
evidence for non-Newtonian gravity. j j Phys. Rev. Lett. 1990. V. 64.
P. 1204-1206.
[119] Jensen M.H., BakP., Bohr T. Complete devil's staircase, fractal dimension,
and universality of mode-locking structure in the circle map. jj
Phys. Rev. Lett. 1983. V. 50 P. 1637-1641.
[120] JensenM.H., BakP., Bohr T. Transition to chaos by interaction of
resonances in dissipative systems, j j Phys. Rev. 1984. V. A30. P. 1960-1969.
[121] Jensen M.H., Kadanoff L. P., LibchaberA., ProcacciaL, StavansJ. Global
universality at the onset of chaos, jj Phys. Rev. Lett. 1985. V. 55 P. 2798-
2801.
[122] Jensen R. V., MyerC.R. Images of the critical points of nonlinear maps, jj
Phys. Rev. 1985. V. A32 P. 1222-1224.
[123] Jones D. Abstract concrete, jj Nature. 1988. V. 332. P. 310.
[124] JuleszB., SlepianD., SondhiM.M. Correction of astigmatism by lens
rotation and image processing, j j J. Opt. Soc. Am. 1969, V. 8 P. 485.
[125] KacM. Enigmas of Chance. N. Y.: Harper & Row, 1985.
[126] KatzA., DuneauM. Quasiperiodic patterns and icosahedral symmetry, jj
J. Phys. 1986. V.47. P. 181-196.
[127] Kelly J. L. A new interpretation of information rate, jj Bell Syst. Tech. J.
1956. V.35. P. 917-926.
[128] KestenH. Percolation Theory and Ergodic Theory of Infinite Particle
Systems. N.Y.: Springer, 1987. [Русский пер.: КестенХ. Теория проса-
просачивания для математиков. М.: Мир, 1986.]
[129] KimS Inversions. Peterborough, N. Н.: Byte Books, McGraw-Hill, 1981.
[130] KleeV., Wagon S. New and Old Unsolved Problems in Plane Geometry and
Number Theory. Washington, D.C.: Mathematical Association of America,
1989.
[131] Klein В., Bivensl. Proof without words, j j Mathematics Magazine. 1988.
V.61. P. 219.
[132] KohlrauschR. Uber das Dellman'sche Elektrometer. j j Annalen der Physik
und Chemie (Poggendorf), 1847. V.III-12, P. 353-405.
[133] KohlrauschR. Theorie des elektrischen Ruckstandes in der Leidener
Flasche. jj Annalen der Physik und Chemie (Poggendorf), 1854. V. IV-
91, P. 56-82, 179-214.
[134] KolbM., BotetR., JullienR. Scaling of kinetically growing clusters, jj
Phys. Rev. Lett. 1983. V. 51. P. 1123-1126.
[135] KoplowitzJ., Sundar Raj A. P. A robust filtering algorihm for subpixel
reconstruction of chain coded line drawings, j j IEEE Trans. Pattern
Analysis and Machine Analysis, 1987. V. 9. P. 451-457.
Литература 503
[136] LandauL.D., LifschitzE.M. Mechanics. Oxford: Pergamon Press, 1976,
sec. 10. [Русский оригинал: Ландау Л. Д., ЛифшицЕ. М. Теоретическая
физика; т.1. Механика. М.: Наука, 1988. Изд. 4-е, испр.]
[137] LapidusM. L., Fleckinger-PelleJ. Tambour fractal: vers une resolution de la
conjecture de Weyl-Berry pour les valeurs propres du laplacien. j j Compt.
Rend. Acad. Sci. Paris Math. 1988. V. 306. Ser. I. P. 171-175.
[138] LaskarJ. A numerical experiment on the chaotic behavior of the solar
system. I/ Nature. 1989. V. 338. P. 237-238.
[139] Lauterborn W., Cramer E. Subharmonic route to chaos observed in
acoustics. I/ Phys. Rev. Lett. 1981. V. 47. P. 1445-1448.
[140] Lauterborn W., Holzfuss J. Evidence for a low-dimensional strange attractor
in acoustic turbulence. Ц Phys. Lett. 1986. V.A115. P. 369-372.
[141] Lauterborn W., ParlitzU. Methods of chaos physics and their application
to acoustics. // J. Acoust. Soc. Am. 1988. V. 84. P. 1975-1993.
[142] LawtonJ.H. More time means more variation. // Nature. 1988. V. 334.
P. 563.
[143] Leibniz G.-W. Principia Philosphiae, More Geometrico Demonstrata. Это
замечательное сочинение Лейбница, написанное в 1714 г. и известное
более под названием «Монадология», было впервые опубликовано в 1720-
1721 гг. Несколько академий и ученых обществ и поныне работают над
изданием полного собрания сочинения Лейбница. [Русский пер.: Лейб-
Лейбниц Г.-В. Сочинения в четырех томах; т.1. М.: Мысль, 1982. С. 413-
429.]
[144] Leopold L. В. Rivers. // Am. Scientist. 1962. V. 50. P. 511-537.
[145] Levin L., Steinhardt P. J. Quasicrystals: A new class of ordered structures.
I/ Phys. Rev. Lett. 1984. V. 53. P. 2477-2480.
[146] LiT.-Y., YorkeJ. A. Period three implies chaos. Ц Am. Math. Monthly.
1975. V.82. P. 985-992.
[147] LibchaberA., Maurer J. Une experience de Rayleigh-Benard de geometrie
reduite; Multiplication, Accrochage et demultiplication de frequences. //
J.Phys. (Paris) Coll. 1980. V.41. P.C3-51.
[148] Lindemeyer A. Mathematical models of cellular interactions in development.
I/ J. Theor. Biol. 1968. V. 18. P. 280-315.
[149] LiuS.H. Fractal model for the ас-response of a rough interface. //
Phys. Rev. Lett. 1985. V. 55. P. 529-532.
[150] Lorentz E. N. Noisy periodicity and reverse bifurcation. В книге:
HellemanR. H. G. Nonlinear Dynamics. (Annals of the New York Academy
of Sciences) 1980. V. 357. P. 282-291.
[151] LovejoyS. Area-perimeter relation for rain and cloud areas. // Science.
1982. V.216. P. 185-187.
504 Литература
[152] Lovejoy S., Mandelbrot В. В. Fractal properties of rain, and a fractal model.
I/ Tellus. 1985. V. 37A. P. 209-232.
[153] Mackey A. Crystallography and the Penrose pattern. // Physica. 1982.
V.114A. P. 609-613.
[154] Mallows C. Conway's Challenging Sequence. 11 Am. Math. Monthly. 1991.
V.98. P. 5-20.
[155] Mandelbrot В. В. On the theory of word frequencies and on related
Markovian models of discourse. В книге: JacobsonR. (ed.) Structures of
Language and Its Mathematical Aspects. N. Y.: American Mathematical
Society, 1961.
[156] Mandelbrot В. В. The stable Paretian income distribution when the
apparent exponent is near zero. // Int. Econ. Rev. 1963. V. 4. P. 111-115.
[157] Mandelbrot В. В. The variation of certain speculative stock prices. // J. Bus.
(Chicago). 1963. V. 36. P. 394-419.
[158] Mandelbrot B. B. New methods in statistical economics. // J. Polit. Econ.
1963. V. 71. P. 421-440.
[159] Mandelbrot В. В. Intermittent turbulence in self-similar cascades:
Divergence of high moments and dimension of the carrier. // J. Fluid
Mech. 1974. V. 62. P. 331-358.
[160] Mandelbrot В. В. Fractal aspects of the iteration z —У \z(l — z) for complex A
and z. В книге: HellemanR. H. G. (ed.) Nonlinear dynamics. (Annals of the
New York Academy of Sciences). 1980. V. 357. P. 249-259.
[161] Mandelbrot В. В. The Fractal Geometry of Nature, updated and augmented.
N. Y.: W. H. Freeman, 1983.
[162] Mandelbrot B. B. Fractals and Multifractals, Selecta Vol.1. N.Y.: Springer,
1991.
[163] Mandelbrot В. В., PassojaD., PaullayA. Fractal character of fracture
surfaces of metal. // Nature. 1984. V. 308. P. 721-722.
[164] Mandelbrot В. В., WallisJ.R. Some long-run properties of geophysical
records. И Water Resources Research. 1969. V. 5. P. 321-340.
[165] Martin J. E., HurdA. J. Scattering from fractals. // J. Appl. Crystallog.
1987. V. 20. P. 61-78.
[166] Martin S., Martienssen W. Circle maps and mode locking in the driven
electrical conductivity of barium sodium niobate crystals. // Phys. Rev. Lett.
1986. V. 56. P. 1522-1525.
[167] MathewsM.V., Pierce J. R., Reeves A., Roberts L. Theoretical and
experimental exploration of the Bohlen-Pierce scale. // J. Acoust. Soc. Am.
1988. V. 84. P. 1214-1222.
[168] MayR. M. How many species are there on earth? // Science. 1988. V. 214.
P. 1441-1449.
Литература 505
[169] MannevilleP., BoccaraN., VichniacG. Y., BidauxR. (eds.) Cellular
Automata and Modeling of Complex Physical Systems. Berlin: Springer,
1989.
[170] McGraw-Hill Encyclopedia of Science and Technology. N. Y.: McGraw-Hill,
1971.
[171] MeakinP. Formation of fractal clusters and networks by irreversible
diffusion-limited aggregation, j j Phys. Rev. Lett. 1983. V. 51. P. 1119-1122.
[172] MeakinP. Scaling properties for the growth probability measure and
harmonic measure of fractals, jj Phys. Rev. 1987. V. A35. P. 2234-2245.
[173] MeakinP., Coniglio A., Stanley H. E., WittenT. A. Scaling properties for the
surfaces of fractal and nonfractal objects: An infinite hierarchy of critical
exponents, jj Phys. Rev. 1986. V. A34. P. 3325-3340.
[174] MeakinP., Stanley H. E., Coniglio A., WittenT. A. Surfaces, interfaces and
screening of fractal structures, jj Phys. Rev. 1985. V. A32. P. 2364-2369.
[175] MeinhardtH. Models of Biological Pattern Formation. London: Academic
Press, 1982.
[176] MeinhardtH., KlingerM. A model for pattern formation on the shells of
molluscs, jj J. Theor. Biol. 1987. V. 126. P. 63-89.
[177] Mekjian A. Z. Model of a fragmentation process and its power-law behavior.
jj Phys. Rev. Lett. 1990. V. 64. P. 2125-2128.
[178] MeneveauC, SreenivasanK.R. Simple multifractal cascade model for fully
developed turbulence, j j Phys. Rev. Lett. 1987. V. 59. P. 1424-1427.
[179] MengerK. Selected Papers in Logic and Foundations, Didactics and
Economics. Boston: Reidel, 1979.
[180] MetropolisN., SteinM. L., SteinP. R. On finite limit sets for
transformations of the unit interval, jj J. Combinatorial Theory.
1973. V. (A) 15. P. 25-44.
[181] MoonF. C. Fractal boundary for chaos in a two-state mechanical oscillator.
jj Phys. Rev. Lett. 1984. V. 53. P. 962-964.
[182] Morse M. Recurrent geodesies on a surface of negative curvature, j j
Trans. Am. Math. Soc. 1921. V. 22. P. 84-100.
[183] NauenbergM., SchellnhuberH. J. Analytic evolution of the multifractal
properties of a Newtonian Julia set. jj Phys. Rev. Lett. 1989. V. 62. P. 1807-
1810.
[184] NiemeyerL., PietroneroL., WiesmannH. J. Fractal dimension of dielectric
breakdown, jj Phys. Rev. Lett. 1984. V. 52. P. 1033-1040.
[185] NiemeyerL., PietroneroL., WiesmannH. J. Response to comments on paper
on dielectric breakdown, jj Phys. Rev. Lett. 1986. V. 57. P. 649-650.
[186] OnodaG.Y., Toner J. Fractal dimensions of model particle packings having
multiple generations of agglomerations, j j Comm. Am. Ceramic Soc. 1986.
V. 69. P. C-278-C-279.
506 Литература
[187] OttinoJ.M. The mixing of fluids, jj Scientific American, January 1989.
V. 260. P. 40-49.
[188] PageW. Proof without words: Geometric sums, jj Mathematics Magazine.
1981. V. 54. P. 201.
[189] Pais A. Subtle Is the Lord ... Oxford: Clarendon Press, 1982. [Русский
пер.: Пайс А. Научная деятельность и жизнь Альберта Эйнштейна. М.:
Наука, 1989.]
[190] ParetoV. Oeuvres Completes. Geneva: Droz, 1896.
[191] Pauling L. Apparent icosahedral symmetry is due to directed multiple
twinning of cubic crystals, jj Nature. 1985. V. 317. P. 512-514.
[192] PeitgenH.-O., PriiferM., RichterP.H. Phase transitions and Julia sets.
В книге: EbelingW., PeschelM. (eds.) Lotka - Volterra Approach to
Cooperation and Competition in Dynamical Systems. Berlin: Akademie-
Verlag, 1985.
[193] PeitgenH.-O., RichterP. Harmonie in Chaos und Kosmos: Bilder aus der
Theorie der dynamischen Systeme. Bremen: Die Sparkasse in Bremen, 1984.
[194] PeitgenH.-O., RichterP.H. The Beauty of Fractals. Berlin: Springer, 1986.
[195] PeitgenH.-O., RichterP.H. Fraktale und die Theorie der Phasenubergange.
jj Phys. Blatter. 1986. V. 42. P. 9-22.
[196] PeitgenH.-O., SaupeD. The Science of Fractal Images. N. Y.: Springer,
1988.
[197] Penrose R. The role of aesthetics in pure and applied mathematical research.
jj Bull. Inst. Math. & Its Appl. 1974. V. 10. P. 266-271. (См. также
Penrose R. Pentaplexity: A class of nonperiodic tilings of the plane, jj
Math. Intelligencer. 1979. V. 2. P. 32-37.)
[198] PfeiferP., AvnirD. Chemistry in noninteger dimensions between two and
three, jj J. Chem.Phys. 1983. V. 79. P. 3558-3565. Erratum: ibid., 1984.
V.80. P. 4573.
[199] Pierce J. R. The Science of Musical Sound. N. Y.: Scienific American Books,
W. H. Freeman, 1983.
[200] PietroneroL., SiebesmaA.P. Self-similarity of fluctuations in random
multiplicative processes, jj Phys. Rev. Lett. 1986. V. 57. P. 1098-1101.
[201] PinkhamR. S. On the distrbution of the first significant digits, jj
Ann. Math. Stat. 1962. V. 32. P. 1223-1230.
[202] ProcacciaL, ThomaeS., TressorC. First return maps as a unified
renormalization scheme for dynamical systems, j j Phys. Rev. 1987. V. A35.
P. 1884-1900.
[203] Prusinkiewicz P. Application of L-systems to computer imagery. В кни-
книге: EhrigH., NaglM., RosenfeldA., RozenbergG. (eds.) Graph Grammars
and Their Application to Computer Science. 3rd Int. Workshop. Berlin:
Литература 507
Springer, 1987. (Series «Lecture Notes in Computer Science», V. 291.)
P. 534-548.
[204] PurcellE. M. Life at low Reynolds number, jj Amer.J.Phys. 1977. V. 45.
P. 3-11.
[205] PurkertW., IlgaudsH.J. Georg Cantor. Basel / Boston: Birkhauser, 1987.
[206] PyensonL. The Young Einstein. Bristol / Boston: Hilger, 1985.
[207] RaimiR. A. The first digit problem, jj Am. Math. Monthly. 1976. V. 83.
P. 521-538.
[208] RamanujanS. Modular equations and approximations to тг. //
Quart. J. Math. 1914. V. 45. P. 350-372.
[209] RammalR., TouloseG., VirasoroM. A. Ultrametricity for physicists, jj
Rev. Mod. Phys. 1986. V. 58. P. 765-788.
[210] RedfearnA., PimmS.L. // Ecological Monogr. 1988. V. 58. P. 39-55.
[211] RenyiA. On a new axiomatic theory of probability, jj Acta Mathematica
Hungarica. 1955. V. 6. P. 285-335.
[212] RichterP., ScholzH.-J. Der goldene Schnitt in der Natur. В книге:
KiippersB.-O. (ed.) Ordnung aus dem Chaos. Miinchen: Piper, 1987.
P. 175-214.
[213] RissetJ.-C. Paradoxes de hauteur. Proc. 7th Int. Cong. Acoustics, paper
S10. P. 20. Budapest: 1971.
[214] RissetJ.-C. Jugements relatifs de hauteur, jj Compt. Rend. Acad. Sci.
Paris. 1975. V. B281 P. 289-292.
[215] RoschkeJ. Eine Analyse der nichtlinearen EEG-Dynamik. Dissertation.
Gottingen: 1987.
[216] RosenfeldA., KimC. E. How a digital computer can tell whether a line is
straight, jj Am. Math. Monthly. 1982. V. 89. P. 230-235.
[217] Rouse H., InceS. History of Hydraulics. Iowa Inst. of Hydraulics, 1957. (По-
(Повторное издание: N. Y.: Dover Publ., 1963.)
[218] SagherY. Counting the rationale, jj Amer. Math. Monthly. 1981. V.96.
P. 823.
[219] Salem J., Wolfram S. Thermodynamics and hydrodynamics of cellular
automata. В книге: Wolfram S. (ed.) Theory and Application of Cellular
Automata. Singapore / Teaneck, N.J.: World Scientific, 1986, P. 362-366.
[220] SanzJ.L.C., HinkleE. В., Jain А. К. Radon and Projection Transform-
Based Computer Vision. Berlin / N. Y.: Springer, 1988.
[221] SchaeferD.W., MartinJ. E., WiltziusP., CannellD. S. Fractal geometry of
colloidal aggregates, jj Phys. Rev. Lett. 1984. V. 52. P. 2371-2374.
[222] Schroder M. Die statistischen Parameter der Frequenzkurven von grossen
Ra'umen. jj Acustica (Beiheft2). V. 4. P. 594-600. Английский перевод:
SchroederM. R. Statistical parameters of the frequency response curves of
large rooms, jj J. Audio Eng. Soc. 1987. V. 35. P. 299-306.
508 Литература
[223] SchroederM.R. Improvement of acoustic feedback stability. jj
J. Acoust. Soc. Amer. 1964. V. 36. P. 1718-1724.
[224] SchroederM. R. Determination of the geometry of the human vocal tract by
acoustic measurements. jj J. Acoust. Soc. Amer. 1967. V. 41. P. 1002-1010.
[225] SchroederM.R. Images from computers and microfilm plotters, jj
Comm. Assoc. Comp.-Mach. V. 12. P. 95-101. (См. также: Schroeder M. R.
Images from computers, j j IEEE Spectrum, March 1969. V. 6. P. 66-78.
[226] SchroederM.R. Digital simulation of sound transmission in reverberated
spaces, jj J. Acoust. Soc. Amer. 1970. V. 47. P. 424-431.
[227] SchroederM.R. An integrable model for the basilar membrane, jj
J. Acoust. Soc. Amer. 1973. V. 53. P. 429-433.
[228] SchroederM.R. Auditory paradox based on fractal waveform, jj
J. Acoust. Soc. Amer. 1986. V. 79. P. 186-189.
[229] SchroederM.R. Statistical parameters of the frequency response curves of
large rooms, jj J. Audio. Eng. Soc. 1987. V. 53. P. 299-306.
[230] SchroederM.R. Number Theory in Science and Communication, with
applications in Cryptography, Physics, Digital Information, Computing,
and Self-Similarity. 2nd enlarged ed. Berlin / N. Y.: Springer, 1990.
[231] SchroederM.R., AtalB.S. Stochastic coding of speech signals at very low
bit rates: The importance of speech prediction, j j Speech Comm. 1985. V. 4.
P. 155-162.
[232] SchroederM.R., AtalB.S., SesslerG. M., WestJ. E. Acoustical
measurements in Philharmonic Hall (New York), jj J. Acoust. Soc. Am.
1966. V. 40. P. 434-440.
[233] SchroederM.R., GottlobD., Siebrasse F. K. Comparative study of European
concert halls: Correlation of subjective preference with geometric and
acoustic parameters, j j J. Acoust. Soc. Amer. 1974. V. 56. P. 1195-1201.
[234] Schuster H. G. Deterministic Chaos. Weinheim: Physik-Verlag, 1984. [Русс-
[Русский пер.: Шустер Г. Детерминированный хаос. Введение. М.: Мир, 1988.]
[235] Sessler G. M. Electrets. Berlin: Springer, 1980.
[236] Shannon С. Е. Prediction and entropy of printed English. Bell Syst. Tech. J.
1951. V. 30. P. 50-64. [Русский пер.: Шеннон К. Предсказание и энтро-
энтропия английского печатного текста // Работы по теории информации
и кибернетики. М.: ИЛ. 1968. С. 669-686.]
[237] Shannon СЕ. Computers and automata. Proc. IRE. 1953. V. 41. P. 1235-
1241.
[238] Sharkovski A. N. Coexistence of cycles of a continuous map of a line into
ilself. jj Ukrain. Math. Zeitschrift. 1964. V. 16. P. 61-71. [Русский ориги-
оригинал: Шарковский А. Н. Существование циклов непрерывного преобразо-
преобразования прямой в себя. Укр. мат. журнал. 1964. Т. 26. №1. С. 61-71.]
Литература 509
[239] ShechtmanD., BlechL, GratiasD., CahnJ.W. Metallic phase with
longe-range orientational order and no translational symmetry, j j
Phys. Rev. Lett. 1984. V. 53. P. 1951-1953.
[240] ShenkerS.J. Scaling behavior in a map of a circle onto itself: Empirical
results. I/ Physica (Utrecht). 1982. V. 5D. P. 405-411.
[241] Shepard R. N. The analysis of proximities: Multidimensional scaling with
unknown distance function. // Psychometrica. 1962. V. 27. P. 125-140, 219-
246.
[242] Shepard R. N. Circularity in pitch judgement. // J. Acoust. Soc. Am. 1964.
V. 36. P. 2346-2353.
[243] Singer D. Stable orbits and bifurcations of maps of the interval. // SIAM
J. Appl. Math. 1978. V. 35. P. 260-267.
[244] Slater P. The analysis of personal preferences. // Br. J. Stat. Psychol. 1960.
V.8. P. 119-135.
[245] SloaneN. J. A. A Handbook of Integer Sequences. N. Y.: Academic Press,
1973.
[246] Smale S. Differentiable dynamical systems. 11 Bull. Am. Math. Soc. 1967.
V. 73. P. 747-817. [Русский пер.: Смейл С. Дифференцируемые динами-
динамические системы. // УМН. 1970. Т. 25, N 1. С. 113-185.]
[247] Stanley H. E., MeakinP. Multifractal phenomena in physics and chemistry.
I/ Nature. 1988. V. 335. P. 405-409.
[248] Stanley H. E., OstrowskyN. (eds.) On Growth and Form: Fractal and Non-
Fractal Patterns in Physics. Dordrecht: NATO ASI, Martinus Nijhoff, 1985.
[249] StaufferD. Introduction to Percolation Theory. London: Taylor & Francis,
1985.
[250] Stevens S. S. On predicting exponent for cross-modality matches. // Percep.
Psychophys. 1969. V. 6. P. 251-256.
[251] Stokes J. P., WeitzD.A., GollubJ. P., Dougherty A., RobbinsM.O.,
Chaikin P. M., Lindsay H. M. Interfacial stability of immiscible displacement
in a porous medium. // Phys. Rev. Lett. 1986. V. 57. P. 1718-1721.
[252] SutnerK. Linear cellular automata and the Garden-of-Eden. // Math.
Intelligencer. 1989. V. 11. P. 49-53.
[253] SuwaN., TakahashiT. Morphological and morphometrical analysis of
circulation in hypertension and ischemia kidney. Munich: Urban &
Schwarzenberg, 1971.
[254] TangC., BakP. Critical exponents and scaling relations for self-organized
critical phenomena. /'/ Phys. Rev. Lett. 1988. V. 60. P. 2347-2350.
[255] Thomas J., KasameyerP., FacklerO., FelskeD., Harris R., KammeraadJ.,
MillettM., MuggeM. Testing the inverse-square law of gravity on 465-m
tower. I/ Phys. Rev. Lett. 1989. V. 63. P. 1902-1905.
510 Литература
[256] Thompson D'A. W. On growth and Form. Cambridge: Cambridge
University Press, 1961.
[257] Thue A. Uber die gegenseitige Lage gleicher Teile gewisser Zeichenreihen.
I/ K. Nord. Vid. Skrifter I Math. Nat. (Oslo). 1906. V. 7. P. 1-22.
[258] ToffoliT., MargolusN. Cellular Automata Machines. Cambridge, Mass.:
MIT Press, 1985.
[259] UlamS. Sets, Numbers, and Universes. Cambridge, Mass.: MIT Press, 1974.
[260] UlrichS. Schdtze deutscher Kunst. Munich: Bertelsmann, 1972.
[261] Verhulst P.-F. Recherches mathematiques sur la loi d'accroissement de la
population. I/ Nouv. Mem. de l'Acad. Roy. des Sciences et Belles-Lettres
de Bruxelles. 1845. V. XVIII.8. P. 1-38.
[262] VichniacG. Simulating physics with cellular automata. j j Physica. 1984.
V. 10D. P. 96-115.
[263] Vichniac G. Cellular automata models of disorder and organization. В кни-
книге: Bienenstock, Fogelman SoulieF., WeisbuchG. (eds.) Disordered Systems
and Biological Organization. Berlin: Springer, 1986, P. 1-20.
[264] VilenkinA. Cosmic strings. j j Scientific American, December 1987. V. 257.
P. 52-60.
[265] von BoehmJ., BakP. Devil's stairs and the commensurate-incommensurate
transitions in GeSb. // Phys. Rev. Lett. 1979. V. 42. P. 122-125.
[266] von SaarloosW., KurtzeD. A. Location of zeros in the complex temperature
plane: Absence of Lee-Young theorem. // J. Phys. 1987. V. A17. P. 1301-
1311.
[267] VossR. F. Random fractal forgeries. В книге: EarnshawR. A (ed.)
Fundamental Algorithms for Computer Graphics. Berlin / N. Y.: Springer,
1985.
[268] VossR.F. Fractals in nature: From characterization to simulation. В книге:
PeitgenH.-O., SaupeD. The Science of Fractal Images. N. Y.: Springer,
1988.
[269] VossR. F., Clark J. 1// noise in music: Music from 1// noise. //
J. Acoust. Soc. Amer. 1978. V. 63. P. 258-263.
[270] Wagon S. Is n normal? 11 Math. Intelligencer. 1985. V. 7. P. 65-67.
[271] WangN., ChenH., KuoK.H. Two-dimensional quasicrystal with eightfold
rotational symmetry. // Phys. Rev. Lett. 1987. V. 59. P. 1010-1013.
[272] Weiner J. The Next One Hundred Years: Shaping the Fate of Our Living
Earth. N.Y.: Bantam, 1990.
[273] WeitzD. A., OliveriaM. Fractal structures formed by kinetic aggregation of
aqueous gold colloids, j j Phys. Rev. Lett. 1984. V. 52. P. 1433-1436.
[274] WermanM., WuA., MelterR. A. Recognition and characterization of
digitized curves, j j Pattern Recognition Lett. 1987. V. 5. P. 207-213.
Литература 511
[275] WeylH. Symmetrie. Basel: Birkhaiiser, 1981. [Русский перевод с более
раннего американского издания: Вейль Г. Симметрия. М.: Наука, 1968.]
[276] WilsonT. A. Design of the bronchial tree, jj Nature. 1967. V. 213. P. 668-
669.
[277] Wisdom J. Chaotic dynamics in the solar system. (Urey Prize Lecture). j j
Icarus. 1987. V.72. P. 241.
[278] WisdomJ., PealeS., MignardF. The chaotic rotation of Hyperion. jj
Icarus. 1983. V. 58. P. 137-152.
[279] WittenT. A., Sander L. M. Diffusion-limited aggregation: A Kinetic critical
phenomenon, jj Phys. Rev. Lett. 1983. V.47. P. 1400-1403. (См. также
Phys. Rev. V. B27. P. 5686-5697.
[280] Wolfram S. Cellular automata as models of complexity, jj Nature. 1984.
V.341. P. 419-424.
[281] Wolfram S. (ed.) Theory and Application of Cellular Automata. Singapore
/ Teaneck, N.J.: World Scientific, 1986.
[282] YangC.N., LeeT. D. Statistical theory of equations of state and phase
transitions, jj Phys. Rev. 1952. V. 87. P. 404-418.
[283] ZiaR. K. P., Dallas W. J. A simple derivation of quasi-crystalline spectra.
jj J. Phys. A: Math. Gen. 1985. V. 18. P. L341-L345.
[284] Zimmerman M. H. Hydraulic architecture of some diffuse-porous trees, jj
Can. J. Botany, 1978. V. 56. P. 2286-2295.
[285] Zipf G. K. Human Behavior and the Principle of Least Effort. Cambridge,
Mass.: Addison-Wesley, 1949.
[286] ZweigG., LipesR., Pierce J. R. The cochlear compromise, j j J. Acoust. Soc.
Amer. 1976. V. 59. P. 975-982.
Предметный указатель
«Абстрактное в конкретном» 296
Авнир, Д. 310
Автомат клеточный 469, 479
— с конечным числом состояний 376
Агломерация, самоподобная 286
Агрегация кластерная 305
— коллоидная 308
— ограниченная диффузией 261, 263,
267, 305
Адамар, Ж. 381
Аддамс, Ч. 125
Аккорд 143
Алгоритм быстрый 484
— поглощающий (жадный) 279
— пятикратный 337
— с конечным числом состояний 337
— сверхбыстрый 337
— черепаший 338
Альварес, Л. В. 63, 153
Альфер, Р. А. 166
Амплитуда, вероятности 207
Анализ состояния рынка 180
— спектральный, высокочастотный
113
— статистический 112
Андерсон, Ф.У. 408, 464
Андерсона, локализация 131, 464
Антенна логопериодическая 129, 135
— телевизионная, самоподобная 130
Антигармоника орбиты 368
Апериодичность 316, 346, 391, 397
Арнольд, В. И. 238, 424
Арнольда, языки 237, 238, 424, 427
Аррениус, С. А. 175
Артефакт, статистический 184
Артикулятор 80
Атомная единица длины 163
AT&T Bell Laboratories 96, 206
Аттрактор 73, 231, 320, 353
— Энона 331
— странный 54, 57, 267, 274, 275, 330
Бак, П. 489
Барнсли, М. 56, 341
Барьер, потенциальный 175
Бассейн, испытательный 110
Батлер, Д. 439
Бах, И. С. 148, 156
Бейл, X. Д. 309
Беранек, Л. Л. 116
Бернулли, Д. 203
Бернулли, И. 203
Бернулли, Н. 203
Бернулли, Я. 203
Берри, М.В. 54, 75
Бессель, Ф. В. 234
Биржа товарная 178
— фондовая 178, 180
Биркгоф, Дж. Д. 108, 158
Битти, пара 90
Бифуркации удвоения периода 362
— точка сгущения 384
Бифуркация 169, 350, 352
— касательная 374, 375
— обратная 363
Блуждание, случайное 200, 201, 445
Бозе, Ш.Н. 427
Бозе, конденсация 427
Бозон 427
Больцано, Б. 36, 251
Больцман, Л. 30, 195, 198
Большой Взрыв 156
Предметный указатель
513
Бор, Н. 408
Боте, Р. 305
БПФ см. Преобразование Фурье,
быстрое
Броун, Р. 181, 194
Булиган, Ж. 75
Вакуум 164
— квантовомеханический 164
— классический 164
Валери, П. 99
ван дер Поль, Б. 158
Вариации, популяции 184
Вебер, В. 111, 176
Вебер, Э. Г. 111
Вейерштрасс, К. 30, 142, 198
Вейль, Г. 41, 74
Вейтц, Д. А. 305
Вектор временной 187
— частот 187
Венте, Э. Ч. 113
Вероятность ошибки 181, 208
— переходная 206
Вес, кажущийся 112
Взаимодействие автокаталитическое
482
— антиферромагнитное 410, 414, 459
— локальное 470
— пятое 63, 154
— спиновое 458
— ядерное 154, 489
сильное 154
слабое 154
Визенфельд, К. 489
Вильсон, Р. 166
Винер, Н. 195, 200
Волна звуковая, поперечная 122
— кругополяризованная 135
Волокно, оптическое 218
Вольфрам, С. 469
Восприимчивость, магнитная 448
Восприятие, человеческое 64, 70
Воспроизведение, звука 122
Время жизни 490
— завершения 214
— когерентности 164
— наблюдения 184
— реверберации 114, 116, 176
— характеристическое 451
Вселенная 144, 166, 193, 209, 212
Выигрыш, ожидаемый 201, 204
Вычет, квадратичный 123, 310
Вычисления безошибочные 132
— в реальном времени 207
— рекурсивные 146
Вязкие языки, образование 265, 289
Гёдель, К. 240
Газ, решеточный 470
Гай, Р. К. 202
Гайзель, Т. 177
Галилей, Г. 102, 106, 153, 223
Гальтон, Ф. 203
Гальтона, доска 203
Гармоника орбиты 368
Гаусс, К.Ф. 111, 167, 176, 233, 284
Gedanken-эксперимент 162
Гейзенберг, В. 156
Геометрия легких 170
Георг III 284
Герман, Р. 166
Гиббс, Дж. У. 273
Гидродинамика 108, 111, 470
Гильберт, Д. 74
Гильберта, огибающая 157
Гирер, А. 481
Голография 164, 202
Гравитация 104, 107, 154
— квантовая 154
Граница 73
— между двумя государствами 71
— фрактальная 320
Грассбергер, П. 306, 357, 447
Графика, компьютерная 96, 326
Громкость 64, 111
— субъективная 64
514
Предметный указатель
Гроссман, С. 356
Группа, контрольная 203
Гюйгенс, X. 233
да Винчи, Л. 168
Данные десятичные 167
— параллельная обработка 229, 459,
470
— самоподобные 166
— упорядочение 203
Дарвин, Ч. 203
Движение броуновское 130, 180, 186,
194, 198, 199
— ограниченное 107
— хаотическое 250
Двойной дракон 83, 85
де Вис, Х.Й. 252
де Гааз, В. Й. 388
Дедекинд, Р. 225
Деление атомных ядер 452
Делитель, наибольший общий 313, 412
Дендрит 266
Дёниц, К. 63
Дерево Кэли 131, 299, 448, 461
— Фарея 25, 429, 433
— бронхиальное 169
— самоподобное 68, 170
— филогенетическое 131
Детерминизм 228
Дефляция 345, 394, 399
Джонс, Д. 296
Диаграмма состояний 454
Диаконис, П. 167
Диапазон аудиочастот 111, 143
Динамика нелинейная 453
— символическая 227, 347, 359, 367,
369, 414, 436
— численности населения 228
Дисплеи, буквенно-цифровые 388
Диссипация энергии 102
Дифракция 78, 391, 404
— Фраунгофера 78
— волновая 309
— звука 122
— на фракталах 78, 307
— фрактальная 78
Дифференцирование, дробное 186
Диффузия 264, 446, 479
— детерминированная 327
Длина видимая 112
— когерентности 164
— корреляционная 62, 77, 447, 450,
457, 465
— периода нечетная 369
четная 372
— планковская 63, 156
— свободного пробега, средняя 197
— серии 95
— характеристическая см. Размер,
характеристический
Доказательство «посмотри и убедись»
139
— основанное на самоподобии 139
Домен магнитный 479
— спиновый 479
Дрейф 479
— генов 479
Дресс, А. В.М. 486
Дроби, унимодулярные 428
Дробь двоичная, предпериодическая
315
— непрерывная 87, 89, 96, 137, 147,
150, 167, 297, 406, 416, 419, 430, 492
— правильная 84
Ду, Б.-С. 227
Дуади, А. 383, 384, 386
Емкость информационная, шеннонов-
ская 181
— канала, информационная 181, 206,
208
Жидкости, несмешивающиеся 266
Жидкость, надкритическая 458
Жюлиа, Г. 72, 384
Жюльен, Р. 305
Предметный указатель
515
Зависимость долгосрочная 182
— от частоты, иррациональная 297
Задача нелинейная 319
— о «единице в каждой клетке» 480
— о синхронизации 394
— о трех телах 432
— обратная 79
— ханойская башня 313
Закон Вебера 111
— Вебера-Фехнера 111
— Кеплера, третий 107
— Планка 254
— Ципфа 65
— арксинуса 202, 378
— больших чисел 195
— всемирного тяготения, Ньютона
107, 151, 154
— гиперболический 66, 157, 163, 176
— обратных квадратов 63
— повторного логарифма 338
— подобия см. Закон, скейлинговый
— скейлинговый 102, 286, 420, 421,
441
— степенной 60, 63, 151, 249, 298, 444,
451, 490
однородный 63, 151, 157, 174
Замощение, апериодическое 402
Затухание, звука 176
Заупе, Д. 188, 321
Звезда, двойная 54
Звук высота 141, 174
— монофонический 122
— музыкальный 144, 149
— парадоксальный 141
— стереофонический 122
Звукопроизводство в человеческой
речи 79
Земля 432
Зеркала, параллельные 127
Игра «Жизнь» 471
— «Королеву — в угол» 90
— азартная 203, 205, 209, 275
— бросание монеты 201, 205
— в хаос 54
— на деньги 181, 205, 206, 208, 275,
276
— продолжительность 279
— сэра Пинского 46
Избыточность 67, 179
Изинг, Э. 458
Излучение космическое фоновое 166
— лазерное 164, 255, 402
дифракционная картина 402
— рентгеновское 188, 305
— черного тела 74, 166, 254
Изображение кодирование 95
— получение 187, 188
— раздвоение 214
— сканирование 35
Импеданс входной 79, 297
— характеристический 297
Инвариантность масштабная 174,
391, 422
— относительно сложения 215
— при преобразованиях Лоренца 27
— степенных законов 490
Инструмент, хорошо темперирован-
темперированный 149
Инструменты, музыкальные 77, 116,
148
Интеграл, эллиптический 337
Интегрирование дробное 186
— полуцелое 186
Интенсивность звука 64
— радарного сигнала 63
Интервал ловушка 231
— носителя 269
— синхронизации частот 238, 430
Интерполяция орбит 368
Интерпретация, черепашья 338
Интерференция, случайная 114
Инфляция 344
Исследования акустические 64
— слуха 79, 174
Источник без памяти 454
516
Предметный указатель
— марковский 454
— стационарный 455
Исчезновение динозавров 153
Итерации 71, 311, 336
— «запертые» 374
— Ньютона 71, 313, 319
Йорк, Дж.А. 362, 375
Каданов, Л. П. 453
Казус, теоретико-числовой 148, 150
Кантор, Г. 40, 220, 251, 317
Каскад, самоподобный 363
Кассини, щели 407
Кац, М. 160, 220
Качество звучания 115, 116, 120
Квазар 214
Квазикристалл 95, 389, 391, 399, 401,
406, 408, 415
— двумерный 402
Квазипериодичность 408
Кванты, мёссбауэровские 162
Квинта, чистая 146
Келли, Дж.Л. 208
Кеплер, И. 361
Китайские коробочки 124
Кларк, Д. С. 30
Кластер несущий 466
— перколяционный 61, 62
Клейн, Ф. 30, 195, 198
Клетки, рост и гибель 473
Код Гензеля 132
— Грея 36, 364
— цепной 95
Коллоид, фрактальный 309
Кольб, М. 305
Компьютер аналоговый 207
— клеточный 470
— цифровой 207
Конвертор, каталитический 486
Констанция (норманская королева)
127
Конуэй, Дж.Х. 93, 96, 428, 471
Конфигурация райский сад 481
— спинов 414, 420
Концентрация, критическая 448
Концертные залы, акустика 74, 109,
113, 117, 176
Корень, первообразный 310
Корреляция, пространственная 327
Космология 75
Кости, игральные 177
Коши, О. Л. 216
Коши, случайная величина 217
Коэффициент ветвления 169, 254
— диффузии 198
— подобия 138, 174, 210, 228
примитивный 138
— скейлинга см. Коэффициент, подо-
подобия
— угловой 92, 94
Крамер, Э. 359
Кранмер, Т. 165
Кривая Гильберта 24, 33
— Гильберта, заполняющая про-
пространство 364
— дракона 82
— заполняющая плоскую фигуру 35
— фон Коха 30, 100
Кривизна, отрицательная 347
Крик, Ф. 383
Кристалл жидкий 388
— периодический 389
Кристаллы, рост 261
Критичность, самоорганизующаяся
489
Кронекер, Л. 311
Куст на ветру 340
Кэли, А. 72
Лавджой, С. 304
Лагранжиан 105
Ландшафт, фрактальный 190
Лапидус, М.Л. 75
Лаутерборн, В. 359
Леви, П. 211
Предметный указатель
517
Леви, полет 211
Лейбниц, Г. В. 186, 482
Леонардо, Пизанский см. Фибонач-
Фибоначчи, Л.
Лестница сатанинская 237
— чертова 25, 229, 277, 410
Леттвин, Дж. 176
Ли, С. 108
Ли, Т.-Я. 362, 375
Ли, Ц. Д. 460
Либхабер, Р. 359
Ливень, космический 155
Лигнит 309
Линдеман, Ф. 311, 317
Линденмайер, А. 339
Линза гравитационная 214
— цилиндрическая, вращающаяся
188
Линия, береговая 189
Липшиц, Й. 117
Лиувилль, Ж. 131, 317
Лифсон, Ш. 25
Лихтенберг, Г. К. 280, 284
Лихтенберга, фигура 261, 284
Логарифм Цеха 310
— дискретный 123
Лопиталь, Ж. Ф.А. де 200
Лоренц, X. А. 73
Магнетизм 165
Мандельброт, Б. Б. 24, 31, 156, 169,
182, 194, 221, 243, 261, 304, 382
Манин, Ю.И. 387
Марков, А. А. 200
Маркс, К. 200
Масса покоя 154
— электрона 155, 163
Масштаб длины, естественный 63
— изменение 63
— характеристический 489
Масштабирование в психологии 111,
115
— психоакустическое 112
Масштабно-инвариантный 490
Математическое ожидание, условное
214
Материя, темная 214
Матрешки 124, 482
Маурер, Й. 359
Машина, угадывающая (Шеннона)
205
Мёбиуса, лист 51
Медиана 205, 216
Медианта 426
Мезон 155
Мейнхардт, X. 481
Менгер, К. 242
Менгера, губка 242
Мера Лебега 244, 375
— Лебега, ненулевая 247
— нулевая 40
Меркурий 425, 432
Метод Монте-Карло 60, 469
— диагональный 223
— касательных, Ньютона 71
— проекций 400
Метрополис, Н. 469
Механизм универсальный 165
— энергопотерь 110
Механика квантовая 162, 186
— классическая 206
— небесная 107
— нелинейная 234
— статистическая 273, 292
Микин, П. 261, 264, 305
Микрофон, конденсаторный 113
Минковский, Г. 75
Минковского площадь 75
— сосиска 75, 283
Множество «стертой средней трети»
40
— Жюлиа 24, 72, 319, 383
заполненное 384
мультифрактальное 322
— Мандельброта 361, 381, 384
— Фату 72
518
Предметный указатель
— вполне разрывное 221
— замкнутое 221
— инвариантное 225
— канторово 24, 36, 40, 143, 210, 212,
221, 225, 228, 241, 244, 274, 285,
299, 357, 411, 491
троичное 62
— несчетное 40, 220, 317
— самоподобное 222, 267
— связное 384
— совершенное 221
— счетное 223, 427
— точечное 40
Множитель, простой 459
Мода нормальная 77
— резонансная 110
Модель лесного пожара 440
— подобная 109
— точно разрешимая 464
— трубчатая 168
Молекулы, столкновения 198
Молния 264
Момент, угловой 106
Морс, М. 342, 343, 347
МТ см. Последовательность Морса-
Туэ
Музыка белая 158
— коричневая 158
— розовая 158
Мультифрактал 251, 257, 258, 267,
270, 274, 322, 425
Мэллоуз, К. 97
Мюон 155
Нарушение взаимозаместимости 104
— подобия 104
— симметрии 479
Натяжение, поверхностное 266
Науэнберг, М. 322
Невязка, пифагорейская 148
Недифференцируемость 195
Независимость от масштаба 61, 63,
101, 156, 160, 221
Нейрон 388
— слуховой 131
Нейтрино 155, 214
Нейтрон 305
Нелинейность 237
Неоднозначность, артикуляционная
80
Неопределенность 112, 163
Непредсказуемость 228, 321, 379
Неразрешимость в теории чисел 240
Нерв, слуховой 112, 174
Неустойчивость, гидродинамическая
266
Нефть, добыча 289
Ним Витхофа 90
— фибоначчиев 89
НОД см. Делитель, наибольший об-
общий
Носитель аттрактора 267
— мультифрактала 258
— фрактального множества 322
— фрактальный 267
Ньютон, И. 107, 314
Облака 303
Область притяжения 55, 56, 71, 246,
274, 319
— свободная от нулей 210
Обратная связь, акустическая 115
Объект, квазизвездный 214
ОДА см. Агрегация, ограниченная
диффузией
Окисление, каталитическое 486
Окно 3-периода 362, 376
— периодичности 247, 361, 364, 376
Окрестность, иерархическая 461
Октава 144, 146, 148, 174
Оливериа, М. 305
Омограф 69
Опалесценция, критическая 453
Оператор утроения периода 368
Орбита 73, 227, 315, 350
— апериодическая 247
Предметный указатель
519
— дочерняя 368
— обратная 321
— сверхустойчивая 350, 353, 359,
369, 380, 436
— хаотическая 330
Осаждение, электролитическое 306
Основание, комплексное 83
Осциллятор «порабощенный» 432
— линейный 106
— нелинейный 106
Осцилляторы, связанные 414, 432
Отношение гиромагнитное, электро-
электрона 388
— масштабов 111
— частот 144, 233, 238, 426
рациональное 234, 433
синхронизирующее 427
Отображение «одногорбое» (унимо-
(унимодальное) 360
— Пуанкаре 319
— Энона 331
— взаимно однозначное 225
— гауссово 88
— гиперболическое 88
— двоичного сдвига 377
— итерированное 225, 392, 406
— квадратичное 274, 348, 377
трижды итерированное 375
— конформное 384, 467
— кошка Арнольда 333, 335
— кроличье 94
— логарифмическое 130
— обратное 54, 73, 320
— окружности 237, 423, 427
критическое 434, 437
— палатка 225, 372, 377
хаотическое 377
— пилообразное 326
— подкова Смейла 331
— унимодальное 361, 366
— хаотическое 315
Оценка, субъективная 116
Оцифровка 95
Пагельс, X. 453
Пайтген, Х.-О. 321, 386, 460
Паллада 233
Панели, акустические 116
Парабола, логистическая 274, 348, 361
Парадокс 144, 214, 215
— акустический 141
— восприятия 142
— неевклидов 36
— петербургский 203
— фрактальный 38
Парамагнетик 440
Параметр порядка 441
— роста 348, 356
— связи 238
— субъективный 111
Парето, В. 65
Партия в шахматы, бесконечно длин-
длинная 347
Паскаля, треугольник 45, 486
Пассойя, Д. 302
Паули, В. 302, 445
Пеано, Дж. 36, 251
Пензиас, А. 166
Пенроуза, мозаика 344, 402
Передача звука 113
— информации, безошибочная 208
— энергии, с малыми потерями 218
Переименование 345
— блоков 345, 394, 399. 421
Перекрестные искажения, компенса-
компенсация 120
Перемежаемость 374
Перемешивание, хаотическое 328
Перенормировка 453, 465
— пространственная 466
Перепонка, основная 130, 131, 174
Переход к хаосу 436
— фазовый 448, 453
Периметр 74, 449
— фрактальный 84
Период обращения 107, 233
Периодичность 145, 410
520
Предметный указатель
Периоды обращения, соизмеримые
407
Перколяция 60, 77, 439, 450
— по связям 60, 462
— по узлам 60
— порог 60, 439
— проникновение 449
Перрен, Ж. Б. 31, 194, 199
Перселл, Э. М. 111
Пи-мезон 155
Пион 155
Пирс, Дж. Р. 149, 165
Плавление 165
Плитка, фрактальная 36
Плоскость временная 187
— гауссова 72
— комплексная 73
— частот 187
Плотность вещества 166
— излучения 166
— мод 77
Плутон 52
Побережье, фрактальное 281
Поведение, алгебраическое 464
Поверхность внутренняя, фракталь-
фрактальная 309
— раздела, фрактальная 296, 299
— рассеивающая звук 122
— рассеяния 122
— шероховатая 298
— эквипотенциальная 264
Поглощение 110
— звука 109
Подмножество мультифрактала 258
— фрактальное 258
Подобие 99, 122, 452
— статистическое 197
Подсчет клеток 283, 292
Показатель Липшица-Гёльдера 258,
259
— Ляпунова 319
— Херста 183, 190
— Шварцшильда 105
— дробный 151, 165
— критический 444, 445, 447, 458,
466, 490
— массовый 62
— скейлинга 248, 267, 441
— спектральный 184, 189
Покрытие, нечетное 481
Поле безопасное 91
— внешнее 490
— конечное 123
— электромагнитное 110, 254
Полинг, Л. 390
Полином, примитивный 123, 310
Полле, А. 302
Полоса хаотическая 363, 372
— частот, критическая 112
Полость микроволновая 110
— электромагнитная 110, 254
Полупроводник 64, 175
Полутон 141, 143, 148
Помехи, радиолокационные 78
Порождение новых орбит 365
Порядок Шарковского 25, 364, 369
— ближний 394
— дальний 93, 346, 389, 390, 394, 397
— универсальный 368
Последовательность а 366, 373
— Битти 90, 93, 395, 415
— Конуэя 98
— Морса-Туэ 25, 343, 360, 367
— индексов 395, 398
— кроличья 92, 393, 397, 399, 406, 420
— пекаря 359
— самоподобная 484
— самопорождающая 344
— секущая 94
— символов 361
— случайная 206, 456
Постоянная Больцмана 175
— Морса-Туэ 317, 361, 384
— Планка 162
— Фейгенбаума 25, 364
— кроличья 93
Предметный указатель
521
Постоянные, фундаментальные физи-
физические 164
Потенциал, электрический 264
Потепление, глобальное 184
Правило Де Моргана 244
— большинства 478
— дифференцирования, цепное 351
Предпочтения, акустические 118
Предсказание линейное 179
— остатки 179
— погоды 228
Представление, визуальное 434
Преобразование Адамара 313
— Гильберта 157
— Лежандра 273
— Радона 188
— Радона, обратное 188
— Фурье 186, 216, 347
быстрое 313
двумерное 187
обратное 186, 218
— аффинное 57
— пекаря 328
— сжимающее 58
Преобразователь, цифроаналоговый
141
Приближение Вентцеля-Крамерса-
Бриллюэна 131
— рациональное 147
Принцип Гюйгенса 233
— включения-исключения 243
— неопределенности, Гейзенберга
101, 113, 162
— подобия 107
Приращение, независимое 199
Притяжение, ньютоновское 107
Проводник,суперионный 235
Продолжительность игры, ожидае-
ожидаемая 201, 279
Проекция 245
Произведение Эйлера, бесконечное
145
— декартово 240
— прямое 244, 313
Прокачча, И. 304
Прообраз 72, 320
Пропускная способность канала см.
Емкость канала, информационная
Пространство вложения 445
— восприятий 119
— вычисляющее 469
— гильбертово 162
— предпочтений 118
— ультраметрическое 132
— фазовое 330, 347, 409
траектория 414
— четырехмерное 75
Пространство-время 75
Профиль скорости звука 218
Процесс Винера 195
— Маркова-Винера 200
— инновационный 172, 179
— марковский 206, 453
— перемешивания 328
— пуассоновский 112
— релаксационный 175
— случайный, мультипликативный
255, 259
— статистически самоподобный 160,
197
— точечный 208
Прусинкевич, П. 340
Психоакустика 111, 174
Психофизика 111
Пуанкаре, А. 52, 251
Пфайфер, П. 310
Раби, И. 155
Равновесие, неустойчивое 335
Равнораспределение энергии 199
Радиус Шварцшильда 104
— боровский 163
Разбиение, самоподобное 36, 37
Различие 99, 118, 119
Различия, едва заметные 112
522
Предметный указатель
Разложение по степеням простых чи-
чисел 224
Разлом 302
Размах интерквартильный 215, 219
— нормированный 182
Размер атома 163, 164
— кластера 60
— характеристический 64, 156, 444
Размерность Минковского 286
— Минковского-Булигана 75
— Хаусдорфа 24, 33, 39, 189, 197, 210,
240, 242, 244, 267, 274, 281, 286,
301, 302, 357, 426, 488, 491
— вложения 294
— евклидова 38, 190, 326
— информационная 260, 272, 274, 292
— корреляционная 272, 290
— массовая 284
— обобщенная 269
— поверхности 189
— подобия 286, 491
— спектральная 77
— топологическая 211
— фрактальная 41, 211, 219, 257, 258,
269, 409, 449, 459
Разорение 209
— безопасные временные промежут-
промежутки 210
— игрока 200
Разряд, электрический 261
Рамануджан, Ш. 314, 336
Ранг слова 65, 68
Распад, радиоактивный 489
Распознавание образов 95
Распределение Бозе-Эйнштейна 254,
427
— Коши 216
— Пуассона 255
— вероятностей 253, 269
нормальное 163
— галактик 209, 212, 452
— гауссово 163, 188, 215
— геометрическое 254
— гиперболическое 175
— инвариантное 216, 318, 378
— кумулятивное 232
— масс 79
— первого знака 166
— самоаффинное 253, 255
— самоподобное 214
— стационарное 318
— степенное 151
— ступенчатое 232
Распространение, многолучевое 115
Рассел, Б. 387
Рассеяние звука 176
— нейтронов 309
— рентгеновского излучения 308,
309
Расстояние, межконтинентальное
218
Расходимость, числовая 321
Реакция каталитическая 306
— поверхностная 197
Реальность атомов 199
Резисторы, остовные 60
Резонанс 74
— зала 114
Резонатор, линейный 216
Реконструкция 109
Реньи, А. 269
Репеллер 73, 321, 353
Решение, подобное 109
Решетка Бете 131, 448, 461
— атомная 459
— гиперкубическая 402
— дифракционная, фрактальная 310
— иерархическая 459
— квадратная 59, 93, 400, 440, 462
— квазипериодическая 95, 399, 401
— кристаллическая 78
— кроличья 400
— перенормированная 466
— самоподобная 459
— треугольная 448, 462, 465
— фазоотражательная 123, 310
Предметный указатель
523
— фрактальная 445
Риман, Б. 429
Рихтер, П.Х. 386, 460
Розенфельд, А. 95
Рост, фрактальный 265
Рулетка 181, 206
Рэлея-Бенара, конвекция 359
Ряд Грегори-Лейбница 336
— временной 294
Самоаффинность 209, 237
Самоаффинный 160, 174, 197
Самоорганизация 453
Самоподобие 62, 73, 82, 98, 178, 209,
254, 281, 311, 331, 340, 353, 357,
360, 395, 398, 422, 425, 440, 452,
453, 459, 465, 482, 484, 488
— асимптотическое 146
— в архитектуре 127
— статистическое 209
Сандер, Л. М. 264
Сатурн 407, 432
Свертка 186-188
Сверхпроводимость 78, 427
Сверхрешетка 467
Сверхузел 466
Связь болтающаяся 60
— между ближайшими соседями 458
— нелинейная 414, 427
Сдвиг, влево 96
Селл, Дж. 117
Серпинский, В. 42
Серпинского, ковер 24, 42, 488
Сеть, нейронная 388, 464
Сечение Пуанкаре 414
— благородное 407, 433, 438, 492
— золотое 87, 89, 92, 93, 136, 141, 298,
391, 407, 408, 415, 420, 431, 433,
437, 494
— серебряное 85, 89, 138, 407, 418
Сигнал речевой 179
— самоподобный парадоксальный
143
Сила влекущая 110
— межатомная 64
Силы, приливные 432
Симметрия восьмого порядка 407
— вращательная 387
— двенадцатого порядка 407
— запрещенная 387, 406
— пятого порядка 387, 407, 416, 420
— трансляционная 389
Синхронизация двух осцилляторов
233
— мод 233, 235, 237, 425, 438
— психовизуальная 434
— фаз 233
Система гамильтонова 177, 334
— динамическая 227
— итерированных функций 58, 341
— нелинейная 250
— нелинейная динамическая 246,
272, 330, 347
— неупорядоченная 388, 464
— планет 54
— солнечная 407
— сосудистая 169
— счисления 83
двоичная 223, 229, 482
комплексная 84
троичная 222, 223, 229
— хаотическая 228, 272
— цифровая 145
Скейлинг 456
— см. также Подобие и Инвариант-
Инвариантность, масштабная
— конечномерный 449
— многопараметрический 118
— самоподобный 436
Складывание бумаги 80
Скопление 208
Скорость 65
— реакции 487
— роста 181, 267
— теплового движения 198
— частицы 470
524
Предметный указатель
— эффективная 235
Слияние рек 168
Слой, пограничный, вязкий 110
Слух, человеческий 79, 130, 144
Слуховой отдел коры головного мозга
295
Смолуховский, М. 194
Соотношение неопределенности 164
— обратное, для преобразования по-
подобия 162
— степенное 111
Состояние «рисующей черепахи» 338
— критическое 489
— минимально устойчивое 490
Спектр Фурье 174
— атомный 165
— мощности 172, 174, 175, 199
— мультифрактальный 259, 273, 275,
426, 437
Спектроскопия мёссбауэровская 164
— нейтронная 164
Спин 410, 458
— Изинга 410, 412, 414, 421, 458, 479
— квазипериодический 420
Спираль, логарифмическая 83, 107,
132, 135
Сравнение, попарное 118
Среда, безэховая 120
Среднее 205
— арифметико-геометрическое 336
Статистика нестандартная 219
— фотонов 427
Стекло металлическое 388
— спиновое 388, 412, 464
Стивене, С. С. 111
Столкновение трех тел 54
Строй музыкальный 150
— темперированный 148
— традиционный 150
— хорошо темперированный 128
Структура дерева 168
— иерархическая 131, 323
— лазерных голограмм, пятнистая
115
— молекулярная 309
— сверхтонкая 165
Струны, космические 193
Стэнли, X. Э. 264
Суперкомпьютер 228, 337, 459
Сцепление 186
Тан, Ч. 489
Твердое тело, аморфное 388
Телефон, сотовый 115
Температура абсолютная 175, 199
— критическая 458
Тень, рентгеновская 79
Теорема Пифагора 25
— вириала 107, 163
— центральная предельная 215, 218
Теория вероятности 215, 232
— графов 461
— информации 66, 180, 208, 292
Шеннона см. Теория, информа-
информации
— относительности 163
общая 75
специальная 28
уточнение 164
— потенциала 264
— ренорм-групп 345, 394, 436, 458
— связи 180
— теплоты, молекулярная 194
— чисел 147
Теплоемкость, удельная 74, 448
Термодинамика 273
Томе, С. 356
Томография 188
— компьютерная 79, 187, 188
Томпсон, Д'Арси 102
Точка Кюри 440, 465
— Серпинского 50, 52
— граничная 72
— критическая 166, 444
— неподвижная 315, 349
Предметный указатель
525
гиперболическая 333
сверхустойчивая 350
— периодическая 51, 336
— сгущения 364
— седловая 333
Точность конечная 89, 379
— числовая 321
Тракт, вокальный 79
Транзитивность 112
Трансфер-матрица 120
Трение 110, 207
Тритава 149
Турбулентность 228, 260, 409
Туэ, А. 343
Тяготение 63
Уайтхед, А. Н. 387
Угол внешний 384
— золотой 434
— рассеяния 309
Удвоение громкости 111
Удвоение периода 275, 353, 356
Уилсон, К. 453
Уиттен, Т. А. 264
УКВ-связь 303
Улам, С. 469
Универсальность 424, 445, 448, 458,
490
Уолл-стрит 178
Уравнение Лапласа 264
— Максвелла 468
— Ферхюльста 349
— движения 105
— дифференциальное, в частных
производных 109
— диффузии 198
— разностное 200
Усилитель, параметрический 233
Устойчивость 407
Ухо, внутреннее 64, 110, 112, 174
Фалконер, К. Дж. 245
Фармер, Дж. Д. 249
Фату, П. 72, 384
Федер, Й. 281
Фейгенбаум, М. 355
Фейнман, Р. 162
Феномен, фрактальный 489
Ферхюльст, П.-Ф. 348
Фехнер, Г. Т. 111
Фибоначчи, Л. 92, 128, 392
Физика, нелинейная 432
Фильтр, цифровой 347
Фильтрация, обратная 120
Фишер, М. 453
Флекингер-Пелле, Й. 75
Флуктуация в вакууме 164
— статистическая 113
— энергии 164
фон Кох, X. 30
фон Коха, снежинка 24
фон Нейман, Дж. 469
Фонон 77
Формирование биологических конфи-
конфигураций 481
Формы, биологические 338
Фосс, Р. Ф. 158, 177, 188
Фотография, цветная 105
Фотон 77, 155, 254
Фрактал колеблющийся 78
— поверхностный 308
— рассеяния 78
— реальный 280
— самоаффинный 256
— случайный 59, 261
— толстый 246
Фрактон 78
Фридрих II 127
Фуллер, Р. Б. 45
Функция sine 145
— Вейерштрасса 142, 143, 195
— Мёбиуса 51
— Эйлера 429
— дзета- 429
— квадратичная, потенциальной
энергии 106
526
Предметный указатель
— кусочно-линейная 326
— недифференцируемая 195, 198
— непрерывная 195
— производящая 200, 347
— распределения 273
— рациональная 72, 320
от частоты 297
— самоаффинная 277
— ступенчатая 95, 229
— универсальная 444
— характеристическая 216
— энтропийная 181, 256
Хаббард, Дж. X. 383, 384
Хаббл, Э. 439
Халмош, П. Р. 127
Хаос 52, 89, 178, 375, 408, 438
— детерминированный 46, 54, 227,
228, 295, 378, 409, 435
— полный 377
— пространственный 409
Характеристика частотная 113, 116
максимум 115
флуктуации 113
Хаттон, Э. Ф. 172
Хаусдорф, Ф. 24, 33
Хвост, хаотический 89
Хентшель, X. Г. Э. 304
Хенце, X. 404
Херст, X. Э. 182, 185
Хирцебрух, Ф. 206
Хогарт, В. 284
Хокинг, С. 145
Холдейн, Дж. Б. С. 32, 102
Хофштадтер, Д. Р. 311
Центр, слуховой 112
Цепь случайная резистивная 465
— электрическая 296
«лестничного» типа 297
Ципф, Дж. К. 65
Цифра, самая значащая 167
Цузе, К. 469
Частота затягивание 233
— использования слова 65
— пространственная 308
Частоты несоизмеримые 398
— синхронизированные 234
— соизмеримые 414
Часы солнечные 244
— солнечные, цифровые 244
Черные дыры 214
Четность 361, 475
Чеширский кот 473
Чингиз-хан 63
Числа Каталана 202
— Лиувилля 316
— Люка 234, 407, 419
— Фибоначчи 85, 92, 136, 234, 335,
392, 396, 420, 431, 493
— алгебраические 223
иррациональные 318
— вещественные 223
— взаимно простые 148, 412
— иррациональные 89, 147, 311, 316,
318, 419
квадратичные 408
кубические 494
— рациональные 223
— трансфинитные 41
— трансцендентные 318
Число 220
— тг 336
— «самое иррациональное» 432
— Рейнольдса 110, 359
— безразмерное 111
— вращения 415, 420, 435, 437
реальное 238, 423, 427
формальное 237, 423, 427
— двоичное, периодическое 315
— иррациональное ненормальное 317
нормальное 316
— координационное 448
— молекул 199
— почти благородное 492
— простое 148
Предметный указатель
527
— псевдослучайное 337
— случайное 177
— эквивалентное 438, 492
Чтение по губам 79
Чувствительность к параметру 250
Чудновски, Г. 337
Чудновски, Д. 337
Шансы 206, 275, 276
Шварца, производная 369
Шварцшильд, К. 104
Шельнхубер, X. Й. 322
Шенкер, С.Дж. 425, 438
Шеннон, К. Э. 66, 180, 205, 456
Шепард, Р.Н. 141
Шефер, Д. В. 305
Шехтман, Д. 389
Шиша, О. 30
Шмидт, П. В. 309
Шмитт, Ф. О. 70
Штауффер, Д. 439, 450, 465
Штраусе, Э. 25
Штрубе, X. В. 404, 491
Шум 1// 64, 374
— белый 160, 172
— в области частот 114
— гауссов 182
— интенсивность 65
— коричневый 158, 160, 173
— розовый 64, 160, 174, 177
— случайный 409
— снижение 123
— степенной 178
— тепловой 172
— черный 173, 182
Эгглтон, Р. Б. 202
Эйнштейн, А. 23, 25, 28, 193, 194, 198,
199, 214, 254, 388, 427
Эйнштейн, Я. 25
Эйфель, Г. 43
Экономика 65
Электромагнетизм 154
Электронограмма 389
Электропроводность 298
Электростатика 384
Электроэнцефалограмма 294
Элемент, с сосредоточенными пара-
параметрами 296
Энергия кинетическая 107
— потенциальная 105, 106
Энон, М. 231, 232
Энтропия 66, 269, 273, 292
— Колмогорова 272
— обобщенная 269
— перекрестная 180
Эрмит, Ш. 30, 317
Эстетика, экспериментальная 111
Эффект Мёссбауэра 336
— парниковый 185
Эшер, М. К. 42, 457
ЭЭГ см. Электроэнцефалограмма
Юкава, X. 155
Юлес, Б. 188
Юпитер 234
Явление, критическое 166, 465
Язык, обезьяний 67, 68
Ян, Ч.Н. 460
Яркость, субъективная 111, 141
Манфред Шредер
Фракталы, хаос, степенные законы
Миниатюры из бесконечного рая
Дизайнер М. В. Ботя
Технический редактор А. В. Широбоков
Корректор М. А. Ложкина
Подписано в печать 29.03.01. Формат 60 х 84У16.
Печать офсетная. Усл. печ. л. 30,69. Уч. изд. л. 30,73.
Гарнитура Computer Modern Roman. Бумага офсетная № 1.
Тираж 1500 экз. Заказ №
Научно-издательский центр «Регулярная и хаотическая динамика»
426057, г. Ижевск, ул. Пастухова, 13.
Лицензия на издательскую деятельность ЛУ № 084 от 03.04.00.
http://rcd.ru E-mail: borisov@uni.udm.ru
Отпечатано в полном соответствии с качеством
предоставленных диапозитивов в ГИПП «Вятка».
610033, г. Киров, ул. Московская, 122.