Текст
начальныя ОСНОВАНІЯ
алгебры.
НАЧАЛЬНЫЯ ОСНОВАНІЯ
ц му
АЛГЕБРЫ,
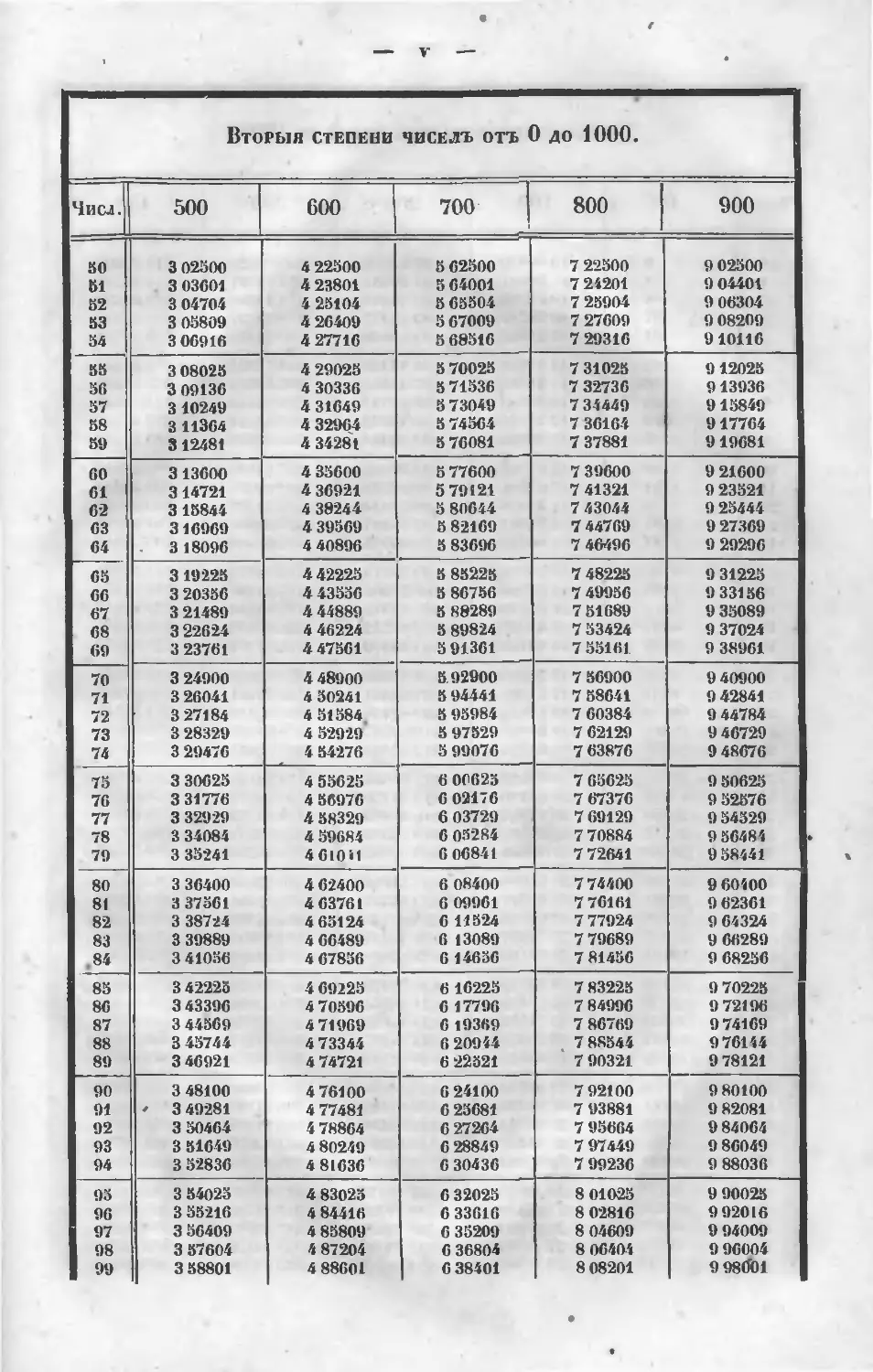
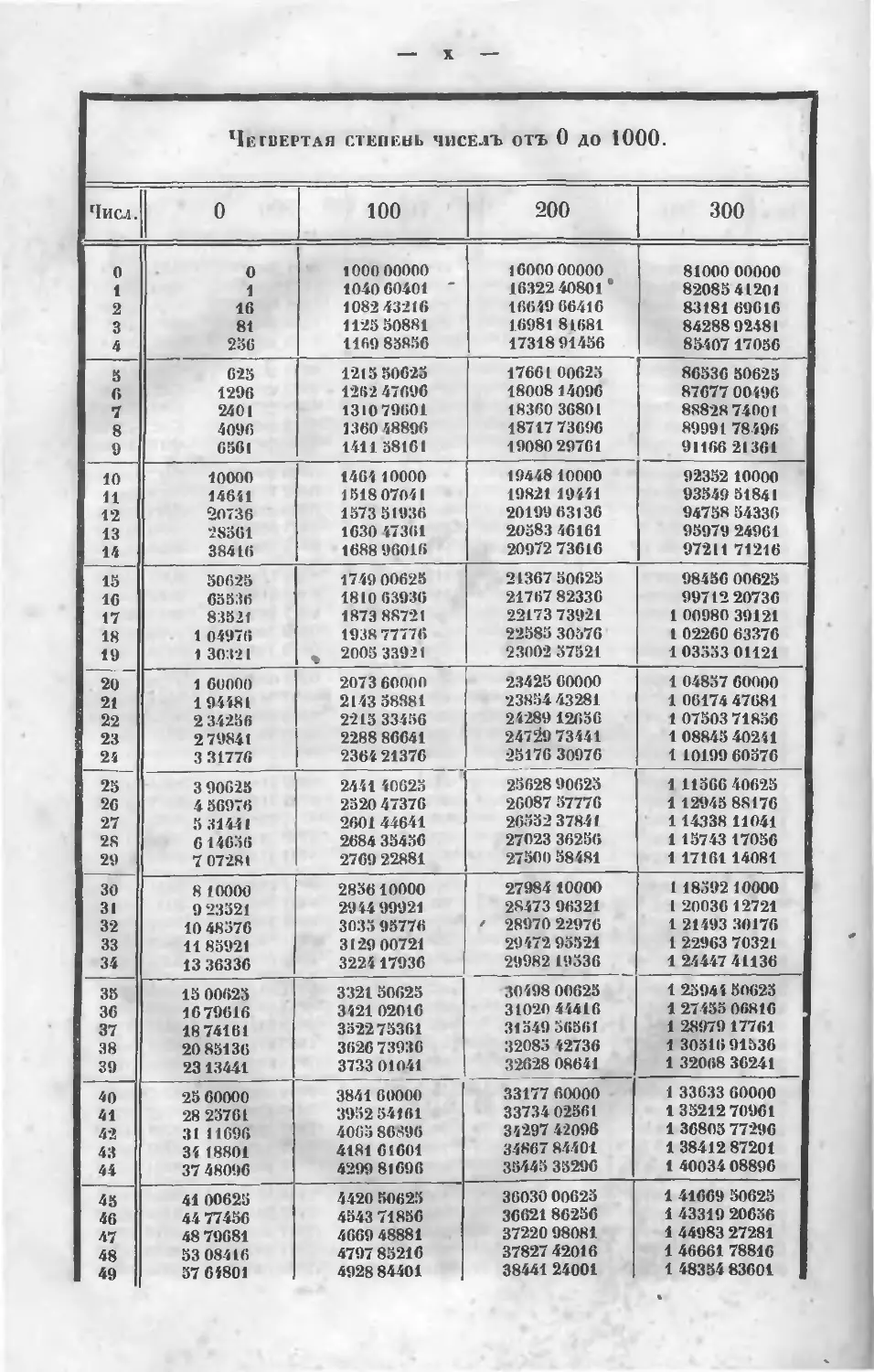
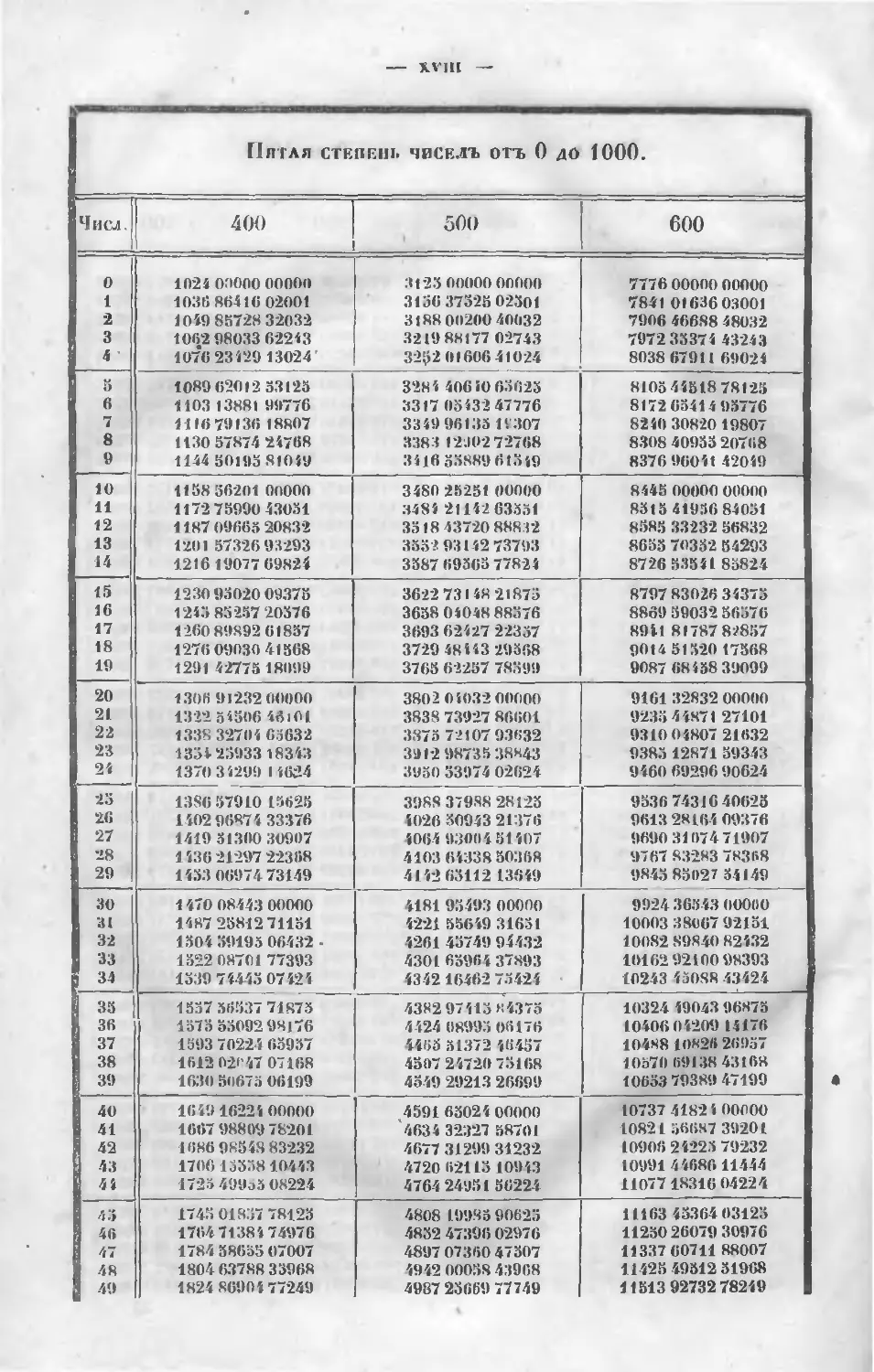
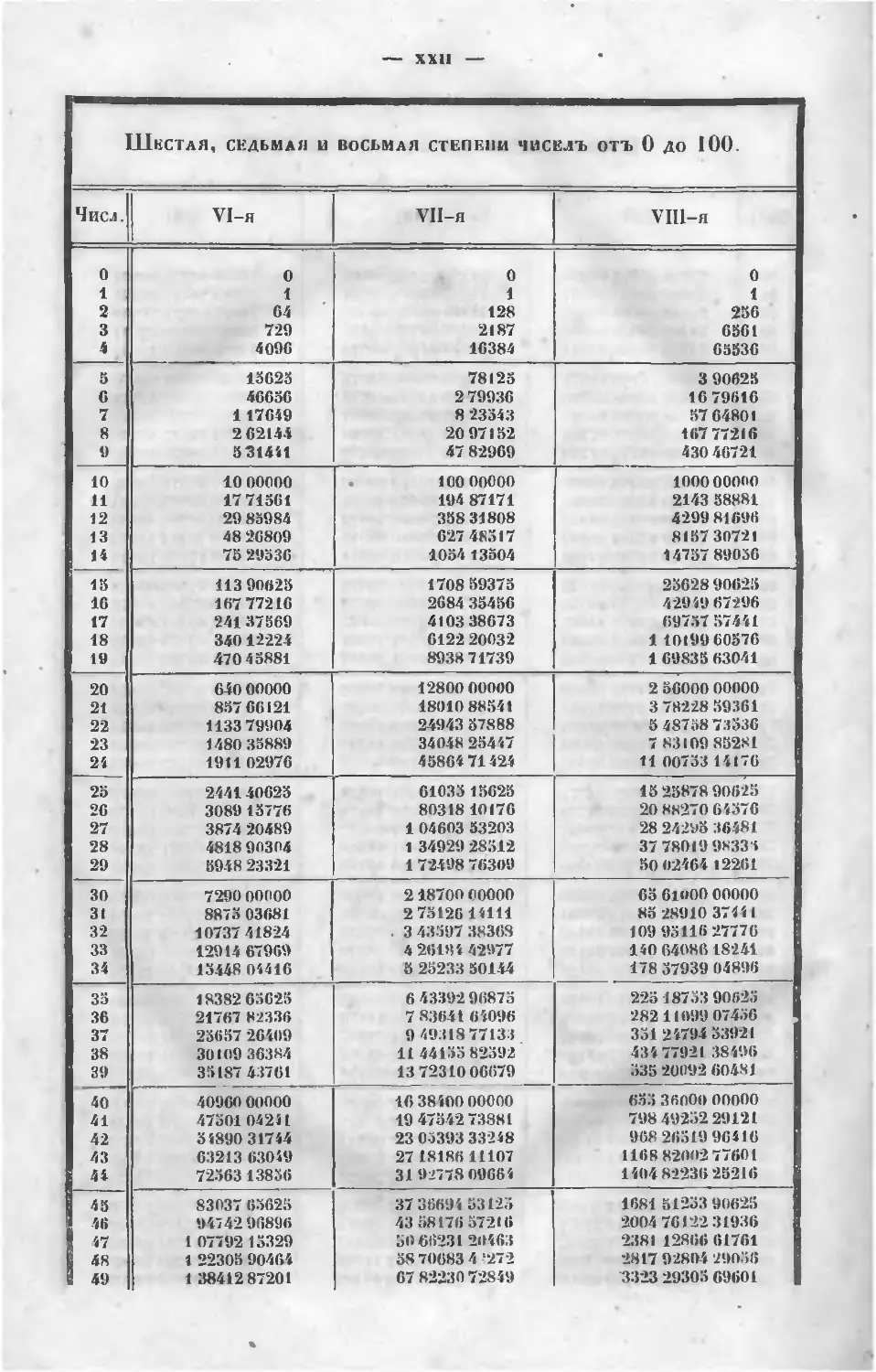
П ТАБЛИЦАМИ СТЕПЕНЕЙ ЧИСЕЛЪ
отъ 1 до 1ООО.
СОСТАВЛЕНЫ
Н. Т- 'іТі&лоьъімъ.
ВЪ ТИПОГРАФІИ ЯКОВА тркя.
1853.
ПЕЧАТАТЬ ПОЗВОЛЯЕТСЯ".
съ тѣмъ, чтобы по отпечатаніи представлено было въ Ценсурный Комитетъ
узаконенное число экземпляровъ. С. Петербургъ, 28 Января 1853 года.
ИЗДАВІВ КВИГОПРОД4ВЦА С. ЛОСКГТОВА.
ПРЕДИСЛОВІЕ.
Курсъ начальныхъ основаній Алгебры, предлагаемый здѣсв благосклон-
ному вниманію почитателей математическихъ наукъ, составленъ мною
не по какой ни есть извѣстной программѣ, принятой въ русскихъ Учеб-
ныхъ Заведеніяхъ, и не въ такомъ объемѣ, въ какомъ преподается въ
нихъ начальная Алгебра. У меня не было цѣли дать этой книгѣ назна-
ченіе спеціальное; а потому и планъ для изложенія предметовъ, которы-
ми я предположилъ ограничиться въ этомъ курсѣ, принятъ такой, какой
собственно для меня показался удобнѣе.
Всѣ извѣстныя Алгебры на русскомъ языкѣ, признаваемыя у насъ
лучшими составлены Французскими авторами, каковы: Лакроа, Фраи-
керъ, Гуроонъ, Іеф.ебіоръ-де~Фурси. Мейеръ и Шоке, и нроч. II дѣй-
ствительно, онѣ ведутъ учащагося къ цѣли, по видимому, путемъ удоб-
«» . I, •
нѣншимъ, отличаются краткостію, легкимъ изложеніемъ предметовъ,
печатаются (на Французскомъ языкѣ) изящно. Предметы излагаются въ
нихъ почти одни и тѣ же, разность замѣчается только въ расположеніи
предметовъ Науки, въ полнотѣ и обработкѣ различныхъ статей.
Во всѣхъ нѣмецкихъ курсахъ даже начальной Алгебры, какіе мнѣ слу-
чалось читать, я находилъ нетолько иной способъ обработки предметовъ,
но другое число предметовъ, чѣмъ я и воспользовался отчасти для со-
ставленія моего курса. Такимъ образомъ, не нарушая системы, я изло-
жилъ совсѣмъ отдѣльно Сиіітактику (теорчо переложеній, сочетаній, и
проч.); за нею ввелъ начальныя основанія Математической теоріи вѣ-
роятностей, въ такомъ размѣрѣ, въ какомъ находилъ ее почти во всѣхъ
начальныхъ Алгебрахъ у нѣмецкихъ авторовъ, чего совсѣмъ нѣтъ въ но-
вѣйшихъ Алгебрахъ Французскихъ. Въ заключеніе, я помѣстилъ способъ
рѣшенія численныхъ уравненій высшихъ степеней съ одною извѣстною.
Для этого надлежало сообщить общія понятія о функціяхъ съ одною пере-
мѣнною, и показать только тѣ ихъ свойства, которыя особенно полезны
для рѣшенія таковыхъ уравненій. А какъ это и было окончательною
статьею, то не счелъ я нужнымъ говорить о дѣлимости многочленныхъ
VI
раціональныхъ Функцій, о симметрическихъ Функціяхъ, объ исключеніи
неизвѣстной между данными уравненіями высокихъ степеней, и о всемъ,
что отъ этого зависитъ. По сей причина выпущены изъ моего курса
нѣкоторыя теоремы, помѣщаемыя въ новѣйшихъ иностранныхъ курсахъ,
которыя превосходны въ теоріи, но затруднительны для начинаю-
щихъ, либо до крайности утомительны въ практикѣ. Въ замѣнъ этого, я
принялъ другой путь, короче ведущій къ достиженію цѣли, мною пред-
положенной, — способы менѣе сложные, на Дѣлѣ удобоисполнимые.
Любознательнаго читателя прошу не считать излишнимъ, что я въ
начальныхъ основаніяхъ Алгебры, изложивши теорію уравненій высшихъ
степеней съ одною неизвѣстною, много распространился надъ рѣшеніемъ
численныхъ уравненій. Это сдѣлано по уваженію единственно къ новымъ
способамъ вычисленія корней дѣйствительныхъ несоизмѣримыхъ, такъ и
мнимыхъ, каковы: способъ Ньютоновъ исправленный, и способъ Фогеля.
Послѣдній способъ еще недавно сдѣлался извѣстенъ, да и первый совсѣмъ
не въ томъ видѣ излагается въ разныхъ курсахъ, какъ здѣсь. Кромѣ того,
что эти способы отличаются вѣрностію и особенною простотою, они любо-
пытны и по одной своей новости. Но, чтобы можно было ими пользоваться
безъ утомительности при разрѣшеніи численныхъ уравненій, не превы-
шающихъ 10-й степени, я составилъ двѣ таблицы, изъ которыхъ въ одной
находятся первыя пять степеней чиселъ отъ 1 до 1000; а во второп—слѣ-
дующія пять степеней, но только для чиселъ "вузначныхъ отъ 1 до 100.
Ни въ одномъ курсѣ не находилъ я таблицъ этого рода (кромѣ таблицъ
квадратовъ и кубовъ), а между тѣмъ, онѣ чрезвычайно полезны не только
для быстраго вычисленія корней численныхъ уравненій, но и во множе-
ствѣ другихъ случаевъ какъ въ Алгебрѣ, такъ и въ другихъ іычисле-
ніяхъ, гдѣ логариѳмы оказываются • недостаточными. Таблицы эти
составлены тщательно и повѣрены Не смотря на это, а не осмѣли-
ваюсь утверждать, .чтобъ не остались въ нихъ гдѣ нибудь погрѣшности,
а потому желательно, чтобы,, для общей пользы, кто ни есть, хотя изъ
одного любопытства, занялся ихъ повѣркою. Всяьая открытая погрѣш-
ность будетъ принята мною съ Злагодарност ю.
Н. Щ.
ОГЛАВЛЕНІЕ.
ВВЕДЕНІЕ.
ПЕРВОНАЧАЛЬНЫЯ ПОНЯТІЯ И ОПРЕДѢЛЕНІЯ.
СТРДН.
Предметъ Алгебры. Общіе знаки для чиселъ. Знаки сложенія, вычитанія,
умноженія и дѣленія. КоеФИціенты. Степени и показатели ихъ. . . 1
Алгебрическія количества, ихъ члены; количества одночленныя, двучленныя,
и проч., и многочленныя. Многочлены однородные и смѣшанные. Степени
однородныхъ многочленовъ. Сокращеніе много членовъ чиезъ совокупленіе
подобныхъ членовъ въ одинъ. Употребленіе скобокъ..................3
АЛГЕБРИЧЕСКІЯ ДѢЙСТВІЯ.
ГЛАВА ПЕРВАЯ.
СЛОЖЕНІЕ И ВЫЧИТАНІЯ АЛГЕБРИЧЕСКИХЪ КОЛИЧЕСТВЪ.
Сложеніе одночленовъ и многочленовъ...............................7
Вычитаніе. Правило знаковъ при выметаніи многочленовъ.............8
Общія понятія о количествахъ отрицательныхъ, и ихъ значеніи въ раз-
ныхъ случаяхъ.....................................................9
Умноженіе одночленовъ. Правила коеФиціентовъ, показателей и знаковъ.
Доказателство, что аЬ~Ьа .............. 11
Умноженіе многоченовъ. Общее правило.............................14
Примѣры ......................................................... —
Дѣленіе одночленовъ. Правила коеФиціентовъ, знаковъ и показателей при
дѣленіи..........................................................13
Показатели нуль и отрицательные..................................18
Дѣленіе многочленовъ. Общее правило..............................19
Примѣры..........................................................20
Дѣлимость чиселъ. Начала, по которымъ заключаютъ о дѣлимости . . 24
Дѣлимость степеней и двучленовъ..................................27
Обшгй наибольшій дѣлитель, и его разысканіе между одночленами и
многочленами Примѣры.............................................29
Алгебрическія дроби. Неизмѣняемость дроби отъ помноженія или раздѣле-
нія обѣихъ ея частей на одно и тоже число........................33
Сокращеніе дробей: чрезъ постепенное исключеніе общихъ множителей, и
посредствомъ общаго наибольшаго дѣлителя. Примѣры................35
Приведеніе дробей къ общему знаменателю .........................37
VIII
СТРЛН.
Сложеніе, вычитаніе, умноженіе и дѣленіе дробей; примѣры для сокращенія
дробныхъ выводовъ...........................................38
измѣненіе дроби отъ сложенія (или вычитанія) обѣихъ ея частей съ какимъ
ни есть числомъ...................,..........................40
•
ГЛАВА ВТОРАЯ.
УРАВНЕНІЯ И НЕРАВЕНСТВА.
Общія понятія объ уравненіяхъ; раздѣленіе уравненій..........42
I. Уравненія первой степени съ одною неизвѣстною.
Приведеніе уравненія въ простѣйшій видъ чрезъ перенесеніе членовъ его
изъ одной части въ другую, и освобожденіе отъ дробей. Общее правило
для рѣшенія сихъ уравненій...................................44
Примѣры......................................................45
Различіе уравненій отъ явныхъ равенствъ......................47
Изслѣдованіе рѣшенія общаго уравненія первой степени съ одною неиз-
вѣстною. Рѣшенія—, —. Случаи, когда рѣшеніе - не означаетъ неопре-
дѣленности ................................................48
Задачи . ... : ................ 51
... о О
Символическія рѣшенія задачъ: отрицательныя, —, ихъ значенія. . . 58
II. Уравненіе первой степени съ двумя, тремя, и болѣе неизвѣст-
ными, когда число неизвѣстныхъ равно числу уравненіи
Рѣшенія опредѣленныя.........................................60
Рѣшенія этихъ уравненій 1) по способу подстановлешя, 2) по способу срав-
нія, 3) по способу сокращенія чрезъ сложеніе и вычитаніе, и 4) по спо-
собу Безу....................................................61
Общій способъ................................................70
Задачи.......................................................75
Замѣчанія относительно рѣшеній отрицательныхъ, нулевыхъ, . Задача
о курьерахъ...............'..................................83
Выводъ начала неопредѣленныхъ предстоящихъ...................89
III. О НЕРАВЕНСТВАХЪ.
Дѣйствія надъ неравенствами . •.............................. 90
Приложеніе, неравенствъ къ изслѣдованію Формулъ..............93
IV. Уравненія съ двумя, тремя и больше, неизвѣстными, когда число
НЕИЗВѢСТНЫХЪ БОЛѢЕ ЧИСЛА ДАННЫХЪ УРАВНЕНІЙ.
Неопредѣленный анализъ 4-й степени ........... 96
Рѣшеніе уравненія ах-+-Ьу—с въ цѣлыхъ, положительнымъ числахъ . . 97
Задачи...................................................... —
IX
СТРЛВ.
ГЛАВА ТРЕТЬЯ.
НЕПРЕРЫВНЫЯ ДРОБИ.
Непрерывныя дроби: конечныя, безконечныя и періодическія.........105
Разложеніе обыкновенной дроби въ непрерывную.....................106
Переходъ отъ непрерывной дроби къ обыкновенной...................107
Законъ составленія послѣдующихъ приближеній изъ предшествующихъ . 108
Слѣдствія: полная величина непрерывной дроби всегда находится между
каждыми двумя послѣдовательными къ пей приближеніями.............109
Виды разностей между послѣдовательными дробями приближеній, когда
числители членовъ приближенія какія ни есть, пли когда они всѣ единицы. 111
Степень приближенія къ непрерывной дроби.........................114
Прибавленіе..............'.......................................115
Приведеніе непрерывной періодической дроби въ уравненіе второй сте-
пени ............................................................117
ГЛАВА ЧЕТВЕРТАЯ.
ВОЗВЫШЕНІЕ АЛГЕБРИЧЕСКИХЪ КОЛИЧЕСТВЪ ВЪ КВАДРАТЪ.
Составленіе квадратовъ...........................................117
Извлеченія квадратнаго корня изъ цѣлыхъ чиселъ...................119
Приближенные корпи изъ чиселъ неполныхъ квадратовъ; ихъ полученіе: 1)
посредствомъ дробей десятичныхъ, 2) дробей обыкновенныхъ, и 3) по-
средствомъ'дробей непрерывныхъ.....................,.............124
Квадратные корни изъ дробныхъ чиселъ........................... 129
Квадратные корни изъ алгебрическихъ одночленовъ..................130
Счисленіе коренныхъ количествъ второй степени....................131
Освобожденіе дробныхъ выраженій отъ квадратныхъ корней въ знамена-
теляхъ ........................................................ 133
Извлеченіе корней квадратныхъ изъ многочленовъ ........ 134
ГЛАВА ПЯТАЯ.
А. УРАВНЕНІЯ ВТОРОЙ СТЕПЕНИ СЪ ОДНОЮ НЕИЗВѢСТНОЮ
1) Уравпіе двучленное...........................................137
2) Полное уравненіе 2-й степени; его рѣшеніе....................138
Составъ квадратнаго уравненія изъ его корней.....................141
Изслѣдованіе корней полнаго уравненія ...... 142
- - общаго уравненія ах2-г-Ьл-ь-с—0..................143
Задачи...........................................................145
В. УРАВНЕНІЯ 2-й СТЕПЕНИ СЪ ДВУМЯ НЕНЗВѢСТНЫМП. КОГДА ЧИСЛО
НЕИЗВѢСТНЫХЪ РАВНО ЧИСЛУ ДАННЫХЪ УРАВНЕНІЙ.
Задачи......................................................... .148
Приведеніе тричленныхъ уравненій и, вообще,
-+-</=0 въ уравненія второй степени. ..........................152
Неопредѣленный анализъ 2-й степени, когда число неизвѣстныхъ болѣе
числа уравненій. Рѣшенія наибольшія и наименьшія.................154
Задачи...........................................................156
X
СТРАВ.
, ГЛАВА ШЕСТАЯ.
ВОЗВЫШЕНІЕ ОДНОЧЛЕНОВЪ И МНОГОЧЛЕНОВЪ ВЪ ТРЕТЬЮ СТЕПЕНЬ.
Извлеченія кубичнаго корня изъ чиселъ полныхъ кубовъ, и неполныхъ.
Вычисленіе приближеннаго корня въ послѣднемъ случаѣ посредствомъ
десятичныхъ дробей................................................159
Извлеченія кубическаго корня изъ алгебрическихъ количествъ одночлен-
ныхъ и многочленныхъ..............................................165
Уравненія третьей степени-, неполныя и полныя.....................168
1) Корни уравненія аз3—с=0......................................—
2) Показать, что уравненіе х3±Ьх—с=0 имѣетъ хотя одинъ дѣйствнтель
ный корень, и вывесть условіе, по которому всегда можно угнать, когда въ
этомъ уравненіи всѣ корни дѣйствительные, и когда только одинъ. . .170
3) Приведеніе уравненія хі-і-ахі-і-с—й къ г3+а'г+с'=0...........171
4) Рѣшенія полнаго уравненія а?-і-ах2-і-Ьх-і-с—0 по способу Кардана . 172
Рѣшеніе общаго уравненія 4-й степени по способу Де карта . . . .174-
Задачи ..........................................................175
ГЛАВА СЕДЬМАЯ.
О ВОЗВЫШЕНІИ ВЪ СТЕПЕНИ ВООБЩЕ, И ИЗВЛЕЧЕНІИ КОРНЕЙ.
I. Степени одночленовъ съ показэтелями цѣлыми.....................177
Переходъ отъ степеней одночленовъ къ ихъ корнямъ..................178
А. Корни изъ полныхъ степеней; корни раціональные и мнимые . * . . - 179
В. Корни изъ неполныхъ степеней; показатели дробные, числа и количества
неизвлекомыя..................................................... 180
Переносъ радикала дроби въ одинъ числитель или въ знаменатель . . .182
Подведеніе множите-.ей при корнѣ подъ коренной знакъ................—
Приведеніе коренныхъ количествъ къ общему коренному показателю . .183
Счисленіе коренныхъ количествъ; сложеніе и вычитаніе, умноженіе и дѣ-
леніе ..............................................................—
Возвышеніе въ степени коренныхъ одночленовъ.......................185
Извлеченіе корней изъ коренныхъ одночленовъ.......................186
Употребленіе дробныхъ показателей вмѣсто коренныхъ знаковъ . . . .187
Примѣчаніе.......................’................................188
Возвышеніе въ степени, умноженіе и дѣленіе корней мнимыхъ .... —
Дѣйствія надъ мнимыми выраженіями, вида а-і-/3 V—1................189
Модуль выраженія а±(і —1. Свойства модулей........................190
т тп
Значеніе выраженій у, --------—, —-----г—, въ случаѣ а— Ь . . .191
а—о а—о а—о
II. Степени количествъ двучленныхъ и многочленныхъ. Ньютоновъ
биномъ (а-\-х}п, когда показатель п бываетъ цѣлый илн дробь, положи-
тельный или отрицательный.........................................192
Приложеніе Ньютонова биномнческаго ряда къ возвышенію въ степени ко-
личествъ двучленныхъ, тричленныхъ и, вообще, многочленныхъ . . .196
Вычисленіе кормой изъ чиселъ посредствомъ ряда Ньютонова бинома. При-
3 В ____ 100____
мѣры. У10, V 24-0, Ѵіо...................................................200
Степени двучлена а-+-Ъ —...................................................202
XI
" СТРЛН.
Приведеніе суммы ѴаЧ-Л V—1± Ѵа—Ь V— 1 къ виду |/А± ѴК, гдѣ А и
В суть количества дѣйствительныя..........................................203
Непосредственное приведеніе Формулы Ѵа±В |/~і къ виду а±6 V — 1;
слѣдствія изъ этого.....................................................204
Возвышеніе мнимыхъ выраженій; V—1, V—1, V—V — 1, V—1, и т.
д. въ цѣлыя степени...............................................206
ГЛАВА ОСЬМАЯ.
ТЕОРІЯ ЛОГАРИѲМОВЪ.
Общія понятія.............................................208
Свойства логариѳмовъ......................................209
Превращеніе логариѳмовъ одной системы въ логариѳмы другой. Модуль . .212
Спосооы вычисленія логариѳмовъ: А. Посредствомъ непрерывныхъ дробей. —
В. посредствомъ разложенія логариѳма въ рядъ. Логариѳмы Неперовы
(гиперболическіе, натуральные)..........................214
Отношеніе малыхъ разностей между логариѳмами..............217
Обыкновенные или Бригговы логариѳмы изъ цѣлыхъ чиселъ и десятич-
ныхъ дробей. Значеніе характеристики въ обоихъ случаяхъ . . . .218
Логариѳмы изъ обыковениыхъ дробей. Ариѳметическое дополненіе . . . 220
Расположеніе и употребленіе обыкновенныхъ логариѳмовъ Каллета, гдѣ объ-
ясняется: 1) какъ наіодить логариѳмъ данному числу, цѣлому или дроби,
и 2) какъ находить число данному логариѳму, будетъ ли его характери-
стика положительная или отрицательная.....................220
Основаніе Неперовыхъ логариѳмовъ..................' . . . 226
Примѣненіе логариѳмовъ къ ариѳметическгімъ исчисленіямъ: умноже-
нію, дѣленію, возвышенію въ степени и извлеченію корней .... 227
Недостаточность логариѳмовъ съ 7-ю десятичными; предѣлъ ихъ точности.
Способъ находить логариѳмъ какому угодно большому числу. Способъ
находить всякому логариѳму число соотвѣтственное, имѣющее точность
во многихъ десятичныхъ..................................229
Примѣненіе логариѳмовъ къ вычисленію алгебрическихъ формулъ . . 234
При иѣненіе логариѳмовъ къ рѣшенію неоі'редіьленно-степенныхъ ура-
вненій .................... —
ГЛАВА ДЕВЯТАЯ.
О ПРОГРЕССІЯХЪ.
А. Прогрессія ариѳметическая: возрастающая и убывающая .... 236
Послѣдній членъ 1~а-ы (п—1) прогрессіи. Суммы членовъ
прогрессіи. Выводы изъ этихъ Формулъ..............................238
Задачи..............................................................239
Суммоваиіе степеней членовъ прогрессіи ариѳметической . ... . 241
Суммоваиіе рядовъ чиселъ фгггурныхъ: треугольныхъ, треугольныхъ-пира-
мидальныхъ, квадратныхъ и квадратныхъ-пирамидальныхъ................243
Разложеніе даннаго числа на*два, на три и болѣе чиселъ цѣлыхъ и поло-
жительныхъ всевозможными образами, и выводъ суммы этихъ разложс ній. 246
XII
стрлн.
В. Прогрессія геометрическая: возрастающая и убывающая...........248
Выраженіе 1~адп~1 ея послѣдняго члена.............................249
„ Іо—а а(ап—1)
Сумма ---------——-------- членовъ прогрессіи......................250
у—1 д—1
Выводы изъ этихъ Форму іъ.........................................—
Задачи............................................................252
а
Сумма ----------членовъ прогрессіи, убывающей до безконечности . . .
Выраженіе всякаго числа посредствомъ безконечнаго ряда членовъ прогрес-
сіи убывающей.........................................................
Обращеніе періодической дроби въ конечную, изъ которой опа произошла.
253
254
ГЛАВА ДЕСЯТАЯ.
/
ПРИЛОЖЕНІЕ ПРОГРЕССІИ И ЛОГАРИѲМОВЪ КЪ ВЫЧИСЛЕНІЮ ПРОЦЕНТОВЪ
И ДОХОДОВЪ РАЗЛИЧНАГО РОДА.
Вопросъ первый. Найти будущую цѣну капитала А, отданнаго въ ростъ па п
лѣтъ, по г-| съ рубля въ годъ..................................256
Выводы изъ Формулы 5—А (1+г)”.....................................—
Задачи...........................................................257
Величина 6—А=А[(1-ы)"—1]—В дохода съ капитала А, обращавшагося
п лѣтъ по г~ съ рубля. Задачи..................................259
Объ учётѣ........................................................262
Вопросъ второй. Найти будущую цѣну капитала А по прошествіи п годовъ
его обращенія, по г-| съ рубля, когда каждогодно будутъ прилагаться къ
нему пли вычитаться изь него, неравныя либо равныя суммы .... 263
Выводы изъ Формулы 5~Агс"=ь у (ю“ — 1)...........................—
Задачи.........................................................265
Общія понятія о вдовьихъ и сиротскихъ кассахъ, временныхъ и пожизнен-
ныхъ доходахъ..................................................270
Случай; когда капиталъ А увеличивается, или уменьшается, количествомъ а
періодически чрезъ годовъ......................................273
ГЛАВА ОДИНАДЦАТАЯ.
(Сиитактика).
ПЕРЕЛОЖЕНІЯ, СОЧЕТАНІЯ И РАЗЛИЧНЫЯ СОЕДИНЕНІЯ ПЗЪ ДАННАГО
ЧИСЛА БУКВЪ, И ОПРЕДѢЛЕНІЕ ИХЪ СУММЫ.
Число перемѣщеній, изъ даннаго числа буквъ: 4) когда буквы неравны
и 2) когда между нами есть нѣкоторыя равныя..........................274
Число сочетаній изъ п буквъ, по двѣ, но три, и т. д. 1) безъ повторенія,
и 2) съ повтореніями каждой буквы....................................277
Число различныхъ совокупленій изъ даннаго числа п буквъ: 4) безъ по-
втореній, и 2) съ повтореніями каждой буквы..........................279
Задачи............................................................. 281
хш
ГЛАВА ДВѢНАДЦАТАЯ.
НАЧАЛЬНЫЯ ПОНЯТІЯ ОБЪ ИСЧИСЛЕНІИ В ѢРОЯТНОСТЕЙ.
1. Вѣроятность простая, абсолютная. Примѣры..................284
2. Вѣроятность относительная. . 292
3. Вѣроятности сложныя: а) что изъ двухъ, или болѣе возможныхъ
случаяхъ произойдетъ хотя одинъ.............................293
Ь) Вѣроятность встрѣчи возможныхъ случаевъ въ послѣдованіи двухъ или
нѣсколькихъ современныхъ событій, либо ихъ появленіе одинъ за другимъ
•непосредственно въ ходу извѣстнаго числа явленій.......... 294-
4 Вѣроятность явленій, одно другимъ замѣняемыхъ..............299
Возрастаніе вѣроятности случая въ слѣдствіи повторенія того же дѣйствія,
наприм. опыта, игры, и проч.................................302
Примѣненіе сложной вѣроятности \Ѵ=1—(1—м>)(1——го").... къ
опредѣленію вѣроятнаго продолженія жизни двухъ, или болѣе, особъ въ
данный промежутокъ времени...................................—
5. Вѣроятность явленій въ повторяемыхъ опытахъ............. 304.
Примѣры . . . . ..... .306
ГЛАВА ТРИНАДЦАТАЯ.
О ФУНКЦІЯХЪ ВООБЩЕ.
Общія понятія Раздѣленіе Функцій 1) на алгебрическія, цѣлыя, дробныя,
раціональныя и ирраціональныя, и 2) на Функціи трансцендентныя . .310
Непрерывность всякой Функціи цѣлой, раціональной; разрывъ непрерывно-
сти въ Функціяхъ другихъ видовъ........................................311
I. Овщііі видъ цѣлой раціональной функціи сь одною перемѣнною:
ас"Ч-Ал;п_*Ч-....-1-Ѵ, и ея свойства:..................................313
1) Отъ уменьшенія перемѣнной х, послѣдній членъ И можетъ сдѣлаться
болѣе суммы всѣхъ прочихъ; 2) отъ увеличенія г, первый членъ мо-
жетъ превзойти сумму всѣхъ прочихъ........................................
3) Видъ Функціи отъ измѣненія х въ х-Ъ-Іѵ . ......................315
Производные многочлены....................................................
Приращеніе [(х-Ѵ-/і)—[(х) измѣненной Функціи. Оно, съ уменьшеніемъ Л,
можетъ сдѣлаться менѣе всякой данной величины. Отсюда заключеніе, что
взякая цѣлая, раціональная Функція не иначе переходитъ изъ положитель-
наго результата въ отрицательный, какъ переступая чрезъ нуль . . .317
Примѣры..................... ............................
Наибольшія п наименьшія величины этихъ Функцій........319
II. Разложеніе цѣлой многочленной и раціональной функціи въ непре-
рывную дробь...................................... 322
III. Разложеніе неопредѣленно-степенной функціи ах въ рядъ, распо-
ложенный по степенямъ ея перемѣнной х . . . ..........304.
а —а
Значеніе —— , когда х=ъ............................. 326
X—я
Л(1+а;)_(Р1ч-5)
«начеше------------> когда х—і.......... —
х—я
IV. Обращенія рядовъ функцій съ одною перемѣнною...............—
Выраженіе всякаго числа рядомъ, расположеннымъ по степенямъ его лога-
риѳма ........................................................328
«V —
стгав.
ГЛАВА ЧЕТЫРНАДЦАТАЯ/
ТЕОРІЯ УРАВНЕНІЙ ВЫСШИХЪ СТЕПЕНЕЙ СЪ ОДНОЮ НЕИЗВѢСТНОЮ.
Общія понятія. Уравненія раціональныя, икъ общій видь; уравненіе ирра-
ціональное. Корень уравненія. Рѣшеніе алгебрическое и численное . . 329
Всякое уравненіе, имѣющее видъ цѣлой раціональной Функціи, имѣетъ ко-
рень «-4-6 і/—1, гдѣ а, Ь, числа дѣйствительныя, которыя въ частнымъ
случаяхъ могутъ быть нулями (теорема Коши).......................... .330
Если х~а корень уравненія, то оно дѣлится па х—а безъ остатка . . . 333
Число корней въ уравненіи...............................................334
Если р-+-уѴ—1 корень уравненія, тоир—у 1^—1 будетъ его корнемъ . 335
Составъ уравненія изъ его корней........................................336
Зависимость знаковъ предъ членами уравненія отъ его дѣйствитель-
ныхъ корней, и обратно................................................338
Перемѣны и повторенія знаковъ между членами уравненія....................—
Преобразованіе ((х)—0 въ /\-х)=0.......................................339
Полное число перемѣнъ въ данномъ уравненіи [(х)п—П и его /’(-гс)т=О
не можетъ быть больше показателя т степени, или больше числа его
корней................................................................340
Всякое полное уравненіе ]\х)—0 можетъ имѣть положительныхъ корней не
болѣе того, сколько въ /‘(х)—0, и небольше отрицательныхъ корней,
сколько въ /‘(-ж)з=0 находится перемѣнъ. А если всѣ его корни дѣйстви-
тельные, то оно имѣетъ точно такое число положительныхъ корней, сколь-
ко перемѣнъ въ /’(ж)=0, и столько отрицательныхъ, сколько перемѣнъ
ьъ /’(-х)=0. (Декартово правило)...................................342
Признаки дѣйствительныхъ корней въ уравненіяхъ.
1. Когда уравненіе отъ какихъ внбудь двухъ подстановленій а,/?, обра-
щается- въ два результата съ противными знаками, то между ними на-
ходится 1, 3, 5......или вообще, нечётное число корней; но если оба
результата съ равными знаками, то между а, @ либо нѣтъ корней, либо
есть чётное число корней...........................................345
2. Всякое уравненіе нечётной степени имѣетъ по крайней мѣрѣ одинъ дѣй-
ствительный корень...................................................346
3. Всякое уравненіе чётной степени, съ отрицательнымъ послѣднимъ чле-
номъ, имѣетъ по крайней мѣрѣ два дѣйствительные корня съ против-
ными знаками.........................................................347
4. Когда въ уравненіи сумма коеФИЦіентовъ положительныхъ равна или
менѣе суммы отрицательныхъ..........................................—
5 Всякое уравненіе нечётной степени, имѣющее послѣдній членъ положи-
тельный, и въ которомъ сумма коеФііціентовъ положительныхъ менѣе сум-
мы отрицательныхъ, имѣетъ три дѣйствительные корня...................348
Признаки мнимыхъ корней, открываемые въ уравненіяхъ посредствомъ
Декартова правила....................................................—
Если сумма \Ѵ всѣхъ перемѣнъ въ /’(х)”з=0 и /'(-а:)т—0 меньше показателя
т,степени; то т—\Ѵ показываетъ число мнимыхъ корней..................—
Число т—АѴ мнимыхъ корней въ уравненіяхъ неполныхъ зависитъ отъ каж-
дой изъ послѣдовательныхъ разностей п—ге, п'—между числомъ не-
СТРЛН.
достающихъ членовъ и числомъ перемѣнъ между ними. Оно равно сумнѣ
этихъ частныхъ разностей. Опредѣленіе мнимыхъ корней по тѣмъ разно-
стямъ ...........................................................349
(."учаи, когда въ уравненіи недостаетъ одного члена между членами раз-
личныхъ знаковъ, и между членами равныхъ знаковъ . . • . . . . 350
Присі тствіе мнимыхъ корней въ уравненіяхъ полныхъ, открываемое чрезъ
введеніе одного или двухъ произвольныхъ положительныхъ корней . . —
Преобразованіе уравненій.
Преобразовать данное уравненіе такъ:
Л. Чтобы корни его сдѣлались въ т разъ болѣе или менѣе.............354
В. Чтобъ исключались изъ него дробные коеФіщіенты..................355
С. Чтобы коеФиціенты двухъ его произвольныхъ членовъ сдѣлались равными,
либо получили данное отношеніе. Примѣчаніе...........................—
I). Чтобы корни новаго уравненія были квадратами корней даннаго . • .356
Е. Чтобы корни его имѣли величины обратныя корнямъ даннаго. Обратное
уравненіе..........................................................357
Уравненіе возвратное...............................................358
Е. Чтобы корни его были числомъ Л менѣе или болѣе корней даннаго. . . —
С. Чтобъ уничтожился второй членъ (исключеніе втораго члена нзъ уравне-
нія) ..............................................................360
Признаки мнимыхъ корней, выводимые, изъ разсматриванія коеФиціентовъ
даннаго уравненія по крюпері ямъ Ньютона........................361
Примѣры............................................................366
ГЛАВА ПЯТНАДЦАТАЯ.
РѢШЕНІЕ ЧИСЛЕННЫХЪ УРАВНЕНІЙ ВЫСШИХЪ СТЕПЕНЕЙ СЪ ОДНОЮ
НЕИЗВѢСТНОЮ.
А. Предѣлы корней.................................................367
Розысканіе высшаго предѣла корней по способу Ньютона . ... . 368
Вспомогательные способы: 1) Маклореневъ, 2) способъ Брета, 3) чрезъ
образованіе даннаго уравненія......................................370
Зависимость предѣла Ь отъ величины отрицательныхъ коеФиціептовъ втора-
го и третьяго членовъ уравненія....................................373
Зависимость Ь отъ повторенія знака -+- предъ первыми членами уравненія. —
Предѣлы въ уравненіяхъ, вида:
8-ч-....-і-1)=0 ......... 375
ап — ах*~* —Ь®”—*— с’(яп—Зч-я"—ч-1)=0....................376
хп—ахп~і-і^Ьхп~г—с3(яп—,ч-я:п—*ч-....ч-І=0............. 377
Примѣры............................................................378
Нижній предѣлъ положительныхъ корней...............................380
В. Розысканіе И ОТДѢЛЕНІЕ КОРНЕЙ СОИЗМѢРИМЫХЪ: *
а) по способу обыкновенному, 6) по способу Бретшнейдера . ... . 381
Примѣры............................................................386
Соизмѣримые дробные корни..........................................388
С. Розысканіе и отдѣленіе равныхъ корней........................389
XVI
стрлп.
В. Исключеніе равныхъ корней, имѣющихъ і.ротивные знаки, какъ дѣй-
ствительныхъ ч-а,—а, такъ и мнимыхъ ± |/—а ....... 393
Е. Возвратныя уравненія. Пониженіе степени возвр. уравненія, когда оно
чётной степени, и когда нечётной степени......................... 395
Примѣненіе къ уравненіямъ двучленнымъ. Примѣры...................398
Е. Отдѣленіе корней несоизмѣримыхъ въ [(х)~0 по способу Фуръе,
основанное на постепенномъ уменьшеніи его корней, полагая х—а-г-я,
и на замѣченныхъ при этомъ потеряхъ перемѣнъ знаковъ въ членахъ
ряда [(а-і-я)=д . . ......................................400
Законъ, которому слѣдуютъ измѣненія знаковъ предъ Ѳ(а), Ѳі(°),
въ ряду Да-+-а)=0, когда въ данномъ уравненіи нѣтъ равныхъ корней . 402
Признаки мнимыхъ корней: а} въ случаѣ уничтоженія одной изъ Функціи
въ ряду /'(а-ь^)=0. Примѣры.......................................405
А) Когда, отъ какого нибудь подстановлепія ж—а, уничтожается сряду нѣ-
сколько Функцій. Порядокъ знаковъ вт рядахъ Ѳ(а—я), Ѳ(а), Ѳ(а-і-я); чи-
сло уносимыхъ перемѣнъ при переходѣ отъ а—г къ а-і-я; правило двой-
наго знака для уничтожившихся Функцій. Число мнимыхъ корней въ пре
дѣлахъ а—я, а-і-я . .........................................406
Примѣры..........................................................409
С. Способы вычисленія несоизмѣримыхъ корней.
I. Способъ Лагранжевъ посредствомъ непрерывныхъ дробей,. . . . .411
II Способъ Ньютоновъ исправленный Розысканіе приближенной величины
корня чрезъ обращеніе ряда /ГаЧ-А)=0, имѣющей видъ х=а-і-(к. В,
С, В,......)......................................................414
Примѣры: 1) для вычисленія корня посредствомъ одного ряда . . . .417
2) для вычисленія его посредствомъ двухъ рядовъ, и болѣе . . . . .419
Примѣры ......................................................... —
Способъ раздѣлять корни весьма близкіе одинъ къ другому. Примѣрь . . 433
Способы отличать дѣйствительные корни отъ мнимыхъ, когда они заключа-
ются въ тѣсных ь предѣлахъ, и потому остаются неизвѣстными . . . 437
Примѣры............................................................—
III. Вычисленіе дѣйствительныхъ корней чрезъ разложеніе преобразованна-
го уравненія въ непрерывную дробь. Способъ Фогеля ...... 441
Послѣдовательныя приближенія къ корню............................443
Признаки мнимости корня............................................—
Примѣры..........................................................444
IV. Вычисленіе пары мнимыхъ корней, по способу Фогеля, ц по общей
Формулѣ х=ач-(А, В, С,.. ). Примѣры............................447
Способъ раздѣлять пары мнимыхъ корней, когда они заключаются въ тѣс-
ныхъ предѣлахъ....................................................460
Приведеніе ирраціональныхъ уравненій въ раціональныя Начальныя понятія. 464
Таблицы........................................................ 469
ІІЛЧАЛМІЫЯ ОСІІѲВАПП! АЛГЕБРЫ.
пвдмгатамыя повятія и опмдѣмвія.
Я. Алгебра есть общая Ариѳметика. Опа показываетъ самые общіе способы
исчисленія количествъ, и общіе способы рѣшенія вопросовъ, къ нимъ относя-
щихся ’).
Въ пей числа, изображающія величины различныхъ количествъ, замѣняются
буквами французской либо греческой азбуки: а, Ь, с..., х, у, я; а, /?, у,
«У.... Каждая буква можетъ представлять какое угодно число цѣлое пли дробь,
отвлеченное нли именованное.
Однородныя, или чѣмъ пибудь сходныя количества, въ Алгебрѣ очень часто
пишутся отпою буквою, а для различія ихъ величины, ставятся знаки надъ, этою
буквою, либо малыя цифры внизу ея съ правой стороны, ыаіжим. а', а", а'".;
это выговаривается: а со знакомъ, съ двѵшя знаками, съ тремя знаками, и
проч. Также пишутъ аі} а2, а3........ и выговариваютъ: а одинъ, а два,
а три, п т. д.
Какъ для теоретическаго изложенія алгебрическихъ дѣйствій, такъ и для об-
щаго рѣшенія задачъ, можпо брать какія угодно буквы вмѣсто чиселъ. СлѣдѴва-
телыю, одна и та же буква въ разнородныхъ задачахъ будетъ имѣть различныя
значенія; по, въ одной п той же задачѣ каждая буква отдѣльно должна изобра-
жать какое пгбудь опредѣленное количество, чѣмъ нпбудь различное отъ всякаго
другаго.
Сложеніе, вычитаніе, умноженіе п дѣленіе между буквенными количествами
въ Алгебрѣ изображается тѣми же знаками, что ц въ обыкновепной Ариѳметикѣ:
-+-, —, х или (•), и
*) До Г. X- Алгебра не была извѣстна. Она появляется въ 4-мъ вѣкѣ послѣ Р. X. въ
твореніяхъ ДіоФавта, александрійскаго ученаго, состоявшихъ изъ 13 книгъ, изъ коихъ
шесть дош іи до насъ.
1
2
Такимъ образомъ сумма изъ а, Ь, с, изображается чрезъ а-ьбн-с, и выго-
варивается: а сложенное съ 6 и с, или а плюсъ Ь плюсъ с.
Для вычитанія Ь изъ а, пишутъ а—Ь, и выговариваютъ; а безъ 6, или а
минусъ 6.
Дѣленіе а на 6 изображается чрезъ
а : Ъ, или .
ь
Умноженіе буквенныхъ количествъ дѣлается такъ: пишутся эти количества
одно подлѣ другаго, и между ними ставится знакъ X или (•)» нлп короче: ста-
вятся помножаемыя буквы одна подлѣ другой безъ всякаго знака. Напримѣръ:
ау^6\с=а.і).с=аЬс, этимъ и означено, что а помножено на Ъ и па с.
Нельзя дѣлать этого сокращенія между числами. Наприм. 5X2 и 52 имѣютъ
совершенно различныя значенія.
3. Когда буквенное количество помножается на численнаго множителя, то
этотъ послѣдній ставится просто подлѣ буквеннаго съ лѣвой стороны, и назы
вается его предстоящемъ или коефіщіентомъ. Напримѣръ:
^'Ха=Иа,-1Хр=^р:
• з
здѣсь 4 коефиціентъ при а, ^-коефиціентъ при р.
Коефиціентъ показываетъ, сколько разъ буквенное количество, при немъ
стоящее, или какая часть его берется. Такъ,
4а=а->-о-ь"-+-а;
3 111
тР=тР-^тР-^тР
Когда коефиціентъ стоитъ предъ произведеніемъ нѣсколькихъ буквъ, то пока
зываетъ, сколько разъ (или какая часть) берется все это произведеніе. Наприм.
ЗаЪс—аЬс-ѵ-аЬс-л-аЬс.
Есячая отдѣльная буква имѣетъ при себѣ коэфиціентомъ 4-цу; только ее пе
пишутъ, а всегда подразумѣваютъ, ибо само собою попятно, что а=1.а.
При самыхъ общихъ рѣшеніяхъ вопросовъ, коефиціенты предъ искомыми или
неизвѣстными количествами также означаются буквами, изображающими какія
пибудь отвлеченныя ччела. Наприм. если въ выраженіи
аж3-+-ож2-ьса;->-гі=0
одно х неизвѣстно, то извѣстная числа а, Ь, с, .... называются коэфиціентами.
41. Степени и показатели ихъ. Отъ умноженія количества самаго па себя
получаются произведенія называемыя степенями того количества. Степени
различаются по числу равныхъ множителей, взятыхъ для ихъ составленія.
Одинъ множитель а представляетъ первую степень этого количества. Произве-
деніе двухъ равныхъ множителей «Ха—а« называется второю степенью отъ а;
произведеніе трехъ равныхъ множителей а X аХа—ааа составляетъ третью
степень отъ а, и т. л.
3
Для сокращенія, пишутъ букву а одинъ разъ, и надъ нею съ правой стороны
ставятъ показатель, то есть, число, показывающее, сколько разъ ята буква
взята множителемъ для составленія степени, или какой опа степени. Посему,
пишутъ аа=а2, и произносятъ: а второй степени, или а квадратъ; ааа=а3~
а третьей степени, или а кубъ; ааааа^о5—а пятой степени.
Ежели степень состоитъ изъ чисда п множителей а, то пишется ааааа....
~ап, и выговаривается а и-ой степени.
Такимъ образомъ,
ааааЪЬЪсс падобно писать а4 6’ с*.
5. Всякое количества а, возвышаемое въ степень, называется основаніемъ,
производителемъ, или корнемъ этой степени
Не должно смѣшивать показателя степени буквеннаго количества съ его
коефпціентомъ. Наприм. За не равно а3; потому что
За—ач-ач-а, а3—ала.
Всякая буква имѣетъ показателемъ 1-пу; но этотъ показатель не пишется, а
только всегда подразумѣвается. Наприм. а=а’.
6. Знаки сравненія. — Для сравненія величины однородныхъ количествъ
употребляются:
а) Знакъ равенства, =, который ставится между равными количествами;
паприм. 2а-+-3а=5а.
б) Знаки неравенства, >, <, которые выговариваются: больше, меньше.
Напримѣръ, если нужно показать, что а больше Ь, и с меньше Л, то пишется
а>6: с<(7,-
отверстіе знака всегда обращается къ большему количеству.
3. При алгебрическихъ дѣйствіяхъ чаще, всего употребляются равенства.
Главное свойство равенства между количествами выражается слѣдующею аксіо-
мою: равенство между равными количествами не перемѣнится, если мы
произведемъ какія нибудь равныя дѣйствія надъ ними, напримѣръ, если
придадимъ къ нимъ по ровну, или отнимемъ по ровну, если ихъ помножимъ илп
раздѣлимъ на равныя количества, если возвысимъ въ равныя степени, и проч.
АЛГЕБРИЧЕСКІЯ КОЛИЧЕСТВА.
8. Алгебрическими, т. е. буквенными, количествами называются выраженія,
которыхъ составляющія части пзображе.іы буквами, и соединены между собою
знаками различныхъ дѣйствій, таковы наприм.:
г л аі о іа3— 76’
5а, Ьа о, За—2о-»-с, —-——, и пгоч.
9. Члены.—Членами алгебрическаго количества называются количества,
его составляющія, соединенныя между собою знаками -4-или—.
4
Члены бываютъ положительные или отрицаталыіыс, смотря потому, ка-
кіе знаки находятся предъ ихъ коефиціептами, -ь или —.
Если количество начинается положительнымъ членомъ, то предъ этимъ чле-
номъ пе пижется знакъ -+-, а только всегда подразумѣвается. Напрчм.
3а®6=м-3а®6
Въ выраженіи 2а2—36-+-5с—й члены 2а2, 5с, положительные; — 36
и —(I члены отрицательные (вычитаемые).
Ю. Количества одночленныя, двучленныя, и проч. — Алгебрическія
количества, по числу членовъ ихъ составляющихъ, бываютъ одночленныя,
двучленныя (биномы), трехчленныя, п. вообще, многочленныя (поли-
номы). Напримѣръ:
3
5а, , суть колпч. одночленныя;
А-+-1), ЗаЬ2—іагп, 7Ьгс-і-^, количества двучленныя,
_ 2 . & аЬ
2а — количество трехчленное;
«ис-ьбж’-ьсж’-ьйж4-ь.... количество многочленное, или многочленъ.
<1. Многочленъ называется однороднымъ, если всѣ его члены состоятъ
изъ равнаго числа буквенныхъ множителей; въ противномъ случаѣ, онъ назы-
вается вмѣшаннымъ, неоднороднымъ. Напримѣръ:
4
аЬг—Збс’-ъ- -д тпр, количество однородное;
аб®—тп-+-р, количество неоднородное.
1®. Однородное количество бываетъ первой степени, второй степени, третьей
степени, и проч., когда всѣ члены его содержатъ по одному буквенному мно-
жителю, или по два, по три, и т. д. Напримѣръ:
„ , 2с
За-ьб---д-, количество первой степени;
За-—Ьй— ^-ст,----------второй степени;
За^р-ч-Ьд?—~ст,--------третьей степени.
13. Значеніе многочлена ни сколько не перемѣнится, въ какомъ бы порядкѣ
ни были написаны его члены. Напримѣръ:
За~Ь—каЬ9-+- 2ЪА можно написать:
263—іаЬ°-+-За^Ь, или
За2Ь-ч- 2Ь3—4аЬ*, или
— 5.а62ч-3а®6-+- 2Й;
потому что, отъ этой перестановки, пе перемѣняется условіе, что За*6 п 26’
надобно сложить, и изъ суммы вычесть 4а6*.
Основываясь на этомъ свойствѣ, въ Алгебрѣ весьма часто располагаютъ мно-
5
гочлены по возрастающимъ или убывающимъ степенямъ какой ниоудь буквы,
общей многимъ членамъ ихъ. Напримѣръ, количество
3 аіг—3 а26н-а3—6’
можно расположить по уменьшающимся степенямъ буквы а, и найдется:
а3—3а36ч-3а62—63;
оно въ тоже время расположилось по возрастающимъ степепямъ'буквы Ь, но въ
сущности нисколько не перемѣнилось.
14. Члены подобные. —Въ многочленѣ могутъ быть члены подобные или
неподобные. Члены подобные всѣ состоятъ изъ однѣхъ и тѣхъ же буквъ, имѣю-
щихъ соотвѣтственно равныхъ показателей; только ихъ знаки и коефиціенты мо-
гутъ быть какіе угодію. Напрпмѣръ, въ многочленѣ
а26ч-5а36—
три первые члена подобны, по четвертый имъ не подобенъ, потому что его буквы
а и Ь имѣютъ другихъ показателей.
15. Сокращеніе многочленовъ.—Многочлены, въ которыхъ находятся по-
добные члены, можно приводить въ простѣйшій видъ, т. е. сокращать, соеди-
няя подобные члены, чрезъ сложеніе пли вычитаніе, въ одинъ членъ, а именно:
1) Если подобные члены будутъ съ равными знаками, то надобно сложить
одни ихъ коефиціенты, предъ суммою поставить ихъ общій знакъ, а буквы напи-
сать тѣ же, какія находятся въ одномъ членѣ. Наприм.:
- За-ь4а—7 а,
іт—Ир—Зр=іт—г»р,
2а368ч-10а3б2=12а36]!,
5тп2—За26— 7а26=5тпа—ІОа’6,
з п , 2 п - 17 , .
---, «V— — а5с =—... абс .
4 3 12
2) Если подобные члены съ противными знаками, то надобно сложить сперва
члены положительные, потомъ члены отрицательные, вычесть меньшую сумму
изъ большей, и предъ остаткомъ поставить знакъ большаго количества. По-
слѣднее понятно изъ слѣдующихъ примѣровъ:
6 а— 4аг=2а,
6а— 6а—О,
6 а—10а_—4а.
(ибо 6а — 10а=6а——4а; во 6а—6а=0, посему 6а—10а=—4а).
Примѣры. 6а“А?—4а’63-ьЗагб3—а263=
=9аа63—5аа6’-4а2б3;
8а-Ь— 15а26ч-6а2А—14^!»—15а26=—а26.
14». Всякое алгебрическое выраженіе обращается въ численное (иумериче-
скос), если выразить его буквы числами, подставить этп числа на мѣста буквъ,
и произвести ариѳметическія дѣйствія, показанныя знаками.
6
Примѣръ. — Найти численную величину количества Зав63, полагая а—
Ъ=-2.
Опа будетъ:
3а*ба=3. 4*. 23=3. 16. 8=384.
4 2
Примѣръ.—Найти численную величину для аЬ*—д-6с*, полагая а=10,
6=3, с=4-
Она будетъ:
4.10. 3*—|. 3.1=72-4=714
ЯЭ". Очень часто нужно бываетъ только показать, что надъ цѣлымъ много-
членомъ должно произвести какое нпбудь дѣйствіе; тогда этотъ многочленъ ста-
вятъ между скобками,и предъ скобкою ставятъ знакъ требуемаго дѣйствія На-
примѣръ, желая показать, что многочленъ За—6-*-2с надобно вычесть изъ
5</, пишутъ:
о(1—(За—6н-2с);
если тотъ-же многочленъ надобно помножить на 5а*6, то пишутъ:
(За—6-ь2с)5а*6.
Для помноженія а-+-Ь па а—Ь, пишутъ-
(ач-А) (а—А);
для возвышенія ач-А въ квадратъ, пишутъ:
(а-+ 6)’, и проч.
АЛГЕБРИЧЕСКІЯ ДѢЙСТВІЯ
ГЛАВА ПЕРВАЯ.
СЛОЖЕНІЕ И ВЫЧИТАНІЕ АЛГЕБРИЧЕСКИХЪ КОЛИЧЕСТВЪ.
Я8. Сложеніе.—Для сложенія алгебрическихъ количествъ, надобно только
нависать ати количества съ ихъ знаками въ одну строку, и потомъ сократить,
если будутъ подобные члены, то и получится искомая сумма. Напримѣръ: сумма
количествъ За2б, 5аба, 26, найдется
За2бн-5абач-26.
Сумма членовъ 2а2, — Зб2, будетъ
2а2—36’.
Здѣсь предъ Зб2 удержанъ знакъ — , потому что ято придаваемое количество
отрицательное. Справедливость этого можно еще доказать тѣмъ, что, если изъ
суммы двухъ количествъ вычесть одно изъ нихъ, то должно остаться другое: отни-
мите же 2а2 изъ 2а2—362, остается именно другое количество — Зб2. Слѣ-
довательно, при сложеніи 2а2 съ — Зб2, долженъ быть сохраненъ знакъ
— предъ Зб2.
Поэтому въ Алгебрѣ суммою вообще называется совокупность членовъ съ
равными или различными знаками, и, для отличія, называется алгебрическою
суммою.
Примѣръ. Сумма количествъ За3-+-2аб2-ьб3 и 5аб2-ь2а3 найдется:
З.а3-+-2а6’-+-Л3-ь5а62-ь2а3;
а, соединивъ подобные члены
За’ч-2аэ =5а3,
2а62ч-5аб2=7аб",
получится также сумма, только сокращенная*
йаЧ-Та^ч-б1.
8
19, II въ Алгебрѣ, подоено тому какъ въ Ариѳметикѣ, при сложеніи много-
членовъ, пишутъ эти слагаемыя количества однѣ подъ другими, проводятъ подъ
ними горизонта іьную черту; потомъ ищутъ подобные члены, начиная съ пер-
ваго; такіе члены приводятъ въ одинъ, который и пишутъ подъ чертою; а послѣ
приписываютъ туда же п члены неподобные съ ихъ знаками.
Примѣръ. — Сложить количества:
7ж3—бжу-ьз2
бжу—9с3—Зж’
3;-2-+-2жу
Найдется сумма 4ж3—5з*.
/
Примѣръ. — Сложить:
» 8 4 8 К 1
• иіи — а и — э »
0 5 х
2 2 8 1
а п —тті — т~
Сумма: пів3 -+- ! а‘п — 5 |
Здѣсь, для сокращенія подобныхъ членовъ | тп* и — тп\ вычтенъ коефи-
э 2 1
ціенть втораго члена изъ коефиціента перваго, то есть, взято — —у = —'
Далѣе, изъ а1п вычтенъ членъ а^п, то есть, взято 4— * , и проч.
90. Вычитаніе. Для вычитанія одного количества изъ другаго, надобно пе-
ремѣнить знаки у всѣхъ членовъ вычитаемаго, и написать оное подлѣ умень-
шаемаго въ одну строку, а потомъ сократить, если будутъ члены подобные, то
и найдется искомая разность.
Это правило можно объяснить слѣдующими примѣрами вычитанія одночлен-
ныхъ количествъ:
1) Изъ За3 вычесть 5аі. Разность бу ютъ
За3—5аЪ.
2) Изъ а вычесть — 6 Разность будетъ
ан-6.
Для доказательства точности этого вывода, замѣтимъ, что Ь — Ъ — 0, и что
уменьшаемое а не перемѣнится, если придадимъ къ нему этотъ нуль:
а=а-ь0=ач-6—Ь;
а потомъ отсюда отнимемъ — Ь, и останется
ач-6.
3) Іізъ а вычесть Ь — с; получится разность
а—6-+-с.
Ибо, а=а-ьО^іа-ь6—6-ьс—с;
9
отсюда вычитаю -+Ь—с, то есть, уничтожаю два члена -+-1> и —с, и полу-
чаю искомую разность а—Іі-+-с.
Этимъ и доказано правило, что, при вычитаніи, надобно у всѣхъ членовъ
количества вычитаемаго перемѣнить знаки, и съ этими знаками написать подлѣ
уменьшаемаго.
5?і. При вычитаніи многочленовъ, дѣйствіе располагаютъ какъ въ Ариоме-
тпкѣ: пишутъ вычитаемое подъ уменьшаемымъ , проводятъ подъ нимъ черту, пе-
ремѣняютъ знаки у всѣхъ членовъ вычитаемаго, сокращаютъ подобные члены,
если они есть, и, что получится, ставятъ подъ чертою; туда же сносятъ и члены
несократимые.
Примѣръ. Изъ 10б8с—15бс‘-ь20с3 вычесть 10с3—Ьс*—2Ьгс.
Для этого перемѣнимъ знаки предъ всѣми членами вычитаемаго, подпишемъ
подъ уменьшаемымъ, и сократимъ-
і№с-156с*-ь20с3
—10с3-ь Ьс2ч-2^с •
разность 1262с—14бс2-ь10с3.
Примѣръ. Изъ 1 тп' -г-а4га—5^-вычесть а*п — — тп* — —.
1 , 1 Ь а 4 3 4
Перемѣнивъ знаки въ вычитаемомъ, напишемъ его подъ уменьшаемымъ, и
сократимъ:
і , 1 , „з
-тп -ь ц- а п—5л-
6 о 4
, . 2 2 1
— а п+ „ тп і —
з 4
В , 4 2 К1
разность = тп1—п—
Я®. Остатки отрицательные, количества отрицательныя.—Въ Ал-
гебрѣ отрицательные остатки происходятъ при вычитаніи большихъ количествъ
пзь меньшихъ. Такъ, если надобно изъ 2а вычесть 5а; то всё-таки вычитаютъ
меньшее изъ большаго, и предъ остаткомь ставятъ знакъ —,
2а—5а=— За.
Ибо это все тоже, что 2а—2а—За; ио 2а—2а=0, слѣдовательно оста-
токъ будетъ —За.
Если изъ 10 станемъ послѣдовательныя вычитать 8, 9, 10,’Н, 12, 13, ...
10, 10, 10, 10, 10, 10, ....
8, 9, 10, 11, 12, 13, ...
2, 1, 0,-1,—2,-3, ....
получатся остатки 2, 1,0,—1,—2,—3....., которые, по общему объ пвхъ
понятію, должны быть тѣмъ меньшіе, чѣмъ вычитаемое число болѣе, то есть:
1 <2, 0 <1, —1 <0, —2 <—1, —3 <—2, и такъ далѣе.
Отсюда заключаютъ, что всякій отрицательный остатокъ меньше пуля; изъ
10
двухъ отрицательныхъ остатковъ тотъ менѣе , котораго чисіенная величина (взя-
тая безъ знака) болѣе.
93. Однакожъ, это заключеніе отнюдь нельзя принимать за общій смыслъ
«всѣхъ отрицательныхъ коіичествъ. Безъ надлежащаго истолкованія, выраженіе
—і <0 противорѣчитъ здравому смыслу: меньше нуля ничего себѣ предста-
вить нельзя, иначе надобно самое ничто признать за нѣкоторое измѣримое коли-
чество. Такимъ же образомъ и выраженіе —3 <—2 противорѣчитъ здравому
_ — 3
смыслу, и приводитъ къ нелѣпости, оудто бы —— должно ныть дробью, а не
цѣлымъ числомъ.
Изъ этого видно, что выраженія—I <0 и —3<—2, имѣютъ смыслъ
не самый общій, а какой именно, это требуетъ объясненія.
Въ отвлеченныхъ числахъ, вообще положительный остатокъ означаетъ
избытокъ уменьшаемаго числа предъ вычитаемымъ, а остатокъ отрица-
тельный показываетъ избытокъ вычитаемаго числа предъ уменьшаемымъ, ко-
торый остался только потому, что вычитать было не изъ чего; стало-быть, онъ
• есть результатъ недоконченнаго вычитанія. Оттого, остатокъ отрицатель-
ный, будучи прилагаемъ ко всякому положительному числу а, уменьшаетъ оное,
тогда какъ пуль, придаваемый къ а, не производитъ въ немъ никакой перемѣны,
такъ что
а—і <а-4-0;
отъ этого неравенства отнявъ по а, найдемъ
— 1 <0.
Очевидно также, что а—3<а—2; а отнявъ но а съ обѣихъ сторонъ,
будетъ
—3 <—2.
П такъ, выраженіе 0> — 1 имѣетъ тотъ смыслъ, что нуль, придаваемый ко
всякому положительному числу, даетъ результатъ болѣе, нежели когда придадимъ
—1 къ этому числу. Смыслъ выраженія —2>—3 тотъ, что —2, придаваемое
къ положительному числу, дастъ результатъ болѣе, нежели когда придадимъ къ
нему — 3. Такъ падобііо разсуждать объ отрицательныхъ остаткахъ въ числахъ
отвлеченныхъ.
Но, въ числахъ именованныхъ отрицательныя количества — а, — 2а,
— За,.....имѣютъ разныя значенія, и увеличиваются точно также, какъ и
положительныя количества, а, 2а, За..., чему множество можно представить
примѣровъ. Такъ, если кто нкбудь дѣлаетъ два шага впередъ и 5 назадъ, то ре-
зультатъ его движенія 3 — 5 = — 2 шага показываетъ, что онъ идетъ не
впередъ, а назадъ. Если я выигрываю ,'і рублей, а проигрываю 8 рублей, то
результатъ моей игры 5 — 8 =— 3 руоля показываетъ, сколько я долженъ за-
платить Если кто нибудь, купивши товару на 15 рублей, заплатилъ только 10
11
рублей, то результатомъ этой покупки 10 —15=—5 будетъ составлять долгъ,
который надобно заплатить рано или поздо., и который тѣмъ больше, чѣмъ болѣе
было бы взято товару. Въ Аналитической Геометріи, для опредѣленія мѣста то-
чекъ принимаются ординаты (извѣстныя прямыя липіп) положительныя о отрица-
тельныя, возрастающія нерѣдко до безконечности. Въ Механикѣ, силы, дѣй-
ствующія въ одну сторону, принимаются за положительныя, а дѣйствующія въ
противную сторону за отрицательныя.
Сдѣлаемъ еще замѣчаніе о нулѣ, который получается при вычитаніи.
Онъ, въ различныхъ случаяхъ вычитанія, бываетъ абсолютный илп только
относительный, условный.
Изъ абсолютнаго нуля вычитать ничего нельзя, 0 — а = — а означаетъ не-
возможность. Такъ нуль градусовъ па гигрометрѣ показываетъ совершенное от-
сутствіе паровъ въ воздухѣ, и отрицательные градусы рѣшительно не возможны.
Нуль условный или относительный не означаетъ совершеннаго отсутствія того
количества, о которомъ идетъ рѣчь; по берется какъ начало, какъ всходная
точка, отъ которой мы соглашаемся начинать считать большія илп меньшія части
этого количества, по обѣ ея стороны, особливо когда мы не знаемъ этому коли-
честву пи начала, пи копна, или когда око возрастаетъ отъ безконечно малаго къ
безконечно большому. Къ такимъ количествамъ относятся: пространство, время,
нѣкоторыя силы. Вотъ примѣры: Окружность круга пе имѣетъ пи начала, пи
конца, а потому н берется произвольная точка за начало, гдѣ ставится нуль, и
отъ него дуги круга считаются въ одну сторону за положительныя, а дуги въ
противную сторону — за отрицательныя. На земномъ шарѣ каждый меридіанъ
можно взять первымъ, и отъ него считать всѣ долготы на востокъ за положи-
тельныя, а па западъ — за отрицательныя. На термометрахъ Реѳмюровомъ и
Фарепгейтовомъ нули градусовъ занимаютъ разныя мѣста, такъ что 0° Реом.
= 32° Фарепгейговымъ, и проч. Слѣдовательно, нуль условный, относитель-
ный, не означаетъ отсутствія количества, но только всходную точку, отъ которой
согласились вести счетъ этому количеству, г
УМНОЖЕНІЕ.
/ иноженів одночленовъ. При умноженіи одночленовъ должно наблю-
дать слѣдующія правила относительно ихъ знаковъ, предстоящихъ, буквъ и пока-
зателей;
I) Коефнціенты должно перемножить одинъ па другой, чтобъ получить коефи-
ціевтъ для произведенія.
2) Разныя буквы написать одну подлѣ другой безъ всякаго знака въ какомъ
угодно порядкѣ, а всего іу чшс въ порядкѣ алфавитномъ.
При шьръ. ІЬ<У(5Ьаі=2ЮаІ)С(1.
12
Ибо, произведеніе пе перемѣнится, если переставить множители въ какомъ
угодно порядкѣ, какъ это извѣстно еще изъ Ариѳметики *); посему, можемъ
паписаты
4-ас'У5Ь(1=:^.5ас'уЬсІ=:20аЬс(1.
3) Если помножаются равныя буквы съ какими ни есть показателями, то на-
добно сложить показатели; сумма ихъ будетъ показателемъ этой буквы въ про-
изведеніи.
Примѣръ. ' а*Х°3—
потому что а*—аа, а3=ааа; стало-быть,
а2Ха3=:«аХааа=::а®-
II вообще, ат. ап — ат~лп, гдѣ т, п, цѣлыя числа.
Примѣръ. ЗаЧ3с]'у(&аЬЧ^=#Л.а\а.Ь\Ь\с.с\й.[=№а3Ьъсі<]ф
Примѣръ. тп X п^гг’рУ ~ прд&=
2 4 3 29ч . 3 Л 9 *»
К • Т т-тп •п\п.р.р.ц6 — -тпрц.
4) Если множимое и множите іь имѣютъ равные знаки -+- и -ь, либо — и —,
то произведеніе должно имѣть знакъ -ь; а если знаки ихъ различны + в —,
либо — и -+-, то произведеніе должно имѣть знакъ —. Это послѣднее правило
требуетъ объясненія.
"] Въ Ариѳметикѣ это правило выводится изъ умноженія чиселъ соизмѣримыхъ. Въ
Алгебрѣ, гдѣ каждая буква можетъ означить количества какія угодно: соизмѣримыя, не-
соизмѣримыя, даже мнимыя, какъ 5 видимъ впослѣдствіи, правило это требуетъ общаго
доказательства.
Доказательство. Очевидно, что. иаприм. а2Ха’=а3Ха2^=а*Ха; ибо это толщ, что
аа.ааа—ааа.аа- -аааа.а=ая. Слѣдовательно, ат Ха«=ат_если
т и п суть числа цѣлыя. И такъ, если аЬ не равно Ьа, то пусть
оІі=Ъат |
__а^„ 1 гдѣ т, п неизвѣстныя цѣлыя числа.
Эти равенства можно написать
аІі—Ьа.а”^'
Ъа—аЪ.Ь"—1.
Подставивъ первое равепство во второе, получаемъ:
Ьа=Ъа.1=Ъа.а”‘~ ’Ь*1-1;
откуда видно, что ат~1 Ь”~ ' = 1. Теперь возмемъ
а =а, помножимъ
на а”1—Чп~1
атЪп~’=а, это помножимъ
на 6 =6
а^Ьп—аЪ.
Цѣлыя числа т, п, удовлетворяющія этому равенству, возможны только'
т=п=1.
Отсюда заключаемъ, что
что и доказать слѣдовало.
13
Очевидно, что если бы дано было помножить а-+-6 на с, надлежало бы пе-
ремножить оба члена множимаго на с, и произведеніе сложить:
(ан-6)с=ас-ьбс.
Это дѣйствіе совершенно таково же, что и въ Ариѳметикѣ, когда помножаютъ
число состоящее изъ согепъ, десятковъ и единицъ: тогда помножаются на дан-
ный множитель единицы, десятки и соніи множимаго, и всѣ полученныя частныя
произведенія слагаются въ одну сумму.
Помножимъ теперь а—6 па с, то есть, отыщемъ произведеніе (а—6)с:
оно будетъ ас — 6с.
Для доказательства возмемъ а>6, и положимъ, что а—6-і-й; будемъ
имѣть:
(а—б)с=:(6-+-й-^б)с=йс.
А какъ всякій членъ долженъ быть помноженъ на с, то будетъ также
бсчсіс—6(-+-с)=сІс.
Отъ равныхъ количествъ отнимемъ по <1с, останется
6с—6(-ьс',—0.
Но чтобъ вто двучленное произведеніе уничтожилось, необходимо, чтобъ
было—б(-ьсі——6с; ибо только тогда Ьс—6с=0.
Этимъ доказано, что —6(ч-с)——6с.
Теперь, обратно: помножитъ с па а—6, полагая а=6-+-(1:
с(а—6)—с(6-+-<1—6)=сЛ, пли
с6-+-с(1-і-с(—6)=сй.
Отъ равныхъ количествъ отбросивъ по сй, останется сб-ьс(—б)~0.
Это возможно лишь тогда, когда -+-с(—6)=—сб, чтобъ было сб—с6=0.
Отсюда видно, что плюсъ на минусъ даетъ въ произведеніи минусъ.
Для доказательства, что —&Х—с=-+-6с, возмемъ тотъ же двучленъ
а—6 и помножимъ на—с, предполагая, что а=6-+-<1; будемъ имѣть про-
изведеніе
(а—6)(—с}=(6- ыі—Ь)(—с)_—с).
А помноживъ каждый членъ множимаго б-ьй—6 на множитель — с, и
замѣчая, что 6(—с)_—6с, -+ —с)~—сіс, какъ было доказано, полу-
чимъ еще
—сб—с<1—6(—с)~—с<1.
Отъ равныхъ количествъ отнимемъ но —ссі, останется
—6с—6(—с)=0.
Но этотъ двучленъ уничтожится лишь тогда, когда при — 6с будетъ стоять
-+-6с, то есть, когда будетъ —6(—с)—-+-6с.
Этимъ и доказано, что минусъ на минусъ даетъ въ произведеніи плюсъ.
14
Гримпры: 1) 0,25а7?сХ— | с?Ьс=.-— а464с8.
7 7
2) Зш8пХ—5тн2Х—6 тпр=-* пі'п'р.
Здѣсь надлежало сперва помножить коефпціентъ 3 па — 5, что даетъ — 15;
а это помножить еще на — чтобъ получить коефиціепъ 4 произведенія.
3) — ^ат6пс3(і X ап&сУй* —— у а’’’4 и6п-*-2сг-*-3 <1»-+ •
36 Умноженіе многочленовъ. Для умноженія одного многочлена па дру
гой. надобно помножить всѣ члены множимаго па каждый членъ множителя,
сложить всѣ полученныя частныя произведенія, и сократить, если будутъ подоб-
ные члены. Самое же дѣйствіе располагаютъ такъ, какъ видно изъ слѣдующихъ
примѣровъ:
I) Помножить За’б’с—4а36Д8
на 5а4Л8—2а7>8с8
г
15я6б®с—20аг6’й8 |
—6а46йс3-г-8ѵаб3сЧ8 | пР°,Ізведрп,я-
Здѣсь пѣтъ подобныхъ членовъ, слѣдовательно искомое произведеніе
^аЧЧ—^аЧЧ^—^ЪЧ^аЧ^^.
Когда множимое и множитель имѣютъ- въ своихъ членахъ равныя буквы съ
разными показателями, то полезно располагать ихъ напередъ по убывающимъ сте-
пенямъ какой нибудь одной буквы. Тогда и частныя произведенія расположатся
по убывающимъ степенямъ той же буквы. Для легчайшаго сокращенія общаго
произведенія, располагаютъ частныя произведенія такъ, чтобы члены съ равны-
ми степенями стояли одни подъ другими; между ними должны находиться подоб-
ные члены, если только они есть дѣйствительно.
2) Помножить 4гс8-ь6л:«/-г-9у8 на 2л:—Зу.
Здѣсь множимое и множитель расположены по убывающимъ степенямъ буквы
х: мы расположимъ и частныя произведенія по степенямъ тойже буквы:
4л?8-+-6а?уч-9у8
• 2 л:—Зу
8аГ-+-12а?8ун-18жу8
—12ж8*/—18жу8—27у’
произведеніе =8я3—27у3
З'і Помволіпть - т3с— »г с8-ь-* тсг на шс8 — « т'с-
> 2 4 Ъ 3 э
Для большаго удобства, расположимъ множимое и множитель по степенямъ
буквы с, п потомъ будемъ умножать
15
* 3 1 5 3 1 3
- йіс — т с + . т с
о л
2 , « ,
~ тс — -.то
л &
1-1 1
12т’с°—шѴ-ь-д пі4с’
1 з . 1 . з 2 > •
— т с4ч- -ц пі4с — -5 пгс
1 , 5 4 3 4 8 4 3 2 5 ,
.^пг сэ—,-^пг с’+.-^т’с’— - иг с .
1 2і 13 Іо Э
23. Если «лены множимаго однородны между собою, и члены множителя
также между собою однородны, то и всѣ члены произведенія должны быть одно-
родными потому что они будутъ состоять изъ равнаго числа буквенныхъ множи-
телей. Это можно видѣть изъ всѣхъ примѣровъ, которые ппедставлепы здѣсь
для умноженія многочленовъ.
28. Если члены множимаго и множителя имѣютъ равныя буквы, и располо-
жены по уменьшающимся степенямъ какой пп есть одной изъ нихъ, то никогда
не можетъ быть, чтобы первый членъ произведенія сократился съ какимъ ппбудь
другимъ членомъ, потому что въ немъ одномъ будетъ находиться высшая сте-
пень этой буквы. Напримѣръ:
а8 ч аѢ і рі’ ч Ь1
аг — 2ао -+- //
а6ч- а*1> ч- аѴ -+- аа68
— 2а4А—ЗаѴ—2а’А8—2а6*
ч аѴ ч' аѴ ч- «А4 ч- Ъ6
а:‘ — аЧ) — аЬ* ч 65.
Здѣсь множимое п множитель расположены были по убывающимъ степенямъ
буквы а, и по возрастающимъ степенямъ буквы Ъ; отъ того получилось и про-
изведеніе, расположеннпое по степенямъ тѣхъ же буквъ. Первый членъ а5 про-
изведеніи содержитъ высшую степень буквы а, равпо какъ и послѣдній членъ /г’
высшую степень буквы Ь; оттого нп которой изъ нихъ сократиться не могъ.
Мы увидимъ, что на этомъ свойствѣ основывается отыскиваніе членовъ
частнаго числа при дѣленіи многочленовъ.
29. Умноженіе служитъ для возвышенія въ степени количествъ одночлен-
ны) ъ. Объ этомъ предметѣ подробно будемъ говорить въ послѣдствіи; а теперь
представимъ только пѣкоторые частные случаи, весьма часто встрѣчающіеся, и
которые надобно знатъ на память всякому учащемуся; это суть произведенія:
(ач-6)(ач-Ь), (а—б)(а—о;, (ач-А)(в—Ь).
16
а-А-Ь а—Ь а-А-Ь
а-А-Ь а—Ь а-+-Ь
а^-А-аб а'—аЬ а*-А-аІ>
-А-аЬ-А-Ьг —аЬ-+-Ъ‘ —аЬ—ь'
а1-А-2аЬ-Д‘ аг—2аЪ+Ьг а1—!>г
И такъ, (а-г-Ь) (ач-б)=(а-ьб)’=а’-ь2а&-і-6’,
(а—Ь '(а—6)=(а—6)’—а1—2аЬ-±-Ьг,
(йч-б)(а—/<)=аэ—б2;
то есть: квадратъ суммы двухъ количествъ а п Ъ равенъ квадрату пер-
ваго -А-удвоенное произведеніе первою на второе, и-А~квадратъ втораго.
Квадратъ разности двухъ количествъ равенъ квадрату ііерваго, безъ
удвоеннаго произведенія перваго на второе, и -ь квадратъ втораго.
Сумма двухъ количествъ, помноженная на разность ихъ, равна раз-
ности ихъ квадрагповъ.
Зная па память ати выводы, надобно стараться непосредственно примѣнять |
ихъ ко всякимъ случаямъ такого рода, не прибѣгая къ дѣйствію умноженія.
Такъ:
(За5б3с-ь5бс’<2)2=9а46сс’-ьЗО«7/с3<2-4-2562с1(Іі,
Кат'—х-иіп’) =Да8и?—-%пЛг+'*‘ т’п»,
\о 6/25 а оЬ 3
Ь*с-г-Зтп) 6!с—Зя»і)=^ 64с*—9т!п~,
(2хтч~5уп)(2хт—5ха)=4хгт~25уІа.
ДЪЛЕНІЕ.
30. Въ Алгебрѣ, какъ и въ Ариѳметикѣ, дѣленіемъ называется такое дѣй-
ствіе, посредствомъ котораго находятъ частное число по даннымъ дѣлимому и
дѣлителю. Слѣдовательно дѣленіе заключаетъ въ себѣ разложеніе дѣлимаго коли-
чества па двухъ производящихъ его множителей, пзъ которыхъ одинъ данъ—эго
дѣлитель, п другой ищется — это частное.
ЗС. Дѣленіе одночленовъ. — При дѣленіи одночленныхъ количествъ, на-
добно соб подать правила относительно знаковъ, коефиціентовъ, буквъ и показа-
телей.
1. Если дѣлимое и дѣлитель имѣютъ равные знаки, то частное должно имѣть
знакъ -+- ; если же у дѣлимаго и дѣлителя знаки различные, то частное должно
имѣть знакъ — .
2. Надобно коефпціелтъ дѣлимаго раздѣлить на коефнціентъ дѣлителя.
3. Если въ дѣлимомъ п дѣлителѣ находятся равныя буквы съ различными
показателями, то должно показатель дѣлителя вычесть пзъ показателя дѣлимаго,
получится показатель той же буквы въ частномъ.
17
ЛГЕНД>
□»ЧьСНОЙ
Жни. >
Г 6И9
КОНИНУ
\АК>
4. Буквы, ощція дѣлимому и дѣлителю, съ равными показателями, гіаамліо
исключить.
Всѣ сіи правила легко доказываются одною повѣркою дѣленія, состоящею
въ томъ, что частное, помноженное на дѣлитель, должно произвести дѣлимое съ
его знакомъ, слѣдующимъ образомъ:
а) При раздѣленіи аЬ на Ь, частное должно быть
аЪ
— —а,
тутъ частное а, помноженное на дѣлитель Ь, дѣйствительно произведетъ дѣли-
мое аЬ.
При раздѣленіи -+-аЬ на —Ь,
—аЬ
12«6 _
— 3«;
а(,
частное =——=—а->
—ь
потому что дѣлитель —Ь только отъ умноженія на —а можетъ произвести
дѣлимое -+-аЬ
При раздѣленіи —аЬ па -+-Ь,
— аЬ
частное = —г- = —а,
-+-Ь
по той же причинѣ, что -а-Ь только на —а помноженное даетъ —аЬ.
При раздѣленіи —аЬ на —і>,
частное = -
о, только —Ь на -ч-а даетъ —аЬ_
Ь) При раздѣленіи 12аЬ на ЬЪ,
частное = ,
40
потому что ЗаХ4^=12а6. Здѣсь, для полученія коефиціента 3 въ частномъ,
надлежало раздѣлить 12 на 4.
с) Теперь раздѣлимъ а5 па а3, гдѣ дѣлимое и дѣлитель суть разныя степени
одного и того же количества а. Частное должно быть
— =а ;
потому что а* только отъ помноженія на а’ даетъ
а’Ха’—а54-—а5.
Очевидно, что показатель 2 = 5 — 3, и что можно было написать
а’ 8_3
~і=а =а’.
ая _
Докажемъ теперь, что вообще ___
—— а
и
ат
Для зтого положимъ, что—=аж, гдѣ показатель частнаго неизвѣстенъ,
сдѣлаемъ повѣрку;
>
— 18 —
Но, чтобы это равенство могло быть, необходимо нужно равенство пока-
зателей:
п-+-ж=іи; отсюда вычтемъ п,
--П——П
х=т—п
Слѣдовательно, — — аЯ!=ат~п.
’ а"
И такъ, при дѣленіи, надобно вычитать показатель дѣлителя изъ показателя
дѣлимаго, если въ нихъ находятся равныя буквы.
<1) Равныя буквы съ равными показателями въ дѣлимомъ и дѣлителѣ надобно
иск почать просто какъ равныхъ множителей; потому что частное отъ этого не
должно перемѣниться. Такъ:
п 12а ЪѴ „ ,,, -
Примѣры: —^^-=3а 6 с3;
6«3&ъ5: ^-авЬхв — 8ахв;
а*п+і —аВп-,= —а^
атхт'м' : ахт-і=а”'-іх^і.
318. Дѣленіе одночленовъ нацѣло невозможно: 1) когда коефиціентъ дѣли-
маго не дѣлится па коефиціентъ дѣлителя безъ остатка; 2) копа показатель ка-
кой ни есть буквы дѣлимаго менѣе показателя той же буквы въ дѣлителѣ; 3)
когда дѣлитель содержитъ въ себѣ такія буквы, какихъ нѣтъ въ дѣлимомъ. #
Во всѣхъ этихъ случаяхъ частное изображается дробью, которую надобно
только сократить чрезъ исключеніе всѣхъ множителей общихъ дѣлимому и дѣли-
телю. Напримѣръ:
2ОаЛЬіса _ іаЧе
16а®6с’р® Зс’р®
33. Показатели нуль и отрицательные.—Мы знаемъ, что =а”’—".
При этомъ дѣленіи могутъ встрѣтиться три случая: т^>п, т~п, т<п. Въ
первомъ случаѣ показатель т—п частнаго будетъ положительный; во второмъ
показатель т—п—0 • въ третьемъ т—п— — ,
Намъ извѣстно, что такое а возвышенное въ положительную степень; дока
* 6о—і а-«—Д-.
-г- -• -♦ а
а) Когда т=п, то выраженіе 7т~а”' ” обращается ъъ-^=ат~”'=ав. Но
ат
знаемъ, что — =1; слѣдовательно я°=1.
И такъ, всякое количе^тЪю, возвышенное въ нуль, равно единицѣ.
19
8—Е.
Ы Отрицательный показатель бываетъ при раздѣленіи меныпей степени на
большую той же буквы. Наприм.
о5 ___ з__к_ __.)
— = а* ~а 2.
“ - и/ ,и
г аъ ааа . . 1
Но, поелику- =по сокращеніи, ооращается въ—, то, очевидно, что
—2 1
а ——г-
Вообще же это -доказывается такъ:
ат
а ~а» ’
положивъ т —О, найдется тотчасъ
а” а"
И такъ, отрицательная степень количества равна единицѣ, раздѣ-
ленной на ту же степень положительную.
31. Выраженіе а0 употребляется въ тѣхъ случаяхъ, когда хотятъ сохранить
въ частномъ числѣ всѣ сокращающіяся буквы. А выраженіе а~п служитъ для
того, чтобы буквы или числа, находящіяся въ знаменателѣ дроби, перенести въ
числитель, или наоборотъ.
Примѣръ.
3я26°с^3н2.
5а’62с
24>п2п-р< з..—і______*Р
ЪтѴр*
10а’"
-~іт 8п Ір~
_ 10
—ц- т
Примѣръ.
тѵ’п
Примѣръ.
Послѣ этого понятны будутъ и слѣдующіе примѣры умноженія и дѣленія ко-
ічествъ, съ положительными и отрицательными показателями:
ат
4) д”,а-"=Д-=а”-".
2) а-т.а'-п=-— — ———а~(’п*п’
/ атая П«Ч-п
3) а’":а-‘=а”‘-м‘.
4) а~т .а~"—а~т+".
Все это оправдывается повѣркою. Такъ, въ послѣднемъ примѣрѣ,
а-"‘=а-"Ха~'"^=а~’'~т^п=а-'п.
35. Дѣленіе многочленовъ. Раздѣлить одинъ многочленъ на другой зна-
читъ найти частное, т, е третій многочленъ такой, который, будучи умноженъ
па дѣлителя, произвелъ бы дѣлимое.
36. Изъ этого опредѣленія видно, что дѣлитель и частное должны содержать
въ себѣ только такія буквы, какія находятся въ дѣлимомъ; и что дѣленіе безъ
остатка невозможно, если въ дѣлителѣ есть хотя одна буква, не находящаяся въ
дѣлимомъ.
Теперь представимъ себѣ, что частное уже найдено, что дѣлитель п частное
20
расположены по убывающимъ степенямъ одной какой ни есть буквы, л перемно-
жены между собою; то получится дѣлимое, также расположенное по убываю-
щимъ степенямъ этой буквы, н первый членъ этого произведенія одинъ будетъ
заключать въ себѣ ея высшую степень (88), слѣдовательно ни съ которымъ не
сократится. Отсюда заключаемъ обратно, что если раздѣлить первый членъ
зтого произведенія (какъ дѣлимаго) на первый членъ дѣлителя, то необходимо
получится первый членъ частнаго. Это свойство приводитъ насъ къ слѣдующему
правилу дѣленія многочленовъ:
Прежде всего должно расположить члепы дѣлимаго и дѣлителя по убываю-
щимъ степенямъ одной буквы; написать дѣлитель съ правой стороны дѣлимаго,
п отдѣлить ихъ вертикальною чертою. Потомъ раздѣлить первый членъ дѣлимаго
на первый членъ дѣлители, наблюдая извѣстныя правила относительно знаковъ,
коефиціентовъ, буквъ и показателей; — получится первый членъ частнаго, на
который надобно помножить всѣ члены дѣлителя. Къ остатку должно снести
всѣ прочіе члены дѣлимаго, расположивъ ихъ по степенямъ все той же буквы,
и раздѣлить первый членъ остатка на первый членъ дѣлителя; получится вто-
рой членъ частнаго, на который надобно помножить всего дѣлителя, и произве-
деніе вычесть изъ дѣлимаго, и т. д. продолжать, пока въ остаткѣ не получится
ничего, или выйдетъ остатокъ, котораго пи одинъ членъ не дѣлится на первый
членъ дѣлителя. Тогда этотъ остатокъ приписывается къ частному, проводится
Шѵдч> щимъ черта, я подъ нею ставится дѣлитель.
Примѣры:
4) Раздѣлить 8а’—10а’6-+-7а68—36’ на 2а8—абч-6’.
Для этого я располагаю дѣлимое и
буквы а:
Д лимов.
8 а3—10а26ч-7а62—363
—8а3-+- 4а26—4а68
— ба’бч-Заб’—363
дѣлитель по убывающимъ степенямъ
Дили-гвль.
2а1—аМ'
4-а—36=частное.
-+- 6агЬ—
О
Дѣлю первый членъ 8а3 дѣлимаго на первый членъ 2а* дѣлителя; отчего
получаю первый членъ 4а частнаго, который пишу подъ чертою дѣлителя. По-
множаю дѣлитель па 4а: ,
(2а’ — е6-+-6’) 4а=8а’— 4-а’6-ь4а&’,
и это произведеніе вычитаю изъ дѣлимаго. Остатокъ —6а26-+-3а6"—36’ распо-
лагаю по степенямъ буквы а, и дѣли —ба’б на 2а". Получаю второй членъ
—36 частнаго, на который также помножаю весь дѣлитель
(2а‘—а6ч-6’)(—36)=- 6а’6ч-3а68—361,
21
и это произведеніе вычитаю изъ дѣлимаго. Въ остаткѣ нуль; слѣдовательно
4а—36 и есть полное частиее число.
Вѣрно ли исполнено дѣленіе, это повѣряется чрезъ умноженіе дѣлителя на
частное: въ произведеніи непремѣнно должно получиться дѣлимое, т. е.:
(2а1 *—аМ3) (4а—36)=8а3— 10а*6-+-7а6’—36’.
2) Раздѣлить {\а3Ь3—4а46—Заб* на За6н-2а*—Ь1
Расположимъ дѣлимое и дѣлитель по степенямъ буквы а.-
Дѣлимое.
— МММ—ЗаЬ1
+ і6>ЫсТ —2а3Ь3
Дѣлитель.
2а*-+-3а6—6’
—
— 2а*6ч-3а6’= частное.
6а’6*-ь9а86’ —За6‘
—ба’б*—9а'б’ -+-3а6‘
3)
0
Дѣлимое. Дѣлитель.
6ае—24&64—72а63—546е За’ч-6а6’ч-96’
— 6а6— 12а46*— 18а®63 2а’—4а6’—66’
— 12а46’-18аѴ—24а26‘—72а65— 5М
12а*6*-+-24а’64-ь36аб5
—18а’6’—Збаб5—546е
ч-18а’63-+-36 а65-ь546е
0~
4) 30®’“— 25^+1№-125 а;*"
—30ж1"‘—50л?“+п
Зо^-ь-ба;"
7К/гп*
1 Ож™—25аЛ+- о --
Зх ”-1-5.2"
—7 5а?*"*" +-7 5а;”‘—125а:’"
ч75х’'”"-і-125а;”‘
Остатокъ — -ь75а>’“
Въ э’омъ примѣрѣ получился остатокъ 75а?**, нераздѣлимый на двучленнаго
дѣлителя; оттого частное найдено ІОа?"1—25о;"ч---— —
ЗжтаЧ-&Гп«
33- Въ Алгебрѣ встрѣчается множество случаевъ, гдѣ нужно бываетъ от-
дѣлять изъ даннаго многочлена множитель общій всѣмъ (или только нѣ-
которымъ) его членамъ, и ставить его внѣ скобокъ. Для этого надобно со-
врать всѣхъ множителей, общихъ всѣмъ членамъ даннаго количества, перемно-
жить ихъ между собою, и на произведеніе раздѣлить все это количество: полу-
чится частное, въ которомъ не будетъ ни одного множителя общаго всѣмъ ега
22
членамъ. Тогда эго частное заключаютъ въ скобки, а внѣ скобокъ ставится об-
щій дѣлитель въ видѣ множителя.
Примѣръ. —Положимъ, что изъ количества 12а563— 15а36° нужно отдѣ-
лить общій множитель, и вынесть за скобки. — Здѣсь тотчасъ видно, что мно-
жители общіе обоимъ членамъ суть 3, а2, Ь3. Составимъ изъ нихъ произведеніе
За’63, и па него раздѣлимъ данное количество:
> 12«3Ь3—15а2Ьс , . „.,
-----~та —56 ; слѣдовательно
12а563—' ЯЬ‘?Л=(4а5—56’)3а56*.
Примѣръ. х-і-ах*—Ъх3—х (і-г-ал? —6а;’).
Нерѣдко нужно бываетъ выносить ыіѣ скобокъ общій множитель съ знакомъ—;
тогда непремѣнно должны перемѣниться знаки всѣхъ членовъ, остающихся вііу
трп скобокъ. Напримѣръ, во всѣхъ членахъ количества —<аЬ-+-а —а31>3
находится общій множитель «6; чтобы вынесть его за скобки сь знакомъ—,
раздѣлимъ это количество на —аЬ; получится’.
------—I—а&ч-аЧг; посему
-ьа’62—а363— -«6(1- -аб-ьа’б').
—2/и-ьЗта;——ш(2—За;).
— »?—2—— 1 (т-ь2)= —(т-ь2).
Примѣръ.
Примѣръ.
Въ послѣднемъ примѣрѣ вынесена за скобки —1 какъ общій множитель.
Надобно прпучпться непосредственно и скоро выносить общихъ множителей
внѣ скобокъ, не.прибѣгая къ извѣстнымъ пріемамъ дѣленія, что возможно, по- •
тому что въ членахъ алгебрическихъ количествъ общіе множители очевидны, и
отдѣленіе пхъ не составляетъ никакой трудности
38. Мы примѣнимъ это обстоятельство къ дѣленію такихъ многочленовъ, ко-
торые, бывъ расположены по унывающимъ степенямъ какой угодно буквы, содер-
жатъ равныя степени этой буквы въ нѣсколькихъ членахъ. Здѣсь необходимо
нужно во всѣхъ членахъ дѣлимаго и дѣлителя, имѣющихъ юдііу и ту же степень
этой буквы, вывесть ее за скобки въ видѣ множителя, и потомъ производить
дѣленіе по общему правилу (ЗС), считая каждую алгебрическую сумму чле-
новъ въ скобкахъ за коеФиціепть предъ тою буквою.
Примѣръ. — Раздѣлить
12а362—27а3с’-ь2а’6іс-+-За26с’- 6а6‘с-ь9а6с’—6’с’
па 2а26-ьЗа$с—6с.
Расположивъ дѣлимое и дѣлитель по степенямъ буквы а, я замѣчаю, что сте-
пей» «’, а2, а, находятся въ нѣсколькихъ членахъ того и другаго; поточу вы-
ношу эти степени внѣ скобокъ, а именно.
(426’—27с’)а’-ь(262сч-36с’)а2—(66-’с-96с1)а—6Ѵ,
(26-г-3с)а°—6с.
ІЗ
Для сбереженія мѣста ори дѣленіи, пишется, вмѣсто каждой пары скобокъ,
одна вертикальная черта; съ лѣвой стороны ея ставятся члены, бывшіе въ скоб-
кахъ, одинъ надъ другимъ, а съ правой стороны — общій ихъ множитель:
Дѣлимое.
Дѣлитель.
126’ а3-ь26’с а8—66’с а—6’с’ (26-+-3с)а’—6с
—27с’ -+-36с’ н-Эбс® (66—9с)а-ьйс
—126’ а3-ь66’с а і Аі
-+-27с’ —96с’
Остатокъ )-ь26’с а’—6’с’
| -ьЗбс8 - • .11
—26’с а2-+-6'с’
—36с’
О
Дѣлю (126’—27с’)а’ па (26-ьЗс)а8, и нахожу частное (66—9с)а.
Помножаю это частное па дѣлитель и вычитаю изъ дѣлимаго. Остатокъ
(26’сч-36с’)а8—6’с’ дѣлю также на (2д-ьЗс)а2, и нахожу частное Ьс. Помно-
жаю дѣлитель па Ьс, и произведеніе вычитаю изъ дѣлимаго. Въ остаткѣ 'мулы
едѣдовательпо полное частное —(66—9с)а-+-6с.
Примѣръ. Раздѣлить
10сг*-+-5а®6- -1 оас+ЗаЬ3— УаЬс— 56'с-Ы 5йс*
на 5а8-ьЗа6 —56с.
Частное получится 2а-і-6—Зс.
Примѣръ. Раздѣлить
6а’6-ь11а6с—За’с—4а6®—66®с на 2а6-+-36с—ас.
Частное получится За—26,
39. Независимо отъ коефиціептоьъ и знаковъ предъ ними, дѣленіе безъ
остатка (нацѣло) одного количества на другое невозможно 1) одночленнаго ко-
личества на двучленное и многочленное вообще; 2) когда дѣлимое количество
меньшей степени относительно дѣлителя; 3) когда дѣлитель содержитъ хотя одну
букву, которой нѣтъ въ дѣлимомъ; 4) когда члены дѣлимаго однородны между
собою, а члены дѣлителя разнородны; 5) если хотя одна 5} ква дѣлимаго будетъ
иеньшей степени относительно той же буквы въ дѣлителѣ; 6) если первый членъ
дѣлимаго, или первый членъ какого либо остатка, не будетъ дѣлиться на нерзыйі
членъ дѣлителя; и 7) если первый членъ дѣлимаго, иля какого ппбудь остатка,
будетъ собсгвсшо одночленомъ, а первый членъ дѣіителя будетъ двойнымъ (въ
видѣ бинома), на примѣръ: дѣлимое яж’ч-б.г’н-сж-ыс,
дѣлитель (а-і-Ь)х’-+~Ьх-+-с.
24
Для алгебрическихъ дѣйствій гораздо полезнѣе знать случаи дѣлимости однихъ
количествъ на другія, и обстоятельства, при которыхъ они имѣютъ мѣсто; но
здѣсь нельзя говорить объ этомъ подробно, а между тѣмъ общія начала дѣлимо-
сти чиселъ знать необходимо нужно.
О ДѢЛИМОСТИ ЧИСЕЛЪ.
<О. Изъ Ариѳметики извѣстно, что всякое число называется кратнымъ
другаго, если оно можетъ на него дѣлиться безъ остатка. Наприм. 21, которое
равно 3X7, есть кратное трехъ и семи.
ЛЯ. Число называется первымъ, если оно можетъ дѣлиться только само на
себя и на единицу. Таковы числа: 1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,.
Два числа называются первыми между собою, если имѣютъ только еди-
ницу общимъ дѣлителемъ. Наприм. числа 12 и 35 суть первыя между собсю,
потому что
12=2. 2. 3. 1,
35=5. 7. 1,
имѣютъ общимъ множителемъ 1 -цу.
Такого же рода бываютъ и количества алгебрическія.
Количество также называется кратнымъ другаго, если оно дѣлится па это
второе безъ остатка. Наприм. 6асбч-11абс—За’с—4аб*—бб’с, которое равно
(2абч-3бс—ас)(3а—26), есть кратное двучлена За—2Ь. Количество назы-
вается первымъ, если оно дѣлится только на себя и на единицу. Два количе-
ства называются первыми между собою, если имѣютъ только единицу общимъ
множителемъ.
ЛЭ. О дѣлимости чиселъ въ Алгебрѣ заключаютъ по тѣмъ же началамъ, ка-
кія излагаются въ Ариѳметикѣ. Мы здѣсь повторимъ ихъ въ общихъ выра-
женіяхъ.
1) Если нѣсколько чиселъ А, В, С,... имѣютъ общій множитель И, то
и алгебрическая сумма ихъ имѣетъ тотъ же множитель.
Положимъ, что, отъ раздѣленія А, В, С,.... на Б, произойдутъ частныя
у, (/, у",-.-, такъ что
А=</І), В=9'В, С;—7'1),....; то сумма
Ач-Вч-Сч-... =(уч-у/ч-д'"ч-.. ,
очевидно, имѣетъ тотъ же множитель 1).
2) Ежели сумма или разность двухъ чиселъ и одно изъ нихъ дѣлятся
на <1 безъ остатка, то и другое число раздѣлится на <1. — Пусть сумма
А±В=«ий дѣлится на Л, 4
и В=нсІ » » ;
25
къ этой суммѣ придадимъ :рВ=::4=пй; получится:
А— тік± пй=\т^п)й.
Откуда видно, что А есть кратное гі.
3) Произведеніе нѣсколькихъ чиселъ АВС дѣлится на В белъ остат-
ка, если хотя одно илъ нихъ, наприм. А, дѣлится на О.
Пусть ^-=9, или А—9В, тс произведеніе
АВС=дВВС
очевидно раздѣлится на В. -
Слѣдствія.—Изъ 2) и 3) заключаемъ: а) если дѣлимое А и дѣлитель В
дѣлятся па какое нибудь число И нацѣло, то и остатокъ г также раздѣлится на
О. Въ самомъ дѣлѣ, положимъ, что А—тВ, В=пВ, и что, отъ раздѣленія А
на В, получится частное д, и остатокъ г; то
Д—дВ-+-г, или тВ^г^.пВч-г;
а поелику А=эиВ и В=пВ дѣлятся на И, то, по 2), необходимо раздѣ-
лится па 1) и остатокъ г.
Ь) Обратно: если дѣлитель В и остатокъ г содержатъ въ себѣ общій мно-
житель В, то и дѣлимое А будетъ содержать въ себѣ тотъ же множитель В.
Это очевидно.
с) Но если дѣлимое А и дѣлитель В суть первые между собою, то дѣли-
тель и остатокъ тоже будутъ между собою первыми. Ибо если между А и В
пѣтъ общаго множителя, кромѣ 1 -цы, то не будетъ его и въ послѣднемъ членѣ г
равенства А—дВч-г.
Въ этомъ случаѣ, отъ раздѣленія дѣлителя В на первый остатокъ г, полу-
чится второй остатокъ г', который будетъ первымъ съ г; отъ раздѣленія перваго
остатка г на второй г', получится третій остатокъ г", который также будетъ
первымъ съ г'. Продолжая такимъ образомъ, мы получимъ рядъ остатковъ
которые будутъ всѣ между собою первые, и постепенно уменьшающіеся; изъ
нихъ послѣдній не уничтожающійся остатокъ будетъ=1.
Пусть д1, 9", д'", д"",.... суть частныя отъ послѣдовательныхъ дѣленій В
па г, г па /, г1 па г", г" на г'"...., такъ что
В_—д’г-л-г',
г=д"г'ч-г",
гІ=дтгИ-+-гт,
гп=дтгіи^_гтг и проч_
Положимъ, что гп"=о, стало-быть, дѣленіе кончено, и г"—д""т"1 или
т~-ц-і=.д”", то необходимо иначе вышло бы, что г" дѣлится безъ остатка
иа число А какъ г"'дѣлитъ само себя и г" нацѣло, то оно раздѣлило
26
бы и / нацѣло (въ предпослѣднемъ равенствѣ), чему быть нельзя, потому что
дѣлимое г' и остатокъ г"' суть первые между собою. II такъ, послѣдній не
уничтожаювйііся остатокъ /"=4.
4) Если какое нибудъ число В дѣлитъ нацѣло произведеніе АВ
двухъ чиселъ А и В, и есть первое съ однимъ изъ нихъ, накрим. съ А,
то оно непремѣнно раздѣлитъ нацѣло другое число В.
Для доказательства, будемъ дѣлить А на 1), потомъ дѣлителя В на первый
остатокъ, первый остатокъ па второй, второй на третій и т. д., пока въ остаткѣ
получится І-ца; при семъ назовемъ у, у','у", у’",.... частныя отъ этихъ дѣ-
леній, и соотвѣтственные остатки г, г', г", г’",... первый, второй, третій......;
то получится рядъ равенствъ:
А=дВ-ы
В=у,г-+-г/,
г=с/'гІч-^,і
г,—у'"іі'-і-г"', и проч
Пусть /"=1; это будетъ послѣдній неуничтожающійся остатокъ. Всѣ этп
равенства помножимъ теперь па второе данное число В:
-<11і «<т я <
Поелику АВ,
раздѣлится на В,
1) АВ: _д.ВВч-Зг.
2) Вгч-Вг',
3) Вп=д'/.Вг,-+-Вг",
4) В/=д'".Вг"-і-В.1.
въ 1), дѣлится на В по положенію, д.ВВ также, то и Вг
ВВ, во 2), я д'.Вг дѣлятся на В, то и членъ Вг' раздѣ-
лится; въ 3) Вг и д .Вг дѣлятся па В, слѣдовательно и Вг"; наконецъ, Вг' в
у"'.^'1 дѣлятся на В, то н В раздѣлится на В. Это послѣднее и доказать
было нужно.
Примѣръ: Произведеніе 50X78=31/00 дѣлится на 13 и даетъ част-
ное 300; множитель 50 и 43 суть первые между собою; слѣдовательно 78 лѣ-
чится па 13. П въ саномъ дѣлѣ,
78:13=6.
Слѣдствіе !—е. Всякое число В, первое съ каждымъ множителемъ произ-
веденія АВС, есть первое л съ самимъ этимъ прозведеніемъ. Ибо, если бы оно
могло раздѣлить АВС безъ остатка, то необходимо раздѣлило бы одинъ изъ еро
множителей, что невозможно. Такъ 12X13=156; число 5 есть первое съ
42 и 13; оно первое н съ произведеніемъ 156.
Слѣдствіе 2-е. Всякое число В первое съ а есть также первое и совсѣм»
его степенями а2, а3, а*,.а”.
Слѣдствіе 3-е. Если числа а, 6, суть первыя между собою, то и степени
ихъ а’, Ь\ а’, Ь'Л,.... суть числа между собою первыя. Ибо, если бы пашеіса
— 27
множитель, способный раздѣлить а8, 63 безъ остатка, то онъ раздѣлилъ бы
также а и 6, что невозможно.
5) Псиное число А, которое дѣлится на какія нибудь числа Г), В'.
первыя межиу собою, раздѣлится и на ихъ произведеніе Бр7.
п А А ,
Положимъ, что - ~у, —=ц.
Изъ перваго имѣемъ А=<;В; подставимъ это во второе, получится:
А 7 О .
в,—-^=7—Чѣлому;
по В, IУ, первыя между собою, слѣдовательно будетъ
Ч А
о/ = інр = Цѣлому
6) Всякое произведеніе И =аЬсд. состоящее только изъ первыхъ
чиселъ а, 6, с, (I,..., какъ множителей, не можетъ быть выражено про-
изведеніе иъ а/ЗуЗ,..., другихъ также простыхъ чиселъ а, у, 8,......
Пусть а/)сс1....=а/ЗуЗ....
Въ слѣдствіе сего равенства, множитель а, долженъ дѣлить 4^ одинъ изъ
множителей произведенія аЬсЛ....; а какъ всѣ этн множители суть первые, то
это возможно лишь тогда, когда одинъ изъ пихь будетъ ~а. Пусть «=«.
Исключивъ этихъ равныхъ множителей, останется равенство
ЬсЛ....=/Зуб....-
въ немъ /? долженъ быть также равенъ Ь, с, либо й..., и т. а. Пзъ этого
питію, что множители двухъ такихъ произведеніи должны быть равны каждый
каждому. Слѣдовательно число М только одинакимъ образомъ можетъ быть раз-
ложено іы простыхъ своихъ множителей.
Мы не будемъ говорить здѣсь о частныхъ случаяхъ дѣлимости чиселъ на 2,
3, 4, 5, 7, 9, II ....; объ этомъ достаточно излагается въ, курсахъ обыкно-
венной Арпометяки но обратимъ вниманіе на дѣлимость нѣкоторыхъ частныхъ
количествъ, весьма часто встрѣчающихся въ алгебрическихъ дѣйствіяхъ.
ДѢЛИМОСТЬ СТЕПЕНЕЙ И ДВУЧЛЕНОВЪ.
43. При раздѣленіи многочленовъ па одночлены, тотчасъ бываетъ видно,
можетъ ли быть произведено это дѣленіе точнымъ образомъ, пли нѣтъ; по этого
нельзя напередъ угадывать ври дѣленіи многочлена на многочленъ. Есть однакоже
случаи явной дѣлимости количествъ, которыя нужно знать учащимся.
1) Всякая степень дѣлится безъ остатка на ея корень.— Сюда о сно-
ся гея простѣйшіе, намъ извѣстные случаи:
(а*ч~ 2а Іг-і-Ь*}: (а -+-Ь)—(« ч-6) 8: (а -і-Ь)=а ч-б;
(а8—2а6ч 68):(а—6)—(а—6/: (о—6}_ _а—Ь
(ач-6)“: (ач-6)—(«ч-6 у-1.
28
2) Разность одинакихъ степеней двухъ количествъ дѣлится безъ
остатка на разность ихъ корней. Наприм.
а! —Ьг-. а—б=(ач-б) (а—б) : (а—Ь ]==а-+-Ь;
а’—б’:а—Ь—а’н- аЬ~г-Ьг;
а*—Ь*'.а—б=а3-+-а’бч~ аб’-і-б8;
а5—б5: а—Ь=а4-г-а3Ь-г-а*Ьг-г-аб3-г-Ь*;
ат—Ьт :а—Ь=ап~ *-ьа”—Іб-р-а"‘-3бЧ-... .-ьб”—
Во всѣхъ этихъ случаяхъ, частное имѣетъ столько членовъ, сколько
единицъ въ показателѣ т дѣлимаго.
Нельзя здѣсь не замѣтить особеннаго, весьма простаго порядка, по которому
происходятъ члены частнаго одинъ послѣ другаго. Однообразное ихъ происхожденіе
такъ явно, что, нашедши два или три такихъ члена, можно по одной аналогіи смѣло
писать прочіе члены, уменьшая показатель буквы а, и увеличивая показатель буквы
Ь единицею. Этотъ порядокъ называется закономъ происхожденія членовъ.
3) Разность равныхъ четныхъ степеней двухъ колгічествъ дѣлится
безъ остатка на сумму ихъ корней.
а*—Ьі:а-+-б=(а-+-Ъ)(а—Ь):ач-Ь=а—б;
а*—Ь*: а-і-б=а3—а'Ь-г-аЬ*— б3
—б”п:а-р-б=а”"_1—а”п_^б-^-а”п_8б^—б”"_‘;
ас —б’=(а3)*—(б*)1 дѣлится на а8ч-б*;
а”"—Ь,-п дѣлится ат-^бп.
4) Сумма двухъ равныхъ нечетныхъ степеней дѣлится безъ остат-
ка на сумму ихъ корней.
а-г-Ь -.а-г-іі—~1;
а!-г~Ь3:ач-Ь=аг— аб-л-Ь';
аъ-і-Ьъ: ач-б=а4—а’бч-а’б’—а б8-і-б4;
Отсюда видно также, что раздѣлятся безъ остатка:
а’-+-б8 на а’ч-б; ибо а6ч-б8=і(а’)8-+-б8;
а10-ьб3 на а’-ьб;
а’ч-б6 на а’-ьб’; и проч.
АЛ. Всѣ эти случаи дѣлимости очень часто употребляются для разложенія
двучленовъ и даже иногда многочленовъ на ихъ множителей.
Такъ: а1—б’=(а-ьб)(а—б),
а3 —б3 =(а—б)(а*ч-«б-ьб’),
а4 —б4 =(а—б) (а’-д-а’бч-аб’-р-б3),
ат~ Ьт=(а—б)(а”'-1-р-а"-,б-р-а”—3б’-+-....-+-б’"“'),
а3 -ьб3 =(ач-б)(а’—нбч-б*), и проч.
29
Примѣры для разложенія многочленовъ на игъ множителей:
а) —7а4с-+-14а’бс—ІаЪ’с.
Здѣсь находимъ сперва —7а’с общимъ множителемъ, который и вынесемъ
внѣ скобокъ:
—7а’с(а’—2абч-6’).
Но а’—2а6-+-6’=(а—6)’, то
—7а‘с-і-і4а’6с—7а’б’с=^—7а’с(а—6)’
Ь) Возмемъ еще 24а5б’4-81а'б3;
вынесемъ внѣ скобокъ общій множитель ЗаЬг\ получится
МЬ^^аѢ^ЗаѢ^а^іЬ3).
Но, 8а’=(2а)’, 276’—(36)’; поэтому можно 8а’ч-27б’ разложить еще на
множителей, дѣля на 2а-ь-36:
8(Лі-276’:2ач36=:4.а’—бабн-96’.
Такимъ образомъ получаемъ
24аБб’4-8а'бБ=За’6’(2а-+-36) (4а’—6а6ч-9б*).
с) Иногда полезно брать члены съ общими множителями, по два, по три.
выносить этихъ множителей за скобки, и такимъ образомъ открывать двучлен-
ныхъ, трнчленныхъ,.... множителей даннаго многочлена.
Примѣръ. &у-і+-9уі^-і-2ру-і-3рх.
Здѣсь нѣтъ ни одного множителя, общаго всѣмъ членамъ, но есть множители
общіе членамъ первому и третьему, также второму и четвертому, а потому
испытаемъ отдѣлить ихъ:
2у(3у2-+-р)-+-32(3ух-ь-р).
Этимъ дѣйствіемъ тотчасъ обнаружился общій двучленный множитель Зуг-ь-р,
который вынесемъ за скобки; получится
(22,4-3^(32/^).
Примѣръ, а3—а3Ь-+-аЬг—Ь3~а3{а—6)ч~6’(а—б)—(а’4-б’)(а—Ъ).
Примѣръ. а5-ьа46-і-2а’6’ч~2а^’-і-а64-і-6'—
=а‘(ач~6)-і-2а’6,(а-і-6)ч~б*(а-+-6)=
=(а4-6)(а‘ч-2а’6’-ь6‘)=(а-ь6)(а’ч-6’)’.
Примѣръ. х3—3 аж’ч-З а*х—а3=х3—а3— 3 ах [х—а)=
=(х,ч~ах-р-аі) (х—а)—Зах[х—а )=
—(ж2—2аям-а’)(а: —а)=(х—а)’.
ОБЩІЙ НАИБОЛЬШІЙ ДѢЛИТЕЛЬ.
*
Д5. Общимъ наибольшимъ дѣлителемъ двухъ чиселъ называется произведе-
ніе, состоящее изъ множителей общихъ атимъ числамъ.
30
416. Въ одночленахъ этотъ наибольшій дѣлитель почти очевиденъ, и его ро-
зысканіс не составляетъ никакой трудности. Положимъ, что надобно найти та-
кой дѣлитель между 60а364с й п 14 НгіѴ.
Отыщемъ напередъ общій наибольшій дѣлитель между нредстоящимп 60 и
144: онъ будетъ 12. А послѣ того уже видно, что наименьшія данныя стсненп
с3, общихъ буквъ, суть общіе мпожнтслп обоихъ одночленовъ. Слѣдова-
тельно, искомый общій наибольшій дѣлитель, какъ произведеніе изъ всѣхъ об-
щихъ множителей, будетъ
12а'64с3.
413. Розысканіе общаго наибольшаго дѣлителя въ многоч.!енахъ гораздо
сложнѣе, и основывается на слѣдующихъ началахъ дѣлимости (45В, слѣдст ):
а) Если въ дѣлимомъ АП и дѣлителѣ ВП есть общій множитель П, то опь
находится и въ остаткѣ г, какой получится отъ раздѣленія АП па ВП; ибо
тогда
АП=</.ВПч-г, пли
А^.Вч-^,
гдѣ 7 частное; и очевидно, что ~ должно быть цѣлымъ количествомъ.
Если общій дѣлптель пахо/ится въ ВП п остаткѣ г, то онъ долженъ быть и
въ остаткѣ г', какой получится отъ раздѣленія ВП иа г, и т. д.
И обратно, если общій дѣлптель находится въ остаткѣ г и дѣлителѣ ВП, то
онъ находится и въ дѣлимомъ АП.
Ь) Сверхъ того, общій дѣлптель не перемѣнится, если одно лапное количество
АП помножить на количество М, первое со вторымъ ВП, или помножить ВП
на М первое съ АП. Отъ этого получатся АПМ, ВП; по, будемъ лп искать
общій наибольшій дѣлитель между АП и ВП, плп между Ѵ1УІ1) и ВО, опъ по-
лучится всё тотъ же I).
с) Общій наибольшій дѣлитель не перемѣнится, если раздѣлить АО на коли-
чество первое съ. ВП, или раздѣлить ВП па количество — положимъ В, первое
съ АП: тогда получатся АО и О вмѣсто АО и ВО, по общій наибольшій дѣ-
литель П останется тотъ же.
41». На этпхъ началахъ основано слѣдующее правило для розысками общаго
наибольшаго дѣлителя:
Надобно сперва вынесть за скобки множителей, общихъ всѣмъ членамъ одного
и общихъ всѣмъ членамъ другаго даннаго многочлена. Отдѣлить многочлены,
оставшіеся внутри скобокъ, и расположить ихъ но убывающимъ степенямъ одной
буквы. Принять за дѣлимое тотъ многочленъ, въ кодеромъ эта буква высшей
степени, и дѣлить его на другой многочленъ. Можетъ случиться, что первый
членъ дѣлимаго не будетъ дѣлиться на первый членъ дѣлителя; тогда надобно
I
31
помножить дѣлимое иа такое число или количество, первое съ дѣлителемъ, кото-
рое бы сдѣлало первый членъ дѣлимаго кратнымъ перваго члена дѣлителя, и
тогда дѣлить. Когда получится остатокъ низшей степени противъ дѣлителя, то,
исключивъ изъ пего множители общіе всѣмъ его членамъ, должно принять его
за дѣлитель, а прежній дѣлитель за дѣлимое, и производить дѣленіе. Отъ этого
получится второй остатокъ. На этотъ второй остатокъ надобно дѣлить первый,
и такъ далѣе продолжать, пока остатка совсѣмъ не будетъ. Тогда послѣдній
дѣлитель и будетъ общимъ дѣлателемъ двухъ данныхъ многочленовъ Га бывъ
помноженъ на произведеніе множителей, вынесенныхъ внѣ скобокъ, при самомъ
началѣ дѣйствія, составитъ общій наибольшій дѣіптель этихъ многочленовъ.
Если же получится остатокъ, пе содержащій главной буквы, по степенямъ кото-
рой были расположены многочлены, то эти многочлены пе имѣютъ общаго много-
членнаго дѣлителя. А если, сверхъ того, пе окажется и общихъ множителей
между числами и буквами, вынесенными внѣ скобокъ вначалѣ дѣйствія; то
многочлены не имѣютъ между собою никакого общаго множители, и суть нервые
между собою.
49. Руководствуясь этимъ правиломъ, поищемъ общій наибольшій дѣлитель
между
Юа’б*—26а26у-г-12аб2г/2, и
21аѴ—42а'Ь2уч-7абѴ—1462г/3.
Сперва вынесемъ за скобки множителей, общихъ всѣмъ членамъ перваго, и
всѣмъ членамъ втораго мпогочлена:
2аб2(5а’—1 Зау-ь-бу/'),
762(3а3— ба^-ьаг/"— 2г/3),
и возмемъ 5а2—13ау-і-6г/2
За3— 6а’г/-ь-аг/2—2/.
Расположивъ эти многочлены п>> уменьшающимся степенямъ буквы а, примемъ
За3—ба'у-ьаг/2—2</’ за дѣлимое, и 5а2—ІЗауч-ьу' за дѣлитель; а чтобы
дѣленіе было возможно безъ дробей, помножимъ дѣлимое на 5:
15а’— ЗОа’у-і-5аг/2—'Ог/3 5а5—ІЗау-і-б?/2
—15а’-+- 39а?</—18аг/’
За, 9у
9а~у— ІЗоу*—1 Оу3, помножимъ на 5:
4 5 а2 г/— 65ау2—50г/3, продолжаемъ дѣіить
—45а2уч-117аг/2—54г/3
52аг/2—104г/3, выключимъ 52 г/’:
52г/2(а—2у).
Примемъ теперь 5а2—13аг/ч-б.ѵ2 за дѣлимое, а Сокращенный остатокъ а—2г/
за дѣлитель-
32
5а’—ІЗауч-бу* а—2у
—5а’ч~10ау 5а—Зу
— Зауч-6у8
-і Зау—бу’
О
II такъ, а—2у есть общій наибольшій дѣлитель многочленовъ 5а’—ІЗауч-
ч-6у’ и За’—ба’уч-лу’—2у3. А раздѣливъ тотъ и другой на а—$>у, получимъ
5а’— 1 Зау-ьбу’—(5а—Зу) (а—2у),
За’— 6а’уч-ау’—2у’= (За’ч-у’) (а—2у).
Полные же данные многочлены получатся, помноживъ первый на 2а6’, а вто-
рой на 76’;
2а6’(5л—Зу) (а—2у)—2а(5а—Зу) (а—2у)6’,
76’(3а’-ьу’)(а—2у)=7(3а’ч-у2)(а—2у)6’.
Изъ этого видно, что общій наибольшій дѣлитель полныхъ данныхъ многочле-
новъ есть
(а—2у)6’.
Примѣръ для упражненія.—Многочлены
6ж’—а3—Нж’— 8аж,
іх*—а*-і~агхі —ІОаа;3,
имѣютъ общій наибольшій дѣлитель х*—2ах—аг.
Слѣдующій примѣръ открываетъ нѣкоторыя замѣчанія, служащія дополне-
ніемъ къ общему правилу. Предлагается найти общій наибольшій дѣлитель между
За’—іаЬ— 8ас—і-Ь*—8Ьс—Зс’, и
6а’ч-7а6—13асч-26’—96сч-5с’.
Расположимъ эти многочлены по убывающимъ степенямъ буквы а, и соеди-
нимъ въ одну сумму члены, содержащіе первую степень буквы а, а члены,
совсѣмъ ее не содержащіе, въ другую сумму, написавъ ту и другую вертикаль-
ными рядами (38):
ба’ч- 71 ач-2Ьг —13с —96с ч-5с’ За’—46 а—46’ —8с —86с —Зс’
ба’ч- 86 ач- 86’ 2
-ьібс ч-166с
ч- 6с’
ч-156 ач-106* |
-і- Зс ч- 7Ьс(56чч;)Зач-106’ч-76счч;’.
Ч- с’)
33
Получивши сстатокъ съ меньшею степенью буквы а относительно дѣ іителя,
надлежало бы теперь помножить весь дѣлитель на 56-ьс, и принять его за дѣ-
лимое. Но, здѣсь надобно еще увѣриться, не находится ли этотъ множитель
56-ы въ 10Л*ч~76с-ь-с’, чего нельзя знать, пе раздѣливъ это количество на
5б-ьг.
10ЬІч-76с-ьс* 56-ьс
Эбсч-с1
—ЪЬс—е
О
Чрезъ это дѣленіе находимъ, что 1065ч-76сн-е*=(56-і-с)(26н-с), и за-
ключаемъ, что остатокъ, выше найденный,
За(56ч-с)-ь106’-і-76с-ьс,=(56ч-с) (За-+-2б-ьс).
Общій наибольшій дѣлитель, если онъ находится, долженъ быть только въ
3«ч-26ч~с, потому что другой множитель 56-4-с не имѣетъ буквы а.
И такъ, станемъ дѣлить прежній дѣлитель на Зач-21>-+-с:
За2—46 а—462
—8с —86с
—Зс2
|3 а—і—2 6-^-с
а—(26-ьЗс)
—За2—26 а
-66 а—462
—9с —86с
—Зс2
=:—3а(26-+-3с)—462—86с—Зс2
-+-66 а-ь465
-+-9с -+-26с
-+-66с
-*-Зс2
О
Посему, За-+-26-ьс и есть искомый общій наибольшій дѣлитель.
АЛГЕБРИЧЕСКІЯ ДРОБИ.
50. Когда дѣленіе одного количества па другое бываетъ невозможно, тогда
это дѣйствіе только обозначается; ставить дълптеля подъ дѣлимымъ и проводятъ
между ними горизонтальную черту. Такія выраженія называются алгебрически-
„ тт 2д6» За2—6 т,
ми дробями. Наприм. -——• Въ нихъ дѣлимое называется числите-
1 вС’>(* 5с—і—ор
лемъ, а дѣлитель знаменателемъ дроби.
з
34
ЛЛ. Надъ алгебрическими дробями производятся всѣ тѣ же дѣйствія, что и
надъ дробями ариѳметическими, потому что ихъ г іавнѣЛлиія свойства тѣ же
самыя
Дробь увеличится, если увеличить ея числитель: но она уменьшится чрезъ
уменьшеніе числителя:
сч-П’ а
——>—, потому что дѣлимое ач-т> а.
а—т .а и
—-—потому что дѣлимое а—т <«.
Дробь уменьшится, если увеличить ея знаменатель; но она увеличится отъ
уменьшенія знаменателя:
а л ,
, потому что дѣлитель оч-с>о,
----> , --- — --- 6----С<6.
б—с ь9
Дробь не перемѣнитъ величины своей, если помножить, или раздѣ-
лить, ея числитель и знаменатель на о/Ліс и то же число.
- - а ,
Для доказательства, возмемъ дрооь у, и назовемъ буквою у частное, отъ раз-
дѣленія а па Ъ, тр есть:
с
і=9-
Дѣлимое а равно дѣлителю, помноженному па частное, то есть:
а~од.
Это равенство помнояснмъ на произвольное число п; будемъ имѣть:
ап~ Ьд.п—ЬцУ' </.
а что равенство раздѣлимъ па Ьп, и будетъ
ап а
Ьп~—Я—Ь'
Обратно:
Въ самокъ дѣлѣ,
а
(1 Пі
Т'
а Ь . , , „
положимъ т=1’ 0Т,;Уда ^~ут, о~(/т. Раздѣ-
лимъ одно равенство на другое:
а______________________________________дт
Ь '
,т . „ ат а
Но, пзъ предыдущаго свойства, знаемъ, что посему
6 у’ Ь
т
35
Эти два свойства служатъ для сокращенія дробей, и также для приведенія ихъ
къ общему знаменателю въ различныхъ дѣйствіяхъ
59. Сокращеніе дробей. — Сократить дробь значитъ привесть ее въ про-
стѣйшій видъ чрезъ исключеніе множителей общихъ ея числителю и знаменателю.
5Л. Въ ороби одночленной множители, общіе числителю и знаменателю,
очевидны; и потому приведеніе дроби въ простѣйшій видъ очень легко.
12а36’с ЗЛ.аЧ’с _________ 3
32ав67с3 8.4.а3а36’Ь3с.с 8а*63с’
Столь же легко сократить дробь, у которой одинъ числитель, или одинъ зна-
менатель, состоитъ изъ нѣсколькихъ членовъ: тогда общіе множители, если
они есть, должны быть въ каждомъ членѣ, безъ чею и сокращеніе пе возможно.
Ьа30в ______ Ьа3Ь3:2аЬ3 __________ За“6
Примѣръ. 4а3Ь3с-4-10ой* (4авЬ’‘с-+-10оЬв):2Ы«» 2а<м-ЗЬ3’
54. Дроби многочленами можно сокращать или чрезъ постепенное исклю-
ченіе множителей, общихъ числителю и знаменателю, пли посредствомъ общаго
наибольшаго дѣлителя.
Для постепеннаго сокращенія, надобно вынесть внѣ скобокъ множители общіе
всѣмъ членамъ числи геля, и общіе всѣмъ членамъ знаменателя,-и сдѣлать между
ними сокращеніе. Потомъ смотрѣть, оставшіеся многочлены не составляютъ ли
квадратовъ отъ суммы или разности двучленовъ, пе имѣютъ ли вида а3—Ьг,
а‘—А‘,.... а’-ъ-А8, а8ч-А8,....; и если это окажется, то разложить ихъ на мно-
жители (С4), и тогда сократить, буде можно.
п „ 1аа3— ЗОа36-і-ГЗ'іЬ“
Примѣръ Сократить -г.—
Отдѣлимъ множители общіе всѣмъ членамъ, и сдѣлаемъ между ними сокра-
щеніе:
1оаГав—2а6-і-63) В ,ав—ЗаІ-ьО3
24ав(а3—Ь3) Ча * а3—63 Г
Но, знаемъ, что а’—2«А-ьА8— (и—А/, а’—&*=(«-+-&)(«—А); то
5 .а2—2а6-ь(Л 5(а— Ь'р ____ 5(а—Ь)
8а \ а2—Ь~ ’ 8а(а-і-6)(а — Ь) 8а(ач-6)
Примѣръ. Сократить
Зйі5П-4-Згл2П
6ш3п2—бпт2’
Сперва находимъ
Згміл( т-і-1) пі (т-+-1)
вЛтв(тпв--1) 2п(«Гв- Г)'
А какъ т’—І=(т-ь1)(т—1), то
Примѣръ.
т (т -і-І) т
2п(пГ—I) 2п(т—1) ’
Xе—1 ___ (а:3нь 1 )(ж3—1)
Xя—а:3-і-я:в—1 а:3(а:2—1)-і-а:в—1
___(а:3-4-1)(а:3—1)____(а:—1 )(&’-) 1
(зЛч-ІДя2-!) (ж-|)(яч-1) —-г-ьГ
- 36 —
Примѣръ.
Примѣръ.
я:4—2л:3у-і-®8у8 я:8(я:8—Вя:у-і-у8)
®4—2я:8у8-і-1/4 (я:8—у8)8
х*(х—уР _______ х*
(я?ч-у)*(х—у)8 (ям-у)8 '
За3-ч-аЬ«—6д8Ь—263 За»(а—2Ь)-л-Ь8(д-2Ь)
<щ'_аЬ«_Д8а4і-+-2Ь» 9а(е—2Ь)-Ь‘(а-2Ь)
_(За8-ьЬ8)(а-26,
(«а4-Ь4)(а—26?
а ьоелпку 9а*—6*— (За’-+-^“)(За’—Ь'}, то
За8-+-Ь8__ 1
І9а< Ь4 — ЗаѴб8 ’
Въ этомъ пос іѣднемъ примѣрѣ употребленъ способъ отдѣленія общихъ мно-
жителей, показанный въ (44,3).
55. Самый общій способъ сокращенія дробей производится посредствомъ
общаго наибольшаго дѣлителя въ числителѣ и знаменателѣ данной дроби.
Дли этого падобно найти этотъ наибольшій дѣлитель, потопъ раздѣлить на вего
числитель е знаменатель данной дроби: она сразу получитъ простѣйшій видъ,
потому что исключатся всѣ множители общіе числителю и знаменателю.
Положимъ, что нужно сократить дробь:
С®5—а3—11 ах9—Яа*х
іх*—а’-і-а‘х‘—ІОах3
Расположимъ обѣ часта этой дроби по убываю.цимъ степенямъ бухвы х:
6х3—1Іая:8—Ва8®— а3
4х*—10аа:3-+-а8а:8—а4
и прш емъ знаменателп за дѣлимое, а числитель за дѣлитель. Но, чтобы первый
членъ 4-а* могъ безъ остатка раздѣлиться на ба3, помножимъ все дѣлимое па 3:
12ж*—30аа3ч- За’а*—За* ба3—Паа’—8а’а—а3
—12а*-4-22а'с3-+-16а*а*ч-2а3а 2а,_4°
—8аа3-+-19а’а’ч- 2а3а—За*, помножимъ на 3;
—24-аа‘Іч-57а’а’ч- 6а3а—9а*
4-24-аа3—44а’а’—32а3а—4-а*
теперь раздѣлимъ:
ІЗа’а’—26а3а—13а\ исключимъ 13а’;
а’— 2аа—а*.
ба*—Паа’—8а’а—а3 а’—2аа—а*
—6а3-4-12аа’ч-6ага ба-ьо
ахе—2а*%—а3
—ах^-г-Яа^х-і-а3
О
37
П такъ, а?—Чах—а* есть общій наибольшій дѣлитель данной дроби. Раздѣ-
ливъ на него ея числитель и знаменатель, получится простѣйшая дробь:
бх-і-а
4х3—2ах-л-а3 ’
56. Приведеніе дробей къ общему знаменателю. Для этого надобно *
каждую данную дробь помножить на произведеніе знаменателей всѣхъ прочихъ
дробей; отчего величины дробей не перемѣнится, но апамеьатели сдѣлаются рав-
ными. Положимъ, что надобно привесть кі общему знаменателю дроби:
а с е
7' а '7
По совершеніи дѣйствія, получатся дроби-
а.і/ с.й/ в.ЬН
77/ ’ 7/ ’ 77/ '
съ равными знаменателями.
&9. Часто бываетъ, что знаменатели данныхъ дробей имѣютъ общихъ мно-
жителей; тогда падобно стараться приводить дроби къ наименьшему общему
знаменателю. Для этого берутся высшія степени всѣхъ множителей въ знаме-
нателгхъ, составляется дзъ нихъ произведеніе, которое и будетъ искомымъ об-
щимъ знаменателемъ. Потомъ смотрятъ, какихъ множителей недостаетъ въ зна-
менателѣ первой дроби, необходимыхъ для составленія этого общаго знаменателя;
на тѣхъ множителей и помножаютъ обѣ части той дроби. Такимъ же образомъ
поступаютъ со второю, трстьею, и т. д. дробями; отчего всѣ онѣ получатъ общій
знаменатель самый меньшій Наприм. дроби:
За а/ ІЛ
Шс' ’ вь'с а ’ зьс® ’
имѣютъ общихъ множителей въ знаменателяхъ. Высшія степени множителей сихъ
/
знаменателей суть: 24, 3, 6'*, с3, <1. Общимъ знаменателемъ будетъ 12б'*с3гі.
Но, чтобы первая дробь получила этотъ знамена гель, надобно помножить обѣ ея
части на ЗІЛІ, во второй на 2с, въ третьей на 4б“с<і. Сдѣлавъ это, получатся
дроби съ общимъ знаменателемъ:
2/с 16Ь5сгіА
12д4сМ , 12Ь4с5€і 9 126*сМ ’
Приведеніе дробей къ общему знаменателю обыкновенно употребляется при
сравненія дробей, при ихъ сложеніи п вычитаніи.
58. Слозкеніе и вычитаніе дробей дѣлается такъ же, какъ и въ Ариѳме-
тикѣ. 1) Если дроби съ равными знаменателями, то слагаются (или вычитаются)
ихъ числители, а подъ суммою (ели разностью) пишется ихъ общій знамена гель»
Для объясненія возмемъ дроби:
а о с *
р> р*
<8
® __ & ____ I с »»
положимъ, что — =д, р—ч > р=ч 9 откуда
а—рц, Ь=рц', с=рц".
Сложимъ ати равенства:
а-і-Ь-і-с—р (уч- у'-л-у"),
и сумму раздѣлимъ на р, получи гея
ач-Л-і-с ... а Ь е
~дЧЧЧ-(/'=-Ч-1—.
р------------------------7 р р р
Если данныя дроби съ разными знаменателями, то сперва приводятся къ обще
му знаменателю, потомъ берется алгебрическая сумма числителей и дѣлится на
общій знаменатель,
гг а с е а.ЛС с.Ъ? е.Ь<1 аНГ-і-ЬсГ— Іхів
Примѣръ. р-^а-7= ъл( а!Г~Щ щ’
Цѣлое число а изобразить въ видѣ дроби съ знаменаніеіемъ Ь. — Для
итого надобно только помножить ато число а и раздѣлить па Ь:
а=^.
ь
59. Дробное число, состоящее изъ цѣлаго, совокупленнаго съ дробью
сложеніемъ или вычитаніемъ, обратить въ неправильную дробь.—Пусть
это число
ь
іп
Обратимъ цѣлое а въ дробь съ знаменателемъ т; потомъ сложимъ числителей,
и подъ алгебрическою суммою напишемъ ихъ общій знаменатель:
ат
а=—, слѣ ювател ыіо
ш ’
. Ь ат , Ь ат-+-Ь
а~ь =- -± ——;
ін т т т
' с8—і—1
Примѣръ. Сложить а—I съ въ одну дробь.
, сЧІ (а — I )(оч- 1)ч-г8ч-1 а8ч-с8
а---* Ч-----’-------------- - =-----—
ачЧ оч—1 ач-1
Ь3 а3
Примѣръ. аі-+-аЪ-і-Ь1-і-------- = —
1 Г , а—о а—Ь
п /-» /чі 18а-4-461 186*-8а’
Примѣръ. ^а-^^ЗЬ—^-)=---------------------— ч-------
_Зба»6ч-86чЧ54а68-13а’
18оЬ
,, і2а68ч-36с8\ /4а8Ь-ЗЬ8с,
_(2аЬ8чЗЬс8)(4ач-Ь)—(4а86-368с)(2Ь-с)
(2Ь—с)(4ач-Ь)
_2_12аЬс8ч-2аЬ5ч-6Ь5с-«-4а86с
8а6—4асч-268—Ьс
39
Примѣръ.
68—«с (а'-л-Ь*)
ач------------—-------—
л-і-с а—с
аъ—ас'-л-аЬ*—аас—/Лс-+-ас"—а’—лЬ8— а’с—Ь’с
«“—с8
(2а“с->-268с) 2с(а8-ь68)
—с8 ' с8—а8
60. Изъ неправильной дроби исключить цѣлое количество. — Это
возможно въ такой дроби, у которой числитель и знаменатель могутъ быть рас-
положены но степенямъ одной и той же буквы, и притомъ когда хотя одинъ пер-
вый членъ числителя можетъ точнымъ образомъ дѣлиться на первый членъ зна-
менателя. Тогда надобно въ самомъ дѣлѣ дѣлить числите ль на знаменателя, пока
получится остатокъ, котораго первый членъ не можетъ дѣлиться па первый
членъ дѣлителя. Тогда этотъ остатокъ надобно приписать къ частному, про-
весть подъ нимъ черту, и подписать дѣлителя.
Примѣръ. Исключить цѣлое изъ дроби
За:8-+-7л:—2
Раздѣливъ числитель на знаменатель, получаемъ
я?—Зх’ч-Тх—2 , 2ж-+-1
-т8—2а:-ьЗ а?8—2а>+-3
61. Для умноженія дроби на дробь, надобно взять произведеніе всѣхъ
числителей и раздѣлить на произведеніе знаменателей.
Положимъ, что даны дроби ~=т,~— п, м что требуется найти произведеніе
і/'а'
Взявъ равенства. а==.Ьт, с=Дп, перемножимъ между собою:
ас—6т. бп—Ьб.тп,
и раздѣлимъ на Ьд, получится
ас а . ,с
,^=:тп=-.У~-,
м ь а ’
что и слѣдовало доказать.
При помножевіп нѣсколькихъ дробей между собою надобно напередъ исклю-
чать множителей, общихъ произведенію числителей п произведенію знамена-
телей; отчего все дѣйствіе сократится, и найдется простѣйшій выводъ.
^7 2а8Ь ч х36с8 „ х8ст с8
Зс7П8/ч10ап8гч7«8Ь8 7атп8
Примѣръ. {I -1-V. 2^’ у 20Ь”+_*—
Примѣръ. 2йа;3п-1 і2а"+т __ 3„>. .X ,=20а-.х'-
Примѣръ. ш-І 1 и8_вЬ-і Ь8 *~Ь’- ' а-і-Ь ^т8—1
40
Въ этомъ примѣрѣ я замѣчаю напередъ, что
а*—(а—Ь),
а’ч- 6в=(«-4-6) («і—аб-+-А’),
т*—1 =(т-+-1)(т—1);
а сдѣлавъ подстановленіе, тотчасъ нахожу простѣйшій выводъ произведенія
а — Ь
(оч-6)(»в—1,
<*И, Для раздѣленія дроби на дробь надобно помножить дробь дѣлимі»
па обращенную дробь дѣлителя.
а с
Положимъ, что нужно раздѣлить ^—Р на & то есть, наѣти частное
а с р
Ь '4 Ц
Дѣлимое равно частному, номножендоад на дѣлитель; слѣдовательно
ь~ д^а'
„ - а
Это равенство помножимъ на дрооь —, получится
ву< Р\/С-Ѵ- ?- - • —•
Ьд 6 <Ь ’
чѣмъ и доказано правило дѣлена.
Если <1=1, то
’ о о ' 4 с
если 6=1,
то
а
Ьс’
й а&
Примѣръ.
Пргімѣръ.
Примѣръ.
а е
Т:~а—1
2йж3п—1 12ап+т 12«Ѣс*п
За’~- ‘ Зх’^і 36а®" ‘
4ап 27а:« 9а! _Л ,
-5— - : —=20аэж3.
Зх ап~~^ ба
іба8 , 20а3Ьа 15ав чх4аЬ-ьЗс» За^^ай-ьЗс?,
За8—ТЬ8 ’ 4аЬ-ьЗс8 Гі8—ТЬ гоа-1!8'”^?8'3<Г8—7Ь8,
Примѣръ. Сократить дробное выраженіе:
а'—Ъ*,
ЗЬ—а
аа(а8-і-ЬаХЬ-ь36)
__(аа—Ьа8-і-Ь8а— Ьа)(д°-ьаЬ -алч-Ь) , а*—Ь* а'—Ь*
4а“(а2ч-Ь’‘) 4ая
63. Въ заключеніе статьи о дробяхъ, разсмотримъ еще одно изъ ихъ
свойствъ.
Если къ числителю и знаменателю 'правильной дроби придать по~
ровну, то она увеличится, а если вычесть по-ровну, то уменьшится.
41
Дробь же непразіі іыіая, въ такихъ случаяхъ, получаетъ измѣненія совсѣмъ
противныя. •
Возмемъ дробь къ обѣимъ частямъ ея придадимъ с; получится По-
томъ раздѣлимъ въ самой вещи ач- с на Ьч-с, выйдетъ
яч-с а ,Ь—а,с ,,,
н^=б'+~(лТс)гГ.........
Очевидно, что эта дробь не равна
.И дроби пряви^ыищ знаменатель й>п, Ь—а=-ь; слѣдовательно будетъ
а .6—а \п . а
б ’’ 4-с 'Ь ' I)
У др.оби неправильной, Ь<а, Ь—«=—; отчего будетъ
о іа—Ъ і с _,а
Ь ' Ь—і—с / Ь ’
то есть, дробь сдѣлается менѣе. Обратное дѣйствіе очевидно само собою.
6*1. Помножимъ числитель и знаменатель дроби на произвольное цѣлое
число п\ величина ея неперсг'ѣнитсь, в будетъ потомъ внесемъ ап, оп,
вмѣсто а, Ь, въ формулу («); получится выводъ совсѣмъ другой:
япч-я ап п(Ь — а) с а (Ь—а) с
——- — —|— ----- • — |—------- -
6пч~с Ьп Ьп-і-с Ьп Ь Ьпч-с Ь
изъ котораго видно, что въ правильной дроби
япч-с яч-с /6—а \с іЬ—а.с
----<5-----, потому ЧТО разность (т-) — <(-—) —.
Ьпч-с ^бч-с і 1 'Ьпч-с'Ь ^'Ьч-с/Ь
Если п взять очень вдлцко, то разность сдѣлается очень мала, и может ь
быть сдѣлана менѣе всякой даішоц величины. Нацрем.
для а=2, Ь~3., с=10, п=і, будетъ
2ч-і0_ 2 іо
Зч 10 3 "*~39‘
. ЛАЛ „ 2010 2 1
для «=1000, найдется—= -+-з5з,
.ллллл 20О010 2 1
для «=100000, ......... И такъ далѣе.
Сдѣдовательно, если п будетъ безконечно великѣ, то разность (’ ' полу-
чится безконечно малою, т. е совсѣмъ уничтожится, и тогда останется только
- 2 _
данная дрооь -. Это значитъ, что конечная величина с предъ безконечною ап,
и также Ьп, совсѣмъ исчезнетъ, потому что не сдѣлаетъ вь пей ни какой
перемѣны.
42
ГЛАВА ВТОРАЯ
УРАВНЕНІЯ.
Общія понятія и опредѣленія.
СіЯ. Два неравныя, впрочемъ однородныя, количества можно всегда при
вести во взаимное равенство, если одно изъ нихъ, или оба вмѣстѣ, измѣнить
чрезъ сложеніе, вычитаніе, умноженіе, дѣленіе, или возвышеніе въ степень, и
нроч. посредствомъ вводнаго третьяго количества. Величина этого послѣдняго
часто бываетъ не очевидна, и потому неизвѣстна, однако же алгебрически
возможна.
Такъ, напримѣръ, числа 3 и 9 неравны; но ихъ можно привесть въ ра-
венство:
а) Чрезъ сложеніе меньшаго числа 3 съ нѣкоторымъ числомъ х, чтобы вышло
3-г х—9; гдѣ, очевидно, ж=б.
Ь) Чрезъ умноженіе: Зж_9; гдѣ х=3.
с) Чрезъ возвышеніе въ степень: Зж=9. Здѣсь х=2, потому что 3’=9.
Число 30 сдѣлается равно 10, чрезъ вычитаніе: 30—ж=20, гдѣ .г=20;
чрезъ дѣленіе: ^=10, взявъ х—3.
<»<». Уравненіемъ называется всякое алгебрическое выраженіе, въ которомъ
символически означены всѣ дѣйствія, посредствомъ коихъ требуется привесть
одни данныя количества въ равенство съ другими посредствомъ одного, по
крайней мѣрѣ, неизвѣстнаго. Оно, въ то же время, заключаетъ въ себѣ и всѣ
условія, показывающія намъ, какъ надобно преобразовать его чтобы найти это
неизвѣстное, выразить оное въ количествахъ данныхъ.
Такимъ образомъ: 30—х=20, есть уравненіе, показывающее., что надобно
число 30 превратить въ 20, чрезъ вычитаніе третьяго неизвѣстнаго х;
30
——10, 3^=9, суть уравненія: въ первомъ требуется 30 превратить въ 10
посредствомъ дѣленія, а во второмъ —какъ получить число 9 пзъ 3 чрезъ воз-
вышеніе въ степень.
Вообще же, всякія два количества, паприм. а-л-Ь—с, іі-л-е, могутъ быть
приводимы въ равенство посредствомъ неизвѣстнаго х, различными способами,
какъ то:
а-з-Ьх—-=зі-л-ех, или
X 9
Ь , е
о.гі- ——с=ал и проч.
43
вЗ. Количества, раздѣленныя знакомъ =, называются частями уравне-
нія, Каждая часть можетъ состоять изъ одного или нѣсколькихъ членовъ, сое-
диненныхъ между собою знаками -+- и — Неизвѣстная величина х ъожетъ
оыіь въ одной части уравненія, иля въ обѣихъ, и притомъ въ нѣкоторыхъ чле
нахъ, или во всѣхъ. Наприм.
2-+-Зх=17—5х,
Ь , е •
ахч——ах--------
X X*
Извѣстный или данныя количества въ уравненіяхъ означаются цифрами или
буквами а, Ь, с,... т, п, р,. .; а неизвѣстныя количества — послѣдними бук-
вами французскаго алфавита.
в8. Уравненія бываютъ численныя и буквенныя. Въ первыхъ всѣ из-
вѣстныя величины означены цифрами, а во вторыхъ буквами. Наприм.
2ч-3о:=43—5х, уравненіе численное;
ач-Ьх— с —бх, уравненіе буквенное.
Уравненіе, въ которомъ неизвѣстная находится въ показателѣ степени, на-
зывается неопредѣленно-степеннымъ. Наприм. <1^=6.
СО. Уравненія различаются по степени неизвѣстной, въ нихь находящейся.
Онѣ бываютъ первой степени, второй степени, третьей,...., и вообще
п-ой степени, когда неизвѣстная х, не находясь нигдѣ въ знаменателѣ, будетъ
имѣть высшею степенью первую, вторую, третью, и іи, вообще, л-'°, На-
примѣръ
ач-і>х~.с—бх, уравненіе первой степени;
ах‘ ч-Ьх~с, уравненіе второй степени;
аа;”-+-б«п_1-г-сл:п-®-т-.-ьз=0 уравненіе и оі| степени.
Уравненія всякихъ степеней различаются еще по числу неизвѣстныхъ: онѣ
бываютъ съ одною неизвѣстною, иногда съ двумя, тремя, и т. д. Наприм.
ач-Ъх-гіС—бх, уравненіе съ одною неизвѣстною;
ахч-Ьу=с, уравненіе съ двумя неизвѣстными х, у.
30. Рѣшить уравненіе значитъ найти всѣ величины его неизвѣстной х,
которыя удовлетворяютъ ему, то есть, будучи подставлены въ уравненіе па мѣсто
х, дѣлаютъ первую часть его тожественно равною второй. Оттого неизвѣстная
въ уравненіи называется величиною искомою, корнемъ уравненія.
Число рѣшеній, то есть, число корней въ нѣкоторыхъ уравненіяхъ бываетъ
опредѣленное, наприм. одно, два, три...; но есть уравненія, допускающія безко
ночное число рѣшеній.
44
I. УРАВНЕНІЕ ПЕРВОЙ СТЕПЕНИ СЪ ОДНОЮ НЕИЗВѢСТНОЮ.
71. Для .разрѣшенія уравненія первой степени съ одною неизвѣстной?, на-
добно преобразовать его такъ, чтобы въ первой его части осталась одна эта
неизвѣстная съ знакомъ ч~, а всѣ извѣстныя величины перенесены въ другую
часть уравненія, безъ нарушенія равенства между этими частями,
7Я. Возмемъ сперва самыя простыя уравненія:
а?-+-а_б, х— с=.Л, рх—ц, —/»,
въ которыхъ неизвѣстная х находится въ первой части и соединена съ одною
пзъ данныхъ посредствомъ сложенія, вычитанія, умноженія и дѣленія.
Чтобъ найти неизвѣстную х изъ уравненій х-ь-а=Ь, х—х=иІ, надобно
перепости нзвѣстиъи члены -+-а, —с, соединенные съ нею сложеніемъ и
вычитаніемъ, во вторую чаешь уравненія съ противнымъ знакомъ, п
будетъ:
х—Л-ггг-ч
Въ сачоцт. дѣлѣ, равенство частей перва-гг уравненія ве излѣщітея, если от-
пять отъ обѣихъ его частей членъ а, то есть, взять
ач-а—а~Ь—а.
Но а—»д=0; посему х=1>—а .
Равенство также сохранятся, если къ обѣимъ частямъ втораго уравненія прі
дадимъ членъ ч- с:
с _-е.
Цо —сч-с=0; слѣдовательно, х=іі+-с.
Такимъ образомъ, въ первомъ уравненіи, членъ -+-а перешелъ во "горую
часть съ знакомъ —; а во вторимъ уравненіи членъ —с перешелъ во вто-
рую часть его со знакомъ -ь.
Въ третьемъ уравненіи ра—ц неизвѣстная х освободится отъ множителя
р чрезъ раздѣленіе обѣихъ частей на р, отчего иавенстве ге перемѣнится-.
<7 д
—_______, или х=- .
Ѵ Р Р
Въ четвертомъ уравненіи неизвѣстная х освободится отъ дѣлителя
р чрезъ помноженіе обѣихъ частей па р; отчего равенство не нарушится:
- .р=}ір, или х=1ір.
Если неизвѣстная по (учится съ злакомъ го надобно первмяіілть знаки
во всѣхт членахъ уравнсіія, чтобъ получить х съ знакомъ ч- Такъ, напрпм.,
изъ уравненія
а—х=Ь, находимъ
—хг^Ь—а.
45
Но чтобы неизвѣстная х сдѣлалась положительною, помножимъ обѣ части
сравненія на —1:
(—х}(—іу_=(Ь—а)(—1); тогда получимъ
~а—Ь,
уравненіе то же, только перемѣнились знаки предъ всѣми его членами
33. Иногда неизвѣстная х найдется скорѣе, если оставимъ ее во второй
части уравненія, или даже перенесемъ ее во вторую часть, а всѣ извѣстныя —
въ первую часть его. Напримѣръ:
а=х—Ь.
Здѣсь, конечно, лучше перенести •—о въ первую часть уравненія съ про-
тивнымъ знакомъ, и будетъ
ач-б-
а это все то же, что х~а-+-Ь.
Примѣръ. р—х=д-і-'2х.
Здѣсь лучше перенести х во вторую часть, а д въ первую часть, и будетъ
р—д=х-+-2х=- Зх;
‘ а это всё равно, что Зх—р—д.
Потомъ, раздѣливъ обѣ части на 3, получимъ
За; р—о р—а
т==_, ИЛИа=—
Послѣ этихъ частныхъ и простѣйшихъ случаевъ рѣшенія уравненій первой
степени съ одною неизвѣстною, не трудно уже лереіітп къ общему правилу рѣ-
шенія сихъ уравненій, сколь бы ни были онѣ сложны.
34. Общее правило.—1) Надобно сперва освободить данное уравненіе отъ
дробей, привесть всѣ его члены къ общему знаменателю, и этотъ знаменатель
отбросить. 2) Потомъ перенесть всѣ извѣстные члены въ первую часть урав-
ненія съ противными знаками, а всѣ неизвѣстные во вторую, либо наоборотъ.
3)* Сдѣлать сокращеніе, соединивъ извѣстные члены въ одинъ, и также всѣ
члены неизвѣстные въ одинъ членъ: тогда получится уравненіе, вида ах=б.
4) Освооодить неизвѣстное х оть цредстоящиго мпожителі, раздѣливъ на него
обѣ части уравненія. Послѣ всего этого, неизвѣстная х опредѣлится совершенно,
выразится во всѣхъ количествахъ данныхъ.
Примѣръ. Разрѣшить уравненіе
4 2
, ~^х—3=5-+-3-я:.
о 3
Приведемъ всѣ члены къ общему знаменателю:
12а;—4 В 7Вн-10а:
іа ів
46
Отпросимъ общій знаменатель; потому что двѣ равныя дроби, съ равными
знаменателями, должны имѣть равныхъ числителей:
12 а?—45=75ч- 10а:.
Перенесемъ неизвѣстные члены въ нерву ю часть уравненія съ противными
знаками, а извѣстные во вторую:
12.г—І0а=75ч-45,
а, по сокращеніи, будетъ
2.г=120.
Наконецъ, освободимъ невзвѣсгное х отъ множителя 2, раздѣливъ обѣ части
уравненія на 2, и получится
=60.
Такова величина неизвѣстной.
35. Повѣрка. — Для избѣжанія погрѣшностей, надобно рѣшеніе каждаго
уравненія повѣрять, а именно: подставить найденную величину въ данное урав-
неніе вмѣсто неизвѣстной х. Если рѣшеніе вѣрно, то первая часть должна выитп
тожественно равною второй.—Такъ мы имѣли уравненіе
іх 2
—3=э-і-^х, и нашли а?=60,
подставимъ 60 на мѣсто х, получится
4-60—3=5-4-“-60, или
М2—3=5-ь2.2О.
45=45.
Отсюда заключаемъ, что рѣшеніе было сдѣлано вѣрно.
Примѣръ. Рѣшить уравненіе:
х—2рх-ѣ‘ідг~3р!>д,‘-—р*х.
Здѣсь пѣтъ дробей; а потому перенесемъ тотчасъ члены съ неизвѣстною х
въ первую часть уравненія, а члены извѣстные во вторую часть съ противными
знаками:
х— 2рх-ѣргх=3ріді—Зд‘.
Вынесемъ общихъ множителей х п Здг за скобки;
.%-( I—2/>ч-р8)=Зд1(р8—1).
Раздѣлимъ обѣ части на многочленъ 1—2рч-р2, помножающій неизвѣстную
х, получится
... Ѵ(р2-‘) _ з<гір -О
1—2/>-г-₽2 (р— I)2 ’
ѵ___Зд2(р~ѣі)
~ Р-* '
Примѣръ. Рѣшить уравненіе:
। (Зяч-а)іа
іх—іі ЪЬ—а
47
Приведемъ сперва къ общему знаменателю, и отбросимъ его:
20Ьх—5Ьг—15Ьх—5аЬ—Іахч-аЬч-Захч-(Г=16ах‘—ІаЬ
Нерепесемъ всѣ неизвѣстные члены въ нервую часть уравненія а всѣ из-
вѣстные во вторую, и сократимъ, найдется:
5Ьх—17ах=5Ь*—а'.
Вынесемъ общій множитель х ннѣ скобокъ:
(56—17п^=56?—
Наконецъ, раздѣлимъ обѣ части на 5Ь—17а, получится
йб2— а2
56^177
Примѣры <).ія упражненія:
I) (а—.г)’—2(а—6).гч-тс,=:(-^^)..т;
За2
найдется ®=12пД-
.... аІ> а А пЪ
2) -----------—-----1 - ; .-г---
' (а— .т}(Ь— а-) а—я- Ь—.т а-е-Ь
,р а я1 । ,т__ 1 । 1 1 ач-А-і-с
' 1 а Ь с аЬ ас Ьс' ' «іАч-аг-ч-Ьс
,. 1 —а а—1 I «ч-1
4) — =-------1---------: .г— — .
2 я .т/.т-і-Л) а — I
5) <±±1Ѵі6=^,-ьІ6х;3--0,І.
' 1—X 1— X 7
9в. Примѣчаніе—Надобно различать уравненія отъ явныхъ равенствъ.
Равенства суть такія выраженія численныя или буквенныя, соединенныя зна
комъ=, которыя довольно сократить, чтобы получить первую часть тождествен-
но равною второй.
Наприм. • 63 : 9~7,
За-ь7а=Л0«,
76—46ч-с^:36ч-с, и проч.
суть равенства явныя.
Онѣ отъ уравненій отличаются еяіе тѣмъ, что, принимая въ иихъ одну букву
за неизвѣстную, а всѣ прокія за количества данныя, мы пе можемъ отсюда найти
яту неизвѣстную: она всегда получится равна только самоіі себѣ и пи отъ чего
независима.
По поелику равенства, по формѣ своеч, сходны съ уравненіями, то онѣ не-
рѣдко могутъ быть смѣшиваемы съ уравненіями. Напри».
1(3-^)—т
48
весьма походитъ па уравненіе: по стоитъ только дѣйствительно помножить па
3----(или какъ нь есть сократить), то найдется:
2 2
х—з=іс—'з , откуда
2 2 Л Л
х—«=д—или 0=0.
Неизвѣстная х осталась неопредѣленною.
МЗСЛЬДОВАІНЕ РѢШЕНІЯ ОБЩАГО УРАВНЕНІЯ ПЕРВОЙ СТЕПЕНИ СЪ ОДНОЮ
НЕИЗВѢСТНОЮ.
і'З. Самый общій видъ уравненія первой степени съ одною неизвѣстною
тотъ, когда члены неизвѣстные и члены извѣстные находятся въ обѣихъ частяхъ
его, а именно: •
ах-і-Ъ~сх-+-(І;
Изъ итого уравненія находимъ
__(1~Ь
а—с '
Здѣсь неизвѣстная х зависитъ отъ частныхъ величинъ а, Ь, с, (I; она измѣ-
няется съ перемѣною сихъ послѣднихъ Давая всевозможно различныя величины
этимъ, количествамъ, можно открыть всѣ измѣненія, какія неизвѣстная х спо-
собна принимать иа себя, и ея переходы пзъ однихъ состояній въ другія. Раз-
смотрѣніе таковыхъ измѣненій называется изслѣдываніемъ, которое мы п при
ложимъ къ выводу
а—ь
а—с '
Прежде всего открывается намъ: 4) что всякое уравненіе первой степени съ
одною неизвѣстною имѣетъ только одио рѣшеніе; потому что — даетъ одно
число.
2) Рѣшеніе найдется положительное, когда будетъ въ одно время </> Ь, а> с,
либо и а<с; это очевидно.
3) ж=0, если 4=6, но а не равно е.
4) Рѣшеніе получится отрицательное, когда 4> Ь и а <с, либо когда сі <Ъ,
а>с.
5) Рѣшеніе выйдетъ если 4—Ъ^зп, и а=с.—Этотъ символическій
выводъ показываетъ, что долженъ быть безконечно большимъ, и что въ
этомъ случаѣ уравненію нельзя удовлетворить ни какими конечными величинами
Въ самомъ дѣлѣ, вообразимъ себѣ, что разность а—с постепенно уменьшается,
і
напр. положимъ а—с=10; тогда
49
Л—6 т , „
гг—---=-т— =1 Ѵіг
а—с —
іо
для а—с=—*~, а?—1000 т;
1000
I
для а—с~700оо00> х—ЮОООООт, и т. д.
Слѣдовательно, если а—с сдѣлается чрезмѣрно мало, то х сдѣлается чрез-
мѣрно великъ; а потому, когда а—с—0, то есть, безконечно мало, то
долженъ сдѣлаться безконечно-великъ.
II такъ, всякое количество, раздѣленное на нуль, равняется безконечности.
Такое количество изображается знакомъ оо, и пишется:
т
х=о=с° •
Отсюда обратно заключаемъ: а) что безконечность,помноженная на нуль,
представляетъ всякую величину конечную,
т= со ХО;
Ь) Что всякая величина конечная, раздѣленная на безконечно боль-
шую, даетъ нуль въ частномъ числѣ; ибо изъ предыдущаго имѣемъ
0.
СО
Выраженіе ~ показываетъ, что въ данномъ уравненіи находится какая-
нибудь несообразность, несовмѣстность, и вообще нелѣпое требованіе.
II дѣйствительно, если въ
ах-і-Ь=сх-е -д,
возмемъ а—с, то должно быть и Ь=б, илп А—6=0. А какъ мы, принявъ
а—с, хотимъ, чтобы было А—Ъ=т, а пе равно пулю; то рѣшеніе х=~лобна-
ружило, что, при такомъ условіи, нельзя удовлетворить уравненію ни какими
конечными величинами, потому что это условіе невозможно.
6) Выводъ ж= ^обратится въ если возмемъ А=Ь и а=~с. Это симво-
лическое рѣшеніе означаетъ неопредѣленность, т. е. что, при такомъ предпо-
ложеніи, можно удовлетворить данному уравненію всякими величинами, взятыми
па мѣсто х. И въ самомъ дѣлѣ, тогда
ах-ь-Ь~ ~вх-і-Л=:ах-+ Ь
представляетъ не уравненіе, но тождественное равенство двухъ выраженій, ко-
торое тѣмъ и отличается отъ уравненія, что изъ него нельзя опредѣлить х; по-
тому что здѣсь всякая величина, взятая на мѣсто х, удовлетворяетъ равенству
!78. Однако же не надобно всегда заключать, что уравненіе допускаетъ не-
опредѣленность. то есть, всѣ возможныя числа для х, когда получится выводъ
д
50
Это обстоятельство можетъ произойти еще и тогда, когда въ числите іѣ и
знаменателѣ дробнаго вывода находится общій множитель, который при частномъ
предположеніи обращается въ пуль, и въ то же время обращаетъ х въ По-
этому, надобно стараться сократить дробный выводъ, найденный для х, выклю-
чивъ всѣ множители, общіе его числителю и знаменателю, и тогда дѣлать желае-
мое предположеніе.
Наприм. выводъ ~иРи положеніи а=и, обращается въ -.только
потому, что эта дробь яе сокращена, что въ ел числителѣ и знаменателѣ пахо
дптся множитель а— Ь; ибо,
а3—«6“ а(а4—Л») а(а-і-Ь)(а—6;
Х~-----;— = --------— —------—------ .
и—Ь а —о а —о
Сдѣлавъ сокращеніе, остапечн х=а(а-г-Ь), и тогда, для п=6, найдется
т—2а’, рѣпіеіёе опредѣленное.
Примѣръ. Разрѣшивъ уравненіе (&о)
х—2рх-ь35'"=:3 р"(^—ргх,
3«4(р4-1)
мы майлн
Полагая р—I, окажется именно отъ того, что пробное выраженіе здѣсь
но сокращено, и содержитъ въ числителѣ и зпаменателі; общій множитель р —1;
потому пто
Примѣръ.
л Зу'^Гр--! — *) 3</4(р-і~1)
р4—ІІр-ЬІ (р — I)4 р-і
Въ сокращенную дробь подставимъ , найдемъ
Зѵ4(р-И) (!</•“
х~----------—— — оо,
о о ’
рѣшеніе хотя символическое, но все же опредѣленпое.
18а4с—12«6с-+-2Ь4с
Х~~ >
при положеніи Ь~За, обращается въ а цртому надобно попробовать сократить
этотъ выводъ. Сначала найдется
2с(9о4—бя&н 64)
х— - - ---——; потомъ
3/(Ь-—2 іа")
2с(3а— Ьр
ЗДі н-Зап-ьѴо4}(г.—Та)
—2сГЗа—Ь)
Теперь положимъ 6=3а, получится #=0, рѣшеніе опредѣленное.
51
3 А Д А Ч И.
39. Задачею въ Алгебрѣ называемся всякой вопросъ, въ которомъ предла-
гаются условія, словесно выражающія связь (отношеніе, зависимость) между нѣ-
которыми количествами данными, и нѣкоторыми неизвѣстными, и требуется
найти послѣднія посредствомъ первыхъ, то есть, разпѣшпть задачу.
Но, если рѣшеніе задачи состоитъ въ томъ, чтобы выразить ея неизвѣстныя
количества посредствомъ надлежащаго совокупленія коли іествъ дачныхъ, то
само собою видно, что связь между количествами даппымп и неизвѣстными задачи
должна изобразиться однимъ плп нѣсколькими уравненіями, изъ которыхъ тѣ
неизвѣстныя и найдутся; онѣ будутъ удовлетворять уравненіямъ, т. е. всѣмъ
требуемымъ условіямъ задачи, и потому будутъ ея рѣшеніями.
Изъ сего видно, что рѣшеніе алгебрическаго вопроса производится двумя дѣй-
ствіями: 1) приведеніемъ задачи въ уравненіе. и 2) разрѣшеніемъ этого
уравненія.
80. Разрѣшеніе уравненія первой степени съ одною неизвѣстною не имѣетъ
никакихъ трудностей; но приведеніе задачи въ уравненіе не имѣетъ опредѣлен-
ныхъ правилъ; оно требуетъ навыка и остроты ума. Только передѣлавъ многіе
примѣры, можно приучиться довольно скоро угадывать, какія въ данномъ вопросѣ
находятся количества данныя и неизвѣстныя, сколько ихъ, какія, по условіямъ
задачи, находятся между ними отношенія явныя или неявныя, и какимп алге-
брическими дѣйствіями надлежитъ выразить сіи отношенія, чтобы составилось
уравненіе. Впрочемъ, во всѣхь курсахъ Алгебры, для привиденія задачи въ
уравненіе, совѣтуютъ пользоваться слѣдующимъ общимъ правиломъ:
Надобно отыскать въ задачѣ всѣ величины данныя, и всѣ величины искомыя,
и, означивъ сіи послѣднія буквами х, у, х,..., ппедноложить, что задача будто
рѣшена, что эти неизвѣстныя найдены. Послѣ того надобно, посредствомъ алге-
брическихъ знаковъ, выразить всѣ отношенія, всѣ дѣйствія надъ количествами
данными и искомыми, означенныя въ задачѣ, какія должно произвести, чтобы
повѣрить величины неизвѣстныхъ: тогда уравненіе составится сямо собою; оста-
нется только разрѣшить его.
Но, чтобы сдѣлать въ этомъ навыкъ. разсмотримъ рѣшеніе нѣсколькихъ
задачъ.
81. Задача 1. Найти два числа, которыхъ сукна а, « разность Ь,
извѣстны.
Пусть ® большее число, то а—& будетъ число меныпее. Разность между
ними =Ь; посему
52
х—(а—х}=1), или
х—а-+-х=Ь,
%&=а-+-Ь
х=-^Ъ^ большее число.
Меньшее число =а—х=а------
__а—Ь
2 ’
И такъ, большее число равно полусуммѣ, а меньшее полуразности
данныхъ чиселъ а и Ъ. Наприм. если а=36, 6=10, то
. __36-4-10 — -
большее число =——=23,
36-10
меньшее....———=13.
Эти числа удовлетворяютъ вопросу; потому что сумма х.—93-»-{ 3—36, а
разность 23—13=10.
Задача 2.—Найти число, которое, бывъ сложено съ своею полови-
ною, и его тремя пятыми, составило бы 105.
Пусть это число =ЗС, то
1
его половина =^«,
3
его три пятыя = -х, —
э
1 3 . АГ
сумма а=Ю5.
Отсюда, 10.тч-5жч-6я=1050, или
21ж=1050,
«=50.
Таково искомое число. II въ самомъ дѣлѣ,
50ч- ~ .50-^.50=105, или
50ч-25ч-30=105.
Задача 3.— Отецъ въ духовномъ завѣщаніи оставилъ *-имѣнія сыну,
7 имѣнія дочери, а остальныя 3000 руб. серебр. вдовѣ, матери ихъ;
спрашивается, какъ велико это имѣніе, и по скольку должны полу-
чить сынъ и дочь?
Пусть х все имѣніе: очевидно, что если взять одну треть имѣнія и его
двѣ пятыя доли, да 3000 рублей, то сумма должна составить все имѣніе;
посему,
ь жч- ѵ ам-3000=ж.
3 5
61
По этому, когда дается нѣсколько уравненій, содержащихъ въ себѣ такое же
число неизвѣстныхъ, надобно прежде всего привесть ихъ въ простѣйшій, одно-
обра&пый видъ, освободивъ отъ знаменателей, и исключивъ общихъ множителей
въ каждомъ: тогда уравненія тожественныя, если онѣ будутъ, сами собою обна-
ружатся.
3) Наконецъ, когда уравненія приведены въ простѣйшій видъ, и члены ихъ
расположены однообразно, надобно смотрѣть, чтобы онѣ были совмѣстны, не
противорѣчивы. Для примѣра, возмемъ уравненія
2-т—3?/~4,
10ж—15у=30;
раздѣлимъ второе на общаго множителя 5, получится 2ж—Зу—6. Очевидно,
что второе уравненіе несовмѣстно съ первымъ, потому что состоитъ съ нимъ
въ явномъ противорѣчіе. Такія уравненія совсѣмъ негодятся для опредѣленія не-
извѣстныхъ х, у.
*. Уравненія съ двумя неизвѣстными.
88. Для разрѣшенія двухъ уравненій съ двумя неизвѣстными первой степени,
надобно сперва каждому изъ нихъ дать общій видъ ва;-+Ъу=с, гдѣ х, у суть
неизвѣстныя, а, Ь, с, числа цѣлыя.
Для этого должпо освоподить уравненія отъ знаменателей, въ каждомъ изъ
нихъ перенесть члены съ неизвѣстными въ первую часть уравненія, а извѣст-
ные — во вторую, и сдѣлать всѣ возможныя сокращенія. Потомъ два уравне-
нія, приведенныя уже въ простѣйшій видъ, надобно совокупить между собою
такъ, чтобъ исключилась одна изъ извѣстныхъ, и составилось бы одно уравне-
ніе съ одною неизвѣстною, откуда она и опредѣлится. А получивши одну изъ
неизвѣстныхъ, легко найдется и другая.
89. Способовъ исключенія неизвѣстной изъ данныхъ уравненій находится
четыре: 1) способъ подстановленія, 2) способъ сравненія, 3) способъ сокраще-
нія чрезъ сложеніе и вычитаніе, и 4) способъ Бе.зу чрезъ введеніе произволь-
ныхъ множителей.
Пусть данныя уравненія:
5® 5 у
30—63/ " 5 Ю—’
7а—9 6-7®
1—У У
Первое уравненіе приведется къ общему знаменателю, если помножимъ обѣ
части дроби * на 5—у, и обѣ части дроби 10^.2у 'на 3.
Отбросивъ общій знаменатель 30—бу, по сокращеніи, получится:
1) 5ач-2у=25.
62
Помноживъ обѣ части втораго уравненія, первую на у а вторію ца 1—у,
найдемъ сперва
7ху—9у=$—7х— &у-і-7ху,
а, по сокращеніи, останется
2) 7х—Зу=6.
Приложимъ теперь всѣ помянутые способы исключенія къ разрѣшенію этихъ
уравненій 1) п 2)
90./Носпособу побстановми-я. — Будемъ искать неизвѣстную .г изъ
перваго уравненія, предполагая,, будто у данъ, и найденное выраженіе для а? под-
ставимъ во второе уравненіе: тогда всклочится х, п останется одно уравненіе
съ однимъ неизвѣстнымъ у, откудо оно и сыщется.
Пзъ перваго уравненія имѣемъ:
25—2і/
ж—------
5
это выраженіе подставимъ во 2-е уравненіе на мѣсто т; наіі іется
7(25-21,) „ „
- - —6, плп
8 а ’
17 5—1 ку— 1‘5у=3 0; откуда
145=29у, и
?/=5.
Наведши ?/=5, подставимъ это въ первое уравненіе 5ж-т-2у=25: выйдетъ
5ж-ь-10=25; откуда
а?—3.
Можно у~5 подставить во второе уравненіе 7х—Зу—6; получится
7.г—15=6, откуда
также ж=3.
91. Но способу сравненіи. — Надобно освободить одну неизвѣстную х
(либо у) изъ обоихъ уравненій, предполагая, будто другая извѣстна, и потомъ
сравнить между собою два выраженія, найденныя для тогда исключится х, и
составится одно уравненіе съ одною неизвѣстною у. откуда она и опредѣлится.
Примѣръ тотъ же:
5жч-2у=25, .'•>
7 х—‘Зу—6
Пзъ перваго уравненія находимъ
25—21/
Х— 5~ ’
бч-Зу
изъ втораго, ж=——.
Эти выраженія должны быть равны между собою, а потому сравнимъ ихъ:
25—21/__________________________6ч-3у
“і 7 ‘
- 63 -
Полученное уравненіе, съ одною неизвѣстною у, освободимъ от<> знаменате-
лей, и разрѣшимъ:
175—14у=30-ь15у, или
—29у=—145; откуда
У— 5-
Чиілі 5 подставимъ па мѣсто у въ первое уравненіе 5.г-4-2у=25, получимъ
\5ж-+10=25, откуда
х=3.
По способу сокртпеиін чрезъ сложеніе и вычитаніе. — Надобно
въ обоихъ уравненіяхъ сдѣлать равными коефлпгенты предъ тою пеизвѣстарю.
которую хотимъ напередъ исключить, помноживъ первое уравненіе' на к№ш
ціептъ этой неизвѣстной во второмъ, а второе уравненіе — на коефиціентъ рей
же неизвѣстной въ первомъ уравненіи Получивши оба уравпр-пя съ равными
коефиціептами предъ одною неизвѣстною, надобно ихъ сложись, если этн коефи
ціенты съ различными знаками, либо вычесть одно изъ другаго, если они съ
равными знаками: тогда исключвтся одна неизвѣстная, и получится одно урав-
неніе съ одною неизвѣстною, которая отсюда и опредѣлится Примѣръ сотъ же;
5лм-2у=25 3
7л"—Зу~ 6 2
Исключимъ сперва неизвѣстную у. Коеіриірепты этой неизвѣстной суть: 2 въ
первомъ п 3 во второмъ; мы сдѣлаемъ ихъ равными, если помножимъ первое па
3, а второе на 2; получатся:
15л>+-6у=75і сложимъ, истому что бу и —бу съ противности
14 г—6у=121 знаками.
29л=87, откуда
х=3- V • /
Такимъ же образомъ можно исключитъ ,неизвѣстную х, чтобы найти у. Опа
имѣетъ коефнціенты 5. и 7; чтобъ сдѣлаѣь ихъ равными, помножимъ первое
уравненіе на 7, а второе па 5:
35я-+-14у=175 ( вынемъ второе изъ іи>а^-14у= 175
35^—15у= 301 перваго. ^35^ч-15у=—30
7 у 29у= 145
7 ' У=5 (*).
__... __-____ , -V
’) Этотъ способъ исключенія неизвѣстной ничѣмъ не разнится отъ способа чрезъ раздѣ-
леніе одного уравненія на другое безъ остатка. Въ саломъ дѣлѣ, данныя уравненія
можно нанисать текъ:
5хч-2у—25=0.
1х—Зу— 6=0.
64
Способъ исключенія чрезъ сложеніе и вычитаніе особенно выгоденъ въ тѣхъ
случаяхъ, когда коефиціенты одной и той же неизвѣстной бываютъ кратными
одинъ другаго, или равными.
Примѣръ: За—4у= 8,
6гг-ь у =25. ,
Здѣсь коефиціенты предъ х, и предъ у, суть кратные одинъ другаго; а по-
тому, для исключенія у, довольно помножить второе уравненіе на 4 и сложить
съ первымъ:
За—іу—8,
24д:-+-4у=100
27а=Ю8, отсюда а=4.
А для исключенія а, и опредѣленія у, довольно помножить первое данное
уравненіе на 2, и вычесть изъ втораго:
6а—8г/=16,
6а-+- у =25.
Вычтемъ верхнее изъ нижняго, получится
9у=9; откуда у=1.
Способъ этотъ дѣлается еще проще, когда коефиціенты одинакихъ неизвѣст-
ныхъ равны.
Примѣръ. Наити два числа, коихъ сумма —а, и разность ~Ь.
Пусть первое число х, второе у; то должно быть
ж-ьу=а
х—у=Ь
сложимъ
С2х~а-+-Ъ
а-і-Ь
= первое число.
А чтобъ найти у, возмемъ опять*
. л-+-у=а | вычтемъ нижнее | а-ьуг=а
х—у—Ь і изъ верхняго | —х-ѵ-у=—Ь
2у=а—Ь
а—Ь
у=^Г
Теперь раздѣлимъ первое уравненіе на второе; а чтобы не имѣть дробей въ частномъ,
то помножимъ первое на коеФиціентъ 7 предъ -т:
35*4-142/—175 7*—Зу—6
- 35*4-152/4- 30 "5
29у—И5=0.
Остатокъ долженъ быть равенъ нулю, потому что дѣлимое и дѣлитель равны нулю.
Изъ этого остатка нахожу
14» к
у =----=5.
* 29
65
1>3. По способу Безу. — Надобно помножить одно изъ данныхъ уравненій
па произвольное неопредѣленное число т; потомъ, изъ этого уравненія вычесть
второе. Получится одно уравненіе съ двумя неизвѣстными и трстьсю произ-
вольною неопредѣленною величиною т, которую мы ввели, и которою можемъ
располагать какъ намъ угодно. Теперь, чтобъ исключить у и опредѣлить х, по-
ложимъ весь алгебрическій коеФЯціентъ предъ у равнымъ нулю: тогда получатся
два простѣйшія уравненія съ х и т, изъ которыхъ сперва найдется т, а по-
томъ х.
Возмемъ самый общій примѣръ*.
въ которомъ а', Ь', с' различны отъ а, Ь, с. Помножимъ первое на произвольное
число т, и вычтемъ изъ него второе, выйдетъ*.
(ат—а') #-+-( Ьт—Ь') у=ст—с'.
Въ этомъ уравненіи хотя двѣ неизвѣстныя; но за то находится произвольное
число т, которое состоитъ въ нашемъ распоряженіи.
Чему бы мы ли положили т равнымъ, мы ничего пе перемѣнимъ въ задачѣ,
потому что на него помножено все первое уравненіе. Для исключенія у, надобно
т взять такимъ, чтобы коефвціентъ Ьт—Ь' обратился въ нуль. Тогда будемъ
и нѣть
Слѣдовательно,
слѣдовательно,
Ьт—6*=0, и (ат—а')а^=ст'—с', откуда
ст—с!
ат—а'
Л пзъ условнаго уравненія, Ът—Ь'=&, находимъ
„___ь'.
ь’
ь>
с.-—•—с'
Ь • - сЬ> —Ьс>
Ъ< аЪ1—Ъа1
а. г—а1
о
Такимъ же образомъ можемъ исключить х и найти у; для этого, въ уранпеніи
(ат—а!]х-+-(Ьт—Ь'^у—ст—с'
положимъ ат—а'_О, и останется*.
(Ът—Ь')=ст—с', откуда
ст—с>
У Ът-Ъ1
Теперь условное уравненіе ат—а—О другое; изъ пего получится и другое
значеніе для т, а именно*.
а1
тг= —;
а
а1
с.------------------------------------с'
У=------;--, ИЛИ
а'
І>- -V
а
&
66
__са'—ас' ас1—са\
Ъа'—аЬ1 аЬ1—Ъа>
Выведенныя нами двѣ формулы:
__сЪ'—Ъс1 ___ас1—са1
аЪ1—Ъа1' У__аЬ1—Ъа1
суть общія для разрѣшенія всѣхъ уравненій съ двумя неизвѣстными. Мы примѣ-
нимъ ихъ къ рѣшенію уравненіи:
5ж-ь2у=25
7 я—Зу— 6.
Чтобы прямо получить величины для х п у по означеннымъ формуламъ,
должно сравнить данныя численныя уравненія съ общпмті алгебппческпмп
ах-+-Ъу~с, а'х-і-Ь'у—с!п положить
а=5, Ь— 2, с=25,
а!=7,Ъ'=—3,с'=6;
котомъ подставить эти числа въ формулы, и получится-
_сЪ/-Ьс> __—23.3—2.6 __ 87 __9
Х=аЬ'-Ьа' — 5.3-2.7 29
__ас'-саі _ 3.0—25.7 143 __
аЬ'—Ьа' — -3.3- 2.7__________~29_Э ’
Впрочемъ, прп разрѣшеніи численныхъ уравненій, надобно избирать такой
способъ, посредствомъ котораго легче п скорѣе можно достигнуть цѣли
9. сравненія съ тремя, п болѣе, неизвѣстными
Всѣ способы, употребляемые для разрѣшенія уравненій съ двумя не-
извѣстными, служатъ п для рѣшенія опредѣленныхъ уравненій первой степени
съ тремя и болѣе неизвѣстными. Возмемъ трп уравненія:
2 1
3-я+ У-3*=23-
5х—6у-+-3с=15,
8 у—
Прежде всего надобно освободить ихъ отъ знаменателей, и потомъ сократятъ,
если можно. Здѣсь третье уравненіе дѣлится все на 2; и такъ
1) 2ам-3у— я= 8,
2) 5х—бу-ьЗгзсІЭ,
3) Зж-ь2з= 7.
а) Рѣшеніе по способу подстановлеіия. — Освободимъ одну какую вп
будь неизвѣстную пзъ одного уравненія, н ея выраженіе подставимъ въ два дру-
гія уравненія: тогда зта неизвѣстная исключится, и останутся два уравненія съ
двумя неизвѣстными, пзъ которыхъ п найдутся сіи послѣднія такимъ же пли
другимъ способомъ. Здѣсь проще всего освободить я пзъ 1) уравненія-
х- 2.?-- Зу—8.
67
Подставимъ это выраженіе вмѣсто г во 2) и 3) уравненія:
—6у-ьЗ(2ж-ьЗу—8)=15,
4у—3а:-+-2(2л:-і-3у—8)= 7.
Сдѣлавъ надлежащее сокращеніе, находимъ:
Иа:ч-3у=39,
10?/ч- 3=23,
два уравненія съ двумя неизвѣстными. Изъ послѣдняго имѣемъ х=23—Юг/
Это подставимъ въ первое, и выйдетъ
11(23—10^)-ьЗу=39,
одно уравненіе съ однимъ неизвѣстнымъ; изъ пего найдется у=2.
Эту величину подставимъ, въ выраженіе
а=23—Юу, получится а=3.
Наконецъ, подставивъ на мѣсто у, х, ихъ найденныя величины, въ
2=2я -+-3у—8; выйдетъ
г=2.3-+-3.2—8, пли г=4.
Что рѣшеніе точно, это оправдывается повѣркою, подставивъ у—2, ж=3,
2=4, наприм. въ 3) уравненіе:
4у —Зх і 2л=7,
4.2—3.3-+-2.4=7,
8— 9-+-8 =7.
Ь) По способу сравненія. — Надобно освободить одну изъ неизвѣстныхъ
изъ всѣхъ трехъ уравненій; потомъ сравнить ея первое выраженіе со вторымъ
и третьимъ, тогда зта неизвѣстная исключится, и получатся два уравненія съ
двумя неизвѣстными, п проч.
Примѣръ тотъ же:
2о-ьЗу— .-= о,
5х—6у-«-Зг=15,
41/—Зхч-22= 7.
Освободимъ 2 изъ всѣхъ трехъ уравненій
2=2я-+-3у— 8 изъ перваго,
15 — 5л -+ Суу „
2=-------------,ізъ втораго,
7 — 4и ч- За
я—-----— - изъ третьяго
Сравнимъ первое выраженіе со вторымъ и съ третьимъ, получатся:
2ж-4_зу-8 = 1±=^,
2жн_3у-8 =
только два уравненіи съ двумя неизвѣстными х, у; онѣ, по сокращеніи, будутъ
68
Нхн- 3у=39,
жн-10у=23.
Освободимъ х пзъ этихъ обоихъ уравненій:
х=^^-, ж=23—4 Оу,
и сравнимъ между собою:
^=13" — 23— Юу, или
39—Зу =253— И Оу,
одно уравненіе съ одною неизвѣстною у, пзъ котораго и найдется у=2;
а потомъ, изъ х~23—Юу, получимъ ахх=3;
и наконецъ, пзъ я=2жч-3у—8, выйдетъ х=і.
с) По способу сокращенія. — Положимъ, что надобно исключить неиз- -
вѣстную -г: для этого надобію сдѣлать равными коефиціепты при х во всѣхъ
уравненіяхъ, чрезъ помноженіе каждаго уравненія па произведеніе коефпціен-
товъ этой неизвѣстной х въ прочихъ уравненіяхъ. Послѣ того, должно сложить,
либо вычесть, первое уравненіе со вторымъ и съ третьимъ, такъ чтобы х ис-
клточился; и останутся два уравненія съ двумя неизвѣстными у, х, и проч.
Беремъ тотъ же примѣръ:
2ам-3у— 5= 8 2.3=6,
5я—6у-+-3я=15 2.1=2,
іу—^хн-^— 7 3.4=3,
Чтобъ исключить х, помножимъ первое уравненіе на произведеніе 2.3=6
коефиціентовъ, стоящихъ при г въ двухъ прочихъ уравненіяхъ; помножимъ вто-
рое па 2.1=3, третье на 3.1=3’
12х ч-4 8у— 6я=4> 8,
Юж—42у-+-6я=30,
42у— 9ж-і-6г=21,
Теперь коефиціенты при х равны, только не съ одинакими знаками; а потому,
для исключенія -, надобно сложить первое уравненіе со вторымъ, а потомъ съ
третьимъ, получатся:
2йвч- 6у=78,
3.гч-30у=69,
пли: •
Пжч- 3у=39 10
ж-+- 10у=23 3
два уравненія съ двумя неизвѣстными. Помножимъ первое изъ нихъ па 10,
второе на 3, п вычтемъ, чтобъ исключить у; останется:
1 07^=321, откуда =3.
Послѣ чего паіідутся у п х такимъ же или другимъ способомъ.
69
Пѣтъ необходимости, чтобы всѣ три неизвѣстныя были въ каждомъ изъ трехъ
уравненій; довольно и того, что три неизвѣстныя будутъ, какъ ни есть, нахо-
диться въ трехъ уравненіяхъ.
Примѣръ: 2л—у—%— 0,|4.
5л—2з=20,
4>у—ж=10.
Помножимъ первое на 4 и сложимъ съ третьимъ, чтобъ исключить у, выйдетъ:
7х—42=10,
сюда припишемъ второе.... 5л—2г=20;
послѣднее помножимъ на 2, и вычтемъ изъ него первое; останется:
Зл=ЗО, л=10.
Вставимъ это въ третье уравненіе 4«/—=10, найдется:
—10=10, у=5.
Подставимъ л=Ю, у=із, въ самое первое уравненіе:
2л—у—2=0, получится
20—5—2=0, 2=15.
Для повѣрки, внесемъ величины л,2, во второе уравненіе 5 л—22=20, будетъ
50—30=20;
слѣдовательно, рѣшеніе вѣрно.
95. По способу Безу. — Чтобъ исключить двѣ неизвѣстныя величины изъ
трехъ уравненій, надобно ввести въ нихъ два нронзвотьные, неопредѣленные
множителя, которыми можемъ располагать, какъ намъ угодно, а именно: помно-
жимъ первое уравненіе па произвольный множитель т, второе на п; сложимъ
два первыя уравненія, а третье пзъ нихъ вычтемъ. Получится одно уравненіе
со всѣми тремя неизвѣстными и съ двумя произвольными т п п. Произвольные
множители можемъ взять такнмп, чтобы алгебрическіе коефиціенты прп у в 2
сдѣлались равными пулю. Отъ этого получатся три уравненія, изъ которыхъ
легко найдутся т, п в х, и проч.
Для примѣра возмемъ три общихъ уравненія:
«л-+- Ъу-+- сг—<1 т
а'х-і-Ь'у-і-с'х^д! п
а"х-\ Ь"у-і-сІІ^=:дІ"
Помноживъ первое на произвольную неопредѣленную т, второе на п, сло-
жимъ эти уравненія, и вычтемъ изъ суммы ихъ третье уравненіе, получится:
(а)...(ат-ьа'п—а'')х-і-(Ьт-+-ЬІп—1>")у-і-(ст-+-с'п—с,г)і=(1т-4-і1'Й—й".
Двѣ произвольныя т, п, возмемъ такнмп, чтобы алгебрическіе коефиціенты
при у и г обратились въ нуль; отчего получатся
70
условныя уравненія: Ьт-і-Ь н—Ь"=0,
стч- с'н—с0;
останется (ат-г-а'п—а")х=(Іт-+-Л,п—А", откуда
Ат 4-Л'п—А1'
.г—--------------.
ат-і-а/п—аЧ
Что касается до т, п, онѣ теперь найдутся изъ условныхъ уравненій, а
именно, будутъ:
— (VсЧ—ЪЧс>} _—(Ъ!>с—ЬсЧ)
т —' Ье'—Ь'с П Ьс-Ыс '
Онѣ, будучи подставлены въ выраженіе для х, по сокращеніи, даютъ
__а(ьісіі—ъіісі)-^-аі{ъі'с—Ьг.іі)-ѵ-ач{Ъсі—ъ'с)
а(І>'сЧ—Ь11 с> )-+-а< (Ъ11 с——Ъ'с)‘
Такпмъ же образомъ найдется неизвѣстное у: для этого надобно изъ общаго
уравненія (а) исключить х и г, положивъ
ит+и'п—а"=0, ст-і-с'п—с"=0; останется
__<Тт-ьгі^п — ЛЧ
Ът-і-Ьгп—ЪЧ'
При этомъ условіи, найдутся для т п п другія величины:
—(а'сЧ—аЧс1} —ІаЧс—асЧ)
т= - -— ---------, П—---------—-—,
ас1—и'с ас<—а'с
которыя надлежитъ подставить въ выраженіе для у, и получится
(Ца'сЧ—аЧс'І-і-а'ІаЧс—асЧі-і-іІЧіасІ—а'с)
У Ь(а'сЧ—а.Чс,)-і-Ъ,(аЧе—асЧ)-+-ЪЧ^акі—аіс) ‘
Наконецъ, чтобъ получить з, уравняемъ пулю коефпціенты при # и у въ об-
щемъ уравненіи (а);
ат-і-а'п—а"—О, біи-ьб'п—6"=:0; останется
• ___гіт-ьгі'я—г?//
стч-с/п—с"
Здѣсь пзь условныхъ уравненій найдутся
—{Ь'а'Ъ—а'Ъ") —(1>Ча~Ъа")
Ъа' — Ъ'а ’ Ъа>—Ѵа ’
отчего выраженіе для з обратится въ
_____________А{Ъ'аЧ — Ъ'1 а^-і-Л' (1>ч а — І>аЧ}-+-г]Ч'ЪаГ—Ь'а)
с{Ь'аЧ—Ьпа<(ЬЧа—Ъа<')ч-сЧ(Ьа1 — !>'а) ‘
«
96. При одномъ взглядѣ на выводы х, у, открывается, что между скоб-
ками въ числителѣ и знаменателѣ каждаго находятся соотвѣтственно равные дву-
члены (наприм. въ послѣднемъ выводѣ видимъ двучлены Ъ'а"—//'а', Ь"а—Ьа",
Ьа'—Ъ’а въ числителѣ и зпйменатеіѣ), а внѣ скобокъ этпхъ двучленовъ, но всѣхъ
числителяхъ, буквы (1, і', Л". Внѣ скобокъ тѣхъ же двучленовъ, находящихся въ
знаменателѣ для х, стоятъ коефпціенты а, а', а", этой неизвѣстной; для у его
коефиціенты Ь, Ъ', Ъ"} и для 2 его коефпціенты с, с', с”.
71
Внимательное наблюденіе за порядкомъ буквъ, составляющихъ тотъ плп дру-
гой выводъ, показало возможность писать дробныя выраженія для х, у и не-
посредственно, слѣдующимъ образомъ:
Напишемъ коефиціепты, а, 1), с, а', У с', I іо три раза, для каждой не-
ИЗиѢСТНОЙ ВЪ ПОрЯДКѣ Для х. а Ь с Ь Для у. а с с Для х. ь а
а' V с' У а' с' с1 Ъ' а!
а" V' с" Ь" а1' с" с" Ъ"' а"
а Ь с 1)' а с с Ъ ' а
а1 ' 1/ </ У ' а! с' с' ' У а'
а!' ' Ь" с" А" ’ а" ' с" с"’ ' Ь" 'а"
а ь с ь а с с -ь а
а' У с' А' а' с1 с' У а'
а!' Ь" с" а" с" с" V а"
Теперь, для полученія х, начнемъ съ его знаменателя: возмемъ среднія буквы
а, а', а", въ первой колоннѣ коефиціентовъ, .и отъ каждой протянемъ косвенно
по двѣ линіи, вверхъ и вппзъ, чрезъ три буквы, какъ здѣсь показано; тогда линіи
внизъ опредѣлятъ множителей для трехъ членовъ положительныхъ, а линіи
вверхъ—множителей для трехъ членовъ отрицательныхъ знаменателя, а именно:
аЪ'с"—аЬ 'с'-+-а'Ъпс—и!Ъс"-і-а"Ъс'—а"Ь'с, или
а(Ь'с"—Ъ"с)-+-а'(Ъ"с—Ѵе).
А чтобъ получить числитель, надобно только взять й, <!', й", вмѣсто
а, а', а".
Точно также найдутся числители и знаменатели для у и * изъ второй и-
третьей колонны коефиціентовъ.
Приложимъ это къ разрѣшенію уравненій:
Зж-+-і!«/—&=. 8,
5 а:—3?/н-3г=33,
7%-+- у ч-5.г=65,
72
Напишемъ коефиціенты Для а>. въ порядкѣ: Дл и у- Для *.
3 2 —4 2 3 —4 —4 2 3
5 7 —3 4 3 5 —3 4 5 7’ 3 5 3 5 ^3 4 ’ 5 7
з 2 ’ —4 2’ 3 ' —4 —4* 2 ’ 3
5’ —3 3 —з' б’ 3 з’ —з' 5
7’ 4 '5 4’ 7 ’б б’ 4 *7
3 ’ 2 — 4 2 3 —4 4 *2 ’з
5 —3 ’з —3 5 д 3 —3 ’б
7 4 5 4 7 5 5 4 7
Отсюда прймо получаемъ:
_ 8(—15—3)4-33(—4—10)4-65(6—12) _
х 3(—16—3)4- 5(—4—10)4- 7(6—12)
__8.18-33.14-65.6
— —3.18— 6.14— 7.6 ’
8(25—21)-і-33(—28—15)4-63(94-20) _
^~Щ25—21) — 3(—28—16)4- 1(94-20)
_ 8.4—33.434-65.29 __
2.4-ь 3.434-4.29 ’
8(—21—6)4-33(3—14)4-65(104-9) __
5 -4(—21—5)4-3(3—14)4-5(104-9)
— 8.26—33.114-66.19 ,
—---------------------=4.
4.26-3.114-5.19
Что рѣшенія о=6, «/=3, я=4 вѣрны, это оправдывается повѣркою надъ
какпмъ угодно даннымъ уравненіемъ.
9?. іГадобпо еще замѣтить, что дробныя выраженія для х,*у, 2, выведен-
ныя изъ трехъ уравненія съ тремя-, неизвѣстными, различаются только^ своими
числителями, .а зиаменэтедь пмѣ^у> общій. Въ самомъ дѣлѣ, рели уничтожить
4і?обки йъ вы|Тйжёіііп для ж, и‘въ каждомъ членѣ расположить буквы по порядку
Ч^;,\цадоід\ад.ъ цимі^то н^е'яъ.спервіК'1 - -ч •'
73
м'с"-ас'ь"-^-са'Ъ"—ъа'с"-^Ьс'а"—сЬ'а"
_______________________________________
аЬ'с"—ас'Ь"-\-са'Ь"—Ьа'с"-і-Ьс'а"—сЬ'а"’
Послѣ того, уничтожимъ скобки въ дробныхъ выраженіяхъ для у и г, и пе-
ремѣнимъ знаки во всѣхъ членахъ ихъ числителей и.знаменателей; найдутся:
—ас' Л''-ъ-са'й"—Иа'с"-і-Яс'а''—сЛ'а"
У аЬ'с" — ас'Ь"-\-са'Ь"— Ьа'с"-\-Ьс'а"—сЬ'а" '
~__аЬ'г!"— ай'Ь"-ь-сІа'Ь"—Ьа'сІ"-і-ЬА'а"—йЬ'а"
аЬ'с" — ас'Ь”-ѵ-са'Ь" — Ьа'с"-+-Ьс'а" —сЬ'а'' ’
98. Употребленіе одинакихъ буквъ, отличающихся только знаками, для вы-
раженія коефиціентовъ предъ тою пли другою неизвѣстною въ данныхъ уравне-
ніяхъ, привело къ открытію способа (притомъ самаго общаго для уравненія со
многими неизвѣстными), писать выводы для ж, у, х,... па память, не прибѣгая
къ непосредственному, довольно продолжительному, ихъ выводу. Начнемъ съ
уравненій съ двумя неизвѣстными:
ах -і-Ъу—і
а'х-і-Уу—с'-,
сЬ’—Ьс' ас'—са'
онѣ даютъ: х~ -, у= .
аб' —Ъа/ '* аЬ'—оа'
гдѣ видно, что общій знаменатель составленъ изъ однихъ коефиціентовъ а, а',
Ь, Ь', предъ х, у; что числители составлены изъ этого знаменателя, взявшп с, с'
вмѣсто а, а', для х, и тѣ же с, с1, вмѣсто Ъ, Ъ', для у.
Теперь возмемъ три уравненія съ тремя неизвѣстными х, у, г, въ которыхъ
а, а', а", коефиціепты для ж,
ь, V, Ь", - . -у,
с, с', с", - - 2.
Для составленія общаго знаменателя, возмемъ члены, аЬ, Ъа, знаменателя
выводовъ для х, у, предыдущаго случая (выпустивъ па время знаки надъ бук-
вами); припишемъ къ каждому члепу букву с сперва па третьемъ мѣстѣ, то
есть, справа, потомъ на второмъ (въ средппъ), п на третьемъ (слѣва), полу-
чатся тройныя содппепія:
аЪс, асЪ, саЪ\ Ьас, Ъса, сЪа,
который соединимъ поперемѣппо знаками ч~ и —:
аЬс—асЪч-саЬ—Ьас-і-Ъса—сЪа.
Наконецъ, поставимъ одинъ знакъ надъ второю буквою, іГ два надъ третьей) въ
каждомъ членѣ; составится общій знаменатель:
аЬ'с!'—асІЬ"~і-са,Ь1'—Ъа'сІІ~\-ЪсІа,!—сЪ'а". .
Для полученія числителя неизвѣстной ж, замѣнимъ буквы а, а', а" знаме-
нателя буквами й, іѴ, А"; для полученія числителя неизвѣстной у замѣнимъ
буквы 1>, V, Ь" знаменателя буквами (I, й', й", а для я замѣнимъ с, с', с" зна-
менателя тѣми же буквами (1, <1', (I".
74
Точно по такому же механизму составляются пробныя выраженія для х,
у, г, и, если даны четыре уравненія съ четырьмя неизвѣстными
ах ч- Ъу ч си ч- йи ~е,
а'х-і-Ь у -і-с'г -а-Н'н —е',
а"х-л-Ь"у -А-с"г>-і-й"и —е",
а",х-А-Ь,"у-А-с"Іх-А-д,'"и—еІ".
Здѣсь неизвѣстныя х, у, а, и, изобразятся дробями, имѣющими общій зна-
менатель. Этотъ знаменатель .мы найдемъ съ помощію знаменателя (взятаго безъ
знаковъ надъ буквами)
аЬс—асЬ-\-сЬа—Іас-+-Ъса—сЬа
предыдущаго случая, когда были даны три уравненія съ тремя неизвѣстными
Къ каждому члену припишемъ справа коефиціентъ Л новой неизвѣстной и\ по-
томъ подвинемъ его влѣво черезъ одну букву, черезъ двѣ, и черезъ всѣ три;
отъ сего каждый трех-буквенный членъ произведетъ четыре члена о четырехъ
буквахъ, а шесть членовъ произведутъ 24 члена. Эти члены надобно написать
въ одну строку, соединивъ ихъ поперемѣнно знаками ч- п —, п въ каждомъ,
начиная слѣва, поставить одинъ, два, три члена, соотвѣтственно надъ второю,
гретьею н четвертою буквами; составится общій знаменатель:
а Ъ'с"Л"'-— а Ь'й"с'"-А-а й'Ь"с"'— й а'Ь"с"'
—асЪ''аг''ч-ас\ІѴ,—сі(1'сѢ№ч-(ІагсѢг!'
^сиЪ''й,''—са'&Ѣ'''^-с(1'а''ЬІ''—йс'и’,Ь'''
—Ьа'с,,іІ'"~і-Ьа,й"оі!'—^Ь(1,а,Іс"\' -аЬ'а"с'"
-а-Ьс'а4 (1!"—Ьс'й"а,"-і-Ъй’с"а'"—Лі>'с"а!"
—сЬ'а"дпІ^сЬ'й"а"’—сд!Ь"а”'-А-йс'Ь"а"'.
Изъ этого общаго знаменателя составятся тотчасъ чпслители; надобно только
I (
въ немъ взять
е вмѣсто а для числителя неизвѣстной х,
е1 - а' - - у,
я е" — а" - - - г,
е'" _ а"' - - и.
Какое бы число нп было уравненій со столькпмп же неизвѣстными, составъ
этпхъ неизвѣстныхъ дѣлается по одному п тому же закону. Лапласъ доказалъ
общность этого закона въ Запискахъ Академіи Наукъ еще 4772 года.
Примѣчаніе. — Если дано будетъ уравненій болѣе числа неизвѣстныхъ ве-
личинъ: тогда, для опредѣленія этихъ неизвѣстныхъ, избирается столько
уравненій, сколько есть неизвѣстныхъ; остальныя же уравненія назы-
ваются условными, которымъ найденныя величины неизвѣстныхъ должны
удовлетворять; въ противномъ случаѣ, такія уравненія называются несо-
вмѣстными, потому что’ не согласуются между собою, даютъ неизвѣст-
нымъ величины различныя, чего не должно быть.
75
Положимъ, что даны: ах-і-Ьу — с,
а'х-і-Ѵу—с'
а!'х-\-Ь"у=с".
Для опредѣленія х, у, довольно двухъ первыхъ уравнев ій, изъ которыхъ
находимъ:
сЬ'—Ьс1 ас'—са>
аЬ1—аІЬ’ аЬ'—Ьа!'
Третье уравненіе аа!'~і-Ьу"=с" условное, которому па ііденпыя величи-
ны х, у должны удовлетворять. Сдѣлавъ это додстаіювлеьпе, наіідется:
а"{сЬ'—Ьсг}-і-Ъ'г(ас'—са')=с!'(аЬ'—Ьа!}.
Если этого равенства не будетъ, то данныя уравненія ле совмѣстны,
и не годятся всѣ вмѣстѣ для рѣшенія вопроса.
3 А Д А Ч 11,
РѢНІхЖкЛ* ІіОСР|ЛСТЬфГЬ ІПРЕДЪЛЕІІНЫХЪ УРАВНЕНІЙ 1-Й СТЕПЕНИ СЪ ДВУМЯ,
ТРЕМЯ, И БОЛѢЕ, НЕИЗВѢСТНЫМИ.
* ’
1СО. Задача 1. — Гувернёръ, раздавая воспитанникамъ бумагу для
письма, замгыпнлъ, что, если дать каждому по /2 листовъ, то у
него не достанетъ 15 листовъ; такъ онъ далъ по 10 листовъ, и у него
осталось 35 листовъ. Спрашивается: сколько было всѣхъ воспитанни-
ковъ, и сколько у гувернера было бумаги?
Въ этоіі задачѣ находилъ двѣ неизвѣстныя величины; число воспитанниковъ
и количество бумаги. II такъ, пусть
х число воспитанниковъ,
у число листовъ бумаги.
Еслг. выдавать по 42 листовъ па х воспитанниковъ, что составитъ 12а; ли-
стовъ. то у листовъ бумаги будетъ мало; къ нимъ надобно прибавить 15 листовъ,
которыхъ не достаетъ. Слѣдовательно. ,
12а?=«/ч-15.
Когда же выдадимъ по 10 листовъ на х воспитанниковъ, то есть, 10а;
листовъ, то всеіі бумаги у листовъ будетъ много; останется 35 листовъ, кото-
рыя надобно вычесть пзъ у. Посему,
10а?=г/—35.
Вычетши второе уравненіе пзъ перваго, наіідется:
2а?—50; откуда
х—25 воспитанниковъ
Это подставивъ во второе уравненіе, получится:
250=«/—35; а отсюда
у—285 листовъ бумаги.
76
Задача 2. — Сколько намъ лѣтъ? спросилъ сынъ отца своею, кото-
рый отвѣчалъ: твои лѣта теперь составляютъ треть моихъ, а шесто
лѣтъ тому назаоъ они составляли только четверть моихъ лѣтъ. —
Сколько же лѣтъ каждому игъ нихъ?
Пусть х годы отца,
у - сыиа.
По первому условію, у=
Шесть лѣтъ назадъ, отцу было х—6 лѣтъ,
сыну..................... у—6 лѣтъ;
и тогда лѣта сына были у—6=*- (х—6).
Для рѣшенія, подставимъ первое уравненіе во второе :
—6), или
4-х—72=3х—18; отсюда
=54 года отцу,
у.- 54=18 лѣтъ сыну.
Задача 3. У разносчика спросили: сколько у нею яблокъ въ двухъ
корзинкахъ? Онъ отвѣчалъ, отгадайте: если изъ первой корзинки пере-
ложить во вторую пять яблокъ, то въ обѣихъ будетъ поровну; а если
изъ второй переложить въ первую 10 яблокъ, то въ первой сдѣлается
вдвое больше, нежели во второй
Пусть х число яблокъ въ первой корзинкѣ;
у - - во второй.
По первому условію:
х— 5=у-г-5, по второму,
ж-ь10=2 (у—10).
Вычтемъ верхнее уравненіе пзъ нижняго, и сократимъ, получится
15=у—25, откуда
«/=40 яблокъ.
Это подставимъ въ первое уравненіе:
х—5=40-ь5,
«=50 яблокъ.
П такъ, въ первой корзинкѣ было 50 яблокъ, а во второй 40; а въ обѣихъ
вмѣстѣ 90.
Задача 4. — Подрядчикъ платитъ 23 руб. серебромъ за ІО рабо-
чихъ дней маляру и за 16 дней плотнику; потомъ, не перемѣняя цѣны,
платитъ 15 руб. серебромъ за слѣдующіе 6* дней маляру и 1'2 дней
77
плотнику. Спрашивается, сколько получаетъ въ день .маляръ, и сколько
плотникъ ?
Пусть ж дневная плата маляру,
у - - плотнику.
За і 0 дней первому слѣдуетъ 1 Ох рублей,
За іб дней рторому - 1 бу - ,
что составляетъ:
1) 1 Ож-ч -16у=23;
а во второй разъ:
6ж-+-12у=15, или
2) 2х-+- 4-у= 5.
Помножимъ второе уравненіе па 4, и вычтемъ изъ перваго, останется:
2х=3, или
х=1,50 рубля.
Потомъ, помножимъ второе уравненіе на 5, и вычтемъ изъ него первое, выйдетъ:
4у=2,
у=0,50 рубля.
П такъ, маляръ получаетъ 1 руб. 50 копѣекъ серебромъ, а плотникъ только
50 копѣекъ, въ каждый депь.
Задача 5. — Два купца продали нѣкоторый товаръ, одинъ по 8 ру-
блей за пудъ, а другой по 9 рублей. Первый говоритъ: еслибы я про-
далъ еще треть твоего товару по своей цѣнѣ, то получилъ бы 2-56
рублей; а другой отвѣчаетъ: еслибы я продалъ еще * твоего товару
по моей цѣнѣ, то получилъ бы 210 рублей. Требуется узнать, сколько
пудовъ продалъ тотъ и другой, и на какую сумму?
Пусть первый продать х пудовъ,
и второй - у пудовъ.
Если къ первому числу придать д- втораго, то за весь товаръ, по 8 рублей
за пудъ, первый получилъ бы
(жч- з у) 8=256 рублей.
Л если ко второму числу у придать перваго, то за весь товаръ, по 9 ру-
блей за пудъ, второй купецъ получилъ бы
(ун- ж)9=270 рублей.
Эти два уравненія можно сократить, первое па 8, а второе на 9; онѣ, по со-
кращеніи, будутъ:
ж-Ц-У=32,
у-ь|-ж=30.
78
или
З. г-+- «/=96 |
, । вычтемъ нижнее
«/-Ьт--г=30'
и 4
1
114 «3=66, откуда
.7—24 пуда
1
Подставимъ 81 о въ «/н-уа=:30, найдется
у—24 пуда.
II такъ оба купца продалп одинакое число пудовъ. *
первый получилъ . 24.8=192 рубля,
а второй 24.9=216 -
Задача 6. -- Купецъ имѣетъ два сорта чаю, по 2* руб. сере'бр. за
фунтъ, и по рубля за фуптъ; онъ щселаепіи оба сорта смѣшать
въ такомъ содерзкан, і, чтобы вышло 100 фунтовъ, по 3 рубля сер. за
фунтъ. Спрашивается: сколько фунтовъ надобно взять перваго < орта,
и сколько втораго для составленія смѣси?
Пусть нужно взять х фунтовъ перваго сорта,
у - втораго сорта,
а всего: 1) ж-+-«/=100 фунтовъ.
л шунтовъ перваго сорта стоитъ 29 х рублей,
„з
у - втораго - - 3, у
100 Фунтовъ смѣси по 3 рубля будутъ стоить 300 рублей; слѣдовательно
• 1 а
2;2 хч-3^у= 300, плп
2) 10 х+15 «/=1200
Помноживъ первое уравненіе на 10, п вычтемъ пзъ втооаго, найдется:
5^=200, или
у= 40 Фунтовъ
Послѣ того, пз'іь жч-«/=100, получимъ:
х=100—у~1 00—40
х= 60 фунтовъ
Стало-быть, д. ія составленія требуемой смѣси, надобно взять 60 фунтовъ
чар> перваго сорта, и 40 фунтовъ втораго.
Задача 7. — Нѣкто, имѣя капиталъ 25000 рублей серебромъ, одну
часть ею отдаеіпъ въ проценты по 5°- со 100 въ годъ, а другую но 4"-,
и со всего ятою капитала получаетъ въ годъ /130 руб.Іен процентовъ.
Узнать, какъ велики эти части капитала?
79
Пусть х первая часть, по 5",
у вторая часть, по 4^.
Обѣ части составляютъ весь капиталъ
1) я-ьу—25009 рублеіі.
Годовые проценты съ этихъ частей капитала найдутся изъ пропорцій:
100 :
Сумма этихъ процентовъ равна 1160 рублямъ; посему
- 4160, илп
100 100
2) 5ж-ь 4у =116000.
Помножимъ первое уравненіе на і, п вычтемъ пзъ втораго:
5х-ь4у=116000
&х-+-Ьу= 1 000 О О
а = 16000
Это подставимъ въ а:-4-у=25000, найдется
у— 9000.
С .ѣдователыю первая часть капитала 16000, а вторая 9000 руб. серебромъ.
Задача Я — Три ората должны заплатитъ общій долгъ въ .5000
рублей, по ни одинъ изъ нихъ не имѣетъ столько денегъ, чтобы, могъ
заплатить весь долгъ. Первый говоритъ второму: дай мнѣ половину
твоихъ денегъ, я заплачу, весь долгъ; второй говоритъ третьему: дай
мнѣ треть твоихъ денегъ, я также заплачу весь долгъ; если первый,
дастъ, третьему четверть своихъ денегъ, то и онъ берется заплатитъ.
Спрашивается, сколько денегъ было у каждаго?
Здѣсь находятся три неизвѣстныя, а именно:
х рублей у перваго брата,
у - у втораго,
г - у третьяго.
По условіямъ задачи, тотчасъ составятся три уравненія.
хч-~у=5000, или 2жч-у=ЮООО,
у-ь^=5000, Зуч-=15000,
гч-1а=5000, 4я-+-л;=20000.
4
Помножимъ второе уравненіе па 4, п вычтемъ изъ него третье, останется:
42у—я;=40000;
80
это помножимъ на 2, и сложимъ съ первымъ, получится:
25^=90000, откуда
. у— 3600 рублей.
Потомъ, изъ 2хч-у= 10000 найдется
я— 3200 рублей;
а зто подставивъ въ 20000, поіучпмъ
4200 рублей.
И такъ, первый братъ имѣетъ 3200 рублей, второй 3600 руб., а третій
4200 рублей.
. Задача 9. — Куплено 60 четвертей ржи, 30 четвертей ячменя и 45
четвертей пшеницы на 525 рублей серебромъ; во второй разъ куплено
80 четвертей ржи, 40 чет. ячменя и 50 четв. пшеницы, по тѣмъ же
цѣнамъ, на 650 руб. серебромъ, въ третій разъ куплено 70 чет. ржи,
20 ячменя и 35 пшеницы, на 465 рублей серебромъ. Узнать, сколько
'ублей платили за четверть ржи, четверть ячменя, и пшеницы ?
Положимъ, что платили:
х рублей за четверть ржи,
у - - ячмепя, •
х - - - пшеницы.
Слѣдовательно, въ первомъ случаѣ,
60 чет. ржи стоятъ 60ж рублей,
30 чет. ячменя - 30г/ -
45 чет. пшеницы - 45.й -,
а все вмѣстѣ:
60ам-30у-ч-45я=525 рублей,.
Во втузомъ случаѣ нашли бы:
8 0ам-40ун-50;х—650;
въ третьемъ: 70я,-+-20ун-355=465
пли:
1) 4ж-+-2у н- Зя= 35,
2) 8жч-4у н- 5х= 65,
3) Мх-і-іу н- 7г— 93.
Помноживъ первое уравненіе па 2, и, вычтя изъ пего второе, получимъ сразу:
я=5 рублей серебромъ.
Это подставимъ во 2) и 3), и вычтемъ 2) изъ 3), найдется:
6ж-ьЮ=28
»
х~3 руб. серебромъ.
Чрезъ подстановлепіе х^-3, х=5, въ первое уравненіе, полуппмъ. наконецъ,
У~4 руб.
81
Отсюда заключаемъ, что за четверть ржи платили 3 рубля, за ячмень 1, а
за пшеницу 5 рублей серебромъ.
Задача 1С. — Нѣкто держитъ въ рукѣ три карты, между кото-
рыми нѣтъ ни одной фигуры, и говоритъ; у меня на двухъ первыхъ кар-
тахъ столько очковъ, сколько на третьей и егце 15; на первой и третьей
столько очковъ, сколько на второй и еще 5; а на второй и третьей
столько, сколько на первой безъ одного. Узнать: какіе эти карты/
Пусть х число очковъ на первой картѣ,
у - - на второй
% - - на третьей
Здѣсь получаются уравненія:
1) ж-Н/—л-і-15,
2) хч-^—уч- 5,
3) 1
Уравненія: 1)ч-2) даютъ а"=іО,
1)н-3) - у= 7,
2) 4- 3) - *= 2.
И такъ, эти карты: десятка, семерка и двойка.
Задача 11. — Находятся три капитала въ обращеніи: изъ нихъ
первый приноситъ извѣстные годовые проценты; другой капиталъ 2о00
рублями болѣе, его проценты со 100 единицею болѣе, и приноситъ го-
довой доходъ 200 рублями болѣе; третій капиталъ 3150 рублями
болѣе перваго, имѣетъ годовые проценты со 100 двумя единицами бо-
лѣе перваго, и приноситъ годовой доходъ 315 рублями больше перваго.
Требуется узнать, какъ велики эти капиталы, ц какъ велики съ нихъ
годовые проценты?
Пусть х первый капиталъ, у его проценты со 100;
то второй капиталъ долженъ быть
ж-ь2500, (у-ьі) его проц. со 100;
третій капиталъ
жч-3750, (у-+-2) - - - -
Годовые проценты съ этнхъ капиталовъ получатся изъ пропорціи:
100 : х=у :
юо
100 : ая-2500=у-+-1 :
100 : ж-ь3750=у-4-2 :
* 1ПП
ъ
82
А какъ проценты втораго капитала 200 рублями, и третьяго капитала 375
рублями болѣе перваго, то слѣдуетъ, что
(®-ѵ2500)(у-+-1) ау 1ОО —100 (я:-4-3730)(у-і-2) ау „ 100 - 100 ' 37э-
Отсюда получаемъ: 2500«/+- а?=17500, 3750у+-2ж=30000, или 5000у+-2ж=35000 і 3750«/+-2д=30000 | вычтемъ иижнее
1250у=5000,
У=* рубі §
у+-1=5 - -
«/-+-2=6 - -
Слѣдовательно, первый капиталъ находился въ обращеніи но 4-“, второй
по 5 третій по 6 А подставивъ у=4 въ уравненіе,
2500у+-я=:17500, найдемъ:
ж= 7500 руб. капиталъ первый,
ам-2500=10000 руб. капиталъ второй,
а?+-3 750=11250 руб. капиталъ третій.
Задача 12. — Опредѣлить постоянныя числа А, В, С, въ данномъ
уравненіе,
Лм В/!ч С(Я=М,
въ которомъ I и М величины перемѣнныя, одна отъ другой зависимыя,
когда извѣстно, что
для /=5, М= 1,
для /=10, М=10,
для /=15, М=30.
По первому значенію для і п М, имѣемъ
5А+-25В+- 125С= 1,
по второму, 10А+-100В+-1000С=Ю,
по третьему, 15А+-225В+-3375С=30,
пли:
А+- 5В -+- 25С = ц,
А+-10В+-100С=1,
А-ч-15В+-225С=2.
83
Вычтемъ первое уравненіе изъ втораго и третьяго, останется:
5В-+- 75 С= і, или Вч-15С~ ‘
5 25
10В-+-200С—' В-ь20С=—.
и ’ во
Изъ разности послѣднихъ уравненіи найдемъ:
5С—во» ьли С—йо’
Послѣ того, изъ уравненія, Вч-20С=г:-^-, получится:
В—А фпс— ®________А —’
30 -уЬ— 30 — 25 — іо’
Наконецъ, А~1—40В—100С=—А.
Для повѣрки, подставимъ найденныя числа въ уравненіе,
5А-+-35Вч-125С=^і, найдется:
10 25 125
------ка— -Ь “— , ИЛИ
5 О 280 ’
2 2 — •
И такъ рѣшеніе сдѣлано вѣрно.
Слѣдовательно данное уравненіе имѣетъ видъ:
Ч‘*г»‘’ч-і‘'=м-
Этотъ случай относится къ простому интерполированію рядовъ чиселъ,
возрастающихъ или убывающихъ по неизвѣстному закону, получаемыхъ изъ ка-
кихъ ии есть наблюденій разсматриваемаго явленія, посредствомъ которыхъ же:
лаютъ открыть законъ зтого явлеігя.
Изслѣдованіе формулъ , получаемыхъ чрезъ разрѣшеніе общихъ
уравненій первой сгепейи съ двумя НЕпзвѣстпйіми. Рѣшенія отрица-
а О
ТЕЛЬНЫЯ, ф, о, И НУЛЕВЫЯ.
1Ол_. Какъ при разрѣшеніи задачъ съ одною неизвѣстного, такъ и со многими
неизвѣстными, могутъ получаться рѣшенія положите іыіыя и отрицательныя, рѣ-
. а 0 '
шешя символическія^-, и сверхъ того рѣшенія пулевыя.
а) Одни только рѣшенія положительныя разрѣшаютъ вопросъ въ прямомъ
смыслѣ, въ какомъ предполагалось по даннымъ его условіямъ.
Ь) Отрицательныя рѣшенія показываютъ, что въ задачѣ находятся какія '
иибудь условія невозможныя, которымъ нельзя удовлетворить рѣшеніями поло-
жительными. Опѣ показываетъ также, какъ надобно измѣнить вопросъ, чтобы
всѣ рѣшенія были прямыя, положительныя, а именно, должно предъ неизвѣстною,
которая получилась съ знакомъ —, перемѣнить знакъ во всѣхъ уравне-
ніяхъ (85).
84
с) Рѣшеніе х= ьо также показываетъ, что въ задачѣ находятся усло-
вія противорѣчивыя или одно съ другимъ несогласныя, отъ которыхъ одно урав-
неніе дѣлается несовмѣстно съ другимъ. Для доказательства этого, возмемъ
только два уравненія:
ах-і-Ъу^^с,
а'х-ь-Ъ'у^с',
пзъ ньт-прыхъ (93) мы нашли я=~~Ц-,,
' ! аІ>‘—аЫ
_ асі—саі
У аЬ1— ЪаІ'
Полежимъ аЪ'—а'Ъ:=О, или получатся въ одно время х—<» , оо.
А, , аЬ'
чтобъ открыть, отчего это произошло, подставимъ а'=— во второе урав-
неніе; найдется:
аЬ'а: ___ <
—-----ѵ-Ь'у—с', ПЛИ
. Ьс'
ах-ь-Ъу=
Сравнивая это послѣднее съ первымъ даннымъ уравненіемъ, находимъ, что
здѣсь должно быть — =с, пли сЬ'—6с'=0. А какъ этого условія въ задачѣ
пѣтъ, то и слѣдуетъ, что два такія данныя уравненія несовмѣстны одно съ
другимъ.
Подобная же несовмѣстность откроется, если взять а=0, а'=0, либо 6=0,
6'=0. Въ первомъ случаѣ, гс=оо , у=-, а во второмъ у=оо , я:=^.
Принимая въ разсмотрѣніе только второй случай, уравненія сдѣлаются:
ах—с, а'х~с', или
с __________________________________с'
Х= а ~ а' ’
Этого равенства не было дано; слѣдовательно и уравненія несовмѣстны между
собою.
4) Рѣшеніе показываетъ: 1) либо неопредѣленность задачи,
2) либо что находится общій множитель въ числителѣ и знаменателѣ дробныхъ
выраженій для х, у, который для частнаго нредноложенія обращается въ нуль.
Это послѣднее мы видѣли (38); а потому разсмотримъ только первый случай.
Для сего, въ выраженіяхъ:
__сЬг — Ъс9 ас9—са9
аЬг—Ьа." аЬг—Ъаг ’
положимъ сЪ'—Ьс' п а6'=6а'; найдется х= ® , и въ то же время у= ? ; ибо,
если уравненіе сЪ'=.Ьс' раздѣлить на а6'=6а', то выйдетъ = ^,,или ас'~са!,
ас1—са'—О.
85
Въ слѣдствіе условій сЪ'=Ьс', аЬ^Ьа', откуда а'= с=
второе данное уравненіе а'х-е-Ь'у—с' обращается
аЬ'а .
въ —----г-Ь'у=Сг, Или
, Ьс'
ах-г-оу= — =с.
3 ь1
Слѣдовательно, при этомъ условіи, второе уравненіе выходитъ тождественно
съ первымъ, то есть, мы собственно имѣемъ только одно уравненіе съ двумя
неизвѣстными, а пе два. Но одного уравненія съ двумя неизвѣстными недоста-
точно для опредѣленія неизвѣстныхъ, отчего оно называется неопредѣленнымъ, а
потому вопросъ токого рода заключаетъ въ себѣ неопредѣленность.
е) Наконецъ, если взять с=0, с'=0, въ уравненіяхъ:
ах-л-Ьу—с
а'х-+-Ъ'у~с',
сЬ'—Ьс' Л ас'—а'е Л
то получимъ: Х—--—,т=0, у=—:—тг =0.
11 а'Ъ—а'Ь ’ 3 аЪ’—а'Ь
Здѣсь открывается также несовмѣстность; потому что данныя уравненія обра-
щаются въ
ах-+-Ъу—§, или агс——Ъу
а'х-е-Ь'у—Ъ а'х~—Ь'у, откуда
~ , или аЬ'=а'Ь.
а' ь' ’
Но этого равенства въ задачѣ нѣтъ, чѣмъ и доказывается несовмѣстность
уравненій.
о о
А еслибъ и это условіе, аЬ'=а'Ь, было дано; то получили бы х— - ,у = -,
зависящія отъ того, что тогда мы имѣли бы не два уравненія, а только одно
ах-і-Ьу=0 неопредѣленное.
Къ такимъ же слѣдствіямъ мы дошли бы, разсматривая символическія рѣше-
нія уравненій съ тремя и болѣе неизвѣстными.
Слѣдующая задача, при различнымъ условіяхъ, представляетъ рѣшенія вся-
каго рода.
103. Задача.—Два курьера выѣхали въ одно время изъ двухъ раз-
ныхъ мѣстъ А и В, и ѣдутъ по одной дорогѣ оба въ сторону В. Пер-
вый изъ нихъ проѣзжаетъ въ каждый часъ по т верстъ, а второй по п
верстъ. Узнать: на какомъ разстояніи АВ первый курьеръ догонитъ
втораго?
х
ІѴ В
а у
86
Назовемъ АВ—а извѣстное разстояніе между А и В; пусть В мѣсто, гдѣ
первый курьеръ догонитъ втораго, и положимъ АВ=х, ВК~^: то будемъ
имѣть:
' 4) х—ж=(і-
Первый курьеръ проѣзжаетъ т верстъ въ 1 часъ, то х верстъ проѣдетъ въ
нѣкоторое время I, которое найдется изъ пропорціи:
®
т: х—1 : і, 1=—.
’ т
Второй проѣзжаетъ п верстъ въ 1 часъ, слѣдовательно у верстъ проѣдетъ во
время А какъ времена ѣзды обоихъ курьеровъ равны, то
* X у
— = плп
т п ’
пх—ту, пли
2) пх—ту—О.
Разрѣшивъ уравненія 1) п 2), найдется:
ат ап
Х=-----, .
т—п ° т—п
Пока тп>п, оба рѣшенія остаются положительными, слѣдовательао
прямыми. Оба курьера съѣдутся въ мѣстѣ В, которое отстоитъ отъ мѣста А на
разстояніи п, а отъ В на разстояніи —чему и быть должно, потому что
задній курьеръ ѣдетъ скорѣе передняго, и непремѣнно гдѣ ннбудь догонитъ.
Но, если, т<п, то есть, скорость ѣзды задняго курьера менѣе скорости пе-
редняго, то обѣ неизвѣстныя получатся отрицательными:
—ат — ап
, 1/ =--‘
п—т п—т
Этимъ рѣшеніемъ и обличается то невозможное требованіе, чтобы первый
курьеръ догналъ втораго, когда онъ ѣдетъ меиеннѣе; по, съ тѣмъ вмѣстѣ, ука-
зывается, какъ надобно перемѣнить условія задачи, чтобы рѣшенія вышли по-
ложительными. Надлежитъ только перемѣнить знаки предъ х, у, въ данныхъ
уравненіяхъ, тогда будетъ:
—х-+-у=.а, или у—х —а, и
пх—ту—0,
и въ такомъ случаѣ надобно заставить обоихъ курьеровъ ѣхать не къ К, по въ
противную сторону, къ IV; разумѣется, что тогда курьеръ В догонитъ курьера
А, потому что ѣдетъ скорѣе
Теперь положимъ т=п, плп т—п—0, то получится:
№ ат ап ап
Х= ---- . Ч—---------= •
т—п О ” т—п О
Это символическое рѣшеніе произошло оть невозможнаго требованія въ за
дачѣ, чтобы первый курьеръ догналъ втораго, когда они ѣдутъ съ равными ско-
ростями.
87
Ежели т и п неравны, по а=0, то есть, что оба курьера выѣзжаютъ
изъ одного мѣста, то очевидно, что ихъ точка соединенія можетъ быть только
на этомъ мѣстѣ, и нигдѣ болѣе, потому что ихъ скорости различны. Въ этомъ
случаѣ
х=-------=А), у= -----=0.
Наконецъ, ежели а=0, и т=.п, то рѣшенія обратятся въ
о о
о ’ о'
п показываютъ здѣсь неопредѣленность въ задачѣ, потому что уравненія удо-
влетворяются всякими числами, взятыми на мѣсто х, у. Опа произошла отъ
того, что мы заставили курьеровъ выѣхать изъ одного мѣста (ибо а=0) въ одну
сторону и съ равными скоростями (іц=п), и хотимъ знать, гдѣ они съѣдутся
между собою. Очевидно, что они всегда будутъ ѣхать одинъ подлѣ другаго,, точка
съѣзда ихъ будетъ па всякомъ разстояніи х или у; оттого эти разстоянія опре-
дѣлились въ символическихъ выражейіяхѣ.
Задача.—Найти два такія числа х, у, чтобъ было
а С
х~ - . 4=0+
V
Изъ нихъ получаемъ:
1) ху=а
2) ху=Ьх-ѣс;
слѣдовательно, Ь с-+-с=а, откуда
О’ С 1 \ •
х= —это подставимъ въ 1):
,а—с,
ху— (- Л -)у—а, отсюда
а.Ь
У——
° а—с
Если взять а=с, то найдутся:
а аЬ
а=0, у= —=фо;
оттого- что, при этомъ условіи, выходитъ
ху~а ।
, несовмѣстность.
ху^=охч-а |
II подавно нельзя брать с> а; въ этомъ случаѣ
—(г— а} —аЬ
Х=-------, у=- ,
. 6 * с—а.
обѣ неизвѣстныя отрицательны.
Если 6=0, то =оо , у=0; тогда уравненія: ху=а, ху=Ьх-ѣс,
обращаются въ з#=а, ху=х; откуда «=с.
По, поелику а пе равно с; то символическое рѣшеніе показываетъ опять не-
совмѣстность уравненій
88
103. Мы знаемъ, что если въ уравненіяхъ съ двумя неизвѣстными,
ах-+-Ьу—с, а'х-+-Ь'у=с',
положить с=0, с'_0, то получатся:
сЬ'—Ьс' „ ас'—са' „
= • м —0, у= , =0.
аЬ—Ъа' ° аЪ'—Ьаг
Но, и въ уравненіяхъ съ тремя неизвѣстными:
ах -і-Ьу -+- сг— й,
а'л -і-Ъ'у-і-^я—д!,
а" х-+Ъ"у-і-с"я
положивши <2=0, гі'=О, <І"=0, получили бы =0, у=0, х=0; потому что
числители дробныхъ выраженій для х, у, г, помножены па й, й', й" (95).
Тоже самое получили бы мы и изъ всякой системы опредѣленныхъ уравненій
со многими неизвѣстными, въ которыхъ нѣтъ ни одного извѣстнаго члена. Всѣ
такія уравненія будутъ между собою несовмѣстны. Это общее правило приводитъ
васъ къ слѣдующему общему заключенію:
Если дано уравненіе
Ан-Вяч-Ос’-ъ Вл'3-ь... .=0,
расположенное по степенямъ нѣкоторой перемѣнной величины х, котораго кое-
фиціенты А, В, С, Б,... неизвѣстны и независимы отъ х, то какія бы числа
мы ни взяли на мѣсто х для опредѣленія коефпціентовъ, всегда получится:
А=0, В=0, С=0, Б=0„...
1О1. Это можно выводить и пе изъ общихъ формулъ. Возмемъ, напримѣръ,
уравненіе
АеВлм
только съ четырьмя неизвѣстными косфпціентами А, В, С, В, и представимъ,
что перемѣнное количество х обратилось въ у, я, и; то, для опредѣленія четы-
рехъ коефпціентовъ, получатся четыре уравненія-
1) А-д-Ва?-д-Сс!-4-В.г3=0
2) Лч-Вуч-Су8 4-Вг/3=0
. 3) Ач-В-гч-С^ч-Вя—О
4) Ач-Внч-Сн8ч-В«3=О.
Станемъ послѣдовательно вычитать изъ перваго уравненія второе, третье и
четвертое:
1)-2) в^-^н-С^—^)ч-В(л:э-?/3)=0
1)—3) В(ж—х)ч-С(л?8—2®)-ьВ(л:3—х”)=0
1)—4) В(я-«)ч-С(гс’—м2)-ьВ(гс —«3)=0.
89
Раздѣлимъ первое изъ сихъ уравненій на х—у, второе на х— г, третье
на х—и:
ВчС (ж—і—у)—і—В (гс8ччсуч-у8)=О
Вч-С {гсч-х )ч-В (хгч-хх-+-га)=0
Вч-С(л:ч-г/)ч-В (ж,ч-гсмч-м!)=0.
Здѣсь вычтемъ второе и третье уравненія изъ перваго:
С(у--2 | ЧІ>(Ху-і-у*-Х2 —х*)=0
С(у—?()ч-В(жуч-у8—хи—«*)=0
или
Сч-В (іч-уч-х) =0
Сч-В (жч-уч-н)=0.
Чрезъ взаимное вычитаніе послѣднихъ, находимъ:
В(х—и)=0.
Но какъ х—и не нуль, то необходимо В=0.
Послѣ сего, изъ Сч-В(жч-уч-х)=0, выходитъ С=0; пзъ Вч-С(гсч-у)-ь
ч-В(я> ччсуч-у’)=0 слѣдуетъ, что В=0; а наконецъ изъ (Ѵч-Вхч-Сж’ч-
ч-Вж’=0 получается А=0.
Изъ всего этого проистекаетъ общій законъ относительно равенства много-
членовъ :
Два многочлена, расположенные по степенямъ одной и той же буквы
х, представляющей нѣкоторую перемѣнную величину, могутъ быть
равны между собою, при всякихъ измѣненіяхъ х, только тогда, когда
численные коефиціенты, помножающіе равныя степени х, будутъ равны
между собою.
Положимъ, что должны быть равны между собою многочлены
АчВл ч-О !ч І).г3ч-...=ач-6я:ч-ся:/ч-гіж3ч-....,
независимо отъ величинъ перемѣнной х, которыхъ коефпціенты А, В, С...,
а, Ь, с,... ностоянны и независимы отъ х; то, перенеся всѣ члены въ одну
часть уравненія
(А—а)ч-(В—5)а;ч-(С—с)агч-(В—й)гс’ч-... .=0,
мы приводимся къ предыдущему случаю; и чтобъ это равенство могло быть для
всякой величины, какую бы х ни получилъ, необходимо нужно
А—а=0, В—6=0, С—с=0, В—і/=0,...
Этотъ простой я весьма замѣчательный закопъ открытъ первоначально Де-
картомъ, и весьма часто употребляется въ Алгебрѣ. Нельзя говорить теперь
объ его употребленіяхъ; по мы увидимъ ихъ впослѣдствіи. Онъ извѣстенъ водъ
именемъ начала неопредѣленныхъ предстоящихъ.
90
ІИ. НЕРАВЕНСТВА. ИЗСЛѢДЫВАНІЕ ФОРМУЛЪ ПОСРЕДСТВОМЪ
НЕРАВЕНСТВЪ.
105. До сихъ поръ мы изслѣдывали формулы, выводимыя изъ различныхъ
вопросовъ, только чрезъ измѣненіе величины данныхъ количествъ, означаемыхъ
буквами а, Ь, с,....; но тѣ же формулы можно еще изслѣдывать другимъ обра-
зомъ, а именно: искать, при какихъ данныхъ неизвѣстная можетъ сдѣлаться
положительною или отрицательною, цѣлою илп дробью, и въ какихъ предѣлахъ
данная формула имѣетъ это свойство. Для сего надобно умѣть данныя количе-
ства подчинять желаемымъ условіямъ равенства или неравенства, и изъ этихъ
условій стараться, посредствомъ преобразованій, найти предѣлы, между кото-
рыми тѣ количества могутъ удовлетворять нашимъ требованіямъ. Мы знаемъ
главнѣйшія преобразованія равенствъ; теперь разсмотримъ свойства неравенствъ,
ихъ преобразованія и начальныя употребленія.
106. Когда сличаются между собою количества неравныя, то, обыкновенно,
пишутся сряду, и отдѣляются знакомъ > (больше), либо < (меньше): выра-
женіе такого рода называется неравенствомъ. Напрпш.
ан-2б> 5с—й, или
5 с—й<а-+-26.
Все количество, по лѣпую сторону знака > или <, называется первою ча-
стію неравенства, а количество съ правой стороны — второю часпг'ю не-
равенства.
Тѣ же самые знаки употребляются иногда перечеркнутые, и и выгова-
риваются : не больше, не меньше. Напримѣръ, если надобно означить, чтобы
число а было не больше 40 и пе менѣе 3, то пишется:
а>10, а-ф^З.
109. Части неравенства могутъ быть обѣ положительныя, плп обѣ отрица-
тельныя, либо одна положительная, а другая отрицательная. Наприм.
а>б, —р">—д, 8>—г;
только нельзя написать —•'>«, потому что всякое количество отрицательное
менѣе положительнаго.
108. Надъ неравенствами можно дѣлать почти всѣ тѣ же преобразованія,
какія дѣлаются надъ равенствами или уравненіями; но есть нѣкоторыя Йреобра
зованія, только пмъ свойственныя.
I) II6 оѵіьимъ частямъ неравенства можно придавать, или изъ нихъ
вычитать, равныя количества; отъ этого знакъ неравенства не пере-
мѣняется. Напримѣръ, если 15> 8, то и
91
45ч- 5>8ч- 5, то есть, 20>13;
15— 5>8— 5, - - 10> 3;
15—18>8—?8, -----------3>—10-
Если —5 <—3, то и —5ч-7 <—Зч-7, или 2 <4
—5—2 <— 3—2, или —7<—5.
Это свойство показываетъ, что можно всѣ члены неравенства переносить
въ первую или во вторую часть его, съ противными знаками, какъ въ уравне-
ніяхъ. Нанрим. 7> 3 можно панпсать 7—3> 0;
—10<—6 можно написать 0<10—6, или 40—6>0.
2) Можно обѣ части неравенства' помножить или раздѣлить на
какое угодно положительное число; отъ этого знакъ неравенства не пе-
ремѣнится.
Нанрим. если а <6, то и ат>Ьт, это очевидно.
3) Знакъ неравенства перемѣнится, пли это неравенство помножить
или раздѣлить на какое ни есть отрицательное число. — Напримѣръ,
а. Ь
если а> Ь, ат> Ьт, —>—; то, перенеся части послѣднихъ двухъ въ противныя
стороны, получимъ:
, Ь а
—от>—ат,-------->----: то есть,
—ат<—ѵт,--------<----, или
’ т иг’
«(—т)<6(—т),
11 такъ, отъ помноженія неравенства а> 6, и отъ раздѣленія па —т, знакъ
неравенства перемѣнился. Примѣры: І2> 6, —10>—15;
по 12(—2)<6(—2), то есть, —24 <—12;
—ю —іа „
, то есть, 2<3.
Отсюда видно, что, при перемѣнѣ знаковъ вредъ всѣми членами неравенства
(т. е. при помпожепіп на —1), должно перемѣнять и самый знакъ неравенства.
Иапрпм. 5>2, по —5<—2.
4) Положительны я неравенства согласныя, то есть, имѣющія тотъ же
знакъ > или <, можно слагать между собою, перемножать и возвы-
шать въ положительныя степени, какъ равенства или уравненія, безъ
перезиыіы знака неравенства. Напрнм. если
а> а', 6> V. с> с', то и
ан-6 і-с> а'ч-б'ч-с'; также и
аЛс> а'Ь'с'.
А полагая а~Ь~с, а:—1)'=с', найдется:
а’><Л
Все это очевидно, и не требуетъ пи какихъ объясненій
92
Если въ неравенствѣ находится одна часть положительная, а другая
отрицательная, то его знакъ не перемѣнится при возвышеніи въ сте-
пени нечётныя; но можетъ перемѣниться отъ возвышенія въ степени
чётныя. Наприм. 5>—3, 5*>(—2)®;
по 5>— 7, 5*<(—7)*.
Знакъ неравенства всегда перемѣняется отъ возвышенія обѣихъ ча-
стей еъ степени отрицательныя.
Наприм. если а>6, то а-3<6-3; это потому, что
, 1 , . 1.
а 3 = Ь 3 ——’
ая Ь!
по а> Ь, слѣдовательно <р-
5) Нельзя позволить вычитать одно неравенство изъ другаго, имѣющаго тотъ
же знакъ; потому что большая часть неравенства уменьшаемаго можетъ иногда
скорѣе истощиться, нежели меньшая, и тогда знакъ неравенства долженъ пере-
мѣниться. Напримѣръ, если станемъ
изъ 5> 3 8> 7
вычитать 3> 2 6> 2, получимъ
2> 1 2<5.
6) Но, можно вычитать одно неравенство изъ другаго, имѣющаго
противный знакъ; отъ этого составится неравенство, имѣющее знакъ
неравенства уменьшаемаго. — Для доказательства, возмемъ
а> Ъ, с<^д,.
Но, если с меньше д, то можно положить —к, и это равенство вычесть
изъ а>Ъ; получится:
а—с> Ь—сі-і-к, слѣдовательно, и подавно
а—с> Ь—<і
7) Неравенства между числами положительными, имѣющія различ-
ные знаки, можно дѣлить одно на другое; въ частномъ помучится не-
равенство съ тѣмъ же знакомъ, какой былъ въ неравенствѣ дѣлимомъ.
Напримѣръ, если а>6, с<й, то будетъ
а Ь
а.
Въ самомъ дѣлѣ, положимъ стй—к, и на это равенство раздѣлимъ а >6;
а Ь
будетъ:
Но вторая дробь сдѣлается еще меньше, если увеличить ея знаменатель, от-
. , п Ь
оросивъ п; слѣдовательно ->-•
93
109. Изъ четырехъ первыхъ свойствъ видно, 1) что всякое дробное нера-
венство можно приводить къ общему знаменателю, и этотъ знаменатель отбра-
сывать, какъ въ равенствахъ или уравненіяхъ; 2) что, перенося члены изъ одной
части неравенства въ другую съ противными знаками, можно освободить какой
угодно членъ, а изъ этого члена какую угодно букву отъ ея коефиціеііта (чрезъ
дѣленіе). Для примѣра, положимъ, что надобно освободить х изъ неравенства
2а -+-6 Ій—с
зс
Приведемъ обѣ части къ общему знаменателю, и откинемъ его :
5б(2ж-ьб)> Зс(4й—с), или
106ж-ь56’> 12с(І—Зс®; отсюда
10&с>12сй—56®—Зс\ и, наконецъ,
І2сй—В6’-3с!
х>-----іо*----•
110. Приложимъ теперь свойства неравенствъ къ изслѣдыванію формулъ,
выводимыхъ изъ рѣшенія алгебрическихъ вопросовъ съ одною и съ двумя неиз-
вѣстными. <
1) Дана формула х~ <0 паити, какія цѣлыя числа падоопо брать
вмѣсто а, чтобъ х оставался всегда положительнымъ, и въ какихъ предѣлахъ?
Для этого падобпо, чтобъ числитель и знаменатель бы..п оба положительные
или оба отрицательные; а потому
2ан-4> 0, либо 2ач-4 <0
10—За>0 10—За<0.
Изъ первыхъ двухъ неравенствъ имѣемъ: а> —2, а <3 *; а изь двухъ послѣд-
нихъ: а <—2, а> 3Этотъ послѣдній выводъ заключаетъ въ себѣ противорѣчіе,
и потому невозможность; а выводъ первый даетъ настоящіе предѣлы, между ко-
торыми заключаются всѣ цѣлые числа, дѣлающія х положительнымъ. Предѣлъ
—2 называется нижнимъ, а предѣлъ 3* высшимъ. Въ самомъ дѣлѣ, взявши
числа —1, О, 1, 2, 3, на мѣсто а, получится:
2 2 в
*=Гз’Г’7’ 2’ 10*
Вообще, если предѣлы имѣютъ противные знаки, и нѣтъ противорѣ-
чія, то всѣ положительны я величины для х зависятъ отъ чиселъ, за-
ключающихся только между этими предѣлами.
п » , 4—2а ,
2 Дана формула х~ —_3а; паити, какш надобно брать числа цѣлыя, поло-
жительныя, на мѣсто а, чтобъ х оставался положительнымъ, и въ какихъ пре-
дѣлахъ?
Беру опять: 4— 2а>0, 'либо 4—2а <0,
10—За>0 10—За<0;
и нахожу: а<2, а<3з , и также а>2, а>3*.
94
, Такимъ образомъ получились два предѣла въ сторону знака <, и два предѣла
въ сторону зпака > ; изъ нихъ предѣлъ <33 включается въ нижнемъ <2, а
предѣлъ > 2 включаетсп нъ высшемъ > З3 . Пачппап отъ этихъ предѣловъ <2
и >3^, можно брать всѣ числа для а, чтобы х оставался положительнымъ.
3) Если, при изслѣдованіи формулы, встрѣтится такое противорѣ-
чіе, которое нельзя исправить г перемѣною знака неравенства въ чи-
слителѣ и-зиаменателѣ, то оно покажетъ, что для х нѣтъ ни одного
рѣшенія положительнаго. Для примѣра возмемъ формулу:
аМ-1
аГ==2а—аа—7
Въ пей а*-4-4>0 возмо'жпо, но 2а—а!—1>0 невозможно, потому что
2а—о —1=—(а—4)* существенно <0. Но, если знаменатель меньше пуля,
то нельзя взять а’ч-1 <0. II такъ, х не имѣетъ положительныхъ рѣшеній, какое
бы число пи взяли па мѣсто а.
4) Найти, для какихъ цѣлыхъ чиселъ а и Ь формула
13—2а—36
аг=--------
За —5—6
даетъ рѣшенія положительпын.
Для этого возмемъ сперва 15—2а—36>0.
За— 5 — Ъ > 0.
Члены За, —2а, съ противными знаками; ихъ можно исключить, по-
множивъ первое неравенство па 2, а второе па 3, и сложивъ; получится
35—И6> 0,откуда
6<3Г1-
Нельзя исключить Ъ такимъ же образомъ, потому что члены —36, —Ь въ
неравенствахъ съ равными знаками; но можемъ найти
ів—зь
а>-——изъ перваго неравенства,
3-+-Б
а>-у изъ втораго неравенства.
Если Ъ не пуль, то оно —.1,2,3.
Для Ъ=А, а <6 и >2, то есть. а=3, 4, 5;
6=2, а<4* и >2;,, то есть, а—2, 3, 4;
6=3, а<3 и >2?, то есть, а=2.
О
95
Если взять 15—2а—ЗЬ <0, За—5—6<0, то нашли бы:
6> 3 —, а>— - - и < напримѣръ,
для Ь=5, а>0, а <5.
5) Найти, для какихъ чиселъ а и Ь формула о1— 3^1.5' Дастъ рѣшенія по-
ложительныя, которыя больше 1-цы?
Возмемъ: 8—2а-і 6>0, 2Ь—За—5>0, и еще
8—2а-ь6> 26—За—5.
Изъ послѣдняго находимъ: 13—і—а—6>0, а отсюда
а>6—13, или
За> 36—39;
Изъ втораго неравенства получаемъ За<26—5. Это послѣднее можно вы-
честь изъ 3а>36—39, потому что имѣютъ противные знаки; останется:
0>6—34, или 6 <34.
Потомъ возмемъ неравенство 26—За—5>0, и вычтемъ изъ него 6 <34.
помноживъ зто на 2; останется:
—За—5>—68, или За-ь5<68; откуда
а <21.
2
Таковы предѣлы для 6 и а. Положимъ а=20, 6=30; найдется х=і~.
г, , ' сЬ'—с'Ь ас'—а'с
6) Возмемъ формулы х=—,——, у— —т-, выведенныя изъ уравненіи
' 1 г аЬ'—а’Ь1 17. аЬ'—а'Ь
ах-і-Ьу^с, а'®-ь6';/=с', и поищемъ условія, при которыхъ будетъ х>у,
предполагая х, у, положительными.
Для этого возмемъ сперва
сЬ’У-с'Ь, ас'>а'с, аЬ’>а'Ь, либо с6'<с'6, ас'<а'с, аЬ'<а'Ь
сЬ'—с'Ь^>ас'—а'с. и сЬ1—с'Ь <ас'
Раздѣливъ сЬ'>с'Ь па а'с-^ас', найдется третье условіе аЬ'уа'Ь (либо
аЬ'<а'Ь пзъ условій обратныхъ). Изъ этого видно, что достаточны только
условія:
а) а6'>а'6, сЬ'—с'Ь^хіс'—а'с, либо /?) аЬ'<а'Ь и сб'—с’Ь<ас'—а'с.
Взявши произвольно пять чиселъ- а, а', 6, 6', с, и пріискавъ къ пимъ
шестое с', чтобъ удовлетворялось неравенство а) или /?), составятся два уравне-
нія, въ которыхъ х, у, будутъ положительными, и понтомъ ж>у.
96
В. КОГДА ЧИСЛО НЕИЗВѢСТНЫХЪ БОЛѢЕ ЧИСЛА УРАВНЕНІЙ. НЕОПРЕДѢЛЕН-
НЫЙ АНАЛИЗЪ ПЕРВОЙ СТЕПЕНИ.
111. Предположимъ, что для разрѣшенія какого нибудь вопроса дано будетъ
число неизвѣстныхъ болѣе числа уравненій: такой вопросъ останется неопредѣ-
леннымъ, потому что число уравненій недостаточно будетъ для опредѣленія
этихъ неизвѣстныхъ. Положимъ, напримѣръ, что даны два уравненія съ тремя
неизвѣстными х, у, х: изъ этихъ уравненій можно исключить только одну не-
извѣстную, наприм. х, и тогда выйдетъ одно уравненіе съ двумя неизвѣстными
х, у, изъ котораго нельзя опредѣлить пи ту, пи дугую, потому что одна изъ нихъ
всегда будетъ выражаться посредствомъ другой.
Пусть дано уравненіе 2^ч-3ж=5. Изъ него имѣемъ Но
этотъ у все-же неопредѣ чепъ, потому что х неизвѣстенъ. Оттого, если давать
неизвѣстной х различныя опредѣленныя величины, столько же разныхъ вели-
чинъ получится и для у. Наприм.
полагая а—0, 1, 2, 3,....
1 1
найдется ?/=2—, 1, —-, —2,....
Каждая величина для х, и ей соотвѣтственная величина для у, удовлетво-
ряютъ данному уравненію. Слѣдовательно, уравненія съ двумя неизвѣстными
(/опускаютъ безчисленное множество рѣшеніи.
Поелику у совершенно зависитъ отъ х, и -измѣняется съ перемѣною сего
послѣдняго; то говорятъ, что у есть функція отъ х, и на оборотъ. Числа
2, 3, 5, въ уравненіи 2уч-3а?=5, называются постоянными, а х, у, пере-
мѣнными.
1158. Хотя уравненія такого рода допускаютъ безчисленное множество рѣ-
шеній; но, въ задачахъ, очень часто необходимо нужно бываетъ ограничивать
это множество рѣшеній слѣдующими условіями: е
1) Чтобы рѣшенія были прямыя, т. е. положительныя; 2) чтобы всѣ онѣ
были цѣлыя; и 3) чтобы величина одной изъ пеизвѣстпыхъ была не больше, или
пе менѣе нѣкоторой данной.
Этими условіями весьма ограничивается число рѣшеній, такъ что оно бываетъ
иногда безконечное, но часто получается небольшое число рѣшеній, и даже пи
одного. Такъ, напримѣръ, въ предыдущемъ уравненіи 2і/-і-3«с=:5, всѣхъ рѣ-
шеніи безчисленное множество; но рѣшеній цѣлыхъ и положительныхъ для х, у,
тТглы:'іо'одио,-а именно; х=:1, у—1. -
97
113. Вотъ признакъ, по которому можно угадывать сразу, допускаетъ ли
даппое уравненіе, ах-+-Ьу=с, рѣшенія въ цѣлыхъ числахъ, или пѣтъ:
Оно не допускаетъ рѣшеній въ цѣлыхъ числахъ, когда коефиціенпіы
а, Ь, предъ неизвѣстными имѣютъ ооийй множитель, а извѣстный
членъ с его не содержитъ.
Пусть этотъ общій множитель Іі, такъ что а—а'Іі, Ь^хЬ'Іі; тогда уравненіе
ах-\~Ьу—с обращается въ а'Ііх-+-Ь'Ііу=:с, или
а'х ч- Ь'у = ' -.
Если а', //, цѣлыя числа, с и Іі числа первыя между собою; то дробь не-
сократимая. Какое бы цѣлое число мы пи взяли па мѣсто у, всегда х полу-
чится дробнымъ. Слѣдовательно, такое уравненіе не допускаетъ ни одного рѣ-
шенія, гдѣ бы въ одно вр^мя х, у, были цѣлыми. Таково наприм. уравненіе
6ж—12у=7;
и такія уравненія надобно тотчасъ оставлять безъ разыскиванія цѣлыхъ рѣшеній,
потому^ что оно ихъ не содержитъ.
ІИ. Найти всѣ рѣшенія цѣлыя и положительныя, удовлетворяю-
щая данному уравненію, ал-*-Ьух=.с, съ двумя неизвѣстными.
Надобно изъ этого уравненія освободить ту неизвѣстную, при которой нахо-
дится меньшій коефиціентъ, раздѣливши па него всѣ члены дѣйствительно: тогда
эта неизвѣстная, вообще, выразится цѣлыми членами и при нихъ дробями. А
какъ дробей не должно быть, то надобно соединить ихъ вмѣстѣ, и сумму ихъ
означить буквою I, представляющею цѣлое число. Такимъ образомъ получится
второе уравненіе съ меньшими коефиціентами, содержащее вторую неизвѣстную,
и новую неизвѣстную I. Пзъ этого втораго уравненія надобно освободить вторую
неизвѣстную, раздѣливъ дѣйствительно всѣ члены пася коефпціенты: она также
выразится цѣлыми членами и дробями при нпхъ. Дроби падооно соединить вмѣстѣ,
и сумму ихъ означить другою буквою I', представляющею также нѣкоторое цѣлое
число. Отъ сего получится третье уравненіе, содержащее только I, і'. Пзъ
этого уравненія должно освободить I, отдѣлить цѣлые члены оі ь дробей, и сумму
дробей означить буквою I", п продолжать все то же дѣйствіе до тѣхъ поръ, пока
одна изъ буквъ Іп выразится одними цѣлыми членами. Тогда, возвращаясь
отъ послѣдняго уравненія къ предпослѣднему, отъ этого къ слѣдующему, п
дѣлая въ нихъ подстановлепія, мы наконецъ дойдемъ до того, что неизвѣстныя
х, у, выразятся также цѣлыми членами, содержащими числа и самую послѣд-
нюю букву .
Получивши эти выводы, падобноу По способу неравенствъ, (Ю), отыскать
предѣлы, между которыми послѣдняя‘бита іп+і даетъ-въ одно время для
7
98
х, у, рѣшенія положительныя: между этими предѣлами будутъ находиться всѣ
искомыя рѣшенія.
Задача.' 1.—Раздѣлить число /54 на двѣ части А и В такія, чтобы
первая дѣлилась безъ остатка на 5, а вторая на 13.
Пусть А:5=ж, В: 13=у; то
А=5я?. В=13у.
Но, А-1-В=124; слѣдовательно,
5^4-1 Зу=124.
Освободимъ х, при которомъ стоитъ меньшій коефиціентъ,
124—іЗу 4 а 3
х=—-— =24-+- - —2у— —у, или
д;=24—2у-ь^.
__ , 4—Зи
Поелику х должно быть цѣлое, то —-— не должно быть дрооью: а потому ва-
зогемъ его буквою I, отчего выйдетъ:
1) а=24—2у-і-1, и условное уравненіе
которое освободимъ отъ знаменателя, 51=4—Зу, и изъ котораго найдемъ у:
4—31 . .1-21
’ 1—21
Но у цѣлое число, то и дробное выраженіе —— должно быть цѣлымъ чи-
сломъ, которое посему назовемъ буквою I'; получится
2) у=1—1-+-11,
4—2^
и второе условное уравненіе 1 ———, или З1'=1—21, откуда освободимъ
Но н і цѣлое число, а потому и —— должно представлять нѣкоторое цѣлое
же число, которое назовемъ буквою і"; тогда будемъ имѣть:
3) і=—і'ч-і1',
1~г' .іг *
и новое условное уравненіе —— — изъ котораго найдется:
4) 1'.=1—21".
Такимъ образомъ і' выразилось цѣлыми членами. Возвращаясь назадъ, под-
ставимъ въ 3) уравненіе на мѣсто I' его величину, получимъ:
і=—14-31".
Величины I, і', подставимъ въ 2) уравненіе, и наконецъ величины у и і1 въ
1) уравненіе, найдутся:
у=3—51",
*=174-13<".
Ѵ9
Нашедши для х, у, выраженія въ цѣлыхъ членахъ и въ функціи нѣкотораго
цѣлаго числа I", поищемъ теперь предѣлы для і", между которыми должно брать
для него цѣлыя числа, чтобы найти для х, у, всѣ рѣшенія цѣлыя и положи-
тельныя.
Для этого надобно составить неравенства:
3— 5«">0, откуда
17ч-13/">0 <">—и
Изъ этого видно, что для і" можно брать цѣлыя числа только 0, и —1.
Въ самомъ дѣлѣ,
для 1= 1, 0, —1, —2,... получится:
у=— 2, 3, 8, 13,...
х= 30, 17, 4, —9,...
Здѣсь возможны только два рѣшенія въ числахъ цѣлыхъ и положительныхъ,
а именно:
у=3, х=17,
либо у=8, &= 4.
Слѣдовательно, число 124 можно двоякимъ образомъ раздѣлить на двѣ такія
части А и В, чтобы первая дѣлилась безъ остатка на 5, а вторая на 13.
Въ первомъ случаѣ:
А= 5-г= 5.17= 85
В—13у=13. 3— 39
А+-В=124.
Во втор жъ случаѣ
А= 5Х= 5.4= 20
В=13у=13.8=104
Ач-В=124.
Задача 2. Промѣнять 100 рублей серебромъ на кредитные билеты
въ 3 и 5 рублей серебромъ.
Пусть х число билетовъ въ 3 рубля,
у - - - 5 - ; то
3®-і-5у=100 .
Освободимъ х, у котораго меньшее предстоящее:
100-3& 00 1-2^
^=—з—=33-з/-і——
1__2у
А какъ х должно быть цѣлое число, то —должно быть такъ же цѣлое,
которое и назовемъ буквою I; получится:
1) а=33—у-+-1, і=^^, или
3/=1—2у.
100
Изъ послѣдняго уравненія освободимъ у:
' 1 — 31 1-1
у— —--------1-\-И ПОЛОЖИМЪ
2 2
„ , . 1—1
2) у=—1-+-1, и I——отсюда
3) 1=А— 2і'.
Сдѣлавъ подстановленіе въ уравненія 2) и 1), получимъ, наконецъ
х= 35—5/',
У=— і+з/'.
Числа х, у, должны быть цѣлыя и положительныя, слѣдовательно:
35—5/'>0, откуда /'<7,
—1чЗ/>0 /'>’•
о
Откуда видно, что цѣлыя числа для /' можно брать только 1, 2, 3, 4, 5, (5,
и тогда получинъ: /' = 1, 2, 3, 4, 5, 6;
х = 30, 25, 20, 15, 10, 5;
у — 2, 5, 8, 11, 14. 17.
ІІ такъ, шестью только разными способами можно размѣнять 100 руб. сере-
бромъ на кредитные билеты въ 3 и въ 5 руб. серебромъ; то есть, можно взять
30 первыхъ и 2 вторыхъ, либо 25 первыхъ и 5 вторыхъ, и т. д. Все это оправ-
дывается повѣркою; наприм. если я возму 10 билетовъ трехоублевыхъ и 44
пятирублевыхъ, то сумма ахъ дастъ:
10.3 4-14.5=30-4-70=100 руб.
115. Если даны два уравненія съ тремя неизвѣстными х, у, г то на-
добно исключить изъ нихъ сперва одну х, и получится одно уравненіе съ двумя
неизвѣстными. Для отысканія всѣхъ рѣшеній цѣлыхъ и положительныхъ,
надобно, по предыдущему способу, выразить неизвѣстныя х, у, цѣлыми членами
въ функціи нѣкотораго цѣлаго числа /, подставить ихъ въ одно изъ данныхъ
уравненій : получится п третья неизвѣстная г, выраженная въ томъ же /. На-
конецъ, надобно отыскать предѣлы, между которыми должно брать цѣлыя числа
для /, лтобы получить для х, у, х, всѣ рѣшенія цѣлыя и положительныя. Все
это можно лучше видѣть изъ слѣдующихъ задачъ:
Задача. — На 38.5 рублей куплено стульевъ, креселъ н столовъ, а
именно: по 5 рублей за стулъ, по П руб. за кресло, и по (ІО руб. за
столъ. При этомъ число стульевъ было втрое болѣе числа креселъ и сто-
ловъ. Спрашивается сколько эісе куплено каждой этой мебели?
Пусть х число стульевъ,
у - креселъ,
х - столовъ.
101
По условію, число стульевъ было втрое болѣе числа креселъ и столовъ;
посему,
х=3(у-і-2)І или
1) х—Зу—Зя=0; а за нихъ заплачено
2) 5х-ь17у-н60г=385 рублей.
Вотъ два уравненія съ тремя неизвѣстными, гдѣ х, у, г, должны быть цѣ-
лыми числами и положительными.
Исключимъ х, помноживъ 1) уравненіе на 5, и, вычтя его изъ втораго,
останется;
32^-4-75^=385, откуда
385-752 1—11с
1/=—=12-2г-ь—, или
(а) 12—2г-ь/, полагая 1= , илп
321=1—1 Ь, и
*=—3/~* ИТ-
Но а цѣлое число, то и положимъ
1-ЬІ
(Ь) 2=—З/ч-/', взявъ і'= откуда
(с) 1=111'—I.
Эго подставимъ въ (Ь) и (а), найдется:
2=3—32/',
3=5-4-75/', и, наконецъ,
а=3^-4-й)=24.-4-129/'.
Для того, чтобы х, у, г, были числами цѣлыми и положительными, надобно:
3— 32/'>0, или /'< Д
о* «
5-ь 75/'> 0 /’>—~
і о
24
21-4-129/'>0 /'> —
Откуда видно, что можно взять только /'=0; и тогда найдется: у.—2 А, у=5,
2=3. Сталп-быть, куплено двѣ дюжины стульевъ, 5 креселъ, и 3 стола.
Задача. — У крестпчінина спросили: сколько арбузовъ ъиъ везетъ
въ городъ? Онъ отвѣчалъ: если считать -ихъ по десяткамъ, то оста-
пется 7;а если считать дюжинами,то останется 9: а всѣхъ менѣеЮО.
Пусть х число десятковъ ароузовъ,
х - дюжинъ,
2 полное число всѣхъ арбузовъ.
Считая по десяткамъ, нашли бы полное чисто арбузовъ е=1 О.т-4-7; а считая
дюжинами, выйдетъ полное число л=12.у-4-9. Посему:
— 102 —
16.г-ь7=12у-ь9. или
10л=12у-4-2, или, короче:
§х—
Освобождаю х, и нахожу
Но кйкъ х число цѣлое, то беру
1) х—у-л-і, полагая і=
а изъ этого условнаго уравненія нахожу:
2) у=5і—1; посему,
3) х=^і— 1.
Теперь полное число ароузовъ будетъ:
г=~\ О-а-’—1—7=10(6/—1)—і—7, или
4) =60/—3<100
А чтобъ х, уѵ я, были числами цѣлыми и положительными, надобно:
6/—1> 0, пли />^-
51—1>0, і>^
60/—3 <100 1<~-
Откуда видно, что только /=1 годится для рѣшенія задачи. И въ самомъ дѣлѣ,
для і= О, I, 2,....
х=— 1, 5, 11,....
у——1, 4, 9....
=—3, 57, 117,....
Полное число я <100; стало-быть, одно рѣшеніе 57 годится, и значитъ, что
у крестьянина 57 арбузовъ.
116. Трудность рѣшенія неопредѣленныхъ вопросовъ увеличивается съ
увеличеніемъ Числа неизвѣстныхъ безъ увеличенія числа уравненій. Это оче-
видно само собою. А какъ при этомъ должно поступать, покажетъ слѣдующій
примѣръ.
Задача.—Раздѣлить число 95 на четыре части такія, чтобы сумма
первой съ удвоенной второю относилась къ суммѣ третьей части съ
утроенною четвертою, какъ 3 : 5.
Пусть х, у, я, и, части первая, вторая, третья и четвертая. По условіямъ
вопроса должно быть:
4) х-\~у-^г,-+~и—с2Ъ, и
ж-+-2у:2-4-За=3:5, или
2) 5а>4-Юу~Зі-4-9гі.
— 103 —
Помножимъ первое уравненіе на 3, и сложимъ со вторымъ; то, по сокраще-
ніи, останется
8а?н-4 Зу—75=6«,
одно уравненіе съ тремя неизвѣстными».
Отсюда освободимъ к, при которомъ находится меньшій коефиціентъ:
_ , _ 2гг-+-и—3
. М=Я?-4-2у—12-4----б------.
Но какъ « число цѣлое, то положимъ
_ . г» 2гг-і-и—3
М=Я?-4-2у 12-4-/, взявъ /=-------—, или
6/=2а?ч-у—3.
Отсюда имѣемъ:
1) у=3ч-6/—2яг,
2) к=43/—6—За?,
3) я=25—а?—у—м=28-+-4х—19/.
Поищемъ теперь предѣлы для I, взявъ неравенства:
3-4-6/—2х> О, ] 2
13/—6—За?> О,
28-і-4х—19/>0.
Помноживъ первое неравенство на 2, и сложивъ съ третьимъ, будетъ
34—7/>0,’или /<5.
Помножимъ первое неравенство на 3, а второе на 2, и вычтемъ первое изъ
втораго, найдетса:
32г—21>‘Э, или <> =
32
И такъ, можно брать дла I только цѣлыя числа 4, 2, 3, 4.
1) Полагая /=І,
будетъ: у—9—2а?
и=7—За?
м=9-і-4а?
Посему, здѣсь можно брать а?=1
Для а?—
У=
м=
Предѣлы для х:
х>~ 2*-.
2, найдется:
5,
I,
и 2.
1,
7,
4,
2=13, 47.
2) Полагая /=2,
будетъ: у—15—2х
и =20—За?
2=Ь,х—10
Предѣлы для х:
*<6р
х>~\.
104 —
Посему, можно брать х=3, 5, 6.
Для х— 3, 4, 5, 6, найдутся:
у— 9, 7, 5, 3,
н=11, 8, 5, 2,
я= 2, 6, 10, 14.
3) Полагая 1=3,
Предѣлы для а>:
оудетъ: у=21—2х
М=33—За? I
2=4л?т-29 х>7Т'
Посему, можно брать л?=8, 9, 10.
Для ж=8, 9, 10, найдутся-
У=5, 3, 1,
ы=9, 6, 3,
5=3, 7, 11.
4) Полагая /=4,
Предѣлы для я;
найдемъ: у=27—2х
ы=46—За? Ж>12.
5=4а?—48
Слѣдовательно, можно взять только а?=13.
Для а?=13, получимъ:
У=
м= 7,
а—- 4.
И такъ, десятью способами можно раздѣлить число 25 на четыре части х,
у, 5, и, такія^ чтобы а?н-2у.5-і-3м=3 :5. Для повѣрки, возмемъ хотя послѣд-
нее рѣшеніе, гдѣ я=13, у=1, и=7, 5=4.
Сумма этихъ чиселъ 13-ь1ч-7-ь4=25; а требуемое отноженіе
13-ь2:4-ь21=3:5, или
15:25=3:5,
чіо совершенію вѣрно.
Задача, разсмотрѣнная нами, весьма хорошо показываетъ употребленіе нера-
венствъ въ изслѣдованіяхъ (анализѣ), п заслуживаетъ того, чтобы учащіеся за-
нялись ея рѣшеніемъ.
— 105 —
ГЛАВА ТРЕТЬЯ.
НЕПРЕРЫВНЫЯ ДРОБИ.
•13. Непрерывною дробью называется такая, у которой знаменатель ка-
кое нибудь цѣлое число, сложенное съ дробью; у этой дроби опять знаменатель
цѣлое число съ дробью, и т. д. Такова паприм. дробь
Частныя дроби ^,...., входящія въ составъ непрерывной дроби, назы-
ваются ея членами приближенія, и считаются: первый членъ, второй, третій,
И НрОЧ.
•
118. Непрерывная дробь называется простою, когда ччслителп всѣхъ ея
дробныхъ членовъ суть едпнипы; нанрим.
1 или
ач- 1----- 2ч- 1—--------------
с-І ------ Зч-----------------
Она бываетъ также конечною и безконечною. Конечная дробь состоитъ изъ
опредѣленнаго числа дробныхъ членовъ, а дробь безконечная имѣетъ безчисленное
множество таковыхъ членовъ. Нанрим.
і
дробь конечная, имѣющая три члена приближенія.
119. Безконечная непрерывная дробь называется періодическою, если нѣ-
которые изъ ея членовъ возвращаются всегда въ одномъ и томъ же порядкѣ; въ
дроби неперіодической этого не бываетъ. Паприм.
і
і
ач ------—
6ч-...,
дробь періодическая, въ которой два члена повторяются безпрестанно въ одномъ
я томъ же порядкѣ.
106 —
Здѣсь мы будемъ разсматривать однѣ простыя непрерывныя дроби, копенныя
или безконечныя.
430. Всякая простая дробь обыкновенная можетъ быть превращена въ
непрерывную дробь конечную; и, на оборотъ, всякая непрерывная дробь конеч-
ная происходитъ отъ какой нибудь дроби обыкновенной, соизмѣримой съ едини-
те . 100
нею. Напримѣръ, для превращенія дроби въ непрерывную, надооно раздѣлить
ея числитель и знаменатель на числитель 400; получится:
іоо__1
347 ~ 47
^іоб
Числитель и знаменатель дроби раздѣлитъ на ея числитель 4>7, найдется:
47 __ 1
100 ’ 6~'
2 ^47
»» е л
Числитель и знаменатель дроби раздѣлимъ на ея числитель 6, выйдетъ:
о____і______
47 в
Наконецъ, “ = '
к”
Дробь-1 имѣетъ числителемъ 1-цу, оттого и не можетъ уже далѣе разла-
гаться въ непрерывную дробь.
Послѣ этого, будемъ подставлять выраженія послѣдующихъ дробей въ пред-
шествующія, начиная съ послѣдней, и найдется:
6 ____і
"47 1
? О
47 __I
іоо ” Г
2-ь-
1
К
100 __ 1
317 І
Зч---------------
"+’й
Такимъ образомъ обыкновенная Дробь вся разложена въ непрерывную, я
состоитъ изъ пяти членовъ приближенія.
107 —
191. Разсматривая приведеніе дроби въ непрерывную, находимъ, что
иы сперва дѣлили большее число 347 на меньшее 100, получили частное 3,
I остатокъ 47. Потомъ, дѣлили прежній дѣлитель 100 па этотъ первый
остатокъ 47; получили частное 2 и второй остатокъ 6. Послѣ того, дѣлили
второй остатокъ на третій, третій на четвертый, и т. д., пока не получилось
въ остаткѣ ничего. Это дѣйствіе совершенно то же, какое употребляется для
розыскавія общаго наибольшаго дѣлителя между 100 и 347. Частныя
числа 3, 2, 7, 1, 5, полученныя такимъ образомъ, дѣлаются знаменателями
послѣдовательныхъ членовъ приближенія непрерывной дроби.
Отсюда видно, что дробь —, или всякая другая несократимая, скорѣе всего
разложглся въ непрерывную дробь чрезъ розысканіе общаго наибольшаго дѣли-
теля между ея числителемъ и знаменателемъ:
Отъ сего тотчасъ получатся всѣ знаменатели членовъ приближенія для непре-
рывной дроби, и она будетъ:
тоо__1_______
Переходъ отъ непрерывной дроби къ обыкновенной; законъ соста-
вленія СЕЙ ПОСЛѢДНЕЙ ИЗЪ ЧЛЕНОВЪ ПРИБЛИЖЕНІЯ ПЕРВОЙ.
199. Назовемъ чрезъ — полное выраженіе непрерывной дроби , и пусть бу-
детъ ея общій видъ
т ___х
п У
а-ь-
п
с_|-------
(
.......
е-ь-...
гдѣ а, Ь, с, х, у}г,и,.... цѣлыя числа, и прчтомъ ж<а,у<6, г<с.................
Поелику мы не можемъ взять безконечное число членовъ приближенія непре-
рывной дроби, чтобъ найти ея полную величину —, то будемъ къ ней прибли-
жаться, бравъ достаточное число членовъ, ея составляющихъ.
— 108 -
Первая приближенная дробь къ найдется, взявши одинъ первый членъ не-
прерывной дроби, и откинувъ всѣ прочіе: она будетъ
ТП, X
чнс.
чле
Вторая приближенная дробь получится, взявъ два первые члена, и откшіуи иот
всѣ нрочіе; или, все равно, взявши а-і-~ на мѣсто а въ нервомъ приближеніи мо.т
получится:
•п„ х Ъх
— 3=-------=-------- Т
п, у аЬ-і-у
а-і—
Ъ
Третья приближенная дробь получится, когда возмемъ три первые члена, от-
кинувъ прочіе; или, все то же, когда подставимъ б-ь— вмѣсто о во второе при-
ближеніе:
«п, х
6 ь-
с
сЬхч-хг
Ъх.с-іх.в
аЬс-ь-іу- і-аі {аЬ л-д}с-і-а.і ‘
Четвертое приближеніе найдется, взявъ четыре члена непрерывной дроби,*
или, все равно, подставивъ въ найденное третье приближеніе сч-
п будетъ: •
вмѣсто с,
и такъ далѣе.
а ч
взят
лучі
т<
верт
тл х ' д,'
* ач----------- (аЬ-ы/' I с-+-
Ь-ь2---------
и
д.
т, Ъсйх-+-Ьхи-і-<1хг
п, аІ>сі1-+-а6и-і~асІг-і-ссІу-і-уи
(Ьса>-+-хг <1 +-Ъхи
(аЬс-і-ах-і-су)іІч (аЬ-і-у)и
ч-аі
193. Закопъ составленія приближеніи. — Разсматривая приближенныя
дроби: первую, вторую, третью и четвертую, открывается, что всякая послѣ
дующая дробь составляется изъ двухъ предшествующихъ по весьма простои)
закону
х Ъх Ъх.с-ь-х.г
а * аЬ-і-у’ (иЪч-у)с-л-а.г
а именно: третья дробь составлена пзъ первыхъ двухъ такимъ образомъ, та
и та
торо
есть
мея;
п вос
чет/
2
и
а
Н-ТІ
»
С
109 —
числитель и знаменатель второй дроби помножены на знаменатель с третьяго
члена р а числитель и знаменатель первой дроби на числитель х втого члена,
Ъх.с х.г _
(аЬ-ѵ-у)с’ а.г'
потомъ взята сумма числителеіГ, и раздѣлена на сумму знаменателей отчего и
получилось
т. Ьх.с-л-х.г тх-нпл
— =. —-------------, или короче, —----------.
п3 (абч-у)с-і-аг п2с-ьп,г
Возмемъ теперь дроби вторую, третью и четвертую:
Ьх Ъсх- і-хх (Ьсх-і-хх)<1-і-Ъх.и
сЬ-ѵ-у’ аЬс-і-су-ь-ах’ (аЬс-і-ах-і-су)(1~і-(аЬ-і-у)и-
и здѣсь, для полученія четвертой дроби, надобно помножить числитель и знаме-
патель третьей дроои па знаменатель а четвертаго члена — непрерывной дроби,
а числитель и знаменатель второй дроби на числитель и этого члена; потомъ
взять сумму числителей и раздѣлить на сумму ихъ знаменателей; отчего п по-
лучилось :
т4 (Ьсх-о-хх)й-о-Ьх.и _____________ »п3Л-і-т2г
п, [оЬсч-ах-і-су)(1-і-(аЬ-о-у)іі п34-ьп2г
Точно также получается пятая приближенная дробь посредствомъ третьей и чет-
вертой. Для этого, въ четвертую дробь надобно внести <1 вмѣсто <2, п найдется:
пи —) -+-»ПоЫ
т„ ' е' (т3й-»-т4и)е-і-т31
п, / (і (п.,'-і-пи«;е-ьп31
”» \а^)
А какъ ті(1-+-тіи=т4и, п3ѵ.-+-п^ит=.піг то
т<в-ц-т3С
пв п,еч-п31
итакъ далѣе. Слѣдственно пятая дробь составилась но тому же закопу, по ко-
торому составлена четвертая и третья; стало-быть, этотъ законъ составленія
есть общій и для всѣхъ нрочнхъ приближеній.
Слѣдствіе Iе. Полная величина непрерывной дроби всегда заключается
между каждыми двумя ея послѣдовательными приближеніями, такъ что
и вообще, всѣ приближенныя дроби нечетнаго порядка больше —, а дроби
четнаго порядка < Въ самомъ дѣлѣ, если
110 —
, . & ЧП, - ТЛ и х
то первое нрполижеше - = _> —, потому что у дроби — уменьшенъ знаме-
натель.
Далѣе, возмемъ
и замѣтимъ, что
т. . тп
то есть, — < — ’
’ и, я.
А_„_„ ”*•>.’’« тп тп, тп.
какъ — > —; то ясно, что ~ заключается между — и —.
я । п п * п , п,
Потомъ возмемъ третій членъ приближенія; онъ будетъ
слѣдовательно:
— 111
тп . т
то есть, — > —.
пл п
ТТ л ЯІ
Но видѣли, что — < -,.
яа п
_ е п
стало-быть, полная дробь — заключается между двумя послѣдовательными къ
ией приближеніями — и —, и такъ далѣе. Очевидно также, что всѣ орибли-
П3
. _ т т
женія нечетнаго порядка больше —, а четнаго порядка меньше —.
Слѣдствіе 2-е. — Отъ зтого, послѣдующія приближенія, вычитлсмыя изъ
ближайшихъ имъ предшествующихъ, даютъ разности поперемѣнно положитель-
ныя и отпицательныя, и каждая разность равна произведенію числителей членовъ
прибіиженія, раздѣленному на произведеніе знаменателей сравниваемыхъ дробей.
Эти разности становятся тѣмъ меньше, чѣмъ высшихъ разрядовъ бываютъ срав-
ягвземыя приближенныя дробя.
Такимъ образомъ находимъ:
Ш, ЯЦ _______ X Ьх _______ । ух _________ ух .
п, п, а аЬ-ь-у а(чЪ-ь-у) п,*1»*
«п4 тп, Ьх (Ялям-хі) ауі
п, п, аЬ-ь-у аЬс-^-ах-і-су (аЪ-^-у)(аЬс-+-ая-л-су)
______хух^
ПЛ*
«п, т4 Ъсх-і-хх {ЪсЛх-і-Ьхи-і-Лхі
п3 п, аЬс-+-ая-*-ус аЬсй-^-аЬи-л-айг л-сЛу-ь-уи
хуги
"Л*
нашли бы также, что
тп. тя хугиі
—-----=--------------—, И т. д.
п, п, пчп„
И такъ, всякая разность изображается дробью, у которой знаменатели равенъ
произведеніе знаменателей сравнительныхъ дробей, а числитель равенъ произве-
денію числителей членовъ приближенія, входящихъ въ эти дроби
Сверхъ того, видно, что вторая разность менѣе пергой
ху
(вЬ-*-у)(аЬс-4-аи-су) вСТЬ
г 1
а<>с-і-аг-ьсу а’
потому что Я— или <с, и а, 6, с, у, суть числа цѣлый. Потомъ, яашля бы
также, что
хуѵи, хуг и і
-----<_-------, ИЛИ — <? —.
п,п, пап,-----п4 " па
То есть, послѣдующія разности становятся тѣмъ меньше, чѣмъ высшихъ по-
рядковъ бываи тъ сравниваемыя дроби.
112 —
Слѣдствіе 3-е. — Чаще всего встрѣчаются непрерывныя дроби, въ кото-
рыхъ всѣ числители членовъ приближенія суть единицы, то есть,
х—у~х=и—...................................—4; тогда
ІИ _ 1
с-ь-----
гіч-.—
Въ такомъ случаѣ, послѣдовательными приближеніями будутъ
т, 1 гпа Ь гп3 Ьс-ьі
п, а ' аЬ-4-1 ’ пя (аЬч-1)с-+-а ’
тп, (Ьс-і-1)Л-4-6
— = —Г—и такъ далѣе.
п, (аЬч-1)Л-4-ай-4-аЬч-1
Здѣсь составленіе в_сякой приближенной дроби изъ двухъ ей предшествующимъ
еще проще. Напримѣръ: третье приближеніе - , составлено изъ втораго
ь 1 ., ,
——и перваго числитель и знаменатель второй дроби помножены на знамена-
тель с третьяго члена потомъ взята сумма (Ьсч-4) числителей и раздѣлена
на сумму (абч-І)сч-а знаменателей. Точно также составлено четвертое при-
ближеніе посредствомъ втораго и третьяго.
І.Ж. Этотъ законъ подаетъ весьма легкій способъ находить всѣ послѣдова-
тельныя приближенія къ непрерывной дроби, будетъ ли она конечная или безко-
нечная. Пусть
т 1
Возмемъ двѣ первыя приближенныя дроби:
11 ___ 7
2 И ~ Г~ 15’
2,<~
поставимъ ихъ въ одной строкѣ; надъ второю дробью, и надъ мѣстами, послѣ-
дующихъ дробей: третьей, четвертой, и т. д., напишемъ знаменатели 1, 5, 40,
6, третьяго, четвертаго и т. д. членовъ, то есть:
і б іо б
1 7 8 47 478 2915
2 ’ 15* 17’ ІОО’ 1017’ вГб2
Потомъ, руководствуясь означеннымъ закономъ, найдемъ третье приближеніе:
7.1-+-1 _ 8
15.1-4-2 17’
113
четвертое приближеніе
пятое приближеніе....
и, наконецъ,.........
5.8 7-7 ___ 47
5.17-7-15 100 ’
10.47-7 8 478
ІО. 1ОС * 17 1017 ’
6 478-х 47 ____2915
6ЛО17-Т- 100 6202'
195. Разности между приближенными дробями, получаемыя чрезъ вычита-
ніе каждой послѣдующей дроби изъ предшествующей, будутъ:
т, п, «4 «з т, п. т». 1 . — — ч , откуда —»?2п1=ч->; Ш. 1 I , іилі„—— 1; 77, - 1 = ч , и/»и4—ПІК.П.— I 1; 71, плп,’ 84 43 тпв 1 = , тлі.—— 1; »» «4и» 46
тт Шг-і-і ____ - 1
пг Пг+і пгпг+і
Отсюда заключаемъ:
а) Поепику всякая разность іи5п3—т3я2=—1,
или »«3и4—т4п3=ч-1,
изображается единицею, то между т2п3, т3п2, также между т3и4, т4п3, не мо-
жетъ быть ни какихъ общихъ множителей кромѣ единицы; слѣдовательно, всѣ
послѣдовательныя приближеніи ~ ~ " > п~,"‘ СУГЬДР°6И несократимыя.
. . ,г . т, тп.. т. т.
и) Послѣдующія разности ---------— ----........... имѣютъ поперемѣнно
знаки ч- и —; каждая разность изображается дробью, у которой числитель
единица, а знаменатель произведеніе знаменателей сравниваемыхъ дробей.
с) Поелику знаменатели п1, пг, п3, становятся постепенно болѣе и
болѣе; то послѣдовательныя разности ч--------,-------, ч- -,... между прп-
ближепіями дѣлаются менѣе и менѣе.
а) А какъ полная величина — непрерывной дроби заключается между —
вг. ти. т, „ іпг
и — , между — и —, и т. д., и воооще между — и---------, она менѣе всѣхъ
П, •’ п2 п5 ' П, . Пг+1
нриолпжевій нечетнаго порядка, а болѣе приближеній четнаго порядка; то раз-
ііі
пости ч------,............. чч-----, можно назвать предѣлами погрѣшпостеп
п,п2 71,71,' ПгПг-^і
, ... т 1т . . т
оныхъ приближеніи къ —. 11 въ самомъ дѣлѣ, если вмѣсто — возмемъ — или
—, то сдѣлаемъ погрѣшность менѣе нежели — И вообще, если вмѣсто
8
— 114 —
т Шг ^гі . . .
— возмемъ — или---------, то сдѣлаемъ погрѣшность менѣе нежели =-------------.
П Пг Пг-Ы ПгЯг-+-1
1 *
Но ПГ<П,+1, то, взявши пг вмѣсто пг+1, получится дробь ± —> ——-1
т
слѣдовательно и подавно можно сказать, что если вмѣсто — взять —, то сдѣ-
п пг
лаемъ погрѣшность менѣе нежели ± Эта послѣдняя дробь и берется ооык-
повенно для приблизительнаго выраженія предѣла погрѣшности.
Для примѣра, возмемъ дробь
. т 1
п~ “' ~ І
2ч--------
7ч-1______
1
1ч--------
м 1
5ч----------
1
10ч-----•
6
Ея послѣдовательныя приближенія были (124)
^- = *- =0,500000........>-
п1 2 п
^ = ^ =0,466666...........<-
15 п
— = ~ =0,470588..........>-
пг 17 ’ п
= ~ =0,470000.........<-
п4 100 ’ п
=4^7 =0,4700098......> — '
п6 1017 п
=^ =0,47000967....=—.
п„ 0202 ’ п
п ш 47
Если вмѣсто — возмемъ то сдѣлаемъ погрѣшность менѣе нежели
—0,0001. И въ самомъ дѣлѣ, разность
~ — =0,47000967.... —0,4700000
1 =0,00000967.... <0,0004.
12<». Составимъ послѣдовательныя разности:
- 1 1
1
пі п,и,
т. 1
пъ
- 1 1
п4 1 ПЪП4
тг тг+ч , 1
—-----------= — -----------, и сложимъ, то получится:
Пг Иг-ьі «гМг-+-|
115 —
і
т. Шт-і-і 1111
_' - — --1----------. /НН —
П,___________________________________________П(Па П*Пъ пъп4 плпй '*
Если ------=— , то отсюда найдется:
Пг-ьі П
т________т, 1 1 1 ____ 1
п п, п,па па»і3 ......пгпг+і
Слѣдовательно, всякая обыкновенная дробь, или дробь, разложенная въ не-
прерывную, изображается рядомъ простыхъ дробей по весьма очевидному закону,
нетребующему изъясненія,
гг _ , т 2915 1
іакимъ ооразомъ дробь — = , для котороіі —- — —, и сверхъ того
п{=2, яа=15, «3=17, и4=100, яв=1017, изобразится рядомъ:
2915____1 11 11 1
0202 2 2Л5 -|_ 15.17 17 100 "+" 100.101/ 1017.6202 *
199. Непрерывныя дроби имѣютъ многія полезныя употребленія: 1) для
вычисленія дробей несоизмѣримыхъ которыхъ полнаго выраженія мы получить
пе можемъ, но къ которымъ можемъ приближаться такъ близко, какъ угодно,
и на всякомъ шагу знать степень приближенія; 2) для простѣйшаго- приближен-
наго выраженія такихъ обыкновенныхъ дробей, которыхъ числитель и знамена-
тель велики, и суть первые между собою. Такъ, напримѣръ, еслибы хотѣли мы,
, 2915 , -
вмѣсто дроби ^2 ’ получить весьма близкую къ неи дробь, только гораздо про-
стѣйшую, и удобнѣе удержимую въ памяти; то, разложивъ ее въ непрерывную
іробь:
2915 _ 1
6202 Г~
2ч----------------
74-2______
1
1-1 Г-
54----------
104- -
нашли бы ея приближенія:
1
478
1017 ’
7 Я 47
2’ 15’ 17’ ІОО’
47
и потомъ взяли бы, наприм. — = 0,17 вмѣсто
менѣе 0,0001.
2915 ,
——; погрѣшность была бы
Прибавленіе. — Иногда нужно бываетъ найти приближенную вели-
чину непрерывной дроби
т
п
у
а----------
г
Ь----*-----
и
, с~ а-'-.
116
иъ такомъ случаѣ надобно обратиться къ формуламъ общимъ (1ЯЗ), и подста-
вить въ нпхъ —у, —г, —и, —.... вмѣсто у, г, и,...., то послѣдовательныя
приближенія найдутся:
юі, я: __ Ьх
п, а п2 аЬ—у ’
тъ Ьсх—хг Ьх.с—х.г тчс—т,г
пв «6с—су—аг {аЬ—у)с—а.т. Пці;—п,г ’
т, т.Л—пм
также — = - --------,
п, п^а—п2»«
тя т.е—т.і
- = —--------, и т. д.
п„ пАе—пъ1
„ - , т.
Слѣдовательно, здѣсь всякая послѣдующая приолижешіая дрооь, паприм. —г
т,
составляется также изъ двухъ предшествующпхт -» ~ • и.также числитель и
„ т. . г
знаменатель дроои — помножаются на знаменатель с слѣдующаго члена —, а
с
- т>
числитель и знаменатель дроои — на г, потомъ берется разность числите-
лей и дѣлится на разность знаменателей.
Разности между послѣдовательными приближеніями-
т, тп2
«і
♦П9 хуг
п« пз ~
7И_ т4 хуги
п, пъп4
тоже имѣютъ поперемѣнно знаки +и —; только порядокъ знаковъ совер-
шенно обратный порядку ихъ въ прежнемъ общемъ случаѣ.
Для а>=«/=г=и=....=1,
т,________________ 1 т2 6
п, а ’ пг ' аЬ—1 ’
ш3 б.с—1 __тас—т,
п, (аЬ—і)с—а пяс—п, ’
и, т3 1
Пя П(Па ’
»па »п3___ 1
«» пъ~~ п»пз ’
^39. Непрерывная безконечная дробь изображается такимъ же рядомъ,
только имѣющимъ безконечное число членовъ, посредствомъ которыхъ она при-
ближается къѴвоеійучлредІйіу,-Никогда -егтгчіе достигая. \1?есьма замѣчательно/
117
что предѣлъ всякой безконечной, непрерывной дроби періодической вы-
ражается корнемъ уравненія 2-й степени. Такъ наприм. дробь
очевидно, можно написать:
ь
х — -----------------------------------; откуда
а-+-л ’
х“ч- ах =Ь, уравненіе второй степени.
Возмемъ еще дробь х = 6 ——
ач—------
а -ь.—.
гдѣ иер:* дъ состоитъ изъ двухъ членовъ приближенія. Эту дробь также можно
написать:
’ откуда
а'Ьч-Ьх
X — ------Г, > 11
аа ч ахч-р'
ахіч-{аа>ч-ЬІ—й1х=а'Ь,
также уравненіе 2-й степени.
Нашли бы также, что непрерывная періодическая дробь съ тремя, четырьмя,
и болѣе, членами приближенія, также зависитъ отъ разрѣшенія уравненія 2-й
степени.
ГЛАВА ЧЕТВЕРТАЯ.
О ВОЗВЫШЕНІЙ АЛГЕБРИЧЕСКИХЪ КОЛИЧЕСТВЪ ВЪ КВАДРАТЪ
И ИЗВЛЕЧЕНІИ КОРНЕЙ КВАДРАТНЫХЪ.
130. Для возвышенія даннаго количества въ квадратъ, иадооно помножить
оное само на себя.
Если количество одночленное, то при этомъ надобно. 1) возвысить въ
квадратъ его предстоящее; 2) помножить на 2 показатели всѣхъ его буквенных ь
множителей; 3) предъ произведеніемъ поставить знакъ ч-, будеі ь-ли данное
количество положительное или отрицательное. 4) Если данное количество дробь,
118
то, для возвышенія въ квадратъ, надобно взять квадратъ ея числителя и раздѣ
лить на квадратъ знаменателя.
Все это основывается на извѣстныхъ правилахъ умноженія, кань видно изъ
слѣдующихъ примѣровъ:
а) (5аѴ)8 = 5а868 X 5а863 = 25а‘66;
Ь) (—6а")8= (—6а") (—6а") = 36а8";
,3«ьу ___ЗаЬ» ѵ 3«Ь» Эа’Ь*
431. Для возвышенія въ квадратъ количества многочленнаго, надобно от-
крыть законъ, по которому оно производится. А дли этого станемъ постепенно
возвышать въ квадратъ количество двучленное, трехчленное, и т. д.
Мы знаемъ, что
(ач-6)! = а8ч2аАч/г;
теперь возмемъ количество а-+-6-ч-с, и примемъ а-ч-б за одинъ членъ, то ква-
дратъ его найдется:
(а-ч-бч-с) = (ач-Ь)8ч-2(а-+-6)сч-с8
= а8ч-2аб-ч-6'-ч-2(а-ч-6)с-і-с8.
То есть: квадратъ трехчленнаго количества а-г-Ь-г-с равенъ квадрату
двучлена (а-г-Ь), сложенному съ удвоеннымъ произведеніемъ этого дву-
члена на третіи членъ с, и -ь квадратъ третьяго члена.
Возмемъ, далѣе, четырехчленное количество а-г-Ь-г-с-г-И, примемъ его
а-+-Ь-г-с за одинъ членъ; то квадратъ его получится:
(а-+-6-+-сч-й)8 = (а-+-6ч-с)8-+-2(а-т-6-ьс/<І-+-іГ
- а8-+-2а6-»-оіч-2(а-4-6)с-і-с8ч-2(а-ь6ч-е)</ч-гі2. "
Здѣсь также видимъ, что квадратъ четырехчленнаго количества равенъ
квадрату количества трехчленнаго, (а-ь-Ь-г-с)*, сложенному съ двойнымъ
произведеніемъ этого тричлена на четвертый членъ, и -+- квадратъ чет-
вертаго члена. — Этотъ законъ мы нашли бы ври возвышеніи въ квадратъ ко-
личества пятичленнаго, шестпчленпаго, и т. д., и узнали бы, что, съ прибавле-
ніемъ новаго члена Л къ данному многочлену, прибавляется къ квадрату этого
многочлена удвоенное произведеніе суммы всѣхъ его членовъ на этотъ новый, и
квадратъ новаго члена.
433. Приложимъ этот ь способъ къ возвышенію въ квадратъ какого ни
есть многозначнаго числа, наприм. 235. Для сего, разложимъ это число на
сотни, десятки и единицы:
235‘2=:(200ч-ЗѲч-5)8 ;
сравнимъ съ квадратомъ тричлена
(а-ьбч-с)2 = а2ч-2а6ч-6 ч-2(ач-6)с-і-с8,
— 119 —
полагая 200=а, 30=6, 5=с ; откроется, что 235’ должно состоятъ изъ ква-
драта сотенъ, ч- удвоеннаго произведенія сотенъ на десятки, -+- квадрата де-
сятковъ, -+- удвоеннаго произведенія сотенъ и десятковъ па единицы, и +- ква-
драта единицъ, то есть:
(235)’=200’-ь2.200.30ч-30’ч-2.280.5-4-5’.
Но, 200’ = 40000
2.200.30 = 12000
30’= 900
2.230.5 = 2300
5’= 25
Посему, 235’ = 55125.
Мы знаемъ, что квадратъ дроби равенъ квадрату ея числителя раздѣленному
на квадратъ знаменателя. А здѣсь замѣтимъ только: 1) что, для возвышенія въ
квадратъ цѣлаго числа съ дробью, надобно привесть это дробное число сперва
въ неправильную дробь, и потомъ возвышать въ эту степень. Наприм.
— 289
X*5 В ' — ' — 5^-5 — 53
2) Квадратъ десятичной дроби получается какъ квадратъ изъ цѣлаго числа.
Онъ долженъ содержать въ себѣ десятичныхъ знаковъ вдвое болѣе, нежели
сколько ихъ было въ данной дроби. Напр.
(2,53)’= 2,53X2,53—6,4009.
А. Извлеченіе корня квадратнаго изъ чиселъ.
133. Извлеченіемъ квадратнаго корня изъ даннаго количества назы-
вается дѣйствіе, посредствомъ котораго ищется такой множитель, котораго ква-
дратъ равенъ этому количеству. Этотъ искомый мноя'итель называется корнемъ
квадратнымъ того количества. Такъ наприм. корень квадратный изъ 4а’ есть
2а; потому что 2аХ2а=4а’.
13Д. Часто нужно бываетъ только показать, что надобно извлечь квадрат-
ный корень изъ даннаго количества; въ такомъ случаѣ употребляется коренной
знакъ \/ , или просто Vх . Подъ пимъ пишется то количество, кото-
раго корень квадратный ищется. Наприм.
Ѵ/4аг=2а, і/ІО".
Эго выговаривается: корень квадратный изъ 4а’, корень квадратный изъ 10
135. Изъ цѣлыхъ чиселъ. — Для извлеченія корней квадратныхъ изъ
цѣлыхъ чиселъ, надобно звать квадраты первыхъ чиселъ; — они находятся
въ слѣдующей табличкѣ:
120 —
Корни: 1, 2, 3, 4, 5, 6, 7 8, 9 10
Квадраты: I, 4, 9, 16, 25, 36, 49, 64, 81 100,
изъ которой видно, что квадрату числа однозначнаго или двузначнаго соотвѣт-
ствуетъ корень однозначный, что самому меньшему трехзиачному числу 100 со-
отвѣтствуетъ корень 10, самое меньшее двузначное число; что не всякое число
полный квадратъ. Такъ напримѣръ, число 30 заключается между полными ква-
дратами 25 и 36, а его корень заключается между 5 и 6.
136. Корни изъ неполныхъ квадратовъ называются неизвлекомымн, ирра-
ціональными, т. е. несоизмѣримыми съ единицею; потому что не могутъ
быть выражены точнымъ образомъ ни цѣлыми числами, пп дробными. — II въ
самомъ дѣлѣ ѴЗО >5 и <6, а потому долженъ изобразиться нѣкоторымъ дроб-
м
пылъ числомъ гдѣ М, суть первыя между собою, и М>Гх. II танъ, пусть
ГЗО^;
возмемъ квадратъ этого равенства :
зо--.
— №
Числа М, IV, первыя между сооою, потому что дрооь несократимая; то и
числа М’, №!, также будутъ первыми между собою. (43, слѣдст. 2). Стало-
- м»
оыть, дрооь - не можетъ оыть сокращена, и не можетъ ооратиться въ цѣлое
число 30. А это и показываетъ, что і/ЗО есть число ирраціональное, несоизмѣ-
римое съ единицею. Оно пе можетъ быть найдено точнымъ образомъ; по мы
увидимъ, что Ложно находить его приближенныя величины, какія угодно.
139. Квадратные корпи изъ чиселъ отрицательныхъ называются невозмозк-
іііііліі, мнимыми, наприм. V—'<; потому что пѣтъ такого числа положитель-
наго или отрицательнаго, котораго квадратъ былъ бы отрицательный. По этому
>іы будемъ говорить здѣсь о корняхъ изъ чиселъ и количествъ положительныхъ.
138. Прежде извлеченія квадратнаго корпя пзъ числа, содержащаго три,
четыре, пли болѣе цифръ, надобно сначала узнать, сколько цифръ должно быть
въ его корнѣ. А для этого сравниваютъ данное число съ квадратами.
'102=100, 1008=10000, 10002=Ч000000. и проч,,
п смотрятъ, между какими изъ этпхь квадратовъ оно заключается. Положимъ,
что дано число 5625. Это число находится между 100 и 10000, слѣдовательно
корень его падаетъ между 10 и 100; стало-быть, искомый корень двузначный,
то есть, состоитъ изъ десятковъ п единицъ; по этому, данное число 5625 должно
содержать въ себѣ квадратъ десятковъ, удвоенное произведеніе десятковъ
корня на е/о единицы, и квадр тъ единицъ, и можетъ быть сравнено съ
121
'квадратомъ двучлена (п-ьб)’, въ которомъ а означаетъ десятки а Ь единицы
корпя, т. е.
5625=а8-ь2а6-ь68.
Отыскиваніе же цифръ корпя Ьроизводится, начиная съ цифры высшаго раз-
ряда, а именно: надобно сперва найти десятки а корня, и квадратъ ихъ вычесть
пзъ 5625; получится остатокъ:
5625—а9- 2а6-т-й8—(2ач-6) Ь.
Потомъ надобно взять удвоенное произведеніе 2аб десятковъ на искомыя еди-
ницы, п раздѣлить па удвоенные десятки 2« корня; получатся 2аЬ : 2а=6
единицы корня. Эти единицы Ь надобно пипдать къ 2а, и сумму 2цч-Ь поиво-
жить на Ъ; произведеніе (2а-ьЬ)6=2ай-+-Ь2 будетъ остальною частію даннаго
квадрата, которую и вычтешь изъ 5625—«8. Если данное число 5625 полный
квадратъ, то остатокъ будетъ пуль:
5625—а8—2а6 — і8—0.
139. Узнавши порядокъ извлеченія корпя, я пишу данное число 5625, про-
вожу съ правой стороны вертикальную черту:
Квадратъ. 56,25 49 Коренъ. 75
72,5 725 14 дес. -+-5 едип. =145 Х5
О
и говорю: квадратъ десятковъ нроизводитъ не менѣе какъ сотни, то н надобно
искать его нь сотняхъ. Для этою отдѣляю единицы и десятки занятою, а нахо-
жу, чго ближайшій меньшій квадратъ, содержащійся въ 56. есть 4-9, которому
соотвѣтствуетъ корень 7 десятковъ. Число 7 десятковъ ставлю но правую сто-
рону вергикалыіой черты; для повѣрки беру 78=49, и вычитаю изъ 56. Къ
остатку 7 сношу остальные 25. Въ зтомъ числѣ 725 должны находиться удво-
енное произведеніе десятковъ корпя на единицы и квадратъ единицъ. По, какъ
удвоенное произведеніе десятковъ па единицы даетъ пе м-епѣе какъ десятки; то
я отдѣляю 5 единицъ запятою, помножаю 7 десятковь корня на 2, и на произве-
деніе Н дѣлю 72. Частное 5 ставлю па мѣстѣ единицъ корня. Для повѣрки,
придаю эти 5 единицъ къ 14 десяткамъ, чго составить 145; помножаю это всс
на 5, чтобы заразъ подучить удвоенное произведеніе десятковъ на единицы и
квадратъ единицъ корна, и нахожу 725. Эго вычитаю изъ 725 Остатокъ пуль;
слѣдовательно,
1/5627—75.
122 —
140. Такимъ же образомъ надобно поступать, когда данпое число имѣетъ
болѣе четырехъ цифръ. Положимъ, что требуется извлечь квадратный корень
изъ 54-756. Это число заключается между 100^=10000 и 10002=1000000;
стало-быть, его корень содержится между 100 и 1000, то есть, состоитъ изъ
трехъ цифръ: изъ сотенъ, десятковъ и единицъ, и можетъ быть сравнено съ ква-
дратомъ тричленаа-ьб-ьс, 54 7 562=(а-ьб-+-с)2=а2-+-2а6-і-6і-+-2(а-+-б)с-+-с2,
гдѣ а означаетъ искомыя сотни корня, Ь его десятки и с единицы.
Квадратъ. 5,47,56 4 Корень. 234
14,7 43
129 3
185,6 464
1856 4
0
И такъ, данцое число 54-756 должно состоять изъ квадрата сотенъ и десят-
ковъ, изъ удвоеннаго произведенія сотенъ и десятковъ на единицы и квадрата
единицъ. Но, поелику квадратъ десятковъ производитъ не менѣе какъ сотни, гдѣ
его должно искать, то отдѣлимъ десятки и единицы занятою. Квадратъ сотенъ
производитъ не менѣе, какъ десяткп тысячи, въ которыхъ его надобно искать,
то отдѣлимъ тысячи и сотни запятою. Поступая такимъ образомъ, мы раздѣ-
лимъ все данное число на классы отъ правой руки къ лѣвой, въ каждомъ по двѣ
цифры; только въ послѣднемъ классѣ можетъ быть и одна цифра. Число клас-
совъ всегда показываетъ число цифръ корня.'
Замѣтивъ это, я ищу квадратъ сотенъ въ 5; ему соотвѣтствуетъ ближайшій
корень 2 сотни. Беру 22=4, и вычитаю изъ 5; къ остатку сношу слѣдующій
классъ 4-7. Въ числѣ 14-7 сотенъ должны заключаться 2аін-б’, то есть, удвоен-
ное произведеніе сотенъ корпя па его десяткп, и квадратъ десятковъ. А какъ
удвоенное произведеніе сотенъ на десяткп даетъ тысячи и должно въ нихъ за-
ключаться; то я отдѣляю цифру 7 сотепъ запятою, удвояю 2 сотни корпя,
что составитъ 4- сотни; дѣлю 14 на 4. Частное 3 десятка ставлю подлѣ 2 со-
тепъ корня, и также подлѣ 4; число 43 помножаю на 3, п произведеніе вы-
читаю изъ 147. Къ остатку 18 сношу послѣдній классъ 56. Во всемъ этомъ
остаткѣ 1856 должны находиться 2(а-+-6)с-+-с2, то есть, удвоенное произведеніе
сотенъ и десятковъ корня на его единицы, и квадратъ единицъ. А чтобы найти
единицы корпя, я отдѣляю 6 единицъ остатка запятою, удвояю 23 десятка,
что составитъ ' 6; дѣлю 185 і,а 46, и частное 4 единицы ставлю подлѣ 23 де-
123 —
сяіковъ корня, и подлѣ 46. Число 464 помножаю на 4, и произведеніе 1856
вычитаю изъ 1856. Въ остаткѣ нуль; слѣдовательно,
051756=234.
141. Ежели случится, что, по снесеніи класса, остатокъ съ первою цифрою
этого класса будетъ менѣе удвоеннаго произведенія цифръ корня; то должно въ кор-
нѣ поставить нуль, снести подъ черту слѣдующій классъ, и продолжать извлеченіе.
Примѣръ. Найти 1/1162084.
Квадратъ. 1,16,20,84 1 Корень. 1078
1,6 2 208
162,0 ‘ 207 8
1449 7 1664
1718,4 2148
' 17184 8
0
По раздѣленіи даннаго числа на классы, видно, что въ корнѣ его должны
быть четыре цифры. Поставивъ 1 тысячу въ корнѣ, и вычтя ея квадратъ изъ
перваго класса, я сношу классъ 16, отдѣляю 6 запятою, удвояю цифру коряя,
и нахожу, что 2 въ 1 не содержится: изъ этого заключаю, что нѣтъ сотенъ въ
корнѣ; а потому ставлю нуль на ихъ мѣстѣ, и сношу слѣдующій классъ. Въ
числѣ 1620 отдѣляю послѣднюю цифру запятою, и, удвоивъ число 10 сотенъ
корня, дѣлю 162 на 20 для того, чтобъ отыскать десятки корня.—Хотя 20 во
162 содержится 8 разъ; но ежели 8 поставимъ подлѣ 20, и число 208 домно-
жимъ па 8, то выйдетъ 1664 произведеніе > 1620. Это показываетъ, что
цифра 8 велика: посему возмемъ 7, и остальное дѣйствіе окончимъ, какъ
было показано въ предыдущихъ примѣрахъ. Найдется
ѴТТб2084=1078.
148. Всего чаще случается, что, по снесеніи всѣхъ классовъ, и по получе-
ніи всѣхъ цифръ корня, получится остатокъ отъ даннаго числа; то надобно за-
ключить, что это число неполный кяадратъ, и что его корня .нельзя получить
точнымъ образомъ.
Примѣръ: 3,49 1 18
24,9 28
224 8
25
124 —
Въ этомъ примърѣ, по снесеніи класса 49. и но удвоеніи десятковъ корня,
видно, что, хотя 2 въ 24 содержится 12 разъ, но не только нельзя взять 12,
даже 9 было бы еще велико (ибо 29X9=261); потому взята цифра 8, и полу-
чился остатокъ 25. Очевидно, что 18 есть неполный корень изъ 349.
443. Хотя цѣлыя числа, неполные квадраты, не имѣютъ себѣ точныхъ кор-
ней; однако же всегда можно искать приближенныя величины такихъ корней
различными способами: 1) носредс рвомъ дробей десятичныхъ, 2) посредствомъ
дробей обыкновенныхъ, 3) посредствомъ дробей непрерывныхъ.
а) Посредствомъ дробей десятичныхъ. — Это самый обыкновенный и
самый употребительной способъ отыскиванія приблиа:еішой величины корня.
Для сего, надобно къ данному числу приписать съ правой стороны
столько нулей, .сколько нужно, чтобъ число ихъ было вдвое болѣе
числа десятичныхъ знаковъ, требуемыхъ въ приближенномъ корнѣ, и
потомъ извлекать корень какъ изъ цѣлаго числа. По окончаніи дѣй-
ствія, отдѣлить въ корнѣ столько десятичныхъ, сколько ихъ требо-
валось.
Примѣръ. — Найти V 7, приближенный и точный только въ трехъ Деся-
тичныхъ.
Приписываю къ числу 7 шесть нулей; потомъ дѣлю все па классы, и извле-
каю корень какъ изъ цѣлаго числа:
7,00,00,00 2645
30,0 46
276 6
240,0 524
2096 4
3040,0 5285
26425 5
3975
Въ полученномъ числѣ 2645 отдѣляю три десятичныхъ знака, н нахожу
1/7=2,645 приближенный и точный только въ тысячныхъ доляхъ.
Примѣръ.— Найти V 5,2, приближенный до двухъ десятичныхь
Здѣсь приписываю три пуля съ правой стороны числа 5,2, чтобы вышло че-
тыре десятичныхъ; потомъ дѣлю па классы, и извлекаю корень какъ изъ цѣлаго
числа:
125 —
5,20,00 4 228
12,0 42
84 2
360,0 448
3584 8
16 •
Отдѣляю въ корнѣ двѣ десятичныя, и нахожу
1^2—2,28....
Примѣры: 1/2=1,4142....
ИГ—1,7320....
1/5=2,2360....
Ь) Посредствомъ обыкновенныхъ дробей.—Положимъ, что изъ числа 'Ѵ
і
неполнаго квадрата, надобпо извлечь корень приближенный до Для этого воз-
мемъ я*, помножимъ и раздѣлимъ на него число IV:
изъ обѣихъ частей равенства извлечемъ корпи:
Мы знаемъ, что квадратъ дроби равенъ квадрату ея числителя, раздѣленному на
квадратъ знаменателя; то, обратно, для извлеченія корпя квадратнаго изъ дроби,
надобно взять корень изъ числителя и раздѣлить на корень изъ знаменателя.
Посему,
_ і/к.п® і/кй®
Ѵ'К = -==- =----------
|/п® П
Найдемъ ИѴп’ только въ цѣлыхъ числахъ, откинувъ дроби, и пусть |/]Ѵ»г’=цг
то будемъ имѣть:
|/Й >” и
п п
. 10—1—1 іѵ 1 іѵ 10-4-1
А какъ —---------= ~, то очевидно, что взятъ ли - или---- за корень
п п п п п 1
приближенный къ і/ГѴ, погрѣшность будетъ менѣе нежели на —.
Примѣръ.—Найти квадратный корень изъ 10, приближенный до
10.125® _ Ѵ'юігв®___ 1/156250
125® 125 125 ’
ищу 1/156250=395, )держивая однѣ цѣлыя числа, откинувъ .дробя; и за-
ключаю, что
Беру |/10=
— 126 —
і/Тпх. 393 393
' Н° < 125’
396 395 1
Разность ^3 — 125 = І25‘ Слѣдовательно, найденный приближенный корень
398 ./Гл 1
разнится отъ истиннаго ѵ 10 менѣе, нежели на
с) Посредствомъ дробей непрерывныхъ. — Весьма замѣчательно, что
корень квадратный изъ числа неполнаго квадрата выражается непрерывною
періодическою дробью (!»»). Положимъ, что данное число, изъ котораго хо-
тимъ извлечь корень, разлагается на а’-ьб; то можно взять
і/аМ-б^а-ьж,
гдѣ ж<1. Отсюда х= —а.
Это выраженіе помножимъ и раздѣлимъ на і/а^-ьбч-а; получится:
ь
х~ |/а^ь6ч-а-
Сюда внесемъ а-+-х на мѣсто Ѵ'сг+Ь, найдется:
ь
х =--------------------------------
2ач-х
На мѣсто х въ знаменателѣ подставимъ
ь
х ь
2а-»--—
2ач-а:
Посему, Vа*-і-Ь=.а-+-х=а-і--—-
2ач-----------------------------------
„ 6
2ач-----
Ъ
2а-»-ж ’
, и такъ далѣе.
Если Ъ—2, то
і
і
ач------
„ 1
9а і----
1
ач—
Пусть Ь=а; тогда
Ѵа8-ьб—«+- -——
2ч------
2ач-----—
2ч-.----
2а-ч-....
П вообще, если между Ь и 2а есть общі і множитель, непрерывная дробь
должна быть періодическою, съ двумя повторяющимся членами приближенія.
Примѣръ.—Найти приближенный посредствомъ непрерывной дроби.
Замѣчая, что Ѵ/5=Ѵ/28-ь1, имѣю тотчасъ:
— 127 —
1/5=24--—
4ч----
1
*' Ч
4ч- —
Ограничиваясь только четырьмя членами приближенія, найдется:
1^=2^=2,23606...,
305 •
1 1
который разнится отъ истиннаго менѣе нежели на —— = —--, и потому
(ЗОо) 1)3025
имѣетъ точность въ пяти десятичныхъ.
Примѣръ. — Найти ѴТТ, приближенный до стотысячныхъ долей включи-
тельно, посредствомъ непрерывной дроби.
і/ГГ= Ѵ'Зіч5=«-і- Ч-
6-ч-----
-3+-* —
Зч--
-ч
Зч-
Здѣсь послѣдовательныя приближенія къ дроби корня:
3 6
1 б 19 120
3 ’ 19’ б5=’ 379’
Взявъ послѣднюю дробь, получаемъ:
^=3^,
который разнится отъ истиннаго менѣе, нежели на * слѣдовательно ме-
(о79)а
нѣе нежели на -0000 - часть единицы.
Примѣръ.—Найти 1^19 приближенный посредствомъ непрерывной дроби.
8-ь ----
_______
8ч-3-__
Здѣсь послѣдовательныя приближенія къ дроби корня (193):
3 8
3 24 201 1680
8 ’ 67 560 ’ 468І’"’
3 8
Взявъ послѣднюю дробь, имѣемъ:
1/19=4—.
4681
128 —
Этотъ корень разнится отъ истиннаго менѣе нежели на 3([0
Приближеніе получается скорѣе, когда числители членовъ непрерывной
дроби суть едииипы, или значительно менѣе знаменателей; а потому полезно
бываетъ преобразовать данпый корень такъ, чтобы онъ выразился непрерывною
дробью такого рода. Напримѣръ, мы гораздо скорѣе получимъ приближенный
|/19, взявъ
1/19=4113-+
1/19= V —= ^71;
V 9 3
потому что 171=169-+-2=132-»-2. Отъ этого
2— - I
2 ’
26ч- ------і
26-і-.... )
1
1—
13-+--—
26ч-----—
13ч- —
26-+-....
Примѣръ.—1/43= 1/36-ь7=6 + -———
12 *--у
12 +- ~
Но лучше взять:
Ѵ'43= 41/43.4= 41/172= 4 і/ІЗ-2
2 2
_ 1
2
2
3
26-г -----\
3 I
26Ч-26^-г|
Взявъ три члена приближенія, найдется корень
4(13,1148770...)
точный въ семи десятичныхъ.
Иногда можно поступать такъ, какъ показываетъ слѣдующій примѣръ.
Найти |/3 приближенный посредствомъ непрерывной дроби.
1/3=1/22—1=2— — 4—
4--------
4— 1______
4—-------
4—....
Здѣсь приближенныя дроби, которыя надобяо вычитать изъ 2, суть:
4 4
1 4 18 53
4 ’ 15’ 56’ 209’"'
Взявъ послѣднюю дробь, мы получимъ:
— 129 —
/3=2— —1,732052....,
который будетъ разниться отъ истиннаго менѣе, нежели на =0,000023.
II въ самомъ дѣлѣ, непосредственное извлеченіе даетъ *
/3=1,732050....,
и разность оказывается только въ милліонныхъ доляхъ.
1Л4. Изъ дробей. — Корень квадратный изъ дроби равняется коршо изъ
числителя, раздѣленному на корень пзъ знаменателя. Нанрим.:
« /~9 ___ / 9 ___з
Приближенные корни изъ дробей, неполныхъ квадратовъ, отыскиваются
тѣми же спосооами, какіе показаны для полученія ихъ изъ цѣлыхъ чиселъ.
4) Данную дробь превращаютъ въ десятичную, и пзъ ятой десятичной извле-
каютъ корень, какъ изъ цѣлаго числа, до столькихъ десятичныхъ, сколько по-
требуется.
Примѣръ. —Найти у/^5, приближенный до трехъ десятичныхъ.
Обращаю эту дробь въ десятичную:
-5=0,42857142....;
беру только шесть десятичныхъ, отбросивъ всѣ прочія; дѣлю на классы, и из-
влекаю корень какъ изъ цѣлаго числа:
42,85,71 36 654
68,5 р 125
625 5
607,1 1304
5216 4
855
Въ найденномъ корнѣ отдѣляю три десятичныхъ знака, и получаю:
у/ у =0,654
точный только въ этихъ десятичныхъ.
2) Можно употребить и дроби обыкновенныя для полученія приближеннаго
квадратнаго корня изъ данной дроби. Для итого надобно сдѣчать знаменатель ея
полнымъ квадратомъ, помноживъ обѣ части дроби на знаменатель; тогда оста-
нется дѣлать приближенное извлеченіе собственно изъ числителя-. Паприм.:
= */Гб1.
2 . / 23 Ѵ 23
7 V 7 V тГ
9
130 —
Извлекши корень изъ 161 только до двухъ десятичныхъ, иы получимъ 12,69.
Г л л « , 12,69 1269
Слѣдовательно, приближенный корень будетъ—— = _,00-.
’ * 1269 ^ « / о2
А какъ 7оо < V 7 ’
1270 . /92
Я 700 > V 37 ’
1270 1269 1 1269
и разность——— —— ; то, взявъ на мѣсто полнаго корня, мы
г 700 700 700 ’ 700 г
сдѣлаемъ погрѣшность меяѣе, нежели па
3) Можно также употребить и дроби непрерывныя для извлеченія прибли-
женнаго квадратнаго корня изъ данной дроби, какъ видно изъ слѣдующаго образ-
ца, гдѣ требуется извлечь корень изъ —.
5
Для этого дѣлаю знаменатель полнымъ квадратомъ:
Беру четыре члена приближенія къ дроби, прилагаемой къ 4; нахожу послѣ-
1 8 17 114
2’ :.' зб’ зоз’’“‘
довательно:
Ограничиваясь послѣднею дробью, получаю-
*8- = і (4+И) =«»»♦«••••
гдѣ вѣрны всѣ 5 десятичныхъ.
В. Корни квадратные изъ одночленныхъ алгебрическихъ количествъ
145. Мы знаемъ, что для составленія квадрата изъ одночлена, надобно
зчть произведеніе квадратовъ всѣхъ его множителей, иль, другими словами,
взять квадратъ его коефгціента и помножить на 2 показатели всѣхъ его буквен-
ныхъ множителей. -Наприм.
(5а3Ъгс)-=5а’6-сХ5а36-е=5'(а;)’(^)!с’=25а 6‘с*.
Отсюда заключаемъ обратна, что корень квадратный изъ одночлена ра-
венъ произведенію квадратныхъ корней изъ его множителей; и что для
131
полученія втого корня надобно поступить ш«ратнымъ путемъ: извлечь корень
квадратный изъ коефиціенкі, и раздѣлить на 2 показатель каждой его буквы.
Посему,
|/25авб4с2=: /25. №. №. №=5а3Ь*с.
іів. Для извлеченія квадратнаго корня изъ дроби, надобно такимъ же обра-
зомъ извлекать корень изъ числителя и знаменателя. Наприм.
2а6‘
ЗгЫ*
іаѴ _
9^1*
115. Корень квадратный называется
одночлена, если его коефиці інтъ или какіе нчбудь его буквенные множетели не
п ишые квадраты. Наприм.
/5а8 и Ѵка№,
оба корня неизвлекомые. Впрочемъ такіе корни могутъ быть приводимы въ про-
стѣйшій видъ, если въ нихъ находятся нѣкоторые множители полные квадраты.
Въ такомъ случаѣ можно эти квадраты отдѣлись, извлечь пзъ нихъ корни, и,
что получится, вынесть за радикалъ въ видѣ множителя. Такъ:
Ѵ/5?—|/5|/а2=а|/5;
|47б8= №а№ №=2аЪ №.
Посредствомъ этого дѣйствія коренныя выраженія дробныя получаютъ иногда
значительное сокращеніе. Наприм.
За2. /Й8 За2. / 2.4.62Ь 1. ГЁ>
іЬ >/ 9а8с 46 у Эаѣа.с 2 \/ ас'
Обратно: можно всегда множитель, стоящій предъ радикаломъ, внести подъ
коренной знакъ; надобно Только возвысить его въ квадратъ, и написать множи-
телемъ подъ корнемъ. Наприм.
неизвлекомымъ изъ алгебрическаго
И это обстоятельство подаетъ иногда возможность приводи гь въ простѣйшій
видъ одночленныя алгебрическія дроби. Наприм.
„ , в / с * / 36а262<: 1/і О А
6а6\/ — =>/ „ . = ѴІ2обс.
у ааЬ
Счисленіе коренныхъ количествъ второй степени.
118. Ояо показываетъ способъ слагать, вычитать, умножать и дѣлить ко -
ренныя количества 2-й степени.
Для большей удобности, мы начнемъ сь умноженія и дѣленія.
132 —
а) Для умноженія или раздѣленія одного кореннаго количества па другое, на-
добно помножить или раздѣлить однѣ ихъ подкоренныя количества, и написать
подъ однимъ радикаломъ Такъ, /аХ ѴЬ— ѴаЬ\
__ В /а
г
Зт< очевидно изъ того, что /а6=Ѵа. Ѵь, и что \/ — = -
X 6 \/ь
Примѣръ. За /26Х^а /86= | а2/26.86=| а’.46=6а26.
Примѣръ. 2а/276 ^/36=2а ,| =5а/9=15а.
О возвышеніи коренныхъ количествъ, какъ дѣйствительныхъ, такъ п мнимыхъ,
мы будемъ говорить впослѣдствіи, въ общемъ трактатѣ о коренныхъ количе-
ствахъ- а здѣсь замѣтимъ только, что
( Ѵау—а, и (/=-а)2=—а.
Ь) Для сложенія пли вычитанія коренныхъ количествъ 2-й степени, на-
добно написать эти количества въ строку, соединить знаками -+- или —, и по-
томъ сократить, если можно. Сокращеніе дѣлается только между членами по-
добными, то есть, такчми, которыхъ нодкоренпыя количества совершенно равны
между собою. Тогда слагаются или вычитаются одни множители при радика-
лахъ, а коренное количество, какъ общій множитель, выносится внѣ скобокъ
Нанрим.
3 /5Д»-ь4 /оа6=(Зч-4-) /5?6=7 /5^6,•
5 /276—4Ѵ2а6=і/2а6;
7аѴрііЭаІ ч=(7а±5а)/р.
Но, чтобы точно знать, находятся ли подобные члены въ дапіюіі алгебриче-
ской суммѣ, надобно, всякой разъ, приводить ея члены въ простѣйшій видъ,
извлекая квадратные корни изъ всѣхъ множителей—полныхъ квадратовъ, нахо-
дящихся нодъ радикаломъ, и вынося ьти корни за радикалъ въ видѣ множителей.
Тогда, подобные члены, если они есть, сами собою, обнаружатся. Нанрим.
За /86Ѵ-+- /2М=6а6с /2 н-(1 №ь=(ЪаЬ+<1} /2б";
2/50-+-3 1/32—5 /18=10 /2-42 /2—15 /2=7 /2.
4^9. Такимъ же образомъ производится счисленіе и между коренными ко-
личествами дробными. Только относительно дробей надобно сдѣлать особое и
весьма нужное замѣчаніе. Когда одночленная дробь имѣетъ коренное количество
въ знаменателѣ, то всегда можно уничтожить радикалъ въ знаменателѣ, чрезъ
помноженіе обѣихъ ея частей на это коренное количество.
— 133
2
Примѣры: 1)
___— 1 \/о
/2 /2 /2 2 ’
3 3/5 3/5___________
—= =—- —=------------=3 |/о,05.
2/5 2 /5./б Ю
3)
=5.
При сложеніи и вычитаніи такихъ дробныхъ количествъ, надобно всегда осво-
бодить ихъ знаменатели отъ радикаловъ, потомъ привести въ простѣйшій видъ
щипальные члены, и подобные члены сократить.
Примѣры: 2аЬ н-3 Ѵа3Ь=2аЬ'^/ " +-3а V аЬ—§а ѴаЬ\
_ЙУ^=3о( ѵіі].
/аб /бс аЬ Ъг. К
150. Извѣстное свойство, что (а-ьб)(а—б)=а’—6!, очень часто употре-
бляется для освобожденія знаменателей дробей отъ коренныхъ количествъ вго-
рой степени, если эти знаменатели двучленные, трехчленные, и т. д.
Примѣры•
I) Если
найдется:
дана дробь .у~, то, помноживъ обѣ ея частя на разность 1— 1^2,
- -------=/2—1.
(1-+- /2)С<— /2}
2)
3)
1 - /2 (1— /2)( 1 1 /2)
а V ,|_і" /г)
/б— /с
Ь—с
і
і
X
/у)8 — і х-+-у—х+-2 уху
(X — У -2)
5)
(ЖЧ-?/—2?— бау
—— =3 (ѴЗч- /2— 1).
И- К
При сложен и п вычитаніи такихъ дробей всегда надобно освобождать ихъ
знаменатели отъ радикаловъ показаннымъ епчеобомъ, а потомъ приводить къ об-
щему знаменателю и сокращать. Напримѣръ:
1 5 6 1
Зн /7 4 4—/11 /7-2 2
—4+ /11 — 2 1/7 - -4— ‘ (V 7—5) =4ч- V11—3 |//.
131 —
Извлеченіе квадратнаго корня изъ количествъ многочленныхъ.
151. Здѣсь берутся такіе многочлены, которые дѣйствительно суть полныя
вторыя степени. Во всѣхъ другихъ случаяхъ непосредственное извлеченіе квад-
ратнаго корня почти безполезно. Поэтому надобно напередъ знать нѣкоторые
признаки для многочленовъ — неполныхъ квадратовъ.
1-е. Всякое количество двучленное не можетъ быть полнымъ квадратомъ; по-
тому что квадратъ одночленнаго количества состоитъ изъ одного члена; квадратъ
двучленнаго количества состоитъ изъ трехъ членовъ, а квадратъ трехчленнаго
количества,
(ач-6-ьс)5=а8ч-2аб-ьб*-ь2 (ач-^)сч-с8,
содержитъ шесть членовъ.
2-е. Многочленное количество, освобожденное отъ множителя общаго всѣмъ
его членамъ, и неимѣющее въ членахъ своихъ радикальныхъ количествъ, будучи
расположено по степенямъ одной буквы, не будетъ полнымъ квадратомъ, если
его первый и послѣдній члены неполные квадраты. — Другіе признаки непол-
ноты квадратовъ открываются при самомъ дѣйствіи извлеченія квадратнаго
корпя.
151В. Изв теченіе корня квадратнаго пзъ многочленовъ ничѣмъ не разнится
отъ извлеченія его изъ чиселъ. Оно также производится порядкомъ, совершенно
обратнымъ тому, по которому составляетсн квадратъ. Надобно послѣдовательно
отыскивать члены корня, составлять изъ нихъ члены квадрата, и вычитать изъ
даннаго многочлена. Если, по исключеніи веѣхъ членовъ квадрата, сосгавлешіаго
изъ суммы членовъ корня, въ остаткѣ не получится ничего, то найденный
корень, и будетъ искомымъ. Все же это дѣйствіе производится слѣдующимъ
образомъ.
1) Располагаютъ данный многочленъ по убывающимъ степенямъ одной его
буквы, извлекаютъ квадратный корень пзъ перваго члена: получится первый
членъ корня, который записываютъ съ правой стороны даннаго количества, и
отдѣляютъ отъ него вертикальною чертою. 2) Этотъ первый членъ корня возвы-
шаютъ въ квадратъ и вычитаютъ изъ даннаго многочлена. Въ полученномъ
остаткѣ должны находиться: удвоенное произведеніе перваго члена корня на вто-
рой неизвѣстный, и еще другіе члены, какіе должны быть въ полномъ квадратѣ.
3) Удвонвъ первый членъ корпя, дѣлятъ на чего первый членъ остатка;—полу-
чаютъ второй членъ корня. 4) Составляютъ удвоенное произведеніе перваго
члена корня на второй, и квадратъ втораго члена, и вычитаютъ изъ дѣлимаго
количества. Если остатка не будетъ, то значитъ корень найденъ, и дѣйствіе
кончено. Но, положимъ, что выйдетъ остатокъ; въ такомъ случаѣ онъ доляіенъ
содержать въ себѣ удвоенное произведеніе перваго и втораго членовъ корня ва
135
третій неизвѣстный, и квадратъ третьяго члена. Посему, 5) третій членъ
найдется, если мы раздѣлимъ остатокъ на удвоенное произведеніе обоихъ чле-
новъ корня. Тогда надобно будетъ составить удвоенное произведеніе перваго и
втораго членовъ корня на этотъ третій и квадратъ третьяго члена, и вычесть
изъ дѣлимаго. Если остатка не получится, то дѣйствіе кончено, п корень най-
денъ. Но, если будетъ остатокъ, то онъ опять долженъ содержать въ себѣ удво-
енное произведеніе трехъ членовъ корня на четвертый неизвѣстный, и квадратъ
четвертаго члена, который надобно будетъ искать также, какъ мы искали
третій членъ, и проч.
Можетъ случиться, что, послѣ какого нибудь вычитанія, получится въ
остаткѣ число членовъ менѣе числа членовъ корня, либо этотъ остатокъ не мо-
жетъ дѣлиться на удвоенное произведеніе всѣхъ найденныхъ членовъ корня;
тогда прямо надобно зак почить, что данное количество неполный квадратъ, и что
корень его неизвлекомый.
Примѣръ. Извлечь квадратный корень пзъ 46"-ь9а®—І2а6.
Расположимъ это количество по степенямъ буквы а:
Квадратъ.
9а*—12а6-ь46®
—9а’
остатокъ —12а6-4-46®
-+-12а6—46®
Корень.
За—26
6а—26 '
—26
О
Квадратный парень изъ перваго члена 9а® есть За. напишемъ его за верти
кальною чертою съ правой стороны, возвысимъ въ квадратъ, (За)*=9а®, и
вычтемъ изъ даннаго многочлена. Остатокъ —12а6ч-46® долженъ содержать
въ себѣ удвоенное произведеніе перваго члена корня на второй, и квадратъ вто-
раго члена. Чтобы найти второй членъ корня, помножимъ первый членъ За
корня на 2, и на троизведеніе 6а раздѣлимъ первый членъ —12а6 остатка ; —
найдется —26 второй членъ корня. Для повѣрки, припишемъ—26 къ 6а, и все
это помножимъ па—26: тогда 6аХ(—26) дастъ —12а6 удвоенное произведе-
ніе перваго члена корня на второй, а —26Х —26=46® квадратъ втораго члена.
Это произведеніе—42а6ч-46® вычтемъ пзъ дѣлимаго. Въ остаткѣ пуль; слѣдо-
вательно данное количество 9а®—42а6ч-46 полный квадратъ, происходящій
отъ корни За—26. Посему, можно написать:
1/9а*— 42а6ч-46®=3 а—26.
Примѣръ. Извлечь квадратный корень изъ
8а6’—4а36-ь46‘-ьа‘.
— 136 —
Расположивъ этотъ многочленъ ио степенямъ буквы а,
КвАДРАІТ . а*—4а86ч-8а68 ч-46' —а‘ Корень. а»_2(,6—26®
—4а86ч-8а68ч-46‘ ь4а86—4а®6® 2а®—2а6 —2а6
—4а®6’ч-8а68ч-46‘ ч-4а®6®—8а68—46* 2а'—4а6—26’ —26®
О
говорю: корень квадратный изъ перваго члена а4 даннаго количества есть а’;—
это первый членъ корня. Беру (а*)’=а’, вычитаю изъ даннаго многочлена, и
весь остатокъ сношу подъ горизонтальную черту. Первый членъ —іа* 3Ь дѣлю
на 2а®; нахожу второй членъ —2аЪ корпя. Этотъ членъ записываю на своемъ
мѣстѣ; сверхъ того, придаю его къ дѣлителю 2а®, сумму 2а®—2а6 помножаю
на —2а6, и произведеніе —4а86ч-4а®6® вычитаю изъ дѣлимаго. Остатотъ
—4а®6'-+-8а68ч-46‘ дѣлю на 2(а2—2а6)=2а®—4а6; получаю —26® третій
членъ корня. Этотъ членъ приписываю къ 2а®—4а6, сумму 2а®—4а6—26®
помножаю на —26®, и произведеніе вычитаю ьзъ дѣлимаго. Въ остаткѣ нуль;
слѣдовательно искомый квадратный корень
' а*—2а6—26®. '
Примѣръ.
Квадратъ. Корень
тра’64— а68с®---аЬ^-ѵ- 4- 6®с‘-4-6с®-г-1 —аЬ‘--4 Ьс*—1
3 3 4 3 2
4 Ш
— ѵа6
—^-аб’с®—4 6®с‘ч-6с®-+-1
-+-ѵа68с®—4^с‘
3 Ф
—уа62-+-6с®ч-1
ч-^ аЬ'—6с —1
О
—аб®—4 ^с’
з ч
±„6®—6с®—1
137 —
ГЛАВА ПЯТАЯ.
А. УРАВНЕНІЯ ВТОРОЙ СТЕПЕНИ СЪ ОДНОЮ НЕИЗВѢСТНОЮ.
153. Уравненіями второй степени называются такія, которыя, по осво-
божденіи отъ знаменателей, имѣютъ въ своихъ членахъ неизвѣстную х не выше
какъ во второй степени. Онѣ бываютъ полныя и неполныя. Полное уравненіе
состоитъ изъ трехъ членовъ: въ первомъ находится квадратъ неизвѣстной, во
второмъ членѣ первая степень неизвѣстной, и третій членъ независимый отъ
втой неизвѣстной. Слѣдовательно оно имѣетъ видъ
аа?*ч-6ж-4-с=0.
Если же будетъ с=0, или 6—0, то оно сдѣлается двучленнымъ, неполнымъ-
ах1-і-Ьх—(), либо ая®-4-с=0.
Уравненія двучленныя.
151. Двучленное уравненіе ах*-ыЬх=0 разлагается на два множителя.
(аа>+-б)л;=0,
и можетъ быть удовлетворено, полагая ж=0, либо ах-+-Ь=0; откуда х— —
а
Слѣдовательно, оно имѣетъ два корня:
0, и-----.
о
Двучленное уравненіе ах‘—Ь=0 также имѣетъ два корня, и разрѣшается
очень просто. Пзъ него находимъ:
х*— А—0.
а
Возьмемъ тогда будетъ
"-(у/4)‘=°-
Разность квадратовъ равна суммѣ корней, помноженной па ихъ разность;
посему,
Х*— ( \/ а ) “(*+ V / « )(Х—\/Ьа )=°-
Этому уравненію можно удовлетворить, полагая:
_ / ь / ь
х—I/ ”="0, либо агн-1/ 0; откуда
- 138 —
Таковы два корни уравненія; они оба вмѣстѣ пишутся формулою:
и получаются просто, чрезъ извлеченіе квадратнаго корня изъ обѣихъ частей
• і »
уравненія х .
Эти корни могутъ быть оба дѣйствительные, или оба мнимые, смотря по то-
му, будетъ ли извѣстный членъ Ь отрицательнымъ или положительнымъ въ
данномъ уравненіи.
Примѣръ 1. Возмемъ численное уравненіе:
3—2®’’ 15 „
=---5а?;
X------------X
освободимъ отъ зпаменителей:
3—2х—15—5а?*, или
За?*=12 ; отсюда
а?*=4, или а?2—4=(а?-+-2)(а?—2)=0.
Этому удовлетворимъ, полагая ж=2, или х=—2. Таковы корни даннаго
уравненія. Они пишутся одною формулою:
х=±1^==Ь2.
Примѣръ 2. Уравненіе За?14-12=5а?’-ь62 даетъ
—2а?!=50, или х‘=—25; откуда
а?=±5р/22Г.
Здѣсь оба корня мнимые. Они произошли отъ явной н ілѣпости въ 5 равненіи,
гдѣ требуется, чтобы За?*-+-12 было равно 5а?!-ь62, когда За?*<5а?*, и
42<62.
Однакоже оба корня удовлетворяютъ уравненію. Наприм., если врять
х= —5 V—1, и подставить въ данное уравненіе, то найдется тожественное
равенство:
—3.25-ь 12= — 5.25ч-62
—63= — 63.
Полное у равненіе второй степени.
Я55. Оно содержите въ себѣ члены со степенями а?*, а, х° неизвѣстной;
таково
«а?*-+-ба?4-са?1'=0, или, просто
аа?*-+-ба?-+-с=0.
Его можно сдѣлать проще, освободивъ х* отъ коефиціепта а:
139 —
о о
и, для краткости, положивъ - =р, а—(Г, тогда найдется
хг-+-рх-ічр=:0,
общее уравненіе 2-й степени въ самомъ простомъ его видѣ.
_ .28,1
Для примѣра, приведемъ къ этому виду уравненіе —- х— — х — —-2л.
и О 2
Сперва освободимъ отъ знаменателей:
4о?—5о?*=3—12х; отсюда
0=5л?!—4а?-ьЗ—12л, или
5л5—16л-+-3=0, и, наконецъ,
,16 з
л-----Л-4- —=0.
о 5
Это уравненіе совершенно сходствуетъ съ х'-і-ря-г-у—О.
15в. Рѣшеніе общаго уравненія второй степени. — Сперва надобно
данное уравненіе ах‘~і-Ьх-+-с—0 привесть къ общему виду
хг-г-рх-і-у—О,
ь с
полагай р=—> (І~~а * П0Т0ВІЪ перевести извѣстный членъ у во вторую часть:
лг-+-рл——ч,
и сдѣлать первую часть полнымъ квадратомъ отъ л-ь—р, что возможно,
лл
потому что
(а>+-уР) — ж*ч-рл-ъ \р*.
Сюда внесемъ х'-ь-рт^—у, и получится тотчасъ:
(ж-*-|р)8=—?+4р — Ір— ч-
Это можно написать:
Разность этихъ квадратовъ разложимъ на сумму и разность ихъ корней:
(л-Цр+у/ у/3)— 0.
Этому уравненію удовлетворимъ, полагая
4р’—5—0, или а?-ь|рчЛ/ ±р»_у-о,
откуда
аР-^у/ -Р1—9. либо л——ур—у/ -^-р*—у
140 -
Таковы два корня даннаго уравненія; ихъ пишутъ общею формулою:
Ж=—2 Р:1\/ уР -Ч )
Рѣшеніе полнаго уравненіе 2-й степени такъ часто встрѣчается, что уча
щимсл поставляется въ обязанность знать на память формулу:
' 1 , * /1 г
^=-уР±Ѵ тРг-Ч>
которою выражаются ооа корня уравненія. Опа выговаривается такъ:
Неизвѣстная равна половинѣ коефиціента предъ первою степенью х,
взятаго съ противнымъ знакомъ, плюсъ или минусъ коренъ квадратный
изъ квадрата этой половины безъ извѣстнаго члена у.
Для уравненія х'—рх—у=О, гдѣ р и у отрицательные, корнями будутъ:
Для уравненія ж*—Рх-*~у, гдѣ одно р отрицательное, корнями будутъ:
и проч.
Если на мѣсто р и у взягь Р=~, Ч=~> найдется:
і4>«—4ОС
ГС= ------------
2а
самый общій выводъ для выраженія обоихъ корней уравненія ах*-і-6х-^-с=0.
Примѣръ 1. Разрѣшить х*—6лн-5=0.
Здѣсь —5=3±2. Слѣдовательно, гс—5, либо х—1.
Примѣръ 2. Найти корни уравненія:
3^4-7^—6—0.
Освооодимъ сперва хг отъ коефиціента 3:
7
ГС—2—0; отсюда
Посему, корни уравненія : - и —3.
*) Открытіе сего рѣшенія Карданъ приписываетъ арабу Могамеду Бенъ Муза,
жившему въ 9-мъ вѣкѣ по Р. X., въ царствованіе Алмамуна.
141
Примѣръ#. —2х—^-хі-і-~х— 8.
У о о
Освобождаю отъ знаменателей:
5."»: —18.т=3яг ч-бя—72, или
х*— 12.гч-36=0; отсюда
х =6± 1^36—36 = 6~Ь0.
Здѣсь оба корня получились равные: одинъ 6ч-0=6, другой 6—0~6. Слѣ-
довательно, данное уравненіе (х — 6)8=0.
Примѣръ 4. Дано $хг—І2а?ч-8=0, или
8 і 8 „
—-3 жч-—=0; отсюда
я—А(1±/_ І).
Оба корни мнимые.
Составъ квадратнаго уравненія изъ его корней.
Теперь мы знаемъ, что общее уравненіе я^н-р-г-ч-#—0 имѣетъ два корня,
которые, для краткости, назовемъ буквами к, к':
* • / 1 2 >.
х——^р-^-у ~уР ~Ч=к,
1 » / 1 2 ,1
х^—^р—у -уР ~Ч=к,
и состоитъ изъ произведенія множителей:
х -+-^Р—у/ ур“—<7=0, или х—к =0,
жч--* рч- у/ур2 * * * * *—-(/:=0, х—к'—О, то есть:
а?’ч-ря:чч7= (х—к) (х—к') — х*—(к-і-к^х-і-кк'=0;
отсюда заключаемъ, что
р=—(к-+-к'), у~кк'.
Стало-быть, коефиціентъ р втораго члена уравненія равенъ суммѣ
корней, взятой съ противнымъ знакомъ, а извѣстный членъ у равенъ
произведенію корней.
Этотъ выводъ показываетъ легкій способъ составлять всякое уравненіе 2-ой
степени изъ данныхъ его корней.
Положимъ, что надобно составить уравненіе, котораго корни 5 и —2. По-
лагая Ін=5, к1——2, найдется:
р—_ — (5—2)=—3,
у—кк’=—10;
142 —
это подставимъ въ общее уравненіе:
х’-+-раН-<7=0; получится уравненіе
ж’—Зя;—10=0,
котораго корни 5 и —2.
Примѣръ. Составить уравненіе изъ корней А=3-+-2 V—I, /г'=3—2 V— I.
Здѣсь р=—6, д=13; посему,
я’—6я-+-13=0.
Изслѣдованіе корней полнаго уравненія второй степени.
458. Мы знаемъ, что оба корня уравненія л,-+-;)жч~д=0 выражаются
формулою:
і * /~і —р±
х = — -р±\/ ^рг—д =-------------з-----
Эти корни могутъ быть дѣйствительные или мнимые, оба положительные или
оба отрицательные, одинъ положительный, а другой отрицательный, равные илп
неравные.
Оба корня бываютъ дѣйствительными, если подкоренное количество р —4>у
>0, или р*—4д=0, какой бы знакъ ни былъ предъ р\ въ противномъ случаѣ,
они оба мнимые. Это очевидно.
459. Положимъ, что уравненіе содержитъ корни дѣйствительные; тогда
остается еще опредѣлить, какіе они: положительные или отрицательные. Знаки
предъ дѣйствительными корнями совершенно зависятъ отъ знаковъ предъ коефи-
ціентами р и у, слѣдовательно отъ знаковъ предъ членами уравненія; это знаемъ
мы изъ самаго состава уравненія ж!ч-ра?-ьд=0, гдѣ р=—{к-+-к'), д—кк'.
Намъ остается еще открыть очевидные признаки, по которымъ бы можно было,
при одномъ взглядѣ па уравненіе, узнавать эти знаки предъ корнями.
Для этого замѣтимъ предварительно, что во всякомъ уравненіи, расположен-
номъ по степенямъ ею неизвѣстной, всякіе два члена, взятые сряду, могутъ
имѣть знаки противные (-4---либо-----г-), илп знаки равные (н—ь или
-----). Послѣдованіе членовъ съ противными знаками называетсн перемѣною,
а послѣдованіе членовъ съ равными знаками называетсн повтореніемъ.
Такъ, уравненіе х^-г-рх-і-д—О имѣетъ только повторенія знаковъ, и пи од-
ной перемѣны. Уравненіе х1—рх-+-д=.О имѣетъ двѣ перемѣны, и ни одного
повторенія. Уравненіе хг±рх—д=0 имѣетъ одну перемѣну и одно повтореніе,
какой бы пи былъ знакъ предъ рх.'
460. Въ полномъ уравненіи второй степени число дѣйствительныхъ
положительныхъ корней всегда равно числу въ немъ перемѣнъ, а число
корней отрицательныхъ равно числу повтореній. Это общее правило легко
и просто вытекаетъ изъ разсматриванія состава р и д.
— 1-13 —
4) Когда уравненіе имѣетъ двѣ перемѣны, т. е. когда р отрицательное, а
д положительное; тогда оба корпя к, к', положите лыіые: во-первыхъ, пото-
му, что ихъ произведеніе кк'=-+-у положительное, слѣдовательно, оба корня
съ равными знаками; а во-вторыхъ, чтобы р——(кг+-к') было отрицательнымъ,
надобно, чтобъ к, к', были положительными.
2) Когда уравненіе имѣетъ два повторенія, или ни .одной перемѣны, т. е
когда р и д оба положительные; тогда оба корня к, кг, отрицательные. Ибо,
положительное произведеніе ккг~-+-у показываетъ, что оба горня съ рав-
ными знаками; а чтобы р=— (к-+-кг) сдѣлалось также положительнымъ, на-
добно, чтобы к, кг, были отрицательными; тогда
р=— (—к—к!) =-ь (Л-ьЛ').
3) Если уравненіе имѣетъ одну перемѣну и одно повтореніе, слѣдовательно
у отрицательное; то, каковъ бы ни былъ знакъ предъ р, одинъ корень урав-
ненія будетъ положительнымъ, а другой отрицательнымъ. Ибо, произве-
деніе двухъ дѣйствительныхъ корней,
кк'= — д,
не можетъ сдѣлаться иначе отрицательнымъ, какъ въ единственномъ случаѣ,
когда эти корни съ противными знаками.
4) Если въ уравненіи аз’-4-рам-д-г-О найдется р*—4д=0, то оно имѣетъ
оба корня равные. Потому что
р’=**-+4'*-+-2ЛЛ'
4д—Ькк'
рі—Ьу=кі+к!і—ЫкІ=(к--к'У=() ;
откуда А=4'.
Это, впрочемъ, видно непосредственно изъ
-Р± Ѵр^—^ч і , Л
-Г—-= — Т?±0-
Слѣдовательно, уравненіе обращается въ
х^-ь-рх-ь- у р’р)!—0.
161. Возмемъ теперь общее уравненіе:
аж’-ь-йж-ьс—0.
и его рѣшеніе:
—Ьхі: \/Ь4—Лас
X = ' За
Здѣсь дѣйствительные корни возможны только въ случаѣ Ь!>4ас, или
б’=:4ас. Знаки предъ этими корнями опредѣляются числомъ перемѣнъ и повто-
реній, по правилу, показанному для ж*-ь-рх-ьд=0. Но, давая частныя значенія
коефиціентамъ а, Ь, с,въ общей формулѣ, которою выражаются корни уравненія,
— 144 —
мы приводимся иногда къ рѣшеніямъ символическимъ, которыя требуютъ объ-
ясненія.
1) Возмемъ с—-0; получится:
—Ь=ьб
корнями уравненія будутъ 0 и —
2) Для 6—0, получится аз = ±у/ 22^
—Ь=ь |/і®—іас _Ъ±Ь
3) Если а- =0, то формула х = --------— обращается въ х— ——. Въ
2а "
* 0 —26
этомъ случаѣ, одинъ корень —, а другой ——.
Для объясненія этого си иволяческаго рѣшенія, освободимъ числитель формулы
— Ь± VИ*—іас
Х= 2^
отъ радикала, помноживъ обѣ части дроби па —бгр ѴЬ' —-Іас, получится;
-2с
а; =---- - .
Ь=р VЬ®—4ас
4) Теперь возмемъ а=0, и найдется аз — '
Слѣдовательно, одинъ корень х ——а другой
—2с
х =—— —
о
И въ самомъ дѣлѣ, данному уравненію,
аА*-і-Ьх-і-с=.О,
можно дать видъ вч--^-ь^=0, раздѣливъ его на х*. Для а=0, первое обра-
щается въ 1)х-+-с=0, откуда х— — а второе въ у ч- ^=0,
чему удовлетворимъ, полагая х~со .
5) Наконецъ, возмемъ а=0, Ъ=О, въ формулѣ
— Ьгь —іпс
Х~------ ------,
2а
О тт ,
получится х— у для оооихъ корней. Чтооы понять это символическое иыраже
ніе корней, преобразуемъ эту формулу, какъ было показано,
—2с
ВЪ X =. ---; ,
6®—4ас
и положимъ а=0, Ъ—0; для обоихъ корней найдется
— 14-5 —
II дѣйствительно, если аа?-+-6я:-+-с=0 раздѣлимъ на хг, то получимъ
ь е Л
ач-----і- —=0;
х ж’
а потомъ положимъ а=0, 6=0; найдется
О,
х*
чему удовлетворимъ, полагая только х =оо .
1С 8. -- ЗАДАЧИ.
Задача {. — Найти среднее пропорціональное число между а и 6.
Пусть это число х; оно должно удовлетворять пропорціи а : х=х : Ь, изъ
которой I
х*=аЬ, х=±Ѵ'аЬ.
Если а=рч-д V7—1, 6=р—у V—1, то среднимъ пропорціональнымъ между
этими мнимыми найдется
х~ \/р^ч-у*
іисло существенно дѣйствительное.
Задача 2. — Найти такое число, котораго квадратъ, сложенный
съ квадратомъ его половины и еще съ квадратомъ его трети, составилъ
бы сумму 196.
Пусть это число х. По условію задачи должно быть
-+-(у х ) =196, или
я/(1-і-^-+- *)=196; откуда
, 196.36 ,
х*——— , а аз=±12.
Задача 3. — Раздѣлитъ число 60 на двѣ части такія , чтобъ
произведеніе ихъ равнялось 500.
Пусть х первая часть, то будетъ 60—х вторая часть; по условію должна
быть
я:(60—я:)=500, или
60ж—я:*=500, или
х*—60жг! —500; откуда
ж=30± 1/900—500=3 0±20.
И такъ, первая часть я:=50, либо 10,
а вторая 60—л?=10, либо 50
Въ обоихъ случаяхъ произведеніе 50.10=500.
Задача 4. — Найти такое чис,іо, на клпорос надобно раздѣлить
130 такъ, чтобъ получить частное равное дѣлителю олорсешіому съ 5,
и остатокъ равный тому же дѣлителю безъ 5.
іо
—.146 -
Пусть х искомый дѣлитель; то
х-с-5 будетъ частное,
х—5 » остатокъ.
Слѣдовъгельно, 134Э=а;(ле-ь-5)-д-ле—5, пли
ж*-»-6=135; откуда
х=. —3± Ѵ^І 3 5= — 3± 12.
П такъ, я=9, либо х=.—15
Задача 5. — Портной купилъ нѣсколько аршинъ сукна за 60 руб.
серебромъ. Если бы за тѣ же деньги онъ купилъ 4 аршина болѣе, то
каждый аршинъ обошелся бы ему половиною рубля дешевле. Спраши-
вается: сколько аршинъ куплено, и по какой цѣнѣ?
Положимъ, что куплено х аршинъ сукна за 60 рублей; въ этомъ случаѣ,
ко I , , , , *
цѣна одного аршина =—. А если бы куплено было 4 аршина болѣе, то есть,
ям- і- за тѣ же 60 рублей, то каждый аршппъ стоилъ бы ~По условію за-
дачи, послѣдняя цѣна менѣе первой половиною рубля; слѣдовательно,
60 60 А
---------- =0,5.
х гг-і-4
Освободивъ это уравненіе отъ знаменателей, найдется:
60а?-+-240—60ж=0,5х*-ь-0,5.4ж, илп
х =480, откуда
х= —2± 1/484= —2-»-22.
Пзъ найденныхъ двухъ корней 20 и —24 единъ только 20 разрѣшаетъ за-
дачу въ прямомъ смыслѣ; корень-же отрицательный надобно отбросить
И такъ, куплено 20 аршппъ сукна, и каждый аршинъ по —=3 руб. серебр.
Задача 6. — По окончити нѣкоторой, работы, спросили у работ-
никовъ: сколько ихъ было всѣхъ, и сколько они дней работали? Они.
отвѣчали', насъ было столько, сколько дней мы работали; а если, бы
къ намъ прибавили еще четырехъ работниковъ, то всю работу окончи-
ли бы въ 2 дня. Узнать, сколько же ихъ было?
Пусть х число работниковъ, и х число дней; а еслибъ было азч-4 работіп.
ковъ, то работа окончилась бы въ 2 дня. Здѣсь между числомъ работниковъ и
числомъ дней должно быть отношеніе обратное, то есть:
ч Х-+-4 : х=х : 2; откуда
а?*=2а;-ь8, пли х*—2х=8, ѣ
. '' „ а=4=НѴ Н78=1іі3>. ' '
। * . ч г \ »- ,,4» *
•'-<Под.б^рд'елі,нь*'-корйй.,''4 показываетъ' что было 4 работниковъ и 4 дня
работы.
147
Задача 7.—Банкиръ принимаетъ въ учётъ два векселя: одинъ въ
8193 рубля, которому срокъ платежа чрезъ 9 мѣсяцевъ; а другой еъ
7500 рублей, которому срокъ чрезъ 8 мѣсяцевъ Пра этомъ онъ даетъ
за первый 1200 рублей болѣе нежели за второй. Узнать, какъ велики
годовые проценты съ этихъ векселей?
Пусть х годовые проценты со 100 въ мѣсяцъ, или 12ж проценты въ годъ;
то 9ж и 8а? будутъ процентами за 9 и 8 мѣсяцевъ. Поэтому, каждые 100
рублей, по прошествіи 9 и 8 мѣсяцевъ, сдѣлаются 100-ь9а: и ЮО-ь-Йа:, и ко-
торыя банкиръ принимаетъ за 100; а въ какую цѣну принимаетъ онъ вексель-
ныя суммы 8793 и 7500 руб., это найдется пзъ пропорціи:
100-+-9ж : 100=8793 : ,
ІОО ь9®
100-ь8ж : 100=7500 : ,
100-4-8®
гдѣ четвертые члены и представляютъ настоящія цЬны векселей, за которыя
принимаетъ ихъ банкиръ. По условію задачи:
879300 750000 , „„ „
- „------, п - - - = 12^0, или
# 100-4-9® 100-1-8®
2931 2500 ,
-----------------_ 4.
100н-9® 100-4-8®
Освободивъ отъ знаменателей, и сокративъ уравненіе на 4, останется:
72х"ч-1463о=775, или
2 1463
775
х — — ; и наконецъ
і іі
72
-731,5
X -
—?7І,5=Ь768,6О
72
„ — 731,5±768,60
Посему, і2о: =
6
Возмемъ одинъ положительный корень, который рѣшаетъ задачу въ прямомъ
ея смыслѣ, получится:
12х—6,2
И такъ, оба векселя приняты въ учётъ по 6,2 процентовъ въ годъ.
В. УРАВНЕНІЯ 2-й СТЕПЕНИ СЪ ДВУМЯ НЕИЗВѢСТНЫМИ, КОГДА ЧИСЛО
УРАВНЕНІЙ РАВНО ЧИСЛУ НЕИЗВѢСТНЫХЪ. РѢШЕНІЯ ОПРЕДѢЛЕННЫЯ.
1СЗ. Для разрѣшенія уравненіи второй степени съ двумя неизвѣстными,
надобно имѣть два уравненія, п, посредствомъ извѣстныхъ способовъ (90),
исключить изъ нихъ одну неизвѣстную; останется одно уравненіе только со вто-
рою неизвѣстною.- Но, чтобы это послѣднее было не выше 2-й степени, и
— 148 —
могло быть разрѣшено по извѣстнымъ доселѣ правиламъ, надобно, чтобъ одно
пзъ данныхъ уравненій было второй степени, а другое первой степени.
Задача 1. — Найти два числа, которыхъ разность 8, а произве-
деніе 20.
Пусть эти числа х, у, то
х—у= 8,
ху=20.
Изъ перваго уравненія находимъ х=зу-+-%; это подставимъ во второе, по-
лучится :
у*-ь-8у=20; откуда
у =—^16-1-20=—4±6.
Слѣдовательно і/=2, либо —Ю.
Для у=2, найдется х=г/ч-8= 10;
для у=—10, х=у+-Ъ=—2.
Задача 2. — Найти два числа, коихъ произведеніе ~а, а ихъ сум-
ма, раздѣленная на разность, =хЬ.
Пусть эти числа я, у; то должно быть
хи—а, --------------------------= о.
. у
Пзъ втораго уравненія находимъ:
х-+-у=Ьх—Ьу, или
у(1ч-Ь)=я:(Ь—1), и
а>(Ъ—1)
6-+-1 ’
Это и подставимъ въ первое уравненіе:
ж8(Ь—1)
- — а'> 0ТКУДа
х—і-і
V ь—і
Таково первое число. Второе же число у — ^, то есть:
_____» / б—1_____, Д /0(6—1)
У Яд/ а(Ь=Ы) у 6ч-1
Паприм. если а=7, 6=8, то
х=±з, у =
слѣдовательно, х=3, либо—3;
у —у, либо —у •
Если положить Ь—1; то найдутся х = ± оо ,
у = ±0.
— 149 -
Для объясненія этихъ рѣшеній, обратимся къ данному уравненію В
Для Ь=1, оно будетъ ^^=1. Очевидно, что ему иначе нельзя удовлетво-
рить, какъ взявъ у—0, каковъ бы х ни былъ; а чтобъ удовлетворить уравненію
ху~Ь, когда у=0, надобно взять ж=оо ; потому что нуль, помноженный на
безконечность, выражаетъ всякое конечное число (3*9^, з).
Задача 3. — Найти два такихъ числа, коихъ размоетъ квадра-
товъ равна у*, а разность между произведеніями перваго на а и вто-
раго на Ь равна я.
Назвавши чрезъ х, у, эти два числа, по условію задачи имѣемъ:
я*—у8=д8,
ах—Ъу=з.
Изъ втораго уравненія получаемъ:
«А/ —_____________________________ -
а
это подставимъ въ первое, найдется:
Ру1 +-2Ь««-*-$2 , ,
-------------------У = Ч . или
6*у-+-2о«у-+-а —а^—а^у*, или
(а8—б8)у8—2б«у=«8—а8д8; отсюда ’
Ьв±а V *2—<?2(“2—Ь2) ч
V______________________________________________а*—Ь*
Таково одно изъ чиселъ. Другое же число х получится:
_ а« =Ь Ъ \/»2—Ч2(“2—Ь2)
Х
Для отстраненія символическихъ рѣшеній, могущихъ произойти въ случаѣ
а—Ь, освободимъ числители отъ радикаловъ. Для этого помножимъ обѣ частп
дробнаго выраженія х на аззрб ѵяг—у* (а*—Ь*), а обѣ части дробнаго выра-
женія у на бв^ра рэ8—д^а8—б8), и сократимъ па а8—Ь8; тогда получатся:
ЬѴ <~«2
ж ~----------- - — ,
в«н=ь ^/«2—в2(а2—6’)
«Ч2—«2
у =--------- - • -
|/«2—52(а2—Ь2)
Розыщемъ теперь, когда эти рѣшенія возможны, и въ какихъ предѣлахъ онѣ
положительны.
Очевидно, что рѣшенія эти возможны только въ предположеніи «8>д’(а8—б8);
илп = д8(а8—б8); въ противномъ случаѣ онѣ всѣ мнимыя.
Чтожъ касается до того, при ьакихъ условіяхъ, и въ какихъ предѣлахъ, дпм-
159 —
ствителиіые корни х, у, будутъ положітелъиьіми, это зависитъ отъ част-
ныхъ величинъ для а, Ь, д, з.
На самомъ предѣлѣ, съ котораго корни начинаютъ быть возможными, го есть.
когда «*—у’(а!—Ь*), получаемъ
Ь2п2ч-«2 о2«2—«2
х — —" У ъ— •
аз ’ '> Ы
Здѣсь корень х положительпый а у только тогда будетъ положительнымъ,
когда а2д*>з’, или а9>з, каково бы ни было отношеніе между а и Ъ.
Для опредѣленія условій, дѣлающихъ положительными х, у, въ случаѣ
5!>д’(а*—Ь*), возмемъ сперва эти корни съ знакомъ -+-, то есть:
Ь2й2-м2
Я7 - - ~~ _ ,
аз-і-Ь ^/з2—д'-!а2—Ъ2)
а2д2—з2
У — -------- —-------
' Ъз~+-Ъ |/52_,^(а2—Ь2)
И здѣсь также, очевидно, х положительный; у также положительный, когда
ад>5.
Даже, если взять ад—$, то найдеіся-
ЬѴ-+-«2_(а2-*-»2]}2 _
Х йз-+-Ъ-ц (а2-ь&2,5
І' = 0.
Таковъ предѣлъ положите іы.ыхъ рѣшеній для х, у, взятыхъ сь знакомъ
Онѣ пе зависятъ отъ а и Ь, а только отъ условія ад > з.
Возмемъ теперь х п у съ знакомъ —, то есть:
ЬУ-ьз2____________
аз - Ь [/з2—д2{а2-іГ)
а2а2 —з°
У = —2------ —
6«—а 0і2-дв(а2—Ь2)
Эти рѣшенія зависятъ отъ а, Ь, д, 8. •
Возмемъ а> 6; тогда будетъ а^ьѴь*, и подавно аь^ЪѴі*—д\а*—6*).
Слѣдовательно х будетъ положительнымъ.
Корень у будетъ ьологкптелыіымъ. когда
а9>з, и б.ОиіЛѵ—<р\а*—I)*}, или
&Ѵ>аѴ—аѴ(а2—6!), или
а’9’(У—62)> (а‘—
слѣдовательно, при томъ же условіи а^>з.
Снъ будетъ также положительнымъ при ад < з.
Если взять ад=^8', тогда х будетъ положительныйь, потому что а>6,
аз>б |/з*, и проч.; другое же число будетъ
_ а*д2—з2 (ад-ь«)(ад—«) 2«
Ьз—адЬ —Ь[ад—і) Ь
отрицательное.
151
А чтобъ узнать, съ какого предѣла у дѣлается отрицательнымъ, уравняемъ
нулю его знаменатель, т. е. возмемъ
Ьз=а V?—уЦа~—ІЛ), нли
—а’^8(а2—А*), или
0=(а2——6*); откуда
(.г_а’9«)(а5_-62)=0.
Поелику л=ад не даетъ предѣла, то надобно взять а=6. Вотъ съ какого
случая у начинаетъ быть отрицательнымъ.
Для этого предѣла а—Ь, становятся
6Ѵ-+-*2
X —------------ 00,
а&—а»
аѴ—з*
« —--------~ оо.
17 Ьг—
Возмемъ, наконецъ, а<6. Въ этомъ случаѣ,
_ Ь2д2-ы2
аЬ—Ь |/«2-+-д2(62—а2У,
а2д2— «2
I/ =-------- •
Ьз—а ^/«2~ьд2(Ь2—а2) ’
х отрицательный, потому что, для а<б, будетъ а$<ЬѴ$*> и 'подавно
а$<Ь ѴѴ-ь-д^б*—а*); у также будетъ отрицательнымъ, ибо, необходимо
6л> а {Ь*—аг), откуда
ЬѴ>Л*+аѴ(62—а’)
(62—а’)л’> а8д2(62—а2)
л*>аѴ;
слѣдовательно, знаменатель будетъ положительнымъ, по числитель ад1—$* дѣ-
лается отрицательнымъ.
Задача 4. Данное число а раздѣлитъ на двѣ такія части,чтобы ква-
драты ихъ находились въ данномъ отношеніи т ; 1.
Пусть первая часть х, то вторая часть а—л . По условію задачи.должно быть
<г2 то
------ - — =т; отсюда
(а—я")2 1 ’
—= ± Ѵв
а—х
х—±аѴт^рхѴт, или
(1 ± Ѵт) х= ±а Ѵт
±а V т ткат
Такова первая часть. Вторая часть будетъ
а Ѵ'т а
а—х=ат^-------— —-----
1±і/то 1± I
15? —
Если взять т— I, то получится:
« , —«
для первой части—, лиоо —•=—оо;
2. О
а , -ьа
для второй части — , лиоо —- = -+-се.
Здѣсь, очевидно, годится только одно рѣшеніе. Но, любопытно дать себѣ
отчетъ въ томъ, какъ второе рѣшеніе удовлетворяетъ уравненію
ж’=и».(а—х*=(а—х)1.
Для этого раздѣлимъ все на х*, получится:
і=(“—1)!,
чему и нельзя иначе удовлетворить, какъ полагая х~±оо.
Этою задачею рѣшаются нѣкоторые практическіе вопросы, какъ то: і) На
прямой линіи, соединяющей двіь свѣтящія точки различной яркости,
найти точку, которая тѣми точками освѣщается равно. 2) На пря-
мой линіи, соединяющей центры двухъ неравныхъ массъ, найти точку,
которая бы равно притягивалась этими массами. Въ такомъ случаѣ чи-
сло т выражаетъ данное отношеніе между яркостями свѣта точекъ, или между
величинами притяженій тѣхъ массъ. Яркость же свѣта, равно какъ и нрптяжепіо
массъ, измѣняется въ обратномъ содержаніи квадратовъ разстояній отъ свѣтя-
щихъ точекъ или центровъ массъ.
•
Приведеніе тричлепныхъ уравненій х^-і-рхі-і-д=(), и, вообще
х2т-і-рхт-л-д—0, въ уравненія второй степени.
56.<. Уравненіе 0 четвертой степепп весьма просто приво-
дится въ уравненіе 2-й степени, и легко можетъ быть разрѣшено. Для этого
надобно только положить хг—у, слѣдовательно х*=у2, и это подставить; по-
лучится,
</‘-+-руч-?=0,
уравненіе второй степени, изъ котораго найдется:
Задача.—Данное число а разложить на два такіе множителя,
чтобы сумма ихъ квадратовъ равнялась Ь*.
Пусть эти множители х, у, то, по условію задачи, должно быть:
ху=а. хг-ѵ-у’=Ь'
153
Пзь перваго уравненія нахожу у — , и это подставляю во второе:
' 1Л
х- ч —. = отсюда
ч- а* -+- Ь*х*, или
аз‘ — 68л:8ч-а8=0.
Для разрѣшенія этого уравненія, полагаю ж8=у, и нахожу:
у1—Ьу-і-а —О, откуда
у=і
/1
слѣдовательно, х = ± \/ - Ь ± ж /* м____„«
» 2 • у *
а а
Послѣ сего найдется у = - =-- _ — —т •
Х ± Ь ± 6*-а»
2 *
Въ этихъ выраженіяхъ заключаются четыре корня, а именно:
Смотря потому, будетъ ли у 68>а8, или <а8, всѣ корпи будутъ дѣйстви-
тельные, или мнимые.
165. Возмемъ теперь тричленпое уравненіе
х* т-+-рх ”‘ч-(/=0,
гдѣ т число цѣлое положительное. Если положить х’"=у! взять этого квадратъ
хІт=у*, и подставить, то получится уравненіе 2-й степени
у8ч-руч-д'=0; откуда
у=4 р =*=
и, наконецъ, х =.
154 —
Въ общей теоріи уравненій мы покажемъ, сколько такое уравненіе можетъ
имѣть корней дѣйствительныхъ и мнимыхъ, и какъ можно ихъ отыскивать. А
теперь намъ достаточно знать, что можно уравненіи такого ища понижать во
вторую степень, и находить по крайней мѣрѣ два ихъ корня.
Неопрёдълеинь.п анализъ 2-й степени. Рѣшенія наибольшія и наи-
меньшія.
<6С. Эти уравнен.я, вообще, допускаютъ безчисленное множество рѣшеній,
между которыми могутъ быть дѣйствительныя и мнимыя, цѣлыя и дробныя, со-
измѣримыя и несоизмѣримыя, положительныя и отрицательныя. Но, это мно-
жество рѣшеній весьма часто въ задачахъ ограничивается условіями: 1) чтобы
всѣ рѣшен.я были дѣйствительныя, и притомъ положительныя, цѣлыя, или
дробныя—соизмѣримыя; 2) чтобы одна пзъ неизвѣстныхъ была ие больше или не
менѣе данной величины; 3) чтобы которая-пибудь пзъ неизвѣстныхъ была наи-
большею либо наименьшею.
169. Въ неопредѣленныхъ уравненіяхъ первой степени не бываетъ рѣшеній
мнимыхъ, нѣтъ также конечныхъ рѣшеній паиболыпих и наименьшихъ; по въ
неопредѣленныхъ уравненіяхъ 2-й степени, и степеней высшихъ, онѣ часто слу-
чаются, а потому мы собственно займемся розыскапіемъ этихъ рѣшеній, ограни-
чиваясь уравпепіями только со двумя неизвѣстными.
Для примѣра, возмемъ уравненіе хіч-у*=5, изъ котораго
у = ±\/5—х*.
Если возмемъ у съ знакомъ ч-, и будемъ перемѣнной х давать возрастающія
величины:
х — — 3, — /б,' — 2, — 1, 0, 1, 2, Ѵ5. 3,....,
то получимъ соотвѣтственныя рѣшенія:
у = Ѵ^^, О, 1, 2, ИГ 2. 1, О, V—Т,....
Здѣсь видно, что всѣ дѣйствительныя рѣшенія заключаются въ предѣлахъ огъ
х= — 1^5 до х= ч-0); а, внѣ этихъ предѣловъ, всѣ у суть мнимыя Рѣше
пій цѣлыхъ положительныхъ для х, у, только два.
Сверхъ того, въ ряду дѣйствительныхъ рѣшеній, у имѣетъ одно наибольшее,
соотвѣтственное наименьшему и два павыепыпихъ, соотвѣтственныя
х— — і/5 и ч-0).
Возмемъ еще уравненіе »/=Зч-(л?—2/.
Оно допускаетъ безчисленное множество рѣшеній въ числахъ цѣлыхъ и поі
жительныхъ. Ибо, для
х = — 1, 0, 1, 2, 3, 4, 5,....
12, 7, 4, 3, 4, 7, 12,....
155 —
Но и въ числѣ этихъ рѣшеній находится одно, у==3, самое меньшее. Слѣдо-
вательно, если бы требовалось, изъ всѣхъ рѣшеній для у, найти наименьшее,
то мы получили бы это одно. ' I
1<*8. Только та неизвѣстная, которая выражается квадратнымъ корнемъ
изъ другой, можетъ сдѣлаться мнимою. Какія дѣйствительны я величины
соотвѣтствуютъ этой неизвѣстной подкоренной, и въ какихъ предѣлахь, найти
петрудио: стоитъ только все количество подъ корнемъ уравнять нулю, и найти
отсюда вторую неизвѣстную. Величина сей неизвѣстной будетъ предѣломъ дѣй-
ствительныхъ рѣшеній для первой неизвѣстной, и въ тоже время наибольшею
либо наименьшею для второй.
Посему, чтобъ отыскать, имѣетъ ли функція
у=3н-(а?—2)’
наибольшую пли наименьшую величину, вадобпо разрѣшить это уравненіе отно-
сительно х, и найти предѣлъ, при которомъ х становится дѣйствительнымъ:
(х—2)*=у—3, отсюда
х=^~Ѵу—3.
Всѣ числа х будутъ дѣйствительныя, когда станемъ у брать только отъ 3 до со ;
менѣе 3 взять нельзя, иначе х сдѣлается мнимымъ. Пзъ этого видно, что для у
соотвѣтствуетъ наименьшая величина 3, которую мы и нашли бы, полагая
подкореппое количество у—3=0. Въ этомъ случаѣ х=2. П такъ, для ж=2,
соотвѣтствуетъ у=3= тінітит .
Примѣръ. По данному уравненію
у8—10а?у-т-26а?8—49=0,
найти, при какихъ величинахъ х, перемѣнная у дѣлается наибольшею или наи-
меньшею.
Разрѣшаю это уравненіе относительпо х:
. 10а" у 49 —у*
X --- —----- —--- ,
2В 26 ’
V 46 26—у3
Х ~ 26 ’
Здѣсь тотчасъ видно, что у* можно брать отъ 0 до 49.26, и пе болѣе, иначе
х сдѣлается мнимымъ Слѣдовательно у допускаетъ тахгтит, которое найдется
изъ уравненія:
49 26 — у‘=0, или
у— ±і/49.26= ±35 (почти).
Примѣръ. Опредѣлить, имѣетъ ли функція
х-+-а
У — ~7=
у х—а
наибольшую или наименьшую величину?
156
Освобождаю отъ знаменателя, и возвышаю въ квадратъ
а;8-і-2аа:-ьа8=у8(а?—а)=ху*—оу2, или
х*-+-(2а—у*)х=—а*—ау1- отсюда
Подкоренное количество показываетъ, что у* можно брать отъ оо до 8а, и
отнюдь не менѣе; слѣдовательно у имѣетъ тіпітит, которое мы найдемъ, по-
лагая у*—8а=0; откуда
у — ± Ѵѣа— тіпітит.
?/у—2а 8а—2а Л
Бъ этомъ случаѣ ——=—-— — За.
Задача. Данное число а раздѣлить на два такихъ множителя, чтобы
сумма ихъ была наименьшею.
Пусть х первый множитель числа а, то вторымъ будетъ ~. Сумму ихъ на-
зовемъ чрезъ у-, получится уравненіе:
х = у, откуда
а?8—хуч-а=0,
1 /1
*= Т У±ѴІ У~а-
Очевидно, что нельзя взять — у < а; слѣдовательно, сумма у имѣетъ наи-
меньшую величину, которую найдемъ, положивъ ~ у8—а=0; откуда
у —
Такова наименьшая сумма у. Въ этомъ случаѣ, первымъ множителемъ числа
а будетъ
х — \ У =^=^а,
а а <— ѵ
вторымъ множителемъ — = ± уа_
И такъ, данное число а надобно раздѣлить на два равные множителя, изъ
коихъ каждый = ±Ѵа^.
Задача. Данное число 2а раздѣлить на двѣ такія части, чтобы
произведеніе ихъ было наибольшимъ.
Пусть первая часть х, то второю будетъ 2а—х. Назовемъ искомое произве-
деніе буквою у; оно будетъ
у—а? (2а—а?).
А чтобы найти, когда это произведеніе сдѣлается наибольшимъ, отыщемъ х:
онъ получился:
х — а ± Ѵа*—у.
157
Самая большая величина для у есть а8; въ семъ случаѣ, х=.а, это первая
часть, и вторая 2а—хт=а. Слѣдовательно, данное число 2а надобно раздѣ-
лить на двѣ равныя части, чтобы произведеніе ихъ было наибольшее.
Задача. — Данное число 2а раздѣлить на двѣ такія части, чтобы
сумма ихъ квадратовъ была наименьшею.
Пусть х первая часть, 2а—х вторая, а сумма ихъ квадратовъ ; то
ж’-ьіа2—іа^-Ч отсюда
Нельзя взять у у < а*, или у <2а*; посему, у=2а* и есть наименьшее. Въ
этомъ случаѣ, х=а, 2а—х=а. Слѣдовательно, и здѣсь надобно 2а раздѣлить
пополамъ.
1в9. Можетъ случиться, что количество подкоренное будетъ трехчленное,
вида у*-+-ру-л-д, и для у найдутся двѣ величины, одна положительная, а другая
отрицательная: тогда первая будетъ тіпітит, въ ряду чиселъ положитель-
ныхъ а вторая тахітит, въ ряду чиселъ отрицательныхъ.
Обратно, если подкоренной тричленъ будетъ вида Ц—ру—у*, то положитель-
ная величина для у будетъ тахітит въ ряду чиселъ положительныхъ, а отри-
цательная — тіпітит въ ряду чиселъ отрицательныхъ.
г^л_6з?_|—69
Для примѣра, возмемъ у = 2а,_10— •
Освободимъ отъ знаменателя:
х*—6ж-ь69=(2я?—10)у, или
х*—(6-ь2у)я:ч-І0у-і-69=:0; откуда
х —3-+-у± Ѵу*—Ьу—60.
Положимъ у'—4-у—60—0, и отсюда найдемъ:
у=10, либо у— —6.
Пзъ этого видно, что у пельзи брать <10, иначе х сдѣлается мнимымъ;
посему, у—10, есть наименьшее въ ряду чиселъ положительныхъ. Нельзя
также брать у>—6, паприм.—5,—3,—1, 0; стало-быть, у——6 есть
наибольшее въ ряду чиселъ отрицательныхъ.
158
ГААГА ШЕСТАЯ.
ВОЗВЫШЕНІЕ КОЛИЧЕСТВЪ ОДНОЧЛЕННЫХЪ И МНОГОЧЛЕННЫХЪ ВЪ
ТРЕТЬЮ СТЕПЕНЬ.
190. Возвысить въ кубъ даппое количество значитъ составить произведеніе
пзъ трехъ равныхъ ему множителей. Наприм. количество 5ай* имѣетъ третью
степень 5аЪі'^5аЬі'^5аЬі=1^зе3Ьв.
• При возвышеніи въ кубъ положительнаго количества пли отрицательнаго, и
самый кубъ получается соотвѣтственно положительный или отрицательный.
Напримѣръ:
(—5ай’)3=—125а3й“.
Здѣсь берутся въ разсмотрѣніе только дѣйствительныя количества.
191. Для возвышенія двучленнаго количества въ третью степень, возмемъ
квадратъ двучлена (а-+-Ьу=а!‘-+-І2аЪ-і-оі, и помножимъ на ач-й; получится:
(ач-й)8(ач-й)=(ач-й)3=(авч-2айч-й2)(ач-й)=а3ч-Завйч-Зай’ч-й3.
Посему, кубъ дву члена равенъ кубу перваго члена, сложенному съ
утроеннымъ произведеніемъ квадрата перваго члена на второіі, сло-
женному съ утроеннымъ произведеніемъ перваго члена на квадратъ вто-
рою, и съ кубомъ втораго члена.
Послѣ этого нетрудно получить кубъ тричлена ач йч-с. Положимъ ач-й=А,
то сперва получится:
(Ач-с)3==А3ч-ЗА8сч-ЗАс8=е3;
сюда подставимъ А~а-+-Ъ, п выйдетъ:
(ач-йч-с) З=(а-+-Ь) ,чч-3 (ач-й) 8сч-3 (ач-й) с’ч-с3, или
=а3ч-3 а8йч-3 лй2ч-йэч~3 (ач-й Ѵсч-3 (ач-й) с’ч-с’.
Слѣдовательно, кубъ тричлена равенъ кубу его первыхъ двухъ членовъ, сло-
женному съ утроеннымъ произведеніемъ квадрата этихъ двухъ членовъ на третій,
сложенному съ утроеннымъ произведеніемъ первыхъ двухъ членовъ па квадратъ
третьяго, и съ кубомъ третьяго члена.
Нашли бы также, что
(ач-йч-сч-й)~(ач-йч-с)3ч-3 (ач-й-ьс Д/ч-3(ач-йч-с)сГччі3
=га3ч-3а®йч-3ай8ч-й3ч-3(ач-й)8сч-3(ач-й)с8ч-с3ч-
ч-З (ач -йч-с) Мч-З (ач-йч-с і й8ч- іі3.
• 918. Зная законъ составленія куба изъ многочлена, можемъ его примѣнитъ
тотчасъ къ составленію куба всякаго многозначнаго числа. Положимъ,
что дано найти (423)’. Разложимъ это число на сотни, десятки и единицы:
(423)3=(4.00ч-20-нЗ)3,
и сравнимъ съ (ач-йч-с)3, полагая а=400, й=20, с=3.
159 —
Но, (ан-б-і-с)3_^а:'-ь3а’б-ь3а68-і-63-і-3(а-і-6)8с-і-3(а-ь6)с8-і-с3; посему
кубъ отъ 423 долженъ, быть равенъ кубу сотенъ, -+- утроенному произведенію
квадрата сотенъ на десятки, -+- утроенному произведенію сотенъ на квадратъ
десятковъ, -+- кубу десятковъ, -+- утроенному произведенію квадрата сотенъ и
десятковъ на единицы, -+- утроенному произведенію сотенъ и десятковъ па ква-
дратъ единицъ, и кубу единицъ, то есть:
(423)’:=40П3-ь3.4008.20-ь3.400.208-ь203-ь3.42 08.Зч-3.420.3Ч-33
или: 4003=64 0 0 0 0 0 0
3.4008.20— 9600000
3.400.20*= 280000
203= 8000
3.420\3 = 1587600
3 420.З8 = 41340
З3 = 27
Посему, (423)3=75486967.
Относительно дробей замѣтимъ только: 1) что кубъ дроби равенъ кубу ея
числителя, раздѣленному на кубъ знаменателя. Напр.
/З.з з з з З5 _ 27
'4* 4'4 4 43 64'
2) Кубъ десятичной дроби составляется также, какъ изт цѣлаго числа- для
итого отбрасываютъ запятую, то есть, обращаютъ дробь въ цѣлое число, возвы-
шаютъ оное въ третью степень; а потомъ въ произведеніи отдѣляютъ десятич-
ныхъ знаковъ втрое болѣе, нежели сколько ихъ было въ данной дроби. Паприм.
(2,5)3=І5,625.
Здѣсь я отдѣлилъ три десятичные знака, потому что (2,5)3=2,5Х2,5Х2,5;
а произведеніе должно имѣть столько десятичныхъ знаковъ, скоіько ихъ нахо-
дится во всѣхъ его производителяхъ.
Извлеченіе кубичнаго корпя изъ чиселъ.
133. Извлеченіемъ корня кубичнаго изъ даннаго количества называется
дѣйствіе, посредствомъ котораго, ищется такой множитель, котораго кубъ ра-
венъ этому количеству. Этотъ искомый множитель называется корнемъ кубич-
цымъ того количества. Такъ паприм. кореиь кубичный изъ 27а3 есть За; по-
тому что ЗсХЗаХЗа=27а3.
Когда нужно только показать, что мы беремъ кубичный кореиь даннаго ко-
8,---------------------------------------------------
личества; въ такомъ случаѣ употребляется коренной знакъ ѵ ; подъ этимъ
знакомъ и пишется данное количество. Паприм.
, 27а3=За, ^20?'
и выговаривается корень кубичный пзъ 27а3, корень кубичный изъ 20.
— 160
13А. Изъ цѣлыхъ чиселъ. — Для извлеченіи кубичныхъ корней изъ цѣ-
лыхъ чиселъ, надобно знать кубы первыхъ девяти чиселъ,
слѣдующей табличкѣ:
Корпи: 1, 2, 3, 4, 5, 6, 7, 8, 9,
Кубы: 1, 8, 27, 64, 125, 216, 343, 512, 729,
кои находятся въ
10.
1000.
т
изъ которой видно, что кубу однозначнаго, двузначнаго или трехзначнаго числа,
соотвѣтствуетъ корень только однозначный; что самому меньшему четырехзнач-
ному числу 1000 соотвѣтствуетъ корень 10, .самое меньшее число двузначное;
что не всякое число есть полный кубъ. Такъ наприм. число 100 заключается
между полными кубами 64 и 125; слѣдовательно, корень его находится между
4 и 5. Корни изъ неполныхъ кубовъ называются неизвлекомыми, ирраціо-
нальными, несоизмѣримыми съ единицею; они не могутъ быть выражены
точнымъ образомъ ни цѣлыми числами, пи дробями. Въ самомъ дѣлѣ V 100>4 и
<5; а потому долженъ изобразиться нѣкоторымъ дробнымъ числомъ гдѣ
и п суть первыя между собоір, и тп>и. И такъ, пусть
Ѵ/Гоб’=-‘;
п
возмемъ кубъ зтого равенства:
100 ~
п5
- - т
числа т, п, суть первыя между собою, потому что дробь - несократимая;
и числа т*, п3, также будутъ первыми между собою. Стало-быть, дробь ,~
можетъ быть сокращена, и не можетъ обратиться въ цѣлое число 100. А этимъ
и доказывается, что 1/100 есть число ирраціональное, несоизмѣримое съ еди-
ницею. Онъ не можетъ быть найденъ точнымъ образомъ; но, увидимъ, что можно
находить его приближенныя величины, какія угодію.
то
ие
135. Приступая къ извлеченію кубичнаго корпя изъ цѣлаго числа, со-
стоящаго изъ четырехъ, пяти пли болѣе цифръ, надобно сперва опредѣлить,
сколько цифръ должно быть въ этомъ корнѣ. Для сего, данное число сравниваютъ
съ полными кубами
ІО3—1000,
1003—1000000,
10003=100 0 0 0 0 0 00, п проч.,
и смотрятъ, между какими изъ этихъ кубовъ оно заключается. Положимъ, что
данное число 103823. Это число находится между 1000 и 1000000 полными
кубами; слѣдовательно корень его падаетъ между 10 и 100; стало быть‘ этотъ
корень двузначный, состояньи изъ десятковъ и единицъ. Посему, данное число
103823 должно содержать въ себѣ: кубъ десятковъ корня, утроенное про-
изведеніе квадрата десятковъ на единицы, утроенное произведеніе де-
161
сятковъ на квадратъ единицъ, и кубъ единицъ, и можетъ быть сравнено
съ кубомъ двучлена (а-ь-6)3, въ которомъ а означаетъ десятки, а Ъ единицы
корня.. то есть,
103823=(а-і-6)3
=а3ч-За‘6-і-За68-І-63.
Отыскиваніе же цифръ корня производится, начиная съ единицъ высшаго
разряда, а именно: надобно сперва найти десяткп а корня, и куоъ десятковъ вы-
честь изъ 103823; получится остатокъ:
103823—а3=Загі-ьЗаб8-і-6\
Потомъ надобно взять утроенное произведеніе іагЬ квадрата десятковъ на
искомыя единицы Ь, и раздѣлить па утроенное произведеніе За8 квадрата десят-
ковъ; получатся За86 : За!=6 единицы корня. Для повѣрки, надобно составить
За86, Заб1, и Ьв, п вычесть пзъ 103823—а3. Если данное число поапый
кубъ, то остатокъ будетъ нуль:
103823—а*—За’б—За&8—63=0.
Узнавши порядокъ извлеченія корня, я пишу данное число 103823, провожу
съ правой стороны его вертикальную черту,
Кубъ. 103,823 64 Коревь. 47
398,23 3.48.7=336 3.48=48 сотенъ 7
622,3 3.4.78=588
343 73=343
О
и говорю: кубъ десятковъ производитъ не менѣе какъ тысячи,то и надобно искать
его въ тысячахъ. Для этого отдѣляю въ данномъ числѣ послѣднія три цифры
запятою, и нахожу, что меньшій самый близкій кубъ къ 103 есть 64, которому
соотвѣтствуетъ корень 4 десятка. Число 4 десятка пишу по правую сторону
вертикальной черты; а, для повѣрки, беру 43=64, и вычитаю изъ 103. Къ
остатку 39 сношу остальныя цифры 823. Въ этомъ остаткѣ должны быть:
утроенное произведеніе квадрата десятковъ корня на его единицы, утроенное
произведеніе десятковъ корпя на квадратъ единицъ, и кубъ единицъ. Но, какъ
утроенное произведеніе квадрата десятковъ производитъ не менѣе, какъ
сотни, слѣдовательно и содержится въ сотняхъ; то я отдѣляю 23 запятою. со-
ставляю 3.48—48 сотенъ, и на это число дѣлю 398; частное 7 ставлю па
мѣстѣ единицъ корпя. Для повѣрки, составляю:
іі
162
3(4 дес.)8.7=336 сот., вычитаю изъ сотень,
3(4 дес.).78=э88 дес., вычитаю изъ десятковъ;
73=343 едип., вычитаю изъ единицъ.
Въ остаткѣ нудь; слѣдовательно,
V Го'З 823=47.
134». Точно также надобно поступать, если данное число будетъ содержать
большее число цифръ.
Положимъ, что надобно извлечь кубичный корень изъ 8741816.
Напередъ я замѣчаю, что это число заключается между
юо3—1000000, и
10003=1000000000,
слѣдовательно, его корень находится между 100 и 1000, то есть, содержитъ три
цифры: сотни, десятки и единицы. Оно можетъ быть сравнено съ (ан-6-ь-с)*=
=а3н-За’6н-Заб*ч-//ч-3(ан-6)8с-4-3(а-+-б)саЧ-с3, гдѣ а означаетъ сотни кор-
ня, Ь его десяткп и с единицы. А какъ 103=1000, 1003=1000000; то кубъ
его десятковъ надобно искать въ тысячахъ, которыя и отдѣлимъ запятою; кубъ
его сотенъ заключается въ милліонахъ, то и 8 милліоновъ отдѣлимъ запятою.
Поступая такимъ образомъ, данное число раздѣлится отъ правой руки къ лѣвой
па классы по три цифры; послѣдній классъ можетъ имѣть и менѣе трехъ цифръ.
Въ пашемъ примѣрѣ, послѣдній классъ имѣетъ одну цисрру,
8,741,816;
при этомъ, число классовъ всегда показываетъ число цифръ корпя. Вотъ
почему поставляется за правило, прежде извлеченія кубическаго корня, дѣлить
данное число на классы, чтобы тотчасъ узнать число цифръ корня, и потомъ
уже дѣлать извлеченіе.
Корень. Кубъ.
8,741,816 206
23=8
7,41
7418,16
3.20*.6=7200
2181,6
3.20.68=2160
3.28=12
3.208=1200
Х6
246
63=216
' 6~
Корень кубическій изъ 8 милліоновъ есгь 2 сотни. Эти двѣ сотни пишу за
вертикальною чертою беру 2’=8, и вычитаю изъ 8 милліоновъ даннаго чисіа
163
Сношу полъ черту слѣдующій классъ 741 тысячъ, въ которомъ должно быть
утроенное произведеніе квадрата сотенъ корня на его искомые десятки, утроен-
ные сотни на квадратъ десятковъ, и кубъ десятковъ. Чтобы отыскать десятки кор-
ня, беру 3.2’, отдѣляю.41 занятою, и дѣлю 7 па 12. А какъ 7 нельзя дѣлить
нацѣло на 12, то заключаю, что десятковъ нѣтъ въ корнѣ; ставлю на мѣстѣ
ихъ нуль; сношу подъ черту слѣдующій классъ 816, п отдѣляю двѣ послѣднія
цифры запятою. Во всемъ числѣ 741816 должны быть: утроенное произведеніе
квадрата сотенъ и десятковъ корня па его искомыя единицы, утроенное произ-
веденіе сотенъ и десятковъ на квадратъ единицъ, и кубъ единицъ. Чтобы найти
единицы, отдѣляю 16 запятою, беру 3.20’=1200, ина это число дѣлю 7418;
нахожу частное 6 единицъ корня, которыя записываю въ корнѣ. Для повѣрки
составляю:
3.20’.6=7200 сотенъ, и вычитаю изъ сотенъ;
3.20.6’=2160 десят., и вычитаю изъ десятковъ;
6’= 216 единицъ, и вычитаю-изъ едішницъ.
Въ остаткѣ нуль; слѣдовательно данное число полный кубъ, и что
V 8741816=206.
Но, если и послѣ этого нашелся бы остатокъ болѣе нуля, то мы заключили
бы, что данное число неполный кубъ, и что онъ имѣетъ корень пеизвлекоыый, 4
несоизмѣримый съ единицею.
133. Изъ чиселъ—неполныхъ кубовъ нельзя находить точныхъ корней, то
есть, нельзя ихъ выразить нн цѣлыми числами, ни конечными дробями (134);
однакоже всегда можно искать приближенныя величины такихъ корней, столь
близкія къ истиннымъ, сколько угодно, выражая сіи приближенія посредствомъ
дробей обыкновенныхъ, или десятичныхъ.
1) Положимъ, что мы хотимъ найти |7]Ѵ, приближенный до-. Въ такомъ
3 /—
з /Хп® 1 8 /____
случаѣ дѣлаемъ уІѴ = = - ѴдѴп3; лзвіекаемъ корень изъ Ми’, при-
ближенный только въ цѣлыхъ числахъ, отбрасывай дробь, и пусть эта цѣлая
часть =го; то будемъ имѣть,
юч-1
п ’
разность —------ = Итакъ, взять ли — или за приближенный корень,
погрѣшность будетъ менѣе нежели на -.
Примѣръ: Найти ѵіО, приближенный до
Беру 1^10 = Ѵ71 °-120’ = X ѴТ7280000.
164 —
*Ло
Нахожу V 17280000=2714-дробь; отбрасываю дробь, и получаю:
271 ' 272
> ім’ ио < "По’
272 271 1 , .. 271
разность — — — = —. Посему, если за приолпженныи корень возмемъ —
272 ... і
плп - - погрѣшность будетъ менѣе нежели на —.
ІхѴ 120
2) Гораздо чаще и обыкновеннѣе разыскиваются приближенные корпи пзъ
чиселъ—неполныхъ кубовъ посредствомъ десятичныхъ дробей. При семъ надобно
помнить, что въ данномъ кубѣ надобно дѣлать или брать десятичныхъ знаковъ
втрое болѣе, нежели сколько ихъ желаемъ получить въ его приближенномъ
корнѣ.
Наприм. въ кубѣ
(2,34,3=2 34X2.34X2,34
должно быть шестъ десятичныхъ, потому что столько десятичныхъ во всѣхъ
его множителяхъ; въ корнѣ же 2,34 находится тоіько два десятичные знака.
Примѣръ —Найти V 82,32, приближенный до двухъ десятичныхъ.
Къ данному числу 82,32 приписываю сперва четыре нуля, чтобы вышло
шесть десятичныхъ; потомъ, раздѣливъ на классы, извлекаю корень, какъ изъ
цѣлаго числа:
Кубъ. Корень.
82,320,000 43=64 435
183,20 3.42.3=144 3.42=48 3
392,0
3 4.3’=108
2840
3’= 27
28130,00
3.438.5=27735
3950,0
3.43.5’=3225 .
7250
3.43'=5547
5
53= 125
7125
Въ найденномъ корнѣ отдѣляю два десятичныхъ знака , и нахожу
3_____
Ѵ»2,32=4,35..., имѣющій точность только въ двухъ десятичныхъ.
165 —
198. Ллв дробей.—Совершенно такимъ же образомъ извлекаются прибли-
женные корпи изъ обыкновенныхъ дробей, если онѣ неполные кубы: превра-
щаютъ данпую дробь въ десятичную, п извлекаютъ изъ нея кубичный корень
какъ изъ цѣлаго числа, не обращая вниманія на запятую, какъ видно изъ слѣ-
дующаго примѣра.
3 /
Примѣръ.—Найти к/~-> приближенный до двухъ десятичныхъ.
2
Сперва нахожу, что — = 0,6666666..беру шесть десятичныхъ, отки
о
ну въ прочія, и извлекаю корень какъ изъ цѣлаго числа:
666,666 87
8’=512
4546,66 3.82=192
3.82.7=1344 Х7
2026,6
3.8.72=1176
8506
7’= 343
8163
Отдѣляю въ найденномъ корнѣ два десятичные знака, и нахоліу;
3 /
. /2
\/|=0,87...,
точный только въ двухъ десятичныхъ.
Примѣры: — |/0,6=0,843....
Ѵ'0ДЙ)05=0,079...
Извлеченіе корпя кубичнаго изъ алгебрическихъ ко.імчесів ь.
199. Мы впдѣлн, что для возвышенія одночленнаго количества въ третью
степень, надобно возвысить въ эту степень его предстоящее и помлоя.лть па 3
показатели всѣхъ его буквенныхъ множителей, напр.
(5аЬ2)*=125а8Ь6;
то заключаемъ обратно, что для извлеченія корня кубичнаго изъ одночленнаго
количества, надобно извлечь его изъ коефиціента, а показатели буквенныхъ мно-
жителей раздѣлить па 3:
\/і^5а3Ъе = 5да Ьз = 5аЬ8.
166
Что касается до знака предъ коефпціеитомъ корня, то онъ будетъ -+- или —,
смотря потому, будетъ 'ли данное количество положительное или отрицательное.
Наприм.
Ѵ/8аг=2а, [/^8а3——2а.
«»О. Одиочленное количество имѣетъ корень неизвіекомый, если коефи-
ціентъ его неполный кубъ, или показатель какого ни есть буквеннаго его мно-
жителя не дѣлится на показатель корня 3.
Я8І. Для извлеченія корпя кубическаго изъ многочленовъ, предлагаются
обыкновенно такіе многочлены, которые дѣйствительно суть полные кубы. Во вся-
кихъ другихъ случаяхъ непосредственное извлеченіе корня не представляетъ
пользы. По этому надобно напередъ знать нѣкоторые признаки для многочле-
новъ — неполныхъ кубовъ.
1) Всякое количество двучленное или трехчленное не можетъ быть полнымъ
кубомъ; потому что кубъ двучленнаго количества содержитъ уже четыре члена:
(а-ьб)3=а3-ьЗа26-і-Зчі2-ьб3.
2) Многочленное количество, расположенное по убывающимъ степенямъ
одной буквы, освобожденное отъ множителей общихъ всѣмъ его членамъ, и не
имѣющее коренныхъ количествъ, не будетъ полнымъ кубомъ, если его первый
и послѣдній члены не будутъ полными кубами.
. Другіе признаки неполноты куба открываются при извлеченіи корпя.
Извлеченіе корня кубичнаго изъ многочленовъ ничѣмъ пе разнится отъ
извлеченія его изъ чиселъ, только гораздо проще. Оно также производится по-
рядкомъ, совершенно обратнымъ тому, по которому составляется кубь двучлен-
наго или трехчленнаго количества. Надобно послѣдовательно отыскивать члены
корня, составлять изъ нихъ члены куба, и вычитать изъ даннаго количества.
Если, по исключеніи всѣхъ членовъ куба, соотвѣтственнаго корню двучленному,
трехчлевному, или какой найдется, въ остаткѣ пе получится ничего; то найден-
ный корень и будетъ искомымъ. Самое же дѣйствіе производятъ такъ:
1) Располагаютъ данное количество по убывающимъ степенямъ одной его
буквы, извлекаютъ корень кубичный изъ перваго члена; — получится первый
членъ корня, который записываютъ съ правой стороны даннаго количества, и
отдѣляютъ отъ него вертикальною чертою. 2) Возвышаютъ этотъ первый членъ
корня въ третью степень, и вычитаютъ изъ даннаго количества; — получится
остатокъ, въ которомъ должны1 находиться: утроенное произведеніе квадрата
перваго члена корпя на второй, утроенное произведеніе перваго члена корня на
квадратъ втораго, и кубъ втораго члена. 3) Берутъ квадратъ перваго члена
корня, помножаютъ его на 3, и на это произведеніе дѣлятъ первый членъ
167
Остатка; получится второй членъ корня. 4) Для повѣрки, составляютъ утроен-
ное произведеніе квадрата перваго члена корня на второй, утроенное произведеніе
перваго члена на квадратъ втораго в кубъ втораго члена, и сумму э^ихъ чле-
новъ вычитаютъ изъ дѣлимаго числа. Если остатка не будетъ то значитъ, что
корень найденъ, и дѣйствіе кончено. По, если получится остатокъ, то онъ дол-
женъ содержать въ себѣ утроенное произведеніе квадрата перваго и втораго чле-
новъ корня на третій, утроенное произведеніе перваго и втораго членовъ на
квадратъ третьяго, и кубъ третьяго члена; по сему, 5) третій членъ корня
наіідется, если раздѣлимъ первый членъ остатка на утроенное произведеніе
квадрата перваго и втораго членовъ корня, для повѣрки, надобно составить
утроенное произведеніе перваго п втораго членовъ корня на третій, утроенное
произведеніе перваго и втораго членовъ на квадратъ третьяго, и кубъ третьяго
члена, и все это вычесть изъ дѣлимаго. Если остатка не будетъ; то корень
найденъ и дѣйствіе копчено. Но, если и послѣ того выйдетъ остатокъ, то онъ
долженъ содержать въ себѣ утроенное произведеніе квадрата трехъ членовъ
корня на четвертый неизвѣстный, утроенное произведеніе трехъ членовъ корня
па квадратъ четвертаго, п кубъ четвертаго члена; а четвертый членъ найдется
точно также, какъ мы отыскивали третіи членъ, и проч. 6) Если, послѣ какого-
нибудь вычитанія, получится остатокъ одночленный или двучленный, пли, вообще,
такой, въ которомт не могутъ заключаться остальныя части куба, когда приба-
вится къ корню еще членъ; то заключаемъ, что данное количество не полный
лубъ, котораго корень получить нельзя точнымъ образомъ.
Примѣръ. Извлечь корень кубичный изъ
27а3—8і’-ь36аА2—МЬ.
Расположивъ это количество по убывающимъ степенямъ буквы а,
Кубъ. Коривъ.
27а3—54«24ч-36а^— 863 За—2і
—27а3
—5іа26-ь-36аЬ2—8б3 27а2
ч-54а26-36аЬ-4-863
О
возмемъ корень куоичный гзъ 27а‘; онъ будетъ За. Напишемъ его за вертикаль-
ною чертою, возвысимъ въ кубъ, в вычтемъ изъ даннаго количества. Получится
остатокъ—5/ы»2б-і-36а62—8Ь3, въ которомъ должны содержаться: утроенное
произведеніе квадрата перваго члена За корня па неизвѣстный второй утроенное
произведеніе перваго члена на квадратъ втораго, и кубъ втораго члена корня.
Чтобы найти второй членъ корня, влзмемъ 3(3а)’=27а2, и раздѣлимъ на него
іервый членъ —54а’б остатка; найдется —2Ь второй членъ корпя, который и
іапишемъ подлѣ За, А, для повѣрки, составимъ три члена куба:
168 —
3(3а)*(—2б)ч-3(3а)(—2Ь)2-+-(—2Ь)3=
= — 54а2Ьч-36аЬ2—8б3,
и все это вычтемъ изъ дѣлимаго. Въ остаткѣ нуль; слѣдовательно За—2б есть
полный корень, а данное количество полный кубъ отъ За—2Ь, и можно на-
писать:
Р'27^’_54а’М6аЬ2—8Ь3=За—2Ь.
Такъ надобно извлекать кубичные корни и изъ другихъ многочленовъ.
Уравпепія третьей степени.
183. Эти уравненія бываютъ полныя и неполный. Полное уравненіе 3-й
степени должно имѣть четыре члена, гдѣ неизвѣстная ж находится въ степеняхъ
ж3, ж2, х, хй. Общій видъ его:
ж3ч-аж*-ь6ж-ьс=г0.
По если будетъ а—0, или 6=0, или вдругъ а~0 и 6=^0, то получатся
уравненія неполныя:
ж3-ьбж-ьс=0,
ж’ч-аж2-+-сг=0,
ж3-ьс=0.
Ни одно изъ пихъ пе можетъ имѣть дѣйствительнаго корня положитель-
наго, когда коефиціепты а, Ъ, с, положительные: ибо никакое положительное
число, взятое па мѣсто ж, не можетъ обратить въ пуль ни одно изъ этихъ урав
неніи. Но, если хотя только послѣдній членъ с будетъ отрицательнымъ, то
каждое изъ этихъ уравненій будетъ имѣть по крайней мѣрѣ одинъ дѣйствитель-
ный корень, и притомъ положительный.
18Л. Рѣшеніе сихъ уравненій начнемъ съ простѣйшаго:
ж3—с—0.
Пзъ него нахѵдимъ тотчасъ первый дѣйствительный корень:
а___________________________________
ѴС.
Слѣдовательно,#—ѵс=0. На это равенство раздѣлимъ данное уравненіе;
получится.
ЗС*—С 3 3 _
х_ = х?-+-х усч- |/с2; откуда
ж3—с=(«2-ьж Ѵ^с-ь |/с2)(ж— і/с)—0.
3.—
Отсюда видно, что данное уравненіе удовлетворится не только дли ж— У с=0,
но и для
ж'ч-ж Ѵсч- і/с^О;
а изъ этого послѣдняго найдутся еще два корня:
169 —
__ Ѵ/С(і±Ѵ/-з)
2
Опи также удовлетворяютъ уравненію х3—с=0, и притомъ оба мпіімые.
І85. Возмемъ теперь уравненіе
х3—Ъх—с=0.
Оно имѣетъ непремѣнно одинъ дѣйствительный корень положительный, кото-
рый не трудно и вычислить по приближенію, когда с < Ѵь *). Для этого раздѣ-
лимъ данное уравненіе па х:
х^—Ь-і-^ и извлечемъ корень;
х := Ѵ^б-ч- —;
во вторую часть подставимъ ѴЬ-ь-с- вмѣсто х,
х —ѴЬ-і- с-—-------------------------
147?.
а?’
сюда опять подставимъ Ѵ^б-г-вмѣсто х,
и такъ далѣе. Этимъ способомъ корень уравненія выразится посредствомъ ради-
кальной непрерывной дроби, и можетъ быть вычисленъ по приближенію до про-
извольной степени точности, какъ видно изъ слѣдующаго примѣра:
’) Если с^> V ь, то надобно преобразовать уравненіе, положивъ х—ть-, получится:
-2-=о.
гл» тъ
с Ъ
Теперь сдѣлаемъ — х' —, или с <"4пг, отсюда
«п5 т»
1Ос
Слѣдовательно, если ззять т =—то получится уравненіе:
6
Ь’.г | Ь®
ІООс® 1000с® ’
I5 . 6®
въ которомъ-------<---------.
1000с® 100с»
Этому уравненію можно найти л, какь теперь же увидимъ; а потомъ найдется
корень
и для самаго даннаго уравненія.
170 —
Это уравненіе имѣетъ дѣйствительный корень между числами 2 и 3; потому что
ж=2 обращаетъ уравненіе въ — 1,
— — въ И-14».
А чтобы вычислитъ этотъ корень, раздѣлимъ уравненіе па «, и извлечемъ
квадратный корень-
Корень х заключается между 2 и 3, то, для перваго приближенія, возмемъ
а?=2, и подставимъ во вторую часть, получится:
х — /4/5=2,1213....
Это приближеніе подставимъ въ \/4ч-^, получится новое приближеніе къ
корню:
ж=У/4'-,-2Т2ІЗ=2’1134-5-’
- /, 1 ..
которое, въ свою очередь, внесемъ въ 1/ 4ч-—, и найдется:
х=\/4ч---------—=2,1149....
— У 2,11345 ’
Такъ получился приближенный корень даннаго уравненія, точный въ трехъ
десятичныхъ; а продолжая дѣйствіе, можемъ его вычислить до какой угодно сте-
пени точности.
186. II такъ, уравненіе ха—Ъх—с±=0 имѣетъ дѣйствительный корень;
пусть этотъ корень а=а, х—а=0, и
а*—аЬ—с=0.
Вычтемъ послѣднее равенство изъ да.інаго уравненія:
Xй—а"—Ь(х-—а')=0;
раздѣлимъ на х—а—О, останется:
:г2ч-аж-і-а—6=0, откуда
—а± ѵіь—за»
Х 2 '
Таковы остальные два корня. Они оба мнимые, когда возметса коефиціентъ Ь
съ противнымъ знакомъ, и даннымъ уравненіемъ будетъ хг-у-Ьх—с=0. Но въ
уравненіи,
х3 — Ьх—с=0,
вти два корня дѣйствительные, когда
46 > За2, или 46=3а!, или вообще 46 </ За8.
Сему условію можно дать другой, самый общій видъ, помноживъ обѣ части ра-
венства на а, и внеся а3=6ач-с;
— 171
4Ьаг йа3,
4іа=ЗЬач-Зс; откуда
, „ Зс
іа=3с, и а==—.
О
Теперь это внесемъ въ 4б^3а!, получится:
, /, л- 27с*
4о<р —, или
Ь5 с®
ЭТ <ЬѴ
Вотъ условіе, при которомъ остальные два корня будутъ дѣйствительными;
с2 Ь3
въ противномъ же случаѣ, когда — > —, уравненіе имѣетъ одинъ первый ко-
4- х 7
рень дѣйствительный, а прочіе два мнимые.
Повторимъ здѣсь паши выводы: 1) когда уравненіе ал-+-Ъх±с=і() имѣетъ
коефиціентъ Ь положительный, то содержитъ въ себѣ одинъ корень
\ < «- Ч Г>\ 9 С®
дѣйствительный и два мнимые; 2) если же о~—, и при томъ — у,
то въ уравненіи всѣ корни дѣйствительные. Что касается до послѣдняго
члена с, то корни вовсе не зависятъ отъ его знака, потому что, въ условіи,
членъ этоть входитъ во второй степени.
ІЙЭ'. Третье неполное уравненіе,
х3ч-ах2-ьс=0,
і
легко приводится къ предыдущему, взявши х~-; отчего получится:
і і
— -+-а-ьс=0, или
г» г® I
1 -ЬЯ2-4-с23=0, ИЛИ
С 1 г\
2 ч ' .я-ь — —О, или, наконецъ,
23-ь-6/2-ь-с/—О,
а 1 .
полагая — — о' — ~с'.
с с
Корни этого уравнепія всѣ дѣйствительные, когда - . с' въ противномъ
случаѣ, одинъ дѣйствительный и два мнимые. А подставивъ па мѣсто Ъ' и с' ихъ
значенія, найдется:
1 1,1а3
~. — т> —. —, то есть:
4 с® ^27 с3 ’
27с <4а3, или = 4а3.
Таково условіе для даннаго уравненія а:3-і-ааЛ+-с=0, чтобы всѣ его корни
были дѣйствительные; въ противномъ случаѣ, оно имѣетъ два корня мнимые.
Рѣшеніе полнаго уравненія
ж3н-аа;2-ьба;-ьс=О
приводитъ къ рѣшенію предыдущаго уравненія а;3-ь/»'гч-с —0, потому что второй
172 —
второй членъ всегда можно исключить изъ уравненія. Для этого довольно взягь
X—г—у, то есть, ровною новой неизвѣстной 2 безъ коефиціеита втораго
члена, раздѣленнаго на степень 3 уравненія, и поставить въ данное уравненіе:
3 . п 1 2 О3
х =х2 — ая‘ч----а г——
3 27
з 9 2 о а~
ч-аж _ Ч-«2-------а ач-—
ч-ігх = Ьх—~
-+-с = -I- с
х*-(~а*-Ь)^а3-^+&).
Такимъ образомъ получилось уравненіе, вида
2=ч-б2-ьс'=0,
пе имѣющее втораго члена. Если разрѣшить оное, пашедши его корни 2, то по-
лучатся и корни полнаго уравненія
а
-----------------------------------
Корнп х будутъ дѣйствительные или мнимые, смотря по тому, будутъ ли та-
ковыми корпи 2.
489. Кардановъ способъ. — Можно выразить корпи уравненія 3-іі сте-
пени посредствомъ извѣстной связи коефиціентовъ различныхъ его членовъ, по-
добно тому, какъ выражаются корни уравненій 2-й степени
Для этого берется уравненіе
х3-і-Ьх-ьс=0 ,
освобожденное отъ втораго члена по способу, предъ симъ показанному.
Положимъ, что одинъ изъ его корней будетъ
Ж=у-Т-2 *),
) Можно и не исключать второй членъ изъ уравненія зсМ-аа2-в-{іж-ьс=О;
но тогда надобно положить, что его корень х~у-л г-ь-и;
потомъ взять а—у=х-+-и, возвысить въ кубъ:
я5—3.тг2/-ь-Зя-?/“—у5=23+-3іи(2-ь-и)ч-ц5
=23-і-3зи(а:—у}н-и3
Отсюда
а:3—Заяу~+-3х(уя—хи)—х3—Зхиуч-и’-^-у3.
Сравнивъ это уравненіе съ даннымъ, получимъ:
Зд=а, 3(уя —г«)=6, г3-+-и3-і-2/3—8ии/=—с
Изъ этихъ трехъ уравненій найдутся:
173 —
гдѣ у и а двѣ его неизвѣстныя части, которыя надобно отыскать. Возвысимъ
это въ кубъ; получится:
х3= у‘ч-Зуг(у-ьг)ч-28, или
а:8= у8Ч-Зу2ЖЧ-28, или
х3—3 ухх—у3—-28=0.
Это уравненіе во всемъ должно быть тожественно съ даннымъ д?’ч-бя:ч-с=О;
слѣдовательно должно быть:
--3»/2 — 6 , ИЛИ 2 — ~ , И
Л > Зу ’
у3-і-23= —с.
Въ послѣднее подставимъ па мѣсто 2 его величину, получится.
, ь®
и--------------------------------— —с, пли
* 27у» ’
в В «>’
/ч-су8 = - . -
Для разрѣшенія этого уравненія, положимъ у3—і, у3—і\ получится:
, ь®
г + сі — — , откуда
г=
Такова первая часть корня; а
дется вторая часть:
ь®
; и, наконецъ,
8
Ѵс I 1 / са &3
~2~У
подставивъ ее вь уравненіе у3-+-28——с, най-
V 2 Ѵ 4 27
Взявъ только верхній згакъ для у и г, получится:
«=ѵ
Ь® • / с Ь®
27Ч-Ѵ/ ЗГ ~~* *~27’ 1
полное выраженіе корпя даннаго уравненія. Корень этотъ дѣйствительный, когда
6г=ч-; но, въ семъ случаѣ, два другіе корпя мнимые, какъ мы это видѣли выше.
Онъ будетъ дѣйствительнымъ и тогда, когда Ь~—, и притомъ когда
с® „ ь®
— < ; и знаемъ, что чѣмъ с мепѣе относительно о, тѣмъ скорѣе можно его
вычислить пзъ выраженія
гакпмъ образомъ составится корень т=у-+-7-ьи.
ІІолагая а=0, нашли бы: у = 0.
2
с“ Ь® __ с_ 1 / с» Ь®
2~ у 4 ~^27 ’ " ~ '2^Ѵ Т-Ь27 ’
•) Іеронимъ Карданъ, уроженецъ миланскій, врачъ и математикъ болонскій, 16 го вѣка,
сдѣлалъ только извѣстнымъ это рѣшеніе. Открытіе же онаго самъ онъ приписываетъ
Сципіону Феррео, болонскому ученому.
174 —
Въ этомъ случаѣ и два остальные корня будутъ дѣйствительные, что также
намъ извѣстно (18в). Отсюда заключаемъ, что формула
всегда представляетъ корень дѣйствительный, не смотря на то, что обѣ части
са Ь®
его, въ случаѣ ----— <0, кажУтся мнимыми. Слѣдовательно, она допускаетъ
такое преобразованіе, отъ котораго ея мнимость уничтожается, въ чемъ и дѣй-
ствительно увѣримся скоро, когда будемъ говорить о возвышеніи двучленовъ и
многочленовъ въ различныя степени цѣлыя и дробныя,
Одинъ взглядъ на эту формулу показываетъ, что вычисленіе корня посред-
ствомъ ея пе только затруднительно, но, безъ преобразованія, даже невозможно,
с2 А®
когда-
#90. Рѣшеніе общаго уравненія 4-іі степени.
Есть нѣсколько способовъ для разрѣшенія полнаго уравненія 4-й степени.
Феррари, ученикъ Кардановъ, и Рафаель Бомбелли, въ 16 мъ вѣкѣ,открыли
первые къ тому способы; въ 47-мъ вѣкѣ Декартъ, и въ концѣ 18-го вѣка
Эйлеръ представили свои. Посредствомъ всѣхъ ихъ рѣшеніе уравненія 4-й
степени приводится ьъ рѣшенію уравненія 3-й степени. Мы разсмотримъ спо-
собъ Декартовъ.
Для этого возмемъ уравненіе х4-+-аж’-і-бх-і-с=О
безъ втораго члена, который всегда можно исключить но тому же правилу, ка-
кое показано было (Й88) при разрѣшеніи уравненія 3-й степени. Попытаемся
разложить это уравненіе на два квадратныхъ, вида:
х‘-4-тх-+-п—§, я?—тх-і-р—0, полагая
ж4-4-ах*-і-6х-4-с=:(х2-і-тх-і-п)(х’—
—т2)х*-+-(?ир—тп^-і-пр—О.
Чрезъ сравненіе коефиціентовъ равныхъ степеней отъ х, получаемъ:
1) п-і-р—т'—а, 2) ипр—тп=Ь, 3) пр=с.
Изъ 1) находимъ п-+-р=а-+-т*, сложимъ и потомъ
- 2) р—и—— . вычтемъ;
2р=(а-ьт2)-і-^ перемножимъ и
2п~ (а-ьт2)—Ь— подставимъ пр=х
№
4с=а,ч-2ат’-кт4------откуда
175 —
гп’-ч-2ат*-ч-(аі—4с)т’— б’=0.
Послѣ этого, возмемъ т*=у, получится:
у3-+-^ау'-+- {а‘—4>с)у—б*=0.
Такимъ образомъ опредѣленіе у приведено къ рѣшенію уравненія 3-й степе-
ни. Изъ этого уравненія найдется по крайней мѣрѣ одинъ дѣйствительный и при-
томъ положительный корень у, потому что послѣдній членъ —Ь* существенно
отрицательный; посредствомъ этого корня опредѣлится дѣйствительная величина
т— Ѵу, и получится:
п=^ (а-ьт’)—, р = 1 (а-ьш*)ч-,
2 ѵ 2т ’ г 2 ' '2т’
стало-быть, опредѣлятся уравненія
яЛ+-та;-+-п=0, а:’—»пж-4-^=0, и ихъ корни
которые будутъ корнями даннаго уравненія.
Примѣръ. Пусть дано уравненіе
ж’ч-3 ж*ч-6л,-+-10=0,
въ которомъ а=3, Ь=&, с=Ю, что и подставимъ въ
у’ч-2ау‘ч-(аі—4с) у—6*=0; найдется
у’-ч-бу*—31 у—36=0.
Корни этого уравненія суть: —1, ч-4, и —9;
стало-быть, т= /у= V—1, либо =2, либо =3 Vх—1.
Взявъ т=2, получатся:
четыре корня даннаго уравненія.
Замѣчательно, что если взять т— Ѵ^—1, или —3 |/—1, то и въ этихъ
случаяхъ корни будутъ тѣ же.
Такъ, длят=1/—1, корень
только по виду разллчается отъ —но въ сущности ему равенъ, въ
чемъ легко увѣриться слѣдующею повѣркою: положимъ
«1* * 1 1 1-*» І-* ьо ю 1 1 сл сл =—1+ Vх—1, или =—2-4-3
176 —
это возвысимъ въ квадратъ:
—42 5=4—9—42 V—1=—5—12 /—1.
Слѣдовательно, уравненіе 4-й степени допускаетъ не болѣе какъ четыре
корни.
Задача.—Найтпі- три числа, составляющія непрерывную геометри-
ческую пропорцію, коихъ сумма =40, а произведеніе перваго на вто
рое =6.
6
Пусть второе число =х, то первымъ будетъ ; третье число найдется изъ
пропорціи
6
—: х—х : трет, число,
имешю,будетъ = ^. Сумма чиселъ =40, посегіу,
6 а3
х-г- — ч--—= 40, откуда
ж‘ч-6ж’—60жч-36=0.
Сравнивъ съ общимъ уравненіемъ,
ж4ч-аж‘-і-6ж-і-с=0, получимъ
а=6, Ь=—6Л, с=26; отъ этого
у’ч-2ау’ч-(ая—4с)у—б*=0 обращается въ
уьч-42у‘—108у—3600=0.
Отсюда исключимъ второй членъ, полагая у=х—4; найдется:
28—156г—3040=0.
Корень этого уравненія, по формулѣ Кардана, будетъ
в Г-------------------------8 /-----------------------
2=1/ 4 520ч- 01520’—52’ч-V/ 4520—04520’—52э.
=48, 0....
Посему, у=ті—х—4=14,
т =014=3,74....
Таково первое число Вторымъ числомъ будетъ— = 1,94...., третьимъ
*с
^=4,96......
Сумма чиселъ =3,10ч-1,94ч-4.96=10.
Примѣчаніе. Безполезно останавливать учащихся надъ рѣшеніемъ задачь,
относящихся къ уравненіямъ 3-й и 4-Й степени, но правиламъ Кардана п Де-
карта. Алгебра имѣетъ превосходные способы рѣшенія чпслеппыхъ уравненій
всякихъ степеней, которые будутъ изложены въ своемъ мѣстѣ.
177 —
ГЛАВА СЕДЬМАЯ.
I. О ВОЗВЫШЕНІИ ВЪ СТЕПЕНИ ОДНОЧЛЕННЫХЪ АЛГЕБРИЧЕСКИХЪ
КОЛИЧЕСТВЪ, И ИЗВЛЕЧЕНІИ КОРНЕЙ ВООБЩЕ.
200. Извѣстно, что степени происходятъ отъ помноженія количества самаго
на себя, и различаются во числу равныхъ множителей, пзъ которыхъ они со-
ставляются чрезъ зто умноженіе.
Одно количество а представляетъ первую его степень; произведеніе двухъ
такихъ количествъ аХа=а’ составляетъ вторую степень или квадратъ отъ а:
произведеніе трехъ множителей а'^а'/^а—аі составляетъ третью степень отъ
а, и такъ далѣе; наконецъ, произведеніе, составленное изъ п такихъ множите-
лей, то есть, аааа....—а", называется .і-ю степенью отъ а
Количество, возвышаемое въ степень, называется корнемъ этой степени. Оно
можетъ быть цѣлое или дробь, положительное или отрицательное, и вообще ка-
кое угодно. Показатели степеней также бываютъ положительные или отрица-
тельные, цѣлые или дробные, и даже во всякихъ возможныхъ видахъ
Степени одночленныхъ количествъ съ показателями цѣлыми.
201. Наблюдая правила знаковъ, предстоящихъ и показателей буквъ, из-
вѣстныя намъ изъ умноженія, и примѣняя ихъ къ возвышенію одночленовъ въ
различныя степени, само собою открывается слѣдующее правило:
Для возвышенія одночленнаго количества въ степень, надобно: 1) воз-
высить въ эту степень коефиціентъ его; 2) умножить показатель
каждой его буквы на показатель степени; 3) поставить предъ выво-
домъ знакъ если показатель степени чётный; если же онъ нечёт-
ный, то поставить тотъ знакъ,' какой былъ предъ количествомъ, воз-
вышаемымъ въ степено.
Положимъ, что надобно возвысить количества 2айс, а’, а’*, первое въ
третью степень, второе въ четвертую, а третье въ н-ю.
Сіи степени будутъ:
(2абс)3=2абсХ2абсХ2абс—23а3б’с3;
(а3) 4=а’Ха’Ха’Ха —а'—а* ’ ‘;
(ат)п=ат. а”. ат...=атп.
12
178 —
Примѣры.
Степени четныя. Степени нечетныя.
(Заб2с’)5=9агб4с’, (Забіс’)і,=27аѴс1’,
(2аб’)4=і6а4б“, (2дг»’)в=32авб*в,
(_4.аЕб3)®=16аі6\ (—іа‘Ь)3=—64.а’б’,
(_ 5а^)-»= ' 7 25а*ов
і —64а®63’
И вообще, пусть п означаетъ всякое цѣлое число, то 2п будетъ изображать
всякое число четное, а 2и-М всякое число нечетное; по этоту условію,
(±а)8п=аіп, (±0)’"**= ±аіп+1,
(±«)-«"=2 —1—-.
\ ' д5п \ / н- ц2п-Н
Къ «тому присовокупимъ еще:
(ат)“п=-А- =а~тп\
’ ' (а")”
—— =а~пп;
' > (ат)" ’
1 1
(а“тѴ"=-------=--------—атп.
\ / (а“)" а~тп
808. Дробь возвысится въ данную степень, если возвысимъ ея чи-
слитель и знаменатель въ эту степень, наблюдая тоже правило относи-
тельно знаковъ.
Примѣры:
/ а \т_____а а а ___ат
’Т' Т‘ ~Ъ‘ ~Ь........... 6”’
/2а2Ьѵ*___2а2Ь 2а26_4а*Ь2
'Зсгі3' ЗсД3 X Зсгі5 ЭЛІ®’
<2а!Ьѵз 8я®63 . , ЗЛ**Ѵ» 27Л®Іс3
*зёй 27см” V ЫдЧ'’
(—Ѵр^3.*__ 623. р®?12 ,ЗЬ2с\-‘__ 23гі®Р
' г«2 ) гЧ“ ’ \а<Г(’) ~9Ё 'с®"'
Переходъ отъ степеней одночленныхъ количествъ къ ихъ корнямъ.
803. Обратный переходъ отъ степени къ ея корню называется извлече-
ніемъ корня. Это дѣйствіе изображается кореннымъ знакомъ і/ , который
ставятъ съ лѣвой стороны количества, изъ коего желаютъ извлечь корень. А
какъ степени бываютъ различны, то и корпи, извлекаемые изъ пихъ, также
бываютъ различны. Для этого различія ставится надъ корнемъ показатель,
то есть, число, показывающее какой степени нужно получить корень. Нанрим.
» --- в,---- .
V , ѵ ; это выговаривается: корень третьей степени, корень пятой степени.
Только не ставится показателъ надъ корнемъ второй степени; но его всегда надобно
подразумѣвать, нанрим. Ѵ'а — Ѵа.
— 179 —
8О4К Вообще, извлечь корень п-ой степени изъ даннаго количества зна-
читъ найти тотъ его производитель, который, будучи возвышенъ въ п-ю степень,
превратился бы въ это количество. Такимъ образомъ находимъ, что
|/4=2, |/9?=3а, Й7=3, V 125^Г°=5аб2.
здѣсь ?, За, 3, 5аЬ~ суть искомые корни, потому что 2“—4, (3«/=Л».*,
33=27, (5а6!)3=125а36°.
805. Количество, стоящее подъ знакомъ корпя, называется подкореннымъ.
Оно можетъ быть цѣлое или дробь, положительное или отрицательное. Пока-
затель корня можетъ быть чётный плп нечетный, и также положительный,
либо отрицательный. Коефиціентъ и буквенные множители подкореннаго коли-
чества могутъ быть полными степенями искомаго корня, плп неполными.
А. КОРПИ ИЗЪ ПОЛНЫХЪ СТЕПЕНЕЙ. ПОКАЗАТЕЛИ ПЪЛЫЕ; КОРНИ РАЦІО-
НАЛЬНЫЕ И МНИМЫЕ.
806. Поелику извлеченіе корня составляетъ переходъ отъ степени къ ея
корню, то оно и производится дѣйствіемъ совершенно обратнымъ возвышенію ко-
личества въ степень, а именно:
Чтобъ извлечь корень изъ одночленнаго количества положительнаго,
4) надобно извлечь этлотъ корень изъ численнаго коефиціента; 2) раздѣ-
лить показатель каждой буквы на показатель корня; 3) поставить
предъ выводомъ два знака ± , если показателъ корня чётный; если же
онъ нечётный, то поставить знакъ ч-
Это правило очевидно: ибо извѣстно, что для возвышенія количества въ сте-
пень, надобно возвысить въ эту степень коесрпціентъ его, и помножить показа-
тели буквъ на показатель степени; то, обратно, при извлеченіи корня, должно
найти корень изъ коефиціента, и раздѣлить показатели каждой буквы на показа-
тель корня. Наприм.
1/27Лв=Заб!.
Предъ корнемъ нечётной степени ставится знакъ -ч- ; потому что положитель-
ное количество, возвышаемое въ нечётную степень, даетъ количество также
положительное. Но предъ корнемъ чётной степени надобно поставить ± ,
наприм.
ѴІ=ЙЬ2;
потому что (ч-2)‘=4, и (—2)‘=4, то есть, оба числа -+-2, —2, даютъ ту
же степень 4, и оба должны быть считаемы корнями второй степени изъ 4.
Точно также извлекаются нечётные корни изъ количествъ отрицатель-
ныхъ; по тогда и предъ выводомъ ставится знакъ — , потому что отрицатель-
ный корень, въ какую бы нечётную степень возвышенъ ни былъ, даетъ степень
отрицательную.
— 180 —
Примѣры:
Ѵ^а1Ьісі-=±ЧаЪісі-, Ѵ'27^Ь^=ч-ЗаЬк ,
Ѵ'ВІаѴс^ ±ЗабѴ; Ѵ'—27а86’св= —Зай’с*.
Ѵ4.6’с’=±-^—.
к і — — 26с5
90®. Но, изъ отрицательнаго количества нельзя извлечь ни одного
корня съ чётнымъ показателемъ; потому что пѣтъ такого числа, положи-
тельнаго илп отрицательнаго, котораго бы чётная степень была отрицательною.
Такіе корни называются невозможными, мнимыми. Наприм. для V—9 нель-
зя взять ни ч-З, ни —'3; потому что 3*=9, (—3)’=:-+-9. Стало-быть, V—9
невозможенъ, и представляетъ выраженіе мнимое.
909. Для извлеченія корня изъ дроби, надобно извлечь этотъ ко-
рень изъ числителя и знаменателя; поточу что всякая дробь возвышается
въ степень чрезъ возвышеніе въ степень ея числителя и знамепителн.
Примѣры :
____________________ 8,---
8аЧ>е ѴЯа1^8 2а6*
~~ ~ '
16а*_____!_2а / _ аЬ2
816*с8 ЗЬс4 ’ |/ 32р'Ѵ0 2р4з* '
В. КОРНИ ИЗЪ НЕПОЛНЫХЪ степеней, показатели дробные, числа и
КОЛИЧЕСТВА НЕИЗВЛЕКОМЫЯ.
909. Корень называется неизвлекомымъ, еслч все подкоренное количе-
’ ство не будетъ степенью кратною радикальнаго показателя. Такихъ корней на-
ходится безчисленное множество; ихъ называютъ также ирраціональными, не-
соизмѣримыми съ единицею, потому что ихъ величины не могутъ быть выра
жены тоннымъ образомъ ни цѣлыми числами, ни дробями. — Это было дока-
зано (1Э>4) относительно корней квадратныхъ и кубичныхъ;но точно также дока-
зывается и относительно всякихъ неизвлекомыхъ корней.
Корень изъ буквеннаго количества также называется неизвлекомымъ, если
показатели его буквъ не дѣлятся точнымъ образомъ на показатель извлекаемаго
корня. — Тогда это дѣленіе только обозначается: пишутъ подкоренное количе-
ство безъ радикала, съ дробнымъ показателемъ, какой получится отъ
раздѣленія показателя подкореннаго количества на показатель корня.
Наприм.:
Ѵа2—а«, Vх—а=(—а)‘, V—ба’б3=—б“авб‘.
181
31®. Докажемъ, что, вообще, Ѵ/ат~ап.
п,----------------
Положимъ, что Ѵат=ах, гдѣ х есть неизвѣстный показатель, который
надобно найти. Возвысимъ это равенство въ и-ю степень; получится:
ат=(ах)п=апх.
Для этого равенства необходимо нужно
пх=.т; откуда
т
п
п___ т
Слѣдовательно, Ѵа/"=аіС=а ".
Если п показатель отрицательный, то
—---------------------- п------ I —я»
Ѵат = ѵ а~т~ -— — а "
|/ ат
И, вообще, для чётныхъ корней ,
вп-- т
V а" — ± аъ ;
для нечётныхъ корней
Изъ этого видно, что знаменатель всякаго дробнаго показателя замѣняетъ
коренной знакъ, у котораго показателемъ этотъ самый знаменатель, и что оба
эти знакоположеігія служатъ къ выраженію несоизмѣримыхъ, ирраціональныхъ
количествъ.
211. Докажемъ еще, что корень изъ произведеніи равенъ произведенію
корней изъ всѣхъ его множителей:
Для сего положимъ, что
\/а,пЬг—ь, возвысимъ въ степень п,
атЬгг=8п; раздѣлимъ на 1>г,
ат=г, ; извлечемъ V
ьг
Ѵат-
V3 з
т Г п.--*
:а м. Ь” — ѴапЬ’
Ѵ 'б
Отсюдав — V
Слѣдствіе. Если »>—п, то
\/апЬ'~ Ѵа". ѴЬг^=а \^ЪТ—аЪ”.
Это показываетъ, что, если подкоренное количество можно разложить
на двѣ группы множителей, изъ коихъ одни—полныя степени, и дру-
182
гіе неполныя; то илъ первыхъ можно извлечь корень особо, и, что по-
лучится, вынесть за радикалъ въ видѣ множителя, а послѣдніе оставить
подъ радикаломъ, либо дать имъ дробныхъ показателей безъ радикала.
Примѣры:
і) .
Здѣсь и замѣчаю, что 2і—23.3, а*=аа.а, 6‘=63.б3; посему:
ѴІІаФс3 = = Ѵ/23а363ХЗ«6*Х'г
— ЗабсѴЗаб*.
С/> » /8аЬ“ . / Д».2« 6’ Ь____26» « /2аЬ
V Ис’сі7 V 3». с».сгі6<1 Зс<Р V с<1 '
3) V—а“ =: 0і4(—а) — ± а V—а.
«іг. При извлеченіи корня изъ дроби неполной степени, мѣлено всегда
дѣлать, чтобы коренной знакъ оставался только въ числителѣ, пли
въ одномъ знаменателѣ; потому что подкоренная дробь не перемѣнитъ вели-
чины своей, если оба члена ея помножить на знаменатель, либо на числитель,
столько разъ, сколько нужно, чтобы тотъ либо другой сдѣлался полною степенью.
*813. Подведеніе подъ коренной знакъ.— Мы уже знаемъ, что Ѵа"—а, •
Ѵр^=р« , и обратно, а=Ѵб? , р~» = Ѵр" ; изъ этого заключаемъ, что
всякое количество можно внести подъ коренной знакъ: для этого надобно только
возвысить оное въ такую степень, каковъ показатель надъ кореннымъ знакомъ,
п написать подъ этимъ радикаломъ. Это дѣйствіе часто нужно бываетъ дѣлать
съ числами и оуквеиными множителями, помножающими корпи Такъ, наприм.
2 Ѵа = , ЗаЬ3 \/с = \/27а*Ьес.
Если показатель корня нечётный, то знакъ —, буде онъ есть, можно вно-
сить подъ корень или оставлять за корнемъ. Нанрим.
—2а2Ѵ^ = — ѴМЬ* = V—8аТ.
— 183 —
Но, при чётномъ показателѣ корня, знакъ —, если онъ есть, надобно всегда
оставлять за радикаломъ; иначе этотъ знакъ можетъ исчезнуть, и выводъ поте-
ряетъ настоящій смыслъ.
9ЛЛ, Коренное количество не перемѣнитъ величины своей, если помножить
(или раздѣлить) на одно и то же число показате іь корня и показатели всѣхъ мно-
жителей, составляющихъ все подкоренное количество. Наприм.
і4г = І^атк, потому что Ѵат =.а~"~а к ; а это все тоже, что
п пк--
Уат - Ѵатк.
Также и обратно: {/д*»; потому что
2 пп т п___
[/апп — а™ - ап - І/ат.
Примѣръ. \/аН)*св — ѴаЬ'с3 = ЬсѴас.
Отсюда видно, что коренныя количества, у которыхъ коренные
знаки съ разными показателями, могутъ бытъ приводимы къ одному
оощему коренному показателю, подобно тому, какъ приводятся дроби къ об-
щему знаменателю. Для этого надобно помножить показатель каждаго отдѣльнаго
корня и показатели подкоренныхъ его множителей на произведеніе показателей
прочихъ корней; отъ этого, какъ знаемъ, пе перемѣнится величина кореннаго
количества.
В _ * 4__
Примѣръ. Привесть V а8 и ѴЬ1 къ одному коренному показателю. Для этого
помножимъ ооа показателя перваго количества па 4, а оба показателя втораго
на 3, и получится:
Это приведеніе часто бываетъ нужно въ Алгебрѣ.
Счисленіе коренныхъ количествъ.
• ’
245. Оно показываетъ способы дѣлать сложеніе, вычитаніе, умноженіе,
дѣленіе, возвышеніе въ степени, и проч., надъ коренными количествами какъ
несоизмѣримыми, такъ и мнимыми.
216. Сложеніе и вычитаніе. — Количества, состоящія изъ коренныхъ
членовъ, слагаются и вычитаются по тѣмъ же правиламъ, какія показаны для
сложеніе и вычитанія одночленовъ и многочленовъ, пеимѣющихъ корней. Наир.,
чтобы сложить і/а съ VЬ— Ѵс, надобно только написать Ѵа-^ѴЬ-Ѵс-, а
если бы требовалось вычесть послѣднее изъ перваго, то надлежало бы пере-
мѣнить знаки предъ его членами, и написать:
Ѵа—\/Ь-^\/с.
184 —
"Если встрѣтятся подобные кореиные члены, то надобно ихъ сокращать,
чрезъ сложеніе иля вычитаніе ихъ коефиціентовъ, стоящихъ предъ радикалами.
Здѣсь подобнымг членами называются тѣ, у которыхъ корни съ равными по-
казателями, и подкоренныя количества, состоящія только пзъ множителей не
извлекомыхъ, также равныя. Таковы, наприм.
2аѴЬ и 36*ѴЬ, или урѴ'йр и 2ссІ*У/57І.
Слагая два первыя, найдемѣ сумму:
2а /б-ьЗб* /б=(2а-г-3б’і У6;
а сдѣлавъ вычитаніе между двумя послѣдними, получимъ:
Ір 2с<Г ^=(1р-2сс1‘} 7'5/.
Примѣръ. \/ач-\/б-і-3 Ѵа—5 Ѵа—4 ѴЬт=Л( Ѵа— Ѵб).
Примѣръ. V аЬ*—р \/а№-+-9ѴаІ/—(1—р-ь/ Ѵаі)*.
Э19. Подобные коренные члены не всегда бываютъ очевидны; а потому, для
открытія ихъ, надобно всякой разъ приводить всѣ коренные члены, слагаемые
или вычитаемые, къ простѣйшему виду, вынося За радикалы все, изъ чего можно
извлечь соотвѣтствующій корень: тогда подобные члепы, если они есть, сами
собою обнаружатся.
Примѣры:
1)
/75—2 \/3= /3?25—2 /3=3 /3.
2)
3)
26 /аб’-ьЗ /а’=(2бгч-3а) /а.
6 Ѵа^—аЬ х/ѵП^аЬ Ѵ'Р—ЗаЬ №=<2аЬ Ѵ&-
81®. Умноженіе и дѣленіе. — При умноженіи, а также и при дѣленіи
одночленныхъ, коренныхъ количествъ, надооно смотрѣть, имѣютъ ли коренные
знаки ихъ равныхъ показателей, или нѣтъ; сверхъ того, ати корни дѣйствитель-
ные или мнимые. Разсмотримъ сперва корни дѣйствительные:
Извѣстно, 1) что корень изъ произведенія равенъ произведенію корней изъ
всѣхъ его множителей (/аб = У а. ѴЬ); 2) что корень изъ дроби получается,
извлекая его отдѣльно изъ числителя и знаменателя I V “ — I отсюла
' * 9 і/„
заключаемъ обратно, что
Уа у7>—Уаб, и
7 ч
185 -
Изъ этого видно, что, для умноженія и раздѣленія коренныхъ количествъ
съ равными коренными показателями,надобно помножитьили раздѣлить
однѣ ихъ подкоренныя количества; предъ произведеніемъ, или частнымъ
числомъ, поставить общій радикалъ съ тѣмъ же показателемъ, и по-
томъ сократить, если можно. Предстоящія предъ коренными знаками
перемножаются, или дѣлятся, только между собою, и, что получит-
ся, ставится за радикаломъ въ видѣ множителя.
Примѣры:
1)
2)
3)
4)
5)
/6X 0= і/б0=2 іА5.
За Ѵ'ШЫЯаЬ \^Ь3=ПаѢ'.
Ѵіі_2.» />2__ 1__ \/ч. 1/2
3 Ѵм 3 ' 24 3/2 3 /2. І2 6
1563с Ѵа*: 36* Ѵа=56с Ѵа.
219. Для перемноженія или раздѣленія коренныхъ количествъ съ разными
показателями, надобно сперва привесть ихъ къ общему коренному пока-
зателю (211), и потомъ дѣлать умноженіе или дѣленіе по сказанному пра-
вилу (218).
Примѣры:
1)
2)
т п .— тп тпп. »пп------.
ѴрХ ^9— ѵрп- ѵ<Г= Ѵргут.
Ѵ%аГ. \/1М3— Ѵ&а3Ьв. ѴиІаѴ
—_Ѵ'28.2і.9а761’=2а6а ^18а’.
3)
4.)
8 3 __ 30 _______
а0>’ уа3»’ / а"Ь" ао______
5) —= V ѴаЪ\
И6. уаеЬв
220. Возвышеніе въ степени. — Для возвышенія одночленнаго кореннаго
количества въ степень, надобно возвысить въ эту степень его предстоящее и
подкоренную величину, оставить эту послѣднюю подъ тѣмъ же радикаломъ, и
потомъ сократить, буде можно. Напримѣръ:
186
( Ѵ'а) —\/ап; потому что
1 *л \п т ш ___________
( у а) = уа. у а. уа.,.., п разъ,
— У'а.а.а.... = і/ап.
Примѣры
1) (За У2Ъ*у=9а* &№=№& Уы.
Извлеченіе корней.—Для извлеченія корня изъ кореннаго количе-
ства, надобно написать подкоренное количество подъ однимъ радикалолъ, только
радикальный показатель умножить на показатель новаго извлекаемаго корня.
Паприм.
ТПп --
= Ѵр.
Для доказательства, положимъ, что
возвысимъ вто равенство въ степень т, найдется
Ур = г;
а это возвысимъ въ степень п, и будетъ
Р — Г .
Изъ послѣдняго равенства извлечемъ корень степени тп, получится
чѣмъ и доказано правило извлеченія.
3 /б /—- ' 7--
Примѣры: 1) V/ 1/2а’ = V2а’;
«) = ‘^’-
3) Уз5 = у/і/25= ѵ'э = 2,236 ...
4) ^2 = 1,259....
5) ^27 = У -732:..
п __ тп___ П / т/~ •)тпу —
Ѵр — Ѵр, и 1/ Ѵр = Ѵр, то
Поелику
187
Отсюда заключаемъ, ч\о, все равно, извлечь ли изъ даннаго количества сна-
чала корень и-ой степени и йотомъ корень гп-ой степени, или на оборотъ, вы-
водъ получится одинъ и тотъ же.
І.римѣръ: 8/ 8/_ \/ Ѵа6 = Ѵа3=а, и
• \/\^= Ѵ^=а.
При умноженіи, дѣленіи, возвышеніи въ степени, и проч. радикаль-
ныхъ количествъ, мы вездѣ употребляли корепные знаки вмѣсто дробныхъ по-
казателей. Но, если бы мы хотѣли употребить дробные показатели вмѣсто ра-
дикаловъ, то съ ними надлежало бы поступить точно также, какъ и съ цѣлыми
показателями, то есть: при умноженіи равныхъ буквъ, падооно слагать ихъ дроб
иые показатели; при дѣленіи равныхъ буквъ надобно вычитать показатель дѣ-
лителя изъ показателя дѣлимаго, и проч, Все это легко доказать слѣдующимъ
образомъ:
1 1 ѵл.— чл.— тп.— тп.----
а) мы знаемъ, что а*.а« = Ѵа . Ѵа= V а" . V а™ =
ѵ» п - т-ні і <
= Ѵа ‘ ^п=а
Ь) Извѣстно также, что ; а»= |?а" : \/ат =
щп . п—щ 1 1
= V а"~т = а "» = а" ".
1 Н
с) Что (а ) =а-", это ясно пзъ того, что
/ 1 2. А
\а,и* — а™ . . а<«....п разъ,
2 А+.........._ А
(1т т тп _Дт,
( _! 1 1 / 1 1 &
(1) Дла доказательства же того, что положимъ, что (а«»)п=а \
и это возвысимъ въ степень п; найдется:
1 , Ххп пх
ат — (а ) ~а .
По это равенство возможно только тогда, когда
і
пх — —; откуда
і
х — —.
тп
Таковъ искомый показатель.
Примѣръ/-*
1) а1 . а1* = а‘ ‘ = а“ — а ‘- а . а4 — а Ѵа.
8 у 8 1 7 15_
2) а’.а-8 —: «3 8 _ о16— а Ѵа1.
- 1 ‘ ? А іб _
3) а‘ : а3 = л8 8 = а,8= а Ѵа*.
— 188 —
Д _ 8 1 В _ « _ 1__1 і _в /
4. ) ав.Ь * а~ .№ — ав * : Ь 8 — а™ : Ь 8 — V —
' ѵ 6,в
5) (За'бІ)8 —^1аЪ\ = 27аб. &?= 27аб ѴЬ.
' « •_ і ,
6) (16а*б8с0)’ = (28.2а*6’св)’ = 2іс*(2а’)3 = 2Ьс* /2а*.
48483. Примѣчаніе. Относительно возвышенія въ степени и извлеченія
корней сдѣлаемъ еще нѣкоторыя замѣчанія.
4) Отъ постепеннаго возвышенія цѣлаго числа а въ цѣлыя степени, оно без-
престанно увеличивается, и когда показатель п=ск> , то и а"—сл.
I
2) Отъ постепеннаго возвышенія правильной дроби — въ цѣлыя степени п,
получаются числа, безпрерывно уменьшающіяся, и приближающіяся къ нулю.
1 1
Когда степень и— со, то а" = со, а =0.
' а а”
3) Отъ пос "ѣдовательпаго извлеченія корней изъ цѣлаго числа а, полу-
чаются корни постепенно меньшіе, которые безпрестанно приближаются къ
4-цѣ, никогда ее не достигая. Надобно извлечь корень безконечно большой сте-
пени, чтобы онъ сдѣлался равенъ единицѣ. Въ самомъ дѣлѣ, если въ /а — а«
і і
положить п — со, то получится — = — —0, и оттого а°=1.
4) Отъ послѣдовательнаго извлеченія корней изъ правильной дроби по-
получаются числа увеличивающіяся и привлекающіяся къ 1-цѣ, которую и
_ "/ і і
имѣютъ своимъ предѣломъ. Ибо, если въ у — положить и = оо, то
а«
0, «°=1,-0=4.
п оо а°
Всѣ сіи замѣчанія относятся собственно къ корнямъ дѣйствительнымъ.
48484. Возвышеніе въ степени, умноженіе и дѣленіе корней мнимыхъ.—
Сложеніе и вычитаніе между корнями мнимыми дѣлается совершенно такъ же.
какъ между корнями дѣйствительными. Возвышеніе въ степени, умноженіе и
дѣленіе между этими корнями производится по тѣмъ же правиламъ, какія видѣли
мы для корней дѣйствительныхъ: только здѣсь должйо наблюдать большую осто-
рожность относительно знаковъ (—) подъ радикаломъ, безъ которой учащіеся
легко могутъ войти въ недоразумѣніе, и потерять истинную дорогу. Вотъ пра-
вила для этого:
Возвышеніе въ чётную степень надобно сначала изобразить знакомъ,
сократитъ показатель корня съ показателемъ степени, и послѣ того
дѣйствительно возвысить уже подкоренное количество въ степень, ка-
кая останется послѣ этого сокращенія.—-Но если мнимый корень воз-
вышается въ нечётную степень 2п+1, то надобно сперва возвысить
- 189 -
«ю въ четную степень 2и, м ату степень помножить еще на данный
корень.
Примѣры:
V — а ~(У/—а)*= V—а,
(у/—ау-|/р^у=_а,
( Ѵ/^)’=( Х/^}~ Ѵ^=—а Ѵ—\,
(і/—а)‘— (і/—а)*( V—а)‘=—аХ—а~а*,
( у/^)'=( V— л)‘+1=а8 V—Г,
(і/—а)°=( V—а)‘+,=—а8, и проч.
Чрезъ умноженіе или дѣленіе дѣйствительнаго корня па мнимый
всегда получается выраженіе мнимое; но, отъ взаимнаго перемноженія или раздѣ-
ленія двухъ мнимыхъ одночленовъ, могутъ получиться количества какъ дѣй-
ствительныя, такъ и мнимыя.
Примѣры для умноженія:
1) V—а.ѴТі—у/—иЬ.
2) Ѵ—а = Ѵа. У/—1X ѴЬ.. /—1= Ѵ^Ь.(^=4)’=— ѴцЬ.
3) у/—а. Ѵ^=— Ѵ'Ь2. Ѵа. У/^Г~— /—1
4) і/—а. і/—а = V—а8.
5) у/~а. У7^0Г Ѵ'Г.
6) у/2^. у<=б= у/^А °Ѵ^Ь{ V1)8= — Ѵа3Ь.
7) у/_0. |/—б— у<^‘. у/=^= ѴаѢ3. у/(— 1 )’=— ѴаѢ3.
Примѣры для дѣленія:
ЯЗД». Дѣйствія надъ мнимыми выраженіями, вида а-+-/3 ѵ—1.
Отъ сложенія, вычитанія, умноженія и дѣленія таковыхъ количествъ между
собою, получаются результаты того же самаго вида:
— 190 —
(ач-/? V—1 )ч-(а'ч-/?' Vх—1)=(ач-а')ч-(/Зч-/3') Ѵ'—1;
(ач-/? (а'ч-/3' V—Г)=(а—а')ч-(/3—/3') [/—Г;
I ач-/? V— 1) X («/-+7?/ V — 1 )=аа'ч-/3а' V— 1 ч-а/3' V — 1 —/3/3'
=(аа'—/?/?')-ъ-(/Эа'ч-а/3')
—1 (ач-/?і/—1}(а'—/3'Vх—1) аа'ч-/?/?'ч- (/За'—а[Зі}Ѵ—1_
а'-*-/?' V —7~(а'ч-/?' \/'~Г) (а’—/3' Ѵ'^Т) ~ а'^З’^
_ аа'-+-/?/3' (/За'—а/З* 1) ./
~ а’2 * * * *+{3'2 ’ Ѵ~~1 ’
Всѣ сіи выводы суть вида ач-б Vх—1.
Очевидно также, что, и ось возвышенія ач-/?і/=1 въ цѣлыя степени, по-
лучатся выводы того же вида. Потому что возвысить ач-/3 V—1 въ п ю сте-
пень, надвбно это количество іюмножвгь само на еебя п—1 разъ.
Впослѣдствіи мы увидимъ, что и отъ извлеченія корней изъ ач-/3 Vх—1, т.
е. отъ возвышенія этого количества въ степени дробныя, получается выводъ
ач-б Vх—1 того же вида.
99Я. Модуль выраженія а±0\/-—1. Свойства, модулей.—При
извлеченіи квадратнаго корня изъ суммы двухъ количествъ а и /3, выводъ
ч-і/аМ-/?* называется модулемъ выраженія ач-/? Vх—1 .Такимъ образомъ, для
Зч-4 1/—1 модуль = ч-Ѵ9ч-16=ч-5. Снъ есть не что иное, какъ среднее
пропорціональное между Зч-4 Vх—1 и 3—4-і/—1.
Два мнимыя выраженія ач-/? V—1, а—/3|/—1, различающіяся между со-
бою только знакомъ предъ коефиціептомъ /3 мнимаго членя, называются сопря-
женными; потому что онѣ имѣютъ одинъ и тотъ же модуль.
Этн модули имѣютъ нѣкоторыя замѣчательныя свойства:
1) Модуль произведеніи двухъ мнимыхъ множителей, равняется про-
изведенію ихъ модулеіі.
Въ самомъ дѣлѣ, мы уже знаемъ, что
(ач-/3 —1 )(а'ч-/3' V—1)=(аа'—/3/3'}ч-(а/3'ч-/?а') р—1; а модуль это-
го произведенія равенъ
і/[аа'—/3р')1-^(а/3'ч-/?а')*= 0г'а'-ч-/?8/?'8ч-а73'8ч-/?ва'г
= Ѵха’(а',ч-/3'8)ч-/3\а'^'2)
= і/і^+ДП (аяч-/3^= Ѵа^ч# і/а^ч-Д”.
2) Модуль частнаго числа двухъ мнимыхъ выраженій ач-/?і/^—I,
а'ч-уЗ'і/—1, равняется частному числу ихъ модулеіі.
Пусть а"-\-(3" Vх—1 частное число отъ раздѣленія а-+-/3 Vх—I на
а'ч/З' |/_ і ; то будетъ
ач-/? |/—1 =(«'ч-/?' 1/^4) [а"-ь-ІЗ" /—1),
— 191
и, стало-быть,
Ѵа+І3‘= откуда
,-------
\/аг^р"
3) Чтобы мнимое выраженіе а+р\/—1 было равно нулю надобно
чтобы было, въ одно время, а—О и или чтобы ею модуль
-+-Ѵ/ІьЭт=0.
Для доказательства, положимъ
а-т-/3 \/—1—0, или
а— —р ; откуда
«М-/3*—0;
С?
Пусть также — = п, или а—/Зп: стало-быть,
/ЗѴ-ь/32=/9>*-М)=0.
Но, и’ч-1, какъ дѣйствительное отвлеченное число, не можетъ быть=0, то
должно быть /3=0, а слѣдовательно и «=0, и і/аМ-уЗ^О. II обратно, если
модуль |/а4ч-/3—0, то очевидно, что а—0, /3=0, и «ч-/3 Г7—1—0.
4) Чтобы произведеніе мнимыхъ множителей равнялось нулю, доста-
точно, если одинъ изъ этихъ множителей сдѣлается нулемъ.
Ибо, произведеніе многихъ мнимыхъ множителей имѣетъ видъ а-ь/3—1;
а чтобъ это произведеніе уничтожилось, довольно если модуль его обратится въ
нуль. Но, мы знаемъ, что этотъ модуль равняется произведенію модулей всѣхъ
множителей, составляющихъ давпое произведеніе; а эти модули суть количества
дѣйствительныя, такъ что ихъ произведеніе не можетъ сдѣлаться нулемъ, пока
одинъ-изъ нихъ не обратится въ нуль; но тогда и мнимый множитель, соотвѣт-
ственный сему множителю, будетъ равенъ нулю, и уничтожитъ все данное про-
изведеніе,
тп т
Л о"—Л" д—"—6—" а «—Ъ п ,
О значеніи выраженіи ~, —-—— , д ь , въ случаѣ а=о.
338. Хотя каждая изъ этихъ дробей, для а=Ь, обращается въ ; однако
же это не означаетъ ихъ неопредѣленности, потому что каждая дробь содержитъ
множитель а—Ь въ своемъ числителѣ и знаменателѣ. Надобно только исключить
этотъ множитель и тогда дробь, для а=Ь, получитъ настоящее свое значеніе.
Доказательство. — 1) Пусть показатель п число цѣлое, положительное;
то знаемъ (ЛЗ, 2), что
пП_______________Ъп
...............................
а—Ь в
гдѣ число членовъ п. Теперь положимъ Ь=а; получится
количество опредѣленное.
— 192 -
2) Возмемъ теперь дробь
а—п—Ь— т
о—Ь ’
въ которой показатель —т число цѣлое, отрицательное. Мы знаемъ, что
_ 1 1
а ”*= — , Ь т= — ; подставимъ это, и сократимъ, найдется:
а~т — Ъ—т 1 ат — Ъ™
а—Ь атЬт ' а—Ь
Теперь положимъ Ь~а, и припомнимъ изъ предыдущаго, что въ этомъ слу-
чаѣ дробь ~а_ь обратится въ тат~і; отъ этого получится
3) Далѣе: возмемъ дробь
а'п—Ът
ап—Ьп ’
въ которой т, п, числа цѣлыя положительныя. Эту дробь написать такъ:
ат — Ьт(о—Ь)(о”—’-с-д ..-ьЬ"1—*)
ап—Ьп (а—Ъ)(ап~ *-+-ап~~
Исключивъ общій множитель а—Ъ, положимъ Ъ=а, получится-
ат—Ът тат~1 т ________
— - —--------— — . а .
о"—6” па”—1 п
4) Наконецъ, дробь съ показателями дробными
/1ч т ГІ.\т'
дп—ь»аѵ‘/ —
очевидно, приводится къ случаю 3); слѣдовательно она, для &=а, обращается въ
т! — — 1
«У > п
выраженіе также опредѣленное. ।
Д. СТЕПЕНИ КОЛИЧЕСТВЪ ДВУЧЛЕННЫХЪ И МНОГОЧІЕННЫХЪ.
НЬЮТОНОВЪ БИНОМЪ.
229. Двучленное количество а-л-х, будучи возвышаемо послѣдовательно въ
степени цѣлыя, даетъ:
(а-ьл:)4=а-ьл;,
(а-ьл?)і==а8-ь2аж-4-.г ,
(ач-я) 3=а3ч-3 «’жчЗ а.г’ччг3,'
Это показываетъ, что степень двучлена, вообще, изображается радомъ, рас-
положеннымъ по степенямъ обоихъ его членовъ, а именно: по убывающимъ сте-
пенямъ перваго члена а, и по возрастающимъ степенямъ втораго члена х. Слѣ-
довательно, для возвышенія двучлена ач-х въ степень п, должна быть нѣкоторая
общая формула, вида:
(аччс)"—а"ч-Аа’“_1жч-Вап-' а:*ч-Са"~’я:3ч-... ,-+-х",
гдѣ п показатель степени* А,В,С,.... нѣкоторые постоянные коефиціенты, не-
засисимые отъ х и а, в которые остается только опредѣлить.
193 —
Такаа формула дѣйствительно есть, и притомъ она одна и таже, каковъ бы
аи былъ показатель и, цѣлый или дробный, положительный или отрицательный.
Постараемся вывесть эту формулу въ самомъ общемъ ея видѣ, т. е. принимая
п какимъ угодно числомъ. А чтобы проще и удобнѣе этого достигнуть,
вынесемъ а” внѣ скобокъ:
, . я1." /. Аж Ва?» €»5
-4-----
апі
отбросимъ на время общій множитель а", и положилъ — =у, получится:
(1ч-у)"=1-ч-Ауч-В/ч-С/ч-..................ч-уя.
Здѣсь коефиціепты А,В,С,.... также независимы отъ у, но они зависятъ
отъ показатели и; слѣдовательно они останутся совершенно тѣ же, если у пере-
мѣнится въ к, а п останется тотъ же:
(1ч-я)п=1ч- Аяч-іВ*’ч-С.г3ч-... .ччЛ
Вычтемъ этотъ рядъ изъ предыдущаго, и разность раздѣломъ на у—з
(1ч-у)я-(1ч-г)я=А(у-г)ч-В(/-г’)ч-^3-^3)ч-....ч-(у“-Г),-
= Ач-В(уч-г)ч-С(угч-уач-гІ)ч-.........................
Теперь, дли краткости, положимъ:
\.-л-у—и |
. } и вычтемъ,
4ч-гз=ы1 ,
у—г=и—ил ; то будетъ
^=Ач-В(^ч-г)ч-С(уМч/гч-^)ч-.........
Но, поелику г взято произвольно, то и положимъ тогда будетъ »,—ч,
и, каково бы ни была степень п, цѣлая или дробная, положительная пли отри-
цательная, дробь ^и_~ обратится въ ни"-1, какъ было доказано (Я®В). Слѣдо-
вательно, мы получимъ
пы"-1—Ач-2В7/ч-ЗСг/’ч-ІОг/3ч-....
Это равенство помножимъ на и, и потомъ подставимъ 1ч у~и:
пи’—м( Ач-2 В^ч-ЗСу’ч-'Шу’ч-....),
п(1ч-^я=(4чч/)(Ач-2Вг/ч-ЗС?/гч-іВ?/3ч-....), или
п (1 ч-Ауч-Ву’ч-Су8ч-.
,.)=Ач-2В уч-ЗС /ч-4В
ч-Л ч-2В ч-ЗС
/-ь
Такимъ образомъ, мы получили два равные многочлена, расположенные по
степенямъ одной и той же буквы у. Коефиціепты ихъ вовсе независимы отъ ?/;
а потому, дли равенства сихъ' многочленовъ, должны быть равны коеіЬпціспты
равныхъ степепей отъ у (10-1), то есть:
13
194
\.~п, откуда А=п
2В-+ А=Ап, ЗСі2В~Гш, Р А(п—1) п(п—1) 2 —1.2 ’ г В(п—2) п(п — і](п—2/ Е 3 1 . 2 . 3 ’ р п(п—1)(п—2)(п—3) 1.2 . 3 .4
Такъ опредѣляются коефиціенты А,В,С....; законъ ихъ составленія изъ по-
казателя п столь простъ и очевиденъ, что не имѣетъ надобности въ объясне-
ніи. Посему,
п(п—1)я2 п(я— 1)(п-2) а п(п—1)(п—2)(п—3)
1.2 ^ + 1 . 2 . 3 У 1 . 2 . 3 . 4 Н"“
Теперь возмемъ опять у— — , и помножимъ обѣ части равенства на а"; по-
лучится:
п(п—1) п(п— 1)(п—2) х
1 . 2 ' а* 1 .2. 3 ' ...)’
(А)....[а-+-л')"=а"-+-п.<іп -”-2<
1 • 2 «3
Такова общая формула, служапіая для возвышенія всякаго двучлена въ какія
угодно степени. Она извѣстна подъ именемъ Ньютонова бинома; потому что
была открыта славнымъ англійскимъ ученымъ Ньютономъ.
330. Разсматривая эту формулу находимъ.
4) Показатели буквы а, начиная съ перваго члена ап ряда, въ каждомъ его
послѣдующемъ членѣ уменьшаются единицею, а показателю буквы х на столько
же увеличиваются, такъ что сумма показателей остается постоянна и равна п,
2) Каждый послѣдующій членъ ряда составляется изъ предшествующаго
(паприм. изъ 3-го члена а"“*ж* составленъ
, .. п(п—1)(п—2) ,
4-и членъ -— -----—- а” 3х3)
1.2.3 '
такимъ образомъ, что членъ предшествующій помножается на показатель его
буквы а, и дѣлятся на число членовъ, предшествующихъ искомому члену послѣ-
дующему; степень буквы а еіишіцею уменьшается, а степень буквы х единицею
увеличивается.
3) Во всякомъ членѣ число вычитаемое изъ показателя буквы а, степепь
буквы х, и наибольшій множитель въ знаменателѣ, равны .числу членовъ пред-
шествующихъ, и потому равны между собою; а наибольшая цифра, вычитаемая
изъ п въ численномъ коефиціенгѣ, единицею менѣе. Слѣдовательно, если взять
г членовъ сряду, то слѣдующій (гч-1)й членъ будетъ:
г , т п(п—1)(п-2)....(п-іч-1) „_г г
——~-г у, х.
195 —
Онъ Называется общимъ членомъ, потому что посредствомъ его можно нахо-
дить всякій членъ, занимающій какое угодно мѣсто въ ряду Ньютонова бинома.
Наприм. для полученія 4-го члена, должно положить п найдется:
т п(п— 1)(п—2) „_3 з
1 .2.3’ й - •
4) При показателѣ п цѣломъ и полоэкателыіомъ^пхьА. пе безконеченъ:
онъ оканчивается членомъ х" и содержитъ пч-1 членовъ. Въ самомъ дѣлѣ,
общій членъ (а) возможенъ до тѣхъ поръ, пока въ его коефиціентѣ самый мень-
шій множитель т—гчі>0, или когда пч-1>г. Если же взять г=пч-1,
то этотъ коефиціентъ обратится въ пуль, и соотвѣтственнаго члена не будетъ,
Послѣдующихъ членовъ также не будетъ, потому что всякій послѣдующій членъ
составляется изъ предшествующаго. Послѣдній членъ ряда получится, взявъ
=п; тогда
_п(п-1)(п-2)....2 -1 .
1.2. 3......п—1)п а
А какъ здѣсь п показываетъ число всѣхъ членовъ предшествующихъ, то во
всемъ ряду находится пч-1 членовъ. Очевидно, что, грп показателѣ п чётномъ,
число членовъ должно быть нечётное; а, при показателѣ нечётномъ — число
членовъ чётное.
5) При показателѣ л цѣломъ и положительному, всякіе два члена ряда (Л',
равно отстоящіе отъ его концовъ, имѣютъ равные коефиціепты; это видно йзъ
того, что «ч-ж=жч-а, и
(а-ьж)'—(жч-а)п. Но,
(ач-а:)п=а"ч-па"_1а;ч-р*~ а”“’а:’ч-....ч-Ва8а?’‘“*ч-8оа?’'~1ч-а;я,
(жч-а)я=жяччіа;я~1ач-- — ж"-1а*ч-... .ч-Вж5а"“’ч-8.га’,_1ч-о’‘
г=в”-4-8а;а"К1-+-Лл:Іа"_8ч-... .ч аб~іа*-+-ііх,'~іа-і~хп.
Эгп многочлены расположены теперь по степенямъ буквы х, и должны оста-
ваться равными для всякой величины х\ а котому коефпціенты равныхъ степе-
ней х должны быть равны между собою. Слѣдовательно 8=п, В — г
ИТ. д., и потому
і о т-ж),‘^=а,‘ч-па,|~1я;ч- и?п~41 о'—^ч-.. - і ? а1хп~тч-пах'г~1ч-х".
' 1 1.2 1.2
. п(п— 1) п(п— і)Гп—2)
Ь) Сверхъ того, коефиціепты I, п, 12 > 3 • ,...., слѣдуя отъ
обоихъ концовъ ряда, возрастаютъ до его средины; такъ что, при показателѣ и
чётномъ, наибольшій коефиціентъ находится въ среднемъ членѣ, а при п нечёт-
номъ, два средніе члена имѣютъ равные наибольшіе коефиціепты. Сумма же
всѣхъ коефиціептовъ равна 2”; она получится, взявъ отчего (ач-д?)я
обратится въ рядъ
2"=1ч-пч-^У ч- ....
1.2 1.2.3 1.2
- 196 -
состоящій изъ однихъ коефиціентовъ общаго ряда. А полагая
п=1, 2, 3, 4, 5, 6, 7, 8, 9, 10,....,
получатся величины коефиціентовъ каждаго члена, соотвѣтственныя степенямъ
і, 2, 3, 4,.... бинома (ач-ж)”, которые здѣсь найдены, и расположены въ
вертикальныхъ строкахъ:
п=1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...
коефиціепты для всѣхъ членовъ:
1, 1, 1, 1, 1, 1, 1, 4, 1, 4,
1, 2, 3, 1, 5, 6, 7, 8, 9, ю, ‘
1, 3, 6, 10, 15, 21, 28, 36, 45,
1, 4, ю, 20, 35, 56, 84, 120,
1, 5, 15, 35, 70, 126, 210,
1, 6, 21, 56, 126, 251,
1, 7, 28, 84. 210,
1, 8, 36, 120,
331. И такъ, при показателѣ п цѣломъ и положительномъ, рядъ би-
номіи Ныотопа будетъ:
А)... (ач-ж)’_а"ч-па"~'хч:-~^ ^а”-8ж’ч-.ч-р^-^а8ж"_8ч-паж"~|ччі:"
„г, X тЦп — ІУіХХ* п(п — І)/Х ч“—5 /Х\”~1 Ж’Ч
—аНч-п.-------1-- (—) чч?.(— ) ч—-I.
I а 1.2 ' а1 1 . 2 ' а / ' а а’Ч
Для возвышенія бинома ач-ж въ отрицательную степень, надобно взять
только —п вмѣсто п, и получится:
„ 1г. П.® п(п-+-
В).....+ГГ2
х* п(пчЧ)(п-і-2)
а*- 1.2.3
Для возвышенія въ дроОную степень, надобно въ рядъ А) подставить —
вмѣсто п, и будетъ.
С).... (ач-ж)» = атг[іч-^
ж х*
а 1.2 пв 1 . 2 3 и
Двѣ послѣднія формулы имѣютъ безчисленное множество членовъ: потому что
,, , . п(пчЧ) п(ш-1)(тм-2)
въ перврй ни одинъ изъ ея коефиціентовъ п, -—-—, -—------------—.... пе мо-
жетъ сдѣлаться нулемъ, сколько бы членовъ мы пи взяли; а во второй, коефи-
„ т т , т ,,
ціеіпы составляются изъ множителей ,---------1,--------2,..., изъ коихъ также
п п п
ни одинъ пе можетъ обратиться въ пуль, потому что ^- < 1.
333. Приложеніе Ньютонова биномическсио ряда къ возвышенію
въ степени количествъ двучленныхъ, трехчленныхъ, четыречлениыхъ,
и, вообще, многочленныхъ.
Примѣръ. Найти 3-ю и 5-ю степени двучлена ач-ж.
197 —
Беру формулу:
(ач-я)Л=а’,ч-поя-1«;ч- |1 *~1 «"“’ж’ч- ^Г*,“1КП“2' а—»ж».
и полагаю сперва п=3, а потомъ иг=5; нахожу:
(а-4-ж) 8~а3ч-3 а’жч-З аж’ч-ж8;
, в с 8 І В-4.3 . 8 5.4.3.2 . В.4.3.2.1 с ,
(«+*)-“ ч-5а х+ —.а х ч- — а х ах а х :
или:
(ач-а;)'=а’ч-5а‘жч-1 ОсЛс’ч-10а“гг8ч-5аж4ч-ж *).
Примѣръ. Возвысить двучленъ (ач-л;) въ степень
Беру формулу С), и полагаю — = -.
(ач-ж)з=а8 [1ч-
2 а: 1 х*
3 ’ а 9
1 хъ
Ь 81 ‘ а3
Примѣръ. Возвысить а—х въ степень п.
Для этого вь ряду А) надобно только взять —х вмѣсто и получится-
(а—х)п^=а"—пап іам-"{”
аГ^х1— п(п-і)(г.-^ ±д.
1 • л • о
83»3». Положимъ теперь,
для возвышенія въ степень
что дано трехчленное количество сч-бч-с
п, то есть, требуется панти (ач-бч-с)".
•) Сдѣлаемъ здѣсь одно полезное замѣчаніе. Въ ряду (а-+-а:}8 возмемъ какой ни есть
членъ, напримѣръ,
5.4.3
——- . «Ат3,
1.2.3
внесемъ въ его числитель всѣ множители 5, 4, 3, 2, 1, и, какіе множители войдутъ лиш-
ніе, тѣ введемъ въ знаменатель, чтобы величина члена пе перемѣнилась; тогда получится:
5.4.3.2.1
1.2.3.1.2 • а*Х*'
Тотчасъ видно, что, въ знаменателѣ, множители 3 и 2, которыми оканчиваются двѣ
группы 1.2.3, 1.2, произведеній, равны показателямъ буквъ хна этого члена. Согласно
съ этнмъ, можно написать общій членъ
п(п—1)(п—2)........2.1
-----------------—-------Лп—гхг
1.2. 3..... 1.2.3...(и—г)
Это замѣчаніе употребляется иногда для опредѣленія коефиціента, когда извѣстно
только произведеніе ап~гхг для члена изъ ряда биноміи Ньютона. Для этого надобно
помнить, что сумма показателей п—т-ѵ-г п, равна степени бинома, и потомъ поставить
въ числителѣ всѣ множители п(п—1)(п—2/...3.2.1, а въ знаменателѣ—произведеніе изъ
н(п— 1)(п—2)...г, и п(п— 1)(п—2)....(п—г), и сократить. Положимъ, нанрим., что надобно
найти предстоящее къ еъх° члена, взятаго изъ биноміи Ньютона. Для этого, слагаю
Зн-5—8, и получаю степень; потомъ беру
8.7.6.5.4.3.2.1
-____________________ке
1 . 2.3.1.2.3.4 . В
Таковъ будетъ искомый коеФиціентъ; а искомый членъ будетъ =5ба‘л8.
198 —
Для этого положимъ сперва Ь-і-с=х, получится:
(ач-ж)"=а’’ч-паи“*«ч- а"-5л?ч- ”(п~Т-)(-п~72) а"“’ж’ч-....;
а потомъ внесемъ сюда я=бч-с:
(ач-бч-с)”=а’,ч-па"’\бч-с)ч-^^)а"-!(бч-с)Іч-^=^^а"-3(бч-б)3ч-.
Накопецъ, составимъ степени
(Ьч-с) 5=б2ч-2 Ьс-і-с*,
(6ч-с)3=6Ч-36‘сч-3&с8ч-с3,
подставимъ и сократимъ, и то получится весь рядъ, выражающій п-ю степепь
трпчлепа ач-бч-с. А этотъ рядъ послужитъ для возвышенія въ ту же степень
количества четыречленнаго а-< Ь-+-с-+-й. Для этого надобно только во всемъ
ряду подставить счч/ вмѣсто с, и найдется (ач-бч-сч-ч/)"; и такъ далѣе.
Примѣчаніе. — Не входя въ подробное разсмотрѣніе закопа происхожденія
послѣдовательныхъ членовъ ряда (ачбч-сччіч-....)", я замѣчу только, что,
по даннымъ буквеннымъ множителямъ какого ни есть члена этого ряда, числея-
ный коефиціентъ его найдется по тому же правилу, какое показано въ замѣчаніи
(®3®) для членовъ биноміп Ньютона. Положимъ, что надобно найти коефиціентъ
для о,Ѵсг одного изъ членовъ (ач-бч~с)7. Составимъ четыре произведенія, со-
отвѣтственно числамъ 7, 3, 2, 2, а именно:
7.6 5.4.3.2.1, 3.2.1, 2.1, 2.1;
поставимъ первое въ числителѣ, и всѣ прочіе въ знаменателѣ, и найдется иско-
мый коефиціентъ
7.6.5.4.3.2Д
3.2.1 2.1.2.1
Коефиціентъ для произведенія а6Ьс нашли бы
7.6.8.4.3.2.1
------------- =42:
ьЪ 4.5.1.1 ’
коефиціентъ для а4бс’ будетъ
7 6 8.4.3.2 1 .п„
. .... ,.-,-гк-=*05.
Справедливость этого закона не трудно повѣрить, надобно только дѣйствитель-
но возвысить ач-бч-с въ п-ю степень, и сравнить члены подобные тѣмъ,
какіе мы брали.
®34. Формула (Іч-жр^іччпжч-у т-^ х‘+....+тх'п~і+х’",
гдѣ т цѣлое число первоначальное, приводитъ къ замѣчательному свойству
чиселъ. Перенесемъ 1, хт, въ первую часть равенства
Іі . 1 *) 2 , . 1
1.2 ....... ’
найдется, что вторая часть дѣлится безъ остатка па т, а слѣдовательно
. 1 +-а і™—1—х" также дѣлится па т.
— 199
Положимъ, что 4ч-л=А, х=А—4, и подставимъ:
А"1—1 — (А— 1)
Это выраженіе дѣлится на т для всякой величины цѣлаго числа А; слѣдо-
вательно для А—1, А—2, А—3...., А—А. Взявъ эти числа вмѣсто А въ
выраженіе
А"*—1—(А—4)“, найдется рядъ выпаженій, дѣ-
(А—1)"—1—(А—2)”' лимыхъ на т, которыя и
(А—2)т—1—(А—3)т сложимъ;
(А—3 1—(А—і)т
(А—Ан-1) ”*—1 —(А—А)т
нолучптся сумма А"—А—(А—А)’’,=А™—А, раздѣлимая па т.
.. А,п—А АгА™-1 —1)
Итакъ, —-— : : ———-----— цѣлому числу.
Если т число первоначальное, А цѣлое неспособное раздѣлиться па т,
то долженъ раздѣлиться на т двучленъ А’"-1—1. При этихъ условіяхъ,
А”1—1
------— цѣлому.
ТТ тт о 4 -л 1О«-1 99
примѣръ. Полагая пі=3, А~4 0, найдется —-—= - —33.
О о
Это замѣчательное свойство дѣлимости открыто Ферматѵмъ, остроумнѣй-
шимъ французскимъ математикомъ 47-го вѣка. Изъ него слѣдуетъ, что поелику
»п~1 т—1
А”-1—1=(А“ч-4)(А~—1);
то одинъ изъ двучленныхъ множителей, на которые разлагается А"1-1—4, не-
премѣнно дѣлится на первое число т. Манрим. пусть А—10, ?и=7; то
А™-’—1 10в-1 (105-ьІ)(10=—і).
т 7 7 ’
множитель 4О8—і—1=4ОО4 дѣлится па 7.
Если изъ А"”1—4 вычесть выраженіе В”1-1—4, гдѣ также А и В пе дѣлятся
па т, то получится разность А’"-1—В™-1, дѣлимая на пі.
Примѣръ. Пусть А=10, В=5, »н=3;
А»—1—В”—1 10’—3’ 73
— —_—
т--------------------3-3
Пусть А=3, В=2, іи=5, то
А’—і-В"— * 3’-2’ Я1—16 63
т ~ ~~ “ 3 ~
Очевидно также, что, отъ раздѣленія А”1-1 иа т, въ остаткѣ получится-+-1;
стало быть, и отъ раздѣленія (А”1-1)® остатокъ будетъ ч-1?—1. Если отъ раз-
дѣленія Аг па т, остатокъ =К; то и отъ раздѣленія Аг(А”*_1)г остатокъ бу-
детъ К. Если Аг(А"*~‘)г—А8» То А', раздѣленный па первое число п, дастъ
также остатокъ Н.
— 200 —
935. Вычисленіе всякихъ корней изъ чиселъ посредствомъ ряда
Ньютонова бинома.
Дія полученія желаемаго корня изъ даннаго числа, разлагаютъ оное на двѣ
части, изъ коихъ первая, сколько возможно большая, была бы полною степенью,
а другая мепыпая, служащая дополненіемъ первой къ данному числу; подста-
вимъ ихъ на мѣсто а и а; въ формулу
(ач-ж)"=а”-ьп. а"~'х-ь- —Ц— а"~8а:*ч-....
__ „г. пх п(1 —п) / х \ 8 п(1—П)(2—П) , X х 8 .
I а 1.2 'а' 1.2.3 V а /
Положимъ, что а—об, х~д, я=—, получится:
(«+Л-! . А' ч-иа-ч (Ъ‘_
' > 1 Г аг 1 . 2.г4 \аг) 1.2 . З.г3 \аТ'
1.(г—1)(2г—1)(3г—1) Л.1 •
1 . 2 . 3 . 4.г* ‘ -+-••••]•
Примѣръ. Найти КіО.
Кубъ, ближайшій къ 10, есть 8=2’; посему можно взять Ѵ40=Ѵ 8-ь2=
=(8-ь2)з, и положить «г=8, <5=2, г=3. Сдѣлавъ подстановленіе, по-
лучимъ.
(8^=2(1-ГЫ-^І4 —-)•
Четыре члена, вычисленные, даютъ корень
^10=2,4 547....
который имѣетъ всю точность только въ тысячныхъ доляхъ.
Примѣръ. Найти ѵ240.
і___
Здѣсь я замѣчаю, что 240 близко къ 243=3 , то и беру Ѵ240=
Б_______ 1
Ѵ243—3=(243—3)«.
Полагая «=243, <5=—3, г=5; нахожу:
Для вычитанія, беру только три первые члена ряда, и получаю
^240=2,9925515....,
корень точный въ шести десятичныхъ.
936. По видимому, трудность этого способа извлеченія корней становится
велика, когда коренной показатель великъ, а подкоренное число мало и разла-
гается на двѣ части невыгодно для вычисленія.
Б ___
Положимъ, что нужно получить VI0. Здѣсь олижайшее разложеніе:
10=1 “-+-9, или
10=32—22=2Й—22;
— 201
изъ нихъ первое совсѣмъ нельзя употребить, я второе невыгодно для вы-
численіи.
Въ такомъ случаѣ надобно данное число 10 обратить въ дробь, помноживъ и
раздѣливъ оное на 5-ю степень другаго однозначнаго или двузначнаго числа;
отчего числитель сдѣлается довольно великъ, и можетъ быть раздѣленъ па двѣ
части, изъ коихъ одна, самая большая, будетъ полною пятою степенью. Такъ,
если помножить 10 на 12'=248832 (см. таблицу степеней чиселъ двузнач-
ныхъ, приложенную въ концѣ книги); то выйдетъ дробное число
Ю 125 ’
котораго числитель 24 88323 0=196-+-12221=24 7 6 0 9 9ч-<2221;
слѣдовательно, і/10 =
Теперь положимъ «=19, $=12221, г=5,
~ = 0,004935887....; паІІ,Яо,
1 ‘ ---19 г 1 $ 2 , * 6 /$ ч3
— у«ч-$=—[1ч-- • — -3(—) Ч- •••]•
Ограничившись только четырьмя членами этого ряда, получимъ.
^16=1,5848931924....=! О0'1.
точный въ 10-ти десятичныхъ; а взявъ большее число членовъ нашли бы
корень-
10°'*=!,58489.31924.61113.4851, въ которомъ точны всѣ 20 цифръ.
195-ь12221
12“
Ѵ/10=
Чтобы видѣть всю выгоду этого способа извлеченія корней, предложимъ себѣ
іоо.-----------
примѣръ: найти Ѵ/Ю=10°г01. Для этого возмемъ сперва
1/10^= 10“л= і/1,58489.31924.61113.4851....,
и нашедши его точнымъ до четырехъ десятичныхъ, 1,2589, составимъ
(1,2589)8=1,58482921, и разложимъ подкоренное количество такъ
10°'*= Ѵ/(1,2589)--+-0,0000639824611134851
гдѣ а8=1,58482921,$=0,00006.39824.6і113.4851.
^=0,00004.03718.33577.
«“
Чрезъ вычисленіе трехъ членовъ ряда, найдется
10°‘=1,25892 54117.94167.2104
корень, точный въ 13-ти десятичныхъ. Здѣсь онъ вычисленъ до 20- ти цифръ,
принимая большее число членовъ ряда.
— •202 —
Пзъ этого числа извлечемъ квадратный корень
Ѵ/ІОБ7’г=4Оо'°в= 1/1,25892.54117.94167.2104
= 1,122018454301963....
Остается теперь найти
1^= 10°'01= 1^1,1220184543....
Здѣсь можно было-бы взять 1,122018... = 1“ч-0,122018..., и вычислять
искомый корень посредствомъ ряда
іч-ѵ-0,122018...—^(0,122018...)’ч-...;
О 25
но приближеніе къ этому корню будетъ медленное; а потому, вычисливши только
два члена этого ряда, которые даютъ 1,0244...., возмемъ отсюда 1,02, воз-
высимъ это въ пятую степень *):
(4,02)®= 1,1040808032, и составимъ
1/171220184543....= {/(1,02)‘+0,0179376511... .=
= 1,02 [1+0,2. |-0,08. (^/ч- 0,048
гдѣ «“—(1,02“= 1,1040808032, 5=0,0179376511....
5 А *
-=0,01624667...., =0,000263954....,
(^)’= 0,0000042884....
'а '
Вычисливши четыре члена, получимъ:
10°'°‘=1,0232929946....,
гдѣ вѣрны восемь десятичныхъ **).
Этотъ способъ надобно употреблять всякой разъ, когда требуется получить
корень точный во многихъ десятичныхъ. Если же нужно имѣть корень пеболь-
ше, какъ о шести цифрахъ, въ такомъ случаѣ легче и благонадежнѣе вычислять
его посредствомъ логариомовъ, о которыхъ скоро говорить будемъ.
Я39. Степени двучлена а±ЛѴ—1. — Всякая степень двучлена
а±Ь і/—1 приводится къ виду а-+-@Ѵ—1, гдѣ а и @ суть величины дѣйстви-
тельныя. Ибо, если взять рядъ
/ п п—1 П(П—і)
(ач-ж) =а ч- па х-і--—
' ' 1.2
а’—’.
п(п—1) (п—2) ,
1.2.3 а
*) Смотри таблицу степеней трехзначныхъ чиселъ, помѣщенную въ концѣ книги.
’*) Извлекая квадратн. корень изъ ІО0'”, и потомъ корень пятой степени, мы получи-
ли бы ІО0'001; такимъ же способамъ нашли бы ю0'003*, іо0'0000’, и т. д. Такимъ образомъ
Д. иіюрманъ (въ Оснабрюкѣ) вычислилъ таблицу степеней числа 10 отъ ІО0'1 до
Юо^сооооілюі. рМе НапбЬисіі <1ег аП^ешешеп АгііЬшеІік ѵоп ₽. И. С. Едеп. Вегііп. 1846.
— 203 —
и, положивъ х=Ь V—I, слѣдовательно «’= — Ьг, х3= — Ь3 \/— I, х‘=б‘,
х3=Ьъ V— 1,...., подставить, и отдѣлить члены дѣйствительные отъ мнимыхъ,
то найдется:
(ач-б Vх—4)"= а"— а’-2б!-+- а"~‘б‘....
1.2 1 • 2 . 3 • 4
то есть, (а-+-Ь V—4)’_а-ь/ЭІ/—1, означая чрезъ а алгебрическую сумму
всѣхъ членовъ дѣйствительныхъ, и чрезъ /9 сумму членовъ, помноженныхъ
на Vх—1.
Отъ перемѣны Ь на —Ь, ничего не перемѣнится, кромѣ знака предъ /9, и слѣ-
довательно получіцся:
(а—Ь V—I )"=«—/9 Ѵ—\.
Изъ этого заключаемъ далѣе, что сумма
(а-+-Ь Vх—4)"-ь(а—Ь Vх-—І)”=2а=
—, "(п-1)(п-2)(п-3) ,Ь I»
—а і1 і.2 и; і. 2 . з . 4 '7'—••••]
есть количество дѣйствительное; а разность
(а-ьб |/=4)"—(а—Ь і/=^1)"г=2/9 |/—1 выраженіе мнимое.
Примѣры:
(а-ьб ѴХ^4)2ч-(а—Ь Vх—4)!=2(а!—б’).
(ач-б Vх—1 У—(а—Ь Ѵ^іу^аЬ ‘/—4.
(а-л-Ъ Vх—4)3ч-(а—Ь |4==4)3=2а(а2—Зб!).
(ач-б V—I)3—(а—Ь |/^=4.)8=2(3а2б—б3) Vх—!.
(а-+4 Vх—4)‘ч-(а—Ь Vх—4)*=(а*— бгч-2аб)(а2—б2—2аб).
1 (Ау....!
Послѣднее выраженіе совершенно сходствуетъ съ выраженіемъ корня урав-
неній 3-й степени (18»). Оно доказываетъ, что этотъ корень всегда дѣйстви-
тельный, потому что не зависитъ отъ Vх—1
938. Приведеніе суммы ^ач-б Vх—4 ± —Ь V—4 къ виду,
^Аіі/В, гдѣ А и В суть количества дѣйствительныя.
Назовемъ эту сумму буквою х:
х— а-+Ъ Iх — 4 ± а—Ь Vх— I,
н возвысимъ въ кваіратъ; получится:
х _2а±2 Ѵі/ч-б2, откуда
л~ 1^2а±2 і/а’н-б2, то есть,
і/ан-б Vх— 4± а—Ь V—1= |/аЧТ2.
- 204 -
Здѣсь 2 і/аЛ4-6 ’> 2а; стадо-быть, для знака ч-, эта сумма есть количество
дѣйствительное, а для знака —, оно представляетъ выраженіе мнимое.
Примѣры:
Ѵ/Зч_2|/22Г+. ^3—2 V 6-4-2 І/ІЗ.
ѴЗч-41ч- ^3—4
239. Непосредственное приведеніе формулы V А±В і/—1 къ виду
а±ьѴ,—1.
Для атого положимъ
'/А±ВѴ/—1=агк6 1/—1,
гдѣ а и Ъ суть нѣкоторыя числа, которыя найти надобно. Возвысимъ это равен-
ство въ квадратъ:
А±В Vх—1=а*—6’±2а6 [/—1.
Сравнимъ члены дѣйствительные съ дѣйствительными, и мнимые съ мни-
мыми:
а’—Ь\=А, 2аЬ=В.
ва
Изъ втораго равенства находимъ 6’= —; это подставимъ въ первое;
і в* . , . , в»
а — — =А; отсюда а—Аа~-~,
№ 4
а!=’ А±’ ѴбѴчЛП,
А изъ а!—б’ггА, получаемъ Ьг=а*—А, или
,, А± іЛѵ і в2 .
о =------------—А; откуда
—А± ѴСаМ-В’
2 ’
Здѣсь і/Л’ч-В’>А; слѣдовательно, для знака+, найденный числа О, А,
суть дѣйствительныя; а для знака —, онѣ оба мнимыя. Но, какой бы знакъ ни
былъ, въ обоихъ случаяхъ
А±В Vх—1—а±б Vх—1,
какъ это выведено было посредствомъ ряда Ньютоновой бйноміи. Настоящее
преобразованіе приводитъ къ нѣкоторымъ замѣчательнымъ слѣдствіямъ.
— 205 -
1=а±6|/—1, то и
А±В
и такъ далѣе, гдѣ а, Ь, а', Ь'} а”, Ь", числа дѣйствительныя, положительныя
или отрицательныя
Слѣдствіе 2. Положимъ А=:0, В=І, получатся:
у/ Ач-В 0=1 = Vх 0=1, у/ А—В 0=1= ^—0=1.
При семъ найдутся:
у/ А— В V—і=а—Ь Vх—1, сдѣлаются:
Vх 0Г?- Ѵ-1= ± (0 н-0. Vх-!).
0— 0—7= ± (0 - . 0=1).
Замѣтимъ далѣе, что
Если изъ этихъ двухъ выраженій извлечь квадратный корень, то найдется
7 0=і= Ѵ=7= 0 ч-0 . 0=1,
Vх—Vх—д—Vх—V——1/0 Vх—1, какъ сей часъ это
видѣли.
Vх—1=у/ ѵ/і-ь-ѵ/і/—!
= ^(1+71)4-^(1-0) хѵ7-1.
и такъ далѣе.
— 206 -»
5 т.---_ -
Отсюда заключаемъ вообще, что всякое выраженіе ѵ±и—4, гдѣ 2т цѣ-
лое четное число, приводится къ виду а±/?|/—1, гдѣ а и /? суть числа дѣй-
ствительныя.
240. Возвышеніе въ цѣлыя степени мнимыхъ выраженіи \/—1,
——V—I, Vх—1,ит. д.
Руководствуясь правиломъ, показаннымъ для возвышенія въ степени мнимыхъ
одночленовъ, первыя четыре степени для V—4 найдутся:
(ч- р-1) *= Vх—4; (ч- V—1 )'^=—4; (ч-V7—1)*=— V7—1; (-+- ^—4) 1;
слѣдующія четыре степени: 5, 6, 7, 8, которыя составляются изъ 4ч-4, 4ч-2,
4ч-3, 4ч-4, будутъ также
ч-Ѵ7—4, — 4, — V—4, чЛ;
степени 9, 40, 4 4, 12, опять будутъ соотвѣтственно тѣ же, и, вообще, каж-
дыя четыре слѣдующія степени будутъ соотвѣтственно періодически все
тѣ же самыя четыре, и могутъ быть изображены общими формулами:
(ч-1/^4 ч-Ѵ7—4; (ч-Ѵ7—— 1;
(ч-Vх—4 )*-*= — Vх—1; (ч- V7— 1ч-4.
Для возвышенія въ цѣлыя степени —V7—4, найдутся также четыре фор-
мулы:
П выраженія V—4=Ѵ7ѴХ—Л, и V7—Vх—1, имѣютъ степени цѣлыя воз-
вращающіяся періодически, только чрезъ каждыя восемь, а именно:
(Ѵ7ѵС=і)‘=ѵ/і_І-^.Ѵ=і,
(/^’^-ѵ^ч-ѵ^ѵСл,
(Ѵ7^)6--/-- 1/А.рСЛ,
(Ѵ'^) = _|/=т,
{V = н-4
= Ѵ7*—Ѵ7!^,
(і7—|/±Т)’=—і/^г,
(Vх——4,
(= - Vх* ч- |/і V-1,
(V— 4)в— ч-1/=4,
(Vх—р/^Г)7= і4 ч— ѵ4-1/~4,
- 207 —
Слѣдующія степени 9, 10, 11, 12, 13, 14, 15, 16, совершенію тѣ же, что
1, 2, 3, 4, 5, 6, 7, 8, какъ для * V—1, такъ и для — V—1, потому что
9=8ч-1, 10=8-4-2,....
Не худо замѣтить, что во всякой степени отъ V—1 и V— V-—1 дѣй-
ствительныя части ихъ совершенно тѣ же, а всѣ мнимыя отличаются' только
противными знаками.
811. Степени, найденныя для ±1^—1, суть вмѣстѣ сте-
пенями и для ѵ± У7—1; потому что
рСГГ = V У7—1 — /у/—1 —• У7—1;
_ у/ у/—у = _ ѵсу ;
ѵ—і = VѴ^і =\/ ѵ=і—у7— і = -+- ѵ|. у/—Г?
ѵ/-ѵ'=т=ѵ/-ѵс±г=^-у/і. у/^г.
Гораздо сложнѣе выражаются степени количества
= у/іѴЗл = /у/Ач-уЛ . У7—!, дао, слѣдс. 2).
у/і-4-уЛу/^Т;
(у/-1)3= у/(ѵ/і+у/<.ѵ/=1)э= Ѵ/-У/А-+-Ѵі.1/^і
= ѵ/^(іТН)-4- /КI ^Н)Х ѵ7-^,
и такъ далѣе.
— 208
ГЛАВА ОІЬМАЯ.
ТЕОРІЯ ЛОГАРИѲМОВЪ.
=(10,м)'
=(10,в'*)8
=(іол‘)‘
= 1/10
=(ібм)в
=іомхіо°"
9А9. Всякое уравненіе аж=г/, въ которомъ неизвѣстная х находится показате-
лемъ степени, называется неопредѣленно-степеннымъ. Оно показываетъ, что
можно получатъ всякія числа у чрезъ возвышеніе даннаго числа а вб нѣко-
торыя опредѣленныя степени, лишь бы число а было больше или мень-
ше единицы. Для примѣра, возмемъ частный случай 10®, и будемъ полагать:
«=0, 1, 2, 3, 4,......; найдется
аа,=1, 10, 100, 1000, 10000,......
Измѣняя надлежащимъ образомъ показатель х, можно получить всѣ числа
промежуточныя между 1 и 10, между 10 м 100, и т д. Напримѣръ, если на-
мѣсто х возмемъ дроби 0,1; 0,2; 0,3; 0,4;.... 0,9, между 0 и 1, и вос-
пользуемся примѣрами, показанными въ (®Жв), то получимъ довольно легко:
10° =1 •
10®'*=1,25892541....
4 0®'*=1,58489319...
10°'3=1,99526231...
10°'=2,51188642..
10°'8=3,16227766..
10°'в=3,98107170..
10®'7=5,01187336..
10®'в=6,30957344..
10®'’=7,94328234..
10' =10.
Можно получить числа, когда показатель х измѣняется отъ одной до одной
сотой, потому что мы нашли 10°'01=1,02329299...:
10°'ІІ=10°'І.10°'®1
10®'и=10м.10°'®!
1Оо,ІЗ= ІО®'1.!©®'®8
10о'!1=10°-!.100'01
10°'2'=10°'!.1Ѳм’
10°' 13— 100'5.100'03
Точно также можно получить и числа промежуточныя между 10 и 100, по-
лагая ®=1,1; 1,2; 1,3; 1,4;....1,9:
10м=10.100,1=12,5892541...
10І'!=10.10°',=15,8489319...
10І,8=10.10°'8=19,9526231...
10м=10.10®-’=79,4328234....
— 209 —
Э43. Въ общемъ выраженіи ат число а можетъ быть цѣлое или дробь,
степень х можетъ быть положительною или отрицательною.
Когда а больше единицы, то всѣ числа у, большія единицы, получатся
чрезъ возвышеніе а въ положительныя степени, цѣлыя или дробныя, въ
естественномъ порядкѣ ихъ послѣдованія. Паприм.
для ®=0, 1, 2, 3, 4,...., найдемъ числа,
а°, а1, аг, а3, а4,....
Всѣ числа, меньшія единицы, получатся чрезъ возвышеніе а въ сте-
лены отрицательныя, цѣлыя или дробныя. Потому что, для
ж=0, —4, —2, —3,........
а^—І, а~1, а~3, а~3,....или
. 1 і і
1, — , — , — ,.....
а а2 а3
Когда а меньше единицы, то, отъ возвышенія его въ степени положи-
тельныя (цѣлыя или дробныя), по пучатся всѣ числа дробныя. Ибо, если
, і
а дрооь равная у; то, полагая
ж=0, 1,2, 3,..... найдемъ
х і ііі
а ьг ’ Т’ ь2’ ь3’.
• А Г 1
А отъ возвышенія дроби а— - въ степени отрицательныя, получат-
ся всѣ числа, большій 1-цы.
Ибо, для ж = 0, —1, —2,—3,.... будетъ
х 1 . 1 11
а —ЬХ—6-1’ 6-” 4-»’............ ПЛИ
1, ь, ь\, ь3....
9ЛА. Степень х, въ которую надобно возвысить постоянное число
а, чтобъ получить данное число у, называется логариѳмомъ этого
числа у. Постоянное же число а называется основаніемъ логариѳмовъ.
А какъ всякое число, большее либо меньшее единицы, можно взять за основа-
ніе, то различныхъ системъ логариѳмовъ находится безчисленное мно-
жество.
Логариомъ, для сокращенія, пишется знакомъ Іо§ или I. Сряду подлѣ зтого
знака ставится то число, которое должно получиться отъ возвышенія основанія
въ степень, равную этому логарпому.
2Й?. Свойства логариѳмовъ. — 1) Во всякой системѣ логариѳмовъ,
логариѳмъ основанія равенъ единицѣ, а логариѳмъ единицы равенъ нулю.
Пбо, если въ уравненіи ах — у
положить х=1, то у —а',
х — 0, »/ = а°= 1;
а какъ 1о§ у~х, то 1о§ а = 1, 1од1= 0.
14
210 —
2) Если основаніе а >1, то логариѳмы для цѣлыхъ чиселъ у поло-
жительные, а логариѳмы дробей — отрицательные. Потому что всѣ цѣ-
лыя числа
у=~Л, а, а1, а3,...оо ,
получатся не иначе, какъ полагая
я=:0г 1, 2, 3,.....оо ;
а для полученія всѣхъ дробей надобно брать показатель х отрицательнымъ:
а = --=дробиу
3) Во всякой системѣ, гдѣ основаніе > /, логариѳмъ безконечно боль-
шаго числа также безконечно великъ, а логариѳмъ нуля равенъ отрица-
тельной безконечности. — Очевидно, что если въ уравненіи ах~у поло-
жить ж=оо , то выйдетъ число у—^ , а какъ я:=Іоду, то Іодоо —со .
Также, если въ а “=—=у, положить х~ оо, то будетъ у— — — 0;
а®
стало-быть,
1оду=—х обратится въ
1о§0=—со .
Аогаргіѳмъ произведенія нѣсколькихъ множителей равенъ суммѣ ло-
гариѳмовъ этихъ множителей, то есть:
ІодууУ^Іоду-ьІоду'-ьІод?/".
Для доказательства примемъ а за основаніе системы логариѳмовъ, и поло-
жимъ, что
ах=у, ах'—у', ах"=у", гдѣ
а—Іоду, я/т^Іоду', х,г=\о^уи;
перемножимъ ах на а®' и на ах", _іслучится:
ах+х'^х"~уу'у", гдѣ также
х-і-х,-г-х,,-=Ао^)ууІуп, или
Іодуу'у"—Іоду-ьіоду'ч-іоду".
5) Логариѳмъ частнаго числа, или дроби равенъ логариѳму дѣли-
маго безъ логариѳма дѣлителя, гг.іи логариѳму числител я безъ логариѳма
знаменателя.
Возмемъ а®=у, ах'=у', гдѣ .г=Іоду, а/=!осУ; и раздѣлимъ ах на ах',
будетъ
ра-_.т—,Ѵ_
V
Откуда, слѣдуетъ, что х—я/=іое —, или
в
/о9 у7=3,Ое.Ѵ—,Оё/-
- 211
6) Логариѳмъ степени какого ни есть числа равенъ логариѳму этого
числа, помноженному на показатель степени, то есть:
]о{гуп~п.]о(гу.
Это слѣдуетъ изъ того, что
•Іо^з/г/у"... .=Іоо-у-+-Іо{Уч-ІО!у,-і-.
Положимъ, что число всѣхъ множителей п, и что у^у’—у11—то и
выйдетъ
Іо§г/"=1о8г/-4-Іо*уЧ-1о!82/-ь... — п. Іо§у.
7) Логариѳмъ всякаго корня равенъ логариѳму подкореннаго числа,
раздѣленнаго на показатель корня, то есть:
1о§ |/у=А.Іоёу.
Для объясненія, положимъ, что ѵу=х, возвысимъ это въ степень п, п
возмемъ логарпомъ степени:
у~х", 1оду=«1о§гг; откуда
Іо§я: или 1о§ Ѵу~ — 1о§у.
«16. Эти свойства показываютъ, что если принять за основаніе кокое-пи-
будь одно число а, м вычислить какимъ нибудь образомъ логариѳмы х для вся-
кихъ чиселъ у, такъ чтобы по данному логариѳму, можно было тотчасъ нахо-
дить число ему соотвѣтственное, и, по данному числу, находить его логариѳмъ;
то можно будетъ всѣ трудныя вычисленія замѣнить простѣйшими:
а) Умноженіе сложеніемъ. Положимъ, что я желаю найти произведеніе
УУ'У'-- беру
]о^уу'у"—Іо^з/ч-Іо^'-т-Іо^";
отыскиваю въ таблицѣ Іо§з/, 1о<т^/, Іо^", и складываю; получится 1о$уу'уп.
Этому логариѳму нахожу соотвѣтственное число въ таблицѣ: оно и бу-
детъ —уу^у".
Ь) Дѣленіе замѣнится вычитаніемъ логариѳмовъ. Такъ, чтобы найти
V
частное -г, возмемъ
ѵ
'°о ^-=1о?у— 1о§з/';
въ таблицѣ найдемъ Іодтд/, 1о^', и возмемъ ихъ разность, получится Іоц у~; тогда
останется только пайги число, этому логариѳму соотвѣтственное, изъ таблицы;
оно и будетъ
с) Возвышеніе числа въ степень замѣнится умноженіемъ его логариѳма
на показатель степени; потому что
Іоуу’— пІо&У-
Взявъ произведеніе п.1о§і/, мы получимъ 1о§у*; а число ему соотвѣтствен-
ное, пріисканное зъ таблицѣ, и будетъ у".
212 —
<!) Извлеченіе корней приведется къ дѣленію логариѳма подкореннаго
числа на показатель корня.
,°8у-
Раздѣливши Іод у на показатель п, мы получимъ искомый логариѳмъ; а число,
ему соотвѣтственное, найденное въ таблицѣ, бу іетъ у у.
ЭЪЗ. Логариѳмы имѣютъ еще то замѣчательное свойство, что логариѳмы
одной системы легко могутъ быть превращаемы въ логариѳмы другой
(вычисляемые по другому основанію).
Положимъ, что данъ логариѳмъ числа IV, вычисленный по основанію а, пзъ
уравненія аг=]Ѵ; а мы хотимъ имѣть логариѳмъ этого же числа изъ уравненія
гдѣ Ь другое основаніе,' которое и должно быть возвышено въ иную сте-
пень х', чтобы могло обратиться въ тоже число ]Ѵ.
Означивши логариѳмы первой системы чрезъ 1о§, а логариѳмы второй чрезъ
1б§, будемъ имѣть: •
а?—1оп]\т, по основанію а.
по основанію Ь,
Возмемъ еще логариѳмъ уравненія принимая а за основаніе:
а/Іо§б=1о^К; отсюда
а:'—І6ц№= —5-г .ІоцК.
й 10^6 6
П такъ, показатель х' или Ід^К, въ который надобно возвысить другое осно-
ваніе Ь, чтобъ получить то же число И, найдется, если взять 1о§К и Іо§6 по
первому основанію, н раздѣлить первый па послѣдній.
1 1
Постоянную дробь { — называютъ модулемъ, и означаютъ буквою М=^^-
Слѣдственно, для перехода отъ одной системы логариѳмовъ къ
другой Ьх'~№, надобно логариѳмъ первой системы помножить на
модуль.
Посему, довольно имѣть одну таблицу логариѳмовъ чиселъ, по какой ші есть
опредѣленной системѣ; посредствомъ ея можно будетъ находить логариѳмы тѣхъ
же чиселъ по всякой другой.
СПОСОБЫ ВЫЧИСЛЕНІЯ ЛОГАРИѲМОВЪ.
А. Посредствомъ непрерывныхъ дробей
9Л». По данному основанію, можно находить логариѳмъ всякаго числа
точно, или приближенно, съ помощію непрерывныхъ дробей, какъ видно изъ
слѣдующаго примѣра.
— 213 —
Возмемъ за основаніе число 4 0, и поищемъ степень х, въ которую надобно
возвысить это число, чтобы оно превратилось въ 17. Для этого надобно разрѣ-
шить уравненіе
10*=17,
или найти Іо§4 7=х.
Будемъ число 40 возвышать послѣдовательно въ степени 1, 2, 3,..., и
смотрѣть, не обратится ли оно въ 17; тогда показатель и былъ бы найденъ. Но
это, вообще, случается очень рѣдко; а потому надобно возвышать основаніе въ
эти степени до тѣхъ поръ, пока полі чатся два числа: одно ближайшее меньшее
17-тп, а другое ближайшее къ нему большее.
Взявъ ж=1, х~2, найдемъ числа
1О'=1О, 108=100.
Данное число 17 заключается между 10 и 100; стало-быть, искомый показа-
тель х находится между 1 и 2, то есть, онъ долженъ быть равенъ единицѣ съ
1 1
нѣкоторою дробью. Назовемъ эту дробь чрезъ — , слѣдоват. з=1-+- —; тогда
уравненіе 10^=17 обратится въ
101-ь^ = 10.10^=17, откуда 10^=1,7; а отсюда
(1,7^=10.
Такъ мы получили новое уравненіе, того же вида, что и данное. Изъ него
точно также будемъ искать показатель у.
Полагая у~=1, 2, 3, 4, 5, найдетси что
(1,7/<10, (1,7)°> 10;
слѣдовательно, у>4, по <5, и можно положите
^4-ь\
(4,7у=(<,7)\(І,7)и=10, и .
1 ІО
(1,7)*=—.=1,1973;
откуда 1,1973^=4,7.
Въ этомъ новомъ уравненіи беремъ =1, 2, 3,...., и находимъ что
4,4973’<1,7; 1,19733>1,7;
1
откуда заключаемъ, что =2-ч- —, то есть:
1,4973’. 1,1973“ =1,7; откуда
1,1973*“ = ^=1,1863, и
(1,1863)“= 1,1973.
Здѣсь снова беру м = 0, 1,_2,...., и нахожу
- 214 -
4,1863 <1,1973,
1,1863®> 1,1973.
„ . 1
Слѣдовательно и = 1ч— , и такъ далѣе.
Такимъ образомъ мы получимъ рядъ чиселъ:
, 1 ,1 г> 1 , 1
ас=1ч-----, у— 'і-і-, х=2ч----, г<—1ч- , ..
у і и ѵ
ксгорыя, чрезъ подстановленіе, совокупляются въ одиу непрерывную дробь
1
4-і-------
1
2 ч-------
1
ѵ
. , 1
Для прлплижешя, откинемъ дробь —; найдется послѣдовательно:
ы=1,
і і
_г=2ч--т=2ч- =3,
и і
, 1 , 1 13
1=4-4- ^ -=4.-ь 3 = -3,
ГС—ІЧ 1 = 1 ч— 1 = 1,2307....
У 13
Такова приближенная величина показателя х\ въ эту степень надобно воз-
высить число 10, чтобъ получить число весьма близкое къ 17. Чѣмъ болѣе
возмемъ членовъ приближенія для непрерывной дроби, тѣмъ вѣрнѣе получит-
ся х. Въ нашемъ примѣрѣ х=: 1,2307.... имѣетъ всю точность въ тысячныхъ
доляхъ.
Впрочемъ этотъ непосредственный способъ вычисленія логариѳмовъ, повиди-
мому самый простои, до крайности утомителенъ, особливо когда въ уравненіяхъ,
вида аР^у, числа а и у велики.
В. Посредствомъ разложенія логариѳма въ рядъ.
ИЛ9. Возмемъ число Іч-ж, въ которомъ х есть членъ перемѣнный. Испы-
таемъ, нельзя лн логариѳмъ этого числа разложить въ убывающій рядъ, распо-
ложенный по степенямъ перемѣнной х, вида:
Іоѵ (І-ьжі— Ад-ч-В^ч-С^ч-В^ч-....
Въ этомъ ряду не должно быть члева, несодержащаго х, потому что для
а;—0, 1о^(1ч-0)=0. Его неизвѣстные коефиціепты А, В, С, Б,.... предпола-
гаются независимыми отъ перемѣнной х\ они остаются тѣми же, какъ бы х ни
измѣпялся. Слѣдовательно, если вмѣсто х взять г, получится также
1о§( 1ч-г)=А2ч-Вг’ч-Сг5ч-Вх4ч-....
Вычтемъ этотъ рядъ пзъ перваго:
1°2( 1ч-х)—Іо^Г Іч-г)—1о^ —~А(х—х)ч-В(гс’—лг)ч-С(л;’—х8)ч-....
— 215 —
Но, 1о§ посему этотъ послѣдній разложится въ рядъ
точно также, какъ и первые:
1оё(1-ь- ^)=А«ч-В(^-2)’ч-С(^-г)’ч-....»
04 Гч-і 1-4-г' 1-+-2 'І-і-г'
и мы будемъ имѣть равенство
а раздѣливъ обѣ части уравненія па х—5, останется:
А В(®—г) С(дг—г)® 4 т>/ .
і“^7 ' Ті^г,у. +- "(ІДІірг -+-• • • =Ач-В(ам-я)-4-С(я; -4-^ч-г )-ь....
Число х взято произвольно, то и положимъ &~х\ останется:
- - —Ач-23я;- ьЗСж’ч-іПя-’-ь....
1-4-л:
А какъ —— =А—Ах-і-Ах*—ЛаЛ-ь...., то
1-+-Л: ’
А—Ах-л-Ахв—Ахг... .=А-ь2Вжч-ЗСа?8н-4Вж5ч-...,
Для равенства этихъ многочленовъ необходимо нужно, чтобы коефиціенты
равныхъ степеней отъ х были равны между собою (104), то есть:
А=А, 2В=— А, ЗС=А, 411——А,....,
пли: А=4, В=—-А, С—-А, Г)~—
2 ’ з
Законъ составленія коефиціентовъ изъ А очевиденъ; посему
• 1о^(1-і-я;)=Ая:—4-Ая:8-1-4“ Аж8—....
2» о
. , а® хг х* х*
=А(х-^ +- т-7 + і-.
Въ этомъ раду осталось одно только предстоящее А неопредѣленнымъ: гакъ
и быть должно, потому что мы получили рядъ, пезависиііыіі отъ системы лога-
риомовъ, въ которомъ необходимо долженъ быть такой множитель, который бы
отличалъ одну систему логариомовъ отъ другой, посредствомъ котораго можно
было бы переходить отъ одной системы къ другой. Таковъ и есть здѣсь множи-
тель А; онъ не что ипое, какъ модуль.
950. Найденный рядъ
1о§( 1 ч-л)=А (х — 4" х*— 4"х -ь’ • •)
надоено еще сдѣлать сколь возможно болѣе убывающимъ, для удобнѣйшаго вы
численія логариомовъ по какой нибудь системѣ. Для этого возмемъ въ немъ—х
вмѣсто х:
1оё( 1— ж)=А(- х— 1 х1— 4- х*— х‘—....),
и этотъ рядъ вычтемъ изъ предыдущаго:
216
Іо8(1ч-аз)—1о§(1—а?)=2А(я<ч-у ч-^ ч- у+....), или
. ,1ч-.Ті , . , я-1 а?“ а?’
Іо§ !— =2А^-* *- 3 -' .>Г'Т~'- • •)
Послѣ сего положимъ І^=1ч- откуда найдемъ
пччіа,. —пч-2- -па"—хх, и
X
Х= ---.
2пч-х
Это подставимъ въ послѣднее выраженіе логариѳма;
Іоп(1ч---)=2А(-------ь——----------------,ч-....): отсюда
Іог (пч-г)=1оепч-2Аі—-------г- —-—- ч- —а
ь ' ° '2пч-г 3(2пч-г)’ о(2п-і-г)“ '
А какъ величины п и х произвольны, то одну нзъ нихъ можно взять равною
чему угодно. Мы положимъ =1, отчего рядъ сдѣлается весьма убывающимъ:
1оё(пч-1)=1о8пч-2А(-^-ч- 3-^-3 ч- 3-^А_ ч-
и совершенно удобнымъ для вычисленія логариомовъ чиселъ 2, 3, 4,...., слѣ-
дующихъ въ естественномъ порядкѣ, по какой угодно системѣ.
95 Я. Найденная формула показываетъ, что логариомы всѣхъ системъ отли-
чаются только модулемъ А. Для вычисленія логариомовъ мы возмемъ сперва
такую систему, въ которой А=1; для отличія означимъ ихъ чрезъ /'; тогда бу-
демъ имѣть •
/'(ІЧ-п) ГпЧ-2(2п^1 I 3(2^,р 1 в(2пч-1)‘
Полагая послѣдовательно:
п=1, найдется 1'2—д,6931.4718...
п=2, - /'3=1,0986.1228...
п—3, - /'4=1,3862.9436...
п=4, - /'5=1,6094.3791...
п=5, /-6=1,7917.5946... .
п=6, - /'7=«,9459.1014...
п—7, - . /'7=2,0794.4154...
п=8, - /'9=2,1972.2457...
п=9, - /'10=2,3025.8509...*).
*) Вычисленіе становится тѣмъ легче чѣмъ болѣе число п; напримѣръ для п^ЮО, полу
чили бы:
* зійір * 5₽і *-•)
Въ этомъ ряду довольно взять оону перчую дробь, чтобъ получить логариѳмъ, точный
въ 6 десятичныхъ.
— 217 —
Непосредственно изъ этой формулы довольно вычислить логариѳмы первыхъ
чиселъ: 2, 3, 5, 7,.11, 43, 17, 19, 23.-...; потому что прочія цѣлыя числа
иропсходятъ отъ перемноженія первыхъ чиселъ между собою, а логариѳмы ихъ
отъ сложенія логариѳмовъ множителей. Наприм.
ІЧь=1'2я =21'2,
1'6=Р2.3= 1'2+ГЗ,
1!8=1'23 =31'2,
I' 10=Г2.5—Г2-+-/'5, п такъ далѣе.
858. Система логариѳмовъ, вычисленная по формулѣ, въ которой Л—1,
называется натуральною, также Нвперовою, по имени шотландскаго барона
Непера, который считается изобрѣтателемъ логариѳмовъ (1614 года). Какое
основаніе оныхъ логариѳмовъ, это мы увидимъ скоро.
Помножая эти логариѳмы на такой илп другой модуль, мы легко перейдемъ
отъ неперовыхъ логариѳмовъ ко всякой другой системѣ ихъ, напримѣръ: по-
1
множая ихъ на модуль получится новая система логариѳмовъ отъ основа-
. 1 1
нія 3; помножая пейеровы логариѳмы на — или на —, получится система ло-
гариѳмовъ отъ основанія 5 либо 10.
858. Во всякой системѣ логариѳмовъ, разности между числами
(если только онѣ очень малы) пропорціональны разностямъ между лога-
риѳмами тіьхъ чиселъ.
Для вывода этого полезнаго свойства, возмемъ общую формулу;
І0ё(и-і-г)-1оё +....).
Отъ этого логариѳма перейдемъ къ другому, взявши у вмѣсто л; будемъ
имѣть также
(п+у)-1оё «=2А(- н- -і 3-^-5 ч-....).
Если числа у, г-, суть малыя дроби, то въ этихъ рядахъ можно отбросить всѣ
• г. 2 3/
степени гну, высшія первой, а въ членахъ -,п-4—, ^п-^у’ выпустить у, г, въ
знаменателяхъ, предполагая, что они весьма малы сравнительно съ 2п. Сдѣланъ
это, раздѣлимъ одну формулу на другую, то и получится отношеніе:
ІО" (п+-1)—Іорп а (пн-а)—п
Іо" (пни/)—Іоцп у (пни/) — п ’
то есть: разности между логариѳмами пропорціональны разностямъ между чи-
слами ихъ.
— 218 —
Обыкновенные или Бригговы логариѳмы.
Логариѳмы, принятые для всѣхъ вычисленій, имѣютъ основаніемъ
число 10. Они называются обыкновенными, также Бригговыліи, по имени
Генриха Бригга, лондонскаго профессора, который большую часть ихъ вычислилъ
(съ 1618 по 1624 годъ), и ввелъ въ употребленіе.
Ихъ можно вычислять непосредственно чрезъ разрѣшеніе уравненія Ю3=К,
но гораздо проще чрезъ помноженіе неперовыхъ логариѳмовъ на модуль
1 і
777о — о зпо-якпа — 0,43429.44819.... Такъ, напримѣръ, мы видѣли, что не-
перовъ /'2=0,69314718; то обыкновенный логариѳмъ числа 2 будетъ
1оё2=^=ё^=0’301029";
1о8 3=Йб = Й5^=°^771215’
И такъ далѣе.
• Преимущества этихъ логариѳмовъ легко открыть, разсматривая ихь
производство изъ уравненія
10^=К.
Если брать а?=0, 1, 2, 3, 4.....
найдутся: К=1, Ю, 100, 1000, 10000,....
А полагая ж=0, —1, —2, —3, —4,....
получимъ: №=1; 0,1; 0,01; 0,001; 0,0001;....
Посему, 1од1=0, Іод 10=1, Іод 100=2, Іод 1000=3,....
Іод 0,1 = —1. Іод 0,01 = —2, Іод 0,001= —3, Іод 0,0001=—4,
и такъ далѣе.
Отсюда заключаемъ: 1) что логариѳмы всѣхъ цѣлыхъ чиселъ, возрастаю-
щихъ отъ 1 до со , суть числа положительныя, также возрастающія отъ О
до оо ; а логариѳмы дробей — отрицательныя.
2) Всякое цѣлое однозначное число, взятое между 1 и 10, имѣетъ лога-
риѳмѣ дробный, заключающійся между 0 и 1. Всякое цѣлое число двузначное,
взятое между 10 и 100, имѣетъ лѳгариолъ между 1 и 2, который долженъ
быть =1-+-дробь. Всякое цѣлое трехзначное число, взятое, между 100 и 1000,
имѣетъ логариѳмъ между 2 и 3, который долженъ быть =2-ь дробь, и т д.
И вообще, если цѣлое число (исключая полныя степени основанія 10) содер-
житъ п цифръ, то логариѳмъ его состоитъ изъ п—1 единицъ, сопровождае-
мыхъ несоизмѣримою десятичною дробью. Паприм. число 3578, которое заклю-
чается между 1000 и 10000, или между ІО8 и 10‘, имѣетъ логариѳмъ
=3-ьдробь.
— 219 — ,
Цѣлая часть логариѳма называется характеристикою; потопу что она
вѣрно показываетъ, какой высшій разрядъ единицъ содержитъ въ себѣ число,
этому логариѳму соотвѣтственное, т. е. сколько цифръ содержитъ оно въ своей
цѣлой части. Наприм., если у даннаго логариѳма'характеристика 3, то ему со-
отвѣтствуетъ число, содержащее четыре цифры, т. е. одною болѣе противъ
числа цифръ характеристики. — Посему-то почти во всѣхъ таблицахъ
обыкновенныхъ логариѳмовъ совсѣмъ не ставятъ характеристики, и нѣтъ въ томъ
надобности, она и безъ того всегда очевидна. Десятичная дробь логариѳма, со-
провождающая характеристику, называется мантиссою.
3) Если извѣстенъ логариѳмъ какого ни есть числа,’ то логариѳмъ этого же
числа, увеличеннаго въ 40, 100, 1000,... разъ, получится, придавъ къ его
характеристикѣ 1, 3,... Положимъ, что извѣстенъ Іода; то
Іод 10а=1од 10-+-Іода =1ч-Іода,
Іод 10ва= 1о^ Ю’ч- Іода =2-ь Іода,
іод 1О’а= Іод 10“-ь Іода =3-ь Іода.
Примѣръ: Іод 345600000=Іод 3456.10'=
=1од ІО'ч- Іод 3456=5ч- Іод 3456.
И обратно: по извѣстному Іода, можемъ тотчасъ найти логариѳмъ числа въ
10, 100, 1000,... разъ меньшаго, надобно только изъ его характеристики вы-
честь 1, 2, 3,...; ибо
Іод==1ода— Іод 10=1ода—1,
1о§^=1ода—21од 10=1ода—2,
4 Іод ^= Іода—п!од10=1ода—п.
Примѣръ:
Іод 3578=3,5536403, то
Іод 35780=4,5536403,
Іод 357800=5,5536403,
Іод 357,8=2,5536403,
Іод 3,578=0,5536403,
Іод 0,3578=3,5536403—4=0,5536403—1,
Іод 0,0003578=3,5536403—7=0,5536403—4.
Отсюда видно, что въ этихъ случаяхъ одна характеристика измѣняется,
а десятичная часть логариѳма остается постоянною.
356. При вычисленіяхъ пе вычитаютъ всего положительнаго логариѳма изъ
отрицательнаго большаго числа, но только одну его характеристику; отъ этого
получится одна только характеристика отрицательная. Ее пишутъ на
— 220 —
своемъ мѣстѣ, а надъ пею ставятъ знакъ минусъ. Въ нашемъ послѣднемъ при-
мѣрѣ будетъ
3,5536403—7=4,5536403.
Употребленіемъ сего знака и показывается, что здѣсь одна характеристика
отрицательная, а мантисса положительная.
35>. Ариѳметическое дополненіе. — Мы знаемъ, что, вообще,
1о§-^= Іой «—Ь.
Если і>а, то и 1о§ б>1о§ а; слѣдовательно, 1о§ ^-будетъ отрицательнымъ.
Въ вычисленіяхъ избѣгаютъ логьриомогъ отрицательныхъ, на тотъ конецъ, что-
бы пе дѣлать вычитанія между десятичными долями логариѳмовъ, а только одно
сложеніе. Для этого употребляется такъ называемое ариѳметическое допол-
неніе, которое дѣлается такъ: къ вычитаемому логариѳму придается 40 и отни-
мается 10:
1о§у = 1о§ а-ь10—1о§ Ь—10;
берется на самомъ дѣлѣ разность 10—1о§і, она-то и называется дополненіемъ
Іо^б до 10 и пишется доп. 1о§6: такимъ образомъ получится
1о§=- = 1о§ ач-доп. 1о§ Ь—10,
и вычитаніе межйу логариѳмами обратится въ сложеніе.
Дополненіе же даннаго логариѳма до 10 получается, вычитая первую съ пра-
вой стороны зиачущую цифру изъ 10, а всѣ нрочія изъ 9. Если логариѳмъ
оканчивается нулями, то они пишутся и въ дополненіи. Это дѣйствіе такъ про-
сто, что дополненіе пишутъ обыкновенно прямо, смотря на данныя логариѳмъ.
Наприм.
для 3,4012306
дополненіе =6,5987694.
Повѣрка здѣсь самая легкая: она дѣлается чрезъ сложеніе логариѳма съ до-
полненіемъ отъ лѣвой рукн къ правой. При этомъ сумма единицъ каждаго раз-
ряда должна выйти 9, а послѣдняго разряда 10.
Расположеніе и употребленіе таблицъ обыкновенныхъ логариѳмовъ.
358. Въ употребленіи находится нѣсколько' логариѳмическихъ таблицъ.
Лучшими признаются таблицы Паллета и Вега, вычисленныя до семидесигич-
ныхъ, и малыя таблицы Лаланда, вычисленныя до пяти десятичныхъ. Всѣ онѣ
имѣютъ однообразное расположеніе^ а потому довольно разсмотрѣть однѣ кото-
рыя нибудь: мы возмемъ таблицы Каллета.
__ 221
859. Таблицы логариѳмовъ Каллета вычислены для чиселъ отъ 1 до
108000. Начиная отъ 1 до 1200 онѣ вычислены до 8 десятичныхъ, и располо
жены такъ, что во всякой вертикальной графѣ подъ литерою И (ношЬге число)
находятся числа, а въ слѣдующей графѣ подъ знакомъ Іод, противъ каждаго
числа находится его логариѳмъ безъ характеристики, потому что она и безъ
таблицъ всегда извѣстна. Разностей между логариѳмами не показано.
Далѣе принято расположеніе другое. Въ колоннѣ подъ литерою IV, слѣдуютъ,
какъ и прежде, всѣ числа отъ 1020 до 10800, а въ слѣдующей колоннѣ, подъ
цифрою 0, пхъ логариѳмы, какъ видно здѣсь въ табличкѣ.
И. 1 0 1 0 3 4 5 6 7 8 9 <1ІП'.
2583 412.1244 1412 1580 1748 1917 2085 2253 2421 2589 2757
84 2925 3093 3261 3429 3597 3765 3933 4101 4269 4437 168
2585 4605 4773 4941 5109 5277 5445 5613 5781 5949 6117 1 17
86 6285 6453 6621 6789 6957 7125 7293 7461 7629 7796 2 34
87 7964 8132 8300 8468 8636 8804 8971 9139 9307 9475 3 50
88 9643 9811 9978 4 67
413. 0146 0314 0482 0649 0817 0985 1153 5 84
89 1321 1*88 1656 1824 1991 2159 2327 2495 2662 2830 6 101
2590 2998 3165 3333 3501 3668 3836 4004 4171 4339 4507 7 118
В ді 4674 4842 5009 51 77 5345 5512 5680 л847 60 <5 6(82 8 134І
92 6350 6518 6685 6853 7020 7188 7355 7523 7690 7858 9 1511
| 93 8025 8193 8360 8528 8695 8863 9030 9197 9365 9531|
Поелику три первыя десятичныя для нѣсколькихъ послѣдовательныхъ чиселъ
остаются однѣ и тѣ же, то онѣ поставлены только противъ перваго изъ этихъ
чиселъ, а прочія четыре десяточныя поставлены противъ каждаго числа особо,
и должны быть присоединяемы къ тремъ первымъ Паприм
1о§ 2785=3,412.4605
1о§ 2589=3,413.1321.
Для чиселъ 10801, 10802, 10803,... до послѣдняго 108000, единицы ихъ
1, 2, 3, 4,.... 9, находятся въ первой верхней горизонтальной графѣ па каждой
страницѣ. Для каждаго такого числа первыя трн десятичныя логариѳма его на-
ходятся въ вертикальной колоннѣ поіъ цифрою 0, а послѣдніе четыре въ одной
же съ нимт горизонтальной строкѣ, только въ вертикальной колоннѣ подъ цифрою
его единицъ. Напримѣръ:
— 222 -
1о8 25853=4,412.5109
1о§ 25886=4,413.0649
1о§ 25929=4,413.7858.
Такъ находятся логариѳмы всѣхъ чиселъ отъ 10800 до 108000.
2«О. Эта же таблична служитъ и для нахожденія логариомовъ чиселъ, боль-
шихъ 108000. Пусть требуется найти логариѳмъ числа 2588274. Этого числа
нѣтъ въ таблицахъ Каллета. Чтобы найти его логариѳмъ, надобно отіѣлить за-
нятою пять цифръ съ лѣвой руки: отчего выіііетъ число 25882,73; потомъ
найти въ таблицѣ числа 25883, 25882, ближайшее большее и ближайшее мень-
шее къ 25882,73, выписать ихъ логариѳмы, и замѣтить табличную разность Г)
между сими логариѳмами:
1о§ 25883=4,413.0146
Іо§ 25882=4,412 9978
П=!68 десятимилліовныхъ.
Число 25882,73 заключается между 25803 и 25882, то и логариѳмъ его
находится между 4,413.0146 и 4,412.9978; онъ менѣе перваго, поболѣе
втораго. А чтобъ отыскать дробь, которую надобно придать къ меньшему лога-
риѳму, и получить 1о§.25882,73, надобно составить пропорцію по тону свой-
ству (3.53), что разности между числами (если онѣ малы) пропорціональ-
ны разностямъ между ихъ логариѳмами. Но разности:
25883—25882=1,
25882,73—25822=0,73,
1о§ 25883—Іоц 25882=Б=168; назовемъ неизвѣстную разность
1о§25882,73—1о§ 25882=^. Эта послѣдняя разность найдется
изъ пропорціи:
1 : 0,73=П : <1=168 : откуда
<1=168.0,73=122,64, пли, приближенію,
=123 десятимилліонныхъ.
Придавъ 123 къ логариѳму 4,412.9978ближайшаго меньшаго числа, получится:
Іо§ 25882,73=4.413.0101; и наконецъ,
1о§ 2588273=6,413.0101.
361. Таблицы Каллета и Вега облегчаютъ вычисленіе I) п іі. Въ нихъ, въ
послѣдней вертикальной колоннѣ, подъ знакомъ (ИЦ. показана табличная раз
ность П=Іб8 между послѣдовательными логариѳмами. Подъ нею находятся двѣ
малыя вертикальныя графы, изъ коихъ въ первой цифры 1, 2, 3,.... 9 озна-
чаютъ одну десятую, двѣ десятыхъ, три десятыхъ, и т. д. единицы, а во вто-
рой — разности имъ пропорціональныя, которыя надобно придавать къ ближаіі-
— 223 —
шѳму меньшему логариѳму, если данное число содержитъ шесть цифръ или бо-
лѣе. Такимъ образомъ, чтобы получить логариѳмъ числа 25882,73, я ищу ло-
гариѳмъ ближайшаго меіАшаго числа
1о§ 25882=4,412.9978;
потомъ, въ колоппѣ бі(Т. нахожу, что для 7 десятыхъ соотвѣтствуетъ приращеніе
логариѳма 118=168X^,7, для 3 сотыхъ —приращеніе 5,0=1.68X0,03. а
для 0,73 сотыхъ оно =118-1-5=123 десятпмилліонныхъ, которое и надобно
придать къ 4,412,9978; получатся:
1о§ 25882,73=4,413.0101,
и слѣдовательно, 1о§ 2588273=6,413.0101.
969. Логаритіы дробей.—Если дана обыкновенная дробь, напр. то
надобно взять логариѳмъ ея числителя, и вычесть изъ иего логариѳмъ знамена-
теля, или, лучше, придать къ нему дополненіе логариѳма знаменателя до 10:
К
=4 * 2 * * 5 * * 8 *—1о8167
=0,698.97000 -2,222.71647;
логариѳмъ получится отрицательный. Но тутъ всегда лучше дѣлать одну харак-
теристику отрицательною, бравъ дополненіе вычитаемаго логариѳма до 10, а
именно *):
1о§-|у =0,698.97000-ьЮ—2,222.71647—10, или
=0,698.97000-4-7,777.28353—10
=8,476,25353—10=2.476 25353.
Примѣчаніе. Если бы этотъ логариѳмъ понадобилось раздѣлить еще па 7,
то есть, получить
') Можно, если угодно, употребить и вычитаніе логариѳма знаменателя изъ логариѳма
числителя; только надобно напередъ придать къ характеристикѣ логариѳма числителя
столько единицъ, чтобы онъ сдѣлался болѣе логариѳма знаменателя, но за то столько
же единицъ поставить съ знакомъ минусъ, и потомъ вычитать. Напримѣръ: найти
2 8
108 Т’ ,0*92Й:
Іов 2=0,301.0300=1,301.0300—1
Іое 3=0,477.1212=0,477.1212
. 2
Іов у =0,823.9088—1
ІОВ 8=0,903 0900=4,903 0900—4
. Іов 9243=3,968.8130=3,963.8130 „
8
=0,937.2770 -4
Но, при вычисленіяхъ по логариѳмамь, сложеніе предпочитается вычитанію, какъ по ,
большей простотѣ, такъ и для единообразія.
— 224 —
-1 . о 8,476.23353—10
- І0Ц — =------------— ,
7 ° 167 7
то непремѣнно надобно измѣнить характеристику 8 и вычитаемое 10, такъ
чтобы это послѣднее раздѣлилось на 7 безъ остатка.
Въ пашемъ примѣрѣ довольно дли этого отнять по 3 отъ 8 и 10, и выйдетъ:
1 , 5 0,476.25333-7
Т1оёш=----------1----
=0,782.32197—1.
Положимъ теперь, что надобно найти логариѳмъ десятичной дроби, на-
примѣръ: 0,00437582.
Эта дробь 0,00437582 = __437д82 ,•
* ’ іоооооооо’
а Іод7^82п =1од 437582—8.
6 ІОООООООО
Слѣдовательно, надобно у десятичной дроби отнятъ запятую, найти
логариѳмъ цѣлаго числа, какое получится, « изъ него вычесть столько
единицъ, сколько было всѣхъ десятгічныхъ знаковъ.
Чтобъ отыскать Іод 437582, беру только Іод 43748,2; нахожу въ табли-
цахъ ближайшій меньшій логариѳмъ
Іод 43758 =4,641.0575
придаю 0,2.................20=й, и получаю
Іод 4-3758,2=4,641.0595; посему
Іод 437582=5,641.0595, и наконецъ
Іод 0,00437582=5,641.0595—8
=3,641.0595.
Э63. Вопросъ обратный. — Найти число, соотвѣтственное данному ло-
гариѳму.
1) Когда характеристика положительная. — Не обращая вниманія на
характеристику, надобно искать данный логарисмъ между логариѳмами чиселъ о
пяти цифрахъ: его три нервна цифры искать въ вертикальной колоннѣ подъ циф-
рою 0, а четыре послѣднія въ ближайшихъ строкахъ между числами, стоящичи въ
колоннахъ подъ цифрами 0, 1, 2, 3,.... 9. Быть можетъ, что сыщется весь
логариѳмъ въ таблицѣ; тогда тотчасъ найдется и число ему соотвѣтственное: его
десятки, сотни, тысячи, и проч. будутъ находиться въ колоннѣ подъ литерою М
въ той горизонтальной строкѣ, въ которой стоятъ его четыре послѣднія цифры,
а единицы —- надъ вертикальною колонною; въ которой находятся эти послѣднія
цифры. Тогда останется только отдѣлить въ немъ столько цифръ для цѣлаго,
сколько того требуетъ характеристика даннаго логариѳма.
Положимъ, что данъ логариѳмъ
1,735.2794;
— 22г —
этотъ логариѳмъ я нахожу весь въ таблицахъ, и пмепио-
4,735.2794=108 54360;
посему, 1,735.2794=1о§ 54,360.
II такъ, искомое число =54,36.
Рѣдко однако же случается, чтобы данный логариѳмъ находился весь въ таб-
лицахъ: тогда надобно искать, между какими смежными логариѳмами онъ заклю-
чается; его число будетъ заключаться между числами этихъ логариѳмовъ, и
найдется, если къ ближайшему меньшему числу придать разность между
даннымъ и ближайшимъ меньшимъ логариѳмами, раздѣленную на таб-
личную разность логариѳмовъ ближайшаго большаго и близка йша: о
меньшаю, какъ видно изъ слѣдующаго примѣра:
Данъ 1о<г №=3,412.3687, найти число №.
Не обращая вниманія на характеристику, я ищу десятичную часть логариѳма
между логариѳмами, соотвѣтственными числамъ о пяти цифрахъ, и нахожу
что мантисса даннаго логариѳма заключается между
412.3765, при нихъ числа 25845
412.3597 '25844
Б = 168 1
Беру разность </=90 между логариѳмомъ даннымъ и ближайшимъ меньшимъ,
н составляю пропорцію:
168 : 90=1 : б; откуда
«=ж=°>51-
Придаю эту дробь къ числу 25844 ближайшему меньшему, и нахожу
25844,54. А какъ данный логариѳмъ имѣетъ характеристику 3, то искомое
число будетъ
№=2584,454.
Табличная разность и пропорціональныя числа, помѣщенныя въ таблицахъ
Каллета подъ знакомъ сіііГ. , облегчаютъ вычисленіе прибавочной дроби къ блп
жавшему меньшему числу, слѣдующимъ образомъ, нашедши разность «2=90
между логариѳмомъ даннымъ и ближайшимъ меньшимъ, я ищу ее во второй ма-
лой графѣ въ колоннѣ <1І1Г., и тамъ нахожу ближайшее меньшее число 84, соот-
вѣтственное 5 десятымъ; а разность 90—84=6 близка къ 6,7, чему соотвѣт-
ствуетъ 4 сотыхъ. Придавъ 0,5-+-0,04=0,54 къ ближайшему меньшему цъло-
му числу 25844, найдется 25844,54. А какъ характеристика даннаго лога-
риѳма =3, то искомое число
№=2584,454.
2) Если у даннаго логариѳма характеристика отрицательная, то соот-
вѣтственное число будетъ нѣкоторою правильною дробью. Чтобы найти згу
15
— 226 —
дробь, надобно отбросить характеристику, поставивъ нуль иа ея мѣсто, и этом^
логариѳму отыскать соотвѣтственное число; потомъ въ этомъ числѣ перенесть
запятую влѣво на столько знаковъ, сколько находилось единицъ въ от-
рицательной характеристикѣ; то и получится число, соотвѣтственное дан-
ному логариѳму.
Примѣръ. Данъ логариѳмъ 3,413.6305=1о§ К; найти его число К.
Откинувъ его характеристику 3, или лучше, написавъ 3,413.6305=
=0,4-13.6305—3, ищу число, соотвѣтственное 0,413.6305.
Этого логариѳма нѣтъ въ таблицахъ; посему беру логариѳмъ ближайшій меньшій
0,413.6182, при немъ число 25919
и разпость й=123 между этимъ логариѳмомъ и даннымъ. Ищу эту разность
въ колоннѣ подъ знакомъ йіГГ. во второй малой графѣ; нахожу число 118 бли-
жайшее меньшее, соотвѣтственное приращенію 7 десятымъ; остатокъ 123—•
118=5,0 соотвѣтствуетъ приращенію 3 сотымъ. Наконецъ, придаю сумму
сихъ приращеній 0,7-+-0,03=0,73 къ ближайшему меньшему числу 25919,
что составитъ 25919,73. Слѣдовательно,
0,413.6305=1о§ 2,591973,
а' 3,413.6305=1оё 2,591973—1о§ 1000
=1о8Аы^-=1оё- 0,002591973.
Итакъ, искомая дробь №=0,002591973.
2«і. Въ заключеніе, разрѣшимъ вопросъ, какъ найти основаніе Пеперо-
<выхъ логариѳмовъ.
П /сть это основаніе =е; основаніе обыкновенныхъ логариѳмовъ =10. Со-
ставимъ уравненіе
е*=1$;
возмемъ его логариѳмъ по таблицамъ Непера,
10=2,302.5851,
и логариѳмъ х 1оое=1о§ 10=1, но таблицамъ Бригга.
Отсюда найдется:
,оёе= 7 = 2,зо2383і =0,4-342945....
Остается теперь найти число е, соотвѣтственное найденному логариѳму. По
таблицамъ находимъ ближайшій меньшій логариѳмъ 0,4342814, которому соот-
вѣтствуетъ число 27182. Разность между этимт логариѳмомъ и даннымъ
=131=128-+-3. Въ колоннѣ ЛІГ. находимъ, что для 128 соотвѣтствуетъ при-
бавокъ 0,8 къ числу 27182, а для 3 прибавокъ 0,018. Посему, искомое чи-
сло е, то есть, основаніе Неперовыхъ логариѳмовъ
=2,7182818.....
вѣрное въ 7 десятичныхъ.
227 —
Примѣненіе логариѳмовъ къ ариѳметическимъ исчисленіямъ.
365. За исключеніемъ сложенія и вычитанія, логариѳмы употребляются съ
величайшею пользою для скораго исполненія всякихъ другихъ ариѳметическихъ
дѣйствій, какъ бы онѣ сложны пи были; потому что, съ помощію логариѳмовъ,
умноженіе приводится къ сложенію логариѳмовъ, дѣленіе къ вычитанію, возвы-
шеніе въ степени къ простому умноженію, а извлеченіе корней къ дѣленію (216).
А. Умноженіе и дѣленіе. — Положимъ, что падобно найти произведеніе
___________________________ 389 2456
х 1748” 3725 ’
Возмемъ логариѳмъ этого произведенія:
1о§#=Іо§ 389-ьІод 24-56ч-доп. Іод 1748-ьдоп. Іод 3725—20.
1од389=2,589.9496
Іо§24-56=3,390.2284
доп. 1о§174-8=6,757.4-586
доп. Іо§3725=6,4-28.8737
19,166.5103
Посему Іод #=19,166.5103—20
= 0,166.5103—1
Отыщемъ число этому логариѳму. Въ таблицахъ найдется ближайшій мень-
шій логариѳмъ 0,166.4-893=102 1,4-672; разность табличная И=296, а раз-
ность между этимъ логариѳмомъ и даннымъ =210. Слѣдовательно, прпоавокъ къ
числу 1,4-672 будетъ
<У= — = 0,7.
296
Это же мы нашли бы въ колоннѣ Лі[[. во второй малой графѣ, подъ таблич-
ною разностью 296, гдѣ находится число 207, весьма близкое къ 210, и кото-
рому соотвѣтствуетъ прибавочное число 7 десятыхъ.
И такъ, 1одж=1од 1,46727—Іод 10
=1од 0,14-6727,
и требуемое произведеніе #=0,146727, вѣрное только въ этихъ десятичныхъ.
Примѣры:
“Х’ =0,003630562;
^^=0,™;
42,6. 1,531._ 426 153.1
• 0,629.0.0359 6,29. 3,59 ,-ОО-
В. Возвышеніе въ степени.—Оно производится по формулѣ
Іод а”=п1ода.
Примѣръ. Пайти приближенно пятую стегень числа 3,567, Положимъ
— 228 —
я=(3,567)“, и возмемъ
1о§я=5Іо§3,567.
1о§3,567=0,552.3031
5 ІоеЗ,567=2,761.5155=іо8 х
•Въ таблицѣ находимъ 2,761.5144=1о§577,45
<1=11
Таблич. разность Б=76; прибавокъ къ ближайшему меньшему числу
11
— -^-=0,14. Слѣдовательно, искомое число
ж=3,5678=577,4514....
Примѣръ. Найти я=0,05754 °'7.
1о8’л= ^(3,759.9699—5)
= ^(8,759.9699—10)
= 7(0,875.99699—1)
= 6,131.9789—7
= 0,131.9789—1.
Этому найдется число ж=0,0135123.
С. Извлеченіе корней. — Оно дѣлается по формулѣ
1о^ Ѵа~ —.Іоц а.
Б______—
Примѣръ. Найти х=\/375,743.
1о§ ж= у-1о§ 375,743.
Въ таблицахъ Каллета нахожу
1о§ 375,74=2,574.8874.
Табличная разность Н=116, разность чиселъ (1=0,3, которой соотвѣт-
ствуетъ пропорціональный прибавокъ 116.0,3=35; посему,
2,574.8874
35
2,574.8909= 1о§ 375,743.
1о§ х= 1.1о§ 375,743= у . 2,574,8909 -
=0,514,9982;
и найдется ж=3,27339...
Примѣръ. Вычислить хв=і5^/ (^=) •
1о§ ж= 15ч- у (1о§ Зч-дон 1о§ 3575—10).
229
Сначала вычислимъ послѣдній членъ:
Іое 3=0,477.1213» ЛА
& !—10
доп. Іѳ§ 3575=6,446.72401
6,923.8453 —Ю
ХЗ
20,771.5359 — 30, или
0,771,5359 — 10
у (0,771.5359—10)=0,154.3072 — 2;
сюда придадимъ 1о§ 15=1,17 6.0913
1о§ж=0,330.3985 — 1
въ таблицахъ нахожу 0,330.3935 = 1о§ 2,1399
*= 50|ц
0=203 в —
посему, ж=0,2139925.
Примѣры:'
5
Б
1) 1,8у/1 = = =ола9 5636_)
найдется
у = 0,850283.
803 __0,9454076—3 _32,9454076- 35
91056 35 35
=0,941.2973-1
Этому соотвѣтствуетъ число 0,873569.
„ . /Щ74
3) \/-т== 0,8132616; .
У 1/9
У у/4, ^,73625=1,242761;
і/ 5/
V 162 1/8135,724
5)-------—-----=6,461020.
Мантисса у всякаго логариома, вообще, есть нѣкоторая несоизмѣримая
дробь, имѣющая безчисленное множество десятичныхъ. Въ логариѳмическихъ же
таблицахъ это число десятичныхъ ограничено. Такъ, въ таблицахъ Каллета есть
обыкновенные и Неперовы логариомы чиселъ отъ 1 до 1097, имѣющіе 61 деся-
тичныхъ, и логариомы чиселъ отъ 1 до 1200 о двадцати десятичныхъ; но самые
обширные и наиболѣе употребительные логариѳмы обыкновенные чиселъ отъ 1
— 230 —
до-108000 съ семью десятичными. Осьмая же десятичная со всѣми прочими, за
малостію, отброшена; только если она была 5 или болѣе, то седьмая десятичная
увеличена единицею своего разряда. Слѣдовательно, была лй просто отброшена
8-я десятичная, если опа <5, или при этомъ увеличена 7-я единицею, въ обоихъ
случаяхъ сдѣлана погрѣшность, котород высшій предѣлъ—±0,00000005. Эта
погрѣшность имѣетъ вліяніе только па седьмую цифру числа, соотвѣтственнаго
логариому, и не болѣе. Но она можетъ сдѣлаться гораздо большею: Ч) отъ сло-
женія нѣсколькихъ логариѳмовъ. Напримѣръ, если сложить 10 логариѳмовъ,
то погрѣшность перейдетъ на шестую десятичную, и, въ самомъ невыгодномъ
случаѣ, можетъ сдѣлаться равною 0,00000!; а погрѣшность въ числѣ начнется
съ шестой или седьмой цифры. 2) Отъ помноженія логариѳма на большія
числа. Такимъ образомъ, отъ помноженія па 100, погрѣшность въ логариѳмѣ
будетъ ощутительна въ нятой десятичной, а въ числѣ она начнется съ пятой или
шестой цифры.
Болѣе точные логариѳмы можно брать изъ таблицы съ 20-ю десятичными; но
все же нельзя изъ таблицъ получить числа вѣрнаго даже только съ 8-ю цифрами.
Для примѣра, возвысимъ число 2 въ 64—ю степень съ помощію логариѳмовъ:
Іо§2м=6!. 1оё2—64.ХО, 3010300
19,265.9200.
Этому логариому соотвѣтствуетъ число
264=184-46.75000.00000.00000,
въ которомъ погрѣшность начинается съ седьмой цифры.
Взявши логариѳмъ съ девятью десятичными:
1ой 2=0,301029995,
64-1о§ 2=19,2059197,
мы получимъ число 18446,74-000.00000.00000, въ которомъ вѣрны всѣ семь
цифръ; мѣста же недостающихъ цифръ заняты пулями.
Ябв. Есть однакоже довольно удобный споеобь вычислять логариѳмъ како-
го пи есть числа, а до многихъ десятичныхъ. Для этого въ Каллетовыхъ табли-
цахъ находятся таблицы I, II и 111 логариѳмовъ съ 20-ю десятичными для чи-
селъ, тамъ показанныхъ; надобно только умѣть логариѳмъ всякаго даннаго числа
выразить посредствомъ какого нибудь изъ этпхъ логариѳмовъ, и придать надле-
жащую поправку.
Возмемъ число а, котораго пѣтъ въ таблицахъ 1, II и III, и которое пе начи-
нается первыми пятью цифрами, составляющими числа второй таблицы, отдѣ-
лимъ пять цифръ у этого числа отъ лѣвой руки къ правой; это отдѣленное число
раздѣлимъ на 1,01, до трехъ десятичныхъ въ частномъ числѣ, и па это частное
у раздѣлимъ данное число а. Пусть
— =га, 1о«5 а— Іоіт д ъ- Іѳ§ п.
231
Такимъ образомъ искомый югариѳмъ отъ а выразится посредствомъ Іо^у,
находящагося въ таблицѣ I, и Іо§л, который надобно вычислить. Для этого, изъ
таблицы II возмемъ число пч-я ближайшее большее къ и; возмемъ ихъ сумму
и разность:
, ?іч-хч-п=2пч-г, пч-х—п=х,
и въ ряду (2.50)
М™)=Ьёп+2М[^г -+- 3(2^,+--К
или, 1о<т(ц-+-я)=]о§пч-2М8, полагая
г х3 [ __
2п-ьх 3(2п-ч г)3 ’
вычислимъ 8, ограничиваясь однимъ, пли только двумя членами- тогда най-
дется:
1о§е= 1о§(и-нг)—2Й18, и слѣдовательно
1о§а=1о§у-+-1о§( пч-х)—2М8.
Для облегченія помноженій модуля М на 28, у Каллета находится табличка
(почти предъ самымъ началомъ таблицъ логариомовъ синусовъ, косинусовъ
и проч.) подъ заглавіемъ: ТаЫе рпиг сопѵегііг Іех Іодагііктех ЪурегЬоІідие»
еп Іодагііктех ѵиідаігех, въ которой помѣщены всѣ произведенія модуля
М=0,43429.44819.03251.82765
па цѣлыя однозначныя и двузначныя числа.
Примѣръ. Найти логариомъ числа
0=3,14159.26535.89793 23846....,
точный въ 15-ти десятичныхъ.
Беру 3,1415 и дѣлю па 1,01; получаю частное у=3,11. На это час піое
дѣлю данное число:
— - =1,01015.84095.14402.97057=»;
. 3,11
въ таблицѣ II нахожу ближайшее большее число 1,01016=п-+-я. Слѣдовательно,
2п-т-«=2,02031.84005.14402.97057,
2=0,00000.15904.85597.02943,
--- =0,00000.07872.45015.21110,3 „
2» •' =8
- **— =0,00000.00000.00000.00016,3
З(2пч-х)3 ’
8=0,00000.07872.45015.21126,6
28=0,00000,15744.90030.42253.
Этимъ числомъ помножаю модуль М, ограничиваясь 15-ю десятичными, и
нахожу
2М8=0,00000.06837.92331.6....
- 232 —
Изъ формулы Іод (пч-г)=Іод Н-+-2М8 получаю
Іод п=1од (пч-2)—2М8;
а изъ л - ~п, имѣю Іод а=1од 3,11^-Ьд и:
Іод 3,11=0,49276.03890.26837, (изъ таб. 1),
Іод (пч-2)=0,00439.01674.59628, (изъ таб II)
0,49715.05564.86465
2М8=0,00000.06837.92332 *
0,49714.98726.94133
Таковъ логариѳмъ лапнаго числа, точный въ 15-тп десятичныхъ.
Розысканіе логариѳма будетъ короче, если его первыя пять или шесть цифръ
составляютъ число, находимое въ таб. И, ибо тогда у=1, 1оду=О, Іода=1одн.
Слѣдовательно, надобно только будетъ паіітп къ числу а=п, въ таб. II, число
п-ъ-2 ближайшее большее, вычислить 8, потомъ 2Й18, и проч.
2<г®. Есть также способъ находить и весьма многозначное число х, соот-
вѣтственное данному логариѳму. Вотъ въ чемъ онъ заключается:
Если первыя пять десятичныхъ даннаго Іода; не находятся между 00432 іі
00509, чѣмъ начинаются мантиссы всѣхъ логариѳмовъ таблицы II, то надобно
изъ этого логариѳма вычесть первыя пять цифръ 0,00432 логариѳма числа
1,01; къ остатку Іодж—0,00432 пріискать ближайшій меньшій 1од(ж—я) въ
таб. II или I, н вычесть его изъ даппаго Іода;.
Пусть Іода;—Іод(а;—2)=В..
Къ этому остатку пріискать въ таб. II логариѳмъ Іод(ж—2—д/) ближайшій
меньшій, вычесть пзъ него, и положить
Іодж—1од(ж—2)—Іод(ж—2 —У)=1одп,
что составитъ: Іодж=Іод(ж—з)(ж—г—2')и,
слѣдовательно, ж=(ж—г)(ж—2—г')п.
Послѣ этого, надобно только найти п, что уже не трудно сдѣлать по формулѣ
____________. Іоя»* 1 (ІодпѴ 1 |1о{;п\3
п— М ТУ 1.2.3
которую мы выведемъ впослѣдствіи; а теперь возмемъ ее безъ вывода только для
того, чтобы послѣ пе возвращаться къ предмету, позчапіе котораго теперь же
особенно полезно и кстати.
Примѣръ. Пусть данъ
1одж=0,49714.98726.9ИЗЗ...
—0,00432
0,49282.98726.94 іЗЗ...
Пзъ таб. II нахожу ближайшій меньшій логариѳмъ:
Іод 3,11=0,49276.03890.26837.5055;
- 233 —
беру разность
Іо^—іоа 3,11=0,00438.04836.67926...
Отсюда вычитаю ближайшій меньшій логариѳмъ, взятый изъ таб. И, именно
1о§ 1,01015=0,00438.58681.74054,309,
и получаю остатокъ
Іоё«—|оё. 3,11—Іоё 1,01015=0,00000.36154.93243,039...=1ойп.
Отсюда: 1=1о§(3,11Х'1»01015Х«). и
ж=3,11ХЪ01015Хп.
Раздѣливши Іо^н на модуль М=0,43429.... (что дѣлать легко ири помощи
другой таблички у Каллета, подъ заглавіемъ: ТаЫероиг сопѵегііг Іез Іодагіік-
пісз ѵиідаігев еп Іод. 1'урегЬоІідиез), получимъ.
1ч-^-=1,00000.83249.80842.94014.4
^(^У=0,00000.00000.34652.65301,5
А^"|3=о,00000.00000.00000.09616.1
и=1,00000.83250.15495.68932?
Взявъ произведеніе «=3,11Х1.О1О15ХП, найдется искомое число
«=3,14159.26535.89793.23846. ...
точное въ 20-ти десятичныхъ.
969. Гораздо проще можно найти число/соотвѣтственное такому логариому,
котораго первыя пять цифръ, находятся въ таб. И между 00432 и О0509. Изъ
логариѳма такого числа х надобно вычесть логариѳмъ числа ближайшаго мень-
шаго х—2, и остатокъ означить чрезъ Іорп:
1оц«—іо§(«—з)=1о§п; откуда
Іо§«=Іод(«—х)н, и «=(ж—л)п.
Пусть, Іо§«=5,00446.59127.70547.507...
Іое(®—я)=1о§ 101033=5,00446.32488.03359.618
Іо§«—Іоіт(«-і-2)=0,00000.26639.67187.88 9=Іо§*і
«=ЮЮЗЗ.п
1-ь 2^ =1,00000.61740.11133
4Й"У=0,00000.00000.18813
ч \ м /
1,00000.61740.29946. ~?зг;
посему, «=101033X1.000006174029946
=101033,619739447....,
число, точное во всѣхъ 15-ти цифрахъ.
— 234 —
58ЭУ. Примѣненіе логариѳмовъ къ вычисленію алгебрическихъ формулъ.
1. Когда формула данная разлагается в? простѣйшіе одночленные или много-
членные множители. Примѣръ:
Р (а2—6«)3а
®— »—--—— '
Замѣчая, что а’-4-6*=(а-+-6)(а—Ь), легко найдется
1о§ж=Іо§ Ѵ^а*—65) За—1о§ V (р-*~д)Ь*=
__І08(а-+-6)-і-1о(?(о—Ь)-+-1о8 З-ьІо^а ІовГр-ь?)—21ов&
2 ~3~’
2. Когда формула не разлагается на простѣйшіе одпочлевные и многочленные
множители и дѣлители, какъ наприм.
а3Ьч-с’
Зр2Ь—4{2е ’
тогда въ числителѣ и знаменателѣ надобно вынесть внѣ скобокъ такіе одночлен-
ные множители, чтобы сдѣлать внутри снобовъ одаобувоенными хотя во одному
члену. Такъ, можно взять
с* 4и2с
вотомъ для краткости положить — = т,
п;
составится
а3 . , бч-п-
^Хзб^Г’и
1о§х=3 Іо^а-ь1од(б-+-пг)—2 Іо^р—Іо§(36—п).
Что касается до т и п, то ихъ надобно напередъ вычислить каждое особо
изъ условныхъ уравненій, то есть--
1о§пі~41о§с—3 1о<та,
Іо§п=1о§4 -+-2 Іо^-г-Іо^с—2 1о§р.
Отсюда найдутся числа т, п; а послѣ того уже легко найти 1о§ж, и самое х.
Впрочемъ, всѣ формулы, состоящія изъ алгебрической суммы членовъ, не-
разложимыя на простѣйшіе множители п дѣлители, вообще, считаются неудоб-
ными для вычисленія по логариѳмамъ, потому что вычисленіе становится
продолжительнымъ. Оттого, гдѣ можно, стараются замѣнить ихъ другими, болѣе
къ тому способными.
Л9Л. Примѣненіе къ рѣшенію неопредѣленно-степенныхъ уравненіи.
Неопредѣленно-степенныя уравненія бываютъ различныхъ порядковъ и сте-
пеней. Такъ:
ах~р уравненіе первой степени и перваго порядка,
цЬа-—_ - - втораго порядка.
ах*=г.... I
Д уравненія второй степени .
— 235 —
Уравненія этихъ порядковъ и степеней очень легко рѣшаются при помощи
логариѳмовъ.
Для рѣшенія а^^р, возмемъ х Іо§а=Іо§р;
Іовр
отсюда х= -— .
Іова
Для рѣшенія а®’—г, возмемъ также х* Іо§а=Іо§г; откуда
3) Для аяР+Ьх-і-с _ находимъ
, , і°в*
х -ьоа:-ьс=------; откуда
1«в« ________________
х= - 4 Ь ± і/ТбГЦ72 _с.
* у 4 іо^а
Ьх
4) Наконецъ, изъ а° =^[, получимъ Іо§а=Іо§у;
возмемъ вторично логариомъ:
а;1оцб-ь1оіг.'о§а=Іост Іовд; а отсюда
__Іов Іову—1°" І°В°
Іовб
Примѣры для упражненія-.
а^пЬр^д=11; отсюда ^^ІовЛ-пІова-^
•’* иііо^ач-ріоо-б.
х /—
— ; отсюда ж=1±2
а'
0,96г=0,6382393; ж=11.
ІоцЬ—Іо^а
Іова
25,5Т= 1/25549.25614; ^=3,133902
1/1.024=4752,31 ; ж=558,5236.
Зіа:~* .0,172л"=3. О^б*-1; ж=90,48.
949. -Даны уравненія:
х,у г . хіУ г , х,у г .
а Ь-'с =П, аЬ^ — Л„
найти х, у, г.
Для эгого возмемъ логариѳмы уравненій :
#!о§а ч-уіо^б -+-хІоцс =1о§/і,
л:1о2а1н-і/Іо^61-+-:г1оігс1=1о$/і1,
жіоца^т/іооб^хіо^с^іод/ц.
Отсюда уже нетрудно найти х, у, х, по извѣстнымъ намъ способамъ (9і)
рѣшенія трехъ уравненій съ тремя неизвѣстными.
236
ГЛАВА ДЕВЯТАЯ.
. • О ПРОГРЕССІЯХЪ.
А. Прогрессія ариѳметическая.
И'іЗ. Ариѳметическою или равноразностною прогрессіею называется
такой рядъ чиселъ, или членовъ вообще, въ которомъ всякія два смежныя члена
имѣютъ одну и ту же разность.
Опа бываетъ возрастающею или убывающею, смотря потому, возрастаютъ
или убываютъ ея послѣдовательные члены. Въ прогрессіи возрастающей раз-
ность эта положительная, потому что въ пей каждый послѣдующій членъ со-
ставляется изъ члена предшествующаго, сложеннаго съ разностью; а въ прогрес-
са убывающей разность отрицательная, потому что каждый ея членъ послѣ-
дующій равенъ предшествующему безъ этой разности. Такимъ образомъ, рядъ
1, 3, 5, 7, 9, 11, 13, 15,....
представляетъ прогрессію возрастающую, въ которой разность между послѣдо-
вательными членами равна 2. А рядъ
25, 22, 19, 16, 13, 10, 7,4, 1,
представляетъ прогрессію убывающую, иъ которой разность между послѣдова-
тельными членами =: —3.
Когда хотятъ показать, что рядъ чиселъ составляетъ прогрессію
ариометическую, то пишутъ эти числа въ одну строку, отдѣляютъ ихъ точками,
и предъ рядомъ ставятъ знакъ -7. Напрмм
ѵ 1. 3: 5. 7. 9. 11. 13....,
7-25. 22. 19. 16. 13. 10. 7. 4. 1,
или, вообще,
4- а. Ь. с. й. е...к. I.
если члены а, Ь, с, й, с,..к, I, составляютъ прогрессію ариѳметическую.
Такая прогресія выговаривается: а безъ Ь равно Ь безъ с, распо с безъ й,
разно й безъ е, и проч., такъ что въ пей всякіе три члепа, сряду взятые,
составляютъ ариометическую пропорцію *).
*) О пропорціяхъ ариѳметической и геометрической достаточно излагается въ началь-
ной Ариѳметикѣ; оттого онѣ и пропущены въ Алгебрѣ.
•237
9Я& При общемъ разсмотрѣніи этой прогрессіи, мы всегда будемъ изобра-
жать ея члены буквами, какъ показано, будемъ означать всегда:
чрезъ а первый членъ прогрессіи,
I послѣдній ея членъ,
п число всѣхъ ея членовъ,
г разность между послѣдовательными членами,
8 сумма всѣхъ членовъ прогрессіи.
По этому, въ возрастающей прогрессіи
4- а. Ь. с. <1. к. I, будемъ имѣть:
Ь=ач-г=а-ь-г,
с=Ь-+-г=Ог+-2г,
Л=с-+-г=:а-± Зг,
гдѣ видно, что каждый членъ равенъ первому, сложенному съ разностью, по-
множенною на число предшествовавшихъ ему членовъ. Слѣдовательно, послѣд-
ігй, т. е. п-й членъ будетъ
1) 1~а-+-г{п—1).
Онъ въ убывающей прогрессіи будетъ 1=а—г(п—1).
Послѣдній членъ называется также общимъ членомъ, потому что служитъ
для опредѣленія величины каждаго члена вообще. Для примѣра, положимъ, что
надобно найти десятый членъ прогрессіи
4-1. 3. 5. 7. 9. 11....,
гдѣ а=1, г=2, м=10. Сдѣлавъ подстаповленія въ 1—а-л-г(п—1), найдется
/=1-ь2(10—1)=19. Таковъ десятый членъ этой прогрессіи.
376. Всякая возрастающая прогрессія, будучи написана въ обратномъ по-
рядкѣ, превращается въ убывающую. Наприм.
4- 1. 3. 5. 7. 9. 11. 13. 15,
4-15.13.11.9.7. 5. 3. 1.
Если гтп двѣ прогрессіи сложить почленно, то получится рядъ равныхъ
членовъ:
4- 16. 16. 16. 16..
II вообще, въ ариѳметической прогрессіи сумма крайнихъ членовъ
равна суммѣ двухъ какихъ угодно членовъ, равно отъ нихъ от-
стоящихъ
Потому что сумма крайнихъ =а-+-1,
второй членъ отъ начала =ач-г і
— - огъ конца =/—г |
сумма —а-і-1:
— 238 —
третій членъ отъ начала ~а-+-2г
- - отъ конца =.!—2г
сумма =а-ь/,
и такъ далѣе.
Л'9'8. Найтп сумму извѣстнаго числа членовъ прогрессіи
4- а. Ь. с. й.і. к. I,
гдѣ а первый членъ, I послѣдній, разность г, число членовъ п.
Означивъ эту сумму чрезъ 8, она должна быть
8—о—Г-6-+-С—.. —г г-+-к-г /, нлп
8= 1-г-к-+-г -ь...-ьсн-6-+-а.
Сложимъ эти два ряда почленно
28=(ач-/)-+-(д-ь/с)-+-(сч-г)-+-.-+-(/і-+-Ь)-ь(/-+-а);
а какъ а-+-к=Ь-і-к=.с-ьг=.., а число членовъ п, то будетъ:
28=п(ач-1), откуда
2) .... 8=^.п
И такъ, сумма членовъ ариѳметической прогрессіи равна полусуммѣ
перваго члена съ послѣднимъ, умноженной на число членовъ.
Примѣръ. Найти сумму 20-ти членовъ прогрессіи 4-1. 4. 7. 10. 13..'..,
въ которой а~1, г=3, п=20.
Вопервыхъ, ищу послѣдній членъ
1—а-і-г{п—1)=1-ьЗ(20—1)—58;
а потомъ, 8=(1~^88)2Цг=590.
Такова сумма 20-ти членовъ этой прогрессіи.
Формулы /=а-ы(п—1), 8—(~^)п, содержатъ въ себѣ пять коли-
чествъ: а, I, г, п, 8, и служатъ для рѣшенія всѣхъ вопросовъ относительно
прогрессіи ариометической, гдѣ, по даннымъ тремъ изъ этихъ количествъ,
ищутся два остальныя. А чтобы рѣшенія были возможныя и прямыя, необходимо
нѵжно, чтобы ьти количества были оѣиствителыіыя, и сверхъ гого, чтобы п
было цѣлое положительное. Такихъ вопросовъ десять; рѣшеніе пхъ вообще
очень просто, а потому мы ограничимся только случаями болѣе сложными.
1. Даны г, п, 8, найти а и I.
Беремъ уравненія к=а-+-г(п—1, 8=(^І^)п:
изъ перваго находимъ I—а~г(п—1) }
28 ? СЛОЖИМЪ
изъ втораго |
2^25-*-пг(я—1).
п *
— 239 —
, 28-+-пг(п—1)
отсюда /=-----------;
2п
а если вычтемъ верхнее изъ нижняго, то получится:
п 28—пг(п—1)
2а=------!----и
п
28—г'п—1)п
а=------.
2п
2. Даны I, п, 8, найти а, г.
28
Изъ втораго уравненія имѣемъ а-+-/= —, и
28 -Іп
а=-------, .
п
. І—а 2(яІ—8)
а изъ перваго уравненія: г=—- — —.
3. Даны а, г, 8, найти I, п.
Изъ второй формулы получаемъ п(а-ь/)=28; сюда внесемъ /=а-ы(п—!):
п(2а-ьпг—г) =28, или
2аѣ+п*г—пг=28, илп
. (2а—г) 28
» -ь п = -; откуда
' г—2а± |/(г—2а)«ч-8г8 ’
П 2г '
А послѣ сего найдется и /=а-4-г(п—1).
4. Даны I, г, 8, найти а и п.
„ л, , , 28-+-пг(п—1)
Изъ 1) беру I—-----------, и нахожу
_ гч-21± Ѵ'^гч-гіУ'-вгВ
П 2г *
а потомъ, а=7-ы(п—1).
339. Задача.—Даны два числа а и I, вставить между пнми т чле-
новъ, которые бы, вмѣстѣ съ данными, составили ариѳметическую
прогрессію.
Здѣсь извѣстны члены: первый а, послѣдній I, и число ѣ всѣхъ членовъ, кото-
рое .= т-+-2; надобно только найти разность г, которую тотчасъ получимъ изъ
формулы 7=а-ч-г(м—1):
_ I—а___ I —а
и—1 иіч-1
Отсюда заключаемъ, что если первый членъ а, то второй =ач-----тре-
2(1—а) *”
тчі =ач-----—, и т. д.
гл-»Ч
Примѣръ. Вставить три члена между 1 и 2.
Тутъ а=1, /=2, »п=3; посему
і-а і
»= —— = —.
т-ьі 4
— 240
Стало-быть, выйдетъ погрессія:
4-1. г. і|. і;-. 2.
Задача.—Работники нанялись вырыть колодезь, съ такимъ условіемъ, что-
бы за первый аршинъ глубины колодца было имъ заплачено 22 коп. се-
ребромъ; за второй 25-л-ІО коп. сер., за третій 2.5-е220 коп. серебр.,
и т. д., прибавляя за каждый аршинъ углубленія все по 10 коп. серебр.
По окончаніи работы они получили 10 руб. серебромъ за весь свой
трудъ. Спрашивается, сколько аршинъ глубины они вырыли?
Здѣсь платы за каждый аршинъ углубленія возрастаютъ въ прогрессіи
4 25.35.45....,
въ которой даны а=25, г=10, и сумма 8=16 руб. =1600 коп. серебр., вы-
данная работпикамъ; требуется найти число п членовъ, то есть, число аршинъ
глубины колодца, и послѣдній членъ I. Для этого имѣемъ формулы:
г—2а± /(г—2а)’-+-8г8 „
«=--------------------- . Н
2г
/=а-ы(«—1).
Сдѣлавъ подстановлеціе, найдется
«=16 аршипъ, и
/=175 коп. серебромъ.
И такъ, глубина колодца была 16 аршипъ.
Задача. — Лѣсной участокъ, содержати”! въ себѣ 50000 кубич. футовъ
лѣспаго запасу съ 2^ годоваго прироста, назначается въ равномѣрную вырубку
въ теченіе 10 лѣтъ, по равной части, т. е. по ——=5000 куоич. футовъ въ
годъ; сюда подобно еще причислить годовой приростъ, 50000X^2=1000, ко-
торый уменьшается по мѣрѣ уменьшенія запаса: требуется паіітн весь 10-лѣт-
пій приростъ и полную годовую вырубку лѣса.
Въ концѣ 1-го года приростъ 1000 отъ 50000
— 2-го - - 900 » 45000
— 3-го - - 800 » 40000
- 4-го - — 700 35000
— 5-го - — 600 » 30000
— 6-го - — 500 25000
— 7-го - — 400 20000
— 8-го - — 300 15000-
- 9-го - — 200 10000
- 10-го - — 100 » 5000
— 11 -го - — 0 » 0
Здѣсь годовые приросты составляютъ убывающую прогрессію. Хотя число
членовъ ея 11, по, для исчисленія всего прироста, надобно взять только 10 члс-
241
новъ, потому что вырубка производится не въ концѣ каждаго года, но въ его
продолженіе, слѣдовательно, въ промежутки между 1 и 2, 2 и 3, 3 и 4,...., а
такихъ промежутковъ 10. Посему, сумма приростовъ
(1000-ь0)™=5000,
да всего лѣсу, без’ь прироста, было 50000; стало-быть, вырублено будетъ
всей массы дерева 55000 кубич. футовъ. Годовая вырубка =—®<^>—=5500 ку-
бическихъ футовъ.
Задача. Поденщикъ нанялся работать съ такимъ условіемъ, чтобы
ему за первый день работы заплатили 1 копѣйку серебромъ, за второй
4 'копѣйки, за третій 7 копѣекъ, и т. д. все увеличивая плату по
3 копѣйки серебромъ за каждый послѣдующій день. По прошествіи
16 дней, онъ кончилъ работу; спрашивается: сколько денегъ надобно
ему выдать?
Въ этой задачѣ также находится прогрессія
М . 4 . 7 . 10....,
въ которой а—1, п—26, т=3. Посему
/=1-ьЗ(26—1)=76,
8=(1-+-76)^—1001 коп. сереб.
Слѣдовательно, ему надобно заплатить почти ровно 10 руб. серебромъ.
Судідіоваіпе степеней членовъ прогрессіи ариометическоіі
990. Возмемъ ариѳметическую прогрессію
*- а.Ь.с б......I,
въ которой число членовъ п, разность г, послѣдній членъ
/=(а-ы(и—1),
8,а-ьі
=(——)л;
возвысимъ всѣ ея члены въ т-ю степень, и постараемся найти ихъ сумму
8т=ат-+-Ьтч-стч-бт-і-... .н-Г.
Мы знаемъ, что 6—ач-г, с=й-+-г, б=сч-г,.... 1=к-+-г; посему,
' 7 1.2 1.2.3
с-=(«н-г)-=6--м»6—г+ 6.-Ѵч_.
ѵ ' 1.2 1.2.0
І'=(1и-г)-=к‘-мпк—*іч-7"’ “е—Ѵ-+-7”. <ІІт3 2> ...
' / 1.2 1 • л> • о
16
__ 242 __
Сложимъ всѣ сіи равенства, и, для краткости, назовемъ:
80—а°-ь6°- ьс°-ь... ,-+-Г=п,
8,г=а-+-Ь -ьс н-....н-/,
8,п_1=а”,-1-ь6”’_1-ьс”‘~1-ь... ,
8т=ат-ь6‘-ьс-4-7”*:
то получится рядъ
въ которою содержатся всѣ суммы отъ 8„_, до 80 включительно.
®8в. Посредствомъ этого ряда можно находить суммы всѣхъ степеней чле
новъ данной прогрессіи слѣдующимъ образомъ:
а) Возмемъ т— 1; найдется:
I—а~г(30—Г), откуда 80— —' 4-1;
а какъ /=а-ч-г(п—1), откуда I—а~г{п—1), то
„ г(п— 1)-»г
80— —п.
Ь) Положимъ »п=2; будемъ имъть:
/*—а’=2г(8,- —/)-4-г’(80—/°);
отсюда найдемъ:
с <- г(і—а)
8,—I— —„-----------— ; слѣдовательно,
1 . 2г 2г ’
Р—а* г(1-+-а)__(Іч-а)(1—а-ы)
~2г~ * 2г~ 2г ’
но изъ 1~а-і-г(п—1) получается /—№-ч~г=гп, то
с___(І-і-а)пг _(а-і 1)п
2 г 2~ '
с) Полагая т='3, находимъ:
Г—а?'=3>(82—/2)-ьЗг (8,—/)-ы8(80—
откуда получится 8, въ функціи отъ 8, и 80.
й) Для т=і, иашли бы:
Г—О‘=4г(83—/^6^(8,—/а)4-4г3(81—/)-ы'(8с—7я),
откуда 8, опредѣлится посредствомъ 8„ 8,, 80: и такъ далѣе.
Для примѣра, возмемъ прогрессію натуральныхъ чиселъ 1, 2, 3, 4, 5,....п,
и поищемъ суммы квадратовъ, кубовъ,.... ея п первыхъ членовъ.
Здѣсь а=1, іг=1, 1—п, 8р=п; посему,
- 243 -
., с п(пн-1) п? п
1)8,— - —-тч-_
с, с г па—1 (*і®—п) (п—1)
2) 8 —п’-+- —-------1-г-' — 1-—', или
с _ 2пМ-Зп®-+-п___п(п +-1 )(2п-ь1)
о8—
6 1.2 ;
3) 83=п’-+- 2^1 -_2
[п®—п)
(п-1)
—, ИЛИ
4
С п’-с-2пМ-п® п«(п-Ы)® с ,
&3 Д 4 —(ЙС
Примѣръ. 1 3+23-ь-33-ь43=( 1-+-2-ьЗ-н4)2.
твч- ИТ и, 1*
Суммованіе рядовъ чиселъ фигурные. —Такія, числа получаются
чрезъ сложеніе двухъ, трехъ, четырехъ, и т. д. членовъ ариѳметической прогрес-
сіи, у которой первый членъ 1-ца, разность — цѣлое число. Изъ полученнаго
ряда такимъ же образомъ составляется другой, а изъ этого третій, и т. д.
Возмемъ сперва чрогресию натуральныхъ чиселъ,
ѵ 1.2.3.4...5.6.7.8.9.......п.
Чрезъ постепенное сложеніе членовъ ея. получится первый ряд •>:
1) і, 3, 6, 10, 15, 21, 28,....;
изъ этого составится в,порой ряоъ:
2) 1, 4, 10, 20, 35, 56, 84....;
а отсюда третій:
3)’ 1, 5, 15, 35, 70, 126, 210,....
Числа перваго ряда называются треугольными; потому что онѣ точно пред-
ставляютъ намъ суммы равныхъ тѣлъ, напримѣръ ядеръ, расположенныхъ на
плоскости въ видѣ треугольниковъ:
Числа втораго ряда называются треугольными пирамидальными; потому
что онѣ представляютъ намъ суммы предыдущихъ слоевъ ядеръ, наложенныхъ
одинъ на другой, и составляющихъ треугольныя пирамиды.
Сумма ряда, ѵ 1.2.3.4.5.6.7....п, есть
с ________________________ (пч-1> _ п’н п
~Г2~ —Т-
Эта сумаа будетъ общимъ членомъ ряда 1, 3, 6, 10,.... чиселъ тре-
угольныхъ, которыя дѣйствительно получатся, если возмемъ 1, 2, 3,.
на мѣсто п-
— 214 —
1
2
1
И »
Возмемъ сумму,
1
и означимъ ее
і
чрезъ 8
П
«,8,= ^
1(82-+-8і)=1ч-3ч-6ч-.. ..ч-8і=8д.
2 1 3 я®—я □
8,=-----------• какъ это “ИДѣли (881) выше; посему,
с __ 1 /2п3-ьЗп2-+-п п!-+-п!
ЬА— 2 ( 6 ' 2" )
1 /2п3ч-6п2-Мп\
= 2(— 6 - )’ИЛИ
_ п=ч-3п’-ь2п _ п(п-^1)(п-+-2) • Т Г И
— 6 1 . 2 . 3 •
Такова сумма рода членовъ треугольныхъ чиселъ. Эта сумма необходима
будетъ общимъ членомъ рида чиселъ треугольныхъ пирамидальныхъ, въ чемъ
легко увѣриться, подставляя числа 1, 2, 3, 4,.... на мѣсто п:
1(Г-+-З.Г-+-2.1)=1
1 «г
- (25-ьЗ.22-+-2.2)—4 Возмемъ сумму, и дадимъ еі і
-і(33-і-3 32-+-2.3)=10
знакъ 8Д.
|-(п3-і-3.п2-+-2.п) =8Д
-(83-І-38.-+-28,)—1-ь4ч-1 0-ь. .. .ч-8Л—8Д.
тт о п,-ь2пв-і-п2 с 2п’-і-3п’-ьп с п’-і-п
Но, 83=------------, 8,—-------------, 8,= —— ; посему,
„ ___ 1 /п4-ь2п,-ьп’ 2т *-Зп2-ч-п 2п’-+-2пі
6 ‘ 4 1 2" 4 2 '
п’ч-бп’-ьіі Л*Ч -6п
— --------------- , или
п >
__п(пч-1)(пч-2)(п-і-3)
А 1.2.3 . 4 ’
Это и есть сумма чиселъ треугольныхъ пирамидальныхъ.
883. Возмемъ теперь прѵгрессію
<1.3.5.7.9.11........................2п—1.
Она даетъ происхожденіе фигурш-иъ числамъ другап класса, а именно:
1) 1, 4, 9, 16, 25, 36....
2) 1, 5, 14, 30, 55, 91....
— 245 —
Числа перваго ряда называются квадратными; потому что ими можно пред-
ставлять суммы круглыхъ тѣлъ (напримѣръ яді ръ', раскладывающихся на плоско-
сти точно въ видѣ квадратовъ:
9 у 9 9] 9 9 9 1 • • • • |
•* ; . ' 1
9 9 9 9 9 9 9
л 9 • • 9
Числа же втораго ряда называются квадратными пирамидальными; пото-
му что, чрезъ сложеніе тѣхъ квадратныхъ слоевъ одинъ на другой, начиная съ
послѣдняго до перваго, составляется пирамида съ квадратнымъ основаніемъ. ,
Сумма прогрессіи ѵ 1.3.5.7....2»—1, имѣющей число членовъ п, бу-
детъ 8,= -)«~нг- Она будетъ общвмъ членомъ ряда чиселъ фигур-
ныхъ квадратныхъ 1, 4, 9, 16,....п2, которыя мы дѣйствительно получимъ,
подставляя въ нее числа 1, 2. 3, 4,.... па мѣсто п:
1*=1
2 ~4 Возмемъ сумму, и да-
32=Д
димъ ей знакъ 8а. *
п*=п*
82=1н-4-ь9~ь. .. .ч-п,=8[-|.
,, . с 2п3-ьЗг5 ьп
Но, видѣли выше, чю 8,—-------- —, то и
2п3-ьЗпв-ьп_п(п-ьі)(п-ь2)
ё —1.2.3 '
Такова сумма чиселъ квадратныхъ; она будетъ общимъ членомъ для ряда
чиселъ четыреугольныхъ пирамидальныхъ 1, 5, 14, 30,...И дѣйствительно,
в:явъ 1, 2, 3,.... на мѣсто п, получаемъ "
* (2,Гч-3.1<і-1)=: 1
-*-(2.23ч-3.2!-ь2)— 5 Возмемъ сумму, и дла нее
’(2.35ч-3.3!-ь3)~14
знакъ 8В
у(2.п’ч-3.п2ч-и)=8а'
у(283ч-38, іь8І)=1-ь5-ь14-ь... ,ч-8в=8и, или
„ _______ 1 /2п’-ь4п3-ь2пв 6п3-ь9пв-ьЗп па-ьп.
0 6\ 4 1 6~ Ь 2
Сдѣлавъ сокращеніе, получимъ сумму
__п*-ьЗп3-ьЗпв-ь2п_п(п-ь1)7н-ь2)
Г2 — ЗЛ
чиселъ квадратныхъ пирамидальныхъ.
— 246 —
Послѣ этого можно найти сумму членовъ ряда
8—«ч-2а!-ьЗо?ч-4а‘ч-.'.. ч-иа"
Этотъ рядъ разлагается на два:
8=ач-а’ч-а3ч-... .ч-а"ч-а[а ь2<гч-3а3ч-... .чДп—1 )а"_‘].
4 із п а—а"-*-1
А какъ ач-а ч-а ч-....ч-а = ———, въ чемъ можемъ увѣриться посред-
ствомъ дѣленія, сверхъ того, рядъ в
ач- 2а!ч-3а3-ь... ,ч-(«—1 )а"_1=8—па”; го
8— -^^-—ьа(8—иап); откуда
ос »-ні а"4-1 —а о —па’14’4
а8—8=па’ьн1----------— -------- — ,
а—1 а—1 4
и, наконецъ,
__ а—(П-+-1 )а’'4"<-е-паП4-2
— (-^1?
вй5. Здѣсь предложимъ себѣ вопросъ о разложеніи цѣлаго положительнаго
числа на данное число цѣлыхъ частей всевозможными образами, и о нахожденіи
суммы таковыхъ разложеніііі.
' Данное число,а разложить на два цѣлыя и положительныя числа
всевозможными образами, и найти сумму разложеніи.
Пусть х, у, эти цѣлыя части; то
х-ь-у— а, откуда
У—а—х. , в' 1 ш I!
Если х должно быть цѣлымъ положительнымъ числомъ, то его можно взять
только х=1, 2. 3,.....а—1,
и тогда, у~а—1, а-—2, а—3,......2, 1.
С іѣдоьательно, число п всѣхъ разложеніи =а—1.
2) Данное число а разложить но три цѣлыя положительныя чисти
всевозможными образами, и найти сумму таковы къ разложеній.
Пусть эти цѣлыя части х, у, я, то
жч-уч-г=а, откуда
а=а— х—У-
Возмемъ сперва: х=1, ', 1, ..1
У=1, 2, 3, .. Число рѣшеній
то 0 а 1 а сс а—4,.. .. 1 а—2.
Потомъ возмемъ. а:—2, 2, 2, .. ..2
у—1, 2, 3, .. а—3
то а—3, а—4, а—5,.. ..1 *
Послѣ того: х=3, 3, 3, ...3
2, 3, .. а—4.
х~ а—4, а—5, а—6,.. ...1
247
И такъ далѣе продолжаемъ, пока получится предпослѣднее число рѣшеній
а—(а—2) =2, а послѣднее а—(ач-1)=1. Посему, искомое число рѣшеній
8=1 ч-2ч-3ч-.., .ч-(а—4 )ч-^а—3)ч-(а—2)
(а — і)(а — 2) Г(п-І-І) ,
= —-------- = - -, полагая а—2—п.
1 • х
Если раздѣляемое число а=7, то сумма его разложеній на три цѣлыя чи-
, б.з , „
сла будетъ —=15, а именно:
Числа рфшпній.
5
а?=1, 1, 1, 1, 1
у={, 2, 3, 4, 5
г=5, 4, 3, 2, 1
4
2. 2, 2, 2,
1, 2, 3, 4
4, 3, 2, I
3
зИГз?
4, 2, 3
3, 2, 1
2
4, 4
1, 2
2, 1
И такъ, число рѣшеній =1ч-2ч-3ч-4ч-5=15.
3) Цѣлое число а раздѣлитъ на четыре части цѣлыя и
ныя, и найти сумму разложеній. — Если эти части х, у, д
х-+-у-+-а-+-и~а; откуда
I
5
1
1
иаложителъ-
, и, то
и—а—х—у—г.
Числа Р11ШВН1Й.
І.(а-З) 1 а 4ч- а—4—2(а—4)
Беру: а=1, 1.. . 1 1, 1,.... ...1 2, 2, ..2
у—1, 1 ..1 2, 2,.... ...2 1, 1, 1
2=1 , 2, 1, 2,.... -4 1, 2,
то и—а—3, а—4,.. .1 1 а—4, а —5. ...1 а— 4, а—5,.. 1
а— 5ч-а -5ч-а— 5=3(а—5)
®=1, 1,.....1
У=3, 3,.....3
г=1, 2....а—5
и—а—5, а—6...1
2, 2,.......2
2, 2,.......2
1, 2.. о—5
а—5, а—6....1
3, 3.....
1, 1,.....
1, 2,.....а—5
а—5, а—6,...1
и такъ далѣе. Послѣднее число рѣшеній будетъ (а—3)[а—(а—1)]=(а—3)1,
тоже что первое, а предпослѣднее (а—4) [а -(а—2)]=(а—4)2, тоже что
второе. А потому, сумма всѣхъ рѣшеній
8=1(а—-3)ч-2(а—4)ч-3(а—5)ч-....ч-(а—4)2ч-(а—3)1.
Этотъ рядъ разлагается на слѣдующіе:
(а—3)ч-(а—4}ч-(п—5)ч-.. ,ч-3ч -2ч-1
ч-(а—4)ч-(а—5)ч-.. .ч-3ч-2ч-1
ч-( а—5)ч-.. .ч-3ч-2ч-'1
ч Зч-2ч-1
ч-2ч-1
ч-І
число рядовъ
а—3.
— 248 -
і.
Слагая суммы этихъ рядовъ снизу вверхъ, получимъ:
8—11-3-Л-ь... .ч-
1. 2
Но мы уже знаемъ, (4883), что эта сумма
с___(а—1)(а—2)(а—3)
8—' 1 . 2.-------3“’ ”ЛИ
с п(и-ь1)(п-і-2) .
Ь=-— -------—, полагая а—3=н.
Нашли бы также, что сумма рѣшеній, отъ раздѣленія цѣлаго числа а на 5 цѣ-
лыхъ частей, будетъ
(а — 1)(о—2)(а—3)(а —4)
Т . 2~". 3 ? 4 ’
н такъ далѣе.
Примѣръ. Разложить число 9 на четыре цѣлыя, положительныя числа
всевозможными образами, и найти сумму этихъ разложеній.
(а—1)'«—2)(а—3) 8. 7. 6
Эта сумма будетъ = —-------------— = = 56.
В. Прогрессія геометрическая.
88в. Геометрическою прогрессіею называется такой рядъ чиселъ, въ кочо-
ромъ каждый членъ послѣдующій равенъ предшествующему, помноженному на
постоянное число, называемое знаменателемъ содержанія. Она бываетъ воз-
растающею или убывающею, смотря потому, каковъ ея знаменатель содержа-
нія, больше единицы, или <4. Такимъ образомъ, рядъ:
4, 3, 9, 27, 81,....
есть прогрессія геометрическая возрастающая, въ которой знаменатель содер-
жанія 7=3,
ряды: 46, 4, 1, -, іе,....
6; 0,6; 0,06; 0,006;...
0.54; 0,0054; 0,000054;....
і
суть прогрессіи убывающія; въ первомъ знаменатель содержаніи ~ , во второмъ
0,1, а ьъ третьемъ 0,01
2:'4С. Для отличія отъ прогрессій ариометической, члены геометрической
прогрессіи пишутся въ одну строку, и отдѣляются знаками дѣленія, а передъ
рядомъ ставится знакъ то есть:
-н- 1 : 3 ; 9 : 27 : 81
С-16:4:1 |
П воооще, если числа а, 1>, с. составляютъ прогрессію геометриче-
скую, то она пишется:
а : Ь : с ; сі ;.I,
— 249 —
и выговаривается: а относится къ I), какъ Ь къ с, какъ с къ й, и проч.,
такъ что въ ней всякіе три члена, взятые сряду, составляютъ непрерывную
геометрическую пропорцію:
а : Ь=Ь : с~с : Л =......
Впередъ всегда будетъ означать:
чрезъ а первый членъ прогрессіи,
7 постьдпій ея членъ,
д знаменатель содержанія,
п число членовъ прогрессіи, и
8 сумму ея членовъ.
883. Въ геометрической прогрессіи каждый членъ равенъ первому
ея члену, помноженному на знаменатель содержанія, возвышенный въ
степень равную числу предшествующихъ членочъ. Это очень просто выво-
дится изъ разсматриванія происхожденія каждаго члена прогрессіи
а : Ь : с : й :..I,
изъ перваго ея члена:
Если знаменатель содержанія д, и число членовъ п, то имѣемъ:
о. а . а у
Ь=адр=ад,
с—Ьд—ад2,
<1=сд=ад3,
Законъ составленія членовъ изъ перваго очевиденъ; такъ, ианрим. третій
членъ с составленъ изъ а, помноженнаго на д второй степени; четвертый
членъ сі равенъ также а, помноженному на д третьей степени, и т. д. Слѣ-
довательно, послѣдній или п-ый членъ I будетъ
1)....1—адп~1г.
Послѣдній членъ называется также общимъ, потому что служитъ длн нахож-
денія вснкаго члена прогрессіи, когда а, д и п даны. Положимъ, что хотимъ
найти 7-ой членъ прогрессіи,
-Н- 3 : 6 : 12 :...,
въ которой п=3, ?=2, п=7; то
/=а?’-'=3 26“'=192.
Примѣръ. Найти 10-й членъ прогрессіи
-Н-25: 5 : 1 : у :.....,
гдѣ а=25, д= — , н=10. Онъ будетъ
78123 ’
— Й50 —
58®®. Найти сумму всѣхъ членовъ прогрессіи геометрической.
-’4- а : Ь : с : й :.к : I,
въ которой послѣдній членъ I, п число членовъ, и знаменатель содержанія </
Искомая сумма должна быть
8-~—о—мЬ- г—сі <1—і—... . і іі і І.
Составимъ равенства:
І)~ад, с=Ьд, Л=сд, е~йд,...., 1=^кц, и сложимъ;
получится: Ь-г-с-г~'і-г-....-і-1—[а-і-Ь~г-с-і ..-+-к)д;
а это все тоже, что 8—а—(8—/)д, откуда
__ ^9 . (і — ід
2)...8= .или 8— —- .
д-1 1— <1
Этому выраженію суммы можно дать еще иной видъ, подставивъ ад"~*;
отчего найдется:
3) ....8^__г=_.,Или
4) ....8= ^=“-“-^1.
1 —9 1—д
Формула 3) служитъ для нахожденія суммы прогрессіи возрастающей, въ
которой ^>1; а формула 4) служитъ для вычисленія суммы членовъ прогрессіи
убывающей, гдѣ у<1.
Примѣръ. Найти сумку десяти членовъ прогрессіи
: : 3 : 6 : 12 : 24
въ которой а=3, у=2, п—10. Она будетъ
8=“^' ;,=34^"=зоео
9—1 2—1
Примѣръ. -—Найти сумму семи членовъ прогрессіи
...........................................
д а(1—д"і 18(1 не?) 20 8®
1—9 81 '
5899. Найденныя формулы:
1=ад”-‘, 8=^,8=
* 9-1 9-1 ’
содержатъ пять величинъ: а, I, д, п, 8, и служатъ для рѣшенія всѣхъ задачъ
относящихся къ прогрессіямъ геометрическимъ, гдѣ, по даннымъ тремъ величи-
намъ, требуется найти двѣ остальныя. Такихъ задачъ десять.
1) Даны а, I, п, найти д и 8.
Я--1 /
Изъ первой формулы нахожу э и вычисляю по логариомамъ:
1°89= Іоё«);
а потомъ беру 8= .
251
2) Даны а, I, д, найти п, 8.
Вторая формула даетъ прямо 8=-^_“.
Возмемъ логариомъ первой формулы;
Іодач-(эт—1)Іо§9; отсюда
. Гор/—1о'»л
П~ ІІ---.
1084
3) Даны а, I, 8, найги ии д.
Изъ второй формулы получается д= ~ ; а^потомъ, изъ первой
ІО87
4) Даны а, п, у, найти I, и 8.
1=ад 8=-(9- *’ .
1 ч~і
5) Даны а, д, 8, найти п, I.
Изъ «торой формулы находимъ 1~ ; а
Іо?/—Іова
изъ первой П=-----;-----4-1.
г 1<>84
6) Даны а, п, 8, наити / и д.
Изъ третьей формулы выводится:
ад"—894-8—
Отсюда надобно искать д\ а потомъ
7) Даны I, п, 8, найти а и д.
Изъ первой формулы нахожу «-= ; это подставляю въ третью, и получаю:
8— —
2”“
(8—1)дп—8дп-1-ьІ—0.
Нашедши д изъ этого уравненія, получится;
1
а=-------
<Іп~і
8) Даны I, п, д, наити а, 8.
Чп~1 ’ 4—1
9) Даны I, д, 8, найти а, п.
Изъ втораго уравненія найдется: а=д1—\д—1)8; а потомъ
. ІО8І—1«8а
изъ перваго п—1ч------.
10) Даны п, д, 8, найти а, I.
Беру а— ^—7 , подставляю въ третью формулу, и получаю:
9'*— 11
---- ; а отсюда
1 ц—1'
- 252 —
/?п—
откуда
ЗП
8= —
г—
1 =
дп—1
Послѣ чего найдется а= . Послѣднее вычисляю по логариѳмамъ:
Іо^а=1о§і— (п—1 )1о .
Только задачи 6-я и 7-я не могутъ быть теперь разрѣшены, потому что ихъ
неизвѣстныя зависятъ отъ рѣшенія уравненій высокихъ степеней, о которыхъ
мы еще ничего не знаемъ.
Задача. Даны два числа а и I, вставить между ними т членовъ,
которые бы совокупно съ тѣми составили геометрическую прогрессію.
Въ этой прогрессіи первый членъ а, послѣдній I, число членовъ т-ч-1=«;
знаменатель содержанія найдется изъ формулы /=05"-*, и будетъ ’
«Ш-і/
«=Ѵг
Посредствомъ его легко уже составятся всѣ члены прогрессіи, котовыя на-
добно вставить между а и I, а именно:
ЯіЧ-1 / ТПЧ-1 / ТП-і-1 у
а, а\/Ь, а\/-, Л/*,.............I
V а г а3 у а.3
11
Если а=1, 1=2, т=М, то «=13, и д=Ѵ'2;
1о8д= .1о§ 2=0,0231562,
5=1,05946....
И такъ, членами прогрессіи будутъ:
44 1 : 1,05946 : 1,18921 : 1,25992 : 1,33484 : 4,41421 :
1,49831 : 1,58780 : 1,68169 : 1,78180 : 1,88775 : 2.
Эти числа выражаютъ высоты всѣхъ 13-ти полутоновъ, заключающихся въ
октавѣ хроматической гаммы, т. е. числа сотрясеній, ихъ производящихъ отъ
перваго полутона С\ до послѣдняго С, включительно.
390. Прогрессіи, какъ возрастающія такъ и убывающія, могутъ состоять
изъ опредѣленнаго или безконечнаго числа членовъ.
а(о'”—1) .
Формула 8= показываетъ, что въ прогрессіи возрастающей; гдѣ
5>1, съ увеличеніемъ числа членовъ п, увеличивается дп, а слѣдовательно и
8, такъ что эта сумма можетъ превзойти всякое данное число. Для п=оо',
будетъ 5"=оо , и 8=<» .
с а—ад" а ад"
391. Формула э=- = у—-—«иредѣляющая сумму прогрес-
сіи убывающей, гдѣ д <1, показываетъ, что, съ увеличеніемъ числа п чле-
новъ, дробь д" безпрестанно уменьшается, и можетъ сдѣлаться менѣе всякаго
— 253 —
даннаго числа. Отъ этого сумма 8 приближается къ предѣлу , никогда его
не достигая. Развѣ когда возмемъ п—оо , тогда 9" обратится въ нуль, и сумма
прогрессіи сдѣлается равна сему предѣлу,
1-я '
Впрочемъ можно получить ее л непосредственно; надобно только помножить рядъ
8—ач-а9-і-а9’-ьа93-ь.... на д, и
вычесть изъ него произведеніе
98=а9-ьа9!-ьа93-і-....;
получится остатокъ 8—д8~а, изъ котораго
8— ~.
і-д
Справедливость ьгого вывода можно повѣрить чрезъ непосредственное раздѣ-
леніе а на 1—д. Отъ этого получится также
~ —ач-а9-ьа9"ч -адпч-... .=8,
геометрическая прогрессія безконечная, и притомъ убывающая, потому что 9<1.
Слѣдовательно, сумма всѣхъ членовъ безконечной геометрической про-
грессіи, убывающей, равна первому ея члену, раздѣленному на единицу
безъ знаменателя содержанія.
Примѣръ. Найти сумму прогрессіи
8-2-ь2 -ь2ч-
Положивъ а=2, д= - , найдется 8=
2
81 '
-3
2
27
2
1 —
Если вмѣсто 7 взять —то получится:
=а—а9-ьа?8—а?“-ь....
5МЮ. Эти два рада могутъ быть употреблены для выраженія всякаго числа
а посредствомъ безконечнаго ряда, котораго члены убываютъ въ прогрессіи гео-
метрической и расположены по степенямъ какой угодно дроби д; потому что
изъ перваго ряда мы тотчасъ имѣемъ
а=(1—9)(а-ьа9-ьа98-ь-а93-ь-....), или
4 =( 1 — 9) (|
Полагая у, у,...., найдется:
254
а помножая тотъ или другой рядъ на какую угодно дробь, мы выразамъ ее ря
домъ, расположеннымъ по степенямъ дроби этого ряда, наприм.:
1 — 1 /л . 1 . 1 1 \
2 3 ’ 3 9 + 2 ’
3 4 4 4-4» > ч.ш.ги-.лв;!
» 1 ? / 1
”8 2'4 ~5 4 5’ іі - )
Положимъ, что надобно дробь - изобразить рядомъ, расположеннымъ по сте
, 2 „ 2
пенямъ дроби - ; тогда падоопо взять 7= - въ ряду ' п
1=(1—г)Цч-д-4-9'Ч-7*-ь...),
і
и все помножить на - ; найдется:
5
Этимъ же способомъ дроби —,«д:, —______ легко обращаются въ деся-
» ѵ ѵ У У У
ТИЧНЫЯ - I
1 =1(|—‘-)(|+1+Л+--‘-+.
9 9 ѵ 1О/Ѵ 10 100 1000
= — -ь— н—-—н....=0,11111...
10 100 юоо ’
1 1 [Л 1 1 1 1
99 99' 100^ 1 100 * 100» 1 100’ 1
= 0,010101..
и такъ далѣе
10П
23
очевидно есть прогрессія, гдѣ а=-^, д=
5ВЭЗ. Рядъ ач-а</-ьад,!-+-а98ч-....= служить также для обращенія
всякой періодической дроби въ конечную, изъ которой она произошла; по-
тому что періодическая дробь состоитъ изъ періодовъ, слѣдующихъ въ безконечной
убывающей прогрессіи Напримѣръ: дробь
О 2323°3 — — -ь —— д 23 і
" юо іоо» ^чоо®
і
стало быть,
100
88
100 23
і____1. — 99'
100
Такова обыкновенная дробь, изъ которой произошла та періодическая.
8= —
і-д
Рядъ у^=н—ау-і-ад'—ад"-ь....
приводитъ насъ къ общему заключенію, что всякая алгебрическая дрооь вида.
а а-+-Ьх а-л-^х-і-сх^
а'-і-І/'х і'-і-б'х-і-с'х4 ’ а'-л-Ъ1 х-і-с'х^-і-Щхг ’ ’ ’ ’ ’
255 —
можетъ быть разложена въ рядъ, въ которомъ каждый членъ равенъ алгебри-
ческой суммѣ извѣстнаго числа предыдущихъ ему членовъ, умноженныхъ на
нѣкоторое постоянное количество. Такъ, <
а
а а' а аЫх аЬ,9а?
— ---- —-------— — —----------1--— —..,,
а'ч-б'ж Ъ'х а7 а'9 а73
1ч----—
• а*
ЬГЯ!
Здѣсь каждый членъ состоитъ изъ предыдущаго, помноженнаго на--------—.
_ „ 1-+-Ъх а Ьх і, ,
;юбь-;—п--------гт— ,----------ь , — полагая р=о'-і-с,л.
а’-ь-Ь ’х-ѵ-с'х4 а'-і-рх и'-ѵ-рх
1Т а а а ѵх а р2®2
Но, - — - ------, -..........
а'-ъ-рх а' аг а а' а'*
Ьх Ьх Ьх ѵх Ьх />2®2
— == —,-----------^т -*—; - —---------- ; то
а'-і-рх а' а' а а’ и'2
а Ьх а Ьх іа Ьхі рх ,а Ьх,\р*х*
а'-і-рх а'-л-рх а' а1 'а' а'* а1 *а' а'' а/2
или:
а-+-Ъх _____ а-+-Ьх Ьх.іЬ'х-г-с'х^. іа-+-Ъх, іЪ'хч с,х‘і\
а'-і-Ъ'х-і-с'х2 а1 X а' Д а' / \ а' ' а '
Явно, что этотъ рядъ есть прогрессія, въ которой знаменатель содер-
6'с-і-са?2
жапія =-------------.
а
Ряды такого рода называются возвратпммн Но объ нихъ я ничего болѣе
говорить не буду.
256
ГЛАВА ДЕСЯТАЯ.
ПРИЛОЖЕНІЕ ПРОГРЕССІЙ И ЛОГАРПѲМОВ7» КЪ ВЫЧИСЛЕНІЮ
ПРОЦЕНТОВЪ.
Я9.>. Нельзя исчислить всѣхъ случаевъ употребленія геометрической про-
грессіи въ наукахъ и общежитіи: довольно, если покажемъ ихъ употребленіе
при вычисленіи процентовъ. Это вычисленіе встрѣчается во множествѣ слу-
чаевъ: при денежныхъ вк іадахъ па приращеніе процентами; при ссудѣ напита
ловъ частнымъ лицамъ по векселямъ или подъ залоги; при постепенной уплатѣ
долговъ и при учетѣ процентовъ; при расчетѣ доходовъ отъ фабрикъ и ману-
фактуръ; при опредѣленіи выгодъ различныхъ компаній, составляющихся на
акціяхъ; при исчисленіи временныхъ или пожизненныхъ доходовъ отъ капита-
ловъ, вносимыхъ въ страховыя обществя, или другія учрежденія, въ пользу ка-
кихъ ни есть лицъ; въ лѣсоводствѣ, для исчисленія прироста и размноженія
лѣса, и при придажѣ или покупкѣ онаго съ уплатою по срокамъ, и проч. и проч.
Алгебра не входитъ въ разсмотрѣніе всего этого, но показываетъ только начала;
подробпое же развитіе и примѣненіе ихъ надобно читать въ особыхъ сочиненіяхъ,
показывающихъ частное примѣненіе прогрессій и логариѳмовъ къ тому или дру-
гому роду случаевъ. Къ сочиненіямъ этого рада относятся: Руководство къ
Политической Ариѳметикѣ, составленное Г. Вруномъ. Одесса 1845,—
сочиненіе весьма замѣчательное и полезное; Лѣсная Математика, съ изло-
женіемъ правилъ межеванія, таксаціи и вычисленія цѣнности лѣсовъ, Г. Ке-
нига, переведенная съ нѣмецкаго Грешищевымъ. С.-Петербургъ. 4841.
ЭД><>. Вопросъ первый. — Капиталъ А рублей отданъ въ ростъ на
приращеніе своими процентами, по съ одного рубля въ годъ; найти
какъ великъ сдѣлается этотъ капиталъ черезъ п годовъ?
По прошествіи перваго года, I рубль превратится въ 1-ы, а капиталъ А
превратится въ А (1-ы); эта сумма остается на второй годъ. Послѣ втораго
года также 4 рубль сдѣлается 1-ы, а капиталъ А(1-+-г) превратится въ
А(1ч-г)(1ч-г)=А(4-ы)’. Послѣ третьяго года, капиталъ А(1ч-г) получитъ
цѣну А(1ч-г)3, и т. д Слѣдовательно, послѣ п годовъ, начальный капиталъ А
превратится въ
8_=А(1-+-г)"...(1).
— 257 —
Изъ четырехъ количествъ 8, А, г, п, входящихъ въ эту формулу, можно
находить каждое, когда три прочія извѣстны. Вычисленіе же дѣлается всегда
по логариѳмамъ:
Іо{т8=Іо2А-+-п1о§( 1-ь-г) .... (2}.
Отсюда:
16§Л=Іо§8—п1о§ (1 - ы*1.... (3);
И=1о°8--2^А.........(4.);
. , , іог§—іо^л
Іоё(1н-г)=...-...........(5).
Задача 1. — Начти будущую цѣну капитала 20000 рублей, полу-
женнаго въ Коммерческій Банкъ для приращенія процентами на 12
лѣтъ, по 0,04-^ съ одного рубля.
Здѣсь А=20000, п=12, ?=0,04;
Іо^8=1о§20000-+- 12 1о§(1,04).
Іод 20000=4,301.0300
12.1о§ 1,04=0,204.4001
4^505.4301=1оё8;
откуда 8=32020,64 рублей. Таковъ будетъ капиталъ А по прошествіи 12
годовъ.
Если же этотъ капиталъ А будетъ въ обращеніи 12 лѣтъ -+-156 дней; то,
превративъ дни въ годы, найдемъ:
п=12+з?о=12-нзогод'ь )’
будущая цѣна капитала получится изъ
і ч
Іо§ 8=1о§ А-+-(12ч~—) 1о§ (1,04)
=1о§ А-ьІ 2 Іод 1,04-+- з >
=4,505.4301-+-^ Іод 1,04=4,512.8112,
чему соотвѣтствуетъ число 32569,50 рублей.
Задача 2. — Лѣсной округъ, содержащій 68160 квадратныхъ саже-
ней лѣсу, и большое количество земли для лѣсонасажденія, стараніемъ
лѣсовода увеличивается каждогодно на 4’ требуется узнать, какъ
великъ этотъ лѣсъ сдѣлается чрезъ 12'годовъ, если его не вырубаютъ?
8=68760(1,0475)^=120000 квадр. саж.
=50 десятинъ.
*) Въ Коммерческомъ Банкѣ, для разсчета процентовъ, принимается мѣсяцъ въ 30
дней, слѣдовете/ьно годъ въ 360 дней.
17
258 —
Задача 3. — Колонія изъ 1000 человѣкъ, поселившаяся въ мѣстѣ
удобномъ для жительства, умножается въ каждый мѣсяцъ по^^^олгь
на человѣка; спрашивается: какъ она будетъ многолюдна чрезъ 100
лѣтъ?
8=1000(1,001)1200=1318 человѣкъ.
Задача 4. — Опредѣлить настоящій капиталъ А, который надобно
отдать въ ломбардъ для пряращенія процентами, по 0,04^ съ рубля въ
годъ, чтобы онъ, по прошествіи 10 годовъ обратился въ 6000 рублей.
Здѣсь 8=6000, п=10, /=0.04, а искомый капиталъ А, который най-
демъ изъ (3):
Іод А= Іод 8—п Іод (1-ы)= ІодбООО—10. Іод1,04.
Іод 6000=3,778.1513
10 Іод 1,04=0.170.3334
3,607.8 і79=ІодА; откуда
А=4053,39 рублей.
Задача 5. — Пайпги, во сколько лѣтъ напита’ъ 1.5000 рублей, от-
данный въ ростъ по 0,04°- съ рубля въ годъ, обратится въ 20000
рублей?
Здѣсь А=15000, 8=20000, г=0,04, а неизвѣстно время и годовъ; то
изъ (4) найдется:
1о"8—ІОцА. Іо" 20000—І05ІНООГ
І08(1-ь-г) Іо^І.Оі
О Ш.9887
0^917.0333 >3 Г0ДЯ‘
Примѣчаній Обыкновенные проценты съ рубля въ годъ бываютъ 0,025;
0,03; 0,035,0,04; 0,045; 0,05; 0,055; 0,06. Логариомы годовой цѣны
1-го рубля въ задачахъ этого рода встрѣчаются безпрестанно. Для облегченія
дѣйствій, эти логариомы помѣщаются здѣсь:
Іод 1,025=0,010.7238.65; Іод 1,045=0,019.1162.90
Іод 1,03 =0,012.8372.25; Іод 1,05 =0,021 1892.99
Іод 1,035—0,014.9403.50; Іод 1,055=0,023.2524.60
Іод 1,04 =0,017.0333.39; Іод 1,06 =0,025.3058.65
Задача 6. — Иаити, во сколько лѣтъ капиталъ А, отданный въ
ростъ по съ рубля, удвоится?
Будущій капиталъ долженъ быть =2А; посему надобно положить
8=А(1-.-г)и=2А откуда
(1-ь-г)’=2, и
»= - 1062
ІО8 (1-ы)
— 259 —
т, л Л, 0,301.0300
Если г=0,04, то п— - •—=17,673 года.
0,01і«ОоЗо *
Во столько времени капиталъ удвоится.
Задача 7.—Два капитала 2735 руб. и 2260 руб. отданы въ ростъ
въ одно время, первый по 0,06^-, а второй по 0,06— съ рубля въ годъ;
найти, чрезъ сколько лѣтъ второй капиталъ, возрастающій быстрѣе,
сдѣлается равенъ первому, и какъ великъ будетъ каждый изъ нихъ?
Положимъ, чіо они сдѣлаются равными чрезъ п годовъ: тогда первый капи-
талъ превратится въ 2735.1,04”, а второй въ 2260.1,06”, и будетъ
2735.1,04"=2260.1,06”. Отсюда
_________ Іоц 2735-1оі> 2260
П ’ ІО" 1,06— 1о& 1,04
0,082.8489
= годовъ-
Слѣдовательно второй капиталъ сдѣлается равенъ первому почти ровно чрезъ
10 лѣтъ. Величину же капитала въ это время найдемъ изъ 2260 1,06|0'м, взяв-
ши логариѳмъ зтого произведенія:
Іо§ 2260-+-10,02 1о§ 1,06
=3,354.1084-4-10,02X0,025.30587
=3,607.6732,
чему соотвѣтствуетъ число 4052,03 рубля. Такимъ сдѣлается каждый капиталъ
чрезъ 10 годовъ.
399. Если изъ будущаго капитала 8=А( 1-4-г)” вычесть начальный капи-
талъ А, то найдется весь доходъ
8—Л=А[(1ч-г)”—1]=В...........(6),
который получится чрезъ п годовъ съ капитала А. Отсюда найдется
. в
1 (1-+-г,п—1
«настоящій капиталъ А, который можетъ принести доходъ В чрезъ п годовъ.
Можно искать также число годовъ, или годовые проценты изъ выраженія:
(ІЧ-г) "= —д—, ВЗЯВЪ
п 1о§(1-ы)=1од(Л-4-В)—1о§А....(8).
Задача 1. — Капиталъ 2516 рублей, находясь въ обращеніи 12 го-
довъ, принесъ доходу 2000,76 рублей; узнать, какіе были проценты
съ рубля въ годъ?
Сложивъ А=2514
съ В—2000,73
А-ьВ=4514,73,
подставляю въ (8), и нахожу:
— 260 —
1о§ (1-ы)=—3^^ =0,021.1893;
1 ++=1,05; г=0,05.
Таковы были искомые проценты.
Задача 2.—Съ недвижимаго имѣнія получался постоянно доходъ Л
чрезъ каждые н годовъ; а теперь этотъ же доходъ полученъ въ концѣ
п—к лѣтъ, то есть, к годами ранѣе срока; требуется наіппи настоя-
щую цѣну этому имѣнію?
Доходъ В, который нолучепъ чрезъ п—к годовъ, въ концѣ п-го года, то есть,
по прошествіи остальныхъ к годовъ, будетъ стоить
В(Г+-г)*=В'.
. Настоящая же цѣна его найдется по (7):
. к' __ ПИ-нг/
(1-г 1 (1-1-г)"—1....'
Вотъ чего стоитъ теперь это имѣніе, предполагая, что доходъ К постоянно
будетъ съ него получаться чрезъ п—к годовъ, или доходъ И' чрезъ каждые
п годовъ.
Задача 3.—Лѣсоводъ, производя правильно лѣсонасажденіе и поруб-
ку лѣса, находитъ, что шесть ею мелкихъ лѣсосѣковъ, въ продолженіе
каждыхъ 20 годовъ, будутъ приносить ему слѣдующіе перемежающіеся
доходы:
въ 4, 5 и 6-й годы..... по 100 руб. серебр
въ 14 и 15-й годы .....по 160 - -
въ 20-й годъ...........по 85 -
Онъ желаетъ знать настоящую цѣну всѣмъ этимъ лѣсосѣкамъ, въ
началѣ наступающаго 20ти-лѣтняго періода, считая по 0,05^ съ
рубля въ годъ.
Доходъ 100 рублей 4-го года, въ концѣ 20ти-лѣтняго періода, то есть, по
прошествіи 16-ти лѣтъ, дѣлается......400(1,05)‘“=218,287
100 руб. 5-го года сдѣлается 100(1,05)“=207,893
- - 6-го - 100(1,05)‘4=197,993
160 - 14-го - 160(1,05)“ =214,416
- - 15-го - 160(1,05)“ =204,2048
85 - 20-го - 85X1= 85
Сумма......=1127,7938
Этотъ 20ти-лѣтній перемежающійся доходъ, въ началѣ сего періода имѣетъ
настоящую цѣну:
1127,7938 1127,7938 „
(і,оз)’°—і “1,6533 6/6,1 руб еи.
— 261
Задача 4.—Найти капиталъ 8, который наообно положитъ въ Лом-
бардъ въ пользу четырехъ наслѣдниковъ, изъ когіхъ первому п' лѣтъ,
второму п", третьему п'", четвертому п"", чтобы каждый изъ нихъ,
достигши возраста п годовъ, могъ получить з рублей.
Пусть а, Ь, с, б, настоящія пѣны участковъ этихъ наслѣдниковъ, ихъ сум-
ма а-ь-6-ьс-ь-(Е.:8 настоящая цѣна капитала. Возрастъ п лѣтъ совершится:
первому наслѣднику чрезъ п—п' годовъ, второму чрезъ п—п", третьему чрезъ
п—п'", четвертому чрезъ п—п"". При этомъ возрастѣ сдѣлаются:
участокъ перваго=а( 1,04)’—=з, эли: а(І,04)л=з(1,04)я/,
- втораго=1>(1,04)’—=з, Ь(1,04)"=8(1,04)"",
- третьяго=с(1,О4)’1_,'"' = а, с(1,04)п=8(1,04Л""',
- четвертаго=й(1^-"""=з, гі(1,04)п=.->(1;04)""",
Отсюда:
(а-ьбч-с-ѵ<1)(1,04)”=8(1,04)п=э (1,04”'ч-1 ,04”"ч-1,04’‘"'ч-1,04”""),
„ _з(І,04ГІ,-+-1,04в"-Ы ,04""'-Ы,04’'"")
~ (Тэ+)”
Таково отношеніе между 5 и з, въ которомъ, по данному з, всегда найдется 8,
и обратно.
' 23
Пусть первому наслѣднику п' =16 лѣтъ, второму 12| = у, третьему 10 и
четвертому — года; и положимъ, что они, при двадцатилѣтиемъ возрастѣ,
должны получить по 10000 рублей каждый; то будетъ п=20, и 5=10000.
Искомый капиталъ будетъ:
8= ^-^^(104ів-ь(1.04):г-т-1,04“,-г-1,043).
Іо§ 1,04=0,017.03334
16 Іо§ 1,04=0,272,5334, его число 1,87299;
- 1о§ 1,04=0,212,9167.......1,63274;
10 1о§ 1,04=0,170,3334,.....1,48024;
1о§ 1,04=0,130,5889,......1,35079;
Сумма=6,336?6
5,_С3367.6
*УГ ,с Г)“ъ ’
1о§ 63367.6=4,801.8672
20 1о§ 1,04=0,340.6668
4,461.2004=1о§8.
Отсюда, 8=28920,14.
Таковь искомый капиталъ, который теперь надобно положить на приращеніе
процентами, чтобы каждый наслѣдникъ, при 20ги-лѣтнемт возрастѣ, могъ по
лучить 10000 рублей.
— 262 —
Настоящія же цѣны а, Ъ, с, <1, участковъ найдутся изъ отношеній:
а(1,04)2О=«(1,04)‘,і, Ь(1,04)2°=8(1,04)|І
с(1,04)!о=«(1,04)‘оІ <і(1,04)20=«(1 ,04)т,
а именно: а=8548,04
Ь='7451,61
с=6755,64
<1=6164,84.
298. Кома уплачивается какой ни есть вексель до срока, въ немъ означен-
наго, то, ври атомъ, должнику дѣлается соразмѣрное вознагражденіе, называе-
мое учётомъ. Учётъ состоитъ въ исключеніи процентовъ изъ вексельной сум-
мы за все остальное время до срока, или дѣлается по какому ни есть иному
условію съ кредиторомъ.
Положимъ, что вексель, который чрезъ п лѣтъ стоитъ 8 рублей, уплачи-
вается к годами ранѣе срока, то есть, по прошествіи п—к годовъ. Назовемъ
чрезъ его проценты съ рубля въ годъ, которые надобно исключить изъ век-
сельной суммы 8 за остальное время до срока; то настоящая цѣпа векселю, ко-
торую надобно заплатить кредитору, найдется, раздѣливъ 8 на (1-ы)А.
Въ самомъ дѣлѣ, начальный капиталь А, чрезъ п годовъ, сдѣлался бы
8=А(1-ы)"; онъ же чрезъ п—к годовъ былъ бы только 8,=А(1ч-г)п-Л
Отсюда =(1-ы)А, 8'=(Т|^.
Такова должна быть плата за вексель. Разность 8—8'покажетъ величину учёта.
Задача 1. — Вексель въ 4.572,.5 рублей уплачивается тремя годами
ранѣе срока, съ учётомъ по 0,0-5^ съ рубля въ годъ', требуется найти
ею цѣпу къ этому времени уплаты.
4Л2Д
(І.ОэГ
Іое 8'=1о§ 4572,5—3 1о§(1,05)
=3,596.5858 •
8'=3949,89 рублей.
Такова цѣна векселю за три года до срока.
Величина же учёта =8-—8'=622,61 рублей.
Задача 2. —Лѣсной участокъ, отъ насажденія въ немъ лѣса, чрезъ
Ю лѣтъ имѣетъ цѣну бцО рублей серебромъ. Этотъ же участокъ,
чрезъ каждые 20 лѣтъ потомъ можетъ приносить дохооу ТОО руб.
серебромъ, и требуетъ каждогоднаго расхода 7 руб. серебромъ. Спра-
шивается: какъ велика настоящая цѣна этому учистку, т. е. цѣна
въ началѣ перваго года.
— 263
Перемежающійся доходъ 700 рублей, имѣющій ноступить чрезъ 30, 50,
70,.... лѣтъ, въ началѣ 10-го года, при 0,05^- процентахъ въ годъ, имѣетъ
цѣну (стран. 260, зад. 3.)
700 700 /до ОПК
(Т^ТГ = да=4'23’395 РУ°’
Сюда придадимъ цѣпу участка —400 » , ®
получится 823,395 руб.
вся цѣна участка въ концѣ Юто года. Теперь, чтобы найти его цѣну въ началѣ
перваго года, надобно сдѣлать учётъ за 10 лѣтъ-
^=®=505’50 РУМеЙ-
Пзъвтого падобпо исключить расходъ 7X20=140 рублей во исѣ 20 лѣтъ- то и
получится
505,50—140=2365,50 руб. сер.,
настоящая цѣна лѣснаго участка.
399. Вопросъ второй. — Капиталъ А отданъ въ ростъ по г-^ съ
рубля въ годъ,и сверхъ того увеличивается (либо уменьшается) въ концѣ
!-го, 2 го, 3-го,.... года соотвгьтственно количествами а„ а2, а3,... а,„
рублей, кромѣ процентовъ, которые къ нему причисляются; поити,
какъ великъ сдіьлается весь этотъ капиталъ по прошествіи п годовъ?
Капиталъ А чрезъ п годовъ сдѣлается А(1-ы)”;
- - а, - п—1 - - аДІч-г)"-1,
- - а, - и—2 - - аг(1-ы)"-8,
- - - 1 - - а„_і(1ч-г),
- - а„ 0 - - ап.
Слѣдовательно, весь капиталъ, въ копцѣ п годовъ будетъ:
8=А(1ч-г)’Н^а1(1ч-г)п“1ч-а2(Лч-г)”_*ч-.... |,
или, полагай для краткости 1-+-г=го, будетъ:
8=Аго”'і(аІіо"~,ч-а2го"~М-... .-ьа„_1іо-ьа„).
Если а1=а2=а8=....=а, то
8=Аго”±а(го"_,-ьго"_*ч-...............-ыгч-1), или
8=Аіо"±у(го”—1)..........(1)
Знакъ ч- соотвѣтствуетъ случаю, когда капиталъ А каждогодно ^вели-шнается
постоянною суммою а; есіи же онъ каждогодно уменьшается этою суммою, то
надобно взять знакъ —.
Если, по прошествіи п годовъ, не вносится прибавочная сумма а, то изъ
найденнаго капитала 8 надобно будетъ вычесть одно а.
-264
Принимая формулу съ знакомъ -+-, получаемъ:
8=Аго"-і-^(го-1)= 1А^^п-а.................(2)
Отсюда:
А=(8ч--)Л—-........(3)
' т ' и-' г ' '
г(Я—А«і’‘)
Іов(8г-ьо)—Іое(Аг-і-а)
І05 и?
300. Но, положимъ, что капиталъ 5 составляется только изъ суммъ
а, а, а,...., вносимыхъ въ началѣ каждаго года, то эти деньги, по проше-
ствіи годовъ
п, п—1, п—2,.........3, 2, 1, обратятся въ
агѵп, агсп~і, аго"-*,....ап;8, агѵ*, агс,
и, въ сложности, составятъ
$—агѵ(гѵ"+1—Іи>п+і-г-.... ч-мЛ4-гоч-1)
—1)
—•—-—-—-, или
8=-^- (гсп+і—го)........(6)
О тсюда: «— —~—....................(7)
Когда ра'вныя суммы а, а, а,..... впосятся въ началѣ каждаго мѣсяца;
тогда п будетъ означать число мѣсяцевъ, г|- проценты съ рубля за каждый мѣ-
сяцъ, и окончательный капиталъ 8 найдется ло формулѣ (6).
30 Д. Если бы нужно было знать величину капитала не по прошествіи п
годовъ, но въ началѣ п-го года; то, въ началѣ годовъ
п, п—1, п—2,..........3, 2, 1,
капиталы а, а, а,...., вносимые каждогодно, сдѣлаются:
аго"^1, агоп+*, аго”+3,..., аго*, аго, а,
и, въ сложности, составятъ
8—а(го"—*ч-го”—?ч-гоп^'8ч-... .ч-пч-1), пли
8= “ (гоп—1)........... (8)
Отсюда: а~- ...............(9)
п Іо^гс—1оц(8г-ьа)—Іо^а....(10)
— 265 —
302. Положимъ теперь, что капиталъ А, отданный въ ростъ по съ
рубля въ годъ, уменьшается каждогодно количествомъ а, и требуется
знать, во сколько лѣтъ онъ совсѣмъ уничтожится.
Тогда надобпо взять формулу (2) съ знакомъ — предъ а, и положить 8=0;
найдется- (Аг—а)го"-ьа=0; откуда
„ а
гѵ =----— , и
а —Аг
Іо^а—1ой(а—Аг) .
П=------:.............(11)
Іорт 4 •
1
А=у (1-
Аг
а— —
(12).
(13).
303. Перейдемъ теперь къ рѣшенію частныхъ задачъ.
Задача 1. — Капиталъ 8000 руб. сереб. отданъ въ Ломбардъ на
приращеніе процентами по 0,04-^- съ рубля въ годъ, и послѣ каждаго
года увеличивается постояннымъ взносомъ 600 рублей; узнать, какъ
великъ онъ будетъ чрезъ 10 лѣтъ?
Возмемъ формулу (2), и въ нее подставимъ А=8п00, а=600, и=10,
і=0,04, го=І-з-г=1,04; получится:
с (Аг-+-а)»о"—а (8000.0,о4-ь600)1,0410-600
о-- --------------------------------------
0,04
=23000.1,0410—15000.
Іоё 23000.1,0410=1о§ 23000-ьЮ 1оё 1,04
=4,532.0612;
втому соотвѣтствуетъ число 34045,60.
П -такъ, 8=34045,60—15000=19045,60 рублей. Такимъ сдѣлается
весь капиталъ чрезъ 10 лѣтъ.
Если въ концѣ 10 го года не внесено 600 рублей, то ихъ падобно выключить,
и получится:
4 904-5,60—600=1844-5,60 рублей.
Задача 2. — Паііти, какой капиталъ надобно отдать въ ростъ,
по 0,04^ съ рубля въ годъ, чтобы онъ, по прошествіи § годовъ обра-
тился въ 10600 рублей, предполагая, что, послѣ каждаго года, онъ
не только будетъ увеличиваться своими процентами, но еще постоян-
нымъ взносомъ по 300 рублей.
Искомый капиталъ А найдется изъ формулы (3),
. о.І а
— 266 —
подставивъ въ нее 8—10000, а=ЗО0, »=0,04, ад=1,0.4; п=8:
17500
(1,04/
7500=5287,10 рублей.
руб.
Задача 3. — Капиталъ 3600 рублей положенъ въ ломбардъ на при-
ращеніе процентами по 0,04-^; требуется найти, по скольку а рублей
надобно вносить каждогодно, чтобы по прошествіи 10 годовъ соста-
вился капиталъ 10000 рублей.—Это рѣшается формулою (4):
__г(8—Ам>п}
подставляя въ нее 8=10000, А=36ОО, и=10, г=0,04, ю=1,04.
_ 0,04(10000—3600.1,04'°)
а ~ 17О4*°—і ’
1о§ 1,04*°=10 1о§ 1,04=0,170.3334,
1,04*°=!,480244; посему
10000—3328,8784 „сп
й=------7=7-------=389,06
12,0061 ’
По стольку надобно вносить каждогодно, чтобы составился капиталъ 10000
рублей чрезъ 10 лѣтъ.
Задача 4. — Найти во сколько лѣтъ капиталъ 12000 рублей, от-
данный въ ростъ по 0,04^ съ рубля въ годъ, и къ которому каждогодно
прибавляется постоянная сумма 600 рублей, обратится въ 30000
рублей.—Неизвѣстное число лѣтъ опредѣляется формулою (5):
І08(8г-ьв)—Іс^(Аг-і-о)
/ — і
подставляя въ нее8=30000, А=12000, а=600,і=0,04, ю=1,04.Найдется:
Іое 18ОО—Іос ЮЯ0 0,221.8487
----------- =
10^ 1,04------------0,017.0333
п=13,024 года.
Во столько лѣтъ составится капиталъ въ 30000 рублей.
Задача 5. — Извогцгікъ вноситъ 10 рублей серебромъ каждый мѣ-
сяцъ въ сберегательную кассу на приращеніе процентами, по 0,01 X
съ рубля въ годъ, и это продолжаетъ непрерывно 12 лѣтъ; спраши-
вается, какъ великъ составится его капиталъ въ концѣ этого времени?
Если 0,04 проценты въ годъ, то проценты въ мѣсяцъ найдутся, розыскнвая,
. - 1
во что ооратится 1 рубль въ мѣсяцъ или въ — часть года, изъ
(1,04)1’=1-ьг1.
Іо§(1-+-г,)=і1-.0,017.03334=0,001.41944;
14-^=1,003273
г,=0,003273.
— 267 —
Послѣ этого, по формулѣ (6) найдется капиталъ
8— “ («Г"1—»),
подставивъ а=10, г,=0,003273, го=1,003273, п=і2 годовъ =144 мѣся-
цевъ, а именно:
с 10.(1,ОО3273І4В-и) 10.0,602827
0,003273 0~003275
=1841,87 рублей серебромъ.
Таковъ составится капиталъ чрезъ 42 лѣтъ.—Если въ послѣдній мѣсяцъ не
было внесено 10-ти рублей, то ихъ надобно исключить изъ втой суммы, и бу-
детъ 1831,87 руб.
Задача 6..—Вдова, получившая въ наслѣдство капиталъ 9875 руб.
серебромъ, отдаетъ его въ ломбардъ по 0,04^ съ рубля въ годъ, и, по
прошествіи каждаго года, намѣрена получать обратно для своего со-
держанія гго 720 руб. серебромъ. С прошиваете я: во сколько лѣтъ весь
этотъ капшпалъ съ процентами уничтожится (выплатится)?
Годовой процентъ съ этого капитала
=9875X0,04=395 рублей.
Если брать, по прошествіи каждаго года, менѣе 395 рублей, то капиталъ
все еще будетъ увеличиваться. Онъ останется неизмѣннымъ, если бы стали
брать одни его проценты годовые 395; но онъ будетъ уменьшаться, если брать
> 395 рублей послѣ каждаго года. По условію задачи, требуется получать
обратно по 720 рублей, по прошествіи каждаго года; стало-быть, капиталъ
9875, не смотря 'ііа его приращеніе процентами, будетъ уменьшаться. Чтобъ
узнать, во сколько лѣтъ онъ весь истощится, возмемъ формулу (11)
Іося—1од(в —Аг)
П—-------,--------,
Іодю
и въ нее подставимъ А=9875, а=720, г=0,04, го=1,04; получится:
_ Іод720—1од(720 —395)
П Іод 1,04
0,345.1491
^™=20 год.ч-3;мѣсяца.
Слѣдовательно, этотъ капиталъ съ процентами уничтожится чрезъ 20 лѣтъ и
3| мѣсяца.
Задача 7. — Фабрикантъ желаетъ огіреоѣлить, какую сумму денегъ
можетъ онъ занять для поправленія своей фабрики, по 0,06 I съ рубля
въ годъ, съ тѣмъ, чтобы погасить весь этотъ долгъ въ 5 лѣтъ, уплачи-
вая по 1500 руб. серебромъ по истеченіи каждаго года?
Тутъ надобно употребить формулу (12)
Д=а(1-±),
Г ' іс"'
268 —
и въ нее подставить а—1500, т=:(і,06, го—1,06, п—5, получится:
А=25000-ту
Іое 25000=4,397.9400
101о? 1,06=0,126.5295
4,271.4105;
этому соотвѣтствуетъ число 18681,46; слѣдовательно,
А=25000—18681,40=6318,6 рублей.
Такія деньги можно занять по условіямъ задачи.
Задача 8.—Купленъ домъ за 1ОООО рублей серебромъ на такомъ
условіи, чтобы при покупкѣ заплатить только 1500 рублей, а
остальной долгъ 8500 рублей съ его процентами, по 0,05-|, уплатить
равными частями въ теченіе 10 лѣтъ, представляя деньги по проше-
ствіи каждаго гида; требуется найти эту каждогодную уплату. —
Мы найдемъ ее по формулѣ (13):
Аг
а р,
і--------
подставивши А=8500, г=0,05, гс=1,05, п=10; и будетъ
8500.0,05 425 . п„ ОЛ ,
а=----------—-- - =1100,80 рублей сереоромъ.
1 —------
(1,05)'°
Такова должна быть каждогодная уплата для погашенія долга 8500 рублей въ
десять лѣтъ.
Задача 9.—Для прорытія и устройство судоходнаго канала исчи-
сленъ расходъ въ 1000000 рублей серебромъ. Компанія капиталистовъ
беретъ на себя исполненіе этого предпріятія, а въ вознагражденіе за
это получаетъ отъ правительства право пользоваться на 100 лѣтг
пошлиною съ судовъ, которыя будутъ ходить по этому каналу. Спра-
шивается: какъ великъ долженъ быть годовой доходъ отъ сей пошлины
для компаніи?
Эта компанія должна каждогодно выручать по крайней мѣрѣ проценты съ
употребленнаго ею милліона рублей, и еіце доходъ для возвращенія этого капи-
тала. Слѣдовательно’, вся предполагаемая выручка должна быть 8г-ьа, означая
чрезъ 8 употребленный милліонъ рублей, чрезъ а сумму каждогодную для его
погашенія. Эту послѣднюю сумму падобно вычислять по формулѣ (7), потому
что деньги па устройство канала потребны вначалѣ каждаго года:
8г
д=-
Положивъ 8=1000000, г=0,05, и=100, гс=1,05, найдемъ:
__1000000X0,05
, а‘ 1,ОЗ'°'—1,О5
— Э69 —
101Іод 1,05=2,140.1192
1,О51о1=138,076; посему,
а=ш7о2б^364’91 РУ6-
8г-ьа=50000ч-3 64,91=50364,91 рублей.
Такова должна быть годовая выручка отъ этого канала, чтобы можно было
чрезъ 100 лѣтъ возвратить милліонъ рублей съ его процентами.
Но, положимъ, что, не смотря па сдѣланную смѣту, правительство пригла-
шаетъ капиталистовъ къ торгу, посредствомъ котораго желаетъ выиграть себѣ
уступку въ числѣ годовъ сбора пошлины съ судовъ по тому каналу. Компанія,
находя смѣту въ 1000000 рублей серебромъ выгодною для себя даже п
при уменьшеніи времени, дѣлаетъ сбавку па 15 лѣтъ. Спрашивается, сколько
выигрываетъ казна отъ этой сбавки во времени, и какъ велика уступка отъ
компаніи?
Назовемъ чрезъ 8' сумму на устройство канала послѣ сбавки во времени. А
поелику компанія все же должна употребить 1000000 рублей на эту постромку;
то выручка съ судоходства по каналу должпа остаться та же 50364,91 руб. се-
ребромъ, только эта выручка теперь должна состоять изъ годовыхъ процентовъ
съ капитала 8' и суммы а', которою къ ней надобно придать, чтобъ возвратить
этотъ капиталъ въ 85 лѣтъ:
8'гч-а—50364,91, откуда
а'=50364,91—8'г.
Капиталъ 8' найдется по формулѣ (6):
+1—го) изъ которой
‘—го);
8'=-(го
8'г=а'(го"+
да изъ 50364,91—8'г, имѣетъ тоже
8Ѵ=50364,91—а'; стало-бьіть,
а'(го,,+1—го)=5 0364,91 —а'; откуда
, 50364,91
а'—----— .
1-г
Теперь положимъ п=85, г=0,05, го=1,05:
50364,91
° (І.Оа.)110—0,05
86 Іод 1,05=1,822.2798; 1,058в=66,41707;
Послѣ сего найдутся проценты:
8^=50364,91—758,88=49606,03.
8'= ^^=992120,6 рублей
— 270 —
Разность 1000000—992120,6=7879,4 рублей серебромъ представляетъ
4
сбавку отъ компаніи, и выигрышъ въ пользу казны. Опа менѣе у процента съ
милліона рублей.
Задача 10. —Мужъ, въ продолженіе 25 годовъ, вносилъ каждогодно
по 32 рубля серебромъ во вдовью кассу *), съ тѣмъ, чтобы, послѣ его
смерти, жена его, четыре года сряду, могла получать нѣкоторый по-
стоянный доходъ изъ этихъ денегъ и ихъ процентовъ. Чрезъ 25 лѣтъ
мужъ умираетъ; вдова его, 4 года сряду, получаете изъ этой кассы, по
368 рублей серебромъ. Спрашивается: сколько выигрываетъ чрезъ это
вдовья касса?
Не обращая вниманія на проценты, мы пашли бы, что мужъ впесъ въ кассу
32X25=80 рубчей серебромъ, а жена его въ 4 года получила
рубля, и вывели бы изъ этого совсѣмъ ложное заключеніе, что вдовья касса
чрезъ это потеряла 1472—80=^2 рубля. Но, принимая въ соображеніе про-
центы по 0,05^ съ рубля въ годъ, найдется, что, въ теченіе 25 годовъ, отъ
каждогодныхъ взносовъ по 32 рубля, составился въ кассѣ капиталъ (8):
8=-(го"—1)= 32(1-’п05^~-1) =640.2,386355
г * 0,05 •
=1527,2672 рублей.
Эта сумма остается еще на 4 года, по 0,05°, только изъ пея выдается
вдовѣ каждогодно по .368 рублей. По прошествіи 4 лѣтъ, изъ этой суммы
останется (1):
8^=1527,2672.1,05*—
4 Іоё 1,05=4X0,021.1893=0,084.7572
Іое 1527,2672=3,183.9150
3,268.6722
число=1856,402,
1,05*=1,21551;
8'=1856,402—1586,154=270,25 рублей.
Слѣдовательно, вдовья касса не только не потеряла, во еще пріобрѣла
270^ рублей.
*) Кассою вдовьею, сиротскою, пенсіонною, называется такое заведеніе, кдуа всякій
можетъ вносить каждогодно опредѣленную сумму денегъ, чтобы, по прошествіи условнаго
срока либо извѣстнаго числа лѣтъ, пріобрѣсть право себѣ или другому лицу (напримѣръ
вдовѣ по смерти ея мужа, сиротѣ, оставшейся послѣ отца или покровителя, который вно-
силъ деньги въ кассу для будущаго ихъ обезпеченія, и проч.) получить отъ этого заведе-
нія опредѣленный доходъ (пенсіонъ). Такіе доходы называются временными. есіиони
простираются на опредѣленное число сроковъ; но они называются пожизненными, если
прекращаются съ жизнію особы, которая пользуется доходомъ. Съ этою цѣлію въ Россіи
существуетъ Общество застрахованія единовременныхъ капиталовъ или пожизненныхъ
доходовъ. См. въ Руководствѣ къ Политической Ариѳметикѣ, Бруна. Одесса. 1845.
— 271
Задача 11. — Какой капиталъ должно отдать въ сохранную казну
на 15 лѣтъ на приращеніе процентами, чтобы послѣ того 20 лѣтъ
пользоваться каждогоднымъ доходомъ 1000 рублей серебромъ.
Назовемъ этотъ капиталъ чрезъ 8', г=Ю,05 проценты съ рубля въ годъ.
Онъ, по прошествіи 15 лѣтъ сдѣлается =8'(1-ы)1“=8'1,05"і; а чтобы онъ
уничтожился чрезъ 20 лѣтъ, когда будемъ брать каждогодно по 1000 рублей,
надобно чтобъ удовлетворялась формула (12), то есть, чтобъ было
8Ч,05«=^°(1-^).
Чрезъ вычисленіе по логариѳмамъ, или по таблицамъ процентовъ, найдется:
1,05‘6=2,07893; ^=0,37689;
8'.2,07893=20000.0,62311,
8'=6000 руб. сер. (почти).
•
Задача 12. — По скольку рублей х надобно вносить каждогодно въ
сохранную казну въ продолженіе п лѣтъ, чтобы потомъ за это можно
было получать каждогодно доходъ а въ продолженіе т лѣтъ, и при-
томъ въ началѣ каждаго года?
Пусть г? проценты съ рубля въ годъ, 1ч-»=го. Каждогодный взносъ х ру-
блей, вначалѣ п-го года, составитъ (8) капиталъ
7 (Ѵ-1);
а каждогодный доходъ а, который за тѣмъ надобно получить въ продолженіе т
годовъ, соотвѣтствуетъ (12) капиталу
-(1— —),
который долженъ быть равенъ предыдущими ; посему
л(цГ-1)=а(1-^)
. 1 X
Х=~^Г ........
Пусть п—25 годовъ, ш=20, а=700 руб. серебромъ, г=0,05; то
ѵ 1.05го'
Х==' Г/)52“—1
1,05аб=3,38636; ^=0,376885;
700.0,623115
х 2,38636 ^82,78 руб.
Таковъ долженъ быть каждогодный вносъ 25 лѣтъ, чтобы можно было
послѣ того получать доходъ 700 рублей серебромъ каждогодно въ продолженіе
20 годовъ-
272 —
Примѣчаніе. Если вту сумму вносилъ мужъ во вдовью кассу для обезпеченія
своей жены, и умеръ по прошествіи 25 годовъ, то касса обязана 20 лѣтъ сряду
производить его вдовѣ пенсію по 700 рублей серебромъ въ годъ.
Если въ формулу (15) подставить, па мѣсто п, вѣроятпое продолженіе жизни
мужа, опредѣляемое по таблицамъ смертности, а вмъсто т вѣроятное про-
долженіе жизни вдовы послѣ него, то опредълвтся годовой взносъ х рублей, ко-
торые мужъ долженъ вносить въ страховое общество или во вдовью кассу, чтобы
вдовѣ, по смерти его, выдавался пожизненный пенсіонъ 700 рублей серебромъ
каждогодно. •
Задача 13. — Г адовой доходъ а рублей, продолжающійся п лѣтъ,
промѣнять на оругой доходъ а', уплатимый въ т лѣтъ.
Пусть г°0 проценты съ рубля въ годъ; то будетъ '
а .. 1 ,
цѣна перваго дохода = - ——),
- втораго - = у(1—
Они равны; слѣдовательно,
а : а'=1 — 1—
гѵт гѵ
Примѣръ: Годовой доходъ 360 руб. серебромъ, простирающійся па 12 лѣтъ,
замѣнить другимъ а!, уплатимымъ въ 7 лѣтъ.—Здѣсь п=12, ш=7, а=360,
1=0,04, ю=1,04;
, 3“(*-гда>
а=
‘-да
=0,624597; = =0,759918,
“--мГоовя-^562’91 РУ°леи‘
Такой-доходъ можно получать въ теченіе 7 годовъ на мѣсто 360 рублей.
Задача 14. — Для обезпеченія чиновниковъ послѣ 32-лѣтней ихъ
службы пожизненною пенсіею- равною половинѣ ихъ жалованья, какіе
проценты надобно удерживать изъ ихъ жалованья во все это время
службы?
Предположимъ, что производство общественныхъ дълъ ^служба) находится въ
самомъ началѣ своего учрежденія, что въ службу вступаютъ имѣющіе возрасті
23 года, и поймемъ за 1-цу средній окладъ жалованья чиновнику. Таблица
— 273 —
смертности Зюсмимха и Баумана *) показываетъ, что изъ 1000 человѣкъ
родившихся, чрезъ 2-3 года остаются въ живыхъ 476. Возмемъ это число 476
за полный комплектъ чиновниковъ. Та же таблица смертности показываетъ, что
изъ этихъ чиновниковъ, чрезъ 32 года, останутся только 255, имѣющихъ
возрастъ 55 лѣтъ. Это число чиновниковъ, по всей вѣроятности, доживетъ до
пожизненной пенсіи. Такимъ образомъ, спустя 32 года послѣ начала службы,
число пожизненныхъ пенсій будетъ простираться до — = 128 окладовъ
жалованья.
Для приведенія въ дѣйствительность этвхъ пенсій, надобно, чтобы пенсіонная
касса, въ 32 года, чрезъ обращеніе вычетовъ взъ жалованья, пріобрѣла капи-
талъ 8, котораго годовой процентъ равнялся бы 128 окладамъ жалованья, безъ
суммы а всѣхъ вычетовъ за послѣдній годъ, то есть:
8=128—а.
Тогда годичная сумма а вычетовъ опредѣлится уравненіемъ:
8г 128—а
а=------;--= -—.—-.
—гѵ гѵп_НІ—
Сюда подставимъ п=32 года, ад=1,05; получимъ
128—а
откуіа
а= /за —25,85 окладовъ жалованья, что состав-
ляетъ почти 5| со всей штатной массы 476 окладовъ.
Разумѣется, что только, по прошествіи 32 лѣтъ, пенсіонная касса должна
начать производить выдачи пенсій; и если она къ этому времени дѣйствительно
въ томъ успѣете, то ея дѣйствіе обезпечено будетъ на будущее время.
304. Случай. — Если капиталъ А, отданный въ ростъ по съ рубля въ
годъ, увеличивается или уменьшается по а рублей не каждогодно, а періоди-
чески чрезъ 5 годовъ, такъ что первый взносъ послѣдуетъ пе послѣ п—1, но
послѣ п—8 годовъ; то, для вычисленія будущей цѣны 8 этого капитала, соста-
вится рвдъ:
8=Аадп±а(адп-5-і-адп-,5-і-адп-85-і-.......ч-ад^-ь!)
Если а означаетъ періодическую уплату, то надобно взять знакъ —. Чтобы
сумма 8 вся выплатилась, должно положить 8=0; тогда найдется:
а(юп—1) А(ад^—1)
Аад— —---------; откуда а=--------— .
ад»—1
’) Собраніе такихъ таблицъ см. въ Руководствѣ къ Политической Ариѳметикѣ Бруиа.
18
— 274 —
Примгръ.—Купленъ лѣсъ за 3000 рублей серебромъ, съ условіемъ, чтобы
покупщикъ выплатилъ эти деньги въ три равные срока, а именно: въ копцѣ 4, 8
и 12 годовъ; узнать, сколько онъ долженъ платить въ эти сроки, полагая про.
центы 0,04 съ рубля въ годъ?
Здѣсь и=12 лѣтъ всей уплаты.
5 —4—годичные сроки;
3000(1,04*—і, 3000.0,16986 .
а= 1_ =і-о.б2ібо =1357’4 РУ6 серебромъ.
1,04»
Такова должна быть періодическая уплата чрезъ каждые 4 года, чтобы по-
гасить весь долгъ въ 3000 рублей серебромъ.
ГЛАВА ОДИНАДЦАТмЯ.
ПЕРЕЛОЖЕНІЯ, СОЧЕТАНІЯ, И РАЗЛИЧНЫЯ СОЕДИНЕНІЯ ИЗЪ ДАННАГО
ЧИСЛА БУКВЪ, II ОПРЕДѢЛЕНІЕ ИХЪ СУММЫ.
?О5. Въ пауьѣ, искусствахъ, и частной жизни вообще, не рѣдко встрѣчают-
ся такіе вопросы, для разрѣшенія когорыхъ необходимо нужно знать, сколько
изъ даннаго числа а, Ь, с,.... предметовъ можно сдѣлать различныхъ перемѣ-
щеній, располагая ихъ одинъ за другимъ; сколько можно сдѣлать всякпхь соче-
таній изъ этяхъ предметовъ, совокупляя ихъ по два, по три, и т. д., или сколь-
ко различныхъ соединеній. Часть Алгебры, въ которой содержится ученіе объ
этомъ предметѣ, называется Сиптактикою. Предметы для переложеній пли
совокупленія изображаются буквами, а въ частныхъ случаяхъ цифрами.
306. АІежду данными предметами а, Ь, с,.... можно дѣлать перестановле-
нія, сочетанія безъ повтореній пли съ повторенія»!в, и различныя соединенія безъ
повтореній либо также съ повтореніями.
Йеремѣщеніями (переложеніями, перестановленіями, Реппиіаііопз) назы-
ваются выводы, получаемые отъ расположенія даннаго числа предметовъ пли
буквъ, однѣхъ за другими, всевозможно различными образами. Въ каждомъ вы-
водѣ находятся всѣ данныя буквы, н<? ихъ расположеніе различно. Напримѣръ
двѣ буквы а, Ь, даютъ только два перемѣщенія аЬ, Ьсг, изъ трехъ буквъ а, Ь, с,
можно сдѣлать только шесть перестановленіи аЬс, асЪ, Ьас, Ьса, саЪ, сЬа.
Э75 —
Сочетаніями (Ѵагіаііопз, аггап^етепв) называются всѣ выводы, какіе мо-
жно получить изъ даннаго числа буквъ, совокупляя ихъ всевозможными образами
по двѣ, по три,... *), напримѣръ пзъ трехь буквъ а, Ь, с, совокупляя ихъ по
двѣ, можно сдѣлать шесть сочетаній
аЬ, ас, Ьс,
Ьа, са, сЬ,
безъ повторенія той же буквы.
Соединеніями (СоіпЬіпаівопв), или различными произведеніями назы-
ваются такія сочетанія взъ даннаго числа буквъ по двѣ, или по три, и т. д.,
которыя состоятъ пзъ равнаго числа буквъ, но различаются одно отъ другаго
хотя одною буквою. Напримѣръ изъ трехъ буквъ а, Ь, с можно составить двой-
ныхъ соединеній, безъ повторенія той же буквы, только три аЬ, ас, Ьс; изъ
четырехъ буквъ а, Ь, с, й, не дѣлая повторенія буквъ, можно составить шесть
двойныхъ сединеній:
аЬ, ас, ад, Ьс, Ьд, сд;
а тропныіъ соединеній будетъ только четыре:
аЬс, аЬд, асд, Ьсй.
309. А. Найти число перемѣщеній изъ даннаго чиста т буквъ.
I) Коіда всѣ т буквъ различны. — Въ этомъ случаѣ число или сумма
перемѣщеніи всегда равна произведенію чиселъ, составляющихъ прогрессію
1, 2, 3,.... до т, то есть.
Р(?и)=1.2.
И дѣйствительно, изъ двухъ буквъ а. Ь, можно сдѣлать два перемѣщенія
аЬ, Ьа, то есть:
Р(2)=1.2
Изъ трехъ буквъ а, Ь, с, можно сдѣлать только шесть перемѣщеній: ибо мы
знаемъ, что буквы Ь, с, даютъ два перемѣщенія Ьс. й; приписавъ къ нимъ па
первомъ мѣстѣ букву а, получатся также два переложенія аЬс, асЬ. А какъ вся-
кая буква можетъ быть поставлена па первомъ мѣстѣ, а всѣхъ буквъ трв; то
очевидно, что число всѣхъ перемѣщеній изъ трехъ буквъ а, Ь, с, будетъ д^а
повторенное три раза, то есть, •
Р(3)=2ХЗ—-і .2.3'.
Изъ четырехъ буквъ можно сдѣлать 24 перестановленія Потому что пзъ
трехъ буквъ Ь. с, д, получаются 6 переложеній; столько же будетъ, если при
каждомъ изъ нихъ поставимъ букву а на первомъ мѣстѣ. А какъ всѣхъ буквъ 4,
*) Такія сочетанія дѣлаются или чрезъ сложеніе буквъ по двѣ, по три,.... или тпліко
чрезъ вычитаніе между ними, чрезъ умноженіе, и проч.
— 276 —
в каждая можетъ быть на первомъ мѣстѣ относительно прочихъ, то число всѣхъ
перемѣщеній будетъ шесть взятое 4 раза, то есть,
Р(4.)=6Х4-=1.2.3.4.
Такимъ же образомъ найдемъ, что изъ пяти буквъ а, Ь, с, Л, е, мож.ю со-
ставить
Р(5)=е1.2.3.4.5 переложеній.
II, наконецъ, вообще изъ п буквъ число переложеній будетъ:
Р(п)=1 23.4....Я.
2) Когда . между данными п буквами находятся нѣкоторыя рав-
ныя.—Возмемъ сочетаніе аааЬсбе, въ которомъ изъ семи буквъ находятся три
равныя. Если бы три первыя буквы ааа были различны, то онѣ сами по себѣ
дали бы шесть разныхъ переложеній. А приписавъ остальныя четыре буквы
ЬсЛе иа послѣднемъ мѣстѣ каждаго изъ этихъ переложеній, мы получили бы
шесть же переложеній изъ всѣхъ 7—ми буквъ, въ которыхъ сочетаніе Ьсйе за-
нимало бы послѣднее мѣсто. Но эти шесть, при равенствѣ трехъ первыхъ, обра-
щаются только въ одно переложеніе. То же самое произойдетъ и со всѣми пере-
ложеніями, въ которыхъ буквы Ь, с, <1, е будутъ расположены въ другомъ по-
рядкѣ, и будутъ занимать другія мѣста. Пзъ этого слѣдуетъ, что въ нашемъ при-
мѣрѣ число перемѣщеній будетъ въ шесть разъ менѣе, нежели въ томъ случаѣ,
когда бы всѣ буквы были разныя. Посему, искомое число переложеній будетъ
Р(7) __ 1.2.3.4.5.6.7
Р(3).і“ Ті .з.і.і.і ‘
Для втораго примѣра возмемъ сочетаніе аааЬЬйе. Въ пемъ, кромѣ трехъ пер-
выхъ буквъ равныхъ, находятся еще двѣ равныя буквы Ь, Ь, вмѣсто различныхъ
Ь, с, какъ было въ предыдущемъ примѣрѣ; а потому два переложенія Ьс, сЬ,
обращаются въ одно, и уменьшаютъ предыдущее число переложеній въ два раза.
Отчего, искомое число переложеній будетъ
Р(7) __ 1.2.3.4.5.6.7
Р(3)Р(2). 1» 1.2.3.1 2Л.'
И вообще, если между п буквами находится одна буква г разъ, другая р разъ,
третья у разъ, то чвсло перемѣщеній будетъ
Р(п) ____ 1.2.3.4..п
Р(Р)Р(?)Р(Г) — 1.2 ..рх«.'2..^.<1.2 ..г •
Примѣръ. — Сочетаніе 111122233333, состоящее изъ 12 цифръ, допу-
скаетъ число переложеній:
_ _5^>_ -Е*8?-..........«________-27720
Р(4)Р(3)Р(5) 1.2. хі.2 3х*-2.3.4.5
Примѣръ.—Слово «Математика» имѣетъ 10 буквъ, изъ которыхъ м и іи
находятся по два раза, и а три раза А потому изъ этихъ буквъ можно сдѣлать
число переложеній:
— 277 —
р(*°) __ 1.2.3.4.8.6.7.8.9.10
Р(2)Р(2)Р(3) І.2.І.2.І.2.3.1.1.1 —
Примѣръ. — Найти число переложеній изъ буквъ имени Імсиііиз
Это число будетъ:
1.2.3.О.6.7.8
• 1.2.3.1.2.3.1.1
В. Найти число всѣхъ сочетаній изъ п буквъ, взятыхъ но двѣ, но три,
□ О ЧЕТЫРЕ, И, ВООБЩЕ, ПО Г БУКВЪ.
1) Безъ повторенія той же буквы въ каждомъ отдѣльномъ сочетаніи.
Возмемъ число п буквъ а, Ь, с, <!,.... для составленія разныхъ сочетаній.
Счвтая по одной буквѣ, получаемъ п разныхъ количествъ.
А чтобы найти всѣ сочетанія этихъ буквъ по двѣ, безъ повтореній, возмемъ
сперва букву а, и припишемъ ее къ каждой изъ прочихъ п—1 буквъ:
а I Ь, с, б, е........
получатся п—1 сочетаній
аЬ.ас,ай,.... по двѣ буквы.
Потомъ возмемъ букву Ъ, и припишемъ ее къ каждой изъ прочихъ п—1 букв ь:
Ь
а, с, Л, е
получается еще п—1 сочетаній
Ьа, Ьс, Ьй...., по двѣ буквы.
Отдѣляя такимъ образомъ каждую букву, и соединяя съ каждою изъ прочихъ,'
получимъ столько разъ п—1 двойныхъ сочетаній, сколько всѣхъ буквъ, то есть,
п{п—1). Это число сочетаній изображается знакомъ
Ѵ,(п)=п(п—1).
Въ немъ находятся пе только различныя двойныя соединенія, но и одинакія,
различающіяся только перестановкою буквъ, таковы: аЬ, Ьа, ас, са, Ьс, сЬ,...
Для полученія всевозможныхъ сочетаній изъ п буквъ по три, безъ повторе-
ній, будемъ брать каждое двойное сочетаніе аЬ, Ьа, ас...., и ко всякому припи-
сывать каждую изъ остальныхъ п—2 буквъ:
аЬ с, й, е п—2 сочетаній въ каждой строкѣ аЬс, аЬ(1, аЬе
Ьа с, й, е Ьас, Ьай, Ьае
ас Ь, й, е асЬ, асй, асе..,..
Ьс а, б, е Ьса, Ьсй, Ьсе
Въ каждой строкѣ получится п—2 сочетаній по три буквы, этихъ строкъ
будетъ п(п—1), потому что столько всѣхъ сочетаній двойныхъ изъ п буквъ;
слѣдовательно число всѣхъ тройныхъ сочетаній будетъ п—2, повторенное
п(п—1) разъ, то есть:
Ѵ,(п)=п(п—1) (п—2).
— 2,8 -
Такимъ же образомъ нашли бы, что число сочетаній изъ п буквъ по четыре
равно
V. (и)=п (п—1) (п—2) (п—3).
II наконецъ, вообще, число сочетаній изъ п буквъ по г, безъ повтореній,
очевидно, будетъ
Ѵг(п)=«(п — і)(п—2)......(п—гч-1).
2) Число сочетеній изъ п буквъ а, Ь, с, й,...., съ повтореніями
каждой.
Для полученія двойныхъ сочетаній съ повтореніями, беру букву а, и къ
ней приписываю каждую изъ п буквъ:
а , а, Ъ, с,... получаю аа, аЬ, ас.....всего п,
Ь [ а, Ь, с,... - Ьа, ЪЬ, Ьс,.... - п,
И такъ, отъ совокупленія каждой буквы, получается п сочетаній; а какъ
всѣхъ буквъ п, то число двойныхъ сочетаній съ повтореніями будетъ «Xй—
Это будемъ писать такъ .
Ѵ±((п))=П*.
Всѣ сочетанія по три буквы, съ повтореніями, найдутся, если ко всѣмъ
двойнымъ сочетаніямъ припишемъ сперва а, потомъ Ь, с,....; отъ этого числа
п8 двойныхъ сочетаній, при переходѣ ихъ въ тройныя, повторится столько разъ,
сколько всѣхъ буквъ а, Ь, с,...., то есть, п разъ; и найдется всѣхъ сочетаній
тройныхъ, съ повтореніями, п8Хп—или
ѴД(п))=п3; ‘
и такъ далѣе. Наконецъ, число всѣхъ сочетаній ’съ повтореніями, изъ п буквъ
по г, очевидно, будетъ
Ѵ,.((п))=пг.
С. Найти число различныхъ, совокупленій или произведеніи (сомвімаі-
5ОИ8) двойныхъ, ТРОЙНЫХЪ,......... ИЗЪ ДАПИАГО числа п БУКВЪ.
1) Число различныхъ совокупленій безъ повтореній.—Опо всегда равно
числу сочетаній, взятыхъ безъ повтореній, раздѣленному па число перемѣщеній,
какое даютъ оуквы, входящія вь каждое сочетаніе. Такъ будетъ число различ-
ныхъ произведеній, безъ повтореній,
п(п —1)
двойныя ь ,
тройныхъ =
п(п—1)(п—2)
1 . 2~. 3 ’
четверныхъ —
п(п—1)(п—2)(п—3;
1.2 .3 . 4
— 279
Въ самомъ дѣлѣ, мы уже знаемъ, что число всѣхъ двойныхъ сочетаній (безъ
повтореній) изъ п буквъ =Ѵ5(п)=п(»г—1); но каждыя двѣ б}квы даютъ
1.2=2 одинакихъ произведеній (аЬ, Ьа, ас, са,....), то очевидно, іто различ-
ныхъ двойныхъ произведеній или совокупленій будетъ вдвое менѣе, то есть,
П(П —<) гч
-—-—. «/го выражается знакомъ
Число всѣхъ сочетаній по три буквы, безъ повторенія, =п(п—1)(п—2).
Но каждыя три буквы даютъ 1.2 3=6 равныхъ перемѣщеній, то есть, равныхъ
тройныхъ сочетаній, отличающихся одною іерестаповкою буквъ; посему раз-
личныхъ тройныхъ совокупленій должно быть въ 6 разъ менѣе, а именно: .
Найдется также число различныхъ произведеній, безъ повторенія, пзъ п
буквъ по 4,
Р п(п — 1)(п—2)(п—3)
С-(П)=Т.7-. з . Г •
И, наконецъ, вообще, число различныхъ совокупленій изъ п буквъ по г, будетъ
Г ! \ ' »Ч‘П—1)(п—2)..(п—г-ьі)
— і 2 . 3...........п
Примгьрб. Найти различныя двойныя и тройныя произведенія изъ чиселъ
1, 2, 3, 4, 5, 6, безъ повтореній.
6.5
Число двойныхъ произведеній будетъ С/І/.б^р^ =15, а именно:
1.2, 1.3, 1.4, 1.5, 1 6
2.3, 2.4, 2.5, 2.6
3.4, 3.5, 3.6
4.5, 4 6
5.6
Число тройныхъ произведеній С3(1„6)= —20, а именно:
1.2.3, 1.2.4, 1.2.5, 1.2.6 і
1.3.4, 1.3.5, 1.3.6 .
1.4.5, 1.4.6 ( — °
1.5.6 )
2.3 4, 2.3.5, 2.3.6 I
2.4.5, 2.4.6 (= 6
2.5.6 )
3.4.5, 3.4.6 I ч
3.5.5 )
4.5.6 |= 1
280
2) Число всевозможно различныхъ совокупленій или произведеній изъ
числа п буквъ, съ повтореніями каждой.
Здѣсь поступимъ такъ:
1. Напишемъ данныя буквы а, Ь, с,... одну подъ другою въ одной верти-
кальной графѣ; число ихъ =п.
2. Будемъ совокуплять каждую букву самое съ собою., и съ каждою изъ буквъ
строкъ предшествующихъ: получатся всѣ двойныя совокупленія съ повторе-
ніями. Число ихъ будетъ =(ч-2ч-3-ь... .
3. Потомъ будемъ совокуплять начальную букву (что въ вертикальной пер-
вой графѣ) каждой горизонтальной строки съ соединеніями двойными, находя-
щимися только въ этой строкѣ и во всѣхъ строкахъ предшествовав-
шихъ: получатсн всѣ соединенія тройныя съ повтореніями. Число ихъ бу-
. о л лл п(п-ь1Цп-»-2)
детъ = Іч-Зч-бч-ІОч-... ; и т. д.
1. 2 » О
а 1 аа; 1. ааа; 1
Ь 1 ЬЬ, аЬ; 2 ЬЬЬ, аЬЬ, ааЬ; 3
с 1 сс, Ьс, ас, 3 ссс, Ьс1, ас1, Ь*с, аЬс, аас; 6
а 1 (Ій, сй, Ьй, ай; 4> Мй, ыГ, .......................... 10
• п
Вездѣ число строкъ —п.
Одинъ взглядъ на эту табличку показываетъ, что въ послѣдовательныхъ стро-
кахъ числа различныхъ двойныхъ соединеній, съ'повтореніями, составляются
чрезъ суммоваиіе ряда членовъ первой степени, изображенныхъ единицами;
числа тройныхъ соединеній въ каждой строкѣ получаются чрезъ суммоваиіе чи-
селъ соединеній двойныхъ, выраженныхъ прогрессіею 1, 2, 3,....п; и т. д.
Стало-быть, сумма различныхъ совокупленій, съ повтореніями,
по одной буквѣ;....=п;
Сумма двойныхъ совокупленій =1ч-2-+-Зч-....п
Сумма тройныхъ совокудленій =Лч-3-+-6ч-10-+-....
___^/пч-1)(п-+-2)
1.2.3
и такъ далѣе.
Для этихъ соединеній, мы употребимъ знаки:
С,((п))—и,
с,((»»=^±ч,
С.((”))=ГГ^ІІ|П^ЗД. • вообще,
— 281
Примѣръ. Найти число двойныхъ и тройныхъ совокупленій изъ пяти чиселъ
1, 2, 3, 4, 5, съ повтореніями.
Число двойныхъ соединеній будетъ
С5((1/,5))=-^|=15, а именно:
11, 12, 13, 14, 15,
22, 23, 24, 25
33, 34, 35
44, 45
55.
А число тройныхъ совокупленій будетъ
С»((1„5))=тѵІ=35, таковы:
1 .ло
111, 112, 113, 114, 415, 222, 223, 224, 225
122, 123, 124, 125 233, 234, 235
133, 134, 135 244, 245
144, 145 255
155
333, 334, 335 444, 445, и 555
344, 345 455
355
309. ЗАДАЧИ,
/. Найти число переложеній изъ пяти буквъ, аЬсіІе, гдѣ буква а зани-
маетъ первое мѣсто, и число тѣхъ, гдѣ аЬ находится на первомъмѣстѣ.
Если а занимаетъ постоянное мѣсто, то остальныя четыре буквы Ь, с, б, е,
дадутъ 1.2.3.4=24 переложенія; а если аЬ занимаетъ первое мѣсто, то буквы
с, А, е, дадутъ 1.2.3=6 перемѣщеній.
2. Даны буквы ааЬЬЬс; найти, сколько можно сдѣлать перемѣщеній,
которыя начинаются буквою а, сколько перемѣщеній начинаются бук-
вою Ь, и сколько буквою с.
Если отнять оукву а, то осгальнын пять дадутъ ————=20 перемѣщеніи;
столько же перемѣщеній будетъ, если къ каждому изъ нихъ приписать сначала
отнятую букву. Если же поставить букву Ь на первомъ мѣстѣ, то она съ про-
1-2. .1.4 □ _ _ т.
чими пятью даетъ =30 перемѣщеніи. Ьуква с, поставленная на пер-
вомъ мѣстѣ, даетъ
- =20 перемѣщеній.
3. Изъ восьми тоновъ СіВЕЕСАНС, діатонической гаммы сколько
можно сдѣлать различныхъ перестановленій?
Отвѣтъ: 1.2.3.4.5.6.7.8=40320 перестановленій.
282 —
4 Изъ четырехъ тоновъ С, Е, 1), С, въ одной октавѣ сколько можно
сдѣлать разныхъ перемѣщеній, предполагая, что каждый изъ нихъ дол-
женъ войти по два раза?
Всѣхъ тоновъ, совокупно съ повторяющимися, будетъ восемь: ССЕЕООСС, а
потому число перемѣщеніи будетъ
1.2.34.3.6.7.8
1.2.1.2.1.2.1.2
•5. Сколькими способами можно раздѣлить между шестью отличив-
шимися воспитанниками шесть наградъ, изъ коихъ одна перваго до-
стоинства, двіь—втораго, а три третьяго достоинства?
_ Р(6) 1.23.4.5.6
Отвѣтъ: =,ат„= = , і » „=60-10 спосооами.
1 1 2.1,2.3
6. Найти, сколько разныхъ видовъ получитъ флагъ, если раскрасить
его па три горизонтальныя поля осьмыо главными красками, употреб-
ляя при этотъ либо краски различныя, либо же и одинакія?
Отвѣтъ: въ первомъ случаѣ Ѵ3(8) =8.7.6=336;
а во второмъ Ѵ3((8))= 83 =512.
7. Изъ 1х членовъ общества, избираются по жребію четверо для ка-
кой ни есть должности; найти, сколько здѣсь можетъ быть разныхъ
случаевъ выбора?
Отвѣтъ: С4(12)=-— - =495 случаевъ.
<9. Паны 10 точекъ въ пространствѣ. расположенныхъ такъ, что
изъ инхъ нѣгпъ даже трехъ, которыя бы находились на одной прямой
линіи: узнать, сколько можно провесть прямыхъ линій отъ каждой ко
всѣмъ прочимъ, или, сколько можно провесть плоскостей чрезъ каждыя
три точки? •
10.9
Отвѣтъ-, всѣхъ линіи 0,(10;=—’2 =45,
и всѣхъ плоскостей С5(10)=-^Ц=І20.
,9. Подрядчикъ, имѣя 6 работниковъ, отпускаетъ каждодневно на нгь-
копгорую постоянную работу только четверыхъ. Онъ платитъ всѣмъ
работникамъ вдругъ всякій разъ, когда они всѣ побываютъ на этой ра-
ѵотіь по равному числу дней. Найти, чрезъ сколько дней надобно имъ
выдавать деньги?
Отвѣтъ: чрезъ ^'~"4 =15 дней.
Если бы при этомъ требовалось узнать, сколько разъ въ эти 15 дней каждый
работникъ долженъ быть на работѣ? отвѣчаю: столько, сколько можно сдѣлать
различныхъ совокупленій изъ остаіьныѵь пяти работниковъ по три, къ которымъ
этотъ шестой присоединяется, то есть, чрезъ
5.4.3 -Л
1.2І=10 ДНеИ
— 283 —
ГЛАВА ДВѢНАДЦАТАЯ.
НАЧАЛЬНЫЯ ПОНЯТІЯ ОБЪ ИСЧИСЛЕНІИ ВѢРОЯТНОСТЕЙ.
309. Въ природѣ находится множество ожидаемыхъ событій, которыхъ бо-
лѣе или менѣе скорое появленіе (исполненіе) зависитъ отъ извѣстнаго числа
случаевъ или обстоятельствъ, равно возможныхъ. О томъ, что извѣстное явте-
ніе или событіе скорѣе произойдетъ, нежели не произойдетъ, мы судимъ по числу
случаевъ, благопріятныхъ его сбыточности, и такимъ образомъ приводимся къ
болѣе или менѣе вѣроятному ожиданію того явленія. Исчисленіе вѣроятностей
состоитъ въ опредѣленіи степени вѣроятности ожидаемаго происшествія. Эго
исчисленіе основано въ половинѣ 17-го вѣка Паскалемъ, Ферматомъ, Гюйген-
сомъ; потомъ оно боліе развито Яковомъ Бернулли, Монмартромъ, Моапромъ,
Д’Аламбертомъ, Эйлеромъ въ 18-ыъ вѣкѣ; а въ 19-мъ вѣкѣ усовершенство-
вано преимущественно Лапласомъ, Гауссомъ, Лежандромъ и Пуасопомь.
310. Для исчисленія вѣроятпостей, надобно имѣть способъ выражать вся-
кую вѣроятность пропорціональнымъ ей числомь. Для этого, простую, абсо-
лютную вѣроятность ожидаемаго событія (явленія, происшествія, приключе-
нія) согласились выражать отношеніемъ всѣхъ случаевъ, благопріятныхъ этому
событію, ко всѣмъ случаямъ, отъ которыхъ оно зависитъ и когорые псѣ равно
возможны. Стало-быгь, ее изображаютъ дробью, у когорой числитель показы-
ваетъ число всѣхъ случаевъ (статочностей), благопріятныхъ исполненію событія,
а знаменатель — число всѣхъ случаевъ возможныхъ. Для примѣра, возмемъ
костяной кубъ, котораго грани отмѣчены очками 1, 2, 3, 4, 5, 6, и броспмъ
его; то вѣроятность, что на верхпей грави куба вскроется опредѣленная цифра,
нанрим. 3, равна ; потому что число случаевъ, благопріятныхъ выхоіу этой
цифры, равно 1-цѣ, а число всѣхъ случаевъ возможныхъ =6. Но, вѣроятность,
что на кубѣ вскроется которое нибудь изъ двухъ данныхъ чиселъ (нанрим. 2
2 1
или 4-), равна — = у, и т. д.
Отсюда видно, что вѣроятность иеполпенія желаемаго или ожидаемаго про-
исшествія становится тѣмъ больше, чѣмъ болѣе становятся числитель, прибли-
жаясь къ равенству съ знаменателемъ, то есть, чѣмъ ближе подходитъ число
случаевъ благопріятныхъ къ равенству съ числомъ всѣхъ статочностей равно-
возможныхъ. Когда между всѣми возможными случаями не будетъ ни одного не-
благопріятнаго ожидаемому происшествію, т. е. когда всѣ случаи благопріятны;
— 284 —
тогда дробь становится единицею, и вѣроятность обращается въ достовѣр-
ноетъ, такъ что единица служитъ символомъ достовѣрности, къ котороИ
чистая вѣроятность можетъ только приближаться болѣе или менѣе.
311. Много находится такихъ явленій въ различныхъ происшествіяхъ, сбы-
точяость которыхъ въ данное время зависитъ отъ извѣстныхъ намъ всѣхъ слу-
чаевъ благопріятныхъ и всѣхъ случаевъ равно-возможныхъ: къ такимъ собы-
тіямъ относится вышеприведенный примѣръ. Опредѣленіе степеней вѣроятности
такихъ событій составляетъ то, что называются исчисленіемъ вѣроятностей,
въ тьсномъ смыслѣ взятомъ, и объ немъ собственно мы говорить будемъ.
Но, если число случаевъ благопріятныхъ, или возможныхъ, илп тѣхъ и другихъ
не совсѣмъ извѣстно, а только извѣстны предѣлы, между которыми всѣ статоч-
ности заключаются, и требуется паити вѣроятность изъ многихъ данныхъ наблю-
деній, приближенно выражающихъ ходъ событія; тогда вопросъ обсуживается
совсѣмъ иначе, по способу наименьшихъ квадратовъ, о чемъ говорить не
будемъ, какъ о предметѣ, требующемъ знаніе высшей Математики *).
Даже и тогда, когда число случаевъ благопріятныхъ событію и число статоч-
ностей возможныхъ бываетъ вполнѣ извѣстно, вѣроятность имѣетъ разные виды;
она бываетъ: простою, относительною, сложною, и проч.
1. Простая или абсолютная вѣроятность.
319. Простая или абсолютная вѣроятность выражается отношеніемъ
числа всѣхъ случаевъ, благопріятныхъ ожидаемому событію, къ числу всѣхъ
случаевъ ранно-возможныхъ. Посему, ежели изъ числа К случаевъ, равно воз-
можныхъ, находится только п случаевъ, благопріятныхъ исполненію какого вв-
есть ожидаемаго происшествія, а —п число случаевъ ему неблагопріят-
ныхъ; то абсолютная вѣроятность въ пользу происшествія будетъ
к
Вѣроятность же, что этого происшествія не воспослѣдуетъ, но оудутъ случаи I
ему противные, и потому называемая вѣроятностью противною ожидаемому ।
событію, будетъ
УѴ'—-I п
М ~ И — Л’
Сумма этихъ обѣихъ вѣроятностей равна единицѣ,
*) Подробное изложеніе о вѣроятностяхъ можно найти въ превосходномъ сочиненіи!
Основанія математической теоріи вѣроятностей, Академика 3. Я. Буняксвскаго.
С. Петербургъ, 18*6 года.
— 285 —
то есть, извѣстности; ибо совершенно извѣстно, что изъ всѣхъ возможныхъ слу-
чаевъ одинъ какой ни есть, благопріятный или неблагопріятный, долженъ
выйти, если только самое происшестіе должно быть необходимо.
Гаданіе объ исполненіи событія, опредѣляемое вѣроятностію, называется
вѣроятнымъ, сомнительнымъ, или.пало вѣроятнымъ, смотря потому, бу-
і і . і
детъ ли эта вѣроятность > -, или — -, или <
Примѣръ. Дана полная, хорошо перемѣшанная колода, состоящая изъ 52
игральныхъ картъ, найти слѣдующія вѣроятности:
1) Вынуть изъиее карту чернаго цвѣта. Здѣсь вѣроятность XV — потому
что картъ чернаго цвѣта во всей колодѣ половина.
13 1
2) Вынуть карту трефовую. Здѣсь XV = —потому что всѣхъ тре-
фовыхъ картъ 13. Противная же вѣроятность, что вынется карта не трефовая,
дѵ,-52-23 _ з
82 4"
12 3
3) Вынуть фигуру. ХѴ= — — —; потому что всѣхъ фигуръ въ колодѣ
12 Вѣроятность XV' противнаго, то есть, что фигура не вынется, будетъ
ѴѴ/-іо_. ю
82 13’
4 1
4) Вынуть тузъ. ХѴ= — = —. Противная вѣроятное™, что тузъ левы-
10
48 12
нется, ХѴ'=- = ^.
5) Вынуть тузъ пиковый. ХѴ= —.
Во всѣхъ этихъ случаяхъ \Ѵ'=І—XV, или ХѴ-ьХѴЪ^І.
Примѣръ.—Возмемъ два игральныхъ куба А и В, которыхъ грани отмѣчены
по порядку очками илн цифрами 1, 2, 3, 4, 5. 6. Если кидать эти два куба
вмѣстѣ, то, вообще, могутъ выпасть на обоихъ кубахъ слѣдующія 36 паръ
цифръ или 36 случаевъ:
АВ
АВ АВ
АВ
АВ
АВ
11
21,
6.1
12
22,
52,
13
23
33
43
24
25
44
35
45
55,
65,
36,
46
56,
1
2
— 286 —
Впрочемъ, и безъ этой таблички знаемъ, что изъ шести цифръ можно сдѣ-
лать число сочетаній по двѣ, съ повтореніями, равное
Ѵ8((1„6))=62=36.
По этому, вѣроятность, что за одинъ разъ выпадутъ: цифра 2 на кубѣ А, и
I
цифра 5 па В, будетъ ѴѴ=- ; потому что всѣхъ случаевъ 36, а 2 и 5 сосг
вѣтствуютъ одному случаю.
Вѣроятность, что за одинъ разъ па обоихъ кубахъ вскроются числа 2 и э. на
какомъ бы кубѣ эти числа пи получились, будетъ ДѴ= - = ; потому что
36 18 4
благопріятныхъ случаевъ можетъ быть два:
можетъ выйти на А число 2, либо 5,
- - В - 5, - 2.
Противная вѣроятность, что за одинъ разъ не вскроются цифры 2 и 5 на
обоихъ кубахъ, будетъ
— — —
36 18*
Но, для частнаго случая, чтобы па обоихъ кубахъ вышли за-разъ два равныя
числа (пашъ), наприм. 2 и 2, вѣроятностью будетъ \Ѵ=^.
Для случая, чтобы сумма чиселъ, выпавгаихь па обоихъ кубахъ, равнялась?,
имѣется шесть благопріятныхъ случаевъ (см. въ табличкѣ по діагональной
строкѣ подъ п° 6); а потому
в =1, и АѴ'=^ = ”.
36 6 х 36 6 .
Для случая, чтобы эта сумма равнялась 5, будетъ ѴѴ= ~ ’ , и
потому что возможны 1 случая благопріятныхъ (см. въ діаго-
нальной строкѣ подъ п° 4) И такъ далѣе.
Вѣроятность, что іга двухъ кубахъ выпадетъ такъ называемый пашъ (два
какія пи есть равныя числа), очевидно,
ЛѴ ' 6 1 30 3
\\ 2= - - = - , и \Ѵ- — —
36 6 ’ 36 6 ’
потому что шесть случаевъ возможны.
Изъ предыдущей таблички еще видно, что изъЗб возможныхъ случаевъ только
въ одномъ случаѣ выпадаетъ сумма 2 на обоихъ кубахъ,
въ 2-хъ - - 3 - -
- 3-хъ - - 4 - -
- 4 -хъ - - 5 - - .
- 5-ти - - - 6 - -
- 6-тн — — - 7 - -
- 5-тп - - - 8 - -
- 4- ъ - - -9 - -
- 3-хъ - - - 10 -
- 2-хъ - - - 41
- 1-мъ - - - 12 - -
287
Откупа видно, что наибольшая вѣроятность соотвѣтствуетъ суммѣ 7, а пан
меньшая суммамъ 2 и 12.
Примѣръ. — Возмемъ теперь три игральные куба А, В. С, и поищемъ вѣ-
роятности для случаевъ: 1) чтобы на всѣхъ кубахъ, брошенныхъ во одно
время, выпала сумма 9; 2) чтобы въ этой суммѣ выпали два равныя
числа; 3) чтобы выпали три равныя числа; 4) чтобы выпали числа
2, 3, 4, на трехъ кубахъ вообще.
,.тт п :іс / Г<7-1)(<Т—2) 8.7
1) Число 9 разлагается па три суммы 28 раз ь (но формулѣ —-— = — =
=28, (см. 084, 2), изъ которыхъ надобно выключить суммы 7-і 1ч-1,1 -ч-7—»-І,
1ч-1ч-7, потому что на кубахъ нѣтъ цифры 7; стало-быть, всѣхъ благопріятныхъ
случаевъ 25, а всѣхъ случаевъ равновозможныхъ на трехъ кубахъ=63=216,
потому что столько можно сдѣлать сочетаній по три, сь повтореніями, изъ 6 пред-
тг ХХТ 23 х*
метовъ. II такъ, ѴѴ= —<- •
2) Чтобы сумма 9 на трехъ брошенныхъ кубахъ состояла изъ двухъ чиселъ
равныхъ, и одного инъ неравнаго, надобно взять только двѣ пары равныхъ чи-
селъ 2ч-2, 4ч-4 (потому что 1ч- Іч-7 по можетъ быть), и придать къ інпгь
соотвѣтственно числа 5 и 1. Сверхъ того, па каждомъ изъ трехъ кубовъ можемъ
выйти одна цифра неравная, и одна изъ цифръ равныхъ, которыхъ число 6;
хѵ 6 1
Т0'Ѵ==^ = §6-
3) Сумма 9 только одинъ разъ составляется изъ трехъ равныхъ цифръ,
1
Зч-Зч-З; а потому ѴѴ= —.
4) Поелику числа 2, 3, 4, даютъ шесть перемѣщеніи 1.2.3; а потому онѣ на
трехъ купахъ могутъ выпасть шестью различными образами; то и ѴѴ=:— =
Сюда же присоединимъ и розыег.анія слѣдующихъ случаевъ вѣроятности.
Вѣроятность, чтобы на трехъ кубахъ, А, В, С, брошенныхъ въ одно
время, выпали три неравныя числа, шія ни есть.
Такъ какъ шесть чиселъ куба, взятыя по три, даюгъ 6.5.4=120 сочетаніи
безъ повтореніи (страя. 277), то искомая вѣроятность будетъ
уѵ— —— -
216 9 *
Вѣроятность, чтобы на тѣхъ же трехъ кубахъ выпали дна каыя
нибудь числа равныя, и одно имъ неравное.— На двухъ кубахъ могутъ вы-
пасть только шесть паръ равныхъ чиселъ, а всякая пара съ каждою изъ осталь-
ныхъ пяти цифръ третьяго куба можетъ быть соединена; то такихъ сочетаній
благопріятныхъ получится 6.5=30. А какъ, сверхъ того, каждый изъ трехъ ку-
бовъ можетъ быть этимъ третьимъ, на которомъ выпадетъ неравное число, то
всѣхъ благопріятныхъ случаевъ будетъ 3X30=90, и потому
XV— «О _ 3
21 5 і2‘
— 288 —
1 . 2
Если бъ мы желали, чтобы при атомъ выпали по крайней мѣрѣ двѣ равныя
цифры (т. е. могутъ быть и всѣ равныя), то Къ предыдущимъ 90 случаямъ
надлежало бы придать еще 6, когда всѣ три равныя числа выпадутъ, и будетъ
ХѴ= 96 _4
216 9 ’
Вѣроятность, чтобы на трехъ кубахъ выпала сумма по крайней
мѣрѣ 14 (она не менѣе, но можетъ быть 15, 16, 17 и 18).— Поелику здѣсь
возможны только пять различныхъ суммъ, то число всѣхъ благопріятныхъ
п(п-+-1)(п-+-2) 5.6.7 __ .
случаевъ -— ----— _ =35, гдѣ п означаетъ число суммъ (стран. 281).
Посему, \Ѵ= почти 1 .
ЛІО о
Вѣроятность, чтобы на трехъ кубахъ выпали три послѣдователь-
ныя числа 123, 234, 345, 456, въ какомъ ни есть порядкѣ. — Каждое
изъ этихъ чиселъ даетъ шесть перемѣщеній безъ повторенія, слѣдовательно чи-
сло всѣхъ благополучныхъ случаевъ будетъ 4X6=24, и искомая вѣроятность
ДѴ= — =1.
216 9
Вѣроятность получить на трехъ брошенныхъ кубахъ четное число, = .
Вѣроятность, чтобы на трехъ кубахъ выпала сумма менѣе 9. Та-
кихъ суммъ шесть: 8, 7, 6, 5, 4, 3. Посему, здѣсь число всѣхъ благопріят-
п(п-+-1)(п-ь2) 6.7.8 к_
ныхъ случаевъ = -—5=— = т—-=5о, и случаевъ возможныхъ 21 о; слѣ-
ИГ 36 7
довательно ѴѴ= -— = — .
лЮ л/
Вѣроятность, что на трехъ кубахъ выйдетъ сумма болѣе 12. Та-
кихъ суммъ также шесть: 13, 14, 15, 16, 17, 18, и также благопріятныхъ
7
случаевъ 56; а потому ѴѴ= — .
Вѣроятность, что ьа трехъ кубахъ выпадетъ сумма между 8 и 13.
Такихъ суммъ четыре: 9, 10, И, 12. Сумма 9 составляется изъ сочетаній
333,441, 522, 342, 351, 621, которыя доставляютъ Іч-Зч-З-і-бнг 6-4-6=25
перемѣщеній; сумма 10 составляется также изъ шести сочетаній: 334, 442,
622, 541, 532, 631, которыя доставляютъ 3-г-3-г-3-і-6ч-6-і-6=27 пере-
мѣщеній; сумма 11 составляется изъ шести сочетаній: 335, 344, 551, 542,
641,632, изъ которыхъ полу чается числр перемѣщеній 3-і-3-г-3-ь6->-6-ь6=27;
а сумму 12 дѣлаютъ шесть сочетаній: 444, 552, 633, 435, 426, 651, изъ
которыхъ находимъ і-г-3ч-3ч-6-г-6ч-6=25 перемѣщеній. Слѣдовательно всѣхъ
случаевъ благопріятныхъ 25ч-27-ь27->-25=104, и вѣроятность
УѴ=Й6 = Й (П°ЧТИ 2І-
Примѣръ.—Найти вѣроятность вынуть изъ полной колоды ,52 картъ
четыре карты одного цвѣта. —Изъ 13 картъ одного цвѣта, взятыхъ но
- 289 —
1.2.3.4
ж .„13.12 11.10
четыре, можно сдѣлать различныхъ соединеніи -—:;; а инкъ всѣхъ цвѣ-
товъ четыре, то всѣхъ такихъ соединеній будетъ вчетверо болѣе, то есть,
4X13.12.11.10 „
—! 2 з 4 • “сѣхъ же случаевъ возможныхъ столько, сколько можно сдѣлать
ег, , 32.51.30.49
разныхъ соединеніи изъ 52 картъ по 4, а именно: — —----посему,,
... 4X13.12.11.10 44
ѴѴгт:--------------—------ .
32.31.30.49 4165
Вѣроятность вынуть четыре карты трефъ, или вообще одной масти,
, 11
будетъ вчетверо менѣе, то есть: .
Вѣроятность вынуть четыре какія нибудь фигуры? — Всѣхъ фнгуръ
12; посему благопріятныхъ случаевъ столько, сколько можно сдѣлать разлпч-
.„ , 12.11.10.9
пыхъ соединеніи изъ 12 по 4, и именно:---------- ; а число случаевъ возмож-
’ і. 2. з .4 '
52.31.30.49
ныхъ = - > посему
-,Т 12.11.10.9 99
ѵѵ — ———— —'------------.
52.31.50.49 54145
Найти вѣроятность вынуть туза, короля, даму и валета. — Здѣсь
число случаевъ благопріятныхъ столько, сколько можно сдѣлать сочетаній съ
повтореніями пзъ 4 картъ по 4, то естр, =4*=4.4 4.4; слѣдовательно,
... 4.4.4.4 X 1.2-3.4 128
ѵѵ —---------------—---------.
52 31.50.49 3*1430
Примѣръ. — Французская лотарея состоитъ изъ 20 билетовъ съ номерами
отъ 1 до 90. Участвующій въ ней избираетъ для себя одинъ или нѣсколько но-
меровъ, и на каждый ставитъ сколько нибудь денегъ съ какимъ ни есть усло-
віемъ, принятымъ въ лотарейпой игрѣ, и отъ котораго зависитъ количество его
выигрыша. Въ каждую игру вынимаются 5 билетовъ изъ 90. Чьи номера будутъ
въ числѣ вынутыхъ, тѣ получаютъ отъ лотареи суммы, болѣе или менѣе значи-
тельныя, соотвѣтствепно условіямъ, какія кто избралъ для себя. Напротивъ, чьи
номера не выйдутъ, тѣ лишаются ставочныхъ денегъ.
Условія, употребительнѣйшія въ этой лотареи, елъдующія:
Одиночка (эстрато} — простой выходъ номера, взятаго играющимъ; тогда
онъ получаетъ въ 15 разъ болѣе ставки.
Амба, — когда условіе.выигрыша состоитъ въ выходѣ обоихъ взятыхъ номе-
ровъ въ одинъ тиражъ; и тогда лотарея платитъ въ 270 разъ болѣе ставки.
Терна, — когда условіе выигрыша состоитъ въ выходѣ трехъ номеровъ, взя-
тыхъ играющимъ, въ одинъ тиражъ: тогда ему платится въ 5500 разъ оолѣе
ставки.
Кватерна, — когда условіемъ выигрыша будетъ выходъ четырехъ номеровъ
въ одичъ тиражъ: тогда лотарея платитъ въ 75000 разъ болѣе ставки.
19
290 —
Пвинтерна,—условіе выхода всѣхъ пяти номеровъ взятыхъ. Въ такомъ слу-
чаѣ лотарея платитъ въ 1000000 разъ болѣе ставки.
Любопытно зпать, какія вѣроятности соотвѣтствуютъ каждому изъ этихъ
выигрышей?
Для эстрато: всѣхъ возможныхъ случаевъ столько, сколько можно сдѣлать
различныхъ соединеній изъ 90 номеровъ по 5; а случаевъ благопріятныхъ, чтобъ
изъ 90 номеровъ вышелъ одинъ, столько, сколько можно сдѣлать различныхъ
' соединеній изъ остальныхъ 89 номеровъ по 4, къ которымъ этотъ пятый померъ
присоединяется:
ХХТ Г1 /Лп\.Г' іс\п\ 89.ЯЯ.Я7.Я6ХЗ 1
'' ~М89) • С5(90)_ 90 89 88 87-86 - •
Такимъ же образомъ найдется:
« ЛѴ=С.(88) :С.(90)=^|^=А,
: С,(80)=д^Х»Х=7А5 ,
для кватерна, АѴ-СД86) : ^(90)=^^ ^ ,
и такъ далѣе.
См. Политическую Ариѳметику Вруна. Одесса. 1845.
Примѣръ. — Въ урнѣ находятся Ь шаровъ голубыхъ и д зеленыхъ; найти
вѣроятность съ одного разу вынуть р шаровъ голубыхъ и у зеленыхъ.—Случаи
равно возможные — это соединенія изъ Ь-х-д шаровъ по /3 +-у. Число /9 шаровъ
голубыхъ можетъ быть вынуто столько разъ, сколько можно сдѣлать различныхъ
соединеній изъ Ь голубыхъ шаровъ 'урны по (3 элементовъ; а число у шаровъ
зеленыхъ можетъ быть вынуто столько разъ, сколько можно сдѣлать различныхъ
соединеній пзъ д зеленыхъ шаровъ по у элементовъ. А поелику каждое соединеніе
шаровъ зеленыхъ съ каждымъ сочетаніемъ шаровъ голубыхъ составляетъ случай
благопріятный для выигрыша, то всѣхъ такихъ случаевъ будетъ Ср(Ь) . Су(^);
число же случаевъ равповозможпыхъ С^-^^Дб-ьд); посему,
уѵ^.с/?(й)-сУ(у)
С/3-^+9) ‘
Вѣроятность такого случая, чтобы за одинъ разъ вынуть /9 шаровъ голубыхъ,
у зеленыхъ, и 3 шаровъ красныхъ изъ числа Ъ шаровъ голубыхъ, д зеленыхъ т
г красныхъ, положенныхъ въ одну урну, паіідется точно такимъ же образомъ:
^ѵ— с/?(й) ‘сГ(9) с$(г)
313. Пари. — Рисковать иа какое пи есть предпріятіе, держать пари
(закладъ) о какомъ нибудь ожидаемомъ произшествіи, что ему будутъ соотвѣт-
ствовать такіе благопріятные случаи, а не другіе, всегда основывается на степени
291
его вѣроятности. Такъ, ослп XV вѣроятность случая, благопріятнаго исполне-
нію произшествія, и 1—XV вѣроятность случая неблагопріятнаго; то можно дер-
жать лари XX противъ 1—XV въ томъ, что для меня выйдетъ скорѣе случай бла-
гопріятный. Для поясненіе, положимъ, что въ урнѣ находятся 100 шаровъ, пзъ
которыхъ 90 бѣлыхъ и 10 черныхъ: вѣроятность, что изъ этой урны вынется
шаръ бѣлый =— ; а противоположная вѣроятность, то есть, что вынет-
10 1
ся первый шаръ черный = — Очевидно, что первая вѣроятность въ 9 разъ
болѣе второй, т. е. въ 9 разъ вѣроятнѣе, что изъ урны вынется скорѣе шаръ
бѣлый, нежели черный, такъ что можно держать пари девять противъ одного,
что въ первый разъ вынется шаръ бѣлый. Денежная ставка въ этомъ случаѣ
должна быть пропорціональна вѣроятиости, если хотимъ, чтобы пари было безо-
бидное, т. е. для обѣихъ партіи равно выгодное. Слѣдовательно, въ нашемъ при-
мѣрѣ, я долженъ ставить 9 рублей противъ 1 рубля, пли 18 противъ 2, п т. д.
Это значитъ, что мой соперникъ обязуется платить мнѣ всякой разъ 1 рубль,
когда изъ урны вынется шаръ бѣлый, между тѣмъ какъ я ему всякой разъ 9 ру-
блей, какъ вынется шаръ черный. При такомъ условіи, счастіе и несчастіе,
выигрышъ и проигрышъ теоретически дѣлятся равно между обѣими партіями.
И дѣйствительно, положимъ, что, согласно съ вѣроятностями, въ 10 игоръ вы-
нется бѣлый шаръ 9 разъ, а черный шаръ одинъ разъ; то, но условію, я получу
отъ соперника 9 рублей за девять выигрышей, и ему заплачу 9 рублей за одпііъ
проигрышъ-, стало-быть, пи одна сторона не выиграетъ и не проиграетъ. По это
такъ надлежитъ расчислять по степени вѣроятностей; а па самомъ дѣлѣ всегда
будетъ между выигрышемъ и проигрышемъ нѣкоторая разность: только эта раз-
ность будетъ становиться тѣмъ менѣе, чѣмъ игра повторяется болѣе. Напримѣръ,
если, послѣ 25 игоръ, разность въ выигрышѣ будетъ 4 рубля, то, послѣ 50, она
сдѣлается нанрим. 2 рубля, а послѣ 100 будетъ только 1 рубль, и т. д. Изъ
этого видно, что денежныя ставки, пропорціональныя вѣроятностямъ, дѣлаютъ
равенство между выигрышемъ и проигрышемъ пе при маломъ числѣ игоръ плл
отдѣльныхъ случаевъ, но при числѣ весьма большомъ.
Л4. Такъ надобно понимать и всѣ выводы, получаемые пзъ вычисленія по
вѣроятностямъ, къ какимъ бы случаямъ оно ни было приложено. Паприм. въ
извѣстныхъ таблицахъ смертности Баумана находимъ, что изъ числа людей,
родившихся въ одинъ и тотъ же годъ, по истеченіи 18 лѣтъ, въ живыхъ оста-
нется только половина. При этомъ однако же отнюдь нельзя сказать, чтобы
изъ двухъ человѣкъ, родившихся въ одинъ годъ, послѣ 18 лѣтъ остался живъ
только одинъ; ни того, что изъ 100 человѣкъ, рожденныхъ въ одно время, послѣ
18 лѣтъ будутъ живы ровно 50 человѣкъ. Въ послѣднемъ случаѣ разность мо-
жетъ быть до 10 или болѣе человѣкъ. Но, если взять 10000 человѣкъ, родив-
— 292 —
шихся въ одинъ годъ, то послѣ 18 лѣтъ разность между числомъ живыхъ и
умершихъ будетъ значительно меньшая; а для милліона людей она можетъ сдѣ-
латься совсѣмъ ничтожною, какъ это и дѣйствительно находятъ въ государствахъ
обширныхъ и многолюдныхъ.
Здѣсь предполагается, что въ ряду годовъ, взятыхъ для вывода степени
смертности, не было большой перемѣны въ обстоятельствахъ, имѣющихъ вліяніе
на размноженіе людей и ихъ смертность. Но, если эти обстоятельства измѣнятся
отъ войпы, моровой язвы, Повальныхъ болѣзней, отъ перемѣны физическихъ и
нравственныхъ причинъ, имѣющихъ вліяніе на рожденіе и смертность людей,
тогда, съ измѣненіемъ причинъ, и послѣдствія выйдутъ другія, на короткое или
продолжительное время.
2. Вѣроятность отпосительнля.
315. Относительною вѣроятностію называется та, которая опредѣляется
чрезъ сравненіе только двухъ пли нѣсколькихъ случаевъ, благопріятныхъ ожи-
даемому происшествію, вовсе пе обращая вниманія на прочіе случаи, могущіе
произойти въ то же время.
Пусть число всѣхъ сбыточностей возможныхъ, изъ колхъ п слу-
чаевъ одного рода, и п' случаевъ другаго: то абсолютная вѣроятность, что про-
изойдетъ случай перваго рода, будетъ, какъ уже знаемъ, и также абсо-
лютная вѣроятность, что выйдетъ случай втораго рода, ѴѴ'_Отсюда слѣ-
дуетъ, что относительная вѣроятность для выхода случаевъ перваго рода,
XV п
5Ѵ = °™Ра
п ____ XV
п-+-п' ХѴ-т-ХХ'"
Она для случаевъ втораго рода отсюда же найдется:
п' хѵ'
п-ьп' ХѴч-ХѴ'"
Посему, относительная вѣроятность какого ни есть случая равна ею
абсолютной вѣроятности, раздѣленной на сумму абсолютныхъ вѣра
ятностей сравниваемыхъ случаевъ.
Примѣръ. Двое играютъ двумя кубами на слѣдующихъ условіяхъ: первый
долженъ выиграть, когда ему выпадетъ сразу 7, а другой — когда у него
вскроется 4 очка, пс обращая вниманія на всѣ прочіе случаи. Въ этомъ пред-
„ 4., 6
положеніи аосолютвая вѣроятность, что выиграетъ первый, и вѣроят-
ность, что выиграетъ второй, (см. табличку стр. 285, на которой видны
числа случаевъ, возможныхъ для того и другаго игрока въ діагональныхъ стро-
кахъ). Отсюда, относительная вѣроятность, что выиграетъ первый,
— 293 —
XV ______ 6 2
ѵѵ ьіг' ІГ ”з ’
и 'К' 3 1.
и что выиграетъ второй, уѵ+лѵ7 = а = Ут
такъ что относительная вѣроятность, перваго къ относительной вѣроятности
втораго содержится, какъ 2:1.
Примѣръ. Въ урнѣ находятся а шаровъ бѣлыхъ, а' красныхъ, а" синихъ,
а"'зеленыхъ, и т. д., коихъ сумма =ач-а,ч-а/,-ьа'"-ь....=А. Простая вѣ-
роятность, что, въ первый разъ, вынется шаръ бѣлый, равна ; она для шара крас-
а’
наго = —, для синяго и т. д. Но относительная вѣроятность, что вы-
нется скорѣе шаръ бѣлый, нежели красный, равна
а ,а а> \. а •
А ’ 'А А ' «-ьа''
а относительная вѣроятность, что вынется прежде шаръ красный, нежели бѣ-
лый, равна
а' іа а' і а'
А ‘ 'А * А ' ач-а> ’
Сумма этихъ обѣихъ вѣроятностей также всегда равна единицѣ.
Пусть а=6 шаровъ бѣлыхъ, а'— 8 красныхъ, а"— 44 синихъ, а'"=12 чер-
ныхъ, а всего 40: то вѣроятность, что вынется скорѣе шаръ бѣлый, нежели
6 3 14 7 . . .
синіи, — 7—77- = —; вѣроятность противнаго = -—т-= 7-; а обѣ вмѣстѣ
’ 6-+14 10 г ’ 6-1-14 Ю
3 7
= — -ь- =4, ибо совершенно извѣстно, что который пибудь изъ этихъ слу-
чаевъ выйдетъ прежде. Но, если вынется шаръ красный или черный, то этимъ
не рѣшается ни чего, и выемъ продолжается.
Примѣръ. Найти вѣроятность, что на трехъ брошенныхъ кубахъ
скорѣе вскроется пашъ. нежели сумма /7. — Всѣхъ случаевъ для пашъ
находится 6, а всѣхъ случаевъ для суммы 17 три (665, 656, 566): посему,
6 2
вѣроятность, что скорѣе вскроется пашъ, = -—-= -; а вѣроятность скорѣе
и 6-4-3 3
1-7 3 1
получить 17, нежели пашъ, = -----= - .
3 ’ ’ 6-ьЗ 3
,, .. 18
Вѣроятность получить скорѣе четное число, нежели пашъ, = 1().
3. Вѣроятности сложныя.
316. Разсмотрѣнныя нами вѣроятности двухъ родовъ простираются толь,.о
на одиночные случаи изъ числа всѣхъ возможныхъ какого ни есть событія; по
можно соединять однѣ вѣроятности съ другими по двѣ, по три, п проч. двоякимъ
образомъ: 1) Взявши два, три, пли болѣе случаевъ, искать вѣроятность, что
одинъ, который нибудь пзъ нихъ, произойдетъ; — эта вѣроятность найдется
чрезъ сложеніе простыхъ вѣроятностей для выхода этихъ случаевъ. 2) Либо,
294 —
искать вѣроятность, что эти случаи произойдутъ въ одно время по два, по
три, или одинъ за другимъ также по два, по три, ; въ такомъ случаѣ
находятъ ее чрезъ умноженіе простыхъ вѣроятностей для этихъ случаевъ.—
Сверхъ того, можно искать вѣроятность, что изъ этихъ парныхъ, тройныхъ,....
случаевъ произойдетъ который ннбудь; тогда ее находятъ чрезъ умноженіе и
сложеніе ихъ вѣроятностей. — Всѣ сіи вѣроятности называются сложными;
размотрпмъ тѣ н другія.
I случай.—Положимъ, что въ ходу какого ннбудь событія считается число
К всѣхъ случаевъ равно возможныхъ; что между ними п случаевъ благопріят-
ныхъ одному явленію, п' случаевъ благопріятныхъ другому, п"—третьему, и
т. д.; назовемъ чрезъ ЛѴ= ” , ... простыя вѣроятности
для этихъ разныхъ случаевъ: то вѣроятность, что изъ этихъ явленій слу-
чится первое либо второе, “ЛѴ-4-ХѴ; что произойдетъ первое, второе либо
третье,
=^Ѵ-+ЛѴ'-ь\Ѵ", и т. д.
Слѣдовательно, вѣроятность, что, изъ нѣсколькихъ равно возмож-
ныхъ явленій, произойдетъ хотя одно, равна суммѣ простыхъ вѣро-
ятностей сихъ явленій.
Примѣръ. — Простая вѣроятность, что на двухъ брошенныхъ кубахъ
вскроется сумма 7, есть \Ѵ=— (см. табличку ла страп. 285 по діагональной
5 4
строкѣ), опа для суммы 8 равна ѴП= —, а для суммы 9 опа АѴ"— —; по-
сему, вѣроятность, что на двухъ кубахъ сразу вскроется сумма 7 или 8, будетъ
6 5 11
\Ѵ-+-\Ѵ'= - ч- “ ;
36 36 36’
чго выпадетъ сумма 8 или 9, вѣроятность будетъ
К Д Л
XV/ , XV//- ° . — 1 .
36 36 4 •
что появится сумма 7 или 9,
хѵ , .
36 36 36 '
Вѣроятность, что надвухъ брошенныхъ кубахъ вскроется сумма 7, 8 либо 9,
будетъ .
ОО оо
Вѣроятность, что па тѣхъ же кубахъ выпадетъ сумма 6, 7, 8 или 9, равна
Зч-6-ѵй-М 20
ОО ОО
И случай. Вѣроятность встрѣчи случаевъ въ ходу двухъ или нѣ-
сколькихъ совре иеічи^съ событій.
Возмемъ сначала два событіи. Пусть IV число всѣхъ возможныхъ, а п чи-
сло благопріятныхъ случаевъ въ первомъ событіи. Означимъ чрезъ К', п', та-
г
— ' 295
кія же числа во второмъ событіи. Простая вѣроятность, что выйдетъ какой ни
есть случай въ пользу перваго событія, не обращая вниманія на случаи втораго,
и такая же вѣроятность для выхода случая въ пользу втораго событія,
«'•
Для большой простоты, положимъ, что IV—4- возможныхъ случая въ первомъ
событіи, которые означимъ буквами а, Ь, с п <1; а изъ нихъ только п=3 въ
нашу пользу, а именно: а, Ъ, с. Во второмъ же событіи №=3 случая возмож-
ныхъ а1, I)', с1, изъ которыхъ только п'=2 въ нашу пользу, именно: а1 и Ь1.
Отъ встрѣчи каждаго изъ № возможныхъ случаевъ перваго событія съ каждымъ
изъ № возможныхъ случаевъ втораго попарно, могутъ произойти №№= 12 воз-
можныхъ паръ; а отъ встрѣчи каждаго изъ п случаевъ перваго событія съ каж
дымъ изъ п' случаевъ втораго, получится пп'—б такихъ встрѣчъ (изъ всѣхъ
12-ти паръ равно возможныхъ); то, вѣроятность XV, что какая нибудь встрѣча,
или пара, благопріятная нашему ожиданію, дѣйствительно произойдетъ, должна
быть АѴ= у. , или ЧѴ=іом'-,
то есть, вѣроятность встрѣчи двухъ такихъ случаевъ равна произведе-
нію гсгс1 простыхъ вѣроятностей этахъ отдѣльныхъ случаевъ.
Къ этимъ двумъ событіямъ присоединимъ еще третіе, которое содержитъ
случаевъ равно возможныхъ, п" случаевъ благопріятныхъ, и, стало быть,
ѵр— — простая вѣроятность для выхода одного изъ этпхъ благопріятныхъ слу-
чаевъ; то встрѣчу благопріятныхъ случаевъ перваго и втораго событія можно
разсматривать за отдѣльный случай, котораго вѣроятность —тп'. Слѣдователь-
но, вѣроятность, что эти три случая встрѣтятся въ одно время (или послѣдуютъ
не иначе какъ одинъ за другимъ), изобразится равенствомъ:
(А)...........\Ѵ=^. или \Ѵ=ад.м/.«о";
и такъ далѣе, для встрѣчи случаевъ четырехъ, пяти, и проч. событій.
Если во всѣхъ этихъ событіяхъ находится равное число № возможныхъ слу-
п пг п"
чаевъ, апростыя вѣроятности для олагопріятныхъ случаевъ
перваго, втораго,.... событій; то для встрѣчи этихъ случаевъ, т. е. для совре-
меннаго ихъ появленія, получится вѣроятность.
.В).........
Примѣръ. Вь двухъ урнахъ А и Б находятся:
3 шара оѣлыхт, , въ В
2 черныхъ,
5 голубыхъ;
БЪ А
і- шара бѣлыхъ,
5 черныхъ,
3 красныхъ;
— 296 —
найти вѣроятность, что изъ обѣихъ урнъ вынутся сразу шаръ голубой изъ Л и
шаръ бѣлый изъ В.
Найдемъ сперва всѣ случаи совокупленія каждаго шара изъ А съ каждымъ
изъ В, равно возможные. Отъ совокупленія одного шара пзъ А съ каждымъ
изъ В (гдѣ 12 шаровъ) получается 12 паръ; а какъ въ А находится всѣхъ
шаровъ 10, то, отъ соединенія ихъ съ шарами В, попарно, получится
12X10=120 паръ. Это и есть число всѣхъ сдучаевъ возможныхъ.
Отъ совокупленія одного голубаго шара изъ А съ каждымъ бѣлымъ шаромъ
изъ В, получатся 4 пары; а какъ въ А находится 5 шаровъ голубыхъ, то, отъ
совокупленія ихъ съ каждымъ бѣлымъ шаромъ въ В, попарно, составится
4X5=20 паръ, благопріятныхъ нашему ожиданію. Посему, искомая вѣроятность
\ѵ= л» = 1.
. 120 6
Вѣроятность, чго сразу вынется шаръ черный изъ А и красный изъ В,
2X3 1
найдется ---= —.
120 20
Вѣроятность, что изъ обѣихъ урнъ вынется по одному бѣлому шару въ одно
зх« 1
ВРеМЯ 120 = ІО ’
1 1 ~ ,
Слѣдовательно, можно держать пари,— : —=:2:1, что скорѣе вындетъ
послѣдній случай, нежели предпосдѣдьій.
3*9. Если въ разныхъ событіяхъ, происходящихъ въ одно время, будетъ
равно не только число М случаевъ возможныхъ, во н число п случаевъ благо-
пріятныхъ каждому явленію, то въ уравненіи (А) всѣ К н также всѣ п будутъ
мейіду собою равны; а потому, вѣроятность \Ѵ, что случай, котораго простая
вѣроятность іе= , произойдетъ т разъ сряду (либо т разъ вдругъ), будетъ
(С)........ЛѴ= (^)"‘, или ѴѴ=адт.
Примѣръ. Простая вѣроятность, что на одной кубической кости выпадетъ
„ 1 .
число 3, равна у ; то вѣроятность, чго это же число выпадетъ два раза
сряду, по уравненію (С), будетъ
\Ѵ= - = — ;
6» 36 ’
а вѣроятность, что зто же число 3 и па томъ же кубѣ вскроется 10 разъ сряду,
\Ѵ=—= —------------------------------------.
6'° 1466176
Воть какъ мала вѣроятность, чтобы могъ выйти такой случай.—Вѣроятность
же противнаго, т. е. что этого случая не будетъ, равна
60466173
1—ѴѴ=т— —
60466176
— 297 -
и чрезвычайно близка къ единицѣ, такъ что соперникъ мой можетъ держать пари,
60 милліоновъ противъ 1, что первый случай, мпѣ благопріятный, не выйдетъ.
Примѣръ. Простая вѣроятность, что на двухъ брошенныхъ кубахъ выпадутъ
сразу числа 3 и 3, какъ извѣстно (стран. 286), равна—; а потому вѣроятность,
что на тѣхъ же кубахъ вскроются два раза сряду числа 3 и 3, будетъ
\Ѵ= — = — .
36» 1296
Примѣръ. Простая вѣроятность, чтобы на двухъ брошенныхъ кубахъ полу-
4 1
чилась сумма очковъ 5 равна — = - ; а вѣроятность, что втоть случай новто-
оЪ У
рится шесть разъ сряду, будетъ
\Ѵ— — = —— .
96 631441
Примѣръ. Положимъ, что какое ни есть происшестне, чрезъ изустныя
преданія отъ одного лица къ другому, отъ этого къ третьему, и т. д., дошло до
насъ отъ 20-го лица; спрашивается, какъ велика вѣроятность этого преданія?
Хотя простая вѣроятность, что каждое изъ сихъ лицъ передавало произше-
9
ствіе вѣрно и полно, будетъ велика, и равняется, наприм. =0,9 ; но
сложная вѣроятность переданнаго такимъ образомъ повѣствованія будетъ только
УѴ=(0,9Г=0,121б;
такъ что можно держать закладъ 1 противъ 8 (почти), что преданіе, полученное
нами отъ 20-го лица, имѣетъ достовѣрность.
Примѣръ. Простая вѣроятность, что на двухъ брошенныхъ кубахъ выпадетъ
сразу сумма 8, какъ извѣстно, равна ; а такая же вѣроятность для суммы 9
4
равна — ; то вѣроятность, что на двухъ кубахъ, брошенныхъ два раза сряду,
получится однажды 8 и однажды 9, по формулѣ (А) найдется:
*=А=0,0454.
Примѣръ. Два игрока А и В бросаютъ до два куба, а третій С бросаетъ
одинъ кубъ; найти вѣроятность, что, въ одно и то же время, А получитъ на
своихъ кубахъ дра равныя числа, В не получитъ равныхъ чиселъ, а С полу-
читъ число 6.
Простая вѣроятность для А равна ,
для В - .
О
для С - і ,
О
а сложная вѣроятность, что эти три случая встрѣтятся въ одно время, будетъ
уѵ—1 “ *—А—о о^зі ‘ '
ѴѴ 6 ’ 6 • 6 216
— 298 -
318. Слѣдующіе примѣры представляютъ случаи совокупленія вѣроятно-
стей I съ вѣроятностями II.
Примѣръ. Въ одной урнѣ находятся 1 шаръ черный и 2 бѣлыхъ, а въ
другой урнѣ—одинъ шаръ черный и 4 бѣлыхъ; найти, какъ велика вѣроятность,
что изъ которой нибудь урны въ первый разъ вынется шаръ бѣлый?
Простая вѣрность, что мы опустимъ руку въ первую урну, равна -д-; а вѣро-
-2
вгность, что изъ пее вынемъ бѣлый шаръ, равна у; посему вѣроятность встрѣчи
этихъ обоихъ случаевъ, или послѣдованія одного за другимъ, будетъ, по формулѣ
(Л), равна 2-з = з-
Такимъ же образомъ найдётся вѣроятность встрѣчи такихъ же двухъ слу-
чаевъ при второй урнѣ
і 4 2
2 8 8 *
«
1 2
А какѣ обѣ вѣроятности - п - соотвѣтствуютъ одному нашему ожиданію, т. е.
о О
одному благопріятному для насъ случаю; то, по 316, искомая сложная вѣроят-
ность должна быть,
хѵ—I 1 . 11 •
2’3 2’8 3 8 18’
Примѣръ. Три урны содержатъ шары:
первая 1 черный и 1 бѣлый,
вторая 1 черный и 2 бѣлые,
третья 3 бѣлые шара;
найти вѣроятность, что изъ которой ннбудь урны въ первый разъ вынется
шаръ бѣлый.
ІТ 5 „.111213121. _.пп
Найдется: \Ѵ= , . - ч- - . - = 5 ч- - ч- 5 =0,722.
Примѣръ. 52 карты разложены на четыре кучки такъ, что находится
въ первой: 10 картъ красныхъ, во второй: 5 красныхъ,
5 черныхъ; 13 черныхъ;
въ третьей: 5 красныхъ, съ четвертой: 6 красныхъ,
4 чериыхъ; . 4 черныхъ;
найти, какъ велика вѣроятность, что изъ которой нибудь кучкн наудачу вы-
нется съ перваго разу красная карта.
Вѣроятность, что я положу руку на какую ннбудь изъ этихъ кучекъ =-; а
вѣроятность, что я выну изъ нее красную карту, будетъ
110 18 ів іб ___________і 21____
4’15_Ь4'18Ч~4'9~Ь4’10 4 * 10 ’ “ '
Рѣшенію этихъ задачъ можно дать общій видъ, полагая, что находится число
урнъ а, изъ коихъ каждая содержитъ т шаровъ бѣлыхъ и п черныхъ, и число
— 299 -
урнъ а', изъ коихъ каждая содержитъ тп' шаровъ бѣлыхъ и п' черныхъ; то вѣ-
роятность, что изъ какой ни есть урны, въ первый разъ, на удачу вынется
шаръ бѣлый, равна
ѵг, а тп а' тп
ѴѴ=-------- . ---1------ . —--
ан-а' т-+-п ач-а' тп'ч-п
4. Вѣроятность для явленіи одно другимъ замѣняемыхъ.
319. Положимъ, что въ послѣдовательномъ ходу извѣстныхъ событій нахо-
дится число К случаевъ равно возможныхъ, изъ нихъ п слу чаевъ благопріятныхъ
для сбыточности явленія А, и п' случаевъ благопріятныхъ явленію В *); то,
назвавъ чрезъ го простую вѣроятность того, что произойдетъ явленіе А, и гю'
вѣроятность въ пользу В, имѣемъ:
п , »>'
"Й ’ ИЛИІС — и •
Опредѣлимъ теперь, какъ велика вѣроятность АѴ, что либо произойдетъ явле-
ніе А, либо явленіе В, если А не случится.
Вѣроятность, что произойдетъ А, —к, стало-быть, вѣроятность, что его не
будетъ, =1—гс; а вѣроятность, что, въ одно время, не случится А, но прои-
зойдетъ В, по II случаю, будетъ
(1-—го)ы/.
По этому, искомая вѣроятность \Ѵ, что либо произойдетъ событіе А, либо,
когда его не будетъ, то произойдетъ В, изобразится (стран. 294) равенствомъ
\ѵ—1 —
=1—(1—го)(1—го')-
Повелимъ это слѣдующимъ примѣромъ:
Вѣроятность, что па двухъ брошенныхъ кубахъ выпадетъ въ первый разъ
сумма 9, или, когда этого не случится, то, по крайней мѣрѣ, во второй разъ
выпадетъ 9.
4
Тутъ простая вѣроятность го=ію— - ,
потому что благопріятныхъ случаевъ четыре: 3-4-6, 4-4-5, 5ч-4, 6-4-3. Посему,
искомою вѣроятностью будетъ
По, вѣроятность, что на этихъ двухъ кубахъ вскроется сначала сумма 9, а
если опа пе выйдетъ, то, по крайней мѣрѣ, сумма 8, будетъ
^-(І-^І-^,234;
потому что здѣсь второму явленію соотвѣтствуетъ пять случаевъ; 2-4-6, 3-4-5,
1-4-4, 5-4-3, 6-1-2.
*) Здѣсь разумѣется, что И > п-т-п'.
— зоо —
320. Положимъ теперь, что находятся три событія, появленію коихъ
соотвѣтствуютъ простыя вѣроятности:
п , п' ,, п"
го= —. го'= —. чкг=. — ;
к ’ л ’ Л
то вѣроятность XV, что выйдетъ случай въ пользу перваго событія, либо, когда
этого не будетъ, то пусть выйдетъ въ пользу втораго, а когда не случится и это-
го, то пусть, по крайней мѣрѣ, выйдетъ случай выгодный для третьяго, найдется
весьма легко слѣдующимъ образомъ.
Положимъ для краткости (319)
х=1—(1—го) (4 —го');
то, очевидно, что искомою вѣроятностью буудетъ:
\Ѵ=1—(1—ж)(1—го");
куда надобно только подставить на мѣсто х его величину, и получится
\Ѵ=1—(1—го)(1—го')(1—го").
Такимъ же образомъ опредѣлится вѣроятность для четырехъ и болѣе событій
одно другимъ замѣняемыхъ.
Примѣръ. Урна содержитъ 20 шаровъ, изъ коихъ 3 бѣлыхъ, 4 черныхъ и
5 голубыхъ; найти вѣроятность, что съ перваго раза вынется шаръ бѣлый, а
если не опъ, то голубой.
Простыя вѣроятности для выхода бѣлаго шара
з
го= ,
2о’
для голубаго го — - , для чернаго го"= Д .
лО 20
Посему, искомая вѣроятность:
\Ѵ=1 — (1— го)(1— го')
' 20'* 20' 20 20 80
Вѣроятность, что вынется шаръ черный, а если пе онъ, то голубой, будетъ:
™=0,4.
Вѣроятность, что вынется шаръ бѣлый, а если не онъ, то черный, а если не
этотъ, то голубой, найдется:
!_(!_«,)™ . 2=0,49.
Примѣръ. Взята колода въ 36 картъ, по 9 листовъ каждой масти; найти
вѣроятность, что, послѣ 2, 3, 4,.... разовъ, вынется карта пиковой масти,
предполагая, что, послѣ каждаго выема, эта вынутая карта откладывается
въ сторону, и, стало-быть, число всѣхъ картъ уменьшается одною, двумя, тре-
мя, и т. д.
9
Вѣроятность, что въ первый разъ вынется пиковая карта, го— . Вѣроят
— ЗС1
ности, что она вынется во второй, въ третій, и т. д. разъ, будутъ: - ,
ю,—а противньія вѣроятности, что такая карта не вынется:
а а
Искомая же сложная вѣроятность ЛѴ будетъ
лѵ=і—(і—іо,)(і—ад±)(і—«’в)
, 3 26 25 , 195 281 _ _
^—4___-—. л 1 — ---------------(> и
4’35 34 476 476 ’
Если бъ мы искали вѣроятность, что послѣ пяти разъ вынется пиковая карта,
то нашли бы:
„г . 195 24 23 . 4485 4
ѴѴ -------. — . -— 1----------— .
476 33 32 20244 5
Примѣръ. Лотарея аллегри состоитъ изъ 100 билетовъ, изъ коихъ 80 пу-
стыхъ и 20 съ выигрышами; узнать, какъ велика вѣроятность, что изъ пяти би-
летовъ, вынимаемыхъ одинъ за другимъ, выиграетъ хотя одинъ?
Здѣсь простыя вѣроятности, что выиграетъ хотя одинъ билетъ, суть:
20 20 20 20 20
ІОО ’ «*= 99 ’ 98 ’ ^=9? ’ 96 і
а вѣроятности противныя:
1—1—1—ад3,....
100 Л Ш)Л‘ 98 Л1 97 Л 96/
19513 41597
Искомая же вѣроятность будетъ
\Ѵ=1—(1—
_ 80 79 78 77 76 . 19513 41597 2.
1 100 ’ 99 ’ 98 ’ 97 ’ 96 61110 61110 3 (почти)-
Примѣръ. Найти вѣроятность, что на двухъ брошенныхъ кубахъ выпадетъ
въ первый разъ сумма 7; если же этого не случится, то второй разъ, а когда и
здѣсь она не получится, то, по крайней мѣрѣ, въ третій разъ.
Такихъ случаевъ, когда на двухъ кубахъ вскроется сумма 7, находится шесть:
1123456
6 I 5 4 3 2 1
Простая вѣроятность, что вскроется сумма 7, будетъ = — ; она остается
таже при каждомъ бросаніи кубовъ; посему искомая вѣроятность будетъ:
91
216 ’
Отъ этого частнаго примѣра можно перейти къ общему. Положимъ,
что, въ какой ни есть игрѣ такого же рода, я имѣю въ свою пользу а стучаевъ
благопріятныхъ, а противъ себя Ь случаевъ неблагопріятныхъ, то вѣроятность,
что, повторяя игру п разъ, я выиграю хотя одинъ разъ, будетъ
XV—1—(1________° 1" _
' ач-6/ — (ач-ЬГ ’
— 302 -
отсюда,
Изъ этого выраженія можно, обратно, искать п, если \Ѵ, а и Ь даны.
Положимъ, что требуется знать, во сколько партій вѣроятность выиграть хотя
одну сдѣлается — . По этому условію имѣемъ:
^-ь^"-6и—1. плп [а^Ь}п=2Ьп-
(а-л-Ь)п 2 ’ ѵ ‘ '
п 1о^ (а-4-6)—1о§ 2н-п 1о§ Ь, и
Іов2
.
Іо^(ан-Ь) —
Для частнаго случая, положимъ, что нужно знать, на сколько игоръ можно
держать пари, что на двухъ игральныхъ кубахъ выпадетъ сумма 12. Здѣсь о=1,
6—35, потому что ан-6=36, и суммѣ 12 соотвѣтствуетъ только одинъ случай:
Іос'2 о.зоюзо
і п=-------- — — —----------
’ 1о§36—ІОКЗ.І 0,012234
П такъ, можно держать пари па 25 игоръ.
Если бы требовалась вѣроятность
(а-ьЬ)”—ьп 2
(ач-Ь)п Т’
то нашлп бы пз=39 игоръ.
399. Выраженіе сложной вѣроятности событій, одно другимъ замѣняемыхъ,
ЛѴЪ= 1—(1—го) (1—го') (1—го")
прилагается непосредственно къ опредѣленію вѣроятнаго продолженія жизни
двухъ, или больше, лицъ въ какой ни есть періодъ времени, при учрежденіи
вдовьихъ либо сиротскихъ кассъ, ооществъ для застрахованія капиталовъ или по-
жизненныхъ доходовъ, а съ тѣмъ вмѣстѣ для вычисленія преміи, какую долженъ
каждогодно вносить страхователь, или покровитель, въ это общество въ пользу
застраховываемаго лица, чтобы, въ случаи смерти страхователя въ теченіе услов-
наго періода времени, общество обязано было выдать этому лпц) извѣстпый ка-
питалъ единовременно, или выдавать ему пожизненный пенсіонъ.
Пусть го вѣроятность, что лицо А, имѣющее а лѣтъ, проживетъ еще р го-
довъ; ѵ1 вѣроятность, что лицо В, имѣющее Ь годовъ, проживетъ также р го-
довъ, и го" вѣроятность, что лицо С, имѣющее с лѣтъ, также проживетъ р
годовъ, и т. д. (Эти вѣроятности можно получать *ізь •'извѣстныхъ таблицъ
смертности); то будемъ имѣть:
гого' вѣроятность, что А и В проживутъ оба р годовъ, которая и принимается
за продолженіе союза этихъ двухъ лицъ; слѣдовательно,
1—гого' будетъ вѣроятностью, что этотъ союзъ не продолжится р лѣтъ, но
что одно изъ двухъ лицъ, А или В, умретъ въ теченіе р годовъ. Далѣе:
го(1—«>') вѣроятность, что чрезъ р годовъ, лицо А будетъ жить, а В будетъ
умершимъ;
303
«/(1—го) вѣроятность, что, послѣ р годовъ, Л будетъ умершимъ, а В будетъ
еще жить; •
(1—ю)(1—го') вѣроятность, что, послѣ р годовъ, оба лица будутъ умершими;
и наконецъ,
1—(1—ю)(1—го') вѣроятность, что, послѣ р годовъ, пе оба лича будутъ умер-
шими, но что во крайней мѣрѣ о^но изъ нихъ будетъ жить.
Такимъ же образомъ найдется;
гмо'го" вѣроятность, что, послѣ р годовъ, всѣ три лица будутъ живыми;
то'(1—го") вѣроятность, что, послѣ того же времени, только Л и В останутся
живы, и С будутъ умершимъ;
(і—и)(1—го')го" вѣроятность, что А и В будутъ умершими, а С будетъ жить;
1—гого'к" вѣроятность, что одно какое ниоудь изъ трехъ лицъ умретъ;
1—(і—«>)(1—»')1—го") вѣроятность, что не всѣ три лица умрутъ, почто
по крайней мѣрѣ одно изъ нихъ будетъ жить;
(і—м>)(1—го')1—го") вѣроятность, что, послѣ р годовъ, не будетъ ни одного
въ живыхъ, и т. д.
Баумакова таблица смертности *) показываетъ, что изъ 1000 человѣкъ, ро-
дившихся въ одинъ годъ, остаются живыми:
491=АІО, послѣ 20 лѣтъ,
439—А,о, - 30 -
374=А40, - 40 -
300=А,„, - 50 -
210=АСО, 60 -
Вѣроятность, что проживетъ еще 20 годовъ человѣкъ, имѣющій нъ настоя-
щее время
20 лѣтъ, будетъ —----= — =0,8=м,
Ав0 чУІ
30 - - — — — 0,7=го'
Азо 439 ’
40 - - -А^— = |1°=0,6=«".
А .о 374
Слѣдовательно, для одновременной жизни двухъ первыхъ лнць, изъ коихъ
одному 20, а другому 30 годовъ, получаются вѣроятности:
.гою'^хО^б *о(1—к>)=0,14
1—н>м>’=0,44 (1—к>)(1—гс'^О.Об
го (1 —к>')=0,24 4—(1 —го) (1 —го')=0 > 9 6
По, если первое лицо А, которому теперь 20 лѣтъ, застраховывается двумя
лицами В и С, изъ коихъ одному 20, а другому 30 лѣтъ; то, для сово-
купной ихъ жизни, и разновременной или одновременной ихъ смерти, найдутся
') См. въ Политической Ариамітикіь Брупа, стран. 155. Одесса, 1845 года.
- 304 —
гг (1—<о') (1—м>")=0,10
(I—и»)—0,02
1—гсгс'ад"—0,66
1—(1—ю)(1—м>')(1—м")—0,98
слѣдующія вѣроятности, на основаніи которыхъ можно вычислять преміи, плати-
мыя страхователямч:
‘іого,ге"=:0
№№,(1—«>")=0,22
(4—го)(1 —м/)м/г=0,04
(1——гс,/)~0,06
и такъ далѣе.
5. Вѣроятности явленій въ повторяемыхъ опытахъ.
ЗЯЗ. Положимъ, что, при повтореніи какого нибудь опыта, возможны
только явленія А и В, что явленіе А возможно въ т случаяхъ, а явленіе В въ
п случаяхъ, и что, при каждомъ повтореній опыта, отношеніе между числами
этвхъ обоихъ случаевъ остается постояннымъ; то вѣроятность, что, послѣ из-
вѣстнаго числа повтореній, выйдетъ тотъ пли другой случай, легко можно нахо-
дить изъ весьма замѣчательнаго ея выраженія.
Начнемъ съ частнаго случая. Возмемъ правильный многогранникъ, имѣющій
т-+-п равныхъ граней, изъ которыхъ т граней отмѣчены буквою А; и и гра-
ней-— буквою В, и положимъ, что этотъ многогранникъ будетъ брошенъ три
раза сряду; то, ясно, что могутъ ва немъ вскрыться слѣдующіе случаи:
Можетъ выйти А три раза....................ААА,
можетъ выйти А два раза, и В однажды.......ААВ,
(а если .порядокъ послѣдованія граней не опредѣленъ, произволенъ,
то это сочетаніе можетъ выйти три раза: ААВ, АВА, ВАА);
можетъ выйти однажды А и два раза В...,АВВ,
(и здѣсь имѣетъ мѣсто предыдущее замѣчаніе);
можетъ выйти В три раза.....................ВВВ.
Означимъ вѣроятности для А и В, соотвѣтственно, буквами а и Ь, то есть:
а~ -Ъ——(это противная вѣроятность относительно А). Сложныя вѣ-
роятяости будутъ:
для 1-го сличая..—ааа—а3; •
- 2-го - —ааЬ-=а3Ь, а когда порядокъ граней произволенъ, то=3а’і;
- 3-го - =аі>Ь—аЬ3, а если порядокъ граней произволенъ,' то г=ЗаЬг;
— '4-го - =Ы>6=Ь3
И такъ, предполагая произвольнымъ порядокъ граней многогранника, ври
троекратномъ повтореніи опыта, вѣроятность, соотвѣтственный всѣмъ воз-
можнымъ случаямъ ихъ выхода, изображаются рядомъ а3, За’6, Заб2, Ь3 членовъ,
составляющихъ разложеніе (а-ьй)3.
— 305 -
381. Разсуждая такимъ же 'образомъ, легко найти отдѣльныя вѣроятности
для всѣхъ случаевъ, могущихъ выйти, когда опытъ повторяется п разъ, по опре-
дѣленному порядку вскрытія граней, а именно:
Чтобы А вышло и разъ и В ни разу...............................а";
либо, чтобы сначала А вышло п—1 разъ и потомъ В однажды........
либо, чтобы сперва А вышло п—2 разъ и потомъ В два рази.... а"-’6”;
либо, чтобы сперва А вышло п—3 раза, и за тѣмъ В три раза...а’,-8б3,
итакъ дал.; или, наконецъ, чтобы А вышло и—р разъиВр разъ... ап-рб₽.
Сложная же вѣроятность, чтобы точно въ этомъ же порядкѣ, при повтореніи
опыта п разъ, А вышло не менѣе п—р и В не болѣе р разъ, найдется (393),
сложивъ всѣ сій вѣроятности.
...-+-ап~рЬр.
Если же порядокъ выхода граней произволенъ, то отдѣльныя вѣроятности
изобразятся членами ряда (а-+-Ь)п, то есть, будутъ:
а”, ^аГ-^Ь, а"-^,......, Ь",
1 1 2»
, . п(п—1)(п—2)....(п—рч-1) ,
гдѣ общій членъ -—-------з------~-----0 ѵ^ѵ изображаетъ вѣроятность того
случая, въ которомъ, при произвольномъ порядкѣ граней, во время п опытовъ,
А можетъ выйти п—р разъ, а В р разъ. А сложная вѣроятность, что, въ
этомъ случаѣ, выйдетъ А неменѣе п—р разъ, а В не болѣе р разъ, изобра-
зится суммою:
о--і_ 2. а—г)-4-п(п--11 а„_РьР
1 1.2 1.2.3 ...........р
И такъ, если ищется вѣроятность, чтобъ, во время п опытовъ, вышло А пе
менѣе п—2 раза, то въ составъ этой вѣроятности должны также входить случаи
и—1 и п выходовъ А. При такомъ условіи, ожидаемая вѣроятность изобра-
зится суммою первыхъ трехъ членовъ помянутаго ряда (ач-6)и; ибо хотимъ,
чтобы А вышло п разъ, или п—1, или п—2 раза, и пе менѣе. — Напротивъ,
вѣроятность, что, во время п опытовъ, А выйдетъ не болѣе п—2 раза,' рав-
няется суммѣ членовъ всего ряда (а-ъ-б)" безъ двухъ его первыхъ членовъ.—
Это же разсужденіе примѣняется и къ В.
335. Поелику , стало-быть и («-ьб)"=1,' то вѣроятность, что А
вскроется не менѣе п—р разъ и не болѣе п—р—1 разъ, во время и опытовъ,
всегда равна 1-цѣ, то есть, достовѣрности, чему и быть должно. •
Очевидно, что, когда, для опредѣленія вѣроятности, потребуется взять сумму
больше половины Членовъ ряда (ач-5)п, «то. ее гораздо легче, найти чрезъ вычи
тапіе суммы меньшаго числа остальныхъ его членовъ изъ единицы.
, . > ѵ(п~ 1) . -
Сверхъ того, поелику .коефиціенты 1, п, »Ц- 1, оиномическаго,
* 1. . л 1
ряд? (а-+-5)”=1 увеличиваются отъ концовъ его къ серединѣ, такъ что. паи-
20
306
большій изъ нихъ соотвѣтствуетъ среднему члену этого ряда при п четномъ, и
два равныхъ наибольшихъ соотвѣтствуютъ двумъ среднимъ членамъ нри п не-
чётномъ, то и вѣроятности, представляемыя сими членами, бываютъ меньшими
или большими.
1. Примѣръ. Найти вѣроятность, что, бросая четыре раза кубическую
кость, мы по іучимъ: а) число 6 однажды, стало-быть, три раза иныя числа;
Ь) тоже число 6 не менѣе двухъ разъ; и, наконецъ, с) тоже число не болѣе
двухъ разъ.
Рѣшеніе.—Здѣсь простая вѣроятность ожидаемаго событія А равна у
а вѣроятность противнаго событія В есть 6= — , и посему,
(а^Ь)п='а-^ЬУ=а^аіЬ^а,‘Ь-^аЬ‘-^Ь\
а) Вѣроятность перваго явленія і ыражается однимъ четвертымъ членомъ это-
го ряда, а именно:
, ,3 , 1 125 125 . 1 1 х
4.а63=4..-.-б=з— (между у и у).
Ь) Вѣроятность втораго случая выражается суммою трехъ первыхъ членовъ
предыдущаго ряда, то есть:
I , «I Л ш 1 43 с-23 19
с) Вѣроятность третьяго случая опредѣляется суммою трехъ послѣднихъ чле-
новъ помянутаго ряда, то есть:
о >М /м о 6.25н-4.125-1-625 425
№ІШаМ'=-----------------------= —.
При этомь, вѣроятность противнаго, что выпадетъ число 6 не менѣе трехъ
г * 43 21 7 П-л л. л. 423 7
разъ, будетъ у. у- = - Ооѣ же вмѣстѣ — - > —=1.
2. Примѣръ. При игрѣ тремя костяными кубами А, В, С, требуется
найти вѣроятность, что, при всякомъ бросаніи кубовъ, на каждомъ изъ нихъ
вскроется: 1) число менѣе 3 или число 6, 2) два раза менѣе 3 и одинъ разъ 6;
или 3) одинъ разъ менѣе 3, и два раза 6; или 4) три раза 6.
Всѣ сіи вѣронтности изображаются членами ряда (ач-6)3^а3-і-За36-ьЗа6’-4-б’,
2 1 1
гдѣ а= — = у (ибо менѣе 3 находятся два случая: 1,2), Ь— 6 .
При этомъ, а^-і-ЗагЪ вѣроятность, что вскроется три раза сряду число менѣе
3, а если этого не случится, то, по крайней мѣрѣ, два раза менѣе 3 и одинъ
разъ 6; она ==—. Далѣе: За^Ь-і-ЗаЬ вѣроятность, что выпадетъ два разя
* число менѣе 3 и одинъ разъ 6, либо 1 разъ менѣе 3 и два раза 6.
\3. У‘Прг мѣръ. «Нейти вѣроятности, что выпадетъ чисЛ'о 6 по крайней мѣрѣ
• одинъ расъ, бросая кубъ 5 разъ сряду.
Он.'(хры^ж»ется 1(ммою ^сѣ"Хъ 4лецовъ ^ад,т-(ач-б)5 безъ послѣдняго, го есть:
— 307 —
Чтобы это же число получить не менѣе трехъ разъ въ пять опоръ, вѣроят-
ность
=аьч-5а46-М0а3б’;
а вѣроятность получить число 6 не болѣетрехъ разъ ~10а3б’-ь10а’Л3-+-5об11
. 1 А 8
гдѣ а= - , о=—
О о
4. Примѣръ. Урна содержитъ въ себѣ 4 шара бѣлыхъ и 6 черныхъ;
найти вѣроятность: а) что, въ шесть разъ сряду, вынутся два шара бѣлыхъ и 4
черныхъ, предполагая, что, послѣ каждаго выема, шаръ опять кладется въ урву;
и Ь) что, въ эти шесть разъ, вынется по крайней мѣрѣ однажды шаръ бѣлый.
4 2
Здѣсь простая вѣроятность вынуть бѣлый шаръ а=. — = — (вѣроятность
событія А); а вѣроятность вынуть шаръ черный 6=-^ = -^-(это длясобытіяВ).
а) Вѣроятность перваго случая выражается пятымъ членомъ ряда (ач-6)3.
Этотъ членъ будетъ вида Аа’64; его коефиціентъ
, 6.5 і з 2.1 .
(“• 232>-
Стало-быть, эта вѣроятность
, 4 81 972 , 1 1 .
^15‘25 ’ 625 = 3125 (ИеЖГУз ИТ)‘
Ь) Вѣроятность втораго случая получится изъ суммы четырехъ членовъ ря-
да (а-+-6)6, то есть:
2'-^6.2“.3-ь13.2* 39-+-20.2’.35 7120 1424
6е 15625 3125 ’
1
немвого менѣе —.
5. Примѣръ. При игрѣ въ орлянку, бросаютъ монету, на котороіі изобра-
женъ съ одной стороны орелъ, а на другой находится надпись (рѣшетка), и кото-
рая не представляетъ ни какой розницы для паденія на тотъ или на другой бокъ;
спрашивается, какъ велика вѣроятность, что, въ двѣ игры сряду, выпадетъ хотя
однажды орелъ?
Искомая вѣроятность, очевидно, состоитъ изъ суммы а*ч-2а6; при чемъ
а=~, , потому что для обоихъ событій А и В, то есть, для паденія тою
2 2
или другою стороною вверхъ, простыя вѣроятности равны. Посему,
а!ч-2аб=4- -ЬТ = Т •
4 4 4
6. Примѣръ. Въ урнѣ положено 6 шаровъ синихъ, 8 красныхъ и 10 зе-
леныхъ: найти вѣроятность, что, въ пять разъ сряду, вынется шаръ опредѣлен-
наго цвѣта, и который опять опускается въ урну.
Простыя вѣроятности для выема шаровъ: синяго а= = у > красна-
, 1 10 5 __
го о = у, зеленаго с= — =. —. Посему, вѣроятность:
- 308 —
а) Не вынуть ни одного зеленаго, стало-быть, вынуть только синіе и красные:
Ъ) Не вынуть ни одного зеленаго, но не менѣе какъ одинъ разъ синій, слѣ-
довательно, не болѣе какъ четыре раза красный:
(ач-Ьу—Ь’=а5-ь-5а46-ь10а* 3Ьг-ѵ10а2Ь’-і-5аЬ4= (’ ь (1)’.
с) Нн одного зеленаго, но не больше какъ 4 раза синій, слѣдовательно, не
менѣе какъ одинъ разъ красный:
(а а =5а7>-г10«3би 10а7/-г 5нб‘-г //— (1 -+- (^) ’•
(I) Вѣроятность вынуть сперва красный шаръ три раза, а потомъ синій два
раза; а если этого не случится, то 2 раза красный и три раза синій въ какомъ
угодно порядкѣ:
(1 №/ 4 \8 / 1 \2/ 4 \8
4 4 +10 4 41 *).
3%(». До сихъ поръ мы брали въ разсмотрѣніе повтореніе только двухъ
событій, и, для опредѣленія вѣроятностей, соотвѣтственныхъ различнымъ слу-
чаямъ выхода этихъ событій, употребляли степень (а-ьй)" бинома; во точно
также надобно употреблять степени многочленовъ для опредѣленія вѣроятностей,
когда нѣсколько событій повторяются.
Положимъ, напримѣръ, что въ урнѣ находятся 3 шара бѣлыхъ, 5 черныхъ, и
4 красныхъ; то вѣроятности всѣхъ возможныхъ случаевъ выхода шаровъ, при
повтореніи выема 4 раза, (предполагая при семъ, что каждый вынутый шаръ
') Если, при повтореніи опыта, послѣ каждаго раза, будетъ уменьшаться число всѣхъ
случаевъ равно возможныхъ (напримѣръ когда шары, послѣдовательно вынимаемые изъ
рны, въ нее не опускаются), то, для опредѣленія вѣроятности событія, употребляются
другія Формулы. Положимъ, что появленіе А возможно въ т случаяхъ, а В въ п случаяхъ,
и т+п=»,то вѣроятность получить А р—д разъ, В д разъ, во время р опытовъ, была бы:
предполагая, что послѣ всякаго выема шаръ опускается опять въ урну. Но, когда, послѣ
(т\р — д
— \ надобно
будетъ взять:
т т — 1 т—2.......[т—(р—
з ' з-1‘ з—2......(я—рч-дч-) ’
(п \д •
— , взять:
1 )
п . (п—1) (п—2)..... (п—дч-1)
—------------------т---------——---------—- , и получили бы
(я—р-ьд)(я-рч-д-1)(я—рч-д—2)....(я—рч-1)
т(т—(р—д)ч-1]п(п—і)....(п—дч !)
р(р—1)....(р—дч-І)
"=і. 2...........г
»(я—1)...........(я—рч-1)
* р(р-і)(р-2)-—(р-«-ьі) , .
гдѣ -— -----5-------------=л коеФиціентъ, который мы вездѣ употребляли.
1 • 2 • V»------а
«г
— 309 —
опять опускается въ урну) выразятся, соотвѣтственно каждому, членами ряда
(ач-і-ьс)*, гдѣ а, Ъ, с суть простыя вѣроятности для выема шаровъ бѣлаго,
чернаго и краснаго.
Такимъ образомъ нашли бы вѣроятность въ ати четыре раза вынуть одинъ
шаръ бѣлый, 2 черныхъ, и 1 красный, равною каЬ*с, гдѣ к— =12,
(см. 232), то есть:
«=12аб’с.
Бѣроятность, что вынется шаръ бѣлый не менѣе двухъ разъ, нашли бы изъ
суммы:
аМЧа86ч-6а’6?-М.а3счЛ2а*6сч--6аѴ,
и такъ далѣе. Для вычисленія, остается только подставить:
• з , в 4
а=12’6=І2’С“І2-
Положимъ, наконецъ, что повторяются событія А, В, С, ......для выхода
коихъ находятся простыя вѣроятности соотвѣтственно а, Ь, с, д,,....; то вѣ-
роятность, что, во время п опытовъ, А выйдетъ а разъ, В /? разъ, С у разъ,
Образъ, и т. д. въ произвольномъ порядкѣ, полагая 8,
выразится членомъ:
кааь№й8....,
въ которомъ коефиціептъ
, п(п—1)(п—2)... 3.2.1
с— і.2...аХ’-2-../?Хі-2--7Х!-
Если положить /с=1, то вѣроятность будетъ ааЬ@сУ ($.... Опа соотвѣт-
ствуетъ тому условію, чтобы событія А, В, С, П...появлялись одно за дру-
гимъ въ порядкѣ опредѣленномъ самою атою формулою.
— 310 —
ГЛАВА ТРИНАДЦАТАЯ.
О ФУНКЦІЯХЪ ВООБЩЕ, ИХЪ РАЗДѢЛЕНІИ, И ПРОЧ.
337. Функціею вообще называется всякое алгебрическое выраженіе, состоя-
щее изъ совокупленія постоянныхъ количествъ съ одною или нѣсколькими величи-
нами перемѣнными. Въ пей постопнныя количества обыкновенно означаются
числами, или начальными буквами а, Ь, с,....; и количества перемѣнныя—
буквами х, у, а,.... Величина (рункпіи измѣняется съ измѣненіемъ ея пере-
мѣнныхъ.
338. Для различу одной функціи отъ другой употребляются общіе знаки
_________________________________________ ах
Г, Л Ѳ, Ѵ>- Такимъ образомъ, функціи Ѵ^ах—х3,~~7==== , можно, для
Ѵа8-я>8
различія, отмѣтить знаками:
V2ах—х3=[(х),
ах
=ГФ-
Такъ изображаются функціи съ одною перемѣнною. Подобнымъ же образомъ
означается функція съ двумя перемѣнными, только при общемъ знак-^пишутся
обѣ перемѣнныя. Напримѣръ: •
2х—Зу3-і-Ь=<р(х, у).
339. Функціи раздѣляются на алгебрическія и трансцендентныя. Алгебри-
ческія функціи тѣ, въ которыхъ количества постоянныя совокуплены съ пере-
мѣнными сложеніемъ, вычитаніемъ, умноженіемъ, возвышеніемъ въ степени
цѣлыя или дробныя, имѣющія постоянныхъ показателей. Таковы, напримѣръ:
ахп-і- —За \/^=С(х),
2х3—у\о$а=[(х,у}.
Функція называется трансцендентною, если находится въ пей хотя одинъ
членъ, въ которомъ перемѣнная соединена съ постоянными какимъ ни есть дру
гимъ дѣйствіемъ, не принадлежащимъ функціи алгебрической. Сюда относятся
функціи неопредѣленио~степенныя', логариѳмическія, и проч. Напримѣръ:
ач-2Іо§ж=Ѳ(ж),
2х3—аЯ—Ѵ (ж).
- 311
330. Алгебрическія функціи раздѣляются еще на цѣлыяидробныя,ъ сверхъ
того на соизмѣримыя (раціональныя) и несоизмѣримыя (ирраціональныя).
Цѣлая функція ни въ одномъ изъ своихъ членовъ не содержитъ перемѣнной
въ знаменателѣ; а функція дробная содержитъ перемѣнную въ знаменателѣ
одного или нѣсколькихъ ея членовъ.
Соизмѣримыя функціи не имѣютъ ни дробныхъ показателей, пи коренныхъ
знаковъ надъ количествами перемѣнными; но функціи несоизмѣримыя имѣютъ
ихъ, и никакими дѣйствіями не могутъ отъ нихъ освободиться.
Такимъ образомъ:
у#5—сх'і-й есть функція цѣлая раціональная,
/ ~ ~ дробная раціональная,
Ѵа*—х' - - гѣлая ирраціональная,
3 .____
, ЗЬ
а-------ч---------- - дрооная ирраціональная.
2—х Ѵ®
331» Всякая функція называется непрерывною, если она, отъ непрерыв-
наго возрастанія ея перемѣнной х, обращается въ результаты дѣйствительные и
конечные, которые возрастаютъ или убываютъ отъ наибольшихъ значеній къ
наименьшимъ также непрерывно, не пропуская ни одной промежуточной величи-
ны, и не дѣлаясь мнимою или безконечною для всѣхъ конечныхъ величинъ ея пе-
ремѣнной.
Это свойство принадлежитъ всякой цѣлой раціональной функціи; потому
что она пе содержитъ перемѣнной въ знаменателѣ, ни коренныхъ знаковъ надъ
перемѣнною. Слѣдовательно, члены этой функціи отъ непрерывнаго возрастанія х
или убыванія, могутъ только возрастать или убывать непрерывно, и отъ взаим-
наго совокупленія давать результаты положительные, отрицательные, или равные
нулю; но для конечныхъ величинъ х, и конечнаго числа членовъ, эта функція
не сдѣлается безконечною, неопредѣленною или мнимою. Для примѣра возмемъ:
/’(я)=ж3—х3—Зх—9;
будемъ въ нее подставлять:
х=— 2,—1, О, 1, 2, 3, 4,.... получится
[(х)= —15, — 8, — 9, —12, —11, 0, 27,....
Непрерывность этой функціи очевидна.
333. Всякая дробная функція раціональная не всегда бываетъ непрерыв-
ною; она, содержа перемѣнную въ знаменателѣ нерѣдко, для копченныхъ ся
величинъ дѣлается безконечною. Напримѣръ:
... . 10—іх
I —----------
' 2—х
- 312 —
9 10
для х=—1, 0, 1,2. 3,..., дѣлается
1 4
Г(я)= у, 5, 6, оо, —4, 0, 2,....
Примѣръ. І\х)~
длнж=І, 2, 3,...., дѣлается
ОС, 3,....
Сверхъ того, функція дробная раціональная очень часто выражается безко-
нечнымъ рядомъ, составляющимъ прогрессію. Наврим.
ах а а . а -
7--- — Т Х---ТТ х 77 X---.. ..
6-ь® 6 6а Ъъ
333. Функція цѣлая ирраціональная, вообще, не бываетъ непрерывна;
разрывъ ея непрерывности часто происходитъ отъ перехода ея изъ дѣйстви-
тельной въ. мнимую. Но, въ частныхъ предѣлахъ, бываетъ непрерывна.
Примѣры:
І\х}= ѵі—х есть функція непрерывная, потому что, для всякой дѣйстви-
тельной величины х, корень нечетной степени изъ 2—х пе можетъ сдѣлаться
ни безконечнымъ, ни мнимымъ.
Но функція /'(«)= ѵ4—х* не непрерывна; ибо, для
X——3. —2, —1, О, і, 2, 3,.... находимъ:
[(х)=^—3, О, Ѵз, 2, ^3, 0, ^=3,....
Опа непрерывна только между предѣлами х=-ь-3, х=—3; а далѣе сихъ
предѣловъ становится мнимою, чѣмъ и нарушается ея непрерывность.
Функція дробная ирраціональная можетъ терять непрерывность пе только отъ
того, что дѣлается иногда мнимою, но и отъ того, что становится безконечною
для конечныхъ величинъ ея перемѣнной. Это очевидно.
Сверхъ того, всякая функція ирраціональная, цѣлая или дробная, весьма
часто выражается безконечнымъ рядомъ. Наврим.
«,----- л
[(х)= Ѵа-+-х = (а+х)п
Число членовъ этого ряда безконечное.
334. Трансцендентныя функціи такжа очень часто бываютъ не непрерывны.
Для примѣра возмемъ
Дляж=1, 2, 3, 4,.... найдется
[(х)=3, оо,-’-, уз,....
— 313 —
Сверхъ того, мы увидимъ, что всякую трапсцендептиую функцію мпжи раз-
ложить въ рядъ, расположенный по степенямъ ея перемѣнной.
1. Общій видъ и свойства цѣлой раціональной функціи съ одною
ПЕРЕМѢННОЮ.
335. Самый общій видъ цѣлой раціональной функціи выражается многочле-
номъ, расположеннымъ по убывающимъ степенямъ его перемѣнной:
/(^^"ч-А^-’ч-Вж"-1-^... .ч-Тан-Ѵ,
гдѣ А, В, С,.... Т, С, суть числа цѣлыя, дробныя, даже ирраціональныя,
вмѣющія предъ собою знаки ч- либо —; нѣкоторыя изъ нихъ могутъ быть
равными нулю. Мы не ставимъ коефиціента предъ хп, потому что его всегда
можно отдѣлить и вынесть за скобки. Разсмотримъ свойства этой функціи.
336. Если уменьшать перемѣнную х, то послѣдній членъ можетъ
сдѣлаться болѣе суммы всѣхъ первыхъ; если же увеличивать х, то
первый членъ можетъ быть сдѣланъ болѣе суммы всѣхъ прочихъ.
Справедливость этого можно видѣть изъ того, что, для ат—О, данная функція
обращается въ послѣдній членъ С. Если же въ данной функціи вынесть ат" внѣ
скобокъ,
/.АВС Т V,
X 1ч- - Ч- —Ч-—, Ч-...Ч------,ч----,
' х гс® гс5 хп—1 хпг
и потомъ взять х — оо; то уничтожатся всѣ члены, кромѣ перваго хп, который
сдѣлается безконечно великъ.
Сверхъ того, первый членъ функціи сдѣлается болѣе суммы всѣхъ
прочихъ ея членовъ, если на мѣсто х подставить самый большій ея
коефиціентъ К, сложенный съ единицею, или больше. Это условіе
пишется такъ:
ат<^Кч-1.
Для краткости • положимъ
Ажп“'-ГВ^’ч-... .ч-Татч-[]=Р;
а для доказательства предложенія, возмемъ случай самый невыгодный, когда
А, В, С,.... Т, С, всѣ равны между собою, и равны РГ; тогда будетъ
Кат"-*ч-Кат"-’ч-... .ч-Катч-РЬ=Р',
и, очевидно, что Р'>Р.
Посему, если успѣемъ доказать, что, длн ат=Річ-1, сдѣлается аО-Р', то и
подавно будетъ ат"> Р. ф
Но РСс"~*ч-РСг"~’ч-... .Кат-ьК—К (жп-*ч-я?"_!ч-... .ч-атч-1)
____________р,
х—1 1
— 314 —
Теперь подставимъ #=Г4-і-1 въ х" и а,_1— — Р', и сравнимъ между со-
бою; найдется:
. ^=^ч-1)", Р'= =(Н-ь1)"-1;
Откуда видно, что ®">Р', а слѣдовательно и
^>Р.
Примѣръ. Въ функціи а?3—5ж*—&х—7 наибольшій коефиціентъ 7: пола-
гая я=7-1-1=8, найдется'512-—320—48—7>0; то есть, первый членъ
сдѣлался болѣе суммы всѣхъ прочихъ.
339. Но, если въ функціи,
а^ч-Аа?"-*-і-Ва?‘—*-і-... .ч-Ѵам-Н,
1
гдѣ 1} не меньше единицы, подставить означая чрезъ также наиболь-
шій коефиціентъ; то послѣдній членъ Н сдѣлается болѣе суммы всѣхъ
прощіхъ.
Для доказательства, положимъ
ж"-+ Аж"-1-і-Вя"_‘-і-. .. .-+-Тж=0,
и возмемъ
многочленъ той же степени, но котораго коефиціенты всѣ равны самому боль-
шому К. Очевидно, что 0'>0; а потому если успѣемъ доказать, что, для
х— дѣлается Н > 0х, то и подавно будетъ Н > О-
Но, 0^1-Цч-Іч-.................................;
— —1
X
1
сюда подставимъ а= найдется:
0,__ И [(І-г-Ку-1]і
Мы предполагали, что 1]<^ 1; слѣдовательно получили:
Н > О', и также
V > О,
что и требовалось доказать.
Примѣръ. Въ функціи,
5аг’ч-8жІ-+-9ж—1,
1 1
наибольшій коефиціентъ 9. Взявъ я:= = —,получится:
0,005н-0,08-і-0,9—1, или
0,985—1;
послѣдній членъ сдѣлался болѣе суммы всѣхъ прочихъ.
- 315 -
339. Производные многочлены. — Разсмотримъ теперь, какое измѣне-
ніе получитъ многочленная, цѣлая, раціональная функція
/'(ж)=ж"н-Аа:”~’ч-Ва:"-’ч-... .н-Тжн-П,
если на мѣсто х подставимъ х-г-к. Она сдѣлается:
/(жЧ-Л)=(жч-7і)”-|-А (жН-Л)п-*Н-В . .-4-Т(жч-/і)-4-Е ;
или, разложивъ степени двучлена жн-Л въ ряды по формулѣ Ньютонова оипома,
и расположивъ всё по возрастающимъ степенямъ бухвы к:
Хп Ч- ПХп~ * ч- А хп~ *ч-(п— 1) А®"—1 ч- Ва"-‘ч-(п—2) Влп- 8 , п(п—1) , Лч- — - а;’*—1 1 . 2 -Ь (П~<Я”'2)Ажп-» 1 . 2 п(п-1) Л«Ч-....Ч- і ? ч-....ч-(п—1)Аж Ч-....Ч- В .4
Лп—8-4-пя:
д«—‘ч-Лп
Вся эта функція приводится къ виду:
/•(а>4-Л)=/(ж)+ 4 ^(ж)./і’н
или, короче:
/(жч-Л)—еч-б1Л-і-&І7і’-ьѲ3/і3-+’... .-нѲі_8Лп-!-і-Ѳи_1/і’‘_‘-і-Лп,
если, для краткости, означимъ коефиціепты различныхъ степеней буквы /і, какъ
разныя функціи отъ х, чрезъ
[(х)—в =а:пч-Аа:п—1ч-Вя:"~іч-....ч-Та:ч-ІТ,
Г(х)=е,=пх”~ *ч-(п—1)Аа>п—’ч-(п—2)Вж’1—8ч-....ч-Т,
1 1
•—/"(л:)=Ѳа= — [л(п—1)®*—’ч-(п — 1)(п—2)Ажп~8ч-(п—2)(п—3)Вж"—$ч-.
1 1.2
-Л-4"'(х)==е,~— [п(п-1)(п-2)я:’‘—3-Нп-1)(п-2)(п-3)Аап-‘ч-(п-2)(п-3)(п-4)Вя;"-»ч-...]
1.2.3 1.2.3
п(п—1)
Ов—1= - — ха-і-(п—1)Аа?ч-В,
1 * 2
6п—1=ПХ-+К.
е„=і-
Происхожденіе и составъ этихъ функцій подлежитъ простому и замѣчательно-
му закону, а именно:
]Г(л?) есть самая даннан функція: она, для простоты и единообразія, означена
также чрезъ Ѳ;
/7(ж), помножающая к, составляется изъ [(х). каждый ея членъ множитсн на
показатель буквы х этого члена, а показатель надъ х уменьшается еди-
ницею;
— 316 —
Р(&), помножающая к', производится изъ /'(ж) также: каждый членъ ея мно-
жится на показатель буквы х того члена, а показатель надъ х уменьшается
единицею;
["'(х), помножающая Л8, производится изъ ("(х) точно также, какъ эта изъ^(«);
и такъ далѣе.
Отъ этого однообразнаго закона происхожденія всякой послѣдующей функціи
изъ предшествующей, функціи ['(х), ["(х), ["'(х),.... называются производ-
ными, также многочленами производными.
Получивши эти производный функціи, для составленія полныхъ коефиціептовъ
Ѳі» Ѳл Ѳ3,.... РВДа> надобно ['(х) раздѣлить на единицу, (ІГ(х) раздѣлить на
1.2, ["'(х).... на 1.2.3, и т. д.
Мы чаще будемъ называть производными функціями коефиціепты О,, О,, 08,....
Составленіе производныхъ функцій изъ данной столь важно для всего послѣ-
дующаго, что всякому учащемуся непремѣнно должно знать оное, и усвоить себѣ
механизмъ произвожденія функцій, передѣлавъ нѣсколько примѣровъ.
Примѣръ. Дана функція:
{\х)-=&=х*—Ьх*-+-5х2—Зж-ь2,
найти всѣ ея производныя, и также ея преобразованіе, когда вмѣсто х возмет-
ся х-+-к.
Онѣ будутъ: !’{х)—^хі—12ж!ч-10ж—3,
11,{х}—\2хі—24а?-ч-10, ["'(х^іх—24, Г"(а;)=24.
Отсюда: ѳ1=Р(х), ѳ^—Г'^х)—^— 12а:-ь5, Ѳа-г=^-^/’,"(х)=Л.х—4,
Такимъ образомъ опредѣлится все преобразованіе данной функціи,то есть, рядъ
—Ѳ-ч—Ѳік-}~з-ч—0в/і3-ч—
- Если вмѣсто к возмемъ —к, то /’(ж) измѣнитсн, и получитъ видъ:
[(х—к)~ 6—бі/і-ч-бі^’-ч-Ѳа/і’-ч-....
*) Дли избѣжанія большихъ чиселъ и дѣйствій надъ ними, въ правтикѣ легче поступать
такъ: по полученіи первой производной о, изъ ѳ, возми производную изъ ѳ, и раздѣли
на 2, получится ѳ2; имѣя 03, возмемъ отъ нее производную, раздѣлимъ на 3, получится о8,
и ь,зоч. Такъ, нашедши в,=4а:’—12а:’ч-10а:—3, говорю:
произв. отъ е, 12ж’—24«ч-10
вв= ------------! --------------= =6ха- 12х-+-й;
X Л
произв. отъ еІ 12а:—12
е5=------з-------=—3— =4®—4}
произв. отъ е5 4
е4— д 4“ •
Я вездѣ буду употреблять этотъ способъ.
— 317 —
339. Разсмотримъ теперь самое измѣненіе функціи [(х) при переходѣ ея
въ Дат-ь-Ті). Это измѣненіе равняется разности:
--0аЛ —Ь-0д/і -4-... Т“7і .
Возмемъ на мѣсто х какую нибудь частную величину а; тогда всѣ функціи
6і, Оі. 03,.... обратятся въ числа, и получится разность:
Да—т-7і) —Да)=б,7т—і—О,к*—г—г—. .. і—А”,
зависящая только отъ перемѣнной 7і. А какъ число членовъ этого ряда опредѣ-
ленное, то приращенію к всегда можно дать такую малую величину, что сумма
Ѳік-г-Ѳікг-+-О3к3-г-....-л-кп, то есть, разность /\а-+-к—Да) можетъ быть
сдѣлана менѣе всякаго даннаго количества е. Въ самомъ дѣлѣ, положимъ,
что для к—д, весь рядъ въ т разъ больше е, то есть, будетъ:
:е;
Ѳ15-4-еІ52-ь....=зпіе, гдѣ т>1, или
бЛ-ѣ-бД2
т т
$
тогда стоитъ только взять — вмѣсто д, и пе обходимо сдѣлается:
т
ѳ,. 4-1-01—5-+"•••• <е-
„іа т5
ЗЛО. Если цѣлая раціональная функція отъ какихъ нибудь
двухъ подстановленій х—а, х=а-г-к, обращается въ два результата
—К и -+-В', съ противными знаками, то, между подстановленіями а,
а-ь-к, находится по крайней'мѣрѣ одно такое, при которомъ эта функ-
ція обращается въ пуль.
Положимъ, что, для х=а, будетъ ({а}——В, а для х=а-+-к, будетъ
[(а-і-к)=[(а)-і-['(а}. к-г-^[^(а).кІ-г-....= -г-В.', или
= —Кч-617и-Ѳ2/і*-і-....=-+-В'
Поелику Да?) непрерывная, то, уменьшая к, можемъ сдѣлать О^г-ьб^і’-ь....
меньше всякаго даннаго числа, слѣдственно и меньше В, такъ что Дан-7і) обра-
тится въ результатъ отрицательный, прежде нежели уничтожится к. А какъ
цѣлая раціональная функція пе иначе переходитъ изъ положительнаго результата
въ отрицательный, какъ переступая чрезъ нуль, то необходимо должно быть та-
кое нодстановлсніе а-г-к' <ач-А, нри которомъ Дач-Л)=0.
3<*. Обратно: если число х=а уничтожаетъ данную [(х), не уничтожая
первой ея производной оп то, при этомъ переходѣ чрезъ нуль, функція перемѣ-
няетъ знакъ свой. Ибо, тогда:
Да?)—Да)=О;
- 318 —
она, для а—к, сдѣлается Да—Л)=——....,
а для а-+-к, она будетъ /'(а-+-К)=^ч-91к-+-9ІкІ-л-....
Приращеніе к всегда можно взять столь малымъ, что первые члены —ѳЛ,
н-0Л, сдѣлаются болѣе суммы всѣхъ послѣднихъ; и тогда знаки для Да—к),
Да-і-к), будутъ одинаки съ знаками этихъ членовъ, т. е. получатся:
Да—Л)= —, ^ач-к)=: ч-_
Слѣдовательно, если, для х=а, будетъ Да)=0, а О, не нуль, то данная
функція, при переходѣ чрезъ нуль, должна перемѣнить знакъ — па и
обратно.
Но, если подстановленіе х—а уничтожаетъ не только Да), но и 0,, не уни-
чтожая Ѳ,; то будемъ юнѣть:
Да)=0, и Ѳі=0,
Да—к)—^—Ѳ3к3-+-....,
Д а ч- /і)~бЛ’-ьб3/і3-+-.
Для приращенія к, довольно малаго, первые члены этихъ рядовъ превзойдутъ
сумму всѣхъ послѣднихъ, и тогда будетъ
Да—Л)= -+-, и І\а-+-к)=: -+- .
Слѣдовательно, въ этомъ случаѣ, данная функція, при переходѣ чрезъ, нуль,
не перемѣняетъ своего знака, но остается положительною пли отрпцательною,
смотря по тому, какой знакъ будетъ у ѲІ, плюсъ или минусъ.
Разсуждай такимъ образомъ, легко опредѣлить знаки для Да—к), [(а-ь-Іі),
когда уничтожаются сряду ѳ, Ѳц, 0г, или Ѳ, 6і, 6к, 63> и такъ далѣе.
Примѣръ. Функція Да?)=о?®—2а?’—5о?ч-6. которой первая производная
О,—За;’—4а?—5, при подстановленіяхъ:
х=— 3, — 2, —1, 0, 1, 2, 3, 4, дѣлается
Да?)=—24. О, 8, 6, 0,-4, 0, 18,
Ѳ,= 34, 15, 2, —5, —4, —1, —10, 27.
Она уничтожается три раза, переходя изъ положительнаго результата въ
отрицательный, и обратно. При этомъ ея первая производная не уничтожается.
Примѣръ. Возмемъ еще функцію
Да?):^1-^’—11а?’—5а?-ь30, и ея первую
производную 01=4а?3-ьЗа?’—22а?—5,
и будемъ подставлять въ ту и другую
х=— 4, —3, —2, —1, 0, 1, 2, 3.
Да?)= 66, 0, 4, 24, 30, 16, 0, 24,....
Ѳ1= —125, —20, 19, 16,—5,—20.—7, 64,....
По видимому, эта функція перешла чрезъ нуль два раза, не перемѣнивъ
своего знака; по, поелику подстановлепія а?=—3 и 2 не уничтожили Ѳо то
слѣдуетъ заключить, что, для нѣкоторыхъ среднихъ подстановлешГ' мйжду
— 319 —
—3, —2, и между 2, 3, [(х) должна имѣть величины отрицательныя. Для
испытанія, беру х=. —|/5 и = і/5, и получаю:
х=— Ь, — 3, —1/5, — 2, — 1, 0, 1, 2, |/5, 3,....
Дя)= 66, 0, 0, 4, 24, 30, 16, 0, 0, 24,....
Ѳ,= ........—20, —14,46;................... —7, 5,54,......
Случайность, что Дж), перешла два раза чрезъ два нуля, не перемѣнивъ
своего знака, и безъ уничтоженія Ѳ1} показываетъ, что между —3, —1^5, и
между 2 и |/5 есть еще числа, для которыхъ Да;) перемѣняетъ свой знакъ.
И въ самомъ дѣлѣ, если взять —2,5 и ж=2,1, тотчасъ найдутся:
Даг)=—2,8..., Цх)= — 0,3,
и такимъ образомъ откроется, что ((х), при всѣхъ ея переходахъ чрезъ пуль,
перемѣняетъ знакъ свой.
ЗЛЗ. Наибольшія (тахіта) и наименьшія (тіпіта) величины этихъ
функцій.
Если [(х), при непрерывномъ ея возрастаніи перемѣнной &, въ какихъ пи
есть предѣлахъ отъ а до Ь, сперва увеличивается, а потомъ уменьшается, то,
разумѣется, что, для какого нибудь опредѣленнаго числа между а и й, эта
функція получаетъ наибольшую величину (тахітит) относительно ея вели-
чинъ, сопредѣльныхъ съ этою. Если же /\х) сначала уменьшается, а по-
томъ увеличивается между предѣлами а и Ъ ея перемѣнной; то она въ этихъ
предѣлахъ получаетъ величину самую меньшую (тіпітит) относительно вели-
чинъ къ ней ближайшихъ, сопредѣльныхъ.
Случается также, что {\х), при непрерывномъ возрастаніи х, сперва увели-
чивается, потомъ уменьшается, а послѣ того снова возрастаетъ и опять начи-
наетъ убывать, и т. д. Такая функція бываетъ нѣсколько разъ наибольшею и
наименьшею.
По функція не имѣетъ пи наибольшей, ии наименьшей величины, если она, съ
возрастаніемъ х, сама возрастаетъ отъ —о© до ч-оо , либо наоборотъ.
3<3. Опредѣленіе условій, при которыхъ данная Да?) дѣлается наибольшею
или наименьшею, составлиетъ особенную важность въ математическомъ анализѣ.
Для этого на мѣсто х возмемъ ближайшія (сопредѣльныя) къ нему величины
агч-й, х—1і. Если тогда окажется, что
Да?ч-/і) <Да?) I то между этими предѣлами
и [(х—Л)</(а?) ( [(х) имѣетъ тахітдт;
а если найдется, что будетъ
Да?ч-/і)>[(х) | то опа имѣетъ
[іх—й)>/’(а?) | тіпітит.
— 320 —
Въ первомъ случаѣ, разности:
/(ам-Л)—[(х) | ,
'; ,' ; обѣ отрицательныя,
[(х-к)— I
а во второмъ, эпѣ обѣ положительныя. Эти условія мы легко откроемъ, взявши •
^ж-+-7і)—- —ь-0,/1—і-0в7і2ч—037ів—і—....,
/’(ж—7і)—/’(ж)— —03Л3-+-.............................
Очевидно, что, для малѣйшихъ приращеній к, эти разности будутъ съ против-
ными знаками: первая будетъ положительною, а вторая отрицательною, если
только не уничтожится б,; слѣдовательно будетъ;
/(жч-Т^^ж), Цх—Л) </\ж).
Въ этомъ случаѣ [(х) не имѣетъ величины ни самой большей, ни самой мень-
шей; но, опа будетъ тахітит или тіпітит, когда, прп этомъ упичтожитси
первая производная безъ уничтоженіи второй; ибо, для Ѳ1=0, будетъ:
({х-і-к}—/'(а:)—037Л+-037Л+-.
^х—к)—[[х)=Ѳікі—Ѳ3к3-г-......
Для к довольно малаго, обѣ разности будутъ положительныя или отрицатель-
ныя, смотря потому, 0,= ч-, или =: — .
Слѣдовательно, всякая величина х, обращающая [(х) въ наибольшую или
наименьшую, должна дѣлать Ѳ,=0, то есть, быть корнемъ этого уравненія.
Нельзя заключать обратно, что всякій корень уравненія 0,=О обращаетъ
/(ж) въ тахітит или тіпітит-, ибо, можетъ случиться, что одинъ пли нѣ-
сколько такихъ корней дѣлаютъ не только Ѳ,=0, но и 03=О, не уничтожая
Ѳ3; отчего разности функцій сдѣлаются:
/(ж-ь7і)— /(ж)= ч-037і’ч-Ѳ47і‘ч-. ...,
Дж—к)—[(%)— —037і3-і-Ѳ47і‘—....,
и, для к довольно малаго, будутъ съ разными знаками: тогда опять /’(ж) не бу-
детъ ни наибольшею, ни наименьшею, однакоже сдѣлается таковою, когда тотъ
же корень уничтожитъ въ тоже время п ѳ3, не уничтожая Ѳ4; и т. д.
И такъ, вообще, чтобы корни уравненія 0,г=:О обращали [(х) въ тахі-
тит или тіпітит, надобно, чтобъ отъ ихъ подставленія въ 0„ 0,, 03,
Ѳ4,.... первая неуничтожающа не я производная была четнаго порядка;
въ противномъ случаѣ, /’(ж) не имѣетъ пи наибольшей, ни наименьшей величины.
ЗАД.Остается еще найти признакъ, по которому можно узнавать, когда корень
х, найденный изъ Ѳ,=0, и удовлетворяющій предыдущимъ условіямъ, обращаетъ
/’(ж) въ тахітит, и когда въ тіпітит. Въ этихъ случаяхъ будутъ разности:
{{х-+-к} —/’(ж)=:Ѳ27і2-+-Ѳ37і3-4-. ..,
/'(ж—к)—/,(ж)=Ѳ3ЛІ—037і3ч-...., либо
[ ,
[(х—к)——Ѳ,7і“ч-....
— 321
Знакиихъ членовъ ѲаЛ’, Ѳ,Л‘, будутъ зависѣть только отъ знаковъ предъ Ѳ,,
б4. Если ч3=—, 64——, то, для к довольно малаго, будетъ
/•(жч-Л) < [х, [(х—к'^Цх).
Если же 0г=ч-, ь, то
Л^ч-Л) >[х, ((х—к) >[&).
Въ нервомъ случаѣ [(х) обращается въ тахітит, а во второмъ въ тіпі-
тит. Этотъ признакъ и открыть нужно было.
Примѣръ. /,(ж)=жІч-4а:ч-2, имѣетъ производныя: Ѳ,—2жч-4, б,=1.
Чтобъ найти, имѣетъ ли эта функція величину наибольшую пли наимень-
шую, возмемъ б,=2жч-4—0; отсюда найдемъ х=.—2. А поелику Ѳ,=1
есть положительная, то /’(ж) допускаетъ тіпітит, для х~ —2, которое и
найдется:
ж’ч-4жч-2=4—8ч~2=—2.
Примѣръ. І\х)=х'—8а?3ч-22ж*—24жч-12, имѣетъ
Ѳ, ~4.г3—24 а-'ч 44ж—24,
Ѳ,=6ж*—24жч-22,
9а=іх— 8, 64—1.
Для опредѣленія ен наибольшихъ и наименьшихъ величинъ, возмемъ то
есть, уравненіе
•г’ч-б^ч-1іх—6=0.
Оно имѣетъ корни 1, 2, 3. Подставимъ эти корни въ 9г; найдется:
для корня 1, Ѳ,= 4, /’(ж) дѣлается тахітит;
для корня 2, Ѳ3——2, /(ж) дѣлается тіпітит;
для корня 3, Ѳ,= 4, — — опять тахітит.
Примѣръ. (\х)—а-+-Ь(х—с)і, или
[[г)=:а-+-Ьх‘‘, полагая х—с~г;
—с)’,
Ѳг =:6кх*=6д(х—с)*, •
Ѳ3—46х "46(ж—с).
= Ь =: Ъ.
Полагая Ѳ1=46(а;—с)3=0, найдется ж=с; отчего сдѣлаются /'(ж)—а, Ѳ{=:0,
Ѳ^=0, Ѳ3—О, 04=6. Слѣдовательно, [{х)—а есть тахітит.
Примѣръ. Но ((х}—а-+-Ъ(х—с)3, не имѣетъ ни наибольшей, ни наименьшей
величины; оттого что, для х~с, дѣлается /’(ж)=а, Ѳ^О, Ѳ3=0, 9с-=.Ь, гдѣ
первая пеуничтожающаяся производная нечетнаго порядка.
— 322
II. Разложеніе цѣлой, многочленной, раціональной функціи въ
НЕПРЕРЫВНУЮ ДРОБЬ.
345. Функціи какъ раціональныя, такъ ирраціональныя и трансцендентныя,
будучи развергнуты въ ряды, расположенные но степенямъ ихъ перемѣнной,
вообще, имѣютъ впдъ:
^(л-)=С0-ьСі^-4-Сіж -+Сажв-4-С4ж4-+-...
Всякая такан функція можетъ быть выражена непрерывною дробью, вида:
/(Ж)=С0-ь^--------
1 ' , алс
1-*--------
а,х
—---------
«4ж
а,ч- —
" «з-ь.
Для этого надобно только неизвѣстные коефиціепты а,, а2, а,,.... выразить
посредствомъ данныхъС„, С„ Ц, С3,...., что и нетрудно исполнить, составивъ
равенство:
Откуда,
_«і________
1ч- а‘Х
а3х
а,ч—------
а2-ь...-
а2С1ж-+-а2С2а;2-ь....
а.ж
к,ь--------
а.х
«2ч----
Это равенство имѣетъ мѣсто для всякаго х, а слѣдовательно п для а;=0;
стало-быть, а,=С.
1 г
Отбросивъ С, и а, изъ равенства 1), и раздѣливъ па х, останется:
С,-іС3.гч-С,г’ч-. .. .і-
а2н—-
«3-і
=0
или:
2) С1С2-і-С1С8^ч-С1С$ж*-+-....-і-
а3 С2ж 4 а3 С3х2-+-«3 С4ж3
“•_«2С,-+-а,Сіам-«іС3жін-
Полагая ®=г0, имѣемъ отсюда С,С8ч-а2Сі=:0, или
ал— —С2.
323 —
Выпустивъ члены С,С2-+-а2С1=О изъ равенства 2), и сокративъ на х, оста-
нется:
СДч-СДям-СДж®-»- ...н-
®зС2-4-а3С3а?-,-а1С4®2ч-.
—С,ч-
а3-+-...
—С2—С2С3д?—С2С4я:!—... .—О; откуда
3) а3С2-і-а3С3а;-ьа3С4ж-ь... .=—(С|—С2С3)С2—(СД—С Д Д*—
__/г г>__р р „8 , С,С3)хч-а4(СгС3 С,С4)ж ~і~....
Здѣсь также, полагая ж=0, найдется-.
а3С^=—(С®—СД)С2; откуда,
а3—СД—С|.
Выпустивъ равные члены изъ равенства 3), и сокративъ на х, получимъ:
4) аяС3-і-«зС4х-ь....=—(С2С3 -СД)С2—(С2С —СДД*—....
«4(С|—С,С3)-»-а4(С2С,—С.С^-ь...
’ а4-ь...
Отсюда, для жгтО, найдется:
(СД-Д)С^—(СД-СД)-а4. и
а4=С1(С2С4—С4);
и такъ далѣе.
Слѣдовательно, искомая непрерывная дробь будетъ:
Лж)=Со-ь2^_
~С.(С,С,-Ф
* _с _ СДСД-С®^
2 С,С3-С|-І-....
Эта дробь имѣетъ свои послѣдовательныя приближенія, между которыми она
т, С,® „
заключается; изъ нихъ первое: — = — =С,.г,
т„ С?®
второе: — = -г—— ,
г п2 с,—с2®
посредствомъ которыхъ найдется третье приближеніе: для этого помножимъ чи-
- ™2 „
слитель и знаменатель дроби — на знаменатель —С2 третьяго члена приоли-
С х
женія, а числитель и знаменатель дроби -у- па числитель (С,С3—С|) того чле-
на, потомъ возмемъ сумму числителей и раздѣлимъ на сумму знаменателей;
тогда, по сокращеніи, получится:
__—С^ям-СС,^—С|)а:2
। —С2-ьС,®
— 324 —
Такимъ же образомъ нашли бы у , и, наконецъ, послѣднее ~ равное всей не-
прерывной дроби. Слѣдовательно, имѣли бы:
Дж)=С0-Ьу.
пг
ІП. О РАЗЛОЖЕНІИ НЕОПРЕДѢЛЕННО—СТЕПЕННОЙ ФУНКЦІИ аХ ВЪ РИДЪ,
РАСПОЛОЖЕННЫЙ ПО СТЕПЕНЯМЪ ЕЯ ПЕРЕМѢННОЙ X.
3X3. Мы знаемъ (333), что функціи дробныя и функціи ирраціональныя
могутъ разлагаться въ безконечные ряды; но и функціи трансцендентныя также
изображаются рядами.
Такъ, мы видѣли, что логариомическая функція,
Я®)—Іо§( 1-ьж)=А(ж— у аг’-ь х3— 1 до4-»-...),
изображается безконечнымъ рядомъ. Покажемъ здѣсь, что всякая неопредѣленно-
степенная функція ах, не смотря на всю ея простоту, также разлагается въ рядъ,
расположенный по степенямъ ея перемѣнной х.
Пусть этотъ рядъ будетъ:
аж~1-ьАлн-Ва?2-ьСя:3н-Шл-+-...................(I),
гдѣ А, В, С, О,.... коефпціенты, независимые отъ х, которые надобно опредѣ-
лить. Первый членъ ряда=1, потому что, для а=0, ах—а°=1 Но, если
предстоящія независимы отъ х, то онѣ останутся тѣ же, когда возмемъ г на
мѣсто х:
а ==іч-Л~-і-В^ ......(2).
Вычтемъ этотъ рядъ изъ предыдущаго:
ах—ах=А.(х—а)-ьЗ(л;!—а’)ч-С(ж3—а3)-ь...., или
)—А(л:—г)ч-В(жа—х!)-ьС(ж3—23)-і-.... (3).
Но, необходимо также будетъ и
а^уЛ-ьА^—г)н-В(*—г)’-ьС(ж—2)3-ь....;
подставимъ это въ (3) строку, найдется:
аг[А(а?—г)-ьВ(я:—2)вч-С(а?—г)3-ь..]=А(а?—г)ч-В(ж8—28)-ьС(«3—23)-ь..
Исключивъ общій множитель х—х, останется:
аг[Ач-В(ж—г)н-С(ж—г)в-ь... .]=Ач-В(ж-+-2)-ъС(я:'1н-а;я-Ь2!)-ь....
Перемѣнная а произвольна, а потому можемъ взять х=х-, получится:
аа:А=А-ь2Влч-ЗСж!-+4В®1 -и....
Сюда подставимъ ах='1ч-Аа?-ьВж8-ьС«3-ь....:
Ач-А’ан-АВаЛч-... .=Ач-2Вж-ьЗСа;!-ь....
I
— 325 —
Для равенства этихъ многочленовъ, необходимо должно быть:
А—А, 2В=А’, ЗС=АВ,....; откуда
А® А3 п А«
В=Ё2’ С=3’Е=П^’ИТ-д-
Посему,
а^І+Аан-^-і-^-ч-..............(4).
;<із. Въ этомъ ряду предстоящее А не могло опредѣлиться, потому что оно
зависитъ отъ частной величины а, и съ ея перемѣною должно измѣняться. А
какъ оно не зависитъ отъ х, то оно останется тѣмъ же, если взять х=1; тогда
найдется:
. А А® А’
с=І+1+_+_+....
Но, чтобъ найти простѣйшее выраженіе зависимости А отъ а, возмемъ снача-
ла А=1; при этомъ а измѣнится и получитъ опредѣленную величину, которую
означимъ чрезъ е:
„111
е=2ч----1----і---ь
2 6 24
=2,718281826459....
Число это тѣмъ замѣчательно, что есть не что иное, какъ основаніе Пейеро-
выхъ логариѳмовъ
Это же самое получится, если въ ряду (4) положить Ая=Л, или х— —; то
есть, будетъ
а А
і і і
2 -Ь О 24
слѣдовательно,
аА~е, или еА=а.
Логариѳмъ этого равенства, по системѣ Пепера, найдется
А=І6б«;
т. е., предстоящее А всегда равно Неперову логариѳму отъ а. Вставивъ это
въ рядъ
«. . . А®ж® А3я3
а = 1-ьАян—— -+- і 2- -ь...., получимъ:
л, , Ѵа Ѵа , Ѵ*а ,
а =1ч--. х+—. х+—.а*+..............
Таковъ искомый рядъ, въ который разлагается неопредѣленно-степенная
функція а®.
Если положить а—с— основанію Неперовыхь логариѳмовъ, слѣдовательно
/'«—1, то получится рядъ
_ , х а?
весьма употребительный въ высшей математикѣ.
(51
— 326 -
х1 >,!1а хъ.1''іа
-а
31*. Въ найденномъ ряду, ’
~ . х.І'а _ _
а~Ц — + — 4-^4-................,
котораго Ра не завист ь отъ х, поставимъ г вмѣсто х\ будемъ имѣть:
. х.І'а
а-1н-~-нТТТ-ьТТ2л-н--
Вычтемъ послѣдній рядъ изъ перваго, и разность раздѣлимъ на х—-я
найдется:
а®—аЕ ,. '(х-у-г) (.т’ч яч-ч-г®}
------=Ра-4-\—. Га-+- 5—х-
X—г 1.2 1.2.3
Теперь положимъ г—®, получится выводъ
О ' 1.2 1.2.3
. хі'а х*Л'9а х
110, МЫ видѣли, ЧТО 1-Н -- -1-
1 1./
— =Ра. аа=а3! .Ра.
о
—а
ТО
349. П обратно, если въ рядъ,
16е(1-ь®)=®—®э— ‘-®4-ь............... (950),
подставить г вмѣсто х,
,6ё(^4-2)—2— 2 в'+'423—уг‘-ь...., вычесть
послѣдній пзъ перваго, и разность раздѣлить на ®—х; получится:
—---------------=1—— (®ч-г)-+- — (®!-+-®г-ьг!)— — (®3н-®!.г....)-ь...;
и йотомъ положить г—®; найдется также
0 . о О . 1
- = 1—®-ь® X Ч-®—....=•-------.
О 1-Ьи,'
Въ обоихъ этихъ случаяхъ, выраженіе^- получило опредѣленное значеніе.
Примѣчаніе. — О рядахъ различныхъ функцій и ихъ подробномъ разсмо-
трѣніи надобно читать въ пространныхъ курсахъ Алгебры. Здѣсь же мы ограни-
чимся только случаями, наиболѣе нужными, для достиженія предположенной
цѣли въ этомъ начальномъ курсѣ Алгебры.
IV". Обращеніе рядовъ функцій съ одною перемѣнною.
350. Обращеніе рядовъ показываетъ способъ, какъ данную функцію, вида
я®-ьб®?-4-с®3-ь(/®4-ь... .=[(&),
расположенную по степенямъ ея перемѣнной ®, преобразовать въ другую, въ
которой бы перемѣнная х обратно была выражена рядомъ расположеннымъ по
степенямъ у.
- 327 —
Пусть этотъ новый рядъ будетъ:
о:=Ауч-В</3ч-С»/!’ч-Пу*-ьЕ^в-ь....,
въ которомъ Л, В, С, В, Е,... постоянныя предстоящія, независимыя отъ х, у,
п которыя подобно опредѣлить. Для этого составимъ различныя степени
У, У\ У3,---- посредствомъ даннаго ряда:
уі=аіхі-+-2аЪхі -і-б* хвч-(2аеч-2/;(1-і-г*]хб-+-.....
-+-2ас
уа=аіув-+-За*Ьх1-і-ЗаІ)г я?ч-(Заі(і-+-$аЬс-і -6?)жв-ь....,
ч-Зас
у‘=а‘л?4-ь4а3бжвч-(6а8б8-ь4а5с)а?6-+-....,
ув=авж'ч-5а‘ітв-ь....,
уе=авхе-і~....;
вставимъ ихъ во второй рядъ, и расположимъ всё по степенямъ х:
О—Аа х-4-АЬ х‘н- Ас
—1 іВа8
-+-2ВаЬ
н-ЗСа8^
-+- Па*
Но, чтобы это равенство могло существовать независимо отъ величины х
надобно, чтобъ было:
Аа—1=0, А6ч-Ва’=0, Асн-2Вад-г-Са3=0,
А(Іч-В62ч-2Васч-ЗСаг/,ч-Па*=0, и проч.
Отсюда найдутся:
. 1 г, —АЬ —Ь , 26*—ас
А — , 13 — ~ , С — л~~ >
а ’ а? а5 а*
5аЬс —ЗЬ5 — а*Л (ЗЬ3ч-а2й—5аЬс)
— -і------, и далѣе,
а' ' ’
°= 1
р___ 14 —а3е—21а!>2с-і-За2с2-»-6о26г7
Ь—-------------------„-------------
ау
(426“—84а6яс-»-28а26св-ь28а262(і—7ая6е—7аясгі-4-аѴ)
Г=
и такъ далѣе.
Слѣдовательно, искомый рядъ будетъ:
1 Ь » /2Ь — ас\ , /’іі6г-і-а*сІ—ЪабсХ ,
а. И‘+ (-)!/-(-------------------)/+
(146’ -21 аЬ-гч-З^с^ч-б^Ьй—а’е) в
а9 У
Если бы данный рядъ былъ
^=аж-і-^х'3-ьса:в-ь....,
то, поступая точно также, нашлп бы
1 Ь . ,ЗЬ’—ас. . /62Ь3-ч-а!й—8аЬсч ,
( V )!/- (----------
— 328 —
Примѣръ 1. Извѣстно, что
у=Іо§(1ч-я)=:М(я;-— х!ч- у ж’— у я*ч-....), гдѣ
М- =0,43429.44819.03251.8.... = модуль. Если бы мы пожелали выразить
число х рядомъ, расположеннымъ по степенямъ у = 1о§ (Іч-т); то, отдѣливъ
модуль М,
у — ~ 1 | 1 ' 3 1_ і
М— 2 3 ~4 Х
сравнимъ зтотъ рядъ съ рядомъ
у=аа?ч-бж8ч-сж3ч-с?а?4ч-. ..., полагая
1,1 у
с— а=—и взявъ — па мѣсто у, подставимъ въ
2
рядъ
г2& — ас\ 3
——) у найдется.
ѵ Vе V5
ч-----------1-----------1-.....или
М 1.2.М2 1.2.3.М3 ’
__1о"(іч-гг) 1о"3(1ч-гг)
х ВТ 1 1.4.М* *“ і•
А если взять 1ч-я=г, или #=2—1, то получимъ
Іоцг» 3
I
х= -
г—1-ьн-— в’ч-- —
М 1.2ѴМ/ 1.2.3
• число расположенное по степеням ь своего логариѳма.
Примѣръ 2.. Пусть требуется данный рядъ
х3 ая
у—а?----------1-------------....
у 1.2.3 1.2.3.4.3
обратить въ а=/(у). Взявъ рядъ у=аам-6х3ч-сж'—
сравнимъ коефиціенты, полагая:
. , і і
а=1, Ь=— — —, с= { 2 и подставимъ въ радъ
1 Ь , /ЗЬ3 — ас\ .
х=а'У~ “Ь Ѵ-—г—) У —••••. найдется:
и и и-
1.«5 1.3.и“ 1.3 З.з/7
= —~ Ч-------------1-------1....
2.3 2.3.5 2.4.0.7
Мы воспользуемся обращеніемъ рядовъ при разрѣшеніи численныхъ уравненій
высокихъ степеней съ одною неизвѣстною.
329
ГЯАЕА ЧЕТЫРНАДЦАТАЯ.
ТЕОРІЯ УРАВНЕНІЙ, ВЫСШИХЪ СТЕПЕНЕЙ, СЪ ОДНОЮ НЕИЗВѢСТНОЮ
351. Уравненія высшихъ степеней съ одною неизвѣстною, несодержащія
трансцендентныхъ функцій въ членахъ своихъ, бываютъ раціональныя и ирра-
ціональныя. Раціональное уравненіе имѣетъ видъ цѣлой раціональной функціи;
члены его содержатъ неизвѣстную х, возвышенную только въ различныя цѣіыя
степени. Оно, будучи расположено по степенямъ неизвѣстной, приводится къ
общему виду.
ж"н-Аж’,-1-і-В"_!ч-... .Тлн-ІЬ:0,
гдѣ п цѣлое число, А, В, С,....Т, I), коефиціенты, независимые отъ я;, ко-
торые здѣсь предполагаются дѣйствительными, цѣлыми или дробными, положи-
тельными или отрицательными; въ числѣ ихъ .могутъ быть и несоизмѣримые,
и даже равные нулю. — Уравненіе •ирраціональное состоитъ изъ членовъ,
между которыми есть такіе, гдѣ неизвѣстная имѣетъ дробныхъ показателей.
Настоящимъ нашимъ предметомъ будутъ уравненія раціональныя, а
цѣлью — ихъ разрѣшеніе. Раціональное уравненіе называется полнымъ,
когда содержитъ всѣ члены отъ степени хп до х°-} въ противномъ случаѣ, оно
неполное.
359. Корнемъ уравненія называется всякое количество, дѣйствительное
члп мнимое, которое, бывъ подставлено на мѣсто х, удовлетворяетъ уравненію,
т. е. дѣлаетъ первую часть его равною второй.
353. Рѣшеніе уравненій бываетъ алгебрическое' и численное. Рѣшить
уравненіе алгебрически значитъ найти формулу, въ которой бы всѣ корни его
выражались въ функціи его коефиціентовъ. Такія формулы*до сихъ поръ из-
вѣстны только для полныхъ уравненій первой, второй, третьей и четвертой сте-
пени. Но, уже формулы, выражающія корни уравненій 3-й п 4-й степени такъ
сложны, что остаются почти безъ употребленія; а между тѣмъ часто бываетъ
нужно рѣшать уравненія, которыхъ степень выше второй. Это обстоятельство
заставило искать общій способъ рѣшепія всякихъ чи< ленныхъ уравненіи по-
средствомъ вычисленія каждаго его корня отдѣльно. Для этого надлежало раз-
смотрѣть общія свойства уравненій и составить общую теерію, которая бы
показывала законъ составленія всякаго уравненія изъ его корней, возможность
— 330 —
давать ему различныя преобразованія чрезъ однообразное измѣненіе корней, от-
дѣлять корни одинъ отъ другаго частными предѣлами, и, наконецъ, вычислять
ихъ. Изъ этой теоріи найдено, что, для вычисленія какого ли есть корпя, отдѣ-
леннаго отъ прочихъ своими предѣлами, надобно сперва дать уравненію особое
преобразованіе; ііашедпш этотъ корень, надобно снова преобразовать уравненіе,
сдѣлать его удобнымъ къ вычисленію другаго корня, и т. д.
Рѣшеніе такого рода называется численнымъ, и совершенно отличается отъ
алгебрическаго, гдѣ всѣ корпи выражаются общею формулою, состоящею изъ
связи коефиціептовъ даннаго уравненія, и отыскиваются чрезъ одно подстано-
вленіе сихъ коефиціентовъ. Для примѣра, возмемъ уравненія:
хі—%ах—Ъ=0, И Xе—2осе—6=0.
Каковы бы пи были а и Ъ въ первомъ уравненіи, оно рѣшается алгебрически;
оба его корня выражаются общею формулою:
х—а±
и получаются чрезъ одно подставленіе чиселъ вмѣсто а и Ь. Но вовсе не таково
другое уравненіе: для него нѣть общей формулы, которая бы сразу опредѣляла
всѣ его корни. Впрочемъ, одинъ корень этого уравненія (таити можемъ, если
6> |/2а; потому что ему можно дать видъ
в /----------------------------------------------------•
аг=2ач-----, а отсюда гх \ /2а н------;
X \ X
8 г Л ’
слѣдовательно, х=Ѵ2а-г----------
I________
|/2а-ь....
и этотъ корень можетъ быть вычисленъ; но, все же этимъ способомъ нельзя
отыскать прочихъ корней.
При изложеніи теоріи раціональныхъ уравненій, мы часто будемъ принимать
ихъ за цѣлыя раціональныя функціи отъ х; а потому, для краткости, будемъ
означать ихъ чрезъ /’(л:)=.0, пли ([х^п—0, если нужно будетъ показать и са-
мую степень т уравненія.
351. Основаніемъ теоріи уравненій служитъ слѣдующая теорема:
Ссяьое уравненіе, имѣющее видъ цѣлоіі-раціоналыюй фунціи, имѣетъ
корень, вида а-л-ЬѴ—1, гдѣ а, Ь, числа дѣйствительныя, которыя, въ
частныхъ случаяхъ, могутъ быть нулями.
А. Возмемъ сперва двучленное уравненіе
приведемъ въ простѣйшій видъ, полагая *=
видъ х*п-Ы—(
тогда это } равненіе получитъ
— 331
откуда непосредственно имѣемъ
т _______________________________ т —
х= V -4-1, х= V—1.
Для т нечётнаго, ііайдутся: ж=н-1, х ——1; то есть, ч-І корень для
хт—1=0, —1 корень для ж”*ч-1=0.
Если показатель гп чётный, то онъ можетъ быть или степень числа 2, или
степень числа 2, помноженная па нечетное число 2»ч-1, то есть:
ти=2г. пли т=2'.(2лч-Г);
и двучленнымъ уравненіемъ будетъ
ж8Г=±1, либо ж* (8”+о=±1.
г 5
Уравненія ж® = ч-1, х3 <2,‘+«>=ч_|} очевидно, имѣютъ корнями ч-І, —1.
Пзъ уравненія х* = —1 непосредственно находимъ
8Г.__
бс=± у—1.
По, извѣстно, что корень такой чётной степени 'ЭЛО, ЭА1) изъ —1
имѣетъ видъ ач-6 \/—1.
Что касается до ж21,,,"+і'=—1, то здѣсь подобно сперва извлечь корень не-
четной степени 2ич-1 изъ обѣихъ частей уравненія, и мы перейдемъ къ преды-
дущему случаю, то есть: .
Іпч-1
х3' =\/ (—1)——1;
а отсюда кореиь четной степени 2* опять будетъ вида
В. Теперь докажемъ, что и всякое уравненіе,
/\ ^=лтч-А^т-‘ч-В^т-!ч-... .ч-Тан-Б=0,
котораго коефиціенты А, В,....Н, суть числа дѣйствительныя, или
мнимыя, имѣетъ корень того же вида а-+-йѴ—1.
Возмемъ я=рч-у У—1, подставимъ въ/7а?)=0, разложимъ всѣ члены
уравненія въ ряды, отдѣлимъ дѣйствительные члены отъ мнимыхъ, назовемъ
первые чрезъ Н=Е(р, <?), а вторые чрезъ V Vх—\==Е'(р,у}. V—1; то бу-
демъ имѣть:
Лрч-у Vх—4)=Нч-Ѵ Vх—!.
Если р-г-у V—1 корень уравненія Дж)=0, то должно выйти ІЗч-Ѵ V—1=0,
то есть, 15=0, Ѵ=0, или модуль ]/Ѵ3-і-Ѵ!=0 3), Остается доказать,
что есть такія числа р, у, которыми производится это равенство.
Вообще говоря, числа, произвольно взятыя па мѣсто у), у, измѣняютъ вели-
чину модуля і/Е’ч-Ѵ2, дѣлая его то больше, то меньше. Но, какъ бы малъ онъ
ші сдѣлался для какихъ пи есть подстановлепій р, у, всегда можно найти дру-
— 332 —
гія величины для р и у, и другой модуль ѴІУ’-ьѴ'8, который будетъ менѣе
ѴЛ]’-ьѴ’; такъ что напменьшпю величиною модуля не можетъ быть другая,
кромѣ нуля, и что./’(ж)=0 должно имѣть корень, вида р-і-цѴ—1.
Для этого возмемъ л^р-ьуі/—1-ье/, гдѣ е количество перемѣнное, спо-
собное сдѣлаться менѣе всякой данной величины, а I неопредѣленная, которою
мы могли бы располагать по нашему произволу. Для подстановленія этой вели-
чины х въ /’(а?)=0, мы перемѣнимъ сначала х въ хч-к; отчего получится:
Л2 Л3
Дж-ь7і)=Л*)-ь/^) .к+Мх). — - ч-Д(ж). — —ь... .-ь/іт;
потомъ, подставимъ въ эту формулу V—1 вмѣсто х, и еі вмѣсто к. Отъ
нтого членъ Г(х), какъ энаемъ, обратится въ Іл-Ѵ І; при чемъ нѣсколько
производныхъ: А(^)=/’1(р-ч-д'і/—Г), А(ж)з=уе{р-ьу И—1),.... могутъ уни-
чтожиться, одпакоже не всѣ; по крайней мѣрѣ кп, не содержащій х, останется.
Лп
Пусть /;(ж) • 4 2 3 п' первый послѣ (\х) неуничтожившійся членъ; слѣдователь-
но, будетъ:
Др-ь»; Ѵ/_І-ь/1)=і;-ьѴ 1/—Г-ь. /Г-ь..,-ь/Г.
Теперь подставимъ еі на мѣсто к, и положимъ, что сдѣлаются:
Др-ь? 1Л^Г-ье/)=П/-ьѴ/
=Кч-8 і/—П
то будемъ имѣть:
ІКьѴ'і/^Іг^Пн-Ѵ Ѵ<=1-ь(К-ь8 1/=4)е"/в-ьСе’,+,/«*‘,
гдѣ Се’‘+*/"+і означаетъ, для краткости, сумму всѣхъ членовъ, помноженныхъ ,
на количество еі, котораго степень выше п-ой.
Поелику I произвольно, то дадимъ ему величину, вида а-ь/ЗѴ —1, такую,
какая получится изъ равенства Г=±1; отдѣлимъ дѣйствительные члены отъ
мнимыхъ; найдется-
Ѵ^ѴіКе'-ьВ'е’4*,
Ѵ'=Ѵ:±38е’,-ьСѴЛ
откуда легко получится:
ІГ-ьѴ'8=П’-ь Ѵ!±2 (ІВ-ьѴ8) е"-ьКе’ѵ+*, нли
1/іКьѴ^
Величину для е можно взять столь малою, іто членъ 2(ІЖ-ьѴ8) сдѣлается
больше суммы всѣхъ членовъ послѣдующихъ, а для /"=-ь1, либо Г=—I,
можетъ быть сдѣланъ всегда отрицательны мъ; тогда сумма а5 всѣхъ членовъ,
слѣдующихъ послѣ Ь8-ьѴ8, будетъ отрицательною, и мы*будемъ имѣть:
то есть,
ИКьѴ8<ѴІЛьѴг;
что и доказать было нужно.
й
— 333 —
Можетъ случиться, что членъ 2(ІЖч-Ѵ8), то есть, ІЖ-+-Ѵ8 уничтожится;
тогда, вмѣсто его, надобно взять членъ, за нимъ слѣдующій, и, чрезъ надлежа-
щее измѣненіе еі, сдѣлать его отрицательнымъ и большимъ суммы всѣхъ по-
слѣдующихъ за нимъ членовъ ряда: результатъ получимъ опять тптъ же.
Если, для х=р-+-д \/—1-ье<, получится модуль і/Ц/8-ьѴ/8> 0; то опять
Шгь же способомъ, можемъ наити для х другую величину р'нн/і/—1-ье'і',
и другой модуль ’ і/С//8-+-Ѵ"8, который будетъ меньше ЦЦ^-ьѴ'8. Продолжая
такимъ образомъ, можно сдѣлать модуль менѣе всякой величины; а это показы-
ваетъ, что необходимо находится такое подстановлепіе х=р"-і-у" V'—І-ье'Ѵ',
которое уничтожаетт модуль, то есть дѣлаетъ 11=0 и Ѵ=0; оно и будетъ кор-
немъ даннаго уравненія. А какъ I", вообще, имѣетъ видъ —1, то
корень отъ этого будетъ
®г=(р//ч-а//е//)-ь(5/'-ь^З//е//) V—1, или
ж=а-ь6 Vх—1, *)
полагая р"-+-а//е//=а, у"-^р"еп—Ь. Въ этомъ видѣ онъ и останется, если не
уничтожатся пи а, ни Ь. Но, если члены р" и а"е", либо члены у" и @"е", бу-
дутъ равны и съ противными знаками, отчего сдѣлается а=0, или 6=0; то
найденный корень будетъ вида х=Ь V—1, либо х=а. Даже можетъ слу-
читься, что въ одно время уничтожатся а и 6, и тогда корень а?=0.
Слѣдовательно, корпи уравненія могутъ быть дѣйствительные и мнимые, тако-
го же вида, какого вида получаются они отъ разрѣшенія уравненій второй и
третьей степени, каковы бы ни были коефиціепты даннаго уравненія. При даль-
нѣйшемъ разсмотрѣніи, мы постоянно будемъ брать уравненія безъ мнимыхъ
коефиціентовъ.
355. Еели к=а корень уравненія,
І(х)’'=Ахпч-Вхп~1ч-Схп-іч-... .ч-Тжч-1=0,
то оно необходимо дѣлится безъ остатка на двучленъ х—а=0, и
обратно.
Пусть ф(х)”~1 частное число, которое получится отъ раздѣленія [(х)п па
х—а, и остатокъ Н, не содержащій х; то будемъ ии*ѣть равенство,
[(ху=(х—а)9>(о:)п_1ч-Н=0.
Но х=а есть корень уравненія; посему
{\а)п=(а—а)9>(а)п-1ч-В=0, откуда
Н=0.
Слѣдовательно /‘(ж)"=0 дѣлится на х—а безъ остатка, такъ что
[(ху=(х—а;д>(ж)п-‘=0.
") Этимъ простымъ и остроумнымъ доказательствомъ Алгебра обязана Французскому
математику Коши.
— 334 —
Иначе это доказывается такъ: подставляютъ въ данное уравненіе /‘(а?)’*—О его
корень а,
Аапч-Ва"-Іч-Сап~2ч-.......-ьТа-іі—0,
и это равенство вычитаютъ пзъ самаго уравненія:
А(ж”—-аЧч-В^"-1—а’-І)-ьС(^-2—а’‘-!)ч-... ,-4-Т(ж—а)=0.
Здѣсь всѣ двучлены х"—ап, —ап~1, х—а, дѣлятся па х—а безъ
остатка (ЛЗ); стало-быть, и данное уравненіе /'(я:)”=0 дѣлится безъ остатка на
х—а. Частное,
Лрг"—с") В(л"— *—ап~*) Срг”—8 йч—2) і о
х— а х—а х—а ’** 3
будетъ полиномъ, одною степенью ниже давнаго уравненія /?(ж)”=0, вида
Да?)"-1=А1®"-,-ьВІ«”-?-ьСІ«"“3-ь. • .ч-Т^О,
который, для сокращенія, назовемъ чрезъ [{х)п~1. А какъ дѣлимое равно дѣли-
телю, помноженному на частное, то
35в. Всякое уравненіе п-ой степени иліьетъ п корней, и не можетъ
имѣть ихъ болѣе.
Пусть данное уравненіе /(а?)"—0. Мы знаемъ, что всякое уравненіе имѣетъ
корень, вида —1, который, для краткости, назовемъ х=а, и что
оно дѣлится безъ остатка на двучленъ х—а. Пусть [(х)"~4 частное отъ раздѣ-
ленія [[х)г на х—а; то
Кх}"=(х—а)
Это равенство удовлетворяется двоякимъ образомъ: полагая х=а, либо
/^)-‘=0.
Но, уравненіе /’(о:)’,_4=0 само необходимо имѣетъ хотя одинъ корень х=Ь;
а потому оно раздѣлится на х—Ь безъ остатка, и дастъ частное, вида /'(а;)"-’,
еще одною степенью ниже. Посему, будемъ имѣть:
• —б)/'(ж)"-8=:0, и слѣдовательно
/(ж)"=(а?- -о}і{х}п~1—{х—а) (х—Ь)[(ху'-і=Ѵ)
чему удовлетворимъ, полагая:
а?—а, х=Ь, либо
Уравнена /\х)п~8=0, въ свою очередь, имѣетъ корень х~с, и можетъ раз-
ложиться па множителей х—с, /"(а")"-3, такъ что
(а?—с)/^)"-8—:0; отчего
СІх)п=(х—а) (а?—Ь) (х—с )/‘(а5)"-8—О.
Этому удовлетворимъ, полагая ,
х=а, х—Ъ, х=с, либо /,(.г)”-3==0.
— 335 -
Такимъ образомъ можно продолжать до тѣхъ поръ, попа послѣднее частное
будетъ въ себѣ содержать х только первой степени, и будетъ, напримѣръ, вида
х—к. Тогда уравненіе /’(х)"=0 разложится на п множителей первой степени,
и. будетъ:
[(ху=.(х—а) (ж—Ь) (х—с).... (х—й)=0.
Оио удовлетворится; взявъ па мѣсто х какую пи есть пзъ п его величинъ,
а, Ь, с,...к, и потому имѣетъ п корней а, Ь, с,...к. Другихъ корней оио не
можетъ имѣть никакихъ, во-первыхъ, потому, что многочленъ [(х)п одинакимъ
образомъ разлагается па простыхъ своихъ множителей (стр. 27); а во-вторыхъ,
если бы находился хотя одинъ множитель го, различный отъ а, Ь, с,....1с; то
произведеніе,
/(ж)п=(ы>—а) (го— Ь) (го—с).... (го—к)
пѳ могло бы сдѣлаться нулемъ, и потому число го не удовлетворило бы
уравненію.
II такъ, данное уравненіе имѣетъ ровно столько корней, различныхъ или рав-
ныхъ, сколпко находится единицъ въ его показателѣ степени: уравненіе первой
степени имѣетъ одинъ корень, уравненіе 2-й степени — два корня, уравненіе
3-й степени — три корпя, и т. д. Пзъ нихъ нѣкоторые могутъ быть дѣйстви-
тельными, а другіе мнимыми.
359. Существованіе мнимыхъ корней въ уравненіяхъ, неимѣющихъ мни-
мыхъ коее/пщіеіітовъ, подлежитъ замѣчательному условію.
Ежели уравненіе /’(ж)=0, безъ мнимыхъ коефиціентовъ, содержитъ
въ себѣ корень р-г-у V—1 , то оно неободимо имѣетъ и корень
р — 7 V—1.
Въ самомъ дѣлѣ, отъ возстановленія корня х=р-+-у V—1,это уравненіе при-
водится къ впду С-+-Ѵ —1=0, гдѣ многочленъ П содержитъ однѣ четныя
степени у, а многочленъ V—нечетныя степени у. Но уравненіе получитъ точно
тотъ же видъ и оіъ подстановлепія х~р—у И—1; разность будетъ только
въ томъ, что перемѣнится знакъ предъ членами нечетныхъ степеней у, то есть
передъ V, и наіідется:
П— V \/—Г.
По, чтобы Ьч-Ѵ V—1 равнялось нулю, надобно []=0 и Ѵ=0; а это усло-
віе дѣлаетъ, въ то же время,
п—ѵѵ/~і=о.
И такъ, /‘(а;)=0 удовлетворяется корнемъ р~+~у V—1 и корнемъ р—у V—1.
Слѣдовательно, мнимые корни въ уравненіяхъ бываютъ не иначе, какъ попарно.
Корпи, составляющіе такую пару, называются сопряженными.
— 336 —
359. Изъ каждой пары сопряженныхъ корней составляется въ уравненіи
простые множители:
х—р—(і V—1,
х—рч-ц Ѵ—'І,
которые, въ совокупности, даютъ произведеніе дѣйствительное, то есть, квад-
ратный многочленъ
(а?—а?8—2рхч~р2ч-дг,
на который уравненіе дѣлится безъ остатка.
Это произведеніе (х—р)*ч-д2 существенно положительное, и не можетъ
сдѣлаться отрицательнымъ ни для какихъ дѣйствительныхъ величинъ р и </.
Составъ уравненія изъ его корней.
359. Чтобъ открыть законъ, по которому составляются коефлціенты послѣ-
довательныхъ членовъ уравненія изъ его корней, возмемъ, для большей простоты
и очевидности, уравненіе 4-й степени:
—а) (а?—Ъ)(х—с)(ж—й)—О,
содержащее четыре корня а, Ь, с, Л, и состоящее изъ четырехъ двучленныхъ:
множителей. Сдѣлавъ умноженіе, получимъ:
—а х3ч-аЬ х2—аЬс хч-аЬсд,—^
—Ь ч-ас —аЬЛ
—с ч-ай —асЛ
—Л ч-Ьс —Ъсй
ч-Ь(1
Ч-С(І
Еслибъ взяли уравненіе пятой степени, состоящее изъ пяти множителей,
. (х—а)(х—Ь)(х—с)(х—Л)(х—е)=й,
то нашлись бы коефиціепты:
2-го члена, —(ач-6ч-сч-йч-е;,
3-го члена, ч-(а6ч-аоч-айч-аеч-6сч-6йч-6еч-сйч-сечч2е),
4-го члена, —(абсч-абйч-абеч-асйч-асеч-асіеч-бсйч-бсеч-бсіечч’йе),
5-го члена, ч-(абсйч абсеч-аЛйеч-ассіеч-бсйе),
6-го члена, — аЬсйе.
Изъ этихъ примѣровъ видно, что:
1) Коефиціентъ 2-го члена уравненія равенъ суммѣ корней, взятой съ отри-
цательнымъ знакомъ;
2) Коефиціентъ 3-го члена равенъ суммѣ всѣхъ различныхъ произведеній
корней, взятыхъ по два;
3) Коефиціентъ 4-го члена равенъ суммѣ всѣхъ различныхт произведеній
корней, взятыхъ по три, и съ противнымъ знакомъ; и т. д.
— 337 —
4-) Коефиціентъ послѣдняго члена, то есть, послѣдній членъ равенъ произве-
денію всѣхъ корней. Его знакъ будетъ ч- или — , смотря по тому, будетъ ли
уравненіе чётной или нечётной степени.
Изъ этого видно, что въ уравненіи, состоящемъ изъ положительныхъ корней,
члены имѣютъ поперемѣнно знаки ч- , — ; а въ уравненіи, состоящемъ изъ
корней отрицательныхъ, всѣ члены положительные.
Дли повѣрки, что этотъ законъ составленія коефиціептовъ справедливъ вооб-
ще, возмемъ уравненіе, состоящее изъ положительныхъ корней,
ж"_Аж"-’н-В’ѵ-2-—Сж^’ч-... .ч-Т,г—Г—0;
введемъ въ пего новый корень к, то есть, помножимъ на х—к', получится:
хп~1—А
—к
,-1] X
—Т/г ч-ЕЬ=О.
—В/г
Ак
Вторая строка этого произведенія, зависящая отъ А, показываетъ ясно, что
всякій новый множитель х—к, введенный въ уравненіе, прибавляетъ ко второму
коефиціенту —А——(ач-бч-с.........) членъ —к; къ третьему коефиціенту
ч-В=абч-асч-айч-...ч-бсч-Мч-... прибавляетъ А/с~(ач-6ч-с...)/с сумму
двойныхъ произведеній корней а, Ъ, с,... на к; и такъ далѣе. Въ послѣднемъ
членѣ корень к входитъ просто какъ множитель.
360. Числа членовъ, изъ которыхъ составляются коефиціенты 2-й,
3-й,...., могутъ быть повѣрены слѣдующимъ образомъ. Возмемъ уравненіе
/(я;)п=(ж—а)(х—Ь)(х—с).... (а-—к}—0,
состоящее изъ я корней. Отъ перемноженія его двучленныхъ множителей по-
лучится:
®"— (ач-Ьч-с...)®’*- 1ч-(аЬч-асч-...ч-6сч-...)®’^-3—(аЬ:ч-оМч-...ч-ЬсЛч-...)®"~3ч-...
....=ЬоЬсгіе...=0.
Сдѣлавъ это, положимъ, что всѣ его корпи равны между собою, а=Ь=:с=:(1=:...;
тогда будемъ имѣть:
(х—а)”=®п— {оч-ач-а. ..^"“‘ч-іа’ч-а
Но, мы знаемъ, что
(х—а)п==х”—пахп~1-і-
слѣдовательно: пч-а -+-а ч-...—па,
і » г п(п-1)
а ч-а ч-о ч-.....— -—
п(п-1}(п-2) ,
1.2 . 3 а ’
...)хп~ ’—(аІч-агч-а1ч-...)я:’1—Зч-...±ая.
я(я-1)(я-2)
1.2.3 °Х ............— ° ’
а*,
,8.-3. „3
Отсюда заключаемъ, что въ общемъ уравненій,
^—Ахп- ‘ч-ВУ-’—С-г’~8-+-...................................................................ч-Тя—11=0,
- 338 -
коефиціентъ А втораго члена состоитъ изъ суммы всѣхъ п корней,
взятой съ противнымъ знакомъ-,
коефиціентъ В третьяго члена состоитъ изъ суммы различныхъ про-
изведеній корней, взятыхъ но два (стр. 279); эта сумма — ;
коефиціентъ С состоитъ изъ суммы произведеній корней, взятыхъ
п(п— 1){п— 2)
по три, которая =г-— ----—; л такъ дглѣе.
Примѣръ. Составить уравненіе изъ корней 2,—3, 5.
Это уравненіе третьей степени; оно равно произведенію
(а;—2)(ж-ьЗ)(а?—5)=0.
Его первый членъ =.с3,
коефиціентъ 2-го члена =—(2—Зч-5)=—4;
коефиціентъ 3-го члена = ч-(—2.3ч-2.5—3.5)= —11;
- - 4-го члена =—2(—3(5=30.
Итакъ, это уравненіе
х3—4а?2—11а?ч-30=0. ’
Для повѣрки, возмемъ х——3, найдется:
—27—36-1-33-1-30=0,
тожественное равенство.
Слѣдствіе. Если уравненіе /’(а?)=0 не имѣетъ втораго члена; это значитъ,
что въ немъ сумма корней положительныхъ равна суммѣ отрицательныхъ. Если
же у него пѣтъ послѣдняго члена со степенью х°, то оно имѣетъ по крайней мѣрѣ
одинъ корень =0. Наприм. х3—4а?=0 не имѣетъ ни втораго члена, ни послѣд-
няго: оно удовлетворяется, полагая а?=0, и также а?=±2. И очевидно, что
сумма корней 0-ь2—2=0, а произведеніе корней 2(—2). 0=0
Зависимость знаковъ предъ членами уравненія отъ его дѣйствитель-
ныхъ корней, и обратно.
Зв*. Коефиціепты различныхъ членовъ уравненія состоятъ изъ совокупле-
нія его корней; слѣдовательно, знаки предъ ними должны зависѣть отъ того, бу-
дутъ ли эти корни положительные или отрицательные, отъ числа и величины
тѣхъ и другихъ.
3<*2. Всякіе два члена въ уравненіи, стоящіе сряду, могутъ имѣть знаки
различные, пли знаки равные. Такой порядокъ знаковъ называется, въ первомъ
случаѣ, перемѣною, а во второмъ случаѣ — повтореніемъ.
Въ полномъ уравненіи п-ой степени, состоящемъ изъ полнаго числа /і 4-1
членовъ, находится и промежутковъ между послѣдовательными знаками его
— 339 —
членовъ; слѣдовательно, въ немъ сумма перемѣнъ и повтореній также равна п,
то есть, равна его степени, пли числу всѣхъ его корней.
Такъ, напримѣръ, въ уравненіи,
+?-2х4—3?-4-ж8— 4ж—5=0,
. находятся три перемѣны знаковъ, и два повторенія, а всего пять.
363. Если послѣдній членъ уравненія (полнаго или неполнаго) положи-
тельный. то оно можетъ пе имѣть пи одной перемѣны, или имѣетъ 2, 4, 6,...
и вообще четное число перемѣнъ. Потому что всякій переходъ отъ положитель-
наго члена къ положительному чрезъ отрицательный членъ даетъ двѣ пере-
мѣны. Наприм.
Ахп—В^ч-Сг""'2.
Если же послѣдній членъ уравненія отрицательный, то оно будетъ имѣть
1, или 3, пли 5. или вообще нечётное число перемѣнъ. Потому что.въ
немъ отъ перваго члена положительнаго до послѣдняго положительнаго число пе-
ремѣнъ четное, а отъ нослѣдняю положительнаго до послѣдняго отрицательнаго
находится еще одна перемѣна; стало-быть, число всѣхъ перемѣнъ нечётное.
361. Всякое уравненіе, состоящее илъ дѣйствительныхъ корней,
отрицательныхъ, имѣетъ однѣ повторенія знаковъ. Наприм. уравненіе,
котораго корни х~—а, х~—Ь, х~—с, то есть,
(ж-ьа) (ж-ьб) (д"-ьс)=0,
очевидно, имѣетъ всѣ члены положительные, слѣдовательно имѣетъ однѣ повто-
ренія.
Всякое уравненіе, состоящее изъ дѣйствительныхъ корней положи-
тельныхъ, имѣетъ однѣ перемѣны знаковъ, и ни одного повторенія. На-
прим. уравненіе (а—а)(х—Ь){х—с)=0, котораго корни ж=а, х~Ь, х—с,
имѣетъ однѣ перемѣны, а именно:
х3—(а-і-/>-л-с]хі-+-(аІ>-г-сг,-г-Ьс)х—аЬс—0;
ооъ этомъ узнали мы еще ранѣе сего, говоря о составѣ уравненія изъ его
корней (359).
365. Отсюда непосредственно открывается легкій способъ, какъ, по дан-
ному уравненію /'(х']~(), найти другое, котораго корни были бы тѣ же,
только съ противными знаками. Для итого довольно только перемѣ.
нить знаки въ /'(а?)=0 предъ членами, занимающими чётныя мѣста
(2-е, 4-е, 6-е,....), считая отъ лѣвой руки къ правой.
Ибо, если вь уравненіи чёюноіі степени 2«,
.7М -С.г2’^,3-4- . .. .ч-Т.ѣ-+-П=0,
— 340 —
взять —х вмѣсто х, то перемѣнятся знаки только предъ членами нечётныхъ
степеней, занимающихъ чётныя мѣста, и получатся:
ж2п_Аа;2п—‘ч-Вж2"-2—Сіп-34-...Тж4-1]=0.
Послѣдній членъ I] не перемѣнитъ знака, потому что полное уравненіе чётной
степени имѣетъ нечётное число членовъ, и потому, послѣдній членъ занимаетъ
мѣсто нечётное.
Если же данное уравненіе нечётной степени,
ж2"+*_1_А.с2"-і-Вжй,-1ч-Сж2п-8-і-. .«.4-Т,г- ІІ,’=О;
то, при перемѣнѣ -г-х въ —х, получится:
—х^-ь-Ах*”—Т.7М-1,—0;
а перемѣнивъ знаки во всѣхъ членахъ, найдется, какъ и прежде,
ж2"+’_Аж8вч-Вл8в-‘—С.г2—?-ь. .. .ч-Тж—П=0
уравненіе, въ которомъ перемѣнились только знаки членовъ, занимающихъ чёт-
ныя мѣста; послѣдній членъ также получилъ перемѣну знака. Корнями этого
уравненія будутъ —а, —Ь, —с,...., если данное /~(х)~0 имѣло корпи
а, Ь, с, ...
Примѣръ. — Уравненіе х3-г-іх!-г-х—6=0 имѣетъ корни -4-1, —2, —3.
Если перемѣнить знаки его втораго и четвертаго членовъ, то получится:
а:8—4^*444-6=0
уравненіе, котораго корни —1, 4-2, 4-3, Для повѣрки, возмемъ а=:3, и най-
дется тожественное равенство
27-364-34-6=0.
Это преобразованіе случается очень часто, а потому, впередъ мы будемъ озна
чать данное уравненіе чрезъ /'(а?)=0, а уравненіе, котораго корни тѣ же, только
съ противными знаками, будемъ изображать чрезъ /’(-ж)=0.
36в. Полное число перемѣнъ въ данномъ уравненіи и въ
ею /'(-а?)”=0. никогда не можетъ бытъ болѣе показателя т степени
уравненія, или болѣе числа его корней.
Для доказательства,возмемъ изъ даннаго уравненія ова какіе ни есть смеж-
ные члена чётной степени, пли оба нечётной степснгі Наименьшая разность
между показателями этихъ членовъ =2 (когда между ивмп не будетъ только
одного члена). Отъ перемѣны х въ —х, чётные члены сохранятъ свои
знаки; отчего въ [(х)п и [(-х)т между ними не будетъ перемѣны, либо бу-
дутъ двѣ, если этн члены были съ противными знаками.
Члены нечётной степени, прп перемѣнѣ ж въ —х, оба перемѣнятъ знаки,
отчего въ /‘(ж)” и [(-х)т между нимп либо не будетъ перемѣны, если онп
были съ равными знаками, либо составятся двѣ перемѣны, если они были съ
противными знаками. Слѣдовательно, въ обоихъ случаяхъ, число перемѣнъ бу-
341
детъ не больше самой меньшей разиости 2 показателей, а п подавно, если эта
разность > 2.
Возмемъ смежные члены, одинъ чётной, а другой нечётной степени:
самая меньшая разность между ихъ показателями =1 (когда между пяти не
пропускается ни одного члена). Если они съ равными знаками, то, при пере
мѣнѣ я въ —х, одинъ только членъ перемѣнитъ свой знакъ, отчего въ /'(«)”*
и Д-ж)” между ннми будетъ одна перемѣна. Если же они съ противными
знаками, стало-быть, имѣютъ перемѣну въ то, для —х, эта перемѣна
въ /'(-ж)’" исчезнетъ; слѣдовательно и здѣсь въ /{х)т и /(-ж)“ между этими
членами будетъ одна перемѣна. Посему и здѣсь, въ обоихъ случаяхъ, число
перемѣнъ не бываетъ больше самой меньшей разности между показателями
смежныхъ членовъ, а и подавно, если эта разность больше 1-цы.
Пусть данное уравненіе
Дх) т=хт-г А ж"'-’,-ьВа:’п-’1-",ч-Сж’п_п'~п''ч-....-+ ІѴч-0.
Пусть ѵ, ѵ1, ѵ",.. . числа перемѣнъ между членами первымъ и вторыми,
вторымъ и третьимъ, третьимъ и четвертымъ,.... какъ въ Дя)т=0, такъ и
въ Д-ж)’п=0, п, п1, п",.... разиости между ихъ показателями; то будемъ
имѣть:
ѵ'^рѣ1, ѵг,^>п",...; откуда
с-ью'-Ы’"-»-.... или
сч-г/-Ы,'//-Ь.... ^)>иі;
потому что въ послЬдаемъ членъ Ож° показатель нуль, то есть, т—п—п1—
—п"—отчего п-ѵ-п'-^-п"-і-....—т.
II такъ, вообще, если V число перемѣнъ въ Да?)"=О,
и V' - - въ /'(-а?)=0,
то Ѵ-+-Ѵ'^>т, что и доказать надлежало.
Эти предварительныя объясненія приводятъ къ заключенію, что число пере-
мѣнъ знаковъ сравненія Дя)=0, и его Д'-ж)—0, можетъ приблизительно, илн
точно, показывать намъ число дѣйствительныхъ его корней, положительныхъ
илп отрицательныхъ. Начнемъ съ простѣйшихъ случаевъ.
ЗС9. Уравненіе, котораго всѣ члены положительные, и въ которомъ
пѣтъ пи одной перемѣны знака, не можетъ имѣть ни одного дѣйствитель-
наго корня, положительнаго. Потому что всякое число -ьа, подставленное
на мѣсто неизвѣстной х, обращаетъ это уравненіе всегда въ результатъ положи-
тельный, а не въ нуль. Слѣдовательно, оно можетъ имѣть только дѣйствитель-
ные і.ории отрицательные, и корни мнимые.
Всякое полное уравненіе {[х)—0, въ которомъ находятся однѣ пере-
мѣны знаковъ, въ которомъ, слѣдовательно, всѣ члены чётнаго порядка огрица-
— 342 —
тельные, а члены нечётнаго порядна положительные, не можетъ имѣть ни
одного дѣйствительнаго корня отрицательнаго. Потому что всякое число
—а, подставленное па мѣсто х въ это уравненіе, перемѣнитъ знаки предъ всѣми
членами—чётными степенями отъ а; отчего во всемъ уравненіи получатся чле-
ны съ равными знаками; сумма ихъ никогда не можетъ быть равна нулю. Стало-
быть, въ этомъ уравненіи [(х)=® могутъ быть корни только положительные и
корни мнимые.
308. Всякое полное уравненіе /’(ж)=0 можетъ имѣть положитель-
ныхъ корней не болѣе того, сколько въ /’(х)=0, и не болѣе отрица-
тельныхъ корней, сколько въ /'(-ж)=0 находится перемѣнъ знаковъ. А
если всѣ его корни дѣйствительные, то оно имѣетъ точно такое число
положительныхъ корней, сколько перемѣнъ въ О, и столько отри-
цательныхъ кдрней, сколько находится перемѣнъ въ /(-а?)=0.
Для доказательства этого важнаго правила, открытаго Декартомъ *). возмемъ
какое пи есть уравненіе, котораго всѣ члены расположены по убывающимъ сте-
пенямъ его неизвѣстной х, и въ которомъ пѣтъ ни одного недостающаго, члена:
. ,-ьКгс^’)—...
.. .ч=8яЛ+‘±(8'аЛ4-.. .-4-С)=0.
Въ немъ находится сперва рйдъ членовъ ж"-4-...ч-Рл:р'1'* положительныхъ,
потомъ рядъ Р,.'Г₽-ч-...-ьС).г'/^1 членовъ отрицательныхъ, за нимъ рядъ
ч-Кжг+1 членовъ положительныхъ, и такъ далѣе. Послѣдняя группа членовъ
±(8'а;'’ч-.. .-+-П) можетъ быть положительною или отрицательною; она имѣетъ
предъ собою группу членовъ съ противнымъ ей знакомъ, изъ которыхъ удержанъ
только послѣдній ч=8л:3+1.
Помножимъ все это уравненіе не х—а=0, то есть, введемъ въ него поло-
жительный корень х~а, и разсмотримъ, какую перемѣну произведетъ онъ въ
знакахъ уравненія. При этомъ мы удержимъ въ произведены. одни первые
члены, которыми явнымъ образомъ начинаются ряды членовъ положительные
пли отрицательные, получаемые отъ помноженія каждой группы членовъ на х;
а отъ умноженія на —а, удержимъ члены, которыми каждая группа оканчи-
вается; и такимъ образомь найдется:
(я>пч-...ч-Ря>,’+,)--(Р'тн-. (О'-Лг-...-+-К®гн-1) —..=г5я:і-1=і:(8'а:іч-...ч-П}
х—а
ч-лЛ^-ь...— Р' хр+1----<2' аЛ^-н....± 8'1 ^‘±....±11*
—... —аР -ьч-а(2 ----...,±а8 | =Ь........=раГІ=О.
Въ этомъ произведеніи хотя неизвѣстно, какіе знаки находятся предъ членами
промежуточными, однако же ясно видно, что, отъ перваго члена аз"+1 до члена
•) Декарто, Французскій математикъ, въ первой половинѣ 17-го вѣка.
— 343 -
степени р-ьі, находится но крайней мѣрѣ олна перемѣна знаковъ (потому что
ати члены явно съ противными знаками); отъ члена степени р-ьі до степени
также находится по крайней мѣрѣ одна перемѣна, и такъ далѣе. Наіідется
такимъ образомъ, что число перемѣнъ въ произведеніи, отъ члена а?"*1 до члена
±(8'-+-а8)ж5+1, равно по крайней мѣрѣ числу ихъ въ данномъ уравненіи отъ
а?" до члена ±8'аЛ Но, въ данномъ уравненіи, начиная отъ члена ±8'а?’ до по-
слѣдняго включительно, нѣтъ пи одной перемѣны; а въ полученномъ произве-
деніи находится по крайней мѣрѣ еще одна, потому что его члены ±(8'-+-о8)жя-к1
и =раН съ противными знаками; слѣдовательно, полояіительный корень .г=а,
введенный въ данное уравненіе, далъ намъ произведеніе, въ которомъ число
перемѣнъ хотя одною болѣе числа ихъ въ данномъ уравненіи.
369. Если число всѣхъ перемѣнъ выйдетъ болѣе числа дѣйствительныхъ
корней, то разность между числомъ перемѣнъ произведенія и числомъ перемѣнъ
множимаго будетъ нечётное число. Положимъ, что множимое /’(ж)=0 было се
послѣднимъ членомъ положительнымъ; то /'(ж)(.с—а)=0 будетъ имѣть
послѣдній членъ отрицательный, и потому будетъ имѣть нечётное число пе-
ремѣнъ: слѣдовательно, разность между первымъ числомъ перемѣнъ и послѣднимъ
будетъ нечётная. Положимъ, что множимое /”(ж)=0 былъ съ послѣднимъ чле-
номъ отрицательнымъ; тогда Д.г)(ж—а)—0 будетъ съ послѣднимъ членомъ
положительнымъ: въ нервомъ число перемѣнъ нечётное, а во второмъ оно
чётное; слѣдовательно, опять разность между числомъ первымъ и послѣднимъ
нечётная.
Но, если, отъ введенія положительнаго корня въ уравненіе [(.г}—0, число его
перемѣнъ сдѣлается одною, тремя, пятью,.... больше; то разность между чи-
сломъ этихъ прибылыхъ перемѣнъ и однимъ введеннымъ корнемъ, будетъ!—1=0,
3—1=2, 5—1=4,.... всегда чётная.
330. Теперь положимъ, что ^(ж)=0 состоитъ изъ положительныхъ корней
а, Ь, с,...., а сверхъ того оно содержитъ еще корпи отрицательные п мнимые;
что произведеніе корней отрицательныхъ и мнимыхъ =<р(ж), и что, посему, все
данное уравненіе /'(а?)=<р(.г)(.г—а)(.г—6)(х—с)....=0: пзъ предыдущаго
слѣдуетъ, что въ <р(ж)(а?—а) будетъ по крайней мѣрѣ одною перемѣною знака,
въ <р(х)(х—а)(ж—6) по крайней мѣрѣ двумя перемѣнами, и т. д. болѣе, нежели
сколько ихъ находится въ <р(дс). Даже, если <р(х) не имѣетъ йн одной перемѣны
знака, то все же многочленъ /’(.?) будетъ имѣть но крайней мѣрѣ столько такихъ
перемѣнъ, сколько въ немъ находится положительныхъ корней а, б, с,.... Если
же нхъ болѣе, то-всегда чётнымъ числомъ больше противъ числа корней ^369).
Преобразуемъ уравненіе /’(т)=0 въ другое /"(-.г)=І, котораго корни тѣ же,
только с.ъ противными знаками; тогда всѣ отрицательные корни перваго <чѣ-
- 344 -
лаются положительными во второмъ, и обратно. Слѣдовательно, уравненіе /’(-ж)=0
также должно имѣть по крайней мѣрѣ столько перемѣнъ знака, сколько будетъ
всѣхъ отрицательныхъ корней въ /’(а?)=0.
II такъ, ноелику всякому положительному корню уравненія /’(я)=0 соотвѣт-
ствуетъ одна перемѣна знака, а всикому отрицательному корню соотвѣтствуетъ
перемѣна знака въ /’(-я?)=0; то заключаемъ обратно, что въ /'(ж)=0 должно
быть пе болѣе дѣйствительныхъ корней, сколько въ У(ж) и /(-«), соотвѣт-
ственно, находится перемѣнъ знака.
в
37Л. Если же данное уравненіе /'(ж)=0 состоитъ изъ однихъ корней
дѣйствительныхъ; то въ немъ будетъ находиться точно столько положи-
тельныхъ корней, сколько перемѣнъ въ /‘(а;)—0, и столько отрицательныхъ,
сколько перемѣнъ въ {\-х)~0, такь что сумма тѣхъ и другихъ равна степени
уравненія.
Для доказательства, положимъ, что уравненіе І(х)т~0 имѣетъ всѣ корпи
дѣйствительные, изъ кояхъ р число корней положительныхъ, п — отрицатель-
ныхъ; то, знаемъ, что сумма нхъ равна показателю т степени уравненія:
р-ь-п—т.
Назовемъ теперь чрезъ V полное число перемѣнъ въ Дж)т=0, и чрезъ V'
полное число перемѣнъ вь ^-х)т=.О- сумма Ѵч-Ѵ7 этихъ перемѣнъ не мо-
жетъ быть больше т, (366); во она пе можетъ быть и меиъе, потому что, при
этихъ двухъ состояніяхъ уравненія, всѣ его корни, какъ дѣйствительные, успѣютъ
быть положительными; а мы знаемъ, что каждый положительный корень произ-
водитъ въ уравненіи не меньше одной перемѣны, и, потому, число всѣхъ пере-
мѣнъ въ {\х)п и /"(-ж)”* не можетъ быть менѣе числа т корней. А когда
Ѵч-Ѵ7 ни больше т, ни менѣе, то значитъ, что
Ѵч-Ѵ—пі, или Ѵ-+-Ѵ7—рч-н.
Но, число перемѣнъ V въ /'(ж)”*=0 не менѣе числа р корней положитель-
ныхъ, и V7 не меньше п, то
Ѵ=р, Ѵ7=п;
въ противномъ случаѣ, для Ѵ>р, было бы V7 <п, чему быть не можно.
И такъ, уравненіе полное пли неполное, состоящее изъ однихъ дѣйстви-
тельныхъ корней, имѣетъ столько положительныхъ корней, сколько перемѣнъ
въ /’(а?)=0, и столько отрицательныхъ, сколько перемѣнъ въ /’(-ж)=0. Сумма
тѣхъ и другихъ перемѣнъ равна степени уравненія.
Примѣръ. Уравненіе хі—5.г3ч-эж8ч-5.г—6—0 имѣетъ корпи 1,—1,2,3.
Вь немъ три перемѣны соотвѣтствуютъ тремъ корнямъ положительнымъ. Его
/’(- ж)=х4ч-м3ч-5ж8——6=0 имѣетъ одну церемѣпѵ. которая соотвѣт-
ствуетъ одному корню отрицательному.
345 —
Признаки дѣйствительныхъ корней въ уравненіяхъ.
352. Изъ того, что данное уравненіе имѣетъ перемѣны знаковъ въ свогхъ
членахъ, нельзя еще заключа гь о присутствіи въ немъ дѣйствительныхъ корней.
Такъ, напримѣръ, полное уравненіе:
х3—Зз?3-ь6л/—5яя-3=0=(а>в—жч-1) (ж’—2ж-ьЗ)
имѣетъ однѣ перемѣны; а между тѣмъ состоитъ только изъ мнимыхъ корней.
Однакоже во многихъ уравненіяхъ представляются весьма простые, и нерѣдко
явные признаки, показывающіе, что онѣ содержатъ хотя по одному дѣйствитель-
ному корню. Ближайшіе изъ этихъ признаковъ слѣдующіе.
353. Если данное уравненіе,
/'(ж)=ж”-ьАтг‘_,-і-В.гп_’ч-. .. .ч-Тж-ь[]=0,
но содержащее мнимыхъ коефпціентовъ, отъ какихъ ни есть двухъ под-
становленій х—п, ісзф, обращается въ два результата съ противными
знаками; это служитъ признакомъ, что между а и (3 находится по
крайней мѣрѣ одинъ дѣйствительный корень этого уравненія.
Ибо, это уравненіе есть непрерывная раціональная функція; слѣд. и пе можетъ
иначе перейти изъ результата положительнаго въ отрицательный, или обратно,
какъ сдѣлавшись сперва нулемъ (3<О). По этому, между а и (3 должно быть
такое нодстановленіе а', для котораго {\х)—0 удовлетворяется; слѣдовательно а7
и будетъ его корнемъ.
Примѣръ. Въ уравненіе
Д х)=2х3—5ж5—20ам-5 0—0, подставляя:
х— 0, 4,2, 3, 4, получимъ:
Дж;=50, 27, 6,-1, 18.
Отъ подстановленій 2, 3,4, уравненіе два раза перемѣнило свой знакъ; слѣ-
довательно одинъ сго корень находится между 2 и 3, а другой между 3 и 4.
П въ самомъ дѣлѣ, корни этого уравненія суть: 2’, Vх!О, —1/10.
Между подстановлепіями, обращающими /(а?)—0 въ результаты съ равными
знаками, корни могутъ быть или нѣтъ. Въ этомъ же примѣрѣ находимъ, что
для х=0, х-^:2, между которыми пѣтъ корней, получились результаты Д0)=50,
/(2)=6, съ равными знаками, и для ж=2, х~і,результаты /'(2)=6,/’(і)=18,
съ равными знаками; однако же между 2 и 4 находятся два дѣйствительные
корпя.
Знаки таковы:, ь результатовъ, равные или различные, зависятъ отъ четнаго
или нечётнаго числа корней, заключающихся между подстановлепіями, взятыми
па мѣсто л, а именно;
— 346 —
335.. Всякія два числа а, (3, между которыми находится нечёткое
число корней, будучи подставлены въ уравненіе, обращаютъ его въ два
результата съ противными знаками; но, оба результата получатся съ
равными знаками, если между а и (3 нѣтъ корней, или есть чётное чи-
сло корней.
•Для доказательства, возмемъ уравненіе:
[(х)={х—а) (х—Ь)Й(х—с).... (ж—к). т>(ж)=0,
котораго корни а, Ь, Ь, Ь, с-,....к, заключаются между подстановленіями а, /3,
а <р(ж) содержитъ въ себѣ всѣ его прочіе корни, которыхъ нѣтъ между ® и /3.
Подставимъ х=а, х—(3\ получатся результаты:
({а}—(а—а)(а—Ь)\а—с).... (а—к).<р(а),
Г{р)=^-а}{р-ЬУ^-с).... ЦЗ-к) ,<р(/3);
гдѣ ф(а), <р(/3), будутъ съ равными знаками; иначе между а и /3 находился бы еще
одинъ корень даннаго уравненія, чего здѣсь не предполагается. Пусть а> /3, и боль-
ше каждаго изъ корней а,б,с,....Л;то Всѣ факторы а—а, а—Ъ,а—с,....а—к,
будутъ положительные, и произведеніе ихъ (а—а)(«—6)3(а—с)....(а—к)
будетъ положительное. Но произведеніе (/3—а)[/3—Ь)г({3—с)..і.(/3—к) будетъ
отрицательное, когда число такихъ факторовъ, т. е. число корней а, Ь, Ь, Ъ,
е,....к, бунеп нечётное; въ противномъ же случаѣ, оно также положительное.
Слѣдовательно, результаты /(«), Д/3), имѣютъ противные знаки, если мсжіу
а и /3, находится нечётное число корней; но они имѣютъ знаки равные, когда
между а и /3 чётное число корней, либо совсѣмъ не будетъ корней.
335. Обратно: если два числа а и /3, взятые на мѣсто х въ [(&•)—й,
даютъ два результата съ противны ліи знаками, то между ними заклю-
чается нечётное число корней (иначе эти результаты были бы съ равными
знаками); если же онѣ даютъ два результата съ равными знаками, то
между ними пѣтъ корней, либо есть чётное число ихъ (иначе два резуль-
тата были бы съ противными знаками)
Мнимые корни, которые въ уравненіяхъ бываютъ попарно, х—р-ь-д V—1,
х—р—дѴ—1, не могутъ имѣть никакого вліянія па знакъ произведенія’
(ж—а)(ж—6)’(.г—с)....(ж—/с).9>(ж)—0: потому что каждая пара ихъ въ
уравненіи составляетъ квадратный множитель (ж—который остается
положительнымъ для всякихъ дѣйствительныхъ величинъ, взятыхъ па мѣсто ж.
336. Всякое уравненіе, нечётной степени '.2п-+ І, имѣетъ, по край-
ней мѣрѣ, одинъ дѣйствительный корень съ противнымъ знакомъ отно-
сительно знака послѣдняго члена.
Для доказательства, возмемъ уравненія
1) ж2,,+*-ь-Ажг"-ь-Вжіп-*ч-....—П=(),
2) .. .4-11—0,
— 347 —
изъ коихъ одно съ послѣднимъ членомъ отрицательнымъ, а другое — съ поло-
жительнымъ. Пусть Ы наибольшій коефиціентъ въ томъ и другомъ.
Въ первомъ, для получится результатъ отрицательный /{0)г=—V; а
для х—№ч-1, первый членъ превзойдетъ сумму всѣхъ прочихъ членовъ, и по-
лучится результатъ положительный Слѣдовательно, уравненіе 1)
имѣетъ дѣйствительный корень между подстановлепіями 0 и ІѴ-ьІ.
Въ уравненіи 2), для ж=0, получается результатъ положительный /‘(О)~ч-С;
а, для х=—(М-+-1), первый членъ его сдѣлается отрицательнымъ, и превзой-
детъ сумму всѣхъ прочихъ членовъ; отъ чего получится отрицательный резуль-
татъ /’(—К—1)=—. Слѣдовательно, между подстановленіями 0 и—(іѴ-ьт)»
находится отрицательный корень.
Въ обоихъ случаяхъ знакъ корпя выходитъ противный знаку послѣдняго
члена С.
300. Всякое уравненіе чётной степени 2п, съ отрицательнымъ по-
слѣднимъ членомъ, имѣетъ, по крайней мѣрѣ, два дѣйствительные
корня, воинъ положительный, а другой отрицательный.
Пусть это уравненіе
/'(ж)=^8"-+-Аж’"-і-ьВж8"~8-т-... .чТж—С=0.
Возмемъ я?=0; останется послѣдній членъ—II.
Если же взять или —(ІѴ-і-1), то, въ обоихъ случаяхъ, пер-
вый членъ останется положительнымъ, и превзойдетъ сумму всѣхъ прочихъ чле-
новъ: по этому, въ обоихъ случаяхъ /'(ж)=0 обратится въ результатъ положи-
тельный. Слѣдовательно, уравненіе имѣетъ два дѣйствительные корня, одинъ
между 0 и ІѴ-і-1, а другой между 0 и — (ІЧ-і-І), изъ коихъ первый—положи-
тельный, а второй отрицательный.
30В. Ежели [Сх)—0, и его таковы, что въ томъ или
другомъ сумма коефиціентовъ положительныхъ менѣе суммы отрица-
тельныхъ, то уравненія нечётной степени имѣетъ по крайней мѣрѣ
одинъ положительный корень, а уравненіе чётной степени — два
корня.
Ибо, для 1, уравненіе обращается въ результатъ отрицательный; а, для
.г=К-ь1, первый членъ уравненія превзойдетъ сумму всѣхъ прочихъ, и полу-
чится результатъ положительный.
По той же причинѣ, въ уравненіи /’(л;)8п=:0 чётной степени найдется поло-
жительный корень а> 1. По, если это уравненіе представить раздѣленнымъ на
х—а, то въ частномъ получится уравненіе Дж)8'’-1—0 нечётной степени, ко-
торое, въ свою очередь, будетъ имѣть хотя одинъ дѣйствительный корень.
— 348 —
339. Всякое уравненіе, въ которомъ сумма коефиц, штовъ положи-
тельныхъ равна суммѣ отрицательныхъ, имѣетъ корнемъ единицу,—
Паприм. х‘—7»-ь6=0. Это очевидно.
390. Всякое уравненіе нечётной степени, имѣющее послѣдній членъ
положительный, и въ которомъ сумма коефпціентовъ положительныхъ
менѣе суммы отрицательныхъ, имѣетъ три дѣйствительные корня.
Первый изъ этихъ корней отрицательный, по причинѣ послѣдняго члена поло-
жительнаго; другой корень положительный, оттого что сумма коефиціептовъ
• положительныхъ менѣе суммы отрицательныхъ. Если эти два корня исключить,
то останется опять уравненіе нечетной степени, двумя степенями ниже, въ ко-
торомъ необходимо находится еще одинъ дѣйствительный корень.
391. Признаки мнимыхъ корней, открываемые въ уравненіяхъ по-
средствомъ Декартова правила знаковъ.
Пусть XV сумма всѣхъ перемѣнъ въ сравненіи /’(.т)т=0 и его /'(-ж)'п=0;
число всѣхъ его корней — т. Извѣстно, что число всѣхъ дѣйствительныхъ кор-
ней бываетъ пе больше XV, а если корни всѣ дѣйствительные, то ихъ число
ш=ХѴ (311). Посему, если найдется, что XV, то данное уравненіе необхо-
димо имѣетъ по крайней мѣрѣ т—XV мнимыхъ корней.
Этимъ признакомъ легко и просто узнается нижній предѣлъ числа мни-
мыхъ корней въ уравненіяхъ неполныхъ.
Примѣръ. Возмемъ [(х)—ха—1=0, и его
І\-х)=х3-ьЛ=0.
Здѣсь ХѴ=1, т—‘і, т—XV—3—1—2. Слѣдовательно, [(х)=0 имѣетъ два
мшімые корня. П въ самомъ дѣлѣ, одинъ кореиь этого уравненіи =1; а, раздѣ
лввшп х3—1=0 на х—1, найдется
ха—ж-ь1=0; откуда
-1±ѴС^З ,
х—--------- , оба корня мнимые.
II вообще, уравненіе чётной степени,
• /'(.г)’п=ж“—1=0,
котораго /’(-«) т=хт—1=0, имѣетъ ХѴ=2. Оно содержитъ, по крайней мѣ-
рѣ, т—2 мнимыхъ корней, и только два дѣйствительные, -+-1 и —1.
Уравненіе нечётной степени —1=0, котораго Д-ж)=Л’т-+-1,
имѣетъ ХѴ=1; оно содержитъ т—ХѴ=т—1 мнимыхъ корней, и только одинъ
дѣйствительный корень л=#1.
Примѣръ. Уравненіе /'(ж)=ж8—аха—6=0, котораго {{~х)—хк-л-ах‘‘—
Ь=0, имѣетъ ХѴ=2, и мнимыхъ корней но крайней мѣрѣ т—ХѴ=Ь—2=6.
— 349 —
393. Въ уравненіяхъ неполныхъ число ш—XV мнимыхъ корней зависятъ
отъ каждой пзъ послѣдовательныхъ разностей между числомъ недостающихъ чле-
новъ и числомъ перемѣнъ, а именно; Разность между показателемъ т сте-
пени уравненія и числомъ XV всѣхъ перемѣнъ въ Дл:)=<) и [(-х)—0
равна суммѣ всѣхъ частныхъ разностей между показателями каждыхъ
двухъ послѣдовательныхъ членовъ и числомъ перемѣнъ между ними.
Возмемъ опять уравненіе
/(ж)=жтч-Ажт-"-ьВл;т-п-п'ч-Сгт-,’-п'-7-+-...=0;
означимъ чрезъ го, го', го",...., сколько найдется перемѣнъ между первымъ и
вторымъ, между вторымъ и третьимъ, третьимъ и четвертымъ,.... членами въ
/(ж) и Д-ж); то будемъ имѣть (Звб)
ти—пн-/»'-ьп"ч-...., ХѴ=го-г-го'-+-го"...
такъ что пг—ХѴ=(п—го)-+-{п'—гх/)ч-(п"—го")-і-....
Ни одна изъ этихъ разностей п—го, п'—го',.... пе можетъ сдѣлаться отри-
цательною (36в) ; однакоже нѣкоторыя изъ нихъ могутъ уничтожиться; и тогда
число т—XV мнимыхъ корней будетъ равно суммѣ всѣхъ неуничтожив-
шихся разностей.
393. Такъ какъ разнести п—го, п'—го',.... независимы одна отъ другой,
то, для опредѣленія т—XX’, каждую изъ нихъ можно искать отдѣльно. Правила
для этого легко найти слѣдующимъ образомъ. Возмемъ двучленныя функціи:
1) Кх}=ахіг+і±Ь, ея Ц-х)=ахіг+1=р:Ъ,
гдѣ недостаетъ 2г членовъ. Въ обоихъ тутъ случаяхъ число перемѣнъ го=1;
число мнимыхъ корней т—го=з2гч-1—гс~2г = числу недостаюгцихъ
членовъ.
2) /\х)=ахіг-і-Ь, ея [(-х)=ахіг-і-Ь.
Здѣсь недостаетъ нечетнаго числа 2г—4 членовъ; го—0; число мнимыхъ
корней т—го—2г—го—2г, единицею больше числа недостающихъ
членовъ.
3) /(ж)=ажВг—Ь, ея І\-х')~ахіг—Ь.
Также недостаетъ 2г—1 членовъ; го=2; число мнимыхъ корней =2г—2,
единицею менѣе числа недостаюгцихъ членовъ.
Теперь, если помножить двучленныя функціи 4), 2), 3) па х”, то полу-
чатся общіе виды всякихъ смежныхъ двухъ членовъ, взятыхъ гдѣ ни есть въ
уравненіи:
х\ах^і±Ь)—ах‘'+і+п±Ьхп, хп{ахіг±Ь)=ах!!г ^±Ьхп.
Въ первомъ недостаетъ также 2г, и во второмъ 2г—1 промежуточныхъ
членовъ. II обратно, легко такіе двучлены приводить къ видамъ 1), 2), 2),
стоитъ только выпесть за скобки общій множитель хп. Счетъ мнимыхъ корней
будетъ совершенно тотъ же, а именно:
— 350 —
1) Когда внутри скобокъ степень х нечётная 2г-ь-1, то число корней
равно числу 2г недостающихъ членовъ.
2) Если внутри скобокъ» х имѣетъ степень чётную 2г, и недостаетъ
2г—1 членовъ; то число мнимыхъ корней =2г или. 2г—2, смотря по-
тому, будутъ ли аиЬ съ равными знаками, или съ знаками различными.
Слѣдовательно, если недостаетъ одного члена между членами равныхъ
знаковъ (стало-быть, 2г—1=1, г=1), то уравненіе имѣетъ 2т=2 мнимые
корня. Если же недостаетъ одного члена между членами разныхъ» знаковъ,
то этимъ не показывается ничего, потому что число мнимыхъ корней выходитъ
2т—2=2—2=0.
Примѣръ. Уравненіе /’(ж)=ж3ч-1 Ож—28=0, котораго /’(-ж)=а;3-і-1 Ож
-1-28=0, имѣетъ Ѵк=1, и число мнимыхъ корней т—ЛѴ=3—1=2. П, въ
самомъ дѣлѣ, его корни:
2и2±±ѵ/-Гз
2
Примѣръ. Въ уравненіи х3—7«-ь6=(ж—1)(а?—2)(ж-г-3)=0, въ кото-
ромъ нѣтъ втораго члена, всѣ корни дѣйствительные.
Но въ уравненіи х3—6я?—7=0, котораго [{-х')=х3—Сжн-7=0, и гдѣ
ЛѴ=3, ът—ѴѴ=3—3=0, находятся мнимые корни, какъ показываетъ из-
.. і 2 б3 7“ 6’ Л
вѣстный (І86) признакъ - г-4- — = — — —> 0.
Предыдущій способъ вовсе недостаточенъ для открытія мнимыхъ кор-
ней въ уравненіяхъ полныхъ. Такъ, напримѣръ, въ уравненіи
/•(х)=х*ч-2х3-г-11х'—20&-+-100=(ж8— 2яч-б) (ж8ч-4я--ь20)=0,
и его 1\-х}=хк—2ж3-4-17ж8-ь20ж-4-100=0,
находится число перемѣнъ \Ѵ=4; т—4Ѵ=4—4=0; а между тѣмь, всѣ
корни эгого уравненія мнимые.
Въ этихъ уравненіяхъ можно узнавать присутствіе мнимыхъ корней, и нахо-
дить нижній предѣлъ числа ихъ, вводя въ уравненіе дѣйствительный корень ±а,
и давая ему такую величину, чтобы въ произведеніи получилось число перемѣнъ
совсѣмъ не то, какое можетъ произойти отъ однихъ корней дѣйствительныхъ;
особливо полезно искать условіе, чтобы въ произведеніи уничтожился хотя одинъ
членъ между членами равныхъ знаковъ.
Пусть /’(л)”*=0 имѣетъ V перемѣнъ. Число дѣйствптелыіыхъ-положитель-
ныхъ его корней пе можетъ быть больше V; онс даже равно V, если корни всѣ
дѣйствительные. Введемъ въ это уравненіе положигпелыіый корень а, помно-
живъ на х—а:
[(х)т(х—а)=0.
Если это уравненіе состоитъ пзъ корней дѣйствительныхъ, то, отъ введенія
корня а, въ немъ должно быть Ѵ-г-1 перемѣнъ, и столько же дѣйствительныхъ-
— 351
положительныхъ корней. Но, положимъ, что въ немъ окажется Ѵч-Л перемѣнъ,
то есть, Ѵч-Л—(Ѵч-1)=/с—1 перемѣнами больше: пи одна изъ этихъ лиш-
нихъ перемѣнъ не могла произойти отъ корней дѣйствительныхъ, а между тѣмъ
онѣ показываютъ присутствіе нѣкоторыхъ корней; — всѣ такіе корни должны
быть мнимые.
Можетъ быть, положительный корень а не откроетъ присутствія мнимыхъ
корней; въ такомъ случаѣ введемъ въ /’(ж)”*=0 корень отрицательный, помно-
живъ на жч-а. Въ произведеніи /г'(ж)'"(жч-а)=0 должно остаться столько же
перемѣнъ V, сколько ихъ было въ данномъ уравненіи 0, если это по-
слѣднее состояло пзъ однихъ дѣйствительныхъ корней. По, положимъ, что въ
[(х)т (х-ь-а)—0 окажется только V—к перемѣнъ, то есть, к перемѣнами мень-
ше; это покажетъ, что въ [(х)т(жч-а)=(), а слѣдовательно и въ /'(ж)т=0
должно быть дѣйствителышхъ-положительныхъ корней менѣе V. Потеря к пе-
ремѣнъ не могла произойти отъ корней дѣйствительныхъ, а только отъ мнимыхъ,
которыхъ число должно быть не меньше к.
Примѣръ. Уравненіе
/'(ж)з=ЙСІІ—ж‘ч-о:3—х*-л-х— 4=0,
въ которомъ находятся пять перемѣнъ, помножимъ на д?ч-а; получится:
—а
—а
Взявъ а—1, найдется хе—4=0, гдѣ четыре перемѣны менѣе, чѣмъ въ
/‘(ж)=0. Слѣдовательно, это послѣднее имѣетъ четыре мнимые корпя и одинъ
дѣйствительный —.1.
Примѣръ. Возмемъ еще уравненіе
Дж)=ж3ч-Зж5ч-12ая-4=0,
гдѣ нѣтъ ни одной перемѣны, стало-быть, ни одного положительнаго корня, и
помножимъ на х—а:
ж4ч-3 д?3ч-12 ж8ч-4 х—4а=0
—а —За —12а
Теперь, если взять а> 3 и <4, то произведеніе получитъ три перемѣны,
тогда какъ, отъ введенія положительнаго корня, должна бы получиться только
одна. Посему, [{х)(х—3)—0, такъ и 0 должна имѣть 3—1~2 мни-
мые корня.
Къ тому же заключенію придемъ, взявъ а=3 (либо а=4): ибо тогда соста-
вится уравненіе:
«‘ч-Зж8—32«—4 2=0,
въ которомъ нѣтъ члена между двумя членами равныхъ знаковъ: а это признакъ,
что оно, также и /(«)—0, имѣетъ два мнимые корпя.
— 352 —
Примѣръ. Уравненіе
а?—8ж3-і-4 Ь^-ьІ Оян-150=0
Помножимъ на ®±а:
хъ—8 «‘-4-15 ж’-ьІО ж’ч-150 х
±а гр8а ±15а ±10а ±150а=0.
Возмемъ нижній знакъ, и дадимъ для а такую величину, чтобы сдѣлалось
45а> 10, 40а<150, напримѣръ, а=1; получится произведеніе:
х*—9ж‘-і-23я?в—5ж!-ь140ж—150=0,
въ которомъ пять перемѣнъ, тогда какъ должно бы выйти только три. Двѣ лиш-
нія перемѣны показываютъ присутствіе двухъ мнимыхъ корней.
385. Очевидно, что посредствомъ вводнаго дѣйствительнаго корпя ±а
можно въ произведеніи Дж)то (ж±а)=0 уничтожить какой угодно средній членъ:
но, для открытія присутствія мнимыхъ корней, надобно, чтобъ уни-
чтожился какой нибудь членъ между членами равныхъ знаковъ, то есть,
чтобы коефиціепты смежныхъ членовъ были оба больше нуля, или меньше
нуля.
Возмемъ произведеніе /‘(ж)4(а:±а)=0 предыдущаго примѣра, съ верхнимъ
знакомъ второй его строки; испытаемъ уничтожить второй его членъ, полагая
а=8. Смежные коефпціенты можно взять только 4>0, 15—8а>0. Но по-
слѣднее условіе не удовлетворяется, потому что 15—8а=15—64 <0; слѣдо-
вательно, здѣсь уничтоженіе втораго члена не показываетъ ничего.
Испытаемъ уничтожить пятый членъ, полагая 10а-ь 150=0; откуда
а=—15. Смежные коефиціепты 10-ь15а<0, 150а<0, показываютъ, что
въ данномъ уравненіи есть пара мнимыхъ корней.
Это же получится и чрезъ уничтоженіе четвертаго члена, принимая нижній
знакъ:
10—15а=0; откуда а==^~ >
смежные коефиціенты 15-ь8а>0, 150—10а>0, оба положительные.
*
П8С>. Если одинъ вводный корень не показываетъ присутствія мнимыхъ кор-
ней, то введемъ въ уравненіе два дѣйствительные корпя, помпоживъ оное па
множитель х‘±ах—6=0, состоящій изъ дѣйствительныхъ корней. Коефиціен-
ты а, 6, какъ произвольные, надобно взять такими, чтобы въ произведеніи
/,(д;)т(а:1±аа:—6)=0 уничтожились два члена сряду или какіе нибудь два
члена, лишъ бы хотя одинъ между членами равныхъ знаковъ.
Примѣръ. Возмемъ уравненіе
х^Зх’-ні 7ж2—20жч-100=0.
— 353 -
и помножимъ на х*±ах—Ь; получитсл
же-ь2|ж*-т-17
±а ±2 а
х — 20
±4 7 а
а?3-4-100 х*
— Ь — 2Ь
ч=20а
— 176
іЮОа'ж
-+- 20б'—1006=0
Испытаемъ уничтожить второй и третій члены зтого произведенія, взявъ
нижній знакъ второй строки, и положивъ . 2—а=0, 17—2а—6—0; откуда
а=2, 6=13. Изъ этого видно, что множитель х*—ах—Ь=х*—2.т—13=0
содержитъ въ себѣ два корпя дѣйствительные, посредствомъ которыхъ уничто-
жаются два члена сряду. Посему, данное уравненіе имѣетъ мнимые корпи.
Коефиціепты смежныхъ членовъ:
1> 0, —20—17а—26 <0,
явно съ противными зваками; слѣдовательно, уничтоженіемъ этихъ членовъ
обличается одна пара мнимыхъ корней.
Испытаемъ теперь уничтожить пятый п шестой члепы произведенія, взявъ
нгіжтй знакъ-.
10 0ч-2 0 о—176=0, — 100а-4-206=0;
откуда ц= , 6=-^ Коефиціепты смежныхъ членовъ: —1006 < О,
13 13
—20—17а—26 < 0, имѣютъ равные знаки; слѣдовательно, уравненіе имѣетъ
4 мнимые корпя.
Испытаемъ еще уничтожить члены второй и шестой, полагая а=2,
206=100а, или 6=10. Коефиціепты ближайшихъ членовъ ко второму: 1> О,
17—2а—6=17—-4—10> 0, оба положительные; а коефиціенты, ближайшіе
къ члену шестому: —1006 <0, 100-4-20а—176=140—170 <0, оба отрица-
тельные. Это также показываетъ, что данное уравненіе имѣетъ 4 мнимые корня.
Примѣръ. Чрезъ введеніе одного дѣйствительнаго корня, нельзя открыть
присутствіе мнимыхъ корней въ уравненіи,
х"—Зж’-ьбж8—5я:-+-3=0.
Помножимъ пное на х’±ах—&=()
хе—ЗІлЛ-т-6
±о| ц^За
—6
.т‘—5 а?3-4-3
±6 а 4:5с
-4-36 —66
гі.За
-4-56
х
—36=0,
и испытаемъ уничтожить члены второй и третій, принимая верхній знакъ:
—Зч-а=0, 6—За—6=0; откуда
а=3, 6=—3.
Коефиціепты смежныхъ членовъ:
1>0, —5ч-6а-4-ЗЛ=—5-4-18—9> О,
имѣютъ равные знаки; слѣдовательно, произведеніе имѣетъ четыре мнимые
корня, изъ коихъ два принадлежатъ данному уравненію? а два другіе множителю
ж’ч-ая:—6=«8-4-Зл?-4-3=0 .
23
— 354 —
Преобразованія уравненій.
399. Оно состоитъ въ томъ, чтобъ, не разрѣшая даннаго уравненія, умѣть
превратить его въ другое, котораго корни съ корнями даннаго уравненія имѣли
бы желаемое отношеніе.
Такъ, мы знаемъ превращать всякое уравненіе [(х)=0 въ другое уравненіе
[[-х)=0, котораго корни тѣ же, только съ протпвнымп знаками. Кромѣ этого
случая, можно давать уравненію многія другія преобразованія; я ограничусь только
тѣми изъ нихъ, которыя состоятъ въ измѣненіи корней уравненія чрезъ совоку-
пленіе ихъ съ какимъ ни есть числомъ посредствомъ начальныхъ алгебрическихъ
дѣйствій, каковы: сложеніе, вычитаніе, умноженіе и дѣленіе. Всѣ эти преобра-
зованія служатъ къ тому, чтобы посредствомъ ихъ можно было открывать при-
знаки, доставляющіе памъ ближайшее понятіе о числѣ корней дѣйствительныхъ
и мнимыхъ всякаго даннаго уравненія. Онѣ же понадобятся памъ, впослѣдствіи,
для нахожденія предѣловъ, между которыми находятся всѣ корни уравненія, для
отдѣленія ихъ частными предѣлами и для вычисленія корней.
А. Данное уравненіе преобразовать въ другое, котораго бы корни
были въ т разъ больше или меньше корней даннагч.
Пусть данное уравненіе
&’-ьАж‘-+-Ва?8ч--С;г’+ І)жч-Е“0.
Возмемъ ж= ~У> и подставимъ; получится:
уь-з-т А 2/‘-+-иг*Ву8-4-т3Су*-4-т‘Пу-і-т’Е=0,
уравненіе, котораго корни въ т разъ болѣе корней даннаго,‘потому что здѣсь
у=тх.
А если въ данное уравненіе подставить х=ту, то получится:
тп!^в-4-Ат‘у‘-4-Вт3у’-ьСт8у’-4-Пту-4-Е=:0, или
, А . В . С , I) Е
уравненіе, котораго корни въ т разъ менѣе корней того даннаго; потому что
здѣсь У=^-
Это преобразованіе можпо иногда употреблять для открытія присутствія дѣй-
ствительныхъ корней въ уравненіяхъ. Нанрим., въ уравненіи
а?— 15ж3-ь20ж’-»-3 Оям-6 0=0,
ни изъ чего не видно, что есть дѣйствительные корни; но стоитъ только умень-
шить его корпи въ 5, или 10 разъ, полагая х=ту=:і0у, то получится
1,5^0,2у’-+-0,03з/ч-0,006=0
уравненіе, въ которомъ сумма коефиціентовъ положительныхъ 1,236 менѣе от-
рицательнаго коефиціента 1,5. Слѣдовательно, ру)=О и /'(ж)=0 имѣютъ во два
корня дѣйствительныхъ. Остальные же два корня мнимые, въ чемъ легко увѣ-
риться, введя въ /’(а>)=0 множитель х—а, и положивъ а=2.
- 355 —
получится новое уравненіе
коефиціепта
—0.
найдемъ
косфи-
между
В. Изъ даннаго уравненія исключить дробные коефиціепты, чрезъ
увеличеніе ею корней.
Для этого надобно найти общій знаменатель 0 всѣхъ дробныхъ коефиціентлвъ
даннаго уравненія/’(ж)=гО, и положить ж=-.у;
/(у)=0, въ которомъ не будетъ ни одного дробнаго
Пусть даппое уравненіе
» а ц Л а с Л
хЧ-----х5-і---ягч- - л-ь —
р Ц т $
Общій знаменатель дробныхъ коефиціентовъ О=рдгз. Возмемъ х———, под-
ставимъ въ уравненіе, и получится
у*-і-адгяуя=Ьрідгіеіу--і-срядяіля*у-і-брядягя$*=О,
уравненіе, въ которомъ нѣтъ дробей.
Примѣръ. х3— у ж’-ь- х— =0.
Здѣсь общій знаменатель дробей 0=6; посему, взявъ х~~у,
уравненіе уг—4у!-ь18у—180=0,
въ которомъ пѣтъ дробей; его корпи въ 6 разъ болѣе корней даннаго.
С. Данное уравненіе преобразовать въ другое, такъ чтобы
ціенты двухъ членовъ сдѣлались равными, или получили бы
собою данное отношеніе.
Пусть дано уравненіе
/(.а?)=:ж4-ь-ал:’-ь-бгг’-і-га:-ьй=О.
Возмемъ х— ~.у, получится
[(у]-=уі-і-атуя-і-Ьтіуя-і-стяу^-йті=:і).
Поелику т произвольно, то и можно всегда взять его такимъ, чтобы два кое-
фиціента сдѣлались равными, или получили бы данное отношеніе. Для этого на-
добно ихъ сравнить, изъ равенства найти т, и подставить въ Дуу=О, то и по-
лучится желаемое преобразованіе.
Такимъ образомъ, для равенства коефиціевтовъ перваго и втораго, надобно взять
і . •
1~опі, откуда т— -; для равенства коефпціентовъ перваго съ третьимъ, на-
добно взять 1=бт*, откуда т= ; для равенства перваго съ четвертымъ,
1—с»і3, откуда тп——5—, и т. д.; а для равенства коефиціентовъ втораго и чет-
Vе . ,
8 /Я „ а /°
вертаго, ат~ст , откуда т^\/ ~ . И дѣйствительно, если взять ж=у\р
подставить въ данное уравненіе, то получится уравненіе
* 1 /° з аЬ і < /° Л
у+а Ѵс-у+^-у^Ѵ .
въ которомъ коефиціенты 2-го и 4-го членовъ равны.
356 —
Но, поло кимъ, '.то это же уравненіе надобно преобразовать въ другое, въ
которомъ бы коефиціепты втораго и четвертаго членовъ получили между со
бою отношеніе 2 :'3; тогда надобно составить процорпію,
ат : ст3=2 : 3; отсюда найти
Это число и надобно подстивпть въ [&)—0, чтобъ получить желаемое пре-
образованіе
Число т, посредствомъ котораго уравненіе [[у)=0 получаетъ тотъ или дру-
гой видъ, будемъ впередъ называть числомъ Лреобразовательнымъ.
Если преобразовать данное уравненіе такъ, чтобы коефиціентъ перваго
члена, и коефиціентъ члена, дающій наибольшее преобразовательное
число т, обратились въ единицы, то коефиціенты всѣхъ прочихъ чле-
новъ сдѣлаются дробями, меньшими единицы.
Пусть данное уравненіе
х1ч-ахгч-Ъх‘ -ьс.т-ь4=0.
Дтя сравненія коефпціента перваго со вторымъ, либо третьимъ, либо четвер-
тымъ, ит. д., надобно брать преобразовательный числа, соотвѣтственно:
а, ѴЬ, Ѵ'с, ѴЛ,-...
Положимъ, что изъ этихъ чиселъ самое большое Ѵд. Возмемъ х—у ѴЬ, и
подставимъ въ уравненіе; найдется
. а с а
У + Ѵьу -^ьѴъ-У^^’
уравненіе, въ которомъ коефиціепты перваго и третьяго членовъ единицы; а
прочіе коефиціепты—правильныя дроби. Въ самомъ дѣлѣ,
а</б, а потому- -
Ѵ,с<Ѵ/6, илп с<ЬѴЪ, а потому < 1;
*/ / а
Ѵ(1<ѵь. или 4 <А’, а питому р < 4 .
П. Данное уравненіе преобразовать въ другое, котораго бы
корни были квадратами корней перваго.
Зго преобразованіе можно сдѣлать чрезъ одно перемноженіе даннаго уравненія
І'(х)=-0 па его Д-я:)=0. Ибо, если
у’(ж)=(.т—а)(х—Ь)(х—с).... =0, то
[(-х)=(х-і-а)(х-і-Ьух-і-с').... —0;
/'(а?)Д-.т)=:(а:—а8)(ж’—б2)(ж’—с1).... —0.
Послѣднее уравненіе имѣетъ степень вдвое выше степени даннаго; члены его
содержатъ однѣ чётныя степени х.
— 357 —
Теперь положимъ ®8=г; то и получится
—а8) (г—Ь ) (г—с8)..=0,
уравненіе, котораго корпи а8, 6’, с8,. суть квадраты корней а, Ъ, с,..
даннаго /’(®)—0.
Есть много уравненій, въ которыхъ это преобразованіе открываетъ мнимые
корни. Въ уравненіи ([х)[{-х')=0 могутъ быть только положительные
дѣйствительные корни, и корни мнимые-, оттого, если окажутся въ немъ
повторенія знаковъ, то онѣ единственно будутъ зависѣть отъ присутствія мни-
мыхъ корней.
Примѣръ. /’(®)—®‘—3®3-4-6®8—5х—3=0,
/,(-®)=®‘ч-3®8-4-6®8-4-5®—3=0;
[(х)(‘(-х)=х8-і-3хв—61 ®8ч-9=0.
Въ послѣднемъ уравненіи уничтожился второй членъ Между членами равныхъ
знаковъ; сверхъ того, уничтожились три члена «ряду между За:” и —61®’; слѣ-
довательно въ немъ находится двѣ пары мнимыхъ корней, пзъ коихъ одна при-
надлежитъ данному уравненію /’(о:)=0, а другая для Д-®)=0.
Примѣръ. х1-і-2х3-і- 17®8—20®ч-1 00=0=/’(®),
/(-®)=®‘—2®!-+Л 7®8-ь20®ч-100=0;
/'(®)^-®)=®ач-30.®°ч-596®‘-+-3000®8ч-10000=0.
Въ послѣднемъ уравненіи уничтожились четыре члена, каждый между членами
равныхъ знаковъ; слѣдовательно въ немъ находится четыре пары мнимыхъ кор •
пей, изъ которыхъ двѣ пары принадлежатъ данному уравненію.
Рѣдко однако же можно пользоваться этимъ способомъ, безъ другихъ вспомо-
гательныхъ преобразованій. Присутствіе корней дѣйствительныхъ часто скры
ваетъ признаки корней мнимыхъ.
Е. По данному уравненію /’(®)=0, составитъ другое, котораго бы
1
корни имѣли величины — , обратныя корнямъ того даннаго.
Дл,і втого надобно въ /’(®)=0 подставлть - мѣсто Л, и полученное уравне-
ніе 7=0 привесть въ простѣйшій видъ.
Пусть дано уравненіе /(®)=®‘-ьА®3-ьВ®8-ьС®-+-П=0,
котораго корни а, Ь, с, й, л гдѣ А=—(ач-бч-сч-й), В=абч-асч-айч-6сч-
Ы-і-сй, С=—[абс-і-аЫ-і-асА-і-Ьсй'), Т)=аЬсЛ. Взявъ— вмѣсто х, най-
дется: /(-^ )=П®"ч-С®8ч-В®‘ч-А®ч-1=0, или
. С 8 В , А 1 „
9 в ~°-
Это и есть искомое уравненіе. Въ самомъ дѣлѣ, въ немъ
с ___ /і і і в__________2. 2. 2. 2. 2. 2
і7 ~~* а Ь с "+” Д I ’ В аЬ ас ай Ьс Ъй сй ’
а ______< і д | і _2а 2 — 1_
1) 'абс аЬй асй Ьсіі'1 В аЬсй ’
— 358 -
Очевидно, обратное уравненіе 0 имѣетъ столько же корней дѣйстви-
тельныхъ и мнимыхъ, сколько ихъ находится въ данномъ [(х)—0.
Обратное уравненіе во многихъ затруднительныхъ случаяхъ служитъ для
отличія корней дѣйствительныхъ отъ мнимыхъ; и на оборотъ.
Примѣръ. Уравненіе [(х)=х*—7ам-7=0 имѣетъ одинъ корень отри-
цательный и два неизвѣстные корня. Чтобъ узнать какіе они, возмемъ
/(~)=:7л;а—7ж-ьі=0, или
х3—ХЧ- у =0,
1 .. 1 1 1
и подставимъ х= — ; найдется — — — -+- — результатъ отрицательный. А
ль о л 7
если взять я=.О или 1, то выйдетъ результатъ -+-~ И такъ, это уравненіе,
кромѣ отрицательнаго корня, имѣетъ еще два дѣйствительные корпя, одинъ
между а?=0 и у , другой между у и 1. Слѣдовательно и данное уравненіе
{’(х)=0 имѣетъ всѣ корни дѣйствительные.
. Уравненіе возвратное. Если помножить /'(ж)—0 на )=0,то составится
уравненіе )=0, въ которомъ для каждаго корня х находятся обратный
1
ему корень —.
Примѣръ. {\х)=ахгч-Ьх*ч-схч-<1=();
обратное уравненіе ^-^=бх'ч-схіч-Ьхч-а=О;
искомое уравненіе /’(«). )=0 найдется
аЛхвч-{асч-ЬД)хіч-[аЬч-Ьсч-С(1)хіч-(а*ч-Ьч-сі-^-д,)х,іч-
ч-^аЬч-Ьсч-с^х^ч-^асч-Ьіі^хч-аіІ—О.
Оно отличается тѣмъ, что коефиціепты членовъ, равно отстоящіе отъ перваго
и послѣдняго, равны между собою. Такія уравненія называются возвратными,
потому что коефиціенты первой половины такого уравненія возвращаются обрат-
нымъ порядкомъ во второй его половинѣ.
Е. Данное уравненіе преобразовать въ другое, котораго бы корни
были числомъ к менѣе или болѣе корней даннаго.
Пусть это уравненіе:
/{ж)=Соа?"-і-С1ж"_1ч-С,ж’‘_’н-... .ч-С„_,ж’-ьС„_1а;-і-Сп=О
ЕЛИ,
или,
а^*-+-Ая:п“1-ьВ^~’ч-... .ч-8«’-ьТж-+-ІІ=0,
С, д Са о Сп—і гр Сп у]
полагая Г =А} -Т—=1, — =И.
Ъ0 ъо ’-'о ''о
359
Въ вто уравненіе подставимъ х=к-+-у:
(Л_ьу)»_І-А(/м-у)»-‘ч-В(Л+у)”-«ч-..........ч-Т(М-у)ч-ІІ=0;
разложимъ всѣ степени двучлена к-+-у въ ряды (®31), и все уравненіе распо-
ложимъ по возрастающимъ степенямъ у.
Л”-+- ’ пЛ"—1 -+-АЛ"-*-+-(п—1)АЛ"—8 !/-+- п(п—1) 1 . 2 (п-1Цп-2) 1 . 2 Л"—’ АЛ"—8 •-Т72- кі ..-+-(п—1}АЛ уп~ 3-ѵ-пЛ
-+- ВЛ,,-*-»-(п—2) ВЛ"-8 ч- (п-2)(п-3) 1 . 2 ВЛ"-’ В 1
-♦-ТЛ Т
ч-СГ.
Коефпціенты при у, у*..... суть не что иное, какъ производные многочлены
(339) изъ даннаго уравненія, въ которыхъ я замѣненъ буквою к.
Для сокращеннаго ихъ выраженія, назовемъ:
б =/Г-ьА/іп-'ч-В/Г-!-г-... .-ьТ/м-Е,
е1=іпкп~1ч-{п—1) АЛ"-!ч-(п—2(ВЛп-8ч-....,
__п(п—1)ЛП—*-+-(п—ІЦп—2) АЛП~
6,—
е-‘=ГПГ ЛЧ-(«-1)АЛ-4-В,
&_1=пЛч-А,
Ѳ„=1-
Отъ этого преобразованное уравненіе приметъ видъ:
' е-»-біУ-ьѳ,у’ч-б3у8-ь... .ч-б„ _2у"-8н-б„_Іу’‘~Ч-у"=0,
. или:
уК-і-Ѳп-1уп~1-+-Ѳп-іуп~і-і~. . .ч-бзУ’ч-б^’-ьбіУч-б^О.
Корни этого уравненія менѣе корней данною числомъ Л; потому что равен-
ство х—к-т-у даетъ у=х—к. Слѣдовательно, если а, Ь, с,.... корни даннаго
уравненія /’(ж)=0, то а—к, Ь—к, с—к, будутъ корнями для /’(у)=0,
такъ что
Ѳ„_і=—(а—Л)—(6—і)—(с—Л)—....
б„_2=(а—к)(Ь—к)-ъ-(а—к)с—к)-+-.......
Если взять к съ противнымъ знакомъ, полагая х—у—к, то получили бы
уравненіе, котораго корни у=х-+-к болѣе корней даннаго числомъ к.
Отъ этого преобразованія не измѣняется число мнимыхъ корней въ уравненіи;
но, перемѣняя величину к, можно всѣ положительные корни, одинъ послѣ дру-
гаго, измѣнить въ отрицательные, или наоборотъ.
— зоо —
Примѣръ. Данное уравненіе,
Д ж)=2ж8-4-Зж8—іх—5=0,
преобразовать въ другое, котораго бы корни были двумя единицами болѣе
корней даннаго. Здѣсь надобно взять у=ж-ь2, откуда х=у—2, слѣдовательно
Л= —2. Искомымъ уравненіемъ будетъ:
-ьѳ^ч-е—0.
Но, е =2Л’ч-3/і4—4Л—5= —16-4-12ч-8—5= —1,
0 —6/?-»-6/і—4=24—12—4=8,
б,=6/і-т-3=—12ч-3= —9,
0з=2.
Сдѣлавъ подстаиовленіе, получимъ уравненіе:
2гД-9гД-4-8у—1=0.
Оно удовлетворяется корнемъ =1; стало-быть, с~у—2=1—2=—1 есть
корень даннаго уравненія.
С. Изъ даннаго уравненія исключить второй членъ, то есть, преобра-
зовать это уравненіе въ другое, въ которомъ бы не было втораго члена
Въ данное уравненіе Дж) =0 подставимъ ж=/і-4-у; получится
Опуп-4-бп_1у"~1-4-0п_2у’*“ІІ-4Ч.. ч-бй/8ч-Ѳгу*ч-6Іу-+-б=0,
гдѣ б, б„ б2,.... суть функціи отъ /і.
Послѣ сего, положимъ б„_1=и/и-А=0; отсюда найдется:
Л= — — А.
71
4
Слѣдовательно, надобно взять ж=/и-у=у— — А, чтобъ получить преобра-
зованное уравненіе Д/ы-у)=0, безъ втораго члена.
И такъ, для исключенія 2-го члена изъ уравненія Дж)=0, надобно
вмѣсто х взять другую неизвѣстнук у, придать къ пей коефиціентъ
втораго члена, взятый съ противнымъ знакомъ и раздіьленный на пока-
затель степени уравненія.
Примѣръ. Исключить второй членъ изъ уравненія:
ж8—6«2-4-4«—5=0.
Беру-----, и съ противнымъ знакомъ придаю къ новой неизвѣстной у; полу-
чаю ж=2-4-у. Это вношу въ данное уравненіе; отъ чего оно получитъ видъ:
Ѳ3уі-ЧЪуі-і-Ѳіу-і-Ѳ=П.
Составляю: б=йп—6/і2-4-4Л—5=8—24-4-8— 5=—13,
6,=3/і’—12/іч-4=12—24-4-4= —8,
@2=3/1—6=0, б3=1.
Сдѣлавъ подставозленіе, получаю
у3—8у-4-13=0,
уравненіе безъ втораго члена.
— 361
Примѣръ. Исключить второй членъ изъ уравненія
3®8ч-15ж!-ь-25ж—3:-0.
Сперва освободимъ первый членъ отъ коефиціента 3, раздѣливъ на 3 все
уравненіе:
ж -4-5® ч- — х—4=0;
й 5
потомъ возмемъ ж=-—--ч-у, полагая /«=--— , и, сдѣлавъ все вычисленіе,
о о
какъ было показано, получимъ
Зу’-^=О,
уравненіе, въ которомъ исключились два члена сряду. Слѣдовательно въ мемъ,
какъ и въ данномъ уравненіи, находятся мнимые корпи. Дѣйствительный корень
получится
р/І52
г’
-5 -5-4-^
®=—Ч-у: =------------
388. Признаки мнимыхъ корней. 1) Очевидно, что, если, при уничто-
женіи 2-го члена уравненія, уничтожится коефиціентъ 3-го члена, пли обра-
тится въ результатъ положительный, то/'(/іч-®)=0, а слѣдовательно и /'(ж)=0
будетъ имѣть хотя одну пару мнимыхъ корней. По этому, данное уравненіе
имѣетъ мнимые корни, когда, въ одно время, будетъ:
пйч-А=0, и
/ЛЦп— 1)АЛ-ьВ<0,
Изъ перваго условія возмемъ Л= — ~ А, и подставимъ во второе, полу-
чится:
(^аМ—'Мио,
В-Г^А--
Но, въ общемъ уравненіи,
Свян-С1®" 8ч-С2®" 3ч-....ч-Сп_2®8ч-С„_1®ч-С„^20,
с с •
мы взяли ~ =А, =В,....; слѣдовательно условіе мнимости корней, въ са-
Ц> Ц)
помъ общемъ вгдѣ, будетъ
С, п-і С,
Со< 2и С’ ’ ИЛИ
(«)....... Со С2<^.С?
— 362 —
И такъ, если произведеніе коефиціентовъ перваго и третьяго членовъ
не менѣе квадрата коефиціента члена промежуточнаго, помноженнаго
п—і . .
на — , то въ уравненіи находятся мнимые корни.
2) Изъ общаго уравненія Дж)=0 составимъ обратное {Іх)=0:
СяЖ”-4-С„_,«п-,-+-Сп_1Я:',_’ч-... .Ч-С2ж’-4-СгТ-4-Со==0.
Оно, а слѣдовательно и ((х)=.О будетъ имѣть мнимые корни, если найдется
въ немъ условіе
(р).............с„спд<^. с:_,.
Изъ этого видно, что присутствіе мнимыхъ корней можно искать по условію
(а) изъ трехъ первыхъ членовъ даннаго уравненія, или по условію (/?) изъ
трехъ его членовъ послѣднихъ.
Поелику условіе присутствіи мнимыхъ корней зависитъ отъ трехъ первыхъ,
или трехъ послѣднихъ коефиціентовъ, то мнимость не можетъ уничтожиться
отъ перемѣны степени п уравненія, отъ числа прочихъ его членовъ, и отъ вся-
кихъ измѣненій величины ихъ коефиціентовъ.
3) Отъ подстановленія х—И-^-у въ общее уравненіе /’(ж)=0 оно превра-
щается въ
Ѳп^-+-Ѳ„_^"_'ч-Ѳ„_2уп-’-+-. • .ч-еіуі-л-Ѳіу-^-Ѳ=0,
уравненіе, котораго корни у—х—к, а коефиціепты еп_,, Ѳп_,,.... суть функціи
отъ А, потому что состоятъ изъ извѣстнаго (стр. 359) совокупленія двучленовъ
а—/і, Ь—к, с—к,...., гдѣ а, Ь, с,... корни даннаго уравненія. Слѣдовательно,
о присутствіи мнимыхъ корней въ /’(&)=() можно заключать изъ присутствія та-
ковыхъ же корней въ уравненіяхъ 6=0, бі=0, е,=0,..., составленныхъ изъ Ѳ
и его производныхъ, а это все тоже, что изъ /'(ж)—О и его производныхъ. Но,
какъ всѣ эти уравненія начинаются тѣми же тремя коефиціентами Со, С,, С„
и одинакимъ образомъ производятся послѣдующія изъ предыдущихъ; то во всѣхъ
Л1
ихъ условіе мнимости остается одно и тоже Со С,<}^ С? .
389. Другое дѣло, если изъэтихъуравненій составитьихъобратныя /’(—) =0,
1 ® / 1 \п—®
/Ц—) =0, /Д—) , Тутъ условія мнимости корней будутъ другія; по-
тому что, съ переходомъ отъ [(—) къ теРяютсв послѣдова-
тельно коефпціенты С„, Сп_,,..., и условія мнимости переносятся сперва на С„_,,
С„_„ С„_3, потомъ на С„_2, С„_3, С„_4,..., и т. д. по особенному весьма про-
стому закону, какъ видно изъ слѣдующаго:
Данное уравненіе
*-ь..-ьСп—,®‘-+-Сп—вя’ч-С.,— і®®ч-Сп_.®-+-С.,=О;
— 363 —
его производныя:
^,(х)п—*=пСох"—1-ь(п-1 )С,х"—,-н....-»-4Сп—*®3-+-ЗС„_з®,-+-2С„_1®-і-Сп_1,
^8(х)’—’=п(п-1)Сох'—’ч-(п—1)(п-2)С1х'‘-»ч-...ч-3.і.С„_,ха-+2.3.С„_8гч-2С„_г,
№)п-8=»»(«-1)(»»-2)Соа:”-3-»-.... -1-3.4. 6С„_8я2-ь2.3.4С„_4а:-»-1.2.3аР_8.
Принявъ эти производныя за уравненія, составимъ ихъ уравненія обратныя:
/•(і) =С,1ж’*-ьС„_іх'— .Сп_8х"-2-»-С„_3х—Ц-С,1_і+"-‘і ....-і С,і і-С1) О,
(, (^) =С„_1х"-‘-»-2Сп_,®п-,-»-ЗСп_8а:1—ач-4С„_ѵГ'‘-‘ч-....ч-пСо-О,
(-*) —1.2С„_,х'’-,Іч-2.3С„_ах"-аь3.4С„_ігп-‘ч-__ьп(п-1)Со=О,
Г, (^) =і.2.3С„_8х’—в-+-2.3.4С„_8®"-‘-і-3.4.5Сп_8я'—..=0.
Изъ этихъ уравненій найдутся слѣдующія условія, между коефиціентами дан-
наго уравненія, показывающія въ немъ присутствіе корней мнимыхъ:
Изъ ^)=0,
^А(|Г=0, С„_1.СП_8<^.^.С:_1;
изъа(і)п-’=о, с„_8.с„_.<4-й-с:-з-’
изъ /з (—) =°, С„_3. С„_8<^ у. — • С_;
и такъ далѣе. (Здѣсь коефиціенты С„, Сп_о С„_8,.... С,, Со, берутся съ ихъ
знаками, а коефиціенты недостающихъ членовъ замѣщаются нулями).
Если хотя одно изъ этихъ условій удовлетворяется, то данное уравненіе со-
держитъ мнимые корни. Этимъ однакоже не опредѣляется дѣйствительное число
мнимыхъ корней, хотя бід выполнились всѣ послѣдовательныя условія. Но,
должно замѣтить, что если найденныя условія мнимости будутъ раздѣ-
лены условіями противными, то число паръ мнимыхъ корней откроется
столько, сколько будетъ находиться группъ первыхъ изъ нихъ. Поло-
жимъ, что въ какомъ нибудь уравненіи найдется рядъ условій
(знаки -г- показываютъ условія мнимости, а знаки — условіи противныя), гдѣ
три группы условій для корней мнимыхъ раздѣлены условіями противными; то
должно заключить, въ немъ находится не менѣе трехъ паръ мимыхъ корней.
390, Въ доказательство этого послѣдняго заключеніи, возмемъ уравненіе
какой ни есть чётной степени, нанрим. шестой:
(я:’-ьа)(л:’-ь6)(л:’-ьс)=а:вч-(а-4-б-і-с)а;‘-ь(аЬ-і-асч-бс)я:’-ьабс=0,
въ которомъ всѣ корни мнимые, вида гі V—а, ьсѣ члены положительные, и
нѣтъ членовъ съ нечётными степенями х; назовемъ эти недостающіе члены
О.ж", О.я>3, О.#; откроется пять условій:
— 364 —
ач-бч-с>0, 0<(ач-Ьч-с)’ (ач-6ч-с)(а6ч-асч-6з)>0,
С < ^-(абч-а- ч-6с)’, аб -ьасч-бс)> О,
Ій
изъ коихъ три условія мнимости раздѣлены противными -условіями только по-
тому, что здѣсь три пары мнимыхъ корней, вида ±1/—а.
Это же послѣдованіе условій будетъ находиться и въ уравненіи
(ж!ч-/іа;ч-Л)(ж!ч-бжч-В) (#!ч-сжч-С;=0,
если его тричленные множители всѣ имѣютъ мнимые корни, и если при тонъ
а, Ь, с, будутъ достаточно малы сравнительно съ А, В, С.
Такъ, въ уравненіи
(ж’-Ьажч-А)(ж!-ь6жЧ-В)=ж-+-(ач-6)г3ч-(Ач-Вч-аб)ж’ч-(А6ч-аВ)а:ч-
ч-АВ=0
будутъ условія:
3 1
^Ач-Вч-аб) >-д-,(ач-6)3,......I если а, Ь, довольно
4 I
(ач-б)(А6ч-аВ) <- (Ач-Вч-аб)’, ) малы относительно
АВ(Ач-Вч-аб) >-|(А6ч-аВ)3 А, В.
Назовемъ, для краткости, ач-о_а, Ач-ВА6ч-аВ=/Э, АВ=К,
получится:
ж‘ч-аж3ч-МлгМ-/Зжч-1Ч—0; и это помножимъ
на ж-ьржч-Р
-+-р -і-ир +№р-і-[3р -+-Хрх
чР ч-аР чМРч.ЗРч-М».
Взявъ а, р, р, довольно малыми въ сравненіи съ М, К, Р, получатся также
условія мнимости:
(Мч-Рч-ар) > (а-ъ-р)(/3-4-Мр^-йР) <^(Мч-Рччср)!,
(Мч-Рч-ар) (Кч-МРч-Рр) > ^(Рч-Мрч-аР/,
(/Зч-Мрч-аР) (Крч-/ЭР) <^ч-МРч-/=?р/,
ДОч-МРч-/Зр)МР>^(Ырч-/?Р/,
раздѣленныя условіями противными, какъ и въ нервомъ примѣрѣ. Онѣ суще-
ственно зависятъ отъ мнимыхъ корней, и, бывъ раздѣлены на три группы, пока-
зываютъ присутствіе трехъ паръ этихъ корней.
Если же «, в, р, не будутъ достаточно малы, то условія мнимости корней
могутъ послѣдовать въ иномъ поряднѣ, раздѣлиться на меньшее свело грушъ
условіями противными, и покажу гъ меныьее число паръ мнимыхъ керией. Напри-
мѣръ, въ уравненіи 4-й степени могутъ иногда всѣ трл условія, сряду взятые
— 365 -
погазыі ать мнимость; но, составляя одну группу, онѣ показываютъ'только, что
въ немъ находится по крайней мѣрѣ одна пара мнимыхъ корней.
Особливо повядокъ поперемѣннаго послѣдованія разнородныхъ условій измѣ-
няется въ уравненіи отъ присутствія въ немъ корней дѣйствительныхъ, отъ кото-
рыхъ часто условія мнимости совсѣмъ исчезаютъ. Напримѣръ, въ уравненіи:
ж‘-ьа’«!-+-а‘=0,
3
условія: а’>0, 0<— а4, ае>0, показываютъ присутствіе двухъ паръ мнимыхъ
о
корней; по, введите въ него положительный корень а, помноживъ на х—а,
получится уравненіе:
—аж‘ч-а!ж’—айх!ч-а4л:—ав2=0,
въ которомъ всѣ условія мнимости удовлетворяются: .
а*> ?• а\ а4> А а*, а’> 1 а’, ./> у а8,
О / Л о
и показываютъ только, что въ этомъ уравненіи есть хотя одна пара мнимыхъ
корней.
А въ уравненіи ж3-+-0.л:’—6ж-ьс=:0, гдѣ у>у , и гдѣ, слѣдовательно,
одинъ корень дѣйствительчый, а два мнимые (ІМі), вовсе нѣтъ условій мни-
мости, о которыхъ идетъ рѣчь, потому что,
-б.і <|.о, о.с<4^.
а о
391. Вычисляя дроби:
1 п— 1 2 п—2 3 п—3 । 4 п—4 8 п—3 ... ...
. ѵт» т-—“г>’ѵ—Г, т-—?>••• для уравненій III, IV ,
2 п ’ 3 п—1 4 п—2 3 п—3 6 п—4’ ' л ’
V, VI,.... степеней, найдемъ:
длн Ш, * , у;
іѵ _ А .
’ 8 ’ 9 ’ 8 ’
2
’ 3 ’ 2 ’ 2 3 ’
... й 8 9 8 5
1л 12’15’16’15’12’
Ѵ1Т 3 3 3 3 5 3
н, у, У’ у’ у, у, у ,
Ѵіп 1 * А 16 А ± А •
’ 16’ 7 ’ 8 ’ 25’ 8 ’ 7 ’ 16 ’
іх А I ! 1 1 1 7 4
* ’ 9 ’ 12’ 14’ “3~’ "з ’ 14’ 12’ V’
у 9 16 21 24 25 24 21 16 9
’ 20’ 27’32’33’ 36’35’32’27’ 20 ’
Для розысканія условій мнимости корней въ данномъ уравненіи, надобно взять
рядъ дробей, соотвѣтственныхъ его степени п, написать ихъ, по порядку, надъ
- 366 —
вторымъ, третьимъ, и т. д членами уравненія, и потомъ искать всѣ тѣ усло
вія, какъ видно изъ слѣдующихъ примѣровъ.
„ тт .343
Примѣръ. Написавъ дроби - , — и , надъ вторымъ, третьимъ и четвер-
о У о
тымъ членами уравненія:
находимъ: 4.6>^.9, 3.5<4-36, 6.3>4.^-
о У о
Здѣсь два условія мнимости раздѣлены условіемъ противнымъ; слѣдовательно,
уравненіе имѣетъ двѣ пары мнимыхъ корней.
Примѣръ. Въ уравнейіи:
11 1 2
Xя—Зж4ч-0.ж’-ь4ж’—5жч-6=0
2 12
находимъ условія: 0 <- .9,—ЗЛ<0,—5.0<— .16, 4.6> — .25, изъ кото-
рыхъ одно послѣднее показываетъ мнимость, слѣдовательно въ немъ есть хотя
одна пара мнимыхъ корней.
Примѣръ. Въ уравненіи:
3 В 3 5 8 ®
ж7—ж’’—2жв—Зж‘-ь4ж3—5ж*—6ж—7=0,
-2.1 <~ 1.3>|.4, -2.4<А.9, 3.5>|Л6,
ч я
—6.4<|.25, 5.7>4-36,
три условія мнимости раздѣлены условіями противными, и обнаруживаютъ три
пары мнимыхъ корней.
Примѣръ. Въ уравненіи:
жвч-0.жвн-Зж‘ч-0.ж3н-0.ж*—1 Ож-ь- 5=0,
8 5
условія: 3>0, 0<—.9, 0=0, 0=0, 0<—.400, открываютъ двѣ пары мин-
ныхъ корней. Въ немъ находятся еще два корня дѣйствительные, потому что
сумма коефпціентовъ положительныхъ менѣе суммы отрицательныхъ (338).
Весь этотъ способъ открывать присутствіе мнимыхъ корней принадлежитъ
Ньютону.
— 367 —
ГЛАВА ПЯТНАДЦАТАЯ.
РѢШЕНІЕ ЧИСЛЕННЫХЪ УРАВНЕНІЙ ВЫСШИХЪ СТЕПЕНЕЙ СЪ ОДНОЮ
НЕИЗВѢСТНОЮ.
392. Въ уравненіяхъ высокихъ степеней корни могутъ быть дѣйствитель-
ные-соизмѣримые или несоизмѣримые, и корни мнимые; сверхъ того, тѣ и дру-
гіе всѣ неравные, или нѣкоторые изъ нихъ равные.
Полное рѣшеніе такого уравненія производится посредствомъ нѣсколькихъ
отдѣльныхъ дѣйствій, смотря потому, какіе корни отыскиваются первоначально,
и какіе послѣ. Надобно: 1) найти предѣлы, между которыми заключаются всѣ
дѣйствительные корни уравненія, и кромѣ того — предѣлы для корней положи-
тельныхъ, я отрицательныхъ. 2) Отыскать всѣ корни равные, и исключить ихъ
изъ уравненія, чтобы понизить его степень; 3) отыскать всѣ соизмѣримые корни
неравные, отдѣлить ихъ изъ уравненія, и чрезъ это вторично понизить его сте-
пень: тогда останутся въ уравненіи корни несоизмѣримые и мнимые. 4) Раздѣлить
несоизмѣримые корни частными предѣлами для каждаго; 5) отыскать приближен-
ную величину каждаго несоизмѣримаго корня: и 5) наконецъ, розыскать корни
мнимые.
А. Предѣлы корней.
393. Предѣлами называются два ближайшія числа, между которыми
находятся всѣ дѣйствительные корни уравненія. Для примѣра, положимъ, что
уравненіе имѣетъ слѣдующіе корпи, расположенные въ убывающемъ
порядкѣ:
Весь рядъ этихъ корней заключается между ближайшими цѣлыми числами
5 и —7. Число 5, ближайшее большее, называется высшимъ предѣломъ,
а число —7, ближайшее меньшее, называется нижнимъ предѣломъ всѣхъ
дѣйствительныхъ корней. Сверхъ того, видно, что всѣ положительные корни
заключаются между 5 и 0, а отрицательные—между 0 и—7. Стало-быть, 5 есть
высшій предѣлъ корней положительныхъ, а 0 нижній предѣлъ ихъ; также 0 и
—7 суть предѣлы высшій и низшій для корней отрицательныхъ.
368 —
Если уравненіе /{х)—0 преобразовать въ Д-ж)=0, то его корни останутся
тѣ же, только будутъ съ противными знаками:
4 111
-4,-2,-|,-1,-,-,3,6;
и тогда прежній высшій предѣлъ 5 здѣсь будетъ нижнимъ —5, а низшій пре-
дѣлъ —7 здѣсь обратится въ высшій ч-7.
Впередъ мы часто будемъ означать буквами Ь, —Ь, высшій и низшій пре-
дѣлы для ьсѣхь корней уравненія.
Высшій предѣлъ Ь парней уравненія Цх)—0 отличается тѣмъ
свойствомъ, что, буду іи взятъ на мѣсто х, обращаетъ какъ это урав-
неніе, такъ и всѣ его производныя ДЬ), Д(Ь), Д'(Ь),.... въ результаты
положительные.
Пусть а, Ь, с,.,г±г‘Ѵ—1, —1,...., корни этого уравненія,
дѣйствительные и мнимые; Ь высшій предѣлъ, который больше а, Ь, с,...... то,
Дж)=(ж—а)(ж—Ь}(х—с).... [(ж—г)!ч-г,][(ж— «)ч-л’].. ..=0.
Если на мѣсто ж взять Ь, то всѣ двучленные ицюжители: ж—а, ж—6,....,
простые и квадратные, сдѣлаются положительными, а слѣдовательно и весь
результатъ ДЬ) будетъ положительнымъ. Само собою разумѣется, что всякое
число, которое больше Ь, взятое на мѣсто ж, и подавно обратитъ Дж) въ резуль-
татъ положительный, большій прежняго.
Теперь возмімъ ж=уч-Ь, и подставимъ Дж)—0; получится
Дуч-Ь)=ДЬ)ч-Д(Ь).уч- -Д'(Ь).у-ч-... 0.
А какъ
Дж)=(ж—а)(ж—Ь)(х—с)....[(ж—г) ч-г,]....=0, то и
Дуч-Ь)=(уч-Ь—а)(уч-Ь—Ь)... ,[(уч-Ь—г)ач-г*][...0.
Дѣйствительные корни этого уравненія всѣ отрицательные, потому что разности
Ь—а, Ь—Ь,.... всѣ положительныя; квадратные двучлены (^ч-Ь—г)!ч-г,,....
также состоятъ изъ членовъ положительныхъ; р потому въ Дуч-Ь)=0 пе
должно быть ни одного отрицательнаго члена, ни одной перемѣны знака; слѣдо-
вательно, коефпціенты ДЬ), Д(Ь), Д'(Ь),.... необходимо будутъ всѣ положи-
тельными.
Мы видѣли, что низшій предѣлъ —Ь корней въ Дж)—0 служитъ въ
Д-ж)=0 предѣломъ высшимъ: онъ также, будучи взятъ въ Д-ж) на мѣсто х,
обратитъ это уравненіе и всѣ его производныя въ положительные результаты
Л-М, П-Ь). н-ц -
Обратно: если вмѣсто высшаго предѣла Ь взять число А, меньшее самаго
большаго корня а уравненія Дж)г=0, то въ уравненіи
Дуч -Л)—(уч-Л- -а) (уч-Л—Ь),... —О
— 369 —
будетъ хотя одинъ первый корень положительный, потому что изъ разностей
Л—а, Л—/>,.... по крайней мѣрѣ первая будетъ отрицательною.
Отъ этого въ уравненіи
Лу+л)=з/’(а)-ьГ(^) • т • .=0
должна появиться (Зв8) по крайней мѣрѣ одна перемѣна знака, слѣіова-
тельно, которая нибудь изъ производныхъ ДЛ), /’(Л), .. должна выйти
отрицательною.
395. Отсюда непосредственно проистекаетъ Ньютоновъ способъ нахожде-
нія предѣловъ, высшаго и низшаго, для дѣйствительныхъ корней дан-
наго уравненія /"(а^схО.—Надобно взять всѣ производныя:
подставлять въ нихъ числа 0, 1, 2, 3,..., намѣсто х, начиная съ послѣдней
производной; писать знаки результатовъ отъ лѣвоіі руки къ правой; и эго про*
должать, пока найдется самое меньшее число, которое всѣ многочлены
ГЫ, '&).
обращаетъ въ положительные результаты: это число и будетъ высшимъ предѣ-
ломъ Ь для всѣхъ корней даннаго уравненія. — Потомъ надобно перемѣнить
знаки предъ членами, занимающими чётныя мѣста во всѣхъ тѣхъ многочленахъ,
чтобъ получить уравненіе {[-х}п—0, и его производныя Г(-х), Г'(-х),...•.;
подставлять въ нихъ также 0, 1, 2, 3,...., пока найдется самое меньшее цѣлое
число, которое обращаетъ всѣ сіи функціи въ результаты положительные; это
число будетъ высшимъ предѣломъ для корней уравненія у(-ж)=0, а низшимъ
предѣломъ —I/ для корней уравненія /’(а?)=0. Между найденными предѣлами
Ь, — I/, будутъ находиться всѣ дѣйствительные корни даннаго уравненія.
Примѣръ. Найти предѣлы корней уравненія
/(ж)=Ѳ=а?—5ж8ч-3 0ж!— 12я—15 0=0.
Для зтого составимъ его производныя:
/',(ж)=Ѳі=4я;3-— 15ж!-+-60ж—12,
А С/І[х)=е^ёхі— 15а?ч-30,
7±-зГ(ж)=Ѳ3=4ж-5, Г(^)=Ѳ4=1;
и будемъ въ нихъ подставлять :
Ѳ» ®3 ®1
ж=0, найдутся: -+- — -+- -+- —
=1, - Ч-----іч--------
=2, - ч ч- ч- ч---
=3, - ч- ч- ч- ч- ч-
24
— 370 —
ІІодстановленіе 3 обратило всѣ функціи въ результаты положительные; слѣдо-
вательно, Ь=3 есть ближайшій высшій предѣлъ корней положительныхъ.
Перемѣнимъ знаки на чётныхъ мѣстахъ во всѣхъ ѳ, бп получатся
/(-ж)=Ф =ж'1ч-5ж3ч-30ж’ч-12ж—150=0,
[І(-х)=<р1=і.х3-г-і 5х’ч-60жЧ-12,
6ж!ч-15жч-30,
~/'"(-ж)=ф3=4жч-5, ф4=1;
Сюда подставимъ:
ф, Ф» Ф. Фі ф.
ж=0, получатся: ч—і------1—і---
=1, - ч- ч- ч- ч------
=2, - ч- ч- ч- ч- ч-
Здѣсь число 2 высшимъ предѣломъ корней для /,(-ж)=0; а елѣдовательио
—2 есть низшій предѣлъ корней даннаго .уравненія Дж)=0.
39в. Этотъ способъ имѣетъ всю желаемую точность, только часто бываетъ
утомителенъ въ практикѣ, если предѣлы бываютъ слишкомъ удалены отъ 0, и,
для достиженія къ пимъ, нужно дѣлать много подстановленій. Такъ, напрнм.,
еслибъ даннымъ уравненіемъ было
• ж‘—2ж3—Зж!—8000ж—10000=0.
то’розысканіе предѣловъ, близкихъ къ его корнямъ, по способу Ньютона, со-
ставило бы продолжительную работу. Посему-то, для избѣжанія многихъ лиш-
нихъ, безполезныхъ подстановленій, употребляются разные воспомогательные
способы, посредствомъ которыхъ, въ самыхъ трудныхъ случаяхъ, весьма много
сокращается число подстановленій.
1. Способъ Маклореневъ.—Мы видѣли (336), что всякая цѣлая, раціо-
нальная функція /'(ж) обращается въ положительный результатъ, если взять ея
наибольшій коефиціентъ 14, сложить съ единицею, и сумму 14ч-1 подставить въ
нее на мѣсто х. Слѣдовательно ж=14ч-1 будетъ высшимъ предѣломъ корней
уравненія /'(ж)—0.
Но этотъ способъ выгоденъ лишъ тогда, кигда наибольшій коефиціентъ 14 на-
ходится во второмъ членѣ, и когда послѣдующіе члены, по большой части,
отрицательные; иначе предѣлъ 14ч-1 бываетъ крайне обширенъ, слишкомъ уда-
ленъ отъ корней *). '
2. Способъ Брега.—Высшій предѣлъ корней получится, если раздѣ-
лить каждый отрицательный коефици птъ даннаго уравненія на сумму
*) Этому же неудобству подлежатъ способы Ролля и Вену, помѣщаемые въ курсахъ
Алгебры; а потому не буду и говорить о нихъ.
— 371
всѣхъ предшествовавшихъ ему положительныхъ коефиціентовъ, взять
наибольшее частное, и сложить съ единицею
Замѣтимъ, что
хп—1=(ж"-,-ьжп-*-ьж"-3-ь...н.гн|)(ж—1), откуда
жп—(ж"- лч-ж"~’н-ж"_3-і-... .ч-жч-1 )(ж—!)-+-!,
и доказательство сиособа, для большей ясности, представимъ на уравненіи нятой
степени
Ажвч-Вж‘ч-Сж3—Бж2ч-Еж—Е=0.
Разложимъ положительные члены его въ строки, возмемъ ихъ сумму, и къ
ней придадимъ члены отрицательные, написавъ пхъ подъ членами подобными.
. Ажв—(Аж‘н-Аж3-ь-Аж’н-Лжн-Л)(ж—І)ч-А
Вж‘=....-ь(Вж3-ьВж’-ьВж-+-В)(ж—1)ч-В
Сж3=.........ч-(Сж!ч-Сж-4-С)(ж—1 )ч-С
Еж =...................-і Е (ж—1)ч-Е
(Аж‘-ьА'ж3-ь А"ж’-ь А"жч-А(ж— 1) -т-А'^О
—Г)ж8 —Г
гдѣ А'=А-і-В, А"=Ач-В-ьС, А"'-Ач-Вч-Сч-Е.
Очевидно, что все уравненіе обратится въ результатъ положительный, если
взять ж такимъ, чтобъ уничтожились разности А"(ж—1)—В, А"'(ж—1)—Е,
, , ,т . о г
либо сдѣлались оолыпе нуля, по, если отношеніе , то довольно положить
А"(ж—1) —Б=0, найти отсюда х= ~ ч-1, и подставить ее во вторую
разность, которую назовемъ буквою
А'"(ж—1)—Г=<У;
то получится -4-1—1)—Г=<У, откуда
и Е _<?
А" А'" А'" ’
результатъ положительный; слѣдовательно, разность
А"'(ж—1)—Г > 0.
И такъ, есть высшій предѣлъ корней; онъ равенъ самому большему
отношенію коефиціента отрицательнаго Б къ суммѣ А" всѣхъ предшествующихъ
ему коефиціентовъ положительныхъ, сложенному съ единицею.
Примѣры Въ уравненіи
Зжв -15ж‘ч-22жа— 1 ООж’-ьБОж—450=0,
... 18 „ 100 ,450 , е
изъ отношеніи — =5, — =4, —, самое оолыпее э; стало-быть, высшій
о 25 40о
предѣлъ корней Е=э-ь1=6;
по способу Ньютона, Е=5;
Маклорепя, онъ = — 4-1=151.
212
А въ уравненіи,
За:6—15а:4ч-22а:3—Л 50ж’ч-80а—600=0,
... 18 „ 180 „ 600 , „
гдѣ изъ отношены -=5, -—=6, — , самое оольшее о, предѣломъ оудетъ
3 20 105
6-М=7.
Способъ Бретовъ выгоденъ только тогда, когда въ предшествующихъ членахъ
уравненія находятся довольно большіе положительные коефиціепты; въ против-
номъ случаѣ, онъ почти такъ же невыгоденъ, какъ и способъ Маклореневъ,
чему увидимъ многіе примѣры.
3-іі способъ. — Надобно преобразовать данное уравненіе Дж)=0
такъ, чтобы первый членъ его, и членъ отрицательный, дающій наи-
большее преобразовательное число ы (стр. 356), получили коефиціепты,
равные единицѣ, (полагая х—ау); тогда составится уравненіе у(у)=О, въ
которомъ всѣ прочіе отрицательные члены будутъ съ коефиціеитами, равными
единицѣ или меньшими единицъ. Высшимъ предѣломъ корней этою уравне
нія будетъ 2, а для корней даннаго уравненія Сверхъ того, смотря
но числу, величинѣ и расположенію членовъ положительныхъ и отрицательныхъ,
, п 3 4 8
предѣлъ можно орать 2ы, — ы, уы, — ы,...., ы, и менѣе.
Собственно говоря, надобно только всякой разъ искать высшее преобразова-
тельное число ы, а дѣйствительнаго преобразованія /(«)—О дѣлать не нужно.
Для поясненія этого способа, возмемъ общее уравненіе, вида:
хп—ахп~1—а’ж"-’—а3л:"“3—... .—ап-1х—ап=0,
и положимъ х~ау, тогда оно обратится въ простѣйшее уравненіе
у"—уп-1-уп~'—у"-3—.. • .-у-1=0,
въ которомъ только первый членъ положительный, и всѣ коефиціепты суть еди-
ницы. По способамъ Маклореня и Брета, высшимъ предѣломъ его корней Б=2.
Стало-быть, надобно только умѣть привесть всякое уравненіе къ виду такого,
въ которомъ бы всѣ отрицательные коефпціеиты были единицами и дробями, то
2 необходимо будетъ высшимъ предѣломъ корней уравненія, получившаго этотъ
видъ, Но, извѣстно (стр. 356), что если въ уравненіи /’(ж)=0 взять х—ыу, и
чрезъ это уравнять коефиціентъ его перваго члена съ тѣмъ, который даетъ
наибольшее преобразовательное число ы, то уравненіе непремѣнно получи гъ
желаемый видъ; тогда 2&> и будетъ высшимъ предѣломъ корней для /”(а:)=0.
Примѣръ. Найти высшій предѣлъ корней уравненія
а?‘—6а;3—50а;’—200а1—1000=0.
Для реобразованія этого уравненія въ другое, котораго бы первый и какой ни
есть отрицательный членъ получили равные коефиціепты, беру преобразователь
ныя числа: 6, 1/50, Ѵ200, ИіООО, и нахожу, что изъ нихъ самое большее
|/50=<у; отсюда заключаю, что высшій предѣлъ корней =2ы=2і/50=Н.
373 —
Этотъ предѣлъ не обширенъ, потому что наибольшій корень даннаго уравненія
находится между 12 и 13, въ чемъ окончательно можемъ увѣриться по способу
Ньютона. Для этого составимъ:
Ѳ—а?‘— 6 а?3—5 0а?!—200л?—1000,
Ѳ1=4я3—18а?!—100а:—200,
Ѳ,=6л?!—18л?—50, Ѳ3=4я?—6, Ѳ*—1,
и будемъ пробовать числа меньшія 14:
Ѳ4 з 2 і о
х—13, получатся: -і—і—і—ь -+-
=12, - -ь -+- -ь ч-------
По Маклореню, Брету, Роллю, нашли бы предѣлъ 1001 крайне обширный
и вовсе безполезный.
393. Зависимость предѣла Ь отъ величины отрицательныхъ кое-
фицгентовъ втораго и третьяго членовъ уравненія.
Высшій предѣлъ корней значительно уменьшается отъ уменьшенія отрицатель-
ныхъ коефиціептовъ 2-го и 3-го членовъ уравненія^ между тѣмъ почти пе измѣ-
няется отъ уменьшенія коефиціептовъ всѣхъ остальныхъ членовъ. Для примѣра
возмемъ уравненія:
я?"— і ах"~'----а*хп—‘—а3хп~3—а^х*-3—....—а"=0,
іо ю
а:"—ах"~'—а'х”-*— - (а3л?"-Ч-а‘а^‘-ь....-ьа")=0.
р
з
Первое имѣетъ предѣлъ Ь= -а, вмѣсто 2а; ибо ему можно дать видъ
и, по освобожденіи отъ знаменателя, получить,
ж"~’(л?3— аа?’-ь ^-л3)-ь-а’гИ=0.
' 10 10 1
» И г 9 з й .3
Многочленъ х—- ах -ь —а обращается въ нуль отъ подстановленія х—-а,
а уравненіе—въ положительный результатъ ап+1; слѣдовательно Ь= ~а.
Что же касается до втораго уравненія, то въ немъ можно даже уничтожить
всѣ члены, кромѣ трехъ первыхъ, полагая р — <х>, и высшій предѣлъ все-таки
останется 2а (или ~а въ этомъ крайнемъ случаѣ).
399. Зависимость предѣла Ь отъ повторенія знака ч- предъ пер-
выми членами уравненія.
Если данное уравненіе имѣетъ два, три, четыре,.... первые члеяа положи-
3
тельные, то высшимъ предѣломъ корней довольно брать, соотвѣтственно: у , ,
4 8 _ , .
у«, усо,.... Для доказательства, возмемъ общее уравненіе
374 — ’
1) аѴ-’—а’я:"-3—...-ап=0,
Когорос, чрезъ подстановленіе я=ау, обращается въ
у '~^у"г'1—уп~і—уп~в—-- •1—0.
13
По способу Брета, высшимъ предѣломъ его корней будетъ — -+-1= — ; а
• і 3
для даннаго уравненія 1= —а.
Этотъ же предѣлъ имѣютъ уравненія, въ которыхъ пѣтъ птораго, либо вто-
раго и третьяго членовъ, послѣ которыхъ слѣдуютъ члены отрицательпые.
2) Для уравненія съ тремя первыми членами положительными,
у-^у-^у- ^у- . .-у-1=0,
114
Предѣломъ Ь будетъ 1=
о о
Этотъ же предѣлъ соотвѣтствуетъ корнямъ уравненій:
уп-^^уп~1—уп- —у —3—... 0,
уп-ь-2у"~’—уп~3—уп~*—....—у—1=0.
У"-ь зГ‘—у-8—у-‘—у—1=0.
3) Для уравнепій съ четырьмя положительными членами:
у-‘_...у—1=О,
предѣлъ Ь= — -+-і= у; и такъ далѣе.
4) Очевидно, что Б=4, когда сумма предшествовавшихъ членовъ положитель-
ныхъ равна суммѣ послѣдующихъ членовъ отрицательныхъ; по онъ меньше
1-цы, когда первая сумма болѣе второй. Напримѣръ.
а*-+-х*-і-х*—х—1=0 имѣетъ Е= ~;
О
л3-НГ--4-ж—1=0 - 1=
т
х>^-х—4=0 - Е=^;
О
Все ято не трудно теперь приложить и ко всякому уравненію, давая ему
преобразованіе по< редствомъ наибольшаго преобразовательнаго числа и, какъ
сказано было въ общемъ правилѣ (стр. 372).
• Примѣръ. Въ уравненіи
ж*-ьЗх8—.100^—1000®—10000=0
___________________________ » _____ »_______
преобразовательныя числа: ѵ ЮО, ѴЮ00, Ѵ10000, равны между собою, и
каждое больше 3. Взявъ а=Юу, нахожу:
У 4-ь0, 'іу у'—у—1=0.
Второй членъ положительный; слѣдовательно, въ втомъ уравненіи высшій
предѣлъ корней = у; а въ данномъ уравнеиі і Б= . 10= 15.
И дѣйствительно, наибольшій корень этого уравненія находится между 14 и
15, въ чемъ окончательно можно увѣриться по способѵ Ньютона.
— 375 —
Примѣръ. Уравненіе
х*—400я’—1600а;—10000=0
не имѣетъ втораго и третьяго членовъ, и подходитъ подъ случай 1). Въ немъ
/400 > /1 600 и > /10000; слѣдовательно, его Ь= ѵ /400=|. 7=10.
По Ньютону, нашли бы Ь=9.
Примѣръ. По, уравненіе
• хі-+-1хі—400'с3—г-1 0а:—10000=0,
въ которомъ наибольшее преобразовательное число почти равно коефиціенту вто-
раго положительнаго члена, и въ которомъ два члена положительные находятся
противъ двухъ послѣдующихъ членовъ отрицательныхъ, имѣетъ предѣломъ только
/400=7.
По той же причинѣ, въ уравненіи
хв4-4х?— 15а>8Ч-а:‘—200х-ь-1=0,
гдѣ /15 > 1/200, и весьма близокъ къ предшествующему положительному
коефиціенту 4, и гдѣ также послѣ первыхъ двухъ положительныхъ членовъ.На-
ходятся два отрицательные, высшимъ предѣломъ будетъ /15=4 *). Этотъ
же предѣлъ нашли бы и по способу Ньютона.
Примѣръ. Въ уравненіи
х64-10х”4-60х4—800а;3—20000x4-1=0,
------------------- 3,--- ' ,--
гдѣ /800 > /20000, сверхъ того, /800<10 и близокъ /60, и гдѣ три
первые положительные члена имѣютъ послѣ себя два отрицательные, высшимъ
предѣломъ будетъ /800= . 9=8 (см. случай 4); а по Ньютону, этотъ
предѣлъ =7.
399. Перейдемъ теперь къ разсмотрѣнію другихъ замѣчательныхъ слу-
чаевъ, имѣющихъ нѣкоторую общность.
Въ уравненіяхъ вида:
х"ч=ах"-‘—Цхп-’4-х"-84-х"-‘-ь. .. .4-1 )=0;
х^ах^—Ь =0,
X— 1 •
предѣлъ Ь= ± 4- у/ Ь -+- *
Въ самомъ дѣлѣ, если взять —а, и освободить уравненіе отъ знаменателя
х—1, то получится:
х”~1[хг—(ач-1 )х4-а—6]-г-6=О.
’) О прочихъ положительныхъ членахъ здѣсь вовсе не упоминаю, хотя они собственно
уменьшаютъ предѣлъ.
— 376 —
Теперь довольно положить х*—(а-ь-1 )л-+-а—6=0; отсюда получитсяпредѣлъ:
»=-:-* Ѵм?)’
Примѣръ. Для корней уравненія,
яЛ—Зж’—100л’—100л—100=0,
1= -г \/ Ю0-+- (-~1)’=2-ь ѵТо 1 =12,049.
И въ самомъ дѣлѣ, наибольшій корень его находится между 12 и 12,04-9.
Такъ можно находить предѣлъ Ь во всѣхъ уравненіяхъ, въ которыхъ наиболь-
шее преобразовательное число ы паходптся но второмъ, либо третьемъ членахъ,
и гдѣ прочіе послѣдующіе отрицательные члены равны или менѣе большаго изъ
тѣхъ коефиціентовъ. Вотъ примѣръ:
л'—1 Ол4—268®’—250л’ч-1 70л—300=0. •
Послѣдній членъ 300, хотя больше 268; но, поелику разность пе велика, и
есть положительный членъ 170л, то предѣломъ будетъ
1=5,5-ь- |/26»-ь20=22,5,
вмѣ’сто 2 1/268=32,6, и весьма близокъ къ самому большему корню уравненія,
потому что число 23 уже велико.
400. Въ уравненіяхъ, вида:
а;-—ал"-1—6л-’—с5(л№8-+-ж"-‘-ьл"-“-ь-.. ,.ч-1)=0, или
л”—ал-1—6л—с3 =0,
а-—1
гдѣ 6ф>ас, даже 6=0, предѣлъ І=ач-с, каково бы ни было отношеніе между
а и с. Ибо, это уравненіе, по освобожденіи отъ знаменателя л—-1, обра-
щается въ
ш-’[л3—(а-ь-1 )л’-+-(а—6)лч-6—с3]ч-с’=0;
а отъ подстановлепія 6=ас, л—а-ь-с, многочленъ въ скобкахъ приводится въ
(а—1)с’ результатъ положптельпый, если а<)^1.
Примѣръ. Такъ, уравненіе
л6—6 л'—60л4—1000(л3ч-л*-ь-л-ь-1)=0,
въ которомъ а=6, с=10, 6=60=ас, имѣетъ 1= 1 0-ь-6= 16; между тѣмъ
какъ по третьему общему способу 1=2 V 1000=20.
Примѣръ. Уравненія:
л'—2л4—38л8—8000(л’-ь-л-ь4)=0,
Xе—20л1—3 8л3—8л8—ь-л—ь-1 )=0,
у коихъ, въ первомъ а=2, с=20,
во второмъ а=20, с=2,
а въ обоихъ ас=40, близкое къ 38, имѣютъ предѣломъ І=а-н-с=22. Таковъ
онъ и по способу Ньютона.
— 377 —
* 401. Наконецъ, возмемъ уравненія, вида:
хп—с3(я"-Ч-я;п-‘ч-а;"-е-ь-... ,-ь-1 )=0, ИЛИ
аГ—ах"- ‘-ь-бя"-’—с3 °'‘**(А)>
въ которыхъ четыре первые члена пмѣютъ только перемѣны знаковъ. Въ
нихъ ближайшій большій предѣлъ зависитъ отъ величины а, Ъ, с; и его нахож-
деніе приводится къ слѣдующимъ замѣчательнымъ случаямъ.
а) Взявши Ь общимъ множителемъ третьяго и всѣхъ за нимъ послѣдующихъ
членовъ*.
хп—ахп^-ь-Ь(хп-3— хп~>— ? я"-8—....—^)=0,
о о Ъ'
. с*
и примѣняя сюда способъ Маклореневъ, тотчасъ видно, что Ь=:а или смотря
потому, что больше, лишь бы разность между этими числами была пе меньше
1-цы. въ противномъ случаѣ, предѣломъ будетъ а-ьі либо —-ьі. Такъ, въ
уравненіи
х3—10ж‘-ь-50я8—600ж!—600я—600=0, или
х*— 4 0 х*ч-5 0 (ж8— 12я’—-12а:— 12)=0,
очевидно, предѣлъ Е=12.
с»
Надобно при семъ замѣтить, что если между числами а и у разность ве-
С3
лика, особливо когда у много больше а, то лучше искать предѣлъ по 3-му
общему способу, либо по способу въ § 400.
Ь) Когда 6<^(а—2)(с-ь-1)-ь-1,
<^ас-ьа—2 с—4, или
<^рс’-ь-рс—2с—1, полагая а=рс;
тогда ближайшимъ высшимъ предѣломъ будетъ
4-г-с.
Для доказательства, освободимъ уравненіе (А) отъ знаменателя а;—1; по-
лучится
я;м_8[ж8—(ач-1)я5-+-(а-т-6)<г—б-—с3]-ь-с3=0.
Отъ подстановлеиія а~рс, 6—рс‘ч-рі—2с—1, <я=1-+-с, многочленъ
х3—(а-ь-1)аг-ь-(ач-б)а;—Ь—с3 обратится въ пуль, а данное уравненіе въ по-
ложительный результатъ с3.
с) Когда а>с и Ь<^ас, или хотя 6>с’.
Въ этомъ случаѣ полезно бываетъ вводить въ данное уравненіе отрицательный
6 6
корень —, помноживъ оное на а?-ь —; высшій предѣлъ корней оттого пе пере-
мѣнится, по уравненіе приведется въ такой видъ, что можно къ нему съ боль-
шою выгодою приложить способъ Брета. Предѣлъ Ь получится весьма близокъ
къ наибольшему корню, въ °емъ увѣримся разными примѣрами.
— 378
Примѣръ. Уравненіе,
а?—2л;84-8л;‘—1000т—1500=0,
Имѣетъ а=2, 6=8, с=10. Предалъ Ь его корней найдется По случаю 6); по-
тому что удовлетворяется условіе
6<^(а—2)(С4-1)4-1, и выходитъ
НЗ;
слѣдовательно Б=1-ьс=1-ь 10=11, тоже, что и по способу Ньютона. Въ
самомъ дѣлѣ, взявъ
6 =х‘—2л ’4-8х!—1000л;—1500=0,
Ѳ,=4л:3—6жг4-16х—4000,
61=6л;‘—6хч-8, 6^=4л—2, 6*=4,
И полагая:
4 3 2 16
х=10, получимъ: -+- 4- 4- 4- —
11, - 4- 4- 4- 4- 4-
т. е. наибольшій корень уравненія находится между 40 и 11.
Примѣръ. Уравненіе
х1—20л?4-200я?—1000(х’4-хг4-х4-1 )=0,
въ которомъ а=20, 6=200, с=10, имѣетъ условія всѣхъ трехъ случаевъ.
Но первому а) получается предѣлъ 20. По второму 6), для котораго удовлетво-
ряется условіе
6> (а—2)(с4-1 )-ь1 , то есть,
200> 199,
имѣемъ предѣлъ С4-1=11.
По третьему, для котораго удовлетворяются условія а> с и 6> ас, вводимъ
въ уравненіе множитель х4- — =а?4-10; получится:
а;7—20х’4-200х8—4000л;4— 4000л'8— 4000яГ—1000а;
4-40 —200 4-4000 —40000 —40000 —.................
х1—10х64- 3000л4 —ІЮООх3—ПОООх8—...........
Теперь, по способу Брета, имѣемъ такой же предѣлъ [.=404-1=14.
По способу Ньютона, онъ также =14.
Примѣръ. Въ уравненіи
хв—6х4-+-5 4х’—4 ЗОх*—4 ЗОх—130=0,
а=6, 6=54, с= у 130=5, а>с, 6>ас, также заключаются условія всѣхъ
трехъ случаевъ. По первому, 1=6 ч-1=7; по второму, І=с-4-1=6; по
ь ы п „
третьему, введемъ въ уравненіе множитель Ж4- — =®4- — =8,5, получится:
— 379 -
я?—Сл6-^!^—130 л8— 130а3— 130л
-+-8,5—51 -+-433,5 —1105 —1105 —1105
л'-+-2,5л6-+-303,5л3—1235л’—1235л—1105=0
Отсюда по способу Брета находимъ
-___________________ 1235 ___1235__,
И 2,5-+-ЗОЗ,5 307 + ‘
Примѣръ. Въ уравненіи
хв—12л4-+Л00л3—200л’—200л1—200=0,
а=12, 6=160, с= 1/200=6, а>с, 6>ас, выгоднѣе всего употребить спа-
, , . , „ 16С
сооъ с), помноживъ уравненіе на л-ь13=л-+- —; получится:
л6-ьл6-г-4л4н-1880л3—2800л’—2800л—2600=0.
По способу Брета, найдемъ теперь
' 1.= ™°=2,5.
1880 ’
Повѣрка способомъ Ньютона показываетъ, что дѣйствительно самый большій
корень даннаго уравненія находится между 2,5 и 3.
При всякомъ такомъ случаѣ (когда—<а), уравненіе, отъ помноженія на
ь
теряетъ двѣ перемѣны знаковъ между тремя первыми членами, и въ то
же время обнаруживаетъ присутствіе двухъ мнимыхъ корней.
Примѣръ. Въ уравненіи
л6—173л*-+-2356л3— 10468л’— 14101л—4183=0
3,.. --
имѣемъ а=173, 6=2356, с= |/10468=22; притомъ а>с и 6>с . Помво-
жимъ это уравненіе па л-+-у =л-+-14:
л6—173л6-+-2356л‘—10468л8—14101л’—4183л
-+- 14 —2422 -+-32984 —146551 —.........
х6— 159л6— 66л‘-ь22516л3—160651л!—........
Теперь, по Брету, найдется искомый предѣлъ Ь=159-1-1=160; а по
Ньютону 159.
Примѣръ. Въ уравненіи
лв—378л6-і-38189л4—492368л8—572551л’—213720л—26352=0,
а=378, с=80, 6=38189>ас, о>с; опять выгоппѣе употребить случай с)
для отысканія предѣла, который и найдется
І=1-ь к38~1Т9=197;
а по Ньютону 1=196.
— 380 -
Изъ всего этого видно, что для полученія высшаго предѣла, ближайшаго къ
корнямъ даннаго уравненія, пе довольно прибѣгать къ самымъ общимъ спосо-
бамъ, по надобно принимать въ помощь особенные пріемы, наибольше выгод-
ные, соображаясь съ различными видами уравненій, какіе мы разсматривали
въ п08 399, 39», 399, 400 и 401.
409. Нижнимъ предѣломъ положительныхъ корней даннаго уравне-
нія называется число ближайшее мепьшее къ самому меньшему положительному
корню. Чтобы пайти этотъ предѣлъ, надобно въ данное уравненіе
І'(х)=хп-і-Ахп-1-+-Вхп-і-^... .-+-Тяч-1]=0,
і
подставить х=. -, и освободить отъ знаменателей, то получится
ГЫ=УП+ У-1 -ь | У"-'+... ±!Н- і =0.
Очевидно, что, если а, Ь, с,.... суть корпи уравненія то у~* >
іі і
.... будутъ корнями для /{у)—0; потому что у— — . Наибольшій изъ
всѣхъ корней этого уравненія — будетъ самымъ меньшимъ положительнымъ
1 '
корнемъ даннаго /’(ж)=0, оттого что дробь — будетъ самою большею, когда ея
знаменатель самый меньшій. Посему, если I есть высшій предѣлъ корней для
Цу'і—О, то ~ будетъ низшимъ предѣломъ корней даннаго уравненія /'(ж)=:0.
Для полученія низшаго предѣла корней отрицательныхъ, преобразуемъ дан-
ное уравненіе Д.т)=0 въ /’(-л:)=0, и найдемъ низшій предѣлъ положитель-
ныхъ корней послѣдняго; онъ будетъ низшимъ предѣломъ’ корней отрицатель-
ныхъ для Дж)=0.
Примѣръ, Въ уравненіи,
/\х')~хі— 12ж*-ь20ж—5~0,
высшій предѣлъ положительныхъ корней 11.
Возмемъ х~ —; найдется
у
І'(у}=у3—ьуі-*~ У— у —О-
Въ этомъ послѣднемъ, высшій предѣлъ =4; слѣдовательно, у будетъ низ-
шимъ предѣломъ положительныхъ корней даннаго уравнепія Д.г)—0; стало-
быть, всѣ положительные корни его заключаются между 1І и Отрицатель-
ныхъ же корней нѣтъ, потому что это уравпеніе полное, и содержитъ однѣ пе-
ремѣны знаковъ.
- 381
В. РоЗЫСКАНІЕ И ОТДѢЛЕНІЕ КОРНЕЙ СОИЗМѢРИМЫХЪ.
<03. Соизмѣримые корпи въ уравненіяхъ бываютъ цѣлые и дробные; мы
начнемъ съ первыхъ.
Предварительно докажемъ, что всякое уравненіе, котораго первый членъ
имѣетъ коефиціентомъ единицу, а коефиціенты во всѣхъ прочихъ чле-
нахъ цѣлыя числа, можетъ имѣть соизмѣримые корни только цѣлыя
числа.
Для сего возмемъ уравненіе съ цѣлыми коефнціептами
хт-+-Рхт-'^х’п-І-+-... .-+Т.гі 1=0;
положимъ, что оно имѣетъ соизмѣримый дробный корень и подставимъ его
на мѣсто х, получится:
/7™ л 1П 1 п
^ч-Р.^5 -+-. . -ьТ. -1-1—0.
Ьт ь™—1 ь
Послѣ сего помножимъ все па Ьт~’, и отдѣлимъ первый членъ:
— Рат-‘—Оат-’б—....—Та6,п-’—
Ь
ат
Вторая часть этого равенства получилась вся цѣлою; по этому — не мо-
жетъ быть дробью, а слѣдовательно и данное уравненіе пе можетъ имѣть соиз-
мѣримыхъ дробей сгопми корнями.
<0-6. И такъ, если преобразовать (ЗЙЯ, В) данное уравненіе въ другое, въ
которомъ бы коефпціентомъ перваго члена была 1 -ца, а всѣ прочіе коефиціенты
цѣлыя числа; то всѣ его соизмѣримые корпи будутъ цѣлыми числами. Но, из-
вѣстію, что послѣдній членъ уравненія равенъ произведенію всѣхъ его корней,
и потому долженъ дѣлиться безъ остатка на каждый цѣлый соизмѣримый корень;
слѣдовательно, стоитъ только разложить послѣдній члепъ на всѣ его цѣлые мно-
жители, подставлять каждый пзъ нихъ въ уравненіе, и смотрѣть, который изъ
пихъ будетъ удовлетворять ему, то и найдутся всѣ цѣлые корпи по-одипачкѣ.
Пусть а, а1, а",... найденные корни: чтобъ исключить ихъ изъ даннаго уравне-
нія /'(ж)=0, надобно раздѣлить оное на произведеніе (х—а)(х—а')(х—а")....
Во всѣхъ случаяхъ надобно прежде всегѣ искать высшій и низшій предѣлы
корней положительныхъ и отрицательныхъ, дабы чрезъ это освободиться отъ
лишнихъ подстановлепій.
Такъ, въ уравненіи,
х3—6г’-ь27ж— 38=0,
дѣлителями послѣдняго члена 38 суть числа 1, 2, 19, 38, а высшій предѣлъ
корней 7 (по Брету); стало-быть, надобно пробовать только 1 и 2. Пзъ этихъ
- 382 —
множителей только 2 удовлетворяетъ уравненію и есть его корнемъ. Отрица-
тельныхъ корней нѣтъ, потому что данное уравненіе полное и не имѣетъ ни
одного повторенія знаковъ.
Нашедши корень 2, раздѣлимъ уравненіе на х—2, получится въ частномъ
уравненіе
х*—4а:-ь-19=0,
изъ котораго получимъ остальные два корня
аг=2±і/—15, оба мнимые.
Но этотъ способъ, по видимому, легкій, становится утомителенъ, когда при-
лагается къ уравненію высокой степени, котораго послѣдній членъ разлагается
па большое число множителей, и когда самый большій корень его великъ. Въ
такихъ случаяхъ розысканіе цѣлыхъ корней, соизмѣримыхъ, облегчается слѣ-
дующими способами.
1-й способъ.—Этотъ способъ мы изъяснимъ на уравненіи 4—й степени:
»‘-ь-Ра:8-+-0а:’-+-Вл:-і-8=О
Пусть а корень уравненія; подставимъ его на мѣсто х:
а‘-г-Ра8-ьОа*-ьВач-8=0, или
8——На—Оа’—Ра8—а*; отсюда
8: а~—В—Оа—Ра’—а3.
Частное 8 : а должно быть цѣлымъ числомъ; потому что корень а долженъ
дѣлить послѣдній членъ 8 безъ остатка. — Перенесемъ —В въ первую часть:
(8; а)-+-В:=—Оа—Ра’—а8,
потомъ раздѣлимъ на а:
(8:а-+-В):а——0—Ра—а’.
Здѣсь вторая часть — цѣлое число, то и первая должна быть числомъ цѣ-
лымъ. Перенесемъ -—О въ первую часть, и опять раздѣлимъ на а; будетъ
[(8: а-ь-В): а-»-0]: а——Р—а.
И здѣсь вторая часть—цѣлое число, то и первая должна быть этимъ же чи-
сломъ. Перенесемъ —Р въ первую часть, и снова раздѣлимъ на а; получится:
| [(8:а-4-В):а-ь-0]:а-ьР^:а=—1.
Наконецъ, къ частному, составляющему всю первую часть равенства, пере-
несемъ —1; тогда все должно сдѣлаться равнымъ нулю:
| |(8:а-ьВ):а-#-0]:а-+-Р | :а-ь1=0.
И такъ, чтобъ узнать, будетъ ли корнемъ уравненія одинъ изъ дѣлителей а
его послѣдняго члена 8, надобно:
1) раздѣлить послѣдній членъ 8 на а, и къ цѣлому частному "ислу придать
коефиціентъ члена съ первою степенью неизвѣстной х;
2) полученную сумму 8:ач-В опять раздѣлить на а, и къ частному придать
коефиціентъ члена, въ которомъ находится вторая степень неизвѣстной, х~;
— 383 —
3) эту сумму раздѣлить на а, и къ цѣлому частному придать коефиціентъ,
помножающій х3;
4) продолжать это дѣйствіе до перваго члена уравненія; и если послѣднее
частное, сложенное съ единицею, то есть, коефиціентомъ перваго члена, будетъ
=0, то а непремѣнно корень уравненія.
Если какое нибудь изъ частныхъ дѣленій не будетъ безъ остатка, то надобно
заключить, что а не есть корень уравненія.
Примѣръ. Послѣдній членъ уравненія
#Б+Зж4—35ж3—41 ж*+66ж+7 0=0
имѣетъ дѣлителями 1* 2, 5, 7, 10, 14, 35, 70, и тѣ же числа, взятыя съ
знакомъ минусъ. Высшій предѣлъ корней положительныхъ = 1^35=6, а для
корней отрицательныхъ 10; посему, цѣлые соизмѣримые корни надобно искать
только между числами
1, 2, 5, -1, —2, —5, —1.
Единица не корень уравненія, потому что изъ непосредственнаго подстанов-
ленія видно, что сумма коефиціентовъ положительныхъ не равна суммѣ отрица-
тельныхъ:
1+3—35—41+66+70=140—76=64.
Беру дѣлитель 2; выписываю коефипіепты членовъ уравненія, и розыскпваю,
какъ показываетъ правило,
1, +3,—35,—41,+66, 7 0 част. 35+66= 101 Д«_іитвли: 2 не корень •
част. 14+66= 80 16—41=—25 —5—35=—40 —8+ 3=— 5 5 корень
—1 + 1= О|
а именно: дѣлю 70 на 2; получаю 35 и придаю къ 66.> Сумма 101 не дѣлится
на 2 безъ остатка; слѣдовательно 2 пе корень уравненія.
Беру слѣдующій дѣлитель 5. Ищу 70:5=14; придаю къ 14 коефиціентъ
66, и сумму 80 дѣлю на 5; къ частному +16 придаю —41, и сумму —25
дѣлю на 5; къ частному —5 придаю слѣдующій коефиціентъ —35, и сумму
—40 дѣлю на 5; къ частному —8 придаю коефиціептъ +3, и сумму —5
дѣлю на 5; къ частному —1 придаю +1, и получаю пуль. Слѣдовательно 5
есть корень уравненія.
Для полученія цѣлѣхъ отрицательныхъ корней, перемѣняю знаки на
чётныхъ мѣстахъ членовъ даннаго уравненія; выписываю коефиціепты
1, —3, —35, +41, +66, —70,
— 384 —
и тотчасъ замѣчаю что І-ца корень, потому что сумма коефиціентовъ положи-
тельныхъ равна суммѣ отрицательныхъ.
Беру дилитель 2;
1, —3, —35, -+-41, -+-66, —70 част. —35-1-66 =31 Д-тапткли: 2 не корень
—14-+-66 =52 5 не корень
I I + + I Ні СС О + I I х + СС 4^ ОІ сл — о II II II I I II II ьэ 4^ СП о ч сс го а: 7 корень •
Ищу —70:2=—35; къ частному —35 придаю слѣдующій коефиціентъ
-+-66; и получаю сумму 31, которая не дѣлится безъ остатка на 2. Слѣдова-
тельно, 2 не корень.
Беру множитель 5; ищу —70:5=—14; къ этому —14 придаю 66, и
получаю сумму 52, которая также не дѣлится на 5 Слѣдовательно и 5 не есть
корень.
Наконецъ, беру множитель 7. Ищу —70:7=—10; придаю 66, и с)мму
-+-56 дѣлю на 7; къ частному 8 придаю 41, и сумму 49 дѣлю на 7; частное 7
слагаю съ —35, и сумму —28 дѣлю па 7; частное —4 слагаю съ —3, и
сумму —7 дѣлю на 7; наконецъ, частное —1 слагаю съ -+-1, получаю пуль.
Слѣдовательно 7 корень уравненія /'(-ж)=0.
И такъ, найденные корпи даннаго уравненія суть:
5, —1, —7.
А раздѣливъ /'(я:)=0 на (ж—5)(ж-+-1)(я;-+-7), получится ж2—2=0, откуда
найдутся два остальные корня ж=±|/2, оба несоизмѣримые.
2-й способъ. — Въ 1838 году Бретшнейдеръ предложилъ другой спо-
собъ розысканія цѣлыхъ соизмѣримыхъ корней, имѣющій ту выгоду, что по-
средствомъ его данное уравненіе, въ то же время, и освобождается отъ этихъ
корней.
Онъ основывается на томъ, что всякое уравненіе
аГ-^аіа?~і+а3лп~*+а3хп~гч-... .-г-ап—0
можетъ быть написано такъ:
' [(1.ам-а1)ам-а1]я-ь....ч-а„_1 ^ч-ап=0;
напримѣръ: х4-ьа1лг’-+-аІ.т2-+-а3я:-+-а4=0 есть тоже, что
I [(1.ж-+-а1)ж-+-а,]ям-а3{ам-а4=0
— 385 —
Разложивъ послѣдній членъ а4 па его цѣлые множители 1, «, /?, у,...., те-
перь легко можно каждый такой множитель испытывать чрезъ подстановленіе.
Положимъ, что хотимъ пробовать множитель а-.
Надобно сперва взять І.а-+-а„ и помножить на а, произведеніе (І.а-ьа,)»
сложить со вторымъ коефпціентомъ а2, и все помножить на а, и такъ далѣе
продолжать др послѣдняго члена. Если получится въ результатѣ нуль, это бу-
детъ признакомъ, что а корепь уравненія; а если выйдетъ какой нибудь резуль-
татъ ±11 (онъ тотъ самый, во что обратится /’(я;)=:0 при подстаповленіи а па
мѣсто ж), то а пе корепь.
ЛОЛ. Весьма замѣчательно, что если выйдетъ результатъ =0, мы пе только
узнаемъ, что нашелся корепь а уравненіи, но что, въ тоже время, оно раздѣли-
лось уже па х—а, то есть, понизилось на одну степень. Чтобъ доказать это
послѣднее, возмемъ уравненіе
/(л;)—х3-і-ах3-ѵ-Ъх-ѵ-с=О,
введемъ въ него корень а, помноживъ на х—а\ получится:
Е(л:)=:я;*-ь(а—а)х3-+-(Ь—аа)а;!-ь(с—Ьа)х—ас~0.
Пзъ самаго состава Е(аз) видно, что, для перехода огъ его коефпціентовъ къ
коефиціептамъ Да?)—О, надобно только придать І.а, аа, Ьа, са, соотвѣтствен-
но къ коефиціептамъ а—а, Ь—аа, с—Ьа, —са. Но мы именно это самое и
дѣлаемъ въ показанномъ дѣйствіи, по слѣдующему механизму.
4, а—а, а—аа, с—Ьа, —ас
____ __________________________ 1
О, -ьа, -ьаа, -ьіа, -ьас
а) 1, а, Ь, с, 0 — Да)-
Въ первой строкѣ пишутся коефиціенты даннаго уравненія 0, и подъ
ними проводится черта. Во второй строкѣ на первомъ мѣстѣ ставится нуль. Въ
третьей строкѣ на первомъ мѣстѣ ставится 1-ца, и при ней, съ лѣвой стороны,
испытываемый множитель а). Берется 1.а=а, ставится во второй строкѣ па
второмъ мѣстѣ, и слагается съ коефиціентомъ а—а\ сумма а ставитсн въ
третьей строкѣ на второмъ мѣстѣ. Эта сумма а помножается на а); произведе-
ніе аа ставится во второй строкѣ на третьемъ мѣстѣ, слагается съ коефиціеп-
томъ Ь—аа, и сумма Ь пишется на третьемъ мѣстѣ третьей строки. Это Ь
помножается опять на а), произведеніе -ьба ставится во второй строкѣ подъ
с—іа, слагается съ пимъ, и сумма с пишется на четвертомъ мѣстѣ третьей
строки. Наконецъ, это с помножено на а), произведеніе -ьас подписано подъ
—ас, и сложено; въ результатѣ получился нуль. Стало-быть, Е(а)=0, и а
есть корень уравненія. Здѣсь же находимъ, что въ третьей строкѣ получились
коефиціенты 1, а, Ь, с, членовъ уравненія
о:’-ьаж!-ьіл-ьс=гО=Дж),
25
— 386 —
т. е. мы перешли отъ уравненія Е(х) четвертой степени къ уравненію ((х)
третьей степени, въ которое обращается первое чрезъ раздѣленіе на х—а.
Примѣръ. Найти цѣлые соизмѣримые корни уравненія
Е(ж)=ж’—5ж3—11ж’-ь79ж—84=0,
въ которомъ 84" дѣлится па 1, 2, 3, 4, 6, 7, 12, 11>, 21, 28, 42, 84; пре-
дѣлъ положительныхъ корней =5 (по Ньютону), предѣлъ отрицательныхъ
=—5. Стало-быть, надобно искать корни между числами і, 2, 3, 4, —1,
—2, —3, —4. Для этого выпишемъ коефиціепты уравненія въ одну строку,
проведемъ подъ ними черту, и проч.
1, —5, —II, -4-79, —84.. коефиціепты;
0, -4-2, — 6, —34, -+-90..произведенія 1.2, —3.2,....
-г-2) 1,—3, —17, -і-45, -ь 6=Д2)... суммы—5-ь2, —11—6,...
0, -4-3, — 6, —51, -4-84.. произведенія 1.3, —2.3,....
-4-3) 1, — 2, —17, -4-28, О=ДЗ)... суммы—5-ъ-З, —11 — 6,..
0, +4, + 8, — 36~~
-4-4) 1, 4-2, — 9, — 8=д>(4)
Въ третьей строкѣ послѣдння сумма получилась -4-6; опа показываетъ, во
что обращается [(х) при постановленіи 2 на мѣсто х; отчего тамъ и означено
-4-6=Д2).
Въ четвертой строкѣ, на первомъ мѣстѣ, поставленъ опять 0, а въ пятой
строкѣ па первомъ мѣстѣ 1-ца, и подлѣ нея новый множитель -4-3, взятый для
испытанія. Дѣйствіе производится такъ, какъ бы пе было строкъ второй и
третьей, то есть: берется, 1.3=3, ставится па второмъ мѣстѣ четвертой
строки, слагается съ —5 первой строки; сумма —2 пишется въ пятой строкѣ.
Далѣе, берется снова ЗХ—2=—6, ставится подъ 11, и сумма—17 пи-
шется подъ —6, и такъ далѣе. По окончаніи дѣйствія выходитъ нуль, то есть,
ДЗ)=0: слѣдовательно, 3 есть корень даннаго уравненія. Вмѣстѣ съ этимъ мы
. перешли къ уравненію 3-й степени, котораго коефиціепты 1, —2, —17, -4-28,
то есть, къ
ж3—2ж3—17жч-28=0=<р(ж),
Посему, для испытанія дѣлителя 4, взяты коефиціепты только этого урав-
ненія:
1, —2, —17, -4-28
0, -ь4, -ь 8, —36
4) 1,ч-2,— 9, — 8=<?(4)
Слѣдовательно, 4 пе корень уравненія
387 —
Послѣдній членъ уравненія ф(ж)=0 есть 28—4.7; а потому, для испытанія
отрицательныхъ корпей, беру —4, и коефичіептьі:
1, —2, —17, ч-28
О, —4, ч-24, —28
—4) 1, —6, ч- 7, 0=ф(—4)
Слѣдовательно, —4 корень уравненія; послѣ этого остается уравненіе 2-й
степени,
а?2—бжч-7—О, изъ котораго
яг=3±/2, оба корня несоизмѣримые.
Примѣръ. Поищемъ цѣлые корпи уравненія
/и)=а?“—2а:4— 1 За:"ч-20ж*ч- ЗОіс—36= =0.
Послѣдній его членъ 36 дѣлится на 1, 2, 3, 4, 6, 9, 12, 18, 36.
Предѣлы корпей ч-4 и —4. И такъ, надобно испытывать только числа 1, 2,
3, —1, —2, —3.
1, —2, —із, ч-20, ч-ЗО, —36
о, Ч-І, — 1, —14, -4- 6, ч-36
4-1) 1, — 1, —14, ч- 6, ч-Зб, 0=ДІ), корепь.
0, -4-2, ч- 2. 24 —36
4-2) 1, Ч-І, —12, —18, 0= =ф(2), корень.
0, 4-3) I, -4-3, ч-4, ч 12, 0, О —18= ^(3), не корень.
Для розысканін отрицательныхъ корней, беру
1, Ч-І, —12, —18, 0=ф(а?)
0, —1, 0, ч-І 2
—1) 1, о, —12, _ 6^ф(-1), не корень
0, —2, ч— 2, ч-20
—2) 1, —1, —ю, ч- 2—<р(—2), не корень,
0, —3, -4- 6, 4-18
—3) 1, —2, — 6, 0=ф(-3), корень.
Оставшееся уравненіе х*—2х—6—0, по разрѣшеніи, даетъ а?—1± Ѵ1.
II такъ, корни даннаго уравненія суть: 1, 2, —3, 1ч-/7, 1-/7.
ЛОв. Если уравненіе имѣетъ соизмѣримые корни дробные, то оно необходимо
должно быть вида:
Ал”-ьВл:т“,-+-Сл:’п-!4-... .ч-П=0,
— 388 —
гдѣ А, В, С,....О, цѣлыя числа, не содержащія общаго множителя, и при-
томъ А > 1; такъ что нельзя освободить первый членъ отъ его коефиціента А,
не сдѣлавъ какіе ни есть коефиціепты дробными. Уравненіе,
необходимо будетъ имѣть дроби.
Для розыскапія соизмѣримыхъ дробныхъ корней, освободимъ это уравненіе отъ
дробей, положивъ х— получится
утч-Вут-,-ьАСут-*-ьА2Бут-3-ь... .-ьА”Т]=0,
уравненіе, въ которомъ могутъ быть только цѣлые соизмѣримые корни (кромѣ
несоизмѣримыхъ и мнимыхъ). Теперь отыщемъ цѣлые корпи Ь, V,.этого
уравненія по какому ниоудь способу, тогда изъ ж=-^=—, х — найдут-
ся соизмѣримые дробные корни даннаго уравненія ^(ж)=0.
Примѣръ. — Уравненіе Зж3—2ж*-+-9ж—6=0, очевидно, имѣетъ дробные
корни, изъ которыхъ нѣкоторые могутъ быть соизмѣримы. Для розысканія сихъ
послѣднихъ, освободимъ первый членъ отъ коефиціента 3:
, 2 . 9 6 Л
х— Х -+- ѵ X— — =0;
ООО
. • 1
исключимъ дроби, полагая х~ —у, получится:
?/’—2у*-ь27у—54=0.
Отыщемъ цѣлые корпи этого уравненія, разложивъ послѣдній его членъ 54>
на дѣлители: 1,2, 3, 6, 9, 18, 27, 54>. Высшій предѣлъ корней =3; стало-
быть, надобно пробовать, не будутъ ли корнями числа 1 и 2. (Отрицательныхъ
корней нѣтъ, потому что уравненіе содержитъ однѣ перемѣны знаковъ).
Здѣсь 1 не корень уравненія, потому что сумма коефиціентовъ положитель-
ныхъ не равна суммѣ отрицательныхъ. Но, 2 будетъ корнемъ, потому что
1, —2, -4-27, —54.
0, -+-2, 0, -+-54
2) 1, 0, -+-27, 0=Д2)
Остальнымъ уравненіемъ будетъ
у*ч-27=0, откуда
у=± V—'27=±3 Ѵ—З.
п ' У 2
Слѣдовательно, х— — также
о о
а'=^=±ѵ/^3.
о
2
Такимъ образомъ найденъ соизмѣримый дробный корень у и два мнимые
-+Ѵ—3, — і/—3.
— 389 -
С. РоЗЫСКАНІЕ И ОТДѢЛЕНІЕ РАВНЫХЪ КОРНЕИ.
<03. Равные корни всякаго рода можно находить и отдѣлять изъ уравненій
слѣдующимъ образомъ.
Пусть а, Ь, с,.... I, корни даннаго уравненія
/(ж)=ж"-ьАжп-,ч-Вж"_ ...—(ж—а) (ж—Ь)(х—с).... (ж—/)=0.
Чтобъ узнать, имѣетъ ли оно нѣкоторые корпи равные, подставимъ въ него
ж-4-2 на мѣсто ж; получится:
/’(жЧ-2)=/(ж)Ч-2./,/(ж)н- ^2 /,//(ж)-Г-....Ч-2п_*.д)'(ж)-і-2"_,.д>(ж)-і-2’‘
=(жч-2----а)(ж-4-2—6)(жч-2---с)...., или
=(г-+-ж—а)(2-г-ж—6)(гч-ж—с)...., илп
2П-4-2В-,<р(ж)-Ь... .4- ^/“\ж)Н-2/7(ж)Ч-/’(ж)г=(2Ч-Ж-а)(2-4-Ж-Ь)....
Первая часть этого равенства, очевидно, состоитъ изъ произведенія п такихъ
биномовъ, у коихъ первый членъ 2, а второй ж—а, х—Ь,....; слѣдовательно,
послѣдній членъ его •
/(ж)=:(ж—а\х—Ь)(х—с)... .—О,
равенъ произведенію всѣхъ такихъ вторыхъ членовъ, и есть самое данное
уравненіе.
Первый производный многочленъ Р(ж) въ предпослѣднемъ членѣ состоитъ
изъ суммы различныхъ произведеніи биномовъ ж—а, х—Ь, х—с,...., взя-
. * .. ?(я") „
тыхъ по п—1. А какъ одинъ членъ этой суммы = , другой = и
т. д., то вся сумма ихъ
' 4 • х—а х—Ь х—с х—I
Второй производный многочленъ Л(ж) долженъ состоять изъ суммы различ-
ныхъ произведеній тѣхъ же биномовъ ж—а, х—Ь,.... взятыхъ по п—2; то
эта сумма будетъ
/"(жЪх ----— - I-----—-----ь...., и т. д.
’ ' ' (х—а)(х—Ъ) (х—а)(х—с) ’
Положимъ теперь, что данное уравненіе /’(ж)=0 имѣетъ т равныхъ корней
а—Ъ=.с—...., пли ш равныхъ биномовъ ж—а=х—Ь—х—с=....; тогда
будетъ:
/(ж)=(ж—а)т(ж—і)....(ж—/)=:0, и
Гл;=<^_ь^ч_....ч_2ЦіИЛИ
' х—а х—і х—1
С(х)=т (ж—а)”‘_1 (ж—і).... (ж—/)-ь(ж —а) ”(...) (ж—/)ч-(ж—а) " (ж—г)...
Откуда видно, что /'(ж) и /‘'(ж) имѣютъ общій наибольшій дѣлитель (ж—а)т~1.
Еслибы въ Дж)=0,кромѣ того, были еще р равныхъ корней к; то нашли бы
также, что /"(ж) и Р(х) имѣютъ общимъ Наибольшимъ дѣлителемъ
(ж—а)п~1.[х—Л)р_1; и такъ далѣе.
— 390 —
Изъ этого объясненія слѣдуетъ, что, для отысканія равныхъ корней въ
уравненіи /’(а?)=0, надобно взять ею первый производный многочленъ
потомъ найти между /<х) и ['(х) общій наиболыиіи дѣлитель,
гсоторый и будетъ состоять изъ произведенія разныхъ степеней
биномовъ, содержащихъ равные корни. Положимъ, что этотъ дѣлитель
—(х—а)т-1.(ж——Н®-1; то данное уравненіе содержитъ т равныхъ
корней а, р корней Л, 5 корней г. Тогда надобно будетъ уравненіе раздѣлить на
этотъ общій наибольшій дѣлитель; отчего исключатся изъ него всѣ равные корни,
и степень его понизится на столько единицъ, сколько было всѣхъ этихъ корней.
Уравненіе не имѣетъ равныхъ корней, если между [\х] и Р(х) не найдется
общій наибольшій дѣлитель, зависимый отъ х.
Примѣръ.—Уравненіе /'(л)=а;‘—х3—Зж’-г-.ъе—2=0 даетъ первый про-
изводный многочленъ /''(аг)=4л-3——бж-т-5. Общій наибольшій дѣлитель
между ними найдется а?2—2а?-т-1=(ж—I)2. Изъ этого слѣдуетъ, что въ дан
номъ уравненіи находятся три равные корня л?=1; а, раздѣливъ /(а?)=0 па
(а?—I)8, получится частное х—2=0, откуда яг=2. И такъ, данное уравненіе
состоитъ изъ корней 1, 1, 1, 2.
Такъ сразу опредѣляются равные корни, когда общій папболт шій дѣлитель
бываетъ первой пли второй степени отъ х. Надобно только уравнять его нулю,
и полученное уравненіе первой или второй степени разрѣшить. Если это урав-
неніе первой степени, то его корень въ данномъ уравненіи находится два раза.
Если же это уравненіе второй степени, то изъ него получатся два корня не-
равные либо равные (дѣйствительные пли мнимые): въ первомъ случаѣ, каждый
изъ корней будетъ находиться два раза въ уравненіи /’(лз)=О, а во-второмъ слу-
чаѣ—три раза, какъ это видѣли въ предыдущемъ примѣрѣ.
<08. Но, можетъ случиться, что, между даннымъ уравненіемъ (\х}=і0 и
его производною /’'(ж), общимъ наибольшимъ дѣлителемъ найдется многочленъ вы-
сокой степени; то, для полученія равныхъ корней пооднначкѣ, надобно упо-
требить тотъ же спо’собъ, какъ показываетъ слѣдующее разсмотрѣніе.
Означимъ чрезъ X, произведеніе различныхъ биномовъ первой степени урав-
ненія /’(л:)=0, чрезъ Х2 произведеніе биномовъ первой степени двойныхъ кор
ней, Хя произведеніе биномовъ изъ тройныхъ корней; чрезъ Х4 произведеніе би-
номовъ изъ четверпьіѵъ корней; и предположимъ, что пѣтъ другихъ повторяю-
щихся корней. Тогда будетъ
Л^)=х, х*х’х;=о.
Пусть Б, общій наибольшій дѣлитель между /’(^) и /7(-г); онъ будетъ
X2 х:
(въ пемъ каждый множитель будетъ одною степенью ниже, чѣмъ въ данномъ
уравненіи)
— 391
Возмемъ производную функцію отъ В,, и между ею и В1 отыщемъ общій
наибольшій дѣлитель 1)8; онъ будетъ
і\=х3 Х^.
Взявъ отъ В, также производную, найдемъ между ею и В, общій наибольшій
дѣлитель В3, то есть:
В3=Х4.
Полипомъ Х4 будетъ состоять пзъ однихъ неравныхъ множителей; слѣдова-
тельно В3 будетъ первымъ съ своею производною.
Послѣ этого падобно будетъ дѣлить каждое пзъ предшет гвовавшихъ равенствъ
на послѣдующее, и назовемъ:
М)—д і>,—— —О
I), — Ѵ‘> І)2 —Б,-
гдѣ О-Х.ХДзХ,, 02^Х2Х3Х4, 03=Х3Х4.
А раздѣливъ каждое изъ этихъ равенствъ па послѣдующее, а послѣднее па
Р3=Х4, получпмъ:
Оі ѵ~ Оа у О г. у
о. ь <г» 2> ь; з-
Такимъ образомъ опредѣлится множители Хп Х2, Х3, Х41 и отыщутся всѣ
корпи уравненія /’(л)=0 чрезъ разрѣшеніе частныхъ уравненій:
Х(=0, Х2=0, Х3=0, Х4=0.
Пзъ перваго уравненія получатся простые (различные) корни для /’(л)=0,
изъ втораго — двойные, изъ третьяго — тройные, а изъ четвертаго — чет-
верные.
Для примѣра , возмемъ уравненіе,
хя—7л’—2л°—11 х*—259л4—83л3— б 12л5 -108л—432=0.
Общимъ наибольшимъ дѣлителемъ между этимъ уравпевісмъ и его производ-
ною найдется:
з^-ьЗж—18=1)..
Общимъ наибольшимъ дѣлителемъ между П, и его производною будетъ
х—3=0*.
Пзъ этого видно, что данное уравненіе не содержитъ множителей, возвышен-
ныхъ въ степени высшія третьей; посему,
/"(л)=Х1Х!!Х^=лв—7л7—2лвч-... .=0
П,= ХД2 =л*—7л3н-13л*-і-3л—18,
1)2= X., ~х—3.
Дѣля каждое предшествующее равенство па послѣдующее, получимъ:
Х;Х5Хч=ж4-—15л’ч- Юам-24,
X Д ь.г'Чб;
а дѣля первое изъ этихъ равенствъ на второе, а это послѣднее па Х3=л—3,
найдется •
Х,=л—4, Х»=л2—х—2.
392 —
Послѣ сего разрѣшимъ уравненія:
ж-т-4=0, х*—жн-2=0, х—3=0;
первое даетъ корень х~—4-, который только однажды входитъ въ данное урав-
неніе; второе даетъ корпи —1 и -т-2, которые входитъ въ уравненіе по два
раза; а третье даетъ корень 3, который входитъ въ уравненіе три раза.
Посему,
Дж)=(ж-ь4).(ж-М)2(ж—1)2(ж—3)3=0.
409. Поелику двойной корень уравненія Дж)=0 находится въ Дж) и /'(ж),
всякой тройной корень находится въ Дж), /Дж), Д'^), всякой четверной —7 въ
Дж), Д(ж), Д(ж), Д"(ж), и т. д.; то очевидно, что такой корень х—а} будучи
подставленъ въ Дж) и ея производныя, уничтожитъ сряду столько функцій, на-
чиная съ Дж), сколько будетъ находиться такихъ равныхъ корней въ данномъ
уравненіи. Наприм. если х~а тройной корень въ уравненіи, то непремѣнно по-
лучится Да)=О, Д(а)=О, Д(а)=0; ни одна изъ остальныхъ функцій не уничто-
жится, потому что ни одна изъ нихъ не имѣетъ этого корня.—Такъ,въ уравненіи
Дж)=ж*-ьЗж3—6ж2-ь-28ж—24=0,
котораго производныя суть:
б,—4.ж3-ь9ж’—12жч-28,
Ѳ^бж’-ьбж—6,
03—іжч-3, 04=1,
корень ж=—2 находится три раза, потому что онъ уничтожаетъ не только
Дж), по и двѣ его производныя, то есть, дѣлаетъ Д-2)=0, оД-2^0,
Ѳ,(-2)=0.
Слѣдовательно, число равныхъ корней можно находись п не прибѣгая къ
розыскапію общаго наибольшаго дѣлителя между Дж) и Ѳ,(ж): разложивъ по-
слѣдній членъ уравненія на его дѣлителей, искать (404), который изъ нихъ
удовлетворяетъ уравненію. Если удовлетворяющій множитель повторяется п разъ
въ послѣднемъ членѣ; то надобно смотрѣть, не находится ли онъ п—1 разъ
множителемъ послѣдняго члена функціи б,(ж), п—2 раза множителемъ послѣд-
няго члена б2(ж), п такъ далѣе, и потомъ пробовать, не обращаетъ ли онъ въ
пуль одну первую производную 6/ж), или двѣ производныя б4(ж) и Ѳв(ж), и проч.
Сколько функцій уничтожитъ онъ, начиная съ Дж), столько разъ онъ будетъ
находиться въ данномъ уравненіи:
Примѣръ.—Въ уравненіи
Дж)=ж’—15ж3-і-84ж2—208жч-192=0,
котораго производныя:
61=4ж’—45ж!-+-168ж—208,
б,=6ж2-‘-4-5ж-ь-84’,
б,=4.ж—15, "=1,
- 393 -
послѣдній членъ192=1.2.2.2.2.2.2.3=1.4.4.4.3=1.8.8 3, іц сверхъ того,
въ функціяхъ 0,, 6„ послѣдніе члены —208 и 84 дѣлятся: первый па 4*, а
второй на 4, то число 4 можно пробовать какъ тройной корень. Мы испытаемъ
сперва 2, а потомъ 4.
1,-15, -+-84, —208, -+-192
О, -+- 2, —26, -+-116, —184
2) 1,-13, -+-58, — 92, -+- 8=/(2), пе корень.
О, -+- 4, —44, —1-160, —192
-+-4) 1, —11, -+-40, — 48, 0=/'(4), корень.
О, 4, —28, -+- 48
-+-4) 1, — 7, -+-12, 0=/(4), корень.
О, +- 4, —ТГ
4-4) 1, — 3, 0=/’"(4), корень.
Остальное уравненіе х—3=0. Посему, данное уравненіе =(ж-4)э(я'-3)=0.
И. Исключеніе Равныхъ корней, имѣющихъ противные зііакй, какъ
дѣйствительныхъ -+-а, —а, такъ и мнимыхъ, вида ±Ѵ^—а.
ЛІО. Это разысканіе и исключеніе корней дѣлается очень просто. Если
уравненіе Дз")=О имѣетъ корни -+-а и —а, или корпи -+-Ѵ'—а и —V—а,
то, въ первомъ случаѣ, опо должно дѣлиться безъ остатка па двучленъ, хг—а*,
а во второмъ—на двучленъ а:!-+-а. II такъ, станемъ дѣлить данное уравнепіе на
х'-+-а до тѣхъ поръ, пока получится остатокъ, содержащій только первую сте-
пень буквы х, и члены зависящіе отъ а, то есть, остатокъ вида
ж.Д«)ч-Е(а).
Этотъ остатокъ долженъ быть =0, если уравненіе содержитъ въ себѣ мно-
житель л:’-+-а=0, что возможно только тогда, когда оба члена этого остатка
уничтожатся, и слѣдовательно оба содержать будутъ въ себѣ корень а. По-
ищемъ общій наибольшій дѣлитель между /(а) и Е(а): если его не будетъ, то въ
уравненіи пѣтъ множителя ж’ч-а, и лѣтъ равныхъ корней съ противными зна-
ками; если же найдется этотъ множитель =а—Ь, такъ что будетъ
Да)=(а—Г(а)=(а—6)Е'(а), и
я:/,(а)-ьЕ(а)=[я:/7(а)-і-Р(а)](а-6)=0,
то заключаю, что а—6=0, или а=6.
Такомъ образомъ опредѣлится искомый двучленъ а?±а=0, и искомые два
корня а=± і/±а; а внеся а~Ь нъ частное число, получится уравненіе, осво-
божденное отъ х2±а, слѣдовательно такое, котораго степень понижена двумя
единицами.
394 —
Примѣръ. Пусть данное уравненіе
хв—6х34-1 5х8—40x4-60=0.
Чтобъ узнать, не имѣетъ ли оно множителя х8±», будемъ дѣлитьоноевах14-а:
хя—6х34-15х8—40x4-60 х84-а
—х*—ах3
х3—(а—6)х4-15
—(а-і-6)х34-15хг—40x4-60
4-( а-+-6) х3-ь(а84-6 а) х
15х*-*-(а*4-6а—40)«4- 60
—15х8—15а
(а*4-6а—40)х— (15а—60)=0.
Поищемъ общій наибольшій дѣлитель между а’-ьба—40 и 15(а—4). Онъ
найдется =а—4. А какъ остатокъ =0, то и а—4=0, или а=4. Посему
х84-а=х*4-4; откуда
х=±2 Vх—Г.
Таковы два корня даппаго уравненія.
Частное число х3—(а-ь-6)х4-15 теперь обращается въ
х3—10x4-15=0;
такимъ образомъ данное уравненіе 5-іі степени понижено въ третью степень,
Примѣръ. Станемъ дѣлить на х84-а уравненіе
хя—2хв —26х‘4-58х«4-1 Зх8—200x4-300=0;
получится частное
я4—2х3—(а-ь26)х8-ь(2а4-58)х4-а8-ь26е4-13,
и остатокъ
—(2а’4-58а4-200)х—(а34-26а’-ьіЗа—300)=0.
Общій наибольшій дѣлитель между 2а,4-58а4-200 и а34-2ба84-13а—300
найдется
а 4-29а-ьІ 00=0, откуда
29 . . /29“ 777 -29±21
а=— —±Ѵ ----------100=--------: то есть,
2 » 4 2
а=—25, или а=—4;
х= А, 5, илп х=±2.
Такъ найдены четыре корпя даннаго уравненія. А раздѣливъ уравненіе на
произведеніе (х2—25) (х2—4), мы понизимъ его во вторую степень, а именно,
въ х8—2х4-3=0, гдѣ
х=1± И—2.
Поступая такимъ же образомъ, мы нашли бы. что уравненіе,
хв—Зх’-+-14х*_ 42х34-1 26х2—і 35x4-405=0,
заключаетъ въ себѣ множитель х24-5=0, и понижается въ четвертую степень
х*—Зхь—х!—27x4 -81=0.
— 395 —
Е. Уравненія возвратныя, и пониженіе ихъ степени.
411. Это такія уравненія, въ которыхъ коефиціепты членовъ, равно от-
стоящихъ отъ перваго и послѣдняго, равны между собою. Онѣ имѣютъ общій
видъ:
®’Ч-Ап—‘ВаГ-*-+-... .±Вж’±Аж±1=0.
Это уравненіе отличается тѣмъ свойствомъ, что если а есть его корень,
то в — будетъ также его корнемъ. Всѣ такія уравненія называются возврат-
ными (стр. 358).
Въ самомъ дѣлѣ, возмемъ х=а:
ап-+-А«п-1-+-Ва"-і-ь... ,±Ва’±Ас±1=0,
раздѣлимъ все на а”, и члены уравненія напишемъ въ обратномъ порядкѣ; то
получится равенство
і
а"-‘
— ±А.— ±1=0,
а а
совершенно тоже, что предыдущее, только въ немъ а замѣнено дробью а это
и показываетъ, что — есть также корень уравненія. Что доказано здѣсь отно-
сительно одного корня, то же должно разумѣть и о всѣхъ прочихъ корняхъ /3, у,
8,.... даннаго уравненія.
418. Покажемъ теперь, какимъ образомъ возвратныя уравненія могутъ быть
понижаемы въ степеняхъ своихъ. Возмемъ сперва уравненіе чётной степени,
хе-+-рх‘-і-ух'-і-гх3-і-^хг-і-рх-і-1=Л;
раздѣлимъ всѣ его члены на я;3, то есть, на степень въ половину меньшую,
выйдетъ:
. . Ч Р 1 Л
X -і-рх'-і-ох-1-г-і----1—„ -+- =0, или
* Л X X* ж5
Теперь положимъ хч- ~ и отсюда найдемъ-
1 --„2 0
Ха —**-----
7г
Далѣе возмемъ (ж’-ь -О)(о:ч- —)=а^н-ж-ь — -+- -.-—г3—2з;
х ж*' ' ж' жж5
откуда лгэ-+- ^5=23—Зз.
Эти выводы подставимъ въ данное уравненіе, "случится:
г3—Зг-ьр(х’—2)-ьдг2Ч-г=0, или
23-+-ря8-ь(7—3 )хч-г—2^=0.
— 39<> —
Такимъ образомъ данное уравненіе 6-й степени понижено въ третью степень.
Этимъ способомъ всѣ возвратныя уравненія четныхъ степеней 4, 6, 8, 10,....
можно привесть въ уравненія степеней 2, 3, 1, 5,.... въ половину мепыпихъ
Уравненіе
хе—рх3-+~ух1’—гх3-*-цхг—ра?-+-1=0,
въ которомъ знаки предъ членами слѣдуютъ поперемѣнно ч-, обращается въ
предыдущее возвратное, чрезъ одно подстановленіе х~—у. оно дѣлается
д'ч-ру'ч-ду* —0.
Случаи.—Возвратное уравненіе
хе—рхе-+-ух ‘—цх*-і-рх—1 =0,
неимѣющее средняго члена, можно написать:
(а?6—1)—рх(х°—1)ч-дх°(хг—1)=0.
Оно имѣетъ общій множитель хг—1=0 дающій два корня , а:=±'Я
Исключивъ этотъ мпожитель, получимъ опять возвратное уравнені
х*—ра,-і-(д-+-1)хг—рт-ь1=0, или
~ —р (т+ ^)ч-дч-1=0,
1 » 1 .
которое, отъ подстаповлешя агч- — =2, х ч-— =г—2, ооращается въ
г’—рг-ьа—1 =0;
отсюда получатся двѣ величины для 2, посредствомъ коихъ изъ х-+~ =з най-
дутся остальные четыре корпя даннаго уравненія.
413. Возмемъ теперь уравнепіі нечётной степени,
я'Ч-р.х^ч-да/ч д.г8ч-ра:ч-1=0.
Здѣсь тотчасъ видно, что х——1 есть корень, потому что онъ обращаетъ
уравненіе въ
—Іч-р—дч-д—рч-1=0.
А раздѣливъ данное уравненіе на хч-1, получится:
—Р
^<1
опять возвратное уравненіе, и при томъ чётной степени, которое можетъ быть
понижено во вторую степень, какъ видѣли (418).
Возмемъ еще уравненіе
х^ч-рх^-і-цх3—ухг—рх— 1 =0.
— 397 —
Очекидпо, что оно имѣетъ корнемъ 1-цу; а раздѣливъ его па х—1, найдется
уравненіе
я:‘-ь1 «’-ьѴж’-ьІ л? 4-1=0
ч-р ч-р ч-р
также возвратное, которое можно понизить во вторую степень.
ЛЯЛ. Возвратныя уравненія съ равными коефиціентам” во всѣхъ
членахъ.
Таково уравненіе
о:пч-ж"_І-+-"_8-+-... .4-ж84-х4-1=0.
Въ этомъ видѣ уравненія не только могутъ быть понижаемы въ степеняхъ
своихъ, по даже не рѣдко со всѣмъ разрѣшаемы.
1) Если оно чётной степени, паприм.
а?°-ьа;8-ьа:в-+-а? 4-ис"+жі4-а:і44;’+з’’4-2'4-І =0,
то сперва надобно его раздѣлить на жв; получится:
(жЧ- ІИ*"*- а Н=0
Положивъ хч—~х, найдемъ отсюда хгч—- =х8—2, жэ4- — = хэ— Зх,
х*ч- ~і=г*—4х’-+-2, агвч- — =хв—5г3-ь5х; и, чрезъ подстановлепіе, полу-
чимъ уравненіе пятой степени
хвч-х‘—4-х3—Зх8-ьЗ х4-1=0.
2) Если это уравненіе нечётной степени, то опо, чрезъ разложеніе па
двучленныхъ или тричленныхъ множителей, приводится въ уравненіе возвратное
чётной степени, которое въ свою очередь можно понизить въ его степени, и не-
рѣдко доити такимъ образомъ до его полнаго разрѣшенія.
Пусть дано уравненіе полное
хпч-хгіч-а^3ч-хііч-. .. .-ьо:8-+-ж-ь1=0 ;
оно имѣетъ чётное число членовъ 26=13.2, и можетъ дѣлиться па ам-1, по-
тому что ему можно дать видъ
х^хч-І )-ьаг°(а:-+-'і )-ь... ,-+-а:8(я>+-4 )-ьж-ь1 =0.
Стало-быть, одинъ его кореиь х——1, по отдѣленіи коего, останется
уравненіе
х"ч-х3іч-х™-ь-... .ч,г‘к/ч1 =0.
Послѣ сего, положимъ хг—у, будетъ имѣть
^+уи-+Ув-+Ѵ+-... .-ьу8-ьУ4-1=0.
1
опять уравненіе возвратное четной степени, которое, для уч- - =х, понижает-
ся въ шестую степень -
хв4-хв—5х4—.4хэч-6х8ч-Зх-1=0.
— 398 —
Примѣръ.—У равненіе
Ж8’-+-ж”-Ьж’І4-^°-+-... ,-ъ<г8-Ьж-+-1 —о
имѣетъ 24—3.8 члена; его можно раздѣлить безъ остатка на ж’-+-ж-ьі, по-
тому что оно приводится въ
жп(ж8-ьж-ьі)-ьж‘э(а;8-4-ж-ь1. ,-ь(а;8-+-ж-+-1 )=0. или
(ж8І-+-ж18-+-ж,3-+-ж,8-ьа;84-ж6-ьж5-ь1) (.г8-+-.гн-1 )=0.
Слѣдовательно, ж8-+-жч-1=г0; откуда
ж8,-+-ж’8-+-ж1,і-ьл:<8-+-ж8-+-я:8-+-ж3-ЬІ=О .
Въ послѣдней ь уравпе ли положимъ х3—у, составится возвратное уравненіе
у7-ьу‘4-у3-ьу44-у3-і-у?ч-у-і-І=0,
печётпой стеиепи. Въ немъ число членовъ 8=2.4; у-+-1 будетъ его дѣлителемъ,
потому что опъ приводится въ
(У6-+-У -ьу’-+-<) (у-+-' )=0
Здѣсь полагаю, во-первыхъ, у-і-1=0, или у~—1, и нахожу
х3=у=—1, или ж3-+Л=0;
откуда, ж=—4. Раздѣливъ жэ-ь1 па жч-1, получится
хг—жч-1=0, откуда
Во-вторыхъ, у3-ьу‘-ьу8-+-1=0.
Здѣсь, положивъ уг—2, имѣю
23-+-28-Ь2-ь 1=(егч-1) (г-ь 1 )=0.
то есть, 2-т-1=0. или з=—1:
2*-+-1=0 2=±И—1; а посему,
.Ѵ=іѴг=:Ьр/22і , и также
у~± V—1, и наконецъ
• 3/~ ’/--------------------/ —
а=:|/у=|/±Ѵ—1, и еще
3 ,----- -----
-> - _+; V 4 ---1.
Такъ найдены всѣ корпи даннаго уравненія 23-й степени
Л15. Примѣненіе къ уравненіямъ двучленнымъ.
Всякое двучленное уравненіе
у ±с=0,
и сокращеніе, приводится въ простѣйшее воз-
вратное уравненіе жт±1=0, допускающее пониженіе въ своей степени. Мы
разсмотримъ только это послѣднее, въ его двухъ видахъ.
1Л
подстановленіе
— 399 —
А) гСт-ЬІ=О.
Если степень т нечётная, наприм. тп—5, и
«'-+-1=0;
то корнемъ будетъ х=—1; а раздѣливъ «'-ьі на хч-1, получится
х*—х3ч-хг—хч-'І =0
возвратное уравненіе. Оно, чрезъ подстаповленіе х=—у, обращается въ
у4-+-ѵ/3-+-у2-+-у-ь1=0, или
3/2-+- Л “ЬУ_Ь * -+~І=0.
у2 у •
1 і
Если ВЗЯТЬ уч- у=гі г0 У*4- и это УРавне11*е получитъ видъ
?++—<і=0; откуда
—1± іА
Я— —------.
2
Послѣ этого, изъ уч- - =х найдется уг—уа=—1;
і± Vг?—!і
слѣдовательно, у—-------- —;
Ѵ^і
и, пакопецъ, х~—у—--------------.
Если степень т чётная, наприм. «зо-+-1=О, или «4 •'-+-!4 '=0, то урав-
неніе можетъ дѣлиться безъ остатка на двучленъ четной степени, и здѣсь именно
на «4-ь1, такъ что
«80-»-1=(«,<і—х^ч-х8—хіч-і)(хіч-1)—0.
Посему, имѣемъ; 1) «‘-+-1=0, и
2) х1е—х^ч-х8—«‘-+-1=0.
Изъ перваго получаемъ хг—Л.Ѵ—1,
х~± V— 1;
во второе же подставляемъ х‘——у, и находимъ
у"ч-у 3-+-у! -+-г/-ь1=0
уравненіе возвратное, котораго корни находить умѣемъ (Л19), и такимъ обра-
зомъ все данное уравненіе разрѣшить можемъ.
В) «т—1=0.
Для т нечётнаго первоначальнаго числа, хх=1і будетъ корнемъ уравне-
нія. А раздѣливъ па х—1, получимъ возвратное уравненіе чётной степени, ко-
торую можно понизить на половину. Наприм.
«’—1=0, ,
по раздѣленіи па х— 1, обращается въ
х8ч-х8ч-х‘ -+-я8-+-«3-+-«ч-1=0,
1
которое, при положеніи =г, переходитъ въ
г’-ьз2—2г-ь1=0.
- 400 -
Когда же показатель т не есть первоначальное число, но состоитъ пзъ мно-
жителей р, д, то хт—і=хрСІ—1=0 можно раздѣлить на хр—1 либо хч—1
и вроч.
Примѣръ. Уравненіе
ж,в—1=0
имѣетъ показателемъ 15=3.5; оно можетъ быть раздѣлено на двучленъ х3—1,
а именно будетъ
хи— 1=(х,3-і-хе-і-хе-і-х3^)(х3—1)=0.
Отсюда имѣемъ: 4) а?3—1=(гс’-і-;г-ь1)(ж—1 )=0,
2) ж15-ь-ж3-ьж6-ьх3-і-1=0.
Пзъ перваго получаемъ: х—1=0, или я?=і;
ж’-ч-жн-1=0, откуда
а во второмъ беру х3=у, и нахожу
у4-+-уэ-ь’/’-+-у-^1=0
возвратное уравненіе чётной степени, котораго корни легко пайти можно; а
послѣ того найдутся и корпи я= Ѵу дапнаго уравненія.
Примѣчаніе. — Въ послѣднемъ и прежнихъ примѣрахъ видѣнъ способъ по-
ниженія степеней въ такихъ уравненіяхъ, въ когорыхъ степени неизвѣстной во
всѣхъ членахъ суть кратныя какого ни есть цѣлаго числа, большаго 1-цы. На-
примѣръ, въ уравненіи,
х' 2-ьая:8-+-бж6-+-ся:3-4-^=0,
всѣ степени неизвѣстной суть кратныя числа 3; а потому, довольно взять
вж3=г, чтобы оно понизилось въ четвертую степень
2‘-+-аг3-+-бд;’-+-сй-+-гі=0.
Но объ этомъ способѣ я не говорилъ особо, во первыхъ потому, что онъ оче-
видѣнъ; а во вторыхъ, опъ о іинъ, безъ рѣшенія .уравненій двучленныхъ, недо-
статоченъ. Такъ, въ этомъ примѣрѣ, нашедши корни г, мы должны обратиться
къ рѣшенію уравненія х3—г=0, чтобы найти всѣ корпи х.
Г. Отдѣленіе когнеіі несоизмѣримыхъ.
416. Возмемъ уравненіе /’(а:)=0, освобожденное отъ корней равныхъ и кор-
ней соизмѣримыхъ, состоящее только изъ корней несоизмѣримыхъ и мнимыхъ.
Чрезъ одно подстаіювленіе чиселъ 1, 2, 3,.... пли —1, —2, —3,.... въ это
уравненіе рѣдко можно отдѣлить его несоизмѣримые корни, то есть, узвагь,
между какими частными предѣлами заключается каждый корень отдѣльно.
Ибо, всякія два постановленія а, /3, обращающія уравненіе въ два результата
-+-В, —В', съ противными знаками, показываютъ только, что между а и /3 па-
— 401
ходится нечётное число корней (37 й), и неизвѣстно, одинъ ли тутъ корень,
или три, и болѣе; а подстановленія а', (У, обращающія уравненіе въ результаты
съ равными знаками, показываютъ, что между а' и /3' либо нѣтъ
корней, либо ихъ чётное число, но, какое, тоже неизвѣстно. Посему, необходимо
нужно умѣть открывать признаки, которые бы намъ показывали, при какихъ
подстановленіяхъ мы переступаемъ черезъ одинъ, два, или болѣе корней даннаго
уравненія, чтобъ начать потомъ раздѣлять ихъ тѣснѣйшими предѣлами.
Способы отдѣленія несоизмѣримыхъ корней представлены Лаіранэюемъ, Бю-
даномъ, Штурмомъ *) и Фурье. Всѣ они превосходны въ своихъ теоріяхъ;
но, для практики, я предпочитаю способъ Фурье; а потому объ пемъ собственно
говорить буду.
Л17. Возмемъ общее уравненіе /’(ж)=0, котораго коефиціепты суть дѣй-
ствительныя числа, и которое освобождено отъ равныхъ корней по извѣстнымъ
способамъ (4107); уменьшимъ корпи его числомъ а, подставивъ х=.а-+-%, то,
какъ извѣстно, получится:
жЯ дЪ
.['(а)-}- —^а)^. .-ья"=0,
или, короче:
е(а-+-л)=б(а)-Ь2.ѲІ(а)-т-гі.Ѳг(а)-і-2э.еэ(а)-+-... .-ья"=0.
Корни этого уравненія будутъ а—х—а. Его Ѳ(а), Ѳ8(а), Ѳ8(а),.... совер-
шенно тоже, что 6(лс), Ѳ^х), Ѳг(х),...., только въ нихъ находится а вмѣсто х.
По этой причинѣ, впослѣдствіи, мы часто въ /"(а-ья) будемъ употреблять букву
х вмѣсто перемѣнной а, которая служитъ для уменьшенія корней даннаго урая-
ненія [(х}~0.
Станемъ подставлять сюда числа I, 2, 3,.... а, (3, на мѣсто а-, получится
пядъ уравненій:
гдѣ корни я=х—1;
Ѳ(2)-ьд;.01(2)-і-х,.Ѳ8(2)-ь....-+-5"=О, - - х=х—2;
Ѳ(а)-+-г.Ѳі(а)-ьд;’.е8(а)-ь....ч-й”=О, - - я=х—а;
Ѳ(/3)ч-д; Ѳ1(/3)ч-я\ѳ8(/?)н-....^г’'=0, - - х=х—(3.
Въ нихъ корни я тѣ же, что и въ только уменьшены числами 1, 2,
3,...., а. Р-
Если, при переходѣ отъ х=х—а къ х—/3, то есть, при подстановленіяхъ
а, (3, на мѣсто а, уравненіе ѳ(а-ьа)=0 потеряетъ одну перемѣну знака,
это покажетъ, что первый в притомъ самый меньшій положительный его корень
•) См. Теорію опредѣленныхъ алгебрическихъ уравненій, Сомова; стран. 182,187, и
проч. Москва, 1838.
26
— 402 —
г не только истощился, по даже перешелъ изъ положительнаго въ отрицатель-
ный, в что въ І\х)=г0 самый меньшій корень ж> а, но </?; слѣдовательно,
между подстановлепіями а и р находится нѣкоторое число Ъ, которое дѣлаетъ
х~х—1>=0, или х=Ь; оно и будетъ корнемъ даннаго уравненія, отдѣлив-
шимся отъ прочихъ корней предѣлами а и /3.
Если е(а-+-я)=О, при переходѣ отъ х~х—а къ х—р, потеряетъ двѣ,
три или болѣе перемѣнъ въ порядкѣ знаковъ между ея членами; то два, три, и
вообще столько же корней будетъ заключаться между а и /3 въ данпомъ уравне-
ніи /’(ж)=0.
Л18. Если содержитъ мнимые корни, которые всегда сопряжены
попарно, то рядъ Ѳ(а-ьг) вдругъ теряетъ столько паръ перемѣнъ, сколько паръ
мнимыхъ корней находится между а и р. Потому что, отъ постепеннаго умень-
шенія пары р±у|/—1 мнимыхъ корней числами 1, 2, 3,...,, а, р, оба
корня сразу переходятъ изъ положительныхъ въ отрицательные, в потому вле-
кутъ за собою потерю двухъ перемѣнъ знака въ ряду ѳ(а-»-й)=0.
Х19> Когда уравненіе /(я;)=0 состоитъ изъ однихъ дѣйствительныхъ
корней, между которыми нѣтъ равныхъ, то знаки предъ 0(а), 0,(а),
въ ряду ѳ(а-4-я), при подстзповленіп чиселъ 1, 2, 3,.... на мѣсто а,
слѣдуютъ нѣкоторому опредѣленному закону, который нужно зпать; потому что
всякое отступленіе отъ сего закопа въ другихъ уравненіяхъ служитъ признакомъ
корней мнимыхъ. Для открытія этого закопа подставимъ въ у(а;)=О два числа
а—х, а-ь-х, па мѣсто х, столь близкія между собою, чтобъ между ними не
было пи одного корпя, то получимъ:
для а—х, І'(а—х}=і0{а)~х.0,{а)ч~х,.б.і{а}—.......
плп а-ь-х, [(а-ь-х)=й(а)-і-х Ѳ1(а)-ья8.6'!(а)ч-..
Поелику а не есть корень даннаго уравненія (\х)=:0, то ѳ(а) не равна пулю.
Число х можно взять столь малымъ, что знаки для [{а—х), /(а-ь-я) будутъ
зависѣть отъ знака предъ ихъ первымъ членомъ б(а); слѣдовательно, онѣ бу-
дутъ съ равными знаками. Пзъ этого заключаемъ, что:
I. Функція не перемѣняетъ знака отъ подстановленія въ нее чиселъ,
между которыми нѣтъ ни одного ея корня.
Но, если а корень уравненія /’(ж)=0, то Ѳ(а)=гО, и тогда будетъ:
для а—х, [{а—х)=:—х.01(а)-+-х*.О^а)—
а, /'(а)=б(а)=0,
ач-2, /’(а-ьс)=:-ьг.0(а)-ь-2!.Ѳ1(а)-+-....
Знаки для [{а—х), ((а-ь-х) будутъ зависѣть отъ знака предъ х.ѳ(а), на-
добно только взять х довольно малымъ; сверхъ того,
— 403
ДО УНИЧТОЖЕНІЯ. НОСЛЬ УНИЧТОЖЕНІЯ.
рели 01(а)=-і-, то /'(«—з)=—, /(я-ье)—н
» Ѳі(а)=—, то У(а—с)=-ь, /’(а-г-з)=—.
Отсюда заключаемъ:
II. Функціи Да?)=О, несодержащая ровныхъ корней, при всякомъ
переходѣ чрезъ нуль, перемѣняетъ свои знакъ н- на —, или — на -+
III. Функція Дх)=0, до уничтоженія своего, имѣетъ знакъ против-
ный съ своею производною О^а), а послѣ уничтоженія —знакъ равный
съ своею производною. Отъ зтого порядокъ знаковъ долженъ быть:
Оі 0 0. ѳ
для а—-і-------, либо-----1
а, і 0 — 0
Я~4—Д», —Н -+~ — --
Стало-быть, если Ѳ{х), 0/ж), при подстаповленіп какого пи есть числа а3,
имѣютъ равные знаки, то Ѳ\х) до тѣхъ поръ не можетъ уничтожиться, пока
Ѳ,(х] напередъ не перемѣнитъ своего знака, т. е. пока между ѳ(х), не
сдѣлается перемѣны знака отъ слѣдующихъ подстаповленій.
По, чтобы 0,{х) могла перемѣнить свой знакъ, надобно ей самой сперва обра-
титься въ нуль отъ какой ни есть величины а3>а3; а чтооы опа могла уни-
чтожиться, надобно ей самой имѣть знакъ противный съ своею производною 6, (я)
при нѣкоторомъ подстановлепіи а, > аі. Послѣ этого уничтоженія функціи
0,(ж), старшая фупк я 0(а?) будетъ имѣть возможность уничтожиться при какомъ
нибудь подстаповленій а > а, > а8 > а3.
Напримѣръ, порядокъ знаковъ можетъ быть таковъ:
о. О. о Число перем. Число корней
для «3. —) — 4
а„ -+- °і — 1 0 0
а„ -+- 1 4
а, -+- 1 , 0) 0
> а, н н- 0 0
гдѣ 6—0(ж) не прежде получила возможность уничтожиться, какъ послѣ уни-
чтоженія Оі или перемѣны съ нею знака.
Примѣръ. Отдѣлить корни уравненія
0—г3—7ж-+-7:-0.
Составимъ коефиціенты ряда ѳ(«-Ь2), или, проще, ряда О(ж-т-е), удерживая
букву х вмѣсто а, и подразумѣвая, что здѣсь х различенъ отъ х въ данномъ
уравненіи; они получатся:
0=®3—ІХ-+-7,
, Оі=3л3—7, ^=3ж, 03=1.
404 —
Предѣлы корней даннаго уравненія суть 2 и —4; и такъ беру:
Ѳз @і 6
Число Число
перси, корней.
=1
--/2>
=2,
2
2
1
О
О
1
1
Подстановленіе а?=0 показываетъ, что рядъ ѳ(л?ч-г) имѣетъ двѣ перемѣны,
и что данное уравненіе содержитъ два положительные корня.
При подстановленіи ж=1, остались тѣ же двѣ перемѣны; онѣ показываютъ,
что между предѣлами 0 и 1 нѣтъ ни одного корня уравненія.
Подстановленіе 2 уничтожило обѣ перемѣны; стало-быть, между < и 2 на-
ходятся два корня.
Для раздѣленія этихъ корней частными предѣлами взято и въ ряду
осталась одна перемѣна, соотвѣственная одному корню. Такимъ обра-
зомъ мы совершенно узнали, что одинъ корень уравненія находится между пре-
. . 3 „ 3 .
дѣлами 1 и —, а другой между -= и 2.
А ли
Для отдѣленія одного отрицательнаго корня, беру
Ѳ(-а?)=ж3—7х—7=0; составляю
Ѳ=«”—7х—7,
е,=3я:’—7, б2=3я:, 68=1.
Чбсло Число
02 02 02 00 перем. корней.
Для ж=0, нахожу -4-0 1 0
=2, - -Ь 4- 4- — 1 0
=3, - 4-4-4 1 л
—4, - 4- 4- 4- 4- 0 1
Слѣдовательно отрицательный корень даннаго уравненія находится между —3
и —4.
Примѣръ. Отдѣлить корни уравненія
Ѳ=х1—5т3-в-2 Ож—3 0=0,
котораго производныя:
08=5^—15^4-20,
08=10^—15», Ѳ3=10^—5, 04=5ж, Ѳв=1.
Полагая Ѳ8=О, 02=О, имѣемъ отсюда ж=±1/1, а;=±І^ти корни
возмемъ въ число подстановленій какъ отрицательныхъ, такъ и положитель-
ныхъ :
— 405 —
Число Число
ѳ, б*
д Персіи, корней.
уравненія только одинъ дѣйствительный между
Изъ пяти корней даннаго
/з /з
1/- и 2, и двѣ пары мнимыхъ: одна соотвѣтствуетъ предѣлу —\/~
у 2 у 2
. /з
предѣлу -4-1/ г , потому что въ оооихъ случаяхъ встрѣчаемъ
ж/ А
а другая
бз бз 61
-4- 0 (см. 420).
Сверхъ того, находимъ шесть случаевъ, отмѣченныхъ скобками, гдѣ функціи,
при переходѣ чрезъ нуль, перемѣняютъ свой знакъ, при чемъ всякая старшая
функція до уничтоженія своего имѣетъ знакъ противный съ своею производною,
а мослѣ уничтоженія — знакъ равный съ этою производною.
Д2О. Признаки мнимыхъ корней — Положимъ, что данное уравненіе
Да;)—О, освобожденное отъ равныхъ корней, состоитъ пзъ корней дѣй-
ствительныхъ и мнимыхъ, или изъ однихъ мнимыхъ, то въ пемъ присутствіе -
мнимыхъ корней обнаруживается слѣдующими признаками:
1) Когда, отт какого ни есть подстановленія х=а-+-х, въ уравненіи
0(а-4-г)=б(а)-і-2.б1(а)-*-х8.Ѳ,(а)ч-... ,-4-хп=0
уничтожится какая нибудь средняя функція такъ, что смежныя съ нею функціи
останутся съ равными знаками, наприм.
Ѳ. б. б0
-+- 0 ч-, или
— О —.
Это противорѣчіе закону измѣненія знаковъ, свойственному корнямъ дѣйстви-
тельнымъ (<19), покажетъ, что 6(ач-г)=0 имѣетъ по крайней мѣрѣ одну пару
мнимыхъ корней. Такая же пара корней будетъ и въ данномъ уравнепів Дж)=0;
ибо, если корень я=х—а будетъ мнимымъ для б(ач-г)=0, то х будетъ мни-
мымъ для Да?)—О
— 506 —
2) Когда въ уравненіи,
Ѳ(ач-х)=:Ѳ(а)ч-2.01(а)ч-г’.О2(а)ч-... .ч-з”=0,
уничтожатся сряду два члена, или болѣе, отъ уничтоженія среднихъ функціи, то
оно, а слѣдовательно и /’(ж)=0, имѣетъ мнимые корни (2ЯЗ).
4211. Число функцій, сряду уничтожившихся отъ какого ни есть подстапов-
ленія а, ведетъ къ заключенію о числѣ мнимыхъ корней, соотвѣтственныхъ
этому предѣлу; надобно только найти, сколько О(ач-г) въ этомъ случаѣ теряетъ
перемѣнъ знаковъ между своими членами. Но тутъ встрѣчается затруднен.,
какіе знаки надобно приписать этимъ нулевымъ функціямъ, для счета потерян-
ныхъ перемѣнъ. Для разрѣшенія этого недоумѣнія, разсмотримъ, въ какомъ
случаѣ могутъ уничтожиться нѣсколько функцій сряду, и какіе знаки онѣ дол-
жны имѣть-до своего уничтоженія, и послѣ уничтоженія.
Отъ частнаго подстаповленій а въ 0(ач-г)=0, уничтожаются всѣ тѣ функ-
ціи, которыя имѣютъ равные корни а, пли суть кратныя двучлена х—а. Сего
не можетъ произойти съ 6(ж) и ОДж), потому что данное уравненіе 0(ж)=0
предполагается свободно отъ равныхъ корпей; но можетъ быть во всѣхъ сред-
нихъ функціяхъ.
Число множителей х—а въ уничтожающихся функціяхъ не будетъ равное
(409), напримѣръ: если уничтожились четыре функціи сряду, то старшая
имѣетъ множителемъ (х—а)4, вторая послѣ нее (х—а)3, третья (-г—а)2, а
младшая х—а. Всѣ члены ряда б(ач-з), у которыхъ эти множители
чётныхъ степеней (х—а)2, (х—а)4,...., не перемѣнятъ своихъ зна-
ковъ, но каждый членъ сохранитъ свой знакъ до и послѣ своего уничтоженія.
Отъ этого происходитъ, что:
а) уничтоженіе сряду четнаго числа среднихъ функцій уноситъ
всегда столько же перемѣнъ знаковъ; Ь) а уничтоженіе нечётнаго числа
функцій уноситъ число перемѣнъ единицею больше, когда у смежныхъ
съ ними функцій знаки равные, или единицею меньше, когда у смеж-
ныхъ функцій знаки различные.
Для объясненія, положимъ, что число функцій, сряду уничтожавшихся, чёт-
ное, папрмм. четыре: Ѳ2, Ѳ3, Ѳ4, Ѳв, и что смежныя съ ними, уцѣлѣвшія функціи
Ѳ, и Ѳ„, имѣютъ знаки равные, то порядокъ знаковъ будетъ таковъ:
В * 3 1 1 03*311
для а—х, ч- 1---- —і—ь пли: -— ч---ч------—
а, ч- О О О 0 ч- — 0 0 0 0 —
а-г-г, ч-І—т ч—і—і- — — — —-------
чет. чет.
При этомъ смежныя, уцѣлѣвшія функціи 0,, 0в, удержатъ свой знакъ до
уничтоженія 0,; 63, б4, 6„ и послѣ ихъ уничтоженія, потому что между предѣ-
— 407 —
лани а—х, ач-х, функціи 0„ 68, не имѣютъ корней. Чтожъ касается до про-
межуточныхъ, то:
0„ должна получить знакъ различный отъ знака ея производной Ѳе до уничто-
женія, и одинакій съ нею послѣ уничтоженія (419);
04, съ чётною степенью (х—а)8 сохранитъ свой знакъ до и послѣ своего
уничтоженія;
08, до исчезанія своего, должна получить зЪакъ противный съ 64, а послѣ ис-
чезанія знакъ съ нею равный; и такъ далѣе.
Отъ этого, число перемѣнъ знаковъ, 'до исчезанія, выходитъ равно числу
уничтожившихся функцій, т. е. четыре, а послѣ исчезанія не остается ни
одной.
Посему, когда смежныя, неуппчтожпвшіяся функціи бываютъ съ равными
знаками, то чётное число исчезающихъ сряду функцій уноситъ изъ ряда 6(«ч-х)
столько же перемѣнъ знаковъ; въ нашемъ примѣрѣ было четыре.
Но, если, при уничтоженіи сряду чётнаго числа функцій, смежныя не
уничтожившіяся функціи будутъ съ разными знаками, наприм. 0,——,
06~ч-; то порядокъ знаковъ будетъ:
д
Б 4 3 11
для а—г, ч----ч- — ч— ’—
а, -4- 0 0 0 0 —
ач-х, -4- -ч- -ч- -ч- ч- —
чет. чет.
Здѣсь, до уничтоженія среднихъ ф}нкцій, находимъ пять перемѣнъ отъ Ѳ,
до 0о, а послѣ уничтоженіи одну, разность =5—1мг4. Слѣдовательно и здѣсь
чётное число сряду уничтожающихся функцій уноситъ столько же перемѣнъ,
сколько такихъ функцій.
Теперь положимъ, что, для х=а, уничтожится сряду нечетное число
функціи, наприм. три: Ѳ8, 63, Ѳ4, и положимъ, что смежныя неупичтожив-
шіяся функціи будутъ сс равными знаками, наприм. 6,=ч-, Ѳе=:ч-, или
обратно; то порядокъ знаковъ въ рядахъ Ѳ(а--г), Ѳ(а), Ѳ(ач-х), будетъ:
»
Ѳв * 3 1 I
для а—х, -і-----1-----ь
а, -4- 0 0 0 -4-
0-4-2, н—і—і—і—і-
чет.
Здѣсь было четыре перемѣны до уничтоженія среднихъ функцій, а послѣ
уничтоженія—пи одной: слѣдовательно, число унесенныхъ перемѣнъ едини-
цею больше числа уничтожившихся функцій, т. е. 4, но все же четное
число.
— 408 —
Наконецъ, положимъ, что, при нечетномъ числѣ исчезающихъ функцій,
смежныя неуничтожающіяся функціи ѳп Ѳв, имѣютъ знаки различные, наприм.
Ѳі=—, бв=-+, или обратно; то порядокъ знаковъ будетъ:
4 321
для а—х, -і----1-------
а, + 0 0 0 —
ач-х, -і—і—і—і----,
гдѣ видно, что, до исчезанія среднихъ функцій, было дари перемѣны, а послѣ
исчезанія — одна; разность =3—1=2. Слѣдовательно, число унесенныхъ
перемѣнъ единицею менѣе числа уничтожившихся функціи, и есть также
чётное.
Не трудно замѣтить, что во всѣхъ этихъ случаяхъ, начиная съ младшей
неуничтожающейся функціи, въ нижнемъ ряду, подъ нулями, всѣ функціи имѣютъ
знаки равные; а въ ряду верхнемъ/ надъ нулями, идутъ знаки поперемѣнно,
ч----, либо----+; всѣ же прочія функціи не перемѣняютъ своихъ знаковъ.
<22. Теперь видно, что, въ случаѣ уничтоженія нѣсколькихъ функцій сряду
въ уравненіи ѳ(ач-х)=0, отъ какого пи есть частнаго подстановленія а, потерю
числа перемѣнъ знаковъ надобно искать, составивши два ряда знаковъ для этихъ
функцій, которые бы соотвѣтствовали предѣламъ а—«, ач-а, безконечно близ-
кимъ къ а, слѣдующимъ образомъ:
1) Написать рядъ знаковъ, полученныхъ отъ подстановленія а; а подъ нимъ,
отъ лѣвой руки къ правой, повторить каждый знакъ, который не нуль. Встрѣ-
тивши нуль, надобно поставить подъ нимъ знакъ предыдущій, и повторить его,
пока встрѣтится не нуль. Это дѣйствіе провесть по всей строкѣ; тогда и соста-
вится рядъ знаковъ для предѣла а-і-а.
2) Для составленія ряда знаковъ, соотвѣтственнаго предѣлу а—а, надобно
написать сверху, начиная отъ лѣвой руки, каждый знакъ ряда (а), который
не нуль; а встрѣтивши пулъ, поставить надъ намъ знакъ противный
предшествовавшему, и это дѣйствіе исполнить по всей строкѣ; то и соста-
вится рядъ знаковъ для предѣла а—а.
Положимъ, что для х=а, рядъ функцій получилъ знаки:
013 Іі 11 10 887 6 0 4 8 2 10
ч-ч-О О 0 — 0 Оч---------------------0 — 0 +
Замѣнимъ его слѣдующими рядами, соотвѣтственными предѣламъ а—«, ач-а,
какъ показываетъ правило:
ч-ч------1--------1----1----1------+ ч-, для а—а,
ч-ч-О 0 0 — 0 0ч------0 — Оч-, а,
ч-ч-ч-ч-ч--------------1-------------ь, а-і-а,
- 409 —
ели, короче:
ч—(-000 — ОО—і--0 — 0 для а.
Разность между числомъ перемѣнъ знаковъ ряда верхняго, и числомъ пере-
мѣнъ нижняго, покажетъ все число перемѣнъ, потерянныхъ отъ уничтоженія
функцій между предѣлами а—«, и а-+-а, и такое же число мнимыхъ корней.
Въ самомъ дѣлѣ, мы предполагали, что а—а, а-+-а, чрезмѣрно близки къ а, и
что между этими предѣлами нѣтъ ни одною дѣйствительнаго корня
даннаго уравненія; стало-быть, при переходѣ отъ а—а къ а-+-а, уравненіе
Ѳ(ач-г)—О не должно терять ни одной перемѣны, если всѣ его корни дѣйстви -
тельные. А какъ эти потери находятся, и число ихъ показываетъ число нѣко-
торыхъ корней между а—а и а-+-а, то всѣ сіи корни должны быть мнимые.
Въ нашемъ примѣрѣ, для предѣла а—а, находится 10 перемѣнъ, а для
ач-а вышло только 4. Разность 10—4=6 показываетъ число мнимыхъ корней
между этими предѣлами.
Примѣръ. Отдѣлить корни уравненія,
Ѳ(а?)=а;‘—6а;3ч-12а?’—30а?ч-35=0.
Здѣсь всѣ корпи положительные, потому что нѣтъ повторенія знаковъ,
шій предѣлъ корней 6. Составимъ коефиціенты ряда ѳ(а>+-2)=0:
0 =а?‘—6.гяч-12а?’—ЗОжч-35.
б,=4а?3—18а?гч-24а?—30,
б,—6а;’—18а?ч-12, ѳ3=4а?—6, Ѳ^і;
лотомъ будемъ подставлять:
Выс-
Ѳ* 3 > 1 о
а?=0; ПОЛуЧИМЪ Ч-----1-----(
=1, - ч------О — ч
--/2»
=2,
=3,
=4,
=5,
Число
перем.
4
2
2
1
1
1
О
Число
корней.
2
О
1
О
О
1
Пзъ числа послѣдовательныхъ перемѣнъ и ихъ разностей видно, что данное
з
уравненіе имѣетъ по одному дѣйствительному корню между 4 и 5, между - и
2, и еще два корпя между 0 и 1. Послѣдніе два корня мнимые; потому что, при
уничтоженіи 0г, смежныя функціи ѳ„ ѳ„ остались съ равными знаками, чего
не можетъ быть при корняхъ дѣйствительныхъ.
Примѣръ. Отдѣлить корни уравненія
0=®'—5а?ч-135а?—245=0.
— 410 —
Составляю: Ѳ,=:5ж*—20ж3ч-135,
Ѳ,=10ж3—ЗОж8,
6и—10ж?—20ж, ѳ*=5ж—5. Ѳ3=1.
Ѳв * з і і о Число корней.
Беру: ж=0, ч-----О 0 ч-------5—3=2 мним.
=2, ч-ч- 0 — ч-—
=3, ч-ч- ч- О 0 —
-Ь +
=4, ч-ч-ч-ч-ч-ч-
0
3—1=2 мним
1
И такъ, это уравненіе имѣетъ всѣ корни положительные, пзъ коихъ два
мнимые между 0 и 1, два мнимые между 2 и 3, и одпнъ дѣйствительный
между 3 и 4.
Примѣръ. Возмемъ еще уравненіе,
Ѳ=ж,0=рЗ 10ж7±8 7 5ж3=рі2 7 9ж—45678=0.
Для отдѣленія его корней, составимъ:
Ѳ1= 10ж8=р2170ж°±2625ж8ч=1279,’
Ѳ.= 45ж3=р65{0ж3±2625ж,
Ѳ3=120ж7=р1 0850ж-тІ7.875,
Ѳ4=210ж6гр10850ж3,
Ѳ3=252ж3=рб510ж8, Ѳ3=210ж*^2170ж,
Ѳ7=120ж“=р310, Ѳ3=45ж8, Ѳ8=10ж, Ѳ10=1.
(Верхній знакъ соотвѣтствуетъ корнямъ положительнымъ ч-ж, а нижній —
корнямъ отрицательнымъ —ж). Для отдѣленія корней положительныхъ,
будемъ брать:
Ѳ10 8733*311 о Число корней.
ж=0, ч-О 0 — 0 0 0 ч- 0-----7—3=4.
-+ 4- — — — +
=1,4- ч-ч----------------------3—1=2.
=6, ч-ч- ч-ч-ч- ч-ч-ч- ч-ч- — 1
=7,4- ч-ч-ч- ч-ч- ч-ч-ч-ч- -ь
Для корней отрицательныхъ:
ж=0, ч-О 0 + 0 0 0 — Оч-----
_і / , .......... .
-/2, Ч- +- +- Н Ь + -1-1---
=1,.........+ + _ьч_ч__
=3,..................4-Ч--
=4,..................ч-ч-
3—1=2
1.
— 411
Эти ряды знаковъ показываютъ, что данпое уравненіе имѣетъ одинъ дѣйстви-
тельный корень между предѣлами 6 и 7. другой — между —3 и —4; подста-
новленіе а?=0 открываетъ четыре мпимые корня; сверхъ того, находятся два
і
корня между предѣлами 0 и 1, и два между —-и —1 Послѣдніе четыре
корня должны быть также мнимые; потому что, между этими предѣлами, въ
обоихъ случаяхъ 0о не перемѣняетъ знака (—); оттого, при уничтоженіи 0„ Ѳ3,
между предѣлами положительными, непремѣнно ігдѣетъ мѣсто случай
— О—;
а между предѣлами отрицательными
ч- 0 ч-, либо *
— О —.
С. Способы вычисленія несоизмѣримыхъ корней.
1. Способъ Лагранжевъ.
123. Лагранжъ показалъ, что можно вычислять несоизмѣримые корни, по
приближенію, посредствомъ непрерывныхъ дробей. Вотъ въ чемъ состоитъ этотъ
замѣчательный способъ.
Положимъ, что одинъ пзъ корней даннаго уравненія Да?)—О заключается
, 1
между предѣлами а и ач-1, то можно положить, что этотъ корень аг=ач- -, гдѣ
-^-добавочная дробь, и гдѣ 1. А подставивъ его въ уравненіе, мы получимъ:
Ѳ-4-6,. - ч-Ѳ.. \ч-Ѳ3.-^ч-...-.ч- О,,-,.-1 ч- ' — 0, или
‘у 3 а/5 " 1 Уп-1 уп ’
Ѳ- 2Л+А . ,ч-13=0=Ду).
Получивши это уравненіе, станемъ искать, между какими предѣлами Ь и 6ч-1
находится его корень, большій единицы. Этотъ корень будетъ только одинъ:
ибо, еслибъ ихъ было два, три,..;, то значило бы, что, между предѣлами а и
ач-1 находится пе одинъ корень, но также два либо три, чему быть нельзя.
П такъ, положимъ, что, между Ь и 6ч-1, корнемъ будетъ:
у=6ч- ~>
а у>’
гдѣ —, добавочная дробь, и «/'> 1. Отъ сего уравненіе Ду)=О преобразуется
въ /'(у')=0, которое также будетъ имѣтъ только одинъ корень большій единицы.
Если этотъ корень лежитъ между с и сч-1, то положимъ:
, 1
у — сч- — :
а у"
тогда уравненіе ДУ)=О превратится въ Въ этомъ уравненіи положи-
тельный корень, большій 1-цы, будетъ между й и йч-1; слѣдовательно, можно
, і
взять у=а~і- г ,~,, и такъ далѣе
412 —
Этимъ способомъ корень даннаго уравненія выразится непрерывною дробью,
і
х=ач-----------------------------—
Г~
сч-----
и можетъ быть найденъ такъ приближенно, какъ будетъ угодно.
Приложимъ этотъ способъ къ уравненію
—За?—4=0,
котораго одинъ корень заключается между 2 и 3. Для сего возмемъ:
а?=2-+-—,
У
подставимъ въ /’(а?)=0; получится новое уравненіе, вида:
Ѳу3-+-Ѳіу’-+-Ѳ.у-+-Ѳз=о=/Ь);
коефиціенты его найдутся:
Ѳ=х3— За?-4= — 2
Ѳ__2^,,_2 ___ д чрезъ подстановленіе
б,=3а? — 6 2 на мѣсто а?.
Ѳ-А = 1
Слѣдовательно:
Ду)= —2у3-4-9у!-+-6у-+-1=0, или
2у3—9у*—бу—1=0.
Въ этомъ уравненіи корень, бблыніі 1-цы, находится между 5 и 6; а потому
возмемъ.
г 1
у-- -І)Н—,,
И у,
подставимъ въ Ду)=О, получится:
0(у')=6у'3-+-О1у,’-+-О8у3-+-О3=О, гдѣ
Ѳ =2у3—9у‘—бу—1= —6
б— бу*— 18у— 6 = 54 п°Дставляя
—бу 9 21 д па м^сто у
Ѳ—2 = 2
Отъ сего /’(у') обращается въ
Ду')=6у'3—54у'!—21 у'—2=0.
Въ этомъ уравненіи корень, большій 1-цы, находится между 9 и 10; возмемъ
у— 9-+- 4,.
а у/
Тогда Ду')=О обратится въ
/(у")=е.у"3ч-Ѳ1.у"2ч-0,.у"+Ѳ,=О,
гдѣ, отъ подстановленія 9 на мѣсто у, найдутся:
Ѳ=6у'я—54у'8—21 у7—2= —191, е1=18у'*—108^—21=465,
Ѳя=18у'—54=108, Ѳ3=6; слѣдовательно,
/(у")=191у"а—465у"5—108у"— 6=0.
— 413 —
Корень этого уравненія, большій 1-цы, лежитъ между 2 и 3; возмемъ
у"—<2-і- получится:
Ему найдутся коефиціенты:.
О =191зГ—465з/"‘—108г/"—6= —574, Ѳ^бУЗу"1—ЭЗОу"—108=324,
(^—57 Зу"—465=681, О3=191, полагая у"=2.
Посему,
/’(2/"/)=5742/"'8— 3242/"'5—6 81 у"'— 191=0.
Здѣсь корень находится между I и 2, то есть,
1
у'"=1ч—--, и такъ далѣе.
Слѣдовательно,
У — 9-ь - ѵ
2ч----------------
1Ч* у""
.г=2-ь-—-—
і
9ч-------
2ч-------—
і
Откинувъ дробь нашли бы корень
ж=2-ь^=2,1958....,
143 '
различающійся отъ полной его величины, менѣе нежели на
Способъ Лагранжевъ примѣняется и къ нахожденію корней соизмѣримыхъ.
Въ такомъ случаѣ дробный корень изображается конечною непрерывною дробью.
Жаль, что этотъ прекрасный способъ часто бываетъ утомителенъ въ прак-
тикѣ, когда члены новыхъ уравненій [(у), [{у1}, [(у").... начинаютъ получать
слишкомъ большіе коефиціенты, и число членовъ велико.
II. Способъ Ньютоновъ исправленный.
Л9Л. Пусть а и Ь два предѣла, между которыми находится только одинъ
дѣйствительный корень даннаго уравненія положимъ, что эти пре-
— ш -
1
дѣлы такъ близки одинъ къ другому, что разность между ними Ь—а<Ір,п что
искомый корень больше а и менѣе Ь. Означимъ чрезъ А ту самую дробь, кото-
рую надобно придать къ а, чтобъ получить истинную величину ач-к корня, и
вставимъ это въ данное уравненіе на мѣсто х, тогда получится извѣстный рядъ
(!)..../’(ач-й)=б(а)ч-/т.0,(а)ч-/і2.02(а)ч-/г’.03(а)ч-....ч-/іп=0
=0ч-01Л-+-02Лі-+-Ѳ8/і8-ь. ...
Поелику дробь Л довольно мала, то можно считать этотъ- рядъ значительно
скоро убывающимъ, и, для вывода приближенной величины к, отбросить всѣ
члены, содержащіе степени /і’, Л’, Л*,....-. останется уравненіе первой степени,
Ѳ(а)ч-/і.0і(а)=0, откуда
к=-
0,(«)
Придавъ эту дробь къ а, получится первая величина, приближенная къ корню,
і е(«) і
х—ач-п—а--------------------------------- , ~а.
О,(а)
Для полученія второй величины, болѣе близкой къ корню, положимъ, что
полнымъ корнемъ будетъ х=агч-к'; внесемъ а' и к' въ рядъ (1) на мѣсто а и
к, и, отбросивъ члены съ к12, к13,.... к'п, получимъ вторую поправку для кор-
ня: отчего теперь второю приближенною величиною корня будетъ
Такимъ образомъ можно искать третье, четвертое, и т. д. приближенія къ
корню.
Таковъ способъ Ньютоновъ для вычисленія корней. Недостатки его оче-
видны: 1) не всегда легко сблизить предѣлы а, Ь, до такой степени, чтобы
разность Ь—а сдѣлалась менѣе —; 2) не всегда также и достаточно Ь—
чтобы можно было начать смѣло приближаться къ корню. Оттого всегда остается
неизвѣстно, сколько десятичныхъ знаковъ дроби А, к1 или к" принадлежатъ
собственно корню, и откуда начинается его неточность. По этой причинѣ, почти
всякой разъ надобно повѣрять найденную величину корня, вставляя ее въ
/(ж)=0, и смотрѣть, какой получится результатъ, положительный или отрица-
тельный, большій или мёнын'й; а это составляетъ утомительную и нерѣдко без-
полезную работу
Можно сказать, что въ Ньютоновомъ способѣ заключается только его начало,
а недостаетъ продолженія и окончанія. Для пополненія его находятся разные спо-
собы, изъ которыхъ мы разсмотримъ только два: 1) обращеніе ряда [{ач~к)—0,
и 2) разложеніе его въ непрерывную дробь.
А. Чрезъ обращеніе ряда /’(а-ь/і)=0.
4585. Возмемъ рядъ (1), отдѣлимъ его первый членъ:
—Ѳ(а)=А.Ѳ1(а)-ьА2.Ѳ2(а)-ь/іл.Ѳ;.(а)-+-....-+-Л"7
— 415 —
или, будемъ впередъ писать короче и удобнѣе, какъ дѣлали это прежде:
Обратимъ этотъ рядъ въ другой, расположенный по степенямъ Ѳ, какъ было
□оказано (350) ; найдется:
.____.6 еа/еѵ . Лв^—
ЗОа-ч-ф,—5е,М;
6І
\ в;
—Зо,0.20-
в3.
а именно:
в, П-
а
полагая о=—.
7 е.
Для сокращеннаго выраженія этого ряда, будемъ называть послѣдовательные
члены его буквами А, В, С, Б,
в . е,
9=-=А, —
* о, е,
А какъ знаки предъ сими членами могутъ быть весьма различные, то будемъ
писать алгебрическую сумму этихъ членовъ просто;
Л=(А, В, С, П,„.).
Мы скоро увидимъ, какъ опредѣляются эти знаки изъ сущности даннаго урав-
ненія и его б, Ѳ2,.....Стало-быть, искомымъ корнемъ будетъ
или-
о;=а-ьЛ=:а(А, В, С, В,....)
4*26. Разсматривая этотъ рядъ, видно тотчасъ, что посредствомъ его можно
находить величину корня такъ приближенную, какъ будетъ угодно; надобно толь-
ко сдѣлать его довольно убывающимъ. А для этого должно сблизить предѣлы а
I X Ѳ _ — і 'х Ѳа
и о корня до того, чтобы — —§ сдѣлать дробью близкою къ — ; чтооы — сдѣ-
(2ѳ2 ѲД
Д °
не имѣлъ вліянія на сотыя доли д *), ьли, по крайней мѣрѣ, чтобы удовлетвори-
лись условія: первое, то есть,
к ' е, в
3 В# 2 Ѳ, у'
г< -.о , или—|------< —, или.
' в, 7 ’ в* 9, в ’
(п).- <-.
' е, е« е
Достигши этихъ условій предварительными пробами, можно смѣло искать при-
ближенную величину корня съ какого угодно предѣла, меньшаго или большаго,
/М
второе,
') Нанрим. если $=0,2, то надобно, чтобъ —.^а<Т),05.
6|
— 416 —
какъ будетъ выгоднѣе: послѣдовательныя цифры корня будутъ вычисляться до-
вольно быстро. Сколько цифръ будетъ принадлежать собственно корню, это по-
кажутъ первые три члена ряда Л=(А, В, С,....); па какую десятичную перва-
го члена А=7=-^~ будутъ имѣть вліяніе второй и третій члены ряда, до этой
десятичной корень будетъ непремѣнно точенъ. Такъ мы найдемъ первое при-
ближеніе
хг^.а-+-к—а!.
Для втораго приближенія къ корню, возмемъ х=а'-ь-кг, опредѣлимъ значенія
для новыхъ О, Ѳі, 021....*), составимъ поправочный рядъ
»'=»’ ..........................
тогда найдется второе приближеніе къ корню
х=аІ-ѵ-кІ=а,-^-[д, — или
а=а*ч-(А, В, С, П,....)=а"
Если этого недостаточно, то можно, совершенно тѣмъ же путемъ, искать
третье приближеніе, полагая а?=а',-ьЛ", опредѣляя новыя значенія для 6,
Ѳ„ б8,....; и найдется:
а;=а"-4-/і"=а"-+-(д, ^~д3,....).
При послѣдовательныхъ вычисленіяхъ поправокъ к, к!, к",.... изъ ихъ ря-
довъ, довольно бываетъ брать только два первые члена каждаго ряда, иногда
третій; а прочіе, какъ малозначащіе, отбрасывать. Впрочемъ, можно искать
всю поправку Л и изъ одного ряда, если члены его убываютъ достаточно скоро,
и числа къ тому удобны, какъ это увидимъ изъ многихъ примѣровъ.
<37. Знаки предъ членами ряда,
к=д, ''Ѵ, — —)д’,....=А, В, С, П,...
в, \ е* еіР г > і > >
зависятъ отъ знаковъ предъ Ѳ, Ѳ„ Ѳ8, Ѳ8,...., и на нихъ надобно обращать стро-
гое вниманіе. А чтобы не затрудняться въ этихъ знакахъ при вычисленіи трехъ
первыхъ членовъ А, В, С, какъ самыхъ важныхъ, надобно имѣть предъ собою
табличку слѣдующихъ случаевъ, могущихъ встрѣтиться
I.
Когда 0=—, Ѳ,= -ь, Ѳ2=-ь і
или Ѳг=-ь, 0,=—, Ѳ,=— |
тогда к=А—Вч-С—.
*) Только для простоты и единообразія какъ во второмъ, такъ и въ слѣдующихъ вычи-
сленіяхъ приближеній, буду употреблять всё тѣ же буквы 0,' Ѳ,, 69. что и въ началь-
номъ ряду; но ихъ дѣйствительныя значенія теперь будутъ совсѣмъ другія.
— 417
П.
Когда Ѳ=-1-, 02=-ь
или 0=—, Ѳ,=—, Ѳ8=—
Ш.
тогда к=—А—В—С.
Когда 0=4-, 0,=—, 08=-ь
или 0=—, 19,= -ь, 02=—
IV.
тогда /і=А4-В4-С ....
Во
Когда 0=4-, Ѳ,=4-, 02=— |
или 0=—, 0,=—, 02= -ь
всѣхъ этихъ случаяхъ предполагается, что
тогда /г=—А-ьВ—С....
2ѳ* е3
—»-----величина положитель-
0, о.
пая; въ противномъ случаѣ знакъ предъ членомъ С перемѣнится. По этому, при
вычисленіи членовъ А, В, С, сооіиѣтственно тому или другому встрѣтившемуся
случаю, надобно только ѳ, 0„ 02, принимать за положительные, а 0, должно
вводить въ третій членъ съ своимъ знакомъ.
4ИВ8. Примѣры для вычисленія корней изъ одного ряда,
□?=а4-Л=а-і-(А, В, С,....).
1. Примѣръ.—Уравненіе /,(ж)=ж3—2ж—5=0 имѣетъ дѣйствительный
корень между предѣлами 2 и 3; поищемъ его приближенную величину,
составивъ:
0=а;’—2а;—5=0, 0,=За;2—2, 02=3а;, Ѳ{=4.
Подстановленіе ж=2 даетъ:
0=—1, 0і=Ю, 0,=6, 0^=1.
Этому случаю соотвѣтствуетъ поправочной рядъ,
Л=А—В-ьС—...., или
. е_ Р»’ ел/Ѵі8 /ЁЁІ вМзѴѳ у
1 6і еде./^іе’ е,Де,/ ѵ? ѲІ Ае,) ...............
слѣдовательно число 2, взятое вмѣсто корня л, мало, и должно быть увеличено
рядомъ к.
Члены этого ряда убываютъ оыстро, потому что условія убыванія:
- < -, — < —, или 0,06 <1,
е, е ю і ’ ’
2в« е» - е, 12 і . ю 61 .
~ёі ё? < е ’ іо 7Г < і ’ или боо<' ’
весьма выгодно удовлетворяются. Посему, испытаемъ вычислить а;=2-ьЛ изъ
одного ряда для Л. А для этого заготовимъ:
- = 4; =0,1: — =0,6; - =0,1; отчего
е, ю е, е,
—[—У=0,006; [2еН-6*у.в Ѵ=о,00062;
еде,/ ’ \ е* Де,/
^5еі-Ие.6»6»у?_у—000078, и проч.
27
— 418 —
Ограничиваясь этими четырьмя членами, получаемъ
ж=2+0,1—0,006+0,00062—0,000078
=2,094542,
кореиь приближенный въ четырехъ десятичныхъ.
Если бы мы съ самаго начала взяли 2,1 вмѣсто 2 для перваго приближеніи;
то нашли бы 0=0,062; Ѳ,=11,23; 02=6,3; Ѳ,=1, и сразу получили бы
ж=2,1—А—В—С— (см. II случай)
_2 ._____________________в* б.з ( с.і у
’ 11230 11,23 11230/
=2,1—0,00543188—0,00001655— ...
=2,0945517....
корепь точный во всѣхъ семи десятичныхъ, въ чемъ можно увѣриться чрезъ вы-
численіе слѣдующаго члена поправки.
2. Примѣръ.—Въ уравиеніи
х3—іх—1=0.
Наибольшій положительный кореиь заключается между предѣлами 2 и 3, и
весьма близокъ къ 2,
потому что. для ж=2, получается 0=—=-1,
а для ж=3, - 0=14.
И такъ, взявъ 0=ж3—4ж—1, и его производныя:
Ѳ,=3ж’—4, Ѳ2=3ж, 0,=1,
внесемъ ж=2; получатся;
о=—і, е— 8, о2=б, ѳ8=і.
Этому случаю соотвѣтствуетъ поправочный рядъ
Л--В+С—1)+....,
которымъ надобно увеличить взятое число 2, чтобъ получить искомый корепь.
Члены этого ряда также достаточно убываютъ, потому что условія убыванія:
|> Ѳ’8<8или °>094-<1/
0. 0. 0 8 6^1’ 6
выгодно удовлетворяются; слѣдовательно можно пробовать, нельзя ли вычислить
корень ж=2+/і изъ одного ряда, составивъ:
— 1 — А & — 1 6» _ 1
0. 8 — Ѵ’ 0,“" 4’ б,-' 8’
ЭД2=—0,0 И 72=В;
йі'Ѳі»
г2е,-е,е.
,ве’—36,6,8,
I е*
-у-=0,001953=С;
64.8 ’
= -^-=0,0004005=0.
262141
— 419
Слѣдовательно, гс=2-ьА—Вн-С—Б-ь.... будетъ
ж=2-ь0,125—0,01172н-0,001953—0,000406-ь....
=2,114827....,
гдѣ точны по крайней мѣрѣ три десятичныхъ.
Эго розысканіе корпя бываетъ неудобно въ тѣхъ случаяхъ, когда приближеніе
слѣдуетъ медленно, что замѣтно уже при вычисленіи послѣдняго корня. Въ та-
комъ случаѣ, нашедши величину корня, приближенную до одной плп до двухъ
ея десятичныхъ, надобно внести ее въ б, О,, 65.,...- и искать слѣдующее прибли-
женіе изъ новаго ряда
я=а'+А'=а'+[-, Г^ —.... '
Іо, о.'о,' ’ ' о, о/'о/ ’ ь
ограничиваясь вычисленіемъ поправки Іі изъ ея первыхъ двухъ членовъ, а
иногда изъ трехъ.
Примѣръ для упражненія:
5^-4-2фс—30=0.
Это уравненіе имѣетъ (стр. 404) одинъ дѣйствительный корень между 1 и 2.
Предположеніе #=2, даетъ 6=2, 6 ,=40, Ѳ2=50, 6^=15; ^-=^о=0,05=А,
В= 0,003125, С=0,00028125, и проч., и получится кореньж=1,9л659....
вѣрный въ четырехъ десятичныхъ.
Примѣчаніе.—При разрѣшеніи уравненіи высокихъ степеней, обыкновенно
представляется утомительное дѣло возвышать въ степени числа однозначныя
и двузначныя. Употребленіе логариомовъ для этой цѣли весьма полезно, только
часто бываетъ недостаточно. По этой причинѣ, въ концѣ, книги приложена
таблица пяти первыхъ степеней чиселъ отъ 1 до 1ООО и десяти
степеней чиселъ отъ ! до ЮО, составленная съ большою тщательностію.
Съ ея пособіемъ легко точнымъ образомъ находить 6, 6,, Ѳ,,.’.если только
степень уравненія пе выше десятой; а тогда уже, для полученія"отношеній —
Ѳ» Ѳ|
?,.... и членовъ А, В, С,.... можно,употребить и логариомы, предполагая,
что ищемъ корень, приближенный не болѣе, какъ въ 5 или 6 десятичныхъ. Все
это мы увидимъ изъ слѣдующихъ примѣровъ.
/199. Примѣры' для вычисленія корней посредствомъ дву^ъ и болѣе•
приближеній.
I. Примѣръ. — Возмемъ уравненіе
6=а?3—7ач-5.=0,
котораго производныя суть:
бі=3а?—7, б,=3х, о8=1,
и котораго два дѣйствительные поюжптельные корня находятся между 0 и 1,
между 2 и 3, какъ видно изъ слѣдующей таблички знаковъ предъ 6, Ѳ„ 62,,...
— 420 —
Ѳ8 Ѳі Ѳі ѳ
Для я=0, ч-О-------ь
=1, ч-ч--------
=2, ч- ч- ч----
=3, ч- ч- ч- ч-
Корень между 0 и 1 ближе къ 1-цѣ, нежели къ 0; потому что,
для ж=0, получается Ѳ=5,
адляж=1, - 0=—1-
Сверхъ того, а=1 обращаетъ ѳ, б,, ѳ2, о,, въ
0=—1, Ѳ,=—4, 02=3, Ѳ8=1.
Этому случаю соотвѣтствуетъ (стр. 417) поправка
к=—Ач-В—Сч-....
Ея чіены убываютъ, одяакоже не слишкомъ быстро, потому что условія убыванія
е„ е, з 4 .
ё<Ѵ Т<Т’ илиі6<1>и
25_^ е. А_1<А, или1<1
в, «, в 4 3^1 24
удовлетворяются не довольно выгодно для вычисленія корпя изъ одного ряда А. По
этому, для перваго приближенія, вычислимъ только два первые члена сего ряда:
А=’-=4=0,25! В=^У=А^0,047....;
получится
ж=1—0,25ч-0,047....=0,80....
Для вычисленія второй величины, приближенной къ корню, возмемъ ж=0,8;
г—0,64; ж8=0,Ь12; подставимъ это въ 0, Ѳ2, б2, Ѳ8, получатся:
Ѳ=—0,088; 0,=—5,08; Ѳ,=2,4; Ѳ.=1.
И здѣсь поправка остается того же вида,
к=—Ач-В—С....;
члены ея и подавно убываютъ; для вычисленія ихъ употребимъ логарпомы.
1о§ 0=1,041.3927 д. 1о$ Ѳ2=7,197.2263—10 1о§ ѳ,=2,477.1213 7,197.2263—10
Іое А =0,238.6190— 2 Іо§ А8=0,477.2380— 4 А=0,01732280 1ор|’ =0,674.3476— 1 0,477.2380— 4 Іо§ В=0,151.5856— 4 В=0,000141760
Членъ С= будетъ весьма малъ, потому что Іо§ А8=0,715.8570—6 даетъ
А’=0,0000052; посему корень
ж=0,800141760—0,01732280
=0,78281896,
долженъ быть точенъ въ пяти десятичныхъ, чѣмъ и ограничимся.
— 421
Дли полученія приближенной величины корня, мезкду предѣлами 2 и 3,
нахожу сперва, что
х== 2 даетъ Ѳ=г. —1,
х=і - 0=11,
и заключаю, что этотъ корень близокъ къ 2. >
Взявши ж=2, нахожу:
ь—— 1, Ѳ,=5, 0,7=6, б8=1.
Этому случаю соотвѣтствуетъ коренная поправка /і=А—Вч-С...., которой
члены убываютъ не очень быстро, потому что уже первое условіе убыванія:
е» е, 6 6 ..
^<Р Т<5> "»<’>
удовлетворяется не довольно выгодно.
Первый членъ этого ряда А— у =0,2. Если ограничимся этимъ членомъ,
то найдется первое приближеніе къ корню
ж=2,2,
которое возмемъ лая отысканія втораго приближенія. При семъ найдутся:
жЕ—4,84-; ж3=10,64.8; 0=0,248; ѳ,=7,520; 0—6,6; Ѳ,=1.
Здѣсь поправочнымъ рядомъ будетъ:
1і= — А—В—С—......;
для вычисленія его членовъ употребимъ логариѳмы:
Іод 0=0,394.4517—1 Іод 9—0,819.5439
д. Іод ѳ,=0,123.7826—1 0,123.7826—1
Іод А=0,518.2343—2 Іод ^=0,943 3265—1
2 Іод А=0,036.4686—3 * ' 0,036.4686—3
3 Іод А=0,554.7521—5 ] в=0,979.7951—4
А=0,0 1297880 В=О,00095454
—— е І(п ='а—=^‘
2 Іод у =0,886.6530—I Іод у1 =0,123.7826
=0,301.0300 в» — о 132979=/?
е,
Іод «=0,187.6830
а=1,540571
—0,132979=3
'.а—/3=1,407592, Іод («—/?)=0,183.9167
3 Іод А=0,554.7521—5
Іод 0=0,738.6688—5
0=0,000054785.
— 422 —
I •
0,0329785
Посему х=2,2— <0,00095454
ІО,000054786
0,033987826
х=2,166012174
корень точный по крайней мѣрѣ въ пяти десятичныхъ.
Остается найти отрицательный корень даннаго уравненія. А для втого
возмемъ*.
С(-х}—х3—1х—5=0, откуда
Ѳ,=3л2-—7, $^=.3х, 08=і.
'3310
Для а=0, получится Ч-1-----
=2, - і-і- ч--------
=3, - ч- -ь ч- ч-
Слѣдовательно корень находится между 2 и 3, и притомъ ближе къ 3, потому
что, для х—'З, находимъ:
Ѳ=1, б1=20, 02=9, Ѳ,=1-
Здѣсь коренная поправка такъ же
/<——А—В—С—....;
, , . еа в а
ея члены быстро убываютъ; потому что условіе уоывапія у <у, 2() < 20, пли
0,0^2 <1, очень выгодно удовлетворяется. А какъ ори этомъ числа для Ѳ, Ѳп
б2, б8, весьма просты и удобны для вычисленія членовъ А, В, С,.... даже безъ
помощи логариомовъ; то будемъ вычислять корень пзъ одного ряда. Для этого
найдутся: м
у =0,05=А; (|)=0,0025; (4 )’=0,000125;
®?=0,45; ^=0,05; В= 4^=0,001^,
Р( У, 0, ' Ѳ '
<Мт| -4;)(4)‘=°’0(,’,Ш775-
.0,05
Посему, корень #=3— <0,001125
ІО,000043775
лс=3—0,051168775=2,94 8831225;
а для даннаго уравненія /,(ж)=0,
ж=—2,948831225.
гдѣ вѣрны по крайней мѣрѣ пять десятичныхъ.
Точность рѣшенія этого уравненія оправдывается тою повѣркою, что сумма его
корней, взятая съ противнымъ знакомъ, почти точно равна коефиціенту втораго
члена уравненія, то есть, нулю;
- 423 —
0,78281895 I
2 16601КОРИИ ппюжительпьіе
сумма=2,948831124
—2,948831225 корень отрицательный
сумма почтп=0.
2. Примѣръ. — Пусть данное уравненіе:
Ѳ=«‘-+-20х’—72ж®—850ж-+-625=0,
и его производныя:
0,=4«’-+-6О«'—444а?—850,
08=6х!-+-6О«—72,
03=4«-ь2О, 04=1.
Для от"ѣленін его корней, подставляю:
* 8 і 1 О
I корень
__У । । ___(__( । 1 корень
и нахожу, что оно имѣетъ два положительные корня между предѣлами 0, 1, и
между 6 и 7. Отыщемъ эти корпи.
Подстановленіе «=0 даетъ 0=625,
х=1 - 6=280;
стало-быть, корень ближе къ 1 нежели къ 0; а испытывая подстановленія 0,6;
0,7; 0,8, найдется, что самое выгоднѣйшее изъ нихъ 0,7, потому что дѣлаетъ
. е
самымъ меньшимъ отношеніе — , а именно даетъ:
0=-+-1,8201; 0.= —920,028; 0,= —27,06.
Этому подстановленію соотвѣтствуетъ коренная поправка
/і=А—В-+-С.... (стр. 416),
которой члены столь быстро убываютъ, что смѣло можно вычислять ее съ
одного раза.
1оё 0=0,260.0952
д. 1оё Ѳ,=7,036.1989—10
1о§ А=0,296.2941—3
2 Іо§ А=0,592.5882 —6
А=0,00197831
1о§ Ѳ—1,432.3278
д.І08б.=7,036.1989—10
Посему, «=0,70197831—0,000000115
=0,701978195
корень, точный въ осьми десятичныхъ.
0,468.5267—2
2 1оёА=0,592.5882—6
1ое В-—0,061.1149—7
В=0,00000011511.
— 424 -
Второй коренъ, между предѣлами 6 и 7, ближе къ 7, потому что
«=6 даетъ 0= —1451
х—1 - 6= -+- 408.
И такъ, взявъ «=7, находимъ:
6=408, 6,=2454, Ѳ8=642, 6,=48;
слѣдовательно, коренная поправка
к~— А—В—С....
Ея члены очевидно убываютъ, однако же не довольно быстро; а потому, нашедши
первый членъ А= у =0,166...., воспользуемся имъ однимъ для полученія
первой приближенной величины къ корню:
х=7—0,166....=6,8....,
и, для полученія втораго приближенія, возмемъ «=6,8. Степени этого числа
найдемъ въ таблицѣ:
«*=46,24; «8=314,432; «‘=2138,1376;
а сдѣлавъ подстановленія, получимъ:
б=—57,5024; Ѳ,=2202,928; 6—613,44; Ѳг=47,2.
Коренная поправка:
/г,—А—Вч-С—.,..= у — у(
Члены ея такъ быстро убываютъ, что
1о§ 6=1,759.6860
д. 1о§ ©.=6,656.9996—10
1о§ А=0,416.6856—2
21о§ А=0,833.3712—4
3 1о§ А=0,250.0568—4
А=0,02610270
в V
0.)'
=0,889.5434—2
1о§ 2=0,301.0300
26*
0,190.5734—1
:0,155086=а
—0,021426=/?
0,133660=а—/? •
1о§ (а—/Э)=0,126.0015—1
3 1оё А=0,250.0568—5
ѳ,) *“ ( ѳ* е.
можно смѣло вычислять ея три члена:
1о§ 6—2,787.7721
д. 1о§ Ѳ,=6,656.9996—10
0,444.7717—1
2 1о§ А=0,833.3712—4
Іод В=0,278.1429—4
В=0,000189723
1о§ Ѳ,=1,673.9420
д. 1о§ 6 —6,656.999.6—10
0,330.9416—2
у =/3=0,021426
0,376.0683—6=1ойС
С=0,0000023826.
— 425
Слѣдовательно,
«=6,8261027—0,00018972+0,00000238
=6,82591536
корень точный почти во всѣхъ десятичныхъ.
Дли вычисленія отрицательныхъ корней, беру:
/•(-«)=«‘—20«’—72«і-+-850«-+-625=0=Ѳ,
Ѳ1=4«’—60а?—144«-і-850,
б8=6а?—60а:—72, Ѳ,=4«—20, 64=1.
Здѣсь корпи находятся между предѣлами 6 и 7, и предѣлами 21 и 22.
Испытывая подстановленія а=6, х—1, найдется, что корень между этими
предѣлами ближе къ 6, нежели къ 7; потому что «=6 дѣлаетъ:
е=-+-Ю9, е,=—ізіо, е ——216,
чему соотвѣтствуетъ поправка:
Л=А—В-ьС.......
Хотя члены этой поправки убываютъ, потому что условіе у < убыванія
хорошо удовлетворяется; но, чтобъ ускорить вычисленіе, возмемъ^- =0,0832..
за первую приближенную поправку, найдемъ первую приближенную величину
корня:
«=6,0832....,
и, для вычисленія второй приближенной величины, положимъ «=6,08. Въ
таблицѣ найдемъ:
«’=36,9664; «’=224,755712; «‘=1366,51472896;
а чрезъ подстановл^піе получимъ:
6=2,8-1968896; 6,= —1344,481152; Ѳ,— —215,0016; 03=4,32.
Этому подстановлевію соотвѣтствуетъ поправка /і=А—В-і-С; мы можемъ
смѣло вычислять ея члены, потому что они убываютъ весьма быстро:
Іо§ 6=0,450.2012 д. Іо§ 64=0,871.4453—4 1о§ 6. =2,332.4400 0,871.4453—4
Іо§ А=0,321.6465—3 2 1о§ А=0,643.2930—6 1о§ =0,203.8853—1 0,643.2930—6 1оё В=0,847.1783—7
А=0,002097233; В= 0,0000007034
Посему. «=6,08ч~А—В
=6,0820965288.
Послѣдній корень находится между предѣлами 21 и 22, п притомъ нѣсколько
ближе къ 21, потому что подстаповленіе х=21 дѣлаетъ:
0=—4016, Ѳ,=8410, 08=1314, Ѳ3=64, Ѳ4=1,
— 426 —
чему соотвѣтствуетъ поправка:
Л=А—Вч-С....,
Ѳ О’
которой члены убываютъ, потому что условіе убыванія -*< —удовлетворяется,
Оі о
д
по убываютъ медленно. Слѣдующая цифра корпя ~ =0,5 (около). Чтобъ осво-
Оі
бодить себя отъ лишнихъ цифръ при розыскаши слѣдующихъ приближеній,
уменьшимъ корни уравненія предѣломъ 21, полагая «=21-+-2, что сдѣлать уже
легко, потому что Ѳ, Ѳ1Г Ѳг, Ѳ3, 6, всѣ готовы; найдется*
24-ь64х3ч-1 3142*4-84102—4016=0,
0—іг5-і-1922*4-262824-8410,
к~1
Возмемъ 2=0,5, получится:
6=525,5625; 0^772,^ 6.=1411,5.
Коренная поправка будетъ:
Л=—А—В—С—....
Хотя ея члены довольно хорошо убываютъ, потому что уже первый членъ
А = —=0,054....; однакоже, чтобы воспользоваться всею выгодою таблицъ
б,
степеней для быстрѣйшаго вычисленія искомаго корня, возмемъ лучше за первую
приближенную величину корня:
2=0,5—0,054....=0,446;
выпишемъ изъ нашей таблицы*
я®=0,198916; 23=0,088716536; 24=0,639567575056;
тогда легко получатся:
6=1,953049879; Ѳ,=9620,546738; ©,=1400,8255.
Соотвѣтственная поправка того же вида
к=— А— В—С;
быстрое убываніе ч деновъ ея показываетъ, что можно сразу вычислиті искомый
корень, вѣрный до пяти или шести десятичныхъ:
1о§ 6=0,290.7133
д.Іо§ 6,=0,016.8003—4
1оё А=0,307.5136—4; .4=0,00020301
2 1о§ А=0,615.0272—8.
Не вычисляю второй членъ В, потому что онъ начнется съ девятой деся-
тичной. Слѣдовательно,
2=0,446—0,00020301=0,44579699;
«=214-2=21,44579699.
Точность рѣшенія повѣряется тѣмъ, что сумма корней, взятая съ противнымъ
знакомъ, почти равна коефиціету 20 втораго члена уравненія:
427
Корой иоложиткльиыв.
0,70197819
6,82591536
7,52789355
Корри отрицігкльиык
— 6,08209654
—21-44579699
—27,52789353;
сумма —(7,52789355—27,52789353) почти точно равна 20.—Большей точ-
ности отъ употребленія логариѳмовъ и ожидать нельзя, да и едваіи гдѣ нужно.
Превращеніе /(аг)=О, въ /(г)=0, чрезъ уменьшеніе корней перваго уравне-
нія предѣломъ 21 ясно показываетъ оборотъ, который надобпо дать вычисленію
корпя, если хотимъ пользоваться таблицами степеней двузначныхъ чиселъ, сдѣ-
лать весь трудъ легкимъ и даже занимательнымъ. Этотъ простой оборотъ мы
вездѣ будемъ употреблять, гдѣ онъ понадобится.
3. Примѣръ.—Возмемъ уравненіе
0=®'—420ж±800=0,
котораго 6,=5ѵс‘—420, 08=1О.т’, Ѳ3=10а/, Ѳ—5ж, 6В=1. Отдѣлимъ его
корни:
Для КОРНЕЙ положительныхъ.
Б * 3 8 1 » О
II II II II й уэ ьэ о + + + + + + + + ++ <=>1 + + + +» + + + + + °| + 11 1 1 + 1 1 + + 2 мнимые 1 1
Для КОРНЕЙ ОТРИЦАТЕЛЬНЫХЪ X— 1, ч 1 1 1 1 х~5, ч—і—і—і—і- ч- 1
Слѣдовательно, данное уравненіе имѣетъ два мнимые корня между 0 и 1, и
Три корня дѣйствительные, изъ коихъ два положительные между предѣлами 1 и
2, между 3 и 4, и отрицательный корень между —4 и —5.
Чтобы найти первый дѣйствительный корень между 1 и 2, дѣлаю нодста-
повленія:
я=1, и нахожу: 6= 381, Ѳі——415,....
х~2, - - 0= — 8, 6,= —340, 6±=80, б3—40.
Тотчасъ видно, что корепь весьма близокъ къ 2; коренная поправка здѣсь
Іі=_— Ач-В—С-+-...............
_____а । е_ іг . ‘_,2в]_бз \ /ѳ \ ’
бі”еі'9і’ (о?
Члены ея убываютъ такъ быстро, что смѣло можемъ вычислять ее изъ одно-
го ряда.‘
- 428 —
Іо# 6=0,903.0900 1о§ е2=1,903.0900
д. Іое ^=7,468.5211 —10 7,468.5211 — 10
1о§ А=0,371.6111— 2 1о§-=0,371.6111—1 61-
2 1о§ А=0,743.2222—4 2 1о§ А=0,743.2222—4
3 1о§ А=0,1 14.8333—5 1ое В=0,114.8333—4
А=0,0235294 В=0,000130266
2 1о§ ^-=0,743.2222—2 Іо§ 6—1,602.0600
0,301.0300 7,468.5211—10
1о§ «=0,044.2522—1 Іо§ /3=0,070.5811—1
«=0,100727 /3=0,117647
/3=0,117647
а—[і=~0,016920, Іое (Д—«)=0,228.4004—2
3 Іое А=0,114.8333—5
• 1оё С=0,343.2337—7
С= —0,000000220411.
Поелику С получилось отрицательное, то коренная поправка сдѣлается
Л= —Ач-В-і-С, и слѣдовательно
о=2—0,0235294-4-0,000130266
-+-0.0000002204
х=1,97660754,
гдѣ вѣрны всѣ десятичныя,
Второй корень уравненія находится между 3 и 4, и близокъ къ 4, потому
что подстановлевія
х=3 I 9=— 217, 61=—215,
а=4 . даютъ: е_ е _ 660, 0 _64.0
Для я=4, поправочный рядъ будетъ (стр. 417),
/(=—А—В—С—
• но онъ убываетъ слабо, хотя условіе убыванія - < и удовлетворяется. По
Ѳ 144
атому, ограничившись первымъ членомъ А= — — —=0,21....,возмемъза
первое приближеніе къ корню
а=4—0,2=3,8;
изъ таблицы найдемъ степени:
ж8=14,44; ж8=54,872; ж‘=208,5136; х8=792,35168.
Отъ этого получатся:
6=—3,64832; Ѳ,=622 568; Ѳ2=548,72; Ѳ3=144,4, и проч.
- 429 -
Коренною поправкою будетъ рядъ
Л=А—В-+-С................................,
котораго члены быстро убываютъ, и подаютъ надежду вычислить корень окон-
чательно:
Іо§ 6=0,562.0929 Іо§ 6—2,739.3508
д. 1о§ 6—7,205.8132—10 7,205.8132—10
1о§ А=0.767.9061—3 =0,945.1640—1
2 !о§ А=0,535.9122—5 2 Іое А=0,535.9122—5
3 Іо§ А=0,303.8183—7 Іо§ В=0,481.0762—5
А=0,0058601 8=0,000030274
2 1оё ^=0,890.3280—1 1ое 6,=2,159.5672
0,301.0300 7,205.8132—10
1о§ а =0,191.3580 Іоё/9=0,365.3804—1
а=1,55368 /9=0,23194
а—/9=1,32174, Іо* (а—/9)=0,121.1461
3 1о§ А—0,303.8483—7
1о§ С=0,424.9644—7
С=0,00000026605
Посему «=3,8058601—0,0000303-4-0,000000266;
«=3,80583246.
Отрицательный корень уравненія находится между предѣлами 4 и 5, и при-
томъ ближе къ 5, потому что подстановленіе ,г=5 даетъ:
6=225, Ѳ1=2705, Ѳв=1250, Ѳ8=250, и проч.
Коренная поправка изображается рядомъ
Л=—А—В—С—....
котораго члены явно убываютъ значительно быстро. Но чтобы сразу вычислить
корень, мы воспользуемся только первымъ членомъ
най-
демъ первое приближеніе къ корню
, е
А=- =0,07947.
ві
«=5—0,0831—=4,916
А какъ отсюда вычитаются еще члены В и С, то, для слѣдующаго прибли-
женія, возмемъ «=4, найдемъ въ таблицахъ степени этого числа:
«’=24,01; «’=117,649; «‘=576,4801; «ь=2824,75249.
Сдѣлавъ подстановлевія, получимъ:
Ѳ= — 33,24751; ^=2462,4005; 6—1176,46; Ѳ3=240,1; и проч.
Этому соотвѣтствуетъ коренная поправка
/і=А—Вч-С....
430
Іо^-=0,130.4006—2
2 1о§^ =0,260.8012—4
3 1оё ^=0,391.2018—6
®-=А=0,01350205
2 108^=0,358.4596—1
0,301 0300
Іо8о=0,659.4896—I;
о—0,456551
0,097872=/?
о—/?=0,358679;
Іо§^ =0,679.2298—1
0,260.8012—4
1о§ В=0,940.0310—5
В=0,0000871026.
1о8 Ѳ3=2,382.0170
6,608.6 414—10
І08 /3=0,990.6584—2
/3=0,097872
Іод (о—/?)=0,554.7061—1
3 Іод А=0,391.2018—6
1о8 С=0,945.9079—7
С=0,00000088289
Посему, ж=4,91350205—0,0000871026
4-0,0000008829
0=4,91341583.....
Остаются два корня мнимые. Но, если уравненіе имѣетъ не болѣе, какъ
одну пару этихъ корпей, то ихъ всегда можно найти пзъ его втораго и послѣд-
няго членовъ съ помощію всѣхъ найденныхъ дѣйствительныхъ корней.
Пусть /)-«-(/V7—1, р—ч Vх— і, эти мнимые корпи: они опредѣлятся, если
успѣемъ найти двѣ ихъ неизвѣстныя р и д.
Для этого возмемъ всѣ дѣйствительные корни: 1,97660754; 3,80583246
—4,91341583.
Данное уравненіе пе имѣетъ втораго члена; слѣдовательно, сумма его корней
должна быть =0, то есть:
2/ы-1,97660754-ьЗ,80583246—4,91341583=0;
откуда р=—0,43451209.
Послѣдній членъ уравненія равенъ произведенію всѣхъ корпей, взятому съ
противнымъ знакомъ, то есть:
(/Л+Ѵ)-1,97660754.3,80583246 . 4,91341583=800.
Отсюда, /?-ь5®=2 1,6440....
Но, р®=1,8880!....-, слѣдоватильпо,
7і=21,6440.... —1,88801.... =19,75599,
9 =±1/19,755990 =±4,44477....
Посему искомою парою корней будетъ
ж=—0,43451209±4,44477.... і/-=Г. ' ’
— 431
4. Примѣръ. — Уравненіе
л,о—310л7-+-875л8—1279л—45678=0,
котораго производныя:
Ѳ1=10ж’—2170л6ч-2625х8—1279,
Ѳ,=45л8—6510лЧ-2625л,
Ѳ,=120х7— 10850х‘-+-875, 04=210лс— 10850л;8,
0в=252л5—6510л8, 06=210л‘—2170л,
07=120л3, Ѳ— 45 л8, Ѳ9=10л, 01о=1,
имѣтъ только два дѣйствительные корня между 6 и 7, и между —3 и —4, а
всѣ прочіе мнимые (стр. 410). Поищемъ корень между 6 и 7.
Этотъ корень ближе къ 7, нежели къ 6; потому что нодстановленіе л=6
даетъ 0=—, 0,=-г-, и, независимо отъ знаковъ, 6 > 0,.
Подстановленіе г—7 даетъ-.
0=27422413. 6,=148365086; Ѳ±=І 50020850, гдѣ Ѳ<0,.
Коренною поправкою здѣсь будетъ рядъ Л=—А—В—С—, котораго члены
убываютъ, однакоже не быстро; а потому, па первый разъ, вычислимъ только
два члена А и В:
1о§ 0=7,438.1057 . 1о§ 0Г=8,176.1515
д. 1о§ 0,=1,828.6683—іо’ 1,828.6683—10
Іоо А—0,266 7740—1
2 1о§ А=0,533.5480—2
А=0,18483....
Посему л=7—
| 0,18483...
[ 0,03454...
0,004.8198
0,533.5480—2 .
Іоо В=0,539.3678—2
В=0,034543.
л=7— 0,21937=6,7806....
гдѣ вѣрна только первая десятичная.
Хотя второй десятичной мы собственно не знаемъ, однакоже она, вѣроятно,
больше 0,05; а потому, для вычисленія второй приближенной величины корня,
возмемъ
л=6,8;
отыщемъ въ таблицахъ степени этого числа, сохраняя при нихъ цѣлыя числа, и
столько десятичныхъ знаковъ, сколько разрядовъ единицъ содержитъ въ себѣ
коефиціентъ того или другаго вычисляемаго члена; а именно, возмемъ:
л’°=211392282,0;
— 310л7=—310X672298,881=—208412653,1;
ч- 875л3=875Х314,432=275128,0;
—1279л =—1279X6,8=—8697,2;
найдется 0=3200382
432
10х8=310871002,96;
—2170«6=—2170X98867,4826=—214542437,24;
2625х8=2625Х46,24=121380,00;
• Ѳ ,=96448666,7
45^=45X4571632,396=205723457,844;
—6510«в=— 6510X14539,336=—94651075,41;
2625х =17850,0;
02=И 1090232.
120ж7=120Хб72298,882=80675865,82;
—10850«‘=—10850X2138,1376=—23198792,96;
6^=57477948.
1о§ 6=6,505,2017 д. 1о§ 6 —2,015.7037—10 Іоа Ѳ2=8,045,6758 2,015,7037—10
1о§ А=0,520.9054—2 2 1о§ А=0,041.8108—3 31о§ А=0,562.7162—5; А=0,0331822 ' 1о§—=0,061.3795 61 0,041.8108—3 1о8 В=0,103,1903—3 В=0,0012682
2 1о§ ^=0,122.7590 '• 0,301.0300 1о§ е,=7,759.5012 2,015.7037—10
• Іо§ «=0,423.7890 а=2,653310 а—/3=2,057367; }0§ /3=0,775.2049—1 /3=0,595943 1о§(«—/э)=0,313.3136 0,562.7162—5 1оеС=0,876.0298—5 С=0,000075167.
Коренная поправка /і=—А—В—С ...; посему
(0,0331822
«=6,8— 0,0012682
|0,0000752
=6,8 — 0,0345256
«=6,7654744 •
Таковъ искомый корень; онъ точенъ въ пяти десятичныхъ
Примѣръ для упражненія:
х*—I Огк3—і—20«®—30«-+-15=0; его корни
0,734881....; —4,1067466; 2,4069308....;
—0,482468±1,40708 |/—Г.
— 433 —
ЛіГС. Иногда уравненіе имѣетъ .корни столь близкіе одинъ къ другому, что
различіе между ими начинается въ сотыхъ либо тысячныхъ доляхъ единицы;
тогда обыкнояенно считается трудностью отдѣленіе одного корня отъ другаго.
Способъ, представленный здѣсь для вычисленія корней, подаетъ однакоже
возможность находить такіе корни, не имѣя надобности въ предварительномъ
ихъ раздѣленіи. Для этого довольно, если мы успѣемъ найти два предѣла, между
которыми находятся такіе корни, столь близкіе, что разность между этими пре-
дѣлами, а слѣдовательно между предѣломъ и ближайшимъ къ нему корнемъ, бу-
і , . . .
детъ — или менѣе, и будетъ выгодно удовлетворяться условіе уоыванія попра-
вочнаго ряда /і=(А, В, С...). Тогда можпо прямо начать приближаться къ кор-
нямъ, взявши предѣлъ, который къ нимъ ближе, что узнать легко, потому что
онъ обращаетъ данное /'(ж)=0 въ меньшій результатъ, и доставляетъ выгодпѣіішеѳ
условіе убыванія коренной поправки. Надобно только строго наблюдать за тѣмъ,
какія десятичныя, получаемыя чрезъ вычисленіе, принадлежатъ пскомому корпю,
ближайшему къ взятому предѣлу: тогда этотъ корень самъ собою отдѣлится отъ
другихъ и легко можетъ быть вычисленъ. А чтобы можно было пользоваться
таблицею степеней чиселъ, то, нашедши предѣлы а и Ь, между которыми лежатъ
корни, полезно иногда преобразовать данное уравненіе ;іъ другое, котораго бы
корни были менѣе предѣломъ а, и потомъ продолжать приближеніе.
Примѣръ. — Уравненіе
о-’-ь н 102х-ь 181 =0
имѣетъ два дѣйствительные корня между 3 и 4; эти корпи суть 3,213128;
3,229521. Они различаются менѣе чѣмъ двумя сотыми. Попробуемъ найти по-
ложепіе сихъ корней, взявши
Ѳ=о:3Ч-11 х5— 102о-ЬІ81,
Ѳ,=3ж’-ь22ж—102, ѳ2=3ж-ь11, ѳ,=1
а 8 і о
л=0, ч—і-----ч-
=1, -I—I-----ь
=3, -і—і-----ь
-”4 । —ь- -1
2 корпя неизвѣстн.
Для о=3, получаемъ 6=1; 6,=—9; Ѳ5=20; Ѳ,=1;
о=4, - 6—13; Ѳ1=34.; Ѳ,=23;
Слѣдовательно оба корня заключаются между 3 и 4, и весьма близки къ 3;
а потому для перваго приближенія возмемъ сначала ж=3,2, а потомъ о=3,3.
Для я=3,2; а?—10,24; о:’=32,768, находимъ:
6=0,008; Ѳ4=—0,880; ѳ2=20,6; Ѳ3—1-
Ддя о=3,3; я:*=1О,79; о'8=35,957, будутъ:
6=0,127; 6^3,27; ѳ«=20,9; С3=1.
28
- 431 —
Въ первомъ ряду функцій остаются двѣ перемѣны знаковъ, а во второмъ пи
одной; стало-быть, оба корня паходятся между предѣлами 3,2 и 3,3, и оба
близки къ 3,2, потому что это падстаневлеше обращаетъ 6 въ результатъ
0,008, близкій къ пулю. П такъ, взявши предѣлъ 3,2, начнемъ искать бли-
жайшій къ нему корень:
®- = -^-=-„ =0,0090909....=А;
0, 880 110 ’
04__2060 _618. е^е V_ 515 _____ 515
І/ ~88 22’ еДе, / 22. \ 2109 266200-'
11=0,0019346.
Ограничившись этими двумя членами поправки 7і=А-ь-Вч-С-4-...., найдемъ
#=3,2-ь0,009090....4-0,00193464-....
=3,211025.....
гдѣ можно считать вѣрными только двѣ десятичныя.
Для слѣдующаго приближенія возмемъ #=3,21; найдемъ въ нашихъ табли-
цахъ #*=10,3041, #3=33,076161; подставимъ въ 6, Ѳ1г 6»; получатся:
6=0,001261; 0!=—0,4677; е5—20,63; Ѳ,=1;
® =0,0026961; (ееУ=0,0000072693;
^=4-44,109; ЙМ—0,00032064.
#=3,21-ь0,00269614-0,00032064=3,21301674.'...
Послѣ сего, взяли бы #=3,123, и т. д.
Но, въ этихъ случаяхъ выгоднѣе поступать такъ: уменьшить корпи уравне-
нія ближайшимъ предѣломъ 3,2, полагая #=3,24-2; это весьма удобно, потому
что 6, Ѳ„ 62, Ѳ„ уже ютовы; тогда получится:
г34-20,6з!—0,8824-0,008=0, откуда
6—32*4-41,2^—0,88; 6=324-20,6; Ѳ8=1.
Сюда подставимъ 2=0,01; найдутся,
6=0,001261; Ѳ,=—0,4677; ѳа=20,63; 6—1.
1о§ 9=0,100.7151т— 3 1о§ ѳ—1,314.4992 0,330 0326
г л. 1о§ 6 —0,330.0326
1о§А=0,430.7477—3 1,61-4,5318
2 Іоіг А=0,861.4954—6 0,861.4954—6
А=0,0026961. 1о§В=0,506.0272-4
4 В=0,0003206.
Слѣдовательно, 2=0,014-0,00629614-0,0003206
=0,0130167.
— 435 —
Здѣсь вѣрны три десятичныя; я потому, для слѣдующаго приближенія, возмемъ
2=0,013; изъ таблицъ найдемъ 2*=0,000169; 23=0,000002197; и тогда
получатся:
6=0,000043597; ѳ4=—0,343893; Ѳ8=20,639.
Іоп 6=0,639.4566—5
д. 1о§ 6,=0,463.5764
1о§ А=0,103.0330—4
21о§ А=0,206.0660—8
А—0,00012677
1о§ Ѳ,=1,314.6887
0,463.5764
1,778.2651
0,206 0660—8
Іод В=0,984.3311—7
В=0.0ѵ000096456.
Поправочная формула все таже 7і=А+В+Сч-....; посему,
2=0,01312677+0,00000096456
=0,01312773; и слѣдовательно
ж=3,2ч-2=3,21312773....
Второй корень находится между 3,213.... и 3,3; для приближенія къ
нему, возмемъ ж=3,25. При этомъ уменьшимъ опять корпи уравненія числомъ
3,2, то есть, возмемъ уже готовое уравненіе,
23ч-20,б25—0,882+0,008=0, и его производныя:
• 323-і-41,2.2—0,88; Згч-20,6; и проч., и положимъ
2=3,25—3,2=0,05; 23=0,0025; 28=0,000125, найдутся:
6=0,015625; Ѳ1=4,1875; Ѳ,=20,75; 6^1.
Здѣсь коренная поправка Л=—А—В—С—....; члены ея очевидно убы-
ваютъ, а потому вычислимъ сперва два члена-
1о§ 6=0,193 8200—2
д. 1о§ Ѳ4=0,925.3664—1
ІопА=0,П 9.1864—2
2 Іо8 А=0,238.3728— 4
А=0,0131579
1о§ Ѳ,=1,317.0181
0,925 3664—1
1,242.3845
0,238.3728—4
Іоц В=0,480.7573—3
В=О,0030252
2=0,05—
0,0131579 1
0,0030252 [ — 0,0338169....
Считая вѣрными только двѣ десятичныя, возмемъ для слѣдующаго приближе-
нія 2=0,03; 2!=0,0009; 23=0,000027; тогда будутъ:
0=0,000167; 6^=0,3587; Ѳ~20,69; 0,=!.
Коренная поправка опять та же к= —А—В—С.
— 430 —
10^9 =0,222.7465—4
д. Іо§ 6,=:0,445.2686
1о§ А=0,667.9851—4
2 1о§ А=0,335.9702—7
" А=0,00046450
10,000464501
• * ’ 10,00001252$
Слѣдовательно, ж=3,2-ьх=3,229522.
1о^ Ѳ~ 1 315.7605
0,445.2686
1,761.0291
0,335 9702—7
1о§- В=о,096.9993—5
В=0,00001252
=ѵ,029522....
Такимъ образомъ отдѣлились корни одинъ отъ другаго, хотя и не были предва-
рительно раздѣлены частными предѣлами.
Вотъ еще примѣры такого же рода:
1) 100х3—500x^600x^63=0;
2) 250ж8—102ж 4-25-4-0;
3) ІѲОж8—162іж-і-2512=0.
&ЗА« Само собою разумѣется, что и дѣйствительные корни всякаго двучлен-
наго уравненія хт—р=0 можно также вычислять по общей формулѣ,
I ві ’ в1\₽1 Л V в’ 61 / ' Ві } ‘
надобно только разложить число р на двѣ части а.' и 8 (полагая р=аг-л-6),
чтобы первая, сколь возмояшо большая, была полною г-іо степенью, а другая
меньшая была ей дополненіемъ къ числу р. Въ этомъ случаѣ, общая формула,
выражающая кореиь, обращается въ рядъ Ньютонова бинома, какой употребляется
для возвышенія двучленныхъ количествъ въ степени дробныя, и слѣдовательно,
для извлеченія корней изъ чиселъ (®35), то есть, въ рядъ
ж= І/р=(аг-4-<5) -а-+-1. —
г ат *
(г-1) 81 (г-1)(2г-1)
1.2.г4 ’ а4г-‘ ~+" 1.2.3 . г»
а’г-1
е__і_ о . Мь К Г~1 5^__________________________
в* г аг—1’ Ѳі\0,) 1.2.г4* а4г—*’
такъ что
_ 6,у9, ?_(г-1)(2г~1)
к е? е, Де,/ 1-2.3 ‘ ‘ ’
Для доказательства возмемъ:
0=хг—р=х'—аг—5=0, и производныя
Ѳ — гх , Ѳ,=-——-.х 63=——-———.х , и такъ далѣе;
и положимъ х=а; то будетъ:
0___г(г-1)(г-2)
Ѳ»^Г. 2 . 3 “
— 437 —
Коренная поправка должна быть Л—А—Вч-С—1)ч-.. ., гдѣ
А=- — -
е, г.ат~1 ’
.. ба ді О—а~* __ г-і Д»
’е, ’ 1.2 ' т*.аіт—* і.2.г’' о?т—*’
г—Уѵ—IГг~1)*-“-* (г- 1)(г-2)С -«| «5‘
\е} е,>' | 2 і . 2 . з і’ г‘аіг—1
__(г—1)(2г—1) д*
1.2 З.г“ ’ л ’
и такъ далѣе.
Отсюда заключаемъ, что формула
ж=а-ь(А, В, С, П,....)
есть самая общая для вычисленія дѣйствительныхъ корней уравненій всякихъ
высшихъ степеней; она заключаетъ въ себѣ и рядъ Ньютонова бинома, изобра-
жающій извлеченіе корней изъ чиселъ, какъ только частный случай. Мы
скоро увидимъ, что эту же формулу можно употребить и для вычисленія корней
мнимыхъ.
Способы отличатъ мнимые корни отъ дѣйствительныхъ, когда они за-
ключаются въ тѣсныхъ предѣлахъ, и потому остаются неизвѣстными.
АПЪ. При отдѣленіи корней даннаго уравненія ѳ(ж)=0 чрезъ подстановленіе
чиселъ 1, 2, 3,....—1,—2,—3,.... на мѣсто х въ 6, Ѳі, 0г, 68,...., перѣдко
въ какой пи есть строкѣ знаковъ уничтожаются сряду двѣ перемѣны, п слѣдо-
вательно обнаруживается присутствіе двухъ корней. Пока эти корпи пе раздѣ-
лены частными предѣлами, до тѣхъ воръ остается неизвѣстнымъ, какіе опи, дѣй-
ствительные пли мнимые. Для разрѣшенія этого недоумѣнія, прежде всего должно
къ уравненію приложить способы, показанные въ ЗШ, 38<, 389, служащіе
для открытія мнимыхъ корней. Если же эти способы окажутся недостаточны длп
указанія полнаго числа зтихъ корней, тогда надобно прибѣгнуть къ сближенію пре-
дѣловъ, заключающихъ неизвѣстные корни уравненія, и къ вычисленію одного
изъ сихъ корней, принимая его за дѣйствительный, и смотрѣть, какова будетъ
его поправка Л=(А-т-В-ьС-ь....).
Если она, при каждомъ сближеніи предѣловъ, становится меньше, то здѣсь
оба корня дѣйствительные, и легко могутъ быть вычислены; по они мнимые,
когда эта поправка начнетъ увеличиваться и удалять насъ отъ корней, несмотря
на послѣдовательное сближеніе предѣловъ, между которыми, явію, считать ихъ
надобно.
Примѣръ. Отдѣляя положительные корпи уравненія
Ѳ=х*—5жі-і-4-л’-+-2—0, пѣ
ер='ьх3—1 Ожч-4,
б,—6 л:’—5, Ѳ3=Лх, 6*=1, находймъ:
— 438 —
4 3 2 10
для х=0, -+- 0-1—ь
—1» '—1—1----1
=2, 4- ч- ч- ч- ч
2 неизвѣст. корня
два неизвѣстные корня между 1 и 2. Чтобъ узнать, какіе это корни, дѣйстви-
тельные или мнимые, станемъ сближать ихъ предѣлы, гзявшп ж=1,3; полу-
чится:
^=1,69; ^=2,197; ^‘=2,8561;
0=1,6061; 0,= —0,212; 0^=5,14; е3=5,2.
Порядокъ этвхъ знаковъ показываетъ, что неизвѣстные корни находятся
между 1,3 и 2, и коренная поправка
А=Ач-Вч-Сч-....
_1,6061 _ 5,14 ,1,6061 _
0,212 4 0.2І2І0.212 )
=7,5759...4-1391,55....4-.-...
х=1,3-ь7,5759.. .4-1391,55.=1400,426....
И такъ, подстановленіе 1,3, которое должно быть ближе къ корнямъ, вдругъ
удалило насъ отъ нихъ на великое разстояніе. Изъ этого заключаемъ, что между
предѣлами 1 и 2 находится пара корней мнимыхъ.
<33. Другой способъ. — Положимъ, что между предѣлами а и Ъ уничто-
жились двѣ перемѣны знаковъ между Ѳ„, 6„_и Ѳ„_8, и чрезъ то открылось при-
сутствіе двухъ неизвѣстныхъ корпей въ данномъ уравнепіп. Мы можемъ точно
опредѣлить родъ этихъ корней, разыскивая наименьшую величину, какую при-
пимаетъ старшая функція 6„ въ зтяхъ предѣлахъ. Для этого возмемъ Ѳп_4=0,
отыщемъ’ дѣйствительный корень этого уравненія между предѣлами а и 6; под-
ставимъ его въ 6„_8, и будемъ смотрѣть, не будетъ ля 0,,_=ч-; въ такомъ слу-
чаѣ 6П имѣетъ наименьшую величину, которую и надобно найти, подставивъ этотъ
корень въ Ѳ„. Наименьшая величина получится 6П= 4-, 0, либо —. Два первые
результата покажутъ, что, въ предѣлахъ а и б, данное уравненіе содер-
житъ пару мпимыхъ корней; а результатъ 6„=— покажетъ, что тутъ пѣтъ
мнимыхъ.
Этимъ способомъ хорошо пользоваться всякой разъ, когда Ѳ„_4=0 бываетъ
невысокой степени отъ х, и легко можетъ быть разрѣшено алгебрическп, не
прибѣгая къ общему выраженію корпя ж=а4-(А4-В4-С4-....). Во всякомъ же
другомъ случаѣ онъ затруднителенъ, и тогда лучше употребить предыдущій спо-
собъ чрезъ сближеніе предѣловъ.
При :ѣръ. л?’—7хч-7=0 имѣетъ
Ѳ^Згг—7, 02=3л?, 03=і.
439
Для
3 8 10
я=0, ч 0--і
=1, ч— ч----і-
=2, ч- ч- ч- ч-
2 неизв. корпя.
Чтобъ узнать, какіе неизвѣстные корни лежатъ между предѣлами 1 и 2, беру
6і—Зж8—7=0; нахожу ®=у/|»; это подставляю въ 62=3ж, получаю
68=ч-: стало-быть, данное уравненіе имѣетъ тіпітит, а именно:
ж(ж8—7)ч-7=уЛ (I — 7^ч-7= —0,0986....
результатъ отрицательный; слѣдовательно въ предѣлахъ 1 и 2 находятся корпи
дѣйствительные.
Примѣръ. Мы видѣли, что уравненіе
Ѳ=ж8ч-11«!—102лзч-181=0, (<ЗО),
имѣетъ два неизвѣстные корня между 3 и 4; по эти корни дѣйствительные,
потому что 01=Зж8ч-22а:—102=0, будучи разрѣшено, даетъ мнимые корни,
и тѣмъ показываетъ, что 6=0 пе имѣетъ наимепьшей величины.
Примѣръ. Ѳ=х‘— 10х8ч-25а:ч-30=0, имѣетъ
б,=5ж4—30ж!ч-25,
68=10ж3—30ж,
б8=і0ж8—ю, е4=5іс, ѳ,=і.
В 4 3 $ 1 О
Для ж=0, ч- 0 — 0 ч—і
=1, ч-ч- 0 — 0 ч-
2 неизвѣстные корня.
=2, ч— ч— ч-
—3, ч—і—н
Беру: 0і=5ж*—:30л:!ч-25=0, илп
ж4—6й“ч-5=0; откуда
аА=3±/9^-5=Ѵ^,
ж = Ѵ/5, либо я=1.
Изъ этихъ корней только заключается въ предѣлахъ 2 и 3; его и под-
ставимъ въ Ѳг, получится 10?—30а:=10.г(а?—3)=10ж(5—3)=ч-. Поло-
жительный результатъ показываетъ, что 6=0 имѣетъ тіпітит между 2 и 3, ко-
торое найдется: Ѳ=а?(ж‘—10л,!ч-25)ч-30=к'25—50ч-25;Ч-30=30.
Этотъ положительный результатъ показываетъ, чго между 2 и 3 находится
пара мнимыхъ корней.
Примѣръ. Ѳ =ж’—10л:3ч-50л—100=0,
0,=5'.г4—30ж8ч-50,
62=10х3—ЗО^с,
О3=10^—10, Ѳ4=5л, 6ь=1.
— 440 —
5 4 9 2 1 0 •
Для т=0, + 0 — 0 ч-------
=1, чч 0 - ч- — _
2 коизвѣстные корпя
=2, Ч- Ч 4- Ч- Ч-----:
__п | 1 | _|_ _| ( 1 корень.
Здѣсь между предѣлами 1 и 2 лежатъ два іп извѣстные корня, какъ видно
изъ порядка знаковъ функцій 0,, 68. Для опредѣленія рода этихъ корней, беру
Ѳ8=40л3—30®=0; отсюда нахожу:
а?=3, между 4 и 2.
Этотъ корень дѣлаетъ 6,= ч-, слЬдовательпо Ѳі обращаетъ въ тіпітит,
которое найдется положительное и =ч-5; стало-быть, неизвѣстные корпи суть
мнимые.
Примѣръ. 6 —Зт‘ч-1 От1—20тч-З0=0,
О—6т'— 12т3ч-20х—20,
Ѳ8=45т*— 4 8т*ч-4О,
03=20т3—12т, Ѳ—15т8—3, 06=6т, 6в=і
Эти строки знаковъ показываютъ двѣ пары неизвѣстныхъ корней: одну
между % и 4, другую между 4 и 2. Первую опредѣлить легко, взявши
03=20х8—42т=0, откуда т=\/А. Этотъ корень подставимъ въ Ѳ4;
у 5
иаіідется:
15т8—3=-|—3=6
результатъ положительный; слѣдовательно Ѳ8 имѣетъ тіпітит, которое найдется
также положительное:
4 5т*—18т8ч-10=——----------- ч-10=4 - .
25 3 О
Л такъ, между % и 1 находятся корпи мнимые.
Но, для опредѣленія корней между 1 и 2, надобно прибѣгнуть къ способу сбли-
женія этихъ предѣловъ, потому что 0, полипомъ высокой степени.
Поелику т=1 даетъ 0=18, а
т=2, — 6=46,
то видно, что корни лежатъ ближе къ 1, нежели къ 2; а потому возмемъ:
т=1,2; я’=1,44; ж3—1,728; т*=2,0736; т'=2,48832; ®’=2,985984;
— 441
найдутся:
Ѳ=17,166 ...; 0,= —1,806....; ^=38,512....
Порядокъ знаковъ показываетъ, что корня должны заключаться между 1,2 и
2; поправочная формула Л=Ач-В-+-С....
Но, уже первый членъ А= — ==У,5.... дѣлаетъ .т=1,2-і-У,5....
1 О| А,п06
=10,7...., и выводитъ его не только изъ предѣловъ 1 и 2, но даже за предѣлъ
всѣхь корней уравненія. Слѣдовательно, между 1 и 2, въ уравненіи находятся
также корни мнимые.
III. Вычисленіе корней чрезъ разложеніе преобразованнаго уравненія
ВЬ НЕПРЕРЫВНУЮ дробь.
434. Этотъ замѣчательный способъ представленъ Фогелемъ, лейпцигскимъ
математикомъ, 1845 года *), и примѣненъ къ рѣшенію всякаго уравненія съ
одною неизвѣстною, будетъ ли оно имѣть видъ многочленной функціи, цѣлой,
раціональной, или функціи трансцендентной, лишь бы имѣло конечное число
членовъ. Мы приложимъ его только къ уравненіямъ, вида
р'х) . ,-д-8.г-ьТ=0 ,
гдѣ А, В, С,.... суть числа дѣйствительныя.
Надобно, 1) отдѣлить корпи этого уравненія своими предѣлами (по спо-
собу 414, 418, 419); 2) потомъ взять между предѣлами а а 6 разыскиваемаго
корня число /і среднее или ближайшее къ корню, и, положивъ ж=А-ьх, подста-
вить въ уравненіе /'(ж)=0; тогда это уравненіе превратится въ полное уравненіе:
Л/іч-г)—Сй і-С,2-і-С-з2-і-С328-і-....-і-х", или
ДЛ-ьа)=0-г-01.г-ь6і.л!-і-ез.28-і-... .-ЬЛ",
означая данное уравненіе и его производныя припитымъ нами знакоположеніемъ:
Со=2, €,=6,, с8=е,........
3) Послѣ того надобно обратить это уравненіе въ непрерывную дробь:
=0
по извѣстному памъ способу (345).
Послѣдовательными приближеніями къ дроби будутъ:
1ГГІ ।
первое — =< .^=0,2,
»?ІО
второе — =
пг
С?г 6,г
С| --В, ѲдХ.
тп5 — С,Свг-г-(СІС,—— 0і0гг-ѵ-(ѳ,0-—
третье — — ---—-——-— —----------=----———
—С2-і-С32 —0й“*-Ѳ5я
, п проч.
*) См. Е'пІНесЬип^ еіпег питегіасЬеп СспсніІ-АиГІоаип^ аііег ЬоЬсгеп епДІісЬси СІеі-
сііипцеп, ѵоп десісг ЬеІіеЬідеп аІ^еЬгаіасЬса ипй Ігапасепбепіен І’огпі, три А. Г. Ѵо^еІ;
пеие Аиа^аЬс. 1847.
— 442 —
Если ограничимся этими тремя приближеніями, и внесемъ ихъ въ ДЛч-г)
вмѣсто полной дроби , сперва одно, потомъ другое и третье, то получимъ:
Ѳч-0,г=0, или —0=6,2;
Оч——0, и
в,—е2г
-е2-ье3г ’
а, по освобожденіи отъ знаменателей, будетъ:
1) 04-0,5=0,
2) 00,—(00,—0?)г=0,
3) — 0б.ч-(Ѳ6— Ѳ108)г-ь(ѲІ03—Ѳ2)х!=О.
-535. Этихъ трехъ уравненій достаточно для вычисленія корня ж=Лч-2 до
такой степени точности, до какой угодно.
Изъ уравненій 1) и 2) найдутся приближенныя поправки г корня х, которыя
для различія назовемъ г, и г8:
— е
2,= — ,
в'
— 061__________ —О
2_______________— ее,-і-е? 1,0,4-э, ’ *
Для разрѣшенія третьяго уравненія, и для отысканія третьей поправки 53 раз-
дѣлимъ его сперва на Ѳ,08:
-е , (е ѳ> А
е, \ ѳ. оа )
положимъ для краткости.
е2 в, ,
— —а, да возмемъ
9, ’ е» ’
2і---(1 4-2, ^53—I
і (1-1-г,Ь)г, г,
3 Ь-а Ь-а
а здѣсь положимъ6 =2с, —— ~й; тогда уравненіе приметъ простѣйшій
о —а Ь—а
8
— =2,, то получится:
23=С, или
;0;
видъ:
—2с53ччі=0, откуда
53=с± Кс2—4.
Такова третья поправка, дающая третье приближеніе къ корню.
При вычисленіи дѣйствительнаго корпя х—к-і-г, ищутся только двѣ пер-
выя его поправки 2, и г8, третья же необходима только при вычислепіл корней
мнимыхъ, какъ это будетъ показано въ своемъ мѣстѣ.
А34». Послѣдовательны я приближенія къ корню. — Когда уравненіе
приведено къ виду:
/•1/і-Ьі)=!54-б ,2 4-65254-0323-і-. .. .Ч-5И=0, .
— 443 —
то ищутся, по предыдущимъ формуламъ, двѣ приближенныя величины х( и х5,
берется средняя между ими‘/2(5,4-^)=/»,, и принимается за б нижайшую къ
истинной. Потомъ означается чрезъ т новая поправка, дополняющая А, до я, т. е.
полагается х=АІч-т; отчего получается х=к-і-кі-+-г=^а-і-г. Это подставимъ
въ начальное уравненіе, найдется:
/'(а-ы)=5ч-Ѳ1гч-е2г'!-і-Ѳ3г’-+-... .=0;
изъ этого уравненія получатся двѣ приближенныя величины для г, то есть, г и
гг коихъ среднюю означимъ чрезъ кг. Послѣ того положимъ г=А3-г-«,
гдѣ « означаетъ новую поправку; слѣдовательно, вмѣсто л:=:Ач-А|-ьг=:а-ы,
ближайшею величиною къ корню будетъ:
х=к-і~ку-і--кі-+-82=ІЗ-і-$.
Эту новую величину для ж подставимъ опять въ начальное уравненіе
получится новое уравненіе:
4-. . .=0,
откуда, въ свою очередъ, найдутся двѣ приближенныя поправки л, и «2, кото-
рыхъ средняя величина пусть—А3. Тогда снова надобно будетъ взять
«_А3-+4, то есть, х=2к-і~к1-і-к1-і-к3-+-іІ—
Продолжая такимъ образомъ, можно вычислить для х величину его такъ
точно, какъ будетъ надобно.
<39. Должно замѣтить, что хотя искомая коренная поправка считается бли-
жайшею къ полусуммѣ найденныхъ приближеній; однакожъ это не всегда спра-
ведливо. А какъ этого нельзя знать напередъ, то все же надобно брать среднее
отъ обоихъ, которое во всѣхъ случаяхт ведетъ къ желаемой цѣли.
<39. Когда вычисленныя приближенныя поправки бываютъ правильныя
дроби, тогда выгоднѣе брать вторую вмѣсто средней отъ обѣихъ; потому что
послѣдующія приближенныя дроби бываютъ ближе къ той поправкѣ, которая
ищется.
<39. Что касается до знака предъ х, когда мы переходимъ отъ /’(ж)=0
къ ДА-т-х)—О, то онъ зависитъ отъ знаковъ предъ 6 и Ѳ,- Если эти знаки бу-
—е ,
дутъ равные, то поправка х,= — будетъ всегда отрицательною; если же
ві
Ѳ и О, съ противными знаками, то поправка х2 будетъ положительною.
Пзъ этихъ поправокъ, положительныхъ или отрицательныхъ, тотчасъ будетъ
видно, будетъ ли х малъ пли великъ.
«О. Признаки мнимости корней. — Если между какими ни есть близ-
кими предѣлами окажутся неизвѣстные корни, то самое вычисленіе одного изъ
нихъ покажетъ, какіе они, дѣйствительные или мнимые. 1) Положимъ, что изъ
двухъ найденныхъ приближеній х, и «3 одно будетъ положительное, а другое
отрицательное, то сначала все-таки надобно взять среднее п,
— 444 —
подставивъ х=кі- і-г въданнпе уравненіе, вычислить новыя приближенныя вели-
• чины г{ и г, поправокъ. Если и послѣ то‘"о найдутся г, и гг съ противны ми зна-
ками, то должны заключите, что искомый корень мнимый. Можетъ случиться
также, что первыя величины я, и г, получатся съ рапными знаками, равно какъ
и вторыя приближенія Гі и гг съ равными -знаками; а между тѣмъ вти вторыя
будутъ болѣе разниться между собою, нежели первыя, слѣдовательно будутъ
насъ удалять отъ корни, а не приближать къ нему: это обстоятельство также
служитъ признакомъ мнимости корня.
ААЛ. Поелику въ данномъ уравненіи ('(х]=.О могутъ быть въ одно время
корни дѣйствительные и мнимые; то сначала должно розыекать соизмѣримые
дѣйствительные корни, и корпи вида + ^±0, —Ѵ±Ь, и исключить ихъ изъ
уравненія; останется уравненіе съ корнями несоизмѣримыми и корнями мнимыми
вида р±:д Vх—4.
АЛѢ. Приступая къ частнымъ примѣрамъ, припомнимъ себѣ, что мы озна-
чили чрезъ
Дж)=0 данное начальное уравненіе,
/‘(/і-ьз)=0+012+Ѳ1г3+0823+. - • .=0
вто же уравненіе измѣненное чрезъ подстановленіе х=к-е-я.
Первое приближеніе къ корню, пли первая его поправка
-8
;
второе приближеніе, илп вторая поправка
—о
третье приближеніе х3~с±Ѵ сг-
й._
5,
____ , _________, п /1— — .
Ь — а ’ Ь—а’ 0 ’
Примѣръ.—Мы нашли (стр. 410), что уравненіе
х"—35ж—245—0,
котораго производныя:
б,—5ж—20л8+135,
Ѳ,—10а?—10л3, 08з=10я:2—20л, 64—5л—5, Ѳ3=1,
имѣетъ одинъ дѣйствительный корень между 3 и 4, а всѣ нрочіе корни мнимые.
Этотъ корень ближе къ 4, нежели къ 3, потому что
х—3 даетъ 0=—2. Ѳ,=0, Ѳа=0, Ѳ8=зЗО,....
х=Л - 0—39, 0 —135, 0—160,....
Пробуя числа 3,3; 3,4; 3,5, находимъ что 3,4 даетъ меньшее отпошеніе-
ві'
Степени этого числа найдутся пзъ таблицъ:
а=3,4; я3=11,56; 39,304; а?=133,6336; л8—454,35424.
— 445 —
Они даютъ 6=0,1868; Ѳ,=17,088; 0^—16,21; отсюда •
первое приближеніе =—0,0І089887=г(;
, —0 —0,1868 .
второе приближеніе ——— = - „„ ——0,01126380.
г 1 2,6,-+-0, 16,081036 ’
Взявъ второе приближеніе, какъ ближайшее къ истинной величинѣ поправки
корпя, пахожу
ж=3,4—0,01126380=3,3887371....,
гдѣ вѣрны по крайней мѣрѣ три десятичныя; а потому, для слѣдующаго приоли-
женія къ корню, #еру ж=3,388+г=а-+-г.
Степени числа 3,388 нельзя найти въ нашихъ таблицахъ; посему надобно ихъ
составить непосредственно, или получить посредствомъ логариѳмовъ
найдутся*
1оё 3,388=0,529.9434
2 іоё а=1,059.8868
3 Іо;? а~1,589.8302
4 1о§ «=2,419.7736
5 1о§ а=2,649.7170
3,388=а
11,4785 =а8
38,8893 =а8
131,757....=а‘
446,392 =а‘
Ѳ=—0,013; &,=15,999; 0,=44,538;
2±=г,=0,0008125;
Взявъ послѣднее приближеніе, найдемъ
ж=3,388+0,00081066=3,38881066.
=0,00081066=,.
Равенство приближеній г, и г, въ пяти десятичныхъ даетъ право заключить,
что найденный корень точенъ въ пяти десятичныхъ. Но, употребивъ логариомы
для полученія степеней числа 3,388, мы никакъ не могли съ достаточною точ-
ностію найти самый важный результатъ Ѳ——0,013: а потому и не можемъ
считать найденный корень вѣрнымъ далѣе четырехъ десятичныхъ.
Примѣръ. —У равненіе
О—а:1—2 0ж’+10ж— 1 —О,
котораго производныя
Ѳ,=5х— 60а?+10,
Ѳ— 10ж8— 60, 03=10ж—20, 64=5ж, Ѳв=1,
имѣетъ положительные корни между 0 и 0,5, между 0,5 и 1, между 4 и 5, и
отрицательные между 0 и —1, и между —4 и —5.
Поищемъ корень между 0,5 и 1. Для этого возмемъ я=0,7+г; получится.
0=—0,692; г— =0,0380.
Ѳ,=—18,200; 1 0>692
—38,570; о,оз8хзь.57—і8,2 0,0413.
Беру второе приближеніе, и нахожу
=0,7—0,0413=0,6587.
— 446 -
Для полученія второй приближенной величины корпя, возмемъ л=0,66-ы=
—а-+-г; по таблицамъ степеней найдемъ:
а'=0,4356; аэ=0,287496; а4=0,18974736; а*=0,12523 326;
получатся:
Ѳ=—0,024687, ^=—0,001619=
0,=—15,187263, • га=—0,001628.
Ѳ-—36,725040,
Взявши второе приближеніе, имѣю
ж=0,66—0,001628=0,6583765',
корень точный, по крайней мѣрѣ, въ четырехъ десятичпыхъ.
Теперь будемъ искать корепь между 4 и 5, и на первый разъ возмемъ
а?=4,5-г-=/?-г-г ;
/3’=20,25; /38=91,125; /3‘=410,0625; /9В=1845,28125.
найдутся:
.6=66,78125; 6,=845,3125; Ѳ4=641,25; отсюда
г,=—0,0790029,
г~-0,084040=—^®-,
2^Е,-ьг8)=—0,08152; посему
ж=4,5—0,08152=4,41848.
Для слѣдующаго приближенія беру:
вычисляю степени по логариѳмамъ:
1оё 4,418=0,645.2257
2 1о&=1,290.4414
3 108=1,935.6671
4 1о§=2,580.8828
5 108=.3,226.1085
4,418 =у
19,5183=/
86,2317=/
380,9630=/$
1683,090 =/
0=1,637; ©,=743,717; 0^=597,237;
г,=~| = —0,002199,
-=—0,002203;
г,о8 <-е,
посему, а;=4,418—0,002203=4,415797, корень точный непремѣнно въ че-
тырехъ десятичпыхъ.
Примѣръ. — Возмемъ еще уравненіе:
^—420^800=0,
которое мы рѣшали (стр. 427), и поищемъ его коренъ между 3 п 4. Составивъ:
Ѳ,=5я‘—420; 0,=1Оя8; 0а=Юя8; 04=5ж; Ѳ,=1,
— 447
положимъ, ж—3,8—1—2 (потому что корень гораздо ближе къ 4, нежели къ 3,
какъ видѣли это на страп. 428); тогда получимъ (см. тамъ же):
Ѳ=—3,64832; 0^=622,568; 0^=548,720.
Отсюда:
2——*-=0,0058601
2,= -^ =0,005570
8 яА-і-01
слѣдовательно «=3,8+0,005715=3,805745, гдѣ точны только три деся-
1(2^2^=0,005715;
точныя.
Для слѣдующаго приближенія къ корню, беру
ж=3,805-ы=а-ы;
вычисляю степени числа 3,805 по логариѳмамъ:
Іое 3,805=0,580.3547
21о§=1,460.7094
3 1о§= 1,741.0641
4 1оё=2,321.4188
5 1оё=2,901-.7735
©=—0,521; 01=628,О65;
3,805 =а
14,478 =«
55,(Л89=а3
209,6130=а‘
| 797,5785=а‘
Ѳ±=550,889;
г,=0,000829; г8=0,000828; слѣдовательно,
«=3,805828.
«3. Этихъ примѣровъ достаточно, чтобъ видѣть, какъ вычисляются дѣй-
ствительные корни по способу Фогеля. Сей способъ ничѣмъ не легче Ньютонова
исправленнаго (4йА); для него также нужно искать 0, 08, ѳ8; но онъ уступаетъ
ему тѣмъ, 1) что тамъ не рѣдко сразу можно найти три, четыре и болѣе членовъ
приближенія, и вычислить корень изъ одного ряда; 2) что для него недостаточно
имѣть таблицы степеней двузначныхъ чиселъ, а часто надобно степени чиселъ
трехзначныхъ и четырезначпыхъ составлять непосредственно, что весьма уто-
мительно; либо искать ихъ посредствомъ логариѳмовъ, а они тоже не всегда
удовлетворительны. По этимъ причинамъ, для вычисленія корней дѣйствитель-
ныхъ, лучше употреблять способъ, предъ симъ изложеппый, нежели этотъ.
Однако же, способъ Фогеля превосходитъ всѣ другіе тѣмъ, что подаетъ воз-
можность довольно удобно вычислять корни мнимые, раздѣленные своими пре-
дѣлами, и прилагается также хорошо къ разрѣшенію трансцендентныхъ уравненій
всякаго рода. Мы разсмотримъ только вычисленіе корней мнимыхъ.
.IV*. Вычисленіе мнимыхъ корней уравненія съ одного непівъстного.
«41. Освободивши данное уравненіе отъ корней соизмѣримыхъ, и корней
вида «=Ѵ/±а («О), останется уравненіе /(«)=0, состоящее изъ корней не-
соизмѣримыхъ, и корней мнимыхъ, имѣющихъ полный видъ р±л/ V—1.
- 448 —
Пйры мнимыхъ корней въ этомъ уравненіи могутъ случиться отдѣленныя отъ
другихъ извѣстными предѣлами, или неотдѣленныя. Чтобы вычислить вару кор-
ней, открытую между какими ни есть предѣлами, возмемъ число Л между сими
предѣлами, либо одинъ изъ этгѵь предѣловъ, и, положивъ вставимъ
• въ Дж)=:0; найдется:
^’(Л-ьг)=ібч-Ѳ,хч-б3хг-ьѲ823ч-..-4-2"=0.
Обративъ это уравненіе въ непрерывную дробь, найдемъ ея третье приближе-
ніе; а изъ него получимъ третью приближенную поправку корня
г3=^с±
Положимъ, что сразу выйдетъ Vс1—іі мнимымъ: тогда надобно будетъ тот-
часъ взять
х=к-+-с-і- Ѵсг—(1-і-т=а-+-р V—І-4-г,
составить
Да-ь/9 V—1-і-г)=Ѳч-в1гч-Ѳ3гг-+-б3г®-і-.. ..=0,
пайти двѣпервыя приближенныя поправки г,, г3, и взять */ч (г,-ы8)— V—1;
получится первая приближенная величина корня
^(ач-а'М/Зч-ДЗ {/—1.
Для отысканія втораго приближенія къ корню, возмемъ
х—а"ч-р" V—1ч-5,
составимъ опять
Да"ч-/3" Vх—'Іч-л)=Ѳ-+-61.'5-і-Ѳ35га-03я8ч-... .=0;
найдемъ двѣ новыя приближенныя поправки л, и «3 корня, и ‘/8(в,ч-л3)і—а!''-+-
; получится вторая приближенная величина корня
іс=|а"-+-а'")-ь(/9"-ь/3"') V7—Г;
и такъ далѣе.
ПіГи этихъ вычисленіяхъ, оба члена корня довольно скоро приближаются къ
своимъ истиннымъ величинамъ, и могутъ быть вычисляемы до произвольной сте-
пени точности.
Можетъ случиться, что, отъ под становленія х=к-+-% въ третья
поправка
г3=с± Ѵ^с’—<1
пе будетъ мнимою, не смотря па то, что к взято въ предѣлахъ мнимыхъ корней;
тогда надобно взять —1)-4-я, составить
ДА-ь /—1-+-г)=еч-ѳ,г=ѳ2«’-+-....;
поправки г, и гг непремѣнно получатся мнимыми, п третья поправка с3 будетъ
ненужна. Такимъ образомъ найдется средняя поправка и первая при-
ближенная величина корня ж=з(Ач-а)-ь-(1-+-^) —1=а'-+-/Зу Vх-—1. Послѣ се-
го надобно положить я^а'-ь/З'Vх—1ч-г, и искать вторую приближенную вели-
чину корня, какъ было сказано выше.
- 449 -
145. При этомъ весь трудъ состоять будетъ въ вычисленіи выраженій, вида:
(а-+/5 Ѵ'— 1) (а'-ьб7 Vх—1), и степеней двучлена ач-0 V—1.
р-ь? И-1
Но, (а-+-0Vх—1)(а'-ь/3’ Vх—Г)=:(а«'—/9/3')-ь(а/3'-+а'/3)
а+р V-1 _ «+/3 Vх-1
|/— і р-»-г|/—і
р-д [/—і (ар-+-/Зд)~і-(/Зр—ад) [/—1
р-</ Ѵ~1 ра-+г8
а возвышеніе двучлена —1 въ различныя степени дѣлается по биноміи
Ньютона, или, гораздо легче, по извѣстной тригонометрической формулѣ Моавра:
(со8а-+8Іпа. Vх—1)п=со8на-ь8Інпа. V—1.
Въ этомъ случаѣ, составляютъ равенство
а-+-(3 Vх—1=()(со8ѵ-ь8Іпѵ. 1^=4), полагая
а=осойи, /?=е8Іпо, и а!-ь/9’—і»4;
отсюда вычисляютъ 2 по логариѳмамъ.
Внеся табличный радіусъ В=1010 въ условныя формулы, получаютъ изъ нихъ
ак . ЛК
СО-Ф=----, 51ПП= С—,
<? <?
1о§ со8«=Іодач-!0—1о§@, іод 8Іпг>=1о§/?-ь10—1о§^:
отсюда находятъ величину дуги ѵ въ градусахъ, минутахъ и секундахъ, не болѣе.
Получивши ѵ, берутъ 2ѵ, Зп, 4ѵ,....; ищутъ () совЗг? и @88Ів2г>, (>* 3С0832 и
(>88ІпЗО, и т. д. Такимъ образомъ вычислятся всѣ степени:
(«-Т-/3 Vх—I)8—е*С082ѵ-Ьу’5Іп2». И— 1,
(«-+-/Э И— 1)3=г(?3С083«-Ь()88ІпЗг V—1,
(а-ь/З Vх—1)‘=@‘со8Й>-ье‘віп4«л Vх—!, и проч.;
послѣ чего легко найдутся 6, Ѳо Ѳ2,....
Все это лучше можно видѣть изъ слѣдующихъ примѣровъ.
Примѣръ 1. Уравненіе 0~хі—2д;+-2=0, котораго производныя
Ѳ,—іа;8—2,
Ѳ2~6х8, Ѳ —4а;, Ѳ4— 1,
имѣетъ всѣ корни мнимые, изъ коихъ одна мара находится въ предѣлахъ 0 и 1 *);
потому что подстановленіе
04 3 2 1 0
— -+-
я:=0, даетъ + 00---------ь
я:=1, ... + +- -ь -+
Чтобы найти эту пару, возмемъ х~ 1-+-г; получатся:
') Мнимость этихъ корней слѣдуетъ изъ того, что №)=О и С(-х}=0 допускаютъ
3 ,-------------------------------------------------------
положительное тіпітит. Ибо, изъ 61==о. получается к= 1/0,8;
отчего 0а=н-; В=а?(а:5—2)-і-2=(0,а-2] у/оЛ+2= —1,5 |/0Л+2.
А это результатъ положительный.
29
— 450 —
0=1; О.=2; 0=6; Ѳ3=4; 6=^=|;
®4 , 7 е і
а=-=3; 6—а= —-; 2,=—— = —- ;
./ гі _ 3 »(*+*,& _ 1 .
1*- ~ ' V--- . — — --- .
Ь — а 14 ’ Ь—а 1 ’
третьею приближенною поправкою корня будетъ:
г3=с+ -' + У ~ = —0,14286+0,4403 Ѵ~і;
слѣдовательно, первая приближенная величина корня будетъ:
а=1+2=0,85714+0,4403 Vх—1.
Для вычисленія слѣдующаго приближенія къ корню, возмемъ:
я=0,86+0,44 V—1+т=а+г;
чрезъ непосредственное возвышеніе въ степени найдемъ:
а2=0,54-6+0,7568 Vх—1,
а8=0,13657+0,8911
а4=—0,27463+0,82643 Vх—1.
Эти степени подставимъ въ ѳ, 0П Ѳ„.... на мѣсто х, получатся
0=0,00537—0,05357 |/^Т,
Ѳ,= —1,45372+3,564.4Ѵ—1,
Ѳ2=3,27600+4,5408 V— 1.
Отсюда, первою поправкою корня будетъ:
0,00337—0,05337 V—1 тп—п V—і р • ь? V—і {ТПр-4~Пу)-4-(тП^—ПП) —1
Гі 1,43372 — 3.3644 ^/-1 ~ р-д ^/—Г р-ѵ-д Р1-^3
Іоц пг=0,729.9743—3,
1о§ /=0,162.4808
~0,892.4551—3
тр—0,0078065
пд=0,1909450
1о§ «=0,728.9216—2
Іое д=0,551.9864
* 0,280.9080—1
0,1987515=тр+«5.
!о§ «1=0,729,9743—3, 1о§ «=0,728.9216—2
1о§ 5=0,551.9864 1о§ р=0,162.4808
0,281.9607—2 0,891.4024—2
№5=0,019140 »гр=0,07787б
0.019140
тд- -пр~—0,058736
2 Іод р=0,324.9616, 2 1о§ 5=1,103.9728
р‘=2,1133 0 58=12,70 51
р2+52=14,8184.
— 451
0,198751-0,05874 Vх-! _ к-1
'* 14,8184 <1
1ое й—0,298.3071—1, 1о§ /=0,768.9339—2
доп. 1о§ </=0,829.1986—2 0,829.1986—2
0,127.5057—2 0,598.1325—3
0,013412, 0,003964.
II такъ, первая поправка:
г,=0,013412—0,003964 /=1.
Ито рою поправкою будетъ:
-О, ОО337-І-О, О3337і/~1
Г,—-------------------7=---------------7=----
(0,013412—0,ОО3964р/ — 1](3,276-+ 5,5408 /—1 )-+-&,
С Л с' </'
Вычислимъ первый членъ знаменателя, по формулѣ:
—с'еі) V—-4:
1о§ с=0,127 5057—12, Іое </=0,598.1325—3
1ое с—0,515.3439 Іод </'=0,657.1324
0,642.8496—2 0,255.2649—2
«/=0,043939 </</'=0,018000
с</4-</Д'=0.061939
Іод с=0,127.5057—2
Іод </'=0,657.1324
0,784.6381—2
«/'=0,060903
— 0,012986
Іод <1=0,598.1325—3
Іод </=0,515.3439
0,113.4764—2
</</=0,012986
0,047917=г</'—</
Искомымъ произведеніемъ будетъ:
0,04394ч-0,04792
Ѳ,= —1,453724-3,56440 Vх-
—1,409784-3,61232 Vх-
Посему,
_ 0,00337 - 0,03337 Ѵ^—1 т—п V— 1.
~ 1^40978 —3,61232 р_г
Іод тп=0,729 9743—3,
Іод р=.0,149.1514
0,879.1257—3
іпр=0.0075705
тр-+-пд=0,201081
1; гъ пему придадимъ:
1
І
гр-+-<2 V—1 (тор-е п^}-^-[т^~пр) \^ — 1
рн-? |/—1 Рѵ-і-92
1о§ и=0,728,9216—2
1оё д—0,557.7850
0,286.7066—1
пд=О, 193511
— 452
1оё т—0,729.9743—3,
1о§ 9=0,557.7850
1о§ п=0,728.9216—2
1о§ р=0,149.<514
0,878.0730—2
пР=0,075522
2 15,03628
102 4=0,303.3711—1,
доп. 1о2 /і=0,822.8597—2
0,287.7593
тз=0,0193981
тд—пр= —0,056124.
2102 р=0,298.3028, 2 Іод 3=1,115.5700
р’=1,98748 з2=13,04880
р2ч-32=15,03628.
О.2О1О81-О.О56124 1/-1 і—и |/—1
Л
Іод «=0,749.1486—2
0,822 8597—2
0,572.0083—3
0,003732
0,126.2308—«
0,013373
И такъ, вторая поправка корня:
г—0,013373—0,003732 Ѵ'—і;
мы возмемъ ее, какъ ближайшую къ истинной, и найдется приближенная вели-
чина корня:
_| 0,8600004-0,44000 Vх— 1
Ж ) 0,013373—0,00373 Ѵ^І
х= 0,873373-1-0,43627 1/—1;
оба члена корня имѣютъ всю точность по крайней мѣрѣ въ трехъ десятичныхъ.
«6. Вычисленіе тоіі же пары корней по общей формулѣ:
ж=/і4-(А, В, С,....).
Когда уже найдены Ѳ, Ѳ,, 6„ б3,...., то коренную поправку можно искать по
извѣстной намъ обшей формулѣ,
МО Ѳа , 03\ з -
7.'д ' Го?-"оЛ ’•••]’ а имеино:
нашедши первую приближенную величину корпя а=0,86-1-0,44 Vх—1 изъ
третьяго приближенія й3=с-ь Ѵс8—<1, и вычисливши необходимо нужныя сте-
пени этого двучлена, мы получили:
Ѳ =0,00537—0,05357 Ѵ—К
Ѳ,= —1,45372-1-3,5644 1/—1,
ѳ8=3,276004-4,5408 V— 1.
Послѣ этого надобно найти первый членъ Л=9= • поправочнаго ряда, ко-
торый и найденъ:
А=0,013412—0,003964 V—1= — г,.
- 453 —
р,/ 0 \4
Второй членъ В=-------1—) поправочнаго ряда будетъ:
(3,276-1-4,8408 V—1)(0,013412—0.003964 V— I)4 _
В—-----------------——------------------------
1,48372—3,8644 V— 1
а-ь/? V— і; г (ар~Рд)ч-(ад+Рр) V—1
Іод а=0,515.3439,
Іод р—0,462.4808
0,677.8247
ар=4,762380
ар—Рд= —11,48282.
Іод «=0,515.3439
Іод 9=0,551 9864
Р'-—^а!р>Ѵ— 1)
Іод /3=0,657.1324
Іод 9=0,551.9864
1,209.1188'
(39=16,18520
4,067.3303
ад— 44,67700,
ад-л-Рд—І8,27805,
р8ч-98=14,8184 (это найдено выше);
слѣдовательно, дробь
Іод /3=0,657.1324
Іод р=0,162.4808
0,849.6132
/9р=6,601055,
а-ь/Э V— 1 —11,48282-1-18,27803 V— 1
ю—</ у/—1 14,8184
= —0,770854-1-1,23347 4/—1, и
В= —(0,770854—1,23347 /—1)(а1*—Р'*—2а'р> у/—1).
210(7 а'=0,255.0114—4,
а'*=0,00017989,
агі—^=0,00016418
Іод а'=0,127.5057—2
1од/3'=0,598.1325—3
Іод 2=0,301.0300
2 (о? /3'—0,196.2650—5
/3/8=0,00001571
0,026.6682—4;
В=—(0,770854—1,23347 /-
к I
=(кт—Іп)-
Іод /(=0,886.9721—1.
Іод №=0,215.3203—4,
0,102.2924—4,
Ш=0,00012646,
кт—Іп— —0,00000469
2а^'=0,00010633
’1)(0,0001642—0,0001063 V—1)
т п
{кп-+-1т} |/— 1
Іод /=0,091.1285
Іод п=0,026.6682—4
0,117.7967—4
/«=0,00013115,
— 454 —
Іо8 /—0,886.9721 -1, Іо8 /=0,091.1285
Іо§ и=0,026.6682—4, Іо^ т=0,215.3203—4
0,913.6403—5 0,306.4488—4
- Ли=0,00008196, /т=0,00020251,
Ь4-/т=0,00028448;
В= 4-0,000005-4-0,0002845 У—1
Поправки А и В найдены съ тѣми знаками, какіе онѣ должны имѣть въ
общемъ ряду, а потому ихъ надобно придать съ этими знаками, и будетъ;
(0,8600004-0,440000 Ѵ—Х
х^<0,013412—0,003965
(0,0000054-0,000286 V—1
х= 0,8734174-0,436320
корень точный по крайней мѣрѣ въ трехъ десятичныхъ обоихъ его членовъ.
Представленное здѣсь подробное вычисленіе пары мнимыхъ корней показы-
ваетъ, что оно вчетверо или впятеро продолжите іыіѣе вычисденія двухъ кор-
ней дѣйствительныхъ, несоизмѣримыхъ, по какому угодно способу. Однакоже,
нельзя сказать, чтобъ оно было трудно; потому что все дѣло состоитъ въ прі-
искиваніи логариомовъ, и чиселъ для логариомовъ, въ сложеніи и вычитаніи.
Примѣръ 2.Уравненіе 0=жв—5а?4-135.г—245=0,котораго производныя:
6,=5^— 20ж34-135, Ѳ—10 л3— 30л:8,
08—10х8—20л, О4—5Ж—5, 6—1,
имѣетъ пару мнимыхъ корней между предѣлами 2 и 3 (стр. 410). Чтобы найти
5 5
одну пару корней, возмемъ % 4-3)= у, и положимъ л=у-ьх; получатся:
ѳ( у 4-х)=Ѳ4-Ѳ1Х4-68Х84-б3Х84-... .=0,
—165 ' 285 —128 25
6 ~зГ’ 61 Чв’’ °8—2:
е __іі ,____ в8__—80___—2 ___ѳа___—іоо
2‘ “е’ 38 ’ 125 ~б ’ а ~Ѳ~ 07 ’
. 2 ІОО 386 , г . п.„-п
& а— У4-87 288: —йТТЧ 21373;
=%(1- ” . 4) ^=0,32642.
Третьимъ приближеніемъ рада будетъ:
х3=с4- у/с8—с/=0,3 2642-ь у/0,10655—0,21373^
=0,326424-0,3274 у/— 1.
Посему, я;=2,54-х3=2,82642-ь0,3274 Ѵ—~1.
Для розыскапія слѣдующей приближенной величины корня, возмемъ:
л=2,8-ь0,3 у/—І4-г=а4-г,
откинувъ всѣ прочія десятичныя дроби, на вѣрность которыхъ положиться нельзя.
455
Чрезъ непосредственное возвышеніе въ степени найдутся:
а*=7,75+-1,68/—/_
/=21,1964-7,02 1.
а‘=5 7,2401 4-26,04 /—1,
/=157,46028-4-90,08403 /—1.
Подставивъ это на мѣсто х, хг, /,.... въ О, Ѳ,, 6,,...., получимъ:
0 = —0,74022-4-0,38403 Ѵ—І,
0,= —2,7195—10,3800^/—1,
6 ——20,54-ь19,89 /—1.
Отсюда первая поправка корня/.
_ 0,74022- 0,38403 /—1 1.9732-1-8,7273 /-1
‘ —(2,71934-10,38/^1) 115,1407
или г,—0,017137-4-0,07578/•—!.
Второю поправкою будетъ:
0,74022 —0,38403 /—1
7* —~----------------------------------------
’ (0,017137-1-0,07578 /^1)(—20,54-4-19,89 /—1)4-0,
0,74022—0.38403 /—1 1,06384-10,34172 /—1
—(4,0787544-11,593665 -4 155,4241
г8=0,0068442-1-0,066539 /—1.
Взявъ эго приближеніе, какъ болѣе вѣрное, найдем^:
ж=2,84-0,3 /—1-4-г
=2,8068445-1-0,36639 /—1.
Для полу”енія слѣдующей приближенной величины корня, возмемъ:
х=2,807-4-0,366 /—І4-8=а-+-/3 /—І4-8=/с4-8.
Отъ этого получится рядъ: ,
Ѳ(«4-Д /-1-4-8)=04-6 ,84-6/4-0/-+-... —О,
въ которомъ Ѳ, 04, О,,,.... опредѣлятся, если успѣемъ вычислить степени дву-
члена а-ь/З /—-1. Эти степени можно искать непосредственно съ помощію
логариомовъ, или вычислять по формулѣ Моавра:
(созгм-БІпгі. V—1 )"=со8пг?4-8Іп?м\ /—І.
Мы употребимъ этотъ послѣдній способъ.
Для сего положимъ:
«=2,807, /3=0,366; отсюда найдемъ:
а’4-/32=8,013205=/
. 1о8 6=0,451.9031, 3 Іо* 6=1,355.7094
21о§б=О,9О3.8О63, 4 1оё 6=1,807.6126
51о§ 6=2,259,5157.
— 456 —
2.807.К . О ЗЯ6.К
сойі)——-—, $іпг=—;
о е
10,448.2424+10,
Іо8 соб«= 19,548.0969—40,
9,996.3393; отсюда
ѵ= 7° 25' 45", 4ѵ=29° 43' ’ О"
2п=14° 51'30", 5г=37° 8'45"
Зѵ=22° 17' 15<_
Для вычисленія степеней а+Д У^-*-1, возмемъ формулу
(а+/3 V—1)"=()"(со8ад+ыпда. У/—Ч).
1о§(?’со8 2г= 0,903.8063, , ,.а 9,985.2301—10 1о8С81п-г— 0,903.8063 9,408.9688—10
а- іо^с’соб Зі>— 0,889.0364 =7,74526, 1>= 1,355.7094 9,966.2790—10 І0^й1п3”— 0,312.7751 =2,05482. 1,355.7094 9,578.9305—10
[о§(э1соь4п— 1,321.9884 «'=20,9889, Ь': 1,807.6126, 9,938.7635—10 Іоее8,п4г’— 0,934 6399 =8,6028. 1,807.6126 9,695.2288—10
Іо§@'со55г>= 1,746.3761 а"=55,7670 Ь”= 2,259.5157, , в [9,901.5134-10 ,0^™= 1,502.8414 31,8303 12,259.5157 19.780.9261—10
2,161.0292 2,040.4418
а'"=144,887, ' ____^"=109,^59.
Посему, Л=2,807+0,366 у/—1=а+/3 у/—1,
/с8=7,74526+2,05482 у/— 1,
/?=20,9889+8,6028 Vх—1_,
/с‘=55,7670+31,8303 у/—1,
/св=144,887+109,759 /—1.
Эти степени подставимъ въ 6, О,, 68,.... на мѣсто х, хі, я:8...., получатся:
0=—0,003+0,0175 Ѵ7—!,
Ѳ(=—5,943—12,9045 V— 1.
Послѣ этого найдется первая поправка корня
0,003-0.0178 у/—1 ___0,208-1-0,14272 У7—-1
51 —(8,9ІЗ-ь12,9О45 Г^Т) 201,8153
«,= 0,0010305+0,000707 У7—1.
— 457 —
Посему ж—2.807-1-0,366 |/—1-ч-я,
=2,80803-1-0,36671 V—І,
Этотъ приближенный корень имѣетъ всю точность по крайней мѣрѣ въ
трехъ десятичныхъ.
Мнимые корни второй пары суть отрицательные. Это видно изъ того, что
сумма корней, взятая съ противнымъ знакомъ, должна быть равна коефиціенту
— 5 втораго члена даннаго уравненія. ‘Слѣдовательно, если вторая пара
—р±ц \/—1, то должно удовлетворяться равенство
2р=2Х2,80803-1-3,3888... .=5; откуда
р——2,0026....
Послѣ сего, можно пайти у изъ послѣдняго члена 245 уравненія, и получится:
_у=2,2370;
р±91/—1=—2,0026±2,2370 V— 1.
Примѣръ 3. Возмемъ еще уравненіе,
Ѳ=я;10—9.г8—б.г-ь20: =0, котораго производныя:
е(=10я:в—27«’—6,
е8=45ж8—27ж,
03=120.г7—9,
е4=2Южв, ев=252жв, е6=2Юж‘, е7=і20ж8,
еа=і.5ж*, ее=Юж, е10=і,
имѣетъ всѣ корпи мнимые, какъ видно изъ порядка знаковъ предъ Ѳ, 01;
когда будемъ измѣнять величину неизвѣстной х:
10 0676Б4 8 8 10
л=0, даетъ-ь 000000 — 0------------------г 10—2=8
х 1, — і - —і— і - і - —і— —г- і - —і— —і— — —і— 2
——2, — —1— —1— -1— —1---1— —1— —1— —1— —1— -1- —Г
гдѣ видно, что въ предѣлахъ 0 и 1 находятся восемь корней мнимыхъ, и
два Веизвѣстные корня между 1 и 2, которые также мнимые, что можно
повѣрить, разыскивая дѣйствительный корень между 1 и 2 чрезъ сбли-
женіе сихъ предѣловъ. Для вычисленія же этой пары корней, замѣтимъ на-
передъ, что
ж=1 даетъ 0=-і-6,
ж=2 - (3=960.
слѣдовательно корни лежатъ ближе къ 1 нежели къ 2; а потому, на первый
случай, возмемъ
ж=1,3ч-я; получится рядъ,
О(1,34-я)=О-ьОіг-ь08г84-03я34-.=0. •
— 458 -
Изъ таблицъ степеней найдемъ:
4,3я—1.69; 1,33=2,197; 1,37=6,27485; і,3*=8,15731;
1,Зе=10.6045...; 1,3*°=13,78585;
а чрезъ непосредственное вычисленіе получимъ:
6=6,2128; 61=54,415; Ѳ—331,97895; Ѳа=743,982....
* Отсюда, х,= - = —0,1142;
я8=—0,096414-0,143 /—1,
и приближенною величиною корня будетъ
я=1,3—0,09641-ь0,143 V—1
=1,203594-0,143 |/—1.
Для слѣдующаго приближенія къ корню, возмемъ
Л=і,2044-0,143 /----І4-Г=«4-/3 /—І4-Г,
и постараемся опредѣлить коефиціенты ряда
Ѳ(й4-/3 /—І4-г)=Ѳ1г4-Ѳ1г4-Ѳ8г’ч-Ѳ,г34-.полагая
«=1,204, /9=0,143,
е8=а’4-Д’=1,470063;
Іо8 5=0,083.6680;
2 Іо8 5=0,167.3360,
3 1о8 5=0,251,0040,
7 Іо8 5=0,585,6760,
8 1о§ 5=0,669.3440,
9 1о§ 5=0,753.0120,
10 1о§ 5=0,836.6800,
Отсюда получаемъ:
ѵ= 6° 46' 20",
21=13° 32' 40",
31=20° 19' О",
71=47° 24' 20",
1.204.В
СО81>= - ---
, 10,080.62654-10
ІОЦ СО81)= I
ь 10,916.3320—10
9,996.9585-
, . 10,155.33604-10
Іо8 ыпі>_|8 діб 33й0_10
9,071.6680
81=54° 10'40"
9і=60° 57' О"
10і)=67° 43' 20".
Вычисленіе степеней двучлена «4-/9 /—1:
Іо§ 58сов2і=
0,167.3360,
9,987.7505—10
0,157.0865
а=1,43577
1о§ 588Іп 2і)=0,167.3360
9,369.5861-10
0,536.9221—10
6=0,344288.
- 45'.)
, , „ 10,251.0040 іо8 е «*з^|,>972.Ж7_10 . .. о (0,251.0040 °8 6 5Ш 3”— | 9,540.5903—10
0,223.1087 0,791.594»
а'=і, 67151, 6'=0,618863.
, , , 10,583.6760, 9,830 , „ (0,585.6760 1о8 е 8іп 7ѵ_| (|,8С6 9738—10
0,416.1393 0,452.6498
а"=2,60699, 6"=2,83563.
, . ‘ (0,669 3440, С С0Б 9,767.3579—10 , 8. „ (0,669.3440 е 8Ш 8ѵ~) 9,908.9335—10
0,436.7019 1 0,578.2775
с"'=2,73340, Ѵ'—Ч, 78684.
, „ п 10,753.0120, р соя 9і>_[9 б8б 25і2_10 , в. г (0,753.0120 1ойе ыи 9і)_ 10 д41 б090_10
0,439.2662 0,694.6210
а""=2,74958, 6""=4,95018.
(0,836.6800, 1о§е сов 1°ѵ__| 9 578 7507—ю , .о ,.л 10,836.6800 1оёе 8іи10і>—19>966 3092—10
0,415.4307 0,802 9892
а'""=2,60274, 6"'"=6,35315.
Нашедши всѣ нужныя степени двучлена а-ь/Зі/—1, подставимъ ихъ въ б,
6П 6,,....; получатся:
6—0,33515—0,07?617 Vх—І,
Ѳ,= —17,2704-4.0,2060 Ѵ7—1,
6^90,495-4-166,6468 Vх—!.
Первою поправкою корня будетъ:
0,33818 —0,074617 |/—Г
г,=-----------------------, ИЛИ
17,27—40,2060 у— 1
8,788214-12,18662 |/=4
Г —-----------------------
1914,773
=0,004-58974-0,006364-5 Vх—!.
Второю поправкою будетъ:
-0,338184-0,07462 V— 1
Гг—----------—---------------—-----------------------
(0,00458974-0,0063655 у-1Д90,4954-166,6468 [/—1)4-6,
— 460 —
Опа найдется
9,104534-12,58756 Ѵ—і
р —_____________________
’ 2047,089
=0,004-4-75-1-0.00614.9 Vх- 1.
Взявъ эту поправку, какъ ближайшую къ истинной, найдется приближенный
корень: ___
11,2(И000ч-0,и30001
0,004475-1-0,00614-9 У7—1
х= 1,2084-75-1-0,14-914-9 V—1,
точный по крайней мѣрѣ въ трехъ десятичныхъ.
ЛЛЭ. Способъ отдѣлять пары мнимыхъ корней даннаго уравненія.—
При розыскапіи частныхъ предѣловъ корней, часто находятъ нѣсколько паръ
мнимыхъ корней между подстановлепіями а, а-4-і==&, различающимися только
единицею: эти корни, обыкновенно, опускаются безъ всякаго вниманія, потому
что въ рѣшеніи задачь не имѣютъ ни какого достоинства. Но, еслибъ намъ по-
надобилось, хотя изъ любопытства, вычислить и всѣ мнимые корни, то нужно
было бы сдѣлать такія подстаповленій въ данное уравненіе, чтобы каждая пара
корней отдѣлилась отъ другой. Во многихъ случаяхъ можно употребить слѣдую-
щій способъ: надобно данное уравненіе преобразовать въ другое, котораго бы
корпи были больше корпей даннаго высшимъ предѣломъ 6, полагая х~—Ь-і-у;
тогда составится уравненіе /‘(г/)=0, въ ко горомъ почти всѣ корпи будутъ поло-
жительные. За тѣмъ надобно увеличить корни этого уравненія въ 10 разъ, по-
лагая У~^ ; составится уравненіе /,(.х)=0. въ которое и надобно подставлять
х=1, 2,..., 10, 20,... пары мнимыхъ корней раздѣлятся, если дѣйствитель-
ные члены ихъ разнились между собою не менѣе, какъ въ десятыхъ доляхъ еди-
ницы. Послѣ чего тотчасъ найдутся числа у и х, которыми отдѣляются нары
корней въ [(у)—0 и /’(л;)=0, Но если окажется и въ уравненіи /’(х)=0 нѣ-
сколько паръ корней между предѣлами- а' и Ь'=аІ-+-'1, то и въ этомъ уравненіи
надобно увеличить корни числомъ 6', и повторить все тоже дѣйствіе надъ /’(х)=0,
какое было надъ /’(зс)=0. Поступая такимъ образомъ, цѣль будетъ достигнута,
исключая тѣ случаи, когда дѣйствительныя части нѣкоторыхъ наръ будутъ рав-
ными, какъ видѣли это въ уравненіяхъ возвратныхъ и двучленныхъ.
Примѣръ. —Намъ извѣстно (стр. 4-4-9), что уравненіе ж4—2л-ь2=0 со-
стоитъ изъ двухъ паръ мнимыхъ корней, показываемыхъ нодстаповленіями 0 и 1.
Чтобъ раздѣлить эти корни, увеличимъ и.\ъ предѣломъ 1, дабы чрезъ это сдѣлать
обѣ пары положительными, полагая
ЗС= — 1-Ь-у,
тогда получатся: $=хі—2л-ь2= >, б1=4х3—2= —6, бІ=6х’=6, 08=
—4-, 01=1; и составится уравненіе
</’—іу^-і-бу*— 61/4-5=0;
- 461
корни этого уравнена увеличимъ въ 10 разъ, полагая у—^> наіідется:
Ф=е‘—40234-60028—600^-4-50000=0,
Ф1=4г3—1 ЗОг’ч-1200х—6000,
<-р8=б2-—12024-600,
ф3=4я—40, 714=1.
Теперь будемъ брать:
4 8 8 1 4
2= 0, найдется 4----1----г
= 9, ....... 4-----1----ь
=10.......... -4-0 0-----4-
=11, ........ 4- 4- 4-4-4-
1 пара;
1 пара.
Пзъ этого порядка знаковъ видно, что два мнимые корня находятся мея:ду
подстановленіямп 9 и 10, и два между 10 и 11; отсюда съ большею вѣроят-
ностію заключаемъ, что дѣйствительный членъ первой пары ’2,=94-Л, а второй
2п=104-А, означая чрезъ Л и к нѣкоторыя числа, меньшія 1-ды.
Отсюда видно, что, для первой пары,
у= *0> Для второй у= 1.
<1 <1,1;
слѣдовательно, въ данномъ уравненіи, для первой пары корней
х=—І4-у<1, для второй ж=—І4-у> 1.
II такъ, предѣлы 0 и 1 обличаютъ двѣ пары корней, положительную и отри-
цательную. Мы вычисляли пару корней положительныхъ, и нашли 0,87337..
±0,4362.....|/—1. Если вторая пара =р±дѴ—1, то сумма всѣхъ корней
должна быть 2р4-2Х87337....=0, откуда
р=—0,87337....
Таковъ дѣйствительный членъ второй пары. Коефиціентъ же д легко вычи-
слить изъ состава послѣдняго члена 2 уравненія.
Примѣръ. Уравненіе
0=Х—Зжэ4-6ж*—5.г 4-3=0,
котораго производныя:
д1=4х3—9 Х54-12 Ж4-5,
б,=6;г’—9л>4-6, Ѳ8=4ж—3, 0*=1,
даетъ для ж=—1,
ж=0,
ж=1,
2 пары.
Въ немъ двѣ неизвѣстныя пары корней суть пары мнимыя (стр. 353). Для
раздѣленія ихъ, положимъ х=—1±у; найдутся-
е4=1, е3=—7, Ѳ,=21, 0 ,=—26, 0=18.
7^4-21 у’—26^4-18=0.
- 462 —
Увеличимъ кории этого уравненія въ 10 разъ, взявши у— и составимъ
производныя:
д>=24—70х3-і-2! 00х8—2600024-180000=0,
д>,=4.25—210г!-ь4.2002—26000,
«р—бх*—210x4-2100,
—70, д>4=1.
Теперь будемъ дѣвать подстановленія:
4 » ? 1 о
2— 0, 4— 4— * 4—
—10, 4—4---------4-
-11, -Ь — 4- -Р4- 1 иаГа-
—1 / . 4— -- 4- 4— 4— .
’ 1 пара.
, ---18, 4— 4— 4- 4— 4—
Этимп подстановлепіями пары мнимыхъ корней весьма хорошо раздѣлились:
одна заключается въ предѣлахъ 10 и II, другая въ предѣлахъ 17 и 18. По
этому у= заключается между 1 и 1,1, и также 1,7 и 1,8; слѣдовательно,
х——І4-у заключается между 0 и 0,1 для одной пары мпймыхъ корней, а для
другой между 0,7 и 0,8.
Примѣръ. Уравненіе
Ѳ=«7—«<ь50«’—2«*4-20=0,
котораго производныя.
Ѳі=7 х*—6жв4-150л11 —4«,
6^=21 «‘—1537*4-150л,
0а=35«‘—20«84-50,
е4=35«3—15«’, е.=2і«8—б«, е—7ж—1, ѳ7=1,
имѣетъ шесть корней между предѣлами:
«=0, 4--------0 0 ч-------0 4-,
-—1, 4— 4— 4— 4- 4- 4— 4— 4—,
и всѣ эти корни мпимые. Для раздѣленія паръ сихъ корней возмемъ «=—1-4-у;
получится:
0,=1, Ое——8, 0К=27, 04=—50, 03=105, 0,=—188,
Ѳ,=167, Ѳо=—34;
у7—8^4-27^“—50^*4-105/—188у84-167з/—34=0.
Потомъ сдѣлаемъ у— —; составится новое уравненіе, и его производныя:
д'>=х’—80хв-і-27.10’.х“—В0.105г4ч-105.10*г’—188.1О8ге4-167.1О<!г—34.10’;
9>,=:7г6—480гв4-133.10’х4—200.10’х34-313.10’г5—376.10ях4-167.10с;
9>е=21г“—12ООг‘-і-37ОО0г=—300000г" ьЗіЗООСОг—18800000;
9>»=ЗВг*—160<)г’-+-27000г*. 20ООО0Х4-1050000;
д>4=33г3—1200х24-135о0х—30000;
9>а=21г4—480г-*-2700; <р6=7г- 80; ф7=4.
— 463 —
Дѣлая подстановленія з=0, 1, 2...., получимъ слѣдующіе знаки для ре-
зультатовъ:
я— 0, ч----1------1----1----
= 9, ч----1-----1-----н —
=10, ч-------0 0ч--------+- ч-
=11, ч-------------н ч- ч— ч-
=и, +
=15, -ъ-ч-4-Ч-Ч-Ч-Ч-Ч-
откуда видно, что между 9 и 10 находится дѣйствительный корень, и тамъ
же находится первая пара мнимыхъ корней; вторая мара мнимыхъ соотвѣтствуетъ
предѣламъ 10 и 11; третья пара между 14 и 15. Слѣдовательно, дѣйствитель-
ный корень данпаго уравненія
х——1ч-у=—1ч- есть отрицатателыіый.
Первая пара мнимыхъ корней соотвѣтствуетъ тому же преіѣлу; вторая пара
соотвѣтствуетъ предѣламъ 0 и 1, а третья между
х=—14-1,4=0,4 и 0,5. .
Такимъ образомъ раздѣлены всѣ пары мнимыхъ корней; остается только не-
извѣстно, какіе корни соотвѣтствуютъ подстановленію я=0, положительные или
отрицательные. Нельзя утвердительно говорить, что въ положительныхъ предѣ-
лахъ находятся непремѣнно пары положительныя; потому что эти предѣлы зави-
симы не отъ однихъ дѣйствительныхъ членовъ корней, но также и отъ членовъ
мнимыхъ, а эта зависимость остается неизвѣстною. Для окончательнаго заклю-
ченія, надобно пробовать вычислять пары корней по способу, который намъ уже
извѣстенъ.
Для упражненія въ раздѣленіи паръ мнимыхъ корней, предлагаю уравненіе:
10^—11 а“ч-45я‘—3 Оіс’ч-6 1 ж2—3 0яч-25=0 ,
котораго корни всѣ мнимые, и заключаются въ предѣлахъ я>=0, л=1. Руко-
водствуясь показаннымъ способомъ, найдется:
между 7 и 8, я2 между 10 и 11, а, между 11 и 12. Слѣдовательно:
х1 между —0,3 и —0,2,
ха ' - 0 и ч-0,1,
т. - 1,1 и 1,2.
«8. Но этотъ способъ раздѣленія паръ мнимыхъ корней недостаточенъ въ
томъ случаѣ, когда, при какомъ внесть подстановленіи, уничтожаются мноі’я
производныя сряду Таково, напримѣръ, уравненіе
Ѳ=л7—Юж?—20=0,
- 46-4
въ которомъ шесть мнимыхъ корней.Оио имѣетъ: ©,=73?'—20а?, Ѳ,=:21 а?6—10,
Ѳз=35а?\ 94—35а?’, Ѳв=21а?2. Ѳв=7а?, Ѳ7=1, откуда находимъ,
для а?=0,
=1,
=2,
ч- 0 0 0 0 — 0 —
6 мнпм.
1.
Здѣсь для раздѣленія трехъ паръ мнимыхъ корней надлежало бы обратиться
къ самымъ общимъ способамъ, о которыхъ здѣсь говорить не буду, какъ о пред-
метахъ, выходящихъ изъ предѣловъ начальныхъ основаній Алгебры, и болѣе
любопытныхъ по своимъ теоріямъ, нежели удобопримѣнимыхъ п полезвыхъ для
практики.
О вычисленіи несоизмѣримыхъ корней по способу Горнера, см. Віе Ткеогіе
ипЛ Ли[1бчипд Лег Іібкегп аІдеЬгаіаскеп ипй йсг ігапзсепііепіеп СІеіскііп-
деп, ікеогеіізск ипй рга^іиск Ьеагкеііеі ѵоп Вг. С. Н. Зскпине; Вганн-
ясЬѵтеі§, 1850, стран 185—279. Способъ Веддле, тамъ же, стран. 280—303.
Опредѣленіе и вычисленіе мнимыхъ корней, по способамъ Лагранжа и Рутер-
форда, тамъ же, стран. 343—362.
Приведеніе ирраціональныхъ уравненіи въ раціональныя.
<19. Уравненіе называется ирраціональнымъ, если въ одномъ или нѣсколь-
кихъ его членахъ неизвѣстная заключается подъ коренными знаками. Для рѣше-
нія такихъ уравненій надобно ихъ преобразовывать въ другія, не содержащія ра-
дикальныхъ функцій.
Общій способъ этого приведенія достаточно понятенъ изъ слѣдующаго при-
мѣра. Пусть дано ирраціональное уравненіе,
Vа—х — Ѵк—х-+- Ѵх—с— Ѵх—;
въ немъ нѣтъ радикальныхъ знаменателей, потому что всегда можно уравненіе
отъ нихъ освободить.
Для освобожденія же отъ радикаловъ, положимъ а—х=у'і, Ь—х=г*,
х—с=и3} х—й=82; найдется:
1) у—х-+-и—и условныя уравненія;
2) г/’ч-д;—«=г0, 3) х‘-+-х—Ь—§
4) і?ч-с—«=0, 5) «2—а?ч-<Ь=0.
Изъ этихъ пяти уравненій надобно только исключить четыре неизвѣстныя,
какія нибудь, наприм. х, х, и, з; останется одно уравненіе Ду)=О съ однимъ
неизвѣстнымъ у, не содержащее радикаловъ. Разрѣшивъ это уравненіе, будемъ
вносить его корпи въ у“ч-х—а—0, наіідется столько же величинъ для х, кото-
рыя надобно подставлять въ данное ирраціональное уравненіе, и смотрѣть, кото-
рыя изъ нихъ ему удовлетворяютъ; онѣ и будутъ его корнями.
461
корни этого уравненія увеличимъ въ 10 разъ, полагая У—~^, найдется:
(р—^—4023ч-600х*— 6000x4-50000=0,
9>1=4х3—120г*+1,200х—6000,
^бх’—120х+600,
<Р3—А-г-—40, <р4=1.
Теперь будемъ брать: ‘ ‘ ‘ ’
х= 0, найдется ч-----1----ь
— с _»_____।____|_ .
1 ....... 1 пара;
=10........... ч- 0 0 — ч- ।
=11.......... + + + +і
Изъ этого порядка знаковъ видно, что два мнимые корня находятся между
подстаповлепіями 9 и 10, и два между 10 и 11; отсюда съ большою вѣроят-
ностію заключаемъ, что дѣйствительный членъ первой пары э,=9ч-/і, а второй
х,=10-ь/с, означая чрезъ /і и к нѣкоторыя числа, меньшія 1-цы.
Отсюда видно, что, для первой пары,
У= ~> 0,9, для второй у= ~> 1
<1 <1,1;
слѣдовательно, въ данномъ уравненіи, для первой нары корней
х~—1-1-у <1, для второй х=—1ч-у> 1.
II такъ, предѣлы 0 и 1 обличаютъ двѣ пары корней, положительную и отри-
цательную. Мы вычисляли пару корней положительныхъ, и нашли 0,87337....
±0,4362 V—1. Если вторая пара=р±у V—1, то сумма всѣхъ корней
должна быть 2р-+-2Х87337....=0, откуда
р=—0,87337....
Таковъ дѣйствительный членъ второй пары. Коефиціентъ же д легко вычи-
слить изъ состава послѣдняго члена 2 уравненія'
Примѣръ. Уравненіе Ѳ=х!—явч-50ж3—2яЛ+-20=0,
котораго производныя: ѳ1=7ж°—бх’ч-150ж‘—4ж,
Ѳ,=21 — 15^' ч-15 0х,
Ѳ,=35х‘—20х3ч-50,
Ѳ4=35л3—15х», Ѳ— 2 Ія2—6ж, Ѳ — 1х— 1, Ѳ7=1,
имѣетъ шесть корней между предѣлами:
а;=0, ч-----0 О-і------0 ч-,
= 1, Ч-Ч-Ч-Ч-Ч-Ч-Ч-Ч-,
и всѣ эти корни мнимые. Для раздѣленія паръ сихъ корней возмемъ х=—1ч-у;
получится:
07=1, Ѳ,=—8, 9В=27, Ѳ——50, 6,3=105, Ѳ——188,
Ѳ,=167, Ѳо=—34;
у’_8ув+27у'—50у‘+105у3—188у’ч-167у—34=0.
зо
- 462 —
гг 7
Потомъ сдѣлаемъ у= —; составится новое уравненіе, и его производныя:
<р=г’-80гв-+-27.10“ тв—ЗО.ІО’г’ч-ІОЗ 10’г3-188.108г2-+-167.10вг—34.10е;
<р1=7ів-480г''ч-135.10!г,-200.10!г8н-3і:> 10«г’—370.10^167.10е;
<Р2=21г“ — 1200г‘-ь 37000г»-3007 О''г2ч-315<>0і'0г—1.4800000;
д\=35г’ -1 і0''г3н-27000г5н-200О0г-+ 1031)000;
ф%=:Ілг5 —1200г’-ь13.Т00г —30000;
<ра=2іг»-480г—2700; <Гвн-7г-80; ф,=1.
Дѣлая подстаповленія х=0, 1, 2---------------------- получимъ слѣдующіе знаки для ре-
зультатовъ: г= О, 4-1.1-1-
= 9, ч---------1-----1-------------ь —
=10, ч---------О 0 ч---------------і-ч-
= 11, 4--------------1- -і 4— ч-
=14, ч-ч-ч-----------ьч-ч-ч-
=15, ч-ч-ч-ч-ч-ч-ч-ч-
откуда видно, что между 9 и 10 находится дѣйствительный корепь, и тамъ
же находится первая пара мнимыхъ корней, вторая пара мнимыхъ соотвѣтствуетъ
предѣламъ 10 п 11; третья пара между 14 и 15. Слѣдовательно, дѣйствитель-
ный корепь даннаго уравненія
х=—1ч-у=—1ч- есть отрпцатательный.
Первая пара мнимыхъ корней соотвѣтствуетъ тому же предѣлу; вторая пара
соотвѣтствуетъ предѣламъ 0 и 1, а третья между
х=—14-1,4=0,4 и 0,5.
Такимъ образомъ раздѣлены всѣ пары мнимыхъ корней; остается только не-
извѣстно, какіе корни соотвѣтствуютъ подстановленію х=0, положительные пли
отрицательные. Нельзя утвердительно говорить, что въ положительныхъ предѣлахъ
находятся непремѣнно пары положительныя; потому что эти предѣлы зависимы не
отъ однихъ дѣйствительныхъ членовъ корней, по также и отъ членовъ мнимыхъ, а
эта зависимость остается неизвѣстною. Для окончательнаго заключенія, надобно
пробовать вычислять пары корней по способу, который палъ уже извѣстенъ.
Для упражненія въ раздѣленіи паръ мнимыхъ корней, предлагаю уравненіе:
1 Охв— I іх’ч-45^— ЗОх’ч-61 іг—30x4-25=0,
котораго корпи всѣ мнимые, и заключаются въ предѣлахъ х=0, х=1. Руко-
водствуясь показаннымъ способомъ, найдется:
м, между 7и8, г, между 10 и 11, з3 между 11 р 12. Слѣдовательпо:
х, между —0,3 п —0,2,
ж, 0 и ч-0,1,
х8 - 1,1 и 1,2.
дде. но этотъ способъ раздѣленія паръ мнимыхъ корней недостаточенъ въ
томъ случаѣ, когда, при какомъ ни есть подстаповлепіи, уничтожаются многія
проиводныя сряду
— 463 —
Таклво, йапригѣръ, уравненіе: Цх)=хв—2х-+-5~0,
которое состоитъ изъ шести мныпыхъ корней. Оно имѣетъ- б1=6ж‘—2,
Ѳ,— 15л4, Ѳ5—20л5, 0.4=І5л2, б.=6л, Ѳ„=І; откуда находимъ-
для л—0, -4-0 0 0 0--------ь 6 мнимыхъ.
Л=1, -4- -4- -4- Н- -4- -4- -4-
Здѣсь, для раздѣленія трехъ паръ мнимыхъ корпей, преобразуемъ /'(х)~О
въ другое уравненіе, котораго бы корни были квадратами ею корней
(стр. 356), перемноживъ /’(л)=0 па /'(-л)=0; получится:
л,2-4-10л“—4лг-4-25=0, или
Ду)—у“-ьІ0уг—4у-ь25=0, полагая х*=у.
Это уравненіе преобразуемъ опять также, помноживъ /"(у) на /"(-у)=0;
получится: у12—50увч-80у‘—16у2ч-625=0, или
Ѳ=хв—50^4-И)?—Ібхч-625, полагая у2=х.
Возмемъ его производныя:
Ѳ1==б2в— 150=4-160х—16,
6^=15г‘—150*4-80,
Ѳ—20і8—50, Ѳ4=15х2, ѲБ=6*, Ѳ,=1.
Отсюда найдемъ;
Такимъ образомъ въ уравненіи Ѳ(=)—0 всѣ три пары раздѣлены, и могутъ
быть вычислены.
Если найдется г~ан-б V—1, то будетъ:
у— V%— ± Vа-і-Ъ V—1,
х= /у— ±\/± V а-г-Ь V—1.
Общій способъ раздѣленія и вычисленія мнимыхъ корней чрезъ составлеші
уравненія изъ квадратовъ разностей корней даннаго можно читать въ Теоріи
опредѣленныхъ алгебрическихъ уравненій высшихъ степеней, Сомова;
Москва, 1838, страи. 130, 131 и 135.
О вычисленіи несоизмѣримыхъ корпей по способу Горнера, см. Віе Ткеогіе
ипй Аи/Іаміпд бег кдкегп аІдеЬгаі^сІіеп ип<1 бе г Ігапзсепбепіеп СІеіскип-
деп, іііеогеііаск ип<1 ргасііисіг ЬеагЬе'ІеІ ѵоп Вг. С. II. Зсіініие; Вганп-
ясЬхѵеі(г, 1850, страи. 185—279 Способъ Веділе, тамъ же, страи. 280—303.
Опредѣленіе и вычисленіе мнимыхъ корпей, по способамъ Лагранжа и Рутер-
форда, тамъ же, стран. 342—362
Слѣдующая таблица полезна для первыхъ Пріемовъ вычисленія мнимыхъ корней.
— 464 —
Степени количества р~*-ц V—1, когда р и ц вршіпмаютъ величины 1,2,3,4,5.
Р=3=1 Р=2, 3=1 Р=І. 3=2 Р=3, з=1 Р=1, 2=3
1 2 3 4 3 6 7 8 і-і |/й 2 |/й -2-1-2 Уй -4-1-0 -4-4 \'-А — вУЙ 8-8 Уй 16 2-ь уй 3-ь 4 У-1 2-ь 11 |/-1 —7-ь 24 |/-1 —38-ь 41 1/-1 — 117-ь 44 |/-1 -278- 29 |/й —327 — 336 |/-1 1-ь 2 Уй —3-ь іУ-І -11- 2|/7-і — 7— 24 У-1 41— 38 Уй 117-ь 44 У- 1 29-ь 278 У-1 -327-ь 336 У~ 3-ь уй 8-ь 6 У-1 18-ь 26 Уй 28-ь 96 У-1 —12-ь 316 У-1 —352-ь 936 У-1 — 1992ч-2436 У-І —8432-ь3376 Уй 1-ь з Уй -8-ь 6 уй -26- 18 Уй 28— 96 Уй 316— 12 Уй 332-ь 936 Уй —2456-ьІ992 Уй -8432-5376 У-1
р=і, з=1 р=1, з=4 р=3, з=1 Р=1. 3=3
1 2 3 4 5 6 7 8 4-ь У-1 13-ь 8 Уй 52-і 47 Уй 161-ь 210 Уй 40і-ь 1121 У-1 493-ь 4888 Уй —2908-ь20047 Уй —31679-1-77280 |/й 1-ь 4 у/Й -із-ь вуй —47— 52 У-1 161— 240 |/й 1121-ь 404 Уй —493-ь 4888 УЛ -20047-ь 2908 Уй —31679—77280 Уй в-ь уй 2і-ь 10 уй 110-ь 74 У-1 476-ь 480 У-1 1900-ь 2876 Уй 6624-ь 16280 Уй 16840-ь 88024 Уй -38214-436960 У-1 1-ь вУй -24-ь 10 Уй -74— 110 Уй 476— 480 Уй 2876-ь 1900 Уй -6624-ь 16280 Уй -88024- 16840 УЙ - 3824—436960 Уй
Р=2, з=3 р=3, 3=2 Р=2, 3=3 р=5, з=2
1 2 3 і В 6 7 Я 2 т- 3 У-1 —З-і- 12 Уй -46ч- 9 У-1 -119— 120 у/-1 122- 597 |/й 2033- 828 У-1 6554-ь 4449 У-1 - 239-1-28566 7-1 3-ь 2 Уй 5-ь 12 Уй —9-ь 46 Уй —119-ь 120 Уй —397-ь 122 У-1 -2033- 828 Уй -4449- 6334 Уй — 239—28560ѴЙ 2-ь 5 Ѵ-І -21-ь 2оуй — 142— 65 41— 810 ѴСі 4282- 1475 Уй 12939-ь 18160 уй - -60422-Ы 16613 уй -703919- 68880 уй 3-ь 2 Уй 21-ь 20 Уй 63-ь 142 У-» 41-ь 840 У-1 — 1473-ь 4282 Уй -13939-ь 18160 Уй -11(і6іЗ-ь60422 Уй —703919-4-68880 УЙ
Если будетъ одно д отрицательное, то въ этой табличкѣ перемѣнятся знаки только
предъ всѣми членами мнимыми.
Если р отрицательное, то перемѣнятся знаки предъ дѣйствительными членами въ не-
чётныхъ степеняхъ, и предъ мнимыми въ степеняхъ чётныхъ.
Если же р и д оба отрицательные, то перемѣнятся знаки предъ обоими членами во
всѣхъ степеняхъ нечётныхъ, что очевидно.
Есл і извѣстный членъ р хотя единицею менѣе коеФиціента д мнимаі члена, то въ
квадратномъ двучленѣ дѣйствительный членъ дѣлается отрицательнымъ.
- 465 —
Приведеніе ирраціональныхъ уравненіи въ раціональныя.
449. Уравненіе называется ирраціональнымъ, если въ одномъ или нѣсколь-
кихъ его членахъ неизвѣстная заключается подъ коренными знаками. Для рѣше-
нія такихъ уравненій, надобно ихъ преобразовывать въ другія, не содержащія ра-
дикальныхъ функцій.
Общій способъ этого приведенія достаточно понятенъ изъ слѣдующаго при-
мѣра. Пусть дано ирраціональное уравнен.е,
Vа—х— ѴЬ—ж-+- Ѵх—с— іЛг—йч-/=0;
въ немъ нѣтъ радикальныхъ знаменателей, потому что всегда можно уравненіе
отъ нихъ освободить.
Для освобожденія же отъ радикаловъ, положимъ а—х=у\ Ъ—х=х*,
х—с=и5, х—^=8*; найдется:
1) у—г-+-и—8-+-[=0, и условныя уравненія;
> 2) у*-+-х—а=0, 3) х‘-кг—6=0 .
4) і/ч-с—іг=0, 5) з*—ж-і-(/=0.
Изъ этихъ пяти уравненій надобно только исключить четыре неизвѣстныя,
какія ннбудь, папрпм. х, х, и, «; останется одно уравненіе /’(г/)=0 съ однимъ
неизвѣстнымъ у, не содержащее радикаловъ. Разрѣшивъ это уравненіе, будемъ
вносить его корни въ уь-+-х—а=0, найдется столько же величинъ для х, кото-
рыя надобно подставлять въ данное ирраціональное уравненіе, и смотрѣть, кото-
рыя изъ нихъ ему удовлетворяютъ; онѣ и будутъ его корнями.
Пзъ этого видно, что, для приведенія ирраціональнаго уравненія въ раціональ-
ное, нужно напередъ знать самые общіе способы исключенія неизвѣстныхъ между
данными уравненіями. Но я совсѣмъ не буду здѣсь излагать этихъ способовъ,
а ограничусь только случаями, въ которыхъ это приведеніе и безъ того можетъ
быть исполнено.
1) Положимъ, что уравненіе содержитъ радикалъ только въ одномъ членѣ:
тогда надобно отдѣлить этотъ членъ, и все уравненіе возвысить въ степень,
означенную показателемъ того корпя.
Примѣръ. Пусть дано уравненіе
ах— ѴЬ—ам-с=0.
і
Отдѣляю радикальный членъ,
ахч-с= іД—х, и возвышаю въ квадратъ:
, аіх3-л-'2асх-і-сі=Ь—х.
Примѣръ. Возмемъ рх--------°— -----д=0.
ь— V в—с
— 46Ь —
Отдѣлимъ радикальную функцію:
п г
рх—у—-----я - ; освободимъ отъ знаменателя,
Ь— V х — с
»,------------
(рх—д}Ь—{рх—у) у х—с~а, или
3________________________
Ьрх—Ьд—а=(рх—д} ух—с.
Возвысимъ въ 3-ю степень, и получится .
{Ьрх—Ьд—а)3~(рх—д)3{х—с)
уравненіе 4-й степени безъ радикаловъ.
2) Положимъ, что уравненіе в вѣетъ радикальныя функціи въ двухъ членахъ,
изъ коихъ одинъ съ показателемъ 2.
Примѣръ. у 2—'X— ух—I —1=0.
3 ,-----------------------
Здѣсь надобно отдѣлить к 2—х:
|/2—я=1-ьі4г— 1, и возвысить въ кубъ,
2—я=Іч-3 |/Д-т-3(ж—1) ; откуда
4—4а=(2-ья) Vх—1.
Теперь возвысимъ въ квадратъ, сократимъ, и найдется:
х3— 13ж’+32ж—20=0.
Этому уравненію удовлетворяетъ корень х=1; онъ же удовлетворяетъ и
радикальному уравненію. Освободивпи найденное уравненіе отъ х—1=0,
получимъ:
хг—12ж-і-20=0, откуда
а?—10, х=2,
которыя только тогда могутъ удовлетворить данному уравненію, когда 1
возмется съ знакомъ ч-.
Возмемъ теперь уравненіе съ овумя какими нибудь радикалами, нанрим.
7----------------------- ’/------
у а—г— у Ь—а?ч-с=0.
Положимъ а—х=^у", или х=а—уп, получится:
3________
у—ѴЬ—ач-упч-с=0; отсюда:
3 _______
у~л~с=ѵЬ—а-+-уп, и наконецъ
у3Ч-Зсу'ч-ЗсгуЧ-с’=6-ЯЧ-у".
Пусть п=5, то будетъ:
у’—у3—Зсу*—Зс*у—с3-і-Ь—а=0.
Положимъ а=4, 6=11, с=1; даннымъ уравненіемъ будетъ:
в з?____________________
1/4-—х— уі 1—хч-1 =0, а преобразованное
Уь-У— Зу— Зуч-6=0.
Этому послѣднему удовлетворяетъ корень у=1. Отъ сего ж=4—у’=4—1=3;
вто число удовлетворяетъ данному уравненію, и есть его корнемъ.
467 —
3) Положимъ, что уравненіе содержитъ -три радикала, изъ коихъ одинъ
съ показателемъ 2. Напримѣръ:
Ѵа—х— ѴЬ—хч- Ѵх—сч-й=0.
Въ этомъ случаѣ также беру:
а—х=у3-, отсюда х=а—у1-, подставляю:
у— ѴЬ—ач-у3ч- Ѵа—с—і/-г-(іг=О; отсюда
________________3 __________
у-+-й~ь- Ѵа—с—у3= ѴЬ—ач-у3.
Для краткости полагаю: у—<1=р, а—с—у3—д, Ь—ач-у3=г; отъ чего
наше уравненіе сдѣлается:
рч- Ѵд= Ѵг,
которое и возвышаю въ кубъ:
р’-рЗр* Ѵдч-Зрдч-д Ѵд—г, или
(3/Л+-?) і4;=(г—р3— Зрд).
Эго возвышаю въ квадратъ:
(3/Л4-7)'д=(г—р3—‘ЗрдУ.
Сюда надобно только подставить, па мѣсто р, д, г, ихъ значенія, потомъ при-
весть въ простѣйшій видъ, то п получится уравненіе безъ радикаловъ, зависящее
только отъ у Нашедши его корни, надобно ихъ подставлять въ х=а—у3, чтобъ
получить всѣ значенія для х, изъ которыхъ нѣкоторыя будутъ удовлетворять
данному уравненію, и потому будутъ его корнями.
Примѣръ. Возмемъ еще уравненіе:
Ѵа—хч- Ѵх—с— Ѵд—хч-{=0.
Положимъ а—х~у3\ отсюда —у3-, подставимъ:
уч- Ѵа—с—у3— Ѵ<1—ач-у3ч^І=0, пли
V а—с—у3= Ѵ(1—ач-у3—(уч-[).
Возвышаю въ кубъ:
с—г/в=а—ач-у* У а—ач-у^—Зіуч-^а—ач-у^ч-Зід-і-^ V гі — а-ьу —
или:
<=—а-т-</Е-т-3(?/н-/’)2] V<1- ач-ув.
Остается все ато возвысить въ квадратъ, чтобъ уничтожился послѣдній
радикалъ.
Пусть а—с=д,—4, [=1; слѣдовательно данное уравненіе:
Ѵ&—хч-Ѵх-----4— Ѵі—Ж-4-1=0,
а условное х=і-—у3. Въ такомъ случаѣ, уравненіе съ однимъ редикаломъ
будетъ:
—і*“-ьЗг/’(1ч-г/)-4-(1-+-у3)=(у,і-4-3-і-6у-і-Зу*) Ѵу\ или
2/+Зу”ч-1ч-Зуч-3/+/=(/ч-3^ч-6^3)ѴУ.
— 468 —
Это возвышаю въ квадратъ, и получаю:
(3!/«ч_2у“ч-г/5ч-ЗуІ-4-Зу-і-1)І=(у“ч-32/’ч-6у-4-3)У,
уравненіе 15-й стевени. Оно удовлетворяется, нолагая у=і; стало-быть,
—у“=3, что удовлетворяетъ данному уравненію, и есть его корнемъ.
Вотъ случаи, въ которыхъ мы можемъ приводить ирраціональныя уравненія
въ раціональныя, и отыскивать ихъ корни, тѣми способами, какіе намъ извѣстны
изъ всего изложеннаго въ этой книгѣ.
ТАБЛИЦЫ
ПЕРВЫХЪ ПЯТИ СТЕПЕНЕЙ ТРЕХЗНАЧНЫХЪ ЧИСЕЛЪ ОТЪ
О ДО 4000, И ПЕРВЫХЪ ДЕСЯТИ СТЕПЕНЕЙ ДВУЗНАЧНЫХЪ
ЧИСЕЛЪ ОТЪ 0 ДО 400.
зі
II
• Вторыя степени чиселъ отъ О до 1000.
сІИСЛ. 0 100 ‘200 300 400
о 0 10000 40000 90000 1 60000
1 і 10201 40401 90601 1 60801
2 4 10404 40804 91204 1 61604
3 9 10609 41209 91809 1 62409
4 16 10816 41616 92416 1 63216
5 25 11025 42025 93025 -1 64025
6. 36 11236 42436 93636 1 64836
7 49 11449 42849 94249 1 65649
8 64 11664 43264 94864 1
9 81 11881 43681 95481 1 07281
10 100 12100 44100 96100 1 68100
11 121 12321 44321 96721 1 68921
12 144 12344 44941 97314 1 69744
13 169 12769 45.169 97969 1 70569
14 190 12996 45796 98596 1 71396
15 223 13225 46223 99225 1 72223
16 256 13456 16656 99886 173036
17 289 13689 47089 1 00489 1 73889
18 324 ' 13924 47524 1 01124 1 74724
19 361 14161 47961 1 0:761 1 73361
20 400 14400 48400 1 02100 1 76500
21 441 14'141 48841 1 0 1041 177241
22 484 14881 49284 1 03684 1 78084
23 529 15129 49729 1 04329 1 78929
24 576 15376 50176 1 04976 1 79776
25 625 15625 50625 1 05625 1 80625
26 15876 51076 1 06276 1 81176
27 729 16129 51529 1 06929 1 82329
28 784 16384 51984 1 07584 1 83184
29 841 16641 52441 1 08241 1 84041
30 900 16900 52900 1 08900 1 84900
31 961 17161 53361 1 09561 I 83761
32 1024 17424 153824 1 10224 1 86624
33 1089 17689 54289 1 10889 1 87489
34 1156 17936 54756 1 11556 1 88356
35 1225 18225 55225 1 12225 1 89225
36 1296 18496 55696 1 12896 1 90096
37 1369 18769 56109 1 13369 1 90969
38 1444 19044 5664 4 1 14244 1 91844
39 1521 19321 57121 1 14921 1 92721
40 1600 19600 57600 1 15600 1 93600
41 1681 19881 38081 1 16281 1 94481
42 1764 20164 58564 116964 1 95364
43 184» 20449 59049 117649 1 96249
44 1936 20736 59536 1 18336 1 97136
45 ' 2025 21025 60025 1 19025 1 98025
46 2116 21316 60516 1 19716 1 98916
47 2209 21609 61009 1 20409 1 99809
48 2304 /21904 61504 1 21104 2 00704
49 2401 22201 62001 1 21801 2 01601
III
Ві'ОРЫЯ СТЕПЕНИ ЧИСЕЛЪ ОТЪ
0 ло 1000. •
Числ. 0 100 200 300 400
80 2500 22500 62500 1 22500 2 02300
51 2601 22801 63001 1 23201 2 03401
52 2704 23104 6350 і 1 23904 2 04304
53 2809 23409 64009 1 24609 2 05209
54 2916 23716 64516 1 253 і 6 2 06116
55 3025 24025 65025 1 26025 2 07025
56 3136 24336 65536 1 26736 2 07936
57 3249 24649 66049 1 27449 2 08849
58 3364 24964 66564 1 28164 2 09764
59 3481 25281 67081 1 28881 210681
60 3600 25600 67600 1 29600 211600
61 3721 25921 68121 1 30321 212521
62 3844 26244 68644 1 31044 213444
63 3969 26569 69169 1 31769 211369
64 4096 26896 69696 1 32496 215296
65 4225 27225 70225 1 33225 216225
66 4356 27556 70756 1 33956 217156
67 4489 27889 71289 1 34689 2 18089
68 4624 28224 71824 1 35424 219024
69 4761 28561 72361 1 361&1 219961
70 4900 28900 72900 1 36900 2 20900
71 5041 29241 73441 1 37641 2 21841
72 5184 29584 73984 1 38384 2 22784
73 5329 29929 74529 1 39129 2 23729
74 5476 30276 75076 1 39876 2 24676
75 5625 30625 75625 1 40625 2 25625
76 5776 30976 76176 1 41376 2 26376
77 5929 31329 76729 1 42129 2 27529
78 6084 31684 77284 1 42884 2 28484
79 6241 32041 77841 1 43641 2 29441
80 6400 32400 78400 1 44400 2 30400
81 6561 32761 78961 1 45161 2 31361
82 6724 33124 79524 1 45924 2 32324
83 6889 33489 80089 1 46689 2 33289
84 7036 33856 80656 1 47456 2 34256
85 7225 34225 81225 1 48225 2 35225
86 7396 34596 81796 1 48996 2 36196
87 7369 34969 82369 149769 2 37169
88 7744 35344 82944 1 50544 2 38144
89 7921 35721 83521 1 31321 2 39121
90 8100 36100 84100 1 32100 2 40100
91 8281 36481 84681 1 52881 2 41081
92 8464 36864 83264 1 53664 2 42064
93 8649 37249 ' 85849 1 54449 2 43049
94 8836 37636 86436 1 55236 2 44036
95 9025 38025 87025 1 56023 2 45025
96 9216 38416 87616 1 56816 2 46616
97 9409 38809 88209 1 57609 2 47009
98 9604 39204 88804 1 58404 2 48004 ’
99 9801 39601 89401 1 59201 2 49001
IV
Вторыя степени ЧИСЕЛЪ ОТЪ 0 ДО 1000.
Числ. 500 600 700 800 900
0 2 50000 3 60000 4 90000 6 40000 810000
1 2 51001 3 61201 4 91401 6 41601 811801
2 2 52004 3 62404 4 92801 6 43204 813604
3 2 53009 3 63609 4 94209 6 4 4809 8 1 5409
4 2 54016 3 64816 4 95616 6 46416 817216
В 2 55025 3 66025 4 97025 6 48025 819025
6 2 56036 3 67236 4 98436 • 6 49636 8 20836
7 2 57049 3 68449 4 99849 6 51249 8 22649
8 2 58064 3 69664 5 01264 6 52864 8 24464
9 2 59081 3 70881 5 02681 6 54481 8 26281
10 2 60100 3 72100 5 04100 6 56100 8 28100
11 2 64121 3 73321 5 05521 6 57721 8 29921
12 2 62144 3 74544 5 06944 6 59344 8 31744
13 2 63169 3 75769 5 08369 6 60969 8 33569
14 2 64196 3 76996 5 09796 6 62596 8 35396
16 2 65225 3 78225 511225 6 64225 8 37225
16 2 66256 3 79436 512656 6 65856 ' 8 39056
17 2 67289 3 80689 514089 6 67489 8 40889
18 2 68324 3 81924 515524 6 69124 8 42724
19 2 69361 3 83161 516961 6 70761 8 44561
20 2 70400 3 84400 518400 6 72400 8 46400
21 2 71441 3 83641 519841 6 74041 8 48241
22 2 72484 3 86884 5 21284 6 75684 8 50084
23 2 73529 3 88129 5 22729 6 77329 8 51929
24 2 74576 3 89376 5 24176 6 78976 8 53776
23 2 75625 3 90625 5 2562а 6 80625 8 55625
26 2 76076 3 91876 5 27076 6 82276 8 57476
27 2 77729 3 93129 5 28529 6 83929 8 59329
28 2 78784 3 94384 ’5 29984 6 85584 8 61184
29 2 79841 3 95641 531441 6 87241 8 63041
30 2 80900 3 96900 5 32900 6 88900 8 64900
31 2 81961 3 98161 5 34361 6 90561 8 66761
32 2 83024 3 99424 5 35824 6 92224 8 68624
33 2 84089 4 00689 5 37289 6 93889 8 70489
34 2 83156 4 01956 5 38756 6 95556 8 72356
33 2 86225 4 03225 5 40225 6 97225 8 74225
36 2 87296 4 04496 5 41696 6 98896 8 76096
37 2 88369 4 05769 5 43169 7 00569 8 77969
38 2 89444 4 07044 5 44644 7 02244 8 79844
39 2 90321 4 08321 5 46121 7 03921 8 81721-
40 2 91600 4 09600 5 47600 7 05600 8 83600
41 2 92681 410881 5 49081 7 07281 8 85481
42 2 93764 412164 5 50564 7 08914 8 87364
43 294849 413449 5 52049 710649 8 89249
44 2 95936 414736 5 53536 712336 891136
45 2 97025 416025 5 55025 714025 8 93025
46 2 98116 417316 5 56516 7 15716 8 94916
47 2 99209 418609 5 58009 717409 8 96809
48 3 00304 419904 5 59504 719104 8 98704
49 3 01401 4 21201 5 61001 7 20801 9 00601
V
Вторыя степени ЧИСЕЛЪ ОТЪ ) до 1000.
Числ. 500 600 700 800 900
КО 3 02500 4 22500 5 62500 7 22500 9 02500
51 3 03601 4 23801 5 64001 7 24201 9 04401
62 3 04704 4 25104 Б 65504 7 25904 9 06304
63 3 05809 4 26409 5 67009 7 27609 9 08209
54 3 06916 4 27716 5 68516 7 29316 910116
66 3 08025 4 29025 5 70025 7 31025 9 12025
56 3 09136 4 30336 5 71536 7 32736 913936
57 310249 4 31649 5 73049 7 34449 915849
68 311364 4 32964 5 74564 7 36164 917764
69 312481 4 34281 5 76081 7 37881 919681
60 313600 4 35600 Б 77600 7 39600 9 21600
61 314721 4 36921 5 79121 7 41321 9 23521
62 316844 4 38244 5 80644 7 43044 9 25444
63 316969 4 39569 Б 82169 7 44769 9 27369
64 318096 4 40896 5 83696 7 46496 9 29296
65 319225 4 42225 5 85225 7 48225 9 31225
66 3 20356 4 43556 5 86756 7 49956 9 33156
67 3 21489 4 44889 5 88289 7 51689 9 35089
68 3 22624 4 46224 5 89824 7 53424 9 37024
69 3 23761 4 47561 5 91361 7 55161 9 38961
70 3 24900 4 48900 5 92900 7 56900 9 40900
71 3 26041 4 50241 5 94441 7 Б864І 9 42841
72 3 27184 4 51584 5 95984 7 60384 9 44784
73 3 28329 4 52929 5 97529 7 62129 9 46729
74 3 29476 4 54276 5 99076 7 63876 9 48676
75 3 30625 4 55625 6 00625 7 65625 9 50625
76 3 31776 4 56976 6 02176 7 67376 9 52676
77 3 32929 4 58329 6 03729 7 69129 9 54529
78 3 34084 4 59684 6 05284 7 70884 9 56484
79 3 35241 46ЮІІ 6 06841 7 72641 958441
80 3 36400 4 62400 6 08400 7 74400 9 60100
81 3 37661 4 63761 6 09961 7 76161 9 62361
82 3 38724 4 65124 611524 7 77924 9 64324
83 3 39889 4 66489 6 13089 7 79689 9 66289
84 3 41056 4 67856 614656 7 81456 9 68256
85 3 42223 4 69225 616225 7 83225 9 70225
86 3 43396 4 70596 6 1 7796 7 84996 9 72196
87 3 44569 4 71969 619369 7 86769 9 74169
88 3 45744 4 73344 6 20944 7 88544 9 76144
89 3 46921 4 74721 6 22521 7 90321 9 78121
90 3 48100 4 76100 6 24100 7 92100 9 80100
91 ' 3 49281 4 77481 6 25681 7 93881 9 82081
92 3 50464 478864 6 27264 7 95664 9 84064
93 3 51649 4 80249 6 28849 7 97449 9 86049
94 3 52836 4 81636 6 30436 7 99236 9 88036
93 3 54025 4 83025 6 32025 8 01025 9 90025
96 3 55216 4 84416 6 33616 8 02816 9 92016
97 3 56409 4 85809 6 35209 8 04609 9 94009
98 3 57604 4 87204 6 36804 8 06404 9 96004
99 3 58801 4 88601 6 38401 8 08201 9 98661
VI
• Третья степень і ЧИСЕЛЪ ОТЪ 1 ) до 1000.
Числ. 0 100 200 300 400
0 0 10 00000 80 00000 270 00000 640 00000
1 і 10 30301 81 20601 272 70901 644 81201
2 8 10 61208 82 42408 275 43608 649 64808
3 27 10 92727 83 65427 27818127 654 50827
4 64 11 24864 84 89664 280 94464 659 39264
5 125 11 57625 86 15125 283 72625 664 30125
6 216 11 91016 87 41816 286 52616 669 23416
7 343 12 25043 88 69743 289 34443 674 19143
8 512 12 59712 89 98912 292 18112 679 17312
9 729 12 93029 91 29329 295 03629 684 17929
10 1000 13 31000 92 61000 297 91000 689 21000
11 1331 13 67631 93 93931 300 80231 694 26531
12 1728 14 04928 , 95 28128 303 71328 699 34528
13 2197 14 42897 96 63597 306 64297 704 44997
14 2744 14 81544 98 00344 309 59144 709 57944
13 3373 15 20875 99 38375 312 55875 714 73375
16 4096 15 60896 100 77696 315 54496 719 91296
17 4913 16 01613 102 18313 318 55013 725 11713
18 5832 16 43032 103 60232 321 57432 730 34632
19 6859 16 85159 105 03459 324 61759 735 60059
20 8000 17 28000 106 48000 327 68000 740 88000
21 9261 17 71561 107 93861 330 76161 746 18461
22 10648 18 15848 109 41048 333 86248 751 51448
23 12167 18 60867 110 8956'? 336 98267 756 86967
24 13824 19 06624 112 39424 340 12224 762 25024
23 15625 19 53125 113 90625 343 28125 767 65625
26 17576 20 00376 115 43176 346 45976 773 08776
27 19683 20 48383 116 97083 349 65783 778 54483
28 21952 20 97132 118 52352 352 87552 784 02752
29 24389 21 46689 120 08989 356 11289 789 53589
30 27000 21 97000 121 67000 359 37000 795 07000
31 29791 22 48091 123 26391 362 64691 800 62991
32 32768 22 99968 124 87168 . 365 94368 806 21568
33 35937 23 52637 126 49337 369 26037 811 82737
34 39304 24 06104 128 12904 372 59704 817 46504
35 42875 24 60375 129 77875 375 95375 82312875
36 46656 23 15456 131 44256 379 33056 828 81856
37 50653 25 71333 133 12053 382 72753 834 53433
38 54872 26 28072 134 81272 386 14472 840 27672
39 59319 26 85619 136 31919 389 58219 846 04519
40 64000 27 44000 138 24000 393 04000 851 84000
41 68921 28 03221 139 97521 396 51821 837 66121
42 74088 28 63288 141 72488 400 01688 863 50888
43 79507 29 24207 143 48907 403 53607 869 38307
44 85184 29 85984 145 26784 407 07584 875 28384
43 91125 30 48625 147 06125 410 63625 881 21125
46 97336 3112136 148 86936 414 21736 88716536
47 1 03823 31 76523 150 69223 417 81923 893 14623
48 1 10592 32 41792 152 52992 421 44192 899 15392
49* 1 17649 33 07949 154 38249 425 08549 90518849
VII
Третья степень ЧИСЕЛЪ ОТЪ ( до 1000. 1
Числ. 0 100 200 300 400
50 1 25000 33 75000 156 25000 428 75000 911 25000
51 1 32651 34 42951 15813231 432 43551 917 33851
52 1 40608 35 11808 160 03008 436 14208 923 45408
53 1 48877 . 35 81577 161 94277 439 86977 929 59677
54 1 57464 36 52264 163 87064 443 61864 935 76664
55 1 66375 37 23875 165 81373 447 38875 941 96375
56 1 75616 37 96416 167 77216 431 18016 94818816
57 1 85193 38 69893 169 74593 454 99293 934 43993
58 1 95112 39 44312 171 73512 458 82712 960 71912
59 2 05379 40 19679 173 73979 462 68279 967 02579
60 216000 40 96000 173 76000 466 56000 973 36000
61 2 26981 41 73281 177 79581 470 43881 979 72181
62 2 38328 42.51528 179 84728 474 37928 98611128
63 2 50047 43 30747 181 91447 478 32147 992 52847
64 2 62144 44 10944 183 99744 482 28544 998 97344
65 2 74625 44 92125 186 09625 486 27125 1003 44625
66 2 87496 45 74296 188 21095 490 27896 1011 94696
67 3 00763 46 57463 190 34163 494 30863 1018 47563
68 3 14432 47 41632 192 48832 498 36032 1025 03232
69 3 28509 48 26809 194 63109 502 43409 1011 61709
70 3 43000 49 13000 196 83000 506 53000 1038 23000
71 3 57911 50 00211 199 02311 510 64811 1044871II
72 3 73248 30 88448 201 23648 314 78848 1051 34048
73 3 89017 51 77717 203 46417 518 95117 1058 23817
74 4 05224 52 68024 205 70824 52313624 1064 96424
75 4 21875 53 59375 207 96873 527 34373 1071 71875
76 4 38976 54 51776 210 24576 331 37376 1078 50176
77 4 56533 55 45233 212 53933 533 82633 1085 ЗІЗЗЗ
78 4 74552 56 39732 214 84932 540 10132 1092 13352
79 4 93039 57 35339 21717639 544 39939 1099 02239
80 512000 58 32000 219 52000 548 72000 1105 92000
81 5 31441 59 29741 22188041 553 06341 1112 84641
82 5 51368 60 28568 224 25768 557 42968 1119 80168
83 5 71787 61 28487 226 63187 561 81887 1126 78587
84 92704 62 29304 229 06304 566 23104 1133 79904
85 614125 63 31625 231 49125 570 66625 1140 84125
86 636056 64 34836 233 93636 57512436 114791236
87 6 58303 65 39203 236 39903 379 60603 1133 01303
88 6 81472 66 44672 238 87872 58411072 116214272
89 7 04969 67 51269 241 37369 588 63869 1169 30169
90 7 29000 68 59000 243 89000 593 19000 1176 49000
91 7 53571 69 67871 246 42171 597 76471 1183 70771
92 7 78688 70 77888 248 97088 602 36288 1190 93488
93 8 04357 ' 71 89057 231 33757 606 98457 1198 23157
94 8 30584 73 01384 254 12184 611 62984 1205 53784
95 8 57375 74 14875 256 72375 616 29875 1212 87375
96 8 84736 75 29536 259 34336 620 99136 1220 23936
97 912673 76 45373 261 98073 625 70773 1227 63473
98 9 41192 77 62392 264 63592 630 44792 1235 05992
99 9 70299 78 80599 '267 30899 635 21199 1242 51499
VIII
Третья степень ЧИСЕЛЪ ОТЪ । ) ДО 1000.
Числ. 500 600 700 800 900
0 1250 00000 2160 00000 3430 00000 5120 00000 7290 00000
1 1257 51501 2170 81801 344472101 5139 22401 7314 32701
2 1265 06008 2181 67208 3459 48408 5158 49608 7338 70808
3 1272 63527 2192 56227 3474 28927 5177 81627 7363 14327
4 1280 24064 2203 48864 3489 13664 5197 18464 7387 63264
5 1287 87625 2214 45125 3504 02623 5216 60125 7412 17625
6 1295 54216 2225 45016 3518 95816 5236 06616 7436 77416
7 1303 23843 2236 48543 3533 93243 5255 57943 7461 42643
8 1310 96512 2247 55712 3348 94912 5275 14112 748613312
9 1318 72229 2258 66529 3564 00829 5294 75129 7510 89429
10 1326 51000 2269 81000 357911000 5314 41000 ' 7535 71000
11 1334 32831 2280 99131 3594 25431 5334 11731 7560 58031
12 134217728 2292 20928 3609 44128 5353 87328 7585 50528
13 1350 05697 2303 46397 3624 67097 5373 67797 7610 48497
14 1357 96744 2314 75544 3639 94344 5393 53114 7635 51944
18 1365 90875 2326 08375 3653 25875 5413 43375 7660 60875
16 1373 88096 2337 44896 3670 61696 5433 38496 7685 75296
17 1381 88413 2348 85113 3686 01813 5453 38513 7710 95213
18 1389 91832 2360 29032 3701 46232 5473 43432 7736 20632 •
19 1397 98359 2371 76659 3716 94959 5493 53259 7761 51559
20 1406 08000 2383 28000 3732 48000 5513 68000 7786 88000
21 1414 20761 2394 83061 3748 05361 5533 87661 7812 29961
22 1422 36648 2406 41848 3763 67048 5554 12248 7837 77448
23 1430 55667 2418 04367 3779 33067 5574 41767 7863 30467
24 1438 77824 2429 70624 3795 03424 5594 76224 7888 89024
25 1447 03125 2441 40625 3810 78125 5615 15625 7914 53125
26 1455 31576 2453 14376 3826 57176 5635 59976 7940 22776
27 1463 63183 2464 91883 3842 40583 5656 09283 7965 97983
28 1471 97952 2476 73152 3858 28352 5676 63552 7991 78752
29 1480 35889 2488 58189 3874 20489 5797 22789 8017 65089
30 1488 77000 2500 47000 3890 17000 5717 87000 8043 57000
31 1497 21291 2512 39591 390617891 5738 56191 8069 54491
32 1505 68768 2524 33968 3922 23168 5759 30368 8095 57568
33 151419437 2336 36137 3938 32837 5780 09537 8121 66237
34 152273304 2548 40104 3954 16904 5800 93704 8147 80504
35 1531 30375 2360 47875 3970 65375 5821 82875 8174 00375
36 1539 90656 2572 59456 3986 88256 5842 77056 8200 25856
37 1548 54153 2584 74853 4003 15553 5863 76233 8226 56953
38 1557 20872 2596 94072 4019 47272 5884 80472 8252 93672
39 1565 90819 2609 17119 4035 83419 5905 89719 8279 36019
40 1574 64006 2621 44000 4052 24000 5927 04000 8305 84000
41 1583 40421 2633 74721 4068 69021 5948 23321 8332 37621
42 1592 20088 2646 09288 408518488 5969 47688 8358 96888
43 1601 <>3007 2638 47707 4101 72407 5990 77107 8385 61807
44 1609 89184 2670 89984 4118 30784 6012 11584 8412 32384
45 1618 78625 2683 36125 4134 93625 6033 51125 8439 08625
46 1627 71336 2695 86136 4151 60936 6054 95736 8465 90536
47 1636 67323 2708 40023 4168 32723 6076 43423 8492 78123
48 1645 66592 2720 97792 4183 08992 6098 00192 8519 71392
49 1654 69149 2733 59449 4201 89749 6119 60049 854670349
IX
Третья степень ЧИСЕЛЪ ОТЪ 0 ло 1000.
Числ 500 600 700 800 900
ко 1663 75000 2746 23000 4218 75000 6141 25001? 8573 75000
51 1672 84151 2758 94431 4235 64751 6162 95051 8600 85351
52 1681 96608 2771 67808 4252 59008 6184 70208 8628 01408
53 169112377 2784 45077 4269 37777 6206 50477 8655 23177
54 1700 31464 2797 26264 1286 61064 6228 35864 8682 50664
55 1709 53875 2810 11375 4303 68875 6230 26375 8709 83875
56 1718 79616 2823 00416 4320 81216 6272 22016 8737 22816
57 1728 08693 2835 93393 4337 98093 6294 22793 8764 67493
58 1737 41112 2848 90312 435319312 6316 28712 879217912
59 1746 76879 286191179 4372 45479 6338 39779 8819 74079
60 1756 16000 2874 96000 4389 76000 6360 56000 8847 36000
61 1765 58481 2888 04781 4407 11081 6382 77381 8875 03681
62 1775 04328 290117528 1424 30728 6405 03928 8902 77128
63 1784 53547 2914 34247 4141 94947 6427 35647 8930 56347
64 1794 06144 2927 54944 4159 13744 6449 72544 8958 41344
65 1803 62125 2940 79625 4476 97125 6472 14625 8986 32123
66 1813 21496 2954 08296 4494 55096 6494 61896 9014 2869 >
67 1822 84263 2967 40963 4512 17663 6517 14363 9042 31063
68 1832 50432 2980 77632 4529 81832 6539 72032 9070 39232
69 1842 20009 299418309 4517 56609 6562 34909 9098 53209
70 1851 93000 3007 63000 4565 33000 6585 03000 9126 73000
71 1861 69411 3021 11711 4583 МОП 6607 76311 9154 98611
72 1871 49248 3034 64448 1600 99648 6630 54848 9183 30048
73 1881 32517 3048 21217 4618 89917 6633 38617 9211 67317
74 1891 19224 3061 82024 4636 84824 6676 27624 9240 10421
75 1901 09375 3075 46875 4654 84375 6699 21875 9268 59375
76 1911 02976 3089 15776 4672 88576 6722 21376 9297 14176
77 192100033 3102 88733 4690 97433 6747 26133 9325 74833
78 1931 00552 3116 65732 4709 10952 6768 36152 9354 41352
79 1941 04539 3130 46839 4727 29139 6791 51439 9383 13739
80 1951 12000 3144 32000 4715 52000 6814 72000 9411 92000
81 1961 22911 3158 21241 4763 79541 6837 97841 9140 76141
82 1971 37368 3172 14568 478211768 6861 28968 9469 66168
83 1981 55287 318611987 4800 48687 6864 65387 9498 62087
84 1991 76704 320013304 4818 90304 6908 07104 9527 63904
85 2002 01625 3214 19125 4837 36625 6931 54123 9556 71625
86 2012 30056 3228 28856 4855 87656 6953 06156 9585 83256
87 2022 62003 3242 42703 4874 43403 6978 64103 9615 04803
88 2032 97472 3256 60672 4893 03872 700227072 9644 30272
89 2043 36469 3270 82769 4«11,69069 7023 95369 9673 61669
90 2053 79000 3285 09000 4930 39000 7049 69000 9702 99000
91 2064 25071 3299 39371 4949 13671 7073 47971 9732 42271
92 207474688 3313 37888 4967 93088 7097 32288 9761 91488
93 2085 27857 3328 12557 4986 77257 712121937 9791 46657
94 2095 84584 3342 55384 5005 66184 7145 16984 9821 07784
95 2106 448 75 3357 02375 502» 59875 7169 17375 9830 74875
96 2117 08736 3371 53536 5043 58336 7193 23136 9880 47936
97 2127 76173 3386 08873 3062 61573 7217 34273 9910 26973
98 2138 47192 3400 68392 5081 69592 7241 50792 9940 11992
99 2119 21799 3415 7 2099 5100 82399 7265 72699 9970 02999
32
Четвертая степень чиселъ отъ 0 до 1000.
Числ. 0 100 200 300
0 0 1000 00000 16000 00000 81000 00000
1 1 1040 60401 ' 16322 40801 82085 41201
2 16 1082 43216 16649 66416 83181 69616
3 81 1125 50881 16981 81681 84288 92481
4 256 1169 85856 17318 91456 85407 17056
8 625 1215 50625 17661 00625 86536 50625
С> 1296 1262 47696 18008 14096 87677 00496
7 2401 1310 79601 18360 36801 88828 74001
8 4096 1360 48896 18717 73696 89991 78496
9 6561 1411 58161 19080 29761 91166 21361
10 10000 146410000 19448 10000 92352 10000
11 14641 1518 07041 19821 19441 93549 51841
12 20736 1573 51936 20199 63136 94758 54336
13 28561 1630 47361 20583 46161 95979 24961
14 38416 1688 96016 20972 73616 97211 71216
15 50625 1749 00625 21367 50625 98456 00625
16 65536 1810 63936 21767 82336 99712 20736
17 83521 1873 88721 22173 73921 1 00980 39121
18 1 04976 193877776 22585 30576 1 02260 63376
19 1 30321 % 2005 33921 23002 37521 1 03553 01121
20 1 60000 2073 60000 23425 60000 1 04837 60000
21 194481 2143 58881 23854 43281 1 06174 47681
22 2 34256 2215 33456 24289 12656 1 07503 71856
23 2 79841 2288 86641 24729 73441 1 08845 40241
24 3 31776 2364 21376 25176 30976 1 10199 60376
25 3 90625 2441 40625 25628 90623 1 11366 40625
26 4 56976 2520 47376 26087 57776 1 12945 88176
27 5 31441 2601 44641 26532 37841 114338 11041
28 614656 2684 35456 27023 36256 1 15743 17056
29 7 07281 2769 22881 27500 58481 1 17161 14081
30 810000 2856 10000 27984 10000 1 1859210000
31 9 23521 2944 99921 28473 96321 1 20036 12721
32 10 48576 3035 95776 ' 28970 22976 1 21493 30176
33 11 85921 3129 00721 29472 93521 1 22963 70321
34 13 36336 3224 17936 2998219336 1 24447 41136
35 15 00625 3321 50625 30498 00625 1 2394450623
36 16 79616 3421 02016 31020 44416 1 27455 06816
37 18 74161 352275361 31549 56561 1 28979 17761
38 20 85136 3626 73936 32085 42736 1 30316 91536
39 23 13441 3733 01041 32628 08641 1 32068 36241
40 25 60000 3841 60000 33177 60000 1 33633 60000
41 28 25761 3952 54161 33734 02561 1 35212 70961
42 31 11696 4065 86896 31297 42096 1 36805 77296
43 34 18801 418161601 34867 84401 1 38412 87201
44 37 48096 4299 81696 35445 35296 1 40034 08896
45 41 00625 4420 50625 36030 00623 1 41669 50625
46 44 77456 4543 71856 3662186256 1 43319 20636
47 48 79681 4669 48881 37220 98081 1 44983 27281
48 53 08416 4797 85216 37827 42016 1 46661 78816
49 57 64801 4928 84401 38441 24001 1 48354 83601
XI
Четвертая сгепеііі. чиселъ отъ 0 до 100Э
Числ. 0 100 200 ЗОО
во 62 50000 5062 50000 39062 50000 1 50062 50000
51 67 6о20і 5198 85601 39691 26001 1 51784 86401
92 7311616 5337 94816 40327 58016 153622 01216
вз 78 90481 5479 81281 40971 52081 1 55274 02881
54 83 03056 5624 48656 41623 14256 1 57040 99856
55 91 50625 5772 00625 42282 50625 ' 1 58823 00625
Й6 98 34496 5922 40896 42949 67296 1 6062013696
37 105 56001 607373201 43624 70401 1 62432 47601
58 11316496 6232 01296 44307 66096 1 6426010896
59 12117361 6391 28961 44998 60561 1 66103 12161
60 129 60000 6553 601Ю9 45697 60000 1 67961 60000
61 138 45841 6713 9824 46404 70641 1 69835 6’041
62 147 76336 6887 47536 47119 98736 1 7172529936
63 157 52961 7059 11761 47843 50561 1 736)0 69361
64 167 77216 7233 9 4816 48575 32416 1 75551 90016
65 178 50625 7412 00625 49315 50625 1 77489 00625
66 189 74736 7593 33136 50064 11536 1 79442 09936
67 201 51121 7777 96321 5082' 21521 1 81411 26721
68 213 81376 7965 94176 51586 86976 1 83396 59776
69 226 67121 8157 30721 5236114321 1 85398 17921
70 24010000 8352 10000 53144 10000 1 8741610000
71 25411681 8550 36081 53935 80481 189450 44881
72 268 73856 875213056 54736 32256 1 91501 31456
73 283 98241 8957 45041 55545 71841 1 93568 78641
74 299 86576 9166 36176 56364 05776 1 95652 95376
75 316 40625 9378 90625 57191 40625 1 97753 90625
76 333 62176 9595 12576 58027 82976 1 99871 73376
77 351 53041 9815 06241 58873 39441 2 02006.12641
78 37015056 10038 75856 59728 16656 2 04158 37456
79 389 50081 10266 25681 60592 21281 2 06327 36881
80 409 60000 10497 бОчОО 61465 60000 2 08513 66000-
81 430 46721 10732 83121 62348 39521 2 10717 15921 •
82 452 12176 10971 99376 63240 66576 21293813776
83 474 58321 11215 13121 64142 47921 . 2 15176 62721
84 497 87136 11462 28736 65053 90336 2 17432 71936
83 522 00625 11713 50625 65975 00625 2 19706 50625
86 547 00816 11968 8з216 66905 85616 2 21998 08016
87 572 89761 12228 30961 67846 52*61 2 24307 53361
88 599 69536 12491 98336 68797 07136 2 26634 95936
89 627 42241 12759 89841 69757 57441 2 28980 45041
90 65610000 1303210000 70728 10000 2 31344 10000
91 685 74961 13308 63.161 71708 71761 2 33726 00161
92 716 39296 13589 54496 72699 49696 2 36126 24896
93 748 05201 13874 88001 73700 50801 2 38544 93601
94 780 74896 14164 68496 74711 82096 2 4098215696
95 814 50625 14459 00625 75733 50625 2 43438 00625
96 849 34636 14757 89056 7676а 63456 2 45912 57856
97 885 29281 15061 3848І 77808 27681 2 48405 96881
98 922 36816 15369 53616 78861 50416 2 50918 27216
99 960 59601 15682 39201 79925 38801 2 5344958401
XII
Четвертая степень чиселъ отъ 0 до 1000.
Числ. 400 500 600
0 2 56000 00000 6 25000 00000 12 96000 00000
1 2 58569 61601 6 30015 02001 13 04661 62401
2 2 61158 52816 6 35060 16016 1313366 59216
3 2 63766 83281 6 40135 54081 13 22115 04881
4 2 66394 62656 6 45241 28256 13 30907 13856
8 2 69042 00625 6 50377 50625 13 39743 00625
в 2 71709 06896 6 55544 33296 13 48622 79696
7 2 7 4395 91201 6 60741 88401 13 57546 65601
8 2 77102 63296 6 65970 28096 13 66514 72896
9 2 79829 32961 6 71229 64561 13 7552716161
10 2 82576 ІООоо 6 7652010000 13 8458410000
11 2 85343 04241 6 81841 76641 13 93685 69041
12 2 88130 25536 6 87194 76736 14 02832 07936
13 2 90937 83761 6 92579 22561 14 12023 41361 С
14 293765 88816 6 97995 26416 14 21259 84016
15 2 96614 50625 7 03443 06625 14 30541 50625
16 2 99483 79136 7 08922 57536 14 39868 55936
17 3 02373 8 '321 7 14434 09521 14 49241 14721
18 3 05284 76176 7 19977 68976 14 58059 41776
1!) 3 08216 64721 7 25553 48321 14 68123 51921
20 3 11169 60000 7 31161 60000 14 77633 60000
21 3 14143 72081 7 36802 16481 14 87189 80881
22 317139 11056 7 42475 30256 14 96792 29456
23 3 20155 87041 7 48181 13841 15 06441 20641'
24 3 2319410176 7 53919’9776 15 16136 69376
25 3 26253 90625 7 59691 40625 15 25878 90625
26 3 29335 38576 7 65496 08976 15 35667 99376
27 3 32438 64241 7 71333 97441 15 45504 10641
28 3 35563 77856 7 77205 18656 15 55387 39456
29 3 38710 89681 7 83109 85281 15 65318 00881
30 3 41880 10000 7 89048 10000 15 7529610000
31 3 45071 49121 7 95020 0552. 15 85321 81921
32 3 48283 17376 8 01025 84576 15 95395 31776
33 3 51521 25121 8 07065 59921 16 05516 74721
34 3 54779 82736 8 13139 44336 1615(186 25936
35 3 58061 00625 8 19247 50625 16 25904 00625
36 3 61364 89216 8 253«9 91616 16 3617014016
37 3 6469158961 8 3'566 80161 16 46484 81361
38 3 68041 20336 8 37778 29136 16 56848 17936
39 3 71413 83841 8 44024 51441 16 67260 39041
40 3 74809 60000 8 50305 6ОО00 16 77721 60000
41 3 78228 59361 8 56621 67761 16 88231 96161
42 3 81670 9 2496 8 62972 87696 16 98791 62896
43 3 85136 70001 8 69359 32801 17 09400 75601
44 3 88626 02496 8 7578116096 17 20059 49696
45 3 92139 00625 8 82238 50625 17 30768 00625
46 3 95675 75056 8 88731 49456 17 41526 43856
47 3 99236 36 481 8 95260 25681 17 62334 94881
48 4 02820 95616 9 01X24 92416 17 63193 6921..
49 4 06429 63201 9 08425 62801 17 7410282401
XIII
Четвертая степень чиселъ отъ 0 до 1000.
Числ. 400 500 600
30 410062 ЙОООО 9 15062 50000 17 83062 50000
31 4137*9 66801 9 2173а 67201 17 91ИП2 87601
32 4 17401 24416 9 28445 27616 18 07134 10816
33 4 21107 33681 9 33191 44481 18 18246 33281
54 4 24838 03456 9 41974 31056 18 29409 76636
53 4 28593 30625 9 48794 00625 18 40624 50623
56 4 32373 80096 9 55650 66496 18 51890 72896
37 4 36179 04801 9 62544 12001 18 63208 39201
58 4 4П009 33696 9 69473 50496 18 74378 25296
59 4 43864 83761 9 76443 73361 18 83999 86961
60 4 47745 60000 9 8а 449 60000 18 97473 60000
61 4 51651 73441 9 90493 07841 19 08999 60241
62 4 53583 41136 9 97574 32836 19 29378 03536
63 4 39340 68161 10 04693 46961 19 32209 03761
64 4 63523 67616 1011850 63216 19 43892 82816
63 4 67332 30625 1019046 00625 19 55629 30625
66 4 71367 28336 10 26279 66736 19 67419 25136
67 4 7562811921 10 33551 77121 19 79262 22321
68 4 7971512376 10 40862 45376 1991158 58176
69 4 83828 41321 10 4821Д 85121 20 03108 48721
70 4 87968 10000 10 53600 10000 201511210000
71 4 92134 29281 10 63027 33681 20 27161, 58081
72 4 96327 10656 10 70493 69356 20 39281 09056
73 5 00546 65441 10 77999 32241 20 51146 79041
74 3 04793 04976 10 83544 34576 20 63666 84176
75 5 09066 40625 10 93128 90623 20 73941 40623
76 5 13366 83776 110073314176 20 88270 64376
77 5 17694 43841 110841719041 21 00634 72241
78 5 22049 38236 11 1612119056 21 130*8 79856
79 3 2643 1 72481 11 23863 28081 21 23588 03681
80 3 30841 60000 11 31649 60000 21 38137 60000
81 3 3527912321 11 39474 28721 21 5074'2 63121
82 5 39744 40976 11 47339 58176 21 63403 33376
83 5 44237 37521 11 53245 32321 21 76119 87121
84 5 48738 73536 11 63191 93136 21 88892 36736
83 5 53308 00623 11 71179 50625 22 01721 00625
86 5 57885 30416 11 79208 12816 22 14605 95216
87 5 6249134561 11 87277 95761 22 27347 36961
88 5 67125 64736 11 93389 13536 22 40543 42336
89 571788 52641 12 03341 80241 22 33600 27841
90 5 76480 10000 121173610000 22 66712 10000
91 5 81200 48361 12 19972 16961 22 “9881 05361
92 5 85949 80096 12 28250 13296 22 9310? 30496
93 5 90728 16401 12 36570 19201 23 06391 02001
94 5 95335 69296 12 44932 <2896 23 « 9732 36496
95 6 00372 60625 12 5333“ 00623 23 3313150625
| 96 6 05238 72256 12 61784 06656 23 46588 61036
В 97 6 10134 46081 12 70273 75281 23 60103 84481
1 98 6 15059 84016 12 78806 20816 * 23 73677 37616
| 99 6 20014 98001 12 87381 37601 23 87309 37201
XIV
Четвертая степень чиселъ отъ 0 до 1000.
Числ. 700 800 900
о 24 01000 00000 40 96000 00000 65 61000 00000
1 2414749 42801 41 16518 43201 65 90208 63601
2 24 28557 82416 41 37113 85616 66 19514 68816
3 24 42425 35681 41 57786 46481 66 48918 37281
4 24 5635219456 417853645056 66 78419 90656
б 24 70338 50625 41 99364 00625 67 08019 50625
6 24 84384 46096 42 20269 32496 67 37717 38896
7 24 98490 22801 42 41252 60001 67 67513 77201
8 2512655 97696 42 62314 02496 67 97408 87296
9 25 26881 87761 42 83453 79361 68 27402 90961
10 25 41168 10000 43 04672 10000 68 57496 10000
11 25 55514 81441 43 25969 13841 68 87688 66241
12 25 69922 19136 43 47345 10336 69 17980 81536
13 25 84390 40161 43 6880018961 69 4837277761
14 25 98919 61616 43 90334 59216 69 78864 76816
15 2613510 00625 44 11948 50625 70 09457 00625
16 26 28161 74336 44 3364212736 70 40149 71136
17 26 42874 99921 44 55415 65121 70 70943 10321
18 26 57649 94576 44 77269 27376 71 01837 40176
19 26 72486 75521 4499303 19121 71 32832 82721
20 26 87385 60000 45 21217 60000 71 63929 60000
21 27 02346 65281 45 43312 69681 71 95127 94081
22 27 17370 08656 45 65488 67856 72 26428 07056
23 27 32456 07441 45 87745 74241 72 57830 21041
24 27 47604 78976 46 10084 08576 72 89334 58176
25 27 62816 40625 46 32503 90625 73 20941 40625
26 27 78091 09776 46 55005 40176 73 52650 90576
27 27 93429 03841 46 77588 77041 73 84463 30241
28 28 08830 40256 47 00254 21056 74 16378 81856
29 28 24295 36481 47 23001 92081 74 48397 67681
30 28 39824 10000 47 45832 Ю00О 74 80520 10000
31 28 55416 78321 47 68744 94721 75 12746^1121
32 28 71073 58976 47 91740 66176 75 45076 53376
33 28 86794 69521 48 14819 44321 75 77510 99121
34 29 02580 27536 48 37981 49136 76 10049 90736
35 29 18430 50625 48 61227 00625 76 42693 50625
36 29 34345 56416 48 84556 18816 76 75442 01216
37 29 50325 62561 49 07969 23761 77 08295 64961
38 29 66370 86736 49 31466 35336 77 41254 64336
39 29 82481 46641 49 5504.7 74241 77 74319 21841
40 2998657 60009 49 78713 60000 78 07489 60000
41 3014899 44561 50 02464 12961 78 40766 01361
42 30 31207 18096 50 26299 53296 78 74148 68496
43 30 47580 98401 50 50220 01201 79 07637 84001
44 30 64021 03296 50 74225 76896 79 41233 70496
45 30 80527 50625 50 98317 00625 79 74936 50625
46 30 97100 58256 51 22493 92656 80 08746 47056
47 31 13740 44081 51 46736 73281 80 42663 82481
48 31 30447 26016 51 71105 62816 80 76688 79616
49 31 47221 22001 5195540 81601 8110821 61201
XV
Четвертая степень чиселъ отъ 0 ДО 1000.
Числ. 700 800 900
30 31 52 53 54 31 64062 50000 31 80971 28001 31 07947 74016 3214992 06081 32 32104 42256 52 20062 50000 52 44670 88401 52 69366 17216 52 94148 56881 5319018 27856 81 45062 50000 81 79411 68801 82 13869 40416 82 48435 87681 82 83111 33456
55 56 57 58 39 32 49283 00625 32 66333 99296 32 83831 56401 33 01237 90096 33 1869.1 18561 53 43975 50625 53 69020 45696 53 94153 33601 54 19374 34896 54 44683 70161 83 17896 00625 83 52790 12096 83 87793 90801 84 22907 59..96 84 58131 41761
60 61 62 63 64 33 36217 60000 33 538И 32641 33 71474 54736 33 89207 44561 34 07010 20416 54 70081 60000 54 95568 25041 55 211 43 85936 55 46808 63361 55 72562 78016 84 93465 60000 85 28910 37441 85 641'15 97136 86 00132 62161 86 35910 55616
63 66 67 68 69 34 24883 00625 34 42826 03536 3 4 6083Ѵ 47521 34 78923 50976 34 97078 32321 55 98406 50625 56 24340 01936 56 50363 52721 56 76477 23776 57 02681 35921 86 71800 00625 87 07801 20336 87 43914 37921 87 80139 76576 88 16477 59521
70 71 72 73 35 15304 10000 35 33601 02481 35 51969 28256 35 70409 05841 35 88920 53776 57 28976 10000 57 55361 66881 57 81838 27456 58 08406 12641 58 35065 43376 88 52928 10000 88 89491 51281 89 26108 06636 89 62957 99441 89 99861 52976
73 76 77 78 79 36 07503 90625 36 26159 3 4976 36 44887 05441 36 63687 20656 36 82559 99281 58 61816 40625 58 88659 25376 59 15594 18641 59 42621 41456 59 69741 14881 90 36878 90625 90 74010 35776 91 1Г256 11841 91 48616 42236 91 86091 50481
80 81 82 83 84 37 01505 60000 37 -20524 21521 37 39616 02576 37 58781 21921 37 78019 98336 59 96953 60000 6024258 97921 60 51657 49776 60 79149 36721 61 06734 79936 92 23681 60000 926138694321 92 99207 76976 93 37144 31521 93 73196 81536
85 86 87 88 89 37 97332 50625 38 16718 97616 38 36179 58161 38 55714 51136 38 75323 95441 6134414 00625 61 62187 20016 61 90054 59361 62 18016 39936 62 46072 83041 94 13365 50625 94 51650 62116 94 90052 40561 95 28571 08736 93 67206 90641
90 91 '9'2 93 94 38 95008 10000 39 1 4767 1 3761 39 3 4601 25696 39 54510 64801 39 74495 50096 6274224 10000 63 02470 42161 63 30812 00896 63 59249 07601 63 87781 83696 96 03960 16000 96 44830 90561 96 83819 56096 97 22926 30401 97 62131 37296
95 96 97 98 99 39 94556 00625 4014692 35456 40 34904 73681 40 55193 34416 40 75558 36801 64 16410 50625 64 45135 29856 64 73956 42881 65 02874 11216 65 31888 56401 98 01493 00625 98 40957 44256 1 98 80538 92081 99 20239 68016 996005996001 |
XVI
Пятыя СТЕПЕНИ ЧИСЕЛЪ отъ 0 до 1000.
Числ. 0 100 . 200 300
0 0 1 00000 00000 32 06060 00000 243 00000 00000
1 1 1 03101 00501 32 80804 01001 247 07709 01501
2 32 1 10408 08032 33 63232 16032 251 20872 24032
3 243 1 15927 40743 3 4 47308 81243 255 39544 21743
4 1024 1 21665 20024 35 33058 57024 259 63779 85024
б 3125 1 27628 15625 36 20506 28125 263 93634 40625
6 7776 1 33822 55776 37 09677 03776 1’68 29163 51776
7 16807 1 4025517307 38 00396'17807 272 70423 18307
8 32768 1 46932 80768 38 93289 28768 277 17469 76768
9 59049 1 53862 39К49 39 87782 20049 281 70360 00549
10 1 00000 1 61051 00000 40 84161 00000 286 29151 00000
11 161051 1 68505 81551 41 82272 02051 290 93900 22551
12 2 48832 1 76234 16832 42 82321 84832 295 64665 32832
13 3 71293 1 84243 51793 43 84277 32291 300 41505 12793
14 5 37824 1 92541 45824 44 88165 53824 305 24477 61824
15 7 59375 2 01135 71875 45 94013 84373 310 13641 96875
16 10 48576 21013416576 47 01849 84576 31В 09057 52576
17 1419857 2 19244 80357 48 11701 40857 320 10784 01357
18 18 89368 2 28775 77568 49 23596 65568 325 18881 53568
1» 24 76099 2 38635 36399 50 37563 97099 330 33410 57599
20 32 00000 2 48832 00000 51 53632 00000 335 54432 00000
21 40 84101 2 59374 24601 52 71829 65101 340 82007 05601
22 51 53632 2 70270 81632 53 92186 09632 346 16197 37632
23 64 36343 2 81530 56843 55 14730 77343 351 57064 97843
24 79 62624 2 93162 50624 56 39493 38624 357 04672 26624
2В 95 65625 3 05175 78125 57 56503 90625 362 59082 03125
26 118 81376 3 1757 9 69376 58 95792 57376 368 20357 45376
27 143 48007 3 30383 69407 60 27389 89907 373 88562 10407
28 172 10368 3 43597 38368 61 61326 66368 379 63759 94368
29 205 11149 3 57230 51649 62 97633 92149 383 46015 32649
30 243 00000 3 71293 00000 64 36343 00000 391 35193 00000
31 286 29151 3 85794 89651 65 77485 50151 397 3195810651
32 335 54132 4 00746 42432 67 21093 30132 40 1 35776 18432
33 394 35393 4 16157 95893 68 67198 56393 409 4691316893
34 454 35124 4 32040 03424 70 15833 71424 415 65435 39424
36 525 21875 4 48403 34375 71 67031 46873 421 91409 59375
36 604 66176 4 63258 71176 73 20824 82176 428 24902 90176
37 693 43957 4 82617 24457 74 77247 04957 4.14 35982 85457
38 792 35168 5 00490 03168 76 3633171168 441 14717 39168
39 902 24199 5 18888 44699 77 98112 65199 447 71174 85699
40 1024 00000 5 37824 00000 79 62624 00000 454 35124 00000
41 1158 56201 5 57308 36701 81 29900 17201 461 07533 97701
42 1306 91232 5 77353 39232 82 99975 8723? 467 87574 35232
43 1470 08413 5 97971 08943 84 72886 09443 474 75615 09943
44 1649 10224 6 19173 64224 86 48666 12224 481 71726 60224
45 1845'^8125 6 40973 40625 88 27351 53125 488 75979 65623
46 2059 62976 6 63382 90976 90 08978 18976 495 88445 46976
47 229? 43097 6 86414 85507 9193582 26007 503 09195 66507
48 2548 03968 7 10082 11968 93 81200 19968 510 38302 27968
49 >824 75249 7 34397 75749 95". 1868 76249 517 75837 76749
XVII
Пятая степень чиселъ отъ 0 до 1000.
Числ. 0 100 200 1 ЗОО
во 3123 ООООО 7 39375 ООООО 97 65625 ООООО 525 21875 ООООО
ВІ 3450 25231 7 85027 25751 99 62506 26251 532 76487 26751 I
52 3802 04032 81136812032 101 62550 20032 540 39748 28032
53 4181 95493 8 38411 35993 103 65794 76493 548 11732 16993
54 439 1 63024 8 66170 9302-4 105 72278 21024 55э 92513 49024
55 5032 84373 8 94660 96875 107 82039 09375 563 82167 21875
56 5507 31776 9 23895 79776 109 93116 27776 571 80768 73776
57 6016 92057 9 33889 92557 11211548 93037 579 88393 93557
58 6563 56768 9 8-4658 0-4768 114 31376 52768 388 05119 00768
5» 7149 24299 1016213 04799 116 54638 85299 596 31020 65799
60 7776 <10000 10 48576 ООООО 118 81376 00000 604 66176 00000
61 8445 96301 10 81736 16801 121 11628 37301 6/ 3 10662 57801
62 916132832 11 15771 00832 123 45436 68832 621 64558 36832
63 992-4 36343 11 30636 17043 125 82841 97543 630 27941 78043
64 10737-41824 11 86367 -49824 128 23885 57824 639 00891 65824
65 11602 90625 12 22981 03125 130 68609 15625 647 83487 28125
66 12523 32576 12 60493 00576 133 17054 68376 6 >6 7580 36576
67 13501 25107 12 98919 83607 133 69264 46107 665 77935 06607
68 14539 33568 13 38278 21568 138 25281 09568 674 89947 97568
60 13640 31349 13 78384 91849 140 85147 52349 684 11928 12849
70 16807 ООООО 14 19859 ООООО 143 48907 ООООО 693 43957 ООООО
71 18042 29351 14 6211169851 14616603 10351 702 86116 50851
72 19349 17632 15 05366 45632 148 88279 73632 712 38489 01632
73 20730 71593 15 49638 92093 151 63981 12593 722 01157 33093
74 22190 06624 15 94946 94624 154 43751 82624 731 74204 70624
73 23730 4687В 16 41308 59375 157 27636 71875 741 57714 84375
76 25355 25376 16 88742 13376 16015681 01376 751 51771 89376
77 27067 84137 17 37266 04637 163 07930 25157 761 56460 43637
78 28871 74368 17 86899 02368 166 04430 30368 771 71863 58368
79 30770 56399 18 37659 96899 169 05227 37399 781 98072 77899
80 32768 ООООО 18 89568 ООООО 17210368 00000 792 35168 ООООО
81 34867 84401 19 42642 44901. 175 19899 05401 802 83237 65901
82 37073 98432 19 96902 86432 178 33867 74432 813 42368 62432
83 39390 40643 20 52369 01143 181 52321 61643 82412648 22143
84 -41821 19424 21 09060 87424 184 75308 55424 834 9 НВ 4 23424
83 44370 53125 21 66998 656 ’5 188 02876 78125 845 87004 90625
86 47042 70176 22 26202 78176 191 35074 86176 836 91258 94176
87 49842 09207 22 86693 89707 19471951 70207 868 07015 50707
88 5277319168 23 48492 87168 19813556 55168 879 34364 23168
89 55840 59439 24 11620 79949 201 59939 00149 890 73395 20949
90 59049 ООООО 24 76099 ООООО 205 11149 ООООО 902 24199 00000
91 62403 21431 25 41949 01931 208 67236 82451 913 1'6866 62951
92 65908 15231 26 09192 63232 212 28253 11232 925 61489 59232
93 69368 83693 26 77831 84193 215 91248 84693 937 48159 85193
94 73390 40224 27 47948 88224 219 65275 36’24 949 46969 84224
95 77.578 09375 28 19506 21875 223 41384 34375 961 58012 46875
96 81537 26976 28 92546 54976 227 22627 82976 973 81381 10976
97 85873 40287 29 67092 80737 211 09058 21257 986 17169 61757
98 90392 07968 30 43168 15968 235 00728 23968 998 6547 2 31968
99 95099 00499 31 20796 00999 238 97691 01499 1011 26384 01999
33
хѵін
ГІПТА11 СТЕПЕНЬ ЧИСЕЛЪ отъ О до 1000.
Числ.
400
50(1
600
О
1
2
3
4
о
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
46
47
48
49
1024 ООООО ООООО
1036 36416 02001
1049 85728 32032
1062 98033 62243
1076 23429 13024'
1089 62012 53123
1103 13881 90776
1116 79136 18807
ИЗО 57874 24768
1144 30195 81019
1158 56201 ООООО
1172 75090 43051
1187 09665 20832
12111 57326 93293
1216 19077 69824
1230 95020 09373
1243 85257 20376
1260 89892 61857
1276 09030 41368
1291 42775 1809»
1306 91232 00000
1322 54506 46101
1338 32704 65632
1354 2593318343
1370 31299 11624
1386 57910 15625
1 402 9687 4 33376
1419 51300 30907
1 436 21297 22368
1433 06974 73149
1470 08443 ООООО
1487 25812 71151
1504 39195 06432
1522 08701 77393
1539 74415 07424
1557 56537 71875
1373 53092 98(76
1593 70224 63957
1612 02' 47 07168
1630 50675 06199
1649 16224 ООООО
1667 98809 78201
1686 98548 83232
1706 13358 10443
1725 4*3935 08224
1745 01837 78123
176471384 74976
1784 58655 0*7007
1804 63788 33968
1824 8690 4 77249
3125 00000 00000
3156 37525 02501
3188 00200 4О(і32
3219 88177 02743
32{52 01606 41024
3284 40610 65625
3317 05532 47776
3349 96133 11'307
3383 12.102 72768
3416 55889 61549
3480 25251 ООООО
3484 21142 63551
3518 43720 88832
3352 93142 73793
3587 69363 77824
3622 73148 2(875
3658 04048 88376
3693 62427 22357
3729 48443 29368
3765 62257 7839»
380’0 4032 00000
3838 73927 86601
3875 7 ’107 93632
3912 98735 38843
3950 53974 02624
3988 37988 28125
4026 30943 21376
4064 93004 51407
4103 64338 50368
4142 65112 13649
4181 95493 ООООО
4221 55649 31631
4261 45749 94432
4301 63964 37893
4342 16462 75424
4382 97415 84375
4424 (18995 06176
4465 51372 46457
4507 24720 75168
4349 29213 26699
4591 65024 ООООО
4634 32327 58701
4677 31299 31232
4720 62113 10943
4764 24951 56224
4808 199.85 90625
4832 47396 02976
4897 07360 47507
4942 00058 43968
4987 23669 77749
7776 ООООО ООООО
7841 01636 03001
7906 46688 48032
7972 33374 43243
8038 67911 69024
8103 44318 78125
8172 63414 93776
8240 30820 19807
8308 40935 20768
8376 96041 42049
8445 ООООО ООООО
8313 41036 84031
8383 >3232 36832
8633 “0332 34293
8726 33341 83824
8797 83026 34375
886» 59032 56576
8941 81787 8/857
9014 51520 17568
9087 68458 39099
9161 32832 ООООО
9235 44871 27101
9310 04807 21632
9385 12871 59343
9460 69296 90624
9536 74316 40623
9613 28164 09376
9690 310/4 71907
9767 83283 78368
9845 85027 54149
9924 36543 ООООО
10003 3 8067 92131
10082 89840 82132
10162 92100 98393
10243 43088 43424
10624 49043 96875
10406 0 4209 14176
10488 10826 26957
10570 69138 43168
10633 79389 47199
10737 4182 4 ООООО
10821 56687 39201
10906 24223 79232
10991 4*686 11444
11077 18316 04224
ІИ63 43364 03123
11230 26079 30976
11337 60711 88007
11423 49312 31968
11313 92732 78249
Пятая степень чиселъ отъ 0 до 1000.
Числ 400 500 ООО
50
51
52
53
54
1845 28125 ООООО
1865 87570 27231
1886 65362 36032
1907 61623 57493
1928 76476 77024
55
56
57
58
59
1950 10045 34375
1971 62453 23776
1993 33824 94057
2015 24285 48768
2037 33960 46299
5032 84375 ООООО
5079 76355 27751
5125 01729 44032
5171 60868 97993
5218 53768 05024
5265 80673 46875
5313 41769 71776
5361 37241 94557
5409 67275 96768
5458 32058 26799
11602 90625 00000
11692 43442 28251
11782 31438 52032
11873 14868 38493
11964 33987 3302.4
12056 09051 59375
12148 4031819776
12241 28044 93057
12334 72490 44768
12428 73914 07299
60
61
62
63
64
2059 62976 00000
2082 11458 78301
2104 79336 04832
2127 67335 58543
2150 74985 73824
5507 31776 ООООО
5556 66616 98801
5606 36769 72832
5656 42423 39043
5706 83767 81824
65
66
67
68
69
2174 02615 40625
2197 50354 04576
2221 18331 67107
2245 06678 85568
2269 15526 73349
5757 60993 53125
5808 74291 72576
5860 23854 27607
5912 09873 73368
5964 32543 33849
70
71
72
73
74
2293 45007 00000
2317 95251 91351
2312 66394 29632
2467 58367 53593
2392 71905 58624
6016 9 ’037 00000
6069 88609 31851
6123 22395 57632
6176 93611 74093
6231 02434 46624
12523 32576 ООООО
12618 48737 19301
12714 227.79 408.72
12810 54605 19543
12907 44837 89824
13004 93621 65625
13103 01221 40376
13201 67902 88107
13300 93932 61568
13400 79577.94349
13501 23107 ООООО
13602 30788 72351
13703 96892 83632
13806 23689 94393
13909 11451 34624
75
76
77
78
79
2418 06542 96873
2443 62014 77376
2469 40256 66157
2495 39604 86368
2521 60796 18399
6285 49121 09375
6340 33809 65376
6395 56718 86657
6431 18048 14368
6507 17997 5889»
80
81
82
83
84
2548 03968 00000
2574 69258 26401
2601 56805 50432
2628 66748 82643
2653 99227 91424
6563 56768 00000
6620 34360 86901
6677 31578 38432
6735 08023 43143
6793 04099 39424
14012 60419 2(875
14116 70956 53376
14221 432-47 07137
14326 77595 42368
14432 74276 99399
14539 33368 00(100
14646 55745 47401
14754 41037 26432
14862 89872 03643
14972 02379 27424
85
86
87
88
89
2683 54383 03125
2711 32353 02176
2739 33285 31207
2767 57315 91168
2796 04589 41449
6851 40011 15625
6910 15963 10176
6969 32161 11707
7028 88811 39168
7088 86121 61949
15081 78889 28125
15192 19683 18176
15363 25042 92207
15414 95’51 27168
15527 30591 82449
90
91
92
93
94
2824 75249 00000
2853 69138 43451
2882 87302 07232
2912 28984 85693
2941 94632 32224
7149 24299 00ООО
7210 03352 23951
7271 24090 35232
7332 86123 86193
7394 89862 80224
13640 31349 ООООО
15753 97808 0 4431
15868 30233 03232
13983 2О7<’ 86693
16098 94261 2822'»
95
96
97
98
99
2971 84390 59375
3091 98406 38976
3032 36827 02257
3062 99800 39968
3093 87475 02499
7437 35318 71873
75 ’0 23303 66976
7583 53430 42737
7647 26112 47968
7711 41564 02999
16215 26306 84375
16332 25672 9497(1
16449 92379 83257
16568 26808 55968
16687 29251 03449
XX
Пятая степень чиселъ отъ 0 до 1000.
Числ. 700 800 900
о 16807 00000 00000 32768 00000 00000 59049 00000 00000
1 16927 39349 03501 32973 31264 04001 59377 77981 0'301
2 17048 47592 56032 33179 65312 64032 59708 02248 72032
3 17170 25025 83743 33387 02531 24243 60039 73290 647-43
4 17292 71944 97024 33595 43306 25024 60372 91393 53024
5 17415 88616 90625 33804 8802“ 03125 60707 57653 15623
6 17539 75429 43776 34015 37075 91776 61043 71954 39776
7 17664 32591 20307 34226 90848 20807 61381 34991 21307
8 17789 60431 68768 34439 49732 16768 61720 47236 64768
9 17915 59251 22549 34653 14119 03049 62061 0824-4 83549
10 180-12 29351 00000 34867 84401 00000 62403 21-451 00000
11 18169 71033 04551 35083 60971 23051 62746 84371 45551
12 18297 84600 24832 33300 44223 92832 ' 63091 98303 60832
13 18426 70356 34793 35518 34534 15293 63436 64343 95793
14 18556 28605 93824 35737 32358 01824 63786 82398 09824
15 18686 59634 46875 33957 38032 39375 64136 53160 71873
16 18817 63808 24576 36178 51975 92376 64487 77133 60576
17 18949 41374 43357 36400 74587 03837 64340 54823 64357
18 19081 92661 05568 36624 06265 93568 -6.И94 86734 81308
19 • 19215 17976 99599 36848 47413 60099 65530 73368 20399
20 19349 176.12 00000 37073 98432 00000 65908 13232 00000
21 19483 91936 67601 37300 59724 08101 66267 12833 48601
22 19619 41202 49632 37528 31693 77632 66627 66681 05632
23 19755 65741 79843 37757 14746 00343 66989 77284 208-43
24 19892 65867 78624 37987 09286 66624 67353 43133 34624
20030 41894 53125 38218 15722 65625 67718 70800 78123
і 23 20168 94136 97376 38450 34461 83376 68083 54738 73376
27 20308 22910 92407 38683 65913 12907 68433 97481 33407
1 28 20448 28533 06368 38918 10486 34368 68823 99543 62368
29 20589 11320 91649 39153 68592 35149 69193 61441 75649
30 20730 71593 00000 39390 40643 00000 69568 83693 00000
31 20873 09668 52651 39628 2705113151 69943 668) 5 73631
32 21016 25867 70432 39867 28230 58432 70320 11329 46432
। 33 21160 20511 58893 -40107 44596 19393 70698 17754 79893
34 21304 93922 11424 40348 76563 79424 71077 866 іЗ 47424
35 21450 46422 09375 40391 24330 21875 71-459 18428 34375
36 21596 78335 22176 40834 88973 30176 7184213723 38176
37 21743 89986 07457 -41079 70251 87937 72226 73023 68457
1 38 21891 81700 11168 41325 68803 79168 72612 96853 47168
39 22040 53803 67699 41372 85035 88199 73ОО0 83746 08699 [
-40 22190 06524 00000 4182119424 00000 7-3390 40224 00000
41 22340 40489 19701 42070 72333 00201 73781 60818 80701
42 22491 55728 27232 -42321 -44206 75232 74174 48061 23232
43 22643 52671 11943 42573 33470 12-4-43 74569 02483 12943
44 22796 31648 5-2224 -42826 46349 00224 74965 2-4617 48224
45 22949 92992 15625 43080 77870 28125 73363 1-4998 -40625
46 23104 37034 58976 43335 29861 86976 737 6 2 7416114976
-47 23259 64109 28507 -43593 02932 69007 76164 02642 09307
48 23415 74550 59968 43850 97572 67968 76367 00978 75968
49 23572 68693 78749 , 44110 1413279249 76971 69709 79.49
XXI
Пятая степень чиселъ отъ 0 до 1000.
Числ. 700 800 900
во 23730 46875 00000 44370 53125 00000 77378 09373 00000
Ві 23889 09431 28751 4463214922 29251 77786 20515 29751
52 24048 36700 60032 44894 99978 68032 78196 03672 76032
63 24208 89021 78993 45159 08729 1 9493 78607 59390 59993
64 24370 06734 61024 45424 41609 89024 79020 88213 17024
65 2433210179 71875 45690 99057 84375 79435 90683 96876
56 24694 99698 67776 43958 81511 15776 79852 67333 63776
57 24838 75633 93557 46227 89408 96057 8027118769 96557
58 23023 38328 92768 46498 23191 40768 80691 43477 88768
59 25188 881’27 87799 46769 83299 68299 81113 48029 48799
60 26333 25376 00000 47042 70176 00000 81537 26976 00000
61 26322 60419 39801 47316 84263 60301 81962 82869 80801
62 25690 63605 08832 47592 26006 76832 82390 16264 44832
63 25839 63281 00043 47868 95850 80343 82819 27714 61043
64 26029'55795 97824 48'46 94242 05824 832501777613824
65 26200 35499 78125 48426 2(627 90625 83682 87006 03125
66 26372 04743 08376 48706 78456 76576 84117 35962 44376
67 26544 63877 48607 48988 65178 09107 84553 63204 69607
68 2671813255 49368 49271 82242 37568 84991 73293 25568
69 26892 53230 54849 49556 30101 15349 83431 66789 75849
70 27067 84157 00000 49842 09207 00000 85873 40257 00000
71 27244 0639012861 50128 20013 53351 86316 96238 93851
72 27421 20286 13632 50417 62975 41632 86762 35360 69632
73 27599 26202 15093 50707 38348 35593 87209 58128 56093
74 27778 24496 22624 509984718910624 87658 65129 98624
75 27958 15327 34375 51290 89355 46875 8ЯІО9 56933 59373
76 28138 99655 41376 51584 65306 29374 88362 34109 17376
/ / 28320 77241 27657 31879 76101 48157 89016 97227 68637
78 28503 48646 76368 52176 21601 98368 89473 46861 26368
79 28687 14234 39899 52474 02469 80399 89931 83583 20899
80 28871 74368 00000 52773 19168 00000 90392 07968 00000
81 29057 29112 07901 53073 72160 68401 90854 20391 28901
8-2 29243 79732 14432 53375 61913 02432 91318 22029 90432
83 29431 25694 64143 53678 88891 24643 9178412861 85143
81 29619 67666 95424 53983 53362 63424 92251 93666 31424
85 29809 06017 40625 54289 56395 53125 92721 65023 65625
86 29999 41113 26176 54596 97859 34176 93193 27315 42176
87 30190 73330 72707 54905 78424 53207 93666 81724 33707
88 30383 03034 95168 55215 98562 63168 94142 2823431168
89 30576 30600 02949 53327 58746 23449 94619 67630 43949
90 30770 56399 00000 55840 59449 ООООО 93099 00499 ООООО
91 30965 80803 84931 36135 01145 65431 93580 27427 43931
9'2 31162 04193 51232 56470 84311 99232 96063 49004 47232
93 31359 26943 87193 56788 09424 87693 96348 33819 88193
94 31537 49427 76224 57106 76962 24224 97035 78464 72224
95 31756 72024 96873 57426 87«03 09375 97524 87531 21875
96 31936 95114 22976 57748 41227 50976 98015 93612 78976
97 3215819075 23737 38071 38916 64267 98308 97304 047ВД
98 32360 44288 63068 58393 80932 71968 99003 99200 79968
99 32563 71136 03999 58721 67819 04499 99300 99900 04999
— XXII
Шестая, седьмая и ВОСЬМАЯ СТЕПЕНИ ЧИСЕЛЪ ОТЪ 0 ДО 100.
Числ. ѴІ-я ѴП-я ѴШ-я
0 0 0 0
1 1 1 1
2 64 128 236
3 729 2187 6561
4 4096 16384 65536
3 13623 78125 3 90625
6 46636 2 79936 16 79616
7 117649 8 23343 57 64801
8 2 62144 20 97152 167 77216
0 3 31441 47 82969 430 46721
10 10 00000 100 00000 1000 00000
11 17 71361 194 87171 2143 38881
12 29 83984 358 31808 4299 81696
13 48 26809 627 48517 8157 30721
14 75 29336 1034 13304 14757 89036
15 113 90623 1708 59373 26628 90625
16 167 77216 2684 35456 42959 67296
17 24137369 4103 38673 69757 57441
18 34012224 6122 20032 1 ЮІ99 60576
19 470 43881 8938 71739 1 69835 63041
20 640 00000 12800 00000 2 56000 00000
21 837 66121 18010 88541 3 78228 59361
22 1133 79904 24943 37888 5 48758 73536
23 1 480 33889 34048 25447 7 83109 85281
24 1911 02976 45864 71424 11 00733 14176
23 2441 40623 61033 15625 15 25878 90625
26 308913776 80318 10176 20 88270 64376
27 3874 20489 1 04603 53203 28 24295 36481
28 4318 90304 1 34929 28512 37 78019 9833 4
29 3948 23321 1 72498 76309 50 02464 12261
30 7290 00000 218700 00000 63 6И>00 00000
31 8873 03681 2 75126 14111 85 28910 37 441
32 10737 41824 3 43597 38368 109 95116 27776
33 12944 67969 4 26184 42977 140 64086 18241
34 13448 04416 5 25233 501-44 178 37939 04896
33 18382 63623 6 43392 96875 225 18753 90625
36 21767 82336 7 83641 64096 282 11099 О74.»6
37 23657 26409 9 49318 77133 331 24794 53921
38 30109 36384 11 44135 82392 43477921 38496
39 35187 43761 13 72310 06679 335 20092 60481
40 40960 00000 16 38400 00000 653 36000 00000
41 47501 04241 19 47542 73881 798 49252 29121
42 31890 31744 23 05393 33248 968 26319 96416
43 63213 63049 27 18186 11107 1168 82002 77601
44 7236313836 31 9'778 09664 1404 82236 25216
43 83037 65625 37 36694 53125 1681 51233 90625
46 94742 96896 43 58176 57216 2004 76122 31936
47 1 07792 13329 50 66231 20463 2381 12866 61761
48 1 22505 90464 58 70683 4 272 2817 92804 29036
б 49 1 38412 87201 67 82230 72849 3323 29305 69601
XXIII
Шестая, седьмая и ВОСЬМАЯ СТЕПЕНИ ЧИСЕЛЪ ОТЪ 0 ДО 100.
—— —1
Числ. ѴІ-я ѴІІ-я ѴШ-я
50 ' 1 56250 00000 78 12500 00С00 3906 23000 00003
51 1 75962 87801 89 74106 77831 4376 79443 70401
52 1 97706 09664 102 80717 02528 5343 97285 31 456
53 2 21643 61129 117 47111 39837 6223 96904 11361
54 2 4794911296 133 89232 09984 723019613 391^6
55 2 76806 40625 152 24332 34375 8373 39378 90625
56 3 08409 79456 172 70948 49536 9671 73113 74016
57 3 42964 47249 193 48974 93193 11142 91371 12001
58 3 80686 92344 220 79841 67352 12806 30817 18016
39 4 21805 33641 248 86514 84819 14683 04376 04321
60 4 63560 О0000 279 93600 00000 16796 16000 00000
61 5 15203 74361 314 27428 36021 19170 73129 97281
62 5 66002 35584 352 16146 06208 21834 01033 84896
63 6 25233 02209 393 89806 39167 24815 57802 67321
64 6 87194 76736 439 80463 11104 28147 49767 10636
65 7 54188 90625 490 22273 90625 31864 48128 90623
66 8 26539 50016 545 51607 01056 36004 62062 69696
67 9 04583 82169 606 07116 03323 4060676775 36641
68 9 88674 82624 672 29888 18432 45716 32396 53376
69 10 79181 63081 744 63332 52539 51379 83744 28641
70 1176490 00000 823 34300 00000 57648 01000 00000
71 12 81002 83921 909 51201 5839І 64373 33312 45761
72 13 93140 69504 1003 06130 04288 72220 41363 08736
73 1513342 26289 1104 73985 19097 80646 00918 94081
74 16 42064 90176 1215 12802 73024 89919 47402 03776
75 17 79783 13623 1334 83886 71873 100112 91303 90623
76 19 26999 28576 1464 31943 71776 1 11303 47874 34976
77 20 84223 80089 1604 83232 66833 123373 62913 47681
78 22 51996 00704 1736 55688 34912 1 37011 43706 83136
79 24 30874 53521 1920 39089 86159 1 51710 88099 06561
80 26 21440 00000 2097 13200 00000 1 67772 16000 ОО000
81 28 24295 36481 2287 67924 54961 1 83302 01888 51841
82 30 40066 71424 2492 83470 56768 2 04414 08586 54976
83 32 69403 73369 2713 6.(309 89627 2 23229 22321 39041
84 3512980 31616 2930 90346 55744 2 47875 89110 82496
83 37 71495 15625 3205 77088 28125 2 72490 52703 90625
86 40 45672 35136 3479 27822 21696 2 99217 92710 65856
87 43 36262 01009 3772 54794 87783 3 28211 67154 37121
88 46 44040 86784 4086 75596 36992 3 5963 4 52480 53296
89 49 69812 90961 4423 13348 93329 3 93638 88037 02081
90 53 14410 00000 4782 96900 00000 4 30467 2100010000
91 56 78692 32041 5167 61019 35731 4 70252 52761 51521
92 60 63530 01344 5578 46601 23648 513218 87313 75016
93 64 69901 83449 6017 00870 60757 5 59381 80966 50401
94 68 98697 81056 6484 77594 19264 6 09368 93834 10816
93 73 50918 90623 6983 37296 09373 6 63420 43128 90623
96 78 27577 89696 7314 47478 10816 7 21389 57898 38336
97 83 29720 04929 8079 82844 78113 7 83743 33943 76961
98 88 58423 8086 4 8681 23333 24672 8 50763 02238 17856
99 94 14801 49401 9320 63347 90699 9 22744 69442 79201
-- XXIV
Девятая и десятая степени чиселъ отъ 0 до 100.
Числ. XI-Я Х-Я
0 0 0
1 1 1
2 312 1024
3 19683 59049
4. 2 62144 10 48576
5 19 33123 97 63625
6 100 71696 604 30176
7 403 53607 2824 75249
8 134217728 10737 41824
9 3874 20489 * 34867 84401
10 1000000000 1 О0000 00000
11 23379 17691 2 59374 24601
12 3139780332 6 19173 64224
13 1 06044 99373 13 78384 91849
14 2 06610 46784 28 92346 54976
15 3 84433 39373 57 66503 90625
16 6 87194 76736 109 95116 27776
17 11 85878 76497 201 59939 00449
18 19 83592 90368 357 04672 26624
19 32 26876 97779 613 10662 37801
20 31 20000 00000 1024 ООоОО 00000
21 79 42800 46581 1667 98809 78201
22 120 72629 17792 2635 99227 91424
23 ГО 11526 61463 4(42 65112 13649
24 264 18073 40224 6340 33809 65376
23 381 46972 65623 9536 74316 40625
26 542 93036 78976 14116 70956 53376
27 762 53974 84987 2058911320 94649
28 105; 84559 53408 ♦ 29619 67666 95424
29 1450 71459 75869 42070 72333 00201
30 1968 ЗО0О0 00000 59049 00000 00000
31 2643 96221 60671 81962 82869 80801
32 3318 43720 88832 1 12589 99068 42624
33 4641 14844 01953 1 53(37 89852 64449
34 6071 69927 66464 2 06437 77540 59776
33 7881 56386 71875 2 7383 ч 73335 15623
36 10153 99566 68416 3 656(5 84400 62976
37 12996 17397 95077 4 80858 43724 17849
38 16521 61012 62848 6 27821 18479 88224
39 20872 83611 38739 8 14040 60831 91601
40 26214 40000 00000 10 48.176 00000 00000
41 32738 19343 93961 13 42265 93101 52401
42 40667 138.18 49472 17 08019 81216 77824
43 502.19 26119 36843 21 61148 23132 84249
44 6181218395 09504 27 19736 09384 18176
75668 06425 78125 34 05062 89160 13625
46 92219 0(626 69056 42 42074 74827 76576
47 1 11913 04731 02767 52 59913 22358 30049'
48 1 33260 34605 94688 64 92506 21085 43024
49 1 62841 33979 10449 79 79226 62976 12001
XXV
Девятая и десятая степени чиселъ отъ 0 до 101).
Числ. ІХ-я Х-Я
30 1 95312 50000 00000 97 65625 00000 00000
.31 2 33416 51730 90451 119 04242 38276 13001
82 2 77990 58836 35712 144 55510 59490 57024
53 3 29976 35918 02133 174 88747 0363513049
54 3 90430 59123 13344 210 83251 92649 20576
55 4 60536 65839 84375 253 29516 21191 40625
56 6 41616 94481 44896 303 30348 90961 14176
57 6 3515619553 84057 362 03333 14538 91249
58 7 42765 87396 44928 430 80420 68994 05824
59 8 66299 58186 5 4939 51111675 33006 41401
60 10 07169 60000 00000 604 30176 00000 00000
61 1169414 60928 34141 713 34291 16628 82601
62 13 53708 65462 63552 839 29936 58683 40224
63 15 63381 41568 53823 984 93029 18817 90849
64 18 01439 85094 81984 1132 92130 46068 46976
65 20 71191 28378 90625 1346 27433 44628 90625
66 23 76268 00137 99936 1568 53688 09(07 95776
67 27 20663 43962 94947 1822 83780 43517 61449
68 31 08710 02964 29Й68 2113 92282 6(572 10624
69 35 45208 78355 76229 2446 19*06 06547 59801
70 40 35360 70000 ООООО 2824 75249 00000 00000
71 45 84850 07184 49031 3255 24335 10098 81201
72 51 99869 78142 28992 3743 90624 26244 87424
73 58 87158 67082 67913 4297 62382 97033 57642
74 66 54041 07750 79424 4923 99039 73558 77376
78 75 08168 62792 96875 5631 35147 09472 (>3625
76 84 59064 38465 78176 6428 88893 23399 41376
77 95 15169 44491 71437 7326 68047 25862 00649
78 106 86892 09132 84608 8335 77583 12361 99424
79 119 85159 59826 18319 9468 27608 26268 47201
80 134 21772 80000 ООООО 10737 4182 4 0 0000 ООООО
81 150 09463 52969 99121 12157 66543 90369 28801
82- 167 61955 04097 08032 13744 80313 35960 58624
.83 186 94025 52675 40403 15516 04118 72058 53449
84 203 21574 85309 29664 17490 02287 65980 91629
85 231 61694 62832 03125 19637 4043 40722 65623
86 257 32741 73116 63616 22130 15788 88030 70976
87 285 54415 42430 29527 24842 34141 91435 68819
88 316 47838 18288 66048 27850 09760 09402 12224
89 350 35640 37074 85209 31181 71992 99661 83601
90 387 42048 90000 00000 34867 84401 00000 00000
91 427 92980 01297 88411 38941 61181 18107 43401
92 47216136 32865 56672 3438 84342 23632 13824
93 520 41108 29884 87293 18398 23071 79293 18249
94 572 99480 22286 16704 53861 51140 94899 70176
95 630 249401'7246 09375 59873 69392 38378 90623
96 692 53399 58244 80256 66483 26359 91301 04576
97 766 23105 86343 65217 73742 41268 94928 26049
98 833 74776 21301 49888 81707 28068 87546 8ООЧ4
99 913 51724 74836 40.899 00438 20730 08804 49001
XXVI
Въ таблицахъ первыхъ пяти степеней чиселъ отъ 1 до 1000, единицы и
десятки этихъ чиселъ помѣщены въ первой вертикальной графѣ, а сотни — въ
первой горизонтальной строкѣ. Степень каждаго однозначнаго или двузначнаго
числа находится противъ него во второй вертикальной графѣ; а степень каждаго
трехзначнаго числа — подъ его сотнями въ вертикальной графѣ, гдѣ оиа пере-
сѣкается строкою горизонтальною, содержащею десятки и единицы. Пояснимъ
это примѣрами:
Найти 61*. Въ таблицѣ пятыхъ степеней, въ первой графѣ, ищу число
67, и прямо противъ него нахожу пятую его степень 1350125107.
Найти 361*. Въ той же таблицѣ беру вертикальную графу подъ числомъ
300, и горизонтальную строку, въ которой стоитъ число 67: гдѣ онѣ встрѣ-
чаются, тамъ и находится 6657793506607=367'.
Таблица степеней; шестой, седьмой,.... десятой, для чиселъ Двузначныхъ,
понятна и безъ объясненія.
Г БИБЛИОТЕКА>
К0МШПН1Ш
< АКАДБМИИ. >
ЗАМѢЧЕННЫЯ ПОГРѢШНОСТИ
Стран. Строка. Напечатано: Слѣдуете читать:
11 4 сверху положительныя о положительныя и
12 23 . ап~ і.ап+і.(іп—і.ап+і— а"*—І.ап+І=ат~ і.а"+3
18 13 » 3«363с3 ЗаЧ3с3
Л 6 снизу (д-ьд'ч-2"....)С
26 18 > АЭ АВ
29 9 сверху ЗаЬ3 ЗаЧ3
35 6аЧ3 6аЧ3
4о363сч-10оЬ3 4а363с-г 10аЬ“
— 5 снизу Зт’п Зт3п
37 10 сверху с.Ь?
42 16 . 30—®=20 30—я:=10
68 16 снизу 2.1=3 2.1=2
86 9 », пж—11>у ту—пх
92 4 сверху 53> (—7)’ 53> (—7)’
106 10 . раздѣлитъ раздѣлимъ
иі,іі-ып2і тяй-ыпаи
109 14 *
л3й-4-паи
П3Й-|-П82
110 X ТИ.
2 • — уменьшенъ знаменатель — знаменатель меньше «!
119 11 - 55125 55225
121 14 снизу а нахожу и нахожу
132 5 сверху Зто Это
149 6 > разноеть разность
— 6 снизу о®3 а3}3
167 11 сверху перваго квадрата перваго
Ь3 6»
173 8 снизу 27~
1 1
178 19 -
(ап}п (а—*»)"
180 1 и 2 св. ЪаЪгс ЗаЬѴ
184 10 снизу а і/ аГ
186 9 сверху радикалоль радикаломъ
— 15 =гт
т ! -
186 2 снизу у/ѴГ \7^;
200 13 » къ 243=3 къ 243—3
208 3 10°'® 10®<*
Стран. Стропа. Напечатано; Слѣдуетъ читать.
213 221 13 сверху завлючается заключается
8 снизу 2785 2585
223 11 сверху Логариѳиы Логариѳмы
229 9 снизу 3) 3)^—
7 . 162 126
254 256 264 1 сверху 15 снизу 18 > выразамь рада «>п+1—1ісп+* выразимъ рода
270 278 282 288 289 298 301 12 и 14 св. 7 сверху 13 » 13 . 18, 6 и 1 снизу 15 снизу' 6 сверху 10 > і. - 80 сочетеній при этотъ благополучныхъ лотарея лотерейной вѣрность 800 сочетаній при этомъ благопріятныхъ лоттерея лоттерейной вѣроятность
322 Лотарея Лоттерея
*г » развергнуты развернуты
325 330 7 снизу 18 сверху І'а Т2 Ь>, 1,га ТГ
335 353 15 снизу 12 саерху веободимо необходимо
звакаыи знаками
355 2 снизу V? “Vх?
356 358 363 370 6 сверху подстивить подставить
11 снизу 7 » 8 . обратнымъ въ немъ кигда тѣмъ жо что въ немъ когда
373 10 и 11 снизу 9 9
385 18 снизу "'“іо а—аСС 10 6—а«
391 1 » а—4 агч-4
444 13 .
447 10 . е удовлетворительны е, достаточны